"router/client/src/v3/sharded_client.rs" did not exist on "fec0167a123eddc60891320dd263e974671ad1c9"
v1.0
Showing
Too many changes to show.
To preserve performance only 176 of 176+ files are displayed.
383 KB
nbs/imgs_models/tft_grn.png
0 → 100644
52.6 KB
nbs/imgs_models/tft_vsn.png
0 → 100644
68 KB
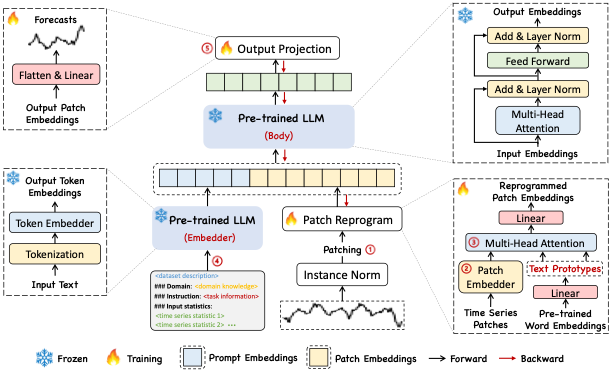
nbs/imgs_models/timellm.png
0 → 100644
93.2 KB
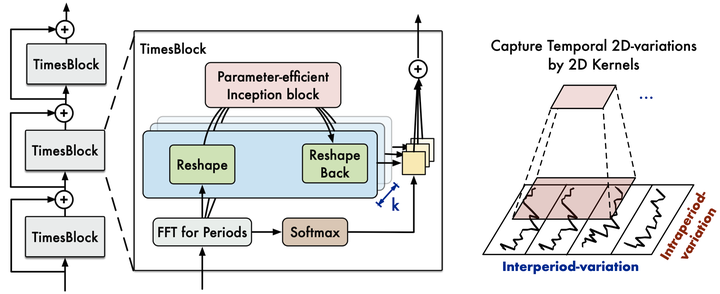
nbs/imgs_models/timesnet.png
0 → 100644
93.6 KB
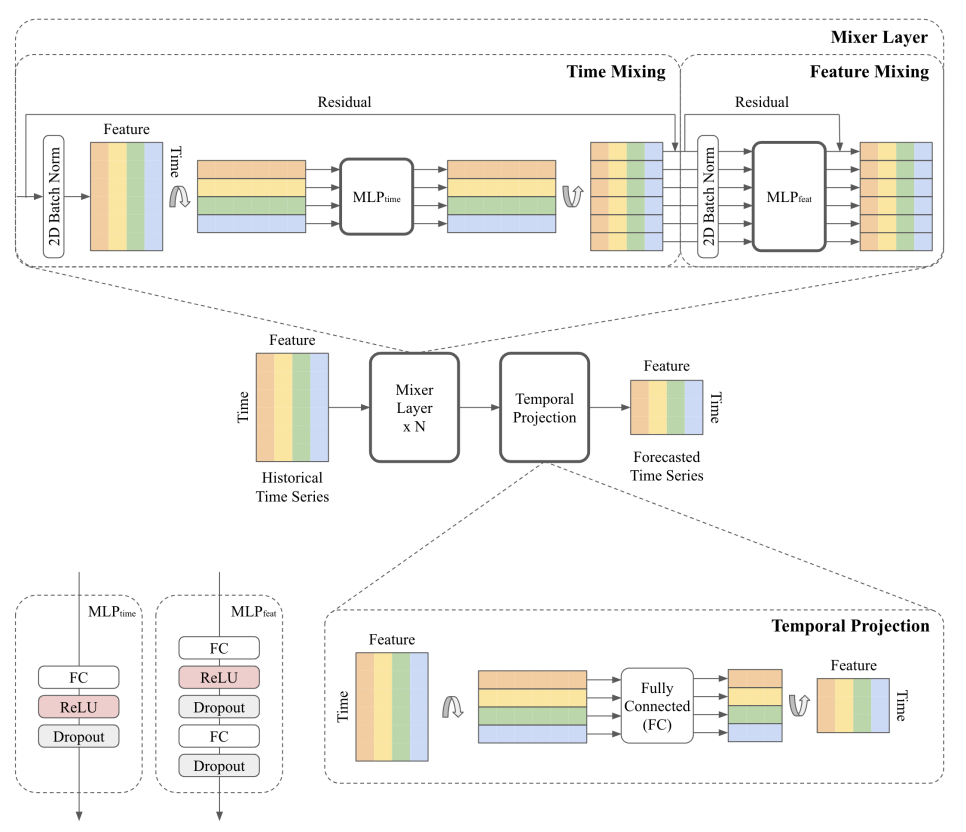
nbs/imgs_models/tsmixer.png
0 → 100644
103 KB
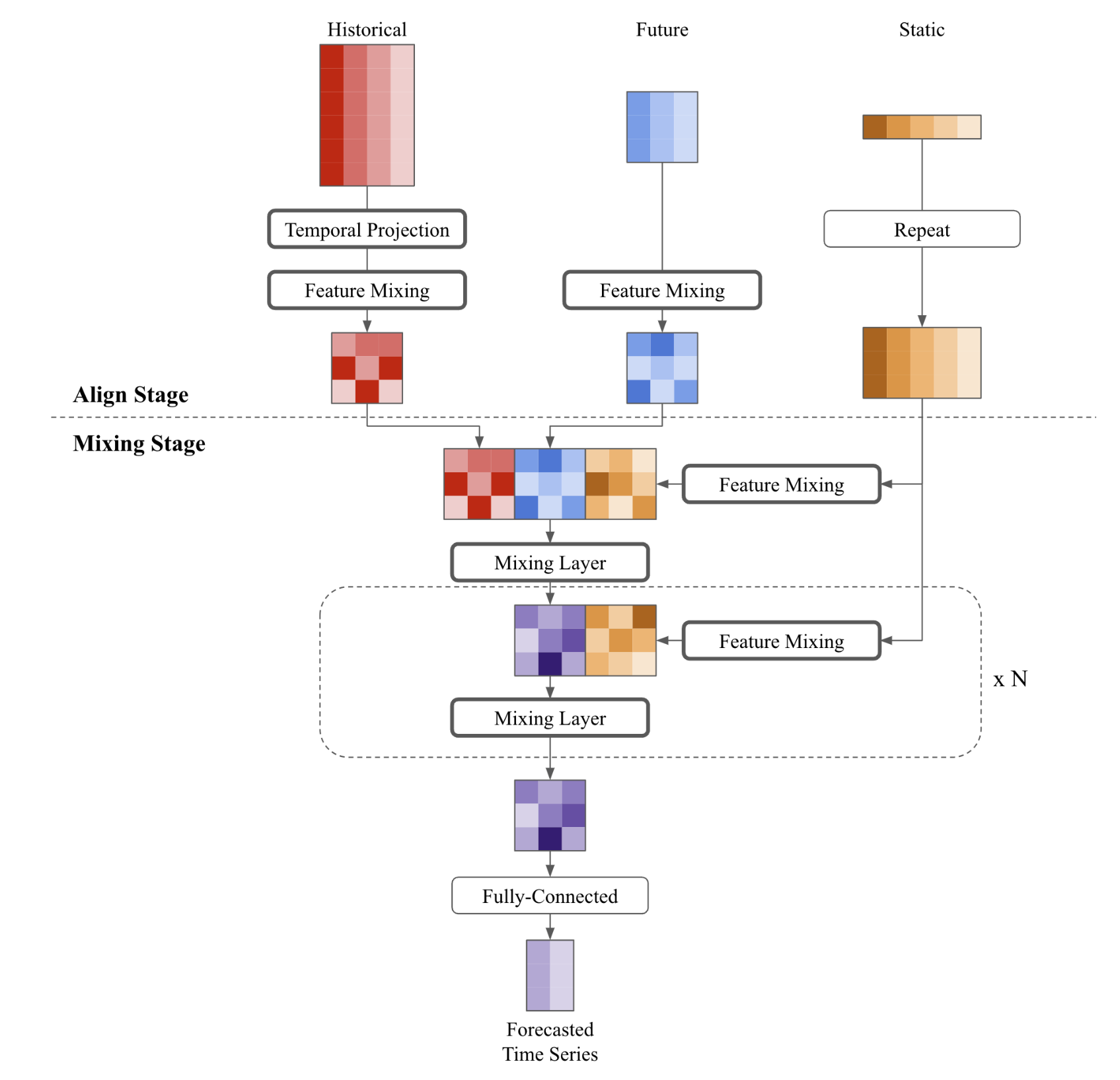
nbs/imgs_models/tsmixerx.png
0 → 100644
134 KB
173 KB
nbs/index.ipynb
0 → 100644
nbs/losses.numpy.ipynb
0 → 100644
nbs/losses.pytorch.ipynb
0 → 100644
nbs/mint.json
0 → 100644
nbs/models.autoformer.ipynb
0 → 100644
nbs/models.bitcn.ipynb
0 → 100644
nbs/models.deepar.ipynb
0 → 100644
nbs/models.dilated_rnn.ipynb
0 → 100644
nbs/models.dlinear.ipynb
0 → 100644
nbs/models.fedformer.ipynb
0 → 100644
nbs/models.gru.ipynb
0 → 100644
nbs/models.hint.ipynb
0 → 100644