readme
parents
Showing
60.5 KB
58.9 KB
71 KB
1.49 MB
177 KB
89.6 KB
285 KB
188 KB
94.3 KB
230 KB
282 KB
190 KB
37.5 KB

60.5 KB

58.9 KB

71 KB

1.49 MB

177 KB

89.6 KB

285 KB
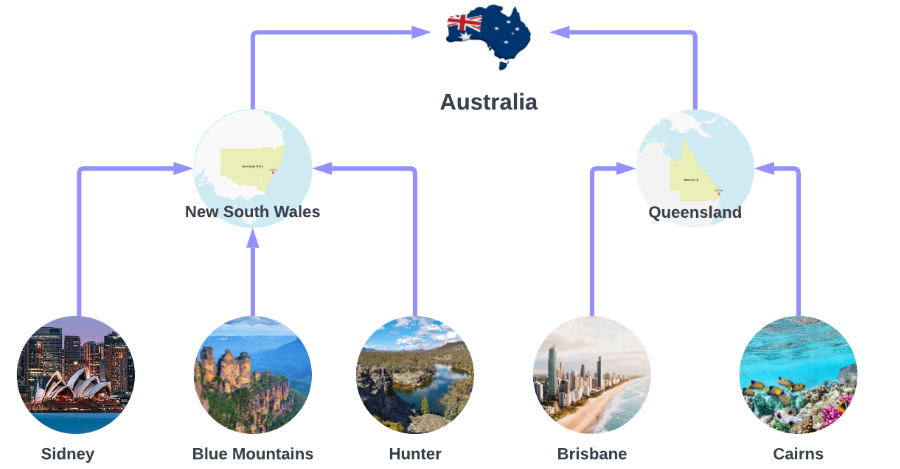
188 KB
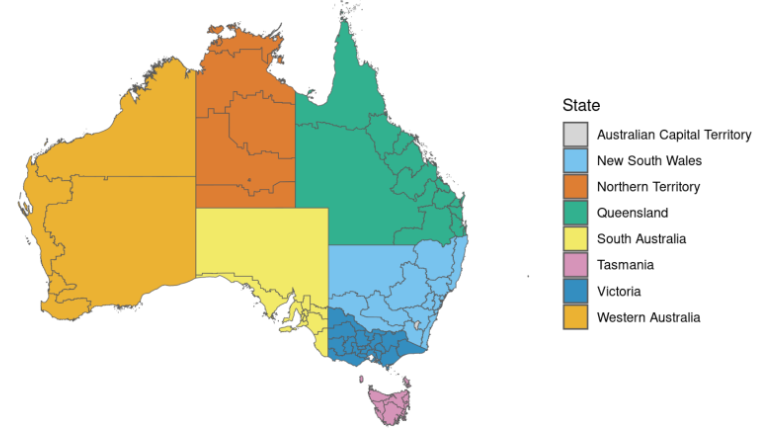
94.3 KB

230 KB
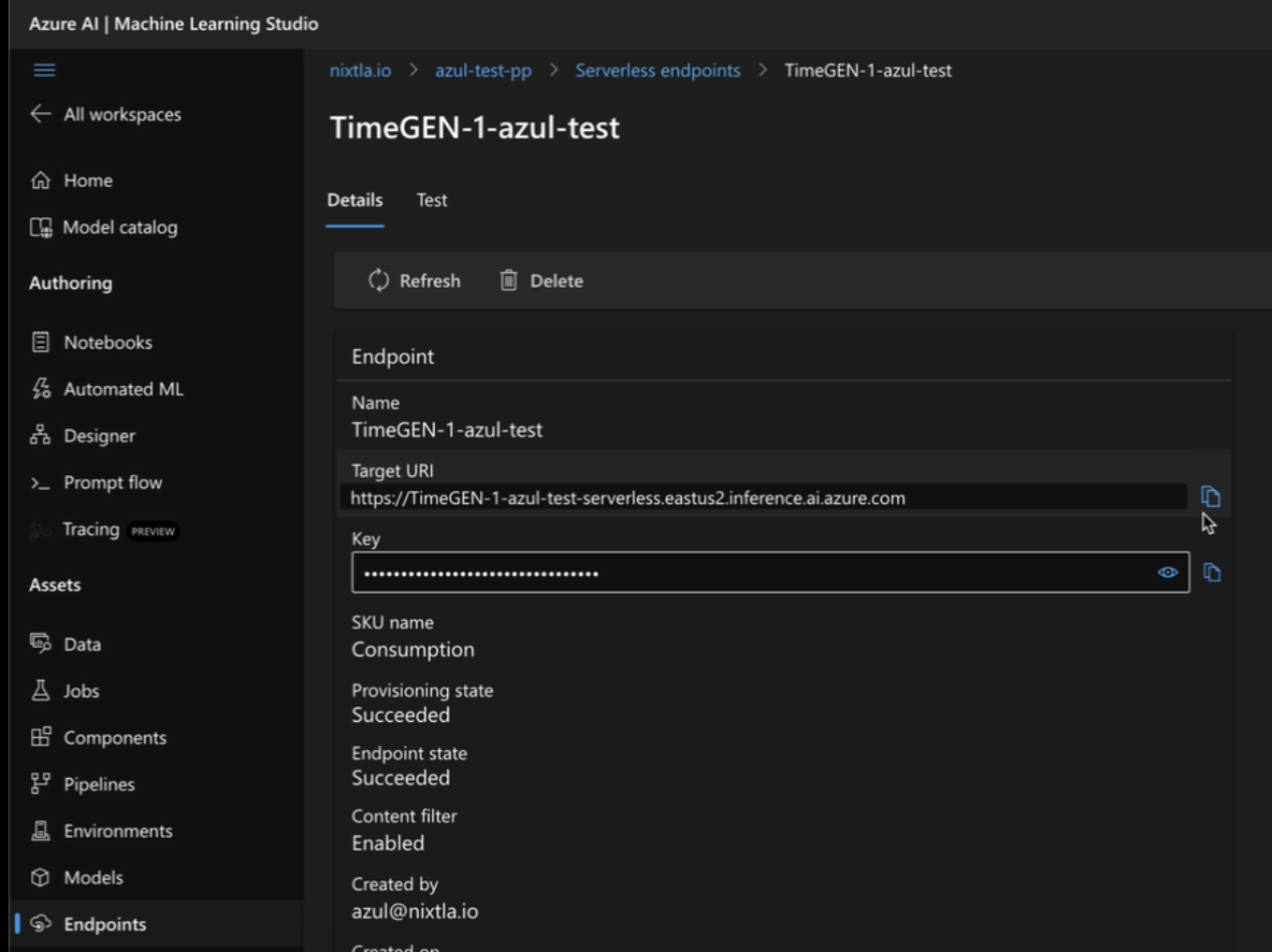
282 KB
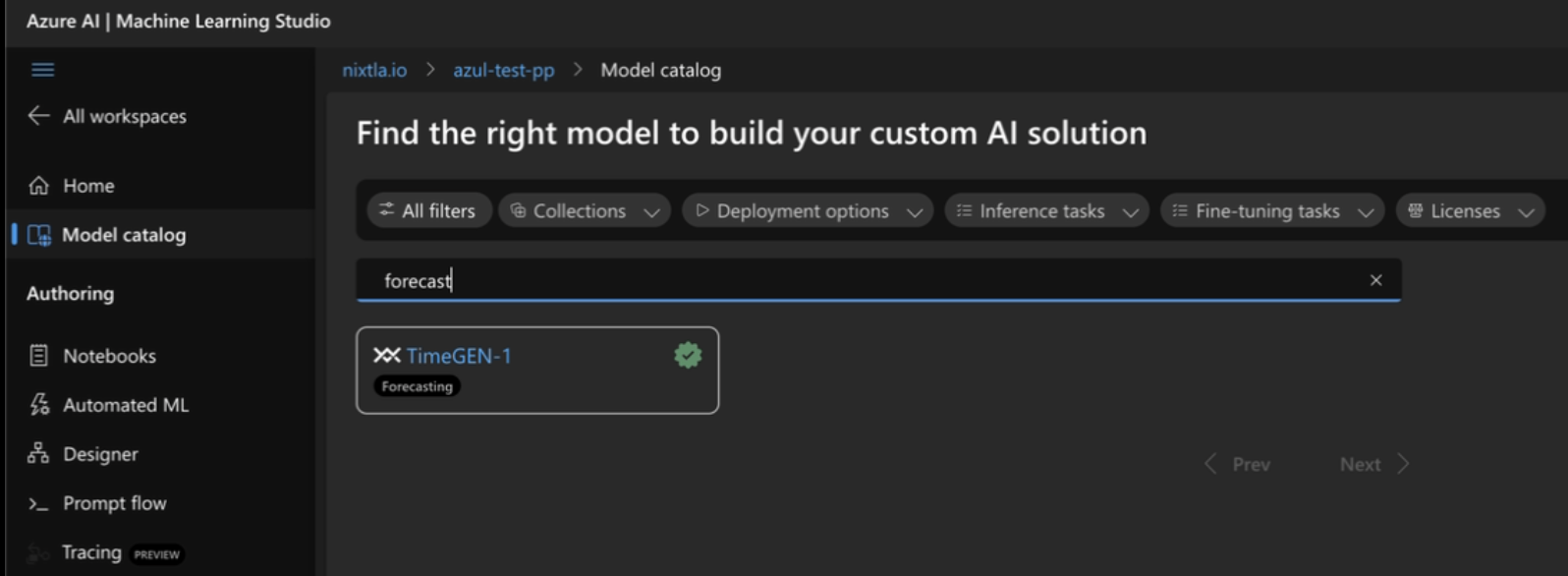
190 KB

37.5 KB