# Search-o1
动态获取和整合外部知识,无需训练即可赋予开源模型CoT“慢思考”能力,属于推理版o1。
## 论文
`Search-o1: Agentic Search-Enhanced Large Reasoning Models`
- https://arxiv.org/abs/2501.05366
## 模型结构
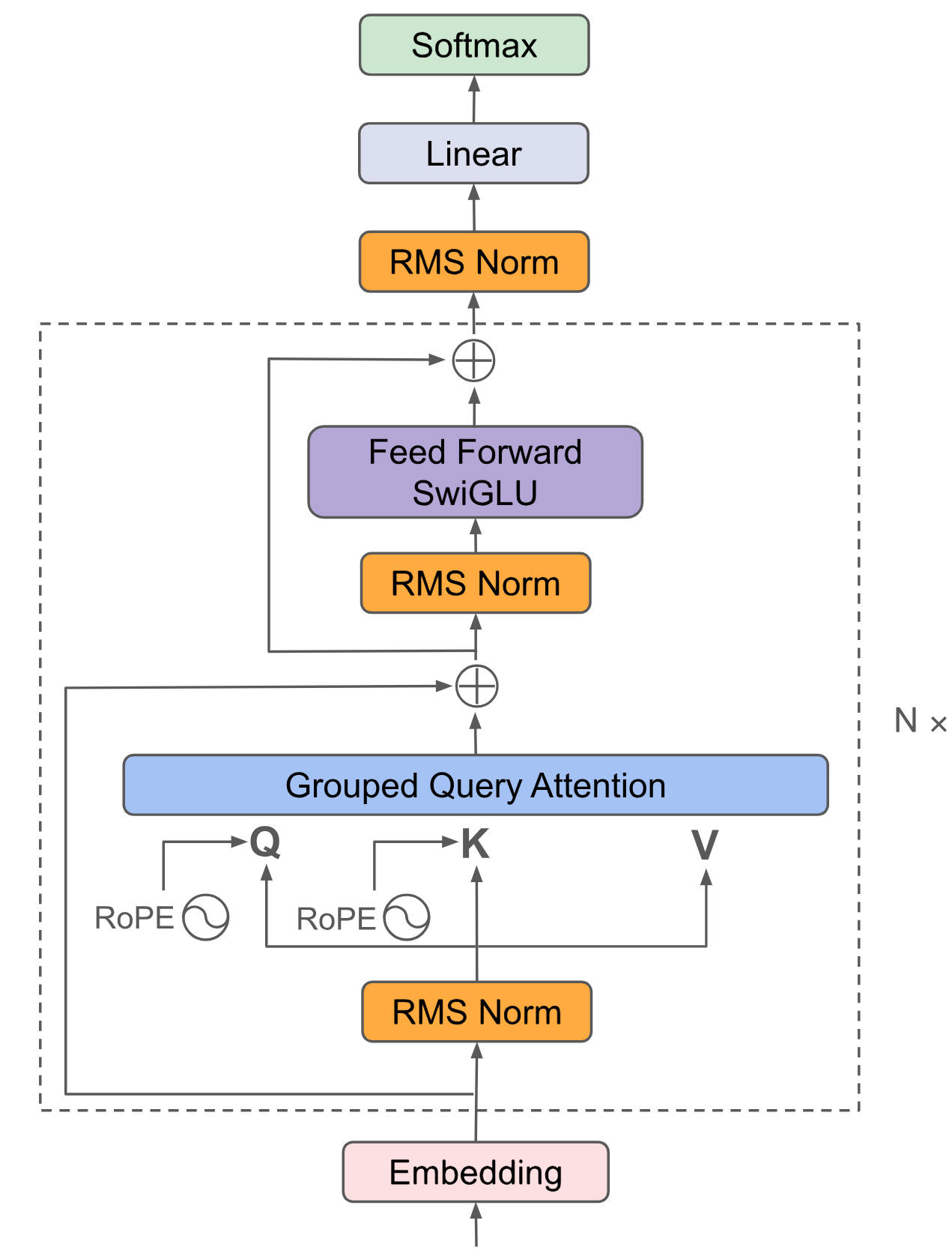
本项目实验效果时LLM模型采用Qwen2.5 作为示例,模型结构类似Llama系列,采用极简Decoder-only结构,Llama源自基本的transformer结构,主体为attention(QKV自点积)+ffn(全连接),最后外加一个softmax进行概率转换输出即可,为了使数据分布归一化方便训练收敛,在attention、ffn、softmax前分别再加一个RMS Norm。
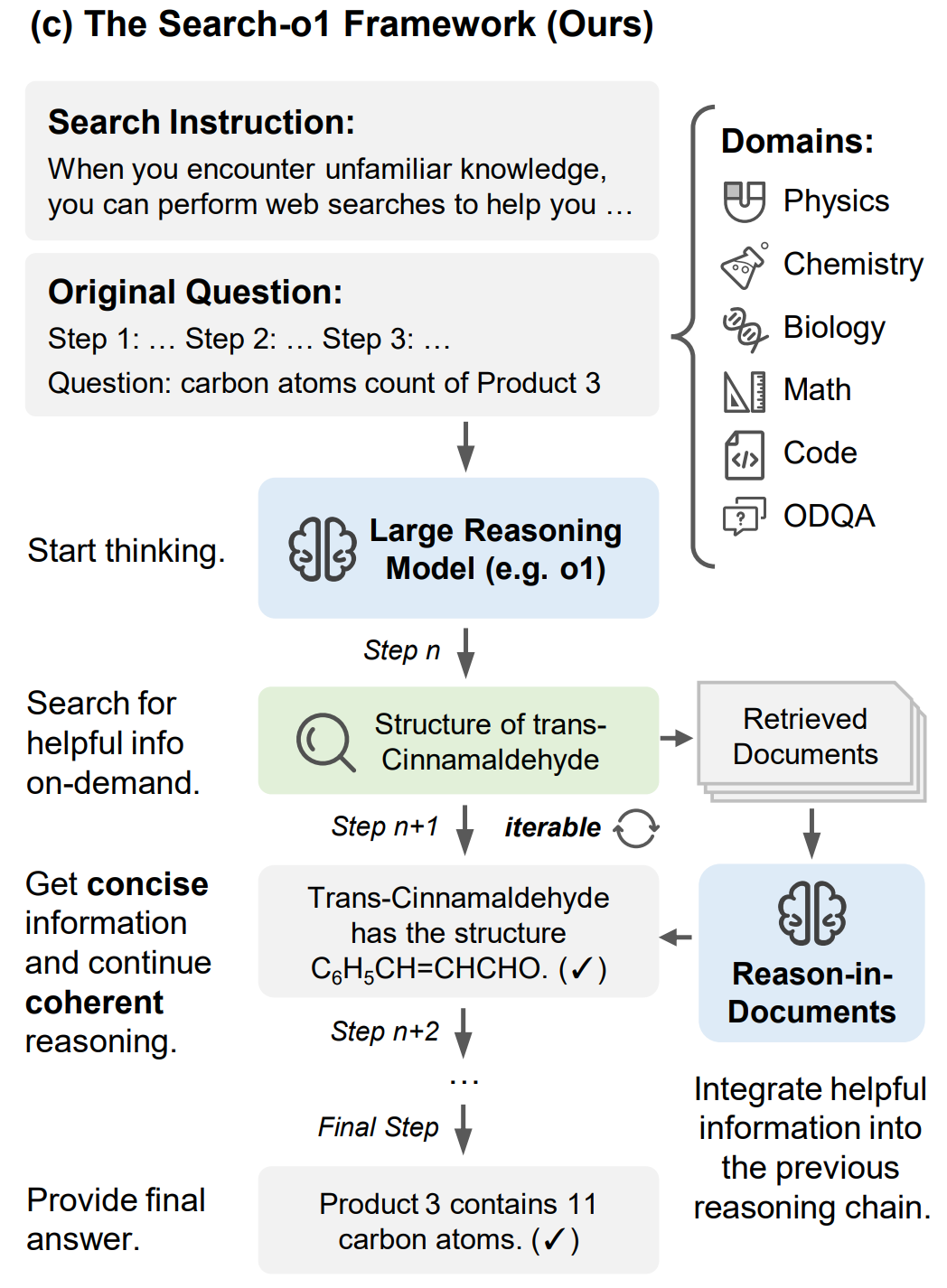
## 算法原理
通过集成自主检索增强生成机制和文档内推理模块,实现了在推理过程中动态获取和整合外部知识的能力,同时,确保推理过程的连贯性和逻辑一致性。
## 环境配置
```
mv Search-o1_pytorch Search-o1 # 去框架名后缀
```
### Docker(方法一)
```
docker pull image.sourcefind.cn:5000/dcu/admin/base/pytorch:2.3.0-py3.10-dtk24.04.3-ubuntu20.04
# 为以上拉取的docker的镜像ID替换,本镜像为:b272aae8ec72
docker run -it --shm-size=64G -v $PWD/Search-o1:/home/Search-o1 -v /opt/hyhal:/opt/hyhal:ro --privileged=true --device=/dev/kfd --device=/dev/dri/ --group-add video --name searcho1 bash
cd /home/Search-o1
pip install -r requirements.txt
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```
### Dockerfile(方法二)
```
cd cd /home/Search-o1/docker
docker build --no-cache -t searcho1:latest .
docker run --shm-size=64G --name searcho1 -v /opt/hyhal:/opt/hyhal:ro --privileged=true --device=/dev/kfd --device=/dev/dri/ --group-add video -v $PWD/../../Search-o1:/home/Search-o1 -it searcho1 bash
# 若遇到Dockerfile启动的方式安装环境需要长时间等待,可注释掉里面的pip安装,启动容器后再安装python库:pip install -r requirements.txt。
cd /home/Search-o1
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```
### Anaconda(方法三)
1、关于本项目DCU显卡所需的特殊深度学习库可从光合开发者社区下载安装:
- https://developer.sourcefind.cn/tool/
```
DTK驱动:dtk24.04.3
python:python3.10
torch:2.3.0
torchvision:0.18.1
torchaudio:2.1.2
triton:2.1.0
vllm:0.6.2
flash-attn:2.6.1
deepspeed:0.14.2
apex:1.3.0
xformers:0.0.25
transformers:4.48.0
```
`Tips:以上dtk驱动、python、torch等DCU相关工具版本需要严格一一对应。`
2、其它非特殊库参照requirements.txt安装
```
cd /home/Search-o1
pip install -r requirements.txt
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```
## 数据集
项目中提供实验性的迷你数据集`AIME`与`GPQA`(两个数据集的问题都难度很大)可直接使用,预处理代码参照][`data_pre_precess.ipynb`](./data/data_pre_precess.ipynb),数据集格式处理成`*.json`。
数据的完整目录结构如下:
```
/home/Search-o1/data
├── AIME
├── test.json
...
├── GPQA
├── diamond.json
...
```
## 训练
无
## 推理
### 单机多卡
**Search-o1 (Ours)**
```bash
python scripts/run_search_o1.py \
--dataset_name aime \
--split test \
--max_search_limit 5 \
--max_turn 10 \
--top_k 10 \
--max_doc_len 3000 \
--use_jina True \
--model_path "YOUR_MODEL_PATH" \
--jina_api_key "YOUR_JINA_API_KEY" \
--bing_subscription_key "YOUR_BING_SUBSCRIPTION_KEY"
```
以上命令为参考命令,无法直接运行,完整使用`Search-o1`的功能需要花钱购买jina和bing搜索引擎的api_key,如有需求可自行购买服务,额外费用与本算法无关,本步骤不含外部搜索的可用api_key,仅供使用方法示例,故无外网搜索功能:
```
sh searcho1_gen.sh # 项目中采用Qwen2.5-72B-Instruct进行示例,建议不要采用小型模型,效果不如大型模型。
# 注:项目中默认的bing_subscription_key为无效api_key,故无法获取网络数据,仅供参考。
```
更多资料可参考源项目的[`README_origin`](./README_origin.md)
## result
由于无有效api_key,无法获取网络数据,此推理效果仅供参考示例,以方便读者了解项目使用方法:
`输入: `
[`test.json`](./data/AIME/test.json)
```
{
"id": 0,
"Problem_ID": 60,
"Question": "Every morning Aya goes for a $9$-kilometer-long walk and stops at a coffee shop afterwards. When she walks at a constant speed of $s$ kilometers per hour, the walk takes her 4 hours, including $t$ minutes spent in the coffee shop. When she walks $s+2$ kilometers per hour, the walk takes her 2 hours and 24 minutes, including $t$ minutes spent in the coffee shop. Suppose Aya walks at $s+\\frac{1}{2}$ kilometers per hour. Find the number of minutes the walk takes her, including the $t$ minutes spent in the coffee shop.",
"Solution": "$\\frac{9}{s} + t = 4$ in hours and $\\frac{9}{s+2} + t = 2.4$ in hours.\nSubtracting the second equation from the first, we get, \n$\\frac{9}{s} - \\frac{9}{s+2} = 1.6$\nMultiplying by $(s)(s+2)$, we get \n$9s+18-9s=18=1.6s^{2} + 3.2s$\nMultiplying by 5/2 on both sides, we get\n$0 = 4s^{2} + 8s - 45$\nFactoring gives us \n$(2s-5)(2s+9) = 0$, of which the solution we want is $s=2.5$.\nSubstituting this back to the first equation, we can find that $t = 0.4$ hours.\nLastly, $s + \\frac{1}{2} = 3$ kilometers per hour, so\n$\\frac{9}{3} + 0.4 = 3.4$ hours, or $\\framebox{204}$ minutes\n-Failure.net\nThe amount of hours spent while walking on the first travel is $\\frac{240-t}{6}$. Thus, we have the equation $(240-t)(s) = 540$, and by the same logic, the second equation yields $(144-t)(s+2) = 540$. We have $240s-st = 540$, and $288+144s-2t-st = 540$. We subtract the two equations to get $96s+2t-288 = 0$, so we have $48s+t = 144$, so $t = 144-48s$, and now we have $(96+48s)(s) = 540$. The numerator of $s$ must evenly divide 540, however, $s$ must be less than 3. We can guess that $s = 2.5$. Now, $2.5+0.5 = 3$. Taking $\\frac{9}{3} = 3$, we find that it will take three hours for the 9 kilometers to be traveled. The t minutes spent at the coffeeshop can be written as $144-48(2.5)$, so t = 24. $180 + 24 = 204$. -sepehr2010",
"answer": "204"
},
...
```
参考`outputs/runs.baselines/aime.qwen2.5-72b.search_o1/test.*.json`
`输出:`
```
{
"id": 0,
"Problem_ID": 60,
"Question": "<|im_start|>system\nYou are Qwen, created by Alibaba Cloud. You are a helpful assistant.<|im_end|>\n<|im_start|>user\nYou are a reasoning assistant with the ability to perform web searches to help you answer the user's question accurately. You have special tools:\n\n- To perform a search: write <|begin_search_query|> your query here <|end_search_query|>.\nThen, the system will search and analyze relevant web pages, then provide you with helpful information in the format <|begin_search_result|> ...search results... <|end_search_result|>.\n\nYou can repeat the search process multiple times if necessary. The maximum number of search attempts is limited to 5.\n\nOnce you have all the information you need, continue your reasoning.\n\nExample:\nQuestion: \"How do you compute the integral of e^(x^2) dx?\"\nAssistant thinking steps:\n- I might need to look up techniques for integrating e^(x^2).\n\nAssistant:\n<|begin_search_query|>methods to integrate e^(x^2)<|end_search_query|>\n\n(System returns processed information from relevant web pages)\n\nAssistant continues reasoning with the new information...\n\nRemember:\n- Use <|begin_search_query|> to request a web search and end with <|end_search_query|>.\n- When done searching, continue your reasoning.\n\nPlease answer the following math question. You should think step by step to solve it.\n\nProvide your final answer in the format \\boxed{YOUR_ANSWER}.\n\nQuestion:\nEvery morning Aya goes for a $9$-kilometer-long walk and stops at a coffee shop afterwards. When she walks at a constant speed of $s$ kilometers per hour, the walk takes her 4 hours, including $t$ minutes spent in the coffee shop. When she walks $s+2$ kilometers per hour, the walk takes her 2 hours and 24 minutes, including $t$ minutes spent in the coffee shop. Suppose Aya walks at $s+\\frac{1}{2}$ kilometers per hour. Find the number of minutes the walk takes her, including the $t$ minutes spent in the coffee shop.\n\n<|im_end|>\n<|im_start|>assistant\n",
"Solution": "$\\frac{9}{s} + t = 4$ in hours and $\\frac{9}{s+2} + t = 2.4$ in hours.\nSubtracting the second equation from the first, we get, \n$\\frac{9}{s} - \\frac{9}{s+2} = 1.6$\nMultiplying by $(s)(s+2)$, we get \n$9s+18-9s=18=1.6s^{2} + 3.2s$\nMultiplying by 5/2 on both sides, we get\n$0 = 4s^{2} + 8s - 45$\nFactoring gives us \n$(2s-5)(2s+9) = 0$, of which the solution we want is $s=2.5$.\nSubstituting this back to the first equation, we can find that $t = 0.4$ hours.\nLastly, $s + \\frac{1}{2} = 3$ kilometers per hour, so\n$\\frac{9}{3} + 0.4 = 3.4$ hours, or $\\framebox{204}$ minutes\n-Failure.net\nThe amount of hours spent while walking on the first travel is $\\frac{240-t}{6}$. Thus, we have the equation $(240-t)(s) = 540$, and by the same logic, the second equation yields $(144-t)(s+2) = 540$. We have $240s-st = 540$, and $288+144s-2t-st = 540$. We subtract the two equations to get $96s+2t-288 = 0$, so we have $48s+t = 144$, so $t = 144-48s$, and now we have $(96+48s)(s) = 540$. The numerator of $s$ must evenly divide 540, however, $s$ must be less than 3. We can guess that $s = 2.5$. Now, $2.5+0.5 = 3$. Taking $\\frac{9}{3} = 3$, we find that it will take three hours for the 9 kilometers to be traveled. The t minutes spent at the coffeeshop can be written as $144-48(2.5)$, so t = 24. $180 + 24 = 204$. -sepehr2010",
"answer": "204",
"Output": "To solve the problem, we need to determine the value of \\( t \\) and then use it to find the total time Aya spends walking and in the coffee shop when she walks at \\( s + \\frac{1}{2} \\) kilometers per hour.\n\nFirst, let's set up the equations based on the information given:\n\n1. When Aya walks at a speed of \\( s \\) kilometers per hour, the walk takes her 4 hours, including \\( t \\) minutes spent in the coffee shop.\n2. When Aya walks at a speed of \\( s + 2 \\) kilometers per hour, the walk takes her 2 hours and 24 minutes, including \\( t \\) minutes spent in the coffee shop.\n\n### Step 1: Convert all times to hours\n- 4 hours is already in hours.\n- 2 hours and 24 minutes can be converted to hours: \\( 2 + \\frac{24}{60} = 2.4 \\) hours.\n\n### Step 2: Set up the equations\nLet \\( T_1 \\) be the time spent walking at speed \\( s \\) and \\( T_2 \\) be the time spent walking at speed \\( s + 2 \\).\n\nFrom the first condition:\n\\[ T_1 + \\frac{t}{60} = 4 \\]\nSince \\( T_1 = \\frac{9}{s} \\):\n\\[ \\frac{9}{s} + \\frac{t}{60} = 4 \\]\n\nFrom the second condition:\n\\[ T_2 + \\frac{t}{60} = 2.4 \\]\nSince \\( T_2 = \\frac{9}{s + 2} \\):\n\\[ \\frac{9}{s + 2} + \\frac{t}{60} = 2.4 \\]\n\n### Step 3: Solve the system of equations\nWe have:\n\\[ \\frac{9}{s} + \\frac{t}{60} = 4 \\]\n\\[ \\frac{9}{s + 2} + \\frac{t}{60} = 2.4 \\]\n\nSubtract the second equation from the first:\n\\[ \\left( \\frac{9}{s} + \\frac{t}{60} \\right) - \\left( \\frac{9}{s + 2} + \\frac{t}{60} \\right) = 4 - 2.4 \\]\n\\[ \\frac{9}{s} - \\frac{9}{s + 2} = 1.6 \\]\n\n### Step 4: Simplify the equation\n\\[ 9 \\left( \\frac{1}{s} - \\frac{1}{s + 2} \\right) = 1.6 \\]\n\\[ 9 \\left( \\frac{(s + 2) - s}{s(s + 2)} \\right) = 1.6 \\]\n\\[ 9 \\left( \\frac{2}{s(s + 2)} \\right) = 1.6 \\]\n\\[ \\frac{18}{s(s + 2)} = 1.6 \\]\n\\[ 18 = 1.6s(s + 2) \\]\n\\[ 18 = 1.6s^2 + 3.2s \\]\n\\[ 1.6s^2 + 3.2s - 18 = 0 \\]\n\n### Step 5: Solve the quadratic equation\nDivide the entire equation by 1.6:\n\\[ s^2 + 2s - 11.25 = 0 \\]\n\nUse the quadratic formula \\( s = \\frac{-b \\pm \\sqrt{b^2 - 4ac}}{2a} \\):\n\\[ s = \\frac{-2 \\pm \\sqrt{2^2 - 4 \\cdot 1 \\cdot (-11.25)}}{2 \\cdot 1} \\]\n\\[ s = \\frac{-2 \\pm \\sqrt{4 + 45}}{2} \\]\n\\[ s = \\frac{-2 \\pm \\sqrt{49}}{2} \\]\n\\[ s = \\frac{-2 \\pm 7}{2} \\]\n\nThis gives us two solutions:\n\\[ s = \\frac{5}{2} = 2.5 \\]\n\\[ s = \\frac{-9}{2} = -4.5 \\]\n\nSince speed cannot be negative, we have:\n\\[ s = 2.5 \\]\n\n### Step 6: Find \\( t \\)\nSubstitute \\( s = 2.5 \\) back into one of the original equations:\n\\[ \\frac{9}{2.5} + \\frac{t}{60} = 4 \\]\n\\[ 3.6 + \\frac{t}{60} = 4 \\]\n\\[ \\frac{t}{60} = 0.4 \\]\n\\[ t = 0.4 \\times 60 \\]\n\\[ t = 24 \\]\n\n### Step 7: Calculate the total time when \\( s = 2.5 + 0.5 = 3 \\)\n\\[ T = \\frac{9}{3} + \\frac{24}{60} \\]\n\\[ T = 3 + 0.4 \\]\n\\[ T = 3.4 \\]\n\nConvert 3.4 hours to minutes:\n\\[ 3.4 \\times 60 = 204 \\]\n\nThus, the total time Aya spends walking and in the coffee shop when she walks at \\( s + \\frac{1}{2} \\) kilometers per hour is \\(\\boxed{204}\\) minutes.",
"Pred_Answer": "204",
"Metrics": {
"is_valid_answer": true,
"acc": 1,
"em": 1,
"f1": 1.0,
"math_equal": true
}
},
...
```
### 精度
DCU与GPU精度一致,推理框架:pytorch。
## 应用场景
### 算法类别
`对话问答`
### 热点应用行业
`制造,广媒,金融,能源,医疗,家居,教育`
## 预训练权重
Hugging Face下载地址为:[Qwen/Qwen2.5-72B-Instruct](https://huggingface.co/Qwen/Qwen2.5-72B-Instruct)
## 源码仓库及问题反馈
- http://developer.sourcefind.cn/codes/modelzoo/search-o1_pytorch.git
## 参考资料
- https://github.com/sunnynexus/Search-o1.git


