diff --git a/docs/README.md b/docs/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..35ed10589b0d052fd7e35d657d8c9ff0eddf5025
--- /dev/null
+++ b/docs/README.md
@@ -0,0 +1,17 @@
+# Public docs for TensorFlow Models
+
+This directory contains the top-level public documentation for
+[TensorFlow Models](https://github.com/tensorflow/models)
+
+This directory is mirrored to https://tensorflow.org/tfmodels, and is mainly
+concerned with documenting the tools provided in the `tensorflow_models` pip
+package (including `orbit`).
+
+Api-reference pages are
+[available on the site](https://www.tensorflow.org/api_docs/more).
+
+The
+[Official Models](https://github.com/tensorflow/models/blob/master/official/projects)
+and [Research Models](https://github.com/tensorflow/models/blob/master/research)
+directories are not described in detail here, refer to the individual project
+directories for more information.
diff --git a/docs/index.md b/docs/index.md
new file mode 100644
index 0000000000000000000000000000000000000000..2b1535a71fe395924a01b62b2668c6d8e94a89b7
--- /dev/null
+++ b/docs/index.md
@@ -0,0 +1,140 @@
+# Model Garden overview
+
+The TensorFlow Model Garden provides implementations of many state-of-the-art
+machine learning (ML) models for vision and natural language processing (NLP),
+as well as workflow tools to let you quickly configure and run those models on
+standard datasets. Whether you are looking to benchmark performance for a
+well-known model, verify the results of recently released research, or extend
+existing models, the Model Garden can help you drive your ML research and
+applications forward.
+
+The Model Garden includes the following resources for machine learning
+developers:
+
+- [**Official models**](#official) for vision and NLP, maintained by Google
+ engineers
+- [**Research models**](#research) published as part of ML research papers
+- [**Training experiment framework**](#training_framework) for fast,
+ declarative training configuration of official models
+- [**Specialized ML operations**](#ops) for vision and natural language
+ processing (NLP)
+- [**Model training loop**](#orbit) management with Orbit
+
+These resources are built to be used with the TensorFlow Core framework and
+integrate with your existing TensorFlow development projects. Model
+Garden resources are also provided under an [open
+source](https://github.com/tensorflow/models/blob/master/LICENSE) license, so
+you can freely extend and distribute the models and tools.
+
+Practical ML models are computationally intensive to train and run, and may
+require accelerators such as Graphical Processing Units (GPUs) and Tensor
+Processing Units (TPUs). Most of the models in Model Garden were trained on
+large datasets using TPUs. However, you can also train and run these models on
+GPU and CPU processors.
+
+## Model Garden models
+
+The machine learning models in the Model Garden include full code so you can
+test, train, or re-train them for research and experimentation. The Model Garden
+includes two primary categories of models: *official models* and *research
+models*.
+
+### Official models {:#official}
+
+The [Official Models](https://github.com/tensorflow/models/tree/master/official)
+repository is a collection of state-of-the-art models, with a focus on
+vision and natural language processing (NLP).
+These models are implemented using current TensorFlow 2.x high-level
+APIs. Model libraries in this repository are optimized for fast performance and
+actively maintained by Google engineers. The official models include additional
+metadata you can use to quickly configure experiments using the Model Garden
+[training experiment framework](#training_framework).
+
+### Research models {:#research}
+
+The [Research Models](https://github.com/tensorflow/models/tree/master/research)
+repository is a collection of models published as code resources for research
+papers. These models are implemented using both TensorFlow 1.x and 2.x. Model
+libraries in the research folder are supported by the code owners and the
+research community.
+
+## Training experiment framework {:#training_framework}
+
+The Model Garden training experiment framework lets you quickly assemble and run
+training experiments using its official models and standard datasets. The
+training framework uses additional metadata included with the Model Garden's
+official models to allow you to configure models quickly using a declarative
+programming model. You can define a training experiment using Python commands in
+the
+[TensorFlow Model library](https://www.tensorflow.org/api_docs/python/tfm/core)
+or configure training using a YAML configuration file, like this
+[example](https://github.com/tensorflow/models/blob/master/official/vision/configs/experiments/image_classification/imagenet_resnet50_tpu.yaml).
+
+The training framework uses
+[`tfm.core.base_trainer.ExperimentConfig`](https://www.tensorflow.org/api_docs/python/tfm/core/base_trainer/ExperimentConfig)
+as the configuration object, which contains the following top-level
+configuration objects:
+
+- [`runtime`](https://www.tensorflow.org/api_docs/python/tfm/core/base_task/RuntimeConfig):
+ Defines the processing hardware, distribution strategy, and other
+ performance optimizations
+- [`task`](https://www.tensorflow.org/api_docs/python/tfm/core/config_definitions/TaskConfig):
+ Defines the model, training data, losses, and initialization
+- [`trainer`](https://www.tensorflow.org/api_docs/python/tfm/core/base_trainer/TrainerConfig):
+ Defines the optimizer, training loops, evaluation loops, summaries, and
+ checkpoints
+
+For a complete example using the Model Garden training experiment framework, see
+the [Image classification with Model Garden](vision/image_classification.ipynb)
+tutorial. For information on the training experiment framework, check out the
+[TensorFlow Models API documentation](https://tensorflow.org/api_docs/python/tfm/core).
+If you are looking for a solution to manage training loops for your model
+training experiments, check out [Orbit](#orbit).
+
+## Specialized ML operations {:#ops}
+
+The Model Garden contains many vision and NLP operations specifically designed
+to execute state-of-the-art models that run efficiently on GPUs and TPUs. Review
+the TensorFlow Models Vision library API docs for a list of specialized
+[vision operations](https://www.tensorflow.org/api_docs/python/tfm/vision).
+Review the TensorFlow Models NLP Library API docs for a list of
+[NLP operations](https://www.tensorflow.org/api_docs/python/tfm/nlp). These
+libraries also include additional utility functions used for vision and NLP data
+processing, training, and model execution.
+
+## Training loops with Orbit {:#orbit}
+
+There are two default options for training TensorFlow models:
+
+* Use the high-level Keras
+[Model.fit](https://www.tensorflow.org/api_docs/python/tf/keras/Model#fit)
+function. If your model and training procedure fit the assumptions of Keras'
+`Model.fit` (incremental gradient descent on batches of data) method this can
+be very convenient.
+* Write a custom training loop
+[with keras](https://www.tensorflow.org/guide/keras/writing_a_training_loop_from_scratch),
+or [without](https://www.tensorflow.org/guide/core/logistic_regression_core).
+You can write a custom training loop with low-level TensorFlow methods such as
+`tf.GradientTape` or `tf.function`. However, this approach requires a lot of
+boilerplate code, and doesn't do anything to simplify distributed training.
+
+Orbit tries to provide a third option in between these two extremes.
+
+Orbit is a flexible, lightweight library designed to make it easier to
+write custom training loops in TensorFlow 2.x, and works well with the Model
+Garden [training experiment framework](#training_framework). Orbit handles
+common model training tasks such as saving checkpoints, running model
+evaluations, and setting up summary writing. It seamlessly integrates with
+`tf.distribute` and supports running on different device types, including CPU,
+GPU, and TPU hardware. The Orbit tool is also [open
+source](https://github.com/tensorflow/models/blob/master/orbit/LICENSE), so you
+can extend and adapt to your model training needs.
+
+The Orbit guide is available [here](orbit/index.ipynb).
+
+Note: You can customize how the Keras API executes training. Mainly you must
+override the `Model.train_step` method or use `keras.callbacks` like
+`callbacks.ModelCheckpoint` or `callbacks.TensorBoard`. For more information
+about modifying the behavior of `train_step`, check out the
+[Customize what happens in Model.fit](https://www.tensorflow.org/guide/keras/customizing_what_happens_in_fit)
+page.
diff --git a/docs/nlp/_guide_toc.yaml b/docs/nlp/_guide_toc.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..5d90c4232a46b6afcd0236a0bdc324258591729e
--- /dev/null
+++ b/docs/nlp/_guide_toc.yaml
@@ -0,0 +1,7 @@
+toc:
+- heading: TensorFlow Models - NLP
+ style: divider
+- title: "Overview"
+ path: /tfmodels/nlp
+- title: "Customize a transformer encoder"
+ path: /tfmodels/nlp/customize_encoder
diff --git a/docs/nlp/customize_encoder.ipynb b/docs/nlp/customize_encoder.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..3d81f084d6c8d824188ee5acdf1719113a62fa46
--- /dev/null
+++ b/docs/nlp/customize_encoder.ipynb
@@ -0,0 +1,596 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Bp8t2AI8i7uP"
+ },
+ "source": [
+ "##### Copyright 2022 The TensorFlow Authors."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "cellView": "form",
+ "id": "rxPj2Lsni9O4"
+ },
+ "outputs": [],
+ "source": [
+ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
+ "# you may not use this file except in compliance with the License.\n",
+ "# You may obtain a copy of the License at\n",
+ "#\n",
+ "# https://www.apache.org/licenses/LICENSE-2.0\n",
+ "#\n",
+ "# Unless required by applicable law or agreed to in writing, software\n",
+ "# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
+ "# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
+ "# See the License for the specific language governing permissions and\n",
+ "# limitations under the License."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6xS-9i5DrRvO"
+ },
+ "source": [
+ "# Customizing a Transformer Encoder"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Mwb9uw1cDXsa"
+ },
+ "source": [
+ "
"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "iLrcV4IyrcGX"
- },
- "source": [
- "## Learning objectives\n",
- "\n",
- "The [TensorFlow Models NLP library](https://github.com/tensorflow/models/tree/master/official/nlp/modeling) is a collection of tools for building and training modern high performance natural language models.\n",
- "\n",
- "The [TransformEncoder](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/networks/encoder_scaffold.py) is the core of this library, and lots of new network architectures are proposed to improve the encoder. In this Colab notebook, we will learn how to customize the encoder to employ new network architectures."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "YYxdyoWgsl8t"
- },
- "source": [
- "## Install and import"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "fEJSFutUsn_h"
- },
- "source": [
- "### Install the TensorFlow Model Garden pip package\n",
- "\n",
- "* `tf-models-official` is the stable Model Garden package. Note that it may not include the latest changes in the `tensorflow_models` github repo. To include latest changes, you may install `tf-models-nightly`,\n",
- "which is the nightly Model Garden package created daily automatically.\n",
- "* `pip` will install all models and dependencies automatically."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "thsKZDjhswhR"
- },
- "source": [
- "!pip install -q tf-models-official==2.4.0"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "hpf7JPCVsqtv"
- },
- "source": [
- "### Import Tensorflow and other libraries"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "my4dp-RMssQe"
- },
- "source": [
- "import numpy as np\n",
- "import tensorflow as tf\n",
- "\n",
- "from official.modeling import activations\n",
- "from official.nlp import modeling\n",
- "from official.nlp.modeling import layers, losses, models, networks"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "vjDmVsFfs85n"
- },
- "source": [
- "## Canonical BERT encoder\n",
- "\n",
- "Before learning how to customize the encoder, let's firstly create a canonical BERT enoder and use it to instantiate a `BertClassifier` for classification task."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "Oav8sbgstWc-"
- },
- "source": [
- "cfg = {\n",
- " \"vocab_size\": 100,\n",
- " \"hidden_size\": 32,\n",
- " \"num_layers\": 3,\n",
- " \"num_attention_heads\": 4,\n",
- " \"intermediate_size\": 64,\n",
- " \"activation\": activations.gelu,\n",
- " \"dropout_rate\": 0.1,\n",
- " \"attention_dropout_rate\": 0.1,\n",
- " \"max_sequence_length\": 16,\n",
- " \"type_vocab_size\": 2,\n",
- " \"initializer\": tf.keras.initializers.TruncatedNormal(stddev=0.02),\n",
- "}\n",
- "bert_encoder = modeling.networks.BertEncoder(**cfg)\n",
- "\n",
- "def build_classifier(bert_encoder):\n",
- " return modeling.models.BertClassifier(bert_encoder, num_classes=2)\n",
- "\n",
- "canonical_classifier_model = build_classifier(bert_encoder)"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "Qe2UWI6_tsHo"
- },
- "source": [
- "`canonical_classifier_model` can be trained using the training data. For details about how to train the model, please see the colab [fine_tuning_bert.ipynb](https://github.com/tensorflow/models/blob/master/official/colab/fine_tuning_bert.ipynb). We skip the code that trains the model here.\n",
- "\n",
- "After training, we can apply the model to do prediction.\n"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "csED2d-Yt5h6"
- },
- "source": [
- "def predict(model):\n",
- " batch_size = 3\n",
- " np.random.seed(0)\n",
- " word_ids = np.random.randint(\n",
- " cfg[\"vocab_size\"], size=(batch_size, cfg[\"max_sequence_length\"]))\n",
- " mask = np.random.randint(2, size=(batch_size, cfg[\"max_sequence_length\"]))\n",
- " type_ids = np.random.randint(\n",
- " cfg[\"type_vocab_size\"], size=(batch_size, cfg[\"max_sequence_length\"]))\n",
- " print(model([word_ids, mask, type_ids], training=False))\n",
- "\n",
- "predict(canonical_classifier_model)"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "PzKStEK9t_Pb"
- },
- "source": [
- "## Customize BERT encoder\n",
- "\n",
- "One BERT encoder consists of an embedding network and multiple transformer blocks, and each transformer block contains an attention layer and a feedforward layer."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "rmwQfhj6fmKz"
- },
- "source": [
- "We provide easy ways to customize each of those components via (1)\n",
- "[EncoderScaffold](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/networks/encoder_scaffold.py) and (2) [TransformerScaffold](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/transformer_scaffold.py)."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "xsMgEVHAui11"
- },
- "source": [
- "### Use EncoderScaffold\n",
- "\n",
- "`EncoderScaffold` allows users to provide a custom embedding subnetwork\n",
- " (which will replace the standard embedding logic) and/or a custom hidden layer class (which will replace the `Transformer` instantiation in the encoder)."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "-JBabpa2AOz8"
- },
- "source": [
- "#### Without Customization\n",
- "\n",
- "Without any customization, `EncoderScaffold` behaves the same the canonical `BertEncoder`.\n",
- "\n",
- "As shown in the following example, `EncoderScaffold` can load `BertEncoder`'s weights and output the same values:"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "ktNzKuVByZQf"
- },
- "source": [
- "default_hidden_cfg = dict(\n",
- " num_attention_heads=cfg[\"num_attention_heads\"],\n",
- " intermediate_size=cfg[\"intermediate_size\"],\n",
- " intermediate_activation=activations.gelu,\n",
- " dropout_rate=cfg[\"dropout_rate\"],\n",
- " attention_dropout_rate=cfg[\"attention_dropout_rate\"],\n",
- " kernel_initializer=tf.keras.initializers.TruncatedNormal(0.02),\n",
- ")\n",
- "default_embedding_cfg = dict(\n",
- " vocab_size=cfg[\"vocab_size\"],\n",
- " type_vocab_size=cfg[\"type_vocab_size\"],\n",
- " hidden_size=cfg[\"hidden_size\"],\n",
- " initializer=tf.keras.initializers.TruncatedNormal(0.02),\n",
- " dropout_rate=cfg[\"dropout_rate\"],\n",
- " max_seq_length=cfg[\"max_sequence_length\"]\n",
- ")\n",
- "default_kwargs = dict(\n",
- " hidden_cfg=default_hidden_cfg,\n",
- " embedding_cfg=default_embedding_cfg,\n",
- " num_hidden_instances=cfg[\"num_layers\"],\n",
- " pooled_output_dim=cfg[\"hidden_size\"],\n",
- " return_all_layer_outputs=True,\n",
- " pooler_layer_initializer=tf.keras.initializers.TruncatedNormal(0.02),\n",
- ")\n",
- "\n",
- "encoder_scaffold = modeling.networks.EncoderScaffold(**default_kwargs)\n",
- "classifier_model_from_encoder_scaffold = build_classifier(encoder_scaffold)\n",
- "classifier_model_from_encoder_scaffold.set_weights(\n",
- " canonical_classifier_model.get_weights())\n",
- "predict(classifier_model_from_encoder_scaffold)"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "sMaUmLyIuwcs"
- },
- "source": [
- "#### Customize Embedding\n",
- "\n",
- "Next, we show how to use a customized embedding network.\n",
- "\n",
- "We firstly build an embedding network that will replace the default network. This one will have 2 inputs (`mask` and `word_ids`) instead of 3, and won't use positional embeddings."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "LTinnaG6vcsw"
- },
- "source": [
- "word_ids = tf.keras.layers.Input(\n",
- " shape=(cfg['max_sequence_length'],), dtype=tf.int32, name=\"input_word_ids\")\n",
- "mask = tf.keras.layers.Input(\n",
- " shape=(cfg['max_sequence_length'],), dtype=tf.int32, name=\"input_mask\")\n",
- "embedding_layer = modeling.layers.OnDeviceEmbedding(\n",
- " vocab_size=cfg['vocab_size'],\n",
- " embedding_width=cfg['hidden_size'],\n",
- " initializer=tf.keras.initializers.TruncatedNormal(stddev=0.02),\n",
- " name=\"word_embeddings\")\n",
- "word_embeddings = embedding_layer(word_ids)\n",
- "attention_mask = layers.SelfAttentionMask()([word_embeddings, mask])\n",
- "new_embedding_network = tf.keras.Model([word_ids, mask],\n",
- " [word_embeddings, attention_mask])"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "HN7_yu-6O3qI"
- },
- "source": [
- "Inspecting `new_embedding_network`, we can see it takes two inputs:\n",
- "`input_word_ids` and `input_mask`."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "fO9zKFE4OpHp"
- },
- "source": [
- "tf.keras.utils.plot_model(new_embedding_network, show_shapes=True, dpi=48)"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "9cOaGQHLv12W"
- },
- "source": [
- "We then can build a new encoder using the above `new_embedding_network`."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "mtFDMNf2vIl9"
- },
- "source": [
- "kwargs = dict(default_kwargs)\n",
- "\n",
- "# Use new embedding network.\n",
- "kwargs['embedding_cls'] = new_embedding_network\n",
- "kwargs['embedding_data'] = embedding_layer.embeddings\n",
- "\n",
- "encoder_with_customized_embedding = modeling.networks.EncoderScaffold(**kwargs)\n",
- "classifier_model = build_classifier(encoder_with_customized_embedding)\n",
- "# ... Train the model ...\n",
- "print(classifier_model.inputs)\n",
- "\n",
- "# Assert that there are only two inputs.\n",
- "assert len(classifier_model.inputs) == 2"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "Z73ZQDtmwg9K"
- },
- "source": [
- "#### Customized Transformer\n",
- "\n",
- "User can also override the [hidden_cls](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/networks/encoder_scaffold.py#L103) argument in `EncoderScaffold`'s constructor to employ a customized Transformer layer.\n",
- "\n",
- "See [ReZeroTransformer](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/rezero_transformer.py) for how to implement a customized Transformer layer.\n",
- "\n",
- "Following is an example of using `ReZeroTransformer`:\n"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "uAIarLZgw6pA"
- },
- "source": [
- "kwargs = dict(default_kwargs)\n",
- "\n",
- "# Use ReZeroTransformer.\n",
- "kwargs['hidden_cls'] = modeling.layers.ReZeroTransformer\n",
- "\n",
- "encoder_with_rezero_transformer = modeling.networks.EncoderScaffold(**kwargs)\n",
- "classifier_model = build_classifier(encoder_with_rezero_transformer)\n",
- "# ... Train the model ...\n",
- "predict(classifier_model)\n",
- "\n",
- "# Assert that the variable `rezero_alpha` from ReZeroTransformer exists.\n",
- "assert 'rezero_alpha' in ''.join([x.name for x in classifier_model.trainable_weights])"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "6PMHFdvnxvR0"
- },
- "source": [
- "### Use [TransformerScaffold](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/transformer_scaffold.py)\n",
- "\n",
- "The above method of customizing `Transformer` requires rewriting the whole `Transformer` layer, while sometimes you may only want to customize either attention layer or feedforward block. In this case, [TransformerScaffold](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/transformer_scaffold.py) can be used.\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "D6FejlgwyAy_"
- },
- "source": [
- "#### Customize Attention Layer\n",
- "\n",
- "User can also override the [attention_cls](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/transformer_scaffold.py#L45) argument in `TransformerScaffold`'s constructor to employ a customized Attention layer.\n",
- "\n",
- "See [TalkingHeadsAttention](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/talking_heads_attention.py) for how to implement a customized `Attention` layer.\n",
- "\n",
- "Following is an example of using [TalkingHeadsAttention](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/talking_heads_attention.py):"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "nFrSMrZuyNeQ"
- },
- "source": [
- "# Use TalkingHeadsAttention\n",
- "hidden_cfg = dict(default_hidden_cfg)\n",
- "hidden_cfg['attention_cls'] = modeling.layers.TalkingHeadsAttention\n",
- "\n",
- "kwargs = dict(default_kwargs)\n",
- "kwargs['hidden_cls'] = modeling.layers.TransformerScaffold\n",
- "kwargs['hidden_cfg'] = hidden_cfg\n",
- "\n",
- "encoder = modeling.networks.EncoderScaffold(**kwargs)\n",
- "classifier_model = build_classifier(encoder)\n",
- "# ... Train the model ...\n",
- "predict(classifier_model)\n",
- "\n",
- "# Assert that the variable `pre_softmax_weight` from TalkingHeadsAttention exists.\n",
- "assert 'pre_softmax_weight' in ''.join([x.name for x in classifier_model.trainable_weights])"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "kuEJcTyByVvI"
- },
- "source": [
- "#### Customize Feedforward Layer\n",
- "\n",
- "Similiarly, one could also customize the feedforward layer.\n",
- "\n",
- "See [GatedFeedforward](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/gated_feedforward.py) for how to implement a customized feedforward layer.\n",
- "\n",
- "Following is an example of using [GatedFeedforward](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/layers/gated_feedforward.py)."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "XAbKy_l4y_-i"
- },
- "source": [
- "# Use TalkingHeadsAttention\n",
- "hidden_cfg = dict(default_hidden_cfg)\n",
- "hidden_cfg['feedforward_cls'] = modeling.layers.GatedFeedforward\n",
- "\n",
- "kwargs = dict(default_kwargs)\n",
- "kwargs['hidden_cls'] = modeling.layers.TransformerScaffold\n",
- "kwargs['hidden_cfg'] = hidden_cfg\n",
- "\n",
- "encoder_with_gated_feedforward = modeling.networks.EncoderScaffold(**kwargs)\n",
- "classifier_model = build_classifier(encoder_with_gated_feedforward)\n",
- "# ... Train the model ...\n",
- "predict(classifier_model)\n",
- "\n",
- "# Assert that the variable `gate` from GatedFeedforward exists.\n",
- "assert 'gate' in ''.join([x.name for x in classifier_model.trainable_weights])"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "a_8NWUhkzeAq"
- },
- "source": [
- "### Build a new Encoder using building blocks from KerasBERT.\n",
- "\n",
- "Finally, you could also build a new encoder using building blocks in the modeling library.\n",
- "\n",
- "See [AlbertEncoder](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/networks/albert_encoder.py) as an example:\n"
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "xsiA3RzUzmUM"
- },
- "source": [
- "albert_encoder = modeling.networks.AlbertEncoder(**cfg)\n",
- "classifier_model = build_classifier(albert_encoder)\n",
- "# ... Train the model ...\n",
- "predict(classifier_model)"
- ],
- "execution_count": null,
- "outputs": []
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "MeidDfhlHKSO"
- },
- "source": [
- "Inspecting the `albert_encoder`, we see it stacks the same `Transformer` layer multiple times."
- ]
- },
- {
- "cell_type": "code",
- "metadata": {
- "id": "Uv_juT22HERW"
- },
- "source": [
- "tf.keras.utils.plot_model(albert_encoder, show_shapes=True, dpi=48)"
- ],
- "execution_count": null,
- "outputs": []
- }
- ]
-}
\ No newline at end of file
diff --git a/official/colab/nlp/nlp_modeling_library_intro.ipynb b/official/colab/nlp/nlp_modeling_library_intro.ipynb
deleted file mode 100644
index e4ce780c96bfbf679c91891f38b08ac3b0bb983e..0000000000000000000000000000000000000000
--- a/official/colab/nlp/nlp_modeling_library_intro.ipynb
+++ /dev/null
@@ -1,544 +0,0 @@
-{
- "cells": [
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "80xnUmoI7fBX"
- },
- "source": [
- "##### Copyright 2020 The TensorFlow Authors."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "cellView": "form",
- "id": "8nvTnfs6Q692"
- },
- "outputs": [],
- "source": [
- "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
- "# you may not use this file except in compliance with the License.\n",
- "# You may obtain a copy of the License at\n",
- "#\n",
- "# https://www.apache.org/licenses/LICENSE-2.0\n",
- "#\n",
- "# Unless required by applicable law or agreed to in writing, software\n",
- "# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
- "# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
- "# See the License for the specific language governing permissions and\n",
- "# limitations under the License."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "WmfcMK5P5C1G"
- },
- "source": [
- "# Introduction to the TensorFlow Models NLP library"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "cH-oJ8R6AHMK"
- },
- "source": [
- "\u003ctable class=\"tfo-notebook-buttons\" align=\"left\"\u003e\n",
- " \u003ctd\u003e\n",
- " \u003ca target=\"_blank\" href=\"https://www.tensorflow.org/official_models/nlp/nlp_modeling_library_intro\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/tf_logo_32px.png\" /\u003eView on TensorFlow.org\u003c/a\u003e\n",
- " \u003c/td\u003e\n",
- " \u003ctd\u003e\n",
- " \u003ca target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/models/blob/master/official/colab/nlp/nlp_modeling_library_intro.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" /\u003eRun in Google Colab\u003c/a\u003e\n",
- " \u003c/td\u003e\n",
- " \u003ctd\u003e\n",
- " \u003ca target=\"_blank\" href=\"https://github.com/tensorflow/models/blob/master/official/colab/nlp/nlp_modeling_library_intro.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" /\u003eView source on GitHub\u003c/a\u003e\n",
- " \u003c/td\u003e\n",
- " \u003ctd\u003e\n",
- " \u003ca href=\"https://storage.googleapis.com/tensorflow_docs/models/official/colab/nlp/nlp_modeling_library_intro.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/download_logo_32px.png\" /\u003eDownload notebook\u003c/a\u003e\n",
- " \u003c/td\u003e\n",
- "\u003c/table\u003e"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "0H_EFIhq4-MJ"
- },
- "source": [
- "## Learning objectives\n",
- "\n",
- "In this Colab notebook, you will learn how to build transformer-based models for common NLP tasks including pretraining, span labelling and classification using the building blocks from [NLP modeling library](https://github.com/tensorflow/models/tree/master/official/nlp/modeling)."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "2N97-dps_nUk"
- },
- "source": [
- "## Install and import"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "459ygAVl_rg0"
- },
- "source": [
- "### Install the TensorFlow Model Garden pip package\n",
- "\n",
- "* `tf-models-official` is the stable Model Garden package. Note that it may not include the latest changes in the `tensorflow_models` github repo. To include latest changes, you may install `tf-models-nightly`,\n",
- "which is the nightly Model Garden package created daily automatically.\n",
- "* `pip` will install all models and dependencies automatically."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "Y-qGkdh6_sZc"
- },
- "outputs": [],
- "source": [
- "!pip install -q tf-models-official==2.4.0"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "e4huSSwyAG_5"
- },
- "source": [
- "### Import Tensorflow and other libraries"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "jqYXqtjBAJd9"
- },
- "outputs": [],
- "source": [
- "import numpy as np\n",
- "import tensorflow as tf\n",
- "\n",
- "from official.nlp import modeling\n",
- "from official.nlp.modeling import layers, losses, models, networks"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "djBQWjvy-60Y"
- },
- "source": [
- "## BERT pretraining model\n",
- "\n",
- "BERT ([Pre-training of Deep Bidirectional Transformers for Language Understanding](https://arxiv.org/abs/1810.04805)) introduced the method of pre-training language representations on a large text corpus and then using that model for downstream NLP tasks.\n",
- "\n",
- "In this section, we will learn how to build a model to pretrain BERT on the masked language modeling task and next sentence prediction task. For simplicity, we only show the minimum example and use dummy data."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "MKuHVlsCHmiq"
- },
- "source": [
- "### Build a `BertPretrainer` model wrapping `BertEncoder`\n",
- "\n",
- "The [BertEncoder](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/networks/bert_encoder.py) implements the Transformer-based encoder as described in [BERT paper](https://arxiv.org/abs/1810.04805). It includes the embedding lookups and transformer layers, but not the masked language model or classification task networks.\n",
- "\n",
- "The [BertPretrainer](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/models/bert_pretrainer.py) allows a user to pass in a transformer stack, and instantiates the masked language model and classification networks that are used to create the training objectives."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "EXkcXz-9BwB3"
- },
- "outputs": [],
- "source": [
- "# Build a small transformer network.\n",
- "vocab_size = 100\n",
- "sequence_length = 16\n",
- "network = modeling.networks.BertEncoder(\n",
- " vocab_size=vocab_size, num_layers=2, sequence_length=16)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "0NH5irV5KTMS"
- },
- "source": [
- "Inspecting the encoder, we see it contains few embedding layers, stacked `Transformer` layers and are connected to three input layers:\n",
- "\n",
- "`input_word_ids`, `input_type_ids` and `input_mask`.\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "lZNoZkBrIoff"
- },
- "outputs": [],
- "source": [
- "tf.keras.utils.plot_model(network, show_shapes=True, dpi=48)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "o7eFOZXiIl-b"
- },
- "outputs": [],
- "source": [
- "# Create a BERT pretrainer with the created network.\n",
- "num_token_predictions = 8\n",
- "bert_pretrainer = modeling.models.BertPretrainer(\n",
- " network, num_classes=2, num_token_predictions=num_token_predictions, output='predictions')"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "d5h5HT7gNHx_"
- },
- "source": [
- "Inspecting the `bert_pretrainer`, we see it wraps the `encoder` with additional `MaskedLM` and `Classification` heads."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "2tcNfm03IBF7"
- },
- "outputs": [],
- "source": [
- "tf.keras.utils.plot_model(bert_pretrainer, show_shapes=True, dpi=48)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "F2oHrXGUIS0M"
- },
- "outputs": [],
- "source": [
- "# We can feed some dummy data to get masked language model and sentence output.\n",
- "batch_size = 2\n",
- "word_id_data = np.random.randint(vocab_size, size=(batch_size, sequence_length))\n",
- "mask_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "type_id_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "masked_lm_positions_data = np.random.randint(2, size=(batch_size, num_token_predictions))\n",
- "\n",
- "outputs = bert_pretrainer(\n",
- " [word_id_data, mask_data, type_id_data, masked_lm_positions_data])\n",
- "lm_output = outputs[\"masked_lm\"]\n",
- "sentence_output = outputs[\"classification\"]\n",
- "print(lm_output)\n",
- "print(sentence_output)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "bnx3UCHniCS5"
- },
- "source": [
- "### Compute loss\n",
- "Next, we can use `lm_output` and `sentence_output` to compute `loss`."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "k30H4Q86f52x"
- },
- "outputs": [],
- "source": [
- "masked_lm_ids_data = np.random.randint(vocab_size, size=(batch_size, num_token_predictions))\n",
- "masked_lm_weights_data = np.random.randint(2, size=(batch_size, num_token_predictions))\n",
- "next_sentence_labels_data = np.random.randint(2, size=(batch_size))\n",
- "\n",
- "mlm_loss = modeling.losses.weighted_sparse_categorical_crossentropy_loss(\n",
- " labels=masked_lm_ids_data,\n",
- " predictions=lm_output,\n",
- " weights=masked_lm_weights_data)\n",
- "sentence_loss = modeling.losses.weighted_sparse_categorical_crossentropy_loss(\n",
- " labels=next_sentence_labels_data,\n",
- " predictions=sentence_output)\n",
- "loss = mlm_loss + sentence_loss\n",
- "print(loss)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "wrmSs8GjHxVw"
- },
- "source": [
- "With the loss, you can optimize the model.\n",
- "After training, we can save the weights of TransformerEncoder for the downstream fine-tuning tasks. Please see [run_pretraining.py](https://github.com/tensorflow/models/blob/master/official/nlp/bert/run_pretraining.py) for the full example.\n",
- "\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "k8cQVFvBCV4s"
- },
- "source": [
- "## Span labeling model\n",
- "\n",
- "Span labeling is the task to assign labels to a span of the text, for example, label a span of text as the answer of a given question.\n",
- "\n",
- "In this section, we will learn how to build a span labeling model. Again, we use dummy data for simplicity."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "xrLLEWpfknUW"
- },
- "source": [
- "### Build a BertSpanLabeler wrapping BertEncoder\n",
- "\n",
- "[BertSpanLabeler](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/models/bert_span_labeler.py) implements a simple single-span start-end predictor (that is, a model that predicts two values: a start token index and an end token index), suitable for SQuAD-style tasks.\n",
- "\n",
- "Note that `BertSpanLabeler` wraps a `BertEncoder`, the weights of which can be restored from the above pretraining model.\n"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "B941M4iUCejO"
- },
- "outputs": [],
- "source": [
- "network = modeling.networks.BertEncoder(\n",
- " vocab_size=vocab_size, num_layers=2, sequence_length=sequence_length)\n",
- "\n",
- "# Create a BERT trainer with the created network.\n",
- "bert_span_labeler = modeling.models.BertSpanLabeler(network)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "QpB9pgj4PpMg"
- },
- "source": [
- "Inspecting the `bert_span_labeler`, we see it wraps the encoder with additional `SpanLabeling` that outputs `start_position` and `end_postion`."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "RbqRNJCLJu4H"
- },
- "outputs": [],
- "source": [
- "tf.keras.utils.plot_model(bert_span_labeler, show_shapes=True, dpi=48)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "fUf1vRxZJwio"
- },
- "outputs": [],
- "source": [
- "# Create a set of 2-dimensional data tensors to feed into the model.\n",
- "word_id_data = np.random.randint(vocab_size, size=(batch_size, sequence_length))\n",
- "mask_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "type_id_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "\n",
- "# Feed the data to the model.\n",
- "start_logits, end_logits = bert_span_labeler([word_id_data, mask_data, type_id_data])\n",
- "print(start_logits)\n",
- "print(end_logits)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "WqhgQaN1lt-G"
- },
- "source": [
- "### Compute loss\n",
- "With `start_logits` and `end_logits`, we can compute loss:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "waqs6azNl3Nn"
- },
- "outputs": [],
- "source": [
- "start_positions = np.random.randint(sequence_length, size=(batch_size))\n",
- "end_positions = np.random.randint(sequence_length, size=(batch_size))\n",
- "\n",
- "start_loss = tf.keras.losses.sparse_categorical_crossentropy(\n",
- " start_positions, start_logits, from_logits=True)\n",
- "end_loss = tf.keras.losses.sparse_categorical_crossentropy(\n",
- " end_positions, end_logits, from_logits=True)\n",
- "\n",
- "total_loss = (tf.reduce_mean(start_loss) + tf.reduce_mean(end_loss)) / 2\n",
- "print(total_loss)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "Zdf03YtZmd_d"
- },
- "source": [
- "With the `loss`, you can optimize the model. Please see [run_squad.py](https://github.com/tensorflow/models/blob/master/official/nlp/bert/run_squad.py) for the full example."
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "0A1XnGSTChg9"
- },
- "source": [
- "## Classification model\n",
- "\n",
- "In the last section, we show how to build a text classification model.\n"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "MSK8OpZgnQa9"
- },
- "source": [
- "### Build a BertClassifier model wrapping BertEncoder\n",
- "\n",
- "[BertClassifier](https://github.com/tensorflow/models/blob/master/official/nlp/modeling/models/bert_classifier.py) implements a [CLS] token classification model containing a single classification head."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "cXXCsffkCphk"
- },
- "outputs": [],
- "source": [
- "network = modeling.networks.BertEncoder(\n",
- " vocab_size=vocab_size, num_layers=2, sequence_length=sequence_length)\n",
- "\n",
- "# Create a BERT trainer with the created network.\n",
- "num_classes = 2\n",
- "bert_classifier = modeling.models.BertClassifier(\n",
- " network, num_classes=num_classes)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "8tZKueKYP4bB"
- },
- "source": [
- "Inspecting the `bert_classifier`, we see it wraps the `encoder` with additional `Classification` head."
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "snlutm9ZJgEZ"
- },
- "outputs": [],
- "source": [
- "tf.keras.utils.plot_model(bert_classifier, show_shapes=True, dpi=48)"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "yyHPHsqBJkCz"
- },
- "outputs": [],
- "source": [
- "# Create a set of 2-dimensional data tensors to feed into the model.\n",
- "word_id_data = np.random.randint(vocab_size, size=(batch_size, sequence_length))\n",
- "mask_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "type_id_data = np.random.randint(2, size=(batch_size, sequence_length))\n",
- "\n",
- "# Feed the data to the model.\n",
- "logits = bert_classifier([word_id_data, mask_data, type_id_data])\n",
- "print(logits)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "w--a2mg4nzKm"
- },
- "source": [
- "### Compute loss\n",
- "\n",
- "With `logits`, we can compute `loss`:"
- ]
- },
- {
- "cell_type": "code",
- "execution_count": null,
- "metadata": {
- "id": "9X0S1DoFn_5Q"
- },
- "outputs": [],
- "source": [
- "labels = np.random.randint(num_classes, size=(batch_size))\n",
- "\n",
- "loss = tf.keras.losses.sparse_categorical_crossentropy(\n",
- " labels, logits, from_logits=True)\n",
- "print(loss)"
- ]
- },
- {
- "cell_type": "markdown",
- "metadata": {
- "id": "mzBqOylZo3og"
- },
- "source": [
- "With the `loss`, you can optimize the model. Please see [run_classifier.py](https://github.com/tensorflow/models/blob/master/official/nlp/bert/run_classifier.py) or the colab [fine_tuning_bert.ipynb](https://github.com/tensorflow/models/blob/master/official/colab/fine_tuning_bert.ipynb) for the full example."
- ]
- }
- ],
- "metadata": {
- "colab": {
- "collapsed_sections": [],
- "name": "Introduction to the TensorFlow Models NLP library",
- "private_outputs": true,
- "provenance": [],
- "toc_visible": true
- },
- "kernelspec": {
- "display_name": "Python 3",
- "name": "python3"
- }
- },
- "nbformat": 4,
- "nbformat_minor": 0
-}
diff --git a/official/common/__init__.py b/official/common/__init__.py
index a25710c222e3327cb20e000db5df5c5651c4a2cc..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1 100644
--- a/official/common/__init__.py
+++ b/official/common/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/common/dataset_fn.py b/official/common/dataset_fn.py
index 4ac16a31b555588368a6c0aba73adbe62a95c2eb..52138d717a0e9a7bdb2ad1c0006966916ecf9910 100644
--- a/official/common/dataset_fn.py
+++ b/official/common/dataset_fn.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,7 +28,8 @@
# ==============================================================================
"""Utility library for picking an appropriate dataset function."""
-from typing import Any, Callable, Union, Type
+import functools
+from typing import Any, Callable, Type, Union
import tensorflow as tf
@@ -38,5 +39,6 @@ PossibleDatasetType = Union[Type[tf.data.Dataset], Callable[[tf.Tensor], Any]]
def pick_dataset_fn(file_type: str) -> PossibleDatasetType:
if file_type == 'tfrecord':
return tf.data.TFRecordDataset
-
+ if file_type == 'tfrecord_compressed':
+ return functools.partial(tf.data.TFRecordDataset, compression_type='GZIP')
raise ValueError('Unrecognized file_type: {}'.format(file_type))
diff --git a/official/common/distribute_utils.py b/official/common/distribute_utils.py
index c48d68d6d93111e0959c9bbfde1e767fc673a979..bce9bf25ad5f4ea5dec88b61735af69a88d6133f 100644
--- a/official/common/distribute_utils.py
+++ b/official/common/distribute_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -96,7 +96,7 @@ def get_distribution_strategy(distribution_strategy="mirrored",
num_packs=1,
tpu_address=None,
**kwargs):
- """Return a DistributionStrategy for running the model.
+ """Return a Strategy for running the model.
Args:
distribution_strategy: a string specifying which distribution strategy to
@@ -119,7 +119,7 @@ def get_distribution_strategy(distribution_strategy="mirrored",
**kwargs: Additional kwargs for internal usages.
Returns:
- tf.distribute.DistibutionStrategy object.
+ tf.distribute.Strategy object.
Raises:
ValueError: if `distribution_strategy` is "off" or "one_device" and
`num_gpus` is larger than 1; or `num_gpus` is negative or if
diff --git a/official/common/distribute_utils_test.py b/official/common/distribute_utils_test.py
index 8e49d366651de0d891c72b4494d743d052e4f749..f06ee3ba628b7b4fe385a73311fbf453f5e3c0e6 100644
--- a/official/common/distribute_utils_test.py
+++ b/official/common/distribute_utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/common/flags.py b/official/common/flags.py
index 01ddf57af3872b0ad6f425602b5029ece9def707..5e15856416945708bda5fbab5110bb83f838c667 100644
--- a/official/common/flags.py
+++ b/official/common/flags.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -45,7 +45,8 @@ def define_flags():
default=None,
enum_values=[
'train', 'eval', 'train_and_eval', 'continuous_eval',
- 'continuous_train_and_eval', 'train_and_validate'
+ 'continuous_train_and_eval', 'train_and_validate',
+ 'train_and_post_eval'
],
help='Mode to run: `train`, `eval`, `train_and_eval`, '
'`continuous_eval`, `continuous_train_and_eval` and '
diff --git a/official/common/registry_imports.py b/official/common/registry_imports.py
index 06f3384db6283cbef08070f3678d0afe36e50c08..eb9af692a4ad144260807623b4b0e6b8ebac11e4 100644
--- a/official/common/registry_imports.py
+++ b/official/common/registry_imports.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,7 +14,7 @@
"""All necessary imports for registration."""
# pylint: disable=unused-import
+from official import vision
from official.nlp import tasks
from official.nlp.configs import experiment_configs
from official.utils.testing import mock_task
-from official.vision import beta
diff --git a/official/common/streamz_counters.py b/official/common/streamz_counters.py
index ab3df36ce6077d2dafd25eb199fc0370852795e5..5def620ec752922e68e97811451b9aa47c21e01a 100644
--- a/official/common/streamz_counters.py
+++ b/official/common/streamz_counters.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/__init__.py b/official/core/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..48624e238c195b7b65a075113815bd8b6b682be3 100644
--- a/official/core/__init__.py
+++ b/official/core/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,3 +12,20 @@
# See the License for the specific language governing permissions and
# limitations under the License.
+"""Core is shared by both `nlp` and `vision`."""
+
+from official.core import actions
+from official.core import base_task
+from official.core import base_trainer
+from official.core import config_definitions
+from official.core import exp_factory
+from official.core import export_base
+from official.core import file_writers
+from official.core import input_reader
+from official.core import registry
+from official.core import savedmodel_checkpoint_manager
+from official.core import task_factory
+from official.core import tf_example_builder
+from official.core import tf_example_feature_key
+from official.core import train_lib
+from official.core import train_utils
diff --git a/official/core/actions.py b/official/core/actions.py
index 20453a829689b0d6cbd5735df936afea2bca6c12..4d51d30943674685d24912d6d64f7170b88be6c3 100644
--- a/official/core/actions.py
+++ b/official/core/actions.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,7 +21,6 @@ from absl import logging
import gin
import orbit
import tensorflow as tf
-import tensorflow_model_optimization as tfmot
from official.core import base_trainer
from official.core import config_definitions
@@ -52,6 +51,8 @@ class PruningAction:
optimizer: `tf.keras.optimizers.Optimizer` optimizer instance used for
training. This will be used to find the current training steps.
"""
+ # TODO(b/221490190): Avoid local import when the bug is fixed.
+ import tensorflow_model_optimization as tfmot # pylint: disable=g-import-not-at-top
self._optimizer = optimizer
self.update_pruning_step = tfmot.sparsity.keras.UpdatePruningStep()
self.update_pruning_step.set_model(model)
@@ -201,7 +202,7 @@ def get_train_actions(
"""Gets train actions for TFM trainer."""
train_actions = []
# Adds pruning callback actions.
- if hasattr(params.task, 'pruning'):
+ if hasattr(params.task, 'pruning') and params.task.pruning:
train_actions.append(
PruningAction(
export_dir=model_dir,
diff --git a/official/core/actions_test.py b/official/core/actions_test.py
index 017fa606d2fd57e797d320d8acc6fd9c5062f512..a42360b66ad8878f18449045ecf768dcd685af96 100644
--- a/official/core/actions_test.py
+++ b/official/core/actions_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/base_task.py b/official/core/base_task.py
index db29395d66eb24f0ea0465838ea5947c2545fb6b..56b9bc4392effcaa9a9acd4ee1c7c7ac80604e50 100644
--- a/official/core/base_task.py
+++ b/official/core/base_task.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,6 +14,7 @@
"""Defines the base task abstraction."""
import abc
+import functools
from typing import Optional
from absl import logging
@@ -22,9 +23,12 @@ import tensorflow as tf
from official.core import config_definitions
from official.modeling import optimization
from official.modeling import performance
+from official.modeling.privacy import configs
+from official.modeling.privacy import ops
OptimizationConfig = optimization.OptimizationConfig
RuntimeConfig = config_definitions.RuntimeConfig
+DifferentialPrivacyConfig = configs.DifferentialPrivacyConfig
class Task(tf.Module, metaclass=abc.ABCMeta):
@@ -65,18 +69,35 @@ class Task(tf.Module, metaclass=abc.ABCMeta):
@classmethod
def create_optimizer(cls, optimizer_config: OptimizationConfig,
- runtime_config: Optional[RuntimeConfig] = None):
+ runtime_config: Optional[RuntimeConfig] = None,
+ dp_config: Optional[DifferentialPrivacyConfig] = None):
"""Creates an TF optimizer from configurations.
Args:
optimizer_config: the parameters of the Optimization settings.
runtime_config: the parameters of the runtime.
+ dp_config: the parameter of differential privacy.
Returns:
A tf.optimizers.Optimizer object.
"""
+ gradient_transformers = None
+ if dp_config is not None:
+ logging.info("Adding differential privacy transform with config %s.",
+ dp_config.as_dict())
+ noise_stddev = dp_config.clipping_norm * dp_config.noise_multiplier
+ gradient_transformers = [
+ functools.partial(
+ ops.clip_l2_norm, l2_norm_clip=dp_config.clipping_norm),
+ functools.partial(
+ ops.add_noise, noise_stddev=noise_stddev)
+ ]
+
opt_factory = optimization.OptimizerFactory(optimizer_config)
- optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+ optimizer = opt_factory.build_optimizer(
+ opt_factory.build_learning_rate(),
+ gradient_transformers=gradient_transformers
+ )
# Configuring optimizer when loss_scale is set in runtime config. This helps
# avoiding overflow/underflow for float16 computations.
if runtime_config:
@@ -101,9 +122,11 @@ class Task(tf.Module, metaclass=abc.ABCMeta):
ckpt_dir_or_file = self.task_config.init_checkpoint
logging.info("Trying to load pretrained checkpoint from %s",
ckpt_dir_or_file)
- if tf.io.gfile.isdir(ckpt_dir_or_file):
+ if ckpt_dir_or_file and tf.io.gfile.isdir(ckpt_dir_or_file):
ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
if not ckpt_dir_or_file:
+ logging.info("No checkpoint file found from %s. Will not load.",
+ ckpt_dir_or_file)
return
if hasattr(model, "checkpoint_items"):
diff --git a/official/core/base_trainer.py b/official/core/base_trainer.py
index a45ea9b9988e34e96e5267266ef863dcb8b48342..4ac35b47da2dd70dc5b7fdc584519f68899db66d 100644
--- a/official/core/base_trainer.py
+++ b/official/core/base_trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -33,57 +33,6 @@ ExperimentConfig = config_definitions.ExperimentConfig
TrainerConfig = config_definitions.TrainerConfig
-class Recovery:
- """Built-in model blowup recovery module.
-
- Checks the loss value by the given threshold. If applicable, recover the
- model by reading the checkpoint on disk.
- """
-
- def __init__(self,
- loss_upper_bound: float,
- checkpoint_manager: tf.train.CheckpointManager,
- recovery_begin_steps: int = 0,
- recovery_max_trials: int = 3):
- self.recover_counter = 0
- self.recovery_begin_steps = recovery_begin_steps
- self.recovery_max_trials = recovery_max_trials
- self.loss_upper_bound = loss_upper_bound
- self.checkpoint_manager = checkpoint_manager
-
- def should_recover(self, loss_value, global_step):
- if tf.math.is_nan(loss_value):
- return True
- if (global_step >= self.recovery_begin_steps and
- loss_value > self.loss_upper_bound):
- return True
- return False
-
- def maybe_recover(self, loss_value, global_step):
- """Conditionally recovers the training by triggering checkpoint restoration.
-
- Args:
- loss_value: the loss value as a float.
- global_step: the number of global training steps.
-
- Raises:
- RuntimeError: when recovery happens more than the max number of trials,
- the job should crash.
- """
- if not self.should_recover(loss_value, global_step):
- return
- self.recover_counter += 1
- if self.recover_counter > self.recovery_max_trials:
- raise RuntimeError(
- "The loss value is NaN or out of range after training loop and "
- f"this happens {self.recover_counter} times.")
- # Loads the previous good checkpoint.
- checkpoint_path = self.checkpoint_manager.restore_or_initialize()
- logging.warning(
- "Recovering the model from checkpoint: %s. The loss value becomes "
- "%f at step %d.", checkpoint_path, loss_value, global_step)
-
-
class _AsyncTrainer(orbit.StandardTrainer, orbit.StandardEvaluator):
"""Trainer class for both sync and async Strategy."""
@@ -370,6 +319,11 @@ class Trainer(_AsyncTrainer):
"""Accesses the training checkpoint."""
return self._checkpoint
+ @property
+ def checkpoint_exporter(self):
+ """Accesses the checkpoint exporter."""
+ return self._checkpoint_exporter
+
def train_loop_end(self):
"""See base class."""
self.join()
diff --git a/official/core/base_trainer_test.py b/official/core/base_trainer_test.py
index e50a5bcb7c2889e2aceda3b82c8916b65718eb05..10cf98e32bae7d2c88b0c7794fa6f3a76626fb92 100644
--- a/official/core/base_trainer_test.py
+++ b/official/core/base_trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -150,30 +150,6 @@ class MockAsyncTrainer(trainer_lib._AsyncTrainer):
return self.eval_global_step.numpy()
-class RecoveryTest(tf.test.TestCase):
-
- def test_recovery_module(self):
- ckpt = tf.train.Checkpoint(v=tf.Variable(1, dtype=tf.int32))
- model_dir = self.get_temp_dir()
- manager = tf.train.CheckpointManager(ckpt, model_dir, max_to_keep=1)
- recovery_module = trainer_lib.Recovery(
- loss_upper_bound=1.0,
- checkpoint_manager=manager,
- recovery_begin_steps=1,
- recovery_max_trials=1)
- self.assertFalse(recovery_module.should_recover(1.1, 0))
- self.assertFalse(recovery_module.should_recover(0.1, 1))
- self.assertTrue(recovery_module.should_recover(1.1, 2))
-
- # First triggers the recovery once.
- recovery_module.maybe_recover(1.1, 10)
-
- # Second time, it raises.
- with self.assertRaisesRegex(
- RuntimeError, 'The loss value is NaN .*'):
- recovery_module.maybe_recover(1.1, 10)
-
-
class TrainerTest(tf.test.TestCase, parameterized.TestCase):
def setUp(self):
@@ -343,7 +319,9 @@ class TrainerTest(tf.test.TestCase, parameterized.TestCase):
self.assertFalse(trainer.optimizer.dynamic)
self.assertEqual(trainer.optimizer.initial_scale, loss_scale)
else:
- self.assertIsInstance(trainer.optimizer, tf.keras.optimizers.SGD)
+ self.assertIsInstance(
+ trainer.optimizer,
+ (tf.keras.optimizers.SGD, tf.keras.optimizers.legacy.SGD))
metrics = trainer.train(tf.convert_to_tensor(5, dtype=tf.int32))
self.assertIn('training_loss', metrics)
diff --git a/official/core/config_definitions.py b/official/core/config_definitions.py
index 3bca789b5221d7e51ed112cfa753613febae11c7..abc09953c36c6952c669bd101d4b966cc7fb3155 100644
--- a/official/core/config_definitions.py
+++ b/official/core/config_definitions.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,6 +19,7 @@ from typing import Optional, Sequence, Union
from official.modeling.hyperparams import base_config
from official.modeling.optimization.configs import optimization_config
+from official.modeling.privacy import configs as dp_configs
OptimizationConfig = optimization_config.OptimizationConfig
@@ -61,7 +62,7 @@ class DataConfig(base_config.Config):
tf_data_service_address: The URI of a tf.data service to offload
preprocessing onto during training. The URI should be in the format
"protocol://address", e.g. "grpc://tf-data-service:5050". It can be
- overridden by `FLAGS.tf_data_service` flag in the binary.
+ overridden by `FLAGS.tf_data_service` flag in the binary.
tf_data_service_job_name: The name of the tf.data service job. This argument
makes it possible for multiple datasets to share the same job. The default
behavior is that the dataset creates anonymous, exclusively owned jobs.
@@ -74,7 +75,35 @@ class DataConfig(base_config.Config):
decoding when loading dataset from TFDS. Use comma to separate multiple
features. The main use case is to skip the image/video decoding for better
performance.
+ enable_shared_tf_data_service_between_parallel_trainers: A bool. When set to
+ true, only a single tf.data service will be started, and it will be shared
+ between all the trainer run simultaneously, e.g. using vizier to tune
+ hyperparameters. This will save CPU and RAM resources compared to running
+ separate tf.data service for each trainer. Notice that if batch size is
+ different for different trainers, the field
+ apply_tf_data_service_before_batching also needs to be true so that only a
+ single tf.data service instance will be created. In this case, tf.data
+ service will be applied before batching operation. So make sure to not
+ apply any processing steps after batching (e.g. in postprocess_fn) since
+ they wouldn't be paralleled by tf.data service and may slow down your
+ tf.data pipeline. When using shared tf.data service, the tf.data dataset
+ must be infinite, and slow trainer may skip certain training examples.
+ More details about shared tf.data service can be found at:
+ https://www.tensorflow.org/api_docs/python/tf/data/experimental/service#sharing_tfdata_service_with_concurrent_trainers.
+ apply_tf_data_service_before_batching: A bool. If set to True, tf.data
+ service will be applied before batching operation. This is useful to make
+ sure only a single tf.data service instance is created when
+ enable_shared_tf_data_service_between_parallel_trainers is true and batch
+ size is changing between parallel trainers.
+ trainer_id: A string. The id of the trainer if there are multiple parallel
+ trainer running at the same time, e.g. in vizier tuning case. It will be
+ automatically set if this field is needed. Users does not need to set it
+ when creating experiment configs.
seed: An optional seed to use for deterministic shuffling/preprocessing.
+ prefetch_buffer_size: An int specifying the buffer size of prefetch
+ datasets. If None, the buffer size is autotuned. Specifying this is useful
+ in case autotuning uses up too much memory by making the buffer size too
+ high.
"""
input_path: Union[Sequence[str], str, base_config.Config] = ""
tfds_name: str = ""
@@ -94,7 +123,11 @@ class DataConfig(base_config.Config):
tfds_data_dir: str = ""
tfds_as_supervised: bool = False
tfds_skip_decoding_feature: str = ""
+ enable_shared_tf_data_service_between_parallel_trainers: bool = False
+ apply_tf_data_service_before_batching: bool = False
+ trainer_id: Optional[str] = None
seed: Optional[int] = None
+ prefetch_buffer_size: Optional[int] = None
@dataclasses.dataclass
@@ -189,8 +222,8 @@ class TrainerConfig(base_config.Config):
is only used continuous_train_and_eval and continuous_eval modes. Default
value is 1 hrs.
train_steps: number of train steps.
- validation_steps: number of eval steps. If `None`, the entire eval dataset
- is used.
+ validation_steps: number of eval steps. If -1, the entire eval dataset is
+ used.
validation_interval: number of training steps to run between evaluations.
best_checkpoint_export_subdir: if set, the trainer will keep track of the
best evaluation metric, and export the corresponding best checkpoint under
@@ -240,11 +273,17 @@ class TrainerConfig(base_config.Config):
@dataclasses.dataclass
class TaskConfig(base_config.Config):
+ """Config passed to task."""
init_checkpoint: str = ""
model: Optional[base_config.Config] = None
train_data: DataConfig = DataConfig()
validation_data: DataConfig = DataConfig()
name: Optional[str] = None
+ # Configs for differential privacy
+ # These configs are only effective if you use create_optimizer in
+ # tensorflow_models/official/core/base_task.py
+ differential_privacy_config: Optional[
+ dp_configs.DifferentialPrivacyConfig] = None
@dataclasses.dataclass
diff --git a/official/core/exp_factory.py b/official/core/exp_factory.py
index b10d49acbdaeee211194ed0c018cb91493d74d21..fef7444987715944026926875fe0edeec67704ab 100644
--- a/official/core/exp_factory.py
+++ b/official/core/exp_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/export_base.py b/official/core/export_base.py
index a300a120d7ce42346c59cf796c07c689f32447c8..0ee9163d725b0a7f0139803cc2296d21663bb86b 100644
--- a/official/core/export_base.py
+++ b/official/core/export_base.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -68,8 +68,17 @@ class ExportModule(tf.Module, metaclass=abc.ABCMeta):
if inference_step is not None:
self.inference_step = functools.partial(inference_step, model=self.model)
else:
- self.inference_step = functools.partial(
- self.model.__call__, training=False)
+ if issubclass(type(model), tf.keras.Model):
+ # Default to self.model.call instead of self.model.__call__ to avoid
+ # keras tracing logic designed for training.
+ # Since most of Model Garden's call doesn't not have training kwargs
+ # or the default is False, we don't pass anything here.
+ # Please pass custom inference step if your model has training=True as
+ # default.
+ self.inference_step = self.model.call
+ else:
+ self.inference_step = functools.partial(
+ self.model.__call__, training=False)
self.preprocessor = preprocessor
self.postprocessor = postprocessor
diff --git a/official/core/export_base_test.py b/official/core/export_base_test.py
index c76dfa326dafbec1b13dda9854ed8944149fa589..e08a4a420f98cdd5711029fb0ab04829a2ba7625 100644
--- a/official/core/export_base_test.py
+++ b/official/core/export_base_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/file_writers.py b/official/core/file_writers.py
new file mode 100644
index 0000000000000000000000000000000000000000..dd8446bbe8b01286bc244f1f5e2e0e0d23daeb58
--- /dev/null
+++ b/official/core/file_writers.py
@@ -0,0 +1,80 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""File writer functions for dataset preparation, infra validation, and unit tests."""
+
+import io
+from typing import Optional, Sequence, Union
+
+import tensorflow as tf
+
+
+def write_small_dataset(examples: Sequence[Union[tf.train.Example,
+ tf.train.SequenceExample]],
+ output_path: str,
+ file_type: str = 'tfrecord') -> None:
+ """Writes `examples` to a file at `output_path` with type `file_type`.
+
+ CAVEAT: This function is not recommended for writing large datasets, since it
+ will loop through `examples` and perform write operation sequentially.
+
+ Args:
+ examples: List of tf.train.Example or tf.train.SequenceExample.
+ output_path: Output path for the dataset.
+ file_type: A string indicating the file format, could be: 'tfrecord',
+ 'tfrecords', 'tfrecord_compressed', 'tfrecords_gzip', 'riegeli'. The
+ string is case insensitive.
+ """
+ file_type = file_type.lower()
+
+ if file_type == 'tfrecord' or file_type == 'tfrecords':
+ _write_tfrecord(examples, output_path)
+ elif file_type == 'tfrecord_compressed' or file_type == 'tfrecords_gzip':
+ _write_tfrecord(examples, output_path,
+ tf.io.TFRecordOptions(compression_type='GZIP'))
+ elif file_type == 'riegeli':
+ _write_riegeli(examples, output_path)
+ else:
+ raise ValueError(f'Unknown file_type: {file_type}')
+
+
+def _write_tfrecord(examples: Sequence[Union[tf.train.Example,
+ tf.train.SequenceExample]],
+ output_path: str,
+ options: Optional[tf.io.TFRecordOptions] = None) -> None:
+ """Writes `examples` to a TFRecord file at `output_path`.
+
+ Args:
+ examples: A list of tf.train.Example.
+ output_path: Output path for the dataset.
+ options: Options used for manipulating TFRecord files.
+ """
+ with tf.io.TFRecordWriter(output_path, options) as writer:
+ for example in examples:
+ writer.write(example.SerializeToString())
+
+
+def _write_riegeli(examples: Sequence[Union[tf.train.Example,
+ tf.train.SequenceExample]],
+ output_path: str) -> None:
+ """Writes `examples` to a Riegeli file at `output_path`.
+
+ Args:
+ examples: A list of tf.train.Example.
+ output_path: Output path for the dataset.
+ """
+ with io.FileIO(output_path, 'wb') as fileio:
+ import riegeli # pylint: disable=g-import-not-at-top
+ with riegeli.RecordWriter(fileio) as writer:
+ writer.write_messages(examples)
diff --git a/official/core/file_writers_test.py b/official/core/file_writers_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..a281964f1ee547ed0601f9bc3360a697e4486d90
--- /dev/null
+++ b/official/core/file_writers_test.py
@@ -0,0 +1,53 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for file_writers."""
+
+import os
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.core import file_writers
+from official.core import tf_example_builder
+
+
+class FileWritersTest(tf.test.TestCase, parameterized.TestCase):
+
+ def setUp(self):
+ super().setUp()
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_bytes_feature('foo', 'Hello World!')
+ self._example = example_builder.example
+
+ @parameterized.parameters('tfrecord', 'TFRecord', 'tfrecords',
+ 'tfrecord_compressed', 'TFRecord_Compressed',
+ 'tfrecords_gzip')
+ def test_write_small_dataset_success(self, file_type):
+ temp_dir = self.create_tempdir()
+ temp_dataset_file = os.path.join(temp_dir.full_path, 'train')
+ file_writers.write_small_dataset([self._example], temp_dataset_file,
+ file_type)
+ self.assertTrue(os.path.exists(temp_dataset_file))
+
+ def test_write_small_dataset_unrecognized_format(self):
+ file_type = 'bar'
+ temp_dir = self.create_tempdir()
+ temp_dataset_file = os.path.join(temp_dir.full_path, 'train')
+ with self.assertRaises(ValueError):
+ file_writers.write_small_dataset([self._example], temp_dataset_file,
+ file_type)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/core/input_reader.py b/official/core/input_reader.py
index 736172b6a25723d6419cbfc267f567b242483a1e..76933fbbb3fac4e80f521b98c39dd4586aa10061 100644
--- a/official/core/input_reader.py
+++ b/official/core/input_reader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -160,22 +160,44 @@ def _read_tfds(tfds_builder: tfds.core.DatasetBuilder,
"""Reads a dataset from tfds."""
# No op if exist.
tfds_builder.download_and_prepare()
-
- read_config = tfds.ReadConfig(
- interleave_cycle_length=cycle_length,
- interleave_block_length=block_length,
- input_context=input_context,
- shuffle_seed=seed)
decoders = {}
if tfds_skip_decoding_feature:
for skip_feature in tfds_skip_decoding_feature.split(','):
decoders[skip_feature.strip()] = tfds.decode.SkipDecoding()
- dataset = tfds_builder.as_dataset(
- split=tfds_split,
- shuffle_files=is_training,
- as_supervised=tfds_as_supervised,
- decoders=decoders,
- read_config=read_config)
+ if tfds_builder.info.splits:
+ num_shards = len(tfds_builder.info.splits[tfds_split].file_instructions)
+ else:
+ # The tfds mock path often does not provide splits.
+ num_shards = 1
+ if input_context and num_shards < input_context.num_input_pipelines:
+ # The number of files in the dataset split is smaller than the number of
+ # input pipelines. We read the entire dataset first and then shard in the
+ # host memory.
+ read_config = tfds.ReadConfig(
+ interleave_cycle_length=cycle_length,
+ interleave_block_length=block_length,
+ input_context=None,
+ shuffle_seed=seed)
+ dataset = tfds_builder.as_dataset(
+ split=tfds_split,
+ shuffle_files=is_training,
+ as_supervised=tfds_as_supervised,
+ decoders=decoders,
+ read_config=read_config)
+ dataset = dataset.shard(input_context.num_input_pipelines,
+ input_context.input_pipeline_id)
+ else:
+ read_config = tfds.ReadConfig(
+ interleave_cycle_length=cycle_length,
+ interleave_block_length=block_length,
+ input_context=input_context,
+ shuffle_seed=seed)
+ dataset = tfds_builder.as_dataset(
+ split=tfds_split,
+ shuffle_files=is_training,
+ as_supervised=tfds_as_supervised,
+ decoders=decoders,
+ read_config=read_config)
if is_training and not cache:
dataset = dataset.repeat()
@@ -270,6 +292,8 @@ class InputReader:
self._transform_and_batch_fn = transform_and_batch_fn
self._postprocess_fn = postprocess_fn
self._seed = params.seed
+ self._prefetch_buffer_size = (
+ params.prefetch_buffer_size or tf.data.experimental.AUTOTUNE)
# When tf.data service is enabled, each data service worker should get
# different random seeds. Thus, we set `seed` to None.
@@ -282,13 +306,36 @@ class InputReader:
self._enable_tf_data_service = (
params.enable_tf_data_service and params.tf_data_service_address)
self._tf_data_service_address = params.tf_data_service_address
+ self._enable_shared_tf_data_service_between_parallel_trainers = (
+ params.enable_shared_tf_data_service_between_parallel_trainers)
+ self._apply_tf_data_service_before_batching = (
+ params.apply_tf_data_service_before_batching)
+ self._trainer_id = params.trainer_id
if self._enable_tf_data_service:
# Add a random seed as the tf.data service job name suffix, so tf.data
# service doesn't reuse the previous state if TPU worker gets preempted.
+ # It's necessary to add global batch size into the tf data service job
+ # name because when tuning batch size with vizier and tf data service is
+ # also enable, the tf data servce job name should be different for
+ # different vizier trials since once batch size is changed, from the
+ # tf.data perspective, the dataset is a different instance, and a
+ # different job name should be used for tf data service. Otherwise, the
+ # model would read tensors from the incorrect tf data service job, which
+ # would causes dimension mismatch on the batch size dimension.
self._tf_data_service_job_name = (
- params.tf_data_service_job_name + str(self.static_randnum))
+ f'{params.tf_data_service_job_name}_bs{params.global_batch_size}_'
+ f'{self.static_randnum}')
self._enable_round_robin_tf_data_service = params.get(
'enable_round_robin_tf_data_service', False)
+ if self._enable_shared_tf_data_service_between_parallel_trainers:
+ # When shared tf.data service is enabled, only a single tf.data service
+ # instance should be created and shared between parallel trainers. If
+ # the global batch size is different across trainers,
+ # params.apply_tf_data_service_before_batching should be set to true
+ # because tf.data service with different batch sizes will be considered
+ # separate tf.data service instances.
+ self._tf_data_service_job_name = (
+ f'{params.tf_data_service_job_name}_{self.static_randnum}')
@property
def tfds_info(self) -> tfds.core.DatasetInfo:
@@ -411,6 +458,19 @@ class InputReader:
dataset = dataset.repeat()
dataset = dataset.shuffle(self._shuffle_buffer_size, seed=self._seed)
+ # Applies tf.data service before batching operations. This is useful when
+ # tf.data service is shared between parallel trainers, and batch size is
+ # changing between parallel trainers. Then batch size is changing, tf.data
+ # services will be considered different instances if applied after batching
+ # operations, which make it difficult to share between parallel trainers.
+ # However, if there are additional expensive operations in
+ # self._transform_and_batch_fn and self._postprocess_fn, the entire tf.data
+ # pipeline could be slowed down. In this case, try to move these dataset
+ # operations into early stages if possible.
+ if (self._enable_shared_tf_data_service_between_parallel_trainers and
+ self._apply_tf_data_service_before_batching):
+ dataset = self._maybe_apply_data_service(dataset, input_context)
+
if self._transform_and_batch_fn is not None:
dataset = self._transform_and_batch_fn(dataset, input_context)
else:
@@ -436,13 +496,18 @@ class InputReader:
num_consumers = input_context.num_input_pipelines * (
replicas_per_input_pipeline)
range_dataset = tf.data.Dataset.range(replicas_per_input_pipeline)
+ tfds_kwargs = {
+ 'processing_mode': 'parallel_epochs',
+ 'service': self._tf_data_service_address,
+ 'job_name': self._tf_data_service_job_name,
+ 'num_consumers': num_consumers
+ }
+ if self._enable_shared_tf_data_service_between_parallel_trainers:
+ raise ValueError('Shared tf.data service does not support round-robin'
+ ' tf.data service.')
dataset = range_dataset.map(lambda i: dataset.apply( # pylint: disable=g-long-lambda
tf.data.experimental.service.distribute(
- processing_mode='parallel_epochs',
- service=self._tf_data_service_address,
- job_name=self._tf_data_service_job_name,
- consumer_index=base_consumer_index + i,
- num_consumers=num_consumers)))
+ consumer_index=base_consumer_index + i, **tfds_kwargs)))
# Use parallel interleave to read multiple batches from a tf.data
# service worker in parallel.
dataset = dataset.interleave(
@@ -451,11 +516,21 @@ class InputReader:
num_parallel_calls=replicas_per_input_pipeline,
deterministic=True)
else:
+ tfds_kwargs = {
+ 'processing_mode': 'parallel_epochs',
+ 'service': self._tf_data_service_address,
+ 'job_name': self._tf_data_service_job_name,
+ }
+ if self._enable_shared_tf_data_service_between_parallel_trainers:
+ tfds_kwargs.update({
+ 'processing_mode':
+ tf.data.experimental.service.ShardingPolicy.OFF,
+ 'cross_trainer_cache':
+ tf.data.experimental.service.CrossTrainerCache(
+ trainer_id=self._trainer_id)
+ })
dataset = dataset.apply(
- tf.data.experimental.service.distribute(
- processing_mode='parallel_epochs',
- service=self._tf_data_service_address,
- job_name=self._tf_data_service_job_name))
+ tf.data.experimental.service.distribute(**tfds_kwargs))
return dataset
def read(self,
@@ -463,16 +538,17 @@ class InputReader:
dataset: Optional[tf.data.Dataset] = None) -> tf.data.Dataset:
"""Generates a tf.data.Dataset object."""
if dataset is None:
- dataset = self._read_data_source(
- self._matched_files, self._dataset_fn, input_context,
- self._tfds_builder)
+ dataset = self._read_data_source(self._matched_files, self._dataset_fn,
+ input_context, self._tfds_builder)
dataset = self._decode_and_parse_dataset(dataset, self._global_batch_size,
input_context)
dataset = _maybe_map_fn(dataset, self._postprocess_fn)
- dataset = self._maybe_apply_data_service(dataset, input_context)
+ if not (self._enable_shared_tf_data_service_between_parallel_trainers and
+ self._apply_tf_data_service_before_batching):
+ dataset = self._maybe_apply_data_service(dataset, input_context)
if self._deterministic is not None:
options = tf.data.Options()
- options.experimental_deterministic = self._deterministic
+ options.deterministic = self._deterministic
dataset = dataset.with_options(options)
- return dataset.prefetch(tf.data.experimental.AUTOTUNE)
+ return dataset.prefetch(self._prefetch_buffer_size)
diff --git a/official/core/registry.py b/official/core/registry.py
index f349710b54f082c8e5d2843b23210c16c8a59023..5fdaf48ad8753d0454e930b77ddccfb6bc26c156 100644
--- a/official/core/registry.py
+++ b/official/core/registry.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,6 +13,7 @@
# limitations under the License.
"""Registry utility."""
+from absl import logging
def register(registered_collection, reg_key):
@@ -54,8 +55,16 @@ def register(registered_collection, reg_key):
leaf_reg_key = reg_key
if leaf_reg_key in collection:
- raise KeyError("Function or class {} registered multiple times.".format(
- leaf_reg_key))
+ if "beta" in fn_or_cls.__module__:
+ # TODO(yeqing): Clean this temporary branch for beta.
+ logging.warn(
+ "Duplicate registeration of beta module "
+ "name %r new %r old %r", reg_key, collection[leaf_reg_key],
+ fn_or_cls.__module__)
+ return fn_or_cls
+ else:
+ raise KeyError("Function or class {} registered multiple times.".format(
+ leaf_reg_key))
collection[leaf_reg_key] = fn_or_cls
return fn_or_cls
diff --git a/official/core/registry_test.py b/official/core/registry_test.py
index 0d0639c6b10d5f9d587593d52dd6f2458c83bcd5..559b918e1e2b7d511c3c5076da5fe2e099938b1b 100644
--- a/official/core/registry_test.py
+++ b/official/core/registry_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/savedmodel_checkpoint_manager.py b/official/core/savedmodel_checkpoint_manager.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b6df5fe32ebb94f463bcb9285ca7acd2c4fc516
--- /dev/null
+++ b/official/core/savedmodel_checkpoint_manager.py
@@ -0,0 +1,244 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Custom checkpoint manager that also exports saved models."""
+
+import os
+import re
+import time
+from typing import Callable, List, Mapping, Optional, Union
+
+from absl import logging
+import tensorflow as tf
+
+SAVED_MODULES_PATH_SUFFIX = 'saved_modules'
+
+
+def make_saved_modules_directory_name(checkpoint_name: str) -> str:
+ return f'{checkpoint_name}_{SAVED_MODULES_PATH_SUFFIX}'
+
+
+class SavedModelCheckpointManager(tf.train.CheckpointManager):
+ """A CheckpointManager that also exports `SavedModel`s."""
+
+ def __init__(self,
+ checkpoint: tf.train.Checkpoint,
+ directory: str,
+ max_to_keep: int,
+ modules_to_export: Optional[Mapping[str, tf.Module]] = None,
+ keep_checkpoint_every_n_hours: Optional[int] = None,
+ checkpoint_name: str = 'ckpt',
+ step_counter: Optional[tf.Variable] = None,
+ checkpoint_interval: Optional[int] = None,
+ init_fn: Optional[Callable[[], None]] = None):
+ """See base class."""
+ super().__init__(
+ checkpoint=checkpoint,
+ directory=directory,
+ max_to_keep=max_to_keep,
+ keep_checkpoint_every_n_hours=keep_checkpoint_every_n_hours,
+ checkpoint_name=checkpoint_name,
+ step_counter=step_counter,
+ checkpoint_interval=checkpoint_interval,
+ init_fn=init_fn)
+ self._modules_to_export = modules_to_export
+ self._savedmodels = self.get_existing_savedmodels()
+
+ def save(self,
+ checkpoint_number: Optional[int] = None,
+ check_interval: bool = True,
+ options: Optional[tf.train.CheckpointOptions] = None):
+ """See base class."""
+ checkpoint_path = super().save(
+ checkpoint_number=checkpoint_number,
+ check_interval=check_interval,
+ options=options)
+ if not checkpoint_path: # Nothing got written.
+ return
+ if not self._modules_to_export: # No modules to export.
+ logging.info('Skip saving SavedModel due to empty modules_to_export.')
+ return checkpoint_path
+
+ # Save the models for the checkpoint that just got written.
+ saved_modules_directory = make_saved_modules_directory_name(checkpoint_path)
+ for model_name, model in self._modules_to_export.items():
+ signatures = getattr(model, 'saved_model_signatures', None)
+ tf.saved_model.save(
+ obj=model,
+ export_dir=os.path.join(saved_modules_directory, model_name),
+ signatures=signatures)
+
+ saved_modules_directories_to_keep = [
+ make_saved_modules_directory_name(ckpt) for ckpt in self.checkpoints
+ ]
+ existing_saved_modules_dirs = self.get_existing_savedmodels()
+
+ self._savedmodels = []
+ # Keep savedmodels in the same order as checkpoints (from oldest to newest).
+ for saved_modules_dir_to_keep in saved_modules_directories_to_keep:
+ if saved_modules_dir_to_keep in existing_saved_modules_dirs:
+ self._savedmodels.append(saved_modules_dir_to_keep)
+
+ for existing_saved_modules_dir in existing_saved_modules_dirs:
+ if existing_saved_modules_dir not in self._savedmodels:
+ tf.io.gfile.rmtree(existing_saved_modules_dir)
+
+ return checkpoint_path
+
+ def get_existing_savedmodels(self) -> List[str]:
+ """Gets a list of all existing SavedModel paths in `directory`.
+
+ Returns:
+ A list of all existing SavedModel paths.
+ """
+ saved_modules_glob = make_saved_modules_directory_name(
+ self._checkpoint_prefix + '-*')
+ return tf.io.gfile.glob(saved_modules_glob)
+
+ @property
+ def latest_savedmodel(self) -> Union[str, None]:
+ """The path of the most recent SavedModel in `directory`.
+
+ Returns:
+ The latest SavedModel path. If there are no SavedModels, returns `None`.
+ """
+ if self._savedmodels:
+ return self._savedmodels[-1]
+ return None
+
+ @property
+ def savedmodels(self) -> List[str]:
+ """A list of managed SavedModels.
+
+ Returns:
+ A list of SavedModel paths, sorted from oldest to newest.
+ """
+ return self._savedmodels
+
+ @property
+ def modules_to_export(self) -> Union[Mapping[str, tf.Module], None]:
+ return self._modules_to_export
+
+ def get_savedmodel_number_from_path(self,
+ savedmodel_path: str) -> Union[int, None]:
+ """Gets the savedmodel_number/checkpoint_number from savedmodel filepath.
+
+ The savedmodel_number is global step when using with orbit controller.
+
+ Args:
+ savedmodel_path: savedmodel directory path.
+
+ Returns:
+ Savedmodel number or None if no matched pattern found in savedmodel path.
+ """
+ pattern = rf'\d+_{SAVED_MODULES_PATH_SUFFIX}$'
+ savedmodel_number = re.search(pattern, savedmodel_path)
+ if savedmodel_number:
+ savedmodel_number = savedmodel_number.group()
+ return int(savedmodel_number[:-len(SAVED_MODULES_PATH_SUFFIX) - 1])
+ return None
+
+ def savedmodels_iterator(self,
+ min_interval_secs: float = 0,
+ timeout: Optional[float] = None,
+ timeout_fn: Optional[Callable[[], bool]] = None):
+ """Continuously yield new SavedModel files as they appear.
+
+ The iterator only checks for new savedmodels when control flow has been
+ reverted to it. The logic is same to the `train.checkpoints_iterator`.
+
+ Args:
+ min_interval_secs: The minimum number of seconds between yielding
+ savedmodels.
+ timeout: The maximum number of seconds to wait between savedmodels. If
+ left as `None`, then the process will wait indefinitely.
+ timeout_fn: Optional function to call after a timeout. If the function
+ returns True, then it means that no new savedmodels will be generated
+ and the iterator will exit. The function is called with no arguments.
+
+ Yields:
+ String paths to latest SavedModel files as they arrive.
+ """
+ savedmodel_path = None
+ while True:
+ new_savedmodel_path = self.wait_for_new_savedmodel(
+ savedmodel_path, timeout=timeout)
+ if new_savedmodel_path is None:
+ if not timeout_fn:
+ # timed out
+ logging.info('Timed-out waiting for a savedmodel.')
+ return
+ if timeout_fn():
+ # The timeout_fn indicated that we are truly done.
+ return
+ else:
+ # The timeout_fn indicated that more savedmodels may come.
+ continue
+ start = time.time()
+ savedmodel_path = new_savedmodel_path
+ yield savedmodel_path
+ time_to_next_eval = start + min_interval_secs - time.time()
+ if time_to_next_eval > 0:
+ time.sleep(time_to_next_eval)
+
+ def wait_for_new_savedmodel(
+ self,
+ last_savedmodel: Optional[str] = None,
+ seconds_to_sleep: float = 1.0,
+ timeout: Optional[float] = None) -> Union[str, None]:
+ """Waits until a new savedmodel file is found.
+
+ Args:
+ last_savedmodel: The last savedmodel path used or `None` if we're
+ expecting a savedmodel for the first time.
+ seconds_to_sleep: The number of seconds to sleep for before looking for a
+ new savedmodel.
+ timeout: The maximum number of seconds to wait. If left as `None`, then
+ the process will wait indefinitely.
+
+ Returns:
+ A new savedmodel path, or None if the timeout was reached.
+ """
+ logging.info('Waiting for new savedmodel at %s', self._directory)
+ stop_time = time.time() + timeout if timeout is not None else None
+
+ last_savedmodel_number = 0
+ if last_savedmodel:
+ last_savedmodel_number = self.get_savedmodel_number_from_path(
+ last_savedmodel)
+
+ while True:
+ if stop_time is not None and time.time() + seconds_to_sleep > stop_time:
+ return None
+
+ existing_savedmodels = {}
+ for savedmodel_path in self.get_existing_savedmodels():
+ savedmodel_number = self.get_savedmodel_number_from_path(
+ savedmodel_path)
+ if savedmodel_number is not None:
+ existing_savedmodels[savedmodel_number] = savedmodel_path
+
+ # Find the first savedmodel with larger step number as next savedmodel.
+ savedmodel_path = None
+ existing_savedmodels = dict(sorted(existing_savedmodels.items()))
+ for savedmodel_number in existing_savedmodels:
+ if savedmodel_number > last_savedmodel_number:
+ savedmodel_path = existing_savedmodels[savedmodel_number]
+ break
+
+ if savedmodel_path:
+ logging.info('Found new savedmodel at %s', savedmodel_path)
+ return savedmodel_path
+ else:
+ time.sleep(seconds_to_sleep)
diff --git a/official/core/savedmodel_checkpoint_manager_test.py b/official/core/savedmodel_checkpoint_manager_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..8fcb51f3b59f0ec91cfc82ad377b75307ce75806
--- /dev/null
+++ b/official/core/savedmodel_checkpoint_manager_test.py
@@ -0,0 +1,114 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+import time
+from typing import Iterable
+
+import tensorflow as tf
+
+from official.core import savedmodel_checkpoint_manager
+
+
+def _models_exist(checkpoint_path: str, models: Iterable[str]) -> bool:
+ for model_name in models:
+ if not tf.io.gfile.isdir(
+ os.path.join(
+ savedmodel_checkpoint_manager.make_saved_modules_directory_name(
+ checkpoint_path), model_name)):
+ return False
+ return True
+
+
+class CheckpointManagerTest(tf.test.TestCase):
+
+ def _create_manager(self, max_to_keep: int = 1) -> tf.train.CheckpointManager:
+ """Sets up SavedModelCheckpointManager object.
+
+ Args:
+ max_to_keep: max number of savedmodels to keep.
+
+ Returns:
+ created savedmodel manager.
+ """
+ models = {
+ 'model_1':
+ tf.keras.Sequential(
+ layers=[tf.keras.layers.Dense(8, input_shape=(16,))]),
+ 'model_2':
+ tf.keras.Sequential(
+ layers=[tf.keras.layers.Dense(16, input_shape=(32,))]),
+ }
+ checkpoint = tf.train.Checkpoint()
+ manager = savedmodel_checkpoint_manager.SavedModelCheckpointManager(
+ checkpoint=checkpoint,
+ directory=self.get_temp_dir(),
+ max_to_keep=max_to_keep,
+ modules_to_export=models)
+ return manager
+
+ def test_max_to_keep(self):
+ manager = self._create_manager()
+ models = manager.modules_to_export
+ first_path = manager.save()
+ second_path = manager.save()
+
+ savedmodel = savedmodel_checkpoint_manager.make_saved_modules_directory_name(
+ manager.latest_checkpoint)
+ self.assertEqual(savedmodel, manager.latest_savedmodel)
+ self.assertTrue(_models_exist(second_path, models.keys()))
+ self.assertFalse(_models_exist(first_path, models.keys()))
+
+ def test_returns_none_after_timeout(self):
+ manager = self._create_manager()
+ start = time.time()
+ ret = manager.wait_for_new_savedmodel(
+ None, timeout=1.0, seconds_to_sleep=0.5)
+ end = time.time()
+ self.assertIsNone(ret)
+ # We've waited 0.5 second.
+ self.assertGreater(end, start + 0.5)
+ # The timeout kicked in.
+ self.assertLess(end, start + 0.6)
+
+ def test_saved_model_iterator(self):
+ manager = self._create_manager(max_to_keep=2)
+ self.assertIsNotNone(manager.save(checkpoint_number=1))
+ self.assertIsNotNone(manager.save(checkpoint_number=2))
+ self.assertIsNotNone(manager.save(checkpoint_number=3))
+
+ # Savedmodels are in time order.
+ expected_savedmodels = manager.savedmodels
+ # Order not guaranteed.
+ existing_savedmodels = manager.get_existing_savedmodels()
+ savedmodels = list(manager.savedmodels_iterator(timeout=3.0))
+ self.assertEqual(savedmodels, expected_savedmodels)
+ self.assertEqual(set(savedmodels), set(existing_savedmodels))
+
+ def test_saved_model_iterator_timeout_fn(self):
+ manager = self._create_manager()
+ timeout_fn_calls = [0]
+
+ def timeout_fn():
+ timeout_fn_calls[0] += 1
+ return timeout_fn_calls[0] > 3
+
+ results = list(
+ manager.savedmodels_iterator(timeout=0.1, timeout_fn=timeout_fn))
+ self.assertEqual([], results)
+ self.assertEqual(4, timeout_fn_calls[0])
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/core/task_factory.py b/official/core/task_factory.py
index f5862462e0da94ad183e8bb7a5d60a7cad6e1b79..4dee1fe2e21fa5a9a0503392c57121e8f160796e 100644
--- a/official/core/task_factory.py
+++ b/official/core/task_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/test_utils.py b/official/core/test_utils.py
index 015373699c5c5917e9f866686d5817a791155d01..7edeff7c632102ed4d3480b58ac4d9f2ba5b5f88 100644
--- a/official/core/test_utils.py
+++ b/official/core/test_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/core/tf_example_builder.py b/official/core/tf_example_builder.py
new file mode 100644
index 0000000000000000000000000000000000000000..862926fff1c2dd6e772a345d1a5c5fd79c146870
--- /dev/null
+++ b/official/core/tf_example_builder.py
@@ -0,0 +1,144 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Builder class for preparing tf.train.Example."""
+
+# https://www.python.org/dev/peps/pep-0563/#enabling-the-future-behavior-in-python-3-7
+from __future__ import annotations
+
+from typing import Mapping, Sequence, Union
+
+import numpy as np
+import tensorflow as tf
+
+BytesValueType = Union[bytes, Sequence[bytes], str, Sequence[str]]
+
+_to_array = lambda v: [v] if not isinstance(v, (list, np.ndarray)) else v
+_to_bytes = lambda v: v.encode() if isinstance(v, str) else v
+_to_bytes_array = lambda v: list(map(_to_bytes, _to_array(v)))
+
+
+class TfExampleBuilder(object):
+ """Builder class for preparing tf.train.Example.
+
+ Read API doc at https://www.tensorflow.org/api_docs/python/tf/train/Example.
+
+ Example usage:
+ >>> example_builder = TfExampleBuilder()
+ >>> example = (
+ example_builder.add_bytes_feature('feature_a', 'foobarbaz')
+ .add_ints_feature('feature_b', [1, 2, 3])
+ .example)
+ """
+
+ def __init__(self) -> None:
+ self._example = tf.train.Example()
+
+ @property
+ def example(self) -> tf.train.Example:
+ """Returns a copy of the generated tf.train.Example proto."""
+ return self._example
+
+ @property
+ def serialized_example(self) -> str:
+ """Returns a serialized string of the generated tf.train.Example proto."""
+ return self._example.SerializeToString()
+
+ def set(self, example: tf.train.Example) -> TfExampleBuilder:
+ """Sets the example."""
+ self._example = example
+ return self
+
+ def reset(self) -> TfExampleBuilder:
+ """Resets the example to an empty proto."""
+ self._example = tf.train.Example()
+ return self
+
+ ###### Basic APIs for primitive data types ######
+ def add_feature_dict(
+ self, feature_dict: Mapping[str, tf.train.Feature]) -> TfExampleBuilder:
+ """Adds the predefined `feature_dict` to the example.
+
+ Note: Please prefer to using feature-type-specific methods.
+
+ Args:
+ feature_dict: A dictionary from tf.Example feature key to
+ tf.train.Feature.
+
+ Returns:
+ The builder object for subsequent method calls.
+ """
+ for k, v in feature_dict.items():
+ self._example.features.feature[k].CopyFrom(v)
+ return self
+
+ def add_feature(self, key: str,
+ feature: tf.train.Feature) -> TfExampleBuilder:
+ """Adds predefined `feature` with `key` to the example.
+
+ Args:
+ key: String key of the feature.
+ feature: The feature to be added to the example.
+
+ Returns:
+ The builder object for subsequent method calls.
+ """
+ self._example.features.feature[key].CopyFrom(feature)
+ return self
+
+ def add_bytes_feature(self, key: str,
+ value: BytesValueType) -> TfExampleBuilder:
+ """Adds byte(s) or string(s) with `key` to the example.
+
+ Args:
+ key: String key of the feature.
+ value: The byte(s) or string(s) to be added to the example.
+
+ Returns:
+ The builder object for subsequent method calls.
+ """
+ return self.add_feature(
+ key,
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(value=_to_bytes_array(value))))
+
+ def add_ints_feature(self, key: str,
+ value: Union[int, Sequence[int]]) -> TfExampleBuilder:
+ """Adds integer(s) with `key` to the example.
+
+ Args:
+ key: String key of the feature.
+ value: The integer(s) to be added to the example.
+
+ Returns:
+ The builder object for subsequent method calls.
+ """
+ return self.add_feature(
+ key,
+ tf.train.Feature(int64_list=tf.train.Int64List(value=_to_array(value))))
+
+ def add_floats_feature(
+ self, key: str, value: Union[float, Sequence[float]]) -> TfExampleBuilder:
+ """Adds float(s) with `key` to the example.
+
+ Args:
+ key: String key of the feature.
+ value: The float(s) to be added to the example.
+
+ Returns:
+ The builder object for subsequent method calls.
+ """
+ return self.add_feature(
+ key,
+ tf.train.Feature(float_list=tf.train.FloatList(value=_to_array(value))))
diff --git a/official/core/tf_example_builder_test.py b/official/core/tf_example_builder_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..880b965b300d71cf23528f173c8ad90efbad1396
--- /dev/null
+++ b/official/core/tf_example_builder_test.py
@@ -0,0 +1,165 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tf_example_builder.
+
+See `test_add_image_matrix_feature_with_fake_image` for the typical structure of
+a unit test.
+"""
+
+from absl.testing import parameterized
+import tensorflow as tf
+from official.core import tf_example_builder
+
+
+class TfExampleBuilderTest(tf.test.TestCase, parameterized.TestCase):
+
+ def test_init_an_empty_example(self):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example = example_builder.example
+ self.assertProtoEquals('', example)
+
+ def test_init_an_empty_serialized_example(self):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example = example_builder.serialized_example
+ self.assertProtoEquals('', example)
+
+ def test_add_feature(self):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_feature(
+ 'foo',
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(value=[b'Hello World!'])))
+ example = example_builder.example
+ # Use proto text to show how the entire proto would look like.
+ self.assertProtoEquals(
+ """
+ features: {
+ feature: {
+ key: "foo"
+ value: {
+ bytes_list: {
+ value: "Hello World!"
+ }
+ }
+ }
+ }""", example)
+
+ def test_add_feature_dict(self):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_feature_dict({
+ 'foo':
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(value=[b'Hello World!'])),
+ 'bar':
+ tf.train.Feature(
+ int64_list=tf.train.Int64List(value=[299, 792, 458]))
+ })
+ example = example_builder.example
+ # Use proto text to show how the entire proto would look like.
+ self.assertProtoEquals(
+ """
+ features: {
+ feature: {
+ key: "foo"
+ value: {
+ bytes_list: {
+ value: "Hello World!"
+ }
+ }
+ }
+ feature: {
+ key: "bar"
+ value: {
+ int64_list: {
+ value: 299
+ value: 792
+ value: 458
+ }
+ }
+ }
+ }""", example)
+
+ @parameterized.named_parameters(
+ ('single_bytes', b'Hello World!', b'Hello World!'),
+ ('single_string', 'Hello World!', b'Hello World!'))
+ def test_add_single_byte_feature(self, value, expected_value):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_bytes_feature('foo', value)
+ example = example_builder.example
+ # Use constructor to easily work with test parameters.
+ self.assertProtoEquals(
+ tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ 'foo':
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(
+ value=[expected_value]))
+ })), example)
+
+ @parameterized.named_parameters(
+ ('multiple_bytes', [b'Hello World!', b'Good Morning!'
+ ], [b'Hello World!', b'Good Morning!']),
+ ('multiple_sring', ['Hello World!', 'Good Morning!'
+ ], [b'Hello World!', b'Good Morning!']))
+ def test_add_multiple_bytes_feature(self, values, expected_values):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_bytes_feature('foo', values)
+ example = example_builder.example
+ self.assertProtoEquals(
+ tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ 'foo':
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(
+ value=expected_values))
+ })), example)
+
+ @parameterized.named_parameters(
+ ('single_integer', 123, [123]),
+ ('multiple_integers', [123, 456, 789], [123, 456, 789]))
+ def test_add_ints_feature(self, value, expected_value):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_ints_feature('bar', value)
+ example = example_builder.example
+ self.assertProtoEquals(
+ tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ 'bar':
+ tf.train.Feature(
+ int64_list=tf.train.Int64List(value=expected_value))
+ })), example)
+
+ @parameterized.named_parameters(
+ ('single_float', 3.14, [3.14]),
+ ('multiple_floats', [3.14, 1.57, 6.28], [3.14, 1.57, 6.28]))
+ def test_add_floats_feature(self, value, expected_value):
+ example_builder = tf_example_builder.TfExampleBuilder()
+ example_builder.add_floats_feature('baz', value)
+ example = example_builder.example
+ self.assertProtoEquals(
+ tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ 'baz':
+ tf.train.Feature(
+ float_list=tf.train.FloatList(value=expected_value))
+ })), example)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/core/tf_example_feature_key.py b/official/core/tf_example_feature_key.py
new file mode 100644
index 0000000000000000000000000000000000000000..e9d3a1d76d26ca1d8097f3dca714bc1602342369
--- /dev/null
+++ b/official/core/tf_example_feature_key.py
@@ -0,0 +1,62 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Data classes for tf.Example proto feature keys.
+
+Feature keys are grouped by feature types. Key names follow conventions in
+go/tf-example.
+"""
+import dataclasses
+import functools
+from typing import Optional
+
+# Disable init function to use the one defined in base class.
+dataclass = functools.partial(dataclasses.dataclass(init=False))
+
+
+@dataclass
+class TfExampleFeatureKeyBase:
+ """Base dataclass for defining tf.Example proto feature keys.
+
+ This class defines the logic of adding prefix to feature keys. Subclasses
+ will define feature keys for a specific feature type in data fields.
+
+ NOTE: Please follow subclass examples in this module to define feature keys
+ for a new feature type.
+ """
+
+ def __init__(self, prefix: Optional[str] = None):
+ """Instantiates the feature key class.
+
+ Adds a string prefix to all fields of a feature key instance if `prefix` is
+ not None nor empty.
+
+ Example usage:
+
+ >>> test_key = EncodedImageFeatureKey()
+ >>> test_key.encoded
+ image/encoded
+ >>> test_key = EncodedImageFeatureKey('prefix')
+ >>> test_key.encoded
+ prefix/image/encoded
+
+ Args:
+ prefix: A prefix string that will be added before the feature key string
+ with a trailing slash '/'.
+ """
+ if prefix:
+ for field in dataclasses.fields(self):
+ key_name = field.name
+ key_value = getattr(self, key_name)
+ setattr(self, key_name, f'{prefix}/{key_value}')
diff --git a/official/core/tf_example_feature_key_test.py b/official/core/tf_example_feature_key_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..295369468707d548cf40556bfe8e422c430ef04e
--- /dev/null
+++ b/official/core/tf_example_feature_key_test.py
@@ -0,0 +1,49 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tf_example_feature_key."""
+import dataclasses
+import inspect
+from absl.testing import absltest
+from absl.testing import parameterized
+
+from official.core import tf_example_feature_key
+
+
+@tf_example_feature_key.dataclass
+class TestFeatureKey(tf_example_feature_key.TfExampleFeatureKeyBase):
+ test: str = 'foo/bar'
+
+
+class TfExampleFeatureKeyTest(parameterized.TestCase):
+
+ def test_add_prefix_success(self):
+ test_key = TestFeatureKey('prefix')
+ self.assertEqual(test_key.test, 'prefix/foo/bar')
+
+ @parameterized.parameters(None, '')
+ def test_add_prefix_skip_success(self, prefix):
+ test_key = TestFeatureKey(prefix)
+ self.assertEqual(test_key.test, 'foo/bar')
+
+ def test_all_feature_key_classes_are_valid(self):
+ for _, obj in inspect.getmembers(tf_example_feature_key):
+ if inspect.isclass(obj):
+ self.assertTrue(dataclasses.is_dataclass(obj))
+ self.assertTrue(
+ issubclass(obj, tf_example_feature_key.TfExampleFeatureKeyBase))
+
+
+if __name__ == '__main__':
+ absltest.main()
diff --git a/official/core/train_lib.py b/official/core/train_lib.py
index 5f548ea722591bb878e468647b449426105ec74b..93afe0d7c55538aebfa3ac75f50eb7d3bf4ca555 100644
--- a/official/core/train_lib.py
+++ b/official/core/train_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,7 +15,7 @@
"""TFM common training driver library."""
# pytype: disable=attribute-error
import os
-from typing import Any, Mapping, Optional, Tuple
+from typing import Any, Mapping, Optional, Tuple, List
# Import libraries
@@ -32,6 +32,226 @@ from official.core import train_utils
maybe_create_best_ckpt_exporter = train_utils.maybe_create_best_ckpt_exporter
+class OrbitExperimentRunner:
+ """Runs experiment with Orbit training loop.
+
+ The default experiment runner for model garden experiments. User can
+ customize the experiment pipeline by subclassing this class and replacing
+ components or functions.
+
+ For example, an experiment runner with customized checkpoint manager:
+
+ ```python
+ class MyExpRunnerWithExporter(AbstractExperimentRunner):
+ def _maybe_build_checkpoint_manager(sefl):
+ return MyCheckpointManager(*args)
+
+ # In user code
+ MyExpRunnerWithExporter(**needed_kwargs).run(mode)
+ ```
+
+ Similar override can be done to other components.
+ """
+
+ def __init__(
+ self,
+ distribution_strategy: tf.distribute.Strategy,
+ task: base_task.Task,
+ mode: str,
+ params: config_definitions.ExperimentConfig,
+ model_dir: str,
+ run_post_eval: bool = False,
+ save_summary: bool = True,
+ train_actions: Optional[List[orbit.Action]] = None,
+ eval_actions: Optional[List[orbit.Action]] = None,
+ trainer: Optional[base_trainer.Trainer] = None,
+ controller_cls=orbit.Controller
+ ):
+ """Constructor.
+
+ Args:
+ distribution_strategy: A distribution strategy.
+ task: A Task instance.
+ mode: A 'str', specifying the mode. Can be 'train', 'eval',
+ 'train_and_eval' or 'continuous_eval'.
+ params: ExperimentConfig instance.
+ model_dir: A 'str', a path to store model checkpoints and summaries.
+ run_post_eval: Whether to run post eval once after training, metrics logs
+ are returned.
+ save_summary: Whether to save train and validation summary.
+ train_actions: Optional list of Orbit train actions.
+ eval_actions: Optional list of Orbit eval actions.
+ trainer: the base_trainer.Trainer instance. It should be created within
+ the strategy.scope().
+ controller_cls: The controller class to manage the train and eval process.
+ Must be a orbit.Controller subclass.
+ """
+ self.strategy = distribution_strategy or tf.distribute.get_strategy()
+ self._params = params
+ self._model_dir = model_dir
+ self._mode = mode
+ self._run_post_eval = run_post_eval
+
+ self._trainer = trainer or self._build_trainer(
+ task,
+ train='train' in mode,
+ evaluate=('eval' in mode) or run_post_eval)
+ assert self.trainer is not None
+ self._checkpoint_manager = self._maybe_build_checkpoint_manager()
+ self._controller = self._build_controller(
+ trainer=self.trainer if 'train' in mode else None,
+ evaluator=self.trainer,
+ save_summary=save_summary,
+ train_actions=train_actions,
+ eval_actions=eval_actions,
+ controller_cls=controller_cls)
+
+ @property
+ def params(self) -> config_definitions.ExperimentConfig:
+ return self._params
+
+ @property
+ def model_dir(self) -> str:
+ return self._model_dir
+
+ @property
+ def trainer(self) -> base_trainer.Trainer:
+ return self._trainer
+
+ @property
+ def checkpoint_manager(self) -> tf.train.CheckpointManager:
+ return self._checkpoint_manager
+
+ @property
+ def controller(self) -> orbit.Controller:
+ return self._controller
+
+ def _build_trainer(self, task: base_task.Task, train: bool,
+ evaluate: bool) -> base_trainer.Trainer:
+ """Create trainer."""
+ with self.strategy.scope():
+ trainer = train_utils.create_trainer(
+ self.params,
+ task,
+ train=train,
+ evaluate=evaluate,
+ checkpoint_exporter=self._build_best_checkpoint_exporter())
+ return trainer
+
+ def _build_best_checkpoint_exporter(self):
+ return maybe_create_best_ckpt_exporter(self.params, self.model_dir)
+
+ def _maybe_build_checkpoint_manager(
+ self) -> Optional[tf.train.CheckpointManager]:
+ """Maybe create a CheckpointManager."""
+ assert self.trainer is not None
+ if self.trainer.checkpoint:
+ if self.model_dir is None:
+ raise ValueError('model_dir must be specified, but got None')
+ checkpoint_manager = tf.train.CheckpointManager(
+ self.trainer.checkpoint,
+ directory=self.model_dir,
+ max_to_keep=self.params.trainer.max_to_keep,
+ step_counter=self.trainer.global_step,
+ checkpoint_interval=self.params.trainer.checkpoint_interval,
+ init_fn=self.trainer.initialize)
+ else:
+ checkpoint_manager = None
+ return checkpoint_manager
+
+ def _build_controller(self,
+ trainer,
+ evaluator,
+ save_summary: bool = True,
+ train_actions: Optional[List[orbit.Action]] = None,
+ eval_actions: Optional[List[orbit.Action]] = None,
+ controller_cls=orbit.Controller) -> orbit.Controller:
+ """Builds a Orbit controler."""
+ train_actions = [] if not train_actions else train_actions
+ if trainer:
+ train_actions += actions.get_train_actions(
+ self.params,
+ trainer,
+ self.model_dir,
+ checkpoint_manager=self.checkpoint_manager)
+
+ eval_actions = [] if not eval_actions else eval_actions
+ if evaluator:
+ eval_actions += actions.get_eval_actions(self.params, evaluator,
+ self.model_dir)
+
+ controller = controller_cls(
+ strategy=self.strategy,
+ trainer=trainer,
+ evaluator=evaluator,
+ global_step=self.trainer.global_step,
+ steps_per_loop=self.params.trainer.steps_per_loop,
+ checkpoint_manager=self.checkpoint_manager,
+ summary_dir=os.path.join(self.model_dir, 'train') if
+ (save_summary) else None,
+ eval_summary_dir=os.path.join(
+ self.model_dir, self.params.trainer.validation_summary_subdir) if
+ (save_summary) else None,
+ summary_interval=self.params.trainer.summary_interval if
+ (save_summary) else None,
+ train_actions=train_actions,
+ eval_actions=eval_actions)
+ return controller
+
+ def run(self) -> Tuple[tf.keras.Model, Mapping[str, Any]]:
+ """Run experiments by mode.
+
+ Returns:
+ A 2-tuple of (model, eval_logs).
+ model: `tf.keras.Model` instance.
+ eval_logs: returns eval metrics logs when run_post_eval is set to True,
+ otherwise, returns {}.
+ """
+ mode = self._mode
+ params = self.params
+ logging.info('Starts to execute mode: %s', mode)
+ with self.strategy.scope():
+ if mode == 'train' or mode == 'train_and_post_eval':
+ self.controller.train(steps=params.trainer.train_steps)
+ elif mode == 'train_and_eval':
+ self.controller.train_and_evaluate(
+ train_steps=params.trainer.train_steps,
+ eval_steps=params.trainer.validation_steps,
+ eval_interval=params.trainer.validation_interval)
+ elif mode == 'eval':
+ self.controller.evaluate(steps=params.trainer.validation_steps)
+ elif mode == 'continuous_eval':
+
+ def timeout_fn():
+ if self.trainer.global_step.numpy() >= params.trainer.train_steps:
+ return True
+ return False
+
+ self.controller.evaluate_continuously(
+ steps=params.trainer.validation_steps,
+ timeout=params.trainer.continuous_eval_timeout,
+ timeout_fn=timeout_fn)
+ else:
+ raise NotImplementedError('The mode is not implemented: %s' % mode)
+
+ num_params = train_utils.try_count_params(self.trainer.model)
+ if num_params is not None:
+ logging.info('Number of trainable params in model: %f Millions.',
+ num_params / 10.**6)
+
+ flops = train_utils.try_count_flops(self.trainer.model)
+ if flops is not None:
+ logging.info('FLOPs (multi-adds) in model: %f Billions.',
+ flops / 10.**9 / 2)
+
+ if self._run_post_eval or mode == 'train_and_post_eval':
+ with self.strategy.scope():
+ return self.trainer.model, self.controller.evaluate(
+ steps=params.trainer.validation_steps)
+ else:
+ return self.trainer.model, {}
+
+
def run_experiment(
distribution_strategy: tf.distribute.Strategy,
task: base_task.Task,
@@ -40,6 +260,8 @@ def run_experiment(
model_dir: str,
run_post_eval: bool = False,
save_summary: bool = True,
+ train_actions: Optional[List[orbit.Action]] = None,
+ eval_actions: Optional[List[orbit.Action]] = None,
trainer: Optional[base_trainer.Trainer] = None,
controller_cls=orbit.Controller
) -> Tuple[tf.keras.Model, Mapping[str, Any]]:
@@ -55,6 +277,8 @@ def run_experiment(
run_post_eval: Whether to run post eval once after training, metrics logs
are returned.
save_summary: Whether to save train and validation summary.
+ train_actions: Optional list of Orbit train actions.
+ eval_actions: Optional list of Orbit eval actions.
trainer: the base_trainer.Trainer instance. It should be created within the
strategy.scope().
controller_cls: The controller class to manage the train and eval process.
@@ -66,85 +290,17 @@ def run_experiment(
eval_logs: returns eval metrics logs when run_post_eval is set to True,
otherwise, returns {}.
"""
-
- with distribution_strategy.scope():
- if not trainer:
- trainer = train_utils.create_trainer(
- params,
- task,
- train='train' in mode,
- evaluate=('eval' in mode) or run_post_eval,
- checkpoint_exporter=maybe_create_best_ckpt_exporter(
- params, model_dir))
-
- if trainer.checkpoint:
- if model_dir is None:
- raise ValueError('model_dir must be specified, but got None')
- checkpoint_manager = tf.train.CheckpointManager(
- trainer.checkpoint,
- directory=model_dir,
- max_to_keep=params.trainer.max_to_keep,
- step_counter=trainer.global_step,
- checkpoint_interval=params.trainer.checkpoint_interval,
- init_fn=trainer.initialize)
- else:
- checkpoint_manager = None
-
- controller = controller_cls(
- strategy=distribution_strategy,
- trainer=trainer if 'train' in mode else None,
- evaluator=trainer,
- global_step=trainer.global_step,
- steps_per_loop=params.trainer.steps_per_loop,
- checkpoint_manager=checkpoint_manager,
- summary_dir=os.path.join(model_dir, 'train') if (save_summary) else None,
- eval_summary_dir=os.path.join(model_dir,
- params.trainer.validation_summary_subdir) if
- (save_summary) else None,
- summary_interval=params.trainer.summary_interval if
- (save_summary) else None,
- train_actions=actions.get_train_actions(
- params, trainer, model_dir, checkpoint_manager=checkpoint_manager),
- eval_actions=actions.get_eval_actions(params, trainer, model_dir))
-
- logging.info('Starts to execute mode: %s', mode)
- with distribution_strategy.scope():
- if mode == 'train':
- controller.train(steps=params.trainer.train_steps)
- elif mode == 'train_and_eval':
- controller.train_and_evaluate(
- train_steps=params.trainer.train_steps,
- eval_steps=params.trainer.validation_steps,
- eval_interval=params.trainer.validation_interval)
- elif mode == 'eval':
- controller.evaluate(steps=params.trainer.validation_steps)
- elif mode == 'continuous_eval':
-
- def timeout_fn():
- if trainer.global_step.numpy() >= params.trainer.train_steps:
- return True
- return False
-
- controller.evaluate_continuously(
- steps=params.trainer.validation_steps,
- timeout=params.trainer.continuous_eval_timeout,
- timeout_fn=timeout_fn)
- else:
- raise NotImplementedError('The mode is not implemented: %s' % mode)
-
- num_params = train_utils.try_count_params(trainer.model)
- if num_params is not None:
- logging.info('Number of trainable params in model: %f Millions.',
- num_params / 10.**6)
-
- flops = train_utils.try_count_flops(trainer.model)
- if flops is not None:
- logging.info('FLOPs (multi-adds) in model: %f Billions.',
- flops / 10.**9 / 2)
-
- if run_post_eval:
- with distribution_strategy.scope():
- return trainer.model, trainer.evaluate(
- tf.convert_to_tensor(params.trainer.validation_steps))
- else:
- return trainer.model, {}
+ runner = OrbitExperimentRunner(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=mode,
+ params=params,
+ model_dir=model_dir,
+ run_post_eval=run_post_eval,
+ save_summary=save_summary,
+ train_actions=train_actions,
+ eval_actions=eval_actions,
+ trainer=trainer,
+ controller_cls=controller_cls,
+ )
+ return runner.run()
diff --git a/official/core/train_lib_test.py b/official/core/train_lib_test.py
index 9c27054d539b009e43ba6f2e9b846d49e02357a1..dd87f5fee4ec4f74f391b63eaaf0fd2ea0aaac1b 100644
--- a/official/core/train_lib_test.py
+++ b/official/core/train_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -117,6 +117,61 @@ class TrainTest(tf.test.TestCase, parameterized.TestCase):
model_dir=model_dir,
run_post_eval=run_post_eval)
+ @combinations.generate(
+ combinations.combine(
+ distribution_strategy=[
+ strategy_combinations.default_strategy,
+ strategy_combinations.cloud_tpu_strategy,
+ strategy_combinations.one_device_strategy_gpu,
+ ],
+ flag_mode=['train', 'eval', 'train_and_eval'],
+ run_post_eval=[True, False]))
+ def test_end_to_end_class(self, distribution_strategy, flag_mode,
+ run_post_eval):
+ model_dir = self.get_temp_dir()
+ flags_dict = dict(
+ experiment='mock',
+ mode=flag_mode,
+ model_dir=model_dir,
+ params_override=json.dumps(self._test_config))
+ with flagsaver.flagsaver(**flags_dict):
+ params = train_utils.parse_configuration(flags.FLAGS)
+ train_utils.serialize_config(params, model_dir)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ _, logs = train_lib.OrbitExperimentRunner(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=flag_mode,
+ params=params,
+ model_dir=model_dir,
+ run_post_eval=run_post_eval).run()
+
+ if 'eval' in flag_mode:
+ self.assertTrue(
+ tf.io.gfile.exists(
+ os.path.join(model_dir,
+ params.trainer.validation_summary_subdir)))
+ if run_post_eval:
+ self.assertNotEmpty(logs)
+ else:
+ self.assertEmpty(logs)
+ self.assertNotEmpty(
+ tf.io.gfile.glob(os.path.join(model_dir, 'params.yaml')))
+ if flag_mode == 'eval':
+ return
+ self.assertNotEmpty(
+ tf.io.gfile.glob(os.path.join(model_dir, 'checkpoint')))
+ # Tests continuous evaluation.
+ _, logs = train_lib.OrbitExperimentRunner(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode='continuous_eval',
+ params=params,
+ model_dir=model_dir,
+ run_post_eval=run_post_eval).run()
+
@combinations.generate(
combinations.combine(
distribution_strategy=[
@@ -148,12 +203,12 @@ class TrainTest(tf.test.TestCase, parameterized.TestCase):
task.build_losses = build_losses
with self.assertRaises(RuntimeError):
- train_lib.run_experiment(
+ train_lib.OrbitExperimentRunner(
distribution_strategy=distribution_strategy,
task=task,
mode=flag_mode,
params=params,
- model_dir=model_dir)
+ model_dir=model_dir).run()
@combinations.generate(
combinations.combine(
@@ -194,12 +249,12 @@ class TrainTest(tf.test.TestCase, parameterized.TestCase):
task.build_losses = build_losses
- model, _ = train_lib.run_experiment(
+ model, _ = train_lib.OrbitExperimentRunner(
distribution_strategy=distribution_strategy,
task=task,
mode=flag_mode,
params=params,
- model_dir=model_dir)
+ model_dir=model_dir).run()
after_weights = model.get_weights()
for left, right in zip(before_weights, after_weights):
self.assertAllEqual(left, right)
diff --git a/official/core/train_utils.py b/official/core/train_utils.py
index 7672661b569d4ce72758f396118f2e3ed6632c3c..94d7bd70d32bbe3061bd6b0e47fa8165e8815c15 100644
--- a/official/core/train_utils.py
+++ b/official/core/train_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,6 +15,7 @@
"""Training utils."""
import copy
import dataclasses
+import inspect
import json
import os
import pprint
@@ -35,6 +36,9 @@ from official.core import exp_factory
from official.modeling import hyperparams
+BEST_CHECKPOINT_NAME = 'best_ckpt'
+
+
def get_leaf_nested_dict(d: Dict[str, Any], keys: List[str]) -> Dict[str, Any]:
"""Get leaf from a dictionary with arbitrary depth with a list of keys.
@@ -101,7 +105,6 @@ def maybe_create_best_ckpt_exporter(params: config_definitions.ExperimentConfig,
return best_ckpt_exporter
-# TODO(b/180147589): Add tests for this module.
class BestCheckpointExporter:
"""Keeps track of the best result, and saves its checkpoint.
@@ -138,7 +141,7 @@ class BestCheckpointExporter:
checkpoint,
directory=self._export_dir,
max_to_keep=1,
- checkpoint_name='best_ckpt')
+ checkpoint_name=BEST_CHECKPOINT_NAME)
return self._checkpoint_manager
@@ -209,6 +212,28 @@ class BestCheckpointExporter:
return tf.train.latest_checkpoint(self._export_dir)
+def create_optimizer(task: base_task.Task,
+ params: config_definitions.ExperimentConfig
+ ) -> tf.keras.optimizers.Optimizer:
+ """A create optimizer util to be backward compatability with new args."""
+ if 'dp_config' in inspect.signature(task.create_optimizer).parameters:
+ dp_config = None
+ if hasattr(params.task, 'differential_privacy_config'):
+ dp_config = params.task.differential_privacy_config
+ optimizer = task.create_optimizer(
+ params.trainer.optimizer_config, params.runtime,
+ dp_config=dp_config)
+ else:
+ if hasattr(params.task, 'differential_privacy_config'
+ ) and params.task.differential_privacy_config is not None:
+ raise ValueError('Differential privacy config is specified but '
+ 'task.create_optimizer api does not accept it.')
+ optimizer = task.create_optimizer(
+ params.trainer.optimizer_config,
+ params.runtime)
+ return optimizer
+
+
@gin.configurable
def create_trainer(params: config_definitions.ExperimentConfig,
task: base_task.Task,
@@ -219,8 +244,7 @@ def create_trainer(params: config_definitions.ExperimentConfig,
"""Create trainer."""
logging.info('Running default trainer.')
model = task.build_model()
- optimizer = task.create_optimizer(params.trainer.optimizer_config,
- params.runtime)
+ optimizer = create_optimizer(task, params)
return trainer_cls(
params,
task,
diff --git a/official/core/train_utils_test.py b/official/core/train_utils_test.py
index 2010736aa2a9285bc55e4cd5194db297431f1385..dbc49d2b7d504967da04c1134a5abd91fb44494b 100644
--- a/official/core/train_utils_test.py
+++ b/official/core/train_utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,6 +13,7 @@
# limitations under the License.
"""Tests for official.core.train_utils."""
+import json
import os
import pprint
@@ -138,5 +139,60 @@ class TrainUtilsTest(tf.test.TestCase):
self.assertEqual(params_from_obj.trainer.validation_steps, 11)
+class BestCheckpointExporterTest(tf.test.TestCase):
+
+ def test_maybe_export(self):
+ model_dir = self.create_tempdir().full_path
+ best_ckpt_path = os.path.join(model_dir, 'best_ckpt-1')
+ metric_name = 'test_metric|metric_1'
+ exporter = train_utils.BestCheckpointExporter(
+ model_dir, metric_name, 'higher')
+ v = tf.Variable(1.0)
+ checkpoint = tf.train.Checkpoint(v=v)
+ ret = exporter.maybe_export_checkpoint(
+ checkpoint, {'test_metric': {'metric_1': 5.0}}, 100)
+ with self.subTest(name='Successful first save.'):
+ self.assertEqual(ret, True)
+ v_2 = tf.Variable(2.0)
+ checkpoint_2 = tf.train.Checkpoint(v=v_2)
+ checkpoint_2.restore(best_ckpt_path)
+ self.assertEqual(v_2.numpy(), 1.0)
+
+ v = tf.Variable(3.0)
+ checkpoint = tf.train.Checkpoint(v=v)
+ ret = exporter.maybe_export_checkpoint(
+ checkpoint, {'test_metric': {'metric_1': 6.0}}, 200)
+ with self.subTest(name='Successful better metic save.'):
+ self.assertEqual(ret, True)
+ v_2 = tf.Variable(2.0)
+ checkpoint_2 = tf.train.Checkpoint(v=v_2)
+ checkpoint_2.restore(best_ckpt_path)
+ self.assertEqual(v_2.numpy(), 3.0)
+
+ v = tf.Variable(5.0)
+ checkpoint = tf.train.Checkpoint(v=v)
+ ret = exporter.maybe_export_checkpoint(
+ checkpoint, {'test_metric': {'metric_1': 1.0}}, 300)
+ with self.subTest(name='Worse metic no save.'):
+ self.assertEqual(ret, False)
+ v_2 = tf.Variable(2.0)
+ checkpoint_2 = tf.train.Checkpoint(v=v_2)
+ checkpoint_2.restore(best_ckpt_path)
+ self.assertEqual(v_2.numpy(), 3.0)
+
+ def test_export_best_eval_metric(self):
+ model_dir = self.create_tempdir().full_path
+ metric_name = 'test_metric|metric_1'
+ exporter = train_utils.BestCheckpointExporter(model_dir, metric_name,
+ 'higher')
+ exporter.export_best_eval_metric({'test_metric': {'metric_1': 5.0}}, 100)
+ with tf.io.gfile.GFile(os.path.join(model_dir, 'info.json'),
+ 'rb') as reader:
+ metric = json.loads(reader.read())
+ self.assertAllEqual(
+ metric,
+ {'test_metric': {'metric_1': 5.0}, 'best_ckpt_global_step': 100.0})
+
+
if __name__ == '__main__':
tf.test.main()
diff --git a/official/legacy/README.md b/official/legacy/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ced1fce05dfcd8308d7bec8b01186a8804bc074f
--- /dev/null
+++ b/official/legacy/README.md
@@ -0,0 +1,5 @@
+Models in this `legacy` directory are mainly are used for benchmarking the
+models.
+
+Please note that the models in this `legacy` directory are not supported like
+the models in official/nlp and official/vision.
diff --git a/official/legacy/__init__.py b/official/legacy/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/__init__.py
+++ b/official/legacy/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/nlp/albert/README.md b/official/legacy/albert/README.md
similarity index 100%
rename from official/legacy/nlp/albert/README.md
rename to official/legacy/albert/README.md
diff --git a/official/legacy/albert/__init__.py b/official/legacy/albert/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/legacy/albert/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/legacy/albert/configs.py b/official/legacy/albert/configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..7baf693aee884d71021e55f64b6477bdd397ed68
--- /dev/null
+++ b/official/legacy/albert/configs.py
@@ -0,0 +1,50 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""The ALBERT configurations."""
+
+import six
+
+from official.legacy.bert import configs
+
+
+class AlbertConfig(configs.BertConfig):
+ """Configuration for `ALBERT`."""
+
+ def __init__(self, num_hidden_groups=1, inner_group_num=1, **kwargs):
+ """Constructs AlbertConfig.
+
+ Args:
+ num_hidden_groups: Number of group for the hidden layers, parameters in
+ the same group are shared. Note that this value and also the following
+ 'inner_group_num' has to be 1 for now, because all released ALBERT
+ models set them to 1. We may support arbitary valid values in future.
+ inner_group_num: Number of inner repetition of attention and ffn.
+ **kwargs: The remaining arguments are the same as above 'BertConfig'.
+ """
+ super(AlbertConfig, self).__init__(**kwargs)
+
+ # TODO(chendouble): 'inner_group_num' and 'num_hidden_groups' are always 1
+ # in the released ALBERT. Support other values in AlbertEncoder if needed.
+ if inner_group_num != 1 or num_hidden_groups != 1:
+ raise ValueError("We only support 'inner_group_num' and "
+ "'num_hidden_groups' as 1.")
+
+ @classmethod
+ def from_dict(cls, json_object):
+ """Constructs a `AlbertConfig` from a Python dictionary of parameters."""
+ config = AlbertConfig(vocab_size=None)
+ for (key, value) in six.iteritems(json_object):
+ config.__dict__[key] = value
+ return config
diff --git a/official/legacy/bert/README.md b/official/legacy/bert/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..cf4062a6dc39567e048232f84218ccd71e19b6fc
--- /dev/null
+++ b/official/legacy/bert/README.md
@@ -0,0 +1,395 @@
+# BERT (Bidirectional Encoder Representations from Transformers)
+
+**WARNING**: We are on the way to deprecate most of the code in this directory.
+Please see
+[this link](../g3doc/tutorials/bert_new.md)
+for the new tutorial and use the new code in `nlp/modeling`. This README is
+still correct for this legacy implementation.
+
+The academic paper which describes BERT in detail and provides full results on a
+number of tasks can be found here: https://arxiv.org/abs/1810.04805.
+
+This repository contains TensorFlow 2.x implementation for BERT.
+
+## Contents
+ * [Contents](#contents)
+ * [Pre-trained Models](#pre-trained-models)
+ * [Restoring from Checkpoints](#restoring-from-checkpoints)
+ * [Set Up](#set-up)
+ * [Process Datasets](#process-datasets)
+ * [Fine-tuning with BERT](#fine-tuning-with-bert)
+ * [Cloud GPUs and TPUs](#cloud-gpus-and-tpus)
+ * [Sentence and Sentence-pair Classification Tasks](#sentence-and-sentence-pair-classification-tasks)
+ * [SQuAD 1.1](#squad-1.1)
+
+
+## Pre-trained Models
+
+We released both checkpoints and tf.hub modules as the pretrained models for
+fine-tuning. They are TF 2.x compatible and are converted from the checkpoints
+released in TF 1.x official BERT repository
+[google-research/bert](https://github.com/google-research/bert)
+in order to keep consistent with BERT paper.
+
+
+### Access to Pretrained Checkpoints
+
+Pretrained checkpoints can be found in the following links:
+
+**Note: We have switched BERT implementation
+to use Keras functional-style networks in [nlp/modeling](../modeling).
+The new checkpoints are:**
+
+* **[`BERT-Large, Uncased (Whole Word Masking)`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/wwm_uncased_L-24_H-1024_A-16.tar.gz)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Large, Cased (Whole Word Masking)`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/wwm_cased_L-24_H-1024_A-16.tar.gz)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Uncased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/uncased_L-12_H-768_A-12.tar.gz)**:
+ 12-layer, 768-hidden, 12-heads, 110M parameters
+* **[`BERT-Large, Uncased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16.tar.gz)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/cased_L-12_H-768_A-12.tar.gz)**:
+ 12-layer, 768-hidden, 12-heads , 110M parameters
+* **[`BERT-Large, Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/cased_L-24_H-1024_A-16.tar.gz)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Multilingual Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/multi_cased_L-12_H-768_A-12.tar.gz)**:
+ 104 languages, 12-layer, 768-hidden, 12-heads, 110M parameters
+
+We recommend to host checkpoints on Google Cloud storage buckets when you use
+Cloud GPU/TPU.
+
+### Restoring from Checkpoints
+
+`tf.train.Checkpoint` is used to manage model checkpoints in TF 2. To restore
+weights from provided pre-trained checkpoints, you can use the following code:
+
+```python
+init_checkpoint='the pretrained model checkpoint path.'
+model=tf.keras.Model() # Bert pre-trained model as feature extractor.
+checkpoint = tf.train.Checkpoint(model=model)
+checkpoint.restore(init_checkpoint)
+```
+
+Checkpoints featuring native serialized Keras models
+(i.e. model.load()/load_weights()) will be available soon.
+
+### Access to Pretrained hub modules.
+
+Pretrained tf.hub modules in TF 2.x SavedModel format can be found in the
+following links:
+
+* **[`BERT-Large, Uncased (Whole Word Masking)`](https://tfhub.dev/tensorflow/bert_en_wwm_uncased_L-24_H-1024_A-16/)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Large, Cased (Whole Word Masking)`](https://tfhub.dev/tensorflow/bert_en_wwm_cased_L-24_H-1024_A-16/)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Uncased`](https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/)**:
+ 12-layer, 768-hidden, 12-heads, 110M parameters
+* **[`BERT-Large, Uncased`](https://tfhub.dev/tensorflow/bert_en_uncased_L-24_H-1024_A-16/)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Cased`](https://tfhub.dev/tensorflow/bert_en_cased_L-12_H-768_A-12/)**:
+ 12-layer, 768-hidden, 12-heads , 110M parameters
+* **[`BERT-Large, Cased`](https://tfhub.dev/tensorflow/bert_en_cased_L-24_H-1024_A-16/)**:
+ 24-layer, 1024-hidden, 16-heads, 340M parameters
+* **[`BERT-Base, Multilingual Cased`](https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/)**:
+ 104 languages, 12-layer, 768-hidden, 12-heads, 110M parameters
+* **[`BERT-Base, Chinese`](https://tfhub.dev/tensorflow/bert_zh_L-12_H-768_A-12/)**:
+ Chinese Simplified and Traditional, 12-layer, 768-hidden, 12-heads,
+ 110M parameters
+
+## Set Up
+
+```shell
+export PYTHONPATH="$PYTHONPATH:/path/to/models"
+```
+
+Install `tf-nightly` to get latest updates:
+
+```shell
+pip install tf-nightly-gpu
+```
+
+With TPU, GPU support is not necessary. First, you need to create a `tf-nightly`
+TPU with [ctpu tool](https://github.com/tensorflow/tpu/tree/master/tools/ctpu):
+
+```shell
+ctpu up -name --tf-version=”nightly”
+```
+
+Second, you need to install TF 2 `tf-nightly` on your VM:
+
+```shell
+pip install tf-nightly
+```
+
+## Process Datasets
+
+### Pre-training
+
+There is no change to generate pre-training data. Please use the script
+[`../data/create_pretraining_data.py`](../data/create_pretraining_data.py)
+which is essentially branched from [BERT research repo](https://github.com/google-research/bert)
+to get processed pre-training data and it adapts to TF2 symbols and python3
+compatibility.
+
+Running the pre-training script requires an input and output directory, as well as a vocab file. Note that max_seq_length will need to match the sequence length parameter you specify when you run pre-training.
+
+Example shell script to call create_pretraining_data.py
+```
+export WORKING_DIR='local disk or cloud location'
+export BERT_DIR='local disk or cloud location'
+python models/official/nlp/data/create_pretraining_data.py \
+ --input_file=$WORKING_DIR/input/input.txt \
+ --output_file=$WORKING_DIR/output/tf_examples.tfrecord \
+ --vocab_file=$BERT_DIR/wwm_uncased_L-24_H-1024_A-16/vocab.txt \
+ --do_lower_case=True \
+ --max_seq_length=512 \
+ --max_predictions_per_seq=76 \
+ --masked_lm_prob=0.15 \
+ --random_seed=12345 \
+ --dupe_factor=5
+```
+
+### Fine-tuning
+
+To prepare the fine-tuning data for final model training, use the
+[`../data/create_finetuning_data.py`](../data/create_finetuning_data.py) script.
+Resulting datasets in `tf_record` format and training meta data should be later
+passed to training or evaluation scripts. The task-specific arguments are
+described in following sections:
+
+* GLUE
+
+Users can download the
+[GLUE data](https://gluebenchmark.com/tasks) by running
+[this script](https://gist.github.com/W4ngatang/60c2bdb54d156a41194446737ce03e2e)
+and unpack it to some directory `$GLUE_DIR`.
+Also, users can download [Pretrained Checkpoint](#access-to-pretrained-checkpoints) and locate on some directory `$BERT_DIR` instead of using checkpoints on Google Cloud Storage.
+
+```shell
+export GLUE_DIR=~/glue
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+
+export TASK_NAME=MNLI
+export OUTPUT_DIR=gs://some_bucket/datasets
+python ../data/create_finetuning_data.py \
+ --input_data_dir=${GLUE_DIR}/${TASK_NAME}/ \
+ --vocab_file=${BERT_DIR}/vocab.txt \
+ --train_data_output_path=${OUTPUT_DIR}/${TASK_NAME}_train.tf_record \
+ --eval_data_output_path=${OUTPUT_DIR}/${TASK_NAME}_eval.tf_record \
+ --meta_data_file_path=${OUTPUT_DIR}/${TASK_NAME}_meta_data \
+ --fine_tuning_task_type=classification --max_seq_length=128 \
+ --classification_task_name=${TASK_NAME}
+```
+
+* SQUAD
+
+The [SQuAD website](https://rajpurkar.github.io/SQuAD-explorer/) contains
+detailed information about the SQuAD datasets and evaluation.
+
+The necessary files can be found here:
+
+* [train-v1.1.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/train-v1.1.json)
+* [dev-v1.1.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/dev-v1.1.json)
+* [evaluate-v1.1.py](https://github.com/allenai/bi-att-flow/blob/master/squad/evaluate-v1.1.py)
+* [train-v2.0.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/train-v2.0.json)
+* [dev-v2.0.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/dev-v2.0.json)
+* [evaluate-v2.0.py](https://worksheets.codalab.org/rest/bundles/0x6b567e1cf2e041ec80d7098f031c5c9e/contents/blob/)
+
+```shell
+export SQUAD_DIR=~/squad
+export SQUAD_VERSION=v1.1
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export OUTPUT_DIR=gs://some_bucket/datasets
+
+python ../data/create_finetuning_data.py \
+ --squad_data_file=${SQUAD_DIR}/train-${SQUAD_VERSION}.json \
+ --vocab_file=${BERT_DIR}/vocab.txt \
+ --train_data_output_path=${OUTPUT_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
+ --meta_data_file_path=${OUTPUT_DIR}/squad_${SQUAD_VERSION}_meta_data \
+ --fine_tuning_task_type=squad --max_seq_length=384
+```
+
+Note: To create fine-tuning data with SQUAD 2.0, you need to add flag `--version_2_with_negative=True`.
+
+## Fine-tuning with BERT
+
+### Cloud GPUs and TPUs
+
+* Cloud Storage
+
+The unzipped pre-trained model files can also be found in the Google Cloud
+Storage folder `gs://cloud-tpu-checkpoints/bert/keras_bert`. For example:
+
+```shell
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export MODEL_DIR=gs://some_bucket/my_output_dir
+```
+
+Currently, users are able to access to `tf-nightly` TPUs and the following TPU
+script should run with `tf-nightly`.
+
+* GPU -> TPU
+
+Just add the following flags to `run_classifier.py` or `run_squad.py`:
+
+```shell
+ --distribution_strategy=tpu
+ --tpu=grpc://${TPU_IP_ADDRESS}:8470
+```
+
+### Sentence and Sentence-pair Classification Tasks
+
+This example code fine-tunes `BERT-Large` on the Microsoft Research Paraphrase
+Corpus (MRPC) corpus, which only contains 3,600 examples and can fine-tune in a
+few minutes on most GPUs.
+
+We use the `BERT-Large` (uncased_L-24_H-1024_A-16) as an example throughout the
+workflow.
+For GPU memory of 16GB or smaller, you may try to use `BERT-Base`
+(uncased_L-12_H-768_A-12).
+
+```shell
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export MODEL_DIR=gs://some_bucket/my_output_dir
+export GLUE_DIR=gs://some_bucket/datasets
+export TASK=MRPC
+
+python run_classifier.py \
+ --mode='train_and_eval' \
+ --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
+ --train_data_path=${GLUE_DIR}/${TASK}_train.tf_record \
+ --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
+ --bert_config_file=${BERT_DIR}/bert_config.json \
+ --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
+ --train_batch_size=4 \
+ --eval_batch_size=4 \
+ --steps_per_loop=1 \
+ --learning_rate=2e-5 \
+ --num_train_epochs=3 \
+ --model_dir=${MODEL_DIR} \
+ --distribution_strategy=mirrored
+```
+
+Alternatively, instead of specifying `init_checkpoint`, you can specify
+`hub_module_url` to employ a pretraind BERT hub module, e.g.,
+` --hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-24_H-1024_A-16/1`.
+
+After training a model, to get predictions from the classifier, you can set the
+`--mode=predict` and offer the test set tfrecords to `--eval_data_path`.
+Output will be created in file called test_results.tsv in the output folder.
+Each line will contain output for each sample, columns are the class
+probabilities.
+
+```shell
+python run_classifier.py \
+ --mode='predict' \
+ --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
+ --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
+ --bert_config_file=${BERT_DIR}/bert_config.json \
+ --eval_batch_size=4 \
+ --model_dir=${MODEL_DIR} \
+ --distribution_strategy=mirrored
+```
+
+To use TPU, you only need to switch distribution strategy type to `tpu` with TPU
+information and use remote storage for model checkpoints.
+
+```shell
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export TPU_IP_ADDRESS='???'
+export MODEL_DIR=gs://some_bucket/my_output_dir
+export GLUE_DIR=gs://some_bucket/datasets
+export TASK=MRPC
+
+python run_classifier.py \
+ --mode='train_and_eval' \
+ --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
+ --train_data_path=${GLUE_DIR}/${TASK}_train.tf_record \
+ --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
+ --bert_config_file=${BERT_DIR}/bert_config.json \
+ --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
+ --train_batch_size=32 \
+ --eval_batch_size=32 \
+ --steps_per_loop=1000 \
+ --learning_rate=2e-5 \
+ --num_train_epochs=3 \
+ --model_dir=${MODEL_DIR} \
+ --distribution_strategy=tpu \
+ --tpu=grpc://${TPU_IP_ADDRESS}:8470
+```
+
+Note that, we specify `steps_per_loop=1000` for TPU, because running a loop of
+training steps inside a `tf.function` can significantly increase TPU utilization
+and callbacks will not be called inside the loop.
+
+### SQuAD 1.1
+
+The Stanford Question Answering Dataset (SQuAD) is a popular question answering
+benchmark dataset. See more in [SQuAD website](https://rajpurkar.github.io/SQuAD-explorer/).
+
+We use the `BERT-Large` (uncased_L-24_H-1024_A-16) as an example throughout the
+workflow.
+For GPU memory of 16GB or smaller, you may try to use `BERT-Base`
+(uncased_L-12_H-768_A-12).
+
+```shell
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export SQUAD_DIR=gs://some_bucket/datasets
+export MODEL_DIR=gs://some_bucket/my_output_dir
+export SQUAD_VERSION=v1.1
+
+python run_squad.py \
+ --input_meta_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_meta_data \
+ --train_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
+ --predict_file=${SQUAD_DIR}/dev-v1.1.json \
+ --vocab_file=${BERT_DIR}/vocab.txt \
+ --bert_config_file=${BERT_DIR}/bert_config.json \
+ --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
+ --train_batch_size=4 \
+ --predict_batch_size=4 \
+ --learning_rate=8e-5 \
+ --num_train_epochs=2 \
+ --model_dir=${MODEL_DIR} \
+ --distribution_strategy=mirrored
+```
+
+Similarily, you can replace `init_checkpoint` FLAG with `hub_module_url` to
+specify a hub module path.
+
+`run_squad.py` writes the prediction for `--predict_file` by default. If you set
+the `--model=predict` and offer the SQuAD test data, the scripts will generate
+the prediction json file.
+
+To use TPU, you need switch distribution strategy type to `tpu` with TPU
+information.
+
+```shell
+export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
+export TPU_IP_ADDRESS='???'
+export MODEL_DIR=gs://some_bucket/my_output_dir
+export SQUAD_DIR=gs://some_bucket/datasets
+export SQUAD_VERSION=v1.1
+
+python run_squad.py \
+ --input_meta_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_meta_data \
+ --train_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
+ --predict_file=${SQUAD_DIR}/dev-v1.1.json \
+ --vocab_file=${BERT_DIR}/vocab.txt \
+ --bert_config_file=${BERT_DIR}/bert_config.json \
+ --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
+ --train_batch_size=32 \
+ --learning_rate=8e-5 \
+ --num_train_epochs=2 \
+ --model_dir=${MODEL_DIR} \
+ --distribution_strategy=tpu \
+ --tpu=grpc://${TPU_IP_ADDRESS}:8470
+```
+
+The dev set predictions will be saved into a file called predictions.json in the
+model_dir:
+
+```shell
+python $SQUAD_DIR/evaluate-v1.1.py $SQUAD_DIR/dev-v1.1.json ./squad/predictions.json
+```
+
+
diff --git a/official/legacy/bert/__init__.py b/official/legacy/bert/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1
--- /dev/null
+++ b/official/legacy/bert/__init__.py
@@ -0,0 +1,15 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
diff --git a/official/nlp/bert/bert_cloud_tpu.md b/official/legacy/bert/bert_cloud_tpu.md
similarity index 100%
rename from official/nlp/bert/bert_cloud_tpu.md
rename to official/legacy/bert/bert_cloud_tpu.md
diff --git a/official/nlp/bert/bert_models.py b/official/legacy/bert/bert_models.py
similarity index 98%
rename from official/nlp/bert/bert_models.py
rename to official/legacy/bert/bert_models.py
index a1061e6c893a64183ae1a83d8fcd6cd4fb1e3ec8..21d095174cc3c8af00ae2b2a0a601c1dae8d3f6b 100644
--- a/official/nlp/bert/bert_models.py
+++ b/official/legacy/bert/bert_models.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,9 +17,9 @@
import gin
import tensorflow as tf
import tensorflow_hub as hub
-from official.legacy.nlp.albert import configs as albert_configs
+from official.legacy.albert import configs as albert_configs
+from official.legacy.bert import configs
from official.modeling import tf_utils
-from official.nlp.bert import configs
from official.nlp.modeling import models
from official.nlp.modeling import networks
diff --git a/official/nlp/bert/bert_models_test.py b/official/legacy/bert/bert_models_test.py
similarity index 95%
rename from official/nlp/bert/bert_models_test.py
rename to official/legacy/bert/bert_models_test.py
index 8c4a52a20d343e3d7cc5f0ccac250d5f4f036667..e64c013c40d2724e02ffbf1ab75b2269928fb000 100644
--- a/official/nlp/bert/bert_models_test.py
+++ b/official/legacy/bert/bert_models_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,8 +14,8 @@
import tensorflow as tf
-from official.nlp.bert import bert_models
-from official.nlp.bert import configs as bert_configs
+from official.legacy.bert import bert_models
+from official.legacy.bert import configs as bert_configs
from official.nlp.modeling import networks
diff --git a/official/legacy/bert/common_flags.py b/official/legacy/bert/common_flags.py
new file mode 100644
index 0000000000000000000000000000000000000000..32ad7059f04e7b17a894de8305df353e3304440e
--- /dev/null
+++ b/official/legacy/bert/common_flags.py
@@ -0,0 +1,125 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Defining common flags used across all BERT models/applications."""
+
+from absl import flags
+import tensorflow as tf
+
+from official.utils import hyperparams_flags
+from official.utils.flags import core as flags_core
+
+
+def define_common_bert_flags():
+ """Define common flags for BERT tasks."""
+ flags_core.define_base(
+ data_dir=False,
+ model_dir=True,
+ clean=False,
+ train_epochs=False,
+ epochs_between_evals=False,
+ stop_threshold=False,
+ batch_size=False,
+ num_gpu=True,
+ export_dir=False,
+ distribution_strategy=True,
+ run_eagerly=True)
+ flags_core.define_distribution()
+ flags.DEFINE_string('bert_config_file', None,
+ 'Bert configuration file to define core bert layers.')
+ flags.DEFINE_string(
+ 'model_export_path', None,
+ 'Path to the directory, where trainined model will be '
+ 'exported.')
+ flags.DEFINE_string('tpu', '', 'TPU address to connect to.')
+ flags.DEFINE_string(
+ 'init_checkpoint', None,
+ 'Initial checkpoint (usually from a pre-trained BERT model).')
+ flags.DEFINE_integer('num_train_epochs', 3,
+ 'Total number of training epochs to perform.')
+ flags.DEFINE_integer(
+ 'steps_per_loop', None,
+ 'Number of steps per graph-mode loop. Only training step '
+ 'happens inside the loop. Callbacks will not be called '
+ 'inside. If not set the value will be configured depending on the '
+ 'devices available.')
+ flags.DEFINE_float('learning_rate', 5e-5,
+ 'The initial learning rate for Adam.')
+ flags.DEFINE_float('end_lr', 0.0,
+ 'The end learning rate for learning rate decay.')
+ flags.DEFINE_string('optimizer_type', 'adamw',
+ 'The type of optimizer to use for training (adamw|lamb)')
+ flags.DEFINE_boolean(
+ 'scale_loss', False,
+ 'Whether to divide the loss by number of replica inside the per-replica '
+ 'loss function.')
+ flags.DEFINE_boolean(
+ 'use_keras_compile_fit', False,
+ 'If True, uses Keras compile/fit() API for training logic. Otherwise '
+ 'use custom training loop.')
+ flags.DEFINE_string(
+ 'hub_module_url', None, 'TF-Hub path/url to Bert module. '
+ 'If specified, init_checkpoint flag should not be used.')
+ flags.DEFINE_bool('hub_module_trainable', True,
+ 'True to make keras layers in the hub module trainable.')
+ flags.DEFINE_string(
+ 'sub_model_export_name', None,
+ 'If set, `sub_model` checkpoints are exported into '
+ 'FLAGS.model_dir/FLAGS.sub_model_export_name.')
+ flags.DEFINE_bool('explicit_allreduce', False,
+ 'True to use explicit allreduce instead of the implicit '
+ 'allreduce in optimizer.apply_gradients(). If fp16 mixed '
+ 'precision training is used, this also enables allreduce '
+ 'gradients in fp16.')
+ flags.DEFINE_integer('allreduce_bytes_per_pack', 0,
+ 'Number of bytes of a gradient pack for allreduce. '
+ 'Should be positive integer, if set to 0, all '
+ 'gradients are in one pack. Breaking gradient into '
+ 'packs could enable overlap between allreduce and '
+ 'backprop computation. This flag only takes effect '
+ 'when explicit_allreduce is set to True.')
+
+ flags_core.define_log_steps()
+
+ # Adds flags for mixed precision and multi-worker training.
+ flags_core.define_performance(
+ num_parallel_calls=False,
+ inter_op=False,
+ intra_op=False,
+ synthetic_data=False,
+ max_train_steps=False,
+ dtype=True,
+ loss_scale=True,
+ all_reduce_alg=True,
+ num_packs=False,
+ tf_gpu_thread_mode=True,
+ datasets_num_private_threads=True,
+ enable_xla=True,
+ fp16_implementation=True,
+ )
+
+ # Adds gin configuration flags.
+ hyperparams_flags.define_gin_flags()
+
+
+def dtype():
+ return flags_core.get_tf_dtype(flags.FLAGS)
+
+
+def use_float16():
+ return flags_core.get_tf_dtype(flags.FLAGS) == tf.float16
+
+
+def get_loss_scale():
+ return flags_core.get_loss_scale(flags.FLAGS, default_for_fp16='dynamic')
diff --git a/official/legacy/bert/configs.py b/official/legacy/bert/configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..bbded1932654a9884e1404ab9543b7955d494aef
--- /dev/null
+++ b/official/legacy/bert/configs.py
@@ -0,0 +1,104 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""The main BERT model and related functions."""
+
+import copy
+import json
+
+import six
+import tensorflow as tf
+
+
+class BertConfig(object):
+ """Configuration for `BertModel`."""
+
+ def __init__(self,
+ vocab_size,
+ hidden_size=768,
+ num_hidden_layers=12,
+ num_attention_heads=12,
+ intermediate_size=3072,
+ hidden_act="gelu",
+ hidden_dropout_prob=0.1,
+ attention_probs_dropout_prob=0.1,
+ max_position_embeddings=512,
+ type_vocab_size=16,
+ initializer_range=0.02,
+ embedding_size=None,
+ backward_compatible=True):
+ """Constructs BertConfig.
+
+ Args:
+ vocab_size: Vocabulary size of `inputs_ids` in `BertModel`.
+ hidden_size: Size of the encoder layers and the pooler layer.
+ num_hidden_layers: Number of hidden layers in the Transformer encoder.
+ num_attention_heads: Number of attention heads for each attention layer in
+ the Transformer encoder.
+ intermediate_size: The size of the "intermediate" (i.e., feed-forward)
+ layer in the Transformer encoder.
+ hidden_act: The non-linear activation function (function or string) in the
+ encoder and pooler.
+ hidden_dropout_prob: The dropout probability for all fully connected
+ layers in the embeddings, encoder, and pooler.
+ attention_probs_dropout_prob: The dropout ratio for the attention
+ probabilities.
+ max_position_embeddings: The maximum sequence length that this model might
+ ever be used with. Typically set this to something large just in case
+ (e.g., 512 or 1024 or 2048).
+ type_vocab_size: The vocabulary size of the `token_type_ids` passed into
+ `BertModel`.
+ initializer_range: The stdev of the truncated_normal_initializer for
+ initializing all weight matrices.
+ embedding_size: (Optional) width of the factorized word embeddings.
+ backward_compatible: Boolean, whether the variables shape are compatible
+ with checkpoints converted from TF 1.x BERT.
+ """
+ self.vocab_size = vocab_size
+ self.hidden_size = hidden_size
+ self.num_hidden_layers = num_hidden_layers
+ self.num_attention_heads = num_attention_heads
+ self.hidden_act = hidden_act
+ self.intermediate_size = intermediate_size
+ self.hidden_dropout_prob = hidden_dropout_prob
+ self.attention_probs_dropout_prob = attention_probs_dropout_prob
+ self.max_position_embeddings = max_position_embeddings
+ self.type_vocab_size = type_vocab_size
+ self.initializer_range = initializer_range
+ self.embedding_size = embedding_size
+ self.backward_compatible = backward_compatible
+
+ @classmethod
+ def from_dict(cls, json_object):
+ """Constructs a `BertConfig` from a Python dictionary of parameters."""
+ config = BertConfig(vocab_size=None)
+ for (key, value) in six.iteritems(json_object):
+ config.__dict__[key] = value
+ return config
+
+ @classmethod
+ def from_json_file(cls, json_file):
+ """Constructs a `BertConfig` from a json file of parameters."""
+ with tf.io.gfile.GFile(json_file, "r") as reader:
+ text = reader.read()
+ return cls.from_dict(json.loads(text))
+
+ def to_dict(self):
+ """Serializes this instance to a Python dictionary."""
+ output = copy.deepcopy(self.__dict__)
+ return output
+
+ def to_json_string(self):
+ """Serializes this instance to a JSON string."""
+ return json.dumps(self.to_dict(), indent=2, sort_keys=True) + "\n"
diff --git a/official/legacy/bert/export_tfhub.py b/official/legacy/bert/export_tfhub.py
new file mode 100644
index 0000000000000000000000000000000000000000..69dd49865e2490a77624374e48976b48bfabeae5
--- /dev/null
+++ b/official/legacy/bert/export_tfhub.py
@@ -0,0 +1,139 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""A script to export BERT as a TF-Hub SavedModel.
+
+This script is **DEPRECATED** for exporting BERT encoder models;
+see the error message in by main() for details.
+"""
+
+from typing import Text
+
+# Import libraries
+from absl import app
+from absl import flags
+from absl import logging
+import tensorflow as tf
+from official.legacy.bert import bert_models
+from official.legacy.bert import configs
+
+FLAGS = flags.FLAGS
+
+flags.DEFINE_string("bert_config_file", None,
+ "Bert configuration file to define core bert layers.")
+flags.DEFINE_string("model_checkpoint_path", None,
+ "File path to TF model checkpoint.")
+flags.DEFINE_string("export_path", None, "TF-Hub SavedModel destination path.")
+flags.DEFINE_string("vocab_file", None,
+ "The vocabulary file that the BERT model was trained on.")
+flags.DEFINE_bool(
+ "do_lower_case", None, "Whether to lowercase. If None, "
+ "do_lower_case will be enabled if 'uncased' appears in the "
+ "name of --vocab_file")
+flags.DEFINE_enum("model_type", "encoder", ["encoder", "squad"],
+ "What kind of BERT model to export.")
+
+
+def create_bert_model(bert_config: configs.BertConfig) -> tf.keras.Model:
+ """Creates a BERT keras core model from BERT configuration.
+
+ Args:
+ bert_config: A `BertConfig` to create the core model.
+
+ Returns:
+ A keras model.
+ """
+ # Adds input layers just as placeholders.
+ input_word_ids = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name="input_word_ids")
+ input_mask = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name="input_mask")
+ input_type_ids = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name="input_type_ids")
+ transformer_encoder = bert_models.get_transformer_encoder(
+ bert_config, sequence_length=None)
+ sequence_output, pooled_output = transformer_encoder(
+ [input_word_ids, input_mask, input_type_ids])
+ # To keep consistent with legacy hub modules, the outputs are
+ # "pooled_output" and "sequence_output".
+ return tf.keras.Model(
+ inputs=[input_word_ids, input_mask, input_type_ids],
+ outputs=[pooled_output, sequence_output]), transformer_encoder
+
+
+def export_bert_tfhub(bert_config: configs.BertConfig,
+ model_checkpoint_path: Text,
+ hub_destination: Text,
+ vocab_file: Text,
+ do_lower_case: bool = None):
+ """Restores a tf.keras.Model and saves for TF-Hub."""
+ # If do_lower_case is not explicit, default to checking whether "uncased" is
+ # in the vocab file name
+ if do_lower_case is None:
+ do_lower_case = "uncased" in vocab_file
+ logging.info("Using do_lower_case=%s based on name of vocab_file=%s",
+ do_lower_case, vocab_file)
+ core_model, encoder = create_bert_model(bert_config)
+ checkpoint = tf.train.Checkpoint(
+ model=encoder, # Legacy checkpoints.
+ encoder=encoder)
+ checkpoint.restore(model_checkpoint_path).assert_existing_objects_matched()
+ core_model.vocab_file = tf.saved_model.Asset(vocab_file)
+ core_model.do_lower_case = tf.Variable(do_lower_case, trainable=False)
+ core_model.save(hub_destination, include_optimizer=False, save_format="tf")
+
+
+def export_bert_squad_tfhub(bert_config: configs.BertConfig,
+ model_checkpoint_path: Text,
+ hub_destination: Text,
+ vocab_file: Text,
+ do_lower_case: bool = None):
+ """Restores a tf.keras.Model for BERT with SQuAD and saves for TF-Hub."""
+ # If do_lower_case is not explicit, default to checking whether "uncased" is
+ # in the vocab file name
+ if do_lower_case is None:
+ do_lower_case = "uncased" in vocab_file
+ logging.info("Using do_lower_case=%s based on name of vocab_file=%s",
+ do_lower_case, vocab_file)
+ span_labeling, _ = bert_models.squad_model(bert_config, max_seq_length=None)
+ checkpoint = tf.train.Checkpoint(model=span_labeling)
+ checkpoint.restore(model_checkpoint_path).assert_existing_objects_matched()
+ span_labeling.vocab_file = tf.saved_model.Asset(vocab_file)
+ span_labeling.do_lower_case = tf.Variable(do_lower_case, trainable=False)
+ span_labeling.save(hub_destination, include_optimizer=False, save_format="tf")
+
+
+def main(_):
+ bert_config = configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ if FLAGS.model_type == "encoder":
+ deprecation_note = (
+ "nlp/bert/export_tfhub is **DEPRECATED** for exporting BERT encoder "
+ "models. Please switch to nlp/tools/export_tfhub for exporting BERT "
+ "(and other) encoders with dict inputs/outputs conforming to "
+ "https://www.tensorflow.org/hub/common_saved_model_apis/text#transformer-encoders"
+ )
+ logging.error(deprecation_note)
+ print("\n\nNOTICE:", deprecation_note, "\n")
+ export_bert_tfhub(bert_config, FLAGS.model_checkpoint_path,
+ FLAGS.export_path, FLAGS.vocab_file, FLAGS.do_lower_case)
+ elif FLAGS.model_type == "squad":
+ export_bert_squad_tfhub(bert_config, FLAGS.model_checkpoint_path,
+ FLAGS.export_path, FLAGS.vocab_file,
+ FLAGS.do_lower_case)
+ else:
+ raise ValueError("Unsupported model_type %s." % FLAGS.model_type)
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/legacy/bert/export_tfhub_test.py b/official/legacy/bert/export_tfhub_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..68146fb58146c489abcabc62b6c15514c1cb28d7
--- /dev/null
+++ b/official/legacy/bert/export_tfhub_test.py
@@ -0,0 +1,108 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests official.nlp.bert.export_tfhub."""
+
+import os
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+import tensorflow_hub as hub
+
+from official.legacy.bert import configs
+from official.legacy.bert import export_tfhub
+
+
+class ExportTfhubTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters("model", "encoder")
+ def test_export_tfhub(self, ckpt_key_name):
+ # Exports a savedmodel for TF-Hub
+ hidden_size = 16
+ bert_config = configs.BertConfig(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ intermediate_size=32,
+ max_position_embeddings=128,
+ num_attention_heads=2,
+ num_hidden_layers=1)
+ bert_model, encoder = export_tfhub.create_bert_model(bert_config)
+ model_checkpoint_dir = os.path.join(self.get_temp_dir(), "checkpoint")
+ checkpoint = tf.train.Checkpoint(**{ckpt_key_name: encoder})
+ checkpoint.save(os.path.join(model_checkpoint_dir, "test"))
+ model_checkpoint_path = tf.train.latest_checkpoint(model_checkpoint_dir)
+
+ vocab_file = os.path.join(self.get_temp_dir(), "uncased_vocab.txt")
+ with tf.io.gfile.GFile(vocab_file, "w") as f:
+ f.write("dummy content")
+
+ hub_destination = os.path.join(self.get_temp_dir(), "hub")
+ export_tfhub.export_bert_tfhub(bert_config, model_checkpoint_path,
+ hub_destination, vocab_file)
+
+ # Restores a hub KerasLayer.
+ hub_layer = hub.KerasLayer(hub_destination, trainable=True)
+
+ if hasattr(hub_layer, "resolved_object"):
+ # Checks meta attributes.
+ self.assertTrue(hub_layer.resolved_object.do_lower_case.numpy())
+ with tf.io.gfile.GFile(
+ hub_layer.resolved_object.vocab_file.asset_path.numpy()) as f:
+ self.assertEqual("dummy content", f.read())
+ # Checks the hub KerasLayer.
+ for source_weight, hub_weight in zip(bert_model.trainable_weights,
+ hub_layer.trainable_weights):
+ self.assertAllClose(source_weight.numpy(), hub_weight.numpy())
+
+ seq_length = 10
+ dummy_ids = np.zeros((2, seq_length), dtype=np.int32)
+ hub_outputs = hub_layer([dummy_ids, dummy_ids, dummy_ids])
+ source_outputs = bert_model([dummy_ids, dummy_ids, dummy_ids])
+
+ # The outputs of hub module are "pooled_output" and "sequence_output",
+ # while the outputs of encoder is in reversed order, i.e.,
+ # "sequence_output" and "pooled_output".
+ encoder_outputs = reversed(encoder([dummy_ids, dummy_ids, dummy_ids]))
+ self.assertEqual(hub_outputs[0].shape, (2, hidden_size))
+ self.assertEqual(hub_outputs[1].shape, (2, seq_length, hidden_size))
+ for source_output, hub_output, encoder_output in zip(
+ source_outputs, hub_outputs, encoder_outputs):
+ self.assertAllClose(source_output.numpy(), hub_output.numpy())
+ self.assertAllClose(source_output.numpy(), encoder_output.numpy())
+
+ # Test that training=True makes a difference (activates dropout).
+ def _dropout_mean_stddev(training, num_runs=20):
+ input_ids = np.array([[14, 12, 42, 95, 99]], np.int32)
+ inputs = [input_ids, np.ones_like(input_ids), np.zeros_like(input_ids)]
+ outputs = np.concatenate(
+ [hub_layer(inputs, training=training)[0] for _ in range(num_runs)])
+ return np.mean(np.std(outputs, axis=0))
+
+ self.assertLess(_dropout_mean_stddev(training=False), 1e-6)
+ self.assertGreater(_dropout_mean_stddev(training=True), 1e-3)
+
+ # Test propagation of seq_length in shape inference.
+ input_word_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ input_mask = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ input_type_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ pooled_output, sequence_output = hub_layer(
+ [input_word_ids, input_mask, input_type_ids])
+ self.assertEqual(pooled_output.shape.as_list(), [None, hidden_size])
+ self.assertEqual(sequence_output.shape.as_list(),
+ [None, seq_length, hidden_size])
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/bert/input_pipeline.py b/official/legacy/bert/input_pipeline.py
similarity index 99%
rename from official/nlp/bert/input_pipeline.py
rename to official/legacy/bert/input_pipeline.py
index 0c0f7615c37142ca039ad9fc68d98776a6b6b7b8..045f16ce76b165cbc329b8a2459b5f575a52eaae 100644
--- a/official/nlp/bert/input_pipeline.py
+++ b/official/legacy/bert/input_pipeline.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/bert/model_saving_utils.py b/official/legacy/bert/model_saving_utils.py
similarity index 97%
rename from official/nlp/bert/model_saving_utils.py
rename to official/legacy/bert/model_saving_utils.py
index 1d69750878bd8a89482958874b5f059193f6d7f5..6a0d7074972ac8f5c78c1bec135b5bcd2586e317 100644
--- a/official/nlp/bert/model_saving_utils.py
+++ b/official/legacy/bert/model_saving_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,10 +15,9 @@
"""Utilities to save models."""
import os
-
+import typing
from absl import logging
import tensorflow as tf
-import typing
def export_bert_model(model_export_path: typing.Text,
diff --git a/official/nlp/bert/model_training_utils.py b/official/legacy/bert/model_training_utils.py
similarity index 99%
rename from official/nlp/bert/model_training_utils.py
rename to official/legacy/bert/model_training_utils.py
index 8cc11993bab397442c927ddcd399c2c620093205..f7c8e443be3798dd2d9670d11d0c789a91459768 100644
--- a/official/nlp/bert/model_training_utils.py
+++ b/official/legacy/bert/model_training_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/bert/model_training_utils_test.py b/official/legacy/bert/model_training_utils_test.py
similarity index 98%
rename from official/nlp/bert/model_training_utils_test.py
rename to official/legacy/bert/model_training_utils_test.py
index 544b66834002d09dfabd90169e6f53fa9f2bbaf3..298c9282c859ee288540b497ba63838ca6cf6242 100644
--- a/official/nlp/bert/model_training_utils_test.py
+++ b/official/legacy/bert/model_training_utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -25,8 +25,8 @@ import tensorflow as tf
from tensorflow.python.distribute import combinations
from tensorflow.python.distribute import strategy_combinations
-from official.nlp.bert import common_flags
-from official.nlp.bert import model_training_utils
+from official.legacy.bert import common_flags
+from official.legacy.bert import model_training_utils
common_flags.define_common_bert_flags()
diff --git a/official/legacy/bert/run_classifier.py b/official/legacy/bert/run_classifier.py
new file mode 100644
index 0000000000000000000000000000000000000000..6e9ea466bcee0ec228bf9be5b43f5393307e30c8
--- /dev/null
+++ b/official/legacy/bert/run_classifier.py
@@ -0,0 +1,515 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""BERT classification or regression finetuning runner in TF 2.x."""
+
+import functools
+import json
+import math
+import os
+
+# Import libraries
+from absl import app
+from absl import flags
+from absl import logging
+import gin
+import tensorflow as tf
+from official.common import distribute_utils
+from official.legacy.bert import bert_models
+from official.legacy.bert import common_flags
+from official.legacy.bert import configs as bert_configs
+from official.legacy.bert import input_pipeline
+from official.legacy.bert import model_saving_utils
+from official.modeling import performance
+from official.nlp import optimization
+from official.utils.misc import keras_utils
+
+flags.DEFINE_enum(
+ 'mode', 'train_and_eval', ['train_and_eval', 'export_only', 'predict'],
+ 'One of {"train_and_eval", "export_only", "predict"}. `train_and_eval`: '
+ 'trains the model and evaluates in the meantime. '
+ '`export_only`: will take the latest checkpoint inside '
+ 'model_dir and export a `SavedModel`. `predict`: takes a checkpoint and '
+ 'restores the model to output predictions on the test set.')
+flags.DEFINE_string('train_data_path', None,
+ 'Path to training data for BERT classifier.')
+flags.DEFINE_string('eval_data_path', None,
+ 'Path to evaluation data for BERT classifier.')
+flags.DEFINE_string(
+ 'input_meta_data_path', None,
+ 'Path to file that contains meta data about input '
+ 'to be used for training and evaluation.')
+flags.DEFINE_integer('train_data_size', None, 'Number of training samples '
+ 'to use. If None, uses the full train data. '
+ '(default: None).')
+flags.DEFINE_string('predict_checkpoint_path', None,
+ 'Path to the checkpoint for predictions.')
+flags.DEFINE_integer(
+ 'num_eval_per_epoch', 1,
+ 'Number of evaluations per epoch. The purpose of this flag is to provide '
+ 'more granular evaluation scores and checkpoints. For example, if original '
+ 'data has N samples and num_eval_per_epoch is n, then each epoch will be '
+ 'evaluated every N/n samples.')
+flags.DEFINE_integer('train_batch_size', 32, 'Batch size for training.')
+flags.DEFINE_integer('eval_batch_size', 32, 'Batch size for evaluation.')
+
+common_flags.define_common_bert_flags()
+
+FLAGS = flags.FLAGS
+
+LABEL_TYPES_MAP = {'int': tf.int64, 'float': tf.float32}
+
+
+def get_loss_fn(num_classes):
+ """Gets the classification loss function."""
+
+ def classification_loss_fn(labels, logits):
+ """Classification loss."""
+ labels = tf.reshape(labels, [-1])
+ log_probs = tf.nn.log_softmax(logits, axis=-1)
+ one_hot_labels = tf.one_hot(
+ tf.cast(labels, dtype=tf.int32), depth=num_classes, dtype=tf.float32)
+ per_example_loss = -tf.reduce_sum(
+ tf.cast(one_hot_labels, dtype=tf.float32) * log_probs, axis=-1)
+ return tf.reduce_mean(per_example_loss)
+
+ return classification_loss_fn
+
+
+def get_dataset_fn(input_file_pattern,
+ max_seq_length,
+ global_batch_size,
+ is_training,
+ label_type=tf.int64,
+ include_sample_weights=False,
+ num_samples=None):
+ """Gets a closure to create a dataset."""
+
+ def _dataset_fn(ctx=None):
+ """Returns tf.data.Dataset for distributed BERT pretraining."""
+ batch_size = ctx.get_per_replica_batch_size(
+ global_batch_size) if ctx else global_batch_size
+ dataset = input_pipeline.create_classifier_dataset(
+ tf.io.gfile.glob(input_file_pattern),
+ max_seq_length,
+ batch_size,
+ is_training=is_training,
+ input_pipeline_context=ctx,
+ label_type=label_type,
+ include_sample_weights=include_sample_weights,
+ num_samples=num_samples)
+ return dataset
+
+ return _dataset_fn
+
+
+def run_bert_classifier(strategy,
+ bert_config,
+ input_meta_data,
+ model_dir,
+ epochs,
+ steps_per_epoch,
+ steps_per_loop,
+ eval_steps,
+ warmup_steps,
+ initial_lr,
+ init_checkpoint,
+ train_input_fn,
+ eval_input_fn,
+ training_callbacks=True,
+ custom_callbacks=None,
+ custom_metrics=None):
+ """Run BERT classifier training using low-level API."""
+ max_seq_length = input_meta_data['max_seq_length']
+ num_classes = input_meta_data.get('num_labels', 1)
+ is_regression = num_classes == 1
+
+ def _get_classifier_model():
+ """Gets a classifier model."""
+ classifier_model, core_model = (
+ bert_models.classifier_model(
+ bert_config,
+ num_classes,
+ max_seq_length,
+ hub_module_url=FLAGS.hub_module_url,
+ hub_module_trainable=FLAGS.hub_module_trainable))
+ optimizer = optimization.create_optimizer(initial_lr,
+ steps_per_epoch * epochs,
+ warmup_steps, FLAGS.end_lr,
+ FLAGS.optimizer_type)
+ classifier_model.optimizer = performance.configure_optimizer(
+ optimizer,
+ use_float16=common_flags.use_float16())
+ return classifier_model, core_model
+
+ # tf.keras.losses objects accept optional sample_weight arguments (eg. coming
+ # from the dataset) to compute weighted loss, as used for the regression
+ # tasks. The classification tasks, using the custom get_loss_fn don't accept
+ # sample weights though.
+ loss_fn = (tf.keras.losses.MeanSquaredError() if is_regression
+ else get_loss_fn(num_classes))
+
+ # Defines evaluation metrics function, which will create metrics in the
+ # correct device and strategy scope.
+ if custom_metrics:
+ metric_fn = custom_metrics
+ elif is_regression:
+ metric_fn = functools.partial(
+ tf.keras.metrics.MeanSquaredError,
+ 'mean_squared_error',
+ dtype=tf.float32)
+ else:
+ metric_fn = functools.partial(
+ tf.keras.metrics.SparseCategoricalAccuracy,
+ 'accuracy',
+ dtype=tf.float32)
+
+ # Start training using Keras compile/fit API.
+ logging.info('Training using TF 2.x Keras compile/fit API with '
+ 'distribution strategy.')
+ return run_keras_compile_fit(
+ model_dir,
+ strategy,
+ _get_classifier_model,
+ train_input_fn,
+ eval_input_fn,
+ loss_fn,
+ metric_fn,
+ init_checkpoint,
+ epochs,
+ steps_per_epoch,
+ steps_per_loop,
+ eval_steps,
+ training_callbacks=training_callbacks,
+ custom_callbacks=custom_callbacks)
+
+
+def run_keras_compile_fit(model_dir,
+ strategy,
+ model_fn,
+ train_input_fn,
+ eval_input_fn,
+ loss_fn,
+ metric_fn,
+ init_checkpoint,
+ epochs,
+ steps_per_epoch,
+ steps_per_loop,
+ eval_steps,
+ training_callbacks=True,
+ custom_callbacks=None):
+ """Runs BERT classifier model using Keras compile/fit API."""
+
+ with strategy.scope():
+ training_dataset = train_input_fn()
+ evaluation_dataset = eval_input_fn() if eval_input_fn else None
+ bert_model, sub_model = model_fn()
+ optimizer = bert_model.optimizer
+
+ if init_checkpoint:
+ checkpoint = tf.train.Checkpoint(model=sub_model, encoder=sub_model)
+ checkpoint.read(init_checkpoint).assert_existing_objects_matched()
+
+ if not isinstance(metric_fn, (list, tuple)):
+ metric_fn = [metric_fn]
+ bert_model.compile(
+ optimizer=optimizer,
+ loss=loss_fn,
+ metrics=[fn() for fn in metric_fn],
+ steps_per_execution=steps_per_loop)
+
+ summary_dir = os.path.join(model_dir, 'summaries')
+ summary_callback = tf.keras.callbacks.TensorBoard(summary_dir)
+ checkpoint = tf.train.Checkpoint(model=bert_model, optimizer=optimizer)
+ checkpoint_manager = tf.train.CheckpointManager(
+ checkpoint,
+ directory=model_dir,
+ max_to_keep=None,
+ step_counter=optimizer.iterations,
+ checkpoint_interval=0)
+ checkpoint_callback = keras_utils.SimpleCheckpoint(checkpoint_manager)
+
+ if training_callbacks:
+ if custom_callbacks is not None:
+ custom_callbacks += [summary_callback, checkpoint_callback]
+ else:
+ custom_callbacks = [summary_callback, checkpoint_callback]
+
+ history = bert_model.fit(
+ x=training_dataset,
+ validation_data=evaluation_dataset,
+ steps_per_epoch=steps_per_epoch,
+ epochs=epochs,
+ validation_steps=eval_steps,
+ callbacks=custom_callbacks)
+ stats = {'total_training_steps': steps_per_epoch * epochs}
+ if 'loss' in history.history:
+ stats['train_loss'] = history.history['loss'][-1]
+ if 'val_accuracy' in history.history:
+ stats['eval_metrics'] = history.history['val_accuracy'][-1]
+ return bert_model, stats
+
+
+def get_predictions_and_labels(strategy,
+ trained_model,
+ eval_input_fn,
+ is_regression=False,
+ return_probs=False):
+ """Obtains predictions of trained model on evaluation data.
+
+ Note that list of labels is returned along with the predictions because the
+ order changes on distributing dataset over TPU pods.
+
+ Args:
+ strategy: Distribution strategy.
+ trained_model: Trained model with preloaded weights.
+ eval_input_fn: Input function for evaluation data.
+ is_regression: Whether it is a regression task.
+ return_probs: Whether to return probabilities of classes.
+
+ Returns:
+ predictions: List of predictions.
+ labels: List of gold labels corresponding to predictions.
+ """
+
+ @tf.function
+ def test_step(iterator):
+ """Computes predictions on distributed devices."""
+
+ def _test_step_fn(inputs):
+ """Replicated predictions."""
+ inputs, labels = inputs
+ logits = trained_model(inputs, training=False)
+ if not is_regression:
+ probabilities = tf.nn.softmax(logits)
+ return probabilities, labels
+ else:
+ return logits, labels
+
+ outputs, labels = strategy.run(_test_step_fn, args=(next(iterator),))
+ # outputs: current batch logits as a tuple of shard logits
+ outputs = tf.nest.map_structure(strategy.experimental_local_results,
+ outputs)
+ labels = tf.nest.map_structure(strategy.experimental_local_results, labels)
+ return outputs, labels
+
+ def _run_evaluation(test_iterator):
+ """Runs evaluation steps."""
+ preds, golds = list(), list()
+ try:
+ with tf.experimental.async_scope():
+ while True:
+ probabilities, labels = test_step(test_iterator)
+ for cur_probs, cur_labels in zip(probabilities, labels):
+ if return_probs:
+ preds.extend(cur_probs.numpy().tolist())
+ else:
+ preds.extend(tf.math.argmax(cur_probs, axis=1).numpy())
+ golds.extend(cur_labels.numpy().tolist())
+ except (StopIteration, tf.errors.OutOfRangeError):
+ tf.experimental.async_clear_error()
+ return preds, golds
+
+ test_iter = iter(strategy.distribute_datasets_from_function(eval_input_fn))
+ predictions, labels = _run_evaluation(test_iter)
+
+ return predictions, labels
+
+
+def export_classifier(model_export_path, input_meta_data, bert_config,
+ model_dir):
+ """Exports a trained model as a `SavedModel` for inference.
+
+ Args:
+ model_export_path: a string specifying the path to the SavedModel directory.
+ input_meta_data: dictionary containing meta data about input and model.
+ bert_config: Bert configuration file to define core bert layers.
+ model_dir: The directory where the model weights and training/evaluation
+ summaries are stored.
+
+ Raises:
+ Export path is not specified, got an empty string or None.
+ """
+ if not model_export_path:
+ raise ValueError('Export path is not specified: %s' % model_export_path)
+ if not model_dir:
+ raise ValueError('Export path is not specified: %s' % model_dir)
+
+ # Export uses float32 for now, even if training uses mixed precision.
+ tf.keras.mixed_precision.set_global_policy('float32')
+ classifier_model = bert_models.classifier_model(
+ bert_config,
+ input_meta_data.get('num_labels', 1),
+ hub_module_url=FLAGS.hub_module_url,
+ hub_module_trainable=False)[0]
+
+ model_saving_utils.export_bert_model(
+ model_export_path, model=classifier_model, checkpoint_dir=model_dir)
+
+
+def run_bert(strategy,
+ input_meta_data,
+ model_config,
+ train_input_fn=None,
+ eval_input_fn=None,
+ init_checkpoint=None,
+ custom_callbacks=None,
+ custom_metrics=None):
+ """Run BERT training."""
+ # Enables XLA in Session Config. Should not be set for TPU.
+ keras_utils.set_session_config(FLAGS.enable_xla)
+ performance.set_mixed_precision_policy(common_flags.dtype())
+
+ epochs = FLAGS.num_train_epochs * FLAGS.num_eval_per_epoch
+ train_data_size = (
+ input_meta_data['train_data_size'] // FLAGS.num_eval_per_epoch)
+ if FLAGS.train_data_size:
+ train_data_size = min(train_data_size, FLAGS.train_data_size)
+ logging.info('Updated train_data_size: %s', train_data_size)
+ steps_per_epoch = int(train_data_size / FLAGS.train_batch_size)
+ warmup_steps = int(epochs * train_data_size * 0.1 / FLAGS.train_batch_size)
+ eval_steps = int(
+ math.ceil(input_meta_data['eval_data_size'] / FLAGS.eval_batch_size))
+
+ if not strategy:
+ raise ValueError('Distribution strategy has not been specified.')
+
+ if not custom_callbacks:
+ custom_callbacks = []
+
+ if FLAGS.log_steps:
+ custom_callbacks.append(
+ keras_utils.TimeHistory(
+ batch_size=FLAGS.train_batch_size,
+ log_steps=FLAGS.log_steps,
+ logdir=FLAGS.model_dir))
+
+ trained_model, _ = run_bert_classifier(
+ strategy,
+ model_config,
+ input_meta_data,
+ FLAGS.model_dir,
+ epochs,
+ steps_per_epoch,
+ FLAGS.steps_per_loop,
+ eval_steps,
+ warmup_steps,
+ FLAGS.learning_rate,
+ init_checkpoint or FLAGS.init_checkpoint,
+ train_input_fn,
+ eval_input_fn,
+ custom_callbacks=custom_callbacks,
+ custom_metrics=custom_metrics)
+
+ if FLAGS.model_export_path:
+ model_saving_utils.export_bert_model(
+ FLAGS.model_export_path, model=trained_model)
+ return trained_model
+
+
+def custom_main(custom_callbacks=None, custom_metrics=None):
+ """Run classification or regression.
+
+ Args:
+ custom_callbacks: list of tf.keras.Callbacks passed to training loop.
+ custom_metrics: list of metrics passed to the training loop.
+ """
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_param)
+
+ with tf.io.gfile.GFile(FLAGS.input_meta_data_path, 'rb') as reader:
+ input_meta_data = json.loads(reader.read().decode('utf-8'))
+ label_type = LABEL_TYPES_MAP[input_meta_data.get('label_type', 'int')]
+ include_sample_weights = input_meta_data.get('has_sample_weights', False)
+
+ if not FLAGS.model_dir:
+ FLAGS.model_dir = '/tmp/bert20/'
+
+ bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+
+ if FLAGS.mode == 'export_only':
+ export_classifier(FLAGS.model_export_path, input_meta_data, bert_config,
+ FLAGS.model_dir)
+ return
+
+ strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=FLAGS.distribution_strategy,
+ num_gpus=FLAGS.num_gpus,
+ tpu_address=FLAGS.tpu)
+ eval_input_fn = get_dataset_fn(
+ FLAGS.eval_data_path,
+ input_meta_data['max_seq_length'],
+ FLAGS.eval_batch_size,
+ is_training=False,
+ label_type=label_type,
+ include_sample_weights=include_sample_weights)
+
+ if FLAGS.mode == 'predict':
+ num_labels = input_meta_data.get('num_labels', 1)
+ with strategy.scope():
+ classifier_model = bert_models.classifier_model(
+ bert_config, num_labels)[0]
+ checkpoint = tf.train.Checkpoint(model=classifier_model)
+ latest_checkpoint_file = (
+ FLAGS.predict_checkpoint_path or
+ tf.train.latest_checkpoint(FLAGS.model_dir))
+ assert latest_checkpoint_file
+ logging.info('Checkpoint file %s found and restoring from '
+ 'checkpoint', latest_checkpoint_file)
+ checkpoint.restore(
+ latest_checkpoint_file).assert_existing_objects_matched()
+ preds, _ = get_predictions_and_labels(
+ strategy,
+ classifier_model,
+ eval_input_fn,
+ is_regression=(num_labels == 1),
+ return_probs=True)
+ output_predict_file = os.path.join(FLAGS.model_dir, 'test_results.tsv')
+ with tf.io.gfile.GFile(output_predict_file, 'w') as writer:
+ logging.info('***** Predict results *****')
+ for probabilities in preds:
+ output_line = '\t'.join(
+ str(class_probability)
+ for class_probability in probabilities) + '\n'
+ writer.write(output_line)
+ return
+
+ if FLAGS.mode != 'train_and_eval':
+ raise ValueError('Unsupported mode is specified: %s' % FLAGS.mode)
+ train_input_fn = get_dataset_fn(
+ FLAGS.train_data_path,
+ input_meta_data['max_seq_length'],
+ FLAGS.train_batch_size,
+ is_training=True,
+ label_type=label_type,
+ include_sample_weights=include_sample_weights,
+ num_samples=FLAGS.train_data_size)
+ run_bert(
+ strategy,
+ input_meta_data,
+ bert_config,
+ train_input_fn,
+ eval_input_fn,
+ custom_callbacks=custom_callbacks,
+ custom_metrics=custom_metrics)
+
+
+def main(_):
+ custom_main(custom_callbacks=None, custom_metrics=None)
+
+
+if __name__ == '__main__':
+ flags.mark_flag_as_required('bert_config_file')
+ flags.mark_flag_as_required('input_meta_data_path')
+ flags.mark_flag_as_required('model_dir')
+ app.run(main)
diff --git a/official/nlp/bert/run_pretraining.py b/official/legacy/bert/run_pretraining.py
similarity index 96%
rename from official/nlp/bert/run_pretraining.py
rename to official/legacy/bert/run_pretraining.py
index 3390d335d2ccedfec7f19fe5da4a79bad95c52d3..6a1b1d7a59b7d51231d129244ee5809a93a5a05b 100644
--- a/official/nlp/bert/run_pretraining.py
+++ b/official/legacy/bert/run_pretraining.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,13 +21,13 @@ from absl import logging
import gin
import tensorflow as tf
from official.common import distribute_utils
+from official.legacy.bert import bert_models
+from official.legacy.bert import common_flags
+from official.legacy.bert import configs
+from official.legacy.bert import input_pipeline
+from official.legacy.bert import model_training_utils
from official.modeling import performance
from official.nlp import optimization
-from official.nlp.bert import bert_models
-from official.nlp.bert import common_flags
-from official.nlp.bert import configs
-from official.nlp.bert import input_pipeline
-from official.nlp.bert import model_training_utils
flags.DEFINE_string('input_files', None,
diff --git a/official/legacy/bert/run_squad.py b/official/legacy/bert/run_squad.py
new file mode 100644
index 0000000000000000000000000000000000000000..ee63bc96f7318941c3e4638fdf0fe076edf90f7d
--- /dev/null
+++ b/official/legacy/bert/run_squad.py
@@ -0,0 +1,148 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Run BERT on SQuAD 1.1 and SQuAD 2.0 in TF 2.x."""
+
+import json
+import os
+import time
+
+# Import libraries
+from absl import app
+from absl import flags
+from absl import logging
+import gin
+import tensorflow as tf
+from official.common import distribute_utils
+from official.legacy.bert import configs as bert_configs
+from official.legacy.bert import run_squad_helper
+from official.nlp.data import squad_lib as squad_lib_wp
+from official.nlp.tools import tokenization
+from official.utils.misc import keras_utils
+
+
+flags.DEFINE_string('vocab_file', None,
+ 'The vocabulary file that the BERT model was trained on.')
+
+# More flags can be found in run_squad_helper.
+run_squad_helper.define_common_squad_flags()
+
+FLAGS = flags.FLAGS
+
+
+def train_squad(strategy,
+ input_meta_data,
+ custom_callbacks=None,
+ run_eagerly=False,
+ init_checkpoint=None,
+ sub_model_export_name=None):
+ """Run bert squad training."""
+ bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ init_checkpoint = init_checkpoint or FLAGS.init_checkpoint
+ run_squad_helper.train_squad(strategy, input_meta_data, bert_config,
+ custom_callbacks, run_eagerly, init_checkpoint,
+ sub_model_export_name=sub_model_export_name)
+
+
+def predict_squad(strategy, input_meta_data):
+ """Makes predictions for the squad dataset."""
+ bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ tokenizer = tokenization.FullTokenizer(
+ vocab_file=FLAGS.vocab_file, do_lower_case=FLAGS.do_lower_case)
+ run_squad_helper.predict_squad(
+ strategy, input_meta_data, tokenizer, bert_config, squad_lib_wp)
+
+
+def eval_squad(strategy, input_meta_data):
+ """Evaluate on the squad dataset."""
+ bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ tokenizer = tokenization.FullTokenizer(
+ vocab_file=FLAGS.vocab_file, do_lower_case=FLAGS.do_lower_case)
+ eval_metrics = run_squad_helper.eval_squad(
+ strategy, input_meta_data, tokenizer, bert_config, squad_lib_wp)
+ return eval_metrics
+
+
+def export_squad(model_export_path, input_meta_data):
+ """Exports a trained model as a `SavedModel` for inference.
+
+ Args:
+ model_export_path: a string specifying the path to the SavedModel directory.
+ input_meta_data: dictionary containing meta data about input and model.
+
+ Raises:
+ Export path is not specified, got an empty string or None.
+ """
+ bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ run_squad_helper.export_squad(model_export_path, input_meta_data, bert_config)
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_param)
+
+ with tf.io.gfile.GFile(FLAGS.input_meta_data_path, 'rb') as reader:
+ input_meta_data = json.loads(reader.read().decode('utf-8'))
+
+ if FLAGS.mode == 'export_only':
+ export_squad(FLAGS.model_export_path, input_meta_data)
+ return
+
+ # Configures cluster spec for multi-worker distribution strategy.
+ if FLAGS.num_gpus > 0:
+ _ = distribute_utils.configure_cluster(FLAGS.worker_hosts, FLAGS.task_index)
+ strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=FLAGS.distribution_strategy,
+ num_gpus=FLAGS.num_gpus,
+ all_reduce_alg=FLAGS.all_reduce_alg,
+ tpu_address=FLAGS.tpu)
+
+ if 'train' in FLAGS.mode:
+ if FLAGS.log_steps:
+ custom_callbacks = [keras_utils.TimeHistory(
+ batch_size=FLAGS.train_batch_size,
+ log_steps=FLAGS.log_steps,
+ logdir=FLAGS.model_dir,
+ )]
+ else:
+ custom_callbacks = None
+
+ train_squad(
+ strategy,
+ input_meta_data,
+ custom_callbacks=custom_callbacks,
+ run_eagerly=FLAGS.run_eagerly,
+ sub_model_export_name=FLAGS.sub_model_export_name,
+ )
+ if 'predict' in FLAGS.mode:
+ predict_squad(strategy, input_meta_data)
+ if 'eval' in FLAGS.mode:
+ eval_metrics = eval_squad(strategy, input_meta_data)
+ f1_score = eval_metrics['final_f1']
+ logging.info('SQuAD eval F1-score: %f', f1_score)
+ summary_dir = os.path.join(FLAGS.model_dir, 'summaries', 'eval')
+ summary_writer = tf.summary.create_file_writer(summary_dir)
+ with summary_writer.as_default():
+ # TODO(lehou): write to the correct step number.
+ tf.summary.scalar('F1-score', f1_score, step=0)
+ summary_writer.flush()
+ # Also write eval_metrics to json file.
+ squad_lib_wp.write_to_json_files(
+ eval_metrics, os.path.join(summary_dir, 'eval_metrics.json'))
+ time.sleep(60)
+
+
+if __name__ == '__main__':
+ flags.mark_flag_as_required('bert_config_file')
+ flags.mark_flag_as_required('model_dir')
+ app.run(main)
diff --git a/official/nlp/bert/run_squad_helper.py b/official/legacy/bert/run_squad_helper.py
similarity index 97%
rename from official/nlp/bert/run_squad_helper.py
rename to official/legacy/bert/run_squad_helper.py
index d4cee884a0d90d2b8cb312494a95e7d3d6b2d08b..be2e97dac5f1c3968fd0a720e7526c66b1f458f7 100644
--- a/official/nlp/bert/run_squad_helper.py
+++ b/official/legacy/bert/run_squad_helper.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,16 +21,16 @@ import os
from absl import flags
from absl import logging
import tensorflow as tf
+from official.legacy.bert import bert_models
+from official.legacy.bert import common_flags
+from official.legacy.bert import input_pipeline
+from official.legacy.bert import model_saving_utils
+from official.legacy.bert import model_training_utils
from official.modeling import performance
from official.nlp import optimization
-from official.nlp.bert import bert_models
-from official.nlp.bert import common_flags
-from official.nlp.bert import input_pipeline
-from official.nlp.bert import model_saving_utils
-from official.nlp.bert import model_training_utils
-from official.nlp.bert import squad_evaluate_v1_1
-from official.nlp.bert import squad_evaluate_v2_0
from official.nlp.data import squad_lib_sp
+from official.nlp.tools import squad_evaluate_v1_1
+from official.nlp.tools import squad_evaluate_v2_0
from official.utils.misc import keras_utils
diff --git a/official/nlp/bert/serving.py b/official/legacy/bert/serving.py
similarity index 97%
rename from official/nlp/bert/serving.py
rename to official/legacy/bert/serving.py
index 7e27869c74b30ae5ce1a8a9b75760d0d8013640a..1666435aa8f2d6bb575814bf2ba612a4ed371880 100644
--- a/official/nlp/bert/serving.py
+++ b/official/legacy/bert/serving.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,8 +18,8 @@ from absl import app
from absl import flags
import tensorflow as tf
-from official.nlp.bert import bert_models
-from official.nlp.bert import configs
+from official.legacy.bert import bert_models
+from official.legacy.bert import configs
flags.DEFINE_integer(
"sequence_length", None, "Sequence length to parse the tf.Example. If "
diff --git a/official/legacy/detection/__init__.py b/official/legacy/detection/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/__init__.py
+++ b/official/legacy/detection/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/__init__.py b/official/legacy/detection/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/configs/__init__.py
+++ b/official/legacy/detection/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/base_config.py b/official/legacy/detection/configs/base_config.py
index 32b8bcc1be551c249cafeab6706ae3bc58cc2d08..e274d91adc01d0f96200bdbd3fe1b1853adb525a 100644
--- a/official/legacy/detection/configs/base_config.py
+++ b/official/legacy/detection/configs/base_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/factory.py b/official/legacy/detection/configs/factory.py
index 3de8fcd2b0df72b2a15d80f8e3166784de26f855..d14f4b4e766a033da6c79fd5c83c9b375e58f03e 100644
--- a/official/legacy/detection/configs/factory.py
+++ b/official/legacy/detection/configs/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/maskrcnn_config.py b/official/legacy/detection/configs/maskrcnn_config.py
index 71af35021258b1a89b9937305e6a98c7f6d017dc..275cbf5e608434dc014f7ee30d589079568d0259 100644
--- a/official/legacy/detection/configs/maskrcnn_config.py
+++ b/official/legacy/detection/configs/maskrcnn_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/olnmask_config.py b/official/legacy/detection/configs/olnmask_config.py
index a12ce5a7f5aa4cdd488c5a70dac8bde5fb314d3f..74e786c1fef4a56639819c89f4282cc3044ee643 100644
--- a/official/legacy/detection/configs/olnmask_config.py
+++ b/official/legacy/detection/configs/olnmask_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/retinanet_config.py b/official/legacy/detection/configs/retinanet_config.py
index 73c288a6460b62f9eacd79d617fdda46ab754b7e..d3bd1ef19eb017be70c370bbc9fe1b2bee3ca122 100644
--- a/official/legacy/detection/configs/retinanet_config.py
+++ b/official/legacy/detection/configs/retinanet_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/configs/shapemask_config.py b/official/legacy/detection/configs/shapemask_config.py
index 30bc9ae92c4bf07906af1e1c5ad9006bd5dc921c..321a364f624e5dc98a257b494f18ec7dd33dbd39 100644
--- a/official/legacy/detection/configs/shapemask_config.py
+++ b/official/legacy/detection/configs/shapemask_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/__init__.py b/official/legacy/detection/dataloader/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/dataloader/__init__.py
+++ b/official/legacy/detection/dataloader/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/anchor.py b/official/legacy/detection/dataloader/anchor.py
index 4853cb1b7a0e19741f5d00904bc075184f048fc1..a5d90ed6c1d3d5d7910f1ac8ba8690f3113890e3 100644
--- a/official/legacy/detection/dataloader/anchor.py
+++ b/official/legacy/detection/dataloader/anchor.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,7 +22,7 @@ import collections
import tensorflow as tf
from official.legacy.detection.utils import box_utils
-from official.vision.beta.ops import iou_similarity
+from official.vision.ops import iou_similarity
from official.vision.utils.object_detection import argmax_matcher
from official.vision.utils.object_detection import balanced_positive_negative_sampler
from official.vision.utils.object_detection import box_list
diff --git a/official/legacy/detection/dataloader/factory.py b/official/legacy/detection/dataloader/factory.py
index 4623fd1ed401291929382c8a370599ac3477c667..3bc8985eb432971020891426c11795a309269770 100644
--- a/official/legacy/detection/dataloader/factory.py
+++ b/official/legacy/detection/dataloader/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/input_reader.py b/official/legacy/detection/dataloader/input_reader.py
index 601db93d84e9166d6c87cd42553ce76242af1b9f..4ffa729eda15c9a4ff983b04d4b4b157907c824c 100644
--- a/official/legacy/detection/dataloader/input_reader.py
+++ b/official/legacy/detection/dataloader/input_reader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/maskrcnn_parser.py b/official/legacy/detection/dataloader/maskrcnn_parser.py
index c7c156d43e36d170f9c16221a441ea15d0f5ed45..f69fa3260f05bba8853f9a3bca731c0edfd9f4d2 100644
--- a/official/legacy/detection/dataloader/maskrcnn_parser.py
+++ b/official/legacy/detection/dataloader/maskrcnn_parser.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/mode_keys.py b/official/legacy/detection/dataloader/mode_keys.py
index d6fdd9008bd4491ebec171d25c14d517ca3647c6..93eb7d3ad9e106d7f90a735a939d7626ebf594eb 100644
--- a/official/legacy/detection/dataloader/mode_keys.py
+++ b/official/legacy/detection/dataloader/mode_keys.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/olnmask_parser.py b/official/legacy/detection/dataloader/olnmask_parser.py
index 6749095319d6a0fcdedcfd39912f069c32b9b25a..b569d66be72d6004bdfef43a92c7b98bc3fe6027 100644
--- a/official/legacy/detection/dataloader/olnmask_parser.py
+++ b/official/legacy/detection/dataloader/olnmask_parser.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/retinanet_parser.py b/official/legacy/detection/dataloader/retinanet_parser.py
index 5de59ca2c1891509c977ec7dbfdefa9d853ab3d1..55058af79ddbdd7aa5d771212a53ce802e46aeeb 100644
--- a/official/legacy/detection/dataloader/retinanet_parser.py
+++ b/official/legacy/detection/dataloader/retinanet_parser.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/shapemask_parser.py b/official/legacy/detection/dataloader/shapemask_parser.py
index f8a99d018e6f551b2ad482f5454a1ac0c0233c5c..5feeb21d430bd40f20b64872baef124e7ed2ecbd 100644
--- a/official/legacy/detection/dataloader/shapemask_parser.py
+++ b/official/legacy/detection/dataloader/shapemask_parser.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/dataloader/tf_example_decoder.py b/official/legacy/detection/dataloader/tf_example_decoder.py
index e6472a36b9a31a8e8a98cecf10a6abf8ccb03985..9e65509ce156b23f28b7fdfb0fdf1b49993137ce 100644
--- a/official/legacy/detection/dataloader/tf_example_decoder.py
+++ b/official/legacy/detection/dataloader/tf_example_decoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/evaluation/__init__.py b/official/legacy/detection/evaluation/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/evaluation/__init__.py
+++ b/official/legacy/detection/evaluation/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/evaluation/coco_evaluator.py b/official/legacy/detection/evaluation/coco_evaluator.py
index 4469af50cb943b4a8640f1d3ba2a1753e8c565d0..222763b5e4090e66dce19bfaed735a92a3566d24 100644
--- a/official/legacy/detection/evaluation/coco_evaluator.py
+++ b/official/legacy/detection/evaluation/coco_evaluator.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/evaluation/coco_utils.py b/official/legacy/detection/evaluation/coco_utils.py
index 03e90c05582b4f4dfda362d14cd1cfc23626d23f..6c3692d011a83c16fb060f3a712f270a9c95f011 100644
--- a/official/legacy/detection/evaluation/coco_utils.py
+++ b/official/legacy/detection/evaluation/coco_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/evaluation/factory.py b/official/legacy/detection/evaluation/factory.py
index 93f18f1e42511cd02963ea27b9f59aa03f026316..b47de01f9e155b995c53c2b63ecb5fef4d01949b 100644
--- a/official/legacy/detection/evaluation/factory.py
+++ b/official/legacy/detection/evaluation/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/executor/__init__.py b/official/legacy/detection/executor/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/executor/__init__.py
+++ b/official/legacy/detection/executor/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/executor/detection_executor.py b/official/legacy/detection/executor/detection_executor.py
index 19dae201fad5d7c4b73ba518959aec765cd3d913..396de52cd6246adea9280b1b6728ec4c5eba5b4f 100644
--- a/official/legacy/detection/executor/detection_executor.py
+++ b/official/legacy/detection/executor/detection_executor.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/executor/distributed_executor.py b/official/legacy/detection/executor/distributed_executor.py
index 4079488107fdf85f441be2458e56b2d140a0d388..529e8d813bce0fbf482b719b95be4f064965df27 100644
--- a/official/legacy/detection/executor/distributed_executor.py
+++ b/official/legacy/detection/executor/distributed_executor.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -683,8 +683,14 @@ class DistributedExecutor(object):
if not checkpoint_path:
raise ValueError('checkpoint path is empty')
reader = tf.compat.v1.train.NewCheckpointReader(checkpoint_path)
- current_step = reader.get_tensor(
- 'optimizer/iter/.ATTRIBUTES/VARIABLE_VALUE')
+ if reader.has_tensor('optimizer/iter/.ATTRIBUTES/VARIABLE_VALUE'):
+ # Legacy keras optimizer iteration.
+ current_step = reader.get_tensor(
+ 'optimizer/iter/.ATTRIBUTES/VARIABLE_VALUE')
+ else:
+ # New keras optimizer iteration.
+ current_step = reader.get_tensor(
+ 'optimizer/_iterations/.ATTRIBUTES/VARIABLE_VALUE')
logging.info('Checkpoint file %s found and restoring from '
'checkpoint', checkpoint_path)
status = checkpoint.restore(checkpoint_path)
diff --git a/official/legacy/detection/main.py b/official/legacy/detection/main.py
index 224f5440a65f89b05f30d359d6eb610bca4adde0..9071e7c990cbb15c89d12ef84109fb6cfd1694a9 100644
--- a/official/legacy/detection/main.py
+++ b/official/legacy/detection/main.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/__init__.py b/official/legacy/detection/modeling/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/modeling/__init__.py
+++ b/official/legacy/detection/modeling/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/__init__.py b/official/legacy/detection/modeling/architecture/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/modeling/architecture/__init__.py
+++ b/official/legacy/detection/modeling/architecture/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/factory.py b/official/legacy/detection/modeling/architecture/factory.py
index 94d48c694e4bd14892af0d7a288f22ae849f225a..4b755200e1109f9efbfa9e0d03a9d69f156300ff 100644
--- a/official/legacy/detection/modeling/architecture/factory.py
+++ b/official/legacy/detection/modeling/architecture/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/fpn.py b/official/legacy/detection/modeling/architecture/fpn.py
index 725e78ea7006da81f3b1b70070ce90c2249fbfb1..6b9edf6dfe3a81eee493f67bd84ec849d3782de2 100644
--- a/official/legacy/detection/modeling/architecture/fpn.py
+++ b/official/legacy/detection/modeling/architecture/fpn.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/heads.py b/official/legacy/detection/modeling/architecture/heads.py
index d30c7ea8cbefac9720c9be5e2d83ef59bf4aaf98..430cb01d79df90d0e9b2d8844d6fa33a1d8bdfcd 100644
--- a/official/legacy/detection/modeling/architecture/heads.py
+++ b/official/legacy/detection/modeling/architecture/heads.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/identity.py b/official/legacy/detection/modeling/architecture/identity.py
index 778297f8919f8a90875c69ce1f11ef5dfd9fc95f..7d3280dbd5e4b01b01bd27fca3cf72cbe6521053 100644
--- a/official/legacy/detection/modeling/architecture/identity.py
+++ b/official/legacy/detection/modeling/architecture/identity.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/nn_blocks.py b/official/legacy/detection/modeling/architecture/nn_blocks.py
index 69a0d28261997eddbd9826d7681edbe95940e9c9..ab61d3239a95cc37dd953edc0b97014539dfc975 100644
--- a/official/legacy/detection/modeling/architecture/nn_blocks.py
+++ b/official/legacy/detection/modeling/architecture/nn_blocks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/nn_ops.py b/official/legacy/detection/modeling/architecture/nn_ops.py
index e4c389c671b5c23e48ee8061b83f63c31a6f643e..70f47c9af0bf2e9b9939a12f2c6bcd474bd945ff 100644
--- a/official/legacy/detection/modeling/architecture/nn_ops.py
+++ b/official/legacy/detection/modeling/architecture/nn_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/resnet.py b/official/legacy/detection/modeling/architecture/resnet.py
index 370e86b50e3b84f57a84f6de44cba89a41357d6a..0a8182bfe4a62e182526fbbd4d3b778b4e29478a 100644
--- a/official/legacy/detection/modeling/architecture/resnet.py
+++ b/official/legacy/detection/modeling/architecture/resnet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/architecture/spinenet.py b/official/legacy/detection/modeling/architecture/spinenet.py
index 7975a0aeb36a96e2c2081104292dbd3036cffd2e..ea86a70f28dc33f3c714636b8889e16cb3528ce7 100644
--- a/official/legacy/detection/modeling/architecture/spinenet.py
+++ b/official/legacy/detection/modeling/architecture/spinenet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
# ==============================================================================
"""Implementation of SpineNet model.
diff --git a/official/legacy/detection/modeling/base_model.py b/official/legacy/detection/modeling/base_model.py
index e7f0c54853a2b9ba3294f56abcdd4be811d32d6d..aa84f4682634f7bf637116a15224293c029fec60 100644
--- a/official/legacy/detection/modeling/base_model.py
+++ b/official/legacy/detection/modeling/base_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/checkpoint_utils.py b/official/legacy/detection/modeling/checkpoint_utils.py
index 237cdf8f2dab8fa57c4b80dca6d04f46dbeef051..1765a059c30d3a2095b0f1f2809372e8ed0153bb 100644
--- a/official/legacy/detection/modeling/checkpoint_utils.py
+++ b/official/legacy/detection/modeling/checkpoint_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/factory.py b/official/legacy/detection/modeling/factory.py
index 028bdde4b0685457333af3e10c210dd8e1c6008f..3d852b8d040d9694f2a47e436deb53c288622de9 100644
--- a/official/legacy/detection/modeling/factory.py
+++ b/official/legacy/detection/modeling/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/learning_rates.py b/official/legacy/detection/modeling/learning_rates.py
index 85a06f5a02b8897112b9954c314ec9929b422fda..bbd34873981ea9f3a5981cbe8a6a7285ca561bab 100644
--- a/official/legacy/detection/modeling/learning_rates.py
+++ b/official/legacy/detection/modeling/learning_rates.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -61,7 +61,7 @@ class CosineLearningRateWithLinearWarmup(
"""Class to generate learning rate tensor."""
def __init__(self, total_steps, params):
- """Creates the consine learning rate tensor with linear warmup."""
+ """Creates the cosine learning rate tensor with linear warmup."""
super(CosineLearningRateWithLinearWarmup, self).__init__()
self._total_steps = total_steps
assert isinstance(params, (dict, params_dict.ParamsDict))
diff --git a/official/legacy/detection/modeling/losses.py b/official/legacy/detection/modeling/losses.py
index 02e2632ae60c9da49f58c1239964d2f1104b52f8..f3423993390ea7cc3173b8d2f71ff1f9588556c5 100644
--- a/official/legacy/detection/modeling/losses.py
+++ b/official/legacy/detection/modeling/losses.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/maskrcnn_model.py b/official/legacy/detection/modeling/maskrcnn_model.py
index a381bd0ce2ac44381f47b466015f5d891c9077b0..576457b612228683ecbdcdbabbb6a131a77432be 100644
--- a/official/legacy/detection/modeling/maskrcnn_model.py
+++ b/official/legacy/detection/modeling/maskrcnn_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/olnmask_model.py b/official/legacy/detection/modeling/olnmask_model.py
index 8e8b080da2752624d60b13fca41846d1b843870f..255ff86e4f6c8921bcf6513d6000a3823e39a36b 100644
--- a/official/legacy/detection/modeling/olnmask_model.py
+++ b/official/legacy/detection/modeling/olnmask_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/optimizers.py b/official/legacy/detection/modeling/optimizers.py
index ce434495571a219deea79296fecd5cf1a60c8a93..d8ff456aa7767d3bc9bf64ff89c82739ceb0d5fc 100644
--- a/official/legacy/detection/modeling/optimizers.py
+++ b/official/legacy/detection/modeling/optimizers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/retinanet_model.py b/official/legacy/detection/modeling/retinanet_model.py
index 7433179f7303239c51fd9a43715437682d630603..7e87717cc9e934a0413301939a5cf92e932bb9e7 100644
--- a/official/legacy/detection/modeling/retinanet_model.py
+++ b/official/legacy/detection/modeling/retinanet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/modeling/shapemask_model.py b/official/legacy/detection/modeling/shapemask_model.py
index b8b7f37422cb7618cc199ec1e90ecde82f9a9724..6d01e122b0b1f0d9251c040cd8ca0c505681b838 100644
--- a/official/legacy/detection/modeling/shapemask_model.py
+++ b/official/legacy/detection/modeling/shapemask_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/__init__.py b/official/legacy/detection/ops/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/ops/__init__.py
+++ b/official/legacy/detection/ops/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/nms.py b/official/legacy/detection/ops/nms.py
index 0beb7e3850612e261e41a0b2634224b3aab93e88..24fdcef87bcc03d0e24950b56422c70f27bffd1b 100644
--- a/official/legacy/detection/ops/nms.py
+++ b/official/legacy/detection/ops/nms.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/postprocess_ops.py b/official/legacy/detection/ops/postprocess_ops.py
index bd11fe964f30242952d5a8cd2536cff721732e3c..8b4a8b6d9f05298937eec6c6a8e9c6493b7c908a 100644
--- a/official/legacy/detection/ops/postprocess_ops.py
+++ b/official/legacy/detection/ops/postprocess_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/roi_ops.py b/official/legacy/detection/ops/roi_ops.py
index 6abdeadc6b2135efecc8b0fa5f54a182e0a93485..7aeb1a91b1f51a15bd88ca0c153f748edcdf41de 100644
--- a/official/legacy/detection/ops/roi_ops.py
+++ b/official/legacy/detection/ops/roi_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/spatial_transform_ops.py b/official/legacy/detection/ops/spatial_transform_ops.py
index 4b7d7ecde48ca8dd1eeb4f7356a1642583b1754d..db9cf98fb80f711aee86a74c548f49a985b5de3e 100644
--- a/official/legacy/detection/ops/spatial_transform_ops.py
+++ b/official/legacy/detection/ops/spatial_transform_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/ops/target_ops.py b/official/legacy/detection/ops/target_ops.py
index db1ea313a9e981ecd0f709b2272eff520255bf3b..7b8e208b99b245a5389c2a197b1e2b6be780925e 100644
--- a/official/legacy/detection/ops/target_ops.py
+++ b/official/legacy/detection/ops/target_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/__init__.py b/official/legacy/detection/utils/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/detection/utils/__init__.py
+++ b/official/legacy/detection/utils/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/box_utils.py b/official/legacy/detection/utils/box_utils.py
index bc95fa8e3602d49f922fb135531e95078942b7c1..f52b4d52c1280e2d1a028cf29552225189e0fb63 100644
--- a/official/legacy/detection/utils/box_utils.py
+++ b/official/legacy/detection/utils/box_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/class_utils.py b/official/legacy/detection/utils/class_utils.py
index cbf806f11070736c17de79dd63240e9a626808d9..fe5525c692657270aacc70d4ec27ba262b95102c 100644
--- a/official/legacy/detection/utils/class_utils.py
+++ b/official/legacy/detection/utils/class_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/dataloader_utils.py b/official/legacy/detection/utils/dataloader_utils.py
index 8cdbc54a05c061cbe1cf719594007875deac64a8..a3a34eb658b242fb2c7d81c1d93aa92ccb19d454 100644
--- a/official/legacy/detection/utils/dataloader_utils.py
+++ b/official/legacy/detection/utils/dataloader_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/input_utils.py b/official/legacy/detection/utils/input_utils.py
index e194d3ca728f418e181f45a5add6fd8b8db21967..12b7c0be168baa047d2084386aaaeab9556eba17 100644
--- a/official/legacy/detection/utils/input_utils.py
+++ b/official/legacy/detection/utils/input_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/detection/utils/mask_utils.py b/official/legacy/detection/utils/mask_utils.py
index 926c829b81b35b11ca53a5a3d351d0ebca36205e..deb86a51605f73af4ea9b71d0bd1c3a4d7095f87 100644
--- a/official/legacy/detection/utils/mask_utils.py
+++ b/official/legacy/detection/utils/mask_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/README.md b/official/legacy/image_classification/README.md
index bc64b791db828a3ce4ccb2539f993e397641717f..6d9231b4848f55a69395d047f3ec33674ac59599 100644
--- a/official/legacy/image_classification/README.md
+++ b/official/legacy/image_classification/README.md
@@ -1,9 +1,9 @@
# Image Classification
-**Warning:** the features in the `image_classification/` folder have been fully
-integrated into vision/beta. Please use the [new code base](../../vision/beta/README.md).
+**Warning:** the features in the `image_classification/` directory have been
+fully integrated into the [new code base](https://github.com/tensorflow/models/tree/benchmark/official/vision/modeling/backbones).
-This folder contains TF 2.0 model examples for image classification:
+This folder contains TF 2 model examples for image classification:
* [MNIST](#mnist)
* [Classifier Trainer](#classifier-trainer), a framework that uses the Keras
@@ -17,8 +17,7 @@ For more information about other types of models, please refer to this
## Before you begin
Please make sure that you have the latest version of TensorFlow
-installed and
-[add the models folder to your Python path](/official/#running-the-models).
+installed and add the models folder to your Python path.
### ImageNet preparation
@@ -70,6 +69,7 @@ available GPUs at each host.
To download the data and run the MNIST sample model locally for the first time,
run one of the following command:
+
```bash
python3 mnist_main.py \
--model_dir=$MODEL_DIR \
@@ -79,9 +79,11 @@ python3 mnist_main.py \
--num_gpus=$NUM_GPUS \
--download
```
+
To train the model on a Cloud TPU, run the following command:
+
```bash
python3 mnist_main.py \
--tpu=$TPU_NAME \
@@ -91,10 +93,10 @@ python3 mnist_main.py \
--distribution_strategy=tpu \
--download
```
+
Note: the `--download` flag is only required the first time you run the model.
-
## Classifier Trainer
The classifier trainer is a unified framework for running image classification
models using Keras's compile/fit methods. Experiments should be provided in the
@@ -111,6 +113,8 @@ be 64 * 8 = 512, and for a v3-32, the global batch size is 64 * 32 = 2048.
### ResNet50
#### On GPU:
+
+
```bash
python3 classifier_trainer.py \
--mode=train_and_eval \
@@ -121,12 +125,15 @@ python3 classifier_trainer.py \
--config_file=configs/examples/resnet/imagenet/gpu.yaml \
--params_override='runtime.num_gpus=$NUM_GPUS'
```
+
To train on multiple hosts, each with GPUs attached using
[MultiWorkerMirroredStrategy](https://www.tensorflow.org/api_docs/python/tf/distribute/experimental/MultiWorkerMirroredStrategy)
please update `runtime` section in gpu.yaml
(or override using `--params_override`) with:
+
+
```YAML
# gpu.yaml
runtime:
@@ -135,12 +142,16 @@ runtime:
num_gpus: $NUM_GPUS
task_index: 0
```
+
+
By having `task_index: 0` on the first host and `task_index: 1` on the second
and so on. `$HOST1` and `$HOST2` are the IP addresses of the hosts, and `port`
can be chosen any free port on the hosts. Only the first host will write
TensorBoard Summaries and save checkpoints.
#### On TPU:
+
+
```bash
python3 classifier_trainer.py \
--mode=train_and_eval \
@@ -152,9 +163,31 @@ python3 classifier_trainer.py \
--config_file=configs/examples/resnet/imagenet/tpu.yaml
```
+
+
+### VGG-16
+
+#### On GPU:
+
+
+```bash
+python3 classifier_trainer.py \
+ --mode=train_and_eval \
+ --model_type=vgg \
+ --dataset=imagenet \
+ --model_dir=$MODEL_DIR \
+ --data_dir=$DATA_DIR \
+ --config_file=configs/examples/vgg/imagenet/gpu.yaml \
+ --params_override='runtime.num_gpus=$NUM_GPUS'
+```
+
+
+
### EfficientNet
**Note: EfficientNet development is a work in progress.**
#### On GPU:
+
+
```bash
python3 classifier_trainer.py \
--mode=train_and_eval \
@@ -166,8 +199,11 @@ python3 classifier_trainer.py \
--params_override='runtime.num_gpus=$NUM_GPUS'
```
+
#### On TPU:
+
+
```bash
python3 classifier_trainer.py \
--mode=train_and_eval \
@@ -178,6 +214,7 @@ python3 classifier_trainer.py \
--data_dir=$DATA_DIR \
--config_file=configs/examples/efficientnet/imagenet/efficientnet-b0-tpu.yaml
```
+
Note that the number of GPU devices can be overridden in the command line using
`--params_overrides`. The TPU does not need this override as the device is fixed
diff --git a/official/legacy/image_classification/__init__.py b/official/legacy/image_classification/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/image_classification/__init__.py
+++ b/official/legacy/image_classification/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/augment.py b/official/legacy/image_classification/augment.py
index f322d31dac6ecc1e282566134720d42261a9b7fc..add7ed631ca2b6e856e726c4e2254826362769b1 100644
--- a/official/legacy/image_classification/augment.py
+++ b/official/legacy/image_classification/augment.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/augment_test.py b/official/legacy/image_classification/augment_test.py
index e5498a9c4778173a62bc9596187ff4623ed03753..139e10195b497d5123d9a492cb15ad4c5c98af03 100644
--- a/official/legacy/image_classification/augment_test.py
+++ b/official/legacy/image_classification/augment_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/callbacks.py b/official/legacy/image_classification/callbacks.py
index a4934ed88f7db280d1ffd9ad57346f68a5395d5e..061826dbd05bb3d08ae00b6d257bc96f6060badc 100644
--- a/official/legacy/image_classification/callbacks.py
+++ b/official/legacy/image_classification/callbacks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Common modules for callbacks."""
from __future__ import absolute_import
from __future__ import division
diff --git a/official/legacy/image_classification/classifier_trainer.py b/official/legacy/image_classification/classifier_trainer.py
index 5dc1b78e3acdc7d9ae10441411d21018a178cdad..66577f6079e00b8dfee76d686ad96a5283096f9c 100644
--- a/official/legacy/image_classification/classifier_trainer.py
+++ b/official/legacy/image_classification/classifier_trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Runs an Image Classification model."""
import os
@@ -32,6 +31,7 @@ from official.legacy.image_classification.configs import configs
from official.legacy.image_classification.efficientnet import efficientnet_model
from official.legacy.image_classification.resnet import common
from official.legacy.image_classification.resnet import resnet_model
+from official.legacy.image_classification.vgg import vgg_model
from official.modeling import hyperparams
from official.modeling import performance
from official.utils import hyperparams_flags
@@ -43,6 +43,7 @@ def get_models() -> Mapping[str, tf.keras.Model]:
return {
'efficientnet': efficientnet_model.EfficientNet.from_name,
'resnet': resnet_model.resnet50,
+ 'vgg': vgg_model.vgg16,
}
diff --git a/official/legacy/image_classification/classifier_trainer_test.py b/official/legacy/image_classification/classifier_trainer_test.py
index fd304cdbae84db73d177729fbbd6338d9ecf4baf..2be5d85727f0847a69b3e43477be5dd2bd42cd29 100644
--- a/official/legacy/image_classification/classifier_trainer_test.py
+++ b/official/legacy/image_classification/classifier_trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,13 +12,8 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Unit tests for the classifier trainer models."""
-from __future__ import absolute_import
-from __future__ import division
-from __future__ import print_function
-
import functools
import json
@@ -53,6 +48,7 @@ def distribution_strategy_combinations() -> Iterable[Tuple[Any, ...]]:
model=[
'efficientnet',
'resnet',
+ 'vgg',
],
dataset=[
'imagenet',
@@ -149,6 +145,7 @@ class ClassifierTest(tf.test.TestCase, parameterized.TestCase):
model=[
'efficientnet',
'resnet',
+ 'vgg',
],
dataset='imagenet',
dtype='float16',
@@ -193,6 +190,7 @@ class ClassifierTest(tf.test.TestCase, parameterized.TestCase):
model=[
'efficientnet',
'resnet',
+ 'vgg',
],
dataset='imagenet',
dtype='bfloat16',
diff --git a/official/legacy/image_classification/classifier_trainer_util_test.py b/official/legacy/image_classification/classifier_trainer_util_test.py
index 634548159aaa569850ba2eb2b2a2e234e5ec0125..19a05fa678bc47ac838e08b05042c1ce41af526f 100644
--- a/official/legacy/image_classification/classifier_trainer_util_test.py
+++ b/official/legacy/image_classification/classifier_trainer_util_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Unit tests for the classifier trainer models."""
from __future__ import absolute_import
diff --git a/official/legacy/image_classification/configs/__init__.py b/official/legacy/image_classification/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/image_classification/configs/__init__.py
+++ b/official/legacy/image_classification/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/configs/base_configs.py b/official/legacy/image_classification/configs/base_configs.py
index 22c9e0b3f181d3efb4ced2b76ad35ed453533ef2..7fd230b418efb4cde7551a3bfa48dc4e6c5e241e 100644
--- a/official/legacy/image_classification/configs/base_configs.py
+++ b/official/legacy/image_classification/configs/base_configs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Definitions for high level configuration groups.."""
import dataclasses
diff --git a/official/legacy/image_classification/configs/configs.py b/official/legacy/image_classification/configs/configs.py
index a11f7f23f799d5051309756455e6a8f0da6826eb..87fb5df5b6f7780ba31890c513a1ea92e05de03c 100644
--- a/official/legacy/image_classification/configs/configs.py
+++ b/official/legacy/image_classification/configs/configs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,11 +12,7 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Configuration utils for image classification experiments."""
-from __future__ import absolute_import
-from __future__ import division
-from __future__ import print_function
import dataclasses
@@ -24,6 +20,7 @@ from official.legacy.image_classification import dataset_factory
from official.legacy.image_classification.configs import base_configs
from official.legacy.image_classification.efficientnet import efficientnet_config
from official.legacy.image_classification.resnet import resnet_config
+from official.legacy.image_classification.vgg import vgg_config
@dataclasses.dataclass
@@ -92,12 +89,38 @@ class ResNetImagenetConfig(base_configs.ExperimentConfig):
model: base_configs.ModelConfig = resnet_config.ResNetModelConfig()
+@dataclasses.dataclass
+class VGGImagenetConfig(base_configs.ExperimentConfig):
+ """Base configuration to train vgg-16 on ImageNet."""
+ export: base_configs.ExportConfig = base_configs.ExportConfig()
+ runtime: base_configs.RuntimeConfig = base_configs.RuntimeConfig()
+ train_dataset: dataset_factory.DatasetConfig = dataset_factory.ImageNetConfig(
+ split='train', one_hot=False, mean_subtract=True, standardize=True)
+ validation_dataset: dataset_factory.DatasetConfig = dataset_factory.ImageNetConfig(
+ split='validation', one_hot=False, mean_subtract=True, standardize=True)
+ train: base_configs.TrainConfig = base_configs.TrainConfig(
+ resume_checkpoint=True,
+ epochs=90,
+ steps=None,
+ callbacks=base_configs.CallbacksConfig(
+ enable_checkpoint_and_export=True, enable_tensorboard=True),
+ metrics=['accuracy', 'top_5'],
+ time_history=base_configs.TimeHistoryConfig(log_steps=100),
+ tensorboard=base_configs.TensorBoardConfig(
+ track_lr=True, write_model_weights=False),
+ set_epoch_loop=False)
+ evaluation: base_configs.EvalConfig = base_configs.EvalConfig(
+ epochs_between_evals=1, steps=None)
+ model: base_configs.ModelConfig = vgg_config.VGGModelConfig()
+
+
def get_config(model: str, dataset: str) -> base_configs.ExperimentConfig:
"""Given model and dataset names, return the ExperimentConfig."""
dataset_model_config_map = {
'imagenet': {
'efficientnet': EfficientNetImageNetConfig(),
'resnet': ResNetImagenetConfig(),
+ 'vgg': VGGImagenetConfig(),
}
}
try:
diff --git a/official/legacy/image_classification/configs/examples/vgg16/imagenet/gpu.yaml b/official/legacy/image_classification/configs/examples/vgg16/imagenet/gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..33c5a4e36a71fd975ddb57e298fa87d65c66555a
--- /dev/null
+++ b/official/legacy/image_classification/configs/examples/vgg16/imagenet/gpu.yaml
@@ -0,0 +1,46 @@
+# Training configuration for VGG-16 trained on ImageNet on GPUs.
+# Reaches > 72.8% within 90 epochs.
+# Note: This configuration uses a scaled per-replica batch size based on the number of devices.
+runtime:
+ distribution_strategy: 'mirrored'
+ num_gpus: 1
+ batchnorm_spatial_persistent: true
+train_dataset:
+ name: 'imagenet2012'
+ data_dir: null
+ builder: 'records'
+ split: 'train'
+ image_size: 224
+ num_classes: 1000
+ num_examples: 1281167
+ batch_size: 128
+ use_per_replica_batch_size: true
+ dtype: 'float32'
+ mean_subtract: true
+ standardize: true
+validation_dataset:
+ name: 'imagenet2012'
+ data_dir: null
+ builder: 'records'
+ split: 'validation'
+ image_size: 224
+ num_classes: 1000
+ num_examples: 50000
+ batch_size: 128
+ use_per_replica_batch_size: true
+ dtype: 'float32'
+ mean_subtract: true
+ standardize: true
+model:
+ name: 'vgg'
+ optimizer:
+ name: 'momentum'
+ momentum: 0.9
+ epsilon: 0.001
+ loss:
+ label_smoothing: 0.0
+train:
+ resume_checkpoint: true
+ epochs: 90
+evaluation:
+ epochs_between_evals: 1
diff --git a/official/legacy/image_classification/dataset_factory.py b/official/legacy/image_classification/dataset_factory.py
index 28012996c5d2f4dd6883798a372bc275b678bc0d..19a757046b36e92dcd5d16461a4e5e8da312e1b6 100644
--- a/official/legacy/image_classification/dataset_factory.py
+++ b/official/legacy/image_classification/dataset_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Dataset utilities for vision tasks using TFDS and tf.data.Dataset."""
from __future__ import absolute_import
from __future__ import division
diff --git a/official/legacy/image_classification/efficientnet/__init__.py b/official/legacy/image_classification/efficientnet/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/image_classification/efficientnet/__init__.py
+++ b/official/legacy/image_classification/efficientnet/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/efficientnet/common_modules.py b/official/legacy/image_classification/efficientnet/common_modules.py
index 0a61aa9fbf1ad53e0621e30f7444cd52692b8bdc..28be696204787c53838def5dc3474556a96161e9 100644
--- a/official/legacy/image_classification/efficientnet/common_modules.py
+++ b/official/legacy/image_classification/efficientnet/common_modules.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/efficientnet/efficientnet_config.py b/official/legacy/image_classification/efficientnet/efficientnet_config.py
index b031e2aa24d3b2d7207ad56ee83834c4be0cf1ca..148851cf687e722a76d6a848a7e0e33017a44ff6 100644
--- a/official/legacy/image_classification/efficientnet/efficientnet_config.py
+++ b/official/legacy/image_classification/efficientnet/efficientnet_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Configuration definitions for EfficientNet losses, learning rates, and optimizers."""
from __future__ import absolute_import
from __future__ import division
diff --git a/official/legacy/image_classification/efficientnet/efficientnet_model.py b/official/legacy/image_classification/efficientnet/efficientnet_model.py
index aa8948207c0be59e0c493dcfc239fed132b3f2a5..a9aa243b0377d2517a16af05c7db7177de42bc41 100644
--- a/official/legacy/image_classification/efficientnet/efficientnet_model.py
+++ b/official/legacy/image_classification/efficientnet/efficientnet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Contains definitions for EfficientNet model.
[1] Mingxing Tan, Quoc V. Le
diff --git a/official/legacy/image_classification/efficientnet/tfhub_export.py b/official/legacy/image_classification/efficientnet/tfhub_export.py
index 6afd6daf72a7732184be0546c8bc22164ce2b222..67971f81ff51181eb4749d488233bc5bbabde53e 100644
--- a/official/legacy/image_classification/efficientnet/tfhub_export.py
+++ b/official/legacy/image_classification/efficientnet/tfhub_export.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -43,8 +43,8 @@ def export_tfhub(model_path, hub_destination, model_name):
image_input = tf.keras.layers.Input(
shape=(None, None, 3), name="image_input", dtype=tf.float32)
x = image_input * 255.0
- ouputs = efficientnet_model.efficientnet(x, config)
- hub_model = tf.keras.Model(image_input, ouputs)
+ outputs = efficientnet_model.efficientnet(x, config)
+ hub_model = tf.keras.Model(image_input, outputs)
ckpt = tf.train.Checkpoint(model=hub_model)
ckpt.restore(model_path).assert_existing_objects_matched()
hub_model.save(
diff --git a/official/legacy/image_classification/learning_rate.py b/official/legacy/image_classification/learning_rate.py
index 72f7e95187521eeebefa1e698ca5382f10642e88..248cc8472e15e7c5695a3efb962d11cfc650ccdf 100644
--- a/official/legacy/image_classification/learning_rate.py
+++ b/official/legacy/image_classification/learning_rate.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Learning rate utilities for vision tasks."""
from __future__ import absolute_import
from __future__ import division
@@ -78,7 +77,7 @@ class CosineDecayWithWarmup(tf.keras.optimizers.schedules.LearningRateSchedule):
"""Class to generate learning rate tensor."""
def __init__(self, batch_size: int, total_steps: int, warmup_steps: int):
- """Creates the consine learning rate tensor with linear warmup.
+ """Creates the cosine learning rate tensor with linear warmup.
Args:
batch_size: The training batch size used in the experiment.
diff --git a/official/legacy/image_classification/learning_rate_test.py b/official/legacy/image_classification/learning_rate_test.py
index c3d757081ef7e3078a82a910242a6277e1b9372f..77dc65c571f451c9dce2c28ab64695ab6f63fc86 100644
--- a/official/legacy/image_classification/learning_rate_test.py
+++ b/official/legacy/image_classification/learning_rate_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/mnist_main.py b/official/legacy/image_classification/mnist_main.py
index 9462c6ae1a9c9e15ecd352da10500a7bc1e3a8fb..cf60631444ee7a693457fb52cdd57b2b33a5ca47 100644
--- a/official/legacy/image_classification/mnist_main.py
+++ b/official/legacy/image_classification/mnist_main.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/mnist_test.py b/official/legacy/image_classification/mnist_test.py
index f79773a4ce02a5eb8eb455155f64f35f7d85a661..384a6a9abb3f4b751752a626ebb3bfe7ad8de3b3 100644
--- a/official/legacy/image_classification/mnist_test.py
+++ b/official/legacy/image_classification/mnist_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/optimizer_factory.py b/official/legacy/image_classification/optimizer_factory.py
index dfddb79524582c2a2b11d649c21b097aa221ef5e..ad6ad30d26403e7d523742c1fad5c063638e2ae3 100644
--- a/official/legacy/image_classification/optimizer_factory.py
+++ b/official/legacy/image_classification/optimizer_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -48,7 +48,7 @@ def build_optimizer(
`ExponentialMovingAverage`.
Returns:
- A tf.keras.Optimizer.
+ A tf.keras.optimizers.legacy.Optimizer.
Raises:
ValueError if the provided optimizer_name is not supported.
@@ -60,12 +60,12 @@ def build_optimizer(
if optimizer_name == 'sgd':
logging.info('Using SGD optimizer')
nesterov = params.get('nesterov', False)
- optimizer = tf.keras.optimizers.SGD(
+ optimizer = tf.keras.optimizers.legacy.SGD(
learning_rate=base_learning_rate, nesterov=nesterov)
elif optimizer_name == 'momentum':
logging.info('Using momentum optimizer')
nesterov = params.get('nesterov', False)
- optimizer = tf.keras.optimizers.SGD(
+ optimizer = tf.keras.optimizers.legacy.SGD(
learning_rate=base_learning_rate,
momentum=params['momentum'],
nesterov=nesterov)
@@ -74,7 +74,7 @@ def build_optimizer(
rho = params.get('decay', None) or params.get('rho', 0.9)
momentum = params.get('momentum', 0.9)
epsilon = params.get('epsilon', 1e-07)
- optimizer = tf.keras.optimizers.RMSprop(
+ optimizer = tf.keras.optimizers.legacy.RMSprop(
learning_rate=base_learning_rate,
rho=rho,
momentum=momentum,
@@ -84,7 +84,7 @@ def build_optimizer(
beta_1 = params.get('beta_1', 0.9)
beta_2 = params.get('beta_2', 0.999)
epsilon = params.get('epsilon', 1e-07)
- optimizer = tf.keras.optimizers.Adam(
+ optimizer = tf.keras.optimizers.legacy.Adam(
learning_rate=base_learning_rate,
beta_1=beta_1,
beta_2=beta_2,
diff --git a/official/legacy/image_classification/optimizer_factory_test.py b/official/legacy/image_classification/optimizer_factory_test.py
index 059d1a267a6b160a2fc6e0d7fa42ae706b0c1e42..e0974505790221768988cf52207cfb0f79f871ed 100644
--- a/official/legacy/image_classification/optimizer_factory_test.py
+++ b/official/legacy/image_classification/optimizer_factory_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/preprocessing.py b/official/legacy/image_classification/preprocessing.py
index 346c8fc8b5b3469ad0cf596f006b7a7517b469c5..78b58243afb8466423eb9e67da0e59c024bb4c0e 100644
--- a/official/legacy/image_classification/preprocessing.py
+++ b/official/legacy/image_classification/preprocessing.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/resnet/__init__.py b/official/legacy/image_classification/resnet/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/image_classification/resnet/__init__.py
+++ b/official/legacy/image_classification/resnet/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/resnet/common.py b/official/legacy/image_classification/resnet/common.py
index 4d57fe8cac460ab12a1822837032267a95001204..a6581d2fb831abe6776391f911aa87a18fb3dd36 100644
--- a/official/legacy/image_classification/resnet/common.py
+++ b/official/legacy/image_classification/resnet/common.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -81,17 +81,18 @@ class PiecewiseConstantDecayWithWarmup(
def _get_learning_rate(self, step):
"""Compute learning rate at given step."""
+ step = tf.cast(step, dtype=tf.float32)
+ warmup_steps = tf.cast(self.warmup_steps, dtype=tf.float32)
with tf.name_scope('PiecewiseConstantDecayWithWarmup'):
def warmup_lr(step):
- return self.rescaled_lr * (
- tf.cast(step, tf.float32) / tf.cast(self.warmup_steps, tf.float32))
+ return self.rescaled_lr * (step / warmup_steps)
def piecewise_lr(step):
return tf.compat.v1.train.piecewise_constant(step, self.step_boundaries,
self.lr_values)
- return tf.cond(step < self.warmup_steps, lambda: warmup_lr(step),
+ return tf.cond(step < warmup_steps, lambda: warmup_lr(step),
lambda: piecewise_lr(step))
def get_config(self):
@@ -105,10 +106,14 @@ class PiecewiseConstantDecayWithWarmup(
}
-def get_optimizer(learning_rate=0.1):
+def get_optimizer(learning_rate=0.1, use_legacy_optimizer=True):
"""Returns optimizer to use."""
# The learning_rate is overwritten at the beginning of each step by callback.
- return tf.keras.optimizers.SGD(learning_rate=learning_rate, momentum=0.9)
+ if use_legacy_optimizer:
+ return tf.keras.optimizers.legacy.SGD(
+ learning_rate=learning_rate, momentum=0.9)
+ else:
+ return tf.keras.optimizers.SGD(learning_rate=learning_rate, momentum=0.9)
def get_callbacks(pruning_method=None,
diff --git a/official/legacy/image_classification/resnet/imagenet_preprocessing.py b/official/legacy/image_classification/resnet/imagenet_preprocessing.py
index 86ba3ed98084987ea5d63edf8fd5f515d58fba93..d60107035da30806411d8905614ba3bfda49d9e2 100644
--- a/official/legacy/image_classification/resnet/imagenet_preprocessing.py
+++ b/official/legacy/image_classification/resnet/imagenet_preprocessing.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/resnet/resnet_config.py b/official/legacy/image_classification/resnet/resnet_config.py
index f06cfed82b17619c05738ecc2a0fc47fdd0c36a2..9c40628216278b6df465fa5c5c494962bd8306c9 100644
--- a/official/legacy/image_classification/resnet/resnet_config.py
+++ b/official/legacy/image_classification/resnet/resnet_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Configuration definitions for ResNet losses, learning rates, and optimizers."""
from __future__ import absolute_import
from __future__ import division
diff --git a/official/legacy/image_classification/resnet/resnet_ctl_imagenet_main.py b/official/legacy/image_classification/resnet/resnet_ctl_imagenet_main.py
index 910879b446252461e5df09562009079611c86a68..963f5b1522f3d93c764fe33cd6ebbf11e9a44170 100644
--- a/official/legacy/image_classification/resnet/resnet_ctl_imagenet_main.py
+++ b/official/legacy/image_classification/resnet/resnet_ctl_imagenet_main.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,6 +22,7 @@ from absl import app
from absl import flags
from absl import logging
import orbit
+import json
import tensorflow as tf
from official.common import distribute_utils
from official.legacy.image_classification.resnet import common
diff --git a/official/legacy/image_classification/resnet/resnet_model.py b/official/legacy/image_classification/resnet/resnet_model.py
index bd5ec8eb74850ed9aad8a9a3537a1d5e9283b4fd..545d06ecc9a49d815497dfebdccd7b9df59cb305 100644
--- a/official/legacy/image_classification/resnet/resnet_model.py
+++ b/official/legacy/image_classification/resnet/resnet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/resnet/resnet_runnable.py b/official/legacy/image_classification/resnet/resnet_runnable.py
index 209117a1ab232fc3c0a1d568eaae56025ead867e..c8f9ade935f9711abbb7f229a025bb5cd79421b6 100644
--- a/official/legacy/image_classification/resnet/resnet_runnable.py
+++ b/official/legacy/image_classification/resnet/resnet_runnable.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/resnet/tfhub_export.py b/official/legacy/image_classification/resnet/tfhub_export.py
index a18360c9e8e2e6ab8455d8fa0e6b23d899ddd5ef..1d7d743ddeb11992cbc2f7c3ce0bda312e6a3108 100644
--- a/official/legacy/image_classification/resnet/tfhub_export.py
+++ b/official/legacy/image_classification/resnet/tfhub_export.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/test_utils.py b/official/legacy/image_classification/test_utils.py
index 8d7180c9d4e10c3241c4d6dd31d2cd013439df7a..871ac7e30f07c772134f54587cb657099361065b 100644
--- a/official/legacy/image_classification/test_utils.py
+++ b/official/legacy/image_classification/test_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/image_classification/vgg/__init__.py b/official/legacy/image_classification/vgg/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1
--- /dev/null
+++ b/official/legacy/image_classification/vgg/__init__.py
@@ -0,0 +1,15 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
diff --git a/official/legacy/image_classification/vgg/vgg_config.py b/official/legacy/image_classification/vgg/vgg_config.py
new file mode 100644
index 0000000000000000000000000000000000000000..0bf936744fae71a63aa4f80553e5025d30cb68ae
--- /dev/null
+++ b/official/legacy/image_classification/vgg/vgg_config.py
@@ -0,0 +1,44 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configuration definitions for VGG losses, learning rates, and optimizers."""
+
+import dataclasses
+from official.legacy.image_classification.configs import base_configs
+from official.modeling.hyperparams import base_config
+
+
+@dataclasses.dataclass
+class VGGModelConfig(base_configs.ModelConfig):
+ """Configuration for the VGG model."""
+ name: str = 'VGG'
+ num_classes: int = 1000
+ model_params: base_config.Config = dataclasses.field(default_factory=lambda: { # pylint:disable=g-long-lambda
+ 'num_classes': 1000,
+ 'batch_size': None,
+ 'use_l2_regularizer': True
+ })
+ loss: base_configs.LossConfig = base_configs.LossConfig(
+ name='sparse_categorical_crossentropy')
+ optimizer: base_configs.OptimizerConfig = base_configs.OptimizerConfig(
+ name='momentum', epsilon=0.001, momentum=0.9, moving_average_decay=None)
+ learning_rate: base_configs.LearningRateConfig = (
+ base_configs.LearningRateConfig(
+ name='stepwise',
+ initial_lr=0.01,
+ examples_per_epoch=1281167,
+ boundaries=[30, 60],
+ warmup_epochs=0,
+ scale_by_batch_size=1. / 256.,
+ multipliers=[0.01 / 256, 0.001 / 256, 0.0001 / 256]))
diff --git a/official/legacy/image_classification/vgg/vgg_model.py b/official/legacy/image_classification/vgg/vgg_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..b93e22555c5d5dddb3c3de1faa6f866680b66b32
--- /dev/null
+++ b/official/legacy/image_classification/vgg/vgg_model.py
@@ -0,0 +1,269 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""VGG16 model for Keras.
+
+Adapted from tf.keras.applications.vgg16.VGG16().
+
+Related papers/blogs:
+- https://arxiv.org/abs/1409.1556
+"""
+
+import tensorflow as tf
+
+layers = tf.keras.layers
+
+
+def _gen_l2_regularizer(use_l2_regularizer=True, l2_weight_decay=1e-4):
+ return tf.keras.regularizers.L2(
+ l2_weight_decay) if use_l2_regularizer else None
+
+
+def vgg16(num_classes,
+ batch_size=None,
+ use_l2_regularizer=True,
+ batch_norm_decay=0.9,
+ batch_norm_epsilon=1e-5):
+ """Instantiates the VGG16 architecture.
+
+ Args:
+ num_classes: `int` number of classes for image classification.
+ batch_size: Size of the batches for each step.
+ use_l2_regularizer: whether to use L2 regularizer on Conv/Dense layer.
+ batch_norm_decay: Moment of batch norm layers.
+ batch_norm_epsilon: Epsilon of batch borm layers.
+
+ Returns:
+ A Keras model instance.
+
+ """
+ input_shape = (224, 224, 3)
+ img_input = layers.Input(shape=input_shape, batch_size=batch_size)
+
+ x = img_input
+
+ if tf.keras.backend.image_data_format() == 'channels_first':
+ x = layers.Permute((3, 1, 2))(x)
+ bn_axis = 1
+ else: # channels_last
+ bn_axis = 3
+ # Block 1
+ x = layers.Conv2D(
+ 64, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block1_conv1')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv1')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 64, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block1_conv2')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv2')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.MaxPooling2D((2, 2), strides=(2, 2), name='block1_pool')(x)
+
+ # Block 2
+ x = layers.Conv2D(
+ 128, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block2_conv1')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv3')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 128, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block2_conv2')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv4')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.MaxPooling2D((2, 2), strides=(2, 2), name='block2_pool')(x)
+
+ # Block 3
+ x = layers.Conv2D(
+ 256, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block3_conv1')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv5')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 256, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block3_conv2')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv6')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 256, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block3_conv3')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv7')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.MaxPooling2D((2, 2), strides=(2, 2), name='block3_pool')(x)
+
+ # Block 4
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block4_conv1')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv8')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block4_conv2')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv9')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block4_conv3')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv10')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.MaxPooling2D((2, 2), strides=(2, 2), name='block4_pool')(x)
+
+ # Block 5
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block5_conv1')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv11')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block5_conv2')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv12')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Conv2D(
+ 512, (3, 3),
+ padding='same',
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='block5_conv3')(
+ x)
+ x = layers.BatchNormalization(
+ axis=bn_axis,
+ momentum=batch_norm_decay,
+ epsilon=batch_norm_epsilon,
+ name='bn_conv13')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.MaxPooling2D((2, 2), strides=(2, 2), name='block5_pool')(x)
+
+ x = layers.Flatten(name='flatten')(x)
+ x = layers.Dense(
+ 4096,
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='fc1')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Dropout(0.5)(x)
+ x = layers.Dense(
+ 4096,
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='fc2')(
+ x)
+ x = layers.Activation('relu')(x)
+ x = layers.Dropout(0.5)(x)
+ x = layers.Dense(
+ num_classes,
+ kernel_regularizer=_gen_l2_regularizer(use_l2_regularizer),
+ name='fc1000')(
+ x)
+
+ x = layers.Activation('softmax', dtype='float32')(x)
+
+ # Create model.
+ return tf.keras.Model(img_input, x, name='vgg16')
diff --git a/official/legacy/nlp/albert/__init__.py b/official/legacy/nlp/albert/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/legacy/nlp/albert/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/legacy/nlp/albert/configs.py b/official/legacy/nlp/albert/configs.py
deleted file mode 100644
index 6fd6fdff7b97e7a0dce385eb4edd22de6d23b6d0..0000000000000000000000000000000000000000
--- a/official/legacy/nlp/albert/configs.py
+++ /dev/null
@@ -1,50 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""The ALBERT configurations."""
-
-import six
-
-from official.nlp.bert import configs
-
-
-class AlbertConfig(configs.BertConfig):
- """Configuration for `ALBERT`."""
-
- def __init__(self, num_hidden_groups=1, inner_group_num=1, **kwargs):
- """Constructs AlbertConfig.
-
- Args:
- num_hidden_groups: Number of group for the hidden layers, parameters in
- the same group are shared. Note that this value and also the following
- 'inner_group_num' has to be 1 for now, because all released ALBERT
- models set them to 1. We may support arbitary valid values in future.
- inner_group_num: Number of inner repetition of attention and ffn.
- **kwargs: The remaining arguments are the same as above 'BertConfig'.
- """
- super(AlbertConfig, self).__init__(**kwargs)
-
- # TODO(chendouble): 'inner_group_num' and 'num_hidden_groups' are always 1
- # in the released ALBERT. Support other values in AlbertEncoder if needed.
- if inner_group_num != 1 or num_hidden_groups != 1:
- raise ValueError("We only support 'inner_group_num' and "
- "'num_hidden_groups' as 1.")
-
- @classmethod
- def from_dict(cls, json_object):
- """Constructs a `AlbertConfig` from a Python dictionary of parameters."""
- config = AlbertConfig(vocab_size=None)
- for (key, value) in six.iteritems(json_object):
- config.__dict__[key] = value
- return config
diff --git a/official/legacy/transformer/__init__.py b/official/legacy/transformer/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/transformer/__init__.py
+++ b/official/legacy/transformer/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/attention_layer.py b/official/legacy/transformer/attention_layer.py
index db6e95b1a293795614f86aa7041ca767b990f099..e966ce143237309b35969c9839cb4cb32908d071 100644
--- a/official/legacy/transformer/attention_layer.py
+++ b/official/legacy/transformer/attention_layer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,6 +17,8 @@ import math
import tensorflow as tf
+from official.modeling import tf_utils
+
class Attention(tf.keras.layers.Layer):
"""Multi-headed attention layer."""
@@ -50,27 +52,27 @@ class Attention(tf.keras.layers.Layer):
attention_initializer = _glorot_initializer(input_shape.as_list()[-1],
self.hidden_size)
- self.query_dense_layer = tf.keras.layers.experimental.EinsumDense(
+ self.query_dense_layer = tf.keras.layers.EinsumDense(
"BTE,ENH->BTNH",
output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
+ kernel_initializer=tf_utils.clone_initializer(attention_initializer),
bias_axes=None,
name="query")
- self.key_dense_layer = tf.keras.layers.experimental.EinsumDense(
+ self.key_dense_layer = tf.keras.layers.EinsumDense(
"BTE,ENH->BTNH",
output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
+ kernel_initializer=tf_utils.clone_initializer(attention_initializer),
bias_axes=None,
name="key")
- self.value_dense_layer = tf.keras.layers.experimental.EinsumDense(
+ self.value_dense_layer = tf.keras.layers.EinsumDense(
"BTE,ENH->BTNH",
output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
+ kernel_initializer=tf_utils.clone_initializer(attention_initializer),
bias_axes=None,
name="value")
output_initializer = _glorot_initializer(self.hidden_size, self.hidden_size)
- self.output_dense_layer = tf.keras.layers.experimental.EinsumDense(
+ self.output_dense_layer = tf.keras.layers.EinsumDense(
"BTNH,NHE->BTE",
output_shape=(None, self.hidden_size),
kernel_initializer=output_initializer,
diff --git a/official/legacy/transformer/beam_search_v1.py b/official/legacy/transformer/beam_search_v1.py
index 2c8537e63b20e718b15dfcd042f3263212af8c08..533cc01b211503a00502f71f06fc20cfb9f7b270 100644
--- a/official/legacy/transformer/beam_search_v1.py
+++ b/official/legacy/transformer/beam_search_v1.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/compute_bleu.py b/official/legacy/transformer/compute_bleu.py
index dbad8cbf0859ce2f24cfe792e639b4457b6a9037..c1b01e11a97b445c8da3733539911509307864f7 100644
--- a/official/legacy/transformer/compute_bleu.py
+++ b/official/legacy/transformer/compute_bleu.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/compute_bleu_test.py b/official/legacy/transformer/compute_bleu_test.py
index aed006e345246927dc72f76b76c8bb78333ae28e..24159248eb2472407dbbde2843bc9d7c7268c06f 100644
--- a/official/legacy/transformer/compute_bleu_test.py
+++ b/official/legacy/transformer/compute_bleu_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/data_download.py b/official/legacy/transformer/data_download.py
index 1b9b8f784c874cc8c4b0ba82a2ef23ddd2d2fb42..4731e82a22b268b8d9b13bfd85ff369f0207d44d 100644
--- a/official/legacy/transformer/data_download.py
+++ b/official/legacy/transformer/data_download.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -188,7 +188,7 @@ def download_and_extract(path, url, input_filename, target_filename):
Full paths to extracted input and target files.
Raises:
- OSError: if the the download/extraction fails.
+ OSError: if the download/extraction fails.
"""
# Check if extracted files already exist in path
input_file = find_file(path, input_filename)
diff --git a/official/legacy/transformer/data_pipeline.py b/official/legacy/transformer/data_pipeline.py
index 1d9f242172cadcd38fefbc900658b914483b3b24..484c8e97a59e1c32582daa0982eb1f0dcbb08e2c 100644
--- a/official/legacy/transformer/data_pipeline.py
+++ b/official/legacy/transformer/data_pipeline.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/embedding_layer.py b/official/legacy/transformer/embedding_layer.py
index 69f3861ce6745bab0f62f29c2213fe53f99183c2..398a950df2b8f35628f5bf6192cab61c50912972 100644
--- a/official/legacy/transformer/embedding_layer.py
+++ b/official/legacy/transformer/embedding_layer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/ffn_layer.py b/official/legacy/transformer/ffn_layer.py
index 26f0a15f69c50abee6f95dd40928e844ece1c691..8e24a1e8428fb8c2659b5d6cca2ffc7cb32423d9 100644
--- a/official/legacy/transformer/ffn_layer.py
+++ b/official/legacy/transformer/ffn_layer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/metrics.py b/official/legacy/transformer/metrics.py
index 38330aa471c7f7384a3f42abb7eefc5a62a48d94..b469e6c6f67d70678534baf82521ab54c52a911d 100644
--- a/official/legacy/transformer/metrics.py
+++ b/official/legacy/transformer/metrics.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/misc.py b/official/legacy/transformer/misc.py
index 255a6b336c4081cffc148e3343b2119e3e959258..ff8930a6601680fb46469fb0e4ff1445e8670003 100644
--- a/official/legacy/transformer/misc.py
+++ b/official/legacy/transformer/misc.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/model_params.py b/official/legacy/transformer/model_params.py
index 0764d5e9a0d2e97754943cd61574b1c24469a0ae..70e464be20abd4b2ed02201b0397b13e3c87ac42 100644
--- a/official/legacy/transformer/model_params.py
+++ b/official/legacy/transformer/model_params.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/model_utils.py b/official/legacy/transformer/model_utils.py
index 6e163b97361cb7f071314909aaa1fc1e52ae6bfd..36095238822a0439f4bd7986ecaf038c76126319 100644
--- a/official/legacy/transformer/model_utils.py
+++ b/official/legacy/transformer/model_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/model_utils_test.py b/official/legacy/transformer/model_utils_test.py
index e6223c62b87a0055c9e8aa7269756c82fbf734b9..0758caa18707997f2766926dc95846da6ed82ba8 100644
--- a/official/legacy/transformer/model_utils_test.py
+++ b/official/legacy/transformer/model_utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/optimizer.py b/official/legacy/transformer/optimizer.py
index b27a6f07a4b73723be6f28d257bc3abcfbca43de..70e96ab6baddce4f326949891c056de9890e0e45 100644
--- a/official/legacy/transformer/optimizer.py
+++ b/official/legacy/transformer/optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer.py b/official/legacy/transformer/transformer.py
index da449a267ef7c3f870d03b96780bfc9cece88352..ed5d874900d863e73281ca6fb449d7acaa3d68cf 100644
--- a/official/legacy/transformer/transformer.py
+++ b/official/legacy/transformer/transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer_forward_test.py b/official/legacy/transformer/transformer_forward_test.py
index b3c2c54c07d1890b30d35126d50e74b47050242f..5efdc4178f4cd87470a8bc5ddf24a930e5e2e443 100644
--- a/official/legacy/transformer/transformer_forward_test.py
+++ b/official/legacy/transformer/transformer_forward_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer_layers_test.py b/official/legacy/transformer/transformer_layers_test.py
index 16b7482d39ebf6fb745c94eafa414ab0b0b234e4..c20804439654a2f8f4be09eb5b040958f9a3657d 100644
--- a/official/legacy/transformer/transformer_layers_test.py
+++ b/official/legacy/transformer/transformer_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer_main.py b/official/legacy/transformer/transformer_main.py
index 38fc3cff2ebc9dc8a732a40ea17d96f34b4be822..ec1e7634045c95c2ab86fd1f34f41429673f0299 100644
--- a/official/legacy/transformer/transformer_main.py
+++ b/official/legacy/transformer/transformer_main.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer_main_test.py b/official/legacy/transformer/transformer_main_test.py
index ec1c5ac188f5bf85c07f36215c44c76684f062b2..82077858102fe9e344cbe9cfcbd3ce63695d360b 100644
--- a/official/legacy/transformer/transformer_main_test.py
+++ b/official/legacy/transformer/transformer_main_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/transformer_test.py b/official/legacy/transformer/transformer_test.py
index 7b3ecc5ab008ad7ac07e77f7b3afc80e5a4cd1dd..a6cedb48e1d4b3be0cfcce079733f9b1eab78e0c 100644
--- a/official/legacy/transformer/transformer_test.py
+++ b/official/legacy/transformer/transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/translate.py b/official/legacy/transformer/translate.py
index 5f88e015ba1ef68044e0a53d69979af951d8bed3..abbf82f5f1a166fe30d2be7521b8e2891fbdb0e8 100644
--- a/official/legacy/transformer/translate.py
+++ b/official/legacy/transformer/translate.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/utils/__init__.py b/official/legacy/transformer/utils/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/legacy/transformer/utils/__init__.py
+++ b/official/legacy/transformer/utils/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/utils/metrics.py b/official/legacy/transformer/utils/metrics.py
index ec1cad0b409cfb69535dce15fab1d531d7811391..23261ac474a8f1d5a924a1e48f380a5483a3f15d 100644
--- a/official/legacy/transformer/utils/metrics.py
+++ b/official/legacy/transformer/utils/metrics.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/utils/tokenizer.py b/official/legacy/transformer/utils/tokenizer.py
index 6a992a324f3b0c651d219f4f2cc081a274d87db4..9533846d2fc4d7d74194806e3a7cbee73a198639 100644
--- a/official/legacy/transformer/utils/tokenizer.py
+++ b/official/legacy/transformer/utils/tokenizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/transformer/utils/tokenizer_test.py b/official/legacy/transformer/utils/tokenizer_test.py
index e75cbd1e6333551d57f4910246e98097bacaf16f..2b582b99c6f7b6e07693c177fbb655231621aa55 100644
--- a/official/legacy/transformer/utils/tokenizer_test.py
+++ b/official/legacy/transformer/utils/tokenizer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/xlnet/README.md b/official/legacy/xlnet/README.md
similarity index 100%
rename from official/nlp/xlnet/README.md
rename to official/legacy/xlnet/README.md
diff --git a/official/legacy/xlnet/__init__.py b/official/legacy/xlnet/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1
--- /dev/null
+++ b/official/legacy/xlnet/__init__.py
@@ -0,0 +1,15 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
diff --git a/official/nlp/xlnet/classifier_utils.py b/official/legacy/xlnet/classifier_utils.py
similarity index 98%
rename from official/nlp/xlnet/classifier_utils.py
rename to official/legacy/xlnet/classifier_utils.py
index cb8acee087dc58596159d1b11ddf7c09299038dc..27aaf4ade1840a380ce054e8ab6705afe42b2b08 100644
--- a/official/nlp/xlnet/classifier_utils.py
+++ b/official/legacy/xlnet/classifier_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,7 +16,7 @@
from absl import logging
-from official.nlp.xlnet import data_utils
+from official.legacy.xlnet import data_utils
SEG_ID_A = 0
SEG_ID_B = 1
diff --git a/official/legacy/xlnet/common_flags.py b/official/legacy/xlnet/common_flags.py
new file mode 100644
index 0000000000000000000000000000000000000000..b1ee5c3e86d8815576d89f26ed459e229adfb9cd
--- /dev/null
+++ b/official/legacy/xlnet/common_flags.py
@@ -0,0 +1,142 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Common flags used in XLNet model."""
+
+from absl import flags
+
+flags.DEFINE_string("master", default=None, help="master")
+flags.DEFINE_string(
+ "tpu",
+ default=None,
+ help="The Cloud TPU to use for training. This should be "
+ "either the name used when creating the Cloud TPU, or a "
+ "url like grpc://ip.address.of.tpu:8470.")
+flags.DEFINE_bool(
+ "use_tpu", default=True, help="Use TPUs rather than plain CPUs.")
+flags.DEFINE_string("tpu_topology", "2x2", help="TPU topology.")
+flags.DEFINE_integer(
+ "num_core_per_host", default=8, help="number of cores per host")
+
+flags.DEFINE_string("model_dir", default=None, help="Estimator model_dir.")
+flags.DEFINE_string(
+ "init_checkpoint",
+ default=None,
+ help="Checkpoint path for initializing the model.")
+flags.DEFINE_bool(
+ "init_from_transformerxl",
+ default=False,
+ help="Init from a transformerxl model checkpoint. Otherwise, init from the "
+ "entire model checkpoint.")
+
+# Optimization config
+flags.DEFINE_float("learning_rate", default=1e-4, help="Maximum learning rate.")
+flags.DEFINE_float("clip", default=1.0, help="Gradient clipping value.")
+flags.DEFINE_float("weight_decay_rate", default=0.0, help="Weight decay rate.")
+
+# lr decay
+flags.DEFINE_integer(
+ "warmup_steps", default=0, help="Number of steps for linear lr warmup.")
+flags.DEFINE_float("adam_epsilon", default=1e-8, help="Adam epsilon.")
+flags.DEFINE_float(
+ "lr_layer_decay_rate",
+ default=1.0,
+ help="Top layer: lr[L] = FLAGS.learning_rate."
+ "Lower layers: lr[l-1] = lr[l] * lr_layer_decay_rate.")
+flags.DEFINE_float(
+ "min_lr_ratio", default=0.0, help="Minimum ratio learning rate.")
+
+# Training config
+flags.DEFINE_integer(
+ "train_batch_size",
+ default=16,
+ help="Size of the train batch across all hosts.")
+flags.DEFINE_integer(
+ "train_steps", default=100000, help="Total number of training steps.")
+flags.DEFINE_integer(
+ "iterations", default=1000, help="Number of iterations per repeat loop.")
+
+# Data config
+flags.DEFINE_integer(
+ "seq_len", default=0, help="Sequence length for pretraining.")
+flags.DEFINE_integer(
+ "reuse_len",
+ default=0,
+ help="How many tokens to be reused in the next batch. "
+ "Could be half of `seq_len`.")
+flags.DEFINE_bool("uncased", False, help="Use uncased inputs or not.")
+flags.DEFINE_bool(
+ "bi_data",
+ default=False,
+ help="Use bidirectional data streams, "
+ "i.e., forward & backward.")
+flags.DEFINE_integer("n_token", 32000, help="Vocab size")
+
+# Model config
+flags.DEFINE_integer("mem_len", default=0, help="Number of steps to cache")
+flags.DEFINE_bool("same_length", default=False, help="Same length attention")
+flags.DEFINE_integer("clamp_len", default=-1, help="Clamp length")
+
+flags.DEFINE_integer("n_layer", default=6, help="Number of layers.")
+flags.DEFINE_integer("d_model", default=32, help="Dimension of the model.")
+flags.DEFINE_integer("d_embed", default=32, help="Dimension of the embeddings.")
+flags.DEFINE_integer("n_head", default=4, help="Number of attention heads.")
+flags.DEFINE_integer(
+ "d_head", default=8, help="Dimension of each attention head.")
+flags.DEFINE_integer(
+ "d_inner",
+ default=32,
+ help="Dimension of inner hidden size in positionwise "
+ "feed-forward.")
+flags.DEFINE_float("dropout", default=0.1, help="Dropout rate.")
+flags.DEFINE_float("dropout_att", default=0.1, help="Attention dropout rate.")
+flags.DEFINE_bool("untie_r", default=False, help="Untie r_w_bias and r_r_bias")
+flags.DEFINE_string(
+ "ff_activation",
+ default="relu",
+ help="Activation type used in position-wise feed-forward.")
+flags.DEFINE_string(
+ "strategy_type",
+ default="tpu",
+ help="Activation type used in position-wise feed-forward.")
+flags.DEFINE_bool("use_bfloat16", False, help="Whether to use bfloat16.")
+
+# Parameter initialization
+flags.DEFINE_enum(
+ "init_method",
+ default="normal",
+ enum_values=["normal", "uniform"],
+ help="Initialization method.")
+flags.DEFINE_float(
+ "init_std", default=0.02, help="Initialization std when init is normal.")
+flags.DEFINE_float(
+ "init_range", default=0.1, help="Initialization std when init is uniform.")
+
+flags.DEFINE_integer(
+ "test_data_size", default=12048, help="Number of test data samples.")
+flags.DEFINE_string(
+ "train_tfrecord_path",
+ default=None,
+ help="Path to preprocessed training set tfrecord.")
+flags.DEFINE_string(
+ "test_tfrecord_path",
+ default=None,
+ help="Path to preprocessed test set tfrecord.")
+flags.DEFINE_integer(
+ "test_batch_size",
+ default=16,
+ help="Size of the test batch across all hosts.")
+flags.DEFINE_integer(
+ "save_steps", default=1000, help="Number of steps for saving checkpoint.")
+FLAGS = flags.FLAGS
diff --git a/official/nlp/xlnet/data_utils.py b/official/legacy/xlnet/data_utils.py
similarity index 99%
rename from official/nlp/xlnet/data_utils.py
rename to official/legacy/xlnet/data_utils.py
index 58ffdbffc2c287064b2f98a5e04a70cc8020ff34..0048832d6eae6e1b470fbcfc45a17ec424a4d0fa 100644
--- a/official/nlp/xlnet/data_utils.py
+++ b/official/legacy/xlnet/data_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/xlnet/optimization.py b/official/legacy/xlnet/optimization.py
new file mode 100644
index 0000000000000000000000000000000000000000..2d394eaefba5be4d86757e798a4466a2f9b99457
--- /dev/null
+++ b/official/legacy/xlnet/optimization.py
@@ -0,0 +1,98 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Functions and classes related to optimization (weight updates)."""
+
+from absl import logging
+import tensorflow as tf
+from official.nlp import optimization
+
+
+class WarmUp(tf.keras.optimizers.schedules.LearningRateSchedule):
+ """Applys a warmup schedule on a given learning rate decay schedule."""
+
+ def __init__(self,
+ initial_learning_rate,
+ decay_schedule_fn,
+ warmup_steps,
+ power=1.0,
+ name=None):
+ super(WarmUp, self).__init__()
+ self.initial_learning_rate = initial_learning_rate
+ self.warmup_steps = warmup_steps
+ self.power = power
+ self.decay_schedule_fn = decay_schedule_fn
+ self.name = name
+
+ def __call__(self, step):
+ with tf.name_scope(self.name or "WarmUp") as name:
+ # Implements polynomial warmup. i.e., if global_step < warmup_steps, the
+ # learning rate will be `global_step/num_warmup_steps * init_lr`.
+ global_step_float = tf.cast(step, tf.float32)
+ warmup_steps_float = tf.cast(self.warmup_steps, tf.float32)
+ warmup_percent_done = global_step_float / warmup_steps_float
+ warmup_learning_rate = (
+ self.initial_learning_rate *
+ tf.math.pow(warmup_percent_done, self.power))
+ return tf.cond(
+ global_step_float < warmup_steps_float,
+ lambda: warmup_learning_rate,
+ lambda: self.decay_schedule_fn(step - self.warmup_steps),
+ name=name)
+
+ def get_config(self):
+ return {
+ "initial_learning_rate": self.initial_learning_rate,
+ "decay_schedule_fn": self.decay_schedule_fn,
+ "warmup_steps": self.warmup_steps,
+ "power": self.power,
+ "name": self.name
+ }
+
+
+def create_optimizer(init_lr,
+ num_train_steps,
+ num_warmup_steps,
+ min_lr_ratio=0.0,
+ adam_epsilon=1e-8,
+ weight_decay_rate=0.0):
+ """Creates an optimizer with learning rate schedule."""
+ # Implements linear decay of the learning rate.
+ learning_rate_fn = tf.keras.optimizers.schedules.PolynomialDecay(
+ initial_learning_rate=init_lr,
+ decay_steps=num_train_steps - num_warmup_steps,
+ end_learning_rate=init_lr * min_lr_ratio)
+ if num_warmup_steps:
+ learning_rate_fn = WarmUp(
+ initial_learning_rate=init_lr,
+ decay_schedule_fn=learning_rate_fn,
+ warmup_steps=num_warmup_steps)
+ if weight_decay_rate > 0.0:
+ logging.info(
+ "Using AdamWeightDecay with adam_epsilon=%.9f weight_decay_rate=%.3f",
+ adam_epsilon, weight_decay_rate)
+ optimizer = optimization.AdamWeightDecay(
+ learning_rate=learning_rate_fn,
+ weight_decay_rate=weight_decay_rate,
+ beta_1=0.9,
+ beta_2=0.999,
+ epsilon=adam_epsilon,
+ exclude_from_weight_decay=["LayerNorm", "layer_norm", "bias"],
+ include_in_weight_decay=["r_s_bias", "r_r_bias", "r_w_bias"])
+ else:
+ logging.info("Using Adam with adam_epsilon=%.9f", (adam_epsilon))
+ optimizer = tf.keras.optimizers.legacy.Adam(
+ learning_rate=learning_rate_fn, epsilon=adam_epsilon)
+
+ return optimizer, learning_rate_fn
diff --git a/official/nlp/xlnet/preprocess_classification_data.py b/official/legacy/xlnet/preprocess_classification_data.py
similarity index 98%
rename from official/nlp/xlnet/preprocess_classification_data.py
rename to official/legacy/xlnet/preprocess_classification_data.py
index e8d42fa4e61541fed4532caffcc012edcc8254bc..d517e486b039baa506acb21a85a0b97e9dd965f2 100644
--- a/official/nlp/xlnet/preprocess_classification_data.py
+++ b/official/legacy/xlnet/preprocess_classification_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -26,8 +26,8 @@ import numpy as np
import tensorflow as tf
import sentencepiece as spm
-from official.nlp.xlnet import classifier_utils
-from official.nlp.xlnet import preprocess_utils
+from official.legacy.xlnet import classifier_utils
+from official.legacy.xlnet import preprocess_utils
flags.DEFINE_bool(
diff --git a/official/nlp/xlnet/preprocess_pretrain_data.py b/official/legacy/xlnet/preprocess_pretrain_data.py
similarity index 99%
rename from official/nlp/xlnet/preprocess_pretrain_data.py
rename to official/legacy/xlnet/preprocess_pretrain_data.py
index 3facc98f5941320379bd75688deeb626572db52d..aaf60ba5e4a8c1dc2ddcc5865247e8edce418bd0 100644
--- a/official/nlp/xlnet/preprocess_pretrain_data.py
+++ b/official/legacy/xlnet/preprocess_pretrain_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,7 +28,7 @@ import numpy as np
import tensorflow.compat.v1 as tf
import sentencepiece as spm
-from official.nlp.xlnet import preprocess_utils
+from official.legacy.xlnet import preprocess_utils
FLAGS = flags.FLAGS
diff --git a/official/nlp/xlnet/preprocess_squad_data.py b/official/legacy/xlnet/preprocess_squad_data.py
similarity index 97%
rename from official/nlp/xlnet/preprocess_squad_data.py
rename to official/legacy/xlnet/preprocess_squad_data.py
index e1d49565067c57611d8613a6d14e5e4bf221b1fc..e99177c838e8dda1a8bf1e2ca639325b67e76afc 100644
--- a/official/nlp/xlnet/preprocess_squad_data.py
+++ b/official/legacy/xlnet/preprocess_squad_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -25,7 +25,7 @@ from absl import logging
import tensorflow as tf
import sentencepiece as spm
-from official.nlp.xlnet import squad_utils
+from official.legacy.xlnet import squad_utils
flags.DEFINE_integer(
"num_proc", default=1, help="Number of preprocessing processes.")
diff --git a/official/nlp/xlnet/preprocess_utils.py b/official/legacy/xlnet/preprocess_utils.py
similarity index 98%
rename from official/nlp/xlnet/preprocess_utils.py
rename to official/legacy/xlnet/preprocess_utils.py
index 5c714a0c1fdd3a7cddd9c0a63fc09c80bc08627e..19cae9174c27848d673070d11f3926be8bdf1ded 100644
--- a/official/nlp/xlnet/preprocess_utils.py
+++ b/official/legacy/xlnet/preprocess_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/legacy/xlnet/run_classifier.py b/official/legacy/xlnet/run_classifier.py
new file mode 100644
index 0000000000000000000000000000000000000000..258e6116ab3537384c9785ce31ec2f92478e57e6
--- /dev/null
+++ b/official/legacy/xlnet/run_classifier.py
@@ -0,0 +1,187 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""XLNet classification finetuning runner in tf2.0."""
+
+import functools
+# Import libraries
+from absl import app
+from absl import flags
+from absl import logging
+
+import numpy as np
+import tensorflow as tf
+# pylint: disable=unused-import
+from official.common import distribute_utils
+from official.legacy.xlnet import common_flags
+from official.legacy.xlnet import data_utils
+from official.legacy.xlnet import optimization
+from official.legacy.xlnet import training_utils
+from official.legacy.xlnet import xlnet_config
+from official.legacy.xlnet import xlnet_modeling as modeling
+
+flags.DEFINE_integer("n_class", default=2, help="Number of classes.")
+flags.DEFINE_string(
+ "summary_type",
+ default="last",
+ help="Method used to summarize a sequence into a vector.")
+
+FLAGS = flags.FLAGS
+
+
+def get_classificationxlnet_model(model_config,
+ run_config,
+ n_class,
+ summary_type="last"):
+ model = modeling.ClassificationXLNetModel(
+ model_config, run_config, n_class, summary_type, name="model")
+ return model
+
+
+def run_evaluation(strategy,
+ test_input_fn,
+ eval_steps,
+ model,
+ step,
+ eval_summary_writer=None):
+ """Run evaluation for classification task.
+
+ Args:
+ strategy: distribution strategy.
+ test_input_fn: input function for evaluation data.
+ eval_steps: total number of evaluation steps.
+ model: keras model object.
+ step: current train step.
+ eval_summary_writer: summary writer used to record evaluation metrics. As
+ there are fake data samples in validation set, we use mask to get rid of
+ them when calculating the accuracy. For the reason that there will be
+ dynamic-shape tensor, we first collect logits, labels and masks from TPU
+ and calculate the accuracy via numpy locally.
+
+ Returns:
+ A float metric, accuracy.
+ """
+
+ def _test_step_fn(inputs):
+ """Replicated validation step."""
+
+ inputs["mems"] = None
+ _, logits = model(inputs, training=False)
+ return logits, inputs["label_ids"], inputs["is_real_example"]
+
+ @tf.function
+ def _run_evaluation(test_iterator):
+ """Runs validation steps."""
+ logits, labels, masks = strategy.run(
+ _test_step_fn, args=(next(test_iterator),))
+ return logits, labels, masks
+
+ test_iterator = data_utils.get_input_iterator(test_input_fn, strategy)
+ correct = 0
+ total = 0
+ for _ in range(eval_steps):
+ logits, labels, masks = _run_evaluation(test_iterator)
+ logits = strategy.experimental_local_results(logits)
+ labels = strategy.experimental_local_results(labels)
+ masks = strategy.experimental_local_results(masks)
+ merged_logits = []
+ merged_labels = []
+ merged_masks = []
+
+ for i in range(strategy.num_replicas_in_sync):
+ merged_logits.append(logits[i].numpy())
+ merged_labels.append(labels[i].numpy())
+ merged_masks.append(masks[i].numpy())
+ merged_logits = np.vstack(np.array(merged_logits))
+ merged_labels = np.hstack(np.array(merged_labels))
+ merged_masks = np.hstack(np.array(merged_masks))
+ real_index = np.where(np.equal(merged_masks, 1))
+ correct += np.sum(
+ np.equal(
+ np.argmax(merged_logits[real_index], axis=-1),
+ merged_labels[real_index]))
+ total += np.shape(real_index)[-1]
+ accuracy = float(correct) / float(total)
+ logging.info("Train step: %d / acc = %d/%d = %f", step, correct, total,
+ accuracy)
+ if eval_summary_writer:
+ with eval_summary_writer.as_default():
+ tf.summary.scalar("eval_acc", float(correct) / float(total), step=step)
+ eval_summary_writer.flush()
+ return accuracy
+
+
+def get_metric_fn():
+ train_acc_metric = tf.keras.metrics.SparseCategoricalAccuracy(
+ "acc", dtype=tf.float32)
+ return train_acc_metric
+
+
+def main(unused_argv):
+ del unused_argv
+ strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=FLAGS.strategy_type,
+ tpu_address=FLAGS.tpu)
+ if strategy:
+ logging.info("***** Number of cores used : %d",
+ strategy.num_replicas_in_sync)
+ train_input_fn = functools.partial(data_utils.get_classification_input_data,
+ FLAGS.train_batch_size, FLAGS.seq_len,
+ strategy, True, FLAGS.train_tfrecord_path)
+ test_input_fn = functools.partial(data_utils.get_classification_input_data,
+ FLAGS.test_batch_size, FLAGS.seq_len,
+ strategy, False, FLAGS.test_tfrecord_path)
+
+ total_training_steps = FLAGS.train_steps
+ steps_per_loop = FLAGS.iterations
+ eval_steps = int(FLAGS.test_data_size / FLAGS.test_batch_size)
+ eval_fn = functools.partial(run_evaluation, strategy, test_input_fn,
+ eval_steps)
+ optimizer, learning_rate_fn = optimization.create_optimizer(
+ FLAGS.learning_rate,
+ total_training_steps,
+ FLAGS.warmup_steps,
+ adam_epsilon=FLAGS.adam_epsilon)
+ model_config = xlnet_config.XLNetConfig(FLAGS)
+ run_config = xlnet_config.create_run_config(True, False, FLAGS)
+ model_fn = functools.partial(get_classificationxlnet_model, model_config,
+ run_config, FLAGS.n_class, FLAGS.summary_type)
+ input_meta_data = {}
+ input_meta_data["d_model"] = FLAGS.d_model
+ input_meta_data["mem_len"] = FLAGS.mem_len
+ input_meta_data["batch_size_per_core"] = int(FLAGS.train_batch_size /
+ strategy.num_replicas_in_sync)
+ input_meta_data["n_layer"] = FLAGS.n_layer
+ input_meta_data["lr_layer_decay_rate"] = FLAGS.lr_layer_decay_rate
+ input_meta_data["n_class"] = FLAGS.n_class
+
+ training_utils.train(
+ strategy=strategy,
+ model_fn=model_fn,
+ input_meta_data=input_meta_data,
+ eval_fn=eval_fn,
+ metric_fn=get_metric_fn,
+ train_input_fn=train_input_fn,
+ init_checkpoint=FLAGS.init_checkpoint,
+ init_from_transformerxl=FLAGS.init_from_transformerxl,
+ total_training_steps=total_training_steps,
+ steps_per_loop=steps_per_loop,
+ optimizer=optimizer,
+ learning_rate_fn=learning_rate_fn,
+ model_dir=FLAGS.model_dir,
+ save_steps=FLAGS.save_steps)
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/nlp/xlnet/run_pretrain.py b/official/legacy/xlnet/run_pretrain.py
similarity index 93%
rename from official/nlp/xlnet/run_pretrain.py
rename to official/legacy/xlnet/run_pretrain.py
index 80ab0bd4d1c500c92e2d97106fb3e3eab0d0b33e..311f283a9cb46f72eb9adc7e3b509e1a482348be 100644
--- a/official/nlp/xlnet/run_pretrain.py
+++ b/official/legacy/xlnet/run_pretrain.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -24,12 +24,12 @@ from absl import logging
import tensorflow as tf
# pylint: disable=unused-import
from official.common import distribute_utils
-from official.nlp.xlnet import common_flags
-from official.nlp.xlnet import data_utils
-from official.nlp.xlnet import optimization
-from official.nlp.xlnet import training_utils
-from official.nlp.xlnet import xlnet_config
-from official.nlp.xlnet import xlnet_modeling as modeling
+from official.legacy.xlnet import common_flags
+from official.legacy.xlnet import data_utils
+from official.legacy.xlnet import optimization
+from official.legacy.xlnet import training_utils
+from official.legacy.xlnet import xlnet_config
+from official.legacy.xlnet import xlnet_modeling as modeling
flags.DEFINE_integer(
"num_predict",
diff --git a/official/legacy/xlnet/run_squad.py b/official/legacy/xlnet/run_squad.py
new file mode 100644
index 0000000000000000000000000000000000000000..29a5c5c451c929b35f68b754771e6a8aab1d3df2
--- /dev/null
+++ b/official/legacy/xlnet/run_squad.py
@@ -0,0 +1,295 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""XLNet SQUAD finetuning runner in tf2.0."""
+
+import functools
+import json
+import os
+import pickle
+
+# Import libraries
+from absl import app
+from absl import flags
+from absl import logging
+
+import tensorflow as tf
+# pylint: disable=unused-import
+import sentencepiece as spm
+from official.common import distribute_utils
+from official.legacy.xlnet import common_flags
+from official.legacy.xlnet import data_utils
+from official.legacy.xlnet import optimization
+from official.legacy.xlnet import squad_utils
+from official.legacy.xlnet import training_utils
+from official.legacy.xlnet import xlnet_config
+from official.legacy.xlnet import xlnet_modeling as modeling
+
+flags.DEFINE_string(
+ "test_feature_path", default=None, help="Path to feature of test set.")
+flags.DEFINE_integer("query_len", default=64, help="Max query length.")
+flags.DEFINE_integer("start_n_top", default=5, help="Beam size for span start.")
+flags.DEFINE_integer("end_n_top", default=5, help="Beam size for span end.")
+flags.DEFINE_string(
+ "predict_dir", default=None, help="Path to write predictions.")
+flags.DEFINE_string(
+ "predict_file", default=None, help="Path to json file of test set.")
+flags.DEFINE_integer(
+ "n_best_size", default=5, help="n best size for predictions.")
+flags.DEFINE_integer("max_answer_length", default=64, help="Max answer length.")
+# Data preprocessing config
+flags.DEFINE_string(
+ "spiece_model_file", default=None, help="Sentence Piece model path.")
+flags.DEFINE_integer("max_seq_length", default=512, help="Max sequence length.")
+flags.DEFINE_integer("max_query_length", default=64, help="Max query length.")
+flags.DEFINE_integer("doc_stride", default=128, help="Doc stride.")
+
+FLAGS = flags.FLAGS
+
+
+class InputFeatures(object):
+ """A single set of features of data."""
+
+ def __init__(self,
+ unique_id,
+ example_index,
+ doc_span_index,
+ tok_start_to_orig_index,
+ tok_end_to_orig_index,
+ token_is_max_context,
+ input_ids,
+ input_mask,
+ p_mask,
+ segment_ids,
+ paragraph_len,
+ cls_index,
+ start_position=None,
+ end_position=None,
+ is_impossible=None):
+ self.unique_id = unique_id
+ self.example_index = example_index
+ self.doc_span_index = doc_span_index
+ self.tok_start_to_orig_index = tok_start_to_orig_index
+ self.tok_end_to_orig_index = tok_end_to_orig_index
+ self.token_is_max_context = token_is_max_context
+ self.input_ids = input_ids
+ self.input_mask = input_mask
+ self.p_mask = p_mask
+ self.segment_ids = segment_ids
+ self.paragraph_len = paragraph_len
+ self.cls_index = cls_index
+ self.start_position = start_position
+ self.end_position = end_position
+ self.is_impossible = is_impossible
+
+
+# pylint: disable=unused-argument
+def run_evaluation(strategy, test_input_fn, eval_examples, eval_features,
+ original_data, eval_steps, input_meta_data, model,
+ current_step, eval_summary_writer):
+ """Run evaluation for SQUAD task.
+
+ Args:
+ strategy: distribution strategy.
+ test_input_fn: input function for evaluation data.
+ eval_examples: tf.Examples of the evaluation set.
+ eval_features: Feature objects of the evaluation set.
+ original_data: The original json data for the evaluation set.
+ eval_steps: total number of evaluation steps.
+ input_meta_data: input meta data.
+ model: keras model object.
+ current_step: current training step.
+ eval_summary_writer: summary writer used to record evaluation metrics.
+
+ Returns:
+ A float metric, F1 score.
+ """
+
+ def _test_step_fn(inputs):
+ """Replicated validation step."""
+
+ inputs["mems"] = None
+ res = model(inputs, training=False)
+ return res, inputs["unique_ids"]
+
+ @tf.function
+ def _run_evaluation(test_iterator):
+ """Runs validation steps."""
+ res, unique_ids = strategy.run(
+ _test_step_fn, args=(next(test_iterator),))
+ return res, unique_ids
+
+ test_iterator = data_utils.get_input_iterator(test_input_fn, strategy)
+ cur_results = []
+ for _ in range(eval_steps):
+ results, unique_ids = _run_evaluation(test_iterator)
+ unique_ids = strategy.experimental_local_results(unique_ids)
+
+ for result_key in results:
+ results[result_key] = (
+ strategy.experimental_local_results(results[result_key]))
+ for core_i in range(strategy.num_replicas_in_sync):
+ bsz = int(input_meta_data["test_batch_size"] /
+ strategy.num_replicas_in_sync)
+ for j in range(bsz):
+ result = {}
+ for result_key in results:
+ result[result_key] = results[result_key][core_i].numpy()[j]
+ result["unique_ids"] = unique_ids[core_i].numpy()[j]
+ # We appended a fake example into dev set to make data size can be
+ # divided by test_batch_size. Ignores this fake example during
+ # evaluation.
+ if result["unique_ids"] == 1000012047:
+ continue
+ unique_id = int(result["unique_ids"])
+
+ start_top_log_probs = ([
+ float(x) for x in result["start_top_log_probs"].flat
+ ])
+ start_top_index = [int(x) for x in result["start_top_index"].flat]
+ end_top_log_probs = ([
+ float(x) for x in result["end_top_log_probs"].flat
+ ])
+ end_top_index = [int(x) for x in result["end_top_index"].flat]
+
+ cls_logits = float(result["cls_logits"].flat[0])
+ cur_results.append(
+ squad_utils.RawResult(
+ unique_id=unique_id,
+ start_top_log_probs=start_top_log_probs,
+ start_top_index=start_top_index,
+ end_top_log_probs=end_top_log_probs,
+ end_top_index=end_top_index,
+ cls_logits=cls_logits))
+ if len(cur_results) % 1000 == 0:
+ logging.info("Processing example: %d", len(cur_results))
+
+ output_prediction_file = os.path.join(input_meta_data["predict_dir"],
+ "predictions.json")
+ output_nbest_file = os.path.join(input_meta_data["predict_dir"],
+ "nbest_predictions.json")
+ output_null_log_odds_file = os.path.join(input_meta_data["predict_dir"],
+ "null_odds.json")
+
+ results = squad_utils.write_predictions(
+ eval_examples, eval_features, cur_results, input_meta_data["n_best_size"],
+ input_meta_data["max_answer_length"], output_prediction_file,
+ output_nbest_file, output_null_log_odds_file, original_data,
+ input_meta_data["start_n_top"], input_meta_data["end_n_top"])
+
+ # Log current results.
+ log_str = "Result | "
+ for key, val in results.items():
+ log_str += "{} {} | ".format(key, val)
+ logging.info(log_str)
+ with eval_summary_writer.as_default():
+ tf.summary.scalar("best_f1", results["best_f1"], step=current_step)
+ tf.summary.scalar("best_exact", results["best_exact"], step=current_step)
+ eval_summary_writer.flush()
+ return results["best_f1"]
+
+
+def get_qaxlnet_model(model_config, run_config, start_n_top, end_n_top):
+ model = modeling.QAXLNetModel(
+ model_config,
+ run_config,
+ start_n_top=start_n_top,
+ end_n_top=end_n_top,
+ name="model")
+ return model
+
+
+def main(unused_argv):
+ del unused_argv
+ strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=FLAGS.strategy_type,
+ tpu_address=FLAGS.tpu)
+ if strategy:
+ logging.info("***** Number of cores used : %d",
+ strategy.num_replicas_in_sync)
+ train_input_fn = functools.partial(data_utils.get_squad_input_data,
+ FLAGS.train_batch_size, FLAGS.seq_len,
+ FLAGS.query_len, strategy, True,
+ FLAGS.train_tfrecord_path)
+
+ test_input_fn = functools.partial(data_utils.get_squad_input_data,
+ FLAGS.test_batch_size, FLAGS.seq_len,
+ FLAGS.query_len, strategy, False,
+ FLAGS.test_tfrecord_path)
+
+ total_training_steps = FLAGS.train_steps
+ steps_per_loop = FLAGS.iterations
+ eval_steps = int(FLAGS.test_data_size / FLAGS.test_batch_size)
+
+ optimizer, learning_rate_fn = optimization.create_optimizer(
+ FLAGS.learning_rate,
+ total_training_steps,
+ FLAGS.warmup_steps,
+ adam_epsilon=FLAGS.adam_epsilon)
+ model_config = xlnet_config.XLNetConfig(FLAGS)
+ run_config = xlnet_config.create_run_config(True, False, FLAGS)
+ input_meta_data = {}
+ input_meta_data["start_n_top"] = FLAGS.start_n_top
+ input_meta_data["end_n_top"] = FLAGS.end_n_top
+ input_meta_data["lr_layer_decay_rate"] = FLAGS.lr_layer_decay_rate
+ input_meta_data["predict_dir"] = FLAGS.predict_dir
+ input_meta_data["n_best_size"] = FLAGS.n_best_size
+ input_meta_data["max_answer_length"] = FLAGS.max_answer_length
+ input_meta_data["test_batch_size"] = FLAGS.test_batch_size
+ input_meta_data["batch_size_per_core"] = int(FLAGS.train_batch_size /
+ strategy.num_replicas_in_sync)
+ input_meta_data["mem_len"] = FLAGS.mem_len
+ model_fn = functools.partial(get_qaxlnet_model, model_config, run_config,
+ FLAGS.start_n_top, FLAGS.end_n_top)
+ eval_examples = squad_utils.read_squad_examples(
+ FLAGS.predict_file, is_training=False)
+ if FLAGS.test_feature_path:
+ logging.info("start reading pickle file...")
+ with tf.io.gfile.GFile(FLAGS.test_feature_path, "rb") as f:
+ eval_features = pickle.load(f)
+ logging.info("finishing reading pickle file...")
+ else:
+ sp_model = spm.SentencePieceProcessor()
+ sp_model.LoadFromSerializedProto(
+ tf.io.gfile.GFile(FLAGS.spiece_model_file, "rb").read())
+ spm_basename = os.path.basename(FLAGS.spiece_model_file)
+ eval_features = squad_utils.create_eval_data(
+ spm_basename, sp_model, eval_examples, FLAGS.max_seq_length,
+ FLAGS.max_query_length, FLAGS.doc_stride, FLAGS.uncased)
+
+ with tf.io.gfile.GFile(FLAGS.predict_file) as f:
+ original_data = json.load(f)["data"]
+ eval_fn = functools.partial(run_evaluation, strategy, test_input_fn,
+ eval_examples, eval_features, original_data,
+ eval_steps, input_meta_data)
+
+ training_utils.train(
+ strategy=strategy,
+ model_fn=model_fn,
+ input_meta_data=input_meta_data,
+ eval_fn=eval_fn,
+ metric_fn=None,
+ train_input_fn=train_input_fn,
+ init_checkpoint=FLAGS.init_checkpoint,
+ init_from_transformerxl=FLAGS.init_from_transformerxl,
+ total_training_steps=total_training_steps,
+ steps_per_loop=steps_per_loop,
+ optimizer=optimizer,
+ learning_rate_fn=learning_rate_fn,
+ model_dir=FLAGS.model_dir,
+ save_steps=FLAGS.save_steps)
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/nlp/xlnet/squad_utils.py b/official/legacy/xlnet/squad_utils.py
similarity index 99%
rename from official/nlp/xlnet/squad_utils.py
rename to official/legacy/xlnet/squad_utils.py
index 44a7b7deed0935ccc7991d8390a7922a48e02206..641e8818f48bcef581bcc4c508c042170b5c8423 100644
--- a/official/nlp/xlnet/squad_utils.py
+++ b/official/legacy/xlnet/squad_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -32,8 +32,8 @@ import numpy as np
import six
import tensorflow as tf
-from official.nlp.xlnet import data_utils
-from official.nlp.xlnet import preprocess_utils
+from official.legacy.xlnet import data_utils
+from official.legacy.xlnet import preprocess_utils
SPIECE_UNDERLINE = u"▁"
diff --git a/official/nlp/xlnet/training_utils.py b/official/legacy/xlnet/training_utils.py
similarity index 98%
rename from official/nlp/xlnet/training_utils.py
rename to official/legacy/xlnet/training_utils.py
index 45afaa76d621046d37cb39d5c4acdd509f98c3da..5fd924e8bbf8bba1b3c17f80f9c145673a793bbb 100644
--- a/official/nlp/xlnet/training_utils.py
+++ b/official/legacy/xlnet/training_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,8 +21,8 @@ from typing import Any, Callable, Dict, Optional, Text
from absl import logging
import tensorflow as tf
-from official.nlp.bert import model_training_utils
-from official.nlp.xlnet import data_utils
+from official.legacy.bert import model_training_utils
+from official.legacy.xlnet import data_utils
# pytype: disable=attribute-error
# pylint: disable=g-bare-generic,unused-import
diff --git a/official/nlp/xlnet/xlnet_config.py b/official/legacy/xlnet/xlnet_config.py
similarity index 98%
rename from official/nlp/xlnet/xlnet_config.py
rename to official/legacy/xlnet/xlnet_config.py
index c0f51955b57289884fc522cc02c3d3db6404bf76..d8ee7e6a07fac9000535969e3bb4a0f5493ed31e 100644
--- a/official/nlp/xlnet/xlnet_config.py
+++ b/official/legacy/xlnet/xlnet_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/xlnet/xlnet_modeling.py b/official/legacy/xlnet/xlnet_modeling.py
similarity index 99%
rename from official/nlp/xlnet/xlnet_modeling.py
rename to official/legacy/xlnet/xlnet_modeling.py
index b48aff4e795444c176cc862dcb98b01e76c39c7d..f03354f62ab4cb266fa8d4fcb93a96b46711579a 100644
--- a/official/nlp/xlnet/xlnet_modeling.py
+++ b/official/legacy/xlnet/xlnet_modeling.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,9 +18,8 @@ import copy
import warnings
import tensorflow as tf
-
+from official.legacy.xlnet import data_utils
from official.nlp.modeling import networks
-from official.nlp.xlnet import data_utils
def gelu(x):
diff --git a/official/modeling/__init__.py b/official/modeling/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/modeling/__init__.py
+++ b/official/modeling/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/__init__.py b/official/modeling/activations/__init__.py
index 086e1fb975f8517dcff3c020f5fd932f6e55edc7..24c0d2606c19d752cde41fc05076920ee88c1b6d 100644
--- a/official/modeling/activations/__init__.py
+++ b/official/modeling/activations/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,6 +14,7 @@
"""Activations package definition."""
from official.modeling.activations.gelu import gelu
+from official.modeling.activations.mish import mish
from official.modeling.activations.relu import relu6
from official.modeling.activations.sigmoid import hard_sigmoid
from official.modeling.activations.swish import hard_swish
diff --git a/official/modeling/activations/gelu.py b/official/modeling/activations/gelu.py
index a73294aa5493747af66d9bbbc2cc26914600d7cf..1ca79ebb662c3924d82b712de31e92c985334a40 100644
--- a/official/modeling/activations/gelu.py
+++ b/official/modeling/activations/gelu.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/gelu_test.py b/official/modeling/activations/gelu_test.py
index cfe1950d9f112c3c33421c410ecdd4ceedd6f1d7..727a714e38bbab2e2549a49441f3ce0282eeaf21 100644
--- a/official/modeling/activations/gelu_test.py
+++ b/official/modeling/activations/gelu_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/mish.py b/official/modeling/activations/mish.py
new file mode 100644
index 0000000000000000000000000000000000000000..063a4a737bf811061b021e845fa10df3b74ccba5
--- /dev/null
+++ b/official/modeling/activations/mish.py
@@ -0,0 +1,38 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Self Regularized Non-Monotonic Activation Function."""
+
+import tensorflow as tf
+
+from tensorflow_addons.utils import types
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+def mish(x: types.TensorLike) -> tf.Tensor:
+ """Mish activation function.
+
+ Mish: A Self Regularized Non-Monotonic Activation Function
+ https://arxiv.org/pdf/1908.08681.pdf
+
+ Mish(x) = x * tanh(ln(1+e^x))
+
+ Args:
+ x: A `Tensor` representing preactivation values.
+
+ Returns:
+ The activation value.
+ """
+ x = tf.convert_to_tensor(x)
+ return x * tf.tanh(tf.nn.softplus(x))
diff --git a/official/modeling/activations/mish_test.py b/official/modeling/activations/mish_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..15eff91d160cc0ef3677e440ebd005c95043f499
--- /dev/null
+++ b/official/modeling/activations/mish_test.py
@@ -0,0 +1,32 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for the customized Mish activation."""
+
+import tensorflow as tf
+
+from tensorflow.python.keras import keras_parameterized # pylint: disable=g-direct-tensorflow-import
+from official.modeling import activations
+
+
+@keras_parameterized.run_all_keras_modes
+class MishTest(keras_parameterized.TestCase):
+
+ def test_mish(self):
+ x = tf.constant([1.0, 0.0])
+ self.assertAllClose([0.86509839, 0.0], activations.mish(x))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/modeling/activations/relu.py b/official/modeling/activations/relu.py
index b3941b2f3462fa6a3eea28e023a4450bcc070797..410be29d266d6b5b06f221ebe9588abf70e952a2 100644
--- a/official/modeling/activations/relu.py
+++ b/official/modeling/activations/relu.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/relu_test.py b/official/modeling/activations/relu_test.py
index 215f189ea9a00ed93bf012d33429fd82b3dc7ca6..45a8339e2a2c8cf1e95608d322eef92a127359d8 100644
--- a/official/modeling/activations/relu_test.py
+++ b/official/modeling/activations/relu_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/sigmoid.py b/official/modeling/activations/sigmoid.py
index 277463040e784325f2b47a5492c98d6e3283ad08..a3fc77fa5eaad267a9ce70e1fd0e0ddb5d753d4d 100644
--- a/official/modeling/activations/sigmoid.py
+++ b/official/modeling/activations/sigmoid.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/sigmoid_test.py b/official/modeling/activations/sigmoid_test.py
index 6aad90ef3645b08708dbfde155654070c40d72ce..e5a1a61f97faead4fd53387cab05b3cecd79fe76 100644
--- a/official/modeling/activations/sigmoid_test.py
+++ b/official/modeling/activations/sigmoid_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/swish.py b/official/modeling/activations/swish.py
index ea79985e3006f1400350601d9b857e947287ace1..3d9372370ceb91c8fb7d762e6fb97834304d8b69 100644
--- a/official/modeling/activations/swish.py
+++ b/official/modeling/activations/swish.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/activations/swish_test.py b/official/modeling/activations/swish_test.py
index 3cb9495d8d19a3b89e4a9b2db0679090ac1e3e9d..1eb5fa2a94f8466425906aeff600c851e19e7b08 100644
--- a/official/modeling/activations/swish_test.py
+++ b/official/modeling/activations/swish_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/experimental/tf2_utils_2x_wide.py b/official/modeling/fast_training/experimental/tf2_utils_2x_wide.py
index 16940cffa153104ca9839d80bd0021acc8bdf2fe..af0760277ae8ce08bfbee9d253b5beea392a5eb9 100644
--- a/official/modeling/fast_training/experimental/tf2_utils_2x_wide.py
+++ b/official/modeling/fast_training/experimental/tf2_utils_2x_wide.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/experimental/tf2_utils_2x_wide_test.py b/official/modeling/fast_training/experimental/tf2_utils_2x_wide_test.py
index 25d6e7628d16dfcc83cc6608da73d5ef31834751..2b95110b606f685669e775fcc82447ced775a253 100644
--- a/official/modeling/fast_training/experimental/tf2_utils_2x_wide_test.py
+++ b/official/modeling/fast_training/experimental/tf2_utils_2x_wide_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/policies.py b/official/modeling/fast_training/progressive/policies.py
index b4f7c3f018bbf45896ca3eb5b3a327dcd9b4dfb7..52c3e73b486b20e88c32e96774303aa5f16e7f01 100644
--- a/official/modeling/fast_training/progressive/policies.py
+++ b/official/modeling/fast_training/progressive/policies.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/train.py b/official/modeling/fast_training/progressive/train.py
index f547ac9a56b0843abce6f2cdeccd6c2cd9d55217..612a485c6b48fe0bcdbe9bc0fa1fd36f282edd0d 100644
--- a/official/modeling/fast_training/progressive/train.py
+++ b/official/modeling/fast_training/progressive/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/train_lib.py b/official/modeling/fast_training/progressive/train_lib.py
index baa132e197bb621b276c7a6471d07fb402a804c0..1fdb1d1c23c03152741ba8572df2dc40a43cd072 100644
--- a/official/modeling/fast_training/progressive/train_lib.py
+++ b/official/modeling/fast_training/progressive/train_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/train_lib_test.py b/official/modeling/fast_training/progressive/train_lib_test.py
index f91faf902ebad5a7af92907fd434f585a580bf3c..fdc35b2e823b13642dd36b71def9ec7c9dfbea84 100644
--- a/official/modeling/fast_training/progressive/train_lib_test.py
+++ b/official/modeling/fast_training/progressive/train_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/trainer.py b/official/modeling/fast_training/progressive/trainer.py
index 685ec395045469c1120be0d02f6575e1b65fc070..af24af52787a98e34a6a4179a8a7177f62539bd8 100644
--- a/official/modeling/fast_training/progressive/trainer.py
+++ b/official/modeling/fast_training/progressive/trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/fast_training/progressive/trainer_test.py b/official/modeling/fast_training/progressive/trainer_test.py
index a0c5d82a55dc94fc5c6f16dfe94f047b56ebf05f..d38e1757caa6a7400658515c1c99560b38366206 100644
--- a/official/modeling/fast_training/progressive/trainer_test.py
+++ b/official/modeling/fast_training/progressive/trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -226,9 +226,13 @@ class TrainerWithMaskedLMTaskTest(tf.test.TestCase, parameterized.TestCase):
task = TestPolicy(None, config.task)
trainer = trainer_lib.ProgressiveTrainer(config, task, self.get_temp_dir())
if mixed_precision_dtype != 'float16':
- self.assertIsInstance(trainer.optimizer, tf.keras.optimizers.SGD)
+ self.assertIsInstance(
+ trainer.optimizer,
+ (tf.keras.optimizers.SGD, tf.keras.optimizers.legacy.SGD))
elif mixed_precision_dtype == 'float16' and loss_scale is None:
- self.assertIsInstance(trainer.optimizer, tf.keras.optimizers.SGD)
+ self.assertIsInstance(
+ trainer.optimizer,
+ (tf.keras.optimizers.SGD, tf.keras.optimizers.legacy.SGD))
metrics = trainer.train(tf.convert_to_tensor(5, dtype=tf.int32))
self.assertIn('training_loss', metrics)
diff --git a/official/modeling/fast_training/progressive/utils.py b/official/modeling/fast_training/progressive/utils.py
index 192170cb87825de6972ab4a85a6b556ee40600c4..2bfd1d6be264390f52596b5cbbd82328e89ba964 100644
--- a/official/modeling/fast_training/progressive/utils.py
+++ b/official/modeling/fast_training/progressive/utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,10 +18,10 @@ from absl import logging
import tensorflow as tf
# pylint: disable=g-direct-tensorflow-import
-from tensorflow.python.training.tracking import tracking
+from tensorflow.python.trackable import autotrackable
-class VolatileTrackable(tracking.AutoTrackable):
+class VolatileTrackable(autotrackable.AutoTrackable):
"""A util class to keep Trackables that might change instances."""
def __init__(self, **kwargs):
diff --git a/official/modeling/grad_utils.py b/official/modeling/grad_utils.py
index 1113d39d5e6f19c9c8fba9e8d8b5c3f99e4e6fba..22479e6ff3bd40dd1fb900fda9145318129aaaa2 100644
--- a/official/modeling/grad_utils.py
+++ b/official/modeling/grad_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/grad_utils_test.py b/official/modeling/grad_utils_test.py
index cc9c1912be268c9952c979564eacce6d0c0ed4a8..ded7794ab58c6f0a3e8f18222a7886ffd23a0e83 100644
--- a/official/modeling/grad_utils_test.py
+++ b/official/modeling/grad_utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/__init__.py b/official/modeling/hyperparams/__init__.py
index bcbc0aedd3d6013c14c641d9e61a0a717f188ec5..5503ad8e478ce624bb94219b4bc58c35387b30a9 100644
--- a/official/modeling/hyperparams/__init__.py
+++ b/official/modeling/hyperparams/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/base_config.py b/official/modeling/hyperparams/base_config.py
index f0afca0909eb0a63d54ae83b4d5fc44515a30c1e..f68b16b3645bde31152ff19f05cc2955bf374f1f 100644
--- a/official/modeling/hyperparams/base_config.py
+++ b/official/modeling/hyperparams/base_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/base_config_test.py b/official/modeling/hyperparams/base_config_test.py
index 21d0aaa1c3ee56884505e4ab5f72bc0212ceb74d..b27352af895300cf2aecaabc4a14baa7a2ef4790 100644
--- a/official/modeling/hyperparams/base_config_test.py
+++ b/official/modeling/hyperparams/base_config_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/oneof.py b/official/modeling/hyperparams/oneof.py
index 61591496eb41de44e6de9eb248c4460498a9a078..298b94fdab532c79037781f19f5a0f579aa05aa7 100644
--- a/official/modeling/hyperparams/oneof.py
+++ b/official/modeling/hyperparams/oneof.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/oneof_test.py b/official/modeling/hyperparams/oneof_test.py
index 2cde73c1545dd04894d0353b22e6254922717829..2ac29869a7aab025d75bae915d793eec0a716294 100644
--- a/official/modeling/hyperparams/oneof_test.py
+++ b/official/modeling/hyperparams/oneof_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/hyperparams/params_dict.py b/official/modeling/hyperparams/params_dict.py
index 76b0446f0ef407488464b1590a1f63765c8bde54..8da29ad7ddecabe6d6dd0f90da0f7fd4283314c9 100644
--- a/official/modeling/hyperparams/params_dict.py
+++ b/official/modeling/hyperparams/params_dict.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -41,15 +41,15 @@ _PARAM_RE = re.compile(
_CONST_VALUE_RE = re.compile(r'(\d.*|-\d.*|None)')
-# Yaml loader with an implicit resolver to parse float decimal and exponential
+# Yaml LOADER with an implicit resolver to parse float decimal and exponential
# format. The regular experission parse the following cases:
# 1- Decimal number with an optional exponential term.
# 2- Integer number with an exponential term.
# 3- Decimal number with an optional exponential term.
# 4- Decimal number.
-LOADER = yaml.SafeLoader
-LOADER.add_implicit_resolver(
+_LOADER = yaml.SafeLoader
+_LOADER.add_implicit_resolver(
'tag:yaml.org,2002:float',
re.compile(r'''
^(?:[-+]?(?:[0-9][0-9_]*)\\.[0-9_]*(?:[eE][-+]?[0-9]+)?
@@ -288,42 +288,42 @@ class ParamsDict(object):
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v != right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
elif '!=' in restriction:
tokens = restriction.split('!=')
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v == right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
elif '<' in restriction:
tokens = restriction.split('<')
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v >= right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
elif '<=' in restriction:
tokens = restriction.split('<=')
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v > right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
elif '>' in restriction:
tokens = restriction.split('>')
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v <= right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
elif '>=' in restriction:
tokens = restriction.split('>=')
_, left_v, _, right_v = _get_kvs(tokens, params_dict)
if left_v < right_v:
raise KeyError(
- 'Found inconsistncy between key `{}` and key `{}`.'.format(
+ 'Found inconsistency between key `{}` and key `{}`.'.format(
tokens[0], tokens[1]))
else:
raise ValueError('Unsupported relation in restriction.')
@@ -332,7 +332,7 @@ class ParamsDict(object):
def read_yaml_to_params_dict(file_path: str):
"""Reads a YAML file to a ParamsDict."""
with tf.io.gfile.GFile(file_path, 'r') as f:
- params_dict = yaml.load(f, Loader=LOADER)
+ params_dict = yaml.load(f, Loader=_LOADER)
return ParamsDict(params_dict)
@@ -453,7 +453,7 @@ def override_params_dict(params, dict_or_string_or_yaml_file, is_strict):
nested_csv_str_to_json_str(dict_or_string_or_yaml_file))
except ValueError:
pass
- params_dict = yaml.load(dict_or_string_or_yaml_file, Loader=LOADER)
+ params_dict = yaml.load(dict_or_string_or_yaml_file, Loader=_LOADER)
if isinstance(params_dict, dict):
params.override(params_dict, is_strict)
else:
diff --git a/official/modeling/hyperparams/params_dict_test.py b/official/modeling/hyperparams/params_dict_test.py
index 248a81652a496266fb9656d40f77e665e8606f10..145590a4c2ce03b0c578b50c0188d9a7b549ceda 100644
--- a/official/modeling/hyperparams/params_dict_test.py
+++ b/official/modeling/hyperparams/params_dict_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/__init__.py b/official/modeling/multitask/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/modeling/multitask/__init__.py
+++ b/official/modeling/multitask/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/base_model.py b/official/modeling/multitask/base_model.py
index 835d7e3443dd8991c32eb12c570479640b58487a..6db013400f5e93a817a7828c635f33956a660d60 100644
--- a/official/modeling/multitask/base_model.py
+++ b/official/modeling/multitask/base_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -43,3 +43,12 @@ class MultiTaskBaseModel(tf.Module):
def initialize(self):
"""Optional function that loads a pre-train checkpoint."""
return
+
+ def build(self):
+ """Builds the networks for tasks to make sure variables are created."""
+ # Try to build all sub tasks.
+ for task_model in self._sub_tasks.values():
+ # Assumes all the tf.Module models are built because we don't have any
+ # way to check them.
+ if isinstance(task_model, tf.keras.Model) and not task_model.built:
+ _ = task_model(task_model.inputs)
diff --git a/official/modeling/multitask/base_trainer.py b/official/modeling/multitask/base_trainer.py
index 45cdb6cdde32866c31f23804df8b1efac521eee8..e3bf18718ed7adaa476af4f8aea9b30b3b820603 100644
--- a/official/modeling/multitask/base_trainer.py
+++ b/official/modeling/multitask/base_trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/base_trainer_test.py b/official/modeling/multitask/base_trainer_test.py
index 2427ff85f2af4c79fb3f7f3cc40c9fc82c0a7e61..2eb5acd252f5054f438aa2def1c6ea16e771c8db 100644
--- a/official/modeling/multitask/base_trainer_test.py
+++ b/official/modeling/multitask/base_trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/configs.py b/official/modeling/multitask/configs.py
index 453db3475072086606f0a979758524c5f789d454..a77d2c0956030a8899a8474627416e319ddfbd39 100644
--- a/official/modeling/multitask/configs.py
+++ b/official/modeling/multitask/configs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,6 +19,7 @@ import dataclasses
from official.core import config_definitions as cfg
from official.modeling import hyperparams
+from official.modeling.privacy import configs as dp_configs
@dataclasses.dataclass
@@ -35,6 +36,8 @@ class MultiTaskConfig(hyperparams.Config):
init_checkpoint: str = ""
model: hyperparams.Config = None
task_routines: Tuple[TaskRoutine, ...] = ()
+ differential_privacy_config: Optional[
+ dp_configs.DifferentialPrivacyConfig] = None
@dataclasses.dataclass
diff --git a/official/modeling/multitask/evaluator.py b/official/modeling/multitask/evaluator.py
index c896e2c8811c828c2eb0199ae5ade8103ce65184..9433a318afb51b459079fdad9af3edcf1c1a4613 100644
--- a/official/modeling/multitask/evaluator.py
+++ b/official/modeling/multitask/evaluator.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/evaluator_test.py b/official/modeling/multitask/evaluator_test.py
index 4725e63e5f996fa3432557906dd8548f08e99c53..660adcfc34fe957fdc5531334156e0391cdb4665 100644
--- a/official/modeling/multitask/evaluator_test.py
+++ b/official/modeling/multitask/evaluator_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/interleaving_trainer.py b/official/modeling/multitask/interleaving_trainer.py
index 1bc943dfb99696fbdcc3ec3517a9bbf7aea51e34..180e00ceeed14499bd290951908d8e7e8e179bf7 100644
--- a/official/modeling/multitask/interleaving_trainer.py
+++ b/official/modeling/multitask/interleaving_trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -31,7 +31,9 @@ class MultiTaskInterleavingTrainer(base_trainer.MultiTaskBaseTrainer):
multi_task: multitask.MultiTask,
multi_task_model: Union[tf.keras.Model,
base_model.MultiTaskBaseModel],
- optimizer: tf.optimizers.Optimizer,
+ optimizer: Union[tf.optimizers.Optimizer,
+ tf.keras.optimizers.experimental.Optimizer,
+ tf.keras.optimizers.legacy.Optimizer],
task_sampler: sampler.TaskSampler,
trainer_options=None):
super().__init__(
@@ -69,6 +71,13 @@ class MultiTaskInterleavingTrainer(base_trainer.MultiTaskBaseTrainer):
name: orbit.utils.create_global_step() for name in self.multi_task.tasks
}
+ # If the new Keras optimizer is used, we require all model variables are
+ # created before the training and let the optimizer to create the slot
+ # variable all together.
+ if isinstance(optimizer, tf.keras.optimizers.experimental.Optimizer):
+ multi_task_model.build()
+ optimizer.build(multi_task_model.trainable_variables)
+
def task_step_counter(self, name):
return self._task_step_counters[name]
diff --git a/official/modeling/multitask/interleaving_trainer_test.py b/official/modeling/multitask/interleaving_trainer_test.py
index a2b1da1b60d983817b029128737ce11275dfb549..6f871713ca7074444553e5c751dfc0d11cb35923 100644
--- a/official/modeling/multitask/interleaving_trainer_test.py
+++ b/official/modeling/multitask/interleaving_trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/multitask.py b/official/modeling/multitask/multitask.py
index 85a345382a33871bd587767166f73faef8454595..4a1b5d07bf6c0d2356b8046f15eac4953e561f64 100644
--- a/official/modeling/multitask/multitask.py
+++ b/official/modeling/multitask/multitask.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,9 +23,11 @@ from official.core import task_factory
from official.modeling import optimization
from official.modeling.multitask import base_model
from official.modeling.multitask import configs
+from official.modeling.privacy import configs as dp_configs
OptimizationConfig = optimization.OptimizationConfig
RuntimeConfig = config_definitions.RuntimeConfig
+DifferentialPrivacyConfig = dp_configs.DifferentialPrivacyConfig
class MultiTask(tf.Module, metaclass=abc.ABCMeta):
@@ -93,9 +95,11 @@ class MultiTask(tf.Module, metaclass=abc.ABCMeta):
@classmethod
def create_optimizer(cls,
optimizer_config: OptimizationConfig,
- runtime_config: Optional[RuntimeConfig] = None):
+ runtime_config: Optional[RuntimeConfig] = None,
+ dp_config: Optional[DifferentialPrivacyConfig] = None):
return base_task.Task.create_optimizer(
- optimizer_config=optimizer_config, runtime_config=runtime_config)
+ optimizer_config=optimizer_config, runtime_config=runtime_config,
+ dp_config=dp_config)
def joint_train_step(self, task_inputs,
multi_task_model: base_model.MultiTaskBaseModel,
@@ -134,10 +138,10 @@ class MultiTask(tf.Module, metaclass=abc.ABCMeta):
self.tasks[name].process_metrics(task_metrics[name], labels, outputs,
**kwargs)
- # Scales loss as the default gradients allreduce performs sum inside
- # the optimizer.
- scaled_loss = total_loss / tf.distribute.get_strategy(
- ).num_replicas_in_sync
+ # Scales loss as the default gradients allreduce performs sum inside
+ # the optimizer.
+ scaled_loss = total_loss / tf.distribute.get_strategy(
+ ).num_replicas_in_sync
tvars = multi_task_model.trainable_variables
grads = tape.gradient(scaled_loss, tvars)
optimizer.apply_gradients(list(zip(grads, tvars)))
diff --git a/official/modeling/multitask/task_sampler.py b/official/modeling/multitask/task_sampler.py
index 1c365a9df09866636f3a6bfa4ef78be8dd8ff624..5e062bd45b5c2ca8f1df515f75981736e17acc83 100644
--- a/official/modeling/multitask/task_sampler.py
+++ b/official/modeling/multitask/task_sampler.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/task_sampler_test.py b/official/modeling/multitask/task_sampler_test.py
index 5b4695049952dab250f9fdac3d6bfd134e2c644d..8b3d95ff462ccbea07fd618165a97c2ae52e034d 100644
--- a/official/modeling/multitask/task_sampler_test.py
+++ b/official/modeling/multitask/task_sampler_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/multitask/test_utils.py b/official/modeling/multitask/test_utils.py
index aa831223817b4968615f5aa87c1e3fbc39021218..166608f43aee8a9fa529bdd05aace2302b55e8e5 100644
--- a/official/modeling/multitask/test_utils.py
+++ b/official/modeling/multitask/test_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,6 +28,8 @@ class MockFooModel(tf.keras.Model):
super().__init__(*args, **kwargs)
self._share_layer = shared_layer
self._foo_specific_layer = tf.keras.layers.Dense(1)
+ self.inputs = {"foo": tf.keras.Input(shape=(2,), dtype=tf.float32),
+ "bar": tf.keras.Input(shape=(2,), dtype=tf.float32)}
def call(self, inputs):
self.add_loss(tf.zeros((1,), dtype=tf.float32))
@@ -39,11 +41,13 @@ class MockFooModel(tf.keras.Model):
class MockBarModel(tf.keras.Model):
+ """A mock model can only consume 'bar' inputs."""
def __init__(self, shared_layer, *args, **kwargs):
super().__init__(*args, **kwargs)
self._share_layer = shared_layer
self._bar_specific_layer = tf.keras.layers.Dense(1)
+ self.inputs = {"bar": tf.keras.Input(shape=(2,), dtype=tf.float32)}
def call(self, inputs):
self.add_loss(tf.zeros((2,), dtype=tf.float32))
diff --git a/official/modeling/multitask/train_lib.py b/official/modeling/multitask/train_lib.py
index 62b022030937660720aed2d4417355f86a6fd7c8..920acbfcfa01664c89cdeb2aa66fb93c8ba3ed1b 100644
--- a/official/modeling/multitask/train_lib.py
+++ b/official/modeling/multitask/train_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,7 +15,7 @@
"""Multitask training driver library."""
# pytype: disable=attribute-error
import os
-from typing import Any, List, Optional, Tuple
+from typing import Any, List, Mapping, Optional, Tuple, Union
from absl import logging
import orbit
import tensorflow as tf
@@ -44,8 +44,12 @@ def run_experiment(
mode: str,
params: configs.MultiTaskExperimentConfig,
model_dir: str,
- trainer: base_trainer.MultiTaskBaseTrainer = None
-) -> base_model.MultiTaskBaseModel:
+ run_post_eval: bool = False,
+ trainer: base_trainer.MultiTaskBaseTrainer = None,
+ best_ckpt_exporter_creator: Optional[Any] = train_utils
+ .maybe_create_best_ckpt_exporter
+) -> Union[base_model.MultiTaskBaseModel, Tuple[base_model.MultiTaskBaseModel,
+ Mapping[Any, Any]]]:
"""Runs train/eval configured by the experiment params.
Args:
@@ -56,8 +60,11 @@ def run_experiment(
or 'continuous_eval'.
params: ExperimentConfig instance.
model_dir: A 'str', a path to store model checkpoints and summaries.
+ run_post_eval: Whether to run post eval once after training, metrics logs
+ are returned.
trainer: (optional) A multi-task trainer to use. If none is provided, a
default one will be created based on `params`.
+ best_ckpt_exporter_creator: A functor for creating best checkpoint exporter.
Returns:
model: `base_model.MultiTaskBaseModel` instance.
@@ -66,8 +73,7 @@ def run_experiment(
is_training = 'train' in mode
is_eval = 'eval' in mode
with distribution_strategy.scope():
- optimizer = task.create_optimizer(params.trainer.optimizer_config,
- params.runtime)
+ optimizer = train_utils.create_optimizer(task, params)
kwargs = dict(multi_task=task, multi_task_model=model, optimizer=optimizer)
if params.trainer.trainer_type == 'interleaving':
sampler = task_sampler.get_task_sampler(params.trainer.task_sampler,
@@ -83,8 +89,7 @@ def run_experiment(
model=model,
eval_steps=eval_steps,
global_step=trainer.global_step if is_training else None,
- checkpoint_exporter=train_utils.maybe_create_best_ckpt_exporter(
- params, model_dir))
+ checkpoint_exporter=best_ckpt_exporter_creator(params, model_dir))
else:
evaluator = None
@@ -95,7 +100,6 @@ def run_experiment(
checkpoint = evaluator.checkpoint
global_step = evaluator.global_step
- # TODO(hongkuny,haozhangthu): Revisit initialization method.
checkpoint_manager = tf.train.CheckpointManager(
checkpoint,
directory=model_dir,
@@ -140,7 +144,11 @@ def run_experiment(
else:
raise NotImplementedError('The mode is not implemented: %s' % mode)
- return model
+ if run_post_eval:
+ return model, evaluator.evaluate(
+ tf.convert_to_tensor(params.trainer.validation_steps)) # pytype: disable=bad-return-type # typed-keras
+ else:
+ return model
def run_experiment_with_multitask_eval(
@@ -153,7 +161,10 @@ def run_experiment_with_multitask_eval(
model_dir: str,
run_post_eval: bool = False,
save_summary: bool = True,
- trainer: Optional[core_lib.Trainer] = None) -> Tuple[Any, Any]:
+ trainer: Optional[core_lib.Trainer] = None,
+ best_ckpt_exporter_creator: Optional[Any] = train_utils
+ .maybe_create_best_ckpt_exporter,
+) -> Tuple[Any, Any]:
"""Runs train/eval configured by the experiment params.
Args:
@@ -170,6 +181,7 @@ def run_experiment_with_multitask_eval(
trainer: the core_lib.Trainer instance. It should be created within the
strategy.scope(). If not provided, an instance will be created by default
if `mode` contains 'train'.
+ best_ckpt_exporter_creator: A functor for creating best checkpoint exporter.
Returns:
model: `tf.keras.Model` instance.
@@ -183,8 +195,7 @@ def run_experiment_with_multitask_eval(
config=params,
task=train_task,
model=train_task.build_model(),
- optimizer=train_task.create_optimizer(params.trainer.optimizer_config,
- params.runtime),
+ optimizer=train_utils.create_optimizer(train_task, params),
train=True,
evaluate=False)
else:
@@ -200,8 +211,7 @@ def run_experiment_with_multitask_eval(
model=model,
global_step=trainer.global_step if is_training else None,
eval_steps=eval_steps,
- checkpoint_exporter=train_utils.maybe_create_best_ckpt_exporter(
- params, model_dir))
+ checkpoint_exporter=best_ckpt_exporter_creator(params, model_dir))
else:
evaluator = None
diff --git a/official/modeling/multitask/train_lib_test.py b/official/modeling/multitask/train_lib_test.py
index 6f90a47f3dca42381bf0024fc8c22a835d3dfd52..acdefa584e7ec13765ef88d2068c61ca1ea528f9 100644
--- a/official/modeling/multitask/train_lib_test.py
+++ b/official/modeling/multitask/train_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -58,8 +58,9 @@ class TrainLibTest(tf.test.TestCase, parameterized.TestCase):
strategy_combinations.one_device_strategy_gpu,
],
mode='eager',
+ optimizer=['sgd_experimental', 'sgd'],
flag_mode=['train', 'eval', 'train_and_eval']))
- def test_end_to_end(self, distribution_strategy, flag_mode):
+ def test_end_to_end(self, distribution_strategy, optimizer, flag_mode):
model_dir = self.get_temp_dir()
experiment_config = configs.MultiTaskExperimentConfig(
task=configs.MultiTaskConfig(
@@ -70,6 +71,7 @@ class TrainLibTest(tf.test.TestCase, parameterized.TestCase):
task_name='bar', task_config=test_utils.BarConfig()))))
experiment_config = params_dict.override_params_dict(
experiment_config, self._test_config, is_strict=False)
+ experiment_config.trainer.optimizer_config.optimizer.type = optimizer
with distribution_strategy.scope():
test_multitask = multitask.MultiTask.from_config(experiment_config.task)
model = test_utils.MockMultiTaskModel()
diff --git a/official/modeling/optimization/__init__.py b/official/modeling/optimization/__init__.py
index ee2b99603b0caf5338c0ecd1b78ef0b1577b64c1..c02b2b9a9133c49c0482e52ac51bd3623f5b9117 100644
--- a/official/modeling/optimization/__init__.py
+++ b/official/modeling/optimization/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/optimization/adafactor_optimizer.py b/official/modeling/optimization/adafactor_optimizer.py
index cea09bda415a7375172d781df3b7f84b3a9da322..b7f1944e61e41f411035a6b61c3d4b6a293a9cbe 100644
--- a/official/modeling/optimization/adafactor_optimizer.py
+++ b/official/modeling/optimization/adafactor_optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/optimization/configs/__init__.py b/official/modeling/optimization/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/modeling/optimization/configs/__init__.py
+++ b/official/modeling/optimization/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/optimization/configs/learning_rate_config.py b/official/modeling/optimization/configs/learning_rate_config.py
index 3904b53dacb83fcb7b85793271f63ee304ad32c0..9af3cb673f8475ef6a77a36d04763e02cb29a9cf 100644
--- a/official/modeling/optimization/configs/learning_rate_config.py
+++ b/official/modeling/optimization/configs/learning_rate_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -216,14 +216,14 @@ class StepCosineLrConfig(base_config.Config):
"""Configuration for stepwise learning rate decay.
This class is a container for the piecewise cosine learning rate scheduling
- configs. It will configure an instance of StepConsineDecayWithOffset keras
+ configs. It will configure an instance of StepCosineDecayWithOffset keras
learning rate schedule.
```python
boundaries: [100000, 110000]
values: [1.0, 0.5]
lr_decayed_fn = (
- lr_schedule.StepConsineDecayWithOffset(
+ lr_schedule.StepCosineDecayWithOffset(
boundaries,
values))
```
@@ -243,7 +243,7 @@ class StepCosineLrConfig(base_config.Config):
[boundaries[n], end] -> values[n+1] to 0.
offset: An int. The offset applied to steps. Defaults to 0.
"""
- name: str = 'StepConsineDecayWithOffset'
+ name: str = 'StepCosineDecayWithOffset'
boundaries: Optional[List[int]] = None
values: Optional[List[float]] = None
offset: int = 0
diff --git a/official/modeling/optimization/configs/optimization_config.py b/official/modeling/optimization/configs/optimization_config.py
index 1bf87e420fb7e36a45f233520baec398d04a8057..f6caf069b3701c0ffbd8edc946b3db916eb89398 100644
--- a/official/modeling/optimization/configs/optimization_config.py
+++ b/official/modeling/optimization/configs/optimization_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -45,8 +45,14 @@ class OptimizerConfig(oneof.OneOfConfig):
"""
type: Optional[str] = None
sgd: opt_cfg.SGDConfig = opt_cfg.SGDConfig()
+ sgd_experimental: opt_cfg.SGDExperimentalConfig = (
+ opt_cfg.SGDExperimentalConfig())
adam: opt_cfg.AdamConfig = opt_cfg.AdamConfig()
+ adam_experimental: opt_cfg.AdamExperimentalConfig = (
+ opt_cfg.AdamExperimentalConfig())
adamw: opt_cfg.AdamWeightDecayConfig = opt_cfg.AdamWeightDecayConfig()
+ adamw_experimental: opt_cfg.AdamWeightDecayExperimentalConfig = (
+ opt_cfg.AdamWeightDecayExperimentalConfig())
lamb: opt_cfg.LAMBConfig = opt_cfg.LAMBConfig()
rmsprop: opt_cfg.RMSPropConfig = opt_cfg.RMSPropConfig()
lars: opt_cfg.LARSConfig = opt_cfg.LARSConfig()
diff --git a/official/modeling/optimization/configs/optimization_config_test.py b/official/modeling/optimization/configs/optimization_config_test.py
index 02b99f592e9ba4f66ccd9e906eee5158b2b1b13e..6fc11fea0223cccf5a8920ae0c99d7753761e253 100644
--- a/official/modeling/optimization/configs/optimization_config_test.py
+++ b/official/modeling/optimization/configs/optimization_config_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/optimization/configs/optimizer_config.py b/official/modeling/optimization/configs/optimizer_config.py
index a4696d26548b491d1131211e418a5f0468411291..300d5c440a15c09fda72e55f0456e4bbb0a22eb8 100644
--- a/official/modeling/optimization/configs/optimizer_config.py
+++ b/official/modeling/optimization/configs/optimizer_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -54,6 +54,27 @@ class SGDConfig(BaseOptimizerConfig):
momentum: float = 0.0
+# TODO(b/216129465): Merge this config with SGDConfig after the experimental
+# optimizer graduates.
+@dataclasses.dataclass
+class SGDExperimentalConfig(BaseOptimizerConfig):
+ """Configuration for SGD optimizer.
+
+ The attributes for this class matches the arguments of
+ `tf.keras.optimizer.experimental.SGD`.
+
+ Attributes:
+ name: name of the optimizer.
+ nesterov: nesterov for SGD optimizer.
+ momentum: momentum for SGD optimizer.
+ jit_compile: if True, jit compile will be used.
+ """
+ name: str = "SGD"
+ nesterov: bool = False
+ momentum: float = 0.0
+ jit_compile: bool = False
+
+
@dataclasses.dataclass
class RMSPropConfig(BaseOptimizerConfig):
"""Configuration for RMSProp optimizer.
@@ -115,6 +136,30 @@ class AdamConfig(BaseOptimizerConfig):
amsgrad: bool = False
+@dataclasses.dataclass
+class AdamExperimentalConfig(BaseOptimizerConfig):
+ """Configuration for experimental Adam optimizer.
+
+ The attributes for this class matches the arguments of
+ `tf.keras.optimizer.experimental.Adam`.
+
+ Attributes:
+ name: name of the optimizer.
+ beta_1: decay rate for 1st order moments.
+ beta_2: decay rate for 2st order moments.
+ epsilon: epsilon value used for numerical stability in Adam optimizer.
+ amsgrad: boolean. Whether to apply AMSGrad variant of this algorithm from
+ the paper "On the Convergence of Adam and beyond".
+ jit_compile: if True, jit compile will be used.
+ """
+ name: str = "Adam"
+ beta_1: float = 0.9
+ beta_2: float = 0.999
+ epsilon: float = 1e-07
+ amsgrad: bool = False
+ jit_compile: bool = False
+
+
@dataclasses.dataclass
class AdamWeightDecayConfig(BaseOptimizerConfig):
"""Configuration for Adam optimizer with weight decay.
@@ -145,6 +190,32 @@ class AdamWeightDecayConfig(BaseOptimizerConfig):
gradient_clip_norm: float = 1.0
+@dataclasses.dataclass
+class AdamWeightDecayExperimentalConfig(BaseOptimizerConfig):
+ """Configuration for Adam optimizer with weight decay.
+
+ Attributes:
+ name: name of the optimizer.
+ beta_1: decay rate for 1st order moments.
+ beta_2: decay rate for 2st order moments.
+ epsilon: epsilon value used for numerical stability in the optimizer.
+ amsgrad: boolean. Whether to apply AMSGrad variant of this algorithm from
+ the paper "On the Convergence of Adam and beyond".
+ weight_decay: float. Weight decay rate. Default to 0.
+ global_clipnorm: A positive float. Clips the gradients to this maximum
+ L2-norm. Default to 1.0.
+ jit_compile: if True, jit compile will be used.
+ """
+ name: str = "AdamWeightDecayExperimental"
+ beta_1: float = 0.9
+ beta_2: float = 0.999
+ epsilon: float = 1e-07
+ amsgrad: bool = False
+ weight_decay: float = 0.0
+ global_clipnorm: float = 1.0
+ jit_compile: bool = False
+
+
@dataclasses.dataclass
class LAMBConfig(BaseOptimizerConfig):
"""Configuration for LAMB optimizer.
@@ -266,3 +337,5 @@ class AdafactorConfig(BaseOptimizerConfig):
min_dim_size_to_factor: int = 128
epsilon1: float = 1e-30
epsilon2: float = 1e-3
+ weight_decay: Optional[float] = None
+ include_in_weight_decay: Optional[str] = None
diff --git a/official/modeling/optimization/ema_optimizer.py b/official/modeling/optimization/ema_optimizer.py
index c4f44d7124d888a7b0403442b1f57385d820e789..95557d5f3776c1ea094b4ee2f944e3b6c562f95d 100644
--- a/official/modeling/optimization/ema_optimizer.py
+++ b/official/modeling/optimization/ema_optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,7 +21,7 @@ import tensorflow as tf
# pylint: disable=protected-access
-class ExponentialMovingAverage(tf.keras.optimizers.Optimizer):
+class ExponentialMovingAverage(tf.keras.optimizers.legacy.Optimizer):
"""Optimizer that computes an exponential moving average of the variables.
Empirically it has been found that using the moving average of the trained
diff --git a/official/modeling/optimization/lars_optimizer.py b/official/modeling/optimization/lars_optimizer.py
index ac15042756c02c3d3e2da22419cac2e04522b57e..ce67a10f966cb1f2d2a385a4b8c728b52464a623 100644
--- a/official/modeling/optimization/lars_optimizer.py
+++ b/official/modeling/optimization/lars_optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,7 +22,7 @@ import tensorflow as tf
# pylint: disable=protected-access
-class LARS(tf.keras.optimizers.Optimizer):
+class LARS(tf.keras.optimizers.legacy.Optimizer):
"""Layer-wise Adaptive Rate Scaling for large batch training.
Introduced by "Large Batch Training of Convolutional Networks" by Y. You,
diff --git a/official/modeling/optimization/legacy_adamw.py b/official/modeling/optimization/legacy_adamw.py
new file mode 100644
index 0000000000000000000000000000000000000000..c1c57e280d58ecac3f83c355b1aa4478d670f1b3
--- /dev/null
+++ b/official/modeling/optimization/legacy_adamw.py
@@ -0,0 +1,139 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Adam optimizer with weight decay that exactly matches the original BERT."""
+
+import re
+
+from absl import logging
+import tensorflow as tf
+
+
+class AdamWeightDecay(tf.keras.optimizers.legacy.Adam):
+ """Adam enables L2 weight decay and clip_by_global_norm on gradients.
+
+ [Warning!]: Keras optimizer supports gradient clipping and has an AdamW
+ implementation. Please consider evaluating the choice in Keras package.
+
+ Just adding the square of the weights to the loss function is *not* the
+ correct way of using L2 regularization/weight decay with Adam, since that will
+ interact with the m and v parameters in strange ways.
+
+ Instead we want to decay the weights in a manner that doesn't interact with
+ the m/v parameters. This is equivalent to adding the square of the weights to
+ the loss with plain (non-momentum) SGD.
+ """
+
+ def __init__(self,
+ learning_rate=0.001,
+ beta_1=0.9,
+ beta_2=0.999,
+ epsilon=1e-7,
+ amsgrad=False,
+ weight_decay_rate=0.0,
+ include_in_weight_decay=None,
+ exclude_from_weight_decay=None,
+ gradient_clip_norm=1.0,
+ name='AdamWeightDecay',
+ **kwargs):
+ super(AdamWeightDecay, self).__init__(learning_rate, beta_1, beta_2,
+ epsilon, amsgrad, name, **kwargs)
+ self.weight_decay_rate = weight_decay_rate
+ self.gradient_clip_norm = gradient_clip_norm
+ self._include_in_weight_decay = include_in_weight_decay
+ self._exclude_from_weight_decay = exclude_from_weight_decay
+ logging.info('AdamWeightDecay gradient_clip_norm=%f', gradient_clip_norm)
+
+ def _prepare_local(self, var_device, var_dtype, apply_state):
+ super(AdamWeightDecay, self)._prepare_local(var_device, var_dtype, # pytype: disable=attribute-error # typed-keras
+ apply_state)
+ apply_state[(var_device, var_dtype)]['weight_decay_rate'] = tf.constant(
+ self.weight_decay_rate, name='adam_weight_decay_rate')
+
+ def _decay_weights_op(self, var, learning_rate, apply_state):
+ do_decay = self._do_use_weight_decay(var.name)
+ if do_decay:
+ return var.assign_sub(
+ learning_rate * var *
+ apply_state[(var.device, var.dtype.base_dtype)]['weight_decay_rate'],
+ use_locking=self._use_locking)
+ return tf.no_op()
+
+ def apply_gradients(self,
+ grads_and_vars,
+ name=None,
+ experimental_aggregate_gradients=True):
+ grads, tvars = list(zip(*grads_and_vars))
+ if experimental_aggregate_gradients and self.gradient_clip_norm > 0.0:
+ # when experimental_aggregate_gradients = False, apply_gradients() no
+ # longer implicitly allreduce gradients, users manually allreduce gradient
+ # and passed the allreduced grads_and_vars. For now, the
+ # clip_by_global_norm will be moved to before the explicit allreduce to
+ # keep the math the same as TF 1 and pre TF 2.2 implementation.
+ (grads, _) = tf.clip_by_global_norm(
+ grads, clip_norm=self.gradient_clip_norm)
+ return super(AdamWeightDecay, self).apply_gradients(
+ zip(grads, tvars),
+ name=name,
+ experimental_aggregate_gradients=experimental_aggregate_gradients)
+
+ def _get_lr(self, var_device, var_dtype, apply_state):
+ """Retrieves the learning rate with the given state."""
+ if apply_state is None:
+ return self._decayed_lr_t[var_dtype], {}
+
+ apply_state = apply_state or {}
+ coefficients = apply_state.get((var_device, var_dtype))
+ if coefficients is None:
+ coefficients = self._fallback_apply_state(var_device, var_dtype)
+ apply_state[(var_device, var_dtype)] = coefficients
+
+ return coefficients['lr_t'], dict(apply_state=apply_state)
+
+ def _resource_apply_dense(self, grad, var, apply_state=None):
+ lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
+ decay = self._decay_weights_op(var, lr_t, apply_state)
+ with tf.control_dependencies([decay]):
+ return super(AdamWeightDecay,
+ self)._resource_apply_dense(grad, var, **kwargs) # pytype: disable=attribute-error # typed-keras
+
+ def _resource_apply_sparse(self, grad, var, indices, apply_state=None):
+ lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
+ decay = self._decay_weights_op(var, lr_t, apply_state)
+ with tf.control_dependencies([decay]):
+ return super(AdamWeightDecay,
+ self)._resource_apply_sparse(grad, var, indices, **kwargs) # pytype: disable=attribute-error # typed-keras
+
+ def get_config(self):
+ config = super(AdamWeightDecay, self).get_config()
+ config.update({
+ 'weight_decay_rate': self.weight_decay_rate,
+ })
+ return config
+
+ def _do_use_weight_decay(self, param_name):
+ """Whether to use L2 weight decay for `param_name`."""
+ if self.weight_decay_rate == 0:
+ return False
+
+ if self._include_in_weight_decay:
+ for r in self._include_in_weight_decay:
+ if re.search(r, param_name) is not None:
+ return True
+
+ if self._exclude_from_weight_decay:
+ for r in self._exclude_from_weight_decay:
+ if re.search(r, param_name) is not None:
+ return False
+ return True
diff --git a/official/modeling/optimization/lr_schedule.py b/official/modeling/optimization/lr_schedule.py
index 5f62f10b11501003c3f066c748811fc19f5882ec..b4846d7aeca69243a763f89f5878c1d7f14005bb 100644
--- a/official/modeling/optimization/lr_schedule.py
+++ b/official/modeling/optimization/lr_schedule.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,7 +23,7 @@ import tensorflow as tf
def _make_offset_wrapper(new_class_name: str, base_lr_class):
"""Generates a offset wrapper of learning rate schedule.
- It will returns a subclass of the the `base_lr_class`, the subclass takes an
+ It will returns a subclass of the `base_lr_class`, the subclass takes an
`offset` argument in the constructor. When the new class instance is called,
the behavior is:
new_class_object(step) = base_lr_class_object(step - offset)
@@ -386,11 +386,11 @@ class PowerDecayWithOffset(tf.keras.optimizers.schedules.LearningRateSchedule):
}
-class StepConsineDecayWithOffset(
+class StepCosineDecayWithOffset(
tf.keras.optimizers.schedules.LearningRateSchedule):
"""Stepwise cosine learning rate decay with offset.
- Learning rate is equivalent to one or more consine decay(s) starting and
+ Learning rate is equivalent to one or more cosine decay(s) starting and
ending at each interval.
ExampleL
@@ -399,7 +399,7 @@ class StepConsineDecayWithOffset(
boundaries: [100000, 110000]
values: [1.0, 0.5]
lr_decayed_fn = (
- lr_schedule.StepConsineDecayWithOffset(
+ lr_schedule.StepCosineDecayWithOffset(
boundaries,
values))
```
@@ -412,7 +412,7 @@ class StepConsineDecayWithOffset(
boundaries,
values,
offset: int = 0,
- name: str = "StepConsineDecayWithOffset"):
+ name: str = "StepCosineDecayWithOffset"):
"""Initialize configuration of the learning rate schedule.
Args:
@@ -444,7 +444,7 @@ class StepConsineDecayWithOffset(
] + [0])
def __call__(self, global_step):
- with tf.name_scope(self.name or "StepConsineDecayWithOffset"):
+ with tf.name_scope(self.name or "StepCosineDecayWithOffset"):
global_step = tf.cast(global_step - self.offset, tf.float32)
lr_levels = self.values
lr_steps = self.boundaries
diff --git a/official/modeling/optimization/lr_schedule_test.py b/official/modeling/optimization/lr_schedule_test.py
index bafd8be1fad277cfd66579e6336e23493337730a..df74db692eb2226fd639cd5cdac18ae3abbe162d 100644
--- a/official/modeling/optimization/lr_schedule_test.py
+++ b/official/modeling/optimization/lr_schedule_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/optimization/optimizer_factory.py b/official/modeling/optimization/optimizer_factory.py
index 4f5b8929b0d87bcb6a8023e85e49df238cd3228e..8ceb6a33307ab648725e314f0429426102b89929 100644
--- a/official/modeling/optimization/optimizer_factory.py
+++ b/official/modeling/optimization/optimizer_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,22 +23,38 @@ from official.modeling.optimization import slide_optimizer
from official.modeling.optimization import adafactor_optimizer
from official.modeling.optimization import ema_optimizer
from official.modeling.optimization import lars_optimizer
+from official.modeling.optimization import legacy_adamw
from official.modeling.optimization import lr_schedule
from official.modeling.optimization.configs import optimization_config as opt_cfg
-from official.nlp import optimization as nlp_optimization
-OPTIMIZERS_CLS = {
- 'sgd': tf.keras.optimizers.SGD,
- 'adam': tf.keras.optimizers.Adam,
- 'adamw': nlp_optimization.AdamWeightDecay,
+# Optimizer CLS to be used in both legacy and new path.
+SHARED_OPTIMIZERS = {
+ 'sgd_experimental': tf.keras.optimizers.experimental.SGD,
+ 'adam_experimental': tf.keras.optimizers.experimental.Adam,
+ 'adamw': legacy_adamw.AdamWeightDecay,
+ 'adamw_experimental': tf.keras.optimizers.experimental.AdamW,
'lamb': tfa_optimizers.LAMB,
- 'rmsprop': tf.keras.optimizers.RMSprop,
'lars': lars_optimizer.LARS,
- 'adagrad': tf.keras.optimizers.Adagrad,
'slide': slide_optimizer.SLIDE,
'adafactor': adafactor_optimizer.Adafactor,
}
+LEGACY_OPTIMIZERS_CLS = {
+ 'sgd': tf.keras.optimizers.legacy.SGD,
+ 'adam': tf.keras.optimizers.legacy.Adam,
+ 'rmsprop': tf.keras.optimizers.legacy.RMSprop,
+ 'adagrad': tf.keras.optimizers.legacy.Adagrad,
+}
+LEGACY_OPTIMIZERS_CLS.update(SHARED_OPTIMIZERS)
+
+NEW_OPTIMIZERS_CLS = {
+ 'sgd': tf.keras.optimizers.experimental.SGD,
+ 'adam': tf.keras.optimizers.experimental.Adam,
+ 'rmsprop': tf.keras.optimizers.experimental.RMSprop,
+ 'adagrad': tf.keras.optimizers.experimental.Adagrad,
+}
+NEW_OPTIMIZERS_CLS.update(SHARED_OPTIMIZERS)
+
LR_CLS = {
'stepwise': lr_schedule.PiecewiseConstantDecayWithOffset,
'polynomial': lr_schedule.PolynomialDecayWithOffset,
@@ -47,7 +63,7 @@ LR_CLS = {
'power': lr_schedule.DirectPowerDecay,
'power_linear': lr_schedule.PowerAndLinearDecay,
'power_with_offset': lr_schedule.PowerDecayWithOffset,
- 'step_cosine_with_offset': lr_schedule.StepConsineDecayWithOffset,
+ 'step_cosine_with_offset': lr_schedule.StepCosineDecayWithOffset,
}
WARMUP_CLS = {
@@ -56,8 +72,13 @@ WARMUP_CLS = {
}
-def register_optimizer_cls(
- key: str, optimizer_config_cls: tf.keras.optimizers.Optimizer):
+def register_optimizer_cls(key: str,
+ optimizer_config_cls: Union[
+ tf.keras.optimizers.Optimizer,
+ tf.keras.optimizers.legacy.Optimizer,
+ tf.keras.optimizers.experimental.Optimizer
+ ],
+ use_legacy_optimizer: bool = True):
"""Register customize optimizer cls.
The user will still need to subclass data classes in
@@ -66,10 +87,16 @@ def register_optimizer_cls(
Args:
key: A string to that the optimizer_config_cls is registered with.
optimizer_config_cls: A class which inherits tf.keras.optimizers.Optimizer.
+ use_legacy_optimizer: A boolean that indicates if using legacy optimizers.
"""
- if key in OPTIMIZERS_CLS:
- raise ValueError('%s already registered in OPTIMIZER_CLS.' % key)
- OPTIMIZERS_CLS[key] = optimizer_config_cls
+ if use_legacy_optimizer:
+ if key in LEGACY_OPTIMIZERS_CLS:
+ raise ValueError('%s already registered in LEGACY_OPTIMIZERS_CLS.' % key)
+ LEGACY_OPTIMIZERS_CLS[key] = optimizer_config_cls
+ else:
+ if key in NEW_OPTIMIZERS_CLS:
+ raise ValueError('%s already registered in NEW_OPTIMIZERS_CLS.' % key)
+ NEW_OPTIMIZERS_CLS[key] = optimizer_config_cls
class OptimizerFactory:
@@ -84,6 +111,8 @@ class OptimizerFactory:
(4) Build optimizer.
This is a typical example for using this class:
+
+ ```
params = {
'optimizer': {
'type': 'sgd',
@@ -103,6 +132,7 @@ class OptimizerFactory:
opt_factory = OptimizerFactory(opt_config)
lr = opt_factory.build_learning_rate()
optimizer = opt_factory.build_optimizer(lr)
+ ```
"""
def __init__(self, config: opt_cfg.OptimizationConfig):
@@ -155,11 +185,15 @@ class OptimizerFactory:
def build_optimizer(
self,
lr: Union[tf.keras.optimizers.schedules.LearningRateSchedule, float],
+ gradient_aggregator: Optional[Callable[
+ [List[Tuple[tf.Tensor, tf.Tensor]]], List[Tuple[tf.Tensor,
+ tf.Tensor]]]] = None,
gradient_transformers: Optional[List[Callable[
- [List[Tuple[tf.Tensor, tf.Tensor]]], List[Tuple[tf.Tensor, tf.Tensor]]
- ]]] = None,
+ [List[Tuple[tf.Tensor, tf.Tensor]]], List[Tuple[tf.Tensor,
+ tf.Tensor]]]]] = None,
postprocessor: Optional[Callable[[tf.keras.optimizers.Optimizer],
- tf.keras.optimizers.Optimizer]] = None):
+ tf.keras.optimizers.Optimizer]] = None,
+ use_legacy_optimizer: bool = True):
"""Build optimizer.
Builds optimizer from config. It takes learning rate as input, and builds
@@ -169,6 +203,7 @@ class OptimizerFactory:
Args:
lr: A floating point value, or a
tf.keras.optimizers.schedules.LearningRateSchedule instance.
+ gradient_aggregator: Optional function to overwrite gradient aggregation.
gradient_transformers: Optional list of functions to use to transform
gradients before applying updates to Variables. The functions are
applied after gradient_aggregator. The functions should accept and
@@ -176,9 +211,11 @@ class OptimizerFactory:
global_clipnorm should not be set when gradient_transformers is passed.
postprocessor: An optional function for postprocessing the optimizer. It
takes an optimizer and returns an optimizer.
+ use_legacy_optimizer: A boolean that indicates if using legacy optimizers.
Returns:
- tf.keras.optimizers.Optimizer instance.
+ `tf.keras.optimizers.legacy.Optimizer` or
+ `tf.keras.optimizers.experimental.Optimizer` instance.
"""
optimizer_dict = self._optimizer_config.as_dict()
@@ -191,18 +228,39 @@ class OptimizerFactory:
del optimizer_dict['global_clipnorm']
optimizer_dict['learning_rate'] = lr
+ if gradient_aggregator is not None:
+ optimizer_dict['gradient_aggregator'] = gradient_aggregator
if gradient_transformers is not None:
optimizer_dict['gradient_transformers'] = gradient_transformers
- optimizer = OPTIMIZERS_CLS[self._optimizer_type](**optimizer_dict)
+ if use_legacy_optimizer:
+ optimizer = LEGACY_OPTIMIZERS_CLS[self._optimizer_type](**optimizer_dict)
+ else:
+ if 'decay' in optimizer_dict:
+ raise ValueError(
+ '`decay` is deprecated in new Keras optimizer, please reflect the '
+ 'decay logic in `lr` or set `use_legacy_optimizer=True` to use the '
+ 'legacy optimizer.')
+ optimizer = NEW_OPTIMIZERS_CLS[self._optimizer_type](**optimizer_dict)
if self._use_ema:
+ if not use_legacy_optimizer:
+ raise ValueError(
+ 'EMA can only work with the legacy optimizer, please set '
+ '`use_legacy_optimizer=True`.')
optimizer = ema_optimizer.ExponentialMovingAverage(
optimizer, **self._ema_config.as_dict())
if postprocessor:
optimizer = postprocessor(optimizer)
- assert isinstance(optimizer, tf.keras.optimizers.Optimizer), (
- 'OptimizerFactory.build_optimizer returning a non-optimizer object: '
- '{}'.format(optimizer))
-
- return optimizer
+ if isinstance(optimizer, tf.keras.optimizers.Optimizer):
+ return optimizer
+ # The following check makes sure the function won't break in older TF
+ # version because of missing the experimental/legacy package.
+ if hasattr(tf.keras.optimizers, 'experimental'):
+ if isinstance(optimizer, tf.keras.optimizers.experimental.Optimizer):
+ return optimizer
+ if hasattr(tf.keras.optimizers, 'legacy'):
+ if isinstance(optimizer, tf.keras.optimizers.legacy.Optimizer):
+ return optimizer
+ raise TypeError('OptimizerFactory.build_optimizer returning a '
+ 'non-optimizer object: {}'.format(optimizer))
diff --git a/official/modeling/optimization/optimizer_factory_test.py b/official/modeling/optimization/optimizer_factory_test.py
index e0cc714483b5a06464436b94b3e2ffe1cf65364a..4d23c2cd4574f9d4a2ecc31b3fb126ebce9c5316 100644
--- a/official/modeling/optimization/optimizer_factory_test.py
+++ b/official/modeling/optimization/optimizer_factory_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -37,7 +37,7 @@ class OptimizerFactoryTest(tf.test.TestCase, parameterized.TestCase):
}
}
}
- optimizer_cls = optimizer_factory.OPTIMIZERS_CLS[optimizer_type]
+ optimizer_cls = optimizer_factory.LEGACY_OPTIMIZERS_CLS[optimizer_type]
expected_optimizer_config = optimizer_cls().get_config()
expected_optimizer_config['learning_rate'] = 0.1
@@ -49,6 +49,72 @@ class OptimizerFactoryTest(tf.test.TestCase, parameterized.TestCase):
self.assertIsInstance(optimizer, optimizer_cls)
self.assertEqual(expected_optimizer_config, optimizer.get_config())
+ @parameterized.parameters(('sgd'), ('rmsprop'), ('adam'), ('adamw'), ('lamb'),
+ ('lars'), ('adagrad'))
+ def test_new_optimizers(self, optimizer_type):
+ params = {
+ 'optimizer': {
+ 'type': optimizer_type
+ },
+ 'learning_rate': {
+ 'type': 'constant',
+ 'constant': {
+ 'learning_rate': 0.1
+ }
+ }
+ }
+ optimizer_cls = optimizer_factory.NEW_OPTIMIZERS_CLS[optimizer_type]
+ expected_optimizer_config = optimizer_cls().get_config()
+ expected_optimizer_config['learning_rate'] = 0.1
+
+ opt_config = optimization_config.OptimizationConfig(params)
+ if optimizer_type == 'sgd':
+ # Delete unsupported arg `decay` from SGDConfig.
+ delattr(opt_config.optimizer.sgd, 'decay')
+ opt_factory = optimizer_factory.OptimizerFactory(opt_config)
+ lr = opt_factory.build_learning_rate()
+ optimizer = opt_factory.build_optimizer(
+ lr, postprocessor=lambda x: x, use_legacy_optimizer=False)
+
+ self.assertIsInstance(optimizer, optimizer_cls)
+ self.assertEqual(expected_optimizer_config, optimizer.get_config())
+
+ def test_gradient_aggregator(self):
+ params = {
+ 'optimizer': {
+ 'type': 'adam',
+ },
+ 'learning_rate': {
+ 'type': 'constant',
+ 'constant': {
+ 'learning_rate': 1.0
+ }
+ }
+ }
+ opt_config = optimization_config.OptimizationConfig(params)
+ opt_factory = optimizer_factory.OptimizerFactory(opt_config)
+ lr = opt_factory.build_learning_rate()
+
+ # Dummy function to zero out gradients.
+ zero_grads = lambda gv: [(tf.zeros_like(g), v) for g, v in gv]
+
+ optimizer = opt_factory.build_optimizer(lr, gradient_aggregator=zero_grads)
+ if isinstance(optimizer, tf.keras.optimizers.experimental.Optimizer):
+ self.skipTest('New Keras optimizer does not support '
+ '`gradient_aggregator` arg.')
+
+ var0 = tf.Variable([1.0, 2.0])
+ var1 = tf.Variable([3.0, 4.0])
+
+ grads0 = tf.constant([1.0, 1.0])
+ grads1 = tf.constant([1.0, 1.0])
+
+ grads_and_vars = list(zip([grads0, grads1], [var0, var1]))
+ optimizer.apply_gradients(grads_and_vars)
+
+ self.assertAllClose(np.array([1.0, 2.0]), var0.numpy())
+ self.assertAllClose(np.array([3.0, 4.0]), var1.numpy())
+
@parameterized.parameters((None, None), (1.0, None), (None, 1.0))
def test_gradient_clipping(self, clipnorm, clipvalue):
params = {
@@ -107,6 +173,25 @@ class OptimizerFactoryTest(tf.test.TestCase, parameterized.TestCase):
optimizer_factory.OptimizerFactory(
optimization_config.OptimizationConfig(params))
+ def test_wrong_return_type(self):
+ optimizer_type = 'sgd'
+ params = {
+ 'optimizer': {
+ 'type': optimizer_type
+ },
+ 'learning_rate': {
+ 'type': 'constant',
+ 'constant': {
+ 'learning_rate': 0.1
+ }
+ }
+ }
+
+ opt_config = optimization_config.OptimizationConfig(params)
+ opt_factory = optimizer_factory.OptimizerFactory(opt_config)
+ with self.assertRaises(TypeError):
+ _ = opt_factory.build_optimizer(0.1, postprocessor=lambda x: None)
+
# TODO(b/187559334) refactor lr_schedule tests into `lr_schedule_test.py`.
@@ -418,7 +503,7 @@ class OptimizerFactoryTest(tf.test.TestCase, parameterized.TestCase):
}
}
}
- expected_lr_step_values = [[0, 0.0], [5000, 1e-4/2.0], [10000, 1e-4],
+ expected_lr_step_values = [[0, 0.0], [5000, 1e-4 / 2.0], [10000, 1e-4],
[20000, 9.994863e-05], [499999, 5e-05]]
opt_config = optimization_config.OptimizationConfig(params)
opt_factory = optimizer_factory.OptimizerFactory(opt_config)
@@ -434,10 +519,12 @@ class OptimizerFactoryRegistryTest(tf.test.TestCase):
class MyClass():
pass
+
optimizer_factory.register_optimizer_cls('test', MyClass)
- self.assertIn('test', optimizer_factory.OPTIMIZERS_CLS)
+ self.assertIn('test', optimizer_factory.LEGACY_OPTIMIZERS_CLS)
with self.assertRaisesRegex(ValueError, 'test already registered.*'):
optimizer_factory.register_optimizer_cls('test', MyClass)
+
if __name__ == '__main__':
tf.test.main()
diff --git a/official/modeling/optimization/slide_optimizer.py b/official/modeling/optimization/slide_optimizer.py
index c1975a3111e109bbb0e40dfb45cb04bc98246ad2..8bbd468746149ffe20cee9ff6f40de1071630327 100644
--- a/official/modeling/optimization/slide_optimizer.py
+++ b/official/modeling/optimization/slide_optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/performance.py b/official/modeling/performance.py
index c1b23714e2b949db97ffc7fe3ba90aa521a36428..3c6f6d15a564494e0307fb9e6af43309fe00c3a1 100644
--- a/official/modeling/performance.py
+++ b/official/modeling/performance.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/modeling/privacy/__init__.py b/official/modeling/privacy/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/modeling/privacy/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/modeling/privacy/configs.py b/official/modeling/privacy/configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8d4692a563c1e458e7cdccd60419491e8cf952c
--- /dev/null
+++ b/official/modeling/privacy/configs.py
@@ -0,0 +1,26 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs for differential privacy."""
+import dataclasses
+
+from official.modeling.hyperparams import base_config
+
+
+@dataclasses.dataclass
+class DifferentialPrivacyConfig(base_config.Config):
+ # Applied to the gradients
+ # Setting to a large number so nothing is clipped.
+ clipping_norm: float = 100000000.0 # 10^9
+ noise_multiplier: float = 0.0
diff --git a/official/modeling/privacy/configs_test.py b/official/modeling/privacy/configs_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..485e4e5c4acb9b1187f4df0fe99ee2d745749f86
--- /dev/null
+++ b/official/modeling/privacy/configs_test.py
@@ -0,0 +1,41 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for configs."""
+
+import tensorflow as tf
+from official.modeling.privacy import configs
+
+
+class ConfigsTest(tf.test.TestCase):
+
+ def test_clipping_norm_default(self):
+ clipping_norm = configs.DifferentialPrivacyConfig().clipping_norm
+ self.assertEqual(100000000.0, clipping_norm)
+
+ def test_noise_multiplier_default(self):
+ noise_multiplier = configs.DifferentialPrivacyConfig().noise_multiplier
+ self.assertEqual(0.0, noise_multiplier)
+
+ def test_config(self):
+ dp_config = configs.DifferentialPrivacyConfig(
+ clipping_norm=1.0,
+ noise_multiplier=1.0,
+ )
+ self.assertEqual(1.0, dp_config.clipping_norm)
+ self.assertEqual(1.0, dp_config.noise_multiplier)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/modeling/privacy/ops.py b/official/modeling/privacy/ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..8b0247020855158ba5bf65fc53f75d436106ab64
--- /dev/null
+++ b/official/modeling/privacy/ops.py
@@ -0,0 +1,42 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Ops for differential privacy (gradient) transforms."""
+
+from typing import List, Tuple
+import tensorflow as tf
+
+
+def clip_l2_norm(grads_vars: List[Tuple[tf.Tensor, tf.Tensor]],
+ l2_norm_clip: float) -> List[Tuple[tf.Tensor, tf.Tensor]]:
+ """Clip gradients by global norm."""
+
+ gradients = []
+ variables = []
+ for (g, v) in grads_vars:
+ gradients.append(g)
+ variables.append(v)
+ clipped_gradients = tf.clip_by_global_norm(gradients, l2_norm_clip)[0]
+ return list(zip(clipped_gradients, variables))
+
+
+def add_noise(grads_vars: List[Tuple[tf.Tensor, tf.Tensor]],
+ noise_stddev: float) -> List[Tuple[tf.Tensor, tf.Tensor]]:
+ """Add noise to gradients."""
+ ret = []
+ for (g, v) in grads_vars:
+ noise = tf.random.normal(tf.shape(g), stddev=noise_stddev)
+ ret.append((g + noise, v))
+ return ret
+
diff --git a/official/modeling/privacy/ops_test.py b/official/modeling/privacy/ops_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..4f5d580c75fe0bbcaebda5f0a912625d27792898
--- /dev/null
+++ b/official/modeling/privacy/ops_test.py
@@ -0,0 +1,52 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for ops."""
+
+from unittest import mock
+
+import tensorflow as tf
+
+from official.modeling.privacy import ops
+
+
+class OpsTest(tf.test.TestCase):
+
+ def test_clip_l2_norm(self):
+ x = tf.constant([4.0, 3.0])
+ y = tf.constant([[12.0]])
+ tensors = [(x, x), (y, y)]
+ clipped = ops.clip_l2_norm(tensors, 1.0)
+ for a, b in zip(clipped, tensors):
+ self.assertAllClose(a[0], b[0] / 13.0) # sqrt(4^2 + 3^2 + 12 ^3) = 13
+ self.assertAllClose(a[1], b[1])
+
+ @mock.patch.object(tf.random,
+ 'normal',
+ autospec=True)
+ def test_add_noise(self, mock_random):
+ x = tf.constant([0.0, 0.0])
+ y = tf.constant([[0.0]])
+ tensors = [(x, x), (y, y)]
+ mock_random.side_effect = [tf.constant([1.0, 1.0]), tf.constant([[1.0]])]
+ added = ops.add_noise(tensors, 10.0)
+ for a, b in zip(added, tensors):
+ self.assertAllClose(a[0], b[0] + 1.0)
+ self.assertAllClose(a[1], b[1])
+ _, kwargs = mock_random.call_args
+ self.assertEqual(kwargs['stddev'], 10.0)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/modeling/tf_utils.py b/official/modeling/tf_utils.py
index e151b7386ab1c6d62c16aa13394e30cadb7036fa..cdde227cb4b4da5bc9e645d84e5b5770ccabf6f3 100644
--- a/official/modeling/tf_utils.py
+++ b/official/modeling/tf_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,6 +14,7 @@
"""Common TF utilities."""
+import functools
import six
import tensorflow as tf
@@ -82,19 +83,22 @@ def is_special_none_tensor(tensor):
return tensor.shape.ndims == 0 and tensor.dtype == tf.int32
-def get_activation(identifier, use_keras_layer=False):
- """Maps a identifier to a Python function, e.g., "relu" => `tf.nn.relu`.
+def get_activation(identifier, use_keras_layer=False, **kwargs):
+ """Maps an identifier to a Python function, e.g., "relu" => `tf.nn.relu`.
It checks string first and if it is one of customized activation not in TF,
the corresponding activation will be returned. For non-customized activation
names and callable identifiers, always fallback to tf.keras.activations.get.
Prefers using keras layers when use_keras_layer=True. Now it only supports
- 'relu', 'linear', 'identity', 'swish'.
+ 'relu', 'linear', 'identity', 'swish', 'mish', 'leaky_relu', and 'gelu'.
Args:
identifier: String name of the activation function or callable.
use_keras_layer: If True, use keras layer if identifier is allow-listed.
+ **kwargs: Keyword arguments to use to instantiate an activation function.
+ Available only for 'leaky_relu' and 'gelu' when using keras layers.
+ For example: get_activation('leaky_relu', use_keras_layer=True, alpha=0.1)
Returns:
A Python function corresponding to the activation function or a keras
@@ -110,8 +114,11 @@ def get_activation(identifier, use_keras_layer=False):
"swish": "swish",
"sigmoid": "sigmoid",
"relu6": tf.nn.relu6,
+ "leaky_relu": functools.partial(tf.nn.leaky_relu, **kwargs),
"hard_swish": activations.hard_swish,
"hard_sigmoid": activations.hard_sigmoid,
+ "mish": activations.mish,
+ "gelu": functools.partial(tf.nn.gelu, **kwargs),
}
if identifier in keras_layer_allowlist:
return tf.keras.layers.Activation(keras_layer_allowlist[identifier])
@@ -122,6 +129,7 @@ def get_activation(identifier, use_keras_layer=False):
"relu6": activations.relu6,
"hard_sigmoid": activations.hard_sigmoid,
"identity": activations.identity,
+ "mish": activations.mish,
}
if identifier in name_to_fn:
return tf.keras.activations.get(name_to_fn[identifier])
@@ -201,3 +209,85 @@ def safe_mean(losses):
total = tf.reduce_sum(losses)
num_elements = tf.cast(tf.size(losses), dtype=losses.dtype)
return tf.math.divide_no_nan(total, num_elements)
+
+
+def get_replica_id():
+ """Gets replica id depending on the environment."""
+ context = tf.distribute.get_replica_context()
+ if context is not None:
+ return context.replica_id_in_sync_group
+ else:
+ raise RuntimeError("Unknown replica context. The `get_replica_id` method "
+ "relies on TF 2.x tf.distribute API.")
+
+
+def cross_replica_concat(value, axis, name="cross_replica_concat"):
+ """Concatenates the given `value` across (GPU/TPU) cores, along `axis`.
+
+ In general, each core ("replica") will pass a
+ replica-specific value as `value` (corresponding to some element of a
+ data-parallel computation taking place across replicas).
+
+ The resulting concatenated `Tensor` will have the same shape as `value` for
+ all dimensions except `axis`, where it will be larger by a factor of the
+ number of replicas. It will also have the same `dtype` as `value`.
+
+ The position of a given replica's `value` within the resulting concatenation
+ is determined by that replica's replica ID. For
+ example:
+
+ With `value` for replica 0 given as
+
+ 0 0 0
+ 0 0 0
+
+ and `value` for replica 1 given as
+
+ 1 1 1
+ 1 1 1
+
+ the resulting concatenation along axis 0 will be
+
+ 0 0 0
+ 0 0 0
+ 1 1 1
+ 1 1 1
+
+ and this result will be identical across all replicas.
+
+ Note that this API only works in TF2 with `tf.distribute`.
+
+ Args:
+ value: The `Tensor` to concatenate across replicas. Each replica will have a
+ different value for this `Tensor`, and these replica-specific values will
+ be concatenated.
+ axis: The axis along which to perform the concatenation as a Python integer
+ (not a `Tensor`). E.g., `axis=0` to concatenate along the batch dimension.
+ name: A name for the operation (used to create a name scope).
+
+ Returns:
+ The result of concatenating `value` along `axis` across replicas.
+
+ Raises:
+ RuntimeError: when the batch (0-th) dimension is None.
+ """
+ with tf.name_scope(name):
+ context = tf.distribute.get_replica_context()
+ # Typically this could be hit only if the tensor is derived from a
+ # dataset with finite epochs and drop_remainder=False, where the last
+ # batch could of different batch size and then the dim-0 is of dynamic
+ # shape.
+ if value.shape.as_list()[0] is None:
+ raise RuntimeError(f"{value} has unknown batch.")
+ return context.all_gather(value, axis=axis)
+
+
+def clone_initializer(initializer):
+ # Keras initializer is going to be stateless, which mean reusing the same
+ # initializer will produce same init value when the shapes are the same.
+ if isinstance(initializer, tf.keras.initializers.Initializer):
+ return initializer.__class__.from_config(initializer.get_config())
+ # When the input is string/dict or other serialized configs, caller will
+ # create a new keras Initializer instance based on that, and we don't need to
+ # do anything
+ return initializer
diff --git a/official/modeling/tf_utils_test.py b/official/modeling/tf_utils_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..4013cd938d127766853c553584786aa2b05dcc97
--- /dev/null
+++ b/official/modeling/tf_utils_test.py
@@ -0,0 +1,107 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tf_utils."""
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from tensorflow.python.distribute import combinations
+from tensorflow.python.distribute import strategy_combinations
+from official.modeling import tf_utils
+
+
+def all_strategy_combinations():
+ return combinations.combine(
+ strategy=[
+ strategy_combinations.cloud_tpu_strategy,
+ strategy_combinations.mirrored_strategy_with_two_gpus,
+ ],
+ mode='eager',
+ )
+
+
+class TFUtilsTest(tf.test.TestCase, parameterized.TestCase):
+
+ @combinations.generate(all_strategy_combinations())
+ def test_cross_replica_concat(self, strategy):
+ num_cores = strategy.num_replicas_in_sync
+
+ shape = (2, 3, 4)
+
+ def concat(axis):
+
+ @tf.function
+ def function():
+ replica_value = tf.fill(shape, tf_utils.get_replica_id())
+ return tf_utils.cross_replica_concat(replica_value, axis=axis)
+
+ return function
+
+ def expected(axis):
+ values = [np.full(shape, i) for i in range(num_cores)]
+ return np.concatenate(values, axis=axis)
+
+ per_replica_results = strategy.run(concat(axis=0))
+ replica_0_result = per_replica_results.values[0].numpy()
+ for value in per_replica_results.values[1:]:
+ self.assertAllClose(value.numpy(), replica_0_result)
+ self.assertAllClose(replica_0_result, expected(axis=0))
+
+ replica_0_result = strategy.run(concat(axis=1)).values[0].numpy()
+ self.assertAllClose(replica_0_result, expected(axis=1))
+
+ replica_0_result = strategy.run(concat(axis=2)).values[0].numpy()
+ self.assertAllClose(replica_0_result, expected(axis=2))
+
+ @combinations.generate(all_strategy_combinations())
+ def test_cross_replica_concat_gradient(self, strategy):
+ num_cores = strategy.num_replicas_in_sync
+
+ shape = (10, 5)
+
+ @tf.function
+ def function():
+ replica_value = tf.random.normal(shape)
+ with tf.GradientTape() as tape:
+ tape.watch(replica_value)
+ concat_value = tf_utils.cross_replica_concat(replica_value, axis=0)
+ output = tf.reduce_sum(concat_value)
+ return tape.gradient(output, replica_value)
+
+ per_replica_gradients = strategy.run(function)
+ for gradient in per_replica_gradients.values:
+ self.assertAllClose(gradient, num_cores * tf.ones(shape))
+
+ @parameterized.parameters(('relu', True), ('relu', False),
+ ('leaky_relu', False), ('leaky_relu', True),
+ ('mish', True), ('mish', False), ('gelu', True))
+ def test_get_activations(self, name, use_keras_layer):
+ fn = tf_utils.get_activation(name, use_keras_layer)
+ self.assertIsNotNone(fn)
+
+ @combinations.generate(all_strategy_combinations())
+ def test_get_leaky_relu_layer(self, strategy):
+ @tf.function
+ def forward(x):
+ fn = tf_utils.get_activation(
+ 'leaky_relu', use_keras_layer=True, alpha=0.1)
+ return strategy.run(fn, args=(x,)).values[0]
+
+ got = forward(tf.constant([-1]))
+ self.assertAllClose(got, tf.constant([-0.1]))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/nightly_requirements.txt b/official/nightly_requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..41f805823b5e6395e7cb061a844f2f4f207cded1
--- /dev/null
+++ b/official/nightly_requirements.txt
@@ -0,0 +1,29 @@
+six
+google-api-python-client>=1.6.7
+kaggle>=1.3.9
+numpy>=1.20
+oauth2client
+pandas>=0.22.0
+psutil>=5.4.3
+py-cpuinfo>=3.3.0
+scipy>=0.19.1
+tensorflow-hub>=0.6.0
+tensorflow-model-optimization>=0.4.1
+tensorflow-datasets
+tfa-nightly
+gin-config
+tf_slim>=1.1.0
+Cython
+matplotlib
+# Loader becomes a required positional argument in 6.0 in yaml.load
+pyyaml>=5.1,<6.0
+# CV related dependencies
+opencv-python-headless==4.5.2.52
+Pillow
+pycocotools
+# NLP related dependencies
+seqeval
+sentencepiece
+sacrebleu
+# Projects/vit dependencies
+immutabledict
diff --git a/official/nlp/MODEL_GARDEN.md b/official/nlp/MODEL_GARDEN.md
index 5d590a9337cf9cb84294eff5ca1da7a74984e375..09294e942e8d6a2e001f36b0f3650a8496bfe69f 100644
--- a/official/nlp/MODEL_GARDEN.md
+++ b/official/nlp/MODEL_GARDEN.md
@@ -2,53 +2,69 @@
## Introduction
-This TF-NLP library provides a collection of scripts for the training and
-evaluation of transformer-based models, on various tasks such as sentence
+The TF-NLP library provides a collection of scripts for training and
+evaluating transformer-based models, on various tasks such as sentence
classification, question answering, and translation. Additionally, we provide
checkpoints of pretrained models which can be finetuned on downstream tasks.
### How to Train Models
-Model Garden can be easily installed using PIP
-(`pip install tf-models-nightly`). After installation, check out
+Model Garden can be easily installed with
+`pip install tf-models-nightly`. After installation, check out
[this instruction](https://github.com/tensorflow/models/blob/master/official/nlp/docs/train.md)
on how to train models with this codebase.
-## Available Tasks
-There are two available model configs (we will add more) under
-`configs/experiments/`:
+By default, the experiment runs on GPUs. To run on TPUs, one should overwrite
+`runtime.distribution_strategy` and set the tpu address. See [RuntimeConfig](https://github.com/tensorflow/models/blob/master/official/core/config_definitions.py) for details.
+
+In general, the experiments can run with the folloing command by setting the
+corresponding `${TASK}`, `${TASK_CONFIG}`, `${MODEL_CONFIG}`.
+```
+EXPERIMENT=???
+TASK_CONFIG=???
+MODEL_CONFIG=???
+EXRTRA_PARAMS=???
+MODEL_DIR=??? # a-folder-to-hold-checkpoints-and-logs
+python3 train.py \
+ --experiment=${EXPERIMENT} \
+ --mode=train_and_eval \
+ --model_dir=${MODEL_DIR} \
+ --config_file=${TASK_CONFIG} \
+ --config_file=${MODEL_CONFIG} \
+ --params_override=${EXRTRA_PARAMS}
+```
+
+* `EXPERIMENT` can be found under `configs/`
+* `TASK_CONFIG` can be found under `configs/experiments/`
+* `MODEL_CONFIG` can be found under `configs/models/`
+
+#### Order of params override:
+1. `train.py` looks up the registered `ExperimentConfig` with `${EXPERIMENT}`
+2. Overrides params in `TaskConfig` in `${TASK_CONFIG}`
+3. Overrides params `model` in `TaskConfig` with `${MODEL_CONFIG}`
+4. Overrides any params in `ExperimentConfig` with `${EXTRA_PARAMS}`
+
+Note that
+1. `${TASK_CONFIG}`, `${MODEL_CONFIG}`, `${EXTRA_PARAMS}` can be optional when EXPERIMENT default is enough.
+2. `${TASK_CONFIG}`, `${MODEL_CONFIG}`, `${EXTRA_PARAMS}` are only guaranteed to be compatible to it's `${EXPERIMENT}` that defines it.
+
+## Experiments
+
+| NAME | EXPERIMENT | TASK_CONFIG | MODEL_CONFIG | EXRTRA_PARAMS |
+| ----------------- | ------------------------ | ------- | -------- | ----------- |
+| BERT-base GLUE/MNLI-matched finetune | [bert/sentence_prediction](https://github.com/tensorflow/models/blob/master/official/nlp/configs/finetuning_experiments.py) | [glue_mnli_matched.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiments/glue_mnli_matched.yaml) | [bert_en_uncased_base.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/models/bert_en_uncased_base.yaml) | data and bert-base hub inittask.train_data.input_path=/path-to-your-training-data,task.validation_data.input_path=/path-to-your-val-data,task.hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/4 |
+| BERT-base GLUE/MNLI-matched finetune | [bert/sentence_prediction](https://github.com/tensorflow/models/blob/master/official/nlp/configs/finetuning_experiments.py) | [glue_mnli_matched.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiments/glue_mnli_matched.yaml) | [bert_en_uncased_base.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/models/bert_en_uncased_base.yaml) | data and bert-base ckpt inittask.train_data.input_path=/path-to-your-training-data,task.validation_data.input_path=/path-to-your-val-data,task.init_checkpoint=gs://tf_model_garden/nlp/bert/uncased_L-12_H-768_A-12/bert_model.ckpt |
+| BERT-base SQuAD v1.1 finetune | [bert/squad](https://github.com/tensorflow/models/blob/master/official/nlp/configs/finetuning_experiments.py) | [squad_v1.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiments/squad_v1.yaml) | [bert_en_uncased_base.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/models/bert_en_uncased_base.yaml) | data and bert-base hub inittask.train_data.input_path=/path-to-your-training-data,task.validation_data.input_path=/path-to-your-val-data,task.hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/4 |
+|ALBERT-base SQuAD v1.1 finetune | [bert/squad](https://github.com/tensorflow/models/blob/master/official/nlp/configs/finetuning_experiments.py) | [squad_v1.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiments/squad_v1.yaml) | [albert_base.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/models/albert_base.yaml)| data and albert-base hub inittask.train_data.input_path=/path-to-your-training-data,task.validation_data.input_path=/path-to-your-val-data,task.hub_module_url=https://tfhub.dev/tensorflow/albert_en_base/3 |
+| Transformer-large WMT14/en-de scratch |[wmt_transformer/large](https://github.com/tensorflow/models/blob/master/official/nlp/configs/wmt_transformer_experiments.py)| | | ende-32k sentencepiecetask.sentencepiece_model_path='gs://tf_model_garden/nlp/transformer_wmt/ende_bpe_32k.model' |
-| Dataset | Task | Config | Example command |
-| ----------------- | ------------------------ | ------- | ---- |
-| GLUE/MNLI-matched | bert/sentence_prediction | [glue_mnli_matched.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiments/glue_mnli_matched.yaml) | finetune BERT-base on this task PARAMS=runtime.distribution_strategy=mirrored PARAMS=${PARAMS},task.train_data.input_path=/path-to-your-training-data/ PARAMS=${PARAMS},task.hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/4
python3 train.py \\ --experiment=bert/squad \\ --mode=train \\ --model_dir=/a-folder-to-hold-checkpoints-and-logs/ \\ --config_file=configs/models/bert_en_uncased_base.yaml \\ --config_file=configs/experiments/squad_v1.yaml \\ --params_override=${PARAMS} |
-
-One example on how to use the config file: if you want to work on the SQuAD
-question answering task, set
-`--config_file=configs/experiments/squad_v1.yaml` and
-`--experiment=bert/squad`
-as arguments to `train.py`.
-
-## Available Model Configs
-
-There are two available model configs (we will add more) under
-`configs/models/`:
-
-| Model | Config | Pretrained checkpoint & Vocabulary | TF-HUB SavedModel | Example command |
-| ------------ | ------- | ---------------------------------- | ----------------- | --------------- |
-| BERT-base | [bert_en_uncased_base.yaml](https://github.com/tensorflow/models/blob/master/official/nlp/configs/models/bert_en_uncased_base.yaml) | [uncased_L-12_H-768_A-12](https://storage.googleapis.com/tf_model_garden/nlp/bert/v3/uncased_L-12_H-768_A-12.tar.gz) | [uncased_L-12_H-768_A-12](https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/) | finetune on SQuAD v1.1 PARAMS=runtime.distribution_strategy=mirrored PARAMS=${PARAMS},task.train_data.input_path=/path-to-your-training-data/ PARAMS=${PARAMS},task.hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/4
python3 train.py \\ --experiment=bert/squad \\ --mode=train \\ --model_dir=/a-folder-to-hold-checkpoints-and-logs/ \\ --config_file=configs/models/albert_base.yaml \\ --config_file=configs/experiments/squad_v1.yaml \\ --params_override=${PARAMS} |
-
-One example on how to use the config file: if you want to train an ALBERT-base
-model, set `--config_file=configs/models/albert_base.yaml` as an argument to
-`train.py`.
## Useful links
[How to Train Models](https://github.com/tensorflow/models/blob/master/official/nlp/docs/train.md)
-[List of Pretrained Models](https://github.com/tensorflow/models/blob/master/official/nlp/docs/pretrained_models.md)
+[List of Pretrained Models for finetuning](https://github.com/tensorflow/models/blob/master/official/nlp/docs/pretrained_models.md)
[How to Publish Models](https://github.com/tensorflow/models/blob/master/official/nlp/docs/tfhub.md)
diff --git a/official/nlp/README.md b/official/nlp/README.md
index 6b095251f65a9cda91aa32fc5582f27e0bda64e4..46ac10f814a1818cdb4d271c8ed14463e44b9e4f 100644
--- a/official/nlp/README.md
+++ b/official/nlp/README.md
@@ -1,28 +1,33 @@
-# TensorFlow NLP Modelling Toolkit
+# TF-NLP Model Garden
-This codebase provides a Natrual Language Processing modeling toolkit written in
+⚠️ Disclaimer: All datasets hyperlinked from this page are not owned or
+distributed by Google. The dataset is made available by third parties. Please
+review the terms and conditions made available by the third parties before using
+the data.
+
+This codebase provides a Natural Language Processing modeling toolkit written in
[TF2](https://www.tensorflow.org/guide/effective_tf2). It allows researchers and
developers to reproduce state-of-the-art model results and train custom models
to experiment new research ideas.
## Features
-* Reusable and modularized modeling building blocks
-* State-of-the-art reproducible
-* Easy to customize and extend
-* End-to-end training
-* Distributed trainable on both GPUs and TPUs
+* Reusable and modularized modeling building blocks
+* State-of-the-art reproducible
+* Easy to customize and extend
+* End-to-end training
+* Distributed trainable on both GPUs and TPUs
## Major components
### Libraries
We provide modeling library to allow users to train custom models for new
-research ideas. Detailed intructions can be found in READMEs in each folder.
+research ideas. Detailed instructions can be found in READMEs in each folder.
* [modeling/](modeling): modeling library that provides building blocks
(e.g.,Layers, Networks, and Models) that can be assembled into
- transformer-based achitectures .
+ transformer-based architectures.
* [data/](data): binaries and utils for input preprocessing, tokenization,
etc.
@@ -30,27 +35,29 @@ research ideas. Detailed intructions can be found in READMEs in each folder.
We provide SoTA model implementations, pre-trained models, training and
evaluation examples, and command lines. Detail instructions can be found in the
-READMEs for specific papers.
+READMEs for specific papers. Below are some papers implemented in the repository
+and more NLP projects can be found in the
+[`projects`](https://github.com/tensorflow/models/tree/master/official/projects)
+folder:
-1. [BERT](MODEL_GARDEN.md#available-model-configs): [BERT: Pre-training of Deep Bidirectional Transformers for
- Language Understanding](https://arxiv.org/abs/1810.04805) by Devlin et al.,
- 2018
+1. [BERT](MODEL_GARDEN.md#available-model-configs): [BERT: Pre-training of Deep
+ Bidirectional Transformers for Language
+ Understanding](https://arxiv.org/abs/1810.04805) by Devlin et al., 2018
2. [ALBERT](MODEL_GARDEN.md#available-model-configs):
[A Lite BERT for Self-supervised Learning of Language Representations](https://arxiv.org/abs/1909.11942)
by Lan et al., 2019
-3. [XLNet](xlnet):
+3. [XLNet](MODEL_GARDEN.md):
[XLNet: Generalized Autoregressive Pretraining for Language Understanding](https://arxiv.org/abs/1906.08237)
by Yang et al., 2019
-4. [Transformer for translation](transformer):
+4. [Transformer for translation](MODEL_GARDEN.md#available-model-configs):
[Attention Is All You Need](https://arxiv.org/abs/1706.03762) by Vaswani et
al., 2017
### Common Training Driver
We provide a single common driver [train.py](train.py) to train above SoTA
-models on popluar tasks. Please see [docs/train.md](docs/train.md) for
-more details.
-
+models on popular tasks. Please see [docs/train.md](docs/train.md) for more
+details.
### Pre-trained models with checkpoints and TF-Hub
diff --git a/official/nlp/__init__.py b/official/nlp/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/nlp/__init__.py
+++ b/official/nlp/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/bert/README.md b/official/nlp/bert/README.md
deleted file mode 100644
index 037ff0b1ff8c6ea22bcf692bb8f786320b7d2d48..0000000000000000000000000000000000000000
--- a/official/nlp/bert/README.md
+++ /dev/null
@@ -1,395 +0,0 @@
-# BERT (Bidirectional Encoder Representations from Transformers)
-
-**WARNING**: We are on the way to deprecate most of the code in this directory.
-Please see
-[this link](https://github.com/tensorflow/models/blob/master/official/nlp/docs/train.md)
-for the new tutorial and use the new code in `nlp/modeling`. This README is
-still correct for this legacy implementation.
-
-The academic paper which describes BERT in detail and provides full results on a
-number of tasks can be found here: https://arxiv.org/abs/1810.04805.
-
-This repository contains TensorFlow 2.x implementation for BERT.
-
-## Contents
- * [Contents](#contents)
- * [Pre-trained Models](#pre-trained-models)
- * [Restoring from Checkpoints](#restoring-from-checkpoints)
- * [Set Up](#set-up)
- * [Process Datasets](#process-datasets)
- * [Fine-tuning with BERT](#fine-tuning-with-bert)
- * [Cloud GPUs and TPUs](#cloud-gpus-and-tpus)
- * [Sentence and Sentence-pair Classification Tasks](#sentence-and-sentence-pair-classification-tasks)
- * [SQuAD 1.1](#squad-1.1)
-
-
-## Pre-trained Models
-
-We released both checkpoints and tf.hub modules as the pretrained models for
-fine-tuning. They are TF 2.x compatible and are converted from the checkpoints
-released in TF 1.x official BERT repository
-[google-research/bert](https://github.com/google-research/bert)
-in order to keep consistent with BERT paper.
-
-
-### Access to Pretrained Checkpoints
-
-Pretrained checkpoints can be found in the following links:
-
-**Note: We have switched BERT implementation
-to use Keras functional-style networks in [nlp/modeling](../modeling).
-The new checkpoints are:**
-
-* **[`BERT-Large, Uncased (Whole Word Masking)`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/wwm_uncased_L-24_H-1024_A-16.tar.gz)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Large, Cased (Whole Word Masking)`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/wwm_cased_L-24_H-1024_A-16.tar.gz)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Uncased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/uncased_L-12_H-768_A-12.tar.gz)**:
- 12-layer, 768-hidden, 12-heads, 110M parameters
-* **[`BERT-Large, Uncased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16.tar.gz)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/cased_L-12_H-768_A-12.tar.gz)**:
- 12-layer, 768-hidden, 12-heads , 110M parameters
-* **[`BERT-Large, Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/cased_L-24_H-1024_A-16.tar.gz)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Multilingual Cased`](https://storage.googleapis.com/cloud-tpu-checkpoints/bert/keras_bert/multi_cased_L-12_H-768_A-12.tar.gz)**:
- 104 languages, 12-layer, 768-hidden, 12-heads, 110M parameters
-
-We recommend to host checkpoints on Google Cloud storage buckets when you use
-Cloud GPU/TPU.
-
-### Restoring from Checkpoints
-
-`tf.train.Checkpoint` is used to manage model checkpoints in TF 2. To restore
-weights from provided pre-trained checkpoints, you can use the following code:
-
-```python
-init_checkpoint='the pretrained model checkpoint path.'
-model=tf.keras.Model() # Bert pre-trained model as feature extractor.
-checkpoint = tf.train.Checkpoint(model=model)
-checkpoint.restore(init_checkpoint)
-```
-
-Checkpoints featuring native serialized Keras models
-(i.e. model.load()/load_weights()) will be available soon.
-
-### Access to Pretrained hub modules.
-
-Pretrained tf.hub modules in TF 2.x SavedModel format can be found in the
-following links:
-
-* **[`BERT-Large, Uncased (Whole Word Masking)`](https://tfhub.dev/tensorflow/bert_en_wwm_uncased_L-24_H-1024_A-16/)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Large, Cased (Whole Word Masking)`](https://tfhub.dev/tensorflow/bert_en_wwm_cased_L-24_H-1024_A-16/)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Uncased`](https://tfhub.dev/tensorflow/bert_en_uncased_L-12_H-768_A-12/)**:
- 12-layer, 768-hidden, 12-heads, 110M parameters
-* **[`BERT-Large, Uncased`](https://tfhub.dev/tensorflow/bert_en_uncased_L-24_H-1024_A-16/)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Cased`](https://tfhub.dev/tensorflow/bert_en_cased_L-12_H-768_A-12/)**:
- 12-layer, 768-hidden, 12-heads , 110M parameters
-* **[`BERT-Large, Cased`](https://tfhub.dev/tensorflow/bert_en_cased_L-24_H-1024_A-16/)**:
- 24-layer, 1024-hidden, 16-heads, 340M parameters
-* **[`BERT-Base, Multilingual Cased`](https://tfhub.dev/tensorflow/bert_multi_cased_L-12_H-768_A-12/)**:
- 104 languages, 12-layer, 768-hidden, 12-heads, 110M parameters
-* **[`BERT-Base, Chinese`](https://tfhub.dev/tensorflow/bert_zh_L-12_H-768_A-12/)**:
- Chinese Simplified and Traditional, 12-layer, 768-hidden, 12-heads,
- 110M parameters
-
-## Set Up
-
-```shell
-export PYTHONPATH="$PYTHONPATH:/path/to/models"
-```
-
-Install `tf-nightly` to get latest updates:
-
-```shell
-pip install tf-nightly-gpu
-```
-
-With TPU, GPU support is not necessary. First, you need to create a `tf-nightly`
-TPU with [ctpu tool](https://github.com/tensorflow/tpu/tree/master/tools/ctpu):
-
-```shell
-ctpu up -name --tf-version=”nightly”
-```
-
-Second, you need to install TF 2 `tf-nightly` on your VM:
-
-```shell
-pip install tf-nightly
-```
-
-## Process Datasets
-
-### Pre-training
-
-There is no change to generate pre-training data. Please use the script
-[`../data/create_pretraining_data.py`](../data/create_pretraining_data.py)
-which is essentially branched from [BERT research repo](https://github.com/google-research/bert)
-to get processed pre-training data and it adapts to TF2 symbols and python3
-compatibility.
-
-Running the pre-training script requires an input and output directory, as well as a vocab file. Note that max_seq_length will need to match the sequence length parameter you specify when you run pre-training.
-
-Example shell script to call create_pretraining_data.py
-```
-export WORKING_DIR='local disk or cloud location'
-export BERT_DIR='local disk or cloud location'
-python models/official/nlp/data/create_pretraining_data.py \
- --input_file=$WORKING_DIR/input/input.txt \
- --output_file=$WORKING_DIR/output/tf_examples.tfrecord \
- --vocab_file=$BERT_DIR/wwm_uncased_L-24_H-1024_A-16/vocab.txt \
- --do_lower_case=True \
- --max_seq_length=512 \
- --max_predictions_per_seq=76 \
- --masked_lm_prob=0.15 \
- --random_seed=12345 \
- --dupe_factor=5
-```
-
-### Fine-tuning
-
-To prepare the fine-tuning data for final model training, use the
-[`../data/create_finetuning_data.py`](../data/create_finetuning_data.py) script.
-Resulting datasets in `tf_record` format and training meta data should be later
-passed to training or evaluation scripts. The task-specific arguments are
-described in following sections:
-
-* GLUE
-
-Users can download the
-[GLUE data](https://gluebenchmark.com/tasks) by running
-[this script](https://gist.github.com/W4ngatang/60c2bdb54d156a41194446737ce03e2e)
-and unpack it to some directory `$GLUE_DIR`.
-Also, users can download [Pretrained Checkpoint](#access-to-pretrained-checkpoints) and locate on some directory `$BERT_DIR` instead of using checkpoints on Google Cloud Storage.
-
-```shell
-export GLUE_DIR=~/glue
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-
-export TASK_NAME=MNLI
-export OUTPUT_DIR=gs://some_bucket/datasets
-python ../data/create_finetuning_data.py \
- --input_data_dir=${GLUE_DIR}/${TASK_NAME}/ \
- --vocab_file=${BERT_DIR}/vocab.txt \
- --train_data_output_path=${OUTPUT_DIR}/${TASK_NAME}_train.tf_record \
- --eval_data_output_path=${OUTPUT_DIR}/${TASK_NAME}_eval.tf_record \
- --meta_data_file_path=${OUTPUT_DIR}/${TASK_NAME}_meta_data \
- --fine_tuning_task_type=classification --max_seq_length=128 \
- --classification_task_name=${TASK_NAME}
-```
-
-* SQUAD
-
-The [SQuAD website](https://rajpurkar.github.io/SQuAD-explorer/) contains
-detailed information about the SQuAD datasets and evaluation.
-
-The necessary files can be found here:
-
-* [train-v1.1.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/train-v1.1.json)
-* [dev-v1.1.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/dev-v1.1.json)
-* [evaluate-v1.1.py](https://github.com/allenai/bi-att-flow/blob/master/squad/evaluate-v1.1.py)
-* [train-v2.0.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/train-v2.0.json)
-* [dev-v2.0.json](https://rajpurkar.github.io/SQuAD-explorer/dataset/dev-v2.0.json)
-* [evaluate-v2.0.py](https://worksheets.codalab.org/rest/bundles/0x6b567e1cf2e041ec80d7098f031c5c9e/contents/blob/)
-
-```shell
-export SQUAD_DIR=~/squad
-export SQUAD_VERSION=v1.1
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export OUTPUT_DIR=gs://some_bucket/datasets
-
-python ../data/create_finetuning_data.py \
- --squad_data_file=${SQUAD_DIR}/train-${SQUAD_VERSION}.json \
- --vocab_file=${BERT_DIR}/vocab.txt \
- --train_data_output_path=${OUTPUT_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
- --meta_data_file_path=${OUTPUT_DIR}/squad_${SQUAD_VERSION}_meta_data \
- --fine_tuning_task_type=squad --max_seq_length=384
-```
-
-Note: To create fine-tuning data with SQUAD 2.0, you need to add flag `--version_2_with_negative=True`.
-
-## Fine-tuning with BERT
-
-### Cloud GPUs and TPUs
-
-* Cloud Storage
-
-The unzipped pre-trained model files can also be found in the Google Cloud
-Storage folder `gs://cloud-tpu-checkpoints/bert/keras_bert`. For example:
-
-```shell
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export MODEL_DIR=gs://some_bucket/my_output_dir
-```
-
-Currently, users are able to access to `tf-nightly` TPUs and the following TPU
-script should run with `tf-nightly`.
-
-* GPU -> TPU
-
-Just add the following flags to `run_classifier.py` or `run_squad.py`:
-
-```shell
- --distribution_strategy=tpu
- --tpu=grpc://${TPU_IP_ADDRESS}:8470
-```
-
-### Sentence and Sentence-pair Classification Tasks
-
-This example code fine-tunes `BERT-Large` on the Microsoft Research Paraphrase
-Corpus (MRPC) corpus, which only contains 3,600 examples and can fine-tune in a
-few minutes on most GPUs.
-
-We use the `BERT-Large` (uncased_L-24_H-1024_A-16) as an example throughout the
-workflow.
-For GPU memory of 16GB or smaller, you may try to use `BERT-Base`
-(uncased_L-12_H-768_A-12).
-
-```shell
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export MODEL_DIR=gs://some_bucket/my_output_dir
-export GLUE_DIR=gs://some_bucket/datasets
-export TASK=MRPC
-
-python run_classifier.py \
- --mode='train_and_eval' \
- --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
- --train_data_path=${GLUE_DIR}/${TASK}_train.tf_record \
- --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
- --bert_config_file=${BERT_DIR}/bert_config.json \
- --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
- --train_batch_size=4 \
- --eval_batch_size=4 \
- --steps_per_loop=1 \
- --learning_rate=2e-5 \
- --num_train_epochs=3 \
- --model_dir=${MODEL_DIR} \
- --distribution_strategy=mirrored
-```
-
-Alternatively, instead of specifying `init_checkpoint`, you can specify
-`hub_module_url` to employ a pretraind BERT hub module, e.g.,
-` --hub_module_url=https://tfhub.dev/tensorflow/bert_en_uncased_L-24_H-1024_A-16/1`.
-
-After training a model, to get predictions from the classifier, you can set the
-`--mode=predict` and offer the test set tfrecords to `--eval_data_path`.
-Output will be created in file called test_results.tsv in the output folder.
-Each line will contain output for each sample, columns are the class
-probabilities.
-
-```shell
-python run_classifier.py \
- --mode='predict' \
- --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
- --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
- --bert_config_file=${BERT_DIR}/bert_config.json \
- --eval_batch_size=4 \
- --model_dir=${MODEL_DIR} \
- --distribution_strategy=mirrored
-```
-
-To use TPU, you only need to switch distribution strategy type to `tpu` with TPU
-information and use remote storage for model checkpoints.
-
-```shell
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export TPU_IP_ADDRESS='???'
-export MODEL_DIR=gs://some_bucket/my_output_dir
-export GLUE_DIR=gs://some_bucket/datasets
-export TASK=MRPC
-
-python run_classifier.py \
- --mode='train_and_eval' \
- --input_meta_data_path=${GLUE_DIR}/${TASK}_meta_data \
- --train_data_path=${GLUE_DIR}/${TASK}_train.tf_record \
- --eval_data_path=${GLUE_DIR}/${TASK}_eval.tf_record \
- --bert_config_file=${BERT_DIR}/bert_config.json \
- --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
- --train_batch_size=32 \
- --eval_batch_size=32 \
- --steps_per_loop=1000 \
- --learning_rate=2e-5 \
- --num_train_epochs=3 \
- --model_dir=${MODEL_DIR} \
- --distribution_strategy=tpu \
- --tpu=grpc://${TPU_IP_ADDRESS}:8470
-```
-
-Note that, we specify `steps_per_loop=1000` for TPU, because running a loop of
-training steps inside a `tf.function` can significantly increase TPU utilization
-and callbacks will not be called inside the loop.
-
-### SQuAD 1.1
-
-The Stanford Question Answering Dataset (SQuAD) is a popular question answering
-benchmark dataset. See more in [SQuAD website](https://rajpurkar.github.io/SQuAD-explorer/).
-
-We use the `BERT-Large` (uncased_L-24_H-1024_A-16) as an example throughout the
-workflow.
-For GPU memory of 16GB or smaller, you may try to use `BERT-Base`
-(uncased_L-12_H-768_A-12).
-
-```shell
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export SQUAD_DIR=gs://some_bucket/datasets
-export MODEL_DIR=gs://some_bucket/my_output_dir
-export SQUAD_VERSION=v1.1
-
-python run_squad.py \
- --input_meta_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_meta_data \
- --train_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
- --predict_file=${SQUAD_DIR}/dev-v1.1.json \
- --vocab_file=${BERT_DIR}/vocab.txt \
- --bert_config_file=${BERT_DIR}/bert_config.json \
- --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
- --train_batch_size=4 \
- --predict_batch_size=4 \
- --learning_rate=8e-5 \
- --num_train_epochs=2 \
- --model_dir=${MODEL_DIR} \
- --distribution_strategy=mirrored
-```
-
-Similarily, you can replace `init_checkpoint` FLAG with `hub_module_url` to
-specify a hub module path.
-
-`run_squad.py` writes the prediction for `--predict_file` by default. If you set
-the `--model=predict` and offer the SQuAD test data, the scripts will generate
-the prediction json file.
-
-To use TPU, you need switch distribution strategy type to `tpu` with TPU
-information.
-
-```shell
-export BERT_DIR=gs://cloud-tpu-checkpoints/bert/keras_bert/uncased_L-24_H-1024_A-16
-export TPU_IP_ADDRESS='???'
-export MODEL_DIR=gs://some_bucket/my_output_dir
-export SQUAD_DIR=gs://some_bucket/datasets
-export SQUAD_VERSION=v1.1
-
-python run_squad.py \
- --input_meta_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_meta_data \
- --train_data_path=${SQUAD_DIR}/squad_${SQUAD_VERSION}_train.tf_record \
- --predict_file=${SQUAD_DIR}/dev-v1.1.json \
- --vocab_file=${BERT_DIR}/vocab.txt \
- --bert_config_file=${BERT_DIR}/bert_config.json \
- --init_checkpoint=${BERT_DIR}/bert_model.ckpt \
- --train_batch_size=32 \
- --learning_rate=8e-5 \
- --num_train_epochs=2 \
- --model_dir=${MODEL_DIR} \
- --distribution_strategy=tpu \
- --tpu=grpc://${TPU_IP_ADDRESS}:8470
-```
-
-The dev set predictions will be saved into a file called predictions.json in the
-model_dir:
-
-```shell
-python $SQUAD_DIR/evaluate-v1.1.py $SQUAD_DIR/dev-v1.1.json ./squad/predictions.json
-```
-
-
diff --git a/official/nlp/bert/__init__.py b/official/nlp/bert/__init__.py
deleted file mode 100644
index a25710c222e3327cb20e000db5df5c5651c4a2cc..0000000000000000000000000000000000000000
--- a/official/nlp/bert/__init__.py
+++ /dev/null
@@ -1,15 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-
diff --git a/official/nlp/bert/common_flags.py b/official/nlp/bert/common_flags.py
deleted file mode 100644
index f622ab1e2f45b4d33af8e13230580cbb08d33820..0000000000000000000000000000000000000000
--- a/official/nlp/bert/common_flags.py
+++ /dev/null
@@ -1,125 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Defining common flags used across all BERT models/applications."""
-
-from absl import flags
-import tensorflow as tf
-
-from official.utils import hyperparams_flags
-from official.utils.flags import core as flags_core
-
-
-def define_common_bert_flags():
- """Define common flags for BERT tasks."""
- flags_core.define_base(
- data_dir=False,
- model_dir=True,
- clean=False,
- train_epochs=False,
- epochs_between_evals=False,
- stop_threshold=False,
- batch_size=False,
- num_gpu=True,
- export_dir=False,
- distribution_strategy=True,
- run_eagerly=True)
- flags_core.define_distribution()
- flags.DEFINE_string('bert_config_file', None,
- 'Bert configuration file to define core bert layers.')
- flags.DEFINE_string(
- 'model_export_path', None,
- 'Path to the directory, where trainined model will be '
- 'exported.')
- flags.DEFINE_string('tpu', '', 'TPU address to connect to.')
- flags.DEFINE_string(
- 'init_checkpoint', None,
- 'Initial checkpoint (usually from a pre-trained BERT model).')
- flags.DEFINE_integer('num_train_epochs', 3,
- 'Total number of training epochs to perform.')
- flags.DEFINE_integer(
- 'steps_per_loop', None,
- 'Number of steps per graph-mode loop. Only training step '
- 'happens inside the loop. Callbacks will not be called '
- 'inside. If not set the value will be configured depending on the '
- 'devices available.')
- flags.DEFINE_float('learning_rate', 5e-5,
- 'The initial learning rate for Adam.')
- flags.DEFINE_float('end_lr', 0.0,
- 'The end learning rate for learning rate decay.')
- flags.DEFINE_string('optimizer_type', 'adamw',
- 'The type of optimizer to use for training (adamw|lamb)')
- flags.DEFINE_boolean(
- 'scale_loss', False,
- 'Whether to divide the loss by number of replica inside the per-replica '
- 'loss function.')
- flags.DEFINE_boolean(
- 'use_keras_compile_fit', False,
- 'If True, uses Keras compile/fit() API for training logic. Otherwise '
- 'use custom training loop.')
- flags.DEFINE_string(
- 'hub_module_url', None, 'TF-Hub path/url to Bert module. '
- 'If specified, init_checkpoint flag should not be used.')
- flags.DEFINE_bool('hub_module_trainable', True,
- 'True to make keras layers in the hub module trainable.')
- flags.DEFINE_string(
- 'sub_model_export_name', None,
- 'If set, `sub_model` checkpoints are exported into '
- 'FLAGS.model_dir/FLAGS.sub_model_export_name.')
- flags.DEFINE_bool('explicit_allreduce', False,
- 'True to use explicit allreduce instead of the implicit '
- 'allreduce in optimizer.apply_gradients(). If fp16 mixed '
- 'precision training is used, this also enables allreduce '
- 'gradients in fp16.')
- flags.DEFINE_integer('allreduce_bytes_per_pack', 0,
- 'Number of bytes of a gradient pack for allreduce. '
- 'Should be positive integer, if set to 0, all '
- 'gradients are in one pack. Breaking gradient into '
- 'packs could enable overlap between allreduce and '
- 'backprop computation. This flag only takes effect '
- 'when explicit_allreduce is set to True.')
-
- flags_core.define_log_steps()
-
- # Adds flags for mixed precision and multi-worker training.
- flags_core.define_performance(
- num_parallel_calls=False,
- inter_op=False,
- intra_op=False,
- synthetic_data=False,
- max_train_steps=False,
- dtype=True,
- loss_scale=True,
- all_reduce_alg=True,
- num_packs=False,
- tf_gpu_thread_mode=True,
- datasets_num_private_threads=True,
- enable_xla=True,
- fp16_implementation=True,
- )
-
- # Adds gin configuration flags.
- hyperparams_flags.define_gin_flags()
-
-
-def dtype():
- return flags_core.get_tf_dtype(flags.FLAGS)
-
-
-def use_float16():
- return flags_core.get_tf_dtype(flags.FLAGS) == tf.float16
-
-
-def get_loss_scale():
- return flags_core.get_loss_scale(flags.FLAGS, default_for_fp16='dynamic')
diff --git a/official/nlp/bert/configs.py b/official/nlp/bert/configs.py
deleted file mode 100644
index 950c32d0bfad3e06f3d14baf042a916de2eb2828..0000000000000000000000000000000000000000
--- a/official/nlp/bert/configs.py
+++ /dev/null
@@ -1,104 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""The main BERT model and related functions."""
-
-import copy
-import json
-
-import six
-import tensorflow as tf
-
-
-class BertConfig(object):
- """Configuration for `BertModel`."""
-
- def __init__(self,
- vocab_size,
- hidden_size=768,
- num_hidden_layers=12,
- num_attention_heads=12,
- intermediate_size=3072,
- hidden_act="gelu",
- hidden_dropout_prob=0.1,
- attention_probs_dropout_prob=0.1,
- max_position_embeddings=512,
- type_vocab_size=16,
- initializer_range=0.02,
- embedding_size=None,
- backward_compatible=True):
- """Constructs BertConfig.
-
- Args:
- vocab_size: Vocabulary size of `inputs_ids` in `BertModel`.
- hidden_size: Size of the encoder layers and the pooler layer.
- num_hidden_layers: Number of hidden layers in the Transformer encoder.
- num_attention_heads: Number of attention heads for each attention layer in
- the Transformer encoder.
- intermediate_size: The size of the "intermediate" (i.e., feed-forward)
- layer in the Transformer encoder.
- hidden_act: The non-linear activation function (function or string) in the
- encoder and pooler.
- hidden_dropout_prob: The dropout probability for all fully connected
- layers in the embeddings, encoder, and pooler.
- attention_probs_dropout_prob: The dropout ratio for the attention
- probabilities.
- max_position_embeddings: The maximum sequence length that this model might
- ever be used with. Typically set this to something large just in case
- (e.g., 512 or 1024 or 2048).
- type_vocab_size: The vocabulary size of the `token_type_ids` passed into
- `BertModel`.
- initializer_range: The stdev of the truncated_normal_initializer for
- initializing all weight matrices.
- embedding_size: (Optional) width of the factorized word embeddings.
- backward_compatible: Boolean, whether the variables shape are compatible
- with checkpoints converted from TF 1.x BERT.
- """
- self.vocab_size = vocab_size
- self.hidden_size = hidden_size
- self.num_hidden_layers = num_hidden_layers
- self.num_attention_heads = num_attention_heads
- self.hidden_act = hidden_act
- self.intermediate_size = intermediate_size
- self.hidden_dropout_prob = hidden_dropout_prob
- self.attention_probs_dropout_prob = attention_probs_dropout_prob
- self.max_position_embeddings = max_position_embeddings
- self.type_vocab_size = type_vocab_size
- self.initializer_range = initializer_range
- self.embedding_size = embedding_size
- self.backward_compatible = backward_compatible
-
- @classmethod
- def from_dict(cls, json_object):
- """Constructs a `BertConfig` from a Python dictionary of parameters."""
- config = BertConfig(vocab_size=None)
- for (key, value) in six.iteritems(json_object):
- config.__dict__[key] = value
- return config
-
- @classmethod
- def from_json_file(cls, json_file):
- """Constructs a `BertConfig` from a json file of parameters."""
- with tf.io.gfile.GFile(json_file, "r") as reader:
- text = reader.read()
- return cls.from_dict(json.loads(text))
-
- def to_dict(self):
- """Serializes this instance to a Python dictionary."""
- output = copy.deepcopy(self.__dict__)
- return output
-
- def to_json_string(self):
- """Serializes this instance to a JSON string."""
- return json.dumps(self.to_dict(), indent=2, sort_keys=True) + "\n"
diff --git a/official/nlp/bert/export_tfhub.py b/official/nlp/bert/export_tfhub.py
deleted file mode 100644
index 833e7c10582f9252f59b3b7584a5bcca0b6f4991..0000000000000000000000000000000000000000
--- a/official/nlp/bert/export_tfhub.py
+++ /dev/null
@@ -1,139 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""A script to export BERT as a TF-Hub SavedModel.
-
-This script is **DEPRECATED** for exporting BERT encoder models;
-see the error message in by main() for details.
-"""
-
-from typing import Text
-
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-import tensorflow as tf
-from official.nlp.bert import bert_models
-from official.nlp.bert import configs
-
-FLAGS = flags.FLAGS
-
-flags.DEFINE_string("bert_config_file", None,
- "Bert configuration file to define core bert layers.")
-flags.DEFINE_string("model_checkpoint_path", None,
- "File path to TF model checkpoint.")
-flags.DEFINE_string("export_path", None, "TF-Hub SavedModel destination path.")
-flags.DEFINE_string("vocab_file", None,
- "The vocabulary file that the BERT model was trained on.")
-flags.DEFINE_bool(
- "do_lower_case", None, "Whether to lowercase. If None, "
- "do_lower_case will be enabled if 'uncased' appears in the "
- "name of --vocab_file")
-flags.DEFINE_enum("model_type", "encoder", ["encoder", "squad"],
- "What kind of BERT model to export.")
-
-
-def create_bert_model(bert_config: configs.BertConfig) -> tf.keras.Model:
- """Creates a BERT keras core model from BERT configuration.
-
- Args:
- bert_config: A `BertConfig` to create the core model.
-
- Returns:
- A keras model.
- """
- # Adds input layers just as placeholders.
- input_word_ids = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name="input_word_ids")
- input_mask = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name="input_mask")
- input_type_ids = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name="input_type_ids")
- transformer_encoder = bert_models.get_transformer_encoder(
- bert_config, sequence_length=None)
- sequence_output, pooled_output = transformer_encoder(
- [input_word_ids, input_mask, input_type_ids])
- # To keep consistent with legacy hub modules, the outputs are
- # "pooled_output" and "sequence_output".
- return tf.keras.Model(
- inputs=[input_word_ids, input_mask, input_type_ids],
- outputs=[pooled_output, sequence_output]), transformer_encoder
-
-
-def export_bert_tfhub(bert_config: configs.BertConfig,
- model_checkpoint_path: Text,
- hub_destination: Text,
- vocab_file: Text,
- do_lower_case: bool = None):
- """Restores a tf.keras.Model and saves for TF-Hub."""
- # If do_lower_case is not explicit, default to checking whether "uncased" is
- # in the vocab file name
- if do_lower_case is None:
- do_lower_case = "uncased" in vocab_file
- logging.info("Using do_lower_case=%s based on name of vocab_file=%s",
- do_lower_case, vocab_file)
- core_model, encoder = create_bert_model(bert_config)
- checkpoint = tf.train.Checkpoint(
- model=encoder, # Legacy checkpoints.
- encoder=encoder)
- checkpoint.restore(model_checkpoint_path).assert_existing_objects_matched()
- core_model.vocab_file = tf.saved_model.Asset(vocab_file)
- core_model.do_lower_case = tf.Variable(do_lower_case, trainable=False)
- core_model.save(hub_destination, include_optimizer=False, save_format="tf")
-
-
-def export_bert_squad_tfhub(bert_config: configs.BertConfig,
- model_checkpoint_path: Text,
- hub_destination: Text,
- vocab_file: Text,
- do_lower_case: bool = None):
- """Restores a tf.keras.Model for BERT with SQuAD and saves for TF-Hub."""
- # If do_lower_case is not explicit, default to checking whether "uncased" is
- # in the vocab file name
- if do_lower_case is None:
- do_lower_case = "uncased" in vocab_file
- logging.info("Using do_lower_case=%s based on name of vocab_file=%s",
- do_lower_case, vocab_file)
- span_labeling, _ = bert_models.squad_model(bert_config, max_seq_length=None)
- checkpoint = tf.train.Checkpoint(model=span_labeling)
- checkpoint.restore(model_checkpoint_path).assert_existing_objects_matched()
- span_labeling.vocab_file = tf.saved_model.Asset(vocab_file)
- span_labeling.do_lower_case = tf.Variable(do_lower_case, trainable=False)
- span_labeling.save(hub_destination, include_optimizer=False, save_format="tf")
-
-
-def main(_):
- bert_config = configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- if FLAGS.model_type == "encoder":
- deprecation_note = (
- "nlp/bert/export_tfhub is **DEPRECATED** for exporting BERT encoder "
- "models. Please switch to nlp/tools/export_tfhub for exporting BERT "
- "(and other) encoders with dict inputs/outputs conforming to "
- "https://www.tensorflow.org/hub/common_saved_model_apis/text#transformer-encoders"
- )
- logging.error(deprecation_note)
- print("\n\nNOTICE:", deprecation_note, "\n")
- export_bert_tfhub(bert_config, FLAGS.model_checkpoint_path,
- FLAGS.export_path, FLAGS.vocab_file, FLAGS.do_lower_case)
- elif FLAGS.model_type == "squad":
- export_bert_squad_tfhub(bert_config, FLAGS.model_checkpoint_path,
- FLAGS.export_path, FLAGS.vocab_file,
- FLAGS.do_lower_case)
- else:
- raise ValueError("Unsupported model_type %s." % FLAGS.model_type)
-
-
-if __name__ == "__main__":
- app.run(main)
diff --git a/official/nlp/bert/export_tfhub_test.py b/official/nlp/bert/export_tfhub_test.py
deleted file mode 100644
index 77030dd3fde7d4c4d73bea0fdea017848b1e253f..0000000000000000000000000000000000000000
--- a/official/nlp/bert/export_tfhub_test.py
+++ /dev/null
@@ -1,108 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Tests official.nlp.bert.export_tfhub."""
-
-import os
-
-from absl.testing import parameterized
-import numpy as np
-import tensorflow as tf
-import tensorflow_hub as hub
-
-from official.nlp.bert import configs
-from official.nlp.bert import export_tfhub
-
-
-class ExportTfhubTest(tf.test.TestCase, parameterized.TestCase):
-
- @parameterized.parameters("model", "encoder")
- def test_export_tfhub(self, ckpt_key_name):
- # Exports a savedmodel for TF-Hub
- hidden_size = 16
- bert_config = configs.BertConfig(
- vocab_size=100,
- hidden_size=hidden_size,
- intermediate_size=32,
- max_position_embeddings=128,
- num_attention_heads=2,
- num_hidden_layers=1)
- bert_model, encoder = export_tfhub.create_bert_model(bert_config)
- model_checkpoint_dir = os.path.join(self.get_temp_dir(), "checkpoint")
- checkpoint = tf.train.Checkpoint(**{ckpt_key_name: encoder})
- checkpoint.save(os.path.join(model_checkpoint_dir, "test"))
- model_checkpoint_path = tf.train.latest_checkpoint(model_checkpoint_dir)
-
- vocab_file = os.path.join(self.get_temp_dir(), "uncased_vocab.txt")
- with tf.io.gfile.GFile(vocab_file, "w") as f:
- f.write("dummy content")
-
- hub_destination = os.path.join(self.get_temp_dir(), "hub")
- export_tfhub.export_bert_tfhub(bert_config, model_checkpoint_path,
- hub_destination, vocab_file)
-
- # Restores a hub KerasLayer.
- hub_layer = hub.KerasLayer(hub_destination, trainable=True)
-
- if hasattr(hub_layer, "resolved_object"):
- # Checks meta attributes.
- self.assertTrue(hub_layer.resolved_object.do_lower_case.numpy())
- with tf.io.gfile.GFile(
- hub_layer.resolved_object.vocab_file.asset_path.numpy()) as f:
- self.assertEqual("dummy content", f.read())
- # Checks the hub KerasLayer.
- for source_weight, hub_weight in zip(bert_model.trainable_weights,
- hub_layer.trainable_weights):
- self.assertAllClose(source_weight.numpy(), hub_weight.numpy())
-
- seq_length = 10
- dummy_ids = np.zeros((2, seq_length), dtype=np.int32)
- hub_outputs = hub_layer([dummy_ids, dummy_ids, dummy_ids])
- source_outputs = bert_model([dummy_ids, dummy_ids, dummy_ids])
-
- # The outputs of hub module are "pooled_output" and "sequence_output",
- # while the outputs of encoder is in reversed order, i.e.,
- # "sequence_output" and "pooled_output".
- encoder_outputs = reversed(encoder([dummy_ids, dummy_ids, dummy_ids]))
- self.assertEqual(hub_outputs[0].shape, (2, hidden_size))
- self.assertEqual(hub_outputs[1].shape, (2, seq_length, hidden_size))
- for source_output, hub_output, encoder_output in zip(
- source_outputs, hub_outputs, encoder_outputs):
- self.assertAllClose(source_output.numpy(), hub_output.numpy())
- self.assertAllClose(source_output.numpy(), encoder_output.numpy())
-
- # Test that training=True makes a difference (activates dropout).
- def _dropout_mean_stddev(training, num_runs=20):
- input_ids = np.array([[14, 12, 42, 95, 99]], np.int32)
- inputs = [input_ids, np.ones_like(input_ids), np.zeros_like(input_ids)]
- outputs = np.concatenate(
- [hub_layer(inputs, training=training)[0] for _ in range(num_runs)])
- return np.mean(np.std(outputs, axis=0))
-
- self.assertLess(_dropout_mean_stddev(training=False), 1e-6)
- self.assertGreater(_dropout_mean_stddev(training=True), 1e-3)
-
- # Test propagation of seq_length in shape inference.
- input_word_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
- input_mask = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
- input_type_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
- pooled_output, sequence_output = hub_layer(
- [input_word_ids, input_mask, input_type_ids])
- self.assertEqual(pooled_output.shape.as_list(), [None, hidden_size])
- self.assertEqual(sequence_output.shape.as_list(),
- [None, seq_length, hidden_size])
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/bert/run_classifier.py b/official/nlp/bert/run_classifier.py
deleted file mode 100644
index b7ee5be8afe27549803ba22901d5e4a3cffc8cce..0000000000000000000000000000000000000000
--- a/official/nlp/bert/run_classifier.py
+++ /dev/null
@@ -1,515 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""BERT classification or regression finetuning runner in TF 2.x."""
-
-import functools
-import json
-import math
-import os
-
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-import gin
-import tensorflow as tf
-from official.common import distribute_utils
-from official.modeling import performance
-from official.nlp import optimization
-from official.nlp.bert import bert_models
-from official.nlp.bert import common_flags
-from official.nlp.bert import configs as bert_configs
-from official.nlp.bert import input_pipeline
-from official.nlp.bert import model_saving_utils
-from official.utils.misc import keras_utils
-
-flags.DEFINE_enum(
- 'mode', 'train_and_eval', ['train_and_eval', 'export_only', 'predict'],
- 'One of {"train_and_eval", "export_only", "predict"}. `train_and_eval`: '
- 'trains the model and evaluates in the meantime. '
- '`export_only`: will take the latest checkpoint inside '
- 'model_dir and export a `SavedModel`. `predict`: takes a checkpoint and '
- 'restores the model to output predictions on the test set.')
-flags.DEFINE_string('train_data_path', None,
- 'Path to training data for BERT classifier.')
-flags.DEFINE_string('eval_data_path', None,
- 'Path to evaluation data for BERT classifier.')
-flags.DEFINE_string(
- 'input_meta_data_path', None,
- 'Path to file that contains meta data about input '
- 'to be used for training and evaluation.')
-flags.DEFINE_integer('train_data_size', None, 'Number of training samples '
- 'to use. If None, uses the full train data. '
- '(default: None).')
-flags.DEFINE_string('predict_checkpoint_path', None,
- 'Path to the checkpoint for predictions.')
-flags.DEFINE_integer(
- 'num_eval_per_epoch', 1,
- 'Number of evaluations per epoch. The purpose of this flag is to provide '
- 'more granular evaluation scores and checkpoints. For example, if original '
- 'data has N samples and num_eval_per_epoch is n, then each epoch will be '
- 'evaluated every N/n samples.')
-flags.DEFINE_integer('train_batch_size', 32, 'Batch size for training.')
-flags.DEFINE_integer('eval_batch_size', 32, 'Batch size for evaluation.')
-
-common_flags.define_common_bert_flags()
-
-FLAGS = flags.FLAGS
-
-LABEL_TYPES_MAP = {'int': tf.int64, 'float': tf.float32}
-
-
-def get_loss_fn(num_classes):
- """Gets the classification loss function."""
-
- def classification_loss_fn(labels, logits):
- """Classification loss."""
- labels = tf.reshape(labels, [-1])
- log_probs = tf.nn.log_softmax(logits, axis=-1)
- one_hot_labels = tf.one_hot(
- tf.cast(labels, dtype=tf.int32), depth=num_classes, dtype=tf.float32)
- per_example_loss = -tf.reduce_sum(
- tf.cast(one_hot_labels, dtype=tf.float32) * log_probs, axis=-1)
- return tf.reduce_mean(per_example_loss)
-
- return classification_loss_fn
-
-
-def get_dataset_fn(input_file_pattern,
- max_seq_length,
- global_batch_size,
- is_training,
- label_type=tf.int64,
- include_sample_weights=False,
- num_samples=None):
- """Gets a closure to create a dataset."""
-
- def _dataset_fn(ctx=None):
- """Returns tf.data.Dataset for distributed BERT pretraining."""
- batch_size = ctx.get_per_replica_batch_size(
- global_batch_size) if ctx else global_batch_size
- dataset = input_pipeline.create_classifier_dataset(
- tf.io.gfile.glob(input_file_pattern),
- max_seq_length,
- batch_size,
- is_training=is_training,
- input_pipeline_context=ctx,
- label_type=label_type,
- include_sample_weights=include_sample_weights,
- num_samples=num_samples)
- return dataset
-
- return _dataset_fn
-
-
-def run_bert_classifier(strategy,
- bert_config,
- input_meta_data,
- model_dir,
- epochs,
- steps_per_epoch,
- steps_per_loop,
- eval_steps,
- warmup_steps,
- initial_lr,
- init_checkpoint,
- train_input_fn,
- eval_input_fn,
- training_callbacks=True,
- custom_callbacks=None,
- custom_metrics=None):
- """Run BERT classifier training using low-level API."""
- max_seq_length = input_meta_data['max_seq_length']
- num_classes = input_meta_data.get('num_labels', 1)
- is_regression = num_classes == 1
-
- def _get_classifier_model():
- """Gets a classifier model."""
- classifier_model, core_model = (
- bert_models.classifier_model(
- bert_config,
- num_classes,
- max_seq_length,
- hub_module_url=FLAGS.hub_module_url,
- hub_module_trainable=FLAGS.hub_module_trainable))
- optimizer = optimization.create_optimizer(initial_lr,
- steps_per_epoch * epochs,
- warmup_steps, FLAGS.end_lr,
- FLAGS.optimizer_type)
- classifier_model.optimizer = performance.configure_optimizer(
- optimizer,
- use_float16=common_flags.use_float16())
- return classifier_model, core_model
-
- # tf.keras.losses objects accept optional sample_weight arguments (eg. coming
- # from the dataset) to compute weighted loss, as used for the regression
- # tasks. The classification tasks, using the custom get_loss_fn don't accept
- # sample weights though.
- loss_fn = (tf.keras.losses.MeanSquaredError() if is_regression
- else get_loss_fn(num_classes))
-
- # Defines evaluation metrics function, which will create metrics in the
- # correct device and strategy scope.
- if custom_metrics:
- metric_fn = custom_metrics
- elif is_regression:
- metric_fn = functools.partial(
- tf.keras.metrics.MeanSquaredError,
- 'mean_squared_error',
- dtype=tf.float32)
- else:
- metric_fn = functools.partial(
- tf.keras.metrics.SparseCategoricalAccuracy,
- 'accuracy',
- dtype=tf.float32)
-
- # Start training using Keras compile/fit API.
- logging.info('Training using TF 2.x Keras compile/fit API with '
- 'distribution strategy.')
- return run_keras_compile_fit(
- model_dir,
- strategy,
- _get_classifier_model,
- train_input_fn,
- eval_input_fn,
- loss_fn,
- metric_fn,
- init_checkpoint,
- epochs,
- steps_per_epoch,
- steps_per_loop,
- eval_steps,
- training_callbacks=training_callbacks,
- custom_callbacks=custom_callbacks)
-
-
-def run_keras_compile_fit(model_dir,
- strategy,
- model_fn,
- train_input_fn,
- eval_input_fn,
- loss_fn,
- metric_fn,
- init_checkpoint,
- epochs,
- steps_per_epoch,
- steps_per_loop,
- eval_steps,
- training_callbacks=True,
- custom_callbacks=None):
- """Runs BERT classifier model using Keras compile/fit API."""
-
- with strategy.scope():
- training_dataset = train_input_fn()
- evaluation_dataset = eval_input_fn() if eval_input_fn else None
- bert_model, sub_model = model_fn()
- optimizer = bert_model.optimizer
-
- if init_checkpoint:
- checkpoint = tf.train.Checkpoint(model=sub_model, encoder=sub_model)
- checkpoint.read(init_checkpoint).assert_existing_objects_matched()
-
- if not isinstance(metric_fn, (list, tuple)):
- metric_fn = [metric_fn]
- bert_model.compile(
- optimizer=optimizer,
- loss=loss_fn,
- metrics=[fn() for fn in metric_fn],
- steps_per_execution=steps_per_loop)
-
- summary_dir = os.path.join(model_dir, 'summaries')
- summary_callback = tf.keras.callbacks.TensorBoard(summary_dir)
- checkpoint = tf.train.Checkpoint(model=bert_model, optimizer=optimizer)
- checkpoint_manager = tf.train.CheckpointManager(
- checkpoint,
- directory=model_dir,
- max_to_keep=None,
- step_counter=optimizer.iterations,
- checkpoint_interval=0)
- checkpoint_callback = keras_utils.SimpleCheckpoint(checkpoint_manager)
-
- if training_callbacks:
- if custom_callbacks is not None:
- custom_callbacks += [summary_callback, checkpoint_callback]
- else:
- custom_callbacks = [summary_callback, checkpoint_callback]
-
- history = bert_model.fit(
- x=training_dataset,
- validation_data=evaluation_dataset,
- steps_per_epoch=steps_per_epoch,
- epochs=epochs,
- validation_steps=eval_steps,
- callbacks=custom_callbacks)
- stats = {'total_training_steps': steps_per_epoch * epochs}
- if 'loss' in history.history:
- stats['train_loss'] = history.history['loss'][-1]
- if 'val_accuracy' in history.history:
- stats['eval_metrics'] = history.history['val_accuracy'][-1]
- return bert_model, stats
-
-
-def get_predictions_and_labels(strategy,
- trained_model,
- eval_input_fn,
- is_regression=False,
- return_probs=False):
- """Obtains predictions of trained model on evaluation data.
-
- Note that list of labels is returned along with the predictions because the
- order changes on distributing dataset over TPU pods.
-
- Args:
- strategy: Distribution strategy.
- trained_model: Trained model with preloaded weights.
- eval_input_fn: Input function for evaluation data.
- is_regression: Whether it is a regression task.
- return_probs: Whether to return probabilities of classes.
-
- Returns:
- predictions: List of predictions.
- labels: List of gold labels corresponding to predictions.
- """
-
- @tf.function
- def test_step(iterator):
- """Computes predictions on distributed devices."""
-
- def _test_step_fn(inputs):
- """Replicated predictions."""
- inputs, labels = inputs
- logits = trained_model(inputs, training=False)
- if not is_regression:
- probabilities = tf.nn.softmax(logits)
- return probabilities, labels
- else:
- return logits, labels
-
- outputs, labels = strategy.run(_test_step_fn, args=(next(iterator),))
- # outputs: current batch logits as a tuple of shard logits
- outputs = tf.nest.map_structure(strategy.experimental_local_results,
- outputs)
- labels = tf.nest.map_structure(strategy.experimental_local_results, labels)
- return outputs, labels
-
- def _run_evaluation(test_iterator):
- """Runs evaluation steps."""
- preds, golds = list(), list()
- try:
- with tf.experimental.async_scope():
- while True:
- probabilities, labels = test_step(test_iterator)
- for cur_probs, cur_labels in zip(probabilities, labels):
- if return_probs:
- preds.extend(cur_probs.numpy().tolist())
- else:
- preds.extend(tf.math.argmax(cur_probs, axis=1).numpy())
- golds.extend(cur_labels.numpy().tolist())
- except (StopIteration, tf.errors.OutOfRangeError):
- tf.experimental.async_clear_error()
- return preds, golds
-
- test_iter = iter(strategy.distribute_datasets_from_function(eval_input_fn))
- predictions, labels = _run_evaluation(test_iter)
-
- return predictions, labels
-
-
-def export_classifier(model_export_path, input_meta_data, bert_config,
- model_dir):
- """Exports a trained model as a `SavedModel` for inference.
-
- Args:
- model_export_path: a string specifying the path to the SavedModel directory.
- input_meta_data: dictionary containing meta data about input and model.
- bert_config: Bert configuration file to define core bert layers.
- model_dir: The directory where the model weights and training/evaluation
- summaries are stored.
-
- Raises:
- Export path is not specified, got an empty string or None.
- """
- if not model_export_path:
- raise ValueError('Export path is not specified: %s' % model_export_path)
- if not model_dir:
- raise ValueError('Export path is not specified: %s' % model_dir)
-
- # Export uses float32 for now, even if training uses mixed precision.
- tf.keras.mixed_precision.set_global_policy('float32')
- classifier_model = bert_models.classifier_model(
- bert_config,
- input_meta_data.get('num_labels', 1),
- hub_module_url=FLAGS.hub_module_url,
- hub_module_trainable=False)[0]
-
- model_saving_utils.export_bert_model(
- model_export_path, model=classifier_model, checkpoint_dir=model_dir)
-
-
-def run_bert(strategy,
- input_meta_data,
- model_config,
- train_input_fn=None,
- eval_input_fn=None,
- init_checkpoint=None,
- custom_callbacks=None,
- custom_metrics=None):
- """Run BERT training."""
- # Enables XLA in Session Config. Should not be set for TPU.
- keras_utils.set_session_config(FLAGS.enable_xla)
- performance.set_mixed_precision_policy(common_flags.dtype())
-
- epochs = FLAGS.num_train_epochs * FLAGS.num_eval_per_epoch
- train_data_size = (
- input_meta_data['train_data_size'] // FLAGS.num_eval_per_epoch)
- if FLAGS.train_data_size:
- train_data_size = min(train_data_size, FLAGS.train_data_size)
- logging.info('Updated train_data_size: %s', train_data_size)
- steps_per_epoch = int(train_data_size / FLAGS.train_batch_size)
- warmup_steps = int(epochs * train_data_size * 0.1 / FLAGS.train_batch_size)
- eval_steps = int(
- math.ceil(input_meta_data['eval_data_size'] / FLAGS.eval_batch_size))
-
- if not strategy:
- raise ValueError('Distribution strategy has not been specified.')
-
- if not custom_callbacks:
- custom_callbacks = []
-
- if FLAGS.log_steps:
- custom_callbacks.append(
- keras_utils.TimeHistory(
- batch_size=FLAGS.train_batch_size,
- log_steps=FLAGS.log_steps,
- logdir=FLAGS.model_dir))
-
- trained_model, _ = run_bert_classifier(
- strategy,
- model_config,
- input_meta_data,
- FLAGS.model_dir,
- epochs,
- steps_per_epoch,
- FLAGS.steps_per_loop,
- eval_steps,
- warmup_steps,
- FLAGS.learning_rate,
- init_checkpoint or FLAGS.init_checkpoint,
- train_input_fn,
- eval_input_fn,
- custom_callbacks=custom_callbacks,
- custom_metrics=custom_metrics)
-
- if FLAGS.model_export_path:
- model_saving_utils.export_bert_model(
- FLAGS.model_export_path, model=trained_model)
- return trained_model
-
-
-def custom_main(custom_callbacks=None, custom_metrics=None):
- """Run classification or regression.
-
- Args:
- custom_callbacks: list of tf.keras.Callbacks passed to training loop.
- custom_metrics: list of metrics passed to the training loop.
- """
- gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_param)
-
- with tf.io.gfile.GFile(FLAGS.input_meta_data_path, 'rb') as reader:
- input_meta_data = json.loads(reader.read().decode('utf-8'))
- label_type = LABEL_TYPES_MAP[input_meta_data.get('label_type', 'int')]
- include_sample_weights = input_meta_data.get('has_sample_weights', False)
-
- if not FLAGS.model_dir:
- FLAGS.model_dir = '/tmp/bert20/'
-
- bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
-
- if FLAGS.mode == 'export_only':
- export_classifier(FLAGS.model_export_path, input_meta_data, bert_config,
- FLAGS.model_dir)
- return
-
- strategy = distribute_utils.get_distribution_strategy(
- distribution_strategy=FLAGS.distribution_strategy,
- num_gpus=FLAGS.num_gpus,
- tpu_address=FLAGS.tpu)
- eval_input_fn = get_dataset_fn(
- FLAGS.eval_data_path,
- input_meta_data['max_seq_length'],
- FLAGS.eval_batch_size,
- is_training=False,
- label_type=label_type,
- include_sample_weights=include_sample_weights)
-
- if FLAGS.mode == 'predict':
- num_labels = input_meta_data.get('num_labels', 1)
- with strategy.scope():
- classifier_model = bert_models.classifier_model(
- bert_config, num_labels)[0]
- checkpoint = tf.train.Checkpoint(model=classifier_model)
- latest_checkpoint_file = (
- FLAGS.predict_checkpoint_path or
- tf.train.latest_checkpoint(FLAGS.model_dir))
- assert latest_checkpoint_file
- logging.info('Checkpoint file %s found and restoring from '
- 'checkpoint', latest_checkpoint_file)
- checkpoint.restore(
- latest_checkpoint_file).assert_existing_objects_matched()
- preds, _ = get_predictions_and_labels(
- strategy,
- classifier_model,
- eval_input_fn,
- is_regression=(num_labels == 1),
- return_probs=True)
- output_predict_file = os.path.join(FLAGS.model_dir, 'test_results.tsv')
- with tf.io.gfile.GFile(output_predict_file, 'w') as writer:
- logging.info('***** Predict results *****')
- for probabilities in preds:
- output_line = '\t'.join(
- str(class_probability)
- for class_probability in probabilities) + '\n'
- writer.write(output_line)
- return
-
- if FLAGS.mode != 'train_and_eval':
- raise ValueError('Unsupported mode is specified: %s' % FLAGS.mode)
- train_input_fn = get_dataset_fn(
- FLAGS.train_data_path,
- input_meta_data['max_seq_length'],
- FLAGS.train_batch_size,
- is_training=True,
- label_type=label_type,
- include_sample_weights=include_sample_weights,
- num_samples=FLAGS.train_data_size)
- run_bert(
- strategy,
- input_meta_data,
- bert_config,
- train_input_fn,
- eval_input_fn,
- custom_callbacks=custom_callbacks,
- custom_metrics=custom_metrics)
-
-
-def main(_):
- custom_main(custom_callbacks=None, custom_metrics=None)
-
-
-if __name__ == '__main__':
- flags.mark_flag_as_required('bert_config_file')
- flags.mark_flag_as_required('input_meta_data_path')
- flags.mark_flag_as_required('model_dir')
- app.run(main)
diff --git a/official/nlp/bert/run_squad.py b/official/nlp/bert/run_squad.py
deleted file mode 100644
index 8cafb917620abe6d969fecb563c3794bc78afc00..0000000000000000000000000000000000000000
--- a/official/nlp/bert/run_squad.py
+++ /dev/null
@@ -1,148 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Run BERT on SQuAD 1.1 and SQuAD 2.0 in TF 2.x."""
-
-import json
-import os
-import time
-
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-import gin
-import tensorflow as tf
-from official.common import distribute_utils
-from official.nlp.bert import configs as bert_configs
-from official.nlp.bert import run_squad_helper
-from official.nlp.bert import tokenization
-from official.nlp.data import squad_lib as squad_lib_wp
-from official.utils.misc import keras_utils
-
-
-flags.DEFINE_string('vocab_file', None,
- 'The vocabulary file that the BERT model was trained on.')
-
-# More flags can be found in run_squad_helper.
-run_squad_helper.define_common_squad_flags()
-
-FLAGS = flags.FLAGS
-
-
-def train_squad(strategy,
- input_meta_data,
- custom_callbacks=None,
- run_eagerly=False,
- init_checkpoint=None,
- sub_model_export_name=None):
- """Run bert squad training."""
- bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- init_checkpoint = init_checkpoint or FLAGS.init_checkpoint
- run_squad_helper.train_squad(strategy, input_meta_data, bert_config,
- custom_callbacks, run_eagerly, init_checkpoint,
- sub_model_export_name=sub_model_export_name)
-
-
-def predict_squad(strategy, input_meta_data):
- """Makes predictions for the squad dataset."""
- bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- tokenizer = tokenization.FullTokenizer(
- vocab_file=FLAGS.vocab_file, do_lower_case=FLAGS.do_lower_case)
- run_squad_helper.predict_squad(
- strategy, input_meta_data, tokenizer, bert_config, squad_lib_wp)
-
-
-def eval_squad(strategy, input_meta_data):
- """Evaluate on the squad dataset."""
- bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- tokenizer = tokenization.FullTokenizer(
- vocab_file=FLAGS.vocab_file, do_lower_case=FLAGS.do_lower_case)
- eval_metrics = run_squad_helper.eval_squad(
- strategy, input_meta_data, tokenizer, bert_config, squad_lib_wp)
- return eval_metrics
-
-
-def export_squad(model_export_path, input_meta_data):
- """Exports a trained model as a `SavedModel` for inference.
-
- Args:
- model_export_path: a string specifying the path to the SavedModel directory.
- input_meta_data: dictionary containing meta data about input and model.
-
- Raises:
- Export path is not specified, got an empty string or None.
- """
- bert_config = bert_configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- run_squad_helper.export_squad(model_export_path, input_meta_data, bert_config)
-
-
-def main(_):
- gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_param)
-
- with tf.io.gfile.GFile(FLAGS.input_meta_data_path, 'rb') as reader:
- input_meta_data = json.loads(reader.read().decode('utf-8'))
-
- if FLAGS.mode == 'export_only':
- export_squad(FLAGS.model_export_path, input_meta_data)
- return
-
- # Configures cluster spec for multi-worker distribution strategy.
- if FLAGS.num_gpus > 0:
- _ = distribute_utils.configure_cluster(FLAGS.worker_hosts, FLAGS.task_index)
- strategy = distribute_utils.get_distribution_strategy(
- distribution_strategy=FLAGS.distribution_strategy,
- num_gpus=FLAGS.num_gpus,
- all_reduce_alg=FLAGS.all_reduce_alg,
- tpu_address=FLAGS.tpu)
-
- if 'train' in FLAGS.mode:
- if FLAGS.log_steps:
- custom_callbacks = [keras_utils.TimeHistory(
- batch_size=FLAGS.train_batch_size,
- log_steps=FLAGS.log_steps,
- logdir=FLAGS.model_dir,
- )]
- else:
- custom_callbacks = None
-
- train_squad(
- strategy,
- input_meta_data,
- custom_callbacks=custom_callbacks,
- run_eagerly=FLAGS.run_eagerly,
- sub_model_export_name=FLAGS.sub_model_export_name,
- )
- if 'predict' in FLAGS.mode:
- predict_squad(strategy, input_meta_data)
- if 'eval' in FLAGS.mode:
- eval_metrics = eval_squad(strategy, input_meta_data)
- f1_score = eval_metrics['final_f1']
- logging.info('SQuAD eval F1-score: %f', f1_score)
- summary_dir = os.path.join(FLAGS.model_dir, 'summaries', 'eval')
- summary_writer = tf.summary.create_file_writer(summary_dir)
- with summary_writer.as_default():
- # TODO(lehou): write to the correct step number.
- tf.summary.scalar('F1-score', f1_score, step=0)
- summary_writer.flush()
- # Also write eval_metrics to json file.
- squad_lib_wp.write_to_json_files(
- eval_metrics, os.path.join(summary_dir, 'eval_metrics.json'))
- time.sleep(60)
-
-
-if __name__ == '__main__':
- flags.mark_flag_as_required('bert_config_file')
- flags.mark_flag_as_required('model_dir')
- app.run(main)
diff --git a/official/nlp/bert/tf1_checkpoint_converter_lib.py b/official/nlp/bert/tf1_checkpoint_converter_lib.py
deleted file mode 100644
index 035a694385abfede7314188e38ab6801b6fef70a..0000000000000000000000000000000000000000
--- a/official/nlp/bert/tf1_checkpoint_converter_lib.py
+++ /dev/null
@@ -1,201 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-r"""Convert checkpoints created by Estimator (tf1) to be Keras compatible."""
-
-import numpy as np
-import tensorflow.compat.v1 as tf # TF 1.x
-
-# Mapping between old <=> new names. The source pattern in original variable
-# name will be replaced by destination pattern.
-BERT_NAME_REPLACEMENTS = (
- ("bert", "bert_model"),
- ("embeddings/word_embeddings", "word_embeddings/embeddings"),
- ("embeddings/token_type_embeddings",
- "embedding_postprocessor/type_embeddings"),
- ("embeddings/position_embeddings",
- "embedding_postprocessor/position_embeddings"),
- ("embeddings/LayerNorm", "embedding_postprocessor/layer_norm"),
- ("attention/self", "self_attention"),
- ("attention/output/dense", "self_attention_output"),
- ("attention/output/LayerNorm", "self_attention_layer_norm"),
- ("intermediate/dense", "intermediate"),
- ("output/dense", "output"),
- ("output/LayerNorm", "output_layer_norm"),
- ("pooler/dense", "pooler_transform"),
-)
-
-BERT_V2_NAME_REPLACEMENTS = (
- ("bert/", ""),
- ("encoder", "transformer"),
- ("embeddings/word_embeddings", "word_embeddings/embeddings"),
- ("embeddings/token_type_embeddings", "type_embeddings/embeddings"),
- ("embeddings/position_embeddings", "position_embedding/embeddings"),
- ("embeddings/LayerNorm", "embeddings/layer_norm"),
- ("attention/self", "self_attention"),
- ("attention/output/dense", "self_attention/attention_output"),
- ("attention/output/LayerNorm", "self_attention_layer_norm"),
- ("intermediate/dense", "intermediate"),
- ("output/dense", "output"),
- ("output/LayerNorm", "output_layer_norm"),
- ("pooler/dense", "pooler_transform"),
- ("cls/predictions", "bert/cls/predictions"),
- ("cls/predictions/output_bias", "cls/predictions/output_bias/bias"),
- ("cls/seq_relationship/output_bias", "predictions/transform/logits/bias"),
- ("cls/seq_relationship/output_weights",
- "predictions/transform/logits/kernel"),
-)
-
-BERT_PERMUTATIONS = ()
-
-BERT_V2_PERMUTATIONS = (("cls/seq_relationship/output_weights", (1, 0)),)
-
-
-def _bert_name_replacement(var_name, name_replacements):
- """Gets the variable name replacement."""
- for src_pattern, tgt_pattern in name_replacements:
- if src_pattern in var_name:
- old_var_name = var_name
- var_name = var_name.replace(src_pattern, tgt_pattern)
- tf.logging.info("Converted: %s --> %s", old_var_name, var_name)
- return var_name
-
-
-def _has_exclude_patterns(name, exclude_patterns):
- """Checks if a string contains substrings that match patterns to exclude."""
- for p in exclude_patterns:
- if p in name:
- return True
- return False
-
-
-def _get_permutation(name, permutations):
- """Checks whether a variable requires transposition by pattern matching."""
- for src_pattern, permutation in permutations:
- if src_pattern in name:
- tf.logging.info("Permuted: %s --> %s", name, permutation)
- return permutation
-
- return None
-
-
-def _get_new_shape(name, shape, num_heads):
- """Checks whether a variable requires reshape by pattern matching."""
- if "self_attention/attention_output/kernel" in name:
- return tuple([num_heads, shape[0] // num_heads, shape[1]])
- if "self_attention/attention_output/bias" in name:
- return shape
-
- patterns = [
- "self_attention/query", "self_attention/value", "self_attention/key"
- ]
- for pattern in patterns:
- if pattern in name:
- if "kernel" in name:
- return tuple([shape[0], num_heads, shape[1] // num_heads])
- if "bias" in name:
- return tuple([num_heads, shape[0] // num_heads])
- return None
-
-
-def create_v2_checkpoint(model,
- src_checkpoint,
- output_path,
- checkpoint_model_name="model"):
- """Converts a name-based matched TF V1 checkpoint to TF V2 checkpoint."""
- # Uses streaming-restore in eager model to read V1 name-based checkpoints.
- model.load_weights(src_checkpoint).assert_existing_objects_matched()
- if hasattr(model, "checkpoint_items"):
- checkpoint_items = model.checkpoint_items
- else:
- checkpoint_items = {}
-
- checkpoint_items[checkpoint_model_name] = model
- checkpoint = tf.train.Checkpoint(**checkpoint_items)
- checkpoint.save(output_path)
-
-
-def convert(checkpoint_from_path,
- checkpoint_to_path,
- num_heads,
- name_replacements,
- permutations,
- exclude_patterns=None):
- """Migrates the names of variables within a checkpoint.
-
- Args:
- checkpoint_from_path: Path to source checkpoint to be read in.
- checkpoint_to_path: Path to checkpoint to be written out.
- num_heads: The number of heads of the model.
- name_replacements: A list of tuples of the form (match_str, replace_str)
- describing variable names to adjust.
- permutations: A list of tuples of the form (match_str, permutation)
- describing permutations to apply to given variables. Note that match_str
- should match the original variable name, not the replaced one.
- exclude_patterns: A list of string patterns to exclude variables from
- checkpoint conversion.
-
- Returns:
- A dictionary that maps the new variable names to the Variable objects.
- A dictionary that maps the old variable names to the new variable names.
- """
- with tf.Graph().as_default():
- tf.logging.info("Reading checkpoint_from_path %s", checkpoint_from_path)
- reader = tf.train.NewCheckpointReader(checkpoint_from_path)
- name_shape_map = reader.get_variable_to_shape_map()
- new_variable_map = {}
- conversion_map = {}
- for var_name in name_shape_map:
- if exclude_patterns and _has_exclude_patterns(var_name, exclude_patterns):
- continue
- # Get the original tensor data.
- tensor = reader.get_tensor(var_name)
-
- # Look up the new variable name, if any.
- new_var_name = _bert_name_replacement(var_name, name_replacements)
-
- # See if we need to reshape the underlying tensor.
- new_shape = None
- if num_heads > 0:
- new_shape = _get_new_shape(new_var_name, tensor.shape, num_heads)
- if new_shape:
- tf.logging.info("Veriable %s has a shape change from %s to %s",
- var_name, tensor.shape, new_shape)
- tensor = np.reshape(tensor, new_shape)
-
- # See if we need to permute the underlying tensor.
- permutation = _get_permutation(var_name, permutations)
- if permutation:
- tensor = np.transpose(tensor, permutation)
-
- # Create a new variable with the possibly-reshaped or transposed tensor.
- var = tf.Variable(tensor, name=var_name)
-
- # Save the variable into the new variable map.
- new_variable_map[new_var_name] = var
-
- # Keep a list of converter variables for sanity checking.
- if new_var_name != var_name:
- conversion_map[var_name] = new_var_name
-
- saver = tf.train.Saver(new_variable_map)
-
- with tf.Session() as sess:
- sess.run(tf.global_variables_initializer())
- tf.logging.info("Writing checkpoint_to_path %s", checkpoint_to_path)
- saver.save(sess, checkpoint_to_path, write_meta_graph=False)
-
- tf.logging.info("Summary:")
- tf.logging.info(" Converted %d variable name(s).", len(new_variable_map))
- tf.logging.info(" Converted: %s", str(conversion_map))
diff --git a/official/nlp/bert/tf2_encoder_checkpoint_converter.py b/official/nlp/bert/tf2_encoder_checkpoint_converter.py
deleted file mode 100644
index 9fced5daee95479c28cffd2b63dffcf6f2d90408..0000000000000000000000000000000000000000
--- a/official/nlp/bert/tf2_encoder_checkpoint_converter.py
+++ /dev/null
@@ -1,160 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""A converter from a V1 BERT encoder checkpoint to a V2 encoder checkpoint.
-
-The conversion will yield an object-oriented checkpoint that can be used
-to restore a BertEncoder or BertPretrainerV2 object (see the `converted_model`
-FLAG below).
-"""
-
-import os
-
-from absl import app
-from absl import flags
-
-import tensorflow as tf
-from official.modeling import tf_utils
-from official.nlp.bert import configs
-from official.nlp.bert import tf1_checkpoint_converter_lib
-from official.nlp.modeling import models
-from official.nlp.modeling import networks
-
-FLAGS = flags.FLAGS
-
-flags.DEFINE_string("bert_config_file", None,
- "Bert configuration file to define core bert layers.")
-flags.DEFINE_string(
- "checkpoint_to_convert", None,
- "Initial checkpoint from a pretrained BERT model core (that is, only the "
- "BertModel, with no task heads.)")
-flags.DEFINE_string("converted_checkpoint_path", None,
- "Name for the created object-based V2 checkpoint.")
-flags.DEFINE_string("checkpoint_model_name", "encoder",
- "The name of the model when saving the checkpoint, i.e., "
- "the checkpoint will be saved using: "
- "tf.train.Checkpoint(FLAGS.checkpoint_model_name=model).")
-flags.DEFINE_enum(
- "converted_model", "encoder", ["encoder", "pretrainer"],
- "Whether to convert the checkpoint to a `BertEncoder` model or a "
- "`BertPretrainerV2` model (with mlm but without classification heads).")
-
-
-def _create_bert_model(cfg):
- """Creates a BERT keras core model from BERT configuration.
-
- Args:
- cfg: A `BertConfig` to create the core model.
-
- Returns:
- A BertEncoder network.
- """
- bert_encoder = networks.BertEncoder(
- vocab_size=cfg.vocab_size,
- hidden_size=cfg.hidden_size,
- num_layers=cfg.num_hidden_layers,
- num_attention_heads=cfg.num_attention_heads,
- intermediate_size=cfg.intermediate_size,
- activation=tf_utils.get_activation(cfg.hidden_act),
- dropout_rate=cfg.hidden_dropout_prob,
- attention_dropout_rate=cfg.attention_probs_dropout_prob,
- max_sequence_length=cfg.max_position_embeddings,
- type_vocab_size=cfg.type_vocab_size,
- initializer=tf.keras.initializers.TruncatedNormal(
- stddev=cfg.initializer_range),
- embedding_width=cfg.embedding_size)
-
- return bert_encoder
-
-
-def _create_bert_pretrainer_model(cfg):
- """Creates a BERT keras core model from BERT configuration.
-
- Args:
- cfg: A `BertConfig` to create the core model.
-
- Returns:
- A BertPretrainerV2 model.
- """
- bert_encoder = _create_bert_model(cfg)
- pretrainer = models.BertPretrainerV2(
- encoder_network=bert_encoder,
- mlm_activation=tf_utils.get_activation(cfg.hidden_act),
- mlm_initializer=tf.keras.initializers.TruncatedNormal(
- stddev=cfg.initializer_range))
- # Makes sure the pretrainer variables are created.
- _ = pretrainer(pretrainer.inputs)
- return pretrainer
-
-
-def convert_checkpoint(bert_config,
- output_path,
- v1_checkpoint,
- checkpoint_model_name="model",
- converted_model="encoder"):
- """Converts a V1 checkpoint into an OO V2 checkpoint."""
- output_dir, _ = os.path.split(output_path)
- tf.io.gfile.makedirs(output_dir)
-
- # Create a temporary V1 name-converted checkpoint in the output directory.
- temporary_checkpoint_dir = os.path.join(output_dir, "temp_v1")
- temporary_checkpoint = os.path.join(temporary_checkpoint_dir, "ckpt")
-
- tf1_checkpoint_converter_lib.convert(
- checkpoint_from_path=v1_checkpoint,
- checkpoint_to_path=temporary_checkpoint,
- num_heads=bert_config.num_attention_heads,
- name_replacements=tf1_checkpoint_converter_lib.BERT_V2_NAME_REPLACEMENTS,
- permutations=tf1_checkpoint_converter_lib.BERT_V2_PERMUTATIONS,
- exclude_patterns=["adam", "Adam"])
-
- if converted_model == "encoder":
- model = _create_bert_model(bert_config)
- elif converted_model == "pretrainer":
- model = _create_bert_pretrainer_model(bert_config)
- else:
- raise ValueError("Unsupported converted_model: %s" % converted_model)
-
- # Create a V2 checkpoint from the temporary checkpoint.
- tf1_checkpoint_converter_lib.create_v2_checkpoint(model, temporary_checkpoint,
- output_path,
- checkpoint_model_name)
-
- # Clean up the temporary checkpoint, if it exists.
- try:
- tf.io.gfile.rmtree(temporary_checkpoint_dir)
- except tf.errors.OpError:
- # If it doesn't exist, we don't need to clean it up; continue.
- pass
-
-
-def main(argv):
- if len(argv) > 1:
- raise app.UsageError("Too many command-line arguments.")
-
- output_path = FLAGS.converted_checkpoint_path
- v1_checkpoint = FLAGS.checkpoint_to_convert
- checkpoint_model_name = FLAGS.checkpoint_model_name
- converted_model = FLAGS.converted_model
- bert_config = configs.BertConfig.from_json_file(FLAGS.bert_config_file)
- convert_checkpoint(
- bert_config=bert_config,
- output_path=output_path,
- v1_checkpoint=v1_checkpoint,
- checkpoint_model_name=checkpoint_model_name,
- converted_model=converted_model)
-
-
-if __name__ == "__main__":
- app.run(main)
diff --git a/official/nlp/configs/__init__.py b/official/nlp/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/nlp/configs/__init__.py
+++ b/official/nlp/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/configs/bert.py b/official/nlp/configs/bert.py
index cf78de0388bf76b68cd6df8cc656842bbfc90b64..e712aae2cf3afbc78dc8d33e41fa6abbfe3842ce 100644
--- a/official/nlp/configs/bert.py
+++ b/official/nlp/configs/bert.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -41,3 +41,5 @@ class PretrainerConfig(base_config.Config):
cls_heads: List[ClsHeadConfig] = dataclasses.field(default_factory=list)
mlm_activation: str = "gelu"
mlm_initializer_range: float = 0.02
+ # Currently only used for mobile bert.
+ mlm_output_weights_use_proj: bool = False
diff --git a/official/nlp/configs/electra.py b/official/nlp/configs/electra.py
index 5e62297667a470fd192779d8dc7f5c5117836804..0c55e50e5e81b5ef88bc4fa115b4c9ed9dd9409a 100644
--- a/official/nlp/configs/electra.py
+++ b/official/nlp/configs/electra.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/configs/encoders.py b/official/nlp/configs/encoders.py
index bc44c899b5cf905c9c50b6fe567f23414c2d0d68..90a5d47d11df7f0709ac1aef4c899b60ef820d2c 100644
--- a/official/nlp/configs/encoders.py
+++ b/official/nlp/configs/encoders.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,9 +16,9 @@
Includes configurations and factory methods.
"""
-from typing import Optional
-
import dataclasses
+from typing import Optional, Sequence
+
import gin
import tensorflow as tf
@@ -26,7 +26,7 @@ from official.modeling import hyperparams
from official.modeling import tf_utils
from official.nlp.modeling import layers
from official.nlp.modeling import networks
-from official.nlp.projects.bigbird import encoder as bigbird_encoder
+from official.projects.bigbird import encoder as bigbird_encoder
@dataclasses.dataclass
@@ -221,6 +221,50 @@ class XLNetEncoderConfig(hyperparams.Config):
two_stream: bool = False
+@dataclasses.dataclass
+class QueryBertConfig(hyperparams.Config):
+ """Query BERT encoder configuration."""
+ vocab_size: int = 30522
+ hidden_size: int = 768
+ num_layers: int = 12
+ num_attention_heads: int = 12
+ hidden_activation: str = "gelu"
+ intermediate_size: int = 3072
+ dropout_rate: float = 0.1
+ attention_dropout_rate: float = 0.1
+ max_position_embeddings: int = 512
+ type_vocab_size: int = 2
+ initializer_range: float = 0.02
+ embedding_size: Optional[int] = None
+ output_range: Optional[int] = None
+ return_all_encoder_outputs: bool = False
+ # Pre/Post-LN Transformer
+ norm_first: bool = False
+
+
+@dataclasses.dataclass
+class FNetEncoderConfig(hyperparams.Config):
+ """FNet encoder configuration."""
+ vocab_size: int = 30522
+ hidden_size: int = 768
+ num_layers: int = 12
+ num_attention_heads: int = 12
+ inner_activation: str = "gelu"
+ inner_dim: int = 3072
+ output_dropout: float = 0.1
+ attention_dropout: float = 0.1
+ max_sequence_length: int = 512
+ type_vocab_size: int = 2
+ initializer_range: float = 0.02
+ embedding_width: Optional[int] = None
+ output_range: Optional[int] = None
+ return_all_encoder_outputs: bool = False
+ # Pre/Post-LN Transformer
+ norm_first: bool = False
+ use_fft: bool = False
+ attention_layers: Sequence[int] = ()
+
+
@dataclasses.dataclass
class EncoderConfig(hyperparams.OneOfConfig):
"""Encoder configuration."""
@@ -233,6 +277,8 @@ class EncoderConfig(hyperparams.OneOfConfig):
mobilebert: MobileBertEncoderConfig = MobileBertEncoderConfig()
reuse: ReuseEncoderConfig = ReuseEncoderConfig()
xlnet: XLNetEncoderConfig = XLNetEncoderConfig()
+ query_bert: QueryBertConfig = QueryBertConfig()
+ fnet: FNetEncoderConfig = FNetEncoderConfig()
# If `any` is used, the encoder building relies on any.BUILDER.
any: hyperparams.Config = hyperparams.Config()
@@ -513,6 +559,54 @@ def build_encoder(config: EncoderConfig,
recursive=True)
return networks.EncoderScaffold(**kwargs)
+ if encoder_type == "query_bert":
+ embedding_layer = layers.FactorizedEmbedding(
+ vocab_size=encoder_cfg.vocab_size,
+ embedding_width=encoder_cfg.embedding_size,
+ output_dim=encoder_cfg.hidden_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ name="word_embeddings")
+ return networks.BertEncoderV2(
+ vocab_size=encoder_cfg.vocab_size,
+ hidden_size=encoder_cfg.hidden_size,
+ num_layers=encoder_cfg.num_layers,
+ num_attention_heads=encoder_cfg.num_attention_heads,
+ intermediate_size=encoder_cfg.intermediate_size,
+ activation=tf_utils.get_activation(encoder_cfg.hidden_activation),
+ dropout_rate=encoder_cfg.dropout_rate,
+ attention_dropout_rate=encoder_cfg.attention_dropout_rate,
+ max_sequence_length=encoder_cfg.max_position_embeddings,
+ type_vocab_size=encoder_cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ output_range=encoder_cfg.output_range,
+ embedding_layer=embedding_layer,
+ return_all_encoder_outputs=encoder_cfg.return_all_encoder_outputs,
+ dict_outputs=True,
+ norm_first=encoder_cfg.norm_first)
+
+ if encoder_type == "fnet":
+ return networks.FNet(
+ vocab_size=encoder_cfg.vocab_size,
+ hidden_size=encoder_cfg.hidden_size,
+ num_layers=encoder_cfg.num_layers,
+ num_attention_heads=encoder_cfg.num_attention_heads,
+ inner_dim=encoder_cfg.inner_dim,
+ inner_activation=tf_utils.get_activation(encoder_cfg.inner_activation),
+ output_dropout=encoder_cfg.output_dropout,
+ attention_dropout=encoder_cfg.attention_dropout,
+ max_sequence_length=encoder_cfg.max_sequence_length,
+ type_vocab_size=encoder_cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ output_range=encoder_cfg.output_range,
+ embedding_width=encoder_cfg.embedding_width,
+ embedding_layer=embedding_layer,
+ norm_first=encoder_cfg.norm_first,
+ use_fft=encoder_cfg.use_fft,
+ attention_layers=encoder_cfg.attention_layers)
+
bert_encoder_cls = networks.BertEncoder
if encoder_type == "bert_v2":
bert_encoder_cls = networks.BertEncoderV2
diff --git a/official/nlp/configs/encoders_test.py b/official/nlp/configs/encoders_test.py
index 3b6bf6198b1757861e56258841b0c58d1951d806..6012c55fe9bab058945b5fa707de0734846cb56e 100644
--- a/official/nlp/configs/encoders_test.py
+++ b/official/nlp/configs/encoders_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ import tensorflow as tf
from official.modeling import hyperparams
from official.nlp.configs import encoders
from official.nlp.modeling import networks
-from official.nlp.projects.teams import teams
+from official.projects.teams import teams
class EncodersTest(tf.test.TestCase):
diff --git a/official/nlp/configs/experiment_configs.py b/official/nlp/configs/experiment_configs.py
index 2b52d5b4b7fda4bfd487310b0bd39a255117968a..006d6d7d5582aef228f499c35d14a3c85fb893e5 100644
--- a/official/nlp/configs/experiment_configs.py
+++ b/official/nlp/configs/experiment_configs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,4 +17,3 @@
from official.nlp.configs import finetuning_experiments
from official.nlp.configs import pretraining_experiments
from official.nlp.configs import wmt_transformer_experiments
-from official.nlp.projects.teams import teams_experiments
diff --git a/official/nlp/configs/experiments/wiki_books_pretrain.yaml b/official/nlp/configs/experiments/wiki_books_pretrain.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..bff3cbb73a1ec6466ade7f985f7dfaf550722371
--- /dev/null
+++ b/official/nlp/configs/experiments/wiki_books_pretrain.yaml
@@ -0,0 +1,48 @@
+task:
+ init_checkpoint: ''
+ model:
+ cls_heads: [{activation: tanh, cls_token_idx: 0, dropout_rate: 0.1, inner_dim: 768, name: next_sentence, num_classes: 2}]
+ train_data:
+ drop_remainder: true
+ global_batch_size: 512
+ input_path: '[Your proceed wiki data path]*,[Your proceed books data path]*'
+ is_training: true
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: true
+ validation_data:
+ drop_remainder: false
+ global_batch_size: 512
+ input_path: '[Your proceed wiki data path]-00000-of-00500,[Your proceed books data path]-00000-of-00500'
+ is_training: false
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: true
+trainer:
+ checkpoint_interval: 20000
+ max_to_keep: 5
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ cycle: false
+ decay_steps: 1000000
+ end_learning_rate: 0.0
+ initial_learning_rate: 0.0001
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 10000
+ type: polynomial
+ steps_per_loop: 1000
+ summary_interval: 1000
+ train_steps: 1000000
+ validation_interval: 1000
+ validation_steps: 64
diff --git a/official/nlp/configs/finetuning_experiments.py b/official/nlp/configs/finetuning_experiments.py
index d87c9655e5118b6d8322ec2513d554c3eebdbf6b..23833d4cf49a01a315edbc3d153fde7570cba487 100644
--- a/official/nlp/configs/finetuning_experiments.py
+++ b/official/nlp/configs/finetuning_experiments.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/configs/pretraining_experiments.py b/official/nlp/configs/pretraining_experiments.py
index 024c6fcfb281a467ceaaffa1cdbdf07fdae5a95a..1eedb87828054729eb621b3dc6241e491a14899d 100644
--- a/official/nlp/configs/pretraining_experiments.py
+++ b/official/nlp/configs/pretraining_experiments.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/configs/wmt_transformer_experiments.py b/official/nlp/configs/wmt_transformer_experiments.py
index eb85b76c5a94505de9c4e7e2e11a563abce5a645..bdef599fa428e3f76e5810bb8fcf7d5a7fa4af92 100644
--- a/official/nlp/configs/wmt_transformer_experiments.py
+++ b/official/nlp/configs/wmt_transformer_experiments.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
# pylint: disable=g-doc-return-or-yield,line-too-long
"""WMT translation configurations."""
diff --git a/official/nlp/continuous_finetune_lib.py b/official/nlp/continuous_finetune_lib.py
index 6fe851741c0f631ea18f80b9bf259c551e7f2561..988b62c60328f46cf371a563f37e3ff0867743d2 100644
--- a/official/nlp/continuous_finetune_lib.py
+++ b/official/nlp/continuous_finetune_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/continuous_finetune_lib_test.py b/official/nlp/continuous_finetune_lib_test.py
index 08ee381dce133d73e18e697b938cab92d04f2ff0..6ed727d73e26521af15fd540b1486bd933dbf0b0 100644
--- a/official/nlp/continuous_finetune_lib_test.py
+++ b/official/nlp/continuous_finetune_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/README.md b/official/nlp/data/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..2a706d7be7f99974a097ca128e890589c8cdb826
--- /dev/null
+++ b/official/nlp/data/README.md
@@ -0,0 +1,4 @@
+This directory contains binaries and utils required for input preprocessing,
+tokenization, etc that can be used with model building blocks available in
+NLP modeling library [nlp/modelling](https://github.com/tensorflow/models/tree/master/official/nlp/modeling)
+to train custom models and validate new research ideas.
diff --git a/official/nlp/data/__init__.py b/official/nlp/data/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/nlp/data/__init__.py
+++ b/official/nlp/data/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/classifier_data_lib.py b/official/nlp/data/classifier_data_lib.py
index 0ba9dcf9a055ab9a3e5206f251d45d2ea41a2661..3e95caf719b83ec1c21faa60889385f519af8b72 100644
--- a/official/nlp/data/classifier_data_lib.py
+++ b/official/nlp/data/classifier_data_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -24,7 +24,7 @@ from absl import logging
import tensorflow as tf
import tensorflow_datasets as tfds
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
class InputExample(object):
@@ -187,6 +187,8 @@ class AxProcessor(DataProcessor):
def _create_examples_tfds(self, dataset, set_type):
"""Creates examples for the training/dev/test sets."""
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -218,6 +220,8 @@ class ColaProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/cola", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -312,6 +316,8 @@ class MnliProcessor(DataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/mnli", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -343,6 +349,8 @@ class MrpcProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/mrpc", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -453,6 +461,8 @@ class QnliProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/qnli", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -484,6 +494,8 @@ class QqpProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/qqp", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -517,6 +529,8 @@ class RteProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/rte", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -548,6 +562,8 @@ class SstProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/sst2", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -574,6 +590,8 @@ class StsBProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/stsb", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
@@ -742,6 +760,8 @@ class WnliProcessor(DefaultGLUEDataProcessor):
"""Creates examples for the training/dev/test sets."""
dataset = tfds.load(
"glue/wnli", split=set_type, try_gcs=True).as_numpy_iterator()
+ dataset = list(dataset)
+ dataset.sort(key=lambda x: x["idx"])
examples = []
for i, example in enumerate(dataset):
guid = "%s-%s" % (set_type, i)
diff --git a/official/nlp/data/classifier_data_lib_test.py b/official/nlp/data/classifier_data_lib_test.py
index c1db1a3d03f7b6daaa4816decb653814c675f3e2..f7a517da0a2a92442da1dcb16afc9230938b20e6 100644
--- a/official/nlp/data/classifier_data_lib_test.py
+++ b/official/nlp/data/classifier_data_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,8 +21,8 @@ from absl.testing import parameterized
import tensorflow as tf
import tensorflow_datasets as tfds
-from official.nlp.bert import tokenization
from official.nlp.data import classifier_data_lib
+from official.nlp.tools import tokenization
def decode_record(record, name_to_features):
diff --git a/official/nlp/data/create_finetuning_data.py b/official/nlp/data/create_finetuning_data.py
index 01f2deaecde56e9927eb41452fd896539932d123..be1b6b444a09539a7d5b07aec908f168d03049ac 100644
--- a/official/nlp/data/create_finetuning_data.py
+++ b/official/nlp/data/create_finetuning_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,7 +22,6 @@ import os
from absl import app
from absl import flags
import tensorflow as tf
-from official.nlp.bert import tokenization
from official.nlp.data import classifier_data_lib
from official.nlp.data import sentence_retrieval_lib
# word-piece tokenizer based squad_lib
@@ -30,10 +29,10 @@ from official.nlp.data import squad_lib as squad_lib_wp
# sentence-piece tokenizer based squad_lib
from official.nlp.data import squad_lib_sp
from official.nlp.data import tagging_data_lib
+from official.nlp.tools import tokenization
FLAGS = flags.FLAGS
-# TODO(chendouble): consider moving each task to its own binary.
flags.DEFINE_enum(
"fine_tuning_task_type", "classification",
["classification", "regression", "squad", "retrieval", "tagging"],
diff --git a/official/nlp/data/create_pretraining_data.py b/official/nlp/data/create_pretraining_data.py
index 93b7723d125a6e4916a8a595ef4c5a4b470bdcc9..4d5eae4de05ba10f0a5f4294d3f7957279eef0a5 100644
--- a/official/nlp/data/create_pretraining_data.py
+++ b/official/nlp/data/create_pretraining_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -24,7 +24,7 @@ from absl import flags
from absl import logging
import tensorflow as tf
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
FLAGS = flags.FLAGS
diff --git a/official/nlp/data/create_pretraining_data_test.py b/official/nlp/data/create_pretraining_data_test.py
index 79a38ba8506ac428d48188f0eb4fbf2ce26b4422..da50d5479e458035f9e4379bf20ae6d1f5309432 100644
--- a/official/nlp/data/create_pretraining_data_test.py
+++ b/official/nlp/data/create_pretraining_data_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/create_xlnet_pretraining_data.py b/official/nlp/data/create_xlnet_pretraining_data.py
index 363164fcae001a61da53b0bb6e0afb9f4e92fd42..3657962fd19a90159eb3e0e5b5a4a21694dea628 100644
--- a/official/nlp/data/create_xlnet_pretraining_data.py
+++ b/official/nlp/data/create_xlnet_pretraining_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,6 +14,7 @@
"""Create LM TF examples for XLNet."""
+import dataclasses
import json
import math
import os
@@ -28,11 +29,10 @@ from absl import app
from absl import flags
from absl import logging
-import dataclasses
import numpy as np
import tensorflow as tf
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
special_symbols = {
"": 0,
diff --git a/official/nlp/data/create_xlnet_pretraining_data_test.py b/official/nlp/data/create_xlnet_pretraining_data_test.py
index 5630411a7eb0e92b2baf6e203547d1c9063ebd79..6a3b96833edfd23f0740ce8b7498c00df03d970e 100644
--- a/official/nlp/data/create_xlnet_pretraining_data_test.py
+++ b/official/nlp/data/create_xlnet_pretraining_data_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/data_loader.py b/official/nlp/data/data_loader.py
index 2b181270658f42f0819f01fbed5af7989b1d3e5d..b962d5f97405300f26512305fc4b96e6699bf5a2 100644
--- a/official/nlp/data/data_loader.py
+++ b/official/nlp/data/data_loader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/data_loader_factory.py b/official/nlp/data/data_loader_factory.py
index 9602ea295283e5490d1bcb5cc67df9f99ebdb0ca..f3a2decb8c5ea3871490d0b551151c86d6887fcf 100644
--- a/official/nlp/data/data_loader_factory.py
+++ b/official/nlp/data/data_loader_factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/data_loader_factory_test.py b/official/nlp/data/data_loader_factory_test.py
index 8aa86757df64a445692ce4bf8ff64e6649b6dfa6..518717a3f37d49b67974e5a66e6f308a1532f971 100644
--- a/official/nlp/data/data_loader_factory_test.py
+++ b/official/nlp/data/data_loader_factory_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/dual_encoder_dataloader.py b/official/nlp/data/dual_encoder_dataloader.py
index af9f1090fceda600373ef785d91fd215e8621fd8..1818d07f0bccb20b94489a14542d8e1bbab42bb3 100644
--- a/official/nlp/data/dual_encoder_dataloader.py
+++ b/official/nlp/data/dual_encoder_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -124,7 +124,7 @@ class DualEncoderDataLoader(data_loader.DataLoader):
raise ValueError('Expected {} to start with {}'.format(string, old))
def _switch_key_prefix(d, old, new):
- return {_switch_prefix(key, old, new): value for key, value in d.items()}
+ return {_switch_prefix(key, old, new): value for key, value in d.items()} # pytype: disable=attribute-error # trace-all-classes
model_inputs = _switch_key_prefix(
self._bert_tokenize(record, self._left_text_fields),
diff --git a/official/nlp/data/dual_encoder_dataloader_test.py b/official/nlp/data/dual_encoder_dataloader_test.py
index 358b0d9635c747a72e0e8f40951f11eb2c5755a0..bebdc1531ef169a93aaa5a1e6c460330db5b6376 100644
--- a/official/nlp/data/dual_encoder_dataloader_test.py
+++ b/official/nlp/data/dual_encoder_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/pretrain_dataloader.py b/official/nlp/data/pretrain_dataloader.py
index dbb7953c3fd7f1562d7b3ec07c58b09eefef8e25..f2a33cd4277cdfac1a71894beb6369ef22d8500a 100644
--- a/official/nlp/data/pretrain_dataloader.py
+++ b/official/nlp/data/pretrain_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/pretrain_dataloader_test.py b/official/nlp/data/pretrain_dataloader_test.py
index 5f3807c907ad9cbb2007425ac13bba620491dce6..ce7f216f9af78ce5d4cc70095444745a1db98ae9 100644
--- a/official/nlp/data/pretrain_dataloader_test.py
+++ b/official/nlp/data/pretrain_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/pretrain_dynamic_dataloader.py b/official/nlp/data/pretrain_dynamic_dataloader.py
index c1de4ba54b86a3386708e3f56b76e8e3726c397d..ab61445468070a674bf5c66a63f7ee83eb5ed4dc 100644
--- a/official/nlp/data/pretrain_dynamic_dataloader.py
+++ b/official/nlp/data/pretrain_dynamic_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -79,17 +79,29 @@ class PretrainingDynamicDataLoader(pretrain_dataloader.BertPretrainDataLoader):
def _decode(self, record: tf.Tensor):
"""Decodes a serialized tf.Example."""
name_to_features = {
- 'input_ids': tf.io.VarLenFeature(tf.int64),
'input_mask': tf.io.VarLenFeature(tf.int64),
- 'segment_ids': tf.io.VarLenFeature(tf.int64),
'masked_lm_positions': tf.io.VarLenFeature(tf.int64),
'masked_lm_ids': tf.io.VarLenFeature(tf.int64),
'masked_lm_weights': tf.io.VarLenFeature(tf.float32),
}
+ if self._params.use_v2_feature_names:
+ input_ids_key = 'input_word_ids'
+ segment_key = 'input_type_ids'
+ name_to_features.update({
+ input_ids_key: tf.io.VarLenFeature(tf.int64),
+ segment_key: tf.io.VarLenFeature(tf.int64),
+ })
+ else:
+ input_ids_key = 'input_ids'
+ segment_key = 'segment_ids'
+ name_to_features.update({
+ input_ids_key: tf.io.VarLenFeature(tf.int64),
+ segment_key: tf.io.VarLenFeature(tf.int64),
+ })
if self._use_next_sentence_label:
name_to_features['next_sentence_labels'] = tf.io.FixedLenFeature([1],
tf.int64)
- dynamic_keys = ['input_ids', 'input_mask', 'segment_ids']
+ dynamic_keys = [input_ids_key, 'input_mask', segment_key]
if self._use_position_id:
name_to_features['position_ids'] = tf.io.VarLenFeature(tf.int64)
dynamic_keys.append('position_ids')
@@ -102,7 +114,7 @@ class PretrainingDynamicDataLoader(pretrain_dataloader.BertPretrainDataLoader):
# sequence length dimension.
# Pad before the first non pad from the back should not be removed.
mask = tf.math.greater(
- tf.math.cumsum(example['input_ids'], reverse=True), 0)
+ tf.math.cumsum(example[input_ids_key], reverse=True), 0)
for key in dynamic_keys:
example[key] = tf.boolean_mask(example[key], mask)
diff --git a/official/nlp/data/pretrain_dynamic_dataloader_test.py b/official/nlp/data/pretrain_dynamic_dataloader_test.py
index 188e6d495b71acc2699b82f71a86acb5efbf99f5..3927b7993559f89dc63133a1f1dd913d55fb8675 100644
--- a/official/nlp/data/pretrain_dynamic_dataloader_test.py
+++ b/official/nlp/data/pretrain_dynamic_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/question_answering_dataloader.py b/official/nlp/data/question_answering_dataloader.py
index 0f721ed773a927e8caa8c3cfbaa5cf2ef6c896e5..171c0d3b228f48a4264a2b1b67704a6b54efe11f 100644
--- a/official/nlp/data/question_answering_dataloader.py
+++ b/official/nlp/data/question_answering_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/question_answering_dataloader_test.py b/official/nlp/data/question_answering_dataloader_test.py
index c853bc080cddf9fc5c26a0f7f21cff19088bad9f..9767ef0a7c1d68fa7d87f5a4f71da20b9f2f092b 100644
--- a/official/nlp/data/question_answering_dataloader_test.py
+++ b/official/nlp/data/question_answering_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/sentence_prediction_dataloader.py b/official/nlp/data/sentence_prediction_dataloader.py
index 3517edfb9757f26869522d5c40b1c01f256de8e0..c601b9d72d5f9aaba658edb68b6c413648780aaa 100644
--- a/official/nlp/data/sentence_prediction_dataloader.py
+++ b/official/nlp/data/sentence_prediction_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/sentence_prediction_dataloader_test.py b/official/nlp/data/sentence_prediction_dataloader_test.py
index 876b9d421d26a06d8442570a65a60e63022c2fd1..d4f0d8559b10c2871fc8daf38af19ad90a8c77a6 100644
--- a/official/nlp/data/sentence_prediction_dataloader_test.py
+++ b/official/nlp/data/sentence_prediction_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/sentence_retrieval_lib.py b/official/nlp/data/sentence_retrieval_lib.py
index 0bfd8e4dec5afba3eb00ff23e3f75a0cc5818958..947dbb77949789f9564e610e7398051dc7b63d70 100644
--- a/official/nlp/data/sentence_retrieval_lib.py
+++ b/official/nlp/data/sentence_retrieval_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,8 +17,8 @@
import os
from absl import logging
-from official.nlp.bert import tokenization
from official.nlp.data import classifier_data_lib
+from official.nlp.tools import tokenization
class BuccProcessor(classifier_data_lib.DataProcessor):
diff --git a/official/nlp/data/squad_lib.py b/official/nlp/data/squad_lib.py
index e96838664c38db4f6cdc2d39f10ad68baeac25e5..2d198e6c1b442f68446d998be4eb8a9c9354a828 100644
--- a/official/nlp/data/squad_lib.py
+++ b/official/nlp/data/squad_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -25,7 +25,7 @@ import six
from absl import logging
import tensorflow as tf
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
class SquadExample(object):
diff --git a/official/nlp/data/squad_lib_sp.py b/official/nlp/data/squad_lib_sp.py
index 021193d4114004adceb5a0197a46842cd9d4601b..abd4abfbc09ca8f97db977294249cf250655658e 100644
--- a/official/nlp/data/squad_lib_sp.py
+++ b/official/nlp/data/squad_lib_sp.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,7 +28,7 @@ from absl import logging
import numpy as np
import tensorflow as tf
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
class SquadExample(object):
diff --git a/official/nlp/data/tagging_data_lib.py b/official/nlp/data/tagging_data_lib.py
index f6b9c19744be9b6b3730e65dd24c1e19730f8e47..c73d7108a9b2f41a1288295cbe27663a30de0ccc 100644
--- a/official/nlp/data/tagging_data_lib.py
+++ b/official/nlp/data/tagging_data_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,8 @@ import os
from absl import logging
import tensorflow as tf
-from official.nlp.bert import tokenization
from official.nlp.data import classifier_data_lib
+from official.nlp.tools import tokenization
# A negative label id for the padding label, which will not contribute
# to loss/metrics in training.
diff --git a/official/nlp/data/tagging_data_lib_test.py b/official/nlp/data/tagging_data_lib_test.py
index afbfebdef30586faa1ec0f362ee15d10461df1c3..6a1679f5e28f497a9bccff9bef9e684636a45247 100644
--- a/official/nlp/data/tagging_data_lib_test.py
+++ b/official/nlp/data/tagging_data_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,8 @@ import random
from absl.testing import parameterized
import tensorflow as tf
-from official.nlp.bert import tokenization
from official.nlp.data import tagging_data_lib
+from official.nlp.tools import tokenization
def _create_fake_file(filename, labels, is_test):
diff --git a/official/nlp/data/tagging_dataloader.py b/official/nlp/data/tagging_dataloader.py
index daecb8e3d8c75e2a6127f9be2892fd504d1a4385..f02d49ab94b59cfda325d41c37eba537cffdb578 100644
--- a/official/nlp/data/tagging_dataloader.py
+++ b/official/nlp/data/tagging_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/tagging_dataloader_test.py b/official/nlp/data/tagging_dataloader_test.py
index 2ff5fc7f2fa9e2715cac68a9648a2dd920405a60..3d2be5e97c33fde79bb6ab9f44d8874d940ca92b 100644
--- a/official/nlp/data/tagging_dataloader_test.py
+++ b/official/nlp/data/tagging_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/train_sentencepiece.py b/official/nlp/data/train_sentencepiece.py
index 4d3b05c46472e55c9b804da2aa45dabfd4867b7f..5b9f944dbeea6452c0c21baedf03b3e24d463f05 100644
--- a/official/nlp/data/train_sentencepiece.py
+++ b/official/nlp/data/train_sentencepiece.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -36,7 +36,7 @@ from sentencepiece import SentencePieceTrainer
FLAGS = flags.FLAGS
flags.DEFINE_string("output_model_path", None,
- "Path to save the the sentencepiece model.")
+ "Path to save the sentencepiece model.")
flags.mark_flag_as_required("output_model_path")
flags.DEFINE_string("tfds_dir", None, "Directory of the tfds.")
diff --git a/official/nlp/data/wmt_dataloader.py b/official/nlp/data/wmt_dataloader.py
index e0521ad47805b05b83287248f9db80dd1881e140..e801e9d74334d75cc944add173e55ed2bffc1686 100644
--- a/official/nlp/data/wmt_dataloader.py
+++ b/official/nlp/data/wmt_dataloader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/data/wmt_dataloader_test.py b/official/nlp/data/wmt_dataloader_test.py
index a4454d96d889504251d50070863b9447b2263648..82e56f599d2ea6ead153448521cd8f0ed38ee4e8 100644
--- a/official/nlp/data/wmt_dataloader_test.py
+++ b/official/nlp/data/wmt_dataloader_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/docs/README.md b/official/nlp/docs/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..5e4cd05342e2e78268ac73ab882e9ae58f476a74
--- /dev/null
+++ b/official/nlp/docs/README.md
@@ -0,0 +1,13 @@
+This directory contain guides to help users to train NLP models.
+
+1. [Training guide](train.md) explain the steps to follow for training NLP
+models on GPU and TPU.
+
+2. [Pretrained_models guide](pretrained_models.md) explain how to load
+pre-trained NLP models (baselines and checkpoints) that can be finetuned
+further depending on application.
+
+3. [TF-Hub guide](tfhub.md) explain how to use TF-NLP's
+[export_tfhub](https://github.com/tensorflow/models/blob/master/official/nlp/tools/export_tfhub.py)
+tool to export pre-trained Transformer encoders to SavedModels format that are
+suitable for publication on TF Hub.
diff --git a/official/nlp/docs/train.md b/official/nlp/docs/train.md
index f2c5245bf6a80af8ff27450494677dbc62dbe925..5a07901cdeb41c54ff279b6c76dea1cec4e8d55d 100644
--- a/official/nlp/docs/train.md
+++ b/official/nlp/docs/train.md
@@ -1,12 +1,14 @@
# Model Garden NLP Common Training Driver
-[train.py](https://github.com/tensorflow/models/blob/master/official/nlp/train.py) is the common training driver that supports multiple
+[train.py](https://github.com/tensorflow/models/blob/master/official/nlp/train.py)
+is the common training driver that supports multiple
NLP tasks (e.g., pre-training, GLUE and SQuAD fine-tuning etc) and multiple
models (e.g., BERT, ALBERT, MobileBERT etc).
## Experiment Configuration
-[train.py] is driven by configs defined by the [ExperimentConfig](https://github.com/tensorflow/models/blob/master/official/core/config_definitions.py)
+[train.py](https://github.com/tensorflow/models/blob/master/official/nlp/train.py)
+is driven by configs defined by the [ExperimentConfig](https://github.com/tensorflow/models/blob/master/official/core/config_definitions.py)
including configurations for `task`, `trainer` and `runtime`. The pre-defined
NLP related [ExperimentConfig](https://github.com/tensorflow/models/blob/master/official/core/config_definitions.py) can be found in
[configs/experiment_configs.py](https://github.com/tensorflow/models/blob/master/official/nlp/configs/experiment_configs.py).
@@ -78,7 +80,9 @@ setting `task.validation_data.input_path` in `PARAMS`.
## Run on Cloud TPUs
-Next, we will describe how to run the [train.py](https://github.com/tensorflow/models/blob/master/official/nlp/train.py) on Cloud TPUs.
+Next, we will describe how to run
+the [train.py](https://github.com/tensorflow/models/blob/master/official/nlp/train.py)
+on Cloud TPUs.
### Setup
First, you need to create a `tf-nightly` TPU with
@@ -99,7 +103,9 @@ pip3 install --user -r official/requirements.txt
### Fine-tuning Sentence Classification with BERT from TF-Hub
-This example fine-tunes BERT-base from TF-Hub on the the Multi-Genre Natural
+
+
+This example fine-tunes BERT-base from TF-Hub on the Multi-Genre Natural
Language Inference (MultiNLI) corpus using TPUs.
Firstly, you can prepare the fine-tuning data using
@@ -163,8 +169,12 @@ python3 train.py \
You can monitor the training progress in the console and find the output
models in `$OUTPUT_DIR`.
+
+
### Fine-tuning SQuAD with a pre-trained BERT checkpoint
+
+
This example fine-tunes a pre-trained BERT checkpoint on the
Stanford Question Answering Dataset (SQuAD) using TPUs.
The [SQuAD website](https://rajpurkar.github.io/SQuAD-explorer/) contains
@@ -219,4 +229,73 @@ python3 train.py \
```
-Note: More examples about pre-training will come soon.
+### Pre-train a BERT from scratch
+
+
+
+This example pre-trains a BERT model with Wikipedia and Books datasets used by
+the original BERT paper.
+The [BERT repo](https://github.com/tensorflow/models/blob/master/official/nlp/data/create_pretraining_data.py)
+contains detailed information about the Wikipedia dump and
+[BookCorpus](https://yknzhu.wixsite.com/mbweb). Of course, the pre-training
+recipe is generic and you can apply the same recipe to your own corpus.
+
+Please use the script
+[`create_pretraining_data.py`](https://github.com/tensorflow/models/blob/master/official/nlp/data/create_pretraining_data.py)
+which is essentially branched from [BERT research repo](https://github.com/google-research/bert)
+to get processed pre-training data and it adapts to TF2 symbols and python3
+compatibility.
+
+Running the pre-training script requires an input and output directory, as well
+as a vocab file. Note that `max_seq_length` will need to match the sequence
+length parameter you specify when you run pre-training.
+
+```shell
+export WORKING_DIR='local disk or cloud location'
+export BERT_DIR='local disk or cloud location'
+python models/official/nlp/data/create_pretraining_data.py \
+ --input_file=$WORKING_DIR/input/input.txt \
+ --output_file=$WORKING_DIR/output/tf_examples.tfrecord \
+ --vocab_file=$BERT_DIR/wwm_uncased_L-24_H-1024_A-16/vocab.txt \
+ --do_lower_case=True \
+ --max_seq_length=512 \
+ --max_predictions_per_seq=76 \
+ --masked_lm_prob=0.15 \
+ --random_seed=12345 \
+ --dupe_factor=5
+```
+
+Then, you can update the yaml configuration file, e.g.
+`configs/experiments/wiki_books_pretrain.yaml` to specify your data paths and
+update masking-related hyper parameters to match with your specification for
+the pretraining data. When your data have multiple shards, you can
+use `*` to include multiple files.
+
+To train different BERT sizes, you need to adjust:
+
+```
+model:
+ cls_heads: [{activation: tanh, cls_token_idx: 0, dropout_rate: 0.1, inner_dim: 768, name: next_sentence, num_classes: 2}]
+```
+
+to match the hidden dimensions.
+
+Then, you can start the training and evaluation jobs, which runs the
+[`bert/pretraining`](https://github.com/tensorflow/models/blob/master/official/nlp/configs/pretraining_experiments.py#L51)
+experiment:
+
+```shell
+export OUTPUT_DIR=gs://some_bucket/my_output_dir
+export PARAMS=$PARAMS,runtime.distribution_strategy=tpu
+
+python3 train.py \
+ --experiment=bert/pretraining \
+ --mode=train_and_eval \
+ --model_dir=$OUTPUT_DIR \
+ --config_file=configs/models/bert_en_uncased_base.yaml \
+ --config_file=configs/experiments/wiki_books_pretrain.yaml \
+ --tpu=${TPU_NAME} \
+ --params_override=$PARAMS
+```
+
+Note: More examples about pre-training with TFDS datesets will come soon.
diff --git a/official/nlp/finetuning/binary_helper.py b/official/nlp/finetuning/binary_helper.py
index 7e0ffc610a1f853f567bae18c4c794ad43f86075..10ad91e9377eb042add8724478e72648376577ee 100644
--- a/official/nlp/finetuning/binary_helper.py
+++ b/official/nlp/finetuning/binary_helper.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/finetuning/glue/flags.py b/official/nlp/finetuning/glue/flags.py
index 0f684fc916fb178cdaa542855ce3cffaa8627a9d..0ad161bc662a2aadcd3cbe0dde008931809613cd 100644
--- a/official/nlp/finetuning/glue/flags.py
+++ b/official/nlp/finetuning/glue/flags.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/finetuning/glue/run_glue.py b/official/nlp/finetuning/glue/run_glue.py
index aa1b047f3e6413e84e7f5882cbfcef26e3c2cad3..d1e67aa695d883592d5b648ee5fcd9539c429923 100644
--- a/official/nlp/finetuning/glue/run_glue.py
+++ b/official/nlp/finetuning/glue/run_glue.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -55,9 +55,9 @@ EVAL_METRIC_MAP = {
'AX': 'matthews_corrcoef',
'COLA': 'matthews_corrcoef',
'MNLI': 'cls_accuracy',
- 'MRPC': 'cls_accuracy',
+ 'MRPC': 'f1',
'QNLI': 'cls_accuracy',
- 'QQP': 'cls_accuracy',
+ 'QQP': 'f1',
'RTE': 'cls_accuracy',
'SST-2': 'cls_accuracy',
'STS-B': 'pearson_spearman_corr',
@@ -93,11 +93,16 @@ def _override_exp_config_by_flags(exp_config, input_meta_data):
binary_helper.override_sentence_prediction_task_config,
num_classes=input_meta_data['num_labels'],
metric_type='matthews_corrcoef')
- elif FLAGS.task_name in ('MNLI', 'MRPC', 'QNLI', 'QQP', 'RTE', 'SST-2',
+ elif FLAGS.task_name in ('MNLI', 'QNLI', 'RTE', 'SST-2',
'WNLI'):
override_task_cfg_fn = functools.partial(
binary_helper.override_sentence_prediction_task_config,
num_classes=input_meta_data['num_labels'])
+ elif FLAGS.task_name in ('QQP', 'MRPC'):
+ override_task_cfg_fn = functools.partial(
+ binary_helper.override_sentence_prediction_task_config,
+ metric_type='f1',
+ num_classes=input_meta_data['num_labels'])
elif FLAGS.task_name in ('STS-B',):
override_task_cfg_fn = functools.partial(
binary_helper.override_sentence_prediction_task_config,
diff --git a/official/nlp/finetuning/superglue/flags.py b/official/nlp/finetuning/superglue/flags.py
index 7c2f0ba72b43c65895b5ba89c5156ef9db3a0714..68457ea379be2c76efc3dc519a379da210ae9687 100644
--- a/official/nlp/finetuning/superglue/flags.py
+++ b/official/nlp/finetuning/superglue/flags.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/finetuning/superglue/run_superglue.py b/official/nlp/finetuning/superglue/run_superglue.py
index 01025a88f93fabc06f6da0d00f148aaf815c9af2..773abbd0315440f023aa70f31457252c61aaefc1 100644
--- a/official/nlp/finetuning/superglue/run_superglue.py
+++ b/official/nlp/finetuning/superglue/run_superglue.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/metrics/__init__.py b/official/nlp/metrics/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/nlp/metrics/__init__.py
+++ b/official/nlp/metrics/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/metrics/bleu.py b/official/nlp/metrics/bleu.py
index 7a17db6d870f2981116e70b5556bd7a785c84476..01c6ae5faa2fc5eeafab4cd793c1cd3db3def4f4 100644
--- a/official/nlp/metrics/bleu.py
+++ b/official/nlp/metrics/bleu.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/metrics/bleu_test.py b/official/nlp/metrics/bleu_test.py
index e410ae80598a47ee660a56ae1ba8c73df20389c5..9097ad8fd2ccb5e3cf9299addaf5f6b11aefe776 100644
--- a/official/nlp/metrics/bleu_test.py
+++ b/official/nlp/metrics/bleu_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/README.md b/official/nlp/modeling/README.md
index 99c7c361f9716b380a9287306558b872238afa7e..05a90248b6dfb176591386e1aac38064c40cbf67 100644
--- a/official/nlp/modeling/README.md
+++ b/official/nlp/modeling/README.md
@@ -20,8 +20,7 @@ examples.
* [`losses`](losses) contains common loss computation used in NLP tasks.
Please see the colab
-[nlp_modeling_library_intro.ipynb]
-(https://colab.sandbox.google.com/github/tensorflow/models/blob/master/official/colab/nlp/nlp_modeling_library_intro.ipynb)
+[NLP modeling library intro.ipynb](https://colab.sandbox.google.com/github/tensorflow/models/blob/master/docs/nlp/index.ipynb)
for how to build transformer-based NLP models using above primitives.
Besides the pre-defined primitives, it also provides scaffold classes to allow
@@ -44,8 +43,7 @@ custom hidden layer (which will replace the Transformer instantiation in the
encoder).
Please see the colab
-[customize_encoder.ipynb]
-(https://colab.sandbox.google.com/github/tensorflow/models/blob/master/official/colab/nlp/customize_encoder.ipynb)
+[customize_encoder.ipynb](https://colab.sandbox.google.com/github/tensorflow/models/blob/master/docs/nlp/customize_encoder.ipynb)
for how to use scaffold classes to build noval achitectures.
BERT and ALBERT models in this repo are implemented using this library.
diff --git a/official/nlp/modeling/__init__.py b/official/nlp/modeling/__init__.py
index 3beacedc96f26caa1db985256fd460b7ba3e543f..6159d986d397e381878b89ba46810cb1f5726989 100644
--- a/official/nlp/modeling/__init__.py
+++ b/official/nlp/modeling/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/README.md b/official/nlp/modeling/layers/README.md
index fb4069abd5bad9e8617f3cd74ec51fe9be262c60..54c00661ffd3f49dbd7f7ddfda9fb9bac00770fa 100644
--- a/official/nlp/modeling/layers/README.md
+++ b/official/nlp/modeling/layers/README.md
@@ -13,7 +13,7 @@ assemble new `tf.keras` layers or models.
["Big Bird: Transformers for Longer Sequences"](https://arxiv.org/abs/2007.14062).
* [CachedAttention](attention.py) implements an attention layer with cache
- used for auto-agressive decoding.
+ used for auto-aggressive decoding.
* [KernelAttention](kernel_attention.py) implements a group of attention
mechansim that express the self-attention as a linear dot-product of
diff --git a/official/nlp/modeling/layers/__init__.py b/official/nlp/modeling/layers/__init__.py
index f8f475d40a50d8f05d49e49ee24a6855c1ee13a7..27a161b69cf19ea8ed9a4cbc1452b6fcaaf8bc93 100644
--- a/official/nlp/modeling/layers/__init__.py
+++ b/official/nlp/modeling/layers/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,9 @@ They can be used to assemble new `tf.keras` layers or models.
from official.nlp.modeling.layers.attention import *
from official.nlp.modeling.layers.bigbird_attention import BigBirdAttention
from official.nlp.modeling.layers.bigbird_attention import BigBirdMasks
+from official.nlp.modeling.layers.block_diag_feedforward import BlockDiagFeedforward
from official.nlp.modeling.layers.cls_head import *
+from official.nlp.modeling.layers.factorized_embedding import FactorizedEmbedding
from official.nlp.modeling.layers.gated_feedforward import GatedFeedforward
from official.nlp.modeling.layers.gaussian_process import RandomFeatureGaussianProcess
from official.nlp.modeling.layers.kernel_attention import KernelAttention
@@ -28,11 +30,19 @@ from official.nlp.modeling.layers.kernel_attention import KernelMask
from official.nlp.modeling.layers.masked_lm import MaskedLM
from official.nlp.modeling.layers.masked_softmax import MaskedSoftmax
from official.nlp.modeling.layers.mat_mul_with_margin import MatMulWithMargin
+from official.nlp.modeling.layers.mixing import FourierTransformLayer
+from official.nlp.modeling.layers.mixing import HartleyTransformLayer
+from official.nlp.modeling.layers.mixing import LinearTransformLayer
+from official.nlp.modeling.layers.mixing import MixingMechanism
from official.nlp.modeling.layers.mobile_bert_layers import MobileBertEmbedding
from official.nlp.modeling.layers.mobile_bert_layers import MobileBertMaskedLM
from official.nlp.modeling.layers.mobile_bert_layers import MobileBertTransformer
from official.nlp.modeling.layers.multi_channel_attention import *
from official.nlp.modeling.layers.on_device_embedding import OnDeviceEmbedding
+from official.nlp.modeling.layers.pack_optimization import PackBertEmbeddings
+from official.nlp.modeling.layers.pack_optimization import StridedTransformerEncoderBlock
+from official.nlp.modeling.layers.pack_optimization import StridedTransformerScaffold
+from official.nlp.modeling.layers.per_dim_scale_attention import PerDimScaleAttention
from official.nlp.modeling.layers.position_embedding import PositionEmbedding
from official.nlp.modeling.layers.position_embedding import RelativePositionBias
from official.nlp.modeling.layers.position_embedding import RelativePositionEmbedding
@@ -41,6 +51,7 @@ from official.nlp.modeling.layers.relative_attention import TwoStreamRelativeAtt
from official.nlp.modeling.layers.reuse_attention import ReuseMultiHeadAttention
from official.nlp.modeling.layers.reuse_transformer import ReuseTransformer
from official.nlp.modeling.layers.rezero_transformer import ReZeroTransformer
+from official.nlp.modeling.layers.routing import *
from official.nlp.modeling.layers.self_attention_mask import SelfAttentionMask
from official.nlp.modeling.layers.spectral_normalization import *
from official.nlp.modeling.layers.talking_heads_attention import TalkingHeadsAttention
@@ -49,7 +60,8 @@ from official.nlp.modeling.layers.text_layers import BertTokenizer
from official.nlp.modeling.layers.text_layers import FastWordpieceBertTokenizer
from official.nlp.modeling.layers.text_layers import SentencepieceTokenizer
from official.nlp.modeling.layers.tn_transformer_expand_condense import TNTransformerExpandCondense
-from official.nlp.modeling.layers.transformer import *
+from official.nlp.modeling.layers.transformer import Transformer
+from official.nlp.modeling.layers.transformer import TransformerDecoderBlock
from official.nlp.modeling.layers.transformer_encoder_block import TransformerEncoderBlock
from official.nlp.modeling.layers.transformer_scaffold import TransformerScaffold
from official.nlp.modeling.layers.transformer_xl import TransformerXL
diff --git a/official/nlp/modeling/layers/attention.py b/official/nlp/modeling/layers/attention.py
index 9b13b89695d2e869b723270d5ac6ed929a3d1369..9d874d7bff8c9d7bb828b365bfccfdbc1ffc16e9 100644
--- a/official/nlp/modeling/layers/attention.py
+++ b/official/nlp/modeling/layers/attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,13 +18,13 @@ import math
import tensorflow as tf
-EinsumDense = tf.keras.layers.experimental.EinsumDense
+EinsumDense = tf.keras.layers.EinsumDense
MultiHeadAttention = tf.keras.layers.MultiHeadAttention
@tf.keras.utils.register_keras_serializable(package="Text")
class CachedAttention(tf.keras.layers.MultiHeadAttention):
- """Attention layer with cache used for auto-agressive decoding.
+ """Attention layer with cache used for autoregressive decoding.
Arguments are the same as `tf.keras.layers.MultiHeadAttention` layer.
"""
diff --git a/official/nlp/modeling/layers/attention_test.py b/official/nlp/modeling/layers/attention_test.py
index e09f88980cc60d35a40b755c45cad1a802dbfadc..1f3d73d164ae5686c0cbbb18fb3e2c1d51c10d56 100644
--- a/official/nlp/modeling/layers/attention_test.py
+++ b/official/nlp/modeling/layers/attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/bigbird_attention.py b/official/nlp/modeling/layers/bigbird_attention.py
index 4d3c662442965bf88018247a90fa37e0f331cfa5..8f6f3d614713ec87db5b1a6557382e4da9776e45 100644
--- a/official/nlp/modeling/layers/bigbird_attention.py
+++ b/official/nlp/modeling/layers/bigbird_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/bigbird_attention_test.py b/official/nlp/modeling/layers/bigbird_attention_test.py
index adafa9316e26610c868bbcd8c5cd735c46d5ad35..3764ce49db67a8e6c7c48b3be76890da4cc3b8ff 100644
--- a/official/nlp/modeling/layers/bigbird_attention_test.py
+++ b/official/nlp/modeling/layers/bigbird_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/block_diag_feedforward.py b/official/nlp/modeling/layers/block_diag_feedforward.py
new file mode 100644
index 0000000000000000000000000000000000000000..a781d7afa231c34066ff0ab8837aef312e96d1a4
--- /dev/null
+++ b/official/nlp/modeling/layers/block_diag_feedforward.py
@@ -0,0 +1,172 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Keras-based gated feedforward layer."""
+# pylint: disable=g-classes-have-attributes
+from typing import Optional
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+
+class BlockDiagFeedforward(tf.keras.layers.Layer):
+ """Block diagonal feedforward layer.
+
+ This layer replaces the weight matrix of the output_dense layer with a block
+ diagonal matrix to save layer parameters and FLOPs. A linear mixing layer can
+ be added optionally to improve layer expressibility.
+
+ Args:
+ intermediate_size: Size of the intermediate layer.
+ intermediate_activation: Activation for the intermediate layer.
+ dropout: Dropout probability for the output dropout.
+ num_blocks: The number of blocks for the block diagonal matrix of the
+ output_dense layer.
+ apply_mixing: Apply linear mixing if True.
+ kernel_initializer: Initializer for dense layer kernels.
+ bias_initializer: Initializer for dense layer biases.
+ kernel_regularizer: Regularizer for dense layer kernels.
+ bias_regularizer: Regularizer for dense layer biases.
+ activity_regularizer: Regularizer for dense layer activity.
+ kernel_constraint: Constraint for dense layer kernels.
+ bias_constraint: Constraint for dense layer kernels.
+ """
+
+ def __init__(
+ self,
+ intermediate_size: int,
+ intermediate_activation: str,
+ dropout: float,
+ num_blocks: int = 1,
+ apply_mixing: bool = True,
+ kernel_initializer: str = "glorot_uniform",
+ bias_initializer: str = "zeros",
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ activity_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ kernel_constraint: Optional[tf.keras.constraints.Constraint] = None,
+ bias_constraint: Optional[tf.keras.constraints.Constraint] = None,
+ **kwargs): # pylint: disable=g-doc-args
+ super().__init__(**kwargs)
+ self._intermediate_size = intermediate_size
+ self._intermediate_activation = intermediate_activation
+ self._dropout = dropout
+ self._num_blocks = num_blocks
+ self._apply_mixing = apply_mixing
+
+ if intermediate_size % num_blocks != 0:
+ raise ValueError("Intermediate_size (%d) isn't a multiple of num_blocks "
+ "(%d)." % (intermediate_size, num_blocks))
+
+ self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
+ self._bias_initializer = tf.keras.initializers.get(bias_initializer)
+ self._kernel_regularizer = tf.keras.regularizers.get(kernel_regularizer)
+ self._bias_regularizer = tf.keras.regularizers.get(bias_regularizer)
+ self._activity_regularizer = tf.keras.regularizers.get(activity_regularizer)
+ self._kernel_constraint = tf.keras.constraints.get(kernel_constraint)
+ self._bias_constraint = tf.keras.constraints.get(bias_constraint)
+
+ def build(self, input_shape):
+ hidden_size = input_shape.as_list()[-1]
+
+ common_kwargs = dict(
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activity_regularizer=self._activity_regularizer,
+ kernel_constraint=self._kernel_constraint,
+ bias_constraint=self._bias_constraint)
+
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
+ "abc,cde->abde",
+ output_shape=(None, self._num_blocks,
+ self._intermediate_size // self._num_blocks),
+ bias_axes="de",
+ name="intermediate",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
+ **common_kwargs)
+
+ policy = tf.keras.mixed_precision.global_policy()
+ if policy.name == "mixed_bfloat16":
+ # bfloat16 causes BERT with the LAMB optimizer to not converge
+ # as well, so we use float32.
+ policy = tf.float32
+ self._intermediate_activation_layer = tf.keras.layers.Activation(
+ self._intermediate_activation, dtype=policy)
+
+ self._output_dense = tf.keras.layers.EinsumDense(
+ "abde,deo->abdo",
+ output_shape=(None, self._num_blocks, hidden_size // self._num_blocks),
+ bias_axes="do",
+ name="output",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
+ **common_kwargs)
+
+ if self._apply_mixing:
+ self._output_mixing = tf.keras.layers.EinsumDense(
+ "abdo,de->abeo",
+ output_shape=(None, self._num_blocks,
+ hidden_size // self._num_blocks),
+ name="output_mixing",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
+ **common_kwargs)
+ self._output_reshape = tf.keras.layers.Reshape((-1, hidden_size))
+
+ self._output_dropout = tf.keras.layers.Dropout(rate=self._dropout)
+
+ def get_config(self):
+ config = {
+ "intermediate_size":
+ self._intermediate_size,
+ "intermediate_activation":
+ self._intermediate_activation,
+ "dropout":
+ self._dropout,
+ "num_blocks":
+ self._num_blocks,
+ "apply_mixing":
+ self._apply_mixing,
+ "kernel_initializer":
+ tf.keras.initializers.serialize(self._kernel_initializer),
+ "bias_initializer":
+ tf.keras.initializers.serialize(self._bias_initializer),
+ "kernel_regularizer":
+ tf.keras.regularizers.serialize(self._kernel_regularizer),
+ "bias_regularizer":
+ tf.keras.regularizers.serialize(self._bias_regularizer),
+ "activity_regularizer":
+ tf.keras.regularizers.serialize(self._activity_regularizer),
+ "kernel_constraint":
+ tf.keras.constraints.serialize(self._kernel_constraint),
+ "bias_constraint":
+ tf.keras.constraints.serialize(self._bias_constraint)
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs):
+ intermediate_output = self._intermediate_dense(inputs)
+ intermediate_output = self._intermediate_activation_layer(
+ intermediate_output)
+ layer_output = self._output_dense(intermediate_output)
+ if self._apply_mixing:
+ layer_output = self._output_mixing(layer_output)
+ layer_output = self._output_reshape(layer_output)
+ layer_output = self._output_dropout(layer_output)
+
+ return layer_output
diff --git a/official/nlp/modeling/layers/block_diag_feedforward_test.py b/official/nlp/modeling/layers/block_diag_feedforward_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..e9b5b4e5e48e05f95a69b7b6c19377cf8d176243
--- /dev/null
+++ b/official/nlp/modeling/layers/block_diag_feedforward_test.py
@@ -0,0 +1,119 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for Keras-based gated feedforward layer."""
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from tensorflow.python.keras import keras_parameterized # pylint: disable=g-direct-tensorflow-import
+from official.nlp.modeling.layers import block_diag_feedforward
+
+
+# This decorator runs the test in V1, V2-Eager, and V2-Functional mode. It
+# guarantees forward compatibility of this code for the V2 switchover.
+@keras_parameterized.run_all_keras_modes
+class BlockDiagFeedforwardTest(keras_parameterized.TestCase):
+
+ def tearDown(self):
+ super(BlockDiagFeedforwardTest, self).tearDown()
+ tf.keras.mixed_precision.set_global_policy("float32")
+
+ @parameterized.parameters(
+ (1, True, "float32"),
+ (1, True, "mixed_float16"),
+ (1, False, "float32"),
+ (1, False, "mixed_float16"),
+ (2, True, "float32"),
+ (2, True, "mixed_float16"),
+ (2, False, "float32"),
+ (2, False, "mixed_float16"),
+ )
+ def test_layer_creation(self, num_blocks, apply_mixing, dtype):
+ tf.keras.mixed_precision.set_global_policy(dtype)
+ kwargs = dict(
+ intermediate_size=128,
+ intermediate_activation="relu",
+ dropout=0.1,
+ num_blocks=num_blocks,
+ apply_mixing=apply_mixing,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros")
+ test_layer = block_diag_feedforward.BlockDiagFeedforward(**kwargs)
+
+ sequence_length = 64
+ width = 128
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+ # The default output of a transformer layer should be the same as the input.
+ self.assertEqual(data_tensor.shape.as_list(), output_tensor.shape.as_list())
+
+ @parameterized.parameters(
+ (1, True, "float32"),
+ (1, True, "mixed_float16"),
+ (1, False, "float32"),
+ (1, False, "mixed_float16"),
+ (2, True, "float32"),
+ (2, True, "mixed_float16"),
+ (2, False, "float32"),
+ (2, False, "mixed_float16"),
+ )
+ def test_layer_invocation(self, num_blocks, apply_mixing, dtype):
+ tf.keras.mixed_precision.set_global_policy(dtype)
+ kwargs = dict(
+ intermediate_size=16,
+ intermediate_activation="relu",
+ dropout=0.1,
+ num_blocks=num_blocks,
+ apply_mixing=apply_mixing,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros")
+ test_layer = block_diag_feedforward.BlockDiagFeedforward(**kwargs)
+
+ sequence_length = 16
+ width = 32
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+
+ # Create a model from the test layer.
+ model = tf.keras.Model(data_tensor, output_tensor)
+
+ # Invoke the model on test data.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ output_data = model.predict(input_data)
+ self.assertEqual(output_data.shape, (batch_size, sequence_length, width))
+
+ def test_get_config(self):
+ kwargs = dict(
+ intermediate_size=16,
+ intermediate_activation="relu",
+ dropout=0.1,
+ num_blocks=2,
+ apply_mixing=True,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros")
+ test_layer = block_diag_feedforward.BlockDiagFeedforward(**kwargs)
+ new_layer = block_diag_feedforward.BlockDiagFeedforward.from_config(
+ test_layer.get_config())
+
+ self.assertAllEqual(test_layer.get_config(), new_layer.get_config())
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/cls_head.py b/official/nlp/modeling/layers/cls_head.py
index 85720df56d404674efcb62888ba3c15d1b11a9a2..2ea2a3eab08708f83c1fdbe263175b6902997f74 100644
--- a/official/nlp/modeling/layers/cls_head.py
+++ b/official/nlp/modeling/layers/cls_head.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -57,12 +57,14 @@ class ClassificationHead(tf.keras.layers.Layer):
self.dense = tf.keras.layers.Dense(
units=self.inner_dim,
activation=self.activation,
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name="pooler_dense")
self.dropout = tf.keras.layers.Dropout(rate=self.dropout_rate)
self.out_proj = tf.keras.layers.Dense(
- units=num_classes, kernel_initializer=self.initializer, name="logits")
+ units=num_classes,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
+ name="logits")
def call(self, features: tf.Tensor, only_project: bool = False):
"""Implements call().
@@ -146,14 +148,15 @@ class MultiClsHeads(tf.keras.layers.Layer):
self.dense = tf.keras.layers.Dense(
units=inner_dim,
activation=self.activation,
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name="pooler_dense")
self.dropout = tf.keras.layers.Dropout(rate=self.dropout_rate)
self.out_projs = []
for name, num_classes in cls_list:
self.out_projs.append(
tf.keras.layers.Dense(
- units=num_classes, kernel_initializer=self.initializer,
+ units=num_classes,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name=name))
def call(self, features: tf.Tensor, only_project: bool = False):
@@ -277,7 +280,7 @@ class GaussianProcessClassificationHead(ClassificationHead):
if use_gp_layer:
self.out_proj = gaussian_process.RandomFeatureGaussianProcess(
self.num_classes,
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name="logits",
**self.gp_layer_kwargs)
@@ -361,3 +364,97 @@ def extract_spec_norm_kwargs(kwargs):
return dict(
iteration=kwargs.pop("iteration", 1),
norm_multiplier=kwargs.pop("norm_multiplier", .99))
+
+
+class PerQueryDenseHead(tf.keras.layers.Layer):
+ """Pooling head used for EncT5 style models.
+
+ This module projects each query to use a different projection.
+
+ For a input shape= [bs, num_queries, hidden_size], it projects each query to
+ (features). Ending up with shape= [bs, num_queries, features].
+
+ For example, for classification with a few classes, one may use num_queries
+ as 1 and features as number of classes. For multilabel classification, one
+ may use num_queries as number of classes and features as 2. So each query
+ represents a binary classification of one label.
+ """
+
+ def __init__(self,
+ num_queries: int,
+ features: int,
+ use_bias: bool = False,
+ kernel_initializer: str = "glorot_uniform",
+ **kwargs):
+ """Initializes the `PerQueryDenseHead`.
+
+ Args:
+ num_queries: number of queries (the learnable embeddings in the input
+ sequences) from the decoder.
+ features: int with numbers of output features. Each query with be
+ projected to this number with a different projection.
+ use_bias: whether to add a bias to the output.
+ kernel_initializer: Initializer for dense layer kernels.
+ **kwargs: Keyword arguments.
+ """
+ super().__init__(**kwargs)
+ self.num_queries = num_queries
+ self.features = features
+
+ self.use_bias = use_bias
+ self.kernel_initializer = tf.keras.initializers.get(kernel_initializer)
+
+ def build(self, input_shape):
+ input_shape = tf.TensorShape(input_shape)
+ # Hidden size.
+ last_dim = tf.compat.dimension_value(input_shape[-1])
+
+ self.hidden_size = last_dim
+ self.kernel = self.add_weight(
+ "kernel",
+ shape=[self.num_queries, last_dim, self.features],
+ initializer=self.kernel_initializer,
+ dtype=self.dtype,
+ trainable=True)
+ if self.use_bias:
+ self.bias = self.add_weight(
+ "bias",
+ shape=[
+ self.num_queries,
+ self.features,
+ ],
+ dtype=self.dtype,
+ trainable=True)
+ else:
+ self.bias = None
+
+ def call(self, inputs: tf.Tensor) -> tf.Tensor:
+ """Implements call().
+
+ Args:
+ inputs: a rank-3 Tensor of shape= [bs, num_queries, hidden_size].
+
+ Returns:
+ A Tensor, shape= [batch size, num_queries, features].
+ """
+
+ outputs = tf.einsum("bqh,qhf->bqf", inputs, self.kernel)
+ if self.use_bias:
+ outputs += self.bias
+ return outputs
+
+ def get_config(self):
+ config = {
+ "num_queries":
+ self.num_queries,
+ "features":
+ self.features,
+ "kernel_initializer":
+ tf.keras.activations.serialize(self.kernel_initializer),
+ }
+ config.update(super(PerQueryDenseHead, self).get_config())
+ return config
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
diff --git a/official/nlp/modeling/layers/cls_head_test.py b/official/nlp/modeling/layers/cls_head_test.py
index 4c640baf414df279b4e59585fc5fd32e6589cfd0..a0bfe15ae8bd5d45843d554239df05572639298f 100644
--- a/official/nlp/modeling/layers/cls_head_test.py
+++ b/official/nlp/modeling/layers/cls_head_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -199,5 +199,29 @@ class GaussianProcessClassificationHead(tf.test.TestCase,
self.assertEqual(layer_config["norm_multiplier"], 1.)
self.assertEqual(layer_config["num_inducing"], 512)
+
+class PerQueryDenseHeadTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.named_parameters(("single_query", 1, 3, False),
+ ("multi_queries", 10, 2, False),
+ ("with_bias", 10, 2, True))
+ def test_layer_invocation(self, num_queries, features, use_bias):
+ batch_size = 5
+ hidden_size = 10
+ layer = cls_head.PerQueryDenseHead(
+ num_queries=num_queries, features=features, use_bias=use_bias)
+ inputs = tf.zeros(
+ shape=(batch_size, num_queries, hidden_size), dtype=tf.float32)
+ outputs = layer(inputs)
+ self.assertEqual(outputs.shape, [batch_size, num_queries, features])
+
+ def test_layer_serialization(self):
+ layer = cls_head.PerQueryDenseHead(
+ num_queries=10, features=2, use_bias=True)
+ new_layer = cls_head.PerQueryDenseHead.from_config(layer.get_config())
+
+ # If the serialization was successful, the new config should match the old.
+ self.assertAllEqual(layer.get_config(), new_layer.get_config())
+
if __name__ == "__main__":
tf.test.main()
diff --git a/official/nlp/modeling/layers/factorized_embedding.py b/official/nlp/modeling/layers/factorized_embedding.py
new file mode 100644
index 0000000000000000000000000000000000000000..f19a4ce7883857038d2a4fab56c17e5f83bf0205
--- /dev/null
+++ b/official/nlp/modeling/layers/factorized_embedding.py
@@ -0,0 +1,76 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""A factorized embedding layer."""
+# pylint: disable=g-classes-have-attributes
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.nlp.modeling.layers import on_device_embedding
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class FactorizedEmbedding(on_device_embedding.OnDeviceEmbedding):
+ """A factorized embeddings layer for supporting larger embeddings.
+
+ Arguments:
+ vocab_size: Number of elements in the vocabulary.
+ embedding_width: Width of word embeddings.
+ output_dim: The output dimension of this layer.
+ initializer: The initializer to use for the embedding weights. Defaults to
+ "glorot_uniform".
+ use_one_hot: Whether to use tf.one_hot over tf.gather for the embedding
+ lookup. Defaults to False (that is, using tf.gather). Setting this option
+ to True may improve performance, especially on small vocabulary sizes, but
+ will generally require more memory.
+ scale_factor: Whether to scale the output embeddings. Defaults to None (that
+ is, not to scale). Setting this option to a float will let values in
+ output embeddings multiplied by scale_factor.
+ """
+
+ def __init__(self,
+ vocab_size: int,
+ embedding_width: int,
+ output_dim: int,
+ initializer='glorot_uniform',
+ use_one_hot=False,
+ scale_factor=None,
+ **kwargs):
+ super().__init__(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ initializer=initializer,
+ use_one_hot=use_one_hot,
+ scale_factor=scale_factor,
+ **kwargs)
+ self._output_dim = output_dim
+
+ def get_config(self):
+ config = {'output_dim': self._output_dim}
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def build(self, input_shape):
+ self._embedding_projection = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=self._output_dim,
+ bias_axes=None,
+ kernel_initializer=tf_utils.clone_initializer(self._initializer),
+ name='embedding_projection')
+ super().build(input_shape)
+
+ def call(self, inputs):
+ output = super().call(inputs)
+ return self._embedding_projection(output)
diff --git a/official/nlp/modeling/layers/factorized_embedding_test.py b/official/nlp/modeling/layers/factorized_embedding_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..686ed7c749512f367887299f389d39476c49dde7
--- /dev/null
+++ b/official/nlp/modeling/layers/factorized_embedding_test.py
@@ -0,0 +1,70 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for FactorizedEmbedding layer."""
+
+import numpy as np
+import tensorflow as tf
+
+from official.nlp.modeling.layers import factorized_embedding
+
+
+class FactorizedEmbeddingTest(tf.test.TestCase):
+
+ def test_layer_creation(self):
+ vocab_size = 31
+ embedding_width = 27
+ output_dim = 45
+ test_layer = factorized_embedding.FactorizedEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ output_dim=output_dim)
+ # Create a 2-dimensional input (the first dimension is implicit).
+ sequence_length = 23
+ input_tensor = tf.keras.Input(shape=(sequence_length), dtype=tf.int32)
+ output_tensor = test_layer(input_tensor)
+
+ # The output should be the same as the input, save that it has an extra
+ # embedding_width dimension on the end.
+ expected_output_shape = [None, sequence_length, output_dim]
+ self.assertEqual(expected_output_shape, output_tensor.shape.as_list())
+ self.assertEqual(output_tensor.dtype, tf.float32)
+
+ def test_layer_invocation(self):
+ vocab_size = 31
+ embedding_width = 27
+ output_dim = 45
+ test_layer = factorized_embedding.FactorizedEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ output_dim=output_dim)
+ # Create a 2-dimensional input (the first dimension is implicit).
+ sequence_length = 23
+ input_tensor = tf.keras.Input(shape=(sequence_length), dtype=tf.int32)
+ output_tensor = test_layer(input_tensor)
+
+ # Create a model from the test layer.
+ model = tf.keras.Model(input_tensor, output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 3
+ input_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ output = model.predict(input_data)
+ self.assertEqual(tf.float32, output.dtype)
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/gated_feedforward.py b/official/nlp/modeling/layers/gated_feedforward.py
index 2de2940658c68c9cd324df339a8f90a1d0038c12..630ba5e772eda765ea1e9d34aee18dd7dcba7e54 100644
--- a/official/nlp/modeling/layers/gated_feedforward.py
+++ b/official/nlp/modeling/layers/gated_feedforward.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,9 @@
import gin
import tensorflow as tf
+from official.modeling import tf_utils
+from official.nlp.modeling.layers import util
+
@tf.keras.utils.register_keras_serializable(package="Text")
@gin.configurable
@@ -55,9 +58,9 @@ class GatedFeedforward(tf.keras.layers.Layer):
"""
def __init__(self,
- intermediate_size,
- intermediate_activation,
- dropout,
+ inner_dim=768,
+ inner_activation=tf_utils.get_activation("gelu"),
+ dropout=0.0,
use_gate=True,
apply_output_layer_norm=True,
num_blocks=1,
@@ -70,9 +73,12 @@ class GatedFeedforward(tf.keras.layers.Layer):
kernel_constraint=None,
bias_constraint=None,
**kwargs):
- super(GatedFeedforward, self).__init__(**kwargs)
- self._intermediate_size = intermediate_size
- self._intermediate_activation = intermediate_activation
+ inner_dim = kwargs.pop("intermediate_size", inner_dim)
+ inner_activation = kwargs.pop("intermediate_activation", inner_activation)
+ util.filter_kwargs(kwargs)
+ super().__init__(**kwargs)
+ self._inner_dim = inner_dim
+ self._inner_activation = inner_activation
self._dropout = dropout
self._use_gate = use_gate
self._num_blocks = num_blocks
@@ -95,15 +101,13 @@ class GatedFeedforward(tf.keras.layers.Layer):
hidden_size = input_shape.as_list()[-1]
common_kwargs = dict(
- kernel_initializer=self._kernel_initializer,
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
kernel_constraint=self._kernel_constraint,
bias_constraint=self._bias_constraint)
self._intermediate_dense = []
- self._intermediate_activation_layers = []
+ self._inner_activation_layers = []
self._gate_dense = []
self._output_dense = []
self._output_dropout = []
@@ -116,29 +120,41 @@ class GatedFeedforward(tf.keras.layers.Layer):
activation_policy = tf.float32
for i in range(self._num_blocks):
self._intermediate_dense.append(
- tf.keras.layers.experimental.EinsumDense(
+ tf.keras.layers.EinsumDense(
"abc,cd->abd",
- output_shape=(None, self._intermediate_size),
+ output_shape=(None, self._inner_dim),
bias_axes="d",
name="intermediate_%d" % i,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(
+ self._bias_initializer),
**common_kwargs))
- self._intermediate_activation_layers.append(
+ self._inner_activation_layers.append(
tf.keras.layers.Activation(
- self._intermediate_activation, dtype=activation_policy))
+ self._inner_activation, dtype=activation_policy))
if self._use_gate:
self._gate_dense.append(
- tf.keras.layers.experimental.EinsumDense(
+ tf.keras.layers.EinsumDense(
"abc,cd->abd",
- output_shape=(None, self._intermediate_size),
+ output_shape=(None, self._inner_dim),
bias_axes="d",
name="gate_%d" % i,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(
+ self._bias_initializer),
**common_kwargs))
self._output_dense.append(
- tf.keras.layers.experimental.EinsumDense(
+ tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
name="output_%d" % i,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(
+ self._bias_initializer),
**common_kwargs))
self._output_dropout.append(tf.keras.layers.Dropout(rate=self._dropout))
# Use float32 in layernorm for numeric stability.
@@ -152,10 +168,10 @@ class GatedFeedforward(tf.keras.layers.Layer):
def get_config(self):
config = {
- "intermediate_size":
- self._intermediate_size,
- "intermediate_activation":
- self._intermediate_activation,
+ "inner_dim":
+ self._inner_dim,
+ "inner_activation":
+ self._inner_activation,
"dropout":
self._dropout,
"use_gate":
@@ -179,7 +195,7 @@ class GatedFeedforward(tf.keras.layers.Layer):
"bias_constraint":
tf.keras.constraints.serialize(self._bias_constraint)
}
- base_config = super(GatedFeedforward, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def call(self, inputs):
@@ -187,7 +203,7 @@ class GatedFeedforward(tf.keras.layers.Layer):
for i in range(self._num_blocks):
layer_input = layer_output
intermediate_output = self._intermediate_dense[i](layer_input)
- intermediate_output = self._intermediate_activation_layers[i](
+ intermediate_output = self._inner_activation_layers[i](
intermediate_output)
if self._use_gate:
gated_linear = self._gate_dense[i](layer_input)
diff --git a/official/nlp/modeling/layers/gated_feedforward_test.py b/official/nlp/modeling/layers/gated_feedforward_test.py
index 46d4f4bb258cf6ea6726679c0d730ac37da50461..6ba2c20053dd5a8da8e2166066c9f541b5b5df9c 100644
--- a/official/nlp/modeling/layers/gated_feedforward_test.py
+++ b/official/nlp/modeling/layers/gated_feedforward_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -44,8 +44,8 @@ class GatedFeedforwardTest(keras_parameterized.TestCase):
def test_layer_creation(self, use_gate, num_blocks, dropout_position, dtype):
tf.keras.mixed_precision.set_global_policy(dtype)
kwargs = dict(
- intermediate_size=128,
- intermediate_activation="relu",
+ inner_dim=128,
+ inner_activation="relu",
dropout=0.1,
use_gate=use_gate,
num_blocks=num_blocks,
@@ -76,8 +76,8 @@ class GatedFeedforwardTest(keras_parameterized.TestCase):
dtype):
tf.keras.mixed_precision.set_global_policy(dtype)
kwargs = dict(
- intermediate_size=16,
- intermediate_activation="relu",
+ inner_dim=16,
+ inner_activation="relu",
dropout=0.1,
use_gate=use_gate,
num_blocks=num_blocks,
@@ -104,8 +104,8 @@ class GatedFeedforwardTest(keras_parameterized.TestCase):
def test_serialize_deserialize(self):
kwargs = dict(
- intermediate_size=16,
- intermediate_activation="relu",
+ inner_dim=16,
+ inner_activation="relu",
dropout=0.1,
use_gate=False,
num_blocks=4,
diff --git a/official/nlp/modeling/layers/gaussian_process.py b/official/nlp/modeling/layers/gaussian_process.py
index 3729d8ee6cfaebe3b6c0a077cc3ee7706295bb10..618000577f1f74f943bcd0b5774b095e71f0a651 100644
--- a/official/nlp/modeling/layers/gaussian_process.py
+++ b/official/nlp/modeling/layers/gaussian_process.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Definitions for random feature Gaussian process layer."""
import math
import tensorflow as tf
@@ -117,7 +116,7 @@ class RandomFeatureGaussianProcess(tf.keras.layers.Layer):
name: (string) Layer name.
**gp_output_kwargs: Additional keyword arguments to dense output layer.
"""
- super(RandomFeatureGaussianProcess, self).__init__(name=name, dtype=dtype)
+ super().__init__(name=name, dtype=dtype)
self.units = units
self.num_inducing = num_inducing
@@ -227,7 +226,7 @@ class RandomFeatureGaussianProcess(tf.keras.layers.Layer):
"""Resets covariance matrix of the GP layer.
This function is useful for reseting the model's covariance matrix at the
- begining of a new epoch.
+ beginning of a new epoch.
"""
self._gp_cov_layer.reset_precision_matrix()
@@ -381,7 +380,7 @@ class LaplaceRandomFeatureCovariance(tf.keras.layers.Layer):
"""Resets precision matrix to its initial value.
This function is useful for reseting the model's covariance matrix at the
- begining of a new epoch.
+ beginning of a new epoch.
"""
precision_matrix_reset_op = self.precision_matrix.assign(
self.initial_precision_matrix)
diff --git a/official/nlp/modeling/layers/gaussian_process_test.py b/official/nlp/modeling/layers/gaussian_process_test.py
index 37958fa742326dc7cde6e1c4625c2b4ba77d2a2d..7a9a56fe452c1bf924e1bb2a069e801604b06a52 100644
--- a/official/nlp/modeling/layers/gaussian_process_test.py
+++ b/official/nlp/modeling/layers/gaussian_process_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for Gaussian process functions."""
import os
import shutil
diff --git a/official/nlp/modeling/layers/kernel_attention.py b/official/nlp/modeling/layers/kernel_attention.py
index 6f8d41ad4b673ed83b3dd9a6ef0afbea3eb1803d..2a175f871b189ba4b1b110ea242affac29985f4e 100644
--- a/official/nlp/modeling/layers/kernel_attention.py
+++ b/official/nlp/modeling/layers/kernel_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,8 @@ import functools
import math
import tensorflow as tf
+from official.modeling import tf_utils
+
_NUMERIC_STABLER = 1e-6
@@ -39,6 +41,236 @@ class KernelMask(tf.keras.layers.Layer):
return mask
+def pad_to_chunk_length(tensor, axis, chunk_length, padding=None):
+ """Pads a tensor so that shape[axis] is divisible by chunk_length.
+
+ Args:
+ tensor: Input tensor to pad.
+ axis: Axis to pad along.
+ chunk_length: The output tensor will have shape[axis] divisible by
+ chunk_length.
+ padding: Pad the input tensor across the axis from either left or right if
+ padding is set to "left" or "right"; applies no padding if padding is set
+ to None. In the latter case, the axis dimension of the input tensor must
+ be divisible by the chunk_length.
+
+ Returns:
+ Padded tensor with shape[axis] divisible by chunk_length.
+ """
+ if padding is None:
+ return tensor
+ shape = tf.shape(tensor)
+ rank = tf.rank(tensor)
+ if axis < 0:
+ axis += rank
+ axis_length = shape[axis]
+ pad_length = -axis_length % chunk_length
+ if padding == "right":
+ axis_paddings = [[0, pad_length]]
+ elif padding == "left":
+ axis_paddings = [[pad_length, 0]]
+ else:
+ raise ValueError(
+ "Illegal padding value; must be one of \"left\", \"right\" or None.")
+ paddings = tf.concat([
+ tf.zeros([axis, 2], dtype=tf.int32), axis_paddings,
+ tf.zeros([rank - axis - 1, 2], dtype=tf.int32)
+ ],
+ axis=0)
+ return tf.pad(tensor, paddings)
+
+
+def split_tensor_into_chunks(tensor, axis, chunk_length):
+ """Reshape tensor along given axis using chunk_length.
+
+ Args:
+ tensor: Input tensor.
+ axis: Reshape tensor along this axis.
+ chunk_length: Split the axis into [axis/chunk_length, chunk_length]
+
+ Returns:
+ Reshaped tensor.
+ """
+ shape = tf.shape(tensor)
+ num_chunks = shape[axis] // chunk_length
+ new_shape = tf.concat(
+ [shape[:axis], [num_chunks, chunk_length], shape[(axis + 1):]], axis=0)
+ return tf.reshape(tensor, new_shape)
+
+
+def rectangular_window_sum(tensor, window_length):
+ """Summarizes tensor elements over a sliding rectangular window.
+
+ Sums elements of the input tensor of shape [B, T', C', H, dim]
+ across a rectangular window sliding along the dimension T'.
+
+ Args:
+ tensor: Tensor of shape `[B, T', C', H, dim]`.
+ window_length: The length of the rectangular window.
+
+ Returns:
+ A tensor of shape [B, T', C', H, dim] containing sums over the
+ window.
+ """
+ tensor_cumsum = tf.cumsum(tensor, axis=-4)
+ tensor_winsum = tensor_cumsum - tf.pad(
+ tensor_cumsum,
+ [[0, 0], [window_length, 0], [0, 0], [0, 0], [0, 0]])[:, :-window_length]
+ return tensor_winsum
+
+
+def weighted_window_sum(tensor, window_length, window_weights):
+ """Summarizes tensor elements over a sliding weighted window.
+
+ Computes a weighted sum of elements of the input tensor of shape [B,
+ T', C', H, dim] across a window sliding along the dimension T'.
+
+ Args:
+ tensor: Tensor of shape `[B, T', C', H, dim]`.
+ window_length: The length of the window.
+ window_weights: Tensor of shape [window_length] containing window weights.
+
+ Returns:
+ A tensor of shape [B, T', C', H, dim] containing sums over the
+ window.
+ """
+ # Flatten the last three dimensions of the [B, T', C', H, dim] shape
+ # into a single channels dimension.
+ tensor_shape = tf.shape(tensor)
+ tensor_2d = tf.reshape(tensor, [tensor_shape[0], tensor_shape[1], 1, -1])
+
+ # Apply the same weights to all channels.
+ conv_filter = tf.tile(
+ tf.reshape(window_weights, [-1, 1, 1, 1]),
+ multiples=[1, 1, tf.shape(tensor_2d)[-1], 1])
+ tensor_winsum_2d = tf.nn.depthwise_conv2d(
+ tensor_2d,
+ conv_filter,
+ strides=[1, 1, 1, 1],
+ padding=[[0, 0], [window_length - 1, 0], [0, 0], [0, 0]])
+
+ # Unflatten the channels dimension into the original shape.
+ tensor_winsum = tf.reshape(tensor_winsum_2d, tensor_shape)
+ return tensor_winsum
+
+
+def causal_windowed_performer_attention(query_matrix,
+ key_matrix,
+ value_matrix,
+ chunk_length,
+ window_length,
+ window_decay=None,
+ padding=None,
+ cache=None):
+ """Applies windowed causal kernel attention with query, key, value tensors.
+
+ We partition the T-length input sequence into N chunks, each of
+ chunk_length tokens (thus: T = N * chunk_length). Within each chunk,
+ we apply bidirectional (non-causal) Performers’ implicit attention
+ and we model relationships between different chunks using
+ Performers’ causal attention. We consider windowed causal variant of
+ performer, where the current chunk attends only to the window of
+ window_length of the most recent chunks.
+
+ Below is an example with T=9, chunk_length=3, window_length=2. In
+ this example 1 indicates attention is computed between the pair
+ while 0 indicates attention is not computed between the pairs:
+
+ 111000000
+ 111000000
+ 111000000
+ 111111000
+ 111111000
+ 111111000
+ 000111111
+ 000111111
+ 000111111
+
+ User can ensure sequence_length is divisible by chunk_length or use
+ padding="left"/"right" to pad the sequence length either at the left
+ or right respectively and make it divisible by chunk_length.
+
+ Args:
+ query_matrix: Kernel query `Tensor` of shape `[B, T, H, dim]`.
+ key_matrix: Kernel key `Tensor` of shape `[B, T, H, dim]`.
+ value_matrix: Value `Tensor` of shape `[B, T, H, out_dim]`.
+ chunk_length: Length of each chunk in tokens.
+ window_length: Length of attention window in chunks.
+ window_decay: Float window decay factor or `None`. If set, exponentially
+ decay past attention window values by this factor before summation.
+ padding: Pad the query, value and key input tensors across the axis from
+ either left or right if padding is set to "left" or "right"; apply no
+ padding if padding is set to None. In the latter case, the axis dimension
+ of the query, value and key input tensors must be divisible by the
+ chunk_length.
+ cache: Cache to accumulate history in memory. Used at inferecne time
+ (streaming, decoding) for causal attention.
+
+ Returns:
+ Window causal performer attention of shape `[B, T, H, out_dim]`.
+ """
+ if cache is None: # Training
+ old_shape = tf.shape(value_matrix)
+
+ query_matrix = pad_to_chunk_length(query_matrix, -3, chunk_length, padding)
+ key_matrix = pad_to_chunk_length(key_matrix, -3, chunk_length, padding)
+ value_matrix = pad_to_chunk_length(value_matrix, -3, chunk_length, padding)
+
+ new_shape = tf.shape(value_matrix)
+ chunked_query_matrix = split_tensor_into_chunks(
+ query_matrix, -3,
+ chunk_length) # [-1, T//chunk_length, chunk_length, N, dim]
+ chunked_key_matrix = split_tensor_into_chunks(
+ key_matrix, -3,
+ chunk_length) # [-1, T//chunk_length, chunk_length, N, dim]
+ chunked_value_matrix = split_tensor_into_chunks(
+ value_matrix, -3,
+ chunk_length) # [-1, T//chunk_length, chunk_length, N, out_dim]
+
+ kp_v = tf.einsum("BTCHD,BTCHO->BTHDO", chunked_key_matrix,
+ chunked_value_matrix)
+
+ k_sum = tf.math.reduce_sum(chunked_key_matrix, axis=-3, keepdims=True)
+
+ if window_decay is None:
+ kp_v_winsum = rectangular_window_sum(kp_v, window_length)
+ k_winsum = rectangular_window_sum(k_sum, window_length)
+ else:
+ # Compute exponentially decaying weights.
+ decaying_weights = tf.math.pow(
+ tf.convert_to_tensor(window_decay, dtype=value_matrix.dtype),
+ tf.range(window_length - 1, -1, delta=-1, dtype=value_matrix.dtype))
+ kp_v_winsum = weighted_window_sum(kp_v, window_length, decaying_weights)
+ k_winsum = weighted_window_sum(k_sum, window_length, decaying_weights)
+
+ numerator = tf.einsum(
+ "BTCHD,BTHDO->BTCHO", chunked_query_matrix, kp_v_winsum)
+
+ k_winsum = tf.squeeze(k_winsum, -3)
+ denominator = tf.einsum("BTCHD,BTHD->BTCH", chunked_query_matrix, k_winsum)
+ denominator = tf.expand_dims(denominator, -1) + _NUMERIC_STABLER
+ attention = numerator / denominator
+ attention = tf.reshape(attention, new_shape)
+
+ start = tf.zeros([len(old_shape)], dtype=old_shape.dtype)
+ attention = tf.slice(attention, start, old_shape)
+
+ # Queued window cache (drop instead of decay) not yet supported.
+ else: # Streaming
+
+ if window_decay is None or window_decay > 1.0 or window_decay < 0.0:
+ raise ValueError("window_decay should be in (0.0, 1.0) and not None.")
+ kv = window_decay * cache["kv"] + tf.einsum(
+ "BTHD,BTHO->BHOD", key_matrix, value_matrix)
+ cache["kv"] = kv
+ k_sum = window_decay * cache["k_sum"] + tf.reduce_sum(key_matrix, axis=1)
+ cache["k_sum"] = k_sum
+ denominator = tf.einsum("BTHD,BHD->BTH", query_matrix, k_sum)
+ attention = tf.einsum("BTHD,BHOD,BTH->BTHO", query_matrix, kv,
+ 1.0 / (denominator + _NUMERIC_STABLER))
+ return attention
+
+
def create_projection_matrix(m, d, seed=None):
r"""Constructs the matrix of random projections.
@@ -56,8 +288,8 @@ def create_projection_matrix(m, d, seed=None):
The matrix of random projections of the shape [m, d].
"""
nb_full_blocks = math.ceil(m / d)
- block_list = tf.TensorArray(tf.float32,
- size=tf.cast(nb_full_blocks, dtype=tf.int32))
+ block_list = tf.TensorArray(
+ tf.float32, size=tf.cast(nb_full_blocks, dtype=tf.int32))
stateful = False
if seed is None:
stateful = True
@@ -85,11 +317,13 @@ def create_projection_matrix(m, d, seed=None):
return tf.linalg.matmul(tf.linalg.diag(multiplier), final_matrix)
-def _generalized_kernel(x, projection_matrix, f, h):
+def _generalized_kernel(x, y, is_query, projection_matrix, f, h):
"""Generalized kernel in RETHINKING ATTENTION WITH PERFORMERS.
Args:
x: The feature being transformed with shape [B, T, N ,H].
+ y: The extra stats-tensor of shape [B, T, N ,H].
+ is_query: True if x is a query-tensor.
projection_matrix: The matrix with shape [M, H] that we projecct x to, where
M is the number of projections.
f: A non-linear function applied on x or projected x.
@@ -99,7 +333,8 @@ def _generalized_kernel(x, projection_matrix, f, h):
Returns:
Transformed feature.
"""
-
+ del y
+ del is_query
if projection_matrix is None:
return h(x) * f(x)
else:
@@ -108,8 +343,124 @@ def _generalized_kernel(x, projection_matrix, f, h):
tf.cast(tf.shape(projection_matrix)[0], tf.float32))
+def expplus(data_orig,
+ other_data,
+ is_query,
+ projection_matrix=None,
+ numerical_stabilizer=0.000001,
+ normalize_data=True,
+ numerical_renormalizer=True,
+ extra_renormalize_exp_fun=False):
+ """FAVOR++ mechanism from the CRT paper: https://arxiv.org/abs/2205.15317 .
+
+ Args:
+ data_orig: data tensor of shape [B,T,H,D] for which random features aree to
+ be computed
+ other_data: additional tensor of the shape [B,F,H,D] used to collect stats
+ to determine the exact instantiation of the random feature mechanism
+ is_query: boolean indicating whether tensor is a query tensor
+ projection_matrix: tensor of the shape [M,D] encoding random projections for
+ random features (M stands for the number of random features)
+ numerical_stabilizer: numerical stabilizer for the kernel features
+ normalize_data: whether to sqrt-d-normalize queries/keys as in the regular
+ attention
+ numerical_renormalizer: whether to apply additional renormalization for
+ numerical stability
+ extra_renormalize_exp_fun: extra renormalizer for the exponential mapping
+ applied to construct random features
+
+ Returns:
+ Random feature map tensor for the unbiased softmax-kernel estimation.
+ """
+
+ data = data_orig
+ if projection_matrix is None:
+ return data_orig
+ projection_matrix = tf.cast(projection_matrix, data.dtype)
+ if normalize_data:
+ data_normalizer = 1.0 / tf.math.sqrt(
+ (tf.math.sqrt(tf.dtypes.cast(data.shape[-1], data.dtype))))
+ else:
+ data_normalizer = 1.0
+ lengths = tf.math.square(data)
+ lengths = tf.reduce_sum(lengths, axis=tf.keras.backend.ndim(data) - 1)
+ lengths = tf.expand_dims(lengths, axis=tf.keras.backend.ndim(data) - 1)
+ lengths = tf.math.sqrt(lengths)
+ data /= lengths
+ ratio = 1.0 / tf.math.sqrt(
+ tf.dtypes.cast(projection_matrix.shape[0], data.dtype))
+ data_dash = tf.einsum("blhd,md->blhm", data_normalizer * data,
+ projection_matrix)
+ diag_data = tf.math.square(data)
+ diag_data = tf.math.reduce_sum(
+ diag_data, axis=tf.keras.backend.ndim(data) - 1)
+ diag_data = (diag_data / 2.0) * data_normalizer * data_normalizer
+ diag_data = tf.expand_dims(diag_data, axis=tf.keras.backend.ndim(data) - 1)
+
+ # Calculating coefficients A, B of the FAVOR++ mechanism:
+ _, l, _, _ = tf_utils.get_shape_list(data_orig)
+
+ l = tf.cast(l, dtype=tf.float32)
+ first_sum_of_squares = tf.math.square(data)
+ first_sum_of_squares = tf.math.reduce_sum(
+ first_sum_of_squares, axis=(1, -1), keepdims=True)
+ first_sum_of_squares *= (data_normalizer * data_normalizer)
+ first_sum_of_squares /= l # data.shape[1]
+ second_sum_of_squares = tf.math.square(other_data)
+ second_sum_of_squares = tf.math.reduce_sum(
+ second_sum_of_squares, axis=(1, -1), keepdims=True)
+ second_sum_of_squares *= (data_normalizer * data_normalizer)
+ second_sum_of_squares /= l # other_data.shape[1]
+ data_sum = tf.math.reduce_sum(data, axis=(1,), keepdims=True)
+ other_data_sum = tf.math.reduce_sum(other_data, axis=(1,), keepdims=True)
+ d_prod = tf.einsum("blhd,blhd->blh", data_sum, other_data_sum)
+ d_prod = tf.expand_dims(d_prod, axis=-1)
+ d_prod *= (data_normalizer * data_normalizer)
+ d_prod *= (2.0 / (l * l))
+ ave = first_sum_of_squares + second_sum_of_squares + d_prod
+ dim = projection_matrix.shape[-1]
+ a_coeff = (1.0 / (4.0 * ave)) * (
+ tf.math.sqrt((2.0 * ave + dim) *
+ (2.0 * ave + dim) + 8.0 * dim * ave) - 2.0 * ave - dim)
+ a_coeff = (1.0 - 1.0 / a_coeff) / 8.0
+ b_coeff = tf.math.sqrt(1.0 - 4.0 * a_coeff)
+ d_coeff = tf.math.pow(1.0 - 4.0 * a_coeff, dim / 4.0)
+ a_coeff = tf.stop_gradient(a_coeff)
+ b_coeff = tf.stop_gradient(b_coeff)
+ d_coeff = tf.stop_gradient(d_coeff)
+
+ # Calculating diag_omega for the FAVOR++ mechanism:
+ diag_omega = tf.math.square(projection_matrix)
+ diag_omega = tf.math.reduce_sum(
+ diag_omega, axis=tf.keras.backend.ndim(projection_matrix) - 1)
+ diag_omega = tf.expand_dims(diag_omega, axis=0)
+ diag_omega = tf.expand_dims(diag_omega, axis=0)
+ diag_omega = tf.expand_dims(diag_omega, axis=0)
+ diag_omega = a_coeff * diag_omega
+
+ if numerical_renormalizer:
+ if is_query:
+ last_dims_t = (len(data_dash.shape) - 1,)
+ stab = b_coeff * tf.math.reduce_max(
+ data_dash, axis=last_dims_t, keepdims=True)
+ else:
+ stab = b_coeff * tf.math.reduce_max(data_dash, keepdims=True)
+ if extra_renormalize_exp_fun:
+ extra_stab = tf.reduce_max(diag_data, axis=1, keepdims=True)
+ stab = tf.math.maximum(stab, extra_stab)
+ data_dash = ratio * d_coeff * (
+ tf.math.exp(b_coeff * data_dash - stab - diag_data + diag_omega) +
+ numerical_stabilizer)
+ else:
+ data_dash = ratio * d_coeff * (
+ tf.math.exp(b_coeff * data_dash - diag_data + diag_omega) +
+ numerical_stabilizer)
+
+ return data_dash
+
+
# pylint: disable=g-long-lambda
-_TRANSFORM_MAP = {
+_CAUSAL_SUPPORT_TRANSFORM_MAP = {
"elu":
functools.partial(
_generalized_kernel,
@@ -117,19 +468,22 @@ _TRANSFORM_MAP = {
h=lambda x: 1),
"relu":
functools.partial(
- _generalized_kernel, f=tf.keras.activations.relu, h=lambda x: 1),
+ _generalized_kernel,
+ # Improve numerical stability and avoid NaNs in some cases by adding
+ # a tiny epsilon.
+ f=lambda x: tf.keras.activations.relu(x) + 1e-3,
+ h=lambda x: 1),
"square":
- functools.partial(
- _generalized_kernel, f=tf.math.square, h=lambda x: 1),
+ functools.partial(_generalized_kernel, f=tf.math.square, h=lambda x: 1),
"exp":
functools.partial(
_generalized_kernel,
# Avoid exp explosion by shifting.
- f=lambda x: tf.math.exp(
- x - tf.math.reduce_max(x, axis=[1, 2, 3], keepdims=True)),
- h=lambda x: tf.math.exp(
- -0.5 * tf.math.reduce_sum(
- tf.math.square(x), axis=-1, keepdims=True)),),
+ f=lambda x: tf.math.exp(x - tf.math.reduce_max(
+ x, axis=[1, 2, 3], keepdims=True)),
+ h=lambda x: tf.math.exp(-0.5 * tf.math.reduce_sum(
+ tf.math.square(x), axis=-1, keepdims=True)),
+ ),
"expmod":
functools.partial(
_generalized_kernel,
@@ -142,6 +496,16 @@ _TRANSFORM_MAP = {
"identity":
functools.partial(_generalized_kernel, f=lambda x: x, h=lambda x: 1)
}
+
+_NON_CAUSAL_SUPPORT_TRANSFORM_MAP = {
+ "expplus": expplus,
+}
+
+_TRANSFORM_MAP = {
+ **_CAUSAL_SUPPORT_TRANSFORM_MAP,
+ **_NON_CAUSAL_SUPPORT_TRANSFORM_MAP
+}
+
# pylint: enable=g-long-lambda
@@ -154,6 +518,9 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
(https://arxiv.org/abs/2009.14794)
- exp (Lemma 1, positive), relu
- random/deterministic projection
+ Chefs' Random Tables: Non-Trigonometric Random Features
+ (https://arxiv.org/abs/2205.15317)
+ - expplus (OPRF mechanism)
Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention
(https://arxiv.org/abs/2006.16236)
@@ -178,13 +545,19 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
is_short_seq=False,
begin_kernel=0,
scale=None,
+ scale_by_length=False,
+ use_causal_windowed=False,
+ causal_chunk_length=1,
+ causal_window_length=3,
+ causal_window_decay=None,
+ causal_padding=None,
**kwargs):
r"""Constructor of KernelAttention.
Args:
- feature_transform: A non-linear transform of the keys and quries.
- Possible transforms are "elu", "relu", "square", "exp", "expmod",
- "identity".
+ feature_transform: A non-linear transform of the keys and queries.
+ Possible transforms are "elu", "relu", "square", "exp", "expplus",
+ "expmod", "identity".
num_random_features: Number of random features to be used for projection.
if num_random_features <= 0, no production is used before transform.
seed: The seed to begin drawing random features. Once the seed is set, the
@@ -194,12 +567,28 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
redraw: Whether to redraw projection every forward pass during training.
The argument is only effective when num_random_features > 0.
is_short_seq: boolean predicate indicating whether input data consists of
- very short sequences or not; in most cases this should be False
- (default option).
+ very short sequences or not; in most cases this should be False (default
+ option).
begin_kernel: Apply kernel_attention after this sequence id and apply
softmax attention before this.
scale: The value to scale the dot product as described in `Attention Is
All You Need`. If None, we use 1/sqrt(dk) as described in the paper.
+ scale_by_length: boolean predicate indicating whether additionally scale
+ the dot product based on key length. Set as log_512^(n) to stablize
+ attention entropy against length. Refer to
+ https://kexue.fm/archives/8823 for details.
+ use_causal_windowed: If true perform windowed causal attention. See
+ causal_windowed_performer_attention function docstring for more details.
+ causal_chunk_length: Length of each chunk in tokens.
+ causal_window_length: Length of attention window in chunks.
+ causal_window_decay: Float window decay factor or `None`. If set,
+ exponentially decay past attention window values by this factor before
+ summation.
+ causal_padding: Pad the query, value and key input tensors across the axis
+ from either left or right if padding is set to "left" or "right"; apply
+ no padding if padding is set to None. In the latter case, the axis
+ dimension of the query, value and key input tensors must be divisible by
+ the chunk_length.
**kwargs: The same arguments `MultiHeadAttention` layer.
"""
if feature_transform not in _TRANSFORM_MAP:
@@ -214,6 +603,7 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
self._redraw = redraw
self._is_short_seq = is_short_seq
self._begin_kernel = begin_kernel
+ self._scale_by_length = scale_by_length
# We use the seed for two scenarios:
# 1. inference
# 2. no redraw
@@ -228,6 +618,14 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
self._projection_matrix = create_projection_matrix(
self._num_random_features, self._key_dim,
tf.constant([self._seed, self._seed + 1]))
+ self.use_causal_windowed = use_causal_windowed
+ self.causal_chunk_length = causal_chunk_length
+ self.causal_window_length = causal_window_length
+ self.causal_window_decay = causal_window_decay
+ self.causal_padding = causal_padding
+ if self.use_causal_windowed and self._is_short_seq:
+ raise ValueError(
+ "use_causal_windowed and short_seq methods are mutually exclusive")
def _compute_attention(self,
query,
@@ -236,6 +634,7 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
feature_transform,
is_short_seq,
attention_mask=None,
+ cache=None,
training=False,
numeric_stabler=_NUMERIC_STABLER):
"""Applies kernel attention with query, key, value tensors.
@@ -252,9 +651,11 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
is_short_seq: boolean predicate indicating whether input data consists of
short or long sequences; usually short sequence is defined as having
length L <= 1024.
- attention_mask: a boolean mask of shape `[B, S]`, that prevents
- attenting to masked positions. Note that the mask is only appied to
- the keys. User may want to mask the output if query contains pads.
+ attention_mask: a boolean mask of shape `[B, S]`, that prevents attenting
+ to masked positions. Note that the mask is only appied to the keys. User
+ may want to mask the output if query contains pads.
+ cache: Cache to accumulate history in memory. Used at inferecne time
+ (streaming, decoding) for causal attention.
training: Python boolean indicating whether the layer should behave in
training mode (adding dropout) or in inference mode (doing nothing).
numeric_stabler: A scalar value added to avoid divide by 0.
@@ -263,6 +664,7 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
attention_output: Multi-headed outputs of attention computation.
"""
projection_matrix = None
+
if self._num_random_features > 0:
if self._redraw and training:
projection_matrix = create_projection_matrix(self._num_random_features,
@@ -270,35 +672,53 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
else:
projection_matrix = self._projection_matrix
+ if self._scale_by_length:
+ scale = tf.math.log(tf.reduce_sum(attention_mask,
+ axis=-1)) * self._scale / math.log(512)
+ scale = tf.reshape(scale, [-1, 1, 1, 1])
+ else:
+ scale = self._scale
if is_short_seq:
# Note: Applying scalar multiply at the smaller end of einsum improves
# XLA performance, but may introduce slight numeric differences in
# the Transformer attention head.
- query = query * self._scale
+ query = query * scale
else:
# Note: we suspect spliting the scale to key, query yields smaller
# approximation variance when random projection is used.
# For simplicity, we also split when there's no random projection.
- key *= math.sqrt(self._scale)
- query *= math.sqrt(self._scale)
+ key *= tf.math.sqrt(scale)
+ query *= tf.math.sqrt(scale)
- key = _TRANSFORM_MAP[feature_transform](key, projection_matrix)
- query = _TRANSFORM_MAP[feature_transform](query, projection_matrix)
+ key_prime = _TRANSFORM_MAP[feature_transform](key, query, False,
+ projection_matrix)
+ query_prime = _TRANSFORM_MAP[feature_transform](query, key, True,
+ projection_matrix)
if attention_mask is not None:
- key = tf.einsum("BSNH,BS->BSNH", key, attention_mask)
+ key_prime = tf.einsum("BSNH,BS->BSNH", key_prime, attention_mask)
if is_short_seq:
- attention_scores = tf.einsum("BTNH,BSNH->BTSN", query, key)
+ attention_scores = tf.einsum("BTNH,BSNH->BTSN", query_prime, key_prime)
attention_scores = tf.nn.softmax(attention_scores, axis=2)
attention_output = tf.einsum("BTSN,BSNH->BTNH", attention_scores, value)
+ elif self.use_causal_windowed:
+ attention_output = causal_windowed_performer_attention(
+ query_prime,
+ key_prime,
+ value,
+ chunk_length=self.causal_chunk_length,
+ window_length=self.causal_window_length,
+ window_decay=self.causal_window_decay,
+ padding=self.causal_padding,
+ cache=cache)
else:
- kv = tf.einsum("BSNH,BSND->BNDH", key, value)
+ kv = tf.einsum("BSNH,BSND->BNDH", key_prime, value)
denominator = 1.0 / (
- tf.einsum("BTNH,BNH->BTN", query, tf.reduce_sum(key, axis=1)) +
- _NUMERIC_STABLER)
- attention_output = tf.einsum(
- "BTNH,BNDH,BTN->BTND", query, kv, denominator)
+ tf.einsum("BTNH,BNH->BTN", query_prime,
+ tf.reduce_sum(key_prime, axis=1)) + _NUMERIC_STABLER)
+ attention_output = tf.einsum("BTNH,BNDH,BTN->BTND", query_prime, kv,
+ denominator)
return attention_output
def _build_from_signature(self, query, value, key=None):
@@ -313,15 +733,12 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
kernel_constraint=self._kernel_constraint,
bias_constraint=self._bias_constraint)
self._output_dense_softmax = self._make_output_dense(
- self._query_shape.rank - 1, common_kwargs,
+ self._query_shape.rank - 1,
+ common_kwargs,
name="attention_output_softmax")
self._dropout_softmax = tf.keras.layers.Dropout(rate=self._dropout)
- def call(self,
- query,
- value,
- key=None,
- attention_mask=None,
+ def call(self, query, value, key=None, attention_mask=None, cache=None,
training=False):
"""Compute attention with kernel mechanism.
@@ -330,15 +747,32 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
value: Value `Tensor` of shape `[B, S, dim]`.
key: Optional key `Tensor` of shape `[B, S, dim]`. If not given, will use
`value` for both `key` and `value`, which is the most common case.
- attention_mask: a boolean mask of shape `[B, S]`, that prevents
- attenting to masked positions. Note that the mask is only appied to
- the keys. User may want to mask the output if query contains pads.
+ attention_mask: a boolean mask of shape `[B, S]`, that prevents attenting
+ to masked positions. Note that the mask is only appied to the keys. User
+ may want to mask the output if query contains pads.
+ cache: Cache to accumulate history in memory. Used at inferecne time
+ (streaming, decoding) for causal attention.
training: Python boolean indicating whether the layer should behave in
training mode (adding dropout) or in inference mode (doing nothing).
Returns:
Multi-headed outputs of attention computation.
"""
+ if cache is not None:
+ if training:
+ raise ValueError(
+ "Cache is not supported when training is True.")
+ if not self.use_causal_windowed:
+ raise ValueError(
+ "Cache is not supported for non use_causal_windowed case.")
+ if self._begin_kernel:
+ raise ValueError(
+ "Cache is not supported when begin_kernel is set since the bahvior "
+ "is too complicated.")
+ if self._feature_transform in _NON_CAUSAL_SUPPORT_TRANSFORM_MAP:
+ raise ValueError("Cache is not supported for feature_transform %s" %
+ (self._feature_transform))
+
if not self._built_from_signature:
self._build_from_signature(query=query, value=value, key=key)
if key is None:
@@ -357,25 +791,26 @@ class KernelAttention(tf.keras.layers.MultiHeadAttention):
if self._begin_kernel > 0:
attention_output_softmax = self._compute_attention(
- query[:, :self._begin_kernel],
- key, value, "identity", True, attention_mask, training)
+ query[:, :self._begin_kernel], key, value, "identity", True,
+ attention_mask, training)
attention_output_softmax = self._dropout_softmax(attention_output_softmax)
attention_output_softmax = self._output_dense_softmax(
attention_output_softmax)
attention_output_kernel = self._compute_attention(
- query[:, self._begin_kernel:],
- key, value, self._feature_transform, self._is_short_seq,
- attention_mask, training)
+ query[:, self._begin_kernel:], key, value, self._feature_transform,
+ self._is_short_seq, attention_mask, training)
attention_output_kernel = self._dropout_layer(attention_output_kernel)
- attention_output_kernel = self._output_dense(
- attention_output_kernel)
+ attention_output_kernel = self._output_dense(attention_output_kernel)
attention_output = tf.concat(
[attention_output_softmax, attention_output_kernel], axis=1)
else:
- attention_output = self._compute_attention(
- query, key, value, self._feature_transform,
- self._is_short_seq, attention_mask, training)
+ attention_output = self._compute_attention(query, key, value,
+ self._feature_transform,
+ self._is_short_seq,
+ attention_mask,
+ cache,
+ training)
# This is actually dropping out entire tokens to attend to, which might
# seem a bit unusual, but is taken from the original Transformer paper.
attention_output = self._dropout_layer(attention_output)
diff --git a/official/nlp/modeling/layers/kernel_attention_test.py b/official/nlp/modeling/layers/kernel_attention_test.py
index 947704fb31dacc76da81af27a6c38328525353e6..fa86b71b96b0c48f93d9ec947dd64e9b04e8f059 100644
--- a/official/nlp/modeling/layers/kernel_attention_test.py
+++ b/official/nlp/modeling/layers/kernel_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,7 +21,7 @@ import tensorflow as tf
from official.nlp.modeling.layers import kernel_attention as attention
-_FEATURE_TRANSFORM = ['relu', 'elu', 'exp']
+_FEATURE_TRANSFORM = ["relu", "elu", "exp", "expplus"]
_REDRAW = [True, False]
_TRAINING = [True, False]
_IS_SHORT_SEQ = [True, False]
@@ -30,9 +30,67 @@ _BEGIN_KERNEL = [0, 512]
class KernelAttentionTest(tf.test.TestCase, parameterized.TestCase):
+ # expplus is only designed for bi-directional use case.
+ # exp can be numeric unstable.
@parameterized.parameters(itertools.product(
- _FEATURE_TRANSFORM, [127], _TRAINING, [True, False],
- _IS_SHORT_SEQ, _BEGIN_KERNEL))
+ ["relu", "elu"], [1, 4], [0.9]))
+ def test_causal_windowed_attention_projection_streaming(
+ self, feature_transform, causal_chunk_length, causal_weight_decay):
+ num_heads = 12
+ key_dim = 64
+ seq_length = 16
+ num_chunks = seq_length // causal_chunk_length
+ causal_window_length = num_chunks
+ batch_size = 2
+ training = False
+ num_random_features = 0
+ test_layer = attention.KernelAttention(
+ num_heads=num_heads,
+ key_dim=key_dim,
+ feature_transform=feature_transform,
+ num_random_features=num_random_features,
+ redraw=False,
+ is_short_seq=False,
+ begin_kernel=False,
+ use_causal_windowed=True,
+ causal_chunk_length=causal_chunk_length,
+ causal_window_length=causal_window_length,
+ causal_window_decay=causal_weight_decay,
+ causal_padding=None,
+ )
+ query = tf.random.normal(
+ shape=(batch_size, seq_length, key_dim), seed=2)
+ value = query
+ encoder_inputs_mask = tf.ones((batch_size, seq_length), dtype=tf.int32)
+ masks = tf.cast(encoder_inputs_mask, dtype=tf.float32)
+ output = test_layer(
+ query=query,
+ value=value,
+ attention_mask=masks,
+ training=training)
+ dim = num_random_features if num_random_features > 0 else key_dim
+ kv_cache = tf.zeros(
+ (batch_size, num_heads, dim, dim))
+ k_sum_cache = tf.zeros((batch_size, num_heads, dim))
+ stream_output = []
+ cache = {"kv": kv_cache, "k_sum": k_sum_cache}
+ for i in range(num_chunks):
+ stream_output.append(
+ test_layer(
+ query=query[:, i * causal_chunk_length:(i + 1) *
+ causal_chunk_length, :],
+ value=value[:, i * causal_chunk_length:(i + 1) *
+ causal_chunk_length, :],
+ attention_mask=masks[:, i * causal_chunk_length:(i + 1) *
+ causal_chunk_length],
+ cache=cache,
+ training=training))
+ stream_output = tf.concat(stream_output, axis=1)
+ self.assertAllClose(output, stream_output)
+
+ @parameterized.parameters(
+ itertools.product(_FEATURE_TRANSFORM, [127], _TRAINING, [True, False],
+ _IS_SHORT_SEQ, _BEGIN_KERNEL))
def test_attention_projection(
self, feature_transform, num_random_features, training, redraw, is_short,
begin_kernel):
@@ -60,6 +118,41 @@ class KernelAttentionTest(tf.test.TestCase, parameterized.TestCase):
training=training)
self.assertEqual(output.shape, [batch_size, seq_length, key_dim])
+ @parameterized.parameters(
+ itertools.product(["relu", "exp"], [127], _TRAINING, [True, False],
+ [0], [None, 0.97], [None, "left", "right"]))
+ def test_causal_windowed_attention_projection(
+ self, feature_transform, num_random_features, training, redraw,
+ begin_kernel, causal_window_decay, causal_padding):
+ num_heads = 12
+ key_dim = 64
+ seq_length = 1024
+ batch_size = 2
+ test_layer = attention.KernelAttention(
+ num_heads=num_heads,
+ key_dim=key_dim,
+ feature_transform=feature_transform,
+ num_random_features=num_random_features,
+ redraw=redraw,
+ is_short_seq=False,
+ begin_kernel=begin_kernel,
+ use_causal_windowed=True,
+ causal_chunk_length=8,
+ causal_window_length=3,
+ causal_window_decay=causal_window_decay,
+ causal_padding=causal_padding)
+ query = tf.random.normal(
+ shape=(batch_size, seq_length, key_dim))
+ value = query
+ encoder_inputs_mask = tf.zeros((batch_size, seq_length), dtype=tf.int32)
+ masks = tf.cast(encoder_inputs_mask, dtype=tf.float32)
+ output = test_layer(
+ query=query,
+ value=value,
+ attention_mask=masks,
+ training=training)
+ self.assertEqual(output.shape, [batch_size, seq_length, key_dim])
+
@parameterized.parameters(itertools.product(
_FEATURE_TRANSFORM, [0], _TRAINING, [False],
_IS_SHORT_SEQ, _BEGIN_KERNEL))
@@ -90,15 +183,41 @@ class KernelAttentionTest(tf.test.TestCase, parameterized.TestCase):
training=training)
self.assertEqual(output.shape, [batch_size, seq_length, key_dim])
+ @parameterized.parameters([128, 512])
+ def test_attention_scale_by_length(self, seq_length):
+ num_heads = 12
+ key_dim = 64
+ batch_size = 2
+ test_layer = attention.KernelAttention(
+ num_heads=num_heads,
+ key_dim=key_dim,
+ num_random_features=0,
+ scale_by_length=True)
+ query = tf.random.normal(
+ shape=(batch_size, seq_length, key_dim))
+ value = query
+ encoder_inputs_mask = tf.ones((batch_size, seq_length), dtype=tf.int32)
+ masks = tf.cast(encoder_inputs_mask, dtype=tf.float32)
+ output_scale_by_length = test_layer(
+ query=query, value=value, attention_mask=masks)
+
+ test_layer._scale_by_length = False
+ output_no_scale_by_length = test_layer(
+ query=query, value=value, attention_mask=masks)
+ if seq_length == 512: # Equals because log(seq_length, base=512) = 1.0
+ self.assertAllClose(output_scale_by_length, output_no_scale_by_length)
+ else:
+ self.assertNotAllClose(output_scale_by_length, output_no_scale_by_length)
+
def test_unsupported_feature_transform(self):
- with self.assertRaisesRegex(ValueError, 'Unsupported feature_transform.*'):
- _ = attention.KernelAttention(feature_transform='test')
+ with self.assertRaisesRegex(ValueError, "Unsupported feature_transform.*"):
+ _ = attention.KernelAttention(feature_transform="test")
def test_redraw_true_no_projection(self):
with self.assertRaisesRegex(
- ValueError, 'There is nothing to redraw when num_random_features.*'):
+ ValueError, "There is nothing to redraw when num_random_features.*"):
_ = attention.KernelAttention(
- num_heads=2, key_dim=64, feature_transform='elu',
+ num_heads=2, key_dim=64, feature_transform="elu",
num_random_features=0, redraw=True)
def test_config(self):
@@ -107,7 +226,7 @@ class KernelAttentionTest(tf.test.TestCase, parameterized.TestCase):
test_layer = attention.KernelAttention(
num_heads=num_heads,
key_dim=key_dim,
- feature_transform='exp',
+ feature_transform="exp",
num_random_features=128,
is_short_seq=True)
new_layer = attention.KernelAttention.from_config(
@@ -115,5 +234,25 @@ class KernelAttentionTest(tf.test.TestCase, parameterized.TestCase):
# If the serialization was successful, the new config should match the old.
self.assertAllEqual(test_layer.get_config(), new_layer.get_config())
-if __name__ == '__main__':
+ def test_rectangular_window_sum(self):
+ x = tf.ones([2, 5, 2, 2, 2])
+ winsum = attention.rectangular_window_sum(x, 3)
+ self.assertEqual(winsum.shape, x.shape)
+ self.assertAllClose(
+ tf.tile(
+ tf.reshape([1., 2., 3., 3., 3.], [1, -1, 1, 1, 1]),
+ [2, 1, 2, 2, 2]),
+ winsum)
+
+ def test_weighted_window_sum(self):
+ x = tf.ones([2, 5, 2, 2, 2])
+ winsum = attention.weighted_window_sum(x, 3, [0.01, 0.1, 1.])
+ self.assertEqual(winsum.shape, x.shape)
+ self.assertAllClose(
+ tf.tile(
+ tf.reshape([1., 1.1, 1.11, 1.11, 1.11], [1, -1, 1, 1, 1]),
+ [2, 1, 2, 2, 2]),
+ winsum)
+
+if __name__ == "__main__":
tf.test.main()
diff --git a/official/nlp/modeling/layers/masked_lm.py b/official/nlp/modeling/layers/masked_lm.py
index 9737b22876f01156d8bb7ab2ca38f49a4aa552ec..2d02f71c77a072b637ba93d30b88c9f1592cb18f 100644
--- a/official/nlp/modeling/layers/masked_lm.py
+++ b/official/nlp/modeling/layers/masked_lm.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -47,7 +47,7 @@ class MaskedLM(tf.keras.layers.Layer):
output='logits',
name=None,
**kwargs):
- super(MaskedLM, self).__init__(name=name, **kwargs)
+ super().__init__(name=name, **kwargs)
self.embedding_table = embedding_table
self.activation = activation
self.initializer = tf.keras.initializers.get(initializer)
@@ -73,7 +73,7 @@ class MaskedLM(tf.keras.layers.Layer):
initializer='zeros',
trainable=True)
- super(MaskedLM, self).build(input_shape)
+ super().build(input_shape)
def call(self, sequence_data, masked_positions):
masked_lm_input = self._gather_indexes(sequence_data, masked_positions)
@@ -115,7 +115,8 @@ class MaskedLM(tf.keras.layers.Layer):
flat_offsets = tf.reshape(
tf.range(0, batch_size, dtype=tf.int32) * seq_length, [-1, 1])
- flat_positions = tf.reshape(positions + flat_offsets, [-1])
+ flat_positions = tf.reshape(
+ positions + tf.cast(flat_offsets, positions.dtype), [-1])
flat_sequence_tensor = tf.reshape(sequence_tensor,
[batch_size * seq_length, width])
output_tensor = tf.gather(flat_sequence_tensor, flat_positions)
diff --git a/official/nlp/modeling/layers/masked_lm_test.py b/official/nlp/modeling/layers/masked_lm_test.py
index 53b3b4a22b2696a4e7e8b2566f0691418b8d8e0f..0cd3ce0721a7568b919aab16f2933cb0a07a85d3 100644
--- a/official/nlp/modeling/layers/masked_lm_test.py
+++ b/official/nlp/modeling/layers/masked_lm_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/masked_softmax.py b/official/nlp/modeling/layers/masked_softmax.py
index 06b1994c7b8e5a6a8624130b2a7c6608b2332cf6..51a859027f194d849356ca63144dd643ca0c884f 100644
--- a/official/nlp/modeling/layers/masked_softmax.py
+++ b/official/nlp/modeling/layers/masked_softmax.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -53,7 +53,7 @@ class MaskedSoftmax(tf.keras.layers.Layer):
self._normalization_axes = (-1,)
else:
self._normalization_axes = normalization_axes
- super(MaskedSoftmax, self).__init__(**kwargs)
+ super().__init__(**kwargs)
def call(self, scores, mask=None):
@@ -81,5 +81,5 @@ class MaskedSoftmax(tf.keras.layers.Layer):
'mask_expansion_axes': self._mask_expansion_axes,
'normalization_axes': self._normalization_axes
}
- base_config = super(MaskedSoftmax, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
diff --git a/official/nlp/modeling/layers/masked_softmax_test.py b/official/nlp/modeling/layers/masked_softmax_test.py
index 802b6848211122c29fcbaef4e014f5094dd25939..d6fe410b16421af31ba060dc2344d32abbec7554 100644
--- a/official/nlp/modeling/layers/masked_softmax_test.py
+++ b/official/nlp/modeling/layers/masked_softmax_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/mat_mul_with_margin.py b/official/nlp/modeling/layers/mat_mul_with_margin.py
index 1fe3156caf35e1010f5838173373004add09b819..25f4ed23a1866881d01ec378f9bd63d6a2946643 100644
--- a/official/nlp/modeling/layers/mat_mul_with_margin.py
+++ b/official/nlp/modeling/layers/mat_mul_with_margin.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -36,7 +36,7 @@ class MatMulWithMargin(tf.keras.layers.Layer):
logit_scale=1.0,
logit_margin=0.0,
**kwargs):
- super(MatMulWithMargin, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self.logit_scale = logit_scale
self.logit_margin = logit_margin
@@ -61,7 +61,7 @@ class MatMulWithMargin(tf.keras.layers.Layer):
config = {
'logit_scale': self.logit_scale,
'logit_margin': self.logit_margin}
- config.update(super(MatMulWithMargin, self).get_config())
+ config.update(super().get_config())
return config
@classmethod
diff --git a/official/nlp/modeling/layers/mat_mul_with_margin_test.py b/official/nlp/modeling/layers/mat_mul_with_margin_test.py
index 1ceea013caee4d060e245dcba5bec590c57937da..4a02d51362ee48970a7339b38cf62903030f2800 100644
--- a/official/nlp/modeling/layers/mat_mul_with_margin_test.py
+++ b/official/nlp/modeling/layers/mat_mul_with_margin_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/mixing.py b/official/nlp/modeling/layers/mixing.py
new file mode 100644
index 0000000000000000000000000000000000000000..71975e9836684583273d9ec069490b9901000f96
--- /dev/null
+++ b/official/nlp/modeling/layers/mixing.py
@@ -0,0 +1,283 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Keras-based mixing layers.
+
+Based on the mixing layers use by FNet
+(https://aclanthology.org/2022.naacl-main.319/) and Sparse Mixers
+(https://arxiv.org/abs/2205.12399).
+
+Mixing layers can be used as drop in replacements for self-attention layers. For
+interoperability with attention layers, we use the same `query` and `value` call
+signature.
+
+Note: These mixing layers currently only support encoder stacks. Decoder stacks
+can be supported in the future by utilizing the `value` inputs.
+"""
+
+import enum
+import functools
+from typing import Callable, Tuple, Union
+
+import numpy as np
+from scipy import linalg
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+_Initializer = Union[str, tf.keras.initializers.Initializer]
+
+default_kernel_initializer = tf.keras.initializers.TruncatedNormal(stddev=2e-2)
+
+
+class MixingMechanism(enum.Enum):
+ """Determines the type of mixing layer.
+
+ Possible options:
+ FOURIER: Fourier Transform mixing.
+ LINEAR: Mixing using dense matrix multiplications with learnable weights.
+ HARTLEY: Hartley Transform mixing.
+ """
+ FOURIER = "fourier"
+ HARTLEY = "hartley"
+ LINEAR = "linear"
+
+
+class MixingLayer(tf.keras.layers.Layer):
+ """Mixing layer base class.
+
+ This class cannot be used directly. It just specifies the API for mixing
+ layer subclasses. For interoperability with attention layers, we use the same
+ `query` and `value` call signature.
+
+ Based on the mixing layers use by FNet
+ (https://aclanthology.org/2022.naacl-main.319/) and Sparse Mixers
+ (https://arxiv.org/abs/2205.12399).
+ """
+
+ def __init__(self, name: str = "mixing", **kwargs):
+ """Initializes layer.
+
+ Args:
+ name: Name for layer.
+ **kwargs: Keyword arguments.
+ """
+ super().__init__(name=name, **kwargs)
+
+ def call(self, query: tf.Tensor, value: tf.Tensor, **kwargs) -> tf.Tensor:
+ """Calls the layer.
+
+ Subclasses should return tensors of shape
+ [batch_size, max_seq_length, hidden_dim].
+
+ Args:
+ query: Batch of input embeddings, typically of shape [batch_size,
+ max_seq_length, hidden_dim].
+ value: Unused. Included to match attention layer API.
+ **kwargs: Optional arguments to catch unused attention keyword arguments.
+
+ Raises:
+ NotImplementedError. This class should not be called directly.
+ """
+ raise NotImplementedError("Abstract method")
+
+
+class FourierTransformLayer(MixingLayer):
+ """Fourier Transform layer.
+
+ Applies 2D Fourier Transform over final two dimensions of `query` inputs -
+ typically the sequence and hidden dimensions.
+ """
+
+ def __init__(self,
+ use_fft: bool = False,
+ name: str = "fourier_transform",
+ **kwargs):
+ """Initializes layer.
+
+ Args:
+ use_fft: Whether to use Fast Fourier Transform (True) or the Discrete
+ Fourier Transform (DFT) matrix (False) to compute the Fourier Transform.
+ See _pick_fourier_transform() for recommendations on when to use FFT or
+ DFT.
+ name: Name for layer.
+ **kwargs: Keyword arguments.
+ """
+ super().__init__(name=name, **kwargs)
+ self.use_fft = use_fft
+
+ def build(self, input_shape: Tuple[int, ...]):
+ """Picks the Fourier Transform implementation."""
+ self.fourier_transform = _pick_fourier_transform(
+ self.use_fft,
+ max_seq_length=input_shape[-2],
+ hidden_dim=input_shape[-1])
+
+ def call(self, query: tf.Tensor, value: tf.Tensor, **kwargs) -> tf.Tensor:
+ """Applies layer to `query`.
+
+ Args:
+ query: Batch of input embeddings, typically of shape [batch_size,
+ max_seq_length, hidden_dim].
+ value: Unused. Included to match attention layer API.
+ **kwargs: Optional arguments to catch unused attention keyword arguments.
+
+ Returns:
+ Real part of discrete Fourier Transform of `query` inputs with shape
+ [batch_size, max_seq_length, hidden_dim].
+ """
+ del value # Ignored by encoder-only mixing layers
+ query = tf.cast(query, tf.complex64)
+ return tf.math.real(self.fourier_transform(query))
+
+
+class HartleyTransformLayer(MixingLayer):
+ """Hartley Transform layer.
+
+ Applies 2D Hartley Transform over final two dimensions of `query` inputs -
+ typically the sequence and hidden dimensions.
+ """
+
+ def __init__(self,
+ use_fft: bool = False,
+ name: str = "hartley_transform",
+ **kwargs):
+ """Initializes layer.
+
+ Args:
+ use_fft: Whether to use Fast Fourier Transform (True) or the Discrete
+ Fourier Transform (DFT) matrix (False) to compute the Hartley Transform.
+ See _pick_fourier_transform() for recommendations on when to use FFT or
+ DFT.
+ name: Name for layer.
+ **kwargs: Keyword arguments.
+ """
+ super().__init__(name=name, **kwargs)
+ self.use_fft = use_fft
+
+ def build(self, input_shape: Tuple[int, ...]):
+ """Picks the Fourier Transform implementation."""
+ self.fourier_transform = _pick_fourier_transform(
+ self.use_fft,
+ max_seq_length=input_shape[-2],
+ hidden_dim=input_shape[-1])
+
+ def call(self, query: tf.Tensor, value: tf.Tensor, **kwargs) -> tf.Tensor:
+ """Applies layer to `query`.
+
+ Args:
+ query: Batch of input embeddings, typically of shape [batch_size,
+ max_seq_length, hidden_dim].
+ value: Unused. Included to match attention layer API.
+ **kwargs: Optional arguments to catch unused attention keyword arguments.
+
+ Returns:
+ Real part of discrete Hartley Transform of `query` inputs with shape
+ [batch_size, max_seq_length, hidden_dim].
+ """
+ del value # Ignored by encoder-only mixing layers
+ query = tf.cast(query, tf.complex64)
+ frequencies = self.fourier_transform(query)
+ return tf.math.real(frequencies) - tf.math.imag(frequencies)
+
+
+class LinearTransformLayer(MixingLayer):
+ """Dense, linear transformation layer.
+
+ Applies matrix multiplications over sequence and hidden dimensions.
+ """
+
+ def __init__(self,
+ kernel_initializer: _Initializer = default_kernel_initializer,
+ name: str = "linear_transform",
+ **kwargs):
+ """Initializes layer.
+
+ Args:
+ kernel_initializer: Initialization scheme for kernel.
+ name: Name for layer.
+ **kwargs: Keyword arguments.
+ """
+ super().__init__(name=name, **kwargs)
+ self.kernel_initializer = kernel_initializer
+
+ def build(self, input_shape: Tuple[int, ...]):
+ """Creates the hidden and sequence matrix variables of the layer."""
+ self.mat_hidden = self.add_weight(
+ shape=(input_shape[-1], input_shape[-1]),
+ initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ trainable=True,
+ name="hidden_kernel")
+ self.mat_seq = self.add_weight(
+ shape=(input_shape[-2], input_shape[-2]),
+ initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ trainable=True,
+ name="seq_kernel")
+
+ def call(self, query: tf.Tensor, value: tf.Tensor, **kwargs) -> tf.Tensor:
+ """Applies layer to `query`.
+
+ Args:
+ query: Batch of input embeddings, typically of shape [batch_size,
+ max_seq_length, hidden_dim].
+ value: Unused. Included to match attention layer API.
+ **kwargs: Optional arguments to catch unused attention keyword arguments.
+
+ Returns:
+ Linearly transformed `query` inputs with shape
+ [batch_size, max_seq_length, hidden_dim].
+ """
+ del value # Ignored by encoder-only mixing layers
+
+ return tf.einsum("bij,jk,ni->bnk", query, self.mat_hidden, self.mat_seq)
+
+
+def _pick_fourier_transform(
+ use_fft: bool, max_seq_length: int,
+ hidden_dim: int) -> Callable[[tf.Tensor], tf.Tensor]:
+ """Returns FFT or DFT Fourier Transform implementation.
+
+ On TPUs, we recommend using the Discrete Fourier Transform (DFT) matrix
+ (use_fft=False), except for very long sequence lengths. On GPUs and CPUs, the
+ Fast Fourier Transform (use_fft=True) is generally optimal for all sequence
+ lengths.
+
+ Note: When using the FFT it is recommended to use a sequence length that is a
+ power of 2.
+
+ Args:
+ use_fft: If True, return FFT. Otherwise, return DFT matrix.
+ max_seq_length: Maximum sequence length of inputs. Only used if
+ use_fft=False.
+ hidden_dim: Size of hidden dimension of inputs. Only used if use_fft=False.
+
+ Returns:
+ Fourier Transform.
+ """
+ if use_fft:
+ return tf.signal.fft2d
+ else:
+ dft_mat_seq = linalg.dft(max_seq_length).astype(np.complex64)
+ dft_mat_hidden = linalg.dft(hidden_dim).astype(np.complex64)
+
+ def two_dim_matmul(x: tf.Tensor, matrix_dim_one: tf.Tensor,
+ matrix_dim_two: tf.Tensor) -> tf.Tensor:
+ """Applies 2D matrix multiplication to input tensors of rank >= 2."""
+ return tf.einsum("...ij,jk,ni->...nk", tf.cast(x, tf.complex64),
+ matrix_dim_two, matrix_dim_one)
+
+ return functools.partial(
+ two_dim_matmul,
+ matrix_dim_one=tf.convert_to_tensor(dft_mat_seq),
+ matrix_dim_two=tf.convert_to_tensor(dft_mat_hidden))
diff --git a/official/nlp/modeling/layers/mixing_test.py b/official/nlp/modeling/layers/mixing_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..811525884a889128f27485dfb5e200dcb5ab8958
--- /dev/null
+++ b/official/nlp/modeling/layers/mixing_test.py
@@ -0,0 +1,109 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for mixing.py."""
+
+import numpy as np
+import tensorflow as tf
+
+from official.nlp.modeling.layers import mixing
+
+
+class MixingTest(tf.test.TestCase):
+
+ def test_base_mixing_layer(self):
+ inputs = tf.random.uniform((3, 8, 16),
+ minval=0,
+ maxval=10,
+ dtype=tf.float32)
+
+ with self.assertRaisesRegex(NotImplementedError, "Abstract method"):
+ _ = mixing.MixingLayer()(query=inputs, value=inputs)
+
+ def test_fourier_layer(self):
+ batch_size = 4
+ max_seq_length = 8
+ hidden_dim = 16
+
+ inputs = tf.random.uniform((batch_size, max_seq_length, hidden_dim),
+ minval=0,
+ maxval=10,
+ dtype=tf.float32)
+ outputs = mixing.FourierTransformLayer(use_fft=True)(
+ query=inputs, value=inputs)
+ self.assertEqual(outputs.shape, (batch_size, max_seq_length, hidden_dim))
+
+ def test_hartley_layer(self):
+ batch_size = 3
+ max_seq_length = 16
+ hidden_dim = 4
+
+ inputs = tf.random.uniform((batch_size, max_seq_length, hidden_dim),
+ minval=0,
+ maxval=12,
+ dtype=tf.float32)
+ outputs = mixing.HartleyTransformLayer(use_fft=True)(
+ query=inputs, value=inputs)
+ self.assertEqual(outputs.shape, (batch_size, max_seq_length, hidden_dim))
+
+ def test_linear_mixing_layer(self):
+ batch_size = 2
+ max_seq_length = 4
+ hidden_dim = 3
+
+ inputs = tf.ones((batch_size, max_seq_length, hidden_dim), dtype=tf.float32)
+ outputs = mixing.LinearTransformLayer(
+ kernel_initializer=tf.keras.initializers.Ones())(
+ query=inputs, value=inputs)
+
+ # hidden_dim * (max_seq_length * 1) = 12.
+ expected_outputs = [
+ [
+ [12., 12., 12.],
+ [12., 12., 12.],
+ [12., 12., 12.],
+ [12., 12., 12.],
+ ],
+ [
+ [12., 12., 12.],
+ [12., 12., 12.],
+ [12., 12., 12.],
+ [12., 12., 12.],
+ ],
+ ]
+ np.testing.assert_allclose(outputs, expected_outputs, rtol=1e-6, atol=1e-6)
+
+ def test_pick_fourier_transform(self):
+ # Ensure we don't hit an edge case which exceeds the fixed numerical error.
+ tf.random.set_seed(1)
+ np.random.seed(1)
+
+ batch_size = 3
+ max_seq_length = 4
+ hidden_dim = 8
+
+ fft = mixing._pick_fourier_transform(
+ use_fft=True, max_seq_length=max_seq_length, hidden_dim=hidden_dim)
+ dft_matmul = mixing._pick_fourier_transform(
+ use_fft=False, max_seq_length=max_seq_length, hidden_dim=hidden_dim)
+
+ inputs = tf.random.uniform([batch_size, max_seq_length, hidden_dim])
+ inputs = tf.cast(inputs, tf.complex64)
+
+ np.testing.assert_allclose(
+ fft(inputs), dft_matmul(inputs), rtol=1e-6, atol=1e-6)
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/mobile_bert_layers.py b/official/nlp/modeling/layers/mobile_bert_layers.py
index cc1c5c585a349f82da1dd18e7534b669b97250ab..4c5a33a270a0a5cc99b3a3783f885f4a11528846 100644
--- a/official/nlp/modeling/layers/mobile_bert_layers.py
+++ b/official/nlp/modeling/layers/mobile_bert_layers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,6 +15,8 @@
"""MobileBERT embedding and transformer layers."""
import tensorflow as tf
+from official.modeling import tf_utils
+
from official.nlp.modeling.layers import on_device_embedding
from official.nlp.modeling.layers import position_embedding
@@ -24,7 +26,7 @@ class NoNorm(tf.keras.layers.Layer):
"""Apply element-wise linear transformation to the last dimension."""
def __init__(self, name=None):
- super(NoNorm, self).__init__(name=name)
+ super().__init__(name=name)
def build(self, shape):
kernal_size = shape[-1]
@@ -96,7 +98,7 @@ class MobileBertEmbedding(tf.keras.layers.Layer):
dropout_rate: Dropout rate.
**kwargs: keyword arguments.
"""
- super(MobileBertEmbedding, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self.word_vocab_size = word_vocab_size
self.word_embed_size = word_embed_size
self.type_vocab_size = type_vocab_size
@@ -109,21 +111,21 @@ class MobileBertEmbedding(tf.keras.layers.Layer):
self.word_embedding = on_device_embedding.OnDeviceEmbedding(
self.word_vocab_size,
self.word_embed_size,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(self.initializer),
name='word_embedding')
self.type_embedding = on_device_embedding.OnDeviceEmbedding(
self.type_vocab_size,
self.output_embed_size,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(self.initializer),
name='type_embedding')
self.pos_embedding = position_embedding.PositionEmbedding(
max_length=max_sequence_length,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(self.initializer),
name='position_embedding')
- self.word_embedding_proj = tf.keras.layers.experimental.EinsumDense(
+ self.word_embedding_proj = tf.keras.layers.EinsumDense(
'abc,cd->abd',
output_shape=[None, self.output_embed_size],
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
bias_axes='d',
name='embedding_projection')
self.layer_norm = _get_norm_layer(normalization_type, 'embedding_norm')
@@ -220,7 +222,7 @@ class MobileBertTransformer(tf.keras.layers.Layer):
Raises:
ValueError: A Tensor shape or parameter is invalid.
"""
- super(MobileBertTransformer, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self.hidden_size = hidden_size
self.num_attention_heads = num_attention_heads
self.intermediate_size = intermediate_size
@@ -242,11 +244,11 @@ class MobileBertTransformer(tf.keras.layers.Layer):
self.block_layers = {}
# add input bottleneck
- dense_layer_2d = tf.keras.layers.experimental.EinsumDense(
+ dense_layer_2d = tf.keras.layers.EinsumDense(
'abc,cd->abd',
output_shape=[None, self.intra_bottleneck_size],
bias_axes='d',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='bottleneck_input/dense')
layer_norm = _get_norm_layer(self.normalization_type,
name='bottleneck_input/norm')
@@ -254,11 +256,11 @@ class MobileBertTransformer(tf.keras.layers.Layer):
layer_norm]
if self.key_query_shared_bottleneck:
- dense_layer_2d = tf.keras.layers.experimental.EinsumDense(
+ dense_layer_2d = tf.keras.layers.EinsumDense(
'abc,cd->abd',
output_shape=[None, self.intra_bottleneck_size],
bias_axes='d',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='kq_shared_bottleneck/dense')
layer_norm = _get_norm_layer(self.normalization_type,
name='kq_shared_bottleneck/norm')
@@ -272,7 +274,7 @@ class MobileBertTransformer(tf.keras.layers.Layer):
value_dim=attention_head_size,
dropout=self.attention_probs_dropout_prob,
output_shape=self.intra_bottleneck_size,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='attention')
layer_norm = _get_norm_layer(self.normalization_type,
name='attention/norm')
@@ -284,19 +286,19 @@ class MobileBertTransformer(tf.keras.layers.Layer):
for ffn_layer_idx in range(self.num_feedforward_networks):
layer_prefix = f'ffn_layer_{ffn_layer_idx}'
layer_name = layer_prefix + '/intermediate_dense'
- intermediate_layer = tf.keras.layers.experimental.EinsumDense(
+ intermediate_layer = tf.keras.layers.EinsumDense(
'abc,cd->abd',
activation=self.intermediate_act_fn,
output_shape=[None, self.intermediate_size],
bias_axes='d',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name=layer_name)
layer_name = layer_prefix + '/output_dense'
- output_layer = tf.keras.layers.experimental.EinsumDense(
+ output_layer = tf.keras.layers.EinsumDense(
'abc,cd->abd',
output_shape=[None, self.intra_bottleneck_size],
bias_axes='d',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name=layer_name)
layer_name = layer_prefix + '/norm'
layer_norm = _get_norm_layer(self.normalization_type,
@@ -306,12 +308,12 @@ class MobileBertTransformer(tf.keras.layers.Layer):
layer_norm])
# add output bottleneck
- bottleneck = tf.keras.layers.experimental.EinsumDense(
+ bottleneck = tf.keras.layers.EinsumDense(
'abc,cd->abd',
output_shape=[None, self.hidden_size],
activation=None,
bias_axes='d',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='bottleneck_output/dense')
dropout_layer = tf.keras.layers.Dropout(
self.hidden_dropout_prob,
@@ -445,6 +447,7 @@ class MobileBertMaskedLM(tf.keras.layers.Layer):
activation=None,
initializer='glorot_uniform',
output='logits',
+ output_weights_use_proj=False,
**kwargs):
"""Class initialization.
@@ -455,9 +458,12 @@ class MobileBertMaskedLM(tf.keras.layers.Layer):
uniform initializer.
output: The output style for this layer. Can be either `logits` or
`predictions`.
+ output_weights_use_proj: Use projection instead of concating extra output
+ weights, this may reduce the MLM task accuracy but will reduce the model
+ params as well.
**kwargs: keyword arguments.
"""
- super(MobileBertMaskedLM, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self.embedding_table = embedding_table
self.activation = activation
self.initializer = tf.keras.initializers.get(initializer)
@@ -467,6 +473,7 @@ class MobileBertMaskedLM(tf.keras.layers.Layer):
('Unknown `output` value "%s". `output` can be either "logits" or '
'"predictions"') % output)
self._output_type = output
+ self._output_weights_use_proj = output_weights_use_proj
def build(self, input_shape):
self._vocab_size, embedding_width = self.embedding_table.shape
@@ -474,15 +481,22 @@ class MobileBertMaskedLM(tf.keras.layers.Layer):
self.dense = tf.keras.layers.Dense(
hidden_size,
activation=self.activation,
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='transform/dense')
if hidden_size > embedding_width:
- self.extra_output_weights = self.add_weight(
- 'extra_output_weights',
- shape=(self._vocab_size, hidden_size - embedding_width),
- initializer=self.initializer,
- trainable=True)
+ if self._output_weights_use_proj:
+ self.extra_output_weights = self.add_weight(
+ 'output_weights_proj',
+ shape=(embedding_width, hidden_size),
+ initializer=tf_utils.clone_initializer(self.initializer),
+ trainable=True)
+ else:
+ self.extra_output_weights = self.add_weight(
+ 'extra_output_weights',
+ shape=(self._vocab_size, hidden_size - embedding_width),
+ initializer=tf_utils.clone_initializer(self.initializer),
+ trainable=True)
elif hidden_size == embedding_width:
self.extra_output_weights = None
else:
@@ -507,10 +521,16 @@ class MobileBertMaskedLM(tf.keras.layers.Layer):
if self.extra_output_weights is None:
lm_data = tf.matmul(lm_data, self.embedding_table, transpose_b=True)
else:
- lm_data = tf.matmul(
- lm_data,
- tf.concat([self.embedding_table, self.extra_output_weights], axis=1),
- transpose_b=True)
+ if self._output_weights_use_proj:
+ lm_data = tf.matmul(
+ lm_data, self.extra_output_weights, transpose_b=True)
+ lm_data = tf.matmul(lm_data, self.embedding_table, transpose_b=True)
+ else:
+ lm_data = tf.matmul(
+ lm_data,
+ tf.concat([self.embedding_table, self.extra_output_weights],
+ axis=1),
+ transpose_b=True)
logits = tf.nn.bias_add(lm_data, self.bias)
masked_positions_length = masked_positions.shape.as_list()[1] or tf.shape(
diff --git a/official/nlp/modeling/layers/mobile_bert_layers_test.py b/official/nlp/modeling/layers/mobile_bert_layers_test.py
index 3edeec0539a1f8cf74e0063b50246f5fcbc764ae..b5c3c5e3fd3d1a27758bcd8397165ca01256f8df 100644
--- a/official/nlp/modeling/layers/mobile_bert_layers_test.py
+++ b/official/nlp/modeling/layers/mobile_bert_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/moe.py b/official/nlp/modeling/layers/moe.py
new file mode 100644
index 0000000000000000000000000000000000000000..06dcbbaee1ef34150a29860d667c42494adacd34
--- /dev/null
+++ b/official/nlp/modeling/layers/moe.py
@@ -0,0 +1,761 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Mixture of Experts layers and their routing mechanisms."""
+
+import dataclasses
+from typing import Any, Callable, Optional, Tuple
+
+from absl import logging
+import numpy as np
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+
+_InitializerType = tf.keras.initializers.Initializer
+
+
+_DEFAULT_KERNEL_INITIALIZER = tf.keras.initializers.TruncatedNormal(stddev=2e-2)
+_DEFAULT_BIAS_INITIALIZER = tf.keras.initializers.Zeros()
+
+
+################## Routers (gating functions) ##################
+
+
+def _router_z_loss(router_logits: tf.Tensor) -> float:
+ """Computes router z-loss.
+
+ The router z-loss was introduced in Designing Effective Sparse Expert Models
+ (https://arxiv.org/abs/2202.08906). It encourages router logits to remain
+ small in an effort to improve stability.
+
+ Args:
+ router_logits: [num_groups, tokens_per_group, num_experts] router
+ logits.
+
+ Returns:
+ Scalar router z-loss .
+ """
+ num_groups, tokens_per_group, _ = router_logits.shape
+
+ log_z = tf.math.reduce_logsumexp(router_logits, axis=-1)
+ z_loss = log_z**2
+ return tf.math.reduce_sum(z_loss) / (num_groups * tokens_per_group)
+
+
+@dataclasses.dataclass
+class RouterMask:
+ """Dispatch and combine arrays for expert routing with masked matmuls.
+
+ Attributes:
+ dispatch_mask:
+ [num_groups, tokens_per_group, num_experts, expert_capacity]
+ dispatch array that is 1 if the token gets routed to the
+ corresponding expert, and 0 otherwise.
+ combine_array:
+ [num_groups, tokens_per_group, num_experts, expert_capacity]
+ combine array used for combining expert outputs and
+ scaling with router probability.
+ """
+ dispatch_mask: tf.Tensor
+ combine_array: tf.Tensor
+
+RouterOutput = RouterMask
+
+
+class Router(tf.keras.layers.Layer):
+ """Abstract base router class, defining router API and inner workings.
+
+ Computations are performed in float32 for stability, and returned after
+ conversion according to the precision policy. See the discussion of
+ "selective precision" in https://arxiv.org/abs/2101.03961.
+
+ Uses Keras add_loss() and add_metric() APIs.
+
+ Attributes:
+ num_experts: Number of experts, used to check consistency with
+ FeedForwardExperts.
+ jitter_noise: Amplitude of jitter noise applied to router logits.
+ router_weights: Dense layer that computes logits for all tokens, which are
+ then used as expert or token weights.
+ """
+
+ def __init__(
+ self,
+ num_experts: int,
+ *,
+ jitter_noise: float = 0.0,
+ use_bias: bool = True,
+ kernel_initializer: _InitializerType = _DEFAULT_KERNEL_INITIALIZER,
+ bias_initializer: _InitializerType = _DEFAULT_BIAS_INITIALIZER,
+ name: str = "router",
+ dtype: Any = tf.float32,
+ **kwargs):
+ """Init.
+
+ Args:
+ num_experts: Number of experts.
+ jitter_noise: Amplitude of jitter noise applied to router logits.
+ use_bias: Whether or not to use the bias term in computing the router
+ weights.
+ kernel_initializer: Kernel initializer for router weights.
+ bias_initializer: Bias initializer for router weights.
+ name: Layer name.
+ dtype: The dtype of the layer's computations and weights. tf.float32 is
+ recommended for stability.
+ **kwargs: Forwarded to super.
+ """
+ super().__init__(name=name, dtype=dtype, **kwargs)
+
+ self.num_experts = num_experts # Used to check consistency with
+ # FeedForwardExperts.
+ self.jitter_noise = jitter_noise
+
+ self.router_weights = tf.keras.layers.Dense(
+ num_experts,
+ use_bias=use_bias,
+ kernel_initializer=tf_utils.clone_initializer(kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(bias_initializer),
+ name="router_weights",
+ dtype=dtype)
+
+ def call(self,
+ inputs: tf.Tensor,
+ *,
+ expert_capacity: int,
+ training: Optional[bool] = None) -> RouterOutput:
+ """Computes dispatch and combine arrays for routing to experts.
+
+ Args:
+ inputs: Inputs to send to experts of shape
+ [num_groups, tokens_per_group, hidden_dim].
+ expert_capacity: Each group will send this many tokens to each expert.
+ training: If true, apply jitter noise during routing. If not provided
+ taken from tf.keras.backend.
+
+ Returns:
+ Router indices or mask arrays (depending on router type).
+ """
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ # inputs shape [num_groups, tokens_per_group, hidden_dim]
+ router_probs, router_logits = self._compute_router_probabilities(
+ inputs, apply_jitter=training)
+ # router_probs [num_groups, tokens_per_group, num_experts]
+ # router_logits [num_groups, tokens_per_group, num_experts]
+ router_z_loss = _router_z_loss(router_logits)
+ self.add_loss(router_z_loss)
+ self.add_metric(router_z_loss, name="router_z_loss")
+
+ routing_instructions = self._compute_routing_instructions(
+ router_probs, expert_capacity)
+ return routing_instructions
+
+ def _compute_router_probabilities(
+ self, inputs: tf.Tensor,
+ apply_jitter: bool) -> Tuple[tf.Tensor, tf.Tensor]:
+ """Computes router probabilities from input tokens.
+
+ Args:
+ inputs: Inputs from which router probabilities are computed, shape
+ [num_groups, tokens_per_group, hidden_dim].
+ apply_jitter: If true, apply jitter noise.
+
+ Returns:
+ - [num_groups, tokens_per_group, num_experts] probabilities for
+ each token and expert. Used for routing tokens to experts.
+ - [num_groups, tokens_per_group, num_experts] raw router logits.
+ Used for computing router z-loss.
+ """
+ if apply_jitter and self.jitter_noise > 0:
+ inputs *= tf.random.uniform(
+ inputs.shape,
+ minval=1.0 - self.jitter_noise,
+ maxval=1.0 + self.jitter_noise,
+ dtype=inputs.dtype)
+ # inputs , router_logits
+ router_logits = self.router_weights(inputs)
+ router_probs = tf.keras.activations.softmax(router_logits, axis=-1)
+ return router_probs, router_logits
+
+ def _compute_routing_instructions(self, router_probs: tf.Tensor,
+ expert_capacity: int) -> RouterOutput:
+ """Computes instructions for routing inputs to experts."""
+ raise NotImplementedError(
+ "Router is an abstract class that should be subclassed.")
+
+
+class MaskedRouter(Router):
+ """Abstract base router class for masked matmul dispatch routers.
+
+ MaskedRouter(s) return RouterMask(s) containing a dispatch mask and combine
+ array for sending and receiving (via masked matmuls) inputs and outputs to and
+ from experts.
+
+ Routing using masked matmuls is generally faster than scatter-based routing on
+ TPUs.
+
+ Uses Keras add_loss() and add_metric() APIs.
+ """
+
+ def _compute_routing_instructions(self, router_probs: tf.Tensor,
+ expert_capacity: int) -> RouterMask:
+ """Computes masks for the top-k experts per token.
+
+ Args:
+ router_probs: [num_groups, tokens_per_group, num_experts]
+ probabilities used to determine the routing of tokens to the experts.
+ expert_capacity: Each group will send this many tokens to each expert.
+
+ Returns:
+ Router mask arrays.
+ """
+ raise NotImplementedError(
+ "MaskedRouter is an abstract class that should be subclassed.")
+
+
+class ExpertsChooseMaskedRouter(MaskedRouter):
+ """Masked matmul router using experts choose tokens assignment.
+
+ This router uses the same mechanism as in Mixture-of-Experts with Expert
+ Choice (https://arxiv.org/abs/2202.09368): each expert selects its top
+ expert_capacity tokens. An individual token may be processed by multiple
+ experts or none at all.
+
+ Note: "experts choose routing" should not be used in decoder blocks because it
+ breaks the autoregressive behavior, leading to a mismatch between training
+ (teacher forcing) and inference (autoregressive decoding).
+
+ Uses Keras add_loss() and add_metric() APIs.
+ """
+
+ def _compute_routing_instructions(self, router_probs: tf.Tensor,
+ expert_capacity: int) -> RouterMask:
+ """Computes masks for the highest probability token per expert.
+
+ Args:
+ router_probs: [num_groups, tokens_per_group, num_experts]
+ probabilities used to determine the routing of tokens to the experts.
+ expert_capacity: Each group will send this many tokens to each expert.
+
+ Returns:
+ Dispatch and combine arrays for routing with masked matmuls.
+ """
+ num_groups, tokens_per_group, _ = router_probs.shape
+ router_probs_t = tf.transpose(router_probs, perm=[0, 2, 1])
+ # router_probs_t: [num_groups, num_experts, tokens_per_group]
+
+ # Top expert_capacity router probability and corresponding token indices for
+ # each expert.
+ # Shapes [num_groups, num_experts, expert_capacity]
+ expert_gate, expert_index = tf.math.top_k(
+ router_probs_t, k=expert_capacity, sorted=False)
+
+ # Convert to one-hot mask of expert indices for each token in each group.
+ # Shape: [num_groups, num_experts, expert_capacity, tokens_per_group].
+ dispatch_mask = tf.one_hot(
+ expert_index, tokens_per_group, dtype=router_probs.dtype)
+
+ # Move axes to conform with shape expected by MoeLayer API.
+ # Shape: [num_groups, tokens_per_group, num_experts, expert_capacity]
+ dispatch_mask = tf.transpose(dispatch_mask, perm=[0, 3, 1, 2])
+
+ # The combine array will be used for combining expert outputs, scaled by the
+ # router probabilities.
+ # Shape: [num_groups, num_experts, tokens_per_group, expert_capacity]
+ combine_array = tf.einsum(
+ "...ec,...tec->...tec",
+ expert_gate,
+ dispatch_mask)
+
+ # Add load balancing loss.
+ # Each expert is choosing tokens until it reaches full capacity, so we don't
+ # need an auxiliary loading balancing loss for expert choice routing.
+ self.add_metric(0.0, name="load_balancing_loss")
+
+ # Gather expert metrics.
+ # Number of tokens that were dispatched to at least one expert.
+ num_tokens = num_groups * tokens_per_group
+ num_tokens_dispatched_somewhere = tf.math.reduce_sum(tf.math.reduce_max(
+ dispatch_mask, axis=(-1, -2)))
+ fraction_tokens_left_behind = 1.0 - num_tokens_dispatched_somewhere / float(
+ num_tokens)
+ # Total number of tokens that were dispatched (one token could be
+ # dispatched to multiple experts).
+ num_tokens_dispatched = tf.math.reduce_sum(dispatch_mask)
+ # Of the tokens dispatched, how confident was the router in its routing?
+ router_confidence = tf.math.reduce_sum(
+ combine_array) / num_tokens_dispatched
+
+ expert_usage = 1.0 # Experts fully utilized when "expert choose tokens"
+
+ self.add_metric(fraction_tokens_left_behind,
+ name="fraction_tokens_left_behind")
+ self.add_metric(router_confidence, name="router_confidence")
+ self.add_metric(expert_usage, name="expert_usage")
+
+ # Return to default dtype now that router computation is complete.
+ dtype = tf.keras.mixed_precision.global_policy().compute_dtype
+ dispatch_mask = tf.cast(dispatch_mask, dtype)
+ combine_array = tf.cast(combine_array, dtype)
+ output = RouterMask(dispatch_mask, combine_array)
+ return output
+
+
+################## Model layers ##################
+
+
+class FeedForward(tf.keras.layers.Layer):
+ """Feed-forward layer - position independent, dense, nonlinear transformation.
+
+ Typically used in an MLP Transformer block.
+ """
+
+ def __init__(
+ self,
+ d_ff: int,
+ *,
+ dropout_rate: float = 0.1,
+ activation: Callable[[tf.Tensor],
+ tf.Tensor] = tf.keras.activations.gelu,
+ kernel_initializer: _InitializerType = _DEFAULT_KERNEL_INITIALIZER,
+ bias_initializer: _InitializerType = _DEFAULT_BIAS_INITIALIZER,
+ name: str = "feed_forward",
+ **kwargs):
+ """Initializes layer.
+
+ Args:
+ d_ff: Dimension of feed-forward layer.
+ dropout_rate: The dropout probability.
+ activation: (Nonlinear) transform applied in layer.
+ kernel_initializer: Initialization scheme for kernel.
+ bias_initializer: Initialization scheme for bias.
+ name: Layer name.
+ **kwargs: Forwarded to super.
+ """
+ super().__init__(name=name, **kwargs)
+ self.activation = activation
+ self.kernel_initializer = kernel_initializer
+ self.bias_initializer = bias_initializer
+
+ self.intermediate_layer = tf.keras.layers.Dense(
+ d_ff,
+ kernel_initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self.bias_initializer),
+ name="intermediate")
+ self.dropout_layer = tf.keras.layers.Dropout(dropout_rate)
+
+ def build(self, input_shape: Tuple[int, int, int]):
+ """Creates the input shape dependent output weight variables."""
+ self.output_layer = tf.keras.layers.Dense(
+ input_shape[-1],
+ kernel_initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self.bias_initializer),
+ name="output")
+
+ def call(self,
+ inputs: tf.Tensor,
+ *,
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Applies layer to inputs.
+
+ Args:
+ inputs: Batch of input embeddings, of shape
+ [batch_size, seq_len, hidden_dim].
+ training: Only apply dropout during training.
+
+ Returns:
+ Transformed inputs with the same shape as inputs
+ [batch_size, seq_len, hidden_dim].
+ """
+ x = self.intermediate_layer(inputs)
+ x = self.activation(x)
+ x = self.output_layer(x)
+ x = self.dropout_layer(x, training=training)
+ return x
+
+
+class FeedForwardExperts(tf.keras.layers.Layer):
+ """Feed-forward layer with multiple experts.
+
+ Note that call() takes inputs with shape
+ [num_groups, num_experts, expert_capacity, hidden_dim]
+ which is different from the usual [batch_size, seq_len, hidden_dim] used by
+ the FeedForward layer.
+
+ The experts are independent FeedForward layers of the
+ same shape, i.e. the kernel doesn't have shape [hidden_dim, out_dim], but
+ [num_experts, hidden_dim, out_dim].
+ """
+
+ def __init__(
+ self,
+ num_experts: int,
+ d_ff: int,
+ *,
+ dropout_rate: float = 0.1,
+ activation: Callable[[tf.Tensor],
+ tf.Tensor] = tf.keras.activations.gelu,
+ kernel_initializer: _InitializerType = _DEFAULT_KERNEL_INITIALIZER,
+ bias_initializer: _InitializerType = _DEFAULT_BIAS_INITIALIZER,
+ name: str = "experts",
+ **kwargs):
+ """Initializes layer.
+
+ Args:
+ num_experts: Number of experts (i.e. number of independent feed-forward
+ blocks).
+ d_ff: Dimension of feed-forward layer of each expert.
+ dropout_rate: The dropout probability (expert_dropout_rate).
+ activation: (Nonlinear) transform applied in layer.
+ kernel_initializer: Initialization scheme for kernel.
+ bias_initializer: Initialization scheme for bias.
+ name: Layer name.
+ **kwargs: Forwarded to super.
+ """
+ super().__init__(name=name, **kwargs)
+ self.num_experts = num_experts
+ self.activation = activation
+ self.kernel_initializer = kernel_initializer
+ self.bias_initializer = bias_initializer
+
+ self.intermediate_layer = tf.keras.layers.EinsumDense(
+ "gech,ehf->gecf",
+ output_shape=(self.num_experts, None, d_ff),
+ bias_axes="ef",
+ kernel_initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self.bias_initializer),
+ name="intermediate")
+ self.dropout_layer = tf.keras.layers.Dropout(dropout_rate)
+
+ def build(self, input_shape: Tuple[int, int, int, int]):
+ """Creates the input shape dependent output weight variables."""
+ if input_shape[1] != self.num_experts:
+ raise ValueError(
+ f"Input shape {input_shape} is inconsistent with num_experts "
+ f"{self.num_experts}.")
+
+ self.output_layer = tf.keras.layers.EinsumDense(
+ "gecf,efh->gech",
+ output_shape=(self.num_experts, None, input_shape[-1]),
+ bias_axes="eh",
+ kernel_initializer=tf_utils.clone_initializer(self.kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self.bias_initializer),
+ name="output")
+
+ def call(self,
+ inputs: tf.Tensor,
+ *,
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Applies layer to inputs.
+
+ Args:
+ inputs: Inputs of shape
+ [num_groups, num_experts, expert_capacity, hidden_dim].
+ training: Only apply dropout during training.
+
+ Returns:
+ Transformed inputs with the same shape as inputs
+ [num_groups, num_experts, expert_capacity, hidden_dim].
+ """
+ x = self.intermediate_layer(inputs)
+ x = self.activation(x)
+ x = self.output_layer(x)
+ x = self.dropout_layer(x, training=training)
+ return x
+
+
+class MoeLayer(tf.keras.layers.Layer):
+ """Sparse MoE layer with per-token routing.
+
+ In this TF implementation, all experts need to fit onto a single device
+ allowing for batch parallelism only.
+
+ Uses Keras add_loss() and add_metric() APIs.
+
+ Attributes:
+ num_experts: Number of experts (i.e. number of independent feed-forward
+ blocks).
+ """
+
+ def __init__(
+ self,
+ experts: FeedForwardExperts,
+ router: MaskedRouter,
+ *,
+ train_capacity_factor: float = 1.0,
+ eval_capacity_factor: float = 1.0,
+ min_expert_capacity: int = 4,
+ max_group_size: int = 4096,
+ strict_group_size: bool = False,
+ name: str = "moe",
+ **kwargs):
+ """Init.
+
+ Args:
+ experts: Instance of FeedForwardExperts. Needs to have the same
+ num_experts as the router.
+ router: Instance of MaskedRouter to route the tokens to
+ the different experts.
+ train_capacity_factor: Scaling factor to increase the expert token
+ capacity during training. This factor plays an analogous, but slightly
+ different, role depending on the routing assignment algorithm:
+ - For "tokens choose" routing, the capacity factor only affects the
+ maximum number of tokens that an expert will process. It does not
+ affect how many experts a given token is routed to; see the
+ num_selected_experts attributes of "tokens choose" routers.
+ - For "experts choose" routing, because experts always fill their
+ buffer, increasing the capacity factor will increase the number of
+ tokens that an expert will process AND will indirectly increase the
+ number of experts that a given token is routed to.
+ eval_capacity_factor: As above, but used during evaluation.
+ min_expert_capacity: Minimum token processing capacity for each expert.
+ max_group_size: The total number of tokens on each device is subdivided
+ into groups of this size. Router computations are then performed on a
+ per-group basis. A larger group size will result in slower but more
+ accurate top-k and sorting computations, whereas a smaller group size
+ will result in faster but more approximate (and potentially less stable)
+ routing choices. Note that actual group size may be smaller than
+ max_group_size for consistency with the number of experts and tokens;
+ see also `strict_group_size` attribute. In practice,
+ we find that imperfect routing choices are tolerable and recommend
+ choosing a group size on the order of 4096 tokens, although this number
+ will vary based on model configuration and size.
+ strict_group_size: If True, fail if unable to set the token group size
+ equal to max_group_size. If False (default), the actual group size may
+ be smaller than max_group_size for consistency with the number of
+ experts and tokens.
+ name: Layer name.
+ **kwargs: Forwarded to super.
+ """
+ super().__init__(name=name, **kwargs)
+ self._experts = experts
+ self._router = router
+
+ self.num_experts = experts.num_experts
+ assert experts.num_experts == router.num_experts
+
+ self._train_capacity_factor = train_capacity_factor
+ self._eval_capacity_factor = eval_capacity_factor
+ self._max_group_size = max_group_size
+ self._min_expert_capacity = min_expert_capacity
+ self._strict_group_size = strict_group_size
+
+ def call(self,
+ inputs: tf.Tensor,
+ *,
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Applies MoeLayer.
+
+ Args:
+ inputs: Batch of input embeddings of shape
+ [batch_size, seq_length, hidden_dim].
+ training: Only apply dropout and jitter noise during training. If not
+ provided taken from tf.keras.backend.
+
+ Returns:
+ Transformed inputs with same shape as inputs:
+ [batch_size, seq_length, hidden_dim].
+
+ Raises:
+ ValueError if we cannot find a group_size satisfying given requirements.
+ """
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ # inputs shape [batch_size, seq_length, hidden_dim]
+ per_device_batch_size, seq_length, hidden_dim = inputs.shape
+ num_tokens = per_device_batch_size * seq_length
+ num_groups = self._num_groups(num_tokens, self._max_group_size)
+ tokens_per_group = num_tokens // num_groups
+
+ if training:
+ capacity_factor = self._train_capacity_factor
+ else:
+ capacity_factor = self._eval_capacity_factor
+ # Each group will send expert_capacity tokens to each expert.
+ expert_capacity = int(
+ round(capacity_factor * tokens_per_group / self.num_experts))
+ expert_capacity = max(expert_capacity, self._min_expert_capacity)
+ logging.info(
+ "Selected expert_capacity=%d for num_experts=%d and training=%r.",
+ expert_capacity, self.num_experts, training)
+
+ # Reshape batch and sequence/token dimensions for expert routing.
+ x = tf.reshape(inputs, (num_groups, tokens_per_group, hidden_dim))
+
+ x = self._mask_and_dispatch_to_experts(x, expert_capacity, training)
+
+ # Return to original input shape.
+ x = tf.reshape(x, (per_device_batch_size, seq_length, hidden_dim))
+ return x
+
+ def _num_groups(self, num_tokens: int, max_group_size: int) -> int:
+ """Returns the number of token routing groups.
+
+ Note that the quantities are local to the device.
+
+ We select the smallest num_groups such that:
+ - num_groups >= num_tokens / max_group_size (ensuring the group size is no
+ larger than max_group_size),
+ - num_tokens % num_groups = 0 (ensuring that the group size evenly divides
+ into the num_tokens),
+
+ Args:
+ num_tokens: Number of tokens from input batch.
+ max_group_size: Maximum size of each token routing group. Actual group
+ size may end up being smaller unless strict_group_size==True.
+
+ Returns:
+ Number of token routing groups.
+
+ Raises:
+ ValueError if we cannot find a group_size satisfying the above
+ requirements.
+ """
+ # Increase the number of groups (and decrease the group size) until we have
+ # a viable number of groups.
+ min_num_groups = int(np.ceil(num_tokens / max_group_size))
+ num_groups = min_num_groups
+ while num_groups < num_tokens and num_tokens % num_groups != 0:
+ num_groups += 1
+
+ group_size = num_tokens // num_groups
+ logging.info(
+ "Selected group_size=%d and num_groups=%d for input num_tokens=%d, "
+ "max_group_size=%d, num_experts=%d.",
+ group_size, num_groups, num_tokens, max_group_size, self.num_experts)
+
+ if group_size < self._min_expert_capacity:
+ raise ValueError(
+ f"Local (per-device) group_size {group_size} is smaller than "
+ f"min_expert_capacity {self._min_expert_capacity}, which is probably "
+ "not intended. Please increase max_group_size {max_group_size} to"
+ " seq_length or increase batch_size or decrease min_expert_capacity.")
+
+ if self._strict_group_size and group_size != self._max_group_size:
+ raise ValueError(
+ f"Selected group_size={group_size} is less than the "
+ f"max_group_size={max_group_size}. Exiting because strict mode is "
+ "active (strict_group_size=True)")
+
+ return num_groups
+
+ def _mask_and_dispatch_to_experts(self, inputs: tf.Tensor,
+ expert_capacity: int,
+ training: bool) -> tf.Tensor:
+ """Wraps expert masked routing and dispatching algorithm.
+
+ This algorithm takes the following steps:
+ (1) Compute dispatch mask and combine array using self._router.
+ (2) Dispatch inputs to experts based on dispatch mask.
+ (3) Recombine individual expert outputs using combine array.
+
+ Args:
+ inputs: [num_groups, tokens_per_group, hidden_dim] inputs to
+ send to experts.
+ expert_capacity: Each group will send this many tokens to each expert.
+ training: If true, apply jitter noise during routing and dropout
+ during expert computation.
+
+ Returns:
+ [num_groups, num_tokens_per_group, hidden_dim] outputs from
+ experts.
+ """
+ # Shape [num_groups, tokens_per_group, num_experts, expert_capacity]
+ router_mask = self._router(
+ inputs,
+ expert_capacity=expert_capacity,
+ training=training)
+
+ # Shape [num_groups, num_experts, expert_capacity, hidden_dim]
+ expert_inputs = tf.einsum(
+ "gth,gtec->gech",
+ inputs,
+ router_mask.dispatch_mask)
+
+ expert_outputs = self._experts(expert_inputs, training=training)
+
+ # Shape [num_groups, tokens_per_group, hidden_dim]
+ combined_outputs = tf.einsum(
+ "gech,gtec->gth",
+ expert_outputs,
+ router_mask.combine_array)
+
+ return combined_outputs
+
+
+class MoeLayerWithBackbone(tf.keras.layers.Layer):
+ """Sparse MoE layer plus a FeedForward layer evaluated for all tokens.
+
+ Uses Keras add_loss() and add_metric() APIs.
+ """
+
+ def __init__(
+ self,
+ moe: MoeLayer,
+ backbone_d_ff: int,
+ *,
+ dropout_rate: float = 0.1,
+ activation: Callable[[tf.Tensor],
+ tf.Tensor] = tf.keras.activations.gelu,
+ kernel_initializer: _InitializerType = _DEFAULT_KERNEL_INITIALIZER,
+ bias_initializer: _InitializerType = _DEFAULT_BIAS_INITIALIZER,
+ name: str = "moe_with_backbone",
+ **kwargs):
+ """Init.
+
+ Args:
+ moe: Instance of MoeLayer with experts and router.
+ backbone_d_ff: Dimension of feed-forward layer of a lightweight backbone,
+ which is evaluated for all tokens.
+ dropout_rate: Dropout rate for the backbone.
+ activation: (Nonlinear) transform applied in the backbone.
+ kernel_initializer: Initialization scheme for kernels in the backbone.
+ bias_initializer: Initialization scheme for biases in the backbone.
+ name: Layer name.
+ **kwargs: Forwarded to super.
+ """
+ super().__init__(name=name, **kwargs)
+ self._moe = moe
+
+ self._backbone = FeedForward(
+ backbone_d_ff,
+ dropout_rate=dropout_rate,
+ activation=activation,
+ kernel_initializer=tf_utils.clone_initializer(kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(bias_initializer),
+ name="backbone")
+
+ def call(self,
+ inputs: tf.Tensor,
+ *,
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Applies MoeLayerWithBackbone layer.
+
+ Args:
+ inputs: Batch of input embeddings of shape
+ [batch_size, seq_length, hidden_dim].
+ training: Only apply dropout and jitter noise during training. If not
+ provided taken from tf.keras.backend.
+
+ Returns:
+ Transformed inputs with same shape as inputs:
+ [batch_size, seq_length, hidden_dim].
+ """
+ return self._backbone(
+ inputs, training=training) + self._moe(
+ inputs, training=training)
diff --git a/official/nlp/modeling/layers/moe_test.py b/official/nlp/modeling/layers/moe_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..47c10175e578c017d72fa91ceef4937b68a691e8
--- /dev/null
+++ b/official/nlp/modeling/layers/moe_test.py
@@ -0,0 +1,255 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for moe.py."""
+
+import ml_collections
+import numpy as np
+import tensorflow as tf
+
+from official.nlp.modeling.layers import moe
+
+
+def small_config() -> ml_collections.ConfigDict:
+ """Creates a small model config that can be used by all tests."""
+ config = ml_collections.ConfigDict()
+
+ config.d_ff = 32
+ config.dropout_rate = 0.1
+
+ config.num_experts = 2
+ config.expert_d_ff = 33
+ config.expert_dropout_rate = 0.1
+ config.jitter_noise = 0.1
+ config.train_capacity_factor = 1.0
+ config.eval_capacity_factor = 1.0
+ config.min_expert_capacity = 1
+ config.max_group_size = 9
+
+ config.backbone_d_ff = 13
+ return config
+
+
+def make_input_ones(batch_size: int = 2,
+ seq_length: int = 10,
+ hidden_dim: int = 7) -> tf.Tensor:
+ return tf.ones((batch_size, seq_length, hidden_dim), dtype=tf.float32)
+
+
+def make_experts_input_ones(num_groups: int = 1,
+ num_experts: int = 2,
+ expert_capacity: int = 5,
+ hidden_dim: int = 7) -> tf.Tensor:
+ return tf.ones((num_groups, num_experts, expert_capacity, hidden_dim),
+ dtype=tf.float32)
+
+
+class MoeTest(tf.test.TestCase):
+
+ def tearDown(self):
+ super().tearDown()
+ tf.keras.mixed_precision.set_global_policy('float32')
+
+ def test_router_z_loss_dtype(self):
+ x = tf.constant([[[10.0, 5.0]]], dtype=tf.float32)
+ y = moe._router_z_loss(x)
+ expected = (5 + np.log(np.exp(5) + 1))**2
+ self.assertAllClose(expected, y, atol=1e-7)
+
+ x = tf.constant([[[10.0, 5.0]]], dtype=tf.bfloat16)
+ y = moe._router_z_loss(x)
+ expected = 100.0
+ self.assertAllClose(expected, y, atol=1e-7)
+
+ def test_router_z_loss_shape(self):
+ x = make_input_ones(2, 5, 7)
+ y = moe._router_z_loss(x)
+ expected = (np.log(7) + 1)**2
+ self.assertAllClose(expected, y, atol=1e-7)
+
+ def test_experts_choose_masked_router_dtype_shape(self):
+ tf.keras.mixed_precision.set_global_policy('mixed_bfloat16')
+ num_groups = 2
+ tokens_per_group = 3
+ hidden_dim = tokens_per_group
+ num_experts = tokens_per_group
+ expert_capacity = 2
+ x = np.zeros([num_groups, tokens_per_group, hidden_dim])
+ x[0, 0, 0] += 1
+ x[0, :2, :2] += 1
+ x[1, 1:, 1:] += 1
+ x[1, -1, -1] += 1
+
+ router = moe.ExpertsChooseMaskedRouter(
+ num_experts=num_experts,
+ jitter_noise=0.1,
+ use_bias=True,
+ kernel_initializer=tf.keras.initializers.get('identity'),
+ bias_initializer=tf.keras.initializers.get('ones'))
+ router_mask = router(x, expert_capacity=expert_capacity, training=False)
+
+ self.assertDTypeEqual(router_mask.dispatch_mask, tf.bfloat16)
+ self.assertDTypeEqual(router_mask.combine_array, tf.bfloat16)
+
+ expect_shape = [num_groups, tokens_per_group, num_experts, expert_capacity]
+ self.assertEqual(expect_shape, router_mask.dispatch_mask.shape)
+ self.assertEqual(expect_shape, router_mask.combine_array.shape)
+
+ # top_k call may not be sorted, so can't compare the output directly
+ # Check that the output contains only 0s and 1s
+ out_dm = router_mask.dispatch_mask.numpy()
+ self.assertSetEqual({0, 1}, set(out_dm.flatten().astype(np.int32)))
+ # Check that the right tokens for selected
+ out_dm_indices = np.dot(
+ out_dm.transpose((0, 2, 3, 1)), np.arange(tokens_per_group))
+ # Shape [num_groups, num_experts, expert_capacity]
+ self.assertSetEqual({0, 1}, set(out_dm_indices[0, 0, :].astype(np.int32)))
+ self.assertSetEqual({1, 2}, set(out_dm_indices[0, 1, :].astype(np.int32)))
+ self.assertSetEqual({1, 2}, set(out_dm_indices[0, 2, :].astype(np.int32)))
+ self.assertSetEqual({0, 1}, set(out_dm_indices[1, 0, :].astype(np.int32)))
+ self.assertSetEqual({0, 1}, set(out_dm_indices[1, 1, :].astype(np.int32)))
+ self.assertSetEqual({1, 2}, set(out_dm_indices[1, 2, :].astype(np.int32)))
+
+ out_ca = router_mask.combine_array.numpy()
+ out_ca = np.dot(out_ca, np.ones((expert_capacity,)))
+
+ expected_combine_array = np.array(
+ [[[0.66, 0.0, 0.0], [0.42, 0.42, 0.16], [0.0, 0.33, 0.33]],
+ [[0.33, 0.33, 0.0], [0.16, 0.42, 0.42], [0.0, 0.0, 0.66]]])
+ self.assertAllClose(expected_combine_array, out_ca, atol=1e-2)
+
+ def test_feed_forward_shape_and_vars(self):
+ config = small_config()
+ layer = moe.FeedForward(d_ff=config.d_ff, dropout_rate=config.dropout_rate)
+ inputs = make_input_ones()
+ outputs = layer(inputs)
+ self.assertAllEqual(tf.shape(inputs), tf.shape(outputs))
+ var_names = sorted([v.name for v in layer.trainable_variables])
+ self.assertAllEqual(['feed_forward/intermediate/bias:0',
+ 'feed_forward/intermediate/kernel:0',
+ 'feed_forward/output/bias:0',
+ 'feed_forward/output/kernel:0'], var_names)
+
+ def test_feed_forward_manual(self):
+ config = small_config()
+ layer = moe.FeedForward(
+ d_ff=config.d_ff,
+ dropout_rate=config.dropout_rate,
+ activation=tf.keras.activations.relu,
+ kernel_initializer=tf.keras.initializers.get('ones'),
+ bias_initializer=tf.keras.initializers.get('ones'))
+ inputs = make_input_ones(1, 2, 3)
+ outputs = layer(inputs, training=False)
+ manual_outputs = tf.constant([[[129.0, 129.0, 129.0],
+ [129.0, 129.0, 129.0]]])
+ self.assertAllClose(manual_outputs, outputs, atol=1e-7)
+
+ def test_feed_forward_experts_shape_and_vars(self):
+ config = small_config()
+ layer = moe.FeedForwardExperts(
+ num_experts=config.num_experts,
+ d_ff=config.expert_d_ff,
+ dropout_rate=config.expert_dropout_rate)
+ inputs = make_experts_input_ones()
+ outputs = layer(inputs)
+ self.assertAllEqual(tf.shape(inputs), tf.shape(outputs))
+ var_names = sorted([v.name for v in layer.trainable_variables])
+ self.assertAllEqual(['experts/intermediate/bias:0',
+ 'experts/intermediate/kernel:0',
+ 'experts/output/bias:0',
+ 'experts/output/kernel:0'], var_names)
+
+ def test_feed_forward_experts_manual(self):
+ config = small_config()
+ layer = moe.FeedForwardExperts(
+ num_experts=1,
+ d_ff=config.expert_d_ff,
+ dropout_rate=config.expert_dropout_rate,
+ activation=tf.keras.activations.relu,
+ kernel_initializer=tf.keras.initializers.get('ones'),
+ bias_initializer=tf.keras.initializers.get('ones'))
+ inputs = make_experts_input_ones(1, 1, 2, 3)
+ outputs = layer(inputs, training=False)
+ manual_outputs = tf.constant([[[[133.0, 133.0, 133.0],
+ [133.0, 133.0, 133.0]]]])
+ self.assertAllClose(manual_outputs, outputs, atol=1e-7)
+
+ def test_moe_layer(self):
+ config = small_config()
+ experts = moe.FeedForwardExperts(
+ num_experts=config.num_experts,
+ d_ff=config.expert_d_ff,
+ dropout_rate=config.expert_dropout_rate)
+ router = moe.ExpertsChooseMaskedRouter(
+ config.num_experts,
+ jitter_noise=config.jitter_noise)
+ moe_layer = moe.MoeLayer(
+ experts,
+ router,
+ train_capacity_factor=config.train_capacity_factor,
+ eval_capacity_factor=config.eval_capacity_factor,
+ max_group_size=config.max_group_size,
+ min_expert_capacity=config.min_expert_capacity)
+
+ inputs = make_input_ones()
+ with self.assertLogs('absl', level='INFO') as cm:
+ outputs = moe_layer(inputs, training=True)
+ self.assertAllEqual(tf.shape(inputs), tf.shape(outputs))
+
+ self.assertEqual(cm.output, [
+ ('INFO:absl:Selected group_size=5 and num_groups=4 for input '
+ 'num_tokens=20, max_group_size=9, num_experts=2.'),
+ ('INFO:absl:Selected expert_capacity=2 for num_experts=2 and '
+ 'training=True.')])
+
+ var_names = sorted([v.name for v in moe_layer.trainable_variables])
+ self.assertAllEqual(['moe/experts/intermediate/bias:0',
+ 'moe/experts/intermediate/kernel:0',
+ 'moe/experts/output/bias:0',
+ 'moe/experts/output/kernel:0',
+ 'moe/router/router_weights/bias:0',
+ 'moe/router/router_weights/kernel:0'], var_names)
+ self.assertLen(moe_layer.losses, 1)
+ metrics = [metric.name for metric in moe_layer.metrics]
+ self.assertSetEqual(
+ {
+ 'router_z_loss', 'load_balancing_loss',
+ 'fraction_tokens_left_behind', 'router_confidence', 'expert_usage'
+ }, set(metrics))
+
+ def test_moe_layer_with_backbone(self):
+ config = small_config()
+ experts = moe.FeedForwardExperts(
+ num_experts=config.num_experts,
+ d_ff=config.expert_d_ff,
+ dropout_rate=config.expert_dropout_rate)
+ router = moe.ExpertsChooseMaskedRouter(
+ config.num_experts,
+ jitter_noise=config.jitter_noise)
+ moe_layer = moe.MoeLayer(
+ experts,
+ router,
+ train_capacity_factor=config.train_capacity_factor,
+ eval_capacity_factor=config.eval_capacity_factor,
+ max_group_size=config.max_group_size,
+ min_expert_capacity=config.min_expert_capacity)
+ layer = moe.MoeLayerWithBackbone(moe_layer, config.backbone_d_ff)
+
+ inputs = make_input_ones()
+ outputs = layer(inputs)
+ self.assertAllEqual(tf.shape(inputs), tf.shape(outputs))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/multi_channel_attention.py b/official/nlp/modeling/layers/multi_channel_attention.py
index dfdf7274c9b8d30a514b1dfc9b43a9e4533e31d5..94c22aee3330f4eb7f221447547124f969dec3f8 100644
--- a/official/nlp/modeling/layers/multi_channel_attention.py
+++ b/official/nlp/modeling/layers/multi_channel_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,7 @@
import math
import tensorflow as tf
+
from official.modeling import tf_utils
from official.nlp.modeling.layers import masked_softmax
@@ -48,7 +49,7 @@ class VotingAttention(tf.keras.layers.Layer):
kernel_constraint=None,
bias_constraint=None,
**kwargs):
- super(VotingAttention, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._num_heads = num_heads
self._head_size = head_size
self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
@@ -60,26 +61,28 @@ class VotingAttention(tf.keras.layers.Layer):
def build(self, unused_input_shapes):
common_kwargs = dict(
- kernel_initializer=self._kernel_initializer,
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
kernel_constraint=self._kernel_constraint,
bias_constraint=self._bias_constraint)
- self._query_dense = tf.keras.layers.experimental.EinsumDense(
+ self._query_dense = tf.keras.layers.EinsumDense(
"BAE,ENH->BANH",
output_shape=(None, self._num_heads, self._head_size),
bias_axes="NH",
name="query",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
- self._key_dense = tf.keras.layers.experimental.EinsumDense(
+ self._key_dense = tf.keras.layers.EinsumDense(
"BAE,ENH->BANH",
output_shape=(None, self._num_heads, self._head_size),
bias_axes="NH",
name="key",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
- super(VotingAttention, self).build(unused_input_shapes)
+ super().build(unused_input_shapes)
def call(self, encoder_outputs, doc_attention_mask):
num_docs = tf_utils.get_shape_list(encoder_outputs, expected_rank=[4])[1]
@@ -120,7 +123,7 @@ class MultiChannelAttention(tf.keras.layers.MultiHeadAttention):
"""
def _build_attention(self, rank):
- super(MultiChannelAttention, self)._build_attention(rank) # pytype: disable=attribute-error # typed-keras
+ super()._build_attention(rank) # pytype: disable=attribute-error # typed-keras
self._masked_softmax = masked_softmax.MaskedSoftmax(mask_expansion_axes=[2])
def call(self,
diff --git a/official/nlp/modeling/layers/multi_channel_attention_test.py b/official/nlp/modeling/layers/multi_channel_attention_test.py
index 2831fc29a5c9f32dcdfba189427fb4d7cbd9f31b..8c022046756b0ce6c106ca21664813adfd8ca4c3 100644
--- a/official/nlp/modeling/layers/multi_channel_attention_test.py
+++ b/official/nlp/modeling/layers/multi_channel_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/on_device_embedding.py b/official/nlp/modeling/layers/on_device_embedding.py
index 3d2faa45fe09c2b5e05a67d346d328d10310e96e..6cc5a05b4fe2fd3ca9e92e1979ba6e6bd1e56bf7 100644
--- a/official/nlp/modeling/layers/on_device_embedding.py
+++ b/official/nlp/modeling/layers/on_device_embedding.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -47,7 +47,7 @@ class OnDeviceEmbedding(tf.keras.layers.Layer):
scale_factor=None,
**kwargs):
- super(OnDeviceEmbedding, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._vocab_size = vocab_size
self._embedding_width = embedding_width
self._initializer = initializer
@@ -62,7 +62,7 @@ class OnDeviceEmbedding(tf.keras.layers.Layer):
"use_one_hot": self._use_one_hot,
"scale_factor": self._scale_factor,
}
- base_config = super(OnDeviceEmbedding, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def build(self, input_shape):
@@ -72,7 +72,7 @@ class OnDeviceEmbedding(tf.keras.layers.Layer):
initializer=self._initializer,
dtype=tf.float32)
- super(OnDeviceEmbedding, self).build(input_shape)
+ super().build(input_shape)
def call(self, inputs):
flat_inputs = tf.reshape(inputs, [-1])
diff --git a/official/nlp/modeling/layers/on_device_embedding_test.py b/official/nlp/modeling/layers/on_device_embedding_test.py
index b724130a181f0666ab6f8f49e27c88f51727f8a5..373cfdb6d3dc8a366939a804c31dea7ecee7734c 100644
--- a/official/nlp/modeling/layers/on_device_embedding_test.py
+++ b/official/nlp/modeling/layers/on_device_embedding_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/pack_optimization.py b/official/nlp/modeling/layers/pack_optimization.py
new file mode 100644
index 0000000000000000000000000000000000000000..2c35faac0f2a2b6a1fec9d5c2d99c950fca13785
--- /dev/null
+++ b/official/nlp/modeling/layers/pack_optimization.py
@@ -0,0 +1,250 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Pack sequence optimization on accelerators."""
+from typing import Dict
+import tensorflow as tf
+from official.modeling import tf_utils
+from official.nlp.modeling.layers import rezero_transformer
+from official.nlp.modeling.layers import self_attention_mask
+from official.nlp.modeling.layers import transformer_encoder_block
+from official.nlp.modeling.layers import transformer_scaffold
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class PackBertEmbeddings(tf.keras.layers.Layer):
+ """Performs packing tricks for BERT inputs to improve TPU utilization."""
+
+ def __init__(self, pack_sequences: int, **kwargs):
+ super().__init__(**kwargs)
+ self.pack_sequences = pack_sequences
+
+ def call(self, input_embeddings: tf.Tensor,
+ input_mask: tf.Tensor) -> Dict[str, tf.Tensor]:
+ batch_size, seq_len, embedding_dim = tf_utils.get_shape_list(
+ input_embeddings, expected_rank=3)
+ reduced_batch_size = batch_size // self.pack_sequences
+ packed_seq_len = self.pack_sequences * seq_len
+ packed_embeddings = tf.reshape(
+ input_embeddings, [reduced_batch_size, packed_seq_len, embedding_dim])
+ input_mask = tf.reshape(input_mask, [reduced_batch_size, packed_seq_len])
+ example_ids = 1 + tf.range(self.pack_sequences)
+ # Shape: [batch_size, seq_len, pack_sequences].
+ example_ids = tf.tile(example_ids[None, :, None],
+ [reduced_batch_size, 1, seq_len])
+ example_ids = tf.reshape(example_ids, [reduced_batch_size, packed_seq_len])
+ example_ids = tf.where(
+ tf.math.equal(input_mask, 0), tf.zeros_like(example_ids), example_ids)
+ packing_mask = tf.cast(
+ tf.equal(
+ tf.expand_dims(example_ids, 2), tf.expand_dims(example_ids, 1)),
+ dtype=tf.bool)
+
+ attention_mask = self_attention_mask.get_mask(
+ packed_embeddings, input_mask, dtype=tf.bool)
+
+ combined_attention_mask = tf.cast(
+ tf.math.logical_and(attention_mask, packing_mask), tf.float32)
+
+ return dict(
+ packed_embeddings=packed_embeddings,
+ combined_attention_mask=combined_attention_mask)
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class StridedTransformerEncoderBlock(
+ transformer_encoder_block.TransformerEncoderBlock):
+ """Transformer layer for packing optimization to stride over inputs."""
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if self._output_range is not None:
+ raise ValueError('StridedTransformerEncoderBlock does not '
+ 'support `output_range` argument.')
+
+ def call(self, inputs, stride: tf.Tensor):
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError('Unexpected inputs to %s with length at %d' %
+ (self.__class__, len(inputs)))
+ else:
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ if self._norm_first:
+ source_tensor = input_tensor[:, ::stride, :]
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm_kv(key_value)
+ target_tensor = input_tensor[:, ::stride, :]
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, ::stride, :]
+
+ if key_value is None:
+ key_value = input_tensor
+ attention_output = self._attention_layer(
+ query=target_tensor, value=key_value, attention_mask=attention_mask)
+ attention_output = self._attention_dropout(attention_output)
+
+ if self._norm_first:
+ # Important to not combine `self._norm_first` and
+ # `self._use_query_residual` into one if clause because else is only for
+ # `_norm_first == False`.
+ if self._use_query_residual:
+ attention_output = source_tensor + attention_output
+ else:
+ if self._use_query_residual:
+ attention_output = target_tensor + attention_output
+ attention_output = self._attention_layer_norm(attention_output)
+
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self._output_layer_norm(attention_output)
+ inner_output = self._intermediate_dense(attention_output)
+ inner_output = self._intermediate_activation_layer(inner_output)
+ inner_output = self._inner_dropout_layer(inner_output)
+ layer_output = self._output_dense(inner_output)
+ layer_output = self._output_dropout(layer_output)
+
+ if self._norm_first:
+ return source_attention_output + layer_output
+
+ layer_output = tf.cast(layer_output, tf.float32)
+ return self._output_layer_norm(layer_output + attention_output)
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class StridedReZeroTransformer(rezero_transformer.ReZeroTransformer):
+ """ReZeroTransformer for packing optimization to stride over inputs."""
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if self._output_range is not None:
+ raise ValueError(f'{self.__class__} does not '
+ 'support `output_range` argument.')
+
+ def call(self, inputs, stride: tf.Tensor):
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError(f'Unexpected inputs to {self.__class__} with '
+ f'length at {len(inputs)}.')
+ else:
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ target_tensor = input_tensor[:, ::stride, :]
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, ::stride, :]
+
+ if key_value is None:
+ key_value = input_tensor
+
+ attention_output = self._attention_layer(
+ query=target_tensor, value=key_value, attention_mask=attention_mask)
+ attention_output = self._attention_dropout(attention_output)
+ attention_output = target_tensor + self._rezero_a * attention_output
+ if self._use_layer_norm:
+ attention_output = self._attention_layer_norm(attention_output)
+ else:
+ attention_output = tf.cast(attention_output, tf.float32)
+
+ intermediate_output = self._intermediate_dense(attention_output)
+ intermediate_output = self._inner_activation_layer(intermediate_output)
+ layer_output = self._output_dense(intermediate_output)
+ layer_output = self._output_dropout(layer_output)
+ layer_output = attention_output + tf.cast(self._rezero_a_ffn * layer_output,
+ tf.float32)
+ if self._use_layer_norm:
+ layer_output = self._output_layer_norm(layer_output)
+
+ return layer_output
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class StridedTransformerScaffold(transformer_scaffold.TransformerScaffold):
+ """TransformerScaffold for packing optimization to stride over inputs."""
+
+ def call(self, inputs, stride: tf.Tensor, training=None):
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError('Unexpected inputs to %s with length at %d' %
+ (self.__class__, len(inputs)))
+ else:
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ if key_value is None:
+ key_value = input_tensor
+
+ if self._norm_first:
+ source_tensor = input_tensor[:, ::stride, :]
+ input_tensor = self._attention_layer_norm(input_tensor, training=training)
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, ::stride, :]
+ target_tensor = input_tensor[:, ::stride, :]
+
+ attention_output = self._attention_layer(
+ query=target_tensor,
+ value=key_value,
+ attention_mask=attention_mask,
+ training=training)
+ attention_output = self._attention_dropout(
+ attention_output, training=training)
+
+ if self._norm_first:
+ attention_output = source_tensor + attention_output
+ else:
+ attention_output = self._attention_layer_norm(
+ target_tensor + attention_output, training=training)
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self._output_layer_norm(
+ attention_output, training=training)
+
+ if self._feedforward_block is None:
+ intermediate_output = self._intermediate_dense(attention_output)
+ intermediate_output = self._intermediate_activation_layer(
+ intermediate_output)
+ layer_output = self._output_dense(intermediate_output, training=training)
+ layer_output = self._output_dropout(layer_output, training=training)
+ layer_output = tf.cast(layer_output, tf.float32)
+ if self._norm_first:
+ layer_output = source_attention_output + layer_output
+ else:
+ layer_output = self._output_layer_norm(
+ layer_output + attention_output, training=training)
+ else:
+ if self._norm_first:
+ # if norm_first, assume the feedforward block will not apply layer norm
+ layer_output = self._feedforward_block(
+ attention_output, training=training)
+ layer_output += source_attention_output
+ else:
+ # if not norm_first, assume that the feedforwad does apply layer norm
+ layer_output = self._feedforward_block(
+ attention_output, training=training)
+
+ return layer_output
diff --git a/official/nlp/modeling/layers/pack_optimization_test.py b/official/nlp/modeling/layers/pack_optimization_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..c475c4c33621d34a784905f3ada023380c9fead1
--- /dev/null
+++ b/official/nlp/modeling/layers/pack_optimization_test.py
@@ -0,0 +1,66 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for pack_optimization."""
+
+import tensorflow as tf
+from official.nlp.modeling.layers import pack_optimization
+
+
+class PackOptimizationTest(tf.test.TestCase):
+
+ def test_bert_embedding_packing(self):
+ batch_size, seq_len, embed_dim = 2, 4, 8
+ pack_sequences = 2
+ token_and_position_embed = tf.ones((batch_size, seq_len, embed_dim),
+ dtype=tf.float32)
+ input_mask = tf.ones((batch_size, seq_len), dtype=tf.int32)
+
+ layer = pack_optimization.PackBertEmbeddings(pack_sequences=pack_sequences)
+ outputs = layer(token_and_position_embed, input_mask)
+ self.assertEqual(outputs["packed_embeddings"].shape, (1, 8, embed_dim))
+ self.assertEqual(outputs["combined_attention_mask"].shape, (1, 8, 8))
+
+ def test_strided_transformer_encoder_block(self):
+ inputs = tf.zeros((2, 4, 8), dtype=tf.float32)
+ attention_mask = tf.ones((2, 4, 4), dtype=tf.float32)
+ transformer = pack_optimization.StridedTransformerEncoderBlock(
+ num_attention_heads=2, inner_dim=4, inner_activation="relu")
+ outputs = transformer([inputs, attention_mask],
+ stride=tf.constant(2, dtype=tf.int32))
+ self.assertEqual(outputs.shape, (2, 2, 8))
+
+ def test_strided_rezero_transformer(self):
+ inputs = tf.zeros((2, 4, 8), dtype=tf.float32)
+ attention_mask = tf.ones((2, 4, 4), dtype=tf.float32)
+ transformer = pack_optimization.StridedReZeroTransformer(
+ num_attention_heads=2, inner_dim=4, inner_activation="relu")
+ outputs = transformer([inputs, attention_mask],
+ stride=tf.constant(2, dtype=tf.int32))
+ self.assertEqual(outputs.shape, (2, 2, 8))
+
+ def test_strided_scaffold(self):
+ inputs = tf.zeros((2, 4, 8), dtype=tf.float32)
+ attention_mask = tf.ones((2, 4, 4), dtype=tf.float32)
+ test_layer = pack_optimization.StridedTransformerScaffold(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation="relu")
+ outputs = test_layer([inputs, attention_mask],
+ stride=tf.constant(2, dtype=tf.int32))
+ self.assertEqual(outputs.shape, (2, 2, 8))
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/per_dim_scale_attention.py b/official/nlp/modeling/layers/per_dim_scale_attention.py
new file mode 100644
index 0000000000000000000000000000000000000000..0930b8d65a3d8f688777f6b48b9614977e8a5ba3
--- /dev/null
+++ b/official/nlp/modeling/layers/per_dim_scale_attention.py
@@ -0,0 +1,101 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Keras-based attention layer with learnable per dim scaling."""
+import gin
+import numpy as np
+import tensorflow as tf
+
+
+@gin.configurable
+@tf.keras.utils.register_keras_serializable(package='Text')
+class PerDimScaleAttention(tf.keras.layers.MultiHeadAttention):
+ """Learn scales for individual dims.
+
+ It can improve quality but might hurt training stability.
+ """
+
+ def _build_from_signature(self, query, value, key=None):
+ super()._build_from_signature(query=query, value=value, key=key) # pytype: disable=attribute-error
+ self._scale_dim = self._key_dim
+ with tf.init_scope():
+ self.per_dim_scale = self.add_weight(
+ name='per_dim_scale',
+ shape=(self._scale_dim,),
+ initializer='zeros',
+ dtype=self.dtype,
+ trainable=True)
+
+ def _scale_query(self, query):
+ # 1.0/tf.nn.softplus(0.0) = 1.442695041. Hard code this number so that we
+ # can avoid unnecessary XLA op fusion mess on TPU.
+ r_softplus_0 = 1.442695041
+ scale = tf.constant(
+ r_softplus_0 / np.sqrt(float(self._scale_dim)), dtype=query.dtype)
+
+ scale *= tf.nn.softplus(self.per_dim_scale)
+ return query * scale
+
+ def _compute_attention(self,
+ query,
+ key,
+ value,
+ attention_mask=None,
+ training=None):
+ query = self._scale_query(query)
+
+ attention_scores = tf.einsum(self._dot_product_equation, key, query)
+
+ attention_scores = self._masked_softmax(attention_scores, attention_mask)
+
+ attention_scores_dropout = self._dropout_layer(
+ attention_scores, training=training)
+
+ # `context_layer` = [B, T, N, H]
+ attention_output = tf.einsum(self._combine_equation,
+ attention_scores_dropout, value)
+ return attention_output, attention_scores
+
+ def call(
+ self,
+ query,
+ value,
+ key=None,
+ attention_mask=None,
+ return_attention_scores=False,
+ training=None,
+ ):
+ if not self._built_from_signature:
+ self._build_from_signature(query=query, value=value, key=key)
+ if key is None:
+ key = value
+
+ # N = `num_attention_heads`
+ # H = `size_per_head`
+ # `query` = [B, T, N ,H]
+ query = self._query_dense(query)
+
+ # `key` = [B, S, N, H]
+ key = self._key_dense(key)
+
+ # `value` = [B, S, N, H]
+ value = self._value_dense(value)
+
+ attention_output, attention_scores = self._compute_attention(
+ query, key, value, attention_mask, training)
+ attention_output = self._output_dense(attention_output)
+
+ if return_attention_scores:
+ return attention_output, attention_scores
+ return attention_output
diff --git a/official/nlp/modeling/layers/per_dim_scale_attention_test.py b/official/nlp/modeling/layers/per_dim_scale_attention_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..a5e61ab128fea3b1b0323352c120db32d09b9119
--- /dev/null
+++ b/official/nlp/modeling/layers/per_dim_scale_attention_test.py
@@ -0,0 +1,52 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for PerDimScaleAttention."""
+
+import tensorflow as tf
+
+from official.nlp.modeling.layers import per_dim_scale_attention as attention
+
+
+class PerDimScaleAttentionTest(tf.test.TestCase):
+
+ def test_attention(self):
+ num_heads = 12
+ key_dim = 64
+ seq_length = 1024
+ batch_size = 2
+ test_layer = attention.PerDimScaleAttention(
+ num_heads=num_heads, key_dim=key_dim)
+ query = tf.random.normal(
+ shape=(batch_size, seq_length, key_dim * num_heads))
+ value = query
+ output = test_layer(query=query, value=value)
+ self.assertEqual(output.shape,
+ [batch_size, seq_length, key_dim * num_heads])
+
+ def test_config(self):
+ num_heads = 12
+ key_dim = 64
+ test_layer = attention.PerDimScaleAttention(
+ num_heads=num_heads, key_dim=key_dim)
+ print(test_layer.get_config())
+ new_layer = attention.PerDimScaleAttention.from_config(
+ test_layer.get_config())
+
+ # If the serialization was successful, the new config should match the old.
+ self.assertAllEqual(test_layer.get_config(), new_layer.get_config())
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/position_embedding.py b/official/nlp/modeling/layers/position_embedding.py
index 8e2744b791d007bd762ca20c51f1498da6864a1e..8f27460d9e4fbc3e78fbb1d2479b1da1adb25deb 100644
--- a/official/nlp/modeling/layers/position_embedding.py
+++ b/official/nlp/modeling/layers/position_embedding.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -53,7 +53,7 @@ class PositionEmbedding(tf.keras.layers.Layer):
seq_axis=1,
**kwargs):
- super(PositionEmbedding, self).__init__(**kwargs)
+ super().__init__(**kwargs)
if max_length is None:
raise ValueError(
"`max_length` must be an Integer, not `None`."
@@ -81,7 +81,7 @@ class PositionEmbedding(tf.keras.layers.Layer):
shape=[weight_sequence_length, width],
initializer=self._initializer)
- super(PositionEmbedding, self).build(input_shape)
+ super().build(input_shape)
def call(self, inputs):
input_shape = tf.shape(inputs)
diff --git a/official/nlp/modeling/layers/position_embedding_test.py b/official/nlp/modeling/layers/position_embedding_test.py
index 6593d428e6ef17c6ac99fb7bca28c2b71a67e6a1..f9f170854212e89b23fa7e3f598ab744b7b36d91 100644
--- a/official/nlp/modeling/layers/position_embedding_test.py
+++ b/official/nlp/modeling/layers/position_embedding_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/relative_attention.py b/official/nlp/modeling/layers/relative_attention.py
index be18c9d1eb0bdedab8b7bd07964b5aefadcfbe61..ffa1369796aab7cec23c9269f2c0f942ba16849e 100644
--- a/official/nlp/modeling/layers/relative_attention.py
+++ b/official/nlp/modeling/layers/relative_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -98,14 +98,14 @@ class MultiHeadRelativeAttention(tf.keras.layers.MultiHeadAttention):
`[B, L, dim]`.
segment_matrix: Optional `Tensor` representing segmentation IDs used in
XLNet of shape `[B, S, S + M]`.
- segment_encoding: Optional `Tensor` representing the segmentation
- encoding as used in XLNet of shape `[2, num_heads, dim]`.
- segment_attention_bias: Optional trainable bias parameter added to the
- query had when calculating the segment-based attention score used in
- XLNet of shape `[num_heads, dim]`.
+ segment_encoding: Optional `Tensor` representing the segmentation encoding
+ as used in XLNet of shape `[2, num_heads, dim]`.
+ segment_attention_bias: Optional trainable bias parameter added to the query
+ had when calculating the segment-based attention score used in XLNet of
+ shape `[num_heads, dim]`.
state: Optional `Tensor` of shape `[B, M, E]` where M is the length of the
- state or memory.
- If passed, this is also attended over as in Transformer XL.
+ state or memory. If passed, this is also attended over as in Transformer
+ XL.
attention_mask: A boolean mask of shape `[B, T, S]` that prevents attention
to certain positions.
"""
@@ -144,7 +144,7 @@ class MultiHeadRelativeAttention(tf.keras.layers.MultiHeadAttention):
with tf.init_scope():
einsum_equation, _, output_rank = _build_proj_equation(
key_shape.rank - 1, bound_dims=1, output_dims=2)
- self._encoding_dense = tf.keras.layers.experimental.EinsumDense(
+ self._encoding_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=_get_output_shape(output_rank - 1,
[self._num_heads, self._key_dim]),
@@ -255,8 +255,8 @@ class MultiHeadRelativeAttention(tf.keras.layers.MultiHeadAttention):
Args:
query: attention input.
value: attention input.
- content_attention_bias: A trainable bias parameter added to the query
- head when calculating the content-based attention score.
+ content_attention_bias: A trainable bias parameter added to the query head
+ when calculating the content-based attention score.
positional_attention_bias: A trainable bias parameter added to the query
head when calculating the position-based attention score.
key: attention input.
@@ -264,8 +264,8 @@ class MultiHeadRelativeAttention(tf.keras.layers.MultiHeadAttention):
value.
segment_matrix: Optional `Tensor` representing segmentation IDs used in
XLNet.
- segment_encoding: Optional `Tensor` representing the segmentation
- encoding as used in XLNet.
+ segment_encoding: Optional `Tensor` representing the segmentation encoding
+ as used in XLNet.
segment_attention_bias: Optional trainable bias parameter added to the
query had when calculating the segment-based attention score used in
XLNet.
@@ -394,22 +394,22 @@ class TwoStreamRelativeAttention(MultiHeadRelativeAttention):
content_stream: The content representation, commonly referred to as h.
This serves a similar role to the standard hidden states in
Transformer-XL.
- content_attention_bias: A trainable bias parameter added to the query
- head when calculating the content-based attention score.
+ content_attention_bias: A trainable bias parameter added to the query head
+ when calculating the content-based attention score.
positional_attention_bias: A trainable bias parameter added to the query
head when calculating the position-based attention score.
- query_stream: The query representation, commonly referred to as g.
- This only has access to contextual information and position, but not
- content. If not provided, then this is MultiHeadRelativeAttention with
+ query_stream: The query representation, commonly referred to as g. This
+ only has access to contextual information and position, but not content.
+ If not provided, then this is MultiHeadRelativeAttention with
self-attention.
relative_position_encoding: relative positional encoding for key and
value.
- target_mapping: Optional `Tensor` representing the target mapping used
- in partial prediction.
+ target_mapping: Optional `Tensor` representing the target mapping used in
+ partial prediction.
segment_matrix: Optional `Tensor` representing segmentation IDs used in
XLNet.
- segment_encoding: Optional `Tensor` representing the segmentation
- encoding as used in XLNet.
+ segment_encoding: Optional `Tensor` representing the segmentation encoding
+ as used in XLNet.
segment_attention_bias: Optional trainable bias parameter added to the
query head when calculating the segment-based attention score.
state: (default None) optional state. If passed, this is also attended
@@ -417,8 +417,8 @@ class TwoStreamRelativeAttention(MultiHeadRelativeAttention):
content_attention_mask: (default None) Optional mask that is added to
content attention logits. If state is not None, the mask source sequence
dimension should extend M.
- query_attention_mask: (default None) Optional mask that is added to
- query attention logits. If state is not None, the mask source sequence
+ query_attention_mask: (default None) Optional mask that is added to query
+ attention logits. If state is not None, the mask source sequence
dimension should extend M.
Returns:
@@ -496,4 +496,3 @@ class TwoStreamRelativeAttention(MultiHeadRelativeAttention):
query_attention_output = self._output_dense(query_attention_output)
return content_attention_output, query_attention_output
-
diff --git a/official/nlp/modeling/layers/relative_attention_test.py b/official/nlp/modeling/layers/relative_attention_test.py
index b092bc6740c187e482ae6ebe4917f81ed67c40c3..d07093f72af1f63e680466b67b7119467866de41 100644
--- a/official/nlp/modeling/layers/relative_attention_test.py
+++ b/official/nlp/modeling/layers/relative_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/reuse_attention.py b/official/nlp/modeling/layers/reuse_attention.py
index 6e36a7154366cb33c3a3ff1251bae2962c75d05e..75778cdc9ea8ed79f87c9cbcdd77ebbb11e02f10 100644
--- a/official/nlp/modeling/layers/reuse_attention.py
+++ b/official/nlp/modeling/layers/reuse_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,6 +22,8 @@ import string
import numpy as np
import tensorflow as tf
+from official.modeling import tf_utils
+
_CHR_IDX = string.ascii_lowercase
@@ -221,7 +223,7 @@ class ReuseMultiHeadAttention(tf.keras.layers.Layer):
kernel_constraint=None,
bias_constraint=None,
**kwargs):
- super(ReuseMultiHeadAttention, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._num_heads = num_heads
self._key_dim = key_dim
self._value_dim = value_dim if value_dim else key_dim
@@ -299,7 +301,7 @@ class ReuseMultiHeadAttention(tf.keras.layers.Layer):
"key_shape": self._key_shape,
"value_shape": self._value_shape,
}
- base_config = super(ReuseMultiHeadAttention, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
@classmethod
@@ -347,8 +349,6 @@ class ReuseMultiHeadAttention(tf.keras.layers.Layer):
self._key_shape = tf.TensorShape(key)
common_kwargs = dict(
- kernel_initializer=self._kernel_initializer,
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -362,42 +362,61 @@ class ReuseMultiHeadAttention(tf.keras.layers.Layer):
if self._reuse_heads < self._num_heads:
einsum_equation, bias_axes, output_rank = _build_proj_equation(
free_dims, bound_dims=1, output_dims=2)
- self._query_dense = tf.keras.layers.experimental.EinsumDense(
+ self._query_dense = tf.keras.layers.EinsumDense(
einsum_equation,
- output_shape=_get_output_shape(output_rank - 1, [
- self._num_heads - self._reuse_heads, self._key_dim]),
+ output_shape=_get_output_shape(
+ output_rank - 1,
+ [self._num_heads - self._reuse_heads, self._key_dim]),
bias_axes=bias_axes if self._use_bias else None,
name="query",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
einsum_equation, bias_axes, output_rank = _build_proj_equation(
self._key_shape.rank - 1, bound_dims=1, output_dims=2)
- self._key_dense = tf.keras.layers.experimental.EinsumDense(
+ self._key_dense = tf.keras.layers.EinsumDense(
einsum_equation,
- output_shape=_get_output_shape(output_rank - 1, [
- self._num_heads - self._reuse_heads, self._key_dim]),
+ output_shape=_get_output_shape(
+ output_rank - 1,
+ [self._num_heads - self._reuse_heads, self._key_dim]),
bias_axes=bias_axes if self._use_bias else None,
name="key",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
einsum_equation, bias_axes, output_rank = _build_proj_equation(
self._value_shape.rank - 1, bound_dims=1, output_dims=2)
self._value_dense = []
if self._reuse_heads > 0:
- self._value_dense.append(tf.keras.layers.experimental.EinsumDense(
- einsum_equation,
- output_shape=_get_output_shape(
- output_rank - 1, [self._reuse_heads, self._value_dim]),
- bias_axes=bias_axes if self._use_bias else None,
- name="value_reuse",
- **common_kwargs))
+ self._value_dense.append(
+ tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(
+ output_rank - 1, [self._reuse_heads, self._value_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="value_reuse",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(
+ self._bias_initializer),
+ **common_kwargs))
if self._reuse_heads < self._num_heads:
- self._value_dense.append(tf.keras.layers.experimental.EinsumDense(
- einsum_equation,
- output_shape=_get_output_shape(output_rank - 1, [
- self._num_heads - self._reuse_heads, self._value_dim]),
- bias_axes=bias_axes if self._use_bias else None,
- name="value_new",
- **common_kwargs))
+ self._value_dense.append(
+ tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(
+ output_rank - 1,
+ [self._num_heads - self._reuse_heads, self._value_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="value_new",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(
+ self._bias_initializer),
+ **common_kwargs))
# Builds the attention computations for multi-head dot product attention.
# These computations could be wrapped into the keras attention layer once
@@ -434,18 +453,20 @@ class ReuseMultiHeadAttention(tf.keras.layers.Layer):
output_shape = [self._query_shape[-1]]
einsum_equation, bias_axes, output_rank = _build_proj_equation(
free_dims, bound_dims=2, output_dims=len(output_shape))
- return tf.keras.layers.experimental.EinsumDense(
+ return tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=_get_output_shape(output_rank - 1, output_shape),
bias_axes=bias_axes if (use_bias and self._use_bias) else None,
name=name,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
def _build_attention(self, rank):
"""Builds multi-head dot-product attention computations.
This function builds attributes necessary for `_compute_attention` to
- costomize attention computation to replace the default dot-product
+ customize attention computation to replace the default dot-product
attention.
Args:
diff --git a/official/nlp/modeling/layers/reuse_attention_test.py b/official/nlp/modeling/layers/reuse_attention_test.py
index 0da8cf5e31742366f50c0e1370d8de1a638aa9cb..fe9e71d2f06c09f3467c14a9a13f7e87f8e8a236 100644
--- a/official/nlp/modeling/layers/reuse_attention_test.py
+++ b/official/nlp/modeling/layers/reuse_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/reuse_transformer.py b/official/nlp/modeling/layers/reuse_transformer.py
index 38736ea4242148ed08513acdae9c55e358187930..79f304bc8a09c35d989f4be78d73306c350998e1 100644
--- a/official/nlp/modeling/layers/reuse_transformer.py
+++ b/official/nlp/modeling/layers/reuse_transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,6 +14,8 @@
"""Keras-based TransformerEncoder block layer."""
import tensorflow as tf
+
+from official.modeling import tf_utils
from official.nlp.modeling.layers import reuse_attention as attention
@@ -131,7 +133,8 @@ class ReuseTransformer(tf.keras.layers.Layer):
self._attention_initializer = tf.keras.initializers.get(
attention_initializer)
else:
- self._attention_initializer = self._kernel_initializer
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
self._attention_axes = attention_axes
def build(self, input_shape):
@@ -156,7 +159,6 @@ class ReuseTransformer(tf.keras.layers.Layer):
else:
self._attention_head_size = self._head_size
common_kwargs = dict(
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -168,6 +170,7 @@ class ReuseTransformer(tf.keras.layers.Layer):
dropout=self._attention_dropout,
use_bias=self._use_bias,
kernel_initializer=self._attention_initializer,
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
attention_axes=self._attention_axes,
reuse_attention=self._reuse_attention,
use_relative_pe=self._use_relative_pe,
@@ -184,11 +187,12 @@ class ReuseTransformer(tf.keras.layers.Layer):
axis=-1,
epsilon=self._norm_epsilon,
dtype=tf.float32))
- self._intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=(None, self._inner_dim),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="intermediate",
**common_kwargs)
policy = tf.keras.mixed_precision.global_policy()
@@ -201,12 +205,13 @@ class ReuseTransformer(tf.keras.layers.Layer):
self._inner_activation, dtype=policy)
self._inner_dropout_layer = tf.keras.layers.Dropout(
rate=self._inner_dropout)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._output_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=(None, hidden_size),
bias_axes="d",
name="output",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
self._output_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
# Use float32 in layernorm for numeric stability.
diff --git a/official/nlp/modeling/layers/reuse_transformer_test.py b/official/nlp/modeling/layers/reuse_transformer_test.py
index 40526ecb3c76ca5abbcc432b94abbc10c2852199..0376906e909e736528938f4ec1e0fc554ac30f2b 100644
--- a/official/nlp/modeling/layers/reuse_transformer_test.py
+++ b/official/nlp/modeling/layers/reuse_transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -68,7 +68,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
# Invoke the model on test data. We can't validate the output data itself
# (the NN is too complex) but this will rule out structural runtime errors.
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
_ = model.predict(input_data)
@@ -89,7 +89,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
# Invoke the model on test data. We can't validate the output data itself
# (the NN is too complex) but this will rule out structural runtime errors.
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
# The attention mask should be of shape (batch, from_seq_len, to_seq_len),
# which here is (batch, sequence_length, sequence_length)
@@ -104,7 +104,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
width = 80
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
mask_data = np.random.randint(
2, size=(batch_size, sequence_length, sequence_length))
@@ -121,7 +121,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
new_layer.set_weights(test_layer.get_weights())
new_output_tensor, _ = new_layer([input_data, mask_data])
self.assertAllClose(
- new_output_tensor, output_tensor[:, 0:1, :], atol=0.002, rtol=0.25)
+ new_output_tensor, output_tensor[:, 0:1, :], atol=0.002, rtol=0.01)
def test_layer_output_range_with_relative_pe(self, transformer_cls):
test_layer = transformer_cls(
@@ -131,7 +131,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
width = 80
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
mask_data = np.random.randint(
2, size=(batch_size, sequence_length, sequence_length))
@@ -149,7 +149,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
new_layer.set_weights(test_layer.get_weights())
new_output_tensor, _ = new_layer([input_data, mask_data])
self.assertAllClose(
- new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
+ new_output_tensor, output_tensor[:, 0:1, :], atol=0.002, rtol=0.01)
def test_layer_output_range_without_mask(self, transformer_cls):
test_layer = transformer_cls(
@@ -159,7 +159,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
width = 80
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
output_tensor, _ = test_layer(input_data)
@@ -175,7 +175,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
new_layer.set_weights(test_layer.get_weights())
new_output_tensor, _ = new_layer(input_data)
self.assertAllClose(
- new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
+ new_output_tensor, output_tensor[:, 0:1, :], atol=0.002, rtol=0.01)
def test_layer_output_range_with_pre_norm(self, transformer_cls):
test_layer = transformer_cls(
@@ -185,7 +185,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
width = 80
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
mask_data = np.random.randint(
2, size=(batch_size, sequence_length, sequence_length))
@@ -203,7 +203,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
new_layer.set_weights(test_layer.get_weights())
new_output_tensor, _ = new_layer([input_data, mask_data])
self.assertAllClose(
- new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
+ new_output_tensor, output_tensor[:, 0:1, :], atol=0.002, rtol=0.01)
def test_layer_invocation_with_float16_dtype(self, transformer_cls):
tf.keras.mixed_precision.set_global_policy('mixed_float16')
@@ -223,7 +223,7 @@ class ReuseTransformerLayerTest(tf.test.TestCase, parameterized.TestCase):
# Invoke the model on test data. We can't validate the output data itself
# (the NN is too complex) but this will rule out structural runtime errors.
batch_size = 6
- input_data = (10 * np.random.random_sample(
+ input_data = (np.random.random_sample(
(batch_size, sequence_length, width)))
# The attention mask should be of shape (batch, from_seq_len, to_seq_len),
# which here is (batch, sequence_length, sequence_length)
@@ -368,7 +368,7 @@ class ReuseTransformerArgumentTest(tf.test.TestCase, parameterized.TestCase):
# Invoke the model on test data. We can't validate the output data itself
# (the NN is too complex) but this will rule out structural runtime errors.
batch_size = 6
- input_data = 10 * np.random.random_sample(
+ input_data = np.random.random_sample(
(batch_size, sequence_length, width))
# The attention mask should be of shape (batch, from_seq_len, to_seq_len),
# which here is (batch, sequence_length, sequence_length)
@@ -404,7 +404,7 @@ class ReuseTransformerArgumentTest(tf.test.TestCase, parameterized.TestCase):
# Invoke the model on test data. We can't validate the output data itself
# (the NN is too complex) but this will rule out structural runtime errors.
batch_size = 6
- input_data = (10 * np.random.random_sample(
+ input_data = (np.random.random_sample(
(batch_size, sequence_length, width)))
# The attention mask should be of shape (batch, from_seq_len, to_seq_len),
# which here is (batch, sequence_length, sequence_length)
diff --git a/official/nlp/modeling/layers/rezero_transformer.py b/official/nlp/modeling/layers/rezero_transformer.py
index 6a9fb1a66459d81a9c5a8c0b8d305c1c917aa84b..6796345c60da38457015bd6454bb7ba4918d390e 100644
--- a/official/nlp/modeling/layers/rezero_transformer.py
+++ b/official/nlp/modeling/layers/rezero_transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,10 +14,13 @@
"""Keras-based rezero-transformer block layer (Transformer with ReZero)."""
# pylint: disable=g-classes-have-attributes
+from typing import Optional
+from absl import logging
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers import util
@@ -33,8 +36,10 @@ class ReZeroTransformer(tf.keras.layers.Layer):
Args:
num_attention_heads: Number of attention heads.
- intermediate_size: Size of the intermediate layer.
- intermediate_activation: Activation for the intermediate layer.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network.
dropout_rate: Dropout probability for the post-attention and output dropout.
attention_dropout_rate: Dropout probability for within the attention layer.
output_range: the sequence output range, [0, output_range) by slicing the
@@ -52,8 +57,8 @@ class ReZeroTransformer(tf.keras.layers.Layer):
def __init__(self,
num_attention_heads,
- intermediate_size,
- intermediate_activation,
+ inner_dim=768,
+ inner_activation=tf_utils.get_activation("gelu"),
dropout_rate=0.0,
attention_dropout_rate=0.0,
output_range=None,
@@ -72,12 +77,19 @@ class ReZeroTransformer(tf.keras.layers.Layer):
attention_dropout_rate = kwargs.pop("attention_dropout",
attention_dropout_rate)
dropout_rate = kwargs.pop("output_dropout", dropout_rate)
+ inner_dim = kwargs.pop("intermediate_size", inner_dim)
+ inner_activation = kwargs.pop("intermediate_activation", inner_activation)
util.filter_kwargs(kwargs)
- super(ReZeroTransformer, self).__init__(**kwargs)
+ super().__init__(**kwargs)
+
+ # Deprecation warning.
+ if output_range is not None:
+ logging.warning("`output_range` is avaliable as an argument for `call()`."
+ "The `output_range` as __init__ argument is deprecated.")
self._num_heads = num_attention_heads
- self._intermediate_size = intermediate_size
- self._intermediate_activation = intermediate_activation
+ self._inner_dim = inner_dim
+ self._inner_activation = inner_activation
self._attention_dropout_rate = attention_dropout_rate
self._dropout_rate = dropout_rate
self._output_range = output_range
@@ -121,8 +133,6 @@ class ReZeroTransformer(tf.keras.layers.Layer):
"heads (%d)" % (hidden_size, self._num_heads))
self._attention_head_size = int(hidden_size // self._num_heads)
common_kwargs = dict(
- kernel_initializer=self._kernel_initializer,
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -133,6 +143,8 @@ class ReZeroTransformer(tf.keras.layers.Layer):
key_dim=self._attention_head_size,
dropout=self._attention_dropout_rate,
name="self_attention",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
self._attention_dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
if self._use_layer_norm:
@@ -144,11 +156,13 @@ class ReZeroTransformer(tf.keras.layers.Layer):
axis=-1,
epsilon=1e-12,
dtype=tf.float32))
- self._intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
- output_shape=(None, self._intermediate_size),
+ output_shape=(None, self._inner_dim),
bias_axes="d",
name="intermediate",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
policy = tf.keras.mixed_precision.global_policy()
if policy.name == "mixed_bfloat16":
@@ -156,13 +170,15 @@ class ReZeroTransformer(tf.keras.layers.Layer):
# as well, so we use float32.
# TODO(b/154538392): Investigate this.
policy = tf.float32
- self._intermediate_activation_layer = tf.keras.layers.Activation(
- self._intermediate_activation, dtype=policy)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._inner_activation_layer = tf.keras.layers.Activation(
+ self._inner_activation, dtype=policy)
+ self._output_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
name="output",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
self._output_dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
if self._use_layer_norm:
@@ -185,16 +201,16 @@ class ReZeroTransformer(tf.keras.layers.Layer):
trainable=True,
dtype=tf.float32)
- super(ReZeroTransformer, self).build(input_shape)
+ super().build(input_shape)
def get_config(self):
config = {
"num_attention_heads":
self._num_heads,
- "intermediate_size":
- self._intermediate_size,
- "intermediate_activation":
- self._intermediate_activation,
+ "inner_dim":
+ self._inner_dim,
+ "inner_activation":
+ self._inner_activation,
"dropout_rate":
self._dropout_rate,
"attention_dropout_rate":
@@ -220,7 +236,7 @@ class ReZeroTransformer(tf.keras.layers.Layer):
"bias_constraint":
tf.keras.constraints.serialize(self._bias_constraint),
}
- base_config = super(ReZeroTransformer, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def reset_rezero(self):
@@ -228,7 +244,7 @@ class ReZeroTransformer(tf.keras.layers.Layer):
if not self._share_rezero:
self._rezero_a_ffn.assign(0.)
- def call(self, inputs):
+ def call(self, inputs, output_range: Optional[tf.Tensor] = None) -> tf.Tensor:
if isinstance(inputs, (list, tuple)):
if len(inputs) == 2:
input_tensor, attention_mask = inputs
@@ -241,10 +257,12 @@ class ReZeroTransformer(tf.keras.layers.Layer):
else:
input_tensor, key_value, attention_mask = (inputs, None, None)
- if self._output_range:
- target_tensor = input_tensor[:, 0:self._output_range, :]
+ if output_range is None:
+ output_range = self._output_range
+ if output_range:
+ target_tensor = input_tensor[:, 0:output_range, :]
if attention_mask is not None:
- attention_mask = attention_mask[:, 0:self._output_range, :]
+ attention_mask = attention_mask[:, 0:output_range, :]
else:
target_tensor = input_tensor
@@ -261,8 +279,7 @@ class ReZeroTransformer(tf.keras.layers.Layer):
attention_output = tf.cast(attention_output, tf.float32)
intermediate_output = self._intermediate_dense(attention_output)
- intermediate_output = self._intermediate_activation_layer(
- intermediate_output)
+ intermediate_output = self._inner_activation_layer(intermediate_output)
layer_output = self._output_dense(intermediate_output)
layer_output = self._output_dropout(layer_output)
# During mixed precision training, attention_output is from layer norm and
diff --git a/official/nlp/modeling/layers/rezero_transformer_test.py b/official/nlp/modeling/layers/rezero_transformer_test.py
index 48d680f922002718416948ed7a1b9c14a5f40737..cb949c8cbdd29a557b1c1cd4ab8f3ce6458bc674 100644
--- a/official/nlp/modeling/layers/rezero_transformer_test.py
+++ b/official/nlp/modeling/layers/rezero_transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -128,6 +128,9 @@ class TransformerWithReZeroLayerTest(keras_parameterized.TestCase):
new_output_tensor = new_layer([input_data, mask_data])
self.assertAllClose(new_output_tensor, output_tensor[:, 0:1, :])
+ output_tensor = test_layer([input_data, mask_data], output_range=1)
+ self.assertAllClose(new_output_tensor, output_tensor, atol=5e-5, rtol=0.003)
+
def test_separate_qkv(self):
test_layer = rezero_transformer.ReZeroTransformer(
num_attention_heads=2,
diff --git a/official/nlp/modeling/layers/routing.py b/official/nlp/modeling/layers/routing.py
new file mode 100644
index 0000000000000000000000000000000000000000..ce0b6875ab2051f64b8ac243654cf269db8410b6
--- /dev/null
+++ b/official/nlp/modeling/layers/routing.py
@@ -0,0 +1,125 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Layers for Mixture of Experts (MoE) routing.
+
+For MoE routing, we need to separate a set of tokens to sets of tokens.
+Later on, different sets of tokens can potentially go to different experts.
+"""
+
+import tensorflow as tf
+
+
+@tf.keras.utils.register_keras_serializable(package="Text")
+class TokenImportanceWithMovingAvg(tf.keras.layers.Layer):
+ """Routing based on per-token importance value."""
+
+ def __init__(self,
+ vocab_size,
+ init_importance,
+ moving_average_beta=0.995,
+ **kwargs):
+ self._vocab_size = vocab_size
+ self._init_importance = init_importance
+ self._moving_average_beta = moving_average_beta
+ super().__init__(**kwargs)
+
+ def build(self, input_shape):
+ self._importance_embedding = self.add_weight(
+ name="importance_embed",
+ shape=(self._vocab_size),
+ initializer=tf.keras.initializers.Constant(self._init_importance),
+ trainable=False)
+
+ def get_config(self):
+ config = {
+ "vocab_size":
+ self._vocab_size,
+ "init_importance":
+ self._init_importance,
+ "moving_average_beta":
+ self._moving_average_beta,
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def update_token_importance(self, token_ids, importance):
+ token_ids = tf.reshape(token_ids, shape=[-1])
+ importance = tf.reshape(importance, shape=[-1])
+
+ beta = self._moving_average_beta
+ old_importance = tf.gather(self._importance_embedding, token_ids)
+ self._importance_embedding.assign(tf.tensor_scatter_nd_update(
+ self._importance_embedding,
+ tf.expand_dims(token_ids, axis=1),
+ old_importance * beta + tf.cast(importance * (1.0 - beta),
+ dtype=tf.float32)))
+
+ def call(self, inputs):
+ return tf.gather(self._importance_embedding, inputs)
+
+
+@tf.keras.utils.register_keras_serializable(package="Text")
+class SelectTopK(tf.keras.layers.Layer):
+ """Select top-k + random-k tokens according to importance."""
+
+ def __init__(self,
+ top_k=None,
+ random_k=None,
+ **kwargs):
+ self._top_k = top_k
+ self._random_k = random_k
+ super().__init__(**kwargs)
+
+ def get_config(self):
+ config = {
+ "top_k":
+ self._top_k,
+ "random_k":
+ self._random_k,
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs):
+ if self._random_k is None:
+ # Pure top-k, not randomness.
+ pos = tf.argsort(inputs, direction="DESCENDING")
+ selected = tf.slice(pos, [0, 0], [-1, self._top_k])
+ not_selected = tf.slice(pos, [0, self._top_k], [-1, -1])
+ elif self._top_k is None:
+ # Pure randomness, no top-k.
+ pos = tf.argsort(tf.random.uniform(shape=tf.shape(inputs)),
+ direction="DESCENDING")
+ selected = tf.slice(pos, [0, 0], [-1, self._random_k])
+ not_selected = tf.slice(pos, [0, self._random_k], [-1, -1])
+ else:
+ # Top-k plus randomness.
+ pos = tf.argsort(inputs, direction="DESCENDING")
+ selected_top_k = tf.slice(pos, [0, 0], [-1, self._top_k])
+ pos_left = tf.slice(pos, [0, self._top_k], [-1, -1])
+
+ # Randomly shuffle pos_left
+ sort_index = tf.argsort(
+ tf.random.uniform(shape=tf.shape(pos_left)),
+ direction="DESCENDING")
+ pos_left = tf.gather(pos_left, sort_index, batch_dims=1, axis=1)
+
+ selected_rand = tf.slice(pos_left, [0, 0], [-1, self._random_k])
+ not_selected = tf.slice(pos_left, [0, self._random_k], [-1, -1])
+
+ selected = tf.concat([selected_top_k, selected_rand], axis=1)
+
+ # Return the indices of selected and not-selected tokens.
+ return selected, not_selected
diff --git a/official/nlp/modeling/layers/routing_test.py b/official/nlp/modeling/layers/routing_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..8d124187f3cd780abadd961cc87c737ad9e034b5
--- /dev/null
+++ b/official/nlp/modeling/layers/routing_test.py
@@ -0,0 +1,59 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for routing."""
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from official.nlp.modeling.layers import routing
+
+
+class TokenImportanceTest(tf.test.TestCase, parameterized.TestCase):
+
+ def test_token_importance(self):
+ token_importance_embed = routing.TokenImportanceWithMovingAvg(
+ vocab_size=4,
+ init_importance=10.0,
+ moving_average_beta=0.995)
+ importance = token_importance_embed(np.array([[0, 1], [2, 3]]))
+ self.assertAllClose(importance, np.array([[10.0, 10.0], [10.0, 10.0]]))
+ token_importance_embed.update_token_importance(
+ token_ids=np.array([[0, 1]]),
+ importance=np.array([[0.0, 0.0]]))
+ importance = token_importance_embed(np.array([[0, 1], [2, 3]]))
+ self.assertAllClose(importance, np.array([[9.95, 9.95], [10.0, 10.0]]))
+
+
+class TopKSelectionTest(tf.test.TestCase, parameterized.TestCase):
+
+ def test_top_k_selection(self):
+ token_selection = routing.SelectTopK(top_k=2)
+ selected, _ = token_selection(np.array([[0, 1, 2, 3], [4, 3, 2, 1]]))
+ self.assertAllClose(selected, np.array([[3, 2], [0, 1]]))
+
+ def test_random_k_selection(self):
+ token_selection = routing.SelectTopK(random_k=2)
+ selected, _ = token_selection(np.array([[0, 1, 2, 3], [4, 3, 2, 1]]))
+ self.assertAllClose(selected.shape, (2, 2))
+
+ def test_top_k_random_k(self):
+ token_selection = routing.SelectTopK(top_k=1, random_k=1)
+ selected, _ = token_selection(np.array([[0, 1, 2, 3], [4, 3, 2, 1]]))
+ self.assertAllClose(selected.shape, (2, 2))
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/layers/self_attention_mask.py b/official/nlp/modeling/layers/self_attention_mask.py
index cd538bed0b8e6b2bc42bc616154e2d35fe7e4db7..e2c99d7a3f7c56547338e7e56d13fe0557f2d4d0 100644
--- a/official/nlp/modeling/layers/self_attention_mask.py
+++ b/official/nlp/modeling/layers/self_attention_mask.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,10 +13,38 @@
# limitations under the License.
"""Keras layer that creates a self-attention mask."""
-
+from typing import Optional
import tensorflow as tf
+def get_mask(inputs: tf.Tensor,
+ to_mask: tf.Tensor,
+ dtype: Optional[tf.DType] = None) -> tf.Tensor:
+ """Gets a 3D self-attention mask.
+
+ Args:
+ inputs: from_tensor: 2D or 3D Tensor of shape [batch_size, from_seq_length,
+ ...].
+ to_mask: int32 Tensor of shape [batch_size, to_seq_length].
+ dtype: the output Tensor dtype.
+
+ Returns:
+ float Tensor of shape [batch_size, from_seq_length, to_seq_length].
+ """
+ from_shape = tf.shape(inputs)
+ batch_size = from_shape[0]
+ from_seq_length = from_shape[1]
+ dtype = inputs.dtype if dtype is None else dtype
+
+ to_shape = tf.shape(to_mask)
+ to_seq_length = to_shape[1]
+
+ to_mask = tf.cast(
+ tf.reshape(to_mask, [batch_size, 1, to_seq_length]), dtype=dtype)
+
+ return tf.broadcast_to(to_mask, [batch_size, from_seq_length, to_seq_length])
+
+
@tf.keras.utils.register_keras_serializable(package='Text')
class SelfAttentionMask(tf.keras.layers.Layer):
"""Create 3D attention mask from a 2D tensor mask.
@@ -33,26 +61,4 @@ class SelfAttentionMask(tf.keras.layers.Layer):
if isinstance(inputs, list) and to_mask is None:
to_mask = inputs[1]
inputs = inputs[0]
- from_shape = tf.shape(inputs)
- batch_size = from_shape[0]
- from_seq_length = from_shape[1]
-
- to_shape = tf.shape(to_mask)
- to_seq_length = to_shape[1]
-
- to_mask = tf.cast(
- tf.reshape(to_mask, [batch_size, 1, to_seq_length]),
- dtype=inputs.dtype)
-
- # We don't assume that `from_tensor` is a mask (although it could be). We
- # don't actually care if we attend *from* padding tokens (only *to* padding)
- # tokens so we create a tensor of all ones.
- #
- # `broadcast_ones` = [batch_size, from_seq_length, 1]
- broadcast_ones = tf.ones(
- shape=[batch_size, from_seq_length, 1], dtype=inputs.dtype)
-
- # Here we broadcast along two dimensions to create the mask.
- mask = broadcast_ones * to_mask
-
- return mask
+ return get_mask(inputs, to_mask)
diff --git a/official/nlp/modeling/layers/spectral_normalization.py b/official/nlp/modeling/layers/spectral_normalization.py
index 175150c8ab683238e6cf89d8c87c7cb8b6e23862..aa81dbe1f0946dd55061c8c5fddcbcac29b8fefa 100644
--- a/official/nlp/modeling/layers/spectral_normalization.py
+++ b/official/nlp/modeling/layers/spectral_normalization.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -74,21 +74,20 @@ class SpectralNormalization(tf.keras.layers.Wrapper):
if not isinstance(layer, tf.keras.layers.Layer):
raise ValueError('`layer` must be a `tf.keras.layer.Layer`. '
'Observed `{}`'.format(layer))
- super(SpectralNormalization, self).__init__(
+ super().__init__(
layer, name=wrapper_name, **kwargs)
def build(self, input_shape):
- super(SpectralNormalization, self).build(input_shape)
+ super().build(input_shape)
self.layer.kernel._aggregation = self.aggregation # pylint: disable=protected-access
self._dtype = self.layer.kernel.dtype
self.w = self.layer.kernel
self.w_shape = self.w.shape.as_list()
- self.uv_initializer = tf.initializers.random_normal()
self.v = self.add_weight(
shape=(1, np.prod(self.w_shape[:-1])),
- initializer=self.uv_initializer,
+ initializer=tf.initializers.random_normal(),
trainable=False,
name='v',
dtype=self.dtype,
@@ -96,7 +95,7 @@ class SpectralNormalization(tf.keras.layers.Wrapper):
self.u = self.add_weight(
shape=(1, self.w_shape[-1]),
- initializer=self.uv_initializer,
+ initializer=tf.initializers.random_normal(),
trainable=False,
name='u',
dtype=self.dtype,
@@ -194,10 +193,11 @@ class SpectralNormalizationConv2D(tf.keras.layers.Wrapper):
raise ValueError(
'layer must be a `tf.keras.layer.Conv2D` instance. You passed: {input}'
.format(input=layer))
- super(SpectralNormalizationConv2D, self).__init__(layer, **kwargs)
+ super().__init__(layer, **kwargs)
def build(self, input_shape):
- self.layer.build(input_shape)
+ if not self.layer.built:
+ self.layer.build(input_shape)
self.layer.kernel._aggregation = self.aggregation # pylint: disable=protected-access
self._dtype = self.layer.kernel.dtype
@@ -221,11 +221,10 @@ class SpectralNormalizationConv2D(tf.keras.layers.Wrapper):
self.in_shape = (uv_dim, in_height, in_width, in_channel)
self.out_shape = (uv_dim, out_height, out_width, out_channel)
- self.uv_initializer = tf.initializers.random_normal()
self.v = self.add_weight(
shape=self.in_shape,
- initializer=self.uv_initializer,
+ initializer=tf.initializers.random_normal(),
trainable=False,
name='v',
dtype=self.dtype,
@@ -233,13 +232,13 @@ class SpectralNormalizationConv2D(tf.keras.layers.Wrapper):
self.u = self.add_weight(
shape=self.out_shape,
- initializer=self.uv_initializer,
+ initializer=tf.initializers.random_normal(),
trainable=False,
name='u',
dtype=self.dtype,
aggregation=self.aggregation)
- super(SpectralNormalizationConv2D, self).build()
+ super().build()
def call(self, inputs):
u_update_op, v_update_op, w_update_op = self.update_weights()
diff --git a/official/nlp/modeling/layers/spectral_normalization_test.py b/official/nlp/modeling/layers/spectral_normalization_test.py
index e2162ac6c2ab860eeabdba42889ccbd0d9fdb97a..41b1f5c4fe5a5d2c26560cf26151014fa680fe0e 100644
--- a/official/nlp/modeling/layers/spectral_normalization_test.py
+++ b/official/nlp/modeling/layers/spectral_normalization_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -66,7 +66,7 @@ class NormalizationTest(tf.test.TestCase, parameterized.TestCase):
spectral_norm_computed = _compute_spectral_norm(normalized_kernel)
spectral_norm_expected = self.norm_multiplier
self.assertAllClose(
- spectral_norm_computed, spectral_norm_expected, atol=5e-2)
+ spectral_norm_computed, spectral_norm_expected, atol=1e-1)
# Test that the normalized layer is K-Lipschitz. In particular, if the layer
# is a function f, then ||f(x1) - f(x2)||_2 <= K * ||(x1 - x2)||_2, where K
diff --git a/official/nlp/modeling/layers/talking_heads_attention.py b/official/nlp/modeling/layers/talking_heads_attention.py
index bddfacaa86d1dea6afd7ec67b4608d15cfc36a81..5a939cd0963b29cb2e5222cc8d569906507b7fcb 100644
--- a/official/nlp/modeling/layers/talking_heads_attention.py
+++ b/official/nlp/modeling/layers/talking_heads_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,6 +20,8 @@ import string
import gin
import tensorflow as tf
+from official.modeling import tf_utils
+
_CHR_IDX = string.ascii_lowercase
@@ -87,7 +89,7 @@ class TalkingHeadsAttention(tf.keras.layers.MultiHeadAttention):
self._pre_softmax_weight = self.add_weight(
"pre_softmax_weight",
shape=(self._num_heads, self._num_heads),
- initializer=self._kernel_initializer,
+ initializer=tf_utils.clone_initializer(self._kernel_initializer),
regularizer=self._kernel_regularizer,
constraint=self._kernel_constraint,
dtype=self.dtype,
@@ -95,7 +97,7 @@ class TalkingHeadsAttention(tf.keras.layers.MultiHeadAttention):
self._post_softmax_weight = self.add_weight(
"post_softmax_weight",
shape=(self._num_heads, self._num_heads),
- initializer=self._kernel_initializer,
+ initializer=tf_utils.clone_initializer(self._kernel_initializer),
regularizer=self._kernel_regularizer,
constraint=self._kernel_constraint,
dtype=self.dtype,
diff --git a/official/nlp/modeling/layers/talking_heads_attention_test.py b/official/nlp/modeling/layers/talking_heads_attention_test.py
index 579384bb754952187682bb8dcfdb74fe9e0b6478..6f14e2023c25e13d883ebd1949864fb328652699 100644
--- a/official/nlp/modeling/layers/talking_heads_attention_test.py
+++ b/official/nlp/modeling/layers/talking_heads_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/text_layers.py b/official/nlp/modeling/layers/text_layers.py
index 299901d2df7504ef207f4adcf3149c9cac700350..60b2f11a7a6d7db024fe42bb416cccf5bdeaea18 100644
--- a/official/nlp/modeling/layers/text_layers.py
+++ b/official/nlp/modeling/layers/text_layers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,14 +14,16 @@
"""Keras Layers for BERT-specific preprocessing."""
# pylint: disable=g-import-not-at-top
-from typing import Any, Dict, List, Optional, Union
+from typing import Any, Dict, List, Mapping, Optional, Text, Union
from absl import logging
import tensorflow as tf
try:
+ # pytype: disable=import-error
import tensorflow_text as text
from tensorflow_text.python.ops import bert_tokenizer
+ # pytype: enable=import-error
except ImportError:
text = None
bert_tokenizer = None
@@ -57,7 +59,7 @@ def _truncate_row_lengths(ragged_tensor: tf.RaggedTensor,
class BertTokenizer(tf.keras.layers.Layer):
- """Wraps BertTokenizer with pre-defined vocab as a Keras Layer.
+ """Wraps TF.Text's BertTokenizer with pre-defined vocab as a Keras Layer.
Attributes:
tokenize_with_offsets: If true, calls
@@ -71,8 +73,9 @@ class BertTokenizer(tf.keras.layers.Layer):
def __init__(self, *,
vocab_file: str,
- lower_case: bool,
+ lower_case: Optional[bool] = None,
tokenize_with_offsets: bool = False,
+ tokenizer_kwargs: Optional[Mapping[Text, Any]] = None,
**kwargs):
"""Initialize a `BertTokenizer` layer.
@@ -81,15 +84,18 @@ class BertTokenizer(tf.keras.layers.Layer):
This is a text file with newline-separated wordpiece tokens.
This layer initializes a lookup table from it that gets used with
`text.BertTokenizer`.
- lower_case: A Python boolean forwarded to `text.BertTokenizer`.
+ lower_case: Optional boolean forwarded to `text.BertTokenizer`.
If true, input text is converted to lower case (where applicable)
before tokenization. This must be set to match the way in which
- the `vocab_file` was created.
+ the `vocab_file` was created. If passed, this overrides whatever value
+ may have been passed in `tokenizer_kwargs`.
tokenize_with_offsets: A Python boolean. If true, this layer calls
`text.BertTokenizer.tokenize_with_offsets()` instead of plain
`text.BertTokenizer.tokenize()` and outputs a triple of
`(tokens, start_offsets, limit_offsets)`
insead of just tokens.
+ tokenizer_kwargs: Optional mapping with keyword arguments to forward to
+ `text.BertTokenizer`'s constructor.
**kwargs: Standard arguments to `Layer()`.
Raises:
@@ -111,8 +117,11 @@ class BertTokenizer(tf.keras.layers.Layer):
self._special_tokens_dict = self._create_special_tokens_dict(
self._vocab_table, vocab_file)
super().__init__(**kwargs)
- self._bert_tokenizer = text.BertTokenizer(
- self._vocab_table, lower_case=lower_case)
+ tokenizer_kwargs = dict(tokenizer_kwargs or {})
+ if lower_case is not None:
+ tokenizer_kwargs["lower_case"] = lower_case
+ self._bert_tokenizer = text.BertTokenizer(self._vocab_table,
+ **tokenizer_kwargs)
@property
def vocab_size(self):
diff --git a/official/nlp/modeling/layers/text_layers_test.py b/official/nlp/modeling/layers/text_layers_test.py
index 0608863ca8f8e933005c760ef597e5a8200d666e..d3bc63352c1c9cd519944f8f5561218723cd050b 100644
--- a/official/nlp/modeling/layers/text_layers_test.py
+++ b/official/nlp/modeling/layers/text_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,6 +19,7 @@ import tempfile
import numpy as np
import tensorflow as tf
+from tensorflow import estimator as tf_estimator
from sentencepiece import SentencePieceTrainer
from official.nlp.modeling.layers import text_layers
@@ -120,10 +121,10 @@ class BertTokenizerTest(tf.test.TestCase):
def model_fn(features, labels, mode):
del labels # Unused.
- return tf.estimator.EstimatorSpec(mode=mode,
+ return tf_estimator.EstimatorSpec(mode=mode,
predictions=features["input_word_ids"])
- estimator = tf.estimator.Estimator(model_fn=model_fn)
+ estimator = tf_estimator.Estimator(model_fn=model_fn)
outputs = list(estimator.predict(input_fn))
self.assertAllEqual(outputs, np.array([[2, 6, 3, 0],
[2, 4, 5, 3]]))
@@ -231,10 +232,10 @@ class SentencepieceTokenizerTest(tf.test.TestCase):
def model_fn(features, labels, mode):
del labels # Unused.
- return tf.estimator.EstimatorSpec(mode=mode,
+ return tf_estimator.EstimatorSpec(mode=mode,
predictions=features["input_word_ids"])
- estimator = tf.estimator.Estimator(model_fn=model_fn)
+ estimator = tf_estimator.Estimator(model_fn=model_fn)
outputs = list(estimator.predict(input_fn))
self.assertAllEqual(outputs, np.array([[2, 8, 3, 0],
[2, 12, 3, 0]]))
@@ -537,10 +538,10 @@ class FastWordPieceBertTokenizerTest(tf.test.TestCase):
def model_fn(features, labels, mode):
del labels # Unused.
- return tf.estimator.EstimatorSpec(mode=mode,
+ return tf_estimator.EstimatorSpec(mode=mode,
predictions=features["input_word_ids"])
- estimator = tf.estimator.Estimator(model_fn=model_fn)
+ estimator = tf_estimator.Estimator(model_fn=model_fn)
outputs = list(estimator.predict(input_fn))
self.assertAllEqual(outputs, np.array([[2, 6, 3, 0],
[2, 4, 5, 3]]))
diff --git a/official/nlp/modeling/layers/tn_expand_condense.py b/official/nlp/modeling/layers/tn_expand_condense.py
index c4bd08c5dcadc02defe46e0e2bb23e369ffd389b..406044cda65cb92a12a185141ec2c9bcb576f945 100644
--- a/official/nlp/modeling/layers/tn_expand_condense.py
+++ b/official/nlp/modeling/layers/tn_expand_condense.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,6 +17,8 @@
from typing import List, Optional, Text, Any, Dict
import tensorflow as tf
+from official.modeling import tf_utils
+
Layer = tf.keras.layers.Layer
activations = tf.keras.activations
initializers = tf.keras.initializers
@@ -64,7 +66,7 @@ class TNExpandCondense(Layer):
if 'input_shape' not in kwargs and 'input_dim' in kwargs:
kwargs['input_shape'] = (kwargs.pop('input_dim'),)
- super(TNExpandCondense, self).__init__(**kwargs)
+ super().__init__(**kwargs)
assert proj_multiplier in [
2, 4, 6, 8, 10, 12
@@ -84,7 +86,7 @@ class TNExpandCondense(Layer):
'The last dimension of the inputs to `TNExpandCondense` '
'should be defined. Found `None`.')
- super(TNExpandCondense, self).build(input_shape)
+ super().build(input_shape)
self.proj_size = self.proj_multiplier * input_shape[-1]
@@ -98,24 +100,24 @@ class TNExpandCondense(Layer):
name='w1',
shape=(input_shape[-1], input_shape[-1]),
trainable=True,
- initializer=self.kernel_initializer)
+ initializer=tf_utils.clone_initializer(self.kernel_initializer))
self.w2 = self.add_weight(
name='w2',
shape=(128, (128 * (self.proj_size // input_shape[-1]))),
trainable=True,
- initializer=self.kernel_initializer)
+ initializer=tf_utils.clone_initializer(self.kernel_initializer))
self.w3 = self.add_weight(
name='w3',
shape=(128 * (self.proj_size // input_shape[-1]), 128),
trainable=True,
- initializer=self.kernel_initializer)
+ initializer=tf_utils.clone_initializer(self.kernel_initializer))
self.w4 = self.add_weight(
name='w4',
shape=(input_shape[-1] // 128, 128, input_shape[-1]),
trainable=True,
- initializer=self.kernel_initializer)
+ initializer=tf_utils.clone_initializer(self.kernel_initializer))
if self.use_bias:
self.bias = self.add_weight(
@@ -176,5 +178,5 @@ class TNExpandCondense(Layer):
getattr(self, initializer_arg))
# Get base config
- base_config = super(TNExpandCondense, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
diff --git a/official/nlp/modeling/layers/tn_expand_condense_test.py b/official/nlp/modeling/layers/tn_expand_condense_test.py
index ae39b8550252537fb44e42406f5051641eecd893..09ec2a86a2bd217e9ab1a1e2814053fb90a7629b 100644
--- a/official/nlp/modeling/layers/tn_expand_condense_test.py
+++ b/official/nlp/modeling/layers/tn_expand_condense_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,6 @@ import os
from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-# pylint: disable=g-direct-tensorflow-import
-from tensorflow.python.keras.testing_utils import layer_test
from official.nlp.modeling.layers.tn_expand_condense import TNExpandCondense
@@ -45,13 +43,9 @@ class TNLayerTest(tf.test.TestCase, parameterized.TestCase):
@parameterized.parameters((768, 6), (1024, 2))
def test_keras_layer(self, input_dim, proj_multiple):
- self.skipTest('Disable the test for now since it imports '
- 'keras.testing_utils, will reenable this test after we '
- 'fix the b/184578869')
- # TODO(scottzhu): Reenable after fix b/184578869
data = np.random.normal(size=(100, input_dim))
data = data.astype(np.float32)
- layer_test(
+ tf.keras.__internal__.utils.layer_test(
TNExpandCondense,
kwargs={
'proj_multiplier': proj_multiple,
@@ -64,9 +58,9 @@ class TNLayerTest(tf.test.TestCase, parameterized.TestCase):
@parameterized.parameters((768, 6), (1024, 2))
def test_train(self, input_dim, proj_multiple):
+ tf.keras.utils.set_random_seed(0)
data = np.random.randint(10, size=(100, input_dim))
model = self._build_model(data, proj_multiple)
- tf.random.set_seed(0)
model.compile(
optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])
@@ -81,7 +75,7 @@ class TNLayerTest(tf.test.TestCase, parameterized.TestCase):
@parameterized.parameters((768, 6), (1024, 2))
def test_weights_change(self, input_dim, proj_multiple):
- tf.random.set_seed(0)
+ tf.keras.utils.set_random_seed(0)
data = np.random.randint(10, size=(100, input_dim))
model = self._build_model(data, proj_multiple)
model.compile(
diff --git a/official/nlp/modeling/layers/tn_transformer_expand_condense.py b/official/nlp/modeling/layers/tn_transformer_expand_condense.py
index c244fcb1cd051a88eebd363dace39914745c582c..53705a1faa486cfd08c94a4bcde131f97539dabe 100644
--- a/official/nlp/modeling/layers/tn_transformer_expand_condense.py
+++ b/official/nlp/modeling/layers/tn_transformer_expand_condense.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,6 +19,7 @@
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers.tn_expand_condense import TNExpandCondense
@@ -77,7 +78,7 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
intermediate_dropout=0.0,
attention_initializer=None,
**kwargs):
- super(TNTransformerExpandCondense, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._num_heads = num_attention_heads
self._intermediate_size = intermediate_size
@@ -100,7 +101,8 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
self._attention_initializer = tf.keras.initializers.get(
attention_initializer)
else:
- self._attention_initializer = self._kernel_initializer
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
def build(self, input_shape):
input_tensor = input_shape[0] if len(input_shape) == 2 else input_shape
@@ -128,7 +130,6 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
"heads (%d)" % (hidden_size, self._num_heads))
self._attention_head_size = int(hidden_size // self._num_heads)
common_kwargs = dict(
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -140,6 +141,7 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
dropout=self._attention_dropout_rate,
use_bias=self._use_bias,
kernel_initializer=self._attention_initializer,
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="self_attention",
**common_kwargs)
self._attention_dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
@@ -168,7 +170,7 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
epsilon=self._norm_epsilon,
dtype=tf.float32)
- super(TNTransformerExpandCondense, self).build(input_shape)
+ super().build(input_shape)
def get_config(self):
config = {
@@ -209,7 +211,7 @@ class TNTransformerExpandCondense(tf.keras.layers.Layer):
"attention_initializer":
tf.keras.initializers.serialize(self._attention_initializer)
}
- base_config = super(TNTransformerExpandCondense, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def call(self, inputs):
diff --git a/official/nlp/modeling/layers/tn_transformer_test.py b/official/nlp/modeling/layers/tn_transformer_test.py
index a21193e7c7b10b2aef1ae3b0e68c74e191149e2e..af52661a99b72d2559cd5d4d949e508de07121f8 100644
--- a/official/nlp/modeling/layers/tn_transformer_test.py
+++ b/official/nlp/modeling/layers/tn_transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/transformer.py b/official/nlp/modeling/layers/transformer.py
index 8026aaaa328ef8301ef67844f4c8a1d8ab12675b..338edf24724c1d4f33f71bcde903e3a531ad3766 100644
--- a/official/nlp/modeling/layers/transformer.py
+++ b/official/nlp/modeling/layers/transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,9 +15,11 @@
"""Keras-based transformer block layer."""
# pylint: disable=g-classes-have-attributes
+from absl import logging
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers import attention
from official.nlp.modeling.layers import multi_channel_attention
from official.nlp.modeling.layers import transformer_encoder_block
@@ -31,6 +33,9 @@ class Transformer(transformer_encoder_block.TransformerEncoderBlock):
This layer implements the Transformer from "Attention Is All You Need".
(https://arxiv.org/abs/1706.03762).
+ **Warning: this layer is deprecated. Please don't use it. Use the
+ `TransformerEncoderBlock` layer instead.**
+
Args:
num_attention_heads: Number of attention heads.
intermediate_size: Size of the intermediate layer.
@@ -97,6 +102,8 @@ class Transformer(transformer_encoder_block.TransformerEncoderBlock):
inner_dropout=intermediate_dropout,
attention_initializer=attention_initializer,
**kwargs)
+ logging.warning("The `Transformer` layer is deprecated. Please directly "
+ "use `TransformerEncoderBlock`.")
def get_config(self):
return {
@@ -226,7 +233,8 @@ class TransformerDecoderBlock(tf.keras.layers.Layer):
self._attention_initializer = tf.keras.initializers.get(
attention_initializer)
else:
- self._attention_initializer = self._kernel_initializer
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
if self.multi_channel_cross_attention:
self._cross_attention_cls = multi_channel_attention.MultiChannelAttention
else:
@@ -244,7 +252,6 @@ class TransformerDecoderBlock(tf.keras.layers.Layer):
"heads (%d)" % (hidden_size, self.num_attention_heads))
self.attention_head_size = int(hidden_size) // self.num_attention_heads
common_kwargs = dict(
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -256,14 +263,17 @@ class TransformerDecoderBlock(tf.keras.layers.Layer):
key_dim=self.attention_head_size,
dropout=self.attention_dropout_rate,
use_bias=self._use_bias,
- kernel_initializer=self._attention_initializer,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._attention_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="self_attention",
**common_kwargs)
- self.self_attention_output_dense = tf.keras.layers.experimental.EinsumDense(
+ self.self_attention_output_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="output",
**common_kwargs)
self.self_attention_dropout = tf.keras.layers.Dropout(
@@ -281,7 +291,9 @@ class TransformerDecoderBlock(tf.keras.layers.Layer):
dropout=self.attention_dropout_rate,
output_shape=hidden_size,
use_bias=self._use_bias,
- kernel_initializer=self._attention_initializer,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._attention_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="attention/encdec",
**common_kwargs)
@@ -295,22 +307,24 @@ class TransformerDecoderBlock(tf.keras.layers.Layer):
dtype="float32"))
# Feed-forward projection.
- self.intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self.intermediate_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, self.intermediate_size),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="intermediate",
**common_kwargs)
self.intermediate_activation_layer = tf.keras.layers.Activation(
self.intermediate_activation)
self._intermediate_dropout_layer = tf.keras.layers.Dropout(
rate=self._intermediate_dropout)
- self.output_dense = tf.keras.layers.experimental.EinsumDense(
+ self.output_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="output",
**common_kwargs)
self.output_dropout = tf.keras.layers.Dropout(rate=self.dropout_rate)
diff --git a/official/nlp/modeling/layers/transformer_encoder_block.py b/official/nlp/modeling/layers/transformer_encoder_block.py
index 49e0e0cbee4315da573b1045c9fe38f6436fd6b9..b7634fbd2c77afc05eb7a8db64d58caad1b55b78 100644
--- a/official/nlp/modeling/layers/transformer_encoder_block.py
+++ b/official/nlp/modeling/layers/transformer_encoder_block.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,9 +13,11 @@
# limitations under the License.
"""Keras-based TransformerEncoder block layer."""
-
+from typing import Any, Optional
+from absl import logging
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers import util
@@ -54,9 +56,32 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
inner_dropout=0.0,
attention_initializer=None,
attention_axes=None,
+ use_query_residual=True,
+ key_dim=None,
+ value_dim=None,
+ output_last_dim=None,
+ diff_q_kv_att_layer_norm=False,
+ return_attention_scores=False,
**kwargs):
"""Initializes `TransformerEncoderBlock`.
+ Note: If `output_last_dim` is used and `use_query_residual` is `True`, the
+ `output_last_dim`'s value must equal the first input's last dimension for
+ the query residual connection to work. This is because the residual
+ connection after the multi-head-attention requires their dimensions to
+ match. If `use_query_residual` is `False`, the `output_last_dim` dictactes
+ the last dimension of the output of this module and the
+ multi-head-attention.
+
+ E.g. let's say input dims are `[batch_size, seq_dim, input_last_dim]`.
+ Scenario 1: If `output_last_dim` is not `None`, then the output dims of this
+ module would be `[batch_size, seq_dim, output_last_dim]`. Note `key_dim` is
+ overriden by `output_last_dim`.
+ Scenario 2: If `output_last_dim` is `None` and `key_dim` is not `None`, then
+ the output dims of this module would be `[batch_size, seq_dim, key_dim]`.
+ Scenario 3: If the `output_last_dim` and `key_dim` are both `None`, the
+ output dims would be `[batch_size, seq_dim, input_last_dim]`.
+
Args:
num_attention_heads: Number of attention heads.
inner_dim: The output dimension of the first Dense layer in a two-layer
@@ -88,17 +113,35 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
kernel.
attention_axes: axes over which the attention is applied. `None` means
attention over all axes, but batch, heads, and features.
+ use_query_residual: Toggle to execute residual connection after attention.
+ key_dim: `key_dim` for the `tf.keras.layers.MultiHeadAttention`. If
+ `None`, we use the first `input_shape`'s last dim.
+ value_dim: `value_dim` for the `tf.keras.layers.MultiHeadAttention`.
+ output_last_dim: Final dimension of the output of this module. This also
+ dictates the value for the final dimension of the multi-head-attention.
+ When it's `None`, we use, in order of decreasing precedence, `key_dim` *
+ `num_heads` or the first `input_shape`'s last dim as the output's last
+ dim.
+ diff_q_kv_att_layer_norm: If `True`, create a separate attention layer
+ norm layer for query and key-value if `norm_first` is `True`. Invalid to
+ set to `True` if `norm_first` is `False`.
+ return_attention_scores: If `True`, the output of this layer will be a
+ tuple and additionally contain the attention scores in the shape of
+ `[batch_size, num_attention_heads, seq_dim, seq_dim]`.
**kwargs: keyword arguments.
"""
util.filter_kwargs(kwargs)
super().__init__(**kwargs)
+ # Deprecation warning.
+ if output_range is not None:
+ logging.warning("`output_range` is available as an argument for `call()`."
+ "The `output_range` as __init__ argument is deprecated.")
+
self._num_heads = num_attention_heads
self._inner_dim = inner_dim
self._inner_activation = inner_activation
- self._attention_dropout = attention_dropout
self._attention_dropout_rate = attention_dropout
- self._output_dropout = output_dropout
self._output_dropout_rate = output_dropout
self._output_range = output_range
self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
@@ -112,13 +155,24 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
self._norm_first = norm_first
self._norm_epsilon = norm_epsilon
self._inner_dropout = inner_dropout
+ self._use_query_residual = use_query_residual
+ self._key_dim = key_dim
+ self._value_dim = value_dim
+ self._output_last_dim = output_last_dim
+ self._diff_q_kv_att_layer_norm = diff_q_kv_att_layer_norm
+ self._return_attention_scores = return_attention_scores
if attention_initializer:
self._attention_initializer = tf.keras.initializers.get(
attention_initializer)
else:
- self._attention_initializer = self._kernel_initializer
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
self._attention_axes = attention_axes
+ if self._diff_q_kv_att_layer_norm and not self._norm_first:
+ raise ValueError("Setting `diff_q_and_kv_attention_layer_norm` to True"
+ "when `norm_first` is False is invalid.")
+
def build(self, input_shape):
if isinstance(input_shape, tf.TensorShape):
input_tensor_shape = input_shape
@@ -133,27 +187,35 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
einsum_equation = "...bc,cd->...bd"
hidden_size = input_tensor_shape[-1]
if hidden_size % self._num_heads != 0:
- raise ValueError(
+ logging.warning(
"The input size (%d) is not a multiple of the number of attention "
- "heads (%d)" % (hidden_size, self._num_heads))
- self._attention_head_size = int(hidden_size // self._num_heads)
+ "heads (%d)", hidden_size, self._num_heads)
+ if self._key_dim is None:
+ self._key_dim = int(hidden_size // self._num_heads)
+ if self._output_last_dim is None:
+ last_output_shape = hidden_size
+ else:
+ last_output_shape = self._output_last_dim
+
common_kwargs = dict(
- bias_initializer=self._bias_initializer,
- kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
kernel_constraint=self._kernel_constraint,
bias_constraint=self._bias_constraint)
self._attention_layer = tf.keras.layers.MultiHeadAttention(
num_heads=self._num_heads,
- key_dim=self._attention_head_size,
- dropout=self._attention_dropout,
+ key_dim=self._key_dim,
+ value_dim=self._value_dim,
+ dropout=self._attention_dropout_rate,
use_bias=self._use_bias,
kernel_initializer=self._attention_initializer,
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
attention_axes=self._attention_axes,
+ output_shape=self._output_last_dim,
name="self_attention",
**common_kwargs)
- self._attention_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ self._attention_dropout = tf.keras.layers.Dropout(
+ rate=self._attention_dropout_rate)
# Use float32 in layernorm for numeric stability.
# It is probably safe in mixed_float16, but we haven't validated this yet.
self._attention_layer_norm = (
@@ -162,11 +224,21 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
axis=-1,
epsilon=self._norm_epsilon,
dtype=tf.float32))
- self._intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self._attention_layer_norm_kv = self._attention_layer_norm
+ if self._diff_q_kv_att_layer_norm:
+ self._attention_layer_norm_kv = (
+ tf.keras.layers.LayerNormalization(
+ name="self_attention_layer_norm_kv",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype=tf.float32))
+
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=(None, self._inner_dim),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
name="intermediate",
**common_kwargs)
policy = tf.keras.mixed_precision.global_policy()
@@ -179,14 +251,16 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
self._inner_activation, dtype=policy)
self._inner_dropout_layer = tf.keras.layers.Dropout(
rate=self._inner_dropout)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._output_dense = tf.keras.layers.EinsumDense(
einsum_equation,
- output_shape=(None, hidden_size),
+ output_shape=(None, last_output_shape),
bias_axes="d",
name="output",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
- self._output_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ self._output_dropout = tf.keras.layers.Dropout(
+ rate=self._output_dropout_rate)
# Use float32 in layernorm for numeric stability.
self._output_layer_norm = tf.keras.layers.LayerNormalization(
name="output_layer_norm",
@@ -194,7 +268,7 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
epsilon=self._norm_epsilon,
dtype=tf.float32)
- super(TransformerEncoderBlock, self).build(input_shape)
+ super().build(input_shape)
def get_config(self):
config = {
@@ -234,22 +308,35 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
self._inner_dropout,
"attention_initializer":
tf.keras.initializers.serialize(self._attention_initializer),
- "attention_axes": self._attention_axes,
+ "attention_axes":
+ self._attention_axes,
+ "use_query_residual":
+ self._use_query_residual,
+ "key_dim":
+ self._key_dim,
+ "value_dim":
+ self._value_dim,
+ "output_last_dim":
+ self._output_last_dim,
+ "diff_q_kv_att_layer_norm":
+ self._diff_q_kv_att_layer_norm,
}
- base_config = super(TransformerEncoderBlock, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
- def call(self, inputs):
+ def call(self, inputs: Any, output_range: Optional[tf.Tensor] = None) -> Any:
"""Transformer self-attention encoder block call.
Args:
- inputs: a single tensor or a list of tensors.
- `input tensor` as the single sequence of embeddings.
- [`input tensor`, `attention mask`] to have the additional attention
- mask.
- [`query tensor`, `key value tensor`, `attention mask`] to have separate
- input streams for the query, and key/value to the multi-head
- attention.
+ inputs: a single tensor or a list of tensors. `input tensor` as the single
+ sequence of embeddings. [`input tensor`, `attention mask`] to have the
+ additional attention mask. [`query tensor`, `key value tensor`,
+ `attention mask`] to have separate input streams for the query, and
+ key/value to the multi-head attention.
+ output_range: the sequence output range, [0, output_range) for slicing the
+ target sequence. `None` means the target sequence is not sliced. If you
+ would like to have no change to the model training, it is better to only
+ set the `output_range` for serving.
Returns:
An output tensor with the same dimensions as input/query tensor.
@@ -266,33 +353,50 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
else:
input_tensor, key_value, attention_mask = (inputs, None, None)
- if self._output_range:
+ if output_range is None:
+ output_range = self._output_range
+ if output_range:
if self._norm_first:
- source_tensor = input_tensor[:, 0:self._output_range, :]
+ source_tensor = input_tensor[:, 0:output_range, :]
input_tensor = self._attention_layer_norm(input_tensor)
if key_value is not None:
- key_value = self._attention_layer_norm(key_value)
- target_tensor = input_tensor[:, 0:self._output_range, :]
+ key_value = self._attention_layer_norm_kv(key_value)
+ target_tensor = input_tensor[:, 0:output_range, :]
if attention_mask is not None:
- attention_mask = attention_mask[:, 0:self._output_range, :]
+ attention_mask = attention_mask[:, 0:output_range, :]
else:
if self._norm_first:
source_tensor = input_tensor
input_tensor = self._attention_layer_norm(input_tensor)
if key_value is not None:
- key_value = self._attention_layer_norm(key_value)
+ key_value = self._attention_layer_norm_kv(key_value)
target_tensor = input_tensor
if key_value is None:
key_value = input_tensor
- attention_output = self._attention_layer(
- query=target_tensor, value=key_value, attention_mask=attention_mask)
+
+ if self._return_attention_scores:
+ attention_output, attention_scores = self._attention_layer(
+ query=target_tensor,
+ value=key_value,
+ attention_mask=attention_mask,
+ return_attention_scores=True)
+ else:
+ attention_output = self._attention_layer(
+ query=target_tensor, value=key_value, attention_mask=attention_mask)
attention_output = self._attention_dropout(attention_output)
+
if self._norm_first:
- attention_output = source_tensor + attention_output
+ # Important to not combine `self._norm_first` and
+ # `self._use_query_residual` into one if clause because else is only for
+ # `_norm_first == False`.
+ if self._use_query_residual:
+ attention_output = source_tensor + attention_output
else:
- attention_output = self._attention_layer_norm(target_tensor +
- attention_output)
+ if self._use_query_residual:
+ attention_output = target_tensor + attention_output
+ attention_output = self._attention_layer_norm(attention_output)
+
if self._norm_first:
source_attention_output = attention_output
attention_output = self._output_layer_norm(attention_output)
@@ -303,9 +407,14 @@ class TransformerEncoderBlock(tf.keras.layers.Layer):
layer_output = self._output_dropout(layer_output)
if self._norm_first:
- return source_attention_output + layer_output
+ layer_output = source_attention_output + layer_output
+ else:
+ # During mixed precision training, layer norm output is always fp32 for
+ # now. Casts fp32 for the subsequent add.
+ layer_output = tf.cast(layer_output, tf.float32)
+ layer_output = self._output_layer_norm(layer_output + attention_output)
- # During mixed precision training, layer norm output is always fp32 for now.
- # Casts fp32 for the subsequent add.
- layer_output = tf.cast(layer_output, tf.float32)
- return self._output_layer_norm(layer_output + attention_output)
+ if self._return_attention_scores:
+ return layer_output, attention_scores
+ else:
+ return layer_output
diff --git a/official/nlp/modeling/layers/transformer_encoder_block_test.py b/official/nlp/modeling/layers/transformer_encoder_block_test.py
index bb9c4f1e38b36f988ecd32fc9816f236a6322320..ca929e9741fe01db3fbf9d9e3f29dce19bd96364 100644
--- a/official/nlp/modeling/layers/transformer_encoder_block_test.py
+++ b/official/nlp/modeling/layers/transformer_encoder_block_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,8 +23,7 @@ from official.nlp.modeling.layers.transformer_encoder_block import TransformerEn
@keras_parameterized.run_all_keras_modes
-@parameterized.named_parameters(
- ('base', TransformerEncoderBlock))
+@parameterized.named_parameters(('base', TransformerEncoderBlock))
class TransformerEncoderBlockLayerTest(keras_parameterized.TestCase):
def tearDown(self):
@@ -117,18 +116,22 @@ class TransformerEncoderBlockLayerTest(keras_parameterized.TestCase):
new_layer = transformer_cls(
num_attention_heads=10,
inner_dim=2048,
- inner_activation='relu',
- output_range=1)
- _ = new_layer([input_data, mask_data])
+ inner_activation='relu')
+ _ = new_layer([input_data, mask_data], output_range=1)
new_layer.set_weights(test_layer.get_weights())
- new_output_tensor = new_layer([input_data, mask_data])
+ new_output_tensor = new_layer([input_data, mask_data], output_range=1)
self.assertAllClose(
new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
+ output_tensor = test_layer([input_data, mask_data], output_range=1)
+ self.assertAllClose(new_output_tensor, output_tensor, atol=5e-5, rtol=0.003)
+
def test_layer_output_range_without_mask(self, transformer_cls):
test_layer = transformer_cls(
- num_attention_heads=10, inner_dim=2048,
- inner_activation='relu', norm_first=True)
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu',
+ norm_first=True)
sequence_length = 21
width = 80
@@ -143,18 +146,19 @@ class TransformerEncoderBlockLayerTest(keras_parameterized.TestCase):
num_attention_heads=10,
inner_dim=2048,
inner_activation='relu',
- output_range=1,
norm_first=True)
- _ = new_layer(input_data)
+ _ = new_layer(input_data, output_range=1)
new_layer.set_weights(test_layer.get_weights())
- new_output_tensor = new_layer(input_data)
+ new_output_tensor = new_layer(input_data, output_range=1)
self.assertAllClose(
new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
def test_layer_output_range_with_pre_norm(self, transformer_cls):
test_layer = transformer_cls(
- num_attention_heads=10, inner_dim=2048,
- inner_activation='relu', norm_first=True)
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu',
+ norm_first=True)
sequence_length = 21
width = 80
@@ -171,14 +175,16 @@ class TransformerEncoderBlockLayerTest(keras_parameterized.TestCase):
num_attention_heads=10,
inner_dim=2048,
inner_activation='relu',
- output_range=1,
norm_first=True)
- _ = new_layer([input_data, mask_data])
+ _ = new_layer([input_data, mask_data], output_range=1)
new_layer.set_weights(test_layer.get_weights())
- new_output_tensor = new_layer([input_data, mask_data])
+ new_output_tensor = new_layer([input_data, mask_data], output_range=1)
self.assertAllClose(
new_output_tensor, output_tensor[:, 0:1, :], atol=5e-5, rtol=0.003)
+ output_tensor = test_layer([input_data, mask_data], output_range=1)
+ self.assertAllClose(new_output_tensor, output_tensor, atol=5e-5, rtol=0.003)
+
def test_layer_invocation_with_float16_dtype(self, transformer_cls):
tf.keras.mixed_precision.set_global_policy('mixed_float16')
test_layer = transformer_cls(
@@ -252,6 +258,155 @@ class TransformerEncoderBlockLayerTest(keras_parameterized.TestCase):
self.assertEqual(output.shape, q_tensor.shape)
+@keras_parameterized.run_all_keras_modes
+class TransformerEncoderBlockLayerTestWithoutParams(keras_parameterized.TestCase
+ ):
+
+ def tearDown(self):
+ super(TransformerEncoderBlockLayerTestWithoutParams, self).tearDown()
+ tf.keras.mixed_precision.set_global_policy('float32')
+
+ def test_raises_invalid_arg_error_when_q_kv_dims_are_different(self):
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation='relu',
+ norm_first=True)
+ # Forward path.
+ q_tensor = tf.zeros([2, 4, 16], dtype=tf.float32)
+ kv_tensor = tf.zeros([2, 8, 32], dtype=tf.float32)
+ dummy_mask = tf.zeros([2, 4, 8], dtype=tf.float32)
+ inputs = [q_tensor, kv_tensor, dummy_mask]
+ with self.assertRaises(tf.errors.InvalidArgumentError):
+ test_layer(inputs)
+
+ @parameterized.named_parameters(('output_range_not_none', 2),
+ ('output_range_none', None))
+ def test_needs_diff_q_kv_att_layer_norm_to_be_true_for_diff_q_and_kv_dims(
+ self, output_range):
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation='relu',
+ norm_first=True)
+ # Forward path.
+ q_tensor = tf.zeros([2, 4, 16], dtype=tf.float32)
+ kv_tensor = tf.zeros([2, 8, 32], dtype=tf.float32)
+ dummy_mask = tf.zeros([2, 4, 8], dtype=tf.float32)
+ inputs = [q_tensor, kv_tensor, dummy_mask]
+ with self.assertRaises(tf.errors.InvalidArgumentError):
+ test_layer(inputs, output_range=output_range)
+
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation='relu',
+ diff_q_kv_att_layer_norm=True,
+ norm_first=True)
+ # Forward path.
+ test_layer(inputs)
+
+ @parameterized.named_parameters(('norm_first_is_true', True),
+ ('norm_first_is_false', False))
+ def test_use_query_residual_false_removes_add_op(self, norm_first):
+ graph_with_res = tf.Graph()
+ with graph_with_res.as_default():
+ layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation='relu',
+ norm_first=norm_first)
+ inputs = tf.keras.Input(shape=(None, None, 2))
+ outputs = layer(inputs)
+ tf.keras.Model(inputs=inputs, outputs=outputs)
+
+ graph_without_res = tf.Graph()
+ with graph_without_res.as_default():
+ layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=128,
+ inner_activation='relu',
+ norm_first=norm_first,
+ use_query_residual=False)
+ inputs = tf.keras.Input(shape=(None, None, 2))
+ outputs = layer(inputs)
+ tf.keras.Model(inputs=inputs, outputs=outputs)
+ graph_with_res_names = {x.name for x in graph_with_res.get_operations()}
+ graph_without_res_names = {
+ x.name for x in graph_without_res.get_operations()
+ }
+
+ self.assertIn('transformer_encoder_block/add',
+ list(graph_with_res_names - graph_without_res_names)[0])
+ self.assertEmpty(graph_without_res_names - graph_with_res_names)
+
+ @parameterized.named_parameters(('key_dim_is_none', None, 128, 2, 128 // 2),
+ ('key_dim_is_not_none', 30, 128, 2, 30))
+ def test_key_dim(self, key_dim, q_tensor_last_dim, some_num_attention_heads,
+ expected):
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ key_dim=key_dim)
+
+ q_tensor = tf.zeros([2, 4, q_tensor_last_dim], dtype=tf.float32)
+ kv_tensor = tf.zeros([2, 8, 32], dtype=tf.float32)
+ dummy_mask = tf.zeros([2, 4, 8], dtype=tf.float32)
+ test_layer([q_tensor, kv_tensor, dummy_mask])
+
+ self.assertEqual(expected,
+ test_layer._attention_layer.get_config()['key_dim'])
+
+ @parameterized.named_parameters(
+ ('output_last_dim_is_none_use_query_residual_false', False, None, 128,
+ 128),
+ ('output_last_dim_is_none_use_query_residual_true', True, None, 128, 128),
+ ('output_last_dim_is_not_none', False, 30, 128, 30))
+ def test_output_last_dim(self, use_query_residual, output_last_dim,
+ q_tensor_last_dim, expected):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ # Must be false for multi-head output to be different from
+ # first input's last dim
+ use_query_residual=use_query_residual,
+ output_last_dim=output_last_dim)
+
+ q_tensor = tf.zeros([2, 4, q_tensor_last_dim], dtype=tf.float32)
+ kv_tensor = tf.zeros([2, 8, 32], dtype=tf.float32)
+ dummy_mask = tf.zeros([2, 4, 8], dtype=tf.float32)
+ output = test_layer([q_tensor, kv_tensor, dummy_mask])
+
+ self.assertEqual(output.numpy().shape[-1], expected)
+
+ @parameterized.named_parameters(('value_dim_is_none', None, 128, 2, 128 // 2),
+ ('value_dim_is_not_none', 30, 128, 2, 30))
+ def test_value_dim(self, value_dim, q_tensor_last_dim,
+ some_num_attention_heads, expected):
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ value_dim=value_dim)
+
+ q_tensor = tf.zeros([2, 4, q_tensor_last_dim], dtype=tf.float32)
+ kv_tensor = tf.zeros([2, 8, 32], dtype=tf.float32)
+ dummy_mask = tf.zeros([2, 4, 8], dtype=tf.float32)
+ test_layer([q_tensor, kv_tensor, dummy_mask])
+
+ self.assertEqual(expected,
+ test_layer._attention_layer.get_config()['value_dim'])
+
+
@keras_parameterized.run_all_keras_modes
class TransformerArgumentTest(keras_parameterized.TestCase):
@@ -277,6 +432,138 @@ class TransformerArgumentTest(keras_parameterized.TestCase):
output = encoder_block(inputs)
self.assertEqual(output.shape, (2, 4, hidden_size))
+ def test_norm_first_false_and_diff_q_kv_att_layer_norm_true_raises(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ with self.assertRaises(ValueError):
+ TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ norm_first=False,
+ diff_q_kv_att_layer_norm=True)
+
+ def test_diff_q_kv_att_layer_norm_is_part_of_config_1(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ norm_first=False)
+ self.assertIn('diff_q_kv_att_layer_norm', encoder.get_config())
+ self.assertFalse(encoder.get_config()['diff_q_kv_att_layer_norm'])
+
+ def test_diff_q_kv_att_layer_norm_is_part_of_config_2(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ norm_first=True,
+ diff_q_kv_att_layer_norm=True)
+ self.assertIn('diff_q_kv_att_layer_norm', encoder.get_config())
+ self.assertTrue(encoder.get_config()['diff_q_kv_att_layer_norm'])
+
+ def test_use_query_residual_is_part_of_config_1(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation)
+ self.assertIn('use_query_residual', encoder.get_config())
+ self.assertTrue(encoder.get_config()['use_query_residual'])
+
+ def test_use_query_residual_is_part_of_config_2(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ use_query_residual=False)
+ self.assertIn('use_query_residual', encoder.get_config())
+ self.assertFalse(encoder.get_config()['use_query_residual'])
+
+ def test_key_dim_is_part_of_config_1(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation)
+ self.assertIn('key_dim', encoder.get_config())
+ self.assertIsNone(encoder.get_config()['key_dim'])
+
+ def test_key_dim_is_part_of_config_2(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ key_dim = 10
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ key_dim=key_dim)
+ self.assertIn('key_dim', encoder.get_config())
+ self.assertEqual(key_dim, encoder.get_config()['key_dim'])
+
+ def test_value_dim_is_part_of_config_1(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation)
+ self.assertIn('value_dim', encoder.get_config())
+ self.assertIsNone(encoder.get_config()['value_dim'])
+
+ def test_value_dim_is_part_of_config_2(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ value_dim = 10
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ value_dim=value_dim)
+ self.assertIn('value_dim', encoder.get_config())
+ self.assertEqual(value_dim, encoder.get_config()['value_dim'])
+
+ def test_output_last_dim_is_part_of_config_1(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation)
+ self.assertIn('output_last_dim', encoder.get_config())
+ self.assertIsNone(encoder.get_config()['output_last_dim'])
+
+ def test_output_last_dim_is_part_of_config_2(self):
+ some_num_attention_heads = 2
+ some_inner_dim = 32
+ some_inner_activation = 'relu'
+ output_last_dim = 10
+ encoder = TransformerEncoderBlock(
+ num_attention_heads=some_num_attention_heads,
+ inner_dim=some_inner_dim,
+ inner_activation=some_inner_activation,
+ output_last_dim=output_last_dim)
+ self.assertIn('output_last_dim', encoder.get_config())
+ self.assertEqual(output_last_dim, encoder.get_config()['output_last_dim'])
+
def test_get_config(self):
num_attention_heads = 2
encoder_block = TransformerEncoderBlock(
@@ -290,7 +577,12 @@ class TransformerArgumentTest(keras_parameterized.TestCase):
norm_epsilon=1e-6,
inner_dropout=0.1,
attention_initializer=tf.keras.initializers.RandomUniform(
- minval=0., maxval=1.))
+ minval=0., maxval=1.),
+ use_query_residual=False,
+ key_dim=20,
+ value_dim=30,
+ output_last_dim=40,
+ diff_q_kv_att_layer_norm=True)
encoder_block_config = encoder_block.get_config()
new_encoder_block = TransformerEncoderBlock.from_config(
encoder_block_config)
@@ -319,6 +611,88 @@ class TransformerArgumentTest(keras_parameterized.TestCase):
# The default output of a transformer layer should be the same as the input.
self.assertEqual(data_tensor.shape.as_list(), output_tensor.shape.as_list())
+ @parameterized.parameters(
+ {
+ 'output_dropout': 0.1,
+ 'attention_dropout': 0.2,
+ 'inner_dropout': 0.3
+ }, {
+ 'output_dropout': 0.0,
+ 'attention_dropout': 0.2,
+ 'inner_dropout': 0.3
+ }, {
+ 'output_dropout': 0.1,
+ 'attention_dropout': 0.0,
+ 'inner_dropout': 0.3
+ }, {
+ 'output_dropout': 0.1,
+ 'attention_dropout': 0.2,
+ 'inner_dropout': 0.0
+ })
+ def test_dropout_config(self, output_dropout, attention_dropout,
+ inner_dropout):
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=2,
+ inner_dim=32,
+ inner_activation='relu',
+ output_dropout=output_dropout,
+ attention_dropout=attention_dropout,
+ inner_dropout=inner_dropout)
+ seq_len = 21
+ hidden_size = 512
+ input_tensor = tf.keras.Input(shape=(seq_len, hidden_size))
+ _ = test_layer(input_tensor)
+
+ true_output_dropout = test_layer._output_dropout.get_config()['rate']
+ true_attention_dropout = test_layer._attention_dropout.get_config()['rate']
+ true_inner_dropout = test_layer._inner_dropout_layer.get_config()['rate']
+ self.assertEqual(true_output_dropout, output_dropout)
+ self.assertEqual(true_attention_dropout, attention_dropout)
+ self.assertEqual(true_inner_dropout, inner_dropout)
+
+ @parameterized.named_parameters(
+ (
+ 'return_attention_scores_is_false',
+ False,
+ ),
+ (
+ 'return_attention_scores_is_true',
+ True,
+ ),
+ )
+ def test_return_attention_scores(self, return_attention_scores):
+ num_attention_heads = 7
+ sequence_length = 21
+ width = 80
+
+ test_layer = TransformerEncoderBlock(
+ num_attention_heads=num_attention_heads,
+ inner_dim=2048,
+ inner_activation='relu',
+ return_attention_scores=return_attention_scores)
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+
+ expected_layer_output_shape = [None, sequence_length, width]
+ expected_attention_scores_shape = [
+ None, num_attention_heads, sequence_length, sequence_length
+ ]
+
+ if return_attention_scores:
+ self.assertIsInstance(output_tensor, tuple)
+ self.assertEqual(len(output_tensor), 2)
+ # First is the standard output.
+ self.assertEqual(output_tensor[0].shape.as_list(),
+ expected_layer_output_shape)
+ # Second is the attention scores.
+ self.assertEqual(output_tensor[1].shape.as_list(),
+ expected_attention_scores_shape)
+ else:
+ # Only the standard layer output.
+ self.assertEqual(output_tensor.shape.as_list(),
+ expected_layer_output_shape)
+
if __name__ == '__main__':
tf.test.main()
diff --git a/official/nlp/modeling/layers/transformer_scaffold.py b/official/nlp/modeling/layers/transformer_scaffold.py
index 4f6de71ceafe5b40442ae68c9bffb2e90cfa7c5b..6b46a4b8123c24495b888f0cd3245c50615c4aec 100644
--- a/official/nlp/modeling/layers/transformer_scaffold.py
+++ b/official/nlp/modeling/layers/transformer_scaffold.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,7 +19,9 @@ from absl import logging
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers import attention
+from official.nlp.modeling.layers import util
@tf.keras.utils.register_keras_serializable(package="Text")
@@ -37,8 +39,10 @@ class TransformerScaffold(tf.keras.layers.Layer):
Args:
num_attention_heads: Number of attention heads.
- intermediate_size: Size of the intermediate layer.
- intermediate_activation: Activation for the intermediate layer.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network.
attention_cls: A class to instantiate attention layer, or a layer instance.
attention_cfg: The config with which to instantiate `attention_cls`. Ignored
if attention_cls is a layer instance or None. If `attention_cls` is a
@@ -58,8 +62,8 @@ class TransformerScaffold(tf.keras.layers.Layer):
Ignored if feedforward_cls is a layer instance or is None. If
`feedforward_cls` is a class, but `feedforward_cfg` is None, following
kwargs will be used to instantiate the feedforward instance: {
- "intermediate_size": intermediate_size,
- "intermediate_activation": intermediate_activation,
+ "inner_dim": inner_dim,
+ "inner_activation": inner_activation,
"dropout": dropout_rate,
"name": "feedforward" }.
dropout_rate: Dropout probability for the post-attention and output dropout.
@@ -75,8 +79,8 @@ class TransformerScaffold(tf.keras.layers.Layer):
def __init__(self,
num_attention_heads,
- intermediate_size,
- intermediate_activation,
+ inner_dim=768,
+ inner_activation=tf_utils.get_activation("gelu"),
attention_cls=attention.MultiHeadAttention,
attention_cfg=None,
feedforward_cls=None,
@@ -92,7 +96,10 @@ class TransformerScaffold(tf.keras.layers.Layer):
kernel_constraint=None,
bias_constraint=None,
**kwargs):
- super(TransformerScaffold, self).__init__(**kwargs)
+ inner_dim = kwargs.pop("intermediate_size", inner_dim)
+ inner_activation = kwargs.pop("inner_activation", inner_activation)
+ util.filter_kwargs(kwargs)
+ super().__init__(**kwargs)
self._attention_cfg = attention_cfg
self._attention_cls = attention_cls
@@ -100,8 +107,8 @@ class TransformerScaffold(tf.keras.layers.Layer):
self._feedforward_cfg = feedforward_cfg
self._norm_first = norm_first
self._num_heads = num_attention_heads
- self._intermediate_size = intermediate_size
- self._intermediate_activation = intermediate_activation
+ self._inner_dim = inner_dim
+ self._inner_activation = inner_activation
self._attention_dropout_rate = attention_dropout_rate
self._dropout_rate = dropout_rate
self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
@@ -112,9 +119,15 @@ class TransformerScaffold(tf.keras.layers.Layer):
self._bias_constraint = tf.keras.constraints.get(bias_constraint)
def build(self, input_shape):
- input_tensor_shape = input_shape[0] if (
- len(input_shape) == 2) else input_shape
- input_tensor_shape = tf.TensorShape(input_tensor_shape)
+ if isinstance(input_shape, tf.TensorShape):
+ input_tensor_shape = input_shape
+ elif isinstance(input_shape, (list, tuple)):
+ input_tensor_shape = tf.TensorShape(input_shape[0])
+ else:
+ raise ValueError(
+ "The type of input shape argument is not supported, got: %s" %
+ type(input_shape))
+
if len(input_tensor_shape.as_list()) != 3:
raise ValueError(
"TransformerScaffold expects a three-dimensional input of "
@@ -127,8 +140,6 @@ class TransformerScaffold(tf.keras.layers.Layer):
self._attention_head_size = int(hidden_size // self._num_heads)
common_kwargs = dict(
- kernel_initializer=self._kernel_initializer,
- bias_initializer=self._bias_initializer,
kernel_regularizer=self._kernel_regularizer,
bias_regularizer=self._bias_regularizer,
activity_regularizer=self._activity_regularizer,
@@ -145,6 +156,9 @@ class TransformerScaffold(tf.keras.layers.Layer):
return instance_or_cls(**config)
default_attention_cfg = {
+ "kernel_initializer": tf_utils.clone_initializer(
+ self._kernel_initializer),
+ "bias_initializer": tf_utils.clone_initializer(self._bias_initializer),
"num_heads": self._num_heads,
"key_dim": self._attention_head_size,
"dropout": self._attention_dropout_rate,
@@ -158,8 +172,15 @@ class TransformerScaffold(tf.keras.layers.Layer):
if self._feedforward_cls is not None:
default_feedforward_cfg = {
- "intermediate_size": self._intermediate_size,
- "intermediate_activation": self._intermediate_activation,
+ "kernel_initializer": tf_utils.clone_initializer(
+ self._kernel_initializer),
+ "bias_initializer": tf_utils.clone_initializer(
+ self._bias_initializer),
+ "inner_dim": self._inner_dim,
+ "inner_activation": self._inner_activation,
+ # TODO(hongkuny): try to update all ffn block args.
+ "intermediate_size": self._inner_dim,
+ "intermediate_activation": self._inner_activation,
"dropout": self._dropout_rate,
"name": "feedforward",
}
@@ -184,11 +205,14 @@ class TransformerScaffold(tf.keras.layers.Layer):
dtype=tf.float32))
if self._feedforward_block is None:
- self._intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
- output_shape=(None, self._intermediate_size),
+ output_shape=(None, self._inner_dim),
bias_axes="d",
name="intermediate",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
policy = tf.keras.mixed_precision.global_policy()
if policy.name == "mixed_bfloat16":
@@ -197,12 +221,15 @@ class TransformerScaffold(tf.keras.layers.Layer):
# TODO(b/154538392): Investigate this.
policy = tf.float32
self._intermediate_activation_layer = tf.keras.layers.Activation(
- self._intermediate_activation, dtype=policy)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._inner_activation, dtype=policy)
+ self._output_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
name="output",
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ bias_initializer=tf_utils.clone_initializer(self._bias_initializer),
**common_kwargs)
self._output_dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
@@ -210,7 +237,7 @@ class TransformerScaffold(tf.keras.layers.Layer):
self._output_layer_norm = tf.keras.layers.LayerNormalization(
name="output_layer_norm", axis=-1, epsilon=1e-12, dtype=tf.float32)
- super(TransformerScaffold, self).build(input_shape)
+ super().build(input_shape)
logging.info("%s configs: %s", self.__class__.__name__, self.get_config())
def get_config(self):
@@ -221,10 +248,10 @@ class TransformerScaffold(tf.keras.layers.Layer):
self._feedforward_block,
"num_attention_heads":
self._num_heads,
- "intermediate_size":
- self._intermediate_size,
- "intermediate_activation":
- self._intermediate_activation,
+ "inner_dim":
+ self._inner_dim,
+ "inner_activation":
+ self._inner_activation,
"dropout_rate":
self._dropout_rate,
"attention_dropout_rate":
@@ -246,21 +273,31 @@ class TransformerScaffold(tf.keras.layers.Layer):
"bias_constraint":
tf.keras.constraints.serialize(self._bias_constraint)
}
- base_config = super(TransformerScaffold, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def call(self, inputs, training=None):
- if isinstance(inputs, (list, tuple)) and len(inputs) == 2:
- input_tensor, attention_mask = inputs
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError("Unexpected inputs to %s with length at %d" %
+ (self.__class__, len(inputs)))
else:
- input_tensor, attention_mask = (inputs, None)
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ if key_value is None:
+ key_value = input_tensor
if self._norm_first:
source_tensor = input_tensor
input_tensor = self._attention_layer_norm(input_tensor, training=training)
attention_output = self._attention_layer(
- query=input_tensor, value=input_tensor, attention_mask=attention_mask,
+ query=input_tensor, value=key_value, attention_mask=attention_mask,
training=training)
attention_output = self._attention_dropout(attention_output,
training=training)
@@ -298,7 +335,9 @@ class TransformerScaffold(tf.keras.layers.Layer):
training=training)
layer_output += source_attention_output
else:
- # if not norm_first, assume that the feedforwad does apply layer norm
+ # Attention: if not norm_first, assume that the feedforwad does apply
+ # layer norm. The feedford also apply residual connection. Please
+ # read the `GatedFeedforward` as a concrete example.
layer_output = self._feedforward_block(attention_output,
training=training)
diff --git a/official/nlp/modeling/layers/transformer_scaffold_test.py b/official/nlp/modeling/layers/transformer_scaffold_test.py
index 5267a27efd627e3418ab76526505ec2b4617147d..d72cbf0ff716b1d4f7b38e15d3b28c3f48db9b99 100644
--- a/official/nlp/modeling/layers/transformer_scaffold_test.py
+++ b/official/nlp/modeling/layers/transformer_scaffold_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -58,7 +58,7 @@ class ValidatedFeedforwardLayer(tf.keras.layers.Layer):
def build(self, input_shape):
hidden_size = input_shape.as_list()[-1]
- self._feedforward_dense = tf.keras.layers.experimental.EinsumDense(
+ self._feedforward_dense = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
@@ -99,8 +99,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -134,8 +134,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
feedforward_cls=ValidatedFeedforwardLayer,
feedforward_cfg=feedforward_layer_cfg,
num_attention_heads=10,
- intermediate_size=None,
- intermediate_activation=None)
+ inner_dim=None,
+ inner_activation=None)
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -165,8 +165,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -194,8 +194,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -236,8 +236,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cfg=attention_layer_cfg,
feedforward_cls=feedforward_layer,
num_attention_heads=10,
- intermediate_size=None,
- intermediate_activation=None)
+ inner_dim=None,
+ inner_activation=None)
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -280,8 +280,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -322,8 +322,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -363,8 +363,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu',
+ inner_dim=2048,
+ inner_activation='relu',
kernel_initializer=tf.keras.initializers.TruncatedNormal(stddev=0.02))
# Create a 3-dimensional input (the first dimension is implicit).
@@ -392,8 +392,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
attention_cls=ValidatedAttentionLayer,
attention_cfg=attention_layer_cfg,
num_attention_heads=10,
- intermediate_size=2048,
- intermediate_activation='relu')
+ inner_dim=2048,
+ inner_activation='relu')
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
@@ -458,8 +458,8 @@ class TransformerLayerTest(keras_parameterized.TestCase):
feedforward_cls=ValidatedFeedforwardLayer,
feedforward_cfg=feedforward_layer_cfg,
num_attention_heads=10,
- intermediate_size=None,
- intermediate_activation=None)
+ inner_dim=None,
+ inner_activation=None)
# Create a 3-dimensional input (the first dimension is implicit).
data_tensor = tf.keras.Input(shape=(sequence_length, width))
diff --git a/official/nlp/modeling/layers/transformer_test.py b/official/nlp/modeling/layers/transformer_test.py
index 0c6c472ec4dfc643450b2d584ce3fdb3f34dffa5..8ee11b9196f6be20cadd22b477d7535740b4207f 100644
--- a/official/nlp/modeling/layers/transformer_test.py
+++ b/official/nlp/modeling/layers/transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/transformer_xl.py b/official/nlp/modeling/layers/transformer_xl.py
index 748957398c923bf0069d7ad0f41c486b9c8ac947..462d80c25341f489840b9a6969ba94565a1c32ab 100644
--- a/official/nlp/modeling/layers/transformer_xl.py
+++ b/official/nlp/modeling/layers/transformer_xl.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,7 @@ from absl import logging
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling.layers import relative_attention
@@ -102,7 +103,7 @@ class TransformerXLBlock(tf.keras.layers.Layer):
**kwargs):
"""Initializes TransformerXLBlock layer."""
- super(TransformerXLBlock, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._vocab_size = vocab_size
self._num_heads = num_attention_heads
self._head_size = head_size
@@ -148,7 +149,7 @@ class TransformerXLBlock(tf.keras.layers.Layer):
value_dim=self._head_size,
dropout=self._attention_dropout_rate,
use_bias=False,
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
name="rel_attn")
self._attention_dropout = tf.keras.layers.Dropout(
rate=self._attention_dropout_rate)
@@ -157,30 +158,30 @@ class TransformerXLBlock(tf.keras.layers.Layer):
axis=-1,
epsilon=self._norm_epsilon,
dtype=tf.float32)
- self._inner_dense = tf.keras.layers.experimental.EinsumDense(
+ self._inner_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, self._inner_size),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
name="inner")
self._inner_activation_layer = tf.keras.layers.Activation(
self._inner_activation)
self._inner_dropout_layer = tf.keras.layers.Dropout(
rate=self._inner_dropout)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._output_dense = tf.keras.layers.EinsumDense(
"abc,cd->abd",
output_shape=(None, hidden_size),
bias_axes="d",
name="output",
- kernel_initializer=self._kernel_initializer)
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer))
self._output_dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
self._output_layer_norm = tf.keras.layers.LayerNormalization(
name="output_layer_norm",
axis=-1,
epsilon=self._norm_epsilon)
- super(TransformerXLBlock, self).build(input_shape)
+ super().build(input_shape)
def get_config(self):
config = {
@@ -209,7 +210,7 @@ class TransformerXLBlock(tf.keras.layers.Layer):
"inner_dropout":
self._inner_dropout,
}
- base_config = super(TransformerXLBlock, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def call(self,
@@ -370,7 +371,7 @@ class TransformerXL(tf.keras.layers.Layer):
inner_activation="relu",
**kwargs):
"""Initializes TransformerXL."""
- super(TransformerXL, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._vocab_size = vocab_size
self._initializer = initializer
@@ -398,17 +399,17 @@ class TransformerXL(tf.keras.layers.Layer):
"content_attention_bias",
shape=attention_bias_shape,
dtype=tf.float32,
- initializer=self._initializer)
+ initializer=tf_utils.clone_initializer(self._initializer))
self.positional_attention_bias = self.add_weight(
"positional_attention_bias",
shape=attention_bias_shape,
dtype=tf.float32,
- initializer=self._initializer)
+ initializer=tf_utils.clone_initializer(self._initializer))
self.segment_attention_bias = self.add_weight(
"segment_attention_bias",
shape=attention_bias_shape,
dtype=tf.float32,
- initializer=self._initializer)
+ initializer=tf_utils.clone_initializer(self._initializer))
self.transformer_xl_layers = []
for i in range(self._num_layers):
@@ -460,7 +461,7 @@ class TransformerXL(tf.keras.layers.Layer):
"inner_activation":
self._inner_activation,
}
- base_config = super(TransformerXL, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def call(self,
diff --git a/official/nlp/modeling/layers/transformer_xl_test.py b/official/nlp/modeling/layers/transformer_xl_test.py
index 94945c962a0a1e897340770005b6c9678e28a050..375d96ec8ff15f8caad4cfdc826978c9fc4f84b8 100644
--- a/official/nlp/modeling/layers/transformer_xl_test.py
+++ b/official/nlp/modeling/layers/transformer_xl_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/layers/util.py b/official/nlp/modeling/layers/util.py
index d9562e24d47ffe8aada5602115b3cb894fdcabd7..a3a7820712ab1dd1283c2a6219f32191a5ec13c5 100644
--- a/official/nlp/modeling/layers/util.py
+++ b/official/nlp/modeling/layers/util.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/losses/__init__.py b/official/nlp/modeling/losses/__init__.py
index cdd2c29f1b50d965af0202b86e2b0cf34e679315..2cb70ee5e5a50116dfae4312c06e6c1717cbec23 100644
--- a/official/nlp/modeling/losses/__init__.py
+++ b/official/nlp/modeling/losses/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy.py b/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy.py
index d777800c611cb83ae5a04c2394ce89cecef50e51..81c9b38c544c4787e17e6ef9fcbd79a8cc6665ff 100644
--- a/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy.py
+++ b/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy_test.py b/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy_test.py
index f890d5b7e35c8dd50747554dcf99dd752449c890..3acab53394bd00e7cf1b7d28bbef66eae08ab341 100644
--- a/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy_test.py
+++ b/official/nlp/modeling/losses/weighted_sparse_categorical_crossentropy_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/__init__.py b/official/nlp/modeling/models/__init__.py
index 456d06629f4a43da39b2bfa1fb5e6707b54b7787..afe28858b0bf739fb6c268cbe0f3ed4827c37458 100644
--- a/official/nlp/modeling/models/__init__.py
+++ b/official/nlp/modeling/models/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_classifier.py b/official/nlp/modeling/models/bert_classifier.py
index 72a29b24ad010fc0540f39383cac340f1dfecd9b..105f00497a07fb1f3a7df836f20a40658b8fa4d0 100644
--- a/official/nlp/modeling/models/bert_classifier.py
+++ b/official/nlp/modeling/models/bert_classifier.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_classifier_test.py b/official/nlp/modeling/models/bert_classifier_test.py
index 52d3157827eb9670e6b54a0d6d0c74e88905701b..98c4d8287f2eaca7ab0fa95b701589b5957f6312 100644
--- a/official/nlp/modeling/models/bert_classifier_test.py
+++ b/official/nlp/modeling/models/bert_classifier_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_pretrainer.py b/official/nlp/modeling/models/bert_pretrainer.py
index dc75da76d937858c70d06337cff945455396af6d..f9bdf7ac6a14fc72e00b18cfc203ce7d626bf559 100644
--- a/official/nlp/modeling/models/bert_pretrainer.py
+++ b/official/nlp/modeling/models/bert_pretrainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,6 +22,7 @@ from absl import logging
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
from official.nlp.modeling import networks
@@ -102,7 +103,7 @@ class BertPretrainer(tf.keras.Model):
masked_lm = layers.MaskedLM(
embedding_table=embedding_table,
activation=activation,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
output=output,
name='cls/predictions')
lm_outputs = masked_lm(
@@ -111,7 +112,7 @@ class BertPretrainer(tf.keras.Model):
classification = networks.Classification(
input_width=cls_output.shape[-1],
num_classes=num_classes,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
output=output,
name='classification')
sentence_outputs = classification(cls_output)
@@ -199,6 +200,7 @@ class BertPretrainerV2(tf.keras.Model):
self._config = {
'encoder_network': encoder_network,
'mlm_initializer': mlm_initializer,
+ 'mlm_activation': mlm_activation,
'classification_heads': classification_heads,
'name': name,
}
diff --git a/official/nlp/modeling/models/bert_pretrainer_test.py b/official/nlp/modeling/models/bert_pretrainer_test.py
index 152dce89d3efec8a9f949559b64d5f13aafad780..869777372215ed7eac8877d71597e8936cea4672 100644
--- a/official/nlp/modeling/models/bert_pretrainer_test.py
+++ b/official/nlp/modeling/models/bert_pretrainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_span_labeler.py b/official/nlp/modeling/models/bert_span_labeler.py
index a444ebbf9cc3839693daa0dc3c8bc097e7397c41..5edc62967b8414a5ae3f8f0b09e647ad2fc85f1a 100644
--- a/official/nlp/modeling/models/bert_span_labeler.py
+++ b/official/nlp/modeling/models/bert_span_labeler.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_span_labeler_test.py b/official/nlp/modeling/models/bert_span_labeler_test.py
index 59d0e256c921d8ece1396a71e7c5d6ca30f8055a..9f9da14c30f7eeaf7bbc90299a905af0d353d698 100644
--- a/official/nlp/modeling/models/bert_span_labeler_test.py
+++ b/official/nlp/modeling/models/bert_span_labeler_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_token_classifier.py b/official/nlp/modeling/models/bert_token_classifier.py
index 340d92fd662103393514415489e22c8d5dac0d76..6375aa4b61c58a836f54d01e7a99a4e2dfe399c9 100644
--- a/official/nlp/modeling/models/bert_token_classifier.py
+++ b/official/nlp/modeling/models/bert_token_classifier.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/bert_token_classifier_test.py b/official/nlp/modeling/models/bert_token_classifier_test.py
index 8af0897638d850a25590b475ae7be65365271343..83765f5fed5e76efd3a7d1822e92b069ec800d2a 100644
--- a/official/nlp/modeling/models/bert_token_classifier_test.py
+++ b/official/nlp/modeling/models/bert_token_classifier_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/dual_encoder.py b/official/nlp/modeling/models/dual_encoder.py
index 7fa496e89623c88866b2183b39ba67fb4c4e156b..b5b948c11a1a65d4f57ef4263c43caa64abdac0b 100644
--- a/official/nlp/modeling/models/dual_encoder.py
+++ b/official/nlp/modeling/models/dual_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/dual_encoder_test.py b/official/nlp/modeling/models/dual_encoder_test.py
index 30d3d4793554ac16426de31bd635aefb8c1525fe..699277966d294b059f8d94b7f0a79564a51fb222 100644
--- a/official/nlp/modeling/models/dual_encoder_test.py
+++ b/official/nlp/modeling/models/dual_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/electra_pretrainer.py b/official/nlp/modeling/models/electra_pretrainer.py
index dcbbc552175625455edb0395a686d2a254419ddc..19db3cc04063608729aeb730894df67e4bf05f8e 100644
--- a/official/nlp/modeling/models/electra_pretrainer.py
+++ b/official/nlp/modeling/models/electra_pretrainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -96,21 +96,22 @@ class ElectraPretrainer(tf.keras.Model):
self.masked_lm = layers.MaskedLM(
embedding_table=generator_network.get_embedding_table(),
activation=mlm_activation,
- initializer=mlm_initializer,
+ initializer=tf_utils.clone_initializer(mlm_initializer),
output=output_type,
name='generator_masked_lm')
self.classification = layers.ClassificationHead(
inner_dim=generator_network.get_config()['hidden_size'],
num_classes=num_classes,
- initializer=mlm_initializer,
+ initializer=tf_utils.clone_initializer(mlm_initializer),
name='generator_classification_head')
self.discriminator_projection = tf.keras.layers.Dense(
units=discriminator_network.get_config()['hidden_size'],
activation=mlm_activation,
- kernel_initializer=mlm_initializer,
+ kernel_initializer=tf_utils.clone_initializer(mlm_initializer),
name='discriminator_projection_head')
self.discriminator_head = tf.keras.layers.Dense(
- units=1, kernel_initializer=mlm_initializer)
+ units=1,
+ kernel_initializer=tf_utils.clone_initializer(mlm_initializer))
def call(self, inputs):
"""ELECTRA forward pass.
diff --git a/official/nlp/modeling/models/electra_pretrainer_test.py b/official/nlp/modeling/models/electra_pretrainer_test.py
index d5d44fa49d005720a13a6752c6af119e99709d31..23864934993ce269c38cb91dd01e64e2d0eae3b7 100644
--- a/official/nlp/modeling/models/electra_pretrainer_test.py
+++ b/official/nlp/modeling/models/electra_pretrainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/seq2seq_transformer.py b/official/nlp/modeling/models/seq2seq_transformer.py
index 3ec765f7afce40f90b4ca3d61340afe4d0fd22bd..d33e690250ed88a72432f4dece04364f5fa703e4 100644
--- a/official/nlp/modeling/models/seq2seq_transformer.py
+++ b/official/nlp/modeling/models/seq2seq_transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/seq2seq_transformer_test.py b/official/nlp/modeling/models/seq2seq_transformer_test.py
index 85e7672fc556d982fc907f5592ed0a785560fafc..f45f5f3cef669b1200354e8216bbe6c408cbe123 100644
--- a/official/nlp/modeling/models/seq2seq_transformer_test.py
+++ b/official/nlp/modeling/models/seq2seq_transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/t5.py b/official/nlp/modeling/models/t5.py
index 61f90971044581f4bd03b5293151b515c4dea209..acd7fc648ddfad83f114885484fad6c5f7fc991f 100644
--- a/official/nlp/modeling/models/t5.py
+++ b/official/nlp/modeling/models/t5.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -55,6 +55,7 @@ class Module(tf.Module):
initializer: Initializer,
dtype: tf.DType = tf.float32,
**kwargs):
+ initializer = tf_utils.clone_initializer(initializer)
return tf.Variable(initializer(shape, dtype=dtype, **kwargs), name=name)
def read_variable(self,
@@ -588,7 +589,8 @@ class MultiHeadAttention(Module):
init_std_rescaling = tf.math.sqrt(tf.cast(self.d_kv, dtype=self.dtype))
query_w_init = (
lambda *args, **kwargs: ( # pylint: disable=g-long-lambda
- weight_initializer(*args, **kwargs) / init_std_rescaling))
+ tf_utils.clone_initializer(weight_initializer)(
+ *args, **kwargs) / init_std_rescaling))
self.q = Linear3D(
self.d_model,
self.d_kv,
@@ -1004,6 +1006,7 @@ class T5TransformerParams:
num_heads: int
d_ff: int
vocab_size: int
+ target_vocab_size: Optional[int] = None
dropout_rate: float = 0.0
layer_norm_epsilon: float = 1e-6
shared_embedding: bool = False
@@ -1020,6 +1023,9 @@ class T5TransformerParams:
num_decoder_layers: Optional[int] = None
one_hot_embedding: bool = True
layer_sharing: bool = False
+ # If true, uses one relative embedding for all encoder layers and one for all
+ # decoder layers. Otherwise, have relative embedding for each layer.
+ use_shared_relative_position_bias: bool = True
class Encoder(Module):
@@ -1048,17 +1054,34 @@ class Encoder(Module):
self.input_embed = shared_embedding
# Creates an alias to the input embed for encoder-only models.
self.word_embed = self.input_embed
- self.relative_embedding = RelativePositionEmbedding(
- num_heads=self.config.num_heads,
- relative_attention_num_buckets=self.config
- .relative_attention_num_buckets,
- relative_attention_max_distance=self.config
- .relative_attention_max_distance,
- bidirectional=self.config.bidirectional,
- embeddings_initializer=self.config.relative_embeddings_initializer,
- dtype=self.dtype,
- compute_dtype=self.compute_dtype,
- name="relative_posemb")
+ if config.use_shared_relative_position_bias:
+ self.relative_embedding = RelativePositionEmbedding(
+ num_heads=self.config.num_heads,
+ relative_attention_num_buckets=self.config
+ .relative_attention_num_buckets,
+ relative_attention_max_distance=self.config
+ .relative_attention_max_distance,
+ bidirectional=self.config.bidirectional,
+ embeddings_initializer=self.config.relative_embeddings_initializer,
+ dtype=self.dtype,
+ compute_dtype=self.compute_dtype,
+ name="relative_posemb")
+ else:
+ self.relative_embeddings = []
+ for layer_idx in range(self.config.num_layers):
+ relative_embedding = RelativePositionEmbedding(
+ num_heads=self.config.num_heads,
+ relative_attention_num_buckets=self.config
+ .relative_attention_num_buckets,
+ relative_attention_max_distance=self.config
+ .relative_attention_max_distance,
+ bidirectional=self.config.bidirectional,
+ embeddings_initializer=self.config
+ .relative_embeddings_initializer,
+ dtype=self.dtype,
+ compute_dtype=self.compute_dtype,
+ name=f"relative_posemb_{layer_idx}")
+ self.relative_embeddings.append(relative_embedding)
self.input_dropout = Dropout(self.config.dropout_rate,)
self.encoder_layers = []
for layer_idx in range(self.config.num_layers):
@@ -1086,12 +1109,38 @@ class Encoder(Module):
self.output_dropout = Dropout(self.config.dropout_rate,)
@tf.Module.with_name_scope
- def __call__(self, inputs, encoder_mask=None, training=False):
+ def get_relpos_bias(self,
+ input_length: int,
+ dense_inputs: tf.Tensor,
+ layer_idx: Optional[int] = None) -> tf.Tensor:
+ if self.config.use_shared_relative_position_bias:
+ position_bias = self.relative_embedding(input_length, input_length)
+ else:
+ position_bias = self.relative_embeddings[layer_idx](input_length,
+ input_length)
+ if dense_inputs is not None:
+ # Here we ignore relative position bias for dense embeddings.
+ # TODO(yejiayu): If we proceed to video use cases, rework this part.
+ dense_input_length = tf_utils.get_shape_list(dense_inputs)[1]
+ # Position bias shape: [batch, 1, len, len]
+ paddings = tf.constant([[0, 0], [0, 0], [0, dense_input_length],
+ [0, dense_input_length]])
+ position_bias = tf.pad(position_bias, paddings, "CONSTANT")
+ return position_bias
+
+ @tf.Module.with_name_scope
+ def __call__(self,
+ inputs=None,
+ encoder_mask=None,
+ dense_inputs=None,
+ training=False):
"""Applies Transformer model on the inputs.
Args:
- inputs: input data
+ inputs: input word ids. Optional if dense data are provided.
encoder_mask: the encoder self-attention mask.
+ dense_inputs: dense input data. Concat after the embedding if word ids
+ are provided.
training: whether it is training pass, affecting dropouts.
Returns:
@@ -1101,14 +1150,26 @@ class Encoder(Module):
if encoder_mask is not None:
encoder_mask = tf.cast(encoder_mask, self.compute_dtype)
cfg = self.config
- x = self.input_embed(inputs, one_hot=cfg.one_hot_embedding)
+ inputs_array = []
+ if inputs is not None:
+ inputs_array.append(
+ self.input_embed(inputs, one_hot=cfg.one_hot_embedding))
+ if dense_inputs is not None:
+ inputs_array.append(dense_inputs)
+ if not inputs_array:
+ raise ValueError("At least one of inputs and dense_inputs must not be "
+ "None.")
+ x = tf.concat(inputs_array, axis=1)
tensor_shape = tf_utils.get_shape_list(x)
tensor_shape[-2] = 1
x = self.input_dropout(x, noise_shape=tensor_shape, training=training)
- input_length = tf_utils.get_shape_list(inputs)[1]
- position_bias = self.relative_embedding(input_length, input_length)
+ if inputs is not None:
+ input_length = tf_utils.get_shape_list(inputs)[1]
+ else:
+ input_length = 0
for i in range(cfg.num_layers):
+ position_bias = self.get_relpos_bias(input_length, dense_inputs, i)
x = self.encoder_layers[i](
x,
attention_mask=encoder_mask,
@@ -1133,11 +1194,15 @@ class Decoder(Module):
self.compute_dtype = compute_dtype
if self.config.num_decoder_layers is None:
self.config.num_decoder_layers = self.config.num_layers
+ if not hasattr(
+ self.config,
+ "target_vocab_size") or self.config.target_vocab_size is None:
+ self.config.target_vocab_size = self.config.vocab_size
with self.name_scope:
# Target Embedding.
if shared_embedding is None:
self.target_embed = Embed(
- vocab_size=self.config.vocab_size,
+ vocab_size=self.config.target_vocab_size,
features=self.config.d_model,
embeddings_initializer=self.config.vocab_embeddings_initializer,
dtype=self.dtype,
@@ -1147,17 +1212,34 @@ class Decoder(Module):
self.target_embed = shared_embedding
self.target_dropout = Dropout(self.config.dropout_rate,)
# Position bias for the target self attention.
- self.relative_embedding = RelativePositionEmbedding(
- num_heads=self.config.num_heads,
- relative_attention_num_buckets=self.config
- .relative_attention_num_buckets,
- relative_attention_max_distance=self.config
- .relative_attention_max_distance,
- bidirectional=self.config.bidirectional,
- embeddings_initializer=self.config.relative_embeddings_initializer,
- dtype=self.dtype,
- compute_dtype=self.compute_dtype,
- name="relative_posemb")
+ if config.use_shared_relative_position_bias:
+ self.relative_embedding = RelativePositionEmbedding(
+ num_heads=self.config.num_heads,
+ relative_attention_num_buckets=self.config
+ .relative_attention_num_buckets,
+ relative_attention_max_distance=self.config
+ .relative_attention_max_distance,
+ bidirectional=self.config.bidirectional,
+ embeddings_initializer=self.config.relative_embeddings_initializer,
+ dtype=self.dtype,
+ compute_dtype=self.compute_dtype,
+ name="relative_posemb")
+ else:
+ self.relative_embeddings = []
+ for layer_idx in range(self.config.num_decoder_layers):
+ relative_embedding = RelativePositionEmbedding(
+ num_heads=self.config.num_heads,
+ relative_attention_num_buckets=self.config
+ .relative_attention_num_buckets,
+ relative_attention_max_distance=self.config
+ .relative_attention_max_distance,
+ bidirectional=self.config.bidirectional,
+ embeddings_initializer=self.config
+ .relative_embeddings_initializer,
+ dtype=self.dtype,
+ compute_dtype=self.compute_dtype,
+ name=f"relative_posemb_{layer_idx}")
+ self.relative_embeddings.append(relative_embedding)
self.decoder_layers = []
for layer_idx in range(self.config.num_decoder_layers):
if self.config.layer_sharing and layer_idx > 0:
@@ -1185,11 +1267,18 @@ class Decoder(Module):
if not self.config.logits_via_embedding:
self.logits_dense = Linear(
in_features=self.config.d_model,
- out_features=self.config.vocab_size,
+ out_features=self.config.target_vocab_size,
use_bias=False,
dtype=self.dtype,
name="logits")
+ @tf.Module.with_name_scope
+ def get_relpos_bias(self, input_length: int, layer_idx: int) -> tf.Tensor:
+ if self.config.use_shared_relative_position_bias:
+ return self.relative_embedding(input_length, input_length)
+ else:
+ return self.relative_embeddings[layer_idx](input_length, input_length)
+
@tf.Module.with_name_scope
def __call__(self,
decoder_input_tokens,
@@ -1208,7 +1297,7 @@ class Decoder(Module):
encoded: the encoder outputs.
decoder_mask: the decoder self-attention mask.
encoder_decoder_mask: the cross-attention mask.
- decode: Whether to perform autoaggressive decoding.
+ decode: Whether to perform autoregressive decoding.
decode_position: integer, the position to decode.
cache: The cache dictionary of key, value tensors.
max_decode_len: An optional integer specifying the maximum decoding
@@ -1217,7 +1306,10 @@ class Decoder(Module):
training: Whether it is training pass, affecting dropouts.
Returns:
- output of a transformer encoder.
+ output of a transformer encoder including
+ 1. logits: Logits for each word in the vocab.
+ 2. raw_logits: Logits along the moded dimension.
+ 3. cache: Used for decoding in inference mode.
"""
cfg = self.config
# Casts inputs to the dtype.
@@ -1230,12 +1322,14 @@ class Decoder(Module):
tensor_shape = tf_utils.get_shape_list(x)
tensor_shape[-2] = 1
x = self.target_dropout(x, noise_shape=tensor_shape, training=training)
- if cache is not None:
- position_bias = self.relative_embedding(max_decode_len, max_decode_len)
- else:
- input_length = tf_utils.get_shape_list(decoder_input_tokens)[1]
- position_bias = self.relative_embedding(input_length, input_length)
+
for i in range(cfg.num_decoder_layers):
+ if cache is not None:
+ position_bias = self.get_relpos_bias(max_decode_len, i)
+ else:
+ input_length = tf_utils.get_shape_list(decoder_input_tokens)[1]
+ position_bias = self.get_relpos_bias(input_length, i)
+
if cache is None:
x, _ = self.decoder_layers[i](
x,
@@ -1265,7 +1359,7 @@ class Decoder(Module):
logits = logits / math.sqrt(cfg.d_model)
else:
logits = self.logits_dense(output)
- return logits, cache
+ return dict(logits=logits, cache=cache, raw_logits=output)
class T5Transformer(Module):
@@ -1306,33 +1400,72 @@ class T5Transformer(Module):
compute_dtype=self.compute_dtype)
def encode(self,
- encoder_input_tokens,
+ encoder_input_tokens=None,
encoder_segment_ids=None,
+ encoder_dense_inputs=None,
+ encoder_dense_segment_ids=None,
training=False):
- eligible_positions = tf.cast(
- tf.not_equal(encoder_input_tokens, 0), self.compute_dtype)
+ eligible_position_array = []
+ if encoder_input_tokens is not None:
+ eligible_position_array.append(
+ tf.cast(tf.not_equal(encoder_input_tokens, 0), self.compute_dtype))
+ if encoder_dense_inputs is not None:
+ eligible_dense_positions = tf.cast(
+ tf.reduce_any(tf.not_equal(encoder_dense_inputs, 0), axis=-1),
+ self.compute_dtype)
+ eligible_position_array.append(eligible_dense_positions)
+ if not eligible_position_array:
+ raise ValueError("At least one of encoder_input_tokens and"
+ " encoder_dense_inputs must be provided.")
+
+ eligible_positions = tf.concat(eligible_position_array, axis=1)
encoder_mask = make_attention_mask(
eligible_positions, eligible_positions, dtype=tf.bool)
+
+ encoder_segment_id_array = []
if encoder_segment_ids is not None:
+ encoder_segment_id_array.append(encoder_segment_ids)
+ if encoder_dense_segment_ids is not None:
+ encoder_segment_id_array.append(encoder_dense_segment_ids)
+ if encoder_segment_id_array:
+ encoder_segment_ids = tf.concat(encoder_segment_id_array, axis=1)
segment_mask = make_attention_mask(
encoder_segment_ids, encoder_segment_ids, tf.equal, dtype=tf.bool)
encoder_mask = tf.math.logical_and(encoder_mask, segment_mask)
encoder_mask = (1.0 - tf.cast(encoder_mask, self.compute_dtype)) * -1e9
- return self.encoder(encoder_input_tokens, encoder_mask, training=training)
+ return self.encoder(
+ encoder_input_tokens,
+ encoder_mask,
+ encoder_dense_inputs,
+ training=training)
def decode(
self,
encoded,
decoder_target_tokens,
- encoder_input_tokens, # only used for masks
+ encoder_input_tokens=None, # only used for masks
+ encoder_dense_inputs=None,
decoder_input_tokens=None,
encoder_segment_ids=None,
+ encoder_dense_segment_ids=None,
decoder_segment_ids=None,
decode_position=None,
cache=None,
max_decode_len=None,
decode=False,
- training=False):
+ training=False) -> Dict[str, tf.Tensor]:
+ eligible_inputs_array = []
+ if encoder_input_tokens is not None:
+ eligible_inputs = tf.cast(
+ tf.not_equal(encoder_input_tokens, 0), self.compute_dtype)
+ eligible_inputs_array.append(eligible_inputs)
+ if encoder_dense_inputs is not None:
+ eligible_dense_inputs = tf.cast(
+ tf.reduce_any(tf.not_equal(encoder_dense_inputs, 0), axis=-1),
+ self.compute_dtype)
+ eligible_inputs_array.append(eligible_dense_inputs)
+ eligible_inputs = tf.concat(eligible_inputs_array, axis=1)
+
if decode:
# For decoding, the decoder_input_tokens is the decoder_target_tokens.
decoder_input_tokens = decoder_target_tokens
@@ -1342,14 +1475,12 @@ class T5Transformer(Module):
tf.cast(
tf.not_equal(tf.ones_like(decoder_target_tokens), 0),
self.compute_dtype),
- tf.cast(tf.not_equal(encoder_input_tokens, 0), self.compute_dtype),
+ eligible_inputs,
dtype=tf.bool)
else:
# Note that, masks should be created using decoder_target_tokens.
eligible_targets = tf.cast(
tf.not_equal(decoder_target_tokens, 0), self.compute_dtype)
- eligible_inputs = tf.cast(
- tf.not_equal(encoder_input_tokens, 0), self.compute_dtype)
decoder_mask = tf.math.logical_and(
make_attention_mask(
eligible_targets, eligible_targets, dtype=tf.bool),
@@ -1365,6 +1496,9 @@ class T5Transformer(Module):
decoder_segment_ids,
tf.equal,
dtype=tf.bool))
+ if encoder_dense_segment_ids is not None:
+ encoder_segment_ids = tf.concat(
+ [encoder_segment_ids, encoder_dense_segment_ids], axis=1)
encoder_decoder_mask = tf.math.logical_and(
encoder_decoder_mask,
make_attention_mask(
@@ -1376,7 +1510,7 @@ class T5Transformer(Module):
decoder_mask = (1.0 - tf.cast(decoder_mask, self.compute_dtype)) * -1e9
encoder_decoder_mask = (
1.0 - tf.cast(encoder_decoder_mask, self.compute_dtype)) * -1e9
- logits, cache = self.decoder(
+ outputs = self.decoder(
decoder_input_tokens,
encoded,
decode_position=decode_position,
@@ -1386,12 +1520,15 @@ class T5Transformer(Module):
max_decode_len=max_decode_len,
decode=decode,
training=training)
- return dict(logits=logits, encoded=encoded, cache=cache)
+ outputs["encoded"] = encoded
+ return outputs
@tf.Module.with_name_scope
def __call__(self,
- encoder_input_tokens,
- decoder_target_tokens,
+ encoder_input_tokens=None,
+ decoder_target_tokens=None,
+ encoder_dense_inputs=None,
+ encoder_dense_segment_ids=None,
decoder_input_tokens=None,
encoder_segment_ids=None,
decoder_segment_ids=None,
@@ -1401,9 +1538,12 @@ class T5Transformer(Module):
Args:
encoder_input_tokens: input tokens to the encoder.
decoder_target_tokens: target tokens to the decoder.
+ encoder_dense_inputs: input dense vectors to the encoder.
+ encoder_dense_segment_ids: dense input segmentation info for packed
decoder_input_tokens: input tokens to the decoder, only required for
training.
encoder_segment_ids: input segmentation info for packed examples.
+ examples.
decoder_segment_ids: target segmentation info for packed examples.
training: whether it is training pass, affecting dropouts.
@@ -1411,15 +1551,19 @@ class T5Transformer(Module):
a dictionary of logits/cache.
"""
encoded = self.encode(
- encoder_input_tokens,
+ encoder_input_tokens=encoder_input_tokens,
encoder_segment_ids=encoder_segment_ids,
+ encoder_dense_inputs=encoder_dense_inputs,
+ encoder_dense_segment_ids=encoder_dense_segment_ids,
training=training)
outputs = self.decode(
encoded=encoded,
decoder_target_tokens=decoder_target_tokens,
encoder_input_tokens=encoder_input_tokens, # only used for masks.
+ encoder_dense_inputs=encoder_dense_inputs, # only used for masks.
decoder_input_tokens=decoder_input_tokens,
encoder_segment_ids=encoder_segment_ids,
+ encoder_dense_segment_ids=encoder_dense_segment_ids,
decoder_segment_ids=decoder_segment_ids,
training=training)
outputs["encoded"] = encoded
diff --git a/official/nlp/modeling/models/t5_test.py b/official/nlp/modeling/models/t5_test.py
index 86acae973f7351286702735906a5b1c3b55238e8..72e1c8f3428a2620a7cf00525909e5c9b3a0d755 100644
--- a/official/nlp/modeling/models/t5_test.py
+++ b/official/nlp/modeling/models/t5_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -354,6 +354,40 @@ class T5Test(tf.test.TestCase, parameterized.TestCase):
encoded = encoder(tf.zeros((4, 8), dtype=tf.int32))
self.assertEqual(encoded.shape, (4, 8, config.d_model))
+ @parameterized.named_parameters(("bfloat16", tf.bfloat16),
+ ("float32", tf.float32))
+ def test_encoder_with_dense(self, dtype):
+ config = t5.T5TransformerParams(
+ num_layers=2,
+ d_model=4,
+ d_kv=3,
+ num_heads=4,
+ d_ff=16,
+ vocab_size=10,
+ vocab_embeddings_initializer=tf.keras.initializers.Ones(),
+ relative_embeddings_initializer=tf.keras.initializers.Ones())
+ encoder = t5.Encoder(config, compute_dtype=dtype)
+ encoded = encoder(
+ tf.zeros((4, 8), dtype=tf.int32),
+ dense_inputs=tf.ones((4, 2, 4), dtype=dtype))
+ self.assertEqual(encoded.shape, (4, 10, config.d_model))
+
+ @parameterized.named_parameters(("bfloat16", tf.bfloat16),
+ ("float32", tf.float32))
+ def test_encoder_only_dense(self, dtype):
+ config = t5.T5TransformerParams(
+ num_layers=2,
+ d_model=4,
+ d_kv=3,
+ num_heads=4,
+ d_ff=16,
+ vocab_size=10,
+ vocab_embeddings_initializer=tf.keras.initializers.Ones(),
+ relative_embeddings_initializer=tf.keras.initializers.Ones())
+ encoder = t5.Encoder(config, compute_dtype=dtype)
+ encoded = encoder(dense_inputs=tf.ones((4, 2, 4), dtype=dtype))
+ self.assertEqual(encoded.shape, (4, 2, config.d_model))
+
def test_decoder(self):
max_decode_len = 10
config = t5.T5TransformerParams(
@@ -369,7 +403,9 @@ class T5Test(tf.test.TestCase, parameterized.TestCase):
batch_size = 4
targets = tf.zeros((4, 8), dtype=tf.int32)
encoded = tf.zeros((4, 8, config.d_model), dtype=tf.float32)
- logits, cache = decoder(targets, encoded)
+ outputs = decoder(targets, encoded)
+ logits = outputs["logits"]
+ cache = outputs["cache"]
self.assertEqual(logits.shape, (4, 8, config.vocab_size))
cache = {}
@@ -378,13 +414,15 @@ class T5Test(tf.test.TestCase, parameterized.TestCase):
cache[1] = _create_cache(batch_size, max_decode_len, config.num_heads,
config.d_kv)
targets = tf.zeros((4, 1), dtype=tf.int32)
- logits, cache = decoder(
+ outputs = decoder(
targets,
encoded,
decode_position=2,
cache=cache,
decode=True,
max_decode_len=max_decode_len)
+ logits = outputs["logits"]
+ cache = outputs["cache"]
self.assertEqual(logits.shape, (batch_size, 1, config.vocab_size))
for entry in cache.values():
for tensor in entry.values():
@@ -445,6 +483,180 @@ class T5Test(tf.test.TestCase, parameterized.TestCase):
print(v.name, v.shape)
self.assertEqual(v.dtype, tf.float32)
+ @parameterized.named_parameters(
+ ("t5_10_dense", ("relu",), True, 26, False, tf.float32),)
+ def test_transformer_with_dense(self, ffn_activations, logits_via_embedding,
+ expect_num_variables, layer_sharing, dtype):
+ max_decode_len = 10
+ config = t5.T5TransformerParams(
+ num_layers=1,
+ d_model=8,
+ d_kv=4,
+ num_heads=4,
+ d_ff=32,
+ vocab_size=10,
+ shared_embedding=True,
+ layer_sharing=layer_sharing,
+ ffn_activations=ffn_activations,
+ logits_via_embedding=logits_via_embedding)
+ transformer = t5.T5Transformer(config, compute_dtype=dtype)
+
+ self.assertLen(transformer.trainable_variables, expect_num_variables)
+ inputs = tf.convert_to_tensor(
+ np.array([[2, 2, 1, 3, 1, 0], [3, 3, 1, 2, 2, 1]]))
+ segments = tf.convert_to_tensor(
+ np.array([[1, 1, 1, 2, 2, 0], [1, 1, 1, 2, 2, 2]]))
+
+ dense_inputs = tf.convert_to_tensor(np.random.randn(2, 2, 8), dtype=dtype)
+ dense_segments = tf.convert_to_tensor(np.array([[1, 2], [1, 2]]))
+ outputs = transformer(
+ encoder_input_tokens=inputs,
+ encoder_dense_inputs=dense_inputs,
+ decoder_input_tokens=inputs,
+ decoder_target_tokens=inputs,
+ encoder_segment_ids=segments,
+ encoder_dense_segment_ids=dense_segments,
+ decoder_segment_ids=segments)
+ cache = {}
+ batch_size = 2
+ cache[0] = _create_cache(
+ batch_size, max_decode_len, config.num_heads, config.d_kv, dtype=dtype)
+ outputs = transformer.decode(
+ encoder_input_tokens=inputs,
+ encoder_dense_inputs=dense_inputs,
+ encoded=outputs["encoded"],
+ decoder_target_tokens=tf.ones((batch_size, 1), dtype=tf.int32),
+ decode_position=1,
+ decode=True,
+ max_decode_len=max_decode_len,
+ cache=cache)
+ self.assertEqual(outputs["logits"].shape,
+ (batch_size, 1, config.vocab_size))
+ for v in transformer.trainable_variables:
+ print(v.name, v.shape)
+ self.assertEqual(v.dtype, tf.float32)
+
+ @parameterized.named_parameters(
+ ("t5_10_dense_layerwise_relpos",
+ ("relu",), True, 26, False, tf.float32, False, 1),
+ ("t5_10_dense_shared_relpos_d2",
+ ("relu",), True, 39, False, tf.float32, True, 2),
+ ("t5_10_dense_layerwise_relpos_d2",
+ ("relu",), True, 40, False, tf.float32, False, 2),
+ )
+ def test_transformer_with_lw_relpos(self, ffn_activations,
+ logits_via_embedding,
+ expect_num_variables, layer_sharing,
+ dtype, use_shared_relpos,
+ num_decoder_layers):
+ max_decode_len = 10
+ config = t5.T5TransformerParams(
+ num_layers=1,
+ num_decoder_layers=num_decoder_layers,
+ d_model=8,
+ d_kv=4,
+ num_heads=4,
+ d_ff=32,
+ vocab_size=10,
+ shared_embedding=True,
+ layer_sharing=layer_sharing,
+ ffn_activations=ffn_activations,
+ logits_via_embedding=logits_via_embedding,
+ use_shared_relative_position_bias=use_shared_relpos)
+ transformer = t5.T5Transformer(config, compute_dtype=dtype)
+
+ self.assertLen(transformer.trainable_variables, expect_num_variables)
+ inputs = tf.convert_to_tensor(
+ np.array([[2, 2, 1, 3, 1, 0], [3, 3, 1, 2, 2, 1]]))
+ segments = tf.convert_to_tensor(
+ np.array([[1, 1, 1, 2, 2, 0], [1, 1, 1, 2, 2, 2]]))
+
+ dense_inputs = tf.convert_to_tensor(np.random.randn(2, 2, 8), dtype=dtype)
+ dense_segments = tf.convert_to_tensor(np.array([[1, 2], [1, 2]]))
+ outputs = transformer(
+ encoder_input_tokens=inputs,
+ encoder_dense_inputs=dense_inputs,
+ decoder_input_tokens=inputs,
+ decoder_target_tokens=inputs,
+ encoder_segment_ids=segments,
+ encoder_dense_segment_ids=dense_segments,
+ decoder_segment_ids=segments)
+ cache = {}
+ batch_size = 2
+ for i in range(num_decoder_layers):
+ cache[i] = _create_cache(
+ batch_size,
+ max_decode_len,
+ config.num_heads,
+ config.d_kv,
+ dtype=dtype)
+ outputs = transformer.decode(
+ encoder_input_tokens=inputs,
+ encoder_dense_inputs=dense_inputs,
+ encoded=outputs["encoded"],
+ decoder_target_tokens=tf.ones((batch_size, 1), dtype=tf.int32),
+ decode_position=1,
+ decode=True,
+ max_decode_len=max_decode_len,
+ cache=cache)
+ self.assertEqual(outputs["logits"].shape,
+ (batch_size, 1, config.vocab_size))
+ for v in transformer.trainable_variables:
+ print(v.name, v.shape)
+ self.assertEqual(v.dtype, tf.float32)
+
+ @parameterized.named_parameters(
+ ("t5_10", ("relu",), True, 26, False, tf.float32),)
+ def test_transformer_with_dense_only(self, ffn_activations,
+ logits_via_embedding,
+ expect_num_variables, layer_sharing,
+ dtype):
+ max_decode_len = 10
+ config = t5.T5TransformerParams(
+ num_layers=1,
+ d_model=8,
+ d_kv=4,
+ num_heads=4,
+ d_ff=32,
+ vocab_size=10,
+ shared_embedding=True,
+ layer_sharing=layer_sharing,
+ ffn_activations=ffn_activations,
+ logits_via_embedding=logits_via_embedding)
+ transformer = t5.T5Transformer(config, compute_dtype=dtype)
+ self.assertLen(transformer.trainable_variables, expect_num_variables)
+
+ decoder_inputs = tf.convert_to_tensor(
+ np.array([[2, 2, 1, 3, 1, 0], [3, 3, 1, 2, 2, 1]]))
+ decoder_segments = tf.convert_to_tensor(
+ np.array([[1, 1, 1, 2, 2, 0], [1, 1, 1, 2, 2, 2]]))
+
+ dense_inputs = tf.convert_to_tensor(np.random.randn(2, 2, 8), dtype=dtype)
+ dense_segments = tf.convert_to_tensor(np.array([[1, 2], [1, 2]]))
+ outputs = transformer(
+ encoder_dense_inputs=dense_inputs,
+ encoder_dense_segment_ids=dense_segments,
+ decoder_input_tokens=decoder_inputs,
+ decoder_target_tokens=decoder_inputs,
+ decoder_segment_ids=decoder_segments)
+ cache = {}
+ batch_size = 2
+ cache[0] = _create_cache(
+ batch_size, max_decode_len, config.num_heads, config.d_kv, dtype=dtype)
+ outputs = transformer.decode(
+ encoder_dense_inputs=dense_inputs,
+ encoded=outputs["encoded"],
+ decoder_target_tokens=tf.ones((batch_size, 1), dtype=tf.int32),
+ decode_position=1,
+ decode=True,
+ max_decode_len=max_decode_len,
+ cache=cache)
+ self.assertEqual(outputs["logits"].shape,
+ (batch_size, 1, config.vocab_size))
+ for v in transformer.trainable_variables:
+ print(v.name, v.shape)
+ self.assertEqual(v.dtype, tf.float32)
+
@parameterized.named_parameters(
("t5_10", ("relu",), True, 39, tf.float32, 2),
("t5_10_bfloat16", ("relu",), True, 39, tf.bfloat16, 2))
diff --git a/official/nlp/modeling/models/xlnet.py b/official/nlp/modeling/models/xlnet.py
index c359c20e949e15f5d228b7714303a99fed794b30..eea637e03163b4afa7bdec6bf4fbd639ae77eac1 100644
--- a/official/nlp/modeling/models/xlnet.py
+++ b/official/nlp/modeling/models/xlnet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/models/xlnet_test.py b/official/nlp/modeling/models/xlnet_test.py
index 74480a48d9b029fdd7f27f543d490e1f7854bf7f..e22883508da994f2419411a93583754a7c1780a9 100644
--- a/official/nlp/modeling/models/xlnet_test.py
+++ b/official/nlp/modeling/models/xlnet_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/README.md b/official/nlp/modeling/networks/README.md
index b192399a7276ef122725f40d2b0e3d237805e644..b32a30775cd3976635618a1d1d404df50f85743a 100644
--- a/official/nlp/modeling/networks/README.md
+++ b/official/nlp/modeling/networks/README.md
@@ -37,3 +37,8 @@ Generalized Autoregressive Pretraining for Language Understanding"
(https://arxiv.org/abs/1906.08237). It includes embedding lookups,
relative position encodings, mask computations, segment matrix computations and
Transformer XL layers using one or two stream relative self-attention.
+
+* [`FNet`](fnet.py) implements the encoder model from ["FNet: Mixing Tokens with
+Fourier Transforms"](https://aclanthology.org/2022.naacl-main.319/). FNet has
+the same structure as a Transformer encoder, except that all or most of the
+self-attention sublayers are replaced with Fourier sublayers.
diff --git a/official/nlp/modeling/networks/__init__.py b/official/nlp/modeling/networks/__init__.py
index 137bc3ac4f787f32c36e9eed15d026d15ec8199c..0128481d91eb3552ee4ac5970e5a983863e5297c 100644
--- a/official/nlp/modeling/networks/__init__.py
+++ b/official/nlp/modeling/networks/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,6 +23,7 @@ from official.nlp.modeling.networks.bert_encoder import BertEncoder
from official.nlp.modeling.networks.bert_encoder import BertEncoderV2
from official.nlp.modeling.networks.classification import Classification
from official.nlp.modeling.networks.encoder_scaffold import EncoderScaffold
+from official.nlp.modeling.networks.fnet import FNet
from official.nlp.modeling.networks.funnel_transformer import FunnelTransformerEncoder
from official.nlp.modeling.networks.mobile_bert_encoder import MobileBERTEncoder
from official.nlp.modeling.networks.packed_sequence_embedding import PackedSequenceEmbedding
diff --git a/official/nlp/modeling/networks/albert_encoder.py b/official/nlp/modeling/networks/albert_encoder.py
index f7453787bef757beb9380276f82f11acc1b562fe..e7095de4e90d914448c73fc88e1774453377ba11 100644
--- a/official/nlp/modeling/networks/albert_encoder.py
+++ b/official/nlp/modeling/networks/albert_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,7 @@ import collections
import tensorflow as tf
from official.modeling import activations
+from official.modeling import tf_utils
from official.nlp.modeling import layers
@@ -92,13 +93,13 @@ class AlbertEncoder(tf.keras.Model):
embedding_layer = layers.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
word_embeddings = embedding_layer(word_ids)
# Always uses dynamic slicing for simplicity.
position_embedding_layer = layers.PositionEmbedding(
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
max_length=max_sequence_length,
name='position_embedding')
position_embeddings = position_embedding_layer(word_embeddings)
@@ -107,7 +108,7 @@ class AlbertEncoder(tf.keras.Model):
layers.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')(type_ids))
@@ -123,11 +124,11 @@ class AlbertEncoder(tf.keras.Model):
# We project the 'embedding' output to 'hidden_size' if it is not already
# 'hidden_size'.
if embedding_width != hidden_size:
- embeddings = tf.keras.layers.experimental.EinsumDense(
+ embeddings = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')(
embeddings)
@@ -139,7 +140,7 @@ class AlbertEncoder(tf.keras.Model):
inner_activation=activation,
output_dropout=dropout_rate,
attention_dropout=attention_dropout_rate,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='transformer')
encoder_outputs = []
for _ in range(num_layers):
@@ -153,7 +154,7 @@ class AlbertEncoder(tf.keras.Model):
cls_output = tf.keras.layers.Dense(
units=hidden_size,
activation='tanh',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='pooler_transform')(
first_token_tensor)
if dict_outputs:
@@ -172,7 +173,7 @@ class AlbertEncoder(tf.keras.Model):
# created using the Functional API. Once super().__init__ is called, we
# can assign attributes to `self` - note that all `self` assignments are
# below this line.
- super(AlbertEncoder, self).__init__(
+ super().__init__(
inputs=[word_ids, mask, type_ids], outputs=outputs, **kwargs)
config_dict = {
'vocab_size': vocab_size,
diff --git a/official/nlp/modeling/networks/albert_encoder_test.py b/official/nlp/modeling/networks/albert_encoder_test.py
index f3cb60c36f9938397a55d17eef00b19cedfdd819..f7116afc9150f85440d20e85f7548abaa8191c95 100644
--- a/official/nlp/modeling/networks/albert_encoder_test.py
+++ b/official/nlp/modeling/networks/albert_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/bert_dense_encoder.py b/official/nlp/modeling/networks/bert_dense_encoder.py
deleted file mode 100644
index 344e9e0406b8a541de7d035efeb71a5a4a5af50d..0000000000000000000000000000000000000000
--- a/official/nlp/modeling/networks/bert_dense_encoder.py
+++ /dev/null
@@ -1,276 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Transformer-based BERT encoder network with dense features as inputs."""
-# pylint: disable=g-classes-have-attributes
-
-from typing import Any, Callable, Optional, Union
-from absl import logging
-import tensorflow as tf
-
-from official.nlp.modeling import layers
-
-
-_Initializer = Union[str, tf.keras.initializers.Initializer]
-_approx_gelu = lambda x: tf.keras.activations.gelu(x, approximate=True)
-
-
-class BertDenseEncoder(tf.keras.layers.Layer):
- """Bi-directional Transformer-based encoder network with dense features.
-
- This network is the same as the BertEncoder except it also concats dense
- features with the embeddings.
-
- Args:
- vocab_size: The size of the token vocabulary.
- hidden_size: The size of the transformer hidden layers.
- num_layers: The number of transformer layers.
- num_attention_heads: The number of attention heads for each transformer. The
- hidden size must be divisible by the number of attention heads.
- max_sequence_length: The maximum sequence length that this encoder can
- consume. If None, max_sequence_length uses the value from sequence length.
- This determines the variable shape for positional embeddings.
- type_vocab_size: The number of types that the 'type_ids' input can take.
- inner_dim: The output dimension of the first Dense layer in a two-layer
- feedforward network for each transformer.
- inner_activation: The activation for the first Dense layer in a two-layer
- feedforward network for each transformer.
- output_dropout: Dropout probability for the post-attention and output
- dropout.
- attention_dropout: The dropout rate to use for the attention layers within
- the transformer layers.
- initializer: The initialzer to use for all weights in this encoder.
- output_range: The sequence output range, [0, output_range), by slicing the
- target sequence of the last transformer layer. `None` means the entire
- target sequence will attend to the source sequence, which yields the full
- output.
- embedding_width: The width of the word embeddings. If the embedding width is
- not equal to hidden size, embedding parameters will be factorized into two
- matrices in the shape of ['vocab_size', 'embedding_width'] and
- ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
- smaller than 'hidden_size').
- embedding_layer: An optional Layer instance which will be called to generate
- embeddings for the input word IDs.
- norm_first: Whether to normalize inputs to attention and intermediate dense
- layers. If set False, output of attention and intermediate dense layers is
- normalized.
- """
-
- def __init__(
- self,
- vocab_size: int,
- hidden_size: int = 768,
- num_layers: int = 12,
- num_attention_heads: int = 12,
- max_sequence_length: int = 512,
- type_vocab_size: int = 16,
- inner_dim: int = 3072,
- inner_activation: Callable[..., Any] = _approx_gelu,
- output_dropout: float = 0.1,
- attention_dropout: float = 0.1,
- initializer: _Initializer = tf.keras.initializers.TruncatedNormal(
- stddev=0.02),
- output_range: Optional[int] = None,
- embedding_width: Optional[int] = None,
- embedding_layer: Optional[tf.keras.layers.Layer] = None,
- norm_first: bool = False,
- **kwargs):
- # Pops kwargs that are used in V1 implementation.
- if 'dict_outputs' in kwargs:
- kwargs.pop('dict_outputs')
- if 'return_all_encoder_outputs' in kwargs:
- kwargs.pop('return_all_encoder_outputs')
- if 'intermediate_size' in kwargs:
- inner_dim = kwargs.pop('intermediate_size')
- if 'activation' in kwargs:
- inner_activation = kwargs.pop('activation')
- if 'dropout_rate' in kwargs:
- output_dropout = kwargs.pop('dropout_rate')
- if 'attention_dropout_rate' in kwargs:
- attention_dropout = kwargs.pop('attention_dropout_rate')
- super().__init__(**kwargs)
-
- activation = tf.keras.activations.get(inner_activation)
- initializer = tf.keras.initializers.get(initializer)
-
- if embedding_width is None:
- embedding_width = hidden_size
-
- if embedding_layer is None:
- self._embedding_layer = layers.OnDeviceEmbedding(
- vocab_size=vocab_size,
- embedding_width=embedding_width,
- initializer=initializer,
- name='word_embeddings')
- else:
- self._embedding_layer = embedding_layer
-
- self._position_embedding_layer = layers.PositionEmbedding(
- initializer=initializer,
- max_length=max_sequence_length,
- name='position_embedding')
-
- self._type_embedding_layer = layers.OnDeviceEmbedding(
- vocab_size=type_vocab_size,
- embedding_width=embedding_width,
- initializer=initializer,
- use_one_hot=True,
- name='type_embeddings')
-
- self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
- name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
-
- self._embedding_dropout = tf.keras.layers.Dropout(
- rate=output_dropout, name='embedding_dropout')
-
- # We project the 'embedding' output to 'hidden_size' if it is not already
- # 'hidden_size'.
- self._embedding_projection = None
- if embedding_width != hidden_size:
- self._embedding_projection = tf.keras.layers.experimental.EinsumDense(
- '...x,xy->...y',
- output_shape=hidden_size,
- bias_axes='y',
- kernel_initializer=initializer,
- name='embedding_projection')
-
- self._transformer_layers = []
- self._attention_mask_layer = layers.SelfAttentionMask(
- name='self_attention_mask')
- for i in range(num_layers):
- layer = layers.TransformerEncoderBlock(
- num_attention_heads=num_attention_heads,
- inner_dim=inner_dim,
- inner_activation=inner_activation,
- output_dropout=output_dropout,
- attention_dropout=attention_dropout,
- norm_first=norm_first,
- output_range=output_range if i == num_layers - 1 else None,
- kernel_initializer=initializer,
- name='transformer/layer_%d' % i)
- self._transformer_layers.append(layer)
-
- self._pooler_layer = tf.keras.layers.Dense(
- units=hidden_size,
- activation='tanh',
- kernel_initializer=initializer,
- name='pooler_transform')
-
- self._config = {
- 'vocab_size': vocab_size,
- 'hidden_size': hidden_size,
- 'num_layers': num_layers,
- 'num_attention_heads': num_attention_heads,
- 'max_sequence_length': max_sequence_length,
- 'type_vocab_size': type_vocab_size,
- 'inner_dim': inner_dim,
- 'inner_activation': tf.keras.activations.serialize(activation),
- 'output_dropout': output_dropout,
- 'attention_dropout': attention_dropout,
- 'initializer': tf.keras.initializers.serialize(initializer),
- 'output_range': output_range,
- 'embedding_width': embedding_width,
- 'embedding_layer': embedding_layer,
- 'norm_first': norm_first,
- }
- self.inputs = dict(
- input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
- input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
- input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
- dense_inputs=tf.keras.Input(
- shape=(None, embedding_width), dtype=tf.float32),
- dense_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
- dense_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
- )
-
- def call(self, inputs):
- word_embeddings = None
- if isinstance(inputs, dict):
- word_ids = inputs.get('input_word_ids')
- mask = inputs.get('input_mask')
- type_ids = inputs.get('input_type_ids')
- word_embeddings = inputs.get('input_word_embeddings', None)
- dense_inputs = inputs.get('dense_inputs')
- dense_mask = inputs.get('dense_mask')
- dense_type_ids = inputs.get('dense_type_ids')
- else:
- raise ValueError('Unexpected inputs type to %s.' % self.__class__)
-
- if word_embeddings is None:
- word_embeddings = self._embedding_layer(word_ids)
-
- # Concat the dense embeddings at sequence end.
- combined_embeddings = tf.concat([word_embeddings, dense_inputs], axis=1)
- combined_type_ids = tf.concat([type_ids, dense_type_ids], axis=1)
- combined_mask = tf.concat([mask, dense_mask], axis=1)
-
- # absolute position embeddings.
- position_embeddings = self._position_embedding_layer(combined_embeddings)
- type_embeddings = self._type_embedding_layer(combined_type_ids)
-
- embeddings = combined_embeddings + position_embeddings + type_embeddings
- embeddings = self._embedding_norm_layer(embeddings)
- embeddings = self._embedding_dropout(embeddings)
-
- if self._embedding_projection is not None:
- embeddings = self._embedding_projection(embeddings)
-
- attention_mask = self._attention_mask_layer(embeddings, combined_mask)
-
- encoder_outputs = []
- x = embeddings
- for layer in self._transformer_layers:
- x = layer([x, attention_mask])
- encoder_outputs.append(x)
-
- last_encoder_output = encoder_outputs[-1]
- first_token_tensor = last_encoder_output[:, 0, :]
- pooled_output = self._pooler_layer(first_token_tensor)
-
- return dict(
- sequence_output=encoder_outputs[-1],
- pooled_output=pooled_output,
- encoder_outputs=encoder_outputs)
-
- def get_embedding_table(self):
- return self._embedding_layer.embeddings
-
- def get_embedding_layer(self):
- return self._embedding_layer
-
- def get_config(self):
- return dict(self._config)
-
- @property
- def transformer_layers(self):
- """List of Transformer layers in the encoder."""
- return self._transformer_layers
-
- @property
- def pooler_layer(self):
- """The pooler dense layer after the transformer layers."""
- return self._pooler_layer
-
- @classmethod
- def from_config(cls, config, custom_objects=None):
- if 'embedding_layer' in config and config['embedding_layer'] is not None:
- warn_string = (
- 'You are reloading a model that was saved with a '
- 'potentially-shared embedding layer object. If you contine to '
- 'train this model, the embedding layer will no longer be shared. '
- 'To work around this, load the model outside of the Keras API.')
- print('WARNING: ' + warn_string)
- logging.warn(warn_string)
-
- return cls(**config)
diff --git a/official/nlp/modeling/networks/bert_dense_encoder_test.py b/official/nlp/modeling/networks/bert_dense_encoder_test.py
index dcc9e3e8af87267d369785b3dc98dd51aa972ada..a2ed8b1b8b68fa3f3e1fbf7108f49f353238139d 100644
--- a/official/nlp/modeling/networks/bert_dense_encoder_test.py
+++ b/official/nlp/modeling/networks/bert_dense_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,29 +20,30 @@ import numpy as np
import tensorflow as tf
from tensorflow.python.keras import keras_parameterized # pylint: disable=g-direct-tensorflow-import
-from official.nlp.modeling.networks import bert_dense_encoder
+from official.nlp.modeling.networks import bert_encoder
# This decorator runs the test in V1, V2-Eager, and V2-Functional mode. It
# guarantees forward compatibility of this code for the V2 switchover.
@keras_parameterized.run_all_keras_modes
-class BertDenseEncoderTest(keras_parameterized.TestCase):
+class BertEncoderV2Test(keras_parameterized.TestCase):
def tearDown(self):
- super(BertDenseEncoderTest, self).tearDown()
+ super(BertEncoderV2Test, self).tearDown()
tf.keras.mixed_precision.set_global_policy("float32")
def test_dict_outputs_network_creation(self):
hidden_size = 32
sequence_length = 21
dense_sequence_length = 20
- # Create a small dense BertDenseEncoder for testing.
+ # Create a small dense BertEncoderV2 for testing.
kwargs = {}
- test_network = bert_dense_encoder.BertDenseEncoder(
+ test_network = bert_encoder.BertEncoderV2(
vocab_size=100,
hidden_size=hidden_size,
num_attention_heads=2,
num_layers=3,
+ with_dense_inputs=True,
**kwargs)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
@@ -86,12 +87,13 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
sequence_length = 21
dense_sequence_length = 20
# Create a small BertEncoder for testing.
- test_network = bert_dense_encoder.BertDenseEncoder(
+ test_network = bert_encoder.BertEncoderV2(
vocab_size=100,
hidden_size=hidden_size,
num_attention_heads=2,
num_layers=3,
- dict_outputs=True)
+ dict_outputs=True,
+ with_dense_inputs=True)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
@@ -134,12 +136,13 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
dense_sequence_length = 20
tf.keras.mixed_precision.set_global_policy("mixed_float16")
# Create a small BertEncoder for testing.
- test_network = bert_dense_encoder.BertDenseEncoder(
+ test_network = bert_encoder.BertEncoderV2(
vocab_size=100,
hidden_size=hidden_size,
num_attention_heads=2,
num_layers=3,
- dict_outputs=True)
+ dict_outputs=True,
+ with_dense_inputs=True)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
@@ -176,9 +179,8 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
self.assertAllEqual(tf.float16, pooled.dtype)
@parameterized.named_parameters(
- ("all_sequence_encoder_v2", bert_dense_encoder.BertDenseEncoder, None,
- 41),
- ("output_range_encoder_v2", bert_dense_encoder.BertDenseEncoder, 1, 1),
+ ("all_sequence_encoder_v2", bert_encoder.BertEncoderV2, None, 41),
+ ("output_range_encoder_v2", bert_encoder.BertEncoderV2, 1, 1),
)
def test_dict_outputs_network_invocation(
self, encoder_cls, output_range, out_seq_len):
@@ -194,8 +196,9 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
num_attention_heads=2,
num_layers=3,
type_vocab_size=num_types,
- output_range=output_range,
- dict_outputs=True)
+ dict_outputs=True,
+ with_dense_inputs=True,
+ output_range=output_range)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
@@ -276,7 +279,7 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
# Creates a BertEncoder with embedding_width != hidden_size
embedding_width = 16
- test_network = bert_dense_encoder.BertDenseEncoder(
+ test_network = bert_encoder.BertEncoderV2(
vocab_size=vocab_size,
hidden_size=hidden_size,
max_sequence_length=max_sequence_length,
@@ -316,11 +319,12 @@ class BertDenseEncoderTest(keras_parameterized.TestCase):
sequence_length = 21
dense_sequence_length = 20
# Create a small BertEncoder for testing.
- test_network = bert_dense_encoder.BertDenseEncoder(
+ test_network = bert_encoder.BertEncoderV2(
vocab_size=100,
hidden_size=hidden_size,
num_attention_heads=2,
- num_layers=3)
+ num_layers=3,
+ with_dense_inputs=True)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length), dtype=tf.int32)
mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
diff --git a/official/nlp/modeling/networks/bert_encoder.py b/official/nlp/modeling/networks/bert_encoder.py
index 40fbd2da2427907e4f9a0aca3ee1ff1dabf5407e..e9dd91d4bac41931ed50a942a6e22b0e4d8fc2cc 100644
--- a/official/nlp/modeling/networks/bert_encoder.py
+++ b/official/nlp/modeling/networks/bert_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,9 +19,9 @@ from typing import Any, Callable, Optional, Union
from absl import logging
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
-
_Initializer = Union[str, tf.keras.initializers.Initializer]
_Activation = Union[str, Callable[..., Any]]
@@ -48,8 +48,7 @@ class BertEncoderV2(tf.keras.layers.Layer):
num_attention_heads: The number of attention heads for each transformer. The
hidden size must be divisible by the number of attention heads.
max_sequence_length: The maximum sequence length that this encoder can
- consume. If None, max_sequence_length uses the value from sequence length.
- This determines the variable shape for positional embeddings.
+ consume. This determines the variable shape for positional embeddings.
type_vocab_size: The number of types that the 'type_ids' input can take.
inner_dim: The output dimension of the first Dense layer in a two-layer
feedforward network for each transformer.
@@ -74,6 +73,11 @@ class BertEncoderV2(tf.keras.layers.Layer):
norm_first: Whether to normalize inputs to attention and intermediate dense
layers. If set False, output of attention and intermediate dense layers is
normalized.
+ with_dense_inputs: Whether to accept dense embeddings as the input.
+ return_attention_scores: Whether to add an additional output containing the
+ attention scores of all transformer layers. This will be a list of length
+ `num_layers`, and each element will be in the shape [batch_size,
+ num_attention_heads, seq_dim, seq_dim].
"""
def __init__(
@@ -94,6 +98,8 @@ class BertEncoderV2(tf.keras.layers.Layer):
embedding_width: Optional[int] = None,
embedding_layer: Optional[tf.keras.layers.Layer] = None,
norm_first: bool = False,
+ with_dense_inputs: bool = False,
+ return_attention_scores: bool = False,
**kwargs):
# Pops kwargs that are used in V1 implementation.
if 'dict_outputs' in kwargs:
@@ -110,6 +116,8 @@ class BertEncoderV2(tf.keras.layers.Layer):
attention_dropout = kwargs.pop('attention_dropout_rate')
super().__init__(**kwargs)
+ self._output_range = output_range
+
activation = tf.keras.activations.get(inner_activation)
initializer = tf.keras.initializers.get(initializer)
@@ -120,20 +128,20 @@ class BertEncoderV2(tf.keras.layers.Layer):
self._embedding_layer = layers.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
else:
self._embedding_layer = embedding_layer
self._position_embedding_layer = layers.PositionEmbedding(
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
max_length=max_sequence_length,
name='position_embedding')
self._type_embedding_layer = layers.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')
@@ -147,16 +155,17 @@ class BertEncoderV2(tf.keras.layers.Layer):
# 'hidden_size'.
self._embedding_projection = None
if embedding_width != hidden_size:
- self._embedding_projection = tf.keras.layers.experimental.EinsumDense(
+ self._embedding_projection = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')
self._transformer_layers = []
self._attention_mask_layer = layers.SelfAttentionMask(
name='self_attention_mask')
+ self._num_layers = num_layers
for i in range(num_layers):
layer = layers.TransformerEncoderBlock(
num_attention_heads=num_attention_heads,
@@ -165,15 +174,15 @@ class BertEncoderV2(tf.keras.layers.Layer):
output_dropout=output_dropout,
attention_dropout=attention_dropout,
norm_first=norm_first,
- output_range=output_range if i == num_layers - 1 else None,
- kernel_initializer=initializer,
+ return_attention_scores=return_attention_scores,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='transformer/layer_%d' % i)
self._transformer_layers.append(layer)
self._pooler_layer = tf.keras.layers.Dense(
units=hidden_size,
activation='tanh',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='pooler_transform')
self._config = {
@@ -192,11 +201,24 @@ class BertEncoderV2(tf.keras.layers.Layer):
'embedding_width': embedding_width,
'embedding_layer': embedding_layer,
'norm_first': norm_first,
+ 'with_dense_inputs': with_dense_inputs,
+ 'return_attention_scores': return_attention_scores,
}
- self.inputs = dict(
- input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
- input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
- input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32))
+ if with_dense_inputs:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ dense_inputs=tf.keras.Input(
+ shape=(None, embedding_width), dtype=tf.float32),
+ dense_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ dense_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ )
+ else:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32))
def call(self, inputs):
word_embeddings = None
@@ -205,11 +227,22 @@ class BertEncoderV2(tf.keras.layers.Layer):
mask = inputs.get('input_mask')
type_ids = inputs.get('input_type_ids')
word_embeddings = inputs.get('input_word_embeddings', None)
+
+ dense_inputs = inputs.get('dense_inputs', None)
+ dense_mask = inputs.get('dense_mask', None)
+ dense_type_ids = inputs.get('dense_type_ids', None)
else:
raise ValueError('Unexpected inputs type to %s.' % self.__class__)
if word_embeddings is None:
word_embeddings = self._embedding_layer(word_ids)
+
+ if dense_inputs is not None:
+ # Concat the dense embeddings at sequence end.
+ word_embeddings = tf.concat([word_embeddings, dense_inputs], axis=1)
+ type_ids = tf.concat([type_ids, dense_type_ids], axis=1)
+ mask = tf.concat([mask, dense_mask], axis=1)
+
# absolute position embeddings.
position_embeddings = self._position_embedding_layer(word_embeddings)
type_embeddings = self._type_embedding_layer(type_ids)
@@ -224,19 +257,29 @@ class BertEncoderV2(tf.keras.layers.Layer):
attention_mask = self._attention_mask_layer(embeddings, mask)
encoder_outputs = []
+ attention_outputs = []
x = embeddings
- for layer in self._transformer_layers:
- x = layer([x, attention_mask])
+ for i, layer in enumerate(self._transformer_layers):
+ transformer_output_range = None
+ if i == self._num_layers - 1:
+ transformer_output_range = self._output_range
+ x = layer([x, attention_mask], output_range=transformer_output_range)
+ if self._config['return_attention_scores']:
+ x, attention_scores = x
+ attention_outputs.append(attention_scores)
encoder_outputs.append(x)
last_encoder_output = encoder_outputs[-1]
first_token_tensor = last_encoder_output[:, 0, :]
pooled_output = self._pooler_layer(first_token_tensor)
- return dict(
+ output = dict(
sequence_output=encoder_outputs[-1],
pooled_output=pooled_output,
encoder_outputs=encoder_outputs)
+ if self._config['return_attention_scores']:
+ output['attention_scores'] = attention_outputs
+ return output
def get_embedding_table(self):
return self._embedding_layer.embeddings
@@ -299,13 +342,13 @@ class BertEncoder(tf.keras.Model):
This determines the variable shape for positional embeddings.
type_vocab_size: The number of types that the 'type_ids' input can take.
inner_dim: The output dimension of the first Dense layer in a two-layer
- feedforward network for each transformer.
+ feedforward network for each transformer.
inner_activation: The activation for the first Dense layer in a two-layer
- feedforward network for each transformer.
+ feedforward network for each transformer.
output_dropout: Dropout probability for the post-attention and output
- dropout.
- attention_dropout: The dropout rate to use for the attention layers
- within the transformer layers.
+ dropout.
+ attention_dropout: The dropout rate to use for the attention layers within
+ the transformer layers.
initializer: The initialzer to use for all weights in this encoder.
output_range: The sequence output range, [0, output_range), by slicing the
target sequence of the last transformer layer. `None` means the entire
@@ -316,16 +359,20 @@ class BertEncoder(tf.keras.Model):
matrices in the shape of ['vocab_size', 'embedding_width'] and
['embedding_width', 'hidden_size'] ('embedding_width' is usually much
smaller than 'hidden_size').
- embedding_layer: An optional Layer instance which will be called to
- generate embeddings for the input word IDs.
- norm_first: Whether to normalize inputs to attention and intermediate
- dense layers. If set False, output of attention and intermediate dense
- layers is normalized.
+ embedding_layer: An optional Layer instance which will be called to generate
+ embeddings for the input word IDs.
+ norm_first: Whether to normalize inputs to attention and intermediate dense
+ layers. If set False, output of attention and intermediate dense layers is
+ normalized.
dict_outputs: Whether to use a dictionary as the model outputs.
return_all_encoder_outputs: Whether to output sequence embedding outputs of
all encoder transformer layers. Note: when the following `dict_outputs`
argument is True, all encoder outputs are always returned in the dict,
keyed by `encoder_outputs`.
+ return_attention_scores: Whether to add an additional output containing the
+ attention scores of all transformer layers. This will be a list of length
+ `num_layers`, and each element will be in the shape [batch_size,
+ num_attention_heads, seq_dim, seq_dim].
"""
def __init__(
@@ -347,6 +394,7 @@ class BertEncoder(tf.keras.Model):
norm_first=False,
dict_outputs=False,
return_all_encoder_outputs=False,
+ return_attention_scores: bool = False,
**kwargs):
if 'sequence_length' in kwargs:
kwargs.pop('sequence_length')
@@ -384,7 +432,7 @@ class BertEncoder(tf.keras.Model):
embedding_layer_inst = layers.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
else:
embedding_layer_inst = embedding_layer
@@ -392,14 +440,14 @@ class BertEncoder(tf.keras.Model):
# Always uses dynamic slicing for simplicity.
position_embedding_layer = layers.PositionEmbedding(
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
max_length=max_sequence_length,
name='position_embedding')
position_embeddings = position_embedding_layer(word_embeddings)
type_embedding_layer = layers.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')
type_embeddings = type_embedding_layer(type_ids)
@@ -416,11 +464,11 @@ class BertEncoder(tf.keras.Model):
# We project the 'embedding' output to 'hidden_size' if it is not already
# 'hidden_size'.
if embedding_width != hidden_size:
- embedding_projection = tf.keras.layers.experimental.EinsumDense(
+ embedding_projection = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')
embeddings = embedding_projection(embeddings)
else:
@@ -430,11 +478,11 @@ class BertEncoder(tf.keras.Model):
data = embeddings
attention_mask = layers.SelfAttentionMask()(data, mask)
encoder_outputs = []
+ attention_outputs = []
for i in range(num_layers):
- if i == num_layers - 1 and output_range is not None:
+ transformer_output_range = None
+ if i == num_layers - 1:
transformer_output_range = output_range
- else:
- transformer_output_range = None
layer = layers.TransformerEncoderBlock(
num_attention_heads=num_attention_heads,
inner_dim=inner_dim,
@@ -442,11 +490,15 @@ class BertEncoder(tf.keras.Model):
output_dropout=output_dropout,
attention_dropout=attention_dropout,
norm_first=norm_first,
- output_range=transformer_output_range,
- kernel_initializer=initializer,
+ return_attention_scores=return_attention_scores,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='transformer/layer_%d' % i)
transformer_layers.append(layer)
- data = layer([data, attention_mask])
+ data = layer([data, attention_mask],
+ output_range=transformer_output_range)
+ if return_attention_scores:
+ data, attention_scores = data
+ attention_outputs.append(attention_scores)
encoder_outputs.append(data)
last_encoder_output = encoder_outputs[-1]
@@ -457,7 +509,7 @@ class BertEncoder(tf.keras.Model):
pooler_layer = tf.keras.layers.Dense(
units=hidden_size,
activation='tanh',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='pooler_transform')
cls_output = pooler_layer(first_token_tensor)
@@ -466,6 +518,8 @@ class BertEncoder(tf.keras.Model):
pooled_output=cls_output,
encoder_outputs=encoder_outputs,
)
+ if return_attention_scores:
+ outputs['attention_scores'] = attention_outputs
if dict_outputs:
super().__init__(
@@ -478,6 +532,8 @@ class BertEncoder(tf.keras.Model):
else:
sequence_output = outputs['sequence_output']
outputs = [sequence_output, cls_output]
+ if return_attention_scores:
+ outputs.append(attention_outputs)
super().__init__( # pylint: disable=bad-super-call
inputs=[word_ids, mask, type_ids],
outputs=outputs,
@@ -509,6 +565,7 @@ class BertEncoder(tf.keras.Model):
'embedding_layer': embedding_layer,
'norm_first': norm_first,
'dict_outputs': dict_outputs,
+ 'return_attention_scores': return_attention_scores,
}
# pylint: disable=protected-access
self._setattr_tracking = False
@@ -547,3 +604,4 @@ class BertEncoder(tf.keras.Model):
logging.warn(warn_string)
return cls(**config)
+
diff --git a/official/nlp/modeling/networks/bert_encoder_test.py b/official/nlp/modeling/networks/bert_encoder_test.py
index 9b3b0826759b4198d282874d4ad57b17422f769c..7bc9b4f27ffeef29a870510dc8d8a01a629d7056 100644
--- a/official/nlp/modeling/networks/bert_encoder_test.py
+++ b/official/nlp/modeling/networks/bert_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -106,6 +106,42 @@ class BertEncoderTest(keras_parameterized.TestCase):
self.assertAllEqual(tf.float32, all_encoder_outputs[-1].dtype)
self.assertAllEqual(tf.float32, pooled.dtype)
+ @parameterized.named_parameters(
+ ("encoder_v2", bert_encoder.BertEncoderV2),
+ ("encoder_v1", bert_encoder.BertEncoder),
+ )
+ def test_dict_outputs_network_creation_return_attention_scores(
+ self, encoder_cls):
+ hidden_size = 32
+ sequence_length = 21
+ num_attention_heads = 5
+ num_layers = 3
+ # Create a small BertEncoder for testing.
+ test_network = encoder_cls(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=num_attention_heads,
+ num_layers=num_layers,
+ return_attention_scores=True,
+ dict_outputs=True)
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ all_attention_outputs = dict_outputs["attention_scores"]
+
+ expected_data_shape = [
+ None, num_attention_heads, sequence_length, sequence_length
+ ]
+ self.assertLen(all_attention_outputs, num_layers)
+ for data in all_attention_outputs:
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, all_attention_outputs[-1].dtype)
+
@parameterized.named_parameters(
("encoder_v2", bert_encoder.BertEncoderV2),
("encoder_v1", bert_encoder.BertEncoder),
@@ -369,6 +405,34 @@ class BertEncoderTest(keras_parameterized.TestCase):
self.assertAllEqual(tf.float32, all_encoder_outputs[-1].dtype)
self.assertAllEqual(tf.float32, pooled.dtype)
+ def test_attention_scores_output_network_creation(self):
+ hidden_size = 32
+ sequence_length = 21
+ num_attention_heads = 5
+ num_layers = 3
+ # Create a small BertEncoder for testing.
+ test_network = bert_encoder.BertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=num_attention_heads,
+ num_layers=num_layers,
+ return_attention_scores=True)
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ _, _, all_attention_outputs = test_network([word_ids, mask, type_ids])
+
+ expected_data_shape = [
+ None, num_attention_heads, sequence_length, sequence_length
+ ]
+ self.assertLen(all_attention_outputs, num_layers)
+ for data in all_attention_outputs:
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, all_attention_outputs[-1].dtype)
+
def test_network_creation_with_float16_dtype(self):
hidden_size = 32
sequence_length = 21
@@ -481,8 +545,7 @@ class BertEncoderV2CompatibilityTest(tf.test.TestCase):
hidden_size=hidden_size,
num_attention_heads=2,
num_layers=3,
- type_vocab_size=num_types,
- output_range=None)
+ type_vocab_size=num_types)
word_id_data = np.random.randint(
vocab_size, size=(batch_size, sequence_length))
@@ -541,8 +604,7 @@ class BertEncoderV2CompatibilityTest(tf.test.TestCase):
hidden_size=hidden_size,
num_attention_heads=2,
num_layers=3,
- type_vocab_size=num_types,
- output_range=None)
+ type_vocab_size=num_types)
word_id_data = np.random.randint(
vocab_size, size=(batch_size, sequence_length))
diff --git a/official/nlp/modeling/networks/classification.py b/official/nlp/modeling/networks/classification.py
index b91810796e3d9aec66605c6c24a13a46252e6dbf..ce8b1d7048593022e7355de3be2251f531934ebb 100644
--- a/official/nlp/modeling/networks/classification.py
+++ b/official/nlp/modeling/networks/classification.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -74,7 +74,7 @@ class Classification(tf.keras.Model):
('Unknown `output` value "%s". `output` can be either "logits" or '
'"predictions"') % output)
- super(Classification, self).__init__(
+ super().__init__(
inputs=[cls_output], outputs=output_tensors, **kwargs)
# b/164516224
diff --git a/official/nlp/modeling/networks/classification_test.py b/official/nlp/modeling/networks/classification_test.py
index ba0360855ec344225398f1e689dfa08106a42656..3f0551813274c4b8eb0549006b5e3a3e9beeb21f 100644
--- a/official/nlp/modeling/networks/classification_test.py
+++ b/official/nlp/modeling/networks/classification_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/encoder_scaffold.py b/official/nlp/modeling/networks/encoder_scaffold.py
index b71a74b706a93b448b7c2ece8a7bd686cf2d45d8..72130d785a53748bc0f33fc97ce9e3ac2deee3a8 100644
--- a/official/nlp/modeling/networks/encoder_scaffold.py
+++ b/official/nlp/modeling/networks/encoder_scaffold.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,6 +21,7 @@ from absl import logging
import gin
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
@@ -153,14 +154,14 @@ class EncoderScaffold(tf.keras.Model):
embedding_layer = layers.OnDeviceEmbedding(
vocab_size=embedding_cfg['vocab_size'],
embedding_width=embedding_cfg['hidden_size'],
- initializer=embedding_cfg['initializer'],
+ initializer=tf_utils.clone_initializer(embedding_cfg['initializer']),
name='word_embeddings')
word_embeddings = embedding_layer(word_ids)
# Always uses dynamic slicing for simplicity.
position_embedding_layer = layers.PositionEmbedding(
- initializer=embedding_cfg['initializer'],
+ initializer=tf_utils.clone_initializer(embedding_cfg['initializer']),
max_length=embedding_cfg['max_seq_length'],
name='position_embedding')
position_embeddings = position_embedding_layer(word_embeddings)
@@ -168,7 +169,7 @@ class EncoderScaffold(tf.keras.Model):
type_embedding_layer = layers.OnDeviceEmbedding(
vocab_size=embedding_cfg['type_vocab_size'],
embedding_width=embedding_cfg['hidden_size'],
- initializer=embedding_cfg['initializer'],
+ initializer=tf_utils.clone_initializer(embedding_cfg['initializer']),
use_one_hot=True,
name='type_embeddings')
type_embeddings = type_embedding_layer(type_ids)
@@ -243,6 +244,8 @@ class EncoderScaffold(tf.keras.Model):
# like this will create a SliceOpLambda layer. This is better than a Lambda
# layer with Python code, because that is fundamentally less portable.
first_token_tensor = last_layer_output[:, 0, :]
+ pooler_layer_initializer = tf.keras.initializers.get(
+ pooler_layer_initializer)
pooler_layer = tf.keras.layers.Dense(
units=pooled_output_dim,
activation='tanh',
@@ -268,7 +271,7 @@ class EncoderScaffold(tf.keras.Model):
# created using the Functional API. Once super().__init__ is called, we
# can assign attributes to `self` - note that all `self` assignments are
# below this line.
- super(EncoderScaffold, self).__init__(
+ super().__init__(
inputs=inputs, outputs=outputs, **kwargs)
self._hidden_cls = hidden_cls
@@ -303,7 +306,8 @@ class EncoderScaffold(tf.keras.Model):
config_dict = {
'num_hidden_instances': self._num_hidden_instances,
'pooled_output_dim': self._pooled_output_dim,
- 'pooler_layer_initializer': self._pooler_layer_initializer,
+ 'pooler_layer_initializer': tf.keras.initializers.serialize(
+ self._pooler_layer_initializer),
'embedding_cls': self._embedding_network,
'embedding_cfg': self._embedding_cfg,
'layer_norm_before_pooling': self._layer_norm_before_pooling,
diff --git a/official/nlp/modeling/networks/encoder_scaffold_test.py b/official/nlp/modeling/networks/encoder_scaffold_test.py
index 433343ae8fbbe5798b33cff3d3b7a8c544e5e2d7..bc0b02e3cf0f4c69e96a623d6f11ddb58594569a 100644
--- a/official/nlp/modeling/networks/encoder_scaffold_test.py
+++ b/official/nlp/modeling/networks/encoder_scaffold_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/fnet.py b/official/nlp/modeling/networks/fnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..ac9676699425ec31d51b52fac15d40095a79acb4
--- /dev/null
+++ b/official/nlp/modeling/networks/fnet.py
@@ -0,0 +1,355 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""FNet encoder network.
+
+Based on ["FNet: Mixing Tokens with Fourier Transforms"]
+(https://aclanthology.org/2022.naacl-main.319/).
+"""
+# pylint: disable=g-classes-have-attributes
+
+from typing import Any, Callable, Optional, Sequence, Union
+from absl import logging
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.nlp.modeling import layers
+
+_Activation = Union[str, Callable[..., Any]]
+_Initializer = Union[str, tf.keras.initializers.Initializer]
+
+_approx_gelu = lambda x: tf.keras.activations.gelu(x, approximate=True)
+
+
+class FNet(tf.keras.layers.Layer):
+ """FNet encoder network.
+
+ Based on ["FNet: Mixing Tokens with Fourier Transforms"]
+ (https://aclanthology.org/2022.naacl-main.319/). FNet is an efficient
+ Transformer-like encoder network that replaces self-attention sublayers with
+ Fourier sublayers.
+
+ This implementation defaults to the canonical FNet Base model, but the network
+ also supports more general mixing models (e.g. 'Linear', 'HNet') and hybrid
+ models (e.g. 'FNet-Hybrid') models that use both mixing and self-attention
+ layers. The input length is fixed to 'max_sequence_length'.
+
+ Args:
+ vocab_size: The size of the token vocabulary.
+ hidden_size: The size of the transformer hidden layers.
+ num_layers: The number of transformer layers.
+ mixing_mechanism: Type of mixing mechanism used in place of self-attention
+ layers. Defaults to FNet ('Fourier') mixing.
+ use_fft: Only used for spectral mixing mechanims. Determines whether to use
+ Fast Fourier Transform (True) or the Discrete Fourier Transform (DFT)
+ matrix (False; default) to compute the Fourier Transform. See
+ layers.FourierTransformLayer or layers.HartleyTransformLayer for advice.
+ attention_layers: Specifies which layers, if any, should be attention layers
+ in the encoder. The remaining [0, num_layers) setminus attention_layers
+ will use the specified `mixing_mechanism`. If using attention layers, a
+ good rule of thumb is to place them in the final few layers.
+ num_attention_heads: The number of attention heads for each transformer. The
+ hidden size must be divisible by the number of attention heads.
+ max_sequence_length: The only sequence length that this encoder can
+ consume. This determines the variable shape for positional embeddings and
+ the size of the mixing matrices.
+ type_vocab_size: The number of types that the 'type_ids' input can take.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ output_dropout: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout: The dropout rate to use for the attention layers within
+ the transformer layers.
+ initializer: The initializer to use for all weights in this encoder.
+ output_range: The sequence output range, [0, output_range), by slicing the
+ target sequence of the last transformer layer. `None` means the entire
+ target sequence will attend to the source sequence, which yields the full
+ output.
+ embedding_width: The width of the word embeddings. If the embedding width is
+ not equal to hidden size, embedding parameters will be factorized into two
+ matrices in the shape of ['vocab_size', 'embedding_width'] and
+ ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
+ smaller than 'hidden_size').
+ embedding_layer: An optional Layer instance which will be called to generate
+ embeddings for the input word IDs.
+ norm_first: Whether to normalize inputs to attention and intermediate dense
+ layers. If set False, output of attention and intermediate dense layers is
+ normalized.
+ with_dense_inputs: Whether to accept dense embeddings as the input.
+ """
+
+ def __init__(
+ self,
+ vocab_size: int,
+ hidden_size: int = 768,
+ num_layers: int = 12,
+ mixing_mechanism: layers.MixingMechanism = layers.MixingMechanism.FOURIER,
+ use_fft: bool = False,
+ attention_layers: Sequence[int] = (),
+ num_attention_heads: int = 12,
+ max_sequence_length: int = 512,
+ type_vocab_size: int = 16,
+ inner_dim: int = 3072,
+ inner_activation: _Activation = _approx_gelu,
+ output_dropout: float = 0.1,
+ attention_dropout: float = 0.1,
+ initializer: _Initializer = tf.keras.initializers.TruncatedNormal(
+ stddev=0.02),
+ output_range: Optional[int] = None,
+ embedding_width: Optional[int] = None,
+ embedding_layer: Optional[tf.keras.layers.Layer] = None,
+ norm_first: bool = False,
+ with_dense_inputs: bool = False,
+ **kwargs):
+ super().__init__(**kwargs)
+
+ activation = tf.keras.activations.get(inner_activation)
+ initializer = tf.keras.initializers.get(initializer)
+
+ if embedding_width is None:
+ embedding_width = hidden_size
+
+ self._config = {
+ 'vocab_size': vocab_size,
+ 'hidden_size': hidden_size,
+ 'num_layers': num_layers,
+ 'mixing_mechanism': mixing_mechanism,
+ 'use_fft': use_fft,
+ 'attention_layers': attention_layers,
+ 'num_attention_heads': num_attention_heads,
+ 'max_sequence_length': max_sequence_length,
+ 'type_vocab_size': type_vocab_size,
+ 'inner_dim': inner_dim,
+ 'inner_activation': tf.keras.activations.serialize(activation),
+ 'output_dropout': output_dropout,
+ 'attention_dropout': attention_dropout,
+ 'initializer': tf.keras.initializers.serialize(initializer),
+ 'output_range': output_range,
+ 'embedding_width': embedding_width,
+ 'embedding_layer': embedding_layer,
+ 'norm_first': norm_first,
+ 'with_dense_inputs': with_dense_inputs,
+ }
+
+ if embedding_layer is None:
+ self._embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ initializer=tf_utils.clone_initializer(initializer),
+ name='word_embeddings')
+ else:
+ self._embedding_layer = embedding_layer
+
+ self._position_embedding_layer = layers.PositionEmbedding(
+ initializer=tf_utils.clone_initializer(initializer),
+ max_length=max_sequence_length,
+ name='position_embedding')
+
+ self._type_embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=type_vocab_size,
+ embedding_width=embedding_width,
+ initializer=tf_utils.clone_initializer(initializer),
+ use_one_hot=True,
+ name='type_embeddings')
+
+ self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
+ name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
+
+ self._embedding_dropout = tf.keras.layers.Dropout(
+ rate=output_dropout, name='embedding_dropout')
+
+ # We project the 'embedding' output to 'hidden_size' if it is not already
+ # 'hidden_size'.
+ self._embedding_projection = None
+ if embedding_width != hidden_size:
+ self._embedding_projection = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=hidden_size,
+ bias_axes='y',
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='embedding_projection')
+
+ self._transformer_layers = []
+ for layer in range(num_layers):
+ if layer in attention_layers:
+ mixing_layer = layers.MultiHeadAttention(
+ num_heads=num_attention_heads,
+ key_dim=int(hidden_size // num_attention_heads),
+ dropout=attention_dropout,
+ use_bias=True,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='self_attention',
+ )
+ else:
+ mixing_layer = self._init_mixing_sublayer(layer)
+
+ block = layers.TransformerScaffold(
+ num_attention_heads=num_attention_heads,
+ inner_dim=inner_dim,
+ inner_activation=inner_activation,
+ attention_cls=mixing_layer,
+ feedforward_cls=None, # Fallback to default FeedForward class
+ output_dropout=output_dropout,
+ attention_dropout=attention_dropout,
+ norm_first=norm_first,
+ output_range=output_range if layer == num_layers - 1 else None,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='transformer/layer_%d' % layer)
+ self._transformer_layers.append(block)
+
+ self._attention_mask_layer = layers.SelfAttentionMask(
+ name='self_attention_mask')
+
+ self._pooler_layer = tf.keras.layers.Dense(
+ units=hidden_size,
+ activation='tanh',
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='pooler_transform')
+
+ if with_dense_inputs:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ input_mask=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ dense_inputs=tf.keras.Input(
+ shape=(max_sequence_length, embedding_width), dtype=tf.float32),
+ dense_mask=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ dense_type_ids=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ )
+ else:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ input_mask=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(
+ shape=(max_sequence_length,), dtype=tf.int32))
+ self._max_sequence_length = max_sequence_length
+
+ def call(self, inputs):
+ word_embeddings = None
+ if isinstance(inputs, dict):
+ word_ids = inputs.get('input_word_ids')
+ mask = inputs.get('input_mask')
+ type_ids = inputs.get('input_type_ids')
+ word_embeddings = inputs.get('input_word_embeddings', None)
+
+ dense_inputs = inputs.get('dense_inputs', None)
+ dense_mask = inputs.get('dense_mask', None)
+ dense_type_ids = inputs.get('dense_type_ids', None)
+ else:
+ raise ValueError('Unexpected inputs type (%s) to %s.' %
+ (type(inputs), self.__class__))
+
+ if word_embeddings is None:
+ word_embeddings = self._embedding_layer(word_ids)
+
+ if dense_inputs is not None:
+ # Concat the dense embeddings at sequence end.
+ word_embeddings = tf.concat([word_embeddings, dense_inputs], axis=1)
+ type_ids = tf.concat([type_ids, dense_type_ids], axis=1)
+ mask = tf.concat([mask, dense_mask], axis=1)
+
+ seq_length = word_embeddings.shape[1]
+ if seq_length != self._max_sequence_length:
+ raise ValueError('FNet: Sequence length must be the same as '
+ '`max_sequence_length` ({}), but it is {}.'.format(
+ self._max_sequence_length, seq_length))
+
+ # Absolute position embeddings.
+ position_embeddings = self._position_embedding_layer(word_embeddings)
+ type_embeddings = self._type_embedding_layer(type_ids)
+
+ embeddings = word_embeddings + position_embeddings + type_embeddings
+ embeddings = self._embedding_norm_layer(embeddings)
+ embeddings = self._embedding_dropout(embeddings)
+
+ if self._embedding_projection is not None:
+ embeddings = self._embedding_projection(embeddings)
+
+ attention_mask = self._attention_mask_layer(embeddings, mask)
+
+ encoder_outputs = []
+ x = embeddings
+ for layer in self._transformer_layers:
+ x = layer([x, attention_mask])
+ encoder_outputs.append(x)
+
+ last_encoder_output = encoder_outputs[-1]
+ first_token_tensor = last_encoder_output[:, 0, :]
+ pooled_output = self._pooler_layer(first_token_tensor)
+
+ output = dict(
+ sequence_output=encoder_outputs[-1],
+ pooled_output=pooled_output,
+ encoder_outputs=encoder_outputs)
+ return output
+
+ def get_embedding_table(self):
+ return self._embedding_layer.embeddings
+
+ def get_embedding_layer(self):
+ return self._embedding_layer
+
+ def get_config(self):
+ return dict(self._config)
+
+ @property
+ def transformer_layers(self):
+ """List of Transformer layers in the encoder."""
+ return self._transformer_layers
+
+ @property
+ def pooler_layer(self):
+ """The pooler dense layer after the transformer layers."""
+ return self._pooler_layer
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ if 'embedding_layer' in config and config['embedding_layer'] is not None:
+ warn_string = (
+ 'You are reloading a model that was saved with a '
+ 'potentially-shared embedding layer object. If you contine to '
+ 'train this model, the embedding layer will no longer be shared. '
+ 'To work around this, load the model outside of the Keras API.')
+ print('WARNING: ' + warn_string)
+ logging.warn(warn_string)
+
+ return cls(**config)
+
+ def _init_mixing_sublayer(self, layer: int):
+ """Initializes config-dependent mixing sublayer."""
+ if self._config['mixing_mechanism'] == layers.MixingMechanism.FOURIER:
+ mixing_sublayer = layers.FourierTransformLayer(
+ use_fft=self._config['use_fft'], name='fourier_transform')
+ elif self._config['mixing_mechanism'] == layers.MixingMechanism.HARTLEY:
+ mixing_sublayer = layers.HartleyTransformLayer(
+ use_fft=self._config['use_fft'], name='hartley_transform')
+ elif self._config['mixing_mechanism'] == layers.MixingMechanism.LINEAR:
+ mixing_sublayer = layers.LinearTransformLayer(
+ kernel_initializer=tf_utils.clone_initializer(
+ self._config['initializer']),
+ name='linear_transform')
+ else:
+ raise ValueError('Unsupported mixing mechanism: %s' %
+ self._config['mixing_mechanism'])
+
+ return mixing_sublayer
diff --git a/official/nlp/modeling/networks/fnet_test.py b/official/nlp/modeling/networks/fnet_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..09a32e2d13c211152aeddc07b06eb27e8ec4a6d7
--- /dev/null
+++ b/official/nlp/modeling/networks/fnet_test.py
@@ -0,0 +1,119 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for FNet encoder network."""
+
+from typing import Sequence
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.nlp.modeling import layers
+from official.nlp.modeling.networks import fnet
+
+
+class FNetTest(parameterized.TestCase, tf.test.TestCase):
+
+ def tearDown(self):
+ super(FNetTest, self).tearDown()
+ tf.keras.mixed_precision.set_global_policy("float32")
+
+ @parameterized.named_parameters(
+ ("fnet", layers.MixingMechanism.FOURIER, ()),
+ ("fnet_hybrid", layers.MixingMechanism.FOURIER, (1, 2)),
+ ("hnet", layers.MixingMechanism.HARTLEY, ()),
+ ("hnet_hybrid", layers.MixingMechanism.HARTLEY, (1, 2)),
+ ("linear", layers.MixingMechanism.LINEAR, ()),
+ ("linear_hybrid", layers.MixingMechanism.LINEAR, (0,)),
+ ("bert", layers.MixingMechanism.FOURIER, (0, 1, 2)),
+ )
+ def test_network(self, mixing_mechanism: layers.MixingMechanism,
+ attention_layers: Sequence[int]):
+ num_layers = 3
+ hidden_size = 32
+ sequence_length = 21
+ test_network = fnet.FNet(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ max_sequence_length=sequence_length,
+ num_layers=num_layers,
+ mixing_mechanism=mixing_mechanism,
+ attention_layers=attention_layers)
+
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ self.assertIsInstance(test_network.transformer_layers, list)
+ self.assertLen(test_network.transformer_layers, 3)
+ self.assertIsInstance(test_network.pooler_layer, tf.keras.layers.Dense)
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, data.dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+ def test_embeddings_as_inputs(self):
+ hidden_size = 32
+ sequence_length = 21
+ test_network = fnet.FNet(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ max_sequence_length=sequence_length,
+ num_layers=3)
+
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+
+ test_network.build(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ embeddings = test_network.get_embedding_layer()(word_ids)
+
+ # Calls with the embeddings.
+ dict_outputs = test_network(
+ dict(
+ input_word_embeddings=embeddings,
+ input_mask=mask,
+ input_type_ids=type_ids))
+ all_encoder_outputs = dict_outputs["encoder_outputs"]
+ pooled = dict_outputs["pooled_output"]
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertLen(all_encoder_outputs, 3)
+ for data in all_encoder_outputs:
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, all_encoder_outputs[-1].dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/nlp/modeling/networks/funnel_transformer.py b/official/nlp/modeling/networks/funnel_transformer.py
index fd3d10c114f453d5afab515ccc7d89e9533b7bd7..f1957f870196fc8ddd06f1ef57522a8403a3016b 100644
--- a/official/nlp/modeling/networks/funnel_transformer.py
+++ b/official/nlp/modeling/networks/funnel_transformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,6 +20,7 @@ from absl import logging
import numpy as np
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
_Initializer = Union[str, tf.keras.initializers.Initializer]
@@ -226,6 +227,7 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
funnel encoder relies on.
share_rezero: bool. Whether to share ReZero alpha between the attention
layer and the ffn layer. This option is specific to ReZero.
+ with_dense_inputs: Whether to accept dense embeddings as the input.
"""
def __init__(
@@ -251,9 +253,14 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
norm_first: bool = False,
transformer_cls: Union[
str, tf.keras.layers.Layer] = layers.TransformerEncoderBlock,
- share_rezero: bool = True,
+ share_rezero: bool = False,
**kwargs):
super().__init__(**kwargs)
+
+ if output_range is not None:
+ logging.warning('`output_range` is available as an argument for `call()`.'
+ 'The `output_range` as __init__ argument is deprecated.')
+
activation = tf.keras.activations.get(inner_activation)
initializer = tf.keras.initializers.get(initializer)
@@ -264,20 +271,20 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
self._embedding_layer = layers.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
else:
self._embedding_layer = embedding_layer
self._position_embedding_layer = layers.PositionEmbedding(
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
max_length=max_sequence_length,
name='position_embedding')
self._type_embedding_layer = layers.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')
@@ -291,11 +298,11 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
# 'hidden_size'.
self._embedding_projection = None
if embedding_width != hidden_size:
- self._embedding_projection = tf.keras.layers.experimental.EinsumDense(
+ self._embedding_projection = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')
self._transformer_layers = []
@@ -304,6 +311,7 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
# Will raise an error if the string is not supported.
if isinstance(transformer_cls, str):
transformer_cls = _str2transformer_cls[transformer_cls]
+ self._num_layers = num_layers
for i in range(num_layers):
layer = transformer_cls(
num_attention_heads=num_attention_heads,
@@ -314,8 +322,7 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
output_dropout=output_dropout,
attention_dropout=attention_dropout,
norm_first=norm_first,
- output_range=output_range if i == num_layers - 1 else None,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
share_rezero=share_rezero,
name='transformer/layer_%d' % i)
self._transformer_layers.append(layer)
@@ -323,7 +330,7 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
self._pooler_layer = tf.keras.layers.Dense(
units=hidden_size,
activation='tanh',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='pooler_transform')
if isinstance(pool_stride, int):
# TODO(b/197133196): Pooling layer can be shared.
@@ -341,9 +348,6 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
# TODO(b/203665205): unpool_length should be implemented.
if unpool_length != 0:
raise ValueError('unpool_length is not supported by truncated_avg now.')
- # Compute the attention masks and pooling transforms.
- self._pooling_transforms = _create_truncated_avg_transforms(
- max_sequence_length, pool_strides)
else:
raise ValueError('pool_type not supported.')
@@ -357,6 +361,7 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
name='att_input_pool_layer')
self._att_input_pool_layers.append(att_input_pool_layer)
+ self._max_sequence_length = max_sequence_length
self._pool_strides = pool_strides # This is a list here.
self._unpool_length = unpool_length
self._pool_type = pool_type
@@ -402,12 +407,22 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
_transformer_cls2str.get(transformer_cls, str(transformer_cls))
}
- def call(self, inputs):
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32))
+
+ def call(self, inputs, output_range: Optional[tf.Tensor] = None):
# inputs are [word_ids, mask, type_ids]
if isinstance(inputs, (list, tuple)):
logging.warning('List inputs to %s are discouraged.', self.__class__)
if len(inputs) == 3:
word_ids, mask, type_ids = inputs
+ dense_inputs = None
+ dense_mask = None
+ dense_type_ids = None
+ elif len(inputs) == 6:
+ word_ids, mask, type_ids, dense_inputs, dense_mask, dense_type_ids = inputs
else:
raise ValueError('Unexpected inputs to %s with length at %d.' %
(self.__class__, len(inputs)))
@@ -415,10 +430,21 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
word_ids = inputs.get('input_word_ids')
mask = inputs.get('input_mask')
type_ids = inputs.get('input_type_ids')
+
+ dense_inputs = inputs.get('dense_inputs', None)
+ dense_mask = inputs.get('dense_mask', None)
+ dense_type_ids = inputs.get('dense_type_ids', None)
else:
raise ValueError('Unexpected inputs type to %s.' % self.__class__)
word_embeddings = self._embedding_layer(word_ids)
+
+ if dense_inputs is not None:
+ # Concat the dense embeddings at sequence begin so unpool_len can control
+ # embedding not being pooled.
+ word_embeddings = tf.concat([dense_inputs, word_embeddings], axis=1)
+ type_ids = tf.concat([dense_type_ids, type_ids], axis=1)
+ mask = tf.concat([dense_mask, mask], axis=1)
# absolute position embeddings
position_embeddings = self._position_embedding_layer(word_embeddings)
type_embeddings = self._type_embedding_layer(type_ids)
@@ -456,7 +482,9 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
x[:, :self._unpool_length, :],
dtype=pooled_inputs.dtype), pooled_inputs),
axis=1)
- x = layer([query_inputs, x, attention_mask])
+ x = layer([query_inputs, x, attention_mask],
+ output_range=output_range if i == self._num_layers -
+ 1 else None)
# Pools the corresponding attention_mask.
if i < len(self._transformer_layers) - 1:
attention_mask = _pool_and_concat(
@@ -466,25 +494,35 @@ class FunnelTransformerEncoder(tf.keras.layers.Layer):
axes=[1, 2])
encoder_outputs.append(x)
elif self._pool_type == _TRUNCATED_AVG:
+ # Compute the attention masks and pooling transforms.
+ # Note we do not compute this in __init__ due to inference converter issue
+ # b/215659399.
+ pooling_transforms = _create_truncated_avg_transforms(
+ self._max_sequence_length, self._pool_strides)
attention_masks = _create_truncated_avg_masks(mask, self._pool_strides,
- self._pooling_transforms)
+ pooling_transforms)
for i, layer in enumerate(self._transformer_layers):
attention_mask = attention_masks[i]
+ transformer_output_range = None
+ if i == self._num_layers - 1:
+ transformer_output_range = output_range
# Bypass no pooling cases.
if self._pool_strides[i] == 1:
- x = layer([x, x, attention_mask])
+ x = layer([x, x, attention_mask],
+ output_range=transformer_output_range)
else:
pooled_inputs = tf.einsum(
'BFD,FT->BTD',
tf.cast(x[:, self._unpool_length:, :], _get_policy_dtype()
), # extra casting for faster mixed computation.
- self._pooling_transforms[i])
+ pooling_transforms[i])
query_inputs = tf.concat(
values=(tf.cast(
x[:, :self._unpool_length, :],
dtype=pooled_inputs.dtype), pooled_inputs),
axis=1)
- x = layer([query_inputs, x, attention_mask])
+ x = layer([query_inputs, x, attention_mask],
+ output_range=transformer_output_range)
encoder_outputs.append(x)
last_encoder_output = encoder_outputs[-1]
diff --git a/official/nlp/modeling/networks/funnel_transformer_test.py b/official/nlp/modeling/networks/funnel_transformer_test.py
index 26a519d433c4e64fc96a32c78aa767ec215c0ed9..202b07e7319819debb43e2de2110f9faf94bbe18 100644
--- a/official/nlp/modeling/networks/funnel_transformer_test.py
+++ b/official/nlp/modeling/networks/funnel_transformer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -101,6 +101,55 @@ class FunnelTransformerEncoderTest(parameterized.TestCase, tf.test.TestCase):
self.assertAllEqual(tf.float32, data.dtype)
self.assertAllEqual(pooled_dtype, pooled.dtype)
+ def test_network_creation_dense(self):
+ tf.keras.mixed_precision.set_global_policy("mixed_float16")
+ pool_type = "avg"
+
+ hidden_size = 32
+ sequence_length = 21
+ dense_sequence_length = 3
+ pool_stride = 2
+ num_layers = 3
+ # Create a small FunnelTransformerEncoder for testing.
+ test_network = funnel_transformer.FunnelTransformerEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=num_layers,
+ pool_stride=pool_stride,
+ pool_type=pool_type,
+ max_sequence_length=sequence_length + dense_sequence_length,
+ unpool_length=0,
+ transformer_cls="TransformerEncoderBlock")
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+
+ dense_inputs = tf.keras.Input(
+ shape=(dense_sequence_length, hidden_size), dtype=tf.float32)
+ dense_mask = tf.keras.Input(shape=(dense_sequence_length,), dtype=tf.int32)
+ dense_type_ids = tf.keras.Input(
+ shape=(dense_sequence_length,), dtype=tf.int32)
+
+ dict_outputs = test_network(
+ [word_ids, mask, type_ids, dense_inputs, dense_mask, dense_type_ids])
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ self.assertIsInstance(test_network.transformer_layers, list)
+ self.assertLen(test_network.transformer_layers, num_layers)
+ self.assertIsInstance(test_network.pooler_layer, tf.keras.layers.Dense)
+
+ # Stride=2 compresses sequence length to half the size at each layer.
+ # For pool_type = max or avg,
+ # this configuration gives each layer of seq length: 24->12->6->3.
+ expected_data_shape = [None, 3, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
def test_invalid_stride_and_num_layers(self):
hidden_size = 32
num_layers = 3
@@ -180,14 +229,14 @@ class FunnelTransformerEncoderTest(parameterized.TestCase, tf.test.TestCase):
num_attention_heads=2,
num_layers=3,
type_vocab_size=num_types,
- output_range=output_range,
pool_stride=pool_stride,
unpool_length=unpool_length)
# Create the inputs (note that the first dimension is implicit).
word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
- dict_outputs = test_network([word_ids, mask, type_ids])
+ dict_outputs = test_network([word_ids, mask, type_ids],
+ output_range=output_range)
data = dict_outputs["sequence_output"]
pooled = dict_outputs["pooled_output"]
diff --git a/official/nlp/modeling/networks/mobile_bert_encoder.py b/official/nlp/modeling/networks/mobile_bert_encoder.py
index 8f3dcd9f2d22e77a1f6f780eeb560bc006d31ae9..46b2dbb21c00dc8af19f65606f1fd95443c76890 100644
--- a/official/nlp/modeling/networks/mobile_bert_encoder.py
+++ b/official/nlp/modeling/networks/mobile_bert_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -146,7 +146,7 @@ class MobileBERTEncoder(tf.keras.Model):
first_token = tf.squeeze(prev_output[:, 0:1, :], axis=1)
if classifier_activation:
- self._pooler_layer = tf.keras.layers.experimental.EinsumDense(
+ self._pooler_layer = tf.keras.layers.EinsumDense(
'ab,bc->ac',
output_shape=hidden_size,
activation=tf.tanh,
@@ -163,7 +163,7 @@ class MobileBERTEncoder(tf.keras.Model):
encoder_outputs=all_layer_outputs,
attention_scores=all_attention_scores)
- super(MobileBERTEncoder, self).__init__(
+ super().__init__(
inputs=self.inputs, outputs=outputs, **kwargs)
def get_embedding_table(self):
diff --git a/official/nlp/modeling/networks/mobile_bert_encoder_test.py b/official/nlp/modeling/networks/mobile_bert_encoder_test.py
index 2360e7202f87686a83d11bf8d9fd66d1281c1cf1..1b119005b325ab2c3ca46519d5d1bcdda05f971b 100644
--- a/official/nlp/modeling/networks/mobile_bert_encoder_test.py
+++ b/official/nlp/modeling/networks/mobile_bert_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/packed_sequence_embedding.py b/official/nlp/modeling/networks/packed_sequence_embedding.py
index 353c5e88e21bd9708d3e9aceac234de71e9788be..6457e736b15c6e4d588fb90cd5e3cd1c39b674bb 100644
--- a/official/nlp/modeling/networks/packed_sequence_embedding.py
+++ b/official/nlp/modeling/networks/packed_sequence_embedding.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -97,13 +97,13 @@ class PackedSequenceEmbedding(tf.keras.Model):
embedding_layer = layers.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
word_embeddings = embedding_layer(word_ids)
# Always uses dynamic slicing for simplicity.
position_embedding_layer = PositionEmbeddingWithSubSeqMask(
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_dynamic_slicing=True,
max_sequence_length=max_seq_length,
name='position_embedding')
@@ -114,7 +114,7 @@ class PackedSequenceEmbedding(tf.keras.Model):
layers.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')(type_ids))
@@ -128,11 +128,11 @@ class PackedSequenceEmbedding(tf.keras.Model):
embeddings)
if embedding_width != hidden_size:
- embeddings = tf.keras.layers.experimental.EinsumDense(
+ embeddings = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes=None,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')(
embeddings)
@@ -143,7 +143,7 @@ class PackedSequenceEmbedding(tf.keras.Model):
[attention_mask, sub_seq_mask])
outputs = [embeddings, attention_mask]
- super(PackedSequenceEmbedding, self).__init__(
+ super().__init__(
inputs=inputs, outputs=outputs, **kwargs)
# TF does not track immutable attrs which do not contain Trackables,
# so by creating a config namedtuple instead of a dict we avoid tracking it.
@@ -221,7 +221,7 @@ class PositionEmbeddingWithSubSeqMask(tf.keras.layers.Layer):
if 'dtype' not in kwargs:
kwargs['dtype'] = 'float32'
- super(PositionEmbeddingWithSubSeqMask, self).__init__(**kwargs)
+ super().__init__(**kwargs)
if use_dynamic_slicing and max_sequence_length is None:
raise ValueError(
'If `use_dynamic_slicing` is True, `max_sequence_length` must be set.'
@@ -236,7 +236,7 @@ class PositionEmbeddingWithSubSeqMask(tf.keras.layers.Layer):
'initializer': tf.keras.initializers.serialize(self._initializer),
'use_dynamic_slicing': self._use_dynamic_slicing,
}
- base_config = super(PositionEmbeddingWithSubSeqMask, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def build(self, input_shape):
@@ -273,7 +273,7 @@ class PositionEmbeddingWithSubSeqMask(tf.keras.layers.Layer):
shape=[weight_sequence_length, width],
initializer=self._initializer)
- super(PositionEmbeddingWithSubSeqMask, self).build(input_shape)
+ super().build(input_shape)
def call(self, inputs, position_ids=None, sub_sequence_mask=None):
"""Implements call() for the layer.
diff --git a/official/nlp/modeling/networks/packed_sequence_embedding_test.py b/official/nlp/modeling/networks/packed_sequence_embedding_test.py
index bfab20ba33898d66fc6e4e4e8e13b30548ac00bb..64080f3c8f227a4155669e4818686a7e8a977b1c 100644
--- a/official/nlp/modeling/networks/packed_sequence_embedding_test.py
+++ b/official/nlp/modeling/networks/packed_sequence_embedding_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/span_labeling.py b/official/nlp/modeling/networks/span_labeling.py
index efbf69d19216b24b1af492b4eec7a080d8457265..7da8a174e6c5be59b10b996d77b3e5c7e43a4b5a 100644
--- a/official/nlp/modeling/networks/span_labeling.py
+++ b/official/nlp/modeling/networks/span_labeling.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,6 +17,8 @@
import collections
import tensorflow as tf
+from official.modeling import tf_utils
+
def _apply_paragraph_mask(logits, paragraph_mask):
"""Applies a position mask to calculated logits."""
@@ -79,7 +81,7 @@ class SpanLabeling(tf.keras.Model):
# created using the Functional API. Once super().__init__ is called, we
# can assign attributes to `self` - note that all `self` assignments are
# below this line.
- super(SpanLabeling, self).__init__(
+ super().__init__(
inputs=[sequence_data], outputs=output_tensors, **kwargs)
config_dict = {
'input_width': input_width,
@@ -156,12 +158,12 @@ class XLNetSpanLabeling(tf.keras.layers.Layer):
self._end_n_top = end_n_top
self.start_logits_dense = tf.keras.layers.Dense(
units=1,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='predictions/transform/start_logits')
self.end_logits_inner_dense = tf.keras.layers.Dense(
units=input_width,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
activation=activation,
name='predictions/transform/end_logits/inner')
self.end_logits_layer_norm = tf.keras.layers.LayerNormalization(
@@ -169,18 +171,18 @@ class XLNetSpanLabeling(tf.keras.layers.Layer):
name='predictions/transform/end_logits/layernorm')
self.end_logits_output_dense = tf.keras.layers.Dense(
units=1,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='predictions/transform/end_logits/output')
self.answer_logits_inner = tf.keras.layers.Dense(
units=input_width,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
activation=activation,
name='predictions/transform/answer_logits/inner')
self.answer_logits_dropout = tf.keras.layers.Dropout(rate=dropout_rate)
self.answer_logits_output = tf.keras.layers.Dense(
units=1,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
use_bias=False,
name='predictions/transform/answer_logits/output')
diff --git a/official/nlp/modeling/networks/span_labeling_test.py b/official/nlp/modeling/networks/span_labeling_test.py
index 45084520e0cccdb21d6e1aae146a8cb3e2fe9f99..a51a0a7c6ec8c43f1168abb10b2e400e918178ee 100644
--- a/official/nlp/modeling/networks/span_labeling_test.py
+++ b/official/nlp/modeling/networks/span_labeling_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/networks/xlnet_base.py b/official/nlp/modeling/networks/xlnet_base.py
index ce32d3dfdda85cdeec5ef1cad4bf7cfbb8d43787..337fd8259ff7ec873c42b4d177280fb3d5518468 100644
--- a/official/nlp/modeling/networks/xlnet_base.py
+++ b/official/nlp/modeling/networks/xlnet_base.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,7 @@ from absl import logging
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
from official.nlp.modeling.layers import transformer_xl
@@ -383,7 +384,7 @@ class RelativePositionEncoding(tf.keras.layers.Layer):
"""
def __init__(self, hidden_size, **kwargs):
- super(RelativePositionEncoding, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._hidden_size = hidden_size
self._inv_freq = 1.0 / (10000.0**(
tf.range(0, self._hidden_size, 2.0) / self._hidden_size))
@@ -475,7 +476,7 @@ class XLNetBase(tf.keras.layers.Layer):
use_cls_mask=False,
embedding_width=None,
**kwargs):
- super(XLNetBase, self).__init__(**kwargs)
+ super().__init__(**kwargs)
self._vocab_size = vocab_size
self._initializer = initializer
@@ -507,7 +508,7 @@ class XLNetBase(tf.keras.layers.Layer):
self._embedding_layer = layers.OnDeviceEmbedding(
vocab_size=self._vocab_size,
embedding_width=embedding_width,
- initializer=self._initializer,
+ initializer=tf_utils.clone_initializer(self._initializer),
dtype=tf.float32,
name="word_embedding")
self._dropout = tf.keras.layers.Dropout(rate=self._dropout_rate)
@@ -573,7 +574,7 @@ class XLNetBase(tf.keras.layers.Layer):
"embedding_width":
self._embedding_width,
}
- base_config = super(XLNetBase, self).get_config()
+ base_config = super().get_config()
return dict(list(base_config.items()) + list(config.items()))
def get_embedding_lookup_table(self):
@@ -600,7 +601,7 @@ class XLNetBase(tf.keras.layers.Layer):
"target_mapping": target_mapping,
"masked_tokens": masked_tokens
}
- return super(XLNetBase, self).__call__(inputs, **kwargs)
+ return super().__call__(inputs, **kwargs)
def call(self, inputs):
"""Implements call() for the layer."""
@@ -666,7 +667,7 @@ class XLNetBase(tf.keras.layers.Layer):
shape=[self._num_layers, 2, self._num_attention_heads,
self._head_size],
dtype=tf.float32,
- initializer=self._initializer)
+ initializer=tf_utils.clone_initializer(self._initializer))
segment_embedding = self._segment_embedding
segment_matrix = _compute_segment_matrix(
diff --git a/official/nlp/modeling/networks/xlnet_base_test.py b/official/nlp/modeling/networks/xlnet_base_test.py
index 81db32487325b3b61d47afac6217590491067257..c2abda3871189d020b74b77032aa2088da262831 100644
--- a/official/nlp/modeling/networks/xlnet_base_test.py
+++ b/official/nlp/modeling/networks/xlnet_base_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/ops/__init__.py b/official/nlp/modeling/ops/__init__.py
index e21f33273f3801a34073aceecf301e23808727d3..3fec3645836df885429024c3b06c5a1fbc5669a2 100644
--- a/official/nlp/modeling/ops/__init__.py
+++ b/official/nlp/modeling/ops/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,5 +14,7 @@
"""Ops package definition."""
from official.nlp.modeling.ops.beam_search import sequence_beam_search
+from official.nlp.modeling.ops.beam_search import SequenceBeamSearch
+from official.nlp.modeling.ops.sampling_module import SamplingModule
from official.nlp.modeling.ops.segment_extractor import get_next_sentence_labels
from official.nlp.modeling.ops.segment_extractor import get_sentence_order_labels
diff --git a/official/nlp/modeling/ops/beam_search.py b/official/nlp/modeling/ops/beam_search.py
index eddb31212bcd633cb35b9eeb78b49a796f73b2e7..afac4b81e69711dfd446582be3c0e23850968021 100644
--- a/official/nlp/modeling/ops/beam_search.py
+++ b/official/nlp/modeling/ops/beam_search.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -107,18 +107,18 @@ class SequenceBeamSearch(tf.Module):
max_decode_length,
eos_id,
padded_decode,
- dtype=tf.float32):
+ dtype=tf.float32,
+ decoding_name=None):
"""Initialize sequence beam search.
Args:
- symbols_to_logits_fn: A function to provide logits, which is the
- interface to the Transformer model. The passed in arguments are: ids ->
- A tensor with shape [batch_size * beam_size, index]. index -> A
- scalar. cache -> A nested dictionary of tensors [batch_size *
- beam_size, ...].
- The function must return a tuple of logits and the updated cache: logits
- -> A tensor with shape [batch * beam_size, vocab_size]. updated cache
- -> A nested dictionary with the same structure as the input cache.
+ symbols_to_logits_fn: A function to provide logits, which is the interface
+ to the Transformer model. The passed in arguments are: ids -> A tensor
+ with shape [batch_size * beam_size, index]. index -> A scalar. cache ->
+ A nested dictionary of tensors [batch_size * beam_size, ...]. The
+ function must return a tuple of logits and the updated cache: logits ->
+ A tensor with shape [batch * beam_size, vocab_size]. updated cache -> A
+ nested dictionary with the same structure as the input cache.
vocab_size: An integer, the size of the vocabulary, used for topk
computation.
beam_size: An integer, number of beams for beam search.
@@ -130,6 +130,7 @@ class SequenceBeamSearch(tf.Module):
for beam search.
dtype: A tensorflow data type used for score computation. The default is
tf.float32.
+ decoding_name: an optional name for the decoding loop tensors.
"""
self.symbols_to_logits_fn = symbols_to_logits_fn
self.vocab_size = vocab_size
@@ -139,6 +140,7 @@ class SequenceBeamSearch(tf.Module):
self.eos_id = eos_id
self.padded_decode = padded_decode
self.dtype = tf.as_dtype(dtype)
+ self.decoding_name = decoding_name
def search(self, initial_ids, initial_cache):
"""Beam search for sequences with highest scores.
@@ -204,7 +206,7 @@ class SequenceBeamSearch(tf.Module):
candidate_log_probs = _log_prob_from_logits(logits)
# Calculate new log probabilities if each of the alive sequences were
- # extended # by the the candidate IDs.
+ # extended # by the candidate IDs.
# Shape [batch_size, beam_size, vocab_size]
log_probs = candidate_log_probs + tf.expand_dims(alive_log_probs, axis=2)
@@ -370,7 +372,8 @@ class SequenceBeamSearch(tf.Module):
_search_step,
loop_vars=[state],
shape_invariants=[state_shapes],
- parallel_iterations=1))
+ parallel_iterations=1,
+ name=self.decoding_name))
finished_state = finished_state[0]
return self._process_finished_state(finished_state)
@@ -587,7 +590,8 @@ def sequence_beam_search(symbols_to_logits_fn,
max_decode_length,
eos_id,
padded_decode=False,
- dtype="float32"):
+ dtype="float32",
+ decoding_name=None):
"""Search for sequence of subtoken ids with the largest probability.
Args:
@@ -612,13 +616,15 @@ def sequence_beam_search(symbols_to_logits_fn,
beam search.
dtype: A tensorflow data type used for score computation. The default is
tf.float32.
+ decoding_name: an optional name for the decoding loop tensors.
Returns:
Top decoded sequences [batch_size, beam_size, max_decode_length]
sequence scores [batch_size, beam_size]
"""
sbs = SequenceBeamSearch(symbols_to_logits_fn, vocab_size, beam_size, alpha,
- max_decode_length, eos_id, padded_decode, dtype)
+ max_decode_length, eos_id, padded_decode, dtype,
+ decoding_name)
return sbs.search(initial_ids, initial_cache)
diff --git a/official/nlp/modeling/ops/beam_search_test.py b/official/nlp/modeling/ops/beam_search_test.py
index 6b46868c3841437107e8858075b36dfed9bbcd64..89daabe137acf1df77d977eca22f058858a3f3ef 100644
--- a/official/nlp/modeling/ops/beam_search_test.py
+++ b/official/nlp/modeling/ops/beam_search_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -60,10 +60,12 @@ class BeamSearchTests(tf.test.TestCase, parameterized.TestCase):
y)
@parameterized.named_parameters([
- ('padded_decode_true', True),
- ('padded_decode_false', False),
+ ('padded_decode_true_with_name', True, 'decoding'),
+ ('padded_decode_false_with_name', False, 'decoding'),
+ ('padded_decode_true_without_name', True, None),
+ ('padded_decode_false_without_name', False, None),
])
- def test_sequence_beam_search(self, padded_decode):
+ def test_sequence_beam_search(self, padded_decode, name):
# batch_size*beam_size, max_decode_length, vocab_size
probabilities = tf.constant([[[0.2, 0.7, 0.1], [0.5, 0.3, 0.2],
[0.1, 0.8, 0.1]],
@@ -91,7 +93,8 @@ class BeamSearchTests(tf.test.TestCase, parameterized.TestCase):
max_decode_length=3,
eos_id=9,
padded_decode=padded_decode,
- dtype=tf.float32)
+ dtype=tf.float32,
+ decoding_name=name)
self.assertAllEqual([[[0, 1, 0, 1], [0, 1, 1, 2]]], predictions)
diff --git a/official/nlp/modeling/ops/decoding_module.py b/official/nlp/modeling/ops/decoding_module.py
index bfd928f130ed82f839155bdc845a5d7326e1ec2f..e4272936c234703cbf27596894e6f6b2033557c8 100644
--- a/official/nlp/modeling/ops/decoding_module.py
+++ b/official/nlp/modeling/ops/decoding_module.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,14 +15,14 @@
"""Base class for Decoding Strategies (beam_search, top_k, top_p and greedy)."""
import abc
-from typing import Any, Callable, Dict, Tuple
+from typing import Any, Callable, Dict, Optional, Tuple
import tensorflow as tf
from tensorflow.python.framework import dtypes
from official.modeling import tf_utils
-Output = Tuple[tf.Tensor, tf.Tensor]
+Output = Tuple[tf.Tensor, tf.Tensor, Optional[tf.Tensor]]
InternalState = Tuple[tf.Tensor, tf.Tensor, tf.Tensor, Dict]
InitialState = Tuple[Dict[str, Any], Dict[str, Any]]
@@ -46,6 +46,10 @@ class StateKeys:
# the previous iteration.
ALIVE_CACHE = "ALIVE_CACHE"
+ # The initial model state/cache after model processing the initial token.
+ # The cache will be filled if extra_cache_output is true.
+ INITIAL_OUTPUT_CACHE = "INITIAL_OUTPUT_CACHE"
+
# Top finished sequences for each batch item.
# Has shape [batch_size, beam_size, CUR_INDEX + 1]. Sequences that are
# shorter than CUR_INDEX + 1 are padded with 0s.
@@ -108,7 +112,9 @@ class DecodingModule(tf.Module, metaclass=abc.ABCMeta):
def __init__(self,
length_normalization_fn: Callable[[int, tf.DType], float],
- dtype: tf.DType = tf.float32):
+ dtype: tf.DType = tf.float32,
+ decoding_name: Optional[str] = None,
+ extra_cache_output: bool = False):
"""Initialize the Decoding Module.
Args:
@@ -116,31 +122,39 @@ class DecodingModule(tf.Module, metaclass=abc.ABCMeta):
parameter. Function accepts input as length, dtype and returns float.
dtype: A tensorflow data type used for score computation. The default is
tf.float32.
+ decoding_name: an optional name for the decoding loop tensors.
+ extra_cache_output: If true, the first cache will be in the states.
"""
self.length_normalization_fn = length_normalization_fn
self.dtype = tf.as_dtype(dtype)
+ self.decoding_name = decoding_name
def generate(self,
initial_ids: tf.Tensor,
- initial_cache: Dict[str, tf.Tensor]) -> Output:
+ initial_cache: Dict[str, tf.Tensor],
+ initial_log_probs: Optional[tf.Tensor] = None) -> Output:
"""Implements the decoding strategy (beam_search or sampling).
Args:
- initial_ids: initial ids to pass into the symbols_to_logits_fn.
- int tensor with shape [batch_size, 1]
+ initial_ids: initial ids to pass into the symbols_to_logits_fn. int tensor
+ with shape [batch_size, 1]
initial_cache: dictionary for caching model outputs from previous step.
+ initial_log_probs: Optionally initial log probs if there is a prefix
+ sequence we want to start to decode from.
+
Returns:
Tuple of tensors representing
finished_sequence: shape [batch, max_seq_length]
finished_scores: [batch]
+ first_cache: The cache after init token
"""
batch_size = (
initial_ids.shape.as_list()[0]
if self.padded_decode else tf.shape(initial_ids)[0])
- state, state_shapes = self._create_initial_state(initial_ids,
- initial_cache,
- batch_size)
+ state, state_shapes = self._create_initial_state(initial_ids, initial_cache,
+ batch_size,
+ initial_log_probs)
def _generate_step(state):
topk_seq, topk_log_probs, topk_ids, new_cache = self._grow_alive_seq(
@@ -160,6 +174,17 @@ class DecodingModule(tf.Module, metaclass=abc.ABCMeta):
}
new_state.update(alive_state)
new_state.update(finished_state)
+ if self.extra_cache_output:
+ i = state[StateKeys.CUR_INDEX]
+ old_cache = state[StateKeys.INITIAL_OUTPUT_CACHE]
+
+ def update_with_cache(new_state, cache):
+ """Updates new_state with cache."""
+ new_state.update({StateKeys.INITIAL_OUTPUT_CACHE: cache})
+
+ tf.cond(
+ tf.equal(i, 0), lambda: update_with_cache(new_state, new_cache),
+ lambda: update_with_cache(new_state, old_cache))
return [new_state]
finished_state = tf.nest.map_structure(
@@ -169,15 +194,18 @@ class DecodingModule(tf.Module, metaclass=abc.ABCMeta):
_generate_step,
loop_vars=[state],
shape_invariants=[state_shapes],
- parallel_iterations=1))
+ parallel_iterations=1,
+ name=self.decoding_name))
final_state = self._process_finished_state(finished_state[0])
return final_state
@abc.abstractmethod
- def _create_initial_state(self,
- initial_ids: tf.Tensor,
- initial_cache: Dict[str, tf.Tensor],
- batch_size: int) -> InitialState:
+ def _create_initial_state(
+ self,
+ initial_ids: tf.Tensor,
+ initial_cache: Dict[str, tf.Tensor],
+ batch_size: int,
+ initial_log_probs: Optional[tf.Tensor] = None) -> InitialState:
"""Return initial state dictionary and its shape invariants."""
pass
@@ -277,6 +305,3 @@ class DecodingModule(tf.Module, metaclass=abc.ABCMeta):
return dtypes.float16.max
else:
raise AssertionError("Invalid dtype: %s" % self.dtype)
-
-
-
diff --git a/official/nlp/modeling/ops/decoding_module_test.py b/official/nlp/modeling/ops/decoding_module_test.py
index da444ed5394a6fd257663b61c9230be715d7846c..cec2902de716c16900806197339e95bb8fd5194b 100644
--- a/official/nlp/modeling/ops/decoding_module_test.py
+++ b/official/nlp/modeling/ops/decoding_module_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -29,6 +29,7 @@ class TestSubclass(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
def __init__(self,
length_normalization_fn=length_normalization,
+ extra_cache_output=True,
dtype=tf.float32):
super(TestSubclass, self).__init__(
length_normalization_fn=length_normalization, dtype=dtype)
diff --git a/official/nlp/modeling/ops/sampling_module.py b/official/nlp/modeling/ops/sampling_module.py
index dc396b7b1f8182fb7f8b4a76645e8b60f1fe8a2b..12e882421deb033d3f06f1d5d65ac272157788af 100644
--- a/official/nlp/modeling/ops/sampling_module.py
+++ b/official/nlp/modeling/ops/sampling_module.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -55,6 +55,8 @@ def sample_top_k(logits, top_k):
Returns:
Logits with top_k filtering applied.
"""
+ top_k = tf.clip_by_value(
+ top_k, clip_value_min=1, clip_value_max=tf.shape(logits)[-1])
top_k_logits = tf.math.top_k(logits, k=top_k)
indices_to_remove = logits < tf.expand_dims(top_k_logits[0][..., -1], -1)
top_k_logits = set_tensor_by_indices_to_value(logits, indices_to_remove,
@@ -160,7 +162,9 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
top_p=1.0,
sample_temperature=0.0,
enable_greedy: bool = True,
- dtype: tf.DType = tf.float32):
+ dtype: tf.DType = tf.float32,
+ decoding_name: Optional[str] = None,
+ extra_cache_output: bool = False):
"""Initialize sampling module."""
self.symbols_to_logits_fn = symbols_to_logits_fn
self.length_normalization_fn = length_normalization_fn
@@ -174,8 +178,13 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
self.sample_temperature = tf.convert_to_tensor(
sample_temperature, dtype=tf.float32)
self.enable_greedy = enable_greedy
+ self.decoding_name = decoding_name
+ self.extra_cache_output = extra_cache_output
super(SamplingModule, self).__init__(
- length_normalization_fn=length_normalization_fn, dtype=dtype)
+ length_normalization_fn=length_normalization_fn,
+ dtype=dtype,
+ decoding_name=decoding_name,
+ extra_cache_output=extra_cache_output)
def _grow_alive_seq(self,
state: Dict[str, Any],
@@ -241,10 +250,13 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
topk_seq = tf.concat([alive_seq, topk_ids], axis=-1)
return topk_seq, topk_log_probs, topk_ids, new_cache
- def _create_initial_state(self,
- initial_ids: tf.Tensor,
- initial_cache: Dict[str, tf.Tensor],
- batch_size: int) -> decoding_module.InitialState:
+ def _create_initial_state(
+ self,
+ initial_ids: tf.Tensor,
+ initial_cache: Dict[str, tf.Tensor],
+ batch_size: int,
+ initial_log_probs: Optional[tf.Tensor] = None
+ ) -> decoding_module.InitialState:
"""Return initial state dictionary and its shape invariants."""
for key, value in initial_cache.items():
for inner_value in tf.nest.flatten(value):
@@ -264,8 +276,11 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
alive_seq = tf.tile(alive_seq, [1, self.max_decode_length + 1])
# Initial log probabilities with shape [batch_size, 1].
- initial_log_probs = tf.constant([[0.]], dtype=self.dtype)
- alive_log_probs = tf.tile(initial_log_probs, [batch_size, 1])
+ if initial_log_probs is None:
+ initial_log_probs = tf.constant([[0.]], dtype=self.dtype)
+ alive_log_probs = tf.tile(initial_log_probs, [batch_size, 1])
+ else:
+ alive_log_probs = initial_log_probs
alive_cache = initial_cache
@@ -294,16 +309,14 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
decoding_module.StateKeys.CUR_INDEX:
tf.TensorShape([]),
decoding_module.StateKeys.ALIVE_SEQ:
- tf.TensorShape(
- [batch_size, self.max_decode_length + 1]),
+ tf.TensorShape([batch_size, self.max_decode_length + 1]),
decoding_module.StateKeys.ALIVE_LOG_PROBS:
tf.TensorShape([batch_size, 1]),
decoding_module.StateKeys.ALIVE_CACHE:
tf.nest.map_structure(lambda state: state.get_shape(),
alive_cache),
decoding_module.StateKeys.FINISHED_SEQ:
- tf.TensorShape(
- [batch_size, self.max_decode_length + 1]),
+ tf.TensorShape([batch_size, self.max_decode_length + 1]),
decoding_module.StateKeys.FINISHED_SCORES:
tf.TensorShape([batch_size, 1]),
decoding_module.StateKeys.FINISHED_FLAGS:
@@ -318,9 +331,8 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
decoding_module.StateKeys.ALIVE_LOG_PROBS:
tf.TensorShape([None, 1]),
decoding_module.StateKeys.ALIVE_CACHE:
- tf.nest.map_structure(
- decoding_module.get_shape_keep_last_dim,
- alive_cache),
+ tf.nest.map_structure(decoding_module.get_shape_keep_last_dim,
+ alive_cache),
decoding_module.StateKeys.FINISHED_SEQ:
tf.TensorShape([None, None]),
decoding_module.StateKeys.FINISHED_SCORES:
@@ -329,6 +341,22 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
tf.TensorShape([None, 1])
}
+ if self.extra_cache_output:
+ state.update(
+ {decoding_module.StateKeys.INITIAL_OUTPUT_CACHE: alive_cache})
+ if self.padded_decode:
+ state_shape_invariants.update({
+ decoding_module.StateKeys.INITIAL_OUTPUT_CACHE:
+ tf.nest.map_structure(lambda state: state.get_shape(),
+ alive_cache)
+ })
+ else:
+ state_shape_invariants.update({
+ decoding_module.StateKeys.INITIAL_OUTPUT_CACHE:
+ tf.nest.map_structure(decoding_module.get_shape_keep_last_dim,
+ alive_cache),
+ })
+
return state, state_shape_invariants
def _get_new_alive_state(self, new_seq: tf.Tensor, new_log_probs: tf.Tensor,
@@ -422,6 +450,9 @@ class SamplingModule(decoding_module.DecodingModule, metaclass=abc.ABCMeta):
finished_scores)
finished_seq = tf.where(seq_cond, finished_seq, alive_seq)
finished_scores = tf.where(score_cond, finished_scores, alive_log_probs)
+ if self.extra_cache_output:
+ return finished_seq, finished_scores, finished_state[
+ decoding_module.StateKeys.INITIAL_OUTPUT_CACHE]
return finished_seq, finished_scores
def _continue_search(self, state) -> tf.Tensor:
diff --git a/official/nlp/modeling/ops/segment_extractor.py b/official/nlp/modeling/ops/segment_extractor.py
index e01649e4a3deffcd6aa9634da639c26b0c7199a0..8016b65cdd4d826829820936906cf7220a34be34 100644
--- a/official/nlp/modeling/ops/segment_extractor.py
+++ b/official/nlp/modeling/ops/segment_extractor.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/modeling/ops/segment_extractor_test.py b/official/nlp/modeling/ops/segment_extractor_test.py
index 6b4094b87870ab3054f460b150e230f74ab30339..3fb6f5667310370c75e3718d1f39b875422cd07c 100644
--- a/official/nlp/modeling/ops/segment_extractor_test.py
+++ b/official/nlp/modeling/ops/segment_extractor_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/optimization.py b/official/nlp/optimization.py
index 4040b73e9a704859ae30e27bafe6c4bc468f6cc8..13d21f144c7796efee359cb0c5b1afde2fba605b 100644
--- a/official/nlp/optimization.py
+++ b/official/nlp/optimization.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,14 +12,15 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-"""Functions and classes related to optimization (weight updates)."""
-
-import re
+"""Legacy functions and classes related to optimization."""
from absl import logging
import gin
import tensorflow as tf
import tensorflow_addons.optimizers as tfa_optimizers
+from official.modeling.optimization import legacy_adamw
+
+AdamWeightDecay = legacy_adamw.AdamWeightDecay
class WarmUp(tf.keras.optimizers.schedules.LearningRateSchedule):
@@ -70,13 +71,15 @@ def create_optimizer(init_lr,
num_warmup_steps,
end_lr=0.0,
optimizer_type='adamw',
- beta_1=0.9):
+ beta_1=0.9,
+ poly_power=1.0):
"""Creates an optimizer with learning rate schedule."""
# Implements linear decay of the learning rate.
lr_schedule = tf.keras.optimizers.schedules.PolynomialDecay(
initial_learning_rate=init_lr,
decay_steps=num_train_steps,
- end_learning_rate=end_lr)
+ end_learning_rate=end_lr,
+ power=poly_power)
if num_warmup_steps:
lr_schedule = WarmUp(
initial_learning_rate=init_lr,
@@ -105,126 +108,3 @@ def create_optimizer(init_lr,
raise ValueError('Unsupported optimizer type: ', optimizer_type)
return optimizer
-
-
-class AdamWeightDecay(tf.keras.optimizers.Adam):
- """Adam enables L2 weight decay and clip_by_global_norm on gradients.
-
- Just adding the square of the weights to the loss function is *not* the
- correct way of using L2 regularization/weight decay with Adam, since that will
- interact with the m and v parameters in strange ways.
-
- Instead we want to decay the weights in a manner that doesn't interact with
- the m/v parameters. This is equivalent to adding the square of the weights to
- the loss with plain (non-momentum) SGD.
- """
-
- def __init__(self,
- learning_rate=0.001,
- beta_1=0.9,
- beta_2=0.999,
- epsilon=1e-7,
- amsgrad=False,
- weight_decay_rate=0.0,
- include_in_weight_decay=None,
- exclude_from_weight_decay=None,
- gradient_clip_norm=1.0,
- name='AdamWeightDecay',
- **kwargs):
- super(AdamWeightDecay, self).__init__(learning_rate, beta_1, beta_2,
- epsilon, amsgrad, name, **kwargs)
- self.weight_decay_rate = weight_decay_rate
- self.gradient_clip_norm = gradient_clip_norm
- self._include_in_weight_decay = include_in_weight_decay
- self._exclude_from_weight_decay = exclude_from_weight_decay
- logging.info('gradient_clip_norm=%f', gradient_clip_norm)
-
- @classmethod
- def from_config(cls, config):
- """Creates an optimizer from its config with WarmUp custom object."""
- custom_objects = {'WarmUp': WarmUp}
- return super(AdamWeightDecay, cls).from_config(
- config, custom_objects=custom_objects)
-
- def _prepare_local(self, var_device, var_dtype, apply_state):
- super(AdamWeightDecay, self)._prepare_local(var_device, var_dtype, # pytype: disable=attribute-error # typed-keras
- apply_state)
- apply_state[(var_device, var_dtype)]['weight_decay_rate'] = tf.constant(
- self.weight_decay_rate, name='adam_weight_decay_rate')
-
- def _decay_weights_op(self, var, learning_rate, apply_state):
- do_decay = self._do_use_weight_decay(var.name)
- if do_decay:
- return var.assign_sub(
- learning_rate * var *
- apply_state[(var.device, var.dtype.base_dtype)]['weight_decay_rate'],
- use_locking=self._use_locking)
- return tf.no_op()
-
- def apply_gradients(self,
- grads_and_vars,
- name=None,
- experimental_aggregate_gradients=True):
- grads, tvars = list(zip(*grads_and_vars))
- if experimental_aggregate_gradients and self.gradient_clip_norm > 0.0:
- # when experimental_aggregate_gradients = False, apply_gradients() no
- # longer implicitly allreduce gradients, users manually allreduce gradient
- # and passed the allreduced grads_and_vars. For now, the
- # clip_by_global_norm will be moved to before the explicit allreduce to
- # keep the math the same as TF 1 and pre TF 2.2 implementation.
- (grads, _) = tf.clip_by_global_norm(
- grads, clip_norm=self.gradient_clip_norm)
- return super(AdamWeightDecay, self).apply_gradients(
- zip(grads, tvars),
- name=name,
- experimental_aggregate_gradients=experimental_aggregate_gradients)
-
- def _get_lr(self, var_device, var_dtype, apply_state):
- """Retrieves the learning rate with the given state."""
- if apply_state is None:
- return self._decayed_lr_t[var_dtype], {}
-
- apply_state = apply_state or {}
- coefficients = apply_state.get((var_device, var_dtype))
- if coefficients is None:
- coefficients = self._fallback_apply_state(var_device, var_dtype)
- apply_state[(var_device, var_dtype)] = coefficients
-
- return coefficients['lr_t'], dict(apply_state=apply_state)
-
- def _resource_apply_dense(self, grad, var, apply_state=None):
- lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
- decay = self._decay_weights_op(var, lr_t, apply_state)
- with tf.control_dependencies([decay]):
- return super(AdamWeightDecay,
- self)._resource_apply_dense(grad, var, **kwargs) # pytype: disable=attribute-error # typed-keras
-
- def _resource_apply_sparse(self, grad, var, indices, apply_state=None):
- lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
- decay = self._decay_weights_op(var, lr_t, apply_state)
- with tf.control_dependencies([decay]):
- return super(AdamWeightDecay,
- self)._resource_apply_sparse(grad, var, indices, **kwargs) # pytype: disable=attribute-error # typed-keras
-
- def get_config(self):
- config = super(AdamWeightDecay, self).get_config()
- config.update({
- 'weight_decay_rate': self.weight_decay_rate,
- })
- return config
-
- def _do_use_weight_decay(self, param_name):
- """Whether to use L2 weight decay for `param_name`."""
- if self.weight_decay_rate == 0:
- return False
-
- if self._include_in_weight_decay:
- for r in self._include_in_weight_decay:
- if re.search(r, param_name) is not None:
- return True
-
- if self._exclude_from_weight_decay:
- for r in self._exclude_from_weight_decay:
- if re.search(r, param_name) is not None:
- return False
- return True
diff --git a/official/nlp/projects/__init__.py b/official/nlp/projects/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/projects/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/projects/bigbird/__init__.py b/official/nlp/projects/bigbird/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/projects/bigbird/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/projects/bigbird/encoder.py b/official/nlp/projects/bigbird/encoder.py
deleted file mode 100644
index 911d8cca77e95448246ac2ca9d15e3a0fd73d861..0000000000000000000000000000000000000000
--- a/official/nlp/projects/bigbird/encoder.py
+++ /dev/null
@@ -1,238 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Transformer-based text encoder network."""
-# pylint: disable=g-classes-have-attributes
-
-import tensorflow as tf
-
-from official.modeling import activations
-from official.nlp import modeling
-from official.nlp.modeling import layers
-from official.nlp.projects.bigbird import recompute_grad
-from official.nlp.projects.bigbird import recomputing_dropout
-
-
-_MAX_SEQ_LEN = 4096
-
-
-class RecomputeTransformerLayer(layers.TransformerScaffold):
- """Transformer layer that recomputes the forward pass during backpropagation."""
-
- def call(self, inputs, training=None):
- emb, mask = inputs
- def f(*args):
- # recompute_grad can only handle tensor inputs. so we enumerate the
- # nested input [emb, mask] as follows:
- # args[0]: emb
- # args[1]: mask[0] = band_mask
- # args[2]: mask[1] = encoder_from_mask
- # args[3]: mask[2] = encoder_to_mask
- # args[4]: mask[3] = blocked_encoder_mask
- x = super(RecomputeTransformerLayer,
- self).call([args[0], [args[1], args[2], args[3], args[4]]],
- training=training)
- return x
-
- f = recompute_grad.recompute_grad(f)
-
- return f(emb, *mask)
-
-
-@tf.keras.utils.register_keras_serializable(package='Text')
-class BigBirdEncoder(tf.keras.Model):
- """Transformer-based encoder network with BigBird attentions.
-
- *Note* that the network is constructed by
- [Keras Functional API](https://keras.io/guides/functional_api/).
-
- Args:
- vocab_size: The size of the token vocabulary.
- hidden_size: The size of the transformer hidden layers.
- num_layers: The number of transformer layers.
- num_attention_heads: The number of attention heads for each transformer. The
- hidden size must be divisible by the number of attention heads.
- max_position_embeddings: The maximum length of position embeddings that this
- encoder can consume. If None, max_position_embeddings uses the value from
- sequence length. This determines the variable shape for positional
- embeddings.
- type_vocab_size: The number of types that the 'type_ids' input can take.
- intermediate_size: The intermediate size for the transformer layers.
- block_size: int. A BigBird Attention parameter: size of block in from/to
- sequences.
- num_rand_blocks: int. A BigBird Attention parameter: number of random chunks
- per row.
- activation: The activation to use for the transformer layers.
- dropout_rate: The dropout rate to use for the transformer layers.
- attention_dropout_rate: The dropout rate to use for the attention layers
- within the transformer layers.
- initializer: The initialzer to use for all weights in this encoder.
- embedding_width: The width of the word embeddings. If the embedding width is
- not equal to hidden size, embedding parameters will be factorized into two
- matrices in the shape of ['vocab_size', 'embedding_width'] and
- ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
- smaller than 'hidden_size').
- use_gradient_checkpointing: Use gradient checkpointing to trade-off compute
- for memory.
- """
-
- def __init__(self,
- vocab_size,
- hidden_size=768,
- num_layers=12,
- num_attention_heads=12,
- max_position_embeddings=_MAX_SEQ_LEN,
- type_vocab_size=16,
- intermediate_size=3072,
- block_size=64,
- num_rand_blocks=3,
- activation=activations.gelu,
- dropout_rate=0.1,
- attention_dropout_rate=0.1,
- initializer=tf.keras.initializers.TruncatedNormal(stddev=0.02),
- embedding_width=None,
- use_gradient_checkpointing=False,
- **kwargs):
- activation = tf.keras.activations.get(activation)
- initializer = tf.keras.initializers.get(initializer)
-
- if use_gradient_checkpointing:
- tf.keras.layers.Dropout = recomputing_dropout.RecomputingDropout
- layer_cls = RecomputeTransformerLayer
- else:
- layer_cls = layers.TransformerScaffold
-
- self._self_setattr_tracking = False
- self._config_dict = {
- 'vocab_size': vocab_size,
- 'hidden_size': hidden_size,
- 'num_layers': num_layers,
- 'num_attention_heads': num_attention_heads,
- 'max_position_embeddings': max_position_embeddings,
- 'type_vocab_size': type_vocab_size,
- 'intermediate_size': intermediate_size,
- 'block_size': block_size,
- 'num_rand_blocks': num_rand_blocks,
- 'activation': tf.keras.activations.serialize(activation),
- 'dropout_rate': dropout_rate,
- 'attention_dropout_rate': attention_dropout_rate,
- 'initializer': tf.keras.initializers.serialize(initializer),
- 'embedding_width': embedding_width,
- }
-
- word_ids = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name='input_word_ids')
- mask = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name='input_mask')
- type_ids = tf.keras.layers.Input(
- shape=(None,), dtype=tf.int32, name='input_type_ids')
-
- if embedding_width is None:
- embedding_width = hidden_size
- self._embedding_layer = modeling.layers.OnDeviceEmbedding(
- vocab_size=vocab_size,
- embedding_width=embedding_width,
- initializer=initializer,
- name='word_embeddings')
- word_embeddings = self._embedding_layer(word_ids)
-
- # Always uses dynamic slicing for simplicity.
- self._position_embedding_layer = modeling.layers.PositionEmbedding(
- initializer=initializer,
- max_length=max_position_embeddings,
- name='position_embedding')
- position_embeddings = self._position_embedding_layer(word_embeddings)
- self._type_embedding_layer = modeling.layers.OnDeviceEmbedding(
- vocab_size=type_vocab_size,
- embedding_width=embedding_width,
- initializer=initializer,
- use_one_hot=True,
- name='type_embeddings')
- type_embeddings = self._type_embedding_layer(type_ids)
-
- embeddings = tf.keras.layers.Add()(
- [word_embeddings, position_embeddings, type_embeddings])
-
- self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
- name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
-
- embeddings = self._embedding_norm_layer(embeddings)
- embeddings = tf.keras.layers.Dropout(rate=dropout_rate)(embeddings)
-
- # We project the 'embedding' output to 'hidden_size' if it is not already
- # 'hidden_size'.
- if embedding_width != hidden_size:
- self._embedding_projection = tf.keras.layers.experimental.EinsumDense(
- '...x,xy->...y',
- output_shape=hidden_size,
- bias_axes='y',
- kernel_initializer=initializer,
- name='embedding_projection')
- embeddings = self._embedding_projection(embeddings)
-
- self._transformer_layers = []
- data = embeddings
- masks = layers.BigBirdMasks(block_size=block_size)(
- data, mask)
- encoder_outputs = []
- attn_head_dim = hidden_size // num_attention_heads
- for i in range(num_layers):
- layer = layer_cls(
- num_attention_heads,
- intermediate_size,
- activation,
- attention_cls=layers.BigBirdAttention,
- attention_cfg=dict(
- num_heads=num_attention_heads,
- key_dim=attn_head_dim,
- kernel_initializer=initializer,
- from_block_size=block_size,
- to_block_size=block_size,
- num_rand_blocks=num_rand_blocks,
- max_rand_mask_length=max_position_embeddings,
- seed=i),
- dropout_rate=dropout_rate,
- attention_dropout_rate=dropout_rate,
- kernel_initializer=initializer)
- self._transformer_layers.append(layer)
- data = layer([data, masks])
- encoder_outputs.append(data)
-
- outputs = dict(
- sequence_output=encoder_outputs[-1], encoder_outputs=encoder_outputs)
- super().__init__(
- inputs=[word_ids, mask, type_ids], outputs=outputs, **kwargs)
-
- def get_embedding_table(self):
- return self._embedding_layer.embeddings
-
- def get_embedding_layer(self):
- return self._embedding_layer
-
- def get_config(self):
- return self._config_dict
-
- @property
- def transformer_layers(self):
- """List of Transformer layers in the encoder."""
- return self._transformer_layers
-
- @property
- def pooler_layer(self):
- """The pooler dense layer after the transformer layers."""
- return self._pooler_layer
-
- @classmethod
- def from_config(cls, config, custom_objects=None):
- return cls(**config)
diff --git a/official/nlp/projects/bigbird/encoder_test.py b/official/nlp/projects/bigbird/encoder_test.py
deleted file mode 100644
index 5ebab7776b56b1af40539e164fa41c7f016f32e0..0000000000000000000000000000000000000000
--- a/official/nlp/projects/bigbird/encoder_test.py
+++ /dev/null
@@ -1,63 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Tests for official.nlp.projects.bigbird.encoder."""
-
-import numpy as np
-import tensorflow as tf
-
-from official.nlp.projects.bigbird import encoder
-
-
-class BigBirdEncoderTest(tf.test.TestCase):
-
- def test_encoder(self):
- sequence_length = 1024
- batch_size = 2
- vocab_size = 1024
- network = encoder.BigBirdEncoder(
- num_layers=1, vocab_size=1024, max_position_embeddings=4096)
- word_id_data = np.random.randint(
- vocab_size, size=(batch_size, sequence_length))
- mask_data = np.random.randint(2, size=(batch_size, sequence_length))
- type_id_data = np.random.randint(2, size=(batch_size, sequence_length))
- outputs = network([word_id_data, mask_data, type_id_data])
- self.assertEqual(outputs["sequence_output"].shape,
- (batch_size, sequence_length, 768))
-
- def test_save_restore(self):
- sequence_length = 1024
- batch_size = 2
- vocab_size = 1024
- network = encoder.BigBirdEncoder(
- num_layers=1, vocab_size=1024, max_position_embeddings=4096)
- word_id_data = np.random.randint(
- vocab_size, size=(batch_size, sequence_length))
- mask_data = np.random.randint(2, size=(batch_size, sequence_length))
- type_id_data = np.random.randint(2, size=(batch_size, sequence_length))
- inputs = dict(
- input_word_ids=word_id_data,
- input_mask=mask_data,
- input_type_ids=type_id_data)
- ref_outputs = network(inputs)
- model_path = self.get_temp_dir() + "/model"
- network.save(model_path)
- loaded = tf.keras.models.load_model(model_path)
- outputs = loaded(inputs)
- self.assertAllClose(outputs["sequence_output"],
- ref_outputs["sequence_output"])
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/projects/bigbird/experiment_configs.py b/official/nlp/projects/bigbird/experiment_configs.py
deleted file mode 100644
index 35de842102b90429d6755ac589e8bc858e7ae109..0000000000000000000000000000000000000000
--- a/official/nlp/projects/bigbird/experiment_configs.py
+++ /dev/null
@@ -1,100 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Bigbird experiment configurations."""
-# pylint: disable=g-doc-return-or-yield,line-too-long
-from official.core import config_definitions as cfg
-from official.core import exp_factory
-from official.modeling import optimization
-from official.nlp.data import question_answering_dataloader
-from official.nlp.data import sentence_prediction_dataloader
-from official.nlp.tasks import question_answering
-from official.nlp.tasks import sentence_prediction
-
-
-@exp_factory.register_config_factory('bigbird/glue')
-def bigbird_glue() -> cfg.ExperimentConfig:
- r"""BigBird GLUE."""
- config = cfg.ExperimentConfig(
- task=sentence_prediction.SentencePredictionConfig(
- train_data=sentence_prediction_dataloader
- .SentencePredictionDataConfig(),
- validation_data=sentence_prediction_dataloader
- .SentencePredictionDataConfig(
- is_training=False, drop_remainder=False)),
- trainer=cfg.TrainerConfig(
- optimizer_config=optimization.OptimizationConfig({
- 'optimizer': {
- 'type': 'adamw',
- 'adamw': {
- 'weight_decay_rate':
- 0.01,
- 'exclude_from_weight_decay':
- ['LayerNorm', 'layer_norm', 'bias'],
- }
- },
- 'learning_rate': {
- 'type': 'polynomial',
- 'polynomial': {
- 'initial_learning_rate': 3e-5,
- 'end_learning_rate': 0.0,
- }
- },
- 'warmup': {
- 'type': 'polynomial'
- }
- })),
- restrictions=[
- 'task.train_data.is_training != None',
- 'task.validation_data.is_training != None'
- ])
- config.task.model.encoder.type = 'bigbird'
- return config
-
-
-@exp_factory.register_config_factory('bigbird/squad')
-def bigbird_squad() -> cfg.ExperimentConfig:
- r"""BigBird Squad V1/V2."""
- config = cfg.ExperimentConfig(
- task=question_answering.QuestionAnsweringConfig(
- train_data=question_answering_dataloader.QADataConfig(),
- validation_data=question_answering_dataloader.QADataConfig()),
- trainer=cfg.TrainerConfig(
- optimizer_config=optimization.OptimizationConfig({
- 'optimizer': {
- 'type': 'adamw',
- 'adamw': {
- 'weight_decay_rate':
- 0.01,
- 'exclude_from_weight_decay':
- ['LayerNorm', 'layer_norm', 'bias'],
- }
- },
- 'learning_rate': {
- 'type': 'polynomial',
- 'polynomial': {
- 'initial_learning_rate': 8e-5,
- 'end_learning_rate': 0.0,
- }
- },
- 'warmup': {
- 'type': 'polynomial'
- }
- })),
- restrictions=[
- 'task.train_data.is_training != None',
- 'task.validation_data.is_training != None'
- ])
- config.task.model.encoder.type = 'bigbird'
- return config
diff --git a/official/nlp/projects/teams/__init__.py b/official/nlp/projects/teams/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/projects/teams/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/projects/teams/teams_experiments_test.py b/official/nlp/projects/teams/teams_experiments_test.py
deleted file mode 100644
index b4b4448c46ce83a44fdc18c87890bdf0fa0ffe85..0000000000000000000000000000000000000000
--- a/official/nlp/projects/teams/teams_experiments_test.py
+++ /dev/null
@@ -1,38 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-# Lint as: python3
-"""Tests for teams_experiments."""
-
-from absl.testing import parameterized
-import tensorflow as tf
-
-# pylint: disable=unused-import
-from official.common import registry_imports
-# pylint: enable=unused-import
-from official.core import config_definitions as cfg
-from official.core import exp_factory
-
-
-class TeamsExperimentsTest(tf.test.TestCase, parameterized.TestCase):
-
- @parameterized.parameters(('teams/pretraining',))
- def test_teams_experiments(self, config_name):
- config = exp_factory.get_exp_config(config_name)
- self.assertIsInstance(config, cfg.ExperimentConfig)
- self.assertIsInstance(config.task.train_data, cfg.DataConfig)
-
-
-if __name__ == '__main__':
- tf.test.main()
diff --git a/official/nlp/projects/triviaqa/__init__.py b/official/nlp/projects/triviaqa/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/projects/triviaqa/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/projects/triviaqa/train.py b/official/nlp/projects/triviaqa/train.py
deleted file mode 100644
index c4e4c101f9f0034600c955fa0fb218a6253299c2..0000000000000000000000000000000000000000
--- a/official/nlp/projects/triviaqa/train.py
+++ /dev/null
@@ -1,384 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""TriviaQA training script."""
-import collections
-import contextlib
-import functools
-import json
-import operator
-import os
-
-from absl import app
-from absl import flags
-from absl import logging
-import gin
-import tensorflow as tf
-import tensorflow_datasets as tfds
-
-import sentencepiece as spm
-from official.nlp import optimization as nlp_optimization
-from official.nlp.configs import encoders
-from official.nlp.projects.triviaqa import evaluation
-from official.nlp.projects.triviaqa import inputs
-from official.nlp.projects.triviaqa import modeling
-from official.nlp.projects.triviaqa import prediction
-
-flags.DEFINE_string('data_dir', None, 'Data directory for TensorFlow Datasets.')
-
-flags.DEFINE_string(
- 'validation_gold_path', None,
- 'Path to golden validation. Usually, the wikipedia-dev.json file.')
-
-flags.DEFINE_string('model_dir', None,
- 'Directory for checkpoints and summaries.')
-
-flags.DEFINE_string('model_config_path', None,
- 'JSON file containing model coniguration.')
-
-flags.DEFINE_string('sentencepiece_model_path', None,
- 'Path to sentence piece model.')
-
-flags.DEFINE_enum('encoder', 'bigbird',
- ['bert', 'bigbird', 'albert', 'mobilebert'],
- 'Which transformer encoder model to use.')
-
-flags.DEFINE_integer('bigbird_block_size', 64,
- 'Size of blocks for sparse block attention.')
-
-flags.DEFINE_string('init_checkpoint_path', None,
- 'Path from which to initialize weights.')
-
-flags.DEFINE_integer('train_sequence_length', 4096,
- 'Maximum number of tokens for training.')
-
-flags.DEFINE_integer('train_global_sequence_length', 320,
- 'Maximum number of global tokens for training.')
-
-flags.DEFINE_integer('validation_sequence_length', 4096,
- 'Maximum number of tokens for validation.')
-
-flags.DEFINE_integer('validation_global_sequence_length', 320,
- 'Maximum number of global tokens for validation.')
-
-flags.DEFINE_integer('batch_size', 32, 'Size of batch.')
-
-flags.DEFINE_string('master', '', 'Address of the TPU master.')
-
-flags.DEFINE_integer('decode_top_k', 8,
- 'Maximum number of tokens to consider for begin/end.')
-
-flags.DEFINE_integer('decode_max_size', 16,
- 'Maximum number of sentence pieces in an answer.')
-
-flags.DEFINE_float('dropout_rate', 0.1, 'Dropout rate for hidden layers.')
-
-flags.DEFINE_float('attention_dropout_rate', 0.3,
- 'Dropout rate for attention layers.')
-
-flags.DEFINE_float('label_smoothing', 1e-1, 'Degree of label smoothing.')
-
-flags.DEFINE_multi_string(
- 'gin_bindings', [],
- 'Gin bindings to override the values set in the config files')
-
-FLAGS = flags.FLAGS
-
-
-@contextlib.contextmanager
-def worker_context():
- if FLAGS.master:
- with tf.device('/job:worker') as d:
- yield d
- else:
- yield
-
-
-def read_sentencepiece_model(path):
- with tf.io.gfile.GFile(path, 'rb') as file:
- processor = spm.SentencePieceProcessor()
- processor.LoadFromSerializedProto(file.read())
- return processor
-
-
-# Rename old BERT v1 configuration parameters.
-_MODEL_CONFIG_REPLACEMENTS = {
- 'num_hidden_layers': 'num_layers',
- 'attention_probs_dropout_prob': 'attention_dropout_rate',
- 'hidden_dropout_prob': 'dropout_rate',
- 'hidden_act': 'hidden_activation',
- 'window_size': 'block_size',
-}
-
-
-def read_model_config(encoder,
- path,
- bigbird_block_size=None) -> encoders.EncoderConfig:
- """Merges the JSON configuration into the encoder configuration."""
- with tf.io.gfile.GFile(path) as f:
- model_config = json.load(f)
- for key, value in _MODEL_CONFIG_REPLACEMENTS.items():
- if key in model_config:
- model_config[value] = model_config.pop(key)
- model_config['attention_dropout_rate'] = FLAGS.attention_dropout_rate
- model_config['dropout_rate'] = FLAGS.dropout_rate
- model_config['block_size'] = bigbird_block_size
- encoder_config = encoders.EncoderConfig(type=encoder)
- # Override the default config with those loaded from the JSON file.
- encoder_config_keys = encoder_config.get().as_dict().keys()
- overrides = {}
- for key, value in model_config.items():
- if key in encoder_config_keys:
- overrides[key] = value
- else:
- logging.warning('Ignoring config parameter %s=%s', key, value)
- encoder_config.get().override(overrides)
- return encoder_config
-
-
-@gin.configurable(denylist=[
- 'model',
- 'strategy',
- 'train_dataset',
- 'model_dir',
- 'init_checkpoint_path',
- 'evaluate_fn',
-])
-def fit(model,
- strategy,
- train_dataset,
- model_dir,
- init_checkpoint_path=None,
- evaluate_fn=None,
- learning_rate=1e-5,
- learning_rate_polynomial_decay_rate=1.,
- weight_decay_rate=1e-1,
- num_warmup_steps=5000,
- num_decay_steps=51000,
- num_epochs=6):
- """Train and evaluate."""
- hparams = dict(
- learning_rate=learning_rate,
- num_decay_steps=num_decay_steps,
- num_warmup_steps=num_warmup_steps,
- num_epochs=num_epochs,
- weight_decay_rate=weight_decay_rate,
- dropout_rate=FLAGS.dropout_rate,
- attention_dropout_rate=FLAGS.attention_dropout_rate,
- label_smoothing=FLAGS.label_smoothing)
- logging.info(hparams)
- learning_rate_schedule = nlp_optimization.WarmUp(
- learning_rate,
- tf.keras.optimizers.schedules.PolynomialDecay(
- learning_rate,
- num_decay_steps,
- end_learning_rate=0.,
- power=learning_rate_polynomial_decay_rate), num_warmup_steps)
- with strategy.scope():
- optimizer = nlp_optimization.AdamWeightDecay(
- learning_rate_schedule,
- weight_decay_rate=weight_decay_rate,
- epsilon=1e-6,
- exclude_from_weight_decay=['LayerNorm', 'layer_norm', 'bias'])
- model.compile(optimizer, loss=modeling.SpanOrCrossEntropyLoss())
-
- def init_fn(init_checkpoint_path):
- ckpt = tf.train.Checkpoint(encoder=model.encoder)
- ckpt.restore(init_checkpoint_path).assert_existing_objects_matched()
-
- with worker_context():
- ckpt_manager = tf.train.CheckpointManager(
- tf.train.Checkpoint(model=model, optimizer=optimizer),
- model_dir,
- max_to_keep=None,
- init_fn=(functools.partial(init_fn, init_checkpoint_path)
- if init_checkpoint_path else None))
- with strategy.scope():
- ckpt_manager.restore_or_initialize()
- val_summary_writer = tf.summary.create_file_writer(
- os.path.join(model_dir, 'val'))
- best_exact_match = 0.
- for epoch in range(len(ckpt_manager.checkpoints), num_epochs):
- model.fit(
- train_dataset,
- callbacks=[
- tf.keras.callbacks.TensorBoard(model_dir, write_graph=False),
- ])
- ckpt_path = ckpt_manager.save()
- if evaluate_fn is None:
- continue
- metrics = evaluate_fn()
- logging.info('Epoch %d: %s', epoch + 1, metrics)
- if best_exact_match < metrics['exact_match']:
- best_exact_match = metrics['exact_match']
- model.save(os.path.join(model_dir, 'export'), include_optimizer=False)
- logging.info('Exporting %s as SavedModel.', ckpt_path)
- with val_summary_writer.as_default():
- for name, data in metrics.items():
- tf.summary.scalar(name, data, epoch + 1)
-
-
-def evaluate(sp_processor, features_map_fn, labels_map_fn, logits_fn,
- decode_logits_fn, split_and_pad_fn, distribute_strategy,
- validation_dataset, ground_truth):
- """Run evaluation."""
- loss_metric = tf.keras.metrics.Mean()
-
- @tf.function
- def update_loss(y, logits):
- loss_fn = modeling.SpanOrCrossEntropyLoss(
- reduction=tf.keras.losses.Reduction.NONE)
- return loss_metric(loss_fn(y, logits))
-
- predictions = collections.defaultdict(list)
- for _, (features, labels) in validation_dataset.enumerate():
- token_ids = features['token_ids']
- y = labels_map_fn(token_ids, labels)
- x = split_and_pad_fn(features_map_fn(features))
- logits = tf.concat(
- distribute_strategy.experimental_local_results(logits_fn(x)), 0)
- logits = logits[:features['token_ids'].shape[0]]
- update_loss(y, logits)
- end_limit = token_ids.row_lengths() - 1 # inclusive
- begin, end, scores = decode_logits_fn(logits, end_limit)
- answers = prediction.decode_answer(features['context'], begin, end,
- features['token_offsets'],
- end_limit).numpy()
- for _, (qid, token_id, offset, score, answer) in enumerate(
- zip(features['qid'].numpy(),
- tf.gather(features['token_ids'], begin, batch_dims=1).numpy(),
- tf.gather(features['token_offsets'], begin, batch_dims=1).numpy(),
- scores, answers)):
- if not answer:
- continue
- if sp_processor.IdToPiece(int(token_id)).startswith('▁') and offset > 0:
- answer = answer[1:]
- predictions[qid.decode('utf-8')].append((score, answer.decode('utf-8')))
- predictions = {
- qid: evaluation.normalize_answer(
- sorted(answers, key=operator.itemgetter(0), reverse=True)[0][1])
- for qid, answers in predictions.items()
- }
- metrics = evaluation.evaluate_triviaqa(ground_truth, predictions, mute=True)
- metrics['loss'] = loss_metric.result().numpy()
- return metrics
-
-
-def main(argv):
- if len(argv) > 1:
- raise app.UsageError('Too many command-line arguments.')
- gin.parse_config(FLAGS.gin_bindings)
- model_config = read_model_config(
- FLAGS.encoder,
- FLAGS.model_config_path,
- bigbird_block_size=FLAGS.bigbird_block_size)
- logging.info(model_config.get().as_dict())
- # Configure input processing.
- sp_processor = read_sentencepiece_model(FLAGS.sentencepiece_model_path)
- features_map_fn = functools.partial(
- inputs.features_map_fn,
- local_radius=FLAGS.bigbird_block_size,
- relative_pos_max_distance=24,
- use_hard_g2l_mask=True,
- padding_id=sp_processor.PieceToId(''),
- eos_id=sp_processor.PieceToId(''),
- null_id=sp_processor.PieceToId(''),
- cls_id=sp_processor.PieceToId(''),
- sep_id=sp_processor.PieceToId(''))
- train_features_map_fn = tf.function(
- functools.partial(
- features_map_fn,
- sequence_length=FLAGS.train_sequence_length,
- global_sequence_length=FLAGS.train_global_sequence_length),
- autograph=False)
- train_labels_map_fn = tf.function(
- functools.partial(
- inputs.labels_map_fn, sequence_length=FLAGS.train_sequence_length))
- # Connect to TPU cluster.
- if FLAGS.master:
- resolver = tf.distribute.cluster_resolver.TPUClusterResolver(FLAGS.master)
- tf.config.experimental_connect_to_cluster(resolver)
- tf.tpu.experimental.initialize_tpu_system(resolver)
- strategy = tf.distribute.TPUStrategy(resolver)
- else:
- strategy = tf.distribute.MirroredStrategy()
- # Initialize datasets.
- with worker_context():
- _ = tf.random.get_global_generator()
- train_dataset = inputs.read_batches(
- FLAGS.data_dir,
- tfds.Split.TRAIN,
- FLAGS.batch_size,
- shuffle=True,
- drop_final_batch=True)
- validation_dataset = inputs.read_batches(FLAGS.data_dir,
- tfds.Split.VALIDATION,
- FLAGS.batch_size)
-
- def train_map_fn(x, y):
- features = train_features_map_fn(x)
- labels = modeling.smooth_labels(FLAGS.label_smoothing,
- train_labels_map_fn(x['token_ids'], y),
- features['question_lengths'],
- features['token_ids'])
- return features, labels
-
- train_dataset = train_dataset.map(train_map_fn, 16).prefetch(16)
- # Initialize model and compile.
- with strategy.scope():
- model = modeling.TriviaQaModel(model_config, FLAGS.train_sequence_length)
- logits_fn = tf.function(
- functools.partial(prediction.distributed_logits_fn, model))
- decode_logits_fn = tf.function(
- functools.partial(prediction.decode_logits, FLAGS.decode_top_k,
- FLAGS.decode_max_size))
- split_and_pad_fn = tf.function(
- functools.partial(prediction.split_and_pad, strategy, FLAGS.batch_size))
- # Evaluation strategy.
- with tf.io.gfile.GFile(FLAGS.validation_gold_path) as f:
- ground_truth = {
- datum['QuestionId']: datum['Answer'] for datum in json.load(f)['Data']
- }
- validation_features_map_fn = tf.function(
- functools.partial(
- features_map_fn,
- sequence_length=FLAGS.validation_sequence_length,
- global_sequence_length=FLAGS.validation_global_sequence_length),
- autograph=False)
- validation_labels_map_fn = tf.function(
- functools.partial(
- inputs.labels_map_fn,
- sequence_length=FLAGS.validation_sequence_length))
- evaluate_fn = functools.partial(
- evaluate,
- sp_processor=sp_processor,
- features_map_fn=validation_features_map_fn,
- labels_map_fn=validation_labels_map_fn,
- logits_fn=logits_fn,
- decode_logits_fn=decode_logits_fn,
- split_and_pad_fn=split_and_pad_fn,
- distribute_strategy=strategy,
- validation_dataset=validation_dataset,
- ground_truth=ground_truth)
- logging.info('Model initialized. Beginning training fit loop.')
- fit(model, strategy, train_dataset, FLAGS.model_dir,
- FLAGS.init_checkpoint_path, evaluate_fn)
-
-
-if __name__ == '__main__':
- flags.mark_flags_as_required([
- 'model_config_path', 'model_dir', 'sentencepiece_model_path',
- 'validation_gold_path'
- ])
- app.run(main)
diff --git a/official/nlp/serving/__init__.py b/official/nlp/serving/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1
--- /dev/null
+++ b/official/nlp/serving/__init__.py
@@ -0,0 +1,15 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
diff --git a/official/nlp/serving/export_savedmodel.py b/official/nlp/serving/export_savedmodel.py
index d96752ee04f9bcbddc1e6d11f4b731dd0e918b1f..d4da2f5eca596de49a0be663bda9d14197063933 100644
--- a/official/nlp/serving/export_savedmodel.py
+++ b/official/nlp/serving/export_savedmodel.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,12 +13,14 @@
# limitations under the License.
"""A binary/library to export TF-NLP serving `SavedModel`."""
+import dataclasses
import os
from typing import Any, Dict, Text
+
from absl import app
from absl import flags
-import dataclasses
import yaml
+
from official.core import base_task
from official.core import task_factory
from official.modeling import hyperparams
@@ -29,6 +31,7 @@ from official.nlp.tasks import masked_lm
from official.nlp.tasks import question_answering
from official.nlp.tasks import sentence_prediction
from official.nlp.tasks import tagging
+from official.nlp.tasks import translation
FLAGS = flags.FLAGS
@@ -40,7 +43,9 @@ SERVING_MODULES = {
question_answering.QuestionAnsweringTask:
serving_modules.QuestionAnswering,
tagging.TaggingTask:
- serving_modules.Tagging
+ serving_modules.Tagging,
+ translation.TranslationTask:
+ serving_modules.Translation
}
@@ -67,6 +72,12 @@ def define_flags():
flags.DEFINE_bool("convert_tpu", False, "")
flags.DEFINE_multi_integer("allowed_batch_size", None,
"Allowed batch sizes for batching ops.")
+ flags.DEFINE_integer("num_batch_threads", 4,
+ "Number of threads to do TPU batching.")
+ flags.DEFINE_integer("batch_timeout_micros", 100000,
+ "TPU batch function timeout in microseconds.")
+ flags.DEFINE_integer("max_enqueued_batches", 1000,
+ "Max number of batches in queue for TPU batching.")
def lookup_export_module(task: base_task.Task):
@@ -125,21 +136,30 @@ def main(_):
if FLAGS.convert_tpu:
# pylint: disable=g-import-not-at-top
- from cloud_tpu.inference_converter import converter_cli
- from cloud_tpu.inference_converter import converter_options_pb2
+ from cloud_tpu.inference_converter_v2 import converter_options_v2_pb2
+ from cloud_tpu.inference_converter_v2.python import converter
+
tpu_dir = os.path.join(export_dir, "tpu")
- options = converter_options_pb2.ConverterOptions()
+ batch_options = []
if FLAGS.allowed_batch_size is not None:
allowed_batch_sizes = sorted(FLAGS.allowed_batch_size)
- options.batch_options.num_batch_threads = 4
- options.batch_options.max_batch_size = allowed_batch_sizes[-1]
- options.batch_options.batch_timeout_micros = 100000
- options.batch_options.allowed_batch_sizes[:] = allowed_batch_sizes
- options.batch_options.max_enqueued_batches = 1000
- converter_cli.ConvertSavedModel(
- export_dir, tpu_dir, function_alias="tpu_candidate", options=options,
- graph_rewrite_only=True)
-
+ batch_option = converter_options_v2_pb2.BatchOptionsV2(
+ num_batch_threads=FLAGS.num_batch_threads,
+ max_batch_size=allowed_batch_sizes[-1],
+ batch_timeout_micros=FLAGS.batch_timeout_micros,
+ allowed_batch_sizes=allowed_batch_sizes,
+ max_enqueued_batches=FLAGS.max_enqueued_batches
+ )
+ batch_options.append(batch_option)
+
+ converter_options = converter_options_v2_pb2.ConverterOptionsV2(
+ tpu_functions=[
+ converter_options_v2_pb2.TpuFunction(function_alias="tpu_candidate")
+ ],
+ batch_options=batch_options,
+ )
+
+ converter.ConvertSavedModel(export_dir, tpu_dir, converter_options)
if __name__ == "__main__":
define_flags()
diff --git a/official/nlp/serving/export_savedmodel_test.py b/official/nlp/serving/export_savedmodel_test.py
index 2891a9499f65c4e19f3e231b7178c2e98c7c704a..1f1a82a90d219e5c5a53611cffc5904158245bb5 100644
--- a/official/nlp/serving/export_savedmodel_test.py
+++ b/official/nlp/serving/export_savedmodel_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/serving/export_savedmodel_util.py b/official/nlp/serving/export_savedmodel_util.py
index b4363f434b296cdfdadb2392c85b3b423a37a000..8fe163c72e990b68c1c0d76b262f8189167d3045 100644
--- a/official/nlp/serving/export_savedmodel_util.py
+++ b/official/nlp/serving/export_savedmodel_util.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/serving/serving_modules.py b/official/nlp/serving/serving_modules.py
index 3fadde8180f57c091455b9360ade4232fd52d5c2..1621e0de543ee0d53b0f6a7a20f964c708ed2293 100644
--- a/official/nlp/serving/serving_modules.py
+++ b/official/nlp/serving/serving_modules.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,10 +14,12 @@
"""Serving export modules for TF Model Garden NLP models."""
# pylint:disable=missing-class-docstring
+import dataclasses
from typing import Dict, List, Optional, Text
-import dataclasses
import tensorflow as tf
+import tensorflow_text as tf_text
+
from official.core import export_base
from official.modeling.hyperparams import base_config
from official.nlp.data import sentence_prediction_dataloader
@@ -407,3 +409,52 @@ class Tagging(export_base.ExportModule):
signatures[signature_key] = self.serve_examples.get_concrete_function(
tf.TensorSpec(shape=[None], dtype=tf.string, name="examples"))
return signatures
+
+
+class Translation(export_base.ExportModule):
+ """The export module for the translation task."""
+
+ @dataclasses.dataclass
+ class Params(base_config.Config):
+ sentencepiece_model_path: str = ""
+ # Needs to be specified if padded_decode is True/on TPUs.
+ batch_size: Optional[int] = None
+
+ def __init__(self, params, model: tf.keras.Model, inference_step=None):
+ super().__init__(params, model, inference_step)
+ self._sp_tokenizer = tf_text.SentencepieceTokenizer(
+ model=tf.io.gfile.GFile(params.sentencepiece_model_path, "rb").read(),
+ add_eos=True)
+ try:
+ empty_str_tokenized = self._sp_tokenizer.tokenize("").numpy()
+ except tf.errors.InternalError:
+ raise ValueError(
+ "EOS token not in tokenizer vocab."
+ "Please make sure the tokenizer generates a single token for an "
+ "empty string.")
+ self._eos_id = empty_str_tokenized.item()
+ self._batch_size = params.batch_size
+
+ @tf.function
+ def serve(self, inputs) -> Dict[str, tf.Tensor]:
+ return self.inference_step(inputs)
+
+ @tf.function
+ def serve_text(self, text: tf.Tensor) -> Dict[str, tf.Tensor]:
+ tokenized = self._sp_tokenizer.tokenize(text).to_tensor(0)
+ return self._sp_tokenizer.detokenize(
+ self.serve({"inputs": tokenized})["outputs"])
+
+ def get_inference_signatures(self, function_keys: Dict[Text, Text]):
+ signatures = {}
+ valid_keys = ("serve_text")
+ for func_key, signature_key in function_keys.items():
+ if func_key not in valid_keys:
+ raise ValueError("Invalid function key for the module: %s with key %s. "
+ "Valid keys are: %s" %
+ (self.__class__, func_key, valid_keys))
+ if func_key == "serve_text":
+ signatures[signature_key] = self.serve_text.get_concrete_function(
+ tf.TensorSpec(shape=[self._batch_size],
+ dtype=tf.string, name="text"))
+ return signatures
diff --git a/official/nlp/serving/serving_modules_test.py b/official/nlp/serving/serving_modules_test.py
index 16c481c98a8b1bb99887ccb51019b6a8e415a8b4..e967c60662930d851860c72266372a2479f1268a 100644
--- a/official/nlp/serving/serving_modules_test.py
+++ b/official/nlp/serving/serving_modules_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,8 +15,12 @@
"""Tests for nlp.serving.serving_modules."""
import os
+
from absl.testing import parameterized
import tensorflow as tf
+
+from sentencepiece import SentencePieceTrainer
+from official.core import export_base
from official.nlp.configs import bert
from official.nlp.configs import encoders
from official.nlp.serving import serving_modules
@@ -24,6 +28,7 @@ from official.nlp.tasks import masked_lm
from official.nlp.tasks import question_answering
from official.nlp.tasks import sentence_prediction
from official.nlp.tasks import tagging
+from official.nlp.tasks import translation
def _create_fake_serialized_examples(features_dict):
@@ -59,6 +64,33 @@ def _create_fake_vocab_file(vocab_file_path):
outfile.write("\n".join(tokens))
+def _train_sentencepiece(input_path, vocab_size, model_path, eos_id=1):
+ argstr = " ".join([
+ f"--input={input_path}", f"--vocab_size={vocab_size}",
+ "--character_coverage=0.995",
+ f"--model_prefix={model_path}", "--model_type=bpe",
+ "--bos_id=-1", "--pad_id=0", f"--eos_id={eos_id}", "--unk_id=2"
+ ])
+ SentencePieceTrainer.Train(argstr)
+
+
+def _generate_line_file(filepath, lines):
+ with tf.io.gfile.GFile(filepath, "w") as f:
+ for l in lines:
+ f.write("{}\n".format(l))
+
+
+def _make_sentencepeice(output_dir):
+ src_lines = ["abc ede fg", "bbcd ef a g", "de f a a g"]
+ tgt_lines = ["dd cc a ef g", "bcd ef a g", "gef cd ba"]
+ sentencepeice_input_path = os.path.join(output_dir, "inputs.txt")
+ _generate_line_file(sentencepeice_input_path, src_lines + tgt_lines)
+ sentencepeice_model_prefix = os.path.join(output_dir, "sp")
+ _train_sentencepiece(sentencepeice_input_path, 11, sentencepeice_model_prefix)
+ sentencepeice_model_path = "{}.model".format(sentencepeice_model_prefix)
+ return sentencepeice_model_path
+
+
class ServingModulesTest(tf.test.TestCase, parameterized.TestCase):
@parameterized.parameters(
@@ -312,6 +344,48 @@ class ServingModulesTest(tf.test.TestCase, parameterized.TestCase):
with self.assertRaises(ValueError):
_ = export_module.get_inference_signatures({"foo": None})
+ @parameterized.parameters(
+ (False, None),
+ (True, 2))
+ def test_translation(self, padded_decode, batch_size):
+ sp_path = _make_sentencepeice(self.get_temp_dir())
+ encdecoder = translation.EncDecoder(
+ num_attention_heads=4, intermediate_size=256)
+ config = translation.TranslationConfig(
+ model=translation.ModelConfig(
+ encoder=encdecoder,
+ decoder=encdecoder,
+ embedding_width=256,
+ padded_decode=padded_decode,
+ decode_max_length=100),
+ sentencepiece_model_path=sp_path,
+ )
+ task = translation.TranslationTask(config)
+ model = task.build_model()
+
+ params = serving_modules.Translation.Params(
+ sentencepiece_model_path=sp_path, batch_size=batch_size)
+ export_module = serving_modules.Translation(params=params, model=model)
+ functions = export_module.get_inference_signatures({
+ "serve_text": "serving_default"
+ })
+ outputs = functions["serving_default"](tf.constant(["abcd", "ef gh"]))
+ self.assertEqual(outputs.shape, (2,))
+ self.assertEqual(outputs.dtype, tf.string)
+
+ tmp_dir = self.get_temp_dir()
+ tmp_dir = os.path.join(tmp_dir, "padded_decode", str(padded_decode))
+ export_base_dir = os.path.join(tmp_dir, "export")
+ ckpt_dir = os.path.join(tmp_dir, "ckpt")
+ ckpt_path = tf.train.Checkpoint(model=model).save(ckpt_dir)
+ export_dir = export_base.export(export_module,
+ {"serve_text": "serving_default"},
+ export_base_dir, ckpt_path)
+ loaded = tf.saved_model.load(export_dir)
+ infer = loaded.signatures["serving_default"]
+ out = infer(text=tf.constant(["abcd", "ef gh"]))
+ self.assertLen(out["output_0"], 2)
+
if __name__ == "__main__":
tf.test.main()
diff --git a/official/nlp/tasks/__init__.py b/official/nlp/tasks/__init__.py
index e506913b0c22a84006e647058636fe08a7cb894b..cec41dff173e4bd1e5ff9b865344a557b57055c5 100644
--- a/official/nlp/tasks/__init__.py
+++ b/official/nlp/tasks/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/dual_encoder.py b/official/nlp/tasks/dual_encoder.py
index 24c750d9ed547c62976976fcde788fa30089f331..116456b590988f72492217795647bcbc3a25cc77 100644
--- a/official/nlp/tasks/dual_encoder.py
+++ b/official/nlp/tasks/dual_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -187,9 +187,13 @@ class DualEncoderTask(base_task.Task):
def initialize(self, model):
"""Load a pretrained checkpoint (if exists) and then train from iter 0."""
ckpt_dir_or_file = self.task_config.init_checkpoint
- if tf.io.gfile.isdir(ckpt_dir_or_file):
+ logging.info('Trying to load pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+ if ckpt_dir_or_file and tf.io.gfile.isdir(ckpt_dir_or_file):
ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
if not ckpt_dir_or_file:
+ logging.info('No checkpoint file found from %s. Will not load.',
+ ckpt_dir_or_file)
return
pretrain2finetune_mapping = {
diff --git a/official/nlp/tasks/dual_encoder_test.py b/official/nlp/tasks/dual_encoder_test.py
index 96763871f06f5e7d992e79dfe8e0d0f33b6fb020..3e1a72605ae62f7029b8de103a4acd4be1ce0f8d 100644
--- a/official/nlp/tasks/dual_encoder_test.py
+++ b/official/nlp/tasks/dual_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,7 +19,7 @@ import os
from absl.testing import parameterized
import tensorflow as tf
-from official.nlp.bert import configs
+from official.legacy.bert import configs
from official.nlp.configs import bert
from official.nlp.configs import encoders
from official.nlp.data import dual_encoder_dataloader
diff --git a/official/nlp/tasks/electra_task.py b/official/nlp/tasks/electra_task.py
index 6853a2cc246acd79f7ee81c7ba0b843ac2c9bfb3..9473c0d4e0626cef58c23574f68559a6077d3f78 100644
--- a/official/nlp/tasks/electra_task.py
+++ b/official/nlp/tasks/electra_task.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/electra_task_test.py b/official/nlp/tasks/electra_task_test.py
index 4f775d26906dc93f78b3fdd66f1cbb230c558104..4018c9220acef88272ffda2385dd97ee44b92f48 100644
--- a/official/nlp/tasks/electra_task_test.py
+++ b/official/nlp/tasks/electra_task_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/masked_lm.py b/official/nlp/tasks/masked_lm.py
index 8e5802ada291c332ed80d874030b5f36f099f835..f784b141676e0bb55868a4380b1fb2e91064cf99 100644
--- a/official/nlp/tasks/masked_lm.py
+++ b/official/nlp/tasks/masked_lm.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/masked_lm_determinism_test.py b/official/nlp/tasks/masked_lm_determinism_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..d9aa90a041ef04eb0dcf5dc95292a83c15d39e79
--- /dev/null
+++ b/official/nlp/tasks/masked_lm_determinism_test.py
@@ -0,0 +1,103 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests that masked LM models are deterministic when determinism is enabled."""
+
+import tensorflow as tf
+
+from official.nlp.configs import bert
+from official.nlp.configs import encoders
+from official.nlp.data import pretrain_dataloader
+from official.nlp.tasks import masked_lm
+
+
+class MLMTaskTest(tf.test.TestCase):
+
+ def _build_dataset(self, params, vocab_size):
+ def dummy_data(_):
+ dummy_ids = tf.random.uniform((1, params.seq_length), maxval=vocab_size,
+ dtype=tf.int32)
+ dummy_mask = tf.ones((1, params.seq_length), dtype=tf.int32)
+ dummy_type_ids = tf.zeros((1, params.seq_length), dtype=tf.int32)
+ dummy_lm = tf.zeros((1, params.max_predictions_per_seq), dtype=tf.int32)
+ return dict(
+ input_word_ids=dummy_ids,
+ input_mask=dummy_mask,
+ input_type_ids=dummy_type_ids,
+ masked_lm_positions=dummy_lm,
+ masked_lm_ids=dummy_lm,
+ masked_lm_weights=tf.cast(dummy_lm, dtype=tf.float32),
+ next_sentence_labels=tf.zeros((1, 1), dtype=tf.int32))
+
+ dataset = tf.data.Dataset.range(1)
+ dataset = dataset.repeat()
+ dataset = dataset.map(
+ dummy_data, num_parallel_calls=tf.data.experimental.AUTOTUNE)
+ return dataset
+
+ def _build_and_run_model(self, config, num_steps=5):
+ task = masked_lm.MaskedLMTask(config)
+ model = task.build_model()
+ metrics = task.build_metrics()
+ dataset = self._build_dataset(config.train_data,
+ config.model.encoder.get().vocab_size)
+
+ iterator = iter(dataset)
+ optimizer = tf.keras.optimizers.SGD(lr=0.1)
+
+ # Run training
+ for _ in range(num_steps):
+ logs = task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ for metric in metrics:
+ logs[metric.name] = metric.result()
+
+ # Run validation
+ validation_logs = task.validation_step(next(iterator), model,
+ metrics=metrics)
+ for metric in metrics:
+ validation_logs[metric.name] = metric.result()
+
+ return logs, validation_logs, model.weights
+
+ def test_task_determinism(self):
+ config = masked_lm.MaskedLMConfig(
+ init_checkpoint=self.get_temp_dir(),
+ scale_loss=True,
+ model=bert.PretrainerConfig(
+ encoder=encoders.EncoderConfig(
+ bert=encoders.BertEncoderConfig(vocab_size=30522,
+ num_layers=1)),
+ cls_heads=[
+ bert.ClsHeadConfig(
+ inner_dim=10, num_classes=2, name="next_sentence")
+ ]),
+ train_data=pretrain_dataloader.BertPretrainDataConfig(
+ max_predictions_per_seq=20,
+ seq_length=128,
+ global_batch_size=1))
+
+ tf.keras.utils.set_random_seed(1)
+ logs1, validation_logs1, weights1 = self._build_and_run_model(config)
+ tf.keras.utils.set_random_seed(1)
+ logs2, validation_logs2, weights2 = self._build_and_run_model(config)
+
+ self.assertEqual(logs1["loss"], logs2["loss"])
+ self.assertEqual(validation_logs1["loss"], validation_logs2["loss"])
+ for weight1, weight2 in zip(weights1, weights2):
+ self.assertAllEqual(weight1, weight2)
+
+
+if __name__ == "__main__":
+ tf.config.experimental.enable_op_determinism()
+ tf.test.main()
diff --git a/official/nlp/tasks/masked_lm_test.py b/official/nlp/tasks/masked_lm_test.py
index 14774e9859f3389ddb6839a2c1eeacbe4077505e..221fa6c0978a2c890b9e3139021f4cdf7d9642b3 100644
--- a/official/nlp/tasks/masked_lm_test.py
+++ b/official/nlp/tasks/masked_lm_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/question_answering.py b/official/nlp/tasks/question_answering.py
index aee3fab883434c89114a7633ef5fd934d1122eed..d9c7508fe862e2ffd352a63db22be33002abaa5a 100644
--- a/official/nlp/tasks/question_answering.py
+++ b/official/nlp/tasks/question_answering.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,13 +13,13 @@
# limitations under the License.
"""Question answering task."""
+import dataclasses
import functools
import json
import os
from typing import List, Optional
from absl import logging
-import dataclasses
import orbit
import tensorflow as tf
@@ -27,15 +27,15 @@ from official.core import base_task
from official.core import config_definitions as cfg
from official.core import task_factory
from official.modeling.hyperparams import base_config
-from official.nlp.bert import squad_evaluate_v1_1
-from official.nlp.bert import squad_evaluate_v2_0
-from official.nlp.bert import tokenization
from official.nlp.configs import encoders
from official.nlp.data import data_loader_factory
from official.nlp.data import squad_lib as squad_lib_wp
from official.nlp.data import squad_lib_sp
from official.nlp.modeling import models
from official.nlp.tasks import utils
+from official.nlp.tools import squad_evaluate_v1_1
+from official.nlp.tools import squad_evaluate_v2_0
+from official.nlp.tools import tokenization
@dataclasses.dataclass
diff --git a/official/nlp/tasks/question_answering_test.py b/official/nlp/tasks/question_answering_test.py
index aa79e3ae86eaf54dca5318df6fef8ceec48ba703..cc50592a829c35336677bd95ce947523ac3edb5a 100644
--- a/official/nlp/tasks/question_answering_test.py
+++ b/official/nlp/tasks/question_answering_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/sentence_prediction.py b/official/nlp/tasks/sentence_prediction.py
index abc038a000fd6934bddd1a9d96b228ecd7884383..41b39eb6f08e8bba87339219c09aa1e2b1ff97b3 100644
--- a/official/nlp/tasks/sentence_prediction.py
+++ b/official/nlp/tasks/sentence_prediction.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -34,7 +34,7 @@ from official.nlp.modeling import models
from official.nlp.tasks import utils
METRIC_TYPES = frozenset(
- ['accuracy', 'matthews_corrcoef', 'pearson_spearman_corr'])
+ ['accuracy', 'f1', 'matthews_corrcoef', 'pearson_spearman_corr'])
@dataclasses.dataclass
@@ -165,14 +165,17 @@ class SentencePredictionTask(base_task.Task):
compiled_metrics.update_state(labels[self.label_field], model_outputs)
def validation_step(self, inputs, model: tf.keras.Model, metrics=None):
- if self.metric_type == 'accuracy':
- return super(SentencePredictionTask,
- self).validation_step(inputs, model, metrics)
features, labels = inputs, inputs
outputs = self.inference_step(features, model)
loss = self.build_losses(
labels=labels, model_outputs=outputs, aux_losses=model.losses)
logs = {self.loss: loss}
+ if metrics:
+ self.process_metrics(metrics, labels, outputs)
+ if model.compiled_metrics:
+ self.process_compiled_metrics(model.compiled_metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in metrics or []})
+ logs.update({m.name: m.result() for m in model.metrics})
if self.metric_type == 'matthews_corrcoef':
logs.update({
'sentence_prediction': # Ensure one prediction along batch dimension.
@@ -180,7 +183,7 @@ class SentencePredictionTask(base_task.Task):
'labels':
labels[self.label_field],
})
- if self.metric_type == 'pearson_spearman_corr':
+ else:
logs.update({
'sentence_prediction': outputs,
'labels': labels[self.label_field],
@@ -202,18 +205,20 @@ class SentencePredictionTask(base_task.Task):
def reduce_aggregated_logs(self, aggregated_logs, global_step=None):
if self.metric_type == 'accuracy':
return None
+
+ preds = np.concatenate(aggregated_logs['sentence_prediction'], axis=0)
+ labels = np.concatenate(aggregated_logs['labels'], axis=0)
+ if self.metric_type == 'f1':
+ preds = np.argmax(preds, axis=1)
+ return {self.metric_type: sklearn_metrics.f1_score(labels, preds)}
elif self.metric_type == 'matthews_corrcoef':
- preds = np.concatenate(aggregated_logs['sentence_prediction'], axis=0)
preds = np.reshape(preds, -1)
- labels = np.concatenate(aggregated_logs['labels'], axis=0)
labels = np.reshape(labels, -1)
return {
self.metric_type: sklearn_metrics.matthews_corrcoef(preds, labels)
}
elif self.metric_type == 'pearson_spearman_corr':
- preds = np.concatenate(aggregated_logs['sentence_prediction'], axis=0)
preds = np.reshape(preds, -1)
- labels = np.concatenate(aggregated_logs['labels'], axis=0)
labels = np.reshape(labels, -1)
pearson_corr = stats.pearsonr(preds, labels)[0]
spearman_corr = stats.spearmanr(preds, labels)[0]
@@ -223,10 +228,14 @@ class SentencePredictionTask(base_task.Task):
def initialize(self, model):
"""Load a pretrained checkpoint (if exists) and then train from iter 0."""
ckpt_dir_or_file = self.task_config.init_checkpoint
+ logging.info('Trying to load pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+ if ckpt_dir_or_file and tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
if not ckpt_dir_or_file:
+ logging.info('No checkpoint file found from %s. Will not load.',
+ ckpt_dir_or_file)
return
- if tf.io.gfile.isdir(ckpt_dir_or_file):
- ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
pretrain2finetune_mapping = {
'encoder': model.checkpoint_items['encoder'],
diff --git a/official/nlp/tasks/sentence_prediction_test.py b/official/nlp/tasks/sentence_prediction_test.py
index 94d056fee6b059ac96e0de01780de9499d612934..316ff7dabe169133eeb28bd66d56de952936ff40 100644
--- a/official/nlp/tasks/sentence_prediction_test.py
+++ b/official/nlp/tasks/sentence_prediction_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -32,10 +32,12 @@ def _create_fake_dataset(output_path, seq_length, num_classes, num_examples):
writer = tf.io.TFRecordWriter(output_path)
def create_int_feature(values):
- return tf.train.Feature(int64_list=tf.train.Int64List(value=list(values)))
+ return tf.train.Feature(
+ int64_list=tf.train.Int64List(value=np.ravel(values)))
def create_float_feature(values):
- return tf.train.Feature(float_list=tf.train.FloatList(value=list(values)))
+ return tf.train.Feature(
+ float_list=tf.train.FloatList(value=np.ravel(values)))
for i in range(num_examples):
features = {}
@@ -81,7 +83,7 @@ class SentencePredictionTaskTest(tf.test.TestCase, parameterized.TestCase):
functools.partial(task.build_inputs, config.train_data))
iterator = iter(dataset)
- optimizer = tf.keras.optimizers.SGD(lr=0.1)
+ optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)
task.train_step(next(iterator), model, optimizer, metrics=metrics)
model.save(os.path.join(self.get_temp_dir(), "saved_model"))
return task.validation_step(next(iterator), model, metrics=metrics)
@@ -118,7 +120,7 @@ class SentencePredictionTaskTest(tf.test.TestCase, parameterized.TestCase):
dataset = task.build_inputs(config.train_data)
iterator = iter(dataset)
- optimizer = tf.keras.optimizers.SGD(lr=0.1)
+ optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)
task.initialize(model)
task.train_step(next(iterator), model, optimizer, metrics=metrics)
task.validation_step(next(iterator), model, metrics=metrics)
@@ -149,7 +151,7 @@ class SentencePredictionTaskTest(tf.test.TestCase, parameterized.TestCase):
dataset = task.build_inputs(config.train_data)
iterator = iter(dataset)
- optimizer = tf.keras.optimizers.SGD(lr=0.1)
+ optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)
task.train_step(next(iterator), model, optimizer, metrics=metrics)
logs = task.validation_step(next(iterator), model, metrics=metrics)
@@ -160,7 +162,8 @@ class SentencePredictionTaskTest(tf.test.TestCase, parameterized.TestCase):
self.assertLess(loss, 1.0)
@parameterized.parameters(("matthews_corrcoef", 2),
- ("pearson_spearman_corr", 1))
+ ("pearson_spearman_corr", 1),
+ ("f1", 2))
def test_np_metrics(self, metric_type, num_classes):
config = sentence_prediction.SentencePredictionConfig(
metric_type=metric_type,
diff --git a/official/nlp/tasks/tagging.py b/official/nlp/tasks/tagging.py
index bf6a3b7b1828fc9ca7e5d6f1d95f0f3d8f8c224a..5f2a3f64fc28b2a461d75507c479b67f2eff942f 100644
--- a/official/nlp/tasks/tagging.py
+++ b/official/nlp/tasks/tagging.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/tagging_test.py b/official/nlp/tasks/tagging_test.py
index 98ac97627abdbfb89fe6a55ef87b5e6f89c67b1a..e888abb5614583fd167a5e357325e08862b18f1a 100644
--- a/official/nlp/tasks/tagging_test.py
+++ b/official/nlp/tasks/tagging_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/translation.py b/official/nlp/tasks/translation.py
index 736d68e3e8b0ed2f245fcf985bd819cb504973a6..bb9591d461738f3a51bff81c799dd20973463154 100644
--- a/official/nlp/tasks/translation.py
+++ b/official/nlp/tasks/translation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/translation_test.py b/official/nlp/tasks/translation_test.py
index a7f9d1c0902de4aa90cfa95968dfc88fb0a69026..30cd8b7f352a21fd192ac12dfa8dc3b10b8ce4fa 100644
--- a/official/nlp/tasks/translation_test.py
+++ b/official/nlp/tasks/translation_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tasks/utils.py b/official/nlp/tasks/utils.py
index 35be4e3d4546dc29f5b43983687d697967eda4f3..44295e6590b5ef61f21952cdb907c82e1ffc6d6e 100644
--- a/official/nlp/tasks/utils.py
+++ b/official/nlp/tasks/utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tools/__init__.py b/official/nlp/tools/__init__.py
index a25710c222e3327cb20e000db5df5c5651c4a2cc..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1 100644
--- a/official/nlp/tools/__init__.py
+++ b/official/nlp/tools/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tools/export_tfhub.py b/official/nlp/tools/export_tfhub.py
index 0effd56863bbe1fbe956cb25114c1f7705a181a1..e81dabd32fd36fbeaa1d5d0fd4e0cbc610caee90 100644
--- a/official/nlp/tools/export_tfhub.py
+++ b/official/nlp/tools/export_tfhub.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -71,8 +71,8 @@ from absl import app
from absl import flags
import gin
+from official.legacy.bert import configs
from official.modeling import hyperparams
-from official.nlp.bert import configs
from official.nlp.configs import encoders
from official.nlp.tools import export_tfhub_lib
diff --git a/official/nlp/tools/export_tfhub_lib.py b/official/nlp/tools/export_tfhub_lib.py
index 7062e41661e9db9f842bd28368e3ad4147eb6514..ad65fd7643bca24068095a748c8aa906ae0a41fb 100644
--- a/official/nlp/tools/export_tfhub_lib.py
+++ b/official/nlp/tools/export_tfhub_lib.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,8 +28,8 @@ import tensorflow as tf
from tensorflow.core.protobuf import saved_model_pb2
from tensorflow.python.ops import control_flow_ops
# pylint: enable=g-direct-tensorflow-import
+from official.legacy.bert import configs
from official.modeling import tf_utils
-from official.nlp.bert import configs
from official.nlp.configs import encoders
from official.nlp.modeling import layers
from official.nlp.modeling import models
@@ -84,13 +84,13 @@ def _create_model(
"""Creates the model to export and the model to restore the checkpoint.
Args:
- bert_config: A legacy `BertConfig` to create a `BertEncoder` object.
- Exactly one of encoder_config and bert_config must be set.
+ bert_config: A legacy `BertConfig` to create a `BertEncoder` object. Exactly
+ one of encoder_config and bert_config must be set.
encoder_config: An `EncoderConfig` to create an encoder of the configured
type (`BertEncoder` or other).
- with_mlm: A bool to control the second component of the result.
- If True, will create a `BertPretrainerV2` object; otherwise, will
- create a `BertEncoder` object.
+ with_mlm: A bool to control the second component of the result. If True,
+ will create a `BertPretrainerV2` object; otherwise, will create a
+ `BertEncoder` object.
Returns:
A Tuple of (1) a Keras model that will be exported, (2) a `BertPretrainerV2`
@@ -110,7 +110,11 @@ def _create_model(
# Convert from list of named inputs to dict of inputs keyed by name.
# Only the latter accepts a dict of inputs after restoring from SavedModel.
- encoder_inputs_dict = {x.name: x for x in encoder.inputs}
+ if isinstance(encoder.inputs, list) or isinstance(encoder.inputs, tuple):
+ encoder_inputs_dict = {x.name: x for x in encoder.inputs}
+ else:
+ # encoder.inputs by default is dict for BertEncoderV2.
+ encoder_inputs_dict = encoder.inputs
encoder_output_dict = encoder(encoder_inputs_dict)
# For interchangeability with other text representations,
# add "default" as an alias for BERT's whole-input reptesentations.
@@ -129,7 +133,10 @@ def _create_model(
encoder_network=encoder,
mlm_activation=tf_utils.get_activation(hidden_act))
- pretrainer_inputs_dict = {x.name: x for x in pretrainer.inputs}
+ if isinstance(pretrainer.inputs, dict):
+ pretrainer_inputs_dict = pretrainer.inputs
+ else:
+ pretrainer_inputs_dict = {x.name: x for x in pretrainer.inputs}
pretrainer_output_dict = pretrainer(pretrainer_inputs_dict)
mlm_model = tf.keras.Model(
inputs=pretrainer_inputs_dict, outputs=pretrainer_output_dict)
@@ -206,26 +213,28 @@ def export_model(export_path: Text,
encoder_config: An optional `encoders.EncoderConfig` object.
model_checkpoint_path: The path to the checkpoint.
with_mlm: Whether to export the additional mlm sub-object.
- copy_pooler_dense_to_encoder: Whether to copy the pooler's dense layer
- used in the next sentence prediction task to the encoder.
+ copy_pooler_dense_to_encoder: Whether to copy the pooler's dense layer used
+ in the next sentence prediction task to the encoder.
vocab_file: The path to the wordpiece vocab file, or None.
- sp_model_file: The path to the sentencepiece model file, or None.
- Exactly one of vocab_file and sp_model_file must be set.
+ sp_model_file: The path to the sentencepiece model file, or None. Exactly
+ one of vocab_file and sp_model_file must be set.
do_lower_case: Whether to lower-case text before tokenization.
"""
if with_mlm:
- core_model, pretrainer = _create_model(bert_config=bert_config,
- encoder_config=encoder_config,
- with_mlm=with_mlm)
+ core_model, pretrainer = _create_model(
+ bert_config=bert_config,
+ encoder_config=encoder_config,
+ with_mlm=with_mlm)
encoder = pretrainer.encoder_network
# It supports both the new pretrainer checkpoint produced by TF-NLP and
# the checkpoint converted from TF1 (original BERT, SmallBERTs).
checkpoint_items = pretrainer.checkpoint_items
checkpoint = tf.train.Checkpoint(**checkpoint_items)
else:
- core_model, encoder = _create_model(bert_config=bert_config,
- encoder_config=encoder_config,
- with_mlm=with_mlm)
+ core_model, encoder = _create_model(
+ bert_config=bert_config,
+ encoder_config=encoder_config,
+ with_mlm=with_mlm)
checkpoint = tf.train.Checkpoint(
model=encoder, # Legacy checkpoints.
encoder=encoder)
@@ -279,21 +288,26 @@ class BertPackInputsSavedModelWrapper(tf.train.Checkpoint):
# overridable. Having this dynamically determined default argument
# requires self.__call__ to be defined in this indirect way.
default_seq_length = bert_pack_inputs.seq_length
+
@tf.function(autograph=False)
def call(inputs, seq_length=default_seq_length):
return layers.BertPackInputs.bert_pack_inputs(
- inputs, seq_length=seq_length,
+ inputs,
+ seq_length=seq_length,
start_of_sequence_id=bert_pack_inputs.start_of_sequence_id,
end_of_segment_id=bert_pack_inputs.end_of_segment_id,
padding_id=bert_pack_inputs.padding_id)
+
self.__call__ = call
for ragged_rank in range(1, 3):
for num_segments in range(1, 3):
- _ = self.__call__.get_concrete_function(
- [tf.RaggedTensorSpec([None] * (ragged_rank + 1), dtype=tf.int32)
- for _ in range(num_segments)],
- seq_length=tf.TensorSpec([], tf.int32))
+ _ = self.__call__.get_concrete_function([
+ tf.RaggedTensorSpec([None] * (ragged_rank + 1), dtype=tf.int32)
+ for _ in range(num_segments)
+ ],
+ seq_length=tf.TensorSpec(
+ [], tf.int32))
def create_preprocessing(*,
@@ -311,14 +325,14 @@ def create_preprocessing(*,
Args:
vocab_file: The path to the wordpiece vocab file, or None.
- sp_model_file: The path to the sentencepiece model file, or None.
- Exactly one of vocab_file and sp_model_file must be set.
- This determines the type of tokenzer that is used.
+ sp_model_file: The path to the sentencepiece model file, or None. Exactly
+ one of vocab_file and sp_model_file must be set. This determines the type
+ of tokenzer that is used.
do_lower_case: Whether to do lower case.
tokenize_with_offsets: Whether to include the .tokenize_with_offsets
subobject.
- default_seq_length: The sequence length of preprocessing results from
- root callable. This is also the default sequence length for the
+ default_seq_length: The sequence length of preprocessing results from root
+ callable. This is also the default sequence length for the
bert_pack_inputs subobject.
Returns:
@@ -378,7 +392,8 @@ def create_preprocessing(*,
def _move_to_tmpdir(file_path: Optional[Text], tmpdir: Text) -> Optional[Text]:
"""Returns new path with same basename and hash of original path."""
- if file_path is None: return None
+ if file_path is None:
+ return None
olddir, filename = os.path.split(file_path)
hasher = hashlib.sha1()
hasher.update(olddir.encode("utf-8"))
@@ -460,12 +475,17 @@ def _check_no_assert(saved_model_path):
assert_nodes = []
graph_def = saved_model.meta_graphs[0].graph_def
- assert_nodes += ["node '{}' in global graph".format(n.name)
- for n in graph_def.node if n.op == "Assert"]
+ assert_nodes += [
+ "node '{}' in global graph".format(n.name)
+ for n in graph_def.node
+ if n.op == "Assert"
+ ]
for fdef in graph_def.library.function:
assert_nodes += [
"node '{}' in function '{}'".format(n.name, fdef.signature.name)
- for n in fdef.node_def if n.op == "Assert"]
+ for n in fdef.node_def
+ if n.op == "Assert"
+ ]
if assert_nodes:
raise AssertionError(
"Internal tool error: "
diff --git a/official/nlp/tools/export_tfhub_lib_test.py b/official/nlp/tools/export_tfhub_lib_test.py
index d2fade8e9580bb9c7df80de21a523fae38fab0d8..51bb87319d784fd3fbbec5b8e121c23c426f602a 100644
--- a/official/nlp/tools/export_tfhub_lib_test.py
+++ b/official/nlp/tools/export_tfhub_lib_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,21 +20,39 @@ import tempfile
from absl.testing import parameterized
import numpy as np
import tensorflow as tf
+from tensorflow import estimator as tf_estimator
import tensorflow_hub as hub
import tensorflow_text as text
from sentencepiece import SentencePieceTrainer
+from official.legacy.bert import configs
from official.modeling import tf_utils
-from official.nlp.bert import configs
from official.nlp.configs import encoders
from official.nlp.modeling import layers
from official.nlp.modeling import models
from official.nlp.tools import export_tfhub_lib
-def _get_bert_config_or_encoder_config(use_bert_config, hidden_size,
- num_hidden_layers, vocab_size=100):
- """Returns config args for export_tfhub_lib._create_model()."""
+def _get_bert_config_or_encoder_config(use_bert_config,
+ hidden_size,
+ num_hidden_layers,
+ encoder_type="albert",
+ vocab_size=100):
+ """Generates config args for export_tfhub_lib._create_model().
+
+ Args:
+ use_bert_config: bool. If True, returns legacy BertConfig.
+ hidden_size: int.
+ num_hidden_layers: int.
+ encoder_type: str. Can be ['albert', 'bert', 'bert_v2']. If use_bert_config
+ == True, then model_type is not used.
+ vocab_size: int.
+
+ Returns:
+ bert_config, encoder_config. Only one is not None. If
+ `use_bert_config` == True, the first config is valid. Otherwise
+ `bert_config` == None.
+ """
if use_bert_config:
bert_config = configs.BertConfig(
vocab_size=vocab_size,
@@ -46,17 +64,31 @@ def _get_bert_config_or_encoder_config(use_bert_config, hidden_size,
encoder_config = None
else:
bert_config = None
- encoder_config = encoders.EncoderConfig(
- type="albert",
- albert=encoders.AlbertEncoderConfig(
- vocab_size=vocab_size,
- embedding_width=16,
- hidden_size=hidden_size,
- intermediate_size=32,
- max_position_embeddings=128,
- num_attention_heads=2,
- num_layers=num_hidden_layers,
- dropout_rate=0.1))
+ if encoder_type == "albert":
+ encoder_config = encoders.EncoderConfig(
+ type="albert",
+ albert=encoders.AlbertEncoderConfig(
+ vocab_size=vocab_size,
+ embedding_width=16,
+ hidden_size=hidden_size,
+ intermediate_size=32,
+ max_position_embeddings=128,
+ num_attention_heads=2,
+ num_layers=num_hidden_layers,
+ dropout_rate=0.1))
+ else:
+ # encoder_type can be 'bert' or 'bert_v2'.
+ model_config = encoders.BertEncoderConfig(
+ vocab_size=vocab_size,
+ embedding_size=16,
+ hidden_size=hidden_size,
+ intermediate_size=32,
+ max_position_embeddings=128,
+ num_attention_heads=2,
+ num_layers=num_hidden_layers,
+ dropout_rate=0.1)
+ kwargs = {"type": encoder_type, encoder_type: model_config}
+ encoder_config = encoders.EncoderConfig(**kwargs)
return bert_config, encoder_config
@@ -105,13 +137,18 @@ class ExportModelTest(tf.test.TestCase, parameterized.TestCase):
alternative to BertTokenizer).
"""
- @parameterized.named_parameters(("Bert", True), ("Albert", False))
- def test_export_model(self, use_bert):
+ @parameterized.named_parameters(
+ ("Bert_Legacy", True, None), ("Albert", False, "albert"),
+ ("BertEncoder", False, "bert"), ("BertEncoderV2", False, "bert_v2"))
+ def test_export_model(self, use_bert, encoder_type):
# Create the encoder and export it.
hidden_size = 16
num_hidden_layers = 1
bert_config, encoder_config = _get_bert_config_or_encoder_config(
- use_bert, hidden_size, num_hidden_layers)
+ use_bert,
+ hidden_size=hidden_size,
+ num_hidden_layers=num_hidden_layers,
+ encoder_type=encoder_type)
bert_model, encoder = export_tfhub_lib._create_model(
bert_config=bert_config, encoder_config=encoder_config, with_mlm=False)
self.assertEmpty(
@@ -151,8 +188,8 @@ class ExportModelTest(tf.test.TestCase, parameterized.TestCase):
_read_asset(hub_layer.resolved_object.sp_model_file))
# Check restored weights.
- self.assertEqual(len(bert_model.trainable_weights),
- len(hub_layer.trainable_weights))
+ self.assertEqual(
+ len(bert_model.trainable_weights), len(hub_layer.trainable_weights))
for source_weight, hub_weight in zip(bert_model.trainable_weights,
hub_layer.trainable_weights):
self.assertAllClose(source_weight.numpy(), hub_weight.numpy())
@@ -334,8 +371,8 @@ class ExportModelWithMLMTest(tf.test.TestCase, parameterized.TestCase):
# Note that we set `_auto_track_sub_layers` to False when exporting the
# SavedModel, so hub_layer has the same number of weights as bert_model;
# otherwise, hub_layer will have extra weights from its `mlm` subobject.
- self.assertEqual(len(bert_model.trainable_weights),
- len(hub_layer.trainable_weights))
+ self.assertEqual(
+ len(bert_model.trainable_weights), len(hub_layer.trainable_weights))
for source_weight, hub_weight in zip(bert_model.trainable_weights,
hub_layer.trainable_weights):
self.assertAllClose(source_weight, hub_weight)
@@ -473,10 +510,11 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
The absolute filename of the created vocab file.
"""
full_vocab = ["[PAD]", "[UNK]", "[CLS]", "[SEP]"
- ] + ["[MASK]"]*add_mask_token + vocab
+ ] + ["[MASK]"] * add_mask_token + vocab
path = os.path.join(
- tempfile.mkdtemp(dir=self.get_temp_dir(), # New subdir each time.
- prefix=_STRING_NOT_TO_LEAK),
+ tempfile.mkdtemp(
+ dir=self.get_temp_dir(), # New subdir each time.
+ prefix=_STRING_NOT_TO_LEAK),
filename)
with tf.io.gfile.GFile(path, "w") as f:
f.write("\n".join(full_vocab + [""]))
@@ -522,22 +560,30 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
model_prefix=model_prefix,
model_type="word",
input=input_file,
- pad_id=0, unk_id=1, control_symbols=control_symbols,
+ pad_id=0,
+ unk_id=1,
+ control_symbols=control_symbols,
vocab_size=full_vocab_size,
- bos_id=full_vocab_size-2, eos_id=full_vocab_size-1)
- SentencePieceTrainer.Train(
- " ".join(["--{}={}".format(k, v) for k, v in flags.items()]))
+ bos_id=full_vocab_size - 2,
+ eos_id=full_vocab_size - 1)
+ SentencePieceTrainer.Train(" ".join(
+ ["--{}={}".format(k, v) for k, v in flags.items()]))
return model_prefix + ".model"
- def _do_export(self, vocab, do_lower_case, default_seq_length=128,
- tokenize_with_offsets=True, use_sp_model=False,
- experimental_disable_assert=False, add_mask_token=False):
+ def _do_export(self,
+ vocab,
+ do_lower_case,
+ default_seq_length=128,
+ tokenize_with_offsets=True,
+ use_sp_model=False,
+ experimental_disable_assert=False,
+ add_mask_token=False):
"""Runs SavedModel export and returns the export_path."""
export_path = tempfile.mkdtemp(dir=self.get_temp_dir())
vocab_file = sp_model_file = None
if use_sp_model:
- sp_model_file = self._make_sp_model_file(vocab,
- add_mask_token=add_mask_token)
+ sp_model_file = self._make_sp_model_file(
+ vocab, add_mask_token=add_mask_token)
else:
vocab_file = self._make_vocab_file(vocab, add_mask_token=add_mask_token)
export_tfhub_lib.export_preprocessing(
@@ -554,19 +600,24 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
def test_no_leaks(self):
"""Tests not leaking the path to the original vocab file."""
- path = self._do_export(
- ["d", "ef", "abc", "xy"], do_lower_case=True, use_sp_model=False)
+ path = self._do_export(["d", "ef", "abc", "xy"],
+ do_lower_case=True,
+ use_sp_model=False)
with tf.io.gfile.GFile(os.path.join(path, "saved_model.pb"), "rb") as f:
self.assertFalse( # pylint: disable=g-generic-assert
_STRING_NOT_TO_LEAK.encode("ascii") in f.read())
@parameterized.named_parameters(("Bert", False), ("Sentencepiece", True))
def test_exported_callables(self, use_sp_model):
- preprocess = tf.saved_model.load(self._do_export(
- ["d", "ef", "abc", "xy"], do_lower_case=True,
- tokenize_with_offsets=not use_sp_model, # TODO(b/181866850): drop this.
- experimental_disable_assert=True, # TODO(b/175369555): drop this.
- use_sp_model=use_sp_model))
+ preprocess = tf.saved_model.load(
+ self._do_export(
+ ["d", "ef", "abc", "xy"],
+ do_lower_case=True,
+ # TODO(b/181866850): drop this.
+ tokenize_with_offsets=not use_sp_model,
+ # TODO(b/175369555): drop this.
+ experimental_disable_assert=True,
+ use_sp_model=use_sp_model))
def fold_dim(rt):
"""Removes the word/subword distinction of BertTokenizer."""
@@ -575,18 +626,20 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
# .tokenize()
inputs = tf.constant(["abc d ef", "ABC D EF d"])
token_ids = preprocess.tokenize(inputs)
- self.assertAllEqual(fold_dim(token_ids),
- tf.ragged.constant([[6, 4, 5],
- [6, 4, 5, 4]]))
+ self.assertAllEqual(
+ fold_dim(token_ids), tf.ragged.constant([[6, 4, 5], [6, 4, 5, 4]]))
special_tokens_dict = {
k: v.numpy().item() # Expecting eager Tensor, converting to Python.
- for k, v in preprocess.tokenize.get_special_tokens_dict().items()}
- self.assertDictEqual(special_tokens_dict,
- dict(padding_id=0,
- start_of_sequence_id=2,
- end_of_segment_id=3,
- vocab_size=4+6 if use_sp_model else 4+4))
+ for k, v in preprocess.tokenize.get_special_tokens_dict().items()
+ }
+ self.assertDictEqual(
+ special_tokens_dict,
+ dict(
+ padding_id=0,
+ start_of_sequence_id=2,
+ end_of_segment_id=3,
+ vocab_size=4 + 6 if use_sp_model else 4 + 4))
# .tokenize_with_offsets()
if use_sp_model:
@@ -595,92 +648,104 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
else:
token_ids, start_offsets, limit_offsets = (
preprocess.tokenize_with_offsets(inputs))
- self.assertAllEqual(fold_dim(token_ids),
- tf.ragged.constant([[6, 4, 5],
- [6, 4, 5, 4]]))
- self.assertAllEqual(fold_dim(start_offsets),
- tf.ragged.constant([[0, 4, 6],
- [0, 4, 6, 9]]))
- self.assertAllEqual(fold_dim(limit_offsets),
- tf.ragged.constant([[3, 5, 8],
- [3, 5, 8, 10]]))
+ self.assertAllEqual(
+ fold_dim(token_ids), tf.ragged.constant([[6, 4, 5], [6, 4, 5, 4]]))
+ self.assertAllEqual(
+ fold_dim(start_offsets), tf.ragged.constant([[0, 4, 6], [0, 4, 6,
+ 9]]))
+ self.assertAllEqual(
+ fold_dim(limit_offsets), tf.ragged.constant([[3, 5, 8], [3, 5, 8,
+ 10]]))
self.assertIs(preprocess.tokenize.get_special_tokens_dict,
preprocess.tokenize_with_offsets.get_special_tokens_dict)
# Root callable.
bert_inputs = preprocess(inputs)
self.assertAllEqual(bert_inputs["input_word_ids"].shape.as_list(), [2, 128])
- self.assertAllEqual(bert_inputs["input_word_ids"][:, :10],
- tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
- [2, 6, 4, 5, 4, 3, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_word_ids"][:, :10],
+ tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
+ [2, 6, 4, 5, 4, 3, 0, 0, 0, 0]]))
self.assertAllEqual(bert_inputs["input_mask"].shape.as_list(), [2, 128])
- self.assertAllEqual(bert_inputs["input_mask"][:, :10],
- tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
- [1, 1, 1, 1, 1, 1, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_mask"][:, :10],
+ tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
+ [1, 1, 1, 1, 1, 1, 0, 0, 0, 0]]))
self.assertAllEqual(bert_inputs["input_type_ids"].shape.as_list(), [2, 128])
- self.assertAllEqual(bert_inputs["input_type_ids"][:, :10],
- tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
- [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_type_ids"][:, :10],
+ tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
+ [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
# .bert_pack_inputs()
inputs_2 = tf.constant(["d xy", "xy abc"])
token_ids_2 = preprocess.tokenize(inputs_2)
- bert_inputs = preprocess.bert_pack_inputs(
- [token_ids, token_ids_2], seq_length=256)
+ bert_inputs = preprocess.bert_pack_inputs([token_ids, token_ids_2],
+ seq_length=256)
self.assertAllEqual(bert_inputs["input_word_ids"].shape.as_list(), [2, 256])
- self.assertAllEqual(bert_inputs["input_word_ids"][:, :10],
- tf.constant([[2, 6, 4, 5, 3, 4, 7, 3, 0, 0],
- [2, 6, 4, 5, 4, 3, 7, 6, 3, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_word_ids"][:, :10],
+ tf.constant([[2, 6, 4, 5, 3, 4, 7, 3, 0, 0],
+ [2, 6, 4, 5, 4, 3, 7, 6, 3, 0]]))
self.assertAllEqual(bert_inputs["input_mask"].shape.as_list(), [2, 256])
- self.assertAllEqual(bert_inputs["input_mask"][:, :10],
- tf.constant([[1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
- [1, 1, 1, 1, 1, 1, 1, 1, 1, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_mask"][:, :10],
+ tf.constant([[1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
+ [1, 1, 1, 1, 1, 1, 1, 1, 1, 0]]))
self.assertAllEqual(bert_inputs["input_type_ids"].shape.as_list(), [2, 256])
- self.assertAllEqual(bert_inputs["input_type_ids"][:, :10],
- tf.constant([[0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
- [0, 0, 0, 0, 0, 0, 1, 1, 1, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_type_ids"][:, :10],
+ tf.constant([[0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
+ [0, 0, 0, 0, 0, 0, 1, 1, 1, 0]]))
# For BertTokenizer only: repeat relevant parts for do_lower_case=False,
# default_seq_length=10, experimental_disable_assert=False,
# tokenize_with_offsets=False, and without folding the word/subword dimension.
def test_cased_length10(self):
- preprocess = tf.saved_model.load(self._do_export(
- ["d", "##ef", "abc", "ABC"],
- do_lower_case=False, default_seq_length=10,
- tokenize_with_offsets=False,
- use_sp_model=False,
- experimental_disable_assert=False))
+ preprocess = tf.saved_model.load(
+ self._do_export(["d", "##ef", "abc", "ABC"],
+ do_lower_case=False,
+ default_seq_length=10,
+ tokenize_with_offsets=False,
+ use_sp_model=False,
+ experimental_disable_assert=False))
inputs = tf.constant(["abc def", "ABC DEF"])
token_ids = preprocess.tokenize(inputs)
- self.assertAllEqual(token_ids, tf.ragged.constant([[[6], [4, 5]],
- [[7], [1]]]))
+ self.assertAllEqual(token_ids,
+ tf.ragged.constant([[[6], [4, 5]], [[7], [1]]]))
self.assertFalse(hasattr(preprocess, "tokenize_with_offsets"))
bert_inputs = preprocess(inputs)
- self.assertAllEqual(bert_inputs["input_word_ids"],
- tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
- [2, 7, 1, 3, 0, 0, 0, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_mask"],
- tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
- [1, 1, 1, 1, 0, 0, 0, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_type_ids"],
- tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
- [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_word_ids"],
+ tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
+ [2, 7, 1, 3, 0, 0, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_mask"],
+ tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
+ [1, 1, 1, 1, 0, 0, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_type_ids"],
+ tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
+ [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
inputs_2 = tf.constant(["d ABC", "ABC abc"])
token_ids_2 = preprocess.tokenize(inputs_2)
bert_inputs = preprocess.bert_pack_inputs([token_ids, token_ids_2])
# Test default seq_length=10.
- self.assertAllEqual(bert_inputs["input_word_ids"],
- tf.constant([[2, 6, 4, 5, 3, 4, 7, 3, 0, 0],
- [2, 7, 1, 3, 7, 6, 3, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_mask"],
- tf.constant([[1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
- [1, 1, 1, 1, 1, 1, 1, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_type_ids"],
- tf.constant([[0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
- [0, 0, 0, 0, 1, 1, 1, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_word_ids"],
+ tf.constant([[2, 6, 4, 5, 3, 4, 7, 3, 0, 0],
+ [2, 7, 1, 3, 7, 6, 3, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_mask"],
+ tf.constant([[1, 1, 1, 1, 1, 1, 1, 1, 0, 0],
+ [1, 1, 1, 1, 1, 1, 1, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_type_ids"],
+ tf.constant([[0, 0, 0, 0, 0, 1, 1, 1, 0, 0],
+ [0, 0, 0, 0, 1, 1, 1, 0, 0, 0]]))
# XLA requires fixed shapes for tensors found in graph mode.
# Statically known shapes in Python are a particularly firm way to
@@ -689,16 +754,21 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
# inference when applied to fully or partially known input shapes.
@parameterized.named_parameters(("Bert", False), ("Sentencepiece", True))
def test_shapes(self, use_sp_model):
- preprocess = tf.saved_model.load(self._do_export(
- ["abc", "def"], do_lower_case=True,
- tokenize_with_offsets=not use_sp_model, # TODO(b/181866850): drop this.
- experimental_disable_assert=True, # TODO(b/175369555): drop this.
- use_sp_model=use_sp_model))
+ preprocess = tf.saved_model.load(
+ self._do_export(
+ ["abc", "def"],
+ do_lower_case=True,
+ # TODO(b/181866850): drop this.
+ tokenize_with_offsets=not use_sp_model,
+ # TODO(b/175369555): drop this.
+ experimental_disable_assert=True,
+ use_sp_model=use_sp_model))
def expected_bert_input_shapes(batch_size, seq_length):
- return dict(input_word_ids=[batch_size, seq_length],
- input_mask=[batch_size, seq_length],
- input_type_ids=[batch_size, seq_length])
+ return dict(
+ input_word_ids=[batch_size, seq_length],
+ input_mask=[batch_size, seq_length],
+ input_type_ids=[batch_size, seq_length])
for batch_size in [7, None]:
if use_sp_model:
@@ -706,11 +776,9 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
else:
token_out_shape = [batch_size, None, None]
self.assertEqual(
- _result_shapes_in_tf_function(
- preprocess.tokenize,
- tf.TensorSpec([batch_size], tf.string)),
- token_out_shape,
- "with batch_size=%s" % batch_size)
+ _result_shapes_in_tf_function(preprocess.tokenize,
+ tf.TensorSpec([batch_size], tf.string)),
+ token_out_shape, "with batch_size=%s" % batch_size)
# TODO(b/181866850): Enable tokenize_with_offsets when it works and test.
if use_sp_model:
self.assertFalse(hasattr(preprocess, "tokenize_with_offsets"))
@@ -718,8 +786,7 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
self.assertEqual(
_result_shapes_in_tf_function(
preprocess.tokenize_with_offsets,
- tf.TensorSpec([batch_size], tf.string)),
- [token_out_shape] * 3,
+ tf.TensorSpec([batch_size], tf.string)), [token_out_shape] * 3,
"with batch_size=%s" % batch_size)
self.assertEqual(
_result_shapes_in_tf_function(
@@ -737,7 +804,9 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
def test_reexport(self, use_sp_model):
"""Test that preprocess keeps working after another save/load cycle."""
path1 = self._do_export(
- ["d", "ef", "abc", "xy"], do_lower_case=True, default_seq_length=10,
+ ["d", "ef", "abc", "xy"],
+ do_lower_case=True,
+ default_seq_length=10,
tokenize_with_offsets=False,
experimental_disable_assert=True, # TODO(b/175369555): drop this.
use_sp_model=use_sp_model)
@@ -752,35 +821,46 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
inputs = tf.constant(["abc d ef", "ABC D EF d"])
bert_inputs = model2(inputs)
- self.assertAllEqual(bert_inputs["input_word_ids"],
- tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
- [2, 6, 4, 5, 4, 3, 0, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_mask"],
- tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
- [1, 1, 1, 1, 1, 1, 0, 0, 0, 0]]))
- self.assertAllEqual(bert_inputs["input_type_ids"],
- tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
- [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_word_ids"],
+ tf.constant([[2, 6, 4, 5, 3, 0, 0, 0, 0, 0],
+ [2, 6, 4, 5, 4, 3, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_mask"],
+ tf.constant([[1, 1, 1, 1, 1, 0, 0, 0, 0, 0],
+ [1, 1, 1, 1, 1, 1, 0, 0, 0, 0]]))
+ self.assertAllEqual(
+ bert_inputs["input_type_ids"],
+ tf.constant([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
+ [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]]))
@parameterized.named_parameters(("Bert", True), ("Albert", False))
def test_preprocessing_for_mlm(self, use_bert):
"""Combines both SavedModel types and TF.text helpers for MLM."""
# Create the preprocessing SavedModel with a [MASK] token.
- non_special_tokens = ["hello", "world",
- "nice", "movie", "great", "actors",
- "quick", "fox", "lazy", "dog"]
- preprocess = tf.saved_model.load(self._do_export(
- non_special_tokens, do_lower_case=True,
- tokenize_with_offsets=use_bert, # TODO(b/181866850): drop this.
- experimental_disable_assert=True, # TODO(b/175369555): drop this.
- add_mask_token=True, use_sp_model=not use_bert))
+ non_special_tokens = [
+ "hello", "world", "nice", "movie", "great", "actors", "quick", "fox",
+ "lazy", "dog"
+ ]
+
+ preprocess = tf.saved_model.load(
+ self._do_export(
+ non_special_tokens,
+ do_lower_case=True,
+ tokenize_with_offsets=use_bert, # TODO(b/181866850): drop this.
+ experimental_disable_assert=True, # TODO(b/175369555): drop this.
+ add_mask_token=True,
+ use_sp_model=not use_bert))
vocab_size = len(non_special_tokens) + (5 if use_bert else 7)
# Create the encoder SavedModel with an .mlm subobject.
hidden_size = 16
num_hidden_layers = 2
bert_config, encoder_config = _get_bert_config_or_encoder_config(
- use_bert, hidden_size, num_hidden_layers, vocab_size)
+ use_bert_config=use_bert,
+ hidden_size=hidden_size,
+ num_hidden_layers=num_hidden_layers,
+ vocab_size=vocab_size)
_, pretrainer = export_tfhub_lib._create_model(
bert_config=bert_config, encoder_config=encoder_config, with_mlm=True)
model_checkpoint_dir = os.path.join(self.get_temp_dir(), "checkpoint")
@@ -814,8 +894,10 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
self.assertEqual(mask_id, 4)
# A batch of 3 segment pairs.
- raw_segments = [tf.constant(["hello", "nice movie", "quick fox"]),
- tf.constant(["world", "great actors", "lazy dog"])]
+ raw_segments = [
+ tf.constant(["hello", "nice movie", "quick fox"]),
+ tf.constant(["world", "great actors", "lazy dog"])
+ ]
batch_size = 3
# Misc hyperparameters.
@@ -842,18 +924,18 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
selection_rate=0.5, # Adjusted for the short test examples.
unselectable_ids=[start_of_sequence_id, end_of_segment_id]),
mask_values_chooser=text.MaskValuesChooser(
- vocab_size=vocab_size, mask_token=mask_id,
+ vocab_size=vocab_size,
+ mask_token=mask_id,
# Always put [MASK] to have a predictable result.
- mask_token_rate=1.0, random_token_rate=0.0))
+ mask_token_rate=1.0,
+ random_token_rate=0.0))
# Pad to fixed-length Transformer encoder inputs.
- input_word_ids, _ = text.pad_model_inputs(masked_input_ids,
- seq_length,
- pad_value=padding_id)
- input_type_ids, input_mask = text.pad_model_inputs(segment_ids, seq_length,
- pad_value=0)
- masked_lm_positions, _ = text.pad_model_inputs(masked_lm_positions,
- max_selections_per_seq,
- pad_value=0)
+ input_word_ids, _ = text.pad_model_inputs(
+ masked_input_ids, seq_length, pad_value=padding_id)
+ input_type_ids, input_mask = text.pad_model_inputs(
+ segment_ids, seq_length, pad_value=0)
+ masked_lm_positions, _ = text.pad_model_inputs(
+ masked_lm_positions, max_selections_per_seq, pad_value=0)
masked_lm_positions = tf.cast(masked_lm_positions, tf.int32)
num_predictions = int(tf.shape(masked_lm_positions)[1])
@@ -865,7 +947,8 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
# [CLS] nice movie [SEP] great actors [SEP]
[2, 7, 8, 3, 9, 10, 3, 0, 0, 0],
# [CLS] brown fox [SEP] lazy dog [SEP]
- [2, 11, 12, 3, 13, 14, 3, 0, 0, 0]])
+ [2, 11, 12, 3, 13, 14, 3, 0, 0, 0]
+ ])
for i in range(batch_size):
for j in range(num_predictions):
k = int(masked_lm_positions[i, j])
@@ -896,15 +979,17 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
@parameterized.named_parameters(("Bert", False), ("Sentencepiece", True))
def test_special_tokens_in_estimator(self, use_sp_model):
"""Tests getting special tokens without an Eager init context."""
- preprocess_export_path = self._do_export(
- ["d", "ef", "abc", "xy"], do_lower_case=True,
- use_sp_model=use_sp_model, tokenize_with_offsets=False)
+ preprocess_export_path = self._do_export(["d", "ef", "abc", "xy"],
+ do_lower_case=True,
+ use_sp_model=use_sp_model,
+ tokenize_with_offsets=False)
def _get_special_tokens_dict(obj):
"""Returns special tokens of restored tokenizer as Python values."""
if tf.executing_eagerly():
- special_tokens_numpy = {k: v.numpy()
- for k, v in obj.get_special_tokens_dict()}
+ special_tokens_numpy = {
+ k: v.numpy() for k, v in obj.get_special_tokens_dict()
+ }
else:
with tf.Graph().as_default():
# This code expects `get_special_tokens_dict()` to be a tf.function
@@ -913,8 +998,10 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
special_tokens_tensors = obj.get_special_tokens_dict()
with tf.compat.v1.Session() as sess:
special_tokens_numpy = sess.run(special_tokens_tensors)
- return {k: v.item() # Numpy to Python.
- for k, v in special_tokens_numpy.items()}
+ return {
+ k: v.item() # Numpy to Python.
+ for k, v in special_tokens_numpy.items()
+ }
def input_fn():
self.assertFalse(tf.executing_eagerly())
@@ -927,7 +1014,8 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
self.assertIsInstance(v, int, "Unexpected type for {}".format(k))
tokens = tokenize(sentences)
packed_inputs = layers.BertPackInputs(
- 4, special_tokens_dict=special_tokens_dict)(tokens)
+ 4, special_tokens_dict=special_tokens_dict)(
+ tokens)
preprocessing = tf.keras.Model(sentences, packed_inputs)
# Map the dataset.
ds = tf.data.Dataset.from_tensors(
@@ -937,22 +1025,22 @@ class ExportPreprocessingTest(tf.test.TestCase, parameterized.TestCase):
def model_fn(features, labels, mode):
del labels # Unused.
- return tf.estimator.EstimatorSpec(mode=mode,
- predictions=features["input_word_ids"])
+ return tf_estimator.EstimatorSpec(
+ mode=mode, predictions=features["input_word_ids"])
- estimator = tf.estimator.Estimator(model_fn=model_fn)
+ estimator = tf_estimator.Estimator(model_fn=model_fn)
outputs = list(estimator.predict(input_fn))
- self.assertAllEqual(outputs, np.array([[2, 6, 3, 0],
- [2, 4, 5, 3]]))
+ self.assertAllEqual(outputs, np.array([[2, 6, 3, 0], [2, 4, 5, 3]]))
# TODO(b/175369555): Remove that code and its test.
@parameterized.named_parameters(("Bert", False), ("Sentencepiece", True))
def test_check_no_assert(self, use_sp_model):
"""Tests the self-check during export without assertions."""
- preprocess_export_path = self._do_export(
- ["d", "ef", "abc", "xy"], do_lower_case=True,
- use_sp_model=use_sp_model, tokenize_with_offsets=False,
- experimental_disable_assert=False)
+ preprocess_export_path = self._do_export(["d", "ef", "abc", "xy"],
+ do_lower_case=True,
+ use_sp_model=use_sp_model,
+ tokenize_with_offsets=False,
+ experimental_disable_assert=False)
with self.assertRaisesRegex(AssertionError,
r"failed to suppress \d+ Assert ops"):
export_tfhub_lib._check_no_assert(preprocess_export_path)
@@ -963,8 +1051,8 @@ def _result_shapes_in_tf_function(fn, *args, **kwargs):
Args:
fn: A callable.
- *args: TensorSpecs for Tensor-valued arguments and actual values
- for Python-valued arguments to fn.
+ *args: TensorSpecs for Tensor-valued arguments and actual values for
+ Python-valued arguments to fn.
**kwargs: Same for keyword arguments.
Returns:
diff --git a/official/nlp/bert/squad_evaluate_v1_1.py b/official/nlp/tools/squad_evaluate_v1_1.py
similarity index 98%
rename from official/nlp/bert/squad_evaluate_v1_1.py
rename to official/nlp/tools/squad_evaluate_v1_1.py
index a39f571c37b002ab10cfe36a1454827d91512945..795fa471e3dff93f0cc153a2062905bd9ccf52b9 100644
--- a/official/nlp/bert/squad_evaluate_v1_1.py
+++ b/official/nlp/tools/squad_evaluate_v1_1.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/bert/squad_evaluate_v2_0.py b/official/nlp/tools/squad_evaluate_v2_0.py
similarity index 99%
rename from official/nlp/bert/squad_evaluate_v2_0.py
rename to official/nlp/tools/squad_evaluate_v2_0.py
index 12c5a7e3d6b406e45e4f91580f8b4198733db37c..ac02f72bec56dab8bb0c2d9a9cfae908adb1142f 100644
--- a/official/nlp/bert/squad_evaluate_v2_0.py
+++ b/official/nlp/tools/squad_evaluate_v2_0.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/tools/tf1_bert_checkpoint_converter_lib.py b/official/nlp/tools/tf1_bert_checkpoint_converter_lib.py
new file mode 100644
index 0000000000000000000000000000000000000000..b34bd00088f2da866093c72619482a01f15677f4
--- /dev/null
+++ b/official/nlp/tools/tf1_bert_checkpoint_converter_lib.py
@@ -0,0 +1,201 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Convert checkpoints created by Estimator (tf1) to be Keras compatible."""
+
+import numpy as np
+import tensorflow.compat.v1 as tf # TF 1.x
+
+# Mapping between old <=> new names. The source pattern in original variable
+# name will be replaced by destination pattern.
+BERT_NAME_REPLACEMENTS = (
+ ("bert", "bert_model"),
+ ("embeddings/word_embeddings", "word_embeddings/embeddings"),
+ ("embeddings/token_type_embeddings",
+ "embedding_postprocessor/type_embeddings"),
+ ("embeddings/position_embeddings",
+ "embedding_postprocessor/position_embeddings"),
+ ("embeddings/LayerNorm", "embedding_postprocessor/layer_norm"),
+ ("attention/self", "self_attention"),
+ ("attention/output/dense", "self_attention_output"),
+ ("attention/output/LayerNorm", "self_attention_layer_norm"),
+ ("intermediate/dense", "intermediate"),
+ ("output/dense", "output"),
+ ("output/LayerNorm", "output_layer_norm"),
+ ("pooler/dense", "pooler_transform"),
+)
+
+BERT_V2_NAME_REPLACEMENTS = (
+ ("bert/", ""),
+ ("encoder", "transformer"),
+ ("embeddings/word_embeddings", "word_embeddings/embeddings"),
+ ("embeddings/token_type_embeddings", "type_embeddings/embeddings"),
+ ("embeddings/position_embeddings", "position_embedding/embeddings"),
+ ("embeddings/LayerNorm", "embeddings/layer_norm"),
+ ("attention/self", "self_attention"),
+ ("attention/output/dense", "self_attention/attention_output"),
+ ("attention/output/LayerNorm", "self_attention_layer_norm"),
+ ("intermediate/dense", "intermediate"),
+ ("output/dense", "output"),
+ ("output/LayerNorm", "output_layer_norm"),
+ ("pooler/dense", "pooler_transform"),
+ ("cls/predictions", "bert/cls/predictions"),
+ ("cls/predictions/output_bias", "cls/predictions/output_bias/bias"),
+ ("cls/seq_relationship/output_bias", "predictions/transform/logits/bias"),
+ ("cls/seq_relationship/output_weights",
+ "predictions/transform/logits/kernel"),
+)
+
+BERT_PERMUTATIONS = ()
+
+BERT_V2_PERMUTATIONS = (("cls/seq_relationship/output_weights", (1, 0)),)
+
+
+def _bert_name_replacement(var_name, name_replacements):
+ """Gets the variable name replacement."""
+ for src_pattern, tgt_pattern in name_replacements:
+ if src_pattern in var_name:
+ old_var_name = var_name
+ var_name = var_name.replace(src_pattern, tgt_pattern)
+ tf.logging.info("Converted: %s --> %s", old_var_name, var_name)
+ return var_name
+
+
+def _has_exclude_patterns(name, exclude_patterns):
+ """Checks if a string contains substrings that match patterns to exclude."""
+ for p in exclude_patterns:
+ if p in name:
+ return True
+ return False
+
+
+def _get_permutation(name, permutations):
+ """Checks whether a variable requires transposition by pattern matching."""
+ for src_pattern, permutation in permutations:
+ if src_pattern in name:
+ tf.logging.info("Permuted: %s --> %s", name, permutation)
+ return permutation
+
+ return None
+
+
+def _get_new_shape(name, shape, num_heads):
+ """Checks whether a variable requires reshape by pattern matching."""
+ if "self_attention/attention_output/kernel" in name:
+ return tuple([num_heads, shape[0] // num_heads, shape[1]])
+ if "self_attention/attention_output/bias" in name:
+ return shape
+
+ patterns = [
+ "self_attention/query", "self_attention/value", "self_attention/key"
+ ]
+ for pattern in patterns:
+ if pattern in name:
+ if "kernel" in name:
+ return tuple([shape[0], num_heads, shape[1] // num_heads])
+ if "bias" in name:
+ return tuple([num_heads, shape[0] // num_heads])
+ return None
+
+
+def create_v2_checkpoint(model,
+ src_checkpoint,
+ output_path,
+ checkpoint_model_name="model"):
+ """Converts a name-based matched TF V1 checkpoint to TF V2 checkpoint."""
+ # Uses streaming-restore in eager model to read V1 name-based checkpoints.
+ model.load_weights(src_checkpoint).assert_existing_objects_matched()
+ if hasattr(model, "checkpoint_items"):
+ checkpoint_items = model.checkpoint_items
+ else:
+ checkpoint_items = {}
+
+ checkpoint_items[checkpoint_model_name] = model
+ checkpoint = tf.train.Checkpoint(**checkpoint_items)
+ checkpoint.save(output_path)
+
+
+def convert(checkpoint_from_path,
+ checkpoint_to_path,
+ num_heads,
+ name_replacements,
+ permutations,
+ exclude_patterns=None):
+ """Migrates the names of variables within a checkpoint.
+
+ Args:
+ checkpoint_from_path: Path to source checkpoint to be read in.
+ checkpoint_to_path: Path to checkpoint to be written out.
+ num_heads: The number of heads of the model.
+ name_replacements: A list of tuples of the form (match_str, replace_str)
+ describing variable names to adjust.
+ permutations: A list of tuples of the form (match_str, permutation)
+ describing permutations to apply to given variables. Note that match_str
+ should match the original variable name, not the replaced one.
+ exclude_patterns: A list of string patterns to exclude variables from
+ checkpoint conversion.
+
+ Returns:
+ A dictionary that maps the new variable names to the Variable objects.
+ A dictionary that maps the old variable names to the new variable names.
+ """
+ with tf.Graph().as_default():
+ tf.logging.info("Reading checkpoint_from_path %s", checkpoint_from_path)
+ reader = tf.train.NewCheckpointReader(checkpoint_from_path)
+ name_shape_map = reader.get_variable_to_shape_map()
+ new_variable_map = {}
+ conversion_map = {}
+ for var_name in name_shape_map:
+ if exclude_patterns and _has_exclude_patterns(var_name, exclude_patterns):
+ continue
+ # Get the original tensor data.
+ tensor = reader.get_tensor(var_name)
+
+ # Look up the new variable name, if any.
+ new_var_name = _bert_name_replacement(var_name, name_replacements)
+
+ # See if we need to reshape the underlying tensor.
+ new_shape = None
+ if num_heads > 0:
+ new_shape = _get_new_shape(new_var_name, tensor.shape, num_heads)
+ if new_shape:
+ tf.logging.info("Veriable %s has a shape change from %s to %s",
+ var_name, tensor.shape, new_shape)
+ tensor = np.reshape(tensor, new_shape)
+
+ # See if we need to permute the underlying tensor.
+ permutation = _get_permutation(var_name, permutations)
+ if permutation:
+ tensor = np.transpose(tensor, permutation)
+
+ # Create a new variable with the possibly-reshaped or transposed tensor.
+ var = tf.Variable(tensor, name=var_name)
+
+ # Save the variable into the new variable map.
+ new_variable_map[new_var_name] = var
+
+ # Keep a list of converter variables for sanity checking.
+ if new_var_name != var_name:
+ conversion_map[var_name] = new_var_name
+
+ saver = tf.train.Saver(new_variable_map)
+
+ with tf.Session() as sess:
+ sess.run(tf.global_variables_initializer())
+ tf.logging.info("Writing checkpoint_to_path %s", checkpoint_to_path)
+ saver.save(sess, checkpoint_to_path, write_meta_graph=False)
+
+ tf.logging.info("Summary:")
+ tf.logging.info(" Converted %d variable name(s).", len(new_variable_map))
+ tf.logging.info(" Converted: %s", str(conversion_map))
diff --git a/official/nlp/tools/tf2_albert_encoder_checkpoint_converter.py b/official/nlp/tools/tf2_albert_encoder_checkpoint_converter.py
index 57b32a02fa4ac9679029e84d820c8eef8d23042c..4583e4c4c6525b9f9e72d2a78548a43eeb7f8b1f 100644
--- a/official/nlp/tools/tf2_albert_encoder_checkpoint_converter.py
+++ b/official/nlp/tools/tf2_albert_encoder_checkpoint_converter.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,11 +23,11 @@ from absl import app
from absl import flags
import tensorflow as tf
-from official.legacy.nlp.albert import configs
+from official.legacy.albert import configs
from official.modeling import tf_utils
-from official.nlp.bert import tf1_checkpoint_converter_lib
from official.nlp.modeling import models
from official.nlp.modeling import networks
+from official.nlp.tools import tf1_bert_checkpoint_converter_lib
FLAGS = flags.FLAGS
@@ -128,12 +128,12 @@ def convert_checkpoint(bert_config, output_path, v1_checkpoint,
# Create a temporary V1 name-converted checkpoint in the output directory.
temporary_checkpoint_dir = os.path.join(output_dir, "temp_v1")
temporary_checkpoint = os.path.join(temporary_checkpoint_dir, "ckpt")
- tf1_checkpoint_converter_lib.convert(
+ tf1_bert_checkpoint_converter_lib.convert(
checkpoint_from_path=v1_checkpoint,
checkpoint_to_path=temporary_checkpoint,
num_heads=bert_config.num_attention_heads,
name_replacements=ALBERT_NAME_REPLACEMENTS,
- permutations=tf1_checkpoint_converter_lib.BERT_V2_PERMUTATIONS,
+ permutations=tf1_bert_checkpoint_converter_lib.BERT_V2_PERMUTATIONS,
exclude_patterns=["adam", "Adam"])
# Create a V2 checkpoint from the temporary checkpoint.
@@ -144,9 +144,8 @@ def convert_checkpoint(bert_config, output_path, v1_checkpoint,
else:
raise ValueError("Unsupported converted_model: %s" % converted_model)
- tf1_checkpoint_converter_lib.create_v2_checkpoint(model, temporary_checkpoint,
- output_path,
- checkpoint_model_name)
+ tf1_bert_checkpoint_converter_lib.create_v2_checkpoint(
+ model, temporary_checkpoint, output_path, checkpoint_model_name)
# Clean up the temporary checkpoint, if it exists.
try:
diff --git a/official/nlp/tools/tf2_bert_encoder_checkpoint_converter.py b/official/nlp/tools/tf2_bert_encoder_checkpoint_converter.py
new file mode 100644
index 0000000000000000000000000000000000000000..ddbff775faf703eaf6c745cffd0ce9f28142cb20
--- /dev/null
+++ b/official/nlp/tools/tf2_bert_encoder_checkpoint_converter.py
@@ -0,0 +1,160 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""A converter from a V1 BERT encoder checkpoint to a V2 encoder checkpoint.
+
+The conversion will yield an object-oriented checkpoint that can be used
+to restore a BertEncoder or BertPretrainerV2 object (see the `converted_model`
+FLAG below).
+"""
+
+import os
+
+from absl import app
+from absl import flags
+
+import tensorflow as tf
+from official.legacy.bert import configs
+from official.modeling import tf_utils
+from official.nlp.modeling import models
+from official.nlp.modeling import networks
+from official.nlp.tools import tf1_bert_checkpoint_converter_lib
+
+FLAGS = flags.FLAGS
+
+flags.DEFINE_string("bert_config_file", None,
+ "Bert configuration file to define core bert layers.")
+flags.DEFINE_string(
+ "checkpoint_to_convert", None,
+ "Initial checkpoint from a pretrained BERT model core (that is, only the "
+ "BertModel, with no task heads.)")
+flags.DEFINE_string("converted_checkpoint_path", None,
+ "Name for the created object-based V2 checkpoint.")
+flags.DEFINE_string("checkpoint_model_name", "encoder",
+ "The name of the model when saving the checkpoint, i.e., "
+ "the checkpoint will be saved using: "
+ "tf.train.Checkpoint(FLAGS.checkpoint_model_name=model).")
+flags.DEFINE_enum(
+ "converted_model", "encoder", ["encoder", "pretrainer"],
+ "Whether to convert the checkpoint to a `BertEncoder` model or a "
+ "`BertPretrainerV2` model (with mlm but without classification heads).")
+
+
+def _create_bert_model(cfg):
+ """Creates a BERT keras core model from BERT configuration.
+
+ Args:
+ cfg: A `BertConfig` to create the core model.
+
+ Returns:
+ A BertEncoder network.
+ """
+ bert_encoder = networks.BertEncoder(
+ vocab_size=cfg.vocab_size,
+ hidden_size=cfg.hidden_size,
+ num_layers=cfg.num_hidden_layers,
+ num_attention_heads=cfg.num_attention_heads,
+ intermediate_size=cfg.intermediate_size,
+ activation=tf_utils.get_activation(cfg.hidden_act),
+ dropout_rate=cfg.hidden_dropout_prob,
+ attention_dropout_rate=cfg.attention_probs_dropout_prob,
+ max_sequence_length=cfg.max_position_embeddings,
+ type_vocab_size=cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=cfg.initializer_range),
+ embedding_width=cfg.embedding_size)
+
+ return bert_encoder
+
+
+def _create_bert_pretrainer_model(cfg):
+ """Creates a BERT keras core model from BERT configuration.
+
+ Args:
+ cfg: A `BertConfig` to create the core model.
+
+ Returns:
+ A BertPretrainerV2 model.
+ """
+ bert_encoder = _create_bert_model(cfg)
+ pretrainer = models.BertPretrainerV2(
+ encoder_network=bert_encoder,
+ mlm_activation=tf_utils.get_activation(cfg.hidden_act),
+ mlm_initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=cfg.initializer_range))
+ # Makes sure the pretrainer variables are created.
+ _ = pretrainer(pretrainer.inputs)
+ return pretrainer
+
+
+def convert_checkpoint(bert_config,
+ output_path,
+ v1_checkpoint,
+ checkpoint_model_name="model",
+ converted_model="encoder"):
+ """Converts a V1 checkpoint into an OO V2 checkpoint."""
+ output_dir, _ = os.path.split(output_path)
+ tf.io.gfile.makedirs(output_dir)
+
+ # Create a temporary V1 name-converted checkpoint in the output directory.
+ temporary_checkpoint_dir = os.path.join(output_dir, "temp_v1")
+ temporary_checkpoint = os.path.join(temporary_checkpoint_dir, "ckpt")
+
+ tf1_bert_checkpoint_converter_lib.convert(
+ checkpoint_from_path=v1_checkpoint,
+ checkpoint_to_path=temporary_checkpoint,
+ num_heads=bert_config.num_attention_heads,
+ name_replacements=(
+ tf1_bert_checkpoint_converter_lib.BERT_V2_NAME_REPLACEMENTS),
+ permutations=tf1_bert_checkpoint_converter_lib.BERT_V2_PERMUTATIONS,
+ exclude_patterns=["adam", "Adam"])
+
+ if converted_model == "encoder":
+ model = _create_bert_model(bert_config)
+ elif converted_model == "pretrainer":
+ model = _create_bert_pretrainer_model(bert_config)
+ else:
+ raise ValueError("Unsupported converted_model: %s" % converted_model)
+
+ # Create a V2 checkpoint from the temporary checkpoint.
+ tf1_bert_checkpoint_converter_lib.create_v2_checkpoint(
+ model, temporary_checkpoint, output_path, checkpoint_model_name)
+
+ # Clean up the temporary checkpoint, if it exists.
+ try:
+ tf.io.gfile.rmtree(temporary_checkpoint_dir)
+ except tf.errors.OpError:
+ # If it doesn't exist, we don't need to clean it up; continue.
+ pass
+
+
+def main(argv):
+ if len(argv) > 1:
+ raise app.UsageError("Too many command-line arguments.")
+
+ output_path = FLAGS.converted_checkpoint_path
+ v1_checkpoint = FLAGS.checkpoint_to_convert
+ checkpoint_model_name = FLAGS.checkpoint_model_name
+ converted_model = FLAGS.converted_model
+ bert_config = configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ convert_checkpoint(
+ bert_config=bert_config,
+ output_path=output_path,
+ v1_checkpoint=v1_checkpoint,
+ checkpoint_model_name=checkpoint_model_name,
+ converted_model=converted_model)
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/nlp/bert/tokenization.py b/official/nlp/tools/tokenization.py
similarity index 99%
rename from official/nlp/bert/tokenization.py
rename to official/nlp/tools/tokenization.py
index ea1546e3c29f33c593c64a4341366254da328b86..65d2b7717b1adb79b6fbc0cd3f93517582b39e3e 100644
--- a/official/nlp/bert/tokenization.py
+++ b/official/nlp/tools/tokenization.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/bert/tokenization_test.py b/official/nlp/tools/tokenization_test.py
similarity index 97%
rename from official/nlp/bert/tokenization_test.py
rename to official/nlp/tools/tokenization_test.py
index 07759de20b7c6eaf1a964c110da645215c10753a..c67a7e53d44890cd0652fd9cb1cad85cc1c4e024 100644
--- a/official/nlp/bert/tokenization_test.py
+++ b/official/nlp/tools/tokenization_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,7 +18,7 @@ import tempfile
import six
import tensorflow as tf
-from official.nlp.bert import tokenization
+from official.nlp.tools import tokenization
class TokenizationTest(tf.test.TestCase):
diff --git a/official/nlp/train.py b/official/nlp/train.py
index 6d022fdb67ce2d5860076d7f107bae82452c8ba1..feef3d54ea51885ab1dd5bb839885f5df2e3c9fd 100644
--- a/official/nlp/train.py
+++ b/official/nlp/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/transformer/README.md b/official/nlp/transformer/README.md
deleted file mode 100644
index a3aec5f9a052fa4e591df7c477011d626e6f257b..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/README.md
+++ /dev/null
@@ -1,220 +0,0 @@
-# Transformer Translation Model
-This is an implementation of the Transformer translation model as described in
-the [Attention is All You Need](https://arxiv.org/abs/1706.03762) paper. The
-implementation leverages tf.keras and makes sure it is compatible with TF 2.x.
-
-**Warning: the features in the `transformer/` folder have been fully intergrated
-into nlp/modeling.
-Due to its dependencies, we will remove this folder after the model
-garden 2.5 release. The model in `nlp/modeling/models/seq2seq_transformer.py` is
-identical to the model in this folder.**
-
-## Contents
- * [Contents](#contents)
- * [Walkthrough](#walkthrough)
- * [Detailed instructions](#detailed-instructions)
- * [Environment preparation](#environment-preparation)
- * [Download and preprocess datasets](#download-and-preprocess-datasets)
- * [Model training and evaluation](#model-training-and-evaluation)
- * [Implementation overview](#implementation-overview)
- * [Model Definition](#model-definition)
- * [Model Trainer](#model-trainer)
- * [Test dataset](#test-dataset)
-
-## Walkthrough
-
-Below are the commands for running the Transformer model. See the
-[Detailed instructions](#detailed-instructions) for more details on running the
-model.
-
-```
-# Ensure that PYTHONPATH is correctly defined as described in
-# https://github.com/tensorflow/models/tree/master/official#requirements
-export PYTHONPATH="$PYTHONPATH:/path/to/models"
-
-cd /path/to/models/official/nlp/transformer
-
-# Export variables
-PARAM_SET=big
-DATA_DIR=$HOME/transformer/data
-MODEL_DIR=$HOME/transformer/model_$PARAM_SET
-VOCAB_FILE=$DATA_DIR/vocab.ende.32768
-
-# Download training/evaluation/test datasets
-python3 data_download.py --data_dir=$DATA_DIR
-
-# Train the model for 100000 steps and evaluate every 5000 steps on a single GPU.
-# Each train step, takes 4096 tokens as a batch budget with 64 as sequence
-# maximal length.
-python3 transformer_main.py --data_dir=$DATA_DIR --model_dir=$MODEL_DIR \
- --vocab_file=$VOCAB_FILE --param_set=$PARAM_SET \
- --train_steps=100000 --steps_between_evals=5000 \
- --batch_size=4096 --max_length=64 \
- --bleu_source=$DATA_DIR/newstest2014.en \
- --bleu_ref=$DATA_DIR/newstest2014.de \
- --num_gpus=1 \
- --enable_time_history=false
-
-# Run during training in a separate process to get continuous updates,
-# or after training is complete.
-tensorboard --logdir=$MODEL_DIR
-```
-
-## Detailed instructions
-
-
-0. ### Environment preparation
-
- #### Add models repo to PYTHONPATH
- Follow the instructions described in the [Requirements](https://github.com/tensorflow/models/tree/master/official#requirements) section to add the models folder to the python path.
-
- #### Export variables (optional)
-
- Export the following variables, or modify the values in each of the snippets below:
-
- ```shell
- PARAM_SET=big
- DATA_DIR=$HOME/transformer/data
- MODEL_DIR=$HOME/transformer/model_$PARAM_SET
- VOCAB_FILE=$DATA_DIR/vocab.ende.32768
- ```
-
-1. ### Download and preprocess datasets
-
- [data_download.py](data_download.py) downloads and preprocesses the training and evaluation WMT datasets. After the data is downloaded and extracted, the training data is used to generate a vocabulary of subtokens. The evaluation and training strings are tokenized, and the resulting data is sharded, shuffled, and saved as TFRecords.
-
- 1.75GB of compressed data will be downloaded. In total, the raw files (compressed, extracted, and combined files) take up 8.4GB of disk space. The resulting TFRecord and vocabulary files are 722MB. The script takes around 40 minutes to run, with the bulk of the time spent downloading and ~15 minutes spent on preprocessing.
-
- Command to run:
- ```
- python3 data_download.py --data_dir=$DATA_DIR
- ```
-
- Arguments:
- * `--data_dir`: Path where the preprocessed TFRecord data, and vocab file will be saved.
- * Use the `--help` or `-h` flag to get a full list of possible arguments.
-
-2. ### Model training and evaluation
-
- [transformer_main.py](transformer_main.py) creates a Transformer keras model,
- and trains it uses keras model.fit().
-
- Users need to adjust `batch_size` and `num_gpus` to get good performance
- running multiple GPUs.
-
- **Note that:**
- when using multiple GPUs or TPUs, this is the global batch size for all
- devices. For example, if the batch size is `4096*4` and there are 4 devices,
- each device will take 4096 tokens as a batch budget.
-
- Command to run:
- ```
- python3 transformer_main.py --data_dir=$DATA_DIR --model_dir=$MODEL_DIR \
- --vocab_file=$VOCAB_FILE --param_set=$PARAM_SET
- ```
-
- Arguments:
- * `--data_dir`: This should be set to the same directory given to the `data_download`'s `data_dir` argument.
- * `--model_dir`: Directory to save Transformer model training checkpoints.
- * `--vocab_file`: Path to subtoken vocabulary file. If data_download was used, you may find the file in `data_dir`.
- * `--param_set`: Parameter set to use when creating and training the model. Options are `base` and `big` (default).
- * `--enable_time_history`: Whether add TimeHistory call. If so, --log_steps must be specified.
- * `--batch_size`: The number of tokens to consider in a batch. Combining with
- `--max_length`, they decide how many sequences are used per batch.
- * Use the `--help` or `-h` flag to get a full list of possible arguments.
-
- #### Using multiple GPUs
- You can train these models on multiple GPUs using `tf.distribute.Strategy` API.
- You can read more about them in this
- [guide](https://www.tensorflow.org/guide/distribute_strategy).
-
- In this example, we have made it easier to use is with just a command line flag
- `--num_gpus`. By default this flag is 1 if TensorFlow is compiled with CUDA,
- and 0 otherwise.
-
- - --num_gpus=0: Uses tf.distribute.OneDeviceStrategy with CPU as the device.
- - --num_gpus=1: Uses tf.distribute.OneDeviceStrategy with GPU as the device.
- - --num_gpus=2+: Uses tf.distribute.MirroredStrategy to run synchronous
- distributed training across the GPUs.
-
- #### Using Cloud TPUs
-
- You can train the Transformer model on Cloud TPUs using
- `tf.distribute.TPUStrategy`. If you are not familiar with Cloud TPUs, it is
- strongly recommended that you go through the
- [quickstart](https://cloud.google.com/tpu/docs/quickstart) to learn how to
- create a TPU and GCE VM.
-
- To run the Transformer model on a TPU, you must set
- `--distribution_strategy=tpu`, `--tpu=$TPU_NAME`, and `--use_ctl=True` where
- `$TPU_NAME` the name of your TPU in the Cloud Console.
-
- An example command to run Transformer on a v2-8 or v3-8 TPU would be:
-
- ```bash
- python transformer_main.py \
- --tpu=$TPU_NAME \
- --model_dir=$MODEL_DIR \
- --data_dir=$DATA_DIR \
- --vocab_file=$DATA_DIR/vocab.ende.32768 \
- --bleu_source=$DATA_DIR/newstest2014.en \
- --bleu_ref=$DATA_DIR/newstest2014.end \
- --batch_size=6144 \
- --train_steps=2000 \
- --static_batch=true \
- --use_ctl=true \
- --param_set=big \
- --max_length=64 \
- --decode_batch_size=32 \
- --decode_max_length=97 \
- --padded_decode=true \
- --distribution_strategy=tpu
- ```
- Note: `$MODEL_DIR` and `$DATA_DIR` must be GCS paths.
-
- #### Customizing training schedule
-
- By default, the model will train for 10 epochs, and evaluate after every epoch. The training schedule may be defined through the flags:
-
- * Training with steps:
- * `--train_steps`: sets the total number of training steps to run.
- * `--steps_between_evals`: Number of training steps to run between evaluations.
-
- #### Compute BLEU score during model evaluation
-
- Use these flags to compute the BLEU when the model evaluates:
-
- * `--bleu_source`: Path to file containing text to translate.
- * `--bleu_ref`: Path to file containing the reference translation.
-
- When running `transformer_main.py`, use the flags: `--bleu_source=$DATA_DIR/newstest2014.en --bleu_ref=$DATA_DIR/newstest2014.de`
-
- #### Tensorboard
- Training and evaluation metrics (loss, accuracy, approximate BLEU score, etc.) are logged, and can be displayed in the browser using Tensorboard.
- ```
- tensorboard --logdir=$MODEL_DIR
- ```
- The values are displayed at [localhost:6006](localhost:6006).
-
-## Implementation overview
-
-A brief look at each component in the code:
-
-### Model Definition
-* [transformer.py](transformer.py): Defines a tf.keras.Model: `Transformer`.
-* [embedding_layer.py](embedding_layer.py): Contains the layer that calculates the embeddings. The embedding weights are also used to calculate the pre-softmax probabilities from the decoder output.
-* [attention_layer.py](attention_layer.py): Defines the multi-headed and self attention layers that are used in the encoder/decoder stacks.
-* [ffn_layer.py](ffn_layer.py): Defines the feedforward network that is used in the encoder/decoder stacks. The network is composed of 2 fully connected layers.
-
-Other files:
-* [beam_search.py](beam_search.py) contains the beam search implementation, which is used during model inference to find high scoring translations.
-
-### Model Trainer
-[transformer_main.py](transformer_main.py) creates an `TransformerTask` to train and evaluate the model using tf.keras.
-
-### Test dataset
-The [newstest2014 files](https://storage.googleapis.com/tf-perf-public/official_transformer/test_data/newstest2014.tgz)
-are extracted from the [NMT Seq2Seq tutorial](https://google.github.io/seq2seq/nmt/#download-data).
-The raw text files are converted from the SGM format of the
-[WMT 2016](http://www.statmt.org/wmt16/translation-task.html) test sets. The
-newstest2014 files are put into the `$DATA_DIR` when executing `data_download.py`
diff --git a/official/nlp/transformer/__init__.py b/official/nlp/transformer/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/transformer/attention_layer.py b/official/nlp/transformer/attention_layer.py
deleted file mode 100644
index db6e95b1a293795614f86aa7041ca767b990f099..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/attention_layer.py
+++ /dev/null
@@ -1,176 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Implementation of multiheaded attention and self-attention layers."""
-import math
-
-import tensorflow as tf
-
-
-class Attention(tf.keras.layers.Layer):
- """Multi-headed attention layer."""
-
- def __init__(self, hidden_size, num_heads, attention_dropout):
- """Initialize Attention.
-
- Args:
- hidden_size: int, output dim of hidden layer.
- num_heads: int, number of heads to repeat the same attention structure.
- attention_dropout: float, dropout rate inside attention for training.
- """
- if hidden_size % num_heads:
- raise ValueError(
- "Hidden size ({}) must be divisible by the number of heads ({})."
- .format(hidden_size, num_heads))
-
- super(Attention, self).__init__()
- self.hidden_size = hidden_size
- self.num_heads = num_heads
- self.attention_dropout = attention_dropout
-
- def build(self, input_shape):
- """Builds the layer."""
- # Layers for linearly projecting the queries, keys, and values.
- size_per_head = self.hidden_size // self.num_heads
-
- def _glorot_initializer(fan_in, fan_out):
- limit = math.sqrt(6.0 / (fan_in + fan_out))
- return tf.keras.initializers.RandomUniform(minval=-limit, maxval=limit)
-
- attention_initializer = _glorot_initializer(input_shape.as_list()[-1],
- self.hidden_size)
- self.query_dense_layer = tf.keras.layers.experimental.EinsumDense(
- "BTE,ENH->BTNH",
- output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
- bias_axes=None,
- name="query")
- self.key_dense_layer = tf.keras.layers.experimental.EinsumDense(
- "BTE,ENH->BTNH",
- output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
- bias_axes=None,
- name="key")
- self.value_dense_layer = tf.keras.layers.experimental.EinsumDense(
- "BTE,ENH->BTNH",
- output_shape=(None, self.num_heads, size_per_head),
- kernel_initializer=attention_initializer,
- bias_axes=None,
- name="value")
-
- output_initializer = _glorot_initializer(self.hidden_size, self.hidden_size)
- self.output_dense_layer = tf.keras.layers.experimental.EinsumDense(
- "BTNH,NHE->BTE",
- output_shape=(None, self.hidden_size),
- kernel_initializer=output_initializer,
- bias_axes=None,
- name="output_transform")
- super(Attention, self).build(input_shape)
-
- def get_config(self):
- return {
- "hidden_size": self.hidden_size,
- "num_heads": self.num_heads,
- "attention_dropout": self.attention_dropout,
- }
-
- def call(self,
- query_input,
- source_input,
- bias,
- training,
- cache=None,
- decode_loop_step=None):
- """Apply attention mechanism to query_input and source_input.
-
- Args:
- query_input: A tensor with shape [batch_size, length_query, hidden_size].
- source_input: A tensor with shape [batch_size, length_source,
- hidden_size].
- bias: A tensor with shape [batch_size, 1, length_query, length_source],
- the attention bias that will be added to the result of the dot product.
- training: A bool, whether in training mode or not.
- cache: (Used during prediction) A dictionary with tensors containing
- results of previous attentions. The dictionary must have the items:
- {"k": tensor with shape [batch_size, i, heads, dim_per_head],
- "v": tensor with shape [batch_size, i, heads, dim_per_head]} where
- i is the current decoded length for non-padded decode, or max
- sequence length for padded decode.
- decode_loop_step: An integer, step number of the decoding loop. Used only
- for autoregressive inference on TPU.
-
- Returns:
- Attention layer output with shape [batch_size, length_query, hidden_size]
- """
- # Linearly project the query, key and value using different learned
- # projections. Splitting heads is automatically done during the linear
- # projections --> [batch_size, length, num_heads, dim_per_head].
- query = self.query_dense_layer(query_input)
- key = self.key_dense_layer(source_input)
- value = self.value_dense_layer(source_input)
-
- if cache is not None:
- # Combine cached keys and values with new keys and values.
- if decode_loop_step is not None:
- cache_k_shape = cache["k"].shape.as_list()
- indices = tf.reshape(
- tf.one_hot(decode_loop_step, cache_k_shape[1], dtype=key.dtype),
- [1, cache_k_shape[1], 1, 1])
- key = cache["k"] + key * indices
- cache_v_shape = cache["v"].shape.as_list()
- indices = tf.reshape(
- tf.one_hot(decode_loop_step, cache_v_shape[1], dtype=value.dtype),
- [1, cache_v_shape[1], 1, 1])
- value = cache["v"] + value * indices
- else:
- key = tf.concat([tf.cast(cache["k"], key.dtype), key], axis=1)
- value = tf.concat([tf.cast(cache["v"], value.dtype), value], axis=1)
-
- # Update cache
- cache["k"] = key
- cache["v"] = value
-
- # Scale query to prevent the dot product between query and key from growing
- # too large.
- depth = (self.hidden_size // self.num_heads)
- query *= depth**-0.5
-
- # Calculate dot product attention
- logits = tf.einsum("BTNH,BFNH->BNFT", key, query)
- logits += bias
- # Note that softmax internally performs math operations using float32
- # for numeric stability. When training with float16, we keep the input
- # and output in float16 for better performance.
- weights = tf.nn.softmax(logits, name="attention_weights")
- if training:
- weights = tf.nn.dropout(weights, rate=self.attention_dropout)
- attention_output = tf.einsum("BNFT,BTNH->BFNH", weights, value)
-
- # Run the outputs through another linear projection layer. Recombining heads
- # is automatically done --> [batch_size, length, hidden_size]
- attention_output = self.output_dense_layer(attention_output)
- return attention_output
-
-
-class SelfAttention(Attention):
- """Multiheaded self-attention layer."""
-
- def call(self,
- query_input,
- bias,
- training,
- cache=None,
- decode_loop_step=None):
- return super(SelfAttention, self).call(query_input, query_input, bias,
- training, cache, decode_loop_step)
diff --git a/official/nlp/transformer/beam_search_v1.py b/official/nlp/transformer/beam_search_v1.py
deleted file mode 100644
index 2c8537e63b20e718b15dfcd042f3263212af8c08..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/beam_search_v1.py
+++ /dev/null
@@ -1,82 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Beam search to find the translated sequence with the highest probability."""
-
-import tensorflow.compat.v1 as tf
-from official.nlp.modeling.ops import beam_search
-
-_StateKeys = beam_search._StateKeys # pylint: disable=protected-access
-
-
-class SequenceBeamSearch(beam_search.SequenceBeamSearch):
- """Implementation of beam search loop."""
-
- def _process_finished_state(self, finished_state):
- alive_seq = finished_state[_StateKeys.ALIVE_SEQ]
- alive_log_probs = finished_state[_StateKeys.ALIVE_LOG_PROBS]
- finished_seq = finished_state[_StateKeys.FINISHED_SEQ]
- finished_scores = finished_state[_StateKeys.FINISHED_SCORES]
- finished_flags = finished_state[_StateKeys.FINISHED_FLAGS]
-
- # Account for corner case where there are no finished sequences for a
- # particular batch item. In that case, return alive sequences for that batch
- # item.
- finished_seq = tf.where(
- tf.reduce_any(finished_flags, 1), finished_seq, alive_seq)
- finished_scores = tf.where(
- tf.reduce_any(finished_flags, 1), finished_scores, alive_log_probs)
- return finished_seq, finished_scores
-
-
-def sequence_beam_search(symbols_to_logits_fn,
- initial_ids,
- initial_cache,
- vocab_size,
- beam_size,
- alpha,
- max_decode_length,
- eos_id,
- padded_decode=False):
- """Search for sequence of subtoken ids with the largest probability.
-
- Args:
- symbols_to_logits_fn: A function that takes in ids, index, and cache as
- arguments. The passed in arguments will have shape: ids -> A tensor with
- shape [batch_size * beam_size, index]. index -> A scalar. cache -> A
- nested dictionary of tensors [batch_size * beam_size, ...].
- The function must return a tuple of logits and new cache: logits -> A
- tensor with shape [batch * beam_size, vocab_size]. new cache -> A nested
- dictionary with the same shape/structure as the inputted cache.
- initial_ids: An int32 tensor with shape [batch_size]. Starting ids for each
- batch item.
- initial_cache: A dictionary, containing starting decoder variables
- information.
- vocab_size: An integer, the size of the vocabulary, used for topk
- computation.
- beam_size: An integer, the number of beams.
- alpha: A float, defining the strength of length normalization.
- max_decode_length: An integer, the maximum length to decoded a sequence.
- eos_id: An integer, ID of eos token, used to determine when a sequence has
- finished.
- padded_decode: A bool, indicating if max_sequence_length padding is used for
- beam search.
-
- Returns:
- Top decoded sequences [batch_size, beam_size, max_decode_length]
- sequence scores [batch_size, beam_size]
- """
- sbs = SequenceBeamSearch(symbols_to_logits_fn, vocab_size, beam_size, alpha,
- max_decode_length, eos_id, padded_decode)
- return sbs.search(initial_ids, initial_cache)
diff --git a/official/nlp/transformer/compute_bleu.py b/official/nlp/transformer/compute_bleu.py
deleted file mode 100644
index 38c77261973c024acbcb7047c2c49942f15962e1..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/compute_bleu.py
+++ /dev/null
@@ -1,148 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Script to compute official BLEU score.
-
-Source:
-https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/bleu_hook.py
-"""
-
-import re
-import sys
-import unicodedata
-
-from absl import app
-from absl import flags
-from absl import logging
-import six
-from six.moves import range
-import tensorflow as tf
-
-from official.nlp.transformer.utils import metrics
-from official.nlp.transformer.utils import tokenizer
-from official.utils.flags import core as flags_core
-
-
-class UnicodeRegex(object):
- """Ad-hoc hack to recognize all punctuation and symbols."""
-
- def __init__(self):
- punctuation = self.property_chars("P")
- self.nondigit_punct_re = re.compile(r"([^\d])([" + punctuation + r"])")
- self.punct_nondigit_re = re.compile(r"([" + punctuation + r"])([^\d])")
- self.symbol_re = re.compile("([" + self.property_chars("S") + "])")
-
- def property_chars(self, prefix):
- return "".join(
- six.unichr(x)
- for x in range(sys.maxunicode)
- if unicodedata.category(six.unichr(x)).startswith(prefix))
-
-
-uregex = UnicodeRegex()
-
-
-def bleu_tokenize(string):
- r"""Tokenize a string following the official BLEU implementation.
-
- See https://github.com/moses-smt/mosesdecoder/'
- 'blob/master/scripts/generic/mteval-v14.pl#L954-L983
- In our case, the input string is expected to be just one line
- and no HTML entities de-escaping is needed.
- So we just tokenize on punctuation and symbols,
- except when a punctuation is preceded and followed by a digit
- (e.g. a comma/dot as a thousand/decimal separator).
-
- Note that a numer (e.g. a year) followed by a dot at the end of sentence
- is NOT tokenized,
- i.e. the dot stays with the number because `s/(\p{P})(\P{N})/ $1 $2/g`
- does not match this case (unless we add a space after each sentence).
- However, this error is already in the original mteval-v14.pl
- and we want to be consistent with it.
-
- Args:
- string: the input string
-
- Returns:
- a list of tokens
- """
- string = uregex.nondigit_punct_re.sub(r"\1 \2 ", string)
- string = uregex.punct_nondigit_re.sub(r" \1 \2", string)
- string = uregex.symbol_re.sub(r" \1 ", string)
- return string.split()
-
-
-def bleu_wrapper(ref_filename, hyp_filename, case_sensitive=False):
- """Compute BLEU for two files (reference and hypothesis translation)."""
- ref_lines = tokenizer.native_to_unicode(
- tf.io.gfile.GFile(ref_filename).read()).strip().splitlines()
- hyp_lines = tokenizer.native_to_unicode(
- tf.io.gfile.GFile(hyp_filename).read()).strip().splitlines()
- return bleu_on_list(ref_lines, hyp_lines, case_sensitive)
-
-
-def bleu_on_list(ref_lines, hyp_lines, case_sensitive=False):
- """Compute BLEU for two list of strings (reference and hypothesis)."""
- if len(ref_lines) != len(hyp_lines):
- raise ValueError(
- "Reference and translation files have different number of "
- "lines (%d VS %d). If training only a few steps (100-200), the "
- "translation may be empty." % (len(ref_lines), len(hyp_lines)))
- if not case_sensitive:
- ref_lines = [x.lower() for x in ref_lines]
- hyp_lines = [x.lower() for x in hyp_lines]
- ref_tokens = [bleu_tokenize(x) for x in ref_lines]
- hyp_tokens = [bleu_tokenize(x) for x in hyp_lines]
- return metrics.compute_bleu(ref_tokens, hyp_tokens) * 100
-
-
-def main(unused_argv):
- if FLAGS.bleu_variant in ("both", "uncased"):
- score = bleu_wrapper(FLAGS.reference, FLAGS.translation, False)
- logging.info("Case-insensitive results: %f", score)
-
- if FLAGS.bleu_variant in ("both", "cased"):
- score = bleu_wrapper(FLAGS.reference, FLAGS.translation, True)
- logging.info("Case-sensitive results: %f", score)
-
-
-def define_compute_bleu_flags():
- """Add flags for computing BLEU score."""
- flags.DEFINE_string(
- name="translation",
- default=None,
- help=flags_core.help_wrap("File containing translated text."))
- flags.mark_flag_as_required("translation")
-
- flags.DEFINE_string(
- name="reference",
- default=None,
- help=flags_core.help_wrap("File containing reference translation."))
- flags.mark_flag_as_required("reference")
-
- flags.DEFINE_enum(
- name="bleu_variant",
- short_name="bv",
- default="both",
- enum_values=["both", "uncased", "cased"],
- case_sensitive=False,
- help=flags_core.help_wrap(
- "Specify one or more BLEU variants to calculate. Variants: \"cased\""
- ", \"uncased\", or \"both\"."))
-
-
-if __name__ == "__main__":
- define_compute_bleu_flags()
- FLAGS = flags.FLAGS
- app.run(main)
diff --git a/official/nlp/transformer/compute_bleu_test.py b/official/nlp/transformer/compute_bleu_test.py
deleted file mode 100644
index 6160bf66ecfc5f36f18ddf730f96780bda236b50..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/compute_bleu_test.py
+++ /dev/null
@@ -1,72 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Test functions in compute_blue.py."""
-
-import tempfile
-
-import tensorflow as tf
-
-from official.nlp.transformer import compute_bleu
-
-
-class ComputeBleuTest(tf.test.TestCase):
-
- def _create_temp_file(self, text):
- temp_file = tempfile.NamedTemporaryFile(delete=False)
- with tf.io.gfile.GFile(temp_file.name, "w") as w:
- w.write(text)
- return temp_file.name
-
- def test_bleu_same(self):
- ref = self._create_temp_file("test 1 two 3\nmore tests!")
- hyp = self._create_temp_file("test 1 two 3\nmore tests!")
-
- uncased_score = compute_bleu.bleu_wrapper(ref, hyp, False)
- cased_score = compute_bleu.bleu_wrapper(ref, hyp, True)
- self.assertEqual(100, uncased_score)
- self.assertEqual(100, cased_score)
-
- def test_bleu_same_different_case(self):
- ref = self._create_temp_file("Test 1 two 3\nmore tests!")
- hyp = self._create_temp_file("test 1 two 3\nMore tests!")
- uncased_score = compute_bleu.bleu_wrapper(ref, hyp, False)
- cased_score = compute_bleu.bleu_wrapper(ref, hyp, True)
- self.assertEqual(100, uncased_score)
- self.assertLess(cased_score, 100)
-
- def test_bleu_different(self):
- ref = self._create_temp_file("Testing\nmore tests!")
- hyp = self._create_temp_file("Dog\nCat")
- uncased_score = compute_bleu.bleu_wrapper(ref, hyp, False)
- cased_score = compute_bleu.bleu_wrapper(ref, hyp, True)
- self.assertLess(uncased_score, 100)
- self.assertLess(cased_score, 100)
-
- def test_bleu_tokenize(self):
- s = "Test0, 1 two, 3"
- tokenized = compute_bleu.bleu_tokenize(s)
- self.assertEqual(["Test0", ",", "1", "two", ",", "3"], tokenized)
-
- def test_bleu_list(self):
- ref = ["test 1 two 3", "more tests!"]
- hyp = ["test 1 two 3", "More tests!"]
- uncased_score = compute_bleu.bleu_on_list(ref, hyp, False)
- cased_score = compute_bleu.bleu_on_list(ref, hyp, True)
- self.assertEqual(uncased_score, 100)
- self.assertLess(cased_score, 100)
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/transformer/data_download.py b/official/nlp/transformer/data_download.py
deleted file mode 100644
index 5a8b8595fd3031b430ccbc489431d9f7711d982c..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/data_download.py
+++ /dev/null
@@ -1,443 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Download and preprocess WMT17 ende training and evaluation datasets."""
-
-import os
-import random
-import tarfile
-
-# pylint: disable=g-bad-import-order
-
-from absl import app
-from absl import flags
-from absl import logging
-import six
-from six.moves import range
-from six.moves import urllib
-from six.moves import zip
-import tensorflow.compat.v1 as tf
-
-from official.nlp.transformer.utils import tokenizer
-from official.utils.flags import core as flags_core
-# pylint: enable=g-bad-import-order
-
-# Data sources for training/evaluating the transformer translation model.
-# If any of the training sources are changed, then either:
-# 1) use the flag `--search` to find the best min count or
-# 2) update the _TRAIN_DATA_MIN_COUNT constant.
-# min_count is the minimum number of times a token must appear in the data
-# before it is added to the vocabulary. "Best min count" refers to the value
-# that generates a vocabulary set that is closest in size to _TARGET_VOCAB_SIZE.
-_TRAIN_DATA_SOURCES = [
- {
- "url": "http://data.statmt.org/wmt17/translation-task/"
- "training-parallel-nc-v12.tgz",
- "input": "news-commentary-v12.de-en.en",
- "target": "news-commentary-v12.de-en.de",
- },
- {
- "url": "http://www.statmt.org/wmt13/training-parallel-commoncrawl.tgz",
- "input": "commoncrawl.de-en.en",
- "target": "commoncrawl.de-en.de",
- },
- {
- "url": "http://www.statmt.org/wmt13/training-parallel-europarl-v7.tgz",
- "input": "europarl-v7.de-en.en",
- "target": "europarl-v7.de-en.de",
- },
-]
-# Use pre-defined minimum count to generate subtoken vocabulary.
-_TRAIN_DATA_MIN_COUNT = 6
-
-_EVAL_DATA_SOURCES = [{
- "url": "http://data.statmt.org/wmt17/translation-task/dev.tgz",
- "input": "newstest2013.en",
- "target": "newstest2013.de",
-}]
-
-_TEST_DATA_SOURCES = [{
- "url": ("https://storage.googleapis.com/cloud-tpu-test-datasets/"
- "transformer_data/newstest2014.tgz"),
- "input": "newstest2014.en",
- "target": "newstest2014.de",
-}]
-
-# Vocabulary constants
-_TARGET_VOCAB_SIZE = 32768 # Number of subtokens in the vocabulary list.
-_TARGET_THRESHOLD = 327 # Accept vocabulary if size is within this threshold
-VOCAB_FILE = "vocab.ende.%d" % _TARGET_VOCAB_SIZE
-
-# Strings to inclue in the generated files.
-_PREFIX = "wmt32k"
-_TRAIN_TAG = "train"
-_EVAL_TAG = "dev" # Following WMT and Tensor2Tensor conventions, in which the
-# evaluation datasets are tagged as "dev" for development.
-
-# Number of files to split train and evaluation data
-_TRAIN_SHARDS = 100
-_EVAL_SHARDS = 1
-
-
-def find_file(path, filename, max_depth=5):
- """Returns full filepath if the file is in path or a subdirectory."""
- for root, dirs, files in os.walk(path):
- if filename in files:
- return os.path.join(root, filename)
-
- # Don't search past max_depth
- depth = root[len(path) + 1:].count(os.sep)
- if depth > max_depth:
- del dirs[:] # Clear dirs
- return None
-
-
-###############################################################################
-# Download and extraction functions
-###############################################################################
-def get_raw_files(raw_dir, data_source):
- """Return raw files from source.
-
- Downloads/extracts if needed.
-
- Args:
- raw_dir: string directory to store raw files
- data_source: dictionary with
- {"url": url of compressed dataset containing input and target files
- "input": file with data in input language
- "target": file with data in target language}
-
- Returns:
- dictionary with
- {"inputs": list of files containing data in input language
- "targets": list of files containing corresponding data in target language
- }
- """
- raw_files = {
- "inputs": [],
- "targets": [],
- } # keys
- for d in data_source:
- input_file, target_file = download_and_extract(raw_dir, d["url"],
- d["input"], d["target"])
- raw_files["inputs"].append(input_file)
- raw_files["targets"].append(target_file)
- return raw_files
-
-
-def download_report_hook(count, block_size, total_size):
- """Report hook for download progress.
-
- Args:
- count: current block number
- block_size: block size
- total_size: total size
- """
- percent = int(count * block_size * 100 / total_size)
- print(six.ensure_str("\r%d%%" % percent) + " completed", end="\r")
-
-
-def download_from_url(path, url):
- """Download content from a url.
-
- Args:
- path: string directory where file will be downloaded
- url: string url
-
- Returns:
- Full path to downloaded file
- """
- filename = six.ensure_str(url).split("/")[-1]
- found_file = find_file(path, filename, max_depth=0)
- if found_file is None:
- filename = os.path.join(path, filename)
- logging.info("Downloading from %s to %s.", url, filename)
- inprogress_filepath = six.ensure_str(filename) + ".incomplete"
- inprogress_filepath, _ = urllib.request.urlretrieve(
- url, inprogress_filepath, reporthook=download_report_hook)
- # Print newline to clear the carriage return from the download progress.
- print()
- tf.gfile.Rename(inprogress_filepath, filename)
- return filename
- else:
- logging.info("Already downloaded: %s (at %s).", url, found_file)
- return found_file
-
-
-def download_and_extract(path, url, input_filename, target_filename):
- """Extract files from downloaded compressed archive file.
-
- Args:
- path: string directory where the files will be downloaded
- url: url containing the compressed input and target files
- input_filename: name of file containing data in source language
- target_filename: name of file containing data in target language
-
- Returns:
- Full paths to extracted input and target files.
-
- Raises:
- OSError: if the the download/extraction fails.
- """
- # Check if extracted files already exist in path
- input_file = find_file(path, input_filename)
- target_file = find_file(path, target_filename)
- if input_file and target_file:
- logging.info("Already downloaded and extracted %s.", url)
- return input_file, target_file
-
- # Download archive file if it doesn't already exist.
- compressed_file = download_from_url(path, url)
-
- # Extract compressed files
- logging.info("Extracting %s.", compressed_file)
- with tarfile.open(compressed_file, "r:gz") as corpus_tar:
- corpus_tar.extractall(path)
-
- # Return file paths of the requested files.
- input_file = find_file(path, input_filename)
- target_file = find_file(path, target_filename)
-
- if input_file and target_file:
- return input_file, target_file
-
- raise OSError("Download/extraction failed for url %s to path %s" %
- (url, path))
-
-
-def txt_line_iterator(path):
- """Iterate through lines of file."""
- with tf.io.gfile.GFile(path) as f:
- for line in f:
- yield line.strip()
-
-
-def compile_files(raw_dir, raw_files, tag):
- """Compile raw files into a single file for each language.
-
- Args:
- raw_dir: Directory containing downloaded raw files.
- raw_files: Dict containing filenames of input and target data.
- {"inputs": list of files containing data in input language
- "targets": list of files containing corresponding data in target language
- }
- tag: String to append to the compiled filename.
-
- Returns:
- Full path of compiled input and target files.
- """
- logging.info("Compiling files with tag %s.", tag)
- filename = "%s-%s" % (_PREFIX, tag)
- input_compiled_file = os.path.join(raw_dir,
- six.ensure_str(filename) + ".lang1")
- target_compiled_file = os.path.join(raw_dir,
- six.ensure_str(filename) + ".lang2")
-
- with tf.io.gfile.GFile(input_compiled_file, mode="w") as input_writer:
- with tf.io.gfile.GFile(target_compiled_file, mode="w") as target_writer:
- for i in range(len(raw_files["inputs"])):
- input_file = raw_files["inputs"][i]
- target_file = raw_files["targets"][i]
-
- logging.info("Reading files %s and %s.", input_file, target_file)
- write_file(input_writer, input_file)
- write_file(target_writer, target_file)
- return input_compiled_file, target_compiled_file
-
-
-def write_file(writer, filename):
- """Write all of lines from file using the writer."""
- for line in txt_line_iterator(filename):
- writer.write(line)
- writer.write("\n")
-
-
-###############################################################################
-# Data preprocessing
-###############################################################################
-def encode_and_save_files(subtokenizer, data_dir, raw_files, tag, total_shards):
- """Save data from files as encoded Examples in TFrecord format.
-
- Args:
- subtokenizer: Subtokenizer object that will be used to encode the strings.
- data_dir: The directory in which to write the examples
- raw_files: A tuple of (input, target) data files. Each line in the input and
- the corresponding line in target file will be saved in a tf.Example.
- tag: String that will be added onto the file names.
- total_shards: Number of files to divide the data into.
-
- Returns:
- List of all files produced.
- """
- # Create a file for each shard.
- filepaths = [
- shard_filename(data_dir, tag, n + 1, total_shards)
- for n in range(total_shards)
- ]
-
- if all_exist(filepaths):
- logging.info("Files with tag %s already exist.", tag)
- return filepaths
-
- logging.info("Saving files with tag %s.", tag)
- input_file = raw_files[0]
- target_file = raw_files[1]
-
- # Write examples to each shard in round robin order.
- tmp_filepaths = [six.ensure_str(fname) + ".incomplete" for fname in filepaths]
- writers = [tf.python_io.TFRecordWriter(fname) for fname in tmp_filepaths]
- counter, shard = 0, 0
- for counter, (input_line, target_line) in enumerate(
- zip(txt_line_iterator(input_file), txt_line_iterator(target_file))):
- if counter > 0 and counter % 100000 == 0:
- logging.info("\tSaving case %d.", counter)
- example = dict_to_example({
- "inputs": subtokenizer.encode(input_line, add_eos=True),
- "targets": subtokenizer.encode(target_line, add_eos=True)
- })
- writers[shard].write(example.SerializeToString())
- shard = (shard + 1) % total_shards
- for writer in writers:
- writer.close()
-
- for tmp_name, final_name in zip(tmp_filepaths, filepaths):
- tf.gfile.Rename(tmp_name, final_name)
-
- logging.info("Saved %d Examples", counter + 1)
- return filepaths
-
-
-def shard_filename(path, tag, shard_num, total_shards):
- """Create filename for data shard."""
- return os.path.join(
- path, "%s-%s-%.5d-of-%.5d" % (_PREFIX, tag, shard_num, total_shards))
-
-
-def shuffle_records(fname):
- """Shuffle records in a single file."""
- logging.info("Shuffling records in file %s", fname)
-
- # Rename file prior to shuffling
- tmp_fname = six.ensure_str(fname) + ".unshuffled"
- tf.gfile.Rename(fname, tmp_fname)
-
- reader = tf.io.tf_record_iterator(tmp_fname)
- records = []
- for record in reader:
- records.append(record)
- if len(records) % 100000 == 0:
- logging.info("\tRead: %d", len(records))
-
- random.shuffle(records)
-
- # Write shuffled records to original file name
- with tf.python_io.TFRecordWriter(fname) as w:
- for count, record in enumerate(records):
- w.write(record)
- if count > 0 and count % 100000 == 0:
- logging.info("\tWriting record: %d", count)
-
- tf.gfile.Remove(tmp_fname)
-
-
-def dict_to_example(dictionary):
- """Converts a dictionary of string->int to a tf.Example."""
- features = {}
- for k, v in six.iteritems(dictionary):
- features[k] = tf.train.Feature(int64_list=tf.train.Int64List(value=v))
- return tf.train.Example(features=tf.train.Features(feature=features))
-
-
-def all_exist(filepaths):
- """Returns true if all files in the list exist."""
- for fname in filepaths:
- if not tf.gfile.Exists(fname):
- return False
- return True
-
-
-def make_dir(path):
- if not tf.gfile.Exists(path):
- logging.info("Creating directory %s", path)
- tf.gfile.MakeDirs(path)
-
-
-def main(unused_argv):
- """Obtain training and evaluation data for the Transformer model."""
- make_dir(FLAGS.raw_dir)
- make_dir(FLAGS.data_dir)
-
- # Download test_data
- logging.info("Step 1/5: Downloading test data")
- get_raw_files(FLAGS.data_dir, _TEST_DATA_SOURCES)
-
- # Get paths of download/extracted training and evaluation files.
- logging.info("Step 2/5: Downloading data from source")
- train_files = get_raw_files(FLAGS.raw_dir, _TRAIN_DATA_SOURCES)
- eval_files = get_raw_files(FLAGS.raw_dir, _EVAL_DATA_SOURCES)
-
- # Create subtokenizer based on the training files.
- logging.info("Step 3/5: Creating subtokenizer and building vocabulary")
- train_files_flat = train_files["inputs"] + train_files["targets"]
- vocab_file = os.path.join(FLAGS.data_dir, VOCAB_FILE)
- subtokenizer = tokenizer.Subtokenizer.init_from_files(
- vocab_file,
- train_files_flat,
- _TARGET_VOCAB_SIZE,
- _TARGET_THRESHOLD,
- min_count=None if FLAGS.search else _TRAIN_DATA_MIN_COUNT)
-
- logging.info("Step 4/5: Compiling training and evaluation data")
- compiled_train_files = compile_files(FLAGS.raw_dir, train_files, _TRAIN_TAG)
- compiled_eval_files = compile_files(FLAGS.raw_dir, eval_files, _EVAL_TAG)
-
- # Tokenize and save data as Examples in the TFRecord format.
- logging.info("Step 5/5: Preprocessing and saving data")
- train_tfrecord_files = encode_and_save_files(subtokenizer, FLAGS.data_dir,
- compiled_train_files, _TRAIN_TAG,
- _TRAIN_SHARDS)
- encode_and_save_files(subtokenizer, FLAGS.data_dir, compiled_eval_files,
- _EVAL_TAG, _EVAL_SHARDS)
-
- for fname in train_tfrecord_files:
- shuffle_records(fname)
-
-
-def define_data_download_flags():
- """Add flags specifying data download arguments."""
- flags.DEFINE_string(
- name="data_dir",
- short_name="dd",
- default="/tmp/translate_ende",
- help=flags_core.help_wrap(
- "Directory for where the translate_ende_wmt32k dataset is saved."))
- flags.DEFINE_string(
- name="raw_dir",
- short_name="rd",
- default="/tmp/translate_ende_raw",
- help=flags_core.help_wrap(
- "Path where the raw data will be downloaded and extracted."))
- flags.DEFINE_bool(
- name="search",
- default=False,
- help=flags_core.help_wrap(
- "If set, use binary search to find the vocabulary set with size"
- "closest to the target size (%d)." % _TARGET_VOCAB_SIZE))
-
-
-if __name__ == "__main__":
- logging.set_verbosity(logging.INFO)
- define_data_download_flags()
- FLAGS = flags.FLAGS
- app.run(main)
diff --git a/official/nlp/transformer/data_pipeline.py b/official/nlp/transformer/data_pipeline.py
deleted file mode 100644
index 1d9f242172cadcd38fefbc900658b914483b3b24..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/data_pipeline.py
+++ /dev/null
@@ -1,330 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Input pipeline for the transformer model to read, filter, and batch examples.
-
-Two things to note in the pipeline:
-
-1. Batching scheme
-
- The examples encoded in the TFRecord files contain data in the format:
- {"inputs": [variable length array of integers],
- "targets": [variable length array of integers]}
- Where integers in the arrays refer to tokens in the English and German vocab
- file (named `vocab.ende.32768`).
-
- Prior to batching, elements in the dataset are grouped by length (max between
- "inputs" and "targets" length). Each group is then batched such that:
- group_batch_size * length <= batch_size.
-
- Another way to view batch_size is the maximum number of tokens in each batch.
-
- Once batched, each element in the dataset will have the shape:
- {"inputs": [group_batch_size, padded_input_length],
- "targets": [group_batch_size, padded_target_length]}
- Lengths are padded to the longest "inputs" or "targets" sequence in the batch
- (padded_input_length and padded_target_length can be different).
-
- This batching scheme decreases the fraction of padding tokens per training
- batch, thus improving the training speed significantly.
-
-2. Shuffling
-
- While training, the dataset is shuffled in two places in the code. The first
- is the list of training files. Second, while reading records using
- `parallel_interleave`, the `sloppy` argument is used to generate randomness
- in the order of the examples.
-"""
-
-import os
-
-from absl import logging
-import tensorflow as tf
-
-from official.utils.misc import model_helpers
-
-# Buffer size for reading records from a TFRecord file. Each training file is
-# 7.2 MB, so 8 MB allows an entire file to be kept in memory.
-_READ_RECORD_BUFFER = 8 * 1000 * 1000
-
-# Example grouping constants. Defines length boundaries for each group.
-# These values are the defaults used in Tensor2Tensor.
-_MIN_BOUNDARY = 8
-_BOUNDARY_SCALE = 1.1
-
-
-def _load_records(filename):
- """Read file and return a dataset of tf.Examples."""
- return tf.data.TFRecordDataset(filename, buffer_size=_READ_RECORD_BUFFER)
-
-
-def _parse_example(serialized_example):
- """Return inputs and targets Tensors from a serialized tf.Example."""
- data_fields = {
- "inputs": tf.io.VarLenFeature(tf.int64),
- "targets": tf.io.VarLenFeature(tf.int64)
- }
- parsed = tf.io.parse_single_example(serialized_example, data_fields)
- inputs = tf.sparse.to_dense(parsed["inputs"])
- targets = tf.sparse.to_dense(parsed["targets"])
- return inputs, targets
-
-
-def _filter_max_length(example, max_length=256):
- """Indicates whether the example's length is lower than the maximum length."""
- return tf.logical_and(
- tf.size(example[0]) <= max_length,
- tf.size(example[1]) <= max_length)
-
-
-def _get_example_length(example):
- """Returns the maximum length between the example inputs and targets."""
- length = tf.maximum(tf.shape(example[0])[0], tf.shape(example[1])[0])
- return length
-
-
-def _create_min_max_boundaries(max_length,
- min_boundary=_MIN_BOUNDARY,
- boundary_scale=_BOUNDARY_SCALE):
- """Create min and max boundary lists up to max_length.
-
- For example, when max_length=24, min_boundary=4 and boundary_scale=2, the
- returned values will be:
- buckets_min = [0, 4, 8, 16, 24]
- buckets_max = [4, 8, 16, 24, 25]
-
- Args:
- max_length: The maximum length of example in dataset.
- min_boundary: Minimum length in boundary.
- boundary_scale: Amount to scale consecutive boundaries in the list.
-
- Returns:
- min and max boundary lists
-
- """
- # Create bucket boundaries list by scaling the previous boundary or adding 1
- # (to ensure increasing boundary sizes).
- bucket_boundaries = []
- x = min_boundary
- while x < max_length:
- bucket_boundaries.append(x)
- x = max(x + 1, int(x * boundary_scale))
-
- # Create min and max boundary lists from the initial list.
- buckets_min = [0] + bucket_boundaries
- buckets_max = bucket_boundaries + [max_length + 1]
- return buckets_min, buckets_max
-
-
-def _batch_examples(dataset, batch_size, max_length):
- """Group examples by similar lengths, and return batched dataset.
-
- Each batch of similar-length examples are padded to the same length, and may
- have different number of elements in each batch, such that:
- group_batch_size * padded_length <= batch_size.
-
- This decreases the number of padding tokens per batch, which improves the
- training speed.
-
- Args:
- dataset: Dataset of unbatched examples.
- batch_size: Max number of tokens per batch of examples.
- max_length: Max number of tokens in an example input or target sequence.
-
- Returns:
- Dataset of batched examples with similar lengths.
- """
- # Get min and max boundary lists for each example. These are used to calculate
- # the `bucket_id`, which is the index at which:
- # buckets_min[bucket_id] <= len(example) < buckets_max[bucket_id]
- # Note that using both min and max lists improves the performance.
- buckets_min, buckets_max = _create_min_max_boundaries(max_length)
-
- # Create list of batch sizes for each bucket_id, so that
- # bucket_batch_size[bucket_id] * buckets_max[bucket_id] <= batch_size
- bucket_batch_sizes = [int(batch_size) // x for x in buckets_max]
- # bucket_id will be a tensor, so convert this list to a tensor as well.
- bucket_batch_sizes = tf.constant(bucket_batch_sizes, dtype=tf.int64)
-
- def example_to_bucket_id(example_input, example_target):
- """Return int64 bucket id for this example, calculated based on length."""
- seq_length = _get_example_length((example_input, example_target))
-
- # TODO(xunkai): investigate if removing code branching improves performance.
- conditions_c = tf.logical_and(
- tf.less_equal(buckets_min, seq_length), tf.less(seq_length,
- buckets_max))
- bucket_id = tf.reduce_min(tf.where(conditions_c))
- return bucket_id
-
- def window_size_fn(bucket_id):
- """Return number of examples to be grouped when given a bucket id."""
- return bucket_batch_sizes[bucket_id]
-
- def batching_fn(bucket_id, grouped_dataset):
- """Batch and add padding to a dataset of elements with similar lengths."""
- bucket_batch_size = window_size_fn(bucket_id)
-
- # Batch the dataset and add padding so that all input sequences in the
- # examples have the same length, and all target sequences have the same
- # lengths as well. Resulting lengths of inputs and targets can differ.
- return grouped_dataset.padded_batch(bucket_batch_size, ([None], [None]))
-
- return dataset.apply(
- tf.data.experimental.group_by_window(
- key_func=example_to_bucket_id,
- reduce_func=batching_fn,
- window_size=None,
- window_size_func=window_size_fn))
-
-
-def _read_and_batch_from_files(file_pattern,
- batch_size,
- max_length,
- max_io_parallelism,
- shuffle,
- repeat,
- static_batch=False,
- num_replicas=1,
- ctx=None):
- """Create dataset where each item is a dict of "inputs" and "targets".
-
- Args:
- file_pattern: String used to match the input TFRecord files.
- batch_size: Maximum number of tokens per global batch of examples.
- max_length: Maximum number of tokens per example
- max_io_parallelism: Max number of cpu cores for parallel input processing.
- shuffle: If true, randomizes order of elements.
- repeat: Number of times to repeat the dataset. If None, the dataset is
- repeated forever.
- static_batch: Whether the batches in the dataset should have static shapes.
- If True, the input is batched so that every batch has the shape
- [batch_size // max_length, max_length]. If False, the input is grouped by
- length, and batched so that batches may have different
- shapes [N, M], where: N * M <= batch_size M <= max_length In general, this
- setting should be False. Dynamic shapes allow the inputs to be grouped
- so that the number of padding tokens is minimized, and helps model
- training. In cases where the input shape must be static (e.g. running on
- TPU), this setting should be set to True.
- num_replicas: Number of GPUs or other workers. We will generate global
- batches, and each global batch is equally divisible by number of replicas.
- Currently it is only effective when static_batch==True. TODO: make it
- effective when static_batch=False.
- ctx: Input context.
-
- Returns:
- tf.data.Dataset object containing examples loaded from the files.
- """
- dataset = tf.data.Dataset.list_files(file_pattern, shuffle=shuffle)
-
- if ctx and ctx.num_input_pipelines > 1:
- logging.info("Shard %d of the dataset.", ctx.input_pipeline_id)
- dataset = dataset.shard(ctx.num_input_pipelines, ctx.input_pipeline_id)
-
- # Read files and interleave results. When training, the order of the examples
- # will be non-deterministic.
- options = tf.data.Options()
- options.experimental_deterministic = False
- dataset = dataset.interleave(
- _load_records,
- cycle_length=max_io_parallelism,
- num_parallel_calls=tf.data.experimental.AUTOTUNE).with_options(options)
-
- # Parse each tf.Example into a dictionary
- # TODO: Look into prefetch_input_elements for performance optimization. # pylint: disable=g-bad-todo
- dataset = dataset.map(
- _parse_example, num_parallel_calls=tf.data.experimental.AUTOTUNE)
-
- # Remove examples where the input or target length exceeds the maximum length,
- dataset = dataset.filter(lambda x, y: _filter_max_length((x, y), max_length))
-
- if static_batch:
- dataset = dataset.padded_batch(
- # First calculate batch size (token number) per worker, then divide it
- # into sentences, and finally expand to a global batch. It could prove
- # the global batch divisble for distribution strategy.
- int(batch_size // num_replicas // max_length * num_replicas),
- ([max_length], [max_length]),
- drop_remainder=True)
- else:
- # Group and batch such that each batch has examples of similar length.
- # TODO(xunkai): _batch_examples might need to do something special for
- # num_replicas.
- dataset = _batch_examples(dataset, batch_size, max_length)
-
- dataset = dataset.repeat(repeat)
-
- # Prefetch the next element to improve speed of input pipeline.
- dataset = dataset.prefetch(buffer_size=tf.data.experimental.AUTOTUNE)
- return dataset
-
-
-def _generate_synthetic_data(params):
- """Create synthetic data based on the parameter batch size."""
- batch_size = int(params["batch_size"] // params["max_length"])
- length = params["max_length"]
- dataset = model_helpers.generate_synthetic_data(
- input_shape=tf.TensorShape([length]),
- input_value=1,
- input_dtype=tf.int64,
- label_shape=tf.TensorShape([length]),
- label_value=1,
- label_dtype=tf.int64,
- )
- if params["static_batch"]:
- dataset = dataset.batch(batch_size, drop_remainder=True)
- else:
- dataset = dataset.padded_batch(batch_size, ([None], [None]))
- return dataset
-
-
-def train_input_fn(params, ctx=None):
- """Load and return dataset of batched examples for use during training."""
- file_pattern = os.path.join(params["data_dir"] or "", "*train*")
- if params["use_synthetic_data"]:
- return _generate_synthetic_data(params)
- return _read_and_batch_from_files(
- file_pattern,
- params["batch_size"],
- params["max_length"],
- params["max_io_parallelism"],
- shuffle=True,
- repeat=params["repeat_dataset"],
- static_batch=params["static_batch"],
- num_replicas=params["num_gpus"],
- ctx=ctx)
-
-
-def eval_input_fn(params, ctx=None):
- """Load and return dataset of batched examples for use during evaluation."""
- file_pattern = os.path.join(params["data_dir"] or "", "*dev*")
- if params["use_synthetic_data"]:
- return _generate_synthetic_data(params)
- return _read_and_batch_from_files(
- file_pattern,
- params["batch_size"],
- params["max_length"],
- params["max_io_parallelism"],
- shuffle=False,
- repeat=1,
- static_batch=params["static_batch"],
- num_replicas=params["num_gpus"],
- ctx=ctx)
-
-
-def map_data_for_transformer_fn(x, y):
- """Maps data for training, and handles weried behaviors for different vers."""
- # Will transform input x and targets y into tuple(x, y) as new model inputs.
- # For TF v2, the 2nd parameter is omitted to make Keras training work.
- return ((x, y),)
diff --git a/official/nlp/transformer/embedding_layer.py b/official/nlp/transformer/embedding_layer.py
deleted file mode 100644
index 69f3861ce6745bab0f62f29c2213fe53f99183c2..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/embedding_layer.py
+++ /dev/null
@@ -1,102 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Implementation of embedding layer with shared weights."""
-
-import tensorflow as tf
-
-
-class EmbeddingSharedWeights(tf.keras.layers.Layer):
- """Calculates input embeddings and pre-softmax linear with shared weights."""
-
- def __init__(self, vocab_size, hidden_size):
- """Specify characteristic parameters of embedding layer.
-
- Args:
- vocab_size: Number of tokens in the embedding. (Typically ~32,000)
- hidden_size: Dimensionality of the embedding. (Typically 512 or 1024)
- """
- super(EmbeddingSharedWeights, self).__init__()
- self.vocab_size = vocab_size
- self.hidden_size = hidden_size
-
- def build(self, input_shape):
- """Build embedding layer."""
- with tf.name_scope("embedding_and_softmax"):
- # Create and initialize weights. The random normal initializer was chosen
- # arbitrarily, and works well.
- self.shared_weights = self.add_weight(
- "weights",
- shape=[self.vocab_size, self.hidden_size],
- dtype=tf.float32,
- initializer=tf.random_normal_initializer(
- mean=0., stddev=self.hidden_size**-0.5))
- super(EmbeddingSharedWeights, self).build(input_shape)
-
- def get_config(self):
- return {
- "vocab_size": self.vocab_size,
- "hidden_size": self.hidden_size,
- }
-
- def call(self, inputs, mode="embedding"):
- """Get token embeddings of inputs.
-
- Args:
- inputs: An int64 tensor with shape [batch_size, length]
- mode: string, a valid value is one of "embedding" and "linear".
-
- Returns:
- outputs: (1) If mode == "embedding", output embedding tensor, float32 with
- shape [batch_size, length, embedding_size]; (2) mode == "linear", output
- linear tensor, float32 with shape [batch_size, length, vocab_size].
- Raises:
- ValueError: if mode is not valid.
- """
- if mode == "embedding":
- return self._embedding(inputs)
- elif mode == "linear":
- return self._linear(inputs)
- else:
- raise ValueError("mode {} is not valid.".format(mode))
-
- def _embedding(self, inputs):
- """Applies embedding based on inputs tensor."""
- with tf.name_scope("embedding"):
- # Create binary mask of size [batch_size, length]
- embeddings = tf.gather(self.shared_weights, inputs)
- # mask = tf.cast(tf.not_equal(inputs, 0), embeddings.dtype)
- # embeddings *= tf.expand_dims(mask, -1)
- # Scale embedding by the sqrt of the hidden size
- embeddings *= self.hidden_size**0.5
-
- return embeddings
-
- def _linear(self, inputs):
- """Computes logits by running inputs through a linear layer.
-
- Args:
- inputs: A float32 tensor with shape [batch_size, length, hidden_size]
-
- Returns:
- float32 tensor with shape [batch_size, length, vocab_size].
- """
- with tf.name_scope("presoftmax_linear"):
- batch_size = tf.shape(inputs)[0]
- length = tf.shape(inputs)[1]
-
- x = tf.reshape(inputs, [-1, self.hidden_size])
- logits = tf.matmul(x, self.shared_weights, transpose_b=True)
-
- return tf.reshape(logits, [batch_size, length, self.vocab_size])
diff --git a/official/nlp/transformer/ffn_layer.py b/official/nlp/transformer/ffn_layer.py
deleted file mode 100644
index 26f0a15f69c50abee6f95dd40928e844ece1c691..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/ffn_layer.py
+++ /dev/null
@@ -1,71 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Implementation of fully connected network."""
-
-import tensorflow as tf
-
-
-class FeedForwardNetwork(tf.keras.layers.Layer):
- """Fully connected feedforward network."""
-
- def __init__(self, hidden_size, filter_size, relu_dropout):
- """Initialize FeedForwardNetwork.
-
- Args:
- hidden_size: int, output dim of hidden layer.
- filter_size: int, filter size for the inner (first) dense layer.
- relu_dropout: float, dropout rate for training.
- """
- super(FeedForwardNetwork, self).__init__()
- self.hidden_size = hidden_size
- self.filter_size = filter_size
- self.relu_dropout = relu_dropout
-
- def build(self, input_shape):
- self.filter_dense_layer = tf.keras.layers.Dense(
- self.filter_size,
- use_bias=True,
- activation=tf.nn.relu,
- name="filter_layer")
- self.output_dense_layer = tf.keras.layers.Dense(
- self.hidden_size, use_bias=True, name="output_layer")
- super(FeedForwardNetwork, self).build(input_shape)
-
- def get_config(self):
- return {
- "hidden_size": self.hidden_size,
- "filter_size": self.filter_size,
- "relu_dropout": self.relu_dropout,
- }
-
- def call(self, x, training):
- """Return outputs of the feedforward network.
-
- Args:
- x: tensor with shape [batch_size, length, hidden_size]
- training: boolean, whether in training mode or not.
-
- Returns:
- Output of the feedforward network.
- tensor with shape [batch_size, length, hidden_size]
- """
- # Retrieve dynamically known shapes
-
- output = self.filter_dense_layer(x)
- if training:
- output = tf.nn.dropout(output, rate=self.relu_dropout)
- output = self.output_dense_layer(output)
-
- return output
diff --git a/official/nlp/transformer/metrics.py b/official/nlp/transformer/metrics.py
deleted file mode 100644
index 38330aa471c7f7384a3f42abb7eefc5a62a48d94..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/metrics.py
+++ /dev/null
@@ -1,180 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Functions for calculating loss, accuracy, and other model metrics.
-
-Metrics:
- - Padded loss, accuracy, and negative log perplexity. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/metrics.py
- - BLEU approximation. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/bleu_hook.py
- - ROUGE score. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/rouge.py
-"""
-
-import functools
-
-import tensorflow as tf
-
-
-def _pad_tensors_to_same_length(x, y):
- """Pad x and y so that the results have the same length (second dimension)."""
- with tf.name_scope("pad_to_same_length"):
- x_length = tf.shape(x)[1]
- y_length = tf.shape(y)[1]
-
- max_length = tf.maximum(x_length, y_length)
-
- x = tf.pad(x, [[0, 0], [0, max_length - x_length], [0, 0]])
- y = tf.pad(y, [[0, 0], [0, max_length - y_length]])
- return x, y
-
-
-def padded_cross_entropy_loss(logits, labels, smoothing, vocab_size):
- """Calculate cross entropy loss while ignoring padding.
-
- Args:
- logits: Tensor of size [batch_size, length_logits, vocab_size]
- labels: Tensor of size [batch_size, length_labels]
- smoothing: Label smoothing constant, used to determine the on and off values
- vocab_size: int size of the vocabulary
-
- Returns:
- Returns the cross entropy loss and weight tensors: float32 tensors with
- shape [batch_size, max(length_logits, length_labels)]
- """
- with tf.name_scope("loss"):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
-
- # Calculate smoothing cross entropy
- with tf.name_scope("smoothing_cross_entropy"):
- confidence = 1.0 - smoothing
- low_confidence = (1.0 - confidence) / tf.cast(vocab_size - 1, tf.float32)
- soft_targets = tf.one_hot(
- tf.cast(labels, tf.int32),
- depth=vocab_size,
- on_value=confidence,
- off_value=low_confidence)
- xentropy = tf.nn.softmax_cross_entropy_with_logits(
- logits=logits, labels=soft_targets)
-
- # Calculate the best (lowest) possible value of cross entropy, and
- # subtract from the cross entropy loss.
- normalizing_constant = -(
- confidence * tf.math.log(confidence) +
- tf.cast(vocab_size - 1, tf.float32) * low_confidence *
- tf.math.log(low_confidence + 1e-20))
- xentropy -= normalizing_constant
-
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- return xentropy * weights, weights
-
-
-def padded_accuracy(logits, labels):
- """Percentage of times that predictions matches labels on non-0s."""
- with tf.name_scope("padded_accuracy"):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- outputs = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- return tf.cast(tf.equal(outputs, padded_labels), tf.float32), weights
-
-
-def padded_accuracy_topk(logits, labels, k):
- """Percentage of times that top-k predictions matches labels on non-0s."""
- with tf.name_scope("padded_accuracy_topk"):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- effective_k = tf.minimum(k, tf.shape(logits)[-1])
- _, outputs = tf.nn.top_k(logits, k=effective_k)
- outputs = tf.cast(outputs, tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- padded_labels = tf.expand_dims(padded_labels, axis=-1)
- padded_labels += tf.zeros_like(outputs) # Pad to same shape.
- same = tf.cast(tf.equal(outputs, padded_labels), tf.float32)
- same_topk = tf.reduce_sum(same, axis=-1)
- return same_topk, weights
-
-
-def padded_accuracy_top5(logits, labels):
- return padded_accuracy_topk(logits, labels, 5)
-
-
-def padded_sequence_accuracy(logits, labels):
- """Percentage of times that predictions matches labels everywhere (non-0)."""
- with tf.name_scope("padded_sequence_accuracy"):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- outputs = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- not_correct = tf.cast(tf.not_equal(outputs, padded_labels),
- tf.float32) * weights
- axis = list(range(1, len(outputs.get_shape())))
- correct_seq = 1.0 - tf.minimum(1.0, tf.reduce_sum(not_correct, axis=axis))
- return correct_seq, tf.constant(1.0)
-
-
-def padded_neg_log_perplexity(logits, labels, vocab_size):
- """Average log-perplexity excluding padding 0s. No smoothing."""
- num, den = padded_cross_entropy_loss(logits, labels, 0, vocab_size)
- return -num, den
-
-
-class MetricLayer(tf.keras.layers.Layer):
- """Custom a layer of metrics for Transformer model."""
-
- def __init__(self, vocab_size):
- super(MetricLayer, self).__init__()
- self.vocab_size = vocab_size
- self.metric_mean_fns = []
-
- def build(self, input_shape):
- """"Builds metric layer."""
- neg_log_perplexity = functools.partial(
- padded_neg_log_perplexity, vocab_size=self.vocab_size)
- self.metric_mean_fns = [
- (tf.keras.metrics.Mean("accuracy"), padded_accuracy),
- (tf.keras.metrics.Mean("accuracy_top5"), padded_accuracy_top5),
- (tf.keras.metrics.Mean("accuracy_per_sequence"),
- padded_sequence_accuracy),
- (tf.keras.metrics.Mean("neg_log_perplexity"), neg_log_perplexity),
- ]
- super(MetricLayer, self).build(input_shape)
-
- def get_config(self):
- return {"vocab_size": self.vocab_size}
-
- def call(self, inputs):
- logits, targets = inputs[0], inputs[1]
- for mean, fn in self.metric_mean_fns:
- m = mean(*fn(logits, targets))
- self.add_metric(m)
- return logits
-
-
-def transformer_loss(logits, labels, smoothing, vocab_size):
- """Calculates total loss containing cross entropy with padding ignored.
-
- Args:
- logits: Tensor of size [batch_size, length_logits, vocab_size]
- labels: Tensor of size [batch_size, length_labels]
- smoothing: Label smoothing constant, used to determine the on and off values
- vocab_size: int size of the vocabulary
-
- Returns:
- A scalar float tensor for loss.
- """
- xentropy, weights = padded_cross_entropy_loss(logits, labels, smoothing,
- vocab_size)
- return tf.reduce_sum(xentropy) / tf.reduce_sum(weights)
diff --git a/official/nlp/transformer/misc.py b/official/nlp/transformer/misc.py
deleted file mode 100644
index a457e92f754f96547b527bddef016c30efea0cd9..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/misc.py
+++ /dev/null
@@ -1,288 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Misc for Transformer."""
-
-# pylint: disable=g-bad-import-order
-
-from absl import flags
-import tensorflow as tf
-
-from official.nlp.transformer import model_params
-from official.utils.flags import core as flags_core
-from official.utils.misc import keras_utils
-
-FLAGS = flags.FLAGS
-
-PARAMS_MAP = {
- 'tiny': model_params.TINY_PARAMS,
- 'base': model_params.BASE_PARAMS,
- 'big': model_params.BIG_PARAMS,
-}
-
-
-def get_model_params(param_set, num_gpus):
- """Gets predefined model params."""
- if num_gpus > 1:
- if param_set == 'big':
- return model_params.BIG_MULTI_GPU_PARAMS.copy()
- elif param_set == 'base':
- return model_params.BASE_MULTI_GPU_PARAMS.copy()
- else:
- raise ValueError('Not valid params: param_set={} num_gpus={}'.format(
- param_set, num_gpus))
-
- return PARAMS_MAP[param_set].copy()
-
-
-def define_transformer_flags():
- """Add flags and flag validators for running transformer_main."""
- # Add common flags (data_dir, model_dir, etc.).
- flags_core.define_base(num_gpu=True, distribution_strategy=True)
- flags_core.define_performance(
- num_parallel_calls=True,
- inter_op=False,
- intra_op=False,
- synthetic_data=True,
- max_train_steps=False,
- dtype=True,
- loss_scale=True,
- all_reduce_alg=True,
- num_packs=True,
- tf_gpu_thread_mode=True,
- datasets_num_private_threads=True,
- enable_xla=True,
- fp16_implementation=True)
-
- flags_core.define_benchmark()
- flags_core.define_device(tpu=True)
-
- flags.DEFINE_integer(
- name='train_steps',
- short_name='ts',
- default=300000,
- help=flags_core.help_wrap('The number of steps used to train.'))
- flags.DEFINE_integer(
- name='steps_between_evals',
- short_name='sbe',
- default=5000,
- help=flags_core.help_wrap(
- 'The Number of training steps to run between evaluations. This is '
- 'used if --train_steps is defined.'))
- flags.DEFINE_boolean(
- name='enable_time_history',
- default=True,
- help='Whether to enable TimeHistory callback.')
- flags.DEFINE_boolean(
- name='enable_tensorboard',
- default=False,
- help='Whether to enable Tensorboard callback.')
- flags.DEFINE_boolean(
- name='enable_metrics_in_training',
- default=False,
- help='Whether to enable metrics during training.')
- flags.DEFINE_boolean(
- name='enable_mlir_bridge',
- default=False,
- help='Whether to enable the TF to XLA bridge.')
- # Set flags from the flags_core module as 'key flags' so they're listed when
- # the '-h' flag is used. Without this line, the flags defined above are
- # only shown in the full `--helpful` help text.
- flags.adopt_module_key_flags(flags_core)
-
- # Add transformer-specific flags
- flags.DEFINE_enum(
- name='param_set',
- short_name='mp',
- default='big',
- enum_values=PARAMS_MAP.keys(),
- help=flags_core.help_wrap(
- 'Parameter set to use when creating and training the model. The '
- 'parameters define the input shape (batch size and max length), '
- 'model configuration (size of embedding, # of hidden layers, etc.), '
- 'and various other settings. The big parameter set increases the '
- 'default batch size, embedding/hidden size, and filter size. For a '
- 'complete list of parameters, please see model/model_params.py.'))
-
- flags.DEFINE_bool(
- name='static_batch',
- short_name='sb',
- default=False,
- help=flags_core.help_wrap(
- 'Whether the batches in the dataset should have static shapes. In '
- 'general, this setting should be False. Dynamic shapes allow the '
- 'inputs to be grouped so that the number of padding tokens is '
- 'minimized, and helps model training. In cases where the input shape '
- 'must be static (e.g. running on TPU), this setting will be ignored '
- 'and static batching will always be used.'))
- flags.DEFINE_integer(
- name='max_length',
- short_name='ml',
- default=256,
- help=flags_core.help_wrap(
- 'Max sentence length for Transformer. Default is 256. Note: Usually '
- 'it is more effective to use a smaller max length if static_batch is '
- 'enabled, e.g. 64.'))
-
- # Flags for training with steps (may be used for debugging)
- flags.DEFINE_integer(
- name='validation_steps',
- short_name='vs',
- default=64,
- help=flags_core.help_wrap('The number of steps used in validation.'))
-
- # BLEU score computation
- flags.DEFINE_string(
- name='bleu_source',
- short_name='bls',
- default=None,
- help=flags_core.help_wrap(
- 'Path to source file containing text translate when calculating the '
- 'official BLEU score. Both --bleu_source and --bleu_ref must be set. '
- ))
- flags.DEFINE_string(
- name='bleu_ref',
- short_name='blr',
- default=None,
- help=flags_core.help_wrap(
- 'Path to source file containing text translate when calculating the '
- 'official BLEU score. Both --bleu_source and --bleu_ref must be set. '
- ))
- flags.DEFINE_string(
- name='vocab_file',
- short_name='vf',
- default=None,
- help=flags_core.help_wrap(
- 'Path to subtoken vocabulary file. If data_download.py was used to '
- 'download and encode the training data, look in the data_dir to find '
- 'the vocab file.'))
- flags.DEFINE_string(
- name='mode',
- default='train',
- help=flags_core.help_wrap('mode: train, eval, or predict'))
- flags.DEFINE_bool(
- name='use_ctl',
- default=False,
- help=flags_core.help_wrap(
- 'Whether the model runs with custom training loop.'))
- flags.DEFINE_integer(
- name='decode_batch_size',
- default=32,
- help=flags_core.help_wrap(
- 'Global batch size used for Transformer autoregressive decoding on '
- 'TPU.'))
- flags.DEFINE_integer(
- name='decode_max_length',
- default=97,
- help=flags_core.help_wrap(
- 'Max sequence length of the decode/eval data. This is used by '
- 'Transformer autoregressive decoding on TPU to have minimum '
- 'paddings.'))
- flags.DEFINE_bool(
- name='padded_decode',
- default=False,
- help=flags_core.help_wrap(
- 'Whether the autoregressive decoding runs with input data padded to '
- 'the decode_max_length. For TPU/XLA-GPU runs, this flag has to be '
- 'set due the static shape requirement. Although CPU/GPU could also '
- 'use padded_decode, it has not been tested. In addition, this method '
- 'will introduce unnecessary overheads which grow quadratically with '
- 'the max sequence length.'))
- flags.DEFINE_bool(
- name='enable_checkpointing',
- default=True,
- help=flags_core.help_wrap(
- 'Whether to do checkpointing during training. When running under '
- 'benchmark harness, we will avoid checkpointing.'))
- flags.DEFINE_bool(
- name='save_weights_only',
- default=True,
- help=flags_core.help_wrap(
- 'Only used when above `enable_checkpointing` is True. '
- 'If True, then only the model\'s weights will be saved '
- '(`model.save_weights(filepath)`), else the full model is saved '
- '(`model.save(filepath)`)'))
-
- flags_core.set_defaults(
- data_dir='/tmp/translate_ende',
- model_dir='/tmp/transformer_model',
- batch_size=None)
-
- # pylint: disable=unused-variable
- @flags.multi_flags_validator(
- ['bleu_source', 'bleu_ref'],
- message='Both or neither --bleu_source and --bleu_ref must be defined.')
- def _check_bleu_files(flags_dict):
- return (flags_dict['bleu_source'] is None) == (
- flags_dict['bleu_ref'] is None)
-
- @flags.multi_flags_validator(
- ['bleu_source', 'bleu_ref', 'vocab_file'],
- message='--vocab_file must be defined if --bleu_source and --bleu_ref '
- 'are defined.')
- def _check_bleu_vocab_file(flags_dict):
- if flags_dict['bleu_source'] and flags_dict['bleu_ref']:
- return flags_dict['vocab_file'] is not None
- return True
-
- # pylint: enable=unused-variable
-
-
-def get_callbacks():
- """Returns common callbacks."""
- callbacks = []
- if FLAGS.enable_time_history:
- time_callback = keras_utils.TimeHistory(
- FLAGS.batch_size,
- FLAGS.log_steps,
- logdir=FLAGS.model_dir if FLAGS.enable_tensorboard else None)
- callbacks.append(time_callback)
-
- if FLAGS.enable_tensorboard:
- tensorboard_callback = tf.keras.callbacks.TensorBoard(
- log_dir=FLAGS.model_dir)
- callbacks.append(tensorboard_callback)
-
- return callbacks
-
-
-def update_stats(history, stats, callbacks):
- """Normalizes and updates dictionary of stats.
-
- Args:
- history: Results of the training step.
- stats: Dict with pre-existing training stats.
- callbacks: a list of callbacks which might include a time history callback
- used during keras.fit.
- """
-
- if history and history.history:
- train_hist = history.history
- # Gets final loss from training.
- stats['loss'] = float(train_hist['loss'][-1])
-
- if not callbacks:
- return
-
- # Look for the time history callback which was used during keras.fit
- for callback in callbacks:
- if isinstance(callback, keras_utils.TimeHistory):
- timestamp_log = callback.timestamp_log
- stats['step_timestamp_log'] = timestamp_log
- stats['train_finish_time'] = callback.train_finish_time
- if len(timestamp_log) > 1:
- stats['avg_exp_per_second'] = (
- callback.batch_size * callback.log_steps *
- (len(callback.timestamp_log) - 1) /
- (timestamp_log[-1].timestamp - timestamp_log[0].timestamp))
diff --git a/official/nlp/transformer/model_params.py b/official/nlp/transformer/model_params.py
deleted file mode 100644
index 0764d5e9a0d2e97754943cd61574b1c24469a0ae..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/model_params.py
+++ /dev/null
@@ -1,96 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Defines Transformer model parameters."""
-
-import collections
-
-
-BASE_PARAMS = collections.defaultdict(
- lambda: None, # Set default value to None.
-
- # Input params
- default_batch_size=2048, # Maximum number of tokens per batch of examples.
- default_batch_size_tpu=32768,
- max_length=256, # Maximum number of tokens per example.
-
- # Model params
- initializer_gain=1.0, # Used in trainable variable initialization.
- vocab_size=33708, # Number of tokens defined in the vocabulary file.
- hidden_size=512, # Model dimension in the hidden layers.
- num_hidden_layers=6, # Number of layers in the encoder and decoder stacks.
- num_heads=8, # Number of heads to use in multi-headed attention.
- filter_size=2048, # Inner layer dimension in the feedforward network.
-
- # Dropout values (only used when training)
- layer_postprocess_dropout=0.1,
- attention_dropout=0.1,
- relu_dropout=0.1,
-
- # Training params
- label_smoothing=0.1,
- learning_rate=2.0,
- learning_rate_decay_rate=1.0,
- learning_rate_warmup_steps=16000,
-
- # Optimizer params
- optimizer_adam_beta1=0.9,
- optimizer_adam_beta2=0.997,
- optimizer_adam_epsilon=1e-09,
-
- # Default prediction params
- extra_decode_length=50,
- beam_size=4,
- alpha=0.6, # used to calculate length normalization in beam search
-
- # TPU specific parameters
- use_tpu=False,
- static_batch=False,
- allow_ffn_pad=True,
-)
-
-BIG_PARAMS = BASE_PARAMS.copy()
-BIG_PARAMS.update(
- default_batch_size=4096,
-
- # default batch size is smaller than for BASE_PARAMS due to memory limits.
- default_batch_size_tpu=16384,
-
- hidden_size=1024,
- filter_size=4096,
- num_heads=16,
-)
-
-# Parameters for running the model in multi gpu. These should not change the
-# params that modify the model shape (such as the hidden_size or num_heads).
-BASE_MULTI_GPU_PARAMS = BASE_PARAMS.copy()
-BASE_MULTI_GPU_PARAMS.update(
- learning_rate_warmup_steps=8000
-)
-
-BIG_MULTI_GPU_PARAMS = BIG_PARAMS.copy()
-BIG_MULTI_GPU_PARAMS.update(
- layer_postprocess_dropout=0.3,
- learning_rate_warmup_steps=8000
-)
-
-# Parameters for testing the model
-TINY_PARAMS = BASE_PARAMS.copy()
-TINY_PARAMS.update(
- default_batch_size=1024,
- default_batch_size_tpu=1024,
- hidden_size=32,
- num_heads=4,
- filter_size=256,
-)
diff --git a/official/nlp/transformer/model_utils.py b/official/nlp/transformer/model_utils.py
deleted file mode 100644
index 6e163b97361cb7f071314909aaa1fc1e52ae6bfd..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/model_utils.py
+++ /dev/null
@@ -1,121 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Transformer model helper methods."""
-
-import math
-
-import numpy as np
-import tensorflow as tf
-
-# Very low numbers to represent -infinity. We do not actually use -Inf, since we
-# want to be able to multiply these values by zero to get zero. (-Inf * 0 = NaN)
-_NEG_INF_FP32 = -1e9
-_NEG_INF_FP16 = np.finfo(np.float16).min
-
-
-def get_position_encoding(length,
- hidden_size,
- min_timescale=1.0,
- max_timescale=1.0e4):
- """Return positional encoding.
-
- Calculates the position encoding as a mix of sine and cosine functions with
- geometrically increasing wavelengths.
- Defined and formulized in Attention is All You Need, section 3.5.
-
- Args:
- length: Sequence length.
- hidden_size: Size of the
- min_timescale: Minimum scale that will be applied at each position
- max_timescale: Maximum scale that will be applied at each position
-
- Returns:
- Tensor with shape [length, hidden_size]
- """
- # We compute the positional encoding in float32 even if the model uses
- # float16, as many of the ops used, like log and exp, are numerically unstable
- # in float16.
- position = tf.cast(tf.range(length), tf.float32)
- num_timescales = hidden_size // 2
- log_timescale_increment = (
- math.log(float(max_timescale) / float(min_timescale)) /
- (tf.cast(num_timescales, tf.float32) - 1))
- inv_timescales = min_timescale * tf.exp(
- tf.cast(tf.range(num_timescales), tf.float32) * -log_timescale_increment)
- scaled_time = tf.expand_dims(position, 1) * tf.expand_dims(inv_timescales, 0)
- signal = tf.concat([tf.sin(scaled_time), tf.cos(scaled_time)], axis=1)
- return signal
-
-
-def get_decoder_self_attention_bias(length, dtype=tf.float32):
- """Calculate bias for decoder that maintains model's autoregressive property.
-
- Creates a tensor that masks out locations that correspond to illegal
- connections, so prediction at position i cannot draw information from future
- positions.
-
- Args:
- length: int length of sequences in batch.
- dtype: The dtype of the return value.
-
- Returns:
- float tensor of shape [1, 1, length, length]
- """
- neg_inf = _NEG_INF_FP16 if dtype == tf.float16 else _NEG_INF_FP32
- with tf.name_scope("decoder_self_attention_bias"):
- valid_locs = tf.linalg.band_part(
- tf.ones([length, length], dtype=dtype), -1, 0)
- valid_locs = tf.reshape(valid_locs, [1, 1, length, length])
- decoder_bias = neg_inf * (1.0 - valid_locs)
- return decoder_bias
-
-
-def get_padding(x, padding_value=0, dtype=tf.float32):
- """Return float tensor representing the padding values in x.
-
- Args:
- x: int tensor with any shape
- padding_value: int which represents padded values in input
- dtype: The dtype of the return value.
-
- Returns:
- float tensor with same shape as x containing values 0 or 1.
- 0 -> non-padding, 1 -> padding
- """
- with tf.name_scope("padding"):
- return tf.cast(tf.equal(x, padding_value), dtype)
-
-
-def get_padding_bias(x, padding_value=0, dtype=tf.float32):
- """Calculate bias tensor from padding values in tensor.
-
- Bias tensor that is added to the pre-softmax multi-headed attention logits,
- which has shape [batch_size, num_heads, length, length]. The tensor is zero at
- non-padding locations, and -1e9 (negative infinity) at padding locations.
-
- Args:
- x: int tensor with shape [batch_size, length]
- padding_value: int which represents padded values in input
- dtype: The dtype of the return value
-
- Returns:
- Attention bias tensor of shape [batch_size, 1, 1, length].
- """
- with tf.name_scope("attention_bias"):
- padding = get_padding(x, padding_value, dtype)
- attention_bias = padding * _NEG_INF_FP32
- attention_bias = tf.expand_dims(
- tf.expand_dims(attention_bias, axis=1), axis=1)
- return attention_bias
diff --git a/official/nlp/transformer/model_utils_test.py b/official/nlp/transformer/model_utils_test.py
deleted file mode 100644
index 10ddeed8392a77175b82b69c6e628cc1306c607c..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/model_utils_test.py
+++ /dev/null
@@ -1,55 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Test Transformer model helper methods."""
-
-import tensorflow as tf
-
-from official.nlp.transformer import model_utils
-
-NEG_INF = -1e9
-
-
-class ModelUtilsTest(tf.test.TestCase):
-
- def test_get_padding(self):
- x = tf.constant([[1, 0, 0, 0, 2], [3, 4, 0, 0, 0], [0, 5, 6, 0, 7]])
- padding = model_utils.get_padding(x, padding_value=0)
-
- self.assertAllEqual([[0, 1, 1, 1, 0], [0, 0, 1, 1, 1], [1, 0, 0, 1, 0]],
- padding)
-
- def test_get_padding_bias(self):
- x = tf.constant([[1, 0, 0, 0, 2], [3, 4, 0, 0, 0], [0, 5, 6, 0, 7]])
- bias = model_utils.get_padding_bias(x)
- bias_shape = tf.shape(bias)
- flattened_bias = tf.reshape(bias, [3, 5])
-
- self.assertAllEqual(
- [[0, NEG_INF, NEG_INF, NEG_INF, 0], [0, 0, NEG_INF, NEG_INF, NEG_INF],
- [NEG_INF, 0, 0, NEG_INF, 0]], flattened_bias)
- self.assertAllEqual([3, 1, 1, 5], bias_shape)
-
- def test_get_decoder_self_attention_bias(self):
- length = 5
- bias = model_utils.get_decoder_self_attention_bias(length)
-
- self.assertAllEqual(
- [[[[0, NEG_INF, NEG_INF, NEG_INF, NEG_INF],
- [0, 0, NEG_INF, NEG_INF, NEG_INF], [0, 0, 0, NEG_INF, NEG_INF],
- [0, 0, 0, 0, NEG_INF], [0, 0, 0, 0, 0]]]], bias)
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/transformer/optimizer.py b/official/nlp/transformer/optimizer.py
deleted file mode 100644
index b27a6f07a4b73723be6f28d257bc3abcfbca43de..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/optimizer.py
+++ /dev/null
@@ -1,64 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Optimizer from addons and learning rate scheduler."""
-
-import tensorflow as tf
-
-
-class LearningRateSchedule(tf.keras.optimizers.schedules.LearningRateSchedule):
- """Learning rate schedule."""
-
- def __init__(self, initial_learning_rate, hidden_size, warmup_steps):
- """Initialize configuration of the learning rate schedule.
-
- Args:
- initial_learning_rate: A float, the initial learning rate.
- hidden_size: An integer, the model dimension in the hidden layers.
- warmup_steps: An integer, the number of steps required for linear warmup.
- """
- super(LearningRateSchedule, self).__init__()
- self.initial_learning_rate = initial_learning_rate
- self.hidden_size = hidden_size
- self.warmup_steps = warmup_steps
- self.warmup_steps_tensor = tf.cast(warmup_steps, tf.float32)
-
- def __call__(self, global_step):
- """Calculate learning rate with linear warmup and rsqrt decay.
-
- Args:
- global_step: An integer, the current global step used for learning rate
- calculation.
-
- Returns:
- A float, the learning rate needs to be used for current global step.
- """
- with tf.name_scope('learning_rate_schedule'):
- global_step = tf.cast(global_step, tf.float32)
- learning_rate = self.initial_learning_rate
- learning_rate *= (self.hidden_size**-0.5)
- # Apply linear warmup
- learning_rate *= tf.minimum(1.0, global_step / self.warmup_steps_tensor)
- # Apply rsqrt decay
- learning_rate /= tf.sqrt(
- tf.maximum(global_step, self.warmup_steps_tensor))
- return learning_rate
-
- def get_config(self):
- """Get the configuration of the learning rate schedule."""
- return {
- 'initial_learning_rate': self.initial_learning_rate,
- 'hidden_size': self.hidden_size,
- 'warmup_steps': self.warmup_steps,
- }
diff --git a/official/nlp/transformer/transformer.py b/official/nlp/transformer/transformer.py
deleted file mode 100644
index b7ea0fe7f5f9bd6a0c57a6b02642df39e953894a..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer.py
+++ /dev/null
@@ -1,549 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Defines the Transformer model in TF 2.0.
-
-Model paper: https://arxiv.org/pdf/1706.03762.pdf
-Transformer model code source: https://github.com/tensorflow/tensor2tensor
-"""
-
-import tensorflow as tf
-from official.nlp.modeling.layers import position_embedding
-from official.nlp.modeling.ops import beam_search
-from official.nlp.transformer import attention_layer
-from official.nlp.transformer import embedding_layer
-from official.nlp.transformer import ffn_layer
-from official.nlp.transformer import metrics
-from official.nlp.transformer import model_utils
-from official.nlp.transformer.utils.tokenizer import EOS_ID
-
-# Disable the not-callable lint error, since it claims many objects are not
-# callable when they actually are.
-# pylint: disable=not-callable
-
-
-def create_model(params, is_train):
- """Creates transformer model."""
- with tf.name_scope("model"):
- if is_train:
- inputs = tf.keras.layers.Input((None,), dtype="int64", name="inputs")
- targets = tf.keras.layers.Input((None,), dtype="int64", name="targets")
- internal_model = Transformer(params, name="transformer_v2")
- logits = internal_model([inputs, targets], training=is_train)
- vocab_size = params["vocab_size"]
- label_smoothing = params["label_smoothing"]
- if params["enable_metrics_in_training"]:
- logits = metrics.MetricLayer(vocab_size)([logits, targets])
- logits = tf.keras.layers.Lambda(
- lambda x: x, name="logits", dtype=tf.float32)(
- logits)
- model = tf.keras.Model([inputs, targets], logits)
- loss = metrics.transformer_loss(logits, targets, label_smoothing,
- vocab_size)
- model.add_loss(loss)
- return model
-
- else:
- inputs = tf.keras.layers.Input((None,), dtype="int64", name="inputs")
- internal_model = Transformer(params, name="transformer_v2")
- ret = internal_model([inputs], training=is_train)
- outputs, scores = ret["outputs"], ret["scores"]
- return tf.keras.Model(inputs, [outputs, scores])
-
-
-class Transformer(tf.keras.Model):
- """Transformer model with Keras.
-
- Implemented as described in: https://arxiv.org/pdf/1706.03762.pdf
-
- The Transformer model consists of an encoder and decoder. The input is an int
- sequence (or a batch of sequences). The encoder produces a continuous
- representation, and the decoder uses the encoder output to generate
- probabilities for the output sequence.
- """
-
- def __init__(self, params, name=None):
- """Initialize layers to build Transformer model.
-
- Args:
- params: hyperparameter object defining layer sizes, dropout values, etc.
- name: name of the model.
- """
- super(Transformer, self).__init__(name=name)
- self.params = params
- self.embedding_softmax_layer = embedding_layer.EmbeddingSharedWeights(
- params["vocab_size"], params["hidden_size"])
- self.encoder_stack = EncoderStack(params)
- self.decoder_stack = DecoderStack(params)
- self.position_embedding = position_embedding.RelativePositionEmbedding(
- hidden_size=self.params["hidden_size"])
-
- def get_config(self):
- return {
- "params": self.params,
- }
-
- def call(self, inputs, training):
- """Calculate target logits or inferred target sequences.
-
- Args:
- inputs: input tensor list of size 1 or 2.
- First item, inputs: int tensor with shape [batch_size, input_length].
- Second item (optional), targets: None or int tensor with shape
- [batch_size, target_length].
- training: boolean, whether in training mode or not.
-
- Returns:
- If targets is defined, then return logits for each word in the target
- sequence. float tensor with shape [batch_size, target_length, vocab_size]
- If target is none, then generate output sequence one token at a time.
- returns a dictionary {
- outputs: int tensor with shape [batch_size, decoded_length]
- scores: float tensor with shape [batch_size]}
- Even when float16 is used, the output tensor(s) are always float32.
-
- Raises:
- NotImplementedError: If try to use padded decode method on CPU/GPUs.
- """
- inputs = inputs if isinstance(inputs, list) else [inputs]
- if len(inputs) == 2:
- inputs, targets = inputs[0], inputs[1]
- else:
- # Decoding path.
- inputs, targets = inputs[0], None
- if self.params["padded_decode"]:
- if not self.params["num_replicas"]:
- raise NotImplementedError(
- "Padded decoding on CPU/GPUs is not supported.")
- decode_batch_size = int(self.params["decode_batch_size"] /
- self.params["num_replicas"])
- inputs.set_shape([decode_batch_size, self.params["decode_max_length"]])
-
- # Variance scaling is used here because it seems to work in many problems.
- # Other reasonable initializers may also work just as well.
- with tf.name_scope("Transformer"):
- # Calculate attention bias for encoder self-attention and decoder
- # multi-headed attention layers.
- attention_bias = model_utils.get_padding_bias(inputs)
-
- # Run the inputs through the encoder layer to map the symbol
- # representations to continuous representations.
- encoder_outputs = self.encode(inputs, attention_bias, training)
- # Generate output sequence if targets is None, or return logits if target
- # sequence is known.
- if targets is None:
- return self.predict(encoder_outputs, attention_bias, training)
- else:
- logits = self.decode(targets, encoder_outputs, attention_bias, training)
- return logits
-
- def encode(self, inputs, attention_bias, training):
- """Generate continuous representation for inputs.
-
- Args:
- inputs: int tensor with shape [batch_size, input_length].
- attention_bias: float tensor with shape [batch_size, 1, 1, input_length].
- training: boolean, whether in training mode or not.
-
- Returns:
- float tensor with shape [batch_size, input_length, hidden_size]
- """
- with tf.name_scope("encode"):
- # Prepare inputs to the layer stack by adding positional encodings and
- # applying dropout.
- embedded_inputs = self.embedding_softmax_layer(inputs)
- embedded_inputs = tf.cast(embedded_inputs, self.params["dtype"])
- inputs_padding = model_utils.get_padding(inputs)
- attention_bias = tf.cast(attention_bias, self.params["dtype"])
-
- with tf.name_scope("add_pos_encoding"):
- pos_encoding = self.position_embedding(inputs=embedded_inputs)
- pos_encoding = tf.cast(pos_encoding, self.params["dtype"])
- encoder_inputs = embedded_inputs + pos_encoding
-
- if training:
- encoder_inputs = tf.nn.dropout(
- encoder_inputs, rate=self.params["layer_postprocess_dropout"])
-
- return self.encoder_stack(
- encoder_inputs, attention_bias, inputs_padding, training=training)
-
- def decode(self, targets, encoder_outputs, attention_bias, training):
- """Generate logits for each value in the target sequence.
-
- Args:
- targets: target values for the output sequence. int tensor with shape
- [batch_size, target_length]
- encoder_outputs: continuous representation of input sequence. float tensor
- with shape [batch_size, input_length, hidden_size]
- attention_bias: float tensor with shape [batch_size, 1, 1, input_length]
- training: boolean, whether in training mode or not.
-
- Returns:
- float32 tensor with shape [batch_size, target_length, vocab_size]
- """
- with tf.name_scope("decode"):
- # Prepare inputs to decoder layers by shifting targets, adding positional
- # encoding and applying dropout.
- with tf.name_scope("shift_targets"):
- # Shift targets to the right, and remove the last element
- targets = tf.pad(targets, [[0, 0], [1, 0]])[:, :-1]
- decoder_inputs = self.embedding_softmax_layer(targets)
- decoder_inputs = tf.cast(decoder_inputs, self.params["dtype"])
- attention_bias = tf.cast(attention_bias, self.params["dtype"])
- with tf.name_scope("add_pos_encoding"):
- length = tf.shape(decoder_inputs)[1]
- pos_encoding = self.position_embedding(decoder_inputs)
- pos_encoding = tf.cast(pos_encoding, self.params["dtype"])
- decoder_inputs += pos_encoding
- if training:
- decoder_inputs = tf.nn.dropout(
- decoder_inputs, rate=self.params["layer_postprocess_dropout"])
-
- # Run values
- decoder_self_attention_bias = model_utils.get_decoder_self_attention_bias(
- length, dtype=self.params["dtype"])
- outputs = self.decoder_stack(
- decoder_inputs,
- encoder_outputs,
- decoder_self_attention_bias,
- attention_bias,
- training=training)
- logits = self.embedding_softmax_layer(outputs, mode="linear")
- logits = tf.cast(logits, tf.float32)
- return logits
-
- def _get_symbols_to_logits_fn(self, max_decode_length, training):
- """Returns a decoding function that calculates logits of the next tokens."""
- timing_signal = self.position_embedding(
- inputs=None, length=max_decode_length + 1)
- timing_signal = tf.cast(timing_signal, self.params["dtype"])
- decoder_self_attention_bias = model_utils.get_decoder_self_attention_bias(
- max_decode_length, dtype=self.params["dtype"])
-
- def symbols_to_logits_fn(ids, i, cache):
- """Generate logits for next potential IDs.
-
- Args:
- ids: Current decoded sequences. int tensor with shape [batch_size *
- beam_size, i + 1].
- i: Loop index.
- cache: dictionary of values storing the encoder output, encoder-decoder
- attention bias, and previous decoder attention values.
-
- Returns:
- Tuple of
- (logits with shape [batch_size * beam_size, vocab_size],
- updated cache values)
- """
- # Set decoder input to the last generated IDs
- decoder_input = ids[:, -1:]
-
- # Preprocess decoder input by getting embeddings and adding timing signal.
- decoder_input = self.embedding_softmax_layer(decoder_input)
- decoder_input += timing_signal[i]
- if self.params["padded_decode"]:
- bias_shape = decoder_self_attention_bias.shape.as_list()
- self_attention_bias = tf.slice(
- decoder_self_attention_bias, [0, 0, i, 0],
- [bias_shape[0], bias_shape[1], 1, bias_shape[3]])
- else:
- self_attention_bias = decoder_self_attention_bias[:, :, i:i + 1, :i + 1]
-
- decoder_outputs = self.decoder_stack(
- decoder_input,
- cache.get("encoder_outputs"),
- self_attention_bias,
- cache.get("encoder_decoder_attention_bias"),
- training=training,
- cache=cache,
- decode_loop_step=i if self.params["padded_decode"] else None)
- logits = self.embedding_softmax_layer(decoder_outputs, mode="linear")
- logits = tf.squeeze(logits, axis=[1])
- return logits, cache
-
- return symbols_to_logits_fn
-
- def predict(self, encoder_outputs, encoder_decoder_attention_bias, training):
- """Return predicted sequence."""
- encoder_outputs = tf.cast(encoder_outputs, self.params["dtype"])
- if self.params["padded_decode"]:
- batch_size = encoder_outputs.shape.as_list()[0]
- input_length = encoder_outputs.shape.as_list()[1]
- else:
- batch_size = tf.shape(encoder_outputs)[0]
- input_length = tf.shape(encoder_outputs)[1]
- max_decode_length = input_length + self.params["extra_decode_length"]
- encoder_decoder_attention_bias = tf.cast(encoder_decoder_attention_bias,
- self.params["dtype"])
-
- symbols_to_logits_fn = self._get_symbols_to_logits_fn(
- max_decode_length, training)
-
- # Create initial set of IDs that will be passed into symbols_to_logits_fn.
- initial_ids = tf.zeros([batch_size], dtype=tf.int32)
-
- # Create cache storing decoder attention values for each layer.
- # pylint: disable=g-complex-comprehension
- init_decode_length = (
- max_decode_length if self.params["padded_decode"] else 0)
- num_heads = self.params["num_heads"]
- dim_per_head = self.params["hidden_size"] // num_heads
- cache = {
- "layer_%d" % layer: {
- "k":
- tf.zeros(
- [batch_size, init_decode_length, num_heads, dim_per_head],
- dtype=self.params["dtype"]),
- "v":
- tf.zeros(
- [batch_size, init_decode_length, num_heads, dim_per_head],
- dtype=self.params["dtype"])
- } for layer in range(self.params["num_hidden_layers"])
- }
- # pylint: enable=g-complex-comprehension
-
- # Add encoder output and attention bias to the cache.
- cache["encoder_outputs"] = encoder_outputs
- cache["encoder_decoder_attention_bias"] = encoder_decoder_attention_bias
-
- # Use beam search to find the top beam_size sequences and scores.
- decoded_ids, scores = beam_search.sequence_beam_search(
- symbols_to_logits_fn=symbols_to_logits_fn,
- initial_ids=initial_ids,
- initial_cache=cache,
- vocab_size=self.params["vocab_size"],
- beam_size=self.params["beam_size"],
- alpha=self.params["alpha"],
- max_decode_length=max_decode_length,
- eos_id=EOS_ID,
- padded_decode=self.params["padded_decode"],
- dtype=self.params["dtype"])
-
- # Get the top sequence for each batch element
- top_decoded_ids = decoded_ids[:, 0, 1:]
- top_scores = scores[:, 0]
-
- return {"outputs": top_decoded_ids, "scores": top_scores}
-
-
-class PrePostProcessingWrapper(tf.keras.layers.Layer):
- """Wrapper class that applies layer pre-processing and post-processing."""
-
- def __init__(self, layer, params):
- super(PrePostProcessingWrapper, self).__init__()
- self.layer = layer
- self.params = params
- self.postprocess_dropout = params["layer_postprocess_dropout"]
-
- def build(self, input_shape):
- # Create normalization layer
- self.layer_norm = tf.keras.layers.LayerNormalization(
- epsilon=1e-6, dtype="float32")
- super(PrePostProcessingWrapper, self).build(input_shape)
-
- def get_config(self):
- return {
- "params": self.params,
- }
-
- def call(self, x, *args, **kwargs):
- """Calls wrapped layer with same parameters."""
- # Preprocessing: apply layer normalization
- training = kwargs["training"]
-
- y = self.layer_norm(x)
-
- # Get layer output
- y = self.layer(y, *args, **kwargs)
-
- # Postprocessing: apply dropout and residual connection
- if training:
- y = tf.nn.dropout(y, rate=self.postprocess_dropout)
- return x + y
-
-
-class EncoderStack(tf.keras.layers.Layer):
- """Transformer encoder stack.
-
- The encoder stack is made up of N identical layers. Each layer is composed
- of the sublayers:
- 1. Self-attention layer
- 2. Feedforward network (which is 2 fully-connected layers)
- """
-
- def __init__(self, params):
- super(EncoderStack, self).__init__()
- self.params = params
- self.layers = []
-
- def build(self, input_shape):
- """Builds the encoder stack."""
- params = self.params
- for _ in range(params["num_hidden_layers"]):
- # Create sublayers for each layer.
- self_attention_layer = attention_layer.SelfAttention(
- params["hidden_size"], params["num_heads"],
- params["attention_dropout"])
- feed_forward_network = ffn_layer.FeedForwardNetwork(
- params["hidden_size"], params["filter_size"], params["relu_dropout"])
-
- self.layers.append([
- PrePostProcessingWrapper(self_attention_layer, params),
- PrePostProcessingWrapper(feed_forward_network, params)
- ])
-
- # Create final layer normalization layer.
- self.output_normalization = tf.keras.layers.LayerNormalization(
- epsilon=1e-6, dtype="float32")
- super(EncoderStack, self).build(input_shape)
-
- def get_config(self):
- return {
- "params": self.params,
- }
-
- def call(self, encoder_inputs, attention_bias, inputs_padding, training):
- """Return the output of the encoder layer stacks.
-
- Args:
- encoder_inputs: tensor with shape [batch_size, input_length, hidden_size]
- attention_bias: bias for the encoder self-attention layer. [batch_size, 1,
- 1, input_length]
- inputs_padding: tensor with shape [batch_size, input_length], inputs with
- zero paddings.
- training: boolean, whether in training mode or not.
-
- Returns:
- Output of encoder layer stack.
- float32 tensor with shape [batch_size, input_length, hidden_size]
- """
- for n, layer in enumerate(self.layers):
- # Run inputs through the sublayers.
- self_attention_layer = layer[0]
- feed_forward_network = layer[1]
-
- with tf.name_scope("layer_%d" % n):
- with tf.name_scope("self_attention"):
- encoder_inputs = self_attention_layer(
- encoder_inputs, attention_bias, training=training)
- with tf.name_scope("ffn"):
- encoder_inputs = feed_forward_network(
- encoder_inputs, training=training)
-
- return self.output_normalization(encoder_inputs)
-
-
-class DecoderStack(tf.keras.layers.Layer):
- """Transformer decoder stack.
-
- Like the encoder stack, the decoder stack is made up of N identical layers.
- Each layer is composed of the sublayers:
- 1. Self-attention layer
- 2. Multi-headed attention layer combining encoder outputs with results from
- the previous self-attention layer.
- 3. Feedforward network (2 fully-connected layers)
- """
-
- def __init__(self, params):
- super(DecoderStack, self).__init__()
- self.params = params
- self.layers = []
-
- def build(self, input_shape):
- """Builds the decoder stack."""
- params = self.params
- for _ in range(params["num_hidden_layers"]):
- self_attention_layer = attention_layer.SelfAttention(
- params["hidden_size"], params["num_heads"],
- params["attention_dropout"])
- enc_dec_attention_layer = attention_layer.Attention(
- params["hidden_size"], params["num_heads"],
- params["attention_dropout"])
- feed_forward_network = ffn_layer.FeedForwardNetwork(
- params["hidden_size"], params["filter_size"], params["relu_dropout"])
-
- self.layers.append([
- PrePostProcessingWrapper(self_attention_layer, params),
- PrePostProcessingWrapper(enc_dec_attention_layer, params),
- PrePostProcessingWrapper(feed_forward_network, params)
- ])
- self.output_normalization = tf.keras.layers.LayerNormalization(
- epsilon=1e-6, dtype="float32")
- super(DecoderStack, self).build(input_shape)
-
- def get_config(self):
- return {
- "params": self.params,
- }
-
- def call(self,
- decoder_inputs,
- encoder_outputs,
- decoder_self_attention_bias,
- attention_bias,
- training,
- cache=None,
- decode_loop_step=None):
- """Return the output of the decoder layer stacks.
-
- Args:
- decoder_inputs: A tensor with shape [batch_size, target_length,
- hidden_size].
- encoder_outputs: A tensor with shape [batch_size, input_length,
- hidden_size]
- decoder_self_attention_bias: A tensor with shape [1, 1, target_len,
- target_length], the bias for decoder self-attention layer.
- attention_bias: A tensor with shape [batch_size, 1, 1, input_length], the
- bias for encoder-decoder attention layer.
- training: A bool, whether in training mode or not.
- cache: (Used for fast decoding) A nested dictionary storing previous
- decoder self-attention values. The items are:
- {layer_n: {"k": A tensor with shape [batch_size, i, key_channels],
- "v": A tensor with shape [batch_size, i, value_channels]},
- ...}
- decode_loop_step: An integer, the step number of the decoding loop. Used
- only for autoregressive inference on TPU.
-
- Returns:
- Output of decoder layer stack.
- float32 tensor with shape [batch_size, target_length, hidden_size]
- """
- for n, layer in enumerate(self.layers):
- self_attention_layer = layer[0]
- enc_dec_attention_layer = layer[1]
- feed_forward_network = layer[2]
-
- # Run inputs through the sublayers.
- layer_name = "layer_%d" % n
- layer_cache = cache[layer_name] if cache is not None else None
- with tf.name_scope(layer_name):
- with tf.name_scope("self_attention"):
- decoder_inputs = self_attention_layer(
- decoder_inputs,
- decoder_self_attention_bias,
- training=training,
- cache=layer_cache,
- decode_loop_step=decode_loop_step)
- with tf.name_scope("encdec_attention"):
- decoder_inputs = enc_dec_attention_layer(
- decoder_inputs,
- encoder_outputs,
- attention_bias,
- training=training)
- with tf.name_scope("ffn"):
- decoder_inputs = feed_forward_network(
- decoder_inputs, training=training)
-
- return self.output_normalization(decoder_inputs)
diff --git a/official/nlp/transformer/transformer_forward_test.py b/official/nlp/transformer/transformer_forward_test.py
deleted file mode 100644
index 4c8406a32e906bc8683b0a3a744eb5890e665cc9..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer_forward_test.py
+++ /dev/null
@@ -1,157 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Forward pass test for Transformer model refactoring."""
-
-import numpy as np
-
-import tensorflow as tf
-
-from official.nlp.modeling import models
-from official.nlp.transformer import metrics
-from official.nlp.transformer import model_params
-from official.nlp.transformer import transformer
-
-
-def _count_params(layer, trainable_only=True):
- """Returns the count of all model parameters, or just trainable ones."""
- if not trainable_only:
- return layer.count_params()
- else:
- return int(
- np.sum([
- tf.keras.backend.count_params(p) for p in layer.trainable_weights
- ]))
-
-
-def _create_model(params, is_train):
- """Creates transformer model."""
-
- encdec_kwargs = dict(
- num_layers=params["num_hidden_layers"],
- num_attention_heads=params["num_heads"],
- intermediate_size=params["filter_size"],
- activation="relu",
- dropout_rate=params["relu_dropout"],
- attention_dropout_rate=params["attention_dropout"],
- use_bias=False,
- norm_first=True,
- norm_epsilon=1e-6,
- intermediate_dropout=params["relu_dropout"])
- encoder_layer = models.TransformerEncoder(**encdec_kwargs)
- decoder_layer = models.TransformerDecoder(**encdec_kwargs)
-
- model_kwargs = dict(
- vocab_size=params["vocab_size"],
- embedding_width=params["hidden_size"],
- dropout_rate=params["layer_postprocess_dropout"],
- padded_decode=params["padded_decode"],
- decode_max_length=params["decode_max_length"],
- dtype=params["dtype"],
- extra_decode_length=params["extra_decode_length"],
- beam_size=params["beam_size"],
- alpha=params["alpha"],
- encoder_layer=encoder_layer,
- decoder_layer=decoder_layer,
- name="transformer_v2")
-
- if is_train:
- inputs = tf.keras.layers.Input((None,), dtype="int64", name="inputs")
- targets = tf.keras.layers.Input((None,), dtype="int64", name="targets")
- internal_model = models.Seq2SeqTransformer(**model_kwargs)
- logits = internal_model(
- dict(inputs=inputs, targets=targets), training=is_train)
- vocab_size = params["vocab_size"]
- label_smoothing = params["label_smoothing"]
- if params["enable_metrics_in_training"]:
- logits = metrics.MetricLayer(vocab_size)([logits, targets])
- logits = tf.keras.layers.Lambda(
- lambda x: x, name="logits", dtype=tf.float32)(
- logits)
- model = tf.keras.Model([inputs, targets], logits)
- loss = metrics.transformer_loss(logits, targets, label_smoothing,
- vocab_size)
- model.add_loss(loss)
- return model
-
- batch_size = params["decode_batch_size"] if params["padded_decode"] else None
- inputs = tf.keras.layers.Input((None,),
- batch_size=batch_size,
- dtype="int64",
- name="inputs")
- internal_model = models.Seq2SeqTransformer(**model_kwargs)
- ret = internal_model(dict(inputs=inputs), training=is_train)
- outputs, scores = ret["outputs"], ret["scores"]
- return tf.keras.Model(inputs, [outputs, scores])
-
-
-class TransformerForwardTest(tf.test.TestCase):
-
- def setUp(self):
- super(TransformerForwardTest, self).setUp()
- self.params = params = model_params.TINY_PARAMS
- params["batch_size"] = params["default_batch_size"] = 16
- params["hidden_size"] = 12
- params["num_hidden_layers"] = 3
- params["filter_size"] = 14
- params["num_heads"] = 2
- params["vocab_size"] = 41
- params["extra_decode_length"] = 0
- params["beam_size"] = 3
- params["dtype"] = tf.float32
- params["layer_postprocess_dropout"] = 0.0
- params["attention_dropout"] = 0.0
- params["relu_dropout"] = 0.0
-
- def test_forward_pass_train(self):
- # Set input_len different from target_len
- inputs = np.asarray([[5, 2, 1], [7, 5, 0], [1, 4, 0], [7, 5, 11]])
- targets = np.asarray([[4, 3, 4, 0], [13, 19, 17, 8], [20, 14, 1, 2],
- [5, 7, 3, 0]])
-
- # src_model is the original model before refactored.
- src_model = transformer.create_model(self.params, True)
- src_num_weights = _count_params(src_model)
- src_weights = src_model.get_weights()
- src_model_output = src_model([inputs, targets], training=True)
-
- # dest_model is the refactored model.
- dest_model = _create_model(self.params, True)
- dest_num_weights = _count_params(dest_model)
- self.assertEqual(src_num_weights, dest_num_weights)
- dest_model.set_weights(src_weights)
- dest_model_output = dest_model([inputs, targets], training=True)
- self.assertAllEqual(src_model_output, dest_model_output)
-
- def test_forward_pass_not_train(self):
- inputs = np.asarray([[5, 2, 1], [7, 5, 0], [1, 4, 0], [7, 5, 11]])
-
- # src_model is the original model before refactored.
- src_model = transformer.create_model(self.params, False)
- src_num_weights = _count_params(src_model)
- src_weights = src_model.get_weights()
- src_model_output = src_model([inputs], training=False)
-
- # dest_model is the refactored model.
- dest_model = _create_model(self.params, False)
- dest_num_weights = _count_params(dest_model)
- self.assertEqual(src_num_weights, dest_num_weights)
- dest_model.set_weights(src_weights)
- dest_model_output = dest_model([inputs], training=False)
- self.assertAllEqual(src_model_output[0], dest_model_output[0])
- self.assertAllEqual(src_model_output[1], dest_model_output[1])
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/transformer/transformer_layers_test.py b/official/nlp/transformer/transformer_layers_test.py
deleted file mode 100644
index 83e76890548e2c4d40345e1b802e22a7fd645b2d..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer_layers_test.py
+++ /dev/null
@@ -1,125 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Tests for layers in Transformer."""
-
-import tensorflow as tf
-
-from official.nlp.transformer import attention_layer
-from official.nlp.transformer import embedding_layer
-from official.nlp.transformer import ffn_layer
-from official.nlp.transformer import metrics
-
-
-class TransformerLayersTest(tf.test.TestCase):
-
- def test_attention_layer(self):
- hidden_size = 64
- num_heads = 4
- dropout = 0.5
- dim_per_head = hidden_size // num_heads
- layer = attention_layer.SelfAttention(hidden_size, num_heads, dropout)
- self.assertDictEqual(
- layer.get_config(), {
- "hidden_size": hidden_size,
- "num_heads": num_heads,
- "attention_dropout": dropout,
- })
- length = 2
- x = tf.ones([1, length, hidden_size])
- bias = tf.ones([1])
- cache = {
- "k": tf.zeros([1, 0, num_heads, dim_per_head]),
- "v": tf.zeros([1, 0, num_heads, dim_per_head]),
- }
- y = layer(x, bias, training=True, cache=cache)
- self.assertEqual(y.shape, (
- 1,
- length,
- 64,
- ))
- self.assertEqual(cache["k"].shape, (
- 1,
- length,
- num_heads,
- dim_per_head,
- ))
- self.assertEqual(cache["v"].shape, (
- 1,
- length,
- num_heads,
- dim_per_head,
- ))
-
- def test_embedding_shared_weights(self):
- vocab_size = 50
- hidden_size = 64
- length = 2
- layer = embedding_layer.EmbeddingSharedWeights(vocab_size, hidden_size)
- self.assertDictEqual(layer.get_config(), {
- "vocab_size": 50,
- "hidden_size": 64,
- })
-
- idx = tf.ones([1, length], dtype="int32")
- y = layer(idx)
- self.assertEqual(y.shape, (
- 1,
- length,
- hidden_size,
- ))
- x = tf.ones([1, length, hidden_size])
- output = layer(x, "linear")
- self.assertEqual(output.shape, (
- 1,
- length,
- vocab_size,
- ))
-
- def test_feed_forward_network(self):
- hidden_size = 64
- filter_size = 32
- relu_dropout = 0.5
- layer = ffn_layer.FeedForwardNetwork(hidden_size, filter_size, relu_dropout)
- self.assertDictEqual(
- layer.get_config(), {
- "hidden_size": hidden_size,
- "filter_size": filter_size,
- "relu_dropout": relu_dropout,
- })
- length = 2
- x = tf.ones([1, length, hidden_size])
- y = layer(x, training=True)
- self.assertEqual(y.shape, (
- 1,
- length,
- hidden_size,
- ))
-
- def test_metric_layer(self):
- vocab_size = 50
- logits = tf.keras.layers.Input((None, vocab_size),
- dtype="float32",
- name="logits")
- targets = tf.keras.layers.Input((None,), dtype="int64", name="targets")
- output_logits = metrics.MetricLayer(vocab_size)([logits, targets])
- self.assertEqual(output_logits.shape.as_list(), [
- None,
- None,
- vocab_size,
- ])
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/transformer/transformer_main.py b/official/nlp/transformer/transformer_main.py
deleted file mode 100644
index 015c4d7dda1a7153af8ac0f14cdf38a984304e9b..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer_main.py
+++ /dev/null
@@ -1,482 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Train and evaluate the Transformer model.
-
-See README for description of setting the training schedule and evaluating the
-BLEU score.
-"""
-
-import os
-import tempfile
-
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-import tensorflow as tf
-from official.common import distribute_utils
-from official.modeling import performance
-from official.nlp.transformer import compute_bleu
-from official.nlp.transformer import data_pipeline
-from official.nlp.transformer import metrics
-from official.nlp.transformer import misc
-from official.nlp.transformer import optimizer
-from official.nlp.transformer import transformer
-from official.nlp.transformer import translate
-from official.nlp.transformer.utils import tokenizer
-from official.utils.flags import core as flags_core
-from official.utils.misc import keras_utils
-# pylint:disable=logging-format-interpolation
-
-INF = int(1e9)
-BLEU_DIR = "bleu"
-_SINGLE_SAMPLE = 1
-
-
-def translate_and_compute_bleu(model,
- params,
- subtokenizer,
- bleu_source,
- bleu_ref,
- distribution_strategy=None):
- """Translate file and report the cased and uncased bleu scores.
-
- Args:
- model: A Keras model, used to generate the translations.
- params: A dictionary, containing the translation related parameters.
- subtokenizer: A subtokenizer object, used for encoding and decoding source
- and translated lines.
- bleu_source: A file containing source sentences for translation.
- bleu_ref: A file containing the reference for the translated sentences.
- distribution_strategy: A platform distribution strategy, used for TPU based
- translation.
-
- Returns:
- uncased_score: A float, the case insensitive BLEU score.
- cased_score: A float, the case sensitive BLEU score.
- """
- # Create temporary file to store translation.
- tmp = tempfile.NamedTemporaryFile(delete=False)
- tmp_filename = tmp.name
-
- translate.translate_file(
- model,
- params,
- subtokenizer,
- bleu_source,
- output_file=tmp_filename,
- print_all_translations=False,
- distribution_strategy=distribution_strategy)
-
- # Compute uncased and cased bleu scores.
- uncased_score = compute_bleu.bleu_wrapper(bleu_ref, tmp_filename, False)
- cased_score = compute_bleu.bleu_wrapper(bleu_ref, tmp_filename, True)
- os.remove(tmp_filename)
- return uncased_score, cased_score
-
-
-def evaluate_and_log_bleu(model,
- params,
- bleu_source,
- bleu_ref,
- vocab_file,
- distribution_strategy=None):
- """Calculate and record the BLEU score.
-
- Args:
- model: A Keras model, used to generate the translations.
- params: A dictionary, containing the translation related parameters.
- bleu_source: A file containing source sentences for translation.
- bleu_ref: A file containing the reference for the translated sentences.
- vocab_file: A file containing the vocabulary for translation.
- distribution_strategy: A platform distribution strategy, used for TPU based
- translation.
-
- Returns:
- uncased_score: A float, the case insensitive BLEU score.
- cased_score: A float, the case sensitive BLEU score.
- """
- subtokenizer = tokenizer.Subtokenizer(vocab_file)
-
- uncased_score, cased_score = translate_and_compute_bleu(
- model, params, subtokenizer, bleu_source, bleu_ref, distribution_strategy)
-
- logging.info("Bleu score (uncased): %s", uncased_score)
- logging.info("Bleu score (cased): %s", cased_score)
- return uncased_score, cased_score
-
-
-class TransformerTask(object):
- """Main entry of Transformer model."""
-
- def __init__(self, flags_obj):
- """Init function of TransformerMain.
-
- Args:
- flags_obj: Object containing parsed flag values, i.e., FLAGS.
-
- Raises:
- ValueError: if not using static batch for input data on TPU.
- """
- self.flags_obj = flags_obj
- self.predict_model = None
-
- # Add flag-defined parameters to params object
- num_gpus = flags_core.get_num_gpus(flags_obj)
- self.params = params = misc.get_model_params(flags_obj.param_set, num_gpus)
-
- params["num_gpus"] = num_gpus
- params["use_ctl"] = flags_obj.use_ctl
- params["data_dir"] = flags_obj.data_dir
- params["model_dir"] = flags_obj.model_dir
- params["static_batch"] = flags_obj.static_batch
- params["max_length"] = flags_obj.max_length
- params["decode_batch_size"] = flags_obj.decode_batch_size
- params["decode_max_length"] = flags_obj.decode_max_length
- params["padded_decode"] = flags_obj.padded_decode
- params["max_io_parallelism"] = (
- flags_obj.num_parallel_calls or tf.data.experimental.AUTOTUNE)
-
- params["use_synthetic_data"] = flags_obj.use_synthetic_data
- params["batch_size"] = flags_obj.batch_size or params["default_batch_size"]
- params["repeat_dataset"] = None
- params["dtype"] = flags_core.get_tf_dtype(flags_obj)
- params["enable_tensorboard"] = flags_obj.enable_tensorboard
- params["enable_metrics_in_training"] = flags_obj.enable_metrics_in_training
- params["steps_between_evals"] = flags_obj.steps_between_evals
- params["enable_checkpointing"] = flags_obj.enable_checkpointing
- params["save_weights_only"] = flags_obj.save_weights_only
-
- self.distribution_strategy = distribute_utils.get_distribution_strategy(
- distribution_strategy=flags_obj.distribution_strategy,
- num_gpus=num_gpus,
- all_reduce_alg=flags_obj.all_reduce_alg,
- num_packs=flags_obj.num_packs,
- tpu_address=flags_obj.tpu or "")
- if self.use_tpu:
- params["num_replicas"] = self.distribution_strategy.num_replicas_in_sync
- else:
- logging.info("Running transformer with num_gpus = %d", num_gpus)
-
- if self.distribution_strategy:
- logging.info("For training, using distribution strategy: %s",
- self.distribution_strategy)
- else:
- logging.info("Not using any distribution strategy.")
-
- performance.set_mixed_precision_policy(params["dtype"])
-
- @property
- def use_tpu(self):
- if self.distribution_strategy:
- return isinstance(self.distribution_strategy, tf.distribute.TPUStrategy)
- return False
-
- def train(self):
- """Trains the model."""
- params = self.params
- flags_obj = self.flags_obj
- # Sets config options.
- keras_utils.set_session_config(enable_xla=flags_obj.enable_xla)
-
- _ensure_dir(flags_obj.model_dir)
- with distribute_utils.get_strategy_scope(self.distribution_strategy):
- model = transformer.create_model(params, is_train=True)
- opt = self._create_optimizer()
-
- current_step = 0
- checkpoint = tf.train.Checkpoint(model=model, optimizer=opt)
- latest_checkpoint = tf.train.latest_checkpoint(flags_obj.model_dir)
- if latest_checkpoint:
- checkpoint.restore(latest_checkpoint)
- logging.info("Loaded checkpoint %s", latest_checkpoint)
- current_step = opt.iterations.numpy()
-
- if params["use_ctl"]:
- train_loss_metric = tf.keras.metrics.Mean(
- "training_loss", dtype=tf.float32)
- if params["enable_tensorboard"]:
- summary_writer = tf.summary.create_file_writer(
- os.path.join(flags_obj.model_dir, "summary"))
- else:
- summary_writer = tf.summary.create_noop_writer()
- train_metrics = [train_loss_metric]
- if params["enable_metrics_in_training"]:
- train_metrics = train_metrics + model.metrics
- else:
- model.compile(opt)
-
- model.summary()
-
- if self.use_tpu:
- # Different from experimental_distribute_dataset,
- # distribute_datasets_from_function requires
- # per-replica/local batch size.
- params["batch_size"] /= self.distribution_strategy.num_replicas_in_sync
- train_ds = (
- self.distribution_strategy.distribute_datasets_from_function(
- lambda ctx: data_pipeline.train_input_fn(params, ctx)))
- else:
- train_ds = data_pipeline.train_input_fn(params)
- map_data_fn = data_pipeline.map_data_for_transformer_fn
- train_ds = train_ds.map(
- map_data_fn, num_parallel_calls=tf.data.experimental.AUTOTUNE)
- if params["use_ctl"]:
- train_ds_iterator = iter(train_ds)
-
- callbacks = self._create_callbacks(flags_obj.model_dir, params)
-
- # Only TimeHistory callback is supported for CTL
- if params["use_ctl"]:
- callbacks = [cb for cb in callbacks
- if isinstance(cb, keras_utils.TimeHistory)]
-
- @tf.function
- def train_steps(iterator, steps):
- """Training steps function for TPU runs.
-
- Args:
- iterator: The input iterator of the training dataset.
- steps: An integer, the number of training steps.
-
- Returns:
- A float, the loss value.
- """
-
- def _step_fn(inputs):
- """Per-replica step function."""
- inputs, targets = inputs
- with tf.GradientTape() as tape:
- logits = model([inputs, targets], training=True)
- loss = metrics.transformer_loss(logits, targets,
- params["label_smoothing"],
- params["vocab_size"])
- # Scales the loss, which results in using the average loss across all
- # of the replicas for backprop.
- scaled_loss = loss / self.distribution_strategy.num_replicas_in_sync
-
- # De-dupes variables due to keras tracking issues.
- tvars = list({id(v): v for v in model.trainable_variables}.values())
- grads = tape.gradient(scaled_loss, tvars)
- opt.apply_gradients(zip(grads, tvars))
- # For reporting, the metric takes the mean of losses.
- train_loss_metric.update_state(loss)
-
- for _ in tf.range(steps):
- train_loss_metric.reset_states()
- self.distribution_strategy.run(
- _step_fn, args=(next(iterator),))
-
- cased_score, uncased_score = None, None
- cased_score_history, uncased_score_history = [], []
- while current_step < flags_obj.train_steps:
- remaining_steps = flags_obj.train_steps - current_step
- train_steps_per_eval = (
- remaining_steps if remaining_steps < flags_obj.steps_between_evals
- else flags_obj.steps_between_evals)
- current_iteration = current_step // flags_obj.steps_between_evals
-
- logging.info(
- "Start train iteration at global step:{}".format(current_step))
- history = None
- if params["use_ctl"]:
- if not self.use_tpu:
- raise NotImplementedError(
- "Custom training loop on GPUs is not implemented.")
-
- # Runs training steps.
- with summary_writer.as_default():
- for cb in callbacks:
- cb.on_epoch_begin(current_iteration)
- cb.on_batch_begin(0)
-
- train_steps(
- train_ds_iterator,
- tf.convert_to_tensor(train_steps_per_eval, dtype=tf.int32))
- current_step += train_steps_per_eval
- train_loss = train_loss_metric.result().numpy().astype(float)
- logging.info("Train Step: %d/%d / loss = %s", current_step,
- flags_obj.train_steps, train_loss)
-
- for cb in callbacks:
- cb.on_batch_end(train_steps_per_eval - 1)
- cb.on_epoch_end(current_iteration)
-
- if params["enable_tensorboard"]:
- for metric_obj in train_metrics:
- tf.summary.scalar(metric_obj.name, metric_obj.result(),
- current_step)
- summary_writer.flush()
-
- for cb in callbacks:
- cb.on_train_end()
-
- if flags_obj.enable_checkpointing:
- # avoid check-pointing when running for benchmarking.
- checkpoint_name = checkpoint.save(
- os.path.join(flags_obj.model_dir,
- "ctl_step_{}.ckpt".format(current_step)))
- logging.info("Saved checkpoint to %s", checkpoint_name)
- else:
- if self.use_tpu:
- raise NotImplementedError(
- "Keras model.fit on TPUs is not implemented.")
- history = model.fit(
- train_ds,
- initial_epoch=current_iteration,
- epochs=current_iteration + 1,
- steps_per_epoch=train_steps_per_eval,
- callbacks=callbacks,
- # If TimeHistory is enabled, progress bar would be messy. Increase
- # the verbose level to get rid of it.
- verbose=(2 if flags_obj.enable_time_history else 1))
- current_step += train_steps_per_eval
- logging.info("Train history: {}".format(history.history))
-
- logging.info("End train iteration at global step:{}".format(current_step))
-
- if (flags_obj.bleu_source and flags_obj.bleu_ref):
- uncased_score, cased_score = self.eval()
- cased_score_history.append([current_iteration + 1, cased_score])
- uncased_score_history.append([current_iteration + 1, uncased_score])
-
- stats = ({
- "loss": train_loss
- } if history is None else {})
- misc.update_stats(history, stats, callbacks)
- if uncased_score and cased_score:
- stats["bleu_uncased"] = uncased_score
- stats["bleu_cased"] = cased_score
- stats["bleu_uncased_history"] = uncased_score_history
- stats["bleu_cased_history"] = cased_score_history
- return stats
-
- def eval(self):
- """Evaluates the model."""
- distribution_strategy = self.distribution_strategy if self.use_tpu else None
-
- # We only want to create the model under DS scope for TPU case.
- # When 'distribution_strategy' is None, a no-op DummyContextManager will
- # be used.
- with distribute_utils.get_strategy_scope(distribution_strategy):
- if not self.predict_model:
- self.predict_model = transformer.create_model(self.params, False)
- self._load_weights_if_possible(
- self.predict_model,
- tf.train.latest_checkpoint(self.flags_obj.model_dir))
- self.predict_model.summary()
- return evaluate_and_log_bleu(
- self.predict_model, self.params, self.flags_obj.bleu_source,
- self.flags_obj.bleu_ref, self.flags_obj.vocab_file,
- distribution_strategy)
-
- def predict(self):
- """Predicts result from the model."""
- params = self.params
- flags_obj = self.flags_obj
-
- with tf.name_scope("model"):
- model = transformer.create_model(params, is_train=False)
- self._load_weights_if_possible(
- model, tf.train.latest_checkpoint(self.flags_obj.model_dir))
- model.summary()
- subtokenizer = tokenizer.Subtokenizer(flags_obj.vocab_file)
-
- ds = data_pipeline.eval_input_fn(params)
- ds = ds.map(lambda x, y: x).take(_SINGLE_SAMPLE)
- ret = model.predict(ds)
- val_outputs, _ = ret
- length = len(val_outputs)
- for i in range(length):
- translate.translate_from_input(val_outputs[i], subtokenizer)
-
- def _create_callbacks(self, cur_log_dir, params):
- """Creates a list of callbacks."""
- callbacks = misc.get_callbacks()
- if params["enable_checkpointing"]:
- ckpt_full_path = os.path.join(cur_log_dir, "cp-{epoch:04d}.ckpt")
- callbacks.append(
- tf.keras.callbacks.ModelCheckpoint(
- ckpt_full_path, save_weights_only=params["save_weights_only"]))
- return callbacks
-
- def _load_weights_if_possible(self, model, init_weight_path=None):
- """Loads model weights when it is provided."""
- if init_weight_path:
- logging.info("Load weights: {}".format(init_weight_path))
- if self.use_tpu:
- checkpoint = tf.train.Checkpoint(
- model=model, optimizer=self._create_optimizer())
- checkpoint.restore(init_weight_path)
- else:
- model.load_weights(init_weight_path)
- else:
- logging.info("Weights not loaded from path:{}".format(init_weight_path))
-
- def _create_optimizer(self):
- """Creates optimizer."""
- params = self.params
- lr_schedule = optimizer.LearningRateSchedule(
- params["learning_rate"], params["hidden_size"],
- params["learning_rate_warmup_steps"])
- opt = tf.keras.optimizers.Adam(
- lr_schedule,
- params["optimizer_adam_beta1"],
- params["optimizer_adam_beta2"],
- epsilon=params["optimizer_adam_epsilon"])
-
- opt = performance.configure_optimizer(
- opt,
- use_float16=params["dtype"] == tf.float16,
- loss_scale=flags_core.get_loss_scale(
- self.flags_obj, default_for_fp16="dynamic"))
-
- return opt
-
-
-def _ensure_dir(log_dir):
- """Makes log dir if not existed."""
- if not tf.io.gfile.exists(log_dir):
- tf.io.gfile.makedirs(log_dir)
-
-
-def main(_):
- flags_obj = flags.FLAGS
- if flags_obj.enable_mlir_bridge:
- tf.config.experimental.enable_mlir_bridge()
- task = TransformerTask(flags_obj)
-
- # Execute flag override logic for better model performance
- if flags_obj.tf_gpu_thread_mode:
- keras_utils.set_gpu_thread_mode_and_count(
- per_gpu_thread_count=flags_obj.per_gpu_thread_count,
- gpu_thread_mode=flags_obj.tf_gpu_thread_mode,
- num_gpus=flags_obj.num_gpus,
- datasets_num_private_threads=flags_obj.datasets_num_private_threads)
-
- if flags_obj.mode == "train":
- task.train()
- elif flags_obj.mode == "predict":
- task.predict()
- elif flags_obj.mode == "eval":
- task.eval()
- else:
- raise ValueError("Invalid mode {}".format(flags_obj.mode))
-
-
-if __name__ == "__main__":
- logging.set_verbosity(logging.INFO)
- misc.define_transformer_flags()
- app.run(main)
diff --git a/official/nlp/transformer/transformer_main_test.py b/official/nlp/transformer/transformer_main_test.py
deleted file mode 100644
index 79f4e17dc64f5c7d05331116d32c0be4d0f99dc0..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer_main_test.py
+++ /dev/null
@@ -1,193 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Test Transformer model."""
-
-import os
-import re
-import sys
-import unittest
-
-from absl import flags
-from absl.testing import flagsaver
-import tensorflow as tf
-from tensorflow.python.eager import context # pylint: disable=ungrouped-imports
-from official.nlp.transformer import misc
-from official.nlp.transformer import transformer_main
-
-FLAGS = flags.FLAGS
-FIXED_TIMESTAMP = 'my_time_stamp'
-WEIGHT_PATTERN = re.compile(r'weights-epoch-.+\.hdf5')
-
-
-def _generate_file(filepath, lines):
- with open(filepath, 'w') as f:
- for l in lines:
- f.write('{}\n'.format(l))
-
-
-class TransformerTaskTest(tf.test.TestCase):
- local_flags = None
-
- def setUp(self): # pylint: disable=g-missing-super-call
- temp_dir = self.get_temp_dir()
- if TransformerTaskTest.local_flags is None:
- misc.define_transformer_flags()
- # Loads flags, array cannot be blank.
- flags.FLAGS(['foo'])
- TransformerTaskTest.local_flags = flagsaver.save_flag_values()
- else:
- flagsaver.restore_flag_values(TransformerTaskTest.local_flags)
- FLAGS.model_dir = os.path.join(temp_dir, FIXED_TIMESTAMP)
- FLAGS.param_set = 'tiny'
- FLAGS.use_synthetic_data = True
- FLAGS.steps_between_evals = 1
- FLAGS.train_steps = 1
- FLAGS.validation_steps = 1
- FLAGS.batch_size = 4
- FLAGS.max_length = 1
- FLAGS.num_gpus = 1
- FLAGS.distribution_strategy = 'off'
- FLAGS.dtype = 'fp32'
- self.model_dir = FLAGS.model_dir
- self.temp_dir = temp_dir
- self.vocab_file = os.path.join(temp_dir, 'vocab')
- self.vocab_size = misc.get_model_params(FLAGS.param_set, 0)['vocab_size']
- self.bleu_source = os.path.join(temp_dir, 'bleu_source')
- self.bleu_ref = os.path.join(temp_dir, 'bleu_ref')
- self.orig_policy = (
- tf.compat.v2.keras.mixed_precision.global_policy())
-
- def tearDown(self): # pylint: disable=g-missing-super-call
- tf.compat.v2.keras.mixed_precision.set_global_policy(self.orig_policy)
-
- def _assert_exists(self, filepath):
- self.assertTrue(os.path.exists(filepath))
-
- def test_train_no_dist_strat(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- def test_train_save_full_model(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- FLAGS.save_weights_only = False
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- def test_train_static_batch(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- FLAGS.distribution_strategy = 'one_device'
- if tf.test.is_built_with_cuda():
- FLAGS.num_gpus = 1
- else:
- FLAGS.num_gpus = 0
- FLAGS.static_batch = True
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- @unittest.skipUnless(tf.test.is_built_with_cuda(), 'requires GPU')
- def test_train_1_gpu_with_dist_strat(self):
- FLAGS.distribution_strategy = 'one_device'
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- @unittest.skipUnless(tf.test.is_built_with_cuda(), 'requires GPU')
- def test_train_fp16(self):
- FLAGS.distribution_strategy = 'one_device'
- FLAGS.dtype = 'fp16'
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- @unittest.skipUnless(tf.test.is_built_with_cuda(), 'requires GPU')
- def test_train_2_gpu(self):
- if context.num_gpus() < 2:
- self.skipTest(
- '{} GPUs are not available for this test. {} GPUs are available'
- .format(2, context.num_gpus()))
- FLAGS.distribution_strategy = 'mirrored'
- FLAGS.num_gpus = 2
- FLAGS.param_set = 'base'
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- @unittest.skipUnless(tf.test.is_built_with_cuda(), 'requires GPU')
- def test_train_2_gpu_fp16(self):
- if context.num_gpus() < 2:
- self.skipTest(
- '{} GPUs are not available for this test. {} GPUs are available'
- .format(2, context.num_gpus()))
- FLAGS.distribution_strategy = 'mirrored'
- FLAGS.num_gpus = 2
- FLAGS.param_set = 'base'
- FLAGS.dtype = 'fp16'
- t = transformer_main.TransformerTask(FLAGS)
- t.train()
-
- def _prepare_files_and_flags(self, *extra_flags):
- # Make log dir.
- if not os.path.exists(self.temp_dir):
- os.makedirs(self.temp_dir)
-
- # Fake vocab, bleu_source and bleu_ref.
- tokens = [
- "''", "''", "'_'", "'a'", "'b'", "'c'", "'d'", "'a_'", "'b_'",
- "'c_'", "'d_'"
- ]
- tokens += ["'{}'".format(i) for i in range(self.vocab_size - len(tokens))]
- _generate_file(self.vocab_file, tokens)
- _generate_file(self.bleu_source, ['a b', 'c d'])
- _generate_file(self.bleu_ref, ['a b', 'd c'])
-
- # Update flags.
- update_flags = [
- 'ignored_program_name',
- '--vocab_file={}'.format(self.vocab_file),
- '--bleu_source={}'.format(self.bleu_source),
- '--bleu_ref={}'.format(self.bleu_ref),
- ]
- if extra_flags:
- update_flags.extend(extra_flags)
- FLAGS(update_flags)
-
- def test_predict(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- self._prepare_files_and_flags()
- t = transformer_main.TransformerTask(FLAGS)
- t.predict()
-
- @unittest.skipUnless(tf.test.is_built_with_cuda(), 'requires GPU')
- def test_predict_fp16(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- self._prepare_files_and_flags('--dtype=fp16')
- t = transformer_main.TransformerTask(FLAGS)
- t.predict()
-
- def test_eval(self):
- if context.num_gpus() >= 2:
- self.skipTest('No need to test 2+ GPUs without a distribution strategy.')
- if 'test_xla' in sys.argv[0]:
- self.skipTest('TODO(xla): Make this test faster under XLA.')
- self._prepare_files_and_flags()
- t = transformer_main.TransformerTask(FLAGS)
- t.eval()
-
-
-if __name__ == '__main__':
- tf.test.main()
diff --git a/official/nlp/transformer/transformer_test.py b/official/nlp/transformer/transformer_test.py
deleted file mode 100644
index c64686dac034c5d0e1d4f29bf4b378f2b64ef130..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/transformer_test.py
+++ /dev/null
@@ -1,98 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Test Transformer model."""
-
-import tensorflow as tf
-
-from official.nlp.transformer import model_params
-from official.nlp.transformer import transformer
-
-
-class TransformerV2Test(tf.test.TestCase):
-
- def setUp(self):
- super().setUp()
- self.params = params = model_params.TINY_PARAMS
- params["batch_size"] = params["default_batch_size"] = 16
- params["use_synthetic_data"] = True
- params["hidden_size"] = 12
- params["num_hidden_layers"] = 2
- params["filter_size"] = 14
- params["num_heads"] = 2
- params["vocab_size"] = 41
- params["extra_decode_length"] = 2
- params["beam_size"] = 3
- params["dtype"] = tf.float32
-
- def test_create_model_train(self):
- model = transformer.create_model(self.params, True)
- inputs, outputs = model.inputs, model.outputs
- self.assertEqual(len(inputs), 2)
- self.assertEqual(len(outputs), 1)
- self.assertEqual(inputs[0].shape.as_list(), [None, None])
- self.assertEqual(inputs[0].dtype, tf.int64)
- self.assertEqual(inputs[1].shape.as_list(), [None, None])
- self.assertEqual(inputs[1].dtype, tf.int64)
- self.assertEqual(outputs[0].shape.as_list(), [None, None, 41])
- self.assertEqual(outputs[0].dtype, tf.float32)
-
- def test_create_model_not_train(self):
- model = transformer.create_model(self.params, False)
- inputs, outputs = model.inputs, model.outputs
- self.assertEqual(len(inputs), 1)
- self.assertEqual(len(outputs), 2)
- self.assertEqual(inputs[0].shape.as_list(), [None, None])
- self.assertEqual(inputs[0].dtype, tf.int64)
- self.assertEqual(outputs[0].shape.as_list(), [None, None])
- self.assertEqual(outputs[0].dtype, tf.int32)
- self.assertEqual(outputs[1].shape.as_list(), [None])
- self.assertEqual(outputs[1].dtype, tf.float32)
-
- def test_export(self):
- model = transformer.Transformer(self.params, name="transformer_v2")
- export_dir = self.get_temp_dir()
- batch_size = 5
- max_length = 6
-
- class SaveModule(tf.Module):
-
- def __init__(self, model):
- super(SaveModule, self).__init__()
- self.model = model
-
- @tf.function
- def serve(self, x):
- return self.model.call([x], training=False)
-
- save_module = SaveModule(model)
- tensor_shape = (None, None)
- sample_input = tf.zeros((batch_size, max_length), dtype=tf.int64)
- _ = save_module.serve(sample_input)
- signatures = dict(
- serving_default=save_module.serve.get_concrete_function(
- tf.TensorSpec(shape=tensor_shape, dtype=tf.int64, name="x")))
- tf.saved_model.save(save_module, export_dir, signatures=signatures)
- imported = tf.saved_model.load(export_dir)
- serving_fn = imported.signatures["serving_default"]
- all_outputs = serving_fn(sample_input)
- output = all_outputs["outputs"]
- output_shapes = output.shape.as_list()
- self.assertEqual(output_shapes[0], batch_size)
- self.assertEqual(output_shapes[1],
- max_length + model.params["extra_decode_length"])
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/transformer/translate.py b/official/nlp/transformer/translate.py
deleted file mode 100644
index 0c15096aed6b33fea0beb2f0ff76daf1737e09bb..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/translate.py
+++ /dev/null
@@ -1,190 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Translate text or files using trained transformer model."""
-
-# Import libraries
-from absl import logging
-import numpy as np
-import tensorflow as tf
-
-from official.nlp.transformer.utils import tokenizer
-
-_EXTRA_DECODE_LENGTH = 100
-_BEAM_SIZE = 4
-_ALPHA = 0.6
-
-
-def _get_sorted_inputs(filename):
- """Read and sort lines from the file sorted by decreasing length.
-
- Args:
- filename: String name of file to read inputs from.
- Returns:
- Sorted list of inputs, and dictionary mapping original index->sorted index
- of each element.
- """
- with tf.io.gfile.GFile(filename) as f:
- records = f.read().split("\n")
- inputs = [record.strip() for record in records]
- if not inputs[-1]:
- inputs.pop()
-
- input_lens = [(i, len(line.split())) for i, line in enumerate(inputs)]
- sorted_input_lens = sorted(input_lens, key=lambda x: x[1], reverse=True)
-
- sorted_inputs = [None] * len(sorted_input_lens)
- sorted_keys = [0] * len(sorted_input_lens)
- for i, (index, _) in enumerate(sorted_input_lens):
- sorted_inputs[i] = inputs[index]
- sorted_keys[index] = i
- return sorted_inputs, sorted_keys
-
-
-def _encode_and_add_eos(line, subtokenizer):
- """Encode line with subtokenizer, and add EOS id to the end."""
- return subtokenizer.encode(line) + [tokenizer.EOS_ID]
-
-
-def _trim_and_decode(ids, subtokenizer):
- """Trim EOS and PAD tokens from ids, and decode to return a string."""
- try:
- index = list(ids).index(tokenizer.EOS_ID)
- return subtokenizer.decode(ids[:index])
- except ValueError: # No EOS found in sequence
- return subtokenizer.decode(ids)
-
-
-def translate_file(model,
- params,
- subtokenizer,
- input_file,
- output_file=None,
- print_all_translations=True,
- distribution_strategy=None):
- """Translate lines in file, and save to output file if specified.
-
- Args:
- model: A Keras model, used to generate the translations.
- params: A dictionary, containing the translation related parameters.
- subtokenizer: A subtokenizer object, used for encoding and decoding source
- and translated lines.
- input_file: A file containing lines to translate.
- output_file: A file that stores the generated translations.
- print_all_translations: A bool. If true, all translations are printed to
- stdout.
- distribution_strategy: A distribution strategy, used to perform inference
- directly with tf.function instead of Keras model.predict().
-
- Raises:
- ValueError: if output file is invalid.
- """
- batch_size = params["decode_batch_size"]
-
- # Read and sort inputs by length. Keep dictionary (original index-->new index
- # in sorted list) to write translations in the original order.
- sorted_inputs, sorted_keys = _get_sorted_inputs(input_file)
- total_samples = len(sorted_inputs)
- num_decode_batches = (total_samples - 1) // batch_size + 1
-
- def input_generator():
- """Yield encoded strings from sorted_inputs."""
- for i in range(num_decode_batches):
- lines = [
- sorted_inputs[j + i * batch_size]
- for j in range(batch_size)
- if j + i * batch_size < total_samples
- ]
- lines = [_encode_and_add_eos(l, subtokenizer) for l in lines]
- if distribution_strategy:
- for j in range(batch_size - len(lines)):
- lines.append([tokenizer.EOS_ID])
- batch = tf.keras.preprocessing.sequence.pad_sequences(
- lines,
- maxlen=params["decode_max_length"],
- dtype="int32",
- padding="post")
- logging.info("Decoding batch %d out of %d.", i, num_decode_batches)
- yield batch
-
- @tf.function
- def predict_step(inputs):
- """Decoding step function for TPU runs."""
-
- def _step_fn(inputs):
- """Per replica step function."""
- tag = inputs[0]
- val_inputs = inputs[1]
- val_outputs, _ = model([val_inputs], training=False)
- return tag, val_outputs
-
- return distribution_strategy.run(_step_fn, args=(inputs,))
-
- translations = []
- if distribution_strategy:
- num_replicas = distribution_strategy.num_replicas_in_sync
- local_batch_size = params["decode_batch_size"] // num_replicas
- for i, text in enumerate(input_generator()):
- if distribution_strategy:
- text = np.reshape(text, [num_replicas, local_batch_size, -1])
- # Add tag to the input of each replica with the reordering logic after
- # outputs, to ensure the output order matches the input order.
- text = tf.constant(text)
-
- @tf.function
- def text_as_per_replica():
- replica_context = tf.distribute.get_replica_context()
- replica_id = replica_context.replica_id_in_sync_group
- return replica_id, text[replica_id] # pylint: disable=cell-var-from-loop
-
- text = distribution_strategy.run(text_as_per_replica)
- outputs = distribution_strategy.experimental_local_results(
- predict_step(text))
- val_outputs = [output for _, output in outputs]
-
- val_outputs = np.reshape(val_outputs, [params["decode_batch_size"], -1])
- else:
- val_outputs, _ = model.predict(text)
-
- length = len(val_outputs)
- for j in range(length):
- if j + i * batch_size < total_samples:
- translation = _trim_and_decode(val_outputs[j], subtokenizer)
- translations.append(translation)
- if print_all_translations:
- logging.info("Translating:\n\tInput: %s\n\tOutput: %s",
- sorted_inputs[j + i * batch_size], translation)
-
- # Write translations in the order they appeared in the original file.
- if output_file is not None:
- if tf.io.gfile.isdir(output_file):
- raise ValueError("File output is a directory, will not save outputs to "
- "file.")
- logging.info("Writing to file %s", output_file)
- with tf.io.gfile.GFile(output_file, "w") as f:
- for i in sorted_keys:
- f.write("%s\n" % translations[i])
-
-
-def translate_from_text(model, subtokenizer, txt):
- encoded_txt = _encode_and_add_eos(txt, subtokenizer)
- result = model.predict(encoded_txt)
- outputs = result["outputs"]
- logging.info("Original: \"%s\"", txt)
- translate_from_input(outputs, subtokenizer)
-
-
-def translate_from_input(outputs, subtokenizer):
- translation = _trim_and_decode(outputs, subtokenizer)
- logging.info("Translation: \"%s\"", translation)
diff --git a/official/nlp/transformer/utils/__init__.py b/official/nlp/transformer/utils/__init__.py
deleted file mode 100644
index e419af524b5f349fe04abfa820c3cb51b777d422..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/utils/__init__.py
+++ /dev/null
@@ -1,14 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
diff --git a/official/nlp/transformer/utils/metrics.py b/official/nlp/transformer/utils/metrics.py
deleted file mode 100644
index ec1cad0b409cfb69535dce15fab1d531d7811391..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/utils/metrics.py
+++ /dev/null
@@ -1,491 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Functions for calculating loss, accuracy, and other model metrics.
-
-Metrics:
- - Padded loss, accuracy, and negative log perplexity. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/metrics.py
- - BLEU approximation. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/bleu_hook.py
- - ROUGE score. Source:
- https://github.com/tensorflow/tensor2tensor/blob/master/tensor2tensor/utils/rouge.py
-"""
-
-from __future__ import absolute_import
-from __future__ import division
-from __future__ import print_function
-
-import collections
-import math
-
-import numpy as np
-import six
-from six.moves import xrange # pylint: disable=redefined-builtin
-import tensorflow.compat.v1 as tf
-
-
-def _pad_tensors_to_same_length(x, y):
- """Pad x and y so that the results have the same length (second dimension)."""
- with tf.name_scope("pad_to_same_length"):
- x_length = tf.shape(x)[1]
- y_length = tf.shape(y)[1]
-
- max_length = tf.maximum(x_length, y_length)
-
- x = tf.pad(x, [[0, 0], [0, max_length - x_length], [0, 0]])
- y = tf.pad(y, [[0, 0], [0, max_length - y_length]])
- return x, y
-
-
-def padded_cross_entropy_loss(logits, labels, smoothing, vocab_size):
- """Calculate cross entropy loss while ignoring padding.
-
- Args:
- logits: Tensor of size [batch_size, length_logits, vocab_size]
- labels: Tensor of size [batch_size, length_labels]
- smoothing: Label smoothing constant, used to determine the on and off values
- vocab_size: int size of the vocabulary
- Returns:
- Returns the cross entropy loss and weight tensors: float32 tensors with
- shape [batch_size, max(length_logits, length_labels)]
- """
- with tf.name_scope("loss", values=[logits, labels]):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
-
- # Calculate smoothing cross entropy
- with tf.name_scope("smoothing_cross_entropy", values=[logits, labels]):
- confidence = 1.0 - smoothing
- low_confidence = (1.0 - confidence) / tf.cast(vocab_size - 1, tf.float32)
- soft_targets = tf.one_hot(
- tf.cast(labels, tf.int32),
- depth=vocab_size,
- on_value=confidence,
- off_value=low_confidence)
- xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(
- logits=logits, labels=soft_targets)
-
- # Calculate the best (lowest) possible value of cross entropy, and
- # subtract from the cross entropy loss.
- normalizing_constant = -(
- confidence * tf.log(confidence) + tf.cast(vocab_size - 1, tf.float32)
- * low_confidence * tf.log(low_confidence + 1e-20))
- xentropy -= normalizing_constant
-
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- return xentropy * weights, weights
-
-
-def _convert_to_eval_metric(metric_fn):
- """Wrap a metric fn that returns scores and weights as an eval metric fn.
-
- The input metric_fn returns values for the current batch. The wrapper
- aggregates the return values collected over all of the batches evaluated.
-
- Args:
- metric_fn: function that returns scores and weights for the current batch's
- logits and predicted labels.
-
- Returns:
- function that aggregates the scores and weights from metric_fn.
- """
- def problem_metric_fn(*args):
- """Returns an aggregation of the metric_fn's returned values."""
- (scores, weights) = metric_fn(*args)
-
- # The tf.metrics.mean function assures correct aggregation.
- return tf.metrics.mean(scores, weights)
- return problem_metric_fn
-
-
-def get_eval_metrics(logits, labels, params):
- """Return dictionary of model evaluation metrics."""
- metrics = {
- "accuracy": _convert_to_eval_metric(padded_accuracy)(logits, labels),
- "accuracy_top5": _convert_to_eval_metric(padded_accuracy_top5)(
- logits, labels),
- "accuracy_per_sequence": _convert_to_eval_metric(
- padded_sequence_accuracy)(logits, labels),
- "neg_log_perplexity": _convert_to_eval_metric(padded_neg_log_perplexity)(
- logits, labels, params["vocab_size"]),
- }
-
- if not params["use_tpu"]:
- # TPU does not support tf.py_func
- metrics.update({
- "approx_bleu_score": _convert_to_eval_metric(
- bleu_score)(logits, labels),
- "rouge_2_fscore": _convert_to_eval_metric(
- rouge_2_fscore)(logits, labels),
- "rouge_L_fscore": _convert_to_eval_metric(
- rouge_l_fscore)(logits, labels),
- })
-
- # Prefix each of the metric names with "metrics/". This allows the metric
- # graphs to display under the "metrics" category in TensorBoard.
- metrics = {"metrics/%s" % k: v for k, v in six.iteritems(metrics)}
- return metrics
-
-
-def padded_accuracy(logits, labels):
- """Percentage of times that predictions matches labels on non-0s."""
- with tf.variable_scope("padded_accuracy", values=[logits, labels]):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- outputs = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- return tf.cast(tf.equal(outputs, padded_labels), tf.float32), weights
-
-
-def padded_accuracy_topk(logits, labels, k):
- """Percentage of times that top-k predictions matches labels on non-0s."""
- with tf.variable_scope("padded_accuracy_topk", values=[logits, labels]):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- effective_k = tf.minimum(k, tf.shape(logits)[-1])
- _, outputs = tf.nn.top_k(logits, k=effective_k)
- outputs = tf.cast(outputs, tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- padded_labels = tf.expand_dims(padded_labels, axis=-1)
- padded_labels += tf.zeros_like(outputs) # Pad to same shape.
- same = tf.cast(tf.equal(outputs, padded_labels), tf.float32)
- same_topk = tf.reduce_sum(same, axis=-1)
- return same_topk, weights
-
-
-def padded_accuracy_top5(logits, labels):
- return padded_accuracy_topk(logits, labels, 5)
-
-
-def padded_sequence_accuracy(logits, labels):
- """Percentage of times that predictions matches labels everywhere (non-0)."""
- with tf.variable_scope("padded_sequence_accuracy", values=[logits, labels]):
- logits, labels = _pad_tensors_to_same_length(logits, labels)
- weights = tf.cast(tf.not_equal(labels, 0), tf.float32)
- outputs = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- padded_labels = tf.cast(labels, tf.int32)
- not_correct = (tf.cast(tf.not_equal(outputs, padded_labels), tf.float32) *
- weights)
- axis = list(range(1, len(outputs.get_shape())))
- correct_seq = 1.0 - tf.minimum(1.0, tf.reduce_sum(not_correct, axis=axis))
- return correct_seq, tf.constant(1.0)
-
-
-def padded_neg_log_perplexity(logits, labels, vocab_size):
- """Average log-perplexity excluding padding 0s. No smoothing."""
- num, den = padded_cross_entropy_loss(logits, labels, 0, vocab_size)
- return -num, den
-
-
-def bleu_score(logits, labels):
- """Approximate BLEU score computation between labels and predictions.
-
- An approximate BLEU scoring method since we do not glue word pieces or
- decode the ids and tokenize the output. By default, we use ngram order of 4
- and use brevity penalty. Also, this does not have beam search.
-
- Args:
- logits: Tensor of size [batch_size, length_logits, vocab_size]
- labels: Tensor of size [batch-size, length_labels]
-
- Returns:
- bleu: int, approx bleu score
- """
- predictions = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- # TODO: Look into removing use of py_func # pylint: disable=g-bad-todo
- bleu = tf.py_func(compute_bleu, (labels, predictions), tf.float32)
- return bleu, tf.constant(1.0)
-
-
-def _get_ngrams_with_counter(segment, max_order):
- """Extracts all n-grams up to a given maximum order from an input segment.
-
- Args:
- segment: text segment from which n-grams will be extracted.
- max_order: maximum length in tokens of the n-grams returned by this
- methods.
-
- Returns:
- The Counter containing all n-grams upto max_order in segment
- with a count of how many times each n-gram occurred.
- """
- ngram_counts = collections.Counter()
- for order in xrange(1, max_order + 1):
- for i in xrange(0, len(segment) - order + 1):
- ngram = tuple(segment[i:i + order])
- ngram_counts[ngram] += 1
- return ngram_counts
-
-
-def compute_bleu(reference_corpus, translation_corpus, max_order=4,
- use_bp=True):
- """Computes BLEU score of translated segments against one or more references.
-
- Args:
- reference_corpus: list of references for each translation. Each
- reference should be tokenized into a list of tokens.
- translation_corpus: list of translations to score. Each translation
- should be tokenized into a list of tokens.
- max_order: Maximum n-gram order to use when computing BLEU score.
- use_bp: boolean, whether to apply brevity penalty.
-
- Returns:
- BLEU score.
- """
- reference_length = 0
- translation_length = 0
- bp = 1.0
- geo_mean = 0
-
- matches_by_order = [0] * max_order
- possible_matches_by_order = [0] * max_order
- precisions = []
-
- for (references, translations) in zip(reference_corpus, translation_corpus):
- reference_length += len(references)
- translation_length += len(translations)
- ref_ngram_counts = _get_ngrams_with_counter(references, max_order)
- translation_ngram_counts = _get_ngrams_with_counter(translations, max_order)
-
- overlap = dict((ngram,
- min(count, translation_ngram_counts[ngram]))
- for ngram, count in ref_ngram_counts.items())
-
- for ngram in overlap:
- matches_by_order[len(ngram) - 1] += overlap[ngram]
- for ngram in translation_ngram_counts:
- possible_matches_by_order[len(ngram) - 1] += translation_ngram_counts[
- ngram]
-
- precisions = [0] * max_order
- smooth = 1.0
-
- for i in xrange(0, max_order):
- if possible_matches_by_order[i] > 0:
- precisions[i] = float(matches_by_order[i]) / possible_matches_by_order[i]
- if matches_by_order[i] > 0:
- precisions[i] = float(matches_by_order[i]) / possible_matches_by_order[
- i]
- else:
- smooth *= 2
- precisions[i] = 1.0 / (smooth * possible_matches_by_order[i])
- else:
- precisions[i] = 0.0
-
- if max(precisions) > 0:
- p_log_sum = sum(math.log(p) for p in precisions if p)
- geo_mean = math.exp(p_log_sum / max_order)
-
- if use_bp:
- ratio = translation_length / reference_length
- bp = math.exp(1 - 1. / ratio) if ratio < 1.0 else 1.0
- bleu = geo_mean * bp
- return np.float32(bleu)
-
-
-def rouge_2_fscore(logits, labels):
- """ROUGE-2 F1 score computation between labels and predictions.
-
- This is an approximate ROUGE scoring method since we do not glue word pieces
- or decode the ids and tokenize the output.
-
- Args:
- logits: tensor, model predictions
- labels: tensor, gold output.
-
- Returns:
- rouge2_fscore: approx rouge-2 f1 score.
- """
- predictions = tf.cast(tf.argmax(logits, axis=-1), tf.int32)
- # TODO: Look into removing use of py_func # pylint: disable=g-bad-todo
- rouge_2_f_score = tf.py_func(rouge_n, (predictions, labels), tf.float32)
- return rouge_2_f_score, tf.constant(1.0)
-
-
-def _get_ngrams(n, text):
- """Calculates n-grams.
-
- Args:
- n: which n-grams to calculate
- text: An array of tokens
-
- Returns:
- A set of n-grams
- """
- ngram_set = set()
- text_length = len(text)
- max_index_ngram_start = text_length - n
- for i in range(max_index_ngram_start + 1):
- ngram_set.add(tuple(text[i:i + n]))
- return ngram_set
-
-
-def rouge_n(eval_sentences, ref_sentences, n=2):
- """Computes ROUGE-N f1 score of two text collections of sentences.
-
- Source: https://www.microsoft.com/en-us/research/publication/
- rouge-a-package-for-automatic-evaluation-of-summaries/
-
- Args:
- eval_sentences: Predicted sentences.
- ref_sentences: Sentences from the reference set
- n: Size of ngram. Defaults to 2.
-
- Returns:
- f1 score for ROUGE-N
- """
- f1_scores = []
- for eval_sentence, ref_sentence in zip(eval_sentences, ref_sentences):
- eval_ngrams = _get_ngrams(n, eval_sentence)
- ref_ngrams = _get_ngrams(n, ref_sentence)
- ref_count = len(ref_ngrams)
- eval_count = len(eval_ngrams)
-
- # Count the overlapping ngrams between evaluated and reference
- overlapping_ngrams = eval_ngrams.intersection(ref_ngrams)
- overlapping_count = len(overlapping_ngrams)
-
- # Handle edge case. This isn't mathematically correct, but it's good enough
- if eval_count == 0:
- precision = 0.0
- else:
- precision = float(overlapping_count) / eval_count
- if ref_count == 0:
- recall = 0.0
- else:
- recall = float(overlapping_count) / ref_count
- f1_scores.append(2.0 * ((precision * recall) / (precision + recall + 1e-8)))
-
- # return overlapping_count / reference_count
- return np.mean(f1_scores, dtype=np.float32)
-
-
-def rouge_l_fscore(predictions, labels):
- """ROUGE scores computation between labels and predictions.
-
- This is an approximate ROUGE scoring method since we do not glue word pieces
- or decode the ids and tokenize the output.
-
- Args:
- predictions: tensor, model predictions
- labels: tensor, gold output.
-
- Returns:
- rouge_l_fscore: approx rouge-l f1 score.
- """
- outputs = tf.cast(tf.argmax(predictions, axis=-1), tf.int32)
- rouge_l_f_score = tf.py_func(rouge_l_sentence_level, (outputs, labels),
- tf.float32)
- return rouge_l_f_score, tf.constant(1.0)
-
-
-def rouge_l_sentence_level(eval_sentences, ref_sentences):
- """Computes ROUGE-L (sentence level) of two collections of sentences.
-
- Source: https://www.microsoft.com/en-us/research/publication/
- rouge-a-package-for-automatic-evaluation-of-summaries/
-
- Calculated according to:
- R_lcs = LCS(X,Y)/m
- P_lcs = LCS(X,Y)/n
- F_lcs = ((1 + beta^2)*R_lcs*P_lcs) / (R_lcs + (beta^2) * P_lcs)
-
- where:
- X = reference summary
- Y = Candidate summary
- m = length of reference summary
- n = length of candidate summary
-
- Args:
- eval_sentences: The sentences that have been picked by the summarizer
- ref_sentences: The sentences from the reference set
-
- Returns:
- A float: F_lcs
- """
-
- f1_scores = []
- for eval_sentence, ref_sentence in zip(eval_sentences, ref_sentences):
- m = float(len(ref_sentence))
- n = float(len(eval_sentence))
- lcs = _len_lcs(eval_sentence, ref_sentence)
- f1_scores.append(_f_lcs(lcs, m, n))
- return np.mean(f1_scores, dtype=np.float32)
-
-
-def _len_lcs(x, y):
- """Returns the length of the Longest Common Subsequence between two seqs.
-
- Source: http://www.algorithmist.com/index.php/Longest_Common_Subsequence
-
- Args:
- x: sequence of words
- y: sequence of words
-
- Returns
- integer: Length of LCS between x and y
- """
- table = _lcs(x, y)
- n, m = len(x), len(y)
- return table[n, m]
-
-
-def _lcs(x, y):
- """Computes the length of the LCS between two seqs.
-
- The implementation below uses a DP programming algorithm and runs
- in O(nm) time where n = len(x) and m = len(y).
- Source: http://www.algorithmist.com/index.php/Longest_Common_Subsequence
-
- Args:
- x: collection of words
- y: collection of words
-
- Returns:
- Table of dictionary of coord and len lcs
- """
- n, m = len(x), len(y)
- table = dict()
- for i in range(n + 1):
- for j in range(m + 1):
- if i == 0 or j == 0:
- table[i, j] = 0
- elif x[i - 1] == y[j - 1]:
- table[i, j] = table[i - 1, j - 1] + 1
- else:
- table[i, j] = max(table[i - 1, j], table[i, j - 1])
- return table
-
-
-def _f_lcs(llcs, m, n):
- """Computes the LCS-based F-measure score.
-
- Source: http://research.microsoft.com/en-us/um/people/cyl/download/papers/
- rouge-working-note-v1.3.1.pdf
-
- Args:
- llcs: Length of LCS
- m: number of words in reference summary
- n: number of words in candidate summary
-
- Returns:
- Float. LCS-based F-measure score
- """
- r_lcs = llcs / m
- p_lcs = llcs / n
- beta = p_lcs / (r_lcs + 1e-12)
- num = (1 + (beta ** 2)) * r_lcs * p_lcs
- denom = r_lcs + ((beta ** 2) * p_lcs)
- f_lcs = num / (denom + 1e-12)
- return f_lcs
diff --git a/official/nlp/transformer/utils/tokenizer.py b/official/nlp/transformer/utils/tokenizer.py
deleted file mode 100644
index 6a992a324f3b0c651d219f4f2cc081a274d87db4..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/utils/tokenizer.py
+++ /dev/null
@@ -1,660 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Defines Subtokenizer class to encode and decode strings."""
-
-from __future__ import absolute_import
-from __future__ import division
-from __future__ import print_function
-
-import collections
-import re
-import sys
-import unicodedata
-
-from absl import logging
-
-import numpy as np
-import six
-from six.moves import xrange # pylint: disable=redefined-builtin
-import tensorflow as tf
-
-# pylint: disable=g-complex-comprehension
-PAD = ""
-PAD_ID = 0
-EOS = ""
-EOS_ID = 1
-RESERVED_TOKENS = [PAD, EOS]
-
-# Set of characters that will be used in the function _escape_token() (see func
-# docstring for more details).
-# This set is added to the alphabet list to ensure that all escaped tokens can
-# be encoded.
-_ESCAPE_CHARS = set(u"\\_u;0123456789")
-# Regex for the function _unescape_token(), the inverse of _escape_token().
-# This is used to find "\u", "\\", and "\###;" substrings in the token.
-_UNESCAPE_REGEX = re.compile(r"\\u|\\\\|\\([0-9]+);")
-
-_UNDEFINED_UNICODE = u"\u3013"
-
-
-def alphanumeric_char_set():
- return set(
- six.unichr(i)
- for i in xrange(sys.maxunicode)
- if (unicodedata.category(six.unichr(i)).startswith("L") or
- unicodedata.category(six.unichr(i)).startswith("N")))
-
-
-# Set contains all letter and number characters.
-_ALPHANUMERIC_CHAR_SET = alphanumeric_char_set()
-
-# min_count is the minimum number of times a subtoken must appear in the data
-# before before it is added to the vocabulary. The value is found using binary
-# search to obtain the target vocabulary size.
-_MIN_MIN_COUNT = 1 # min value to use when binary searching for min_count
-_MAX_MIN_COUNT = 1000 # max value to use when binary searching for min_count
-
-
-class Subtokenizer(object):
- """Encodes and decodes strings to/from integer IDs."""
-
- def __init__(self, vocab_file, reserved_tokens=None, master_char_set=None):
- """Initializes class, creating a vocab file if data_files is provided."""
- logging.info("Initializing Subtokenizer from file %s.", vocab_file)
-
- if master_char_set is None:
- master_char_set = _ALPHANUMERIC_CHAR_SET
-
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- self.subtoken_list = _load_vocab_file(vocab_file, reserved_tokens)
- self.alphabet = _generate_alphabet_dict(self.subtoken_list)
- self.subtoken_to_id_dict = _list_to_index_dict(self.subtoken_list)
-
- self.max_subtoken_length = 0
- for subtoken in self.subtoken_list:
- self.max_subtoken_length = max(self.max_subtoken_length, len(subtoken))
-
- # Create cache to speed up subtokenization
- self._cache_size = 2**20
- self._cache = [(None, None)] * self._cache_size
- self._master_char_set = master_char_set
-
- @staticmethod
- def init_from_files(vocab_file,
- files,
- target_vocab_size,
- threshold,
- min_count=None,
- file_byte_limit=1e6,
- reserved_tokens=None,
- correct_strip=True,
- master_char_set=None):
- """Create subtoken vocabulary based on files, and save vocab to file.
-
- Args:
- vocab_file: String name of vocab file to store subtoken vocabulary.
- files: List of file paths that will be used to generate vocabulary.
- target_vocab_size: target vocabulary size to generate.
- threshold: int threshold of vocabulary size to accept.
- min_count: int minimum count to use for generating the vocabulary. The min
- count is the minimum number of times a subtoken should appear in the
- files before it is added to the vocabulary. If set to none, this value
- is found using binary search.
- file_byte_limit: (Default 1e6) Maximum number of bytes of sample text that
- will be drawn from the files.
- reserved_tokens: List of string tokens that are guaranteed to be at the
- beginning of the subtoken vocabulary list.
- correct_strip: Whether to convert text to unicode before strip.
- master_char_set: the char set.
-
- Returns:
- Subtokenizer object
- """
- if master_char_set is None:
- master_char_set = _ALPHANUMERIC_CHAR_SET
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- if tf.io.gfile.exists(vocab_file):
- logging.info("Vocab file already exists (%s)", vocab_file)
- else:
- logging.info("Begin steps to create subtoken vocabulary...")
- token_counts = _count_tokens(files, file_byte_limit, correct_strip,
- master_char_set)
- alphabet = _generate_alphabet_dict(token_counts)
- subtoken_list = _generate_subtokens_with_target_vocab_size(
- token_counts, alphabet, target_vocab_size, threshold, min_count,
- reserved_tokens)
- logging.info("Generated vocabulary with %d subtokens.",
- len(subtoken_list))
- _save_vocab_file(vocab_file, subtoken_list)
- return Subtokenizer(vocab_file, master_char_set=master_char_set)
-
- def encode(self, raw_string, add_eos=False):
- """Encodes a string into a list of int subtoken ids."""
- ret = []
- tokens = _split_string_to_tokens(
- native_to_unicode(raw_string), self._master_char_set)
- for token in tokens:
- ret.extend(self._token_to_subtoken_ids(token))
- if add_eos:
- assert EOS in self.subtoken_list, \
- "Can't append 'EOS' because it is not in list of known subtokens."
- ret.append(EOS_ID)
- return ret
-
- def _token_to_subtoken_ids(self, token):
- """Encode a single token into a list of subtoken ids."""
- cache_location = hash(token) % self._cache_size
- cache_key, cache_value = self._cache[cache_location]
- if cache_key == token:
- return cache_value
-
- ret = _split_token_to_subtokens(
- _escape_token(token, self.alphabet), self.subtoken_to_id_dict,
- self.max_subtoken_length)
- ret = [self.subtoken_to_id_dict[subtoken_id] for subtoken_id in ret]
-
- self._cache[cache_location] = (token, ret)
- return ret
-
- def decode(self, subtokens):
- """Converts list of int subtokens ids into a string."""
- if isinstance(subtokens, np.ndarray):
- # Note that list(subtokens) converts subtokens to a python list, but the
- # items remain as np.int32. This converts both the array and its items.
- subtokens = subtokens.tolist()
-
- if not subtokens:
- return ""
-
- assert isinstance(subtokens, list) and isinstance(subtokens[0], int), (
- "Subtokens argument passed into decode() must be a list of integers.")
-
- return _unicode_to_native(
- _join_tokens_to_string(
- self._subtoken_ids_to_tokens(subtokens), self._master_char_set))
-
- def _subtoken_ids_to_tokens(self, subtokens):
- """Convert list of int subtoken ids to a list of string tokens."""
- escaped_tokens = "".join([
- self.subtoken_list[s] for s in subtokens if s < len(self.subtoken_list)
- ])
- escaped_tokens = escaped_tokens.split("_")
-
- # All tokens in the vocabulary list have been escaped (see _escape_token())
- # so each token must be unescaped when decoding.
- ret = []
- for token in escaped_tokens:
- if token:
- ret.append(_unescape_token(token))
- return ret
-
-
-def _save_vocab_file(vocab_file, subtoken_list):
- """Save subtokens to file."""
- with tf.io.gfile.GFile(vocab_file, mode="w") as f:
- for subtoken in subtoken_list:
- f.write("'%s'\n" % _unicode_to_native(subtoken))
-
-
-def _load_vocab_file(vocab_file, reserved_tokens=None):
- """Load vocabulary while ensuring reserved tokens are at the top."""
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- subtoken_list = []
- with tf.io.gfile.GFile(vocab_file, mode="r") as f:
- for line in f:
- subtoken = native_to_unicode(line.strip())
- subtoken = subtoken[1:-1] # Remove surrounding single-quotes
- if subtoken in reserved_tokens:
- continue
- subtoken_list.append(native_to_unicode(subtoken))
- return reserved_tokens + subtoken_list
-
-
-def native_to_unicode(s):
- """Convert string to unicode (required in Python 2)."""
- try: # Python 2
- return s if isinstance(s, unicode) else s.decode("utf-8")
- except NameError: # Python 3
- return s
-
-
-def _unicode_to_native(s):
- """Convert string from unicode to native format (required in Python 2)."""
- try: # Python 2
- return s.encode("utf-8") if isinstance(s, unicode) else s
- except NameError: # Python 3
- return s
-
-
-def _split_string_to_tokens(text, master_char_set):
- """Splits text to a list of string tokens."""
- if not text:
- return []
- ret = []
- token_start = 0
- # Classify each character in the input string
- is_master = [c in master_char_set for c in text]
- for pos in xrange(1, len(text)):
- if is_master[pos] != is_master[pos - 1]:
- token = text[token_start:pos]
- if token != u" " or token_start == 0:
- ret.append(token)
- token_start = pos
- final_token = text[token_start:]
- ret.append(final_token)
- return ret
-
-
-def _join_tokens_to_string(tokens, master_char_set):
- """Join a list of string tokens into a single string."""
- token_is_master = [t[0] in master_char_set for t in tokens]
- ret = []
- for i, token in enumerate(tokens):
- if i > 0 and token_is_master[i - 1] and token_is_master[i]:
- ret.append(u" ")
- ret.append(token)
- return "".join(ret)
-
-
-def _escape_token(token, alphabet):
- r"""Replace characters that aren't in the alphabet and append "_" to token.
-
- Apply three transformations to the token:
- 1. Replace underline character "_" with "\u", and backslash "\" with "\\".
- 2. Replace characters outside of the alphabet with "\###;", where ### is the
- character's Unicode code point.
- 3. Appends "_" to mark the end of a token.
-
- Args:
- token: unicode string to be escaped
- alphabet: list of all known characters
-
- Returns:
- escaped string
- """
- token = token.replace(u"\\", u"\\\\").replace(u"_", u"\\u")
- ret = [c if c in alphabet and c != u"\n" else r"\%d;" % ord(c) for c in token]
- return u"".join(ret) + "_"
-
-
-def _unescape_token(token):
- r"""Replaces escaped characters in the token with their unescaped versions.
-
- Applies inverse transformations as _escape_token():
- 1. Replace "\u" with "_", and "\\" with "\".
- 2. Replace "\###;" with the unicode character the ### refers to.
-
- Args:
- token: escaped string
-
- Returns:
- unescaped string
- """
-
- def match(m):
- r"""Returns replacement string for matched object.
-
- Matched objects contain one of the strings that matches the regex pattern:
- r"\\u|\\\\|\\([0-9]+);"
- The strings can be '\u', '\\', or '\###;' (### is any digit number).
-
- m.group(0) refers to the entire matched string ('\u', '\\', or '\###;').
- m.group(1) refers to the first parenthesized subgroup ('###').
-
- m.group(0) exists for all match objects, while m.group(1) exists only for
- the string '\###;'.
-
- This function looks to see if m.group(1) exists. If it doesn't, then the
- matched string must be '\u' or '\\' . In this case, the corresponding
- replacement ('_' and '\') are returned. Note that in python, a single
- backslash is written as '\\', and double backslash as '\\\\'.
-
- If m.goup(1) exists, then use the integer in m.group(1) to return a
- unicode character.
-
- Args:
- m: match object
-
- Returns:
- String to replace matched object with.
- """
- # Check if the matched strings are '\u' or '\\'.
- if m.group(1) is None:
- return u"_" if m.group(0) == u"\\u" else u"\\"
-
- # If m.group(1) exists, try and return unicode character.
- try:
- return six.unichr(int(m.group(1)))
- except (ValueError, OverflowError) as _:
- return _UNDEFINED_UNICODE
-
- # Use match function to replace escaped substrings in the token.
- return _UNESCAPE_REGEX.sub(match, token)
-
-
-def _count_tokens(files,
- file_byte_limit=1e6,
- correct_strip=True,
- master_char_set=None):
- """Return token counts of words in the files.
-
- Samples file_byte_limit bytes from each file, and counts the words that appear
- in the samples. The samples are semi-evenly distributed across the file.
-
- Args:
- files: List of filepaths
- file_byte_limit: Max number of bytes that will be read from each file.
- correct_strip: Whether to convert text to unicode before strip. This affects
- vocabulary generation for PY2. Sets correct_strip to False in PY2 to
- reproduce previous common public result. Sets correct_strip to True will
- let PY2 and PY3 get a consistent vocabulary.
- master_char_set: the char set.
-
- Returns:
- Dictionary mapping tokens to the number of times they appear in the sampled
- lines from the files.
- """
- if master_char_set is None:
- master_char_set = _ALPHANUMERIC_CHAR_SET
-
- token_counts = collections.defaultdict(int)
-
- for filepath in files:
- with tf.io.gfile.GFile(filepath, mode="r") as reader:
- file_byte_budget = file_byte_limit
- counter = 0
- lines_to_skip = int(reader.size() / (file_byte_budget * 2))
- for line in reader:
- if counter < lines_to_skip:
- counter += 1
- else:
- if file_byte_budget < 0:
- break
- if correct_strip:
- line = native_to_unicode(line)
- line = line.strip()
- file_byte_budget -= len(line)
- counter = 0
-
- # Add words to token counts
- for token in _split_string_to_tokens(
- native_to_unicode(line), master_char_set):
- token_counts[token] += 1
- return token_counts
-
-
-def _list_to_index_dict(lst):
- """Create dictionary mapping list items to their indices in the list."""
- return {item: n for n, item in enumerate(lst)}
-
-
-def _split_token_to_subtokens(token, subtoken_dict, max_subtoken_length):
- """Splits a token into subtokens defined in the subtoken dict."""
- ret = []
- start = 0
- token_len = len(token)
- while start < token_len:
- # Find the longest subtoken, so iterate backwards.
- for end in xrange(min(token_len, start + max_subtoken_length), start, -1):
- subtoken = token[start:end]
- if subtoken in subtoken_dict:
- ret.append(subtoken)
- start = end
- break
- else: # Did not break
- # If there is no possible encoding of the escaped token then one of the
- # characters in the token is not in the alphabet. This should be
- # impossible and would be indicative of a bug.
- raise ValueError("Was unable to split token \"%s\" into subtokens." %
- token)
- return ret
-
-
-def _generate_subtokens_with_target_vocab_size(token_counts,
- alphabet,
- target_size,
- threshold,
- min_count=None,
- reserved_tokens=None):
- """Generate subtoken vocabulary close to the target size."""
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- if min_count is not None:
- logging.info("Using min_count=%d to generate vocab with target size %d",
- min_count, target_size)
- return _generate_subtokens(
- token_counts, alphabet, min_count, reserved_tokens=reserved_tokens)
-
- def bisect(min_val, max_val):
- """Recursive function to binary search for subtoken vocabulary."""
- cur_count = (min_val + max_val) // 2
- logging.info("Binary search: trying min_count=%d (%d %d)", cur_count,
- min_val, max_val)
- subtoken_list = _generate_subtokens(
- token_counts, alphabet, cur_count, reserved_tokens=reserved_tokens)
-
- val = len(subtoken_list)
- logging.info("Binary search: min_count=%d resulted in %d tokens", cur_count,
- val)
-
- within_threshold = abs(val - target_size) < threshold
- if within_threshold or min_val >= max_val or cur_count < 2:
- return subtoken_list
- if val > target_size:
- other_subtoken_list = bisect(cur_count + 1, max_val)
- else:
- other_subtoken_list = bisect(min_val, cur_count - 1)
-
- # Return vocabulary dictionary with the closest number of tokens.
- other_val = len(other_subtoken_list)
- if abs(other_val - target_size) < abs(val - target_size):
- return other_subtoken_list
- return subtoken_list
-
- logging.info("Finding best min_count to get target size of %d", target_size)
- return bisect(_MIN_MIN_COUNT, _MAX_MIN_COUNT)
-
-
-def _generate_alphabet_dict(iterable, reserved_tokens=None):
- """Create set of characters that appear in any element in the iterable."""
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
- alphabet = {c for token in iterable for c in token}
- alphabet |= {c for token in reserved_tokens for c in token}
- alphabet |= _ESCAPE_CHARS # Add escape characters to alphabet set.
- return alphabet
-
-
-def _count_and_gen_subtokens(token_counts, alphabet, subtoken_dict,
- max_subtoken_length):
- """Count number of times subtokens appear, and generate new subtokens.
-
- Args:
- token_counts: dict mapping tokens to the number of times they appear in the
- original files.
- alphabet: list of allowed characters. Used to escape the tokens, which
- guarantees that all tokens can be split into subtokens.
- subtoken_dict: dict mapping subtokens to ids.
- max_subtoken_length: maximum length of subtoken in subtoken_dict.
-
- Returns:
- A defaultdict mapping subtokens to the number of times they appear in the
- tokens. The dict may contain new subtokens.
- """
- subtoken_counts = collections.defaultdict(int)
- for token, count in six.iteritems(token_counts):
- token = _escape_token(token, alphabet)
- subtokens = _split_token_to_subtokens(token, subtoken_dict,
- max_subtoken_length)
-
- # Generate new subtokens by taking substrings from token.
- start = 0
- for subtoken in subtokens:
- for end in xrange(start + 1, len(token) + 1):
- new_subtoken = token[start:end]
- subtoken_counts[new_subtoken] += count
- start += len(subtoken)
-
- return subtoken_counts
-
-
-def _filter_and_bucket_subtokens(subtoken_counts, min_count):
- """Return a bucketed list of subtokens that are filtered by count.
-
- Args:
- subtoken_counts: defaultdict mapping subtokens to their counts
- min_count: int count used to filter subtokens
-
- Returns:
- List of subtoken sets, where subtokens in set i have the same length=i.
- """
- # Create list of buckets, where subtokens in bucket i have length i.
- subtoken_buckets = []
- for subtoken, count in six.iteritems(subtoken_counts):
- if count < min_count: # Filter out subtokens that don't appear enough
- continue
- while len(subtoken_buckets) <= len(subtoken):
- subtoken_buckets.append(set())
- subtoken_buckets[len(subtoken)].add(subtoken)
- return subtoken_buckets
-
-
-def _gen_new_subtoken_list(subtoken_counts,
- min_count,
- alphabet,
- reserved_tokens=None):
- """Generate candidate subtokens ordered by count, and new max subtoken length.
-
- Add subtokens to the candiate list in order of length (longest subtokens
- first). When a subtoken is added, the counts of each of its prefixes are
- decreased. Prefixes that don't appear much outside the subtoken are not added
- to the candidate list.
-
- For example:
- subtoken being added to candidate list: 'translate'
- subtoken_counts: {'translate':10, 't':40, 'tr':16, 'tra':12, ...}
- min_count: 5
-
- When 'translate' is added, subtoken_counts is updated to:
- {'translate':0, 't':30, 'tr':6, 'tra': 2, ...}
-
- The subtoken 'tra' will not be added to the candidate list, because it appears
- twice (less than min_count) outside of 'translate'.
-
- Args:
- subtoken_counts: defaultdict mapping str subtokens to int counts
- min_count: int minumum count requirement for subtokens
- alphabet: set of characters. Each character is added to the subtoken list to
- guarantee that all tokens can be encoded.
- reserved_tokens: list of tokens that will be added to the beginning of the
- returned subtoken list.
-
- Returns:
- List of candidate subtokens in decreasing count order, and maximum subtoken
- length
- """
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- # Create a list of (count, subtoken) for each candidate subtoken.
- subtoken_candidates = []
-
- # Use bucketted list to iterate through subtokens in order of length.
- # subtoken_buckets[i] = set(subtokens), where each subtoken has length i.
- subtoken_buckets = _filter_and_bucket_subtokens(subtoken_counts, min_count)
- max_subtoken_length = len(subtoken_buckets) - 1
-
- # Go through the list in reverse order to consider longer subtokens first.
- for subtoken_len in xrange(max_subtoken_length, 0, -1):
- for subtoken in subtoken_buckets[subtoken_len]:
- count = subtoken_counts[subtoken]
-
- # Possible if this subtoken is a prefix of another token.
- if count < min_count:
- continue
-
- # Ignore alphabet/reserved tokens, which will be added manually later.
- if subtoken not in alphabet and subtoken not in reserved_tokens:
- subtoken_candidates.append((count, subtoken))
-
- # Decrement count of the subtoken's prefixes (if a longer subtoken is
- # added, its prefixes lose priority to be added).
- for end in xrange(1, subtoken_len):
- subtoken_counts[subtoken[:end]] -= count
-
- # Add alphabet subtokens (guarantees that all strings are encodable).
- subtoken_candidates.extend((subtoken_counts.get(a, 0), a) for a in alphabet)
-
- # Order subtoken candidates by decreasing count.
- subtoken_list = [t for _, t in sorted(subtoken_candidates, reverse=True)]
-
- # Add reserved tokens to beginning of the list.
- subtoken_list = reserved_tokens + subtoken_list
- return subtoken_list, max_subtoken_length
-
-
-def _generate_subtokens(token_counts,
- alphabet,
- min_count,
- num_iterations=4,
- reserved_tokens=None):
- """Create a list of subtokens in decreasing order of frequency.
-
- Args:
- token_counts: dict mapping str tokens -> int count
- alphabet: set of characters
- min_count: int minimum number of times a subtoken must appear before it is
- added to the vocabulary.
- num_iterations: int number of iterations to generate new tokens.
- reserved_tokens: list of tokens that will be added to the beginning to the
- returned subtoken list.
-
- Returns:
- Sorted list of subtokens (most frequent first)
- """
- if reserved_tokens is None:
- reserved_tokens = RESERVED_TOKENS
-
- # Use alphabet set to create initial list of subtokens
- subtoken_list = reserved_tokens + list(alphabet)
- max_subtoken_length = 1
-
- # On each iteration, segment all words using the subtokens defined in
- # subtoken_dict, count how often the resulting subtokens appear, and update
- # the dictionary with subtokens w/ high enough counts.
- for i in xrange(num_iterations):
- logging.info("\tGenerating subtokens: iteration %d", i)
- # Generate new subtoken->id dictionary using the new subtoken list.
- subtoken_dict = _list_to_index_dict(subtoken_list)
-
- # Create dict mapping subtoken->count, with additional subtokens created
- # from substrings taken from the tokens.
- subtoken_counts = _count_and_gen_subtokens(token_counts, alphabet,
- subtoken_dict,
- max_subtoken_length)
-
- # Generate new list of subtokens sorted by subtoken count.
- subtoken_list, max_subtoken_length = _gen_new_subtoken_list(
- subtoken_counts, min_count, alphabet, reserved_tokens)
-
- logging.info("\tVocab size: %d", len(subtoken_list))
- return subtoken_list
diff --git a/official/nlp/transformer/utils/tokenizer_test.py b/official/nlp/transformer/utils/tokenizer_test.py
deleted file mode 100644
index f6ef7a08b2490c49410201a5114183f24a87a1e7..0000000000000000000000000000000000000000
--- a/official/nlp/transformer/utils/tokenizer_test.py
+++ /dev/null
@@ -1,204 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Test Subtokenizer and string helper methods."""
-
-import collections
-import tempfile
-
-import tensorflow as tf
-
-from official.nlp.transformer.utils import tokenizer
-
-
-class SubtokenizerTest(tf.test.TestCase):
-
- def _init_subtokenizer(self, vocab_list):
- temp_file = tempfile.NamedTemporaryFile(delete=False)
- with tf.io.gfile.GFile(temp_file.name, "w") as w:
- for subtoken in vocab_list:
- w.write("'%s'" % subtoken)
- w.write("\n")
- return tokenizer.Subtokenizer(temp_file.name, reserved_tokens=[])
-
- def test_encode(self):
- vocab_list = ["123_", "test", "ing_"]
- subtokenizer = self._init_subtokenizer(vocab_list)
- s = "testing 123"
- encoded_list = subtokenizer.encode(s)
- self.assertEqual([1, 2, 0], encoded_list)
-
- def test_decode(self):
- vocab_list = ["123_", "test", "ing_"]
- subtokenizer = self._init_subtokenizer(vocab_list)
- encoded_list = [1, 2, 0] # testing 123
- decoded_str = subtokenizer.decode(encoded_list)
- self.assertEqual("testing 123", decoded_str)
-
- def test_subtoken_ids_to_tokens(self):
- vocab_list = ["123_", "test", "ing_"]
- subtokenizer = self._init_subtokenizer(vocab_list)
- encoded_list = [1, 2, 0] # testing 123
- token_list = subtokenizer._subtoken_ids_to_tokens(encoded_list)
- self.assertEqual([u"testing", u"123"], token_list)
-
-
-class StringHelperTest(tf.test.TestCase):
-
- def test_split_string_to_tokens(self):
- text = "test? testing 123."
-
- tokens = tokenizer._split_string_to_tokens(text,
- tokenizer._ALPHANUMERIC_CHAR_SET)
- self.assertEqual(["test", "? ", "testing", "123", "."], tokens)
-
- def test_join_tokens_to_string(self):
- tokens = ["test", "? ", "testing", "123", "."]
-
- s = tokenizer._join_tokens_to_string(tokens,
- tokenizer._ALPHANUMERIC_CHAR_SET)
- self.assertEqual("test? testing 123.", s)
-
- def test_escape_token(self):
- token = u"abc_\\4"
- alphabet = set("abc_\\u;")
-
- escaped_token = tokenizer._escape_token(token, alphabet)
- self.assertEqual("abc\\u\\\\\\52;_", escaped_token)
-
- def test_unescape_token(self):
- escaped_token = u"Underline: \\u, Backslash: \\\\, Unicode: \\52;"
-
- unescaped_token = tokenizer._unescape_token(escaped_token)
- self.assertEqual("Underline: _, Backslash: \\, Unicode: 4", unescaped_token)
-
- def test_list_to_index_dict(self):
- lst = ["test", "strings"]
-
- d = tokenizer._list_to_index_dict(lst)
- self.assertDictEqual({"test": 0, "strings": 1}, d)
-
- def test_split_token_to_subtokens(self):
- token = "abc"
- subtoken_dict = {"a": 0, "b": 1, "c": 2, "ab": 3}
- max_subtoken_length = 2
-
- subtokens = tokenizer._split_token_to_subtokens(token, subtoken_dict,
- max_subtoken_length)
- self.assertEqual(["ab", "c"], subtokens)
-
- def test_generate_alphabet_dict(self):
- s = ["testing", "123"]
- reserved_tokens = ["???"]
-
- alphabet = tokenizer._generate_alphabet_dict(s, reserved_tokens)
- self.assertIn("?", alphabet)
- self.assertIn("t", alphabet)
- self.assertIn("e", alphabet)
- self.assertIn("s", alphabet)
- self.assertIn("i", alphabet)
- self.assertIn("n", alphabet)
- self.assertIn("g", alphabet)
- self.assertIn("1", alphabet)
- self.assertIn("2", alphabet)
- self.assertIn("3", alphabet)
-
- def test_count_and_gen_subtokens(self):
- token_counts = {"abc": 5}
- alphabet = set("abc_")
- subtoken_dict = {"a": 0, "b": 1, "c": 2, "_": 3}
- max_subtoken_length = 2
-
- subtoken_counts = tokenizer._count_and_gen_subtokens(
- token_counts, alphabet, subtoken_dict, max_subtoken_length)
-
- self.assertIsInstance(subtoken_counts, collections.defaultdict)
- self.assertDictEqual(
- {
- "a": 5,
- "b": 5,
- "c": 5,
- "_": 5,
- "ab": 5,
- "bc": 5,
- "c_": 5,
- "abc": 5,
- "bc_": 5,
- "abc_": 5
- }, subtoken_counts)
-
- def test_filter_and_bucket_subtokens(self):
- subtoken_counts = collections.defaultdict(int, {
- "a": 2,
- "b": 4,
- "c": 1,
- "ab": 6,
- "ac": 3,
- "abbc": 5
- })
- min_count = 3
-
- subtoken_buckets = tokenizer._filter_and_bucket_subtokens(
- subtoken_counts, min_count)
-
- self.assertEqual(len(subtoken_buckets[0]), 0)
- self.assertEqual(set("b"), subtoken_buckets[1])
- self.assertEqual(set(["ab", "ac"]), subtoken_buckets[2])
- self.assertEqual(len(subtoken_buckets[3]), 0)
- self.assertEqual(set(["abbc"]), subtoken_buckets[4])
-
- def test_gen_new_subtoken_list(self):
- subtoken_counts = collections.defaultdict(int, {
- "translate": 10,
- "t": 40,
- "tr": 16,
- "tra": 12
- })
- min_count = 5
- alphabet = set("translate")
- reserved_tokens = ["reserved", "tokens"]
-
- subtoken_list, max_token_length = tokenizer._gen_new_subtoken_list(
- subtoken_counts, min_count, alphabet, reserved_tokens)
-
- # Check that "tra" isn"t in the list (its count should be decremented to 2,
- # so it should not be added to the canddiate list).
- self.assertNotIn("tra", subtoken_list)
-
- self.assertIn("tr", subtoken_list)
- self.assertIn("t", subtoken_list)
-
- self.assertEqual(len("translate"), max_token_length)
-
- def test_generate_subtokens(self):
- token_counts = {"ab": 1, "bc": 3, "abc": 5}
- alphabet = set("abc_")
- min_count = 100
- num_iterations = 1
- reserved_tokens = ["reserved", "tokens"]
-
- vocab_list = tokenizer._generate_subtokens(token_counts, alphabet,
- min_count, num_iterations,
- reserved_tokens)
-
- # Check that reserved tokens are at the front of the list
- self.assertEqual(vocab_list[:2], reserved_tokens)
-
- # Check that each character in alphabet is in the vocab list
- for c in alphabet:
- self.assertIn(c, vocab_list)
-
-
-if __name__ == "__main__":
- tf.test.main()
diff --git a/official/nlp/xlnet/__init__.py b/official/nlp/xlnet/__init__.py
deleted file mode 100644
index a25710c222e3327cb20e000db5df5c5651c4a2cc..0000000000000000000000000000000000000000
--- a/official/nlp/xlnet/__init__.py
+++ /dev/null
@@ -1,15 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-
diff --git a/official/nlp/xlnet/common_flags.py b/official/nlp/xlnet/common_flags.py
deleted file mode 100644
index 549e7b036e8133c6e6e50deea5099404e9ee1dcf..0000000000000000000000000000000000000000
--- a/official/nlp/xlnet/common_flags.py
+++ /dev/null
@@ -1,142 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Common flags used in XLNet model."""
-
-from absl import flags
-
-flags.DEFINE_string("master", default=None, help="master")
-flags.DEFINE_string(
- "tpu",
- default=None,
- help="The Cloud TPU to use for training. This should be "
- "either the name used when creating the Cloud TPU, or a "
- "url like grpc://ip.address.of.tpu:8470.")
-flags.DEFINE_bool(
- "use_tpu", default=True, help="Use TPUs rather than plain CPUs.")
-flags.DEFINE_string("tpu_topology", "2x2", help="TPU topology.")
-flags.DEFINE_integer(
- "num_core_per_host", default=8, help="number of cores per host")
-
-flags.DEFINE_string("model_dir", default=None, help="Estimator model_dir.")
-flags.DEFINE_string(
- "init_checkpoint",
- default=None,
- help="Checkpoint path for initializing the model.")
-flags.DEFINE_bool(
- "init_from_transformerxl",
- default=False,
- help="Init from a transformerxl model checkpoint. Otherwise, init from the "
- "entire model checkpoint.")
-
-# Optimization config
-flags.DEFINE_float("learning_rate", default=1e-4, help="Maximum learning rate.")
-flags.DEFINE_float("clip", default=1.0, help="Gradient clipping value.")
-flags.DEFINE_float("weight_decay_rate", default=0.0, help="Weight decay rate.")
-
-# lr decay
-flags.DEFINE_integer(
- "warmup_steps", default=0, help="Number of steps for linear lr warmup.")
-flags.DEFINE_float("adam_epsilon", default=1e-8, help="Adam epsilon.")
-flags.DEFINE_float(
- "lr_layer_decay_rate",
- default=1.0,
- help="Top layer: lr[L] = FLAGS.learning_rate."
- "Lower layers: lr[l-1] = lr[l] * lr_layer_decay_rate.")
-flags.DEFINE_float(
- "min_lr_ratio", default=0.0, help="Minimum ratio learning rate.")
-
-# Training config
-flags.DEFINE_integer(
- "train_batch_size",
- default=16,
- help="Size of the train batch across all hosts.")
-flags.DEFINE_integer(
- "train_steps", default=100000, help="Total number of training steps.")
-flags.DEFINE_integer(
- "iterations", default=1000, help="Number of iterations per repeat loop.")
-
-# Data config
-flags.DEFINE_integer(
- "seq_len", default=0, help="Sequence length for pretraining.")
-flags.DEFINE_integer(
- "reuse_len",
- default=0,
- help="How many tokens to be reused in the next batch. "
- "Could be half of `seq_len`.")
-flags.DEFINE_bool("uncased", False, help="Use uncased inputs or not.")
-flags.DEFINE_bool(
- "bi_data",
- default=False,
- help="Use bidirectional data streams, "
- "i.e., forward & backward.")
-flags.DEFINE_integer("n_token", 32000, help="Vocab size")
-
-# Model config
-flags.DEFINE_integer("mem_len", default=0, help="Number of steps to cache")
-flags.DEFINE_bool("same_length", default=False, help="Same length attention")
-flags.DEFINE_integer("clamp_len", default=-1, help="Clamp length")
-
-flags.DEFINE_integer("n_layer", default=6, help="Number of layers.")
-flags.DEFINE_integer("d_model", default=32, help="Dimension of the model.")
-flags.DEFINE_integer("d_embed", default=32, help="Dimension of the embeddings.")
-flags.DEFINE_integer("n_head", default=4, help="Number of attention heads.")
-flags.DEFINE_integer(
- "d_head", default=8, help="Dimension of each attention head.")
-flags.DEFINE_integer(
- "d_inner",
- default=32,
- help="Dimension of inner hidden size in positionwise "
- "feed-forward.")
-flags.DEFINE_float("dropout", default=0.1, help="Dropout rate.")
-flags.DEFINE_float("dropout_att", default=0.1, help="Attention dropout rate.")
-flags.DEFINE_bool("untie_r", default=False, help="Untie r_w_bias and r_r_bias")
-flags.DEFINE_string(
- "ff_activation",
- default="relu",
- help="Activation type used in position-wise feed-forward.")
-flags.DEFINE_string(
- "strategy_type",
- default="tpu",
- help="Activation type used in position-wise feed-forward.")
-flags.DEFINE_bool("use_bfloat16", False, help="Whether to use bfloat16.")
-
-# Parameter initialization
-flags.DEFINE_enum(
- "init_method",
- default="normal",
- enum_values=["normal", "uniform"],
- help="Initialization method.")
-flags.DEFINE_float(
- "init_std", default=0.02, help="Initialization std when init is normal.")
-flags.DEFINE_float(
- "init_range", default=0.1, help="Initialization std when init is uniform.")
-
-flags.DEFINE_integer(
- "test_data_size", default=12048, help="Number of test data samples.")
-flags.DEFINE_string(
- "train_tfrecord_path",
- default=None,
- help="Path to preprocessed training set tfrecord.")
-flags.DEFINE_string(
- "test_tfrecord_path",
- default=None,
- help="Path to preprocessed test set tfrecord.")
-flags.DEFINE_integer(
- "test_batch_size",
- default=16,
- help="Size of the test batch across all hosts.")
-flags.DEFINE_integer(
- "save_steps", default=1000, help="Number of steps for saving checkpoint.")
-FLAGS = flags.FLAGS
diff --git a/official/nlp/xlnet/optimization.py b/official/nlp/xlnet/optimization.py
deleted file mode 100644
index d6954ab9fb76b12e37c05b7b8da51505dc72d6cb..0000000000000000000000000000000000000000
--- a/official/nlp/xlnet/optimization.py
+++ /dev/null
@@ -1,98 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""Functions and classes related to optimization (weight updates)."""
-
-from absl import logging
-import tensorflow as tf
-from official.nlp import optimization
-
-
-class WarmUp(tf.keras.optimizers.schedules.LearningRateSchedule):
- """Applys a warmup schedule on a given learning rate decay schedule."""
-
- def __init__(self,
- initial_learning_rate,
- decay_schedule_fn,
- warmup_steps,
- power=1.0,
- name=None):
- super(WarmUp, self).__init__()
- self.initial_learning_rate = initial_learning_rate
- self.warmup_steps = warmup_steps
- self.power = power
- self.decay_schedule_fn = decay_schedule_fn
- self.name = name
-
- def __call__(self, step):
- with tf.name_scope(self.name or "WarmUp") as name:
- # Implements polynomial warmup. i.e., if global_step < warmup_steps, the
- # learning rate will be `global_step/num_warmup_steps * init_lr`.
- global_step_float = tf.cast(step, tf.float32)
- warmup_steps_float = tf.cast(self.warmup_steps, tf.float32)
- warmup_percent_done = global_step_float / warmup_steps_float
- warmup_learning_rate = (
- self.initial_learning_rate *
- tf.math.pow(warmup_percent_done, self.power))
- return tf.cond(
- global_step_float < warmup_steps_float,
- lambda: warmup_learning_rate,
- lambda: self.decay_schedule_fn(step - self.warmup_steps),
- name=name)
-
- def get_config(self):
- return {
- "initial_learning_rate": self.initial_learning_rate,
- "decay_schedule_fn": self.decay_schedule_fn,
- "warmup_steps": self.warmup_steps,
- "power": self.power,
- "name": self.name
- }
-
-
-def create_optimizer(init_lr,
- num_train_steps,
- num_warmup_steps,
- min_lr_ratio=0.0,
- adam_epsilon=1e-8,
- weight_decay_rate=0.0):
- """Creates an optimizer with learning rate schedule."""
- # Implements linear decay of the learning rate.
- learning_rate_fn = tf.keras.optimizers.schedules.PolynomialDecay(
- initial_learning_rate=init_lr,
- decay_steps=num_train_steps - num_warmup_steps,
- end_learning_rate=init_lr * min_lr_ratio)
- if num_warmup_steps:
- learning_rate_fn = WarmUp(
- initial_learning_rate=init_lr,
- decay_schedule_fn=learning_rate_fn,
- warmup_steps=num_warmup_steps)
- if weight_decay_rate > 0.0:
- logging.info(
- "Using AdamWeightDecay with adam_epsilon=%.9f weight_decay_rate=%.3f",
- adam_epsilon, weight_decay_rate)
- optimizer = optimization.AdamWeightDecay(
- learning_rate=learning_rate_fn,
- weight_decay_rate=weight_decay_rate,
- beta_1=0.9,
- beta_2=0.999,
- epsilon=adam_epsilon,
- exclude_from_weight_decay=["LayerNorm", "layer_norm", "bias"],
- include_in_weight_decay=["r_s_bias", "r_r_bias", "r_w_bias"])
- else:
- logging.info("Using Adam with adam_epsilon=%.9f", (adam_epsilon))
- optimizer = tf.keras.optimizers.Adam(
- learning_rate=learning_rate_fn, epsilon=adam_epsilon)
-
- return optimizer, learning_rate_fn
diff --git a/official/nlp/xlnet/run_classifier.py b/official/nlp/xlnet/run_classifier.py
deleted file mode 100644
index f2681e0ce8a714cb4f784430a86f076bdc356676..0000000000000000000000000000000000000000
--- a/official/nlp/xlnet/run_classifier.py
+++ /dev/null
@@ -1,187 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""XLNet classification finetuning runner in tf2.0."""
-
-import functools
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-
-import numpy as np
-import tensorflow as tf
-# pylint: disable=unused-import
-from official.common import distribute_utils
-from official.nlp.xlnet import common_flags
-from official.nlp.xlnet import data_utils
-from official.nlp.xlnet import optimization
-from official.nlp.xlnet import training_utils
-from official.nlp.xlnet import xlnet_config
-from official.nlp.xlnet import xlnet_modeling as modeling
-
-flags.DEFINE_integer("n_class", default=2, help="Number of classes.")
-flags.DEFINE_string(
- "summary_type",
- default="last",
- help="Method used to summarize a sequence into a vector.")
-
-FLAGS = flags.FLAGS
-
-
-def get_classificationxlnet_model(model_config,
- run_config,
- n_class,
- summary_type="last"):
- model = modeling.ClassificationXLNetModel(
- model_config, run_config, n_class, summary_type, name="model")
- return model
-
-
-def run_evaluation(strategy,
- test_input_fn,
- eval_steps,
- model,
- step,
- eval_summary_writer=None):
- """Run evaluation for classification task.
-
- Args:
- strategy: distribution strategy.
- test_input_fn: input function for evaluation data.
- eval_steps: total number of evaluation steps.
- model: keras model object.
- step: current train step.
- eval_summary_writer: summary writer used to record evaluation metrics. As
- there are fake data samples in validation set, we use mask to get rid of
- them when calculating the accuracy. For the reason that there will be
- dynamic-shape tensor, we first collect logits, labels and masks from TPU
- and calculate the accuracy via numpy locally.
-
- Returns:
- A float metric, accuracy.
- """
-
- def _test_step_fn(inputs):
- """Replicated validation step."""
-
- inputs["mems"] = None
- _, logits = model(inputs, training=False)
- return logits, inputs["label_ids"], inputs["is_real_example"]
-
- @tf.function
- def _run_evaluation(test_iterator):
- """Runs validation steps."""
- logits, labels, masks = strategy.run(
- _test_step_fn, args=(next(test_iterator),))
- return logits, labels, masks
-
- test_iterator = data_utils.get_input_iterator(test_input_fn, strategy)
- correct = 0
- total = 0
- for _ in range(eval_steps):
- logits, labels, masks = _run_evaluation(test_iterator)
- logits = strategy.experimental_local_results(logits)
- labels = strategy.experimental_local_results(labels)
- masks = strategy.experimental_local_results(masks)
- merged_logits = []
- merged_labels = []
- merged_masks = []
-
- for i in range(strategy.num_replicas_in_sync):
- merged_logits.append(logits[i].numpy())
- merged_labels.append(labels[i].numpy())
- merged_masks.append(masks[i].numpy())
- merged_logits = np.vstack(np.array(merged_logits))
- merged_labels = np.hstack(np.array(merged_labels))
- merged_masks = np.hstack(np.array(merged_masks))
- real_index = np.where(np.equal(merged_masks, 1))
- correct += np.sum(
- np.equal(
- np.argmax(merged_logits[real_index], axis=-1),
- merged_labels[real_index]))
- total += np.shape(real_index)[-1]
- accuracy = float(correct) / float(total)
- logging.info("Train step: %d / acc = %d/%d = %f", step, correct, total,
- accuracy)
- if eval_summary_writer:
- with eval_summary_writer.as_default():
- tf.summary.scalar("eval_acc", float(correct) / float(total), step=step)
- eval_summary_writer.flush()
- return accuracy
-
-
-def get_metric_fn():
- train_acc_metric = tf.keras.metrics.SparseCategoricalAccuracy(
- "acc", dtype=tf.float32)
- return train_acc_metric
-
-
-def main(unused_argv):
- del unused_argv
- strategy = distribute_utils.get_distribution_strategy(
- distribution_strategy=FLAGS.strategy_type,
- tpu_address=FLAGS.tpu)
- if strategy:
- logging.info("***** Number of cores used : %d",
- strategy.num_replicas_in_sync)
- train_input_fn = functools.partial(data_utils.get_classification_input_data,
- FLAGS.train_batch_size, FLAGS.seq_len,
- strategy, True, FLAGS.train_tfrecord_path)
- test_input_fn = functools.partial(data_utils.get_classification_input_data,
- FLAGS.test_batch_size, FLAGS.seq_len,
- strategy, False, FLAGS.test_tfrecord_path)
-
- total_training_steps = FLAGS.train_steps
- steps_per_loop = FLAGS.iterations
- eval_steps = int(FLAGS.test_data_size / FLAGS.test_batch_size)
- eval_fn = functools.partial(run_evaluation, strategy, test_input_fn,
- eval_steps)
- optimizer, learning_rate_fn = optimization.create_optimizer(
- FLAGS.learning_rate,
- total_training_steps,
- FLAGS.warmup_steps,
- adam_epsilon=FLAGS.adam_epsilon)
- model_config = xlnet_config.XLNetConfig(FLAGS)
- run_config = xlnet_config.create_run_config(True, False, FLAGS)
- model_fn = functools.partial(get_classificationxlnet_model, model_config,
- run_config, FLAGS.n_class, FLAGS.summary_type)
- input_meta_data = {}
- input_meta_data["d_model"] = FLAGS.d_model
- input_meta_data["mem_len"] = FLAGS.mem_len
- input_meta_data["batch_size_per_core"] = int(FLAGS.train_batch_size /
- strategy.num_replicas_in_sync)
- input_meta_data["n_layer"] = FLAGS.n_layer
- input_meta_data["lr_layer_decay_rate"] = FLAGS.lr_layer_decay_rate
- input_meta_data["n_class"] = FLAGS.n_class
-
- training_utils.train(
- strategy=strategy,
- model_fn=model_fn,
- input_meta_data=input_meta_data,
- eval_fn=eval_fn,
- metric_fn=get_metric_fn,
- train_input_fn=train_input_fn,
- init_checkpoint=FLAGS.init_checkpoint,
- init_from_transformerxl=FLAGS.init_from_transformerxl,
- total_training_steps=total_training_steps,
- steps_per_loop=steps_per_loop,
- optimizer=optimizer,
- learning_rate_fn=learning_rate_fn,
- model_dir=FLAGS.model_dir,
- save_steps=FLAGS.save_steps)
-
-
-if __name__ == "__main__":
- app.run(main)
diff --git a/official/nlp/xlnet/run_squad.py b/official/nlp/xlnet/run_squad.py
deleted file mode 100644
index a6126295ec1bd571abf04b90e2713eb43d1df002..0000000000000000000000000000000000000000
--- a/official/nlp/xlnet/run_squad.py
+++ /dev/null
@@ -1,295 +0,0 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
-#
-# Licensed under the Apache License, Version 2.0 (the "License");
-# you may not use this file except in compliance with the License.
-# You may obtain a copy of the License at
-#
-# http://www.apache.org/licenses/LICENSE-2.0
-#
-# Unless required by applicable law or agreed to in writing, software
-# distributed under the License is distributed on an "AS IS" BASIS,
-# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
-# See the License for the specific language governing permissions and
-# limitations under the License.
-
-"""XLNet SQUAD finetuning runner in tf2.0."""
-
-import functools
-import json
-import os
-import pickle
-
-# Import libraries
-from absl import app
-from absl import flags
-from absl import logging
-
-import tensorflow as tf
-# pylint: disable=unused-import
-import sentencepiece as spm
-from official.common import distribute_utils
-from official.nlp.xlnet import common_flags
-from official.nlp.xlnet import data_utils
-from official.nlp.xlnet import optimization
-from official.nlp.xlnet import squad_utils
-from official.nlp.xlnet import training_utils
-from official.nlp.xlnet import xlnet_config
-from official.nlp.xlnet import xlnet_modeling as modeling
-
-flags.DEFINE_string(
- "test_feature_path", default=None, help="Path to feature of test set.")
-flags.DEFINE_integer("query_len", default=64, help="Max query length.")
-flags.DEFINE_integer("start_n_top", default=5, help="Beam size for span start.")
-flags.DEFINE_integer("end_n_top", default=5, help="Beam size for span end.")
-flags.DEFINE_string(
- "predict_dir", default=None, help="Path to write predictions.")
-flags.DEFINE_string(
- "predict_file", default=None, help="Path to json file of test set.")
-flags.DEFINE_integer(
- "n_best_size", default=5, help="n best size for predictions.")
-flags.DEFINE_integer("max_answer_length", default=64, help="Max answer length.")
-# Data preprocessing config
-flags.DEFINE_string(
- "spiece_model_file", default=None, help="Sentence Piece model path.")
-flags.DEFINE_integer("max_seq_length", default=512, help="Max sequence length.")
-flags.DEFINE_integer("max_query_length", default=64, help="Max query length.")
-flags.DEFINE_integer("doc_stride", default=128, help="Doc stride.")
-
-FLAGS = flags.FLAGS
-
-
-class InputFeatures(object):
- """A single set of features of data."""
-
- def __init__(self,
- unique_id,
- example_index,
- doc_span_index,
- tok_start_to_orig_index,
- tok_end_to_orig_index,
- token_is_max_context,
- input_ids,
- input_mask,
- p_mask,
- segment_ids,
- paragraph_len,
- cls_index,
- start_position=None,
- end_position=None,
- is_impossible=None):
- self.unique_id = unique_id
- self.example_index = example_index
- self.doc_span_index = doc_span_index
- self.tok_start_to_orig_index = tok_start_to_orig_index
- self.tok_end_to_orig_index = tok_end_to_orig_index
- self.token_is_max_context = token_is_max_context
- self.input_ids = input_ids
- self.input_mask = input_mask
- self.p_mask = p_mask
- self.segment_ids = segment_ids
- self.paragraph_len = paragraph_len
- self.cls_index = cls_index
- self.start_position = start_position
- self.end_position = end_position
- self.is_impossible = is_impossible
-
-
-# pylint: disable=unused-argument
-def run_evaluation(strategy, test_input_fn, eval_examples, eval_features,
- original_data, eval_steps, input_meta_data, model,
- current_step, eval_summary_writer):
- """Run evaluation for SQUAD task.
-
- Args:
- strategy: distribution strategy.
- test_input_fn: input function for evaluation data.
- eval_examples: tf.Examples of the evaluation set.
- eval_features: Feature objects of the evaluation set.
- original_data: The original json data for the evaluation set.
- eval_steps: total number of evaluation steps.
- input_meta_data: input meta data.
- model: keras model object.
- current_step: current training step.
- eval_summary_writer: summary writer used to record evaluation metrics.
-
- Returns:
- A float metric, F1 score.
- """
-
- def _test_step_fn(inputs):
- """Replicated validation step."""
-
- inputs["mems"] = None
- res = model(inputs, training=False)
- return res, inputs["unique_ids"]
-
- @tf.function
- def _run_evaluation(test_iterator):
- """Runs validation steps."""
- res, unique_ids = strategy.run(
- _test_step_fn, args=(next(test_iterator),))
- return res, unique_ids
-
- test_iterator = data_utils.get_input_iterator(test_input_fn, strategy)
- cur_results = []
- for _ in range(eval_steps):
- results, unique_ids = _run_evaluation(test_iterator)
- unique_ids = strategy.experimental_local_results(unique_ids)
-
- for result_key in results:
- results[result_key] = (
- strategy.experimental_local_results(results[result_key]))
- for core_i in range(strategy.num_replicas_in_sync):
- bsz = int(input_meta_data["test_batch_size"] /
- strategy.num_replicas_in_sync)
- for j in range(bsz):
- result = {}
- for result_key in results:
- result[result_key] = results[result_key][core_i].numpy()[j]
- result["unique_ids"] = unique_ids[core_i].numpy()[j]
- # We appended a fake example into dev set to make data size can be
- # divided by test_batch_size. Ignores this fake example during
- # evaluation.
- if result["unique_ids"] == 1000012047:
- continue
- unique_id = int(result["unique_ids"])
-
- start_top_log_probs = ([
- float(x) for x in result["start_top_log_probs"].flat
- ])
- start_top_index = [int(x) for x in result["start_top_index"].flat]
- end_top_log_probs = ([
- float(x) for x in result["end_top_log_probs"].flat
- ])
- end_top_index = [int(x) for x in result["end_top_index"].flat]
-
- cls_logits = float(result["cls_logits"].flat[0])
- cur_results.append(
- squad_utils.RawResult(
- unique_id=unique_id,
- start_top_log_probs=start_top_log_probs,
- start_top_index=start_top_index,
- end_top_log_probs=end_top_log_probs,
- end_top_index=end_top_index,
- cls_logits=cls_logits))
- if len(cur_results) % 1000 == 0:
- logging.info("Processing example: %d", len(cur_results))
-
- output_prediction_file = os.path.join(input_meta_data["predict_dir"],
- "predictions.json")
- output_nbest_file = os.path.join(input_meta_data["predict_dir"],
- "nbest_predictions.json")
- output_null_log_odds_file = os.path.join(input_meta_data["predict_dir"],
- "null_odds.json")
-
- results = squad_utils.write_predictions(
- eval_examples, eval_features, cur_results, input_meta_data["n_best_size"],
- input_meta_data["max_answer_length"], output_prediction_file,
- output_nbest_file, output_null_log_odds_file, original_data,
- input_meta_data["start_n_top"], input_meta_data["end_n_top"])
-
- # Log current results.
- log_str = "Result | "
- for key, val in results.items():
- log_str += "{} {} | ".format(key, val)
- logging.info(log_str)
- with eval_summary_writer.as_default():
- tf.summary.scalar("best_f1", results["best_f1"], step=current_step)
- tf.summary.scalar("best_exact", results["best_exact"], step=current_step)
- eval_summary_writer.flush()
- return results["best_f1"]
-
-
-def get_qaxlnet_model(model_config, run_config, start_n_top, end_n_top):
- model = modeling.QAXLNetModel(
- model_config,
- run_config,
- start_n_top=start_n_top,
- end_n_top=end_n_top,
- name="model")
- return model
-
-
-def main(unused_argv):
- del unused_argv
- strategy = distribute_utils.get_distribution_strategy(
- distribution_strategy=FLAGS.strategy_type,
- tpu_address=FLAGS.tpu)
- if strategy:
- logging.info("***** Number of cores used : %d",
- strategy.num_replicas_in_sync)
- train_input_fn = functools.partial(data_utils.get_squad_input_data,
- FLAGS.train_batch_size, FLAGS.seq_len,
- FLAGS.query_len, strategy, True,
- FLAGS.train_tfrecord_path)
-
- test_input_fn = functools.partial(data_utils.get_squad_input_data,
- FLAGS.test_batch_size, FLAGS.seq_len,
- FLAGS.query_len, strategy, False,
- FLAGS.test_tfrecord_path)
-
- total_training_steps = FLAGS.train_steps
- steps_per_loop = FLAGS.iterations
- eval_steps = int(FLAGS.test_data_size / FLAGS.test_batch_size)
-
- optimizer, learning_rate_fn = optimization.create_optimizer(
- FLAGS.learning_rate,
- total_training_steps,
- FLAGS.warmup_steps,
- adam_epsilon=FLAGS.adam_epsilon)
- model_config = xlnet_config.XLNetConfig(FLAGS)
- run_config = xlnet_config.create_run_config(True, False, FLAGS)
- input_meta_data = {}
- input_meta_data["start_n_top"] = FLAGS.start_n_top
- input_meta_data["end_n_top"] = FLAGS.end_n_top
- input_meta_data["lr_layer_decay_rate"] = FLAGS.lr_layer_decay_rate
- input_meta_data["predict_dir"] = FLAGS.predict_dir
- input_meta_data["n_best_size"] = FLAGS.n_best_size
- input_meta_data["max_answer_length"] = FLAGS.max_answer_length
- input_meta_data["test_batch_size"] = FLAGS.test_batch_size
- input_meta_data["batch_size_per_core"] = int(FLAGS.train_batch_size /
- strategy.num_replicas_in_sync)
- input_meta_data["mem_len"] = FLAGS.mem_len
- model_fn = functools.partial(get_qaxlnet_model, model_config, run_config,
- FLAGS.start_n_top, FLAGS.end_n_top)
- eval_examples = squad_utils.read_squad_examples(
- FLAGS.predict_file, is_training=False)
- if FLAGS.test_feature_path:
- logging.info("start reading pickle file...")
- with tf.io.gfile.GFile(FLAGS.test_feature_path, "rb") as f:
- eval_features = pickle.load(f)
- logging.info("finishing reading pickle file...")
- else:
- sp_model = spm.SentencePieceProcessor()
- sp_model.LoadFromSerializedProto(
- tf.io.gfile.GFile(FLAGS.spiece_model_file, "rb").read())
- spm_basename = os.path.basename(FLAGS.spiece_model_file)
- eval_features = squad_utils.create_eval_data(
- spm_basename, sp_model, eval_examples, FLAGS.max_seq_length,
- FLAGS.max_query_length, FLAGS.doc_stride, FLAGS.uncased)
-
- with tf.io.gfile.GFile(FLAGS.predict_file) as f:
- original_data = json.load(f)["data"]
- eval_fn = functools.partial(run_evaluation, strategy, test_input_fn,
- eval_examples, eval_features, original_data,
- eval_steps, input_meta_data)
-
- training_utils.train(
- strategy=strategy,
- model_fn=model_fn,
- input_meta_data=input_meta_data,
- eval_fn=eval_fn,
- metric_fn=None,
- train_input_fn=train_input_fn,
- init_checkpoint=FLAGS.init_checkpoint,
- init_from_transformerxl=FLAGS.init_from_transformerxl,
- total_training_steps=total_training_steps,
- steps_per_loop=steps_per_loop,
- optimizer=optimizer,
- learning_rate_fn=learning_rate_fn,
- model_dir=FLAGS.model_dir,
- save_steps=FLAGS.save_steps)
-
-
-if __name__ == "__main__":
- app.run(main)
diff --git a/official/pip_package/setup.py b/official/pip_package/setup.py
index 56087d7c106a70f8e97a542b569571de91d88984..348c277454f5a691a7df4e0a7aa9bd341c01e86e 100644
--- a/official/pip_package/setup.py
+++ b/official/pip_package/setup.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,8 +20,8 @@ import sys
from setuptools import find_packages
from setuptools import setup
-version = '2.7.0'
-tf_version = '2.7.0' # Major version.
+version = '2.10.0'
+tf_version = '2.10.0' # Major version.
project_name = 'tf-models-official'
@@ -74,7 +74,7 @@ setup(
description='TensorFlow Official Models',
long_description=long_description,
author='Google Inc.',
- author_email='no-reply@google.com',
+ author_email='packages@tensorflow.org',
url='https://github.com/tensorflow/models',
license='Apache 2.0',
packages=find_packages(exclude=[
diff --git a/official/projects/README.md b/official/projects/README.md
index 9c94fdd110642ed56a2610f063f54acba9ae045a..fb2768b558fe1601afd741cf2e4bf36d833d4db7 100644
--- a/official/projects/README.md
+++ b/official/projects/README.md
@@ -1,11 +1,31 @@
# TensorFlow Model Garden Modeling Projects
-This directory contains projects using TensorFlow Model Garden Modeling
-libraries.
+This directory contains projects using Modeling libraries of TensorFlow Model
+Garden. More details about each project can be found in the individual
+project folders listed below.
## Projects
-* [NHNet](nhnet):
- [Generating Representative Headlines for News Stories](https://arxiv.org/abs/2001.09386)
- by Gu et al, 2020
-
+* [AssembleNet](./assemblenet/README.md)
+* [BASNet](./basnet/README.md)
+* [BigBird](./bigbird/README.md)
+* [DeepMAC Mask-RCNN](./deepmac_maskrcnn/README.md)
+* [DETR](./detr/README.md)
+* [Edge-TPU for Vision and NLP](./edgetpu/README.md)
+* [Language-agnostic BERT Sentence Embedding](./labse/README.md)
+* [Long-Document Transformer](./longformer/README.md)
+* [MobileBERT](./mobilebert/README.md)
+* [MoViNets](./movinet/README.md)
+* [News Headline Generation Model: NHNet](./nhnet/README.md)
+* [Training with Pruning](./pruning/README.md)
+* [QAT for Computer Vision](./qat/vision/README.md)
+* [Roformer Project](./roformer/README.md)
+* [Training ELECTRA Augmented with Multi-word Selection](./teams/README.md)
+* [NLP example project](./text_classification_example/README.md)
+* [TensorNetwork BERT](./tn_bert/README.md)
+* [Token Dropping for Efficient BERT Pretraining](./token_dropping/README.md)
+* [Spatiotemporal Contrastive Video Representation Learning](./video_ssl/README.md)
+* [Vision Transformer (ViT)](./vit/README.md)
+* [Data-Efficient Image Transformer (DEIT)](./vit/README.md)
+* [Volumetric Models](./volumetric_models/README.md)
+* [YouTube-8M Tensorflow Starter Code](./yt8m/README.md)
diff --git a/official/projects/__init__.py b/official/projects/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/assemblenet/configs/assemblenet.py b/official/projects/assemblenet/configs/assemblenet.py
index e021f3a4bca0a3a30020eb8dd352557c4575f26a..5bbe79b58a84dae09b54d6afd3774b69259f91d3 100644
--- a/official/projects/assemblenet/configs/assemblenet.py
+++ b/official/projects/assemblenet/configs/assemblenet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Definitions for AssembleNet/++ structures.
This structure is a `list` corresponding to a graph representation of the
@@ -40,9 +39,9 @@ from typing import List, Optional, Tuple
from official.core import config_definitions as cfg
from official.core import exp_factory
from official.modeling import hyperparams
-from official.vision.beta.configs import backbones_3d
-from official.vision.beta.configs import common
-from official.vision.beta.configs import video_classification
+from official.vision.configs import backbones_3d
+from official.vision.configs import common
+from official.vision.configs import video_classification
@dataclasses.dataclass
@@ -62,7 +61,7 @@ def flat_lists_to_blocks(model_structures, model_edge_weights):
if node[0] < 0:
block = BlockSpec(level=node[0], temporal_dilation=node[1])
else:
- block = BlockSpec(
+ block = BlockSpec( # pytype: disable=wrong-arg-types
level=node[0],
input_blocks=node[1],
num_filters=node[2],
diff --git a/official/projects/assemblenet/configs/assemblenet_test.py b/official/projects/assemblenet/configs/assemblenet_test.py
index 26fc08edc028982c0e0c6dfa1087078f3c7938b2..f11c21135c0dbb38508d4e3613376cbc9a788336 100644
--- a/official/projects/assemblenet/configs/assemblenet_test.py
+++ b/official/projects/assemblenet/configs/assemblenet_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,13 +12,12 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
from absl.testing import parameterized
import tensorflow as tf
from official.core import config_definitions as cfg
from official.core import exp_factory
from official.projects.assemblenet.configs import assemblenet
-from official.vision.beta.configs import video_classification as exp_cfg
+from official.vision.configs import video_classification as exp_cfg
class AssemblenetTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/assemblenet/modeling/assemblenet.py b/official/projects/assemblenet/modeling/assemblenet.py
index f84f38a854f7f7a9f4fa0e07b978ebe66f012100..3c2417a94e8594b05d72e541006e566eb4a9693d 100644
--- a/official/projects/assemblenet/modeling/assemblenet.py
+++ b/official/projects/assemblenet/modeling/assemblenet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Contains definitions for the AssembleNet [1] models.
Requires the AssembleNet architecture to be specified in
@@ -57,8 +56,8 @@ import tensorflow as tf
from official.modeling import hyperparams
from official.projects.assemblenet.configs import assemblenet as cfg
from official.projects.assemblenet.modeling import rep_flow_2d_layer as rf
-from official.vision.beta.modeling import factory_3d as model_factory
-from official.vision.beta.modeling.backbones import factory as backbone_factory
+from official.vision.modeling import factory_3d as model_factory
+from official.vision.modeling.backbones import factory as backbone_factory
layers = tf.keras.layers
intermediate_channel_size = [64, 128, 256, 512]
diff --git a/official/projects/assemblenet/modeling/assemblenet_plus.py b/official/projects/assemblenet/modeling/assemblenet_plus.py
index 85d7629012080dc642c7558c416416b863869239..c07657bdf1ff54af8024ea0f7ed1aed4ac739d35 100644
--- a/official/projects/assemblenet/modeling/assemblenet_plus.py
+++ b/official/projects/assemblenet/modeling/assemblenet_plus.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -64,8 +64,8 @@ from official.modeling import hyperparams
from official.projects.assemblenet.configs import assemblenet as cfg
from official.projects.assemblenet.modeling import assemblenet as asn
from official.projects.assemblenet.modeling import rep_flow_2d_layer as rf
-from official.vision.beta.modeling import factory_3d as model_factory
-from official.vision.beta.modeling.backbones import factory as backbone_factory
+from official.vision.modeling import factory_3d as model_factory
+from official.vision.modeling.backbones import factory as backbone_factory
layers = tf.keras.layers
diff --git a/official/projects/assemblenet/modeling/assemblenet_plus_test.py b/official/projects/assemblenet/modeling/assemblenet_plus_test.py
index 5eb6ae810e559983f8e7576274c34d4702c72e4a..a2799c0b045eb234b4a60c0d09016026032d5004 100644
--- a/official/projects/assemblenet/modeling/assemblenet_plus_test.py
+++ b/official/projects/assemblenet/modeling/assemblenet_plus_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/assemblenet/modeling/rep_flow_2d_layer.py b/official/projects/assemblenet/modeling/rep_flow_2d_layer.py
index d29968a668d6e6695b4442983239aeacd9b59b61..2b6439342ed06482d756e74570e694a744c040b5 100644
--- a/official/projects/assemblenet/modeling/rep_flow_2d_layer.py
+++ b/official/projects/assemblenet/modeling/rep_flow_2d_layer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Contains definitions for 'Representation Flow' layer [1].
Representation flow layer is a generalization of optical flow extraction; the
diff --git a/official/projects/assemblenet/train.py b/official/projects/assemblenet/train.py
index 3107f807dbaf475aa340e613282d22ab2be0d03c..54b682ef059b1947120062763ce348aab5a2a391 100644
--- a/official/projects/assemblenet/train.py
+++ b/official/projects/assemblenet/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
r"""Training driver.
Commandline:
@@ -29,9 +28,6 @@ from absl import flags
from absl import logging
import gin
-# pylint: disable=unused-import
-from official.common import registry_imports
-# pylint: enable=unused-import
from official.common import distribute_utils
from official.common import flags as tfm_flags
from official.core import task_factory
@@ -42,6 +38,7 @@ from official.modeling import performance
from official.projects.assemblenet.configs import assemblenet as asn_configs
from official.projects.assemblenet.modeling import assemblenet as asn
from official.projects.assemblenet.modeling import assemblenet_plus as asnp
+from official.vision import registry_imports
# pylint: enable=unused-import
FLAGS = flags.FLAGS
diff --git a/official/projects/assemblenet/train_test.py b/official/projects/assemblenet/train_test.py
index c07fa1c63473fac97fcaaab173d1feee18605027..b3fda06790440539fb1767fd6c1dd79e2bb5b9f5 100644
--- a/official/projects/assemblenet/train_test.py
+++ b/official/projects/assemblenet/train_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
import json
import os
import random
@@ -22,7 +21,7 @@ from absl import logging
from absl.testing import flagsaver
import tensorflow as tf
from official.projects.assemblenet import train as train_lib
-from official.vision.beta.dataloaders import tfexample_utils
+from official.vision.dataloaders import tfexample_utils
FLAGS = flags.FLAGS
diff --git a/official/projects/backbone_reuse/README.md b/official/projects/backbone_reuse/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..0981c9e2260c5383df0dd7973427f69bc274d78c
--- /dev/null
+++ b/official/projects/backbone_reuse/README.md
@@ -0,0 +1,41 @@
+# Proper Reuse of Image Classification Features Improves Object Detection
+
+This project brings the backbone freezing training approach into the Mask-RCNN
+architecture. Please see the paper for more details
+\([arxiv](https://arxiv.org/abs/2204.00484) - selected for oral presentation at
+CVPR 2022\).
+
+### Training Mask-Rcnn Models with backbone frozen.
+
+#### Freezing Resnet-RS-101 checkpoint (ImageNet pretrained).
+
+1. Download the ResNet-RS-101 pretrained checkpoint from
+ [TF-Vision Model Garden](https://github.com/tensorflow/models/tree/master/official/vision#resnet-rs-models-trained-with-various-settings),
+ \([checkpoint](https://storage.cloud.google.com/tf_model_garden/vision/resnet-rs/resnet-rs-101-i192.tar.gz)\)
+
+2. Config files used in our Resnet-101 ablations are included in the
+ [configs folder](https://github.com/tensorflow/models/tree/master/official/projects/backbone_reuse/configs/experiments/faster_rcnn).
+ Select one according to the target architecture (FPN, NASFPN, NASFPN +
+ Cascades) and training schedule preference (shorter--72 epochs, or longer
+ --600 epochs).
+
+3. Change the config flag `init_checkpoint` to point to the downloaded file.
+
+You are all set. Follow the standard TFVision Mask-Rcnn training pipeline to
+complete the training.
+
+#### How does it work?
+
+The config files set the task's flag `freeze_backbone: true`. This flag prevents
+the pretrained backbone weights from being updated during the downstream model
+training.
+
+## Citation
+
+```
+@inproceedings{vasconcelos2022backbonefreeze,
+ title = {Proper Reuse of Image Classification Features Improves Object Detection},
+ author = {Cristina Vasconcelos and Vighnesh Birodkar and Vincent Dumoulin},
+ booktitle={CVPR}
+ year={2022},
+```
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..2696f3d0e81b4a3e223ca2d9c78f9847d0e339d5
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_600epochs.yaml
@@ -0,0 +1,38 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ detection_head:
+ num_fcs: 2
+ norm_activation:
+ activation: swish
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [1062734, 1090458]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 1108940
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..423fd2d59cad108db91b02163fe741e4aafa2894
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_72epochs.yaml
@@ -0,0 +1,38 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ detection_head:
+ num_fcs: 2
+ norm_activation:
+ activation: swish
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [88704, 125664]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 133056
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..c6cecb4f8e9e6c3c1b65932f5dc7a9115768b495
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_600epochs.yaml
@@ -0,0 +1,43 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ detection_head:
+ cascade_class_ensemble: true
+ class_agnostic_bbox_pred: true
+ num_fcs: 2
+ input_size: [1280, 1280, 3]
+ norm_activation:
+ activation: swish
+ roi_sampler:
+ cascade_iou_thresholds: [0.7, 0.8]
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [1062734, 1090458]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 1108940
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..482c655c83237f3d3474c87f318e3b4f5d6c3f54
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_fpn_cascade_72epochs.yaml
@@ -0,0 +1,43 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ detection_head:
+ cascade_class_ensemble: true
+ class_agnostic_bbox_pred: true
+ num_fcs: 2
+ input_size: [1280, 1280, 3]
+ norm_activation:
+ activation: swish
+ roi_sampler:
+ cascade_iou_thresholds: [0.7, 0.8]
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [88704, 125664]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 133056
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..1affdaf22e47ab990dee9da9edcdffe7cd078b30
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_600epochs.yaml
@@ -0,0 +1,41 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ detection_head:
+ num_fcs: 2
+ include_mask: false
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: swish
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [1062734, 1090458]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 1108940
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..2c239c96f131cfe277d054e0c41207e885ac4898
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_72epochs.yaml
@@ -0,0 +1,41 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ detection_head:
+ num_fcs: 2
+ include_mask: false
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: swish
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [88704, 125664]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 133056
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..b2378c49499343ebdf7ee814c702552db69b4426
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_600epochs.yaml
@@ -0,0 +1,45 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ detection_head:
+ cascade_class_ensemble: true
+ class_agnostic_bbox_pred: true
+ num_fcs: 2
+ input_size: [1280, 1280, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: swish
+ roi_sampler:
+ cascade_iou_thresholds: [0.7, 0.8]
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [1062734, 1090458]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 1108940
diff --git a/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..061aeeb9ac91cb088db38ca3101a02f7b16d49cd
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/faster_rcnn/fastrcnn_resnet101_nasfpn_cascade_72epochs.yaml
@@ -0,0 +1,45 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ detection_head:
+ cascade_class_ensemble: true
+ class_agnostic_bbox_pred: true
+ num_fcs: 2
+ input_size: [1280, 1280, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: swish
+ roi_sampler:
+ cascade_iou_thresholds: [0.7, 0.8]
+ train_data:
+ global_batch_size: 64
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [88704, 125664]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.16, 0.016, 0.0016]
+ type: stepwise
+ steps_per_loop: 1848
+ summary_interval: 1848
+ train_steps: 133056
diff --git a/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7b4f285b890c43010edbd4968ae74d624825b15f
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_600epochs.yaml
@@ -0,0 +1,34 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ train_data:
+ global_batch_size: 256
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [265684, 272615]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.32, 0.032, 0.0032]
+ type: stepwise
+ steps_per_loop: 462
+ summary_interval: 462
+ train_steps: 277235
diff --git a/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..436f7a0c7f4d6912b0090aa74bf91bf0ad937072
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_fpn_72epochs.yaml
@@ -0,0 +1,34 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: fpn
+ train_data:
+ global_batch_size: 256
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [22176, 31416]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.32, 0.032, 0.0032]
+ type: stepwise
+ steps_per_loop: 462
+ summary_interval: 462
+ train_steps: 33264
diff --git a/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_600epochs.yaml b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_600epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..13db989d4077630769b477e56b0faf1059fccd78
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_600epochs.yaml
@@ -0,0 +1,34 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ train_data:
+ global_batch_size: 256
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [265684, 272615]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.32, 0.032, 0.0032]
+ type: stepwise
+ steps_per_loop: 462
+ summary_interval: 462
+ train_steps: 277235
diff --git a/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_72epochs.yaml b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_72epochs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..74a35ee9a5382e653b048f0bd3c15d9e4faa3294
--- /dev/null
+++ b/official/projects/backbone_reuse/configs/experiments/retinanet/retinanet_resnet101_nasfpn_72epochs.yaml
@@ -0,0 +1,34 @@
+task:
+ # init_checkpoint: 'a_pretrained_backbone_checkpoint'
+ init_checkpoint_modules: backbone
+ freeze_backbone: true
+ model:
+ backbone:
+ resnet:
+ model_id: 101
+ replace_stem_max_pool: true
+ resnetd_shortcut: true
+ scale_stem: true
+ se_ratio: 0.25
+ stem_type: v1
+ type: resnet
+ decoder:
+ type: nasfpn
+ train_data:
+ global_batch_size: 256
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.1
+trainer:
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [22176, 31416]
+ name: PiecewiseConstantDecay
+ offset: 0
+ values: [0.32, 0.032, 0.0032]
+ type: stepwise
+ steps_per_loop: 462
+ summary_interval: 462
+ train_steps: 33264
diff --git a/official/projects/basnet/configs/basnet.py b/official/projects/basnet/configs/basnet.py
index 6a79e370f65c9c010d01483bdb5ce179a8ce3c18..3c971d3ca6615e4e4f0c4534bd39cbdeb6fb4fe7 100644
--- a/official/projects/basnet/configs/basnet.py
+++ b/official/projects/basnet/configs/basnet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ from official.core import config_definitions as cfg
from official.core import exp_factory
from official.modeling import hyperparams
from official.modeling import optimization
-from official.vision.beta.configs import common
+from official.vision.configs import common
@dataclasses.dataclass
diff --git a/official/projects/basnet/configs/basnet_test.py b/official/projects/basnet/configs/basnet_test.py
index 2d0c40ef0cd5bc20855a052231cc78b84249f27e..3e474ab098dcf8e9e5d0674712430b6341da29f3 100644
--- a/official/projects/basnet/configs/basnet_test.py
+++ b/official/projects/basnet/configs/basnet_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/evaluation/metrics.py b/official/projects/basnet/evaluation/metrics.py
index 0126bbc357e23372f7e6d7df5e70ca7c8a845687..88fb5907222fc6471fdc001f712b140f5294c552 100644
--- a/official/projects/basnet/evaluation/metrics.py
+++ b/official/projects/basnet/evaluation/metrics.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/evaluation/metrics_test.py b/official/projects/basnet/evaluation/metrics_test.py
index 26cb7d83551349f376908e2d8a0aec7812362690..e37b0185ff5bbc2d1ef76de8f57e7ca0d37010a4 100644
--- a/official/projects/basnet/evaluation/metrics_test.py
+++ b/official/projects/basnet/evaluation/metrics_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/losses/basnet_losses.py b/official/projects/basnet/losses/basnet_losses.py
index ece1f8646f0573e0b164abc57ba5f40775e3353c..023d3c6358f21add9935648e0225362484cadf1e 100644
--- a/official/projects/basnet/losses/basnet_losses.py
+++ b/official/projects/basnet/losses/basnet_losses.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/modeling/basnet_model.py b/official/projects/basnet/modeling/basnet_model.py
index cdcc978a8f6c989ce44c4bc8a59f186e9951b92b..cef6d456d6433fef9c2456787cc35578a8de4301 100644
--- a/official/projects/basnet/modeling/basnet_model.py
+++ b/official/projects/basnet/modeling/basnet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ import tensorflow as tf
from official.modeling import tf_utils
from official.projects.basnet.modeling import nn_blocks
-from official.vision.beta.modeling.backbones import factory
+from official.vision.modeling.backbones import factory
# Specifications for BASNet encoder.
# Each element in the block configuration is in the following format:
diff --git a/official/projects/basnet/modeling/basnet_model_test.py b/official/projects/basnet/modeling/basnet_model_test.py
index 8f919d7fa5026e17d25409a4d4a67254c8a6b964..8f59904e5d1ba2e4163728c43b9967537e53718a 100644
--- a/official/projects/basnet/modeling/basnet_model_test.py
+++ b/official/projects/basnet/modeling/basnet_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/modeling/nn_blocks.py b/official/projects/basnet/modeling/nn_blocks.py
index c0815ab7094c3ef71873cfc7a71e36f59da0d520..1254c9c78d8d24a8e52086dc930dd19aaa3669c3 100644
--- a/official/projects/basnet/modeling/nn_blocks.py
+++ b/official/projects/basnet/modeling/nn_blocks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/modeling/refunet.py b/official/projects/basnet/modeling/refunet.py
index 0a730f4c7807a381e661c260b460815ad85c78fd..a052adc9ef4802f273fb3c6e4fffb8eb717fd315 100644
--- a/official/projects/basnet/modeling/refunet.py
+++ b/official/projects/basnet/modeling/refunet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/basnet/serving/basnet.py b/official/projects/basnet/serving/basnet.py
index 84c0617c16a40bec3bd2ebef893d16503c796db7..d25f11c18f58fc73de69693bb693a73a52390c4d 100644
--- a/official/projects/basnet/serving/basnet.py
+++ b/official/projects/basnet/serving/basnet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,11 +17,7 @@
import tensorflow as tf
from official.projects.basnet.tasks import basnet
-from official.vision.beta.serving import semantic_segmentation
-
-
-MEAN_RGB = (0.485 * 255, 0.456 * 255, 0.406 * 255)
-STDDEV_RGB = (0.229 * 255, 0.224 * 255, 0.225 * 255)
+from official.vision.serving import semantic_segmentation
class BASNetModule(semantic_segmentation.SegmentationModule):
diff --git a/official/projects/basnet/serving/export_saved_model.py b/official/projects/basnet/serving/export_saved_model.py
index a08a1bf5a470b32974445d10d87aa819259debd4..417beac57fde4999c2bd8f68fc4eb0d7b2e9e79e 100644
--- a/official/projects/basnet/serving/export_saved_model.py
+++ b/official/projects/basnet/serving/export_saved_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -41,7 +41,7 @@ from absl import flags
from official.core import exp_factory
from official.modeling import hyperparams
from official.projects.basnet.serving import basnet
-from official.vision.beta.serving import export_saved_model_lib
+from official.vision.serving import export_saved_model_lib
FLAGS = flags.FLAGS
diff --git a/official/projects/basnet/tasks/basnet.py b/official/projects/basnet/tasks/basnet.py
index 99e97586a80630710c5280515e41f2ecdd19dc09..07332a552590fbad657d67e9aa573b6f24353f74 100644
--- a/official/projects/basnet/tasks/basnet.py
+++ b/official/projects/basnet/tasks/basnet.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -27,13 +27,13 @@ from official.projects.basnet.evaluation import metrics as basnet_metrics
from official.projects.basnet.losses import basnet_losses
from official.projects.basnet.modeling import basnet_model
from official.projects.basnet.modeling import refunet
-from official.vision.beta.dataloaders import segmentation_input
+from official.vision.dataloaders import segmentation_input
def build_basnet_model(
input_specs: tf.keras.layers.InputSpec,
model_config: exp_cfg.BASNetModel,
- l2_regularizer: tf.keras.regularizers.Regularizer = None):
+ l2_regularizer: Optional[tf.keras.regularizers.Regularizer] = None):
"""Builds BASNet model."""
norm_activation_config = model_config.norm_activation
backbone = basnet_model.BASNetEncoder(
@@ -203,8 +203,7 @@ class BASNetTask(base_task.Task):
# For mixed_precision policy, when LossScaleOptimizer is used, loss is
# scaled for numerical stability.
- if isinstance(
- optimizer, tf.keras.mixed_precision.experimental.LossScaleOptimizer):
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
scaled_loss = optimizer.get_scaled_loss(scaled_loss)
tvars = model.trainable_variables
@@ -212,8 +211,7 @@ class BASNetTask(base_task.Task):
# Scales back gradient before apply_gradients when LossScaleOptimizer is
# used.
- if isinstance(
- optimizer, tf.keras.mixed_precision.experimental.LossScaleOptimizer):
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
grads = optimizer.get_unscaled_gradients(grads)
# Apply gradient clipping.
diff --git a/official/projects/basnet/train.py b/official/projects/basnet/train.py
index c65604f5d8bf5cc8d44b88fa132ed838ec833d69..d30321ac37337c14c4d0fc099eacd91e7d76b31e 100644
--- a/official/projects/basnet/train.py
+++ b/official/projects/basnet/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""TensorFlow Model Garden Vision training driver."""
from absl import app
@@ -23,7 +22,7 @@ from official.projects.basnet.configs import basnet as basnet_cfg
from official.projects.basnet.modeling import basnet_model
from official.projects.basnet.modeling import refunet
from official.projects.basnet.tasks import basnet as basenet_task
-from official.vision.beta import train
+from official.vision import train
if __name__ == '__main__':
diff --git a/official/nlp/projects/bigbird/README.md b/official/projects/bigbird/README.md
similarity index 100%
rename from official/nlp/projects/bigbird/README.md
rename to official/projects/bigbird/README.md
diff --git a/official/projects/bigbird/__init__.py b/official/projects/bigbird/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/bigbird/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/bigbird/encoder.py b/official/projects/bigbird/encoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..f0d0af458ab7df8b57bcb294382d345f75e8c579
--- /dev/null
+++ b/official/projects/bigbird/encoder.py
@@ -0,0 +1,238 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Transformer-based text encoder network."""
+# pylint: disable=g-classes-have-attributes
+
+import tensorflow as tf
+
+from official.modeling import activations
+from official.nlp import modeling
+from official.nlp.modeling import layers
+from official.projects.bigbird import recompute_grad
+from official.projects.bigbird import recomputing_dropout
+
+
+_MAX_SEQ_LEN = 4096
+
+
+class RecomputeTransformerLayer(layers.TransformerScaffold):
+ """Transformer layer that recomputes the forward pass during backpropagation."""
+
+ def call(self, inputs, training=None):
+ emb, mask = inputs
+ def f(*args):
+ # recompute_grad can only handle tensor inputs. so we enumerate the
+ # nested input [emb, mask] as follows:
+ # args[0]: emb
+ # args[1]: mask[0] = band_mask
+ # args[2]: mask[1] = encoder_from_mask
+ # args[3]: mask[2] = encoder_to_mask
+ # args[4]: mask[3] = blocked_encoder_mask
+ x = super(RecomputeTransformerLayer,
+ self).call([args[0], [args[1], args[2], args[3], args[4]]],
+ training=training)
+ return x
+
+ f = recompute_grad.recompute_grad(f)
+
+ return f(emb, *mask)
+
+
+@tf.keras.utils.register_keras_serializable(package='Text')
+class BigBirdEncoder(tf.keras.Model):
+ """Transformer-based encoder network with BigBird attentions.
+
+ *Note* that the network is constructed by
+ [Keras Functional API](https://keras.io/guides/functional_api/).
+
+ Args:
+ vocab_size: The size of the token vocabulary.
+ hidden_size: The size of the transformer hidden layers.
+ num_layers: The number of transformer layers.
+ num_attention_heads: The number of attention heads for each transformer. The
+ hidden size must be divisible by the number of attention heads.
+ max_position_embeddings: The maximum length of position embeddings that this
+ encoder can consume. If None, max_position_embeddings uses the value from
+ sequence length. This determines the variable shape for positional
+ embeddings.
+ type_vocab_size: The number of types that the 'type_ids' input can take.
+ intermediate_size: The intermediate size for the transformer layers.
+ block_size: int. A BigBird Attention parameter: size of block in from/to
+ sequences.
+ num_rand_blocks: int. A BigBird Attention parameter: number of random chunks
+ per row.
+ activation: The activation to use for the transformer layers.
+ dropout_rate: The dropout rate to use for the transformer layers.
+ attention_dropout_rate: The dropout rate to use for the attention layers
+ within the transformer layers.
+ initializer: The initialzer to use for all weights in this encoder.
+ embedding_width: The width of the word embeddings. If the embedding width is
+ not equal to hidden size, embedding parameters will be factorized into two
+ matrices in the shape of ['vocab_size', 'embedding_width'] and
+ ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
+ smaller than 'hidden_size').
+ use_gradient_checkpointing: Use gradient checkpointing to trade-off compute
+ for memory.
+ """
+
+ def __init__(self,
+ vocab_size,
+ hidden_size=768,
+ num_layers=12,
+ num_attention_heads=12,
+ max_position_embeddings=_MAX_SEQ_LEN,
+ type_vocab_size=16,
+ intermediate_size=3072,
+ block_size=64,
+ num_rand_blocks=3,
+ activation=activations.gelu,
+ dropout_rate=0.1,
+ attention_dropout_rate=0.1,
+ initializer=tf.keras.initializers.TruncatedNormal(stddev=0.02),
+ embedding_width=None,
+ use_gradient_checkpointing=False,
+ **kwargs):
+ activation = tf.keras.activations.get(activation)
+ initializer = tf.keras.initializers.get(initializer)
+
+ if use_gradient_checkpointing:
+ tf.keras.layers.Dropout = recomputing_dropout.RecomputingDropout
+ layer_cls = RecomputeTransformerLayer
+ else:
+ layer_cls = layers.TransformerScaffold
+
+ self._self_setattr_tracking = False
+ self._config_dict = {
+ 'vocab_size': vocab_size,
+ 'hidden_size': hidden_size,
+ 'num_layers': num_layers,
+ 'num_attention_heads': num_attention_heads,
+ 'max_position_embeddings': max_position_embeddings,
+ 'type_vocab_size': type_vocab_size,
+ 'intermediate_size': intermediate_size,
+ 'block_size': block_size,
+ 'num_rand_blocks': num_rand_blocks,
+ 'activation': tf.keras.activations.serialize(activation),
+ 'dropout_rate': dropout_rate,
+ 'attention_dropout_rate': attention_dropout_rate,
+ 'initializer': tf.keras.initializers.serialize(initializer),
+ 'embedding_width': embedding_width,
+ }
+
+ word_ids = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name='input_word_ids')
+ mask = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name='input_mask')
+ type_ids = tf.keras.layers.Input(
+ shape=(None,), dtype=tf.int32, name='input_type_ids')
+
+ if embedding_width is None:
+ embedding_width = hidden_size
+ self._embedding_layer = modeling.layers.OnDeviceEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ initializer=initializer,
+ name='word_embeddings')
+ word_embeddings = self._embedding_layer(word_ids)
+
+ # Always uses dynamic slicing for simplicity.
+ self._position_embedding_layer = modeling.layers.PositionEmbedding(
+ initializer=initializer,
+ max_length=max_position_embeddings,
+ name='position_embedding')
+ position_embeddings = self._position_embedding_layer(word_embeddings)
+ self._type_embedding_layer = modeling.layers.OnDeviceEmbedding(
+ vocab_size=type_vocab_size,
+ embedding_width=embedding_width,
+ initializer=initializer,
+ use_one_hot=True,
+ name='type_embeddings')
+ type_embeddings = self._type_embedding_layer(type_ids)
+
+ embeddings = tf.keras.layers.Add()(
+ [word_embeddings, position_embeddings, type_embeddings])
+
+ self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
+ name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
+
+ embeddings = self._embedding_norm_layer(embeddings)
+ embeddings = tf.keras.layers.Dropout(rate=dropout_rate)(embeddings)
+
+ # We project the 'embedding' output to 'hidden_size' if it is not already
+ # 'hidden_size'.
+ if embedding_width != hidden_size:
+ self._embedding_projection = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=hidden_size,
+ bias_axes='y',
+ kernel_initializer=initializer,
+ name='embedding_projection')
+ embeddings = self._embedding_projection(embeddings)
+
+ self._transformer_layers = []
+ data = embeddings
+ masks = layers.BigBirdMasks(block_size=block_size)(
+ data, mask)
+ encoder_outputs = []
+ attn_head_dim = hidden_size // num_attention_heads
+ for i in range(num_layers):
+ layer = layer_cls(
+ num_attention_heads,
+ intermediate_size,
+ activation,
+ attention_cls=layers.BigBirdAttention,
+ attention_cfg=dict(
+ num_heads=num_attention_heads,
+ key_dim=attn_head_dim,
+ kernel_initializer=initializer,
+ from_block_size=block_size,
+ to_block_size=block_size,
+ num_rand_blocks=num_rand_blocks,
+ max_rand_mask_length=max_position_embeddings,
+ seed=i),
+ dropout_rate=dropout_rate,
+ attention_dropout_rate=dropout_rate,
+ kernel_initializer=initializer)
+ self._transformer_layers.append(layer)
+ data = layer([data, masks])
+ encoder_outputs.append(data)
+
+ outputs = dict(
+ sequence_output=encoder_outputs[-1], encoder_outputs=encoder_outputs)
+ super().__init__(
+ inputs=[word_ids, mask, type_ids], outputs=outputs, **kwargs)
+
+ def get_embedding_table(self):
+ return self._embedding_layer.embeddings
+
+ def get_embedding_layer(self):
+ return self._embedding_layer
+
+ def get_config(self):
+ return self._config_dict
+
+ @property
+ def transformer_layers(self):
+ """List of Transformer layers in the encoder."""
+ return self._transformer_layers
+
+ @property
+ def pooler_layer(self):
+ """The pooler dense layer after the transformer layers."""
+ return self._pooler_layer
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
diff --git a/official/projects/bigbird/encoder_test.py b/official/projects/bigbird/encoder_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..9b6833720501dab7d0d3258dee5e0826b8987738
--- /dev/null
+++ b/official/projects/bigbird/encoder_test.py
@@ -0,0 +1,63 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for official.nlp.projects.bigbird.encoder."""
+
+import numpy as np
+import tensorflow as tf
+
+from official.projects.bigbird import encoder
+
+
+class BigBirdEncoderTest(tf.test.TestCase):
+
+ def test_encoder(self):
+ sequence_length = 1024
+ batch_size = 2
+ vocab_size = 1024
+ network = encoder.BigBirdEncoder(
+ num_layers=1, vocab_size=1024, max_position_embeddings=4096)
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(2, size=(batch_size, sequence_length))
+ outputs = network([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs["sequence_output"].shape,
+ (batch_size, sequence_length, 768))
+
+ def test_save_restore(self):
+ sequence_length = 1024
+ batch_size = 2
+ vocab_size = 1024
+ network = encoder.BigBirdEncoder(
+ num_layers=1, vocab_size=1024, max_position_embeddings=4096)
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(2, size=(batch_size, sequence_length))
+ inputs = dict(
+ input_word_ids=word_id_data,
+ input_mask=mask_data,
+ input_type_ids=type_id_data)
+ ref_outputs = network(inputs)
+ model_path = self.get_temp_dir() + "/model"
+ network.save(model_path)
+ loaded = tf.keras.models.load_model(model_path)
+ outputs = loaded(inputs)
+ self.assertAllClose(outputs["sequence_output"],
+ ref_outputs["sequence_output"])
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/projects/bigbird/experiment_configs.py b/official/projects/bigbird/experiment_configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..0ad3e4e5820ab5627bfc4a477e10f4274fdb3b33
--- /dev/null
+++ b/official/projects/bigbird/experiment_configs.py
@@ -0,0 +1,100 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Bigbird experiment configurations."""
+# pylint: disable=g-doc-return-or-yield,line-too-long
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+from official.nlp.data import question_answering_dataloader
+from official.nlp.data import sentence_prediction_dataloader
+from official.nlp.tasks import question_answering
+from official.nlp.tasks import sentence_prediction
+
+
+@exp_factory.register_config_factory('bigbird/glue')
+def bigbird_glue() -> cfg.ExperimentConfig:
+ r"""BigBird GLUE."""
+ config = cfg.ExperimentConfig(
+ task=sentence_prediction.SentencePredictionConfig(
+ train_data=sentence_prediction_dataloader
+ .SentencePredictionDataConfig(),
+ validation_data=sentence_prediction_dataloader
+ .SentencePredictionDataConfig(
+ is_training=False, drop_remainder=False)),
+ trainer=cfg.TrainerConfig(
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate':
+ 0.01,
+ 'exclude_from_weight_decay':
+ ['LayerNorm', 'layer_norm', 'bias'],
+ }
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 3e-5,
+ 'end_learning_rate': 0.0,
+ }
+ },
+ 'warmup': {
+ 'type': 'polynomial'
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ config.task.model.encoder.type = 'bigbird'
+ return config
+
+
+@exp_factory.register_config_factory('bigbird/squad')
+def bigbird_squad() -> cfg.ExperimentConfig:
+ r"""BigBird Squad V1/V2."""
+ config = cfg.ExperimentConfig(
+ task=question_answering.QuestionAnsweringConfig(
+ train_data=question_answering_dataloader.QADataConfig(),
+ validation_data=question_answering_dataloader.QADataConfig()),
+ trainer=cfg.TrainerConfig(
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate':
+ 0.01,
+ 'exclude_from_weight_decay':
+ ['LayerNorm', 'layer_norm', 'bias'],
+ }
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 8e-5,
+ 'end_learning_rate': 0.0,
+ }
+ },
+ 'warmup': {
+ 'type': 'polynomial'
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ config.task.model.encoder.type = 'bigbird'
+ return config
diff --git a/official/nlp/projects/bigbird/experiments/glue_mnli_matched.yaml b/official/projects/bigbird/experiments/glue_mnli_matched.yaml
similarity index 100%
rename from official/nlp/projects/bigbird/experiments/glue_mnli_matched.yaml
rename to official/projects/bigbird/experiments/glue_mnli_matched.yaml
diff --git a/official/nlp/projects/bigbird/experiments/squad_v1.yaml b/official/projects/bigbird/experiments/squad_v1.yaml
similarity index 100%
rename from official/nlp/projects/bigbird/experiments/squad_v1.yaml
rename to official/projects/bigbird/experiments/squad_v1.yaml
diff --git a/official/nlp/projects/bigbird/recompute_grad.py b/official/projects/bigbird/recompute_grad.py
similarity index 99%
rename from official/nlp/projects/bigbird/recompute_grad.py
rename to official/projects/bigbird/recompute_grad.py
index d570ba848be467425f6cb3177fb1b8587a25632d..be9424d60316c19b9ba9ec46c997d07868410a41 100644
--- a/official/nlp/projects/bigbird/recompute_grad.py
+++ b/official/projects/bigbird/recompute_grad.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/bigbird/recomputing_dropout.py b/official/projects/bigbird/recomputing_dropout.py
similarity index 96%
rename from official/nlp/projects/bigbird/recomputing_dropout.py
rename to official/projects/bigbird/recomputing_dropout.py
index 3a0cfa31c2143d2dd06505badf7f66a5af658d7a..fb3e565b9662413a9f48584ac325ac15805f7fd3 100644
--- a/official/nlp/projects/bigbird/recomputing_dropout.py
+++ b/official/projects/bigbird/recomputing_dropout.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,8 +17,8 @@
import numpy as np
import tensorflow as tf
-from official.nlp.projects.bigbird import recompute_grad as recompute_grad_lib
-from official.nlp.projects.bigbird import stateless_dropout as stateless_dropout_lib
+from official.projects.bigbird import recompute_grad as recompute_grad_lib
+from official.projects.bigbird import stateless_dropout as stateless_dropout_lib
# Reimplements internal function
diff --git a/official/nlp/projects/bigbird/stateless_dropout.py b/official/projects/bigbird/stateless_dropout.py
similarity index 98%
rename from official/nlp/projects/bigbird/stateless_dropout.py
rename to official/projects/bigbird/stateless_dropout.py
index d61b313b5465d7eb2ada787c70ad97035fd098d4..49941253c646bce30fa173881ee7d04d9ee82b14 100644
--- a/official/nlp/projects/bigbird/stateless_dropout.py
+++ b/official/projects/bigbird/stateless_dropout.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/centernet/README.md b/official/projects/centernet/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..b6a182aa6cc7dc730e31c5362daa1801b125fcb1
--- /dev/null
+++ b/official/projects/centernet/README.md
@@ -0,0 +1,82 @@
+# Centernet
+
+[](https://arxiv.org/abs/1904.07850)
+
+Centernet builds upon CornerNet, an anchor-free model for object detection.
+
+Many other models, such as YOLO and RetinaNet, use anchor boxes. These anchor
+boxes are predefined to be close to the aspect ratios and scales of the objects
+in the training dataset. Anchor-based models do not predict the bounding boxes
+of objects directly. They instead predict the location and size/shape
+refinements to a predefined anchor box. The detection generator then computes
+the final confidences, positions, and size of the detection.
+
+CornerNet eliminates the need for anchor boxes. RetinaNet needs thousands of
+anchor boxes in order to cover the most common ground truth boxes. This adds
+unnecessary complexity to the model which slow down training and create
+imbalances in positive and negative anchor boxes. Instead, CornerNet creates
+heatmaps for each of the corners and pools them together in order to get the
+final detection boxes for the objects. CenterNet removes even more complexity
+by using the center instead of the corners, meaning that only one set of
+heatmaps (one heatmap for each class) is needed to predict the object. CenterNet
+proves that this can be done without a significant difference in accuracy.
+
+
+## Environment setup
+
+The code can be run on multiple GPUs or TPUs with different distribution
+strategies. See the TensorFlow distributed training
+[guide](https://www.tensorflow.org/guide/distributed_training) for an overview
+of `tf.distribute`.
+
+The code is compatible with TensorFlow 2.5+. See requirements.txt for all
+prerequisites, and you can also install them using the following command. `pip
+install -r ./official/requirements.txt`
+
+## Training
+To train the model on Coco, try the following command:
+
+```
+python3 -m official.vision.beta.projects.centernet.train \
+ --mode=train_and_eval \
+ --experiment=centernet_hourglass_coco \
+ --model_dir={MODEL_DIR} \
+ --config_file={CONFIG_FILE}
+```
+
+## Configurations
+
+In the following table, we report the mAP measured on the `coco-val2017` set.
+
+Backbone | Config name | mAP
+:--------------- | :-----------------------------------------------| -------:
+Hourglass-104 | `coco-centernet-hourglass-gpu.yaml` | 40.01
+Hourglass-104 | `coco-centernet-hourglass-tpu.yaml` | 40.5
+
+**Note:** `float16` (`bfloat16` for TPU) is used in the provided configurations.
+
+
+## Cite
+
+[Centernet](https://arxiv.org/abs/1904.07850):
+```
+@article{Zhou2019ObjectsAP,
+ title={Objects as Points},
+ author={Xingyi Zhou and Dequan Wang and Philipp Kr{\"a}henb{\"u}hl},
+ journal={ArXiv},
+ year={2019},
+ volume={abs/1904.07850}
+}
+```
+
+[CornerNet](https://arxiv.org/abs/1808.01244):
+```
+@article{Law2019CornerNetDO,
+ title={CornerNet: Detecting Objects as Paired Keypoints},
+ author={Hei Law and J. Deng},
+ journal={International Journal of Computer Vision},
+ year={2019},
+ volume={128},
+ pages={642-656}
+}
+```
diff --git a/official/projects/centernet/__init__.py b/official/projects/centernet/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/common/__init__.py b/official/projects/centernet/common/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/common/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/common/registry_imports.py b/official/projects/centernet/common/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..49631514340480654dcd7706bda011f3cbedb08c
--- /dev/null
+++ b/official/projects/centernet/common/registry_imports.py
@@ -0,0 +1,22 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""All necessary imports for registration."""
+
+# pylint: disable=unused-import
+from official.projects.centernet.configs import centernet
+from official.projects.centernet.modeling import centernet_model
+from official.projects.centernet.modeling.backbones import hourglass
+from official.projects.centernet.tasks import centernet as centernet_task
+from official.vision import registry_imports
diff --git a/official/projects/centernet/configs/__init__.py b/official/projects/centernet/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/configs/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/configs/backbones.py b/official/projects/centernet/configs/backbones.py
new file mode 100644
index 0000000000000000000000000000000000000000..170aa4969324ef107c9f4a5d156a70d72e746aca
--- /dev/null
+++ b/official/projects/centernet/configs/backbones.py
@@ -0,0 +1,35 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Backbones configurations."""
+
+import dataclasses
+
+from official.modeling import hyperparams
+from official.vision.configs import backbones
+
+
+@dataclasses.dataclass
+class Hourglass(hyperparams.Config):
+ """Hourglass config."""
+ model_id: int = 52
+ input_channel_dims: int = 128
+ num_hourglasses: int = 2
+ initial_downsample: bool = True
+ activation: str = 'relu'
+
+
+@dataclasses.dataclass
+class Backbone(backbones.Backbone):
+ hourglass: Hourglass = Hourglass()
diff --git a/official/projects/centernet/configs/centernet.py b/official/projects/centernet/configs/centernet.py
new file mode 100644
index 0000000000000000000000000000000000000000..14f950e1285334c2a0e19d4a46754c8a464c9d98
--- /dev/null
+++ b/official/projects/centernet/configs/centernet.py
@@ -0,0 +1,226 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""CenterNet configuration definition."""
+
+import dataclasses
+import os
+from typing import List, Optional, Tuple
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.projects.centernet.configs import backbones
+from official.vision.configs import common
+
+
+TfExampleDecoderLabelMap = common.TfExampleDecoderLabelMap
+
+
+@dataclasses.dataclass
+class TfExampleDecoder(hyperparams.Config):
+ regenerate_source_id: bool = False
+
+
+@dataclasses.dataclass
+class DataDecoder(hyperparams.OneOfConfig):
+ type: Optional[str] = 'simple_decoder'
+ simple_decoder: TfExampleDecoder = TfExampleDecoder()
+ label_map_decoder: TfExampleDecoderLabelMap = TfExampleDecoderLabelMap()
+
+
+@dataclasses.dataclass
+class Parser(hyperparams.Config):
+ """Config for parser."""
+ bgr_ordering: bool = True
+ aug_rand_hflip: bool = True
+ aug_scale_min: float = 1.0
+ aug_scale_max: float = 1.0
+ aug_rand_saturation: bool = False
+ aug_rand_brightness: bool = False
+ aug_rand_hue: bool = False
+ aug_rand_contrast: bool = False
+ odapi_augmentation: bool = False
+ channel_means: Tuple[float, float, float] = dataclasses.field(
+ default_factory=lambda: (104.01362025, 114.03422265, 119.9165958))
+ channel_stds: Tuple[float, float, float] = dataclasses.field(
+ default_factory=lambda: (73.6027665, 69.89082075, 70.9150767))
+
+
+@dataclasses.dataclass
+class DataConfig(cfg.DataConfig):
+ """Input config for training."""
+ input_path: str = ''
+ global_batch_size: int = 32
+ is_training: bool = True
+ dtype: str = 'float16'
+ decoder: DataDecoder = DataDecoder()
+ parser: Parser = Parser()
+ shuffle_buffer_size: int = 10000
+ file_type: str = 'tfrecord'
+ drop_remainder: bool = True
+
+
+@dataclasses.dataclass
+class DetectionLoss(hyperparams.Config):
+ object_center_weight: float = 1.0
+ offset_weight: float = 1.0
+ scale_weight: float = 0.1
+
+
+@dataclasses.dataclass
+class Losses(hyperparams.Config):
+ detection: DetectionLoss = DetectionLoss()
+ gaussian_iou: float = 0.7
+ class_offset: int = 1
+
+
+@dataclasses.dataclass
+class CenterNetHead(hyperparams.Config):
+ heatmap_bias: float = -2.19
+ input_levels: List[str] = dataclasses.field(
+ default_factory=lambda: ['2_0', '2'])
+
+
+@dataclasses.dataclass
+class CenterNetDetectionGenerator(hyperparams.Config):
+ max_detections: int = 100
+ peak_error: float = 1e-6
+ peak_extract_kernel_size: int = 3
+ class_offset: int = 1
+ use_nms: bool = False
+ nms_pre_thresh: float = 0.1
+ nms_thresh: float = 0.4
+ use_reduction_sum: bool = True
+
+
+@dataclasses.dataclass
+class CenterNetModel(hyperparams.Config):
+ """Config for centernet model."""
+ num_classes: int = 90
+ max_num_instances: int = 128
+ input_size: List[int] = dataclasses.field(default_factory=list)
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='hourglass', hourglass=backbones.Hourglass(model_id=52))
+ head: CenterNetHead = CenterNetHead()
+ # pylint: disable=line-too-long
+ detection_generator: CenterNetDetectionGenerator = CenterNetDetectionGenerator()
+ norm_activation: common.NormActivation = common.NormActivation(
+ norm_momentum=0.1, norm_epsilon=1e-5, use_sync_bn=True)
+
+
+@dataclasses.dataclass
+class CenterNetDetection(hyperparams.Config):
+ # use_center is the only option implemented currently.
+ use_centers: bool = True
+
+
+@dataclasses.dataclass
+class CenterNetSubTasks(hyperparams.Config):
+ detection: CenterNetDetection = CenterNetDetection()
+
+
+@dataclasses.dataclass
+class CenterNetTask(cfg.TaskConfig):
+ """Config for centernet task."""
+ model: CenterNetModel = CenterNetModel()
+ train_data: DataConfig = DataConfig(is_training=True)
+ validation_data: DataConfig = DataConfig(is_training=False)
+ subtasks: CenterNetSubTasks = CenterNetSubTasks()
+ losses: Losses = Losses()
+ gradient_clip_norm: float = 10.0
+ per_category_metrics: bool = False
+ weight_decay: float = 5e-4
+ # Load checkpoints
+ init_checkpoint: Optional[str] = None
+ init_checkpoint_modules: str = 'all'
+ annotation_file: Optional[str] = None
+
+ def get_output_length_dict(self):
+ task_outputs = {}
+ if self.subtasks.detection and self.subtasks.detection.use_centers:
+ task_outputs.update({
+ 'ct_heatmaps': self.model.num_classes,
+ 'ct_offset': 2,
+ 'ct_size': 2
+ })
+ else:
+ raise ValueError('Detection with center point is only available ')
+ return task_outputs
+
+
+COCO_INPUT_PATH_BASE = 'coco'
+COCO_TRAIN_EXAMPLES = 118287
+COCO_VAL_EXAMPLES = 5000
+
+
+@exp_factory.register_config_factory('centernet_hourglass_coco')
+def centernet_hourglass_coco() -> cfg.ExperimentConfig:
+ """COCO object detection with CenterNet."""
+ train_batch_size = 128
+ eval_batch_size = 8
+ steps_per_epoch = COCO_TRAIN_EXAMPLES // train_batch_size
+
+ config = cfg.ExperimentConfig(
+ task=CenterNetTask(
+ annotation_file=os.path.join(COCO_INPUT_PATH_BASE,
+ 'instances_val2017.json'),
+ model=CenterNetModel(),
+ train_data=DataConfig(
+ input_path=os.path.join(COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=Parser(),
+ shuffle_buffer_size=2),
+ validation_data=DataConfig(
+ input_path=os.path.join(COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ shuffle_buffer_size=2),
+ ),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=150 * steps_per_epoch,
+ validation_steps=COCO_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adam',
+ 'adam': {
+ 'epsilon': 1e-7
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ 'initial_learning_rate': 0.001,
+ 'decay_steps': 150 * steps_per_epoch
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 2000,
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
diff --git a/official/vision/beta/projects/centernet/configs/centernet_test.py b/official/projects/centernet/configs/centernet_test.py
similarity index 84%
rename from official/vision/beta/projects/centernet/configs/centernet_test.py
rename to official/projects/centernet/configs/centernet_test.py
index 93e3b8f02665dcb2e4fc4cca24f18fed426c9256..06fbadd56ab9e64e0eb925913b6846660825c994 100644
--- a/official/vision/beta/projects/centernet/configs/centernet_test.py
+++ b/official/projects/centernet/configs/centernet_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,8 @@ import tensorflow as tf
from official.core import config_definitions as cfg
from official.core import exp_factory
-from official.vision.beta.projects.centernet.common import registry_imports # pylint: disable=unused-import
-from official.vision.beta.projects.centernet.configs import centernet as exp_cfg
+from official.projects.centernet.common import registry_imports # pylint: disable=unused-import
+from official.projects.centernet.configs import centernet as exp_cfg
class CenterNetConfigTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml b/official/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml
similarity index 82%
rename from official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml
rename to official/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml
index 6483de509f3d6f5a632b2dfd4fef6dab128d3332..a4d665e7a91384bf2317da14bedd8fd612ca7398 100644
--- a/official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml
+++ b/official/projects/centernet/configs/experiments/coco-centernet-hourglass-gpu.yaml
@@ -38,11 +38,11 @@ task:
per_category_metrics: false
weight_decay: 0.0005
gradient_clip_norm: 10.0
- annotation_file: 'coco/instances_val2017.json'
- init_checkpoint: '/placer/prod/scratch/home/tf-model-garden-dev/vision/centernet/extremenet_hg104_512x512_coco17/2021-10-19'
+ annotation_file: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/instances_val2017.json'
+ init_checkpoint: gs://tf_model_garden/vision/centernet/extremenet_hg104_512x512_coco17
init_checkpoint_modules: 'backbone'
train_data:
- input_path: 'coco/train*'
+ input_path: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/train*'
drop_remainder: true
dtype: 'float16'
global_batch_size: 64
@@ -57,7 +57,7 @@ task:
aug_rand_contrast: true
odapi_augmentation: true
validation_data:
- input_path: 'coco/val*'
+ input_path: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/val*'
drop_remainder: false
dtype: 'float16'
global_batch_size: 16
diff --git a/official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml b/official/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml
similarity index 80%
rename from official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml
rename to official/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml
index 23456708349b8507a683f9ee24ca60317ba5e42d..5d60831e5ed840bc3d1385929e1b61152f903f03 100644
--- a/official/vision/beta/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml
+++ b/official/projects/centernet/configs/experiments/coco-centernet-hourglass-tpu.yaml
@@ -37,11 +37,11 @@ task:
per_category_metrics: false
weight_decay: 0.0005
gradient_clip_norm: 10.0
- annotation_file: 'coco/instances_val2017.json'
- init_checkpoint: '/placer/prod/scratch/home/tf-model-garden-dev/vision/centernet/extremenet_hg104_512x512_coco17/2021-10-19'
+ annotation_file: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/instances_val2017.json'
+ init_checkpoint: gs://tf_model_garden/vision/centernet/extremenet_hg104_512x512_coco17
init_checkpoint_modules: 'backbone'
train_data:
- input_path: 'coco/train*'
+ input_path: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/train*'
drop_remainder: true
dtype: 'bfloat16'
global_batch_size: 128
@@ -56,14 +56,14 @@ task:
aug_rand_contrast: true
odapi_augmentation: true
validation_data:
- input_path: 'coco/val*'
+ input_path: '/readahead/200M/placer/prod/home/tensorflow-performance-data/datasets/coco/val*'
drop_remainder: false
dtype: 'bfloat16'
- global_batch_size: 16
+ global_batch_size: 64
is_training: false
trainer:
train_steps: 140000
- validation_steps: 78 # 5000 / 16
+ validation_steps: 78 # 5000 / 64
steps_per_loop: 924 # 118287 / 128
validation_interval: 924
summary_interval: 924
diff --git a/official/projects/centernet/dataloaders/__init__.py b/official/projects/centernet/dataloaders/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/dataloaders/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/dataloaders/centernet_input.py b/official/projects/centernet/dataloaders/centernet_input.py
similarity index 96%
rename from official/vision/beta/projects/centernet/dataloaders/centernet_input.py
rename to official/projects/centernet/dataloaders/centernet_input.py
index 373b7a87e364d0fa58350287e14f62aa9d0e10ea..b44d98d213cb88d06010ddc6dc38f90cf4d07f87 100644
--- a/official/vision/beta/projects/centernet/dataloaders/centernet_input.py
+++ b/official/projects/centernet/dataloaders/centernet_input.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,13 +18,13 @@ from typing import Tuple
import tensorflow as tf
-from official.vision.beta.dataloaders import parser
-from official.vision.beta.dataloaders import utils
-from official.vision.beta.ops import box_ops
-from official.vision.beta.ops import preprocess_ops
-from official.vision.beta.projects.centernet.ops import box_list
-from official.vision.beta.projects.centernet.ops import box_list_ops
-from official.vision.beta.projects.centernet.ops import preprocess_ops as cn_prep_ops
+from official.projects.centernet.ops import box_list
+from official.projects.centernet.ops import box_list_ops
+from official.projects.centernet.ops import preprocess_ops as cn_prep_ops
+from official.vision.dataloaders import parser
+from official.vision.dataloaders import utils
+from official.vision.ops import box_ops
+from official.vision.ops import preprocess_ops
CHANNEL_MEANS = (104.01362025, 114.03422265, 119.9165958)
diff --git a/official/projects/centernet/losses/__init__.py b/official/projects/centernet/losses/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/losses/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/losses/centernet_losses.py b/official/projects/centernet/losses/centernet_losses.py
similarity index 98%
rename from official/vision/beta/projects/centernet/losses/centernet_losses.py
rename to official/projects/centernet/losses/centernet_losses.py
index a83f8ae8143b7824f16c6c1f0cd8c29f3ab924aa..4cb7b0fe8d0eb9df1a84da763cd0b8c5eb80f229 100644
--- a/official/vision/beta/projects/centernet/losses/centernet_losses.py
+++ b/official/projects/centernet/losses/centernet_losses.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/centernet/losses/centernet_losses_test.py b/official/projects/centernet/losses/centernet_losses_test.py
similarity index 96%
rename from official/vision/beta/projects/centernet/losses/centernet_losses_test.py
rename to official/projects/centernet/losses/centernet_losses_test.py
index ac1e699a2af4eaab8fbcb6dc5d39201db324388a..3be0341d456b3fb70dea69c5a9055abf80269694 100644
--- a/official/vision/beta/projects/centernet/losses/centernet_losses_test.py
+++ b/official/projects/centernet/losses/centernet_losses_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,7 +17,7 @@
import numpy as np
import tensorflow as tf
-from official.vision.beta.projects.centernet.losses import centernet_losses
+from official.projects.centernet.losses import centernet_losses
LOG_2 = np.log(2)
LOG_3 = np.log(3)
diff --git a/official/projects/centernet/modeling/__init__.py b/official/projects/centernet/modeling/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/modeling/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/modeling/backbones/__init__.py b/official/projects/centernet/modeling/backbones/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/modeling/backbones/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/modeling/backbones/hourglass.py b/official/projects/centernet/modeling/backbones/hourglass.py
similarity index 96%
rename from official/vision/beta/projects/centernet/modeling/backbones/hourglass.py
rename to official/projects/centernet/modeling/backbones/hourglass.py
index b3f5ba394655f3a03ec31f1e7d53612ad8519394..c369e20fc64dbbebe2654ad1174b650daf38dddc 100644
--- a/official/vision/beta/projects/centernet/modeling/backbones/hourglass.py
+++ b/official/projects/centernet/modeling/backbones/hourglass.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,10 +19,10 @@ from typing import Optional
import tensorflow as tf
from official.modeling import hyperparams
-from official.vision.beta.modeling.backbones import factory
-from official.vision.beta.modeling.backbones import mobilenet
-from official.vision.beta.modeling.layers import nn_blocks
-from official.vision.beta.projects.centernet.modeling.layers import cn_nn_blocks
+from official.projects.centernet.modeling.layers import cn_nn_blocks
+from official.vision.modeling.backbones import factory
+from official.vision.modeling.backbones import mobilenet
+from official.vision.modeling.layers import nn_blocks
HOURGLASS_SPECS = {
10: {
diff --git a/official/vision/beta/projects/centernet/modeling/backbones/hourglass_test.py b/official/projects/centernet/modeling/backbones/hourglass_test.py
similarity index 77%
rename from official/vision/beta/projects/centernet/modeling/backbones/hourglass_test.py
rename to official/projects/centernet/modeling/backbones/hourglass_test.py
index 3e5af61024e5503278174a2da0b6a2d3283e50c5..3217608bd360a6ed8fd87a1ec7e118c83a518f32 100644
--- a/official/vision/beta/projects/centernet/modeling/backbones/hourglass_test.py
+++ b/official/projects/centernet/modeling/backbones/hourglass_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,10 +18,10 @@ from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.configs import common
-from official.vision.beta.projects.centernet.common import registry_imports # pylint: disable=unused-import
-from official.vision.beta.projects.centernet.configs import backbones
-from official.vision.beta.projects.centernet.modeling.backbones import hourglass
+from official.projects.centernet.common import registry_imports # pylint: disable=unused-import
+from official.projects.centernet.configs import backbones
+from official.projects.centernet.modeling.backbones import hourglass
+from official.vision.configs import common
class HourglassTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/vision/beta/projects/centernet/modeling/centernet_model.py b/official/projects/centernet/modeling/centernet_model.py
similarity index 97%
rename from official/vision/beta/projects/centernet/modeling/centernet_model.py
rename to official/projects/centernet/modeling/centernet_model.py
index e35adf9ac1dc893d6ad88e0d16aaf9cb8f29546d..3b8de7534b2639af37a9901d6f8912da8f0477af 100644
--- a/official/vision/beta/projects/centernet/modeling/centernet_model.py
+++ b/official/projects/centernet/modeling/centernet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/centernet/modeling/centernet_model_test.py b/official/projects/centernet/modeling/centernet_model_test.py
similarity index 80%
rename from official/vision/beta/projects/centernet/modeling/centernet_model_test.py
rename to official/projects/centernet/modeling/centernet_model_test.py
index 6fa767f3e2c0876c7334a2f32d114b959ba97961..f4dc3cccc6130f7354732c8347a6db43b5617ce5 100644
--- a/official/vision/beta/projects/centernet/modeling/centernet_model_test.py
+++ b/official/projects/centernet/modeling/centernet_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,12 +17,12 @@
from absl.testing import parameterized
import tensorflow as tf
-from official.vision.beta.configs import common
-from official.vision.beta.projects.centernet.configs import backbones
-from official.vision.beta.projects.centernet.modeling import centernet_model
-from official.vision.beta.projects.centernet.modeling.backbones import hourglass
-from official.vision.beta.projects.centernet.modeling.heads import centernet_head
-from official.vision.beta.projects.centernet.modeling.layers import detection_generator
+from official.projects.centernet.configs import backbones
+from official.projects.centernet.modeling import centernet_model
+from official.projects.centernet.modeling.backbones import hourglass
+from official.projects.centernet.modeling.heads import centernet_head
+from official.projects.centernet.modeling.layers import detection_generator
+from official.vision.configs import common
class CenterNetTest(parameterized.TestCase, tf.test.TestCase):
diff --git a/official/projects/centernet/modeling/heads/__init__.py b/official/projects/centernet/modeling/heads/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/modeling/heads/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/modeling/heads/centernet_head.py b/official/projects/centernet/modeling/heads/centernet_head.py
similarity index 93%
rename from official/vision/beta/projects/centernet/modeling/heads/centernet_head.py
rename to official/projects/centernet/modeling/heads/centernet_head.py
index d493076c7149f2ad9cc808c4bf95fdce307b4a43..37703c1c761baac3b3d8ebba446c303748330617 100644
--- a/official/vision/beta/projects/centernet/modeling/heads/centernet_head.py
+++ b/official/projects/centernet/modeling/heads/centernet_head.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,11 +14,11 @@
"""Contains the definitions of head for CenterNet."""
-from typing import Any, Mapping, Dict, List
+from typing import Any, Dict, List, Mapping
import tensorflow as tf
-from official.vision.beta.projects.centernet.modeling.layers import cn_nn_blocks
+from official.projects.centernet.modeling.layers import cn_nn_blocks
class CenterNetHead(tf.keras.Model):
@@ -61,7 +61,6 @@ class CenterNetHead(tf.keras.Model):
self._heatmap_bias = heatmap_bias
self._num_inputs = len(input_levels)
- input_levels = sorted(self._input_specs.keys())
inputs = {level: tf.keras.layers.Input(shape=self._input_specs[level][1:])
for level in input_levels}
outputs = {}
diff --git a/official/vision/beta/projects/centernet/modeling/heads/centernet_head_test.py b/official/projects/centernet/modeling/heads/centernet_head_test.py
similarity index 94%
rename from official/vision/beta/projects/centernet/modeling/heads/centernet_head_test.py
rename to official/projects/centernet/modeling/heads/centernet_head_test.py
index f1497a7e9a9275b1bda18bdd8eeaa368f6ec4c77..269d8c9ba1264634517322326650568715e7b8fe 100644
--- a/official/vision/beta/projects/centernet/modeling/heads/centernet_head_test.py
+++ b/official/projects/centernet/modeling/heads/centernet_head_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,7 +18,7 @@ from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.projects.centernet.modeling.heads import centernet_head
+from official.projects.centernet.modeling.heads import centernet_head
class CenterNetHeadTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/centernet/modeling/layers/__init__.py b/official/projects/centernet/modeling/layers/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/modeling/layers/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks.py b/official/projects/centernet/modeling/layers/cn_nn_blocks.py
similarity index 99%
rename from official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks.py
rename to official/projects/centernet/modeling/layers/cn_nn_blocks.py
index f8d395cb694423026dbed86591fd0e75f9473ed8..eba920e428397a59515abfbdbc1643264aeca84d 100644
--- a/official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks.py
+++ b/official/projects/centernet/modeling/layers/cn_nn_blocks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,7 +18,7 @@ from typing import List, Optional
import tensorflow as tf
-from official.vision.beta.modeling.layers import nn_blocks
+from official.vision.modeling.layers import nn_blocks
def _apply_blocks(inputs, blocks):
diff --git a/official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks_test.py b/official/projects/centernet/modeling/layers/cn_nn_blocks_test.py
similarity index 96%
rename from official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks_test.py
rename to official/projects/centernet/modeling/layers/cn_nn_blocks_test.py
index 5ad90b496567e73ee643b110c3392c2b72324354..b66232d895f6a3561cd108037995641f23419a73 100644
--- a/official/vision/beta/projects/centernet/modeling/layers/cn_nn_blocks_test.py
+++ b/official/projects/centernet/modeling/layers/cn_nn_blocks_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,8 +21,8 @@ from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.modeling.layers import nn_blocks
-from official.vision.beta.projects.centernet.modeling.layers import cn_nn_blocks
+from official.projects.centernet.modeling.layers import cn_nn_blocks
+from official.vision.modeling.layers import nn_blocks
class HourglassBlockPyTorch(tf.keras.layers.Layer):
diff --git a/official/projects/centernet/modeling/layers/detection_generator.py b/official/projects/centernet/modeling/layers/detection_generator.py
new file mode 100644
index 0000000000000000000000000000000000000000..899f97f0c021b4bb608c3e953f09610e634047fb
--- /dev/null
+++ b/official/projects/centernet/modeling/layers/detection_generator.py
@@ -0,0 +1,339 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Detection generator for centernet.
+
+Parses predictions from the CenterNet head into the final bounding boxes,
+confidences, and classes. This class contains repurposed methods from the
+TensorFlow Object Detection API
+in: https://github.com/tensorflow/models/blob/master/research/object_detection
+/meta_architectures/center_net_meta_arch.py
+"""
+
+from typing import Any, Mapping
+
+import tensorflow as tf
+
+from official.projects.centernet.ops import loss_ops
+from official.projects.centernet.ops import nms_ops
+from official.vision.ops import box_ops
+
+
+class CenterNetDetectionGenerator(tf.keras.layers.Layer):
+ """CenterNet Detection Generator."""
+
+ def __init__(self,
+ input_image_dims: int = 512,
+ net_down_scale: int = 4,
+ max_detections: int = 100,
+ peak_error: float = 1e-6,
+ peak_extract_kernel_size: int = 3,
+ class_offset: int = 1,
+ use_nms: bool = False,
+ nms_pre_thresh: float = 0.1,
+ nms_thresh: float = 0.4,
+ **kwargs):
+ """Initialize CenterNet Detection Generator.
+
+ Args:
+ input_image_dims: An `int` that specifies the input image size.
+ net_down_scale: An `int` that specifies stride of the output.
+ max_detections: An `int` specifying the maximum number of bounding
+ boxes generated. This is an upper bound, so the number of generated
+ boxes may be less than this due to thresholding/non-maximum suppression.
+ peak_error: A `float` for determining non-valid heatmap locations to mask.
+ peak_extract_kernel_size: An `int` indicating the kernel size used when
+ performing max-pool over the heatmaps to detect valid center locations
+ from its neighbors. From the paper, set this to 3 to detect valid.
+ locations that have responses greater than its 8-connected neighbors
+ class_offset: An `int` indicating to add an offset to the class
+ prediction if the dataset labels have been shifted.
+ use_nms: A `bool` for whether or not to use non-maximum suppression to
+ filter the bounding boxes.
+ nms_pre_thresh: A `float` for pre-nms threshold.
+ nms_thresh: A `float` for nms threshold.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(CenterNetDetectionGenerator, self).__init__(**kwargs)
+
+ # Object center selection parameters
+ self._max_detections = max_detections
+ self._peak_error = peak_error
+ self._peak_extract_kernel_size = peak_extract_kernel_size
+
+ # Used for adjusting class prediction
+ self._class_offset = class_offset
+
+ # Box normalization parameters
+ self._net_down_scale = net_down_scale
+ self._input_image_dims = input_image_dims
+
+ self._use_nms = use_nms
+ self._nms_pre_thresh = nms_pre_thresh
+ self._nms_thresh = nms_thresh
+
+ def process_heatmap(self,
+ feature_map: tf.Tensor,
+ kernel_size: int) -> tf.Tensor:
+ """Processes the heatmap into peaks for box selection.
+
+ Given a heatmap, this function first masks out nearby heatmap locations of
+ the same class using max-pooling such that, ideally, only one center for the
+ object remains. Then, center locations are masked according to their scores
+ in comparison to a threshold. NOTE: Repurposed from Google OD API.
+
+ Args:
+ feature_map: A Tensor with shape [batch_size, height, width, num_classes]
+ which is the center heatmap predictions.
+ kernel_size: An integer value for max-pool kernel size.
+
+ Returns:
+ A Tensor with the same shape as the input but with non-valid center
+ prediction locations masked out.
+ """
+
+ feature_map = tf.math.sigmoid(feature_map)
+ if not kernel_size or kernel_size == 1:
+ feature_map_peaks = feature_map
+ else:
+ feature_map_max_pool = tf.nn.max_pool(
+ feature_map,
+ ksize=kernel_size,
+ strides=1,
+ padding='SAME')
+
+ feature_map_peak_mask = tf.math.abs(
+ feature_map - feature_map_max_pool) < self._peak_error
+
+ # Zero out everything that is not a peak.
+ feature_map_peaks = (
+ feature_map * tf.cast(feature_map_peak_mask, feature_map.dtype))
+
+ return feature_map_peaks
+
+ def get_top_k_peaks(self,
+ feature_map_peaks: tf.Tensor,
+ batch_size: int,
+ width: int,
+ num_classes: int,
+ k: int = 100):
+ """Gets the scores and indices of the top-k peaks from the feature map.
+
+ This function flattens the feature map in order to retrieve the top-k
+ peaks, then computes the x, y, and class indices for those scores.
+ NOTE: Repurposed from Google OD API.
+
+ Args:
+ feature_map_peaks: A `Tensor` with shape [batch_size, height,
+ width, num_classes] which is the processed center heatmap peaks.
+ batch_size: An `int` that indicates the batch size of the input.
+ width: An `int` that indicates the width (and also height) of the input.
+ num_classes: An `int` for the number of possible classes. This is also
+ the channel depth of the input.
+ k: `int`` that controls how many peaks to select.
+
+ Returns:
+ top_scores: A Tensor with shape [batch_size, k] containing the top-k
+ scores.
+ y_indices: A Tensor with shape [batch_size, k] containing the top-k
+ y-indices corresponding to top_scores.
+ x_indices: A Tensor with shape [batch_size, k] containing the top-k
+ x-indices corresponding to top_scores.
+ channel_indices: A Tensor with shape [batch_size, k] containing the top-k
+ channel indices corresponding to top_scores.
+ """
+ # Flatten the entire prediction per batch
+ feature_map_peaks_flat = tf.reshape(feature_map_peaks, [batch_size, -1])
+
+ # top_scores and top_indices have shape [batch_size, k]
+ top_scores, top_indices = tf.math.top_k(feature_map_peaks_flat, k=k)
+
+ # Get x, y and channel indices corresponding to the top indices in the flat
+ # array.
+ y_indices, x_indices, channel_indices = (
+ loss_ops.get_row_col_channel_indices_from_flattened_indices(
+ top_indices, width, num_classes))
+
+ return top_scores, y_indices, x_indices, channel_indices
+
+ def get_boxes(self,
+ y_indices: tf.Tensor,
+ x_indices: tf.Tensor,
+ channel_indices: tf.Tensor,
+ height_width_predictions: tf.Tensor,
+ offset_predictions: tf.Tensor,
+ num_boxes: int):
+ """Organizes prediction information into the final bounding boxes.
+
+ NOTE: Repurposed from Google OD API.
+
+ Args:
+ y_indices: A Tensor with shape [batch_size, k] containing the top-k
+ y-indices corresponding to top_scores.
+ x_indices: A Tensor with shape [batch_size, k] containing the top-k
+ x-indices corresponding to top_scores.
+ channel_indices: A Tensor with shape [batch_size, k] containing the top-k
+ channel indices corresponding to top_scores.
+ height_width_predictions: A Tensor with shape [batch_size, height,
+ width, 2] containing the object size predictions.
+ offset_predictions: A Tensor with shape [batch_size, height, width, 2]
+ containing the object local offset predictions.
+ num_boxes: `int`, the number of boxes.
+
+ Returns:
+ boxes: A Tensor with shape [batch_size, num_boxes, 4] that contains the
+ bounding box coordinates in [y_min, x_min, y_max, x_max] format.
+ detection_classes: A Tensor with shape [batch_size, num_boxes] that
+ gives the class prediction for each box.
+ num_detections: Number of non-zero confidence detections made.
+ """
+ # TF Lite does not support tf.gather with batch_dims > 0, so we need to use
+ # tf_gather_nd instead and here we prepare the indices for that.
+
+ # shapes of heatmap output
+ shape = tf.shape(height_width_predictions)
+ batch_size, height, width = shape[0], shape[1], shape[2]
+
+ # combined indices dtype=int32
+ combined_indices = tf.stack([
+ loss_ops.multi_range(batch_size, value_repetitions=num_boxes),
+ tf.reshape(y_indices, [-1]),
+ tf.reshape(x_indices, [-1])
+ ], axis=1)
+
+ new_height_width = tf.gather_nd(height_width_predictions, combined_indices)
+ new_height_width = tf.reshape(new_height_width, [batch_size, num_boxes, 2])
+ height_width = tf.maximum(new_height_width, 0.0)
+
+ # height and widths dtype=float32
+ heights = height_width[..., 0]
+ widths = height_width[..., 1]
+
+ # Get the offsets of center points
+ new_offsets = tf.gather_nd(offset_predictions, combined_indices)
+ offsets = tf.reshape(new_offsets, [batch_size, num_boxes, 2])
+
+ # offsets are dtype=float32
+ y_offsets = offsets[..., 0]
+ x_offsets = offsets[..., 1]
+
+ y_indices = tf.cast(y_indices, dtype=heights.dtype)
+ x_indices = tf.cast(x_indices, dtype=widths.dtype)
+
+ detection_classes = channel_indices + self._class_offset
+ ymin = y_indices + y_offsets - heights / 2.0
+ xmin = x_indices + x_offsets - widths / 2.0
+ ymax = y_indices + y_offsets + heights / 2.0
+ xmax = x_indices + x_offsets + widths / 2.0
+
+ ymin = tf.clip_by_value(ymin, 0., tf.cast(height, ymin.dtype))
+ xmin = tf.clip_by_value(xmin, 0., tf.cast(width, xmin.dtype))
+ ymax = tf.clip_by_value(ymax, 0., tf.cast(height, ymax.dtype))
+ xmax = tf.clip_by_value(xmax, 0., tf.cast(width, xmax.dtype))
+ boxes = tf.stack([ymin, xmin, ymax, xmax], axis=2)
+
+ return boxes, detection_classes
+
+ def convert_strided_predictions_to_normalized_boxes(self, boxes: tf.Tensor):
+ boxes = boxes * tf.cast(self._net_down_scale, boxes.dtype)
+ boxes = boxes / tf.cast(self._input_image_dims, boxes.dtype)
+ boxes = tf.clip_by_value(boxes, 0.0, 1.0)
+ return boxes
+
+ def __call__(self, inputs):
+ # Get heatmaps from decoded outputs via final hourglass stack output
+ all_ct_heatmaps = inputs['ct_heatmaps']
+ all_ct_sizes = inputs['ct_size']
+ all_ct_offsets = inputs['ct_offset']
+
+ ct_heatmaps = all_ct_heatmaps[-1]
+ ct_sizes = all_ct_sizes[-1]
+ ct_offsets = all_ct_offsets[-1]
+
+ shape = tf.shape(ct_heatmaps)
+
+ _, width = shape[1], shape[2]
+ batch_size, num_channels = shape[0], shape[3]
+
+ # Process heatmaps using 3x3 max pool and applying sigmoid
+ peaks = self.process_heatmap(
+ feature_map=ct_heatmaps,
+ kernel_size=self._peak_extract_kernel_size)
+
+ # Get top scores along with their x, y, and class
+ # Each has size [batch_size, k]
+ scores, y_indices, x_indices, channel_indices = self.get_top_k_peaks(
+ feature_map_peaks=peaks,
+ batch_size=batch_size,
+ width=width,
+ num_classes=num_channels,
+ k=self._max_detections)
+
+ # Parse the score and indices into bounding boxes
+ boxes, classes = self.get_boxes(
+ y_indices=y_indices,
+ x_indices=x_indices,
+ channel_indices=channel_indices,
+ height_width_predictions=ct_sizes,
+ offset_predictions=ct_offsets,
+ num_boxes=self._max_detections)
+
+ # Normalize bounding boxes
+ boxes = self.convert_strided_predictions_to_normalized_boxes(boxes)
+
+ # Apply nms
+ if self._use_nms:
+ boxes = tf.expand_dims(boxes, axis=-2)
+ multi_class_scores = tf.gather_nd(
+ peaks, tf.stack([y_indices, x_indices], -1), batch_dims=1)
+
+ boxes, _, scores = nms_ops.nms(
+ boxes=boxes,
+ classes=multi_class_scores,
+ confidence=scores,
+ k=self._max_detections,
+ limit_pre_thresh=True,
+ pre_nms_thresh=0.1,
+ nms_thresh=0.4)
+
+ num_det = tf.reduce_sum(tf.cast(scores > 0, dtype=tf.int32), axis=1)
+ boxes = box_ops.denormalize_boxes(
+ boxes, [self._input_image_dims, self._input_image_dims])
+
+ return {
+ 'boxes': boxes,
+ 'classes': classes,
+ 'confidence': scores,
+ 'num_detections': num_det
+ }
+
+ def get_config(self) -> Mapping[str, Any]:
+ config = {
+ 'max_detections': self._max_detections,
+ 'peak_error': self._peak_error,
+ 'peak_extract_kernel_size': self._peak_extract_kernel_size,
+ 'class_offset': self._class_offset,
+ 'net_down_scale': self._net_down_scale,
+ 'input_image_dims': self._input_image_dims,
+ 'use_nms': self._use_nms,
+ 'nms_pre_thresh': self._nms_pre_thresh,
+ 'nms_thresh': self._nms_thresh
+ }
+
+ base_config = super(CenterNetDetectionGenerator, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
diff --git a/official/projects/centernet/ops/__init__.py b/official/projects/centernet/ops/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/ops/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/ops/box_list.py b/official/projects/centernet/ops/box_list.py
similarity index 99%
rename from official/vision/beta/projects/centernet/ops/box_list.py
rename to official/projects/centernet/ops/box_list.py
index 6de3b975d02e36ce88bed06e83772b8ee9c2c0e8..4e93b9fd631f6f37fc89c013e7b1dc2428e686d6 100644
--- a/official/vision/beta/projects/centernet/ops/box_list.py
+++ b/official/projects/centernet/ops/box_list.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/centernet/ops/box_list_ops.py b/official/projects/centernet/ops/box_list_ops.py
similarity index 98%
rename from official/vision/beta/projects/centernet/ops/box_list_ops.py
rename to official/projects/centernet/ops/box_list_ops.py
index 998c32cf0292c41ac535819d74139c6dd8f7cdc3..d419be84af33c3a4d2f271c7822d3e01a3755513 100644
--- a/official/vision/beta/projects/centernet/ops/box_list_ops.py
+++ b/official/projects/centernet/ops/box_list_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,8 +16,8 @@
import tensorflow as tf
-from official.vision.beta.ops import sampling_ops
-from official.vision.beta.projects.centernet.ops import box_list
+from official.projects.centernet.ops import box_list
+from official.vision.ops import sampling_ops
def _copy_extra_fields(boxlist_to_copy_to, boxlist_to_copy_from):
diff --git a/official/vision/beta/projects/centernet/ops/loss_ops.py b/official/projects/centernet/ops/loss_ops.py
similarity index 98%
rename from official/vision/beta/projects/centernet/ops/loss_ops.py
rename to official/projects/centernet/ops/loss_ops.py
index dfb585f6ff632975b8c778eac098f81490707989..db7875c110e71d779cb1f768ed3d1a9ef02d8eb3 100644
--- a/official/vision/beta/projects/centernet/ops/loss_ops.py
+++ b/official/projects/centernet/ops/loss_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,7 +16,7 @@
import tensorflow as tf
-from official.vision.beta.ops import sampling_ops
+from official.vision.ops import sampling_ops
def _get_shape(tensor, num_dims):
diff --git a/official/vision/beta/projects/centernet/ops/nms_ops.py b/official/projects/centernet/ops/nms_ops.py
similarity index 96%
rename from official/vision/beta/projects/centernet/ops/nms_ops.py
rename to official/projects/centernet/ops/nms_ops.py
index c331b62159167464a23912ae8898b11d7de5466c..1da690b6f1a90c9da941882db2512732ad594bc3 100644
--- a/official/vision/beta/projects/centernet/ops/nms_ops.py
+++ b/official/projects/centernet/ops/nms_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,7 +16,7 @@
import tensorflow as tf
-from official.vision.beta.projects.yolo.ops import box_ops
+from official.projects.yolo.ops import box_ops
NMS_TILE_SIZE = 512
diff --git a/official/projects/centernet/ops/preprocess_ops.py b/official/projects/centernet/ops/preprocess_ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..38f16afb3e1c40c597756186ac06235f63fec470
--- /dev/null
+++ b/official/projects/centernet/ops/preprocess_ops.py
@@ -0,0 +1,496 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Preprocessing ops imported from OD API."""
+
+import functools
+
+import tensorflow as tf
+
+from official.projects.centernet.ops import box_list
+from official.projects.centernet.ops import box_list_ops
+
+
+def _get_or_create_preprocess_rand_vars(generator_func,
+ function_id,
+ preprocess_vars_cache,
+ key=''):
+ """Returns a tensor stored in preprocess_vars_cache or using generator_func.
+
+ If the tensor was previously generated and appears in the PreprocessorCache,
+ the previously generated tensor will be returned. Otherwise, a new tensor
+ is generated using generator_func and stored in the cache.
+
+ Args:
+ generator_func: A 0-argument function that generates a tensor.
+ function_id: identifier for the preprocessing function used.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+ key: identifier for the variable stored.
+
+ Returns:
+ The generated tensor.
+ """
+ if preprocess_vars_cache is not None:
+ var = preprocess_vars_cache.get(function_id, key)
+ if var is None:
+ var = generator_func()
+ preprocess_vars_cache.update(function_id, key, var)
+ else:
+ var = generator_func()
+ return var
+
+
+def _random_integer(minval, maxval, seed):
+ """Returns a random 0-D tensor between minval and maxval.
+
+ Args:
+ minval: minimum value of the random tensor.
+ maxval: maximum value of the random tensor.
+ seed: random seed.
+
+ Returns:
+ A random 0-D tensor between minval and maxval.
+ """
+ return tf.random.uniform(
+ [], minval=minval, maxval=maxval, dtype=tf.int32, seed=seed)
+
+
+def _get_crop_border(border, size):
+ """Get the border of cropping."""
+
+ border = tf.cast(border, tf.float32)
+ size = tf.cast(size, tf.float32)
+
+ i = tf.math.ceil(tf.math.log(2.0 * border / size) / tf.math.log(2.0))
+ divisor = tf.pow(2.0, i)
+ divisor = tf.clip_by_value(divisor, 1, border)
+ divisor = tf.cast(divisor, tf.int32)
+
+ return tf.cast(border, tf.int32) // divisor
+
+
+def random_square_crop_by_scale(image,
+ boxes,
+ labels,
+ max_border=128,
+ scale_min=0.6,
+ scale_max=1.3,
+ num_scales=8,
+ seed=None,
+ preprocess_vars_cache=None):
+ """Randomly crop a square in proportion to scale and image size.
+
+ Extract a square sized crop from an image whose side length is sampled by
+ randomly scaling the maximum spatial dimension of the image. If part of
+ the crop falls outside the image, it is filled with zeros.
+ The augmentation is borrowed from [1]
+ [1]: https://arxiv.org/abs/1904.07850
+
+ Args:
+ image: rank 3 float32 tensor containing 1 image ->
+ [height, width, channels].
+ boxes: rank 2 float32 tensor containing the bounding boxes -> [N, 4].
+ Boxes are in normalized form meaning their coordinates vary
+ between [0, 1]. Each row is in the form of [ymin, xmin, ymax, xmax].
+ Boxes on the crop boundary are clipped to the boundary and boxes
+ falling outside the crop are ignored.
+ labels: rank 1 int32 tensor containing the object classes.
+ max_border: The maximum size of the border. The border defines distance in
+ pixels to the image boundaries that will not be considered as a center of
+ a crop. To make sure that the border does not go over the center of the
+ image, we chose the border value by computing the minimum k, such that
+ (max_border / (2**k)) < image_dimension/2.
+ scale_min: float, the minimum value for scale.
+ scale_max: float, the maximum value for scale.
+ num_scales: int, the number of discrete scale values to sample between
+ [scale_min, scale_max]
+ seed: random seed.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+
+
+ Returns:
+ image: image which is the same rank as input image.
+ boxes: boxes which is the same rank as input boxes.
+ Boxes are in normalized form.
+ labels: new labels.
+
+ """
+
+ img_shape = tf.shape(image)
+ height, width = img_shape[0], img_shape[1]
+ scales = tf.linspace(scale_min, scale_max, num_scales)
+
+ scale = _get_or_create_preprocess_rand_vars(
+ lambda: scales[_random_integer(0, num_scales, seed)],
+ 'square_crop_scale',
+ preprocess_vars_cache, 'scale')
+
+ image_size = scale * tf.cast(tf.maximum(height, width), tf.float32)
+ image_size = tf.cast(image_size, tf.int32)
+ h_border = _get_crop_border(max_border, height)
+ w_border = _get_crop_border(max_border, width)
+
+ def y_function():
+ y = _random_integer(h_border,
+ tf.cast(height, tf.int32) - h_border + 1,
+ seed)
+ return y
+
+ def x_function():
+ x = _random_integer(w_border,
+ tf.cast(width, tf.int32) - w_border + 1,
+ seed)
+ return x
+
+ y_center = _get_or_create_preprocess_rand_vars(
+ y_function,
+ 'square_crop_scale',
+ preprocess_vars_cache, 'y_center')
+
+ x_center = _get_or_create_preprocess_rand_vars(
+ x_function,
+ 'square_crop_scale',
+ preprocess_vars_cache, 'x_center')
+
+ half_size = tf.cast(image_size / 2, tf.int32)
+ crop_ymin, crop_ymax = y_center - half_size, y_center + half_size
+ crop_xmin, crop_xmax = x_center - half_size, x_center + half_size
+
+ ymin = tf.maximum(crop_ymin, 0)
+ xmin = tf.maximum(crop_xmin, 0)
+ ymax = tf.minimum(crop_ymax, height - 1)
+ xmax = tf.minimum(crop_xmax, width - 1)
+
+ cropped_image = image[ymin:ymax, xmin:xmax]
+ offset_y = tf.maximum(0, ymin - crop_ymin)
+ offset_x = tf.maximum(0, xmin - crop_xmin)
+
+ oy_i = offset_y
+ ox_i = offset_x
+
+ output_image = tf.image.pad_to_bounding_box(
+ cropped_image, offset_height=oy_i, offset_width=ox_i,
+ target_height=image_size, target_width=image_size)
+
+ if ymin == 0:
+ # We might be padding the image.
+ box_ymin = -offset_y
+ else:
+ box_ymin = crop_ymin
+
+ if xmin == 0:
+ # We might be padding the image.
+ box_xmin = -offset_x
+ else:
+ box_xmin = crop_xmin
+
+ box_ymax = box_ymin + image_size
+ box_xmax = box_xmin + image_size
+
+ image_box = [box_ymin / height, box_xmin / width,
+ box_ymax / height, box_xmax / width]
+ boxlist = box_list.BoxList(boxes)
+ boxlist = box_list_ops.change_coordinate_frame(boxlist, image_box)
+ boxlist, indices = box_list_ops.prune_completely_outside_window(
+ boxlist, [0.0, 0.0, 1.0, 1.0])
+ boxlist = box_list_ops.clip_to_window(boxlist, [0.0, 0.0, 1.0, 1.0],
+ filter_nonoverlapping=False)
+
+ return_values = [output_image,
+ boxlist.get(),
+ tf.gather(labels, indices)]
+
+ return return_values
+
+
+def resize_to_range(image,
+ masks=None,
+ min_dimension=None,
+ max_dimension=None,
+ method=tf.image.ResizeMethod.BILINEAR,
+ pad_to_max_dimension=False,
+ per_channel_pad_value=(0, 0, 0)):
+ """Resizes an image so its dimensions are within the provided value.
+
+ The output size can be described by two cases:
+ 1. If the image can be rescaled so its minimum dimension is equal to the
+ provided value without the other dimension exceeding max_dimension,
+ then do so.
+ 2. Otherwise, resize so the largest dimension is equal to max_dimension.
+
+ Args:
+ image: A 3D tensor of shape [height, width, channels]
+ masks: (optional) rank 3 float32 tensor with shape
+ [num_instances, height, width] containing instance masks.
+ min_dimension: (optional) (scalar) desired size of the smaller image
+ dimension.
+ max_dimension: (optional) (scalar) maximum allowed size
+ of the larger image dimension.
+ method: (optional) interpolation method used in resizing. Defaults to
+ BILINEAR.
+ pad_to_max_dimension: Whether to resize the image and pad it with zeros
+ so the resulting image is of the spatial size
+ [max_dimension, max_dimension]. If masks are included they are padded
+ similarly.
+ per_channel_pad_value: A tuple of per-channel scalar value to use for
+ padding. By default pads zeros.
+
+ Returns:
+ Note that the position of the resized_image_shape changes based on whether
+ masks are present.
+ resized_image: A 3D tensor of shape [new_height, new_width, channels],
+ where the image has been resized (with bilinear interpolation) so that
+ min(new_height, new_width) == min_dimension or
+ max(new_height, new_width) == max_dimension.
+ resized_masks: If masks is not None, also outputs masks. A 3D tensor of
+ shape [num_instances, new_height, new_width].
+ resized_image_shape: A 1D tensor of shape [3] containing shape of the
+ resized image.
+
+ Raises:
+ ValueError: if the image is not a 3D tensor.
+ """
+ if len(image.get_shape()) != 3:
+ raise ValueError('Image should be 3D tensor')
+
+ def _resize_landscape_image(image):
+ # resize a landscape image
+ return tf.image.resize(
+ image, tf.stack([min_dimension, max_dimension]), method=method,
+ preserve_aspect_ratio=True)
+
+ def _resize_portrait_image(image):
+ # resize a portrait image
+ return tf.image.resize(
+ image, tf.stack([max_dimension, min_dimension]), method=method,
+ preserve_aspect_ratio=True)
+
+ with tf.name_scope('ResizeToRange'):
+ if image.get_shape().is_fully_defined():
+ if image.get_shape()[0] < image.get_shape()[1]:
+ new_image = _resize_landscape_image(image)
+ else:
+ new_image = _resize_portrait_image(image)
+ new_size = tf.constant(new_image.get_shape().as_list())
+ else:
+ new_image = tf.cond(
+ tf.less(tf.shape(image)[0], tf.shape(image)[1]),
+ lambda: _resize_landscape_image(image),
+ lambda: _resize_portrait_image(image))
+ new_size = tf.shape(new_image)
+
+ if pad_to_max_dimension:
+ channels = tf.unstack(new_image, axis=2)
+ if len(channels) != len(per_channel_pad_value):
+ raise ValueError('Number of channels must be equal to the length of '
+ 'per-channel pad value.')
+ new_image = tf.stack(
+ [
+ tf.pad( # pylint: disable=g-complex-comprehension
+ channels[i], [[0, max_dimension - new_size[0]],
+ [0, max_dimension - new_size[1]]],
+ constant_values=per_channel_pad_value[i])
+ for i in range(len(channels))
+ ],
+ axis=2)
+ new_image.set_shape([max_dimension, max_dimension, len(channels)])
+
+ result = [new_image, new_size]
+ if masks is not None:
+ new_masks = tf.expand_dims(masks, 3)
+ new_masks = tf.image.resize(
+ new_masks,
+ new_size[:-1],
+ method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
+ if pad_to_max_dimension:
+ new_masks = tf.image.pad_to_bounding_box(
+ new_masks, 0, 0, max_dimension, max_dimension)
+ new_masks = tf.squeeze(new_masks, 3)
+ result.append(new_masks)
+
+ return result
+
+
+def _augment_only_rgb_channels(image, augment_function):
+ """Augments only the RGB slice of an image with additional channels."""
+ rgb_slice = image[:, :, :3]
+ augmented_rgb_slice = augment_function(rgb_slice)
+ image = tf.concat([augmented_rgb_slice, image[:, :, 3:]], -1)
+ return image
+
+
+def random_adjust_brightness(image,
+ max_delta=0.2,
+ seed=None,
+ preprocess_vars_cache=None):
+ """Randomly adjusts brightness.
+
+ Makes sure the output image is still between 0 and 255.
+
+ Args:
+ image: rank 3 float32 tensor contains 1 image -> [height, width, channels]
+ with pixel values varying between [0, 255].
+ max_delta: how much to change the brightness. A value between [0, 1).
+ seed: random seed.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+
+ Returns:
+ image: image which is the same shape as input image.
+ """
+ with tf.name_scope('RandomAdjustBrightness'):
+ generator_func = functools.partial(tf.random.uniform, [],
+ -max_delta, max_delta, seed=seed)
+ delta = _get_or_create_preprocess_rand_vars(
+ generator_func,
+ 'adjust_brightness',
+ preprocess_vars_cache)
+
+ def _adjust_brightness(image):
+ image = tf.image.adjust_brightness(image / 255, delta) * 255
+ image = tf.clip_by_value(image, clip_value_min=0.0, clip_value_max=255.0)
+ return image
+
+ image = _augment_only_rgb_channels(image, _adjust_brightness)
+ return image
+
+
+def random_adjust_contrast(image,
+ min_delta=0.8,
+ max_delta=1.25,
+ seed=None,
+ preprocess_vars_cache=None):
+ """Randomly adjusts contrast.
+
+ Makes sure the output image is still between 0 and 255.
+
+ Args:
+ image: rank 3 float32 tensor contains 1 image -> [height, width, channels]
+ with pixel values varying between [0, 255].
+ min_delta: see max_delta.
+ max_delta: how much to change the contrast. Contrast will change with a
+ value between min_delta and max_delta. This value will be
+ multiplied to the current contrast of the image.
+ seed: random seed.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+
+ Returns:
+ image: image which is the same shape as input image.
+ """
+ with tf.name_scope('RandomAdjustContrast'):
+ generator_func = functools.partial(tf.random.uniform, [],
+ min_delta, max_delta, seed=seed)
+ contrast_factor = _get_or_create_preprocess_rand_vars(
+ generator_func,
+ 'adjust_contrast',
+ preprocess_vars_cache)
+
+ def _adjust_contrast(image):
+ image = tf.image.adjust_contrast(image / 255, contrast_factor) * 255
+ image = tf.clip_by_value(image, clip_value_min=0.0, clip_value_max=255.0)
+ return image
+
+ image = _augment_only_rgb_channels(image, _adjust_contrast)
+ return image
+
+
+def random_adjust_hue(image,
+ max_delta=0.02,
+ seed=None,
+ preprocess_vars_cache=None):
+ """Randomly adjusts hue.
+
+ Makes sure the output image is still between 0 and 255.
+
+ Args:
+ image: rank 3 float32 tensor contains 1 image -> [height, width, channels]
+ with pixel values varying between [0, 255].
+ max_delta: change hue randomly with a value between 0 and max_delta.
+ seed: random seed.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+
+ Returns:
+ image: image which is the same shape as input image.
+ """
+ with tf.name_scope('RandomAdjustHue'):
+ generator_func = functools.partial(tf.random.uniform, [],
+ -max_delta, max_delta, seed=seed)
+ delta = _get_or_create_preprocess_rand_vars(
+ generator_func,
+ 'adjust_hue',
+ preprocess_vars_cache)
+
+ def _adjust_hue(image):
+ image = tf.image.adjust_hue(image / 255, delta) * 255
+ image = tf.clip_by_value(image, clip_value_min=0.0, clip_value_max=255.0)
+ return image
+
+ image = _augment_only_rgb_channels(image, _adjust_hue)
+ return image
+
+
+def random_adjust_saturation(image,
+ min_delta=0.8,
+ max_delta=1.25,
+ seed=None,
+ preprocess_vars_cache=None):
+ """Randomly adjusts saturation.
+
+ Makes sure the output image is still between 0 and 255.
+
+ Args:
+ image: rank 3 float32 tensor contains 1 image -> [height, width, channels]
+ with pixel values varying between [0, 255].
+ min_delta: see max_delta.
+ max_delta: how much to change the saturation. Saturation will change with a
+ value between min_delta and max_delta. This value will be
+ multiplied to the current saturation of the image.
+ seed: random seed.
+ preprocess_vars_cache: PreprocessorCache object that records previously
+ performed augmentations. Updated in-place. If this
+ function is called multiple times with the same
+ non-null cache, it will perform deterministically.
+
+ Returns:
+ image: image which is the same shape as input image.
+ """
+ with tf.name_scope('RandomAdjustSaturation'):
+ generator_func = functools.partial(tf.random.uniform, [],
+ min_delta, max_delta, seed=seed)
+ saturation_factor = _get_or_create_preprocess_rand_vars(
+ generator_func,
+ 'adjust_saturation',
+ preprocess_vars_cache)
+
+ def _adjust_saturation(image):
+ image = tf.image.adjust_saturation(image / 255, saturation_factor) * 255
+ image = tf.clip_by_value(image, clip_value_min=0.0, clip_value_max=255.0)
+ return image
+
+ image = _augment_only_rgb_channels(image, _adjust_saturation)
+ return image
diff --git a/official/vision/beta/projects/centernet/ops/target_assigner.py b/official/projects/centernet/ops/target_assigner.py
similarity index 99%
rename from official/vision/beta/projects/centernet/ops/target_assigner.py
rename to official/projects/centernet/ops/target_assigner.py
index dd1cdc1710cdbed49a8af9e0108d5b837f8e86dc..0bbe39dffe663b2789278c903a0e1cec34321f84 100644
--- a/official/vision/beta/projects/centernet/ops/target_assigner.py
+++ b/official/projects/centernet/ops/target_assigner.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,7 +18,7 @@ from typing import Dict, List
import tensorflow as tf
-from official.vision.beta.ops import sampling_ops
+from official.vision.ops import sampling_ops
def smallest_positive_root(a, b, c):
diff --git a/official/vision/beta/projects/centernet/ops/target_assigner_test.py b/official/projects/centernet/ops/target_assigner_test.py
similarity index 97%
rename from official/vision/beta/projects/centernet/ops/target_assigner_test.py
rename to official/projects/centernet/ops/target_assigner_test.py
index 4d10dc0c65b64d80309b72af59b988630d7b19ce..36de86a4e1f1917e04ceaa6104053fe29c3baa33 100644
--- a/official/vision/beta/projects/centernet/ops/target_assigner_test.py
+++ b/official/projects/centernet/ops/target_assigner_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,8 +17,8 @@
from absl.testing import parameterized
import tensorflow as tf
-from official.vision.beta.ops import preprocess_ops
-from official.vision.beta.projects.centernet.ops import target_assigner
+from official.projects.centernet.ops import target_assigner
+from official.vision.ops import preprocess_ops
class TargetAssignerTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/centernet/tasks/__init__.py b/official/projects/centernet/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/tasks/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/tasks/centernet.py b/official/projects/centernet/tasks/centernet.py
new file mode 100644
index 0000000000000000000000000000000000000000..fae44dae03ebe729403e1cc783c3405edfc2bf63
--- /dev/null
+++ b/official/projects/centernet/tasks/centernet.py
@@ -0,0 +1,425 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Centernet task definition."""
+
+from typing import Any, List, Optional, Tuple
+
+from absl import logging
+import tensorflow as tf
+
+from official.core import base_task
+from official.core import input_reader
+from official.core import task_factory
+from official.projects.centernet.configs import centernet as exp_cfg
+from official.projects.centernet.dataloaders import centernet_input
+from official.projects.centernet.losses import centernet_losses
+from official.projects.centernet.modeling import centernet_model
+from official.projects.centernet.modeling.heads import centernet_head
+from official.projects.centernet.modeling.layers import detection_generator
+from official.projects.centernet.ops import loss_ops
+from official.projects.centernet.ops import target_assigner
+from official.vision.dataloaders import tf_example_decoder
+from official.vision.dataloaders import tfds_factory
+from official.vision.dataloaders import tf_example_label_map_decoder
+from official.vision.evaluation import coco_evaluator
+from official.vision.modeling.backbones import factory
+
+
+@task_factory.register_task_cls(exp_cfg.CenterNetTask)
+class CenterNetTask(base_task.Task):
+ """Task definition for centernet."""
+
+ def build_inputs(self,
+ params: exp_cfg.DataConfig,
+ input_context: Optional[tf.distribute.InputContext] = None):
+ """Build input dataset."""
+ if params.tfds_name:
+ decoder = tfds_factory.get_detection_decoder(params.tfds_name)
+ else:
+ decoder_cfg = params.decoder.get()
+ if params.decoder.type == 'simple_decoder':
+ decoder = tf_example_decoder.TfExampleDecoder(
+ regenerate_source_id=decoder_cfg.regenerate_source_id)
+ elif params.decoder.type == 'label_map_decoder':
+ decoder = tf_example_label_map_decoder.TfExampleDecoderLabelMap(
+ label_map=decoder_cfg.label_map,
+ regenerate_source_id=decoder_cfg.regenerate_source_id)
+ else:
+ raise ValueError('Unknown decoder type: {}!'.format(
+ params.decoder.type))
+
+ parser = centernet_input.CenterNetParser(
+ output_height=self.task_config.model.input_size[0],
+ output_width=self.task_config.model.input_size[1],
+ max_num_instances=self.task_config.model.max_num_instances,
+ bgr_ordering=params.parser.bgr_ordering,
+ channel_means=params.parser.channel_means,
+ channel_stds=params.parser.channel_stds,
+ aug_rand_hflip=params.parser.aug_rand_hflip,
+ aug_scale_min=params.parser.aug_scale_min,
+ aug_scale_max=params.parser.aug_scale_max,
+ aug_rand_hue=params.parser.aug_rand_hue,
+ aug_rand_brightness=params.parser.aug_rand_brightness,
+ aug_rand_contrast=params.parser.aug_rand_contrast,
+ aug_rand_saturation=params.parser.aug_rand_saturation,
+ odapi_augmentation=params.parser.odapi_augmentation,
+ dtype=params.dtype)
+
+ reader = input_reader.InputReader(
+ params,
+ dataset_fn=tf.data.TFRecordDataset,
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def build_model(self):
+ """get an instance of CenterNet."""
+ model_config = self.task_config.model
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + model_config.input_size)
+
+ l2_weight_decay = self.task_config.weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ backbone = factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=model_config.norm_activation,
+ l2_regularizer=l2_regularizer)
+
+ task_outputs = self.task_config.get_output_length_dict()
+ head_config = model_config.head
+ head = centernet_head.CenterNetHead(
+ input_specs=backbone.output_specs,
+ task_outputs=task_outputs,
+ input_levels=head_config.input_levels,
+ heatmap_bias=head_config.heatmap_bias)
+
+ # output_specs is a dict
+ backbone_output_spec = backbone.output_specs[head_config.input_levels[-1]]
+ if len(backbone_output_spec) == 4:
+ bb_output_height = backbone_output_spec[1]
+ elif len(backbone_output_spec) == 3:
+ bb_output_height = backbone_output_spec[0]
+ else:
+ raise ValueError
+ self._net_down_scale = int(model_config.input_size[0] / bb_output_height)
+ dg_config = model_config.detection_generator
+ detect_generator_obj = detection_generator.CenterNetDetectionGenerator(
+ max_detections=dg_config.max_detections,
+ peak_error=dg_config.peak_error,
+ peak_extract_kernel_size=dg_config.peak_extract_kernel_size,
+ class_offset=dg_config.class_offset,
+ net_down_scale=self._net_down_scale,
+ input_image_dims=model_config.input_size[0],
+ use_nms=dg_config.use_nms,
+ nms_pre_thresh=dg_config.nms_pre_thresh,
+ nms_thresh=dg_config.nms_thresh)
+
+ model = centernet_model.CenterNetModel(
+ backbone=backbone,
+ head=head,
+ detection_generator=detect_generator_obj)
+
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loading pretrained checkpoint."""
+ if not self.task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self.task_config.init_checkpoint
+
+ # Restoring checkpoint.
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ if self.task_config.init_checkpoint_modules == 'all':
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.restore(ckpt_dir_or_file)
+ status.assert_consumed()
+ elif self.task_config.init_checkpoint_modules == 'backbone':
+ ckpt = tf.train.Checkpoint(backbone=model.backbone)
+ status = ckpt.restore(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ else:
+ raise ValueError(
+ "Only 'all' or 'backbone' can be used to initialize the model.")
+
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+
+ def build_losses(self,
+ outputs,
+ labels,
+ aux_losses=None):
+ """Build losses."""
+ input_size = self.task_config.model.input_size[0:2]
+ output_size = outputs['ct_heatmaps'][0].get_shape().as_list()[1:3]
+
+ gt_label = tf.map_fn(
+ # pylint: disable=g-long-lambda
+ fn=lambda x: target_assigner.assign_centernet_targets(
+ labels=x,
+ input_size=input_size,
+ output_size=output_size,
+ num_classes=self.task_config.model.num_classes,
+ max_num_instances=self.task_config.model.max_num_instances,
+ gaussian_iou=self.task_config.losses.gaussian_iou,
+ class_offset=self.task_config.losses.class_offset),
+ elems=labels,
+ fn_output_signature={
+ 'ct_heatmaps': tf.TensorSpec(
+ shape=[output_size[0], output_size[1],
+ self.task_config.model.num_classes],
+ dtype=tf.float32),
+ 'ct_offset': tf.TensorSpec(
+ shape=[self.task_config.model.max_num_instances, 2],
+ dtype=tf.float32),
+ 'size': tf.TensorSpec(
+ shape=[self.task_config.model.max_num_instances, 2],
+ dtype=tf.float32),
+ 'box_mask': tf.TensorSpec(
+ shape=[self.task_config.model.max_num_instances],
+ dtype=tf.int32),
+ 'box_indices': tf.TensorSpec(
+ shape=[self.task_config.model.max_num_instances, 2],
+ dtype=tf.int32),
+ }
+ )
+
+ losses = {}
+
+ # Create loss functions
+ object_center_loss_fn = centernet_losses.PenaltyReducedLogisticFocalLoss()
+ localization_loss_fn = centernet_losses.L1LocalizationLoss()
+
+ # Set up box indices so that they have a batch element as well
+ box_indices = loss_ops.add_batch_to_indices(gt_label['box_indices'])
+
+ box_mask = tf.cast(gt_label['box_mask'], dtype=tf.float32)
+ num_boxes = tf.cast(
+ loss_ops.get_num_instances_from_weights(gt_label['box_mask']),
+ dtype=tf.float32)
+
+ # Calculate center heatmap loss
+ output_unpad_image_shapes = tf.math.ceil(
+ tf.cast(labels['unpad_image_shapes'],
+ tf.float32) / self._net_down_scale)
+ valid_anchor_weights = loss_ops.get_valid_anchor_weights_in_flattened_image(
+ output_unpad_image_shapes, output_size[0], output_size[1])
+ valid_anchor_weights = tf.expand_dims(valid_anchor_weights, 2)
+
+ pred_ct_heatmap_list = outputs['ct_heatmaps']
+ true_flattened_ct_heatmap = loss_ops.flatten_spatial_dimensions(
+ gt_label['ct_heatmaps'])
+ true_flattened_ct_heatmap = tf.cast(true_flattened_ct_heatmap, tf.float32)
+
+ total_center_loss = 0.0
+ for ct_heatmap in pred_ct_heatmap_list:
+ pred_flattened_ct_heatmap = loss_ops.flatten_spatial_dimensions(
+ ct_heatmap)
+ pred_flattened_ct_heatmap = tf.cast(pred_flattened_ct_heatmap, tf.float32)
+ total_center_loss += object_center_loss_fn(
+ target_tensor=true_flattened_ct_heatmap,
+ prediction_tensor=pred_flattened_ct_heatmap,
+ weights=valid_anchor_weights)
+
+ center_loss = tf.reduce_sum(total_center_loss) / float(
+ len(pred_ct_heatmap_list) * num_boxes)
+ losses['ct_loss'] = center_loss
+
+ # Calculate scale loss
+ pred_scale_list = outputs['ct_size']
+ true_scale = tf.cast(gt_label['size'], tf.float32)
+
+ total_scale_loss = 0.0
+ for scale_map in pred_scale_list:
+ pred_scale = loss_ops.get_batch_predictions_from_indices(scale_map,
+ box_indices)
+ pred_scale = tf.cast(pred_scale, tf.float32)
+ # Only apply loss for boxes that appear in the ground truth
+ total_scale_loss += tf.reduce_sum(
+ localization_loss_fn(target_tensor=true_scale,
+ prediction_tensor=pred_scale),
+ axis=-1) * box_mask
+
+ scale_loss = tf.reduce_sum(total_scale_loss) / float(
+ len(pred_scale_list) * num_boxes)
+ losses['scale_loss'] = scale_loss
+
+ # Calculate offset loss
+ pred_offset_list = outputs['ct_offset']
+ true_offset = tf.cast(gt_label['ct_offset'], tf.float32)
+
+ total_offset_loss = 0.0
+ for offset_map in pred_offset_list:
+ pred_offset = loss_ops.get_batch_predictions_from_indices(offset_map,
+ box_indices)
+ pred_offset = tf.cast(pred_offset, tf.float32)
+ # Only apply loss for boxes that appear in the ground truth
+ total_offset_loss += tf.reduce_sum(
+ localization_loss_fn(target_tensor=true_offset,
+ prediction_tensor=pred_offset),
+ axis=-1) * box_mask
+
+ offset_loss = tf.reduce_sum(total_offset_loss) / float(
+ len(pred_offset_list) * num_boxes)
+ losses['ct_offset_loss'] = offset_loss
+
+ # Aggregate and finalize loss
+ loss_weights = self.task_config.losses.detection
+ total_loss = (loss_weights.object_center_weight * center_loss +
+ loss_weights.scale_weight * scale_loss +
+ loss_weights.offset_weight * offset_loss)
+
+ if aux_losses:
+ total_loss += tf.add_n(aux_losses)
+
+ losses['total_loss'] = total_loss
+ return losses
+
+ def build_metrics(self, training=True):
+ metrics = []
+ metric_names = ['total_loss', 'ct_loss', 'scale_loss', 'ct_offset_loss']
+ for name in metric_names:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+
+ if not training:
+ if (self.task_config.validation_data.tfds_name
+ and self.task_config.annotation_file):
+ raise ValueError(
+ "Can't evaluate using annotation file when TFDS is used.")
+ self.coco_metric = coco_evaluator.COCOEvaluator(
+ annotation_file=self.task_config.annotation_file,
+ include_mask=False,
+ per_category_metrics=self.task_config.per_category_metrics)
+
+ return metrics
+
+ def train_step(self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ optimizer: tf.keras.optimizers.Optimizer,
+ metrics: Optional[List[Any]] = None):
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+
+ num_replicas = tf.distribute.get_strategy().num_replicas_in_sync
+ with tf.GradientTape() as tape:
+ outputs = model(features, training=True)
+ # Casting output layer as float32 is necessary when mixed_precision is
+ # mixed_float16 or mixed_bfloat16 to ensure output is casted as float32.
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+
+ losses = self.build_losses(outputs['raw_output'], labels)
+
+ scaled_loss = losses['total_loss'] / num_replicas
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ # compute the gradient
+ tvars = model.trainable_variables
+ gradients = tape.gradient(scaled_loss, tvars)
+
+ # get unscaled loss if the scaled loss was used
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ gradients = optimizer.get_unscaled_gradients(gradients)
+
+ if self.task_config.gradient_clip_norm > 0.0:
+ gradients, _ = tf.clip_by_global_norm(gradients,
+ self.task_config.gradient_clip_norm)
+
+ optimizer.apply_gradients(list(zip(gradients, tvars)))
+
+ logs = {self.loss: losses['total_loss']}
+
+ if metrics:
+ for m in metrics:
+ m.update_state(losses[m.name])
+ logs.update({m.name: m.result()})
+
+ return logs
+
+ def validation_step(self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ metrics: Optional[List[Any]] = None):
+ """Validation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+
+ outputs = model(features, training=False)
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+
+ losses = self.build_losses(outputs['raw_output'], labels)
+
+ logs = {self.loss: losses['total_loss']}
+
+ coco_model_outputs = {
+ 'detection_boxes': outputs['boxes'],
+ 'detection_scores': outputs['confidence'],
+ 'detection_classes': outputs['classes'],
+ 'num_detections': outputs['num_detections'],
+ 'source_id': labels['groundtruths']['source_id'],
+ 'image_info': labels['image_info']
+ }
+
+ logs.update({self.coco_metric.name: (labels['groundtruths'],
+ coco_model_outputs)})
+
+ if metrics:
+ for m in metrics:
+ m.update_state(losses[m.name])
+ logs.update({m.name: m.result()})
+ return logs
+
+ def aggregate_logs(self, state=None, step_outputs=None):
+ if state is None:
+ self.coco_metric.reset_states()
+ state = self.coco_metric
+ self.coco_metric.update_state(step_outputs[self.coco_metric.name][0],
+ step_outputs[self.coco_metric.name][1])
+ return state
+
+ def reduce_aggregated_logs(self, aggregated_logs, global_step=None):
+ return self.coco_metric.result()
diff --git a/official/projects/centernet/train.py b/official/projects/centernet/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..62474a33cf0f80242b17d0579d6da4390358844d
--- /dev/null
+++ b/official/projects/centernet/train.py
@@ -0,0 +1,67 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision Centernet trainer."""
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+from official.projects.centernet.common import registry_imports # pylint: disable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/projects/centernet/utils/__init__.py b/official/projects/centernet/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/utils/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/centernet/utils/checkpoints/__init__.py b/official/projects/centernet/utils/checkpoints/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/centernet/utils/checkpoints/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/centernet/utils/checkpoints/config_classes.py b/official/projects/centernet/utils/checkpoints/config_classes.py
similarity index 99%
rename from official/vision/beta/projects/centernet/utils/checkpoints/config_classes.py
rename to official/projects/centernet/utils/checkpoints/config_classes.py
index 12b25d25e2e58de93347f05bfc8470cab445672a..5c67085f9f6f9478e7426ff743c64541afe35e1c 100644
--- a/official/vision/beta/projects/centernet/utils/checkpoints/config_classes.py
+++ b/official/projects/centernet/utils/checkpoints/config_classes.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/centernet/utils/checkpoints/config_data.py b/official/projects/centernet/utils/checkpoints/config_data.py
similarity index 96%
rename from official/vision/beta/projects/centernet/utils/checkpoints/config_data.py
rename to official/projects/centernet/utils/checkpoints/config_data.py
index 302f661f3464e13fdfbadd12fbdc2937c0c387b8..e5cffe83467e492e196dba5fa0550c3655f6cadb 100644
--- a/official/vision/beta/projects/centernet/utils/checkpoints/config_data.py
+++ b/official/projects/centernet/utils/checkpoints/config_data.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,7 +19,7 @@ from typing import Dict, Optional
import numpy as np
-from official.vision.beta.projects.centernet.utils.checkpoints import config_classes
+from official.projects.centernet.utils.checkpoints import config_classes
Conv2DBNCFG = config_classes.Conv2DBNCFG
HeadConvCFG = config_classes.HeadConvCFG
diff --git a/official/vision/beta/projects/centernet/utils/checkpoints/load_weights.py b/official/projects/centernet/utils/checkpoints/load_weights.py
similarity index 92%
rename from official/vision/beta/projects/centernet/utils/checkpoints/load_weights.py
rename to official/projects/centernet/utils/checkpoints/load_weights.py
index 4bc387f4e02509709ac1c4d05d2d2d4c3b473699..e193ef4da24e92da8da877f3acda44a30b37d619 100644
--- a/official/vision/beta/projects/centernet/utils/checkpoints/load_weights.py
+++ b/official/projects/centernet/utils/checkpoints/load_weights.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,11 +14,11 @@
"""Functions used to load the ODAPI CenterNet checkpoint."""
-from official.vision.beta.modeling.backbones import mobilenet
-from official.vision.beta.modeling.layers import nn_blocks
-from official.vision.beta.projects.centernet.modeling.layers import cn_nn_blocks
-from official.vision.beta.projects.centernet.utils.checkpoints import config_classes
-from official.vision.beta.projects.centernet.utils.checkpoints import config_data
+from official.projects.centernet.modeling.layers import cn_nn_blocks
+from official.projects.centernet.utils.checkpoints import config_classes
+from official.projects.centernet.utils.checkpoints import config_data
+from official.vision.modeling.backbones import mobilenet
+from official.vision.modeling.layers import nn_blocks
Conv2DBNCFG = config_classes.Conv2DBNCFG
HeadConvCFG = config_classes.HeadConvCFG
diff --git a/official/vision/beta/projects/centernet/utils/checkpoints/read_checkpoints.py b/official/projects/centernet/utils/checkpoints/read_checkpoints.py
similarity index 98%
rename from official/vision/beta/projects/centernet/utils/checkpoints/read_checkpoints.py
rename to official/projects/centernet/utils/checkpoints/read_checkpoints.py
index 850b3382587e02f41c47d7176f96d7faa097d89a..4128f404600e383fc027323171a8e8c45ade6a3b 100644
--- a/official/vision/beta/projects/centernet/utils/checkpoints/read_checkpoints.py
+++ b/official/projects/centernet/utils/checkpoints/read_checkpoints.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/centernet/utils/tf2_centernet_checkpoint_converter.py b/official/projects/centernet/utils/tf2_centernet_checkpoint_converter.py
similarity index 85%
rename from official/vision/beta/projects/centernet/utils/tf2_centernet_checkpoint_converter.py
rename to official/projects/centernet/utils/tf2_centernet_checkpoint_converter.py
index 33c29efe2c307de51da3ce55fe1b82ff214b270c..d1afcf9d8d30b79403d436cb1d72e92a7f0d1448 100644
--- a/official/vision/beta/projects/centernet/utils/tf2_centernet_checkpoint_converter.py
+++ b/official/projects/centernet/utils/tf2_centernet_checkpoint_converter.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,15 +19,15 @@ from absl import flags
from absl import logging
import tensorflow as tf
-from official.vision.beta.modeling.backbones import factory
-from official.vision.beta.projects.centernet.common import registry_imports # pylint: disable=unused-import
-from official.vision.beta.projects.centernet.configs import backbones
-from official.vision.beta.projects.centernet.configs import centernet
-from official.vision.beta.projects.centernet.modeling import centernet_model
-from official.vision.beta.projects.centernet.modeling.heads import centernet_head
-from official.vision.beta.projects.centernet.modeling.layers import detection_generator
-from official.vision.beta.projects.centernet.utils.checkpoints import load_weights
-from official.vision.beta.projects.centernet.utils.checkpoints import read_checkpoints
+from official.projects.centernet.common import registry_imports # pylint: disable=unused-import
+from official.projects.centernet.configs import backbones
+from official.projects.centernet.configs import centernet
+from official.projects.centernet.modeling import centernet_model
+from official.projects.centernet.modeling.heads import centernet_head
+from official.projects.centernet.modeling.layers import detection_generator
+from official.projects.centernet.utils.checkpoints import load_weights
+from official.projects.centernet.utils.checkpoints import read_checkpoints
+from official.vision.modeling.backbones import factory
FLAGS = flags.FLAGS
diff --git a/official/projects/const_cl/README.md b/official/projects/const_cl/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..488b455fda9e606b51061e597546bc6783a5c4ac
--- /dev/null
+++ b/official/projects/const_cl/README.md
@@ -0,0 +1,5 @@
+# Contextualized Spatial-Temporal Contrastive Learning with Self-Supervision
+
+(WIP) This repository contains the official implementation of
+[Contextualized Spatio-Temporal Contrastive Learning with Self-Supervision](https://arxiv.org/abs/2112.05181)
+in TF2.
diff --git a/official/projects/cots_detector/README.md b/official/projects/cots_detector/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..550382bbcedd3cb48b827f8c803e6bd701ad264f
--- /dev/null
+++ b/official/projects/cots_detector/README.md
@@ -0,0 +1,32 @@
+# Crown-of-Thorns Starfish Detection Pipeline
+
+[](https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb?force_crab_mode=1)
+
+This repository shows how to detect crown-of-thorns starfish (COTS) using a
+pre-trained COTS detector implemented in TensorFlow.
+
+
+
+## Description
+
+Coral reefs are some of the most diverse and important ecosystems in the world,
+however they face a number of rising threats that have resulted in massive
+global declines. In Australia, outbreaks of the coral-eating crown-of-thorns
+starfish (COTS) have been shown to cause major coral loss, with just 15 starfish
+in a hectare being able to strip a reef of 90% of its coral tissue. While COTS
+naturally exist in the Indo-Pacific, overfishing and excess run-off nutrients
+have led to massive outbreaks that are devastating already vulnerable coral
+communities.
+
+Controlling COTS populations is critical to promoting coral growth and
+resilience, so Google teamed up with Australia’s national science agency,
+[CSIRO](https://www.csiro.au/en/), to tackle this problem. We trained ML object
+detection models to help scale underwater surveys, enabling the monitoring and
+mapping out these harmful invertebrates with the ultimate goal of helping
+control teams to address and prioritize outbreaks.
+
+## Get started
+
+[Open the notebook in Colab](https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb?force_crab_mode=1)
+to run the COTS detection pipeline.
diff --git a/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb b/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..f9a790c60a633d7a51b0e11f4a5b8fc74fcadded
--- /dev/null
+++ b/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb
@@ -0,0 +1,1473 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "cellView": "form",
+ "id": "xBH8CcrkV3IU"
+ },
+ "outputs": [],
+ "source": [
+ "#@title Licensed under the Apache License, Version 2.0 (the \"License\");\n",
+ "# you may not use this file except in compliance with the License.\n",
+ "# You may obtain a copy of the License at\n",
+ "#\n",
+ "# https://www.apache.org/licenses/LICENSE-2.0\n",
+ "#\n",
+ "# Unless required by applicable law or agreed to in writing, software\n",
+ "# distributed under the License is distributed on an \"AS IS\" BASIS,\n",
+ "# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.\n",
+ "# See the License for the specific language governing permissions and\n",
+ "# limitations under the License."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "9CzbXNRovpbc"
+ },
+ "source": [
+ "# Crown-of-Thorns Starfish Detection Pipeline"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Lpb0yoNjiWhw"
+ },
+ "source": [
+ "\u003ctable class=\"tfo-notebook-buttons\" align=\"left\"\u003e\n",
+ " \u003ctd\u003e\n",
+ " \u003ca target=\"_blank\" href=\"https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb?force_crab_mode=1\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/colab_logo_32px.png\" /\u003eRun in Google Colab\u003c/a\u003e\n",
+ " \u003c/td\u003e\n",
+ " \u003ctd\u003e\n",
+ " \u003ca target=\"_blank\" href=\"https://github.com/tensorflow/models/blob/master/official/projects/cots_detector/crown_of_thorns_starfish_detection_pipeline.ipynb\"\u003e\u003cimg src=\"https://www.tensorflow.org/images/GitHub-Mark-32px.png\" /\u003eView on GitHub\u003c/a\u003e\n",
+ " \u003c/td\u003e\n",
+ "\u003c/table\u003e"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "GUQ1x137ysLD"
+ },
+ "source": [
+ "Coral reefs are some of the most diverse and important ecosystems in the world , however they face a number of rising threats that have resulted in massive global declines. In Australia, outbreaks of the coral-eating crown-of-thorns starfish (COTS) have been shown to cause major coral loss, with just 15 starfish in a hectare being able to strip a reef of 90% of its coral tissue. While COTS naturally exist in the Indo-Pacific, overfishing and excess run-off nutrients have led to massive outbreaks that are devastating already vulnerable coral communities.\n",
+ "\n",
+ "Controlling COTS populations is critical to promoting coral growth and resilience, so Google teamed up with Australia’s national science agency, [CSIRO](https://www.csiro.au/en/), to tackle this problem. We trained ML object detection models to help scale underwater surveys, enabling the monitoring and mapping out these harmful invertebrates with the ultimate goal of helping control teams to address and prioritize outbreaks."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "jDiIX2xawkJw"
+ },
+ "source": [
+ "## About this notebook\n",
+ "\n",
+ "This notebook tutorial shows how to detect COTS using a pre-trained COTS detector implemented in TensorFlow. On top of just running the model on each frame of the video, the tracking code in this notebook aligns detections from frame to frame creating a consistent track for each COTS. Each track is given an id and frame count. Here is an example image from a video of a reef showing labeled COTS starfish.\n",
+ "\n",
+ "\u003cimg src=\"https://storage.googleapis.com/download.tensorflow.org/data/cots_detection/COTS_detected_sample.png\"\u003e"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "YxCF1t-Skag8"
+ },
+ "source": [
+ "It is recommended to enable GPU to accelerate the inference. On CPU, this runs for about 40 minutes, but on GPU it takes only 10 minutes. (In Colab it should already be set to GPU in the Runtime menu: *Runtime \u003e Change runtime type \u003e Hardware accelerator \u003e select \"GPU\"*)."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "a4R2T97u442o"
+ },
+ "source": [
+ "## Setup \n",
+ "\n",
+ "Install all needed packages."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "5Gs7XvCGlwlj"
+ },
+ "outputs": [],
+ "source": [
+ "# remove the existing datascience package to avoid package conflicts in the colab environment\n",
+ "!pip3 uninstall -y datascience\n",
+ "!pip3 install -q opencv-python\n",
+ "!pip3 install PILLOW"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "w-UQ87240x5R"
+ },
+ "outputs": [],
+ "source": [
+ "# Imports\n",
+ "import base64\n",
+ "import copy\n",
+ "import dataclasses\n",
+ "import glob\n",
+ "import logging\n",
+ "import mimetypes\n",
+ "import os\n",
+ "import pathlib\n",
+ "import subprocess\n",
+ "import time\n",
+ "import textwrap\n",
+ "from typing import Dict, Iterable, List, Optional, Tuple\n",
+ "\n",
+ "from absl import logging as absl_logging\n",
+ "from IPython import display\n",
+ "import cv2\n",
+ "import matplotlib.pyplot as plt\n",
+ "import numpy as np\n",
+ "import PIL.Image\n",
+ "import tensorflow as tf\n",
+ "from tqdm import tqdm"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "gsSclJg4sJbX"
+ },
+ "source": [
+ "Define all needed variables."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "iKMCvnZEXBBT"
+ },
+ "outputs": [],
+ "source": [
+ "model_name = \"cots_1080_v1\" #@param [\"cots_1080_v1\", \"cots_720_v1\"]\n",
+ "test_sequence_name = \"test3\" #@param [\"test1\", \"test2\", \"test3\"]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "ORLJSdLq4-gd"
+ },
+ "outputs": [],
+ "source": [
+ "cots_model = f\"https://storage.googleapis.com/download.tensorflow.org/models/cots_detection/{model_name}.zip\"\n",
+ "\n",
+ "# Alternatively, this dataset can be downloaded through CSIRO's Data Access Portal at https://data.csiro.au/collection/csiro:54830v2\n",
+ "sample_data_link = f\"https://storage.googleapis.com/download.tensorflow.org/data/cots_detection/sample_images.zip\"\n",
+ "\n",
+ "preview_video_path = \"preview.mp4\"\n",
+ "detection_small_video_path = \"COTS_detection.mp4\"\n",
+ "detection_csv_path = \"detections.csv\""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "FNwP3s-5xgaF"
+ },
+ "source": [
+ "You also need to retrieve the sample data. This sample data is made up of a series of chronological images."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "DF_c_ZMXdPRN"
+ },
+ "outputs": [],
+ "source": [
+ "sample_data_path = tf.keras.utils.get_file(origin=sample_data_link)\n",
+ "# Unzip data\n",
+ "!mkdir sample_images\n",
+ "!unzip -o -q {sample_data_path} -d sample_images"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Ghf-4E5-ZiJn"
+ },
+ "source": [
+ "Convert the images to a video file:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "kCdWsbO1afIJ"
+ },
+ "outputs": [],
+ "source": [
+ "tmp_video_path = \"tmp_preview.mp4\"\n",
+ "\n",
+ "filenames = sorted(glob.glob(f\"sample_images/{test_sequence_name}/*.jpg\"))\n",
+ "img = cv2.imread(filenames[0])\n",
+ "height, width, layers = img.shape\n",
+ "size = (width, height)\n",
+ "\n",
+ "video_writer = cv2.VideoWriter(\n",
+ " filename=tmp_video_path,\n",
+ " fourcc=cv2.VideoWriter_fourcc(*\"MP4V\"), \n",
+ " fps=15, \n",
+ " frameSize=size)\n",
+ " \n",
+ "for filename in tqdm(filenames):\n",
+ " img = cv2.imread(filename)\n",
+ " video_writer.write(img)\n",
+ "cv2.destroyAllWindows()\n",
+ "video_writer.release()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "cHsKpPyviWmF"
+ },
+ "source": [
+ "Re-encode the video, and reduce its size (Colab crashes if you try to embed the full size video)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "_li0qe-gh1iT"
+ },
+ "outputs": [],
+ "source": [
+ "subprocess.check_call([\n",
+ " \"ffmpeg\", \"-y\", \"-i\", tmp_video_path,\n",
+ " \"-vf\",\"scale=800:-1\",\n",
+ " \"-crf\", \"18\",\n",
+ " \"-preset\", \"veryfast\",\n",
+ " \"-vcodec\", \"libx264\", preview_video_path])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "2ItoiHyYQGya"
+ },
+ "source": [
+ "The images you downloaded are frames of a movie showing a top view of a coral reef with crown-of-thorns starfish. Use the `base64` data-URL trick to embed the video in this notebook:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "u0fqXQUzdZCu"
+ },
+ "outputs": [],
+ "source": [
+ "def embed_video_file(path: os.PathLike) -\u003e display.HTML:\n",
+ " \"\"\"Embeds a file in the notebook as an html tag with a data-url.\"\"\"\n",
+ " path = pathlib.Path(path)\n",
+ " mime, unused_encoding = mimetypes.guess_type(str(path))\n",
+ " data = path.read_bytes()\n",
+ "\n",
+ " b64 = base64.b64encode(data).decode()\n",
+ " return display.HTML(\n",
+ " textwrap.dedent(\"\"\"\n",
+ " \u003cvideo width=\"640\" height=\"480\" controls\u003e\n",
+ " \u003csource src=\"data:{mime};base64,{b64}\" type=\"{mime}\"\u003e\n",
+ " Your browser does not support the video tag.\n",
+ " \u003c/video\u003e\n",
+ " \"\"\").format(mime=mime, b64=b64))\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "SiOsbr8xePkg"
+ },
+ "outputs": [],
+ "source": [
+ "embed_video_file(preview_video_path)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "9Z0DTbWrZMZ-"
+ },
+ "source": [
+ "Can you se them? there are lots. The goal of the model is to put boxes around all of the starfish. Each starfish will get its own ID, and that ID will be stable as the camera passes over it."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "d0iALUwM0g2p"
+ },
+ "source": [
+ "## Load the model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "fVq6vNBTxM62"
+ },
+ "source": [
+ "Download the trained COTS detection model that matches your preferences from earlier."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "No5jRA1TxXj0"
+ },
+ "outputs": [],
+ "source": [
+ "model_path = tf.keras.utils.get_file(origin=cots_model)\n",
+ "# Unzip model\n",
+ "!mkdir {model_name}\n",
+ "!unzip -o -q {model_path} -d {model_name}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ezyuSHK5ap__"
+ },
+ "source": [
+ "Load trained model from disk and create the inference function `model_fn()`. This might take a little while."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "HXQnNjwl8Beu"
+ },
+ "outputs": [],
+ "source": [
+ "absl_logging.set_verbosity(absl_logging.ERROR)\n",
+ "\n",
+ "tf.config.optimizer.set_experimental_options({'auto_mixed_precision': True})\n",
+ "tf.config.optimizer.set_jit(True)\n",
+ "\n",
+ "model_fn = tf.saved_model.load(model_name).signatures['serving_default']"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "OvLuznhUa7uG"
+ },
+ "source": [
+ "Here's one test image; how many COTS can you see?"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "XmQF_2L_a7Hu"
+ },
+ "outputs": [],
+ "source": [
+ "example_frame_number = 52\n",
+ "image = tf.io.read_file(filenames[example_frame_number])\n",
+ "image = tf.io.decode_jpeg(image)\n",
+ "\n",
+ "# Caution PIL and tf use \"RGB\" color order, while cv2 uses \"BGR\".\n",
+ "PIL.Image.fromarray(image.numpy())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "KSOf4V8WhTHF"
+ },
+ "source": [
+ "## Raw model outputs\n",
+ "\n",
+ "Try running the model on the image. The model expects a batch of images so add an outer `batch` dimension before calling the model.\n",
+ "\n",
+ "Note: The model only runs correctly with a batch size of 1.\n",
+ "\n",
+ "The result is a dictionary with a number of fields. For all fields the first dimension of the shape is the `batch` dimension, "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "iqLHo8h0c2pW"
+ },
+ "outputs": [],
+ "source": [
+ "image_batch = image[tf.newaxis, ...]\n",
+ "result = model_fn(image_batch)\n",
+ "\n",
+ "print(f\"{'image_batch':20s}- shape: {image_batch.shape}\")\n",
+ "\n",
+ "for key, value in result.items():\n",
+ " print(f\"{key:20s}- shape: {value.shape}\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "0xuNoKLCjyDz"
+ },
+ "source": [
+ "The `num_detections` field gives the number of valid detections, but this is always 100. There are always 100 locations that _could_ be a COTS."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "nGCDZJQvkIOL"
+ },
+ "outputs": [],
+ "source": [
+ "print('\\nnum_detections: ', result['num_detections'].numpy())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "cSd7JJYqkPz7"
+ },
+ "source": [
+ "Similarly the `detection_classes` field is always `0`, since the model only detects 1 class: COTS."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "JoY8bJrfkcuS"
+ },
+ "outputs": [],
+ "source": [
+ "print('detection_classes: \\n', result['detection_classes'].numpy())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "X2nVLSOokyog"
+ },
+ "source": [
+ "What actually matters here is the detection scores, indicating the quality of each detection: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "iepEgCc2jsRD"
+ },
+ "outputs": [],
+ "source": [
+ "result['detection_scores'].numpy()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Fn2B0nbplAFy"
+ },
+ "source": [
+ "You need to choose a threshold that determines what counts as a good detection. This frame has a few good detections:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "a30Uyc0WlK2a"
+ },
+ "outputs": [],
+ "source": [
+ "good_detections = result['detection_scores'] \u003e 0.4\n",
+ "good_detections.numpy()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Y_xrbQiAlWrK"
+ },
+ "source": [
+ "## Bounding boxes and detections\n",
+ "\n",
+ "Build a class to handle the detection boxes:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "S5inzqu-4JhT"
+ },
+ "outputs": [],
+ "source": [
+ "@dataclasses.dataclass(frozen=True)\n",
+ "class BBox:\n",
+ " x0: float\n",
+ " y0: float\n",
+ " x1: float\n",
+ " y1: float\n",
+ "\n",
+ " def replace(self, **kwargs):\n",
+ " d = self.__dict__.copy()\n",
+ " d.update(kwargs)\n",
+ " return type(self)(**d)\n",
+ "\n",
+ " @property\n",
+ " def center(self)-\u003e Tuple[float, float]:\n",
+ " return ((self.x0+self.x1)/2, (self.y0+self.y1)/2)\n",
+ " \n",
+ " @property\n",
+ " def width(self) -\u003e float:\n",
+ " return self.x1 - self.x0\n",
+ "\n",
+ " @property\n",
+ " def height(self) -\u003e float:\n",
+ " return self.y1 - self.y0\n",
+ "\n",
+ " @property\n",
+ " def area(self)-\u003e float:\n",
+ " return (self.x1 - self.x0 + 1) * (self.y1 - self.y0 + 1)\n",
+ " \n",
+ " def intersection(self, other)-\u003e Optional['BBox']:\n",
+ " x0 = max(self.x0, other.x0)\n",
+ " y0 = max(self.y0, other.y0)\n",
+ " x1 = min(self.x1, other.x1)\n",
+ " y1 = min(self.y1, other.y1)\n",
+ " if x0 \u003e x1 or y0 \u003e y1:\n",
+ " return None\n",
+ " return BBox(x0, y0, x1, y1)\n",
+ "\n",
+ " def iou(self, other):\n",
+ " intersection = self.intersection(other)\n",
+ " if intersection is None:\n",
+ " return 0\n",
+ " \n",
+ " ia = intersection.area\n",
+ "\n",
+ " return ia/(self.area + other.area - ia)\n",
+ " \n",
+ " def draw(self, image, label=None, color=(0, 140, 255)):\n",
+ " image = np.asarray(image)\n",
+ " cv2.rectangle(image, \n",
+ " (int(self.x0), int(self.y0)),\n",
+ " (int(self.x1), int(self.y1)),\n",
+ " color,\n",
+ " thickness=2)\n",
+ " if label is not None:\n",
+ " cv2.putText(image, str(label), \n",
+ " (int(self.x0), int(self.y0-10)),\n",
+ " cv2.FONT_HERSHEY_SIMPLEX,\n",
+ " 0.9, color, thickness=2)\n",
+ " return image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "2izYMR9Q6Dn0"
+ },
+ "source": [
+ "And a class to represent a `Detection`, with a method to create a list of detections from the model's output:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "tybwY3eaY803"
+ },
+ "outputs": [],
+ "source": [
+ "@dataclasses.dataclass(frozen=True)\n",
+ "class Detection:\n",
+ " \"\"\"Detection dataclass.\"\"\"\n",
+ " class_id: int\n",
+ " score: float\n",
+ " bbox: BBox\n",
+ " threshold:float = 0.4\n",
+ "\n",
+ " def replace(self, **kwargs):\n",
+ " d = self.__dict__.copy()\n",
+ " d.update(kwargs)\n",
+ " return type(self)(**d)\n",
+ "\n",
+ " @classmethod\n",
+ " def process_model_output(\n",
+ " cls, image, detections: Dict[str, tf.Tensor]\n",
+ " ) -\u003e Iterable['Detection']:\n",
+ " \n",
+ " # The model only works on a batch size of 1.\n",
+ " detection_boxes = detections['detection_boxes'].numpy()[0]\n",
+ " detection_classes = detections['detection_classes'].numpy()[0].astype(np.int32)\n",
+ " detection_scores = detections['detection_scores'].numpy()[0]\n",
+ "\n",
+ " img_h, img_w = image.shape[0:2]\n",
+ "\n",
+ " valid_indices = detection_scores \u003e= cls.threshold\n",
+ " classes = detection_classes[valid_indices]\n",
+ " scores = detection_scores[valid_indices]\n",
+ " boxes = detection_boxes[valid_indices, :]\n",
+ " detections = []\n",
+ "\n",
+ " for class_id, score, box in zip(classes, scores, boxes):\n",
+ " detections.append(\n",
+ " Detection(\n",
+ " class_id=class_id,\n",
+ " score=score,\n",
+ " bbox=BBox(\n",
+ " x0=box[1] * img_w,\n",
+ " y0=box[0] * img_h,\n",
+ " x1=box[3] * img_w,\n",
+ " y1=box[2] * img_h,)))\n",
+ "\n",
+ " return detections"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "QRZ9Q5meHl84"
+ },
+ "source": [
+ "## Preview some detections\n",
+ "\n",
+ "Now you can preview the model's output:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Px7AoFCn-psx"
+ },
+ "outputs": [],
+ "source": [
+ "detections = Detection.process_model_output(image, result)\n",
+ "\n",
+ "for n, det in enumerate(detections):\n",
+ " det.bbox.draw(image, label=n+1, color=(255, 140, 0))\n",
+ "\n",
+ "PIL.Image.fromarray(image.numpy())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "B1q_n1xJLm60"
+ },
+ "source": [
+ "That works well for one frame, but to count the number of COTS in a video you'll need to track the detections from frame to frame. The raw detection indices are not stable, they're just sorted by the detection score. Below both sets of detections are overlaid on the second image with the first frame's detections in white and the second frame's in orange, the indices are not aligned. The positions are shifted because of camera motion between the two frames:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "PLtxJFPuLma0"
+ },
+ "outputs": [],
+ "source": [
+ "image2 = tf.io.read_file(filenames[example_frame_number+5]) # five frames later\n",
+ "image2 = tf.io.decode_jpeg(image2)\n",
+ "result2 = model_fn(image2[tf.newaxis, ...])\n",
+ "detections2 = Detection.process_model_output(image2, result2)\n",
+ "\n",
+ "for n, det in enumerate(detections):\n",
+ " det.bbox.draw(image2, label=n+1, color=(255, 255, 255))\n",
+ "\n",
+ "for n, det in enumerate(detections2):\n",
+ " det.bbox.draw(image2, label=n+1, color=(255, 140, 0))\n",
+ "\n",
+ "PIL.Image.fromarray(image2.numpy())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "CoRxLon5MZ35"
+ },
+ "source": [
+ "## Use optical flow to align detections\n",
+ "\n",
+ "The two sets of bounding boxes above don't line up because of camera movement. \n",
+ "To see in more detail how tracks are aligned, initialize the tracker with the first image, and then run the optical flow step, `propagate_tracks`. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "wb_nkcPJJx2t"
+ },
+ "outputs": [],
+ "source": [
+ "def default_of_params():\n",
+ " its=20\n",
+ " eps=0.03\n",
+ " return {\n",
+ " 'winSize': (64,64),\n",
+ " 'maxLevel': 3,\n",
+ " 'criteria': (cv2.TermCriteria_COUNT + cv2.TermCriteria_EPS, its, eps)\n",
+ " }"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "mHVPymG8F2ke"
+ },
+ "outputs": [],
+ "source": [
+ "def propagate_detections(detections, image1, image2, of_params=None):\n",
+ " if of_params is None:\n",
+ " of_params = default_of_params()\n",
+ "\n",
+ " bboxes = [det.bbox for det in detections]\n",
+ " centers = np.float32([[bbox.center for bbox in bboxes]])\n",
+ " widths = np.float32([[bbox.width for bbox in bboxes]])\n",
+ " heights = np.float32([[bbox.height for bbox in bboxes]])\n",
+ "\n",
+ "\n",
+ " new_centers, status, error = cv2.calcOpticalFlowPyrLK(\n",
+ " image1, image2, centers, None, **of_params)\n",
+ "\n",
+ " x0s = new_centers[...,0] - widths/2\n",
+ " x1s = new_centers[...,0] + widths/2\n",
+ " y0s = new_centers[...,1] - heights/2\n",
+ " y1s = new_centers[...,1] + heights/2\n",
+ "\n",
+ " updated_detections = []\n",
+ " for i, det in enumerate(detections):\n",
+ " det = det.replace(\n",
+ " bbox = BBox(x0s[0,i], y0s[0,i], x1s[0,i], y1s[0,i]))\n",
+ " updated_detections.append(det)\n",
+ " return updated_detections"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "dCjgvoZnOcBu"
+ },
+ "source": [
+ "Now keep the white boxes for the initial detections, and the orange boxes for the new set of detections. But add the optical-flow propagated tracks in green. You can see that by using optical-flow to propagate the old detections to the new frame the alignment is quite good. It's this alignment between the old and new detections (between the green and orange boxes) that allows the tracker to make a persistent track for each COTS. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "aeTny8YnHwTw"
+ },
+ "outputs": [],
+ "source": [
+ "image = tf.io.read_file(filenames[example_frame_number])\n",
+ "image = tf.io.decode_jpeg(image).numpy()\n",
+ "image_gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)\n",
+ "\n",
+ "image2 = tf.io.read_file(filenames[example_frame_number+5]) # five frames later\n",
+ "image2 = tf.io.decode_jpeg(image2).numpy()\n",
+ "image2_gray = cv2.cvtColor(image2, cv2.COLOR_BGR2GRAY)\n",
+ "\n",
+ "updated_detections = propagate_detections(detections, image_gray, image2_gray)\n",
+ "\n",
+ "\n",
+ "for det in detections:\n",
+ " det.bbox.draw(image2, color=(255, 255, 255))\n",
+ "\n",
+ "for det in updated_detections:\n",
+ " det.bbox.draw(image2, color=(0, 255, 0))\n",
+ "\n",
+ "for det in detections2:\n",
+ " det.bbox.draw(image2, color=(255, 140, 0))\n",
+ "\n",
+ "PIL.Image.fromarray(image2)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "jbZ-7ICCENWG"
+ },
+ "source": [
+ "## Define **OpticalFlowTracker** class\n",
+ "\n",
+ "These help track the movement of each COTS object across the video frames.\n",
+ "\n",
+ "The tracker collects related detections into `Track` objects. \n",
+ "\n",
+ "The class's init is defined below, it's methods are defined in the following cells.\n",
+ "\n",
+ "The `__init__` method just initializes the track counter (`track_id`), and sets some default values for the tracking and optical flow configurations. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "3j2Ka1uGEoz4"
+ },
+ "outputs": [],
+ "source": [
+ "class OpticalFlowTracker:\n",
+ " \"\"\"Optical flow tracker.\"\"\"\n",
+ "\n",
+ " @classmethod\n",
+ " def add_method(cls, fun):\n",
+ " \"\"\"Attach a new method to the class.\"\"\"\n",
+ " setattr(cls, fun.__name__, fun)\n",
+ "\n",
+ "\n",
+ " def __init__(self, tid=1, ft=3.0, iou=0.5, tt=2.0, bb=32, of_params=None):\n",
+ " # Bookkeeping for the tracks.\n",
+ " # The running track count, incremented for each new track.\n",
+ " self.track_id = tid\n",
+ " self.tracks = []\n",
+ " self.prev_image = None\n",
+ " self.prev_time = None\n",
+ "\n",
+ " # Configuration for the track cleanup logic.\n",
+ " # How long to apply optical flow tracking without getting positive \n",
+ " # detections (sec).\n",
+ " self.track_flow_time = ft * 1000\n",
+ " # Required IoU overlap to link a detection to a track.\n",
+ " self.overlap_threshold = iou\n",
+ " # Used to detect if detector needs to be reset.\n",
+ " self.time_threshold = tt * 1000\n",
+ " self.border = bb\n",
+ "\n",
+ " if of_params is None:\n",
+ " of_params = default_of_params()\n",
+ " self.of_params = of_params\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "yBLSv0Fi_JJD"
+ },
+ "source": [
+ "Internally the tracker will use small `Track` and `Tracklet` classes to organize the data. The `Tracklet` class is just a `Detection` with a timestamp, while a `Track` is a track ID, the most recent detection and a list of `Tracklet` objects forming the history of the track."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "gCQFfAkaY_WN"
+ },
+ "outputs": [],
+ "source": [
+ "@dataclasses.dataclass(frozen=True)\n",
+ "class Tracklet:\n",
+ " timestamp:float\n",
+ " detection:Detection\n",
+ "\n",
+ " def replace(self, **kwargs):\n",
+ " d = self.__dict__.copy()\n",
+ " d.update(kwargs)\n",
+ " return type(self)(**d)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "7qVW1a_YZBgL"
+ },
+ "outputs": [],
+ "source": [
+ "@dataclasses.dataclass(frozen=True)\n",
+ "class Track:\n",
+ " \"\"\"Tracker entries.\"\"\"\n",
+ " id:int\n",
+ " det: Detection\n",
+ " linked_dets:List[Tracklet] = dataclasses.field(default_factory=list)\n",
+ "\n",
+ " def replace(self, **kwargs):\n",
+ " d = self.__dict__.copy()\n",
+ " d.update(kwargs)\n",
+ " return type(self)(**d)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Ntl_4oUp_1nD"
+ },
+ "source": [
+ "The tracker keeps a list of active `Track` objects.\n",
+ "\n",
+ "The main `update` method takes an image, along with the list of detections and the timestamp for that image. On each frame step it performs the following sub-tasks:\n",
+ "\n",
+ "* The tracker uses optical flow to calculate where each `Track` expects to see a new `Detection`.\n",
+ "* The tracker matches up the actual detections for the frame to the expected detections for each Track.\n",
+ "* If a detection doesn't get matched to an existing track, a new track is created for the detection.\n",
+ "* If a track stops getting assigned new detections, it is eventually deactivated. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "koZ0mjFTpiTv"
+ },
+ "outputs": [],
+ "source": [
+ "@OpticalFlowTracker.add_method\n",
+ "def update(self, image_bgr, detections, timestamp):\n",
+ " start = time.time()\n",
+ "\n",
+ " image = cv2.cvtColor(image_bgr, cv2.COLOR_BGR2GRAY)\n",
+ "\n",
+ " # Remove dead tracks.\n",
+ " self.tracks = self.cleanup_tracks(image, timestamp)\n",
+ "\n",
+ " # Run optical flow to update existing tracks.\n",
+ " if self.prev_time is not None:\n",
+ " self.tracks = self.propagate_tracks(image)\n",
+ "\n",
+ " # Update the track list based on the new detections\n",
+ " self.apply_detections_to_tracks(image, detections, timestamp)\n",
+ "\n",
+ " self.prev_image = image\n",
+ " self.prev_time = timestamp\n",
+ "\n",
+ " return self.tracks"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "U-6__zF2CHFS"
+ },
+ "source": [
+ "The `cleanup_tracks` method clears tracks that are too old or are too close to the edge of the image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "HQBj8GihjF3-"
+ },
+ "outputs": [],
+ "source": [
+ "@OpticalFlowTracker.add_method\n",
+ "def cleanup_tracks(self, image, timestamp) -\u003e List[Track]:\n",
+ " image_w = image.shape[1]\n",
+ " image_h = image.shape[0]\n",
+ "\n",
+ " # Assume tracker is invalid if too much time has passed!\n",
+ " if (self.prev_time is not None and\n",
+ " timestamp - self.prev_time \u003e self.time_threshold):\n",
+ " logging.info(\n",
+ " 'Too much time since last update, resetting tracker.')\n",
+ " return []\n",
+ "\n",
+ " # Remove tracks which are:\n",
+ " # - Touching the image edge.\n",
+ " # - Have existed for a long time without linking a real detection.\n",
+ " active_tracks = []\n",
+ " for track in self.tracks:\n",
+ " bbox = track.det.bbox\n",
+ " if (bbox.x0 \u003c self.border or bbox.y0 \u003c self.border or\n",
+ " bbox.x1 \u003e= (image_w - self.border) or\n",
+ " bbox.y1 \u003e= (image_h - self.border)):\n",
+ " logging.info(f'Removing track {track.id} because it\\'s near the border')\n",
+ " continue\n",
+ "\n",
+ " time_since_last_detection = timestamp - track.linked_dets[-1].timestamp\n",
+ " if (time_since_last_detection \u003e self.track_flow_time):\n",
+ " logging.info(f'Removing track {track.id} because it\\'s too old '\n",
+ " f'({time_since_last_detection:.02f}s)')\n",
+ " continue\n",
+ "\n",
+ " active_tracks.append(track)\n",
+ "\n",
+ " return active_tracks"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "DVzNcESxC6vY"
+ },
+ "source": [
+ "The `propagate_tracks` method uses optical flow to update each track's bounding box's position to predict their location in the new image: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "0GycdAflCs6v"
+ },
+ "outputs": [],
+ "source": [
+ "@OpticalFlowTracker.add_method\n",
+ "def propagate_tracks(self, image):\n",
+ " if not self.tracks:\n",
+ " return self.tracks[:]\n",
+ "\n",
+ " detections = [track.det for track in self.tracks]\n",
+ " detections = propagate_detections(detections, self.prev_image, image, self.of_params)\n",
+ "\n",
+ " return [track.replace(det=det) \n",
+ " for track, det in zip(self.tracks, detections)]\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uLbVeetwD0ph"
+ },
+ "source": [
+ "The `apply_detections_to_tracks` method compares each detection to the updated bounding box for each track. The detection is added to the track that matches best, if the match is better than the `overlap_threshold`. If no track is better than the threshold, the detection is used to create a new track. \n",
+ "\n",
+ "If a track has no new detection assigned to it the predicted detection is used."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "j6pfRhDRlApe"
+ },
+ "outputs": [],
+ "source": [
+ "@OpticalFlowTracker.add_method\n",
+ "def apply_detections_to_tracks(self, image, detections, timestamp):\n",
+ " image_w = image.shape[1]\n",
+ " image_h = image.shape[0]\n",
+ "\n",
+ " # Insert new detections.\n",
+ " detected_obj_track_ids = set()\n",
+ "\n",
+ " for detection in detections:\n",
+ " bbox = detection.bbox\n",
+ " if (bbox.x0 \u003c self.border or bbox.y0 \u003c self.border or\n",
+ " bbox.x1 \u003e= image_w - self.border or\n",
+ " bbox.y1 \u003e= image_h - self.border):\n",
+ " logging.debug('Skipping detection because it\\'s close to the border.')\n",
+ " continue\n",
+ "\n",
+ " # See if detection can be linked to an existing track.\n",
+ " linked = False\n",
+ " overlap_index = 0\n",
+ " overlap_max = -1000\n",
+ " for track_index, track in enumerate(self.tracks):\n",
+ " logging.debug('Testing track %d', track_index)\n",
+ " if track.det.class_id != detection.class_id:\n",
+ " continue\n",
+ " overlap = detection.bbox.iou(track.det.bbox)\n",
+ " if overlap \u003e overlap_max:\n",
+ " overlap_index = track_index\n",
+ " overlap_max = overlap\n",
+ "\n",
+ " # Link to existing track with maximal IoU.\n",
+ " if overlap_max \u003e self.overlap_threshold:\n",
+ " track = self.tracks[overlap_index]\n",
+ " self.tracks[overlap_index] = track.replace(det=detection)\n",
+ " track.linked_dets.append(Tracklet(timestamp, detection))\n",
+ " detected_obj_track_ids.add(track.id)\n",
+ " linked = True\n",
+ "\n",
+ " if not linked:\n",
+ " logging.info(f'Creating new track with ID {self.track_id}')\n",
+ " new_track = Track(self.track_id, detection)\n",
+ " new_track.linked_dets.append(Tracklet(timestamp, detection))\n",
+ " detected_obj_track_ids.add(self.track_id)\n",
+ " self.tracks.append(new_track)\n",
+ " self.track_id += 1\n",
+ "\n",
+ " for track in self.tracks:\n",
+ " # If the detector does not find the obj but estimated in the tracker, \n",
+ " # add the estimated one to that tracker's linked_dets\n",
+ " if track.id not in detected_obj_track_ids:\n",
+ " track.linked_dets.append(Tracklet(timestamp, track.det))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "gY0AH-KUHPlC"
+ },
+ "source": [
+ "## Test run the tracker\n",
+ "\n",
+ "So reload the test images, and run the detections to test out the tracker.\n",
+ "\n",
+ "On the first frame it creates and returns one track per detection:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "7Ekkj_XFGdfq"
+ },
+ "outputs": [],
+ "source": [
+ "example_frame_number = 52\n",
+ "image = tf.io.read_file(filenames[example_frame_number])\n",
+ "image = tf.io.decode_jpeg(image)\n",
+ "result = model_fn(image[tf.newaxis, ...])\n",
+ "detections = Detection.process_model_output(image, result)\n",
+ "\n",
+ "tracker = OpticalFlowTracker()\n",
+ "tracks = tracker.update(image.numpy(), detections, timestamp = 0)\n",
+ "\n",
+ "print(f'detections : {len(detections)}') \n",
+ "print(f'tracks : {len(tracks)}')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "WovDYdNMII-n"
+ },
+ "source": [
+ "On the second frame many of the detections get assigned to existing tracks:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "7iFEKwgMGi5n"
+ },
+ "outputs": [],
+ "source": [
+ "image2 = tf.io.read_file(filenames[example_frame_number+5]) # five frames later\n",
+ "image2 = tf.io.decode_jpeg(image2)\n",
+ "result2 = model_fn(image2[tf.newaxis, ...])\n",
+ "detections2 = Detection.process_model_output(image2, result2)\n",
+ "\n",
+ "new_tracks = tracker.update(image2.numpy(), detections2, timestamp = 1000)\n",
+ "\n",
+ "print(f'detections : {len(detections2)}') \n",
+ "print(f'tracks : {len(new_tracks)}')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "dbkedwiVrxnQ"
+ },
+ "source": [
+ "Now the track IDs should be consistent:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "QexJR5gerw6q"
+ },
+ "outputs": [],
+ "source": [
+ "test_img = image2.numpy()\n",
+ "for n,track in enumerate(tracks):\n",
+ " track.det.bbox.draw(test_img, label=n, color=(255, 255, 255))\n",
+ "\n",
+ "for n,track in enumerate(new_tracks):\n",
+ " track.det.bbox.draw(test_img, label=n, color=(255, 140, 0))\n",
+ "\n",
+ "PIL.Image.fromarray(test_img)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "OW5gGixy1osE"
+ },
+ "source": [
+ "## Perform the COTS detection inference and tracking."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "f21596933d08"
+ },
+ "source": [
+ "The main tracking loop will perform the following: \n",
+ "\n",
+ "1. Load the images in order.\n",
+ "2. Run the model on the image.\n",
+ "3. Update the tracker with the new images and detections.\n",
+ "4. Keep information about each track (id, current index and length) analysis or display. \n",
+ "\n",
+ "The `TrackAnnotation` class, below, will collect the data about each track:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "lESJE0qXxubm"
+ },
+ "outputs": [],
+ "source": [
+ "@dataclasses.dataclass(frozen=True)\n",
+ "class TrackAnnotation:\n",
+ " det: Detection\n",
+ " seq_id: int\n",
+ " seq_idx: int\n",
+ " seq_length: Optional[int] = None\n",
+ "\n",
+ " def replace(self, **kwargs):\n",
+ " d = self.__dict__.copy()\n",
+ " d.update(kwargs)\n",
+ " return type(self)(**d)\n",
+ "\n",
+ " def annotation_str(self):\n",
+ " return f\"{self.seq_id} ({self.seq_idx}/{self.seq_length})\"\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "3863fb28cd34"
+ },
+ "source": [
+ "The `parse_image` function, below, will take `(index, filename)` pairs load the images as tensors and return `(timestamp_ms, filename, image)` triples, assuming 30fps"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Dn7efhr0GBGz"
+ },
+ "outputs": [],
+ "source": [
+ "# Read a jpg image and decode it to a uint8 tf tensor.\n",
+ "def parse_image(index, filename):\n",
+ " image = tf.io.read_file(filename)\n",
+ " image = tf.io.decode_jpeg(image)\n",
+ " timestamp_ms = 1000*index/30 # assuming 30fps\n",
+ " return (timestamp_ms, filename, image)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "8f878e4b0852"
+ },
+ "source": [
+ "Here is the main tracker loop. Note that initially the saved `TrackAnnotations` don't contain the track lengths. The lengths are collected in the `track_length_for_id` dict."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "cqN8RGBgVbr4"
+ },
+ "outputs": [],
+ "source": [
+ "# Create a tracker object\n",
+ "tracker = OpticalFlowTracker(tid=1)\n",
+ "# Record tracking responses from the tracker\n",
+ "detection_result = []\n",
+ "# Record the length of each tracking sequence\n",
+ "track_length_for_id = {}\n",
+ "\n",
+ "# Create a data loader\n",
+ "file_list = sorted(glob.glob(f\"sample_images/{test_sequence_name}/*.jpg\"))\n",
+ "list_ds = tf.data.Dataset.from_tensor_slices(file_list).enumerate()\n",
+ "images_ds = list_ds.map(parse_image)\n",
+ "\n",
+ "# Traverse the dataset with batch size = 1, you cannot change the batch size\n",
+ "for timestamp_ms, file_path, images in tqdm(images_ds.batch(1, drop_remainder=True)):\n",
+ " # get detection result\n",
+ " detections = Detection.process_model_output(images[0], model_fn(images))\n",
+ "\n",
+ " # Feed detection results and the corresponding timestamp to the tracker, and then get tracker response\n",
+ " tracks = tracker.update(images[0].numpy(), detections, timestamp_ms[0])\n",
+ " annotations = []\n",
+ " for track in tracks:\n",
+ " anno = TrackAnnotation(\n",
+ " det=track.det,\n",
+ " seq_id = track.id,\n",
+ " seq_idx = len(track.linked_dets)\n",
+ " )\n",
+ " annotations.append(anno)\n",
+ " track_length_for_id[track.id] = len(track.linked_dets)\n",
+ " \n",
+ " detection_result.append((file_path.numpy()[0].decode(), annotations))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "29306d7f32df"
+ },
+ "source": [
+ "Once the tracking loop has completed you can update the track length (`seq_length`) for each annotation from the `track_length_for_id` dict:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "oPSfnQ1o04Rx"
+ },
+ "outputs": [],
+ "source": [
+ "def update_annotation_lengths(detection_result, track_length_for_id):\n",
+ " new_result = []\n",
+ " for file_path, annotations in detection_result:\n",
+ " new_annotations = []\n",
+ " for anno in annotations:\n",
+ " anno = anno.replace(seq_length=track_length_for_id[anno.seq_id])\n",
+ " new_annotations.append(anno)\n",
+ " new_result.append((file_path, new_annotations))\n",
+ " return new_result"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "zda914lv1o_v"
+ },
+ "outputs": [],
+ "source": [
+ "detection_result = update_annotation_lengths(detection_result, track_length_for_id)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "QkpmYRyFAMlM"
+ },
+ "source": [
+ "## Output the detection results and play the result video\n",
+ "\n",
+ "Once the inference is done, we draw the bounding boxes and track information onto each frame's image. Finally, we combine all frames into a video for visualisation."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "gWMJG7g95MGk"
+ },
+ "outputs": [],
+ "source": [
+ "detection_full_video_path = \"COTS_detection_full_size.mp4\"\n",
+ "detect_video_writer = cv2.VideoWriter(\n",
+ " filename=detection_full_video_path,\n",
+ " fourcc=cv2.VideoWriter_fourcc(*\"MP4V\"), \n",
+ " fps=15, \n",
+ " frameSize=size)\n",
+ "\n",
+ "for file_path, annotations in tqdm(detection_result):\n",
+ " image = cv2.imread(file_path)\n",
+ " for anno in annotations:\n",
+ " anno.det.bbox.draw(image, label=anno.annotation_str(), color=(0, 140, 255))\n",
+ " detect_video_writer.write(image)\n",
+ "cv2.destroyAllWindows()\n",
+ "\n",
+ "detect_video_writer.release()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "9s1myz67jcV8"
+ },
+ "outputs": [],
+ "source": [
+ "subprocess.check_call([\n",
+ " \"ffmpeg\",\"-y\", \"-i\", detection_full_video_path,\n",
+ " \"-vf\",\"scale=800:-1\",\n",
+ " \"-crf\", \"18\",\n",
+ " \"-preset\", \"veryfast\",\n",
+ " \"-vcodec\", \"libx264\", detection_small_video_path])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "wsK5cvX5jkL7"
+ },
+ "outputs": [],
+ "source": [
+ "embed_video_file(detection_small_video_path)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "n1oOgMR2zzIl"
+ },
+ "source": [
+ "The output video is now saved as movie at `detection_full_video_path`. You can download your video by uncommenting the following code."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "tyHucK8lbGXk"
+ },
+ "outputs": [],
+ "source": [
+ "#try:\n",
+ "# from google.colab import files\n",
+ "# files.download(detection_full_video_path)\n",
+ "#except ImportError:\n",
+ "# pass"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "collapsed_sections": [],
+ "name": "crown_of_thorns_starfish_detection_pipeline.ipynb",
+ "toc_visible": true
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/official/projects/deepmac_maskrcnn/README.md b/official/projects/deepmac_maskrcnn/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..e0dc3cafa5b837aabb30948c19ff7571d82b8746
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/README.md
@@ -0,0 +1,129 @@
+# Mask R-CNN with deep mask heads
+
+This project brings insights from the DeepMAC model into the Mask-RCNN
+architecture. Please see the paper
+[The surprising impact of mask-head architecture on novel class segmentation](https://arxiv.org/abs/2104.00613)
+for more details.
+
+## Code structure
+
+* This folder contains forks of a few Mask R-CNN files and repurposes them to
+ support deep mask heads.
+* To see the benefits of using deep mask heads, it is important to train the
+ mask head with only groundtruth boxes. This is configured via the
+ `task.model.use_gt_boxes_for_masks` flag.
+* Architecture of the mask head can be changed via the config value
+ `task.model.mask_head.convnet_variant`. Supported values are `"default"`,
+ `"hourglass20"`, `"hourglass52"`, and `"hourglass100"`.
+* The flag `task.model.mask_head.class_agnostic` trains the model in class
+ agnostic mode and `task.allowed_mask_class_ids` controls which classes are
+ allowed to have masks during training.
+* Majority of experiments and ablations from the paper are perfomed with the
+ [DeepMAC model](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/deepmac.md)
+ in the Object Detection API code base.
+
+## Prerequisites
+
+### Prepare dataset
+
+Use [create_coco_tf_record.py](https://github.com/tensorflow/models/blob/master/official/vision/data/create_coco_tf_record.py) to create
+the COCO dataset. The data needs to be store in a
+[Google cloud storage bucket](https://cloud.google.com/storage/docs/creating-buckets)
+so that it can be accessed by the TPU.
+
+### Start a TPU v3-32 instance
+
+See [TPU Quickstart](https://cloud.google.com/tpu/docs/quickstart) for
+instructions. An example command would look like:
+
+```shell
+ctpu up --name --zone --tpu-size=v3-32 --tf-version nightly
+```
+
+This model requires TF version `>= 2.5`. Currently, that is only available via a
+`nightly` build on Cloud.
+
+
+### Install requirements
+
+SSH into the TPU host with `gcloud compute ssh ` and execute the
+following.
+
+```shell
+$ git clone https://github.com/tensorflow/models.git
+$ cd models
+$ pip3 install -r official/requirements.txt
+```
+
+## Training Models
+
+The configurations can be found in the `configs/experiments` directory. You can
+launch a training job by executing.
+
+```shell
+$ export CONFIG=./official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50.yaml
+$ export MODEL_DIR="gs://"
+$ export ANNOTAION_FILE="gs://"
+$ export TRAIN_DATA="gs://"
+$ export EVAL_DATA="gs://"
+# Overrides to access data. These can also be changed in the config file.
+$ export OVERRIDES="task.validation_data.input_path=${EVAL_DATA},\
+task.train_data.input_path=${TRAIN_DATA},\
+task.annotation_file=${ANNOTAION_FILE},\
+runtime.distribution_strategy=tpu"
+
+$ python3 -m official.projects.deepmac_maskrcnn.train \
+ --logtostderr \
+ --mode=train_and_eval \
+ --experiment=deep_mask_head_rcnn_resnetfpn_coco \
+ --model_dir=$MODEL_DIR \
+ --config_file=$CONFIG \
+ --params_override=$OVERRIDES\
+ --tpu=
+```
+
+`CONFIG_FILE` can be any file in the `configs/experiments` directory.
+When using SpineNet models, please specify
+`--experiment=deep_mask_head_rcnn_spinenet_coco`
+
+**Note:** The default eval batch size of 32 discards some samples during
+validation. For accurate vaidation statistics, launch a dedicated eval job on
+TPU `v3-8` and set batch size to 8.
+
+## Configurations
+
+In the following table, we report the Mask mAP of our models on the non-VOC
+classes when only training with masks for the VOC calsses. Performance is
+measured on the `coco-val2017` set.
+
+Backbone | Mask head | Config name | Mask mAP
+:------------| :----------- | :-----------------------------------------------| -------:
+ResNet-50 | Default | `deep_mask_head_rcnn_voc_r50.yaml` | 25.9
+ResNet-50 | Hourglass-52 | `deep_mask_head_rcnn_voc_r50_hg52.yaml` | 33.1
+ResNet-101 | Hourglass-52 | `deep_mask_head_rcnn_voc_r101_hg52.yaml` | 34.4
+SpienNet-143 | Hourglass-52 | `deep_mask_head_rcnn_voc_spinenet143_hg52.yaml` | 38.7
+
+## Checkpoints
+This model takes Image + boxes as input and produces per-box instance
+masks as output.
+
+* [Mask-RCNN SpineNet backbone](https://storage.googleapis.com/tf_model_garden/vision/deepmac_maskrcnn/deepmarc_spinenet.zip)
+
+## See also
+
+* [DeepMAC model](https://github.com/tensorflow/models/blob/master/research/object_detection/g3doc/deepmac.md)
+ in the Object Detection API code base.
+* Project website - [git.io/deepmac](https://google.github.io/deepmac/)
+
+## Citation
+
+```
+@misc{birodkar2021surprising,
+ title={The surprising impact of mask-head architecture on novel class segmentation},
+ author={Vighnesh Birodkar and Zhichao Lu and Siyang Li and Vivek Rathod and Jonathan Huang},
+ year={2021},
+ eprint={2104.00613},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+```
diff --git a/official/projects/deepmac_maskrcnn/__init__.py b/official/projects/deepmac_maskrcnn/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/common/__init__.py b/official/projects/deepmac_maskrcnn/common/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/common/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/common/registry_imports.py b/official/projects/deepmac_maskrcnn/common/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..018e01f61c158ba09ac461397ab1c4ec9cc0cebf
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/common/registry_imports.py
@@ -0,0 +1,18 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Imports to configure Mask R-CNN with deep mask heads."""
+
+# pylint: disable=unused-import
+from official.projects.deepmac_maskrcnn.tasks import deep_mask_head_rcnn
diff --git a/official/projects/deepmac_maskrcnn/configs/__init__.py b/official/projects/deepmac_maskrcnn/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/configs/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn.py b/official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn.py
new file mode 100644
index 0000000000000000000000000000000000000000..932e76dc883597658f0219b74410ef781b7703ae
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn.py
@@ -0,0 +1,196 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configuration for Mask R-CNN with deep mask heads."""
+
+import dataclasses
+import os
+from typing import Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+from official.vision.configs import backbones
+from official.vision.configs import common
+from official.vision.configs import decoders
+from official.vision.configs import maskrcnn as maskrcnn_config
+from official.vision.configs import retinanet as retinanet_config
+
+
+@dataclasses.dataclass
+class DeepMaskHead(maskrcnn_config.MaskHead):
+ convnet_variant: str = 'default'
+
+
+@dataclasses.dataclass
+class DeepMaskHeadRCNN(maskrcnn_config.MaskRCNN):
+ mask_head: Optional[DeepMaskHead] = DeepMaskHead()
+ use_gt_boxes_for_masks: bool = False
+
+
+@dataclasses.dataclass
+class DeepMaskHeadRCNNTask(maskrcnn_config.MaskRCNNTask):
+ """Configuration for the deep mask head R-CNN task."""
+ model: DeepMaskHeadRCNN = DeepMaskHeadRCNN()
+
+
+@exp_factory.register_config_factory('deep_mask_head_rcnn_resnetfpn_coco')
+def deep_mask_head_rcnn_resnetfpn_coco() -> cfg.ExperimentConfig:
+ """COCO object detection with Mask R-CNN with deep mask heads."""
+ global_batch_size = 64
+ steps_per_epoch = int(retinanet_config.COCO_TRAIN_EXAMPLES /
+ global_batch_size)
+ coco_val_samples = 5000
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(mixed_precision_dtype='bfloat16'),
+ task=DeepMaskHeadRCNNTask(
+ init_checkpoint='gs://cloud-tpu-checkpoints/vision-2.0/resnet50_imagenet/ckpt-28080',
+ init_checkpoint_modules='backbone',
+ annotation_file=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'instances_val2017.json'),
+ model=DeepMaskHeadRCNN(
+ num_classes=91, input_size=[1024, 1024, 3], include_mask=True), # pytype: disable=wrong-keyword-args
+ losses=maskrcnn_config.Losses(l2_weight_decay=0.00004),
+ train_data=maskrcnn_config.DataConfig(
+ input_path=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'train*'),
+ is_training=True,
+ global_batch_size=global_batch_size,
+ parser=maskrcnn_config.Parser(
+ aug_rand_hflip=True, aug_scale_min=0.8, aug_scale_max=1.25)),
+ validation_data=maskrcnn_config.DataConfig(
+ input_path=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'val*'),
+ is_training=False,
+ global_batch_size=8)), # pytype: disable=wrong-keyword-args
+ trainer=cfg.TrainerConfig(
+ train_steps=22500,
+ validation_steps=coco_val_samples // 8,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'sgd',
+ 'sgd': {
+ 'momentum': 0.9
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [15000, 20000],
+ 'values': [0.12, 0.012, 0.0012],
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 500,
+ 'warmup_learning_rate': 0.0067
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
+
+
+@exp_factory.register_config_factory('deep_mask_head_rcnn_spinenet_coco')
+def deep_mask_head_rcnn_spinenet_coco() -> cfg.ExperimentConfig:
+ """COCO object detection with Mask R-CNN with SpineNet backbone."""
+ steps_per_epoch = 463
+ coco_val_samples = 5000
+ train_batch_size = 256
+ eval_batch_size = 8
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(mixed_precision_dtype='bfloat16'),
+ task=DeepMaskHeadRCNNTask(
+ annotation_file=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'instances_val2017.json'), # pytype: disable=wrong-keyword-args
+ model=DeepMaskHeadRCNN(
+ backbone=backbones.Backbone(
+ type='spinenet',
+ spinenet=backbones.SpineNet(
+ model_id='49',
+ min_level=3,
+ max_level=7,
+ )),
+ decoder=decoders.Decoder(
+ type='identity', identity=decoders.Identity()),
+ anchor=maskrcnn_config.Anchor(anchor_size=3),
+ norm_activation=common.NormActivation(use_sync_bn=True),
+ num_classes=91,
+ input_size=[640, 640, 3],
+ min_level=3,
+ max_level=7,
+ include_mask=True), # pytype: disable=wrong-keyword-args
+ losses=maskrcnn_config.Losses(l2_weight_decay=0.00004),
+ train_data=maskrcnn_config.DataConfig(
+ input_path=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=maskrcnn_config.Parser(
+ aug_rand_hflip=True, aug_scale_min=0.5, aug_scale_max=2.0)),
+ validation_data=maskrcnn_config.DataConfig(
+ input_path=os.path.join(maskrcnn_config.COCO_INPUT_PATH_BASE,
+ 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ drop_remainder=False)), # pytype: disable=wrong-keyword-args
+ trainer=cfg.TrainerConfig(
+ train_steps=steps_per_epoch * 350,
+ validation_steps=coco_val_samples // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'sgd',
+ 'sgd': {
+ 'momentum': 0.9
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [
+ steps_per_epoch * 320, steps_per_epoch * 340
+ ],
+ 'values': [0.32, 0.032, 0.0032],
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 2000,
+ 'warmup_learning_rate': 0.0067
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None',
+ 'task.model.min_level == task.model.backbone.spinenet.min_level',
+ 'task.model.max_level == task.model.backbone.spinenet.max_level',
+ ])
+ return config
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py b/official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py
similarity index 87%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py
rename to official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py
index 77920be603b84146fc7e648187827918f41ea496..03a7d52747349eb80fcf45685387c89d768f1706 100644
--- a/official/vision/beta/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py
+++ b/official/projects/deepmac_maskrcnn/configs/deep_mask_head_rcnn_config_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,7 +16,7 @@
import tensorflow as tf
-from official.vision.beta.projects.deepmac_maskrcnn.configs import deep_mask_head_rcnn
+from official.projects.deepmac_maskrcnn.configs import deep_mask_head_rcnn
class DeepMaskHeadRcnnConfigTest(tf.test.TestCase):
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_nonvoc_spinenet143_hg52.yaml b/official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_nonvoc_spinenet143_hg52.yaml
similarity index 100%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_nonvoc_spinenet143_hg52.yaml
rename to official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_nonvoc_spinenet143_hg52.yaml
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r101_hg52.yaml b/official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r101_hg52.yaml
similarity index 100%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r101_hg52.yaml
rename to official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r101_hg52.yaml
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50.yaml b/official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50.yaml
similarity index 100%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50.yaml
rename to official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50.yaml
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50_hg52.yaml b/official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50_hg52.yaml
similarity index 100%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50_hg52.yaml
rename to official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_r50_hg52.yaml
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_spinenet143_hg52.yaml b/official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_spinenet143_hg52.yaml
similarity index 100%
rename from official/vision/beta/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_spinenet143_hg52.yaml
rename to official/projects/deepmac_maskrcnn/configs/experiments/deep_mask_head_rcnn_voc_spinenet143_hg52.yaml
diff --git a/official/projects/deepmac_maskrcnn/modeling/__init__.py b/official/projects/deepmac_maskrcnn/modeling/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/modeling/heads/__init__.py b/official/projects/deepmac_maskrcnn/modeling/heads/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/heads/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py b/official/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py
similarity index 99%
rename from official/vision/beta/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py
rename to official/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py
index 8b73140457940d9a45c8f545f0bd085bda0daa8c..b6f3cac996d2d794d0a1e025f44641aa01f01e5a 100644
--- a/official/vision/beta/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py
+++ b/official/projects/deepmac_maskrcnn/modeling/heads/hourglass_network.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads.py b/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads.py
new file mode 100644
index 0000000000000000000000000000000000000000..cec8bd3a49e10dd12e7346ecd7e23d8b759b1583
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads.py
@@ -0,0 +1,311 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Instance prediction heads."""
+
+# Import libraries
+
+from absl import logging
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.deepmac_maskrcnn.modeling.heads import hourglass_network
+
+
+class DeepMaskHead(tf.keras.layers.Layer):
+ """Creates a mask head."""
+
+ def __init__(self,
+ num_classes,
+ upsample_factor=2,
+ num_convs=4,
+ num_filters=256,
+ use_separable_conv=False,
+ activation='relu',
+ use_sync_bn=False,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ class_agnostic=False,
+ convnet_variant='default',
+ **kwargs):
+ """Initializes a mask head.
+
+ Args:
+ num_classes: An `int` of the number of classes.
+ upsample_factor: An `int` that indicates the upsample factor to generate
+ the final predicted masks. It should be >= 1.
+ num_convs: An `int` number that represents the number of the intermediate
+ convolution layers before the mask prediction layers.
+ num_filters: An `int` number that represents the number of filters of the
+ intermediate convolution layers.
+ use_separable_conv: A `bool` that indicates whether the separable
+ convolution layers is used.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ class_agnostic: A `bool`. If set, we use a single channel mask head that
+ is shared between all classes.
+ convnet_variant: A `str` denoting the architecture of network used in the
+ head. Supported options are 'default', 'hourglass20', 'hourglass52'
+ and 'hourglass100'.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(DeepMaskHead, self).__init__(**kwargs)
+ self._config_dict = {
+ 'num_classes': num_classes,
+ 'upsample_factor': upsample_factor,
+ 'num_convs': num_convs,
+ 'num_filters': num_filters,
+ 'use_separable_conv': use_separable_conv,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'norm_momentum': norm_momentum,
+ 'norm_epsilon': norm_epsilon,
+ 'kernel_regularizer': kernel_regularizer,
+ 'bias_regularizer': bias_regularizer,
+ 'class_agnostic': class_agnostic,
+ 'convnet_variant': convnet_variant,
+ }
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._activation = tf_utils.get_activation(activation)
+
+ def _get_conv_op_and_kwargs(self):
+ conv_op = (tf.keras.layers.SeparableConv2D
+ if self._config_dict['use_separable_conv']
+ else tf.keras.layers.Conv2D)
+ conv_kwargs = {
+ 'filters': self._config_dict['num_filters'],
+ 'kernel_size': 3,
+ 'padding': 'same',
+ }
+ if self._config_dict['use_separable_conv']:
+ conv_kwargs.update({
+ 'depthwise_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'pointwise_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'bias_initializer': tf.zeros_initializer(),
+ 'depthwise_regularizer': self._config_dict['kernel_regularizer'],
+ 'pointwise_regularizer': self._config_dict['kernel_regularizer'],
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ })
+ else:
+ conv_kwargs.update({
+ 'kernel_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'bias_initializer': tf.zeros_initializer(),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ })
+
+ return conv_op, conv_kwargs
+
+ def _get_bn_op_and_kwargs(self):
+
+ bn_op = (tf.keras.layers.experimental.SyncBatchNormalization
+ if self._config_dict['use_sync_bn']
+ else tf.keras.layers.BatchNormalization)
+ bn_kwargs = {
+ 'axis': self._bn_axis,
+ 'momentum': self._config_dict['norm_momentum'],
+ 'epsilon': self._config_dict['norm_epsilon'],
+ }
+
+ return bn_op, bn_kwargs
+
+ def build(self, input_shape):
+ """Creates the variables of the head."""
+
+ conv_op, conv_kwargs = self._get_conv_op_and_kwargs()
+
+ self._build_convnet_variant()
+
+ self._deconv = tf.keras.layers.Conv2DTranspose(
+ filters=self._config_dict['num_filters'],
+ kernel_size=self._config_dict['upsample_factor'],
+ strides=self._config_dict['upsample_factor'],
+ padding='valid',
+ kernel_initializer=tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ bias_initializer=tf.zeros_initializer(),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'],
+ name='mask-upsampling')
+
+ bn_op, bn_kwargs = self._get_bn_op_and_kwargs()
+ self._deconv_bn = bn_op(name='mask-deconv-bn', **bn_kwargs)
+
+ if self._config_dict['class_agnostic']:
+ num_filters = 1
+ else:
+ num_filters = self._config_dict['num_classes']
+
+ conv_kwargs = {
+ 'filters': num_filters,
+ 'kernel_size': 1,
+ 'padding': 'valid',
+ }
+ if self._config_dict['use_separable_conv']:
+ conv_kwargs.update({
+ 'depthwise_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'pointwise_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'bias_initializer': tf.zeros_initializer(),
+ 'depthwise_regularizer': self._config_dict['kernel_regularizer'],
+ 'pointwise_regularizer': self._config_dict['kernel_regularizer'],
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ })
+ else:
+ conv_kwargs.update({
+ 'kernel_initializer': tf.keras.initializers.VarianceScaling(
+ scale=2, mode='fan_out', distribution='untruncated_normal'),
+ 'bias_initializer': tf.zeros_initializer(),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ })
+ self._mask_regressor = conv_op(name='mask-logits', **conv_kwargs)
+
+ super(DeepMaskHead, self).build(input_shape)
+
+ def call(self, inputs, training=None):
+ """Forward pass of mask branch for the Mask-RCNN model.
+
+ Args:
+ inputs: A `list` of two tensors where
+ inputs[0]: A `tf.Tensor` of shape [batch_size, num_instances,
+ roi_height, roi_width, roi_channels], representing the ROI features.
+ inputs[1]: A `tf.Tensor` of shape [batch_size, num_instances],
+ representing the classes of the ROIs.
+ training: A `bool` indicating whether it is in `training` mode.
+
+ Returns:
+ mask_outputs: A `tf.Tensor` of shape
+ [batch_size, num_instances, roi_height * upsample_factor,
+ roi_width * upsample_factor], representing the mask predictions.
+ """
+ roi_features, roi_classes = inputs
+ features_shape = tf.shape(roi_features)
+ batch_size, num_rois, height, width, filters = (
+ features_shape[0], features_shape[1], features_shape[2],
+ features_shape[3], features_shape[4])
+ if batch_size is None:
+ batch_size = tf.shape(roi_features)[0]
+
+ x = tf.reshape(roi_features, [-1, height, width, filters])
+
+ x = self._call_convnet_variant(x)
+
+ x = self._deconv(x)
+ x = self._deconv_bn(x)
+ x = self._activation(x)
+
+ logits = self._mask_regressor(x)
+
+ mask_height = height * self._config_dict['upsample_factor']
+ mask_width = width * self._config_dict['upsample_factor']
+
+ if self._config_dict['class_agnostic']:
+ logits = tf.reshape(logits, [-1, num_rois, mask_height, mask_width, 1])
+ else:
+ logits = tf.reshape(
+ logits,
+ [-1, num_rois, mask_height, mask_width,
+ self._config_dict['num_classes']])
+
+ batch_indices = tf.tile(
+ tf.expand_dims(tf.range(batch_size), axis=1), [1, num_rois])
+ mask_indices = tf.tile(
+ tf.expand_dims(tf.range(num_rois), axis=0), [batch_size, 1])
+
+ if self._config_dict['class_agnostic']:
+ class_gather_indices = tf.zeros_like(roi_classes, dtype=tf.int32)
+ else:
+ class_gather_indices = tf.cast(roi_classes, dtype=tf.int32)
+
+ gather_indices = tf.stack(
+ [batch_indices, mask_indices, class_gather_indices],
+ axis=2)
+ mask_outputs = tf.gather_nd(
+ tf.transpose(logits, [0, 1, 4, 2, 3]), gather_indices)
+ return mask_outputs
+
+ def _build_convnet_variant(self):
+
+ variant = self._config_dict['convnet_variant']
+ if variant == 'default':
+ bn_op, bn_kwargs = self._get_bn_op_and_kwargs()
+ self._convs = []
+ self._conv_norms = []
+ for i in range(self._config_dict['num_convs']):
+ conv_name = 'mask-conv_{}'.format(i)
+ conv_op, conv_kwargs = self._get_conv_op_and_kwargs()
+ self._convs.append(conv_op(name=conv_name, **conv_kwargs))
+ bn_name = 'mask-conv-bn_{}'.format(i)
+ self._conv_norms.append(bn_op(name=bn_name, **bn_kwargs))
+
+ elif variant == 'hourglass20':
+ logging.info('Using hourglass 20 network.')
+ self._hourglass = hourglass_network.hourglass_20(
+ self._config_dict['num_filters'], initial_downsample=False)
+
+ elif variant == 'hourglass52':
+ logging.info('Using hourglass 52 network.')
+ self._hourglass = hourglass_network.hourglass_52(
+ self._config_dict['num_filters'], initial_downsample=False)
+
+ elif variant == 'hourglass100':
+ logging.info('Using hourglass 100 network.')
+ self._hourglass = hourglass_network.hourglass_100(
+ self._config_dict['num_filters'], initial_downsample=False)
+
+ else:
+ raise ValueError('Unknown ConvNet variant - {}'.format(variant))
+
+ def _call_convnet_variant(self, x):
+
+ variant = self._config_dict['convnet_variant']
+ if variant == 'default':
+ for conv, bn in zip(self._convs, self._conv_norms):
+ x = conv(x)
+ x = bn(x)
+ x = self._activation(x)
+ return x
+ elif variant == 'hourglass20':
+ return self._hourglass(x)[-1]
+ elif variant == 'hourglass52':
+ return self._hourglass(x)[-1]
+ elif variant == 'hourglass100':
+ return self._hourglass(x)[-1]
+ else:
+ raise ValueError('Unknown ConvNet variant - {}'.format(variant))
+
+ def get_config(self):
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
diff --git a/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads_test.py b/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..20cdc0fcab66ffc23bf465c435454e1b30540247
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/heads/instance_heads_test.py
@@ -0,0 +1,98 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for instance_heads.py."""
+
+# Import libraries
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from official.projects.deepmac_maskrcnn.modeling.heads import instance_heads as deep_instance_heads
+
+
+class MaskHeadTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (1, 1, False),
+ (1, 2, False),
+ (2, 1, False),
+ (2, 2, False),
+ )
+ def test_forward(self, upsample_factor, num_convs, use_sync_bn):
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=3,
+ upsample_factor=upsample_factor,
+ num_convs=num_convs,
+ num_filters=16,
+ use_separable_conv=False,
+ activation='relu',
+ use_sync_bn=use_sync_bn,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ )
+ roi_features = np.random.rand(2, 10, 14, 14, 16)
+ roi_classes = np.zeros((2, 10))
+ masks = mask_head([roi_features, roi_classes])
+ self.assertAllEqual(
+ masks.numpy().shape,
+ [2, 10, 14 * upsample_factor, 14 * upsample_factor])
+
+ def test_serialize_deserialize(self):
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=3,
+ upsample_factor=2,
+ num_convs=1,
+ num_filters=256,
+ use_separable_conv=False,
+ activation='relu',
+ use_sync_bn=False,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ )
+ config = mask_head.get_config()
+ new_mask_head = deep_instance_heads.DeepMaskHead.from_config(config)
+ self.assertAllEqual(
+ mask_head.get_config(), new_mask_head.get_config())
+
+ def test_forward_class_agnostic(self):
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=3,
+ class_agnostic=True
+ )
+ roi_features = np.random.rand(2, 10, 14, 14, 16)
+ roi_classes = np.zeros((2, 10))
+ masks = mask_head([roi_features, roi_classes])
+ self.assertAllEqual(masks.numpy().shape, [2, 10, 28, 28])
+
+ def test_instance_head_hourglass(self):
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=3,
+ class_agnostic=True,
+ convnet_variant='hourglass20',
+ num_filters=32,
+ upsample_factor=2
+ )
+ roi_features = np.random.rand(2, 10, 16, 16, 16)
+ roi_classes = np.zeros((2, 10))
+ masks = mask_head([roi_features, roi_classes])
+ self.assertAllEqual(masks.numpy().shape, [2, 10, 32, 32])
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model.py b/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..488485e2881c28c56d1d755a28929bc36bfef5ed
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model.py
@@ -0,0 +1,221 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Mask R-CNN model."""
+
+from typing import List, Mapping, Optional, Union
+
+# Import libraries
+
+from absl import logging
+import tensorflow as tf
+
+from official.vision.modeling import maskrcnn_model
+
+
+def resize_as(source, size):
+
+ source = tf.transpose(source, (0, 2, 3, 1))
+ source = tf.image.resize(source, (size, size))
+ return tf.transpose(source, (0, 3, 1, 2))
+
+
+class DeepMaskRCNNModel(maskrcnn_model.MaskRCNNModel):
+ """The Mask R-CNN model."""
+
+ def __init__(self,
+ backbone: tf.keras.Model,
+ decoder: tf.keras.Model,
+ rpn_head: tf.keras.layers.Layer,
+ detection_head: Union[tf.keras.layers.Layer,
+ List[tf.keras.layers.Layer]],
+ roi_generator: tf.keras.layers.Layer,
+ roi_sampler: Union[tf.keras.layers.Layer,
+ List[tf.keras.layers.Layer]],
+ roi_aligner: tf.keras.layers.Layer,
+ detection_generator: tf.keras.layers.Layer,
+ mask_head: Optional[tf.keras.layers.Layer] = None,
+ mask_sampler: Optional[tf.keras.layers.Layer] = None,
+ mask_roi_aligner: Optional[tf.keras.layers.Layer] = None,
+ class_agnostic_bbox_pred: bool = False,
+ cascade_class_ensemble: bool = False,
+ min_level: Optional[int] = None,
+ max_level: Optional[int] = None,
+ num_scales: Optional[int] = None,
+ aspect_ratios: Optional[List[float]] = None,
+ anchor_size: Optional[float] = None,
+ use_gt_boxes_for_masks=False,
+ **kwargs):
+ """Initializes the Mask R-CNN model.
+
+ Args:
+ backbone: `tf.keras.Model`, the backbone network.
+ decoder: `tf.keras.Model`, the decoder network.
+ rpn_head: the RPN head.
+ detection_head: the detection head or a list of heads.
+ roi_generator: the ROI generator.
+ roi_sampler: a single ROI sampler or a list of ROI samplers for cascade
+ detection heads.
+ roi_aligner: the ROI aligner.
+ detection_generator: the detection generator.
+ mask_head: the mask head.
+ mask_sampler: the mask sampler.
+ mask_roi_aligner: the ROI alginer for mask prediction.
+ class_agnostic_bbox_pred: if True, perform class agnostic bounding box
+ prediction. Needs to be `True` for Cascade RCNN models.
+ cascade_class_ensemble: if True, ensemble classification scores over all
+ detection heads.
+ min_level: Minimum level in output feature maps.
+ max_level: Maximum level in output feature maps.
+ num_scales: A number representing intermediate scales added on each level.
+ For instances, num_scales=2 adds one additional intermediate anchor
+ scales [2^0, 2^0.5] on each level.
+ aspect_ratios: A list representing the aspect raito anchors added on each
+ level. The number indicates the ratio of width to height. For instances,
+ aspect_ratios=[1.0, 2.0, 0.5] adds three anchors on each scale level.
+ anchor_size: A number representing the scale of size of the base anchor to
+ the feature stride 2^level.
+ use_gt_boxes_for_masks: bool, if set, crop using groundtruth boxes instead
+ of proposals for training mask head
+ **kwargs: keyword arguments to be passed.
+ """
+ super(DeepMaskRCNNModel, self).__init__(
+ backbone=backbone,
+ decoder=decoder,
+ rpn_head=rpn_head,
+ detection_head=detection_head,
+ roi_generator=roi_generator,
+ roi_sampler=roi_sampler,
+ roi_aligner=roi_aligner,
+ detection_generator=detection_generator,
+ mask_head=mask_head,
+ mask_sampler=mask_sampler,
+ mask_roi_aligner=mask_roi_aligner,
+ class_agnostic_bbox_pred=class_agnostic_bbox_pred,
+ cascade_class_ensemble=cascade_class_ensemble,
+ min_level=min_level,
+ max_level=max_level,
+ num_scales=num_scales,
+ aspect_ratios=aspect_ratios,
+ anchor_size=anchor_size,
+ **kwargs)
+
+ self._config_dict['use_gt_boxes_for_masks'] = use_gt_boxes_for_masks
+
+ def call(self,
+ images: tf.Tensor,
+ image_shape: tf.Tensor,
+ anchor_boxes: Optional[Mapping[str, tf.Tensor]] = None,
+ gt_boxes: Optional[tf.Tensor] = None,
+ gt_classes: Optional[tf.Tensor] = None,
+ gt_masks: Optional[tf.Tensor] = None,
+ training: Optional[bool] = None) -> Mapping[str, tf.Tensor]:
+
+ model_outputs, intermediate_outputs = self._call_box_outputs(
+ images=images, image_shape=image_shape, anchor_boxes=anchor_boxes,
+ gt_boxes=gt_boxes, gt_classes=gt_classes, training=training)
+ if not self._include_mask:
+ return model_outputs
+
+ model_mask_outputs = self._call_mask_outputs(
+ model_box_outputs=model_outputs,
+ features=model_outputs['decoder_features'],
+ current_rois=intermediate_outputs['current_rois'],
+ matched_gt_indices=intermediate_outputs['matched_gt_indices'],
+ matched_gt_boxes=intermediate_outputs['matched_gt_boxes'],
+ matched_gt_classes=intermediate_outputs['matched_gt_classes'],
+ gt_masks=gt_masks,
+ gt_classes=gt_classes,
+ gt_boxes=gt_boxes,
+ training=training)
+ model_outputs.update(model_mask_outputs)
+ return model_outputs
+
+ def call_images_and_boxes(self, images, boxes):
+ """Predict masks given an image and bounding boxes."""
+
+ _, decoder_features = self._get_backbone_and_decoder_features(images)
+ boxes_shape = tf.shape(boxes)
+ batch_size, num_boxes = boxes_shape[0], boxes_shape[1]
+ classes = tf.zeros((batch_size, num_boxes), dtype=tf.int32)
+
+ _, mask_probs = self._features_to_mask_outputs(
+ decoder_features, boxes, classes)
+ return {
+ 'detection_masks': mask_probs
+ }
+
+ def _call_mask_outputs(
+ self,
+ model_box_outputs: Mapping[str, tf.Tensor],
+ features: tf.Tensor,
+ current_rois: tf.Tensor,
+ matched_gt_indices: tf.Tensor,
+ matched_gt_boxes: tf.Tensor,
+ matched_gt_classes: tf.Tensor,
+ gt_masks: tf.Tensor,
+ gt_classes: tf.Tensor,
+ gt_boxes: tf.Tensor,
+ training: Optional[bool] = None) -> Mapping[str, tf.Tensor]:
+
+ model_outputs = dict(model_box_outputs)
+ if training:
+ if self._config_dict['use_gt_boxes_for_masks']:
+ mask_size = (
+ self.mask_roi_aligner._config_dict['crop_size'] * # pylint:disable=protected-access
+ self.mask_head._config_dict['upsample_factor'] # pylint:disable=protected-access
+ )
+ gt_masks = resize_as(source=gt_masks, size=mask_size)
+
+ logging.info('Using GT class and mask targets.')
+ model_outputs.update({
+ 'mask_class_targets': gt_classes,
+ 'mask_targets': gt_masks,
+ })
+ else:
+ rois, roi_classes, roi_masks = self.mask_sampler(
+ current_rois, matched_gt_boxes, matched_gt_classes,
+ matched_gt_indices, gt_masks)
+ roi_masks = tf.stop_gradient(roi_masks)
+ model_outputs.update({
+ 'mask_class_targets': roi_classes,
+ 'mask_targets': roi_masks,
+ })
+
+ else:
+ rois = model_outputs['detection_boxes']
+ roi_classes = model_outputs['detection_classes']
+
+ # Mask RoI align.
+ if training and self._config_dict['use_gt_boxes_for_masks']:
+ logging.info('Using GT mask roi features.')
+ roi_aligner_boxes = gt_boxes
+ mask_head_classes = gt_classes
+
+ else:
+ roi_aligner_boxes = rois
+ mask_head_classes = roi_classes
+
+ mask_logits, mask_probs = self._features_to_mask_outputs(
+ features, roi_aligner_boxes, mask_head_classes)
+
+ if training:
+ model_outputs.update({
+ 'mask_outputs': mask_logits,
+ })
+ else:
+ model_outputs.update({
+ 'detection_masks': mask_probs,
+ })
+ return model_outputs
diff --git a/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model_test.py b/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..08e9ab5376f36ac5c753504dfcee67438ab7299e
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/modeling/maskrcnn_model_test.py
@@ -0,0 +1,153 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for maskrcnn_model.py."""
+
+# Import libraries
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from official.projects.deepmac_maskrcnn.modeling import maskrcnn_model
+from official.projects.deepmac_maskrcnn.modeling.heads import instance_heads as deep_instance_heads
+from official.vision.modeling.backbones import resnet
+from official.vision.modeling.decoders import fpn
+from official.vision.modeling.heads import dense_prediction_heads
+from official.vision.modeling.heads import instance_heads
+from official.vision.modeling.layers import detection_generator
+from official.vision.modeling.layers import mask_sampler
+from official.vision.modeling.layers import roi_aligner
+from official.vision.modeling.layers import roi_generator
+from official.vision.modeling.layers import roi_sampler
+from official.vision.ops import anchor
+
+
+def construct_model_and_anchors(image_size, use_gt_boxes_for_masks):
+ num_classes = 3
+ min_level = 3
+ max_level = 4
+ num_scales = 3
+ aspect_ratios = [1.0]
+
+ anchor_boxes = anchor.Anchor(
+ min_level=min_level,
+ max_level=max_level,
+ num_scales=num_scales,
+ aspect_ratios=aspect_ratios,
+ anchor_size=3,
+ image_size=image_size).multilevel_boxes
+ num_anchors_per_location = len(aspect_ratios) * num_scales
+
+ input_specs = tf.keras.layers.InputSpec(shape=[None, None, None, 3])
+ backbone = resnet.ResNet(model_id=50, input_specs=input_specs)
+ decoder = fpn.FPN(
+ min_level=min_level,
+ max_level=max_level,
+ input_specs=backbone.output_specs)
+ rpn_head = dense_prediction_heads.RPNHead(
+ min_level=min_level,
+ max_level=max_level,
+ num_anchors_per_location=num_anchors_per_location)
+ detection_head = instance_heads.DetectionHead(
+ num_classes=num_classes)
+ roi_generator_obj = roi_generator.MultilevelROIGenerator()
+ roi_sampler_obj = roi_sampler.ROISampler()
+ roi_aligner_obj = roi_aligner.MultilevelROIAligner()
+ detection_generator_obj = detection_generator.DetectionGenerator()
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=num_classes, upsample_factor=2)
+ mask_sampler_obj = mask_sampler.MaskSampler(
+ mask_target_size=28, num_sampled_masks=1)
+ mask_roi_aligner_obj = roi_aligner.MultilevelROIAligner(crop_size=14)
+
+ model = maskrcnn_model.DeepMaskRCNNModel(
+ backbone,
+ decoder,
+ rpn_head,
+ detection_head,
+ roi_generator_obj,
+ roi_sampler_obj,
+ roi_aligner_obj,
+ detection_generator_obj,
+ mask_head,
+ mask_sampler_obj,
+ mask_roi_aligner_obj,
+ use_gt_boxes_for_masks=use_gt_boxes_for_masks)
+
+ return model, anchor_boxes
+
+
+class MaskRCNNModelTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (False, False,),
+ (False, True,),
+ (True, False,),
+ (True, True,),
+ )
+ def test_forward(self, use_gt_boxes_for_masks, training):
+ image_size = (256, 256)
+ images = np.random.rand(2, image_size[0], image_size[1], 3)
+ image_shape = np.array([[224, 100], [100, 224]])
+ model, anchor_boxes = construct_model_and_anchors(
+ image_size, use_gt_boxes_for_masks)
+
+ gt_boxes = tf.zeros((2, 16, 4), dtype=tf.float32)
+ gt_masks = tf.zeros((2, 16, 32, 32))
+ gt_classes = tf.zeros((2, 16), dtype=tf.int32)
+ results = model(images.astype(np.uint8),
+ image_shape,
+ anchor_boxes,
+ gt_boxes,
+ gt_classes,
+ gt_masks,
+ training=training)
+
+ self.assertIn('rpn_boxes', results)
+ self.assertIn('rpn_scores', results)
+ if training:
+ self.assertIn('class_targets', results)
+ self.assertIn('box_targets', results)
+ self.assertIn('class_outputs', results)
+ self.assertIn('box_outputs', results)
+ self.assertIn('mask_outputs', results)
+ self.assertEqual(results['mask_targets'].shape,
+ results['mask_outputs'].shape)
+ else:
+ self.assertIn('detection_boxes', results)
+ self.assertIn('detection_scores', results)
+ self.assertIn('detection_classes', results)
+ self.assertIn('num_detections', results)
+ self.assertIn('detection_masks', results)
+
+ @parameterized.parameters(
+ [(1, 5), (1, 10), (1, 15), (2, 5), (2, 10), (2, 15)]
+ )
+ def test_image_and_boxes(self, batch_size, num_boxes):
+ image_size = (640, 640)
+ images = np.random.rand(1, image_size[0], image_size[1], 3).astype(
+ np.float32)
+ model, _ = construct_model_and_anchors(
+ image_size, use_gt_boxes_for_masks=True)
+
+ boxes = np.zeros((1, num_boxes, 4), dtype=np.float32)
+ boxes[:, :, [2, 3]] = 1.0
+ boxes = tf.constant(boxes)
+ results = model.call_images_and_boxes(images, boxes)
+ self.assertIn('detection_masks', results)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/deepmac_maskrcnn/serving/__init__.py b/official/projects/deepmac_maskrcnn/serving/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/serving/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/serving/detection.py b/official/projects/deepmac_maskrcnn/serving/detection.py
new file mode 100644
index 0000000000000000000000000000000000000000..9e3bbfd28892173a015818c0906b7ce3e130a449
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/serving/detection.py
@@ -0,0 +1,139 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Detection input and model functions for serving/inference."""
+
+from typing import Dict, Mapping, Text
+
+import tensorflow as tf
+
+from official.projects.deepmac_maskrcnn.configs import deep_mask_head_rcnn as cfg
+from official.projects.deepmac_maskrcnn.modeling import maskrcnn_model
+from official.projects.deepmac_maskrcnn.tasks import deep_mask_head_rcnn
+from official.vision.ops import box_ops
+from official.vision.serving import detection
+
+
+def reverse_input_box_transformation(boxes, image_info):
+ """Reverse the Mask R-CNN model's input boxes tranformation.
+
+ Args:
+ boxes: A [batch_size, num_boxes, 4] float tensor of boxes in normalized
+ coordinates.
+ image_info: a 2D `Tensor` that encodes the information of the image and the
+ applied preprocessing. It is in the format of
+ [[original_height, original_width], [desired_height, desired_width],
+ [y_scale, x_scale], [y_offset, x_offset]], where [desired_height,
+ desired_width] is the actual scaled image size, and [y_scale, x_scale] is
+ the scaling factor, which is the ratio of
+ scaled dimension / original dimension.
+
+ Returns:
+ boxes: Same shape as input `boxes` but in the absolute coordinate space of
+ the preprocessed image.
+ """
+ # Reversing sequence from Detection_module.serve when
+ # output_normalized_coordinates=true
+ scale = image_info[:, 2:3, :]
+ scale = tf.tile(scale, [1, 1, 2])
+ boxes = boxes * scale
+ height_width = image_info[:, 0:1, :]
+ return box_ops.denormalize_boxes(boxes, height_width)
+
+
+class DetectionModule(detection.DetectionModule):
+ """Detection Module."""
+
+ def _build_model(self):
+
+ if self._batch_size is None:
+ ValueError("batch_size can't be None for detection models")
+ if self.params.task.model.detection_generator.nms_version != 'batched':
+ ValueError('Only batched_nms is supported.')
+ input_specs = tf.keras.layers.InputSpec(shape=[self._batch_size] +
+ self._input_image_size + [3])
+
+ if isinstance(self.params.task.model, cfg.DeepMaskHeadRCNN):
+ model = deep_mask_head_rcnn.build_maskrcnn(
+ input_specs=input_specs, model_config=self.params.task.model)
+ else:
+ raise ValueError('Detection module not implemented for {} model.'.format(
+ type(self.params.task.model)))
+
+ return model
+
+ @tf.function
+ def inference_for_tflite_image_and_boxes(
+ self, images: tf.Tensor, boxes: tf.Tensor) -> Mapping[str, tf.Tensor]:
+ """A tf-function for serve_image_and_boxes.
+
+ Args:
+ images: A [batch_size, height, width, channels] float tensor.
+ boxes: A [batch_size, num_boxes, 4] float tensor containing boxes
+ normalized to the input image.
+
+ Returns:
+ result: A dict containing:
+ 'detection_masks': A [batch_size, num_boxes, mask_height, mask_width]
+ float tensor containing per-pixel mask probabilities.
+ """
+
+ if not isinstance(self.model, maskrcnn_model.DeepMaskRCNNModel):
+ raise ValueError(
+ ('Can only use image and boxes input for DeepMaskRCNNModel, '
+ 'Found {}'.format(type(self.model))))
+
+ return self.serve_image_and_boxes(images, boxes)
+
+ def serve_image_and_boxes(self, images: tf.Tensor, boxes: tf.Tensor):
+ """Function used to export a model that consumes and image and boxes.
+
+ The model predicts the class-agnostic masks at the given box locations.
+
+ Args:
+ images: A [batch_size, height, width, channels] float tensor.
+ boxes: A [batch_size, num_boxes, 4] float tensor containing boxes
+ normalized to the input image.
+
+ Returns:
+ result: A dict containing:
+ 'detection_masks': A [batch_size, num_boxes, mask_height, mask_width]
+ float tensor containing per-pixel mask probabilities.
+ """
+ images, _, image_info = self.preprocess(images)
+ boxes = reverse_input_box_transformation(boxes, image_info)
+ result = self.model.call_images_and_boxes(images, boxes)
+ return result
+
+ def get_inference_signatures(self, function_keys: Dict[Text, Text]):
+ signatures = {}
+
+ if 'image_and_boxes_tensor' in function_keys:
+ def_name = function_keys['image_and_boxes_tensor']
+ image_signature = tf.TensorSpec(
+ shape=[self._batch_size] + [None] * len(self._input_image_size) +
+ [self._num_channels],
+ dtype=tf.uint8)
+ boxes_signature = tf.TensorSpec(shape=[self._batch_size, None, 4],
+ dtype=tf.float32)
+ tf_function = self.inference_for_tflite_image_and_boxes
+ signatures[def_name] = tf_function.get_concrete_function(
+ image_signature, boxes_signature)
+
+ function_keys.pop('image_and_boxes_tensor', None)
+ parent_signatures = super(DetectionModule, self).get_inference_signatures(
+ function_keys)
+ signatures.update(parent_signatures)
+
+ return signatures
diff --git a/official/projects/deepmac_maskrcnn/serving/detection_test.py b/official/projects/deepmac_maskrcnn/serving/detection_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..cd832e2821fcc126e9986faf53733069c146c2f1
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/serving/detection_test.py
@@ -0,0 +1,164 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Test for image detection export lib."""
+
+import io
+import os
+
+from absl.testing import parameterized
+import numpy as np
+from PIL import Image
+import tensorflow as tf
+
+from official.core import exp_factory
+from official.projects.deepmac_maskrcnn.serving import detection
+
+
+class DetectionExportTest(tf.test.TestCase, parameterized.TestCase):
+
+ def _get_detection_module(self, experiment_name, image_size=(640, 640)):
+ params = exp_factory.get_exp_config(experiment_name)
+ params.task.model.backbone.resnet.model_id = 18
+ params.task.model.detection_generator.use_batched_nms = True
+ detection_module = detection.DetectionModule(
+ params, batch_size=1, input_image_size=list(image_size))
+ return detection_module
+
+ def _export_from_module(self, module, input_type, save_directory):
+ signatures = module.get_inference_signatures(
+ {input_type: 'serving_default'})
+ tf.saved_model.save(module, save_directory, signatures=signatures)
+
+ def _get_dummy_input(self, input_type, batch_size, image_size):
+ """Get dummy input for the given input type."""
+ h, w = image_size
+
+ if input_type == 'image_tensor':
+ return tf.zeros((batch_size, h, w, 3), dtype=np.uint8)
+ elif input_type == 'image_bytes':
+ image = Image.fromarray(np.zeros((h, w, 3), dtype=np.uint8))
+ byte_io = io.BytesIO()
+ image.save(byte_io, 'PNG')
+ return [byte_io.getvalue() for b in range(batch_size)]
+ elif input_type == 'tf_example':
+ image_tensor = tf.zeros((h, w, 3), dtype=tf.uint8)
+ encoded_jpeg = tf.image.encode_jpeg(tf.constant(image_tensor)).numpy()
+ example = tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ 'image/encoded':
+ tf.train.Feature(
+ bytes_list=tf.train.BytesList(value=[encoded_jpeg])),
+ })).SerializeToString()
+ return [example for b in range(batch_size)]
+
+ @parameterized.parameters(
+ ('image_tensor', 'deep_mask_head_rcnn_resnetfpn_coco', [640, 640]),
+ ('image_bytes', 'deep_mask_head_rcnn_resnetfpn_coco', [640, 384]),
+ ('tf_example', 'deep_mask_head_rcnn_resnetfpn_coco', [640, 640]),
+ )
+ def test_export(self, input_type, experiment_name, image_size):
+ self.skipTest('a')
+ tmp_dir = self.get_temp_dir()
+ module = self._get_detection_module(experiment_name, image_size)
+
+ self._export_from_module(module, input_type, tmp_dir)
+
+ self.assertTrue(os.path.exists(os.path.join(tmp_dir, 'saved_model.pb')))
+ self.assertTrue(
+ os.path.exists(os.path.join(tmp_dir, 'variables', 'variables.index')))
+ self.assertTrue(
+ os.path.exists(
+ os.path.join(tmp_dir, 'variables',
+ 'variables.data-00000-of-00001')))
+
+ imported = tf.saved_model.load(tmp_dir)
+ detection_fn = imported.signatures['serving_default']
+
+ images = self._get_dummy_input(
+ input_type, batch_size=1, image_size=image_size)
+
+ processed_images, anchor_boxes, image_info = module._build_inputs(
+ tf.zeros((224, 224, 3), dtype=tf.uint8))
+ image_shape = image_info[1, :]
+ image_shape = tf.expand_dims(image_shape, 0)
+ processed_images = tf.expand_dims(processed_images, 0)
+ for l, l_boxes in anchor_boxes.items():
+ anchor_boxes[l] = tf.expand_dims(l_boxes, 0)
+
+ expected_outputs = module.model(
+ images=processed_images,
+ image_shape=image_shape,
+ anchor_boxes=anchor_boxes,
+ training=False)
+ outputs = detection_fn(tf.constant(images))
+
+ self.assertAllClose(outputs['num_detections'].numpy(),
+ expected_outputs['num_detections'].numpy())
+
+ @parameterized.parameters(
+ ('deep_mask_head_rcnn_resnetfpn_coco', [640, 640], 1),
+ ('deep_mask_head_rcnn_resnetfpn_coco', [640, 640], 5),
+ ('deep_mask_head_rcnn_spinenet_coco', [640, 384], 3),
+ ('deep_mask_head_rcnn_spinenet_coco', [640, 384], 9),
+ )
+ def test_export_image_and_boxes(self, experiment_name, image_size, num_boxes):
+ tmp_dir = self.get_temp_dir()
+ module = self._get_detection_module(experiment_name)
+
+ self._export_from_module(module, 'image_and_boxes_tensor', tmp_dir)
+
+ self.assertTrue(os.path.exists(os.path.join(tmp_dir, 'saved_model.pb')))
+ self.assertTrue(
+ os.path.exists(os.path.join(tmp_dir, 'variables', 'variables.index')))
+ self.assertTrue(
+ os.path.exists(
+ os.path.join(tmp_dir, 'variables',
+ 'variables.data-00000-of-00001')))
+
+ imported = tf.saved_model.load(tmp_dir)
+ detection_fn = imported.signatures['serving_default']
+
+ images = self._get_dummy_input(
+ 'image_tensor', batch_size=1, image_size=image_size)
+
+ processed_images, anchor_boxes, image_info = module._build_inputs(
+ tf.zeros(image_size + [3], dtype=tf.uint8))
+
+ image_shape = image_info[1, :]
+ image_shape = image_shape[tf.newaxis]
+ processed_images = processed_images[tf.newaxis]
+ image_info = image_info[tf.newaxis]
+
+ for l, l_boxes in anchor_boxes.items():
+ anchor_boxes[l] = tf.expand_dims(l_boxes, 0)
+
+ boxes = np.zeros((1, num_boxes, 4), dtype=np.float32)
+ boxes[:, :, [2, 3]] = 1.0
+ boxes = tf.constant(boxes)
+
+ denormalized_boxes = detection.reverse_input_box_transformation(
+ boxes, image_info)
+ expected_outputs = module.model.call_images_and_boxes(
+ images=processed_images, boxes=denormalized_boxes)
+ outputs = detection_fn(images=tf.constant(images), boxes=boxes)
+
+ self.assertAllClose(outputs['detection_masks'].numpy(),
+ expected_outputs['detection_masks'].numpy(),
+ rtol=1e-3, atol=1e-3)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/deepmac_maskrcnn/serving/export_saved_model.py b/official/projects/deepmac_maskrcnn/serving/export_saved_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..b88aa70eb8a59a51a29390a6199b214bef924acb
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/serving/export_saved_model.py
@@ -0,0 +1,106 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Deepmac model export binary for serving/inference.
+
+To export a trained checkpoint in saved_model format (shell script):
+
+CHECKPOINT_PATH = XX
+EXPORT_DIR_PATH = XX
+CONFIG_FILE_PATH = XX
+export_saved_model --export_dir=${EXPORT_DIR_PATH}/ \
+ --checkpoint_path=${CHECKPOINT_PATH} \
+ --config_file=${CONFIG_FILE_PATH} \
+ --batch_size=2 \
+ --input_image_size=224,224
+To serve (python):
+export_dir_path = XX
+input_type = XX
+input_images = XX
+imported = tf.saved_model.load(export_dir_path)
+model_fn = imported.signatures['serving_default']
+output = model_fn(input_images)
+"""
+
+from absl import app
+from absl import flags
+
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.projects.deepmac_maskrcnn.serving import detection
+from official.projects.deepmac_maskrcnn.tasks import deep_mask_head_rcnn # pylint: disable=unused-import
+from official.vision.serving import export_saved_model_lib
+
+FLAGS = flags.FLAGS
+
+flags.DEFINE_string('experiment', 'deep_mask_head_rcnn_resnetfpn_coco',
+ 'experiment type, e.g. retinanet_resnetfpn_coco')
+flags.DEFINE_string('export_dir', None, 'The export directory.')
+flags.DEFINE_string('checkpoint_path', None, 'Checkpoint path.')
+flags.DEFINE_multi_string(
+ 'config_file',
+ default=None,
+ help='YAML/JSON files which specifies overrides. The override order '
+ 'follows the order of args. Note that each file '
+ 'can be used as an override template to override the default parameters '
+ 'specified in Python. If the same parameter is specified in both '
+ '`--config_file` and `--params_override`, `config_file` will be used '
+ 'first, followed by params_override.')
+flags.DEFINE_string(
+ 'params_override', '',
+ 'The JSON/YAML file or string which specifies the parameter to be overriden'
+ ' on top of `config_file` template.')
+flags.DEFINE_integer('batch_size', None, 'The batch size.')
+flags.DEFINE_string('input_type', 'image_tensor',
+ ('One of `image_tensor`, `image_bytes`, `tf_example` '
+ 'or `image_and_boxes_tensor`.'))
+flags.DEFINE_string(
+ 'input_image_size', '224,224',
+ 'The comma-separated string of two integers representing the height,width '
+ 'of the input to the model.')
+
+
+def main(_):
+
+ params = exp_factory.get_exp_config(FLAGS.experiment)
+ for config_file in FLAGS.config_file or []:
+ params = hyperparams.override_params_dict(
+ params, config_file, is_strict=True)
+ if FLAGS.params_override:
+ params = hyperparams.override_params_dict(
+ params, FLAGS.params_override, is_strict=True)
+
+ params.validate()
+ params.lock()
+
+ export_module = detection.DetectionModule(
+ params=params,
+ batch_size=FLAGS.batch_size,
+ input_image_size=[int(x) for x in FLAGS.input_image_size.split(',')],
+ num_channels=3)
+
+ export_saved_model_lib.export_inference_graph(
+ input_type=FLAGS.input_type,
+ batch_size=FLAGS.batch_size,
+ input_image_size=[int(x) for x in FLAGS.input_image_size.split(',')],
+ params=params,
+ checkpoint_path=FLAGS.checkpoint_path,
+ export_dir=FLAGS.export_dir,
+ export_module=export_module,
+ export_checkpoint_subdir='checkpoint',
+ export_saved_model_subdir='saved_model')
+
+
+if __name__ == '__main__':
+ app.run(main)
diff --git a/official/projects/deepmac_maskrcnn/tasks/__init__.py b/official/projects/deepmac_maskrcnn/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/tasks/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/deepmac_maskrcnn/tasks/deep_mask_head_rcnn.py b/official/projects/deepmac_maskrcnn/tasks/deep_mask_head_rcnn.py
new file mode 100644
index 0000000000000000000000000000000000000000..f15df962a025f87eac015b267a6bb7483dd7be18
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/tasks/deep_mask_head_rcnn.py
@@ -0,0 +1,194 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Mask R-CNN variant with support for deep mask heads."""
+
+import tensorflow as tf
+
+from official.core import task_factory
+from official.projects.deepmac_maskrcnn.configs import deep_mask_head_rcnn as deep_mask_head_rcnn_config
+from official.projects.deepmac_maskrcnn.modeling import maskrcnn_model as deep_maskrcnn_model
+from official.projects.deepmac_maskrcnn.modeling.heads import instance_heads as deep_instance_heads
+from official.vision.modeling import backbones
+from official.vision.modeling.decoders import factory as decoder_factory
+from official.vision.modeling.heads import dense_prediction_heads
+from official.vision.modeling.heads import instance_heads
+from official.vision.modeling.layers import detection_generator
+from official.vision.modeling.layers import mask_sampler
+from official.vision.modeling.layers import roi_aligner
+from official.vision.modeling.layers import roi_generator
+from official.vision.modeling.layers import roi_sampler
+from official.vision.tasks import maskrcnn
+
+
+# Taken from modeling/factory.py
+def build_maskrcnn(input_specs: tf.keras.layers.InputSpec,
+ model_config: deep_mask_head_rcnn_config.DeepMaskHeadRCNN,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None): # pytype: disable=annotation-type-mismatch # typed-keras
+ """Builds Mask R-CNN model."""
+ norm_activation_config = model_config.norm_activation
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=norm_activation_config,
+ l2_regularizer=l2_regularizer)
+
+ decoder = decoder_factory.build_decoder(
+ input_specs=backbone.output_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ rpn_head_config = model_config.rpn_head
+ roi_generator_config = model_config.roi_generator
+ roi_sampler_config = model_config.roi_sampler
+ roi_aligner_config = model_config.roi_aligner
+ detection_head_config = model_config.detection_head
+ generator_config = model_config.detection_generator
+ num_anchors_per_location = (
+ len(model_config.anchor.aspect_ratios) * model_config.anchor.num_scales)
+
+ rpn_head = dense_prediction_heads.RPNHead(
+ min_level=model_config.min_level,
+ max_level=model_config.max_level,
+ num_anchors_per_location=num_anchors_per_location,
+ num_convs=rpn_head_config.num_convs,
+ num_filters=rpn_head_config.num_filters,
+ use_separable_conv=rpn_head_config.use_separable_conv,
+ activation=norm_activation_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_regularizer=l2_regularizer)
+
+ detection_head = instance_heads.DetectionHead(
+ num_classes=model_config.num_classes,
+ num_convs=detection_head_config.num_convs,
+ num_filters=detection_head_config.num_filters,
+ use_separable_conv=detection_head_config.use_separable_conv,
+ num_fcs=detection_head_config.num_fcs,
+ fc_dims=detection_head_config.fc_dims,
+ activation=norm_activation_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_regularizer=l2_regularizer)
+
+ roi_generator_obj = roi_generator.MultilevelROIGenerator(
+ pre_nms_top_k=roi_generator_config.pre_nms_top_k,
+ pre_nms_score_threshold=roi_generator_config.pre_nms_score_threshold,
+ pre_nms_min_size_threshold=(
+ roi_generator_config.pre_nms_min_size_threshold),
+ nms_iou_threshold=roi_generator_config.nms_iou_threshold,
+ num_proposals=roi_generator_config.num_proposals,
+ test_pre_nms_top_k=roi_generator_config.test_pre_nms_top_k,
+ test_pre_nms_score_threshold=(
+ roi_generator_config.test_pre_nms_score_threshold),
+ test_pre_nms_min_size_threshold=(
+ roi_generator_config.test_pre_nms_min_size_threshold),
+ test_nms_iou_threshold=roi_generator_config.test_nms_iou_threshold,
+ test_num_proposals=roi_generator_config.test_num_proposals,
+ use_batched_nms=roi_generator_config.use_batched_nms)
+
+ roi_sampler_obj = roi_sampler.ROISampler(
+ mix_gt_boxes=roi_sampler_config.mix_gt_boxes,
+ num_sampled_rois=roi_sampler_config.num_sampled_rois,
+ foreground_fraction=roi_sampler_config.foreground_fraction,
+ foreground_iou_threshold=roi_sampler_config.foreground_iou_threshold,
+ background_iou_high_threshold=(
+ roi_sampler_config.background_iou_high_threshold),
+ background_iou_low_threshold=(
+ roi_sampler_config.background_iou_low_threshold))
+
+ roi_aligner_obj = roi_aligner.MultilevelROIAligner(
+ crop_size=roi_aligner_config.crop_size,
+ sample_offset=roi_aligner_config.sample_offset)
+
+ detection_generator_obj = detection_generator.DetectionGenerator(
+ apply_nms=True,
+ pre_nms_top_k=generator_config.pre_nms_top_k,
+ pre_nms_score_threshold=generator_config.pre_nms_score_threshold,
+ nms_iou_threshold=generator_config.nms_iou_threshold,
+ max_num_detections=generator_config.max_num_detections,
+ nms_version=generator_config.nms_version)
+
+ if model_config.include_mask:
+ mask_head = deep_instance_heads.DeepMaskHead(
+ num_classes=model_config.num_classes,
+ upsample_factor=model_config.mask_head.upsample_factor,
+ num_convs=model_config.mask_head.num_convs,
+ num_filters=model_config.mask_head.num_filters,
+ use_separable_conv=model_config.mask_head.use_separable_conv,
+ activation=model_config.norm_activation.activation,
+ norm_momentum=model_config.norm_activation.norm_momentum,
+ norm_epsilon=model_config.norm_activation.norm_epsilon,
+ kernel_regularizer=l2_regularizer,
+ class_agnostic=model_config.mask_head.class_agnostic,
+ convnet_variant=model_config.mask_head.convnet_variant)
+
+ mask_sampler_obj = mask_sampler.MaskSampler(
+ mask_target_size=(
+ model_config.mask_roi_aligner.crop_size *
+ model_config.mask_head.upsample_factor),
+ num_sampled_masks=model_config.mask_sampler.num_sampled_masks)
+
+ mask_roi_aligner_obj = roi_aligner.MultilevelROIAligner(
+ crop_size=model_config.mask_roi_aligner.crop_size,
+ sample_offset=model_config.mask_roi_aligner.sample_offset)
+ else:
+ mask_head = None
+ mask_sampler_obj = None
+ mask_roi_aligner_obj = None
+
+ model = deep_maskrcnn_model.DeepMaskRCNNModel(
+ backbone=backbone,
+ decoder=decoder,
+ rpn_head=rpn_head,
+ detection_head=detection_head,
+ roi_generator=roi_generator_obj,
+ roi_sampler=roi_sampler_obj,
+ roi_aligner=roi_aligner_obj,
+ detection_generator=detection_generator_obj,
+ mask_head=mask_head,
+ mask_sampler=mask_sampler_obj,
+ mask_roi_aligner=mask_roi_aligner_obj,
+ use_gt_boxes_for_masks=model_config.use_gt_boxes_for_masks)
+ return model
+
+
+@task_factory.register_task_cls(deep_mask_head_rcnn_config.DeepMaskHeadRCNNTask)
+class DeepMaskHeadRCNNTask(maskrcnn.MaskRCNNTask):
+ """Mask R-CNN with support for deep mask heads."""
+
+ def build_model(self):
+ """Build Mask R-CNN model."""
+
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + self.task_config.model.input_size)
+
+ l2_weight_decay = self.task_config.losses.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ model = build_maskrcnn(
+ input_specs=input_specs,
+ model_config=self.task_config.model,
+ l2_regularizer=l2_regularizer)
+
+ if self.task_config.freeze_backbone:
+ model.backbone.trainable = False
+
+ return model
diff --git a/official/projects/deepmac_maskrcnn/train.py b/official/projects/deepmac_maskrcnn/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..ac866f51ded4ccfd185d9369432a74f602d44517
--- /dev/null
+++ b/official/projects/deepmac_maskrcnn/train.py
@@ -0,0 +1,71 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver."""
+
+from absl import app
+from absl import flags
+from absl import logging
+
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+# pylint: disable=unused-import
+from official.projects.deepmac_maskrcnn.common import registry_imports
+# pylint: enable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+ logging.info('Training with task %s', task)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/projects/detr/README.md b/official/projects/detr/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..e8860f5e1eb881624608ba2c56b98538e7c7bf1d
--- /dev/null
+++ b/official/projects/detr/README.md
@@ -0,0 +1,46 @@
+# End-to-End Object Detection with Transformers (DETR)
+
+[](https://arxiv.org/abs/2005.12872).
+
+TensorFlow 2 implementation of End-to-End Object Detection with Transformers
+
+⚠️ Disclaimer: All datasets hyperlinked from this page are not owned or
+distributed by Google. The dataset is made available by third parties.
+Please review the terms and conditions made available by the third parties
+before using the data.
+
+## Scripts:
+
+You can find the scripts to reproduce the following experiments in
+detr/experiments.
+
+
+## DETR [COCO](https://cocodataset.org) ([ImageNet](https://www.image-net.org) pretrained)
+
+| Model | Resolution | Batch size | Epochs | Decay@ | Params (M) | Box AP | Dashboard | Checkpoint | Experiment |
+| --------- | :--------: | ----------:| ------:| -----: | ---------: | -----: | --------: | ---------: | ---------: |
+| DETR-ResNet-50 | 1333x1333 |64|300| 200 |41 | 40.6 | [tensorboard](https://tensorboard.dev/experiment/o2IEZnniRYu6pqViBeopIg/#scalars) | [ckpt](https://storage.googleapis.com/tf_model_garden/vision/detr/detr_resnet_50_300.tar.gz) | detr_r50_300epochs.sh |
+| DETR-ResNet-50 | 1333x1333 |64|500| 400 |41 | 42.0| [tensorboard](https://tensorboard.dev/experiment/YFMDKpESR4yjocPh5HgfRw/) | [ckpt](https://storage.googleapis.com/tf_model_garden/vision/detr/detr_resnet_50_500.tar.gz) | detr_r50_500epochs.sh |
+| DETR-ResNet-50 | 1333x1333 |64|300| 200 |41 | 40.6 | paper | NA | NA |
+| DETR-ResNet-50 | 1333x1333 |64|500| 400 |41 | 42.0 | paper | NA | NA |
+| DETR-DC5-ResNet-50 | 1333x1333 |64|500| 400 |41 | 43.3 | paper | NA | NA |
+
+## Need contribution:
+
+* Add DC5 support and update experiment table.
+
+
+## Citing TensorFlow Model Garden
+
+If you find this codebase helpful in your research, please cite this repository.
+
+```
+@misc{tensorflowmodelgarden2020,
+ author = {Hongkun Yu and Chen Chen and Xianzhi Du and Yeqing Li and
+ Abdullah Rashwan and Le Hou and Pengchong Jin and Fan Yang and
+ Frederick Liu and Jaeyoun Kim and Jing Li},
+ title = {{TensorFlow Model Garden}},
+ howpublished = {\url{https://github.com/tensorflow/models}},
+ year = {2020}
+}
+```
diff --git a/official/projects/detr/configs/detr.py b/official/projects/detr/configs/detr.py
new file mode 100644
index 0000000000000000000000000000000000000000..bcdd50e95b0b0f659c10b1566cbdfb254ef1bee2
--- /dev/null
+++ b/official/projects/detr/configs/detr.py
@@ -0,0 +1,277 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""DETR configurations."""
+
+import dataclasses
+import os
+from typing import List, Optional, Union
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.projects.detr import optimization
+from official.projects.detr.dataloaders import coco
+from official.vision.configs import backbones
+from official.vision.configs import common
+
+
+@dataclasses.dataclass
+class DataConfig(cfg.DataConfig):
+ """Input config for training."""
+ input_path: str = ''
+ tfds_name: str = ''
+ tfds_split: str = 'train'
+ global_batch_size: int = 0
+ is_training: bool = False
+ dtype: str = 'bfloat16'
+ decoder: common.DataDecoder = common.DataDecoder()
+ shuffle_buffer_size: int = 10000
+ file_type: str = 'tfrecord'
+ drop_remainder: bool = True
+
+
+@dataclasses.dataclass
+class Losses(hyperparams.Config):
+ class_offset: int = 0
+ lambda_cls: float = 1.0
+ lambda_box: float = 5.0
+ lambda_giou: float = 2.0
+ background_cls_weight: float = 0.1
+ l2_weight_decay: float = 1e-4
+
+
+@dataclasses.dataclass
+class Detr(hyperparams.Config):
+ """Detr model definations."""
+ num_queries: int = 100
+ hidden_size: int = 256
+ num_classes: int = 91 # 0: background
+ num_encoder_layers: int = 6
+ num_decoder_layers: int = 6
+ input_size: List[int] = dataclasses.field(default_factory=list)
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='resnet', resnet=backbones.ResNet(model_id=50, bn_trainable=False))
+ norm_activation: common.NormActivation = common.NormActivation()
+ backbone_endpoint_name: str = '5'
+
+
+@dataclasses.dataclass
+class DetrTask(cfg.TaskConfig):
+ model: Detr = Detr()
+ train_data: cfg.DataConfig = cfg.DataConfig()
+ validation_data: cfg.DataConfig = cfg.DataConfig()
+ losses: Losses = Losses()
+ init_checkpoint: Optional[str] = None
+ init_checkpoint_modules: Union[str, List[str]] = 'all' # all, backbone
+ annotation_file: Optional[str] = None
+ per_category_metrics: bool = False
+
+
+COCO_INPUT_PATH_BASE = 'coco'
+COCO_TRAIN_EXAMPLES = 118287
+COCO_VAL_EXAMPLES = 5000
+
+
+@exp_factory.register_config_factory('detr_coco')
+def detr_coco() -> cfg.ExperimentConfig:
+ """Config to get results that matches the paper."""
+ train_batch_size = 64
+ eval_batch_size = 64
+ num_train_data = COCO_TRAIN_EXAMPLES
+ num_steps_per_epoch = num_train_data // train_batch_size
+ train_steps = 500 * num_steps_per_epoch # 500 epochs
+ decay_at = train_steps - 100 * num_steps_per_epoch # 400 epochs
+ config = cfg.ExperimentConfig(
+ task=DetrTask(
+ init_checkpoint='',
+ init_checkpoint_modules='backbone',
+ model=Detr(
+ num_classes=81,
+ input_size=[1333, 1333, 3],
+ norm_activation=common.NormActivation()),
+ losses=Losses(),
+ train_data=coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='train',
+ is_training=True,
+ global_batch_size=train_batch_size,
+ shuffle_buffer_size=1000,
+ ),
+ validation_data=coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ drop_remainder=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=-1,
+ steps_per_loop=10000,
+ summary_interval=10000,
+ checkpoint_interval=10000,
+ validation_interval=10000,
+ max_to_keep=1,
+ best_checkpoint_export_subdir='best_ckpt',
+ best_checkpoint_eval_metric='AP',
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'detr_adamw',
+ 'detr_adamw': {
+ 'weight_decay_rate': 1e-4,
+ 'global_clipnorm': 0.1,
+ # Avoid AdamW legacy behavior.
+ 'gradient_clip_norm': 0.0
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [decay_at],
+ 'values': [0.0001, 1.0e-05]
+ }
+ },
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ ])
+ return config
+
+
+@exp_factory.register_config_factory('detr_coco_tfrecord')
+def detr_coco_tfrecord() -> cfg.ExperimentConfig:
+ """Config to get results that matches the paper."""
+ train_batch_size = 64
+ eval_batch_size = 64
+ steps_per_epoch = COCO_TRAIN_EXAMPLES // train_batch_size
+ train_steps = 300 * steps_per_epoch # 300 epochs
+ decay_at = train_steps - 100 * steps_per_epoch # 200 epochs
+ config = cfg.ExperimentConfig(
+ task=DetrTask(
+ init_checkpoint='',
+ init_checkpoint_modules='backbone',
+ annotation_file=os.path.join(COCO_INPUT_PATH_BASE,
+ 'instances_val2017.json'),
+ model=Detr(
+ input_size=[1333, 1333, 3],
+ norm_activation=common.NormActivation()),
+ losses=Losses(),
+ train_data=DataConfig(
+ input_path=os.path.join(COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ shuffle_buffer_size=1000,
+ ),
+ validation_data=DataConfig(
+ input_path=os.path.join(COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ drop_remainder=False,
+ )),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=COCO_VAL_EXAMPLES // eval_batch_size,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ validation_interval=5 * steps_per_epoch,
+ max_to_keep=1,
+ best_checkpoint_export_subdir='best_ckpt',
+ best_checkpoint_eval_metric='AP',
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'detr_adamw',
+ 'detr_adamw': {
+ 'weight_decay_rate': 1e-4,
+ 'global_clipnorm': 0.1,
+ # Avoid AdamW legacy behavior.
+ 'gradient_clip_norm': 0.0
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [decay_at],
+ 'values': [0.0001, 1.0e-05]
+ }
+ },
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ ])
+ return config
+
+
+@exp_factory.register_config_factory('detr_coco_tfds')
+def detr_coco_tfds() -> cfg.ExperimentConfig:
+ """Config to get results that matches the paper."""
+ train_batch_size = 64
+ eval_batch_size = 64
+ steps_per_epoch = COCO_TRAIN_EXAMPLES // train_batch_size
+ train_steps = 300 * steps_per_epoch # 300 epochs
+ decay_at = train_steps - 100 * steps_per_epoch # 200 epochs
+ config = cfg.ExperimentConfig(
+ task=DetrTask(
+ init_checkpoint='',
+ init_checkpoint_modules='backbone',
+ model=Detr(
+ num_classes=81,
+ input_size=[1333, 1333, 3],
+ norm_activation=common.NormActivation()),
+ losses=Losses(class_offset=1),
+ train_data=DataConfig(
+ tfds_name='coco/2017',
+ tfds_split='train',
+ is_training=True,
+ global_batch_size=train_batch_size,
+ shuffle_buffer_size=1000,
+ ),
+ validation_data=DataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ drop_remainder=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=COCO_VAL_EXAMPLES // eval_batch_size,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ validation_interval=5 * steps_per_epoch,
+ max_to_keep=1,
+ best_checkpoint_export_subdir='best_ckpt',
+ best_checkpoint_eval_metric='AP',
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'detr_adamw',
+ 'detr_adamw': {
+ 'weight_decay_rate': 1e-4,
+ 'global_clipnorm': 0.1,
+ # Avoid AdamW legacy behavior.
+ 'gradient_clip_norm': 0.0
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [decay_at],
+ 'values': [0.0001, 1.0e-05]
+ }
+ },
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ ])
+ return config
diff --git a/official/projects/detr/configs/detr_test.py b/official/projects/detr/configs/detr_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a3f04d457689b5d8601ef8f8b2941840bcf088d
--- /dev/null
+++ b/official/projects/detr/configs/detr_test.py
@@ -0,0 +1,51 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for detr."""
+
+# pylint: disable=unused-import
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.detr.configs import detr as exp_cfg
+from official.projects.detr.dataloaders import coco
+
+
+class DetrTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(('detr_coco',))
+ def test_detr_configs_tfds(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, exp_cfg.DetrTask)
+ self.assertIsInstance(config.task.train_data, coco.COCODataConfig)
+ config.task.train_data.is_training = None
+ with self.assertRaises(KeyError):
+ config.validate()
+
+ @parameterized.parameters(('detr_coco_tfrecord'), ('detr_coco_tfds'))
+ def test_detr_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, exp_cfg.DetrTask)
+ self.assertIsInstance(config.task.train_data, cfg.DataConfig)
+ config.task.train_data.is_training = None
+ with self.assertRaises(KeyError):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/dataloaders/coco.py b/official/projects/detr/dataloaders/coco.py
new file mode 100644
index 0000000000000000000000000000000000000000..e9c2e5fb37d524ae61664357310a546169595cd3
--- /dev/null
+++ b/official/projects/detr/dataloaders/coco.py
@@ -0,0 +1,157 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""COCO data loader for DETR."""
+
+import dataclasses
+from typing import Optional, Tuple
+import tensorflow as tf
+
+from official.core import config_definitions as cfg
+from official.core import input_reader
+from official.vision.ops import box_ops
+from official.vision.ops import preprocess_ops
+
+
+@dataclasses.dataclass
+class COCODataConfig(cfg.DataConfig):
+ """Data config for COCO."""
+ output_size: Tuple[int, int] = (1333, 1333)
+ max_num_boxes: int = 100
+ resize_scales: Tuple[int, ...] = (
+ 480, 512, 544, 576, 608, 640, 672, 704, 736, 768, 800)
+
+
+class COCODataLoader():
+ """A class to load dataset for COCO detection task."""
+
+ def __init__(self, params: COCODataConfig):
+ self._params = params
+
+ def preprocess(self, inputs):
+ """Preprocess COCO for DETR."""
+ image = inputs['image']
+ boxes = inputs['objects']['bbox']
+ classes = inputs['objects']['label'] + 1
+ is_crowd = inputs['objects']['is_crowd']
+
+ image = preprocess_ops.normalize_image(image)
+ if self._params.is_training:
+ image, boxes, _ = preprocess_ops.random_horizontal_flip(image, boxes)
+
+ do_crop = tf.greater(tf.random.uniform([]), 0.5)
+ if do_crop:
+ # Rescale
+ boxes = box_ops.denormalize_boxes(boxes, tf.shape(image)[:2])
+ index = tf.random.categorical(tf.zeros([1, 3]), 1)[0]
+ scales = tf.gather([400.0, 500.0, 600.0], index, axis=0)
+ short_side = scales[0]
+ image, image_info = preprocess_ops.resize_image(image, short_side)
+ boxes = preprocess_ops.resize_and_crop_boxes(boxes,
+ image_info[2, :],
+ image_info[1, :],
+ image_info[3, :])
+ boxes = box_ops.normalize_boxes(boxes, image_info[1, :])
+
+ # Do croping
+ shape = tf.cast(image_info[1], dtype=tf.int32)
+ h = tf.random.uniform(
+ [], 384, tf.math.minimum(shape[0], 600), dtype=tf.int32)
+ w = tf.random.uniform(
+ [], 384, tf.math.minimum(shape[1], 600), dtype=tf.int32)
+ i = tf.random.uniform([], 0, shape[0] - h + 1, dtype=tf.int32)
+ j = tf.random.uniform([], 0, shape[1] - w + 1, dtype=tf.int32)
+ image = tf.image.crop_to_bounding_box(image, i, j, h, w)
+ boxes = tf.clip_by_value(
+ (boxes[..., :] * tf.cast(
+ tf.stack([shape[0], shape[1], shape[0], shape[1]]),
+ dtype=tf.float32) -
+ tf.cast(tf.stack([i, j, i, j]), dtype=tf.float32)) /
+ tf.cast(tf.stack([h, w, h, w]), dtype=tf.float32), 0.0, 1.0)
+ scales = tf.constant(
+ self._params.resize_scales,
+ dtype=tf.float32)
+ index = tf.random.categorical(tf.zeros([1, 11]), 1)[0]
+ scales = tf.gather(scales, index, axis=0)
+ else:
+ scales = tf.constant([self._params.resize_scales[-1]], tf.float32)
+
+ image_shape = tf.shape(image)[:2]
+ boxes = box_ops.denormalize_boxes(boxes, image_shape)
+ gt_boxes = boxes
+ short_side = scales[0]
+ image, image_info = preprocess_ops.resize_image(
+ image,
+ short_side,
+ max(self._params.output_size))
+ boxes = preprocess_ops.resize_and_crop_boxes(boxes,
+ image_info[2, :],
+ image_info[1, :],
+ image_info[3, :])
+ boxes = box_ops.normalize_boxes(boxes, image_info[1, :])
+
+ # Filters out ground truth boxes that are all zeros.
+ indices = box_ops.get_non_empty_box_indices(boxes)
+ boxes = tf.gather(boxes, indices)
+ classes = tf.gather(classes, indices)
+ is_crowd = tf.gather(is_crowd, indices)
+ boxes = box_ops.yxyx_to_cycxhw(boxes)
+
+ image = tf.image.pad_to_bounding_box(
+ image, 0, 0, self._params.output_size[0], self._params.output_size[1])
+ labels = {
+ 'classes':
+ preprocess_ops.clip_or_pad_to_fixed_size(
+ classes, self._params.max_num_boxes),
+ 'boxes':
+ preprocess_ops.clip_or_pad_to_fixed_size(
+ boxes, self._params.max_num_boxes)
+ }
+ if not self._params.is_training:
+ labels.update({
+ 'id':
+ inputs['image/id'],
+ 'image_info':
+ image_info,
+ 'is_crowd':
+ preprocess_ops.clip_or_pad_to_fixed_size(
+ is_crowd, self._params.max_num_boxes),
+ 'gt_boxes':
+ preprocess_ops.clip_or_pad_to_fixed_size(
+ gt_boxes, self._params.max_num_boxes),
+ })
+
+ return image, labels
+
+ def _transform_and_batch_fn(
+ self,
+ dataset,
+ input_context: Optional[tf.distribute.InputContext] = None):
+ """Preprocess and batch."""
+ dataset = dataset.map(
+ self.preprocess, num_parallel_calls=tf.data.experimental.AUTOTUNE)
+ per_replica_batch_size = input_context.get_per_replica_batch_size(
+ self._params.global_batch_size
+ ) if input_context else self._params.global_batch_size
+ dataset = dataset.batch(
+ per_replica_batch_size, drop_remainder=self._params.drop_remainder)
+ return dataset
+
+ def load(self, input_context: Optional[tf.distribute.InputContext] = None):
+ """Returns a tf.dataset.Dataset."""
+ reader = input_reader.InputReader(
+ params=self._params,
+ decoder_fn=None,
+ transform_and_batch_fn=self._transform_and_batch_fn)
+ return reader.read(input_context)
diff --git a/official/projects/detr/dataloaders/coco_test.py b/official/projects/detr/dataloaders/coco_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..cad38e18c0091d84914449b9fef608134d4a36dc
--- /dev/null
+++ b/official/projects/detr/dataloaders/coco_test.py
@@ -0,0 +1,111 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tensorflow_models.official.projects.detr.dataloaders.coco."""
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+import tensorflow_datasets as tfds
+
+from official.projects.detr.dataloaders import coco
+
+
+def _gen_fn():
+ h = np.random.randint(0, 300)
+ w = np.random.randint(0, 300)
+ num_boxes = np.random.randint(0, 50)
+ return {
+ 'image': np.ones(shape=(h, w, 3), dtype=np.uint8),
+ 'image/id': np.random.randint(0, 100),
+ 'image/filename': 'test',
+ 'objects': {
+ 'is_crowd': np.ones(shape=(num_boxes), dtype=np.bool),
+ 'bbox': np.ones(shape=(num_boxes, 4), dtype=np.float32),
+ 'label': np.ones(shape=(num_boxes), dtype=np.int64),
+ 'id': np.ones(shape=(num_boxes), dtype=np.int64),
+ 'area': np.ones(shape=(num_boxes), dtype=np.int64),
+ }
+ }
+
+
+class CocoDataloaderTest(tf.test.TestCase, parameterized.TestCase):
+
+ def test_load_dataset(self):
+ output_size = 1280
+ max_num_boxes = 100
+ batch_size = 2
+ data_config = coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=False,
+ global_batch_size=batch_size,
+ output_size=(output_size, output_size),
+ max_num_boxes=max_num_boxes,
+ )
+
+ num_examples = 10
+ def as_dataset(self, *args, **kwargs):
+ del args
+ del kwargs
+ return tf.data.Dataset.from_generator(
+ lambda: (_gen_fn() for i in range(num_examples)),
+ output_types=self.info.features.dtype,
+ output_shapes=self.info.features.shape,
+ )
+
+ with tfds.testing.mock_data(num_examples=num_examples,
+ as_dataset_fn=as_dataset):
+ dataset = coco.COCODataLoader(data_config).load()
+ dataset_iter = iter(dataset)
+ images, labels = next(dataset_iter)
+ self.assertEqual(images.shape, (batch_size, output_size, output_size, 3))
+ self.assertEqual(labels['classes'].shape, (batch_size, max_num_boxes))
+ self.assertEqual(labels['boxes'].shape, (batch_size, max_num_boxes, 4))
+ self.assertEqual(labels['id'].shape, (batch_size,))
+ self.assertEqual(
+ labels['image_info'].shape, (batch_size, 4, 2))
+ self.assertEqual(labels['is_crowd'].shape, (batch_size, max_num_boxes))
+
+ @parameterized.named_parameters(
+ ('training', True),
+ ('validation', False))
+ def test_preprocess(self, is_training):
+ output_size = 1280
+ max_num_boxes = 100
+ batch_size = 2
+ data_config = coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=is_training,
+ global_batch_size=batch_size,
+ output_size=(output_size, output_size),
+ max_num_boxes=max_num_boxes,
+ )
+
+ dl = coco.COCODataLoader(data_config)
+ inputs = _gen_fn()
+ image, label = dl.preprocess(inputs)
+ self.assertEqual(image.shape, (output_size, output_size, 3))
+ self.assertEqual(label['classes'].shape, (max_num_boxes))
+ self.assertEqual(label['boxes'].shape, (max_num_boxes, 4))
+ if not is_training:
+ self.assertDTypeEqual(label['id'], int)
+ self.assertEqual(
+ label['image_info'].shape, (4, 2))
+ self.assertEqual(label['is_crowd'].shape, (max_num_boxes))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/dataloaders/detr_input.py b/official/projects/detr/dataloaders/detr_input.py
new file mode 100644
index 0000000000000000000000000000000000000000..2085d56ac848193cd32fa6f60f21d32e1e2cd432
--- /dev/null
+++ b/official/projects/detr/dataloaders/detr_input.py
@@ -0,0 +1,175 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""COCO data loader for DETR."""
+
+from typing import Tuple
+import tensorflow as tf
+
+from official.vision.dataloaders import parser
+
+from official.vision.ops import box_ops
+from official.vision.ops import preprocess_ops
+
+RESIZE_SCALES = (480, 512, 544, 576, 608, 640, 672, 704, 736, 768, 800)
+
+
+class Parser(parser.Parser):
+ """Parse an image and its annotations into a dictionary of tensors."""
+
+ def __init__(self,
+ class_offset: int = 0,
+ output_size: Tuple[int, int] = (1333, 1333),
+ max_num_boxes: int = 100,
+ resize_scales: Tuple[int, ...] = RESIZE_SCALES,
+ aug_rand_hflip=True):
+ self._class_offset = class_offset
+ self._output_size = output_size
+ self._max_num_boxes = max_num_boxes
+ self._resize_scales = resize_scales
+ self._aug_rand_hflip = aug_rand_hflip
+
+ def _parse_train_data(self, data):
+ """Parses data for training and evaluation."""
+ classes = data['groundtruth_classes'] + self._class_offset
+ boxes = data['groundtruth_boxes']
+ is_crowd = data['groundtruth_is_crowd']
+
+ # Gets original image.
+ image = data['image']
+
+ # Normalizes image with mean and std pixel values.
+ image = preprocess_ops.normalize_image(image)
+ image, boxes, _ = preprocess_ops.random_horizontal_flip(image, boxes)
+
+ do_crop = tf.greater(tf.random.uniform([]), 0.5)
+ if do_crop:
+ # Rescale
+ boxes = box_ops.denormalize_boxes(boxes, tf.shape(image)[:2])
+ index = tf.random.categorical(tf.zeros([1, 3]), 1)[0]
+ scales = tf.gather([400.0, 500.0, 600.0], index, axis=0)
+ short_side = scales[0]
+ image, image_info = preprocess_ops.resize_image(image, short_side)
+ boxes = preprocess_ops.resize_and_crop_boxes(boxes, image_info[2, :],
+ image_info[1, :],
+ image_info[3, :])
+ boxes = box_ops.normalize_boxes(boxes, image_info[1, :])
+
+ # Do croping
+ shape = tf.cast(image_info[1], dtype=tf.int32)
+ h = tf.random.uniform([],
+ 384,
+ tf.math.minimum(shape[0], 600),
+ dtype=tf.int32)
+ w = tf.random.uniform([],
+ 384,
+ tf.math.minimum(shape[1], 600),
+ dtype=tf.int32)
+ i = tf.random.uniform([], 0, shape[0] - h + 1, dtype=tf.int32)
+ j = tf.random.uniform([], 0, shape[1] - w + 1, dtype=tf.int32)
+ image = tf.image.crop_to_bounding_box(image, i, j, h, w)
+ boxes = tf.clip_by_value(
+ (boxes[..., :] * tf.cast(
+ tf.stack([shape[0], shape[1], shape[0], shape[1]]),
+ dtype=tf.float32) -
+ tf.cast(tf.stack([i, j, i, j]), dtype=tf.float32)) /
+ tf.cast(tf.stack([h, w, h, w]), dtype=tf.float32), 0.0, 1.0)
+ scales = tf.constant(self._resize_scales, dtype=tf.float32)
+ index = tf.random.categorical(tf.zeros([1, 11]), 1)[0]
+ scales = tf.gather(scales, index, axis=0)
+
+ image_shape = tf.shape(image)[:2]
+ boxes = box_ops.denormalize_boxes(boxes, image_shape)
+ short_side = scales[0]
+ image, image_info = preprocess_ops.resize_image(image, short_side,
+ max(self._output_size))
+ boxes = preprocess_ops.resize_and_crop_boxes(boxes, image_info[2, :],
+ image_info[1, :],
+ image_info[3, :])
+ boxes = box_ops.normalize_boxes(boxes, image_info[1, :])
+
+ # Filters out ground truth boxes that are all zeros.
+ indices = box_ops.get_non_empty_box_indices(boxes)
+ boxes = tf.gather(boxes, indices)
+ classes = tf.gather(classes, indices)
+ is_crowd = tf.gather(is_crowd, indices)
+ boxes = box_ops.yxyx_to_cycxhw(boxes)
+
+ image = tf.image.pad_to_bounding_box(image, 0, 0, self._output_size[0],
+ self._output_size[1])
+ labels = {
+ 'classes':
+ preprocess_ops.clip_or_pad_to_fixed_size(classes,
+ self._max_num_boxes),
+ 'boxes':
+ preprocess_ops.clip_or_pad_to_fixed_size(boxes, self._max_num_boxes)
+ }
+
+ return image, labels
+
+ def _parse_eval_data(self, data):
+ """Parses data for training and evaluation."""
+ classes = data['groundtruth_classes']
+ boxes = data['groundtruth_boxes']
+ is_crowd = data['groundtruth_is_crowd']
+
+ # Gets original image and its size.
+ image = data['image']
+
+ # Normalizes image with mean and std pixel values.
+ image = preprocess_ops.normalize_image(image)
+
+ scales = tf.constant([self._resize_scales[-1]], tf.float32)
+
+ image_shape = tf.shape(image)[:2]
+ boxes = box_ops.denormalize_boxes(boxes, image_shape)
+ gt_boxes = boxes
+ short_side = scales[0]
+ image, image_info = preprocess_ops.resize_image(image, short_side,
+ max(self._output_size))
+ boxes = preprocess_ops.resize_and_crop_boxes(boxes, image_info[2, :],
+ image_info[1, :],
+ image_info[3, :])
+ boxes = box_ops.normalize_boxes(boxes, image_info[1, :])
+
+ # Filters out ground truth boxes that are all zeros.
+ indices = box_ops.get_non_empty_box_indices(boxes)
+ boxes = tf.gather(boxes, indices)
+ classes = tf.gather(classes, indices)
+ is_crowd = tf.gather(is_crowd, indices)
+ boxes = box_ops.yxyx_to_cycxhw(boxes)
+
+ image = tf.image.pad_to_bounding_box(image, 0, 0, self._output_size[0],
+ self._output_size[1])
+ labels = {
+ 'classes':
+ preprocess_ops.clip_or_pad_to_fixed_size(classes,
+ self._max_num_boxes),
+ 'boxes':
+ preprocess_ops.clip_or_pad_to_fixed_size(boxes, self._max_num_boxes)
+ }
+ labels.update({
+ 'id':
+ int(data['source_id']),
+ 'image_info':
+ image_info,
+ 'is_crowd':
+ preprocess_ops.clip_or_pad_to_fixed_size(is_crowd,
+ self._max_num_boxes),
+ 'gt_boxes':
+ preprocess_ops.clip_or_pad_to_fixed_size(gt_boxes,
+ self._max_num_boxes),
+ })
+
+ return image, labels
diff --git a/official/projects/detr/experiments/detr_r50_300epochs.sh b/official/projects/detr/experiments/detr_r50_300epochs.sh
new file mode 100644
index 0000000000000000000000000000000000000000..162f974306bfdaed79cf0f092285bb614ec7fc69
--- /dev/null
+++ b/official/projects/detr/experiments/detr_r50_300epochs.sh
@@ -0,0 +1,6 @@
+#!/bin/bash
+python3 official/projects/detr/train.py \
+ --experiment=detr_coco \
+ --mode=train_and_eval \
+ --model_dir=/tmp/logging_dir/ \
+ --params_override=task.init_checkpoint='gs://tf_model_garden/vision/resnet50_imagenet/ckpt-62400',trainer.train_steps=554400,trainer.optimizer_config.learning_rate.stepwise.boundaries="[369600]"
diff --git a/official/projects/detr/experiments/detr_r50_500epochs.sh b/official/projects/detr/experiments/detr_r50_500epochs.sh
new file mode 100644
index 0000000000000000000000000000000000000000..58036040578a73f35ef663c91aa5ab828c90cb4b
--- /dev/null
+++ b/official/projects/detr/experiments/detr_r50_500epochs.sh
@@ -0,0 +1,6 @@
+#!/bin/bash
+python3 official/projects/detr/train.py \
+ --experiment=detr_coco \
+ --mode=train_and_eval \
+ --model_dir=/tmp/logging_dir/ \
+ --params_override=task.init_checkpoint='gs://tf_model_garden/vision/resnet50_imagenet/ckpt-62400'
diff --git a/official/projects/detr/modeling/detr.py b/official/projects/detr/modeling/detr.py
new file mode 100644
index 0000000000000000000000000000000000000000..a3051aa796e8259d91040bfbf3a7687ddb7efd52
--- /dev/null
+++ b/official/projects/detr/modeling/detr.py
@@ -0,0 +1,297 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Implements End-to-End Object Detection with Transformers.
+
+Model paper: https://arxiv.org/abs/2005.12872
+This module does not support Keras de/serialization. Please use
+tf.train.Checkpoint for object based saving and loading and tf.saved_model.save
+for graph serializaiton.
+"""
+import math
+from typing import Any, List
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.detr.modeling import transformer
+
+
+def position_embedding_sine(attention_mask,
+ num_pos_features=256,
+ temperature=10000.,
+ normalize=True,
+ scale=2 * math.pi):
+ """Sine-based positional embeddings for 2D images.
+
+ Args:
+ attention_mask: a `bool` Tensor specifying the size of the input image to
+ the Transformer and which elements are padded, of size [batch_size,
+ height, width]
+ num_pos_features: a `int` specifying the number of positional features,
+ should be equal to the hidden size of the Transformer network
+ temperature: a `float` specifying the temperature of the positional
+ embedding. Any type that is converted to a `float` can also be accepted.
+ normalize: a `bool` determining whether the positional embeddings should be
+ normalized between [0, scale] before application of the sine and cos
+ functions.
+ scale: a `float` if normalize is True specifying the scale embeddings before
+ application of the embedding function.
+
+ Returns:
+ embeddings: a `float` tensor of the same shape as input_tensor specifying
+ the positional embeddings based on sine features.
+ """
+ if num_pos_features % 2 != 0:
+ raise ValueError(
+ "Number of embedding features (num_pos_features) must be even when "
+ "column and row embeddings are concatenated.")
+ num_pos_features = num_pos_features // 2
+
+ # Produce row and column embeddings based on total size of the image
+ # [batch_size, height, width]
+ attention_mask = tf.cast(attention_mask, tf.float32)
+ row_embedding = tf.cumsum(attention_mask, 1)
+ col_embedding = tf.cumsum(attention_mask, 2)
+
+ if normalize:
+ eps = 1e-6
+ row_embedding = row_embedding / (row_embedding[:, -1:, :] + eps) * scale
+ col_embedding = col_embedding / (col_embedding[:, :, -1:] + eps) * scale
+
+ dim_t = tf.range(num_pos_features, dtype=row_embedding.dtype)
+ dim_t = tf.pow(temperature, 2 * (dim_t // 2) / num_pos_features)
+
+ # Creates positional embeddings for each row and column position
+ # [batch_size, height, width, num_pos_features]
+ pos_row = tf.expand_dims(row_embedding, -1) / dim_t
+ pos_col = tf.expand_dims(col_embedding, -1) / dim_t
+ pos_row = tf.stack(
+ [tf.sin(pos_row[:, :, :, 0::2]),
+ tf.cos(pos_row[:, :, :, 1::2])], axis=4)
+ pos_col = tf.stack(
+ [tf.sin(pos_col[:, :, :, 0::2]),
+ tf.cos(pos_col[:, :, :, 1::2])], axis=4)
+
+ # final_shape = pos_row.shape.as_list()[:3] + [-1]
+ final_shape = tf_utils.get_shape_list(pos_row)[:3] + [-1]
+ pos_row = tf.reshape(pos_row, final_shape)
+ pos_col = tf.reshape(pos_col, final_shape)
+ output = tf.concat([pos_row, pos_col], -1)
+
+ embeddings = tf.cast(output, tf.float32)
+ return embeddings
+
+
+class DETR(tf.keras.Model):
+ """DETR model with Keras.
+
+ DETR consists of backbone, query embedding, DETRTransformer,
+ class and box heads.
+ """
+
+ def __init__(self,
+ backbone,
+ backbone_endpoint_name,
+ num_queries,
+ hidden_size,
+ num_classes,
+ num_encoder_layers=6,
+ num_decoder_layers=6,
+ dropout_rate=0.1,
+ **kwargs):
+ super().__init__(**kwargs)
+ self._num_queries = num_queries
+ self._hidden_size = hidden_size
+ self._num_classes = num_classes
+ self._num_encoder_layers = num_encoder_layers
+ self._num_decoder_layers = num_decoder_layers
+ self._dropout_rate = dropout_rate
+ if hidden_size % 2 != 0:
+ raise ValueError("hidden_size must be a multiple of 2.")
+ self._backbone = backbone
+ self._backbone_endpoint_name = backbone_endpoint_name
+
+ def build(self, input_shape=None):
+ self._input_proj = tf.keras.layers.Conv2D(
+ self._hidden_size, 1, name="detr/conv2d")
+ self._build_detection_decoder()
+ super().build(input_shape)
+
+ def _build_detection_decoder(self):
+ """Builds detection decoder."""
+ self._transformer = DETRTransformer(
+ num_encoder_layers=self._num_encoder_layers,
+ num_decoder_layers=self._num_decoder_layers,
+ dropout_rate=self._dropout_rate)
+ self._query_embeddings = self.add_weight(
+ "detr/query_embeddings",
+ shape=[self._num_queries, self._hidden_size],
+ initializer=tf.keras.initializers.RandomNormal(mean=0., stddev=1.),
+ dtype=tf.float32)
+ sqrt_k = math.sqrt(1.0 / self._hidden_size)
+ self._class_embed = tf.keras.layers.Dense(
+ self._num_classes,
+ kernel_initializer=tf.keras.initializers.RandomUniform(-sqrt_k, sqrt_k),
+ name="detr/cls_dense")
+ self._bbox_embed = [
+ tf.keras.layers.Dense(
+ self._hidden_size, activation="relu",
+ kernel_initializer=tf.keras.initializers.RandomUniform(
+ -sqrt_k, sqrt_k),
+ name="detr/box_dense_0"),
+ tf.keras.layers.Dense(
+ self._hidden_size, activation="relu",
+ kernel_initializer=tf.keras.initializers.RandomUniform(
+ -sqrt_k, sqrt_k),
+ name="detr/box_dense_1"),
+ tf.keras.layers.Dense(
+ 4, kernel_initializer=tf.keras.initializers.RandomUniform(
+ -sqrt_k, sqrt_k),
+ name="detr/box_dense_2")]
+ self._sigmoid = tf.keras.layers.Activation("sigmoid")
+
+ @property
+ def backbone(self) -> tf.keras.Model:
+ return self._backbone
+
+ def get_config(self):
+ return {
+ "backbone": self._backbone,
+ "backbone_endpoint_name": self._backbone_endpoint_name,
+ "num_queries": self._num_queries,
+ "hidden_size": self._hidden_size,
+ "num_classes": self._num_classes,
+ "num_encoder_layers": self._num_encoder_layers,
+ "num_decoder_layers": self._num_decoder_layers,
+ "dropout_rate": self._dropout_rate,
+ }
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
+
+ def _generate_image_mask(self, inputs: tf.Tensor,
+ target_shape: tf.Tensor) -> tf.Tensor:
+ """Generates image mask from input image."""
+ mask = tf.expand_dims(
+ tf.cast(tf.not_equal(tf.reduce_sum(inputs, axis=-1), 0), inputs.dtype),
+ axis=-1)
+ mask = tf.image.resize(
+ mask, target_shape, method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
+ return mask
+
+ def call(self, inputs: tf.Tensor) -> List[Any]:
+ batch_size = tf.shape(inputs)[0]
+ features = self._backbone(inputs)[self._backbone_endpoint_name]
+ shape = tf.shape(features)
+ mask = self._generate_image_mask(inputs, shape[1: 3])
+
+ pos_embed = position_embedding_sine(
+ mask[:, :, :, 0], num_pos_features=self._hidden_size)
+ pos_embed = tf.reshape(pos_embed, [batch_size, -1, self._hidden_size])
+
+ features = tf.reshape(
+ self._input_proj(features), [batch_size, -1, self._hidden_size])
+ mask = tf.reshape(mask, [batch_size, -1])
+
+ decoded_list = self._transformer({
+ "inputs":
+ features,
+ "targets":
+ tf.tile(
+ tf.expand_dims(self._query_embeddings, axis=0),
+ (batch_size, 1, 1)),
+ "pos_embed": pos_embed,
+ "mask": mask,
+ })
+ out_list = []
+ for decoded in decoded_list:
+ decoded = tf.stack(decoded)
+ output_class = self._class_embed(decoded)
+ box_out = decoded
+ for layer in self._bbox_embed:
+ box_out = layer(box_out)
+ output_coord = self._sigmoid(box_out)
+ out = {"cls_outputs": output_class, "box_outputs": output_coord}
+ out_list.append(out)
+ return out_list
+
+
+class DETRTransformer(tf.keras.layers.Layer):
+ """Encoder and Decoder of DETR."""
+
+ def __init__(self, num_encoder_layers=6, num_decoder_layers=6,
+ dropout_rate=0.1, **kwargs):
+ super().__init__(**kwargs)
+ self._dropout_rate = dropout_rate
+ self._num_encoder_layers = num_encoder_layers
+ self._num_decoder_layers = num_decoder_layers
+
+ def build(self, input_shape=None):
+ if self._num_encoder_layers > 0:
+ self._encoder = transformer.TransformerEncoder(
+ attention_dropout_rate=self._dropout_rate,
+ dropout_rate=self._dropout_rate,
+ intermediate_dropout=self._dropout_rate,
+ norm_first=False,
+ num_layers=self._num_encoder_layers)
+ else:
+ self._encoder = None
+
+ self._decoder = transformer.TransformerDecoder(
+ attention_dropout_rate=self._dropout_rate,
+ dropout_rate=self._dropout_rate,
+ intermediate_dropout=self._dropout_rate,
+ norm_first=False,
+ num_layers=self._num_decoder_layers)
+ super().build(input_shape)
+
+ def get_config(self):
+ return {
+ "num_encoder_layers": self._num_encoder_layers,
+ "num_decoder_layers": self._num_decoder_layers,
+ "dropout_rate": self._dropout_rate,
+ }
+
+ def call(self, inputs):
+ sources = inputs["inputs"]
+ targets = inputs["targets"]
+ pos_embed = inputs["pos_embed"]
+ mask = inputs["mask"]
+ input_shape = tf_utils.get_shape_list(sources)
+ source_attention_mask = tf.tile(
+ tf.expand_dims(mask, axis=1), [1, input_shape[1], 1])
+ if self._encoder is not None:
+ memory = self._encoder(
+ sources, attention_mask=source_attention_mask, pos_embed=pos_embed)
+ else:
+ memory = sources
+
+ target_shape = tf_utils.get_shape_list(targets)
+ cross_attention_mask = tf.tile(
+ tf.expand_dims(mask, axis=1), [1, target_shape[1], 1])
+ target_shape = tf.shape(targets)
+ decoded = self._decoder(
+ tf.zeros_like(targets),
+ memory,
+ # TODO(b/199545430): self_attention_mask could be set to None when this
+ # bug is resolved. Passing ones for now.
+ self_attention_mask=tf.ones(
+ (target_shape[0], target_shape[1], target_shape[1])),
+ cross_attention_mask=cross_attention_mask,
+ return_all_decoder_outputs=True,
+ input_pos_embed=targets,
+ memory_pos_embed=pos_embed)
+ return decoded
diff --git a/official/projects/detr/modeling/detr_test.py b/official/projects/detr/modeling/detr_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..90d6d64906c9ae63a84b65a95560dfc5c53bde71
--- /dev/null
+++ b/official/projects/detr/modeling/detr_test.py
@@ -0,0 +1,70 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tensorflow_models.official.projects.detr.detr."""
+import tensorflow as tf
+from official.projects.detr.modeling import detr
+from official.vision.modeling.backbones import resnet
+
+
+class DetrTest(tf.test.TestCase):
+
+ def test_forward(self):
+ num_queries = 10
+ hidden_size = 128
+ num_classes = 10
+ image_size = 640
+ batch_size = 2
+ backbone = resnet.ResNet(50, bn_trainable=False)
+ backbone_endpoint_name = '5'
+ model = detr.DETR(backbone, backbone_endpoint_name, num_queries,
+ hidden_size, num_classes)
+ outs = model(tf.ones((batch_size, image_size, image_size, 3)))
+ self.assertLen(outs, 6) # intermediate decoded outputs.
+ for out in outs:
+ self.assertAllEqual(
+ tf.shape(out['cls_outputs']), (batch_size, num_queries, num_classes))
+ self.assertAllEqual(
+ tf.shape(out['box_outputs']), (batch_size, num_queries, 4))
+
+ def test_get_from_config_detr_transformer(self):
+ config = {
+ 'num_encoder_layers': 1,
+ 'num_decoder_layers': 2,
+ 'dropout_rate': 0.5,
+ }
+ detr_model = detr.DETRTransformer.from_config(config)
+ retrieved_config = detr_model.get_config()
+
+ self.assertEqual(config, retrieved_config)
+
+ def test_get_from_config_detr(self):
+ config = {
+ 'backbone': resnet.ResNet(50, bn_trainable=False),
+ 'backbone_endpoint_name': '5',
+ 'num_queries': 2,
+ 'hidden_size': 4,
+ 'num_classes': 10,
+ 'num_encoder_layers': 4,
+ 'num_decoder_layers': 5,
+ 'dropout_rate': 0.5,
+ }
+ detr_model = detr.DETR.from_config(config)
+ retrieved_config = detr_model.get_config()
+
+ self.assertEqual(config, retrieved_config)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/modeling/transformer.py b/official/projects/detr/modeling/transformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..d1eeb9aa118da33dd087c71cde95c66d0835b4a4
--- /dev/null
+++ b/official/projects/detr/modeling/transformer.py
@@ -0,0 +1,851 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Specialized Transformers for DETR.
+
+the position embeddings are added to the query and key for every self- and
+cross-attention layer.
+"""
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.nlp.modeling import layers
+from official.nlp.modeling import models
+
+
+class TransformerEncoder(tf.keras.layers.Layer):
+ """Transformer encoder.
+
+ Transformer encoder is made up of N identical layers. Each layer is composed
+ of the sublayers:
+ 1. Self-attention layer
+ 2. Feedforward network (which is 2 fully-connected layers)
+ """
+
+ def __init__(self,
+ num_layers=6,
+ num_attention_heads=8,
+ intermediate_size=2048,
+ activation="relu",
+ dropout_rate=0.0,
+ attention_dropout_rate=0.0,
+ use_bias=False,
+ norm_first=True,
+ norm_epsilon=1e-6,
+ intermediate_dropout=0.0,
+ **kwargs):
+ """Initialize a Transformer encoder.
+
+ Args:
+ num_layers: Number of layers.
+ num_attention_heads: Number of attention heads.
+ intermediate_size: Size of the intermediate (Feedforward) layer.
+ activation: Activation for the intermediate layer.
+ dropout_rate: Dropout probability.
+ attention_dropout_rate: Dropout probability for attention layers.
+ use_bias: Whether to enable use_bias in attention layer. If set False,
+ use_bias in attention layer is disabled.
+ norm_first: Whether to normalize inputs to attention and intermediate
+ dense layers. If set False, output of attention and intermediate dense
+ layers is normalized.
+ norm_epsilon: Epsilon value to initialize normalization layers.
+ intermediate_dropout: Dropout probability for intermediate_dropout_layer.
+ **kwargs: key word arguemnts passed to tf.keras.layers.Layer.
+ """
+
+ super(TransformerEncoder, self).__init__(**kwargs)
+ self.num_layers = num_layers
+ self.num_attention_heads = num_attention_heads
+ self._intermediate_size = intermediate_size
+ self._activation = activation
+ self._dropout_rate = dropout_rate
+ self._attention_dropout_rate = attention_dropout_rate
+ self._use_bias = use_bias
+ self._norm_first = norm_first
+ self._norm_epsilon = norm_epsilon
+ self._intermediate_dropout = intermediate_dropout
+
+ def build(self, input_shape):
+ """Implements build() for the layer."""
+ self.encoder_layers = []
+ for i in range(self.num_layers):
+ self.encoder_layers.append(
+ TransformerEncoderBlock(
+ num_attention_heads=self.num_attention_heads,
+ inner_dim=self._intermediate_size,
+ inner_activation=self._activation,
+ output_dropout=self._dropout_rate,
+ attention_dropout=self._attention_dropout_rate,
+ use_bias=self._use_bias,
+ norm_first=self._norm_first,
+ norm_epsilon=self._norm_epsilon,
+ inner_dropout=self._intermediate_dropout,
+ attention_initializer=tf_utils.clone_initializer(
+ models.seq2seq_transformer.attention_initializer(
+ input_shape[2])),
+ name=("layer_%d" % i)))
+ self.output_normalization = tf.keras.layers.LayerNormalization(
+ epsilon=self._norm_epsilon, dtype="float32")
+ super(TransformerEncoder, self).build(input_shape)
+
+ def get_config(self):
+ config = {
+ "num_layers": self.num_layers,
+ "num_attention_heads": self.num_attention_heads,
+ "intermediate_size": self._intermediate_size,
+ "activation": self._activation,
+ "dropout_rate": self._dropout_rate,
+ "attention_dropout_rate": self._attention_dropout_rate,
+ "use_bias": self._use_bias,
+ "norm_first": self._norm_first,
+ "norm_epsilon": self._norm_epsilon,
+ "intermediate_dropout": self._intermediate_dropout
+ }
+ base_config = super(TransformerEncoder, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, encoder_inputs, attention_mask=None, pos_embed=None):
+ """Return the output of the encoder.
+
+ Args:
+ encoder_inputs: A tensor with shape `(batch_size, input_length,
+ hidden_size)`.
+ attention_mask: A mask for the encoder self-attention layer with shape
+ `(batch_size, input_length, input_length)`.
+ pos_embed: Position embedding to add to every encoder layer.
+
+ Returns:
+ Output of encoder which is a `float32` tensor with shape
+ `(batch_size, input_length, hidden_size)`.
+ """
+ for layer_idx in range(self.num_layers):
+ encoder_inputs = self.encoder_layers[layer_idx](
+ [encoder_inputs, attention_mask, pos_embed])
+
+ output_tensor = encoder_inputs
+ output_tensor = self.output_normalization(output_tensor)
+
+ return output_tensor
+
+
+class TransformerEncoderBlock(tf.keras.layers.Layer):
+ """TransformerEncoderBlock layer.
+
+ This layer implements the Transformer Encoder from
+ "Attention Is All You Need". (https://arxiv.org/abs/1706.03762),
+ which combines a `tf.keras.layers.MultiHeadAttention` layer with a
+ two-layer feedforward network. The only difference: position embedding is
+ added to the query and key of self-attention.
+
+ References:
+ [Attention Is All You Need](https://arxiv.org/abs/1706.03762)
+ [BERT: Pre-training of Deep Bidirectional Transformers for Language
+ Understanding](https://arxiv.org/abs/1810.04805)
+ """
+
+ def __init__(self,
+ num_attention_heads,
+ inner_dim,
+ inner_activation,
+ output_range=None,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros",
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activity_regularizer=None,
+ kernel_constraint=None,
+ bias_constraint=None,
+ use_bias=True,
+ norm_first=False,
+ norm_epsilon=1e-12,
+ output_dropout=0.0,
+ attention_dropout=0.0,
+ inner_dropout=0.0,
+ attention_initializer=None,
+ attention_axes=None,
+ **kwargs):
+ """Initializes `TransformerEncoderBlock`.
+
+ Args:
+ num_attention_heads: Number of attention heads.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network.
+ output_range: the sequence output range, [0, output_range) for slicing the
+ target sequence. `None` means the target sequence is not sliced.
+ kernel_initializer: Initializer for dense layer kernels.
+ bias_initializer: Initializer for dense layer biases.
+ kernel_regularizer: Regularizer for dense layer kernels.
+ bias_regularizer: Regularizer for dense layer biases.
+ activity_regularizer: Regularizer for dense layer activity.
+ kernel_constraint: Constraint for dense layer kernels.
+ bias_constraint: Constraint for dense layer kernels.
+ use_bias: Whether to enable use_bias in attention layer. If set False,
+ use_bias in attention layer is disabled.
+ norm_first: Whether to normalize inputs to attention and intermediate
+ dense layers. If set False, output of attention and intermediate dense
+ layers is normalized.
+ norm_epsilon: Epsilon value to initialize normalization layers.
+ output_dropout: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout: Dropout probability for within the attention layer.
+ inner_dropout: Dropout probability for the first Dense layer in a
+ two-layer feedforward network.
+ attention_initializer: Initializer for kernels of attention layers. If set
+ `None`, attention layers use kernel_initializer as initializer for
+ kernel.
+ attention_axes: axes over which the attention is applied. `None` means
+ attention over all axes, but batch, heads, and features.
+ **kwargs: keyword arguments/
+ """
+ super().__init__(**kwargs)
+
+ self._num_heads = num_attention_heads
+ self._inner_dim = inner_dim
+ self._inner_activation = inner_activation
+ self._attention_dropout = attention_dropout
+ self._attention_dropout_rate = attention_dropout
+ self._output_dropout = output_dropout
+ self._output_dropout_rate = output_dropout
+ self._output_range = output_range
+ self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
+ self._bias_initializer = tf.keras.initializers.get(bias_initializer)
+ self._kernel_regularizer = tf.keras.regularizers.get(kernel_regularizer)
+ self._bias_regularizer = tf.keras.regularizers.get(bias_regularizer)
+ self._activity_regularizer = tf.keras.regularizers.get(activity_regularizer)
+ self._kernel_constraint = tf.keras.constraints.get(kernel_constraint)
+ self._bias_constraint = tf.keras.constraints.get(bias_constraint)
+ self._use_bias = use_bias
+ self._norm_first = norm_first
+ self._norm_epsilon = norm_epsilon
+ self._inner_dropout = inner_dropout
+ if attention_initializer:
+ self._attention_initializer = tf.keras.initializers.get(
+ attention_initializer)
+ else:
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
+ self._attention_axes = attention_axes
+
+ def build(self, input_shape):
+ if isinstance(input_shape, tf.TensorShape):
+ input_tensor_shape = input_shape
+ elif isinstance(input_shape, (list, tuple)):
+ input_tensor_shape = tf.TensorShape(input_shape[0])
+ else:
+ raise ValueError(
+ "The type of input shape argument is not supported, got: %s" %
+ type(input_shape))
+ einsum_equation = "abc,cd->abd"
+ if len(input_tensor_shape.as_list()) > 3:
+ einsum_equation = "...bc,cd->...bd"
+ hidden_size = input_tensor_shape[-1]
+ if hidden_size % self._num_heads != 0:
+ raise ValueError(
+ "The input size (%d) is not a multiple of the number of attention "
+ "heads (%d)" % (hidden_size, self._num_heads))
+ self._attention_head_size = int(hidden_size // self._num_heads)
+ common_kwargs = dict(
+ bias_initializer=self._bias_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activity_regularizer=self._activity_regularizer,
+ kernel_constraint=self._kernel_constraint,
+ bias_constraint=self._bias_constraint)
+ self._attention_layer = tf.keras.layers.MultiHeadAttention(
+ num_heads=self._num_heads,
+ key_dim=self._attention_head_size,
+ dropout=self._attention_dropout,
+ use_bias=self._use_bias,
+ kernel_initializer=self._attention_initializer,
+ attention_axes=self._attention_axes,
+ name="self_attention",
+ **common_kwargs)
+ self._attention_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ # Use float32 in layernorm for numeric stability.
+ # It is probably safe in mixed_float16, but we haven't validated this yet.
+ self._attention_layer_norm = (
+ tf.keras.layers.LayerNormalization(
+ name="self_attention_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype=tf.float32))
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=(None, self._inner_dim),
+ bias_axes="d",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ name="intermediate",
+ **common_kwargs)
+ policy = tf.keras.mixed_precision.global_policy()
+ if policy.name == "mixed_bfloat16":
+ # bfloat16 causes BERT with the LAMB optimizer to not converge
+ # as well, so we use float32.
+ # TODO(b/154538392): Investigate this.
+ policy = tf.float32
+ self._intermediate_activation_layer = tf.keras.layers.Activation(
+ self._inner_activation, dtype=policy)
+ self._inner_dropout_layer = tf.keras.layers.Dropout(
+ rate=self._inner_dropout)
+ self._output_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=(None, hidden_size),
+ bias_axes="d",
+ name="output",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ **common_kwargs)
+ self._output_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ # Use float32 in layernorm for numeric stability.
+ self._output_layer_norm = tf.keras.layers.LayerNormalization(
+ name="output_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype=tf.float32)
+
+ super(TransformerEncoderBlock, self).build(input_shape)
+
+ def get_config(self):
+ config = {
+ "num_attention_heads":
+ self._num_heads,
+ "inner_dim":
+ self._inner_dim,
+ "inner_activation":
+ self._inner_activation,
+ "output_dropout":
+ self._output_dropout_rate,
+ "attention_dropout":
+ self._attention_dropout_rate,
+ "output_range":
+ self._output_range,
+ "kernel_initializer":
+ tf.keras.initializers.serialize(self._kernel_initializer),
+ "bias_initializer":
+ tf.keras.initializers.serialize(self._bias_initializer),
+ "kernel_regularizer":
+ tf.keras.regularizers.serialize(self._kernel_regularizer),
+ "bias_regularizer":
+ tf.keras.regularizers.serialize(self._bias_regularizer),
+ "activity_regularizer":
+ tf.keras.regularizers.serialize(self._activity_regularizer),
+ "kernel_constraint":
+ tf.keras.constraints.serialize(self._kernel_constraint),
+ "bias_constraint":
+ tf.keras.constraints.serialize(self._bias_constraint),
+ "use_bias":
+ self._use_bias,
+ "norm_first":
+ self._norm_first,
+ "norm_epsilon":
+ self._norm_epsilon,
+ "inner_dropout":
+ self._inner_dropout,
+ "attention_initializer":
+ tf.keras.initializers.serialize(self._attention_initializer),
+ "attention_axes":
+ self._attention_axes,
+ }
+ base_config = super(TransformerEncoderBlock, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs):
+ """Transformer self-attention encoder block call.
+
+ Args:
+ inputs: a single tensor or a list of tensors. `input tensor` as the single
+ sequence of embeddings. [`input tensor`, `attention mask`] to have the
+ additional attention mask. [`input tensor`, `attention mask`, `query
+ embed`] to have an additional position embedding to add.
+
+ Returns:
+ An output tensor with the same dimensions as input/query tensor.
+ """
+ input_tensor, attention_mask, pos_embed = inputs
+
+ key_value = None
+
+ if self._output_range:
+ if self._norm_first:
+ source_tensor = input_tensor[:, 0:self._output_range, :]
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor[:, 0:self._output_range, :]
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, 0:self._output_range, :]
+ else:
+ if self._norm_first:
+ source_tensor = input_tensor
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor
+
+ if key_value is None:
+ key_value = input_tensor
+ attention_output = self._attention_layer(
+ query=target_tensor + pos_embed,
+ key=key_value + pos_embed,
+ value=key_value,
+ attention_mask=attention_mask)
+ attention_output = self._attention_dropout(attention_output)
+ if self._norm_first:
+ attention_output = source_tensor + attention_output
+ else:
+ attention_output = self._attention_layer_norm(target_tensor +
+ attention_output)
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self._output_layer_norm(attention_output)
+ inner_output = self._intermediate_dense(attention_output)
+ inner_output = self._intermediate_activation_layer(inner_output)
+ inner_output = self._inner_dropout_layer(inner_output)
+ layer_output = self._output_dense(inner_output)
+ layer_output = self._output_dropout(layer_output)
+
+ if self._norm_first:
+ return source_attention_output + layer_output
+
+ # During mixed precision training, layer norm output is always fp32 for now.
+ # Casts fp32 for the subsequent add.
+ layer_output = tf.cast(layer_output, tf.float32)
+ return self._output_layer_norm(layer_output + attention_output)
+
+
+class TransformerDecoder(tf.keras.layers.Layer):
+ """Transformer decoder.
+
+ Like the encoder, the decoder is made up of N identical layers.
+ Each layer is composed of the sublayers:
+ 1. Self-attention layer
+ 2. Multi-headed attention layer combining encoder outputs with results from
+ the previous self-attention layer.
+ 3. Feedforward network (2 fully-connected layers)
+ """
+
+ def __init__(self,
+ num_layers=6,
+ num_attention_heads=8,
+ intermediate_size=2048,
+ activation="relu",
+ dropout_rate=0.0,
+ attention_dropout_rate=0.0,
+ use_bias=False,
+ norm_first=True,
+ norm_epsilon=1e-6,
+ intermediate_dropout=0.0,
+ **kwargs):
+ """Initialize a Transformer decoder.
+
+ Args:
+ num_layers: Number of layers.
+ num_attention_heads: Number of attention heads.
+ intermediate_size: Size of the intermediate (Feedforward) layer.
+ activation: Activation for the intermediate layer.
+ dropout_rate: Dropout probability.
+ attention_dropout_rate: Dropout probability for attention layers.
+ use_bias: Whether to enable use_bias in attention layer. If set `False`,
+ use_bias in attention layer is disabled.
+ norm_first: Whether to normalize inputs to attention and intermediate
+ dense layers. If set `False`, output of attention and intermediate dense
+ layers is normalized.
+ norm_epsilon: Epsilon value to initialize normalization layers.
+ intermediate_dropout: Dropout probability for intermediate_dropout_layer.
+ **kwargs: key word arguemnts passed to tf.keras.layers.Layer.
+ """
+ super(TransformerDecoder, self).__init__(**kwargs)
+ self.num_layers = num_layers
+ self.num_attention_heads = num_attention_heads
+ self._intermediate_size = intermediate_size
+ self._activation = activation
+ self._dropout_rate = dropout_rate
+ self._attention_dropout_rate = attention_dropout_rate
+ self._use_bias = use_bias
+ self._norm_first = norm_first
+ self._norm_epsilon = norm_epsilon
+ self._intermediate_dropout = intermediate_dropout
+
+ def build(self, input_shape):
+ """Implements build() for the layer."""
+ self.decoder_layers = []
+ for i in range(self.num_layers):
+ self.decoder_layers.append(
+ TransformerDecoderBlock(
+ num_attention_heads=self.num_attention_heads,
+ intermediate_size=self._intermediate_size,
+ intermediate_activation=self._activation,
+ dropout_rate=self._dropout_rate,
+ attention_dropout_rate=self._attention_dropout_rate,
+ use_bias=self._use_bias,
+ norm_first=self._norm_first,
+ norm_epsilon=self._norm_epsilon,
+ intermediate_dropout=self._intermediate_dropout,
+ attention_initializer=tf_utils.clone_initializer(
+ models.seq2seq_transformer.attention_initializer(
+ input_shape[2])),
+ name=("layer_%d" % i)))
+ self.output_normalization = tf.keras.layers.LayerNormalization(
+ epsilon=self._norm_epsilon, dtype="float32")
+ super(TransformerDecoder, self).build(input_shape)
+
+ def get_config(self):
+ config = {
+ "num_layers": self.num_layers,
+ "num_attention_heads": self.num_attention_heads,
+ "intermediate_size": self._intermediate_size,
+ "activation": self._activation,
+ "dropout_rate": self._dropout_rate,
+ "attention_dropout_rate": self._attention_dropout_rate,
+ "use_bias": self._use_bias,
+ "norm_first": self._norm_first,
+ "norm_epsilon": self._norm_epsilon,
+ "intermediate_dropout": self._intermediate_dropout
+ }
+ base_config = super(TransformerDecoder, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self,
+ target,
+ memory,
+ self_attention_mask=None,
+ cross_attention_mask=None,
+ cache=None,
+ decode_loop_step=None,
+ return_all_decoder_outputs=False,
+ input_pos_embed=None,
+ memory_pos_embed=None):
+ """Return the output of the decoder layer stacks.
+
+ Args:
+ target: A tensor with shape `(batch_size, target_length, hidden_size)`.
+ memory: A tensor with shape `(batch_size, input_length, hidden_size)`.
+ self_attention_mask: A tensor with shape `(batch_size, target_len,
+ target_length)`, the mask for decoder self-attention layer.
+ cross_attention_mask: A tensor with shape `(batch_size, target_length,
+ input_length)` which is the mask for encoder-decoder attention layer.
+ cache: (Used for fast decoding) A nested dictionary storing previous
+ decoder self-attention values. The items are:
+ {layer_n: {"k": A tensor with shape `(batch_size, i, key_channels)`,
+ "v": A tensor with shape `(batch_size, i, value_channels)`},
+ ...}
+ decode_loop_step: An integer, the step number of the decoding loop. Used
+ only for autoregressive inference on TPU.
+ return_all_decoder_outputs: Return all decoder layer outputs. Note that
+ the outputs are layer normed. This is useful when introducing per layer
+ auxiliary loss.
+ input_pos_embed: A tensor that is added to the query and key of the
+ self-attention layer.
+ memory_pos_embed: A tensor that is added to the query and key of the
+ cross-attention layer.
+
+ Returns:
+ Output of decoder.
+ float32 tensor with shape `(batch_size, target_length, hidden_size`).
+ """
+
+ output_tensor = target
+ decoder_outputs = []
+ for layer_idx in range(self.num_layers):
+ transformer_inputs = [
+ output_tensor, memory, cross_attention_mask, self_attention_mask,
+ input_pos_embed, memory_pos_embed
+ ]
+ # Gets the cache for decoding.
+ if cache is None:
+ output_tensor, _ = self.decoder_layers[layer_idx](transformer_inputs)
+ else:
+ cache_layer_idx = str(layer_idx)
+ output_tensor, cache[cache_layer_idx] = self.decoder_layers[layer_idx](
+ transformer_inputs,
+ cache=cache[cache_layer_idx],
+ decode_loop_step=decode_loop_step)
+ if return_all_decoder_outputs:
+ decoder_outputs.append(self.output_normalization(output_tensor))
+
+ if return_all_decoder_outputs:
+ return decoder_outputs
+ else:
+ return self.output_normalization(output_tensor)
+
+
+class TransformerDecoderBlock(tf.keras.layers.Layer):
+ """Single transformer layer for decoder.
+
+ It has three sub-layers:
+ (1) a multi-head self-attention mechanism.
+ (2) a encoder-decoder attention.
+ (3) a positionwise fully connected feed-forward network.
+ """
+
+ def __init__(self,
+ num_attention_heads,
+ intermediate_size,
+ intermediate_activation,
+ dropout_rate=0.0,
+ attention_dropout_rate=0.0,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros",
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activity_regularizer=None,
+ kernel_constraint=None,
+ bias_constraint=None,
+ use_bias=True,
+ norm_first=False,
+ norm_epsilon=1e-12,
+ intermediate_dropout=0.0,
+ attention_initializer=None,
+ **kwargs):
+ """Initialize a Transformer decoder block.
+
+ Args:
+ num_attention_heads: Number of attention heads.
+ intermediate_size: Size of the intermediate layer.
+ intermediate_activation: Activation for the intermediate layer.
+ dropout_rate: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout_rate: Dropout probability for within the attention
+ layer.
+ kernel_initializer: Initializer for dense layer kernels.
+ bias_initializer: Initializer for dense layer biases.
+ kernel_regularizer: Regularizer for dense layer kernels.
+ bias_regularizer: Regularizer for dense layer biases.
+ activity_regularizer: Regularizer for dense layer activity.
+ kernel_constraint: Constraint for dense layer kernels.
+ bias_constraint: Constraint for dense layer kernels.
+ use_bias: Whether to enable use_bias in attention layer. If set False,
+ use_bias in attention layer is disabled.
+ norm_first: Whether to normalize inputs to attention and intermediate
+ dense layers. If set False, output of attention and intermediate dense
+ layers is normalized.
+ norm_epsilon: Epsilon value to initialize normalization layers.
+ intermediate_dropout: Dropout probability for intermediate_dropout_layer.
+ attention_initializer: Initializer for kernels of attention layers. If set
+ `None`, attention layers use kernel_initializer as initializer for
+ kernel.
+ **kwargs: key word arguemnts passed to tf.keras.layers.Layer.
+ """
+ super().__init__(**kwargs)
+ self.num_attention_heads = num_attention_heads
+ self.intermediate_size = intermediate_size
+ self.intermediate_activation = tf.keras.activations.get(
+ intermediate_activation)
+ self.dropout_rate = dropout_rate
+ self.attention_dropout_rate = attention_dropout_rate
+ self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
+ self._bias_initializer = tf.keras.initializers.get(bias_initializer)
+ self._kernel_regularizer = tf.keras.regularizers.get(kernel_regularizer)
+ self._bias_regularizer = tf.keras.regularizers.get(bias_regularizer)
+ self._activity_regularizer = tf.keras.regularizers.get(activity_regularizer)
+ self._kernel_constraint = tf.keras.constraints.get(kernel_constraint)
+ self._bias_constraint = tf.keras.constraints.get(bias_constraint)
+ self._use_bias = use_bias
+ self._norm_first = norm_first
+ self._norm_epsilon = norm_epsilon
+ self._intermediate_dropout = intermediate_dropout
+ if attention_initializer:
+ self._attention_initializer = tf.keras.initializers.get(
+ attention_initializer)
+ else:
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
+ self._cross_attention_cls = layers.attention.MultiHeadAttention
+
+ def build(self, input_shape):
+ target_tensor_shape = tf.TensorShape(input_shape[0])
+ if len(target_tensor_shape.as_list()) != 3:
+ raise ValueError("TransformerLayer expects a three-dimensional input of "
+ "shape [batch, sequence, width].")
+ hidden_size = target_tensor_shape[2]
+ if hidden_size % self.num_attention_heads != 0:
+ raise ValueError(
+ "The hidden size (%d) is not a multiple of the number of attention "
+ "heads (%d)" % (hidden_size, self.num_attention_heads))
+ self.attention_head_size = int(hidden_size) // self.num_attention_heads
+ common_kwargs = dict(
+ bias_initializer=self._bias_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activity_regularizer=self._activity_regularizer,
+ kernel_constraint=self._kernel_constraint,
+ bias_constraint=self._bias_constraint)
+ # Self attention.
+ self.self_attention = layers.attention.CachedAttention(
+ num_heads=self.num_attention_heads,
+ key_dim=self.attention_head_size,
+ dropout=self.attention_dropout_rate,
+ use_bias=self._use_bias,
+ kernel_initializer=self._attention_initializer,
+ name="self_attention",
+ **common_kwargs)
+ self.self_attention_output_dense = tf.keras.layers.EinsumDense(
+ "abc,cd->abd",
+ output_shape=(None, hidden_size),
+ bias_axes="d",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ name="output",
+ **common_kwargs)
+ self.self_attention_dropout = tf.keras.layers.Dropout(
+ rate=self.dropout_rate)
+ self.self_attention_layer_norm = (
+ tf.keras.layers.LayerNormalization(
+ name="self_attention_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype="float32"))
+ # Encoder-decoder attention.
+ self.encdec_attention = self._cross_attention_cls(
+ num_heads=self.num_attention_heads,
+ key_dim=self.attention_head_size,
+ dropout=self.attention_dropout_rate,
+ output_shape=hidden_size,
+ use_bias=self._use_bias,
+ kernel_initializer=self._attention_initializer,
+ name="attention/encdec",
+ **common_kwargs)
+
+ self.encdec_attention_dropout = tf.keras.layers.Dropout(
+ rate=self.dropout_rate)
+ self.encdec_attention_layer_norm = (
+ tf.keras.layers.LayerNormalization(
+ name="attention/encdec_output_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype="float32"))
+
+ # Feed-forward projection.
+ self.intermediate_dense = tf.keras.layers.EinsumDense(
+ "abc,cd->abd",
+ output_shape=(None, self.intermediate_size),
+ bias_axes="d",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ name="intermediate",
+ **common_kwargs)
+ self.intermediate_activation_layer = tf.keras.layers.Activation(
+ self.intermediate_activation)
+ self._intermediate_dropout_layer = tf.keras.layers.Dropout(
+ rate=self._intermediate_dropout)
+ self.output_dense = tf.keras.layers.EinsumDense(
+ "abc,cd->abd",
+ output_shape=(None, hidden_size),
+ bias_axes="d",
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ name="output",
+ **common_kwargs)
+ self.output_dropout = tf.keras.layers.Dropout(rate=self.dropout_rate)
+ self.output_layer_norm = tf.keras.layers.LayerNormalization(
+ name="output_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype="float32")
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {
+ "num_attention_heads":
+ self.num_attention_heads,
+ "intermediate_size":
+ self.intermediate_size,
+ "intermediate_activation":
+ tf.keras.activations.serialize(self.intermediate_activation),
+ "dropout_rate":
+ self.dropout_rate,
+ "attention_dropout_rate":
+ self.attention_dropout_rate,
+ "kernel_initializer":
+ tf.keras.initializers.serialize(self._kernel_initializer),
+ "bias_initializer":
+ tf.keras.initializers.serialize(self._bias_initializer),
+ "kernel_regularizer":
+ tf.keras.regularizers.serialize(self._kernel_regularizer),
+ "bias_regularizer":
+ tf.keras.regularizers.serialize(self._bias_regularizer),
+ "activity_regularizer":
+ tf.keras.regularizers.serialize(self._activity_regularizer),
+ "kernel_constraint":
+ tf.keras.constraints.serialize(self._kernel_constraint),
+ "bias_constraint":
+ tf.keras.constraints.serialize(self._bias_constraint),
+ "use_bias":
+ self._use_bias,
+ "norm_first":
+ self._norm_first,
+ "norm_epsilon":
+ self._norm_epsilon,
+ "intermediate_dropout":
+ self._intermediate_dropout,
+ "attention_initializer":
+ tf.keras.initializers.serialize(self._attention_initializer)
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def common_layers_with_encoder(self):
+ """Gets layer objects that can make a Transformer encoder block."""
+ return [
+ self.self_attention, self.self_attention_layer_norm,
+ self.intermediate_dense, self.output_dense, self.output_layer_norm
+ ]
+
+ def call(self, inputs, cache=None, decode_loop_step=None):
+ input_tensor, memory, attention_mask, self_attention_mask, input_pos_embed, memory_pos_embed = inputs
+ source_tensor = input_tensor
+ if self._norm_first:
+ input_tensor = self.self_attention_layer_norm(input_tensor)
+ self_attention_output, cache = self.self_attention(
+ query=input_tensor + input_pos_embed,
+ key=input_tensor + input_pos_embed,
+ value=input_tensor,
+ attention_mask=self_attention_mask,
+ cache=cache,
+ decode_loop_step=decode_loop_step)
+ self_attention_output = self.self_attention_dropout(self_attention_output)
+ if self._norm_first:
+ self_attention_output = source_tensor + self_attention_output
+ else:
+ self_attention_output = self.self_attention_layer_norm(
+ input_tensor + self_attention_output)
+ if self._norm_first:
+ source_self_attention_output = self_attention_output
+ self_attention_output = self.encdec_attention_layer_norm(
+ self_attention_output)
+ cross_attn_inputs = dict(
+ query=self_attention_output + input_pos_embed,
+ key=memory + memory_pos_embed,
+ value=memory,
+ attention_mask=attention_mask)
+ attention_output = self.encdec_attention(**cross_attn_inputs)
+ attention_output = self.encdec_attention_dropout(attention_output)
+ if self._norm_first:
+ attention_output = source_self_attention_output + attention_output
+ else:
+ attention_output = self.encdec_attention_layer_norm(
+ self_attention_output + attention_output)
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self.output_layer_norm(attention_output)
+
+ intermediate_output = self.intermediate_dense(attention_output)
+ intermediate_output = self.intermediate_activation_layer(
+ intermediate_output)
+ intermediate_output = self._intermediate_dropout_layer(intermediate_output)
+ layer_output = self.output_dense(intermediate_output)
+ layer_output = self.output_dropout(layer_output)
+ if self._norm_first:
+ layer_output = source_attention_output + layer_output
+ else:
+ layer_output = self.output_layer_norm(layer_output + attention_output)
+ return layer_output, cache
diff --git a/official/projects/detr/modeling/transformer_test.py b/official/projects/detr/modeling/transformer_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..0752403a2a816beca3da2f07b648214228a8cf80
--- /dev/null
+++ b/official/projects/detr/modeling/transformer_test.py
@@ -0,0 +1,263 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for transformer."""
+
+import tensorflow as tf
+
+from official.projects.detr.modeling import transformer
+
+
+class TransformerTest(tf.test.TestCase):
+
+ def test_transformer_encoder_block(self):
+ batch_size = 2
+ sequence_length = 100
+ feature_size = 256
+ num_attention_heads = 2
+ inner_dim = 256
+ inner_activation = 'relu'
+ model = transformer.TransformerEncoderBlock(num_attention_heads, inner_dim,
+ inner_activation)
+ input_tensor = tf.ones((batch_size, sequence_length, feature_size))
+ attention_mask = tf.ones((batch_size, sequence_length, sequence_length),
+ dtype=tf.int64)
+ pos_embed = tf.ones((batch_size, sequence_length, feature_size))
+
+ out = model([input_tensor, attention_mask, pos_embed])
+ self.assertAllEqual(
+ tf.shape(out), (batch_size, sequence_length, feature_size))
+
+ def test_transformer_encoder_block_get_config(self):
+ num_attention_heads = 2
+ inner_dim = 256
+ inner_activation = 'relu'
+ model = transformer.TransformerEncoderBlock(num_attention_heads, inner_dim,
+ inner_activation)
+ config = model.get_config()
+ expected_config = {
+ 'name': 'transformer_encoder_block',
+ 'trainable': True,
+ 'dtype': 'float32',
+ 'num_attention_heads': 2,
+ 'inner_dim': 256,
+ 'inner_activation': 'relu',
+ 'output_dropout': 0.0,
+ 'attention_dropout': 0.0,
+ 'output_range': None,
+ 'kernel_initializer': {
+ 'class_name': 'GlorotUniform',
+ 'config': {
+ 'seed': None}
+ },
+ 'bias_initializer': {
+ 'class_name': 'Zeros',
+ 'config': {}
+ },
+ 'kernel_regularizer': None,
+ 'bias_regularizer': None,
+ 'activity_regularizer': None,
+ 'kernel_constraint': None,
+ 'bias_constraint': None,
+ 'use_bias': True,
+ 'norm_first': False,
+ 'norm_epsilon': 1e-12,
+ 'inner_dropout': 0.0,
+ 'attention_initializer': {
+ 'class_name': 'GlorotUniform',
+ 'config': {'seed': None}
+ },
+ 'attention_axes': None}
+ self.assertAllEqual(expected_config, config)
+
+ def test_transformer_encoder(self):
+ batch_size = 2
+ sequence_length = 100
+ feature_size = 256
+ num_layers = 2
+ num_attention_heads = 2
+ intermediate_size = 256
+ model = transformer.TransformerEncoder(
+ num_layers=num_layers,
+ num_attention_heads=num_attention_heads,
+ intermediate_size=intermediate_size)
+ input_tensor = tf.ones((batch_size, sequence_length, feature_size))
+ attention_mask = tf.ones((batch_size, sequence_length, sequence_length),
+ dtype=tf.int64)
+ pos_embed = tf.ones((batch_size, sequence_length, feature_size))
+ out = model(input_tensor, attention_mask, pos_embed)
+ self.assertAllEqual(
+ tf.shape(out), (batch_size, sequence_length, feature_size))
+
+ def test_transformer_encoder_get_config(self):
+ num_layers = 2
+ num_attention_heads = 2
+ intermediate_size = 256
+ model = transformer.TransformerEncoder(
+ num_layers=num_layers,
+ num_attention_heads=num_attention_heads,
+ intermediate_size=intermediate_size)
+ config = model.get_config()
+ expected_config = {
+ 'name': 'transformer_encoder',
+ 'trainable': True,
+ 'dtype': 'float32',
+ 'num_layers': 2,
+ 'num_attention_heads': 2,
+ 'intermediate_size': 256,
+ 'activation': 'relu',
+ 'dropout_rate': 0.0,
+ 'attention_dropout_rate': 0.0,
+ 'use_bias': False,
+ 'norm_first': True,
+ 'norm_epsilon': 1e-06,
+ 'intermediate_dropout': 0.0
+ }
+ self.assertAllEqual(expected_config, config)
+
+ def test_transformer_decoder_block(self):
+ batch_size = 2
+ sequence_length = 100
+ memory_length = 200
+ feature_size = 256
+ num_attention_heads = 2
+ intermediate_size = 256
+ intermediate_activation = 'relu'
+ model = transformer.TransformerDecoderBlock(num_attention_heads,
+ intermediate_size,
+ intermediate_activation)
+ input_tensor = tf.ones((batch_size, sequence_length, feature_size))
+ memory = tf.ones((batch_size, memory_length, feature_size))
+ attention_mask = tf.ones((batch_size, sequence_length, memory_length),
+ dtype=tf.int64)
+ self_attention_mask = tf.ones(
+ (batch_size, sequence_length, sequence_length), dtype=tf.int64)
+ input_pos_embed = tf.ones((batch_size, sequence_length, feature_size))
+ memory_pos_embed = tf.ones((batch_size, memory_length, feature_size))
+
+ out, _ = model([
+ input_tensor, memory, attention_mask, self_attention_mask,
+ input_pos_embed, memory_pos_embed
+ ])
+ self.assertAllEqual(
+ tf.shape(out), (batch_size, sequence_length, feature_size))
+
+ def test_transformer_decoder_block_get_config(self):
+ num_attention_heads = 2
+ intermediate_size = 256
+ intermediate_activation = 'relu'
+ model = transformer.TransformerDecoderBlock(num_attention_heads,
+ intermediate_size,
+ intermediate_activation)
+ config = model.get_config()
+ expected_config = {
+ 'name': 'transformer_decoder_block',
+ 'trainable': True,
+ 'dtype': 'float32',
+ 'num_attention_heads': 2,
+ 'intermediate_size': 256,
+ 'intermediate_activation': 'relu',
+ 'dropout_rate': 0.0,
+ 'attention_dropout_rate': 0.0,
+ 'kernel_initializer': {
+ 'class_name': 'GlorotUniform',
+ 'config': {
+ 'seed': None
+ }
+ },
+ 'bias_initializer': {
+ 'class_name': 'Zeros',
+ 'config': {}
+ },
+ 'kernel_regularizer': None,
+ 'bias_regularizer': None,
+ 'activity_regularizer': None,
+ 'kernel_constraint': None,
+ 'bias_constraint': None,
+ 'use_bias': True,
+ 'norm_first': False,
+ 'norm_epsilon': 1e-12,
+ 'intermediate_dropout': 0.0,
+ 'attention_initializer': {
+ 'class_name': 'GlorotUniform',
+ 'config': {
+ 'seed': None
+ }
+ }
+ }
+ self.assertAllEqual(expected_config, config)
+
+ def test_transformer_decoder(self):
+ batch_size = 2
+ sequence_length = 100
+ memory_length = 200
+ feature_size = 256
+ num_layers = 2
+ num_attention_heads = 2
+ intermediate_size = 256
+ model = transformer.TransformerDecoder(
+ num_layers=num_layers,
+ num_attention_heads=num_attention_heads,
+ intermediate_size=intermediate_size)
+ input_tensor = tf.ones((batch_size, sequence_length, feature_size))
+ memory = tf.ones((batch_size, memory_length, feature_size))
+ attention_mask = tf.ones((batch_size, sequence_length, memory_length),
+ dtype=tf.int64)
+ self_attention_mask = tf.ones(
+ (batch_size, sequence_length, sequence_length), dtype=tf.int64)
+ input_pos_embed = tf.ones((batch_size, sequence_length, feature_size))
+ memory_pos_embed = tf.ones((batch_size, memory_length, feature_size))
+
+ outs = model(
+ input_tensor,
+ memory,
+ self_attention_mask,
+ attention_mask,
+ return_all_decoder_outputs=True,
+ input_pos_embed=input_pos_embed,
+ memory_pos_embed=memory_pos_embed)
+ self.assertLen(outs, 2) # intermeidate decoded outputs.
+ for out in outs:
+ self.assertAllEqual(
+ tf.shape(out), (batch_size, sequence_length, feature_size))
+
+ def test_transformer_decoder_get_config(self):
+ num_layers = 2
+ num_attention_heads = 2
+ intermediate_size = 256
+ model = transformer.TransformerDecoder(
+ num_layers=num_layers,
+ num_attention_heads=num_attention_heads,
+ intermediate_size=intermediate_size)
+ config = model.get_config()
+ expected_config = {
+ 'name': 'transformer_decoder',
+ 'trainable': True,
+ 'dtype': 'float32',
+ 'num_layers': 2,
+ 'num_attention_heads': 2,
+ 'intermediate_size': 256,
+ 'activation': 'relu',
+ 'dropout_rate': 0.0,
+ 'attention_dropout_rate': 0.0,
+ 'use_bias': False,
+ 'norm_first': True,
+ 'norm_epsilon': 1e-06,
+ 'intermediate_dropout': 0.0
+ }
+ self.assertAllEqual(expected_config, config)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/ops/matchers.py b/official/projects/detr/ops/matchers.py
new file mode 100644
index 0000000000000000000000000000000000000000..56f25585ed21208eaac0d5bc75d8ce731aef03a8
--- /dev/null
+++ b/official/projects/detr/ops/matchers.py
@@ -0,0 +1,489 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tensorflow implementation to solve the Linear Sum Assignment problem.
+
+The Linear Sum Assignment problem involves determining the minimum weight
+matching for bipartite graphs. For example, this problem can be defined by
+a 2D matrix C, where each element i,j determines the cost of matching worker i
+with job j. The solution to the problem is a complete assignment of jobs to
+workers, such that no job is assigned to more than one work and no worker is
+assigned more than one job, with minimum cost.
+
+This implementation builds off of the Hungarian
+Matching Algorithm (https://www.cse.ust.hk/~golin/COMP572/Notes/Matching.pdf).
+
+Based on the original implementation by Jiquan Ngiam .
+"""
+import tensorflow as tf
+from official.modeling import tf_utils
+
+
+def _prepare(weights):
+ """Prepare the cost matrix.
+
+ To speed up computational efficiency of the algorithm, all weights are shifted
+ to be non-negative. Each element is reduced by the row / column minimum. Note
+ that neither operation will effect the resulting solution but will provide
+ a better starting point for the greedy assignment. Note this corresponds to
+ the pre-processing and step 1 of the Hungarian algorithm from Wikipedia.
+
+ Args:
+ weights: A float32 [batch_size, num_elems, num_elems] tensor, where each
+ inner matrix represents weights to be use for matching.
+
+ Returns:
+ A prepared weights tensor of the same shape and dtype.
+ """
+ # Since every worker needs a job and every job needs a worker, we can subtract
+ # the minimum from each.
+ weights -= tf.reduce_min(weights, axis=2, keepdims=True)
+ weights -= tf.reduce_min(weights, axis=1, keepdims=True)
+ return weights
+
+
+def _greedy_assignment(adj_matrix):
+ """Greedily assigns workers to jobs based on an adjaceny matrix.
+
+ Starting with an adjacency matrix representing the available connections
+ in the bi-partite graph, this function greedily chooses elements such
+ that each worker is matched to at most one job (or each job is assigned to
+ at most one worker). Note, if the adjacency matrix has no available values
+ for a particular row/column, the corresponding job/worker may go unassigned.
+
+ Args:
+ adj_matrix: A bool [batch_size, num_elems, num_elems] tensor, where each
+ element of the inner matrix represents whether the worker (row) can be
+ matched to the job (column).
+
+ Returns:
+ A bool [batch_size, num_elems, num_elems] tensor, where each element of the
+ inner matrix represents whether the worker has been matched to the job.
+ Each row and column can have at most one true element. Some of the rows
+ and columns may not be matched.
+ """
+ _, num_elems, _ = tf_utils.get_shape_list(adj_matrix, expected_rank=3)
+ adj_matrix = tf.transpose(adj_matrix, [1, 0, 2])
+
+ # Create a dynamic TensorArray containing the assignments for each worker/job
+ assignment = tf.TensorArray(tf.bool, num_elems)
+
+ # Store the elements assigned to each column to update each iteration
+ col_assigned = tf.zeros_like(adj_matrix[0, ...], dtype=tf.bool)
+
+ # Iteratively assign each row using tf.foldl. Intuitively, this is a loop
+ # over rows, where we incrementally assign each row.
+ def _assign_row(accumulator, row_adj):
+ # The accumulator tracks the row assignment index.
+ idx, assignment, col_assigned = accumulator
+
+ # Viable candidates cannot already be assigned to another job.
+ candidates = row_adj & (~col_assigned)
+
+ # Deterministically assign to the candidates of the highest index count.
+ max_candidate_idx = tf.argmax(
+ tf.cast(candidates, tf.int32), axis=1, output_type=tf.int32)
+
+ candidates_indicator = tf.one_hot(
+ max_candidate_idx,
+ num_elems,
+ on_value=True,
+ off_value=False,
+ dtype=tf.bool)
+ candidates_indicator &= candidates
+
+ # Make assignment to the column.
+ col_assigned |= candidates_indicator
+ assignment = assignment.write(idx, candidates_indicator)
+
+ return (idx + 1, assignment, col_assigned)
+
+ _, assignment, _ = tf.foldl(
+ _assign_row, adj_matrix, (0, assignment, col_assigned), back_prop=False)
+
+ assignment = assignment.stack()
+ assignment = tf.transpose(assignment, [1, 0, 2])
+ return assignment
+
+
+def _find_augmenting_path(assignment, adj_matrix):
+ """Finds an augmenting path given an assignment and an adjacency matrix.
+
+ The augmenting path search starts from the unassigned workers, then goes on
+ to find jobs (via an unassigned pairing), then back again to workers (via an
+ existing pairing), and so on. The path alternates between unassigned and
+ existing pairings. Returns the state after the search.
+
+ Note: In the state the worker and job, indices are 1-indexed so that we can
+ use 0 to represent unreachable nodes. State contains the following keys:
+
+ - jobs: A [batch_size, 1, num_elems] tensor containing the highest index
+ unassigned worker that can reach this job through a path.
+ - jobs_from_worker: A [batch_size, num_elems] tensor containing the worker
+ reached immediately before this job.
+ - workers: A [batch_size, num_elems, 1] tensor containing the highest index
+ unassigned worker that can reach this worker through a path.
+ - workers_from_job: A [batch_size, num_elems] tensor containing the job
+ reached immediately before this worker.
+ - new_jobs: A bool [batch_size, num_elems] tensor containing True if the
+ unassigned job can be reached via a path.
+
+ State can be used to recover the path via backtracking.
+
+ Args:
+ assignment: A bool [batch_size, num_elems, num_elems] tensor, where each
+ element of the inner matrix represents whether the worker has been matched
+ to the job. This may be a partial assignment.
+ adj_matrix: A bool [batch_size, num_elems, num_elems] tensor, where each
+ element of the inner matrix represents whether the worker (row) can be
+ matched to the job (column).
+
+ Returns:
+ A state dict, which represents the outcome of running an augmenting
+ path search on the graph given the assignment.
+ """
+ batch_size, num_elems, _ = tf_utils.get_shape_list(
+ assignment, expected_rank=3)
+ unassigned_workers = ~tf.reduce_any(assignment, axis=2, keepdims=True)
+ unassigned_jobs = ~tf.reduce_any(assignment, axis=1, keepdims=True)
+
+ unassigned_pairings = tf.cast(adj_matrix & ~assignment, tf.int32)
+ existing_pairings = tf.cast(assignment, tf.int32)
+
+ # Initialize unassigned workers to have non-zero ids, assigned workers will
+ # have ids = 0.
+ worker_indices = tf.range(1, num_elems + 1, dtype=tf.int32)
+ init_workers = tf.tile(worker_indices[tf.newaxis, :, tf.newaxis],
+ [batch_size, 1, 1])
+ init_workers *= tf.cast(unassigned_workers, tf.int32)
+
+ state = {
+ "jobs": tf.zeros((batch_size, 1, num_elems), dtype=tf.int32),
+ "jobs_from_worker": tf.zeros((batch_size, num_elems), dtype=tf.int32),
+ "workers": init_workers,
+ "workers_from_job": tf.zeros((batch_size, num_elems), dtype=tf.int32)
+ }
+
+ def _has_active_workers(state, curr_workers):
+ """Check if there are still active workers."""
+ del state
+ return tf.reduce_sum(curr_workers) > 0
+
+ def _augment_step(state, curr_workers):
+ """Performs one search step."""
+
+ # Note: These steps could be potentially much faster if sparse matrices are
+ # supported. The unassigned_pairings and existing_pairings matrices can be
+ # very sparse.
+
+ # Find potential jobs using current workers.
+ potential_jobs = curr_workers * unassigned_pairings
+ curr_jobs = tf.reduce_max(potential_jobs, axis=1, keepdims=True)
+ curr_jobs_from_worker = 1 + tf.argmax(
+ potential_jobs, axis=1, output_type=tf.int32)
+
+ # Remove already accessible jobs from curr_jobs.
+ default_jobs = tf.zeros_like(state["jobs"], dtype=state["jobs"].dtype)
+ curr_jobs = tf.where(state["jobs"] > 0, default_jobs, curr_jobs)
+ curr_jobs_from_worker *= tf.cast(curr_jobs > 0, tf.int32)[:, 0, :]
+
+ # Find potential workers from current jobs.
+ potential_workers = curr_jobs * existing_pairings
+ curr_workers = tf.reduce_max(potential_workers, axis=2, keepdims=True)
+ curr_workers_from_job = 1 + tf.argmax(
+ potential_workers, axis=2, output_type=tf.int32)
+
+ # Remove already accessible workers from curr_workers.
+ default_workers = tf.zeros_like(state["workers"])
+ curr_workers = tf.where(
+ state["workers"] > 0, default_workers, curr_workers)
+ curr_workers_from_job *= tf.cast(curr_workers > 0, tf.int32)[:, :, 0]
+
+ # Update state so that we can backtrack later.
+ state = state.copy()
+ state["jobs"] = tf.maximum(state["jobs"], curr_jobs)
+ state["jobs_from_worker"] = tf.maximum(state["jobs_from_worker"],
+ curr_jobs_from_worker)
+ state["workers"] = tf.maximum(state["workers"], curr_workers)
+ state["workers_from_job"] = tf.maximum(state["workers_from_job"],
+ curr_workers_from_job)
+
+ return state, curr_workers
+
+ state, _ = tf.while_loop(
+ _has_active_workers,
+ _augment_step, (state, init_workers),
+ back_prop=False)
+
+ # Compute new jobs, this is useful for determnining termnination of the
+ # maximum bi-partite matching and initialization for backtracking.
+ new_jobs = (state["jobs"] > 0) & unassigned_jobs
+ state["new_jobs"] = new_jobs[:, 0, :]
+ return state
+
+
+def _improve_assignment(assignment, state):
+ """Improves an assignment by backtracking the augmented path using state.
+
+ Args:
+ assignment: A bool [batch_size, num_elems, num_elems] tensor, where each
+ element of the inner matrix represents whether the worker has been matched
+ to the job. This may be a partial assignment.
+ state: A dict, which represents the outcome of running an augmenting path
+ search on the graph given the assignment.
+
+ Returns:
+ A new assignment matrix of the same shape and type as assignment, where the
+ assignment has been updated using the augmented path found.
+ """
+ batch_size, num_elems, _ = tf_utils.get_shape_list(assignment, 3)
+
+ # We store the current job id and iteratively backtrack using jobs_from_worker
+ # and workers_from_job until we reach an unassigned worker. We flip all the
+ # assignments on this path to discover a better overall assignment.
+
+ # Note: The indices in state are 1-indexed, where 0 represents that the
+ # worker / job cannot be reached.
+
+ # Obtain initial job indices based on new_jobs.
+ curr_job_idx = tf.argmax(
+ tf.cast(state["new_jobs"], tf.int32), axis=1, output_type=tf.int32)
+
+ # Track whether an example is actively being backtracked. Since we are
+ # operating on a batch, not all examples in the batch may be active.
+ active = tf.gather(state["new_jobs"], curr_job_idx, batch_dims=1)
+ batch_range = tf.range(0, batch_size, dtype=tf.int32)
+
+ # Flip matrix tracks which assignments we need to flip - corresponding to the
+ # augmenting path taken. We use an integer tensor here so that we can use
+ # tensor_scatter_nd_add to update the tensor, and then cast it back to bool
+ # after the loop.
+ flip_matrix = tf.zeros((batch_size, num_elems, num_elems), dtype=tf.int32)
+
+ def _has_active_backtracks(flip_matrix, active, curr_job_idx):
+ """Check if there are still active workers."""
+ del flip_matrix, curr_job_idx
+ return tf.reduce_any(active)
+
+ def _backtrack_one_step(flip_matrix, active, curr_job_idx):
+ """Take one step in backtracking."""
+ # Discover the worker that the job originated from, note that this worker
+ # must exist by construction.
+ curr_worker_idx = tf.gather(
+ state["jobs_from_worker"], curr_job_idx, batch_dims=1) - 1
+ curr_worker_idx = tf.maximum(curr_worker_idx, 0)
+ update_indices = tf.stack([batch_range, curr_worker_idx, curr_job_idx],
+ axis=1)
+ update_indices = tf.maximum(update_indices, 0)
+ flip_matrix = tf.tensor_scatter_nd_add(flip_matrix, update_indices,
+ tf.cast(active, tf.int32))
+
+ # Discover the (potential) job that the worker originated from.
+ curr_job_idx = tf.gather(
+ state["workers_from_job"], curr_worker_idx, batch_dims=1) - 1
+ # Note that jobs may not be active, and we track that here (before
+ # adjusting indices so that they are all >= 0 for gather).
+ active &= curr_job_idx >= 0
+ curr_job_idx = tf.maximum(curr_job_idx, 0)
+ update_indices = tf.stack([batch_range, curr_worker_idx, curr_job_idx],
+ axis=1)
+ update_indices = tf.maximum(update_indices, 0)
+ flip_matrix = tf.tensor_scatter_nd_add(flip_matrix, update_indices,
+ tf.cast(active, tf.int32))
+
+ return flip_matrix, active, curr_job_idx
+
+ flip_matrix, _, _ = tf.while_loop(
+ _has_active_backtracks,
+ _backtrack_one_step, (flip_matrix, active, curr_job_idx),
+ back_prop=False)
+
+ flip_matrix = tf.cast(flip_matrix, tf.bool)
+ assignment = tf.math.logical_xor(assignment, flip_matrix)
+
+ return assignment
+
+
+def _maximum_bipartite_matching(adj_matrix, assignment=None):
+ """Performs maximum bipartite matching using augmented paths.
+
+ Args:
+ adj_matrix: A bool [batch_size, num_elems, num_elems] tensor, where each
+ element of the inner matrix represents whether the worker (row) can be
+ matched to the job (column).
+ assignment: An optional bool [batch_size, num_elems, num_elems] tensor,
+ where each element of the inner matrix represents whether the worker has
+ been matched to the job. This may be a partial assignment. If specified,
+ this assignment will be used to seed the iterative algorithm.
+
+ Returns:
+ A state dict representing the final augmenting path state search, and
+ a maximum bipartite matching assignment tensor. Note that the state outcome
+ can be used to compute a minimum vertex cover for the bipartite graph.
+ """
+
+ if assignment is None:
+ assignment = _greedy_assignment(adj_matrix)
+
+ state = _find_augmenting_path(assignment, adj_matrix)
+
+ def _has_new_jobs(state, assignment):
+ del assignment
+ return tf.reduce_any(state["new_jobs"])
+
+ def _improve_assignment_and_find_new_path(state, assignment):
+ assignment = _improve_assignment(assignment, state)
+ state = _find_augmenting_path(assignment, adj_matrix)
+ return state, assignment
+
+ state, assignment = tf.while_loop(
+ _has_new_jobs,
+ _improve_assignment_and_find_new_path, (state, assignment),
+ back_prop=False)
+
+ return state, assignment
+
+
+def _compute_cover(state, assignment):
+ """Computes a cover for the bipartite graph.
+
+ We compute a cover using the construction provided at
+ https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_(graph_theory)#Proof
+ which uses the outcome from the alternating path search.
+
+ Args:
+ state: A state dict, which represents the outcome of running an augmenting
+ path search on the graph given the assignment.
+ assignment: An optional bool [batch_size, num_elems, num_elems] tensor,
+ where each element of the inner matrix represents whether the worker has
+ been matched to the job. This may be a partial assignment. If specified,
+ this assignment will be used to seed the iterative algorithm.
+
+ Returns:
+ A tuple of (workers_cover, jobs_cover) corresponding to row and column
+ covers for the bipartite graph. workers_cover is a boolean tensor of shape
+ [batch_size, num_elems, 1] and jobs_cover is a boolean tensor of shape
+ [batch_size, 1, num_elems].
+ """
+ assigned_workers = tf.reduce_any(assignment, axis=2, keepdims=True)
+ assigned_jobs = tf.reduce_any(assignment, axis=1, keepdims=True)
+
+ reachable_workers = state["workers"] > 0
+ reachable_jobs = state["jobs"] > 0
+
+ workers_cover = assigned_workers & (~reachable_workers)
+ jobs_cover = assigned_jobs & reachable_jobs
+
+ return workers_cover, jobs_cover
+
+
+def _update_weights_using_cover(workers_cover, jobs_cover, weights):
+ """Updates weights for hungarian matching using a cover.
+
+ We first find the minimum uncovered weight. Then, we subtract this from all
+ the uncovered weights, and add it to all the doubly covered weights.
+
+ Args:
+ workers_cover: A boolean tensor of shape [batch_size, num_elems, 1].
+ jobs_cover: A boolean tensor of shape [batch_size, 1, num_elems].
+ weights: A float32 [batch_size, num_elems, num_elems] tensor, where each
+ inner matrix represents weights to be use for matching.
+
+ Returns:
+ A new weight matrix with elements adjusted by the cover.
+ """
+ max_value = tf.reduce_max(weights)
+
+ covered = workers_cover | jobs_cover
+ double_covered = workers_cover & jobs_cover
+
+ uncovered_weights = tf.where(covered,
+ tf.ones_like(weights) * max_value, weights)
+ min_weight = tf.reduce_min(uncovered_weights, axis=[-2, -1], keepdims=True)
+
+ add_weight = tf.where(double_covered,
+ tf.ones_like(weights) * min_weight,
+ tf.zeros_like(weights))
+ sub_weight = tf.where(covered, tf.zeros_like(weights),
+ tf.ones_like(weights) * min_weight)
+
+ return weights + add_weight - sub_weight
+
+
+def assert_rank(tensor, expected_rank, name=None):
+ """Raises an exception if the tensor rank is not of the expected rank.
+
+ Args:
+ tensor: A tf.Tensor to check the rank of.
+ expected_rank: Python integer or list of integers, expected rank.
+ name: Optional name of the tensor for the error message.
+
+ Raises:
+ ValueError: If the expected shape doesn't match the actual shape.
+ """
+ expected_rank_dict = {}
+ if isinstance(expected_rank, int):
+ expected_rank_dict[expected_rank] = True
+ else:
+ for x in expected_rank:
+ expected_rank_dict[x] = True
+
+ actual_rank = len(tensor.shape)
+ if actual_rank not in expected_rank_dict:
+ raise ValueError(
+ "For the tensor `%s`, the actual tensor rank `%d` (shape = %s) is not "
+ "equal to the expected tensor rank `%s`" %
+ (name, actual_rank, str(tensor.shape), str(expected_rank)))
+
+
+def hungarian_matching(weights):
+ """Computes the minimum linear sum assignment using the Hungarian algorithm.
+
+ Args:
+ weights: A float32 [batch_size, num_elems, num_elems] tensor, where each
+ inner matrix represents weights to be use for matching.
+
+ Returns:
+ A bool [batch_size, num_elems, num_elems] tensor, where each element of the
+ inner matrix represents whether the worker has been matched to the job.
+ The returned matching will always be a perfect match.
+ """
+ batch_size, num_elems, _ = tf_utils.get_shape_list(weights, 3)
+
+ weights = _prepare(weights)
+ adj_matrix = tf.equal(weights, 0.)
+ state, assignment = _maximum_bipartite_matching(adj_matrix)
+ workers_cover, jobs_cover = _compute_cover(state, assignment)
+
+ def _cover_incomplete(workers_cover, jobs_cover, *args):
+ del args
+ cover_sum = (
+ tf.reduce_sum(tf.cast(workers_cover, tf.int32)) +
+ tf.reduce_sum(tf.cast(jobs_cover, tf.int32)))
+ return tf.less(cover_sum, batch_size * num_elems)
+
+ def _update_weights_and_match(workers_cover, jobs_cover, weights, assignment):
+ weights = _update_weights_using_cover(workers_cover, jobs_cover, weights)
+ adj_matrix = tf.equal(weights, 0.)
+ state, assignment = _maximum_bipartite_matching(adj_matrix, assignment)
+ workers_cover, jobs_cover = _compute_cover(state, assignment)
+ return workers_cover, jobs_cover, weights, assignment
+
+ workers_cover, jobs_cover, weights, assignment = tf.while_loop(
+ _cover_incomplete,
+ _update_weights_and_match,
+ (workers_cover, jobs_cover, weights, assignment),
+ back_prop=False)
+ return weights, assignment
+
diff --git a/official/projects/detr/ops/matchers_test.py b/official/projects/detr/ops/matchers_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..71c607123a31e6fd185c2d2528a7c17970e3b40a
--- /dev/null
+++ b/official/projects/detr/ops/matchers_test.py
@@ -0,0 +1,95 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for tensorflow_models.official.projects.detr.ops.matchers."""
+
+import numpy as np
+from scipy import optimize
+import tensorflow as tf
+
+from official.projects.detr.ops import matchers
+
+
+class MatchersOpsTest(tf.test.TestCase):
+
+ def testLinearSumAssignment(self):
+ """Check a simple 2D test case of the Linear Sum Assignment problem.
+
+ Ensures that the implementation of the matching algorithm is correct
+ and functional on TPUs.
+ """
+ cost_matrix = np.array([[[4, 1, 3], [2, 0, 5], [3, 2, 2]]],
+ dtype=np.float32)
+ _, adjacency_matrix = matchers.hungarian_matching(tf.constant(cost_matrix))
+ adjacency_output = adjacency_matrix.numpy()
+
+ correct_output = np.array([
+ [0, 1, 0],
+ [1, 0, 0],
+ [0, 0, 1],
+ ], dtype=bool)
+ self.assertAllEqual(adjacency_output[0], correct_output)
+
+ def testBatchedLinearSumAssignment(self):
+ """Check a batched case of the Linear Sum Assignment Problem.
+
+ Ensures that a correct solution is found for all inputted problems within
+ a batch.
+ """
+ cost_matrix = np.array([
+ [[4, 1, 3], [2, 0, 5], [3, 2, 2]],
+ [[1, 4, 3], [0, 2, 5], [2, 3, 2]],
+ [[1, 3, 4], [0, 5, 2], [2, 2, 3]],
+ ],
+ dtype=np.float32)
+ _, adjacency_matrix = matchers.hungarian_matching(tf.constant(cost_matrix))
+ adjacency_output = adjacency_matrix.numpy()
+
+ # Hand solved correct output for the linear sum assignment problem
+ correct_output = np.array([
+ [[0, 1, 0], [1, 0, 0], [0, 0, 1]],
+ [[1, 0, 0], [0, 1, 0], [0, 0, 1]],
+ [[1, 0, 0], [0, 0, 1], [0, 1, 0]],
+ ],
+ dtype=bool)
+ self.assertAllClose(adjacency_output, correct_output)
+
+ def testMaximumBipartiteMatching(self):
+ """Check that the maximum bipartite match assigns the correct numbers."""
+ adj_matrix = tf.cast([[
+ [1, 0, 0, 0, 1],
+ [0, 1, 0, 1, 0],
+ [0, 0, 1, 0, 0],
+ [0, 1, 0, 0, 0],
+ [1, 0, 0, 0, 0],
+ ]], tf.bool)
+ _, assignment = matchers._maximum_bipartite_matching(adj_matrix)
+ self.assertEqual(np.sum(assignment.numpy()), 5)
+
+ def testAssignmentMatchesScipy(self):
+ """Check that the Linear Sum Assignment matches the Scipy implementation."""
+ batch_size, num_elems = 2, 25
+ weights = tf.random.uniform((batch_size, num_elems, num_elems),
+ minval=0.,
+ maxval=1.)
+ weights, assignment = matchers.hungarian_matching(weights)
+
+ for idx in range(batch_size):
+ _, scipy_assignment = optimize.linear_sum_assignment(weights.numpy()[idx])
+ hungarian_assignment = np.where(assignment.numpy()[idx])[1]
+
+ self.assertAllEqual(hungarian_assignment, scipy_assignment)
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/optimization.py b/official/projects/detr/optimization.py
new file mode 100644
index 0000000000000000000000000000000000000000..a9da1740d11a83f3989d85e78c04b04c50773539
--- /dev/null
+++ b/official/projects/detr/optimization.py
@@ -0,0 +1,147 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Customized optimizer to match paper results."""
+
+import dataclasses
+import tensorflow as tf
+from official.modeling import optimization
+from official.nlp import optimization as nlp_optimization
+
+
+@dataclasses.dataclass
+class DETRAdamWConfig(optimization.AdamWeightDecayConfig):
+ pass
+
+
+@dataclasses.dataclass
+class OptimizerConfig(optimization.OptimizerConfig):
+ detr_adamw: DETRAdamWConfig = DETRAdamWConfig()
+
+
+@dataclasses.dataclass
+class OptimizationConfig(optimization.OptimizationConfig):
+ """Configuration for optimizer and learning rate schedule.
+
+ Attributes:
+ optimizer: optimizer oneof config.
+ ema: optional exponential moving average optimizer config, if specified, ema
+ optimizer will be used.
+ learning_rate: learning rate oneof config.
+ warmup: warmup oneof config.
+ """
+ optimizer: OptimizerConfig = OptimizerConfig()
+
+
+# TODO(frederickliu): figure out how to make this configuable.
+# TODO(frederickliu): Study if this is needed.
+class _DETRAdamW(nlp_optimization.AdamWeightDecay):
+ """Custom AdamW to support different lr scaling for backbone.
+
+ The code is copied from AdamWeightDecay and Adam with learning scaling.
+ """
+
+ def _resource_apply_dense(self, grad, var, apply_state=None):
+ lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
+ apply_state = kwargs['apply_state']
+ if 'detr' not in var.name:
+ lr_t *= 0.1
+ decay = self._decay_weights_op(var, lr_t, apply_state)
+ with tf.control_dependencies([decay]):
+ var_device, var_dtype = var.device, var.dtype.base_dtype
+ coefficients = ((apply_state or {}).get((var_device, var_dtype))
+ or self._fallback_apply_state(var_device, var_dtype))
+
+ m = self.get_slot(var, 'm')
+ v = self.get_slot(var, 'v')
+ lr = coefficients[
+ 'lr_t'] * 0.1 if 'detr' not in var.name else coefficients['lr_t']
+
+ if not self.amsgrad:
+ return tf.raw_ops.ResourceApplyAdam(
+ var=var.handle,
+ m=m.handle,
+ v=v.handle,
+ beta1_power=coefficients['beta_1_power'],
+ beta2_power=coefficients['beta_2_power'],
+ lr=lr,
+ beta1=coefficients['beta_1_t'],
+ beta2=coefficients['beta_2_t'],
+ epsilon=coefficients['epsilon'],
+ grad=grad,
+ use_locking=self._use_locking)
+ else:
+ vhat = self.get_slot(var, 'vhat')
+ return tf.raw_ops.ResourceApplyAdamWithAmsgrad(
+ var=var.handle,
+ m=m.handle,
+ v=v.handle,
+ vhat=vhat.handle,
+ beta1_power=coefficients['beta_1_power'],
+ beta2_power=coefficients['beta_2_power'],
+ lr=lr,
+ beta1=coefficients['beta_1_t'],
+ beta2=coefficients['beta_2_t'],
+ epsilon=coefficients['epsilon'],
+ grad=grad,
+ use_locking=self._use_locking)
+
+ def _resource_apply_sparse(self, grad, var, indices, apply_state=None):
+ lr_t, kwargs = self._get_lr(var.device, var.dtype.base_dtype, apply_state)
+ apply_state = kwargs['apply_state']
+ if 'detr' not in var.name:
+ lr_t *= 0.1
+ decay = self._decay_weights_op(var, lr_t, apply_state)
+ with tf.control_dependencies([decay]):
+ var_device, var_dtype = var.device, var.dtype.base_dtype
+ coefficients = ((apply_state or {}).get((var_device, var_dtype))
+ or self._fallback_apply_state(var_device, var_dtype))
+
+ # m_t = beta1 * m + (1 - beta1) * g_t
+ m = self.get_slot(var, 'm')
+ m_scaled_g_values = grad * coefficients['one_minus_beta_1_t']
+ m_t = tf.compat.v1.assign(m, m * coefficients['beta_1_t'],
+ use_locking=self._use_locking)
+ with tf.control_dependencies([m_t]):
+ m_t = self._resource_scatter_add(m, indices, m_scaled_g_values)
+
+ # v_t = beta2 * v + (1 - beta2) * (g_t * g_t)
+ v = self.get_slot(var, 'v')
+ v_scaled_g_values = (grad * grad) * coefficients['one_minus_beta_2_t']
+ v_t = tf.compat.v1.assign(v, v * coefficients['beta_2_t'],
+ use_locking=self._use_locking)
+ with tf.control_dependencies([v_t]):
+ v_t = self._resource_scatter_add(v, indices, v_scaled_g_values)
+ lr = coefficients[
+ 'lr_t'] * 0.1 if 'detr' not in var.name else coefficients['lr_t']
+ if not self.amsgrad:
+ v_sqrt = tf.sqrt(v_t)
+ var_update = tf.compat.v1.assign_sub(
+ var, lr * m_t / (v_sqrt + coefficients['epsilon']),
+ use_locking=self._use_locking)
+ return tf.group(*[var_update, m_t, v_t])
+ else:
+ v_hat = self.get_slot(var, 'vhat')
+ v_hat_t = tf.maximum(v_hat, v_t)
+ with tf.control_dependencies([v_hat_t]):
+ v_hat_t = tf.compat.v1.assign(
+ v_hat, v_hat_t, use_locking=self._use_locking)
+ v_hat_sqrt = tf.sqrt(v_hat_t)
+ var_update = tf.compat.v1.assign_sub(
+ var,
+ lr* m_t / (v_hat_sqrt + coefficients['epsilon']),
+ use_locking=self._use_locking)
+ return tf.group(*[var_update, m_t, v_t, v_hat_t])
+
+optimization.register_optimizer_cls('detr_adamw', _DETRAdamW)
diff --git a/official/projects/detr/tasks/detection.py b/official/projects/detr/tasks/detection.py
new file mode 100644
index 0000000000000000000000000000000000000000..732b1801b881ef1a8060201434c118b1e71c1715
--- /dev/null
+++ b/official/projects/detr/tasks/detection.py
@@ -0,0 +1,402 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""DETR detection task definition."""
+from typing import Optional
+
+from absl import logging
+import tensorflow as tf
+
+from official.common import dataset_fn
+from official.core import base_task
+from official.core import task_factory
+from official.projects.detr.configs import detr as detr_cfg
+from official.projects.detr.dataloaders import coco
+from official.projects.detr.dataloaders import detr_input
+from official.projects.detr.modeling import detr
+from official.projects.detr.ops import matchers
+from official.vision.dataloaders import input_reader_factory
+from official.vision.dataloaders import tf_example_decoder
+from official.vision.dataloaders import tfds_factory
+from official.vision.dataloaders import tf_example_label_map_decoder
+from official.vision.evaluation import coco_evaluator
+from official.vision.modeling import backbones
+from official.vision.ops import box_ops
+
+
+@task_factory.register_task_cls(detr_cfg.DetrTask)
+class DetectionTask(base_task.Task):
+ """A single-replica view of training procedure.
+
+ DETR task provides artifacts for training/evalution procedures, including
+ loading/iterating over Datasets, initializing the model, calculating the loss,
+ post-processing, and customized metrics with reduction.
+ """
+
+ def build_model(self):
+ """Build DETR model."""
+
+ input_specs = tf.keras.layers.InputSpec(shape=[None] +
+ self._task_config.model.input_size)
+
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=self._task_config.model.backbone,
+ norm_activation_config=self._task_config.model.norm_activation)
+
+ model = detr.DETR(backbone,
+ self._task_config.model.backbone_endpoint_name,
+ self._task_config.model.num_queries,
+ self._task_config.model.hidden_size,
+ self._task_config.model.num_classes,
+ self._task_config.model.num_encoder_layers,
+ self._task_config.model.num_decoder_layers)
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loading pretrained checkpoint."""
+ if not self._task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self._task_config.init_checkpoint
+
+ # Restoring checkpoint.
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ if self._task_config.init_checkpoint_modules == 'all':
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.restore(ckpt_dir_or_file)
+ status.assert_consumed()
+ elif self._task_config.init_checkpoint_modules == 'backbone':
+ ckpt = tf.train.Checkpoint(backbone=model.backbone)
+ status = ckpt.restore(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+
+ def build_inputs(self,
+ params,
+ input_context: Optional[tf.distribute.InputContext] = None):
+ """Build input dataset."""
+ if isinstance(params, coco.COCODataConfig):
+ dataset = coco.COCODataLoader(params).load(input_context)
+ else:
+ if params.tfds_name:
+ decoder = tfds_factory.get_detection_decoder(params.tfds_name)
+ else:
+ decoder_cfg = params.decoder.get()
+ if params.decoder.type == 'simple_decoder':
+ decoder = tf_example_decoder.TfExampleDecoder(
+ regenerate_source_id=decoder_cfg.regenerate_source_id)
+ elif params.decoder.type == 'label_map_decoder':
+ decoder = tf_example_label_map_decoder.TfExampleDecoderLabelMap(
+ label_map=decoder_cfg.label_map,
+ regenerate_source_id=decoder_cfg.regenerate_source_id)
+ else:
+ raise ValueError('Unknown decoder type: {}!'.format(
+ params.decoder.type))
+
+ parser = detr_input.Parser(
+ class_offset=self._task_config.losses.class_offset,
+ output_size=self._task_config.model.input_size[:2],
+ )
+
+ reader = input_reader_factory.input_reader_generator(
+ params,
+ dataset_fn=dataset_fn.pick_dataset_fn(params.file_type),
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def _compute_cost(self, cls_outputs, box_outputs, cls_targets, box_targets):
+ # Approximate classification cost with 1 - prob[target class].
+ # The 1 is a constant that doesn't change the matching, it can be ommitted.
+ # background: 0
+ cls_cost = self._task_config.losses.lambda_cls * tf.gather(
+ -tf.nn.softmax(cls_outputs), cls_targets, batch_dims=1, axis=-1)
+
+ # Compute the L1 cost between boxes,
+ paired_differences = self._task_config.losses.lambda_box * tf.abs(
+ tf.expand_dims(box_outputs, 2) - tf.expand_dims(box_targets, 1))
+ box_cost = tf.reduce_sum(paired_differences, axis=-1)
+
+ # Compute the giou cost betwen boxes
+ giou_cost = self._task_config.losses.lambda_giou * -box_ops.bbox_generalized_overlap(
+ box_ops.cycxhw_to_yxyx(box_outputs),
+ box_ops.cycxhw_to_yxyx(box_targets))
+
+ total_cost = cls_cost + box_cost + giou_cost
+
+ max_cost = (
+ self._task_config.losses.lambda_cls * 0.0 +
+ self._task_config.losses.lambda_box * 4. +
+ self._task_config.losses.lambda_giou * 0.0)
+
+ # Set pads to large constant
+ valid = tf.expand_dims(
+ tf.cast(tf.not_equal(cls_targets, 0), dtype=total_cost.dtype), axis=1)
+ total_cost = (1 - valid) * max_cost + valid * total_cost
+
+ # Set inf of nan to large constant
+ total_cost = tf.where(
+ tf.logical_or(tf.math.is_nan(total_cost), tf.math.is_inf(total_cost)),
+ max_cost * tf.ones_like(total_cost, dtype=total_cost.dtype),
+ total_cost)
+
+ return total_cost
+
+ def build_losses(self, outputs, labels, aux_losses=None):
+ """Build DETR losses."""
+ cls_outputs = outputs['cls_outputs']
+ box_outputs = outputs['box_outputs']
+ cls_targets = labels['classes']
+ box_targets = labels['boxes']
+
+ cost = self._compute_cost(
+ cls_outputs, box_outputs, cls_targets, box_targets)
+
+ _, indices = matchers.hungarian_matching(cost)
+ indices = tf.stop_gradient(indices)
+
+ target_index = tf.math.argmax(indices, axis=1)
+ cls_assigned = tf.gather(cls_outputs, target_index, batch_dims=1, axis=1)
+ box_assigned = tf.gather(box_outputs, target_index, batch_dims=1, axis=1)
+
+ background = tf.equal(cls_targets, 0)
+ num_boxes = tf.reduce_sum(
+ tf.cast(tf.logical_not(background), tf.float32), axis=-1)
+
+ # Down-weight background to account for class imbalance.
+ xentropy = tf.nn.sparse_softmax_cross_entropy_with_logits(
+ labels=cls_targets, logits=cls_assigned)
+ cls_loss = self._task_config.losses.lambda_cls * tf.where(
+ background, self._task_config.losses.background_cls_weight * xentropy,
+ xentropy)
+ cls_weights = tf.where(
+ background,
+ self._task_config.losses.background_cls_weight * tf.ones_like(cls_loss),
+ tf.ones_like(cls_loss))
+
+ # Box loss is only calculated on non-background class.
+ l_1 = tf.reduce_sum(tf.abs(box_assigned - box_targets), axis=-1)
+ box_loss = self._task_config.losses.lambda_box * tf.where(
+ background, tf.zeros_like(l_1), l_1)
+
+ # Giou loss is only calculated on non-background class.
+ giou = tf.linalg.diag_part(1.0 - box_ops.bbox_generalized_overlap(
+ box_ops.cycxhw_to_yxyx(box_assigned),
+ box_ops.cycxhw_to_yxyx(box_targets)
+ ))
+ giou_loss = self._task_config.losses.lambda_giou * tf.where(
+ background, tf.zeros_like(giou), giou)
+
+ # Consider doing all reduce once in train_step to speed up.
+ num_boxes_per_replica = tf.reduce_sum(num_boxes)
+ cls_weights_per_replica = tf.reduce_sum(cls_weights)
+ replica_context = tf.distribute.get_replica_context()
+ num_boxes_sum, cls_weights_sum = replica_context.all_reduce(
+ tf.distribute.ReduceOp.SUM,
+ [num_boxes_per_replica, cls_weights_per_replica])
+ cls_loss = tf.math.divide_no_nan(
+ tf.reduce_sum(cls_loss), cls_weights_sum)
+ box_loss = tf.math.divide_no_nan(
+ tf.reduce_sum(box_loss), num_boxes_sum)
+ giou_loss = tf.math.divide_no_nan(
+ tf.reduce_sum(giou_loss), num_boxes_sum)
+
+ aux_losses = tf.add_n(aux_losses) if aux_losses else 0.0
+
+ total_loss = cls_loss + box_loss + giou_loss + aux_losses
+ return total_loss, cls_loss, box_loss, giou_loss
+
+ def build_metrics(self, training=True):
+ """Build detection metrics."""
+ metrics = []
+ metric_names = ['cls_loss', 'box_loss', 'giou_loss']
+ for name in metric_names:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+
+ if not training:
+ self.coco_metric = coco_evaluator.COCOEvaluator(
+ annotation_file=self._task_config.annotation_file,
+ include_mask=False,
+ need_rescale_bboxes=True,
+ per_category_metrics=self._task_config.per_category_metrics)
+ return metrics
+
+ def train_step(self, inputs, model, optimizer, metrics=None):
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+ with tf.GradientTape() as tape:
+ outputs = model(features, training=True)
+
+ loss = 0.0
+ cls_loss = 0.0
+ box_loss = 0.0
+ giou_loss = 0.0
+
+ for output in outputs:
+ # Computes per-replica loss.
+ layer_loss, layer_cls_loss, layer_box_loss, layer_giou_loss = self.build_losses(
+ outputs=output, labels=labels, aux_losses=model.losses)
+ loss += layer_loss
+ cls_loss += layer_cls_loss
+ box_loss += layer_box_loss
+ giou_loss += layer_giou_loss
+
+ # Consider moving scaling logic from build_losses to here.
+ scaled_loss = loss
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ tvars = model.trainable_variables
+ grads = tape.gradient(scaled_loss, tvars)
+ # Scales back gradient when LossScaleOptimizer is used.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ grads = optimizer.get_unscaled_gradients(grads)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ # Multiply for logging.
+ # Since we expect the gradient replica sum to happen in the optimizer,
+ # the loss is scaled with global num_boxes and weights.
+ # To have it more interpretable/comparable we scale it back when logging.
+ num_replicas_in_sync = tf.distribute.get_strategy().num_replicas_in_sync
+ loss *= num_replicas_in_sync
+ cls_loss *= num_replicas_in_sync
+ box_loss *= num_replicas_in_sync
+ giou_loss *= num_replicas_in_sync
+
+ # Trainer class handles loss metric for you.
+ logs = {self.loss: loss}
+
+ all_losses = {
+ 'cls_loss': cls_loss,
+ 'box_loss': box_loss,
+ 'giou_loss': giou_loss,
+ }
+
+ # Metric results will be added to logs for you.
+ if metrics:
+ for m in metrics:
+ m.update_state(all_losses[m.name])
+ return logs
+
+ def validation_step(self, inputs, model, metrics=None):
+ """Validatation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+
+ outputs = model(features, training=False)[-1]
+ loss, cls_loss, box_loss, giou_loss = self.build_losses(
+ outputs=outputs, labels=labels, aux_losses=model.losses)
+
+ # Multiply for logging.
+ # Since we expect the gradient replica sum to happen in the optimizer,
+ # the loss is scaled with global num_boxes and weights.
+ # To have it more interpretable/comparable we scale it back when logging.
+ num_replicas_in_sync = tf.distribute.get_strategy().num_replicas_in_sync
+ loss *= num_replicas_in_sync
+ cls_loss *= num_replicas_in_sync
+ box_loss *= num_replicas_in_sync
+ giou_loss *= num_replicas_in_sync
+
+ # Evaluator class handles loss metric for you.
+ logs = {self.loss: loss}
+
+ predictions = {
+ 'detection_boxes':
+ box_ops.cycxhw_to_yxyx(outputs['box_outputs'])
+ * tf.expand_dims(
+ tf.concat([
+ labels['image_info'][:, 1:2, 0],
+ labels['image_info'][:, 1:2, 1],
+ labels['image_info'][:, 1:2, 0],
+ labels['image_info'][:, 1:2, 1]
+ ],
+ axis=1),
+ axis=1),
+ 'detection_scores':
+ tf.math.reduce_max(
+ tf.nn.softmax(outputs['cls_outputs'])[:, :, 1:], axis=-1),
+ 'detection_classes':
+ tf.math.argmax(outputs['cls_outputs'][:, :, 1:], axis=-1) + 1,
+ # Fix this. It's not being used at the moment.
+ 'num_detections': tf.reduce_sum(
+ tf.cast(
+ tf.math.greater(tf.math.reduce_max(
+ outputs['cls_outputs'], axis=-1), 0), tf.int32), axis=-1),
+ 'source_id': labels['id'],
+ 'image_info': labels['image_info']
+ }
+ ground_truths = {
+ 'source_id': labels['id'],
+ 'height': labels['image_info'][:, 0:1, 0],
+ 'width': labels['image_info'][:, 0:1, 1],
+ 'num_detections': tf.reduce_sum(
+ tf.cast(tf.math.greater(labels['classes'], 0), tf.int32), axis=-1),
+ 'boxes': labels['gt_boxes'],
+ 'classes': labels['classes'],
+ 'is_crowds': labels['is_crowd']
+ }
+ logs.update({'predictions': predictions,
+ 'ground_truths': ground_truths})
+
+ all_losses = {
+ 'cls_loss': cls_loss,
+ 'box_loss': box_loss,
+ 'giou_loss': giou_loss,
+ }
+
+ # Metric results will be added to logs for you.
+ if metrics:
+ for m in metrics:
+ m.update_state(all_losses[m.name])
+ return logs
+
+ def aggregate_logs(self, state=None, step_outputs=None):
+ if state is None:
+ self.coco_metric.reset_states()
+ state = self.coco_metric
+
+ state.update_state(
+ step_outputs['ground_truths'],
+ step_outputs['predictions'])
+ return state
+
+ def reduce_aggregated_logs(self, aggregated_logs, global_step=None):
+ return aggregated_logs.result()
diff --git a/official/projects/detr/tasks/detection_test.py b/official/projects/detr/tasks/detection_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..7e27f4db0ca9e2a095f1b0ae85469cfe38d47f0e
--- /dev/null
+++ b/official/projects/detr/tasks/detection_test.py
@@ -0,0 +1,203 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for detection."""
+
+import numpy as np
+import tensorflow as tf
+import tensorflow_datasets as tfds
+
+from official.projects.detr import optimization
+from official.projects.detr.configs import detr as detr_cfg
+from official.projects.detr.dataloaders import coco
+from official.projects.detr.tasks import detection
+from official.vision.configs import backbones
+
+
+_NUM_EXAMPLES = 10
+
+
+def _gen_fn():
+ h = np.random.randint(0, 300)
+ w = np.random.randint(0, 300)
+ num_boxes = np.random.randint(0, 50)
+ return {
+ 'image': np.ones(shape=(h, w, 3), dtype=np.uint8),
+ 'image/id': np.random.randint(0, 100),
+ 'image/filename': 'test',
+ 'objects': {
+ 'is_crowd': np.ones(shape=(num_boxes), dtype=np.bool),
+ 'bbox': np.ones(shape=(num_boxes, 4), dtype=np.float32),
+ 'label': np.ones(shape=(num_boxes), dtype=np.int64),
+ 'id': np.ones(shape=(num_boxes), dtype=np.int64),
+ 'area': np.ones(shape=(num_boxes), dtype=np.int64),
+ }
+ }
+
+
+def _as_dataset(self, *args, **kwargs):
+ del args
+ del kwargs
+ return tf.data.Dataset.from_generator(
+ lambda: (_gen_fn() for i in range(_NUM_EXAMPLES)),
+ output_types=self.info.features.dtype,
+ output_shapes=self.info.features.shape,
+ )
+
+
+class DetectionTest(tf.test.TestCase):
+
+ def test_train_step(self):
+ config = detr_cfg.DetrTask(
+ model=detr_cfg.Detr(
+ input_size=[1333, 1333, 3],
+ num_encoder_layers=1,
+ num_decoder_layers=1,
+ num_classes=81,
+ backbone=backbones.Backbone(
+ type='resnet',
+ resnet=backbones.ResNet(model_id=10, bn_trainable=False))
+ ),
+ train_data=coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=True,
+ global_batch_size=2,
+ ))
+ with tfds.testing.mock_data(as_dataset_fn=_as_dataset):
+ task = detection.DetectionTask(config)
+ model = task.build_model()
+ dataset = task.build_inputs(config.train_data)
+ iterator = iter(dataset)
+ opt_cfg = optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'detr_adamw',
+ 'detr_adamw': {
+ 'weight_decay_rate': 1e-4,
+ 'global_clipnorm': 0.1,
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [120000],
+ 'values': [0.0001, 1.0e-05]
+ }
+ },
+ })
+ optimizer = detection.DetectionTask.create_optimizer(opt_cfg)
+ task.train_step(next(iterator), model, optimizer)
+
+ def test_validation_step(self):
+ config = detr_cfg.DetrTask(
+ model=detr_cfg.Detr(
+ input_size=[1333, 1333, 3],
+ num_encoder_layers=1,
+ num_decoder_layers=1,
+ num_classes=81,
+ backbone=backbones.Backbone(
+ type='resnet',
+ resnet=backbones.ResNet(model_id=10, bn_trainable=False))
+ ),
+ validation_data=coco.COCODataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=False,
+ global_batch_size=2,
+ ))
+
+ with tfds.testing.mock_data(as_dataset_fn=_as_dataset):
+ task = detection.DetectionTask(config)
+ model = task.build_model()
+ metrics = task.build_metrics(training=False)
+ dataset = task.build_inputs(config.validation_data)
+ iterator = iter(dataset)
+ logs = task.validation_step(next(iterator), model, metrics)
+ state = task.aggregate_logs(step_outputs=logs)
+ task.reduce_aggregated_logs(state)
+
+
+class DetectionTFDSTest(tf.test.TestCase):
+
+ def test_train_step(self):
+ config = detr_cfg.DetrTask(
+ model=detr_cfg.Detr(
+ input_size=[1333, 1333, 3],
+ num_encoder_layers=1,
+ num_decoder_layers=1,
+ backbone=backbones.Backbone(
+ type='resnet',
+ resnet=backbones.ResNet(model_id=10, bn_trainable=False))
+ ),
+ losses=detr_cfg.Losses(class_offset=1),
+ train_data=detr_cfg.DataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=True,
+ global_batch_size=2,
+ ))
+ with tfds.testing.mock_data(as_dataset_fn=_as_dataset):
+ task = detection.DetectionTask(config)
+ model = task.build_model()
+ dataset = task.build_inputs(config.train_data)
+ iterator = iter(dataset)
+ opt_cfg = optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'detr_adamw',
+ 'detr_adamw': {
+ 'weight_decay_rate': 1e-4,
+ 'global_clipnorm': 0.1,
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [120000],
+ 'values': [0.0001, 1.0e-05]
+ }
+ },
+ })
+ optimizer = detection.DetectionTask.create_optimizer(opt_cfg)
+ task.train_step(next(iterator), model, optimizer)
+
+ def test_validation_step(self):
+ config = detr_cfg.DetrTask(
+ model=detr_cfg.Detr(
+ input_size=[1333, 1333, 3],
+ num_encoder_layers=1,
+ num_decoder_layers=1,
+ backbone=backbones.Backbone(
+ type='resnet',
+ resnet=backbones.ResNet(model_id=10, bn_trainable=False))
+ ),
+ losses=detr_cfg.Losses(class_offset=1),
+ validation_data=detr_cfg.DataConfig(
+ tfds_name='coco/2017',
+ tfds_split='validation',
+ is_training=False,
+ global_batch_size=2,
+ ))
+
+ with tfds.testing.mock_data(as_dataset_fn=_as_dataset):
+ task = detection.DetectionTask(config)
+ model = task.build_model()
+ metrics = task.build_metrics(training=False)
+ dataset = task.build_inputs(config.validation_data)
+ iterator = iter(dataset)
+ logs = task.validation_step(next(iterator), model, metrics)
+ state = task.aggregate_logs(step_outputs=logs)
+ task.reduce_aggregated_logs(state)
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/detr/train.py b/official/projects/detr/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..a34da6843b45cbc0f17c5b8166ad92092dd33066
--- /dev/null
+++ b/official/projects/detr/train.py
@@ -0,0 +1,70 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver."""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+# pylint: disable=unused-import
+from official.projects.detr.configs import detr
+from official.projects.detr.tasks import detection
+# pylint: enable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ flags.mark_flags_as_required(['experiment', 'mode', 'model_dir'])
+ app.run(main)
diff --git a/official/projects/edgetpu/nlp/__init__.py b/official/projects/edgetpu/nlp/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/nlp/__init__.py
+++ b/official/projects/edgetpu/nlp/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/configs/__init__.py b/official/projects/edgetpu/nlp/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/nlp/configs/__init__.py
+++ b/official/projects/edgetpu/nlp/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/configs/params.py b/official/projects/edgetpu/nlp/configs/params.py
index fc8a5f4e9d9959f1d793c158dab60b6cf4002e55..39a83ba26eb11075158c4bc6e27ba6a4d7db8435 100644
--- a/official/projects/edgetpu/nlp/configs/params.py
+++ b/official/projects/edgetpu/nlp/configs/params.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_baseline.yaml b/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_baseline.yaml
index 0b7d0563e4e7e80947ebf8f577df78f9f7032229..0b55beeaaed58b7fd3ee1c9ba3390429f3ccc8e0 100644
--- a/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_baseline.yaml
+++ b/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_baseline.yaml
@@ -13,7 +13,7 @@ task:
num_attention_heads: 4
intermediate_size: 512
hidden_activation: relu
- hidden_dropout_prob: 0.0
+ hidden_dropout_prob: 0.1
attention_probs_dropout_prob: 0.1
intra_bottleneck_size: 128
initializer_range: 0.02
diff --git a/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_edgetpu_xxs.yaml b/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_edgetpu_xxs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f1b1bfff412c4e8485e2bcfb7c883b47e834263e
--- /dev/null
+++ b/official/projects/edgetpu/nlp/experiments/downstream_tasks/mobilebert_edgetpu_xxs.yaml
@@ -0,0 +1,23 @@
+# MobileBERT-EdgeTPU-XXS model.
+task:
+ model:
+ encoder:
+ type: mobilebert
+ mobilebert:
+ word_vocab_size: 30522
+ word_embed_size: 128
+ type_vocab_size: 2
+ max_sequence_length: 512
+ num_blocks: 6
+ hidden_size: 512
+ num_attention_heads: 4
+ intermediate_size: 1024
+ hidden_activation: relu
+ hidden_dropout_prob: 0.1
+ attention_probs_dropout_prob: 0.1
+ intra_bottleneck_size: 128
+ initializer_range: 0.02
+ key_query_shared_bottleneck: true
+ num_feedforward_networks: 2
+ normalization_type: no_norm
+ classifier_activation: false
diff --git a/official/projects/edgetpu/nlp/experiments/mobilebert_edgetpu_xxs.yaml b/official/projects/edgetpu/nlp/experiments/mobilebert_edgetpu_xxs.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..86c26569339a5f147f5b9e18f47d5f636f643957
--- /dev/null
+++ b/official/projects/edgetpu/nlp/experiments/mobilebert_edgetpu_xxs.yaml
@@ -0,0 +1,142 @@
+layer_wise_distillation:
+ num_steps: 30000
+ warmup_steps: 0
+ initial_learning_rate: 1.5e-3
+ end_learning_rate: 1.5e-3
+ decay_steps: 30000
+end_to_end_distillation:
+ num_steps: 585000
+ warmup_steps: 20000
+ initial_learning_rate: 1.5e-3
+ end_learning_rate: 1.5e-7
+ decay_steps: 585000
+ distill_ground_truth_ratio: 0.5
+optimizer:
+ optimizer:
+ lamb:
+ beta_1: 0.9
+ beta_2: 0.999
+ clipnorm: 1.0
+ epsilon: 1.0e-06
+ exclude_from_layer_adaptation: null
+ exclude_from_weight_decay: ['LayerNorm', 'bias', 'norm']
+ global_clipnorm: null
+ name: LAMB
+ weight_decay_rate: 0.01
+ type: lamb
+orbit_config:
+ eval_interval: 1000
+ eval_steps: -1
+ mode: train
+ steps_per_loop: 1000
+ total_steps: 825000
+runtime:
+ distribution_strategy: 'tpu'
+student_model:
+ cls_heads: [{'activation': 'tanh',
+ 'cls_token_idx': 0,
+ 'dropout_rate': 0.0,
+ 'inner_dim': 512,
+ 'name': 'next_sentence',
+ 'num_classes': 2}]
+ encoder:
+ mobilebert:
+ attention_probs_dropout_prob: 0.1
+ classifier_activation: false
+ hidden_activation: relu
+ hidden_dropout_prob: 0.0
+ hidden_size: 512
+ initializer_range: 0.02
+ input_mask_dtype: int32
+ intermediate_size: 1024
+ intra_bottleneck_size: 128
+ key_query_shared_bottleneck: true
+ max_sequence_length: 512
+ normalization_type: no_norm
+ num_attention_heads: 4
+ num_blocks: 6
+ num_feedforward_networks: 2
+ type_vocab_size: 2
+ use_bottleneck_attention: false
+ word_embed_size: 128
+ word_vocab_size: 30522
+ type: mobilebert
+ mlm_activation: relu
+ mlm_initializer_range: 0.02
+ mlm_output_weights_use_proj: true
+teacher_model:
+ cls_heads: []
+ encoder:
+ mobilebert:
+ attention_probs_dropout_prob: 0.1
+ classifier_activation: false
+ hidden_activation: gelu
+ hidden_dropout_prob: 0.1
+ hidden_size: 512
+ initializer_range: 0.02
+ input_mask_dtype: int32
+ intermediate_size: 4096
+ intra_bottleneck_size: 1024
+ key_query_shared_bottleneck: false
+ max_sequence_length: 512
+ normalization_type: layer_norm
+ num_attention_heads: 4
+ num_blocks: 24
+ num_feedforward_networks: 1
+ type_vocab_size: 2
+ use_bottleneck_attention: false
+ word_embed_size: 128
+ word_vocab_size: 30522
+ type: mobilebert
+ mlm_activation: gelu
+ mlm_initializer_range: 0.02
+teacher_model_init_checkpoint: gs://**/uncased_L-24_H-1024_B-512_A-4_teacher/tf2_checkpoint/bert_model.ckpt-1
+student_model_init_checkpoint: ''
+train_datasest:
+ block_length: 1
+ cache: false
+ cycle_length: null
+ deterministic: null
+ drop_remainder: true
+ enable_tf_data_service: false
+ global_batch_size: 2048
+ input_path: gs://**/seq_512_mask_20/wikipedia.tfrecord*,gs://**/seq_512_mask_20/books.tfrecord*
+ is_training: true
+ max_predictions_per_seq: 20
+ seq_length: 512
+ sharding: true
+ shuffle_buffer_size: 100
+ tf_data_service_address: null
+ tf_data_service_job_name: null
+ tfds_as_supervised: false
+ tfds_data_dir: ''
+ tfds_name: ''
+ tfds_skip_decoding_feature: ''
+ tfds_split: ''
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: false
+eval_dataset:
+ block_length: 1
+ cache: false
+ cycle_length: null
+ deterministic: null
+ drop_remainder: true
+ enable_tf_data_service: false
+ global_batch_size: 2048
+ input_path: gs://**/seq_512_mask_20/wikipedia.tfrecord-00141-of-00500,gs://**/seq_512_mask_20/books.tfrecord-00141-of-00500
+ is_training: false
+ max_predictions_per_seq: 20
+ seq_length: 512
+ sharding: true
+ shuffle_buffer_size: 100
+ tf_data_service_address: null
+ tf_data_service_job_name: null
+ tfds_as_supervised: false
+ tfds_data_dir: ''
+ tfds_name: ''
+ tfds_skip_decoding_feature: ''
+ tfds_split: ''
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: false
diff --git a/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer.py b/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer.py
index 8e57ef9b17ac4ce22bcd83b138397a3533367528..2adeb246bf054845b9c769786138f274a07e7bb1 100644
--- a/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer.py
+++ b/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer_test.py b/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer_test.py
index 82afbca221f3a4af70f2d43b399394ee61fb607f..b411c4946f3c5ff55400b8f028f704db19279c19 100644
--- a/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer_test.py
+++ b/official/projects/edgetpu/nlp/mobilebert_edgetpu_trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/modeling/__init__.py b/official/projects/edgetpu/nlp/modeling/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/nlp/modeling/__init__.py
+++ b/official/projects/edgetpu/nlp/modeling/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/modeling/edgetpu_layers.py b/official/projects/edgetpu/nlp/modeling/edgetpu_layers.py
index fd1ea5cc7efdabda1a2b3a2ba73204fcc260275e..08900f6acc59960b7a10e445d0a9d64ed2e1cd52 100644
--- a/official/projects/edgetpu/nlp/modeling/edgetpu_layers.py
+++ b/official/projects/edgetpu/nlp/modeling/edgetpu_layers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -123,7 +123,7 @@ class EdgeTPUMultiHeadAttention(tf.keras.layers.MultiHeadAttention):
"""Builds multi-head dot-product attention computations.
This function builds attributes necessary for `_compute_attention` to
- costomize attention computation to replace the default dot-product
+ customize attention computation to replace the default dot-product
attention.
Args:
diff --git a/official/projects/edgetpu/nlp/modeling/edgetpu_layers_test.py b/official/projects/edgetpu/nlp/modeling/edgetpu_layers_test.py
index 477eea25862261224a2a385017b65e7444cd65d9..1ed5570d2d1132c0ea015a1e0ebd2a15aef310db 100644
--- a/official/projects/edgetpu/nlp/modeling/edgetpu_layers_test.py
+++ b/official/projects/edgetpu/nlp/modeling/edgetpu_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/modeling/encoder.py b/official/projects/edgetpu/nlp/modeling/encoder.py
index 0693a0ac1f59912636e6463792316aaedf536e76..ea8e03f2bd6c2fe7d5d929817a7acd5a266f0e0b 100644
--- a/official/projects/edgetpu/nlp/modeling/encoder.py
+++ b/official/projects/edgetpu/nlp/modeling/encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -161,7 +161,7 @@ class MobileBERTEncoder(tf.keras.Model):
first_token = tf.squeeze(prev_output[:, 0:1, :], axis=1)
if classifier_activation:
- self._pooler_layer = tf.keras.layers.experimental.EinsumDense(
+ self._pooler_layer = tf.keras.layers.EinsumDense(
'ab,bc->ac',
output_shape=hidden_size,
activation=tf.tanh,
diff --git a/official/projects/edgetpu/nlp/modeling/model_builder.py b/official/projects/edgetpu/nlp/modeling/model_builder.py
index b78916dd2696b02cd92aab69925053a8ffc95899..de6f1ec597b4c228967c34b9efdc9da83d3c4ac2 100644
--- a/official/projects/edgetpu/nlp/modeling/model_builder.py
+++ b/official/projects/edgetpu/nlp/modeling/model_builder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -85,6 +85,7 @@ def build_bert_pretrainer(pretrainer_cfg: params.PretrainerModelParams,
activation=tf_utils.get_activation(pretrainer_cfg.mlm_activation),
initializer=tf.keras.initializers.TruncatedNormal(
stddev=pretrainer_cfg.mlm_initializer_range),
+ output_weights_use_proj=pretrainer_cfg.mlm_output_weights_use_proj,
name='cls/predictions')
pretrainer = edgetpu_pretrainer.MobileBERTEdgeTPUPretrainer(
diff --git a/official/projects/edgetpu/nlp/modeling/model_builder_test.py b/official/projects/edgetpu/nlp/modeling/model_builder_test.py
index 96461fb31391a90b0c8374feb4e89f1be0444556..159dd2d7b448141388bcec4a0f62bfcda19b7175 100644
--- a/official/projects/edgetpu/nlp/modeling/model_builder_test.py
+++ b/official/projects/edgetpu/nlp/modeling/model_builder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/modeling/pretrainer.py b/official/projects/edgetpu/nlp/modeling/pretrainer.py
index 8a81021c0220d6f4d7047f906c990793a741bc4c..8607f3e817c105ca293b0d56aa0bea4b24f5077a 100644
--- a/official/projects/edgetpu/nlp/modeling/pretrainer.py
+++ b/official/projects/edgetpu/nlp/modeling/pretrainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/modeling/pretrainer_test.py b/official/projects/edgetpu/nlp/modeling/pretrainer_test.py
index 67741cbf69a58414657b7702210eb85057843d8d..e896d0da1a90bdc3bf6d4acac1b434d58e47eb8e 100644
--- a/official/projects/edgetpu/nlp/modeling/pretrainer_test.py
+++ b/official/projects/edgetpu/nlp/modeling/pretrainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/run_mobilebert_edgetpu_train.py b/official/projects/edgetpu/nlp/run_mobilebert_edgetpu_train.py
index 2a9e671f9f1ce89e5184f4395c5a8be369f480b0..812a0d051e686dbd33226c4082b312035938d44d 100644
--- a/official/projects/edgetpu/nlp/run_mobilebert_edgetpu_train.py
+++ b/official/projects/edgetpu/nlp/run_mobilebert_edgetpu_train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/serving/__init__.py b/official/projects/edgetpu/nlp/serving/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/nlp/serving/__init__.py
+++ b/official/projects/edgetpu/nlp/serving/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/serving/export_tflite_squad.py b/official/projects/edgetpu/nlp/serving/export_tflite_squad.py
index acd39198642410bb205995c6155256d63fca87ca..b66c54a84d4d706e5c354f40bda1b5083a6c5099 100644
--- a/official/projects/edgetpu/nlp/serving/export_tflite_squad.py
+++ b/official/projects/edgetpu/nlp/serving/export_tflite_squad.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -135,7 +135,8 @@ def main(argv: Sequence[str]) -> None:
checkpoint = tf.train.Checkpoint(**checkpoint_dict)
checkpoint.restore(FLAGS.model_checkpoint).assert_existing_objects_matched()
- model_for_serving = build_model_for_serving(model)
+ model_for_serving = build_model_for_serving(model, FLAGS.sequence_length,
+ FLAGS.batch_size)
model_for_serving.summary()
# TODO(b/194449109): Need to save the model to file and then convert tflite
diff --git a/official/projects/edgetpu/nlp/serving/export_tflite_squad_test.py b/official/projects/edgetpu/nlp/serving/export_tflite_squad_test.py
index 300c66b353c2573c44d3f4124b4c2fc277c25426..10c1b0d51a89e0476fac683f7c00e47315a54f9b 100644
--- a/official/projects/edgetpu/nlp/serving/export_tflite_squad_test.py
+++ b/official/projects/edgetpu/nlp/serving/export_tflite_squad_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/utils/__init__.py b/official/projects/edgetpu/nlp/utils/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/nlp/utils/__init__.py
+++ b/official/projects/edgetpu/nlp/utils/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/utils/utils.py b/official/projects/edgetpu/nlp/utils/utils.py
index 95604502611c696ca7f8ec1158d29178f93677e1..ea0594a160eaa06af897c9a7cf177bee357159aa 100644
--- a/official/projects/edgetpu/nlp/utils/utils.py
+++ b/official/projects/edgetpu/nlp/utils/utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/nlp/utils/utils_test.py b/official/projects/edgetpu/nlp/utils/utils_test.py
index 37cb0efbd414b89d554370996ea0a2c619e461c0..82131baab74b7f34c3fe72285194109c3c432b1e 100644
--- a/official/projects/edgetpu/nlp/utils/utils_test.py
+++ b/official/projects/edgetpu/nlp/utils/utils_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/README.md b/official/projects/edgetpu/vision/README.md
index d1a4d3fd7d3eb9836b70f53175c1abedd7baa958..5951a20d88039e1e371c6126ca63ae2f613e2232 100644
--- a/official/projects/edgetpu/vision/README.md
+++ b/official/projects/edgetpu/vision/README.md
@@ -78,10 +78,10 @@ models for 224x224 input resolution:
Model (Checkpoint) | Accuracy (int8) | Pixel 6 Edge TPU Latency (ms) | tflite
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | :-------------: | :---------------------------: | :----:
[MobileNetEdgeTPUv2-Tiny](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet-edgetpu-v2-tiny.tar.gz) | 74.66% | 0.78 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet_edgetpu_v2_tiny.tflite)
-[MobileNetEdgeTPUv2-XS](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet-edgetpu-v2-xs.tar.gz) | 75.79% | 0.82 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet_edgetpu_v2_xs.tflite)
-[MobileNetEdgeTPUv2-S](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet-edgetpu-v2-s.tar.gz) | 77.36% | 1.03 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet_edgetpu_v2_s.tflite)
-[MobileNetEdgeTPUv2-M](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet-edgetpu-v2-m.tar.gz) | 78.43% | 1.35 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet_edgetpu_v2_m.tflite)
-[MobileNetEdgeTPUv2-L](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet-edgetpu-v2-l.tar.gz) | 79.00% | 1.64 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/tiny/mobilenet_edgetpu_v2_l.tflite)
+[MobileNetEdgeTPUv2-XS](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/xs/mobilenet-edgetpu-v2-xs.tar.gz) | 75.79% | 0.82 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/xs/mobilenet_edgetpu_v2_xs.tflite)
+[MobileNetEdgeTPUv2-S](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/s/mobilenet-edgetpu-v2-s.tar.gz) | 77.36% | 1.03 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/s/mobilenet_edgetpu_v2_s.tflite)
+[MobileNetEdgeTPUv2-M](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/m/mobilenet-edgetpu-v2-m.tar.gz) | 78.43% | 1.35 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/m/mobilenet_edgetpu_v2_m.tflite)
+[MobileNetEdgeTPUv2-L](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/l/mobilenet-edgetpu-v2-l.tar.gz) | 79.00% | 1.64 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v2/l/mobilenet_edgetpu_v2_l.tflite)
[MobileNetEdgeTPU dm1.0](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p0/mobilenet-edgetpu-dm1p0.tar.gz) | 75.6% | 0.92 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p0/mobilenet_edgetpu.tflite)
[MobileNetEdgeTPU dm1.25](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p25/mobilenet-edgetpu-dm1p25.tar.gz) | 77.06% | 1.20 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p25/mobilenet_edgetpu_dm1p25.tflite)
[MobileNetEdgeTPU dm1.5](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p5/mobilenet-edgetpu-dm1p5.tar.gz) | 75.9% | 1.42 | [link](https://storage.cloud.google.com/tf_model_garden/models/edgetpu/checkpoint_and_tflite/vision/mobilenet-edgetpu-v1/dm1p5/mobilenet_edgetpu_dm1p5.tflite)
diff --git a/official/projects/edgetpu/vision/__init__.py b/official/projects/edgetpu/vision/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/__init__.py
+++ b/official/projects/edgetpu/vision/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/configs/__init__.py b/official/projects/edgetpu/vision/configs/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/configs/__init__.py
+++ b/official/projects/edgetpu/vision/configs/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/configs/mobilenet_edgetpu_config.py b/official/projects/edgetpu/vision/configs/mobilenet_edgetpu_config.py
index 5ce1c3eb49f408ddb78424e121752d1155d4a002..5970e533c5ec9adfb926d9679ec0d8d82ff6d4a9 100644
--- a/official/projects/edgetpu/vision/configs/mobilenet_edgetpu_config.py
+++ b/official/projects/edgetpu/vision/configs/mobilenet_edgetpu_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -24,8 +24,8 @@ from typing import Any, Mapping, Optional
from official.core import config_definitions as cfg
from official.core import exp_factory
from official.modeling import optimization
-from official.vision.beta.configs import common
-from official.vision.beta.configs import image_classification as base_config
+from official.vision.configs import common
+from official.vision.configs import image_classification as base_config
@dataclasses.dataclass
diff --git a/official/projects/edgetpu/vision/configs/semantic_segmentation_config.py b/official/projects/edgetpu/vision/configs/semantic_segmentation_config.py
index dbb5e41502535ad5782e71a39833305e480fd5a1..10012436d963935939252da1ff68d7028b7e05d1 100644
--- a/official/projects/edgetpu/vision/configs/semantic_segmentation_config.py
+++ b/official/projects/edgetpu/vision/configs/semantic_segmentation_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Semantic segmentation configuration definition.
The segmentation model is built using the mobilenet edgetpu v2 backbone and
@@ -25,10 +24,10 @@ from official.core import config_definitions as cfg
from official.core import exp_factory
from official.modeling import hyperparams
from official.modeling import optimization
-from official.vision.beta.configs import backbones
-from official.vision.beta.configs import common
-from official.vision.beta.configs import decoders
-from official.vision.beta.configs import semantic_segmentation as base_cfg
+from official.vision.configs import backbones
+from official.vision.configs import common
+from official.vision.configs import decoders
+from official.vision.configs import semantic_segmentation as base_cfg
@dataclasses.dataclass
diff --git a/official/projects/edgetpu/vision/configs/semantic_segmentation_searched_config.py b/official/projects/edgetpu/vision/configs/semantic_segmentation_searched_config.py
index 44a5a4c04930ae244f2d8e82e22d0319874352ec..87213ff6dc73d977228ca6fe255f69b29f60631a 100644
--- a/official/projects/edgetpu/vision/configs/semantic_segmentation_searched_config.py
+++ b/official/projects/edgetpu/vision/configs/semantic_segmentation_searched_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -26,8 +26,8 @@ from official.core import config_definitions as cfg
from official.core import exp_factory
from official.modeling import hyperparams
from official.modeling import optimization
-from official.vision.beta.configs import backbones
-from official.vision.beta.configs import semantic_segmentation as base_cfg
+from official.vision.configs import backbones
+from official.vision.configs import semantic_segmentation as base_cfg
# ADE 20K Dataset
ADE20K_TRAIN_EXAMPLES = 20210
diff --git a/official/projects/edgetpu/vision/dataloaders/__init__.py b/official/projects/edgetpu/vision/dataloaders/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/dataloaders/__init__.py
+++ b/official/projects/edgetpu/vision/dataloaders/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/dataloaders/classification_input.py b/official/projects/edgetpu/vision/dataloaders/classification_input.py
index 175d1900d0d6bdaade05fabab01e4345348877ff..1c7f532d93b5c34adbbdcc0bffe18d8da77dd834 100644
--- a/official/projects/edgetpu/vision/dataloaders/classification_input.py
+++ b/official/projects/edgetpu/vision/dataloaders/classification_input.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,8 +16,8 @@
# Import libraries
import tensorflow as tf
-from official.vision.beta.dataloaders import classification_input
-from official.vision.beta.ops import preprocess_ops
+from official.vision.dataloaders import classification_input
+from official.vision.ops import preprocess_ops
MEAN_RGB = (0.5 * 255, 0.5 * 255, 0.5 * 255)
STDDEV_RGB = (0.5 * 255, 0.5 * 255, 0.5 * 255)
diff --git a/official/projects/edgetpu/vision/dataloaders/classification_input_test.py b/official/projects/edgetpu/vision/dataloaders/classification_input_test.py
index 437f10b8d418fa03d4ab3a80c4e035ef92b36275..ecd552b072d12809f66f9b28faef970d17fed132 100644
--- a/official/projects/edgetpu/vision/dataloaders/classification_input_test.py
+++ b/official/projects/edgetpu/vision/dataloaders/classification_input_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,8 +17,8 @@
from absl.testing import parameterized
import tensorflow as tf
from official.projects.edgetpu.vision.dataloaders import classification_input
-from official.vision.beta.configs import common
-from official.vision.beta.dataloaders import tfexample_utils
+from official.vision.configs import common
+from official.vision.dataloaders import tfexample_utils
IMAGE_FIELD_KEY = 'image/encoded'
LABEL_FIELD_KEY = 'image/class/label'
diff --git a/official/projects/edgetpu/vision/modeling/__init__.py b/official/projects/edgetpu/vision/modeling/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/modeling/__init__.py
+++ b/official/projects/edgetpu/vision/modeling/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/backbones/__init__.py b/official/projects/edgetpu/vision/modeling/backbones/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/modeling/backbones/__init__.py
+++ b/official/projects/edgetpu/vision/modeling/backbones/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu.py b/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu.py
index 0a2aafe3d554ea745c3ec49a668c609d6af9a279..2fa8d10e59719ca25a7000e3803f903bded0b17f 100644
--- a/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu.py
+++ b/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,7 +22,7 @@ import tensorflow as tf
from official.modeling import hyperparams
from official.projects.edgetpu.vision.modeling.mobilenet_edgetpu_v1_model import MobilenetEdgeTPU
from official.projects.edgetpu.vision.modeling.mobilenet_edgetpu_v2_model import MobilenetEdgeTPUV2
-from official.vision.beta.modeling.backbones import factory
+from official.vision.modeling.backbones import factory
layers = tf.keras.layers
diff --git a/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu_test.py b/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu_test.py
index dea28630eb71878cb9bac789115919e2c2c311f8..9043aeb06089ef93e72c59efc4feb829d1f46a72 100644
--- a/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu_test.py
+++ b/official/projects/edgetpu/vision/modeling/backbones/mobilenet_edgetpu_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for MobileNet."""
# Import libraries
diff --git a/official/projects/edgetpu/vision/modeling/common_modules.py b/official/projects/edgetpu/vision/modeling/common_modules.py
index 878a5702fd3b09d683c1256f8a69f2b4262e1097..284a2e8e46fc3561e833bb5792392c50955b629f 100644
--- a/official/projects/edgetpu/vision/modeling/common_modules.py
+++ b/official/projects/edgetpu/vision/modeling/common_modules.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/custom_layers.py b/official/projects/edgetpu/vision/modeling/custom_layers.py
index 7097fde2e4703c36ae8990cc7d1f43ee95e6b20f..3548dd335785724efd6c2083db7e99ae03ba434c 100644
--- a/official/projects/edgetpu/vision/modeling/custom_layers.py
+++ b/official/projects/edgetpu/vision/modeling/custom_layers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,6 +18,8 @@ import inspect
from typing import Any, MutableMapping, Optional, Union, Tuple
import tensorflow as tf
+from official.modeling import tf_utils
+
class GroupConv2D(tf.keras.layers.Conv2D):
"""2D group convolution as a Keras Layer."""
@@ -168,7 +170,7 @@ class GroupConv2D(tf.keras.layers.Conv2D):
self.add_weight(
name='kernel_{}'.format(g),
shape=self.group_kernel_shape,
- initializer=self.kernel_initializer,
+ initializer=tf_utils.clone_initializer(self.kernel_initializer),
regularizer=self.kernel_regularizer,
constraint=self.kernel_constraint,
trainable=True,
@@ -178,7 +180,7 @@ class GroupConv2D(tf.keras.layers.Conv2D):
self.add_weight(
name='bias_{}'.format(g),
shape=(self.group_output_channel,),
- initializer=self.bias_initializer,
+ initializer=tf_utils.clone_initializer(self.bias_initializer),
regularizer=self.bias_regularizer,
constraint=self.bias_constraint,
trainable=True,
diff --git a/official/projects/edgetpu/vision/modeling/custom_layers_test.py b/official/projects/edgetpu/vision/modeling/custom_layers_test.py
index ef39c563d19c950a48671e74e7f8819f0fa13f9e..c07ce224ee3ab18ad68815c0e0f45b40470e59ee 100644
--- a/official/projects/edgetpu/vision/modeling/custom_layers_test.py
+++ b/official/projects/edgetpu/vision/modeling/custom_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/heads/__init__.py b/official/projects/edgetpu/vision/modeling/heads/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/modeling/heads/__init__.py
+++ b/official/projects/edgetpu/vision/modeling/heads/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/heads/bifpn_head.py b/official/projects/edgetpu/vision/modeling/heads/bifpn_head.py
index ea6ba275b5678d2beefe549c78a3afc491bf478d..7af79d1e55b6449d70604129b0e04ec2ce096f66 100644
--- a/official/projects/edgetpu/vision/modeling/heads/bifpn_head.py
+++ b/official/projects/edgetpu/vision/modeling/heads/bifpn_head.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -670,7 +670,7 @@ class SegClassNet(tf.keras.layers.Layer):
self.min_level = min_level
self.max_level = max_level
self.fullres_output = fullres_output
- self.fullres_conv_transpose = fullres_skip_connections
+ self.fullres_skip_connections = fullres_skip_connections
self.fnode = FNode(
0, # Always use the first level with highest resolution.
@@ -726,7 +726,7 @@ class SegClassNet(tf.keras.layers.Layer):
if self.fullres_output:
for i in reversed(range(self.min_level)):
- if self.config.fullres_skip_connections:
+ if self.fullres_skip_connections:
net = tf.keras.layers.Concatenate()([net, backbone_feats[i + 1]])
net = self.fullres_conv[str(i)](net)
net = self.fullres_conv_transpose[str(i)](net)
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model.py
index c3b4a18cbe13da34fbdeeccb7985e1bfe0d5a1b9..fa3f36cc55aff3c8ab82da242a5be12d12cdf615 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_blocks.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_blocks.py
index 7441db5b721a4a4f18333085bc0a42689e94b76a..29d93d3d92b758582add630fc3eb49d1951b2132 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_blocks.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_blocks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_test.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_test.py
index 775e56620bd1f1c0edda004c4fba5aef71cde6a2..a4ca070a908585349f2ccc86c3b5635da546e6cd 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_test.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v1_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model.py
index 4cb34b94a1abf2801374acd98349ecd50aac0b7e..9321cb47ec6d03068b29316a20382b3c0642ab24 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks.py
index c5aa89d0e81c6a2a3d2463b47323f87e3681e632..a66c72a7c1fc1ec6aa851e42924cf520b6e80f7c 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -26,6 +26,8 @@ from official.modeling.hyperparams import oneof
from official.projects.edgetpu.vision.modeling import common_modules
from official.projects.edgetpu.vision.modeling import custom_layers
+InitializerType = Optional[Union[str, tf.keras.initializers.Initializer]]
+
@dataclasses.dataclass
class BlockType(oneof.OneOfConfig):
@@ -216,6 +218,8 @@ class ModelConfig(base_config.Config):
stem_base_filters: int = 64
stem_kernel_size: int = 5
top_base_filters: int = 1280
+ conv_kernel_initializer: InitializerType = None
+ dense_kernel_initializer: InitializerType = None
blocks: Tuple[BlockConfig, ...] = (
# (input_filters, output_filters, kernel_size, num_repeat,
# expand_ratio, strides, se_ratio, id_skip, fused_conv, conv_type)
@@ -279,7 +283,8 @@ def mobilenet_edgetpu_v2_base(
drop_connect_rate: float = 0.1,
filter_size_overrides: Optional[Dict[int, int]] = None,
block_op_overrides: Optional[Dict[int, Dict[int, Dict[str, Any]]]] = None,
- block_group_overrides: Optional[Dict[int, Dict[str, Any]]] = None):
+ block_group_overrides: Optional[Dict[int, Dict[str, Any]]] = None,
+ topology: Optional[TopologyConfig] = None):
"""Creates MobilenetEdgeTPUV2 ModelConfig based on tuning parameters."""
config = ModelConfig()
@@ -295,7 +300,7 @@ def mobilenet_edgetpu_v2_base(
}
config = config.replace(**param_overrides)
- topology_config = TopologyConfig()
+ topology_config = TopologyConfig() if topology is None else topology
if filter_size_overrides:
for group_id in filter_size_overrides:
topology_config.block_groups[group_id].filters = filter_size_overrides[
@@ -724,6 +729,7 @@ def conv2d_block_as_layers(
use_bias: bool = False,
activation: Any = None,
depthwise: bool = False,
+ kernel_initializer: InitializerType = None,
name: Optional[str] = None) -> List[tf.keras.layers.Layer]:
"""A conv2d followed by batch norm and an activation."""
batch_norm = common_modules.get_batch_norm(config.batch_norm)
@@ -748,11 +754,13 @@ def conv2d_block_as_layers(
sequential_layers: List[tf.keras.layers.Layer] = []
if depthwise:
conv2d = tf.keras.layers.DepthwiseConv2D
- init_kwargs.update({'depthwise_initializer': CONV_KERNEL_INITIALIZER})
+ init_kwargs.update({'depthwise_initializer': kernel_initializer})
else:
conv2d = tf.keras.layers.Conv2D
- init_kwargs.update({'filters': conv_filters,
- 'kernel_initializer': CONV_KERNEL_INITIALIZER})
+ init_kwargs.update({
+ 'filters': conv_filters,
+ 'kernel_initializer': kernel_initializer
+ })
sequential_layers.append(conv2d(**init_kwargs))
@@ -780,12 +788,21 @@ def conv2d_block(inputs: tf.Tensor,
use_bias: bool = False,
activation: Any = None,
depthwise: bool = False,
+ kernel_initializer: Optional[InitializerType] = None,
name: Optional[str] = None) -> tf.Tensor:
"""Compatibility with third_party/car/deep_nets."""
x = inputs
- for layer in conv2d_block_as_layers(conv_filters, config, kernel_size,
- strides, use_batch_norm, use_bias,
- activation, depthwise, name):
+ for layer in conv2d_block_as_layers(
+ conv_filters=conv_filters,
+ config=config,
+ kernel_size=kernel_size,
+ strides=strides,
+ use_batch_norm=use_batch_norm,
+ use_bias=use_bias,
+ activation=activation,
+ depthwise=depthwise,
+ kernel_initializer=kernel_initializer,
+ name=name):
x = layer(x)
return x
@@ -828,6 +845,9 @@ class _MbConvBlock:
use_groupconv = block.conv_type == 'group'
prefix = prefix or ''
self.name = prefix
+ conv_kernel_initializer = (
+ config.conv_kernel_initializer if config.conv_kernel_initializer
+ is not None else CONV_KERNEL_INITIALIZER)
filters = block.input_filters * block.expand_ratio
@@ -851,22 +871,26 @@ class _MbConvBlock:
activation=activation,
name=prefix + 'fused'))
else:
- self.expand_block.extend(conv2d_block_as_layers(
- filters,
- config,
- kernel_size=block.kernel_size,
- strides=block.strides,
- activation=activation,
- name=prefix + 'fused'))
+ self.expand_block.extend(
+ conv2d_block_as_layers(
+ conv_filters=filters,
+ config=config,
+ kernel_size=block.kernel_size,
+ strides=block.strides,
+ activation=activation,
+ kernel_initializer=conv_kernel_initializer,
+ name=prefix + 'fused'))
else:
if block.expand_ratio != 1:
# Expansion phase with a pointwise conv
- self.expand_block.extend(conv2d_block_as_layers(
- filters,
- config,
- kernel_size=(1, 1),
- activation=activation,
- name=prefix + 'expand'))
+ self.expand_block.extend(
+ conv2d_block_as_layers(
+ conv_filters=filters,
+ config=config,
+ kernel_size=(1, 1),
+ activation=activation,
+ kernel_initializer=conv_kernel_initializer,
+ name=prefix + 'expand'))
# Main kernel, after the expansion (if applicable, i.e. not fused).
if use_depthwise:
@@ -876,6 +900,7 @@ class _MbConvBlock:
kernel_size=block.kernel_size,
strides=block.strides,
activation=activation,
+ kernel_initializer=conv_kernel_initializer,
depthwise=True,
name=prefix + 'depthwise'))
elif use_groupconv:
@@ -907,27 +932,30 @@ class _MbConvBlock:
tf.keras.layers.Reshape(se_shape, name=prefix + 'se_reshape'))
self.squeeze_excitation.extend(
conv2d_block_as_layers(
- num_reduced_filters,
- config,
+ conv_filters=num_reduced_filters,
+ config=config,
use_bias=True,
use_batch_norm=False,
activation=activation,
+ kernel_initializer=conv_kernel_initializer,
name=prefix + 'se_reduce'))
self.squeeze_excitation.extend(
conv2d_block_as_layers(
- filters,
- config,
+ conv_filters=filters,
+ config=config,
use_bias=True,
use_batch_norm=False,
activation='sigmoid',
+ kernel_initializer=conv_kernel_initializer,
name=prefix + 'se_expand'))
# Output phase
self.project_block.extend(
conv2d_block_as_layers(
- block.output_filters,
- config,
+ conv_filters=block.output_filters,
+ config=config,
activation=None,
+ kernel_initializer=conv_kernel_initializer,
name=prefix + 'project'))
# Add identity so that quantization-aware training can insert quantization
@@ -993,6 +1021,12 @@ def mobilenet_edgetpu_v2(image_input: tf.keras.layers.Input,
activation = tf_utils.get_activation(config.activation)
dropout_rate = config.dropout_rate
drop_connect_rate = config.drop_connect_rate
+ conv_kernel_initializer = (
+ config.conv_kernel_initializer if config.conv_kernel_initializer
+ is not None else CONV_KERNEL_INITIALIZER)
+ dense_kernel_initializer = (
+ config.dense_kernel_initializer if config.dense_kernel_initializer
+ is not None else DENSE_KERNEL_INITIALIZER)
num_classes = config.num_classes
input_channels = config.input_channels
rescale_input = config.rescale_input
@@ -1010,12 +1044,13 @@ def mobilenet_edgetpu_v2(image_input: tf.keras.layers.Input,
# Build stem
x = conv2d_block(
- x,
- round_filters(stem_base_filters, config),
- config,
+ inputs=x,
+ conv_filters=round_filters(stem_base_filters, config),
+ config=config,
kernel_size=[stem_kernel_size, stem_kernel_size],
strides=[2, 2],
activation=activation,
+ kernel_initializer=conv_kernel_initializer,
name='stem')
# Build blocks
@@ -1061,11 +1096,13 @@ def mobilenet_edgetpu_v2(image_input: tf.keras.layers.Input,
if config.backbone_only:
return backbone_levels
# Build top
- x = conv2d_block(x,
- round_filters(top_base_filters, config),
- config,
- activation=activation,
- name='top')
+ x = conv2d_block(
+ inputs=x,
+ conv_filters=round_filters(top_base_filters, config),
+ config=config,
+ activation=activation,
+ kernel_initializer=conv_kernel_initializer,
+ name='top')
# Build classifier
pool_size = (x.shape.as_list()[1], x.shape.as_list()[2])
@@ -1075,7 +1112,7 @@ def mobilenet_edgetpu_v2(image_input: tf.keras.layers.Input,
x = tf.keras.layers.Conv2D(
num_classes,
1,
- kernel_initializer=DENSE_KERNEL_INITIALIZER,
+ kernel_initializer=dense_kernel_initializer,
kernel_regularizer=tf.keras.regularizers.l2(weight_decay),
bias_regularizer=tf.keras.regularizers.l2(weight_decay),
name='logits')(
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks_test.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..1ad600399d1e38c8eb5311b3a8a91e9c14065452
--- /dev/null
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_blocks_test.py
@@ -0,0 +1,72 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for mobilenet_edgetpu_v2_model_blocks."""
+
+import tensorflow as tf
+
+from official.projects.edgetpu.vision.modeling import custom_layers
+from official.projects.edgetpu.vision.modeling import mobilenet_edgetpu_v2_model_blocks
+
+
+class MobilenetEdgetpuV2ModelBlocksTest(tf.test.TestCase):
+
+ def setUp(self):
+ super().setUp()
+ self.model_config = mobilenet_edgetpu_v2_model_blocks.ModelConfig()
+
+ def test_model_creatation(self):
+ model_input = tf.keras.layers.Input(shape=(224, 224, 1))
+ model_output = mobilenet_edgetpu_v2_model_blocks.mobilenet_edgetpu_v2(
+ image_input=model_input,
+ config=self.model_config)
+ test_model = tf.keras.Model(inputs=model_input, outputs=model_output)
+ self.assertIsInstance(test_model, tf.keras.Model)
+ self.assertEqual(test_model.input.shape, (None, 224, 224, 1))
+ self.assertEqual(test_model.output.shape, (None, 1001))
+
+ def test_model_with_customized_kernel_initializer(self):
+ self.model_config.conv_kernel_initializer = 'he_uniform'
+ self.model_config.dense_kernel_initializer = 'glorot_normal'
+ model_input = tf.keras.layers.Input(shape=(224, 224, 1))
+ model_output = mobilenet_edgetpu_v2_model_blocks.mobilenet_edgetpu_v2(
+ image_input=model_input,
+ config=self.model_config)
+ test_model = tf.keras.Model(inputs=model_input, outputs=model_output)
+
+ conv_layer_stack = []
+ for layer in test_model.layers:
+ if (isinstance(layer, tf.keras.layers.Conv2D) or
+ isinstance(layer, tf.keras.layers.DepthwiseConv2D) or
+ isinstance(layer, custom_layers.GroupConv2D)):
+ conv_layer_stack.append(layer)
+ self.assertGreater(len(conv_layer_stack), 2)
+ # The last Conv layer is used as a Dense layer.
+ for layer in conv_layer_stack[:-1]:
+ if isinstance(layer, custom_layers.GroupConv2D):
+ self.assertIsInstance(layer.kernel_initializer,
+ tf.keras.initializers.GlorotUniform)
+ elif isinstance(layer, tf.keras.layers.Conv2D):
+ self.assertIsInstance(layer.kernel_initializer,
+ tf.keras.initializers.HeUniform)
+ elif isinstance(layer, tf.keras.layers.DepthwiseConv2D):
+ self.assertIsInstance(layer.depthwise_initializer,
+ tf.keras.initializers.HeUniform)
+
+ self.assertIsInstance(conv_layer_stack[-1].kernel_initializer,
+ tf.keras.initializers.GlorotNormal)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_test.py b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_test.py
index 004ffeb79b382e132a80906306f2403bdd614390..7044d7d93e5642176cf298237f92754759fa10c4 100644
--- a/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_test.py
+++ b/official/projects/edgetpu/vision/modeling/mobilenet_edgetpu_v2_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer.py b/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8f80fd8216b0fd5292a22452d43e71ccb7525bc
--- /dev/null
+++ b/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer.py
@@ -0,0 +1,164 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""MultiHeadAttention layer optimized for EdgeTPU.
+
+Compared to tf.keras.layers.MultiHeadAttention, this layer performs query-key
+multiplication instead of key-query multiplication to remove an unnecessary
+transpose.
+"""
+import math
+import string
+from typing import Optional, Tuple
+
+import numpy as np
+import tensorflow as tf
+
+_CHR_IDX = string.ascii_lowercase
+
+
+def _build_attention_equation(
+ rank: int, attn_axes: Tuple[int, ...]) -> Tuple[str, str, int]:
+ """Builds einsum equations for the attention computation.
+
+ Query, key, value inputs after projection are expected to have the shape as:
+ `(bs, , , num_heads, channels)`.
+ `bs` and `` are treated as ``.
+
+ The attention operations can be generalized:
+ (1) Query-key dot product:
+ `(, , num_heads, channels), (,
+ , num_heads, channels) -> (,
+ num_heads, , )`
+ (2) Combination:
+ `(, num_heads, , ),
+ (, , num_heads, channels) -> (, , num_heads, channels)`
+
+ Args:
+ rank: Rank of query, key, value tensors.
+ attn_axes: List/tuple of axes, `[-1, rank)`, that attention will be
+ applied to.
+
+ Returns:
+ Einsum equations.
+ """
+ target_notation = _CHR_IDX[:rank]
+ # `batch_dims` includes the head dim.
+ batch_dims = tuple(np.delete(range(rank), attn_axes + (rank - 1,)))
+ letter_offset = rank
+ source_notation = ""
+ for i in range(rank):
+ if i in batch_dims or i == rank - 1:
+ source_notation += target_notation[i]
+ else:
+ source_notation += _CHR_IDX[letter_offset]
+ letter_offset += 1
+
+ product_notation = "".join([target_notation[i] for i in batch_dims] +
+ [target_notation[i] for i in attn_axes] +
+ [source_notation[i] for i in attn_axes])
+ dot_product_equation = "%s,%s->%s" % (
+ target_notation,
+ source_notation,
+ product_notation,
+ )
+ attn_scores_rank = len(product_notation)
+ combine_equation = "%s,%s->%s" % (
+ product_notation,
+ source_notation,
+ target_notation,
+ )
+ return dot_product_equation, combine_equation, attn_scores_rank
+
+
+class OptimizedMultiHeadAttention(tf.keras.layers.MultiHeadAttention):
+ """MultiHeadAttention with query-key multiplication.
+
+ Currently, this layer only works for self-attention but not for
+ cross-attention. TODO(b/243166060).
+ """
+
+ def _build_attention(self, rank: int) -> None:
+ """Builds multi-head dot-product attention computations.
+
+ This function builds attributes necessary for `_compute_attention` to
+ customize attention computation to replace the default dot-product
+ attention.
+
+ Args:
+ rank: the rank of query, key, value tensors.
+ """
+ if self._attention_axes is None:
+ self._attention_axes = tuple(range(1, rank - 2))
+ else:
+ self._attention_axes = tuple(self._attention_axes)
+ (
+ self._dot_product_equation,
+ self._combine_equation,
+ attn_scores_rank,
+ ) = _build_attention_equation(
+ rank, attn_axes=self._attention_axes)
+ norm_axes = tuple(
+ range(attn_scores_rank - len(self._attention_axes), attn_scores_rank))
+ self._softmax = tf.keras.layers.Softmax(axis=norm_axes)
+ self._dropout_layer = tf.keras.layers.Dropout(rate=self._dropout)
+
+ def _compute_attention(
+ self,
+ query: tf.Tensor,
+ key: tf.Tensor,
+ value: tf.Tensor,
+ attention_mask: Optional[tf.Tensor] = None,
+ training: Optional[bool] = None) -> Tuple[tf.Tensor, tf.Tensor]:
+ """Applies Dot-product attention with query, key, value tensors.
+
+ This function defines the computation inside `call` with projected
+ multi-head Q, K, V inputs. Users can override this function for
+ customized attention implementation.
+
+ Args:
+ query: Projected query `Tensor` of shape `(B, T, N, key_dim)`.
+ key: Projected key `Tensor` of shape `(B, S, N, key_dim)`.
+ value: Projected value `Tensor` of shape `(B, S, N, value_dim)`.
+ attention_mask: a boolean mask of shape `(B, T, S)`, that prevents
+ attention to certain positions. It is generally not needed if the
+ `query` and `value` (and/or `key`) are masked.
+ training: Python boolean indicating whether the layer should behave in
+ training mode (adding dropout) or in inference mode (doing nothing).
+
+ Returns:
+ attention_output: Multi-headed outputs of attention computation.
+ attention_scores: Multi-headed attention weights.
+ """
+ # Note: Applying scalar multiply at the smaller end of einsum improves
+ # XLA performance, but may introduce slight numeric differences in
+ # the Transformer attention head.
+ query = tf.multiply(query, 1.0 / math.sqrt(float(self._key_dim)))
+
+ # Take the dot product between "query" and "key" to get the raw
+ # attention scores.
+ attention_scores = tf.einsum(self._dot_product_equation, query, key)
+
+ attention_scores = self._masked_softmax(attention_scores, attention_mask)
+
+ # This is actually dropping out entire tokens to attend to, which might
+ # seem a bit unusual, but is taken from the original Transformer paper.
+ attention_scores_dropout = self._dropout_layer(
+ attention_scores, training=training)
+
+ # `context_layer` = [B, T, N, H]
+ attention_output = tf.einsum(self._combine_equation,
+ attention_scores_dropout, value)
+ return attention_output, attention_scores
diff --git a/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer_test.py b/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..4d4ca514867fbfd318f4ef9ec3f945fa853bf9d3
--- /dev/null
+++ b/official/projects/edgetpu/vision/modeling/optimized_multiheadattention_layer_test.py
@@ -0,0 +1,81 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for optimized_multiheadattention_layer."""
+
+import numpy as np
+import tensorflow as tf
+
+from official.projects.edgetpu.vision.modeling import optimized_multiheadattention_layer
+
+_BATCH_SIZE = 32
+_SEQ_LEN = 4
+_EMBEDDING_SIZE = 8
+_NUM_HEADS = 2
+_KEY_DIM = 2
+
+
+class OptimizedMultiheadattentionLayerTest(tf.test.TestCase):
+
+ def test_same_output(self):
+ """Tests that OptimizedMultiHeadAttention returns the expected outputs."""
+
+ input_tensor_1 = tf.random.uniform((_BATCH_SIZE, _SEQ_LEN, _EMBEDDING_SIZE))
+ input_tensor_2 = tf.random.uniform((_BATCH_SIZE, _SEQ_LEN, _EMBEDDING_SIZE))
+
+ # Instantiate layer and call with inputs to build.
+ orig_layer = tf.keras.layers.MultiHeadAttention(
+ num_heads=_NUM_HEADS, key_dim=_KEY_DIM)
+ _ = orig_layer(input_tensor_1, input_tensor_2)
+ opt_layer = optimized_multiheadattention_layer.OptimizedMultiHeadAttention(
+ num_heads=_NUM_HEADS, key_dim=_KEY_DIM)
+ _ = opt_layer(input_tensor_1, input_tensor_2)
+
+ # Set the weights of the two layers to be the same.
+ query_dense_weights = np.random.uniform(
+ size=(_EMBEDDING_SIZE, _NUM_HEADS, _KEY_DIM))
+ query_dense_bias = np.random.uniform(size=(_NUM_HEADS, _KEY_DIM))
+ key_dense_weights = np.random.uniform(
+ size=(_EMBEDDING_SIZE, _NUM_HEADS, _KEY_DIM))
+ key_dense_bias = np.random.uniform(size=(_NUM_HEADS, _KEY_DIM))
+ value_dense_weights = np.random.uniform(
+ size=(_EMBEDDING_SIZE, _NUM_HEADS, _KEY_DIM))
+ value_dense_bias = np.random.uniform(size=(_NUM_HEADS, _KEY_DIM))
+ attention_output_dense_weights = np.random.uniform(
+ size=(_NUM_HEADS, _KEY_DIM, _EMBEDDING_SIZE))
+ attention_output_dense_bias = np.random.uniform(size=(_EMBEDDING_SIZE,))
+
+ orig_layer._query_dense.set_weights([query_dense_weights, query_dense_bias])
+ orig_layer._key_dense.set_weights([key_dense_weights, key_dense_bias])
+ orig_layer._value_dense.set_weights([value_dense_weights, value_dense_bias])
+ orig_layer._output_dense.set_weights(
+ [attention_output_dense_weights, attention_output_dense_bias])
+
+ opt_layer._query_dense.set_weights([query_dense_weights, query_dense_bias])
+ opt_layer._key_dense.set_weights([key_dense_weights, key_dense_bias])
+ opt_layer._value_dense.set_weights([value_dense_weights, value_dense_bias])
+ opt_layer._output_dense.set_weights(
+ [attention_output_dense_weights, attention_output_dense_bias])
+
+ # Calculate two sets of attention outputs and scores and compare.
+ orig_attn_output, orig_attn_score = orig_layer(
+ input_tensor_1, input_tensor_2, return_attention_scores=True)
+ opt_attn_output, opt_attn_score = opt_layer(
+ input_tensor_1, input_tensor_2, return_attention_scores=True)
+ self.assertAllClose(orig_attn_output, opt_attn_output)
+ self.assertAllClose(orig_attn_score, opt_attn_score)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/edgetpu/vision/serving/__init__.py b/official/projects/edgetpu/vision/serving/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/serving/__init__.py
+++ b/official/projects/edgetpu/vision/serving/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/serving/export_tflite.py b/official/projects/edgetpu/vision/serving/export_tflite.py
index 3014329e36e4ce547729c97d455eea69d2ac9e76..775b55f4ba9b27e39bddf844676fc0c5590cee7d 100644
--- a/official/projects/edgetpu/vision/serving/export_tflite.py
+++ b/official/projects/edgetpu/vision/serving/export_tflite.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -60,6 +60,8 @@ flags.DEFINE_integer(
'image_size', 224,
'Size of the input image. Ideally should be the same as the image_size used '
'in training config.')
+flags.DEFINE_bool(
+ 'fix_batch_size', True, 'Whether to export model with fixed batch size.')
flags.DEFINE_string(
'output_layer', None,
'Layer name to take the output from. Can be used to take the output from '
@@ -146,9 +148,11 @@ def run_export():
output_layer = model.get_layer(export_config.output_layer)
model = tf.keras.Model(model.input, output_layer.output)
+ batch_size = 1 if FLAGS.fix_batch_size else None
+
model_input = tf.keras.Input(
shape=(export_config.image_size, export_config.image_size, 3),
- batch_size=1)
+ batch_size=batch_size)
model_output = export_util.finalize_serving(model(model_input), export_config)
model_for_inference = tf.keras.Model(model_input, model_output)
diff --git a/official/projects/edgetpu/vision/serving/export_tflite_test.py b/official/projects/edgetpu/vision/serving/export_tflite_test.py
index 179212c5b5f8b5906b2fb505ab32de98882c6034..6a0ae90629c0d6078cab9ae1ac4584a78298bac1 100644
--- a/official/projects/edgetpu/vision/serving/export_tflite_test.py
+++ b/official/projects/edgetpu/vision/serving/export_tflite_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/serving/export_util.py b/official/projects/edgetpu/vision/serving/export_util.py
index a98b149820a24894bf23cdece70cef42ff7885c8..5b208a40f403f796a1c5991069fcb896dc9fc4a3 100644
--- a/official/projects/edgetpu/vision/serving/export_util.py
+++ b/official/projects/edgetpu/vision/serving/export_util.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -31,7 +31,7 @@ from official.projects.edgetpu.vision.modeling import custom_layers
from official.projects.edgetpu.vision.modeling.backbones import mobilenet_edgetpu
from official.projects.edgetpu.vision.tasks import image_classification
from official.projects.edgetpu.vision.tasks import semantic_segmentation as edgetpu_semantic_segmentation
-from official.vision.beta.tasks import semantic_segmentation
+from official.vision.tasks import semantic_segmentation
# pylint: enable=unused-import
MEAN_RGB = [127.5, 127.5, 127.5]
@@ -107,6 +107,12 @@ class ExportConfig(base_config.Config):
def finalize_serving(model_output, export_config):
"""Adds extra layers based on the provided configuration."""
+ if isinstance(model_output, dict):
+ return {
+ key: finalize_serving(model_output[key], export_config)
+ for key in model_output
+ }
+
finalize_method = export_config.finalize_method
output_layer = model_output
if not finalize_method or finalize_method[0] == 'none':
@@ -183,8 +189,7 @@ def representative_dataset_gen(export_config):
"""Gets a python generator of numpy arrays for the given dataset."""
quantization_config = export_config.quantization_config
dataset = tfds.builder(
- quantization_config.dataset_name,
- data_dir=quantization_config.dataset_dir)
+ quantization_config.dataset_name, try_gcs=True)
dataset.download_and_prepare()
data = dataset.as_dataset()[quantization_config.dataset_split]
iterator = data.as_numpy_iterator()
@@ -201,7 +206,8 @@ def configure_tflite_converter(export_config, converter):
"""Common code for picking up quantization parameters."""
quantization_config = export_config.quantization_config
if quantization_config.quantize:
- if quantization_config.dataset_dir is None:
+ if (quantization_config.dataset_dir is
+ None) and (quantization_config.dataset_name is None):
raise ValueError(
'Must provide a representative dataset when quantizing the model.')
converter.optimizations = [tf.lite.Optimize.DEFAULT]
diff --git a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator.py b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator.py
index b28adec43229a755bbff3cf24a9971b953f80d77..c4afb000b018255824dfe401f3d4ded9f248bacd 100644
--- a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator.py
+++ b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_run.py b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_run.py
index 5a8981da05c33b09a840d665c08fbf66dfc4f81b..f74f90ac2fb2e526af9aaa3e90e4f1fcd69f0437 100644
--- a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_run.py
+++ b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_run.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_test.py b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_test.py
index f531069000911cfff0b427e2022ee59981940aee..3fcaffa453701c0b2910b3db1f33a13df3969a17 100644
--- a/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_test.py
+++ b/official/projects/edgetpu/vision/serving/tflite_imagenet_evaluator_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/tasks/__init__.py b/official/projects/edgetpu/vision/tasks/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/edgetpu/vision/tasks/__init__.py
+++ b/official/projects/edgetpu/vision/tasks/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/edgetpu/vision/tasks/image_classification.py b/official/projects/edgetpu/vision/tasks/image_classification.py
index cdb651a61b655daf4569b6a5efe8f4991dc828c1..6559368a2176c8acd5d2510504599635d89f9e2d 100644
--- a/official/projects/edgetpu/vision/tasks/image_classification.py
+++ b/official/projects/edgetpu/vision/tasks/image_classification.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -28,8 +28,8 @@ from official.projects.edgetpu.vision.configs import mobilenet_edgetpu_config as
from official.projects.edgetpu.vision.dataloaders import classification_input
from official.projects.edgetpu.vision.modeling import mobilenet_edgetpu_v1_model
from official.projects.edgetpu.vision.modeling import mobilenet_edgetpu_v2_model
-from official.vision.beta.configs import image_classification as base_cfg
-from official.vision.beta.dataloaders import input_reader_factory
+from official.vision.configs import image_classification as base_cfg
+from official.vision.dataloaders import input_reader_factory
def _copy_recursively(src: str, dst: str) -> None:
@@ -265,7 +265,7 @@ class EdgeTPUTask(base_task.Task):
"""Does forward and backward.
Args:
- inputs: A tuple of of input tensors of (features, labels).
+ inputs: A tuple of input tensors of (features, labels).
model: A tf.keras.Model instance.
optimizer: The optimizer for this training step.
metrics: A nested structure of metrics objects.
@@ -319,7 +319,7 @@ class EdgeTPUTask(base_task.Task):
"""Runs validatation step.
Args:
- inputs: A tuple of of input tensors of (features, labels).
+ inputs: A tuple of input tensors of (features, labels).
model: A tf.keras.Model instance.
metrics: A nested structure of metrics objects.
diff --git a/official/projects/edgetpu/vision/tasks/image_classification_test.py b/official/projects/edgetpu/vision/tasks/image_classification_test.py
index 8916fc92cad9d79bfe5225350fa6950afc18dd86..be250d9d405d8b6f6feac9202520c0b2b78a3a25 100644
--- a/official/projects/edgetpu/vision/tasks/image_classification_test.py
+++ b/official/projects/edgetpu/vision/tasks/image_classification_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for image classification task."""
# pylint: disable=unused-import
@@ -20,11 +19,11 @@ from absl.testing import parameterized
import orbit
import tensorflow as tf
-from official.common import registry_imports
from official.core import exp_factory
from official.modeling import optimization
from official.projects.edgetpu.vision.configs import mobilenet_edgetpu_config
from official.projects.edgetpu.vision.tasks import image_classification
+from official.vision import registry_imports
# Dummy ImageNet TF dataset.
diff --git a/official/projects/edgetpu/vision/tasks/semantic_segmentation.py b/official/projects/edgetpu/vision/tasks/semantic_segmentation.py
index 28477f1bdff4b36b9499808d5d9b0fb3069862c4..d5cac8120fa85fcaaabdb9dd7e7e76426589c4a9 100644
--- a/official/projects/edgetpu/vision/tasks/semantic_segmentation.py
+++ b/official/projects/edgetpu/vision/tasks/semantic_segmentation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -27,11 +27,11 @@ from official.projects.edgetpu.vision.modeling import mobilenet_edgetpu_v1_model
from official.projects.edgetpu.vision.modeling import mobilenet_edgetpu_v2_model
from official.projects.edgetpu.vision.modeling.backbones import mobilenet_edgetpu # pylint: disable=unused-import
from official.projects.edgetpu.vision.modeling.heads import bifpn_head
-from official.vision.beta.dataloaders import input_reader_factory
-from official.vision.beta.dataloaders import segmentation_input
-from official.vision.beta.dataloaders import tfds_factory
-from official.vision.beta.ops import preprocess_ops
-from official.vision.beta.tasks import semantic_segmentation
+from official.vision.dataloaders import input_reader_factory
+from official.vision.dataloaders import segmentation_input
+from official.vision.dataloaders import tfds_factory
+from official.vision.ops import preprocess_ops
+from official.vision.tasks import semantic_segmentation
class ClassMappingParser(segmentation_input.Parser):
diff --git a/official/projects/edgetpu/vision/tasks/semantic_segmentation_test.py b/official/projects/edgetpu/vision/tasks/semantic_segmentation_test.py
index c3c637c02c92a62982d59357b3565ba40c691708..d12eb8dcdcd369370d456ce56816a4e9a52ec7de 100644
--- a/official/projects/edgetpu/vision/tasks/semantic_segmentation_test.py
+++ b/official/projects/edgetpu/vision/tasks/semantic_segmentation_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for semantic segmentation task."""
# pylint: disable=unused-import
@@ -20,12 +19,12 @@ from absl.testing import parameterized
import orbit
import tensorflow as tf
+from official import vision
from official.core import exp_factory
from official.modeling import optimization
from official.projects.edgetpu.vision.configs import semantic_segmentation_config as seg_cfg
from official.projects.edgetpu.vision.configs import semantic_segmentation_searched_config as autoseg_cfg
from official.projects.edgetpu.vision.tasks import semantic_segmentation as img_seg_task
-from official.vision import beta
# Dummy ADE20K TF dataset.
diff --git a/official/projects/edgetpu/vision/train.py b/official/projects/edgetpu/vision/train.py
index 3b4a432e02a6ac71ac1935eee827c7902c628ea6..d08da93810d1274e62d9976e14440d9e75242c25 100644
--- a/official/projects/edgetpu/vision/train.py
+++ b/official/projects/edgetpu/vision/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,16 +12,12 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""TensorFlow Model Garden Vision training for MobileNet-EdgeTPU."""
from absl import app
from absl import flags
import gin
-# pylint: disable=unused-import
-from official.common import registry_imports
-# pylint: enable=unused-import
from official.common import distribute_utils
from official.common import flags as tfm_flags
from official.core import task_factory
@@ -35,6 +31,7 @@ from official.projects.edgetpu.vision.configs import semantic_segmentation_searc
from official.projects.edgetpu.vision.modeling.backbones import mobilenet_edgetpu
from official.projects.edgetpu.vision.tasks import image_classification
from official.projects.edgetpu.vision.tasks import semantic_segmentation
+from official.vision import registry_imports
# pylint: enable=unused-import
FLAGS = flags.FLAGS
diff --git a/official/projects/labse/README.md b/official/projects/labse/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..bb6abcca16d8c27e2376e7c93dfad24abd2a0115
--- /dev/null
+++ b/official/projects/labse/README.md
@@ -0,0 +1,111 @@
+# Language-agnostic BERT Sentence Embedding
+
+The repository contains the implementation and experiment definition of `LaBSE`,
+[Language-agnostic BERT Sentence Embedding](https://arxiv.org/pdf/2007.01852.pdf).
+The implementation is provided by the paper author, Yinfei Yang. Note that,
+the cross-accelerator batch softmax is not implemented by the author, so the
+implementation does not fully reproduce the paper yet.
+
+Due to the data policy, the authors are not able to release the pre-training and
+fine-tuning data for `LaBSE` training.
+
+### Requirements
+
+The starter code requires Tensorflow. If you haven't installed it yet, follow
+the instructions on [tensorflow.org][1].
+This code has been tested with Tensorflow 2.8.0. Going forward,
+we will continue to target the latest released version of Tensorflow.
+
+Please verify that you have Python 3.7+ and Tensorflow 2.8.0 or higher
+installed by running the following commands:
+
+```sh
+python --version
+python -c 'import tensorflow as tf; print(tf.__version__)'
+```
+
+Refer to the [instructions here][2]
+for using the model in this repo. Make sure to add the models folder to your
+Python path.
+
+[1]: https://www.tensorflow.org/install/
+[2]:
+https://github.com/tensorflow/models/tree/master/official#running-the-models
+
+## Data
+
+The pre-training data should be multi-lingual and the format is the same as BERT
+pre-training.
+
+The fine-tuning data follows the format as below:
+
+```text
+{ # (tensorflow.Example)
+ features: {
+ feature: {
+ key : "src_raw"
+ value: {
+ bytes_list: {
+ value: [ "Foo. " ]
+ }
+ }
+ }
+ feature: {
+ key : "tgt_raw"
+ value: {
+ bytes_list: {
+ value: [ "Bar. " ]
+ }
+ }
+ }
+ }
+}
+```
+
+## Train using the config file.
+
+After you generated your pretraining data, run the following command to start
+pretraining:
+
+```bash
+TPU=local
+VOCAB=???
+INIT_CHECKPOINT=???
+PARAMS="task.train_data.input_data=/path/to/train/data"
+PARAMS="${PARAMS},task.train_data.vocab_file=${VOCAB}"
+PARAMS="${PARAMS},task.validation_data.input_path=/path/to/validation/data"
+PARAMS="${PARAMS},task.validation_data.vocab_file=${VOCAB}"
+PARAMS="${PARAMS},task.init_checkpoint=${INIT_CHECKPOINT}"
+PARAMS="${PARAMS},runtime.distribution_strategy=tpu"
+
+python3 train.py \
+ --experiment=labse/train \
+ --config_file=./experiments/labse_bert_base.yaml \
+ --config_file=./experiments/labse_base.yaml \
+ --params_override=${PARAMS} \
+ --tpu=${TPU} \
+ --model_dir=/folder/to/hold/logs/and/models/ \
+ --mode=train_and_eval
+```
+
+## Implementation
+
+We implement the encoder and layers using `tf.keras` APIs in NLP
+modeling library:
+
+ * [dual_encoder.py](https://github.com/tensorflow/models/blob/master/official/nlp/tasks/dual_encoder.py)
+ contains the dual-encoder task used for labse training.
+
+ * [config_labse.py](https://github.com/tensorflow/models/blob/master/official/projects/labse/config_labse.py)
+ registers the labse training experiment.
+
+ * [train.py](https://github.com/tensorflow/models/blob/master/official/projects/labse/train.py)
+ is the program entry.
+
+
+## Pre-trained model through TF-HUB
+
+If you are looking for pre-trained models, please check out:
+https://tfhub.dev/google/LaBSE/2.
+The hub `SavedModel`s are exported through the `export_tfhub.py` in
+this repository.
diff --git a/official/projects/labse/config_labse.py b/official/projects/labse/config_labse.py
new file mode 100644
index 0000000000000000000000000000000000000000..4dba0e32a03c150b324a01bb4f8df217f6908ebe
--- /dev/null
+++ b/official/projects/labse/config_labse.py
@@ -0,0 +1,68 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# pylint: disable=g-doc-return-or-yield,line-too-long
+"""LaBSE configurations."""
+import dataclasses
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+from official.nlp.data import dual_encoder_dataloader
+from official.nlp.tasks import dual_encoder
+
+AdamWeightDecay = optimization.AdamWeightDecayConfig
+PolynomialLr = optimization.PolynomialLrConfig
+PolynomialWarmupConfig = optimization.PolynomialWarmupConfig
+
+
+@dataclasses.dataclass
+class LaBSEOptimizationConfig(optimization.OptimizationConfig):
+ """Bert optimization config."""
+ optimizer: optimization.OptimizerConfig = optimization.OptimizerConfig(
+ type="adamw", adamw=AdamWeightDecay())
+ learning_rate: optimization.LrConfig = optimization.LrConfig(
+ type="polynomial",
+ polynomial=PolynomialLr(
+ initial_learning_rate=1e-4,
+ decay_steps=1000000,
+ end_learning_rate=0.0))
+ warmup: optimization.WarmupConfig = optimization.WarmupConfig(
+ type="polynomial", polynomial=PolynomialWarmupConfig(warmup_steps=10000))
+
+
+@exp_factory.register_config_factory("labse/train")
+def labse_train() -> cfg.ExperimentConfig:
+ r"""Language-agnostic bert sentence embedding.
+
+ *Note*: this experiment does not use cross-accelerator global softmax so it
+ does not reproduce the exact LABSE training.
+ """
+ config = cfg.ExperimentConfig(
+ task=dual_encoder.DualEncoderConfig(
+ train_data=dual_encoder_dataloader.DualEncoderDataConfig(),
+ validation_data=dual_encoder_dataloader.DualEncoderDataConfig(
+ is_training=False, drop_remainder=False)),
+ trainer=cfg.TrainerConfig(
+ optimizer_config=LaBSEOptimizationConfig(
+ learning_rate=optimization.LrConfig(
+ type="polynomial",
+ polynomial=PolynomialLr(
+ initial_learning_rate=3e-5, end_learning_rate=0.0)),
+ warmup=optimization.WarmupConfig(
+ type="polynomial", polynomial=PolynomialWarmupConfig()))),
+ restrictions=[
+ "task.train_data.is_training != None",
+ "task.validation_data.is_training != None"
+ ])
+ return config
diff --git a/official/projects/labse/experiments/labse_base.yaml b/official/projects/labse/experiments/labse_base.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..a2487fd12580478b8854a1e422f1b569752aaeaf
--- /dev/null
+++ b/official/projects/labse/experiments/labse_base.yaml
@@ -0,0 +1,85 @@
+task:
+ hub_module_url: ''
+ model:
+ bidirectional: true
+ max_sequence_length: 32
+ logit_scale: 100
+ logit_margin: 0.3
+ init_checkpoint: 'the pre-trained BERT checkpoint using the labse vocab.'
+ train_data:
+ drop_remainder: true
+ global_batch_size: 4096
+ input_path: 'the path to train partition'
+ left_text_fields: ['src_raw']
+ right_text_fields: ['tgt_raw']
+ vocab_file: 'the path to vocab.txt'
+ lower_case: false
+ is_training: true
+ seq_length: 32
+ sharding: false
+ cycle_length: 4
+ shuffle_buffer_size: 1000
+ tfds_as_supervised: false
+ tfds_data_dir: ''
+ tfds_name: ''
+ tfds_skip_decoding_feature: ''
+ tfds_split: ''
+ validation_data:
+ block_length: 1
+ cache: false
+ cycle_length: 4
+ drop_remainder: false
+ global_batch_size: 32000
+ input_path: 'the path to validation partition'
+ left_text_fields: ['src_raw']
+ right_text_fields: ['tgt_raw']
+ vocab_file: 'the path to vocab.txt'
+ lower_case: false
+ is_training: false
+ seq_length: 32
+ sharding: true
+ shuffle_buffer_size: 1000
+ tfds_as_supervised: false
+ tfds_data_dir: ''
+ tfds_name: ''
+ tfds_skip_decoding_feature: ''
+ tfds_split: ''
+trainer:
+ checkpoint_interval: 1000
+ eval_tf_function: true
+ max_to_keep: 5
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ cycle: false
+ decay_steps: 500000
+ end_learning_rate: 0.0
+ initial_learning_rate: 1.0e-04
+ name: PolynomialDecay
+ power: 1.0
+ type: polynomial
+ optimizer:
+ adamw:
+ amsgrad: false
+ beta_1: 0.9
+ beta_2: 0.999
+ epsilon: 1.0e-05
+ exclude_from_weight_decay: null
+ include_in_weight_decay: null
+ name: AdamWeightDecay
+ weight_decay_rate: 0.0
+ gradient_clip_norm: 100
+ type: adamw
+ warmup:
+ polynomial:
+ name: polynomial
+ power: 1
+ warmup_steps: 5000
+ type: polynomial
+ steps_per_loop: 1000
+ summary_interval: 1000
+ train_tf_function: true
+ train_tf_while_loop: true
+ train_steps: 500000
+ validation_interval: 1000
+ validation_steps: 100
diff --git a/official/projects/labse/experiments/labse_bert_base.yaml b/official/projects/labse/experiments/labse_bert_base.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..bd292cdf5c5b1ef1e2e67432e514fe63d4de2f17
--- /dev/null
+++ b/official/projects/labse/experiments/labse_bert_base.yaml
@@ -0,0 +1,15 @@
+task:
+ model:
+ encoder:
+ bert:
+ attention_dropout_rate: 0.1
+ dropout_rate: 0.1
+ hidden_activation: gelu
+ hidden_size: 768
+ initializer_range: 0.02
+ intermediate_size: 3072
+ max_position_embeddings: 512
+ num_attention_heads: 12
+ num_layers: 12
+ type_vocab_size: 2
+ vocab_size: 501153
diff --git a/official/projects/labse/export_tfhub.py b/official/projects/labse/export_tfhub.py
new file mode 100644
index 0000000000000000000000000000000000000000..6adb53c79840a0b05dd2130cd2529b728a503856
--- /dev/null
+++ b/official/projects/labse/export_tfhub.py
@@ -0,0 +1,161 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Exports the LaBSE model and its preprocessing as SavedModels for TF Hub.
+
+Example usage:
+# Point this variable to your training results.
+# Note that flag --do_lower_case is inferred from the name.
+LaBSE_DIR=
+# Step 1: export the core LaBSE model.
+python3 ./export_tfhub.py \
+ --bert_config_file ${LaBSE_DIR:?}/bert_config.json \
+ --model_checkpoint_path ${LaBSE_DIR:?}/labse_model.ckpt \
+ --vocab_file ${LaBSE_DIR:?}/vocab.txt \
+ --export_type model --export_path /tmp/labse_model
+# Step 2: export matching preprocessing (be sure to use same flags).
+python3 ./export_tfhub.py \
+ --vocab_file ${LaBSE_DIR:?}/vocab.txt \
+ --export_type preprocessing --export_path /tmp/labse_preprocessing
+"""
+
+from typing import Text
+
+from absl import app
+from absl import flags
+from absl import logging
+import tensorflow as tf
+
+from official.legacy.bert import bert_models
+from official.legacy.bert import configs
+from official.nlp.modeling import models
+from official.nlp.tasks import utils
+from official.nlp.tools import export_tfhub_lib
+
+FLAGS = flags.FLAGS
+
+flags.DEFINE_enum("export_type", "model", ["model", "preprocessing"],
+ "The type of model to export")
+flags.DEFINE_string("export_path", None, "TF-Hub SavedModel destination path.")
+flags.DEFINE_string(
+ "bert_tfhub_module", None,
+ "Bert tfhub module to define core bert layers. Needed for --export_type "
+ "model.")
+flags.DEFINE_string(
+ "bert_config_file", None,
+ "Bert configuration file to define core bert layers. It will not be used "
+ "if bert_tfhub_module is set. Needed for --export_type model.")
+flags.DEFINE_string(
+ "model_checkpoint_path", None, "File path to TF model checkpoint. "
+ "Needed for --export_type model.")
+flags.DEFINE_string(
+ "vocab_file", None,
+ "The vocabulary file that the BERT model was trained on. "
+ "Needed for both --export_type model and preprocessing.")
+flags.DEFINE_bool(
+ "do_lower_case", None,
+ "Whether to lowercase before tokenization. If left as None, "
+ "do_lower_case will be enabled if 'uncased' appears in the "
+ "name of --vocab_file. "
+ "Needed for both --export_type model and preprocessing.")
+flags.DEFINE_integer(
+ "default_seq_length", 128,
+ "The sequence length of preprocessing results from "
+ "top-level preprocess method. This is also the default "
+ "sequence length for the bert_pack_inputs subobject."
+ "Needed for --export_type preprocessing.")
+flags.DEFINE_bool(
+ "tokenize_with_offsets", False, # TODO(b/181866850)
+ "Whether to export a .tokenize_with_offsets subobject for "
+ "--export_type preprocessing.")
+flags.DEFINE_bool(
+ "normalize", True,
+ "Parameter of DualEncoder model, normalize the embedding (pooled_output) "
+ "if set to True.")
+
+
+def _get_do_lower_case(do_lower_case, vocab_file):
+ """Returns do_lower_case, replacing None by a guess from vocab file name."""
+ if do_lower_case is None:
+ do_lower_case = "uncased" in vocab_file
+ logging.info("Using do_lower_case=%s based on name of vocab_file=%s",
+ do_lower_case, vocab_file)
+ return do_lower_case
+
+
+def create_labse_model(bert_tfhub_module: Text,
+ bert_config: configs.BertConfig,
+ normalize: bool) -> tf.keras.Model:
+ """Creates a LaBSE keras core model from BERT configuration.
+
+ Args:
+ bert_tfhub_module: The bert tfhub module path. The LaBSE will be built upon
+ the tfhub module if it is not empty.
+ bert_config: A `BertConfig` to create the core model. Used if
+ bert_tfhub_module is empty.
+ normalize: Parameter of DualEncoder model, normalize the embedding (
+ pooled_output) if set to True.
+
+ Returns:
+ A keras model.
+ """
+ if bert_tfhub_module:
+ encoder_network = utils.get_encoder_from_hub(bert_tfhub_module)
+ else:
+ encoder_network = bert_models.get_transformer_encoder(
+ bert_config, sequence_length=None)
+
+ labse_model = models.DualEncoder(
+ network=encoder_network,
+ max_seq_length=None,
+ normalize=normalize,
+ output="predictions")
+ return labse_model, encoder_network # pytype: disable=bad-return-type # typed-keras
+
+
+def export_labse_model(bert_tfhub_module: Text, bert_config: configs.BertConfig,
+ model_checkpoint_path: Text, hub_destination: Text,
+ vocab_file: Text, do_lower_case: bool, normalize: bool):
+ """Restores a tf.keras.Model and saves for TF-Hub."""
+ core_model, encoder = create_labse_model(
+ bert_tfhub_module, bert_config, normalize)
+ checkpoint = tf.train.Checkpoint(encoder=encoder)
+ checkpoint.restore(model_checkpoint_path).assert_existing_objects_matched()
+ core_model.vocab_file = tf.saved_model.Asset(vocab_file)
+ core_model.do_lower_case = tf.Variable(do_lower_case, trainable=False)
+ core_model.save(hub_destination, include_optimizer=False, save_format="tf")
+
+
+def main(_):
+ do_lower_case = export_tfhub_lib.get_do_lower_case(FLAGS.do_lower_case,
+ FLAGS.vocab_file)
+ if FLAGS.export_type == "model":
+ if FLAGS.bert_tfhub_module:
+ bert_config = None
+ else:
+ bert_config = configs.BertConfig.from_json_file(FLAGS.bert_config_file)
+ export_labse_model(FLAGS.bert_tfhub_module, bert_config,
+ FLAGS.model_checkpoint_path, FLAGS.export_path,
+ FLAGS.vocab_file, do_lower_case, FLAGS.normalize)
+ elif FLAGS.export_type == "preprocessing":
+ # LaBSE is still a BERT model, reuse the export_bert_preprocessing here.
+ export_tfhub_lib.export_bert_preprocessing(
+ FLAGS.export_path, FLAGS.vocab_file, do_lower_case,
+ FLAGS.default_seq_length, FLAGS.tokenize_with_offsets)
+ else:
+ raise app.UsageError("Unknown value '%s' for flag --export_type")
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/projects/labse/export_tfhub_test.py b/official/projects/labse/export_tfhub_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..f45c200441c22bc695a7559876f747054695b028
--- /dev/null
+++ b/official/projects/labse/export_tfhub_test.py
@@ -0,0 +1,111 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests LaBSE's export_tfhub."""
+
+import os
+
+# Import libraries
+import numpy as np
+import tensorflow as tf
+import tensorflow_hub as hub
+from official.legacy.bert import configs
+from official.projects.labse import export_tfhub
+
+
+class ExportModelTest(tf.test.TestCase):
+
+ def test_export_model(self):
+ # Exports a savedmodel for TF-Hub
+ hidden_size = 16
+ bert_config = configs.BertConfig(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ intermediate_size=32,
+ max_position_embeddings=128,
+ num_attention_heads=2,
+ num_hidden_layers=1)
+ labse_model, encoder = export_tfhub.create_labse_model(
+ None, bert_config, normalize=True)
+ model_checkpoint_dir = os.path.join(self.get_temp_dir(), "checkpoint")
+ checkpoint = tf.train.Checkpoint(encoder=encoder)
+ checkpoint.save(os.path.join(model_checkpoint_dir, "test"))
+ model_checkpoint_path = tf.train.latest_checkpoint(model_checkpoint_dir)
+
+ vocab_file = os.path.join(self.get_temp_dir(), "uncased_vocab.txt")
+ with tf.io.gfile.GFile(vocab_file, "w") as f:
+ f.write("dummy content")
+
+ hub_destination = os.path.join(self.get_temp_dir(), "hub")
+ export_tfhub.export_labse_model(
+ None, # bert_tfhub_module
+ bert_config,
+ model_checkpoint_path,
+ hub_destination,
+ vocab_file,
+ do_lower_case=True,
+ normalize=True)
+
+ # Restores a hub KerasLayer.
+ hub_layer = hub.KerasLayer(hub_destination, trainable=True)
+
+ if hasattr(hub_layer, "resolved_object"):
+ # Checks meta attributes.
+ self.assertTrue(hub_layer.resolved_object.do_lower_case.numpy())
+ with tf.io.gfile.GFile(
+ hub_layer.resolved_object.vocab_file.asset_path.numpy()) as f:
+ self.assertEqual("dummy content", f.read())
+ # Checks the hub KerasLayer.
+ for source_weight, hub_weight in zip(labse_model.trainable_weights,
+ hub_layer.trainable_weights):
+ self.assertAllClose(source_weight.numpy(), hub_weight.numpy())
+
+ seq_length = 10
+ dummy_ids = np.zeros((2, seq_length), dtype=np.int32)
+ hub_outputs = hub_layer([dummy_ids, dummy_ids, dummy_ids])
+ source_outputs = labse_model([dummy_ids, dummy_ids, dummy_ids])
+
+ self.assertEqual(hub_outputs["pooled_output"].shape, (2, hidden_size))
+ self.assertEqual(hub_outputs["sequence_output"].shape,
+ (2, seq_length, hidden_size))
+ for output_name in source_outputs:
+ self.assertAllClose(hub_outputs[output_name].numpy(),
+ hub_outputs[output_name].numpy())
+
+ # Test that training=True makes a difference (activates dropout).
+ def _dropout_mean_stddev(training, num_runs=20):
+ input_ids = np.array([[14, 12, 42, 95, 99]], np.int32)
+ inputs = [input_ids, np.ones_like(input_ids), np.zeros_like(input_ids)]
+ outputs = np.concatenate([
+ hub_layer(inputs, training=training)["pooled_output"]
+ for _ in range(num_runs)
+ ])
+ return np.mean(np.std(outputs, axis=0))
+
+ self.assertLess(_dropout_mean_stddev(training=False), 1e-6)
+ self.assertGreater(_dropout_mean_stddev(training=True), 1e-3)
+
+ # Test propagation of seq_length in shape inference.
+ input_word_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ input_mask = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ input_type_ids = tf.keras.layers.Input(shape=(seq_length,), dtype=tf.int32)
+ outputs = hub_layer([input_word_ids, input_mask, input_type_ids])
+ self.assertEqual(outputs["pooled_output"].shape.as_list(),
+ [None, hidden_size])
+ self.assertEqual(outputs["sequence_output"].shape.as_list(),
+ [None, seq_length, hidden_size])
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/projects/labse/train.py b/official/projects/labse/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..7e9cc7d11c3df2c7697f607871fcf82c1a45d905
--- /dev/null
+++ b/official/projects/labse/train.py
@@ -0,0 +1,27 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Labse training driver, register labse configs."""
+
+# pylint: disable=unused-import
+from absl import app
+
+from official.common import flags as tfm_flags
+from official.nlp import tasks
+from official.nlp import train
+from official.projects.labse import config_labse
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/longformer/README.md b/official/projects/longformer/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..8db9a3ac8fb11f47c47370138e760e7134c37b65
--- /dev/null
+++ b/official/projects/longformer/README.md
@@ -0,0 +1,50 @@
+# Longformer: The Long-Document Transformer
+
+## Modifications from Huggingface's Implementation
+
+All models require a `global_attention_size` specified in the config, setting a
+global attention for all first `global_attention_size` tokens in any sentence.
+Individual different global attention sizes for sentences are not supported.
+This setting allows running on TPUs where tensor sizes have to be determined.
+
+`_get_global_attn_indices` in `longformer_attention.py` contains how the new
+global attention indices are specified. Changed all `tf.cond` to if
+confiditions, since global attention is specified in the start now.
+
+To load weights from a pre-trained huggingface longformer, run
+`utils/convert_pretrained_pytorch_checkpoint_to_tf.py` to create a checkpoint. \
+There is also a `utils/longformer_tokenizer_to_tfrecord.py` that transformers
+pytorch longformer tokenized data to tf_records.
+
+## Steps to Fine-tune on MNLI
+#### Prepare the pre-trained checkpoint
+Option 1. Use our saved checkpoint of `allenai/longformer-base-4096` stored in cloud storage
+
+```bash
+gsutil cp -r gs://model-garden-ucsd-zihan/longformer-4096 .
+```
+Option 2. Create it directly
+
+```bash
+python3 utils/convert_pretrained_pytorch_checkpoint_to_tf.py
+```
+#### [Optional] Prepare the input file
+```bash
+python3 longformer_tokenizer_to_tfrecord.py
+```
+#### Training
+Here, we use the training data of MNLI that were uploaded to the cloud storage, you can replace it with the input files you generated.
+
+```bash
+TRAIN_DATA=task.train_data.input_path=gs://model-garden-ucsd-zihan/longformer_allenai_mnli_train.tf_record,task.validation_data.input_path=gs://model-garden-ucsd-zihan/longformer_allenai_mnli_eval.tf_record
+INIT_CHECKPOINT=longformer-4096/longformer
+PYTHONPATH=/path/to/model/garden \
+ python3 train.py \
+ --experiment=longformer/glue \
+ --config_file=experiments/glue_mnli_allenai.yaml \
+ --params_override="${TRAIN_DATA},runtime.distribution_strategy=tpu,task.init_checkpoint=${INIT_CHECKPOINT}" \
+ --tpu=local \
+ --model_dir=/path/to/outputdir \
+ --mode=train_and_eval
+```
+This should take ~ 3 hours to run, and give a performance of ~86.
diff --git a/official/projects/longformer/experiments/glue_mnli.yaml b/official/projects/longformer/experiments/glue_mnli.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7c5540cfe9f144efc544570e8aea198e25b363d6
--- /dev/null
+++ b/official/projects/longformer/experiments/glue_mnli.yaml
@@ -0,0 +1,47 @@
+task:
+ hub_module_url: ''
+ model:
+ num_classes: 3
+ encoder:
+ type: any
+ any:
+ max_position_embeddings: 512
+ attention_window: [32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32]
+ global_attention_size: 1
+ metric_type: 'accuracy'
+ train_data:
+ drop_remainder: true
+ global_batch_size: 32
+ input_path: TODO
+ is_training: true
+ seq_length: 128
+ validation_data:
+ drop_remainder: true
+ global_batch_size: 32
+ input_path: TODO
+ is_training: false
+ seq_length: 128
+trainer:
+ checkpoint_interval: 1000
+ continuous_eval_timeout: 7200
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 61359
+ end_learning_rate: 0.0
+ initial_learning_rate: 3.0e-05
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 6136
+ type: polynomial
+ steps_per_loop: 100
+ summary_interval: 100
+ # Training data size 392,702 examples, 5 epochs.
+ train_steps: 61359
+ validation_interval: 2000
+ validation_steps: 307
diff --git a/official/projects/longformer/experiments/glue_mnli_allenai.yaml b/official/projects/longformer/experiments/glue_mnli_allenai.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..c3495786de838efb73fffe0df415e1687132f847
--- /dev/null
+++ b/official/projects/longformer/experiments/glue_mnli_allenai.yaml
@@ -0,0 +1,48 @@
+task:
+ hub_module_url: ''
+ model:
+ num_classes: 3
+ encoder:
+ type: any
+ any:
+ max_position_embeddings: 4098
+ attention_window: [128, 128, 128, 128, 128, 128, 128, 128, 128, 128, 128, 128]
+ global_attention_size: 1
+ vocab_size: 50265
+ metric_type: 'accuracy'
+ train_data:
+ drop_remainder: true
+ global_batch_size: 32
+ input_path: TODO
+ is_training: true
+ seq_length: 512
+ validation_data:
+ drop_remainder: true
+ global_batch_size: 32
+ input_path: TODO
+ is_training: false
+ seq_length: 512
+trainer:
+ checkpoint_interval: 1000
+ continuous_eval_timeout: 7200
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 61359
+ end_learning_rate: 0.0
+ initial_learning_rate: 3.0e-05
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 6136
+ type: polynomial
+ steps_per_loop: 1000
+ summary_interval: 1000
+ # Training data size 392,702 examples, 5 epochs.
+ train_steps: 61359
+ validation_interval: 2000
+ validation_steps: 307
diff --git a/official/projects/longformer/experiments/pretraining_512.yaml b/official/projects/longformer/experiments/pretraining_512.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..152d1356690800b160283075faf6d3ae2e9e8198
--- /dev/null
+++ b/official/projects/longformer/experiments/pretraining_512.yaml
@@ -0,0 +1,74 @@
+task:
+ init_checkpoint: ""
+ model:
+ cls_heads:
+ [
+ {
+ activation: tanh,
+ cls_token_idx: 0,
+ dropout_rate: 0.1,
+ inner_dim: 768,
+ name: next_sentence,
+ num_classes: 2,
+ },
+ ]
+ encoder:
+ type: any
+ any:
+ attention_dropout_rate: 0.1
+ dropout_rate: 0.1
+ embedding_size: 768
+ hidden_activation: gelu
+ hidden_size: 768
+ initializer_range: 0.02
+ intermediate_size: 3072
+ max_position_embeddings: 512
+ num_attention_heads: 12
+ num_layers: 12
+ type_vocab_size: 2
+ vocab_size: 30522
+ attention_window: [32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32, 32]
+ global_attention_size: 1
+ train_data:
+ drop_remainder: true
+ global_batch_size: 256
+ input_path: gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00000-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00001-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00002-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00003-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00004-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00005-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00006-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00007-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00008-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00009-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00010-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00011-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00012-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00013-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00014-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00015-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00016-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00017-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00018-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00019-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00020-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00021-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00022-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00023-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00024-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00025-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00026-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00027-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00028-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00029-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00030-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00031-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00032-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00033-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00034-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00035-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00036-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00037-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00038-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00039-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00040-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00041-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00042-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00043-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00044-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00045-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00046-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00047-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00048-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00049-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00050-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00051-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00052-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00053-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00054-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00055-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00056-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00057-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00058-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00059-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00060-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00061-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00062-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00063-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00064-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00065-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00066-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00067-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00068-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00069-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00070-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00071-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00072-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00073-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00074-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00075-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00076-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00077-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00078-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00079-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00080-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00081-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00082-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00083-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00084-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00085-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00086-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00087-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00088-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00089-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00090-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00091-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00092-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00093-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00094-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00095-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00096-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00097-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00098-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00099-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00100-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00101-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00102-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00103-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00104-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00105-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00106-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00107-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00108-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00109-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00110-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00111-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00112-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00113-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00114-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00115-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00116-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00117-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00118-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00119-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00120-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00121-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00122-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00123-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00124-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00125-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00126-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00127-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00128-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00129-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00130-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00131-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00132-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00133-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00134-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00135-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00136-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00137-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00138-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00139-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00140-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00141-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00142-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00143-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00144-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00145-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00146-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00147-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00148-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00149-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00150-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00151-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00152-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00153-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00154-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00155-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00156-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00157-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00158-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00159-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00160-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00161-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00162-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00163-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00164-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00165-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00166-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00167-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00168-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00169-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00170-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00171-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00172-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00173-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00174-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00175-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00176-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00177-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00178-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00179-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00180-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00181-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00182-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00183-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00184-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00185-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00186-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00187-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00188-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00189-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00190-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00191-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00192-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00193-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00194-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00195-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00196-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00197-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00198-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00199-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00200-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00201-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00202-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00203-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00204-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00205-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00206-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00207-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00208-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00209-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00210-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00211-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00212-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00213-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00214-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00215-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00216-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00217-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00218-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00219-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00220-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00221-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00222-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00223-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00224-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00225-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00226-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00227-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00228-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00229-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00230-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00231-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00232-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00233-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00234-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00235-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00236-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00237-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00238-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00239-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00240-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00241-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00242-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00243-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00244-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00245-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00246-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00247-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00248-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00249-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00250-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00251-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00252-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00253-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00254-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00255-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00256-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00257-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00258-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00259-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00260-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00261-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00262-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00263-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00264-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00265-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00266-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00267-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00268-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00269-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00270-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00271-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00272-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00273-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00274-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00275-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00276-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00277-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00278-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00279-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00280-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00281-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00282-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00283-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00284-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00285-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00286-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00287-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00288-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00289-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00290-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00291-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00292-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00293-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00294-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00295-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00296-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00297-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00298-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00299-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00300-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00301-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00302-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00303-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00304-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00305-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00306-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00307-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00308-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00309-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00310-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00311-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00312-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00313-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00314-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00315-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00316-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00317-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00318-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00319-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00320-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00321-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00322-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00323-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00324-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00325-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00326-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00327-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00328-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00329-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00330-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00331-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00332-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00333-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00334-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00335-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00336-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00337-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00338-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00339-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00340-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00341-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00342-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00343-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00344-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00345-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00346-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00347-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00348-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00349-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00350-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00351-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00352-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00353-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00354-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00355-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00356-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00357-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00358-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00359-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00360-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00361-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00362-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00363-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00364-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00365-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00366-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00367-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00368-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00369-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00370-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00371-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00372-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00373-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00374-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00375-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00376-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00377-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00378-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00379-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00380-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00381-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00382-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00383-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00384-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00385-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00386-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00387-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00388-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00389-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00390-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00391-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00392-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00393-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00394-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00395-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00396-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00397-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00398-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00399-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00400-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00401-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00402-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00403-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00404-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00405-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00406-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00407-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00408-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00409-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00410-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00411-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00412-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00413-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00414-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00415-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00416-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00417-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00418-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00419-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00420-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00421-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00422-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00423-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00424-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00425-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00426-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00427-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00428-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00429-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00430-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00431-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00432-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00433-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00434-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00435-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00436-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00437-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00438-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00439-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00440-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00441-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00442-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00443-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00444-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00445-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00446-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00447-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00448-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00449-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00450-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00451-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00452-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00453-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00454-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00455-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00456-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00457-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00458-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00459-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00460-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00461-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00462-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00463-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00464-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00465-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00466-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00467-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00468-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00469-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00470-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00471-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00472-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00473-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00474-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00475-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00476-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00477-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00478-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00479-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00480-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00481-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00482-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00483-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00484-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00485-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00486-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00487-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00488-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00489-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00490-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00491-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00492-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00493-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00494-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00495-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00496-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00497-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00498-of-00500,gs://tf_model_garden/nlp/data/research_data/bert_pretrain/wikipedia.tfrecord-00499-of-00500
+
+ is_training: true
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+ validation_data:
+ drop_remainder: true
+ global_batch_size: 256
+ input_path: TODO
+ is_training: false
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+trainer:
+ checkpoint_interval: 20000
+ max_to_keep: 5
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ cycle: false
+ decay_steps: 1000000
+ end_learning_rate: 0.0
+ initial_learning_rate: 0.0001
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 10000
+ type: polynomial
+ steps_per_loop: 50
+ summary_interval: 50
+ train_steps: 1000000
+ validation_interval: 1000
+ validation_steps: 64
diff --git a/official/projects/longformer/longformer.py b/official/projects/longformer/longformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..76a491ccb5fd70c35a19aaab6935a13de2bcfcb9
--- /dev/null
+++ b/official/projects/longformer/longformer.py
@@ -0,0 +1,69 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Longformer model configurations and instantiation methods."""
+import dataclasses
+from typing import List
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.modeling.hyperparams import base_config
+from official.nlp.configs import encoders
+from official.projects.longformer.longformer_encoder import LongformerEncoder
+
+
+@dataclasses.dataclass
+class LongformerEncoderConfig(encoders.BertEncoderConfig):
+ """Extra paramerters for Longformer configs.
+
+ Attributes:
+ attention_window: list of ints representing the window size for each layer.
+ global_attention_size: the size of global attention used for each token.
+ pad_token_id: the token id for the pad token
+ """
+ attention_window: List[int] = dataclasses.field(default_factory=list)
+ global_attention_size: int = 0
+ pad_token_id: int = 1
+
+
+@base_config.bind(LongformerEncoderConfig)
+def get_encoder(encoder_cfg: LongformerEncoderConfig):
+ """Gets a 'LongformerEncoder' object.
+
+ Args:
+ encoder_cfg: A 'LongformerEncoderConfig'.
+
+ Returns:
+ A encoder object.
+ """
+ encoder = LongformerEncoder(
+ attention_window=encoder_cfg.attention_window,
+ global_attention_size=encoder_cfg.global_attention_size,
+ vocab_size=encoder_cfg.vocab_size,
+ hidden_size=encoder_cfg.hidden_size,
+ num_layers=encoder_cfg.num_layers,
+ num_attention_heads=encoder_cfg.num_attention_heads,
+ inner_dim=encoder_cfg.intermediate_size,
+ inner_activation=tf_utils.get_activation(encoder_cfg.hidden_activation),
+ output_dropout=encoder_cfg.dropout_rate,
+ attention_dropout=encoder_cfg.attention_dropout_rate,
+ max_sequence_length=encoder_cfg.max_position_embeddings,
+ type_vocab_size=encoder_cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ output_range=encoder_cfg.output_range,
+ embedding_width=encoder_cfg.embedding_size,
+ norm_first=encoder_cfg.norm_first)
+ return encoder
diff --git a/official/projects/longformer/longformer_attention.py b/official/projects/longformer/longformer_attention.py
new file mode 100644
index 0000000000000000000000000000000000000000..f8d884220542b1daea63f7fde77bd7bee8b6c70e
--- /dev/null
+++ b/official/projects/longformer/longformer_attention.py
@@ -0,0 +1,1082 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Longformer attention block. Modified From huggingface/transformers."""
+
+# pylint: disable=g-classes-have-attributes
+
+import math
+import string
+
+import numpy as np
+import tensorflow as tf
+
+from official.modeling.tf_utils import get_shape_list
+
+_CHR_IDX = string.ascii_lowercase
+
+
+def _build_attention_equation(rank, attn_axes):
+ """Builds einsum equations for the attention computation.
+
+ Query, key, value inputs after projection are expected to have the shape as:
+ `(bs, , , num_heads, channels)`.
+ `bs` and `` are treated as ``.
+ The attention operations can be generalized:
+ (1) Query-key dot product:
+ `(, , num_heads, channels), (,
+ , num_heads, channels) -> (,
+ num_heads, , )`
+ (2) Combination:
+ `(, num_heads, , ),
+ (, , num_heads, channels) -> (,
+ , num_heads, channels)`
+ Args:
+ rank: Rank of query, key, value tensors.
+ attn_axes: List/tuple of axes, `[-1, rank)`, that attention will be applied
+ to.
+
+ Returns:
+ Einsum equations.
+ """
+ target_notation = _CHR_IDX[:rank]
+ # `batch_dims` includes the head dim.
+ batch_dims = tuple(np.delete(range(rank), attn_axes + (rank - 1,)))
+ letter_offset = rank
+ source_notation = ""
+ for i in range(rank):
+ if i in batch_dims or i == rank - 1:
+ source_notation += target_notation[i]
+ else:
+ source_notation += _CHR_IDX[letter_offset]
+ letter_offset += 1
+
+ product_notation = "".join([target_notation[i] for i in batch_dims] +
+ [target_notation[i] for i in attn_axes] +
+ [source_notation[i] for i in attn_axes])
+ dot_product_equation = f"{source_notation},{target_notation}->{product_notation}"
+ attn_scores_rank = len(product_notation)
+ combine_equation = f"{product_notation},{source_notation}->{target_notation}"
+ return dot_product_equation, combine_equation, attn_scores_rank
+
+
+def _build_proj_equation(free_dims, bound_dims, output_dims):
+ """Builds an einsum equation for projections inside multi-head attention."""
+ input_str = ""
+ kernel_str = ""
+ output_str = ""
+ bias_axes = ""
+ letter_offset = 0
+ for i in range(free_dims):
+ char = _CHR_IDX[i + letter_offset]
+ input_str += char
+ output_str += char
+
+ letter_offset += free_dims
+ for i in range(bound_dims):
+ char = _CHR_IDX[i + letter_offset]
+ input_str += char
+ kernel_str += char
+
+ letter_offset += bound_dims
+ for i in range(output_dims):
+ char = _CHR_IDX[i + letter_offset]
+ kernel_str += char
+ output_str += char
+ bias_axes += char
+ equation = f"{input_str},{kernel_str}->{output_str}"
+
+ return equation, bias_axes, len(output_str)
+
+
+def _get_output_shape(output_rank, known_last_dims):
+ return [None] * (output_rank - len(known_last_dims)) + list(known_last_dims)
+
+
+@tf.keras.utils.register_keras_serializable(package="Text")
+class LongformerAttention(tf.keras.layers.MultiHeadAttention):
+ """LongformerAttention.
+
+ Args:
+ attention_window: int representing the window size for attention.
+ layer_id: int of the id of the layer.
+ global_attention_size: the size of global attention used for each token.
+ """
+
+ def __init__(self, attention_window, layer_id, global_attention_size,
+ **kwargs):
+ super().__init__(**kwargs)
+ self._layer_id = layer_id
+ self._attention_window = attention_window
+ assert (self._attention_window % 2 == 0), (
+ f"`attention_window` for layer {self._layer_id} has to be an even "
+ f"value. Given {self.attention_window}")
+ assert (self._attention_window > 0), (
+ f"`attention_window` for layer {self._layer_id} has to be positive. "
+ f"Given {self.attention_window}")
+ self._one_sided_attn_window_size = self._attention_window // 2
+ self.global_attention_size = global_attention_size
+
+ def _build_from_signature(self, query, value, key=None):
+ """Builds layers and variables.
+
+ Once the method is called, self._built_from_signature will be set to True.
+ Args:
+ query: Query tensor or TensorShape.
+ value: Value tensor or TensorShape.
+ key: Key tensor or TensorShape.
+ """
+ self._built_from_signature = True
+ if hasattr(query, "shape"):
+ self._query_shape = tf.TensorShape(query.shape)
+ else:
+ self._query_shape = tf.TensorShape(query)
+ if hasattr(value, "shape"):
+ self._value_shape = tf.TensorShape(value.shape)
+ else:
+ self._value_shape = tf.TensorShape(value)
+ if key is None:
+ self._key_shape = self._value_shape
+ elif hasattr(key, "shape"):
+ self._key_shape = tf.TensorShape(key.shape)
+ else:
+ self._key_shape = tf.TensorShape(key)
+
+ common_kwargs = dict(
+ kernel_initializer=self._kernel_initializer,
+ bias_initializer=self._bias_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activity_regularizer=self._activity_regularizer,
+ kernel_constraint=self._kernel_constraint,
+ bias_constraint=self._bias_constraint)
+ # Any setup work performed only once should happen in an `init_scope`
+ # to avoid creating symbolic Tensors that will later pollute any eager
+ # operations.
+ # with tf_utils.maybe_init_scope(self):
+ # TODO(crickwu): check whether tf_utils.maybe_init_scope(self) (keras)
+ # is needed.
+ free_dims = self._query_shape.rank - 1
+ einsum_equation, bias_axes, output_rank = _build_proj_equation(
+ free_dims, bound_dims=1, output_dims=2)
+ self._query_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._key_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="query",
+ **common_kwargs)
+ self._global_query_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._key_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="global_query",
+ **common_kwargs)
+ einsum_equation, bias_axes, output_rank = _build_proj_equation(
+ self._key_shape.rank - 1, bound_dims=1, output_dims=2)
+ self._key_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._key_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="key",
+ **common_kwargs)
+ self._global_key_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._key_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="global_key",
+ **common_kwargs)
+ einsum_equation, bias_axes, output_rank = _build_proj_equation(
+ self._value_shape.rank - 1, bound_dims=1, output_dims=2)
+ self._value_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._value_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="value",
+ **common_kwargs)
+ self._global_value_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=_get_output_shape(output_rank - 1,
+ [self._num_heads, self._value_dim]),
+ bias_axes=bias_axes if self._use_bias else None,
+ name="global_value",
+ **common_kwargs)
+
+ # Builds the attention computations for multi-head dot product attention.
+ # These computations could be wrapped into the keras attention layer once
+ # it support mult-head einsum computations.
+ self._build_attention(output_rank)
+ self._global_dropout_layer = tf.keras.layers.Dropout(rate=self._dropout)
+ # self._output_dense = self._make_output_dense(
+ # free_dims, common_kwargs, "attention_output")
+ self._output_dense = tf.keras.layers.Dense(
+ units=self._num_heads * self._key_dim, name="dense", **common_kwargs)
+
+ def call(self,
+ hidden_states,
+ attention_mask=None,
+ is_index_masked=None,
+ is_index_global_attn=None,
+ training=None):
+ """Applies Dot-product attention with query, key, value tensors.
+
+ This function defines the computation inside `call` with projected
+ multi-head Q, K, V inputs. Users can override this function for customized
+ attention implementation.
+ Args:
+ hidden_states: inputs for generating query, key and value tensors.
+ attention_mask: a boolean mask of shape `(B, T, S)`, that prevents
+ attention to certain positions.
+ is_index_masked: boolean indicating whether the index is masked.
+ is_index_global_attn: boolean indicating whether the index is global
+ attention.
+ training: Python boolean indicating whether the layer should behave in
+ training mode (adding dropout) or in inference mode (doing nothing).
+
+ Returns:
+ attention_output: Multi-headed outputs of attention computation.
+ """
+ if not self._built_from_signature:
+ self._build_from_signature(
+ query=hidden_states, value=hidden_states, key=hidden_states)
+
+ # N = `num_attention_heads`
+ # H = `size_per_head`
+ # `query` = [B, T, N ,H]
+ query = self._query_dense(hidden_states)
+
+ # `key` = [B, S, N, H]
+ key = self._key_dense(hidden_states)
+
+ # `value` = [B, S, N, H]
+ value = self._value_dense(hidden_states)
+
+ # Note: Applying scalar multiply at the smaller end of einsum improves
+ # XLA performance, but may introduce slight numeric differences in
+ # the Transformer attention head.
+ query = tf.multiply(query, 1.0 / math.sqrt(float(self._key_dim)))
+ batch_size, seq_len, num_heads, head_dim = get_shape_list(query)
+
+ # attn_probs = (batch_size, seq_len, num_heads, window*2+1)
+ attn_scores = self._sliding_chunks_query_key_matmul(
+ query, key, self._one_sided_attn_window_size)
+
+ # diagonal mask with zeros everywhere and -inf inplace of padding
+ diagonal_mask = self._sliding_chunks_query_key_matmul(
+ tf.ones(get_shape_list(attention_mask)),
+ attention_mask,
+ self._one_sided_attn_window_size,
+ )
+
+ # pad local attention probs
+ attn_scores += diagonal_mask
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(attn_scores),
+ [
+ batch_size, seq_len, self._num_heads,
+ self._one_sided_attn_window_size * 2 + 1
+ ],
+ message=f"attn_probs should be of size "
+ f"({batch_size}, {seq_len}, {num_heads}, "
+ f"{self._one_sided_attn_window_size * 2 + 1}),"
+ f" but is of size {get_shape_list(attn_scores)}",
+ )
+
+ # compute global attn indices required through out forward fn
+ (
+ max_num_global_attn_indices,
+ is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero,
+ ) = self._get_global_attn_indices(is_index_global_attn,
+ self.global_attention_size)
+ # this function is only relevant for global attention
+ if self.global_attention_size > 0:
+ attn_scores = self._concat_with_global_key_attn_probs(
+ attn_scores=attn_scores,
+ query_vectors=query,
+ key_vectors=key,
+ max_num_global_attn_indices=max_num_global_attn_indices,
+ is_index_global_attn_nonzero=is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero=is_local_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero=is_local_index_no_global_attn_nonzero,
+ )
+ else:
+ pass
+
+ attn_probs = tf.nn.softmax(attn_scores, axis=-1)
+
+ # softmax sometimes inserts NaN if all positions are masked,
+ # replace them with 0
+ # Make sure to create a mask with the proper shape:
+ # if is_global_attn==True => [batch_size, seq_len, self.num_heads,
+ # self.one_sided_attn_window_size * 2 + max_num_global_attn_indices + 1]
+ # if is_global_attn==False => [batch_size, seq_len, self.num_heads,
+ # self.one_sided_attn_window_size * 2 + 1]
+ if self.global_attention_size > 0:
+ masked_index = tf.tile(
+ is_index_masked[:, :, None, None],
+ (1, 1, self._num_heads, self._one_sided_attn_window_size * 2 +
+ max_num_global_attn_indices + 1),
+ )
+ else:
+ masked_index = tf.tile(
+ is_index_masked[:, :, None, None],
+ (1, 1, self._num_heads, self._one_sided_attn_window_size * 2 + 1),
+ )
+
+ attn_probs = tf.where(
+ masked_index,
+ tf.zeros(get_shape_list(masked_index), dtype=attn_probs.dtype),
+ attn_probs,
+ )
+
+ layer_head_mask = None
+ if layer_head_mask is not None:
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(layer_head_mask),
+ [self._num_heads],
+ message=f"Head mask for a single layer should be of size "
+ f"{(self._num_heads)}, but is "
+ f"{get_shape_list(layer_head_mask)}",
+ )
+
+ attn_probs = tf.reshape(layer_head_mask, (1, 1, -1, 1)) * attn_probs
+
+ # apply dropout
+ attn_probs = self._dropout_layer(attn_probs, training=training)
+ value_vectors = tf.reshape(
+ value, (batch_size, seq_len, self._num_heads, self._key_dim))
+
+ # if global attention, compute sum of global and local attn
+ if self.global_attention_size > 0:
+ attn_output = self._compute_attn_output_with_global_indices(
+ value_vectors=value_vectors,
+ attn_probs=attn_probs,
+ max_num_global_attn_indices=max_num_global_attn_indices,
+ is_index_global_attn_nonzero=is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero=is_local_index_global_attn_nonzero,
+ )
+ else:
+ attn_output = self._sliding_chunks_matmul_attn_probs_value(
+ attn_probs, value_vectors, self._one_sided_attn_window_size)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(attn_output),
+ [batch_size, seq_len, self._num_heads, head_dim],
+ message="Unexpected size",
+ )
+
+ attn_output = tf.reshape(
+ attn_output,
+ (batch_size, seq_len, self._num_heads * self._key_dim)) # FIXME
+
+ # compute value for global attention and overwrite to attention output
+ # TODO(crickwu): remove the redundant computation
+ if self.global_attention_size > 0:
+ attn_output, global_attn_probs = self._compute_global_attn_output_from_hidden( # pylint: disable=unused-variable
+ attn_output=attn_output,
+ hidden_states=hidden_states,
+ max_num_global_attn_indices=max_num_global_attn_indices,
+ layer_head_mask=layer_head_mask,
+ is_local_index_global_attn_nonzero=is_local_index_global_attn_nonzero,
+ is_index_global_attn_nonzero=is_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero=is_local_index_no_global_attn_nonzero,
+ is_index_masked=is_index_masked,
+ training=training,
+ )
+ else:
+ global_attn_probs = tf.zeros(
+ (batch_size, self._num_heads, max_num_global_attn_indices, seq_len))
+
+ # make sure that local attention probabilities are set to 0 for indices of
+ # global attn
+ if self.global_attention_size > 0:
+ masked_global_attn_index = tf.tile(
+ is_index_global_attn[:, :, None, None],
+ (1, 1, self._num_heads, self._one_sided_attn_window_size * 2 +
+ max_num_global_attn_indices + 1),
+ )
+ else:
+ masked_global_attn_index = tf.tile(
+ is_index_global_attn[:, :, None, None],
+ (1, 1, self._num_heads, self._one_sided_attn_window_size * 2 + 1),
+ )
+
+ attn_probs = tf.where(
+ masked_global_attn_index,
+ tf.zeros(
+ get_shape_list(masked_global_attn_index), dtype=attn_probs.dtype),
+ attn_probs,
+ )
+
+ # we can return extra information here
+ # (attn_output, attn_probs, global_attn_probs)
+
+ return attn_output
+
+ def get_config(self):
+ config = {
+ "layer_id": self._layer_id,
+ "attention_window": self._one_sided_attn_window_size,
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def _sliding_chunks_query_key_matmul(self, query, key, window_overlap):
+ """Matrix multiplication of query and key tensors.
+
+ This multiplication uses a sliding window attention pattern.
+
+ This implementation splits the input into overlapping chunks of size
+ 2w (e.g. 512 for pretrained Longformer) with an overlap of size
+ window_overlap.
+ Args:
+ query: query tensor.
+ key: key tensor.
+ window_overlap: int.
+ Returns:
+ diagonal_attention_scores: tensor.
+ """
+ batch_size, seq_len, num_heads, head_dim = get_shape_list(query)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ seq_len % (window_overlap * 2),
+ 0,
+ message=f"Sequence length should be multiple of {window_overlap * 2}. "
+ f"Given {seq_len}",
+ )
+ tf.debugging.assert_equal(
+ get_shape_list(query),
+ get_shape_list(key),
+ message=f"Shape of query and key should be equal, but got query: "
+ f"{get_shape_list(query)} and key: {get_shape_list(key)}",
+ )
+
+ chunks_count = seq_len // window_overlap - 1
+
+ # group batch_size and num_heads dimensions into one,
+ # then chunk seq_len into chunks of size window_overlap * 2
+ query = tf.reshape(
+ tf.transpose(query, (0, 2, 1, 3)),
+ (batch_size * num_heads, seq_len, head_dim),
+ )
+ key = tf.reshape(
+ tf.transpose(key, (0, 2, 1, 3)),
+ (batch_size * num_heads, seq_len, head_dim))
+ chunked_query = self._chunk(query, window_overlap)
+ chunked_key = self._chunk(key, window_overlap)
+
+ # matrix multiplication
+ # bcxd: batch_size * num_heads x chunks x 2window_overlap x head_dim
+ # bcyd: batch_size * num_heads x chunks x 2window_overlap x head_dim
+ # bcxy: batch_size * num_heads x chunks x 2window_overlap x 2window_overlap
+ chunked_query = tf.cast(chunked_query, dtype=chunked_key.dtype)
+ chunked_attention_scores = tf.einsum("bcxd,bcyd->bcxy", chunked_query,
+ chunked_key) # multiply
+
+ # convert diagonals into columns
+ paddings = tf.convert_to_tensor([[0, 0], [0, 0], [0, 1], [0, 0]])
+ diagonal_chunked_attention_scores = self._pad_and_transpose_last_two_dims(
+ chunked_attention_scores, paddings)
+
+ # allocate space for the overall attention matrix where the chunks are
+ # combined. The last dimension
+ # has (window_overlap * 2 + 1) columns. The first (window_overlap) columns
+ # are the window_overlap lower triangles (attention from a word to
+ # window_overlap previous words). The following column is attention score
+ # from each word to itself, then
+ # followed by window_overlap columns for the upper triangle.
+
+ # copy parts from diagonal_chunked_attention_scores into the combined matrix
+ # of attentions - copying the main diagonal and the upper triangle
+ # TODO(crickwu): This code is most likely not very efficient and should be
+ # improved.
+ diagonal_attn_scores_up_triang = tf.concat(
+ [
+ diagonal_chunked_attention_scores[:, :, :window_overlap, :
+ window_overlap + 1],
+ diagonal_chunked_attention_scores[:, -1:,
+ window_overlap:, :window_overlap +
+ 1],
+ ],
+ axis=1,
+ )
+
+ # - copying the lower triangle
+ diagonal_attn_scores_low_triang = tf.concat(
+ [
+ tf.zeros(
+ (batch_size * num_heads, 1, window_overlap, window_overlap),
+ dtype=diagonal_chunked_attention_scores.dtype,
+ ),
+ diagonal_chunked_attention_scores[:, :, -(window_overlap + 1):-1,
+ window_overlap + 1:],
+ ],
+ axis=1,
+ )
+ diagonal_attn_scores_first_chunk = tf.concat(
+ [
+ tf.roll(
+ diagonal_chunked_attention_scores,
+ shift=[1, window_overlap],
+ axis=[2, 3],
+ )[:, :, :window_overlap, :window_overlap],
+ tf.zeros(
+ (batch_size * num_heads, 1, window_overlap, window_overlap),
+ dtype=diagonal_chunked_attention_scores.dtype,
+ ),
+ ],
+ axis=1,
+ )
+ first_chunk_mask = (
+ tf.tile(
+ tf.range(chunks_count + 1)[None, :, None, None],
+ (batch_size * num_heads, 1, window_overlap, window_overlap),
+ ) < 1)
+
+ diagonal_attn_scores_low_triang = tf.where(
+ first_chunk_mask,
+ diagonal_attn_scores_first_chunk,
+ diagonal_attn_scores_low_triang,
+ )
+
+ # merging upper and lower triangle
+ diagonal_attention_scores = tf.concat(
+ [diagonal_attn_scores_low_triang, diagonal_attn_scores_up_triang],
+ axis=-1)
+
+ # separate batch_size and num_heads dimensions again
+ diagonal_attention_scores = tf.transpose(
+ tf.reshape(
+ diagonal_attention_scores,
+ (batch_size, num_heads, seq_len, 2 * window_overlap + 1),
+ ),
+ (0, 2, 1, 3),
+ )
+
+ diagonal_attention_scores = self._mask_invalid_locations(
+ diagonal_attention_scores, window_overlap)
+
+ return diagonal_attention_scores
+
+ @staticmethod
+ def _mask_invalid_locations(input_tensor, window_overlap):
+ # create correct upper triangle bool mask
+ mask_2d_upper = tf.reverse(
+ tf.linalg.band_part(
+ tf.ones(shape=(window_overlap, window_overlap + 1)), -1, 0),
+ axis=[0],
+ )
+
+ # pad to full matrix
+ padding = tf.convert_to_tensor(
+ [[0, get_shape_list(input_tensor)[1] - window_overlap],
+ [0, get_shape_list(input_tensor)[3] - window_overlap - 1]])
+
+ # create lower mask
+ mask_2d = tf.pad(mask_2d_upper, padding)
+
+ # combine with upper mask
+ mask_2d = mask_2d + tf.reverse(mask_2d, axis=[0, 1])
+
+ # broadcast to full matrix
+ mask_4d = tf.tile(mask_2d[None, :, None, :],
+ (get_shape_list(input_tensor)[0], 1, 1, 1))
+
+ # inf tensor used for masking
+ inf_tensor = -float("inf") * tf.ones_like(input_tensor)
+
+ # mask
+ input_tensor = tf.where(
+ tf.math.greater(mask_4d, 0), inf_tensor, input_tensor)
+
+ return input_tensor
+
+ def _sliding_chunks_matmul_attn_probs_value(self, attn_probs, value,
+ window_overlap):
+ """Same as _sliding_chunks_query_key_matmul but for attn_probs and value."""
+
+ batch_size, seq_len, num_heads, head_dim = get_shape_list(value)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ seq_len % (window_overlap * 2),
+ 0,
+ message="Seq_len has to be multiple of 2 * window_overlap",
+ )
+ tf.debugging.assert_equal(
+ get_shape_list(attn_probs)[:3],
+ get_shape_list(value)[:3],
+ message="value and attn_probs must have same dims (except head_dim)",
+ )
+ tf.debugging.assert_equal(
+ get_shape_list(attn_probs)[3],
+ 2 * window_overlap + 1,
+ message="attn_probs last dim has to be 2 * window_overlap + 1",
+ )
+
+ chunks_count = seq_len // window_overlap - 1
+
+ # group batch_size and num_heads dimensions into one, then chunk seq_len
+ # into chunks of size 2 window overlap
+ chunked_attn_probs = tf.reshape(
+ tf.transpose(attn_probs, (0, 2, 1, 3)),
+ (
+ batch_size * num_heads,
+ seq_len // window_overlap,
+ window_overlap,
+ 2 * window_overlap + 1,
+ ),
+ )
+
+ # group batch_size and num_heads dimensions into one
+ value = tf.reshape(
+ tf.transpose(value, (0, 2, 1, 3)),
+ (batch_size * num_heads, seq_len, head_dim),
+ )
+
+ # pad seq_len with w at the beginning of the sequence and another window
+ # overlap at the end
+ paddings = tf.convert_to_tensor([[0, 0], [window_overlap, window_overlap],
+ [0, 0]])
+ padded_value = tf.pad(value, paddings, constant_values=-1)
+
+ # chunk padded_value into chunks of size 3 window overlap and an overlap of
+ # size window overlap
+ frame_size = 3 * window_overlap * head_dim
+ frame_hop_size = (get_shape_list(padded_value)[1] * head_dim -
+ frame_size) // chunks_count
+ chunked_value = tf.signal.frame(
+ tf.reshape(padded_value, (batch_size * num_heads, -1)),
+ frame_size,
+ frame_hop_size,
+ )
+ chunked_value = tf.reshape(
+ chunked_value,
+ (batch_size * num_heads, chunks_count + 1, 3 * window_overlap,
+ head_dim),
+ )
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(chunked_value),
+ [
+ batch_size * num_heads, chunks_count + 1, 3 * window_overlap,
+ head_dim
+ ],
+ message="Chunked value has the wrong shape",
+ )
+
+ chunked_attn_probs = self._pad_and_diagonalize(chunked_attn_probs)
+ context = tf.einsum("bcwd,bcdh->bcwh", chunked_attn_probs, chunked_value)
+ context = tf.transpose(
+ tf.reshape(context, (batch_size, num_heads, seq_len, head_dim)),
+ (0, 2, 1, 3),
+ )
+
+ return context
+
+ @staticmethod
+ def _pad_and_transpose_last_two_dims(hidden_states_padded, paddings):
+ """Pads rows and then flips rows and columns."""
+ hidden_states_padded = tf.pad(
+ hidden_states_padded, paddings
+ ) # padding value is not important because it will be overwritten
+ batch_size, chunk_size, seq_length, hidden_dim = get_shape_list(
+ hidden_states_padded)
+ hidden_states_padded = tf.reshape(
+ hidden_states_padded, (batch_size, chunk_size, hidden_dim, seq_length))
+
+ return hidden_states_padded
+
+ @staticmethod
+ def _pad_and_diagonalize(chunked_hidden_states):
+ """Shifts every row 1 step right, converting columns into diagonals.
+
+ Example::
+
+ chunked_hidden_states: [ 0.4983, 2.6918, -0.0071, 1.0492,
+ -1.8348, 0.7672, 0.2986, 0.0285,
+ -0.7584, 0.4206, -0.0405, 0.1599,
+ 2.0514, -1.1600, 0.5372, 0.2629 ]
+ window_overlap = num_rows = 4
+ (pad & diagonalize) =>
+ [ 0.4983, 2.6918, -0.0071, 1.0492, 0.0000, 0.0000, 0.0000
+ 0.0000, -1.8348, 0.7672, 0.2986, 0.0285, 0.0000, 0.0000
+ 0.0000, 0.0000, -0.7584, 0.4206, -0.0405, 0.1599, 0.0000
+ 0.0000, 0.0000, 0.0000, 2.0514, -1.1600, 0.5372, 0.2629 ]
+ Args:
+ chunked_hidden_states: tensor.
+ Returns:
+ padded_hidden_stategs: tensor.
+ """
+ total_num_heads, num_chunks, window_overlap, hidden_dim = get_shape_list(
+ chunked_hidden_states)
+ paddings = tf.convert_to_tensor([[0, 0], [0, 0], [0, 0],
+ [0, window_overlap + 1]])
+
+ chunked_hidden_states = tf.pad(chunked_hidden_states, paddings)
+
+ chunked_hidden_states = tf.reshape(chunked_hidden_states,
+ (total_num_heads, num_chunks, -1))
+ chunked_hidden_states = chunked_hidden_states[:, :, :-window_overlap]
+ chunked_hidden_states = tf.reshape(
+ chunked_hidden_states,
+ (total_num_heads, num_chunks, window_overlap,
+ window_overlap + hidden_dim),
+ )
+ chunked_hidden_states = chunked_hidden_states[:, :, :, :-1]
+
+ return chunked_hidden_states
+
+ @staticmethod
+ def _chunk(hidden_states, window_overlap):
+ """convert into overlapping chunks. Chunk size = 2w, overlap size = w."""
+ batch_size, seq_length, hidden_dim = get_shape_list(hidden_states)
+ num_output_chunks = 2 * (seq_length // (2 * window_overlap)) - 1
+
+ # define frame size and frame stride (similar to convolution)
+ frame_hop_size = window_overlap * hidden_dim
+ frame_size = 2 * frame_hop_size
+ hidden_states = tf.reshape(hidden_states,
+ (batch_size, seq_length * hidden_dim))
+
+ # chunk with overlap
+ chunked_hidden_states = tf.signal.frame(hidden_states, frame_size,
+ frame_hop_size)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(chunked_hidden_states),
+ [batch_size, num_output_chunks, frame_size],
+ message=f"Make sure chunking is correctly applied. `Chunked hidden "
+ f"states should have output dimension"
+ f" {[batch_size, frame_size, num_output_chunks]}, but got "
+ f"{get_shape_list(chunked_hidden_states)}.",
+ )
+
+ chunked_hidden_states = tf.reshape(
+ chunked_hidden_states,
+ (batch_size, num_output_chunks, 2 * window_overlap, hidden_dim),
+ )
+
+ return chunked_hidden_states
+
+ @staticmethod
+ def _get_global_attn_indices(is_index_global_attn, global_attention_size):
+ """Computes global attn indices required throughout forward pass."""
+ # All global attention size are fixed through global_attention_size
+
+ batch_size, _ = get_shape_list(is_index_global_attn)
+
+ max_num_global_attn_indices = global_attention_size
+
+ row_indices = tf.range(batch_size)
+ row_indices = tf.repeat(
+ tf.expand_dims(row_indices, axis=0),
+ repeats=[global_attention_size],
+ axis=0)
+ row_indices = tf.reshape(row_indices,
+ (batch_size * global_attention_size, 1))
+
+ col_indices = tf.range(global_attention_size)
+ col_indices = tf.repeat(
+ tf.expand_dims(col_indices, axis=1), repeats=[batch_size], axis=0)
+
+ is_index_global_attn_nonzero = tf.concat((row_indices, col_indices), axis=1)
+
+ # this is actually same as `is_index_global_attn_nonzero`,
+ # since we assume all global attention are the same size
+ is_local_index_global_attn_nonzero = tf.concat((row_indices, col_indices),
+ axis=1)
+
+ # empty tensor
+ is_local_index_no_global_attn_nonzero = tf.reshape(
+ tf.expand_dims(tf.range(0), axis=1), (0, 2))
+ return (
+ max_num_global_attn_indices,
+ is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero,
+ )
+
+ def _concat_with_global_key_attn_probs(
+ self,
+ attn_scores,
+ key_vectors,
+ query_vectors,
+ max_num_global_attn_indices,
+ is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero,
+ ):
+ batch_size = get_shape_list(key_vectors)[0]
+
+ # select global key vectors
+ global_key_vectors = tf.gather_nd(key_vectors, is_index_global_attn_nonzero)
+
+ # create only global key vectors
+ key_vectors_only_global = tf.scatter_nd(
+ is_local_index_global_attn_nonzero,
+ global_key_vectors,
+ shape=(
+ batch_size,
+ max_num_global_attn_indices,
+ self._num_heads,
+ self._key_dim,
+ ),
+ )
+
+ # (batch_size, seq_len, num_heads, max_num_global_attn_indices)
+ attn_probs_from_global_key = tf.einsum("blhd,bshd->blhs", query_vectors,
+ key_vectors_only_global)
+
+ # (batch_size, max_num_global_attn_indices, seq_len, num_heads)
+ attn_probs_from_global_key_trans = tf.transpose(attn_probs_from_global_key,
+ (0, 3, 1, 2))
+ mask_shape = (
+ get_shape_list(is_local_index_no_global_attn_nonzero)[0],) + tuple(
+ get_shape_list(attn_probs_from_global_key_trans)[-2:])
+ mask = tf.ones(mask_shape) * -10000.0
+ mask = tf.cast(mask, dtype=attn_probs_from_global_key_trans.dtype)
+
+ # scatter mask
+ attn_probs_from_global_key_trans = tf.tensor_scatter_nd_update(
+ attn_probs_from_global_key_trans,
+ is_local_index_no_global_attn_nonzero,
+ mask,
+ )
+
+ # (batch_size, seq_len, num_heads, max_num_global_attn_indices)
+ attn_probs_from_global_key = tf.transpose(attn_probs_from_global_key_trans,
+ (0, 2, 3, 1))
+
+ # concat to attn_probs
+ # (batch_size, seq_len, num_heads, extra attention count + 2*window+1)
+ attn_scores = tf.concat((attn_probs_from_global_key, attn_scores), axis=-1)
+ return attn_scores
+
+ def _compute_attn_output_with_global_indices(
+ self,
+ value_vectors,
+ attn_probs,
+ max_num_global_attn_indices,
+ is_index_global_attn_nonzero,
+ is_local_index_global_attn_nonzero,
+ ):
+ batch_size = get_shape_list(attn_probs)[0]
+
+ # cut local attn probs to global only
+ attn_probs_only_global = attn_probs[:, :, :, :max_num_global_attn_indices]
+
+ # select global value vectors
+ global_value_vectors = tf.gather_nd(value_vectors,
+ is_index_global_attn_nonzero)
+
+ # create only global value vectors
+ value_vectors_only_global = tf.scatter_nd(
+ is_local_index_global_attn_nonzero,
+ global_value_vectors,
+ shape=(
+ batch_size,
+ max_num_global_attn_indices,
+ self._num_heads,
+ self._key_dim,
+ ),
+ )
+
+ # compute attn output only global
+ attn_output_only_global = tf.einsum("blhs,bshd->blhd",
+ attn_probs_only_global,
+ value_vectors_only_global)
+ # reshape attn probs
+ attn_probs_without_global = attn_probs[:, :, :,
+ max_num_global_attn_indices:]
+
+ # compute attn output with global
+ attn_output_without_global = self._sliding_chunks_matmul_attn_probs_value(
+ attn_probs_without_global, value_vectors,
+ self._one_sided_attn_window_size)
+
+ return attn_output_only_global + attn_output_without_global
+
+ def _compute_global_attn_output_from_hidden(
+ self,
+ attn_output,
+ hidden_states,
+ max_num_global_attn_indices,
+ layer_head_mask,
+ is_local_index_global_attn_nonzero,
+ is_index_global_attn_nonzero,
+ is_local_index_no_global_attn_nonzero,
+ is_index_masked,
+ training,
+ ):
+ batch_size, seq_len = get_shape_list(hidden_states)[:2]
+
+ # prepare global hidden states
+ global_attn_hidden_states = tf.gather_nd(hidden_states,
+ is_index_global_attn_nonzero)
+ global_attn_hidden_states = tf.scatter_nd(
+ is_local_index_global_attn_nonzero,
+ global_attn_hidden_states,
+ shape=(batch_size, max_num_global_attn_indices,
+ self._num_heads * self._key_dim),
+ )
+
+ # global key, query, value
+ global_query_vectors_only_global = self._global_query_dense(
+ global_attn_hidden_states)
+ global_key_vectors = self._global_key_dense(hidden_states)
+ global_value_vectors = self._global_value_dense(hidden_states)
+
+ # normalize
+ global_query_vectors_only_global /= tf.math.sqrt(
+ tf.cast(self._key_dim, dtype=global_query_vectors_only_global.dtype))
+ global_query_vectors_only_global = self.reshape_and_transpose(
+ global_query_vectors_only_global, batch_size)
+ global_key_vectors = self.reshape_and_transpose(global_key_vectors,
+ batch_size)
+ global_value_vectors = self.reshape_and_transpose(global_value_vectors,
+ batch_size)
+
+ # compute attn scores
+ global_attn_scores = tf.matmul(
+ global_query_vectors_only_global, global_key_vectors, transpose_b=True)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(global_attn_scores),
+ [batch_size * self._num_heads, max_num_global_attn_indices, seq_len],
+ message=f"global_attn_scores have the wrong size. Size should be"
+ f"{(batch_size * self._num_heads, max_num_global_attn_indices, seq_len)}, "
+ f"but is {get_shape_list(global_attn_scores)}.",
+ )
+
+ global_attn_scores = tf.reshape(
+ global_attn_scores,
+ (batch_size, self._num_heads, max_num_global_attn_indices, seq_len),
+ )
+ global_attn_scores_trans = tf.transpose(global_attn_scores, (0, 2, 1, 3))
+ mask_shape = (get_shape_list(is_local_index_no_global_attn_nonzero)[0],
+ ) + tuple(get_shape_list(global_attn_scores_trans)[-2:])
+ global_attn_mask = tf.ones(mask_shape) * -10000.0
+ global_attn_mask = tf.cast(
+ global_attn_mask, dtype=global_attn_scores_trans.dtype)
+
+ # scatter mask
+ global_attn_scores_trans = tf.tensor_scatter_nd_update(
+ global_attn_scores_trans,
+ is_local_index_no_global_attn_nonzero,
+ global_attn_mask,
+ )
+ global_attn_scores = tf.transpose(global_attn_scores_trans, (0, 2, 1, 3))
+
+ # mask global attn scores
+ attn_mask = tf.tile(is_index_masked[:, None, None, :],
+ (1, get_shape_list(global_attn_scores)[1], 1, 1))
+ global_attn_scores = tf.where(attn_mask, -10000.0, global_attn_scores)
+ global_attn_scores = tf.reshape(
+ global_attn_scores,
+ (batch_size * self._num_heads, max_num_global_attn_indices, seq_len),
+ )
+
+ # compute global attn probs
+ global_attn_probs_float = tf.nn.softmax(global_attn_scores, axis=-1)
+
+ # apply layer head masking
+ if layer_head_mask is not None:
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(layer_head_mask),
+ [self._num_heads],
+ message=f"Head mask for a single layer should be of size "
+ f"{(self._num_heads)}, but is {get_shape_list(layer_head_mask)}",
+ )
+ global_attn_probs_float = tf.reshape(
+ layer_head_mask,
+ (1, -1, 1, 1)) * tf.reshape(global_attn_probs_float,
+ (batch_size, self._num_heads,
+ max_num_global_attn_indices, seq_len))
+ global_attn_probs_float = tf.reshape(
+ global_attn_probs_float,
+ (batch_size * self._num_heads, max_num_global_attn_indices, seq_len))
+
+ # dropout
+ global_attn_probs = self._global_dropout_layer(
+ global_attn_probs_float, training=training)
+
+ # global attn output
+ global_attn_output = tf.matmul(global_attn_probs, global_value_vectors)
+
+ if tf.executing_eagerly():
+ tf.debugging.assert_equal(
+ get_shape_list(global_attn_output),
+ [
+ batch_size * self._num_heads, max_num_global_attn_indices,
+ self._key_dim
+ ],
+ message=f"global_attn_output tensor has the wrong size. Size should be "
+ f"{(batch_size * self._num_heads, max_num_global_attn_indices, self._key_dim)}, "
+ f"but is {get_shape_list(global_attn_output)}.",
+ )
+
+ global_attn_output = tf.reshape(
+ global_attn_output,
+ (batch_size, self._num_heads, max_num_global_attn_indices,
+ self._key_dim),
+ )
+
+ # get only non zero global attn output
+ nonzero_global_attn_output = tf.gather_nd(
+ tf.transpose(global_attn_output, (0, 2, 1, 3)),
+ is_local_index_global_attn_nonzero,
+ )
+ nonzero_global_attn_output = tf.reshape(
+ nonzero_global_attn_output,
+ (get_shape_list(is_local_index_global_attn_nonzero)[0], -1),
+ )
+
+ # overwrite values with global attention
+ attn_output = tf.tensor_scatter_nd_update(attn_output,
+ is_index_global_attn_nonzero,
+ nonzero_global_attn_output)
+
+ global_attn_probs = tf.reshape(
+ global_attn_probs,
+ (batch_size, self._num_heads, max_num_global_attn_indices, seq_len))
+
+ attn_output = self._output_dense(attn_output)
+
+ return attn_output, global_attn_probs
+
+ def reshape_and_transpose(self, vector, batch_size):
+ return tf.reshape(
+ tf.transpose(
+ tf.reshape(vector,
+ (batch_size, -1, self._num_heads, self._key_dim)),
+ (0, 2, 1, 3),
+ ),
+ (batch_size * self._num_heads, -1, self._key_dim),
+ )
diff --git a/official/projects/longformer/longformer_attention_test.py b/official/projects/longformer/longformer_attention_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..9211987e62ab752954bb345f9daf635164cbd12d
--- /dev/null
+++ b/official/projects/longformer/longformer_attention_test.py
@@ -0,0 +1,306 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for official.nlp.projects.longformer.longformer_attention."""
+
+import numpy as np
+import tensorflow as tf
+
+from official.modeling.tf_utils import get_shape_list
+from official.projects.longformer import longformer_attention
+
+
+def _create_mock_attention_data(num_heads,
+ key_dim,
+ value_dim,
+ q_seq_length,
+ kv_seq_length,
+ batch_size,
+ include_mask=False):
+ """Creates mock testing data.
+
+ Args:
+ num_heads: `int`, Number of attention heads.
+ key_dim: `int`, Size of query head.
+ value_dim: `int`, Size of key, value dim.
+ q_seq_length: `int`, query sequence length of the input.
+ kv_seq_length: `int`, key, value sequence length of the input.
+ batch_size: `int`, the batch size.
+ include_mask: optional `bool`, whether or not to include mask data.
+
+ Returns:
+ A dictionary with `str` as keys and `Tensor` as values.
+ """
+ query_shape = (batch_size, q_seq_length, key_dim)
+ value_shape = (batch_size, kv_seq_length, value_dim)
+
+ data = dict(
+ query=tf.random.normal(shape=query_shape),
+ value=tf.random.normal(shape=value_shape),
+ key=tf.random.normal(shape=value_shape))
+
+ total_seq_length = kv_seq_length
+
+ if include_mask:
+ mask_shape = (batch_size, num_heads, q_seq_length, total_seq_length)
+ mask_data = np.random.randint(2, size=mask_shape).astype('float32')
+ mask_data = dict(attention_mask=mask_data)
+ data.update(mask_data)
+
+ return data
+
+
+class LongformerAttentionTest(tf.test.TestCase):
+
+ def setUp(self):
+ super(LongformerAttentionTest, self).setUp()
+ np.random.seed(0)
+ tf.random.set_seed(0)
+
+ def _get_hidden_states(self):
+ return tf.convert_to_tensor(
+ [[
+ [
+ 4.98332758e-01,
+ 2.69175139e00,
+ -7.08081422e-03,
+ 1.04915401e00,
+ -1.83476661e00,
+ 7.67220476e-01,
+ 2.98580543e-01,
+ 2.84803992e-02,
+ ],
+ [
+ -7.58357372e-01,
+ 4.20635998e-01,
+ -4.04739919e-02,
+ 1.59924145e-01,
+ 2.05135748e00,
+ -1.15997978e00,
+ 5.37166397e-01,
+ 2.62873606e-01,
+ ],
+ [
+ -1.69438001e00,
+ 4.17574660e-01,
+ -1.49196962e00,
+ -1.76483717e00,
+ -1.94566312e-01,
+ -1.71183858e00,
+ 7.72903565e-01,
+ -1.11557056e00,
+ ],
+ [
+ 5.44028163e-01,
+ 2.05466114e-01,
+ -3.63045868e-01,
+ 2.41865062e-01,
+ 3.20348382e-01,
+ -9.05611176e-01,
+ -1.92690727e-01,
+ -1.19917547e00,
+ ],
+ ]],
+ dtype=tf.float32,
+ )
+
+ def test_diagonalize(self):
+ hidden_states = self._get_hidden_states()
+ hidden_states = tf.reshape(hidden_states,
+ (1, 8, 4)) # set seq length = 8, hidden dim = 4
+ chunked_hidden_states = longformer_attention.LongformerAttention._chunk(
+ hidden_states, window_overlap=2)
+ window_overlap_size = get_shape_list(chunked_hidden_states)[2]
+ self.assertEqual(window_overlap_size, 4)
+
+ padded_hidden_states = longformer_attention.LongformerAttention._pad_and_diagonalize(
+ chunked_hidden_states)
+
+ self.assertEqual(
+ get_shape_list(padded_hidden_states)[-1],
+ get_shape_list(chunked_hidden_states)[-1] + window_overlap_size - 1)
+
+ # first row => [0.4983, 2.6918, -0.0071, 1.0492, 0.0000, 0.0000, 0.0000]
+ tf.debugging.assert_near(
+ padded_hidden_states[0, 0, 0, :4],
+ chunked_hidden_states[0, 0, 0],
+ rtol=1e-3)
+ tf.debugging.assert_near(
+ padded_hidden_states[0, 0, 0, 4:],
+ tf.zeros((3,), dtype=tf.dtypes.float32),
+ rtol=1e-3)
+
+ # last row => [0.0000, 0.0000, 0.0000, 2.0514, -1.1600, 0.5372, 0.2629]
+ tf.debugging.assert_near(
+ padded_hidden_states[0, 0, -1, 3:],
+ chunked_hidden_states[0, 0, -1],
+ rtol=1e-3)
+ tf.debugging.assert_near(
+ padded_hidden_states[0, 0, -1, :3],
+ tf.zeros((3,), dtype=tf.dtypes.float32),
+ rtol=1e-3)
+
+ def test_pad_and_transpose_last_two_dims(self):
+ hidden_states = self._get_hidden_states()
+ self.assertTrue(get_shape_list(hidden_states), [1, 8, 4])
+
+ # pad along seq length dim
+ paddings = tf.constant([[0, 0], [0, 0], [0, 1], [0, 0]],
+ dtype=tf.dtypes.int32)
+
+ hidden_states = longformer_attention.LongformerAttention._chunk(
+ hidden_states, window_overlap=2)
+ padded_hidden_states = longformer_attention.LongformerAttention._pad_and_transpose_last_two_dims(
+ hidden_states, paddings)
+ self.assertEqual(get_shape_list(padded_hidden_states), [1, 1, 8, 5])
+
+ expected_added_dim = tf.zeros((5,), dtype=tf.dtypes.float32)
+ tf.debugging.assert_near(
+ expected_added_dim, padded_hidden_states[0, 0, -1, :], rtol=1e-6)
+ tf.debugging.assert_near(
+ hidden_states[0, 0, -1, :],
+ tf.reshape(padded_hidden_states, (1, -1))[0, 24:32],
+ rtol=1e-6)
+
+ def test_mask_invalid_locations(self):
+ hidden_states = self._get_hidden_states()
+ batch_size = 1
+ seq_length = 8
+ hidden_size = 4
+ hidden_states = tf.reshape(hidden_states,
+ (batch_size, seq_length, hidden_size))
+ hidden_states = longformer_attention.LongformerAttention._chunk(
+ hidden_states, window_overlap=2)
+
+ hid_states_1 = longformer_attention.LongformerAttention._mask_invalid_locations(
+ hidden_states, 1)
+ hid_states_2 = longformer_attention.LongformerAttention._mask_invalid_locations(
+ hidden_states, 2)
+ hid_states_3 = longformer_attention.LongformerAttention._mask_invalid_locations(
+ hidden_states[:, :, :, :3], 2)
+ hid_states_4 = longformer_attention.LongformerAttention._mask_invalid_locations(
+ hidden_states[:, :, 2:, :], 2)
+
+ self.assertEqual(
+ tf.math.reduce_sum(
+ tf.cast(tf.math.is_inf(hid_states_1), tf.dtypes.int32)), 8)
+ self.assertEqual(
+ tf.math.reduce_sum(
+ tf.cast(tf.math.is_inf(hid_states_2), tf.dtypes.int32)), 24)
+ self.assertEqual(
+ tf.math.reduce_sum(
+ tf.cast(tf.math.is_inf(hid_states_3), tf.dtypes.int32)), 24)
+ self.assertEqual(
+ tf.math.reduce_sum(
+ tf.cast(tf.math.is_inf(hid_states_4), tf.dtypes.int32)), 12)
+
+ def test_chunk(self):
+ hidden_states = self._get_hidden_states()
+ batch_size = 1
+ seq_length = 8
+ hidden_size = 4
+ hidden_states = tf.reshape(hidden_states,
+ (batch_size, seq_length, hidden_size))
+
+ chunked_hidden_states = longformer_attention.LongformerAttention._chunk(
+ hidden_states, window_overlap=2)
+
+ # expected slices across chunk and seq length dim
+ expected_slice_along_seq_length = tf.convert_to_tensor(
+ [0.4983, -0.7584, -1.6944], dtype=tf.dtypes.float32)
+ expected_slice_along_chunk = tf.convert_to_tensor(
+ [0.4983, -1.8348, -0.7584, 2.0514], dtype=tf.dtypes.float32)
+
+ self.assertEqual(get_shape_list(chunked_hidden_states), [1, 3, 4, 4])
+ tf.debugging.assert_near(
+ chunked_hidden_states[0, :, 0, 0],
+ expected_slice_along_seq_length,
+ rtol=1e-3)
+ tf.debugging.assert_near(
+ chunked_hidden_states[0, 0, :, 0],
+ expected_slice_along_chunk,
+ rtol=1e-3)
+
+ def test_layer_local_attn(self):
+ hidden_states = self._get_hidden_states()
+ batch_size, seq_length, _ = hidden_states.shape
+ layer = longformer_attention.LongformerAttention(
+ num_heads=2,
+ key_dim=4,
+ value_dim=4,
+ layer_id=0,
+ attention_window=4,
+ global_attention_size=0,
+ )
+
+ attention_mask = tf.zeros((batch_size, seq_length), dtype=tf.dtypes.float32)
+ is_index_global_attn = tf.math.greater(attention_mask, 1)
+
+ attention_mask = tf.where(
+ tf.range(4)[None, :, None, None] > 1, -10000.0,
+ attention_mask[:, :, None, None])
+ is_index_masked = tf.math.less(attention_mask[:, :, 0, 0], 0)
+
+ output_hidden_states = layer(
+ hidden_states=hidden_states,
+ attention_mask=attention_mask,
+ is_index_masked=is_index_masked,
+ is_index_global_attn=is_index_global_attn,
+ )[0]
+
+ self.assertTrue(output_hidden_states.shape, (1, 4, 8))
+
+ def test_layer_global_attn(self):
+ layer = longformer_attention.LongformerAttention(
+ num_heads=2,
+ key_dim=4,
+ value_dim=4,
+ layer_id=0,
+ attention_window=4,
+ global_attention_size=1,
+ )
+ hidden_states = self._get_hidden_states()
+
+ hidden_states = tf.concat(
+ [self._get_hidden_states(),
+ self._get_hidden_states() - 0.5], axis=0)
+ _, seq_length, _ = hidden_states.shape
+
+ # create attn mask
+ attention_mask_1 = tf.zeros((1, 1, 1, seq_length), dtype=tf.dtypes.float32)
+ attention_mask_2 = tf.zeros((1, 1, 1, seq_length), dtype=tf.dtypes.float32)
+
+ attention_mask_1 = tf.where(
+ tf.range(4)[None, :, None, None] == 0, 10000.0, attention_mask_1)
+ attention_mask_1 = tf.where(
+ tf.range(4)[None, :, None, None] > 2, -10000.0, attention_mask_1)
+ attention_mask_2 = tf.where(
+ tf.range(4)[None, :, None, None] == 0, 10000.0, attention_mask_2)
+ attention_mask = tf.concat([attention_mask_1, attention_mask_2], axis=0)
+
+ is_index_masked = tf.math.less(attention_mask[:, :, 0, 0], 0)
+ is_index_global_attn = tf.math.greater(attention_mask[:, :, 0, 0], 0)
+
+ output_hidden_states = layer(
+ hidden_states=hidden_states,
+ attention_mask=-tf.math.abs(attention_mask),
+ is_index_masked=is_index_masked,
+ is_index_global_attn=is_index_global_attn,
+ )[0]
+
+ self.assertTrue(output_hidden_states.shape, (2, 4, 8))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/longformer/longformer_encoder.py b/official/projects/longformer/longformer_encoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..c5a29dc4496d0574403188837a884a3be8d44112
--- /dev/null
+++ b/official/projects/longformer/longformer_encoder.py
@@ -0,0 +1,365 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Longformer encoder. Modified From huggingface/transformers."""
+
+# pylint: disable=g-classes-have-attributes
+
+from typing import Any, Callable, List, Optional, Union
+
+from absl import logging
+import tensorflow as tf
+
+from official.modeling.tf_utils import get_shape_list
+from official.nlp.modeling import layers
+from official.projects.longformer.longformer_encoder_block import LongformerEncoderBlock
+
+
+_Initializer = Union[str, tf.keras.initializers.Initializer]
+_approx_gelu = lambda x: tf.keras.activations.gelu(x, approximate=True)
+
+
+class LongformerEncoder(tf.keras.layers.Layer):
+ """LongformerEncoder.
+
+ Args:
+ vocab_size: The size of the token vocabulary.
+ attention_window: list of ints representing the window size for each layer.
+ global_attention_size: the size of global attention used for each token.
+ pad_token_id: the token id for the pad token
+ hidden_size: The size of the transformer hidden layers.
+ num_layers: The number of transformer layers.
+ num_attention_heads: The number of attention heads for each transformer. The
+ hidden size must be divisible by the number of attention heads.
+ max_sequence_length: The maximum sequence length that this encoder can
+ consume. If None, max_sequence_length uses the value from sequence length.
+ This determines the variable shape for positional embeddings.
+ type_vocab_size: The number of types that the 'type_ids' input can take.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ output_dropout: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout: The dropout rate to use for the attention layers within
+ the transformer layers.
+ initializer: The initialzer to use for all weights in this encoder.
+ output_range: The sequence output range, [0, output_range), by slicing the
+ target sequence of the last transformer layer. `None` means the entire
+ target sequence will attend to the source sequence, which yields the full
+ output.
+ embedding_width: The width of the word embeddings. If the embedding width is
+ not equal to hidden size, embedding parameters will be factorized into two
+ matrices in the shape of ['vocab_size', 'embedding_width'] and
+ ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
+ smaller than 'hidden_size').
+ embedding_layer: An optional Layer instance which will be called to generate
+ embeddings for the input word IDs.
+ norm_first: Whether to normalize inputs to attention and intermediate dense
+ layers. If set False, output of attention and intermediate dense layers is
+ normalized.
+ """
+
+ def __init__(
+ self,
+ vocab_size: int,
+ attention_window: Union[List[int], int] = 512,
+ global_attention_size: int = 0,
+ pad_token_id: int = 1,
+ hidden_size: int = 768,
+ num_layers: int = 12,
+ num_attention_heads: int = 12,
+ max_sequence_length: int = 512,
+ type_vocab_size: int = 16,
+ inner_dim: int = 3072,
+ inner_activation: Callable[..., Any] = _approx_gelu,
+ output_dropout: float = 0.1,
+ attention_dropout: float = 0.1,
+ initializer: _Initializer = tf.keras.initializers.TruncatedNormal(
+ stddev=0.02),
+ output_range: Optional[int] = None,
+ embedding_width: Optional[int] = None,
+ embedding_layer: Optional[tf.keras.layers.Layer] = None,
+ norm_first: bool = False,
+ **kwargs):
+ super().__init__(**kwargs)
+ # Longformer args
+ self._attention_window = attention_window
+ self._global_attention_size = global_attention_size
+ self._pad_token_id = pad_token_id
+
+ activation = tf.keras.activations.get(inner_activation)
+ initializer = tf.keras.initializers.get(initializer)
+
+ if embedding_width is None:
+ embedding_width = hidden_size
+
+ if embedding_layer is None:
+ self._embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ initializer=initializer,
+ name='word_embeddings')
+ else:
+ self._embedding_layer = embedding_layer
+
+ self._position_embedding_layer = layers.PositionEmbedding(
+ initializer=initializer,
+ max_length=max_sequence_length,
+ name='position_embedding')
+
+ self._type_embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=type_vocab_size,
+ embedding_width=embedding_width,
+ initializer=initializer,
+ use_one_hot=True,
+ name='type_embeddings')
+
+ self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
+ name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
+
+ self._embedding_dropout = tf.keras.layers.Dropout(
+ rate=output_dropout, name='embedding_dropout')
+
+ # We project the 'embedding' output to 'hidden_size' if it is not already
+ # 'hidden_size'.
+ self._embedding_projection = None
+ if embedding_width != hidden_size:
+ self._embedding_projection = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=hidden_size,
+ bias_axes='y',
+ kernel_initializer=initializer,
+ name='embedding_projection')
+
+ self._transformer_layers = []
+ self._attention_mask_layer = layers.SelfAttentionMask(
+ name='self_attention_mask')
+ for i in range(num_layers):
+ layer = LongformerEncoderBlock(
+ global_attention_size=global_attention_size,
+ num_attention_heads=num_attention_heads,
+ inner_dim=inner_dim,
+ inner_activation=inner_activation,
+ attention_window=attention_window[i],
+ layer_id=i,
+ output_dropout=output_dropout,
+ attention_dropout=attention_dropout,
+ norm_first=norm_first,
+ output_range=output_range if i == num_layers - 1 else None,
+ kernel_initializer=initializer,
+ name=f'transformer/layer_{i}')
+ self._transformer_layers.append(layer)
+
+ self._pooler_layer = tf.keras.layers.Dense(
+ units=hidden_size,
+ activation='tanh',
+ kernel_initializer=initializer,
+ name='pooler_transform')
+
+ self._config = {
+ 'vocab_size': vocab_size,
+ 'hidden_size': hidden_size,
+ 'num_layers': num_layers,
+ 'num_attention_heads': num_attention_heads,
+ 'max_sequence_length': max_sequence_length,
+ 'type_vocab_size': type_vocab_size,
+ 'inner_dim': inner_dim,
+ 'inner_activation': tf.keras.activations.serialize(activation),
+ 'output_dropout': output_dropout,
+ 'attention_dropout': attention_dropout,
+ 'initializer': tf.keras.initializers.serialize(initializer),
+ 'output_range': output_range,
+ 'embedding_width': embedding_width,
+ 'embedding_layer': embedding_layer,
+ 'norm_first': norm_first,
+ 'attention_window': attention_window,
+ 'global_attention_size': global_attention_size,
+ 'pad_token_id': pad_token_id,
+ }
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32))
+
+ def call(self, inputs):
+ word_embeddings = None
+ if isinstance(inputs, dict):
+ word_ids = inputs.get('input_word_ids') # input_ids
+ mask = inputs.get('input_mask') # attention_mask
+ type_ids = inputs.get('input_type_ids') # token_type_ids
+ word_embeddings = inputs.get('input_word_embeddings',
+ None) # input_embeds
+ else:
+ raise ValueError(f'Unexpected inputs type to {self.__class__}.')
+
+ (
+ padding_len,
+ word_ids,
+ mask,
+ type_ids,
+ word_embeddings,
+ ) = self._pad_to_window_size(
+ word_ids=word_ids,
+ mask=mask,
+ type_ids=type_ids,
+ word_embeddings=word_embeddings,
+ pad_token_id=self._pad_token_id)
+
+ if word_embeddings is None:
+ word_embeddings = self._embedding_layer(word_ids)
+ # absolute position embeddings.
+ position_embeddings = self._position_embedding_layer(word_embeddings)
+ type_embeddings = self._type_embedding_layer(type_ids)
+
+ embeddings = word_embeddings + position_embeddings + type_embeddings
+ embeddings = self._embedding_norm_layer(embeddings)
+ embeddings = self._embedding_dropout(embeddings)
+
+ if self._embedding_projection is not None:
+ embeddings = self._embedding_projection(embeddings)
+
+ batch_size, seq_len = get_shape_list(mask)
+ # create masks with fixed len global_attention_size
+ mask = tf.transpose(
+ tf.concat(
+ values=[
+ tf.ones(
+ (self._global_attention_size, batch_size), tf.int32) * 2,
+ tf.transpose(mask)[self._global_attention_size:]
+ ],
+ axis=0))
+
+ is_index_masked = tf.math.less(mask, 1)
+
+ is_index_global_attn = tf.transpose(
+ tf.concat(
+ values=[
+ tf.ones((self._global_attention_size, batch_size), tf.bool),
+ tf.zeros((seq_len - self._global_attention_size, batch_size),
+ tf.bool)
+ ],
+ axis=0))
+
+ # Longformer
+ attention_mask = mask
+ extended_attention_mask = tf.reshape(
+ attention_mask, (tf.shape(mask)[0], tf.shape(mask)[1], 1, 1))
+ attention_mask = tf.cast(
+ tf.math.abs(1 - extended_attention_mask), tf.dtypes.float32) * -10000.0
+
+ encoder_outputs = []
+ x = embeddings
+ # TFLongformerEncoder
+ for layer in self._transformer_layers:
+ x = layer([x, attention_mask, is_index_masked, is_index_global_attn])
+ encoder_outputs.append(x)
+
+ last_encoder_output = encoder_outputs[-1]
+ if padding_len > 0:
+ last_encoder_output = last_encoder_output[:, :-padding_len]
+ first_token_tensor = last_encoder_output[:, 0, :]
+ pooled_output = self._pooler_layer(first_token_tensor)
+
+ return dict(
+ sequence_output=last_encoder_output,
+ pooled_output=pooled_output,
+ encoder_outputs=encoder_outputs)
+
+ def get_embedding_table(self):
+ return self._embedding_layer.embeddings
+
+ def get_embedding_layer(self):
+ return self._embedding_layer
+
+ def get_config(self):
+ return dict(self._config)
+
+ @property
+ def transformer_layers(self):
+ """List of Transformer layers in the encoder."""
+ return self._transformer_layers
+
+ @property
+ def pooler_layer(self):
+ """The pooler dense layer after the transformer layers."""
+ return self._pooler_layer
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ if 'embedding_layer' in config and config['embedding_layer'] is not None:
+ warn_string = (
+ 'You are reloading a model that was saved with a '
+ 'potentially-shared embedding layer object. If you contine to '
+ 'train this model, the embedding layer will no longer be shared. '
+ 'To work around this, load the model outside of the Keras API.')
+ print('WARNING: ' + warn_string)
+ logging.warn(warn_string)
+
+ return cls(**config)
+
+ def _pad_to_window_size(
+ self,
+ word_ids,
+ mask,
+ type_ids,
+ word_embeddings,
+ pad_token_id,
+ ):
+ # padding
+ attention_window = max(self._attention_window)
+
+ assert (attention_window %
+ 2 == 0), ('`attention_window` should be an even value.'
+ f'Given {attention_window}')
+
+ input_shape = get_shape_list(
+ word_ids) if word_ids is not None else get_shape_list(word_embeddings)
+ batch_size, seq_len = input_shape[:2]
+
+ if seq_len is not None:
+ padding_len = (attention_window -
+ seq_len % attention_window) % attention_window
+ else:
+ padding_len = 0
+
+ paddings = tf.convert_to_tensor([[0, 0], [0, padding_len]])
+
+ if word_ids is not None:
+ word_ids = tf.pad(word_ids, paddings, constant_values=pad_token_id)
+
+ if word_embeddings is not None:
+
+ def pad_embeddings():
+ word_ids_padding = tf.fill((batch_size, padding_len), self.pad_token_id)
+ word_embeddings_padding = self._embedding_layer(word_ids_padding)
+ return tf.concat([word_embeddings, word_embeddings_padding], axis=-2)
+
+ word_embeddings = tf.cond(
+ tf.math.greater(padding_len, 0), pad_embeddings,
+ lambda: word_embeddings)
+
+ mask = tf.pad(
+ mask, paddings,
+ constant_values=False) # no attention on the padding tokens
+ token_type_ids = tf.pad(
+ type_ids, paddings, constant_values=0) # pad with token_type_id = 0
+
+ return (
+ padding_len,
+ word_ids,
+ mask,
+ token_type_ids,
+ word_embeddings,
+ )
diff --git a/official/projects/longformer/longformer_encoder_block.py b/official/projects/longformer/longformer_encoder_block.py
new file mode 100644
index 0000000000000000000000000000000000000000..1253477d37f69774aa36ea1fe8cbf3b83c12f300
--- /dev/null
+++ b/official/projects/longformer/longformer_encoder_block.py
@@ -0,0 +1,340 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Longformer attention layer. Modified From huggingface/transformers."""
+
+import tensorflow as tf
+from official.projects.longformer.longformer_attention import LongformerAttention
+
+
+@tf.keras.utils.register_keras_serializable(package="Text")
+class LongformerEncoderBlock(tf.keras.layers.Layer):
+ """LongformerEncoderBlock.
+
+ Args:
+ num_attention_heads: Number of attention heads.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network.
+ output_range: the sequence output range, [0, output_range) for slicing the
+ target sequence. `None` means the target sequence is not sliced.
+ kernel_initializer: Initializer for dense layer kernels.
+ bias_initializer: Initializer for dense layer biases.
+ kernel_regularizer: Regularizer for dense layer kernels.
+ bias_regularizer: Regularizer for dense layer biases.
+ activity_regularizer: Regularizer for dense layer activity.
+ kernel_constraint: Constraint for dense layer kernels.
+ bias_constraint: Constraint for dense layer kernels.
+ use_bias: Whether to enable use_bias in attention layer. If set False,
+ use_bias in attention layer is disabled.
+ norm_first: Whether to normalize inputs to attention and intermediate
+ dense layers. If set False, output of attention and intermediate dense
+ layers is normalized.
+ norm_epsilon: Epsilon value to initialize normalization layers.
+ output_dropout: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout: Dropout probability for within the attention layer.
+ inner_dropout: Dropout probability for the first Dense layer in a
+ two-layer feedforward network.
+ attention_initializer: Initializer for kernels of attention layers. If set
+ `None`, attention layers use kernel_initializer as initializer for
+ kernel.
+ attention_axes: axes over which the attention is applied. `None` means
+ attention over all axes, but batch, heads, and features.
+ **kwargs: keyword arguments/
+ """
+
+ def __init__(
+ self,
+ global_attention_size,
+ num_attention_heads,
+ inner_dim,
+ inner_activation,
+ # Longformer
+ attention_window,
+ layer_id=0,
+ output_range=None,
+ kernel_initializer="glorot_uniform",
+ bias_initializer="zeros",
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activity_regularizer=None,
+ kernel_constraint=None,
+ bias_constraint=None,
+ use_bias=True,
+ norm_first=False,
+ norm_epsilon=1e-12,
+ output_dropout=0.0,
+ attention_dropout=0.0,
+ inner_dropout=0.0,
+ attention_initializer=None,
+ attention_axes=None,
+ **kwargs):
+ super().__init__(**kwargs)
+
+ self.global_attention_size = global_attention_size
+ self._num_heads = num_attention_heads
+ self._inner_dim = inner_dim
+ self._inner_activation = inner_activation
+ # Longformer
+ self._attention_window = attention_window
+ self._layer_id = layer_id
+ self._attention_dropout = attention_dropout
+ self._attention_dropout_rate = attention_dropout
+ self._output_dropout = output_dropout
+ self._output_dropout_rate = output_dropout
+ self._output_range = output_range
+ self._kernel_initializer = tf.keras.initializers.get(kernel_initializer)
+ self._bias_initializer = tf.keras.initializers.get(bias_initializer)
+ self._kernel_regularizer = tf.keras.regularizers.get(kernel_regularizer)
+ self._bias_regularizer = tf.keras.regularizers.get(bias_regularizer)
+ self._activity_regularizer = tf.keras.regularizers.get(activity_regularizer)
+ self._kernel_constraint = tf.keras.constraints.get(kernel_constraint)
+ self._bias_constraint = tf.keras.constraints.get(bias_constraint)
+ self._use_bias = use_bias
+ self._norm_first = norm_first
+ self._norm_epsilon = norm_epsilon
+ self._inner_dropout = inner_dropout
+ if attention_initializer:
+ self._attention_initializer = tf.keras.initializers.get(
+ attention_initializer)
+ else:
+ self._attention_initializer = self._kernel_initializer
+ self._attention_axes = attention_axes
+
+ def build(self, input_shape):
+ if isinstance(input_shape, tf.TensorShape):
+ input_tensor_shape = input_shape
+ elif isinstance(input_shape, (list, tuple)):
+ input_tensor_shape = tf.TensorShape(input_shape[0])
+ else:
+ raise ValueError(
+ f"The type of input shape argument is not supported, got: "
+ f"{type(input_shape)}")
+ einsum_equation = "abc,cd->abd"
+ if len(input_tensor_shape.as_list()) > 3:
+ einsum_equation = "...bc,cd->...bd"
+ hidden_size = input_tensor_shape[-1]
+ if hidden_size % self._num_heads != 0:
+ raise ValueError(
+ f"The input size ({hidden_size}) is not a multiple of the number of attention "
+ f"heads ({self._num_heads})")
+ self._attention_head_size = int(hidden_size // self._num_heads)
+ common_kwargs = dict(
+ bias_initializer=self._bias_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activity_regularizer=self._activity_regularizer,
+ kernel_constraint=self._kernel_constraint,
+ bias_constraint=self._bias_constraint)
+ # TFLongformerSelfAttention + TFLongformerSelfOutput.dense
+ self._attention_layer = LongformerAttention(
+ # Longformer
+ layer_id=self._layer_id,
+ global_attention_size=self.global_attention_size,
+ attention_window=self._attention_window,
+ num_heads=self._num_heads,
+ key_dim=self._attention_head_size,
+ dropout=self._attention_dropout,
+ use_bias=self._use_bias,
+ kernel_initializer=self._attention_initializer,
+ attention_axes=self._attention_axes,
+ name="self_attention",
+ **common_kwargs)
+ # TFLongformerSelfOutput.dropout
+ self._attention_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ # Use float32 in layernorm for numeric stability.
+ # It is probably safe in mixed_float16, but we haven't validated this yet.
+ # TFLongformerSelfOutput.Layernorm
+ self._attention_layer_norm = (
+ tf.keras.layers.LayerNormalization(
+ name="self_attention_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype=tf.float32))
+ # TFLongformerIntermediate
+ # TFLongformerIntermediate.dense
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=(None, self._inner_dim),
+ bias_axes="d",
+ kernel_initializer=self._kernel_initializer,
+ name="intermediate",
+ **common_kwargs)
+ policy = tf.keras.mixed_precision.global_policy()
+ if policy.name == "mixed_bfloat16":
+ # bfloat16 causes BERT with the LAMB optimizer to not converge
+ # as well, so we use float32.
+ # TODO(b/154538392): Investigate this.
+ policy = tf.float32
+ # TFLongformerIntermediate.intermediate_act_fn
+ self._intermediate_activation_layer = tf.keras.layers.Activation(
+ self._inner_activation, dtype=policy)
+ self._inner_dropout_layer = tf.keras.layers.Dropout(
+ rate=self._inner_dropout)
+ # TFLongformerOutput
+ # TFLongformerOutput.dense
+ self._output_dense = tf.keras.layers.EinsumDense(
+ einsum_equation,
+ output_shape=(None, hidden_size),
+ bias_axes="d",
+ name="output",
+ kernel_initializer=self._kernel_initializer,
+ **common_kwargs)
+ # TFLongformerOutput.dropout
+ self._output_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
+ # Use float32 in layernorm for numeric stability.
+ # TFLongformerOutput.layernorm
+ self._output_layer_norm = tf.keras.layers.LayerNormalization(
+ name="output_layer_norm",
+ axis=-1,
+ epsilon=self._norm_epsilon,
+ dtype=tf.float32)
+
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {
+ "num_attention_heads":
+ self._num_heads,
+ "inner_dim":
+ self._inner_dim,
+ "inner_activation":
+ self._inner_activation,
+ "output_dropout":
+ self._output_dropout_rate,
+ "attention_dropout":
+ self._attention_dropout_rate,
+ "output_range":
+ self._output_range,
+ "kernel_initializer":
+ tf.keras.initializers.serialize(self._kernel_initializer),
+ "bias_initializer":
+ tf.keras.initializers.serialize(self._bias_initializer),
+ "kernel_regularizer":
+ tf.keras.regularizers.serialize(self._kernel_regularizer),
+ "bias_regularizer":
+ tf.keras.regularizers.serialize(self._bias_regularizer),
+ "activity_regularizer":
+ tf.keras.regularizers.serialize(self._activity_regularizer),
+ "kernel_constraint":
+ tf.keras.constraints.serialize(self._kernel_constraint),
+ "bias_constraint":
+ tf.keras.constraints.serialize(self._bias_constraint),
+ "use_bias":
+ self._use_bias,
+ "norm_first":
+ self._norm_first,
+ "norm_epsilon":
+ self._norm_epsilon,
+ "inner_dropout":
+ self._inner_dropout,
+ "attention_initializer":
+ tf.keras.initializers.serialize(self._attention_initializer),
+ "attention_axes":
+ self._attention_axes,
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs):
+ """Transformer self-attention encoder block call.
+
+ Args:
+ inputs: a single tensor or a list of tensors. `input tensor` as the single
+ sequence of embeddings. [`input tensor`, `attention mask`] to have the
+ additional attention mask. [`query tensor`, `key value tensor`,
+ `attention mask`] to have separate input streams for the query, and
+ key/value to the multi-head attention.
+
+ Returns:
+ An output tensor with the same dimensions as input/query tensor.
+ """
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 4:
+ (
+ input_tensor,
+ attention_mask,
+ is_index_masked,
+ is_index_global_attn,
+ ) = inputs
+ key_value = None
+ elif len(inputs) == 5:
+ assert False # No key_value
+ else:
+ raise ValueError(
+ f"Unexpected inputs to {self.__class__} with length at {len(inputs)}"
+ )
+ else:
+ input_tensor = inputs
+ attention_mask = None
+ is_index_masked = None
+ is_index_global_attn = None
+ key_value = None
+
+ if self._output_range:
+ if self._norm_first:
+ source_tensor = input_tensor[:, 0:self._output_range, :]
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor[:, 0:self._output_range, :]
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, 0:self._output_range, :]
+ if is_index_masked is not None:
+ is_index_masked = is_index_masked[:, 0:self._output_range]
+ if is_index_global_attn is not None:
+ is_index_global_attn = is_index_global_attn[:, 0:self._output_range]
+ else:
+ if self._norm_first:
+ source_tensor = input_tensor
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor
+
+ if key_value is None:
+ key_value = input_tensor
+ attention_output = self._attention_layer(
+ hidden_states=target_tensor,
+ attention_mask=attention_mask,
+ is_index_masked=is_index_masked,
+ is_index_global_attn=is_index_global_attn,
+ )
+ # TFLongformerAttention.TFLongformerSelfOutput.* - {.dense}
+ attention_output = self._attention_dropout(attention_output)
+ if self._norm_first:
+ attention_output = source_tensor + attention_output
+ else:
+ attention_output = self._attention_layer_norm(target_tensor +
+ attention_output)
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self._output_layer_norm(attention_output)
+ # TFLongformerIntermediate
+ inner_output = self._intermediate_dense(attention_output)
+ inner_output = self._intermediate_activation_layer(inner_output)
+ inner_output = self._inner_dropout_layer(inner_output)
+ # TFLongformerOutput
+ layer_output = self._output_dense(inner_output)
+ layer_output = self._output_dropout(layer_output)
+
+ if self._norm_first:
+ return source_attention_output + layer_output
+
+ # During mixed precision training, layer norm output is always fp32 for now.
+ # Casts fp32 for the subsequent add.
+ layer_output = tf.cast(layer_output, tf.float32)
+ return self._output_layer_norm(layer_output + attention_output)
diff --git a/official/projects/longformer/longformer_encoder_test.py b/official/projects/longformer/longformer_encoder_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..cf24d7c926bed5ec94c4f4528a72856ebd3b7d35
--- /dev/null
+++ b/official/projects/longformer/longformer_encoder_test.py
@@ -0,0 +1,97 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for official.nlp.projects.longformer.longformer_encoder."""
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from tensorflow.python.distribute import combinations
+from official.projects.longformer.longformer_encoder import LongformerEncoder
+
+
+class LongformerEncoderTest(parameterized.TestCase, tf.test.TestCase):
+
+ def setUp(self):
+ super(LongformerEncoderTest, self).setUp()
+ np.random.seed(0)
+ tf.random.set_seed(0)
+
+ @combinations.generate(
+ combinations.combine(
+ attention_window=[32, 128], global_attention_size=[0, 1, 2]))
+ def test_encoder(self, attention_window, global_attention_size):
+ sequence_length = 128
+ batch_size = 2
+ vocab_size = 1024
+ hidden_size = 256
+ network = LongformerEncoder(
+ global_attention_size=global_attention_size,
+ vocab_size=vocab_size,
+ attention_window=[attention_window],
+ hidden_size=hidden_size,
+ num_layers=1,
+ num_attention_heads=4,
+ max_sequence_length=512)
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length), dtype=np.int32)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ type_id_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ inputs = {
+ 'input_word_ids': word_id_data,
+ 'input_mask': mask_data,
+ 'input_type_ids': type_id_data,
+ }
+ outputs = network(inputs)
+ self.assertEqual(outputs['sequence_output'].shape,
+ (batch_size, sequence_length, hidden_size))
+
+ @combinations.generate(
+ combinations.combine(
+ norm_first=[True, False], global_attention_size=[0, 1, 2]))
+ def test_norm_first(self, norm_first, global_attention_size):
+ sequence_length = 128
+ batch_size = 2
+ vocab_size = 1024
+ hidden_size = 256
+ network = LongformerEncoder(
+ global_attention_size=global_attention_size,
+ vocab_size=vocab_size,
+ attention_window=[32],
+ hidden_size=hidden_size,
+ num_layers=1,
+ num_attention_heads=4,
+ max_sequence_length=512,
+ norm_first=norm_first)
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length), dtype=np.int32)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ type_id_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ inputs = {
+ 'input_word_ids': word_id_data,
+ 'input_mask': mask_data,
+ 'input_type_ids': type_id_data,
+ }
+ outputs = network(inputs)
+ self.assertEqual(outputs['sequence_output'].shape,
+ (batch_size, sequence_length, hidden_size))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/longformer/longformer_experiments.py b/official/projects/longformer/longformer_experiments.py
new file mode 100644
index 0000000000000000000000000000000000000000..e93672806d849bc7801b3d3f13f44af50b0ea320
--- /dev/null
+++ b/official/projects/longformer/longformer_experiments.py
@@ -0,0 +1,123 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Longformer experiments."""
+# pylint: disable=g-doc-return-or-yield,line-too-long
+import dataclasses
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+from official.nlp.configs import bert
+from official.nlp.configs import encoders
+from official.nlp.data import pretrain_dataloader
+from official.nlp.data import sentence_prediction_dataloader
+from official.nlp.tasks import masked_lm
+from official.nlp.tasks import sentence_prediction
+from official.projects.longformer.longformer import LongformerEncoderConfig
+
+
+AdamWeightDecay = optimization.AdamWeightDecayConfig
+PolynomialLr = optimization.PolynomialLrConfig
+PolynomialWarmupConfig = optimization.PolynomialWarmupConfig
+
+
+@dataclasses.dataclass
+class LongformerOptimizationConfig(optimization.OptimizationConfig):
+ """Longformer optimization configuration."""
+ optimizer: optimization.OptimizerConfig = optimization.OptimizerConfig(
+ type='adamw',
+ adamw=AdamWeightDecay(
+ weight_decay_rate=0.01,
+ exclude_from_weight_decay=['LayerNorm', 'layer_norm', 'bias'],
+ epsilon=1e-6))
+ learning_rate: optimization.LrConfig = optimization.LrConfig(
+ type='polynomial',
+ polynomial=PolynomialLr(
+ initial_learning_rate=1e-4,
+ decay_steps=1000000,
+ end_learning_rate=0.0))
+ warmup: optimization.WarmupConfig = optimization.WarmupConfig(
+ type='polynomial', polynomial=PolynomialWarmupConfig(warmup_steps=10000))
+
+
+@exp_factory.register_config_factory('longformer/pretraining')
+def longformer_pretraining() -> cfg.ExperimentConfig:
+ """Longformer pretraining experiment."""
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(enable_xla=True),
+ task=masked_lm.MaskedLMConfig(
+ model=bert.PretrainerConfig(
+ encoder=encoders.EncoderConfig(
+ type='any', any=LongformerEncoderConfig()),
+ cls_heads=[
+ bert.ClsHeadConfig(
+ inner_dim=768,
+ num_classes=2,
+ dropout_rate=0.1,
+ name='next_sentence')
+ ]),
+ train_data=pretrain_dataloader.BertPretrainDataConfig(
+ use_v2_feature_names=True),
+ validation_data=pretrain_dataloader.BertPretrainDataConfig(
+ use_v2_feature_names=True, is_training=False)),
+ trainer=cfg.TrainerConfig(
+ optimizer_config=LongformerOptimizationConfig(), train_steps=1000000),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
+
+
+@exp_factory.register_config_factory('longformer/glue')
+def longformer_glue() -> cfg.ExperimentConfig:
+ """Longformer glue fine-tuning."""
+ config = cfg.ExperimentConfig(
+ task=sentence_prediction.SentencePredictionConfig(
+ model=sentence_prediction.ModelConfig(
+ encoder=encoders.EncoderConfig(
+ type='any', any=LongformerEncoderConfig())),
+ train_data=sentence_prediction_dataloader
+ .SentencePredictionDataConfig(),
+ validation_data=sentence_prediction_dataloader
+ .SentencePredictionDataConfig(
+ is_training=False, drop_remainder=False)),
+ trainer=cfg.TrainerConfig(
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate':
+ 0.01,
+ 'exclude_from_weight_decay':
+ ['LayerNorm', 'layer_norm', 'bias'],
+ }
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 3e-5,
+ 'end_learning_rate': 0.0,
+ }
+ },
+ 'warmup': {
+ 'type': 'polynomial'
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
diff --git a/official/projects/longformer/train.py b/official/projects/longformer/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5486c1902d8ec61613a88c554f4600fc20c0bcd7
--- /dev/null
+++ b/official/projects/longformer/train.py
@@ -0,0 +1,69 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""A customized training library for the specific task."""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+from official.projects.longformer import longformer_experiments # pylint: disable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu,
+ **params.runtime.model_parallelism())
+
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/projects/longformer/utils/convert_pretrained_pytorch_checkpoint_to_tf.py b/official/projects/longformer/utils/convert_pretrained_pytorch_checkpoint_to_tf.py
new file mode 100644
index 0000000000000000000000000000000000000000..38fcc84e07792f5bc4970b30aba7e61ca20d10f8
--- /dev/null
+++ b/official/projects/longformer/utils/convert_pretrained_pytorch_checkpoint_to_tf.py
@@ -0,0 +1,200 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Converts pre-trained pytorch checkpoint into a tf encoder checkpoint."""
+
+import os
+
+from absl import app
+import numpy as np
+import tensorflow as tf
+import transformers
+
+from official.modeling import tf_utils
+from official.projects.longformer.longformer import LongformerEncoderConfig
+from official.projects.longformer.longformer_encoder import LongformerEncoder
+
+
+def _get_pytorch_longformer_model():
+ pretrained_lm = "allenai/longformer-base-4096"
+
+ model = transformers.AutoModel.from_pretrained(pretrained_lm)
+
+ return {n: p.data.numpy() for n, p in model.named_parameters()}
+
+
+def _create_longformer_model():
+ """Creates a Longformer model."""
+ encoder_cfg = LongformerEncoderConfig
+ encoder_cfg.vocab_size = 50265
+ encoder_cfg.max_position_embeddings = 4098
+ encoder_cfg.attention_window = [2] * encoder_cfg.num_layers
+ encoder_cfg.global_attention_size = 1
+ encoder = LongformerEncoder(
+ attention_window=encoder_cfg.attention_window,
+ global_attention_size=encoder_cfg.global_attention_size,
+ vocab_size=encoder_cfg.vocab_size,
+ hidden_size=encoder_cfg.hidden_size,
+ num_layers=encoder_cfg.num_layers,
+ num_attention_heads=encoder_cfg.num_attention_heads,
+ inner_dim=encoder_cfg.intermediate_size,
+ inner_activation=tf_utils.get_activation(encoder_cfg.hidden_activation),
+ output_dropout=encoder_cfg.dropout_rate,
+ attention_dropout=encoder_cfg.attention_dropout_rate,
+ max_sequence_length=encoder_cfg.max_position_embeddings,
+ type_vocab_size=encoder_cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ output_range=encoder_cfg.output_range,
+ embedding_width=encoder_cfg.embedding_size,
+ norm_first=encoder_cfg.norm_first)
+ return encoder
+
+
+# pylint: disable=protected-access
+def convert(encoder, allenai_model):
+ """Convert AllenAI Longformer to the one in the codebase."""
+ num_layers = encoder._config["num_layers"]
+ num_attention_heads = encoder._config["num_attention_heads"]
+ hidden_size = encoder._config["hidden_size"]
+ head_size = hidden_size // num_attention_heads
+ assert head_size * num_attention_heads == hidden_size
+ encoder._embedding_layer.set_weights(
+ [allenai_model["embeddings.word_embeddings.weight"]])
+ encoder._embedding_norm_layer.set_weights([
+ allenai_model["embeddings.LayerNorm.weight"],
+ allenai_model["embeddings.LayerNorm.bias"]
+ ])
+ encoder._type_embedding_layer.set_weights([
+ np.repeat(
+ allenai_model["embeddings.token_type_embeddings.weight"], 2, axis=0)
+ ])
+ encoder._position_embedding_layer.set_weights(
+ [allenai_model["embeddings.position_embeddings.weight"]])
+ encoder._pooler_layer.set_weights([
+ allenai_model["pooler.dense.weight"], allenai_model["pooler.dense.bias"]
+ ])
+ for layer_num in range(num_layers):
+ encoder._transformer_layers[
+ layer_num]._attention_layer._global_key_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.key_global.weight"].T
+ .reshape(
+ (hidden_size, num_attention_heads, head_size)), allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.key_global.bias"]
+ .reshape((num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._global_query_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.query_global.weight"]
+ .T.reshape((hidden_size, num_attention_heads, head_size)),
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.query_global.bias"]
+ .reshape((num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._global_value_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.value_global.weight"]
+ .T.reshape((hidden_size, num_attention_heads, head_size)),
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.value_global.bias"]
+ .reshape((num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._key_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.key.weight"].T
+ .reshape(
+ (hidden_size, num_attention_heads, head_size)), allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.key_global.bias"]
+ .reshape((num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._query_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.query.weight"].T
+ .reshape((hidden_size, num_attention_heads, head_size)),
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.query.bias"].reshape(
+ (num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._value_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.value.weight"].T
+ .reshape((hidden_size, num_attention_heads, head_size)),
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.self.value.bias"].reshape(
+ (num_attention_heads, head_size))
+ ])
+ encoder._transformer_layers[
+ layer_num]._attention_layer._output_dense.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.output.dense.weight"].T,
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.output.dense.bias"]
+ ])
+ encoder._transformer_layers[layer_num]._attention_layer_norm.set_weights([
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.output.LayerNorm.weight"],
+ allenai_model[
+ f"encoder.layer.{layer_num}.attention.output.LayerNorm.bias"]
+ ])
+ encoder._transformer_layers[layer_num]._intermediate_dense.set_weights([
+ allenai_model[f"encoder.layer.{layer_num}.intermediate.dense.weight"].T,
+ allenai_model[f"encoder.layer.{layer_num}.intermediate.dense.bias"]
+ ])
+ encoder._transformer_layers[layer_num]._output_dense.set_weights([
+ allenai_model[f"encoder.layer.{layer_num}.output.dense.weight"].T,
+ allenai_model[f"encoder.layer.{layer_num}.output.dense.bias"]
+ ])
+ encoder._transformer_layers[layer_num]._output_layer_norm.set_weights([
+ allenai_model[f"encoder.layer.{layer_num}.output.LayerNorm.weight"],
+ allenai_model[f"encoder.layer.{layer_num}.output.LayerNorm.bias"]
+ ])
+
+
+def convert_checkpoint(output_path):
+ """Converts and save the checkpoint."""
+ output_dir, _ = os.path.split(output_path)
+ tf.io.gfile.makedirs(output_dir)
+
+ encoder = _create_longformer_model()
+ allenai_model = _get_pytorch_longformer_model()
+ sequence_length = 128
+ batch_size = 2
+ word_id_data = np.random.randint(
+ 10, size=(batch_size, sequence_length), dtype=np.int32)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ type_id_data = np.random.randint(
+ 2, size=(batch_size, sequence_length), dtype=np.int32)
+ inputs = {
+ "input_word_ids": word_id_data,
+ "input_mask": mask_data,
+ "input_type_ids": type_id_data,
+ }
+ encoder(inputs)
+ convert(encoder, allenai_model)
+ tf.train.Checkpoint(encoder=encoder).write(output_path)
+
+
+def main(_):
+ convert_checkpoint("longformer-4096/longformer")
+
+
+if __name__ == "__main__":
+ app.run(main)
diff --git a/official/projects/longformer/utils/longformer_tokenizer_to_tfrecord.py b/official/projects/longformer/utils/longformer_tokenizer_to_tfrecord.py
new file mode 100644
index 0000000000000000000000000000000000000000..9fc85a391edc7d3beefbc64bbfd51fe04d2f3f73
--- /dev/null
+++ b/official/projects/longformer/utils/longformer_tokenizer_to_tfrecord.py
@@ -0,0 +1,112 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Convert Longformer training examples to Tfrecord."""
+import collections
+import os
+
+import datasets
+import tensorflow as tf
+import transformers
+
+pretrained_lm = "allenai/longformer-base-4096"
+task_name = "mnli"
+save_path = "./"
+
+raw_datasets = datasets.load_dataset("glue", task_name, cache_dir=None)
+label_list = raw_datasets["train"].features["label"].names
+num_labels = len(label_list)
+
+tokenizer = transformers.AutoTokenizer.from_pretrained(
+ pretrained_lm,
+ use_fast=True,
+)
+
+task_to_keys = {
+ "cola": ("sentence", None),
+ "mnli": ("premise", "hypothesis"),
+ "mrpc": ("sentence1", "sentence2"),
+ "qnli": ("question", "sentence"),
+ "qqp": ("question1", "question2"),
+ "rte": ("sentence1", "sentence2"),
+ "sst2": ("sentence", None),
+ "stsb": ("sentence1", "sentence2"),
+ "wnli": ("sentence1", "sentence2"),
+}
+
+sentence1_key, sentence2_key = task_to_keys[task_name]
+padding = "max_length"
+
+# make sure this is the same with model input size.
+max_seq_length = 512
+
+
+def preprocess_function(examples):
+ # Tokenize the texts
+ args = ((examples[sentence1_key],) if sentence2_key is None else
+ (examples[sentence1_key], examples[sentence2_key]))
+ result = tokenizer(
+ *args, padding=padding, max_length=max_seq_length, truncation=True)
+ return result
+
+
+raw_datasets = raw_datasets.map(
+ preprocess_function,
+ batched=True,
+ desc="Running tokenizer on dataset",
+)
+
+train_dataset = raw_datasets["train"]
+eval_dataset = raw_datasets["validation_matched" if task_name ==
+ "mnli" else "validation"]
+
+print("train_dataset", train_dataset[0])
+print("eval_dataset", eval_dataset[0])
+
+
+def file_based_convert_examples_to_features(examples, output_file):
+ """Convert a set of `InputExample`s to a TFRecord file."""
+ tf.io.gfile.makedirs(os.path.dirname(output_file))
+ writer = tf.io.TFRecordWriter(output_file)
+
+ for ex_index, example in enumerate(examples):
+ if ex_index % 10000 == 0:
+ print(f"Writing example {ex_index} of {len(examples)}")
+
+ def create_int_feature(values):
+ f = tf.train.Feature(int64_list=tf.train.Int64List(value=list(values)))
+ return f
+
+ features = collections.OrderedDict()
+ features["input_ids"] = create_int_feature(example["input_ids"])
+ features["input_mask"] = create_int_feature(example["attention_mask"])
+ features["segment_ids"] = create_int_feature([0] *
+ len(example["attention_mask"]))
+ features["label_ids"] = create_int_feature([example["label"]])
+ features["is_real_example"] = create_int_feature([1])
+ features["example_id"] = create_int_feature([example["idx"]])
+
+ tf_example = tf.train.Example(features=tf.train.Features(feature=features))
+ writer.write(tf_example.SerializeToString())
+ writer.close()
+
+
+file_based_convert_examples_to_features(
+ train_dataset,
+ os.path.join(save_path,
+ f"{pretrained_lm.replace('/', '_')}_train.tf_record"))
+file_based_convert_examples_to_features(
+ eval_dataset,
+ os.path.join(save_path,
+ f"{pretrained_lm.replace('/', '_')}_eval.tf_record"))
diff --git a/official/projects/mobilebert/__init__.py b/official/projects/mobilebert/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/mobilebert/__init__.py
+++ b/official/projects/mobilebert/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mobilebert/distillation.py b/official/projects/mobilebert/distillation.py
index 731e32f938226c5233d2683a517e977a91c80d3b..68decad6c92756519226f4ff0c1a1f001962c8ad 100644
--- a/official/projects/mobilebert/distillation.py
+++ b/official/projects/mobilebert/distillation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -238,6 +238,9 @@ class BertDistillationTask(policies.ProgressivePolicy, base_task.Task):
})
opt_factory = optimization.OptimizerFactory(params)
optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+ if isinstance(optimizer, tf.keras.optimizers.experimental.Optimizer):
+ optimizer = tf.keras.__internal__.optimizers.convert_to_legacy_optimizer(
+ optimizer)
return optimizer
diff --git a/official/projects/mobilebert/distillation_test.py b/official/projects/mobilebert/distillation_test.py
index 6b80ebaa30663e93f161e2a0c9afbc25a82701ab..1e6605ac1064929ae5556dd0ff3ed860d6cc6369 100644
--- a/official/projects/mobilebert/distillation_test.py
+++ b/official/projects/mobilebert/distillation_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -153,7 +153,7 @@ class DistillationTest(tf.test.TestCase, parameterized.TestCase):
eval_dataset = bert_distillation_task.get_eval_dataset(stage_id=0)
eval_iterator = iter(eval_dataset)
- optimizer = tf.keras.optimizers.SGD(lr=0.1)
+ optimizer = tf.keras.optimizers.legacy.SGD(learning_rate=0.1)
# test train/val step for all stages, including the last pretraining stage
for stage in range(student_block_num + 1):
diff --git a/official/projects/mobilebert/export_tfhub.py b/official/projects/mobilebert/export_tfhub.py
index 4f065a2a94488f5661fcec0e3405406ae500fbb3..184de577b57b105fe6ea3fd194f460339f4de149 100644
--- a/official/projects/mobilebert/export_tfhub.py
+++ b/official/projects/mobilebert/export_tfhub.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mobilebert/model_utils.py b/official/projects/mobilebert/model_utils.py
index 0cd6448515771f5aa4a06cbe71908a7ac196933d..70be52a4f864822b828e35aa2daf99805ba9a32f 100644
--- a/official/projects/mobilebert/model_utils.py
+++ b/official/projects/mobilebert/model_utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mobilebert/run_distillation.py b/official/projects/mobilebert/run_distillation.py
index 9fb7a9e670d2d191e9add1886443e72e6bdf9444..30aefcf8d7bde410a3c891ba1a567f094154d76c 100644
--- a/official/projects/mobilebert/run_distillation.py
+++ b/official/projects/mobilebert/run_distillation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mobilebert/tf2_model_checkpoint_converter.py b/official/projects/mobilebert/tf2_model_checkpoint_converter.py
index d3333ee31908c63541603ea2f4a1338b523263c1..eae8e8b2d2ad43090f560087b7113e8ca1e661a8 100644
--- a/official/projects/mobilebert/tf2_model_checkpoint_converter.py
+++ b/official/projects/mobilebert/tf2_model_checkpoint_converter.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mobilebert/utils.py b/official/projects/mobilebert/utils.py
index d5c3e4067471de279ce2e3147ef655771447cb57..f9e2a924c6f1def16e2af8c3cd4ae463ff42d583 100644
--- a/official/projects/mobilebert/utils.py
+++ b/official/projects/mobilebert/utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/mosaic/README.md b/official/projects/mosaic/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..d63a22deaa9007d46e07ec59b8cf0e523c91093a
--- /dev/null
+++ b/official/projects/mosaic/README.md
@@ -0,0 +1,121 @@
+# MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded Context
+
+[](https://arxiv.org/abs/2112.11623)
+
+This repository is the official implementation of the following
+paper.
+
+* [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded Context](https://arxiv.org/abs/2112.11623)
+
+## Description
+
+MOSAIC is a neural network architecture for efficient and accurate semantic
+image segmentation on mobile devices. MOSAIC is designed using commonly
+supported neural operations by diverse mobile hardware platforms for flexible
+deployment across various mobile platforms. With a simple asymmetric
+encoder-decoder structure which consists of an efficient multi-scale context
+encoder and a light-weight hybrid decoder to recover spatial details from
+aggregated information, MOSAIC achieves better balanced performance while
+considering accuracy and computational cost. Deployed on top of a tailored
+feature extraction backbone based on a searched classification network, MOSAIC
+achieves a 5% absolute accuracy gain on ADE20K with similar or lower latency
+compared to the current industry standard MLPerf mobile v1.0 models and
+state-of-the-art architectures.
+
+[MLPerf Mobile v2.0]((https://mlcommons.org/en/inference-mobile-20/)) included
+MOSAIC as a new industry standard benchmark model for image segmentation.
+Please see details [here](https://mlcommons.org/en/news/mlperf-inference-1q2022/).
+
+You can also refer to the [MLCommons GitHub repository](https://github.com/mlcommons/mobile_open/tree/main/vision/mosaic).
+
+## History
+
+### Oct 13, 2022
+
+* First release of MOSAIC in TensorFlow 2 including checkpoints that have been
+ pretrained on Cityscapes.
+
+## Maintainers
+
+* Weijun Wang ([weijunw-g](https://github.com/weijunw-g))
+* Fang Yang ([fyangf](https://github.com/fyangf))
+* Shixin Luo ([luotigerlsx](https://github.com/luotigerlsx))
+
+## Requirements
+
+[](https://badge.fury.io/py/tensorflow)
+[](https://badge.fury.io/py/tf-models-official)
+
+## Results
+
+The following table shows the mIoU measured on the `cityscapes` dataset.
+
+| Config | Backbone | Resolution | branch_filter_depths | pyramid_pool_bin_nums | mIoU | Download |
+|-------------------------|:--------------------:|:----------:|:--------------------:|:---------------------:|:-----:|:--------:|
+| Paper reference config | MobileNetMultiAVGSeg | 1024x2048 | [32, 32] | [4, 8, 16] | 75.98 | [ckpt](https://storage.googleapis.com/tf_model_garden/vision/mosaic/MobileNetMultiAVGSeg-r1024-ebf32-nogp.tar.gz) [tensorboard](https://tensorboard.dev/experiment/okEog90bSwupajFgJwGEIw//#scalars) |
+| Current best config | MobileNetMultiAVGSeg | 1024x2048 | [64, 64] | [1, 4, 8, 16] | 77.24 | [ckpt](https://storage.googleapis.com/tf_model_garden/vision/mosaic/MobileNetMultiAVGSeg-r1024-ebf64-gp.tar.gz) [tensorboard](https://tensorboard.dev/experiment/l5hkV7JaQM23EXeOBT6oJg/#scalars) |
+
+* `branch_filter_depths`: the number of convolution channels in each branch at
+ a pyramid level after `Spatial Pyramid Pooling`
+* `pyramid_pool_bin_nums`: the number of bins at each level of the `Spatial
+ Pyramid Pooling`
+
+## Training
+
+It can run on Google Cloud Platform using Cloud TPU.
+[Here](https://cloud.google.com/tpu/docs/how-to) is the instruction of using
+Cloud TPU. Following the instructions to set up Cloud TPU and
+launch training by:
+
+```shell
+EXP_TYPE=mosaic_mnv35_cityscapes
+EXP_NAME="" # You can give any name to the experiment.
+TPU_NAME="" # The name assigned while creating a Cloud TPU
+MODEL_DIR="gs://"
+# Now launch the experiment.
+python3 -m official.projects.mosaic.train \
+ --experiment=$EXP_TYPE \
+ --mode=train \
+ --tpu=$TPU_NAME \
+ --model_dir=$MODEL_DIR \
+ --config_file=official/projects/mosaic/configs/experiments/mosaic_mnv35_cityscapes_tdfs_tpu.yaml
+```
+
+## Evaluation
+
+Please run this command line for evaluation.
+
+```shell
+EXP_TYPE=mosaic_mnv35_cityscapes
+EXP_NAME="" # You can give any name to the experiment.
+TPU_NAME="" # The name assigned while creating a Cloud TPU
+MODEL_DIR="gs://"
+# Now launch the experiment.
+python3 -m official.projects.mosaic.train \
+ --experiment=$EXP_TYPE \
+ --mode=eval \
+ --tpu=$TPU_NAME \
+ --model_dir=$MODEL_DIR \
+ --config_file=official/projects/mosaic/configs/experiments/mosaic_mnv35_cityscapes_tdfs_tpu.yaml
+```
+
+## License
+
+[](https://opensource.org/licenses/Apache-2.0)
+
+This project is licensed under the terms of the **Apache License 2.0**.
+
+## Citation
+
+If you want to cite this repository in your work, please consider citing the
+paper.
+
+```
+@inproceedings{weijun2021mosaic,
+ title={MOSAIC: Mobile Segmentation via decoding Aggregated Information and
+ encoded Context},
+ author={Weijun Wang, Andrew Howard},
+ journal={arXiv preprint arXiv:2112.11623},
+ year={2021},
+}
+```
diff --git a/official/projects/mosaic/configs/experiments/mosaic_mnv35_cityscapes_tfds_tpu.yaml b/official/projects/mosaic/configs/experiments/mosaic_mnv35_cityscapes_tfds_tpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..b2a240050492a8d00ac427d2f2bf48bd39872d80
--- /dev/null
+++ b/official/projects/mosaic/configs/experiments/mosaic_mnv35_cityscapes_tfds_tpu.yaml
@@ -0,0 +1,87 @@
+# Using Tensorflow datasets: 'cityscapes/semantic_segmentation'
+# Some expected flags to use with xmanager launcher:
+# --experiment_type=mosaic_mnv35_cityscapes
+# --tpu_topology=4x4
+# mIoU: 77.24%
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ model:
+ num_classes: 19
+ input_size: [null, null, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetMultiAVGSeg'
+ output_intermediate_endpoints: true
+ output_stride: 16
+ neck:
+ branch_filter_depths: [64, 64]
+ conv_kernel_sizes: [3, 5]
+ pyramid_pool_bin_nums: [1, 4, 8, 16]
+ dropout_rate: 0.0
+ head:
+ num_classes: 19
+ decoder_input_levels: ['3/depthwise', '2/depthwise']
+ decoder_stage_merge_styles: ['concat_merge', 'sum_merge']
+ decoder_filters: [64, 64]
+ decoder_projected_filters: [19, 19]
+ norm_activation:
+ activation: relu
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ init_checkpoint: 'gs://tf_model_garden/vision/mobilenet/v3.5multiavg_seg_float/'
+ init_checkpoint_modules: 'backbone'
+ losses:
+ l2_weight_decay: 1.0e-04
+ train_data:
+ output_size: [1024, 2048]
+ crop_size: [1024, 2048]
+ input_path: ''
+ tfds_name: 'cityscapes/semantic_segmentation'
+ tfds_split: 'train'
+ is_training: true
+ global_batch_size: 32
+ dtype: 'float32'
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ output_size: [1024, 2048]
+ input_path: ''
+ tfds_name: 'cityscapes/semantic_segmentation'
+ tfds_split: 'validation'
+ is_training: false
+ global_batch_size: 32
+ dtype: 'float32'
+ drop_remainder: false
+ resize_eval_groundtruth: true
+trainer:
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 100000
+ initial_learning_rate: 0.1
+ power: 0.9
+ type: polynomial
+ optimizer:
+ sgd:
+ momentum: 0.9
+ type: sgd
+ warmup:
+ linear:
+ name: linear
+ warmup_learning_rate: 0
+ warmup_steps: 925
+ type: linear
+ steps_per_loop: 92 # 2975 / 32 = 92
+ summary_interval: 92
+ train_steps: 100000
+ validation_interval: 92
+ validation_steps: 16 # 500 / 32 = 16
+ checkpoint_interval: 92
+ best_checkpoint_export_subdir: 'best_ckpt'
+ best_checkpoint_eval_metric: 'mean_iou'
+ best_checkpoint_metric_comp: 'higher'
diff --git a/official/projects/mosaic/configs/mosaic_config.py b/official/projects/mosaic/configs/mosaic_config.py
new file mode 100644
index 0000000000000000000000000000000000000000..4435a83d42b2540a5cce7d7ca904507e85729ec3
--- /dev/null
+++ b/official/projects/mosaic/configs/mosaic_config.py
@@ -0,0 +1,218 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configuration definition for Semantic Segmentation with MOSAIC."""
+import dataclasses
+import os
+from typing import List, Optional, Union
+
+import numpy as np
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.vision.configs import common
+from official.vision.configs import semantic_segmentation as seg_cfg
+from official.vision.configs.google import backbones
+
+
+@dataclasses.dataclass
+class MosaicDecoderHead(hyperparams.Config):
+ """MOSAIC decoder head config for Segmentation."""
+ num_classes: int = 19
+ decoder_input_levels: List[str] = dataclasses.field(default_factory=list)
+ decoder_stage_merge_styles: List[str] = dataclasses.field(
+ default_factory=list)
+ decoder_filters: List[int] = dataclasses.field(default_factory=list)
+ decoder_projected_filters: List[int] = dataclasses.field(default_factory=list)
+ encoder_end_level: int = 4
+ use_additional_classifier_layer: bool = False
+ classifier_kernel_size: int = 1
+ activation: str = 'relu'
+ kernel_initializer: str = 'glorot_uniform'
+ interpolation: str = 'bilinear'
+
+
+@dataclasses.dataclass
+class MosaicEncoderNeck(hyperparams.Config):
+ """MOSAIC encoder neck config for segmentation."""
+ encoder_input_level: Union[str, int] = '4'
+ branch_filter_depths: List[int] = dataclasses.field(default_factory=list)
+ conv_kernel_sizes: List[int] = dataclasses.field(default_factory=list)
+ pyramid_pool_bin_nums: List[int] = dataclasses.field(default_factory=list)
+ activation: str = 'relu'
+ dropout_rate: float = 0.1
+ kernel_initializer: str = 'glorot_uniform'
+ interpolation: str = 'bilinear'
+ use_depthwise_convolution: bool = True
+
+
+@dataclasses.dataclass
+class MosaicSemanticSegmentationModel(hyperparams.Config):
+ """MOSAIC semantic segmentation model config."""
+ num_classes: int = 19
+ input_size: List[int] = dataclasses.field(default_factory=list)
+ head: MosaicDecoderHead = MosaicDecoderHead()
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='mobilenet', mobilenet=backbones.MobileNet())
+ neck: MosaicEncoderNeck = MosaicEncoderNeck()
+ norm_activation: common.NormActivation = common.NormActivation(
+ use_sync_bn=True, norm_momentum=0.99, norm_epsilon=0.001)
+
+
+@dataclasses.dataclass
+class MosaicSemanticSegmentationTask(seg_cfg.SemanticSegmentationTask):
+ """The config for MOSAIC segmentation task."""
+ model: MosaicSemanticSegmentationModel = MosaicSemanticSegmentationModel()
+ train_data: seg_cfg.DataConfig = seg_cfg.DataConfig(is_training=True)
+ validation_data: seg_cfg.DataConfig = seg_cfg.DataConfig(is_training=False)
+ losses: seg_cfg.Losses = seg_cfg.Losses()
+ evaluation: seg_cfg.Evaluation = seg_cfg.Evaluation()
+ train_input_partition_dims: List[int] = dataclasses.field(
+ default_factory=list)
+ eval_input_partition_dims: List[int] = dataclasses.field(
+ default_factory=list)
+ init_checkpoint: Optional[str] = None
+ init_checkpoint_modules: Union[
+ str, List[str]] = 'all' # all, backbone, and/or neck.
+ export_config: seg_cfg.ExportConfig = seg_cfg.ExportConfig()
+
+
+# Cityscapes Dataset (Download and process the dataset yourself)
+CITYSCAPES_TRAIN_EXAMPLES = 2975
+CITYSCAPES_VAL_EXAMPLES = 500
+CITYSCAPES_INPUT_PATH_BASE = 'cityscapes/tfrecord'
+
+
+@exp_factory.register_config_factory('mosaic_mnv35_cityscapes')
+def mosaic_mnv35_cityscapes() -> cfg.ExperimentConfig:
+ """Instantiates an experiment configuration of image segmentation task.
+
+ This image segmentation experiment is conducted on Cityscapes dataset. The
+ model architecture is a MOSAIC encoder-decoer. The default backbone network is
+ a mobilenet variant called Mobilenet_v3.5-MultiAvg on top of which the MOSAIC
+ encoder-decoder can be deployed. All detailed configurations can be overridden
+ by a .yaml file provided by the user to launch the experiments. Please refer
+ to .yaml examples in the path of ../configs/experiments/.
+
+ Returns:
+ A particular instance of cfg.ExperimentConfig for MOSAIC model based
+ image semantic segmentation task.
+ """
+ train_batch_size = 16
+ eval_batch_size = 16
+ steps_per_epoch = CITYSCAPES_TRAIN_EXAMPLES // train_batch_size
+ output_stride = 16
+
+ backbone_output_level = int(np.math.log2(output_stride))
+ config = cfg.ExperimentConfig(
+ task=MosaicSemanticSegmentationTask(
+ model=MosaicSemanticSegmentationModel(
+ # Cityscapes uses only 19 semantic classes for train/evaluation.
+ # The void (background) class is ignored in train and evaluation.
+ num_classes=19,
+ input_size=[None, None, 3],
+ backbone=backbones.Backbone(
+ type='mobilenet',
+ mobilenet=backbones.MobileNet(
+ model_id='MobileNetMultiAVGSeg',
+ output_intermediate_endpoints=True,
+ output_stride=output_stride)),
+ neck=MosaicEncoderNeck(
+ encoder_input_level=backbone_output_level,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=[1, 4, 8, 16], # paper default
+ activation='relu',
+ dropout_rate=0.1,
+ kernel_initializer='glorot_uniform',
+ interpolation='bilinear',
+ use_depthwise_convolution=True),
+ head=MosaicDecoderHead(
+ num_classes=19,
+ decoder_input_levels=['3/depthwise', '2/depthwise'],
+ decoder_stage_merge_styles=['concat_merge', 'sum_merge'],
+ decoder_filters=[64, 64],
+ decoder_projected_filters=[19, 19],
+ encoder_end_level=backbone_output_level,
+ use_additional_classifier_layer=False,
+ classifier_kernel_size=1,
+ activation='relu',
+ kernel_initializer='glorot_uniform',
+ interpolation='bilinear'),
+ norm_activation=common.NormActivation(
+ activation='relu',
+ norm_momentum=0.99,
+ norm_epsilon=1e-3,
+ use_sync_bn=True)),
+ losses=seg_cfg.Losses(l2_weight_decay=4e-5),
+ train_data=seg_cfg.DataConfig(
+ input_path=os.path.join(CITYSCAPES_INPUT_PATH_BASE,
+ 'train_fine**'),
+ crop_size=[1024, 2048],
+ output_size=[1024, 2048],
+ is_training=True,
+ global_batch_size=train_batch_size,
+ aug_scale_min=0.5,
+ aug_scale_max=2.0),
+ validation_data=seg_cfg.DataConfig(
+ input_path=os.path.join(CITYSCAPES_INPUT_PATH_BASE, 'val_fine*'),
+ output_size=[1024, 2048],
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ resize_eval_groundtruth=True,
+ drop_remainder=False),
+ # Imagenet pre-trained Mobilenet_v3.5-MultiAvg checkpoint.
+ init_checkpoint='gs://tf_model_garden/vision/mobilenet/v3.5multiavg_seg_float/',
+ init_checkpoint_modules='backbone'),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=100000,
+ validation_steps=CITYSCAPES_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ best_checkpoint_eval_metric='mean_iou',
+ best_checkpoint_export_subdir='best_ckpt',
+ best_checkpoint_metric_comp='higher',
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'sgd',
+ 'sgd': {
+ 'momentum': 0.9
+ }
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 0.1,
+ 'decay_steps': 100000,
+ 'end_learning_rate': 0.0,
+ 'power': 0.9
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 5 * steps_per_epoch,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
diff --git a/official/projects/mosaic/modeling/mosaic_blocks.py b/official/projects/mosaic/modeling/mosaic_blocks.py
new file mode 100644
index 0000000000000000000000000000000000000000..076859bb2425e3f82839fed98527d034610d8909
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_blocks.py
@@ -0,0 +1,885 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Definitions of building blocks for MOSAIC model.
+
+Reference:
+ [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded
+ Context](https://arxiv.org/pdf/2112.11623.pdf)
+"""
+
+from typing import Any, Dict, List, Optional, Tuple, Union
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class MultiKernelGroupConvBlock(tf.keras.layers.Layer):
+ """A multi-kernel grouped convolution block.
+
+ This block is used in the segmentation neck introduced in MOSAIC.
+ Reference:
+ [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded
+ Context](https://arxiv.org/pdf/2112.11623.pdf)
+ """
+
+ def __init__(
+ self,
+ output_filter_depths: Optional[List[int]] = None,
+ kernel_sizes: Optional[List[int]] = None,
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ kernel_initializer: str = 'GlorotUniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ use_depthwise_convolution: bool = True,
+ **kwargs):
+ """Initializes a Multi-kernel Grouped Convolution Block.
+
+ Args:
+ output_filter_depths: A list of integers representing the numbers of
+ output channels or filter depths of convolution groups.
+ kernel_sizes: A list of integers denoting the convolution kernel sizes in
+ each convolution group.
+ use_sync_bn: A bool, whether or not to use sync batch normalization.
+ batchnorm_momentum: A float for the momentum in BatchNorm. Defaults to
+ 0.99.
+ batchnorm_epsilon: A float for the epsilon value in BatchNorm. Defaults to
+ 0.001.
+ activation: A `str` for the activation fuction type. Defaults to 'relu'.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: Kernel regularizer for conv layers. Defaults to None.
+ use_depthwise_convolution: Allows spatial pooling to be separable
+ depthwise convolusions.
+ **kwargs: Other keyword arguments for the layer.
+ """
+ super(MultiKernelGroupConvBlock, self).__init__(**kwargs)
+
+ if output_filter_depths is None:
+ output_filter_depths = [64, 64]
+ if kernel_sizes is None:
+ kernel_sizes = [3, 5]
+ if len(output_filter_depths) != len(kernel_sizes):
+ raise ValueError('The number of output groups must match #kernels.')
+ self._output_filter_depths = output_filter_depths
+ self._kernel_sizes = kernel_sizes
+ self._num_groups = len(self._kernel_sizes)
+ self._use_sync_bn = use_sync_bn
+ self._batchnorm_momentum = batchnorm_momentum
+ self._batchnorm_epsilon = batchnorm_epsilon
+ self._activation = activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._use_depthwise_convolution = use_depthwise_convolution
+ # To apply BN before activation. Putting BN between conv and activation also
+ # helps quantization where conv+bn+activation are fused into a single op.
+ self._activation_fn = tf_utils.get_activation(activation)
+ if self._use_sync_bn:
+ self._bn_op = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._bn_op = tf.keras.layers.BatchNormalization
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ self._group_split_axis = -1
+ else:
+ self._bn_axis = 1
+ self._group_split_axis = 1
+
+ def build(self, input_shape: tf.TensorShape) -> None:
+ """Builds the block with the given input shape."""
+ input_channels = input_shape[self._group_split_axis]
+ if input_channels % self._num_groups != 0:
+ raise ValueError('The number of input channels must be divisible by '
+ 'the number of groups for evenly group split.')
+ self._conv_branches = []
+ if self._use_depthwise_convolution:
+ for i, conv_kernel_size in enumerate(self._kernel_sizes):
+ depthwise_conv = tf.keras.layers.DepthwiseConv2D(
+ kernel_size=(conv_kernel_size, conv_kernel_size),
+ depth_multiplier=1,
+ padding='same',
+ depthwise_regularizer=self._kernel_regularizer,
+ depthwise_initializer=self._kernel_initializer,
+ use_bias=False)
+ # Add BN->RELU after depthwise convolution.
+ batchnorm_op_depthwise = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ activation_depthwise = self._activation_fn
+ feature_conv = tf.keras.layers.Conv2D(
+ filters=self._output_filter_depths[i],
+ kernel_size=(1, 1),
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ # Use list manually as current QAT API does not support sequential model
+ # within a tf.keras.Sequential block, e.g. conv_branch =
+ # tf.keras.Sequential([depthwise_conv, feature_conv, batchnorm_op,])
+ conv_branch = [
+ depthwise_conv,
+ batchnorm_op_depthwise,
+ activation_depthwise,
+ feature_conv,
+ batchnorm_op,
+ ]
+ self._conv_branches.append(conv_branch)
+ else:
+ for i, conv_kernel_size in enumerate(self._kernel_sizes):
+ norm_conv = tf.keras.layers.Conv2D(
+ filters=self._output_filter_depths[i],
+ kernel_size=(conv_kernel_size, conv_kernel_size),
+ padding='same',
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ conv_branch = [norm_conv, batchnorm_op]
+ self._conv_branches.append(conv_branch)
+ self._concat_groups = tf.keras.layers.Concatenate(
+ axis=self._group_split_axis)
+
+ def call(self,
+ inputs: tf.Tensor,
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Calls this group convolution block with the given inputs."""
+ inputs_splits = tf.split(inputs,
+ num_or_size_splits=self._num_groups,
+ axis=self._group_split_axis)
+ output_branches = []
+ for i, x in enumerate(inputs_splits):
+ conv_branch = self._conv_branches[i]
+ # Apply layers sequentially and manually.
+ for layer in conv_branch:
+ if isinstance(layer, tf.keras.layers.Layer):
+ x = layer(x, training=training)
+ else:
+ x = layer(x)
+ # Apply activation function after BN, which also helps quantization
+ # where conv+bn+activation are fused into a single op.
+ x = self._activation_fn(x)
+ output_branches.append(x)
+ x = self._concat_groups(output_branches)
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ config = {
+ 'output_filter_depths': self._output_filter_depths,
+ 'kernel_sizes': self._kernel_sizes,
+ 'num_groups': self._num_groups,
+ 'use_sync_bn': self._use_sync_bn,
+ 'batchnorm_momentum': self._batchnorm_momentum,
+ 'batchnorm_epsilon': self._batchnorm_epsilon,
+ 'activation': self._activation,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'use_depthwise_convolution': self._use_depthwise_convolution,
+ }
+ base_config = super(MultiKernelGroupConvBlock, self).get_config()
+ base_config.update(config)
+ return base_config
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class MosaicEncoderBlock(tf.keras.layers.Layer):
+ """Implements the encoder module/block of MOSAIC model.
+
+ Spatial Pyramid Pooling and Multi-kernel Conv layer
+ SpatialPyramidPoolingMultiKernelConv
+ References:
+ [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded
+ context](https://arxiv.org/pdf/2112.11623.pdf)
+ """
+
+ def __init__(
+ self,
+ encoder_input_level: Optional[Union[str, int]] = '4',
+ branch_filter_depths: Optional[List[int]] = None,
+ conv_kernel_sizes: Optional[List[int]] = None,
+ pyramid_pool_bin_nums: Optional[List[int]] = None,
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ dropout_rate: float = 0.1,
+ kernel_initializer: str = 'glorot_uniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ use_depthwise_convolution: bool = True,
+ **kwargs):
+ """Initializes a MOSAIC encoder block which is deployed after a backbone.
+
+ Args:
+ encoder_input_level: An optional `str` or integer specifying the level of
+ backbone outputs as the input to the encoder.
+ branch_filter_depths: A list of integers for the number of convolution
+ channels in each branch at a pyramid level after SpatialPyramidPooling.
+ conv_kernel_sizes: A list of integers representing the convolution kernel
+ sizes in the Multi-kernel Convolution blocks in the encoder.
+ pyramid_pool_bin_nums: A list of integers for the number of bins at each
+ level of the Spatial Pyramid Pooling.
+ use_sync_bn: A bool, whether or not to use sync batch normalization.
+ batchnorm_momentum: A float for the momentum in BatchNorm. Defaults to
+ 0.99.
+ batchnorm_epsilon: A float for the epsilon value in BatchNorm. Defaults to
+ 0.001.
+ activation: A `str` for the activation function type. Defaults to 'relu'.
+ dropout_rate: A float between 0 and 1. Fraction of the input units to drop
+ out, which will be used directly as the `rate` of the Dropout layer at
+ the end of the encoder. Defaults to 0.1.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: Kernel regularizer for conv layers. Defaults to None.
+ interpolation: The interpolation method for upsampling. Defaults to
+ `bilinear`.
+ use_depthwise_convolution: Use depthwise separable convolusions in the
+ Multi-kernel Convolution blocks in the encoder.
+ **kwargs: Other keyword arguments for the layer.
+ """
+ super().__init__(**kwargs)
+
+ self._encoder_input_level = str(encoder_input_level)
+ if branch_filter_depths is None:
+ branch_filter_depths = [64, 64]
+ self._branch_filter_depths = branch_filter_depths
+ if conv_kernel_sizes is None:
+ conv_kernel_sizes = [3, 5]
+ self._conv_kernel_sizes = conv_kernel_sizes
+ if pyramid_pool_bin_nums is None:
+ pyramid_pool_bin_nums = [1, 4, 8, 16]
+ self._pyramid_pool_bin_nums = pyramid_pool_bin_nums
+ self._use_sync_bn = use_sync_bn
+ self._batchnorm_momentum = batchnorm_momentum
+ self._batchnorm_epsilon = batchnorm_epsilon
+ self._activation = activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._interpolation = interpolation
+ self._use_depthwise_convolution = use_depthwise_convolution
+ self._activation_fn = tf_utils.get_activation(activation)
+
+ if self._use_sync_bn:
+ self._bn_op = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._bn_op = tf.keras.layers.BatchNormalization
+
+ self._dropout_rate = dropout_rate
+ if dropout_rate:
+ self._encoder_end_dropout_layer = tf.keras.layers.Dropout(
+ rate=dropout_rate)
+ else:
+ self._encoder_end_dropout_layer = None
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ self._channel_axis = -1
+ else:
+ self._bn_axis = 1
+ self._channel_axis = 1
+
+ def _get_bin_pool_kernel_and_stride(
+ self,
+ input_size: int,
+ num_of_bin: int) -> Tuple[int, int]:
+ """Calculates the kernel size and stride for spatial bin pooling.
+
+ Args:
+ input_size: Input dimension (a scalar).
+ num_of_bin: The number of bins used for spatial bin pooling.
+
+ Returns:
+ The Kernel and Stride for spatial bin pooling (a scalar).
+ """
+ bin_overlap = int(input_size % num_of_bin)
+ pooling_stride = int(input_size // num_of_bin)
+ pooling_kernel = pooling_stride + bin_overlap
+ return pooling_kernel, pooling_stride
+
+ def build(
+ self, input_shape: Union[tf.TensorShape, Dict[str,
+ tf.TensorShape]]) -> None:
+ """Builds this MOSAIC encoder block with the given single input shape."""
+ input_shape = (
+ input_shape[self._encoder_input_level]
+ if isinstance(input_shape, dict) else input_shape)
+ self._data_format = tf.keras.backend.image_data_format()
+ if self._data_format == 'channels_last':
+ height = input_shape[1]
+ width = input_shape[2]
+ else:
+ height = input_shape[2]
+ width = input_shape[3]
+
+ self._global_pool_branch = None
+ self._spatial_pyramid = []
+
+ for pyramid_pool_bin_num in self._pyramid_pool_bin_nums:
+ if pyramid_pool_bin_num == 1:
+ global_pool = tf.keras.layers.GlobalAveragePooling2D(
+ data_format=self._data_format, keepdims=True)
+ global_projection = tf.keras.layers.Conv2D(
+ filters=max(self._branch_filter_depths),
+ kernel_size=(1, 1),
+ padding='same',
+ activation=None,
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ use_bias=False)
+ batch_norm_global_branch = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ # Use list manually instead of tf.keras.Sequential([])
+ self._global_pool_branch = [
+ global_pool,
+ global_projection,
+ batch_norm_global_branch,
+ ]
+ else:
+ if height < pyramid_pool_bin_num or width < pyramid_pool_bin_num:
+ raise ValueError('The number of pooling bins must be smaller than '
+ 'input sizes.')
+ assert pyramid_pool_bin_num >= 2, (
+ 'Except for the gloabl pooling, the number of bins in pyramid '
+ 'pooling must be at least two.')
+ pool_height, stride_height = self._get_bin_pool_kernel_and_stride(
+ height, pyramid_pool_bin_num)
+ pool_width, stride_width = self._get_bin_pool_kernel_and_stride(
+ width, pyramid_pool_bin_num)
+ bin_pool_level = tf.keras.layers.AveragePooling2D(
+ pool_size=(pool_height, pool_width),
+ strides=(stride_height, stride_width),
+ padding='valid',
+ data_format=self._data_format)
+ self._spatial_pyramid.append(bin_pool_level)
+
+ # Grouped multi-kernel Convolution.
+ self._multi_kernel_group_conv = MultiKernelGroupConvBlock(
+ output_filter_depths=self._branch_filter_depths,
+ kernel_sizes=self._conv_kernel_sizes,
+ use_sync_bn=self._use_sync_bn,
+ batchnorm_momentum=self._batchnorm_momentum,
+ batchnorm_epsilon=self._batchnorm_epsilon,
+ activation=self._activation,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ use_depthwise_convolution=self._use_depthwise_convolution)
+
+ # Encoder's final 1x1 feature projection.
+ # Considering the relatively large #channels merged before projection,
+ # enlarge the projection #channels to the sum of the filter depths of
+ # branches.
+ self._output_channels = sum(self._branch_filter_depths)
+ # Use list manually instead of tf.keras.Sequential([]).
+ self._encoder_projection = [
+ tf.keras.layers.Conv2D(
+ filters=self._output_channels,
+ kernel_size=(1, 1),
+ padding='same',
+ activation=None,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ use_bias=False),
+ self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon),
+ ]
+ # Use the TF2 default feature alignment rule for bilinear resizing.
+ self._upsample = tf.keras.layers.Resizing(
+ height,
+ width,
+ interpolation=self._interpolation,
+ crop_to_aspect_ratio=False)
+ self._concat_layer = tf.keras.layers.Concatenate(axis=self._channel_axis)
+
+ def call(self,
+ inputs: Union[tf.Tensor, Dict[str, tf.Tensor]],
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Calls this MOSAIC encoder block with the given input."""
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+ input_from_backbone_output = (
+ inputs[self._encoder_input_level]
+ if isinstance(inputs, dict) else inputs)
+ branches = []
+ # Original features from the final output of the backbone.
+ branches.append(input_from_backbone_output)
+ if self._spatial_pyramid:
+ for bin_pool_level in self._spatial_pyramid:
+ x = input_from_backbone_output
+ x = bin_pool_level(x)
+ x = self._multi_kernel_group_conv(x, training=training)
+ x = self._upsample(x)
+ branches.append(x)
+ if self._global_pool_branch is not None:
+ x = input_from_backbone_output
+ for layer in self._global_pool_branch:
+ x = layer(x, training=training)
+ x = self._activation_fn(x)
+ x = self._upsample(x)
+ branches.append(x)
+ x = self._concat_layer(branches)
+ for layer in self._encoder_projection:
+ x = layer(x, training=training)
+ x = self._activation_fn(x)
+ if self._encoder_end_dropout_layer is not None:
+ x = self._encoder_end_dropout_layer(x, training=training)
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ config = {
+ 'encoder_input_level': self._encoder_input_level,
+ 'branch_filter_depths': self._branch_filter_depths,
+ 'conv_kernel_sizes': self._conv_kernel_sizes,
+ 'pyramid_pool_bin_nums': self._pyramid_pool_bin_nums,
+ 'use_sync_bn': self._use_sync_bn,
+ 'batchnorm_momentum': self._batchnorm_momentum,
+ 'batchnorm_epsilon': self._batchnorm_epsilon,
+ 'activation': self._activation,
+ 'dropout_rate': self._dropout_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'interpolation': self._interpolation,
+ 'use_depthwise_convolution': self._use_depthwise_convolution,
+ }
+ base_config = super().get_config()
+ base_config.update(config)
+ return base_config
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class DecoderSumMergeBlock(tf.keras.layers.Layer):
+ """Implements the decoder feature sum merge block of MOSAIC model.
+
+ This block is used in the decoder of segmentation head introduced in MOSAIC.
+ It essentially merges a high-resolution feature map of a low semantic level
+ and a low-resolution feature map of a higher semantic level by 'Sum-Merge'.
+ """
+
+ def __init__(
+ self,
+ decoder_projected_depth: int,
+ output_size: Tuple[int, int] = (0, 0),
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ kernel_initializer: str = 'GlorotUniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ **kwargs):
+ """Initialize a sum-merge block for one decoder stage.
+
+ Args:
+ decoder_projected_depth: An integer representing the number of output
+ channels of this sum-merge block in the decoder.
+ output_size: A Tuple of integers representing the output height and width
+ of the feature maps from this sum-merge block. Defaults to (0, 0),
+ where the output size is set the same as the high-resolution branch.
+ use_sync_bn: A bool, whether or not to use sync batch normalization.
+ batchnorm_momentum: A float for the momentum in BatchNorm. Defaults to
+ 0.99.
+ batchnorm_epsilon: A float for the epsilon value in BatchNorm. Defaults to
+ 0.001.
+ activation: A `str` for the activation function type. Defaults to 'relu'.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: Kernel regularizer for conv layers. Defaults to None.
+ interpolation: The interpolation method for upsampling. Defaults to
+ `bilinear`.
+ **kwargs: Other keyword arguments for the layer.
+ """
+ super(DecoderSumMergeBlock, self).__init__(**kwargs)
+
+ self._decoder_projected_depth = decoder_projected_depth
+ self._output_size = output_size
+ self._low_res_branch = []
+ self._upsample_low_res = None
+ self._high_res_branch = []
+ self._upsample_high_res = None
+
+ self._use_sync_bn = use_sync_bn
+ self._batchnorm_momentum = batchnorm_momentum
+ self._batchnorm_epsilon = batchnorm_epsilon
+ self._activation = activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._interpolation = interpolation
+ # Apply BN before activation. Putting BN between conv and activation also
+ # helps quantization where conv+bn+activation are fused into a single op.
+ self._activation_fn = tf_utils.get_activation(activation)
+ if self._use_sync_bn:
+ self._bn_op = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._bn_op = tf.keras.layers.BatchNormalization
+
+ self._bn_axis = (
+ -1
+ if tf.keras.backend.image_data_format() == 'channels_last' else 1)
+ self._channel_axis = (
+ -1
+ if tf.keras.backend.image_data_format() == 'channels_last' else 1)
+ self._add_layer = tf.keras.layers.Add()
+
+ def build(
+ self,
+ input_shape: Tuple[tf.TensorShape, tf.TensorShape]) -> None:
+ """Builds the block with the given input shape."""
+ # Assume backbone features of the same level are concated before input.
+ low_res_input_shape = input_shape[0]
+ high_res_input_shape = input_shape[1]
+ low_res_channels = low_res_input_shape[self._channel_axis]
+ high_res_channels = high_res_input_shape[self._channel_axis]
+
+ if low_res_channels != self._decoder_projected_depth:
+ low_res_feature_conv = tf.keras.layers.Conv2D(
+ filters=self._decoder_projected_depth,
+ kernel_size=(1, 1),
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ self._low_res_branch.extend([
+ low_res_feature_conv,
+ batchnorm_op,
+ ])
+ if high_res_channels != self._decoder_projected_depth:
+ high_res_feature_conv = tf.keras.layers.Conv2D(
+ filters=self._decoder_projected_depth,
+ kernel_size=(1, 1),
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op_high = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ self._high_res_branch.extend([
+ high_res_feature_conv,
+ batchnorm_op_high,
+ ])
+ # Resize feature maps.
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ low_res_height = low_res_input_shape[1]
+ low_res_width = low_res_input_shape[2]
+ high_res_height = high_res_input_shape[1]
+ high_res_width = high_res_input_shape[2]
+ else:
+ low_res_height = low_res_input_shape[2]
+ low_res_width = low_res_input_shape[3]
+ high_res_height = high_res_input_shape[2]
+ high_res_width = high_res_input_shape[3]
+ if (self._output_size[0] == 0 or self._output_size[1] == 0):
+ self._output_size = (high_res_height, high_res_width)
+ if (low_res_height != self._output_size[0] or
+ low_res_width != self._output_size[1]):
+ self._upsample_low_res = tf.keras.layers.Resizing(
+ self._output_size[0],
+ self._output_size[1],
+ interpolation=self._interpolation,
+ crop_to_aspect_ratio=False)
+ if (high_res_height != self._output_size[0] or
+ high_res_width != self._output_size[1]):
+ self._upsample_high_res = tf.keras.layers.Resizing(
+ self._output_size[0],
+ self._output_size[1],
+ interpolation=self._interpolation,
+ crop_to_aspect_ratio=False)
+
+ def call(self,
+ inputs: Tuple[tf.Tensor, tf.Tensor],
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Calls this decoder sum-merge block with the given input.
+
+ Args:
+ inputs: A Tuple of tensors consisting of a low-resolution higher-semantic
+ level feature map from the encoder as the first item and a higher
+ resolution lower-level feature map from the backbone as the second item.
+ training: a `bool` indicating whether it is in `training` mode.
+ Note: the first item of the input Tuple takes a lower-resolution feature map
+ and the second item of the input Tuple takes a higher-resolution branch.
+
+ Returns:
+ A tensor representing the sum-merged decoder feature map.
+ """
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+ x_low_res = inputs[0]
+ x_high_res = inputs[1]
+ if self._low_res_branch:
+ for layer in self._low_res_branch:
+ x_low_res = layer(x_low_res, training=training)
+ x_low_res = self._activation_fn(x_low_res)
+ if self._high_res_branch:
+ for layer in self._high_res_branch:
+ x_high_res = layer(x_high_res, training=training)
+ x_high_res = self._activation_fn(x_high_res)
+ if self._upsample_low_res is not None:
+ x_low_res = self._upsample_low_res(x_low_res)
+ if self._upsample_high_res is not None:
+ x_high_res = self._upsample_high_res(x_high_res)
+ output = self._add_layer([x_low_res, x_high_res])
+ return output
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ config = {
+ 'decoder_projected_depth': self._decoder_projected_depth,
+ 'output_size': self._output_size,
+ 'use_sync_bn': self._use_sync_bn,
+ 'batchnorm_momentum': self._batchnorm_momentum,
+ 'batchnorm_epsilon': self._batchnorm_epsilon,
+ 'activation': self._activation,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'interpolation': self._interpolation,
+ }
+ base_config = super(DecoderSumMergeBlock, self).get_config()
+ base_config.update(config)
+ return base_config
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class DecoderConcatMergeBlock(tf.keras.layers.Layer):
+ """Implements the decoder feature concat merge block of MOSAIC model.
+
+ This block is used in the decoder of segmentation head introduced in MOSAIC.
+ It essentially merges a high-resolution feature map of a low semantic level
+ and a low-resolution feature of a higher semantic level by 'Concat-Merge'.
+ """
+
+ def __init__(
+ self,
+ decoder_internal_depth: int,
+ decoder_projected_depth: int,
+ output_size: Tuple[int, int] = (0, 0),
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ kernel_initializer: str = 'GlorotUniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ **kwargs):
+ """Initializes a concat-merge block for one decoder stage.
+
+ Args:
+ decoder_internal_depth: An integer representing the number of internal
+ channels of this concat-merge block in the decoder.
+ decoder_projected_depth: An integer representing the number of output
+ channels of this concat-merge block in the decoder.
+ output_size: A Tuple of integers representing the output height and width
+ of the feature maps from this concat-merge block. Defaults to (0, 0),
+ where the output size is set the same as the high-resolution branch.
+ use_sync_bn: A bool, whether or not to use sync batch normalization.
+ batchnorm_momentum: A float for the momentum in BatchNorm. Defaults to
+ 0.99.
+ batchnorm_epsilon: A float for the epsilon value in BatchNorm. Defaults to
+ 0.001.
+ activation: A `str` for the activation function type. Defaults to 'relu'.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: Kernel regularizer for conv layers. Defaults to None.
+ interpolation: The interpolation method for upsampling. Defaults to
+ `bilinear`.
+ **kwargs: Other keyword arguments for the layer.
+ """
+ super(DecoderConcatMergeBlock, self).__init__(**kwargs)
+
+ self._decoder_internal_depth = decoder_internal_depth
+ self._decoder_projected_depth = decoder_projected_depth
+ self._output_size = output_size
+ self._upsample_low_res = None
+ self._upsample_high_res = None
+
+ self._use_sync_bn = use_sync_bn
+ self._batchnorm_momentum = batchnorm_momentum
+ self._batchnorm_epsilon = batchnorm_epsilon
+ self._activation = activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._interpolation = interpolation
+ # Apply BN before activation. Putting BN between conv and activation also
+ # helps quantization where conv+bn+activation are fused into a single op.
+ self._activation_fn = tf_utils.get_activation(activation)
+ if self._use_sync_bn:
+ self._bn_op = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._bn_op = tf.keras.layers.BatchNormalization
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ self._channel_axis = -1
+ else:
+ self._bn_axis = 1
+ self._channel_axis = 1
+
+ def build(
+ self,
+ input_shape: Tuple[tf.TensorShape, tf.TensorShape]) -> None:
+ """Builds this block with the given input shape."""
+ # Assume backbone features of the same level are concated before input.
+ low_res_input_shape = input_shape[0]
+ high_res_input_shape = input_shape[1]
+ # Set up resizing feature maps before concat.
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ low_res_height = low_res_input_shape[1]
+ low_res_width = low_res_input_shape[2]
+ high_res_height = high_res_input_shape[1]
+ high_res_width = high_res_input_shape[2]
+ else:
+ low_res_height = low_res_input_shape[2]
+ low_res_width = low_res_input_shape[3]
+ high_res_height = high_res_input_shape[2]
+ high_res_width = high_res_input_shape[3]
+ if (self._output_size[0] == 0 or self._output_size[1] == 0):
+ self._output_size = (high_res_height, high_res_width)
+ if (low_res_height != self._output_size[0] or
+ low_res_width != self._output_size[1]):
+ self._upsample_low_res = tf.keras.layers.Resizing(
+ self._output_size[0],
+ self._output_size[1],
+ interpolation=self._interpolation,
+ crop_to_aspect_ratio=False)
+ if (high_res_height != self._output_size[0] or
+ high_res_width != self._output_size[1]):
+ self._upsample_high_res = tf.keras.layers.Resizing(
+ self._output_size[0],
+ self._output_size[1],
+ interpolation=self._interpolation,
+ crop_to_aspect_ratio=False)
+ # Set up a 3-layer separable convolution blocks, i.e.
+ # 1x1->BN->RELU + Depthwise->BN->RELU + 1x1->BN->RELU.
+ initial_feature_conv = tf.keras.layers.Conv2D(
+ filters=self._decoder_internal_depth,
+ kernel_size=(1, 1),
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op1 = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ activation1 = self._activation_fn
+ depthwise_conv = tf.keras.layers.DepthwiseConv2D(
+ kernel_size=(3, 3),
+ depth_multiplier=1,
+ padding='same',
+ depthwise_regularizer=self._kernel_regularizer,
+ depthwise_initializer=self._kernel_initializer,
+ use_bias=False)
+ batchnorm_op2 = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ activation2 = self._activation_fn
+ project_feature_conv = tf.keras.layers.Conv2D(
+ filters=self._decoder_projected_depth,
+ kernel_size=(1, 1),
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ activation=None,
+ use_bias=False)
+ batchnorm_op3 = self._bn_op(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ activation3 = self._activation_fn
+ self._feature_fusion_block = [
+ initial_feature_conv,
+ batchnorm_op1,
+ activation1,
+ depthwise_conv,
+ batchnorm_op2,
+ activation2,
+ project_feature_conv,
+ batchnorm_op3,
+ activation3,
+ ]
+ self._concat_layer = tf.keras.layers.Concatenate(axis=self._channel_axis)
+
+ def call(self,
+ inputs: Tuple[tf.Tensor, tf.Tensor],
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Calls this concat-merge block with the given inputs.
+
+ Args:
+ inputs: A Tuple of tensors consisting of a lower-level higher-resolution
+ feature map from the backbone as the first item and a higher-level
+ lower-resolution feature map from the encoder as the second item.
+ training: a `Boolean` indicating whether it is in `training` mode.
+
+ Returns:
+ A tensor representing the concat-merged decoder feature map.
+ """
+ low_res_input = inputs[0]
+ high_res_input = inputs[1]
+ if self._upsample_low_res is not None:
+ low_res_input = self._upsample_low_res(low_res_input)
+ if self._upsample_high_res is not None:
+ high_res_input = self._upsample_high_res(high_res_input)
+ decoder_feature_list = [low_res_input, high_res_input]
+ x = self._concat_layer(decoder_feature_list)
+ for layer in self._feature_fusion_block:
+ if isinstance(layer, tf.keras.layers.Layer):
+ x = layer(x, training=training)
+ else:
+ x = layer(x)
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ config = {
+ 'decoder_internal_depth': self._decoder_internal_depth,
+ 'decoder_projected_depth': self._decoder_projected_depth,
+ 'output_size': self._output_size,
+ 'use_sync_bn': self._use_sync_bn,
+ 'batchnorm_momentum': self._batchnorm_momentum,
+ 'batchnorm_epsilon': self._batchnorm_epsilon,
+ 'activation': self._activation,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'interpolation': self._interpolation,
+ }
+ base_config = super(DecoderConcatMergeBlock, self).get_config()
+ base_config.update(config)
+ return base_config
diff --git a/official/projects/mosaic/modeling/mosaic_blocks_test.py b/official/projects/mosaic/modeling/mosaic_blocks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..9e1f168dc165275cb8da1fda8556999b199de86b
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_blocks_test.py
@@ -0,0 +1,100 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for mosaic_blocks."""
+
+# Import libraries
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.mosaic.modeling import mosaic_blocks
+
+
+class MosaicBlocksTest(parameterized.TestCase, tf.test.TestCase):
+
+ def test_multi_kernel_group_conv_block(self):
+ block = mosaic_blocks.MultiKernelGroupConvBlock([64, 64], [3, 5])
+ inputs = tf.ones([1, 4, 4, 448])
+ outputs = block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 4, 4, 128])
+
+ def test_mosaic_encoder_block(self):
+ block = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=4,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=[1, 4, 8, 16])
+ inputs = tf.ones([1, 32, 32, 448])
+ outputs = block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 32, 32, 128])
+
+ def test_mosaic_encoder_block_odd_input_overlap_pool(self):
+ block = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=4,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=[1, 4, 8, 16])
+ inputs = tf.ones([1, 31, 31, 448])
+ outputs = block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 31, 31, 128])
+
+ def test_mosaic_encoder_non_separable_block(self):
+ block = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=4,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=[1, 4, 8, 16],
+ use_depthwise_convolution=False)
+ inputs = tf.ones([1, 32, 32, 448])
+ outputs = block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 32, 32, 128])
+
+ def test_mosaic_decoder_concat_merge_block(self):
+ concat_merge_block = mosaic_blocks.DecoderConcatMergeBlock(64, 32, [64, 64])
+ inputs = [tf.ones([1, 32, 32, 128]), tf.ones([1, 64, 64, 192])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 64, 64, 32])
+
+ def test_mosaic_decoder_concat_merge_block_default_output_size(self):
+ concat_merge_block = mosaic_blocks.DecoderConcatMergeBlock(64, 32)
+ inputs = [tf.ones([1, 32, 32, 128]), tf.ones([1, 64, 64, 192])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 64, 64, 32])
+
+ def test_mosaic_decoder_concat_merge_block_default_output_size_4x(self):
+ concat_merge_block = mosaic_blocks.DecoderConcatMergeBlock(64, 32)
+ inputs = [tf.ones([1, 32, 32, 128]), tf.ones([1, 128, 128, 192])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 128, 128, 32])
+
+ def test_mosaic_decoder_concat_merge_block_default_output_size_4x_rec(self):
+ concat_merge_block = mosaic_blocks.DecoderConcatMergeBlock(64, 32)
+ inputs = [tf.ones([1, 32, 64, 128]), tf.ones([1, 128, 256, 64])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 128, 256, 32])
+
+ def test_mosaic_decoder_sum_merge_block(self):
+ concat_merge_block = mosaic_blocks.DecoderSumMergeBlock(32, [128, 128])
+ inputs = [tf.ones([1, 64, 64, 32]), tf.ones([1, 128, 128, 64])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 128, 128, 32])
+
+ def test_mosaic_decoder_sum_merge_block_default_output_size(self):
+ concat_merge_block = mosaic_blocks.DecoderSumMergeBlock(32)
+ inputs = [tf.ones([1, 64, 64, 32]), tf.ones([1, 128, 128, 64])]
+ outputs = concat_merge_block(inputs)
+ self.assertAllEqual(outputs.shape, [1, 128, 128, 32])
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/mosaic/modeling/mosaic_head.py b/official/projects/mosaic/modeling/mosaic_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..79e16ecf2a4464f4cbf79034fc420f34e44c1c06
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_head.py
@@ -0,0 +1,242 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains definitions of segmentation head of the MOSAIC model."""
+from typing import Any, Dict, List, Mapping, Optional, Tuple, Union
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.mosaic.modeling import mosaic_blocks
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class MosaicDecoderHead(tf.keras.layers.Layer):
+ """Creates a MOSAIC decoder in segmentation head.
+
+ Reference:
+ [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded
+ Context](https://arxiv.org/pdf/2112.11623.pdf)
+ """
+
+ def __init__(
+ self,
+ num_classes: int,
+ decoder_input_levels: Optional[List[str]] = None,
+ decoder_stage_merge_styles: Optional[List[str]] = None,
+ decoder_filters: Optional[List[int]] = None,
+ decoder_projected_filters: Optional[List[int]] = None,
+ encoder_end_level: Optional[int] = 4,
+ use_additional_classifier_layer: bool = False,
+ classifier_kernel_size: int = 1,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ kernel_initializer: str = 'GlorotUniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ **kwargs):
+ """Initializes a MOSAIC segmentation head.
+
+ Args:
+ num_classes: An `int` number of mask classification categories. The number
+ of classes does not include background class.
+ decoder_input_levels: A list of `str` specifying additional
+ input levels from the backbone outputs for mask refinement in decoder.
+ decoder_stage_merge_styles: A list of `str` specifying the merge style at
+ each stage of the decoder, merge styles can be 'concat_merge' or
+ 'sum_merge'.
+ decoder_filters: A list of integers specifying the number of channels used
+ at each decoder stage. Note: this only has affects if the decoder merge
+ style is 'concat_merge'.
+ decoder_projected_filters: A list of integers specifying the number of
+ projected channels at the end of each decoder stage.
+ encoder_end_level: An optional integer specifying the output level of the
+ encoder stage, which is used if the input from the encoder to the
+ decoder head is a dictionary.
+ use_additional_classifier_layer: A `bool` specifying whether to use an
+ additional classifier layer or not. It must be True if the final decoder
+ projected filters does not match the `num_classes`.
+ classifier_kernel_size: An `int` number to specify the kernel size of the
+ classifier layer.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ batchnorm_momentum: A `float` of normalization momentum for the moving
+ average.
+ batchnorm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ interpolation: The interpolation method for upsampling. Defaults to
+ `bilinear`.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(MosaicDecoderHead, self).__init__(**kwargs)
+
+ # Assuming 'decoder_input_levels' are sorted in descending order and the
+ # other setting are listed in the order according to 'decoder_input_levels'.
+ if decoder_input_levels is None:
+ decoder_input_levels = ['3', '2']
+ if decoder_stage_merge_styles is None:
+ decoder_stage_merge_styles = ['concat_merge', 'sum_merge']
+ if decoder_filters is None:
+ decoder_filters = [64, 64]
+ if decoder_projected_filters is None:
+ decoder_projected_filters = [32, 32]
+ self._decoder_input_levels = decoder_input_levels
+ self._decoder_stage_merge_styles = decoder_stage_merge_styles
+ self._decoder_filters = decoder_filters
+ self._decoder_projected_filters = decoder_projected_filters
+ if (len(decoder_input_levels) != len(decoder_stage_merge_styles) or
+ len(decoder_input_levels) != len(decoder_filters) or
+ len(decoder_input_levels) != len(decoder_projected_filters)):
+ raise ValueError('The number of Decoder inputs and settings must match.')
+ self._merge_stages = []
+ for (stage_merge_style, decoder_filter,
+ decoder_projected_filter) in zip(decoder_stage_merge_styles,
+ decoder_filters,
+ decoder_projected_filters):
+ if stage_merge_style == 'concat_merge':
+ concat_merge_stage = mosaic_blocks.DecoderConcatMergeBlock(
+ decoder_internal_depth=decoder_filter,
+ decoder_projected_depth=decoder_projected_filter,
+ output_size=(0, 0),
+ use_sync_bn=use_sync_bn,
+ batchnorm_momentum=batchnorm_momentum,
+ batchnorm_epsilon=batchnorm_epsilon,
+ activation=activation,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer,
+ interpolation=interpolation)
+ self._merge_stages.append(concat_merge_stage)
+ elif stage_merge_style == 'sum_merge':
+ sum_merge_stage = mosaic_blocks.DecoderSumMergeBlock(
+ decoder_projected_depth=decoder_projected_filter,
+ output_size=(0, 0),
+ use_sync_bn=use_sync_bn,
+ batchnorm_momentum=batchnorm_momentum,
+ batchnorm_epsilon=batchnorm_epsilon,
+ activation=activation,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer,
+ interpolation=interpolation)
+ self._merge_stages.append(sum_merge_stage)
+ else:
+ raise ValueError(
+ 'A stage merge style in MOSAIC Decoder can only be concat_merge '
+ 'or sum_merge.')
+
+ # Concat merge or sum merge does not require an additional classifer layer
+ # unless the final decoder projected filter does not match num_classes.
+ final_decoder_projected_filter = decoder_projected_filters[-1]
+ if (final_decoder_projected_filter != num_classes and
+ not use_additional_classifier_layer):
+ raise ValueError('Additional classifier layer is needed if final decoder '
+ 'projected filters does not match num_classes!')
+ self._use_additional_classifier_layer = use_additional_classifier_layer
+ if use_additional_classifier_layer:
+ # This additional classification layer uses different kernel
+ # initializers and bias compared to earlier blocks.
+ self._pixelwise_classifier = tf.keras.layers.Conv2D(
+ name='pixelwise_classifier',
+ filters=num_classes,
+ kernel_size=classifier_kernel_size,
+ padding='same',
+ bias_initializer=tf.zeros_initializer(),
+ kernel_initializer=tf.keras.initializers.RandomNormal(stddev=0.01),
+ kernel_regularizer=kernel_regularizer,
+ bias_regularizer=bias_regularizer,
+ use_bias=True)
+ self._activation_fn = tf_utils.get_activation(activation)
+
+ self._config_dict = {
+ 'num_classes': num_classes,
+ 'decoder_input_levels': decoder_input_levels,
+ 'decoder_stage_merge_styles': decoder_stage_merge_styles,
+ 'decoder_filters': decoder_filters,
+ 'decoder_projected_filters': decoder_projected_filters,
+ 'encoder_end_level': encoder_end_level,
+ 'use_additional_classifier_layer': use_additional_classifier_layer,
+ 'classifier_kernel_size': classifier_kernel_size,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'batchnorm_momentum': batchnorm_momentum,
+ 'batchnorm_epsilon': batchnorm_epsilon,
+ 'kernel_initializer': kernel_initializer,
+ 'kernel_regularizer': kernel_regularizer,
+ 'interpolation': interpolation,
+ 'bias_regularizer': bias_regularizer
+ }
+
+ def call(self,
+ inputs: Tuple[Union[tf.Tensor, Mapping[str, tf.Tensor]],
+ Union[tf.Tensor, Mapping[str, tf.Tensor]]],
+ training: Optional[bool] = None) -> tf.Tensor:
+ """Forward pass of the segmentation head.
+
+ It supports a tuple of 2 elements. Each element is a tensor or a tensor
+ dictionary. The first one is the final (low-resolution) encoder endpoints,
+ and the second one is higher-resolution backbone endpoints.
+ When inputs are tensors, they are from a single level of feature maps.
+ When inputs are dictionaries, they contain multiple levels of feature maps,
+ where the key is the level/index of feature map.
+ Note: 'level' denotes the number of 2x downsampling, defined in backbone.
+
+ Args:
+ inputs: A tuple of 2 elements, each element can either be a tensor
+ representing feature maps or 1 dictionary of tensors:
+ - key: A `str` of the level of the multilevel features.
+ - values: A `tf.Tensor` of the feature map tensors.
+ The first is encoder endpoints, and the second is backbone endpoints.
+ training: a `Boolean` indicating whether it is in `training` mode.
+ Returns:
+ segmentation mask prediction logits: A `tf.Tensor` representing the
+ output logits before the final segmentation mask.
+ """
+
+ encoder_outputs = inputs[0]
+ backbone_outputs = inputs[1]
+ y = encoder_outputs[str(
+ self._config_dict['encoder_end_level'])] if isinstance(
+ encoder_outputs, dict) else encoder_outputs
+ if isinstance(backbone_outputs, dict):
+ for level, merge_stage in zip(
+ self._decoder_input_levels, self._merge_stages):
+ x = backbone_outputs[str(level)]
+ y = merge_stage([y, x], training=training)
+ else:
+ x = backbone_outputs
+ y = self._merge_stages[0]([y, x], training=training)
+
+ if self._use_additional_classifier_layer:
+ y = self._pixelwise_classifier(y)
+ y = self._activation_fn(y)
+
+ return y
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ base_config = super().get_config()
+ base_config.update(self._config_dict)
+ return base_config
+
+ @classmethod
+ def from_config(cls, config: Dict[str, Any]):
+ return cls(**config)
diff --git a/official/projects/mosaic/modeling/mosaic_head_test.py b/official/projects/mosaic/modeling/mosaic_head_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..b8e15969181f6667e2254bbfb30ce9a75ab2b9ef
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_head_test.py
@@ -0,0 +1,63 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for mosaic_head."""
+
+# Import libraries
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.mosaic.modeling import mosaic_head
+
+
+class MosaicBlocksTest(parameterized.TestCase, tf.test.TestCase):
+
+ def test_mosaic_head(self):
+ decoder_head = mosaic_head.MosaicDecoderHead(
+ num_classes=32,
+ decoder_input_levels=['3', '2'],
+ decoder_stage_merge_styles=['concat_merge', 'sum_merge'],
+ decoder_filters=[64, 64],
+ decoder_projected_filters=[32, 32])
+ inputs = [
+ tf.ones([1, 32, 32, 128]), {
+ '2': tf.ones([1, 128, 128, 64]),
+ '3': tf.ones([1, 64, 64, 192])
+ }
+ ]
+ outputs = decoder_head(inputs)
+ self.assertAllEqual(outputs.shape, [1, 128, 128, 32])
+
+ def test_mosaic_head_3laterals(self):
+ decoder_head = mosaic_head.MosaicDecoderHead(
+ num_classes=32,
+ decoder_input_levels=[3, 2, 1],
+ decoder_stage_merge_styles=[
+ 'concat_merge', 'concat_merge', 'sum_merge'
+ ],
+ decoder_filters=[64, 64, 64],
+ decoder_projected_filters=[32, 32, 32])
+ inputs = [
+ tf.ones([1, 32, 32, 128]), {
+ '1': tf.ones([1, 256, 256, 64]),
+ '2': tf.ones([1, 128, 128, 64]),
+ '3': tf.ones([1, 64, 64, 192])
+ }
+ ]
+ outputs = decoder_head(inputs)
+ self.assertAllEqual(outputs.shape, [1, 256, 256, 32])
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/mosaic/modeling/mosaic_model.py b/official/projects/mosaic/modeling/mosaic_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..1d9a750c3da5acae201baf8bdf1e4111014a8432
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_model.py
@@ -0,0 +1,152 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Builds the overall MOSAIC segmentation models."""
+from typing import Any, Dict, Optional, Union
+
+import tensorflow as tf
+from official.projects.mosaic.configs import mosaic_config
+from official.projects.mosaic.modeling import mosaic_blocks
+from official.projects.mosaic.modeling import mosaic_head
+from official.vision.modeling import backbones
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class MosaicSegmentationModel(tf.keras.Model):
+ """A model class for segmentation using MOSAIC.
+
+ Input images are passed through a backbone first. A MOSAIC neck encoder
+ network is then applied, and finally a MOSAIC segmentation head is applied on
+ the outputs of the backbone and neck encoder network. Feature fusion and
+ decoding is done in the segmentation head.
+
+ Reference:
+ [MOSAIC: Mobile Segmentation via decoding Aggregated Information and encoded
+ Context](https://arxiv.org/pdf/2112.11623.pdf)
+ """
+
+ def __init__(self,
+ backbone: tf.keras.Model,
+ head: tf.keras.layers.Layer,
+ neck: Optional[tf.keras.layers.Layer] = None,
+ **kwargs):
+ """Segmentation initialization function.
+
+ Args:
+ backbone: A backbone network.
+ head: A segmentation head, e.g. MOSAIC decoder.
+ neck: An optional neck encoder network, e.g. MOSAIC encoder. If it is not
+ provided, the decoder head will be connected directly with the backbone.
+ **kwargs: keyword arguments to be passed.
+ """
+ super(MosaicSegmentationModel, self).__init__(**kwargs)
+ self._config_dict = {
+ 'backbone': backbone,
+ 'neck': neck,
+ 'head': head,
+ }
+ self.backbone = backbone
+ self.neck = neck
+ self.head = head
+
+ def call(self,
+ inputs: tf.Tensor,
+ training: bool = None) -> Dict[str, tf.Tensor]:
+ backbone_features = self.backbone(inputs)
+
+ if self.neck is not None:
+ neck_features = self.neck(backbone_features, training=training)
+ else:
+ neck_features = backbone_features
+
+ logits = self.head([neck_features, backbone_features], training=training)
+ outputs = {'logits': logits}
+ return outputs
+
+ @property
+ def checkpoint_items(
+ self) -> Dict[str, Union[tf.keras.Model, tf.keras.layers.Layer]]:
+ """Returns a dictionary of items to be additionally checkpointed."""
+ items = dict(backbone=self.backbone, head=self.head)
+ if self.neck is not None:
+ items.update(neck=self.neck)
+ return items
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns a config dictionary for initialization from serialization."""
+ base_config = super().get_config()
+ model_config = base_config
+ model_config.update(self._config_dict)
+ return model_config
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
+
+
+def build_mosaic_segmentation_model(
+ input_specs: tf.keras.layers.InputSpec,
+ model_config: mosaic_config.MosaicSemanticSegmentationModel,
+ l2_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ backbone: Optional[tf.keras.Model] = None,
+ neck: Optional[tf.keras.layers.Layer] = None
+) -> tf.keras.Model:
+ """Builds MOSAIC Segmentation model."""
+ norm_activation_config = model_config.norm_activation
+ if backbone is None:
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=norm_activation_config,
+ l2_regularizer=l2_regularizer)
+
+ if neck is None:
+ neck_config = model_config.neck
+ neck = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=neck_config.encoder_input_level,
+ branch_filter_depths=neck_config.branch_filter_depths,
+ conv_kernel_sizes=neck_config.conv_kernel_sizes,
+ pyramid_pool_bin_nums=neck_config.pyramid_pool_bin_nums,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ batchnorm_momentum=norm_activation_config.norm_momentum,
+ batchnorm_epsilon=norm_activation_config.norm_epsilon,
+ activation=neck_config.activation,
+ dropout_rate=neck_config.dropout_rate,
+ kernel_initializer=neck_config.kernel_initializer,
+ kernel_regularizer=l2_regularizer,
+ interpolation=neck_config.interpolation,
+ use_depthwise_convolution=neck_config.use_depthwise_convolution)
+
+ head_config = model_config.head
+ head = mosaic_head.MosaicDecoderHead(
+ num_classes=model_config.num_classes,
+ decoder_input_levels=head_config.decoder_input_levels,
+ decoder_stage_merge_styles=head_config.decoder_stage_merge_styles,
+ decoder_filters=head_config.decoder_filters,
+ decoder_projected_filters=head_config.decoder_projected_filters,
+ encoder_end_level=head_config.encoder_end_level,
+ use_additional_classifier_layer=head_config
+ .use_additional_classifier_layer,
+ classifier_kernel_size=head_config.classifier_kernel_size,
+ activation=head_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ batchnorm_momentum=norm_activation_config.norm_momentum,
+ batchnorm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_initializer=head_config.kernel_initializer,
+ kernel_regularizer=l2_regularizer,
+ interpolation=head_config.interpolation)
+
+ model = MosaicSegmentationModel(
+ backbone=backbone, neck=neck, head=head)
+ return model
diff --git a/official/projects/mosaic/modeling/mosaic_model_test.py b/official/projects/mosaic/modeling/mosaic_model_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..9ee8d7aa212bc82c3ac4949bf5d8ff0bd01fe862
--- /dev/null
+++ b/official/projects/mosaic/modeling/mosaic_model_test.py
@@ -0,0 +1,108 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for the overall MOSAIC segmentation network modeling."""
+
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from official.projects.mosaic.modeling import mosaic_blocks
+from official.projects.mosaic.modeling import mosaic_head
+from official.projects.mosaic.modeling import mosaic_model
+from official.vision.modeling import backbones
+
+
+class SegmentationNetworkTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (128, [4, 8], [3, 2], ['concat_merge', 'sum_merge']),
+ (128, [1, 4, 8], [3, 2], ['concat_merge', 'sum_merge']),
+ (128, [1, 4, 8], [3, 2], ['sum_merge', 'sum_merge']),
+ (128, [1, 4, 8], [3, 2], ['concat_merge', 'concat_merge']),
+ (512, [1, 4, 8, 16], [3, 2], ['concat_merge', 'sum_merge']),
+ (256, [4, 8], [3, 2], ['concat_merge', 'sum_merge']),
+ (256, [1, 4, 8], [3, 2], ['concat_merge', 'sum_merge']),
+ (256, [1, 4, 8, 16], [3, 2], ['concat_merge', 'sum_merge']),
+ )
+ def test_mosaic_segmentation_model(self,
+ input_size,
+ pyramid_pool_bin_nums,
+ decoder_input_levels,
+ decoder_stage_merge_styles):
+ """Test for building and calling of a MOSAIC segmentation network."""
+ num_classes = 32
+ inputs = np.random.rand(2, input_size, input_size, 3)
+ tf.keras.backend.set_image_data_format('channels_last')
+ backbone = backbones.MobileNet(model_id='MobileNetMultiAVGSeg')
+ encoder_input_level = 4
+
+ neck = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=encoder_input_level,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=pyramid_pool_bin_nums)
+ head = mosaic_head.MosaicDecoderHead(
+ num_classes=num_classes,
+ decoder_input_levels=decoder_input_levels,
+ decoder_stage_merge_styles=decoder_stage_merge_styles,
+ decoder_filters=[64, 64],
+ decoder_projected_filters=[32, 32])
+
+ model = mosaic_model.MosaicSegmentationModel(
+ backbone=backbone,
+ head=head,
+ neck=neck,
+ )
+
+ # Calls the MOSAIC model.
+ outputs = model(inputs)
+ level = min(decoder_input_levels)
+ self.assertAllEqual(
+ [2, input_size // (2**level), input_size // (2**level), num_classes],
+ outputs['logits'].numpy().shape)
+
+ def test_serialize_deserialize(self):
+ """Validate the mosaic network can be serialized and deserialized."""
+ num_classes = 8
+ backbone = backbones.ResNet(model_id=50)
+ neck = mosaic_blocks.MosaicEncoderBlock(
+ encoder_input_level=4,
+ branch_filter_depths=[64, 64],
+ conv_kernel_sizes=[3, 5],
+ pyramid_pool_bin_nums=[1, 4, 8, 16])
+ head = mosaic_head.MosaicDecoderHead(
+ num_classes=num_classes,
+ decoder_input_levels=[3, 2],
+ decoder_stage_merge_styles=['concat_merge', 'sum_merge'],
+ decoder_filters=[64, 64],
+ decoder_projected_filters=[32, 8])
+ model = mosaic_model.MosaicSegmentationModel(
+ backbone=backbone,
+ head=head,
+ neck=neck,
+ )
+
+ config = model.get_config()
+ new_model = mosaic_model.MosaicSegmentationModel.from_config(config)
+
+ # Validate that the config can be forced to JSON.
+ _ = new_model.to_json()
+
+ # If the serialization was successful, the new config should match the old.
+ self.assertAllEqual(model.get_config(), new_model.get_config())
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/mosaic/mosaic_tasks.py b/official/projects/mosaic/mosaic_tasks.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b2af795dde44c8e9cf6cd8b0f8f9aca8acad823
--- /dev/null
+++ b/official/projects/mosaic/mosaic_tasks.py
@@ -0,0 +1,96 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Task definition for image semantic segmentation with MOSAIC models."""
+
+from absl import logging
+import tensorflow as tf
+
+from official.core import task_factory
+from official.projects.mosaic.configs import mosaic_config
+from official.projects.mosaic.modeling import mosaic_model
+from official.vision.tasks import semantic_segmentation as seg_tasks
+
+
+@task_factory.register_task_cls(mosaic_config.MosaicSemanticSegmentationTask)
+class MosaicSemanticSegmentationTask(seg_tasks.SemanticSegmentationTask):
+ """A task for semantic segmentation using MOSAIC model."""
+
+ # Note: the `build_model` is overrided to add an additional `train` flag
+ # for the purpose of indicating the model is built for performing `training`
+ # or `eval`. This is to make sure the model is initialized with proper
+ # `input_shape` if the model will be trained and evaluated in different
+ # `input_shape`. For example, the model is trained with cropping but
+ # evaluated with original shape.
+ def build_model(self, training: bool = True) -> tf.keras.Model:
+ """Builds MOSAIC segmentation model."""
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + self.task_config.model.input_size)
+
+ l2_weight_decay = self.task_config.losses.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ model = mosaic_model.build_mosaic_segmentation_model(
+ input_specs=input_specs,
+ model_config=self.task_config.model,
+ l2_regularizer=l2_regularizer)
+
+ # Note: Create a dummy input and call model instance to initialize.
+ # This ensures all the layers are built; otherwise some layers may be
+ # missing from the model and cannot be associated with variables from
+ # a loaded checkpoint. The input size is determined by whether the model
+ # is built for performing training or eval.
+ if training:
+ input_size = self.task_config.train_data.output_size
+ crop_size = self.task_config.train_data.crop_size
+ if crop_size:
+ input_size = crop_size
+ else:
+ input_size = self.task_config.validation_data.output_size
+ dummy_input = tf.ones(shape=[1] + input_size + [3])
+ model(dummy_input)
+
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loads pretrained checkpoint."""
+ if not self.task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self.task_config.init_checkpoint
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ # Restoring checkpoint.
+ if 'all' in self.task_config.init_checkpoint_modules:
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ else:
+ ckpt_items = {}
+ if 'backbone' in self.task_config.init_checkpoint_modules:
+ ckpt_items.update(backbone=model.backbone)
+ if 'neck' in self.task_config.init_checkpoint_modules:
+ ckpt_items.update(neck=model.neck)
+
+ ckpt = tf.train.Checkpoint(**ckpt_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
diff --git a/official/projects/mosaic/mosaic_tasks_test.py b/official/projects/mosaic/mosaic_tasks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..b6dd9aebd06ebd729d352b3d226eb9c18084e591
--- /dev/null
+++ b/official/projects/mosaic/mosaic_tasks_test.py
@@ -0,0 +1,91 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for mosaic task."""
+# pylint: disable=unused-import
+import os
+
+from absl.testing import parameterized
+import orbit
+import tensorflow as tf
+
+from official import vision
+from official.core import exp_factory
+from official.modeling import optimization
+from official.projects.mosaic import mosaic_tasks
+from official.projects.mosaic.configs import mosaic_config as exp_cfg
+from official.vision.dataloaders import tfexample_utils
+
+
+class MosaicTaskTest(parameterized.TestCase, tf.test.TestCase):
+
+ def _create_test_tfrecord(self, tfrecord_file, example, num_samples):
+ examples = [example] * num_samples
+ tfexample_utils.dump_to_tfrecord(
+ record_file=tfrecord_file, tf_examples=examples)
+
+ @parameterized.parameters(
+ ('mosaic_mnv35_cityscapes', True),
+ ('mosaic_mnv35_cityscapes', False),
+ )
+ def test_semantic_segmentation_task(self, test_config, is_training):
+ """Tests mosaic task for training and eval using toy configs."""
+ input_image_size = [1024, 2048]
+ test_tfrecord_file = os.path.join(self.get_temp_dir(), 'seg_test.tfrecord')
+ example = tfexample_utils.create_segmentation_test_example(
+ image_height=input_image_size[0],
+ image_width=input_image_size[1],
+ image_channel=3)
+ self._create_test_tfrecord(
+ tfrecord_file=test_tfrecord_file, example=example, num_samples=10)
+ config = exp_factory.get_exp_config(test_config)
+ # Modify config to suit local testing
+ config.task.model.input_size = [None, None, 3]
+ config.trainer.steps_per_loop = 1
+ config.task.train_data.global_batch_size = 1
+ config.task.validation_data.global_batch_size = 1
+ config.task.train_data.output_size = [1024, 2048]
+ config.task.validation_data.output_size = [1024, 2048]
+ config.task.train_data.crop_size = [512, 512]
+ config.task.train_data.shuffle_buffer_size = 2
+ config.task.validation_data.shuffle_buffer_size = 2
+ config.task.validation_data.input_path = test_tfrecord_file
+ config.task.train_data.input_path = test_tfrecord_file
+ config.train_steps = 1
+ config.task.model.num_classes = 256
+ config.task.model.head.num_classes = 256
+ config.task.model.head.decoder_projected_filters = [256, 256]
+
+ task = mosaic_tasks.MosaicSemanticSegmentationTask(config.task)
+ model = task.build_model(training=is_training)
+ metrics = task.build_metrics(training=is_training)
+
+ strategy = tf.distribute.get_strategy()
+
+ data_config = config.task.train_data if is_training else config.task.validation_data
+ dataset = orbit.utils.make_distributed_dataset(strategy, task.build_inputs,
+ data_config)
+ iterator = iter(dataset)
+ opt_factory = optimization.OptimizerFactory(config.trainer.optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+
+ if is_training:
+ logs = task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ else:
+ logs = task.validation_step(next(iterator), model, metrics=metrics)
+
+ self.assertIn('loss', logs)
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/mosaic/train.py b/official/projects/mosaic/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea07b6d80ef9030304f87df9670224d7e12f4667
--- /dev/null
+++ b/official/projects/mosaic/train.py
@@ -0,0 +1,103 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Training driver for MOSAIC models."""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import base_trainer
+from official.core import config_definitions
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+# Import MOSAIC libraries to register the model into tf.vision
+# model garden factory.
+# pylint: disable=unused-import
+from official.projects.mosaic import mosaic_tasks
+from official.projects.mosaic.modeling import mosaic_model
+from official.vision import registry_imports
+# pylint: enable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+# Note: we overrided the `build_trainer` due to the customized `build_model`
+# methods in `MosaicSemanticSegmentationTask.
+def _build_mosaic_trainer(params: config_definitions.ExperimentConfig,
+ task: mosaic_tasks.MosaicSemanticSegmentationTask,
+ model_dir: str, train: bool,
+ evaluate: bool) -> base_trainer.Trainer:
+ """Creates custom trainer."""
+ checkpoint_exporter = train_lib.maybe_create_best_ckpt_exporter(
+ params, model_dir)
+ model = task.build_model(train)
+ optimizer = train_utils.create_optimizer(task, params)
+ trainer = base_trainer.Trainer(
+ params,
+ task,
+ model=model,
+ optimizer=optimizer,
+ train=train,
+ evaluate=evaluate,
+ checkpoint_exporter=checkpoint_exporter)
+ return trainer
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+ mosaic_trainer = _build_mosaic_trainer(
+ task=task,
+ params=params,
+ model_dir=model_dir,
+ train='train' in FLAGS.mode,
+ evaluate='eval' in FLAGS.mode)
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir,
+ trainer=mosaic_trainer)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ flags.mark_flags_as_required(['experiment', 'mode', 'model_dir'])
+ app.run(main)
diff --git a/official/projects/movinet/README.md b/official/projects/movinet/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..36bcfe89de5a2cfc53bbbd090801f1e57e7d6a85
--- /dev/null
+++ b/official/projects/movinet/README.md
@@ -0,0 +1,444 @@
+# Mobile Video Networks (MoViNets)
+
+[](https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/movinet/movinet_tutorial.ipynb)
+[](https://tfhub.dev/google/collections/movinet)
+[](https://arxiv.org/abs/2103.11511)
+
+This repository is the official implementation of
+[MoViNets: Mobile Video Networks for Efficient Video
+Recognition](https://arxiv.org/abs/2103.11511).
+
+- **[UPDATE 2022-03-14] Quantized TF Lite models
+ [available on TF Hub](https://tfhub.dev/s?deployment-format=lite&q=movinet)
+ (also [see table](https://tfhub.dev/google/collections/movinet) for
+ quantized performance)**
+
+
+
+
+
+Create your own video plot like the one above with this [Colab notebook](https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/movinet/tools/plot_movinet_video_stream_predictions.ipynb).
+
+## Description
+
+Mobile Video Networks (MoViNets) are efficient video classification models
+runnable on mobile devices. MoViNets demonstrate state-of-the-art accuracy and
+efficiency on several large-scale video action recognition datasets.
+
+On [Kinetics 600](https://deepmind.com/research/open-source/kinetics),
+MoViNet-A6 achieves 84.8% top-1 accuracy, outperforming recent
+Vision Transformer models like [ViViT](https://arxiv.org/abs/2103.15691) (83.0%)
+and [VATT](https://arxiv.org/abs/2104.11178) (83.6%) without any additional
+training data, while using 10x fewer FLOPs. And streaming MoViNet-A0 achieves
+72% accuracy while using 3x fewer FLOPs than MobileNetV3-large (68%).
+
+There is a large gap between video model performance of accurate models and
+efficient models for video action recognition. On the one hand, 2D MobileNet
+CNNs are fast and can operate on streaming video in real time, but are prone to
+be noisy and inaccurate. On the other hand, 3D CNNs are accurate, but are
+memory and computation intensive and cannot operate on streaming video.
+
+MoViNets bridge this gap, producing:
+
+- State-of-the art efficiency and accuracy across the model family (MoViNet-A0
+to A6).
+- Streaming models with 3D causal convolutions substantially reducing memory
+usage.
+- Temporal ensembles of models to boost efficiency even higher.
+
+MoViNets also improve computational efficiency by outputting high-quality
+predictions frame by frame, as opposed to the traditional multi-clip evaluation
+approach that performs redundant computation and limits temporal scope.
+
+
+
+
+
+
+
+
+
+## History
+
+- **2022-03-14** Support quantized TF Lite models and add/update Colab
+notebooks.
+- **2021-07-12** Add TF Lite support and replace 3D stream models with
+mobile-friendly (2+1)D stream.
+- **2021-05-30** Add streaming MoViNet checkpoints and examples.
+- **2021-05-11** Initial Commit.
+
+## Authors and Maintainers
+
+* Dan Kondratyuk ([@hyperparticle](https://github.com/hyperparticle))
+* Liangzhe Yuan ([@yuanliangzhe](https://github.com/yuanliangzhe))
+* Yeqing Li ([@yeqingli](https://github.com/yeqingli))
+
+## Table of Contents
+
+- [Requirements](#requirements)
+- [Results and Pretrained Weights](#results-and-pretrained-weights)
+ - [Kinetics 600](#kinetics-600)
+ - [Kinetics 400](#kinetics-400)
+- [Prediction Examples](#prediction-examples)
+- [TF Lite Example](#tf-lite-example)
+- [Training and Evaluation](#training-and-evaluation)
+- [References](#references)
+- [License](#license)
+- [Citation](#citation)
+
+## Requirements
+
+[](https://github.com/tensorflow/tensorflow/releases/tag/v2.1.0)
+[](https://www.python.org/downloads/release/python-360/)
+
+To install requirements:
+
+```shell
+pip install -r requirements.txt
+```
+
+## Results and Pretrained Weights
+
+[](https://tfhub.dev/google/collections/movinet)
+[](https://tensorboard.dev/experiment/Q07RQUlVRWOY4yDw3SnSkA/)
+
+### Kinetics 600
+
+
+
+
+
+[tensorboard.dev summary](https://tensorboard.dev/experiment/Q07RQUlVRWOY4yDw3SnSkA/)
+of training runs across all models.
+
+The table below summarizes the performance of each model on
+[Kinetics 600](https://deepmind.com/research/open-source/kinetics)
+and provides links to download pretrained models. All models are evaluated on
+single clips with the same resolution as training.
+
+Note: MoViNet-A6 can be constructed as an ensemble of MoViNet-A4 and
+MoViNet-A5.
+
+#### Base Models
+
+Base models implement standard 3D convolutions without stream buffers. Base
+models are not recommended for fast inference on CPU or mobile due to
+limited support for
+[`tf.nn.conv3d`](https://www.tensorflow.org/api_docs/python/tf/nn/conv3d).
+Instead, see the [streaming models section](#streaming-models).
+
+| Model Name | Top-1 Accuracy | Top-5 Accuracy | Input Shape | GFLOPs\* | Checkpoint | TF Hub SavedModel |
+|------------|----------------|----------------|-------------|----------|------------|-------------------|
+| MoViNet-A0-Base | 72.28 | 90.92 | 50 x 172 x 172 | 2.7 | [checkpoint (12 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a0/base/kinetics-600/classification/) |
+| MoViNet-A1-Base | 76.69 | 93.40 | 50 x 172 x 172 | 6.0 | [checkpoint (18 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a1_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a1/base/kinetics-600/classification/) |
+| MoViNet-A2-Base | 78.62 | 94.17 | 50 x 224 x 224 | 10 | [checkpoint (20 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a2_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a2/base/kinetics-600/classification/) |
+| MoViNet-A3-Base | 81.79 | 95.67 | 120 x 256 x 256 | 57 | [checkpoint (29 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a3_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a3/base/kinetics-600/classification/) |
+| MoViNet-A4-Base | 83.48 | 96.16 | 80 x 290 x 290 | 110 | [checkpoint (44 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a4_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a4/base/kinetics-600/classification/) |
+| MoViNet-A5-Base | 84.27 | 96.39 | 120 x 320 x 320 | 280 | [checkpoint (72 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a5_base.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a5/base/kinetics-600/classification/) |
+
+\*GFLOPs per video on Kinetics 600.
+
+#### Streaming Models
+
+Streaming models implement causal (2+1)D convolutions with stream buffers.
+Streaming models use (2+1)D convolution instead of 3D to utilize optimized
+[`tf.nn.conv2d`](https://www.tensorflow.org/api_docs/python/tf/nn/conv2d)
+operations, which offer fast inference on CPU. Streaming models can be run on
+individual frames or on larger video clips like base models.
+
+Note: A3, A4, and A5 models use a positional encoding in the squeeze-excitation
+blocks, while A0, A1, and A2 do not. For the smaller models, accuracy is
+unaffected without positional encoding, while for the larger models accuracy is
+significantly worse without positional encoding.
+
+| Model Name | Top-1 Accuracy | Top-5 Accuracy | Input Shape\* | GFLOPs\*\* | Checkpoint | TF Hub SavedModel |
+|------------|----------------|----------------|---------------|------------|------------|-------------------|
+| MoViNet-A0-Stream | 72.05 | 90.63 | 50 x 172 x 172 | 2.7 | [checkpoint (12 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a0/stream/kinetics-600/classification/) |
+| MoViNet-A1-Stream | 76.45 | 93.25 | 50 x 172 x 172 | 6.0 | [checkpoint (18 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a1_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a1/stream/kinetics-600/classification/) |
+| MoViNet-A2-Stream | 78.40 | 94.05 | 50 x 224 x 224 | 10 | [checkpoint (20 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a2_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a2/stream/kinetics-600/classification/) |
+| MoViNet-A3-Stream | 80.09 | 94.84 | 120 x 256 x 256 | 57 | [checkpoint (29 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a3_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a3/stream/kinetics-600/classification/) |
+| MoViNet-A4-Stream | 81.49 | 95.66 | 80 x 290 x 290 | 110 | [checkpoint (44 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a4_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a4/stream/kinetics-600/classification/) |
+| MoViNet-A5-Stream | 82.37 | 95.79 | 120 x 320 x 320 | 280 | [checkpoint (72 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a5_stream.tar.gz) | [tfhub](https://tfhub.dev/tensorflow/movinet/a5/stream/kinetics-600/classification/) |
+
+\*In streaming mode, the number of frames correspond to the total accumulated
+duration of the 10-second clip.
+
+\*\*GFLOPs per video on Kinetics 600.
+
+Note: current streaming model checkpoints have been updated with a slightly
+different architecture. To download the old checkpoints, insert `_legacy` before
+`.tar.gz` in the URL. E.g., `movinet_a0_stream_legacy.tar.gz`.
+
+##### TF Lite Streaming Models
+
+For convenience, we provide converted TF Lite models for inference on mobile
+devices. See the [TF Lite Example](#tf-lite-example) to export and run your own
+models. We also provide [quantized TF Lite binaries via TF Hub](https://tfhub.dev/s?deployment-format=lite&q=movinet).
+
+For reference, MoViNet-A0-Stream runs with a similar latency to
+[MobileNetV3-Large](https://tfhub.dev/google/imagenet/mobilenet_v3_large_100_224/classification/)
+with +5% accuracy on Kinetics 600.
+
+| Model Name | Input Shape | Pixel 4 Latency\* | x86 Latency\* | TF Lite Binary |
+|------------|-------------|-------------------|---------------|----------------|
+| MoViNet-A0-Stream | 1 x 1 x 172 x 172 | 22 ms | 16 ms | [TF Lite (13 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_stream.tflite) |
+| MoViNet-A1-Stream | 1 x 1 x 172 x 172 | 42 ms | 33 ms | [TF Lite (45 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a1_stream.tflite) |
+| MoViNet-A2-Stream | 1 x 1 x 224 x 224 | 200 ms | 66 ms | [TF Lite (53 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a2_stream.tflite) |
+| MoViNet-A3-Stream | 1 x 1 x 256 x 256 | - | 120 ms | [TF Lite (73 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a3_stream.tflite) |
+| MoViNet-A4-Stream | 1 x 1 x 290 x 290 | - | 300 ms | [TF Lite (101 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a4_stream.tflite) |
+| MoViNet-A5-Stream | 1 x 1 x 320 x 320 | - | 450 ms | [TF Lite (153 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a5_stream.tflite) |
+
+\*Single-frame latency measured on with unaltered float32 operations on a
+single CPU core. Observed latency may differ depending on hardware
+configuration. Measured on a stock Pixel 4 (Android 11) and x86 Intel Xeon
+W-2135 CPU.
+
+### Kinetics 400
+
+We also have checkpoints for Kinetics 400 models available. See the Kinetics 600
+sections for more details. To load checkpoints, set `num_classes=400`.
+
+#### Base Models
+
+| Model Name | Top-1 Accuracy | Top-5 Accuracy | Input Shape | GFLOPs\* | Checkpoint |
+|------------|----------------|----------------|-------------|----------|------------|
+| MoViNet-A0-Base | 69.40 | 89.18 | 50 x 172 x 172 | 2.7 | [checkpoint (12 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_base_k400.tar.gz) |
+| MoViNet-A1-Base | 74.57 | 92.03 | 50 x 172 x 172 | 6.0 | [checkpoint (18 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a1_base_k400.tar.gz) |
+| MoViNet-A2-Base | 75.91 | 92.63 | 50 x 224 x 224 | 10 | [checkpoint (20 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a2_base_k400.tar.gz) |
+| MoViNet-A3-Base | 79.34 | 94.52 | 120 x 256 x 256 | 57 | [checkpoint (29 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a3_base_k400.tar.gz) |
+| MoViNet-A4-Base | 80.64 | 94.93 | 80 x 290 x 290 | 110 | [checkpoint (44 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a4_base_k400.tar.gz) |
+| MoViNet-A5-Base | 81.39 | 95.06 | 120 x 320 x 320 | 280 | [checkpoint (72 MB)](https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a5_base_k400.tar.gz) |
+
+*GFLOPs per video on Kinetics 400.
+
+## Prediction Examples
+
+Please check out our [Colab Notebook](https://colab.research.google.com/github/tensorflow/models/blob/master/official/projects/movinet/movinet_tutorial.ipynb)
+to get started with MoViNets.
+
+This section provides examples on how to run prediction.
+
+For **base models**, run the following:
+
+```python
+import tensorflow as tf
+
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
+
+# Create backbone and model.
+backbone = movinet.Movinet(
+ model_id='a0',
+ causal=False,
+ use_external_states=False,
+)
+model = movinet_model.MovinetClassifier(
+ backbone, num_classes=600, output_states=False)
+
+# Create your example input here.
+# Refer to the paper for recommended input shapes.
+inputs = tf.ones([1, 8, 172, 172, 3])
+
+# [Optional] Build the model and load a pretrained checkpoint
+model.build(inputs.shape)
+
+checkpoint_dir = '/path/to/checkpoint'
+checkpoint_path = tf.train.latest_checkpoint(checkpoint_dir)
+checkpoint = tf.train.Checkpoint(model=model)
+status = checkpoint.restore(checkpoint_path)
+status.assert_existing_objects_matched()
+
+# Run the model prediction.
+output = model(inputs)
+prediction = tf.argmax(output, -1)
+```
+
+For **streaming models**, run the following:
+
+```python
+import tensorflow as tf
+
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
+
+model_id = 'a0'
+use_positional_encoding = model_id in {'a3', 'a4', 'a5'}
+
+# Create backbone and model.
+backbone = movinet.Movinet(
+ model_id=model_id,
+ causal=True,
+ conv_type='2plus1d',
+ se_type='2plus3d',
+ activation='hard_swish',
+ gating_activation='hard_sigmoid',
+ use_positional_encoding=use_positional_encoding,
+ use_external_states=True,
+)
+
+model = movinet_model.MovinetClassifier(
+ backbone,
+ num_classes=600,
+ output_states=True)
+
+# Create your example input here.
+# Refer to the paper for recommended input shapes.
+inputs = tf.ones([1, 8, 172, 172, 3])
+
+# [Optional] Build the model and load a pretrained checkpoint.
+model.build(inputs.shape)
+
+checkpoint_dir = '/path/to/checkpoint'
+checkpoint_path = tf.train.latest_checkpoint(checkpoint_dir)
+checkpoint = tf.train.Checkpoint(model=model)
+status = checkpoint.restore(checkpoint_path)
+status.assert_existing_objects_matched()
+
+# Split the video into individual frames.
+# Note: we can also split into larger clips as well (e.g., 8-frame clips).
+# Running on larger clips will slightly reduce latency overhead, but
+# will consume more memory.
+frames = tf.split(inputs, inputs.shape[1], axis=1)
+
+# Initialize the dict of states. All state tensors are initially zeros.
+init_states = model.init_states(tf.shape(inputs))
+
+# Run the model prediction by looping over each frame.
+states = init_states
+predictions = []
+for frame in frames:
+ output, states = model({**states, 'image': frame})
+ predictions.append(output)
+
+# The video classification will simply be the last output of the model.
+final_prediction = tf.argmax(predictions[-1], -1)
+
+# Alternatively, we can run the network on the entire input video.
+# The output should be effectively the same
+# (but it may differ a small amount due to floating point errors).
+non_streaming_output, _ = model({**init_states, 'image': inputs})
+non_streaming_prediction = tf.argmax(non_streaming_output, -1)
+```
+
+## TF Lite Example
+
+This section outlines an example on how to export a model to run on mobile
+devices with [TF Lite](https://www.tensorflow.org/lite).
+
+[Optional] For streaming models, they are typically trained with
+`conv_type = 3d_2plus1d` for better training throughpouts. In order to achieve
+better inference performance on CPU, we need to convert the `3d_2plus1d`
+checkpoint to make it compatible with the `2plus1d` graph.
+You could achieve this by running `tools/convert_3d_2plus1d.py`.
+
+First, convert to [TF SavedModel](https://www.tensorflow.org/guide/saved_model)
+by running `export_saved_model.py`. For example, for `MoViNet-A0-Stream`, run:
+
+```shell
+python3 export_saved_model.py \
+ --model_id=a0 \
+ --causal=True \
+ --conv_type=2plus1d \
+ --se_type=2plus3d \
+ --activation=hard_swish \
+ --gating_activation=hard_sigmoid \
+ --use_positional_encoding=False \
+ --num_classes=600 \
+ --batch_size=1 \
+ --num_frames=1 \
+ --image_size=172 \
+ --bundle_input_init_states_fn=False \
+ --checkpoint_path=/path/to/checkpoint \
+ --export_path=/tmp/movinet_a0_stream
+```
+
+Then the SavedModel can be converted to TF Lite using the [`TFLiteConverter`](https://www.tensorflow.org/lite/convert):
+
+```python
+saved_model_dir = '/tmp/movinet_a0_stream'
+converter = tf.lite.TFLiteConverter.from_saved_model(saved_model_dir)
+tflite_model = converter.convert()
+
+with open('/tmp/movinet_a0_stream.tflite', 'wb') as f:
+ f.write(tflite_model)
+```
+
+To run with TF Lite using [tf.lite.Interpreter](https://www.tensorflow.org/lite/guide/inference#load_and_run_a_model_in_python)
+with the Python API:
+
+```python
+# Create the interpreter and signature runner
+interpreter = tf.lite.Interpreter('/tmp/movinet_a0_stream.tflite')
+runner = interpreter.get_signature_runner()
+
+# Extract state names and create the initial (zero) states
+def state_name(name: str) -> str:
+ return name[len('serving_default_'):-len(':0')]
+
+init_states = {
+ state_name(x['name']): tf.zeros(x['shape'], dtype=x['dtype'])
+ for x in interpreter.get_input_details()
+}
+del init_states['image']
+
+# Insert your video clip here
+video = tf.ones([1, 8, 172, 172, 3])
+clips = tf.split(video, video.shape[1], axis=1)
+
+# To run on a video, pass in one frame at a time
+states = init_states
+for clip in clips:
+ # Input shape: [1, 1, 172, 172, 3]
+ outputs = runner(**states, image=clip)
+ logits = outputs.pop('logits')
+ states = outputs
+```
+
+Follow the [official guide](https://www.tensorflow.org/lite/guide) to run a
+model with TF Lite on your mobile device.
+
+## Training and Evaluation
+
+Run this command line for continuous training and evaluation.
+
+```shell
+MODE=train_and_eval # Can also be 'train' if using a separate evaluator job
+CONFIG_FILE=official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
+python3 official/projects/movinet/train.py \
+ --experiment=movinet_kinetics600 \
+ --mode=${MODE} \
+ --model_dir=/tmp/movinet_a0_base/ \
+ --config_file=${CONFIG_FILE}
+```
+
+Run this command line for evaluation.
+
+```shell
+MODE=eval # Can also be 'eval_continuous' for use during training
+CONFIG_FILE=official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
+python3 official/projects/movinet/train.py \
+ --experiment=movinet_kinetics600 \
+ --mode=${MODE} \
+ --model_dir=/tmp/movinet_a0_base/ \
+ --config_file=${CONFIG_FILE}
+```
+
+## License
+
+[](https://opensource.org/licenses/Apache-2.0)
+
+This project is licensed under the terms of the **Apache License 2.0**.
+
+## Citation
+
+If you want to cite this code in your research paper, please use the following
+information.
+
+```
+@article{kondratyuk2021movinets,
+ title={MoViNets: Mobile Video Networks for Efficient Video Recognition},
+ author={Dan Kondratyuk, Liangzhe Yuan, Yandong Li, Li Zhang, Matthew Brown, and Boqing Gong},
+ journal={arXiv preprint arXiv:2103.11511},
+ year={2021}
+}
+```
diff --git a/official/projects/movinet/__init__.py b/official/projects/movinet/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/movinet/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/movinet/configs/__init__.py b/official/projects/movinet/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/movinet/configs/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/movinet/configs/movinet.py b/official/projects/movinet/configs/movinet.py
new file mode 100644
index 0000000000000000000000000000000000000000..8db85b03f7c84f413ed87cbf0ef25d6e1b067068
--- /dev/null
+++ b/official/projects/movinet/configs/movinet.py
@@ -0,0 +1,149 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Definitions for MoViNet structures.
+
+Reference: "MoViNets: Mobile Video Networks for Efficient Video Recognition"
+https://arxiv.org/pdf/2103.11511.pdf
+
+MoViNets are efficient video classification networks that are part of a model
+family, ranging from the smallest model, MoViNet-A0, to the largest model,
+MoViNet-A6. Each model has various width, depth, input resolution, and input
+frame-rate associated with them. See the main paper for more details.
+"""
+
+import dataclasses
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.vision.configs import backbones_3d
+from official.vision.configs import common
+from official.vision.configs import video_classification
+
+
+@dataclasses.dataclass
+class Movinet(hyperparams.Config):
+ """Backbone config for Base MoViNet."""
+ model_id: str = 'a0'
+ causal: bool = False
+ use_positional_encoding: bool = False
+ # Choose from ['3d', '2plus1d', '3d_2plus1d']
+ # 3d: default 3D convolution
+ # 2plus1d: (2+1)D convolution with Conv2D (2D reshaping)
+ # 3d_2plus1d: (2+1)D convolution with Conv3D (no 2D reshaping)
+ conv_type: str = '3d'
+ # Choose from ['3d', '2d', '2plus3d']
+ # 3d: default 3D global average pooling.
+ # 2d: 2D global average pooling.
+ # 2plus3d: concatenation of 2D and 3D global average pooling.
+ se_type: str = '3d'
+ activation: str = 'swish'
+ gating_activation: str = 'sigmoid'
+ stochastic_depth_drop_rate: float = 0.2
+ use_external_states: bool = False
+ average_pooling_type: str = '3d'
+ output_states: bool = True
+
+
+@dataclasses.dataclass
+class MovinetA0(Movinet):
+ """Backbone config for MoViNet-A0.
+
+ Represents the smallest base MoViNet searched by NAS.
+
+ Reference: https://arxiv.org/pdf/2103.11511.pdf
+ """
+ model_id: str = 'a0'
+
+
+@dataclasses.dataclass
+class MovinetA1(Movinet):
+ """Backbone config for MoViNet-A1."""
+ model_id: str = 'a1'
+
+
+@dataclasses.dataclass
+class MovinetA2(Movinet):
+ """Backbone config for MoViNet-A2."""
+ model_id: str = 'a2'
+
+
+@dataclasses.dataclass
+class MovinetA3(Movinet):
+ """Backbone config for MoViNet-A3."""
+ model_id: str = 'a3'
+
+
+@dataclasses.dataclass
+class MovinetA4(Movinet):
+ """Backbone config for MoViNet-A4."""
+ model_id: str = 'a4'
+
+
+@dataclasses.dataclass
+class MovinetA5(Movinet):
+ """Backbone config for MoViNet-A5.
+
+ Represents the largest base MoViNet searched by NAS.
+ """
+ model_id: str = 'a5'
+
+
+@dataclasses.dataclass
+class MovinetT0(Movinet):
+ """Backbone config for MoViNet-T0.
+
+ MoViNet-T0 is a smaller version of MoViNet-A0 for even faster processing.
+ """
+ model_id: str = 't0'
+
+
+@dataclasses.dataclass
+class Backbone3D(backbones_3d.Backbone3D):
+ """Configuration for backbones.
+
+ Attributes:
+ type: 'str', type of backbone be used, on the of fields below.
+ movinet: movinet backbone config.
+ """
+ type: str = 'movinet'
+ movinet: Movinet = Movinet()
+
+
+@dataclasses.dataclass
+class MovinetModel(video_classification.VideoClassificationModel):
+ """The MoViNet model config."""
+ model_type: str = 'movinet'
+ backbone: Backbone3D = Backbone3D()
+ norm_activation: common.NormActivation = common.NormActivation(
+ activation=None, # legacy flag, not used.
+ norm_momentum=0.99,
+ norm_epsilon=1e-3,
+ use_sync_bn=True)
+ activation: str = 'swish'
+ output_states: bool = False
+
+
+@exp_factory.register_config_factory('movinet_kinetics600')
+def movinet_kinetics600() -> cfg.ExperimentConfig:
+ """Video classification on Videonet with MoViNet backbone."""
+ exp = video_classification.video_classification_kinetics600()
+ exp.task.train_data.dtype = 'bfloat16'
+ exp.task.validation_data.dtype = 'bfloat16'
+
+ model = MovinetModel()
+ exp.task.model = model
+
+ return exp
diff --git a/official/projects/movinet/configs/movinet_test.py b/official/projects/movinet/configs/movinet_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..6efd069c97f0dfa5bec4e31ed415ffb555dbb234
--- /dev/null
+++ b/official/projects/movinet/configs/movinet_test.py
@@ -0,0 +1,42 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for movinet video classification."""
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.movinet.configs import movinet
+from official.vision.configs import video_classification as exp_cfg
+
+
+class MovinetConfigTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(
+ ('movinet_kinetics600',),)
+ def test_video_classification_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, exp_cfg.VideoClassificationTask)
+ self.assertIsInstance(config.task.model, movinet.MovinetModel)
+ self.assertIsInstance(config.task.train_data, exp_cfg.DataConfig)
+ config.task.train_data.is_training = None
+ with self.assertRaises(KeyError):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
index bd7d3ce92a9d1b5dee6932a0be1e39e0f54e938f..368a5c8ca0d71a80e28d373a1d404fc9c0d242e8 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.2
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml b/official/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml
rename to official/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml
index a144ac56e4df38adbe336e807fbf236ab2d4345d..b8f66ed68ae36be3b2b83e799dc20a9190bcda26 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a0_k600_cpu_local.yaml
@@ -12,6 +12,7 @@ task:
norm_activation:
use_sync_bn: false
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml
index 749f97af2392eedee98fa35c5040bad33bb5cda2..5f678a844d7ecc300ea8d56f7e07f15d3448394e 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a0_stream_k600_8x8.yaml
@@ -24,6 +24,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.2
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml
index 8c097f49b4a06af4fbda6b7c45b1e51b441247fd..f25539d70bf887fc6120ee586ef58b4b6c905ea9 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a1_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml
index 7f6e597368ac380e31f2086708f959917c2e2aa1..3948f3ed1ff4e643c0d1e917f78ea4d5398aee1e 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a1_stream_k600_8x8.yaml
@@ -24,6 +24,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.2
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml
index 575772b9f3e62e2e8a462c7cb08bbb64e8ac44e0..a8728225ae25d081cf494b4bf552535931dd4012 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a2_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml
index d5a1f9d9ebc97745743ff978e3be5d2d6cffb63c..9f707e98d9b9fb8d1fb32ff2957f4172b85ca65c 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a2_stream_k600_8x8.yaml
@@ -24,6 +24,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml
index a4d34314695baa36a74fd515118ae3429cd81d4b..5a729cca8fae791ac57d1d894df3699fd1a78114 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a3_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml
index 3f8336be0678240f7d65244e12496f7e5bee0917..c4778a084aff56282afbeebed6ee7a45d7167a25 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a3_stream_k600_8x8.yaml
@@ -25,6 +25,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml
index 102ccad4f5524a2160b004262bcc34cc2d06680f..e3eb772b80ceaa3c13d311649d6b5ebd860458c9 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a4_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml
index ac72c65f7c5753b09f85aac75790139f1da05e74..0b3b687605c4a6544cff23882ee4503b8cef3b9f 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a4_stream_k600_8x8.yaml
@@ -25,6 +25,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml
index 79c9d209d9177f59e05b1e0b7d81682cdad3197f..560fccab4cdb12890509531b33d7feedddf887e4 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a5_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml
index 13b7c4904c2c4e90021277701951c2e4858953ec..c44f9ba2653c82718932cc1f1ff85b2d5f0bf853 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_a5_stream_k600_8x8.yaml
@@ -25,6 +25,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.5
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml
index b6b190c8acb6f504ac489f9531f8f5af46f7ba65..fde13d342834f0c718b635b4a48e4bcf14940e6b 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_t0_k600_8x8.yaml
@@ -18,6 +18,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.2
+ activation: 'swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/vision/beta/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml b/official/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml
similarity index 98%
rename from official/vision/beta/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml
rename to official/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml
index 9f490e7c3d4049d6ef6d984bcfa2cfaeaf900488..b302850c66985225fa541ce07d735e399959687f 100644
--- a/official/vision/beta/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml
+++ b/official/projects/movinet/configs/yaml/movinet_t0_stream_k600_8x8.yaml
@@ -24,6 +24,7 @@ task:
norm_activation:
use_sync_bn: true
dropout_rate: 0.2
+ activation: 'hard_swish'
train_data:
name: kinetics600
variant_name: rgb
diff --git a/official/projects/movinet/files/jumpingjack.gif b/official/projects/movinet/files/jumpingjack.gif
new file mode 100644
index 0000000000000000000000000000000000000000..9527e431228e519afa0f307121b4d2d54dc69c58
Binary files /dev/null and b/official/projects/movinet/files/jumpingjack.gif differ
diff --git a/official/projects/movinet/files/kinetics_600_labels.txt b/official/projects/movinet/files/kinetics_600_labels.txt
new file mode 100644
index 0000000000000000000000000000000000000000..639e9c91fa8a941ea57942872fae55628d590b42
--- /dev/null
+++ b/official/projects/movinet/files/kinetics_600_labels.txt
@@ -0,0 +1,600 @@
+abseiling
+acting in play
+adjusting glasses
+air drumming
+alligator wrestling
+answering questions
+applauding
+applying cream
+archaeological excavation
+archery
+arguing
+arm wrestling
+arranging flowers
+assembling bicycle
+assembling computer
+attending conference
+auctioning
+backflip (human)
+baking cookies
+bandaging
+barbequing
+bartending
+base jumping
+bathing dog
+battle rope training
+beatboxing
+bee keeping
+belly dancing
+bench pressing
+bending back
+bending metal
+biking through snow
+blasting sand
+blowdrying hair
+blowing bubble gum
+blowing glass
+blowing leaves
+blowing nose
+blowing out candles
+bobsledding
+bodysurfing
+bookbinding
+bottling
+bouncing on bouncy castle
+bouncing on trampoline
+bowling
+braiding hair
+breading or breadcrumbing
+breakdancing
+breaking boards
+breathing fire
+brush painting
+brushing hair
+brushing teeth
+building cabinet
+building lego
+building sandcastle
+building shed
+bull fighting
+bulldozing
+bungee jumping
+burping
+busking
+calculating
+calligraphy
+canoeing or kayaking
+capoeira
+capsizing
+card stacking
+card throwing
+carrying baby
+cartwheeling
+carving ice
+carving pumpkin
+casting fishing line
+catching fish
+catching or throwing baseball
+catching or throwing frisbee
+catching or throwing softball
+celebrating
+changing gear in car
+changing oil
+changing wheel (not on bike)
+checking tires
+cheerleading
+chewing gum
+chiseling stone
+chiseling wood
+chopping meat
+chopping vegetables
+chopping wood
+clam digging
+clapping
+clay pottery making
+clean and jerk
+cleaning gutters
+cleaning pool
+cleaning shoes
+cleaning toilet
+cleaning windows
+climbing a rope
+climbing ladder
+climbing tree
+coloring in
+combing hair
+contact juggling
+contorting
+cooking egg
+cooking on campfire
+cooking sausages (not on barbeque)
+cooking scallops
+cosplaying
+counting money
+country line dancing
+cracking back
+cracking knuckles
+cracking neck
+crawling baby
+crossing eyes
+crossing river
+crying
+cumbia
+curling (sport)
+curling hair
+cutting apple
+cutting nails
+cutting orange
+cutting pineapple
+cutting watermelon
+dancing ballet
+dancing charleston
+dancing gangnam style
+dancing macarena
+deadlifting
+decorating the christmas tree
+delivering mail
+dining
+directing traffic
+disc golfing
+diving cliff
+docking boat
+dodgeball
+doing aerobics
+doing jigsaw puzzle
+doing laundry
+doing nails
+drawing
+dribbling basketball
+drinking shots
+driving car
+driving tractor
+drooling
+drop kicking
+drumming fingers
+dumpster diving
+dunking basketball
+dyeing eyebrows
+dyeing hair
+eating burger
+eating cake
+eating carrots
+eating chips
+eating doughnuts
+eating hotdog
+eating ice cream
+eating spaghetti
+eating watermelon
+egg hunting
+embroidering
+exercising with an exercise ball
+extinguishing fire
+faceplanting
+falling off bike
+falling off chair
+feeding birds
+feeding fish
+feeding goats
+fencing (sport)
+fidgeting
+finger snapping
+fixing bicycle
+fixing hair
+flint knapping
+flipping pancake
+fly tying
+flying kite
+folding clothes
+folding napkins
+folding paper
+front raises
+frying vegetables
+geocaching
+getting a haircut
+getting a piercing
+getting a tattoo
+giving or receiving award
+gold panning
+golf chipping
+golf driving
+golf putting
+gospel singing in church
+grinding meat
+grooming dog
+grooming horse
+gymnastics tumbling
+hammer throw
+hand washing clothes
+head stand
+headbanging
+headbutting
+high jump
+high kick
+historical reenactment
+hitting baseball
+hockey stop
+holding snake
+home roasting coffee
+hopscotch
+hoverboarding
+huddling
+hugging (not baby)
+hugging baby
+hula hooping
+hurdling
+hurling (sport)
+ice climbing
+ice fishing
+ice skating
+ice swimming
+inflating balloons
+installing carpet
+ironing
+ironing hair
+javelin throw
+jaywalking
+jetskiing
+jogging
+juggling balls
+juggling fire
+juggling soccer ball
+jumping bicycle
+jumping into pool
+jumping jacks
+jumpstyle dancing
+karaoke
+kicking field goal
+kicking soccer ball
+kissing
+kitesurfing
+knitting
+krumping
+land sailing
+laughing
+lawn mower racing
+laying bricks
+laying concrete
+laying stone
+laying tiles
+leatherworking
+licking
+lifting hat
+lighting fire
+lock picking
+long jump
+longboarding
+looking at phone
+luge
+lunge
+making a cake
+making a sandwich
+making balloon shapes
+making bubbles
+making cheese
+making horseshoes
+making jewelry
+making paper aeroplanes
+making pizza
+making snowman
+making sushi
+making tea
+making the bed
+marching
+marriage proposal
+massaging back
+massaging feet
+massaging legs
+massaging neck
+massaging person's head
+milking cow
+moon walking
+mopping floor
+mosh pit dancing
+motorcycling
+mountain climber (exercise)
+moving furniture
+mowing lawn
+mushroom foraging
+needle felting
+news anchoring
+opening bottle (not wine)
+opening door
+opening present
+opening refrigerator
+opening wine bottle
+packing
+paragliding
+parasailing
+parkour
+passing American football (in game)
+passing american football (not in game)
+passing soccer ball
+peeling apples
+peeling potatoes
+person collecting garbage
+petting animal (not cat)
+petting cat
+photobombing
+photocopying
+picking fruit
+pillow fight
+pinching
+pirouetting
+planing wood
+planting trees
+plastering
+playing accordion
+playing badminton
+playing bagpipes
+playing basketball
+playing bass guitar
+playing beer pong
+playing blackjack
+playing cello
+playing chess
+playing clarinet
+playing controller
+playing cricket
+playing cymbals
+playing darts
+playing didgeridoo
+playing dominoes
+playing drums
+playing field hockey
+playing flute
+playing gong
+playing guitar
+playing hand clapping games
+playing harmonica
+playing harp
+playing ice hockey
+playing keyboard
+playing kickball
+playing laser tag
+playing lute
+playing maracas
+playing marbles
+playing monopoly
+playing netball
+playing ocarina
+playing organ
+playing paintball
+playing pan pipes
+playing piano
+playing pinball
+playing ping pong
+playing poker
+playing polo
+playing recorder
+playing rubiks cube
+playing saxophone
+playing scrabble
+playing squash or racquetball
+playing tennis
+playing trombone
+playing trumpet
+playing ukulele
+playing violin
+playing volleyball
+playing with trains
+playing xylophone
+poking bellybutton
+pole vault
+polishing metal
+popping balloons
+pouring beer
+preparing salad
+presenting weather forecast
+pull ups
+pumping fist
+pumping gas
+punching bag
+punching person (boxing)
+push up
+pushing car
+pushing cart
+pushing wheelbarrow
+pushing wheelchair
+putting in contact lenses
+putting on eyeliner
+putting on foundation
+putting on lipstick
+putting on mascara
+putting on sari
+putting on shoes
+raising eyebrows
+reading book
+reading newspaper
+recording music
+repairing puncture
+riding a bike
+riding camel
+riding elephant
+riding mechanical bull
+riding mule
+riding or walking with horse
+riding scooter
+riding snow blower
+riding unicycle
+ripping paper
+roasting marshmallows
+roasting pig
+robot dancing
+rock climbing
+rock scissors paper
+roller skating
+rolling pastry
+rope pushdown
+running on treadmill
+sailing
+salsa dancing
+sanding floor
+sausage making
+sawing wood
+scrambling eggs
+scrapbooking
+scrubbing face
+scuba diving
+separating eggs
+setting table
+sewing
+shaking hands
+shaking head
+shaping bread dough
+sharpening knives
+sharpening pencil
+shaving head
+shaving legs
+shearing sheep
+shining flashlight
+shining shoes
+shooting basketball
+shooting goal (soccer)
+shopping
+shot put
+shoveling snow
+shucking oysters
+shuffling cards
+shuffling feet
+side kick
+sign language interpreting
+singing
+sipping cup
+situp
+skateboarding
+ski jumping
+skiing crosscountry
+skiing mono
+skiing slalom
+skipping rope
+skipping stone
+skydiving
+slacklining
+slapping
+sled dog racing
+sleeping
+smashing
+smelling feet
+smoking
+smoking hookah
+smoking pipe
+snatch weight lifting
+sneezing
+snorkeling
+snowboarding
+snowkiting
+snowmobiling
+somersaulting
+spelunking
+spinning poi
+spray painting
+springboard diving
+square dancing
+squat
+standing on hands
+staring
+steer roping
+sticking tongue out
+stomping grapes
+stretching arm
+stretching leg
+sucking lolly
+surfing crowd
+surfing water
+sweeping floor
+swimming backstroke
+swimming breast stroke
+swimming butterfly stroke
+swimming front crawl
+swing dancing
+swinging baseball bat
+swinging on something
+sword fighting
+sword swallowing
+tackling
+tagging graffiti
+tai chi
+talking on cell phone
+tango dancing
+tap dancing
+tapping guitar
+tapping pen
+tasting beer
+tasting food
+tasting wine
+testifying
+texting
+threading needle
+throwing axe
+throwing ball (not baseball or American football)
+throwing discus
+throwing knife
+throwing snowballs
+throwing tantrum
+throwing water balloon
+tickling
+tie dying
+tightrope walking
+tiptoeing
+tobogganing
+tossing coin
+training dog
+trapezing
+trimming or shaving beard
+trimming shrubs
+trimming trees
+triple jump
+twiddling fingers
+tying bow tie
+tying knot (not on a tie)
+tying necktie
+tying shoe laces
+unboxing
+unloading truck
+using a microscope
+using a paint roller
+using a power drill
+using a sledge hammer
+using a wrench
+using atm
+using bagging machine
+using circular saw
+using inhaler
+using puppets
+using remote controller (not gaming)
+using segway
+vacuuming floor
+visiting the zoo
+wading through mud
+wading through water
+waiting in line
+waking up
+walking the dog
+walking through snow
+washing dishes
+washing feet
+washing hair
+washing hands
+watching tv
+water skiing
+water sliding
+watering plants
+waving hand
+waxing back
+waxing chest
+waxing eyebrows
+waxing legs
+weaving basket
+weaving fabric
+welding
+whistling
+windsurfing
+winking
+wood burning (art)
+wrapping present
+wrestling
+writing
+yarn spinning
+yawning
+yoga
+zumba
diff --git a/official/projects/movinet/modeling/__init__.py b/official/projects/movinet/modeling/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/movinet/modeling/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/movinet/modeling/movinet.py b/official/projects/movinet/modeling/movinet.py
new file mode 100644
index 0000000000000000000000000000000000000000..eef9b7f0edae44a4b0a4c23b5b03c42c952fd3cd
--- /dev/null
+++ b/official/projects/movinet/modeling/movinet.py
@@ -0,0 +1,740 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains definitions of Mobile Video Networks.
+
+Reference: https://arxiv.org/pdf/2103.11511.pdf
+"""
+import dataclasses
+import math
+from typing import Dict, Mapping, Optional, Sequence, Tuple, Union
+
+from absl import logging
+import tensorflow as tf
+
+from official.modeling import hyperparams
+from official.projects.movinet.modeling import movinet_layers
+from official.vision.modeling.backbones import factory
+
+# Defines a set of kernel sizes and stride sizes to simplify and shorten
+# architecture definitions for configs below.
+KernelSize = Tuple[int, int, int]
+
+# K(ab) represents a 3D kernel of size (a, b, b)
+K13: KernelSize = (1, 3, 3)
+K15: KernelSize = (1, 5, 5)
+K33: KernelSize = (3, 3, 3)
+K53: KernelSize = (5, 3, 3)
+
+# S(ab) represents a 3D stride of size (a, b, b)
+S11: KernelSize = (1, 1, 1)
+S12: KernelSize = (1, 2, 2)
+S22: KernelSize = (2, 2, 2)
+S21: KernelSize = (2, 1, 1)
+
+# Type for a state container (map)
+TensorMap = Mapping[str, tf.Tensor]
+
+
+@dataclasses.dataclass
+class BlockSpec:
+ """Configuration of a block."""
+
+
+@dataclasses.dataclass
+class StemSpec(BlockSpec):
+ """Configuration of a Movinet block."""
+ filters: int = 0
+ kernel_size: KernelSize = (0, 0, 0)
+ strides: KernelSize = (0, 0, 0)
+
+
+@dataclasses.dataclass
+class MovinetBlockSpec(BlockSpec):
+ """Configuration of a Movinet block."""
+ base_filters: int = 0
+ expand_filters: Sequence[int] = ()
+ kernel_sizes: Sequence[KernelSize] = ()
+ strides: Sequence[KernelSize] = ()
+
+
+@dataclasses.dataclass
+class HeadSpec(BlockSpec):
+ """Configuration of a Movinet block."""
+ project_filters: int = 0
+ head_filters: int = 0
+
+
+# Block specs specify the architecture of each model
+BLOCK_SPECS = {
+ 'a0': (
+ StemSpec(filters=8, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=8,
+ expand_filters=(24,),
+ kernel_sizes=(K15,),
+ strides=(S12,)),
+ MovinetBlockSpec(
+ base_filters=32,
+ expand_filters=(80, 80, 80),
+ kernel_sizes=(K33, K33, K33),
+ strides=(S12, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=56,
+ expand_filters=(184, 112, 184),
+ kernel_sizes=(K53, K33, K33),
+ strides=(S12, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=56,
+ expand_filters=(184, 184, 184, 184),
+ kernel_sizes=(K53, K33, K33, K33),
+ strides=(S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=104,
+ expand_filters=(384, 280, 280, 344),
+ kernel_sizes=(K53, K15, K15, K15),
+ strides=(S12, S11, S11, S11)),
+ HeadSpec(project_filters=480, head_filters=2048),
+ ),
+ 'a1': (
+ StemSpec(filters=16, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=16,
+ expand_filters=(40, 40),
+ kernel_sizes=(K15, K33),
+ strides=(S12, S11)),
+ MovinetBlockSpec(
+ base_filters=40,
+ expand_filters=(96, 120, 96, 96),
+ kernel_sizes=(K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=64,
+ expand_filters=(216, 128, 216, 168, 216),
+ kernel_sizes=(K53, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=64,
+ expand_filters=(216, 216, 216, 128, 128, 216),
+ kernel_sizes=(K53, K33, K33, K33, K15, K33),
+ strides=(S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=136,
+ expand_filters=(456, 360, 360, 360, 456, 456, 544),
+ kernel_sizes=(K53, K15, K15, K15, K15, K33, K13),
+ strides=(S12, S11, S11, S11, S11, S11, S11)),
+ HeadSpec(project_filters=600, head_filters=2048),
+ ),
+ 'a2': (
+ StemSpec(filters=16, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=16,
+ expand_filters=(40, 40, 64),
+ kernel_sizes=(K15, K33, K33),
+ strides=(S12, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=40,
+ expand_filters=(96, 120, 96, 96, 120),
+ kernel_sizes=(K33, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=72,
+ expand_filters=(240, 160, 240, 192, 240),
+ kernel_sizes=(K53, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=72,
+ expand_filters=(240, 240, 240, 240, 144, 240),
+ kernel_sizes=(K53, K33, K33, K33, K15, K33),
+ strides=(S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=144,
+ expand_filters=(480, 384, 384, 480, 480, 480, 576),
+ kernel_sizes=(K53, K15, K15, K15, K15, K33, K13),
+ strides=(S12, S11, S11, S11, S11, S11, S11)),
+ HeadSpec(project_filters=640, head_filters=2048),
+ ),
+ 'a3': (
+ StemSpec(filters=16, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=16,
+ expand_filters=(40, 40, 64, 40),
+ kernel_sizes=(K15, K33, K33, K33),
+ strides=(S12, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=48,
+ expand_filters=(112, 144, 112, 112, 144, 144),
+ kernel_sizes=(K33, K33, K33, K15, K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=80,
+ expand_filters=(240, 152, 240, 192, 240),
+ kernel_sizes=(K53, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=88,
+ expand_filters=(264, 264, 264, 264, 160, 264, 264, 264),
+ kernel_sizes=(K53, K33, K33, K33, K15, K33, K33, K33),
+ strides=(S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=168,
+ expand_filters=(560, 448, 448, 560, 560, 560, 448, 448, 560, 672),
+ kernel_sizes=(K53, K15, K15, K15, K15, K33, K15, K15, K33, K13),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11, S11)),
+ HeadSpec(project_filters=744, head_filters=2048),
+ ),
+ 'a4': (
+ StemSpec(filters=24, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=24,
+ expand_filters=(64, 64, 96, 64, 96, 64),
+ kernel_sizes=(K15, K33, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=56,
+ expand_filters=(168, 168, 136, 136, 168, 168, 168, 136, 136),
+ kernel_sizes=(K33, K33, K33, K33, K33, K33, K33, K15, K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=96,
+ expand_filters=(320, 160, 320, 192, 320, 160, 320, 256, 320),
+ kernel_sizes=(K53, K33, K33, K33, K33, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=96,
+ expand_filters=(320, 320, 320, 320, 192, 320, 320, 192, 320, 320),
+ kernel_sizes=(K53, K33, K33, K33, K15, K33, K33, K33, K33, K33),
+ strides=(S11, S11, S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=192,
+ expand_filters=(640, 512, 512, 640, 640, 640, 512, 512, 640, 768,
+ 640, 640, 768),
+ kernel_sizes=(K53, K15, K15, K15, K15, K33, K15, K15, K15, K15, K15,
+ K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11,
+ S11)),
+ HeadSpec(project_filters=856, head_filters=2048),
+ ),
+ 'a5': (
+ StemSpec(filters=24, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=24,
+ expand_filters=(64, 64, 96, 64, 96, 64),
+ kernel_sizes=(K15, K15, K33, K33, K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=64,
+ expand_filters=(192, 152, 152, 152, 192, 192, 192, 152, 152, 192,
+ 192),
+ kernel_sizes=(K53, K33, K33, K33, K33, K33, K33, K33, K33, K33,
+ K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=112,
+ expand_filters=(376, 224, 376, 376, 296, 376, 224, 376, 376, 296,
+ 376, 376, 376),
+ kernel_sizes=(K53, K33, K33, K33, K33, K33, K33, K33, K33, K33, K33,
+ K33, K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11,
+ S11)),
+ MovinetBlockSpec(
+ base_filters=120,
+ expand_filters=(376, 376, 376, 376, 224, 376, 376, 224, 376, 376,
+ 376),
+ kernel_sizes=(K53, K33, K33, K33, K15, K33, K33, K33, K33, K33,
+ K33),
+ strides=(S11, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=224,
+ expand_filters=(744, 744, 600, 600, 744, 744, 744, 896, 600, 600,
+ 896, 744, 744, 896, 600, 600, 744, 744),
+ kernel_sizes=(K53, K33, K15, K15, K15, K15, K33, K15, K15, K15, K15,
+ K15, K33, K15, K15, K15, K15, K33),
+ strides=(S12, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11, S11,
+ S11, S11, S11, S11, S11, S11)),
+ HeadSpec(project_filters=992, head_filters=2048),
+ ),
+ 't0': (
+ StemSpec(filters=8, kernel_size=K13, strides=S12),
+ MovinetBlockSpec(
+ base_filters=8,
+ expand_filters=(16,),
+ kernel_sizes=(K15,),
+ strides=(S12,)),
+ MovinetBlockSpec(
+ base_filters=32,
+ expand_filters=(72, 72),
+ kernel_sizes=(K33, K15),
+ strides=(S12, S11)),
+ MovinetBlockSpec(
+ base_filters=56,
+ expand_filters=(112, 112, 112),
+ kernel_sizes=(K53, K15, K33),
+ strides=(S12, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=56,
+ expand_filters=(184, 184, 184, 184),
+ kernel_sizes=(K53, K15, K33, K33),
+ strides=(S11, S11, S11, S11)),
+ MovinetBlockSpec(
+ base_filters=104,
+ expand_filters=(344, 344, 344, 344),
+ kernel_sizes=(K53, K15, K15, K33),
+ strides=(S12, S11, S11, S11)),
+ HeadSpec(project_filters=240, head_filters=1024),
+ ),
+}
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class Movinet(tf.keras.Model):
+ """Class to build Movinet family model.
+
+ Reference: https://arxiv.org/pdf/2103.11511.pdf
+ """
+
+ def __init__(self,
+ model_id: str = 'a0',
+ causal: bool = False,
+ use_positional_encoding: bool = False,
+ conv_type: str = '3d',
+ se_type: str = '3d',
+ input_specs: Optional[tf.keras.layers.InputSpec] = None,
+ activation: str = 'swish',
+ gating_activation: str = 'sigmoid',
+ use_sync_bn: bool = True,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_initializer: str = 'HeNormal',
+ kernel_regularizer: Optional[str] = None,
+ bias_regularizer: Optional[str] = None,
+ stochastic_depth_drop_rate: float = 0.,
+ use_external_states: bool = False,
+ output_states: bool = True,
+ average_pooling_type: str = '3d',
+ **kwargs):
+ """MoViNet initialization function.
+
+ Args:
+ model_id: name of MoViNet backbone model.
+ causal: use causal mode, with CausalConv and CausalSE operations.
+ use_positional_encoding: if True, adds a positional encoding before
+ temporal convolutions and the cumulative global average pooling
+ layers.
+ conv_type: '3d', '2plus1d', or '3d_2plus1d'. '3d' configures the network
+ to use the default 3D convolution. '2plus1d' uses (2+1)D convolution
+ with Conv2D operations and 2D reshaping (e.g., a 5x3x3 kernel becomes
+ 3x3 followed by 5x1 conv). '3d_2plus1d' uses (2+1)D convolution with
+ Conv3D and no 2D reshaping (e.g., a 5x3x3 kernel becomes 1x3x3 followed
+ by 5x1x1 conv).
+ se_type: '3d', '2d', '2plus3d' or 'none'. '3d' uses the default 3D
+ spatiotemporal global average pooling for squeeze excitation. '2d'
+ uses 2D spatial global average pooling on each frame. '2plus3d'
+ concatenates both 3D and 2D global average pooling.
+ input_specs: the model input spec to use.
+ activation: name of the main activation function.
+ gating_activation: gating activation to use in squeeze excitation layers.
+ use_sync_bn: if True, use synchronized batch normalization.
+ norm_momentum: normalization momentum for the moving average.
+ norm_epsilon: small float added to variance to avoid dividing by
+ zero.
+ kernel_initializer: kernel_initializer for convolutional layers.
+ kernel_regularizer: tf.keras.regularizers.Regularizer object for Conv2D.
+ Defaults to None.
+ bias_regularizer: tf.keras.regularizers.Regularizer object for Conv2d.
+ Defaults to None.
+ stochastic_depth_drop_rate: the base rate for stochastic depth.
+ use_external_states: if True, expects states to be passed as additional
+ input.
+ output_states: if True, output intermediate states that can be used to run
+ the model in streaming mode. Inputting the output states of the
+ previous input clip with the current input clip will utilize a stream
+ buffer for streaming video.
+ average_pooling_type: The average pooling type. Currently supporting
+ ['3d', '2d', 'none'].
+ **kwargs: keyword arguments to be passed.
+ """
+ block_specs = BLOCK_SPECS[model_id]
+ if input_specs is None:
+ input_specs = tf.keras.layers.InputSpec(shape=[None, None, None, None, 3])
+
+ if conv_type not in ('3d', '2plus1d', '3d_2plus1d'):
+ raise ValueError('Unknown conv type: {}'.format(conv_type))
+ if se_type not in ('3d', '2d', '2plus3d', 'none'):
+ raise ValueError('Unknown squeeze excitation type: {}'.format(se_type))
+
+ self._model_id = model_id
+ self._block_specs = block_specs
+ self._causal = causal
+ self._use_positional_encoding = use_positional_encoding
+ self._conv_type = conv_type
+ self._se_type = se_type
+ self._input_specs = input_specs
+ self._use_sync_bn = use_sync_bn
+ self._activation = activation
+ self._gating_activation = gating_activation
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ if use_sync_bn:
+ self._norm = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._norm = tf.keras.layers.BatchNormalization
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._use_external_states = use_external_states
+ self._output_states = output_states
+ self._average_pooling_type = average_pooling_type
+
+ if self._use_external_states and not self._causal:
+ raise ValueError('External states should be used with causal mode.')
+ if not isinstance(block_specs[0], StemSpec):
+ raise ValueError(
+ 'Expected first spec to be StemSpec, got {}'.format(block_specs[0]))
+ if not isinstance(block_specs[-1], HeadSpec):
+ raise ValueError(
+ 'Expected final spec to be HeadSpec, got {}'.format(block_specs[-1]))
+ self._head_filters = block_specs[-1].head_filters
+
+ state_specs = None
+ if use_external_states:
+ self._set_dtype_policy(input_specs.dtype)
+ state_specs = self.initial_state_specs(input_specs.shape)
+
+ inputs, outputs = self._build_network(input_specs, state_specs=state_specs)
+
+ super(Movinet, self).__init__(inputs=inputs, outputs=outputs, **kwargs)
+
+ self._state_specs = state_specs
+
+ def _build_network(
+ self,
+ input_specs: tf.keras.layers.InputSpec,
+ state_specs: Optional[Mapping[str, tf.keras.layers.InputSpec]] = None,
+ ) -> Tuple[TensorMap, Union[TensorMap, Tuple[TensorMap, TensorMap]]]:
+ """Builds the model network.
+
+ Args:
+ input_specs: the model input spec to use.
+ state_specs: a dict mapping a state name to the corresponding state spec.
+ State names should match with the `state` input/output dict.
+
+ Returns:
+ Inputs and outputs as a tuple. Inputs are expected to be a dict with
+ base input and states. Outputs are expected to be a dict of endpoints
+ and (optional) output states.
+ """
+ state_specs = state_specs if state_specs is not None else {}
+
+ image_input = tf.keras.Input(shape=input_specs.shape[1:], name='inputs')
+
+ states = {
+ name: tf.keras.Input(shape=spec.shape[1:], dtype=spec.dtype, name=name)
+ for name, spec in state_specs.items()
+ }
+
+ inputs = {**states, 'image': image_input}
+ endpoints = {}
+
+ x = image_input
+
+ num_layers = sum(
+ len(block.expand_filters)
+ for block in self._block_specs
+ if isinstance(block, MovinetBlockSpec))
+ stochastic_depth_idx = 1
+ for block_idx, block in enumerate(self._block_specs):
+ if isinstance(block, StemSpec):
+ layer_obj = movinet_layers.Stem(
+ block.filters,
+ block.kernel_size,
+ block.strides,
+ conv_type=self._conv_type,
+ causal=self._causal,
+ activation=self._activation,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ batch_norm_layer=self._norm,
+ batch_norm_momentum=self._norm_momentum,
+ batch_norm_epsilon=self._norm_epsilon,
+ state_prefix='state_stem',
+ name='stem')
+ x, states = layer_obj(x, states=states)
+ endpoints['stem'] = x
+ elif isinstance(block, MovinetBlockSpec):
+ if not (len(block.expand_filters) == len(block.kernel_sizes) ==
+ len(block.strides)):
+ raise ValueError(
+ 'Lengths of block parameters differ: {}, {}, {}'.format(
+ len(block.expand_filters),
+ len(block.kernel_sizes),
+ len(block.strides)))
+ params = list(zip(block.expand_filters,
+ block.kernel_sizes,
+ block.strides))
+ for layer_idx, layer in enumerate(params):
+ stochastic_depth_drop_rate = (
+ self._stochastic_depth_drop_rate * stochastic_depth_idx /
+ num_layers)
+ expand_filters, kernel_size, strides = layer
+ name = f'block{block_idx-1}_layer{layer_idx}'
+ layer_obj = movinet_layers.MovinetBlock(
+ block.base_filters,
+ expand_filters,
+ kernel_size=kernel_size,
+ strides=strides,
+ causal=self._causal,
+ activation=self._activation,
+ gating_activation=self._gating_activation,
+ stochastic_depth_drop_rate=stochastic_depth_drop_rate,
+ conv_type=self._conv_type,
+ se_type=self._se_type,
+ use_positional_encoding=
+ self._use_positional_encoding and self._causal,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ batch_norm_layer=self._norm,
+ batch_norm_momentum=self._norm_momentum,
+ batch_norm_epsilon=self._norm_epsilon,
+ state_prefix=f'state_{name}',
+ name=name)
+ x, states = layer_obj(x, states=states)
+
+ endpoints[name] = x
+ stochastic_depth_idx += 1
+ elif isinstance(block, HeadSpec):
+ layer_obj = movinet_layers.Head(
+ project_filters=block.project_filters,
+ conv_type=self._conv_type,
+ activation=self._activation,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ batch_norm_layer=self._norm,
+ batch_norm_momentum=self._norm_momentum,
+ batch_norm_epsilon=self._norm_epsilon,
+ average_pooling_type=self._average_pooling_type,
+ state_prefix='state_head',
+ name='head')
+ x, states = layer_obj(x, states=states)
+ endpoints['head'] = x
+ else:
+ raise ValueError('Unknown block type {}'.format(block))
+
+ outputs = (endpoints, states) if self._output_states else endpoints
+
+ return inputs, outputs
+
+ def _get_initial_state_shapes(
+ self,
+ block_specs: Sequence[BlockSpec],
+ input_shape: Union[Sequence[int], tf.Tensor],
+ use_positional_encoding: bool = False) -> Dict[str, Sequence[int]]:
+ """Generates names and shapes for all input states.
+
+ Args:
+ block_specs: sequence of specs used for creating a model.
+ input_shape: the expected 5D shape of the image input.
+ use_positional_encoding: whether the model will use positional encoding.
+
+ Returns:
+ A dict mapping state names to state shapes.
+ """
+ def divide_resolution(shape, num_downsamples):
+ """Downsamples the dimension to calculate strided convolution shape."""
+ if shape is None:
+ return None
+ if isinstance(shape, tf.Tensor):
+ # Avoid using div and ceil to support tf lite
+ shape = tf.cast(shape, tf.float32)
+ resolution_divisor = 2 ** num_downsamples
+ resolution_multiplier = 0.5 ** num_downsamples
+ shape = ((shape + resolution_divisor - 1) * resolution_multiplier)
+ return tf.cast(shape, tf.int32)
+ else:
+ resolution_divisor = 2 ** num_downsamples
+ return math.ceil(shape / resolution_divisor)
+
+ states = {}
+ num_downsamples = 0
+
+ for block_idx, block in enumerate(block_specs):
+ if isinstance(block, StemSpec):
+ if block.kernel_size[0] > 1:
+ states['state_stem_stream_buffer'] = (
+ input_shape[0],
+ input_shape[1],
+ divide_resolution(input_shape[2], num_downsamples),
+ divide_resolution(input_shape[3], num_downsamples),
+ block.filters,
+ )
+ num_downsamples += 1
+ elif isinstance(block, MovinetBlockSpec):
+ block_idx -= 1
+ params = list(zip(
+ block.expand_filters,
+ block.kernel_sizes,
+ block.strides))
+ for layer_idx, layer in enumerate(params):
+ expand_filters, kernel_size, strides = layer
+
+ # If we use a 2D kernel, we apply spatial downsampling
+ # before the buffer.
+ if (tuple(strides[1:3]) != (1, 1) and
+ self._conv_type in ['2plus1d', '3d_2plus1d']):
+ num_downsamples += 1
+
+ prefix = f'state_block{block_idx}_layer{layer_idx}'
+
+ if kernel_size[0] > 1:
+ states[f'{prefix}_stream_buffer'] = (
+ input_shape[0],
+ kernel_size[0] - 1,
+ divide_resolution(input_shape[2], num_downsamples),
+ divide_resolution(input_shape[3], num_downsamples),
+ expand_filters,
+ )
+
+ if '3d' in self._se_type:
+ states[f'{prefix}_pool_buffer'] = (
+ input_shape[0], 1, 1, 1, expand_filters,
+ )
+ states[f'{prefix}_pool_frame_count'] = (1,)
+
+ if use_positional_encoding:
+ name = f'{prefix}_pos_enc_frame_count'
+ states[name] = (1,)
+
+ if strides[1] != strides[2]:
+ raise ValueError('Strides must match in the spatial dimensions, '
+ 'got {}'.format(strides))
+
+ # If we use a 3D kernel, we apply spatial downsampling
+ # after the buffer.
+ if (tuple(strides[1:3]) != (1, 1) and
+ self._conv_type not in ['2plus1d', '3d_2plus1d']):
+ num_downsamples += 1
+ elif isinstance(block, HeadSpec):
+ states['state_head_pool_buffer'] = (
+ input_shape[0], 1, 1, 1, block.project_filters,
+ )
+ states['state_head_pool_frame_count'] = (1,)
+
+ return states
+
+ def _get_state_dtype(self, name: str) -> str:
+ """Returns the dtype associated with a state."""
+ if 'frame_count' in name:
+ return 'int32'
+ return self.dtype
+
+ def initial_state_specs(
+ self, input_shape: Sequence[int]) -> Dict[str, tf.keras.layers.InputSpec]:
+ """Creates a mapping of state name to InputSpec from the input shape."""
+ state_shapes = self._get_initial_state_shapes(
+ self._block_specs,
+ input_shape,
+ use_positional_encoding=self._use_positional_encoding)
+
+ return {
+ name: tf.keras.layers.InputSpec(
+ shape=shape, dtype=self._get_state_dtype(name))
+ for name, shape in state_shapes.items()
+ }
+
+ def init_states(self, input_shape: Sequence[int]) -> Dict[str, tf.Tensor]:
+ """Returns initial states for the first call in steaming mode."""
+ state_shapes = self._get_initial_state_shapes(
+ self._block_specs,
+ input_shape,
+ use_positional_encoding=self._use_positional_encoding)
+
+ states = {
+ name: tf.zeros(shape, dtype=self._get_state_dtype(name))
+ for name, shape in state_shapes.items()
+ }
+ return states
+
+ @property
+ def use_external_states(self) -> bool:
+ """Whether this model is expecting input states as additional input."""
+ return self._use_external_states
+
+ @property
+ def head_filters(self):
+ """The number of filters expected to be in the head classifer layer."""
+ return self._head_filters
+
+ @property
+ def conv_type(self):
+ """The expected convolution type (see __init__ for more details)."""
+ return self._conv_type
+
+ def get_config(self):
+ config_dict = {
+ 'model_id': self._model_id,
+ 'causal': self._causal,
+ 'use_positional_encoding': self._use_positional_encoding,
+ 'conv_type': self._conv_type,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'stochastic_depth_drop_rate': self._stochastic_depth_drop_rate,
+ 'use_external_states': self._use_external_states,
+ 'output_states': self._output_states,
+ }
+ return config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
+
+
+@factory.register_backbone_builder('movinet')
+def build_movinet(
+ input_specs: tf.keras.layers.InputSpec,
+ backbone_config: hyperparams.Config,
+ norm_activation_config: hyperparams.Config,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ """Builds MoViNet backbone from a config."""
+ backbone_type = backbone_config.type
+ backbone_cfg = backbone_config.get()
+ if backbone_type != 'movinet':
+ raise ValueError(f'Inconsistent backbone type {backbone_type}')
+ if norm_activation_config.activation is not None:
+ logging.warn('norm_activation is not used in MoViNets, but specified: '
+ '%s', norm_activation_config.activation)
+ logging.warn('norm_activation is ignored.')
+
+ return Movinet(
+ model_id=backbone_cfg.model_id,
+ causal=backbone_cfg.causal,
+ use_positional_encoding=backbone_cfg.use_positional_encoding,
+ conv_type=backbone_cfg.conv_type,
+ se_type=backbone_cfg.se_type,
+ input_specs=input_specs,
+ activation=backbone_cfg.activation,
+ gating_activation=backbone_cfg.gating_activation,
+ output_states=backbone_cfg.output_states,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_regularizer=l2_regularizer,
+ stochastic_depth_drop_rate=backbone_cfg.stochastic_depth_drop_rate,
+ use_external_states=backbone_cfg.use_external_states,
+ average_pooling_type=backbone_cfg.average_pooling_type)
diff --git a/official/vision/beta/projects/movinet/modeling/movinet_layers.py b/official/projects/movinet/modeling/movinet_layers.py
similarity index 94%
rename from official/vision/beta/projects/movinet/modeling/movinet_layers.py
rename to official/projects/movinet/modeling/movinet_layers.py
index 38179e7b3f748bb464bea7e2f5ee5f9284e6b424..af81c4cabb3a28d552411e21502a2b8efd5ec1f8 100644
--- a/official/vision/beta/projects/movinet/modeling/movinet_layers.py
+++ b/official/projects/movinet/modeling/movinet_layers.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Contains common building blocks for MoViNets.
Reference: https://arxiv.org/pdf/2103.11511.pdf
@@ -23,7 +22,7 @@ from typing import Any, Mapping, Optional, Sequence, Tuple, Union
import tensorflow as tf
from official.modeling import tf_utils
-from official.vision.beta.modeling.layers import nn_layers
+from official.vision.modeling.layers import nn_layers
# Default kernel weight decay that may be overridden
KERNEL_WEIGHT_DECAY = 1.5e-5
@@ -93,10 +92,9 @@ class MobileConv2D(tf.keras.layers.Layer):
data_format: Optional[str] = None,
dilation_rate: Union[int, Sequence[int]] = (1, 1),
groups: int = 1,
- activation: Optional[nn_layers.Activation] = None,
use_bias: bool = True,
- kernel_initializer: tf.keras.initializers.Initializer = 'glorot_uniform',
- bias_initializer: tf.keras.initializers.Initializer = 'zeros',
+ kernel_initializer: str = 'glorot_uniform',
+ bias_initializer: str = 'zeros',
kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
activity_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
@@ -105,6 +103,8 @@ class MobileConv2D(tf.keras.layers.Layer):
use_depthwise: bool = False,
use_temporal: bool = False,
use_buffered_input: bool = False, # pytype: disable=annotation-type-mismatch # typed-keras
+ batch_norm_op: Optional[Any] = None,
+ activation_op: Optional[Any] = None,
**kwargs): # pylint: disable=g-doc-args
"""Initializes mobile conv2d.
@@ -117,6 +117,10 @@ class MobileConv2D(tf.keras.layers.Layer):
use_buffered_input: if True, the input is expected to be padded
beforehand. In effect, calling this layer will use 'valid' padding on
the temporal dimension to simulate 'causal' padding.
+ batch_norm_op: A callable object of batch norm layer. If None, no batch
+ norm will be applied after the convolution.
+ activation_op: A callabel object of activation layer. If None, no
+ activation will be applied after the convolution.
**kwargs: keyword arguments to be passed to this layer.
Returns:
@@ -130,7 +134,6 @@ class MobileConv2D(tf.keras.layers.Layer):
self._data_format = data_format
self._dilation_rate = dilation_rate
self._groups = groups
- self._activation = activation
self._use_bias = use_bias
self._kernel_initializer = kernel_initializer
self._bias_initializer = bias_initializer
@@ -142,6 +145,8 @@ class MobileConv2D(tf.keras.layers.Layer):
self._use_depthwise = use_depthwise
self._use_temporal = use_temporal
self._use_buffered_input = use_buffered_input
+ self._batch_norm_op = batch_norm_op
+ self._activation_op = activation_op
kernel_size = normalize_tuple(kernel_size, 2, 'kernel_size')
@@ -156,7 +161,6 @@ class MobileConv2D(tf.keras.layers.Layer):
depth_multiplier=1,
data_format=data_format,
dilation_rate=dilation_rate,
- activation=activation,
use_bias=use_bias,
depthwise_initializer=kernel_initializer,
bias_initializer=bias_initializer,
@@ -175,7 +179,6 @@ class MobileConv2D(tf.keras.layers.Layer):
data_format=data_format,
dilation_rate=dilation_rate,
groups=groups,
- activation=activation,
use_bias=use_bias,
kernel_initializer=kernel_initializer,
bias_initializer=bias_initializer,
@@ -196,7 +199,6 @@ class MobileConv2D(tf.keras.layers.Layer):
'data_format': self._data_format,
'dilation_rate': self._dilation_rate,
'groups': self._groups,
- 'activation': self._activation,
'use_bias': self._use_bias,
'kernel_initializer': self._kernel_initializer,
'bias_initializer': self._bias_initializer,
@@ -229,6 +231,10 @@ class MobileConv2D(tf.keras.layers.Layer):
x = tf.reshape(inputs, input_shape)
x = self._conv(x)
+ if self._batch_norm_op is not None:
+ x = self._batch_norm_op(x)
+ if self._activation_op is not None:
+ x = self._activation_op(x)
if self._use_temporal:
output_shape = [
@@ -357,8 +363,20 @@ class ConvBlock(tf.keras.layers.Layer):
padding = 'causal' if self._causal else 'same'
self._groups = input_shape[-1] if self._depthwise else 1
- self._conv_temporal = None
+ self._batch_norm = None
+ self._batch_norm_temporal = None
+ if self._use_batch_norm:
+ self._batch_norm = self._batch_norm_layer(
+ momentum=self._batch_norm_momentum,
+ epsilon=self._batch_norm_epsilon,
+ name='bn')
+ if self._conv_type != '3d' and self._kernel_size[0] > 1:
+ self._batch_norm_temporal = self._batch_norm_layer(
+ momentum=self._batch_norm_momentum,
+ epsilon=self._batch_norm_epsilon,
+ name='bn_temporal')
+ self._conv_temporal = None
if self._conv_type == '3d_2plus1d' and self._kernel_size[0] > 1:
self._conv = nn_layers.Conv3D(
self._filters,
@@ -394,6 +412,8 @@ class ConvBlock(tf.keras.layers.Layer):
kernel_initializer=self._kernel_initializer,
kernel_regularizer=self._kernel_regularizer,
use_buffered_input=False,
+ batch_norm_op=self._batch_norm,
+ activation_op=self._activation_layer,
name='conv2d')
if self._kernel_size[0] > 1:
self._conv_temporal = MobileConv2D(
@@ -408,6 +428,8 @@ class ConvBlock(tf.keras.layers.Layer):
kernel_initializer=self._kernel_initializer,
kernel_regularizer=self._kernel_regularizer,
use_buffered_input=self._use_buffered_input,
+ batch_norm_op=self._batch_norm_temporal,
+ activation_op=self._activation_layer,
name='conv2d_temporal')
else:
self._conv = nn_layers.Conv3D(
@@ -422,37 +444,26 @@ class ConvBlock(tf.keras.layers.Layer):
use_buffered_input=self._use_buffered_input,
name='conv3d')
- self._batch_norm = None
- self._batch_norm_temporal = None
-
- if self._use_batch_norm:
- self._batch_norm = self._batch_norm_layer(
- momentum=self._batch_norm_momentum,
- epsilon=self._batch_norm_epsilon,
- name='bn')
- if self._conv_type != '3d' and self._conv_temporal is not None:
- self._batch_norm_temporal = self._batch_norm_layer(
- momentum=self._batch_norm_momentum,
- epsilon=self._batch_norm_epsilon,
- name='bn_temporal')
-
super(ConvBlock, self).build(input_shape)
def call(self, inputs):
"""Calls the layer with the given inputs."""
x = inputs
+ # bn_op and activation_op are folded into the '2plus1d' conv layer so that
+ # we do not explicitly call them here.
+ # TODO(lzyuan): clean the conv layers api once the models are re-trained.
x = self._conv(x)
- if self._batch_norm is not None:
+ if self._batch_norm is not None and self._conv_type != '2plus1d':
x = self._batch_norm(x)
- if self._activation_layer is not None:
+ if self._activation_layer is not None and self._conv_type != '2plus1d':
x = self._activation_layer(x)
if self._conv_temporal is not None:
x = self._conv_temporal(x)
- if self._batch_norm_temporal is not None:
+ if self._batch_norm_temporal is not None and self._conv_type != '2plus1d':
x = self._batch_norm_temporal(x)
- if self._activation_layer is not None:
+ if self._activation_layer is not None and self._conv_type != '2plus1d':
x = self._activation_layer(x)
return x
@@ -640,10 +651,13 @@ class StreamConvBlock(ConvBlock):
if self._conv_temporal is None and self._stream_buffer is not None:
x, states = self._stream_buffer(x, states=states)
+ # bn_op and activation_op are folded into the '2plus1d' conv layer so that
+ # we do not explicitly call them here.
+ # TODO(lzyuan): clean the conv layers api once the models are re-trained.
x = self._conv(x)
- if self._batch_norm is not None:
+ if self._batch_norm is not None and self._conv_type != '2plus1d':
x = self._batch_norm(x)
- if self._activation_layer is not None:
+ if self._activation_layer is not None and self._conv_type != '2plus1d':
x = self._activation_layer(x)
if self._conv_temporal is not None:
@@ -653,9 +667,9 @@ class StreamConvBlock(ConvBlock):
x, states = self._stream_buffer(x, states=states)
x = self._conv_temporal(x)
- if self._batch_norm_temporal is not None:
+ if self._batch_norm_temporal is not None and self._conv_type != '2plus1d':
x = self._batch_norm_temporal(x)
- if self._activation_layer is not None:
+ if self._activation_layer is not None and self._conv_type != '2plus1d':
x = self._activation_layer(x)
return x, states
@@ -788,12 +802,14 @@ class StreamSqueezeExcitation(tf.keras.layers.Layer):
states = dict(states) if states is not None else {}
if self._se_type == '3d':
- x, states = self._spatiotemporal_pool(inputs, states=states)
+ x, states = self._spatiotemporal_pool(
+ inputs, states=states, output_states=True)
elif self._se_type == '2d':
x = self._spatial_pool(inputs)
elif self._se_type == '2plus3d':
x_space = self._spatial_pool(inputs)
- x, states = self._spatiotemporal_pool(x_space, states=states)
+ x, states = self._spatiotemporal_pool(
+ x_space, states=states, output_states=True)
if not self._causal:
x = tf.tile(x, [1, tf.shape(inputs)[1], 1, 1, 1])
@@ -885,7 +901,8 @@ class MobileBottleneck(tf.keras.layers.Layer):
x = self._expansion_layer(inputs)
x, states = self._feature_layer(x, states=states)
- x, states = self._attention_layer(x, states=states)
+ if self._attention_layer is not None:
+ x, states = self._attention_layer(x, states=states)
x = self._projection_layer(x)
# Add identity so that the ops are ordered as written. This is useful for,
@@ -1136,18 +1153,20 @@ class MovinetBlock(tf.keras.layers.Layer):
batch_norm_momentum=self._batch_norm_momentum,
batch_norm_epsilon=self._batch_norm_epsilon,
name='projection')
- self._attention = StreamSqueezeExcitation(
- se_hidden_filters,
- se_type=se_type,
- activation=activation,
- gating_activation=gating_activation,
- causal=self._causal,
- conv_type=conv_type,
- use_positional_encoding=use_positional_encoding,
- kernel_initializer=kernel_initializer,
- kernel_regularizer=kernel_regularizer,
- state_prefix=state_prefix,
- name='se')
+ self._attention = None
+ if se_type != 'none':
+ self._attention = StreamSqueezeExcitation(
+ se_hidden_filters,
+ se_type=se_type,
+ activation=activation,
+ gating_activation=gating_activation,
+ causal=self._causal,
+ conv_type=conv_type,
+ use_positional_encoding=use_positional_encoding,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer,
+ state_prefix=state_prefix,
+ name='se')
def get_config(self):
"""Returns a dictionary containing the config used for initialization."""
@@ -1345,6 +1364,7 @@ class Head(tf.keras.layers.Layer):
tf.keras.layers.BatchNormalization,
batch_norm_momentum: float = 0.99,
batch_norm_epsilon: float = 1e-3,
+ average_pooling_type: str = '3d',
state_prefix: Optional[str] = None, # pytype: disable=annotation-type-mismatch # typed-keras
**kwargs):
"""Implementation for video model head.
@@ -1361,6 +1381,8 @@ class Head(tf.keras.layers.Layer):
batch_norm_layer: class to use for batch norm.
batch_norm_momentum: momentum of the batch norm operation.
batch_norm_epsilon: epsilon of the batch norm operation.
+ average_pooling_type: The average pooling type. Currently supporting
+ ['3d', '2d', 'none'].
state_prefix: a prefix string to identify states.
**kwargs: keyword arguments to be passed to this layer.
"""
@@ -1387,8 +1409,16 @@ class Head(tf.keras.layers.Layer):
batch_norm_momentum=self._batch_norm_momentum,
batch_norm_epsilon=self._batch_norm_epsilon,
name='project')
- self._pool = nn_layers.GlobalAveragePool3D(
- keepdims=True, causal=False, state_prefix=state_prefix)
+ if average_pooling_type.lower() == '3d':
+ self._pool = nn_layers.GlobalAveragePool3D(
+ keepdims=True, causal=False, state_prefix=state_prefix)
+ elif average_pooling_type.lower() == '2d':
+ self._pool = nn_layers.SpatialAveragePool3D(keepdims=True)
+ elif average_pooling_type == 'none':
+ self._pool = None
+ else:
+ raise ValueError(
+ '%s average_pooling_type is not supported.' % average_pooling_type)
def get_config(self):
"""Returns a dictionary containing the config used for initialization."""
@@ -1422,7 +1452,11 @@ class Head(tf.keras.layers.Layer):
"""
states = dict(states) if states is not None else {}
x = self._project(inputs)
- return self._pool(x, states=states)
+ if self._pool is not None:
+ outputs = self._pool(x, states=states, output_states=True)
+ else:
+ outputs = (x, states)
+ return outputs
@tf.keras.utils.register_keras_serializable(package='Vision')
diff --git a/official/vision/beta/projects/movinet/modeling/movinet_layers_test.py b/official/projects/movinet/modeling/movinet_layers_test.py
similarity index 80%
rename from official/vision/beta/projects/movinet/modeling/movinet_layers_test.py
rename to official/projects/movinet/modeling/movinet_layers_test.py
index 472ad167571a56473f65f395b9ce2acdac75481f..b4027043c1acaf5a0cc71c8566acadda46c64eb6 100644
--- a/official/vision/beta/projects/movinet/modeling/movinet_layers_test.py
+++ b/official/projects/movinet/modeling/movinet_layers_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,14 +12,13 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for movinet_layers.py."""
from absl.testing import parameterized
import tensorflow as tf
-from official.vision.beta.modeling.layers import nn_layers
-from official.vision.beta.projects.movinet.modeling import movinet_layers
+from official.projects.movinet.modeling import movinet_layers
+from official.vision.modeling.layers import nn_layers
class MovinetLayersTest(parameterized.TestCase, tf.test.TestCase):
@@ -64,6 +63,72 @@ class MovinetLayersTest(parameterized.TestCase, tf.test.TestCase):
self.assertEqual(predicted.shape, expected.shape)
self.assertAllClose(predicted, expected)
+ def test_mobile_conv2d_bn(self):
+ batch_norm_op = tf.keras.layers.BatchNormalization(
+ momentum=0.9,
+ epsilon=1.,
+ name='bn')
+ conv2d = movinet_layers.MobileConv2D(
+ filters=3,
+ kernel_size=(3, 3),
+ strides=(1, 1),
+ padding='same',
+ kernel_initializer='ones',
+ use_bias=False,
+ use_depthwise=False,
+ use_temporal=False,
+ use_buffered_input=True,
+ batch_norm_op=batch_norm_op,
+ )
+
+ inputs = tf.ones([1, 2, 2, 2, 3])
+
+ predicted = conv2d(inputs)
+
+ expected = tf.constant(
+ [[[[[8.48528, 8.48528, 8.48528],
+ [8.48528, 8.48528, 8.48528]],
+ [[8.48528, 8.48528, 8.48528],
+ [8.48528, 8.48528, 8.48528]]],
+ [[[8.48528, 8.48528, 8.48528],
+ [8.48528, 8.48528, 8.48528]],
+ [[8.48528, 8.48528, 8.48528],
+ [8.48528, 8.48528, 8.48528]]]]])
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected)
+
+ def test_mobile_conv2d_activation(self):
+ conv2d = movinet_layers.MobileConv2D(
+ filters=3,
+ kernel_size=(3, 3),
+ strides=(1, 1),
+ padding='same',
+ kernel_initializer='ones',
+ use_bias=False,
+ use_depthwise=False,
+ use_temporal=False,
+ use_buffered_input=True,
+ activation_op=tf.nn.relu6,
+ )
+
+ inputs = tf.ones([1, 2, 2, 2, 3])
+
+ predicted = conv2d(inputs)
+
+ expected = tf.constant(
+ [[[[[6., 6., 6.],
+ [6., 6., 6.]],
+ [[6., 6., 6.],
+ [6., 6., 6.]]],
+ [[[6., 6., 6.],
+ [6., 6., 6.]],
+ [[6., 6., 6.],
+ [6., 6., 6.]]]]])
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected)
+
def test_mobile_conv2d_temporal(self):
conv2d = movinet_layers.MobileConv2D(
filters=3,
@@ -378,6 +443,35 @@ class MovinetLayersTest(parameterized.TestCase, tf.test.TestCase):
self.assertEqual(predicted.shape, expected.shape)
self.assertAllClose(predicted, expected)
+ def test_stream_movinet_block_none_se(self):
+ block = movinet_layers.MovinetBlock(
+ out_filters=3,
+ expand_filters=6,
+ kernel_size=(3, 3, 3),
+ strides=(1, 2, 2),
+ causal=True,
+ se_type='none',
+ state_prefix='test',
+ )
+
+ inputs = tf.range(4, dtype=tf.float32) + 1.
+ inputs = tf.reshape(inputs, [1, 4, 1, 1, 1])
+ inputs = tf.tile(inputs, [1, 1, 2, 1, 3])
+ expected, expected_states = block(inputs)
+
+ for num_splits in [1, 2, 4]:
+ frames = tf.split(inputs, inputs.shape[1] // num_splits, axis=1)
+ states = {}
+ predicted = []
+ for frame in frames:
+ x, states = block(frame, states=states)
+ predicted.append(x)
+ predicted = tf.concat(predicted, axis=1)
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected)
+ self.assertAllEqual(list(expected_states.keys()), ['test_stream_buffer'])
+
def test_stream_classifier_head(self):
head = movinet_layers.Head(project_filters=5)
classifier_head = movinet_layers.ClassifierHead(
diff --git a/official/vision/beta/projects/movinet/modeling/movinet_model.py b/official/projects/movinet/modeling/movinet_model.py
similarity index 88%
rename from official/vision/beta/projects/movinet/modeling/movinet_model.py
rename to official/projects/movinet/modeling/movinet_model.py
index e269306c0c1cf960d73c9c37f4daa36119c9ec9e..0b527f7c159a569358a6a3c52f91366684cc0069 100644
--- a/official/vision/beta/projects/movinet/modeling/movinet_model.py
+++ b/official/projects/movinet/modeling/movinet_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,10 +21,10 @@ from typing import Any, Dict, Mapping, Optional, Sequence, Tuple, Union
from absl import logging
import tensorflow as tf
-from official.vision.beta.modeling import backbones
-from official.vision.beta.modeling import factory_3d as model_factory
-from official.vision.beta.projects.movinet.configs import movinet as cfg
-from official.vision.beta.projects.movinet.modeling import movinet_layers
+from official.projects.movinet.configs import movinet as cfg
+from official.projects.movinet.modeling import movinet_layers
+from official.vision.modeling import backbones
+from official.vision.modeling import factory_3d as model_factory
@tf.keras.utils.register_keras_serializable(package='Vision')
@@ -88,14 +88,13 @@ class MovinetClassifier(tf.keras.Model):
# Move backbone after super() call so Keras is happy
self._backbone = backbone
- def _build_network(
+ def _build_backbone(
self,
backbone: tf.keras.Model,
input_specs: Mapping[str, tf.keras.layers.InputSpec],
state_specs: Optional[Mapping[str, tf.keras.layers.InputSpec]] = None,
- ) -> Tuple[Mapping[str, tf.keras.Input], Union[Tuple[Mapping[ # pytype: disable=invalid-annotation # typed-keras
- str, tf.Tensor], Mapping[str, tf.Tensor]], Mapping[str, tf.Tensor]]]:
- """Builds the model network.
+ ) -> Tuple[Mapping[str, Any], Any, Any]:
+ """Builds the backbone network and gets states and endpoints.
Args:
backbone: the model backbone.
@@ -104,9 +103,9 @@ class MovinetClassifier(tf.keras.Model):
layer, will overwrite the contents of the buffer(s).
Returns:
- Inputs and outputs as a tuple. Inputs are expected to be a dict with
- base input and states. Outputs are expected to be a dict of endpoints
- and (optionally) output states.
+ inputs: a dict of input specs.
+ endpoints: a dict of model endpoints.
+ states: a dict of model states.
"""
state_specs = state_specs if state_specs is not None else {}
@@ -145,7 +144,30 @@ class MovinetClassifier(tf.keras.Model):
mismatched_shapes))
else:
endpoints, states = backbone(inputs)
+ return inputs, endpoints, states
+ def _build_network(
+ self,
+ backbone: tf.keras.Model,
+ input_specs: Mapping[str, tf.keras.layers.InputSpec],
+ state_specs: Optional[Mapping[str, tf.keras.layers.InputSpec]] = None,
+ ) -> Tuple[Mapping[str, tf.keras.Input], Union[Tuple[Mapping[ # pytype: disable=invalid-annotation # typed-keras
+ str, tf.Tensor], Mapping[str, tf.Tensor]], Mapping[str, tf.Tensor]]]:
+ """Builds the model network.
+
+ Args:
+ backbone: the model backbone.
+ input_specs: the model input spec to use.
+ state_specs: a dict of states such that, if any of the keys match for a
+ layer, will overwrite the contents of the buffer(s).
+
+ Returns:
+ Inputs and outputs as a tuple. Inputs are expected to be a dict with
+ base input and states. Outputs are expected to be a dict of endpoints
+ and (optionally) output states.
+ """
+ inputs, endpoints, states = self._build_backbone(
+ backbone=backbone, input_specs=input_specs, state_specs=state_specs)
x = endpoints['head']
x = movinet_layers.ClassifierHead(
diff --git a/official/vision/beta/projects/movinet/modeling/movinet_model_test.py b/official/projects/movinet/modeling/movinet_model_test.py
similarity index 97%
rename from official/vision/beta/projects/movinet/modeling/movinet_model_test.py
rename to official/projects/movinet/modeling/movinet_model_test.py
index 7075b487ebce111a59b7a0321673429f12418b28..3187e38a3f62143dc5f7134d524385d91e902041 100644
--- a/official/vision/beta/projects/movinet/modeling/movinet_model_test.py
+++ b/official/projects/movinet/modeling/movinet_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,15 +12,14 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for movinet_model.py."""
from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.projects.movinet.modeling import movinet
-from official.vision.beta.projects.movinet.modeling import movinet_model
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
class MovinetModelTest(parameterized.TestCase, tf.test.TestCase):
diff --git a/official/projects/movinet/modeling/movinet_test.py b/official/projects/movinet/modeling/movinet_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..0b082c00a62b42a4f7accacc928c47eadb4c4192
--- /dev/null
+++ b/official/projects/movinet/modeling/movinet_test.py
@@ -0,0 +1,225 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for movinet.py."""
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.movinet.modeling import movinet
+
+
+class MoViNetTest(parameterized.TestCase, tf.test.TestCase):
+
+ def test_network_creation(self):
+ """Test creation of MoViNet family models."""
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ network = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ )
+ inputs = tf.keras.Input(shape=(8, 128, 128, 3), batch_size=1)
+ endpoints, states = network(inputs)
+
+ self.assertAllEqual(endpoints['stem'].shape, [1, 8, 64, 64, 8])
+ self.assertAllEqual(endpoints['block0_layer0'].shape, [1, 8, 32, 32, 8])
+ self.assertAllEqual(endpoints['block1_layer0'].shape, [1, 8, 16, 16, 32])
+ self.assertAllEqual(endpoints['block2_layer0'].shape, [1, 8, 8, 8, 56])
+ self.assertAllEqual(endpoints['block3_layer0'].shape, [1, 8, 8, 8, 56])
+ self.assertAllEqual(endpoints['block4_layer0'].shape, [1, 8, 4, 4, 104])
+ self.assertAllEqual(endpoints['head'].shape, [1, 1, 1, 1, 480])
+
+ self.assertNotEmpty(states)
+
+ def test_network_with_states(self):
+ """Test creation of MoViNet family models with states."""
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ backbone = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ use_external_states=True,
+ )
+ inputs = tf.ones([1, 8, 128, 128, 3])
+
+ init_states = backbone.init_states(tf.shape(inputs))
+ endpoints, new_states = backbone({**init_states, 'image': inputs})
+
+ self.assertAllEqual(endpoints['stem'].shape, [1, 8, 64, 64, 8])
+ self.assertAllEqual(endpoints['block0_layer0'].shape, [1, 8, 32, 32, 8])
+ self.assertAllEqual(endpoints['block1_layer0'].shape, [1, 8, 16, 16, 32])
+ self.assertAllEqual(endpoints['block2_layer0'].shape, [1, 8, 8, 8, 56])
+ self.assertAllEqual(endpoints['block3_layer0'].shape, [1, 8, 8, 8, 56])
+ self.assertAllEqual(endpoints['block4_layer0'].shape, [1, 8, 4, 4, 104])
+ self.assertAllEqual(endpoints['head'].shape, [1, 1, 1, 1, 480])
+
+ self.assertNotEmpty(init_states)
+ self.assertNotEmpty(new_states)
+
+ def test_movinet_stream(self):
+ """Test if the backbone can be run in streaming mode."""
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ backbone = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ use_external_states=True,
+ )
+ inputs = tf.ones([1, 5, 128, 128, 3])
+
+ init_states = backbone.init_states(tf.shape(inputs))
+ expected_endpoints, _ = backbone({**init_states, 'image': inputs})
+
+ frames = tf.split(inputs, inputs.shape[1], axis=1)
+
+ states = init_states
+ for frame in frames:
+ output, states = backbone({**states, 'image': frame})
+ predicted_endpoints = output
+
+ predicted = predicted_endpoints['head']
+
+ # The expected final output is simply the mean across frames
+ expected = expected_endpoints['head']
+ expected = tf.reduce_mean(expected, 1, keepdims=True)
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected, 1e-5, 1e-5)
+
+ def test_movinet_stream_nse(self):
+ """Test if the backbone can be run in streaming mode w/o SE layer."""
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ backbone = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ use_external_states=True,
+ se_type='none',
+ )
+ inputs = tf.ones([1, 5, 128, 128, 3])
+
+ init_states = backbone.init_states(tf.shape(inputs))
+ expected_endpoints, _ = backbone({**init_states, 'image': inputs})
+
+ frames = tf.split(inputs, inputs.shape[1], axis=1)
+
+ states = init_states
+ for frame in frames:
+ output, states = backbone({**states, 'image': frame})
+ predicted_endpoints = output
+
+ predicted = predicted_endpoints['head']
+
+ # The expected final output is simply the mean across frames
+ expected = expected_endpoints['head']
+ expected = tf.reduce_mean(expected, 1, keepdims=True)
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected, 1e-5, 1e-5)
+
+ # Check contents in the states dictionary.
+ state_keys = list(init_states.keys())
+ self.assertIn('state_head_pool_buffer', state_keys)
+ self.assertIn('state_head_pool_frame_count', state_keys)
+ state_keys.remove('state_head_pool_buffer')
+ state_keys.remove('state_head_pool_frame_count')
+ # From now on, there are only 'stream_buffer' for the convolutions.
+ for state_key in state_keys:
+ self.assertIn(
+ 'stream_buffer', state_key,
+ msg=f'Expecting stream_buffer only, found {state_key}')
+
+ def test_movinet_2plus1d_stream(self):
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ backbone = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ conv_type='2plus1d',
+ use_external_states=True,
+ )
+ inputs = tf.ones([1, 5, 128, 128, 3])
+
+ init_states = backbone.init_states(tf.shape(inputs))
+ expected_endpoints, _ = backbone({**init_states, 'image': inputs})
+
+ frames = tf.split(inputs, inputs.shape[1], axis=1)
+
+ states = init_states
+ for frame in frames:
+ output, states = backbone({**states, 'image': frame})
+ predicted_endpoints = output
+
+ predicted = predicted_endpoints['head']
+
+ # The expected final output is simply the mean across frames
+ expected = expected_endpoints['head']
+ expected = tf.reduce_mean(expected, 1, keepdims=True)
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected, 1e-5, 1e-5)
+
+ def test_movinet_3d_2plus1d_stream(self):
+ tf.keras.backend.set_image_data_format('channels_last')
+
+ backbone = movinet.Movinet(
+ model_id='a0',
+ causal=True,
+ conv_type='3d_2plus1d',
+ use_external_states=True,
+ )
+ inputs = tf.ones([1, 5, 128, 128, 3])
+
+ init_states = backbone.init_states(tf.shape(inputs))
+ expected_endpoints, _ = backbone({**init_states, 'image': inputs})
+
+ frames = tf.split(inputs, inputs.shape[1], axis=1)
+
+ states = init_states
+ for frame in frames:
+ output, states = backbone({**states, 'image': frame})
+ predicted_endpoints = output
+
+ predicted = predicted_endpoints['head']
+
+ # The expected final output is simply the mean across frames
+ expected = expected_endpoints['head']
+ expected = tf.reduce_mean(expected, 1, keepdims=True)
+
+ self.assertEqual(predicted.shape, expected.shape)
+ self.assertAllClose(predicted, expected, 1e-5, 1e-5)
+
+ def test_serialize_deserialize(self):
+ # Create a network object that sets all of its config options.
+ kwargs = dict(
+ model_id='a0',
+ causal=True,
+ use_positional_encoding=True,
+ use_external_states=True,
+ )
+ network = movinet.Movinet(**kwargs)
+
+ # Create another network object from the first object's config.
+ new_network = movinet.Movinet.from_config(network.get_config())
+
+ # Validate that the config can be forced to JSON.
+ _ = new_network.to_json()
+
+ # If the serialization was successful, the new config should match the old.
+ self.assertAllEqual(network.get_config(), new_network.get_config())
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/movinet/movinet_tutorial.ipynb b/official/projects/movinet/movinet_tutorial.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..a29cc72fac9d799ae03773253b736ccf7dc3cca0
--- /dev/null
+++ b/official/projects/movinet/movinet_tutorial.ipynb
@@ -0,0 +1,1112 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "3E96e1UKQ8uR"
+ },
+ "source": [
+ "# MoViNet Tutorial\n",
+ "\n",
+ "This notebook provides basic example code to build, run, and fine-tune [MoViNets (Mobile Video Networks)](https://arxiv.org/pdf/2103.11511.pdf).\n",
+ "\n",
+ "Pretrained models are provided by [TensorFlow Hub](https://tfhub.dev/google/collections/movinet/) and the [TensorFlow Model Garden](https://github.com/tensorflow/models/tree/master/official/projects/movinet), trained on [Kinetics 600](https://deepmind.com/research/open-source/kinetics) for video action classification. All Models use TensorFlow 2 with Keras for inference and training.\n",
+ "\n",
+ "The following steps will be performed:\n",
+ "\n",
+ "1. [Running base model inference with TensorFlow Hub](#scrollTo=6g0tuFvf71S9\u0026line=8\u0026uniqifier=1)\n",
+ "2. [Running streaming model inference with TensorFlow Hub and plotting predictions](#scrollTo=ADrHPmwGcBZ5\u0026line=4\u0026uniqifier=1)\n",
+ "3. [Exporting a streaming model to TensorFlow Lite for mobile](#scrollTo=W3CLHvubvdSI\u0026line=3\u0026uniqifier=1)\n",
+ "4. [Fine-Tuning a base Model with the TensorFlow Model Garden](#scrollTo=_s-7bEoa3f8g\u0026line=11\u0026uniqifier=1)\n",
+ "\n",
+ "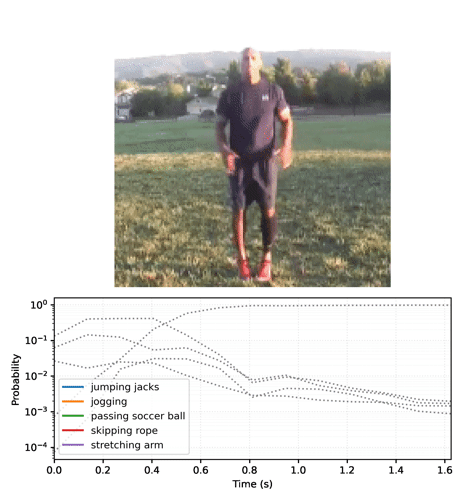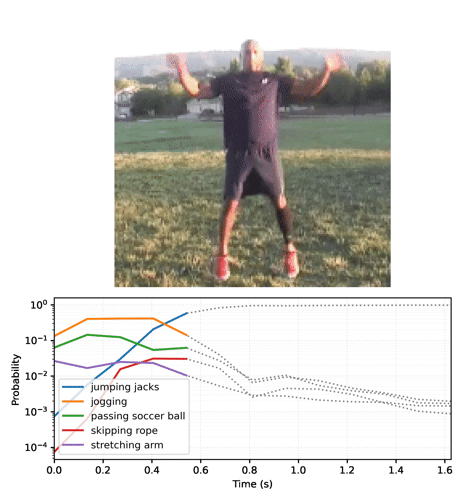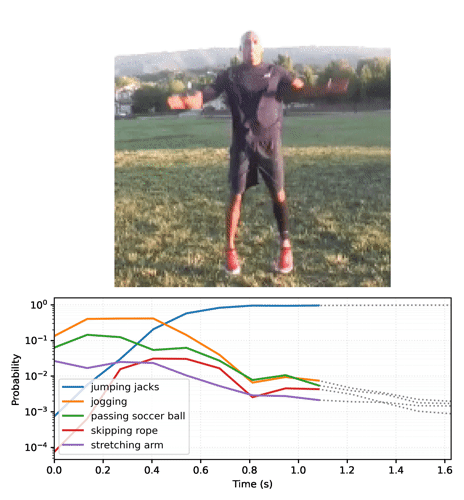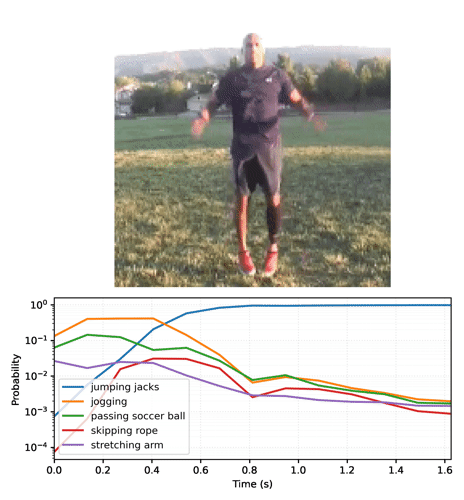\n",
+ "\n",
+ "To generate video plots like the one above, see [section 2](#scrollTo=ADrHPmwGcBZ5\u0026line=4\u0026uniqifier=1)."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "8_oLnvJy7kz5"
+ },
+ "source": [
+ "## Setup\n",
+ "\n",
+ "For inference on smaller models (A0-A2), CPU is sufficient for this Colab. For fine-tuning, it is recommended to run the models using GPUs.\n",
+ "\n",
+ "To select a GPU in Colab, select `Runtime \u003e Change runtime type \u003e Hardware accelerator \u003e GPU` dropdown in the top menu."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "s3khsunT7kWa"
+ },
+ "outputs": [],
+ "source": [
+ "# Install packages\n",
+ "\n",
+ "# tf-models-official is the stable Model Garden package\n",
+ "# tf-models-nightly includes latest changes\n",
+ "!pip install -q tf-models-nightly\n",
+ "\n",
+ "# Install tfds nightly to download ucf101\n",
+ "!pip install -q tfds-nightly\n",
+ "\n",
+ "# Install the mediapy package for visualizing images/videos.\n",
+ "# See https://github.com/google/mediapy\n",
+ "!command -v ffmpeg \u003e/dev/null || (apt update \u0026\u0026 apt install -y ffmpeg)\n",
+ "!pip install -q mediapy\n",
+ "\n",
+ "# Due to a bug, we reinstall opencv\n",
+ "# See https://stackoverflow.com/q/70537488\n",
+ "!pip uninstall -q -y opencv-python-headless\n",
+ "!pip install -q \"opencv-python-headless\u003c4.3\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "dI_1csl6Q-gH"
+ },
+ "outputs": [],
+ "source": [
+ "# Run imports\n",
+ "import os\n",
+ "\n",
+ "import matplotlib as mpl\n",
+ "import matplotlib.pyplot as plt\n",
+ "import mediapy as media\n",
+ "import numpy as np\n",
+ "import PIL\n",
+ "import pandas as pd\n",
+ "import tensorflow as tf\n",
+ "import tensorflow_datasets as tfds\n",
+ "import tensorflow_hub as hub\n",
+ "import tqdm\n",
+ "\n",
+ "mpl.rcParams.update({\n",
+ " 'font.size': 10,\n",
+ "})"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "OnFqOXazoWgy"
+ },
+ "source": [
+ "Run the cell below to define helper functions and create variables."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "cellView": "form",
+ "id": "dx55NK3ZoZeh"
+ },
+ "outputs": [],
+ "source": [
+ "#@title Run this cell to set up some helper code.\n",
+ "\n",
+ "# Download Kinetics 600 label map\n",
+ "!wget https://raw.githubusercontent.com/tensorflow/models/f8af2291cced43fc9f1d9b41ddbf772ae7b0d7d2/official/projects/movinet/files/kinetics_600_labels.txt -O labels.txt -q\n",
+ "\n",
+ "with tf.io.gfile.GFile('labels.txt') as f:\n",
+ " lines = f.readlines()\n",
+ " KINETICS_600_LABELS_LIST = [line.strip() for line in lines]\n",
+ " KINETICS_600_LABELS = tf.constant(KINETICS_600_LABELS_LIST)\n",
+ "\n",
+ "def get_top_k(probs, k=5, label_map=KINETICS_600_LABELS):\n",
+ " \"\"\"Outputs the top k model labels and probabilities on the given video.\"\"\"\n",
+ " top_predictions = tf.argsort(probs, axis=-1, direction='DESCENDING')[:k]\n",
+ " top_labels = tf.gather(label_map, top_predictions, axis=-1)\n",
+ " top_labels = [label.decode('utf8') for label in top_labels.numpy()]\n",
+ " top_probs = tf.gather(probs, top_predictions, axis=-1).numpy()\n",
+ " return tuple(zip(top_labels, top_probs))\n",
+ "\n",
+ "def predict_top_k(model, video, k=5, label_map=KINETICS_600_LABELS):\n",
+ " \"\"\"Outputs the top k model labels and probabilities on the given video.\"\"\"\n",
+ " outputs = model.predict(video[tf.newaxis])[0]\n",
+ " probs = tf.nn.softmax(outputs)\n",
+ " return get_top_k(probs, k=k, label_map=label_map)\n",
+ "\n",
+ "def load_movinet_from_hub(model_id, model_mode, hub_version=3):\n",
+ " \"\"\"Loads a MoViNet model from TF Hub.\"\"\"\n",
+ " hub_url = f'https://tfhub.dev/tensorflow/movinet/{model_id}/{model_mode}/kinetics-600/classification/{hub_version}'\n",
+ "\n",
+ " encoder = hub.KerasLayer(hub_url, trainable=True)\n",
+ "\n",
+ " inputs = tf.keras.layers.Input(\n",
+ " shape=[None, None, None, 3],\n",
+ " dtype=tf.float32)\n",
+ "\n",
+ " if model_mode == 'base':\n",
+ " inputs = dict(image=inputs)\n",
+ " else:\n",
+ " # Define the state inputs, which is a dict that maps state names to tensors.\n",
+ " init_states_fn = encoder.resolved_object.signatures['init_states']\n",
+ " state_shapes = {\n",
+ " name: ([s if s \u003e 0 else None for s in state.shape], state.dtype)\n",
+ " for name, state in init_states_fn(tf.constant([0, 0, 0, 0, 3])).items()\n",
+ " }\n",
+ " states_input = {\n",
+ " name: tf.keras.Input(shape[1:], dtype=dtype, name=name)\n",
+ " for name, (shape, dtype) in state_shapes.items()\n",
+ " }\n",
+ "\n",
+ " # The inputs to the model are the states and the video\n",
+ " inputs = {**states_input, 'image': inputs}\n",
+ "\n",
+ " # Output shape: [batch_size, 600]\n",
+ " outputs = encoder(inputs)\n",
+ "\n",
+ " model = tf.keras.Model(inputs, outputs)\n",
+ " model.build([1, 1, 1, 1, 3])\n",
+ "\n",
+ " return model\n",
+ "\n",
+ "# Download example gif\n",
+ "!wget https://github.com/tensorflow/models/raw/f8af2291cced43fc9f1d9b41ddbf772ae7b0d7d2/official/projects/movinet/files/jumpingjack.gif -O jumpingjack.gif -q\n",
+ "\n",
+ "def load_gif(file_path, image_size=(224, 224)):\n",
+ " \"\"\"Loads a gif file into a TF tensor.\"\"\"\n",
+ " with tf.io.gfile.GFile(file_path, 'rb') as f:\n",
+ " video = tf.io.decode_gif(f.read())\n",
+ " video = tf.image.resize(video, image_size)\n",
+ " video = tf.cast(video, tf.float32) / 255.\n",
+ " return video\n",
+ "\n",
+ "def get_top_k_streaming_labels(probs, k=5, label_map=KINETICS_600_LABELS_LIST):\n",
+ " \"\"\"Returns the top-k labels over an entire video sequence.\n",
+ "\n",
+ " Args:\n",
+ " probs: probability tensor of shape (num_frames, num_classes) that represents\n",
+ " the probability of each class on each frame.\n",
+ " k: the number of top predictions to select.\n",
+ " label_map: a list of labels to map logit indices to label strings.\n",
+ "\n",
+ " Returns:\n",
+ " a tuple of the top-k probabilities, labels, and logit indices\n",
+ " \"\"\"\n",
+ " top_categories_last = tf.argsort(probs, -1, 'DESCENDING')[-1, :1]\n",
+ " categories = tf.argsort(probs, -1, 'DESCENDING')[:, :k]\n",
+ " categories = tf.reshape(categories, [-1])\n",
+ "\n",
+ " counts = sorted([\n",
+ " (i.numpy(), tf.reduce_sum(tf.cast(categories == i, tf.int32)).numpy())\n",
+ " for i in tf.unique(categories)[0]\n",
+ " ], key=lambda x: x[1], reverse=True)\n",
+ "\n",
+ " top_probs_idx = tf.constant([i for i, _ in counts[:k]])\n",
+ " top_probs_idx = tf.concat([top_categories_last, top_probs_idx], 0)\n",
+ " top_probs_idx = tf.unique(top_probs_idx)[0][:k+1]\n",
+ "\n",
+ " top_probs = tf.gather(probs, top_probs_idx, axis=-1)\n",
+ " top_probs = tf.transpose(top_probs, perm=(1, 0))\n",
+ " top_labels = tf.gather(label_map, top_probs_idx, axis=0)\n",
+ " top_labels = [label.decode('utf8') for label in top_labels.numpy()]\n",
+ "\n",
+ " return top_probs, top_labels, top_probs_idx\n",
+ "\n",
+ "def plot_streaming_top_preds_at_step(\n",
+ " top_probs,\n",
+ " top_labels,\n",
+ " step=None,\n",
+ " image=None,\n",
+ " legend_loc='lower left',\n",
+ " duration_seconds=10,\n",
+ " figure_height=500,\n",
+ " playhead_scale=0.8,\n",
+ " grid_alpha=0.3):\n",
+ " \"\"\"Generates a plot of the top video model predictions at a given time step.\n",
+ "\n",
+ " Args:\n",
+ " top_probs: a tensor of shape (k, num_frames) representing the top-k\n",
+ " probabilities over all frames.\n",
+ " top_labels: a list of length k that represents the top-k label strings.\n",
+ " step: the current time step in the range [0, num_frames].\n",
+ " image: the image frame to display at the current time step.\n",
+ " legend_loc: the placement location of the legend.\n",
+ " duration_seconds: the total duration of the video.\n",
+ " figure_height: the output figure height.\n",
+ " playhead_scale: scale value for the playhead.\n",
+ " grid_alpha: alpha value for the gridlines.\n",
+ "\n",
+ " Returns:\n",
+ " A tuple of the output numpy image, figure, and axes.\n",
+ " \"\"\"\n",
+ " num_labels, num_frames = top_probs.shape\n",
+ " if step is None:\n",
+ " step = num_frames\n",
+ "\n",
+ " fig = plt.figure(figsize=(6.5, 7), dpi=300)\n",
+ " gs = mpl.gridspec.GridSpec(8, 1)\n",
+ " ax2 = plt.subplot(gs[:-3, :])\n",
+ " ax = plt.subplot(gs[-3:, :])\n",
+ "\n",
+ " if image is not None:\n",
+ " ax2.imshow(image, interpolation='nearest')\n",
+ " ax2.axis('off')\n",
+ "\n",
+ " preview_line_x = tf.linspace(0., duration_seconds, num_frames)\n",
+ " preview_line_y = top_probs\n",
+ "\n",
+ " line_x = preview_line_x[:step+1]\n",
+ " line_y = preview_line_y[:, :step+1]\n",
+ "\n",
+ " for i in range(num_labels):\n",
+ " ax.plot(preview_line_x, preview_line_y[i], label=None, linewidth='1.5',\n",
+ " linestyle=':', color='gray')\n",
+ " ax.plot(line_x, line_y[i], label=top_labels[i], linewidth='2.0')\n",
+ "\n",
+ "\n",
+ " ax.grid(which='major', linestyle=':', linewidth='1.0', alpha=grid_alpha)\n",
+ " ax.grid(which='minor', linestyle=':', linewidth='0.5', alpha=grid_alpha)\n",
+ "\n",
+ " min_height = tf.reduce_min(top_probs) * playhead_scale\n",
+ " max_height = tf.reduce_max(top_probs)\n",
+ " ax.vlines(preview_line_x[step], min_height, max_height, colors='red')\n",
+ " ax.scatter(preview_line_x[step], max_height, color='red')\n",
+ "\n",
+ " ax.legend(loc=legend_loc)\n",
+ "\n",
+ " plt.xlim(0, duration_seconds)\n",
+ " plt.ylabel('Probability')\n",
+ " plt.xlabel('Time (s)')\n",
+ " plt.yscale('log')\n",
+ "\n",
+ " fig.tight_layout()\n",
+ " fig.canvas.draw()\n",
+ "\n",
+ " data = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)\n",
+ " data = data.reshape(fig.canvas.get_width_height()[::-1] + (3,))\n",
+ " plt.close()\n",
+ "\n",
+ " figure_width = int(figure_height * data.shape[1] / data.shape[0])\n",
+ " image = PIL.Image.fromarray(data).resize([figure_width, figure_height])\n",
+ " image = np.array(image)\n",
+ "\n",
+ " return image, (fig, ax, ax2)\n",
+ "\n",
+ "def plot_streaming_top_preds(\n",
+ " probs,\n",
+ " video,\n",
+ " top_k=5,\n",
+ " video_fps=25.,\n",
+ " figure_height=500,\n",
+ " use_progbar=True):\n",
+ " \"\"\"Generates a video plot of the top video model predictions.\n",
+ "\n",
+ " Args:\n",
+ " probs: probability tensor of shape (num_frames, num_classes) that represents\n",
+ " the probability of each class on each frame.\n",
+ " video: the video to display in the plot.\n",
+ " top_k: the number of top predictions to select.\n",
+ " video_fps: the input video fps.\n",
+ " figure_fps: the output video fps.\n",
+ " figure_height: the height of the output video.\n",
+ " use_progbar: display a progress bar.\n",
+ "\n",
+ " Returns:\n",
+ " A numpy array representing the output video.\n",
+ " \"\"\"\n",
+ " video_fps = 8.\n",
+ " figure_height = 500\n",
+ " steps = video.shape[0]\n",
+ " duration = steps / video_fps\n",
+ "\n",
+ " top_probs, top_labels, _ = get_top_k_streaming_labels(probs, k=top_k)\n",
+ "\n",
+ " images = []\n",
+ " step_generator = tqdm.trange(steps) if use_progbar else range(steps)\n",
+ " for i in step_generator:\n",
+ " image, _ = plot_streaming_top_preds_at_step(\n",
+ " top_probs=top_probs,\n",
+ " top_labels=top_labels,\n",
+ " step=i,\n",
+ " image=video[i],\n",
+ " duration_seconds=duration,\n",
+ " figure_height=figure_height,\n",
+ " )\n",
+ " images.append(image)\n",
+ "\n",
+ " return np.array(images)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6g0tuFvf71S9"
+ },
+ "source": [
+ "## Running Base Model Inference with TensorFlow Hub\n",
+ "\n",
+ "We will load MoViNet-A2-Base from TensorFlow Hub as part of the [MoViNet collection](https://tfhub.dev/google/collections/movinet/).\n",
+ "\n",
+ "The following code will:\n",
+ "\n",
+ "- Load a MoViNet KerasLayer from [tfhub.dev](https://tfhub.dev).\n",
+ "- Wrap the layer in a [Keras Model](https://www.tensorflow.org/api_docs/python/tf/keras/Model).\n",
+ "- Load an example gif as a video.\n",
+ "- Classify the video and print the top-5 predicted classes."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "KZKKNZVBpglJ"
+ },
+ "outputs": [],
+ "source": [
+ "model = load_movinet_from_hub('a2', 'base', hub_version=3)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "7kU1_pL10l0B"
+ },
+ "source": [
+ "To provide a simple example video for classification, we can load a short gif of jumping jacks being performed.\n",
+ "\n",
+ "\n",
+ "\n",
+ "Attribution: Footage shared by [Coach Bobby Bluford](https://www.youtube.com/watch?v=-AxHpj-EuPg) on YouTube under the CC-BY license."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Iy0rKRrT723_"
+ },
+ "outputs": [],
+ "source": [
+ "video = load_gif('jumpingjack.gif', image_size=(172, 172))\n",
+ "\n",
+ "# Show video\n",
+ "print(video.shape)\n",
+ "media.show_video(video.numpy(), fps=5)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "P0bZfrAsqPv2",
+ "outputId": "bd82571f-8dfd-4faf-ed10-e34708b0405d"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "jumping jacks 0.9166437\n",
+ "zumba 0.016020728\n",
+ "doing aerobics 0.008053946\n",
+ "dancing charleston 0.006083599\n",
+ "lunge 0.0035062772\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Run the model on the video and output the top 5 predictions\n",
+ "outputs = predict_top_k(model, video)\n",
+ "\n",
+ "for label, prob in outputs:\n",
+ " print(label, prob)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ADrHPmwGcBZ5"
+ },
+ "source": [
+ "## Run Streaming Model Inference with TensorFlow Hub and Plot Predictions\n",
+ "\n",
+ "We will load MoViNet-A0-Stream from TensorFlow Hub as part of the [MoViNet collection](https://tfhub.dev/google/collections/movinet/).\n",
+ "\n",
+ "The following code will:\n",
+ "\n",
+ "- Load a MoViNet model from [tfhub.dev](https://tfhub.dev).\n",
+ "- Classify an example video and plot the streaming predictions over time."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "tXWR13wthnK5"
+ },
+ "outputs": [],
+ "source": [
+ "model = load_movinet_from_hub('a2', 'stream', hub_version=3)\n",
+ "\n",
+ "# Create initial states for the stream model\n",
+ "init_states_fn = model.layers[-1].resolved_object.signatures['init_states']\n",
+ "init_states = init_states_fn(tf.shape(video[tf.newaxis]))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "YqSkt7l8ltwt",
+ "outputId": "6ccf1dd6-95d1-43b1-efdb-2e931dd3a19d"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "100%|██████████| 13/13 [00:08\u003c00:00, 1.58it/s]\n",
+ "jumping jacks 0.9998123\n",
+ "zumba 0.00011835508\n",
+ "doing aerobics 3.3375818e-05\n",
+ "dancing charleston 4.9819987e-06\n",
+ "finger snapping 3.8673647e-06\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Insert your video clip here\n",
+ "video = load_gif('jumpingjack.gif', image_size=(172, 172))\n",
+ "clips = tf.split(video[tf.newaxis], video.shape[0], axis=1)\n",
+ "\n",
+ "all_logits = []\n",
+ "\n",
+ "# To run on a video, pass in one frame at a time\n",
+ "states = init_states\n",
+ "for clip in tqdm.tqdm(clips):\n",
+ " # Input shape: [1, 1, 172, 172, 3]\n",
+ " logits, states = model.predict({**states, 'image': clip}, verbose=0)\n",
+ " all_logits.append(logits)\n",
+ "\n",
+ "logits = tf.concat(all_logits, 0)\n",
+ "probs = tf.nn.softmax(logits)\n",
+ "\n",
+ "final_probs = probs[-1]\n",
+ "top_k = get_top_k(final_probs)\n",
+ "print()\n",
+ "for label, prob in top_k:\n",
+ " print(label, prob)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Xdox556CtMRb"
+ },
+ "outputs": [],
+ "source": [
+ "# Generate a plot and output to a video tensor\n",
+ "plot_video = plot_streaming_top_preds(probs, video, video_fps=8.)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "NSStKE9klCs3"
+ },
+ "outputs": [],
+ "source": [
+ "# For gif format, set codec='gif'\n",
+ "media.show_video(plot_video, fps=3)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "W3CLHvubvdSI"
+ },
+ "source": [
+ "## Export a Streaming Model to TensorFlow Lite for Mobile\n",
+ "\n",
+ "We will convert a MoViNet-A0-Stream model to [TensorFlow Lite](https://www.tensorflow.org/lite).\n",
+ "\n",
+ "The following code will:\n",
+ "- Load a MoViNet-A0-Stream model.\n",
+ "- Convert the model to TF Lite.\n",
+ "- Run inference on an example video using the Python interpreter."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "KH0j-07KVh06"
+ },
+ "outputs": [],
+ "source": [
+ "# Run imports\n",
+ "from official.vision.configs import video_classification\n",
+ "from official.projects.movinet.configs import movinet as movinet_configs\n",
+ "from official.projects.movinet.modeling import movinet\n",
+ "from official.projects.movinet.modeling import movinet_layers\n",
+ "from official.projects.movinet.modeling import movinet_model\n",
+ "from official.projects.movinet.tools import export_saved_model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "RLkV0xtPvfkY"
+ },
+ "outputs": [],
+ "source": [
+ "# Export to saved model\n",
+ "saved_model_dir = 'model'\n",
+ "tflite_filename = 'model.tflite'\n",
+ "input_shape = [1, 1, 172, 172, 3]\n",
+ "batch_size, num_frames, image_size, = input_shape[:3]\n",
+ "\n",
+ "tf.keras.backend.clear_session()\n",
+ "\n",
+ "# Create the model\n",
+ "input_specs = tf.keras.layers.InputSpec(shape=input_shape)\n",
+ "backbone = movinet.Movinet(\n",
+ " model_id='a0',\n",
+ " causal=True,\n",
+ " conv_type='2plus1d',\n",
+ " se_type='2plus3d',\n",
+ " input_specs=input_specs,\n",
+ " activation='hard_swish',\n",
+ " gating_activation='hard_sigmoid',\n",
+ " use_sync_bn=False,\n",
+ " use_external_states=True)\n",
+ "model = movinet_model.MovinetClassifier(\n",
+ " backbone=backbone,\n",
+ " activation='hard_swish',\n",
+ " num_classes=600,\n",
+ " output_states=True,\n",
+ " input_specs=dict(image=input_specs))\n",
+ "model.build([1, 1, 1, 1, 3])\n",
+ "\n",
+ "# Extract pretrained weights\n",
+ "!wget https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_stream.tar.gz -O movinet_a0_stream.tar.gz -q\n",
+ "!tar -xvf movinet_a0_stream.tar.gz\n",
+ "\n",
+ "checkpoint_dir = 'movinet_a0_stream'\n",
+ "checkpoint_path = tf.train.latest_checkpoint(checkpoint_dir)\n",
+ "\n",
+ "# Convert to saved model\n",
+ "export_saved_model.export_saved_model(\n",
+ " model=model,\n",
+ " input_shape=input_shape,\n",
+ " export_path=saved_model_dir,\n",
+ " causal=True,\n",
+ " bundle_input_init_states_fn=False,\n",
+ " checkpoint_path=checkpoint_path)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "gPg_6eMC8IwF"
+ },
+ "outputs": [],
+ "source": [
+ "# Convert to TF Lite\n",
+ "converter = tf.lite.TFLiteConverter.from_saved_model(saved_model_dir)\n",
+ "tflite_model = converter.convert()\n",
+ "\n",
+ "with open(tflite_filename, 'wb') as f:\n",
+ " f.write(tflite_model)\n",
+ "\n",
+ "# Create the interpreter and signature runner\n",
+ "interpreter = tf.lite.Interpreter(model_path=tflite_filename)\n",
+ "runner = interpreter.get_signature_runner()\n",
+ "\n",
+ "init_states = {\n",
+ " name: tf.zeros(x['shape'], dtype=x['dtype'])\n",
+ " for name, x in runner.get_input_details().items()\n",
+ "}\n",
+ "del init_states['image']"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "-TQ-7oSJIlTA",
+ "outputId": "a15519ff-d08c-40bc-fbea-d3a58169450c"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "jumping jacks 0.9791285\n",
+ "jogging 0.0019550633\n",
+ "riding unicycle 0.0017429002\n",
+ "passing soccer ball 0.0016952101\n",
+ "stretching arm 0.0014458151\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Insert your video clip here\n",
+ "video = load_gif('jumpingjack.gif', image_size=(172, 172))\n",
+ "clips = tf.split(video[tf.newaxis], video.shape[0], axis=1)\n",
+ "\n",
+ "# To run on a video, pass in one frame at a time\n",
+ "states = init_states\n",
+ "for clip in clips:\n",
+ " # Input shape: [1, 1, 172, 172, 3]\n",
+ " outputs = runner(**states, image=clip)\n",
+ " logits = outputs.pop('logits')[0]\n",
+ " states = outputs\n",
+ "\n",
+ "probs = tf.nn.softmax(logits)\n",
+ "top_k = get_top_k(probs)\n",
+ "print()\n",
+ "for label, prob in top_k:\n",
+ " print(label, prob)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "_s-7bEoa3f8g"
+ },
+ "source": [
+ "## Fine-Tune a Base Model with the TensorFlow Model Garden\n",
+ "\n",
+ "We will Fine-tune MoViNet-A0-Base on [UCF-101](https://www.crcv.ucf.edu/research/data-sets/ucf101/).\n",
+ "\n",
+ "The following code will:\n",
+ "\n",
+ "- Load the UCF-101 dataset with [TensorFlow Datasets](https://www.tensorflow.org/datasets/catalog/ucf101).\n",
+ "- Create a simple [`tf.data.Dataset`](https://www.tensorflow.org/api_docs/python/tf/data/Dataset) pipeline for training and evaluation.\n",
+ "- Display some example videos from the dataset.\n",
+ "- Build a MoViNet model and load pretrained weights.\n",
+ "- Fine-tune the final classifier layers on UCF-101 and evaluate accuracy on the validation set."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "o7unW4WVr580"
+ },
+ "source": [
+ "### Load the UCF-101 Dataset with TensorFlow Datasets\n",
+ "\n",
+ "Calling `download_and_prepare()` will automatically download the dataset. This step may take up to 1 hour depending on the download and extraction speed. After downloading, the next cell will output information about the dataset."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "2IHLbPAfrs5P"
+ },
+ "outputs": [],
+ "source": [
+ "# Run imports\n",
+ "import tensorflow_datasets as tfds\n",
+ "\n",
+ "from official.vision.configs import video_classification\n",
+ "from official.projects.movinet.configs import movinet as movinet_configs\n",
+ "from official.projects.movinet.modeling import movinet\n",
+ "from official.projects.movinet.modeling import movinet_layers\n",
+ "from official.projects.movinet.modeling import movinet_model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "FxM1vNYp_YAM"
+ },
+ "outputs": [],
+ "source": [
+ "dataset_name = 'ucf101'\n",
+ "\n",
+ "builder = tfds.builder(dataset_name)\n",
+ "\n",
+ "config = tfds.download.DownloadConfig(verify_ssl=False)\n",
+ "builder.download_and_prepare(download_config=config)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "executionInfo": {
+ "elapsed": 2957,
+ "status": "ok",
+ "timestamp": 1619748263684,
+ "user": {
+ "displayName": "",
+ "photoUrl": "",
+ "userId": ""
+ },
+ "user_tz": 360
+ },
+ "id": "boQHbcfDhXpJ",
+ "outputId": "eabc3307-d6bf-4f29-cc5a-c8dc6360701b"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Number of classes: 101\n",
+ "Number of examples for train: 9537\n",
+ "Number of examples for test: 3783\n",
+ "\n"
+ ]
+ },
+ {
+ "data": {
+ "text/plain": [
+ "tfds.core.DatasetInfo(\n",
+ " name='ucf101',\n",
+ " full_name='ucf101/ucf101_1_256/2.0.0',\n",
+ " description=\"\"\"\n",
+ " A 101-label video classification dataset.\n",
+ " \"\"\",\n",
+ " config_description=\"\"\"\n",
+ " 256x256 UCF with the first action recognition split.\n",
+ " \"\"\",\n",
+ " homepage='https://www.crcv.ucf.edu/data-sets/ucf101/',\n",
+ " data_path='/readahead/128M/placer/prod/home/tensorflow-datasets-cns-storage-owner/datasets/ucf101/ucf101_1_256/2.0.0',\n",
+ " download_size=6.48 GiB,\n",
+ " dataset_size=Unknown size,\n",
+ " features=FeaturesDict({\n",
+ " 'label': ClassLabel(shape=(), dtype=tf.int64, num_classes=101),\n",
+ " 'video': Video(Image(shape=(256, 256, 3), dtype=tf.uint8)),\n",
+ " }),\n",
+ " supervised_keys=None,\n",
+ " splits={\n",
+ " 'test': \u003cSplitInfo num_examples=3783, num_shards=32\u003e,\n",
+ " 'train': \u003cSplitInfo num_examples=9537, num_shards=64\u003e,\n",
+ " },\n",
+ " citation=\"\"\"@article{DBLP:journals/corr/abs-1212-0402,\n",
+ " author = {Khurram Soomro and\n",
+ " Amir Roshan Zamir and\n",
+ " Mubarak Shah},\n",
+ " title = {{UCF101:} {A} Dataset of 101 Human Actions Classes From Videos in\n",
+ " The Wild},\n",
+ " journal = {CoRR},\n",
+ " volume = {abs/1212.0402},\n",
+ " year = {2012},\n",
+ " url = {http://arxiv.org/abs/1212.0402},\n",
+ " archivePrefix = {arXiv},\n",
+ " eprint = {1212.0402},\n",
+ " timestamp = {Mon, 13 Aug 2018 16:47:45 +0200},\n",
+ " biburl = {https://dblp.org/rec/bib/journals/corr/abs-1212-0402},\n",
+ " bibsource = {dblp computer science bibliography, https://dblp.org}\n",
+ " }\"\"\",\n",
+ ")"
+ ]
+ },
+ "execution_count": null,
+ "metadata": {
+ "tags": []
+ },
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "num_classes = builder.info.features['label'].num_classes\n",
+ "num_examples = {\n",
+ " name: split.num_examples\n",
+ " for name, split in builder.info.splits.items()\n",
+ "}\n",
+ "\n",
+ "print('Number of classes:', num_classes)\n",
+ "print('Number of examples for train:', num_examples['train'])\n",
+ "print('Number of examples for test:', num_examples['test'])\n",
+ "print()\n",
+ "\n",
+ "builder.info"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "9cO_BCu9le3r"
+ },
+ "outputs": [],
+ "source": [
+ "# Build the training and evaluation datasets.\n",
+ "\n",
+ "batch_size = 8\n",
+ "num_frames = 8\n",
+ "frame_stride = 10\n",
+ "resolution = 172\n",
+ "\n",
+ "def format_features(features):\n",
+ " video = features['video']\n",
+ " video = video[:, ::frame_stride]\n",
+ " video = video[:, :num_frames]\n",
+ "\n",
+ " video = tf.reshape(video, [-1, video.shape[2], video.shape[3], 3])\n",
+ " video = tf.image.resize(video, (resolution, resolution))\n",
+ " video = tf.reshape(video, [-1, num_frames, resolution, resolution, 3])\n",
+ " video = tf.cast(video, tf.float32) / 255.\n",
+ "\n",
+ " label = tf.one_hot(features['label'], num_classes)\n",
+ " return (video, label)\n",
+ "\n",
+ "train_dataset = builder.as_dataset(\n",
+ " split='train',\n",
+ " batch_size=batch_size,\n",
+ " shuffle_files=True)\n",
+ "train_dataset = train_dataset.map(\n",
+ " format_features,\n",
+ " num_parallel_calls=tf.data.AUTOTUNE)\n",
+ "train_dataset = train_dataset.repeat()\n",
+ "train_dataset = train_dataset.prefetch(2)\n",
+ "\n",
+ "test_dataset = builder.as_dataset(\n",
+ " split='test',\n",
+ " batch_size=batch_size)\n",
+ "test_dataset = test_dataset.map(\n",
+ " format_features,\n",
+ " num_parallel_calls=tf.data.AUTOTUNE,\n",
+ " deterministic=True)\n",
+ "test_dataset = test_dataset.prefetch(2)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "rToX7_Ymgh57"
+ },
+ "source": [
+ "Display some example videos from the dataset."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "KG8Z7rUj06of"
+ },
+ "outputs": [],
+ "source": [
+ "videos, labels = next(iter(train_dataset))\n",
+ "media.show_videos(videos.numpy(), codec='gif', fps=5)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "R3RHeuHdsd_3"
+ },
+ "source": [
+ "### Build MoViNet-A0-Base and Load Pretrained Weights\n",
+ "\n",
+ "Here we create a MoViNet model using the open source code provided in [official/projects/movinet](https://github.com/tensorflow/models/tree/master/official/projects/movinet) and load the pretrained weights. Here we freeze the all layers except the final classifier head to speed up fine-tuning."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "JpfxpeGSsbzJ"
+ },
+ "outputs": [],
+ "source": [
+ "model_id = 'a0'\n",
+ "\n",
+ "tf.keras.backend.clear_session()\n",
+ "\n",
+ "backbone = movinet.Movinet(model_id=model_id)\n",
+ "model = movinet_model.MovinetClassifier(backbone=backbone, num_classes=600)\n",
+ "model.build([1, 1, 1, 1, 3])\n",
+ "\n",
+ "# Load pretrained weights\n",
+ "!wget https://storage.googleapis.com/tf_model_garden/vision/movinet/movinet_a0_base.tar.gz -O movinet_a0_base.tar.gz -q\n",
+ "!tar -xvf movinet_a0_base.tar.gz\n",
+ "\n",
+ "checkpoint_dir = 'movinet_a0_base'\n",
+ "checkpoint_path = tf.train.latest_checkpoint(checkpoint_dir)\n",
+ "checkpoint = tf.train.Checkpoint(model=model)\n",
+ "status = checkpoint.restore(checkpoint_path)\n",
+ "status.assert_existing_objects_matched()\n",
+ "\n",
+ "def build_classifier(backbone, num_classes, freeze_backbone=False):\n",
+ " \"\"\"Builds a classifier on top of a backbone model.\"\"\"\n",
+ " model = movinet_model.MovinetClassifier(\n",
+ " backbone=backbone,\n",
+ " num_classes=num_classes)\n",
+ " model.build([batch_size, num_frames, resolution, resolution, 3])\n",
+ "\n",
+ " if freeze_backbone:\n",
+ " for layer in model.layers[:-1]:\n",
+ " layer.trainable = False\n",
+ " model.layers[-1].trainable = True\n",
+ "\n",
+ " return model\n",
+ "\n",
+ "# Wrap the backbone with a new classifier to create a new classifier head\n",
+ "# with num_classes outputs (101 classes for UCF101).\n",
+ "# Freeze all layers except for the final classifier head.\n",
+ "model = build_classifier(backbone, num_classes, freeze_backbone=True)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ucntdu2xqgXB"
+ },
+ "source": [
+ "Configure fine-tuning with training/evaluation steps, loss object, metrics, learning rate, optimizer, and callbacks.\n",
+ "\n",
+ "Here we use 3 epochs. Training for more epochs should improve accuracy."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "WUYTw48BouTu"
+ },
+ "outputs": [],
+ "source": [
+ "num_epochs = 3\n",
+ "\n",
+ "train_steps = num_examples['train'] // batch_size\n",
+ "total_train_steps = train_steps * num_epochs\n",
+ "test_steps = num_examples['test'] // batch_size\n",
+ "\n",
+ "loss_obj = tf.keras.losses.CategoricalCrossentropy(\n",
+ " from_logits=True,\n",
+ " label_smoothing=0.1)\n",
+ "\n",
+ "metrics = [\n",
+ " tf.keras.metrics.TopKCategoricalAccuracy(\n",
+ " k=1, name='top_1', dtype=tf.float32),\n",
+ " tf.keras.metrics.TopKCategoricalAccuracy(\n",
+ " k=5, name='top_5', dtype=tf.float32),\n",
+ "]\n",
+ "\n",
+ "initial_learning_rate = 0.01\n",
+ "learning_rate = tf.keras.optimizers.schedules.CosineDecay(\n",
+ " initial_learning_rate, decay_steps=total_train_steps,\n",
+ ")\n",
+ "optimizer = tf.keras.optimizers.RMSprop(\n",
+ " learning_rate, rho=0.9, momentum=0.9, epsilon=1.0, clipnorm=1.0)\n",
+ "\n",
+ "model.compile(loss=loss_obj, optimizer=optimizer, metrics=metrics)\n",
+ "\n",
+ "callbacks = [\n",
+ " tf.keras.callbacks.TensorBoard(),\n",
+ "]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "0IyAOOlcpHna"
+ },
+ "source": [
+ "Run the fine-tuning with Keras compile/fit. After fine-tuning the model, we should be able to achieve \u003e85% accuracy on the test set."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "executionInfo": {
+ "elapsed": 982253,
+ "status": "ok",
+ "timestamp": 1619750139919,
+ "user": {
+ "displayName": "",
+ "photoUrl": "",
+ "userId": ""
+ },
+ "user_tz": 360
+ },
+ "id": "Zecc_K3lga8I",
+ "outputId": "e4c5c61e-aa08-47db-c04c-42dea3efb545"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Epoch 1/3\n",
+ "1192/1192 [==============================] - 551s 451ms/step - loss: 2.5050 - top_1: 0.6692 - top_5: 0.8753 - val_loss: 1.6310 - val_top_1: 0.8109 - val_top_5: 0.9701\n",
+ "Epoch 2/3\n",
+ "1192/1192 [==============================] - 533s 447ms/step - loss: 1.3336 - top_1: 0.9024 - top_5: 0.9906 - val_loss: 1.4576 - val_top_1: 0.8451 - val_top_5: 0.9740\n",
+ "Epoch 3/3\n",
+ "1192/1192 [==============================] - 531s 446ms/step - loss: 1.2298 - top_1: 0.9329 - top_5: 0.9943 - val_loss: 1.4351 - val_top_1: 0.8514 - val_top_5: 0.9762\n"
+ ]
+ }
+ ],
+ "source": [
+ "results = model.fit(\n",
+ " train_dataset,\n",
+ " validation_data=test_dataset,\n",
+ " epochs=num_epochs,\n",
+ " steps_per_epoch=train_steps,\n",
+ " validation_steps=test_steps,\n",
+ " callbacks=callbacks,\n",
+ " validation_freq=1,\n",
+ " verbose=1)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "XuH8XflmpU9d"
+ },
+ "source": [
+ "We can also view the training and evaluation progress in TensorBoard."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "9fZhzhRJRd2J"
+ },
+ "outputs": [],
+ "source": [
+ "%reload_ext tensorboard\n",
+ "%tensorboard --logdir logs --port 0"
+ ]
+ }
+ ],
+ "metadata": {
+ "colab": {
+ "collapsed_sections": [],
+ "last_runtime": {
+ "build_target": "//learning/deepmind/dm_python:dm_notebook3",
+ "kind": "private"
+ },
+ "name": "movinet_tutorial.ipynb",
+ "provenance": [
+ {
+ "file_id": "11msGCxFjxwioBOBJavP9alfTclUQCJf-",
+ "timestamp": 1617043059980
+ }
+ ]
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "name": "python"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/official/vision/beta/projects/movinet/requirements.txt b/official/projects/movinet/requirements.txt
similarity index 100%
rename from official/vision/beta/projects/movinet/requirements.txt
rename to official/projects/movinet/requirements.txt
diff --git a/official/projects/movinet/tools/__init__.py b/official/projects/movinet/tools/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/movinet/tools/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/movinet/tools/convert_3d_2plus1d.py b/official/projects/movinet/tools/convert_3d_2plus1d.py
similarity index 91%
rename from official/vision/beta/projects/movinet/tools/convert_3d_2plus1d.py
rename to official/projects/movinet/tools/convert_3d_2plus1d.py
index 4b126150bc9650e8080193f679e8cd8013e2c8fe..0349c6075174f716b3d27f88c58d288cb239ba1b 100644
--- a/official/vision/beta/projects/movinet/tools/convert_3d_2plus1d.py
+++ b/official/projects/movinet/tools/convert_3d_2plus1d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,8 +18,8 @@ from absl import app
from absl import flags
import tensorflow as tf
-from official.vision.beta.projects.movinet.modeling import movinet
-from official.vision.beta.projects.movinet.modeling import movinet_model
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
flags.DEFINE_string(
'input_checkpoint_path', None,
@@ -29,6 +29,8 @@ flags.DEFINE_string(
'Export path to save the saved_model file.')
flags.DEFINE_string(
'model_id', 'a0', 'MoViNet model name.')
+flags.DEFINE_string(
+ 'se_type', '2plus3d', 'MoViNet model SE type.')
flags.DEFINE_bool(
'causal', True, 'Run the model in causal mode.')
flags.DEFINE_bool(
@@ -47,6 +49,7 @@ def main(_) -> None:
model_id=FLAGS.model_id,
causal=FLAGS.causal,
conv_type='2plus1d',
+ se_type=FLAGS.se_type,
use_positional_encoding=FLAGS.use_positional_encoding)
model_2plus1d = movinet_model.MovinetClassifier(
backbone=backbone_2plus1d,
@@ -57,6 +60,7 @@ def main(_) -> None:
model_id=FLAGS.model_id,
causal=FLAGS.causal,
conv_type='3d_2plus1d',
+ se_type=FLAGS.se_type,
use_positional_encoding=FLAGS.use_positional_encoding)
model_3d_2plus1d = movinet_model.MovinetClassifier(
backbone=backbone_3d_2plus1d,
diff --git a/official/vision/beta/projects/movinet/tools/convert_3d_2plus1d_test.py b/official/projects/movinet/tools/convert_3d_2plus1d_test.py
similarity index 84%
rename from official/vision/beta/projects/movinet/tools/convert_3d_2plus1d_test.py
rename to official/projects/movinet/tools/convert_3d_2plus1d_test.py
index d225e13a8704762d0690973d3e13ee4ba11441b7..d2899c9b960ca7991370e2cd991323a091065dba 100644
--- a/official/vision/beta/projects/movinet/tools/convert_3d_2plus1d_test.py
+++ b/official/projects/movinet/tools/convert_3d_2plus1d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,9 +19,9 @@ import os
from absl import flags
import tensorflow as tf
-from official.vision.beta.projects.movinet.modeling import movinet
-from official.vision.beta.projects.movinet.modeling import movinet_model
-from official.vision.beta.projects.movinet.tools import convert_3d_2plus1d
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
+from official.projects.movinet.tools import convert_3d_2plus1d
FLAGS = flags.FLAGS
@@ -36,7 +36,8 @@ class Convert3d2plus1dTest(tf.test.TestCase):
model_3d_2plus1d = movinet_model.MovinetClassifier(
backbone=movinet.Movinet(
model_id='a0',
- conv_type='3d_2plus1d'),
+ conv_type='3d_2plus1d',
+ se_type='2plus3d'),
num_classes=600)
model_3d_2plus1d.build([1, 1, 1, 1, 3])
save_checkpoint = tf.train.Checkpoint(model=model_3d_2plus1d)
diff --git a/official/projects/movinet/tools/export_saved_model.py b/official/projects/movinet/tools/export_saved_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..86be661647760ca88e527446116cc6e481587b62
--- /dev/null
+++ b/official/projects/movinet/tools/export_saved_model.py
@@ -0,0 +1,299 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Exports models to tf.saved_model.
+
+Export example:
+
+```shell
+python3 export_saved_model.py \
+ --export_path=/tmp/movinet/ \
+ --model_id=a0 \
+ --causal=True \
+ --conv_type="3d" \
+ --num_classes=600 \
+ --use_positional_encoding=False \
+ --checkpoint_path=""
+```
+
+Export for TF Lite example:
+
+```shell
+python3 export_saved_model.py \
+ --model_id=a0 \
+ --causal=True \
+ --conv_type=2plus1d \
+ --se_type=2plus3d \
+ --activation=hard_swish \
+ --gating_activation=hard_sigmoid \
+ --use_positional_encoding=False \
+ --num_classes=600 \
+ --batch_size=1 \
+ --num_frames=1 \ # Use a single frame for streaming mode
+ --image_size=172 \ # Input resolution for the model
+ --bundle_input_init_states_fn=False \
+ --checkpoint_path=/path/to/checkpoint \
+ --export_path=/tmp/movinet_a0_stream
+```
+
+To use an exported saved_model, refer to export_saved_model_test.py.
+"""
+
+from typing import Optional, Tuple
+
+from absl import app
+from absl import flags
+import tensorflow as tf
+
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
+
+flags.DEFINE_string(
+ 'export_path', '/tmp/movinet/',
+ 'Export path to save the saved_model file.')
+flags.DEFINE_string(
+ 'model_id', 'a0', 'MoViNet model name.')
+flags.DEFINE_bool(
+ 'causal', False, 'Run the model in causal mode.')
+flags.DEFINE_string(
+ 'conv_type', '3d',
+ '3d, 2plus1d, or 3d_2plus1d. 3d configures the network '
+ 'to use the default 3D convolution. 2plus1d uses (2+1)D convolution '
+ 'with Conv2D operations and 2D reshaping (e.g., a 5x3x3 kernel becomes '
+ '3x3 followed by 5x1 conv). 3d_2plus1d uses (2+1)D convolution with '
+ 'Conv3D and no 2D reshaping (e.g., a 5x3x3 kernel becomes 1x3x3 '
+ 'followed by 5x1x1 conv).')
+flags.DEFINE_string(
+ 'se_type', '3d',
+ '3d, 2d, or 2plus3d. 3d uses the default 3D spatiotemporal global average'
+ 'pooling for squeeze excitation. 2d uses 2D spatial global average pooling '
+ 'on each frame. 2plus3d concatenates both 3D and 2D global average '
+ 'pooling.')
+flags.DEFINE_string(
+ 'activation', 'swish',
+ 'The main activation to use across layers.')
+flags.DEFINE_string(
+ 'classifier_activation', 'swish',
+ 'The classifier activation to use.')
+flags.DEFINE_string(
+ 'gating_activation', 'sigmoid',
+ 'The gating activation to use in squeeze-excitation layers.')
+flags.DEFINE_bool(
+ 'use_positional_encoding', False,
+ 'Whether to use positional encoding (only applied when causal=True).')
+flags.DEFINE_integer(
+ 'num_classes', 600, 'The number of classes for prediction.')
+flags.DEFINE_integer(
+ 'batch_size', None,
+ 'The batch size of the input. Set to None for dynamic input.')
+flags.DEFINE_integer(
+ 'num_frames', None,
+ 'The number of frames of the input. Set to None for dynamic input.')
+flags.DEFINE_integer(
+ 'image_size', None,
+ 'The resolution of the input. Set to None for dynamic input.')
+flags.DEFINE_bool(
+ 'bundle_input_init_states_fn', True,
+ 'Add init_states as a function signature to the saved model.'
+ 'This is not necessary if the input shape is static (e.g., for TF Lite).')
+flags.DEFINE_string(
+ 'checkpoint_path', '',
+ 'Checkpoint path to load. Leave blank for default initialization.')
+
+FLAGS = flags.FLAGS
+
+
+def export_saved_model(
+ model: tf.keras.Model,
+ input_shape: Tuple[int, int, int, int, int],
+ export_path: str = '/tmp/movinet/',
+ causal: bool = False,
+ bundle_input_init_states_fn: bool = True,
+ checkpoint_path: Optional[str] = None) -> None:
+ """Exports a MoViNet model to a saved model.
+
+ Args:
+ model: the tf.keras.Model to export.
+ input_shape: The 5D spatiotemporal input shape of size
+ [batch_size, num_frames, image_height, image_width, num_channels].
+ Set the field or a shape position in the field to None for dynamic input.
+ export_path: Export path to save the saved_model file.
+ causal: Run the model in causal mode.
+ bundle_input_init_states_fn: Add init_states as a function signature to the
+ saved model. This is not necessary if the input shape is static (e.g.,
+ for TF Lite).
+ checkpoint_path: Checkpoint path to load. Leave blank to keep the model's
+ initialization.
+ """
+
+ # Use dimensions of 1 except the channels to export faster,
+ # since we only really need the last dimension to build and get the output
+ # states. These dimensions can be set to `None` once the model is built.
+ input_shape_concrete = [1 if s is None else s for s in input_shape]
+ model.build(input_shape_concrete)
+
+ # Compile model to generate some internal Keras variables.
+ model.compile()
+
+ if checkpoint_path:
+ checkpoint = tf.train.Checkpoint(model=model)
+ status = checkpoint.restore(checkpoint_path)
+ status.assert_existing_objects_matched()
+
+ if causal:
+ # Call the model once to get the output states. Call again with `states`
+ # input to ensure that the inputs with the `states` argument is built
+ # with the full output state shapes.
+ input_image = tf.ones(input_shape_concrete)
+ _, states = model({
+ **model.init_states(input_shape_concrete), 'image': input_image})
+ _ = model({**states, 'image': input_image})
+
+ # Create a function to explicitly set the names of the outputs
+ def predict(inputs):
+ outputs, states = model(inputs)
+ return {**states, 'logits': outputs}
+
+ specs = {
+ name: tf.TensorSpec(spec.shape, name=name, dtype=spec.dtype)
+ for name, spec in model.initial_state_specs(
+ input_shape).items()
+ }
+ specs['image'] = tf.TensorSpec(
+ input_shape, dtype=model.dtype, name='image')
+
+ predict_fn = tf.function(predict, jit_compile=True)
+ predict_fn = predict_fn.get_concrete_function(specs)
+
+ init_states_fn = tf.function(model.init_states, jit_compile=True)
+ init_states_fn = init_states_fn.get_concrete_function(
+ tf.TensorSpec([5], dtype=tf.int32))
+
+ if bundle_input_init_states_fn:
+ signatures = {'call': predict_fn, 'init_states': init_states_fn}
+ else:
+ signatures = predict_fn
+
+ tf.keras.models.save_model(
+ model, export_path, signatures=signatures)
+ else:
+ _ = model(tf.ones(input_shape_concrete))
+ tf.keras.models.save_model(model, export_path)
+
+
+def build_and_export_saved_model(
+ export_path: str = '/tmp/movinet/',
+ model_id: str = 'a0',
+ causal: bool = False,
+ conv_type: str = '3d',
+ se_type: str = '3d',
+ activation: str = 'swish',
+ classifier_activation: str = 'swish',
+ gating_activation: str = 'sigmoid',
+ use_positional_encoding: bool = False,
+ num_classes: int = 600,
+ input_shape: Optional[Tuple[int, int, int, int, int]] = None,
+ bundle_input_init_states_fn: bool = True,
+ checkpoint_path: Optional[str] = None) -> None:
+ """Builds and exports a MoViNet model to a saved model.
+
+ Args:
+ export_path: Export path to save the saved_model file.
+ model_id: MoViNet model name.
+ causal: Run the model in causal mode.
+ conv_type: 3d, 2plus1d, or 3d_2plus1d. 3d configures the network
+ to use the default 3D convolution. 2plus1d uses (2+1)D convolution
+ with Conv2D operations and 2D reshaping (e.g., a 5x3x3 kernel becomes
+ 3x3 followed by 5x1 conv). 3d_2plus1d uses (2+1)D convolution with
+ Conv3D and no 2D reshaping (e.g., a 5x3x3 kernel becomes 1x3x3
+ followed by 5x1x1 conv).
+ se_type:
+ 3d, 2d, or 2plus3d. 3d uses the default 3D spatiotemporal global average
+ pooling for squeeze excitation. 2d uses 2D spatial global average pooling
+ on each frame. 2plus3d concatenates both 3D and 2D global average
+ pooling.
+ activation: The main activation to use across layers.
+ classifier_activation: The classifier activation to use.
+ gating_activation: The gating activation to use in squeeze-excitation
+ layers.
+ use_positional_encoding: Whether to use positional encoding (only applied
+ when causal=True).
+ num_classes: The number of classes for prediction.
+ input_shape: The 5D spatiotemporal input shape of size
+ [batch_size, num_frames, image_height, image_width, num_channels].
+ Set the field or a shape position in the field to None for dynamic input.
+ bundle_input_init_states_fn: Add init_states as a function signature to the
+ saved model. This is not necessary if the input shape is static (e.g.,
+ for TF Lite).
+ checkpoint_path: Checkpoint path to load. Leave blank for default
+ initialization.
+ """
+
+ input_specs = tf.keras.layers.InputSpec(shape=input_shape)
+
+ # Override swish activation implementation to remove custom gradients
+ if activation == 'swish':
+ activation = 'simple_swish'
+ if classifier_activation == 'swish':
+ classifier_activation = 'simple_swish'
+
+ backbone = movinet.Movinet(
+ model_id=model_id,
+ causal=causal,
+ use_positional_encoding=use_positional_encoding,
+ conv_type=conv_type,
+ se_type=se_type,
+ input_specs=input_specs,
+ activation=activation,
+ gating_activation=gating_activation,
+ use_sync_bn=False,
+ use_external_states=causal)
+ model = movinet_model.MovinetClassifier(
+ backbone,
+ num_classes=num_classes,
+ output_states=causal,
+ input_specs=dict(image=input_specs),
+ activation=classifier_activation)
+
+ export_saved_model(
+ model=model,
+ input_shape=input_shape,
+ export_path=export_path,
+ causal=causal,
+ bundle_input_init_states_fn=bundle_input_init_states_fn,
+ checkpoint_path=checkpoint_path)
+
+
+def main(_) -> None:
+ input_shape = (
+ FLAGS.batch_size, FLAGS.num_frames, FLAGS.image_size, FLAGS.image_size, 3)
+ build_and_export_saved_model(
+ export_path=FLAGS.export_path,
+ model_id=FLAGS.model_id,
+ causal=FLAGS.causal,
+ conv_type=FLAGS.conv_type,
+ se_type=FLAGS.se_type,
+ activation=FLAGS.activation,
+ classifier_activation=FLAGS.classifier_activation,
+ gating_activation=FLAGS.gating_activation,
+ use_positional_encoding=FLAGS.use_positional_encoding,
+ num_classes=FLAGS.num_classes,
+ input_shape=input_shape,
+ bundle_input_init_states_fn=FLAGS.bundle_input_init_states_fn,
+ checkpoint_path=FLAGS.checkpoint_path)
+ print(' ----- Done. Saved Model is saved at {}'.format(FLAGS.export_path))
+
+
+if __name__ == '__main__':
+ app.run(main)
diff --git a/official/vision/beta/projects/movinet/export_saved_model_test.py b/official/projects/movinet/tools/export_saved_model_test.py
similarity index 97%
rename from official/vision/beta/projects/movinet/export_saved_model_test.py
rename to official/projects/movinet/tools/export_saved_model_test.py
index cc620c505e2d5d65d2a824cd81acda7c5fa588a9..a06be1c9e5adc4f04d8f32f70aacb45efdde30f2 100644
--- a/official/vision/beta/projects/movinet/export_saved_model_test.py
+++ b/official/projects/movinet/tools/export_saved_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,7 +18,7 @@ from absl import flags
import tensorflow as tf
import tensorflow_hub as hub
-from official.vision.beta.projects.movinet import export_saved_model
+from official.projects.movinet.tools import export_saved_model
FLAGS = flags.FLAGS
diff --git a/official/projects/movinet/tools/plot_movinet_video_stream_predictions.ipynb b/official/projects/movinet/tools/plot_movinet_video_stream_predictions.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..93d09a77bb5ade95a07dc01a6f3fc3e3e2e7088e
--- /dev/null
+++ b/official/projects/movinet/tools/plot_movinet_video_stream_predictions.ipynb
@@ -0,0 +1,393 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "qwBHHt-XvPqn"
+ },
+ "source": [
+ "# Plot MoViNet Video Stream Predictions\n",
+ "\n",
+ "This notebook uses [MoViNets (Mobile Video Networks)](https://github.com/tensorflow/models/tree/master/official/projects/movinet) to predict a human action in a streaming video and outputs a visualization of predictions on each frame.\n",
+ "\n",
+ "Provide a video URL or upload your own to see how predictions change over time. All models can be run on CPU.\n",
+ "\n",
+ "Pretrained models are provided by [TensorFlow Hub](https://tfhub.dev/google/collections/movinet/) and the [TensorFlow Model Garden](https://github.com/tensorflow/models/tree/master/official/projects/movinet), trained on [Kinetics 600](https://deepmind.com/research/open-source/kinetics) for video action classification. All Models use TensorFlow 2 with Keras for inference and training. See the [research paper](https://arxiv.org/pdf/2103.11511.pdf) for more details.\n",
+ "\n",
+ "Example output using [this gif](https://github.com/tensorflow/models/raw/f8af2291cced43fc9f1d9b41ddbf772ae7b0d7d2/official/projects/movinet/files/jumpingjack.gif) as input:\n",
+ "\n",
+ ""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "cellView": "form",
+ "id": "ElvELd9mIfZe"
+ },
+ "outputs": [],
+ "source": [
+ "#@title Run this cell to initialize and setup a [MoViNet](https://github.com/tensorflow/models/tree/master/official/projects/movinet) model.\n",
+ "\n",
+ "\n",
+ "# Install the mediapy package for visualizing images/videos.\n",
+ "# See https://github.com/google/mediapy\n",
+ "!pip install -q mediapy\n",
+ "\n",
+ "# Run imports\n",
+ "import os\n",
+ "import io\n",
+ "\n",
+ "import matplotlib as mpl\n",
+ "import matplotlib.pyplot as plt\n",
+ "import mediapy as media\n",
+ "import numpy as np\n",
+ "import PIL\n",
+ "import pandas as pd\n",
+ "import tensorflow as tf\n",
+ "import tensorflow_datasets as tfds\n",
+ "import tensorflow_hub as hub\n",
+ "import tqdm\n",
+ "from google.colab import files\n",
+ "import urllib.request\n",
+ "\n",
+ "mpl.rcParams.update({\n",
+ " 'font.size': 10,\n",
+ "})\n",
+ "\n",
+ "\n",
+ "# Download Kinetics 600 label map\n",
+ "!wget https://raw.githubusercontent.com/tensorflow/models/f8af2291cced43fc9f1d9b41ddbf772ae7b0d7d2/official/projects/movinet/files/kinetics_600_labels.txt -O labels.txt -q\n",
+ "\n",
+ "with tf.io.gfile.GFile('labels.txt') as f:\n",
+ " lines = f.readlines()\n",
+ " KINETICS_600_LABELS_LIST = [line.strip() for line in lines]\n",
+ " KINETICS_600_LABELS = tf.constant(KINETICS_600_LABELS_LIST)\n",
+ "\n",
+ "def get_top_k(probs, k=5, label_map=KINETICS_600_LABELS):\n",
+ " \"\"\"Outputs the top k model labels and probabilities on the given video.\"\"\"\n",
+ " top_predictions = tf.argsort(probs, axis=-1, direction='DESCENDING')[:k]\n",
+ " top_labels = tf.gather(label_map, top_predictions, axis=-1)\n",
+ " top_labels = [label.decode('utf8') for label in top_labels.numpy()]\n",
+ " top_probs = tf.gather(probs, top_predictions, axis=-1).numpy()\n",
+ " return tuple(zip(top_labels, top_probs))\n",
+ "\n",
+ "def predict_top_k(model, video, k=5, label_map=KINETICS_600_LABELS):\n",
+ " \"\"\"Outputs the top k model labels and probabilities on the given video.\"\"\"\n",
+ " outputs = model.predict(video[tf.newaxis])[0]\n",
+ " probs = tf.nn.softmax(outputs)\n",
+ " return get_top_k(probs, k=k, label_map=label_map)\n",
+ "\n",
+ "def load_movinet_from_hub(model_id, model_mode, hub_version=3):\n",
+ " \"\"\"Loads a MoViNet model from TF Hub.\"\"\"\n",
+ " hub_url = f'https://tfhub.dev/tensorflow/movinet/{model_id}/{model_mode}/kinetics-600/classification/{hub_version}'\n",
+ "\n",
+ " encoder = hub.KerasLayer(hub_url, trainable=True)\n",
+ "\n",
+ " inputs = tf.keras.layers.Input(\n",
+ " shape=[None, None, None, 3],\n",
+ " dtype=tf.float32)\n",
+ "\n",
+ " if model_mode == 'base':\n",
+ " inputs = dict(image=inputs)\n",
+ " else:\n",
+ " # Define the state inputs, which is a dict that maps state names to tensors.\n",
+ " init_states_fn = encoder.resolved_object.signatures['init_states']\n",
+ " state_shapes = {\n",
+ " name: ([s if s \u003e 0 else None for s in state.shape], state.dtype)\n",
+ " for name, state in init_states_fn(tf.constant([0, 0, 0, 0, 3])).items()\n",
+ " }\n",
+ " states_input = {\n",
+ " name: tf.keras.Input(shape[1:], dtype=dtype, name=name)\n",
+ " for name, (shape, dtype) in state_shapes.items()\n",
+ " }\n",
+ "\n",
+ " # The inputs to the model are the states and the video\n",
+ " inputs = {**states_input, 'image': inputs}\n",
+ "\n",
+ " # Output shape: [batch_size, 600]\n",
+ " outputs = encoder(inputs)\n",
+ "\n",
+ " model = tf.keras.Model(inputs, outputs)\n",
+ " model.build([1, 1, 1, 1, 3])\n",
+ "\n",
+ " return model\n",
+ "\n",
+ "# Download example gif\n",
+ "!wget https://github.com/tensorflow/models/raw/f8af2291cced43fc9f1d9b41ddbf772ae7b0d7d2/official/projects/movinet/files/jumpingjack.gif -O jumpingjack.gif -q\n",
+ "\n",
+ "def load_gif(file_path, image_size=(224, 224)):\n",
+ " \"\"\"Loads a gif file into a TF tensor.\"\"\"\n",
+ " with tf.io.gfile.GFile(file_path, 'rb') as f:\n",
+ " video = tf.io.decode_gif(f.read())\n",
+ " video = tf.image.resize(video, image_size)\n",
+ " video = tf.cast(video, tf.float32) / 255.\n",
+ " return video\n",
+ "\n",
+ "def get_top_k_streaming_labels(probs, k=5, label_map=KINETICS_600_LABELS_LIST):\n",
+ " \"\"\"Returns the top-k labels over an entire video sequence.\n",
+ "\n",
+ " Args:\n",
+ " probs: probability tensor of shape (num_frames, num_classes) that represents\n",
+ " the probability of each class on each frame.\n",
+ " k: the number of top predictions to select.\n",
+ " label_map: a list of labels to map logit indices to label strings.\n",
+ "\n",
+ " Returns:\n",
+ " a tuple of the top-k probabilities, labels, and logit indices\n",
+ " \"\"\"\n",
+ " top_categories_last = tf.argsort(probs, -1, 'DESCENDING')[-1, :1]\n",
+ " categories = tf.argsort(probs, -1, 'DESCENDING')[:, :k]\n",
+ " categories = tf.reshape(categories, [-1])\n",
+ "\n",
+ " counts = sorted([\n",
+ " (i.numpy(), tf.reduce_sum(tf.cast(categories == i, tf.int32)).numpy())\n",
+ " for i in tf.unique(categories)[0]\n",
+ " ], key=lambda x: x[1], reverse=True)\n",
+ "\n",
+ " top_probs_idx = tf.constant([i for i, _ in counts[:k]])\n",
+ " top_probs_idx = tf.concat([top_categories_last, top_probs_idx], 0)\n",
+ " top_probs_idx = tf.unique(top_probs_idx)[0][:k+1]\n",
+ "\n",
+ " top_probs = tf.gather(probs, top_probs_idx, axis=-1)\n",
+ " top_probs = tf.transpose(top_probs, perm=(1, 0))\n",
+ " top_labels = tf.gather(label_map, top_probs_idx, axis=0)\n",
+ " top_labels = [label.decode('utf8') for label in top_labels.numpy()]\n",
+ "\n",
+ " return top_probs, top_labels, top_probs_idx\n",
+ "\n",
+ "def plot_streaming_top_preds_at_step(\n",
+ " top_probs,\n",
+ " top_labels,\n",
+ " step=None,\n",
+ " image=None,\n",
+ " legend_loc='lower left',\n",
+ " duration_seconds=10,\n",
+ " figure_height=500,\n",
+ " playhead_scale=0.8,\n",
+ " grid_alpha=0.3):\n",
+ " \"\"\"Generates a plot of the top video model predictions at a given time step.\n",
+ "\n",
+ " Args:\n",
+ " top_probs: a tensor of shape (k, num_frames) representing the top-k\n",
+ " probabilities over all frames.\n",
+ " top_labels: a list of length k that represents the top-k label strings.\n",
+ " step: the current time step in the range [0, num_frames].\n",
+ " image: the image frame to display at the current time step.\n",
+ " legend_loc: the placement location of the legend.\n",
+ " duration_seconds: the total duration of the video.\n",
+ " figure_height: the output figure height.\n",
+ " playhead_scale: scale value for the playhead.\n",
+ " grid_alpha: alpha value for the gridlines.\n",
+ "\n",
+ " Returns:\n",
+ " A tuple of the output numpy image, figure, and axes.\n",
+ " \"\"\"\n",
+ " num_labels, num_frames = top_probs.shape\n",
+ " if step is None:\n",
+ " step = num_frames\n",
+ "\n",
+ " fig = plt.figure(figsize=(6.5, 7), dpi=300)\n",
+ " gs = mpl.gridspec.GridSpec(8, 1)\n",
+ " ax2 = plt.subplot(gs[:-3, :])\n",
+ " ax = plt.subplot(gs[-3:, :])\n",
+ "\n",
+ " if image is not None:\n",
+ " ax2.imshow(image, interpolation='nearest')\n",
+ " ax2.axis('off')\n",
+ "\n",
+ " preview_line_x = tf.linspace(0., duration_seconds, num_frames)\n",
+ " preview_line_y = top_probs\n",
+ "\n",
+ " line_x = preview_line_x[:step+1]\n",
+ " line_y = preview_line_y[:, :step+1]\n",
+ "\n",
+ " for i in range(num_labels):\n",
+ " ax.plot(preview_line_x, preview_line_y[i], label=None, linewidth='1.5',\n",
+ " linestyle=':', color='gray')\n",
+ " ax.plot(line_x, line_y[i], label=top_labels[i], linewidth='2.0')\n",
+ "\n",
+ "\n",
+ " ax.grid(which='major', linestyle=':', linewidth='1.0', alpha=grid_alpha)\n",
+ " ax.grid(which='minor', linestyle=':', linewidth='0.5', alpha=grid_alpha)\n",
+ "\n",
+ " min_height = tf.reduce_min(top_probs) * playhead_scale\n",
+ " max_height = tf.reduce_max(top_probs)\n",
+ " ax.vlines(preview_line_x[step], min_height, max_height, colors='red')\n",
+ " ax.scatter(preview_line_x[step], max_height, color='red')\n",
+ "\n",
+ " ax.legend(loc=legend_loc)\n",
+ "\n",
+ " plt.xlim(0, duration_seconds)\n",
+ " plt.ylabel('Probability')\n",
+ " plt.xlabel('Time (s)')\n",
+ " plt.yscale('log')\n",
+ "\n",
+ " fig.tight_layout()\n",
+ " fig.canvas.draw()\n",
+ "\n",
+ " data = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)\n",
+ " data = data.reshape(fig.canvas.get_width_height()[::-1] + (3,))\n",
+ " plt.close()\n",
+ "\n",
+ " figure_width = int(figure_height * data.shape[1] / data.shape[0])\n",
+ " image = PIL.Image.fromarray(data).resize([figure_width, figure_height])\n",
+ " image = np.array(image)\n",
+ "\n",
+ " return image, (fig, ax, ax2)\n",
+ "\n",
+ "def plot_streaming_top_preds(\n",
+ " probs,\n",
+ " video,\n",
+ " top_k=5,\n",
+ " video_fps=25.,\n",
+ " figure_height=500,\n",
+ " use_progbar=True):\n",
+ " \"\"\"Generates a video plot of the top video model predictions.\n",
+ "\n",
+ " Args:\n",
+ " probs: probability tensor of shape (num_frames, num_classes) that represents\n",
+ " the probability of each class on each frame.\n",
+ " video: the video to display in the plot.\n",
+ " top_k: the number of top predictions to select.\n",
+ " video_fps: the input video fps.\n",
+ " figure_fps: the output video fps.\n",
+ " figure_height: the height of the output video.\n",
+ " use_progbar: display a progress bar.\n",
+ "\n",
+ " Returns:\n",
+ " A numpy array representing the output video.\n",
+ " \"\"\"\n",
+ " video_fps = 8.\n",
+ " figure_height = 500\n",
+ " steps = video.shape[0]\n",
+ " duration = steps / video_fps\n",
+ "\n",
+ " top_probs, top_labels, _ = get_top_k_streaming_labels(probs, k=top_k)\n",
+ "\n",
+ " images = []\n",
+ " step_generator = tqdm.trange(steps) if use_progbar else range(steps)\n",
+ " for i in step_generator:\n",
+ " image, _ = plot_streaming_top_preds_at_step(\n",
+ " top_probs=top_probs,\n",
+ " top_labels=top_labels,\n",
+ " step=i,\n",
+ " image=video[i],\n",
+ " duration_seconds=duration,\n",
+ " figure_height=figure_height,\n",
+ " )\n",
+ " images.append(image)\n",
+ "\n",
+ " return np.array(images)\n",
+ "\n",
+ "def generate_plot(\n",
+ " model,\n",
+ " video_url=None,\n",
+ " resolution=224,\n",
+ " video_fps=25,\n",
+ " display_fps=25):\n",
+ " # Load the video\n",
+ " if not video_url:\n",
+ " video_bytes = list(files.upload().values())[0]\n",
+ " with open('video', 'wb') as f:\n",
+ " f.write(video_bytes)\n",
+ " else:\n",
+ " urllib.request.urlretrieve(video_url, \"video\")\n",
+ "\n",
+ " video = tf.cast(media.read_video('video'), tf.float32) / 255.\n",
+ " video = tf.image.resize(video, [resolution, resolution], preserve_aspect_ratio=True)\n",
+ "\n",
+ " # Create initial states for the stream model\n",
+ " init_states_fn = model.layers[-1].resolved_object.signatures['init_states']\n",
+ " init_states = init_states_fn(tf.shape(video[tf.newaxis]))\n",
+ "\n",
+ " clips = tf.split(video[tf.newaxis], video.shape[0], axis=1)\n",
+ "\n",
+ " all_logits = []\n",
+ "\n",
+ " print('Running the model on the video...')\n",
+ "\n",
+ " # To run on a video, pass in one frame at a time\n",
+ " states = init_states\n",
+ " for clip in tqdm.tqdm(clips):\n",
+ " # Input shape: [1, 1, 172, 172, 3]\n",
+ " logits, states = model.predict({**states, 'image': clip}, verbose=0)\n",
+ " all_logits.append(logits)\n",
+ "\n",
+ " logits = tf.concat(all_logits, 0)\n",
+ " probs = tf.nn.softmax(logits)\n",
+ "\n",
+ " print('Generating the plot...')\n",
+ "\n",
+ " # Generate a plot and output to a video tensor\n",
+ " plot_video = plot_streaming_top_preds(probs, video, video_fps=video_fps)\n",
+ " media.show_video(plot_video, fps=display_fps, codec='gif')\n",
+ "\n",
+ "model_size = 'm' #@param [\"xs\", \"s\", \"m\", \"l\", \"xl\", \"xxl\"]\n",
+ "\n",
+ "model_map = {\n",
+ " 'xs': 'a0',\n",
+ " 's': 'a1',\n",
+ " 'm': 'a2',\n",
+ " 'l': 'a3',\n",
+ " 'xl': 'a4',\n",
+ " 'xxl': 'a5',\n",
+ "}\n",
+ "movinet_model_id = model_map[model_size]\n",
+ "\n",
+ "model = load_movinet_from_hub(\n",
+ " movinet_model_id, 'stream', hub_version=3)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "cellView": "form",
+ "id": "jO6HrPk8pqo8"
+ },
+ "outputs": [],
+ "source": [
+ "#@title Generate a video plot.\n",
+ "\n",
+ "#@markdown You may add a video URL (gif or mp4) or leave the video_url field blank to upload your own file.\n",
+ "video_url = \"https://i.pinimg.com/originals/33/5e/31/335e31bc8ed52511da0cfb4bc44e95c7.gif\" #@param {type:\"string\"}\n",
+ "\n",
+ "#@markdown The base input resolution to the model. A good value is 224, but can change based on model size.\n",
+ "resolution = 224 #@param\n",
+ "#@markdown The fps of the input video.\n",
+ "video_fps = 12 #@param\n",
+ "#@markdown The fps to display the output plot. Depending on the duration of the input video, it may help to use a lower fps.\n",
+ "display_fps = 12 #@param\n",
+ "\n",
+ "generate_plot(\n",
+ " model,\n",
+ " video_url=video_url,\n",
+ " resolution=resolution,\n",
+ " video_fps=video_fps,\n",
+ " display_fps=display_fps)"
+ ]
+ }
+ ],
+ "metadata": {
+ "colab": {
+ "collapsed_sections": [],
+ "last_runtime": {
+ "build_target": "//learning/deepmind/dm_python:dm_notebook3",
+ "kind": "private"
+ },
+ "name": "plot_movinet_video_stream_predictions.ipynb",
+ "provenance": []
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "name": "python"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/official/projects/movinet/tools/quantize_movinet.py b/official/projects/movinet/tools/quantize_movinet.py
new file mode 100644
index 0000000000000000000000000000000000000000..5e34c3c9e524ead11ca144d511f7dee159582be1
--- /dev/null
+++ b/official/projects/movinet/tools/quantize_movinet.py
@@ -0,0 +1,331 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Generates example dataset for post-training quantization.
+
+Example command line to run the script:
+
+```shell
+python3 quantize_movinet.py \
+--saved_model_dir=${SAVED_MODEL_DIR} \
+--saved_model_with_states_dir=${SAVED_MODEL_WITH_STATES_DIR} \
+--output_dataset_dir=${OUTPUT_DATASET_DIR} \
+--output_tflite=${OUTPUT_TFLITE} \
+--quantization_mode='int_float_fallback' \
+--save_dataset_to_tfrecords=True
+```
+
+"""
+
+import functools
+from typing import Any, Callable, Mapping, Optional
+
+from absl import app
+from absl import flags
+from absl import logging
+import numpy as np
+import tensorflow.compat.v2 as tf
+import tensorflow_hub as hub
+
+from official.vision.configs import video_classification as video_classification_configs
+from official.vision.tasks import video_classification
+
+tf.enable_v2_behavior()
+
+FLAGS = flags.FLAGS
+flags.DEFINE_string(
+ 'saved_model_dir', None, 'The saved_model directory.')
+flags.DEFINE_string(
+ 'saved_model_with_states_dir', None,
+ 'The directory to the saved_model with state signature. '
+ 'The saved_model_with_states is needed in order to get the initial state '
+ 'shape and dtype while saved_model is used for the quantization.')
+flags.DEFINE_string(
+ 'output_tflite', '/tmp/output.tflite',
+ 'The output tflite file path.')
+flags.DEFINE_integer(
+ 'temporal_stride', 5,
+ 'Temporal stride used to generate input videos.')
+flags.DEFINE_integer(
+ 'num_frames', 50, 'Input videos number of frames.')
+flags.DEFINE_integer(
+ 'image_size', 172, 'Input videos frame size.')
+flags.DEFINE_string(
+ 'quantization_mode', None,
+ 'The quantization mode. Can be one of "float16", "int8",'
+ '"int_float_fallback" or None.')
+flags.DEFINE_integer(
+ 'num_calibration_videos', 100,
+ 'Number of videos to run to generate example datasets.')
+flags.DEFINE_integer(
+ 'num_samples_per_video', 3,
+ 'Number of sample draw from one single video.')
+flags.DEFINE_boolean(
+ 'save_dataset_to_tfrecords', False,
+ 'Whether to save representative dataset to the disk.')
+flags.DEFINE_string(
+ 'output_dataset_dir', '/tmp/representative_dataset/',
+ 'The directory to store exported tfrecords.')
+flags.DEFINE_integer(
+ 'max_saved_files', 100,
+ 'The maximum number of tfrecord files to save.')
+
+
+def _bytes_feature(value):
+ """Returns a bytes_list from a string / byte."""
+ if isinstance(value, type(tf.constant(0))):
+ value = value.numpy() # BytesList won't unpack string from an EagerTensor.
+ return tf.train.Feature(bytes_list=tf.train.BytesList(value=[value]))
+
+
+def _float_feature(value):
+ """Returns a float_list from a float / double."""
+ return tf.train.Feature(float_list=tf.train.FloatList(value=value))
+
+
+def _int64_feature(value):
+ """Returns an int64_list from a bool / enum / int / uint."""
+ return tf.train.Feature(int64_list=tf.train.Int64List(value=value))
+
+
+def _build_tf_example(feature):
+ return tf.train.Example(
+ features=tf.train.Features(feature=feature)).SerializeToString()
+
+
+def save_to_tfrecord(input_frame: tf.Tensor,
+ input_states: Mapping[str, tf.Tensor],
+ frame_index: int,
+ predictions: tf.Tensor,
+ output_states: Mapping[str, tf.Tensor],
+ groundtruth_label_id: tf.Tensor,
+ output_dataset_dir: str,
+ file_index: int):
+ """Save results to tfrecord."""
+ features = {}
+ features['frame_id'] = _int64_feature([frame_index])
+ features['groundtruth_label'] = _int64_feature(
+ groundtruth_label_id.numpy().flatten().tolist())
+ features['predictions'] = _float_feature(
+ predictions.numpy().flatten().tolist())
+ image_string = tf.io.encode_png(
+ tf.squeeze(tf.cast(input_frame * 255., tf.uint8), axis=[0, 1]))
+ features['image'] = _bytes_feature(image_string.numpy())
+
+ # Input/Output states at time T
+ for k, v in output_states.items():
+ dtype = v[0].dtype
+ if dtype == tf.int32:
+ features['input/' + k] = _int64_feature(
+ input_states[k].numpy().flatten().tolist())
+ features['output/' + k] = _int64_feature(
+ output_states[k].numpy().flatten().tolist())
+ elif dtype == tf.float32:
+ features['input/' + k] = _float_feature(
+ input_states[k].numpy().flatten().tolist())
+ features['output/' + k] = _float_feature(
+ output_states[k].numpy().flatten().tolist())
+ else:
+ raise ValueError(f'Unrecongized dtype: {dtype}')
+
+ tfe = _build_tf_example(features)
+ record_file = '{}/movinet_stream_{:06d}.tfrecords'.format(
+ output_dataset_dir, file_index)
+ logging.info('Saving to %s.', record_file)
+ with tf.io.TFRecordWriter(record_file) as writer:
+ writer.write(tfe)
+
+
+def get_dataset() -> tf.data.Dataset:
+ """Gets dataset source."""
+ config = video_classification_configs.video_classification_kinetics600()
+
+ temporal_stride = FLAGS.temporal_stride
+ num_frames = FLAGS.num_frames
+ image_size = FLAGS.image_size
+ feature_shape = (num_frames, image_size, image_size, 3)
+
+ config.task.validation_data.global_batch_size = 1
+ config.task.validation_data.feature_shape = feature_shape
+ config.task.validation_data.temporal_stride = temporal_stride
+ config.task.train_data.min_image_size = int(1.125 * image_size)
+ config.task.validation_data.dtype = 'float32'
+ config.task.validation_data.drop_remainder = False
+
+ task = video_classification.VideoClassificationTask(config.task)
+
+ valid_dataset = task.build_inputs(config.task.validation_data)
+ valid_dataset = valid_dataset.map(lambda x, y: (x['image'], y))
+ valid_dataset = valid_dataset.prefetch(32)
+ return valid_dataset
+
+
+def stateful_representative_dataset_generator(
+ model: tf.keras.Model,
+ dataset_iter: Any,
+ init_states: Mapping[str, tf.Tensor],
+ save_dataset_to_tfrecords: bool = False,
+ max_saved_files: int = 100,
+ output_dataset_dir: Optional[str] = None,
+ num_samples_per_video: int = 3,
+ num_calibration_videos: int = 100):
+ """Generates sample input data with states.
+
+ Args:
+ model: the inference keras model.
+ dataset_iter: the dataset source.
+ init_states: the initial states for the model.
+ save_dataset_to_tfrecords: whether to save the representative dataset to
+ tfrecords on disk.
+ max_saved_files: the max number of saved tfrecords files.
+ output_dataset_dir: the directory to store the saved tfrecords.
+ num_samples_per_video: number of randomly sampled frames per video.
+ num_calibration_videos: number of calibration videos to run.
+
+ Yields:
+ A dictionary of model inputs.
+ """
+ counter = 0
+ for i in range(num_calibration_videos):
+ if i % 100 == 0:
+ logging.info('Reading representative dateset id %d.', i)
+
+ example_input, example_label = next(dataset_iter)
+ groundtruth_label_id = tf.argmax(example_label, axis=-1)
+ input_states = init_states
+ # split video into frames along the temporal dimension.
+ frames = tf.split(example_input, example_input.shape[1], axis=1)
+
+ random_indices = np.random.randint(
+ low=1, high=len(frames), size=num_samples_per_video)
+ # always include the first frame
+ random_indices[0] = 0
+ random_indices = set(random_indices)
+
+ for frame_index, frame in enumerate(frames):
+ predictions, output_states = model({'image': frame, **input_states})
+ if frame_index in random_indices:
+ if save_dataset_to_tfrecords and counter < max_saved_files:
+ save_to_tfrecord(
+ input_frame=frame,
+ input_states=input_states,
+ frame_index=frame_index,
+ predictions=predictions,
+ output_states=output_states,
+ groundtruth_label_id=groundtruth_label_id,
+ output_dataset_dir=output_dataset_dir,
+ file_index=counter)
+ yield {'image': frame, **input_states}
+ counter += 1
+
+ # update states for the next inference step
+ input_states = output_states
+
+
+def get_tflite_converter(
+ saved_model_dir: str,
+ quantization_mode: str,
+ representative_dataset: Optional[Callable[..., Any]] = None
+) -> tf.lite.TFLiteConverter:
+ """Gets tflite converter."""
+ converter = tf.lite.TFLiteConverter.from_saved_model(
+ saved_model_dir=saved_model_dir)
+ converter.optimizations = [tf.lite.Optimize.DEFAULT]
+
+ if quantization_mode == 'float16':
+ logging.info('Using float16 quantization.')
+ converter.target_spec.supported_types = [tf.float16]
+
+ elif quantization_mode == 'int8':
+ logging.info('Using full interger quantization.')
+ converter.representative_dataset = representative_dataset
+ converter.target_spec.supported_ops = [tf.lite.OpsSet.TFLITE_BUILTINS_INT8]
+ converter.inference_input_type = tf.int8
+ converter.inference_output_type = tf.int8
+
+ elif quantization_mode == 'int_float_fallback':
+ logging.info('Using interger quantization with float-point fallback.')
+ converter.representative_dataset = representative_dataset
+
+ else:
+ logging.info('Using dynamic range quantization.')
+ return converter
+
+
+def quantize_movinet(dataset_fn):
+ """Quantizes Movinet."""
+ valid_dataset = dataset_fn()
+ dataset_iter = iter(valid_dataset)
+
+ # Load model
+ encoder = hub.KerasLayer(FLAGS.saved_model_with_states_dir, trainable=False)
+ inputs = tf.keras.layers.Input(
+ shape=[1, FLAGS.image_size, FLAGS.image_size, 3],
+ dtype=tf.float32,
+ name='image')
+
+ # Define the state inputs, which is a dict that maps state names to tensors.
+ init_states_fn = encoder.resolved_object.signatures['init_states']
+ state_shapes = {
+ name: ([s if s > 0 else None for s in state.shape], state.dtype)
+ for name, state in init_states_fn(
+ tf.constant([1, 1, FLAGS.image_size, FLAGS.image_size, 3])).items()
+ }
+ states_input = {
+ name: tf.keras.Input(shape[1:], dtype=dtype, name=name)
+ for name, (shape, dtype) in state_shapes.items()
+ }
+
+ # The inputs to the model are the states and the video
+ inputs = {**states_input, 'image': inputs}
+ outputs = encoder(inputs)
+ model = tf.keras.Model(inputs, outputs, name='movinet_stream')
+ input_shape = tf.constant(
+ [1, FLAGS.num_frames, FLAGS.image_size, FLAGS.image_size, 3])
+ init_states = init_states_fn(input_shape)
+
+ # config representative_datset_fn
+ representative_dataset = functools.partial(
+ stateful_representative_dataset_generator,
+ model=model,
+ dataset_iter=dataset_iter,
+ init_states=init_states,
+ save_dataset_to_tfrecords=FLAGS.save_dataset_to_tfrecords,
+ max_saved_files=FLAGS.max_saved_files,
+ output_dataset_dir=FLAGS.output_dataset_dir,
+ num_samples_per_video=FLAGS.num_samples_per_video,
+ num_calibration_videos=FLAGS.num_calibration_videos)
+
+ converter = get_tflite_converter(
+ saved_model_dir=FLAGS.saved_model_dir,
+ quantization_mode=FLAGS.quantization_mode,
+ representative_dataset=representative_dataset)
+
+ logging.info('Converting...')
+ tflite_buffer = converter.convert()
+ return tflite_buffer
+
+
+def main(_):
+ tflite_buffer = quantize_movinet(dataset_fn=get_dataset)
+
+ with open(FLAGS.output_tflite, 'wb') as f:
+ f.write(tflite_buffer)
+
+ logging.info('tflite model written to %s', FLAGS.output_tflite)
+
+if __name__ == '__main__':
+ flags.mark_flag_as_required('saved_model_dir')
+ flags.mark_flag_as_required('saved_model_with_states_dir')
+ app.run(main)
diff --git a/official/projects/movinet/train.py b/official/projects/movinet/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..ef42379ec7bc543f3910ed3ba4829ef14734cc5a
--- /dev/null
+++ b/official/projects/movinet/train.py
@@ -0,0 +1,91 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Training driver.
+
+To train:
+
+CONFIG_FILE=official/projects/movinet/configs/yaml/movinet_a0_k600_8x8.yaml
+python3 official/projects/movinet/train.py \
+ --experiment=movinet_kinetics600 \
+ --mode=train \
+ --model_dir=/tmp/movinet/ \
+ --config_file=${CONFIG_FILE} \
+ --params_override="" \
+ --gin_file="" \
+ --gin_params="" \
+ --tpu="" \
+ --tf_data_service=""
+"""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+# Import movinet libraries to register the backbone and model into tf.vision
+# model garden factory.
+# pylint: disable=unused-import
+from official.projects.movinet.modeling import movinet
+from official.projects.movinet.modeling import movinet_model
+from official.vision import registry_imports
+# pylint: enable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ if 'train_and_eval' in FLAGS.mode:
+ assert (params.task.train_data.feature_shape ==
+ params.task.validation_data.feature_shape), (
+ f'train {params.task.train_data.feature_shape} != validate '
+ f'{params.task.validation_data.feature_shape}')
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/vision/beta/projects/movinet/train_test.py b/official/projects/movinet/train_test.py
similarity index 93%
rename from official/vision/beta/projects/movinet/train_test.py
rename to official/projects/movinet/train_test.py
index 5258c50cee9032bb082d3ed25388bcb5f48ef4e2..ad53802ac6593aca986ad40d4cd949f755a86a83 100644
--- a/official/vision/beta/projects/movinet/train_test.py
+++ b/official/projects/movinet/train_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for train.py."""
import json
@@ -24,8 +23,8 @@ from absl import logging
from absl.testing import flagsaver
import tensorflow as tf
-from official.vision.beta.dataloaders import tfexample_utils
-from official.vision.beta.projects.movinet import train as train_lib
+from official.projects.movinet import train as train_lib
+from official.vision.dataloaders import tfexample_utils
FLAGS = flags.FLAGS
diff --git a/official/projects/mtop/README.md b/official/projects/mtop/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..8efe09616216d8e72523c7df2a91120210b0a236
--- /dev/null
+++ b/official/projects/mtop/README.md
@@ -0,0 +1,11 @@
+# MTOP (All Birds with One Stone: Multi-task Text Classification for Efficient Inference with One Forward Pass)
+
+**Note:** This project is a work in progress; please stay tuned.
+
+MTOP is a text encoder multi-task method that can conduct one forward pass to
+make predictions for all tasks. We propose prompt-based modules tailored for
+the multi-task setting and a conditional pooler for flexible task
+representations, and initialization from single task models for effective
+knowledge transfer. Our proposed approach gets superior performance on news
+tasks and the GLUE benchmark. We also release a multi-task news dataset.
+
diff --git a/official/projects/nhnet/README.md b/official/projects/nhnet/README.md
index f838d120fb8bcc419d5eaeb543675eb224cfddbd..88a7d1f9fe40765441b3aed44643c7f2b425cae9 100644
--- a/official/projects/nhnet/README.md
+++ b/official/projects/nhnet/README.md
@@ -36,7 +36,7 @@ will crawl and extract news articles on a local machine.
First, install the `news-please` CLI (requires python 3.x)
```shell
-$ pip3 install news-please
+$ pip3 install news-please==1.4.26
```
Next, run the crawler with our provided [config and URL list](https://github.com/google-research-datasets/NewSHead/releases)
diff --git a/official/projects/nhnet/__init__.py b/official/projects/nhnet/__init__.py
index e419af524b5f349fe04abfa820c3cb51b777d422..310bfb28f0c252bc4a4485325059bff28c5250c2 100644
--- a/official/projects/nhnet/__init__.py
+++ b/official/projects/nhnet/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/configs.py b/official/projects/nhnet/configs.py
index 0f58dce8a9a1304aa00367cc759f6446cbb6a081..fa0a787f9a4a9e81fe0e8c737c9050c0391fd9a6 100644
--- a/official/projects/nhnet/configs.py
+++ b/official/projects/nhnet/configs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/configs_test.py b/official/projects/nhnet/configs_test.py
index 6ed2b24adbed457670fee85e36c0ad75bf9f9631..54678ddecf2703d1aef90d4c70944d7d0a0c6e57 100644
--- a/official/projects/nhnet/configs_test.py
+++ b/official/projects/nhnet/configs_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/decoder.py b/official/projects/nhnet/decoder.py
index c937feac1003bc9b0d0ff00033d44245b6201786..dc1d8e3fd86351fe609ebd1449e83c75b0e28ca9 100644
--- a/official/projects/nhnet/decoder.py
+++ b/official/projects/nhnet/decoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/decoder_test.py b/official/projects/nhnet/decoder_test.py
index 4d70bbadf0a0b67fa6a997bc9181cebbac277ec1..1c0feb81abc7a300128931e1b2d52d4ff416400c 100644
--- a/official/projects/nhnet/decoder_test.py
+++ b/official/projects/nhnet/decoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/evaluation.py b/official/projects/nhnet/evaluation.py
index 8435d2c0a24dab13da3a66a587235fc099c1a77e..c762aeb54897456159a92dd73343af4420207896 100644
--- a/official/projects/nhnet/evaluation.py
+++ b/official/projects/nhnet/evaluation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/input_pipeline.py b/official/projects/nhnet/input_pipeline.py
index d61ea688e2d9dc83083f5ddd1e1df109dc8e65d5..3bfe2bc511370ea4838c67faf58e23d87d56648d 100644
--- a/official/projects/nhnet/input_pipeline.py
+++ b/official/projects/nhnet/input_pipeline.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/models.py b/official/projects/nhnet/models.py
index 96f2ab30c288e54eeef66bfbbba21de721cc109b..6832a96404e7abef73a9502c57c656850e6867f3 100644
--- a/official/projects/nhnet/models.py
+++ b/official/projects/nhnet/models.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/models_test.py b/official/projects/nhnet/models_test.py
index ac4783722a3b49493e262a3f833fcf7c3e116bf4..3f487d08943c54d1cbc3fb5cbb0a31d0b6938543 100644
--- a/official/projects/nhnet/models_test.py
+++ b/official/projects/nhnet/models_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/optimizer.py b/official/projects/nhnet/optimizer.py
index 03375c3b22134e566dd1ce28120a2897cf8a1b1d..85a9a79448d5325fdf272cde406af4441e54d09b 100644
--- a/official/projects/nhnet/optimizer.py
+++ b/official/projects/nhnet/optimizer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/raw_data_process.py b/official/projects/nhnet/raw_data_process.py
index c845b08c2b447fef8f03ba3fe505735bea8850fa..3f5d15eab10df7c7e99b8207132a21cff226d94a 100644
--- a/official/projects/nhnet/raw_data_process.py
+++ b/official/projects/nhnet/raw_data_process.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/raw_data_processor.py b/official/projects/nhnet/raw_data_processor.py
index 73a00ba158cb2aa098516880ef6d18dd1ef2636e..1e3316e8be74cf229c7e817af23089abcea1ab03 100644
--- a/official/projects/nhnet/raw_data_processor.py
+++ b/official/projects/nhnet/raw_data_processor.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,8 +22,8 @@ import urllib.parse
import tensorflow as tf
-from official.nlp.bert import tokenization
from official.nlp.data import classifier_data_lib
+from official.nlp.tools import tokenization
class RawDataProcessor(object):
diff --git a/official/projects/nhnet/trainer.py b/official/projects/nhnet/trainer.py
index 183f05ef01e29b533a5ecbdd2b4075ee8f8df567..35d4eea637c39a80a34afbd3fe9172ba3b5a51f5 100644
--- a/official/projects/nhnet/trainer.py
+++ b/official/projects/nhnet/trainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -120,9 +120,13 @@ class Trainer(tf.keras.Model):
tvars = self.trainable_variables
grads = tape.gradient(scaled_loss, tvars)
self.optimizer.apply_gradients(list(zip(grads, tvars)))
+ if isinstance(self.optimizer, tf.keras.optimizers.experimental.Optimizer):
+ learning_rate = self.optimizer.learning_rate
+ else:
+ learning_rate = self.optimizer._decayed_lr(var_dtype=tf.float32)
return {
"training_loss": loss,
- "learning_rate": self.optimizer._decayed_lr(var_dtype=tf.float32)
+ "learning_rate": learning_rate,
}
diff --git a/official/projects/nhnet/trainer_test.py b/official/projects/nhnet/trainer_test.py
index 6adddbbdba63385da56887fe8268065a1a08a2a0..886c8b4cf2a1773e03f577f089a4ab3dac056845 100644
--- a/official/projects/nhnet/trainer_test.py
+++ b/official/projects/nhnet/trainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/nhnet/utils.py b/official/projects/nhnet/utils.py
index f23b2bef21cd171e432e03eff4e93077c478c076..23c3d571e70e4f1b21d461a56e0fa7bc28bac6e6 100644
--- a/official/projects/nhnet/utils.py
+++ b/official/projects/nhnet/utils.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,8 +18,8 @@ from typing import Optional, Text
from absl import logging
import tensorflow as tf
+from official.legacy.bert import configs
from official.modeling.hyperparams import params_dict
-from official.nlp.bert import configs
from official.projects.nhnet import configs as nhnet_configs
diff --git a/official/projects/panoptic/README.md b/official/projects/panoptic/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ebe1c2a93ddd97c355730239a20f0ee76a8f716b
--- /dev/null
+++ b/official/projects/panoptic/README.md
@@ -0,0 +1,114 @@
+# Panoptic Segmentation
+
+## Description
+
+Panoptic Segmentation combines the two distinct vision tasks - semantic
+segmentation and instance segmentation. These tasks are unified such that, each
+pixel in the image is assigned the label of the class it belongs to, and also
+the instance identifier of the object it is a part of.
+
+## Environment setup
+The code can be run on multiple GPUs or TPUs with different distribution
+strategies. See the TensorFlow distributed training
+[guide](https://www.tensorflow.org/guide/distributed_training) for an overview
+of `tf.distribute`.
+
+The code is compatible with TensorFlow 2.6+. See requirements.txt for all
+prerequisites.
+
+```bash
+$ git clone https://github.com/tensorflow/models.git
+$ cd models
+$ pip3 install -r official/requirements.txt
+$ export PYTHONPATH=$(pwd)
+```
+
+## Preparing Dataset
+```bash
+$ ./official/vision/beta/data/process_coco_panoptic.sh
+```
+
+## Launch Training
+```bash
+$ export MODEL_DIR="gs://"
+$ export TPU_NAME=""
+$ export ANNOTATION_FILE="gs://"
+$ export TRAIN_DATA="gs://"
+$ export EVAL_DATA="gs://"
+$ export OVERRIDES="task.validation_data.input_path=${EVAL_DATA},\
+task.train_data.input_path=${TRAIN_DATA},\
+task.annotation_file=${ANNOTATION_FILE},\
+runtime.distribution_strategy=tpu"
+
+
+$ python3 train.py \
+ --experiment panoptic_fpn_coco \
+ --config_file configs/experiments/r50fpn_1x_coco.yaml \
+ --mode train \
+ --model_dir $MODEL_DIR \
+ --tpu $TPU_NAME \
+ --params_override=$OVERRIDES
+```
+
+## Launch Evaluation
+```bash
+$ export MODEL_DIR="gs://"
+$ export NUM_GPUS=""
+$ export PRECISION=""
+$ export ANNOTATION_FILE="gs://"
+$ export TRAIN_DATA="gs://"
+$ export EVAL_DATA="gs://"
+$ export OVERRIDES="task.validation_data.input_path=${EVAL_DATA}, \
+task.train_data.input_path=${TRAIN_DATA}, \
+task.annotation_file=${ANNOTATION_FILE}, \
+runtime.distribution_strategy=mirrored, \
+runtime.mixed_precision_dtype=$PRECISION, \
+runtime.num_gpus=$NUM_GPUS"
+
+
+$ python3 train.py \
+ --experiment panoptic_fpn_coco \
+ --config_file configs/experiments/r50fpn_1x_coco.yaml \
+ --mode eval \
+ --model_dir $MODEL_DIR \
+ --params_override=$OVERRIDES
+```
+**Note**: The [PanopticSegmentationGenerator](https://github.com/tensorflow/models/blob/ac7f9e7f2d0508913947242bad3e23ef7cae5a43/official/projects/panoptic/modeling/layers/panoptic_segmentation_generator.py#L22) layer uses dynamic shapes and hence generating panoptic masks is not supported on Cloud TPUs. Running evaluation on Cloud TPUs is not supported for the same reason. However, training is supported on both Cloud TPUs and GPUs.
+## Pretrained Models
+### Panoptic FPN
+Backbone | Schedule | Experiment name | Box mAP | Mask mAP | Overall PQ | Things PQ | Stuff PQ | Checkpoints
+:------------| :----------- | :---------------------------| ------- | ---------- | ---------- | --------- | -------- | ------------:
+ResNet-50 | 1x | `panoptic_fpn_coco` | 38.19 | 34.25 | 39.14 | 45.42 | 29.65 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_fpn/panoptic_fpn_1x)
+ResNet-50 | 3x | `panoptic_fpn_coco` | 40.64 | 36.29 | 40.91 | 47.68 | 30.69 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_fpn/panoptic_fpn_3x)
+
+**Note**: Here 1x schedule refers to ~12 epochs
+
+### Panoptic Deeplab
+Backbone | Experiment name | Overall PQ | Things PQ | Stuff PQ | Checkpoints
+:---------------------| :-------------------------------| ---------- | --------- | -------- | ------------:
+Dilated ResNet-50 | `panoptic_deeplab_resnet_coco` | 36.80 | 37.51 | 35.73 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_deeplab/coco/resnet50)
+Dilated ResNet-101 | `panoptic_deeplab_resnet_coco` | 38.39 | 39.47 | 36.75 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_deeplab/coco/resnet101)
+MobileNetV3 Large | `panoptic_deeplab_mobilenetv3_large_coco` | 30.50 | 30.10 | 31.10 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_deeplab/coco/mobilenetv3_large)
+MobileNetV3 Small | `panoptic_deeplab_mobilenetv3_small_coco` | 25.06 | 23.46 | 27.48 | [ckpt](gs://tf_model_garden/vision/panoptic/panoptic_deeplab/coco/mobilenetv3_small)
+
+
+___
+## Citation
+```
+@misc{kirillov2019panoptic,
+ title={Panoptic Feature Pyramid Networks},
+ author={Alexander Kirillov and Ross Girshick and Kaiming He and Piotr Dollár},
+ year={2019},
+ eprint={1901.02446},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+
+@article{Cheng2020PanopticDeepLabAS,
+ title={Panoptic-DeepLab: A Simple, Strong, and Fast Baseline for Bottom-Up Panoptic Segmentation},
+ author={Bowen Cheng and Maxwell D. Collins and Yukun Zhu and Ting Liu and Thomas S. Huang and Hartwig Adam and Liang-Chieh Chen},
+ journal={2020 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
+ year={2020},
+ pages={12472-12482}
+}
+```
diff --git a/official/projects/panoptic/__init__.py b/official/projects/panoptic/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/panoptic/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/panoptic/configs/__init__.py b/official/projects/panoptic/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/panoptic/configs/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/vision/beta/projects/panoptic_maskrcnn/configs/experiments/r50fpn_1x_coco.yaml b/official/projects/panoptic/configs/experiments/r50fpn_1x_coco.yaml
similarity index 100%
rename from official/vision/beta/projects/panoptic_maskrcnn/configs/experiments/r50fpn_1x_coco.yaml
rename to official/projects/panoptic/configs/experiments/r50fpn_1x_coco.yaml
diff --git a/official/vision/beta/projects/panoptic_maskrcnn/configs/experiments/r50fpn_3x_coco.yaml b/official/projects/panoptic/configs/experiments/r50fpn_3x_coco.yaml
similarity index 100%
rename from official/vision/beta/projects/panoptic_maskrcnn/configs/experiments/r50fpn_3x_coco.yaml
rename to official/projects/panoptic/configs/experiments/r50fpn_3x_coco.yaml
diff --git a/official/projects/panoptic/configs/panoptic_deeplab.py b/official/projects/panoptic/configs/panoptic_deeplab.py
new file mode 100644
index 0000000000000000000000000000000000000000..b64fb62410030719d7501cccd18ce1051c28c4ed
--- /dev/null
+++ b/official/projects/panoptic/configs/panoptic_deeplab.py
@@ -0,0 +1,670 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic Deeplab configuration definition."""
+import dataclasses
+import os
+from typing import List, Optional, Union
+
+import numpy as np
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.vision.configs import common
+from official.vision.configs import decoders
+from official.vision.configs import backbones
+
+
+_COCO_INPUT_PATH_BASE = 'coco/tfrecords'
+_COCO_TRAIN_EXAMPLES = 118287
+_COCO_VAL_EXAMPLES = 5000
+
+
+@dataclasses.dataclass
+class Parser(hyperparams.Config):
+ """Panoptic deeplab parser."""
+ ignore_label: int = 0
+ # If resize_eval_groundtruth is set to False, original image sizes are used
+ # for eval. In that case, groundtruth_padded_size has to be specified too to
+ # allow for batching the variable input sizes of images.
+ resize_eval_groundtruth: bool = True
+ groundtruth_padded_size: List[int] = dataclasses.field(default_factory=list)
+ aug_scale_min: float = 1.0
+ aug_scale_max: float = 1.0
+ aug_rand_hflip: bool = True
+ aug_type: common.Augmentation = common.Augmentation()
+ sigma: float = 8.0
+ small_instance_area_threshold: int = 4096
+ small_instance_weight: float = 3.0
+ dtype = 'float32'
+
+
+@dataclasses.dataclass
+class TfExampleDecoder(common.TfExampleDecoder):
+ """A simple TF Example decoder config."""
+ panoptic_category_mask_key: str = 'image/panoptic/category_mask'
+ panoptic_instance_mask_key: str = 'image/panoptic/instance_mask'
+
+
+@dataclasses.dataclass
+class DataDecoder(common.DataDecoder):
+ """Data decoder config."""
+ simple_decoder: TfExampleDecoder = TfExampleDecoder()
+
+
+@dataclasses.dataclass
+class DataConfig(cfg.DataConfig):
+ """Input config for training."""
+ decoder: DataDecoder = DataDecoder()
+ parser: Parser = Parser()
+ input_path: str = ''
+ drop_remainder: bool = True
+ file_type: str = 'tfrecord'
+ is_training: bool = True
+ global_batch_size: int = 1
+
+
+@dataclasses.dataclass
+class PanopticDeeplabHead(hyperparams.Config):
+ """Panoptic Deeplab head config."""
+ level: int = 3
+ num_convs: int = 2
+ num_filters: int = 256
+ kernel_size: int = 5
+ use_depthwise_convolution: bool = False
+ upsample_factor: int = 1
+ low_level: List[int] = dataclasses.field(default_factory=lambda: [3, 2])
+ low_level_num_filters: List[int] = dataclasses.field(
+ default_factory=lambda: [64, 32])
+ fusion_num_output_filters: int = 256
+
+
+@dataclasses.dataclass
+class SemanticHead(PanopticDeeplabHead):
+ """Semantic head config."""
+ prediction_kernel_size: int = 1
+
+
+@dataclasses.dataclass
+class InstanceHead(PanopticDeeplabHead):
+ """Instance head config."""
+ prediction_kernel_size: int = 1
+
+
+@dataclasses.dataclass
+class PanopticDeeplabPostProcessor(hyperparams.Config):
+ """Panoptic Deeplab PostProcessing config."""
+ output_size: List[int] = dataclasses.field(
+ default_factory=list)
+ center_score_threshold: float = 0.1
+ thing_class_ids: List[int] = dataclasses.field(default_factory=list)
+ label_divisor: int = 256 * 256 * 256
+ stuff_area_limit: int = 4096
+ ignore_label: int = 0
+ nms_kernel: int = 7
+ keep_k_centers: int = 200
+ rescale_predictions: bool = True
+
+
+@dataclasses.dataclass
+class PanopticDeeplab(hyperparams.Config):
+ """Panoptic Deeplab model config."""
+ num_classes: int = 2
+ input_size: List[int] = dataclasses.field(default_factory=list)
+ min_level: int = 3
+ max_level: int = 6
+ norm_activation: common.NormActivation = common.NormActivation()
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='resnet', resnet=backbones.ResNet())
+ decoder: decoders.Decoder = decoders.Decoder(type='aspp')
+ semantic_head: SemanticHead = SemanticHead()
+ instance_head: InstanceHead = InstanceHead()
+ shared_decoder: bool = False
+ generate_panoptic_masks: bool = True
+ post_processor: PanopticDeeplabPostProcessor = PanopticDeeplabPostProcessor()
+
+
+@dataclasses.dataclass
+class Losses(hyperparams.Config):
+ label_smoothing: float = 0.0
+ ignore_label: int = 0
+ class_weights: List[float] = dataclasses.field(default_factory=list)
+ l2_weight_decay: float = 1e-4
+ top_k_percent_pixels: float = 0.15
+ segmentation_loss_weight: float = 1.0
+ center_heatmap_loss_weight: float = 200
+ center_offset_loss_weight: float = 0.01
+
+
+@dataclasses.dataclass
+class Evaluation(hyperparams.Config):
+ """Evaluation config."""
+ ignored_label: int = 0
+ max_instances_per_category: int = 256
+ offset: int = 256 * 256 * 256
+ is_thing: List[float] = dataclasses.field(
+ default_factory=list)
+ rescale_predictions: bool = True
+ report_per_class_pq: bool = False
+
+ report_per_class_iou: bool = False
+ report_train_mean_iou: bool = True # Turning this off can speed up training.
+
+
+@dataclasses.dataclass
+class PanopticDeeplabTask(cfg.TaskConfig):
+ """Panoptic deeplab task config."""
+ model: PanopticDeeplab = PanopticDeeplab()
+ train_data: DataConfig = DataConfig(is_training=True)
+ validation_data: DataConfig = DataConfig(
+ is_training=False,
+ drop_remainder=False)
+ losses: Losses = Losses()
+ init_checkpoint: Optional[str] = None
+ init_checkpoint_modules: Union[
+ str, List[str]] = 'all' # all, backbone, and/or decoder
+ evaluation: Evaluation = Evaluation()
+
+
+@exp_factory.register_config_factory('panoptic_deeplab_resnet_coco')
+def panoptic_deeplab_resnet_coco() -> cfg.ExperimentConfig:
+ """COCO panoptic segmentation with Panoptic Deeplab."""
+ train_steps = 200000
+ train_batch_size = 64
+ eval_batch_size = 1
+ steps_per_epoch = _COCO_TRAIN_EXAMPLES // train_batch_size
+ validation_steps = _COCO_VAL_EXAMPLES // eval_batch_size
+
+ num_panoptic_categories = 201
+ num_thing_categories = 91
+ ignore_label = 0
+
+ is_thing = [False]
+ for idx in range(1, num_panoptic_categories):
+ is_thing.append(True if idx <= num_thing_categories else False)
+
+ input_size = [640, 640, 3]
+ output_stride = 16
+ aspp_dilation_rates = [6, 12, 18]
+ multigrid = [1, 2, 4]
+ stem_type = 'v1'
+ level = int(np.math.log2(output_stride))
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(
+ mixed_precision_dtype='bfloat16', enable_xla=True),
+ task=PanopticDeeplabTask(
+ init_checkpoint='gs://tf_model_garden/vision/panoptic/panoptic_deeplab/imagenet/resnet50_v1/ckpt-436800', # pylint: disable=line-too-long
+ init_checkpoint_modules=['backbone'],
+ model=PanopticDeeplab(
+ num_classes=num_panoptic_categories,
+ input_size=input_size,
+ backbone=backbones.Backbone(
+ type='dilated_resnet', dilated_resnet=backbones.DilatedResNet(
+ model_id=50,
+ stem_type=stem_type,
+ output_stride=output_stride,
+ multigrid=multigrid,
+ se_ratio=0.25,
+ last_stage_repeats=1,
+ stochastic_depth_drop_rate=0.2)),
+ decoder=decoders.Decoder(
+ type='aspp',
+ aspp=decoders.ASPP(
+ level=level,
+ num_filters=256,
+ pool_kernel_size=input_size[:2],
+ dilation_rates=aspp_dilation_rates,
+ use_depthwise_convolution=True,
+ dropout_rate=0.1)),
+ semantic_head=SemanticHead(
+ level=level,
+ num_convs=1,
+ num_filters=256,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[64, 32],
+ fusion_num_output_filters=256,
+ prediction_kernel_size=1),
+ instance_head=InstanceHead(
+ level=level,
+ num_convs=1,
+ num_filters=32,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[32, 16],
+ fusion_num_output_filters=128,
+ prediction_kernel_size=1),
+ shared_decoder=False,
+ generate_panoptic_masks=True,
+ post_processor=PanopticDeeplabPostProcessor(
+ output_size=input_size[:2],
+ center_score_threshold=0.1,
+ thing_class_ids=list(range(1, num_thing_categories)),
+ label_divisor=256,
+ stuff_area_limit=4096,
+ ignore_label=ignore_label,
+ nms_kernel=41,
+ keep_k_centers=200,
+ rescale_predictions=True)),
+ losses=Losses(
+ label_smoothing=0.0,
+ ignore_label=ignore_label,
+ l2_weight_decay=0.0,
+ top_k_percent_pixels=0.2,
+ segmentation_loss_weight=1.0,
+ center_heatmap_loss_weight=200,
+ center_offset_loss_weight=0.01),
+ train_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=Parser(
+ aug_scale_min=0.5,
+ aug_scale_max=1.5,
+ aug_rand_hflip=True,
+ aug_type=common.Augmentation(
+ type='autoaug',
+ autoaug=common.AutoAugment(
+ augmentation_name='panoptic_deeplab_policy')),
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0)),
+ validation_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ parser=Parser(
+ resize_eval_groundtruth=False,
+ groundtruth_padded_size=[640, 640],
+ aug_scale_min=1.0,
+ aug_scale_max=1.0,
+ aug_rand_hflip=False,
+ aug_type=None,
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0),
+ drop_remainder=False),
+ evaluation=Evaluation(
+ ignored_label=ignore_label,
+ max_instances_per_category=256,
+ offset=256*256*256,
+ is_thing=is_thing,
+ rescale_predictions=True,
+ report_per_class_pq=False,
+ report_per_class_iou=False,
+ report_train_mean_iou=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=validation_steps,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adam',
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 0.0005,
+ 'decay_steps': train_steps,
+ 'end_learning_rate': 0.0,
+ 'power': 0.9
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 2000,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
+
+
+@exp_factory.register_config_factory('panoptic_deeplab_mobilenetv3_large_coco')
+def panoptic_deeplab_mobilenetv3_large_coco() -> cfg.ExperimentConfig:
+ """COCO panoptic segmentation with Panoptic Deeplab."""
+ train_steps = 200000
+ train_batch_size = 64
+ eval_batch_size = 1
+ steps_per_epoch = _COCO_TRAIN_EXAMPLES // train_batch_size
+ validation_steps = _COCO_VAL_EXAMPLES // eval_batch_size
+
+ num_panoptic_categories = 201
+ num_thing_categories = 91
+ ignore_label = 0
+
+ is_thing = [False]
+ for idx in range(1, num_panoptic_categories):
+ is_thing.append(True if idx <= num_thing_categories else False)
+
+ input_size = [640, 640, 3]
+ output_stride = 16
+ aspp_dilation_rates = [6, 12, 18]
+ level = int(np.math.log2(output_stride))
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(
+ mixed_precision_dtype='float32', enable_xla=True),
+ task=PanopticDeeplabTask(
+ init_checkpoint='gs://tf_model_garden/vision/panoptic/panoptic_deeplab/imagenet/mobilenetv3_large/ckpt-156000',
+ init_checkpoint_modules=['backbone'],
+ model=PanopticDeeplab(
+ num_classes=num_panoptic_categories,
+ input_size=input_size,
+ backbone=backbones.Backbone(
+ type='mobilenet', mobilenet=backbones.MobileNet(
+ model_id='MobileNetV3Large',
+ filter_size_scale=1.0,
+ stochastic_depth_drop_rate=0.0,
+ output_stride=output_stride)),
+ decoder=decoders.Decoder(
+ type='aspp',
+ aspp=decoders.ASPP(
+ level=level,
+ num_filters=256,
+ pool_kernel_size=input_size[:2],
+ dilation_rates=aspp_dilation_rates,
+ use_depthwise_convolution=True,
+ dropout_rate=0.1)),
+ semantic_head=SemanticHead(
+ level=level,
+ num_convs=1,
+ num_filters=256,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[64, 32],
+ fusion_num_output_filters=256,
+ prediction_kernel_size=1),
+ instance_head=InstanceHead(
+ level=level,
+ num_convs=1,
+ num_filters=32,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[32, 16],
+ fusion_num_output_filters=128,
+ prediction_kernel_size=1),
+ shared_decoder=False,
+ generate_panoptic_masks=True,
+ post_processor=PanopticDeeplabPostProcessor(
+ output_size=input_size[:2],
+ center_score_threshold=0.1,
+ thing_class_ids=list(range(1, num_thing_categories)),
+ label_divisor=256,
+ stuff_area_limit=4096,
+ ignore_label=ignore_label,
+ nms_kernel=41,
+ keep_k_centers=200,
+ rescale_predictions=True)),
+ losses=Losses(
+ label_smoothing=0.0,
+ ignore_label=ignore_label,
+ l2_weight_decay=0.0,
+ top_k_percent_pixels=0.2,
+ segmentation_loss_weight=1.0,
+ center_heatmap_loss_weight=200,
+ center_offset_loss_weight=0.01),
+ train_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=Parser(
+ aug_scale_min=0.5,
+ aug_scale_max=2.0,
+ aug_rand_hflip=True,
+ aug_type=common.Augmentation(
+ type='autoaug',
+ autoaug=common.AutoAugment(
+ augmentation_name='panoptic_deeplab_policy')),
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0)),
+ validation_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ parser=Parser(
+ resize_eval_groundtruth=False,
+ groundtruth_padded_size=[640, 640],
+ aug_scale_min=1.0,
+ aug_scale_max=1.0,
+ aug_rand_hflip=False,
+ aug_type=None,
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0),
+ drop_remainder=False),
+ evaluation=Evaluation(
+ ignored_label=ignore_label,
+ max_instances_per_category=256,
+ offset=256*256*256,
+ is_thing=is_thing,
+ rescale_predictions=True,
+ report_per_class_pq=False,
+ report_per_class_iou=False,
+ report_train_mean_iou=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=validation_steps,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adam',
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 0.001,
+ 'decay_steps': train_steps,
+ 'end_learning_rate': 0.0,
+ 'power': 0.9
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 2000,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
+
+
+@exp_factory.register_config_factory('panoptic_deeplab_mobilenetv3_small_coco')
+def panoptic_deeplab_mobilenetv3_small_coco() -> cfg.ExperimentConfig:
+ """COCO panoptic segmentation with Panoptic Deeplab."""
+ train_steps = 200000
+ train_batch_size = 64
+ eval_batch_size = 1
+ steps_per_epoch = _COCO_TRAIN_EXAMPLES // train_batch_size
+ validation_steps = _COCO_VAL_EXAMPLES // eval_batch_size
+
+ num_panoptic_categories = 201
+ num_thing_categories = 91
+ ignore_label = 0
+
+ is_thing = [False]
+ for idx in range(1, num_panoptic_categories):
+ is_thing.append(True if idx <= num_thing_categories else False)
+
+ input_size = [640, 640, 3]
+ output_stride = 16
+ aspp_dilation_rates = [6, 12, 18]
+ level = int(np.math.log2(output_stride))
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(
+ mixed_precision_dtype='float32', enable_xla=True),
+ task=PanopticDeeplabTask(
+ init_checkpoint='gs://tf_model_garden/vision/panoptic/panoptic_deeplab/imagenet/mobilenetv3_small/ckpt-312000',
+ init_checkpoint_modules=['backbone'],
+ model=PanopticDeeplab(
+ num_classes=num_panoptic_categories,
+ input_size=input_size,
+ backbone=backbones.Backbone(
+ type='mobilenet', mobilenet=backbones.MobileNet(
+ model_id='MobileNetV3Small',
+ filter_size_scale=1.0,
+ stochastic_depth_drop_rate=0.0,
+ output_stride=output_stride)),
+ decoder=decoders.Decoder(
+ type='aspp',
+ aspp=decoders.ASPP(
+ level=level,
+ num_filters=256,
+ pool_kernel_size=input_size[:2],
+ dilation_rates=aspp_dilation_rates,
+ use_depthwise_convolution=True,
+ dropout_rate=0.1)),
+ semantic_head=SemanticHead(
+ level=level,
+ num_convs=1,
+ num_filters=256,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[64, 32],
+ fusion_num_output_filters=256,
+ prediction_kernel_size=1),
+ instance_head=InstanceHead(
+ level=level,
+ num_convs=1,
+ num_filters=32,
+ kernel_size=5,
+ use_depthwise_convolution=True,
+ upsample_factor=1,
+ low_level=[3, 2],
+ low_level_num_filters=[32, 16],
+ fusion_num_output_filters=128,
+ prediction_kernel_size=1),
+ shared_decoder=False,
+ generate_panoptic_masks=True,
+ post_processor=PanopticDeeplabPostProcessor(
+ output_size=input_size[:2],
+ center_score_threshold=0.1,
+ thing_class_ids=list(range(1, num_thing_categories)),
+ label_divisor=256,
+ stuff_area_limit=4096,
+ ignore_label=ignore_label,
+ nms_kernel=41,
+ keep_k_centers=200,
+ rescale_predictions=True)),
+ losses=Losses(
+ label_smoothing=0.0,
+ ignore_label=ignore_label,
+ l2_weight_decay=0.0,
+ top_k_percent_pixels=0.2,
+ segmentation_loss_weight=1.0,
+ center_heatmap_loss_weight=200,
+ center_offset_loss_weight=0.01),
+ train_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=Parser(
+ aug_scale_min=0.5,
+ aug_scale_max=2.0,
+ aug_rand_hflip=True,
+ aug_type=common.Augmentation(
+ type='autoaug',
+ autoaug=common.AutoAugment(
+ augmentation_name='panoptic_deeplab_policy')),
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0)),
+ validation_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ parser=Parser(
+ resize_eval_groundtruth=False,
+ groundtruth_padded_size=[640, 640],
+ aug_scale_min=1.0,
+ aug_scale_max=1.0,
+ aug_rand_hflip=False,
+ aug_type=None,
+ sigma=8.0,
+ small_instance_area_threshold=4096,
+ small_instance_weight=3.0),
+ drop_remainder=False),
+ evaluation=Evaluation(
+ ignored_label=ignore_label,
+ max_instances_per_category=256,
+ offset=256*256*256,
+ is_thing=is_thing,
+ rescale_predictions=True,
+ report_per_class_pq=False,
+ report_per_class_iou=False,
+ report_train_mean_iou=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=train_steps,
+ validation_steps=validation_steps,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adam',
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 0.001,
+ 'decay_steps': train_steps,
+ 'end_learning_rate': 0.0,
+ 'power': 0.9
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 2000,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
diff --git a/official/projects/panoptic/configs/panoptic_maskrcnn.py b/official/projects/panoptic/configs/panoptic_maskrcnn.py
new file mode 100644
index 0000000000000000000000000000000000000000..a27bcb7755f2bd34d469ee73b4400cc7324fce3f
--- /dev/null
+++ b/official/projects/panoptic/configs/panoptic_maskrcnn.py
@@ -0,0 +1,259 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic Mask R-CNN configuration definition."""
+
+import dataclasses
+import os
+from typing import List, Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.projects.deepmac_maskrcnn.configs import deep_mask_head_rcnn as deepmac_maskrcnn
+from official.vision.configs import common
+from official.vision.configs import maskrcnn
+from official.vision.configs import semantic_segmentation
+
+
+SEGMENTATION_MODEL = semantic_segmentation.SemanticSegmentationModel
+SEGMENTATION_HEAD = semantic_segmentation.SegmentationHead
+
+_COCO_INPUT_PATH_BASE = 'coco/tfrecords'
+_COCO_TRAIN_EXAMPLES = 118287
+_COCO_VAL_EXAMPLES = 5000
+
+# pytype: disable=wrong-keyword-args
+
+
+@dataclasses.dataclass
+class Parser(maskrcnn.Parser):
+ """Panoptic Mask R-CNN parser config."""
+ # If segmentation_resize_eval_groundtruth is set to False, original image
+ # sizes are used for eval. In that case,
+ # segmentation_groundtruth_padded_size has to be specified too to allow for
+ # batching the variable input sizes of images.
+ segmentation_resize_eval_groundtruth: bool = True
+ segmentation_groundtruth_padded_size: List[int] = dataclasses.field(
+ default_factory=list)
+ segmentation_ignore_label: int = 255
+ panoptic_ignore_label: int = 0
+ # Setting this to true will enable parsing category_mask and instance_mask.
+ include_panoptic_masks: bool = True
+
+
+@dataclasses.dataclass
+class TfExampleDecoder(common.TfExampleDecoder):
+ """A simple TF Example decoder config."""
+ # Setting this to true will enable decoding category_mask and instance_mask.
+ include_panoptic_masks: bool = True
+ panoptic_category_mask_key: str = 'image/panoptic/category_mask'
+ panoptic_instance_mask_key: str = 'image/panoptic/instance_mask'
+
+
+@dataclasses.dataclass
+class DataDecoder(common.DataDecoder):
+ """Data decoder config."""
+ simple_decoder: TfExampleDecoder = TfExampleDecoder()
+
+
+@dataclasses.dataclass
+class DataConfig(maskrcnn.DataConfig):
+ """Input config for training."""
+ decoder: DataDecoder = DataDecoder()
+ parser: Parser = Parser()
+
+
+@dataclasses.dataclass
+class PanopticSegmentationGenerator(hyperparams.Config):
+ """Panoptic segmentation generator config."""
+ output_size: List[int] = dataclasses.field(
+ default_factory=list)
+ mask_binarize_threshold: float = 0.5
+ score_threshold: float = 0.5
+ things_overlap_threshold: float = 0.5
+ stuff_area_threshold: float = 4096.0
+ things_class_label: int = 1
+ void_class_label: int = 0
+ void_instance_id: int = 0
+ rescale_predictions: bool = False
+
+
+@dataclasses.dataclass
+class PanopticMaskRCNN(deepmac_maskrcnn.DeepMaskHeadRCNN):
+ """Panoptic Mask R-CNN model config."""
+ segmentation_model: semantic_segmentation.SemanticSegmentationModel = (
+ SEGMENTATION_MODEL(num_classes=2))
+ include_mask = True
+ shared_backbone: bool = True
+ shared_decoder: bool = True
+ stuff_classes_offset: int = 0
+ generate_panoptic_masks: bool = True
+ panoptic_segmentation_generator: PanopticSegmentationGenerator = PanopticSegmentationGenerator() # pylint:disable=line-too-long
+
+
+@dataclasses.dataclass
+class Losses(maskrcnn.Losses):
+ """Panoptic Mask R-CNN loss config."""
+ semantic_segmentation_label_smoothing: float = 0.0
+ semantic_segmentation_ignore_label: int = 255
+ semantic_segmentation_gt_is_matting_map: bool = False
+ semantic_segmentation_class_weights: List[float] = dataclasses.field(
+ default_factory=list)
+ semantic_segmentation_use_groundtruth_dimension: bool = True
+ semantic_segmentation_top_k_percent_pixels: float = 1.0
+ instance_segmentation_weight: float = 1.0
+ semantic_segmentation_weight: float = 0.5
+
+
+@dataclasses.dataclass
+class PanopticQualityEvaluator(hyperparams.Config):
+ """Panoptic Quality Evaluator config."""
+ num_categories: int = 2
+ ignored_label: int = 0
+ max_instances_per_category: int = 256
+ offset: int = 256 * 256 * 256
+ is_thing: List[float] = dataclasses.field(
+ default_factory=list)
+ rescale_predictions: bool = False
+ report_per_class_metrics: bool = False
+
+
+@dataclasses.dataclass
+class PanopticMaskRCNNTask(maskrcnn.MaskRCNNTask):
+ """Panoptic Mask R-CNN task config."""
+ model: PanopticMaskRCNN = PanopticMaskRCNN()
+ train_data: DataConfig = DataConfig(is_training=True)
+ validation_data: DataConfig = DataConfig(is_training=False,
+ drop_remainder=False)
+ segmentation_evaluation: semantic_segmentation.Evaluation = semantic_segmentation.Evaluation() # pylint: disable=line-too-long
+ losses: Losses = Losses()
+ init_checkpoint: Optional[str] = None
+ segmentation_init_checkpoint: Optional[str] = None
+
+ # 'init_checkpoint_modules' controls the modules that need to be initialized
+ # from checkpoint paths given by 'init_checkpoint' and/or
+ # 'segmentation_init_checkpoint. Supports modules:
+ # 'backbone': Initialize MaskRCNN backbone
+ # 'segmentation_backbone': Initialize segmentation backbone
+ # 'segmentation_decoder': Initialize segmentation decoder
+ # 'all': Initialize all modules
+ init_checkpoint_modules: Optional[List[str]] = dataclasses.field(
+ default_factory=list)
+ panoptic_quality_evaluator: PanopticQualityEvaluator = PanopticQualityEvaluator() # pylint: disable=line-too-long
+
+
+@exp_factory.register_config_factory('panoptic_fpn_coco')
+def panoptic_fpn_coco() -> cfg.ExperimentConfig:
+ """COCO panoptic segmentation with Panoptic Mask R-CNN."""
+ train_batch_size = 64
+ eval_batch_size = 8
+ steps_per_epoch = _COCO_TRAIN_EXAMPLES // train_batch_size
+ validation_steps = _COCO_VAL_EXAMPLES // eval_batch_size
+
+ # coco panoptic dataset has category ids ranging from [0-200] inclusive.
+ # 0 is not used and represents the background class
+ # ids 1-91 represent thing categories (91)
+ # ids 92-200 represent stuff categories (109)
+ # for the segmentation task, we continue using id=0 for the background
+ # and map all thing categories to id=1, the remaining 109 stuff categories
+ # are shifted by an offset=90 given by num_thing classes - 1. This shifting
+ # will make all the stuff categories begin from id=2 and end at id=110
+ num_panoptic_categories = 201
+ num_thing_categories = 91
+ num_semantic_segmentation_classes = 111
+
+ is_thing = [False]
+ for idx in range(1, num_panoptic_categories):
+ is_thing.append(True if idx <= num_thing_categories else False)
+
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(
+ mixed_precision_dtype='float32', enable_xla=True),
+ task=PanopticMaskRCNNTask(
+ init_checkpoint='gs://cloud-tpu-checkpoints/vision-2.0/resnet50_imagenet/ckpt-28080', # pylint: disable=line-too-long
+ init_checkpoint_modules=['backbone'],
+ model=PanopticMaskRCNN(
+ num_classes=91, input_size=[1024, 1024, 3],
+ panoptic_segmentation_generator=PanopticSegmentationGenerator(
+ output_size=[640, 640], rescale_predictions=True),
+ stuff_classes_offset=90,
+ segmentation_model=SEGMENTATION_MODEL(
+ num_classes=num_semantic_segmentation_classes,
+ head=SEGMENTATION_HEAD(
+ level=2,
+ num_convs=0,
+ num_filters=128,
+ decoder_min_level=2,
+ decoder_max_level=6,
+ feature_fusion='panoptic_fpn_fusion'))),
+ losses=Losses(l2_weight_decay=0.00004),
+ train_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ parser=Parser(
+ aug_rand_hflip=True, aug_scale_min=0.8, aug_scale_max=1.25)),
+ validation_data=DataConfig(
+ input_path=os.path.join(_COCO_INPUT_PATH_BASE, 'val*'),
+ is_training=False,
+ global_batch_size=eval_batch_size,
+ parser=Parser(
+ segmentation_resize_eval_groundtruth=False,
+ segmentation_groundtruth_padded_size=[640, 640]),
+ drop_remainder=False),
+ annotation_file=os.path.join(_COCO_INPUT_PATH_BASE,
+ 'instances_val2017.json'),
+ segmentation_evaluation=semantic_segmentation.Evaluation(
+ report_per_class_iou=False, report_train_mean_iou=False),
+ panoptic_quality_evaluator=PanopticQualityEvaluator(
+ num_categories=num_panoptic_categories,
+ ignored_label=0,
+ is_thing=is_thing,
+ rescale_predictions=True)),
+ trainer=cfg.TrainerConfig(
+ train_steps=22500,
+ validation_steps=validation_steps,
+ validation_interval=steps_per_epoch,
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'sgd',
+ 'sgd': {
+ 'momentum': 0.9
+ }
+ },
+ 'learning_rate': {
+ 'type': 'stepwise',
+ 'stepwise': {
+ 'boundaries': [15000, 20000],
+ 'values': [0.12, 0.012, 0.0012],
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 500,
+ 'warmup_learning_rate': 0.0067
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
diff --git a/official/projects/panoptic/dataloaders/panoptic_deeplab_input.py b/official/projects/panoptic/dataloaders/panoptic_deeplab_input.py
new file mode 100644
index 0000000000000000000000000000000000000000..6729c9e0d28692debca454b0e96552986341fdce
--- /dev/null
+++ b/official/projects/panoptic/dataloaders/panoptic_deeplab_input.py
@@ -0,0 +1,359 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Data parser and processing for Panoptic Deeplab."""
+
+from typing import List, Optional
+
+import numpy as np
+import tensorflow as tf
+
+from official.vision.configs import common
+from official.vision.dataloaders import parser
+from official.vision.dataloaders import tf_example_decoder
+from official.vision.ops import augment
+from official.vision.ops import preprocess_ops
+
+
+def _compute_gaussian_from_std(sigma):
+ """Computes the Gaussian and its size from a given standard deviation."""
+ size = int(6 * sigma + 3)
+ x = np.arange(size, dtype=np.float)
+ y = x[:, np.newaxis]
+ x0, y0 = 3 * sigma + 1, 3 * sigma + 1
+ gaussian = tf.constant(
+ np.exp(-((x - x0)**2 + (y - y0)**2) / (2 * sigma**2)),
+ dtype=tf.float32)
+ return gaussian, size
+
+
+class TfExampleDecoder(tf_example_decoder.TfExampleDecoder):
+ """Tensorflow Example proto decoder."""
+
+ def __init__(
+ self,
+ regenerate_source_id: bool,
+ panoptic_category_mask_key: str = 'image/panoptic/category_mask',
+ panoptic_instance_mask_key: str = 'image/panoptic/instance_mask'):
+ super(TfExampleDecoder,
+ self).__init__(
+ include_mask=True,
+ regenerate_source_id=regenerate_source_id)
+ self._panoptic_category_mask_key = panoptic_category_mask_key
+ self._panoptic_instance_mask_key = panoptic_instance_mask_key
+
+ self._panoptic_keys_to_features = {
+ panoptic_category_mask_key:
+ tf.io.FixedLenFeature((), tf.string, default_value=''),
+ panoptic_instance_mask_key:
+ tf.io.FixedLenFeature((), tf.string, default_value='')
+ }
+
+ def decode(self, serialized_example):
+ decoded_tensors = super(TfExampleDecoder,
+ self).decode(serialized_example)
+ parsed_tensors = tf.io.parse_single_example(
+ serialized_example, self._panoptic_keys_to_features)
+
+ category_mask = tf.io.decode_image(
+ parsed_tensors[self._panoptic_category_mask_key], channels=1)
+ instance_mask = tf.io.decode_image(
+ parsed_tensors[self._panoptic_instance_mask_key], channels=1)
+ category_mask.set_shape([None, None, 1])
+ instance_mask.set_shape([None, None, 1])
+
+ decoded_tensors.update({
+ 'groundtruth_panoptic_category_mask': category_mask,
+ 'groundtruth_panoptic_instance_mask': instance_mask
+ })
+ return decoded_tensors
+
+
+class Parser(parser.Parser):
+ """Parser to parse an image and its annotations into a dictionary of tensors."""
+
+ def __init__(
+ self,
+ output_size: List[int],
+ resize_eval_groundtruth: bool = True,
+ groundtruth_padded_size: Optional[List[int]] = None,
+ ignore_label: int = 0,
+ aug_rand_hflip: bool = False,
+ aug_scale_min: float = 1.0,
+ aug_scale_max: float = 1.0,
+ aug_type: Optional[common.Augmentation] = None,
+ sigma: float = 8.0,
+ small_instance_area_threshold: int = 4096,
+ small_instance_weight: float = 3.0,
+ dtype: str = 'float32'):
+ """Initializes parameters for parsing annotations in the dataset.
+
+ Args:
+ output_size: `Tensor` or `list` for [height, width] of output image. The
+ output_size should be divided by the largest feature stride 2^max_level.
+ resize_eval_groundtruth: `bool`, if True, eval groundtruth masks are
+ resized to output_size.
+ groundtruth_padded_size: `Tensor` or `list` for [height, width]. When
+ resize_eval_groundtruth is set to False, the groundtruth masks are
+ padded to this size.
+ ignore_label: `int` the pixel with ignore label will not used for training
+ and evaluation.
+ aug_rand_hflip: `bool`, if True, augment training with random
+ horizontal flip.
+ aug_scale_min: `float`, the minimum scale applied to `output_size` for
+ data augmentation during training.
+ aug_scale_max: `float`, the maximum scale applied to `output_size` for
+ data augmentation during training.
+ aug_type: An optional Augmentation object with params for AutoAugment.
+ sigma: `float`, standard deviation for generating 2D Gaussian to encode
+ centers.
+ small_instance_area_threshold: `int`, small instance area threshold.
+ small_instance_weight: `float`, small instance weight.
+ dtype: `str`, data type. One of {`bfloat16`, `float32`, `float16`}.
+ """
+ self._output_size = output_size
+ self._resize_eval_groundtruth = resize_eval_groundtruth
+ if (not resize_eval_groundtruth) and (groundtruth_padded_size is None):
+ raise ValueError(
+ 'groundtruth_padded_size ([height, width]) needs to be'
+ 'specified when resize_eval_groundtruth is False.')
+ self._groundtruth_padded_size = groundtruth_padded_size
+ self._ignore_label = ignore_label
+
+ # Data augmentation.
+ self._aug_rand_hflip = aug_rand_hflip
+ self._aug_scale_min = aug_scale_min
+ self._aug_scale_max = aug_scale_max
+
+ if aug_type and aug_type.type:
+ if aug_type.type == 'autoaug':
+ self._augmenter = augment.AutoAugment(
+ augmentation_name=aug_type.autoaug.augmentation_name,
+ cutout_const=aug_type.autoaug.cutout_const,
+ translate_const=aug_type.autoaug.translate_const)
+ else:
+ raise ValueError('Augmentation policy {} not supported.'.format(
+ aug_type.type))
+ else:
+ self._augmenter = None
+
+ self._dtype = dtype
+
+ self._sigma = sigma
+ self._gaussian, self._gaussian_size = _compute_gaussian_from_std(
+ self._sigma)
+ self._gaussian = tf.reshape(self._gaussian, shape=[-1])
+ self._small_instance_area_threshold = small_instance_area_threshold
+ self._small_instance_weight = small_instance_weight
+
+ def _resize_and_crop_mask(self, mask, image_info, is_training):
+ """Resizes and crops mask using `image_info` dict."""
+ height = image_info[0][0]
+ width = image_info[0][1]
+ mask = tf.reshape(mask, shape=[1, height, width, 1])
+ mask += 1
+
+ if is_training or self._resize_eval_groundtruth:
+ image_scale = image_info[2, :]
+ offset = image_info[3, :]
+ mask = preprocess_ops.resize_and_crop_masks(
+ mask,
+ image_scale,
+ self._output_size,
+ offset)
+ else:
+ mask = tf.image.pad_to_bounding_box(
+ mask, 0, 0,
+ self._groundtruth_padded_size[0],
+ self._groundtruth_padded_size[1])
+ mask -= 1
+
+ # Assign ignore label to the padded region.
+ mask = tf.where(
+ tf.equal(mask, -1),
+ self._ignore_label * tf.ones_like(mask),
+ mask)
+ mask = tf.squeeze(mask, axis=0)
+ return mask
+
+ def _parse_data(self, data, is_training):
+ image = data['image']
+
+ if self._augmenter is not None and is_training:
+ image = self._augmenter.distort(image)
+
+ image = preprocess_ops.normalize_image(image)
+
+ category_mask = tf.cast(
+ data['groundtruth_panoptic_category_mask'][:, :, 0],
+ dtype=tf.float32)
+ instance_mask = tf.cast(
+ data['groundtruth_panoptic_instance_mask'][:, :, 0],
+ dtype=tf.float32)
+
+ # Flips image randomly during training.
+ if self._aug_rand_hflip and is_training:
+ masks = tf.stack([category_mask, instance_mask], axis=0)
+ image, _, masks = preprocess_ops.random_horizontal_flip(
+ image=image, masks=masks)
+ category_mask = masks[0]
+ instance_mask = masks[1]
+
+ # Resizes and crops image.
+ image, image_info = preprocess_ops.resize_and_crop_image(
+ image,
+ self._output_size,
+ self._output_size,
+ aug_scale_min=self._aug_scale_min if is_training else 1.0,
+ aug_scale_max=self._aug_scale_max if is_training else 1.0)
+
+ category_mask = self._resize_and_crop_mask(
+ category_mask,
+ image_info,
+ is_training=is_training)
+ instance_mask = self._resize_and_crop_mask(
+ instance_mask,
+ image_info,
+ is_training=is_training)
+
+ (instance_centers_heatmap,
+ instance_centers_offset,
+ semantic_weights) = self._encode_centers_and_offets(
+ instance_mask=instance_mask[:, :, 0])
+
+ # Cast image and labels as self._dtype
+ image = tf.cast(image, dtype=self._dtype)
+ category_mask = tf.cast(category_mask, dtype=self._dtype)
+ instance_mask = tf.cast(instance_mask, dtype=self._dtype)
+ instance_centers_heatmap = tf.cast(
+ instance_centers_heatmap, dtype=self._dtype)
+ instance_centers_offset = tf.cast(
+ instance_centers_offset, dtype=self._dtype)
+
+ valid_mask = tf.not_equal(
+ category_mask, self._ignore_label)
+ things_mask = tf.not_equal(
+ instance_mask, self._ignore_label)
+
+ labels = {
+ 'category_mask': category_mask,
+ 'instance_mask': instance_mask,
+ 'instance_centers_heatmap': instance_centers_heatmap,
+ 'instance_centers_offset': instance_centers_offset,
+ 'semantic_weights': semantic_weights,
+ 'valid_mask': valid_mask,
+ 'things_mask': things_mask,
+ 'image_info': image_info
+ }
+ return image, labels
+
+ def _parse_train_data(self, data):
+ """Parses data for training."""
+ return self._parse_data(data=data, is_training=True)
+
+ def _parse_eval_data(self, data):
+ """Parses data for evaluation."""
+ return self._parse_data(data=data, is_training=False)
+
+ def _encode_centers_and_offets(self, instance_mask):
+ """Generates center heatmaps and offets from instance id mask.
+
+ Args:
+ instance_mask: `tf.Tensor` of shape [height, width] representing
+ groundtruth instance id mask.
+ Returns:
+ instance_centers_heatmap: `tf.Tensor` of shape [height, width, 1]
+ instance_centers_offset: `tf.Tensor` of shape [height, width, 2]
+ """
+ shape = tf.shape(instance_mask)
+ height, width = shape[0], shape[1]
+
+ padding_start = int(3 * self._sigma + 1)
+ padding_end = int(3 * self._sigma + 2)
+
+ # padding should be equal to self._gaussian_size which is calculated
+ # as size = int(6 * sigma + 3)
+ padding = padding_start + padding_end
+
+ instance_centers_heatmap = tf.zeros(
+ shape=[height + padding, width + padding],
+ dtype=tf.float32)
+ centers_offset_y = tf.zeros(
+ shape=[height, width],
+ dtype=tf.float32)
+ centers_offset_x = tf.zeros(
+ shape=[height, width],
+ dtype=tf.float32)
+ semantic_weights = tf.ones(
+ shape=[height, width],
+ dtype=tf.float32)
+
+ unique_instance_ids, _ = tf.unique(tf.reshape(instance_mask, [-1]))
+
+ # The following method for encoding center heatmaps and offets is inspired
+ # by the reference implementation available at
+ # https://github.com/google-research/deeplab2/blob/main/data/sample_generator.py # pylint: disable=line-too-long
+ for instance_id in unique_instance_ids:
+ if instance_id == self._ignore_label:
+ continue
+
+ mask = tf.equal(instance_mask, instance_id)
+ mask_area = tf.reduce_sum(tf.cast(mask, dtype=tf.float32))
+ mask_indices = tf.cast(tf.where(mask), dtype=tf.float32)
+ mask_center = tf.reduce_mean(mask_indices, axis=0)
+ mask_center_y = tf.cast(tf.round(mask_center[0]), dtype=tf.int32)
+ mask_center_x = tf.cast(tf.round(mask_center[1]), dtype=tf.int32)
+
+ if mask_area < self._small_instance_area_threshold:
+ semantic_weights = tf.where(
+ mask,
+ self._small_instance_weight,
+ semantic_weights)
+
+ gaussian_size = self._gaussian_size
+ indices_y = tf.range(mask_center_y, mask_center_y + gaussian_size)
+ indices_x = tf.range(mask_center_x, mask_center_x + gaussian_size)
+
+ indices = tf.stack(tf.meshgrid(indices_y, indices_x))
+ indices = tf.reshape(
+ indices, shape=[2, gaussian_size * gaussian_size])
+ indices = tf.transpose(indices)
+
+ instance_centers_heatmap = tf.tensor_scatter_nd_max(
+ tensor=instance_centers_heatmap,
+ indices=indices,
+ updates=self._gaussian)
+
+ centers_offset_y = tf.tensor_scatter_nd_update(
+ tensor=centers_offset_y,
+ indices=tf.cast(mask_indices, dtype=tf.int32),
+ updates=tf.cast(mask_center_y, dtype=tf.float32) - mask_indices[:, 0])
+
+ centers_offset_x = tf.tensor_scatter_nd_update(
+ tensor=centers_offset_x,
+ indices=tf.cast(mask_indices, dtype=tf.int32),
+ updates=tf.cast(mask_center_x, dtype=tf.float32) - mask_indices[:, 1])
+
+ instance_centers_heatmap = instance_centers_heatmap[
+ padding_start:padding_start + height,
+ padding_start:padding_start + width]
+ instance_centers_heatmap = tf.expand_dims(instance_centers_heatmap, axis=-1)
+
+ instance_centers_offset = tf.stack(
+ [centers_offset_y, centers_offset_x],
+ axis=-1)
+
+ return (instance_centers_heatmap,
+ instance_centers_offset,
+ semantic_weights)
diff --git a/official/vision/beta/projects/panoptic_maskrcnn/dataloaders/panoptic_maskrcnn_input.py b/official/projects/panoptic/dataloaders/panoptic_maskrcnn_input.py
similarity index 88%
rename from official/vision/beta/projects/panoptic_maskrcnn/dataloaders/panoptic_maskrcnn_input.py
rename to official/projects/panoptic/dataloaders/panoptic_maskrcnn_input.py
index 4df17b483cf0cd5590c32301b63f7861fc5d2419..ac207e14e5cc81f3978dfbb9f491a99d5f285240 100644
--- a/official/vision/beta/projects/panoptic_maskrcnn/dataloaders/panoptic_maskrcnn_input.py
+++ b/official/projects/panoptic/dataloaders/panoptic_maskrcnn_input.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,50 +16,63 @@
import tensorflow as tf
-from official.vision.beta.dataloaders import maskrcnn_input
-from official.vision.beta.dataloaders import tf_example_decoder
-from official.vision.beta.ops import preprocess_ops
+from official.vision.dataloaders import maskrcnn_input
+from official.vision.dataloaders import tf_example_decoder
+from official.vision.ops import preprocess_ops
class TfExampleDecoder(tf_example_decoder.TfExampleDecoder):
"""Tensorflow Example proto decoder."""
- def __init__(self, regenerate_source_id,
- mask_binarize_threshold, include_panoptic_masks):
+ def __init__(
+ self,
+ regenerate_source_id: bool,
+ mask_binarize_threshold: float,
+ include_panoptic_masks: bool,
+ panoptic_category_mask_key: str = 'image/panoptic/category_mask',
+ panoptic_instance_mask_key: str = 'image/panoptic/instance_mask'):
super(TfExampleDecoder, self).__init__(
include_mask=True,
regenerate_source_id=regenerate_source_id,
mask_binarize_threshold=None)
self._include_panoptic_masks = include_panoptic_masks
+ self._panoptic_category_mask_key = panoptic_category_mask_key
+ self._panoptic_instance_mask_key = panoptic_instance_mask_key
keys_to_features = {
'image/segmentation/class/encoded':
tf.io.FixedLenFeature((), tf.string, default_value='')}
if include_panoptic_masks:
keys_to_features.update({
- 'image/panoptic/category_mask':
+ panoptic_category_mask_key:
tf.io.FixedLenFeature((), tf.string, default_value=''),
- 'image/panoptic/instance_mask':
- tf.io.FixedLenFeature((), tf.string, default_value='')})
+ panoptic_instance_mask_key:
+ tf.io.FixedLenFeature((), tf.string, default_value='')
+ })
self._segmentation_keys_to_features = keys_to_features
+ def decode_segmentation_mask(self, parsed_tensors):
+ segmentation_mask = tf.io.decode_image(
+ parsed_tensors['image/segmentation/class/encoded'], channels=1)
+ segmentation_mask.set_shape([None, None, 1])
+ return segmentation_mask
+
def decode(self, serialized_example):
decoded_tensors = super(TfExampleDecoder, self).decode(serialized_example)
parsed_tensors = tf.io.parse_single_example(
serialized_example, self._segmentation_keys_to_features)
- segmentation_mask = tf.io.decode_image(
- parsed_tensors['image/segmentation/class/encoded'],
- channels=1)
- segmentation_mask.set_shape([None, None, 1])
- decoded_tensors.update({'groundtruth_segmentation_mask': segmentation_mask})
+ decoded_tensors.update({
+ 'groundtruth_segmentation_mask':
+ self.decode_segmentation_mask(parsed_tensors)
+ })
if self._include_panoptic_masks:
category_mask = tf.io.decode_image(
- parsed_tensors['image/panoptic/category_mask'],
+ parsed_tensors[self._panoptic_category_mask_key],
channels=1)
instance_mask = tf.io.decode_image(
- parsed_tensors['image/panoptic/instance_mask'],
+ parsed_tensors[self._panoptic_instance_mask_key],
channels=1)
category_mask.set_shape([None, None, 1])
instance_mask.set_shape([None, None, 1])
@@ -214,18 +227,21 @@ class Parser(maskrcnn_input.Parser):
are supposed to be used in computing the segmentation loss while
training.
"""
+ # (height, width, num_channels = 1)
+ # All the operations below support num_channels >= 1.
segmentation_mask = data['groundtruth_segmentation_mask']
# Flips image randomly during training.
if self.aug_rand_hflip:
masks = data['groundtruth_instance_masks']
+ num_image_channels = data['image'].shape.as_list()[-1]
image_mask = tf.concat([data['image'], segmentation_mask], axis=2)
image_mask, boxes, masks = preprocess_ops.random_horizontal_flip(
image_mask, data['groundtruth_boxes'], masks)
- segmentation_mask = image_mask[:, :, -1:]
- image = image_mask[:, :, :-1]
+ image = image_mask[:, :, :num_image_channels]
+ segmentation_mask = image_mask[:, :, num_image_channels:]
data['image'] = image
data['groundtruth_boxes'] = boxes
@@ -237,14 +253,14 @@ class Parser(maskrcnn_input.Parser):
image_scale = image_info[2, :]
offset = image_info[3, :]
- segmentation_mask = tf.reshape(
- segmentation_mask, shape=[1, data['height'], data['width']])
+ # (height, width, num_channels = 1)
segmentation_mask = tf.cast(segmentation_mask, tf.float32)
# Pad label and make sure the padded region assigned to the ignore label.
# The label is first offset by +1 and then padded with 0.
segmentation_mask += 1
- segmentation_mask = tf.expand_dims(segmentation_mask, axis=3)
+ # (1, height, width, num_channels = 1)
+ segmentation_mask = tf.expand_dims(segmentation_mask, axis=0)
segmentation_mask = preprocess_ops.resize_and_crop_masks(
segmentation_mask, image_scale, self._output_size, offset)
segmentation_mask -= 1
@@ -252,6 +268,7 @@ class Parser(maskrcnn_input.Parser):
tf.equal(segmentation_mask, -1),
self._segmentation_ignore_label * tf.ones_like(segmentation_mask),
segmentation_mask)
+ # (height, width, num_channels = 1)
segmentation_mask = tf.squeeze(segmentation_mask, axis=0)
segmentation_valid_mask = tf.not_equal(
segmentation_mask, self._segmentation_ignore_label)
@@ -284,9 +301,13 @@ class Parser(maskrcnn_input.Parser):
shape [height_l, width_l, 4] representing anchor boxes at each
level.
"""
+
def _process_mask(mask, ignore_label, image_info):
+ # (height, width, num_channels = 1)
+ # All the operations below support num_channels >= 1.
mask = tf.cast(mask, dtype=tf.float32)
- mask = tf.reshape(mask, shape=[1, data['height'], data['width'], 1])
+ # (1, height, width, num_channels = 1)
+ mask = tf.expand_dims(mask, axis=0)
mask += 1
if self._segmentation_resize_eval_groundtruth:
@@ -307,12 +328,14 @@ class Parser(maskrcnn_input.Parser):
tf.equal(mask, -1),
ignore_label * tf.ones_like(mask),
mask)
+ # (height, width, num_channels = 1)
mask = tf.squeeze(mask, axis=0)
return mask
image, labels = super(Parser, self)._parse_eval_data(data)
image_info = labels['image_info']
+ # (height, width, num_channels = 1)
segmentation_mask = _process_mask(
data['groundtruth_segmentation_mask'],
self._segmentation_ignore_label, image_info)
diff --git a/official/projects/panoptic/losses/panoptic_deeplab_losses.py b/official/projects/panoptic/losses/panoptic_deeplab_losses.py
new file mode 100644
index 0000000000000000000000000000000000000000..f109bf9d5414a0003af6c79325cf451f64752270
--- /dev/null
+++ b/official/projects/panoptic/losses/panoptic_deeplab_losses.py
@@ -0,0 +1,148 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Losses used for panoptic deeplab model."""
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.panoptic.ops import mask_ops
+
+EPSILON = 1e-5
+
+
+class WeightedBootstrappedCrossEntropyLoss:
+ """Weighted semantic segmentation loss."""
+
+ def __init__(self, label_smoothing, class_weights, ignore_label,
+ top_k_percent_pixels=1.0):
+ self._top_k_percent_pixels = top_k_percent_pixels
+ self._class_weights = class_weights
+ self._ignore_label = ignore_label
+ self._label_smoothing = label_smoothing
+
+ def __call__(self, logits, labels, sample_weight=None):
+ _, _, _, num_classes = logits.get_shape().as_list()
+
+ logits = tf.image.resize(
+ logits, tf.shape(labels)[1:3],
+ method=tf.image.ResizeMethod.BILINEAR)
+
+ valid_mask = tf.not_equal(labels, self._ignore_label)
+ normalizer = tf.reduce_sum(tf.cast(valid_mask, tf.float32)) + EPSILON
+ # Assign pixel with ignore label to class 0 (background). The loss on the
+ # pixel will later be masked out.
+ labels = tf.where(valid_mask, labels, tf.zeros_like(labels))
+
+ labels = tf.squeeze(tf.cast(labels, tf.int32), axis=3)
+ valid_mask = tf.squeeze(tf.cast(valid_mask, tf.float32), axis=3)
+ onehot_labels = tf.one_hot(labels, num_classes)
+ onehot_labels = onehot_labels * (
+ 1 - self._label_smoothing) + self._label_smoothing / num_classes
+ cross_entropy_loss = tf.nn.softmax_cross_entropy_with_logits(
+ labels=onehot_labels, logits=logits)
+
+ if not self._class_weights:
+ class_weights = [1] * num_classes
+ else:
+ class_weights = self._class_weights
+
+ if num_classes != len(class_weights):
+ raise ValueError(
+ 'Length of class_weights should be {}'.format(num_classes))
+
+ weight_mask = tf.einsum('...y,y->...',
+ tf.one_hot(labels, num_classes, dtype=tf.float32),
+ tf.constant(class_weights, tf.float32))
+ valid_mask *= weight_mask
+
+ if sample_weight is not None:
+ valid_mask *= sample_weight
+
+ cross_entropy_loss *= tf.cast(valid_mask, tf.float32)
+
+ if self._top_k_percent_pixels >= 1.0:
+ loss = tf.reduce_sum(cross_entropy_loss) / normalizer
+ else:
+ loss = self._compute_top_k_loss(cross_entropy_loss)
+ return loss
+
+ def _compute_top_k_loss(self, loss):
+ """Computs top k loss."""
+ batch_size = tf.shape(loss)[0]
+ loss = tf.reshape(loss, shape=[batch_size, -1])
+
+ top_k_pixels = tf.cast(
+ self._top_k_percent_pixels *
+ tf.cast(tf.shape(loss)[-1], dtype=tf.float32),
+ dtype=tf.int32)
+
+ # shape: [batch_size, top_k_pixels]
+ per_sample_top_k_loss = tf.map_fn(
+ fn=lambda x: tf.nn.top_k(x, k=top_k_pixels, sorted=False)[0],
+ elems=loss,
+ parallel_iterations=32,
+ fn_output_signature=tf.float32)
+
+ # shape: [batch_size]
+ per_sample_normalizer = tf.reduce_sum(
+ tf.cast(
+ tf.not_equal(per_sample_top_k_loss, 0.0),
+ dtype=tf.float32),
+ axis=-1) + EPSILON
+ per_sample_normalized_loss = tf.reduce_sum(
+ per_sample_top_k_loss, axis=-1) / per_sample_normalizer
+
+ normalized_loss = tf_utils.safe_mean(per_sample_normalized_loss)
+ return normalized_loss
+
+
+class CenterHeatmapLoss:
+ """Center heatmap loss."""
+
+ def __init__(self):
+ self._loss_fn = tf.losses.mean_squared_error
+
+ def __call__(self, logits, labels, sample_weight=None):
+ _, height, width, _ = labels.get_shape().as_list()
+ logits = tf.image.resize(
+ logits,
+ size=[height, width],
+ method=tf.image.ResizeMethod.BILINEAR)
+
+ loss = self._loss_fn(y_true=labels, y_pred=logits)
+
+ if sample_weight is not None:
+ loss *= sample_weight
+
+ return tf_utils.safe_mean(loss)
+
+
+class CenterOffsetLoss:
+ """Center offset loss."""
+
+ def __init__(self):
+ self._loss_fn = tf.losses.mean_absolute_error
+
+ def __call__(self, logits, labels, sample_weight=None):
+ _, height, width, _ = labels.get_shape().as_list()
+ logits = mask_ops.resize_and_rescale_offsets(
+ logits, target_size=[height, width])
+
+ loss = self._loss_fn(y_true=labels, y_pred=logits)
+
+ if sample_weight is not None:
+ loss *= sample_weight
+
+ return tf_utils.safe_mean(loss)
diff --git a/official/projects/panoptic/modeling/factory.py b/official/projects/panoptic/modeling/factory.py
new file mode 100644
index 0000000000000000000000000000000000000000..d9769c18f91ec40e78e3975aa29288e265e4abaf
--- /dev/null
+++ b/official/projects/panoptic/modeling/factory.py
@@ -0,0 +1,252 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Factory method to build panoptic segmentation model."""
+from typing import Optional
+
+import tensorflow as tf
+
+from official.projects.deepmac_maskrcnn.tasks import deep_mask_head_rcnn
+from official.projects.panoptic.configs import panoptic_deeplab as panoptic_deeplab_cfg
+from official.projects.panoptic.configs import panoptic_maskrcnn as panoptic_maskrcnn_cfg
+from official.projects.panoptic.modeling import panoptic_deeplab_model
+from official.projects.panoptic.modeling import panoptic_maskrcnn_model
+from official.projects.panoptic.modeling.heads import panoptic_deeplab_heads
+from official.projects.panoptic.modeling.layers import panoptic_deeplab_merge
+from official.projects.panoptic.modeling.layers import panoptic_segmentation_generator
+from official.vision.modeling import backbones
+from official.vision.modeling.decoders import factory as decoder_factory
+from official.vision.modeling.heads import segmentation_heads
+
+
+def build_panoptic_maskrcnn(
+ input_specs: tf.keras.layers.InputSpec,
+ model_config: panoptic_maskrcnn_cfg.PanopticMaskRCNN,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ """Builds Panoptic Mask R-CNN model.
+
+ This factory function builds the mask rcnn first, builds the non-shared
+ semantic segmentation layers, and finally combines the two models to form
+ the panoptic segmentation model.
+
+ Args:
+ input_specs: `tf.keras.layers.InputSpec` specs of the input tensor.
+ model_config: Config instance for the panoptic maskrcnn model.
+ l2_regularizer: Optional `tf.keras.regularizers.Regularizer`, if specified,
+ the model is built with the provided regularization layer.
+ Returns:
+ tf.keras.Model for the panoptic segmentation model.
+ """
+ norm_activation_config = model_config.norm_activation
+ segmentation_config = model_config.segmentation_model
+
+ # Builds the maskrcnn model.
+ maskrcnn_model = deep_mask_head_rcnn.build_maskrcnn(
+ input_specs=input_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ # Builds the semantic segmentation branch.
+ if not model_config.shared_backbone:
+ segmentation_backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=segmentation_config.backbone,
+ norm_activation_config=norm_activation_config,
+ l2_regularizer=l2_regularizer)
+ segmentation_decoder_input_specs = segmentation_backbone.output_specs
+ else:
+ segmentation_backbone = None
+ segmentation_decoder_input_specs = maskrcnn_model.backbone.output_specs
+
+ if not model_config.shared_decoder:
+ segmentation_decoder = decoder_factory.build_decoder(
+ input_specs=segmentation_decoder_input_specs,
+ model_config=segmentation_config,
+ l2_regularizer=l2_regularizer)
+ decoder_config = segmentation_decoder.get_config()
+ else:
+ segmentation_decoder = None
+ decoder_config = maskrcnn_model.decoder.get_config()
+
+ segmentation_head_config = segmentation_config.head
+ detection_head_config = model_config.detection_head
+ postprocessing_config = model_config.panoptic_segmentation_generator
+
+ segmentation_head = segmentation_heads.SegmentationHead(
+ num_classes=segmentation_config.num_classes,
+ level=segmentation_head_config.level,
+ num_convs=segmentation_head_config.num_convs,
+ prediction_kernel_size=segmentation_head_config.prediction_kernel_size,
+ num_filters=segmentation_head_config.num_filters,
+ upsample_factor=segmentation_head_config.upsample_factor,
+ feature_fusion=segmentation_head_config.feature_fusion,
+ decoder_min_level=segmentation_head_config.decoder_min_level,
+ decoder_max_level=segmentation_head_config.decoder_max_level,
+ low_level=segmentation_head_config.low_level,
+ low_level_num_filters=segmentation_head_config.low_level_num_filters,
+ activation=norm_activation_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ num_decoder_filters=decoder_config['num_filters'],
+ kernel_regularizer=l2_regularizer)
+
+ if model_config.generate_panoptic_masks:
+ max_num_detections = model_config.detection_generator.max_num_detections
+ mask_binarize_threshold = postprocessing_config.mask_binarize_threshold
+ panoptic_segmentation_generator_obj = (
+ panoptic_segmentation_generator.PanopticSegmentationGeneratorV2(
+ output_size=postprocessing_config.output_size,
+ max_num_detections=max_num_detections,
+ stuff_classes_offset=model_config.stuff_classes_offset,
+ mask_binarize_threshold=mask_binarize_threshold,
+ score_threshold=postprocessing_config.score_threshold,
+ things_overlap_threshold=postprocessing_config
+ .things_overlap_threshold,
+ things_class_label=postprocessing_config.things_class_label,
+ stuff_area_threshold=postprocessing_config.stuff_area_threshold,
+ void_class_label=postprocessing_config.void_class_label,
+ void_instance_id=postprocessing_config.void_instance_id,
+ rescale_predictions=postprocessing_config.rescale_predictions))
+ else:
+ panoptic_segmentation_generator_obj = None
+
+ # Combines maskrcnn, and segmentation models to build panoptic segmentation
+ # model.
+
+ model = panoptic_maskrcnn_model.PanopticMaskRCNNModel(
+ backbone=maskrcnn_model.backbone,
+ decoder=maskrcnn_model.decoder,
+ rpn_head=maskrcnn_model.rpn_head,
+ detection_head=maskrcnn_model.detection_head,
+ roi_generator=maskrcnn_model.roi_generator,
+ roi_sampler=maskrcnn_model.roi_sampler,
+ roi_aligner=maskrcnn_model.roi_aligner,
+ detection_generator=maskrcnn_model.detection_generator,
+ panoptic_segmentation_generator=panoptic_segmentation_generator_obj,
+ mask_head=maskrcnn_model.mask_head,
+ mask_sampler=maskrcnn_model.mask_sampler,
+ mask_roi_aligner=maskrcnn_model.mask_roi_aligner,
+ segmentation_backbone=segmentation_backbone,
+ segmentation_decoder=segmentation_decoder,
+ segmentation_head=segmentation_head,
+ class_agnostic_bbox_pred=detection_head_config.class_agnostic_bbox_pred,
+ cascade_class_ensemble=detection_head_config.cascade_class_ensemble,
+ min_level=model_config.min_level,
+ max_level=model_config.max_level,
+ num_scales=model_config.anchor.num_scales,
+ aspect_ratios=model_config.anchor.aspect_ratios,
+ anchor_size=model_config.anchor.anchor_size)
+ return model
+
+
+def build_panoptic_deeplab(
+ input_specs: tf.keras.layers.InputSpec,
+ model_config: panoptic_deeplab_cfg.PanopticDeeplab,
+ l2_regularizer: Optional[tf.keras.regularizers.Regularizer] = None
+) -> tf.keras.Model:
+ """Builds Panoptic Deeplab model.
+
+
+ Args:
+ input_specs: `tf.keras.layers.InputSpec` specs of the input tensor.
+ model_config: Config instance for the panoptic deeplab model.
+ l2_regularizer: Optional `tf.keras.regularizers.Regularizer`, if specified,
+ the model is built with the provided regularization layer.
+ Returns:
+ tf.keras.Model for the panoptic segmentation model.
+ """
+ norm_activation_config = model_config.norm_activation
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=norm_activation_config,
+ l2_regularizer=l2_regularizer)
+
+ semantic_decoder = decoder_factory.build_decoder(
+ input_specs=backbone.output_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ if model_config.shared_decoder:
+ instance_decoder = None
+ else:
+ # semantic and instance share the same decoder type
+ instance_decoder = decoder_factory.build_decoder(
+ input_specs=backbone.output_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ semantic_head_config = model_config.semantic_head
+ instance_head_config = model_config.instance_head
+
+ semantic_head = panoptic_deeplab_heads.SemanticHead(
+ num_classes=model_config.num_classes,
+ level=semantic_head_config.level,
+ num_convs=semantic_head_config.num_convs,
+ kernel_size=semantic_head_config.kernel_size,
+ prediction_kernel_size=semantic_head_config.prediction_kernel_size,
+ num_filters=semantic_head_config.num_filters,
+ use_depthwise_convolution=semantic_head_config.use_depthwise_convolution,
+ upsample_factor=semantic_head_config.upsample_factor,
+ low_level=semantic_head_config.low_level,
+ low_level_num_filters=semantic_head_config.low_level_num_filters,
+ fusion_num_output_filters=semantic_head_config.fusion_num_output_filters,
+ activation=norm_activation_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_regularizer=l2_regularizer)
+
+ instance_head = panoptic_deeplab_heads.InstanceHead(
+ level=instance_head_config.level,
+ num_convs=instance_head_config.num_convs,
+ kernel_size=instance_head_config.kernel_size,
+ prediction_kernel_size=instance_head_config.prediction_kernel_size,
+ num_filters=instance_head_config.num_filters,
+ use_depthwise_convolution=instance_head_config.use_depthwise_convolution,
+ upsample_factor=instance_head_config.upsample_factor,
+ low_level=instance_head_config.low_level,
+ low_level_num_filters=instance_head_config.low_level_num_filters,
+ fusion_num_output_filters=instance_head_config.fusion_num_output_filters,
+ activation=norm_activation_config.activation,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon,
+ kernel_regularizer=l2_regularizer)
+
+ if model_config.generate_panoptic_masks:
+ post_processing_config = model_config.post_processor
+ post_processor = panoptic_deeplab_merge.PostProcessor(
+ output_size=post_processing_config.output_size,
+ center_score_threshold=post_processing_config.center_score_threshold,
+ thing_class_ids=post_processing_config.thing_class_ids,
+ label_divisor=post_processing_config.label_divisor,
+ stuff_area_limit=post_processing_config.stuff_area_limit,
+ ignore_label=post_processing_config.ignore_label,
+ nms_kernel=post_processing_config.nms_kernel,
+ keep_k_centers=post_processing_config.keep_k_centers,
+ rescale_predictions=post_processing_config.rescale_predictions)
+ else:
+ post_processor = None
+
+ model = panoptic_deeplab_model.PanopticDeeplabModel(
+ backbone=backbone,
+ semantic_decoder=semantic_decoder,
+ instance_decoder=instance_decoder,
+ semantic_head=semantic_head,
+ instance_head=instance_head,
+ post_processor=post_processor)
+
+ return model
diff --git a/official/projects/panoptic/modeling/heads/panoptic_deeplab_heads.py b/official/projects/panoptic/modeling/heads/panoptic_deeplab_heads.py
new file mode 100644
index 0000000000000000000000000000000000000000..93113a333e8644d771b19f9e00a117c3cdfaa55f
--- /dev/null
+++ b/official/projects/panoptic/modeling/heads/panoptic_deeplab_heads.py
@@ -0,0 +1,434 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains definitions for Panoptic Deeplab heads."""
+
+from typing import List, Mapping, Optional, Tuple, Union
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.panoptic.modeling.layers import fusion_layers
+from official.vision.ops import spatial_transform_ops
+
+
+class PanopticDeeplabHead(tf.keras.layers.Layer):
+ """Creates a panoptic deeplab head."""
+
+ def __init__(
+ self,
+ level: Union[int, str],
+ num_convs: int = 2,
+ num_filters: int = 256,
+ kernel_size: int = 3,
+ use_depthwise_convolution: bool = False,
+ upsample_factor: int = 1,
+ low_level: Optional[List[int]] = None,
+ low_level_num_filters: Optional[List[int]] = None,
+ fusion_num_output_filters: int = 256,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ **kwargs):
+ """Initializes a panoptic deeplab head.
+
+ Args:
+ level: An `int` or `str`, level to use to build head.
+ num_convs: An `int` number of stacked convolution before the last
+ prediction layer.
+ num_filters: An `int` number to specify the number of filters used.
+ Default is 256.
+ kernel_size: An `int` number to specify the kernel size of the
+ stacked convolutions before the last prediction layer.
+ use_depthwise_convolution: A bool to specify if use depthwise separable
+ convolutions.
+ upsample_factor: An `int` number to specify the upsampling factor to
+ generate finer mask. Default 1 means no upsampling is applied.
+ low_level: An `int` of backbone level to be used for feature fusion. It is
+ used when feature_fusion is set to `deeplabv3plus`.
+ low_level_num_filters: An `int` of reduced number of filters for the low
+ level features before fusing it with higher level features. It is only
+ used when feature_fusion is set to `deeplabv3plus`.
+ fusion_num_output_filters: An `int` number to specify the number of
+ filters used by output layer of fusion module. Default is 256.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(PanopticDeeplabHead, self).__init__(**kwargs)
+
+ self._config_dict = {
+ 'level': level,
+ 'num_convs': num_convs,
+ 'num_filters': num_filters,
+ 'kernel_size': kernel_size,
+ 'use_depthwise_convolution': use_depthwise_convolution,
+ 'upsample_factor': upsample_factor,
+ 'low_level': low_level,
+ 'low_level_num_filters': low_level_num_filters,
+ 'fusion_num_output_filters': fusion_num_output_filters,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'norm_momentum': norm_momentum,
+ 'norm_epsilon': norm_epsilon,
+ 'kernel_regularizer': kernel_regularizer,
+ 'bias_regularizer': bias_regularizer
+ }
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._activation = tf_utils.get_activation(activation)
+
+ def build(self, input_shape: Union[tf.TensorShape, List[tf.TensorShape]]):
+ """Creates the variables of the head."""
+ kernel_size = self._config_dict['kernel_size']
+ use_depthwise_convolution = self._config_dict['use_depthwise_convolution']
+ random_initializer = tf.keras.initializers.RandomNormal(stddev=0.01)
+ conv_op = tf.keras.layers.Conv2D
+ conv_kwargs = {
+ 'kernel_size': kernel_size if not use_depthwise_convolution else 1,
+ 'padding': 'same',
+ 'use_bias': True,
+ 'kernel_initializer': random_initializer,
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ }
+ bn_op = (tf.keras.layers.experimental.SyncBatchNormalization
+ if self._config_dict['use_sync_bn']
+ else tf.keras.layers.BatchNormalization)
+ bn_kwargs = {
+ 'axis': self._bn_axis,
+ 'momentum': self._config_dict['norm_momentum'],
+ 'epsilon': self._config_dict['norm_epsilon'],
+ }
+
+ self._panoptic_deeplab_fusion = fusion_layers.PanopticDeepLabFusion(
+ level=self._config_dict['level'],
+ low_level=self._config_dict['low_level'],
+ num_projection_filters=self._config_dict['low_level_num_filters'],
+ num_output_filters=self._config_dict['fusion_num_output_filters'],
+ use_depthwise_convolution=self
+ ._config_dict['use_depthwise_convolution'],
+ activation=self._config_dict['activation'],
+ use_sync_bn=self._config_dict['use_sync_bn'],
+ norm_momentum=self._config_dict['norm_momentum'],
+ norm_epsilon=self._config_dict['norm_epsilon'],
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'])
+
+ # Stacked convolutions layers.
+ self._convs = []
+ self._norms = []
+ for i in range(self._config_dict['num_convs']):
+ if use_depthwise_convolution:
+ self._convs.append(
+ tf.keras.layers.DepthwiseConv2D(
+ name='panoptic_deeplab_head_depthwise_conv_{}'.format(i),
+ kernel_size=kernel_size,
+ padding='same',
+ use_bias=True,
+ depthwise_initializer=random_initializer,
+ depthwise_regularizer=self._config_dict['kernel_regularizer'],
+ depth_multiplier=1))
+ norm_name = 'panoptic_deeplab_head_depthwise_norm_{}'.format(i)
+ self._norms.append(bn_op(name=norm_name, **bn_kwargs))
+ conv_name = 'panoptic_deeplab_head_conv_{}'.format(i)
+ self._convs.append(
+ conv_op(
+ name=conv_name,
+ filters=self._config_dict['num_filters'],
+ **conv_kwargs))
+ norm_name = 'panoptic_deeplab_head_norm_{}'.format(i)
+ self._norms.append(bn_op(name=norm_name, **bn_kwargs))
+
+ super().build(input_shape)
+
+ def call(self, inputs: Tuple[Union[tf.Tensor, Mapping[str, tf.Tensor]],
+ Union[tf.Tensor, Mapping[str, tf.Tensor]]],
+ training=None):
+ """Forward pass of the head.
+
+ It supports both a tuple of 2 tensors or 2 dictionaries. The first is
+ backbone endpoints, and the second is decoder endpoints. When inputs are
+ tensors, they are from a single level of feature maps. When inputs are
+ dictionaries, they contain multiple levels of feature maps, where the key
+ is the index of feature map.
+
+ Args:
+ inputs: A tuple of 2 feature map tensors of shape
+ [batch, height_l, width_l, channels] or 2 dictionaries of tensors:
+ - key: A `str` of the level of the multilevel features.
+ - values: A `tf.Tensor` of the feature map tensors, whose shape is
+ [batch, height_l, width_l, channels].
+ training: A bool, runs the model in training/eval mode.
+
+ Returns:
+ A `tf.Tensor` of the fused backbone and decoder features.
+ """
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ x = self._panoptic_deeplab_fusion(inputs, training=training)
+
+ for conv, norm in zip(self._convs, self._norms):
+ x = conv(x)
+ x = norm(x, training=training)
+ x = self._activation(x)
+
+ if self._config_dict['upsample_factor'] > 1:
+ x = spatial_transform_ops.nearest_upsampling(
+ x, scale=self._config_dict['upsample_factor'])
+
+ return x
+
+ def get_config(self):
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(self._config_dict.items()))
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SemanticHead(PanopticDeeplabHead):
+ """Creates a semantic head."""
+
+ def __init__(
+ self,
+ num_classes: int,
+ level: Union[int, str],
+ num_convs: int = 2,
+ num_filters: int = 256,
+ kernel_size: int = 3,
+ prediction_kernel_size: int = 3,
+ use_depthwise_convolution: bool = False,
+ upsample_factor: int = 1,
+ low_level: Optional[List[int]] = None,
+ low_level_num_filters: Optional[List[int]] = None,
+ fusion_num_output_filters: int = 256,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ **kwargs):
+ """Initializes a instance center head.
+
+ Args:
+ num_classes: An `int` number of mask classification categories. The number
+ of classes does not include background class.
+ level: An `int` or `str`, level to use to build head.
+ num_convs: An `int` number of stacked convolution before the last
+ prediction layer.
+ num_filters: An `int` number to specify the number of filters used.
+ Default is 256.
+ kernel_size: An `int` number to specify the kernel size of the
+ stacked convolutions before the last prediction layer.
+ prediction_kernel_size: An `int` number to specify the kernel size of the
+ prediction layer.
+ use_depthwise_convolution: A bool to specify if use depthwise separable
+ convolutions.
+ upsample_factor: An `int` number to specify the upsampling factor to
+ generate finer mask. Default 1 means no upsampling is applied.
+ low_level: An `int` of backbone level to be used for feature fusion. It is
+ used when feature_fusion is set to `deeplabv3plus`.
+ low_level_num_filters: An `int` of reduced number of filters for the low
+ level features before fusing it with higher level features. It is only
+ used when feature_fusion is set to `deeplabv3plus`.
+ fusion_num_output_filters: An `int` number to specify the number of
+ filters used by output layer of fusion module. Default is 256.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(SemanticHead, self).__init__(
+ level=level,
+ num_convs=num_convs,
+ num_filters=num_filters,
+ use_depthwise_convolution=use_depthwise_convolution,
+ kernel_size=kernel_size,
+ upsample_factor=upsample_factor,
+ low_level=low_level,
+ low_level_num_filters=low_level_num_filters,
+ fusion_num_output_filters=fusion_num_output_filters,
+ activation=activation,
+ use_sync_bn=use_sync_bn,
+ norm_momentum=norm_momentum,
+ norm_epsilon=norm_epsilon,
+ kernel_regularizer=kernel_regularizer,
+ bias_regularizer=bias_regularizer,
+ **kwargs)
+ self._config_dict.update({
+ 'num_classes': num_classes,
+ 'prediction_kernel_size': prediction_kernel_size})
+
+ def build(self, input_shape: Union[tf.TensorShape, List[tf.TensorShape]]):
+ """Creates the variables of the semantic head."""
+ super(SemanticHead, self).build(input_shape)
+ self._classifier = tf.keras.layers.Conv2D(
+ name='semantic_output',
+ filters=self._config_dict['num_classes'],
+ kernel_size=self._config_dict['prediction_kernel_size'],
+ padding='same',
+ bias_initializer=tf.zeros_initializer(),
+ kernel_initializer=tf.keras.initializers.RandomNormal(stddev=0.01),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'])
+
+ def call(self, inputs: Tuple[Union[tf.Tensor, Mapping[str, tf.Tensor]],
+ Union[tf.Tensor, Mapping[str, tf.Tensor]]],
+ training=None):
+ """Forward pass of the head."""
+
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+ x = super(SemanticHead, self).call(inputs, training=training)
+ outputs = self._classifier(x)
+ return outputs
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class InstanceHead(PanopticDeeplabHead):
+ """Creates a instance head."""
+
+ def __init__(
+ self,
+ level: Union[int, str],
+ num_convs: int = 2,
+ num_filters: int = 256,
+ kernel_size: int = 3,
+ prediction_kernel_size: int = 3,
+ use_depthwise_convolution: bool = False,
+ upsample_factor: int = 1,
+ low_level: Optional[List[int]] = None,
+ low_level_num_filters: Optional[List[int]] = None,
+ fusion_num_output_filters: int = 256,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ **kwargs):
+ """Initializes a instance center head.
+
+ Args:
+ level: An `int` or `str`, level to use to build head.
+ num_convs: An `int` number of stacked convolution before the last
+ prediction layer.
+ num_filters: An `int` number to specify the number of filters used.
+ Default is 256.
+ kernel_size: An `int` number to specify the kernel size of the
+ stacked convolutions before the last prediction layer.
+ prediction_kernel_size: An `int` number to specify the kernel size of the
+ prediction layer.
+ use_depthwise_convolution: A bool to specify if use depthwise separable
+ convolutions.
+ upsample_factor: An `int` number to specify the upsampling factor to
+ generate finer mask. Default 1 means no upsampling is applied.
+ low_level: An `int` of backbone level to be used for feature fusion. It is
+ used when feature_fusion is set to `deeplabv3plus`.
+ low_level_num_filters: An `int` of reduced number of filters for the low
+ level features before fusing it with higher level features. It is only
+ used when feature_fusion is set to `deeplabv3plus`.
+ fusion_num_output_filters: An `int` number to specify the number of
+ filters used by output layer of fusion module. Default is 256.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(InstanceHead, self).__init__(
+ level=level,
+ num_convs=num_convs,
+ num_filters=num_filters,
+ use_depthwise_convolution=use_depthwise_convolution,
+ kernel_size=kernel_size,
+ upsample_factor=upsample_factor,
+ low_level=low_level,
+ low_level_num_filters=low_level_num_filters,
+ fusion_num_output_filters=fusion_num_output_filters,
+ activation=activation,
+ use_sync_bn=use_sync_bn,
+ norm_momentum=norm_momentum,
+ norm_epsilon=norm_epsilon,
+ kernel_regularizer=kernel_regularizer,
+ bias_regularizer=bias_regularizer,
+ **kwargs)
+ self._config_dict.update({
+ 'prediction_kernel_size': prediction_kernel_size})
+
+ def build(self, input_shape: Union[tf.TensorShape, List[tf.TensorShape]]):
+ """Creates the variables of the instance head."""
+ super(InstanceHead, self).build(input_shape)
+ self._instance_center_prediction_conv = tf.keras.layers.Conv2D(
+ name='instance_centers_heatmap',
+ filters=1,
+ kernel_size=self._config_dict['prediction_kernel_size'],
+ padding='same',
+ bias_initializer=tf.zeros_initializer(),
+ kernel_initializer=tf.keras.initializers.RandomNormal(stddev=0.01),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'])
+
+ self._instance_center_regression_conv = tf.keras.layers.Conv2D(
+ name='instance_centers_offset',
+ filters=2,
+ kernel_size=self._config_dict['prediction_kernel_size'],
+ padding='same',
+ bias_initializer=tf.zeros_initializer(),
+ kernel_initializer=tf.keras.initializers.RandomNormal(stddev=0.01),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'])
+
+ def call(self, inputs: Tuple[Union[tf.Tensor, Mapping[str, tf.Tensor]],
+ Union[tf.Tensor, Mapping[str, tf.Tensor]]],
+ training=None):
+ """Forward pass of the head."""
+
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ x = super(InstanceHead, self).call(inputs, training=training)
+ instance_centers_heatmap = self._instance_center_prediction_conv(x)
+ instance_centers_offset = self._instance_center_regression_conv(x)
+ outputs = {
+ 'instance_centers_heatmap': instance_centers_heatmap,
+ 'instance_centers_offset': instance_centers_offset
+ }
+ return outputs
diff --git a/official/projects/panoptic/modeling/layers/fusion_layers.py b/official/projects/panoptic/modeling/layers/fusion_layers.py
new file mode 100644
index 0000000000000000000000000000000000000000..42db299738d6f444c1ac3223c7863a38a41ebba0
--- /dev/null
+++ b/official/projects/panoptic/modeling/layers/fusion_layers.py
@@ -0,0 +1,180 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains feature fusion blocks for panoptic segmentation models."""
+from typing import Any, Callable, Dict, List, Mapping, Optional, Union
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+
+# Type annotations.
+States = Dict[str, tf.Tensor]
+Activation = Union[str, Callable]
+
+
+class PanopticDeepLabFusion(tf.keras.layers.Layer):
+ """Creates a Panoptic DeepLab feature Fusion layer.
+
+ This implements the feature fusion introduced in the paper:
+ Cheng et al. Panoptic-DeepLab
+ (https://arxiv.org/pdf/1911.10194.pdf)
+ """
+
+ def __init__(
+ self,
+ level: int,
+ low_level: List[int],
+ num_projection_filters: List[int],
+ num_output_filters: int = 256,
+ use_depthwise_convolution: bool = False,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ **kwargs):
+ """Initializes panoptic FPN feature fusion layer.
+
+ Args:
+ level: An `int` level at which the decoder was appled at.
+ low_level: A list of `int` of minimum level to use in feature fusion.
+ num_projection_filters: A list of `int` with number of filters for
+ projection conv2d layers.
+ num_output_filters: An `int` number of filters in output conv2d layers.
+ use_depthwise_convolution: A bool to specify if use depthwise separable
+ convolutions.
+ activation: A `str` name of the activation function.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ interpolation: A `str` interpolation method for upsampling. Defaults to
+ `bilinear`.
+ **kwargs: Additional keyword arguments to be passed.
+ Returns:
+ A `float` `tf.Tensor` of shape [batch_size, feature_height, feature_width,
+ feature_channel].
+ """
+ super(PanopticDeepLabFusion, self).__init__(**kwargs)
+
+ self._config_dict = {
+ 'level': level,
+ 'low_level': low_level,
+ 'num_projection_filters': num_projection_filters,
+ 'num_output_filters': num_output_filters,
+ 'use_depthwise_convolution': use_depthwise_convolution,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'norm_momentum': norm_momentum,
+ 'norm_epsilon': norm_epsilon,
+ 'kernel_regularizer': kernel_regularizer,
+ 'bias_regularizer': bias_regularizer,
+ 'interpolation': interpolation
+ }
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._channel_axis = -1
+ else:
+ self._channel_axis = 1
+ self._activation = tf_utils.get_activation(activation)
+
+ def build(self, input_shape: List[tf.TensorShape]):
+ conv_op = tf.keras.layers.Conv2D
+ conv_kwargs = {
+ 'padding': 'same',
+ 'use_bias': True,
+ 'kernel_initializer': tf.initializers.VarianceScaling(),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ }
+ bn_op = (tf.keras.layers.experimental.SyncBatchNormalization
+ if self._config_dict['use_sync_bn']
+ else tf.keras.layers.BatchNormalization)
+ bn_kwargs = {
+ 'axis': self._channel_axis,
+ 'momentum': self._config_dict['norm_momentum'],
+ 'epsilon': self._config_dict['norm_epsilon'],
+ }
+
+ self._projection_convs = []
+ self._projection_norms = []
+ self._fusion_convs = []
+ self._fusion_norms = []
+ for i in range(len(self._config_dict['low_level'])):
+ self._projection_convs.append(
+ conv_op(
+ filters=self._config_dict['num_projection_filters'][i],
+ kernel_size=1,
+ **conv_kwargs))
+ if self._config_dict['use_depthwise_convolution']:
+ depthwise_initializer = tf.keras.initializers.RandomNormal(stddev=0.01)
+ fusion_conv = tf.keras.Sequential([
+ tf.keras.layers.DepthwiseConv2D(
+ kernel_size=5,
+ padding='same',
+ use_bias=True,
+ depthwise_initializer=depthwise_initializer,
+ depthwise_regularizer=self._config_dict['kernel_regularizer'],
+ depth_multiplier=1),
+ bn_op(**bn_kwargs),
+ conv_op(
+ filters=self._config_dict['num_output_filters'],
+ kernel_size=1,
+ **conv_kwargs)])
+ else:
+ fusion_conv = conv_op(
+ filters=self._config_dict['num_output_filters'],
+ kernel_size=5,
+ **conv_kwargs)
+ self._fusion_convs.append(fusion_conv)
+ self._projection_norms.append(bn_op(**bn_kwargs))
+ self._fusion_norms.append(bn_op(**bn_kwargs))
+
+ def call(self, inputs, training=None):
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ backbone_output = inputs[0]
+ decoder_output = inputs[1][str(self._config_dict['level'])]
+
+ x = decoder_output
+ for i in range(len(self._config_dict['low_level'])):
+ feature = backbone_output[str(self._config_dict['low_level'][i])]
+ feature = self._projection_convs[i](feature)
+ feature = self._projection_norms[i](feature, training=training)
+ feature = self._activation(feature)
+
+ shape = tf.shape(feature)
+ x = tf.image.resize(
+ x, size=[shape[1], shape[2]],
+ method=self._config_dict['interpolation'])
+ x = tf.cast(x, dtype=feature.dtype)
+ x = tf.concat([x, feature], axis=self._channel_axis)
+
+ x = self._fusion_convs[i](x)
+ x = self._fusion_norms[i](x, training=training)
+ x = self._activation(x)
+ return x
+
+ def get_config(self) -> Mapping[str, Any]:
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
diff --git a/official/projects/panoptic/modeling/layers/panoptic_deeplab_merge.py b/official/projects/panoptic/modeling/layers/panoptic_deeplab_merge.py
new file mode 100644
index 0000000000000000000000000000000000000000..764b15e19ef64e58537b8af9b6595756c635a6d5
--- /dev/null
+++ b/official/projects/panoptic/modeling/layers/panoptic_deeplab_merge.py
@@ -0,0 +1,568 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""This file contains functions to post-process Panoptic-DeepLab results.
+
+Note that the postprocessing class and the supporting functions are branched
+from:
+https://github.com/google-research/deeplab2/blob/main/model/post_processor/panoptic_deeplab.py
+with minor changes.
+"""
+
+import functools
+from typing import Dict, List, Text, Tuple
+
+import tensorflow as tf
+
+from official.projects.panoptic.ops import mask_ops
+
+
+def _add_zero_padding(input_tensor: tf.Tensor, kernel_size: int,
+ rank: int) -> tf.Tensor:
+ """Adds zero-padding to the input_tensor."""
+ pad_total = kernel_size - 1
+ pad_begin = pad_total // 2
+ pad_end = pad_total - pad_begin
+ if rank == 3:
+ return tf.pad(
+ input_tensor,
+ paddings=[[pad_begin, pad_end], [pad_begin, pad_end], [0, 0]])
+ else:
+ return tf.pad(
+ input_tensor,
+ paddings=[[0, 0], [pad_begin, pad_end], [pad_begin, pad_end], [0, 0]])
+
+
+def _get_semantic_predictions(semantic_logits: tf.Tensor) -> tf.Tensor:
+ """Computes the semantic classes from the predictions.
+
+ Args:
+ semantic_logits: A tf.tensor of shape [batch, height, width, classes].
+ Returns:
+ A tf.Tensor containing the semantic class prediction of shape
+ [batch, height, width].
+ """
+ return tf.argmax(semantic_logits, axis=-1, output_type=tf.int32)
+
+
+def _get_instance_centers_from_heatmap(
+ center_heatmap: tf.Tensor,
+ center_threshold: float,
+ nms_kernel_size: int,
+ keep_k_centers: int) -> Tuple[tf.Tensor, tf.Tensor]:
+ """Computes a list of instance centers.
+
+ Args:
+ center_heatmap: A tf.Tensor of shape [height, width, 1].
+ center_threshold: A float setting the threshold for the center heatmap.
+ nms_kernel_size: An integer specifying the nms kernel size.
+ keep_k_centers: An integer specifying the number of centers to keep (K).
+ Non-positive values will keep all centers.
+ Returns:
+ A tuple of
+ - tf.Tensor of shape [N, 2] containing N center coordinates (after
+ non-maximum suppression) in (y, x) order.
+ - tf.Tensor of shape [height, width] containing the center heatmap after
+ non-maximum suppression.
+ """
+ # Threshold center map.
+ center_heatmap = tf.where(
+ tf.greater(center_heatmap, center_threshold), center_heatmap, 0.0)
+
+ # Non-maximum suppression.
+ padded_map = _add_zero_padding(center_heatmap, nms_kernel_size, rank=3)
+ pooled_center_heatmap = tf.keras.backend.pool2d(
+ tf.expand_dims(padded_map, 0),
+ pool_size=(nms_kernel_size, nms_kernel_size),
+ strides=(1, 1),
+ padding='valid',
+ pool_mode='max')
+ center_heatmap = tf.where(
+ tf.equal(pooled_center_heatmap, center_heatmap), center_heatmap, 0.0)
+ center_heatmap = tf.squeeze(center_heatmap, axis=[0, 3])
+
+ # `centers` is of shape (N, 2) with (y, x) order of the second dimension.
+ centers = tf.where(tf.greater(center_heatmap, 0.0))
+
+ if keep_k_centers > 0 and tf.shape(centers)[0] > keep_k_centers:
+ topk_scores, _ = tf.math.top_k(
+ tf.reshape(center_heatmap, [-1]), keep_k_centers, sorted=False)
+ centers = tf.where(tf.greater(center_heatmap, topk_scores[-1]))
+
+ return centers, center_heatmap
+
+
+def _find_closest_center_per_pixel(centers: tf.Tensor,
+ center_offsets: tf.Tensor) -> tf.Tensor:
+ """Assigns all pixels to their closest center.
+
+ Args:
+ centers: A tf.Tensor of shape [N, 2] containing N centers with coordinate
+ order (y, x).
+ center_offsets: A tf.Tensor of shape [height, width, 2].
+ Returns:
+ A tf.Tensor of shape [height, width] containing the index of the closest
+ center, per pixel.
+ """
+ height = tf.shape(center_offsets)[0]
+ width = tf.shape(center_offsets)[1]
+
+ x_coord, y_coord = tf.meshgrid(tf.range(width), tf.range(height))
+ coord = tf.stack([y_coord, x_coord], axis=-1)
+
+ center_per_pixel = tf.cast(coord, tf.float32) + center_offsets
+
+ # centers: [N, 2] -> [N, 1, 2].
+ # center_per_pixel: [H, W, 2] -> [1, H*W, 2].
+ centers = tf.cast(tf.expand_dims(centers, 1), tf.float32)
+ center_per_pixel = tf.reshape(center_per_pixel, [height*width, 2])
+ center_per_pixel = tf.expand_dims(center_per_pixel, 0)
+
+ # distances: [N, H*W].
+ distances = tf.norm(centers - center_per_pixel, axis=-1)
+
+ return tf.reshape(tf.argmin(distances, axis=0), [height, width])
+
+
+def _get_instances_from_heatmap_and_offset(
+ semantic_segmentation: tf.Tensor, center_heatmap: tf.Tensor,
+ center_offsets: tf.Tensor, center_threshold: float,
+ thing_class_ids: tf.Tensor, nms_kernel_size: int,
+ keep_k_centers: int) -> Tuple[tf.Tensor, tf.Tensor, tf.Tensor]:
+ """Computes the instance assignment per pixel.
+
+ Args:
+ semantic_segmentation: A tf.Tensor containing the semantic labels of shape
+ [height, width].
+ center_heatmap: A tf.Tensor of shape [height, width, 1].
+ center_offsets: A tf.Tensor of shape [height, width, 2].
+ center_threshold: A float setting the threshold for the center heatmap.
+ thing_class_ids: A tf.Tensor of shape [N] containing N thing indices.
+ nms_kernel_size: An integer specifying the nms kernel size.
+ keep_k_centers: An integer specifying the number of centers to keep.
+ Negative values will keep all centers.
+ Returns:
+ A tuple of:
+ - tf.Tensor containing the instance segmentation (filtered with the `thing`
+ segmentation from the semantic segmentation output) with shape
+ [height, width].
+ - tf.Tensor containing the processed centermap with shape [height, width].
+ - tf.Tensor containing instance scores (where higher "score" is a reasonable
+ signal of a higher confidence detection.) Will be of shape [height, width]
+ with the score for a pixel being the score of the instance it belongs to.
+ The scores will be zero for pixels in background/"stuff" regions.
+ """
+ thing_segmentation = tf.zeros_like(semantic_segmentation)
+ for thing_id in thing_class_ids:
+ thing_segmentation = tf.where(tf.equal(semantic_segmentation, thing_id),
+ 1,
+ thing_segmentation)
+
+ centers, processed_center_heatmap = _get_instance_centers_from_heatmap(
+ center_heatmap, center_threshold, nms_kernel_size, keep_k_centers)
+ if tf.shape(centers)[0] == 0:
+ return (tf.zeros_like(semantic_segmentation), processed_center_heatmap,
+ tf.zeros_like(processed_center_heatmap))
+
+ instance_center_index = _find_closest_center_per_pixel(
+ centers, center_offsets)
+ # Instance IDs should start with 1. So we use the index into the centers, but
+ # shifted by 1.
+ instance_segmentation = tf.cast(instance_center_index, tf.int32) + 1
+
+ # The value of the heatmap at an instance's center is used as the score
+ # for that instance.
+ instance_scores = tf.gather_nd(processed_center_heatmap, centers)
+ # This will map the instance scores back to the image space: where each pixel
+ # has a value equal to the score of its instance.
+ flat_center_index = tf.reshape(instance_center_index, [-1])
+ instance_score_map = tf.gather(instance_scores, flat_center_index)
+ instance_score_map = tf.reshape(instance_score_map,
+ tf.shape(instance_segmentation))
+ instance_score_map *= tf.cast(thing_segmentation, tf.float32)
+
+ return (thing_segmentation * instance_segmentation, processed_center_heatmap,
+ instance_score_map)
+
+
+@tf.function
+def _get_panoptic_predictions(
+ semantic_logits: tf.Tensor, center_heatmap: tf.Tensor,
+ center_offsets: tf.Tensor, center_threshold: float,
+ thing_class_ids: tf.Tensor, label_divisor: int, stuff_area_limit: int,
+ void_label: int, nms_kernel_size: int, keep_k_centers: int
+) -> Tuple[tf.Tensor, tf.Tensor, tf.Tensor, tf.Tensor]:
+ """Computes the semantic class and instance ID per pixel.
+
+ Args:
+ semantic_logits: A tf.Tensor of shape [batch, height, width, classes].
+ center_heatmap: A tf.Tensor of shape [batch, height, width, 1].
+ center_offsets: A tf.Tensor of shape [batch, height, width, 2].
+ center_threshold: A float setting the threshold for the center heatmap.
+ thing_class_ids: A tf.Tensor of shape [N] containing N thing indices.
+ label_divisor: An integer specifying the label divisor of the dataset.
+ stuff_area_limit: An integer specifying the number of pixels that stuff
+ regions need to have at least. The stuff region will be included in the
+ panoptic prediction, only if its area is larger than the limit; otherwise,
+ it will be re-assigned as void_label.
+ void_label: An integer specifying the void label.
+ nms_kernel_size: An integer specifying the nms kernel size.
+ keep_k_centers: An integer specifying the number of centers to keep.
+ Negative values will keep all centers.
+ Returns:
+ A tuple of:
+ - the panoptic prediction as tf.Tensor with shape [batch, height, width].
+ - the centermap prediction as tf.Tensor with shape [batch, height, width].
+ - the instance score maps as tf.Tensor with shape [batch, height, width].
+ - the instance prediction as tf.Tensor with shape [batch, height, width].
+ """
+ semantic_prediction = _get_semantic_predictions(semantic_logits)
+ batch_size = tf.shape(semantic_logits)[0]
+
+ instance_map_lists = tf.TensorArray(
+ tf.int32, size=batch_size, dynamic_size=False)
+ center_map_lists = tf.TensorArray(
+ tf.float32, size=batch_size, dynamic_size=False)
+ instance_score_map_lists = tf.TensorArray(
+ tf.float32, size=batch_size, dynamic_size=False)
+
+ for i in tf.range(batch_size):
+ (instance_map, center_map,
+ instance_score_map) = _get_instances_from_heatmap_and_offset(
+ semantic_prediction[i, ...], center_heatmap[i, ...],
+ center_offsets[i, ...], center_threshold, thing_class_ids,
+ nms_kernel_size, keep_k_centers)
+ instance_map_lists = instance_map_lists.write(i, instance_map)
+ center_map_lists = center_map_lists.write(i, center_map)
+ instance_score_map_lists = instance_score_map_lists.write(
+ i, instance_score_map)
+
+ # This does not work with unknown shapes.
+ instance_maps = instance_map_lists.stack()
+ center_maps = center_map_lists.stack()
+ instance_score_maps = instance_score_map_lists.stack()
+
+ panoptic_prediction = _merge_semantic_and_instance_maps(
+ semantic_prediction, instance_maps, thing_class_ids, label_divisor,
+ stuff_area_limit, void_label)
+ return (panoptic_prediction, center_maps, instance_score_maps, instance_maps)
+
+
+@tf.function
+def _merge_semantic_and_instance_maps(
+ semantic_prediction: tf.Tensor,
+ instance_maps: tf.Tensor,
+ thing_class_ids: tf.Tensor,
+ label_divisor: int,
+ stuff_area_limit: int,
+ void_label: int) -> tf.Tensor:
+ """Merges semantic and instance maps to obtain panoptic segmentation.
+
+ This function merges the semantic segmentation and class-agnostic
+ instance segmentation to form the panoptic segmentation. In particular,
+ the class label of each instance mask is inferred from the majority
+ votes from the corresponding pixels in the semantic segmentation. This
+ operation is first proposed in the DeeperLab paper and adopted by the
+ Panoptic-DeepLab.
+ - DeeperLab: Single-Shot Image Parser, T-J Yang, et al. arXiv:1902.05093.
+ - Panoptic-DeepLab, B. Cheng, et al. In CVPR, 2020.
+ Note that this function only supports batch = 1 for simplicity. Additionally,
+ this function has a slightly different implementation from the provided
+ TensorFlow implementation `merge_ops` but with a similar performance. This
+ function is mainly used as a backup solution when you could not successfully
+ compile the provided TensorFlow implementation. To reproduce our results,
+ please use the provided TensorFlow implementation (i.e., not use this
+ function, but the `merge_ops.merge_semantic_and_instance_maps`).
+
+ Args:
+ semantic_prediction: A tf.Tensor of shape [batch, height, width].
+ instance_maps: A tf.Tensor of shape [batch, height, width].
+ thing_class_ids: A tf.Tensor of shape [N] containing N thing indices.
+ label_divisor: An integer specifying the label divisor of the dataset.
+ stuff_area_limit: An integer specifying the number of pixels that stuff
+ regions need to have at least. The stuff region will be included in the
+ panoptic prediction, only if its area is larger than the limit; otherwise,
+ it will be re-assigned as void_label.
+ void_label: An integer specifying the void label.
+ Returns:
+ panoptic_prediction: A tf.Tensor with shape [batch, height, width].
+ """
+ prediction_shape = semantic_prediction.get_shape().as_list()
+ # This implementation only supports batch size of 1. Since model construction
+ # might lose batch size information (and leave it to None), override it here.
+ prediction_shape[0] = 1
+ semantic_prediction = tf.ensure_shape(semantic_prediction, prediction_shape)
+ instance_maps = tf.ensure_shape(instance_maps, prediction_shape)
+
+ # Default panoptic_prediction to have semantic label = void_label.
+ panoptic_prediction = tf.ones_like(
+ semantic_prediction) * void_label * label_divisor
+
+ # Start to paste predicted `thing` regions to panoptic_prediction.
+ # Infer `thing` segmentation regions from semantic prediction.
+ semantic_thing_segmentation = tf.zeros_like(semantic_prediction,
+ dtype=tf.bool)
+ for thing_class in thing_class_ids:
+ semantic_thing_segmentation = tf.math.logical_or(
+ semantic_thing_segmentation,
+ semantic_prediction == thing_class)
+ # Keep track of how many instances for each semantic label.
+ num_instance_per_semantic_label = tf.TensorArray(
+ tf.int32, size=0, dynamic_size=True, clear_after_read=False)
+ instance_ids, _ = tf.unique(tf.reshape(instance_maps, [-1]))
+ for instance_id in instance_ids:
+ # Instance ID 0 is reserved for crowd region.
+ if instance_id == 0:
+ continue
+ thing_mask = tf.math.logical_and(instance_maps == instance_id,
+ semantic_thing_segmentation)
+ if tf.reduce_sum(tf.cast(thing_mask, tf.int32)) == 0:
+ continue
+ semantic_bin_counts = tf.math.bincount(
+ tf.boolean_mask(semantic_prediction, thing_mask))
+ semantic_majority = tf.cast(
+ tf.math.argmax(semantic_bin_counts), tf.int32)
+
+ while num_instance_per_semantic_label.size() <= semantic_majority:
+ num_instance_per_semantic_label = num_instance_per_semantic_label.write(
+ num_instance_per_semantic_label.size(), 0)
+
+ new_instance_id = (
+ num_instance_per_semantic_label.read(semantic_majority) + 1)
+ num_instance_per_semantic_label = num_instance_per_semantic_label.write(
+ semantic_majority, new_instance_id)
+ panoptic_prediction = tf.where(
+ thing_mask,
+ tf.ones_like(panoptic_prediction) * semantic_majority * label_divisor
+ + new_instance_id,
+ panoptic_prediction)
+
+ # Done with `num_instance_per_semantic_label` tensor array.
+ num_instance_per_semantic_label.close()
+
+ # Start to paste predicted `stuff` regions to panoptic prediction.
+ instance_stuff_regions = instance_maps == 0
+ semantic_ids, _ = tf.unique(tf.reshape(semantic_prediction, [-1]))
+ for semantic_id in semantic_ids:
+ if tf.reduce_sum(tf.cast(thing_class_ids == semantic_id, tf.int32)) > 0:
+ continue
+ # Check stuff area.
+ stuff_mask = tf.math.logical_and(semantic_prediction == semantic_id,
+ instance_stuff_regions)
+ stuff_area = tf.reduce_sum(tf.cast(stuff_mask, tf.int32))
+ if stuff_area >= stuff_area_limit:
+ panoptic_prediction = tf.where(
+ stuff_mask,
+ tf.ones_like(panoptic_prediction) * semantic_id * label_divisor,
+ panoptic_prediction)
+
+ return panoptic_prediction
+
+
+class PostProcessor(tf.keras.layers.Layer):
+ """This class contains code of a Panoptic-Deeplab post-processor."""
+
+ def __init__(
+ self,
+ output_size: List[int],
+ center_score_threshold: float,
+ thing_class_ids: List[int],
+ label_divisor: int,
+ stuff_area_limit: int,
+ ignore_label: int,
+ nms_kernel: int,
+ keep_k_centers: int,
+ rescale_predictions: bool,
+ **kwargs):
+ """Initializes a Panoptic-Deeplab post-processor.
+
+ Args:
+ output_size: A `List` of integers that represent the height and width of
+ the output mask.
+ center_score_threshold: A float setting the threshold for the center
+ heatmap.
+ thing_class_ids: An integer list shape [N] containing N thing indices.
+ label_divisor: An integer specifying the label divisor of the dataset.
+ stuff_area_limit: An integer specifying the number of pixels that stuff
+ regions need to have at least. The stuff region will be included in the
+ panoptic prediction, only if its area is larger than the limit;
+ otherwise, it will be re-assigned as void_label.
+ ignore_label: An integer specifying the void label.
+ nms_kernel: An integer specifying the nms kernel size.
+ keep_k_centers: An integer specifying the number of centers to keep.
+ Negative values will keep all centers.
+ rescale_predictions: `bool`, whether to scale back prediction to original
+ image sizes. If True, image_info is used to rescale predictions.
+ **kwargs: additional kwargs arguments.
+ """
+ super(PostProcessor, self).__init__(**kwargs)
+
+ self._config_dict = {
+ 'output_size': output_size,
+ 'center_score_threshold': center_score_threshold,
+ 'thing_class_ids': thing_class_ids,
+ 'label_divisor': label_divisor,
+ 'stuff_area_limit': stuff_area_limit,
+ 'ignore_label': ignore_label,
+ 'nms_kernel': nms_kernel,
+ 'keep_k_centers': keep_k_centers,
+ 'rescale_predictions': rescale_predictions
+ }
+ self._post_processor = functools.partial(
+ _get_panoptic_predictions,
+ center_threshold=center_score_threshold,
+ thing_class_ids=tf.convert_to_tensor(thing_class_ids),
+ label_divisor=label_divisor,
+ stuff_area_limit=stuff_area_limit,
+ void_label=ignore_label,
+ nms_kernel_size=nms_kernel,
+ keep_k_centers=keep_k_centers)
+
+ def _resize_and_pad_masks(self, mask, image_info):
+ """Resizes masks to match the original image shape and pads to`output_size`.
+
+ Args:
+ mask: a padded mask tensor.
+ image_info: a tensor that holds information about original and
+ preprocessed images.
+ Returns:
+ resized and padded masks: tf.Tensor.
+ """
+ rescale_size = tf.cast(
+ tf.math.ceil(image_info[1, :] / image_info[2, :]), tf.int32)
+ image_shape = tf.cast(image_info[0, :], tf.int32)
+ offsets = tf.cast(image_info[3, :], tf.int32)
+
+ mask = tf.image.resize(
+ mask,
+ rescale_size,
+ method='bilinear')
+ mask = tf.image.crop_to_bounding_box(
+ mask,
+ offsets[0], offsets[1],
+ image_shape[0],
+ image_shape[1])
+ mask = tf.image.pad_to_bounding_box(
+ mask, 0, 0,
+ self._config_dict['output_size'][0],
+ self._config_dict['output_size'][1])
+ return mask
+
+ def _resize_and_pad_offset_mask(self, mask, image_info):
+ """Rescales and resizes offset masks and pads to`output_size`.
+
+ Args:
+ mask: a padded offset mask tensor.
+ image_info: a tensor that holds information about original and
+ preprocessed images.
+ Returns:
+ rescaled, resized and padded masks: tf.Tensor.
+ """
+ rescale_size = tf.cast(
+ tf.math.ceil(image_info[1, :] / image_info[2, :]), tf.int32)
+ image_shape = tf.cast(image_info[0, :], tf.int32)
+ offsets = tf.cast(image_info[3, :], tf.int32)
+
+ mask = mask_ops.resize_and_rescale_offsets(
+ tf.expand_dims(mask, axis=0),
+ rescale_size)[0]
+ mask = tf.image.crop_to_bounding_box(
+ mask,
+ offsets[0], offsets[1],
+ image_shape[0],
+ image_shape[1])
+ mask = tf.image.pad_to_bounding_box(
+ mask, 0, 0,
+ self._config_dict['output_size'][0],
+ self._config_dict['output_size'][1])
+ return mask
+
+ def call(
+ self,
+ result_dict: Dict[Text, tf.Tensor],
+ image_info: tf.Tensor) -> Dict[Text, tf.Tensor]:
+ """Performs the post-processing given model predicted results.
+
+ Args:
+ result_dict: A dictionary of tf.Tensor containing model results. The dict
+ has to contain
+ - segmentation_outputs
+ - instance_centers_heatmap
+ - instance_centers_offset
+ image_info: A tf.Tensor of image infos.
+
+ Returns:
+ The post-processed dict of tf.Tensor, containing the following keys:
+ - panoptic_outputs
+ - category_mask
+ - instance_mask
+ - instance_centers
+ - instance_score
+ """
+ if self._config_dict['rescale_predictions']:
+ segmentation_outputs = tf.map_fn(
+ fn=lambda x: self._resize_and_pad_masks(x[0], x[1]),
+ elems=(result_dict['segmentation_outputs'], image_info),
+ fn_output_signature=tf.float32,
+ parallel_iterations=32)
+ instance_centers_heatmap = tf.map_fn(
+ fn=lambda x: self._resize_and_pad_masks(x[0], x[1]),
+ elems=(result_dict['instance_centers_heatmap'], image_info),
+ fn_output_signature=tf.float32,
+ parallel_iterations=32)
+ instance_centers_offset = tf.map_fn(
+ fn=lambda x: self._resize_and_pad_offset_mask(x[0], x[1]),
+ elems=(result_dict['instance_centers_offset'], image_info),
+ fn_output_signature=tf.float32,
+ parallel_iterations=32)
+ else:
+ segmentation_outputs = tf.image.resize(
+ result_dict['segmentation_outputs'],
+ size=self._config_dict['output_size'],
+ method='bilinear')
+ instance_centers_heatmap = tf.image.resize(
+ result_dict['instance_centers_heatmap'],
+ size=self._config_dict['output_size'],
+ method='bilinear')
+ instance_centers_offset = mask_ops.resize_and_rescale_offsets(
+ result_dict['instance_centers_offset'],
+ target_size=self._config_dict['output_size'])
+
+ processed_dict = {}
+
+ (processed_dict['panoptic_outputs'],
+ processed_dict['instance_centers'],
+ processed_dict['instance_scores'],
+ _) = self._post_processor(
+ tf.nn.softmax(segmentation_outputs, axis=-1),
+ instance_centers_heatmap,
+ instance_centers_offset)
+
+ label_divisor = self._config_dict['label_divisor']
+ processed_dict['category_mask'] = (
+ processed_dict['panoptic_outputs'] // label_divisor)
+ processed_dict['instance_mask'] = (
+ processed_dict['panoptic_outputs'] % label_divisor)
+
+ processed_dict.update({
+ 'segmentation_outputs': result_dict['segmentation_outputs']})
+
+ return processed_dict
+
+ def get_config(self):
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
diff --git a/official/projects/panoptic/modeling/layers/panoptic_segmentation_generator.py b/official/projects/panoptic/modeling/layers/panoptic_segmentation_generator.py
new file mode 100644
index 0000000000000000000000000000000000000000..cecc4661d330076029cf429aece197fdabf1c84d
--- /dev/null
+++ b/official/projects/panoptic/modeling/layers/panoptic_segmentation_generator.py
@@ -0,0 +1,617 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains definition for postprocessing layer to genrate panoptic segmentations."""
+
+from typing import Any, Dict, List, Optional, Tuple
+
+import tensorflow as tf
+
+from official.projects.panoptic.modeling.layers import paste_masks
+from official.vision.ops import spatial_transform_ops
+
+
+def _batch_count_ones(masks: tf.Tensor,
+ dtype: tf.dtypes.DType = tf.int32) -> tf.Tensor:
+ """Counts the ones/trues for each mask in the batch.
+
+ Args:
+ masks: A tensor in shape (..., height, width) with arbitrary numbers of
+ batch dimensions.
+ dtype: DType of the resulting tensor. Default is tf.int32.
+
+ Returns:
+ A tensor which contains the count of non-zero elements for each mask in the
+ batch. The rank of the resulting tensor is equal to rank(masks) - 2.
+ """
+ masks_shape = masks.get_shape().as_list()
+ if len(masks_shape) < 2:
+ raise ValueError(
+ 'Expected the input masks (..., height, width) has rank >= 2, was: %s' %
+ masks_shape)
+ return tf.reduce_sum(tf.cast(masks, dtype), axis=[-2, -1])
+
+
+class PanopticSegmentationGenerator(tf.keras.layers.Layer):
+ """Panoptic segmentation generator layer."""
+
+ def __init__(
+ self,
+ output_size: List[int],
+ max_num_detections: int,
+ stuff_classes_offset: int,
+ mask_binarize_threshold: float = 0.5,
+ score_threshold: float = 0.5,
+ things_overlap_threshold: float = 0.5,
+ stuff_area_threshold: float = 4096,
+ things_class_label: int = 1,
+ void_class_label: int = 0,
+ void_instance_id: int = -1,
+ rescale_predictions: bool = False,
+ **kwargs):
+ """Generates panoptic segmentation masks.
+
+ Args:
+ output_size: A `List` of integers that represent the height and width of
+ the output mask.
+ max_num_detections: `int` for maximum number of detections.
+ stuff_classes_offset: An `int` that is added to the output of the
+ semantic segmentation mask to make sure that the stuff class ids do not
+ ovelap with the thing class ids of the MaskRCNN outputs.
+ mask_binarize_threshold: A `float`
+ score_threshold: A `float` representing the threshold for deciding
+ when to remove objects based on score.
+ things_overlap_threshold: A `float` representing a threshold for deciding
+ to ignore a thing if overlap is above the threshold.
+ stuff_area_threshold: A `float` representing a threshold for deciding to
+ to ignore a stuff class if area is below certain threshold.
+ things_class_label: An `int` that represents a single merged category of
+ all thing classes in the semantic segmentation output.
+ void_class_label: An `int` that is used to represent empty or unlabelled
+ regions of the mask
+ void_instance_id: An `int` that is used to denote regions that are not
+ assigned to any thing class. That is, void_instance_id are assigned to
+ both stuff regions and empty regions.
+ rescale_predictions: `bool`, whether to scale back prediction to original
+ image sizes. If True, image_info is used to rescale predictions.
+ **kwargs: additional kewargs arguments.
+ """
+ self._output_size = output_size
+ self._max_num_detections = max_num_detections
+ self._stuff_classes_offset = stuff_classes_offset
+ self._mask_binarize_threshold = mask_binarize_threshold
+ self._score_threshold = score_threshold
+ self._things_overlap_threshold = things_overlap_threshold
+ self._stuff_area_threshold = stuff_area_threshold
+ self._things_class_label = things_class_label
+ self._void_class_label = void_class_label
+ self._void_instance_id = void_instance_id
+ self._rescale_predictions = rescale_predictions
+
+ self._config_dict = {
+ 'output_size': output_size,
+ 'max_num_detections': max_num_detections,
+ 'stuff_classes_offset': stuff_classes_offset,
+ 'mask_binarize_threshold': mask_binarize_threshold,
+ 'score_threshold': score_threshold,
+ 'things_class_label': things_class_label,
+ 'void_class_label': void_class_label,
+ 'void_instance_id': void_instance_id,
+ 'rescale_predictions': rescale_predictions
+ }
+ super().__init__(**kwargs)
+
+ def build(self, input_shape: tf.TensorShape):
+ grid_sampler = paste_masks.BilinearGridSampler(align_corners=False)
+ self._paste_masks_fn = paste_masks.PasteMasks(
+ output_size=self._output_size, grid_sampler=grid_sampler)
+ super().build(input_shape)
+
+ def _generate_panoptic_masks(
+ self, boxes: tf.Tensor, scores: tf.Tensor, classes: tf.Tensor,
+ detections_masks: tf.Tensor,
+ segmentation_mask: tf.Tensor) -> Dict[str, tf.Tensor]:
+ """Generates panoptic masks for a single image.
+
+ This function implements the following steps to merge instance and semantic
+ segmentation masks described in https://arxiv.org/pdf/1901.02446.pdf
+ Steps:
+ 1. resolving overlaps between different instances based on their
+ confidence scores
+ 2. resolving overlaps between instance and semantic segmentation
+ outputs in favor of instances
+ 3. removing any stuff regions labeled other or under a given area
+ threshold.
+ Args:
+ boxes: A `tf.Tensor` of shape [num_rois, 4], representing the bounding
+ boxes for detected objects.
+ scores: A `tf.Tensor` of shape [num_rois], representing the
+ confidence scores for each object.
+ classes: A `tf.Tensor` of shape [num_rois], representing the class
+ for each object.
+ detections_masks: A `tf.Tensor` of shape
+ [num_rois, mask_height, mask_width, 1], representing the cropped mask
+ for each object.
+ segmentation_mask: A `tf.Tensor` of shape [height, width], representing
+ the semantic segmentation output.
+ Returns:
+ Dict with the following keys:
+ - category_mask: A `tf.Tensor` for category masks.
+ - instance_mask: A `tf.Tensor for instance masks.
+ """
+
+ # Offset stuff class predictions
+ segmentation_mask = tf.where(
+ tf.logical_or(
+ tf.equal(segmentation_mask, self._things_class_label),
+ tf.equal(segmentation_mask, self._void_class_label)),
+ segmentation_mask,
+ segmentation_mask + self._stuff_classes_offset
+ )
+ # sort instances by their scores
+ sorted_indices = tf.argsort(scores, direction='DESCENDING')
+
+ mask_shape = self._output_size + [1]
+ category_mask = tf.ones(mask_shape,
+ dtype=tf.float32) * self._void_class_label
+ instance_mask = tf.ones(
+ mask_shape, dtype=tf.float32) * self._void_instance_id
+
+ # filter instances with low confidence
+ sorted_scores = tf.sort(scores, direction='DESCENDING')
+
+ valid_indices = tf.where(sorted_scores > self._score_threshold)
+
+ # if no instance has sufficient confidence score, skip merging
+ # instance segmentation masks
+ if tf.shape(valid_indices)[0] > 0:
+ loop_end_idx = valid_indices[-1, 0] + 1
+ loop_end_idx = tf.minimum(
+ tf.cast(loop_end_idx, dtype=tf.int32),
+ self._max_num_detections)
+ pasted_masks = self._paste_masks_fn((
+ detections_masks[:loop_end_idx],
+ boxes[:loop_end_idx]))
+
+ # add things segmentation to panoptic masks
+ for i in range(loop_end_idx):
+ # we process instances in decending order, which will make sure
+ # the overlaps are resolved based on confidence score
+ instance_idx = sorted_indices[i]
+
+ pasted_mask = pasted_masks[instance_idx]
+
+ class_id = tf.cast(classes[instance_idx], dtype=tf.float32)
+
+ # convert sigmoid scores to binary values
+ binary_mask = tf.greater(
+ pasted_mask, self._mask_binarize_threshold)
+
+ # filter empty instance masks
+ if not tf.reduce_sum(tf.cast(binary_mask, tf.float32)) > 0:
+ continue
+
+ overlap = tf.logical_and(
+ binary_mask,
+ tf.not_equal(category_mask, self._void_class_label))
+ binary_mask_area = tf.reduce_sum(
+ tf.cast(binary_mask, dtype=tf.float32))
+ overlap_area = tf.reduce_sum(
+ tf.cast(overlap, dtype=tf.float32))
+
+ # skip instance that have a big enough overlap with instances with
+ # higer scores
+ if overlap_area / binary_mask_area > self._things_overlap_threshold:
+ continue
+
+ # fill empty regions in category_mask represented by
+ # void_class_label with class_id of the instance.
+ category_mask = tf.where(
+ tf.logical_and(
+ binary_mask, tf.equal(category_mask, self._void_class_label)),
+ tf.ones_like(category_mask) * class_id, category_mask)
+
+ # fill empty regions in the instance_mask represented by
+ # void_instance_id with the id of the instance, starting from 1
+ instance_mask = tf.where(
+ tf.logical_and(
+ binary_mask,
+ tf.equal(instance_mask, self._void_instance_id)),
+ tf.ones_like(instance_mask) *
+ tf.cast(instance_idx + 1, tf.float32), instance_mask)
+
+ stuff_class_ids = tf.unique(tf.reshape(segmentation_mask, [-1])).y
+ for stuff_class_id in stuff_class_ids:
+ if stuff_class_id == self._things_class_label:
+ continue
+
+ stuff_mask = tf.logical_and(
+ tf.equal(segmentation_mask, stuff_class_id),
+ tf.equal(category_mask, self._void_class_label))
+
+ stuff_mask_area = tf.reduce_sum(
+ tf.cast(stuff_mask, dtype=tf.float32))
+
+ if stuff_mask_area < self._stuff_area_threshold:
+ continue
+
+ category_mask = tf.where(
+ stuff_mask,
+ tf.ones_like(category_mask) * stuff_class_id,
+ category_mask)
+
+ results = {
+ 'category_mask': category_mask[:, :, 0],
+ 'instance_mask': instance_mask[:, :, 0]
+ }
+ return results
+
+ def _resize_and_pad_masks(self, mask, image_info):
+ """Resizes masks to match the original image shape and pads to`output_size`.
+
+ Args:
+ mask: a padded mask tensor.
+ image_info: a tensor that holds information about original and
+ preprocessed images.
+ Returns:
+ resized and padded masks: tf.Tensor.
+ """
+ rescale_size = tf.cast(
+ tf.math.ceil(image_info[1, :] / image_info[2, :]), tf.int32)
+ image_shape = tf.cast(image_info[0, :], tf.int32)
+ offsets = tf.cast(image_info[3, :], tf.int32)
+
+ mask = tf.image.resize(
+ mask,
+ rescale_size,
+ method='bilinear')
+ mask = tf.image.crop_to_bounding_box(
+ mask,
+ offsets[0], offsets[1],
+ image_shape[0],
+ image_shape[1])
+ mask = tf.image.pad_to_bounding_box(
+ mask, 0, 0, self._output_size[0], self._output_size[1])
+ return mask
+
+ def call(self,
+ inputs: tf.Tensor,
+ image_info: Optional[tf.Tensor] = None) -> Dict[str, tf.Tensor]:
+ detections = inputs
+
+ batched_scores = detections['detection_scores']
+ batched_classes = detections['detection_classes']
+ batched_detections_masks = tf.expand_dims(
+ detections['detection_masks'], axis=-1)
+ batched_boxes = detections['detection_boxes']
+ batched_segmentation_masks = tf.cast(
+ detections['segmentation_outputs'], dtype=tf.float32)
+
+ if self._rescale_predictions:
+ scale = tf.tile(
+ tf.cast(image_info[:, 2:3, :], dtype=batched_boxes.dtype),
+ multiples=[1, 1, 2])
+ batched_boxes /= scale
+
+ batched_segmentation_masks = tf.map_fn(
+ fn=lambda x: self._resize_and_pad_masks(x[0], x[1]),
+ elems=(
+ batched_segmentation_masks,
+ image_info),
+ fn_output_signature=tf.float32,
+ parallel_iterations=32)
+ else:
+ batched_segmentation_masks = tf.image.resize(
+ batched_segmentation_masks,
+ size=self._output_size,
+ method='bilinear')
+
+ batched_segmentation_masks = tf.expand_dims(tf.cast(
+ tf.argmax(batched_segmentation_masks, axis=-1),
+ dtype=tf.float32), axis=-1)
+
+ panoptic_masks = tf.map_fn(
+ fn=lambda x: self._generate_panoptic_masks( # pylint:disable=g-long-lambda
+ x[0], x[1], x[2], x[3], x[4]),
+ elems=(
+ batched_boxes,
+ batched_scores,
+ batched_classes,
+ batched_detections_masks,
+ batched_segmentation_masks),
+ fn_output_signature={
+ 'category_mask': tf.float32,
+ 'instance_mask': tf.float32
+ }, parallel_iterations=32)
+
+ for k, v in panoptic_masks.items():
+ panoptic_masks[k] = tf.cast(v, dtype=tf.int32)
+
+ return panoptic_masks
+
+ def get_config(self) -> Dict[str, Any]:
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config: Dict[str,
+ Any]) -> 'PanopticSegmentationGenerator':
+ return cls(**config)
+
+
+class PanopticSegmentationGeneratorV2(tf.keras.layers.Layer):
+ """Panoptic segmentation generator layer V2."""
+
+ def __init__(self,
+ output_size: List[int],
+ max_num_detections: int,
+ stuff_classes_offset: int,
+ mask_binarize_threshold: float = 0.5,
+ score_threshold: float = 0.5,
+ things_overlap_threshold: float = 0.5,
+ stuff_area_threshold: float = 4096,
+ things_class_label: int = 1,
+ void_class_label: int = 0,
+ void_instance_id: int = -1,
+ rescale_predictions: bool = False,
+ **kwargs):
+ """Generates panoptic segmentation masks.
+
+ Args:
+ output_size: A `List` of integers that represent the height and width of
+ the output mask.
+ max_num_detections: `int` for maximum number of detections.
+ stuff_classes_offset: An `int` that is added to the output of the semantic
+ segmentation mask to make sure that the stuff class ids do not ovelap
+ with the thing class ids of the MaskRCNN outputs.
+ mask_binarize_threshold: A `float`
+ score_threshold: A `float` representing the threshold for deciding when to
+ remove objects based on score.
+ things_overlap_threshold: A `float` representing a threshold for deciding
+ to ignore a thing if overlap is above the threshold.
+ stuff_area_threshold: A `float` representing a threshold for deciding to
+ to ignore a stuff class if area is below certain threshold.
+ things_class_label: An `int` that represents a single merged category of
+ all thing classes in the semantic segmentation output.
+ void_class_label: An `int` that is used to represent empty or unlabelled
+ regions of the mask
+ void_instance_id: An `int` that is used to denote regions that are not
+ assigned to any thing class. That is, void_instance_id are assigned to
+ both stuff regions and empty regions.
+ rescale_predictions: `bool`, whether to scale back prediction to original
+ image sizes. If True, image_info is used to rescale predictions.
+ **kwargs: additional kewargs arguments.
+ """
+ self._output_size = output_size
+ self._max_num_detections = max_num_detections
+ self._stuff_classes_offset = stuff_classes_offset
+ self._mask_binarize_threshold = mask_binarize_threshold
+ self._score_threshold = score_threshold
+ self._things_overlap_threshold = things_overlap_threshold
+ self._stuff_area_threshold = stuff_area_threshold
+ self._things_class_label = things_class_label
+ self._void_class_label = void_class_label
+ self._void_instance_id = void_instance_id
+ self._rescale_predictions = rescale_predictions
+
+ self._config_dict = {
+ 'output_size': output_size,
+ 'max_num_detections': max_num_detections,
+ 'stuff_classes_offset': stuff_classes_offset,
+ 'mask_binarize_threshold': mask_binarize_threshold,
+ 'score_threshold': score_threshold,
+ 'things_class_label': things_class_label,
+ 'void_class_label': void_class_label,
+ 'void_instance_id': void_instance_id,
+ 'rescale_predictions': rescale_predictions
+ }
+ super().__init__(**kwargs)
+
+ def call(self,
+ inputs: tf.Tensor,
+ image_info: Optional[tf.Tensor] = None) -> Dict[str, tf.Tensor]:
+ """Generates panoptic segmentation masks."""
+ # (batch_size, num_rois, 4) in absolute coordinates.
+ detection_boxes = tf.cast(inputs['detection_boxes'], tf.float32)
+ # (batch_size, num_rois)
+ detection_classes = tf.cast(inputs['detection_classes'], tf.int32)
+ # (batch_size, num_rois)
+ detection_scores = tf.cast(inputs['detection_scores'], tf.float32)
+ # (batch_size, num_rois, mask_height, mask_width)
+ detections_masks = tf.cast(inputs['detection_masks'], tf.float32)
+ # (batch_size, height, width, num_semantic_classes)
+ segmentation_outputs = tf.cast(inputs['segmentation_outputs'], tf.float32)
+
+ if self._rescale_predictions:
+ # (batch_size, 2)
+ original_size = tf.cast(image_info[:, 0, :], tf.float32)
+ desired_size = tf.cast(image_info[:, 1, :], tf.float32)
+ image_scale = tf.cast(image_info[:, 2, :], tf.float32)
+ offset = tf.cast(image_info[:, 3, :], tf.float32)
+ rescale_size = tf.math.ceil(desired_size / image_scale)
+ # (batch_size, output_height, output_width, num_semantic_classes)
+ segmentation_outputs = (
+ spatial_transform_ops.bilinear_resize_with_crop_and_pad(
+ segmentation_outputs,
+ rescale_size,
+ crop_offset=offset,
+ crop_size=original_size,
+ output_size=self._output_size))
+ # (batch_size, 1, 4)
+ image_scale = tf.tile(image_scale, multiples=[1, 2])[:, tf.newaxis]
+ detection_boxes /= image_scale
+ else:
+ # (batch_size, output_height, output_width, num_semantic_classes)
+ segmentation_outputs = tf.image.resize(
+ segmentation_outputs, size=self._output_size, method='bilinear')
+
+ # (batch_size, output_height, output_width)
+ instance_mask, instance_category_mask = self._generate_instances(
+ detection_boxes, detection_classes, detection_scores, detections_masks)
+
+ # (batch_size, output_height, output_width)
+ stuff_category_mask = self._generate_stuffs(segmentation_outputs)
+
+ # (batch_size, output_height, output_width)
+ category_mask = tf.where((stuff_category_mask != self._void_class_label) &
+ (instance_category_mask == self._void_class_label),
+ stuff_category_mask + self._stuff_classes_offset,
+ instance_category_mask)
+
+ return {'instance_mask': instance_mask, 'category_mask': category_mask}
+
+ def _generate_instances(
+ self, detection_boxes: tf.Tensor, detection_classes: tf.Tensor,
+ detection_scores: tf.Tensor,
+ detections_masks: tf.Tensor) -> Tuple[tf.Tensor, tf.Tensor]:
+ """Generates instance & category masks from instance segmentation outputs."""
+ batch_size = tf.shape(detections_masks)[0]
+ num_rois = tf.shape(detections_masks)[1]
+ mask_height = tf.shape(detections_masks)[2]
+ mask_width = tf.shape(detections_masks)[3]
+ output_height = self._output_size[0]
+ output_width = self._output_size[1]
+
+ # (batch_size, num_rois, mask_height, mask_width)
+ detections_masks = detections_masks * (
+ tf.cast((detection_scores > self._score_threshold) &
+ (detection_classes != self._void_class_label),
+ detections_masks.dtype)[:, :, tf.newaxis, tf.newaxis])
+
+ # Resizes and copies the detections_masks to the bounding boxes in the
+ # output canvas.
+ # (batch_size, num_rois, output_height, output_width)
+ pasted_detection_masks = tf.reshape(
+ spatial_transform_ops.bilinear_resize_to_bbox(
+ tf.reshape(detections_masks, [-1, mask_height, mask_width]),
+ tf.reshape(detection_boxes, [-1, 4]), self._output_size),
+ shape=[-1, num_rois, output_height, output_width])
+
+ # (batch_size, num_rois, output_height, output_width)
+ instance_binary_masks = (
+ pasted_detection_masks > self._mask_binarize_threshold)
+
+ # Sorts detection related tensors by scores.
+ # (batch_size, num_rois)
+ sorted_detection_indices = tf.argsort(
+ detection_scores, axis=1, direction='DESCENDING')
+ # (batch_size, num_rois)
+ sorted_detection_classes = tf.gather(
+ detection_classes, sorted_detection_indices, batch_dims=1)
+ # (batch_size, num_rois, output_height, output_width)
+ sorted_instance_binary_masks = tf.gather(
+ instance_binary_masks, sorted_detection_indices, batch_dims=1)
+ # (batch_size, num_rois)
+ instance_areas = _batch_count_ones(
+ sorted_instance_binary_masks, dtype=tf.float32)
+
+ init_loop_vars = (
+ 0, # i: the loop counter
+ tf.ones([batch_size, output_height, output_width], dtype=tf.int32) *
+ self._void_instance_id, # combined_instance_mask
+ tf.ones([batch_size, output_height, output_width], dtype=tf.int32) *
+ self._void_class_label # combined_category_mask
+ )
+
+ def _copy_instances_loop_body(
+ i: int, combined_instance_mask: tf.Tensor,
+ combined_category_mask: tf.Tensor) -> Tuple[int, tf.Tensor, tf.Tensor]:
+ """Iterates the sorted detections and copies the instances."""
+ # (batch_size, output_height, output_width)
+ instance_binary_mask = sorted_instance_binary_masks[:, i]
+
+ # Masks out the instances that have a big enough overlap with the other
+ # instances with higher scores.
+ # (batch_size, )
+ overlap_areas = _batch_count_ones(
+ (combined_instance_mask != self._void_instance_id)
+ & instance_binary_mask,
+ dtype=tf.float32)
+ # (batch_size, )
+ instance_overlap_threshold_mask = tf.math.divide_no_nan(
+ overlap_areas, instance_areas[:, i]) < self._things_overlap_threshold
+ # (batch_size, output_height, output_width)
+ instance_binary_mask &= (
+ instance_overlap_threshold_mask[:, tf.newaxis, tf.newaxis]
+ & (combined_instance_mask == self._void_instance_id))
+
+ # Updates combined_instance_mask.
+ # (batch_size, )
+ instance_id = tf.cast(
+ sorted_detection_indices[:, i] + 1, # starting from 1
+ dtype=combined_instance_mask.dtype)
+ # (batch_size, output_height, output_width)
+ combined_instance_mask = tf.where(instance_binary_mask,
+ instance_id[:, tf.newaxis, tf.newaxis],
+ combined_instance_mask)
+
+ # Updates combined_category_mask.
+ # (batch_size, )
+ class_id = tf.cast(
+ sorted_detection_classes[:, i], dtype=combined_category_mask.dtype)
+ # (batch_size, output_height, output_width)
+ combined_category_mask = tf.where(instance_binary_mask,
+ class_id[:, tf.newaxis, tf.newaxis],
+ combined_category_mask)
+
+ # Returns the updated loop vars.
+ return (
+ i + 1, # Increment the loop counter i
+ combined_instance_mask,
+ combined_category_mask)
+
+ # (batch_size, output_height, output_width)
+ _, instance_mask, category_mask = tf.while_loop(
+ cond=lambda i, *_: i < num_rois - 1,
+ body=_copy_instances_loop_body,
+ loop_vars=init_loop_vars,
+ parallel_iterations=32,
+ maximum_iterations=num_rois)
+ return instance_mask, category_mask
+
+ def _generate_stuffs(self, segmentation_outputs: tf.Tensor) -> tf.Tensor:
+ """Generates category mask from semantic segmentation outputs."""
+ num_semantic_classes = tf.shape(segmentation_outputs)[3]
+
+ # (batch_size, output_height, output_width)
+ segmentation_masks = tf.argmax(
+ segmentation_outputs, axis=-1, output_type=tf.int32)
+ stuff_binary_masks = (segmentation_masks != self._things_class_label) & (
+ segmentation_masks != self._void_class_label)
+ # (batch_size, num_semantic_classes, output_height, output_width)
+ stuff_class_binary_masks = ((tf.one_hot(
+ segmentation_masks, num_semantic_classes, axis=1, dtype=tf.int32) == 1)
+ & tf.expand_dims(stuff_binary_masks, axis=1))
+
+ # Masks out the stuff class whose area is below the given threshold.
+ # (batch_size, num_semantic_classes)
+ stuff_class_areas = _batch_count_ones(
+ stuff_class_binary_masks, dtype=tf.float32)
+ # (batch_size, num_semantic_classes, output_height, output_width)
+ stuff_class_binary_masks &= tf.greater(
+ stuff_class_areas, self._stuff_area_threshold)[:, :, tf.newaxis,
+ tf.newaxis]
+ # (batch_size, output_height, output_width)
+ stuff_binary_masks = tf.reduce_any(stuff_class_binary_masks, axis=1)
+
+ # (batch_size, output_height, output_width)
+ return tf.where(stuff_binary_masks, segmentation_masks,
+ tf.ones_like(segmentation_masks) * self._void_class_label)
+
+ def get_config(self) -> Dict[str, Any]:
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config: Dict[str,
+ Any]) -> 'PanopticSegmentationGeneratorV2':
+ return cls(**config)
diff --git a/official/vision/beta/projects/panoptic_maskrcnn/modeling/layers/paste_masks.py b/official/projects/panoptic/modeling/layers/paste_masks.py
similarity index 98%
rename from official/vision/beta/projects/panoptic_maskrcnn/modeling/layers/paste_masks.py
rename to official/projects/panoptic/modeling/layers/paste_masks.py
index 1a750be5941a993a49bd7d4a388272cb50dca402..e46ffae8ca362dcc82e0c5e69d70ac59fd00bd8e 100644
--- a/official/vision/beta/projects/panoptic_maskrcnn/modeling/layers/paste_masks.py
+++ b/official/projects/panoptic/modeling/layers/paste_masks.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/panoptic/modeling/panoptic_deeplab_model.py b/official/projects/panoptic/modeling/panoptic_deeplab_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..47ea1d714310f6ea019758bdaf140f29ab21ebd0
--- /dev/null
+++ b/official/projects/panoptic/modeling/panoptic_deeplab_model.py
@@ -0,0 +1,122 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Build Panoptic Deeplab model."""
+from typing import Any, Mapping, Optional, Union
+
+import tensorflow as tf
+from official.projects.panoptic.modeling.layers import panoptic_deeplab_merge
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class PanopticDeeplabModel(tf.keras.Model):
+ """Panoptic Deeplab model."""
+
+ def __init__(
+ self,
+ backbone: tf.keras.Model,
+ semantic_decoder: tf.keras.Model,
+ semantic_head: tf.keras.layers.Layer,
+ instance_head: tf.keras.layers.Layer,
+ instance_decoder: Optional[tf.keras.Model] = None,
+ post_processor: Optional[panoptic_deeplab_merge.PostProcessor] = None,
+ **kwargs):
+ """Panoptic deeplab model initializer.
+
+ Args:
+ backbone: a backbone network.
+ semantic_decoder: a decoder network. E.g. FPN.
+ semantic_head: segmentation head.
+ instance_head: instance center head.
+ instance_decoder: Optional decoder network for instance predictions.
+ post_processor: Optional post processor layer.
+ **kwargs: keyword arguments to be passed.
+ """
+ super(PanopticDeeplabModel, self).__init__(**kwargs)
+
+ self._config_dict = {
+ 'backbone': backbone,
+ 'semantic_decoder': semantic_decoder,
+ 'instance_decoder': instance_decoder,
+ 'semantic_head': semantic_head,
+ 'instance_head': instance_head,
+ 'post_processor': post_processor
+ }
+ self.backbone = backbone
+ self.semantic_decoder = semantic_decoder
+ self.instance_decoder = instance_decoder
+ self.semantic_head = semantic_head
+ self.instance_head = instance_head
+ self.post_processor = post_processor
+
+ def call(
+ self, inputs: tf.Tensor,
+ image_info: tf.Tensor,
+ training: bool = None):
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+
+ backbone_features = self.backbone(inputs, training=training)
+
+ semantic_features = self.semantic_decoder(
+ backbone_features, training=training)
+
+ if self.instance_decoder is None:
+ instance_features = semantic_features
+ else:
+ instance_features = self.instance_decoder(
+ backbone_features, training=training)
+
+ segmentation_outputs = self.semantic_head(
+ (backbone_features, semantic_features),
+ training=training)
+ instance_outputs = self.instance_head(
+ (backbone_features, instance_features),
+ training=training)
+
+ outputs = {
+ 'segmentation_outputs': segmentation_outputs,
+ 'instance_centers_heatmap':
+ instance_outputs['instance_centers_heatmap'],
+ 'instance_centers_offset':
+ instance_outputs['instance_centers_offset'],
+ }
+ if training:
+ return outputs
+
+ if self.post_processor is not None:
+ panoptic_masks = self.post_processor(outputs, image_info)
+ outputs.update(panoptic_masks)
+ return outputs
+
+ @property
+ def checkpoint_items(
+ self) -> Mapping[str, Union[tf.keras.Model, tf.keras.layers.Layer]]:
+ """Returns a dictionary of items to be additionally checkpointed."""
+ items = dict(
+ backbone=self.backbone,
+ semantic_decoder=self.semantic_decoder,
+ semantic_head=self.semantic_head,
+ instance_head=self.instance_head)
+ if self.instance_decoder is not None:
+ items.update(instance_decoder=self.instance_decoder)
+
+ return items
+
+ def get_config(self) -> Mapping[str, Any]:
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
diff --git a/official/vision/beta/projects/panoptic_maskrcnn/modeling/panoptic_maskrcnn_model.py b/official/projects/panoptic/modeling/panoptic_maskrcnn_model.py
similarity index 94%
rename from official/vision/beta/projects/panoptic_maskrcnn/modeling/panoptic_maskrcnn_model.py
rename to official/projects/panoptic/modeling/panoptic_maskrcnn_model.py
index 713ae62b203c3ced67b343eacca7af441285fd49..309f7fa7bf7404be1cfd17481b734a6f90f4e5a0 100644
--- a/official/vision/beta/projects/panoptic_maskrcnn/modeling/panoptic_maskrcnn_model.py
+++ b/official/projects/panoptic/modeling/panoptic_maskrcnn_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,10 +18,10 @@ from typing import List, Mapping, Optional, Union
import tensorflow as tf
-from official.vision.beta.modeling import maskrcnn_model
+from official.projects.deepmac_maskrcnn.modeling import maskrcnn_model
-class PanopticMaskRCNNModel(maskrcnn_model.MaskRCNNModel):
+class PanopticMaskRCNNModel(maskrcnn_model.DeepMaskRCNNModel):
"""The Panoptic Segmentation model."""
def __init__(
@@ -49,7 +49,8 @@ class PanopticMaskRCNNModel(maskrcnn_model.MaskRCNNModel):
max_level: Optional[int] = None,
num_scales: Optional[int] = None,
aspect_ratios: Optional[List[float]] = None,
- anchor_size: Optional[float] = None, # pytype: disable=annotation-type-mismatch # typed-keras
+ anchor_size: Optional[float] = None,
+ use_gt_boxes_for_masks: bool = False, # pytype: disable=annotation-type-mismatch # typed-keras
**kwargs):
"""Initializes the Panoptic Mask R-CNN model.
@@ -94,6 +95,7 @@ class PanopticMaskRCNNModel(maskrcnn_model.MaskRCNNModel):
aspect_ratios=[1.0, 2.0, 0.5] adds three anchors on each scale level.
anchor_size: A number representing the scale of size of the base anchor to
the feature stride 2^level.
+ use_gt_boxes_for_masks: `bool`, whether to use only gt boxes for masks.
**kwargs: keyword arguments to be passed.
"""
super(PanopticMaskRCNNModel, self).__init__(
@@ -115,6 +117,7 @@ class PanopticMaskRCNNModel(maskrcnn_model.MaskRCNNModel):
num_scales=num_scales,
aspect_ratios=aspect_ratios,
anchor_size=anchor_size,
+ use_gt_boxes_for_masks=use_gt_boxes_for_masks,
**kwargs)
self._config_dict.update({
diff --git a/official/projects/panoptic/ops/mask_ops.py b/official/projects/panoptic/ops/mask_ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..9bcc542e8ebf0724f985f95f6082848420b7e4ba
--- /dev/null
+++ b/official/projects/panoptic/ops/mask_ops.py
@@ -0,0 +1,55 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Utility functions for masks."""
+
+import tensorflow as tf
+
+
+def resize_and_rescale_offsets(input_tensor: tf.Tensor, target_size):
+ """Bilinearly resizes and rescales the offsets.
+
+ Reference:
+ https://github.com/google-research/deeplab2/blob/main/model/utils.py#L157
+
+ Args:
+ input_tensor: A tf.Tensor of shape [batch, height, width, 2].
+ target_size: A list or tuple or 1D tf.Tensor that specifies the height and
+ width after resizing.
+
+ Returns:
+ The input_tensor resized to shape `[batch, target_height, target_width, 2]`.
+ Moreover, the offsets along the y-axis are rescaled by a factor equal to
+ (target_height - 1) / (reference_height - 1) and the offsets along the
+ x-axis are rescaled by a factor equal to
+ (target_width - 1) / (reference_width - 1).
+ """
+ input_size_y = tf.shape(input_tensor)[1]
+ input_size_x = tf.shape(input_tensor)[2]
+ dtype = input_tensor.dtype
+
+ scale_y = tf.cast(target_size[0] - 1, dtype=dtype) / tf.cast(
+ input_size_y - 1, dtype=dtype)
+ scale_x = tf.cast(target_size[1] - 1, dtype=dtype) / tf.cast(
+ input_size_x - 1, dtype=dtype)
+
+ target_y, target_x = tf.split(
+ value=input_tensor, num_or_size_splits=2, axis=3)
+ target_y *= scale_y
+ target_x *= scale_x
+ _ = tf.concat([target_y, target_x], 3)
+ return tf.image.resize(
+ input_tensor,
+ size=target_size,
+ method=tf.image.ResizeMethod.BILINEAR)
diff --git a/official/projects/panoptic/serving/export_saved_model.py b/official/projects/panoptic/serving/export_saved_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..9808c64804980f71dc4912a684660a780cd7207d
--- /dev/null
+++ b/official/projects/panoptic/serving/export_saved_model.py
@@ -0,0 +1,130 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Panoptic MaskRCNN model export binary for serving/inference.
+
+To export a trained checkpoint in saved_model format (shell script):
+
+CHECKPOINT_PATH = XX
+EXPORT_DIR_PATH = XX
+CONFIG_FILE_PATH = XX
+export_saved_model --export_dir=${EXPORT_DIR_PATH}/ \
+ --checkpoint_path=${CHECKPOINT_PATH} \
+ --config_file=${CONFIG_FILE_PATH} \
+ --batch_size=2 \
+ --input_image_size=224,224
+To serve (python):
+export_dir_path = XX
+input_type = XX
+input_images = XX
+imported = tf.saved_model.load(export_dir_path)
+model_fn = imported.signatures['serving_default']
+output = model_fn(input_images)
+"""
+
+from absl import app
+from absl import flags
+import tensorflow as tf
+
+from official.core import exp_factory
+from official.modeling import hyperparams
+# pylint: disable=unused-import
+from official.projects.panoptic.configs import panoptic_deeplab as panoptic_deeplab_cfg
+from official.projects.panoptic.configs import panoptic_maskrcnn as panoptic_maskrcnn_cfg
+# pylint: enable=unused-import
+from official.projects.panoptic.modeling import factory
+from official.projects.panoptic.serving import panoptic_deeplab
+from official.projects.panoptic.serving import panoptic_maskrcnn
+# pylint: disable=unused-import
+from official.projects.panoptic.tasks import panoptic_deeplab as panoptic_deeplab_task
+from official.projects.panoptic.tasks import panoptic_maskrcnn as panoptic_maskrcnn_task
+# pylint: enable=unused-import
+from official.vision.serving import export_saved_model_lib
+
+FLAGS = flags.FLAGS
+
+flags.DEFINE_string('model', 'panoptic_maskrcnn',
+ 'model type, one of panoptic_maskrcnn and panoptic_deeplab')
+flags.DEFINE_string('experiment', 'panoptic_fpn_coco',
+ 'experiment type, e.g. panoptic_fpn_coco')
+flags.DEFINE_string('export_dir', None, 'The export directory.')
+flags.DEFINE_string('checkpoint_path', None, 'Checkpoint path.')
+flags.DEFINE_multi_string(
+ 'config_file',
+ default=None,
+ help='YAML/JSON files which specifies overrides. The override order '
+ 'follows the order of args. Note that each file '
+ 'can be used as an override template to override the default parameters '
+ 'specified in Python. If the same parameter is specified in both '
+ '`--config_file` and `--params_override`, `config_file` will be used '
+ 'first, followed by params_override.')
+flags.DEFINE_string(
+ 'params_override', '',
+ 'The JSON/YAML file or string which specifies the parameter to be overriden'
+ ' on top of `config_file` template.')
+flags.DEFINE_integer('batch_size', None, 'The batch size.')
+flags.DEFINE_string('input_type', 'image_tensor',
+ 'One of `image_tensor`, `image_bytes`, `tf_example`.')
+flags.DEFINE_string(
+ 'input_image_size', '224,224',
+ 'The comma-separated string of two integers representing the height,width '
+ 'of the input to the model.')
+
+
+def main(_):
+
+ params = exp_factory.get_exp_config(FLAGS.experiment)
+ for config_file in FLAGS.config_file or []:
+ params = hyperparams.override_params_dict(
+ params, config_file, is_strict=True)
+ if FLAGS.params_override:
+ params = hyperparams.override_params_dict(
+ params, FLAGS.params_override, is_strict=True)
+
+ params.validate()
+ params.lock()
+
+ input_image_size = [int(x) for x in FLAGS.input_image_size.split(',')]
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[FLAGS.batch_size, *input_image_size, 3])
+
+ if FLAGS.model == 'panoptic_deeplab':
+ build_model = factory.build_panoptic_deeplab
+ panoptic_module = panoptic_deeplab.PanopticSegmentationModule
+ elif FLAGS.model == 'panoptic_maskrcnn':
+ build_model = factory.build_panoptic_maskrcnn
+ panoptic_module = panoptic_maskrcnn.PanopticSegmentationModule
+ else:
+ raise ValueError('Unsupported model type: %s' % FLAGS.model)
+
+ model = build_model(input_specs=input_specs, model_config=params.task.model)
+ export_module = panoptic_module(
+ params=params,
+ model=model,
+ batch_size=FLAGS.batch_size,
+ input_image_size=[int(x) for x in FLAGS.input_image_size.split(',')],
+ num_channels=3)
+ export_saved_model_lib.export_inference_graph(
+ input_type=FLAGS.input_type,
+ batch_size=FLAGS.batch_size,
+ input_image_size=input_image_size,
+ params=params,
+ checkpoint_path=FLAGS.checkpoint_path,
+ export_dir=FLAGS.export_dir,
+ export_module=export_module,
+ export_checkpoint_subdir='checkpoint',
+ export_saved_model_subdir='saved_model')
+
+if __name__ == '__main__':
+ app.run(main)
diff --git a/official/projects/panoptic/serving/panoptic_deeplab.py b/official/projects/panoptic/serving/panoptic_deeplab.py
new file mode 100644
index 0000000000000000000000000000000000000000..0c2ad0607be6d25d55b72dc5263a4ce394d36fe9
--- /dev/null
+++ b/official/projects/panoptic/serving/panoptic_deeplab.py
@@ -0,0 +1,103 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic Segmentation input and model functions for serving/inference."""
+
+from typing import List
+
+import tensorflow as tf
+
+from official.core import config_definitions as cfg
+from official.projects.panoptic.modeling import factory
+from official.projects.panoptic.modeling import panoptic_deeplab_model
+from official.vision.serving import semantic_segmentation
+
+
+class PanopticSegmentationModule(
+ semantic_segmentation.SegmentationModule):
+ """Panoptic Deeplab Segmentation Module."""
+
+ def __init__(self,
+ params: cfg.ExperimentConfig,
+ *,
+ model: tf.keras.Model,
+ batch_size: int,
+ input_image_size: List[int],
+ num_channels: int = 3):
+ """Initializes panoptic segmentation module for export."""
+
+ if batch_size is None:
+ raise ValueError('batch_size cannot be None for panoptic segmentation '
+ 'model.')
+ if not isinstance(model, panoptic_deeplab_model.PanopticDeeplabModel):
+ raise ValueError('PanopticSegmentationModule module not '
+ 'implemented for {} model.'.format(type(model)))
+ params.task.train_data.preserve_aspect_ratio = True
+ super(PanopticSegmentationModule, self).__init__(
+ params=params,
+ model=model,
+ batch_size=batch_size,
+ input_image_size=input_image_size,
+ num_channels=num_channels)
+
+ def _build_model(self):
+ input_specs = tf.keras.layers.InputSpec(shape=[self._batch_size] +
+ self._input_image_size + [3])
+
+ return factory.build_panoptic_deeplab(
+ input_specs=input_specs,
+ model_config=self.params.task.model,
+ l2_regularizer=None)
+
+ def serve(self, images: tf.Tensor):
+ """Cast image to float and run inference.
+
+ Args:
+ images: uint8 Tensor of shape [batch_size, None, None, 3]
+
+ Returns:
+ Tensor holding detection output logits.
+ """
+ if self._input_type != 'tflite':
+ with tf.device('cpu:0'):
+ images = tf.cast(images, dtype=tf.float32)
+ images_spec = tf.TensorSpec(
+ shape=self._input_image_size + [3], dtype=tf.float32)
+ image_info_spec = tf.TensorSpec(shape=[4, 2], dtype=tf.float32)
+
+ images, image_info = tf.nest.map_structure(
+ tf.identity,
+ tf.map_fn(
+ self._build_inputs,
+ elems=images,
+ fn_output_signature=(images_spec, image_info_spec),
+ parallel_iterations=32))
+
+ outputs = self.model.call(
+ inputs=images, image_info=image_info, training=False)
+
+ masks = outputs['segmentation_outputs']
+ masks = tf.image.resize(masks, self._input_image_size, method='bilinear')
+ classes = tf.math.argmax(masks, axis=-1)
+ scores = tf.nn.softmax(masks, axis=-1)
+ final_outputs = {
+ 'semantic_logits': masks,
+ 'semantic_scores': scores,
+ 'semantic_classes': classes,
+ 'image_info': image_info,
+ 'panoptic_category_mask': outputs['category_mask'],
+ 'panoptic_instance_mask': outputs['instance_mask'],
+ }
+
+ return final_outputs
diff --git a/official/projects/panoptic/serving/panoptic_maskrcnn.py b/official/projects/panoptic/serving/panoptic_maskrcnn.py
new file mode 100644
index 0000000000000000000000000000000000000000..d62b073259aad4e9a5ce687461f13a17724d1c7e
--- /dev/null
+++ b/official/projects/panoptic/serving/panoptic_maskrcnn.py
@@ -0,0 +1,145 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic Segmentation input and model functions for serving/inference."""
+
+from typing import List
+
+import tensorflow as tf
+
+from official.core import config_definitions as cfg
+from official.projects.panoptic.modeling import panoptic_maskrcnn_model
+from official.vision.serving import detection
+
+
+class PanopticSegmentationModule(detection.DetectionModule):
+ """Panoptic Segmentation Module."""
+
+ def __init__(self,
+ params: cfg.ExperimentConfig,
+ *,
+ model: tf.keras.Model,
+ batch_size: int,
+ input_image_size: List[int],
+ num_channels: int = 3):
+ """Initializes panoptic segmentation module for export."""
+
+ if batch_size is None:
+ raise ValueError('batch_size cannot be None for panoptic segmentation '
+ 'model.')
+ if not isinstance(model, panoptic_maskrcnn_model.PanopticMaskRCNNModel):
+ raise ValueError('PanopticSegmentationModule module not implemented for '
+ '{} model.'.format(type(model)))
+
+ super(PanopticSegmentationModule, self).__init__(
+ params=params,
+ model=model,
+ batch_size=batch_size,
+ input_image_size=input_image_size,
+ num_channels=num_channels)
+
+ def serve(self, images: tf.Tensor):
+ """Cast image to float and run inference.
+
+ Args:
+ images: uint8 Tensor of shape [batch_size, None, None, 3]
+ Returns:
+ Tensor holding detection output logits.
+ """
+ model_params = self.params.task.model
+ with tf.device('cpu:0'):
+ images = tf.cast(images, dtype=tf.float32)
+
+ # Tensor Specs for map_fn outputs (images, anchor_boxes, and image_info).
+ images_spec = tf.TensorSpec(shape=self._input_image_size + [3],
+ dtype=tf.float32)
+
+ num_anchors = model_params.anchor.num_scales * len(
+ model_params.anchor.aspect_ratios) * 4
+ anchor_shapes = []
+ for level in range(model_params.min_level, model_params.max_level + 1):
+ anchor_level_spec = tf.TensorSpec(
+ shape=[
+ self._input_image_size[0] // 2**level,
+ self._input_image_size[1] // 2**level, num_anchors
+ ],
+ dtype=tf.float32)
+ anchor_shapes.append((str(level), anchor_level_spec))
+
+ image_info_spec = tf.TensorSpec(shape=[4, 2], dtype=tf.float32)
+
+ images, anchor_boxes, image_info = tf.nest.map_structure(
+ tf.identity,
+ tf.map_fn(
+ self._build_inputs,
+ elems=images,
+ fn_output_signature=(images_spec, dict(anchor_shapes),
+ image_info_spec),
+ parallel_iterations=32))
+
+ # To overcome keras.Model extra limitation to save a model with layers that
+ # have multiple inputs, we use `model.call` here to trigger the forward
+ # path. Note that, this disables some keras magics happens in `__call__`.
+ detections = self.model.call(
+ images=images,
+ image_info=image_info,
+ anchor_boxes=anchor_boxes,
+ training=False)
+
+ detections.pop('rpn_boxes')
+ detections.pop('rpn_scores')
+ detections.pop('cls_outputs')
+ detections.pop('box_outputs')
+ detections.pop('backbone_features')
+ detections.pop('decoder_features')
+
+ # Normalize detection boxes to [0, 1]. Here we first map them to the
+ # original image size, then normalize them to [0, 1].
+ detections['detection_boxes'] = (
+ detections['detection_boxes'] /
+ tf.tile(image_info[:, 2:3, :], [1, 1, 2]) /
+ tf.tile(image_info[:, 0:1, :], [1, 1, 2]))
+
+ if model_params.detection_generator.apply_nms:
+ final_outputs = {
+ 'detection_boxes': detections['detection_boxes'],
+ 'detection_scores': detections['detection_scores'],
+ 'detection_classes': detections['detection_classes'],
+ 'num_detections': detections['num_detections']
+ }
+ else:
+ final_outputs = {
+ 'decoded_boxes': detections['decoded_boxes'],
+ 'decoded_box_scores': detections['decoded_box_scores']
+ }
+ masks = detections['segmentation_outputs']
+ masks = tf.image.resize(masks, self._input_image_size, method='bilinear')
+ classes = tf.math.argmax(masks, axis=-1)
+ scores = tf.nn.softmax(masks, axis=-1)
+ final_outputs.update({
+ 'detection_masks': detections['detection_masks'],
+ 'semantic_logits': masks,
+ 'semantic_scores': scores,
+ 'semantic_classes': classes,
+ 'image_info': image_info
+ })
+ if model_params.generate_panoptic_masks:
+ final_outputs.update({
+ 'panoptic_category_mask':
+ detections['panoptic_outputs']['category_mask'],
+ 'panoptic_instance_mask':
+ detections['panoptic_outputs']['instance_mask'],
+ })
+
+ return final_outputs
diff --git a/official/projects/panoptic/tasks/__init__.py b/official/projects/panoptic/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/panoptic/tasks/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/projects/panoptic/tasks/panoptic_deeplab.py b/official/projects/panoptic/tasks/panoptic_deeplab.py
new file mode 100644
index 0000000000000000000000000000000000000000..cb6ddf1322ff69e2feff7158700a4d4a0173e267
--- /dev/null
+++ b/official/projects/panoptic/tasks/panoptic_deeplab.py
@@ -0,0 +1,387 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic Deeplab task definition."""
+from typing import Any, Dict, List, Mapping, Optional, Tuple
+
+from absl import logging
+import tensorflow as tf
+
+from official.common import dataset_fn
+from official.core import base_task
+from official.core import task_factory
+from official.projects.panoptic.configs import panoptic_deeplab as exp_cfg
+from official.projects.panoptic.dataloaders import panoptic_deeplab_input
+from official.projects.panoptic.losses import panoptic_deeplab_losses
+from official.projects.panoptic.modeling import factory
+from official.vision.dataloaders import input_reader_factory
+from official.vision.evaluation import panoptic_quality_evaluator
+from official.vision.evaluation import segmentation_metrics
+
+
+@task_factory.register_task_cls(exp_cfg.PanopticDeeplabTask)
+class PanopticDeeplabTask(base_task.Task):
+ """A task for Panoptic Deeplab."""
+
+ def build_model(self):
+ """Builds panoptic deeplab model."""
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + self.task_config.model.input_size)
+
+ l2_weight_decay = self.task_config.losses.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ model = factory.build_panoptic_deeplab(
+ input_specs=input_specs,
+ model_config=self.task_config.model,
+ l2_regularizer=l2_regularizer)
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loads pretrained checkpoint."""
+ if not self.task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self.task_config.init_checkpoint
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ # Restoring checkpoint.
+ if 'all' in self.task_config.init_checkpoint_modules:
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ else:
+ ckpt_items = {}
+ if 'backbone' in self.task_config.init_checkpoint_modules:
+ ckpt_items.update(backbone=model.backbone)
+ if 'decoder' in self.task_config.init_checkpoint_modules:
+ ckpt_items.update(semantic_decoder=model.semantic_decoder)
+ if not self.task_config.model.shared_decoder:
+ ckpt_items.update(instance_decoder=model.instance_decoder)
+
+ ckpt = tf.train.Checkpoint(**ckpt_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+
+ def build_inputs(self,
+ params: exp_cfg.DataConfig,
+ input_context: Optional[tf.distribute.InputContext] = None):
+ """Builds panoptic deeplab input."""
+ decoder_cfg = params.decoder.get()
+
+ if params.decoder.type == 'simple_decoder':
+ decoder = panoptic_deeplab_input.TfExampleDecoder(
+ regenerate_source_id=decoder_cfg.regenerate_source_id,
+ panoptic_category_mask_key=decoder_cfg.panoptic_category_mask_key,
+ panoptic_instance_mask_key=decoder_cfg.panoptic_instance_mask_key)
+ else:
+ raise ValueError('Unknown decoder type: {}!'.format(params.decoder.type))
+
+ parser = panoptic_deeplab_input.Parser(
+ output_size=self.task_config.model.input_size[:2],
+ ignore_label=params.parser.ignore_label,
+ resize_eval_groundtruth=params.parser.resize_eval_groundtruth,
+ groundtruth_padded_size=params.parser.groundtruth_padded_size,
+ aug_scale_min=params.parser.aug_scale_min,
+ aug_scale_max=params.parser.aug_scale_max,
+ aug_rand_hflip=params.parser.aug_rand_hflip,
+ aug_type=params.parser.aug_type,
+ sigma=params.parser.sigma,
+ dtype=params.parser.dtype)
+
+ reader = input_reader_factory.input_reader_generator(
+ params,
+ dataset_fn=dataset_fn.pick_dataset_fn(params.file_type),
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def build_losses(self,
+ labels: Mapping[str, tf.Tensor],
+ model_outputs: Mapping[str, tf.Tensor],
+ aux_losses: Optional[Any] = None):
+ """Panoptic deeplab losses.
+
+ Args:
+ labels: labels.
+ model_outputs: Output logits from panoptic deeplab.
+ aux_losses: auxiliarly loss tensors, i.e. `losses` in keras.Model.
+
+ Returns:
+ The total loss tensor.
+ """
+ loss_config = self._task_config.losses
+ segmentation_loss_fn = (
+ panoptic_deeplab_losses.WeightedBootstrappedCrossEntropyLoss(
+ loss_config.label_smoothing,
+ loss_config.class_weights,
+ loss_config.ignore_label,
+ top_k_percent_pixels=loss_config.top_k_percent_pixels))
+ instance_center_heatmap_loss_fn = panoptic_deeplab_losses.CenterHeatmapLoss(
+ )
+ instance_center_offset_loss_fn = panoptic_deeplab_losses.CenterOffsetLoss()
+
+ semantic_weights = tf.cast(
+ labels['semantic_weights'],
+ dtype=model_outputs['instance_centers_heatmap'].dtype)
+ things_mask = tf.cast(
+ tf.squeeze(labels['things_mask'], axis=3),
+ dtype=model_outputs['instance_centers_heatmap'].dtype)
+ valid_mask = tf.cast(
+ tf.squeeze(labels['valid_mask'], axis=3),
+ dtype=model_outputs['instance_centers_heatmap'].dtype)
+
+ segmentation_loss = segmentation_loss_fn(
+ model_outputs['segmentation_outputs'],
+ labels['category_mask'],
+ sample_weight=semantic_weights)
+ instance_center_heatmap_loss = instance_center_heatmap_loss_fn(
+ model_outputs['instance_centers_heatmap'],
+ labels['instance_centers_heatmap'],
+ sample_weight=valid_mask)
+ instance_center_offset_loss = instance_center_offset_loss_fn(
+ model_outputs['instance_centers_offset'],
+ labels['instance_centers_offset'],
+ sample_weight=things_mask)
+
+ model_loss = (
+ loss_config.segmentation_loss_weight * segmentation_loss +
+ loss_config.center_heatmap_loss_weight * instance_center_heatmap_loss +
+ loss_config.center_offset_loss_weight * instance_center_offset_loss)
+
+ total_loss = model_loss
+ if aux_losses:
+ total_loss += tf.add_n(aux_losses)
+
+ losses = {
+ 'total_loss': total_loss,
+ 'model_loss': model_loss,
+ 'segmentation_loss': segmentation_loss,
+ 'instance_center_heatmap_loss': instance_center_heatmap_loss,
+ 'instance_center_offset_loss': instance_center_offset_loss
+ }
+
+ return losses
+
+ def build_metrics(self, training: bool = True) -> List[
+ tf.keras.metrics.Metric]:
+ """Build metrics."""
+ eval_config = self.task_config.evaluation
+ metrics = []
+ if training:
+ metric_names = [
+ 'total_loss',
+ 'segmentation_loss',
+ 'instance_center_heatmap_loss',
+ 'instance_center_offset_loss',
+ 'model_loss']
+ for name in metric_names:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+
+ if eval_config.report_train_mean_iou:
+ self.train_mean_iou = segmentation_metrics.MeanIoU(
+ name='train_mean_iou',
+ num_classes=self.task_config.model.num_classes,
+ rescale_predictions=False,
+ dtype=tf.float32)
+ else:
+ rescale_predictions = (not self.task_config.validation_data.parser
+ .resize_eval_groundtruth)
+ self.perclass_iou_metric = segmentation_metrics.PerClassIoU(
+ name='per_class_iou',
+ num_classes=self.task_config.model.num_classes,
+ rescale_predictions=rescale_predictions,
+ dtype=tf.float32)
+
+ if self.task_config.model.generate_panoptic_masks:
+ self.panoptic_quality_metric = (
+ panoptic_quality_evaluator.PanopticQualityEvaluator(
+ num_categories=self.task_config.model.num_classes,
+ ignored_label=eval_config.ignored_label,
+ max_instances_per_category=eval_config
+ .max_instances_per_category,
+ offset=eval_config.offset,
+ is_thing=eval_config.is_thing,
+ rescale_predictions=eval_config.rescale_predictions))
+
+ return metrics
+
+ def train_step(
+ self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ optimizer: tf.keras.optimizers.Optimizer,
+ metrics: Optional[List[Any]] = None) -> Dict[str, Any]:
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ images, labels = inputs
+ num_replicas = tf.distribute.get_strategy().num_replicas_in_sync
+
+ with tf.GradientTape() as tape:
+ outputs = model(
+ inputs=images,
+ image_info=labels['image_info'],
+ training=True)
+ outputs = tf.nest.map_structure(
+ lambda x: tf.cast(x, tf.float32), outputs)
+
+ # Computes per-replica loss.
+ losses = self.build_losses(
+ labels=labels,
+ model_outputs=outputs,
+ aux_losses=model.losses)
+ scaled_loss = losses['total_loss'] / num_replicas
+
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ tvars = model.trainable_variables
+ grads = tape.gradient(scaled_loss, tvars)
+ # Scales back gradient when LossScaleOptimizer is used.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ grads = optimizer.get_unscaled_gradients(grads)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ logs = {self.loss: losses['total_loss']}
+
+ if metrics:
+ for m in metrics:
+ m.update_state(losses[m.name])
+
+ if self.task_config.evaluation.report_train_mean_iou:
+ segmentation_labels = {
+ 'masks': labels['category_mask'],
+ 'valid_masks': labels['valid_mask'],
+ 'image_info': labels['image_info']
+ }
+ self.process_metrics(
+ metrics=[self.train_mean_iou],
+ labels=segmentation_labels,
+ model_outputs=outputs['segmentation_outputs'])
+ logs.update({
+ self.train_mean_iou.name:
+ self.train_mean_iou.result()
+ })
+
+ return logs
+
+ def validation_step(
+ self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ metrics: Optional[List[Any]] = None) -> Dict[str, Any]:
+ """Validatation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ images, labels = inputs
+
+ outputs = model(
+ inputs=images,
+ image_info=labels['image_info'],
+ training=False)
+
+ logs = {self.loss: 0}
+ segmentation_labels = {
+ 'masks': labels['category_mask'],
+ 'valid_masks': labels['valid_mask'],
+ 'image_info': labels['image_info']
+ }
+
+ self.perclass_iou_metric.update_state(segmentation_labels,
+ outputs['segmentation_outputs'])
+
+ if self.task_config.model.generate_panoptic_masks:
+ pq_metric_labels = {
+ 'category_mask': tf.squeeze(labels['category_mask'], axis=3),
+ 'instance_mask': tf.squeeze(labels['instance_mask'], axis=3),
+ 'image_info': labels['image_info']
+ }
+ panoptic_outputs = {
+ 'category_mask':
+ outputs['category_mask'],
+ 'instance_mask':
+ outputs['instance_mask'],
+ }
+ logs.update({
+ self.panoptic_quality_metric.name:
+ (pq_metric_labels, panoptic_outputs)})
+ return logs
+
+ def aggregate_logs(self, state=None, step_outputs=None):
+ if state is None:
+ self.perclass_iou_metric.reset_states()
+ state = [self.perclass_iou_metric]
+ if self.task_config.model.generate_panoptic_masks:
+ state += [self.panoptic_quality_metric]
+
+ if self.task_config.model.generate_panoptic_masks:
+ self.panoptic_quality_metric.update_state(
+ step_outputs[self.panoptic_quality_metric.name][0],
+ step_outputs[self.panoptic_quality_metric.name][1])
+
+ return state
+
+ def reduce_aggregated_logs(self, aggregated_logs, global_step=None):
+ result = {}
+ ious = self.perclass_iou_metric.result()
+ if self.task_config.evaluation.report_per_class_iou:
+ for i, value in enumerate(ious.numpy()):
+ result.update({'segmentation_iou/class_{}'.format(i): value})
+
+ # Computes mean IoU
+ result.update({'segmentation_mean_iou': tf.reduce_mean(ious).numpy()})
+
+ if self.task_config.model.generate_panoptic_masks:
+ panoptic_quality_results = self.panoptic_quality_metric.result()
+ for k, value in panoptic_quality_results.items():
+ if k.endswith('per_class'):
+ if self.task_config.evaluation.report_per_class_pq:
+ for i, per_class_value in enumerate(value):
+ metric_key = 'panoptic_quality/{}/class_{}'.format(k, i)
+ result[metric_key] = per_class_value
+ else:
+ continue
+ else:
+ result['panoptic_quality/{}'.format(k)] = value
+
+ return result
diff --git a/official/projects/panoptic/tasks/panoptic_maskrcnn.py b/official/projects/panoptic/tasks/panoptic_maskrcnn.py
new file mode 100644
index 0000000000000000000000000000000000000000..137888c0844ec2f09739a1f18f64cee4839bcf3a
--- /dev/null
+++ b/official/projects/panoptic/tasks/panoptic_maskrcnn.py
@@ -0,0 +1,451 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic MaskRCNN task definition."""
+from typing import Any, Dict, List, Mapping, Optional, Tuple
+
+from absl import logging
+import tensorflow as tf
+
+from official.common import dataset_fn
+from official.core import task_factory
+from official.projects.panoptic.configs import panoptic_maskrcnn as exp_cfg
+from official.projects.panoptic.dataloaders import panoptic_maskrcnn_input
+from official.projects.panoptic.modeling import factory
+from official.vision.dataloaders import input_reader_factory
+from official.vision.evaluation import panoptic_quality_evaluator
+from official.vision.evaluation import segmentation_metrics
+from official.vision.losses import segmentation_losses
+from official.vision.tasks import maskrcnn
+
+
+@task_factory.register_task_cls(exp_cfg.PanopticMaskRCNNTask)
+class PanopticMaskRCNNTask(maskrcnn.MaskRCNNTask):
+
+ """A single-replica view of training procedure.
+
+ Panoptic Mask R-CNN task provides artifacts for training/evalution procedures,
+ including loading/iterating over Datasets, initializing the model, calculating
+ the loss, post-processing, and customized metrics with reduction.
+ """
+
+ def build_model(self) -> tf.keras.Model:
+ """Build Panoptic Mask R-CNN model."""
+
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + self.task_config.model.input_size)
+
+ l2_weight_decay = self.task_config.losses.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ model = factory.build_panoptic_maskrcnn(
+ input_specs=input_specs,
+ model_config=self.task_config.model,
+ l2_regularizer=l2_regularizer)
+
+ if self.task_config.freeze_backbone:
+ model.backbone.trainable = False
+
+ return model
+
+ def initialize(self, model: tf.keras.Model) -> None:
+ """Loading pretrained checkpoint."""
+
+ if not self.task_config.init_checkpoint:
+ return
+
+ def _get_checkpoint_path(checkpoint_dir_or_file):
+ checkpoint_path = checkpoint_dir_or_file
+ if tf.io.gfile.isdir(checkpoint_dir_or_file):
+ checkpoint_path = tf.train.latest_checkpoint(
+ checkpoint_dir_or_file)
+ return checkpoint_path
+
+ for init_module in self.task_config.init_checkpoint_modules:
+ # Restoring checkpoint.
+ if init_module == 'all':
+ checkpoint_path = _get_checkpoint_path(
+ self.task_config.init_checkpoint)
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.read(checkpoint_path)
+ status.expect_partial().assert_existing_objects_matched()
+
+ elif init_module == 'backbone':
+ checkpoint_path = _get_checkpoint_path(
+ self.task_config.init_checkpoint)
+ ckpt = tf.train.Checkpoint(backbone=model.backbone)
+ status = ckpt.read(checkpoint_path)
+ status.expect_partial().assert_existing_objects_matched()
+
+ elif init_module == 'segmentation_backbone':
+ checkpoint_path = _get_checkpoint_path(
+ self.task_config.segmentation_init_checkpoint)
+ ckpt = tf.train.Checkpoint(
+ segmentation_backbone=model.segmentation_backbone)
+ status = ckpt.read(checkpoint_path)
+ status.expect_partial().assert_existing_objects_matched()
+
+ elif init_module == 'segmentation_decoder':
+ checkpoint_path = _get_checkpoint_path(
+ self.task_config.segmentation_init_checkpoint)
+ ckpt = tf.train.Checkpoint(
+ segmentation_decoder=model.segmentation_decoder)
+ status = ckpt.read(checkpoint_path)
+ status.expect_partial().assert_existing_objects_matched()
+
+ else:
+ raise ValueError(
+ "Only 'all', 'backbone', 'segmentation_backbone' and/or "
+ "segmentation_backbone' can be used to initialize the model, but "
+ "got {}".format(init_module))
+ logging.info('Finished loading pretrained checkpoint from %s for %s',
+ checkpoint_path, init_module)
+
+ def build_inputs(
+ self,
+ params: exp_cfg.DataConfig,
+ input_context: Optional[tf.distribute.InputContext] = None
+ ) -> tf.data.Dataset:
+ """Build input dataset."""
+ decoder_cfg = params.decoder.get()
+ if params.decoder.type == 'simple_decoder':
+ decoder = panoptic_maskrcnn_input.TfExampleDecoder(
+ regenerate_source_id=decoder_cfg.regenerate_source_id,
+ mask_binarize_threshold=decoder_cfg.mask_binarize_threshold,
+ include_panoptic_masks=decoder_cfg.include_panoptic_masks,
+ panoptic_category_mask_key=decoder_cfg.panoptic_category_mask_key,
+ panoptic_instance_mask_key=decoder_cfg.panoptic_instance_mask_key)
+ else:
+ raise ValueError('Unknown decoder type: {}!'.format(params.decoder.type))
+
+ parser = panoptic_maskrcnn_input.Parser(
+ output_size=self.task_config.model.input_size[:2],
+ min_level=self.task_config.model.min_level,
+ max_level=self.task_config.model.max_level,
+ num_scales=self.task_config.model.anchor.num_scales,
+ aspect_ratios=self.task_config.model.anchor.aspect_ratios,
+ anchor_size=self.task_config.model.anchor.anchor_size,
+ dtype=params.dtype,
+ rpn_match_threshold=params.parser.rpn_match_threshold,
+ rpn_unmatched_threshold=params.parser.rpn_unmatched_threshold,
+ rpn_batch_size_per_im=params.parser.rpn_batch_size_per_im,
+ rpn_fg_fraction=params.parser.rpn_fg_fraction,
+ aug_rand_hflip=params.parser.aug_rand_hflip,
+ aug_scale_min=params.parser.aug_scale_min,
+ aug_scale_max=params.parser.aug_scale_max,
+ skip_crowd_during_training=params.parser.skip_crowd_during_training,
+ max_num_instances=params.parser.max_num_instances,
+ mask_crop_size=params.parser.mask_crop_size,
+ segmentation_resize_eval_groundtruth=params.parser
+ .segmentation_resize_eval_groundtruth,
+ segmentation_groundtruth_padded_size=params.parser
+ .segmentation_groundtruth_padded_size,
+ segmentation_ignore_label=params.parser.segmentation_ignore_label,
+ panoptic_ignore_label=params.parser.panoptic_ignore_label,
+ include_panoptic_masks=params.parser.include_panoptic_masks)
+
+ reader = input_reader_factory.input_reader_generator(
+ params,
+ dataset_fn=dataset_fn.pick_dataset_fn(params.file_type),
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def build_losses(self,
+ outputs: Mapping[str, Any],
+ labels: Mapping[str, Any],
+ aux_losses: Optional[Any] = None) -> Dict[str, tf.Tensor]:
+ """Build Panoptic Mask R-CNN losses."""
+ params = self.task_config.losses
+
+ use_groundtruth_dimension = (
+ params.semantic_segmentation_use_groundtruth_dimension)
+
+ segmentation_loss_fn = segmentation_losses.SegmentationLoss(
+ label_smoothing=params.semantic_segmentation_label_smoothing,
+ class_weights=params.semantic_segmentation_class_weights,
+ ignore_label=params.semantic_segmentation_ignore_label,
+ gt_is_matting_map=params.semantic_segmentation_gt_is_matting_map,
+ use_groundtruth_dimension=use_groundtruth_dimension,
+ top_k_percent_pixels=params.semantic_segmentation_top_k_percent_pixels)
+
+ instance_segmentation_weight = params.instance_segmentation_weight
+ semantic_segmentation_weight = params.semantic_segmentation_weight
+
+ losses = super(PanopticMaskRCNNTask, self).build_losses(
+ outputs=outputs,
+ labels=labels,
+ aux_losses=None)
+ maskrcnn_loss = losses['model_loss']
+ segmentation_loss = segmentation_loss_fn(
+ outputs['segmentation_outputs'],
+ labels['gt_segmentation_mask'])
+
+ model_loss = (
+ instance_segmentation_weight * maskrcnn_loss +
+ semantic_segmentation_weight * segmentation_loss)
+
+ total_loss = model_loss
+ if aux_losses:
+ reg_loss = tf.reduce_sum(aux_losses)
+ total_loss = model_loss + reg_loss
+
+ losses.update({
+ 'total_loss': total_loss,
+ 'maskrcnn_loss': maskrcnn_loss,
+ 'segmentation_loss': segmentation_loss,
+ 'model_loss': model_loss,
+ })
+ return losses
+
+ def build_metrics(self, training: bool = True) -> List[
+ tf.keras.metrics.Metric]:
+ """Build detection metrics."""
+ metrics = []
+ num_segmentation_classes = (
+ self.task_config.model.segmentation_model.num_classes)
+ if training:
+ metric_names = [
+ 'total_loss',
+ 'rpn_score_loss',
+ 'rpn_box_loss',
+ 'frcnn_cls_loss',
+ 'frcnn_box_loss',
+ 'mask_loss',
+ 'maskrcnn_loss',
+ 'segmentation_loss',
+ 'model_loss'
+ ]
+ for name in metric_names:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+
+ if self.task_config.segmentation_evaluation.report_train_mean_iou:
+ self.segmentation_train_mean_iou = segmentation_metrics.MeanIoU(
+ name='train_mean_iou',
+ num_classes=num_segmentation_classes,
+ rescale_predictions=False,
+ dtype=tf.float32)
+
+ else:
+ if self.task_config.use_coco_metrics:
+ self._build_coco_metrics()
+
+ rescale_predictions = (not self.task_config.validation_data.parser
+ .segmentation_resize_eval_groundtruth)
+
+ self.segmentation_perclass_iou_metric = segmentation_metrics.PerClassIoU(
+ name='per_class_iou',
+ num_classes=num_segmentation_classes,
+ rescale_predictions=rescale_predictions,
+ dtype=tf.float32)
+
+ if self.task_config.model.generate_panoptic_masks:
+ if not self.task_config.validation_data.parser.include_panoptic_masks:
+ raise ValueError('`include_panoptic_masks` should be set to True when'
+ ' computing panoptic quality.')
+ pq_config = self.task_config.panoptic_quality_evaluator
+ self.panoptic_quality_metric = (
+ panoptic_quality_evaluator.PanopticQualityEvaluator(
+ num_categories=pq_config.num_categories,
+ ignored_label=pq_config.ignored_label,
+ max_instances_per_category=pq_config.max_instances_per_category,
+ offset=pq_config.offset,
+ is_thing=pq_config.is_thing,
+ rescale_predictions=pq_config.rescale_predictions))
+
+ return metrics
+
+ def train_step(self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ optimizer: tf.keras.optimizers.Optimizer,
+ metrics: Optional[List[Any]] = None) -> Dict[str, Any]:
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ images, labels = inputs
+ num_replicas = tf.distribute.get_strategy().num_replicas_in_sync
+
+ with tf.GradientTape() as tape:
+ outputs = model(
+ images,
+ image_info=labels['image_info'],
+ anchor_boxes=labels['anchor_boxes'],
+ gt_boxes=labels['gt_boxes'],
+ gt_classes=labels['gt_classes'],
+ gt_masks=(labels['gt_masks'] if self.task_config.model.include_mask
+ else None),
+ training=True)
+ outputs = tf.nest.map_structure(
+ lambda x: tf.cast(x, tf.float32), outputs)
+
+ # Computes per-replica loss.
+ losses = self.build_losses(
+ outputs=outputs, labels=labels, aux_losses=model.losses)
+ scaled_loss = losses['total_loss'] / num_replicas
+
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ tvars = model.trainable_variables
+ grads = tape.gradient(scaled_loss, tvars)
+ # Scales back gradient when LossScaleOptimizer is used.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ grads = optimizer.get_unscaled_gradients(grads)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ logs = {self.loss: losses['total_loss']}
+
+ if metrics:
+ for m in metrics:
+ m.update_state(losses[m.name])
+
+ if self.task_config.segmentation_evaluation.report_train_mean_iou:
+ segmentation_labels = {
+ 'masks': labels['gt_segmentation_mask'],
+ 'valid_masks': labels['gt_segmentation_valid_mask'],
+ 'image_info': labels['image_info']
+ }
+ self.process_metrics(
+ metrics=[self.segmentation_train_mean_iou],
+ labels=segmentation_labels,
+ model_outputs=outputs['segmentation_outputs'])
+ logs.update({
+ self.segmentation_train_mean_iou.name:
+ self.segmentation_train_mean_iou.result()
+ })
+
+ return logs
+
+ def validation_step(self,
+ inputs: Tuple[Any, Any],
+ model: tf.keras.Model,
+ metrics: Optional[List[Any]] = None) -> Dict[str, Any]:
+ """Validatation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ images, labels = inputs
+
+ outputs = model(
+ images,
+ anchor_boxes=labels['anchor_boxes'],
+ image_info=labels['image_info'],
+ training=False)
+
+ logs = {self.loss: 0}
+ if self._task_config.use_coco_metrics:
+ coco_model_outputs = {
+ 'detection_masks': outputs['detection_masks'],
+ 'detection_boxes': outputs['detection_boxes'],
+ 'detection_scores': outputs['detection_scores'],
+ 'detection_classes': outputs['detection_classes'],
+ 'num_detections': outputs['num_detections'],
+ 'source_id': labels['groundtruths']['source_id'],
+ 'image_info': labels['image_info']
+ }
+ logs.update(
+ {self.coco_metric.name: (labels['groundtruths'], coco_model_outputs)})
+
+ segmentation_labels = {
+ 'masks': labels['groundtruths']['gt_segmentation_mask'],
+ 'valid_masks': labels['groundtruths']['gt_segmentation_valid_mask'],
+ 'image_info': labels['image_info']
+ }
+
+ self.segmentation_perclass_iou_metric.update_state(
+ segmentation_labels, outputs['segmentation_outputs'])
+
+ if self.task_config.model.generate_panoptic_masks:
+ pq_metric_labels = {
+ 'category_mask': labels['groundtruths']['gt_panoptic_category_mask'],
+ 'instance_mask': labels['groundtruths']['gt_panoptic_instance_mask'],
+ 'image_info': labels['image_info']
+ }
+ logs.update({
+ self.panoptic_quality_metric.name:
+ (pq_metric_labels, outputs['panoptic_outputs'])})
+ return logs
+
+ def aggregate_logs(self, state=None, step_outputs=None):
+ if state is None:
+ self.segmentation_perclass_iou_metric.reset_states()
+ state = [self.segmentation_perclass_iou_metric]
+ if self.task_config.use_coco_metrics:
+ self.coco_metric.reset_states()
+ state.append(self.coco_metric)
+ if self.task_config.model.generate_panoptic_masks:
+ self.panoptic_quality_metric.reset_states()
+ state.append(self.panoptic_quality_metric)
+
+ if self.task_config.use_coco_metrics:
+ self.coco_metric.update_state(step_outputs[self.coco_metric.name][0],
+ step_outputs[self.coco_metric.name][1])
+
+ if self.task_config.model.generate_panoptic_masks:
+ self.panoptic_quality_metric.update_state(
+ step_outputs[self.panoptic_quality_metric.name][0],
+ step_outputs[self.panoptic_quality_metric.name][1])
+
+ return state
+
+ def reduce_aggregated_logs(self, aggregated_logs, global_step=None):
+ result = super().reduce_aggregated_logs(
+ aggregated_logs=aggregated_logs, global_step=global_step)
+
+ ious = self.segmentation_perclass_iou_metric.result()
+ if self.task_config.segmentation_evaluation.report_per_class_iou:
+ for i, value in enumerate(ious.numpy()):
+ result.update({'segmentation_iou/class_{}'.format(i): value})
+ # Computes mean IoU
+ result.update({'segmentation_mean_iou': tf.reduce_mean(ious).numpy()})
+
+ if self.task_config.model.generate_panoptic_masks:
+ report_per_class_metrics = (
+ self.task_config.panoptic_quality_evaluator.report_per_class_metrics)
+ panoptic_quality_results = self.panoptic_quality_metric.result()
+ for k, value in panoptic_quality_results.items():
+ if k.endswith('per_class'):
+ if report_per_class_metrics:
+ for i, per_class_value in enumerate(value):
+ metric_key = 'panoptic_quality/{}/class_{}'.format(k, i)
+ result[metric_key] = per_class_value
+ else:
+ continue
+ else:
+ result['panoptic_quality/{}'.format(k)] = value
+
+ return result
diff --git a/official/projects/panoptic/train.py b/official/projects/panoptic/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..f8287bd73bed58a43a702a1dbe2fb689a089099e
--- /dev/null
+++ b/official/projects/panoptic/train.py
@@ -0,0 +1,30 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Panoptic MaskRCNN trainer."""
+
+from absl import app
+
+from official.common import flags as tfm_flags
+# pylint: disable=unused-import
+from official.projects.panoptic.configs import panoptic_deeplab
+from official.projects.panoptic.configs import panoptic_maskrcnn
+from official.projects.panoptic.tasks import panoptic_deeplab as panoptic_deeplab_task
+from official.projects.panoptic.tasks import panoptic_maskrcnn as panoptic_maskrcnn_task
+from official.vision import train
+# pylint: enable=unused-import
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/pruning/README.md b/official/projects/pruning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..f5539584614b8acad4fbc25dfe8d772cd0aa69ef
--- /dev/null
+++ b/official/projects/pruning/README.md
@@ -0,0 +1,44 @@
+# Training with Pruning
+[TOC]
+
+⚠️ Disclaimer: All datasets hyperlinked from this page are not owned or
+distributed by Google. The dataset is made available by third parties.
+Please review the terms and conditions made available by the third parties
+before using the data.
+
+## Overview
+
+This project includes pruning codes for TensorFlow models.
+These are examples to show how to apply the Model Optimization Toolkit's
+[pruning API](https://www.tensorflow.org/model_optimization/guide/pruning).
+
+## How to train a model
+
+```bash
+EXPERIMENT=xxx # Change this for your run, for example, 'resnet_imagenet_pruning'
+CONFIG_FILE=xxx # Change this for your run, for example, path of imagenet_resnet50_pruning_gpu.yaml
+MODEL_DIR=xxx # Change this for your run, for example, /tmp/model_dir
+python3 train.py \
+ --experiment=${EXPERIMENT} \
+ --config_file=${CONFIG_FILE} \
+ --model_dir=${MODEL_DIR} \
+ --mode=train_and_eval
+```
+
+## Accuracy
+
+
+
+Comparison of Imagenet top-1 accuracy for the classification models
+
+
+Note: The Top-1 model accuracy is measured on the validation set of [ImageNet](https://www.image-net.org/).
+
+## Pre-trained Models
+
+### Image Classification
+
+Model |Resolution|Top-1 Accuracy (Dense)|Top-1 Accuracy (50% sparsity)|Top-1 Accuracy (80% sparsity)|Config |Download
+----------------------|----------|---------------------|-------------------------|-------------------------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------------------------------------|
+|MobileNetV2 |224x224 |72.768% |71.334% |61.378% |[config](https://github.com/tensorflow/models/blob/master/official/projects/pruning/configs/experiments/image_classification/imagenet_mobilenetv2_pruning_gpu.yaml) |[TFLite(50% sparsity)](https://storage.googleapis.com/tf_model_garden/vision/mobilenet/v2_1.0_float/mobilenet_v2_0.5_pruned_1.00_224_float.tflite), |
+|ResNet50 |224x224 |76.704% |76.61% |75.508% |[config](https://github.com/tensorflow/models/blob/master/official/projects/pruning/configs/experiments/image_classification/imagenet_resnet50_pruning_gpu.yaml) |[TFLite(80% sparsity)](https://storage.googleapis.com/tf_model_garden/vision/resnet50_imagenet/resnet_50_0.8_pruned_224_float.tflite) |
diff --git a/official/projects/pruning/configs/__init__.py b/official/projects/pruning/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..4425d4bd55b14430b52bb8cca8a0d50c61cd329f
--- /dev/null
+++ b/official/projects/pruning/configs/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
+
+from official.projects.pruning.configs import image_classification
diff --git a/official/projects/pruning/configs/experiments/image_classification/imagenet_mobilenetv2_pruning_gpu.yaml b/official/projects/pruning/configs/experiments/image_classification/imagenet_mobilenetv2_pruning_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..af1dca89d30f1967156558bc758ba3bf80095df7
--- /dev/null
+++ b/official/projects/pruning/configs/experiments/image_classification/imagenet_mobilenetv2_pruning_gpu.yaml
@@ -0,0 +1,59 @@
+# MobileNetV2_1.0 ImageNet classification.
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ filter_size_scale: 1.0
+ dropout_rate: 0.1
+ losses:
+ l2_weight_decay: 0
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: 'gs://mlcompass-data/imagenet/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 1024
+ dtype: 'float32'
+ validation_data:
+ input_path: 'gs://mlcompass-data/imagenet/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 1024
+ dtype: 'float32'
+ drop_remainder: false
+ pruning:
+ pretrained_original_checkpoint: 'gs://**/mobilenetv2_gpu/22984194/ckpt-625500'
+ pruning_schedule: 'PolynomialDecay'
+ begin_step: 0
+ end_step: 80000
+ initial_sparsity: 0.2
+ final_sparsity: 0.5
+ frequency: 400
+trainer:
+ # Top1 accuracy 71.33% after 17hr for 8 GPUs with pruning.
+ # Pretrained network without pruning has Top1 accuracy 72.77%
+ train_steps: 125100 # 50 epoch
+ validation_steps: 98
+ validation_interval: 2502
+ steps_per_loop: 2502
+ summary_interval: 2502
+ checkpoint_interval: 2502
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.04
+ decay_steps: 5004
+ decay_rate: 0.85
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/pruning/configs/experiments/image_classification/imagenet_resnet50_pruning_gpu.yaml b/official/projects/pruning/configs/experiments/image_classification/imagenet_resnet50_pruning_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..dfa298a8a44f93bdf17d5a3a3dc55432e0365355
--- /dev/null
+++ b/official/projects/pruning/configs/experiments/image_classification/imagenet_resnet50_pruning_gpu.yaml
@@ -0,0 +1,60 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: 'gs://mlcompass-data/imagenet/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 1024
+ dtype: 'float32'
+ validation_data:
+ input_path: 'gs://mlcompass-data/imagenet/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 1024
+ dtype: 'float32'
+ drop_remainder: false
+ pruning:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+ pruning_schedule: 'PolynomialDecay'
+ begin_step: 0
+ end_step: 40000
+ initial_sparsity: 0.2
+ final_sparsity: 0.8
+ frequency: 40
+trainer:
+ # Top1 accuracy 75.508% after 7hr for 8 GPUs with pruning.
+ # Pretrained network without pruning has Top1 accuracy 76.7%
+ train_steps: 50000
+ validation_steps: 50
+ validation_interval: 1251
+ steps_per_loop: 1251
+ summary_interval: 1251
+ checkpoint_interval: 1251
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.01
+ decay_steps: 2502
+ decay_rate: 0.9
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/pruning/configs/image_classification.py b/official/projects/pruning/configs/image_classification.py
new file mode 100644
index 0000000000000000000000000000000000000000..4ab5952a85f739732ae7a55252f0200e0da9a3f5
--- /dev/null
+++ b/official/projects/pruning/configs/image_classification.py
@@ -0,0 +1,80 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification configuration definition."""
+import dataclasses
+
+from typing import Optional, Tuple
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.vision.configs import image_classification
+
+
+@dataclasses.dataclass
+class PruningConfig(hyperparams.Config):
+ """Pruning parameters.
+
+ Attributes:
+ pretrained_original_checkpoint: The pretrained checkpoint location of the
+ original model.
+ pruning_schedule: A string that indicates the name of `PruningSchedule`
+ object that controls pruning rate throughout training. Current available
+ options are: `PolynomialDecay` and `ConstantSparsity`.
+ begin_step: Step at which to begin pruning.
+ end_step: Step at which to end pruning.
+ initial_sparsity: Sparsity ratio at which pruning begins.
+ final_sparsity: Sparsity ratio at which pruning ends.
+ frequency: Number of training steps between sparsity adjustment.
+ sparsity_m_by_n: Structured sparsity specification. It specifies m zeros
+ over n consecutive weight elements.
+ """
+ pretrained_original_checkpoint: Optional[str] = None
+ pruning_schedule: str = 'PolynomialDecay'
+ begin_step: int = 0
+ end_step: int = 1000
+ initial_sparsity: float = 0.0
+ final_sparsity: float = 0.1
+ frequency: int = 100
+ sparsity_m_by_n: Optional[Tuple[int, int]] = None
+
+
+@dataclasses.dataclass
+class ImageClassificationTask(image_classification.ImageClassificationTask):
+ pruning: Optional[PruningConfig] = None
+
+
+@exp_factory.register_config_factory('resnet_imagenet_pruning')
+def image_classification_imagenet() -> cfg.ExperimentConfig:
+ """Builds an image classification config for the resnet with pruning."""
+ config = image_classification.image_classification_imagenet()
+ task = ImageClassificationTask.from_args(
+ pruning=PruningConfig(), **config.task.as_dict())
+ config.task = task
+ runtime = cfg.RuntimeConfig(enable_xla=False)
+ config.runtime = runtime
+
+ return config
+
+
+@exp_factory.register_config_factory('mobilenet_imagenet_pruning')
+def image_classification_imagenet_mobilenet() -> cfg.ExperimentConfig:
+ """Builds an image classification config for the mobilenetV2 with pruning."""
+ config = image_classification.image_classification_imagenet_mobilenet()
+ task = ImageClassificationTask.from_args(
+ pruning=PruningConfig(), **config.task.as_dict())
+ config.task = task
+
+ return config
diff --git a/official/projects/pruning/configs/image_classification_test.py b/official/projects/pruning/configs/image_classification_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..f52505d27cc3718c8f9161a006bd55c177c6ff0b
--- /dev/null
+++ b/official/projects/pruning/configs/image_classification_test.py
@@ -0,0 +1,48 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for image_classification."""
+# pylint: disable=unused-import
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official import vision
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.pruning.configs import image_classification as pruning_exp_cfg
+from official.vision.configs import image_classification as exp_cfg
+
+
+class ImageClassificationConfigTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(
+ ('resnet_imagenet_pruning',),
+ ('mobilenet_imagenet_pruning'),
+ )
+ def test_image_classification_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, exp_cfg.ImageClassificationTask)
+ self.assertIsInstance(config.task, pruning_exp_cfg.ImageClassificationTask)
+ self.assertIsInstance(config.task.pruning, pruning_exp_cfg.PruningConfig)
+ self.assertIsInstance(config.task.model, exp_cfg.ImageClassificationModel)
+ self.assertIsInstance(config.task.train_data, exp_cfg.DataConfig)
+ config.validate()
+ config.task.train_data.is_training = None
+ with self.assertRaises(KeyError):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/pruning/registry_imports.py b/official/projects/pruning/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..847cca42e1417637cf2268ed1f00840579ea5f37
--- /dev/null
+++ b/official/projects/pruning/registry_imports.py
@@ -0,0 +1,18 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""All necessary imports for registration on pruning project."""
+# pylint: disable=unused-import
+from official.projects.pruning import configs
+from official.projects.pruning.tasks import image_classification
diff --git a/official/projects/pruning/tasks/__init__.py b/official/projects/pruning/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..9320e3087f57565a200bb7ea2b89ed083fabf42f
--- /dev/null
+++ b/official/projects/pruning/tasks/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Modeling package definition."""
+
+from official.projects.pruning.tasks import image_classification
diff --git a/official/projects/pruning/tasks/image_classification.py b/official/projects/pruning/tasks/image_classification.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b81788289af41d38c76b68af7acf5902ea4b49b
--- /dev/null
+++ b/official/projects/pruning/tasks/image_classification.py
@@ -0,0 +1,147 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification task definition."""
+from absl import logging
+import tensorflow as tf
+import tensorflow_model_optimization as tfmot
+
+from official.core import task_factory
+from official.projects.pruning.configs import image_classification as exp_cfg
+from official.vision.modeling.backbones import mobilenet
+from official.vision.modeling.layers import nn_blocks
+from official.vision.tasks import image_classification
+
+
+@task_factory.register_task_cls(exp_cfg.ImageClassificationTask)
+class ImageClassificationTask(image_classification.ImageClassificationTask):
+ """A task for image classification with pruning."""
+ _BLOCK_LAYER_SUFFIX_MAP = {
+ mobilenet.Conv2DBNBlock: ('conv2d/kernel:0',),
+ nn_blocks.BottleneckBlock: (
+ 'conv2d/kernel:0',
+ 'conv2d_1/kernel:0',
+ 'conv2d_2/kernel:0',
+ 'conv2d_3/kernel:0',
+ ),
+ nn_blocks.InvertedBottleneckBlock: (
+ 'conv2d/kernel:0',
+ 'conv2d_1/kernel:0',
+ 'conv2d_2/kernel:0',
+ 'conv2d_3/kernel:0',
+ 'depthwise_conv2d/depthwise_kernel:0',
+ ),
+ nn_blocks.ResidualBlock: (
+ 'conv2d/kernel:0',
+ 'conv2d_1/kernel:0',
+ 'conv2d_2/kernel:0',
+ ),
+ }
+
+ def build_model(self) -> tf.keras.Model:
+ """Builds classification model with pruning."""
+ model = super(ImageClassificationTask, self).build_model()
+ if self.task_config.pruning is None:
+ return model
+
+ pruning_cfg = self.task_config.pruning
+
+ prunable_model = tf.keras.models.clone_model(
+ model,
+ clone_function=self._make_block_prunable,
+ )
+
+ original_checkpoint = pruning_cfg.pretrained_original_checkpoint
+ if original_checkpoint is not None:
+ ckpt = tf.train.Checkpoint(model=prunable_model, **model.checkpoint_items)
+ status = ckpt.read(original_checkpoint)
+ status.expect_partial().assert_existing_objects_matched()
+
+ pruning_params = {}
+ if pruning_cfg.sparsity_m_by_n is not None:
+ pruning_params['sparsity_m_by_n'] = pruning_cfg.sparsity_m_by_n
+
+ if pruning_cfg.pruning_schedule == 'PolynomialDecay':
+ pruning_params['pruning_schedule'] = tfmot.sparsity.keras.PolynomialDecay(
+ initial_sparsity=pruning_cfg.initial_sparsity,
+ final_sparsity=pruning_cfg.final_sparsity,
+ begin_step=pruning_cfg.begin_step,
+ end_step=pruning_cfg.end_step,
+ frequency=pruning_cfg.frequency)
+ elif pruning_cfg.pruning_schedule == 'ConstantSparsity':
+ pruning_params[
+ 'pruning_schedule'] = tfmot.sparsity.keras.ConstantSparsity(
+ target_sparsity=pruning_cfg.final_sparsity,
+ begin_step=pruning_cfg.begin_step,
+ frequency=pruning_cfg.frequency)
+ else:
+ raise NotImplementedError(
+ 'Only PolynomialDecay and ConstantSparsity are currently supported. Not support %s'
+ % pruning_cfg.pruning_schedule)
+
+ pruned_model = tfmot.sparsity.keras.prune_low_magnitude(
+ prunable_model, **pruning_params)
+
+ # Print out prunable weights for debugging purpose.
+ prunable_layers = collect_prunable_layers(pruned_model)
+ pruned_weights = []
+ for layer in prunable_layers:
+ pruned_weights += [weight.name for weight, _, _ in layer.pruning_vars]
+ unpruned_weights = [
+ weight.name
+ for weight in pruned_model.weights
+ if weight.name not in pruned_weights
+ ]
+
+ logging.info(
+ '%d / %d weights are pruned.\nPruned weights: [ \n%s \n],\n'
+ 'Unpruned weights: [ \n%s \n],',
+ len(pruned_weights), len(model.weights), ', '.join(pruned_weights),
+ ', '.join(unpruned_weights))
+
+ return pruned_model
+
+ def _make_block_prunable(
+ self, layer: tf.keras.layers.Layer) -> tf.keras.layers.Layer:
+ if isinstance(layer, tf.keras.Model):
+ return tf.keras.models.clone_model(
+ layer, input_tensors=None, clone_function=self._make_block_prunable)
+
+ if layer.__class__ not in self._BLOCK_LAYER_SUFFIX_MAP:
+ return layer
+
+ prunable_weights = []
+ for layer_suffix in self._BLOCK_LAYER_SUFFIX_MAP[layer.__class__]:
+ for weight in layer.weights:
+ if weight.name.endswith(layer_suffix):
+ prunable_weights.append(weight)
+
+ def get_prunable_weights():
+ return prunable_weights
+
+ layer.get_prunable_weights = get_prunable_weights
+
+ return layer
+
+
+def collect_prunable_layers(model):
+ """Recursively collect the prunable layers in the model."""
+ prunable_layers = []
+ for layer in model.layers:
+ if isinstance(layer, tf.keras.Model):
+ prunable_layers += collect_prunable_layers(layer)
+ if layer.__class__.__name__ == 'PruneLowMagnitude':
+ prunable_layers.append(layer)
+
+ return prunable_layers
diff --git a/official/projects/pruning/tasks/image_classification_test.py b/official/projects/pruning/tasks/image_classification_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..09c5a0aa05a7ef2f144a312aedbe4dbb6c5033db
--- /dev/null
+++ b/official/projects/pruning/tasks/image_classification_test.py
@@ -0,0 +1,201 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for image classification task."""
+
+# pylint: disable=unused-import
+import os
+import tempfile
+
+from absl.testing import parameterized
+import numpy as np
+import orbit
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official import vision
+from official.core import actions
+from official.core import exp_factory
+from official.modeling import optimization
+from official.projects.pruning.tasks import image_classification as img_cls_task
+from official.vision.dataloaders import tfexample_utils
+
+
+class ImageClassificationTaskTest(tf.test.TestCase, parameterized.TestCase):
+
+ def _validate_model_pruned(self, model, config_name):
+
+ pruning_weight_names = []
+ prunable_layers = img_cls_task.collect_prunable_layers(model)
+ for layer in prunable_layers:
+ for weight, _, _ in layer.pruning_vars:
+ pruning_weight_names.append(weight.name)
+ if config_name == 'resnet_imagenet_pruning':
+ # Conv2D : 1
+ # BottleneckBlockGroup : 4+3+3 = 10
+ # BottleneckBlockGroup1 : 4+3+3+3 = 13
+ # BottleneckBlockGroup2 : 4+3+3+3+3+3 = 19
+ # BottleneckBlockGroup3 : 4+3+3 = 10
+ # FullyConnected : 1
+ # Total : 54
+ self.assertLen(pruning_weight_names, 54)
+ elif config_name == 'mobilenet_imagenet_pruning':
+ # Conv2DBN = 1
+ # InvertedBottleneckBlockGroup = 2
+ # InvertedBottleneckBlockGroup1~16 = 48
+ # Conv2DBN = 1
+ # FullyConnected : 1
+ # Total : 53
+ self.assertLen(pruning_weight_names, 53)
+
+ def _check_2x4_sparsity(self, model):
+
+ def _is_pruned_2_by_4(weights):
+ if weights.shape.rank == 2:
+ prepared_weights = tf.transpose(weights)
+ elif weights.shape.rank == 4:
+ perm_weights = tf.transpose(weights, perm=[3, 0, 1, 2])
+ prepared_weights = tf.reshape(perm_weights,
+ [-1, perm_weights.shape[-1]])
+
+ prepared_weights_np = prepared_weights.numpy()
+
+ for row in range(0, prepared_weights_np.shape[0]):
+ for col in range(0, prepared_weights_np.shape[1], 4):
+ if np.count_nonzero(prepared_weights_np[row, col:col + 4]) > 2:
+ return False
+ return True
+
+ prunable_layers = img_cls_task.collect_prunable_layers(model)
+ for layer in prunable_layers:
+ for weight, _, _ in layer.pruning_vars:
+ if weight.shape[-2] % 4 == 0:
+ self.assertTrue(_is_pruned_2_by_4(weight))
+
+ def _validate_metrics(self, logs, metrics):
+ for metric in metrics:
+ logs[metric.name] = metric.result()
+ self.assertIn('loss', logs)
+ self.assertIn('accuracy', logs)
+ self.assertIn('top_5_accuracy', logs)
+
+ def _create_test_tfrecord(self, test_tfrecord_file, num_samples,
+ input_image_size):
+ example = tf.train.Example.FromString(
+ tfexample_utils.create_classification_example(
+ image_height=input_image_size[0], image_width=input_image_size[1]))
+ examples = [example] * num_samples
+ tfexample_utils.dump_to_tfrecord(
+ record_file=test_tfrecord_file, tf_examples=examples)
+
+ @parameterized.parameters(('resnet_imagenet_pruning'),
+ ('mobilenet_imagenet_pruning'))
+ def testTaskWithUnstructuredSparsity(self, config_name):
+ test_tfrecord_file = os.path.join(self.get_temp_dir(), 'cls_test.tfrecord')
+ self._create_test_tfrecord(
+ test_tfrecord_file=test_tfrecord_file,
+ num_samples=10,
+ input_image_size=[224, 224])
+ config = exp_factory.get_exp_config(config_name)
+ config.task.train_data.global_batch_size = 2
+ config.task.validation_data.input_path = test_tfrecord_file
+ config.task.train_data.input_path = test_tfrecord_file
+
+ task = img_cls_task.ImageClassificationTask(config.task)
+ model = task.build_model()
+
+ metrics = task.build_metrics()
+ strategy = tf.distribute.get_strategy()
+
+ dataset = orbit.utils.make_distributed_dataset(strategy, task.build_inputs,
+ config.task.train_data)
+
+ iterator = iter(dataset)
+ opt_factory = optimization.OptimizerFactory(config.trainer.optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+
+ if isinstance(optimizer, optimization.ExponentialMovingAverage
+ ) and not optimizer.has_shadow_copy:
+ optimizer.shadow_copy(model)
+
+ if config.task.pruning:
+ # This is an auxilary initialization required to prune a model which is
+ # originally done in the train library.
+ actions.PruningAction(
+ export_dir=tempfile.gettempdir(), model=model, optimizer=optimizer)
+
+ # Check all layers and target weights are successfully pruned.
+ self._validate_model_pruned(model, config_name)
+
+ logs = task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ self._validate_metrics(logs, metrics)
+
+ logs = task.validation_step(next(iterator), model, metrics=metrics)
+ self._validate_metrics(logs, metrics)
+
+ @parameterized.parameters(('resnet_imagenet_pruning'),
+ ('mobilenet_imagenet_pruning'))
+ def testTaskWithStructuredSparsity(self, config_name):
+ test_tfrecord_file = os.path.join(self.get_temp_dir(), 'cls_test.tfrecord')
+ self._create_test_tfrecord(
+ test_tfrecord_file=test_tfrecord_file,
+ num_samples=10,
+ input_image_size=[224, 224])
+ config = exp_factory.get_exp_config(config_name)
+ config.task.train_data.global_batch_size = 2
+ config.task.validation_data.input_path = test_tfrecord_file
+ config.task.train_data.input_path = test_tfrecord_file
+
+ # Add structured sparsity
+ config.task.pruning.sparsity_m_by_n = (2, 4)
+ config.task.pruning.frequency = 1
+
+ task = img_cls_task.ImageClassificationTask(config.task)
+ model = task.build_model()
+
+ metrics = task.build_metrics()
+ strategy = tf.distribute.get_strategy()
+
+ dataset = orbit.utils.make_distributed_dataset(strategy, task.build_inputs,
+ config.task.train_data)
+
+ iterator = iter(dataset)
+ opt_factory = optimization.OptimizerFactory(config.trainer.optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+
+ if isinstance(optimizer, optimization.ExponentialMovingAverage
+ ) and not optimizer.has_shadow_copy:
+ optimizer.shadow_copy(model)
+
+ # This is an auxiliary initialization required to prune a model which is
+ # originally done in the train library.
+ pruning_actions = actions.PruningAction(
+ export_dir=tempfile.gettempdir(), model=model, optimizer=optimizer)
+
+ # Check all layers and target weights are successfully pruned.
+ self._validate_model_pruned(model, config_name)
+
+ logs = task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ self._validate_metrics(logs, metrics)
+
+ logs = task.validation_step(next(iterator), model, metrics=metrics)
+ self._validate_metrics(logs, metrics)
+
+ pruning_actions.update_pruning_step.on_epoch_end(batch=None)
+ # Check whether the weights are pruned in 2x4 pattern.
+ self._check_2x4_sparsity(model)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/pruning/train.py b/official/projects/pruning/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..e1d6e3c9416232ecefaa7530387bbcb23084e1e5
--- /dev/null
+++ b/official/projects/pruning/train.py
@@ -0,0 +1,29 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver, including Pruning configs.."""
+
+from absl import app
+
+from official.common import flags as tfm_flags
+# To build up a connection with the training binary for pruning, the custom
+# configs & tasks are imported while unused.
+from official.projects.pruning import configs # pylint: disable=unused-import
+from official.projects.pruning.tasks import image_classification # pylint: disable=unused-import
+from official.vision import train
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/qat/vision/README.md b/official/projects/qat/vision/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..cfe4b1a76028b19a10e1f5f916eb577494d7d7d3
--- /dev/null
+++ b/official/projects/qat/vision/README.md
@@ -0,0 +1,63 @@
+# Quantization Aware Training Project for Computer Vision Models
+
+⚠️ Disclaimer: All datasets hyperlinked from this page are not owned or
+distributed by Google. The dataset is made available by third parties.
+Please review the terms and conditions made available by the third parties
+before using the data.
+
+## Overview
+
+This project includes quantization aware training code for Computer Vision
+models. These are examples to show how to apply the Model Optimization Toolkit's
+[quantization aware training API](https://www.tensorflow.org/model_optimization/guide/quantization/training).
+
+Note: Currently, we support a limited number of ML tasks & models (e.g., image
+classification and semantic segmentation)
+We will keep adding support for other ML tasks and models in the next releases.
+
+## How to train a model
+
+```
+EXPERIMENT=xxx # Change this for your run, for example, 'mobilenet_imagenet_qat'
+CONFIG_FILE=xxx # Change this for your run, for example, path of imagenet_mobilenetv2_qat_gpu.yaml
+MODEL_DIR=xxx # Change this for your run, for example, /tmp/model_dir
+$ python3 train.py \
+--experiment=${EXPERIMENT} \
+--config_file=${CONFIG_FILE} \
+--model_dir=${MODEL_DIR} \
+--mode=train_and_eval
+```
+
+## Image Classification
+
+
+
+Comparison of Imagenet top-1 accuracy for the classification models
+
+
+Note: The Top-1 model accuracy is measured on the validation set of [ImageNet](https://www.image-net.org/).
+
+
+### Pre-trained Models
+
+|Model |Resolution|Top-1 Accuracy (FP32)|Top-1 Accuracy (Int8/PTQ)|Top-1 Accuracy (Int8/QAT)|Config |Download |
+|----------------------|----------|---------------------|-------------------------|-------------------------|--------------------------------------------------------------------------------------------------------------------------------------------------------------------|------------------------------------------------------------------------------------------------------------------------------------------------|
+|MobileNetV2 |224x224 |72.782% |72.392% |72.792% |[config](https://github.com/tensorflow/models/blob/master/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu.yaml) |[TFLite(Int8/QAT)](https://storage.googleapis.com/tf_model_garden/vision/mobilenet/v2_1.0_int8/mobilenet_v2_1.00_224_int8.tflite) |
+|ResNet50 |224x224 |76.710% |76.420% |77.200% |[config](https://github.com/tensorflow/models/blob/master/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu.yaml) |[TFLite(Int8/QAT)](https://storage.googleapis.com/tf_model_garden/vision/resnet50_imagenet/resnet_50_224_int8.tflite) |
+|MobileNetV3.5 MultiAVG|224x224 |75.212% |74.122% |75.130% |[config](https://github.com/tensorflow/models/blob/master/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3.5_qat_gpu.yaml)|[TFLite(Int8/QAT)](https://storage.googleapis.com/tf_model_garden/vision/mobilenet/v3.5multiavg_1.0_int8/mobilenet_v3.5multiavg_1.00_224_int8.tflite)|
+
+## Semantic Segmentation
+
+
+Model is pretrained using COCO train set. Two datasets, Pascal VOC segmentation
+dataset and Cityscapes dataset (only for DeepLab v3+), are used to train and
+evaluate models. Model accuracy is measured on full Pascal VOC segmentation
+validation set.
+
+### Pre-trained Models
+
+model | resolution | mIoU | mIoU (FP32) | mIoU (FP16) | mIoU (INT8) | mIoU (QAT INT8) | download (tflite)|
+:------------------------- | :--------: | ----: | ----------: | ----------: | ----------: | --------------: | ----------------:
+MobileNet v2 + DeepLab v3 | 512x512 | 75.27 | 75.30 | 75.32 | 73.95 | 74.68 | [FP32](https://storage.googleapis.com/tf_model_garden/vision/qat/deeplabv3_mobilenetv2_pascal_coco_0.21/model_none.tflite) \| [FP16](https://storage.googleapis.com/tf_model_garden/vision/qat/deeplabv3_mobilenetv2_pascal_coco_0.21/model_fp16.tflite) \| [INT8](https://storage.googleapis.com/tf_model_garden/vision/qat/deeplabv3_mobilenetv2_pascal_coco_0.21model_int8_full.tflite) \| [QAT INT8](https://storage.googleapis.com/tf_model_garden/vision/qat/deeplabv3_mobilenetv2_pascal_coco_0.21/Fmodel_default.tflite)
+MobileNet v2 + DeepLab v3+ | 1024x2048 | 73.82 | 73.84 | 73.65 | 72.33 | 73.49 | [FP32](https://storage.googleapis.com/tf_model_garden/vision/qat/mnv2_deeplabv3plus_cityscapes/model_none.tflite) \| [FP16](https://storage.googleapis.com/tf_model_garden/vision/qat/mnv2_deeplabv3plus_cityscapes/Fmodel_fp16.tflite) \| [INT8](https://storage.googleapis.com/tf_model_garden/vision/qat/mnv2_deeplabv3plus_cityscapes/model_int8_full.tflite) \| [QAT INT8](https://storage.googleapis.com/tf_model_garden/vision/qat/mnv2_deeplabv3plus_cityscapes/Fmodel_default.tflite)
+
diff --git a/official/projects/qat/vision/configs/__init__.py b/official/projects/qat/vision/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..1d3c061ac778f0e1a5dc864cfddb8c7eda3c7aea
--- /dev/null
+++ b/official/projects/qat/vision/configs/__init__.py
@@ -0,0 +1,19 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
+
+from official.projects.qat.vision.configs import image_classification
+from official.projects.qat.vision.configs import retinanet
+from official.projects.qat.vision.configs import semantic_segmentation
diff --git a/official/projects/qat/vision/configs/common.py b/official/projects/qat/vision/configs/common.py
new file mode 100644
index 0000000000000000000000000000000000000000..c370226169e669569ad85b5dfe04402681c400dc
--- /dev/null
+++ b/official/projects/qat/vision/configs/common.py
@@ -0,0 +1,43 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification configuration definition."""
+
+import dataclasses
+from typing import Optional
+
+from official.modeling import hyperparams
+
+
+@dataclasses.dataclass
+class Quantization(hyperparams.Config):
+ """Quantization parameters.
+
+ Attributes:
+ pretrained_original_checkpoint: A string indicate pretrained checkpoint
+ location.
+ change_num_bits: A `bool` indicates whether to manually allocate num_bits.
+ num_bits_weight: An `int` number of bits for weight. Default to 8.
+ num_bits_activation: An `int` number of bits for activation. Default to 8.
+ quantize_detection_decoder: A `bool` indicates whether to quantize detection
+ decoder. It only works for detection model.
+ quantize_detection_head: A `bool` indicates whether to quantize detection
+ head. It only works for detection model.
+ """
+ pretrained_original_checkpoint: Optional[str] = None
+ change_num_bits: bool = False
+ num_bits_weight: int = 8
+ num_bits_activation: int = 8
+ quantize_detection_decoder: bool = False
+ quantize_detection_head: bool = False
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..c22848a5cb5d5017ca0e92b988a1ba23560ba9c0
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu.yaml
@@ -0,0 +1,53 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ filter_size_scale: 1.0
+ dropout_rate: 0.1
+ losses:
+ l2_weight_decay: 0.0000001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 512 # 64 * 8
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 512 # 64 * 8
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/mobilenetv2_gpu/22984194/ckpt-625500'
+trainer:
+ # With below setting, the accuracy of QAT reaches to accuracy 0.7279 after 43 hours with 8 GPUS.
+ train_steps: 250200
+ validation_steps: 98
+ validation_interval: 2502
+ steps_per_loop: 2502
+ summary_interval: 2502
+ checkpoint_interval: 2502
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ decay_rate: 0.9
+ decay_steps: 1251
+ initial_learning_rate: 0.0001
+ name: 'ExponentialDecay'
+ offset: 0
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch256.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch256.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..cf081190d18bbf2e36f2ac674f788e966660c039
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch256.yaml
@@ -0,0 +1,53 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ filter_size_scale: 1.0
+ dropout_rate: 0.0 # changed from 0.2 to 0.0
+ losses:
+ l2_weight_decay: 0.0000001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/mobilenetv2_gpu/22984194/ckpt-625500'
+trainer:
+ # With below setting, the accuracy of QAT reaches Top1-accuracy 0.7251 at 420336 steps after
+ # 1 day 19 hours of training with 8GPUs, which is higher than the result of PTQ in MobileNetV2.
+ train_steps: 1000800 # 200 epochs
+ validation_steps: 196 # NUM_EXAMPLES (50000) // global_batch_size (256)
+ validation_interval: 5004 # 1 epoch
+ steps_per_loop: 5004 # NUM_EXAMPLES (1281167) // global_batch_size (256)
+ summary_interval: 5004 # 1 epoch
+ checkpoint_interval: 5004 # 1 epoch
+ max_to_keep: 200
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.0001
+ decay_steps: 1251 # steps_per_epoch // 4
+ decay_rate: 0.96
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch512.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch512.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..c1ab24a5e7cfe901a8a196b3c97eacb915b97290
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv2_qat_gpu_batch512.yaml
@@ -0,0 +1,53 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ filter_size_scale: 1.0
+ dropout_rate: 0.0 # changed from 0.2 to 0.0
+ losses:
+ l2_weight_decay: 0.0000001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 512
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 512
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/mobilenetv2_gpu/22984194/ckpt-625500'
+trainer:
+ # With below setting, the accuracy of QAT reaches Top1-accuracy 0.7266 at 312750 steps after
+ # 1 day 22 hours of training with 8GPUs, which is higher than the result of PTQ in MobileNetV2.
+ train_steps: 500400 # 200 epochs
+ validation_steps: 98 # NUM_EXAMPLES (50000) // global_batch_size (512)
+ validation_interval: 2502 # 1 epoch
+ steps_per_loop: 2502 # NUM_EXAMPLES (1281167) // global_batch_size (512)
+ summary_interval: 2502 # 1 epoch
+ checkpoint_interval: 2502 # 1 epoch
+ max_to_keep: 200
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.0002
+ decay_steps: 1251 # steps_per_epoch // 2
+ decay_rate: 0.96
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3.5_qat_gpu.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3.5_qat_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..946b034d177ab936addd97180bbdbf7ce6291f3d
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3.5_qat_gpu.yaml
@@ -0,0 +1,53 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetMultiAVG'
+ filter_size_scale: 1.0
+ dropout_rate: 0.3
+ losses:
+ l2_weight_decay: 0.000001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 512
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 512
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/tf2_mhave_nobias_bn_aug05/28334857/ckpt-156000'
+trainer:
+ # With below setting, the accuracy of QAT reaches to accuracy 0.7513 after 30 hours with 8 GPUS.
+ train_steps: 250200
+ validation_steps: 98
+ validation_interval: 2502
+ steps_per_loop: 2502
+ summary_interval: 2502
+ checkpoint_interval: 2502
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ decay_rate: 0.9
+ decay_steps: 1251
+ initial_learning_rate: 0.0004
+ name: 'ExponentialDecay'
+ offset: 0
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3large_qat_tpu.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3large_qat_tpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..d5070c33a6ca6e04d00a356ab5842b6a44b0ee0b
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_mobilenetv3large_qat_tpu.yaml
@@ -0,0 +1,63 @@
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV3Large'
+ filter_size_scale: 1.0
+ dropout_rate: 0.3
+ losses:
+ l2_weight_decay: 1.0e-06 # 1/10 of original value.
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 4096
+ dtype: 'float32'
+ aug_rand_hflip: true
+ drop_remainder: true
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 4096
+ dtype: 'float32'
+ drop_remainder: false
+ aug_rand_hflip: true
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/mobilenetv3_baseline_31/ckpt-156000'
+trainer:
+ # With below setting, the accuracy of QAT reaches to accuracy 0.74.43 after ~2 hours with 4x4 DF.
+ train_steps: 62400
+ validation_steps: 13
+ validation_interval: 312
+ steps_per_loop: 312
+ summary_interval: 312
+ checkpoint_interval: 312
+ optimizer_config:
+ learning_rate:
+ cosine:
+ alpha: 0.0
+ decay_steps: 62400
+ initial_learning_rate: 0.0003 # 1/10 of original lr.
+ name: CosineDecay
+ offset: 0
+ type: cosine
+ optimizer:
+ adamw:
+ amsgrad: false
+ beta_1: 0.9
+ beta_2: 0.999
+ epsilon: 1.0e-07
+ gradient_clip_norm: 1.0
+ weight_decay_rate: 0.0
+ type: adamw
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 0
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..01ab5eb09caf665d803fe719c64cbda0a61206cf
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu.yaml
@@ -0,0 +1,52 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0.0001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+trainer:
+ # With below setting, the accuracy of QAT reaches to Top1-accuracy 0.7720 after 5 days of training
+ # with 8GPUs, which is higher than the non-quantized float32 version Resnet.
+ train_steps: 449280
+ validation_steps: 200
+ validation_interval: 5000
+ steps_per_loop: 5000
+ summary_interval: 5000
+ checkpoint_interval: 5000
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'stepwise'
+ stepwise:
+ boundaries: [150000, 300000, 400000]
+ values: [0.08, 0.008, 0.0008, 0.00008]
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 40000
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..1912477bb79fe35b2efb90df56aeea91cd5a20c1
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast.yaml
@@ -0,0 +1,54 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0.0001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+trainer:
+ # With below setting, the accuracy of QAT reaches to the non-quantized float32 version after
+ # around 160k steps, which takes 1d 15h with 8 GPUS.
+ train_steps: 449280
+ validation_steps: 200
+ validation_interval: 5000
+ steps_per_loop: 5000
+ summary_interval: 5000
+ checkpoint_interval: 5000
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.016
+ decay_steps: 25000
+ decay_rate: 0.5
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 1000
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x4.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x4.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..12d4a2c9921403fbfc86f1eeef6fac6d1c9d1ad3
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x4.yaml
@@ -0,0 +1,57 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0.0001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+ change_num_bits: true
+ num_bits_weight: 4
+ num_bits_activation: 4
+trainer:
+ # With below setting, the accuracy of QAT reaches Top1-accuracy 0.6822 at 205k steps with 8GPUs.
+ # TODO: Please change the configs when training is done.
+ train_steps: 449280
+ validation_steps: 200
+ validation_interval: 5000
+ steps_per_loop: 5000
+ summary_interval: 5000
+ checkpoint_interval: 5000
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.016
+ decay_steps: 25000
+ decay_rate: 0.5
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 1000
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x8.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x8.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..ca739d41497271dcbe3c05b05da841a77ff75b39
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_4x8.yaml
@@ -0,0 +1,57 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0.0001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+ change_num_bits: true
+ num_bits_weight: 4
+ num_bits_activation: 8
+trainer:
+ # With below setting, the accuracy of QAT reaches Top1-accuracy 0.7575 at 220k steps with 8GPUs.
+ # TODO: Please change the configs when training is done.
+ train_steps: 449280
+ validation_steps: 200
+ validation_interval: 5000
+ steps_per_loop: 5000
+ summary_interval: 5000
+ checkpoint_interval: 5000
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.016
+ decay_steps: 25000
+ decay_rate: 0.5
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 1000
diff --git a/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_6x6.yaml b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_6x6.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..88512f6002e81f293a660444b6bf9f6d37aff4e2
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/image_classification/imagenet_resnet50_qat_gpu_fast_6x6.yaml
@@ -0,0 +1,57 @@
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 1001
+ input_size: [224, 224, 3]
+ backbone:
+ type: 'resnet'
+ resnet:
+ model_id: 50
+ losses:
+ l2_weight_decay: 0.0001
+ one_hot: true
+ label_smoothing: 0.1
+ train_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/train*'
+ is_training: true
+ global_batch_size: 256
+ dtype: 'float32'
+ validation_data:
+ input_path: '/readahead/200M/placer/prod/home/distbelief/imagenet-tensorflow/imagenet-2012-tfrecord/valid*'
+ is_training: false
+ global_batch_size: 256
+ dtype: 'float32'
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/resnet_classifier_gpu/ckpt-56160'
+ change_num_bits: true
+ num_bits_weight: 6
+ num_bits_activation: 6
+trainer:
+ # With below setting, the accuracy of QAT reaches Top1-accuracy 0.7607 at 190k steps with 8GPUs.
+ # TODO: Please change the configs when training is done.
+ train_steps: 449280
+ validation_steps: 200
+ validation_interval: 5000
+ steps_per_loop: 5000
+ summary_interval: 5000
+ checkpoint_interval: 5000
+ optimizer_config:
+ optimizer:
+ type: 'sgd'
+ sgd:
+ momentum: 0.9
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ initial_learning_rate: 0.016
+ decay_steps: 25000
+ decay_rate: 0.5
+ staircase: true
+ warmup:
+ type: 'linear'
+ linear:
+ warmup_steps: 1000
diff --git a/official/projects/qat/vision/configs/experiments/retinanet/coco_mobilenetv2_qat_tpu_e2e.yaml b/official/projects/qat/vision/configs/experiments/retinanet/coco_mobilenetv2_qat_tpu_e2e.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7238f9357f1871de54d92d54a81eefbdb1f0d9b3
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/retinanet/coco_mobilenetv2_qat_tpu_e2e.yaml
@@ -0,0 +1,72 @@
+# --experiment_type=retinanet_mobile_coco_qat
+# COCO mAP: 23.02 from QAT training and 21.62 from the TFLite after conversion.
+# QAT only supports float32 tpu due to fake-quant op.
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ losses:
+ l2_weight_decay: 0.0
+ model:
+ anchor:
+ anchor_size: 3
+ aspect_ratios: [0.5, 1.0, 2.0]
+ num_scales: 3
+ backbone:
+ mobilenet:
+ model_id: 'MobileNetV2'
+ filter_size_scale: 1.0
+ type: 'mobilenet'
+ decoder:
+ type: 'fpn'
+ fpn:
+ num_filters: 128
+ use_separable_conv: true
+ use_keras_layer: true
+ head:
+ num_convs: 4
+ num_filters: 128
+ use_separable_conv: true
+ input_size: [256, 256, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: 'relu6'
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ train_data:
+ dtype: 'float32'
+ global_batch_size: 256
+ is_training: true
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ dtype: 'float32'
+ global_batch_size: 256
+ is_training: false
+ drop_remainder: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/coco_mobilenetv2_mobile_tpu/ckpt-277200'
+ quantize_detection_decoder: true
+ quantize_detection_head: true
+trainer:
+ best_checkpoint_eval_metric: AP
+ best_checkpoint_export_subdir: best_ckpt
+ best_checkpoint_metric_comp: higher
+ optimizer_config:
+ learning_rate:
+ type: 'exponential'
+ exponential:
+ decay_rate: 0.96
+ decay_steps: 231
+ initial_learning_rate: 0.5
+ name: 'ExponentialDecay'
+ offset: 0
+ staircase: true
+ steps_per_loop: 462
+ train_steps: 46200
+ validation_interval: 462
+ validation_steps: 20
diff --git a/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_gpu.yaml b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..3bfcfb57d3304d501c85ddd7a6509380d0709b65
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_gpu.yaml
@@ -0,0 +1,64 @@
+# --experiment_type=retinanet_mobile_coco_qat
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+task:
+ losses:
+ l2_weight_decay: 3.0e-05
+ model:
+ anchor:
+ anchor_size: 3
+ aspect_ratios: [0.5, 1.0, 2.0]
+ num_scales: 3
+ backbone:
+ spinenet_mobile:
+ stochastic_depth_drop_rate: 0.2
+ model_id: '49'
+ se_ratio: 0.2
+ use_keras_upsampling_2d: true
+ type: 'spinenet_mobile'
+ decoder:
+ type: 'identity'
+ head:
+ num_convs: 4
+ num_filters: 48
+ use_separable_conv: true
+ input_size: [384, 384, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: 'swish'
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ train_data:
+ dtype: 'float32'
+ global_batch_size: 128
+ is_training: true
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ dtype: 'float32'
+ global_batch_size: 8
+ is_training: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/coco_spinenet49_mobile_tpu/ckpt-277200'
+trainer:
+ checkpoint_interval: 924
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [531300, 545160]
+ values: [0.0016, 0.00016, 0.000016]
+ type: 'stepwise'
+ warmup:
+ linear:
+ warmup_learning_rate: 0.0000335
+ warmup_steps: 4000
+ steps_per_loop: 924
+ train_steps: 554400
+ validation_interval: 924
+ validation_steps: 1250
+ summary_interval: 924
diff --git a/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu.yaml b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..0ce3d5462101fdca40a6800633c45c306d6b1c05
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu.yaml
@@ -0,0 +1,66 @@
+# --experiment_type=retinanet_mobile_coco_qat
+# COCO mAP: 24.7
+# QAT only supports float32 tpu due to fake-quant op.
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ losses:
+ l2_weight_decay: 3.0e-05
+ model:
+ anchor:
+ anchor_size: 3
+ aspect_ratios: [0.5, 1.0, 2.0]
+ num_scales: 3
+ backbone:
+ spinenet_mobile:
+ stochastic_depth_drop_rate: 0.2
+ model_id: '49'
+ se_ratio: 0.2
+ use_keras_upsampling_2d: true
+ type: 'spinenet_mobile'
+ decoder:
+ type: 'identity'
+ head:
+ num_convs: 4
+ num_filters: 48
+ use_separable_conv: true
+ input_size: [384, 384, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: 'swish'
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ train_data:
+ dtype: 'float32'
+ global_batch_size: 128
+ is_training: true
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ dtype: 'float32'
+ global_batch_size: 16
+ is_training: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/coco_spinenet49_mobile_tpu_33884721/ckpt-277200'
+trainer:
+ checkpoint_interval: 924
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [531300, 545160]
+ values: [0.0016, 0.00016, 0.000016]
+ type: 'stepwise'
+ warmup:
+ linear:
+ warmup_learning_rate: 0.0000335
+ warmup_steps: 4000
+ steps_per_loop: 924
+ train_steps: 554400
+ validation_interval: 924
+ validation_steps: 1250
+ summary_interval: 924
diff --git a/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu_e2e.yaml b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu_e2e.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..b4374f9cd6118bee60bd75a6f3dce2c5eb04c15a
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/retinanet/coco_spinenet49_mobile_qat_tpu_e2e.yaml
@@ -0,0 +1,67 @@
+# --experiment_type=retinanet_mobile_coco_qat
+# COCO mAP: 23.2
+# QAT only supports float32 tpu due to fake-quant op.
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ losses:
+ l2_weight_decay: 3.0e-05
+ model:
+ anchor:
+ anchor_size: 3
+ aspect_ratios: [0.5, 1.0, 2.0]
+ num_scales: 3
+ backbone:
+ spinenet_mobile:
+ stochastic_depth_drop_rate: 0.2
+ model_id: '49'
+ se_ratio: 0.2
+ use_keras_upsampling_2d: true
+ type: 'spinenet_mobile'
+ decoder:
+ type: 'identity'
+ head:
+ num_convs: 4
+ num_filters: 48
+ use_separable_conv: true
+ input_size: [384, 384, 3]
+ max_level: 7
+ min_level: 3
+ norm_activation:
+ activation: 'swish'
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ train_data:
+ dtype: 'float32'
+ global_batch_size: 256
+ is_training: true
+ parser:
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ dtype: 'float32'
+ global_batch_size: 16
+ is_training: false
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/coco_spinenet49_mobile_tpu_33884721/ckpt-277200'
+ quantize_detection_head: true
+trainer:
+ checkpoint_interval: 462
+ optimizer_config:
+ learning_rate:
+ stepwise:
+ boundaries: [263340, 272580]
+ values: [0.032, 0.0032, 0.00032]
+ type: 'stepwise'
+ warmup:
+ linear:
+ warmup_learning_rate: 0.00067
+ warmup_steps: 2000
+ steps_per_loop: 462
+ train_steps: 277200
+ validation_interval: 462
+ validation_steps: 625
+ summary_interval: 924
diff --git a/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_gpu.yaml b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_gpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..ca8bf7873cdf53fd202147370e6572ea5a6c4204
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_gpu.yaml
@@ -0,0 +1,81 @@
+# --experiment_type=mnv2_deeplabv3_pascal_qat
+# Use 8 v100 GPUs for training and 4 v100 GPUs for eval.
+# mIoU (unquantized fp32): 74.78
+runtime:
+ distribution_strategy: 'mirrored'
+ mixed_precision_dtype: 'float32'
+ loss_scale: 'dynamic'
+task:
+ model:
+ num_classes: 21
+ input_size: [512, 512, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ output_stride: 16
+ decoder:
+ aspp:
+ dilation_rates: []
+ level: 4
+ pool_kernel_size: null
+ output_tensor: true
+ type: 'aspp'
+ head:
+ feature_fusion: null
+ num_convs: 0
+ norm_activation:
+ activation: relu
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ losses:
+ l2_weight_decay: 4.0e-07 # 1/100 of original value.
+ train_data:
+ output_size: [512, 512]
+ crop_size: [512, 512]
+ input_path: 'gs://**/pascal_voc_seg/train_aug*'
+ is_training: true
+ global_batch_size: 16
+ dtype: 'float32'
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ output_size: [512, 512]
+ input_path: 'gs://**/pascal_voc_seg/val*'
+ is_training: false
+ global_batch_size: 16
+ dtype: 'float32'
+ drop_remainder: false
+ resize_eval_groundtruth: false
+ groundtruth_padded_size: [512, 512]
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/deeplabv3_mobilenetv2_pascal_coco_0.21/29808901/best_ckpt/best_ckpt-54'
+ init_checkpoint: null
+trainer:
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 13240
+ initial_learning_rate: 0.00007 # 1/100 of original lr.
+ power: 0.9
+ type: polynomial
+ optimizer:
+ sgd:
+ momentum: 0.9
+ type: sgd
+ warmup:
+ linear:
+ name: linear
+ warmup_steps: 0 # No warmup
+ type: linear
+ best_checkpoint_eval_metric: 'mean_iou'
+ best_checkpoint_export_subdir: 'best_ckpt'
+ best_checkpoint_metric_comp: 'higher'
+ steps_per_loop: 662
+ summary_interval: 662
+ train_steps: 13240
+ validation_interval: 662
+ validation_steps: 90
+ checkpoint_interval: 662
diff --git a/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_tpu.yaml b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_tpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7776a836436d6d89a8974d1cb8efd5311609a69c
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3_mobilenetv2_pascal_qat_tpu.yaml
@@ -0,0 +1,80 @@
+# --experiment_type=mnv2_deeplabv3_pascal_qat
+# Use 4x2 DF for training and eval.
+# mIoU (unquantized fp32): 74.69
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ model:
+ num_classes: 21
+ input_size: [512, 512, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ output_stride: 16
+ decoder:
+ aspp:
+ dilation_rates: []
+ level: 4
+ pool_kernel_size: null
+ output_tensor: true
+ type: 'aspp'
+ head:
+ feature_fusion: null
+ num_convs: 0
+ norm_activation:
+ activation: relu
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ losses:
+ l2_weight_decay: 4.0e-07 # 1/100 of original value.
+ train_data:
+ output_size: [512, 512]
+ crop_size: [512, 512]
+ input_path: 'gs://**/pascal_voc_seg/train_aug*'
+ is_training: true
+ global_batch_size: 16
+ dtype: 'float32'
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ output_size: [512, 512]
+ input_path: 'gs://**/pascal_voc_seg/val*'
+ is_training: false
+ global_batch_size: 16
+ dtype: 'float32'
+ drop_remainder: false
+ resize_eval_groundtruth: false
+ groundtruth_padded_size: [512, 512]
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/deeplabv3_mobilenetv2_pascal_coco_0.21/29808901/best_ckpt/best_ckpt-54'
+ init_checkpoint: null
+trainer:
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 13240
+ initial_learning_rate: 0.00007 # 1/100 of original lr.
+ power: 0.9
+ type: polynomial
+ optimizer:
+ sgd:
+ momentum: 0.9
+ type: sgd
+ warmup:
+ linear:
+ name: linear
+ warmup_steps: 0 # No warmup
+ type: linear
+ best_checkpoint_eval_metric: 'mean_iou'
+ best_checkpoint_export_subdir: 'best_ckpt'
+ best_checkpoint_metric_comp: 'higher'
+ steps_per_loop: 662
+ summary_interval: 662
+ train_steps: 13240
+ validation_interval: 662
+ validation_steps: 90
+ checkpoint_interval: 662
diff --git a/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3plus_mobilenetv2_cityscapes_qat_tpu.yaml b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3plus_mobilenetv2_cityscapes_qat_tpu.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..b9bdbae6f04be513d195afdd9126e87ee68aed5a
--- /dev/null
+++ b/official/projects/qat/vision/configs/experiments/semantic_segmentation/deeplabv3plus_mobilenetv2_cityscapes_qat_tpu.yaml
@@ -0,0 +1,89 @@
+# --experiment_type=mnv2_deeplabv3plus_cityscapes_qat
+# Use 4x2 DF for training and eval.
+# mIoU (unquantized fp32): 73.84
+runtime:
+ distribution_strategy: 'tpu'
+ mixed_precision_dtype: 'float32'
+task:
+ model:
+ num_classes: 19
+ input_size: [1024, 2048, 3]
+ backbone:
+ type: 'mobilenet'
+ mobilenet:
+ model_id: 'MobileNetV2'
+ output_stride: 16
+ output_intermediate_endpoints: true
+ decoder:
+ aspp:
+ dilation_rates: []
+ level: 4
+ pool_kernel_size: [512, 1024]
+ output_tensor: true
+ type: 'aspp'
+ head:
+ feature_fusion: 'deeplabv3plus'
+ low_level: '2/depthwise'
+ low_level_num_filters: 48
+ level: 4
+ num_convs: 2
+ use_depthwise_convolution: true
+ norm_activation:
+ activation: relu
+ norm_epsilon: 0.001
+ norm_momentum: 0.99
+ use_sync_bn: true
+ losses:
+ l2_weight_decay: 4.0e-07 # 1/100 of original value.
+ train_data:
+ output_size: [1024, 2048]
+ crop_size: []
+ input_path: ''
+ tfds_name: 'cityscapes/semantic_segmentation'
+ tfds_split: 'train'
+ is_training: true
+ global_batch_size: 16
+ dtype: 'float32'
+ aug_rand_hflip: true
+ aug_scale_max: 2.0
+ aug_scale_min: 0.5
+ validation_data:
+ output_size: [1024, 2048]
+ input_path: ''
+ tfds_name: 'cityscapes/semantic_segmentation'
+ tfds_split: 'validation'
+ is_training: false
+ global_batch_size: 16
+ dtype: 'float32'
+ drop_remainder: false
+ resize_eval_groundtruth: true
+ quantization:
+ pretrained_original_checkpoint: 'gs://**/deeplabv3plus_mobilenetv2_cityscapes/29814723/best_ckpt/best_ckpt-408'
+ init_checkpoint: null
+trainer:
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ decay_steps: 20000
+ initial_learning_rate: 0.0001 # 1/100 of original lr.
+ power: 0.9
+ type: polynomial
+ optimizer:
+ sgd:
+ momentum: 0.9
+ type: sgd
+ warmup:
+ linear:
+ name: linear
+ warmup_learning_rate: 0
+ warmup_steps: 0 # No warmup
+ type: linear
+ steps_per_loop: 185
+ summary_interval: 185
+ train_steps: 20000
+ validation_interval: 185
+ validation_steps: 31
+ checkpoint_interval: 185
+ best_checkpoint_export_subdir: 'best_ckpt'
+ best_checkpoint_eval_metric: 'mean_iou'
+ best_checkpoint_metric_comp: 'higher'
diff --git a/official/projects/qat/vision/configs/image_classification.py b/official/projects/qat/vision/configs/image_classification.py
new file mode 100644
index 0000000000000000000000000000000000000000..b3f0356970c99551771084a5e60657919e8c77fa
--- /dev/null
+++ b/official/projects/qat/vision/configs/image_classification.py
@@ -0,0 +1,52 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification configuration definition."""
+
+import dataclasses
+from typing import Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.vision.configs import image_classification
+
+
+@dataclasses.dataclass
+class ImageClassificationTask(image_classification.ImageClassificationTask):
+ quantization: Optional[common.Quantization] = None
+
+
+@exp_factory.register_config_factory('resnet_imagenet_qat')
+def image_classification_imagenet() -> cfg.ExperimentConfig:
+ """Builds an image classification config for the resnet with QAT."""
+ config = image_classification.image_classification_imagenet()
+ task = ImageClassificationTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ config.task = task
+ runtime = cfg.RuntimeConfig(enable_xla=False)
+ config.runtime = runtime
+
+ return config
+
+
+@exp_factory.register_config_factory('mobilenet_imagenet_qat')
+def image_classification_imagenet_mobilenet() -> cfg.ExperimentConfig:
+ """Builds an image classification config for the mobilenetV2 with QAT."""
+ config = image_classification.image_classification_imagenet_mobilenet()
+ task = ImageClassificationTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ config.task = task
+
+ return config
diff --git a/official/projects/qat/vision/configs/image_classification_test.py b/official/projects/qat/vision/configs/image_classification_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..6bddd78f0a9fac28d945a59bc3f959efbc1b71e5
--- /dev/null
+++ b/official/projects/qat/vision/configs/image_classification_test.py
@@ -0,0 +1,48 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for image_classification."""
+# pylint: disable=unused-import
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official import vision
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.projects.qat.vision.configs import image_classification as qat_exp_cfg
+from official.vision.configs import image_classification as exp_cfg
+
+
+class ImageClassificationConfigTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(
+ ('resnet_imagenet_qat',),
+ ('mobilenet_imagenet_qat',),
+ )
+ def test_image_classification_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, qat_exp_cfg.ImageClassificationTask)
+ self.assertIsInstance(config.task.model,
+ exp_cfg.ImageClassificationModel)
+ self.assertIsInstance(config.task.quantization, common.Quantization)
+ self.assertIsInstance(config.task.train_data, exp_cfg.DataConfig)
+ config.task.train_data.is_training = None
+ with self.assertRaisesRegex(KeyError, 'Found inconsistency between key'):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/configs/retinanet.py b/official/projects/qat/vision/configs/retinanet.py
new file mode 100644
index 0000000000000000000000000000000000000000..36dfa4bf8e01bfc090cd47a19ba42560f648efc1
--- /dev/null
+++ b/official/projects/qat/vision/configs/retinanet.py
@@ -0,0 +1,47 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""RetinaNet configuration definition."""
+import dataclasses
+from typing import Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.vision.configs import retinanet
+from official.vision.configs import backbones
+
+
+@dataclasses.dataclass
+class RetinaNetTask(retinanet.RetinaNetTask):
+ quantization: Optional[common.Quantization] = None
+
+
+@exp_factory.register_config_factory('retinanet_mobile_coco_qat')
+def retinanet_mobile_coco() -> cfg.ExperimentConfig:
+ """Generates a config for COCO OD RetinaNet for mobile with QAT."""
+ config = retinanet.retinanet_spinenet_mobile_coco()
+ task = RetinaNetTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ task.model.backbone = backbones.Backbone(
+ type='spinenet_mobile',
+ spinenet_mobile=backbones.SpineNetMobile(
+ model_id='49',
+ stochastic_depth_drop_rate=0.2,
+ min_level=3,
+ max_level=7,
+ use_keras_upsampling_2d=True))
+ config.task = task
+
+ return config
diff --git a/official/projects/qat/vision/configs/retinanet_test.py b/official/projects/qat/vision/configs/retinanet_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..6d7dde0fd3b0fc2d9e244145c371ba2b3d82c601
--- /dev/null
+++ b/official/projects/qat/vision/configs/retinanet_test.py
@@ -0,0 +1,47 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for retinanet."""
+# pylint: disable=unused-import
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official import vision
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.projects.qat.vision.configs import retinanet as qat_exp_cfg
+from official.vision.configs import retinanet as exp_cfg
+
+
+class RetinaNetConfigTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(
+ ('retinanet_mobile_coco_qat',),
+ )
+ def test_retinanet_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, qat_exp_cfg.RetinaNetTask)
+ self.assertIsInstance(config.task.model, exp_cfg.RetinaNet)
+ self.assertIsInstance(config.task.quantization, common.Quantization)
+ self.assertIsInstance(config.task.train_data, exp_cfg.DataConfig)
+ config.validate()
+ config.task.train_data.is_training = None
+ with self.assertRaisesRegex(KeyError, 'Found inconsistency between key'):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/configs/semantic_segmentation.py b/official/projects/qat/vision/configs/semantic_segmentation.py
new file mode 100644
index 0000000000000000000000000000000000000000..0bfe94b4549040f7e54fe956625d25eab5eba6f5
--- /dev/null
+++ b/official/projects/qat/vision/configs/semantic_segmentation.py
@@ -0,0 +1,57 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""RetinaNet configuration definition."""
+import dataclasses
+from typing import Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.vision.configs import semantic_segmentation
+
+
+@dataclasses.dataclass
+class SemanticSegmentationTask(semantic_segmentation.SemanticSegmentationTask):
+ quantization: Optional[common.Quantization] = None
+
+
+@exp_factory.register_config_factory('mnv2_deeplabv3_pascal_qat')
+def mnv2_deeplabv3_pascal() -> cfg.ExperimentConfig:
+ """Generates a config for MobileNet v2 + deeplab v3 with QAT."""
+ config = semantic_segmentation.mnv2_deeplabv3_pascal()
+ task = SemanticSegmentationTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ config.task = task
+ return config
+
+
+@exp_factory.register_config_factory('mnv2_deeplabv3_cityscapes_qat')
+def mnv2_deeplabv3_cityscapes() -> cfg.ExperimentConfig:
+ """Generates a config for MobileNet v2 + deeplab v3 with QAT."""
+ config = semantic_segmentation.mnv2_deeplabv3_cityscapes()
+ task = SemanticSegmentationTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ config.task = task
+ return config
+
+
+@exp_factory.register_config_factory('mnv2_deeplabv3plus_cityscapes_qat')
+def mnv2_deeplabv3plus_cityscapes() -> cfg.ExperimentConfig:
+ """Generates a config for MobileNet v2 + deeplab v3+ with QAT."""
+ config = semantic_segmentation.mnv2_deeplabv3plus_cityscapes()
+ task = SemanticSegmentationTask.from_args(
+ quantization=common.Quantization(), **config.task.as_dict())
+ config.task = task
+ return config
diff --git a/official/projects/qat/vision/configs/semantic_segmentation_test.py b/official/projects/qat/vision/configs/semantic_segmentation_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..55659fe62347d9d4c3eda4fb196c2c0dc676dd38
--- /dev/null
+++ b/official/projects/qat/vision/configs/semantic_segmentation_test.py
@@ -0,0 +1,47 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for retinanet."""
+# pylint: disable=unused-import
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official import vision
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.projects.qat.vision.configs import common
+from official.projects.qat.vision.configs import semantic_segmentation as qat_exp_cfg
+from official.vision.configs import semantic_segmentation as exp_cfg
+
+
+class SemanticSegmentationConfigTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(('mnv2_deeplabv3_pascal_qat',),
+ ('mnv2_deeplabv3_cityscapes_qat',),
+ ('mnv2_deeplabv3plus_cityscapes_qat'))
+ def test_semantic_segmentation_configs(self, config_name):
+ config = exp_factory.get_exp_config(config_name)
+ self.assertIsInstance(config, cfg.ExperimentConfig)
+ self.assertIsInstance(config.task, qat_exp_cfg.SemanticSegmentationTask)
+ self.assertIsInstance(config.task.model, exp_cfg.SemanticSegmentationModel)
+ self.assertIsInstance(config.task.quantization, common.Quantization)
+ self.assertIsInstance(config.task.train_data, exp_cfg.DataConfig)
+ config.validate()
+ config.task.train_data.is_training = None
+ with self.assertRaisesRegex(KeyError, 'Found inconsistency between key'):
+ config.validate()
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/modeling/__init__.py b/official/projects/qat/vision/modeling/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..aa57bbd868386cbe542c0ea680d75d9e01062df8
--- /dev/null
+++ b/official/projects/qat/vision/modeling/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Modeling package definition."""
+
+from official.projects.qat.vision.modeling import layers
diff --git a/official/projects/qat/vision/modeling/factory.py b/official/projects/qat/vision/modeling/factory.py
new file mode 100644
index 0000000000000000000000000000000000000000..81b175e02541abfbd4eaee1d64e84fadafd52a2f
--- /dev/null
+++ b/official/projects/qat/vision/modeling/factory.py
@@ -0,0 +1,267 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Factory methods to build models."""
+# Import libraries
+
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.configs import common
+from official.projects.qat.vision.modeling import segmentation_model as qat_segmentation_model
+from official.projects.qat.vision.modeling.heads import dense_prediction_heads as dense_prediction_heads_qat
+from official.projects.qat.vision.modeling.layers import nn_layers as qat_nn_layers
+from official.projects.qat.vision.n_bit import schemes as n_bit_schemes
+from official.projects.qat.vision.quantization import configs as qat_configs
+from official.projects.qat.vision.quantization import helper
+from official.projects.qat.vision.quantization import schemes
+from official.vision import configs
+from official.vision.modeling import classification_model
+from official.vision.modeling import retinanet_model
+from official.vision.modeling.decoders import aspp
+from official.vision.modeling.decoders import fpn
+from official.vision.modeling.heads import dense_prediction_heads
+from official.vision.modeling.heads import segmentation_heads
+from official.vision.modeling.layers import nn_layers
+
+
+def build_qat_classification_model(
+ model: tf.keras.Model,
+ quantization: common.Quantization,
+ input_specs: tf.keras.layers.InputSpec,
+ model_config: configs.image_classification.ImageClassificationModel,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None
+) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ """Apply model optimization techniques.
+
+ Args:
+ model: The model applying model optimization techniques.
+ quantization: The Quantization config.
+ input_specs: `tf.keras.layers.InputSpec` specs of the input tensor.
+ model_config: The model config.
+ l2_regularizer: tf.keras.regularizers.Regularizer object. Default to None.
+
+ Returns:
+ model: The model that applied optimization techniques.
+ """
+ original_checkpoint = quantization.pretrained_original_checkpoint
+ if original_checkpoint:
+ ckpt = tf.train.Checkpoint(
+ model=model,
+ **model.checkpoint_items)
+ status = ckpt.read(original_checkpoint)
+ status.expect_partial().assert_existing_objects_matched()
+
+ scope_dict = {
+ 'L2': tf.keras.regularizers.l2,
+ }
+ with tfmot.quantization.keras.quantize_scope(scope_dict):
+ annotated_backbone = tfmot.quantization.keras.quantize_annotate_model(
+ model.backbone)
+ if quantization.change_num_bits:
+ backbone = tfmot.quantization.keras.quantize_apply(
+ annotated_backbone,
+ scheme=n_bit_schemes.DefaultNBitQuantizeScheme(
+ num_bits_weight=quantization.num_bits_weight,
+ num_bits_activation=quantization.num_bits_activation))
+ else:
+ backbone = tfmot.quantization.keras.quantize_apply(
+ annotated_backbone,
+ scheme=schemes.Default8BitQuantizeScheme())
+
+ norm_activation_config = model_config.norm_activation
+ backbone_optimized_model = classification_model.ClassificationModel(
+ backbone=backbone,
+ num_classes=model_config.num_classes,
+ input_specs=input_specs,
+ dropout_rate=model_config.dropout_rate,
+ kernel_regularizer=l2_regularizer,
+ add_head_batch_norm=model_config.add_head_batch_norm,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon)
+ for from_layer, to_layer in zip(
+ model.layers, backbone_optimized_model.layers):
+ if from_layer != model.backbone:
+ to_layer.set_weights(from_layer.get_weights())
+
+ with tfmot.quantization.keras.quantize_scope(scope_dict):
+ def apply_quantization_to_dense(layer):
+ if isinstance(layer, (tf.keras.layers.Dense,
+ tf.keras.layers.Dropout,
+ tf.keras.layers.GlobalAveragePooling2D)):
+ return tfmot.quantization.keras.quantize_annotate_layer(layer)
+ return layer
+
+ annotated_model = tf.keras.models.clone_model(
+ backbone_optimized_model,
+ clone_function=apply_quantization_to_dense,
+ )
+
+ if quantization.change_num_bits:
+ optimized_model = tfmot.quantization.keras.quantize_apply(
+ annotated_model,
+ scheme=n_bit_schemes.DefaultNBitQuantizeScheme(
+ num_bits_weight=quantization.num_bits_weight,
+ num_bits_activation=quantization.num_bits_activation))
+
+ else:
+ optimized_model = tfmot.quantization.keras.quantize_apply(
+ annotated_model)
+
+ return optimized_model
+
+
+def _clone_function_for_fpn(layer):
+ if isinstance(layer, (
+ tf.keras.layers.BatchNormalization,
+ tf.keras.layers.experimental.SyncBatchNormalization)):
+ return tfmot.quantization.keras.quantize_annotate_layer(
+ qat_nn_layers.BatchNormalizationWrapper(layer),
+ qat_configs.Default8BitOutputQuantizeConfig())
+ if isinstance(layer, tf.keras.layers.UpSampling2D):
+ return layer
+ return tfmot.quantization.keras.quantize_annotate_layer(layer)
+
+
+def build_qat_retinanet(
+ model: tf.keras.Model, quantization: common.Quantization,
+ model_config: configs.retinanet.RetinaNet) -> tf.keras.Model:
+ """Applies quantization aware training for RetinaNet model.
+
+ Args:
+ model: The model applying quantization aware training.
+ quantization: The Quantization config.
+ model_config: The model config.
+
+ Returns:
+ The model that applied optimization techniques.
+ """
+
+ original_checkpoint = quantization.pretrained_original_checkpoint
+ if original_checkpoint is not None:
+ ckpt = tf.train.Checkpoint(
+ model=model,
+ **model.checkpoint_items)
+ status = ckpt.read(original_checkpoint)
+ status.expect_partial().assert_existing_objects_matched()
+
+ scope_dict = {
+ 'L2': tf.keras.regularizers.l2,
+ 'BatchNormalizationWrapper': qat_nn_layers.BatchNormalizationWrapper,
+ }
+ with tfmot.quantization.keras.quantize_scope(scope_dict):
+ annotated_backbone = tfmot.quantization.keras.quantize_annotate_model(
+ model.backbone)
+ optimized_backbone = tfmot.quantization.keras.quantize_apply(
+ annotated_backbone,
+ scheme=schemes.Default8BitQuantizeScheme())
+ decoder = model.decoder
+ if quantization.quantize_detection_decoder:
+ if not isinstance(decoder, fpn.FPN):
+ raise ValueError('Currently only supports FPN.')
+
+ decoder = tf.keras.models.clone_model(
+ decoder,
+ clone_function=_clone_function_for_fpn,
+ )
+ decoder = tfmot.quantization.keras.quantize_apply(decoder)
+ decoder = tfmot.quantization.keras.remove_input_range(decoder)
+
+ head = model.head
+ if quantization.quantize_detection_head:
+ if not isinstance(head, dense_prediction_heads.RetinaNetHead):
+ raise ValueError('Currently only supports RetinaNetHead.')
+ head = (
+ dense_prediction_heads_qat.RetinaNetHeadQuantized.from_config(
+ head.get_config()))
+
+ optimized_model = retinanet_model.RetinaNetModel(
+ optimized_backbone,
+ decoder,
+ head,
+ model.detection_generator,
+ min_level=model_config.min_level,
+ max_level=model_config.max_level,
+ num_scales=model_config.anchor.num_scales,
+ aspect_ratios=model_config.anchor.aspect_ratios,
+ anchor_size=model_config.anchor.anchor_size)
+
+ if quantization.quantize_detection_head:
+ # Call the model with dummy input to build the head part.
+ dummpy_input = tf.zeros([1] + model_config.input_size)
+ optimized_model(dummpy_input, training=True)
+ helper.copy_original_weights(model.head, optimized_model.head)
+ return optimized_model
+
+
+def build_qat_segmentation_model(
+ model: tf.keras.Model, quantization: common.Quantization,
+ input_specs: tf.keras.layers.InputSpec) -> tf.keras.Model:
+ """Applies quantization aware training for segmentation model.
+
+ Args:
+ model: The model applying quantization aware training.
+ quantization: The Quantization config.
+ input_specs: The shape specifications of input tensor.
+
+ Returns:
+ The model that applied optimization techniques.
+ """
+
+ original_checkpoint = quantization.pretrained_original_checkpoint
+ if original_checkpoint is not None:
+ ckpt = tf.train.Checkpoint(model=model, **model.checkpoint_items)
+ status = ckpt.read(original_checkpoint)
+ status.expect_partial().assert_existing_objects_matched()
+
+ # Build quantization compatible model.
+ model = qat_segmentation_model.SegmentationModelQuantized(
+ model.backbone, model.decoder, model.head, input_specs)
+
+ scope_dict = {
+ 'L2': tf.keras.regularizers.l2,
+ }
+
+ # Apply QAT to backbone (a tf.keras.Model) first.
+ with tfmot.quantization.keras.quantize_scope(scope_dict):
+ annotated_backbone = tfmot.quantization.keras.quantize_annotate_model(
+ model.backbone)
+ optimized_backbone = tfmot.quantization.keras.quantize_apply(
+ annotated_backbone, scheme=schemes.Default8BitQuantizeScheme())
+ backbone_optimized_model = qat_segmentation_model.SegmentationModelQuantized(
+ optimized_backbone, model.decoder, model.head, input_specs)
+
+ # Copy over all remaining layers.
+ for from_layer, to_layer in zip(model.layers,
+ backbone_optimized_model.layers):
+ if from_layer != model.backbone:
+ to_layer.set_weights(from_layer.get_weights())
+
+ with tfmot.quantization.keras.quantize_scope(scope_dict):
+
+ def apply_quantization_to_layers(layer):
+ if isinstance(layer, (segmentation_heads.SegmentationHead,
+ nn_layers.SpatialPyramidPooling, aspp.ASPP)):
+ return tfmot.quantization.keras.quantize_annotate_layer(layer)
+ return layer
+
+ annotated_model = tf.keras.models.clone_model(
+ backbone_optimized_model,
+ clone_function=apply_quantization_to_layers,
+ )
+ optimized_model = tfmot.quantization.keras.quantize_apply(
+ annotated_model, scheme=schemes.Default8BitQuantizeScheme())
+
+ return optimized_model
diff --git a/official/projects/qat/vision/modeling/factory_test.py b/official/projects/qat/vision/modeling/factory_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..ae7aa90c7cbe9557841ec36df3a3190b0d6227b0
--- /dev/null
+++ b/official/projects/qat/vision/modeling/factory_test.py
@@ -0,0 +1,251 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for factory.py."""
+
+# Import libraries
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.qat.vision.configs import common
+from official.projects.qat.vision.modeling import factory as qat_factory
+from official.projects.qat.vision.modeling.heads import dense_prediction_heads as qat_dense_prediction_heads
+from official.vision.configs import backbones
+from official.vision.configs import decoders
+from official.vision.configs import image_classification as classification_cfg
+from official.vision.configs import retinanet as retinanet_cfg
+from official.vision.configs import semantic_segmentation as semantic_segmentation_cfg
+from official.vision.modeling import factory
+from official.vision.modeling.decoders import fpn
+from official.vision.modeling.heads import dense_prediction_heads
+
+
+class ClassificationModelBuilderTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ ('resnet', (224, 224), 5e-5),
+ ('resnet', (224, 224), None),
+ ('resnet', (None, None), 5e-5),
+ ('resnet', (None, None), None),
+ ('mobilenet', (224, 224), 5e-5),
+ ('mobilenet', (224, 224), None),
+ ('mobilenet', (None, None), 5e-5),
+ ('mobilenet', (None, None), None),
+ )
+ def test_builder(self, backbone_type, input_size, weight_decay):
+ num_classes = 2
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None, input_size[0], input_size[1], 3])
+ model_config = classification_cfg.ImageClassificationModel(
+ num_classes=num_classes,
+ backbone=backbones.Backbone(type=backbone_type))
+ l2_regularizer = (
+ tf.keras.regularizers.l2(weight_decay) if weight_decay else None)
+ model = factory.build_classification_model(
+ input_specs=input_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ quantization_config = common.Quantization()
+ _ = qat_factory.build_qat_classification_model(
+ model=model,
+ input_specs=input_specs,
+ quantization=quantization_config,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+
+class RetinaNetBuilderTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ ('spinenet_mobile', 'identity', (640, 640), False, False),
+ ('spinenet_mobile', 'identity', (640, 640), True, False),
+ ('mobilenet', 'fpn', (640, 640), True, False),
+ ('mobilenet', 'fpn', (640, 640), True, True),
+ )
+ def test_builder(self,
+ backbone_type,
+ decoder_type,
+ input_size,
+ quantize_detection_head,
+ quantize_detection_decoder):
+ num_classes = 2
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None, input_size[0], input_size[1], 3])
+
+ if backbone_type == 'spinenet_mobile':
+ backbone_config = backbones.Backbone(
+ type=backbone_type,
+ spinenet_mobile=backbones.SpineNetMobile(
+ model_id='49',
+ stochastic_depth_drop_rate=0.2,
+ min_level=3,
+ max_level=7,
+ use_keras_upsampling_2d=True))
+ elif backbone_type == 'mobilenet':
+ backbone_config = backbones.Backbone(
+ type=backbone_type,
+ mobilenet=backbones.MobileNet(
+ model_id='MobileNetV2',
+ filter_size_scale=1.0))
+ else:
+ raise ValueError(
+ 'backbone_type {} is not supported'.format(backbone_type))
+
+ if decoder_type == 'identity':
+ decoder_config = decoders.Decoder(type=decoder_type)
+ elif decoder_type == 'fpn':
+ decoder_config = decoders.Decoder(
+ type=decoder_type,
+ fpn=decoders.FPN(
+ num_filters=128,
+ use_separable_conv=True,
+ use_keras_layer=True))
+ else:
+ raise ValueError(
+ 'decoder_type {} is not supported'.format(decoder_type))
+
+ model_config = retinanet_cfg.RetinaNet(
+ num_classes=num_classes,
+ input_size=[input_size[0], input_size[1], 3],
+ backbone=backbone_config,
+ decoder=decoder_config,
+ head=retinanet_cfg.RetinaNetHead(
+ attribute_heads=None,
+ use_separable_conv=True))
+
+ l2_regularizer = tf.keras.regularizers.l2(5e-5)
+ # Build the original float32 retinanet model.
+ model = factory.build_retinanet(
+ input_specs=input_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+
+ # Call the model with dummy input to build the head part.
+ dummpy_input = tf.zeros([1] + model_config.input_size)
+ model(dummpy_input, training=True)
+
+ # Build the QAT model from the original model with quantization config.
+ qat_model = qat_factory.build_qat_retinanet(
+ model=model,
+ quantization=common.Quantization(
+ quantize_detection_decoder=quantize_detection_decoder,
+ quantize_detection_head=quantize_detection_head),
+ model_config=model_config)
+
+ if quantize_detection_head:
+ # head become a RetinaNetHeadQuantized when we apply quantization.
+ self.assertIsInstance(qat_model.head,
+ qat_dense_prediction_heads.RetinaNetHeadQuantized)
+ else:
+ # head is a RetinaNetHead if we don't apply quantization on head part.
+ self.assertIsInstance(
+ qat_model.head, dense_prediction_heads.RetinaNetHead)
+ self.assertNotIsInstance(
+ qat_model.head, qat_dense_prediction_heads.RetinaNetHeadQuantized)
+
+ if decoder_type == 'FPN':
+ if quantize_detection_decoder:
+ # FPN decoder become a general keras functional model after applying
+ # quantization.
+ self.assertNotIsInstance(qat_model.decoder, fpn.FPN)
+ else:
+ self.assertIsInstance(qat_model.decoder, fpn.FPN)
+
+
+class SegmentationModelBuilderTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ ('mobilenet', (512, 512), 5e-5),)
+ def test_deeplabv3_builder(self, backbone_type, input_size, weight_decay):
+ num_classes = 21
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None, input_size[0], input_size[1], 3])
+ model_config = semantic_segmentation_cfg.SemanticSegmentationModel(
+ num_classes=num_classes,
+ backbone=backbones.Backbone(
+ type=backbone_type,
+ mobilenet=backbones.MobileNet(
+ model_id='MobileNetV2', output_stride=16)),
+ decoder=decoders.Decoder(
+ type='aspp',
+ aspp=decoders.ASPP(
+ level=4,
+ num_filters=256,
+ dilation_rates=[],
+ spp_layer_version='v1',
+ output_tensor=True)),
+ head=semantic_segmentation_cfg.SegmentationHead(
+ level=4,
+ low_level=2,
+ num_convs=1,
+ upsample_factor=2,
+ use_depthwise_convolution=True))
+ l2_regularizer = (
+ tf.keras.regularizers.l2(weight_decay) if weight_decay else None)
+ model = factory.build_segmentation_model(
+ input_specs=input_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+ quantization_config = common.Quantization()
+ _ = qat_factory.build_qat_segmentation_model(
+ model=model, quantization=quantization_config, input_specs=input_specs)
+
+ @parameterized.parameters(
+ ('mobilenet', (512, 1024), 5e-5),)
+ def test_deeplabv3plus_builder(self, backbone_type, input_size, weight_decay):
+ num_classes = 19
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None, input_size[0], input_size[1], 3])
+ model_config = semantic_segmentation_cfg.SemanticSegmentationModel(
+ num_classes=num_classes,
+ backbone=backbones.Backbone(
+ type=backbone_type,
+ mobilenet=backbones.MobileNet(
+ model_id='MobileNetV2',
+ output_stride=16,
+ output_intermediate_endpoints=True)),
+ decoder=decoders.Decoder(
+ type='aspp',
+ aspp=decoders.ASPP(
+ level=4,
+ num_filters=256,
+ dilation_rates=[],
+ pool_kernel_size=[512, 1024],
+ use_depthwise_convolution=False,
+ spp_layer_version='v1',
+ output_tensor=True)),
+ head=semantic_segmentation_cfg.SegmentationHead(
+ level=4,
+ num_convs=2,
+ feature_fusion='deeplabv3plus',
+ use_depthwise_convolution=True,
+ low_level='2/depthwise',
+ low_level_num_filters=48,
+ prediction_kernel_size=1,
+ upsample_factor=1,
+ num_filters=256))
+ l2_regularizer = (
+ tf.keras.regularizers.l2(weight_decay) if weight_decay else None)
+ model = factory.build_segmentation_model(
+ input_specs=input_specs,
+ model_config=model_config,
+ l2_regularizer=l2_regularizer)
+ quantization_config = common.Quantization()
+ _ = qat_factory.build_qat_segmentation_model(
+ model=model, quantization=quantization_config, input_specs=input_specs)
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/modeling/heads/__init__.py b/official/projects/qat/vision/modeling/heads/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..a7216cab7dc4f51486c6ef516a081d841e1d174e
--- /dev/null
+++ b/official/projects/qat/vision/modeling/heads/__init__.py
@@ -0,0 +1,18 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Lint as: python3
+"""Heads package definition."""
+
+from official.projects.qat.vision.modeling.heads.dense_prediction_heads import RetinaNetHeadQuantized
diff --git a/official/projects/qat/vision/modeling/heads/dense_prediction_heads.py b/official/projects/qat/vision/modeling/heads/dense_prediction_heads.py
new file mode 100644
index 0000000000000000000000000000000000000000..9ffe46f68284f24067506a6b81f8f8d3a5e3595f
--- /dev/null
+++ b/official/projects/qat/vision/modeling/heads/dense_prediction_heads.py
@@ -0,0 +1,438 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains definitions of dense prediction heads."""
+from __future__ import annotations
+
+import copy
+from typing import Any, Dict, List, Mapping, Optional, Union, Type
+
+# Import libraries
+
+import numpy as np
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.modeling import tf_utils
+from official.projects.qat.vision.quantization import configs
+from official.projects.qat.vision.quantization import helper
+
+
+class SeparableConv2DQuantized(tf.keras.layers.Layer):
+ """Quantized SeperableConv2D."""
+
+ def __init__(self,
+ name: Optional[str] = None,
+ last_quantize: bool = False,
+ **conv_kwargs):
+ """Initializes a SeparableConv2DQuantized.
+
+ Args:
+ name: The name of the layer.
+ last_quantize: A `bool` indicates whether add quantization for the output.
+ **conv_kwargs: A keyword arguments to be used for conv and dwconv.
+ """
+
+ super().__init__(name=name)
+ self._conv_kwargs = copy.deepcopy(conv_kwargs)
+ self._name = name
+ self._last_quantize = last_quantize
+
+ def build(self, input_shape: Union[tf.TensorShape, List[tf.TensorShape]]):
+ """Creates the child layers of the layer."""
+ depthwise_conv2d_quantized = helper.quantize_wrapped_layer(
+ tf.keras.layers.DepthwiseConv2D,
+ configs.Default8BitConvQuantizeConfig(
+ ['depthwise_kernel'], [], True))
+ conv2d_quantized = helper.quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.Default8BitConvQuantizeConfig(
+ ['kernel'], [], self._last_quantize))
+
+ dwconv_kwargs = self._conv_kwargs.copy()
+ # Depthwise conv input filters is always equal to output filters.
+ # This filters argument only needed for the point-wise conv2d op.
+ del dwconv_kwargs['filters']
+ dwconv_kwargs.update({
+ 'activation': None,
+ 'use_bias': False,
+ })
+ self.dw_conv = depthwise_conv2d_quantized(name='dw', **dwconv_kwargs)
+
+ conv_kwargs = self._conv_kwargs.copy()
+ conv_kwargs.update({
+ 'kernel_size': (1, 1),
+ 'strides': (1, 1),
+ 'padding': 'valid',
+ 'groups': 1,
+ })
+
+ self.conv = conv2d_quantized(name='pw', **conv_kwargs)
+
+ def call(self, inputs: tf.Tensor) -> tf.Tensor:
+ """Call the separable conv layer."""
+ x = self.dw_conv(inputs)
+ outputs = self.conv(x)
+ return outputs
+
+ def get_config(self) -> Dict[str, Any]:
+ """Returns the config of the layer."""
+ config = self._conv_kwargs.copy()
+ config.update({
+ 'name': self._name,
+ 'last_quantize': self._last_quantize,
+ })
+ return config
+
+ @classmethod
+ def from_config(
+ cls: Type[SeparableConv2DQuantized],
+ config: Dict[str, Any]) -> SeparableConv2DQuantized:
+ """Creates a layer from its config."""
+ return cls(**config)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class RetinaNetHeadQuantized(tf.keras.layers.Layer):
+ """Creates a RetinaNet quantized head."""
+
+ def __init__(
+ self,
+ min_level: int,
+ max_level: int,
+ num_classes: int,
+ num_anchors_per_location: int,
+ num_convs: int = 4,
+ num_filters: int = 256,
+ attribute_heads: Optional[List[Dict[str, Any]]] = None,
+ use_separable_conv: bool = False,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ num_params_per_anchor: int = 4,
+ share_classification_heads: bool = False,
+ **kwargs):
+ """Initializes a RetinaNet quantized head.
+
+ Args:
+ min_level: An `int` number of minimum feature level.
+ max_level: An `int` number of maximum feature level.
+ num_classes: An `int` number of classes to predict.
+ num_anchors_per_location: An `int` number of number of anchors per pixel
+ location.
+ num_convs: An `int` number that represents the number of the intermediate
+ conv layers before the prediction.
+ num_filters: An `int` number that represents the number of filters of the
+ intermediate conv layers.
+ attribute_heads: If not None, a list that contains a dict for each
+ additional attribute head. Each dict consists of 3 key-value pairs:
+ `name`, `type` ('regression' or 'classification'), and `size` (number
+ of predicted values for each instance).
+ use_separable_conv: A `bool` that indicates whether the separable
+ convolution layers is used.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ num_params_per_anchor: Number of parameters required to specify an anchor
+ box. For example, `num_params_per_anchor` would be 4 for axis-aligned
+ anchor boxes specified by their y-centers, x-centers, heights, and
+ widths.
+ share_classification_heads: A `bool` that indicates whethere
+ sharing weights among the main and attribute classification heads. Not
+ used in the QAT model.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ del share_classification_heads
+
+ super().__init__(**kwargs)
+ self._config_dict = {
+ 'min_level': min_level,
+ 'max_level': max_level,
+ 'num_classes': num_classes,
+ 'num_anchors_per_location': num_anchors_per_location,
+ 'num_convs': num_convs,
+ 'num_filters': num_filters,
+ 'attribute_heads': attribute_heads,
+ 'use_separable_conv': use_separable_conv,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'norm_momentum': norm_momentum,
+ 'norm_epsilon': norm_epsilon,
+ 'kernel_regularizer': kernel_regularizer,
+ 'bias_regularizer': bias_regularizer,
+ 'num_params_per_anchor': num_params_per_anchor,
+ }
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._activation = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ def build(self, input_shape: Union[tf.TensorShape, List[tf.TensorShape]]):
+ """Creates the variables of the head."""
+ if self._config_dict['use_separable_conv']:
+ conv_op = SeparableConv2DQuantized
+ else:
+ conv_op = helper.quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.Default8BitConvQuantizeConfig(
+ ['kernel'], ['activation'], False))
+ conv_kwargs = {
+ 'filters': self._config_dict['num_filters'],
+ 'kernel_size': 3,
+ 'padding': 'same',
+ 'bias_initializer': tf.zeros_initializer(),
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ }
+ if not self._config_dict['use_separable_conv']:
+ conv_kwargs.update({
+ 'kernel_initializer': tf.keras.initializers.RandomNormal(
+ stddev=0.01),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ })
+
+ base_bn_op = (tf.keras.layers.experimental.SyncBatchNormalization
+ if self._config_dict['use_sync_bn']
+ else tf.keras.layers.BatchNormalization)
+ bn_op = helper.norm_by_activation(
+ self._config_dict['activation'],
+ helper.quantize_wrapped_layer(
+ base_bn_op, configs.Default8BitOutputQuantizeConfig()),
+ helper.quantize_wrapped_layer(
+ base_bn_op, configs.NoOpQuantizeConfig()))
+
+ bn_kwargs = {
+ 'axis': self._bn_axis,
+ 'momentum': self._config_dict['norm_momentum'],
+ 'epsilon': self._config_dict['norm_epsilon'],
+ }
+
+ # Class net.
+ self._cls_convs = []
+ self._cls_norms = []
+ for level in range(
+ self._config_dict['min_level'], self._config_dict['max_level'] + 1):
+ this_level_cls_norms = []
+ for i in range(self._config_dict['num_convs']):
+ if level == self._config_dict['min_level']:
+ cls_conv_name = 'classnet-conv_{}'.format(i)
+ self._cls_convs.append(conv_op(name=cls_conv_name, **conv_kwargs))
+ cls_norm_name = 'classnet-conv-norm_{}_{}'.format(level, i)
+ this_level_cls_norms.append(bn_op(name=cls_norm_name, **bn_kwargs))
+ self._cls_norms.append(this_level_cls_norms)
+
+ classifier_kwargs = {
+ 'filters': (
+ self._config_dict['num_classes'] *
+ self._config_dict['num_anchors_per_location']),
+ 'kernel_size': 3,
+ 'padding': 'same',
+ 'bias_initializer': tf.constant_initializer(-np.log((1 - 0.01) / 0.01)),
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ }
+ if not self._config_dict['use_separable_conv']:
+ classifier_kwargs.update({
+ 'kernel_initializer': tf.keras.initializers.RandomNormal(stddev=1e-5),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ })
+ self._classifier = conv_op(
+ name='scores', last_quantize=True, **classifier_kwargs)
+
+ # Box net.
+ self._box_convs = []
+ self._box_norms = []
+ for level in range(
+ self._config_dict['min_level'], self._config_dict['max_level'] + 1):
+ this_level_box_norms = []
+ for i in range(self._config_dict['num_convs']):
+ if level == self._config_dict['min_level']:
+ box_conv_name = 'boxnet-conv_{}'.format(i)
+ self._box_convs.append(conv_op(name=box_conv_name, **conv_kwargs))
+ box_norm_name = 'boxnet-conv-norm_{}_{}'.format(level, i)
+ this_level_box_norms.append(bn_op(name=box_norm_name, **bn_kwargs))
+ self._box_norms.append(this_level_box_norms)
+
+ box_regressor_kwargs = {
+ 'filters': (self._config_dict['num_params_per_anchor'] *
+ self._config_dict['num_anchors_per_location']),
+ 'kernel_size': 3,
+ 'padding': 'same',
+ 'bias_initializer': tf.zeros_initializer(),
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ }
+ if not self._config_dict['use_separable_conv']:
+ box_regressor_kwargs.update({
+ 'kernel_initializer': tf.keras.initializers.RandomNormal(
+ stddev=1e-5),
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ })
+ self._box_regressor = conv_op(
+ name='boxes', last_quantize=True, **box_regressor_kwargs)
+
+ # Attribute learning nets.
+ if self._config_dict['attribute_heads']:
+ self._att_predictors = {}
+ self._att_convs = {}
+ self._att_norms = {}
+
+ for att_config in self._config_dict['attribute_heads']:
+ att_name = att_config['name']
+ att_type = att_config['type']
+ att_size = att_config['size']
+ att_convs_i = []
+ att_norms_i = []
+
+ # Build conv and norm layers.
+ for level in range(self._config_dict['min_level'],
+ self._config_dict['max_level'] + 1):
+ this_level_att_norms = []
+ for i in range(self._config_dict['num_convs']):
+ if level == self._config_dict['min_level']:
+ att_conv_name = '{}-conv_{}'.format(att_name, i)
+ att_convs_i.append(conv_op(name=att_conv_name, **conv_kwargs))
+ att_norm_name = '{}-conv-norm_{}_{}'.format(att_name, level, i)
+ this_level_att_norms.append(bn_op(name=att_norm_name, **bn_kwargs))
+ att_norms_i.append(this_level_att_norms)
+ self._att_convs[att_name] = att_convs_i
+ self._att_norms[att_name] = att_norms_i
+
+ # Build the final prediction layer.
+ att_predictor_kwargs = {
+ 'filters':
+ (att_size * self._config_dict['num_anchors_per_location']),
+ 'kernel_size': 3,
+ 'padding': 'same',
+ 'bias_initializer': tf.zeros_initializer(),
+ 'bias_regularizer': self._config_dict['bias_regularizer'],
+ }
+ if att_type == 'regression':
+ att_predictor_kwargs.update(
+ {'bias_initializer': tf.zeros_initializer()})
+ elif att_type == 'classification':
+ att_predictor_kwargs.update({
+ 'bias_initializer':
+ tf.constant_initializer(-np.log((1 - 0.01) / 0.01))
+ })
+ else:
+ raise ValueError(
+ 'Attribute head type {} not supported.'.format(att_type))
+
+ if not self._config_dict['use_separable_conv']:
+ att_predictor_kwargs.update({
+ 'kernel_initializer':
+ tf.keras.initializers.RandomNormal(stddev=1e-5),
+ 'kernel_regularizer':
+ self._config_dict['kernel_regularizer'],
+ })
+
+ self._att_predictors[att_name] = conv_op(
+ name='{}_attributes'.format(att_name), **att_predictor_kwargs)
+
+ super().build(input_shape)
+
+ def call(self, features: Mapping[str, tf.Tensor]):
+ """Forward pass of the RetinaNet quantized head.
+
+ Args:
+ features: A `dict` of `tf.Tensor` where
+ - key: A `str` of the level of the multilevel features.
+ - values: A `tf.Tensor`, the feature map tensors, whose shape is
+ [batch, height_l, width_l, channels].
+
+ Returns:
+ scores: A `dict` of `tf.Tensor` which includes scores of the predictions.
+ - key: A `str` of the level of the multilevel predictions.
+ - values: A `tf.Tensor` of the box scores predicted from a particular
+ feature level, whose shape is
+ [batch, height_l, width_l, num_classes * num_anchors_per_location].
+ boxes: A `dict` of `tf.Tensor` which includes coordinates of the
+ predictions.
+ - key: A `str` of the level of the multilevel predictions.
+ - values: A `tf.Tensor` of the box scores predicted from a particular
+ feature level, whose shape is
+ [batch, height_l, width_l,
+ num_params_per_anchor * num_anchors_per_location].
+ attributes: a dict of (attribute_name, attribute_prediction). Each
+ `attribute_prediction` is a dict of:
+ - key: `str`, the level of the multilevel predictions.
+ - values: `Tensor`, the box scores predicted from a particular feature
+ level, whose shape is
+ [batch, height_l, width_l,
+ attribute_size * num_anchors_per_location].
+ Can be an empty dictionary if no attribute learning is required.
+ """
+ scores = {}
+ boxes = {}
+ if self._config_dict['attribute_heads']:
+ attributes = {
+ att_config['name']: {}
+ for att_config in self._config_dict['attribute_heads']
+ }
+ else:
+ attributes = {}
+
+ for i, level in enumerate(
+ range(self._config_dict['min_level'],
+ self._config_dict['max_level'] + 1)):
+ this_level_features = features[str(level)]
+
+ # class net.
+ x = this_level_features
+ for conv, norm in zip(self._cls_convs, self._cls_norms[i]):
+ x = conv(x)
+ x = norm(x)
+ x = self._activation(x)
+ scores[str(level)] = self._classifier(x)
+
+ # box net.
+ x = this_level_features
+ for conv, norm in zip(self._box_convs, self._box_norms[i]):
+ x = conv(x)
+ x = norm(x)
+ x = self._activation(x)
+ boxes[str(level)] = self._box_regressor(x)
+
+ # attribute nets.
+ if self._config_dict['attribute_heads']:
+ for att_config in self._config_dict['attribute_heads']:
+ att_name = att_config['name']
+ x = this_level_features
+ for conv, norm in zip(self._att_convs[att_name],
+ self._att_norms[att_name][i]):
+ x = conv(x)
+ x = norm(x)
+ x = self._activation(x)
+ attributes[att_name][str(level)] = self._att_predictors[att_name](x)
+
+ return scores, boxes, attributes
+
+ def get_config(self):
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
+
diff --git a/official/projects/qat/vision/modeling/heads/dense_prediction_heads_test.py b/official/projects/qat/vision/modeling/heads/dense_prediction_heads_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..911fb17b56748dea043380fe3745613ebc500fbe
--- /dev/null
+++ b/official/projects/qat/vision/modeling/heads/dense_prediction_heads_test.py
@@ -0,0 +1,92 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Lint as: python3
+"""Tests for dense_prediction_heads.py."""
+
+# Import libraries
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from official.projects.qat.vision.modeling.heads import dense_prediction_heads
+
+
+class RetinaNetHeadQuantizedTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (False, False, False),
+ (False, True, False),
+ (True, False, True),
+ (True, True, True),
+ )
+ def test_forward(self, use_separable_conv, use_sync_bn, has_att_heads):
+ if has_att_heads:
+ attribute_heads = [dict(name='depth', type='regression', size=1)]
+ else:
+ attribute_heads = None
+
+ retinanet_head = dense_prediction_heads.RetinaNetHeadQuantized(
+ min_level=3,
+ max_level=4,
+ num_classes=3,
+ num_anchors_per_location=3,
+ num_convs=2,
+ num_filters=256,
+ attribute_heads=attribute_heads,
+ use_separable_conv=use_separable_conv,
+ activation='relu',
+ use_sync_bn=use_sync_bn,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ )
+ features = {
+ '3': np.random.rand(2, 128, 128, 16),
+ '4': np.random.rand(2, 64, 64, 16),
+ }
+ scores, boxes, attributes = retinanet_head(features)
+ self.assertAllEqual(scores['3'].numpy().shape, [2, 128, 128, 9])
+ self.assertAllEqual(scores['4'].numpy().shape, [2, 64, 64, 9])
+ self.assertAllEqual(boxes['3'].numpy().shape, [2, 128, 128, 12])
+ self.assertAllEqual(boxes['4'].numpy().shape, [2, 64, 64, 12])
+ if has_att_heads:
+ for att in attributes.values():
+ self.assertAllEqual(att['3'].numpy().shape, [2, 128, 128, 3])
+ self.assertAllEqual(att['4'].numpy().shape, [2, 64, 64, 3])
+
+ def test_serialize_deserialize(self):
+ retinanet_head = dense_prediction_heads.RetinaNetHeadQuantized(
+ min_level=3,
+ max_level=7,
+ num_classes=3,
+ num_anchors_per_location=9,
+ num_convs=2,
+ num_filters=16,
+ attribute_heads=None,
+ use_separable_conv=False,
+ activation='relu',
+ use_sync_bn=False,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ )
+ config = retinanet_head.get_config()
+ new_retinanet_head = (
+ dense_prediction_heads.RetinaNetHead.from_config(config))
+ self.assertAllEqual(
+ retinanet_head.get_config(), new_retinanet_head.get_config())
+
diff --git a/official/projects/qat/vision/modeling/layers/__init__.py b/official/projects/qat/vision/modeling/layers/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..534843dd65845190da1dc2e7fa724cb6c9a7f14a
--- /dev/null
+++ b/official/projects/qat/vision/modeling/layers/__init__.py
@@ -0,0 +1,19 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Layers package definition."""
+
+from official.projects.qat.vision.modeling.layers.nn_blocks import BottleneckBlockQuantized
+from official.projects.qat.vision.modeling.layers.nn_blocks import Conv2DBNBlockQuantized
+from official.projects.qat.vision.modeling.layers.nn_blocks import InvertedBottleneckBlockQuantized
diff --git a/official/projects/qat/vision/modeling/layers/nn_blocks.py b/official/projects/qat/vision/modeling/layers/nn_blocks.py
new file mode 100644
index 0000000000000000000000000000000000000000..a5e2c14536321f8feb6c74dcfee38120db30df8b
--- /dev/null
+++ b/official/projects/qat/vision/modeling/layers/nn_blocks.py
@@ -0,0 +1,717 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains quantized neural blocks for the QAT."""
+from typing import Any, Dict, Optional, Sequence, Tuple, Union
+
+# Import libraries
+
+from absl import logging
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.modeling import tf_utils
+from official.projects.qat.vision.modeling.layers import nn_layers as qat_nn_layers
+from official.projects.qat.vision.quantization import configs
+from official.projects.qat.vision.quantization import helper
+from official.vision.modeling.layers import nn_layers
+
+
+# This class is copied from modeling.layers.nn_blocks.BottleneckBlock and apply
+# QAT.
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class BottleneckBlockQuantized(tf.keras.layers.Layer):
+ """A quantized standard bottleneck block."""
+
+ def __init__(self,
+ filters: int,
+ strides: int,
+ dilation_rate: int = 1,
+ use_projection: bool = False,
+ se_ratio: Optional[float] = None,
+ resnetd_shortcut: bool = False,
+ stochastic_depth_drop_rate: Optional[float] = None,
+ kernel_initializer: str = 'VarianceScaling',
+ kernel_regularizer: tf.keras.regularizers.Regularizer = None,
+ bias_regularizer: tf.keras.regularizers.Regularizer = None,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ bn_trainable: bool = True, # pytype: disable=annotation-type-mismatch # typed-keras
+ **kwargs):
+ """Initializes a standard bottleneck block with BN after convolutions.
+
+ Args:
+ filters: An `int` number of filters for the first two convolutions. Note
+ that the third and final convolution will use 4 times as many filters.
+ strides: An `int` block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ dilation_rate: An `int` dilation_rate of convolutions. Default to 1.
+ use_projection: A `bool` for whether this block should use a projection
+ shortcut (versus the default identity shortcut). This is usually `True`
+ for the first block of a block group, which may change the number of
+ filters and the resolution.
+ se_ratio: A `float` or None. Ratio of the Squeeze-and-Excitation layer.
+ resnetd_shortcut: A `bool`. If True, apply the resnetd style modification
+ to the shortcut connection.
+ stochastic_depth_drop_rate: A `float` or None. If not None, drop rate for
+ the stochastic depth layer.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ use_sync_bn: A `bool`. If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ bn_trainable: A `bool` that indicates whether batch norm layers should be
+ trainable. Default to True.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(BottleneckBlockQuantized, self).__init__(**kwargs)
+
+ self._filters = filters
+ self._strides = strides
+ self._dilation_rate = dilation_rate
+ self._use_projection = use_projection
+ self._se_ratio = se_ratio
+ self._resnetd_shortcut = resnetd_shortcut
+ self._use_sync_bn = use_sync_bn
+ self._activation = activation
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._kernel_initializer = kernel_initializer
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+
+ norm_layer = (
+ tf.keras.layers.experimental.SyncBatchNormalization
+ if use_sync_bn else tf.keras.layers.BatchNormalization)
+ self._norm_with_quantize = helper.BatchNormalizationQuantized(norm_layer)
+ self._norm = helper.BatchNormalizationNoQuantized(norm_layer)
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._bn_trainable = bn_trainable
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ if self._use_projection:
+ if self._resnetd_shortcut:
+ self._shortcut0 = tf.keras.layers.AveragePooling2D(
+ pool_size=2, strides=self._strides, padding='same')
+ self._shortcut1 = helper.Conv2DQuantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ else:
+ self._shortcut = helper.Conv2DQuantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=self._strides,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+
+ self._norm0 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+
+ self._conv1 = helper.Conv2DQuantized(
+ filters=self._filters,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm1 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation1 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ self._conv2 = helper.Conv2DQuantized(
+ filters=self._filters,
+ kernel_size=3,
+ strides=self._strides,
+ dilation_rate=self._dilation_rate,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm2 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation2 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ self._conv3 = helper.Conv2DQuantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm3 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation3 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ if self._se_ratio and self._se_ratio > 0 and self._se_ratio <= 1:
+ self._squeeze_excitation = qat_nn_layers.SqueezeExcitationQuantized(
+ in_filters=self._filters * 4,
+ out_filters=self._filters * 4,
+ se_ratio=self._se_ratio,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer)
+ else:
+ self._squeeze_excitation = None
+
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = nn_layers.StochasticDepth(
+ self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = None
+ self._add = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Add(),
+ configs.Default8BitQuantizeConfig([], [], True))
+
+ super(BottleneckBlockQuantized, self).build(input_shape)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'filters': self._filters,
+ 'strides': self._strides,
+ 'dilation_rate': self._dilation_rate,
+ 'use_projection': self._use_projection,
+ 'se_ratio': self._se_ratio,
+ 'resnetd_shortcut': self._resnetd_shortcut,
+ 'stochastic_depth_drop_rate': self._stochastic_depth_drop_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'bn_trainable': self._bn_trainable
+ }
+ base_config = super(BottleneckBlockQuantized, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None) -> tf.Tensor:
+ """Run the BottleneckBlockQuantized logics."""
+ shortcut = inputs
+ if self._use_projection:
+ if self._resnetd_shortcut:
+ shortcut = self._shortcut0(shortcut)
+ shortcut = self._shortcut1(shortcut)
+ else:
+ shortcut = self._shortcut(shortcut)
+ shortcut = self._norm0(shortcut)
+
+ x = self._conv1(inputs)
+ x = self._norm1(x)
+ x = self._activation1(x)
+
+ x = self._conv2(x)
+ x = self._norm2(x)
+ x = self._activation2(x)
+
+ x = self._conv3(x)
+ x = self._norm3(x)
+
+ if self._squeeze_excitation:
+ x = self._squeeze_excitation(x)
+
+ if self._stochastic_depth:
+ x = self._stochastic_depth(x, training=training)
+
+ x = self._add([x, shortcut])
+ return self._activation3(x)
+
+
+# This class is copied from modeling.backbones.mobilenet.Conv2DBNBlock and apply
+# QAT.
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class Conv2DBNBlockQuantized(tf.keras.layers.Layer):
+ """A quantized convolution block with batch normalization."""
+
+ def __init__(
+ self,
+ filters: int,
+ kernel_size: int = 3,
+ strides: int = 1,
+ use_bias: bool = False,
+ use_explicit_padding: bool = False,
+ activation: str = 'relu6',
+ kernel_initializer: str = 'VarianceScaling',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ use_normalization: bool = True,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ **kwargs):
+ """A convolution block with batch normalization.
+
+ Args:
+ filters: An `int` number of filters for the first two convolutions. Note
+ that the third and final convolution will use 4 times as many filters.
+ kernel_size: An `int` specifying the height and width of the 2D
+ convolution window.
+ strides: An `int` of block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ use_bias: If True, use bias in the convolution layer.
+ use_explicit_padding: Use 'VALID' padding for convolutions, but prepad
+ inputs so that the output dimensions are the same as if 'SAME' padding
+ were used.
+ activation: A `str` name of the activation function.
+ kernel_initializer: A `str` for kernel initializer of convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ Default to None.
+ use_normalization: If True, use batch normalization.
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(Conv2DBNBlockQuantized, self).__init__(**kwargs)
+ self._filters = filters
+ self._kernel_size = kernel_size
+ self._strides = strides
+ self._activation = activation
+ self._use_bias = use_bias
+ self._use_explicit_padding = use_explicit_padding
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._use_normalization = use_normalization
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+
+ if use_explicit_padding and kernel_size > 1:
+ self._padding = 'valid'
+ else:
+ self._padding = 'same'
+
+ norm_layer = (
+ tf.keras.layers.experimental.SyncBatchNormalization
+ if use_sync_bn else tf.keras.layers.BatchNormalization)
+ self._norm_with_quantize = helper.BatchNormalizationQuantized(norm_layer)
+ self._norm = helper.BatchNormalizationNoQuantized(norm_layer)
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'filters': self._filters,
+ 'strides': self._strides,
+ 'kernel_size': self._kernel_size,
+ 'use_bias': self._use_bias,
+ 'use_explicit_padding': self._use_explicit_padding,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'use_normalization': self._use_normalization,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon
+ }
+ base_config = super(Conv2DBNBlockQuantized, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ if self._use_explicit_padding and self._kernel_size > 1:
+ padding_size = nn_layers.get_padding_for_kernel_size(self._kernel_size)
+ self._pad = tf.keras.layers.ZeroPadding2D(padding_size)
+ conv2d_quantized = (
+ helper.Conv2DQuantized
+ if self._use_normalization else helper.Conv2DOutputQuantized)
+
+ self._conv0 = conv2d_quantized(
+ filters=self._filters,
+ kernel_size=self._kernel_size,
+ strides=self._strides,
+ padding=self._padding,
+ use_bias=self._use_bias,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ if self._use_normalization:
+ self._norm0 = helper.norm_by_activation(self._activation,
+ self._norm_with_quantize,
+ self._norm)(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+ super(Conv2DBNBlockQuantized, self).build(input_shape)
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None) -> tf.Tensor:
+ """Run the Conv2DBNBlockQuantized logics."""
+ if self._use_explicit_padding and self._kernel_size > 1:
+ inputs = self._pad(inputs)
+ x = self._conv0(inputs)
+ if self._use_normalization:
+ x = self._norm0(x)
+ return self._activation_layer(x)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class InvertedBottleneckBlockQuantized(tf.keras.layers.Layer):
+ """A quantized inverted bottleneck block."""
+
+ def __init__(self,
+ in_filters,
+ out_filters,
+ expand_ratio,
+ strides,
+ kernel_size=3,
+ se_ratio=None,
+ stochastic_depth_drop_rate=None,
+ kernel_initializer='VarianceScaling',
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activation='relu',
+ se_inner_activation='relu',
+ se_gating_activation='sigmoid',
+ se_round_down_protect=True,
+ expand_se_in_filters=False,
+ depthwise_activation=None,
+ use_sync_bn=False,
+ dilation_rate=1,
+ divisible_by=1,
+ regularize_depthwise=False,
+ use_depthwise=True,
+ use_residual=True,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ output_intermediate_endpoints=False,
+ **kwargs):
+ """Initializes an inverted bottleneck block with BN after convolutions.
+
+ Args:
+ in_filters: An `int` number of filters of the input tensor.
+ out_filters: An `int` number of filters of the output tensor.
+ expand_ratio: An `int` of expand_ratio for an inverted bottleneck block.
+ strides: An `int` block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ kernel_size: An `int` kernel_size of the depthwise conv layer.
+ se_ratio: A `float` or None. If not None, se ratio for the squeeze and
+ excitation layer.
+ stochastic_depth_drop_rate: A `float` or None. if not None, drop rate for
+ the stochastic depth layer.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ se_inner_activation: A `str` name of squeeze-excitation inner activation.
+ se_gating_activation: A `str` name of squeeze-excitation gating
+ activation.
+ se_round_down_protect: A `bool` of whether round down more than 10% will
+ be allowed in SE layer.
+ expand_se_in_filters: A `bool` of whether or not to expand in_filter in
+ squeeze and excitation layer.
+ depthwise_activation: A `str` name of the activation function for
+ depthwise only.
+ use_sync_bn: A `bool`. If True, use synchronized batch normalization.
+ dilation_rate: An `int` that specifies the dilation rate to use for.
+ divisible_by: An `int` that ensures all inner dimensions are divisible by
+ this number.
+ dilated convolution: An `int` to specify the same value for all spatial
+ dimensions.
+ regularize_depthwise: A `bool` of whether or not apply regularization on
+ depthwise.
+ use_depthwise: A `bool` of whether to uses fused convolutions instead of
+ depthwise.
+ use_residual: A `bool` of whether to include residual connection between
+ input and output.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ output_intermediate_endpoints: A `bool` of whether or not output the
+ intermediate endpoints.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super(InvertedBottleneckBlockQuantized, self).__init__(**kwargs)
+
+ self._in_filters = in_filters
+ self._out_filters = out_filters
+ self._expand_ratio = expand_ratio
+ self._strides = strides
+ self._kernel_size = kernel_size
+ self._se_ratio = se_ratio
+ self._divisible_by = divisible_by
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._dilation_rate = dilation_rate
+ self._use_sync_bn = use_sync_bn
+ self._regularize_depthwise = regularize_depthwise
+ self._use_depthwise = use_depthwise
+ self._use_residual = use_residual
+ self._activation = activation
+ self._se_inner_activation = se_inner_activation
+ self._se_gating_activation = se_gating_activation
+ self._se_round_down_protect = se_round_down_protect
+ self._depthwise_activation = depthwise_activation
+ self._kernel_initializer = kernel_initializer
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._expand_se_in_filters = expand_se_in_filters
+ self._output_intermediate_endpoints = output_intermediate_endpoints
+
+ norm_layer = (
+ tf.keras.layers.experimental.SyncBatchNormalization
+ if use_sync_bn else tf.keras.layers.BatchNormalization)
+ self._norm_with_quantize = helper.BatchNormalizationQuantized(norm_layer)
+ self._norm = helper.BatchNormalizationNoQuantized(norm_layer)
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ if not depthwise_activation:
+ self._depthwise_activation = activation
+ if regularize_depthwise:
+ self._depthsize_regularizer = kernel_regularizer
+ else:
+ self._depthsize_regularizer = None
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ expand_filters = self._in_filters
+ if self._expand_ratio > 1:
+ # First 1x1 conv for channel expansion.
+ expand_filters = nn_layers.make_divisible(
+ self._in_filters * self._expand_ratio, self._divisible_by)
+
+ expand_kernel = 1 if self._use_depthwise else self._kernel_size
+ expand_stride = 1 if self._use_depthwise else self._strides
+
+ self._conv0 = helper.Conv2DQuantized(
+ filters=expand_filters,
+ kernel_size=expand_kernel,
+ strides=expand_stride,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm0 = helper.norm_by_activation(self._activation,
+ self._norm_with_quantize,
+ self._norm)(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+ if self._use_depthwise:
+ # Depthwise conv.
+ self._conv1 = helper.DepthwiseConv2DQuantized(
+ kernel_size=(self._kernel_size, self._kernel_size),
+ strides=self._strides,
+ padding='same',
+ depth_multiplier=1,
+ dilation_rate=self._dilation_rate,
+ use_bias=False,
+ depthwise_initializer=self._kernel_initializer,
+ depthwise_regularizer=self._depthsize_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm1 = helper.norm_by_activation(self._depthwise_activation,
+ self._norm_with_quantize,
+ self._norm)(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._depthwise_activation_layer = (
+ tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._depthwise_activation,
+ use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig()))
+
+ # Squeeze and excitation.
+ if self._se_ratio and self._se_ratio > 0 and self._se_ratio <= 1:
+ logging.info('Use Squeeze and excitation.')
+ in_filters = self._in_filters
+ if self._expand_se_in_filters:
+ in_filters = expand_filters
+ self._squeeze_excitation = qat_nn_layers.SqueezeExcitationQuantized(
+ in_filters=in_filters,
+ out_filters=expand_filters,
+ se_ratio=self._se_ratio,
+ divisible_by=self._divisible_by,
+ round_down_protect=self._se_round_down_protect,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=self._se_inner_activation,
+ gating_activation=self._se_gating_activation)
+ else:
+ self._squeeze_excitation = None
+
+ # Last 1x1 conv.
+ self._conv2 = helper.Conv2DQuantized(
+ filters=self._out_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+ self._norm2 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = nn_layers.StochasticDepth(
+ self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = None
+ self._add = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Add(),
+ configs.Default8BitQuantizeConfig([], [], True))
+
+ super(InvertedBottleneckBlockQuantized, self).build(input_shape)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'in_filters': self._in_filters,
+ 'out_filters': self._out_filters,
+ 'expand_ratio': self._expand_ratio,
+ 'strides': self._strides,
+ 'kernel_size': self._kernel_size,
+ 'se_ratio': self._se_ratio,
+ 'divisible_by': self._divisible_by,
+ 'stochastic_depth_drop_rate': self._stochastic_depth_drop_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'se_inner_activation': self._se_inner_activation,
+ 'se_gating_activation': self._se_gating_activation,
+ 'se_round_down_protect': self._se_round_down_protect,
+ 'expand_se_in_filters': self._expand_se_in_filters,
+ 'depthwise_activation': self._depthwise_activation,
+ 'dilation_rate': self._dilation_rate,
+ 'use_sync_bn': self._use_sync_bn,
+ 'regularize_depthwise': self._regularize_depthwise,
+ 'use_depthwise': self._use_depthwise,
+ 'use_residual': self._use_residual,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'output_intermediate_endpoints': self._output_intermediate_endpoints
+ }
+ base_config = super(InvertedBottleneckBlockQuantized, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None
+ ) -> Union[tf.Tensor, Tuple[tf.Tensor, Dict[str, tf.Tensor]]]:
+ """Run the InvertedBottleneckBlockQuantized logics."""
+ endpoints = {}
+ shortcut = inputs
+ if self._expand_ratio > 1:
+ x = self._conv0(inputs)
+ x = self._norm0(x)
+ x = self._activation_layer(x)
+ else:
+ x = inputs
+
+ if self._use_depthwise:
+ x = self._conv1(x)
+ x = self._norm1(x)
+ x = self._depthwise_activation_layer(x)
+ if self._output_intermediate_endpoints:
+ endpoints['depthwise'] = x
+
+ if self._squeeze_excitation:
+ x = self._squeeze_excitation(x)
+
+ x = self._conv2(x)
+ x = self._norm2(x)
+
+ if (self._use_residual and self._in_filters == self._out_filters and
+ self._strides == 1):
+ if self._stochastic_depth:
+ x = self._stochastic_depth(x, training=training)
+ x = self._add([x, shortcut])
+
+ if self._output_intermediate_endpoints:
+ return x, endpoints
+ return x
diff --git a/official/projects/qat/vision/modeling/layers/nn_blocks_test.py b/official/projects/qat/vision/modeling/layers/nn_blocks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..be7389b7aedf2b62337bd84fd07d0db757738dfa
--- /dev/null
+++ b/official/projects/qat/vision/modeling/layers/nn_blocks_test.py
@@ -0,0 +1,95 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for nn_blocks."""
+
+from typing import Any, Iterable, Tuple
+# Import libraries
+from absl.testing import parameterized
+import tensorflow as tf
+
+from tensorflow.python.distribute import combinations
+from tensorflow.python.distribute import strategy_combinations
+from official.projects.qat.vision.modeling.layers import nn_blocks
+
+
+def distribution_strategy_combinations() -> Iterable[Tuple[Any, ...]]:
+ """Returns the combinations of end-to-end tests to run."""
+ return combinations.combine(
+ distribution=[
+ strategy_combinations.default_strategy,
+ strategy_combinations.cloud_tpu_strategy,
+ strategy_combinations.one_device_strategy_gpu,
+ ],
+ )
+
+
+class NNBlocksTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (nn_blocks.BottleneckBlockQuantized, 1, False, 0.0, None),
+ (nn_blocks.BottleneckBlockQuantized, 2, True, 0.2, 0.25),
+ )
+ def test_bottleneck_block_creation(self, block_fn, strides, use_projection,
+ stochastic_depth_drop_rate, se_ratio):
+ input_size = 128
+ filter_size = 256
+ inputs = tf.keras.Input(
+ shape=(input_size, input_size, filter_size * 4), batch_size=1)
+ block = block_fn(
+ filter_size,
+ strides,
+ use_projection=use_projection,
+ se_ratio=se_ratio,
+ stochastic_depth_drop_rate=stochastic_depth_drop_rate)
+
+ features = block(inputs)
+
+ self.assertAllEqual(
+ [1, input_size // strides, input_size // strides, filter_size * 4],
+ features.shape.as_list())
+
+ @parameterized.parameters(
+ (nn_blocks.InvertedBottleneckBlockQuantized, 1, 1, None, None),
+ (nn_blocks.InvertedBottleneckBlockQuantized, 6, 1, None, None),
+ (nn_blocks.InvertedBottleneckBlockQuantized, 1, 2, None, None),
+ (nn_blocks.InvertedBottleneckBlockQuantized, 1, 1, 0.2, None),
+ (nn_blocks.InvertedBottleneckBlockQuantized, 1, 1, None, 0.2),
+ )
+ def test_invertedbottleneck_block_creation(
+ self, block_fn, expand_ratio, strides, se_ratio,
+ stochastic_depth_drop_rate):
+ input_size = 128
+ in_filters = 24
+ out_filters = 40
+ inputs = tf.keras.Input(
+ shape=(input_size, input_size, in_filters), batch_size=1)
+ block = block_fn(
+ in_filters=in_filters,
+ out_filters=out_filters,
+ expand_ratio=expand_ratio,
+ strides=strides,
+ se_ratio=se_ratio,
+ stochastic_depth_drop_rate=stochastic_depth_drop_rate,
+ output_intermediate_endpoints=False)
+
+ features = block(inputs)
+
+ self.assertAllEqual(
+ [1, input_size // strides, input_size // strides, out_filters],
+ features.shape.as_list())
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/modeling/layers/nn_layers.py b/official/projects/qat/vision/modeling/layers/nn_layers.py
new file mode 100644
index 0000000000000000000000000000000000000000..139432de61f67325123065a9d07074a427962310
--- /dev/null
+++ b/official/projects/qat/vision/modeling/layers/nn_layers.py
@@ -0,0 +1,794 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains common building blocks for neural networks."""
+
+import enum
+from typing import Callable, Dict, List, Mapping, Optional, Sequence, Tuple, Union, Any
+
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.modeling import tf_utils
+from official.projects.qat.vision.quantization import configs
+from official.projects.qat.vision.quantization import helper
+from official.vision.modeling.decoders import aspp
+from official.vision.modeling.layers import nn_layers
+
+
+# Type annotations.
+States = Dict[str, tf.Tensor]
+Activation = Union[str, Callable]
+
+
+# String constants.
+class FeatureFusion(str, enum.Enum):
+ PYRAMID_FUSION = 'pyramid_fusion'
+ PANOPTIC_FPN_FUSION = 'panoptic_fpn_fusion'
+ DEEPLABV3PLUS = 'deeplabv3plus'
+ DEEPLABV3PLUS_SUM_TO_MERGE = 'deeplabv3plus_sum_to_merge'
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SqueezeExcitationQuantized(
+ helper.LayerQuantizerHelper,
+ tf.keras.layers.Layer):
+ """Creates a squeeze and excitation layer."""
+
+ def __init__(self,
+ in_filters,
+ out_filters,
+ se_ratio,
+ divisible_by=1,
+ use_3d_input=False,
+ kernel_initializer='VarianceScaling',
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activation='relu',
+ gating_activation='sigmoid',
+ round_down_protect=True,
+ **kwargs):
+ """Initializes a squeeze and excitation layer.
+
+ Args:
+ in_filters: An `int` number of filters of the input tensor.
+ out_filters: An `int` number of filters of the output tensor.
+ se_ratio: A `float` or None. If not None, se ratio for the squeeze and
+ excitation layer.
+ divisible_by: An `int` that ensures all inner dimensions are divisible by
+ this number.
+ use_3d_input: A `bool` of whether input is 2D or 3D image.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ gating_activation: A `str` name of the activation function for final
+ gating function.
+ round_down_protect: A `bool` of whether round down more than 10% will be
+ allowed.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+
+ self._in_filters = in_filters
+ self._out_filters = out_filters
+ self._se_ratio = se_ratio
+ self._divisible_by = divisible_by
+ self._round_down_protect = round_down_protect
+ self._use_3d_input = use_3d_input
+ self._activation = activation
+ self._gating_activation = gating_activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ if not use_3d_input:
+ self._spatial_axis = [1, 2]
+ else:
+ self._spatial_axis = [1, 2, 3]
+ else:
+ if not use_3d_input:
+ self._spatial_axis = [2, 3]
+ else:
+ self._spatial_axis = [2, 3, 4]
+
+ def _create_gating_activation_layer(self):
+ if self._gating_activation == 'hard_sigmoid':
+ # Convert hard_sigmoid activation to quantizable keras layers so each op
+ # can be properly quantized.
+ # Formula is hard_sigmoid(x) = relu6(x + 3) * 0.16667.
+ self._add_quantizer('add_three')
+ self._add_quantizer('divide_six')
+ self._relu6 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation('relu6', use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+ else:
+ self._gating_activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(
+ self._gating_activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ def _apply_gating_activation_layer(
+ self, x: tf.Tensor, training: bool) -> tf.Tensor:
+ if self._gating_activation == 'hard_sigmoid':
+ x = self._apply_quantizer('add_three', x + 3.0, training)
+ x = self._relu6(x)
+ x = self._apply_quantizer('divide_six', x * 1.6667, training)
+ else:
+ x = self._gating_activation_layer(x)
+ return x
+
+ def build(self, input_shape):
+ num_reduced_filters = nn_layers.make_divisible(
+ max(1, int(self._in_filters * self._se_ratio)),
+ divisor=self._divisible_by,
+ round_down_protect=self._round_down_protect)
+
+ self._se_reduce = helper.Conv2DQuantized(
+ filters=num_reduced_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=True,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+
+ self._se_expand = helper.Conv2DOutputQuantized(
+ filters=self._out_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=True,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=helper.NoOpActivation())
+
+ self._multiply = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Multiply(),
+ configs.Default8BitQuantizeConfig([], [], True))
+ self._reduce_mean_quantizer = (
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False))
+ self._reduce_mean_quantizer_vars = self._reduce_mean_quantizer.build(
+ None, 'reduce_mean_quantizer_vars', self)
+
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+ self._create_gating_activation_layer()
+
+ self._build_quantizer_vars()
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {
+ 'in_filters': self._in_filters,
+ 'out_filters': self._out_filters,
+ 'se_ratio': self._se_ratio,
+ 'divisible_by': self._divisible_by,
+ 'use_3d_input': self._use_3d_input,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'gating_activation': self._gating_activation,
+ 'round_down_protect': self._round_down_protect,
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs, training=None):
+ x = tf.reduce_mean(inputs, self._spatial_axis, keepdims=True)
+ x = self._reduce_mean_quantizer(
+ x, training, self._reduce_mean_quantizer_vars)
+ x = self._activation_layer(self._se_reduce(x))
+ x = self._apply_gating_activation_layer(self._se_expand(x), training)
+ x = self._multiply([x, inputs])
+ return x
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SegmentationHeadQuantized(tf.keras.layers.Layer):
+ """Creates a segmentation head."""
+
+ def __init__(
+ self,
+ num_classes: int,
+ level: Union[int, str],
+ num_convs: int = 2,
+ num_filters: int = 256,
+ use_depthwise_convolution: bool = False,
+ prediction_kernel_size: int = 1,
+ upsample_factor: int = 1,
+ feature_fusion: Optional[str] = None,
+ decoder_min_level: Optional[int] = None,
+ decoder_max_level: Optional[int] = None,
+ low_level: int = 2,
+ low_level_num_filters: int = 48,
+ num_decoder_filters: int = 256,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ **kwargs):
+ """Initializes a segmentation head.
+
+ Args:
+ num_classes: An `int` number of mask classification categories. The number
+ of classes does not include background class.
+ level: An `int` or `str`, level to use to build segmentation head.
+ num_convs: An `int` number of stacked convolution before the last
+ prediction layer.
+ num_filters: An `int` number to specify the number of filters used.
+ Default is 256.
+ use_depthwise_convolution: A bool to specify if use depthwise separable
+ convolutions.
+ prediction_kernel_size: An `int` number to specify the kernel size of the
+ prediction layer.
+ upsample_factor: An `int` number to specify the upsampling factor to
+ generate finer mask. Default 1 means no upsampling is applied.
+ feature_fusion: One of `deeplabv3plus`, `deeplabv3plus_sum_to_merge`,
+ `pyramid_fusion`, or None. If `deeplabv3plus`, features from
+ decoder_features[level] will be fused with low level feature maps from
+ backbone. If `pyramid_fusion`, multiscale features will be resized and
+ fused at the target level.
+ decoder_min_level: An `int` of minimum level from decoder to use in
+ feature fusion. It is only used when feature_fusion is set to
+ `panoptic_fpn_fusion`.
+ decoder_max_level: An `int` of maximum level from decoder to use in
+ feature fusion. It is only used when feature_fusion is set to
+ `panoptic_fpn_fusion`.
+ low_level: An `int` of backbone level to be used for feature fusion. It is
+ used when feature_fusion is set to `deeplabv3plus`.
+ low_level_num_filters: An `int` of reduced number of filters for the low
+ level features before fusing it with higher level features. It is only
+ used when feature_fusion is set to `deeplabv3plus`.
+ num_decoder_filters: An `int` of number of filters in the decoder outputs.
+ It is only used when feature_fusion is set to `panoptic_fpn_fusion`.
+ activation: A `str` that indicates which activation is used, e.g. 'relu',
+ 'swish', etc.
+ use_sync_bn: A `bool` that indicates whether to use synchronized batch
+ normalization across different replicas.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+
+ self._config_dict = {
+ 'num_classes': num_classes,
+ 'level': level,
+ 'num_convs': num_convs,
+ 'num_filters': num_filters,
+ 'use_depthwise_convolution': use_depthwise_convolution,
+ 'prediction_kernel_size': prediction_kernel_size,
+ 'upsample_factor': upsample_factor,
+ 'feature_fusion': feature_fusion,
+ 'decoder_min_level': decoder_min_level,
+ 'decoder_max_level': decoder_max_level,
+ 'low_level': low_level,
+ 'low_level_num_filters': low_level_num_filters,
+ 'num_decoder_filters': num_decoder_filters,
+ 'activation': activation,
+ 'use_sync_bn': use_sync_bn,
+ 'norm_momentum': norm_momentum,
+ 'norm_epsilon': norm_epsilon,
+ 'kernel_regularizer': kernel_regularizer,
+ 'bias_regularizer': bias_regularizer,
+ }
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+
+ def build(self, input_shape: Sequence[tf.TensorShape]):
+ """Creates the variables of the segmentation head."""
+ # When input_shape is a list/tuple, the first corresponds to backbone
+ # features used for resizing the decoder features (the second) if feature
+ # fusion type is `deeplabv3plus`.
+ backbone_shape = input_shape[0]
+ use_depthwise_convolution = self._config_dict['use_depthwise_convolution']
+ random_initializer = tf.keras.initializers.RandomNormal(stddev=0.01)
+ conv_kwargs = {
+ 'kernel_size': 3 if not use_depthwise_convolution else 1,
+ 'padding': 'same',
+ 'use_bias': False,
+ 'kernel_initializer': random_initializer,
+ 'kernel_regularizer': self._config_dict['kernel_regularizer'],
+ }
+
+ norm_layer = (
+ tf.keras.layers.experimental.SyncBatchNormalization
+ if self._config_dict['use_sync_bn'] else
+ tf.keras.layers.BatchNormalization)
+ norm_with_quantize = helper.BatchNormalizationQuantized(norm_layer)
+ norm_no_quantize = helper.BatchNormalizationNoQuantized(norm_layer)
+ norm = helper.norm_by_activation(self._config_dict['activation'],
+ norm_with_quantize, norm_no_quantize)
+
+ bn_kwargs = {
+ 'axis': self._bn_axis,
+ 'momentum': self._config_dict['norm_momentum'],
+ 'epsilon': self._config_dict['norm_epsilon'],
+ }
+
+ if self._config_dict['feature_fusion'] in [
+ FeatureFusion.DEEPLABV3PLUS, FeatureFusion.DEEPLABV3PLUS_SUM_TO_MERGE
+ ]:
+ # Deeplabv3+ feature fusion layers.
+ self._dlv3p_conv = helper.Conv2DQuantized(
+ kernel_size=1,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(random_initializer),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ name='segmentation_head_deeplabv3p_fusion_conv',
+ filters=self._config_dict['low_level_num_filters'],
+ activation=helper.NoOpActivation())
+
+ self._dlv3p_norm = norm(
+ name='segmentation_head_deeplabv3p_fusion_norm', **bn_kwargs)
+
+ # Segmentation head layers.
+ self._convs = []
+ self._norms = []
+ for i in range(self._config_dict['num_convs']):
+ if use_depthwise_convolution:
+ self._convs.append(
+ helper.DepthwiseConv2DQuantized(
+ name='segmentation_head_depthwise_conv_{}'.format(i),
+ kernel_size=3,
+ padding='same',
+ use_bias=False,
+ depthwise_initializer=tf_utils.clone_initializer(
+ random_initializer),
+ depthwise_regularizer=self._config_dict['kernel_regularizer'],
+ depth_multiplier=1,
+ activation=helper.NoOpActivation()))
+ norm_name = 'segmentation_head_depthwise_norm_{}'.format(i)
+ self._norms.append(norm(name=norm_name, **bn_kwargs))
+ conv_name = 'segmentation_head_conv_{}'.format(i)
+ self._convs.append(
+ helper.Conv2DQuantized(
+ name=conv_name,
+ filters=self._config_dict['num_filters'],
+ activation=helper.NoOpActivation(),
+ **conv_kwargs))
+ norm_name = 'segmentation_head_norm_{}'.format(i)
+ self._norms.append(norm(name=norm_name, **bn_kwargs))
+
+ self._classifier = helper.Conv2DOutputQuantized(
+ name='segmentation_output',
+ filters=self._config_dict['num_classes'],
+ kernel_size=self._config_dict['prediction_kernel_size'],
+ padding='same',
+ bias_initializer=tf.zeros_initializer(),
+ kernel_initializer=tf_utils.clone_initializer(random_initializer),
+ kernel_regularizer=self._config_dict['kernel_regularizer'],
+ bias_regularizer=self._config_dict['bias_regularizer'],
+ activation=helper.NoOpActivation())
+
+ self._upsampling_layer = helper.UpSampling2DQuantized(
+ size=(self._config_dict['upsample_factor'],
+ self._config_dict['upsample_factor']),
+ interpolation='nearest')
+ self._resizing_layer = helper.ResizingQuantized(
+ backbone_shape[1], backbone_shape[2], interpolation='bilinear')
+
+ self._concat_layer = helper.ConcatenateQuantized(axis=self._bn_axis)
+ self._add_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Add(), configs.Default8BitQuantizeConfig([], [], True))
+
+ super().build(input_shape)
+
+ def call(self, inputs: Tuple[Union[tf.Tensor, Mapping[str, tf.Tensor]],
+ Union[tf.Tensor, Mapping[str, tf.Tensor]]]):
+ """Forward pass of the segmentation head.
+
+ It supports both a tuple of 2 tensors or 2 dictionaries. The first is
+ backbone endpoints, and the second is decoder endpoints. When inputs are
+ tensors, they are from a single level of feature maps. When inputs are
+ dictionaries, they contain multiple levels of feature maps, where the key
+ is the index of feature map.
+
+ Args:
+ inputs: A tuple of 2 feature map tensors of shape
+ [batch, height_l, width_l, channels] or 2 dictionaries of tensors:
+ - key: A `str` of the level of the multilevel features.
+ - values: A `tf.Tensor` of the feature map tensors, whose shape is
+ [batch, height_l, width_l, channels].
+
+ Returns:
+ segmentation prediction mask: A `tf.Tensor` of the segmentation mask
+ scores predicted from input features.
+ """
+ if self._config_dict['feature_fusion'] in (
+ FeatureFusion.PYRAMID_FUSION, FeatureFusion.PANOPTIC_FPN_FUSION):
+ raise ValueError(
+ 'The feature fusion method `pyramid_fusion` is not supported in QAT.')
+
+ backbone_output = inputs[0]
+ decoder_output = inputs[1]
+ if self._config_dict['feature_fusion'] in {
+ FeatureFusion.DEEPLABV3PLUS, FeatureFusion.DEEPLABV3PLUS_SUM_TO_MERGE
+ }:
+ # deeplabv3+ feature fusion.
+ x = decoder_output[str(self._config_dict['level'])] if isinstance(
+ decoder_output, dict) else decoder_output
+ y = backbone_output[str(self._config_dict['low_level'])] if isinstance(
+ backbone_output, dict) else backbone_output
+ y = self._dlv3p_norm(self._dlv3p_conv(y))
+ y = self._activation_layer(y)
+ x = self._resizing_layer(x)
+ x = tf.cast(x, dtype=y.dtype)
+ if self._config_dict['feature_fusion'] == FeatureFusion.DEEPLABV3PLUS:
+ x = self._concat_layer([x, y])
+ else:
+ x = self._add_layer([x, y])
+ else:
+ x = decoder_output[str(self._config_dict['level'])] if isinstance(
+ decoder_output, dict) else decoder_output
+
+ for conv, norm in zip(self._convs, self._norms):
+ x = conv(x)
+ x = norm(x)
+ x = self._activation_layer(x)
+ if self._config_dict['upsample_factor'] > 1:
+ # Use keras layer for nearest upsampling so it is QAT compatible.
+ x = self._upsampling_layer(x)
+
+ return self._classifier(x)
+
+ def get_config(self):
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(self._config_dict.items()))
+
+ @classmethod
+ def from_config(cls, config):
+ return cls(**config)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SpatialPyramidPoolingQuantized(nn_layers.SpatialPyramidPooling):
+ """Implements the quantized Atrous Spatial Pyramid Pooling.
+
+ References:
+ [Rethinking Atrous Convolution for Semantic Image Segmentation](
+ https://arxiv.org/pdf/1706.05587.pdf)
+ [Encoder-Decoder with Atrous Separable Convolution for Semantic Image
+ Segmentation](https://arxiv.org/pdf/1802.02611.pdf)
+ """
+
+ def __init__(
+ self,
+ output_channels: int,
+ dilation_rates: List[int],
+ pool_kernel_size: Optional[List[int]] = None,
+ use_sync_bn: bool = False,
+ batchnorm_momentum: float = 0.99,
+ batchnorm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ dropout: float = 0.5,
+ kernel_initializer: str = 'GlorotUniform',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ use_depthwise_convolution: bool = False,
+ **kwargs):
+ """Initializes `SpatialPyramidPooling`.
+
+ Args:
+ output_channels: Number of channels produced by SpatialPyramidPooling.
+ dilation_rates: A list of integers for parallel dilated conv.
+ pool_kernel_size: A list of integers or None. If None, global average
+ pooling is applied, otherwise an average pooling of pool_kernel_size is
+ applied.
+ use_sync_bn: A bool, whether or not to use sync batch normalization.
+ batchnorm_momentum: A float for the momentum in BatchNorm. Defaults to
+ 0.99.
+ batchnorm_epsilon: A float for the epsilon value in BatchNorm. Defaults to
+ 0.001.
+ activation: A `str` for type of activation to be used. Defaults to 'relu'.
+ dropout: A float for the dropout rate before output. Defaults to 0.5.
+ kernel_initializer: Kernel initializer for conv layers. Defaults to
+ `glorot_uniform`.
+ kernel_regularizer: Kernel regularizer for conv layers. Defaults to None.
+ interpolation: The interpolation method for upsampling. Defaults to
+ `bilinear`.
+ use_depthwise_convolution: Allows spatial pooling to be separable
+ depthwise convolusions. [Encoder-Decoder with Atrous Separable
+ Convolution for Semantic Image Segmentation](
+ https://arxiv.org/pdf/1802.02611.pdf)
+ **kwargs: Other keyword arguments for the layer.
+ """
+ super().__init__(
+ output_channels=output_channels,
+ dilation_rates=dilation_rates,
+ use_sync_bn=use_sync_bn,
+ batchnorm_momentum=batchnorm_momentum,
+ batchnorm_epsilon=batchnorm_epsilon,
+ activation=activation,
+ dropout=dropout,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer,
+ interpolation=interpolation,
+ pool_kernel_size=pool_kernel_size,
+ use_depthwise_convolution=use_depthwise_convolution)
+
+ self._activation_fn = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(activation, use_keras_layer=True),
+ configs.Default8BitActivationQuantizeConfig())
+ self._activation_fn_no_quant = (
+ tf_utils.get_activation(activation, use_keras_layer=True))
+
+ def build(self, input_shape):
+ height = input_shape[1]
+ width = input_shape[2]
+ channels = input_shape[3]
+
+ norm_layer = (
+ tf.keras.layers.experimental.SyncBatchNormalization
+ if self._use_sync_bn else tf.keras.layers.BatchNormalization)
+ norm_with_quantize = helper.BatchNormalizationQuantized(norm_layer)
+ norm_no_quantize = helper.BatchNormalizationNoQuantized(norm_layer)
+ norm = helper.norm_by_activation(self._activation, norm_with_quantize,
+ norm_no_quantize)
+
+ self.aspp_layers = []
+
+ conv1 = helper.Conv2DQuantized(
+ filters=self._output_channels,
+ kernel_size=(1, 1),
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer,
+ use_bias=False,
+ activation=helper.NoOpActivation())
+ norm1 = norm(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+
+ self.aspp_layers.append([conv1, norm1])
+
+ for dilation_rate in self._dilation_rates:
+ leading_layers = []
+ kernel_size = (3, 3)
+ if self._use_depthwise_convolution:
+ leading_layers += [
+ helper.DepthwiseConv2DOutputQuantized(
+ depth_multiplier=1,
+ kernel_size=kernel_size,
+ padding='same',
+ depthwise_regularizer=self._kernel_regularizer,
+ depthwise_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ dilation_rate=dilation_rate,
+ use_bias=False,
+ activation=helper.NoOpActivation())
+ ]
+ kernel_size = (1, 1)
+ conv_dilation = leading_layers + [
+ helper.Conv2DQuantized(
+ filters=self._output_channels,
+ kernel_size=kernel_size,
+ padding='same',
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ dilation_rate=dilation_rate,
+ use_bias=False,
+ activation=helper.NoOpActivation())
+ ]
+ norm_dilation = norm(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+
+ self.aspp_layers.append(conv_dilation + [norm_dilation])
+
+ if self._pool_kernel_size is None:
+ pooling = [
+ helper.GlobalAveragePooling2DQuantized(),
+ helper.ReshapeQuantized((1, 1, channels))
+ ]
+ else:
+ pooling = [helper.AveragePooling2DQuantized(self._pool_kernel_size)]
+
+ conv2 = helper.Conv2DQuantized(
+ filters=self._output_channels,
+ kernel_size=(1, 1),
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer,
+ use_bias=False,
+ activation=helper.NoOpActivation())
+ norm2 = norm(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+
+ self.aspp_layers.append(pooling + [conv2, norm2])
+ self._resizing_layer = helper.ResizingQuantized(
+ height, width, interpolation=self._interpolation)
+
+ self._projection = [
+ helper.Conv2DQuantized(
+ filters=self._output_channels,
+ kernel_size=(1, 1),
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer,
+ use_bias=False,
+ activation=helper.NoOpActivation()),
+ norm(
+ axis=self._bn_axis,
+ momentum=self._batchnorm_momentum,
+ epsilon=self._batchnorm_epsilon)
+ ]
+ self._dropout_layer = tf.keras.layers.Dropout(rate=self._dropout)
+ self._concat_layer = helper.ConcatenateQuantized(axis=-1)
+
+ def call(self,
+ inputs: tf.Tensor,
+ training: Optional[bool] = None) -> tf.Tensor:
+ if training is None:
+ training = tf.keras.backend.learning_phase()
+ result = []
+ for i, layers in enumerate(self.aspp_layers):
+ x = inputs
+ for layer in layers:
+ # Apply layers sequentially.
+ x = layer(x, training=training)
+ x = self._activation_fn(x)
+
+ # Apply resize layer to the end of the last set of layers.
+ if i == len(self.aspp_layers) - 1:
+ x = self._resizing_layer(x)
+
+ result.append(tf.cast(x, inputs.dtype))
+ x = self._concat_layer(result)
+ for layer in self._projection:
+ x = layer(x, training=training)
+ x = self._activation_fn(x)
+ return self._dropout_layer(x)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class ASPPQuantized(aspp.ASPP):
+ """Creates a quantized Atrous Spatial Pyramid Pooling (ASPP) layer."""
+
+ def __init__(
+ self,
+ level: int,
+ dilation_rates: List[int],
+ num_filters: int = 256,
+ pool_kernel_size: Optional[int] = None,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ activation: str = 'relu',
+ dropout_rate: float = 0.0,
+ kernel_initializer: str = 'VarianceScaling',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ interpolation: str = 'bilinear',
+ use_depthwise_convolution: bool = False,
+ spp_layer_version: str = 'v1',
+ output_tensor: bool = True,
+ **kwargs):
+ """Initializes an Atrous Spatial Pyramid Pooling (ASPP) layer.
+
+ Args:
+ level: An `int` level to apply ASPP.
+ dilation_rates: A `list` of dilation rates.
+ num_filters: An `int` number of output filters in ASPP.
+ pool_kernel_size: A `list` of [height, width] of pooling kernel size or
+ None. Pooling size is with respect to original image size, it will be
+ scaled down by 2**level. If None, global average pooling is used.
+ use_sync_bn: A `bool`. If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ activation: A `str` activation to be used in ASPP.
+ dropout_rate: A `float` rate for dropout regularization.
+ kernel_initializer: A `str` name of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default is None.
+ interpolation: A `str` of interpolation method. It should be one of
+ `bilinear`, `nearest`, `bicubic`, `area`, `lanczos3`, `lanczos5`,
+ `gaussian`, or `mitchellcubic`.
+ use_depthwise_convolution: If True depthwise separable convolutions will
+ be added to the Atrous spatial pyramid pooling.
+ spp_layer_version: A `str` of spatial pyramid pooling layer version.
+ output_tensor: Whether to output a single tensor or a dictionary of
+ tensor. Default is true.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(
+ level=level,
+ dilation_rates=dilation_rates,
+ num_filters=num_filters,
+ pool_kernel_size=pool_kernel_size,
+ use_sync_bn=use_sync_bn,
+ norm_momentum=norm_momentum,
+ norm_epsilon=norm_epsilon,
+ activation=activation,
+ dropout_rate=dropout_rate,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer,
+ interpolation=interpolation,
+ use_depthwise_convolution=use_depthwise_convolution,
+ spp_layer_version=spp_layer_version,
+ output_tensor=output_tensor,
+ **kwargs)
+
+ self._aspp_layer = SpatialPyramidPoolingQuantized
+
+ def call(self, inputs: Union[tf.Tensor, Mapping[str,
+ tf.Tensor]]) -> tf.Tensor:
+ """Calls the Atrous Spatial Pyramid Pooling (ASPP) layer on an input.
+
+ The output of ASPP will be a dict of {`level`, `tf.Tensor`} even if only one
+ level is present, if output_tensor is false. Hence, this will be compatible
+ with the rest of the segmentation model interfaces.
+ If output_tensor is true, a single tensot is output.
+
+ Args:
+ inputs: A `tf.Tensor` of shape [batch, height_l, width_l, filter_size] or
+ a `dict` of `tf.Tensor` where
+ - key: A `str` of the level of the multilevel feature maps.
+ - values: A `tf.Tensor` of shape [batch, height_l, width_l,
+ filter_size].
+
+ Returns:
+ A `tf.Tensor` of shape [batch, height_l, width_l, filter_size] or a `dict`
+ of `tf.Tensor` where
+ - key: A `str` of the level of the multilevel feature maps.
+ - values: A `tf.Tensor` of output of ASPP module.
+ """
+ level = str(self._config_dict['level'])
+ backbone_output = inputs[level] if isinstance(inputs, dict) else inputs
+ return self.aspp(backbone_output)
+
+
+class BatchNormalizationWrapper(tf.keras.layers.Wrapper):
+ """A BatchNormalizationWrapper that explicitly not folded.
+
+ It just added an identity depthwise conv right before the normalization.
+ As a result, given normalization op just folded into the identity depthwise
+ conv layer.
+
+ Note that it only used when the batch normalization folding is not working.
+ It makes quantize them as a 1x1 depthwise conv layer that just work as same
+ as inference mode for the normalization. (Basically mult and add for the BN.)
+ """
+
+ def call(self, inputs: tf.Tensor, *args: Any, **kwargs: Any) -> tf.Tensor:
+ channels = tf.shape(inputs)[-1]
+ x = tf.nn.depthwise_conv2d(
+ inputs, tf.ones([1, 1, channels, 1]), [1, 1, 1, 1], 'VALID')
+ outputs = self.layer.call(x, *args, **kwargs)
+ return outputs
diff --git a/official/projects/qat/vision/modeling/layers/nn_layers_test.py b/official/projects/qat/vision/modeling/layers/nn_layers_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..002a2e2920ec113e0d62e22ba251cd5a75dc2fcd
--- /dev/null
+++ b/official/projects/qat/vision/modeling/layers/nn_layers_test.py
@@ -0,0 +1,107 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for nn_layers."""
+
+# Import libraries
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.qat.vision.modeling.layers import nn_layers
+
+
+class NNLayersTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ ('deeplabv3plus', 1, 128, 128),
+ ('deeplabv3plus', 2, 128, 128),
+ ('deeplabv3', 1, 128, 64),
+ ('deeplabv3', 2, 128, 64),
+ ('deeplabv3plus_sum_to_merge', 1, 64, 128),
+ ('deeplabv3plus_sum_to_merge', 2, 64, 128),
+ )
+ def test_segmentation_head_creation(self, feature_fusion, upsample_factor,
+ low_level_num_filters, expected_shape):
+ input_size = 128
+ decoder_outupt_size = input_size // 2
+
+ decoder_output = tf.random.uniform(
+ (2, decoder_outupt_size, decoder_outupt_size, 64), dtype=tf.float32)
+ backbone_output = tf.random.uniform((2, input_size, input_size, 32),
+ dtype=tf.float32)
+ segmentation_head = nn_layers.SegmentationHeadQuantized(
+ num_classes=5,
+ level=4,
+ upsample_factor=upsample_factor,
+ low_level=2,
+ low_level_num_filters=low_level_num_filters,
+ feature_fusion=feature_fusion)
+
+ features = segmentation_head((backbone_output, decoder_output))
+
+ self.assertAllEqual([
+ 2, expected_shape * upsample_factor, expected_shape * upsample_factor, 5
+ ], features.shape.as_list())
+
+ @parameterized.parameters(
+ (None, []),
+ (None, [6, 12, 18]),
+ ([32, 32], [6, 12, 18]),
+ )
+ def test_spatial_pyramid_pooling_creation(self, pool_kernel_size,
+ dilation_rates):
+ inputs = tf.keras.Input(shape=(64, 64, 128), dtype=tf.float32)
+ layer = nn_layers.SpatialPyramidPoolingQuantized(
+ output_channels=256,
+ dilation_rates=dilation_rates,
+ pool_kernel_size=pool_kernel_size)
+ output = layer(inputs)
+ self.assertAllEqual([None, 64, 64, 256], output.shape)
+
+ @parameterized.parameters(
+ (3, [6, 12, 18, 24], 128),
+ (3, [6, 12, 18], 128),
+ (3, [6, 12], 256),
+ (4, [], 128),
+ (4, [6, 12, 18], 128),
+ (4, [], 256),
+ )
+ def test_aspp_creation(self, level, dilation_rates, num_filters):
+ input_size = 128 // 2**level
+ tf.keras.backend.set_image_data_format('channels_last')
+ endpoints = tf.random.uniform(
+ shape=(2, input_size, input_size, 64), dtype=tf.float32)
+
+ network = nn_layers.ASPPQuantized(
+ level=level, dilation_rates=dilation_rates, num_filters=num_filters)
+
+ feats = network(endpoints)
+
+ self.assertAllEqual([2, input_size, input_size, num_filters],
+ feats.shape.as_list())
+
+ @parameterized.parameters(False, True)
+ def test_bnorm_wrapper_creation(self, use_sync_bn):
+ inputs = tf.keras.Input(shape=(64, 64, 128), dtype=tf.float32)
+ if use_sync_bn:
+ norm = tf.keras.layers.experimental.SyncBatchNormalization(axis=-1)
+ else:
+ norm = tf.keras.layers.BatchNormalization(axis=-1)
+ layer = nn_layers.BatchNormalizationWrapper(norm)
+ output = layer(inputs)
+ self.assertAllEqual([None, 64, 64, 128], output.shape)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/modeling/segmentation_model.py b/official/projects/qat/vision/modeling/segmentation_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..99511e2275dd5d01b162b503567ea1fb9038e1db
--- /dev/null
+++ b/official/projects/qat/vision/modeling/segmentation_model.py
@@ -0,0 +1,84 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Build segmentation models."""
+from typing import Any, Mapping, Union
+
+# Import libraries
+import tensorflow as tf
+
+layers = tf.keras.layers
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SegmentationModelQuantized(tf.keras.Model):
+ """A Segmentation class model.
+
+ Input images are passed through backbone first. Decoder network is then
+ applied, and finally, segmentation head is applied on the output of the
+ decoder network. Layers such as ASPP should be part of decoder. Any feature
+ fusion is done as part of the segmentation head (i.e. deeplabv3+ feature
+ fusion is not part of the decoder, instead it is part of the segmentation
+ head). This way, different feature fusion techniques can be combined with
+ different backbones, and decoders.
+ """
+
+ def __init__(self, backbone: tf.keras.Model, decoder: tf.keras.layers.Layer,
+ head: tf.keras.layers.Layer,
+ input_specs: tf.keras.layers.InputSpec, **kwargs):
+ """Segmentation initialization function.
+
+ Args:
+ backbone: a backbone network.
+ decoder: a decoder network. E.g. FPN.
+ head: segmentation head.
+ input_specs: The shape specifications of input tensor.
+ **kwargs: keyword arguments to be passed.
+ """
+ inputs = tf.keras.Input(shape=input_specs.shape[1:], name=input_specs.name)
+ backbone_features = backbone(inputs)
+
+ if decoder:
+ backbone_feature = backbone_features[str(decoder.get_config()['level'])]
+ decoder_feature = decoder(backbone_feature)
+ else:
+ decoder_feature = backbone_features
+
+ backbone_feature = backbone_features[str(head.get_config()['low_level'])]
+ x = {'logits': head((backbone_feature, decoder_feature))}
+ super().__init__(inputs=inputs, outputs=x, **kwargs)
+ self._config_dict = {
+ 'backbone': backbone,
+ 'decoder': decoder,
+ 'head': head,
+ }
+ self.backbone = backbone
+ self.decoder = decoder
+ self.head = head
+
+ @property
+ def checkpoint_items(
+ self) -> Mapping[str, Union[tf.keras.Model, tf.keras.layers.Layer]]:
+ """Returns a dictionary of items to be additionally checkpointed."""
+ items = dict(backbone=self.backbone, head=self.head)
+ if self.decoder is not None:
+ items.update(decoder=self.decoder)
+ return items
+
+ def get_config(self) -> Mapping[str, Any]:
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
diff --git a/official/projects/qat/vision/n_bit/__init__.py b/official/projects/qat/vision/n_bit/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..569b809ec7d5e74454e698639ab48b7c1822937b
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/__init__.py
@@ -0,0 +1,21 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
+
+from official.projects.qat.vision.n_bit import configs
+from official.projects.qat.vision.n_bit import schemes
+from official.projects.qat.vision.n_bit.nn_blocks import BottleneckBlockNBitQuantized
+from official.projects.qat.vision.n_bit.nn_blocks import Conv2DBNBlockNBitQuantized
+from official.projects.qat.vision.n_bit.nn_blocks import InvertedBottleneckBlockNBitQuantized
diff --git a/official/projects/qat/vision/n_bit/configs.py b/official/projects/qat/vision/n_bit/configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..941c3690f34f2cb258af65be9226edddab40ec0e
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/configs.py
@@ -0,0 +1,380 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Default 8-bit QuantizeConfigs."""
+from typing import Sequence, Callable, Tuple, Any, Dict
+
+import tensorflow as tf
+import tensorflow_model_optimization as tfmot
+
+
+Quantizer = tfmot.quantization.keras.quantizers.Quantizer
+Layer = tf.keras.layers.Layer
+Activation = Callable[[tf.Tensor], tf.Tensor]
+WeightAndQuantizer = Tuple[tf.Variable, Quantizer]
+ActivationAndQuantizer = Tuple[Activation, Quantizer]
+
+
+class DefaultNBitOutputQuantizeConfig(
+ tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig which only quantizes the output from a layer."""
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ return []
+
+ def set_quantize_weights(self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ pass
+
+ def set_quantize_activations(self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ pass
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ return [
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=self._num_bits_activation, per_axis=False,
+ symmetric=False, narrow_range=False) # activation/output
+ ]
+
+ def get_config(self) -> Dict[str, Any]:
+ return {
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation,
+ }
+
+
+class NoOpQuantizeConfig(tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig which does not quantize any part of the layer."""
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ return []
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ pass
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ pass
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ return []
+
+ def get_config(self) -> Dict[str, Any]:
+ return {
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation,
+ }
+
+
+class DefaultNBitQuantizeConfig(tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig for non recurrent Keras layers."""
+
+ def __init__(self,
+ weight_attrs: Sequence[str],
+ activation_attrs: Sequence[str],
+ quantize_output: bool,
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8):
+ """Initializes a default N-bit quantize config."""
+ self.weight_attrs = weight_attrs
+ self.activation_attrs = activation_attrs
+ self.quantize_output = quantize_output
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ # TODO(pulkitb): For some layers such as Conv2D, per_axis should be True.
+ # Add mapping for which layers support per_axis.
+ self.weight_quantizer = tfmot.quantization.keras.quantizers.LastValueQuantizer(
+ num_bits=num_bits_weight, per_axis=False,
+ symmetric=True, narrow_range=True) # weight
+ self.activation_quantizer = tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=num_bits_activation, per_axis=False,
+ symmetric=False, narrow_range=False) # activation/output
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ """See base class."""
+ return [(getattr(layer, weight_attr), self.weight_quantizer)
+ for weight_attr in self.weight_attrs]
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ """See base class."""
+ return [(getattr(layer, activation_attr), self.activation_quantizer)
+ for activation_attr in self.activation_attrs]
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ """See base class."""
+ if len(self.weight_attrs) != len(quantize_weights):
+ raise ValueError(
+ '`set_quantize_weights` called on layer {} with {} '
+ 'weight parameters, but layer expects {} values.'.format(
+ layer.name, len(quantize_weights), len(self.weight_attrs)))
+
+ for weight_attr, weight in zip(self.weight_attrs, quantize_weights):
+ current_weight = getattr(layer, weight_attr)
+ if current_weight.shape != weight.shape:
+ raise ValueError('Existing layer weight shape {} is incompatible with'
+ 'provided weight shape {}'.format(
+ current_weight.shape, weight.shape))
+
+ setattr(layer, weight_attr, weight)
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ """See base class."""
+ if len(self.activation_attrs) != len(quantize_activations):
+ raise ValueError(
+ '`set_quantize_activations` called on layer {} with {} '
+ 'activation parameters, but layer expects {} values.'.format(
+ layer.name, len(quantize_activations),
+ len(self.activation_attrs)))
+
+ for activation_attr, activation in zip(
+ self.activation_attrs, quantize_activations):
+ setattr(layer, activation_attr, activation)
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ """See base class."""
+ if self.quantize_output:
+ return [self.activation_quantizer]
+ return []
+
+ @classmethod
+ def from_config(cls, config: Dict[str, Any]) -> object:
+ """Instantiates a `DefaultNBitQuantizeConfig` from its config.
+
+ Args:
+ config: Output of `get_config()`.
+
+ Returns:
+ A `DefaultNBitQuantizeConfig` instance.
+ """
+ return cls(**config)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config for this quantize config."""
+ # TODO(pulkitb): Add weight and activation quantizer to config.
+ # Currently it's created internally, but ideally the quantizers should be
+ # part of the constructor and passed in from the registry.
+ return {
+ 'weight_attrs': self.weight_attrs,
+ 'activation_attrs': self.activation_attrs,
+ 'quantize_output': self.quantize_output,
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation
+ }
+
+ def __eq__(self, other):
+ if not isinstance(other, DefaultNBitQuantizeConfig):
+ return False
+
+ return (self.weight_attrs == other.weight_attrs and
+ self.activation_attrs == self.activation_attrs and
+ self.weight_quantizer == other.weight_quantizer and
+ self.activation_quantizer == other.activation_quantizer and
+ self.quantize_output == other.quantize_output)
+
+ def __ne__(self, other):
+ return not self.__eq__(other)
+
+
+class DefaultNBitConvWeightsQuantizer(
+ tfmot.quantization.keras.quantizers.LastValueQuantizer):
+ """Quantizer for handling weights in Conv2D/DepthwiseConv2D layers."""
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ """Construct LastValueQuantizer with params specific for TFLite Convs."""
+
+ super(DefaultNBitConvWeightsQuantizer, self).__init__(
+ num_bits=num_bits_weight, per_axis=True,
+ symmetric=True, narrow_range=True) # weight
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def build(self,
+ tensor_shape: tf.TensorShape,
+ name: str,
+ layer: Layer):
+ """Build min/max quantization variables."""
+ min_weight = layer.add_weight(
+ name + '_min',
+ shape=(tensor_shape[-1],),
+ initializer=tf.keras.initializers.Constant(-6.0),
+ trainable=False)
+ max_weight = layer.add_weight(
+ name + '_max',
+ shape=(tensor_shape[-1],),
+ initializer=tf.keras.initializers.Constant(6.0),
+ trainable=False)
+
+ return {'min_var': min_weight, 'max_var': max_weight}
+
+
+class NoQuantizer(tfmot.quantization.keras.quantizers.Quantizer):
+ """Dummy quantizer for explicitly not quantize."""
+
+ def __call__(self, inputs, training, weights, **kwargs):
+ return tf.identity(inputs)
+
+ def get_config(self):
+ return {}
+
+ def build(self, tensor_shape, name, layer):
+ return {}
+
+
+class DefaultNBitConvQuantizeConfig(DefaultNBitQuantizeConfig):
+ """QuantizeConfig for Conv2D/DepthwiseConv2D layers."""
+
+ def __init__(self,
+ weight_attrs: Sequence[str],
+ activation_attrs: Sequence[str],
+ quantize_output: bool,
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8):
+ """Initializes default N-bit quantization config for the conv layer."""
+ super().__init__(weight_attrs=weight_attrs,
+ activation_attrs=activation_attrs,
+ quantize_output=quantize_output,
+ num_bits_weight=num_bits_weight,
+ num_bits_activation=num_bits_activation)
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ self.weight_quantizer = DefaultNBitConvWeightsQuantizer(
+ num_bits_weight=num_bits_weight,
+ num_bits_activation=num_bits_activation)
+
+
+class DefaultNBitActivationQuantizeConfig(
+ tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig for keras.layers.Activation.
+
+ `keras.layers.Activation` needs a separate `QuantizeConfig` since the
+ decision to quantize depends on the specific activation type.
+ """
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def _assert_activation_layer(self, layer: Layer):
+ if not isinstance(layer, tf.keras.layers.Activation):
+ raise RuntimeError(
+ 'DefaultNBitActivationQuantizeConfig can only be used with '
+ '`keras.layers.Activation`.')
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+ return []
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ if not hasattr(layer.activation, '__name__'):
+ raise ValueError('Activation {} not supported by '
+ 'DefaultNBitActivationQuantizeConfig.'.format(
+ layer.activation))
+
+ # This code is copied from TFMOT repo, but added relu6 to support mobilenet.
+ if layer.activation.__name__ in ['relu', 'relu6', 'swish']:
+ # 'relu' should generally get fused into the previous layer.
+ return [tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=self._num_bits_activation, per_axis=False,
+ symmetric=False, narrow_range=False)] # activation/output
+ elif layer.activation.__name__ in ['linear', 'softmax', 'sigmoid']:
+ return []
+
+ raise ValueError('Activation {} not supported by '
+ 'DefaultNBitActivationQuantizeConfig.'.format(
+ layer.activation))
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config for this quantizer config."""
+ return {
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation,
+ }
+
+
+def _types_dict():
+ return {
+ 'DefaultNBitOutputQuantizeConfig':
+ DefaultNBitOutputQuantizeConfig,
+ 'NoOpQuantizeConfig':
+ NoOpQuantizeConfig,
+ 'DefaultNBitQuantizeConfig':
+ DefaultNBitQuantizeConfig,
+ 'DefaultNBitConvWeightsQuantizer':
+ DefaultNBitConvWeightsQuantizer,
+ 'DefaultNBitConvQuantizeConfig':
+ DefaultNBitConvQuantizeConfig,
+ 'DefaultNBitActivationQuantizeConfig':
+ DefaultNBitActivationQuantizeConfig,
+ }
diff --git a/official/projects/qat/vision/n_bit/configs_test.py b/official/projects/qat/vision/n_bit/configs_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..5390f8d9c47fccde8034604c53e192292c8ee321
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/configs_test.py
@@ -0,0 +1,224 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for configs.py."""
+
+# Import libraries
+
+import numpy as np
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+
+from official.projects.qat.vision.n_bit import configs
+
+
+class _TestHelper(object):
+
+ def _convert_list(self, list_of_tuples):
+ """Transforms a list of 2-tuples to a tuple of 2 lists.
+
+ `QuantizeConfig` methods return a list of 2-tuples in the form
+ [(weight1, quantizer1), (weight2, quantizer2)]. This function converts
+ it into a 2-tuple of lists. ([weight1, weight2]), (quantizer1, quantizer2).
+
+ Args:
+ list_of_tuples: List of 2-tuples.
+
+ Returns:
+ 2-tuple of lists.
+ """
+ list1 = []
+ list2 = []
+ for a, b in list_of_tuples:
+ list1.append(a)
+ list2.append(b)
+
+ return list1, list2
+
+ # TODO(pulkitb): Consider asserting on full equality for quantizers.
+
+ def _assert_weight_quantizers(self, quantizer_list):
+ for quantizer in quantizer_list:
+ self.assertIsInstance(
+ quantizer,
+ tfmot.quantization.keras.quantizers.LastValueQuantizer)
+
+ def _assert_activation_quantizers(self, quantizer_list):
+ for quantizer in quantizer_list:
+ self.assertIsInstance(
+ quantizer,
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer)
+
+ def _assert_kernel_equality(self, a, b):
+ self.assertAllEqual(a.numpy(), b.numpy())
+
+
+class DefaultNBitQuantizeConfigTest(tf.test.TestCase, _TestHelper):
+
+ def _simple_dense_layer(self):
+ layer = tf.keras.layers.Dense(2)
+ layer.build(input_shape=(3,))
+ return layer
+
+ def testGetsQuantizeWeightsAndQuantizers(self):
+ layer = self._simple_dense_layer()
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+ (weights, weight_quantizers) = self._convert_list(
+ quantize_config.get_weights_and_quantizers(layer))
+
+ self._assert_weight_quantizers(weight_quantizers)
+ self.assertEqual([layer.kernel], weights)
+
+ def testGetsQuantizeActivationsAndQuantizers(self):
+ layer = self._simple_dense_layer()
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+ (activations, activation_quantizers) = self._convert_list(
+ quantize_config.get_activations_and_quantizers(layer))
+
+ self._assert_activation_quantizers(activation_quantizers)
+ self.assertEqual([layer.activation], activations)
+
+ def testSetsQuantizeWeights(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(
+ np.ones(layer.kernel.shape.as_list()))
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+ quantize_config.set_quantize_weights(layer, [quantize_kernel])
+
+ self._assert_kernel_equality(layer.kernel, quantize_kernel)
+
+ def testSetsQuantizeActivations(self):
+ layer = self._simple_dense_layer()
+ quantize_activation = tf.keras.activations.relu
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+ quantize_config.set_quantize_activations(layer, [quantize_activation])
+
+ self.assertEqual(layer.activation, quantize_activation)
+
+ def testSetsQuantizeWeights_ErrorOnWrongNumberOfWeights(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(
+ np.ones(layer.kernel.shape.as_list()))
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer, [])
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer,
+ [quantize_kernel, quantize_kernel])
+
+ def testSetsQuantizeWeights_ErrorOnWrongShapeOfWeight(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(np.ones([1, 2]))
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer, [quantize_kernel])
+
+ def testSetsQuantizeActivations_ErrorOnWrongNumberOfActivations(self):
+ layer = self._simple_dense_layer()
+ quantize_activation = tf.keras.activations.relu
+ num_bits_weight = 4
+ num_bits_activation = 4
+
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_activations(layer, [])
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_activations(
+ layer, [quantize_activation, quantize_activation])
+
+ def testGetsResultQuantizers_ReturnsQuantizer(self):
+ layer = self._simple_dense_layer()
+ num_bits_weight = 4
+ num_bits_activation = 4
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ [], [], True, num_bits_weight, num_bits_activation)
+
+ output_quantizers = quantize_config.get_output_quantizers(layer)
+
+ self.assertLen(output_quantizers, 1)
+ self._assert_activation_quantizers(output_quantizers)
+
+ def testGetsResultQuantizers_EmptyWhenFalse(self):
+ layer = self._simple_dense_layer()
+ num_bits_weight = 4
+ num_bits_activation = 4
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ [], [], False, num_bits_weight, num_bits_activation)
+
+ output_quantizers = quantize_config.get_output_quantizers(layer)
+
+ self.assertEqual([], output_quantizers)
+
+ def testSerialization(self):
+ num_bits_weight = 4
+ num_bits_activation = 4
+ quantize_config = configs.DefaultNBitQuantizeConfig(
+ ['kernel'], ['activation'], False, num_bits_weight, num_bits_activation)
+
+ expected_config = {
+ 'class_name': 'DefaultNBitQuantizeConfig',
+ 'config': {
+ 'weight_attrs': ['kernel'],
+ 'activation_attrs': ['activation'],
+ 'quantize_output': False,
+ 'num_bits_weight': 4,
+ 'num_bits_activation': 4
+ }
+ }
+ serialized_quantize_config = tf.keras.utils.serialize_keras_object(
+ quantize_config)
+
+ self.assertEqual(expected_config, serialized_quantize_config)
+
+ quantize_config_from_config = tf.keras.utils.deserialize_keras_object(
+ serialized_quantize_config,
+ module_objects=globals(),
+ custom_objects=configs._types_dict())
+
+ self.assertEqual(quantize_config, quantize_config_from_config)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/n_bit/nn_blocks.py b/official/projects/qat/vision/n_bit/nn_blocks.py
new file mode 100644
index 0000000000000000000000000000000000000000..6f168fab7aa039eec43e7206e509c6a316abfaaa
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/nn_blocks.py
@@ -0,0 +1,799 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains quantized neural blocks for the QAT."""
+from typing import Any, Dict, Optional, Sequence, Union
+
+# Import libraries
+
+from absl import logging
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.modeling import tf_utils
+from official.projects.qat.vision.n_bit import configs
+from official.projects.qat.vision.n_bit import nn_layers as qat_nn_layers
+from official.vision.modeling.layers import nn_layers
+
+
+class NoOpActivation:
+ """No-op activation which simply returns the incoming tensor.
+
+ This activation is required to distinguish between `keras.activations.linear`
+ which does the same thing. The main difference is that NoOpActivation should
+ not have any quantize operation applied to it.
+ """
+
+ def __call__(self, x: tf.Tensor) -> tf.Tensor:
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this object."""
+ return {}
+
+ def __eq__(self, other: Any) -> bool:
+ if not other or not isinstance(other, NoOpActivation):
+ return False
+
+ return True
+
+ def __ne__(self, other: Any) -> bool:
+ return not self.__eq__(other)
+
+
+def _quantize_wrapped_layer(cls, quantize_config):
+ def constructor(*arg, **kwargs):
+ return tfmot.quantization.keras.QuantizeWrapperV2(
+ cls(*arg, **kwargs),
+ quantize_config)
+ return constructor
+
+
+# This class is copied from modeling.layers.nn_blocks.BottleneckBlock and apply
+# QAT.
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class BottleneckBlockNBitQuantized(tf.keras.layers.Layer):
+ """A quantized standard bottleneck block."""
+
+ def __init__(self,
+ filters: int,
+ strides: int,
+ dilation_rate: int = 1,
+ use_projection: bool = False,
+ se_ratio: Optional[float] = None,
+ resnetd_shortcut: bool = False,
+ stochastic_depth_drop_rate: Optional[float] = None,
+ kernel_initializer: str = 'VarianceScaling',
+ kernel_regularizer: tf.keras.regularizers.Regularizer = None,
+ bias_regularizer: tf.keras.regularizers.Regularizer = None,
+ activation: str = 'relu',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ bn_trainable: bool = True,
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8, # pytype: disable=annotation-type-mismatch # typed-keras
+ **kwargs):
+ """Initializes a standard bottleneck block with BN after convolutions.
+
+ Args:
+ filters: An `int` number of filters for the first two convolutions. Note
+ that the third and final convolution will use 4 times as many filters.
+ strides: An `int` block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ dilation_rate: An `int` dilation_rate of convolutions. Default to 1.
+ use_projection: A `bool` for whether this block should use a projection
+ shortcut (versus the default identity shortcut). This is usually `True`
+ for the first block of a block group, which may change the number of
+ filters and the resolution.
+ se_ratio: A `float` or None. Ratio of the Squeeze-and-Excitation layer.
+ resnetd_shortcut: A `bool`. If True, apply the resnetd style modification
+ to the shortcut connection.
+ stochastic_depth_drop_rate: A `float` or None. If not None, drop rate for
+ the stochastic depth layer.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ use_sync_bn: A `bool`. If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ bn_trainable: A `bool` that indicates whether batch norm layers should be
+ trainable. Default to True.
+ num_bits_weight: An `int` number of bits for the weight. Default to 8.
+ num_bits_activation: An `int` number of bits for the weight. Default to 8.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+
+ self._filters = filters
+ self._strides = strides
+ self._dilation_rate = dilation_rate
+ self._use_projection = use_projection
+ self._se_ratio = se_ratio
+ self._resnetd_shortcut = resnetd_shortcut
+ self._use_sync_bn = use_sync_bn
+ self._activation = activation
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._kernel_initializer = kernel_initializer
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+ if use_sync_bn:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.experimental.SyncBatchNormalization,
+ configs.NoOpQuantizeConfig())
+ self._norm_with_quantize = _quantize_wrapped_layer(
+ tf.keras.layers.experimental.SyncBatchNormalization,
+ configs.DefaultNBitOutputQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ else:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.BatchNormalization,
+ configs.NoOpQuantizeConfig())
+ self._norm_with_quantize = _quantize_wrapped_layer(
+ tf.keras.layers.BatchNormalization,
+ configs.DefaultNBitOutputQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ self._bn_trainable = bn_trainable
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ conv2d_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['kernel'], ['activation'], False,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ if self._use_projection:
+ if self._resnetd_shortcut:
+ self._shortcut0 = tf.keras.layers.AveragePooling2D(
+ pool_size=2, strides=self._strides, padding='same')
+ self._shortcut1 = conv2d_quantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ else:
+ self._shortcut = conv2d_quantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=self._strides,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+
+ self._norm0 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+
+ self._conv1 = conv2d_quantized(
+ filters=self._filters,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm1 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation1 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ self._conv2 = conv2d_quantized(
+ filters=self._filters,
+ kernel_size=3,
+ strides=self._strides,
+ dilation_rate=self._dilation_rate,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm2 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation2 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ self._conv3 = conv2d_quantized(
+ filters=self._filters * 4,
+ kernel_size=1,
+ strides=1,
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm3 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ trainable=self._bn_trainable)
+ self._activation3 = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ if self._se_ratio and self._se_ratio > 0 and self._se_ratio <= 1:
+ self._squeeze_excitation = qat_nn_layers.SqueezeExcitationNBitQuantized(
+ in_filters=self._filters * 4,
+ out_filters=self._filters * 4,
+ se_ratio=self._se_ratio,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)
+ else:
+ self._squeeze_excitation = None
+
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = nn_layers.StochasticDepth(
+ self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = None
+ self._add = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Add(),
+ configs.DefaultNBitQuantizeConfig(
+ [], [], True,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ super().build(input_shape)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'filters': self._filters,
+ 'strides': self._strides,
+ 'dilation_rate': self._dilation_rate,
+ 'use_projection': self._use_projection,
+ 'se_ratio': self._se_ratio,
+ 'resnetd_shortcut': self._resnetd_shortcut,
+ 'stochastic_depth_drop_rate': self._stochastic_depth_drop_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'bn_trainable': self._bn_trainable,
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None) -> tf.Tensor:
+ """Run the BottleneckBlockQuantized logics."""
+ shortcut = inputs
+ if self._use_projection:
+ if self._resnetd_shortcut:
+ shortcut = self._shortcut0(shortcut)
+ shortcut = self._shortcut1(shortcut)
+ else:
+ shortcut = self._shortcut(shortcut)
+ shortcut = self._norm0(shortcut)
+
+ x = self._conv1(inputs)
+ x = self._norm1(x)
+ x = self._activation1(x)
+
+ x = self._conv2(x)
+ x = self._norm2(x)
+ x = self._activation2(x)
+
+ x = self._conv3(x)
+ x = self._norm3(x)
+
+ if self._squeeze_excitation:
+ x = self._squeeze_excitation(x)
+
+ if self._stochastic_depth:
+ x = self._stochastic_depth(x, training=training)
+
+ x = self._add([x, shortcut])
+ return self._activation3(x)
+
+
+# This class is copied from modeling.backbones.mobilenet.Conv2DBNBlock and apply
+# QAT.
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class Conv2DBNBlockNBitQuantized(tf.keras.layers.Layer):
+ """A quantized convolution block with batch normalization."""
+
+ def __init__(
+ self,
+ filters: int,
+ kernel_size: int = 3,
+ strides: int = 1,
+ use_bias: bool = False,
+ activation: str = 'relu6',
+ kernel_initializer: str = 'VarianceScaling',
+ kernel_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ bias_regularizer: Optional[tf.keras.regularizers.Regularizer] = None,
+ use_normalization: bool = True,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8,
+ **kwargs):
+ """A convolution block with batch normalization.
+
+ Args:
+ filters: An `int` number of filters for the first two convolutions. Note
+ that the third and final convolution will use 4 times as many filters.
+ kernel_size: An `int` specifying the height and width of the 2D
+ convolution window.
+ strides: An `int` of block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ use_bias: If True, use bias in the convolution layer.
+ activation: A `str` name of the activation function.
+ kernel_initializer: A `str` for kernel initializer of convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2D.
+ Default to None.
+ use_normalization: If True, use batch normalization.
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ num_bits_weight: An `int` number of bits for the weight. Default to 8.
+ num_bits_activation: An `int` number of bits for the weight. Default to 8.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+ self._filters = filters
+ self._kernel_size = kernel_size
+ self._strides = strides
+ self._activation = activation
+ self._use_bias = use_bias
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._use_normalization = use_normalization
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ if use_sync_bn:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.experimental.SyncBatchNormalization,
+ configs.NoOpQuantizeConfig())
+ else:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.BatchNormalization,
+ configs.NoOpQuantizeConfig())
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'filters': self._filters,
+ 'strides': self._strides,
+ 'kernel_size': self._kernel_size,
+ 'use_bias': self._use_bias,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'use_normalization': self._use_normalization,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ conv2d_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['kernel'], ['activation'], False,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ self._conv0 = conv2d_quantized(
+ filters=self._filters,
+ kernel_size=self._kernel_size,
+ strides=self._strides,
+ padding='same',
+ use_bias=self._use_bias,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ if self._use_normalization:
+ self._norm0 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ super(Conv2DBNBlockNBitQuantized, self).build(input_shape)
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None) -> tf.Tensor:
+ """Run the Conv2DBNBlockNBitQuantized logics."""
+ x = self._conv0(inputs)
+ if self._use_normalization:
+ x = self._norm0(x)
+ return self._activation_layer(x)
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class InvertedBottleneckBlockNBitQuantized(tf.keras.layers.Layer):
+ """A quantized inverted bottleneck block."""
+
+ def __init__(self,
+ in_filters,
+ out_filters,
+ expand_ratio,
+ strides,
+ kernel_size=3,
+ se_ratio=None,
+ stochastic_depth_drop_rate=None,
+ kernel_initializer='VarianceScaling',
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activation='relu',
+ se_inner_activation='relu',
+ se_gating_activation='sigmoid',
+ expand_se_in_filters=False,
+ depthwise_activation=None,
+ use_sync_bn=False,
+ dilation_rate=1,
+ divisible_by=1,
+ regularize_depthwise=False,
+ use_depthwise=True,
+ use_residual=True,
+ norm_momentum=0.99,
+ norm_epsilon=0.001,
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8,
+ **kwargs):
+ """Initializes an inverted bottleneck block with BN after convolutions.
+
+ Args:
+ in_filters: An `int` number of filters of the input tensor.
+ out_filters: An `int` number of filters of the output tensor.
+ expand_ratio: An `int` of expand_ratio for an inverted bottleneck block.
+ strides: An `int` block stride. If greater than 1, this block will
+ ultimately downsample the input.
+ kernel_size: An `int` kernel_size of the depthwise conv layer.
+ se_ratio: A `float` or None. If not None, se ratio for the squeeze and
+ excitation layer.
+ stochastic_depth_drop_rate: A `float` or None. if not None, drop rate for
+ the stochastic depth layer.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ se_inner_activation: A `str` name of squeeze-excitation inner activation.
+ se_gating_activation: A `str` name of squeeze-excitation gating
+ activation.
+ expand_se_in_filters: A `bool` of whether or not to expand in_filter in
+ squeeze and excitation layer.
+ depthwise_activation: A `str` name of the activation function for
+ depthwise only.
+ use_sync_bn: A `bool`. If True, use synchronized batch normalization.
+ dilation_rate: An `int` that specifies the dilation rate to use for.
+ divisible_by: An `int` that ensures all inner dimensions are divisible by
+ this number.
+ dilated convolution: An `int` to specify the same value for all spatial
+ dimensions.
+ regularize_depthwise: A `bool` of whether or not apply regularization on
+ depthwise.
+ use_depthwise: A `bool` of whether to uses fused convolutions instead of
+ depthwise.
+ use_residual: A `bool` of whether to include residual connection between
+ input and output.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ num_bits_weight: An `int` number of bits for the weight. Default to 8.
+ num_bits_activation: An `int` number of bits for the weight. Default to 8.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+
+ self._in_filters = in_filters
+ self._out_filters = out_filters
+ self._expand_ratio = expand_ratio
+ self._strides = strides
+ self._kernel_size = kernel_size
+ self._se_ratio = se_ratio
+ self._divisible_by = divisible_by
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._dilation_rate = dilation_rate
+ self._use_sync_bn = use_sync_bn
+ self._regularize_depthwise = regularize_depthwise
+ self._use_depthwise = use_depthwise
+ self._use_residual = use_residual
+ self._activation = activation
+ self._se_inner_activation = se_inner_activation
+ self._se_gating_activation = se_gating_activation
+ self._depthwise_activation = depthwise_activation
+ self._kernel_initializer = kernel_initializer
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._expand_se_in_filters = expand_se_in_filters
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ if use_sync_bn:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.experimental.SyncBatchNormalization,
+ configs.NoOpQuantizeConfig())
+ self._norm_with_quantize = _quantize_wrapped_layer(
+ tf.keras.layers.experimental.SyncBatchNormalization,
+ configs.DefaultNBitOutputQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ else:
+ self._norm = _quantize_wrapped_layer(
+ tf.keras.layers.BatchNormalization,
+ configs.NoOpQuantizeConfig())
+ self._norm_with_quantize = _quantize_wrapped_layer(
+ tf.keras.layers.BatchNormalization,
+ configs.DefaultNBitOutputQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ if not depthwise_activation:
+ self._depthwise_activation = activation
+ if regularize_depthwise:
+ self._depthsize_regularizer = kernel_regularizer
+ else:
+ self._depthsize_regularizer = None
+
+ def build(self, input_shape: Optional[Union[Sequence[int], tf.Tensor]]):
+ """Build variables and child layers to prepare for calling."""
+ conv2d_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['kernel'], ['activation'], False,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ depthwise_conv2d_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.DepthwiseConv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['depthwise_kernel'], ['activation'], False,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ expand_filters = self._in_filters
+ if self._expand_ratio > 1:
+ # First 1x1 conv for channel expansion.
+ expand_filters = nn_layers.make_divisible(
+ self._in_filters * self._expand_ratio, self._divisible_by)
+
+ expand_kernel = 1 if self._use_depthwise else self._kernel_size
+ expand_stride = 1 if self._use_depthwise else self._strides
+
+ self._conv0 = conv2d_quantized(
+ filters=expand_filters,
+ kernel_size=expand_kernel,
+ strides=expand_stride,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm0 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ if self._use_depthwise:
+ # Depthwise conv.
+ self._conv1 = depthwise_conv2d_quantized(
+ kernel_size=(self._kernel_size, self._kernel_size),
+ strides=self._strides,
+ padding='same',
+ depth_multiplier=1,
+ dilation_rate=self._dilation_rate,
+ use_bias=False,
+ depthwise_initializer=self._kernel_initializer,
+ depthwise_regularizer=self._depthsize_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm1 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+ self._depthwise_activation_layer = (
+ tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(self._depthwise_activation,
+ use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)))
+
+ # Squeeze and excitation.
+ if self._se_ratio and self._se_ratio > 0 and self._se_ratio <= 1:
+ logging.info('Use Squeeze and excitation.')
+ in_filters = self._in_filters
+ if self._expand_se_in_filters:
+ in_filters = expand_filters
+ self._squeeze_excitation = qat_nn_layers.SqueezeExcitationNBitQuantized(
+ in_filters=in_filters,
+ out_filters=expand_filters,
+ se_ratio=self._se_ratio,
+ divisible_by=self._divisible_by,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=self._se_inner_activation,
+ gating_activation=self._se_gating_activation,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)
+ else:
+ self._squeeze_excitation = None
+
+ # Last 1x1 conv.
+ self._conv2 = conv2d_quantized(
+ filters=self._out_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=False,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+ self._norm2 = self._norm_with_quantize(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon)
+
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = nn_layers.StochasticDepth(
+ self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = None
+ self._add = tf.keras.layers.Add()
+
+ super().build(input_shape)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this layer."""
+ config = {
+ 'in_filters': self._in_filters,
+ 'out_filters': self._out_filters,
+ 'expand_ratio': self._expand_ratio,
+ 'strides': self._strides,
+ 'kernel_size': self._kernel_size,
+ 'se_ratio': self._se_ratio,
+ 'divisible_by': self._divisible_by,
+ 'stochastic_depth_drop_rate': self._stochastic_depth_drop_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'se_inner_activation': self._se_inner_activation,
+ 'se_gating_activation': self._se_gating_activation,
+ 'expand_se_in_filters': self._expand_se_in_filters,
+ 'depthwise_activation': self._depthwise_activation,
+ 'dilation_rate': self._dilation_rate,
+ 'use_sync_bn': self._use_sync_bn,
+ 'regularize_depthwise': self._regularize_depthwise,
+ 'use_depthwise': self._use_depthwise,
+ 'use_residual': self._use_residual,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[Union[bool, tf.Tensor]] = None) -> tf.Tensor:
+ """Run the InvertedBottleneckBlockNBitQuantized logics."""
+ shortcut = inputs
+ if self._expand_ratio > 1:
+ x = self._conv0(inputs)
+ x = self._norm0(x)
+ x = self._activation_layer(x)
+ else:
+ x = inputs
+
+ if self._use_depthwise:
+ x = self._conv1(x)
+ x = self._norm1(x)
+ x = self._depthwise_activation_layer(x)
+
+ if self._squeeze_excitation:
+ x = self._squeeze_excitation(x)
+
+ x = self._conv2(x)
+ x = self._norm2(x)
+
+ if (self._use_residual and
+ self._in_filters == self._out_filters and
+ self._strides == 1):
+ if self._stochastic_depth:
+ x = self._stochastic_depth(x, training=training)
+ x = self._add([x, shortcut])
+
+ return x
diff --git a/official/projects/qat/vision/n_bit/nn_blocks_test.py b/official/projects/qat/vision/n_bit/nn_blocks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..e5778b4414f4d1acbdd979d4cde11e8fc9fb33ff
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/nn_blocks_test.py
@@ -0,0 +1,99 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for nn_blocks."""
+
+from typing import Any, Iterable, Tuple
+# Import libraries
+from absl.testing import parameterized
+import tensorflow as tf
+
+from tensorflow.python.distribute import combinations
+from tensorflow.python.distribute import strategy_combinations
+from official.projects.qat.vision.n_bit import nn_blocks
+
+
+def distribution_strategy_combinations() -> Iterable[Tuple[Any, ...]]:
+ """Returns the combinations of end-to-end tests to run."""
+ return combinations.combine(
+ distribution=[
+ strategy_combinations.default_strategy,
+ strategy_combinations.cloud_tpu_strategy,
+ strategy_combinations.one_device_strategy_gpu,
+ ],
+ )
+
+
+class NNBlocksTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (nn_blocks.BottleneckBlockNBitQuantized, 1, False, 0.0, None, 4, 4),
+ (nn_blocks.BottleneckBlockNBitQuantized, 2, True, 0.2, 0.25, 4, 4),
+ )
+ def test_bottleneck_block_creation(self, block_fn, strides, use_projection,
+ stochastic_depth_drop_rate, se_ratio,
+ num_bits_weight, num_bits_activation):
+ input_size = 128
+ filter_size = 256
+ inputs = tf.keras.Input(
+ shape=(input_size, input_size, filter_size * 4), batch_size=1)
+ block = block_fn(
+ filter_size,
+ strides,
+ use_projection=use_projection,
+ se_ratio=se_ratio,
+ stochastic_depth_drop_rate=stochastic_depth_drop_rate,
+ num_bits_weight=num_bits_weight,
+ num_bits_activation=num_bits_activation)
+
+ features = block(inputs)
+
+ self.assertAllEqual(
+ [1, input_size // strides, input_size // strides, filter_size * 4],
+ features.shape.as_list())
+
+ @parameterized.parameters(
+ (nn_blocks.InvertedBottleneckBlockNBitQuantized, 1, 1, None, None, 4, 4),
+ (nn_blocks.InvertedBottleneckBlockNBitQuantized, 6, 1, None, None, 4, 4),
+ (nn_blocks.InvertedBottleneckBlockNBitQuantized, 1, 2, None, None, 4, 4),
+ (nn_blocks.InvertedBottleneckBlockNBitQuantized, 1, 1, 0.2, None, 4, 4),
+ (nn_blocks.InvertedBottleneckBlockNBitQuantized, 1, 1, None, 0.2, 4, 4),
+ )
+ def test_invertedbottleneck_block_creation(
+ self, block_fn, expand_ratio, strides, se_ratio,
+ stochastic_depth_drop_rate, num_bits_weight, num_bits_activation):
+ input_size = 128
+ in_filters = 24
+ out_filters = 40
+ inputs = tf.keras.Input(
+ shape=(input_size, input_size, in_filters), batch_size=1)
+ block = block_fn(
+ in_filters=in_filters,
+ out_filters=out_filters,
+ expand_ratio=expand_ratio,
+ strides=strides,
+ se_ratio=se_ratio,
+ stochastic_depth_drop_rate=stochastic_depth_drop_rate,
+ num_bits_weight=num_bits_weight,
+ num_bits_activation=num_bits_activation)
+
+ features = block(inputs)
+
+ self.assertAllEqual(
+ [1, input_size // strides, input_size // strides, out_filters],
+ features.shape.as_list())
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/n_bit/nn_layers.py b/official/projects/qat/vision/n_bit/nn_layers.py
new file mode 100644
index 0000000000000000000000000000000000000000..feef66e7cd0280302c78835c837eafac4b373187
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/nn_layers.py
@@ -0,0 +1,215 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains common building blocks for neural networks."""
+
+from typing import Any, Callable, Dict, Union
+
+import tensorflow as tf
+import tensorflow_model_optimization as tfmot
+
+from official.modeling import tf_utils
+from official.projects.qat.vision.n_bit import configs
+from official.vision.modeling.layers import nn_layers
+
+# Type annotations.
+States = Dict[str, tf.Tensor]
+Activation = Union[str, Callable]
+
+
+class NoOpActivation:
+ """No-op activation which simply returns the incoming tensor.
+
+ This activation is required to distinguish between `keras.activations.linear`
+ which does the same thing. The main difference is that NoOpActivation should
+ not have any quantize operation applied to it.
+ """
+
+ def __call__(self, x: tf.Tensor) -> tf.Tensor:
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this object."""
+ return {}
+
+ def __eq__(self, other: Any) -> bool:
+ return isinstance(other, NoOpActivation)
+
+ def __ne__(self, other: Any) -> bool:
+ return not self.__eq__(other)
+
+
+def _quantize_wrapped_layer(cls, quantize_config):
+ def constructor(*arg, **kwargs):
+ return tfmot.quantization.keras.QuantizeWrapperV2(
+ cls(*arg, **kwargs),
+ quantize_config)
+ return constructor
+
+
+@tf.keras.utils.register_keras_serializable(package='Vision')
+class SqueezeExcitationNBitQuantized(tf.keras.layers.Layer):
+ """Creates a squeeze and excitation layer."""
+
+ def __init__(self,
+ in_filters,
+ out_filters,
+ se_ratio,
+ divisible_by=1,
+ use_3d_input=False,
+ kernel_initializer='VarianceScaling',
+ kernel_regularizer=None,
+ bias_regularizer=None,
+ activation='relu',
+ gating_activation='sigmoid',
+ num_bits_weight=8,
+ num_bits_activation=8,
+ **kwargs):
+ """Initializes a squeeze and excitation layer.
+
+ Args:
+ in_filters: An `int` number of filters of the input tensor.
+ out_filters: An `int` number of filters of the output tensor.
+ se_ratio: A `float` or None. If not None, se ratio for the squeeze and
+ excitation layer.
+ divisible_by: An `int` that ensures all inner dimensions are divisible by
+ this number.
+ use_3d_input: A `bool` of whether input is 2D or 3D image.
+ kernel_initializer: A `str` of kernel_initializer for convolutional
+ layers.
+ kernel_regularizer: A `tf.keras.regularizers.Regularizer` object for
+ Conv2D. Default to None.
+ bias_regularizer: A `tf.keras.regularizers.Regularizer` object for Conv2d.
+ Default to None.
+ activation: A `str` name of the activation function.
+ gating_activation: A `str` name of the activation function for final
+ gating function.
+ num_bits_weight: An `int` number of bits for the weight. Default to 8.
+ num_bits_activation: An `int` number of bits for the weight. Default to 8.
+ **kwargs: Additional keyword arguments to be passed.
+ """
+ super().__init__(**kwargs)
+
+ self._in_filters = in_filters
+ self._out_filters = out_filters
+ self._se_ratio = se_ratio
+ self._divisible_by = divisible_by
+ self._use_3d_input = use_3d_input
+ self._activation = activation
+ self._gating_activation = gating_activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ if not use_3d_input:
+ self._spatial_axis = [1, 2]
+ else:
+ self._spatial_axis = [1, 2, 3]
+ else:
+ if not use_3d_input:
+ self._spatial_axis = [2, 3]
+ else:
+ self._spatial_axis = [2, 3, 4]
+ self._activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ self._gating_activation_layer = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf_utils.get_activation(gating_activation, use_keras_layer=True),
+ configs.DefaultNBitActivationQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+
+ def build(self, input_shape):
+ conv2d_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['kernel'], ['activation'], False,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ conv2d_quantized_output_quantized = _quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.DefaultNBitConvQuantizeConfig(
+ ['kernel'], ['activation'], True,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ num_reduced_filters = nn_layers.make_divisible(
+ max(1, int(self._in_filters * self._se_ratio)),
+ divisor=self._divisible_by)
+
+ self._se_reduce = conv2d_quantized(
+ filters=num_reduced_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=True,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+
+ self._se_expand = conv2d_quantized_output_quantized(
+ filters=self._out_filters,
+ kernel_size=1,
+ strides=1,
+ padding='same',
+ use_bias=True,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ activation=NoOpActivation())
+
+ self._multiply = tfmot.quantization.keras.QuantizeWrapperV2(
+ tf.keras.layers.Multiply(),
+ configs.DefaultNBitQuantizeConfig(
+ [], [], True, num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation))
+ self._reduce_mean_quantizer = (
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=self._num_bits_activation, per_axis=False,
+ symmetric=False, narrow_range=False)) # activation/output
+ self._reduce_mean_quantizer_vars = self._reduce_mean_quantizer.build(
+ None, 'reduce_mean_quantizer_vars', self)
+
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {
+ 'in_filters': self._in_filters,
+ 'out_filters': self._out_filters,
+ 'se_ratio': self._se_ratio,
+ 'divisible_by': self._divisible_by,
+ 'use_3d_input': self._use_3d_input,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ 'activation': self._activation,
+ 'gating_activation': self._gating_activation,
+ 'num_bits_weight': self._num_bits_weight,
+ 'num_bits_activation': self._num_bits_activation
+ }
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs, training=None):
+ x = tf.reduce_mean(inputs, self._spatial_axis, keepdims=True)
+ x = self._reduce_mean_quantizer(
+ x, training, self._reduce_mean_quantizer_vars)
+ x = self._activation_layer(self._se_reduce(x))
+ x = self._gating_activation_layer(self._se_expand(x))
+ x = self._multiply([x, inputs])
+ return x
diff --git a/official/projects/qat/vision/n_bit/schemes.py b/official/projects/qat/vision/n_bit/schemes.py
new file mode 100644
index 0000000000000000000000000000000000000000..31661f89e23335f62be3f3677693cfcef09590d6
--- /dev/null
+++ b/official/projects/qat/vision/n_bit/schemes.py
@@ -0,0 +1,223 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Quantization schemes."""
+from typing import Type
+
+# Import libraries
+
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.n_bit import configs
+from official.projects.qat.vision.n_bit import nn_blocks
+
+keras = tf.keras
+default_n_bit_transforms = tfmot.quantization.keras.experimental.default_n_bit.default_n_bit_transforms
+_LayerNode = tfmot.quantization.keras.graph_transformations.transforms.LayerNode
+_LayerPattern = tfmot.quantization.keras.graph_transformations.transforms.LayerPattern
+_ModelTransformer = tfmot.quantization.keras.graph_transformations.model_transformer.ModelTransformer
+
+_QUANTIZATION_WEIGHT_NAMES = [
+ 'output_max', 'output_min', 'optimizer_step',
+ 'kernel_min', 'kernel_max',
+ 'depthwise_kernel_min', 'depthwise_kernel_max',
+ 'reduce_mean_quantizer_vars_min', 'reduce_mean_quantizer_vars_max']
+
+_ORIGINAL_WEIGHT_NAME = [
+ 'kernel', 'depthwise_kernel',
+ 'gamma', 'beta', 'moving_mean', 'moving_variance',
+ 'bias']
+
+
+class CustomLayerQuantize(
+ tfmot.quantization.keras.graph_transformations.transforms.Transform):
+ """Add QAT support for Keras Custom layer."""
+
+ def __init__(self,
+ original_layer_pattern: str,
+ quantized_layer_class: Type[keras.layers.Layer],
+ num_bits_weight: int = 8,
+ num_bits_activation: int = 8):
+ super().__init__()
+ self._original_layer_pattern = original_layer_pattern
+ self._quantized_layer_class = quantized_layer_class
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def pattern(self) -> _LayerPattern:
+ """See base class."""
+ return _LayerPattern(self._original_layer_pattern)
+
+ def _is_quantization_weight_name(self, name):
+ simple_name = name.split('/')[-1].split(':')[0]
+ if simple_name in _QUANTIZATION_WEIGHT_NAMES:
+ return True
+ if simple_name in _ORIGINAL_WEIGHT_NAME:
+ return False
+ raise ValueError(f'Variable name {simple_name} is not supported on '
+ 'CustomLayerQuantize({self._original_layer_pattern}) '
+ 'transform.')
+
+ def replacement(self, match_layer: _LayerNode) -> _LayerNode:
+ """See base class."""
+ bottleneck_layer = match_layer.layer
+ bottleneck_config = bottleneck_layer['config']
+ bottleneck_config['num_bits_weight'] = self._num_bits_weight
+ bottleneck_config['num_bits_activation'] = self._num_bits_activation
+ bottleneck_names_and_weights = list(match_layer.names_and_weights)
+ quantized_layer = self._quantized_layer_class(
+ **bottleneck_config)
+ dummy_input_shape = [1, 1, 1, 1]
+ quantized_layer.compute_output_shape(dummy_input_shape)
+ quantized_names_and_weights = zip(
+ [weight.name for weight in quantized_layer.weights],
+ quantized_layer.get_weights())
+ match_idx = 0
+ names_and_weights = []
+ for name_and_weight in quantized_names_and_weights:
+ if not self._is_quantization_weight_name(name=name_and_weight[0]):
+ name_and_weight = bottleneck_names_and_weights[match_idx]
+ match_idx = match_idx + 1
+ names_and_weights.append(name_and_weight)
+
+ if match_idx != len(bottleneck_names_and_weights):
+ raise ValueError('{}/{} of Bottleneck weights is transformed.'.format(
+ match_idx, len(bottleneck_names_and_weights)))
+ quantized_layer_config = keras.layers.serialize(quantized_layer)
+ quantized_layer_config['name'] = quantized_layer_config['config']['name']
+ layer_metadata = {
+ 'quantize_config':
+ configs.DefaultNBitOutputQuantizeConfig(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)}
+
+ return _LayerNode(
+ quantized_layer_config,
+ metadata=layer_metadata,
+ names_and_weights=names_and_weights)
+
+
+class QuantizeLayoutTransform(
+ tfmot.quantization.keras.QuantizeLayoutTransform):
+ """Default model transformations."""
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def apply(self, model, layer_quantize_map):
+ """Implement default 8-bit transforms.
+
+ Currently this means the following.
+ 1. Pull activations into layers, and apply fuse activations. (TODO)
+ 2. Modify range in incoming layers for Concat. (TODO)
+ 3. Fuse Conv2D/DepthwiseConv2D + BN into single layer.
+
+ Args:
+ model: Keras model to be quantized.
+ layer_quantize_map: Map with keys as layer names, and values as dicts
+ containing custom `QuantizeConfig`s which may have been passed with
+ layers.
+
+ Returns:
+ (Transformed Keras model to better match TensorFlow Lite backend, updated
+ layer quantize map.)
+ """
+
+ transforms = [
+ default_n_bit_transforms.InputLayerQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.SeparableConv1DQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.SeparableConvQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DReshapeBatchNormReLUQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DReshapeBatchNormActivationQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DBatchNormReLUQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DBatchNormActivationQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DReshapeBatchNormQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.Conv2DBatchNormQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.ConcatTransform6Inputs(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.ConcatTransform5Inputs(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.ConcatTransform4Inputs(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.ConcatTransform3Inputs(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.ConcatTransform(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.LayerReLUQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ default_n_bit_transforms.LayerReluActivationQuantize(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ CustomLayerQuantize(
+ 'Vision>BottleneckBlock',
+ nn_blocks.BottleneckBlockNBitQuantized,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ CustomLayerQuantize(
+ 'Vision>InvertedBottleneckBlock',
+ nn_blocks.InvertedBottleneckBlockNBitQuantized,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation),
+ CustomLayerQuantize(
+ 'Vision>Conv2DBNBlock',
+ nn_blocks.Conv2DBNBlockNBitQuantized,
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)
+ ]
+ return _ModelTransformer(model, transforms, set(layer_quantize_map.keys()),
+ layer_quantize_map).transform()
+
+
+class DefaultNBitQuantizeScheme(tfmot.quantization.keras.experimental
+ .default_n_bit.DefaultNBitQuantizeScheme):
+ """Default N-bit Scheme."""
+
+ def __init__(self, num_bits_weight: int = 8, num_bits_activation: int = 8):
+ super(DefaultNBitQuantizeScheme, self).__init__(
+ num_bits_weight=num_bits_weight,
+ num_bits_activation=num_bits_activation)
+ self._num_bits_weight = num_bits_weight
+ self._num_bits_activation = num_bits_activation
+
+ def get_layout_transformer(self):
+ return QuantizeLayoutTransform(
+ num_bits_weight=self._num_bits_weight,
+ num_bits_activation=self._num_bits_activation)
+
diff --git a/official/projects/qat/vision/quantization/__init__.py b/official/projects/qat/vision/quantization/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..67c06b5c83222383a661fce9c58ce2a763e39c07
--- /dev/null
+++ b/official/projects/qat/vision/quantization/__init__.py
@@ -0,0 +1,15 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
diff --git a/official/projects/qat/vision/quantization/configs.py b/official/projects/qat/vision/quantization/configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..17eeb9c3fcc8a9216da1e5b1f0d73e65ed0b88cb
--- /dev/null
+++ b/official/projects/qat/vision/quantization/configs.py
@@ -0,0 +1,337 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Default 8-bit QuantizeConfigs."""
+from typing import Sequence, Callable, Tuple, Any, Dict
+
+import tensorflow as tf
+import tensorflow_model_optimization as tfmot
+
+
+Quantizer = tfmot.quantization.keras.quantizers.Quantizer
+Layer = tf.keras.layers.Layer
+Activation = Callable[[tf.Tensor], tf.Tensor]
+WeightAndQuantizer = Tuple[tf.Variable, Quantizer]
+ActivationAndQuantizer = Tuple[Activation, Quantizer]
+
+
+class Default8BitOutputQuantizeConfig(tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig which only quantizes the output from a layer."""
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ return []
+
+ def set_quantize_weights(self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ pass
+
+ def set_quantize_activations(self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ pass
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ return [
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False)
+ ]
+
+ def get_config(self) -> Dict[str, Any]:
+ return {}
+
+
+class NoOpQuantizeConfig(tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig which does not quantize any part of the layer."""
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ return []
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ pass
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ pass
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ return []
+
+ def get_config(self) -> Dict[str, Any]:
+ return {}
+
+
+class Default8BitQuantizeConfig(tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig for non recurrent Keras layers."""
+
+ def __init__(self,
+ weight_attrs: Sequence[str],
+ activation_attrs: Sequence[str],
+ quantize_output: bool):
+ """Initializes a default 8bit quantize config."""
+ self.weight_attrs = weight_attrs
+ self.activation_attrs = activation_attrs
+ self.quantize_output = quantize_output
+
+ # TODO(pulkitb): For some layers such as Conv2D, per_axis should be True.
+ # Add mapping for which layers support per_axis.
+ self.weight_quantizer = tfmot.quantization.keras.quantizers.LastValueQuantizer(
+ num_bits=8, per_axis=False, symmetric=True, narrow_range=True)
+ self.activation_quantizer = tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False)
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ """See base class."""
+ return [(getattr(layer, weight_attr), self.weight_quantizer)
+ for weight_attr in self.weight_attrs]
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ """See base class."""
+ return [(getattr(layer, activation_attr), self.activation_quantizer)
+ for activation_attr in self.activation_attrs]
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ """See base class."""
+ if len(self.weight_attrs) != len(quantize_weights):
+ raise ValueError(
+ '`set_quantize_weights` called on layer {} with {} '
+ 'weight parameters, but layer expects {} values.'.format(
+ layer.name, len(quantize_weights), len(self.weight_attrs)))
+
+ for weight_attr, weight in zip(self.weight_attrs, quantize_weights):
+ current_weight = getattr(layer, weight_attr)
+ if current_weight.shape != weight.shape:
+ raise ValueError('Existing layer weight shape {} is incompatible with'
+ 'provided weight shape {}'.format(
+ current_weight.shape, weight.shape))
+
+ setattr(layer, weight_attr, weight)
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ """See base class."""
+ if len(self.activation_attrs) != len(quantize_activations):
+ raise ValueError(
+ '`set_quantize_activations` called on layer {} with {} '
+ 'activation parameters, but layer expects {} values.'.format(
+ layer.name, len(quantize_activations),
+ len(self.activation_attrs)))
+
+ for activation_attr, activation in zip(
+ self.activation_attrs, quantize_activations):
+ setattr(layer, activation_attr, activation)
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ """See base class."""
+ if self.quantize_output:
+ return [self.activation_quantizer]
+ return []
+
+ @classmethod
+ def from_config(cls, config: Dict[str, Any]) -> object:
+ """Instantiates a `Default8BitQuantizeConfig` from its config.
+
+ Args:
+ config: Output of `get_config()`.
+
+ Returns:
+ A `Default8BitQuantizeConfig` instance.
+ """
+ return cls(**config)
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config for this quantize config."""
+ # TODO(pulkitb): Add weight and activation quantizer to config.
+ # Currently it's created internally, but ideally the quantizers should be
+ # part of the constructor and passed in from the registry.
+ return {
+ 'weight_attrs': self.weight_attrs,
+ 'activation_attrs': self.activation_attrs,
+ 'quantize_output': self.quantize_output
+ }
+
+ def __eq__(self, other):
+ if not isinstance(other, Default8BitQuantizeConfig):
+ return False
+
+ return (self.weight_attrs == other.weight_attrs and
+ self.activation_attrs == self.activation_attrs and
+ self.weight_quantizer == other.weight_quantizer and
+ self.activation_quantizer == other.activation_quantizer and
+ self.quantize_output == other.quantize_output)
+
+ def __ne__(self, other):
+ return not self.__eq__(other)
+
+
+class Default8BitConvWeightsQuantizer(
+ tfmot.quantization.keras.quantizers.LastValueQuantizer):
+ """Quantizer for handling weights in Conv2D/DepthwiseConv2D layers."""
+
+ def __init__(self):
+ """Construct LastValueQuantizer with params specific for TFLite Convs."""
+
+ super(Default8BitConvWeightsQuantizer, self).__init__(
+ num_bits=8, per_axis=True, symmetric=True, narrow_range=True)
+
+ def build(self,
+ tensor_shape: tf.TensorShape,
+ name: str,
+ layer: Layer):
+ """Build min/max quantization variables."""
+ min_weight = layer.add_weight(
+ name + '_min',
+ shape=(tensor_shape[-1],),
+ initializer=tf.keras.initializers.Constant(-6.0),
+ trainable=False)
+ max_weight = layer.add_weight(
+ name + '_max',
+ shape=(tensor_shape[-1],),
+ initializer=tf.keras.initializers.Constant(6.0),
+ trainable=False)
+
+ return {'min_var': min_weight, 'max_var': max_weight}
+
+
+class NoQuantizer(tfmot.quantization.keras.quantizers.Quantizer):
+ """Dummy quantizer for explicitly not quantize."""
+
+ def __call__(self, inputs, training, weights, **kwargs):
+ return tf.identity(inputs)
+
+ def get_config(self):
+ return {}
+
+ def build(self, tensor_shape, name, layer):
+ return {}
+
+
+class Default8BitConvQuantizeConfig(Default8BitQuantizeConfig):
+ """QuantizeConfig for Conv2D/DepthwiseConv2D layers."""
+
+ def __init__(self,
+ weight_attrs: Sequence[str],
+ activation_attrs: Sequence[str],
+ quantize_output: bool):
+ """Initializes default 8bit quantization config for the conv layer."""
+ super().__init__(weight_attrs, activation_attrs, quantize_output)
+
+ self.weight_quantizer = Default8BitConvWeightsQuantizer()
+
+
+class Default8BitActivationQuantizeConfig(
+ tfmot.quantization.keras.QuantizeConfig):
+ """QuantizeConfig for keras.layers.Activation.
+
+ `keras.layers.Activation` needs a separate `QuantizeConfig` since the
+ decision to quantize depends on the specific activation type.
+ """
+
+ def _assert_activation_layer(self, layer: Layer):
+ if not isinstance(layer, tf.keras.layers.Activation):
+ raise RuntimeError(
+ 'Default8BitActivationQuantizeConfig can only be used with '
+ '`keras.layers.Activation`.')
+
+ def get_weights_and_quantizers(
+ self, layer: Layer) -> Sequence[WeightAndQuantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+ return []
+
+ def get_activations_and_quantizers(
+ self, layer: Layer) -> Sequence[ActivationAndQuantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+ return []
+
+ def set_quantize_weights(
+ self,
+ layer: Layer,
+ quantize_weights: Sequence[tf.Tensor]):
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ def set_quantize_activations(
+ self,
+ layer: Layer,
+ quantize_activations: Sequence[Activation]):
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ def get_output_quantizers(self, layer: Layer) -> Sequence[Quantizer]:
+ """See base class."""
+ self._assert_activation_layer(layer)
+
+ if not hasattr(layer.activation, '__name__'):
+ raise ValueError('Activation {} not supported by '
+ 'Default8BitActivationQuantizeConfig.'.format(
+ layer.activation))
+
+ # This code is copied from TFMOT repo, but added relu6 to support mobilenet.
+ if layer.activation.__name__ in ['relu', 'relu6', 'swish', 'hard_swish']:
+ # 'relu' should generally get fused into the previous layer.
+ return [tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False)]
+ elif layer.activation.__name__ in [
+ 'linear', 'softmax', 'sigmoid', 'hard_sigmoid'
+ ]:
+ return []
+
+ raise ValueError('Activation {} not supported by '
+ 'Default8BitActivationQuantizeConfig.'.format(
+ layer.activation))
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config for this quantizer config."""
+ return {}
+
+
+def _types_dict():
+ return {
+ 'Default8BitOutputQuantizeConfig':
+ Default8BitOutputQuantizeConfig,
+ 'NoOpQuantizeConfig':
+ NoOpQuantizeConfig,
+ 'Default8BitQuantizeConfig':
+ Default8BitQuantizeConfig,
+ 'Default8BitConvWeightsQuantizer':
+ Default8BitConvWeightsQuantizer,
+ 'Default8BitConvQuantizeConfig':
+ Default8BitConvQuantizeConfig,
+ 'Default8BitActivationQuantizeConfig':
+ Default8BitActivationQuantizeConfig,
+ }
diff --git a/official/projects/qat/vision/quantization/configs_test.py b/official/projects/qat/vision/quantization/configs_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..d23a65e3a1621890bb17e0a5774f737a6a666ed4
--- /dev/null
+++ b/official/projects/qat/vision/quantization/configs_test.py
@@ -0,0 +1,202 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for configs.py."""
+
+# Import libraries
+
+import numpy as np
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+
+from official.projects.qat.vision.quantization import configs
+
+
+class _TestHelper(object):
+
+ def _convert_list(self, list_of_tuples):
+ """Transforms a list of 2-tuples to a tuple of 2 lists.
+
+ `QuantizeConfig` methods return a list of 2-tuples in the form
+ [(weight1, quantizer1), (weight2, quantizer2)]. This function converts
+ it into a 2-tuple of lists. ([weight1, weight2]), (quantizer1, quantizer2).
+
+ Args:
+ list_of_tuples: List of 2-tuples.
+
+ Returns:
+ 2-tuple of lists.
+ """
+ list1 = []
+ list2 = []
+ for a, b in list_of_tuples:
+ list1.append(a)
+ list2.append(b)
+
+ return list1, list2
+
+ # TODO(pulkitb): Consider asserting on full equality for quantizers.
+
+ def _assert_weight_quantizers(self, quantizer_list):
+ for quantizer in quantizer_list:
+ self.assertIsInstance(
+ quantizer,
+ tfmot.quantization.keras.quantizers.LastValueQuantizer)
+
+ def _assert_activation_quantizers(self, quantizer_list):
+ for quantizer in quantizer_list:
+ self.assertIsInstance(
+ quantizer,
+ tfmot.quantization.keras.quantizers.MovingAverageQuantizer)
+
+ def _assert_kernel_equality(self, a, b):
+ self.assertAllEqual(a.numpy(), b.numpy())
+
+
+class Default8BitQuantizeConfigTest(tf.test.TestCase, _TestHelper):
+
+ def _simple_dense_layer(self):
+ layer = tf.keras.layers.Dense(2)
+ layer.build(input_shape=(3,))
+ return layer
+
+ def testGetsQuantizeWeightsAndQuantizers(self):
+ layer = self._simple_dense_layer()
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+ (weights, weight_quantizers) = self._convert_list(
+ quantize_config.get_weights_and_quantizers(layer))
+
+ self._assert_weight_quantizers(weight_quantizers)
+ self.assertEqual([layer.kernel], weights)
+
+ def testGetsQuantizeActivationsAndQuantizers(self):
+ layer = self._simple_dense_layer()
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+ (activations, activation_quantizers) = self._convert_list(
+ quantize_config.get_activations_and_quantizers(layer))
+
+ self._assert_activation_quantizers(activation_quantizers)
+ self.assertEqual([layer.activation], activations)
+
+ def testSetsQuantizeWeights(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(
+ np.ones(layer.kernel.shape.as_list()))
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+ quantize_config.set_quantize_weights(layer, [quantize_kernel])
+
+ self._assert_kernel_equality(layer.kernel, quantize_kernel)
+
+ def testSetsQuantizeActivations(self):
+ layer = self._simple_dense_layer()
+ quantize_activation = tf.keras.activations.relu
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+ quantize_config.set_quantize_activations(layer, [quantize_activation])
+
+ self.assertEqual(layer.activation, quantize_activation)
+
+ def testSetsQuantizeWeights_ErrorOnWrongNumberOfWeights(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(
+ np.ones(layer.kernel.shape.as_list()))
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer, [])
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer,
+ [quantize_kernel, quantize_kernel])
+
+ def testSetsQuantizeWeights_ErrorOnWrongShapeOfWeight(self):
+ layer = self._simple_dense_layer()
+ quantize_kernel = tf.keras.backend.variable(np.ones([1, 2]))
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_weights(layer, [quantize_kernel])
+
+ def testSetsQuantizeActivations_ErrorOnWrongNumberOfActivations(self):
+ layer = self._simple_dense_layer()
+ quantize_activation = tf.keras.activations.relu
+
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_activations(layer, [])
+
+ with self.assertRaises(ValueError):
+ quantize_config.set_quantize_activations(
+ layer, [quantize_activation, quantize_activation])
+
+ def testGetsResultQuantizers_ReturnsQuantizer(self):
+ layer = self._simple_dense_layer()
+ quantize_config = configs.Default8BitQuantizeConfig(
+ [], [], True)
+
+ output_quantizers = quantize_config.get_output_quantizers(layer)
+
+ self.assertLen(output_quantizers, 1)
+ self._assert_activation_quantizers(output_quantizers)
+
+ def testGetsResultQuantizers_EmptyWhenFalse(self):
+ layer = self._simple_dense_layer()
+ quantize_config = configs.Default8BitQuantizeConfig(
+ [], [], False)
+
+ output_quantizers = quantize_config.get_output_quantizers(layer)
+
+ self.assertEqual([], output_quantizers)
+
+ def testSerialization(self):
+ quantize_config = configs.Default8BitQuantizeConfig(
+ ['kernel'], ['activation'], False)
+
+ expected_config = {
+ 'class_name': 'Default8BitQuantizeConfig',
+ 'config': {
+ 'weight_attrs': ['kernel'],
+ 'activation_attrs': ['activation'],
+ 'quantize_output': False
+ }
+ }
+ serialized_quantize_config = tf.keras.utils.serialize_keras_object(
+ quantize_config)
+
+ self.assertEqual(expected_config, serialized_quantize_config)
+
+ quantize_config_from_config = tf.keras.utils.deserialize_keras_object(
+ serialized_quantize_config,
+ module_objects=globals(),
+ custom_objects=configs._types_dict())
+
+ self.assertEqual(quantize_config, quantize_config_from_config)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/quantization/helper.py b/official/projects/qat/vision/quantization/helper.py
new file mode 100644
index 0000000000000000000000000000000000000000..3b8958caa8f1f1dcf1e530a3875b231f3e8949ff
--- /dev/null
+++ b/official/projects/qat/vision/quantization/helper.py
@@ -0,0 +1,179 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Quantization helpers."""
+from typing import Any, Dict
+
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.quantization import configs
+
+
+_QUANTIZATION_WEIGHT_NAMES = [
+ 'output_max', 'output_min', 'optimizer_step', 'kernel_min', 'kernel_max',
+ 'add_three_min', 'add_three_max', 'divide_six_min', 'divide_six_max',
+ 'depthwise_kernel_min', 'depthwise_kernel_max',
+ 'reduce_mean_quantizer_vars_min', 'reduce_mean_quantizer_vars_max',
+ 'quantize_layer_min', 'quantize_layer_max',
+ 'quantize_layer_1_min', 'quantize_layer_1_max',
+ 'quantize_layer_2_min', 'quantize_layer_2_max',
+ 'quantize_layer_3_min', 'quantize_layer_3_max',
+ 'post_activation_min', 'post_activation_max',
+]
+
+_ORIGINAL_WEIGHT_NAME = [
+ 'kernel', 'depthwise_kernel', 'gamma', 'beta', 'moving_mean',
+ 'moving_variance', 'bias'
+]
+
+
+def is_quantization_weight_name(name: str) -> bool:
+ simple_name = name.split('/')[-1].split(':')[0]
+ if simple_name in _QUANTIZATION_WEIGHT_NAMES:
+ return True
+ if simple_name in _ORIGINAL_WEIGHT_NAME:
+ return False
+ raise ValueError('Variable name {} is not supported.'.format(simple_name))
+
+
+def copy_original_weights(original_model: tf.keras.Model,
+ quantized_model: tf.keras.Model):
+ """Helper function that copy the original model weights to quantized model."""
+ original_weight_value = original_model.get_weights()
+ weight_values = quantized_model.get_weights()
+
+ original_idx = 0
+ for idx, weight in enumerate(quantized_model.weights):
+ if not is_quantization_weight_name(weight.name):
+ if original_idx >= len(original_weight_value):
+ raise ValueError('Not enought original model weights.')
+ weight_values[idx] = original_weight_value[original_idx]
+ original_idx = original_idx + 1
+
+ if original_idx < len(original_weight_value):
+ raise ValueError('Not enought quantized model weights.')
+
+ quantized_model.set_weights(weight_values)
+
+
+class LayerQuantizerHelper(object):
+ """Helper class that handles quantizers."""
+
+ def __init__(self, *args, **kwargs):
+ self._quantizers = {}
+ self._quantizer_vars = {}
+ super().__init__(*args, **kwargs)
+
+ def _all_value_quantizer(self):
+ return tfmot.quantization.keras.quantizers.AllValuesQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False)
+
+ def _moving_average_quantizer(self):
+ return tfmot.quantization.keras.quantizers.MovingAverageQuantizer(
+ num_bits=8, per_axis=False, symmetric=False, narrow_range=False)
+
+ def _add_quantizer(self, name, all_value_quantizer=False):
+ if all_value_quantizer:
+ self._quantizers[name] = self._all_value_quantizer()
+ else:
+ self._quantizers[name] = self._moving_average_quantizer()
+
+ def _apply_quantizer(self, name, inputs, training, **kwargs):
+ return self._quantizers[name](
+ inputs, training, self._quantizer_vars[name], **kwargs)
+
+ def _build_quantizer_vars(self):
+ for name in self._quantizers:
+ self._quantizer_vars[name] = self._quantizers[name].build(
+ tensor_shape=None, name=name, layer=self)
+
+
+class NoOpActivation:
+ """No-op activation which simply returns the incoming tensor.
+
+ This activation is required to distinguish between `keras.activations.linear`
+ which does the same thing. The main difference is that NoOpActivation should
+ not have any quantize operation applied to it.
+ """
+
+ def __call__(self, x: tf.Tensor) -> tf.Tensor:
+ return x
+
+ def get_config(self) -> Dict[str, Any]:
+ """Get a config of this object."""
+ return {}
+
+ def __eq__(self, other: Any) -> bool:
+ if not other or not isinstance(other, NoOpActivation):
+ return False
+
+ return True
+
+ def __ne__(self, other: Any) -> bool:
+ return not self.__eq__(other)
+
+
+def quantize_wrapped_layer(cls, quantize_config):
+
+ def constructor(*arg, **kwargs):
+ return tfmot.quantization.keras.QuantizeWrapperV2(
+ cls(*arg, **kwargs), quantize_config)
+
+ return constructor
+
+
+def norm_by_activation(activation, norm_quantized, norm_no_quantized):
+ if activation not in ['relu', 'relu6']:
+ return norm_quantized
+ else:
+ return norm_no_quantized
+
+
+Conv2DQuantized = quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.Default8BitConvQuantizeConfig(['kernel'], ['activation'], False))
+Conv2DOutputQuantized = quantize_wrapped_layer(
+ tf.keras.layers.Conv2D,
+ configs.Default8BitConvQuantizeConfig(['kernel'], ['activation'], True))
+DepthwiseConv2DQuantized = quantize_wrapped_layer(
+ tf.keras.layers.DepthwiseConv2D,
+ configs.Default8BitConvQuantizeConfig(['depthwise_kernel'], ['activation'],
+ False))
+DepthwiseConv2DOutputQuantized = quantize_wrapped_layer(
+ tf.keras.layers.DepthwiseConv2D,
+ configs.Default8BitConvQuantizeConfig(['depthwise_kernel'], ['activation'],
+ True))
+GlobalAveragePooling2DQuantized = quantize_wrapped_layer(
+ tf.keras.layers.GlobalAveragePooling2D,
+ configs.Default8BitQuantizeConfig([], [], True))
+AveragePooling2DQuantized = quantize_wrapped_layer(
+ tf.keras.layers.AveragePooling2D,
+ configs.Default8BitQuantizeConfig([], [], True))
+ResizingQuantized = quantize_wrapped_layer(
+ tf.keras.layers.Resizing, configs.Default8BitQuantizeConfig([], [], True))
+ConcatenateQuantized = quantize_wrapped_layer(
+ tf.keras.layers.Concatenate, configs.Default8BitQuantizeConfig([], [],
+ True))
+UpSampling2DQuantized = quantize_wrapped_layer(
+ tf.keras.layers.UpSampling2D, configs.Default8BitQuantizeConfig([], [],
+ True))
+ReshapeQuantized = quantize_wrapped_layer(
+ tf.keras.layers.Reshape, configs.Default8BitQuantizeConfig([], [], True))
+
+# pylint:disable=g-long-lambda
+BatchNormalizationQuantized = lambda norm_layer: quantize_wrapped_layer(
+ norm_layer, configs.Default8BitOutputQuantizeConfig())
+BatchNormalizationNoQuantized = lambda norm_layer: quantize_wrapped_layer(
+ norm_layer, configs.NoOpQuantizeConfig())
diff --git a/official/projects/qat/vision/quantization/helper_test.py b/official/projects/qat/vision/quantization/helper_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..3f9c372dfdbed81d294b7973c5af9b4d03613d2d
--- /dev/null
+++ b/official/projects/qat/vision/quantization/helper_test.py
@@ -0,0 +1,54 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for helper."""
+import numpy as np
+import tensorflow as tf
+
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.quantization import helper
+
+
+class HelperTest(tf.test.TestCase):
+
+ def create_simple_model(self):
+ return tf.keras.models.Sequential([
+ tf.keras.layers.Dense(8, input_shape=(16,)),
+ ])
+
+ def test_copy_original_weights_for_simple_model_with_custom_weights(self):
+ one_model = self.create_simple_model()
+ one_weights = [np.ones_like(weight) for weight in one_model.get_weights()]
+ one_model.set_weights(one_weights)
+
+ qat_model = tfmot.quantization.keras.quantize_model(
+ self.create_simple_model())
+ zero_weights = [np.zeros_like(weight) for weight in qat_model.get_weights()]
+ qat_model.set_weights(zero_weights)
+
+ helper.copy_original_weights(one_model, qat_model)
+
+ qat_model_weights = qat_model.get_weights()
+ count = 0
+ for idx, weight in enumerate(qat_model.weights):
+ if not helper.is_quantization_weight_name(weight.name):
+ self.assertAllEqual(
+ qat_model_weights[idx], np.ones_like(qat_model_weights[idx]))
+ count += 1
+ self.assertLen(one_model.weights, count)
+ self.assertGreater(len(qat_model.weights), len(one_model.weights))
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/quantization/layer_transforms.py b/official/projects/qat/vision/quantization/layer_transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..c093f92e6dd53a436facdd3829dc367f0c316371
--- /dev/null
+++ b/official/projects/qat/vision/quantization/layer_transforms.py
@@ -0,0 +1,115 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains custom quantization layer transforms."""
+from typing import Any, Type, Mapping, List, Union, Tuple
+
+import tensorflow as tf
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.modeling.layers import nn_blocks as quantized_nn_blocks
+from official.projects.qat.vision.modeling.layers import nn_layers as quantized_nn_layers
+from official.projects.qat.vision.quantization import configs
+from official.projects.qat.vision.quantization import helper
+
+keras = tf.keras
+LayerNode = tfmot.quantization.keras.graph_transformations.transforms.LayerNode
+LayerPattern = tfmot.quantization.keras.graph_transformations.transforms.LayerPattern
+
+_LAYER_NAMES = [
+ 'Vision>Conv2DBNBlock', 'Vision>InvertedBottleneckBlock',
+ 'Vision>SegmentationHead', 'Vision>SpatialPyramidPooling', 'Vision>ASPP'
+]
+
+
+class CustomLayerQuantize(
+ tfmot.quantization.keras.graph_transformations.transforms.Transform):
+ """Add QAT support for Keras Custom layer."""
+
+ def __init__(self, original_layer_pattern: str,
+ quantized_layer_class: Type[keras.layers.Layer]):
+ super(CustomLayerQuantize, self).__init__()
+ self._original_layer_pattern = original_layer_pattern
+ self._quantized_layer_class = quantized_layer_class
+
+ def pattern(self) -> LayerPattern:
+ """See base class."""
+ return LayerPattern(self._original_layer_pattern)
+
+ def _create_layer_metadata(
+ self, layer_class_name: str
+ ) -> Mapping[str, tfmot.quantization.keras.QuantizeConfig]:
+ if layer_class_name in _LAYER_NAMES:
+ layer_metadata = {'quantize_config': configs.NoOpQuantizeConfig()}
+ else:
+ layer_metadata = {
+ 'quantize_config': configs.Default8BitOutputQuantizeConfig()
+ }
+ return layer_metadata
+
+ def _create_dummy_input_shape(
+ self, quantized_layer: tf.keras.layers.Layer
+ ) -> Union[List[int], Tuple[Any, Any]]:
+ dummy_input_shape = [1, 128, 128, 1]
+ # SegmentationHead layer requires a tuple of 2 tensors.
+ if isinstance(quantized_layer,
+ quantized_nn_layers.SegmentationHeadQuantized):
+ dummy_input_shape = ([1, 1, 1, 1], [1, 1, 1, 1])
+ return dummy_input_shape
+
+ def replacement(self, match_layer: LayerNode) -> LayerNode:
+ """See base class."""
+ bottleneck_layer = match_layer.layer
+ bottleneck_config = bottleneck_layer['config']
+ bottleneck_names_and_weights = list(match_layer.names_and_weights)
+ quantized_layer = self._quantized_layer_class(**bottleneck_config)
+ dummy_input_shape = self._create_dummy_input_shape(quantized_layer)
+ quantized_layer.compute_output_shape(dummy_input_shape)
+ quantized_names_and_weights = zip(
+ [weight.name for weight in quantized_layer.weights],
+ quantized_layer.get_weights())
+ match_idx = 0
+ names_and_weights = []
+ for name_and_weight in quantized_names_and_weights:
+ if not helper.is_quantization_weight_name(name=name_and_weight[0]):
+ name_and_weight = bottleneck_names_and_weights[match_idx]
+ match_idx = match_idx + 1
+ names_and_weights.append(name_and_weight)
+
+ if match_idx != len(bottleneck_names_and_weights):
+ raise ValueError('{}/{} of Bottleneck weights is transformed.'.format(
+ match_idx, len(bottleneck_names_and_weights)))
+ quantized_layer_config = keras.layers.serialize(quantized_layer)
+ quantized_layer_config['name'] = quantized_layer_config['config']['name']
+
+ layer_metadata = self._create_layer_metadata(bottleneck_layer['class_name'])
+
+ return LayerNode(
+ quantized_layer_config,
+ metadata=layer_metadata,
+ names_and_weights=names_and_weights)
+
+
+CUSTOM_TRANSFORMS = [
+ CustomLayerQuantize('Vision>BottleneckBlock',
+ quantized_nn_blocks.BottleneckBlockQuantized),
+ CustomLayerQuantize('Vision>InvertedBottleneckBlock',
+ quantized_nn_blocks.InvertedBottleneckBlockQuantized),
+ CustomLayerQuantize('Vision>Conv2DBNBlock',
+ quantized_nn_blocks.Conv2DBNBlockQuantized),
+ CustomLayerQuantize('Vision>SegmentationHead',
+ quantized_nn_layers.SegmentationHeadQuantized),
+ CustomLayerQuantize('Vision>SpatialPyramidPooling',
+ quantized_nn_layers.SpatialPyramidPoolingQuantized),
+ CustomLayerQuantize('Vision>ASPP', quantized_nn_layers.ASPPQuantized)
+]
diff --git a/official/projects/qat/vision/quantization/schemes.py b/official/projects/qat/vision/quantization/schemes.py
new file mode 100644
index 0000000000000000000000000000000000000000..fca03e4cbf96139d488a7be615dbd4f08ffc4f1a
--- /dev/null
+++ b/official/projects/qat/vision/quantization/schemes.py
@@ -0,0 +1,76 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Quantization schemes."""
+# Import libraries
+
+import tensorflow_model_optimization as tfmot
+from official.projects.qat.vision.quantization import layer_transforms
+
+
+default_8bit_transforms = tfmot.quantization.keras.default_8bit.default_8bit_transforms
+
+
+class QuantizeLayoutTransform(
+ tfmot.quantization.keras.QuantizeLayoutTransform):
+ """Default model transformations."""
+
+ def apply(self, model, layer_quantize_map):
+ """Implement default 8-bit transforms.
+
+ Currently this means the following.
+ 1. Pull activations into layers, and apply fuse activations. (TODO)
+ 2. Modify range in incoming layers for Concat. (TODO)
+ 3. Fuse Conv2D/DepthwiseConv2D + BN into single layer.
+
+ Args:
+ model: Keras model to be quantized.
+ layer_quantize_map: Map with keys as layer names, and values as dicts
+ containing custom `QuantizeConfig`s which may have been passed with
+ layers.
+
+ Returns:
+ (Transformed Keras model to better match TensorFlow Lite backend, updated
+ layer quantize map.)
+ """
+
+ transforms = [
+ default_8bit_transforms.InputLayerQuantize(),
+ default_8bit_transforms.SeparableConv1DQuantize(),
+ default_8bit_transforms.SeparableConvQuantize(),
+ default_8bit_transforms.Conv2DReshapeBatchNormReLUQuantize(),
+ default_8bit_transforms.Conv2DReshapeBatchNormActivationQuantize(),
+ default_8bit_transforms.Conv2DBatchNormReLUQuantize(),
+ default_8bit_transforms.Conv2DBatchNormActivationQuantize(),
+ default_8bit_transforms.Conv2DReshapeBatchNormQuantize(),
+ default_8bit_transforms.Conv2DBatchNormQuantize(),
+ default_8bit_transforms.ConcatTransform6Inputs(),
+ default_8bit_transforms.ConcatTransform5Inputs(),
+ default_8bit_transforms.ConcatTransform4Inputs(),
+ default_8bit_transforms.ConcatTransform3Inputs(),
+ default_8bit_transforms.ConcatTransform(),
+ default_8bit_transforms.LayerReLUQuantize(),
+ default_8bit_transforms.LayerReluActivationQuantize()
+ ]
+ transforms += layer_transforms.CUSTOM_TRANSFORMS
+ return tfmot.quantization.keras.graph_transformations.model_transformer.ModelTransformer(
+ model, transforms,
+ set(layer_quantize_map.keys()), layer_quantize_map).transform()
+
+
+class Default8BitQuantizeScheme(
+ tfmot.quantization.keras.default_8bit.Default8BitQuantizeScheme):
+
+ def get_layout_transformer(self):
+ return QuantizeLayoutTransform()
diff --git a/official/projects/qat/vision/registry_imports.py b/official/projects/qat/vision/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..2c93ccd9afebc2b697413e24b36391a6c54344d1
--- /dev/null
+++ b/official/projects/qat/vision/registry_imports.py
@@ -0,0 +1,21 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""All necessary imports for registration on qat project."""
+# pylint: disable=unused-import
+from official.projects.qat.vision import configs
+from official.projects.qat.vision.modeling import layers
+from official.projects.qat.vision.tasks import image_classification
+from official.projects.qat.vision.tasks import retinanet
+from official.projects.qat.vision.tasks import semantic_segmentation
diff --git a/official/projects/qat/vision/serving/export_module.py b/official/projects/qat/vision/serving/export_module.py
new file mode 100644
index 0000000000000000000000000000000000000000..2f24337c0bc954069fa5bc808dc251ef51803b40
--- /dev/null
+++ b/official/projects/qat/vision/serving/export_module.py
@@ -0,0 +1,68 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Export modules for QAT model serving/inference."""
+from absl import logging
+import tensorflow as tf
+
+from official.projects.qat.vision.modeling import factory as qat_factory
+from official.vision import configs
+from official.vision.serving import detection
+from official.vision.serving import image_classification
+from official.vision.serving import semantic_segmentation
+
+
+class ClassificationModule(image_classification.ClassificationModule):
+ """Classification Module."""
+
+ def _build_model(self):
+ model = super()._build_model()
+ input_specs = tf.keras.layers.InputSpec(shape=[self._batch_size] +
+ self._input_image_size + [3])
+ return qat_factory.build_qat_classification_model(
+ model, self.params.task.quantization, input_specs,
+ self.params.task.model)
+
+
+class SegmentationModule(semantic_segmentation.SegmentationModule):
+ """Segmentation Module."""
+
+ def _build_model(self):
+ model = super()._build_model()
+ input_specs = tf.keras.layers.InputSpec(shape=[self._batch_size] +
+ self._input_image_size + [3])
+ return qat_factory.build_qat_segmentation_model(
+ model, self.params.task.quantization, input_specs)
+
+
+class DetectionModule(detection.DetectionModule):
+ """Detection Module."""
+
+ def _build_model(self):
+ if self.params.task.model.detection_generator.nms_version != 'tflite':
+ self.params.task.model.detection_generator.nms_version = 'tflite'
+ logging.info('Set `nms_version` to `tflite` because only TFLite NMS is '
+ 'supported for QAT detection models.')
+
+ model = super()._build_model()
+
+ if isinstance(self.params.task.model, configs.retinanet.RetinaNet):
+ model = qat_factory.build_qat_retinanet(model,
+ self.params.task.quantization,
+ self.params.task.model)
+ else:
+ raise ValueError('Detection module not implemented for {} model.'.format(
+ type(self.params.task.model)))
+
+ return model
diff --git a/official/projects/qat/vision/serving/export_saved_model.py b/official/projects/qat/vision/serving/export_saved_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..85336d2c25afda882446a344702cdae33e6e67b7
--- /dev/null
+++ b/official/projects/qat/vision/serving/export_saved_model.py
@@ -0,0 +1,138 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Vision models export binary for serving/inference.
+
+To export a trained checkpoint in saved_model format (shell script):
+
+EXPERIMENT_TYPE = XX
+CHECKPOINT_PATH = XX
+EXPORT_DIR_PATH = XX
+export_saved_model --experiment=${EXPERIMENT_TYPE} \
+ --export_dir=${EXPORT_DIR_PATH}/ \
+ --checkpoint_path=${CHECKPOINT_PATH} \
+ --batch_size=2 \
+ --input_image_size=224,224
+
+To serve (python):
+
+export_dir_path = XX
+input_type = XX
+input_images = XX
+imported = tf.saved_model.load(export_dir_path)
+model_fn = imported.signatures['serving_default']
+output = model_fn(input_images)
+"""
+from absl import app
+from absl import flags
+
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.projects.qat.vision import registry_imports # pylint: disable=unused-import
+from official.projects.qat.vision.serving import export_module
+from official.vision import configs
+from official.vision.serving import export_saved_model_lib
+
+FLAGS = flags.FLAGS
+
+_EXPERIMENT = flags.DEFINE_string(
+ 'experiment', None, 'experiment type, e.g. retinanet_resnetfpn_coco')
+_EXPORT_DIR = flags.DEFINE_string('export_dir', None, 'The export directory.')
+_CHECKPOINT_PATH = flags.DEFINE_string('checkpoint_path', None,
+ 'Checkpoint path.')
+_CONFIG_FILE = flags.DEFINE_multi_string(
+ 'config_file',
+ default=None,
+ help='YAML/JSON files which specifies overrides. The override order '
+ 'follows the order of args. Note that each file '
+ 'can be used as an override template to override the default parameters '
+ 'specified in Python. If the same parameter is specified in both '
+ '`--config_file` and `--params_override`, `config_file` will be used '
+ 'first, followed by params_override.')
+_PARAMS_OVERRIDE = flags.DEFINE_string(
+ 'params_override', '',
+ 'The JSON/YAML file or string which specifies the parameter to be overriden'
+ ' on top of `config_file` template.')
+_BATCH_SIZE = flags.DEFINE_integer('batch_size', None, 'The batch size.')
+_IMAGE_TYPE = flags.DEFINE_string(
+ 'input_type', 'image_tensor',
+ 'One of `image_tensor`, `image_bytes`, `tf_example` and `tflite`.')
+_INPUT_IMAGE_SIZE = flags.DEFINE_string(
+ 'input_image_size', '224,224',
+ 'The comma-separated string of two integers representing the height,width '
+ 'of the input to the model.')
+_EXPORT_CHECKPOINT_SUBDIR = flags.DEFINE_string(
+ 'export_checkpoint_subdir', 'checkpoint',
+ 'The subdirectory for checkpoints.')
+_EXPORT_SAVED_MODEL_SUBDIR = flags.DEFINE_string(
+ 'export_saved_model_subdir', 'saved_model',
+ 'The subdirectory for saved model.')
+_LOG_MODEL_FLOPS_AND_PARAMS = flags.DEFINE_bool(
+ 'log_model_flops_and_params', False,
+ 'If true, logs model flops and parameters.')
+_INPUT_NAME = flags.DEFINE_string(
+ 'input_name', None,
+ 'Input tensor name in signature def. Default at None which'
+ 'produces input tensor name `inputs`.')
+
+
+def main(_):
+
+ params = exp_factory.get_exp_config(_EXPERIMENT.value)
+ for config_file in _CONFIG_FILE.value or []:
+ params = hyperparams.override_params_dict(
+ params, config_file, is_strict=True)
+ if _PARAMS_OVERRIDE.value:
+ params = hyperparams.override_params_dict(
+ params, _PARAMS_OVERRIDE.value, is_strict=True)
+
+ params.validate()
+ params.lock()
+
+ input_image_size = [int(x) for x in _INPUT_IMAGE_SIZE.value.split(',')]
+
+ if isinstance(params.task,
+ configs.image_classification.ImageClassificationTask):
+ export_module_cls = export_module.ClassificationModule
+ elif isinstance(params.task, configs.retinanet.RetinaNetTask):
+ export_module_cls = export_module.DetectionModule
+ elif isinstance(params.task,
+ configs.semantic_segmentation.SemanticSegmentationTask):
+ export_module_cls = export_module.SegmentationModule
+ else:
+ raise TypeError(f'Export module for {type(params.task)} is not supported.')
+
+ module = export_module_cls(
+ params=params,
+ batch_size=_BATCH_SIZE.value,
+ input_image_size=input_image_size,
+ input_type=_IMAGE_TYPE.value,
+ num_channels=3)
+
+ export_saved_model_lib.export_inference_graph(
+ input_type=_IMAGE_TYPE.value,
+ batch_size=_BATCH_SIZE.value,
+ input_image_size=input_image_size,
+ params=params,
+ checkpoint_path=_CHECKPOINT_PATH.value,
+ export_dir=_EXPORT_DIR.value,
+ export_checkpoint_subdir=_EXPORT_CHECKPOINT_SUBDIR.value,
+ export_saved_model_subdir=_EXPORT_SAVED_MODEL_SUBDIR.value,
+ export_module=module,
+ log_model_flops_and_params=_LOG_MODEL_FLOPS_AND_PARAMS.value,
+ input_name=_INPUT_NAME.value)
+
+
+if __name__ == '__main__':
+ app.run(main)
diff --git a/official/projects/qat/vision/serving/export_tflite.py b/official/projects/qat/vision/serving/export_tflite.py
new file mode 100644
index 0000000000000000000000000000000000000000..884ac0dad26f6caeb332cbdf145c1f01d16c3bb3
--- /dev/null
+++ b/official/projects/qat/vision/serving/export_tflite.py
@@ -0,0 +1,23 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Binary to convert a saved model to TFLite model for the QAT model."""
+
+from absl import app
+
+from official.projects.qat.vision import registry_imports # pylint: disable=unused-import
+from official.vision.serving import export_tflite
+
+if __name__ == '__main__':
+ app.run(export_tflite.main)
diff --git a/official/projects/qat/vision/tasks/__init__.py b/official/projects/qat/vision/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..42350ee0790bca9d71df31c52e7e3940f24f0bc6
--- /dev/null
+++ b/official/projects/qat/vision/tasks/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tasks package definition."""
+
+from official.projects.qat.vision.tasks import image_classification
diff --git a/official/projects/qat/vision/tasks/image_classification.py b/official/projects/qat/vision/tasks/image_classification.py
new file mode 100644
index 0000000000000000000000000000000000000000..20824dcef552e3299bba689a80aa5fafad9d550c
--- /dev/null
+++ b/official/projects/qat/vision/tasks/image_classification.py
@@ -0,0 +1,49 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification task definition."""
+import tensorflow as tf
+
+from official.core import task_factory
+from official.projects.qat.vision.configs import image_classification as exp_cfg
+from official.projects.qat.vision.modeling import factory
+from official.vision.tasks import image_classification
+
+
+@task_factory.register_task_cls(exp_cfg.ImageClassificationTask)
+class ImageClassificationTask(image_classification.ImageClassificationTask):
+ """A task for image classification with QAT."""
+
+ def build_model(self) -> tf.keras.Model:
+ """Builds classification model with QAT."""
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[None] + self.task_config.model.input_size)
+
+ l2_weight_decay = self.task_config.losses.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (tf.keras.regularizers.l2(
+ l2_weight_decay / 2.0) if l2_weight_decay else None)
+
+ model = super(ImageClassificationTask, self).build_model()
+ if self.task_config.quantization:
+ model = factory.build_qat_classification_model(
+ model,
+ self.task_config.quantization,
+ input_specs=input_specs,
+ model_config=self.task_config.model,
+ l2_regularizer=l2_regularizer)
+
+ return model
diff --git a/official/projects/qat/vision/tasks/image_classification_test.py b/official/projects/qat/vision/tasks/image_classification_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..eac971da3236d8e1523eb13830fdc35c243efb70
--- /dev/null
+++ b/official/projects/qat/vision/tasks/image_classification_test.py
@@ -0,0 +1,79 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for image classification task."""
+
+# pylint: disable=unused-import
+import os
+
+from absl.testing import parameterized
+import orbit
+import tensorflow as tf
+
+from official import vision
+from official.core import exp_factory
+from official.modeling import optimization
+from official.projects.qat.vision.tasks import image_classification as img_cls_task
+from official.vision.dataloaders import tfexample_utils
+
+
+class ImageClassificationTaskTest(tf.test.TestCase, parameterized.TestCase):
+
+ def _create_test_tfrecord(self, tfrecord_file, example, num_samples):
+ examples = [example] * num_samples
+ tfexample_utils.dump_to_tfrecord(
+ record_file=tfrecord_file, tf_examples=examples)
+
+ @parameterized.parameters(('resnet_imagenet_qat'),
+ ('mobilenet_imagenet_qat'))
+ def test_task(self, config_name):
+ input_image_size = [224, 224]
+ test_tfrecord_file = os.path.join(self.get_temp_dir(), 'cls_test.tfrecord')
+ example = tf.train.Example.FromString(
+ tfexample_utils.create_classification_example(
+ image_height=input_image_size[0], image_width=input_image_size[1]))
+ self._create_test_tfrecord(
+ tfrecord_file=test_tfrecord_file, example=example, num_samples=10)
+
+ config = exp_factory.get_exp_config(config_name)
+ config.task.train_data.global_batch_size = 2
+ config.task.validation_data.input_path = test_tfrecord_file
+ config.task.train_data.input_path = test_tfrecord_file
+ task = img_cls_task.ImageClassificationTask(config.task)
+ model = task.build_model()
+ metrics = task.build_metrics()
+ strategy = tf.distribute.get_strategy()
+
+ dataset = orbit.utils.make_distributed_dataset(strategy, task.build_inputs,
+ config.task.train_data)
+
+ iterator = iter(dataset)
+ opt_factory = optimization.OptimizerFactory(config.trainer.optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+ logs = task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ for metric in metrics:
+ logs[metric.name] = metric.result()
+ self.assertIn('loss', logs)
+ self.assertIn('accuracy', logs)
+ self.assertIn('top_5_accuracy', logs)
+ logs = task.validation_step(next(iterator), model, metrics=metrics)
+ for metric in metrics:
+ logs[metric.name] = metric.result()
+ self.assertIn('loss', logs)
+ self.assertIn('accuracy', logs)
+ self.assertIn('top_5_accuracy', logs)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/tasks/retinanet.py b/official/projects/qat/vision/tasks/retinanet.py
new file mode 100644
index 0000000000000000000000000000000000000000..5798bdec10b24ff02999a6991ede131771c1c695
--- /dev/null
+++ b/official/projects/qat/vision/tasks/retinanet.py
@@ -0,0 +1,40 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""RetinaNet task definition."""
+import tensorflow as tf
+
+from official.core import task_factory
+from official.projects.qat.vision.configs import retinanet as exp_cfg
+from official.projects.qat.vision.modeling import factory
+from official.vision.tasks import retinanet
+
+
+@task_factory.register_task_cls(exp_cfg.RetinaNetTask)
+class RetinaNetTask(retinanet.RetinaNetTask):
+ """A task for RetinaNet object detection with QAT."""
+
+ def build_model(self) -> tf.keras.Model:
+ """Builds RetinaNet model with QAT."""
+ model = super(RetinaNetTask, self).build_model()
+ # Call the model with dummy input to build the head part.
+ dummpy_input = tf.zeros([1] + self.task_config.model.input_size)
+ model(dummpy_input, training=True)
+
+ if self.task_config.quantization:
+ model = factory.build_qat_retinanet(
+ model,
+ self.task_config.quantization,
+ model_config=self.task_config.model)
+ return model
diff --git a/official/projects/qat/vision/tasks/retinanet_test.py b/official/projects/qat/vision/tasks/retinanet_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..03b3694c94d022964888dcff3fdd5df7fb96cb55
--- /dev/null
+++ b/official/projects/qat/vision/tasks/retinanet_test.py
@@ -0,0 +1,87 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for RetinaNet task."""
+# pylint: disable=unused-import
+import os
+
+from absl.testing import parameterized
+import orbit
+import tensorflow as tf
+
+from official import vision
+from official.core import exp_factory
+from official.modeling import optimization
+from official.projects.qat.vision.tasks import retinanet
+from official.vision.configs import retinanet as exp_cfg
+from official.vision.dataloaders import tfexample_utils
+
+
+class RetinaNetTaskTest(parameterized.TestCase, tf.test.TestCase):
+
+ def _create_test_tfrecord(self, tfrecord_file, example, num_samples):
+ examples = [example] * num_samples
+ tfexample_utils.dump_to_tfrecord(
+ record_file=tfrecord_file, tf_examples=examples)
+
+ @parameterized.parameters(
+ ('retinanet_mobile_coco_qat', True),
+ ('retinanet_mobile_coco_qat', False),
+ )
+ def test_retinanet_task(self, test_config, is_training):
+ """RetinaNet task test for training and val using toy configs."""
+ input_image_size = [384, 384]
+ test_tfrecord_file = os.path.join(self.get_temp_dir(), 'det_test.tfrecord')
+ example = tfexample_utils.create_detection_test_example(
+ image_height=input_image_size[0],
+ image_width=input_image_size[1],
+ image_channel=3,
+ num_instances=10)
+ self._create_test_tfrecord(
+ tfrecord_file=test_tfrecord_file, example=example, num_samples=10)
+ config = exp_factory.get_exp_config(test_config)
+ # modify config to suit local testing
+ config.task.model.input_size = [128, 128, 3]
+ config.trainer.steps_per_loop = 1
+ config.task.train_data.global_batch_size = 1
+ config.task.validation_data.global_batch_size = 1
+ config.task.train_data.shuffle_buffer_size = 2
+ config.task.validation_data.shuffle_buffer_size = 2
+ config.task.validation_data.input_path = test_tfrecord_file
+ config.task.train_data.input_path = test_tfrecord_file
+ config.task.annotation_file = None
+ config.train_steps = 1
+
+ task = retinanet.RetinaNetTask(config.task)
+ model = task.build_model()
+ self.assertLen(model.weights, 2393)
+ metrics = task.build_metrics(training=is_training)
+
+ strategy = tf.distribute.get_strategy()
+
+ data_config = config.task.train_data if is_training else config.task.validation_data
+ dataset = orbit.utils.make_distributed_dataset(strategy, task.build_inputs,
+ data_config)
+ iterator = iter(dataset)
+ opt_factory = optimization.OptimizerFactory(config.trainer.optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+
+ if is_training:
+ task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ else:
+ task.validation_step(next(iterator), model, metrics=metrics)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/qat/vision/tasks/semantic_segmentation.py b/official/projects/qat/vision/tasks/semantic_segmentation.py
new file mode 100644
index 0000000000000000000000000000000000000000..a2c1bd0e972fd2f84c74ff59cb82e916885a1c6e
--- /dev/null
+++ b/official/projects/qat/vision/tasks/semantic_segmentation.py
@@ -0,0 +1,36 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Semantic segmentation task definition."""
+import tensorflow as tf
+
+from official.core import task_factory
+from official.projects.qat.vision.configs import semantic_segmentation as exp_cfg
+from official.projects.qat.vision.modeling import factory
+from official.vision.tasks import semantic_segmentation
+
+
+@task_factory.register_task_cls(exp_cfg.SemanticSegmentationTask)
+class SemanticSegmentationTask(semantic_segmentation.SemanticSegmentationTask):
+ """A task for semantic segmentation with QAT."""
+
+ def build_model(self) -> tf.keras.Model:
+ """Builds semantic segmentation model with QAT."""
+ model = super().build_model()
+ input_specs = tf.keras.layers.InputSpec(shape=[None] +
+ self.task_config.model.input_size)
+ if self.task_config.quantization:
+ model = factory.build_qat_segmentation_model(
+ model, self.task_config.quantization, input_specs)
+ return model
diff --git a/official/projects/qat/vision/train.py b/official/projects/qat/vision/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..453cb9fe4e0addafc929ed661ba75f463f2b03e5
--- /dev/null
+++ b/official/projects/qat/vision/train.py
@@ -0,0 +1,26 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver, including QAT configs.."""
+
+from absl import app
+
+from official.common import flags as tfm_flags
+from official.projects.qat.vision import registry_imports # pylint: disable=unused-import
+from official.vision import train
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/roformer/__init__.py b/official/projects/roformer/__init__.py
index a25710c222e3327cb20e000db5df5c5651c4a2cc..ba97902e7ec1e12871c0fad301b9ce48c92cf1d1 100644
--- a/official/projects/roformer/__init__.py
+++ b/official/projects/roformer/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/roformer.py b/official/projects/roformer/roformer.py
index d0f4da23c19812f9a9662769575f9e48ad4945bd..0474de3dac87fcdd8458bc4ba2aaca1e38aed7e7 100644
--- a/official/projects/roformer/roformer.py
+++ b/official/projects/roformer/roformer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/roformer_attention.py b/official/projects/roformer/roformer_attention.py
index 2eec24db539ccda12d5eab65e414f7f0cbde0d2f..dc3be9507037eea20b4b019a1faa1e6a9b764ad0 100644
--- a/official/projects/roformer/roformer_attention.py
+++ b/official/projects/roformer/roformer_attention.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,7 +16,7 @@
# pylint: disable=g-classes-have-attributes
import tensorflow as tf
-EinsumDense = tf.keras.layers.experimental.EinsumDense
+EinsumDense = tf.keras.layers.EinsumDense
MultiHeadAttention = tf.keras.layers.MultiHeadAttention
diff --git a/official/projects/roformer/roformer_attention_test.py b/official/projects/roformer/roformer_attention_test.py
index 92d6b9001e7df10612278314e3c748471b713751..d131e876a7a645c24bfb778f1846605b7fdad7e5 100644
--- a/official/projects/roformer/roformer_attention_test.py
+++ b/official/projects/roformer/roformer_attention_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/roformer_encoder.py b/official/projects/roformer/roformer_encoder.py
index a81aa17aae9556753ea714d38178205357296ff4..0e683e7f09a183bc79aa7249b764064ec8aaf6f5 100644
--- a/official/projects/roformer/roformer_encoder.py
+++ b/official/projects/roformer/roformer_encoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,6 +19,7 @@ import collections
from absl import logging
import tensorflow as tf
+from official.modeling import tf_utils
from official.nlp.modeling import layers
from official.projects.roformer import roformer_encoder_block
@@ -115,7 +116,7 @@ class RoformerEncoder(tf.keras.Model):
embedding_layer_inst = layers.on_device_embedding.OnDeviceEmbedding(
vocab_size=vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
name='word_embeddings')
else:
embedding_layer_inst = embedding_layer
@@ -125,7 +126,7 @@ class RoformerEncoder(tf.keras.Model):
type_embedding_layer = layers.on_device_embedding.OnDeviceEmbedding(
vocab_size=type_vocab_size,
embedding_width=embedding_width,
- initializer=initializer,
+ initializer=tf_utils.clone_initializer(initializer),
use_one_hot=True,
name='type_embeddings')
type_embeddings = type_embedding_layer(type_ids)
@@ -142,11 +143,11 @@ class RoformerEncoder(tf.keras.Model):
# We project the 'embedding' output to 'hidden_size' if it is not already
# 'hidden_size'.
if embedding_width != hidden_size:
- embedding_projection = tf.keras.layers.experimental.EinsumDense(
+ embedding_projection = tf.keras.layers.EinsumDense(
'...x,xy->...y',
output_shape=hidden_size,
bias_axes='y',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='embedding_projection')
embeddings = embedding_projection(embeddings)
else:
@@ -171,7 +172,7 @@ class RoformerEncoder(tf.keras.Model):
attention_dropout=attention_dropout,
norm_first=norm_first,
output_range=transformer_output_range,
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='roformer/layer_%d' % i)
transformer_layers.append(layer)
data = layer([data, attention_mask])
@@ -185,7 +186,7 @@ class RoformerEncoder(tf.keras.Model):
pooler_layer = tf.keras.layers.Dense(
units=hidden_size,
activation='tanh',
- kernel_initializer=initializer,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
name='pooler_transform')
cls_output = pooler_layer(first_token_tensor)
diff --git a/official/projects/roformer/roformer_encoder_block.py b/official/projects/roformer/roformer_encoder_block.py
index 20826c41e71eca94654d9facdb34f2101af3294b..91714917fc4d4f8517bdfcd13818e32aa10621e4 100644
--- a/official/projects/roformer/roformer_encoder_block.py
+++ b/official/projects/roformer/roformer_encoder_block.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,6 +15,7 @@
"""Roformer TransformerEncoder block layer."""
import tensorflow as tf
+from official.modeling import tf_utils
from official.projects.roformer import roformer_attention
@@ -111,7 +112,8 @@ class RoformerEncoderBlock(tf.keras.layers.Layer):
self._attention_initializer = tf.keras.initializers.get(
attention_initializer)
else:
- self._attention_initializer = self._kernel_initializer
+ self._attention_initializer = tf_utils.clone_initializer(
+ self._kernel_initializer)
self._attention_axes = attention_axes
def build(self, input_shape):
@@ -160,11 +162,11 @@ class RoformerEncoderBlock(tf.keras.layers.Layer):
axis=-1,
epsilon=self._norm_epsilon,
dtype=tf.float32))
- self._intermediate_dense = tf.keras.layers.experimental.EinsumDense(
+ self._intermediate_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=(None, self._inner_dim),
bias_axes="d",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
name="intermediate",
**common_kwargs)
policy = tf.keras.mixed_precision.global_policy()
@@ -177,12 +179,12 @@ class RoformerEncoderBlock(tf.keras.layers.Layer):
self._inner_activation, dtype=policy)
self._inner_dropout_layer = tf.keras.layers.Dropout(
rate=self._inner_dropout)
- self._output_dense = tf.keras.layers.experimental.EinsumDense(
+ self._output_dense = tf.keras.layers.EinsumDense(
einsum_equation,
output_shape=(None, hidden_size),
bias_axes="d",
name="output",
- kernel_initializer=self._kernel_initializer,
+ kernel_initializer=tf_utils.clone_initializer(self._kernel_initializer),
**common_kwargs)
self._output_dropout = tf.keras.layers.Dropout(rate=self._output_dropout)
# Use float32 in layernorm for numeric stability.
diff --git a/official/projects/roformer/roformer_encoder_block_test.py b/official/projects/roformer/roformer_encoder_block_test.py
index f4833f96aa0dfb8cc9dd713d378be04cb5032ab1..99dd2b00c6cbb3a8f7e835093c8f10c1109e7c62 100644
--- a/official/projects/roformer/roformer_encoder_block_test.py
+++ b/official/projects/roformer/roformer_encoder_block_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/roformer_encoder_test.py b/official/projects/roformer/roformer_encoder_test.py
index 7c4d4f5d6081a2ba45b74414fd459a0af62f5cae..7fc77f3cf4e123af1da4f35d29425cd4a0aebb74 100644
--- a/official/projects/roformer/roformer_encoder_test.py
+++ b/official/projects/roformer/roformer_encoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/roformer_experiments.py b/official/projects/roformer/roformer_experiments.py
index a16c26be4a77c52bb3bc5428bfb7710395d5f4b0..cb095847d3d47573763b8b45195e0b823abeb186 100644
--- a/official/projects/roformer/roformer_experiments.py
+++ b/official/projects/roformer/roformer_experiments.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/roformer/train.py b/official/projects/roformer/train.py
index 7bd5dde0b14dba9fe1875e303f44a4daad8fc6b8..6ea0aec4b35cce61b53839f53f82b655132e4d59 100644
--- a/official/projects/roformer/train.py
+++ b/official/projects/roformer/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/s3d/configs/s3d.py b/official/projects/s3d/configs/s3d.py
new file mode 100644
index 0000000000000000000000000000000000000000..1dcd1424c2c92dbff6155c6a8a3cbb427c49ed4a
--- /dev/null
+++ b/official/projects/s3d/configs/s3d.py
@@ -0,0 +1,98 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""S3D model configurations."""
+import dataclasses
+from typing import Text
+
+from official.modeling import hyperparams
+from official.vision.configs import backbones_3d
+from official.vision.configs import video_classification
+
+
+@dataclasses.dataclass
+class S3D(hyperparams.Config):
+ """S3D backbone config.
+
+ Attributes:
+ final_endpoint: Specifies the endpoint to construct the network up to. It
+ can be one of ['Conv2d_1a_7x7', 'MaxPool_2a_3x3', 'Conv2d_2b_1x1',
+ 'Conv2d_2c_3x3', 'MaxPool_3a_3x3', 'Mixed_3b', 'Mixed_3c',
+ 'MaxPool_4a_3x3', 'Mixed_4b', 'Mixed_4c', 'Mixed_4d', 'Mixed_4e',
+ 'Mixed_4f', 'MaxPool_5a_2x2', 'Mixed_5b', 'Mixed_5c']
+ first_temporal_kernel_size: Specifies the temporal kernel size for the first
+ conv3d filter. A larger value slows down the model but provides little
+ accuracy improvement. Must be set to one of 1, 3, 5 or 7.
+ temporal_conv_start_at: Specifies the first conv block to use separable 3D
+ convs rather than 2D convs (implemented as [1, k, k] 3D conv). This is
+ used to construct the inverted pyramid models. 'Conv2d_2c_3x3' is the
+ first valid block to use separable 3D convs. If provided block name is
+ not present, all valid blocks will use separable 3D convs.
+ gating_start_at: Specifies the first conv block to use self gating.
+ 'Conv2d_2c_3x3' is the first valid block to use self gating.
+ swap_pool_and_1x1x1: If True, in Branch_3 1x1x1 convolution is performed
+ first, then followed by max pooling. 1x1x1 convolution is used to reduce
+ the number of filters. Thus, max pooling is performed on less filters.
+ gating_style: Self gating can be applied after each branch and/or after each
+ inception cell. It can be one of ['BRANCH', 'CELL', 'BRANCH_AND_CELL'].
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ temporal_conv_type: It can be one of ['3d', '2+1d', '1+2d', '1+1+1d'] where
+ '3d' is SPATIOTEMPORAL 3d convolution, '2+1d' is SPATIAL_TEMPORAL_SEPARATE
+ with 2D convolution on the spatial dimensions followed by 1D convolution
+ on the temporal dimension, '1+2d' is TEMPORAL_SPATIAL_SEPARATE with 1D
+ convolution on the temporal dimension followed by 2D convolution on the
+ spatial dimensions, and '1+1+1d' is FULLY_SEPARATE with 1D convolutions on
+ the horizontal, vertical, and temporal dimensions, respectively.
+ depth_multiplier: Float multiplier for the depth (number of channels) for
+ all convolution ops. The value must be greater than zero. Typical usage
+ will be to set this value in (0, 1) to reduce the number of parameters or
+ computation cost of the model.
+ """
+ final_endpoint: Text = 'Mixed_5c'
+ first_temporal_kernel_size: int = 3
+ temporal_conv_start_at: Text = 'Conv2d_2c_3x3'
+ gating_start_at: Text = 'Conv2d_2c_3x3'
+ swap_pool_and_1x1x1: bool = True
+ gating_style: Text = 'CELL'
+ use_sync_bn: bool = False
+ norm_momentum: float = 0.999
+ norm_epsilon: float = 0.001
+ temporal_conv_type: Text = '2+1d'
+ depth_multiplier: float = 1.0
+
+
+@dataclasses.dataclass
+class Backbone3D(backbones_3d.Backbone3D):
+ """Configuration for backbones.
+
+ Attributes:
+ type: 'str', type of backbone be used, on the of fields below.
+ s3d: s3d backbone config.
+ """
+ type: str = 's3d'
+ s3d: S3D = S3D()
+
+
+@dataclasses.dataclass
+class S3DModel(video_classification.VideoClassificationModel):
+ """The S3D model config.
+
+ Attributes:
+ type: 'str', type of backbone be used, on the of fields below.
+ backbone: backbone config.
+ """
+ model_type: str = 's3d'
+ backbone: Backbone3D = Backbone3D()
diff --git a/official/projects/s3d/modeling/inception_utils.py b/official/projects/s3d/modeling/inception_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..8ffa051c724bf9a1f204f7ce1678f2474b96c6bc
--- /dev/null
+++ b/official/projects/s3d/modeling/inception_utils.py
@@ -0,0 +1,536 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains modules related to Inception networks."""
+from typing import Callable, Dict, Optional, Sequence, Set, Text, Tuple, Type, Union
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.projects.s3d.modeling import net_utils
+from official.vision.modeling.layers import nn_blocks_3d
+
+INCEPTION_V1_CONV_ENDPOINTS = [
+ 'Conv2d_1a_7x7', 'Conv2d_2c_3x3', 'Mixed_3b', 'Mixed_3c', 'Mixed_4b',
+ 'Mixed_4c', 'Mixed_4d', 'Mixed_4e', 'Mixed_4f', 'Mixed_5b', 'Mixed_5c'
+]
+
+# Mapping from endpoint to branch filters. The endpoint shapes below are
+# specific for input 64x224x224.
+INCEPTION_V1_ARCH_SKELETON = [
+ ('Mixed_3b', [[64], [96, 128], [16, 32], [32]]), # 32x28x28x256
+ ('Mixed_3c', [[128], [128, 192], [32, 96], [64]]), # 32x28x28x480
+ ('MaxPool_4a_3x3', [[3, 3, 3], [2, 2, 2]]), # 16x14x14x480
+ ('Mixed_4b', [[192], [96, 208], [16, 48], [64]]), # 16x14x14x512
+ ('Mixed_4c', [[160], [112, 224], [24, 64], [64]]), # 16x14x14x512
+ ('Mixed_4d', [[128], [128, 256], [24, 64], [64]]), # 16x14x14x512
+ ('Mixed_4e', [[112], [144, 288], [32, 64], [64]]), # 16x14x14x528
+ ('Mixed_4f', [[256], [160, 320], [32, 128], [128]]), # 16x14x14x832
+ ('MaxPool_5a_2x2', [[2, 2, 2], [2, 2, 2]]), # 8x7x7x832
+ ('Mixed_5b', [[256], [160, 320], [32, 128], [128]]), # 8x7x7x832
+ ('Mixed_5c', [[384], [192, 384], [48, 128], [128]]), # 8x7x7x1024
+]
+
+INCEPTION_V1_LOCAL_SKELETON = [
+ ('MaxPool_5a_2x2_local', [[2, 2, 2], [2, 2, 2]]), # 8x7x7x832
+ ('Mixed_5b_local', [[256], [160, 320], [32, 128], [128]]), # 8x7x7x832
+ ('Mixed_5c_local', [[384], [192, 384], [48, 128], [128]]), # 8x7x7x1024
+]
+
+initializers = tf.keras.initializers
+regularizers = tf.keras.regularizers
+
+
+def inception_v1_stem_cells(
+ inputs: tf.Tensor,
+ depth_multiplier: float,
+ final_endpoint: Text,
+ temporal_conv_endpoints: Optional[Set[Text]] = None,
+ self_gating_endpoints: Optional[Set[Text]] = None,
+ temporal_conv_type: Text = '3d',
+ first_temporal_kernel_size: int = 7,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.999,
+ norm_epsilon: float = 0.001,
+ temporal_conv_initializer: Union[
+ Text, initializers.Initializer] = initializers.TruncatedNormal(
+ mean=0.0, stddev=0.01),
+ kernel_initializer: Union[Text,
+ initializers.Initializer] = 'truncated_normal',
+ kernel_regularizer: Union[Text, regularizers.Regularizer] = 'l2',
+ parameterized_conv_layer: Type[
+ net_utils.ParameterizedConvLayer] = net_utils.ParameterizedConvLayer,
+ layer_naming_fn: Callable[[Text], Text] = lambda end_point: None,
+) -> Tuple[tf.Tensor, Dict[Text, tf.Tensor]]:
+ """Stem cells used in the original I3D/S3D model.
+
+ Args:
+ inputs: A 5-D float tensor of size [batch_size, num_frames, height, width,
+ channels].
+ depth_multiplier: A float to reduce/increase number of channels.
+ final_endpoint: Specifies the endpoint to construct the network up to. It
+ can be one of ['Conv2d_1a_7x7', 'MaxPool_2a_3x3', 'Conv2d_2b_1x1',
+ 'Conv2d_2c_3x3', 'MaxPool_3a_3x3'].
+ temporal_conv_endpoints: Specifies the endpoints where to perform temporal
+ convolution.
+ self_gating_endpoints: Specifies the endpoints where to perform self gating.
+ temporal_conv_type: '3d' for I3D model and '2+1d' for S3D model.
+ first_temporal_kernel_size: temporal kernel size of the first convolution
+ layer.
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ temporal_conv_initializer: Weight initializer for temporal convolution
+ inside the cell. It only applies to 2+1d and 1+2d cases.
+ kernel_initializer: Weight initializer for convolutional layers other than
+ temporal convolution.
+ kernel_regularizer: Weight regularizer for all convolutional layers.
+ parameterized_conv_layer: class for parameterized conv layer.
+ layer_naming_fn: function to customize conv / pooling layer names given
+ endpoint name of the block. This is mainly used to creat model that is
+ compatible with TF1 checkpoints.
+
+ Returns:
+ A dictionary from components of the network to the corresponding activation.
+ """
+
+ if temporal_conv_endpoints is None:
+ temporal_conv_endpoints = set()
+ if self_gating_endpoints is None:
+ self_gating_endpoints = set()
+ if use_sync_bn:
+ batch_norm = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ batch_norm = tf.keras.layers.BatchNormalization
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ bn_axis = -1
+ else:
+ bn_axis = 1
+
+ end_points = {}
+ # batch_size x 32 x 112 x 112 x 64
+ end_point = 'Conv2d_1a_7x7'
+ net = tf.keras.layers.Conv3D(
+ filters=net_utils.apply_depth_multiplier(64, depth_multiplier),
+ kernel_size=[first_temporal_kernel_size, 7, 7],
+ strides=[2, 2, 2],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(kernel_initializer),
+ kernel_regularizer=kernel_regularizer,
+ name=layer_naming_fn(end_point))(
+ inputs)
+ net = batch_norm(
+ axis=bn_axis,
+ momentum=norm_momentum,
+ epsilon=norm_epsilon,
+ scale=False,
+ gamma_initializer='ones',
+ name=layer_naming_fn(end_point + '/BatchNorm'))(
+ net)
+ net = tf.nn.relu(net)
+ end_points[end_point] = net
+ if final_endpoint == end_point:
+ return net, end_points
+ # batch_size x 32 x 56 x 56 x 64
+ end_point = 'MaxPool_2a_3x3'
+ net = tf.keras.layers.MaxPool3D(
+ pool_size=[1, 3, 3],
+ strides=[1, 2, 2],
+ padding='same',
+ name=layer_naming_fn(end_point))(
+ net)
+ end_points[end_point] = net
+ if final_endpoint == end_point:
+ return net, end_points
+ # batch_size x 32 x 56 x 56 x 64
+ end_point = 'Conv2d_2b_1x1'
+ net = tf.keras.layers.Conv3D(
+ filters=net_utils.apply_depth_multiplier(64, depth_multiplier),
+ strides=[1, 1, 1],
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(kernel_initializer),
+ kernel_regularizer=kernel_regularizer,
+ name=layer_naming_fn(end_point))(
+ net)
+ net = batch_norm(
+ axis=bn_axis,
+ momentum=norm_momentum,
+ epsilon=norm_epsilon,
+ scale=False,
+ gamma_initializer='ones',
+ name=layer_naming_fn(end_point + '/BatchNorm'))(
+ net)
+ net = tf.nn.relu(net)
+ end_points[end_point] = net
+ if final_endpoint == end_point:
+ return net, end_points
+ # batch_size x 32 x 56 x 56 x 192
+ end_point = 'Conv2d_2c_3x3'
+ if end_point not in temporal_conv_endpoints:
+ temporal_conv_type = '2d'
+ net = parameterized_conv_layer(
+ conv_type=temporal_conv_type,
+ kernel_size=3,
+ filters=net_utils.apply_depth_multiplier(192, depth_multiplier),
+ strides=[1, 1, 1],
+ rates=[1, 1, 1],
+ use_sync_bn=use_sync_bn,
+ norm_momentum=norm_momentum,
+ norm_epsilon=norm_epsilon,
+ temporal_conv_initializer=temporal_conv_initializer,
+ kernel_initializer=tf_utils.clone_initializer(kernel_initializer),
+ kernel_regularizer=kernel_regularizer,
+ name=layer_naming_fn(end_point))(
+ net)
+ if end_point in self_gating_endpoints:
+ net = nn_blocks_3d.SelfGating(
+ filters=net_utils.apply_depth_multiplier(192, depth_multiplier),
+ name=layer_naming_fn(end_point + '/self_gating'))(
+ net)
+ end_points[end_point] = net
+ if final_endpoint == end_point:
+ return net, end_points
+ # batch_size x 32 x 28 x 28 x 192
+ end_point = 'MaxPool_3a_3x3'
+ net = tf.keras.layers.MaxPool3D(
+ pool_size=[1, 3, 3],
+ strides=[1, 2, 2],
+ padding='same',
+ name=layer_naming_fn(end_point))(
+ net)
+ end_points[end_point] = net
+ return net, end_points
+
+
+def _construct_branch_3_layers(
+ channels: int,
+ swap_pool_and_1x1x1: bool,
+ pool_type: Text,
+ batch_norm_layer: tf.keras.layers.Layer,
+ kernel_initializer: Union[Text, initializers.Initializer],
+ kernel_regularizer: Union[Text, regularizers.Regularizer],
+):
+ """Helper function for Branch 3 inside Inception module."""
+ kernel_size = [1, 3, 3] if pool_type == '2d' else [3] * 3
+
+ conv = tf.keras.layers.Conv3D(
+ filters=channels,
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=kernel_initializer,
+ kernel_regularizer=kernel_regularizer)
+ activation = tf.keras.layers.Activation('relu')
+ pool = tf.keras.layers.MaxPool3D(
+ pool_size=kernel_size, strides=[1, 1, 1], padding='same')
+ if swap_pool_and_1x1x1:
+ branch_3_layers = [conv, batch_norm_layer, activation, pool]
+ else:
+ branch_3_layers = [pool, conv, batch_norm_layer, activation]
+ return branch_3_layers
+
+
+class InceptionV1CellLayer(tf.keras.layers.Layer):
+ """A single Tensorflow 2 cell used in the original I3D/S3D model."""
+
+ def __init__(
+ self,
+ branch_filters: Sequence[Sequence[int]],
+ conv_type: Text = '3d',
+ temporal_dilation_rate: int = 1,
+ swap_pool_and_1x1x1: bool = False,
+ use_self_gating_on_branch: bool = False,
+ use_self_gating_on_cell: bool = False,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.999,
+ norm_epsilon: float = 0.001,
+ temporal_conv_initializer: Union[
+ Text, initializers.Initializer] = initializers.TruncatedNormal(
+ mean=0.0, stddev=0.01),
+ kernel_initializer: Union[Text,
+ initializers.Initializer] = 'truncated_normal',
+ kernel_regularizer: Union[Text, regularizers.Regularizer] = 'l2',
+ parameterized_conv_layer: Type[
+ net_utils.ParameterizedConvLayer] = net_utils.ParameterizedConvLayer,
+ **kwargs):
+ """A cell structure inspired by Inception V1.
+
+ Args:
+ branch_filters: Specifies the number of filters in four branches
+ (Branch_0, Branch_1, Branch_2, Branch_3). Single number for Branch_0 and
+ Branch_3. For Branch_1 and Branch_2, each need to specify two numbers,
+ one for 1x1x1 and one for 3x3x3.
+ conv_type: The type of parameterized convolution. Currently, we support
+ '2d', '3d', '2+1d', '1+2d'.
+ temporal_dilation_rate: The dilation rate for temporal convolution.
+ swap_pool_and_1x1x1: A boolean flag indicates that whether to swap the
+ order of convolution and max pooling in Branch_3.
+ use_self_gating_on_branch: Whether or not to apply self gating on each
+ branch of the inception cell.
+ use_self_gating_on_cell: Whether or not to apply self gating on each cell
+ after the concatenation of all branches.
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ temporal_conv_initializer: Weight initializer for temporal convolution
+ inside the cell. It only applies to 2+1d and 1+2d cases.
+ kernel_initializer: Weight initializer for convolutional layers other than
+ temporal convolution.
+ kernel_regularizer: Weight regularizer for all convolutional layers.
+ parameterized_conv_layer: class for parameterized conv layer.
+ **kwargs: keyword arguments to be passed.
+
+ Returns:
+ out_tensor: A 5-D float tensor of size [batch_size, num_frames, height,
+ width, channels].
+ """
+ super(InceptionV1CellLayer, self).__init__(**kwargs)
+
+ self._branch_filters = branch_filters
+ self._conv_type = conv_type
+ self._temporal_dilation_rate = temporal_dilation_rate
+ self._swap_pool_and_1x1x1 = swap_pool_and_1x1x1
+ self._use_self_gating_on_branch = use_self_gating_on_branch
+ self._use_self_gating_on_cell = use_self_gating_on_cell
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._temporal_conv_initializer = temporal_conv_initializer
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._parameterized_conv_layer = parameterized_conv_layer
+ if use_sync_bn:
+ self._norm = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._norm = tf.keras.layers.BatchNormalization
+
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._channel_axis = -1
+ else:
+ self._channel_axis = 1
+
+ def _build_branch_params(self):
+ branch_0_params = [
+ # Conv3D
+ dict(
+ filters=self._branch_filters[0][0],
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer),
+ # norm
+ dict(
+ axis=self._channel_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ scale=False,
+ gamma_initializer='ones'),
+ # relu
+ dict(),
+ ]
+ branch_1_params = [
+ # Conv3D
+ dict(
+ filters=self._branch_filters[1][0],
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer),
+ # norm
+ dict(
+ axis=self._channel_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ scale=False,
+ gamma_initializer='ones'),
+ # relu
+ dict(),
+ # ParameterizedConvLayer
+ dict(
+ conv_type=self._conv_type,
+ kernel_size=3,
+ filters=self._branch_filters[1][1],
+ strides=[1, 1, 1],
+ rates=[self._temporal_dilation_rate, 1, 1],
+ use_sync_bn=self._use_sync_bn,
+ norm_momentum=self._norm_momentum,
+ norm_epsilon=self._norm_epsilon,
+ temporal_conv_initializer=self._temporal_conv_initializer,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer),
+ ]
+ branch_2_params = [
+ # Conv3D
+ dict(
+ filters=self._branch_filters[2][0],
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer),
+ # norm
+ dict(
+ axis=self._channel_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ scale=False,
+ gamma_initializer='ones'),
+ # relu
+ dict(),
+ # ParameterizedConvLayer
+ dict(
+ conv_type=self._conv_type,
+ kernel_size=3,
+ filters=self._branch_filters[2][1],
+ strides=[1, 1, 1],
+ rates=[self._temporal_dilation_rate, 1, 1],
+ use_sync_bn=self._use_sync_bn,
+ norm_momentum=self._norm_momentum,
+ norm_epsilon=self._norm_epsilon,
+ temporal_conv_initializer=self._temporal_conv_initializer,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer)
+ ]
+ branch_3_params = [
+ # Conv3D
+ dict(
+ filters=self._branch_filters[3][0],
+ kernel_size=[1, 1, 1],
+ padding='same',
+ use_bias=False,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ kernel_regularizer=self._kernel_regularizer),
+ # norm
+ dict(
+ axis=self._channel_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ scale=False,
+ gamma_initializer='ones'),
+ # relu
+ dict(),
+ # pool
+ dict(
+ pool_size=([1, 3, 3] if self._conv_type == '2d' else [3] * 3),
+ strides=[1, 1, 1],
+ padding='same')
+ ]
+
+ if self._use_self_gating_on_branch:
+ branch_0_params.append(dict(filters=self._branch_filters[0][0]))
+ branch_1_params.append(dict(filters=self._branch_filters[1][1]))
+ branch_2_params.append(dict(filters=self._branch_filters[2][1]))
+ branch_3_params.append(dict(filters=self._branch_filters[3][0]))
+
+ out_gating_params = []
+ if self._use_self_gating_on_cell:
+ out_channels = (
+ self._branch_filters[0][0] + self._branch_filters[1][1] +
+ self._branch_filters[2][1] + self._branch_filters[3][0])
+ out_gating_params.append(dict(filters=out_channels))
+
+ return [
+ branch_0_params, branch_1_params, branch_2_params, branch_3_params,
+ out_gating_params
+ ]
+
+ def build(self, input_shape):
+ branch_params = self._build_branch_params()
+
+ self._branch_0_layers = [
+ tf.keras.layers.Conv3D(**branch_params[0][0]),
+ self._norm(**branch_params[0][1]),
+ tf.keras.layers.Activation('relu', **branch_params[0][2]),
+ ]
+
+ self._branch_1_layers = [
+ tf.keras.layers.Conv3D(**branch_params[1][0]),
+ self._norm(**branch_params[1][1]),
+ tf.keras.layers.Activation('relu', **branch_params[1][2]),
+ self._parameterized_conv_layer(**branch_params[1][3]),
+ ]
+
+ self._branch_2_layers = [
+ tf.keras.layers.Conv3D(**branch_params[2][0]),
+ self._norm(**branch_params[2][1]),
+ tf.keras.layers.Activation('relu', **branch_params[2][2]),
+ self._parameterized_conv_layer(**branch_params[2][3])
+ ]
+
+ if self._swap_pool_and_1x1x1:
+ self._branch_3_layers = [
+ tf.keras.layers.Conv3D(**branch_params[3][0]),
+ self._norm(**branch_params[3][1]),
+ tf.keras.layers.Activation('relu', **branch_params[3][2]),
+ tf.keras.layers.MaxPool3D(**branch_params[3][3]),
+ ]
+ else:
+ self._branch_3_layers = [
+ tf.keras.layers.MaxPool3D(**branch_params[3][3]),
+ tf.keras.layers.Conv3D(**branch_params[3][0]),
+ self._norm(**branch_params[3][1]),
+ tf.keras.layers.Activation('relu', **branch_params[3][2]),
+ ]
+
+ if self._use_self_gating_on_branch:
+ self._branch_0_layers.append(
+ nn_blocks_3d.SelfGating(**branch_params[0][-1]))
+ self._branch_1_layers.append(
+ nn_blocks_3d.SelfGating(**branch_params[1][-1]))
+ self._branch_2_layers.append(
+ nn_blocks_3d.SelfGating(**branch_params[2][-1]))
+ self._branch_3_layers.append(
+ nn_blocks_3d.SelfGating(**branch_params[3][-1]))
+
+ if self._use_self_gating_on_cell:
+ self.cell_self_gating = nn_blocks_3d.SelfGating(**branch_params[4][0])
+
+ super(InceptionV1CellLayer, self).build(input_shape)
+
+ def call(self, inputs):
+ x = inputs
+ for layer in self._branch_0_layers:
+ x = layer(x)
+ branch_0 = x
+
+ x = inputs
+ for layer in self._branch_1_layers:
+ x = layer(x)
+ branch_1 = x
+
+ x = inputs
+ for layer in self._branch_2_layers:
+ x = layer(x)
+ branch_2 = x
+
+ x = inputs
+ for layer in self._branch_3_layers:
+ x = layer(x)
+ branch_3 = x
+ out_tensor = tf.concat([branch_0, branch_1, branch_2, branch_3],
+ axis=self._channel_axis)
+ if self._use_self_gating_on_cell:
+ out_tensor = self.cell_self_gating(out_tensor)
+ return out_tensor
diff --git a/official/projects/s3d/modeling/inception_utils_test.py b/official/projects/s3d/modeling/inception_utils_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..3fa79658dba0a4d5589201b000fef299aea2f88f
--- /dev/null
+++ b/official/projects/s3d/modeling/inception_utils_test.py
@@ -0,0 +1,84 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.s3d.modeling import inception_utils
+
+
+class InceptionUtilsTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters((1.0, 3, {'Conv2d_1a_7x7', 'Conv2d_2c_3x3'}),
+ (0.5, 5, {'Conv2d_1a_7x7', 'Conv2d_2c_3x3'}),
+ (0.25, 7, {'Conv2d_1a_7x7', 'Conv2d_2c_3x3'}))
+ def test_s3d_stem_cells(self, depth_multiplier, first_temporal_kernel_size,
+ temporal_conv_endpoints):
+ batch_size = 1
+ num_frames = 64
+ height, width = 224, 224
+
+ inputs = tf.keras.layers.Input(
+ shape=(num_frames, height, width, 3), batch_size=batch_size)
+
+ outputs, output_endpoints = inception_utils.inception_v1_stem_cells(
+ inputs,
+ depth_multiplier,
+ 'Mixed_5c',
+ temporal_conv_endpoints=temporal_conv_endpoints,
+ self_gating_endpoints={'Conv2d_2c_3x3'},
+ first_temporal_kernel_size=first_temporal_kernel_size)
+ self.assertListEqual(outputs.shape.as_list(),
+ [batch_size, 32, 28, 28, int(192 * depth_multiplier)])
+
+ expected_endpoints = {
+ 'Conv2d_1a_7x7', 'MaxPool_2a_3x3', 'Conv2d_2b_1x1', 'Conv2d_2c_3x3',
+ 'MaxPool_3a_3x3'
+ }
+ self.assertSetEqual(expected_endpoints, set(output_endpoints.keys()))
+
+ @parameterized.parameters(
+ ('3d', True, True, True),
+ ('2d', False, False, True),
+ ('1+2d', True, False, False),
+ ('2+1d', False, True, False),
+ )
+ def test_inception_v1_cell_endpoint_match(self, conv_type,
+ swap_pool_and_1x1x1,
+ use_self_gating_on_branch,
+ use_self_gating_on_cell):
+ batch_size = 5
+ num_frames = 32
+ channels = 128
+ height, width = 28, 28
+
+ inputs = tf.keras.layers.Input(
+ shape=(num_frames, height, width, channels), batch_size=batch_size)
+
+ inception_v1_cell_layer = inception_utils.InceptionV1CellLayer(
+ [[64], [96, 128], [16, 32], [32]],
+ conv_type=conv_type,
+ swap_pool_and_1x1x1=swap_pool_and_1x1x1,
+ use_self_gating_on_branch=use_self_gating_on_branch,
+ use_self_gating_on_cell=use_self_gating_on_cell,
+ name='test')
+ outputs = inception_v1_cell_layer(inputs)
+
+ # self.assertTrue(net.op.name.startswith('test'))
+ self.assertListEqual(outputs.shape.as_list(),
+ [batch_size, 32, 28, 28, 256])
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/s3d/modeling/net_utils.py b/official/projects/s3d/modeling/net_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ce586da4420d9209ce9ff7bf21943832797b16c6
--- /dev/null
+++ b/official/projects/s3d/modeling/net_utils.py
@@ -0,0 +1,221 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Commonly used TensorFlow 2 network blocks."""
+from typing import Any, Text, Sequence, Union
+
+import tensorflow as tf
+from official.modeling import tf_utils
+
+WEIGHT_INITIALIZER = {
+ 'Xavier': tf.keras.initializers.GlorotUniform,
+ 'Gaussian': lambda: tf.keras.initializers.RandomNormal(stddev=0.01),
+}
+
+initializers = tf.keras.initializers
+regularizers = tf.keras.regularizers
+
+
+def make_set_from_start_endpoint(start_endpoint: Text,
+ endpoints: Sequence[Text]):
+ """Makes a subset of endpoints from the given starting position."""
+ if start_endpoint not in endpoints:
+ return set()
+ start_index = endpoints.index(start_endpoint)
+ return set(endpoints[start_index:])
+
+
+def apply_depth_multiplier(d: Union[int, Sequence[Any]],
+ depth_multiplier: float):
+ """Applies depth_multiplier recursively to ints."""
+ if isinstance(d, int):
+ return int(d * depth_multiplier)
+ else:
+ return [apply_depth_multiplier(x, depth_multiplier) for x in d]
+
+
+class ParameterizedConvLayer(tf.keras.layers.Layer):
+ """Convolution layer based on the input conv_type."""
+
+ def __init__(
+ self,
+ conv_type: Text,
+ kernel_size: int,
+ filters: int,
+ strides: Sequence[int],
+ rates: Sequence[int],
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.999,
+ norm_epsilon: float = 0.001,
+ temporal_conv_initializer: Union[
+ Text, initializers.Initializer] = 'glorot_uniform',
+ kernel_initializer: Union[Text,
+ initializers.Initializer] = 'truncated_normal',
+ kernel_regularizer: Union[Text, regularizers.Regularizer] = 'l2',
+ **kwargs):
+ super(ParameterizedConvLayer, self).__init__(**kwargs)
+ self._conv_type = conv_type
+ self._kernel_size = kernel_size
+ self._filters = filters
+ self._strides = strides
+ self._rates = rates
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ if use_sync_bn:
+ self._norm = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._norm = tf.keras.layers.BatchNormalization
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._channel_axis = -1
+ else:
+ self._channel_axis = 1
+ self._temporal_conv_initializer = temporal_conv_initializer
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+
+ def _build_conv_layer_params(self, input_shape):
+ """Builds params for conv layers."""
+ conv_layer_params = []
+ if self._conv_type == '3d':
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[self._kernel_size] * 3,
+ strides=self._strides,
+ dilation_rate=self._rates,
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ elif self._conv_type == '2d':
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[1, self._kernel_size, self._kernel_size],
+ strides=[1, self._strides[1], self._strides[2]],
+ dilation_rate=[1, self._rates[1], self._rates[2]],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ elif self._conv_type == '1+2d':
+ channels_in = input_shape[self._channel_axis]
+ conv_layer_params.append(
+ dict(
+ filters=channels_in,
+ kernel_size=[self._kernel_size, 1, 1],
+ strides=[self._strides[0], 1, 1],
+ dilation_rate=[self._rates[0], 1, 1],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._temporal_conv_initializer),
+ ))
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[1, self._kernel_size, self._kernel_size],
+ strides=[1, self._strides[1], self._strides[2]],
+ dilation_rate=[1, self._rates[1], self._rates[2]],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ elif self._conv_type == '2+1d':
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[1, self._kernel_size, self._kernel_size],
+ strides=[1, self._strides[1], self._strides[2]],
+ dilation_rate=[1, self._rates[1], self._rates[2]],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[self._kernel_size, 1, 1],
+ strides=[self._strides[0], 1, 1],
+ dilation_rate=[self._rates[0], 1, 1],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._temporal_conv_initializer),
+ ))
+ elif self._conv_type == '1+1+1d':
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[1, 1, self._kernel_size],
+ strides=[1, 1, self._strides[2]],
+ dilation_rate=[1, 1, self._rates[2]],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[1, self._kernel_size, 1],
+ strides=[1, self._strides[1], 1],
+ dilation_rate=[1, self._rates[1], 1],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ conv_layer_params.append(
+ dict(
+ filters=self._filters,
+ kernel_size=[self._kernel_size, 1, 1],
+ strides=[self._strides[0], 1, 1],
+ dilation_rate=[self._rates[0], 1, 1],
+ kernel_initializer=tf_utils.clone_initializer(
+ self._kernel_initializer),
+ ))
+ else:
+ raise ValueError('Unsupported conv_type: {}'.format(self._conv_type))
+ return conv_layer_params
+
+ def _build_norm_layer_params(self, conv_param):
+ """Builds params for the norm layer after one conv layer."""
+ return dict(
+ axis=self._channel_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ scale=False,
+ gamma_initializer='ones')
+
+ def _build_activation_layer_params(self, conv_param):
+ """Builds params for the activation layer after one conv layer."""
+ return {}
+
+ def _append_conv_layer(self, param):
+ """Appends conv, normalization and activation layers."""
+ self._parameterized_conv_layers.append(
+ tf.keras.layers.Conv3D(
+ padding='same',
+ use_bias=False,
+ kernel_regularizer=self._kernel_regularizer,
+ **param,
+ ))
+ norm_layer_params = self._build_norm_layer_params(param)
+ self._parameterized_conv_layers.append(self._norm(**norm_layer_params))
+
+ relu_layer_params = self._build_activation_layer_params(param)
+ self._parameterized_conv_layers.append(
+ tf.keras.layers.Activation('relu', **relu_layer_params))
+
+ def build(self, input_shape):
+ self._parameterized_conv_layers = []
+ for conv_layer_param in self._build_conv_layer_params(input_shape):
+ self._append_conv_layer(conv_layer_param)
+ super(ParameterizedConvLayer, self).build(input_shape)
+
+ def call(self, inputs):
+ x = inputs
+ for layer in self._parameterized_conv_layers:
+ x = layer(x)
+ return x
diff --git a/official/projects/s3d/modeling/net_utils_test.py b/official/projects/s3d/modeling/net_utils_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..d45c1142878f3313da45ad334c842e232cc1bde0
--- /dev/null
+++ b/official/projects/s3d/modeling/net_utils_test.py
@@ -0,0 +1,68 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+from absl import logging
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.s3d.modeling import net_utils
+
+
+class Tf2NetUtilsTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ ('3d', [2, 1, 1], [5, 16, 28, 28, 256]),
+ ('3d', [2, 2, 2], [5, 16, 14, 14, 256]),
+ ('3d', [1, 2, 1], [5, 32, 14, 28, 256]),
+ ('2d', [2, 2, 2], [5, 32, 14, 14, 256]),
+ ('2d', [1, 1, 2], [5, 32, 28, 14, 256]),
+ ('1+2d', [2, 2, 2], [5, 16, 14, 14, 256]),
+ ('1+2d', [2, 1, 1], [5, 16, 28, 28, 256]),
+ ('1+2d', [1, 1, 1], [5, 32, 28, 28, 256]),
+ ('1+2d', [1, 1, 2], [5, 32, 28, 14, 256]),
+ ('2+1d', [2, 2, 2], [5, 16, 14, 14, 256]),
+ ('2+1d', [1, 1, 1], [5, 32, 28, 28, 256]),
+ ('2+1d', [2, 1, 2], [5, 16, 28, 14, 256]),
+ ('1+1+1d', [2, 2, 2], [5, 16, 14, 14, 256]),
+ ('1+1+1d', [1, 1, 1], [5, 32, 28, 28, 256]),
+ ('1+1+1d', [2, 1, 2], [5, 16, 28, 14, 256]),
+ )
+ def test_parameterized_conv_layer_creation(self, conv_type, strides,
+ expected_shape):
+ batch_size = 5
+ temporal_size = 32
+ spatial_size = 28
+ channels = 128
+
+ kernel_size = 3
+ filters = 256
+ rates = [1, 1, 1]
+
+ name = 'ParameterizedConv'
+
+ inputs = tf.keras.Input(
+ shape=(temporal_size, spatial_size, spatial_size, channels),
+ batch_size=batch_size)
+ parameterized_conv_layer = net_utils.ParameterizedConvLayer(
+ conv_type, kernel_size, filters, strides, rates, name=name)
+
+ features = parameterized_conv_layer(inputs)
+ logging.info(features.shape.as_list())
+ logging.info([w.name for w in parameterized_conv_layer.weights])
+
+ self.assertAllEqual(features.shape.as_list(), expected_shape)
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/s3d/modeling/s3d.py b/official/projects/s3d/modeling/s3d.py
new file mode 100644
index 0000000000000000000000000000000000000000..9b76ad177ed43108c3b3a06477871738592eddff
--- /dev/null
+++ b/official/projects/s3d/modeling/s3d.py
@@ -0,0 +1,355 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains the Tensorflow 2 version definition of S3D model.
+
+S3D model is described in the following paper:
+https://arxiv.org/abs/1712.04851.
+"""
+from typing import Any, Dict, Mapping, Optional, Sequence, Text, Tuple, Union
+
+import tensorflow as tf
+
+from official.modeling import hyperparams
+from official.projects.s3d.configs import s3d as cfg
+from official.projects.s3d.modeling import inception_utils
+from official.projects.s3d.modeling import net_utils
+from official.vision.modeling import factory_3d as model_factory
+from official.vision.modeling.backbones import factory as backbone_factory
+
+initializers = tf.keras.initializers
+regularizers = tf.keras.regularizers
+
+
+class S3D(tf.keras.Model):
+ """Class to build S3D family model."""
+
+ def __init__(self,
+ input_specs: tf.keras.layers.InputSpec,
+ final_endpoint: Text = 'Mixed_5c',
+ first_temporal_kernel_size: int = 3,
+ temporal_conv_start_at: Text = 'Conv2d_2c_3x3',
+ gating_start_at: Text = 'Conv2d_2c_3x3',
+ swap_pool_and_1x1x1: bool = True,
+ gating_style: Text = 'CELL',
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.999,
+ norm_epsilon: float = 0.001,
+ temporal_conv_initializer: Union[
+ Text,
+ initializers.Initializer] = initializers.TruncatedNormal(
+ mean=0.0, stddev=0.01),
+ temporal_conv_type: Text = '2+1d',
+ kernel_initializer: Union[
+ Text,
+ initializers.Initializer] = initializers.TruncatedNormal(
+ mean=0.0, stddev=0.01),
+ kernel_regularizer: Union[Text, regularizers.Regularizer] = 'l2',
+ depth_multiplier: float = 1.0,
+ **kwargs):
+ """Constructor.
+
+ Args:
+ input_specs: `tf.keras.layers.InputSpec` specs of the input tensor.
+ final_endpoint: Specifies the endpoint to construct the network up to.
+ first_temporal_kernel_size: Temporal kernel size of the first convolution
+ layer.
+ temporal_conv_start_at: Specifies the endpoint where to start performimg
+ temporal convolution from.
+ gating_start_at: Specifies the endpoint where to start performimg self
+ gating from.
+ swap_pool_and_1x1x1: A boolean flag indicates that whether to swap the
+ order of convolution and max pooling in Branch_3 of inception v1 cell.
+ gating_style: A string that specifies self gating to be applied after each
+ branch and/or after each cell. It can be one of ['BRANCH', 'CELL',
+ 'BRANCH_AND_CELL'].
+ use_sync_bn: If True, use synchronized batch normalization.
+ norm_momentum: A `float` of normalization momentum for the moving average.
+ norm_epsilon: A `float` added to variance to avoid dividing by zero.
+ temporal_conv_initializer: Weight initializer for temporal convolutional
+ layers.
+ temporal_conv_type: The type of parameterized convolution. Currently, we
+ support '2d', '3d', '2+1d', '1+2d'.
+ kernel_initializer: Weight initializer for convolutional layers other than
+ temporal convolution.
+ kernel_regularizer: Weight regularizer for all convolutional layers.
+ depth_multiplier: A float to reduce/increase number of channels.
+ **kwargs: keyword arguments to be passed.
+ """
+
+ self._input_specs = input_specs
+ self._final_endpoint = final_endpoint
+ self._first_temporal_kernel_size = first_temporal_kernel_size
+ self._temporal_conv_start_at = temporal_conv_start_at
+ self._gating_start_at = gating_start_at
+ self._swap_pool_and_1x1x1 = swap_pool_and_1x1x1
+ self._gating_style = gating_style
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._temporal_conv_initializer = temporal_conv_initializer
+ self._temporal_conv_type = temporal_conv_type
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._depth_multiplier = depth_multiplier
+
+ self._temporal_conv_endpoints = net_utils.make_set_from_start_endpoint(
+ temporal_conv_start_at, inception_utils.INCEPTION_V1_CONV_ENDPOINTS)
+ self._self_gating_endpoints = net_utils.make_set_from_start_endpoint(
+ gating_start_at, inception_utils.INCEPTION_V1_CONV_ENDPOINTS)
+
+ inputs = tf.keras.Input(shape=input_specs.shape[1:])
+ net, end_points = inception_utils.inception_v1_stem_cells(
+ inputs,
+ depth_multiplier,
+ final_endpoint,
+ temporal_conv_endpoints=self._temporal_conv_endpoints,
+ self_gating_endpoints=self._self_gating_endpoints,
+ temporal_conv_type=self._temporal_conv_type,
+ first_temporal_kernel_size=self._first_temporal_kernel_size,
+ use_sync_bn=self._use_sync_bn,
+ norm_momentum=self._norm_momentum,
+ norm_epsilon=self._norm_epsilon,
+ temporal_conv_initializer=self._temporal_conv_initializer,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ parameterized_conv_layer=self._get_parameterized_conv_layer_impl(),
+ layer_naming_fn=self._get_layer_naming_fn(),
+ )
+
+ for end_point, filters in inception_utils.INCEPTION_V1_ARCH_SKELETON:
+ net, end_points = self._s3d_cell(net, end_point, end_points, filters)
+ if end_point == final_endpoint:
+ break
+
+ if final_endpoint not in end_points:
+ raise ValueError(
+ 'Unrecognized final endpoint %s (available endpoints: %s).' %
+ (final_endpoint, end_points.keys()))
+
+ super(S3D, self).__init__(inputs=inputs, outputs=end_points, **kwargs)
+
+ def _s3d_cell(
+ self,
+ net: tf.Tensor,
+ end_point: Text,
+ end_points: Dict[Text, tf.Tensor],
+ filters: Union[int, Sequence[Any]],
+ non_local_block: Optional[tf.keras.layers.Layer] = None,
+ attention_cell: Optional[tf.keras.layers.Layer] = None,
+ attention_cell_super_graph: Optional[tf.keras.layers.Layer] = None
+ ) -> Tuple[tf.Tensor, Dict[Text, tf.Tensor]]:
+ if end_point.startswith('Mixed'):
+ conv_type = (
+ self._temporal_conv_type
+ if end_point in self._temporal_conv_endpoints else '2d')
+ use_self_gating_on_branch = (
+ end_point in self._self_gating_endpoints and
+ (self._gating_style == 'BRANCH' or
+ self._gating_style == 'BRANCH_AND_CELL'))
+ use_self_gating_on_cell = (
+ end_point in self._self_gating_endpoints and
+ (self._gating_style == 'CELL' or
+ self._gating_style == 'BRANCH_AND_CELL'))
+ net = self._get_inception_v1_cell_layer_impl()(
+ branch_filters=net_utils.apply_depth_multiplier(
+ filters, self._depth_multiplier),
+ conv_type=conv_type,
+ temporal_dilation_rate=1,
+ swap_pool_and_1x1x1=self._swap_pool_and_1x1x1,
+ use_self_gating_on_branch=use_self_gating_on_branch,
+ use_self_gating_on_cell=use_self_gating_on_cell,
+ use_sync_bn=self._use_sync_bn,
+ norm_momentum=self._norm_momentum,
+ norm_epsilon=self._norm_epsilon,
+ kernel_initializer=self._kernel_initializer,
+ temporal_conv_initializer=self._temporal_conv_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ name=self._get_layer_naming_fn()(end_point))(
+ net)
+ else:
+ net = tf.keras.layers.MaxPool3D(
+ pool_size=filters[0],
+ strides=filters[1],
+ padding='same',
+ name=self._get_layer_naming_fn()(end_point))(
+ net)
+ end_points[end_point] = net
+ if non_local_block:
+ # TODO(b/182299420): Implement non local block in TF2.
+ raise NotImplementedError('Non local block is not implemented yet.')
+ if attention_cell:
+ # TODO(b/182299420): Implement attention cell in TF2.
+ raise NotImplementedError('Attention cell is not implemented yet.')
+ if attention_cell_super_graph:
+ # TODO(b/182299420): Implement attention cell super graph in TF2.
+ raise NotImplementedError('Attention cell super graph is not implemented'
+ ' yet.')
+ return net, end_points
+
+ def get_config(self):
+ config_dict = {
+ 'input_specs': self._input_specs,
+ 'final_endpoint': self._final_endpoint,
+ 'first_temporal_kernel_size': self._first_temporal_kernel_size,
+ 'temporal_conv_start_at': self._temporal_conv_start_at,
+ 'gating_start_at': self._gating_start_at,
+ 'swap_pool_and_1x1x1': self._swap_pool_and_1x1x1,
+ 'gating_style': self._gating_style,
+ 'use_sync_bn': self._use_sync_bn,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'temporal_conv_initializer': self._temporal_conv_initializer,
+ 'temporal_conv_type': self._temporal_conv_type,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'depth_multiplier': self._depth_multiplier
+ }
+ return config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
+
+ @property
+ def output_specs(self):
+ """A dict of {level: TensorShape} pairs for the model output."""
+ return self._output_specs
+
+ def _get_inception_v1_cell_layer_impl(self):
+ return inception_utils.InceptionV1CellLayer
+
+ def _get_parameterized_conv_layer_impl(self):
+ return net_utils.ParameterizedConvLayer
+
+ def _get_layer_naming_fn(self):
+ return lambda end_point: None
+
+
+class S3DModel(tf.keras.Model):
+ """An S3D model builder."""
+
+ def __init__(self,
+ backbone: tf.keras.Model,
+ num_classes: int,
+ input_specs: Mapping[Text, tf.keras.layers.InputSpec],
+ final_endpoint: Text = 'Mixed_5c',
+ dropout_rate: float = 0.0,
+ **kwargs):
+ """Constructor.
+
+ Args:
+ backbone: S3D backbone Keras Model.
+ num_classes: `int` number of possible classes for video classification.
+ input_specs: input_specs: `tf.keras.layers.InputSpec` specs of the input
+ tensor.
+ final_endpoint: Specifies the endpoint to construct the network up to.
+ dropout_rate: `float` between 0 and 1. Fraction of the input units to
+ drop. Note that dropout_rate = 1.0 - dropout_keep_prob.
+ **kwargs: keyword arguments to be passed.
+ """
+ self._self_setattr_tracking = False
+ self._backbone = backbone
+ self._num_classes = num_classes
+ self._input_specs = input_specs
+ self._final_endpoint = final_endpoint
+ self._dropout_rate = dropout_rate
+ self._config_dict = {
+ 'backbone': backbone,
+ 'num_classes': num_classes,
+ 'input_specs': input_specs,
+ 'final_endpoint': final_endpoint,
+ 'dropout_rate': dropout_rate,
+ }
+
+ inputs = {
+ k: tf.keras.Input(shape=v.shape[1:]) for k, v in input_specs.items()
+ }
+ streams = self._backbone(inputs['image'])
+
+ pool = tf.math.reduce_mean(streams[self._final_endpoint], axis=[1, 2, 3])
+ fc = tf.keras.layers.Dropout(dropout_rate)(pool)
+ logits = tf.keras.layers.Dense(**self._build_dense_layer_params())(fc)
+
+ super(S3DModel, self).__init__(inputs=inputs, outputs=logits, **kwargs)
+
+ @property
+ def checkpoint_items(self):
+ """Returns a dictionary of items to be additionally checkpointed."""
+ return dict(backbone=self.backbone)
+
+ @property
+ def backbone(self):
+ return self._backbone
+
+ def get_config(self):
+ return self._config_dict
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ return cls(**config)
+
+ def _build_dense_layer_params(self):
+ return dict(units=self._num_classes, kernel_regularizer='l2')
+
+
+@backbone_factory.register_backbone_builder('s3d')
+def build_s3d(
+ input_specs: tf.keras.layers.InputSpec,
+ backbone_config: hyperparams.Config,
+ norm_activation_config: hyperparams.Config,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None
+) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ """Builds S3D backbone."""
+
+ backbone_type = backbone_config.type
+ backbone_cfg = backbone_config.get()
+ assert backbone_type == 's3d'
+ del norm_activation_config
+
+ backbone = S3D(
+ input_specs=input_specs,
+ final_endpoint=backbone_cfg.final_endpoint,
+ first_temporal_kernel_size=backbone_cfg.first_temporal_kernel_size,
+ temporal_conv_start_at=backbone_cfg.temporal_conv_start_at,
+ gating_start_at=backbone_cfg.gating_start_at,
+ swap_pool_and_1x1x1=backbone_cfg.swap_pool_and_1x1x1,
+ gating_style=backbone_cfg.gating_style,
+ use_sync_bn=backbone_cfg.use_sync_bn,
+ norm_momentum=backbone_cfg.norm_momentum,
+ norm_epsilon=backbone_cfg.norm_epsilon,
+ temporal_conv_type=backbone_cfg.temporal_conv_type,
+ kernel_regularizer=l2_regularizer,
+ depth_multiplier=backbone_cfg.depth_multiplier)
+ return backbone
+
+
+@model_factory.register_model_builder('s3d')
+def build_s3d_model(
+ input_specs: tf.keras.layers.InputSpec,
+ model_config: cfg.S3DModel,
+ num_classes: int,
+ l2_regularizer: tf.keras.regularizers.Regularizer = None
+) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ """Builds S3D model with classification layer."""
+ input_specs_dict = {'image': input_specs}
+ backbone = build_s3d(input_specs, model_config.backbone,
+ model_config.norm_activation, l2_regularizer)
+
+ model = S3DModel(
+ backbone,
+ num_classes=num_classes,
+ input_specs=input_specs_dict,
+ dropout_rate=model_config.dropout_rate)
+ return model
diff --git a/official/projects/s3d/modeling/s3d_test.py b/official/projects/s3d/modeling/s3d_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..d9565aa4700d922d4192452a457578573e072253
--- /dev/null
+++ b/official/projects/s3d/modeling/s3d_test.py
@@ -0,0 +1,106 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for S3D model."""
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.s3d.modeling import s3d
+
+
+class S3dTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (7, 224, 224, 3),
+ (7, 128, 128, 3),
+ (7, 256, 256, 3),
+ (7, 192, 192, 3),
+ (64, 224, 224, 3),
+ (32, 224, 224, 3),
+ (64, 224, 224, 11),
+ (32, 224, 224, 11),
+ )
+ def test_build(self, num_frames, height, width, first_temporal_kernel_size):
+ batch_size = 5
+
+ input_shape = [batch_size, num_frames, height, width, 3]
+ input_specs = tf.keras.layers.InputSpec(shape=input_shape)
+ network = s3d.S3D(
+ input_specs=input_specs
+ )
+ inputs = tf.keras.Input(shape=input_shape[1:], batch_size=input_shape[0])
+ endpoints = network(inputs)
+
+ temporal_1a = (num_frames - 1)//2 + 1
+ expected_shapes = {
+ 'Conv2d_1a_7x7': [5, temporal_1a, height//2, width//2, 64],
+ 'Conv2d_2b_1x1': [5, temporal_1a, height//4, width//4, 64],
+ 'Conv2d_2c_3x3': [5, temporal_1a, height//4, height//4, 192],
+ 'MaxPool_2a_3x3': [5, temporal_1a, height//4, height//4, 64],
+ 'MaxPool_3a_3x3': [5, temporal_1a, height//8, width//8, 192],
+ 'Mixed_3b': [5, temporal_1a, height//8, width//8, 256],
+ 'Mixed_3c': [5, temporal_1a, height//8, width//8, 480],
+ 'MaxPool_4a_3x3': [5, temporal_1a//2, height//16, width//16, 480],
+ 'Mixed_4b': [5, temporal_1a//2, height//16, width//16, 512],
+ 'Mixed_4c': [5, temporal_1a//2, height//16, width//16, 512],
+ 'Mixed_4d': [5, temporal_1a//2, height//16, width//16, 512],
+ 'Mixed_4e': [5, temporal_1a//2, height//16, width//16, 528],
+ 'Mixed_4f': [5, temporal_1a//2, height//16, width//16, 832],
+ 'MaxPool_5a_2x2': [5, temporal_1a//4, height//32, width//32, 832],
+ 'Mixed_5b': [5, temporal_1a//4, height//32, width//32, 832],
+ 'Mixed_5c': [5, temporal_1a//4, height//32, width//32, 1024],
+ }
+
+ output_shapes = dict()
+ for end_point, output_tensor in endpoints.items():
+ output_shapes[end_point] = output_tensor.shape.as_list()
+ self.assertDictEqual(output_shapes, expected_shapes)
+
+ def test_serialize_deserialize(self):
+ # Create a network object that sets all of its config options.
+ kwargs = dict(
+ input_specs=tf.keras.layers.InputSpec(shape=(5, 64, 224, 224, 3)),
+ final_endpoint='Mixed_5c',
+ first_temporal_kernel_size=3,
+ temporal_conv_start_at='Conv2d_2c_3x3',
+ gating_start_at='Conv2d_2c_3x3',
+ swap_pool_and_1x1x1=True,
+ gating_style='CELL',
+ use_sync_bn=False,
+ norm_momentum=0.999,
+ norm_epsilon=0.001,
+ temporal_conv_initializer=tf.keras.initializers.TruncatedNormal(
+ mean=0.0, stddev=0.01),
+ temporal_conv_type='2+1d',
+ kernel_initializer='truncated_normal',
+ kernel_regularizer='l2',
+ depth_multiplier=1.0
+ )
+ network = s3d.S3D(**kwargs)
+
+ expected_config = dict(kwargs)
+ self.assertEqual(network.get_config(), expected_config)
+
+ # Create another network object from the first object's config.
+ new_network = s3d.S3D.from_config(network.get_config())
+
+ # Validate that the config can be forced to JSON.
+ _ = new_network.to_json()
+
+ # If the serialization was successful, the new config should match the old.
+ self.assertAllEqual(network.get_config(), new_network.get_config())
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/s3d/train.py b/official/projects/s3d/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5f1819fc2ea3abe9df5764312120f4cb3ce7a392
--- /dev/null
+++ b/official/projects/s3d/train.py
@@ -0,0 +1,30 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver for S3D."""
+
+from absl import app
+
+from official.common import flags as tfm_flags
+# pylint: disable=unused-import
+from official.projects.s3d.configs.google import s3d as s3d_config
+from official.projects.s3d.modeling import s3d
+from official.projects.s3d.tasks.google import automl_video_classification
+from official.vision import registry_imports
+# pylint: enable=unused-import
+from official.vision import train
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/simclr/README.md b/official/projects/simclr/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..3644532032a78aefdd7376b1669687a93354dd2c
--- /dev/null
+++ b/official/projects/simclr/README.md
@@ -0,0 +1,78 @@
+# Simple Framework for Contrastive Learning
+
+[](https://arxiv.org/abs/2002.05709)
+[](https://arxiv.org/abs/2006.10029)
+
+
+
+## Environment setup
+
+The code can be run on multiple GPUs or TPUs with different distribution
+strategies. See the TensorFlow distributed training
+[guide](https://www.tensorflow.org/guide/distributed_training) for an overview
+of `tf.distribute`.
+
+The code is compatible with TensorFlow 2.4+. See requirements.txt for all
+prerequisites, and you can also install them using the following command. `pip
+install -r ./official/requirements.txt`
+
+## Pretraining
+To pretrain the model on Imagenet, try the following command:
+
+```
+python3 -m official.projects.simclr.train \
+ --mode=train_and_eval \
+ --experiment=simclr_pretraining \
+ --model_dir={MODEL_DIR} \
+ --config_file={CONFIG_FILE}
+```
+
+An example of the config file can be found [here](./configs/experiments/imagenet_simclr_pretrain_gpu.yaml)
+
+
+## Semi-supervised learning and fine-tuning the whole network
+
+You can access 1% and 10% ImageNet subsets used for semi-supervised learning via
+[tensorflow datasets](https://www.tensorflow.org/datasets/catalog/imagenet2012_subset).
+You can also find image IDs of these subsets in `imagenet_subsets/`.
+
+To fine-tune the whole network, refer to the following command:
+
+```
+python3 -m official.projects.simclr.train \
+ --mode=train_and_eval \
+ --experiment=simclr_finetuning \
+ --model_dir={MODEL_DIR} \
+ --config_file={CONFIG_FILE}
+```
+
+An example of the config file can be found [here](./configs/experiments/imagenet_simclr_finetune_gpu.yaml).
+
+## Cite
+
+[SimCLR paper](https://arxiv.org/abs/2002.05709):
+
+```
+@article{chen2020simple,
+ title={A Simple Framework for Contrastive Learning of Visual Representations},
+ author={Chen, Ting and Kornblith, Simon and Norouzi, Mohammad and Hinton, Geoffrey},
+ journal={arXiv preprint arXiv:2002.05709},
+ year={2020}
+}
+```
+
+[SimCLRv2 paper](https://arxiv.org/abs/2006.10029):
+
+```
+@article{chen2020big,
+ title={Big Self-Supervised Models are Strong Semi-Supervised Learners},
+ author={Chen, Ting and Kornblith, Simon and Swersky, Kevin and Norouzi, Mohammad and Hinton, Geoffrey},
+ journal={arXiv preprint arXiv:2006.10029},
+ year={2020}
+}
+```
diff --git a/official/projects/simclr/common/registry_imports.py b/official/projects/simclr/common/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..16b4a55c19eadbe0ba793467306915eb5684ace5
--- /dev/null
+++ b/official/projects/simclr/common/registry_imports.py
@@ -0,0 +1,22 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""All necessary imports for registration."""
+
+# pylint: disable=unused-import
+from official.projects.simclr.configs import simclr
+from official.projects.simclr.losses import contrastive_losses
+from official.projects.simclr.modeling import simclr_model
+from official.projects.simclr.tasks import simclr as simclr_task
+from official.vision import registry_imports
diff --git a/official/vision/beta/projects/simclr/configs/experiments/cifar_simclr_pretrain.yaml b/official/projects/simclr/configs/experiments/cifar_simclr_pretrain.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/cifar_simclr_pretrain.yaml
rename to official/projects/simclr/configs/experiments/cifar_simclr_pretrain.yaml
diff --git a/official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_finetune_gpu.yaml b/official/projects/simclr/configs/experiments/imagenet_simclr_finetune_gpu.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_finetune_gpu.yaml
rename to official/projects/simclr/configs/experiments/imagenet_simclr_finetune_gpu.yaml
diff --git a/official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_finetune_tpu.yaml b/official/projects/simclr/configs/experiments/imagenet_simclr_finetune_tpu.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_finetune_tpu.yaml
rename to official/projects/simclr/configs/experiments/imagenet_simclr_finetune_tpu.yaml
diff --git a/official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_multitask_tpu.yaml b/official/projects/simclr/configs/experiments/imagenet_simclr_multitask_tpu.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_multitask_tpu.yaml
rename to official/projects/simclr/configs/experiments/imagenet_simclr_multitask_tpu.yaml
diff --git a/official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_pretrain_gpu.yaml b/official/projects/simclr/configs/experiments/imagenet_simclr_pretrain_gpu.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_pretrain_gpu.yaml
rename to official/projects/simclr/configs/experiments/imagenet_simclr_pretrain_gpu.yaml
diff --git a/official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_pretrain_tpu.yaml b/official/projects/simclr/configs/experiments/imagenet_simclr_pretrain_tpu.yaml
similarity index 100%
rename from official/vision/beta/projects/simclr/configs/experiments/imagenet_simclr_pretrain_tpu.yaml
rename to official/projects/simclr/configs/experiments/imagenet_simclr_pretrain_tpu.yaml
diff --git a/official/vision/beta/projects/simclr/configs/multitask_config.py b/official/projects/simclr/configs/multitask_config.py
similarity index 90%
rename from official/vision/beta/projects/simclr/configs/multitask_config.py
rename to official/projects/simclr/configs/multitask_config.py
index 8cf00d5afb1dc0bf441ea780ef116b02136a346f..59f6f752a3fe60d3c6d82d8103f7a6e65abed7ce 100644
--- a/official/vision/beta/projects/simclr/configs/multitask_config.py
+++ b/official/projects/simclr/configs/multitask_config.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,10 +20,10 @@ from typing import List, Tuple
from official.core import exp_factory
from official.modeling import hyperparams
from official.modeling.multitask import configs as multitask_configs
-from official.vision.beta.configs import backbones
-from official.vision.beta.configs import common
-from official.vision.beta.projects.simclr.configs import simclr as simclr_configs
-from official.vision.beta.projects.simclr.modeling import simclr_model
+from official.projects.simclr.configs import simclr as simclr_configs
+from official.projects.simclr.modeling import simclr_model
+from official.vision.configs import backbones
+from official.vision.configs import common
@dataclasses.dataclass
diff --git a/official/vision/beta/projects/simclr/configs/multitask_config_test.py b/official/projects/simclr/configs/multitask_config_test.py
similarity index 84%
rename from official/vision/beta/projects/simclr/configs/multitask_config_test.py
rename to official/projects/simclr/configs/multitask_config_test.py
index 666cd759962f0e150a5c29853e6f16659b40c9d7..d4cfded59b3a3d300046b78c01fcf4979629151b 100644
--- a/official/vision/beta/projects/simclr/configs/multitask_config_test.py
+++ b/official/projects/simclr/configs/multitask_config_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,8 +18,8 @@ import tensorflow as tf
from official.core import exp_factory
from official.modeling.multitask import configs as multitask_configs
-from official.vision.beta.projects.simclr.configs import multitask_config as simclr_multitask_config
-from official.vision.beta.projects.simclr.configs import simclr as exp_cfg
+from official.projects.simclr.configs import multitask_config as simclr_multitask_config
+from official.projects.simclr.configs import simclr as exp_cfg
class MultitaskConfigTest(tf.test.TestCase):
diff --git a/official/projects/simclr/configs/simclr.py b/official/projects/simclr/configs/simclr.py
new file mode 100644
index 0000000000000000000000000000000000000000..23c071a8f12650ed1ecc77bcf3476cbc684f9f47
--- /dev/null
+++ b/official/projects/simclr/configs/simclr.py
@@ -0,0 +1,318 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""SimCLR configurations."""
+import dataclasses
+import os
+from typing import List, Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.projects.simclr.modeling import simclr_model
+from official.vision.configs import backbones
+from official.vision.configs import common
+
+
+@dataclasses.dataclass
+class Decoder(hyperparams.Config):
+ decode_label: bool = True
+
+
+@dataclasses.dataclass
+class Parser(hyperparams.Config):
+ """Parser config."""
+ aug_rand_crop: bool = True
+ aug_rand_hflip: bool = True
+ aug_color_distort: bool = True
+ aug_color_jitter_strength: float = 1.0
+ aug_color_jitter_impl: str = 'simclrv2' # 'simclrv1' or 'simclrv2'
+ aug_rand_blur: bool = True
+ parse_label: bool = True
+ test_crop: bool = True
+ mode: str = simclr_model.PRETRAIN
+
+
+@dataclasses.dataclass
+class DataConfig(cfg.DataConfig):
+ """Training data config."""
+ input_path: str = ''
+ global_batch_size: int = 0
+ is_training: bool = True
+ dtype: str = 'float32'
+ shuffle_buffer_size: int = 10000
+ cycle_length: int = 10
+ # simclr specific configs
+ parser: Parser = Parser()
+ decoder: Decoder = Decoder()
+ # Useful when doing a sanity check that we absolutely use no labels while
+ # pretrain by setting labels to zeros (default = False, keep original labels)
+ input_set_label_to_zero: bool = False
+
+
+@dataclasses.dataclass
+class ProjectionHead(hyperparams.Config):
+ proj_output_dim: int = 128
+ num_proj_layers: int = 3
+ ft_proj_idx: int = 1 # layer of the projection head to use for fine-tuning.
+
+
+@dataclasses.dataclass
+class SupervisedHead(hyperparams.Config):
+ num_classes: int = 1001
+ zero_init: bool = False
+
+
+@dataclasses.dataclass
+class ContrastiveLoss(hyperparams.Config):
+ projection_norm: bool = True
+ temperature: float = 0.1
+ l2_weight_decay: float = 0.0
+
+
+@dataclasses.dataclass
+class ClassificationLosses(hyperparams.Config):
+ label_smoothing: float = 0.0
+ one_hot: bool = True
+ l2_weight_decay: float = 0.0
+
+
+@dataclasses.dataclass
+class Evaluation(hyperparams.Config):
+ top_k: int = 5
+ one_hot: bool = True
+
+
+@dataclasses.dataclass
+class SimCLRModel(hyperparams.Config):
+ """SimCLR model config."""
+ input_size: List[int] = dataclasses.field(default_factory=list)
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='resnet', resnet=backbones.ResNet())
+ projection_head: ProjectionHead = ProjectionHead(
+ proj_output_dim=128, num_proj_layers=3, ft_proj_idx=1)
+ supervised_head: SupervisedHead = SupervisedHead(num_classes=1001)
+ norm_activation: common.NormActivation = common.NormActivation(
+ norm_momentum=0.9, norm_epsilon=1e-5, use_sync_bn=False)
+ mode: str = simclr_model.PRETRAIN
+ backbone_trainable: bool = True
+
+
+@dataclasses.dataclass
+class SimCLRPretrainTask(cfg.TaskConfig):
+ """SimCLR pretraining task config."""
+ model: SimCLRModel = SimCLRModel(mode=simclr_model.PRETRAIN)
+ train_data: DataConfig = DataConfig(
+ parser=Parser(mode=simclr_model.PRETRAIN), is_training=True)
+ validation_data: DataConfig = DataConfig(
+ parser=Parser(mode=simclr_model.PRETRAIN), is_training=False)
+ loss: ContrastiveLoss = ContrastiveLoss()
+ evaluation: Evaluation = Evaluation()
+ init_checkpoint: Optional[str] = None
+ # all or backbone
+ init_checkpoint_modules: str = 'all'
+
+
+@dataclasses.dataclass
+class SimCLRFinetuneTask(cfg.TaskConfig):
+ """SimCLR fine tune task config."""
+ model: SimCLRModel = SimCLRModel(
+ mode=simclr_model.FINETUNE,
+ supervised_head=SupervisedHead(num_classes=1001, zero_init=True))
+ train_data: DataConfig = DataConfig(
+ parser=Parser(mode=simclr_model.FINETUNE), is_training=True)
+ validation_data: DataConfig = DataConfig(
+ parser=Parser(mode=simclr_model.FINETUNE), is_training=False)
+ loss: ClassificationLosses = ClassificationLosses()
+ evaluation: Evaluation = Evaluation()
+ init_checkpoint: Optional[str] = None
+ # all, backbone_projection or backbone
+ init_checkpoint_modules: str = 'backbone_projection'
+
+
+@exp_factory.register_config_factory('simclr_pretraining')
+def simclr_pretraining() -> cfg.ExperimentConfig:
+ """Image classification general."""
+ return cfg.ExperimentConfig(
+ task=SimCLRPretrainTask(),
+ trainer=cfg.TrainerConfig(),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+
+@exp_factory.register_config_factory('simclr_finetuning')
+def simclr_finetuning() -> cfg.ExperimentConfig:
+ """Image classification general."""
+ return cfg.ExperimentConfig(
+ task=SimCLRFinetuneTask(),
+ trainer=cfg.TrainerConfig(),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+
+IMAGENET_TRAIN_EXAMPLES = 1281167
+IMAGENET_VAL_EXAMPLES = 50000
+IMAGENET_INPUT_PATH_BASE = 'imagenet-2012-tfrecord'
+
+
+@exp_factory.register_config_factory('simclr_pretraining_imagenet')
+def simclr_pretraining_imagenet() -> cfg.ExperimentConfig:
+ """Image classification general."""
+ train_batch_size = 4096
+ eval_batch_size = 4096
+ steps_per_epoch = IMAGENET_TRAIN_EXAMPLES // train_batch_size
+ return cfg.ExperimentConfig(
+ task=SimCLRPretrainTask(
+ model=SimCLRModel(
+ mode=simclr_model.PRETRAIN,
+ backbone_trainable=True,
+ input_size=[224, 224, 3],
+ backbone=backbones.Backbone(
+ type='resnet', resnet=backbones.ResNet(model_id=50)),
+ projection_head=ProjectionHead(
+ proj_output_dim=128, num_proj_layers=3, ft_proj_idx=1),
+ supervised_head=SupervisedHead(num_classes=1001),
+ norm_activation=common.NormActivation(
+ norm_momentum=0.9, norm_epsilon=1e-5, use_sync_bn=True)),
+ loss=ContrastiveLoss(),
+ evaluation=Evaluation(),
+ train_data=DataConfig(
+ parser=Parser(mode=simclr_model.PRETRAIN),
+ decoder=Decoder(decode_label=True),
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size),
+ validation_data=DataConfig(
+ parser=Parser(mode=simclr_model.PRETRAIN),
+ decoder=Decoder(decode_label=True),
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'valid*'),
+ is_training=False,
+ global_batch_size=eval_batch_size),
+ ),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=500 * steps_per_epoch,
+ validation_steps=IMAGENET_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'lars',
+ 'lars': {
+ 'momentum':
+ 0.9,
+ 'weight_decay_rate':
+ 0.000001,
+ 'exclude_from_weight_decay': [
+ 'batch_normalization', 'bias'
+ ]
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ # 0.2 * BatchSize / 256
+ 'initial_learning_rate': 0.2 * train_batch_size / 256,
+ # train_steps - warmup_steps
+ 'decay_steps': 475 * steps_per_epoch
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ # 5% of total epochs
+ 'warmup_steps': 25 * steps_per_epoch
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+
+@exp_factory.register_config_factory('simclr_finetuning_imagenet')
+def simclr_finetuning_imagenet() -> cfg.ExperimentConfig:
+ """Image classification general."""
+ train_batch_size = 1024
+ eval_batch_size = 1024
+ steps_per_epoch = IMAGENET_TRAIN_EXAMPLES // train_batch_size
+ pretrain_model_base = ''
+ return cfg.ExperimentConfig(
+ task=SimCLRFinetuneTask(
+ model=SimCLRModel(
+ mode=simclr_model.FINETUNE,
+ backbone_trainable=True,
+ input_size=[224, 224, 3],
+ backbone=backbones.Backbone(
+ type='resnet', resnet=backbones.ResNet(model_id=50)),
+ projection_head=ProjectionHead(
+ proj_output_dim=128, num_proj_layers=3, ft_proj_idx=1),
+ supervised_head=SupervisedHead(num_classes=1001, zero_init=True),
+ norm_activation=common.NormActivation(
+ norm_momentum=0.9, norm_epsilon=1e-5, use_sync_bn=False)),
+ loss=ClassificationLosses(),
+ evaluation=Evaluation(),
+ train_data=DataConfig(
+ parser=Parser(mode=simclr_model.FINETUNE),
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size),
+ validation_data=DataConfig(
+ parser=Parser(mode=simclr_model.FINETUNE),
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'valid*'),
+ is_training=False,
+ global_batch_size=eval_batch_size),
+ init_checkpoint=pretrain_model_base,
+ # all, backbone_projection or backbone
+ init_checkpoint_modules='backbone_projection'),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=60 * steps_per_epoch,
+ validation_steps=IMAGENET_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'lars',
+ 'lars': {
+ 'momentum':
+ 0.9,
+ 'weight_decay_rate':
+ 0.0,
+ 'exclude_from_weight_decay': [
+ 'batch_normalization', 'bias'
+ ]
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ # 0.01 × BatchSize / 512
+ 'initial_learning_rate': 0.01 * train_batch_size / 512,
+ 'decay_steps': 60 * steps_per_epoch
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
diff --git a/official/vision/beta/projects/simclr/configs/simclr_test.py b/official/projects/simclr/configs/simclr_test.py
similarity index 86%
rename from official/vision/beta/projects/simclr/configs/simclr_test.py
rename to official/projects/simclr/configs/simclr_test.py
index 5a6518018e33a715a9118eef431e40e14f28fe36..af3dfbf5729f1633c681a7c20c556e7d6dc2fb1f 100644
--- a/official/vision/beta/projects/simclr/configs/simclr_test.py
+++ b/official/projects/simclr/configs/simclr_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,8 @@ import tensorflow as tf
from official.core import config_definitions as cfg
from official.core import exp_factory
-from official.vision.beta.projects.simclr.common import registry_imports # pylint: disable=unused-import
-from official.vision.beta.projects.simclr.configs import simclr as exp_cfg
+from official.projects.simclr.common import registry_imports # pylint: disable=unused-import
+from official.projects.simclr.configs import simclr as exp_cfg
class SimCLRConfigTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/simclr/dataloaders/preprocess_ops.py b/official/projects/simclr/dataloaders/preprocess_ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..081621466e81955cec26634b51bb944c05094b7c
--- /dev/null
+++ b/official/projects/simclr/dataloaders/preprocess_ops.py
@@ -0,0 +1,349 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Preprocessing ops."""
+import functools
+import tensorflow as tf
+
+CROP_PROPORTION = 0.875 # Standard for ImageNet.
+
+
+def random_apply(func, p, x):
+ """Randomly apply function func to x with probability p."""
+ return tf.cond(
+ tf.less(
+ tf.random.uniform([], minval=0, maxval=1, dtype=tf.float32),
+ tf.cast(p, tf.float32)), lambda: func(x), lambda: x)
+
+
+def random_brightness(image, max_delta, impl='simclrv2'):
+ """A multiplicative vs additive change of brightness."""
+ if impl == 'simclrv2':
+ factor = tf.random.uniform([], tf.maximum(1.0 - max_delta, 0),
+ 1.0 + max_delta)
+ image = image * factor
+ elif impl == 'simclrv1':
+ image = tf.image.random_brightness(image, max_delta=max_delta)
+ else:
+ raise ValueError('Unknown impl {} for random brightness.'.format(impl))
+ return image
+
+
+def to_grayscale(image, keep_channels=True):
+ image = tf.image.rgb_to_grayscale(image)
+ if keep_channels:
+ image = tf.tile(image, [1, 1, 3])
+ return image
+
+
+def color_jitter_nonrand(image,
+ brightness=0,
+ contrast=0,
+ saturation=0,
+ hue=0,
+ impl='simclrv2'):
+ """Distorts the color of the image (jittering order is fixed).
+
+ Args:
+ image: The input image tensor.
+ brightness: A float, specifying the brightness for color jitter.
+ contrast: A float, specifying the contrast for color jitter.
+ saturation: A float, specifying the saturation for color jitter.
+ hue: A float, specifying the hue for color jitter.
+ impl: 'simclrv1' or 'simclrv2'. Whether to use simclrv1 or simclrv2's
+ version of random brightness.
+
+ Returns:
+ The distorted image tensor.
+ """
+ with tf.name_scope('distort_color'):
+ def apply_transform(i, x, brightness, contrast, saturation, hue):
+ """Apply the i-th transformation."""
+ if brightness != 0 and i == 0:
+ x = random_brightness(x, max_delta=brightness, impl=impl)
+ elif contrast != 0 and i == 1:
+ x = tf.image.random_contrast(
+ x, lower=1 - contrast, upper=1 + contrast)
+ elif saturation != 0 and i == 2:
+ x = tf.image.random_saturation(
+ x, lower=1 - saturation, upper=1 + saturation)
+ elif hue != 0:
+ x = tf.image.random_hue(x, max_delta=hue)
+ return x
+
+ for i in range(4):
+ image = apply_transform(i, image, brightness, contrast, saturation, hue)
+ image = tf.clip_by_value(image, 0., 1.)
+ return image
+
+
+def color_jitter_rand(image,
+ brightness=0,
+ contrast=0,
+ saturation=0,
+ hue=0,
+ impl='simclrv2'):
+ """Distorts the color of the image (jittering order is random).
+
+ Args:
+ image: The input image tensor.
+ brightness: A float, specifying the brightness for color jitter.
+ contrast: A float, specifying the contrast for color jitter.
+ saturation: A float, specifying the saturation for color jitter.
+ hue: A float, specifying the hue for color jitter.
+ impl: 'simclrv1' or 'simclrv2'. Whether to use simclrv1 or simclrv2's
+ version of random brightness.
+
+ Returns:
+ The distorted image tensor.
+ """
+ with tf.name_scope('distort_color'):
+ def apply_transform(i, x):
+ """Apply the i-th transformation."""
+
+ def brightness_foo():
+ if brightness == 0:
+ return x
+ else:
+ return random_brightness(x, max_delta=brightness, impl=impl)
+
+ def contrast_foo():
+ if contrast == 0:
+ return x
+ else:
+ return tf.image.random_contrast(x, lower=1 - contrast,
+ upper=1 + contrast)
+
+ def saturation_foo():
+ if saturation == 0:
+ return x
+ else:
+ return tf.image.random_saturation(
+ x, lower=1 - saturation, upper=1 + saturation)
+
+ def hue_foo():
+ if hue == 0:
+ return x
+ else:
+ return tf.image.random_hue(x, max_delta=hue)
+
+ x = tf.cond(tf.less(i, 2),
+ lambda: tf.cond(tf.less(i, 1), brightness_foo, contrast_foo),
+ lambda: tf.cond(tf.less(i, 3), saturation_foo, hue_foo))
+ return x
+
+ perm = tf.random.shuffle(tf.range(4))
+ for i in range(4):
+ image = apply_transform(perm[i], image)
+ image = tf.clip_by_value(image, 0., 1.)
+ return image
+
+
+def color_jitter(image, strength, random_order=True, impl='simclrv2'):
+ """Distorts the color of the image.
+
+ Args:
+ image: The input image tensor.
+ strength: the floating number for the strength of the color augmentation.
+ random_order: A bool, specifying whether to randomize the jittering order.
+ impl: 'simclrv1' or 'simclrv2'. Whether to use simclrv1 or simclrv2's
+ version of random brightness.
+
+ Returns:
+ The distorted image tensor.
+ """
+ brightness = 0.8 * strength
+ contrast = 0.8 * strength
+ saturation = 0.8 * strength
+ hue = 0.2 * strength
+ if random_order:
+ return color_jitter_rand(
+ image, brightness, contrast, saturation, hue, impl=impl)
+ else:
+ return color_jitter_nonrand(
+ image, brightness, contrast, saturation, hue, impl=impl)
+
+
+def random_color_jitter(image,
+ p=1.0,
+ color_jitter_strength=1.0,
+ impl='simclrv2'):
+ """Perform random color jitter."""
+ def _transform(image):
+ color_jitter_t = functools.partial(
+ color_jitter, strength=color_jitter_strength, impl=impl)
+ image = random_apply(color_jitter_t, p=0.8, x=image)
+ return random_apply(to_grayscale, p=0.2, x=image)
+
+ return random_apply(_transform, p=p, x=image)
+
+
+def gaussian_blur(image, kernel_size, sigma, padding='SAME'):
+ """Blurs the given image with separable convolution.
+
+
+ Args:
+ image: Tensor of shape [height, width, channels] and dtype float to blur.
+ kernel_size: Integer Tensor for the size of the blur kernel. This is should
+ be an odd number. If it is an even number, the actual kernel size will be
+ size + 1.
+ sigma: Sigma value for gaussian operator.
+ padding: Padding to use for the convolution. Typically 'SAME' or 'VALID'.
+
+ Returns:
+ A Tensor representing the blurred image.
+ """
+ radius = tf.cast(kernel_size / 2, dtype=tf.int32)
+ kernel_size = radius * 2 + 1
+ x = tf.cast(tf.range(-radius, radius + 1), dtype=tf.float32)
+ blur_filter = tf.exp(-tf.pow(x, 2.0) /
+ (2.0 * tf.pow(tf.cast(sigma, dtype=tf.float32), 2.0)))
+ blur_filter /= tf.reduce_sum(blur_filter)
+ # One vertical and one horizontal filter.
+ blur_v = tf.reshape(blur_filter, [kernel_size, 1, 1, 1])
+ blur_h = tf.reshape(blur_filter, [1, kernel_size, 1, 1])
+ num_channels = tf.shape(image)[-1]
+ blur_h = tf.tile(blur_h, [1, 1, num_channels, 1])
+ blur_v = tf.tile(blur_v, [1, 1, num_channels, 1])
+ expand_batch_dim = image.shape.ndims == 3
+ if expand_batch_dim:
+ # Tensorflow requires batched input to convolutions, which we can fake with
+ # an extra dimension.
+ image = tf.expand_dims(image, axis=0)
+ blurred = tf.nn.depthwise_conv2d(
+ image, blur_h, strides=[1, 1, 1, 1], padding=padding)
+ blurred = tf.nn.depthwise_conv2d(
+ blurred, blur_v, strides=[1, 1, 1, 1], padding=padding)
+ if expand_batch_dim:
+ blurred = tf.squeeze(blurred, axis=0)
+ return blurred
+
+
+def random_blur(image, height, width, p=0.5):
+ """Randomly blur an image.
+
+ Args:
+ image: `Tensor` representing an image of arbitrary size.
+ height: Height of output image.
+ width: Width of output image.
+ p: probability of applying this transformation.
+
+ Returns:
+ A preprocessed image `Tensor`.
+ """
+ del width
+
+ def _transform(image):
+ sigma = tf.random.uniform([], 0.1, 2.0, dtype=tf.float32)
+ return gaussian_blur(
+ image, kernel_size=height // 10, sigma=sigma, padding='SAME')
+
+ return random_apply(_transform, p=p, x=image)
+
+
+def distorted_bounding_box_crop(image,
+ bbox,
+ min_object_covered=0.1,
+ aspect_ratio_range=(0.75, 1.33),
+ area_range=(0.05, 1.0),
+ max_attempts=100,
+ scope=None):
+ """Generates cropped_image using one of the bboxes randomly distorted.
+
+ See `tf.image.sample_distorted_bounding_box` for more documentation.
+
+ Args:
+ image: `Tensor` of image data.
+ bbox: `Tensor` of bounding boxes arranged `[1, num_boxes, coords]`
+ where each coordinate is [0, 1) and the coordinates are arranged
+ as `[ymin, xmin, ymax, xmax]`. If num_boxes is 0 then use the whole
+ image.
+ min_object_covered: An optional `float`. Defaults to `0.1`. The cropped
+ area of the image must contain at least this fraction of any bounding
+ box supplied.
+ aspect_ratio_range: An optional list of `float`s. The cropped area of the
+ image must have an aspect ratio = width / height within this range.
+ area_range: An optional list of `float`s. The cropped area of the image
+ must contain a fraction of the supplied image within in this range.
+ max_attempts: An optional `int`. Number of attempts at generating a cropped
+ region of the image of the specified constraints. After `max_attempts`
+ failures, return the entire image.
+ scope: Optional `str` for name scope.
+ Returns:
+ (cropped image `Tensor`, distorted bbox `Tensor`).
+ """
+ with tf.name_scope(scope or 'distorted_bounding_box_crop'):
+ shape = tf.shape(image)
+ sample_distorted_bounding_box = tf.image.sample_distorted_bounding_box(
+ shape,
+ bounding_boxes=bbox,
+ min_object_covered=min_object_covered,
+ aspect_ratio_range=aspect_ratio_range,
+ area_range=area_range,
+ max_attempts=max_attempts,
+ use_image_if_no_bounding_boxes=True)
+ bbox_begin, bbox_size, _ = sample_distorted_bounding_box
+
+ # Crop the image to the specified bounding box.
+ offset_y, offset_x, _ = tf.unstack(bbox_begin)
+ target_height, target_width, _ = tf.unstack(bbox_size)
+ image = tf.image.crop_to_bounding_box(
+ image, offset_y, offset_x, target_height, target_width)
+
+ return image
+
+
+def crop_and_resize(image, height, width):
+ """Make a random crop and resize it to height `height` and width `width`.
+
+ Args:
+ image: Tensor representing the image.
+ height: Desired image height.
+ width: Desired image width.
+
+ Returns:
+ A `height` x `width` x channels Tensor holding a random crop of `image`.
+ """
+ bbox = tf.constant([0.0, 0.0, 1.0, 1.0], dtype=tf.float32, shape=[1, 1, 4])
+ aspect_ratio = width / height
+ image = distorted_bounding_box_crop(
+ image,
+ bbox,
+ min_object_covered=0.1,
+ aspect_ratio_range=(3. / 4 * aspect_ratio, 4. / 3. * aspect_ratio),
+ area_range=(0.08, 1.0),
+ max_attempts=100,
+ scope=None)
+ return tf.image.resize([image], [height, width],
+ method=tf.image.ResizeMethod.BICUBIC)[0]
+
+
+def random_crop_with_resize(image, height, width, p=1.0):
+ """Randomly crop and resize an image.
+
+ Args:
+ image: `Tensor` representing an image of arbitrary size.
+ height: Height of output image.
+ width: Width of output image.
+ p: Probability of applying this transformation.
+
+ Returns:
+ A preprocessed image `Tensor`.
+ """
+
+ def _transform(image): # pylint: disable=missing-docstring
+ image = crop_and_resize(image, height, width)
+ return image
+
+ return random_apply(_transform, p=p, x=image)
diff --git a/official/vision/beta/projects/simclr/dataloaders/simclr_input.py b/official/projects/simclr/dataloaders/simclr_input.py
similarity index 95%
rename from official/vision/beta/projects/simclr/dataloaders/simclr_input.py
rename to official/projects/simclr/dataloaders/simclr_input.py
index 4170b2e681649090810efb049256c2d7c8fe9187..8585f5dada772c5b716a7c940fcaef33c1d10d9b 100644
--- a/official/vision/beta/projects/simclr/dataloaders/simclr_input.py
+++ b/official/projects/simclr/dataloaders/simclr_input.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -40,11 +40,11 @@ from typing import List
import tensorflow as tf
-from official.vision.beta.dataloaders import decoder
-from official.vision.beta.dataloaders import parser
-from official.vision.beta.ops import preprocess_ops
-from official.vision.beta.projects.simclr.dataloaders import preprocess_ops as simclr_preprocess_ops
-from official.vision.beta.projects.simclr.modeling import simclr_model
+from official.projects.simclr.dataloaders import preprocess_ops as simclr_preprocess_ops
+from official.projects.simclr.modeling import simclr_model
+from official.vision.dataloaders import decoder
+from official.vision.dataloaders import parser
+from official.vision.ops import preprocess_ops
class Decoder(decoder.Decoder):
diff --git a/official/vision/beta/projects/simclr/heads/simclr_head.py b/official/projects/simclr/heads/simclr_head.py
similarity index 97%
rename from official/vision/beta/projects/simclr/heads/simclr_head.py
rename to official/projects/simclr/heads/simclr_head.py
index 947fc38e980bc6c089aa786a646241b27be7810b..7dc37f0dbe65790ae04f97227537136e4c017aaf 100644
--- a/official/vision/beta/projects/simclr/heads/simclr_head.py
+++ b/official/projects/simclr/heads/simclr_head.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,11 +14,11 @@
"""SimCLR prediction heads."""
-from typing import Text, Optional
+from typing import Optional, Text
import tensorflow as tf
-from official.vision.beta.projects.simclr.modeling.layers import nn_blocks
+from official.projects.simclr.modeling.layers import nn_blocks
regularizers = tf.keras.regularizers
layers = tf.keras.layers
diff --git a/official/vision/beta/projects/simclr/heads/simclr_head_test.py b/official/projects/simclr/heads/simclr_head_test.py
similarity index 96%
rename from official/vision/beta/projects/simclr/heads/simclr_head_test.py
rename to official/projects/simclr/heads/simclr_head_test.py
index 1c8f92603ad26f3971933017f5e27f517ce48645..1ff7582c82d5c0ae7d3cb10b6172b0b59c222258 100644
--- a/official/vision/beta/projects/simclr/heads/simclr_head_test.py
+++ b/official/projects/simclr/heads/simclr_head_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,7 +17,7 @@ from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.projects.simclr.heads import simclr_head
+from official.projects.simclr.heads import simclr_head
class ProjectionHeadTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/vision/beta/projects/simclr/losses/contrastive_losses.py b/official/projects/simclr/losses/contrastive_losses.py
similarity index 98%
rename from official/vision/beta/projects/simclr/losses/contrastive_losses.py
rename to official/projects/simclr/losses/contrastive_losses.py
index af528265c6e20b9d2a0f519e4f2b92d82a471dc5..f16a7b723f59405ba082febd2e2160738f15b614 100644
--- a/official/vision/beta/projects/simclr/losses/contrastive_losses.py
+++ b/official/projects/simclr/losses/contrastive_losses.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/simclr/losses/contrastive_losses_test.py b/official/projects/simclr/losses/contrastive_losses_test.py
similarity index 94%
rename from official/vision/beta/projects/simclr/losses/contrastive_losses_test.py
rename to official/projects/simclr/losses/contrastive_losses_test.py
index 815a3d01ef8c1906c50d47ba249408af4e029d28..364936ed3caeeb3766ecb1575bbef28b6e5042f5 100644
--- a/official/vision/beta/projects/simclr/losses/contrastive_losses_test.py
+++ b/official/projects/simclr/losses/contrastive_losses_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -17,7 +17,7 @@ from absl.testing import parameterized
import numpy as np
import tensorflow as tf
-from official.vision.beta.projects.simclr.losses import contrastive_losses
+from official.projects.simclr.losses import contrastive_losses
class ContrastiveLossesTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/simclr/modeling/layers/nn_blocks.py b/official/projects/simclr/modeling/layers/nn_blocks.py
new file mode 100644
index 0000000000000000000000000000000000000000..013a7be5201e4a0b15f0c595e22f471ca43098cb
--- /dev/null
+++ b/official/projects/simclr/modeling/layers/nn_blocks.py
@@ -0,0 +1,133 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Contains common building blocks for simclr neural networks."""
+from typing import Text, Optional
+
+import tensorflow as tf
+
+from official.modeling import tf_utils
+
+regularizers = tf.keras.regularizers
+
+
+class DenseBN(tf.keras.layers.Layer):
+ """Modified Dense layer to help build simclr system.
+
+ The layer is a standards combination of Dense, BatchNorm and Activation.
+ """
+
+ def __init__(
+ self,
+ output_dim: int,
+ use_bias: bool = True,
+ use_normalization: bool = False,
+ use_sync_bn: bool = False,
+ norm_momentum: float = 0.99,
+ norm_epsilon: float = 0.001,
+ activation: Optional[Text] = 'relu',
+ kernel_initializer: Text = 'VarianceScaling',
+ kernel_regularizer: Optional[regularizers.Regularizer] = None,
+ bias_regularizer: Optional[regularizers.Regularizer] = None,
+ name='linear_layer',
+ **kwargs):
+ """Customized Dense layer.
+
+ Args:
+ output_dim: `int` size of output dimension.
+ use_bias: if True, use biase in the dense layer.
+ use_normalization: if True, use batch normalization.
+ use_sync_bn: if True, use synchronized batch normalization.
+ norm_momentum: `float` normalization momentum for the moving average.
+ norm_epsilon: `float` small float added to variance to avoid dividing by
+ zero.
+ activation: `str` name of the activation function.
+ kernel_initializer: kernel_initializer for convolutional layers.
+ kernel_regularizer: tf.keras.regularizers.Regularizer object for Conv2D.
+ Default to None.
+ bias_regularizer: tf.keras.regularizers.Regularizer object for Conv2d.
+ Default to None.
+ name: `str`, name of the layer.
+ **kwargs: keyword arguments to be passed.
+ """
+ # Note: use_bias is ignored for the dense layer when use_bn=True.
+ # However, it is still used for batch norm.
+ super(DenseBN, self).__init__(**kwargs)
+ self._output_dim = output_dim
+ self._use_bias = use_bias
+ self._use_normalization = use_normalization
+ self._use_sync_bn = use_sync_bn
+ self._norm_momentum = norm_momentum
+ self._norm_epsilon = norm_epsilon
+ self._activation = activation
+ self._kernel_initializer = kernel_initializer
+ self._kernel_regularizer = kernel_regularizer
+ self._bias_regularizer = bias_regularizer
+ self._name = name
+
+ if use_sync_bn:
+ self._norm = tf.keras.layers.experimental.SyncBatchNormalization
+ else:
+ self._norm = tf.keras.layers.BatchNormalization
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ self._bn_axis = -1
+ else:
+ self._bn_axis = 1
+ if activation:
+ self._activation_fn = tf_utils.get_activation(activation)
+ else:
+ self._activation_fn = None
+
+ def get_config(self):
+ config = {
+ 'output_dim': self._output_dim,
+ 'use_bias': self._use_bias,
+ 'activation': self._activation,
+ 'use_sync_bn': self._use_sync_bn,
+ 'use_normalization': self._use_normalization,
+ 'norm_momentum': self._norm_momentum,
+ 'norm_epsilon': self._norm_epsilon,
+ 'kernel_initializer': self._kernel_initializer,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'bias_regularizer': self._bias_regularizer,
+ }
+ base_config = super(DenseBN, self).get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def build(self, input_shape):
+ self._dense0 = tf.keras.layers.Dense(
+ self._output_dim,
+ kernel_initializer=self._kernel_initializer,
+ kernel_regularizer=self._kernel_regularizer,
+ bias_regularizer=self._bias_regularizer,
+ use_bias=self._use_bias and not self._use_normalization)
+
+ if self._use_normalization:
+ self._norm0 = self._norm(
+ axis=self._bn_axis,
+ momentum=self._norm_momentum,
+ epsilon=self._norm_epsilon,
+ center=self._use_bias,
+ scale=True)
+
+ super(DenseBN, self).build(input_shape)
+
+ def call(self, inputs, training=None):
+ assert inputs.shape.ndims == 2, inputs.shape
+ x = self._dense0(inputs)
+ if self._use_normalization:
+ x = self._norm0(x)
+ if self._activation:
+ x = self._activation_fn(x)
+ return x
diff --git a/official/projects/simclr/modeling/layers/nn_blocks_test.py b/official/projects/simclr/modeling/layers/nn_blocks_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..f8d830dfbf91b58c6fe4be410ab76d346f1f20bb
--- /dev/null
+++ b/official/projects/simclr/modeling/layers/nn_blocks_test.py
@@ -0,0 +1,58 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from absl.testing import parameterized
+
+import tensorflow as tf
+
+from official.projects.simclr.modeling.layers import nn_blocks
+
+
+class DenseBNTest(tf.test.TestCase, parameterized.TestCase):
+
+ @parameterized.parameters(
+ (64, True, True),
+ (64, True, False),
+ (64, False, True),
+ )
+ def test_pass_through(self, output_dim, use_bias, use_normalization):
+ test_layer = nn_blocks.DenseBN(
+ output_dim=output_dim,
+ use_bias=use_bias,
+ use_normalization=use_normalization
+ )
+
+ x = tf.keras.Input(shape=(64,))
+ out_x = test_layer(x)
+
+ self.assertAllEqual(out_x.shape.as_list(), [None, output_dim])
+
+ # kernel of the dense layer
+ train_var_len = 1
+ if use_normalization:
+ if use_bias:
+ # batch norm introduce two trainable variables
+ train_var_len += 2
+ else:
+ # center is set to False if not use bias
+ train_var_len += 1
+ else:
+ if use_bias:
+ # bias of dense layer
+ train_var_len += 1
+ self.assertLen(test_layer.trainable_variables, train_var_len)
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/vision/beta/projects/simclr/modeling/multitask_model.py b/official/projects/simclr/modeling/multitask_model.py
similarity index 91%
rename from official/vision/beta/projects/simclr/modeling/multitask_model.py
rename to official/projects/simclr/modeling/multitask_model.py
index a971e85c89c952cef20c778138ee443fe9443cf3..0c814dba7382a645eb96c71ad8ea751cf0e7a5cb 100644
--- a/official/vision/beta/projects/simclr/modeling/multitask_model.py
+++ b/official/projects/simclr/modeling/multitask_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,15 +14,15 @@
"""Multi-task image multi-taskSimCLR model definition."""
from typing import Dict, Text
-from absl import logging
+from absl import logging
import tensorflow as tf
from official.modeling.multitask import base_model
-from official.vision.beta.modeling import backbones
-from official.vision.beta.projects.simclr.configs import multitask_config as simclr_multitask_config
-from official.vision.beta.projects.simclr.heads import simclr_head
-from official.vision.beta.projects.simclr.modeling import simclr_model
+from official.projects.simclr.configs import multitask_config as simclr_multitask_config
+from official.projects.simclr.heads import simclr_head
+from official.projects.simclr.modeling import simclr_model
+from official.vision.modeling import backbones
PROJECTION_OUTPUT_KEY = 'projection_outputs'
SUPERVISED_OUTPUT_KEY = 'supervised_outputs'
@@ -110,8 +110,9 @@ class SimCLRMTModel(base_model.MultiTaskBaseModel):
pretrained_items = dict(
backbone=self._backbone, projection_head=self._projection_head)
else:
- assert ("Only 'backbone_projection' or 'backbone' can be used to "
- 'initialize the model.')
+ raise ValueError(
+ "Only 'backbone_projection' or 'backbone' can be used to "
+ 'initialize the model.')
ckpt = tf.train.Checkpoint(**pretrained_items)
status = ckpt.read(ckpt_dir_or_file)
diff --git a/official/vision/beta/projects/simclr/modeling/multitask_model_test.py b/official/projects/simclr/modeling/multitask_model_test.py
similarity index 83%
rename from official/vision/beta/projects/simclr/modeling/multitask_model_test.py
rename to official/projects/simclr/modeling/multitask_model_test.py
index 0190145a8974a6ebf8ea834317bf087f7d8676ce..365ae5a3517bc7bc1daef553109cfccbccf6e2c4 100644
--- a/official/vision/beta/projects/simclr/modeling/multitask_model_test.py
+++ b/official/projects/simclr/modeling/multitask_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -18,9 +18,9 @@ import os.path
import tensorflow as tf
-from official.vision.beta.projects.simclr.configs import multitask_config
-from official.vision.beta.projects.simclr.modeling import multitask_model
-from official.vision.beta.projects.simclr.modeling import simclr_model
+from official.projects.simclr.configs import multitask_config
+from official.projects.simclr.modeling import multitask_model
+from official.projects.simclr.modeling import simclr_model
class MultitaskModelTest(tf.test.TestCase):
diff --git a/official/vision/beta/projects/simclr/modeling/simclr_model.py b/official/projects/simclr/modeling/simclr_model.py
similarity index 98%
rename from official/vision/beta/projects/simclr/modeling/simclr_model.py
rename to official/projects/simclr/modeling/simclr_model.py
index 25db8a9f33c2611a4e3aa29da23d209256951d6a..da8a6e3572cfd3ef9e4c9bfb687e4b9151e7058a 100644
--- a/official/vision/beta/projects/simclr/modeling/simclr_model.py
+++ b/official/projects/simclr/modeling/simclr_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/vision/beta/projects/simclr/modeling/simclr_model_test.py b/official/projects/simclr/modeling/simclr_model_test.py
similarity index 89%
rename from official/vision/beta/projects/simclr/modeling/simclr_model_test.py
rename to official/projects/simclr/modeling/simclr_model_test.py
index ee8724ebadec7a44f7acc67bcf5bd8d3734c1da8..42f104be3adef12bdd469d8e078928988b7509c2 100644
--- a/official/vision/beta/projects/simclr/modeling/simclr_model_test.py
+++ b/official/projects/simclr/modeling/simclr_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -14,13 +14,12 @@
"""Test for SimCLR model."""
from absl.testing import parameterized
-
import numpy as np
import tensorflow as tf
-from official.vision.beta.modeling import backbones
-from official.vision.beta.projects.simclr.heads import simclr_head
-from official.vision.beta.projects.simclr.modeling import simclr_model
+from official.projects.simclr.heads import simclr_head
+from official.projects.simclr.modeling import simclr_model
+from official.vision.modeling import backbones
class SimCLRModelTest(parameterized.TestCase, tf.test.TestCase):
diff --git a/official/vision/beta/projects/simclr/multitask_train.py b/official/projects/simclr/multitask_train.py
similarity index 89%
rename from official/vision/beta/projects/simclr/multitask_train.py
rename to official/projects/simclr/multitask_train.py
index 77fb621a87910aca736cab4eba80688f06a278bd..fec106dcac6ce4a8779a8744d24515cec3b36e95 100644
--- a/official/vision/beta/projects/simclr/multitask_train.py
+++ b/official/projects/simclr/multitask_train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -25,9 +25,9 @@ from official.modeling.multitask import multitask
from official.modeling.multitask import train_lib
# pylint: disable=unused-import
-from official.vision.beta.projects.simclr.common import registry_imports
-from official.vision.beta.projects.simclr.configs import multitask_config
-from official.vision.beta.projects.simclr.modeling import multitask_model
+from official.projects.simclr.common import registry_imports
+from official.projects.simclr.configs import multitask_config
+from official.projects.simclr.modeling import multitask_model
# pylint: enable=unused-import
FLAGS = flags.FLAGS
diff --git a/official/projects/simclr/tasks/simclr.py b/official/projects/simclr/tasks/simclr.py
new file mode 100644
index 0000000000000000000000000000000000000000..cf52fa1fbe04c25f19c9a39e3fa8de44d0887736
--- /dev/null
+++ b/official/projects/simclr/tasks/simclr.py
@@ -0,0 +1,635 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image SimCLR task definition.
+
+SimCLR training two different modes:
+- pretrain
+- fine-tuning
+
+For the above two different modes, the following components are different in
+the task definition:
+- training data format
+- training loss
+- projection_head and/or supervised_head
+"""
+from typing import Dict, Optional
+
+from absl import logging
+import tensorflow as tf
+
+from official.core import base_task
+from official.core import config_definitions
+from official.core import input_reader
+from official.core import task_factory
+from official.modeling import optimization
+from official.modeling import performance
+from official.modeling import tf_utils
+from official.projects.simclr.configs import simclr as exp_cfg
+from official.projects.simclr.dataloaders import simclr_input
+from official.projects.simclr.heads import simclr_head
+from official.projects.simclr.losses import contrastive_losses
+from official.projects.simclr.modeling import simclr_model
+from official.vision.modeling import backbones
+
+OptimizationConfig = optimization.OptimizationConfig
+RuntimeConfig = config_definitions.RuntimeConfig
+
+
+@task_factory.register_task_cls(exp_cfg.SimCLRPretrainTask)
+class SimCLRPretrainTask(base_task.Task):
+ """A task for image classification."""
+
+ def create_optimizer(self,
+ optimizer_config: OptimizationConfig,
+ runtime_config: Optional[RuntimeConfig] = None):
+ """Creates an TF optimizer from configurations.
+
+ Args:
+ optimizer_config: the parameters of the Optimization settings.
+ runtime_config: the parameters of the runtime.
+
+ Returns:
+ A tf.optimizers.Optimizer object.
+ """
+ if (optimizer_config.optimizer.type == 'lars' and
+ self.task_config.loss.l2_weight_decay > 0.0):
+ raise ValueError('The l2_weight_decay cannot be used together with lars '
+ 'optimizer. Please set it to 0.')
+
+ opt_factory = optimization.OptimizerFactory(optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+ # Configuring optimizer when loss_scale is set in runtime config. This helps
+ # avoiding overflow/underflow for float16 computations.
+ if runtime_config and runtime_config.loss_scale:
+ optimizer = performance.configure_optimizer(
+ optimizer,
+ use_float16=runtime_config.mixed_precision_dtype == 'float16',
+ loss_scale=runtime_config.loss_scale)
+
+ return optimizer
+
+ def build_model(self):
+ model_config = self.task_config.model
+ input_specs = tf.keras.layers.InputSpec(shape=[None] +
+ model_config.input_size)
+
+ l2_weight_decay = self.task_config.loss.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (
+ tf.keras.regularizers.l2(l2_weight_decay /
+ 2.0) if l2_weight_decay else None)
+
+ # Build backbone
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=model_config.norm_activation,
+ l2_regularizer=l2_regularizer)
+
+ # Build projection head
+ norm_activation_config = model_config.norm_activation
+ projection_head_config = model_config.projection_head
+ projection_head = simclr_head.ProjectionHead(
+ proj_output_dim=projection_head_config.proj_output_dim,
+ num_proj_layers=projection_head_config.num_proj_layers,
+ ft_proj_idx=projection_head_config.ft_proj_idx,
+ kernel_regularizer=l2_regularizer,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon)
+
+ # Build supervised head
+ supervised_head_config = model_config.supervised_head
+ if supervised_head_config:
+ if supervised_head_config.zero_init:
+ s_kernel_initializer = 'zeros'
+ else:
+ s_kernel_initializer = 'random_uniform'
+ supervised_head = simclr_head.ClassificationHead(
+ num_classes=supervised_head_config.num_classes,
+ kernel_initializer=s_kernel_initializer,
+ kernel_regularizer=l2_regularizer)
+ else:
+ supervised_head = None
+
+ model = simclr_model.SimCLRModel(
+ input_specs=input_specs,
+ backbone=backbone,
+ projection_head=projection_head,
+ supervised_head=supervised_head,
+ mode=model_config.mode,
+ backbone_trainable=model_config.backbone_trainable)
+
+ logging.info(model.get_config())
+
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loading pretrained checkpoint."""
+ if not self.task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self.task_config.init_checkpoint
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ # Restoring checkpoint.
+ if self.task_config.init_checkpoint_modules == 'all':
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ elif self.task_config.init_checkpoint_modules == 'backbone':
+ ckpt = tf.train.Checkpoint(backbone=model.backbone)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ else:
+ raise ValueError(
+ "Only 'all' or 'backbone' can be used to initialize the model.")
+
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+
+ def build_inputs(self, params, input_context=None):
+ input_size = self.task_config.model.input_size
+
+ if params.tfds_name:
+ decoder = simclr_input.TFDSDecoder(params.decoder.decode_label)
+ else:
+ decoder = simclr_input.Decoder(params.decoder.decode_label)
+
+ parser = simclr_input.Parser(
+ output_size=input_size[:2],
+ aug_rand_crop=params.parser.aug_rand_crop,
+ aug_rand_hflip=params.parser.aug_rand_hflip,
+ aug_color_distort=params.parser.aug_color_distort,
+ aug_color_jitter_strength=params.parser.aug_color_jitter_strength,
+ aug_color_jitter_impl=params.parser.aug_color_jitter_impl,
+ aug_rand_blur=params.parser.aug_rand_blur,
+ parse_label=params.parser.parse_label,
+ test_crop=params.parser.test_crop,
+ mode=params.parser.mode,
+ dtype=params.dtype)
+
+ reader = input_reader.InputReader(
+ params,
+ dataset_fn=tf.data.TFRecordDataset,
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def build_losses(self,
+ labels,
+ model_outputs,
+ aux_losses=None) -> Dict[str, tf.Tensor]:
+ # Compute contrastive relative loss
+ con_losses_obj = contrastive_losses.ContrastiveLoss(
+ projection_norm=self.task_config.loss.projection_norm,
+ temperature=self.task_config.loss.temperature)
+ # The projection outputs from model has the size of
+ # (2 * bsz, project_dim)
+ projection_outputs = model_outputs[simclr_model.PROJECTION_OUTPUT_KEY]
+ projection1, projection2 = tf.split(projection_outputs, 2, 0)
+ contrast_loss, (contrast_logits, contrast_labels) = con_losses_obj(
+ projection1=projection1, projection2=projection2)
+
+ contrast_accuracy = tf.equal(
+ tf.argmax(contrast_labels, axis=1), tf.argmax(contrast_logits, axis=1))
+ contrast_accuracy = tf.reduce_mean(tf.cast(contrast_accuracy, tf.float32))
+
+ contrast_prob = tf.nn.softmax(contrast_logits)
+ contrast_entropy = -tf.reduce_mean(
+ tf.reduce_sum(contrast_prob * tf.math.log(contrast_prob + 1e-8), -1))
+
+ model_loss = contrast_loss
+
+ losses = {
+ 'contrast_loss': contrast_loss,
+ 'contrast_accuracy': contrast_accuracy,
+ 'contrast_entropy': contrast_entropy
+ }
+
+ if self.task_config.model.supervised_head is not None:
+ outputs = model_outputs[simclr_model.SUPERVISED_OUTPUT_KEY]
+ labels = tf.concat([labels, labels], 0)
+
+ if self.task_config.evaluation.one_hot:
+ sup_loss = tf.keras.losses.CategoricalCrossentropy(
+ from_logits=True, reduction=tf.keras.losses.Reduction.NONE)(labels,
+ outputs)
+ else:
+ sup_loss = tf.keras.losses.SparseCategoricalCrossentropy(
+ from_logits=True, reduction=tf.keras.losses.Reduction.NONE)(labels,
+ outputs)
+ sup_loss = tf.reduce_mean(sup_loss)
+
+ label_acc = tf.equal(
+ tf.argmax(labels, axis=1), tf.argmax(outputs, axis=1))
+ label_acc = tf.reduce_mean(tf.cast(label_acc, tf.float32))
+
+ model_loss = contrast_loss + sup_loss
+
+ losses.update({
+ 'accuracy': label_acc,
+ 'supervised_loss': sup_loss,
+ })
+
+ total_loss = model_loss
+ if aux_losses:
+ reg_loss = tf.reduce_sum(aux_losses)
+ total_loss = model_loss + reg_loss
+
+ losses['total_loss'] = total_loss
+
+ return losses
+
+ def build_metrics(self, training=True):
+
+ if training:
+ metrics = []
+ metric_names = [
+ 'total_loss', 'contrast_loss', 'contrast_accuracy', 'contrast_entropy'
+ ]
+ if self.task_config.model.supervised_head:
+ metric_names.extend(['supervised_loss', 'accuracy'])
+ for name in metric_names:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+ else:
+ k = self.task_config.evaluation.top_k
+ if self.task_config.evaluation.one_hot:
+ metrics = [
+ tf.keras.metrics.CategoricalAccuracy(name='accuracy'),
+ tf.keras.metrics.TopKCategoricalAccuracy(
+ k=k, name='top_{}_accuracy'.format(k))
+ ]
+ else:
+ metrics = [
+ tf.keras.metrics.SparseCategoricalAccuracy(name='accuracy'),
+ tf.keras.metrics.SparseTopKCategoricalAccuracy(
+ k=k, name='top_{}_accuracy'.format(k))
+ ]
+ return metrics
+
+ def train_step(self, inputs, model, optimizer, metrics=None):
+ features, labels = inputs
+
+ # To do a sanity check that we absolutely use no labels when pretraining, we
+ # can set the labels here to zero.
+ if self.task_config.train_data.input_set_label_to_zero:
+ labels *= 0
+
+ if (self.task_config.model.supervised_head is not None and
+ self.task_config.evaluation.one_hot):
+ num_classes = self.task_config.model.supervised_head.num_classes
+ labels = tf.one_hot(labels, num_classes)
+
+ num_replicas = tf.distribute.get_strategy().num_replicas_in_sync
+ with tf.GradientTape() as tape:
+ outputs = model(features, training=True)
+ # Casting output layer as float32 is necessary when mixed_precision is
+ # mixed_float16 or mixed_bfloat16 to ensure output is casted as float32.
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+
+ # Computes per-replica loss.
+ losses = self.build_losses(
+ model_outputs=outputs, labels=labels, aux_losses=model.losses)
+
+ scaled_loss = losses['total_loss'] / num_replicas
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ tvars = model.trainable_variables
+ logging.info('Trainable variables:')
+ for var in tvars:
+ logging.info(var.name)
+ grads = tape.gradient(scaled_loss, tvars)
+ # Scales back gradient when LossScaleOptimizer is used.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ grads = optimizer.get_unscaled_gradients(grads)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ logs = {self.loss: losses['total_loss']}
+
+ for m in metrics:
+ m.update_state(losses[m.name])
+ logs.update({m.name: m.result()})
+
+ return logs
+
+ def validation_step(self, inputs, model, metrics=None):
+ if self.task_config.model.supervised_head is None:
+ raise ValueError(
+ 'Skipping eval during pretraining without supervised head.')
+
+ features, labels = inputs
+ if self.task_config.evaluation.one_hot:
+ num_classes = self.task_config.model.supervised_head.num_classes
+ labels = tf.one_hot(labels, num_classes)
+
+ outputs = model(
+ features, training=False)[simclr_model.SUPERVISED_OUTPUT_KEY]
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+
+ logs = {self.loss: 0}
+
+ if metrics:
+ self.process_metrics(metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in metrics})
+ elif model.compiled_metrics:
+ self.process_compiled_metrics(model.compiled_metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in model.metrics})
+
+ return logs
+
+
+@task_factory.register_task_cls(exp_cfg.SimCLRFinetuneTask)
+class SimCLRFinetuneTask(base_task.Task):
+ """A task for image classification."""
+
+ def create_optimizer(self,
+ optimizer_config: OptimizationConfig,
+ runtime_config: Optional[RuntimeConfig] = None):
+ """Creates an TF optimizer from configurations.
+
+ Args:
+ optimizer_config: the parameters of the Optimization settings.
+ runtime_config: the parameters of the runtime.
+
+ Returns:
+ A tf.optimizers.Optimizer object.
+ """
+ if (optimizer_config.optimizer.type == 'lars' and
+ self.task_config.loss.l2_weight_decay > 0.0):
+ raise ValueError('The l2_weight_decay cannot be used together with lars '
+ 'optimizer. Please set it to 0.')
+
+ opt_factory = optimization.OptimizerFactory(optimizer_config)
+ optimizer = opt_factory.build_optimizer(opt_factory.build_learning_rate())
+ # Configuring optimizer when loss_scale is set in runtime config. This helps
+ # avoiding overflow/underflow for float16 computations.
+ if runtime_config and runtime_config.loss_scale:
+ optimizer = performance.configure_optimizer(
+ optimizer,
+ use_float16=runtime_config.mixed_precision_dtype == 'float16',
+ loss_scale=runtime_config.loss_scale)
+
+ return optimizer
+
+ def build_model(self):
+ model_config = self.task_config.model
+ input_specs = tf.keras.layers.InputSpec(shape=[None] +
+ model_config.input_size)
+
+ l2_weight_decay = self.task_config.loss.l2_weight_decay
+ # Divide weight decay by 2.0 to match the implementation of tf.nn.l2_loss.
+ # (https://www.tensorflow.org/api_docs/python/tf/keras/regularizers/l2)
+ # (https://www.tensorflow.org/api_docs/python/tf/nn/l2_loss)
+ l2_regularizer = (
+ tf.keras.regularizers.l2(l2_weight_decay /
+ 2.0) if l2_weight_decay else None)
+
+ backbone = backbones.factory.build_backbone(
+ input_specs=input_specs,
+ backbone_config=model_config.backbone,
+ norm_activation_config=model_config.norm_activation,
+ l2_regularizer=l2_regularizer)
+
+ norm_activation_config = model_config.norm_activation
+ projection_head_config = model_config.projection_head
+ projection_head = simclr_head.ProjectionHead(
+ proj_output_dim=projection_head_config.proj_output_dim,
+ num_proj_layers=projection_head_config.num_proj_layers,
+ ft_proj_idx=projection_head_config.ft_proj_idx,
+ kernel_regularizer=l2_regularizer,
+ use_sync_bn=norm_activation_config.use_sync_bn,
+ norm_momentum=norm_activation_config.norm_momentum,
+ norm_epsilon=norm_activation_config.norm_epsilon)
+
+ supervised_head_config = model_config.supervised_head
+ if supervised_head_config.zero_init:
+ s_kernel_initializer = 'zeros'
+ else:
+ s_kernel_initializer = 'random_uniform'
+ supervised_head = simclr_head.ClassificationHead(
+ num_classes=supervised_head_config.num_classes,
+ kernel_initializer=s_kernel_initializer,
+ kernel_regularizer=l2_regularizer)
+
+ model = simclr_model.SimCLRModel(
+ input_specs=input_specs,
+ backbone=backbone,
+ projection_head=projection_head,
+ supervised_head=supervised_head,
+ mode=model_config.mode,
+ backbone_trainable=model_config.backbone_trainable)
+
+ logging.info(model.get_config())
+
+ return model
+
+ def initialize(self, model: tf.keras.Model):
+ """Loading pretrained checkpoint."""
+ if not self.task_config.init_checkpoint:
+ return
+
+ ckpt_dir_or_file = self.task_config.init_checkpoint
+ if tf.io.gfile.isdir(ckpt_dir_or_file):
+ ckpt_dir_or_file = tf.train.latest_checkpoint(ckpt_dir_or_file)
+
+ # Restoring checkpoint.
+ if self.task_config.init_checkpoint_modules == 'all':
+ ckpt = tf.train.Checkpoint(**model.checkpoint_items)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ elif self.task_config.init_checkpoint_modules == 'backbone_projection':
+ ckpt = tf.train.Checkpoint(
+ backbone=model.backbone, projection_head=model.projection_head)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ elif self.task_config.init_checkpoint_modules == 'backbone':
+ ckpt = tf.train.Checkpoint(backbone=model.backbone)
+ status = ckpt.read(ckpt_dir_or_file)
+ status.expect_partial().assert_existing_objects_matched()
+ else:
+ raise ValueError(
+ "Only 'all' or 'backbone' can be used to initialize the model.")
+
+ # If the checkpoint is from pretraining, reset the following parameters
+ model.backbone_trainable = self.task_config.model.backbone_trainable
+ logging.info('Finished loading pretrained checkpoint from %s',
+ ckpt_dir_or_file)
+
+ def build_inputs(self, params, input_context=None):
+ input_size = self.task_config.model.input_size
+
+ if params.tfds_name:
+ decoder = simclr_input.TFDSDecoder(params.decoder.decode_label)
+ else:
+ decoder = simclr_input.Decoder(params.decoder.decode_label)
+ parser = simclr_input.Parser(
+ output_size=input_size[:2],
+ parse_label=params.parser.parse_label,
+ test_crop=params.parser.test_crop,
+ mode=params.parser.mode,
+ dtype=params.dtype)
+
+ reader = input_reader.InputReader(
+ params,
+ dataset_fn=tf.data.TFRecordDataset,
+ decoder_fn=decoder.decode,
+ parser_fn=parser.parse_fn(params.is_training))
+
+ dataset = reader.read(input_context=input_context)
+
+ return dataset
+
+ def build_losses(self, labels, model_outputs, aux_losses=None):
+ """Sparse categorical cross entropy loss.
+
+ Args:
+ labels: labels.
+ model_outputs: Output logits of the classifier.
+ aux_losses: auxiliarly loss tensors, i.e. `losses` in keras.Model.
+
+ Returns:
+ The total loss tensor.
+ """
+ losses_config = self.task_config.loss
+ if losses_config.one_hot:
+ total_loss = tf.keras.losses.categorical_crossentropy(
+ labels,
+ model_outputs,
+ from_logits=True,
+ label_smoothing=losses_config.label_smoothing)
+ else:
+ total_loss = tf.keras.losses.sparse_categorical_crossentropy(
+ labels, model_outputs, from_logits=True)
+
+ total_loss = tf_utils.safe_mean(total_loss)
+ if aux_losses:
+ total_loss += tf.add_n(aux_losses)
+
+ return total_loss
+
+ def build_metrics(self, training=True):
+ """Gets streaming metrics for training/validation."""
+ k = self.task_config.evaluation.top_k
+ if self.task_config.evaluation.one_hot:
+ metrics = [
+ tf.keras.metrics.CategoricalAccuracy(name='accuracy'),
+ tf.keras.metrics.TopKCategoricalAccuracy(
+ k=k, name='top_{}_accuracy'.format(k))
+ ]
+ else:
+ metrics = [
+ tf.keras.metrics.SparseCategoricalAccuracy(name='accuracy'),
+ tf.keras.metrics.SparseTopKCategoricalAccuracy(
+ k=k, name='top_{}_accuracy'.format(k))
+ ]
+ return metrics
+
+ def train_step(self, inputs, model, optimizer, metrics=None):
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+ if self.task_config.loss.one_hot:
+ num_classes = self.task_config.model.supervised_head.num_classes
+ labels = tf.one_hot(labels, num_classes)
+
+ num_replicas = tf.distribute.get_strategy().num_replicas_in_sync
+ with tf.GradientTape() as tape:
+ outputs = model(
+ features, training=True)[simclr_model.SUPERVISED_OUTPUT_KEY]
+ # Casting output layer as float32 is necessary when mixed_precision is
+ # mixed_float16 or mixed_bfloat16 to ensure output is casted as float32.
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+
+ # Computes per-replica loss.
+ loss = self.build_losses(
+ model_outputs=outputs, labels=labels, aux_losses=model.losses)
+ # Scales loss as the default gradients allreduce performs sum inside the
+ # optimizer.
+ scaled_loss = loss / num_replicas
+
+ # For mixed_precision policy, when LossScaleOptimizer is used, loss is
+ # scaled for numerical stability.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ scaled_loss = optimizer.get_scaled_loss(scaled_loss)
+
+ tvars = model.trainable_variables
+ logging.info('Trainable variables:')
+ for var in tvars:
+ logging.info(var.name)
+ grads = tape.gradient(scaled_loss, tvars)
+ # Scales back gradient before apply_gradients when LossScaleOptimizer is
+ # used.
+ if isinstance(optimizer, tf.keras.mixed_precision.LossScaleOptimizer):
+ grads = optimizer.get_unscaled_gradients(grads)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ logs = {self.loss: loss}
+ if metrics:
+ self.process_metrics(metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in metrics})
+ elif model.compiled_metrics:
+ self.process_compiled_metrics(model.compiled_metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in model.metrics})
+ return logs
+
+ def validation_step(self, inputs, model, metrics=None):
+ """Validatation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ features, labels = inputs
+ if self.task_config.loss.one_hot:
+ num_classes = self.task_config.model.supervised_head.num_classes
+ labels = tf.one_hot(labels, num_classes)
+
+ outputs = self.inference_step(features,
+ model)[simclr_model.SUPERVISED_OUTPUT_KEY]
+ outputs = tf.nest.map_structure(lambda x: tf.cast(x, tf.float32), outputs)
+ loss = self.build_losses(
+ model_outputs=outputs, labels=labels, aux_losses=model.losses)
+
+ logs = {self.loss: loss}
+ if metrics:
+ self.process_metrics(metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in metrics})
+ elif model.compiled_metrics:
+ self.process_compiled_metrics(model.compiled_metrics, labels, outputs)
+ logs.update({m.name: m.result() for m in model.metrics})
+ return logs
diff --git a/official/projects/simclr/train.py b/official/projects/simclr/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..3114af5c3d2b4be93927a6ab7a70a70df8b3e49d
--- /dev/null
+++ b/official/projects/simclr/train.py
@@ -0,0 +1,66 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision SimCLR trainer."""
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+from official.projects.simclr.common import registry_imports # pylint: disable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ print(FLAGS.experiment)
+ params = train_utils.parse_configuration(FLAGS)
+
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/nlp/projects/teams/README.md b/official/projects/teams/README.md
similarity index 100%
rename from official/nlp/projects/teams/README.md
rename to official/projects/teams/README.md
diff --git a/official/projects/teams/__init__.py b/official/projects/teams/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/teams/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/nlp/projects/teams/experiments/base/glue_mnli.yaml b/official/projects/teams/experiments/base/glue_mnli.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/base/glue_mnli.yaml
rename to official/projects/teams/experiments/base/glue_mnli.yaml
diff --git a/official/nlp/projects/teams/experiments/base/squad_v1.yaml b/official/projects/teams/experiments/base/squad_v1.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/base/squad_v1.yaml
rename to official/projects/teams/experiments/base/squad_v1.yaml
diff --git a/official/nlp/projects/teams/experiments/base/squad_v2.yaml b/official/projects/teams/experiments/base/squad_v2.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/base/squad_v2.yaml
rename to official/projects/teams/experiments/base/squad_v2.yaml
diff --git a/official/nlp/projects/teams/experiments/base/wiki_books_pretrain.yaml b/official/projects/teams/experiments/base/wiki_books_pretrain.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/base/wiki_books_pretrain.yaml
rename to official/projects/teams/experiments/base/wiki_books_pretrain.yaml
diff --git a/official/nlp/projects/teams/experiments/small/glue_mnli.yaml b/official/projects/teams/experiments/small/glue_mnli.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/small/glue_mnli.yaml
rename to official/projects/teams/experiments/small/glue_mnli.yaml
diff --git a/official/nlp/projects/teams/experiments/small/squad_v1.yaml b/official/projects/teams/experiments/small/squad_v1.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/small/squad_v1.yaml
rename to official/projects/teams/experiments/small/squad_v1.yaml
diff --git a/official/nlp/projects/teams/experiments/small/squad_v2.yaml b/official/projects/teams/experiments/small/squad_v2.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/small/squad_v2.yaml
rename to official/projects/teams/experiments/small/squad_v2.yaml
diff --git a/official/nlp/projects/teams/experiments/small/wiki_books_pretrain.yaml b/official/projects/teams/experiments/small/wiki_books_pretrain.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/small/wiki_books_pretrain.yaml
rename to official/projects/teams/experiments/small/wiki_books_pretrain.yaml
diff --git a/official/nlp/projects/teams/experiments/teams_en_uncased_base.yaml b/official/projects/teams/experiments/teams_en_uncased_base.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/teams_en_uncased_base.yaml
rename to official/projects/teams/experiments/teams_en_uncased_base.yaml
diff --git a/official/nlp/projects/teams/experiments/teams_en_uncased_small.yaml b/official/projects/teams/experiments/teams_en_uncased_small.yaml
similarity index 100%
rename from official/nlp/projects/teams/experiments/teams_en_uncased_small.yaml
rename to official/projects/teams/experiments/teams_en_uncased_small.yaml
diff --git a/official/nlp/projects/teams/teams.py b/official/projects/teams/teams.py
similarity index 98%
rename from official/nlp/projects/teams/teams.py
rename to official/projects/teams/teams.py
index e5aed0a7a5235f98ff3a65c01309d1df92681aca..d2833cfe5def06bf7e654889e3c0b1c515fb3418 100644
--- a/official/nlp/projects/teams/teams.py
+++ b/official/projects/teams/teams.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/teams/teams_experiments.py b/official/projects/teams/teams_experiments.py
similarity index 96%
rename from official/nlp/projects/teams/teams_experiments.py
rename to official/projects/teams/teams_experiments.py
index 3c9df9b4d13af417e5d953c8a5bc1fe261f99015..030e1393918786edcf83d346ab227c7bd2c186cd 100644
--- a/official/nlp/projects/teams/teams_experiments.py
+++ b/official/projects/teams/teams_experiments.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
# pylint: disable=g-doc-return-or-yield,line-too-long
"""TEAMS experiments."""
import dataclasses
@@ -24,10 +23,10 @@ from official.nlp.configs import encoders
from official.nlp.data import pretrain_dataloader
from official.nlp.data import question_answering_dataloader
from official.nlp.data import sentence_prediction_dataloader
-from official.nlp.projects.teams import teams
-from official.nlp.projects.teams import teams_task
from official.nlp.tasks import question_answering
from official.nlp.tasks import sentence_prediction
+from official.projects.teams import teams
+from official.projects.teams import teams_task
AdamWeightDecay = optimization.AdamWeightDecayConfig
PolynomialLr = optimization.PolynomialLrConfig
diff --git a/official/nlp/projects/teams/teams_pretrainer.py b/official/projects/teams/teams_pretrainer.py
similarity index 98%
rename from official/nlp/projects/teams/teams_pretrainer.py
rename to official/projects/teams/teams_pretrainer.py
index 727c0184f01067524291b3e760a6b5d9b4f9f5b5..ea8121f9256ff1d0626815eabebe8c33455a7bd2 100644
--- a/official/nlp/projects/teams/teams_pretrainer.py
+++ b/official/projects/teams/teams_pretrainer.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -58,15 +58,16 @@ class ReplacedTokenDetectionHead(tf.keras.layers.Layer):
intermediate_activation=self.activation,
dropout_rate=self.hidden_cfg['dropout_rate'],
attention_dropout_rate=self.hidden_cfg['attention_dropout_rate'],
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='transformer/layer_%d_rtd' % i))
self.dense = tf.keras.layers.Dense(
self.hidden_size,
activation=self.activation,
- kernel_initializer=self.initializer,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='transform/rtd_dense')
self.rtd_head = tf.keras.layers.Dense(
- units=1, kernel_initializer=self.initializer,
+ units=1,
+ kernel_initializer=tf_utils.clone_initializer(self.initializer),
name='transform/rtd_head')
if output not in ('predictions', 'logits'):
diff --git a/official/nlp/projects/teams/teams_pretrainer_test.py b/official/projects/teams/teams_pretrainer_test.py
similarity index 98%
rename from official/nlp/projects/teams/teams_pretrainer_test.py
rename to official/projects/teams/teams_pretrainer_test.py
index 643038509f16ff8a11d0d99e718992fbb26a66c2..9a1fc2029d8bd8a9b7263705a2f4d52376361376 100644
--- a/official/nlp/projects/teams/teams_pretrainer_test.py
+++ b/official/projects/teams/teams_pretrainer_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ from tensorflow.python.keras import keras_parameterized # pylint: disable=g-dir
from official.modeling import activations
from official.nlp.modeling.networks import encoder_scaffold
from official.nlp.modeling.networks import packed_sequence_embedding
-from official.nlp.projects.teams import teams_pretrainer
+from official.projects.teams import teams_pretrainer
# This decorator runs the test in V1, V2-Eager, and V2-Functional mode. It
diff --git a/official/nlp/projects/teams/teams_task.py b/official/projects/teams/teams_task.py
similarity index 98%
rename from official/nlp/projects/teams/teams_task.py
rename to official/projects/teams/teams_task.py
index c14ba0a09f4d8fbfba9dfd1448c494dd32b1d3ff..c8da8c8274395f0d76db1dd2e21e5dd02020a187 100644
--- a/official/nlp/projects/teams/teams_task.py
+++ b/official/projects/teams/teams_task.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,8 +23,8 @@ from official.core import task_factory
from official.modeling import tf_utils
from official.nlp.data import pretrain_dataloader
from official.nlp.modeling import layers
-from official.nlp.projects.teams import teams
-from official.nlp.projects.teams import teams_pretrainer
+from official.projects.teams import teams
+from official.projects.teams import teams_pretrainer
@dataclasses.dataclass
diff --git a/official/nlp/projects/teams/teams_task_test.py b/official/projects/teams/teams_task_test.py
similarity index 92%
rename from official/nlp/projects/teams/teams_task_test.py
rename to official/projects/teams/teams_task_test.py
index 329fd3fe7cd50976d545c13443607af88edf73c3..df3c93a0f92b8b79653d21231aac1d50cc07efd3 100644
--- a/official/nlp/projects/teams/teams_task_test.py
+++ b/official/projects/teams/teams_task_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,8 +19,8 @@ import tensorflow as tf
from official.nlp.configs import encoders
from official.nlp.data import pretrain_dataloader
-from official.nlp.projects.teams import teams
-from official.nlp.projects.teams import teams_task
+from official.projects.teams import teams
+from official.projects.teams import teams_task
class TeamsPretrainTaskTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/teams/train.py b/official/projects/teams/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..b13afe537e514197edcafbc6cdb8e3aae96f7c26
--- /dev/null
+++ b/official/projects/teams/train.py
@@ -0,0 +1,28 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Teams training driver, register Teams configs."""
+
+# pylint: disable=unused-import
+from absl import app
+
+from official.common import flags as tfm_flags
+from official.nlp import tasks
+from official.nlp import train
+from official.projects.teams import teams_experiments
+from official.projects.teams import teams_task
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/text_classification_example/classification_data_loader.py b/official/projects/text_classification_example/classification_data_loader.py
index fea67e026a5d702d853628b2fd233eb54c43ff20..fa142bc03b595a7e24603208fbc0742fbe830cdb 100644
--- a/official/projects/text_classification_example/classification_data_loader.py
+++ b/official/projects/text_classification_example/classification_data_loader.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/text_classification_example/classification_example.py b/official/projects/text_classification_example/classification_example.py
index da0eccb750c43c6ab012617e8071a5d9e01fde98..b8600a4e043f95b4c8b6bc8ad58750d7de88a5ec 100644
--- a/official/projects/text_classification_example/classification_example.py
+++ b/official/projects/text_classification_example/classification_example.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/text_classification_example/classification_example_test.py b/official/projects/text_classification_example/classification_example_test.py
index d26ece724459fc1475ada0998b682e9dda13d71c..4de434f531df9da31f5f2d5586ebf498ae1ec680 100644
--- a/official/projects/text_classification_example/classification_example_test.py
+++ b/official/projects/text_classification_example/classification_example_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/text_classification_example/train.py b/official/projects/text_classification_example/train.py
index bfa28b5c6252775b7e1b04c52140be79b886f49a..c2e8e16558cdd0484e29796957584e225f4ba4ee 100644
--- a/official/projects/text_classification_example/train.py
+++ b/official/projects/text_classification_example/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/tn_bert/README.md b/official/projects/tn_bert/README.md
similarity index 100%
rename from official/nlp/projects/tn_bert/README.md
rename to official/projects/tn_bert/README.md
diff --git a/official/projects/token_dropping/README.md b/official/projects/token_dropping/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..4e8eb007ee1cf9d0e787720e2ffa9c4a72b5e0f1
--- /dev/null
+++ b/official/projects/token_dropping/README.md
@@ -0,0 +1,104 @@
+# Token Dropping for Efficient BERT Pretraining
+
+This is the official implementation of the token dropping method
+[Pang et al. Token Dropping for Efficient BERT Pretraining. ACL 2022](#reference).
+
+Token dropping aims to accelerate the pretraining of transformer
+models such as BERT without degrading its performance on downstream tasks. In
+particular, we drop unimportant tokens starting from an intermediate layer in
+the model, to make the model focus on important tokens more efficiently with its
+limited computational resources. The dropped tokens are later picked up by the
+last layer of the model, so that the model still produces full-length sequences.
+We leverage the already built-in masked language modeling (MLM) loss and its
+dynamics to identify unimportant tokens with practically no computational
+overhead. In our experiments, this simple approach reduces the pretraining cost
+of BERT by 25% while achieving slightly better overall fine-tuning performance
+on standard downstream tasks.
+
+A BERT model pretrained using this token dropping method is not different to
+a BERT model pretrained in the conventional way: a BERT checkpoint pretrained
+with token dropping can be viewed and used as a normal BERT checkpoint, for
+finetuning etc. Thus, this README file only illustrates how to run token
+dropping for pretraining.
+
+### Requirements
+
+The starter code requires Tensorflow. If you haven't installed it yet, follow
+the instructions on [tensorflow.org][1].
+This code has been tested with Tensorflow 2.5.0. Going forward,
+we will continue to target the latest released version of Tensorflow.
+
+Please verify that you have Python 3.6+ and Tensorflow 2.5.0 or higher
+installed by running the following commands:
+
+```sh
+python --version
+python -c 'import tensorflow as tf; print(tf.__version__)'
+```
+
+Refer to the [instructions here][2]
+for using the model in this repo. Make sure to add the models folder to your
+Python path.
+
+[1]: https://www.tensorflow.org/install/
+[2]:
+https://github.com/tensorflow/models/tree/master/official#running-the-models
+
+Then, you need to generate pretraining data. See
+[this instruction]
+(https://github.com/tensorflow/models/blob/27fb855b027ead16d2616dcb59c67409a2176b7f/official/legacy/bert/README.md#pre-training)
+on how to do that.
+
+## Train using the config file.
+
+After you generated your pretraining data, run the following command to start
+pretraining:
+
+```bash
+PARAMS="task.train_data.input_data=/path/to/train/data"
+PARAMS="${PARAMS},task.validation_data.input_path=/path/to/validation/data"
+PARAMS="${PARAMS},runtime.distribution_strategy=tpu"
+
+python3 train.py \
+ --experiment=token_drop_bert/pretraining \
+ --config_file=wiki_books_pretrain_sequence_pack.yaml \
+ --config_file=bert_en_uncased_base_token_drop.yaml \
+ --params_override=${PARAMS} \
+ --tpu=local \
+ --model_dir=/folder/to/hold/logs/and/models/ \
+ --mode=train_and_eval
+```
+
+## Implementation
+
+We implement the encoder and layers using `tf.keras` APIs in NLP
+modeling library:
+
+ * [masked_lm.py](https://github.com/tensorflow/models/blob/master/official/projects/token_dropping/masked_lm.py)
+ contains the BERT pretraining task.
+
+ * [experiment_configs.py](https://github.com/tensorflow/models/blob/master/official/projects/token_dropping/experiment_configs.py)
+ registers the token dropping experiment.
+
+ * [encoder.py](https://github.com/tensorflow/models/blob/master/official/projects/token_dropping/encoder.py)
+ contains the BERT encoder that supports token dropping.
+
+ * [encoder_config.py](https://github.com/tensorflow/models/blob/master/official/projects/token_dropping/encoder_config.py)
+ contains the config and method for instantiating the token dropping BERT
+ encoder.
+
+ * [train.py](https://github.com/tensorflow/models/blob/master/official/projects/token_dropping/train.py)
+ is the program entry.
+
+## Reference
+
+Please cite our paper:
+
+```
+@article{hou2022token,
+ title={Token Dropping for Efficient BERT Pretraining},
+ author={Pang, Richard Yuanzhe and Hou, Le and Zhou, Tianyi and Wu, Yuexin and Song, Xinying and Song, Xiaodan and Zhou, Denny},
+ journal={arXiv preprint arXiv:2203.13240},
+ year={2022}
+}
+```
diff --git a/official/projects/token_dropping/bert_en_uncased_base_token_drop.yaml b/official/projects/token_dropping/bert_en_uncased_base_token_drop.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..718aacb22cec58d7bd74b79a4cd3b8ead4db66be
--- /dev/null
+++ b/official/projects/token_dropping/bert_en_uncased_base_token_drop.yaml
@@ -0,0 +1,26 @@
+task:
+ model:
+ encoder:
+ type: any
+ any:
+ token_allow_list: !!python/tuple
+ - 100 # [UNK]
+ - 101 # [CLS]
+ - 102 # [SEP]
+ - 103 # [MASK]
+ token_deny_list: !!python/tuple
+ - 0 # [PAD]
+ attention_dropout_rate: 0.1
+ dropout_rate: 0.1
+ hidden_activation: gelu
+ hidden_size: 768
+ initializer_range: 0.02
+ intermediate_size: 3072
+ max_position_embeddings: 512
+ num_attention_heads: 12
+ num_layers: 12
+ type_vocab_size: 2
+ vocab_size: 30522
+ token_loss_init_value: 10.0
+ token_loss_beta: 0.995
+ token_keep_k: 256
diff --git a/official/projects/token_dropping/encoder.py b/official/projects/token_dropping/encoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..c83d21f5e0538e19c89258898607e4b24fdf0b30
--- /dev/null
+++ b/official/projects/token_dropping/encoder.py
@@ -0,0 +1,400 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Transformer-based BERT encoder network."""
+# pylint: disable=g-classes-have-attributes
+
+from typing import Any, Callable, Optional, Union, Tuple
+from absl import logging
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.nlp.modeling import layers
+
+
+_Initializer = Union[str, tf.keras.initializers.Initializer]
+_Activation = Union[str, Callable[..., Any]]
+
+_approx_gelu = lambda x: tf.keras.activations.gelu(x, approximate=True)
+
+
+class TokenDropBertEncoder(tf.keras.layers.Layer):
+ """Bi-directional Transformer-based encoder network with token dropping.
+
+ During pretraining, we drop unimportant tokens starting from an intermediate
+ layer in the model, to make the model focus on important tokens more
+ efficiently with its limited computational resources. The dropped tokens are
+ later picked up by the last layer of the model, so that the model still
+ produces full-length sequences. This approach reduces the pretraining cost of
+ BERT by 25% while achieving better overall fine-tuning performance on standard
+ downstream tasks.
+
+ Args:
+ vocab_size: The size of the token vocabulary.
+ hidden_size: The size of the transformer hidden layers.
+ num_layers: The number of transformer layers.
+ num_attention_heads: The number of attention heads for each transformer. The
+ hidden size must be divisible by the number of attention heads.
+ max_sequence_length: The maximum sequence length that this encoder can
+ consume. If None, max_sequence_length uses the value from sequence length.
+ This determines the variable shape for positional embeddings.
+ type_vocab_size: The number of types that the 'type_ids' input can take.
+ inner_dim: The output dimension of the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ inner_activation: The activation for the first Dense layer in a two-layer
+ feedforward network for each transformer.
+ output_dropout: Dropout probability for the post-attention and output
+ dropout.
+ attention_dropout: The dropout rate to use for the attention layers within
+ the transformer layers.
+ token_loss_init_value: The default loss value of a token, when the token is
+ never masked and predicted.
+ token_loss_beta: How running average factor for computing the average loss
+ value of a token.
+ token_keep_k: The number of tokens you want to keep in the intermediate
+ layers. The rest will be dropped in those layers.
+ token_allow_list: The list of token-ids that should not be droped. In the
+ BERT English vocab, token-id from 1 to 998 contains special tokens such as
+ [CLS], [SEP]. By default, token_allow_list contains all of these special
+ tokens.
+ token_deny_list: The list of token-ids that should always be droped. In the
+ BERT English vocab, token-id=0 means [PAD]. By default, token_deny_list
+ contains and only contains [PAD].
+ initializer: The initialzer to use for all weights in this encoder.
+ output_range: The sequence output range, [0, output_range), by slicing the
+ target sequence of the last transformer layer. `None` means the entire
+ target sequence will attend to the source sequence, which yields the full
+ output.
+ embedding_width: The width of the word embeddings. If the embedding width is
+ not equal to hidden size, embedding parameters will be factorized into two
+ matrices in the shape of ['vocab_size', 'embedding_width'] and
+ ['embedding_width', 'hidden_size'] ('embedding_width' is usually much
+ smaller than 'hidden_size').
+ embedding_layer: An optional Layer instance which will be called to generate
+ embeddings for the input word IDs.
+ norm_first: Whether to normalize inputs to attention and intermediate dense
+ layers. If set False, output of attention and intermediate dense layers is
+ normalized.
+ with_dense_inputs: Whether to accept dense embeddings as the input.
+ """
+
+ def __init__(
+ self,
+ vocab_size: int,
+ hidden_size: int = 768,
+ num_layers: int = 12,
+ num_attention_heads: int = 12,
+ max_sequence_length: int = 512,
+ type_vocab_size: int = 16,
+ inner_dim: int = 3072,
+ inner_activation: _Activation = _approx_gelu,
+ output_dropout: float = 0.1,
+ attention_dropout: float = 0.1,
+ token_loss_init_value: float = 10.0,
+ token_loss_beta: float = 0.995,
+ token_keep_k: int = 256,
+ token_allow_list: Tuple[int, ...] = (100, 101, 102, 103),
+ token_deny_list: Tuple[int, ...] = (0,),
+ initializer: _Initializer = tf.keras.initializers.TruncatedNormal(
+ stddev=0.02),
+ output_range: Optional[int] = None,
+ embedding_width: Optional[int] = None,
+ embedding_layer: Optional[tf.keras.layers.Layer] = None,
+ norm_first: bool = False,
+ with_dense_inputs: bool = False,
+ **kwargs):
+ # Pops kwargs that are used in V1 implementation.
+ if 'dict_outputs' in kwargs:
+ kwargs.pop('dict_outputs')
+ if 'return_all_encoder_outputs' in kwargs:
+ kwargs.pop('return_all_encoder_outputs')
+ if 'intermediate_size' in kwargs:
+ inner_dim = kwargs.pop('intermediate_size')
+ if 'activation' in kwargs:
+ inner_activation = kwargs.pop('activation')
+ if 'dropout_rate' in kwargs:
+ output_dropout = kwargs.pop('dropout_rate')
+ if 'attention_dropout_rate' in kwargs:
+ attention_dropout = kwargs.pop('attention_dropout_rate')
+ super().__init__(**kwargs)
+
+ if output_range is not None:
+ logging.warning('`output_range` is available as an argument for `call()`.'
+ 'The `output_range` as __init__ argument is deprecated.')
+
+ activation = tf.keras.activations.get(inner_activation)
+ initializer = tf.keras.initializers.get(initializer)
+
+ if embedding_width is None:
+ embedding_width = hidden_size
+
+ if embedding_layer is None:
+ self._embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=vocab_size,
+ embedding_width=embedding_width,
+ initializer=tf_utils.clone_initializer(initializer),
+ name='word_embeddings')
+ else:
+ self._embedding_layer = embedding_layer
+
+ self._position_embedding_layer = layers.PositionEmbedding(
+ initializer=tf_utils.clone_initializer(initializer),
+ max_length=max_sequence_length,
+ name='position_embedding')
+
+ self._type_embedding_layer = layers.OnDeviceEmbedding(
+ vocab_size=type_vocab_size,
+ embedding_width=embedding_width,
+ initializer=tf_utils.clone_initializer(initializer),
+ use_one_hot=True,
+ name='type_embeddings')
+
+ self._embedding_norm_layer = tf.keras.layers.LayerNormalization(
+ name='embeddings/layer_norm', axis=-1, epsilon=1e-12, dtype=tf.float32)
+
+ self._embedding_dropout = tf.keras.layers.Dropout(
+ rate=output_dropout, name='embedding_dropout')
+
+ # We project the 'embedding' output to 'hidden_size' if it is not already
+ # 'hidden_size'.
+ self._embedding_projection = None
+ if embedding_width != hidden_size:
+ self._embedding_projection = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=hidden_size,
+ bias_axes='y',
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='embedding_projection')
+
+ # The first 999 tokens are special tokens such as [PAD], [CLS], [SEP].
+ # We want to always mask [PAD], and always not to maks [CLS], [SEP].
+ init_importance = tf.constant(token_loss_init_value, shape=(vocab_size))
+ if token_allow_list:
+ init_importance = tf.tensor_scatter_nd_update(
+ tensor=init_importance,
+ indices=[[x] for x in token_allow_list],
+ updates=[1.0e4 for x in token_allow_list])
+ if token_deny_list:
+ init_importance = tf.tensor_scatter_nd_update(
+ tensor=init_importance,
+ indices=[[x] for x in token_deny_list],
+ updates=[-1.0e4 for x in token_deny_list])
+ self._token_importance_embed = layers.TokenImportanceWithMovingAvg(
+ vocab_size=vocab_size,
+ init_importance=init_importance,
+ moving_average_beta=token_loss_beta)
+
+ self._token_separator = layers.SelectTopK(top_k=token_keep_k)
+ self._transformer_layers = []
+ self._num_layers = num_layers
+ self._attention_mask_layer = layers.SelfAttentionMask(
+ name='self_attention_mask')
+ for i in range(num_layers):
+ layer = layers.TransformerEncoderBlock(
+ num_attention_heads=num_attention_heads,
+ inner_dim=inner_dim,
+ inner_activation=inner_activation,
+ output_dropout=output_dropout,
+ attention_dropout=attention_dropout,
+ norm_first=norm_first,
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='transformer/layer_%d' % i)
+ self._transformer_layers.append(layer)
+
+ self._pooler_layer = tf.keras.layers.Dense(
+ units=hidden_size,
+ activation='tanh',
+ kernel_initializer=tf_utils.clone_initializer(initializer),
+ name='pooler_transform')
+
+ self._config = {
+ 'vocab_size': vocab_size,
+ 'hidden_size': hidden_size,
+ 'num_layers': num_layers,
+ 'num_attention_heads': num_attention_heads,
+ 'max_sequence_length': max_sequence_length,
+ 'type_vocab_size': type_vocab_size,
+ 'inner_dim': inner_dim,
+ 'inner_activation': tf.keras.activations.serialize(activation),
+ 'output_dropout': output_dropout,
+ 'attention_dropout': attention_dropout,
+ 'token_loss_init_value': token_loss_init_value,
+ 'token_loss_beta': token_loss_beta,
+ 'token_keep_k': token_keep_k,
+ 'token_allow_list': token_allow_list,
+ 'token_deny_list': token_deny_list,
+ 'initializer': tf.keras.initializers.serialize(initializer),
+ 'output_range': output_range,
+ 'embedding_width': embedding_width,
+ 'embedding_layer': embedding_layer,
+ 'norm_first': norm_first,
+ 'with_dense_inputs': with_dense_inputs,
+ }
+ if with_dense_inputs:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ dense_inputs=tf.keras.Input(
+ shape=(None, embedding_width), dtype=tf.float32),
+ dense_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ dense_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ )
+ else:
+ self.inputs = dict(
+ input_word_ids=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_mask=tf.keras.Input(shape=(None,), dtype=tf.int32),
+ input_type_ids=tf.keras.Input(shape=(None,), dtype=tf.int32))
+
+ def call(self, inputs, output_range: Optional[tf.Tensor] = None):
+ if isinstance(inputs, dict):
+ word_ids = inputs.get('input_word_ids')
+ mask = inputs.get('input_mask')
+ type_ids = inputs.get('input_type_ids')
+
+ dense_inputs = inputs.get('dense_inputs', None)
+ dense_mask = inputs.get('dense_mask', None)
+ dense_type_ids = inputs.get('dense_type_ids', None)
+ else:
+ raise ValueError('Unexpected inputs type to %s.' % self.__class__)
+
+ word_embeddings = self._embedding_layer(word_ids)
+
+ if dense_inputs is not None:
+ # Concat the dense embeddings at sequence end.
+ word_embeddings = tf.concat([word_embeddings, dense_inputs], axis=1)
+ type_ids = tf.concat([type_ids, dense_type_ids], axis=1)
+ mask = tf.concat([mask, dense_mask], axis=1)
+
+ # absolute position embeddings.
+ position_embeddings = self._position_embedding_layer(word_embeddings)
+ type_embeddings = self._type_embedding_layer(type_ids)
+
+ embeddings = word_embeddings + position_embeddings + type_embeddings
+ embeddings = self._embedding_norm_layer(embeddings)
+ embeddings = self._embedding_dropout(embeddings)
+
+ if self._embedding_projection is not None:
+ embeddings = self._embedding_projection(embeddings)
+
+ attention_mask = self._attention_mask_layer(embeddings, mask)
+
+ encoder_outputs = []
+ x = embeddings
+
+ # Get token routing.
+ token_importance = self._token_importance_embed(word_ids)
+ selected, not_selected = self._token_separator(token_importance)
+
+ # For a 12-layer BERT:
+ # 1. All tokens fist go though 5 transformer layers, then
+ # 2. Only important tokens go through 1 transformer layer with cross
+ # attention to unimportant tokens, then
+ # 3. Only important tokens go through 5 transformer layers without cross
+ # attention.
+ # 4. Finally, all tokens go through the last layer.
+
+ # Step 1.
+ for i, layer in enumerate(self._transformer_layers[:self._num_layers // 2 -
+ 1]):
+ x = layer([x, attention_mask],
+ output_range=output_range if i == self._num_layers -
+ 1 else None)
+ encoder_outputs.append(x)
+
+ # Step 2.
+ # First, separate important and non-important tokens.
+ x_selected = tf.gather(x, selected, batch_dims=1, axis=1)
+ mask_selected = tf.gather(mask, selected, batch_dims=1, axis=1)
+ attention_mask_token_drop = self._attention_mask_layer(
+ x_selected, mask_selected)
+
+ x_not_selected = tf.gather(x, not_selected, batch_dims=1, axis=1)
+ mask_not_selected = tf.gather(mask, not_selected, batch_dims=1, axis=1)
+ attention_mask_token_pass = self._attention_mask_layer(
+ x_selected, tf.concat([mask_selected, mask_not_selected], axis=1))
+ x_all = tf.concat([x_selected, x_not_selected], axis=1)
+
+ # Then, call transformer layer with cross attention.
+ x_selected = self._transformer_layers[self._num_layers // 2 - 1](
+ [x_selected, x_all, attention_mask_token_pass],
+ output_range=output_range if self._num_layers // 2 -
+ 1 == self._num_layers - 1 else None)
+ encoder_outputs.append(x_selected)
+
+ # Step 3.
+ for i, layer in enumerate(self._transformer_layers[self._num_layers //
+ 2:-1]):
+ x_selected = layer([x_selected, attention_mask_token_drop],
+ output_range=output_range if i == self._num_layers - 1
+ else None)
+ encoder_outputs.append(x_selected)
+
+ # Step 4.
+ # First, merge important and non-important tokens.
+ x_not_selected = tf.cast(x_not_selected, dtype=x_selected.dtype)
+ x = tf.concat([x_selected, x_not_selected], axis=1)
+ indices = tf.concat([selected, not_selected], axis=1)
+ reverse_indices = tf.argsort(indices)
+ x = tf.gather(x, reverse_indices, batch_dims=1, axis=1)
+
+ # Then, call transformer layer with all tokens.
+ x = self._transformer_layers[-1]([x, attention_mask],
+ output_range=output_range)
+ encoder_outputs.append(x)
+
+ last_encoder_output = encoder_outputs[-1]
+ first_token_tensor = last_encoder_output[:, 0, :]
+ pooled_output = self._pooler_layer(first_token_tensor)
+
+ return dict(
+ sequence_output=encoder_outputs[-1],
+ pooled_output=pooled_output,
+ encoder_outputs=encoder_outputs)
+
+ def record_mlm_loss(self, mlm_ids: tf.Tensor, mlm_losses: tf.Tensor):
+ self._token_importance_embed.update_token_importance(
+ token_ids=mlm_ids, importance=mlm_losses)
+
+ def get_embedding_table(self):
+ return self._embedding_layer.embeddings
+
+ def get_embedding_layer(self):
+ return self._embedding_layer
+
+ def get_config(self):
+ return dict(self._config)
+
+ @property
+ def transformer_layers(self):
+ """List of Transformer layers in the encoder."""
+ return self._transformer_layers
+
+ @property
+ def pooler_layer(self):
+ """The pooler dense layer after the transformer layers."""
+ return self._pooler_layer
+
+ @classmethod
+ def from_config(cls, config, custom_objects=None):
+ if 'embedding_layer' in config and config['embedding_layer'] is not None:
+ warn_string = (
+ 'You are reloading a model that was saved with a '
+ 'potentially-shared embedding layer object. If you contine to '
+ 'train this model, the embedding layer will no longer be shared. '
+ 'To work around this, load the model outside of the Keras API.')
+ print('WARNING: ' + warn_string)
+ logging.warn(warn_string)
+
+ return cls(**config)
diff --git a/official/projects/token_dropping/encoder_config.py b/official/projects/token_dropping/encoder_config.py
new file mode 100644
index 0000000000000000000000000000000000000000..b7809d46f817c03f48d94cc7357a7df12784deac
--- /dev/null
+++ b/official/projects/token_dropping/encoder_config.py
@@ -0,0 +1,67 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Token dropping encoder configuration and instantiation."""
+import dataclasses
+from typing import Tuple
+import tensorflow as tf
+
+from official.modeling import tf_utils
+from official.modeling.hyperparams import base_config
+from official.nlp.configs import encoders
+from official.projects.token_dropping import encoder
+
+
+@dataclasses.dataclass
+class TokenDropBertEncoderConfig(encoders.BertEncoderConfig):
+ token_loss_init_value: float = 10.0
+ token_loss_beta: float = 0.995
+ token_keep_k: int = 256
+ token_allow_list: Tuple[int, ...] = (100, 101, 102, 103)
+ token_deny_list: Tuple[int, ...] = (0,)
+
+
+@base_config.bind(TokenDropBertEncoderConfig)
+def get_encoder(encoder_cfg: TokenDropBertEncoderConfig):
+ """Instantiates 'TokenDropBertEncoder'.
+
+ Args:
+ encoder_cfg: A 'TokenDropBertEncoderConfig'.
+
+ Returns:
+ A 'encoder.TokenDropBertEncoder' object.
+ """
+ return encoder.TokenDropBertEncoder(
+ vocab_size=encoder_cfg.vocab_size,
+ hidden_size=encoder_cfg.hidden_size,
+ num_layers=encoder_cfg.num_layers,
+ num_attention_heads=encoder_cfg.num_attention_heads,
+ intermediate_size=encoder_cfg.intermediate_size,
+ activation=tf_utils.get_activation(encoder_cfg.hidden_activation),
+ dropout_rate=encoder_cfg.dropout_rate,
+ attention_dropout_rate=encoder_cfg.attention_dropout_rate,
+ max_sequence_length=encoder_cfg.max_position_embeddings,
+ type_vocab_size=encoder_cfg.type_vocab_size,
+ initializer=tf.keras.initializers.TruncatedNormal(
+ stddev=encoder_cfg.initializer_range),
+ output_range=encoder_cfg.output_range,
+ embedding_width=encoder_cfg.embedding_size,
+ return_all_encoder_outputs=encoder_cfg.return_all_encoder_outputs,
+ dict_outputs=True,
+ norm_first=encoder_cfg.norm_first,
+ token_loss_init_value=encoder_cfg.token_loss_init_value,
+ token_loss_beta=encoder_cfg.token_loss_beta,
+ token_keep_k=encoder_cfg.token_keep_k,
+ token_allow_list=encoder_cfg.token_allow_list,
+ token_deny_list=encoder_cfg.token_deny_list)
diff --git a/official/projects/token_dropping/encoder_test.py b/official/projects/token_dropping/encoder_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..0cfcb594bf87fc180b764767d987a1fdf2d75f56
--- /dev/null
+++ b/official/projects/token_dropping/encoder_test.py
@@ -0,0 +1,524 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for transformer-based bert encoder network."""
+
+# Import libraries
+from absl.testing import parameterized
+import numpy as np
+import tensorflow as tf
+
+from tensorflow.python.keras import keras_parameterized # pylint: disable=g-direct-tensorflow-import
+from official.nlp.modeling.networks import bert_encoder
+from official.projects.token_dropping import encoder
+
+
+# This decorator runs the test in V1, V2-Eager, and V2-Functional mode. It
+# guarantees forward compatibility of this code for the V2 switchover.
+@keras_parameterized.run_all_keras_modes
+class TokenDropBertEncoderTest(keras_parameterized.TestCase):
+
+ def tearDown(self):
+ super(TokenDropBertEncoderTest, self).tearDown()
+ tf.keras.mixed_precision.set_global_policy("float32")
+
+ def test_dict_outputs_network_creation(self):
+ hidden_size = 32
+ sequence_length = 21
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ self.assertIsInstance(test_network.transformer_layers, list)
+ self.assertLen(test_network.transformer_layers, 3)
+ self.assertIsInstance(test_network.pooler_layer, tf.keras.layers.Dense)
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, data.dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+ def test_dict_outputs_all_encoder_outputs_network_creation(self):
+ hidden_size = 32
+ sequence_length = 21
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ dict_outputs=True,
+ token_keep_k=sequence_length,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ all_encoder_outputs = dict_outputs["encoder_outputs"]
+ pooled = dict_outputs["pooled_output"]
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertLen(all_encoder_outputs, 3)
+ for data in all_encoder_outputs:
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, all_encoder_outputs[-1].dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+ def test_dict_outputs_network_creation_with_float16_dtype(self):
+ hidden_size = 32
+ sequence_length = 21
+ tf.keras.mixed_precision.set_global_policy("mixed_float16")
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=4,
+ dict_outputs=True,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # If float_dtype is set to float16, the data output is float32 (from a layer
+ # norm) and pool output should be float16.
+ self.assertAllEqual(tf.float32, data.dtype)
+ self.assertAllEqual(tf.float16, pooled.dtype)
+
+ @parameterized.named_parameters(
+ ("all_sequence_encoder", None, 21),
+ ("output_range_encoder", 1, 1),
+ )
+ def test_dict_outputs_network_invocation(
+ self, output_range, out_seq_len):
+ hidden_size = 32
+ sequence_length = 21
+ vocab_size = 57
+ num_types = 7
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ dict_outputs=True,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids),
+ output_range=output_range)
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ # Create a model based off of this network:
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+
+ # Invoke the model. We can't validate the output data here (the model is too
+ # complex) but this will catch structural runtime errors.
+ batch_size = 3
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(
+ num_types, size=(batch_size, sequence_length))
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[1], out_seq_len)
+
+ # Creates a BertEncoder with max_sequence_length != sequence_length
+ max_sequence_length = 128
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ max_sequence_length=max_sequence_length,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ dict_outputs=True,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[1], sequence_length)
+
+ # Creates a BertEncoder with embedding_width != hidden_size
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ max_sequence_length=max_sequence_length,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ embedding_width=16,
+ dict_outputs=True,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[-1], hidden_size)
+ self.assertTrue(hasattr(test_network, "_embedding_projection"))
+
+ def test_network_creation(self):
+ hidden_size = 32
+ sequence_length = 21
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ self.assertIsInstance(test_network.transformer_layers, list)
+ self.assertLen(test_network.transformer_layers, 3)
+ self.assertIsInstance(test_network.pooler_layer, tf.keras.layers.Dense)
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, data.dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ inputs = dict(
+ input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids)
+ _ = test_network(inputs)
+
+ def test_all_encoder_outputs_network_creation(self):
+ hidden_size = 32
+ sequence_length = 21
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ return_all_encoder_outputs=True,
+ token_keep_k=sequence_length,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ all_encoder_outputs = dict_outputs["encoder_outputs"]
+ pooled = dict_outputs["pooled_output"]
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertLen(all_encoder_outputs, 3)
+ for data in all_encoder_outputs:
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # The default output dtype is float32.
+ self.assertAllEqual(tf.float32, all_encoder_outputs[-1].dtype)
+ self.assertAllEqual(tf.float32, pooled.dtype)
+
+ def test_network_creation_with_float16_dtype(self):
+ hidden_size = 32
+ sequence_length = 21
+ tf.keras.mixed_precision.set_global_policy("mixed_float16")
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=100,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=4,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ expected_data_shape = [None, sequence_length, hidden_size]
+ expected_pooled_shape = [None, hidden_size]
+ self.assertAllEqual(expected_data_shape, data.shape.as_list())
+ self.assertAllEqual(expected_pooled_shape, pooled.shape.as_list())
+
+ # If float_dtype is set to float16, the data output is float32 (from a layer
+ # norm) and pool output should be float16.
+ self.assertAllEqual(tf.float32, data.dtype)
+ self.assertAllEqual(tf.float16, pooled.dtype)
+
+ @parameterized.named_parameters(
+ ("all_sequence", None, 21),
+ ("output_range", 1, 1),
+ )
+ def test_network_invocation(self, output_range, out_seq_len):
+ hidden_size = 32
+ sequence_length = 21
+ vocab_size = 57
+ num_types = 7
+ # Create a small BertEncoder for testing.
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ # Create the inputs (note that the first dimension is implicit).
+ word_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ mask = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ type_ids = tf.keras.Input(shape=(sequence_length,), dtype=tf.int32)
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids),
+ output_range=output_range)
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+
+ # Create a model based off of this network:
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+
+ # Invoke the model. We can't validate the output data here (the model is too
+ # complex) but this will catch structural runtime errors.
+ batch_size = 3
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(
+ num_types, size=(batch_size, sequence_length))
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[1], out_seq_len)
+
+ # Creates a BertEncoder with max_sequence_length != sequence_length
+ max_sequence_length = 128
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ max_sequence_length=max_sequence_length,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[1], sequence_length)
+
+ # Creates a BertEncoder with embedding_width != hidden_size
+ test_network = encoder.TokenDropBertEncoder(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ max_sequence_length=max_sequence_length,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ embedding_width=16,
+ token_keep_k=2,
+ token_allow_list=(),
+ token_deny_list=())
+ dict_outputs = test_network(
+ dict(input_word_ids=word_ids, input_mask=mask, input_type_ids=type_ids))
+ data = dict_outputs["sequence_output"]
+ pooled = dict_outputs["pooled_output"]
+ model = tf.keras.Model([word_ids, mask, type_ids], [data, pooled])
+ outputs = model.predict([word_id_data, mask_data, type_id_data])
+ self.assertEqual(outputs[0].shape[-1], hidden_size)
+ self.assertTrue(hasattr(test_network, "_embedding_projection"))
+
+
+class TokenDropCompatibilityTest(tf.test.TestCase):
+
+ def tearDown(self):
+ super().tearDown()
+ tf.keras.mixed_precision.set_global_policy("float32")
+
+ def test_checkpoint_forward_compatible(self):
+ batch_size = 3
+
+ hidden_size = 32
+ sequence_length = 21
+ vocab_size = 57
+ num_types = 7
+
+ kwargs = dict(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ output_range=None)
+
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(
+ num_types, size=(batch_size, sequence_length))
+ data = dict(
+ input_word_ids=word_id_data,
+ input_mask=mask_data,
+ input_type_ids=type_id_data)
+
+ old_net = bert_encoder.BertEncoderV2(**kwargs)
+ old_net_outputs = old_net(data)
+ ckpt = tf.train.Checkpoint(net=old_net)
+ path = ckpt.save(self.get_temp_dir())
+ new_net = encoder.TokenDropBertEncoder(
+ token_keep_k=sequence_length,
+ token_allow_list=(),
+ token_deny_list=(),
+ **kwargs)
+ new_ckpt = tf.train.Checkpoint(net=new_net)
+ status = new_ckpt.restore(path)
+ status.assert_existing_objects_matched()
+ # assert_consumed will fail because the old model has redundant nodes.
+ new_net_outputs = new_net(data)
+
+ self.assertAllEqual(old_net_outputs.keys(), new_net_outputs.keys())
+ for key in old_net_outputs:
+ self.assertAllClose(old_net_outputs[key], new_net_outputs[key])
+
+ def test_keras_model_checkpoint_forward_compatible(self):
+ batch_size = 3
+
+ hidden_size = 32
+ sequence_length = 21
+ vocab_size = 57
+ num_types = 7
+
+ kwargs = dict(
+ vocab_size=vocab_size,
+ hidden_size=hidden_size,
+ num_attention_heads=2,
+ num_layers=3,
+ type_vocab_size=num_types,
+ output_range=None)
+
+ word_id_data = np.random.randint(
+ vocab_size, size=(batch_size, sequence_length))
+ mask_data = np.random.randint(2, size=(batch_size, sequence_length))
+ type_id_data = np.random.randint(
+ num_types, size=(batch_size, sequence_length))
+ data = dict(
+ input_word_ids=word_id_data,
+ input_mask=mask_data,
+ input_type_ids=type_id_data)
+
+ old_net = bert_encoder.BertEncoderV2(**kwargs)
+ inputs = old_net.inputs
+ outputs = old_net(inputs)
+ old_model = tf.keras.Model(inputs=inputs, outputs=outputs)
+ old_model_outputs = old_model(data)
+ ckpt = tf.train.Checkpoint(net=old_model)
+ path = ckpt.save(self.get_temp_dir())
+ new_net = encoder.TokenDropBertEncoder(
+ token_keep_k=sequence_length,
+ token_allow_list=(),
+ token_deny_list=(),
+ **kwargs)
+ inputs = new_net.inputs
+ outputs = new_net(inputs)
+ new_model = tf.keras.Model(inputs=inputs, outputs=outputs)
+ new_ckpt = tf.train.Checkpoint(net=new_model)
+ new_ckpt.restore(path)
+
+ new_model_outputs = new_model(data)
+
+ self.assertAllEqual(old_model_outputs.keys(), new_model_outputs.keys())
+ for key in old_model_outputs:
+ self.assertAllClose(old_model_outputs[key], new_model_outputs[key])
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/projects/token_dropping/experiment_configs.py b/official/projects/token_dropping/experiment_configs.py
new file mode 100644
index 0000000000000000000000000000000000000000..3f2fd6a85b7900905bef6b0a48c58ca69c190fe6
--- /dev/null
+++ b/official/projects/token_dropping/experiment_configs.py
@@ -0,0 +1,72 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Token dropping BERT experiment configurations.
+
+Only pretraining configs. Token dropping BERT's checkpoints can be used directly
+for the regular BERT. So you can just use the regular BERT for finetuning.
+"""
+# pylint: disable=g-doc-return-or-yield,line-too-long
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+from official.nlp.configs import bert
+from official.nlp.configs import encoders
+from official.nlp.data import pretrain_dataloader
+from official.projects.token_dropping import encoder_config
+from official.projects.token_dropping import masked_lm
+
+
+@exp_factory.register_config_factory('token_drop_bert/pretraining')
+def token_drop_bert_pretraining() -> cfg.ExperimentConfig:
+ """BERT pretraining with token dropping."""
+ config = cfg.ExperimentConfig(
+ runtime=cfg.RuntimeConfig(enable_xla=True),
+ task=masked_lm.TokenDropMaskedLMConfig(
+ model=bert.PretrainerConfig(
+ encoder=encoders.EncoderConfig(
+ any=encoder_config.TokenDropBertEncoderConfig(
+ vocab_size=30522, num_layers=1, token_keep_k=64),
+ type='any')),
+ train_data=pretrain_dataloader.BertPretrainDataConfig(),
+ validation_data=pretrain_dataloader.BertPretrainDataConfig(
+ is_training=False)),
+ trainer=cfg.TrainerConfig(
+ train_steps=1000000,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate':
+ 0.01,
+ 'exclude_from_weight_decay':
+ ['LayerNorm', 'layer_norm', 'bias'],
+ }
+ },
+ 'learning_rate': {
+ 'type': 'polynomial',
+ 'polynomial': {
+ 'initial_learning_rate': 1e-4,
+ 'end_learning_rate': 0.0,
+ }
+ },
+ 'warmup': {
+ 'type': 'polynomial'
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+ return config
diff --git a/official/projects/token_dropping/masked_lm.py b/official/projects/token_dropping/masked_lm.py
new file mode 100644
index 0000000000000000000000000000000000000000..f159a216d3724b0ceb852d5a7db66fd75c5d9456
--- /dev/null
+++ b/official/projects/token_dropping/masked_lm.py
@@ -0,0 +1,124 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Masked language task."""
+
+import dataclasses
+from typing import Tuple
+import tensorflow as tf
+
+from official.core import task_factory
+from official.nlp.tasks import masked_lm
+
+
+@dataclasses.dataclass
+class TokenDropMaskedLMConfig(masked_lm.MaskedLMConfig):
+ """The model config."""
+ pass
+
+
+@task_factory.register_task_cls(TokenDropMaskedLMConfig)
+class TokenDropMaskedLMTask(masked_lm.MaskedLMTask):
+ """Task object for Mask language modeling."""
+
+ def build_losses(self,
+ labels,
+ model_outputs,
+ metrics,
+ aux_losses=None) -> Tuple[tf.Tensor, tf.Tensor]:
+ """Return the final loss, and the masked-lm loss."""
+ with tf.name_scope('MaskedLMTask/losses'):
+ metrics = dict([(metric.name, metric) for metric in metrics])
+ lm_prediction_losses = tf.keras.losses.sparse_categorical_crossentropy(
+ labels['masked_lm_ids'],
+ tf.cast(model_outputs['mlm_logits'], tf.float32),
+ from_logits=True)
+ lm_label_weights = labels['masked_lm_weights']
+ lm_numerator_loss = tf.reduce_sum(lm_prediction_losses *
+ lm_label_weights)
+ lm_denominator_loss = tf.reduce_sum(lm_label_weights)
+ mlm_loss = tf.math.divide_no_nan(lm_numerator_loss, lm_denominator_loss)
+ metrics['lm_example_loss'].update_state(mlm_loss)
+ if 'next_sentence_labels' in labels:
+ sentence_labels = labels['next_sentence_labels']
+ sentence_outputs = tf.cast(
+ model_outputs['next_sentence'], dtype=tf.float32)
+ sentence_loss = tf.reduce_mean(
+ tf.keras.losses.sparse_categorical_crossentropy(
+ sentence_labels, sentence_outputs, from_logits=True))
+ metrics['next_sentence_loss'].update_state(sentence_loss)
+ total_loss = mlm_loss + sentence_loss
+ else:
+ total_loss = mlm_loss
+
+ if aux_losses:
+ total_loss += tf.add_n(aux_losses)
+ return total_loss, lm_prediction_losses
+
+ def train_step(self, inputs, model: tf.keras.Model,
+ optimizer: tf.keras.optimizers.Optimizer, metrics):
+ """Does forward and backward.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the model, forward pass definition.
+ optimizer: the optimizer for this training step.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ with tf.GradientTape() as tape:
+ outputs = model(inputs, training=True)
+ # Computes per-replica loss.
+ loss, lm_prediction_losses = self.build_losses(
+ labels=inputs,
+ model_outputs=outputs,
+ metrics=metrics,
+ aux_losses=model.losses)
+ model.encoder_network.record_mlm_loss(
+ mlm_ids=inputs['masked_lm_ids'],
+ mlm_losses=lm_prediction_losses)
+ if self.task_config.scale_loss:
+ # Scales loss as the default gradients allreduce performs sum inside the
+ # optimizer.
+ scaled_loss = loss / tf.distribute.get_strategy().num_replicas_in_sync
+ tvars = model.trainable_variables
+ if self.task_config.scale_loss:
+ grads = tape.gradient(scaled_loss, tvars)
+ else:
+ grads = tape.gradient(loss, tvars)
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+ self.process_metrics(metrics, inputs, outputs)
+ return {self.loss: loss}
+
+ def validation_step(self, inputs, model: tf.keras.Model, metrics):
+ """Validatation step.
+
+ Args:
+ inputs: a dictionary of input tensors.
+ model: the keras.Model.
+ metrics: a nested structure of metrics objects.
+
+ Returns:
+ A dictionary of logs.
+ """
+ outputs = self.inference_step(inputs, model)
+ loss, _ = self.build_losses(
+ labels=inputs,
+ model_outputs=outputs,
+ metrics=metrics,
+ aux_losses=model.losses)
+ self.process_metrics(metrics, inputs, outputs)
+ return {self.loss: loss}
diff --git a/official/projects/token_dropping/masked_lm_test.py b/official/projects/token_dropping/masked_lm_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..2c0ea5af948e01c3e89a25a4b14e690a1589d25b
--- /dev/null
+++ b/official/projects/token_dropping/masked_lm_test.py
@@ -0,0 +1,63 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for official.nlp.tasks.masked_lm."""
+
+import tensorflow as tf
+
+from official.nlp.configs import bert
+from official.nlp.configs import encoders
+from official.nlp.data import pretrain_dataloader
+from official.projects.token_dropping import encoder_config
+from official.projects.token_dropping import masked_lm
+
+
+class MLMTaskTest(tf.test.TestCase):
+
+ def test_task(self):
+ config = masked_lm.TokenDropMaskedLMConfig(
+ init_checkpoint=self.get_temp_dir(),
+ scale_loss=True,
+ model=bert.PretrainerConfig(
+ encoder=encoders.EncoderConfig(
+ any=encoder_config.TokenDropBertEncoderConfig(
+ vocab_size=30522, num_layers=1, token_keep_k=64),
+ type="any"),
+ cls_heads=[
+ bert.ClsHeadConfig(
+ inner_dim=10, num_classes=2, name="next_sentence")
+ ]),
+ train_data=pretrain_dataloader.BertPretrainDataConfig(
+ input_path="dummy",
+ max_predictions_per_seq=20,
+ seq_length=128,
+ global_batch_size=1))
+ task = masked_lm.TokenDropMaskedLMTask(config)
+ model = task.build_model()
+ metrics = task.build_metrics()
+ dataset = task.build_inputs(config.train_data)
+
+ iterator = iter(dataset)
+ optimizer = tf.keras.optimizers.SGD(lr=0.1)
+ task.train_step(next(iterator), model, optimizer, metrics=metrics)
+ task.validation_step(next(iterator), model, metrics=metrics)
+
+ # Saves a checkpoint.
+ ckpt = tf.train.Checkpoint(model=model, **model.checkpoint_items)
+ ckpt.save(config.init_checkpoint)
+ task.initialize(model)
+
+
+if __name__ == "__main__":
+ tf.test.main()
diff --git a/official/projects/token_dropping/train.py b/official/projects/token_dropping/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..e84d45f77247a6c10a8c241bfd1f31b7b53a073f
--- /dev/null
+++ b/official/projects/token_dropping/train.py
@@ -0,0 +1,69 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""A customized training binary for running token dropping experiments."""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+from official.projects.token_dropping import experiment_configs # pylint: disable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu,
+ **params.runtime.model_parallelism())
+
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/projects/token_dropping/wiki_books_pretrain.yaml b/official/projects/token_dropping/wiki_books_pretrain.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f585ca353571695f10ecac77e5d90e309d60802d
--- /dev/null
+++ b/official/projects/token_dropping/wiki_books_pretrain.yaml
@@ -0,0 +1,48 @@
+task:
+ init_checkpoint: ''
+ model:
+ cls_heads: [{activation: tanh, cls_token_idx: 0, dropout_rate: 0.1, inner_dim: 768, name: next_sentence, num_classes: 2}]
+ train_data:
+ drop_remainder: true
+ global_batch_size: 512
+ input_path: /path-to-data/wikipedia.tfrecord*,/path-to-data/books.tfrecord*
+ is_training: true
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: true
+ validation_data:
+ drop_remainder: false
+ global_batch_size: 512
+ input_path: /path-to-data/wikipedia.tfrecord*,/path-to-data/books.tfrecord*
+ is_training: false
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: true
+ use_position_id: false
+ use_v2_feature_names: true
+trainer:
+ checkpoint_interval: 20000
+ max_to_keep: 5
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ cycle: false
+ decay_steps: 1000000
+ end_learning_rate: 0.0
+ initial_learning_rate: 0.0001
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 10000
+ type: polynomial
+ steps_per_loop: 1000
+ summary_interval: 1000
+ train_steps: 1000000
+ validation_interval: 1000
+ validation_steps: 64
diff --git a/official/projects/token_dropping/wiki_books_pretrain_sequence_pack.yaml b/official/projects/token_dropping/wiki_books_pretrain_sequence_pack.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..8904d57192c4aa1bb3ea1968f117d04e179ba4d9
--- /dev/null
+++ b/official/projects/token_dropping/wiki_books_pretrain_sequence_pack.yaml
@@ -0,0 +1,48 @@
+task:
+ init_checkpoint: ''
+ model:
+ cls_heads: []
+ train_data:
+ drop_remainder: true
+ global_batch_size: 512
+ input_path: /path-to-packed-data/wikipedia.tfrecord*,/path-to-packed-data/books.tfrecord*
+ is_training: true
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: false
+ use_position_id: false
+ use_v2_feature_names: true
+ validation_data:
+ drop_remainder: false
+ global_batch_size: 512
+ input_path: /path-to-packed-data/wikipedia.tfrecord*,/path-to-packed-data/books.tfrecord*
+ is_training: false
+ max_predictions_per_seq: 76
+ seq_length: 512
+ use_next_sentence_label: false
+ use_position_id: false
+ use_v2_feature_names: true
+trainer:
+ checkpoint_interval: 20000
+ max_to_keep: 5
+ optimizer_config:
+ learning_rate:
+ polynomial:
+ cycle: false
+ decay_steps: 1000000
+ end_learning_rate: 0.0
+ initial_learning_rate: 0.0001
+ power: 1.0
+ type: polynomial
+ optimizer:
+ type: adamw
+ warmup:
+ polynomial:
+ power: 1
+ warmup_steps: 10000
+ type: polynomial
+ steps_per_loop: 1000
+ summary_interval: 1000
+ train_steps: 1000000
+ validation_interval: 1000
+ validation_steps: 64
diff --git a/official/projects/triviaqa/__init__.py b/official/projects/triviaqa/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..310bfb28f0c252bc4a4485325059bff28c5250c2
--- /dev/null
+++ b/official/projects/triviaqa/__init__.py
@@ -0,0 +1,14 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
diff --git a/official/nlp/projects/triviaqa/dataset.py b/official/projects/triviaqa/dataset.py
similarity index 99%
rename from official/nlp/projects/triviaqa/dataset.py
rename to official/projects/triviaqa/dataset.py
index 1623991266b1a2af318ff07874463f9c3047ceb6..706bbb6779bfd34fc483e9279fdaa8ba6ac215bd 100644
--- a/official/nlp/projects/triviaqa/dataset.py
+++ b/official/projects/triviaqa/dataset.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -23,7 +23,7 @@ import six
import tensorflow as tf
import tensorflow_datasets.public_api as tfds
-from official.nlp.projects.triviaqa import preprocess
+from official.projects.triviaqa import preprocess
_CITATION = """
@article{2017arXivtriviaqa,
diff --git a/official/nlp/projects/triviaqa/download_and_prepare.py b/official/projects/triviaqa/download_and_prepare.py
similarity index 94%
rename from official/nlp/projects/triviaqa/download_and_prepare.py
rename to official/projects/triviaqa/download_and_prepare.py
index 98b3e4befd41d74e0f2042636ca9c97afaae2eca..1a3140c3dd840c57a081c358620998829408e123 100644
--- a/official/nlp/projects/triviaqa/download_and_prepare.py
+++ b/official/projects/triviaqa/download_and_prepare.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,7 +21,7 @@ from absl import logging
import apache_beam as beam
import tensorflow_datasets as tfds
-from official.nlp.projects.triviaqa import dataset # pylint: disable=unused-import
+from official.projects.triviaqa import dataset # pylint: disable=unused-import
flags.DEFINE_integer('sequence_length', 4096, 'Max number of tokens.')
diff --git a/official/nlp/projects/triviaqa/evaluate.py b/official/projects/triviaqa/evaluate.py
similarity index 92%
rename from official/nlp/projects/triviaqa/evaluate.py
rename to official/projects/triviaqa/evaluate.py
index 2afdeacd903fa67655b77cc394de6c86bec5e7d5..6d19c58e6062c2c2abf50b517e66484bb2f36b02 100644
--- a/official/nlp/projects/triviaqa/evaluate.py
+++ b/official/projects/triviaqa/evaluate.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ from absl import flags
from absl import logging
import tensorflow as tf
-from official.nlp.projects.triviaqa import evaluation
+from official.projects.triviaqa import evaluation
flags.DEFINE_string('gold_path', None,
'Path to golden validation, i.e. wikipedia-dev.json.')
diff --git a/official/nlp/projects/triviaqa/evaluation.py b/official/projects/triviaqa/evaluation.py
similarity index 98%
rename from official/nlp/projects/triviaqa/evaluation.py
rename to official/projects/triviaqa/evaluation.py
index fb987f4cce3656bac3cb28504d795228ab484f42..80218cab90b0a60e09513268ecf6a2edf39c08c6 100644
--- a/official/nlp/projects/triviaqa/evaluation.py
+++ b/official/projects/triviaqa/evaluation.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/triviaqa/inputs.py b/official/projects/triviaqa/inputs.py
similarity index 99%
rename from official/nlp/projects/triviaqa/inputs.py
rename to official/projects/triviaqa/inputs.py
index 30a2f29e746b5e8f0974bd4ffdd8a32fe434d2af..426a11541107add368ab312a14eefe932d1a7937 100644
--- a/official/nlp/projects/triviaqa/inputs.py
+++ b/official/projects/triviaqa/inputs.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ import tensorflow as tf
import tensorflow_datasets as tfds
from official.modeling import tf_utils
-from official.nlp.projects.triviaqa import dataset # pylint: disable=unused-import
+from official.projects.triviaqa import dataset # pylint: disable=unused-import
def _flatten_dims(tensor: tf.Tensor,
diff --git a/official/nlp/projects/triviaqa/modeling.py b/official/projects/triviaqa/modeling.py
similarity index 98%
rename from official/nlp/projects/triviaqa/modeling.py
rename to official/projects/triviaqa/modeling.py
index 9a2c711352b4248b667ef5c882a5244f84f79de4..4df0f1b2b0173e79e82431ffbfcc382c88dd67ac 100644
--- a/official/nlp/projects/triviaqa/modeling.py
+++ b/official/projects/triviaqa/modeling.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/triviaqa/predict.py b/official/projects/triviaqa/predict.py
similarity index 96%
rename from official/nlp/projects/triviaqa/predict.py
rename to official/projects/triviaqa/predict.py
index bc4f5dad87792f8bb1c80ba4609cbbec526c03c0..16ccdb83faef10793915f0518cda890ef9f1d121 100644
--- a/official/nlp/projects/triviaqa/predict.py
+++ b/official/projects/triviaqa/predict.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -27,9 +27,9 @@ import tensorflow_datasets as tfds
import sentencepiece as spm
from official.nlp.configs import encoders # pylint: disable=unused-import
-from official.nlp.projects.triviaqa import evaluation
-from official.nlp.projects.triviaqa import inputs
-from official.nlp.projects.triviaqa import prediction
+from official.projects.triviaqa import evaluation
+from official.projects.triviaqa import inputs
+from official.projects.triviaqa import prediction
flags.DEFINE_string('data_dir', None, 'TensorFlow Datasets directory.')
diff --git a/official/nlp/projects/triviaqa/prediction.py b/official/projects/triviaqa/prediction.py
similarity index 97%
rename from official/nlp/projects/triviaqa/prediction.py
rename to official/projects/triviaqa/prediction.py
index f9ebd729fa7698bf71af1b4b2efa3a70f79a42ad..f2c96954fabf9b07f304dcd41c08cbce33e4349c 100644
--- a/official/nlp/projects/triviaqa/prediction.py
+++ b/official/projects/triviaqa/prediction.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/nlp/projects/triviaqa/preprocess.py b/official/projects/triviaqa/preprocess.py
similarity index 99%
rename from official/nlp/projects/triviaqa/preprocess.py
rename to official/projects/triviaqa/preprocess.py
index 45406a68f7724b3ec17b4356e890cef67c843574..fb16ef8a058591893f53771324cdc28bfc212ada 100644
--- a/official/nlp/projects/triviaqa/preprocess.py
+++ b/official/projects/triviaqa/preprocess.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -30,8 +30,8 @@ import numpy as np
import tensorflow.io.gfile as gfile
import sentencepiece as spm
-from official.nlp.projects.triviaqa import evaluation
-from official.nlp.projects.triviaqa import sentencepiece_pb2
+from official.projects.triviaqa import evaluation
+from official.projects.triviaqa import sentencepiece_pb2
@dataclasses.dataclass
diff --git a/official/nlp/projects/triviaqa/sentencepiece_pb2.py b/official/projects/triviaqa/sentencepiece_pb2.py
similarity index 99%
rename from official/nlp/projects/triviaqa/sentencepiece_pb2.py
rename to official/projects/triviaqa/sentencepiece_pb2.py
index 518e907792e1dd36d222182f39f3bd49b81afb4f..080682d35d871f264d173813477b83f743b2d776 100755
--- a/official/nlp/projects/triviaqa/sentencepiece_pb2.py
+++ b/official/projects/triviaqa/sentencepiece_pb2.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/triviaqa/train.py b/official/projects/triviaqa/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..ff84f8dc205cba624f7c17cb9bf002bcfb9aa152
--- /dev/null
+++ b/official/projects/triviaqa/train.py
@@ -0,0 +1,384 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TriviaQA training script."""
+import collections
+import contextlib
+import functools
+import json
+import operator
+import os
+
+from absl import app
+from absl import flags
+from absl import logging
+import gin
+import tensorflow as tf
+import tensorflow_datasets as tfds
+
+import sentencepiece as spm
+from official.nlp import optimization as nlp_optimization
+from official.nlp.configs import encoders
+from official.projects.triviaqa import evaluation
+from official.projects.triviaqa import inputs
+from official.projects.triviaqa import modeling
+from official.projects.triviaqa import prediction
+
+flags.DEFINE_string('data_dir', None, 'Data directory for TensorFlow Datasets.')
+
+flags.DEFINE_string(
+ 'validation_gold_path', None,
+ 'Path to golden validation. Usually, the wikipedia-dev.json file.')
+
+flags.DEFINE_string('model_dir', None,
+ 'Directory for checkpoints and summaries.')
+
+flags.DEFINE_string('model_config_path', None,
+ 'JSON file containing model coniguration.')
+
+flags.DEFINE_string('sentencepiece_model_path', None,
+ 'Path to sentence piece model.')
+
+flags.DEFINE_enum('encoder', 'bigbird',
+ ['bert', 'bigbird', 'albert', 'mobilebert'],
+ 'Which transformer encoder model to use.')
+
+flags.DEFINE_integer('bigbird_block_size', 64,
+ 'Size of blocks for sparse block attention.')
+
+flags.DEFINE_string('init_checkpoint_path', None,
+ 'Path from which to initialize weights.')
+
+flags.DEFINE_integer('train_sequence_length', 4096,
+ 'Maximum number of tokens for training.')
+
+flags.DEFINE_integer('train_global_sequence_length', 320,
+ 'Maximum number of global tokens for training.')
+
+flags.DEFINE_integer('validation_sequence_length', 4096,
+ 'Maximum number of tokens for validation.')
+
+flags.DEFINE_integer('validation_global_sequence_length', 320,
+ 'Maximum number of global tokens for validation.')
+
+flags.DEFINE_integer('batch_size', 32, 'Size of batch.')
+
+flags.DEFINE_string('master', '', 'Address of the TPU master.')
+
+flags.DEFINE_integer('decode_top_k', 8,
+ 'Maximum number of tokens to consider for begin/end.')
+
+flags.DEFINE_integer('decode_max_size', 16,
+ 'Maximum number of sentence pieces in an answer.')
+
+flags.DEFINE_float('dropout_rate', 0.1, 'Dropout rate for hidden layers.')
+
+flags.DEFINE_float('attention_dropout_rate', 0.3,
+ 'Dropout rate for attention layers.')
+
+flags.DEFINE_float('label_smoothing', 1e-1, 'Degree of label smoothing.')
+
+flags.DEFINE_multi_string(
+ 'gin_bindings', [],
+ 'Gin bindings to override the values set in the config files')
+
+FLAGS = flags.FLAGS
+
+
+@contextlib.contextmanager
+def worker_context():
+ if FLAGS.master:
+ with tf.device('/job:worker') as d:
+ yield d
+ else:
+ yield
+
+
+def read_sentencepiece_model(path):
+ with tf.io.gfile.GFile(path, 'rb') as file:
+ processor = spm.SentencePieceProcessor()
+ processor.LoadFromSerializedProto(file.read())
+ return processor
+
+
+# Rename old BERT v1 configuration parameters.
+_MODEL_CONFIG_REPLACEMENTS = {
+ 'num_hidden_layers': 'num_layers',
+ 'attention_probs_dropout_prob': 'attention_dropout_rate',
+ 'hidden_dropout_prob': 'dropout_rate',
+ 'hidden_act': 'hidden_activation',
+ 'window_size': 'block_size',
+}
+
+
+def read_model_config(encoder,
+ path,
+ bigbird_block_size=None) -> encoders.EncoderConfig:
+ """Merges the JSON configuration into the encoder configuration."""
+ with tf.io.gfile.GFile(path) as f:
+ model_config = json.load(f)
+ for key, value in _MODEL_CONFIG_REPLACEMENTS.items():
+ if key in model_config:
+ model_config[value] = model_config.pop(key)
+ model_config['attention_dropout_rate'] = FLAGS.attention_dropout_rate
+ model_config['dropout_rate'] = FLAGS.dropout_rate
+ model_config['block_size'] = bigbird_block_size
+ encoder_config = encoders.EncoderConfig(type=encoder)
+ # Override the default config with those loaded from the JSON file.
+ encoder_config_keys = encoder_config.get().as_dict().keys()
+ overrides = {}
+ for key, value in model_config.items():
+ if key in encoder_config_keys:
+ overrides[key] = value
+ else:
+ logging.warning('Ignoring config parameter %s=%s', key, value)
+ encoder_config.get().override(overrides)
+ return encoder_config
+
+
+@gin.configurable(denylist=[
+ 'model',
+ 'strategy',
+ 'train_dataset',
+ 'model_dir',
+ 'init_checkpoint_path',
+ 'evaluate_fn',
+])
+def fit(model,
+ strategy,
+ train_dataset,
+ model_dir,
+ init_checkpoint_path=None,
+ evaluate_fn=None,
+ learning_rate=1e-5,
+ learning_rate_polynomial_decay_rate=1.,
+ weight_decay_rate=1e-1,
+ num_warmup_steps=5000,
+ num_decay_steps=51000,
+ num_epochs=6):
+ """Train and evaluate."""
+ hparams = dict(
+ learning_rate=learning_rate,
+ num_decay_steps=num_decay_steps,
+ num_warmup_steps=num_warmup_steps,
+ num_epochs=num_epochs,
+ weight_decay_rate=weight_decay_rate,
+ dropout_rate=FLAGS.dropout_rate,
+ attention_dropout_rate=FLAGS.attention_dropout_rate,
+ label_smoothing=FLAGS.label_smoothing)
+ logging.info(hparams)
+ learning_rate_schedule = nlp_optimization.WarmUp(
+ learning_rate,
+ tf.keras.optimizers.schedules.PolynomialDecay(
+ learning_rate,
+ num_decay_steps,
+ end_learning_rate=0.,
+ power=learning_rate_polynomial_decay_rate), num_warmup_steps)
+ with strategy.scope():
+ optimizer = nlp_optimization.AdamWeightDecay(
+ learning_rate_schedule,
+ weight_decay_rate=weight_decay_rate,
+ epsilon=1e-6,
+ exclude_from_weight_decay=['LayerNorm', 'layer_norm', 'bias'])
+ model.compile(optimizer, loss=modeling.SpanOrCrossEntropyLoss())
+
+ def init_fn(init_checkpoint_path):
+ ckpt = tf.train.Checkpoint(encoder=model.encoder)
+ ckpt.restore(init_checkpoint_path).assert_existing_objects_matched()
+
+ with worker_context():
+ ckpt_manager = tf.train.CheckpointManager(
+ tf.train.Checkpoint(model=model, optimizer=optimizer),
+ model_dir,
+ max_to_keep=None,
+ init_fn=(functools.partial(init_fn, init_checkpoint_path)
+ if init_checkpoint_path else None))
+ with strategy.scope():
+ ckpt_manager.restore_or_initialize()
+ val_summary_writer = tf.summary.create_file_writer(
+ os.path.join(model_dir, 'val'))
+ best_exact_match = 0.
+ for epoch in range(len(ckpt_manager.checkpoints), num_epochs):
+ model.fit(
+ train_dataset,
+ callbacks=[
+ tf.keras.callbacks.TensorBoard(model_dir, write_graph=False),
+ ])
+ ckpt_path = ckpt_manager.save()
+ if evaluate_fn is None:
+ continue
+ metrics = evaluate_fn()
+ logging.info('Epoch %d: %s', epoch + 1, metrics)
+ if best_exact_match < metrics['exact_match']:
+ best_exact_match = metrics['exact_match']
+ model.save(os.path.join(model_dir, 'export'), include_optimizer=False)
+ logging.info('Exporting %s as SavedModel.', ckpt_path)
+ with val_summary_writer.as_default():
+ for name, data in metrics.items():
+ tf.summary.scalar(name, data, epoch + 1)
+
+
+def evaluate(sp_processor, features_map_fn, labels_map_fn, logits_fn,
+ decode_logits_fn, split_and_pad_fn, distribute_strategy,
+ validation_dataset, ground_truth):
+ """Run evaluation."""
+ loss_metric = tf.keras.metrics.Mean()
+
+ @tf.function
+ def update_loss(y, logits):
+ loss_fn = modeling.SpanOrCrossEntropyLoss(
+ reduction=tf.keras.losses.Reduction.NONE)
+ return loss_metric(loss_fn(y, logits))
+
+ predictions = collections.defaultdict(list)
+ for _, (features, labels) in validation_dataset.enumerate():
+ token_ids = features['token_ids']
+ y = labels_map_fn(token_ids, labels)
+ x = split_and_pad_fn(features_map_fn(features))
+ logits = tf.concat(
+ distribute_strategy.experimental_local_results(logits_fn(x)), 0)
+ logits = logits[:features['token_ids'].shape[0]]
+ update_loss(y, logits)
+ end_limit = token_ids.row_lengths() - 1 # inclusive
+ begin, end, scores = decode_logits_fn(logits, end_limit)
+ answers = prediction.decode_answer(features['context'], begin, end,
+ features['token_offsets'],
+ end_limit).numpy()
+ for _, (qid, token_id, offset, score, answer) in enumerate(
+ zip(features['qid'].numpy(),
+ tf.gather(features['token_ids'], begin, batch_dims=1).numpy(),
+ tf.gather(features['token_offsets'], begin, batch_dims=1).numpy(),
+ scores, answers)):
+ if not answer:
+ continue
+ if sp_processor.IdToPiece(int(token_id)).startswith('▁') and offset > 0:
+ answer = answer[1:]
+ predictions[qid.decode('utf-8')].append((score, answer.decode('utf-8')))
+ predictions = {
+ qid: evaluation.normalize_answer(
+ sorted(answers, key=operator.itemgetter(0), reverse=True)[0][1])
+ for qid, answers in predictions.items()
+ }
+ metrics = evaluation.evaluate_triviaqa(ground_truth, predictions, mute=True)
+ metrics['loss'] = loss_metric.result().numpy()
+ return metrics
+
+
+def main(argv):
+ if len(argv) > 1:
+ raise app.UsageError('Too many command-line arguments.')
+ gin.parse_config(FLAGS.gin_bindings)
+ model_config = read_model_config(
+ FLAGS.encoder,
+ FLAGS.model_config_path,
+ bigbird_block_size=FLAGS.bigbird_block_size)
+ logging.info(model_config.get().as_dict())
+ # Configure input processing.
+ sp_processor = read_sentencepiece_model(FLAGS.sentencepiece_model_path)
+ features_map_fn = functools.partial(
+ inputs.features_map_fn,
+ local_radius=FLAGS.bigbird_block_size,
+ relative_pos_max_distance=24,
+ use_hard_g2l_mask=True,
+ padding_id=sp_processor.PieceToId(''),
+ eos_id=sp_processor.PieceToId(''),
+ null_id=sp_processor.PieceToId(''),
+ cls_id=sp_processor.PieceToId(''),
+ sep_id=sp_processor.PieceToId(''))
+ train_features_map_fn = tf.function(
+ functools.partial(
+ features_map_fn,
+ sequence_length=FLAGS.train_sequence_length,
+ global_sequence_length=FLAGS.train_global_sequence_length),
+ autograph=False)
+ train_labels_map_fn = tf.function(
+ functools.partial(
+ inputs.labels_map_fn, sequence_length=FLAGS.train_sequence_length))
+ # Connect to TPU cluster.
+ if FLAGS.master:
+ resolver = tf.distribute.cluster_resolver.TPUClusterResolver(FLAGS.master)
+ tf.config.experimental_connect_to_cluster(resolver)
+ tf.tpu.experimental.initialize_tpu_system(resolver)
+ strategy = tf.distribute.TPUStrategy(resolver)
+ else:
+ strategy = tf.distribute.MirroredStrategy()
+ # Initialize datasets.
+ with worker_context():
+ _ = tf.random.get_global_generator()
+ train_dataset = inputs.read_batches(
+ FLAGS.data_dir,
+ tfds.Split.TRAIN,
+ FLAGS.batch_size,
+ shuffle=True,
+ drop_final_batch=True)
+ validation_dataset = inputs.read_batches(FLAGS.data_dir,
+ tfds.Split.VALIDATION,
+ FLAGS.batch_size)
+
+ def train_map_fn(x, y):
+ features = train_features_map_fn(x)
+ labels = modeling.smooth_labels(FLAGS.label_smoothing,
+ train_labels_map_fn(x['token_ids'], y),
+ features['question_lengths'],
+ features['token_ids'])
+ return features, labels
+
+ train_dataset = train_dataset.map(train_map_fn, 16).prefetch(16)
+ # Initialize model and compile.
+ with strategy.scope():
+ model = modeling.TriviaQaModel(model_config, FLAGS.train_sequence_length)
+ logits_fn = tf.function(
+ functools.partial(prediction.distributed_logits_fn, model))
+ decode_logits_fn = tf.function(
+ functools.partial(prediction.decode_logits, FLAGS.decode_top_k,
+ FLAGS.decode_max_size))
+ split_and_pad_fn = tf.function(
+ functools.partial(prediction.split_and_pad, strategy, FLAGS.batch_size))
+ # Evaluation strategy.
+ with tf.io.gfile.GFile(FLAGS.validation_gold_path) as f:
+ ground_truth = {
+ datum['QuestionId']: datum['Answer'] for datum in json.load(f)['Data']
+ }
+ validation_features_map_fn = tf.function(
+ functools.partial(
+ features_map_fn,
+ sequence_length=FLAGS.validation_sequence_length,
+ global_sequence_length=FLAGS.validation_global_sequence_length),
+ autograph=False)
+ validation_labels_map_fn = tf.function(
+ functools.partial(
+ inputs.labels_map_fn,
+ sequence_length=FLAGS.validation_sequence_length))
+ evaluate_fn = functools.partial(
+ evaluate,
+ sp_processor=sp_processor,
+ features_map_fn=validation_features_map_fn,
+ labels_map_fn=validation_labels_map_fn,
+ logits_fn=logits_fn,
+ decode_logits_fn=decode_logits_fn,
+ split_and_pad_fn=split_and_pad_fn,
+ distribute_strategy=strategy,
+ validation_dataset=validation_dataset,
+ ground_truth=ground_truth)
+ logging.info('Model initialized. Beginning training fit loop.')
+ fit(model, strategy, train_dataset, FLAGS.model_dir,
+ FLAGS.init_checkpoint_path, evaluate_fn)
+
+
+if __name__ == '__main__':
+ flags.mark_flags_as_required([
+ 'model_config_path', 'model_dir', 'sentencepiece_model_path',
+ 'validation_gold_path'
+ ])
+ app.run(main)
diff --git a/official/projects/unified_detector/README.md b/official/projects/unified_detector/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..31c2980d5a5f52373d77831114b9227ac6805466
--- /dev/null
+++ b/official/projects/unified_detector/README.md
@@ -0,0 +1,163 @@
+# Towards End-to-End Unified Scene Text Detection and Layout Analysis
+
+
+
+[](https://arxiv.org/abs/2203.15143)
+
+Official TensorFlow 2 implementation of the paper `Towards End-to-End Unified
+Scene Text Detection and Layout Analysis`. If you encounter any issues using the
+code, you are welcome to submit them to the Issues tab or send emails directly
+to us: `hiertext@google.com`.
+
+## Installation
+
+### Set up TensorFlow Models
+
+```bash
+# (Optional) Create and enter a virtual environment
+pip3 install --user virtualenv
+virtualenv -p python3 unified_detector
+source ./unified_detector/bin/activate
+
+# First clone the TensorFlow Models project:
+git clone https://github.com/tensorflow/models.git
+
+# Install the requirements of TensorFlow Models and this repo:
+cd models
+pip3 install -r official/requirements.txt
+pip3 install -r official/projects/unified_detector/requirements.txt
+
+# Compile the protos
+# If `protoc` is not installed, please follow: https://grpc.io/docs/protoc-installation/
+export PYTHONPATH=${PYTHONPATH}:${PWD}/research/
+cd research/object_detection/
+protoc protos/string_int_label_map.proto --python_out=.
+```
+
+### Set up Deeplab2
+
+```bash
+# Clone Deeplab2 anywhere you like
+cd
+git clone https://github.com/google-research/deeplab2.git
+
+# Compile the protos
+protoc deeplab2/*.proto --python_out=.
+
+# Add to PYTHONPATH the directory where deeplab2 sits.
+export PYTHONPATH=${PYTHONPATH}:${PWD}
+```
+
+## Running the model on some images using the provided checkpoint.
+
+### Download the checkpoint
+
+Model | Input Resolution | #object query | line PQ (val) | paragraph PQ (val) | line PQ (test) | paragraph PQ (test)
+---------------------------------------------------------------------------------------------------------------------------------- | ---------------- | ------------- | ------------- | ------------------ | -------------- | -------------------
+Unified-Detector-Line ([ckpt](https://storage.cloud.google.com/tf_model_garden/vision/unified_detector/unified_detector_ckpt.tgz)) | 1024 | 384 | 61.04 | 52.84 | 62.20 | 53.52
+
+### Demo on single images
+
+```bash
+# run from `models/`
+python3 -m official.projects.unified_detector.run_inference \
+--gin_file=official/projects/unified_detector/configs/gin_files/unified_detector_model.gin \
+--ckpt_path= \
+--img_file= \
+--output_path=/demo.jsonl \
+--vis_dir=
+
+```
+
+The output will be stored in jsonl in the same hierarchical format as required
+by the evaluation script of the HierText dataset. There will also be
+visualizations of the word/line/paragraph boundaries. Note that, the unified
+detector produces line-level masks and an affinity matrix for grouping lines
+into paragraphs. For visualization purpose, we split each line mask into pixel
+groups which are defined as connected components/pixels. We visualize these
+groups as `words`. They are not necessarily at the word granularity, though. We
+visualize lines and paragraphs as groupings of these `words` using axis-aligned
+bounding boxes.
+
+## Inference and Evaluation on the HierText dataset
+
+### Download the HierText dataset
+
+Clone the [HierText repo](https://github.com/google-research-datasets/hiertext)
+and download the dataset. The `requirements.txt` in this folder already covers
+those in the HierText repo, so there is no need to create a new virtual
+environment again.
+
+### Inference and eval
+
+The following command will run the model on the validation set and compute the
+score. Note that the test set annotation is not released yet, so only validation
+set is used here for demo purposes.
+
+#### Inference
+
+```bash
+# Run from `models/`
+python3 -m official.projects.unified_detector.run_inference \
+--gin_file=official/projects/unified_detector/configs/gin_files/unified_detector_model.gin \
+--ckpt_path= \
+--img_dir= \
+--output_path=/validation_output.jsonl
+
+```
+
+#### Evaluation
+
+```bash
+# Run from `hiertext/`
+python3 eval.py \
+--gt=gt/validation.jsonl \
+--result=/validation_output.jsonl \
+--output=./validation-score.txt \
+--mask_stride=1 \
+--eval_lines \
+--eval_paragraphs \
+--num_workers=0
+
+```
+
+## Train new models.
+
+First, you will need to convert the HierText dataset into TFrecords:
+
+```bash
+# Run from `models/official/projects/unified_detector/data_conversion`
+CUDA_VISIBLE_DEVICES='' python3 convert.py \
+--gt_file=/path/to/gt.jsonl \
+--img_dir=/path/to/image \
+--out_file=/path/to/tfrecords/file-prefix
+
+```
+
+To train the unified detector, run the following script:
+
+```bash
+# Run from `models/`
+python3 -m official.projects.unified_detector.train \
+--mode=train \
+--experiment=unified_detector \
+--model_dir='' \
+--gin_file='official/projects/unified_detector/configs/gin_files/unified_detector_train.gin' \
+--gin_file='official/projects/unified_detector/configs/gin_files/unified_detector_model.gin' \
+--gin_params='InputFn.input_paths = ["/path/to/tfrecords/file-prefix*"]'
+
+```
+
+## Citation
+
+Please cite our [paper](https://arxiv.org/pdf/2203.15143.pdf) if you find this
+work helpful:
+
+```
+@inproceedings{long2022towards,
+ title={Towards End-to-End Unified Scene Text Detection and Layout Analysis},
+ author={Long, Shangbang and Qin, Siyang and Panteleev, Dmitry and Bissacco, Alessandro and Fujii, Yasuhisa and Raptis, Michalis},
+ booktitle={Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition},
+ year={2022}
+}
+```
diff --git a/official/projects/unified_detector/configs/gin_files/unified_detector_model.gin b/official/projects/unified_detector/configs/gin_files/unified_detector_model.gin
new file mode 100644
index 0000000000000000000000000000000000000000..4dfcbc1d71c8d72b4b651a43066c73401e42a8fd
--- /dev/null
+++ b/official/projects/unified_detector/configs/gin_files/unified_detector_model.gin
@@ -0,0 +1,43 @@
+# Defining the unified detector models.
+
+# Model
+## Backbone
+num_slots = 384
+SyncBatchNormalization.momentum = 0.95
+
+get_max_deep_lab_backbone.num_slots = %num_slots
+
+## Decoder
+intermediate_filters = 256
+num_entity_class = 3 # C + 1 (bkg) + 1 (void)
+
+_get_decoder_head.atrous_rates = (6, 12, 18)
+_get_decoder_head.pixel_space_dim = 128
+_get_decoder_head.pixel_space_intermediate = %intermediate_filters
+_get_decoder_head.num_classes = %num_entity_class
+_get_decoder_head.aux_sem_intermediate = %intermediate_filters
+_get_decoder_head.low_level = [
+ {'feature_key': 'res3', 'channels_project': 64,},
+ {'feature_key': 'res2', 'channels_project': 32,},]
+_get_decoder_head.norm_fn = @SyncBatchNormalization
+_get_embed_head.norm_fn = @LayerNorm
+
+# Loss
+# pq loss
+alpha = 0.75
+tau = 0.3
+_entity_mask_loss.alpha = %alpha
+_instance_discrimination_loss.tau = %tau
+_paragraph_grouping_loss.tau = %tau
+_paragraph_grouping_loss.loss_mode = 'balanced'
+
+
+# Other Model setting
+UniversalDetector.mask_threshold = 0.4
+UniversalDetector.class_threshold = 0.5
+UniversalDetector.filter_area = 32
+universal_detection_loss_weights.loss_segmentation_word = 1e0
+universal_detection_loss_weights.loss_inst_dist = 1e0
+universal_detection_loss_weights.loss_mask_id = 1e-4
+universal_detection_loss_weights.loss_pq = 3e0
+universal_detection_loss_weights.loss_para = 1e0
diff --git a/official/projects/unified_detector/configs/gin_files/unified_detector_train.gin b/official/projects/unified_detector/configs/gin_files/unified_detector_train.gin
new file mode 100644
index 0000000000000000000000000000000000000000..384fa4cbbafb3449aec1286281d8b30ff75580a3
--- /dev/null
+++ b/official/projects/unified_detector/configs/gin_files/unified_detector_train.gin
@@ -0,0 +1,22 @@
+# Defining the input pipeline of unified detector.
+
+# ===== ===== Model ===== =====
+# Internal import 2.
+OcrTask.model_fn = @UniversalDetector
+
+# ===== ===== Data pipeline ===== =====
+InputFn.parser_fn = @UniDetectorParserFn
+InputFn.dataset_type = 'tfrecord'
+InputFn.batch_size = 256
+
+# Internal import 3.
+
+UniDetectorParserFn.output_dimension = 1024
+# Simple data augmentation for now.
+UniDetectorParserFn.rot90_probability = 0.0
+UniDetectorParserFn.use_color_distortion = True
+UniDetectorParserFn.crop_min_scale = 0.5
+UniDetectorParserFn.crop_max_scale = 1.5
+UniDetectorParserFn.crop_min_aspect = 0.8
+UniDetectorParserFn.crop_max_aspect = 1.25
+UniDetectorParserFn.max_num_instance = 384
diff --git a/official/projects/unified_detector/configs/ocr_config.py b/official/projects/unified_detector/configs/ocr_config.py
new file mode 100644
index 0000000000000000000000000000000000000000..7500900c16c2f6de5e175bce5524c1708f0e55a3
--- /dev/null
+++ b/official/projects/unified_detector/configs/ocr_config.py
@@ -0,0 +1,78 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""OCR tasks and models configurations."""
+
+import dataclasses
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.modeling import optimization
+
+
+@dataclasses.dataclass
+class OcrTaskConfig(cfg.TaskConfig):
+ train_data: cfg.DataConfig = cfg.DataConfig()
+ model_call_needs_labels: bool = False
+
+
+@exp_factory.register_config_factory('unified_detector')
+def unified_detector() -> cfg.ExperimentConfig:
+ """Configurations for trainer of unified detector."""
+ total_train_steps = 100000
+ summary_interval = steps_per_loop = 200
+ checkpoint_interval = 2000
+ warmup_steps = 1000
+ config = cfg.ExperimentConfig(
+ # Input pipeline and model are configured through Gin.
+ task=OcrTaskConfig(train_data=cfg.DataConfig(is_training=True)),
+ trainer=cfg.TrainerConfig(
+ train_steps=total_train_steps,
+ steps_per_loop=steps_per_loop,
+ summary_interval=summary_interval,
+ checkpoint_interval=checkpoint_interval,
+ max_to_keep=1,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate': 0.05,
+ 'include_in_weight_decay': [
+ '^((?!depthwise).)*(kernel|weights):0$',
+ ],
+ 'exclude_from_weight_decay': [
+ '(^((?!kernel).)*:0)|(depthwise_kernel)',
+ ],
+ 'gradient_clip_norm': 10.,
+ },
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ 'initial_learning_rate': 1e-3,
+ 'decay_steps': total_train_steps - warmup_steps,
+ 'alpha': 1e-2,
+ 'offset': warmup_steps,
+ },
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_learning_rate': 1e-5,
+ 'warmup_steps': warmup_steps,
+ }
+ },
+ }),
+ ),
+ )
+ return config
diff --git a/official/projects/unified_detector/data_conversion/convert.py b/official/projects/unified_detector/data_conversion/convert.py
new file mode 100644
index 0000000000000000000000000000000000000000..ad133cd55cab2021e42ed6d1f72db3aadbd977d7
--- /dev/null
+++ b/official/projects/unified_detector/data_conversion/convert.py
@@ -0,0 +1,66 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""Script to convert HierText to TFExamples.
+
+This script is only intended to run locally.
+
+python3 data_preprocess/convert.py \
+--gt_file=/path/to/gt.jsonl \
+--img_dir=/path/to/image \
+--out_file=/path/to/tfrecords/file-prefix
+
+"""
+
+import json
+import os
+import random
+
+from absl import app
+from absl import flags
+import tensorflow as tf
+import tqdm
+import utils
+
+
+_GT_FILE = flags.DEFINE_string('gt_file', None, 'Path to the GT file')
+_IMG_DIR = flags.DEFINE_string('img_dir', None, 'Path to the image folder.')
+_OUT_FILE = flags.DEFINE_string('out_file', None, 'Path for the tfrecords.')
+_NUM_SHARD = flags.DEFINE_integer(
+ 'num_shard', 100, 'The number of shards of tfrecords.')
+
+
+def main(unused_argv) -> None:
+ annotations = json.load(open(_GT_FILE.value))['annotations']
+ random.shuffle(annotations)
+ n_sample = len(annotations)
+ n_shards = _NUM_SHARD.value
+ n_sample_per_shard = (n_sample - 1) // n_shards + 1
+
+ for shard in tqdm.tqdm(range(n_shards)):
+ output_path = f'{_OUT_FILE.value}-{shard:05}-{n_shards:05}.tfrecords'
+ annotation_subset = annotations[
+ shard * n_sample_per_shard : (shard + 1) * n_sample_per_shard]
+
+ with tf.io.TFRecordWriter(output_path) as file_writer:
+ for annotation in annotation_subset:
+ img_file_path = os.path.join(_IMG_DIR.value,
+ f"{annotation['image_id']}.jpg")
+ tfexample = utils.convert_to_tfe(img_file_path, annotation)
+ file_writer.write(tfexample)
+
+
+if __name__ == '__main__':
+ flags.mark_flags_as_required(['gt_file', 'img_dir', 'out_file'])
+ app.run(main)
diff --git a/official/projects/unified_detector/data_conversion/utils.py b/official/projects/unified_detector/data_conversion/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..a7fee2f56352b552da99ba70bf27a5866ca82991
--- /dev/null
+++ b/official/projects/unified_detector/data_conversion/utils.py
@@ -0,0 +1,182 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Utilities to convert data to TFExamples and store in TFRecords."""
+
+from typing import Any, Dict, List, Tuple, Union
+
+
+import cv2
+import numpy as np
+import tensorflow as tf
+
+
+def encode_image(
+ image_tensor: np.ndarray,
+ encoding_type: str = 'png') -> Union[np.ndarray, tf.Tensor]:
+ """Encode image tensor into byte string."""
+ if encoding_type == 'jpg':
+ image_encoded = tf.image.encode_jpeg(tf.constant(image_tensor))
+ elif encoding_type == 'png':
+ image_encoded = tf.image.encode_png(tf.constant(image_tensor))
+ else:
+ raise ValueError('Invalid encoding type.')
+ if tf.executing_eagerly():
+ image_encoded = image_encoded.numpy()
+ else:
+ image_encoded = image_encoded.eval()
+ return image_encoded
+
+
+def int64_feature(value: Union[int, List[int]]) -> tf.train.Feature:
+ if not isinstance(value, list):
+ value = [value]
+ return tf.train.Feature(int64_list=tf.train.Int64List(value=value))
+
+
+def float_feature(value: Union[float, List[float]]) -> tf.train.Feature:
+ if not isinstance(value, list):
+ value = [value]
+ return tf.train.Feature(float_list=tf.train.FloatList(value=value))
+
+
+def bytes_feature(value: Union[Union[bytes, str], List[Union[bytes, str]]]
+ ) -> tf.train.Feature:
+ if not isinstance(value, list):
+ value = [value]
+ for i in range(len(value)):
+ if not isinstance(value[i], bytes):
+ value[i] = value[i].encode('utf-8')
+ return tf.train.Feature(bytes_list=tf.train.BytesList(value=value))
+
+
+def annotation_to_entities(annotation: Dict[str, Any]) -> List[Dict[str, Any]]:
+ """Flatten the annotation dict to a list of 'entities'."""
+ entities = []
+ for paragraph in annotation['paragraphs']:
+ paragraph_id = len(entities)
+ paragraph['type'] = 3 # 3 for paragraph
+ paragraph['parent_id'] = -1
+ entities.append(paragraph)
+
+ for line in paragraph['lines']:
+ line_id = len(entities)
+ line['type'] = 2 # 2 for line
+ line['parent_id'] = paragraph_id
+ entities.append(line)
+
+ for word in line['words']:
+ word['type'] = 1 # 1 for word
+ word['parent_id'] = line_id
+ entities.append(word)
+
+ return entities
+
+
+def draw_entity_mask(
+ entities: List[Dict[str, Any]],
+ image_shape: Tuple[int, int, int]) -> np.ndarray:
+ """Draw entity id mask.
+
+ Args:
+ entities: A list of entity objects. Should be output from
+ `annotation_to_entities`.
+ image_shape: The shape of the input image.
+ Returns:
+ A (H, W, 3) entity id mask of the same height/width as the image. Each pixel
+ (i, j, :) encodes the entity id of one pixel. Only word entities are
+ rendered. 0 for non-text pixels; word entity ids start from 1.
+ """
+ instance_mask = np.zeros(image_shape, dtype=np.uint8)
+ for i, entity in enumerate(entities):
+ # only draw word masks
+ if entity['type'] != 1:
+ continue
+ vertices = np.array(entity['vertices'])
+ # the pixel value is actually 1 + position in entities
+ entity_id = i + 1
+ if entity_id >= 65536:
+ # As entity_id is encoded in the last two channels, it should be less than
+ # 256**2=65536.
+ raise ValueError(
+ (f'Entity ID overflow: {entity_id}. Currently only entity_id<65536 '
+ 'are supported.'))
+
+ # use the last two channels to encode the entity id.
+ color = [0, entity_id // 256, entity_id % 256]
+ instance_mask = cv2.fillPoly(instance_mask,
+ [np.round(vertices).astype('int32')], color)
+ return instance_mask
+
+
+def convert_to_tfe(img_file_name: str,
+ annotation: Dict[str, Any]) -> tf.train.Example:
+ """Convert the annotation dict into a TFExample."""
+
+ img = cv2.imread(img_file_name)
+ img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
+ h, w, c = img.shape
+ encoded_img = encode_image(img)
+
+ entities = annotation_to_entities(annotation)
+ masks = draw_entity_mask(entities, img.shape)
+ encoded_mask = encode_image(masks)
+
+ # encode attributes
+ parent = []
+ classes = []
+ content_type = []
+ text = []
+ vertices = []
+
+ for entity in entities:
+ parent.append(entity['parent_id'])
+ classes.append(entity['type'])
+ # 0 for annotated; 8 for not annotated
+ content_type.append((0 if entity['legible'] else 8))
+ text.append(entity.get('text', ''))
+ v = np.array(entity['vertices'])
+ vertices.append(','.join(str(float(n)) for n in v.reshape(-1)))
+
+ example = tf.train.Example(
+ features=tf.train.Features(
+ feature={
+ # input images
+ 'image/encoded': bytes_feature(encoded_img),
+ # image format
+ 'image/format': bytes_feature('png'),
+ # image width
+ 'image/width': int64_feature([w]),
+ # image height
+ 'image/height': int64_feature([h]),
+ # image channels
+ 'image/channels': int64_feature([c]),
+ # image key
+ 'image/source_id': bytes_feature(annotation['image_id']),
+ # HxWx3 tensors: channel 2-3 encodes the id of the word entity.
+ 'image/additional_channels/encoded': bytes_feature(encoded_mask),
+ # format of the additional channels
+ 'image/additional_channels/format': bytes_feature('png'),
+ 'image/object/parent': int64_feature(parent),
+ # word / line / paragraph / symbol / ...
+ 'image/object/classes': int64_feature(classes),
+ # text / handwritten / not-annotated / ...
+ 'image/object/content_type': int64_feature(content_type),
+ # string text transcription
+ 'image/object/text': bytes_feature(text),
+ # comma separated coordinates, (x,y) * n
+ 'image/object/vertices': bytes_feature(vertices),
+ })).SerializeToString()
+
+ return example
diff --git a/official/projects/unified_detector/data_loaders/autoaugment.py b/official/projects/unified_detector/data_loaders/autoaugment.py
new file mode 100644
index 0000000000000000000000000000000000000000..26a4d838f47c3fa26717cb02492ecf1282c25682
--- /dev/null
+++ b/official/projects/unified_detector/data_loaders/autoaugment.py
@@ -0,0 +1,753 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""AutoAugment and RandAugment policies for enhanced image preprocessing.
+
+AutoAugment Reference: https://arxiv.org/abs/1805.09501
+RandAugment Reference: https://arxiv.org/abs/1909.13719
+
+This library is adapted from:
+`https://github.com/tensorflow/tpu/blob/master/models/official/efficientnet/autoaugment.py`.
+Several changes are made. They are inspired by the TIMM library:
+https://github.com/rwightman/pytorch-image-models/tree/master/timm/data
+
+Changes include:
+(1) Random Erasing / Cutout is added, and separated from the random augmentation
+ pool (not sampled as an operation).
+(2) For `posterize` and `solarize`, the arguments are changed such that the
+ level of corruption increases as the `magnitude` argument increases.
+(3) `color`, `contrast`, `brightness`, `sharpness` are randomly enhanced or
+ diminished.
+(4) Magnitude is randomly sampled from a normal distribution.
+(5) Operations are applied with a probability.
+"""
+
+import inspect
+import math
+import tensorflow as tf
+import tensorflow_addons.image as tfa_image
+
+# This signifies the max integer that the controller RNN could predict for the
+# augmentation scheme.
+_MAX_LEVEL = 10.
+
+
+def policy_v0():
+ """Autoaugment policy that was used in AutoAugment Paper."""
+ # Each tuple is an augmentation operation of the form
+ # (operation, probability, magnitude). Each element in policy is a
+ # sub-policy that will be applied sequentially on the image.
+ policy = [
+ [('Equalize', 0.8, 1), ('ShearY', 0.8, 4)],
+ [('Color', 0.4, 9), ('Equalize', 0.6, 3)],
+ [('Color', 0.4, 1), ('Rotate', 0.6, 8)],
+ [('Solarize', 0.8, 3), ('Equalize', 0.4, 7)],
+ [('Solarize', 0.4, 2), ('Solarize', 0.6, 2)],
+ [('Color', 0.2, 0), ('Equalize', 0.8, 8)],
+ [('Equalize', 0.4, 8), ('SolarizeAdd', 0.8, 3)],
+ [('ShearX', 0.2, 9), ('Rotate', 0.6, 8)],
+ [('Color', 0.6, 1), ('Equalize', 1.0, 2)],
+ [('Invert', 0.4, 9), ('Rotate', 0.6, 0)],
+ [('Equalize', 1.0, 9), ('ShearY', 0.6, 3)],
+ [('Color', 0.4, 7), ('Equalize', 0.6, 0)],
+ [('Posterize', 0.4, 6), ('AutoContrast', 0.4, 7)],
+ [('Solarize', 0.6, 8), ('Color', 0.6, 9)],
+ [('Solarize', 0.2, 4), ('Rotate', 0.8, 9)],
+ [('Rotate', 1.0, 7), ('TranslateY', 0.8, 9)],
+ [('ShearX', 0.0, 0), ('Solarize', 0.8, 4)],
+ [('ShearY', 0.8, 0), ('Color', 0.6, 4)],
+ [('Color', 1.0, 0), ('Rotate', 0.6, 2)],
+ [('Equalize', 0.8, 4), ('Equalize', 0.0, 8)],
+ [('Equalize', 1.0, 4), ('AutoContrast', 0.6, 2)],
+ [('ShearY', 0.4, 7), ('SolarizeAdd', 0.6, 7)],
+ [('Posterize', 0.8, 2), ('Solarize', 0.6, 10)],
+ [('Solarize', 0.6, 8), ('Equalize', 0.6, 1)],
+ [('Color', 0.8, 6), ('Rotate', 0.4, 5)],
+ ]
+ return policy
+
+
+def policy_vtest():
+ """Autoaugment test policy for debugging."""
+ # Each tuple is an augmentation operation of the form
+ # (operation, probability, magnitude). Each element in policy is a
+ # sub-policy that will be applied sequentially on the image.
+ policy = [
+ [('TranslateX', 1.0, 4), ('Equalize', 1.0, 10)],
+ ]
+ return policy
+
+
+# pylint: disable=g-long-lambda
+blend = tf.function(lambda i1, i2, factor: tf.cast(
+ tfa_image.blend(tf.cast(i1, tf.float32), tf.cast(i2, tf.float32), factor),
+ tf.uint8))
+# pylint: enable=g-long-lambda
+
+
+def random_erase(image,
+ prob,
+ min_area=0.02,
+ max_area=1 / 3,
+ min_aspect=1 / 3,
+ max_aspect=10 / 3,
+ mode='pixel'):
+ """The random erasing augmentations: https://arxiv.org/pdf/1708.04896.pdf.
+
+ This augmentation is applied after image normalization.
+
+ Args:
+ image: Input image after all other augmentation and normalization. It has
+ type tf.float32.
+ prob: Probability of applying the random erasing operation.
+ min_area: As named.
+ max_area: As named.
+ min_aspect: As named.
+ max_aspect: As named.
+ mode: How the erased area is filled. 'pixel' means white noise (uniform
+ dist).
+
+ Returns:
+ Randomly erased image.
+ """
+
+ image_height = tf.shape(image)[0]
+ image_width = tf.shape(image)[1]
+ image_area = tf.cast(image_width * image_height, tf.float32)
+
+ # Sample width, height
+ erase_area = tf.random.uniform([], min_area, max_area) * image_area
+ log_max_target_ar = tf.math.log(
+ tf.minimum(
+ tf.math.divide(
+ tf.math.square(tf.cast(image_width, tf.float32)), erase_area),
+ max_aspect))
+ log_min_target_ar = tf.math.log(
+ tf.maximum(
+ tf.math.divide(erase_area,
+ tf.math.square(tf.cast(image_height, tf.float32))),
+ min_aspect))
+ erase_aspect_ratio = tf.math.exp(
+ tf.random.uniform([], log_min_target_ar, log_max_target_ar))
+ erase_h = tf.cast(tf.math.sqrt(erase_area / erase_aspect_ratio), tf.int32)
+ erase_w = tf.cast(tf.math.sqrt(erase_area * erase_aspect_ratio), tf.int32)
+
+ # Sample (left, top) of the rectangle to erase
+ erase_left = tf.random.uniform(
+ shape=[], minval=0, maxval=image_width - erase_w, dtype=tf.int32)
+ erase_top = tf.random.uniform(
+ shape=[], minval=0, maxval=image_height - erase_h, dtype=tf.int32)
+ pad_right = image_width - erase_w - erase_left
+ pad_bottom = image_height - erase_h - erase_top
+ mask = tf.pad(
+ tf.zeros([erase_h, erase_w], dtype=image.dtype),
+ [[erase_top, pad_bottom], [erase_left, pad_right]],
+ constant_values=1)
+ mask = tf.expand_dims(mask, -1) # [H, W, 1]
+ if mode == 'pixel':
+ fill = tf.random.truncated_normal(
+ tf.shape(image), 0.0, 1.0, dtype=image.dtype)
+ else:
+ fill = tf.zeros(tf.shape(image), dtype=image.dtype)
+
+ should_apply_op = tf.cast(
+ tf.floor(tf.random.uniform([], dtype=tf.float32) + prob), tf.bool)
+ augmented_image = tf.cond(should_apply_op,
+ lambda: mask * image + (1 - mask) * fill,
+ lambda: image)
+ return augmented_image
+
+
+def solarize(image, threshold=128):
+ # For each pixel in the image, select the pixel
+ # if the value is less than the threshold.
+ # Otherwise, subtract 255 from the pixel.
+ return tf.where(image < threshold, image, 255 - image)
+
+
+def solarize_add(image, addition=0, threshold=128):
+ # For each pixel in the image less than threshold
+ # we add 'addition' amount to it and then clip the
+ # pixel value to be between 0 and 255. The value
+ # of 'addition' is between -128 and 128.
+ added_image = tf.cast(image, tf.int64) + addition
+ added_image = tf.cast(tf.clip_by_value(added_image, 0, 255), tf.uint8)
+ return tf.where(image < threshold, added_image, image)
+
+
+def color(image, factor):
+ """Equivalent of PIL Color."""
+ degenerate = tf.image.grayscale_to_rgb(tf.image.rgb_to_grayscale(image))
+ return blend(degenerate, image, factor)
+
+
+def contrast(image, factor):
+ """Equivalent of PIL Contrast."""
+ degenerate = tf.image.rgb_to_grayscale(image)
+ # Cast before calling tf.histogram.
+ degenerate = tf.cast(degenerate, tf.int32)
+
+ # Compute the grayscale histogram, then compute the mean pixel value,
+ # and create a constant image size of that value. Use that as the
+ # blending degenerate target of the original image.
+ hist = tf.histogram_fixed_width(degenerate, [0, 255], nbins=256)
+ mean = tf.reduce_sum(tf.cast(hist, tf.float32)) / 256.0
+ degenerate = tf.ones_like(degenerate, dtype=tf.float32) * mean
+ degenerate = tf.clip_by_value(degenerate, 0.0, 255.0)
+ degenerate = tf.image.grayscale_to_rgb(tf.cast(degenerate, tf.uint8))
+ return blend(degenerate, image, factor)
+
+
+def brightness(image, factor):
+ """Equivalent of PIL Brightness."""
+ degenerate = tf.zeros_like(image)
+ return blend(degenerate, image, factor)
+
+
+def posterize(image, bits):
+ """Equivalent of PIL Posterize. Smaller `bits` means larger degradation."""
+ shift = 8 - bits
+ return tf.bitwise.left_shift(tf.bitwise.right_shift(image, shift), shift)
+
+
+def rotate(image, degrees, replace):
+ """Rotates the image by degrees either clockwise or counterclockwise.
+
+ Args:
+ image: An image Tensor of type uint8.
+ degrees: Float, a scalar angle in degrees to rotate all images by. If
+ degrees is positive the image will be rotated clockwise otherwise it will
+ be rotated counterclockwise.
+ replace: A one or three value 1D tensor to fill empty pixels caused by the
+ rotate operation.
+
+ Returns:
+ The rotated version of image.
+ """
+ # Convert from degrees to radians.
+ degrees_to_radians = math.pi / 180.0
+ radians = degrees * degrees_to_radians
+
+ # In practice, we should randomize the rotation degrees by flipping
+ # it negatively half the time, but that's done on 'degrees' outside
+ # of the function.
+ if isinstance(replace, list) or isinstance(replace, tuple):
+ replace = replace[0]
+ image = tfa_image.rotate(image, radians, fill_value=replace)
+ return image
+
+
+def translate_x(image, pixels, replace):
+ """Equivalent of PIL Translate in X dimension."""
+ return tfa_image.translate_xy(image, [-pixels, 0], replace)
+
+
+def translate_y(image, pixels, replace):
+ """Equivalent of PIL Translate in Y dimension."""
+ return tfa_image.translate_xy(image, [0, -pixels], replace)
+
+
+def autocontrast(image):
+ """Implements Autocontrast function from PIL using TF ops.
+
+ Args:
+ image: A 3D uint8 tensor.
+
+ Returns:
+ The image after it has had autocontrast applied to it and will be of type
+ uint8.
+ """
+
+ def scale_channel(image):
+ """Scale the 2D image using the autocontrast rule."""
+ # A possibly cheaper version can be done using cumsum/unique_with_counts
+ # over the histogram values, rather than iterating over the entire image.
+ # to compute mins and maxes.
+ lo = tf.cast(tf.reduce_min(image), tf.float32)
+ hi = tf.cast(tf.reduce_max(image), tf.float32)
+
+ # Scale the image, making the lowest value 0 and the highest value 255.
+ def scale_values(im):
+ scale = 255.0 / (hi - lo)
+ offset = -lo * scale
+ im = tf.cast(im, tf.float32) * scale + offset
+ im = tf.clip_by_value(im, 0.0, 255.0)
+ return tf.cast(im, tf.uint8)
+
+ result = tf.cond(hi > lo, lambda: scale_values(image), lambda: image)
+ return result
+
+ # Assumes RGB for now. Scales each channel independently
+ # and then stacks the result.
+ s1 = scale_channel(image[:, :, 0])
+ s2 = scale_channel(image[:, :, 1])
+ s3 = scale_channel(image[:, :, 2])
+ image = tf.stack([s1, s2, s3], 2)
+ return image
+
+
+def sharpness(image, factor):
+ """Implements Sharpness function from PIL using TF ops."""
+ orig_image = image
+ image = tf.cast(image, tf.float32)
+ # Make image 4D for conv operation.
+ image = tf.expand_dims(image, 0)
+ # SMOOTH PIL Kernel.
+ kernel = tf.constant([[1, 1, 1], [1, 5, 1], [1, 1, 1]],
+ dtype=tf.float32,
+ shape=[3, 3, 1, 1]) / 13.
+ # Tile across channel dimension.
+ kernel = tf.tile(kernel, [1, 1, 3, 1])
+ strides = [1, 1, 1, 1]
+ with tf.device('/cpu:0'):
+ # Some augmentation that uses depth-wise conv will cause crashing when
+ # training on GPU. See (b/156242594) for details.
+ degenerate = tf.nn.depthwise_conv2d(image, kernel, strides, padding='VALID')
+ degenerate = tf.clip_by_value(degenerate, 0.0, 255.0)
+ degenerate = tf.squeeze(tf.cast(degenerate, tf.uint8), [0])
+
+ # For the borders of the resulting image, fill in the values of the
+ # original image.
+ mask = tf.ones_like(degenerate)
+ padded_mask = tf.pad(mask, [[1, 1], [1, 1], [0, 0]])
+ padded_degenerate = tf.pad(degenerate, [[1, 1], [1, 1], [0, 0]])
+ result = tf.where(tf.equal(padded_mask, 1), padded_degenerate, orig_image)
+
+ # Blend the final result.
+ return blend(result, orig_image, factor)
+
+
+def equalize(image):
+ """Implements Equalize function from PIL using TF ops."""
+
+ def scale_channel(im, c):
+ """Scale the data in the channel to implement equalize."""
+ im = tf.cast(im[:, :, c], tf.int32)
+ # Compute the histogram of the image channel.
+ histo = tf.histogram_fixed_width(im, [0, 255], nbins=256)
+
+ # For the purposes of computing the step, filter out the nonzeros.
+ nonzero = tf.where(tf.not_equal(histo, 0))
+ nonzero_histo = tf.reshape(tf.gather(histo, nonzero), [-1])
+ step = (tf.reduce_sum(nonzero_histo) - nonzero_histo[-1]) // 255
+
+ def build_lut(histo, step):
+ # Compute the cumulative sum, shifting by step // 2
+ # and then normalization by step.
+ lut = (tf.cumsum(histo) + (step // 2)) // step
+ # Shift lut, prepending with 0.
+ lut = tf.concat([[0], lut[:-1]], 0)
+ # Clip the counts to be in range. This is done
+ # in the C code for image.point.
+ return tf.clip_by_value(lut, 0, 255)
+
+ # If step is zero, return the original image. Otherwise, build
+ # lut from the full histogram and step and then index from it.
+ result = tf.cond(
+ tf.equal(step, 0), lambda: im,
+ lambda: tf.gather(build_lut(histo, step), im))
+
+ return tf.cast(result, tf.uint8)
+
+ # Assumes RGB for now. Scales each channel independently
+ # and then stacks the result.
+ s1 = scale_channel(image, 0)
+ s2 = scale_channel(image, 1)
+ s3 = scale_channel(image, 2)
+ image = tf.stack([s1, s2, s3], 2)
+ return image
+
+
+def invert(image):
+ """Inverts the image pixels."""
+ image = tf.convert_to_tensor(image)
+ return 255 - image
+
+
+NAME_TO_FUNC = {
+ 'AutoContrast': autocontrast,
+ 'Equalize': equalize,
+ 'Invert': invert,
+ 'Rotate': rotate,
+ 'Posterize': posterize,
+ 'PosterizeIncreasing': posterize,
+ 'Solarize': solarize,
+ 'SolarizeIncreasing': solarize,
+ 'SolarizeAdd': solarize_add,
+ 'Color': color,
+ 'ColorIncreasing': color,
+ 'Contrast': contrast,
+ 'ContrastIncreasing': contrast,
+ 'Brightness': brightness,
+ 'BrightnessIncreasing': brightness,
+ 'Sharpness': sharpness,
+ 'SharpnessIncreasing': sharpness,
+ 'ShearX': tfa_image.shear_x,
+ 'ShearY': tfa_image.shear_y,
+ 'TranslateX': translate_x,
+ 'TranslateY': translate_y,
+ 'Cutout': tfa_image.random_cutout,
+ 'Hue': tf.image.adjust_hue,
+}
+
+
+def _randomly_negate_tensor(tensor):
+ """With 50% prob turn the tensor negative."""
+ should_flip = tf.cast(tf.floor(tf.random.uniform([]) + 0.5), tf.bool)
+ final_tensor = tf.cond(should_flip, lambda: -tensor, lambda: tensor)
+ return final_tensor
+
+
+def _rotate_level_to_arg(level):
+ level = (level / _MAX_LEVEL) * 30.
+ level = _randomly_negate_tensor(level)
+ return (level,)
+
+
+def _shrink_level_to_arg(level):
+ """Converts level to ratio by which we shrink the image content."""
+ if level == 0:
+ return (1.0,) # if level is zero, do not shrink the image
+ # Maximum shrinking ratio is 2.9.
+ level = 2. / (_MAX_LEVEL / level) + 0.9
+ return (level,)
+
+
+def _enhance_level_to_arg(level):
+ return ((level / _MAX_LEVEL) * 1.8 + 0.1,)
+
+
+def _enhance_increasing_level_to_arg(level):
+ level = (level / _MAX_LEVEL) * .9
+ level = 1.0 + _randomly_negate_tensor(level)
+ return (level,)
+
+
+def _shear_level_to_arg(level):
+ level = (level / _MAX_LEVEL) * 0.3
+ # Flip level to negative with 50% chance.
+ level = _randomly_negate_tensor(level)
+ return (level,)
+
+
+def _translate_level_to_arg(level, translate_const):
+ level = level / _MAX_LEVEL * translate_const
+ # Flip level to negative with 50% chance.
+ level = _randomly_negate_tensor(level)
+ return (level,)
+
+
+def _posterize_level_to_arg(level):
+ return (tf.cast(level / _MAX_LEVEL * 4, tf.uint8),)
+
+
+def _posterize_increase_level_to_arg(level):
+ return (4 - _posterize_level_to_arg(level)[0],)
+
+
+def _solarize_level_to_arg(level):
+ return (tf.cast(level / _MAX_LEVEL * 256, tf.uint8),)
+
+
+def _solarize_increase_level_to_arg(level):
+ return (256 - _solarize_level_to_arg(level)[0],)
+
+
+def _solarize_add_level_to_arg(level):
+ return (tf.cast(level / _MAX_LEVEL * 110, tf.int64),)
+
+
+def _cutout_arg(level, cutout_size):
+ pad_size = tf.cast(level / _MAX_LEVEL * cutout_size, tf.int32)
+ return (2 * pad_size, 2 * pad_size)
+
+
+def level_to_arg(hparams):
+ return {
+ 'AutoContrast':
+ lambda level: (),
+ 'Equalize':
+ lambda level: (),
+ 'Invert':
+ lambda level: (),
+ 'Rotate':
+ _rotate_level_to_arg,
+ 'Posterize':
+ _posterize_level_to_arg,
+ 'PosterizeIncreasing':
+ _posterize_increase_level_to_arg,
+ 'Solarize':
+ _solarize_level_to_arg,
+ 'SolarizeIncreasing':
+ _solarize_increase_level_to_arg,
+ 'SolarizeAdd':
+ _solarize_add_level_to_arg,
+ 'Color':
+ _enhance_level_to_arg,
+ 'ColorIncreasing':
+ _enhance_increasing_level_to_arg,
+ 'Contrast':
+ _enhance_level_to_arg,
+ 'ContrastIncreasing':
+ _enhance_increasing_level_to_arg,
+ 'Brightness':
+ _enhance_level_to_arg,
+ 'BrightnessIncreasing':
+ _enhance_increasing_level_to_arg,
+ 'Sharpness':
+ _enhance_level_to_arg,
+ 'SharpnessIncreasing':
+ _enhance_increasing_level_to_arg,
+ 'ShearX':
+ _shear_level_to_arg,
+ 'ShearY':
+ _shear_level_to_arg,
+ # pylint:disable=g-long-lambda
+ 'Cutout':
+ lambda level: _cutout_arg(level, hparams['cutout_const']),
+ # pylint:disable=g-long-lambda
+ 'TranslateX':
+ lambda level: _translate_level_to_arg(level, hparams['translate_const'
+ ]),
+ 'TranslateY':
+ lambda level: _translate_level_to_arg(level, hparams['translate_const'
+ ]),
+ 'Hue':
+ lambda level: ((level / _MAX_LEVEL) * 0.25,),
+ # pylint:enable=g-long-lambda
+ }
+
+
+def _parse_policy_info(name, prob, level, replace_value, augmentation_hparams):
+ """Return the function that corresponds to `name` and update `level` param."""
+ func = NAME_TO_FUNC[name]
+ args = level_to_arg(augmentation_hparams)[name](level)
+
+ # Add in replace arg if it is required for the function that is being called.
+ # pytype:disable=wrong-arg-types
+ if 'replace' in inspect.signature(func).parameters.keys(): # pylint: disable=deprecated-method
+ args = tuple(list(args) + [replace_value])
+ # pytype:enable=wrong-arg-types
+
+ return (func, prob, args)
+
+
+def _apply_func_with_prob(func, image, args, prob):
+ """Apply `func` to image w/ `args` as input with probability `prob`."""
+ assert isinstance(args, tuple)
+
+ # Apply the function with probability `prob`.
+ should_apply_op = tf.cast(
+ tf.floor(tf.random.uniform([], dtype=tf.float32) + prob), tf.bool)
+ augmented_image = tf.cond(should_apply_op, lambda: func(image, *args),
+ lambda: image)
+ return augmented_image
+
+
+def select_and_apply_random_policy(policies, image):
+ """Select a random policy from `policies` and apply it to `image`."""
+ policy_to_select = tf.random.uniform([], maxval=len(policies), dtype=tf.int32)
+ # Note that using tf.case instead of tf.conds would result in significantly
+ # larger graphs and would even break export for some larger policies.
+ for (i, policy) in enumerate(policies):
+ image = tf.cond(
+ tf.equal(i, policy_to_select),
+ lambda selected_policy=policy: selected_policy(image),
+ lambda: image)
+ return image
+
+
+def build_and_apply_nas_policy(policies, image, augmentation_hparams):
+ """Build a policy from the given policies passed in and apply to image.
+
+ Args:
+ policies: list of lists of tuples in the form `(func, prob, level)`, `func`
+ is a string name of the augmentation function, `prob` is the probability
+ of applying the `func` operation, `level` is the input argument for
+ `func`.
+ image: tf.Tensor that the resulting policy will be applied to.
+ augmentation_hparams: Hparams associated with the NAS learned policy.
+
+ Returns:
+ A version of image that now has data augmentation applied to it based on
+ the `policies` pass into the function.
+ """
+ replace_value = [128, 128, 128]
+
+ # func is the string name of the augmentation function, prob is the
+ # probability of applying the operation and level is the parameter associated
+ # with the tf op.
+
+ # tf_policies are functions that take in an image and return an augmented
+ # image.
+ tf_policies = []
+ for policy in policies:
+ tf_policy = []
+ # Link string name to the correct python function and make sure the correct
+ # argument is passed into that function.
+ for policy_info in policy:
+ policy_info = list(policy_info) + [replace_value, augmentation_hparams]
+
+ tf_policy.append(_parse_policy_info(*policy_info))
+ # Now build the tf policy that will apply the augmentation procedue
+ # on image.
+ def make_final_policy(tf_policy_):
+
+ def final_policy(image_):
+ for func, prob, args in tf_policy_:
+ image_ = _apply_func_with_prob(func, image_, args, prob)
+ return image_
+
+ return final_policy
+
+ tf_policies.append(make_final_policy(tf_policy))
+
+ augmented_image = select_and_apply_random_policy(tf_policies, image)
+ return augmented_image
+
+
+def distort_image_with_autoaugment(image, augmentation_name):
+ """Applies the AutoAugment policy to `image`.
+
+ AutoAugment is from the paper: https://arxiv.org/abs/1805.09501.
+
+ Args:
+ image: `Tensor` of shape [height, width, 3] representing an image.
+ augmentation_name: The name of the AutoAugment policy to use. The available
+ options are `v0` and `test`. `v0` is the policy used for all of the
+ results in the paper and was found to achieve the best results on the COCO
+ dataset. `v1`, `v2` and `v3` are additional good policies found on the
+ COCO dataset that have slight variation in what operations were used
+ during the search procedure along with how many operations are applied in
+ parallel to a single image (2 vs 3).
+
+ Returns:
+ A tuple containing the augmented versions of `image`.
+ """
+ available_policies = {'v0': policy_v0, 'test': policy_vtest}
+ if augmentation_name not in available_policies:
+ raise ValueError('Invalid augmentation_name: {}'.format(augmentation_name))
+
+ policy = available_policies[augmentation_name]()
+ # Hparams that will be used for AutoAugment.
+ augmentation_hparams = dict(cutout_const=100, translate_const=250)
+
+ return build_and_apply_nas_policy(policy, image, augmentation_hparams)
+
+
+# Cutout is implemented separately.
+_RAND_TRANSFORMS = [
+ 'AutoContrast',
+ 'Equalize',
+ 'Invert',
+ 'Rotate',
+ 'Posterize',
+ 'Solarize',
+ 'Color',
+ 'Contrast',
+ 'Brightness',
+ 'Sharpness',
+ 'ShearX',
+ 'ShearY',
+ 'TranslateX',
+ 'TranslateY',
+ 'SolarizeAdd',
+ 'Hue',
+]
+
+# Cutout is implemented separately.
+_RAND_INCREASING_TRANSFORMS = [
+ 'AutoContrast',
+ 'Equalize',
+ 'Invert',
+ 'Rotate',
+ 'PosterizeIncreasing',
+ 'SolarizeIncreasing',
+ 'SolarizeAdd',
+ 'ColorIncreasing',
+ 'ContrastIncreasing',
+ 'BrightnessIncreasing',
+ 'SharpnessIncreasing',
+ 'ShearX',
+ 'ShearY',
+ 'TranslateX',
+ 'TranslateY',
+ 'Hue',
+]
+
+# These augmentations are not suitable for detection task.
+_NON_COLOR_DISTORTION_OPS = [
+ 'Rotate',
+ 'ShearX',
+ 'ShearY',
+ 'TranslateX',
+ 'TranslateY',
+]
+
+
+def distort_image_with_randaugment(image,
+ num_layers,
+ magnitude,
+ mag_std,
+ inc,
+ prob,
+ color_only=False):
+ """Applies the RandAugment policy to `image`.
+
+ RandAugment is from the paper https://arxiv.org/abs/1909.13719,
+
+ Args:
+ image: `Tensor` of shape [height, width, 3] representing an image. The image
+ should have uint8 type in [0, 255].
+ num_layers: Integer, the number of augmentation transformations to apply
+ sequentially to an image. Represented as (N) in the paper. Usually best
+ values will be in the range [1, 3].
+ magnitude: Integer, shared magnitude across all augmentation operations.
+ Represented as (M) in the paper. Usually best values are in the range [5,
+ 30].
+ mag_std: Randomness of magnitude. The magnitude will be sampled from a
+ normal distribution on the fly.
+ inc: Whether to select aug that increases as magnitude increases.
+ prob: Probability of any aug being applied.
+ color_only: Whether only apply operations that distort color and do not
+ change spatial layouts.
+
+ Returns:
+ The augmented version of `image`.
+ """
+ replace_value = [128] * 3
+ augmentation_hparams = dict(cutout_const=40, translate_const=100)
+ available_ops = _RAND_INCREASING_TRANSFORMS if inc else _RAND_TRANSFORMS
+ if color_only:
+ available_ops = list(
+ filter(lambda op: op not in _NON_COLOR_DISTORTION_OPS, available_ops))
+
+ for layer_num in range(num_layers):
+ op_to_select = tf.random.uniform([],
+ maxval=len(available_ops),
+ dtype=tf.int32)
+ random_magnitude = tf.clip_by_value(
+ tf.random.normal([], magnitude, mag_std), 0., _MAX_LEVEL)
+ with tf.name_scope('randaug_layer_{}'.format(layer_num)):
+ for (i, op_name) in enumerate(available_ops):
+ func, _, args = _parse_policy_info(op_name, prob, random_magnitude,
+ replace_value, augmentation_hparams)
+ image = tf.cond(
+ tf.equal(i, op_to_select),
+ # pylint:disable=g-long-lambda
+ lambda s_func=func, s_args=args: _apply_func_with_prob(
+ s_func, image, s_args, prob),
+ # pylint:enable=g-long-lambda
+ lambda: image)
+ return image
diff --git a/official/projects/unified_detector/data_loaders/input_reader.py b/official/projects/unified_detector/data_loaders/input_reader.py
new file mode 100644
index 0000000000000000000000000000000000000000..a850f9ca30b44f53a298d5bde00e5c02629fe11a
--- /dev/null
+++ b/official/projects/unified_detector/data_loaders/input_reader.py
@@ -0,0 +1,270 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Input data reader.
+
+Creates a tf.data.Dataset object from multiple input sstables and use a
+provided data parser function to decode the serialized tf.Example and optionally
+run data augmentation.
+"""
+
+import os
+from typing import Any, Callable, List, Optional, Sequence, Union
+
+import gin
+from six.moves import map
+import tensorflow as tf
+
+from official.common import dataset_fn
+from research.object_detection.utils import label_map_util
+from official.core import config_definitions as cfg
+from official.projects.unified_detector.data_loaders import universal_detection_parser # pylint: disable=unused-import
+
+FuncType = Callable[..., Any]
+
+
+@gin.configurable(denylist=['is_training'])
+class InputFn(object):
+ """Input data reader class.
+
+ Creates a tf.data.Dataset object from multiple datasets (optionally performs
+ weighted sampling between different datasets), parses the tf.Example message
+ using `parser_fn`. The datasets can either be stored in SSTable or TfRecord.
+ """
+
+ def __init__(self,
+ is_training: bool,
+ batch_size: Optional[int] = None,
+ data_root: str = '',
+ input_paths: List[str] = gin.REQUIRED,
+ dataset_type: str = 'tfrecord',
+ use_sampling: bool = False,
+ sampling_weights: Optional[Sequence[Union[int, float]]] = None,
+ cycle_length: Optional[int] = 64,
+ shuffle_buffer_size: Optional[int] = 512,
+ parser_fn: Optional[FuncType] = None,
+ parser_num_parallel_calls: Optional[int] = 64,
+ max_intra_op_parallelism: Optional[int] = None,
+ label_map_proto_path: Optional[str] = None,
+ input_filter_fns: Optional[List[FuncType]] = None,
+ input_training_filter_fns: Optional[Sequence[FuncType]] = None,
+ dense_to_ragged_batch: bool = False,
+ data_validator_fn: Optional[Callable[[Sequence[str]],
+ None]] = None):
+ """Input reader constructor.
+
+ Args:
+ is_training: Boolean indicating TRAIN or EVAL.
+ batch_size: Input data batch size. Ignored if batch size is passed through
+ params. In that case, this can be None.
+ data_root: All the relative input paths are based on this location.
+ input_paths: Input file patterns.
+ dataset_type: Can be 'sstable' or 'tfrecord'.
+ use_sampling: Whether to perform weighted sampling between different
+ datasets.
+ sampling_weights: Unnormalized sampling weights. The length should be
+ equal to `input_paths`.
+ cycle_length: The number of input Datasets to interleave from in parallel.
+ If set to None tf.data experimental autotuning is used.
+ shuffle_buffer_size: The random shuffle buffer size.
+ parser_fn: The function to run decoding and data augmentation. The
+ function takes `is_training` as an input, which is passed from here.
+ parser_num_parallel_calls: The number of parallel calls for `parser_fn`.
+ The number of CPU cores is the suggested value. If set to None tf.data
+ experimental autotuning is used.
+ max_intra_op_parallelism: if set limits the max intra op parallelism of
+ functions run on slices of the input.
+ label_map_proto_path: Path to a StringIntLabelMap which will be used to
+ decode the input data.
+ input_filter_fns: A list of functions on the dataset points which returns
+ true for valid data.
+ input_training_filter_fns: A list of functions on the dataset points which
+ returns true for valid data used only for training.
+ dense_to_ragged_batch: Whether to use ragged batching for MPNN format.
+ data_validator_fn: If not None, used to validate the data specified by
+ input_paths.
+
+ Raises:
+ ValueError for invalid input_paths.
+ """
+ self._is_training = is_training
+
+ if data_root:
+ # If an input path is absolute this does not change it.
+ input_paths = [os.path.join(data_root, value) for value in input_paths]
+
+ self._input_paths = input_paths
+ # Disables datasets sampling during eval.
+ self._batch_size = batch_size
+ if is_training:
+ self._use_sampling = use_sampling
+ else:
+ self._use_sampling = False
+ self._sampling_weights = sampling_weights
+ self._cycle_length = (cycle_length if cycle_length else tf.data.AUTOTUNE)
+ self._shuffle_buffer_size = shuffle_buffer_size
+ self._parser_num_parallel_calls = (
+ parser_num_parallel_calls
+ if parser_num_parallel_calls else tf.data.AUTOTUNE)
+ self._max_intra_op_parallelism = max_intra_op_parallelism
+ self._label_map_proto_path = label_map_proto_path
+ if label_map_proto_path:
+ name_to_id = label_map_util.get_label_map_dict(label_map_proto_path)
+ self._lookup_str_keys = list(name_to_id.keys())
+ self._lookup_int_values = list(name_to_id.values())
+ self._parser_fn = parser_fn
+ self._input_filter_fns = input_filter_fns or []
+ if is_training and input_training_filter_fns:
+ self._input_filter_fns.extend(input_training_filter_fns)
+ self._dataset_type = dataset_type
+ self._dense_to_ragged_batch = dense_to_ragged_batch
+
+ if data_validator_fn is not None:
+ data_validator_fn(self._input_paths)
+
+ @property
+ def batch_size(self):
+ return self._batch_size
+
+ def __call__(
+ self,
+ params: cfg.DataConfig,
+ input_context: Optional[tf.distribute.InputContext] = None
+ ) -> tf.data.Dataset:
+ """Read and parse input datasets, return a tf.data.Dataset object."""
+ # TPUEstimator passes the batch size through params.
+ if params is not None and 'batch_size' in params:
+ batch_size = params['batch_size']
+ else:
+ batch_size = self._batch_size
+
+ per_replica_batch_size = input_context.get_per_replica_batch_size(
+ batch_size) if input_context else batch_size
+
+ with tf.name_scope('input_reader'):
+ dataset = self._build_dataset_from_records()
+ dataset_parser_fn = self._build_dataset_parser_fn()
+
+ dataset = dataset.map(
+ dataset_parser_fn, num_parallel_calls=self._parser_num_parallel_calls)
+ for filter_fn in self._input_filter_fns:
+ dataset = dataset.filter(filter_fn)
+
+ if self._dense_to_ragged_batch:
+ dataset = dataset.apply(
+ tf.data.experimental.dense_to_ragged_batch(
+ batch_size=per_replica_batch_size, drop_remainder=True))
+ else:
+ dataset = dataset.batch(per_replica_batch_size, drop_remainder=True)
+ dataset = dataset.prefetch(tf.data.AUTOTUNE)
+
+ return dataset
+
+ def _fetch_dataset(self, filename: str) -> tf.data.Dataset:
+ """Fetch dataset depending on type.
+
+ Args:
+ filename: Location of dataset.
+
+ Returns:
+ Tf Dataset.
+ """
+
+ data_cls = dataset_fn.pick_dataset_fn(self._dataset_type)
+
+ data = data_cls([filename])
+ return data
+
+ def _build_dataset_parser_fn(self) -> Callable[..., tf.Tensor]:
+ """Depending on label_map and storage type, build a parser_fn."""
+ # Parse the fetched records to input tensors for model function.
+ if self._label_map_proto_path:
+ lookup_initializer = tf.lookup.KeyValueTensorInitializer(
+ keys=tf.constant(self._lookup_str_keys, dtype=tf.string),
+ values=tf.constant(self._lookup_int_values, dtype=tf.int32))
+ name_to_id_table = tf.lookup.StaticHashTable(
+ initializer=lookup_initializer, default_value=0)
+ parser_fn = self._parser_fn(
+ is_training=self._is_training, label_lookup_table=name_to_id_table)
+ else:
+ parser_fn = self._parser_fn(is_training=self._is_training)
+
+ return parser_fn
+
+ def _build_dataset_from_records(self) -> tf.data.Dataset:
+ """Build a tf.data.Dataset object from input SSTables.
+
+ If the input data come from multiple SSTables, use the user defined sampling
+ weights to perform sampling. For example, if the sampling weights is
+ [1., 2.], the second dataset will be sampled twice more often than the first
+ one.
+
+ Returns:
+ Dataset built from SSTables.
+ Raises:
+ ValueError for inability to find SSTable files.
+ """
+ all_file_patterns = []
+ if self._use_sampling:
+ for file_pattern in self._input_paths:
+ all_file_patterns.append([file_pattern])
+ # Normalize sampling probabilities.
+ total_weight = sum(self._sampling_weights)
+ sampling_probabilities = [
+ float(w) / total_weight for w in self._sampling_weights
+ ]
+ else:
+ all_file_patterns.append(self._input_paths)
+
+ datasets = []
+ for file_pattern in all_file_patterns:
+ filenames = sum(list(map(tf.io.gfile.glob, file_pattern)), [])
+ if not filenames:
+ raise ValueError(
+ f'Error trying to read input files for file pattern {file_pattern}')
+ # Create a dataset of filenames and shuffle the files. In each epoch,
+ # the file order is shuffled again. This may help if
+ # per_host_input_for_training = false on TPU.
+ dataset = tf.data.Dataset.list_files(
+ file_pattern, shuffle=self._is_training)
+
+ if self._is_training:
+ dataset = dataset.repeat()
+
+ if self._max_intra_op_parallelism:
+ # Disable intra-op parallelism to optimize for throughput instead of
+ # latency.
+ options = tf.data.Options()
+ options.experimental_threading.max_intra_op_parallelism = 1
+ dataset = dataset.with_options(options)
+
+ dataset = dataset.interleave(
+ self._fetch_dataset,
+ cycle_length=self._cycle_length,
+ num_parallel_calls=self._cycle_length,
+ deterministic=(not self._is_training))
+
+ if self._is_training:
+ dataset = dataset.shuffle(self._shuffle_buffer_size)
+
+ datasets.append(dataset)
+
+ if self._use_sampling:
+ assert len(datasets) == len(sampling_probabilities)
+ dataset = tf.data.experimental.sample_from_datasets(
+ datasets, sampling_probabilities)
+ else:
+ dataset = datasets[0]
+
+ return dataset
diff --git a/official/projects/unified_detector/data_loaders/tf_example_decoder.py b/official/projects/unified_detector/data_loaders/tf_example_decoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..1057cfd4d6c2df8ca7bd2e24069959f7e8108112
--- /dev/null
+++ b/official/projects/unified_detector/data_loaders/tf_example_decoder.py
@@ -0,0 +1,320 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tensorflow Example proto decoder for GOCR."""
+
+from typing import List, Optional, Sequence, Tuple, Union
+
+import tensorflow as tf
+from official.projects.unified_detector.utils.typing import TensorDict
+from official.vision.dataloaders import decoder
+
+
+class TfExampleDecoder(decoder.Decoder):
+ """Tensorflow Example proto decoder."""
+
+ def __init__(self,
+ use_instance_mask: bool = False,
+ additional_class_names: Optional[Sequence[str]] = None,
+ additional_regression_names: Optional[Sequence[str]] = None,
+ num_additional_channels: int = 0):
+ """Constructor.
+
+ keys_to_features is a dictionary mapping the names of the tf.Example
+ fields to tf features, possibly with defaults.
+
+ Uses fixed length for scalars and variable length for vectors.
+
+ Args:
+ use_instance_mask: if False, prevents decoding of the instance mask, which
+ can take a lot of resources.
+ additional_class_names: If not none, a list of additional class names. For
+ additional class name n, named image/object/${n} are expected to be an
+ int vector of length one, and are mapped to tensor dict key
+ groundtruth_${n}.
+ additional_regression_names: If not none, a list of additional regression
+ output names. For additional class name n, named image/object/${n} are
+ expected to be a float vector, and are mapped to tensor dict key
+ groundtruth_${n}.
+ num_additional_channels: The number of additional channels of information
+ present in the tf.Example proto.
+ """
+ self._num_additional_channels = num_additional_channels
+ self._use_instance_mask = use_instance_mask
+
+ self.keys_to_features = {}
+ # Map names in the final tensor dict (output of `self.decode()`) to names in
+ # tf examples, e.g. 'groundtruth_text' -> 'image/object/text'
+ self.name_to_key = {}
+
+ if use_instance_mask:
+ self.keys_to_features.update({
+ 'image/object/mask': tf.io.VarLenFeature(tf.string),
+ })
+
+ # Now we have lists of standard types.
+ # To add new features, just add entries here.
+ # The tuple elements are (example name, tensor name, default value).
+ # If the items_to_handlers part is already set up use None for
+ # the tensor name.
+ # There are other tensor names listed as None which we probably
+ # want to discuss and specify.
+ scalar_strings = [
+ ('image/encoded', None, ''),
+ ('image/format', None, 'jpg'),
+ ('image/additional_channels/encoded', None, ''),
+ ('image/additional_channels/format', None, 'png'),
+ ('image/label_type', 'label_type', ''),
+ ('image/key', 'key', ''),
+ ('image/source_id', 'source_id', ''),
+ ]
+ vector_strings = [
+ ('image/attributes', None, ''),
+ ('image/object/text', 'groundtruth_text', ''),
+ ('image/object/encoded_text', 'groundtruth_encoded_text', ''),
+ ('image/object/vertices', 'groundtruth_vertices', ''),
+ ('image/object/object_type', None, ''),
+ ('image/object/language', 'language', ''),
+ ('image/object/reorderer_type', None, ''),
+ ('image/label_map_path', 'label_map_path', '')
+ ]
+ scalar_ints = [
+ ('image/height', None, 1),
+ ('image/width', None, 1),
+ ('image/channels', None, 3),
+ ]
+ vector_ints = [
+ ('image/object/classes', 'groundtruth_classes', 0),
+ ('image/object/frame_id', 'frame_id', 0),
+ ('image/object/track_id', 'track_id', 0),
+ ('image/object/content_type', 'groundtruth_content_type', 0),
+ ]
+ if additional_class_names:
+ vector_ints += [('image/object/%s' % name, 'groundtruth_%s' % name, 0)
+ for name in additional_class_names]
+ # This one is not yet needed:
+ # scalar_floats = [
+ # ]
+ vector_floats = [
+ ('image/object/weight', 'groundtruth_weight', 0),
+ ('image/object/rbox_tl_x', None, 0),
+ ('image/object/rbox_tl_y', None, 0),
+ ('image/object/rbox_width', None, 0),
+ ('image/object/rbox_height', None, 0),
+ ('image/object/rbox_angle', None, 0),
+ ('image/object/bbox/xmin', None, 0),
+ ('image/object/bbox/xmax', None, 0),
+ ('image/object/bbox/ymin', None, 0),
+ ('image/object/bbox/ymax', None, 0),
+ ]
+ if additional_regression_names:
+ vector_floats += [('image/object/%s' % name, 'groundtruth_%s' % name, 0)
+ for name in additional_regression_names]
+
+ self._init_scalar_features(scalar_strings, tf.string)
+ self._init_vector_features(vector_strings, tf.string)
+ self._init_scalar_features(scalar_ints, tf.int64)
+ self._init_vector_features(vector_ints, tf.int64)
+ self._init_vector_features(vector_floats, tf.float32)
+
+ def _init_scalar_features(
+ self,
+ feature_list: List[Tuple[str, Optional[str], Union[str, int, float]]],
+ ftype: tf.dtypes.DType) -> None:
+ for entry in feature_list:
+ self.keys_to_features[entry[0]] = tf.io.FixedLenFeature(
+ (), ftype, default_value=entry[2])
+ if entry[1] is not None:
+ self.name_to_key[entry[1]] = entry[0]
+
+ def _init_vector_features(
+ self,
+ feature_list: List[Tuple[str, Optional[str], Union[str, int, float]]],
+ ftype: tf.dtypes.DType) -> None:
+ for entry in feature_list:
+ self.keys_to_features[entry[0]] = tf.io.VarLenFeature(ftype)
+ if entry[1] is not None:
+ self.name_to_key[entry[1]] = entry[0]
+
+ def _decode_png_instance_masks(self, keys_to_tensors: TensorDict)-> tf.Tensor:
+ """Decode PNG instance segmentation masks and stack into dense tensor.
+
+ The instance segmentation masks are reshaped to [num_instances, height,
+ width].
+
+ Args:
+ keys_to_tensors: A dictionary from keys to tensors.
+
+ Returns:
+ A 3-D float tensor of shape [num_instances, height, width] with values
+ in {0, 1}.
+ """
+
+ def decode_png_mask(image_buffer):
+ image = tf.squeeze(
+ tf.image.decode_image(image_buffer, channels=1), axis=2)
+ image.set_shape([None, None])
+ image = tf.to_float(tf.greater(image, 0))
+ return image
+
+ png_masks = keys_to_tensors['image/object/mask']
+ height = keys_to_tensors['image/height']
+ width = keys_to_tensors['image/width']
+ if isinstance(png_masks, tf.SparseTensor):
+ png_masks = tf.sparse_tensor_to_dense(png_masks, default_value='')
+ return tf.cond(
+ tf.greater(tf.size(png_masks), 0),
+ lambda: tf.map_fn(decode_png_mask, png_masks, dtype=tf.float32),
+ lambda: tf.zeros(tf.to_int32(tf.stack([0, height, width]))))
+
+ def _decode_image(self,
+ parsed_tensors: TensorDict,
+ channel: int = 3) -> TensorDict:
+ """Decodes the image and set its shape (H, W are dynamic; C is fixed)."""
+ image = tf.io.decode_image(parsed_tensors['image/encoded'],
+ channels=channel)
+ image.set_shape([None, None, channel])
+ return {'image': image}
+
+ def _decode_additional_channels(self,
+ parsed_tensors: TensorDict,
+ channel: int = 3) -> TensorDict:
+ """Decodes the additional channels and set its static shape."""
+ channels = tf.io.decode_image(
+ parsed_tensors['image/additional_channels/encoded'], channels=channel)
+ channels.set_shape([None, None, channel])
+ return {'additional_channels': channels}
+
+ def _decode_boxes(self, parsed_tensors: TensorDict) -> TensorDict:
+ """Concat box coordinates in the format of [ymin, xmin, ymax, xmax]."""
+ xmin = parsed_tensors['image/object/bbox/xmin']
+ xmax = parsed_tensors['image/object/bbox/xmax']
+ ymin = parsed_tensors['image/object/bbox/ymin']
+ ymax = parsed_tensors['image/object/bbox/ymax']
+ return {
+ 'groundtruth_aligned_boxes': tf.stack([ymin, xmin, ymax, xmax], axis=-1)
+ }
+
+ def _decode_rboxes(self, parsed_tensors: TensorDict) -> TensorDict:
+ """Concat rbox coordinates: [left, top, box_width, box_height, angle]."""
+ top_left_x = parsed_tensors['image/object/rbox_tl_x']
+ top_left_y = parsed_tensors['image/object/rbox_tl_y']
+ width = parsed_tensors['image/object/rbox_width']
+ height = parsed_tensors['image/object/rbox_height']
+ angle = parsed_tensors['image/object/rbox_angle']
+ return {
+ 'groundtruth_boxes':
+ tf.stack([top_left_x, top_left_y, width, height, angle], axis=-1)
+ }
+
+ def _decode_masks(self, parsed_tensors: TensorDict) -> TensorDict:
+ """Decode a set of PNG masks to the tf.float32 tensors."""
+
+ def _decode_png_mask(png_bytes):
+ mask = tf.squeeze(
+ tf.io.decode_png(png_bytes, channels=1, dtype=tf.uint8), axis=-1)
+ mask = tf.cast(mask, dtype=tf.float32)
+ mask.set_shape([None, None])
+ return mask
+
+ height = parsed_tensors['image/height']
+ width = parsed_tensors['image/width']
+ masks = parsed_tensors['image/object/mask']
+ masks = tf.cond(
+ pred=tf.greater(tf.size(input=masks), 0),
+ true_fn=lambda: tf.map_fn(_decode_png_mask, masks, dtype=tf.float32),
+ false_fn=lambda: tf.zeros([0, height, width], dtype=tf.float32))
+ return {'groundtruth_instance_masks': masks}
+
+ def decode(self, tf_example_string_tensor: tf.string):
+ """Decodes serialized tensorflow example and returns a tensor dictionary.
+
+ Args:
+ tf_example_string_tensor: A string tensor holding a serialized tensorflow
+ example proto.
+
+ Returns:
+ A dictionary contains a subset of the following, depends on the inputs:
+ image: A uint8 tensor of shape [height, width, 3] containing the image.
+ source_id: A string tensor contains image fingerprint.
+ key: A string tensor contains the unique sha256 hash key.
+ label_type: Either `full` or `partial`. `full` means all the text are
+ fully labeled, `partial` otherwise. Currently, this is used by E2E
+ model. If an input image is fully labeled, we update the weights of
+ both the detection and the recognizer. Otherwise, only recognizer part
+ of the model is trained.
+ groundtruth_text: A string tensor list, the original transcriptions.
+ groundtruth_encoded_text: A string tensor list, the class ids for the
+ atoms in the text, after applying the reordering algorithm, in string
+ form. For example "90,71,85,69,86,85,93,90,71,91,1,71,85,93,90,71".
+ This depends on the class label map provided to the conversion
+ program. These are 0 based, with -1 for OOV symbols.
+ groundtruth_classes: A int32 tensor of shape [num_boxes] contains the
+ class id. Note this is 1 based, 0 is reserved for background class.
+ groundtruth_content_type: A int32 tensor of shape [num_boxes] contains
+ the content type. Values correspond to PageLayoutEntity::ContentType.
+ groundtruth_weight: A int32 tensor of shape [num_boxes], either 0 or 1.
+ If a region has weight 0, it will be ignored when computing the
+ losses.
+ groundtruth_boxes: A float tensor of shape [num_boxes, 5] contains the
+ groundtruth rotated rectangles. Each row is in [left, top, box_width,
+ box_height, angle] order, absolute coordinates are used.
+ groundtruth_aligned_boxes: A float tensor of shape [num_boxes, 4]
+ contains the groundtruth axis-aligned rectangles. Each row is in
+ [ymin, xmin, ymax, xmax] order. Currently, this is used to store
+ groundtruth symbol boxes.
+ groundtruth_vertices: A string tensor list contains encoded normalized
+ box or polygon coordinates. E.g. `x1,y1,x2,y2,x3,y3,x4,y4`.
+ groundtruth_instance_masks: A float tensor of shape [num_boxes, height,
+ width] contains binarized image sized instance segmentation masks.
+ `1.0` for positive region, `0.0` otherwise. None if not in tfe.
+ frame_id: A int32 tensor of shape [num_boxes], either `0` or `1`.
+ `0` means object comes from first image, `1` means second.
+ track_id: A int32 tensor of shape [num_boxes], where value indicates
+ identity across frame indices.
+ additional_channels: A uint8 tensor of shape [H, W, C] representing some
+ features.
+ """
+ parsed_tensors = tf.io.parse_single_example(
+ serialized=tf_example_string_tensor, features=self.keys_to_features)
+ for k in parsed_tensors:
+ if isinstance(parsed_tensors[k], tf.SparseTensor):
+ if parsed_tensors[k].dtype == tf.string:
+ parsed_tensors[k] = tf.sparse.to_dense(
+ parsed_tensors[k], default_value='')
+ else:
+ parsed_tensors[k] = tf.sparse.to_dense(
+ parsed_tensors[k], default_value=0)
+
+ decoded_tensors = {}
+ decoded_tensors.update(self._decode_image(parsed_tensors))
+ decoded_tensors.update(self._decode_rboxes(parsed_tensors))
+ decoded_tensors.update(self._decode_boxes(parsed_tensors))
+ if self._use_instance_mask:
+ decoded_tensors[
+ 'groundtruth_instance_masks'] = self._decode_png_instance_masks(
+ parsed_tensors)
+ if self._num_additional_channels:
+ decoded_tensors.update(self._decode_additional_channels(
+ parsed_tensors, self._num_additional_channels))
+
+ # other attributes:
+ for key in self.name_to_key:
+ if key not in decoded_tensors:
+ decoded_tensors[key] = parsed_tensors[self.name_to_key[key]]
+
+ if 'groundtruth_instance_masks' not in decoded_tensors:
+ decoded_tensors['groundtruth_instance_masks'] = None
+
+ return decoded_tensors
diff --git a/official/projects/unified_detector/data_loaders/universal_detection_parser.py b/official/projects/unified_detector/data_loaders/universal_detection_parser.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a4011360656a68c91d9e723f486975f4a1f0d4c
--- /dev/null
+++ b/official/projects/unified_detector/data_loaders/universal_detection_parser.py
@@ -0,0 +1,606 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Data parser for universal detector."""
+
+import enum
+import functools
+from typing import Any, Tuple
+
+import gin
+import tensorflow as tf
+
+from official.projects.unified_detector.data_loaders import autoaugment
+from official.projects.unified_detector.data_loaders import tf_example_decoder
+from official.projects.unified_detector.utils import utilities
+from official.projects.unified_detector.utils.typing import NestedTensorDict
+from official.projects.unified_detector.utils.typing import TensorDict
+
+
+@gin.constants_from_enum
+class DetectionClass(enum.IntEnum):
+ """As in `PageLayoutEntity.EntityType`."""
+ WORD = 0
+ LINE = 2
+ PARAGRAPH = 3
+ BLOCK = 4
+
+
+NOT_ANNOTATED_ID = 8
+
+
+def _erase(mask: tf.Tensor,
+ feature: tf.Tensor,
+ min_val: float = 0.,
+ max_val: float = 256.) -> tf.Tensor:
+ """Erase the feature maps with a mask.
+
+ Erase feature maps with a mask and replace the erased area with uniform random
+ noise. The mask can have different size from the feature maps.
+
+ Args:
+ mask: an (h, w) binay mask for pixels to erase with. Value 1 represents
+ pixels to erase.
+ feature: the (H, W, C) feature maps to erase from.
+ min_val: The minimum value of random noise.
+ max_val: The maximum value of random noise.
+
+ Returns:
+ The (H, W, C) feature maps, with pixels in mask replaced with noises. It's
+ equal to mask * noise + (1 - mask) * feature.
+ """
+ h, w, c = utilities.resolve_shape(feature)
+ resized_mask = tf.image.resize(
+ tf.tile(tf.expand_dims(tf.cast(mask, tf.float32), -1), (1, 1, c)), (h, w))
+ erased = tf.where(
+ condition=(resized_mask > 0.5),
+ x=tf.cast(tf.random.uniform((h, w, c), min_val, max_val), feature.dtype),
+ y=feature)
+ return erased
+
+
+@gin.configurable(denylist=['is_training'])
+class UniDetectorParserFn(object):
+ """Data parser for universal detector."""
+
+ def __init__(
+ self,
+ is_training: bool,
+ output_dimension: int = 1025,
+ mask_dimension: int = -1,
+ max_num_instance: int = 128,
+ rot90_probability: float = 0.5,
+ use_color_distortion: bool = True,
+ randaug_mag: float = 5.,
+ randaug_std: float = 0.5,
+ randaug_layer: int = 2,
+ randaug_prob: float = 0.5,
+ use_cropping: bool = True,
+ crop_min_scale: float = 0.5,
+ crop_max_scale: float = 1.5,
+ crop_min_aspect: float = 4 / 5,
+ crop_max_aspect: float = 5 / 4,
+ is_shape_defined: bool = True,
+ use_tpu: bool = True,
+ detection_unit: DetectionClass = DetectionClass.LINE,
+ ):
+ """Constructor.
+
+ Args:
+ is_training: bool indicating TRAIN or EVAL.
+ output_dimension: The size of input images.
+ mask_dimension: The size of the output mask. If negative or zero, it will
+ be set the same as output_dimension.
+ max_num_instance: The maximum number of instances to output. If it's
+ negative, padding or truncating will not be performed.
+ rot90_probability: The probability of rotating multiples of 90 degrees.
+ use_color_distortion: Whether to apply color distortions to images (via
+ autoaugment).
+ randaug_mag: (autoaugment parameter) Color distortion magnitude. Note
+ that, this value should be set conservatively, as some color distortions
+ can easily make text illegible e.g. posterize.
+ randaug_std: (autoaugment parameter) Randomness in color distortion
+ magnitude.
+ randaug_layer: (autoaugment parameter) Number of color distortion
+ operations.
+ randaug_prob: (autoaugment parameter) Probabilily of applying each
+ distortion operation.
+ use_cropping: Bool, whether to use random cropping and resizing in
+ training.
+ crop_min_scale: The minimum scale of a random crop.
+ crop_max_scale: The maximum scale of a random crop. If >1, it means the
+ images are downsampled.
+ crop_min_aspect: The minimum aspect ratio of a random crop.
+ crop_max_aspect: The maximum aspect ratio of a random crop.
+ is_shape_defined: Whether to define the static shapes for all features and
+ labels. This must be set to True in TPU training as it requires static
+ shapes for all tensors.
+ use_tpu: Whether the inputs are fed to a TPU device.
+ detection_unit: Whether word or line (or else) is regarded as an entity.
+ The instance masks will be at word or line level.
+ """
+ if is_training and max_num_instance < 0:
+ raise ValueError('In TRAIN mode, padding/truncation is required.')
+
+ self._is_training = is_training
+ self._output_dimension = output_dimension
+ self._mask_dimension = (
+ mask_dimension if mask_dimension > 0 else output_dimension)
+ self._max_num_instance = max_num_instance
+ self._decoder = tf_example_decoder.TfExampleDecoder(
+ num_additional_channels=3, additional_class_names=['parent'])
+ self._use_color_distortion = use_color_distortion
+ self._rot90_probability = rot90_probability
+ self._randaug_mag = randaug_mag
+ self._randaug_std = randaug_std
+ self._randaug_layer = randaug_layer
+ self._randaug_prob = randaug_prob
+ self._use_cropping = use_cropping
+ self._crop_min_scale = crop_min_scale
+ self._crop_max_scale = crop_max_scale
+ self._crop_min_aspect = crop_min_aspect
+ self._crop_max_aspect = crop_max_aspect
+ self._is_shape_defined = is_shape_defined
+ self._use_tpu = use_tpu
+ self._detection_unit = detection_unit
+
+ def __call__(self, value: str) -> Tuple[TensorDict, NestedTensorDict]:
+ """Parsing the data.
+
+ Args:
+ value: The serialized data sample.
+
+ Returns:
+ Two dicts for features and labels.
+ features:
+ 'source_id': id of the sample; only in EVAL mode
+ 'images': the normalized images, (output_dimension, output_dimension, 3)
+ labels:
+ See `_prepare_labels` for its content.
+ """
+ data = self._decoder.decode(value)
+ features = {}
+ labels = {}
+ self._preprocess(data, features, labels)
+ self._rot90k(data, features, labels)
+ self._crop_and_resize(data, features, labels)
+ self._color_distortion_and_normalize(data, features, labels)
+ self._prepare_labels(data, features, labels)
+ self._define_shapes(features, labels)
+ return features, labels
+
+ def _preprocess(self, data: TensorDict, features: TensorDict,
+ unused_labels: TensorDict):
+ """All kinds of preprocessing of the decoded data dict."""
+ # (1) Decode the entity_id_mask: a H*W*1 mask, each pixel equals to
+ # (1 + position) of the entity in the GT entity list. The IDs
+ # (which can be larger than 255) are stored in the last two channels.
+ data['additional_channels'] = tf.cast(data['additional_channels'], tf.int32)
+ entity_id_mask = (
+ data['additional_channels'][:, :, -2:-1] * 256 +
+ data['additional_channels'][:, :, -1:])
+ data['entity_id_mask'] = entity_id_mask
+
+ # (2) Write image id. Used in evaluation.
+ if not self._use_tpu:
+ features['source_id'] = data['source_id']
+
+ # (3) Block mask: area without annotation
+ data['image'] = _erase(
+ data['additional_channels'][:, :, 0],
+ data['image'],
+ min_val=0.,
+ max_val=256.)
+
+ def _rot90k(self, data: TensorDict, unused_features: TensorDict,
+ unused_labels: TensorDict):
+ """Rotate the image, gt_bboxes, masks by 90k degrees."""
+ if not self._is_training:
+ return
+
+ rotate_90_choice = tf.random.uniform([])
+
+ def _rotate():
+ """Rotation.
+
+ These will be rotated:
+ image,
+ rbox,
+ entity_id_mask,
+ TODO(longshangbang): rotate vertices.
+
+ Returns:
+ The rotated tensors of the above fields.
+ """
+ k = tf.random.uniform([], 1, 4, dtype=tf.int32)
+ h, w, _ = utilities.resolve_shape(data['image'])
+ # Image
+ rotated_img = tf.image.rot90(data['image'], k=k, name='image_rot90k')
+ # Box
+ rotate_box_op = functools.partial(
+ utilities.rotate_rboxes90,
+ rboxes=data['groundtruth_boxes'],
+ image_width=w,
+ image_height=h)
+ rotated_boxes = tf.switch_case(
+ k - 1, # Indices start with 1.
+ branch_fns=[
+ lambda: rotate_box_op(rotation_count=1),
+ lambda: rotate_box_op(rotation_count=2),
+ lambda: rotate_box_op(rotation_count=3)
+ ])
+ # Mask
+ rotated_mask = tf.image.rot90(
+ data['entity_id_mask'], k=k, name='mask_rot90k')
+ return rotated_img, rotated_boxes, rotated_mask
+
+ # pylint: disable=g-long-lambda
+ (data['image'], data['groundtruth_boxes'],
+ data['entity_id_mask']) = tf.cond(
+ rotate_90_choice < self._rot90_probability, _rotate, lambda:
+ (data['image'], data['groundtruth_boxes'], data['entity_id_mask']))
+ # pylint: enable=g-long-lambda
+
+ def _crop_and_resize(self, data: TensorDict, unused_features: TensorDict,
+ unused_labels: TensorDict):
+ """Perform random cropping and resizing."""
+ # TODO(longshangbang): resize & translate box as well
+ # TODO(longshangbang): resize & translate vertices as well
+
+ # Get cropping target.
+ h, w = utilities.resolve_shape(data['image'])[:2]
+ left, top, crop_w, crop_h, pad_w, pad_h = self._get_crop_box(
+ tf.cast(h, tf.float32), tf.cast(w, tf.float32))
+
+ # Crop the image. (Pad the images if the crop box is larger than image.)
+ if self._is_training:
+ # padding left, top, right, bottom
+ pad_left = tf.random.uniform([], 0, pad_w + 1, dtype=tf.int32)
+ pad_top = tf.random.uniform([], 0, pad_h + 1, dtype=tf.int32)
+ else:
+ pad_left = 0
+ pad_top = 0
+ cropped_img = tf.image.crop_to_bounding_box(data['image'], top, left,
+ crop_h, crop_w)
+ padded_img = tf.pad(
+ cropped_img,
+ [[pad_top, pad_h - pad_top], [pad_left, pad_w - pad_left], [0, 0]],
+ constant_values=127)
+
+ # Resize images
+ data['resized_image'] = tf.image.resize(
+ padded_img, (self._output_dimension, self._output_dimension))
+ data['resized_image'] = tf.cast(data['resized_image'], tf.uint8)
+
+ # Crop the masks
+ cropped_masks = tf.image.crop_to_bounding_box(data['entity_id_mask'], top,
+ left, crop_h, crop_w)
+ padded_masks = tf.pad(
+ cropped_masks,
+ [[pad_top, pad_h - pad_top], [pad_left, pad_w - pad_left], [0, 0]])
+
+ # Resize masks
+ data['resized_masks'] = tf.image.resize(
+ padded_masks, (self._mask_dimension, self._mask_dimension),
+ method=tf.image.ResizeMethod.NEAREST_NEIGHBOR)
+ data['resized_masks'] = tf.squeeze(data['resized_masks'], -1)
+
+ def _get_crop_box(
+ self, h: tf.Tensor,
+ w: tf.Tensor) -> Tuple[Any, Any, tf.Tensor, tf.Tensor, Any, Any]:
+ """Get the cropping box.
+
+ Args:
+ h: The height of the image to crop. Should be float type.
+ w: The width of the image to crop. Should be float type.
+
+ Returns:
+ A tuple representing (left, top, crop_w, crop_h, pad_w, pad_h).
+ Then in `self._crop_and_resize`, a crop will be extracted with bounding
+ box from top-left corner (left, top) and with size (crop_w, crop_h). This
+ crop will then be padded with (pad_w, pad_h) to square sizes.
+ The outputs also are re-cast to int32 type.
+ """
+ if not self._is_training or not self._use_cropping:
+ # cast back to integers.
+ w = tf.cast(w, tf.int32)
+ h = tf.cast(h, tf.int32)
+ side = tf.maximum(w, h)
+ return 0, 0, w, h, side - w, side - h
+
+ # Get box size
+ scale = tf.random.uniform([], self._crop_min_scale, self._crop_max_scale)
+ max_edge = tf.maximum(w, h)
+ long_edge = max_edge * scale
+
+ sqrt_aspect_ratio = tf.math.sqrt(
+ tf.random.uniform([], self._crop_min_aspect, self._crop_max_aspect))
+ box_h = long_edge / sqrt_aspect_ratio
+ box_w = long_edge * sqrt_aspect_ratio
+
+ # Get box location
+ left = tf.random.uniform([], 0., tf.maximum(0., w - box_w))
+ top = tf.random.uniform([], 0., tf.maximum(0., h - box_h))
+ # Get crop & pad
+ crop_w = tf.minimum(box_w, w - left)
+ crop_h = tf.minimum(box_h, h - top)
+ pad_w = box_w - crop_w
+ pad_h = box_h - crop_h
+ return (tf.cast(left, tf.int32), tf.cast(top, tf.int32),
+ tf.cast(crop_w, tf.int32), tf.cast(crop_h, tf.int32),
+ tf.cast(pad_w, tf.int32), tf.cast(pad_h, tf.int32))
+
+ def _color_distortion_and_normalize(self, data: TensorDict,
+ features: TensorDict,
+ unused_labels: TensorDict):
+ """Distort colors."""
+ if self._is_training and self._use_color_distortion:
+ data['resized_image'] = autoaugment.distort_image_with_randaugment(
+ data['resized_image'], self._randaug_layer, self._randaug_mag,
+ self._randaug_std, True, self._randaug_prob, True)
+ # Normalize
+ features['images'] = utilities.normalize_image_to_range(
+ data['resized_image'])
+
+ def _prepare_labels(self, data: TensorDict, features: TensorDict,
+ labels: TensorDict):
+ """This function prepares the labels.
+
+ These following targets are added to labels['segmentation_output']:
+ 'gt_word_score': A (h, w) float32 mask for textness score. 1 for word,
+ 0 for bkg.
+
+ These following targets are added to labels['instance_labels']:
+ 'num_instance': A float scalar tensor for the total number of
+ instances. It is bounded by the maximum number of instances allowed.
+ It includes the special background instance, so it equals to
+ (1 + entity numbers).
+ 'masks': A (h, w) int32 mask for entity IDs. The value of each pixel is
+ the id of the entity it belongs to. A value of `0` means the bkg mask.
+ 'classes': A (max_num,) int tensor indicating the classes of each
+ instance:
+ 2 for background
+ 1 for text entity
+ 0 for non-object
+ 'masks_sizes': A (max_num,) float tensor for the size of all masks.
+ 'gt_weights': Whether it's difficult / does not have text annotation.
+
+ These following targets are added to labels['paragraph_labels']:
+ 'paragraph_ids': A (max_num,) integer tensor for paragprah id. if `-1`,
+ then no paragraph label for this text.
+ 'has_para_ids': A float scalar; 1.0 if the sample has paragraph labels.
+
+ Args:
+ data: The data dictionary.
+ features: The feature dict.
+ labels: The label dict.
+ """
+ # Segmentation labels:
+ self._get_segmentation_labels(data, features, labels)
+ # Instance labels:
+ self._get_instance_labels(data, features, labels)
+
+ def _get_segmentation_labels(self, data: TensorDict,
+ unused_features: TensorDict,
+ labels: NestedTensorDict):
+ labels['segmentation_output'] = {
+ 'gt_word_score': tf.cast((data['resized_masks'] > 0), tf.float32)
+ }
+
+ def _get_instance_labels(self, data: TensorDict, features: TensorDict,
+ labels: NestedTensorDict):
+ """Generate the labels for text entity detection."""
+
+ labels['instance_labels'] = {}
+ # (1) Depending on `detection_unit`:
+ # Convert the word-id map to line-id map or use the word-id map directly
+ # Word entity ids start from 1 in the map, so pad a -1 at the beginning of
+ # the parent list to counter this offset.
+ padded_parent = tf.concat(
+ [tf.constant([-1]),
+ tf.cast(data['groundtruth_parent'], tf.int32)], 0)
+ if self._detection_unit == DetectionClass.WORD:
+ entity_id_mask = data['resized_masks']
+ elif self._detection_unit == DetectionClass.LINE:
+ # The pixel value is entity_id + 1, shape = [H, W]; 0 for background.
+ # correctness:
+ # 0s in data['resized_masks'] --> padded_parent[0] == -1
+ # i-th entity in plp.entities --> i+1 in data['resized_masks']
+ # --> padded_parent[i+1]
+ # --> data['groundtruth_parent'][i]
+ # --> the parent of i-th entity
+ entity_id_mask = tf.gather(padded_parent, data['resized_masks']) + 1
+ elif self._detection_unit == DetectionClass.PARAGRAPH:
+ # directly segmenting paragraphs; two hops here.
+ entity_id_mask = tf.gather(padded_parent, data['resized_masks']) + 1
+ entity_id_mask = tf.gather(padded_parent, entity_id_mask) + 1
+ else:
+ raise ValueError(f'No such detection unit: {self._detection_unit}')
+ data['entity_id_mask'] = entity_id_mask
+
+ # (2) Get individual masks for entities.
+ entity_selection_mask = tf.equal(data['groundtruth_classes'],
+ self._detection_unit)
+ num_all_entity = utilities.resolve_shape(data['groundtruth_classes'])[0]
+ # entity_ids is a 1-D tensor for IDs of all entities of a certain type.
+ entity_ids = tf.boolean_mask(
+ tf.range(num_all_entity, dtype=tf.int32), entity_selection_mask) # (N,)
+ # +1 to match the entity ids in entity_id_mask
+ entity_ids = tf.reshape(entity_ids, (-1, 1, 1)) + 1
+ individual_masks = tf.expand_dims(entity_id_mask, 0)
+ individual_masks = tf.equal(entity_ids, individual_masks) # (N, H, W), bool
+ # TODO(longshangbang): replace with real mask sizes computing.
+ # Currently, we use full-resolution masks for individual_masks. In order to
+ # compute mask sizes, we need to convert individual_masks to int/float type.
+ # This will cause OOM because the mask is too large.
+ masks_sizes = tf.cast(
+ tf.reduce_any(individual_masks, axis=[1, 2]), tf.float32)
+ # remove empty masks (usually caused by cropping)
+ non_empty_masks_ids = tf.not_equal(masks_sizes, 0)
+ valid_masks = tf.boolean_mask(individual_masks, non_empty_masks_ids)
+ valid_entity_ids = tf.boolean_mask(entity_ids, non_empty_masks_ids)[:, 0, 0]
+
+ # (3) Write num of instance
+ num_instance = tf.reduce_sum(tf.cast(non_empty_masks_ids, tf.float32))
+ num_instance_and_bkg = num_instance + 1
+ if self._max_num_instance >= 0:
+ num_instance_and_bkg = tf.minimum(num_instance_and_bkg,
+ self._max_num_instance)
+ labels['instance_labels']['num_instance'] = num_instance_and_bkg
+
+ # (4) Write instance masks
+ num_entity_int = tf.cast(num_instance, tf.int32)
+ max_num_entities = self._max_num_instance - 1 # Spare 1 for bkg.
+ pad_num = tf.maximum(max_num_entities - num_entity_int, 0)
+ padded_valid_masks = tf.pad(valid_masks, [[0, pad_num], [0, 0], [0, 0]])
+
+ # If there are more instances than allowed, randomly sample some.
+ # `random_selection_mask` is a 0/1 array; the maximum number of 1 is
+ # `self._max_num_instance`; if not bound, it's an array with all 1s.
+ if self._max_num_instance >= 0:
+ padded_size = num_entity_int + pad_num
+ random_selection = tf.random.uniform((padded_size,), dtype=tf.float32)
+ selected_indices = tf.math.top_k(random_selection, k=max_num_entities)[1]
+ random_selection_mask = tf.scatter_nd(
+ indices=tf.expand_dims(selected_indices, axis=-1),
+ updates=tf.ones((max_num_entities,), dtype=tf.bool),
+ shape=(padded_size,))
+ else:
+ random_selection_mask = tf.ones((num_entity_int,), dtype=tf.bool)
+ random_discard_mask = tf.logical_not(random_selection_mask)
+
+ kept_masks = tf.boolean_mask(padded_valid_masks, random_selection_mask)
+ erased_masks = tf.boolean_mask(padded_valid_masks, random_discard_mask)
+ erased_masks = tf.cast(tf.reduce_any(erased_masks, axis=0), tf.float32)
+ # erase text instances that are obmitted.
+ features['images'] = _erase(erased_masks, features['images'], -1., 1.)
+ labels['segmentation_output']['gt_word_score'] *= 1. - erased_masks
+ kept_masks_and_bkg = tf.concat(
+ [
+ tf.math.logical_not(
+ tf.reduce_any(kept_masks, axis=0, keepdims=True)), # bkg
+ kept_masks,
+ ],
+ 0)
+ labels['instance_labels']['masks'] = tf.argmax(kept_masks_and_bkg, axis=0)
+
+ # (5) Write mask size
+ # TODO(longshangbang): replace with real masks sizes
+ masks_sizes = tf.cast(
+ tf.reduce_any(kept_masks_and_bkg, axis=[1, 2]), tf.float32)
+ labels['instance_labels']['masks_sizes'] = masks_sizes
+ # (6) Write classes.
+ classes = tf.ones((num_instance,), dtype=tf.int32)
+ classes = tf.concat([tf.constant(2, tf.int32, (1,)), classes], 0) # bkg
+ if self._max_num_instance >= 0:
+ classes = utilities.truncate_or_pad(classes, self._max_num_instance, 0)
+ labels['instance_labels']['classes'] = classes
+
+ # (7) gt-weights
+ selected_ids = tf.boolean_mask(valid_entity_ids,
+ random_selection_mask[:num_entity_int])
+
+ if self._detection_unit != DetectionClass.PARAGRAPH:
+ gt_text = tf.gather(data['groundtruth_text'], selected_ids - 1)
+ gt_weights = tf.cast(tf.strings.length(gt_text) > 0, tf.float32)
+ else:
+ text_types = tf.concat(
+ [
+ tf.constant([8]),
+ tf.cast(data['groundtruth_content_type'], tf.int32),
+ # TODO(longshangbang): temp solution for tfes with no para labels
+ tf.constant(8, shape=(1000,)),
+ ],
+ 0)
+ para_types = tf.gather(text_types, selected_ids)
+
+ gt_weights = tf.cast(
+ tf.not_equal(para_types, NOT_ANNOTATED_ID), tf.float32)
+
+ gt_weights = tf.concat([tf.constant(1., shape=(1,)), gt_weights], 0) # bkg
+ if self._max_num_instance >= 0:
+ gt_weights = utilities.truncate_or_pad(
+ gt_weights, self._max_num_instance, 0)
+ labels['instance_labels']['gt_weights'] = gt_weights
+
+ # (8) get paragraph label
+ # In this step, an array `{p_i}` is generated. `p_i` is an integer that
+ # indicates the group of paragraph which i-th text belongs to. `p_i` == -1
+ # if this instance is non-text or it has no paragraph labels.
+ # word -> line -> paragraph
+ if self._detection_unit == DetectionClass.WORD:
+ num_hop = 2
+ elif self._detection_unit == DetectionClass.LINE:
+ num_hop = 1
+ elif self._detection_unit == DetectionClass.PARAGRAPH:
+ num_hop = 0
+ else:
+ raise ValueError(f'No such detection unit: {self._detection_unit}. '
+ 'Note that this error should have been raised in '
+ 'previous lines, not here!')
+ para_ids = tf.identity(selected_ids) # == id in plp + 1
+ for _ in range(num_hop):
+ para_ids = tf.gather(padded_parent, para_ids) + 1
+
+ text_types = tf.concat(
+ [
+ tf.constant([8]),
+ tf.cast(data['groundtruth_content_type'], tf.int32),
+ # TODO(longshangbang): tricks for tfes that have not para labels
+ tf.constant(8, shape=(1000,)),
+ ],
+ 0)
+ para_types = tf.gather(text_types, para_ids)
+
+ para_ids = para_ids - 1 # revert to id in plp.entities; -1 for no labels
+ valid_para = tf.cast(tf.not_equal(para_types, NOT_ANNOTATED_ID), tf.int32)
+ para_ids = valid_para * para_ids + (1 - valid_para) * (-1)
+ para_ids = tf.concat([tf.constant([-1]), para_ids], 0) # add bkg
+
+ has_para_ids = tf.cast(tf.reduce_sum(valid_para) > 0, tf.float32)
+
+ if self._max_num_instance >= 0:
+ para_ids = utilities.truncate_or_pad(
+ para_ids, self._max_num_instance, 0, -1)
+ labels['paragraph_labels'] = {
+ 'paragraph_ids': para_ids,
+ 'has_para_ids': has_para_ids
+ }
+
+ def _define_shapes(self, features: TensorDict, labels: TensorDict):
+ """Define the tensor shapes for TPU compiling."""
+ if not self._is_shape_defined:
+ return
+ features['images'] = tf.ensure_shape(
+ features['images'], (self._output_dimension, self._output_dimension, 3))
+ labels['segmentation_output']['gt_word_score'] = tf.ensure_shape(
+ labels['segmentation_output']['gt_word_score'],
+ (self._mask_dimension, self._mask_dimension))
+ labels['instance_labels']['num_instance'] = tf.ensure_shape(
+ labels['instance_labels']['num_instance'], [])
+ if self._max_num_instance >= 0:
+ labels['instance_labels']['masks_sizes'] = tf.ensure_shape(
+ labels['instance_labels']['masks_sizes'], (self._max_num_instance,))
+ labels['instance_labels']['masks'] = tf.ensure_shape(
+ labels['instance_labels']['masks'],
+ (self._mask_dimension, self._mask_dimension))
+ labels['instance_labels']['classes'] = tf.ensure_shape(
+ labels['instance_labels']['classes'], (self._max_num_instance,))
+ labels['instance_labels']['gt_weights'] = tf.ensure_shape(
+ labels['instance_labels']['gt_weights'], (self._max_num_instance,))
+ labels['paragraph_labels']['paragraph_ids'] = tf.ensure_shape(
+ labels['paragraph_labels']['paragraph_ids'],
+ (self._max_num_instance,))
+ labels['paragraph_labels']['has_para_ids'] = tf.ensure_shape(
+ labels['paragraph_labels']['has_para_ids'], [])
diff --git a/official/projects/unified_detector/docs/images/task.png b/official/projects/unified_detector/docs/images/task.png
new file mode 100644
index 0000000000000000000000000000000000000000..342ecef630c424adb051ad46a8ee8bb85f7969e5
Binary files /dev/null and b/official/projects/unified_detector/docs/images/task.png differ
diff --git a/official/projects/unified_detector/external_configurables.py b/official/projects/unified_detector/external_configurables.py
new file mode 100644
index 0000000000000000000000000000000000000000..b10fc66a66256348c09098913352868063d9b76a
--- /dev/null
+++ b/official/projects/unified_detector/external_configurables.py
@@ -0,0 +1,22 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Wrap external code in gin."""
+
+import gin
+import gin.tf.external_configurables
+import tensorflow as tf
+
+# Tensorflow.
+gin.external_configurable(tf.keras.layers.experimental.SyncBatchNormalization)
diff --git a/official/projects/unified_detector/modeling/universal_detector.py b/official/projects/unified_detector/modeling/universal_detector.py
new file mode 100644
index 0000000000000000000000000000000000000000..a076701af78b679ffa3e83fcea5e191b42cec2bf
--- /dev/null
+++ b/official/projects/unified_detector/modeling/universal_detector.py
@@ -0,0 +1,888 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Universal detector implementation."""
+
+from typing import Any, Dict, Optional, Sequence, Tuple, Union
+
+import gin
+import tensorflow as tf
+
+from deeplab2 import config_pb2
+from deeplab2.model.decoder import max_deeplab as max_deeplab_head
+from deeplab2.model.encoder import axial_resnet_instances
+from deeplab2.model.loss import matchers_ops
+from official.legacy.transformer import transformer
+from official.projects.unified_detector.utils import typing
+from official.projects.unified_detector.utils import utilities
+
+
+EPSILON = 1e-6
+
+
+@gin.configurable
+def universal_detection_loss_weights(
+ loss_segmentation_word: float = 1e0,
+ loss_inst_dist: float = 1e0,
+ loss_mask_id: float = 1e-4,
+ loss_pq: float = 3e0,
+ loss_para: float = 1e0) -> Dict[str, float]:
+ """A function that returns a dict for the weights of loss terms."""
+ return {
+ "loss_segmentation_word": loss_segmentation_word,
+ "loss_inst_dist": loss_inst_dist,
+ "loss_mask_id": loss_mask_id,
+ "loss_pq": loss_pq,
+ "loss_para": loss_para,
+ }
+
+
+@gin.configurable
+class LayerNorm(tf.keras.layers.LayerNormalization):
+ """A wrapper to allow passing the `training` argument.
+
+ The normalization layers in the MaX-DeepLab implementation are passed with
+ the `training` argument. This wrapper enables the usage of LayerNorm.
+ """
+
+ def call(self,
+ inputs: tf.Tensor,
+ training: Optional[bool] = None) -> tf.Tensor:
+ del training
+ return super().call(inputs)
+
+
+@gin.configurable
+def get_max_deep_lab_backbone(num_slots: int = 128):
+ return axial_resnet_instances.get_model(
+ "max_deeplab_s",
+ bn_layer=LayerNorm,
+ block_group_config={
+ "drop_path_schedule": "linear",
+ "axial_use_recompute_grad": False
+ },
+ backbone_use_transformer_beyond_stride=16,
+ extra_decoder_use_transformer_beyond_stride=16,
+ num_mask_slots=num_slots,
+ max_num_mask_slots=num_slots)
+
+
+@gin.configurable
+class UniversalDetector(tf.keras.layers.Layer):
+ """Univeral Detector."""
+ loss_items = ("loss_pq", "loss_inst_dist", "loss_para", "loss_mask_id",
+ "loss_segmentation_word")
+
+ def __init__(self,
+ backbone_fn: tf.keras.layers.Layer = get_max_deep_lab_backbone,
+ mask_threshold: float = 0.4,
+ class_threshold: float = 0.5,
+ filter_area: float = 32,
+ **kwargs: Any):
+ """Constructor.
+
+ Args:
+ backbone_fn: The function to initialize a backbone.
+ mask_threshold: Masks are thresholded with this value.
+ class_threshold: Classification heads are thresholded with this value.
+ filter_area: In inference, detections with area smaller than this
+ threshold will be removed.
+ **kwargs: other keyword arguments passed to the base class.
+ """
+ super().__init__(**kwargs)
+
+ # Model
+ self._backbone_fn = backbone_fn()
+ self._decoder = _get_decoder_head()
+ self._class_embed_head, self._para_embed_head = _get_embed_head()
+ self._para_head, self._para_proj = _get_para_head()
+
+ # Losses
+ # self._max_deeplab_loss = _get_max_deeplab_loss()
+ self._loss_weights = universal_detection_loss_weights()
+
+ # Post-processing
+ self._mask_threshold = mask_threshold
+ self._class_threshold = class_threshold
+ self._filter_area = filter_area
+
+ def _preprocess_labels(self, labels: typing.TensorDict):
+ # Preprocessing
+ # Converted the integer mask to one-hot embedded masks.
+ num_instances = utilities.resolve_shape(
+ labels["instance_labels"]["masks_sizes"])[1]
+ labels["instance_labels"]["masks"] = tf.one_hot(
+ labels["instance_labels"]["masks"],
+ depth=num_instances,
+ axis=1,
+ dtype=tf.float32) # (B, N, H, W)
+
+ def compute_losses(
+ self, labels: typing.NestedTensorDict, outputs: typing.NestedTensorDict
+ ) -> Tuple[tf.Tensor, typing.NestedTensorDict]:
+ """Computes the loss.
+
+ Args:
+ labels: A dictionary of ground-truth labels.
+ outputs: Output from self.call().
+
+ Returns:
+ A scalar total loss tensor and a dictionary for individual losses.
+ """
+ loss_dict = {}
+
+ self._preprocess_labels(labels)
+
+ # Main loss: PQ loss.
+ _entity_mask_loss(loss_dict, labels["instance_labels"],
+ outputs["instance_output"])
+ # Auxiliary loss 1: semantic loss
+ _semantic_loss(loss_dict, labels["segmentation_output"],
+ outputs["segmentation_output"])
+ # Auxiliary loss 2: instance discrimination
+ _instance_discrimination_loss(loss_dict, labels["instance_labels"], outputs)
+ # Auxiliary loss 3: mask id
+ _mask_id_xent_loss(loss_dict, labels["instance_labels"], outputs)
+ # Auxiliary loss 4: paragraph grouping
+ _paragraph_grouping_loss(loss_dict, labels, outputs)
+
+ weighted_loss = [self._loss_weights[k] * v for k, v in loss_dict.items()]
+ total_loss = sum(weighted_loss)
+ return total_loss, loss_dict
+
+ def call(self,
+ features: typing.TensorDict,
+ training: bool = False) -> typing.NestedTensorDict:
+ """Forward pass of the model.
+
+ Args:
+ features: The input features: {"images": tf.Tensor}. Shape = [B, H, W, C]
+ training: Whether it's training mode.
+
+ Returns:
+ A dictionary of output with this structure:
+ {
+ "max_deep_lab": {
+ All the max deeplab outputs are here, including both backbone and
+ decoder.
+ }
+ "segmentation_output": {
+ "word_score": tf.Tensor, [B, h, w],
+ }
+ "instance_output": {
+ "cls_logits": tf.Tensor, [B, N, C],
+ "mask_id_logits": tf.Tensor, [B, H, W, N],
+ "cls_prob": tf.Tensor, [B, N, C],
+ "mask_id_prob": tf.Tensor, [B, H, W, N],
+ }
+ "postprocessed": {
+ "classes": A (B, N) tensor for the class ids. Zero for non-firing
+ slots.
+ "binary_masks": A (B, H, W, N) tensor for the N binary masks. Masks
+ for void cls are set to zero.
+ "confidence": A (B, N) float tensor for the confidence of "classes".
+ "mask_area": A (B, N) float tensor for the area of each mask.
+ }
+ "transformer_group_feature": (B, N, C) float tensor (normalized),
+ "para_affinity": (B, N, N) float tensor.
+ }
+
+ Class-0 is for void. Class-(C-1) is for background. Class-1~(C-2) is for
+ valid classes.
+ """
+ # backbone
+ backbone_output = self._backbone_fn(features["images"], training)
+ # split instance embedding and paragraph embedding;
+ # then perform paragraph grouping
+ para_fts = self._get_para_outputs(backbone_output, training)
+ affinity = tf.linalg.matmul(para_fts, para_fts, transpose_b=True)
+ # text detection head
+ decoder_output = self._decoder(backbone_output, training)
+ output_dict = {
+ "max_deep_lab": decoder_output,
+ "transformer_group_feature": para_fts,
+ "para_affinity": affinity,
+ }
+ input_shape = utilities.resolve_shape(features["images"])
+ self._get_semantic_outputs(output_dict, input_shape)
+ self._get_instance_outputs(output_dict, input_shape)
+ self._postprocess(output_dict)
+
+ return output_dict
+
+ def _get_para_outputs(self, outputs: typing.TensorDict,
+ training: bool) -> tf.Tensor:
+ """Apply the paragraph head.
+
+ This function first splits the features for instance classification and
+ instance grouping. Then, the additional grouping branch (transformer layers)
+ is applied to further encode the grouping features. Finally, a tensor of
+ normalized grouping features is returned.
+
+ Args:
+ outputs: output dictionary from the backbone.
+ training: training / eval mode mark.
+
+ Returns:
+ The normalized paragraph embedding vector of shape (B, N, C).
+ """
+ # Project the object embeddings into classification feature and grouping
+ # feature.
+ fts = outputs["transformer_class_feature"] # B,N,C
+ class_feature = self._class_embed_head(fts, training)
+ group_feature = self._para_embed_head(fts, training)
+ outputs["transformer_class_feature"] = class_feature
+ outputs["transformer_group_feature"] = group_feature
+
+ # Feed the grouping features into additional group encoding branch.
+ # First we need to build the attention_bias which is used the standard
+ # transformer encoder.
+ input_shape = utilities.resolve_shape(group_feature)
+ b = input_shape[0]
+ n = int(input_shape[1])
+ seq_len = tf.constant(n, shape=(b,))
+ padding_mask = utilities.get_padding_mask_from_valid_lengths(
+ seq_len, n, tf.float32)
+ attention_bias = utilities.get_transformer_attention_bias(padding_mask)
+ group_feature = self._para_proj(
+ self._para_head(group_feature, attention_bias, None, training))
+ return tf.math.l2_normalize(group_feature, axis=-1)
+
+ def _get_semantic_outputs(self, outputs: typing.NestedTensorDict,
+ input_shape: tf.TensorShape):
+ """Add `segmentation_output` to outputs.
+
+ Args:
+ outputs: A dictionary of outputs.
+ input_shape: The shape of the input images.
+ """
+ h, w = input_shape[1:3]
+ # B, H/4, W/4, C
+ semantic_logits = outputs["max_deep_lab"]["semantic_logits"]
+ textness, unused_logits = tf.split(semantic_logits, [2, -1], -1)
+ # Channel[0:2], textness. c0: non-textness, c1: textness.
+ word_score = tf.nn.softmax(textness, -1, "word_score")[:, :, :, 1:2]
+ word_score = tf.squeeze(tf.image.resize(word_score, (h, w)), -1)
+ # Channel[2:] not used yet
+ outputs["segmentation_output"] = {"word_score": word_score}
+
+ def _get_instance_outputs(self, outputs: typing.NestedTensorDict,
+ input_shape: tf.TensorShape):
+ """Add `instance_output` to outputs.
+
+ Args:
+ outputs: A dictionary of outputs.
+ input_shape: The shape of the input images.
+ These following fields are added to outputs["instance_output"]:
+ "cls_logits": tf.Tensor, [B, N, C].
+ "mask_id_logits": tf.Tensor, [B, H, W, N].
+ "cls_prob": tf.Tensor, [B, N, C], softmax probability.
+ "mask_id_prob": tf.Tensor, [B, H, W, N], softmax probability. They are
+ used in training. Masks are all resized to full resolution.
+ """
+ # Get instance_output
+ h, w = input_shape[1:3]
+ ## Classes
+ class_logits = outputs["max_deep_lab"]["transformer_class_logits"]
+ # The MaX-DeepLab repo uses the last logit for void; but we use 0.
+ # Therefore we shift the logits here.
+ class_logits = tf.roll(class_logits, shift=1, axis=-1)
+ class_prob = tf.nn.softmax(class_logits)
+
+ ## Masks
+ mask_id_logits = outputs["max_deep_lab"]["pixel_space_mask_logits"]
+ mask_id_prob = tf.nn.softmax(mask_id_logits)
+ mask_id_logits = tf.image.resize(mask_id_logits, (h, w))
+ mask_id_prob = tf.image.resize(mask_id_prob, (h, w))
+ outputs["instance_output"] = {
+ "cls_logits": class_logits,
+ "mask_id_logits": mask_id_logits,
+ "cls_prob": class_prob,
+ "mask_id_prob": mask_id_prob,
+ }
+
+ def _postprocess(self, outputs: typing.NestedTensorDict):
+ """Post-process (filtering) the outputs.
+
+ Args:
+ outputs: A dictionary of outputs.
+ These following fields are added to outputs["postprocessed"]:
+ "classes": A (B,N) integer tensor for the class ids.
+ "binary_masks": A (B, H, W, N) tensor for the N binarized 0/1 masks. Masks
+ for void cls are set to zero.
+ "confidence": A (B, N) float tensor for the confidence of "classes".
+ "mask_area": A (B, N) float tensor for the area of each mask. They are
+ used in inference / visualization.
+ """
+ # Get postprocessed outputs
+ outputs["postprocessed"] = {}
+
+ ## Masks:
+ mask_id_prob = outputs["instance_output"]["mask_id_prob"]
+ mask_max_prob = tf.reduce_max(mask_id_prob, axis=-1, keepdims=True)
+ thresholded_binary_masks = tf.cast(
+ tf.math.logical_and(
+ tf.equal(mask_max_prob, mask_id_prob),
+ tf.greater_equal(mask_max_prob, self._mask_threshold)), tf.float32)
+ area = tf.reduce_sum(thresholded_binary_masks, axis=(1, 2)) # (B, N)
+ ## Classification:
+ cls_prob = outputs["instance_output"]["cls_prob"]
+ cls_max_prob = tf.reduce_max(cls_prob, axis=-1) # B, N
+ cls_max_id = tf.cast(tf.argmax(cls_prob, axis=-1), tf.float32) # B, N
+
+ ## filtering
+ c = utilities.resolve_shape(cls_prob)[2]
+ non_void = tf.reduce_all(
+ tf.stack(
+ [
+ tf.greater_equal(area, self._filter_area), # mask large enough.
+ tf.not_equal(cls_max_id, 0), # class-0 is for non-object.
+ tf.not_equal(cls_max_id,
+ c - 1), # class-(c-1) is for background (last).
+ tf.greater_equal(cls_max_prob,
+ self._class_threshold) # prob >= thr
+ ],
+ axis=-1),
+ axis=-1)
+ non_void = tf.cast(non_void, tf.float32)
+
+ # Storing
+ outputs["postprocessed"]["classes"] = tf.cast(cls_max_id * non_void,
+ tf.int32)
+ b, n = utilities.resolve_shape(non_void)
+ outputs["postprocessed"]["binary_masks"] = (
+ thresholded_binary_masks * tf.reshape(non_void, (b, 1, 1, n)))
+ outputs["postprocessed"]["confidence"] = cls_max_prob
+ outputs["postprocessed"]["mask_area"] = area
+
+ def _coloring(self, masks: tf.Tensor) -> tf.Tensor:
+ """Coloring segmentation masks.
+
+ Used in visualization.
+
+ Args:
+ masks: A float binary tensor of shape (B, H, W, N), representing `B`
+ samples, with `N` masks of size `H*W` each. Each of the `N` masks will
+ be assigned a random color.
+
+ Returns:
+ A (b, h, w, 3) float tensor in [0., 1.] for the coloring result.
+ """
+ b, h, w, n = utilities.resolve_shape(masks)
+ palette = tf.random.uniform((1, n, 3), 0.5, 1.)
+ colored = tf.reshape(
+ tf.matmul(tf.reshape(masks, (b, -1, n)), palette), (b, h, w, 3))
+ return colored
+
+ def visualize(self,
+ outputs: typing.NestedTensorDict,
+ labels: Optional[typing.TensorDict] = None):
+ """Visualizes the outputs and labels.
+
+ Args:
+ outputs: A dictionary of outputs.
+ labels: A dictionary of labels.
+ The following dict is added to outputs["visualization"]: {
+ "instance": {
+ "pred": A (B, H, W, 3) tensor for the visualized map in [0,1].
+ "gt": A (B, H, W, 3) tensor for the visualized map in [0,1], if labels
+ is present.
+ "concat": Concatenation of "prediction" and "gt" along width axis, if
+ labels is present. }
+ "seg-text": {... Similar to above, but the shape is (B, H, W, 1).} } All
+ of these tensors have a rank of 4 (B, H, W, C).
+ """
+
+ outputs["visualization"] = {}
+ # 1. prediction
+ # 1.1 instance mask
+ binary_masks = outputs["postprocessed"]["binary_masks"]
+ outputs["visualization"]["instance"] = {
+ "pred": self._coloring(binary_masks),
+ }
+ # 1.2 text-seg
+ outputs["visualization"]["seg-text"] = {
+ "pred":
+ tf.expand_dims(outputs["segmentation_output"]["word_score"], -1),
+ }
+
+ # 2. labels
+ if labels is not None:
+ # 2.1 instance mask
+ # (B, N, H, W) -> (B, H, W, N); the first one is bkg so removed.
+ gt_masks = tf.transpose(labels["instance_labels"]["masks"][:, 1:],
+ (0, 2, 3, 1))
+ outputs["visualization"]["instance"]["gt"] = self._coloring(gt_masks)
+ # 2.2 text-seg
+ outputs["visualization"]["seg-text"]["gt"] = tf.expand_dims(
+ labels["segmentation_output"]["gt_word_score"], -1)
+
+ # 3. concat
+ for v in outputs["visualization"].values():
+ # Resize to make the size align. The prediction always has stride=1
+ # resolution, so we make gt align with pred instead of vice versa.
+ v["concat"] = tf.concat(
+ [v["pred"],
+ tf.image.resize(v["gt"],
+ tf.shape(v["pred"])[1:3])],
+ axis=2)
+
+ @tf.function
+ def serve(self, image_tensor: tf.Tensor) -> typing.NestedTensorDict:
+ """Method to be exported for SavedModel.
+
+ Args:
+ image_tensor: A float32 normalized tensor representing an image of shape
+ [1, height, width, channels].
+
+ Returns:
+ Dict of output:
+ classes: (B, N) int32 tensor == o["postprocessed"]["classes"]
+ masks: (B, H, W, N) float32 tensor == o["postprocessed"]["binary_masks"]
+ groups: (B, N, N) float32 tensor == o["para_affinity"]
+ confidence: A (B, N) float tensor == o["postprocessed"]["confidence"]
+ mask_area: A (B, N) float tensor == o["postprocessed"]["mask_area"]
+ """
+ features = {"images": image_tensor}
+ nn_outputs = self(features, False)
+ outputs = {
+ "classes": nn_outputs["postprocessed"]["classes"],
+ "masks": nn_outputs["postprocessed"]["binary_masks"],
+ "confidence": nn_outputs["postprocessed"]["confidence"],
+ "mask_area": nn_outputs["postprocessed"]["mask_area"],
+ "groups": nn_outputs["para_affinity"],
+ }
+ return outputs
+
+
+@gin.configurable()
+def _get_decoder_head(
+ atrous_rates: Sequence[int] = (6, 12, 18),
+ pixel_space_dim: int = 128,
+ pixel_space_intermediate: int = 256,
+ low_level: Sequence[Dict[str, Union[str, int]]] = ({
+ "feature_key": "res3",
+ "channels_project": 64,
+ }, {
+ "feature_key": "res2",
+ "channels_project": 32,
+ }),
+ num_classes=3,
+ aux_sem_intermediate=256,
+ norm_fn=tf.keras.layers.BatchNormalization,
+) -> max_deeplab_head.MaXDeepLab:
+ """Get the MaX-DeepLab prediction head.
+
+ Args:
+ atrous_rates: Dilation rate for astrou conv in the semantic head.
+ pixel_space_dim: The dimension for the final panoptic features.
+ pixel_space_intermediate: The dimension for the layer before
+ `pixel_space_dim` (i.e. the separable 5x5 layer).
+ low_level: A list of dicts for the feature pyramid in forming the semantic
+ output. Each dict represents one skip-path from the backbone.
+ num_classes: Number of classes (entities + bkg) including void. For example,
+ if we only want to detect word, then `num_classes` = 3 (1 for word, 1 for
+ bkg, and 1 for void).
+ aux_sem_intermediate: Similar to `pixel_space_intermediate`, but for the
+ auxiliary semantic output head.
+ norm_fn: The normalization function used in the head.
+
+ Returns:
+ A MaX-DeepLab decoder head (as a keras layer).
+ """
+
+ # Initialize the configs.
+ configs = config_pb2.ModelOptions()
+ configs.decoder.feature_key = "feature_semantic"
+ configs.decoder.atrous_rates.extend(atrous_rates)
+ configs.max_deeplab.pixel_space_head.output_channels = pixel_space_dim
+ configs.max_deeplab.pixel_space_head.head_channels = pixel_space_intermediate
+ for low_level_config in low_level:
+ low_level_ = configs.max_deeplab.auxiliary_low_level.add()
+ low_level_.feature_key = low_level_config["feature_key"]
+ low_level_.channels_project = low_level_config["channels_project"]
+ configs.max_deeplab.auxiliary_semantic_head.output_channels = num_classes
+ configs.max_deeplab.auxiliary_semantic_head.head_channels = aux_sem_intermediate
+
+ return max_deeplab_head.MaXDeepLab(configs.decoder,
+ configs.max_deeplab, 0, norm_fn)
+
+
+class PseudoLayer(tf.keras.layers.Layer):
+ """Pseudo layer for ablation study.
+
+ The `call()` function has the same argument signature as a transformer
+ encoder stack. `unused_ph1` and `unused_ph2` are place holders for this
+ purpose. When studying the effectiveness of using transformer as the
+ grouping branch, we can use this PseudoLayer to replace the transformer to
+ use as a no-transformer baseline.
+
+ To use a single projection layer instead of transformer, simply set `extra_fc`
+ to True.
+ """
+
+ def __init__(self, extra_fc: bool):
+ super().__init__(name="extra_fc")
+ self._extra_fc = extra_fc
+ if extra_fc:
+ self._layer = tf.keras.Sequential([
+ tf.keras.layers.Dense(256, activation="relu"),
+ tf.keras.layers.LayerNormalization(),
+ ])
+
+ def call(self,
+ fts: tf.Tensor,
+ unused_ph1: Optional[tf.Tensor],
+ unused_ph2: Optional[tf.Tensor],
+ training: Optional[bool] = None) -> tf.Tensor:
+ """See base class."""
+ if self._extra_fc:
+ return self._layer(fts, training)
+ return fts
+
+
+@gin.configurable()
+def _get_embed_head(
+ dimension=256,
+ norm_fn=tf.keras.layers.BatchNormalization
+) -> Tuple[tf.keras.Sequential, tf.keras.Sequential]:
+ """Projection layers to get instance & grouping features."""
+ instance_head = tf.keras.Sequential([
+ tf.keras.layers.Dense(dimension, use_bias=False),
+ norm_fn(),
+ tf.keras.layers.ReLU(),
+ ])
+ grouping_head = tf.keras.Sequential([
+ tf.keras.layers.Dense(dimension, use_bias=False),
+ norm_fn(),
+ tf.keras.layers.ReLU(),
+ ])
+ return instance_head, grouping_head
+
+
+@gin.configurable()
+def _get_para_head(
+ dimension=128,
+ num_layer=3,
+ extra_fc=False) -> Tuple[tf.keras.layers.Layer, tf.keras.layers.Layer]:
+ """Get the additional para head.
+
+ Args:
+ dimension: the dimension of the final output.
+ num_layer: the number of transformer layer.
+ extra_fc: Whether an extra single fully-connected layer is used, when
+ num_layer=0.
+
+ Returns:
+ an encoder and a projection layer for the grouping features.
+ """
+ if num_layer > 0:
+ encoder = transformer.EncoderStack(
+ params={
+ "hidden_size": 256,
+ "num_hidden_layers": num_layer,
+ "num_heads": 4,
+ "filter_size": 512,
+ "initializer_gain": 1.0,
+ "attention_dropout": 0.1,
+ "relu_dropout": 0.1,
+ "layer_postprocess_dropout": 0.1,
+ "allow_ffn_pad": True,
+ })
+ else:
+ encoder = PseudoLayer(extra_fc)
+ dense = tf.keras.layers.Dense(dimension)
+ return encoder, dense
+
+
+def _dice_sim(pred: tf.Tensor, ground_truth: tf.Tensor) -> tf.Tensor:
+ """Dice Coefficient for mask similarity.
+
+ Args:
+ pred: The predicted mask. [B, N, H, W], in [0, 1].
+ ground_truth: The ground-truth mask. [B, N, H, W], in [0, 1] or {0, 1}.
+
+ Returns:
+ A matrix for the losses: m[b, i, j] is the dice similarity between pred `i`
+ and gt `j` in batch `b`.
+ """
+ b, n = utilities.resolve_shape(pred)[:2]
+ ground_truth = tf.reshape(
+ tf.transpose(ground_truth, (0, 2, 3, 1)), (b, -1, n)) # B, HW, N
+ pred = tf.reshape(pred, (b, n, -1)) # B, N, HW
+ numerator = tf.matmul(pred, ground_truth) * 2.
+ # TODO(longshangbang): The official implementation does not square the scores.
+ # Need to do experiment to determine which one is better.
+ denominator = (
+ tf.math.reduce_sum(tf.math.square(ground_truth), 1, keepdims=True) +
+ tf.math.reduce_sum(tf.math.square(pred), 2, keepdims=True))
+ return (numerator + EPSILON) / (denominator + EPSILON)
+
+
+def _semantic_loss(
+ loss_dict: Dict[str, tf.Tensor],
+ labels: tf.Tensor,
+ outputs: tf.Tensor,
+):
+ """Auxiliary semantic loss.
+
+ Currently, these losses are added:
+ (1) text/non-text heatmap
+
+ Args:
+ loss_dict: A dictionary for the loss. The values are loss scalars.
+ labels: The label dictionary containing:
+ `gt_word_score`: (B, H, W) tensor for the text/non-text map.
+ outputs: The output dictionary containing:
+ `word_score`: (B, H, W) prediction tensor for `gt_word_score`
+ """
+ pred = tf.expand_dims(outputs["word_score"], 1)
+ gt = tf.expand_dims(labels["gt_word_score"], 1)
+ loss_dict["loss_segmentation_word"] = 1. - tf.reduce_mean(_dice_sim(pred, gt))
+
+
+@gin.configurable
+def _entity_mask_loss(loss_dict: Dict[str, tf.Tensor],
+ labels: tf.Tensor,
+ outputs: tf.Tensor,
+ alpha: float = gin.REQUIRED):
+ """PQ loss for entity-mask training.
+
+ This method adds the PQ loss term to loss_dict directly. The match result will
+ also be stored in outputs (As a [B, N_pred, N_gt] float tensor).
+
+ Args:
+ loss_dict: A dictionary for the loss. The values are loss scalars.
+ labels: A dict containing: `num_instance` - (B,) `masks` - (B, N, H, W)
+ `classes` - (B, N)
+ outputs: A dict containing:
+ `cls_prob`: (B, N, C)
+ `mask_id_prob`: (B, H, W, N)
+ `cls_logits`: (B, N, C)
+ `mask_id_logits`: (B, H, W, N)
+ alpha: Weight for pos/neg balance.
+ """
+ # Classification score: (B, N, N)
+ # in batch b, the probability of prediction i being class of gt j, i.e.:
+ # score[b, i, j] = pred_cls[b, i, gt_cls[b, j]]
+ gt_cls = labels["classes"] # (B, N)
+ pred_cls = outputs["cls_prob"] # (B, N, C)
+ b, n = utilities.resolve_shape(pred_cls)[:2]
+ # indices[b, i, j] = gt_cls[b, j]
+ indices = tf.tile(tf.expand_dims(gt_cls, 1), (1, n, 1))
+ cls_score = tf.gather(pred_cls, tf.cast(indices, tf.int32), batch_dims=2)
+
+ # Mask score (dice): (B, N, N)
+ # mask_score[b, i, j]: dice-similarity for pred i and gt j in batch b.
+ mask_score = _dice_sim(
+ tf.transpose(outputs["mask_id_prob"], (0, 3, 1, 2)), labels["masks"])
+
+ # Get similarity matrix and matching.
+ # padded mask[b, j, i] = -1 << other scores, if i >= num_instance[b]
+ similarity = cls_score * mask_score
+ padded_mask = tf.cast(tf.reshape(tf.range(n), (1, 1, n)), tf.float32)
+ padded_mask = tf.cast(
+ tf.math.greater_equal(padded_mask,
+ tf.reshape(labels["num_instance"], (b, 1, 1))),
+ tf.float32)
+ # The constant value for padding has no effect.
+ masked_similarity = similarity * (1. - padded_mask) + padded_mask * (-1.)
+ matched_mask = matchers_ops.hungarian_matching(-masked_similarity)
+ matched_mask = tf.cast(matched_mask, tf.float32) * (1 - padded_mask)
+ outputs["matched_mask"] = matched_mask
+ # Pos loss
+ loss_pos = (
+ tf.stop_gradient(cls_score) * (-mask_score) +
+ tf.stop_gradient(mask_score) * (-tf.math.log(cls_score)))
+ loss_pos = tf.reduce_sum(loss_pos * matched_mask, axis=[1, 2]) # (B,)
+ # Neg loss
+ matched_pred = tf.cast(tf.reduce_sum(matched_mask, axis=2) > 0,
+ tf.float32) # (B, N)
+ # 0 for void class
+ log_loss = -tf.nn.log_softmax(outputs["cls_logits"])[:, :, 0] # (B, N)
+ loss_neg = tf.reduce_sum(log_loss * (1. - matched_pred), axis=-1) # (B,)
+
+ loss_pq = (alpha * loss_pos + (1 - alpha) * loss_neg) / n
+ loss_pq = tf.reduce_mean(loss_pq)
+ loss_dict["loss_pq"] = loss_pq
+
+
+@gin.configurable
+def _instance_discrimination_loss(loss_dict: Dict[str, Any],
+ labels: Dict[str, Any],
+ outputs: Dict[str, Any],
+ tau: float = gin.REQUIRED):
+ """Instance discrimination loss.
+
+ This method adds the ID loss term to loss_dict directly.
+
+ Args:
+ loss_dict: A dictionary for the loss. The values are loss scalars.
+ labels: The label dictionary.
+ outputs: The output dictionary.
+ tau: The temperature term in the loss
+ """
+ # The normalized feature, shape=(B, H/4, W/4, D)
+ g = outputs["max_deep_lab"]["pixel_space_normalized_feature"]
+ b, h, w = utilities.resolve_shape(g)[:3]
+ # The ground-truth masks, shape=(B, N, H, W) --> (B, N, H/4, W/4)
+ m = labels["masks"]
+ m = tf.image.resize(
+ tf.transpose(m, (0, 2, 3, 1)), (h, w),
+ tf.image.ResizeMethod.NEAREST_NEIGHBOR)
+ m = tf.transpose(m, (0, 3, 1, 2))
+ # The number of ground-truth instance (K), shape=(B,)
+ num = labels["num_instance"]
+ n = utilities.resolve_shape(m)[1] # max number of predictions
+ # is_void[b, i] = 1 if instance i in batch b is a padded slot.
+ is_void = tf.cast(tf.expand_dims(tf.range(n), 0), tf.float32) # (1, n)
+ is_void = tf.cast(
+ tf.math.greater_equal(is_void, tf.expand_dims(num, 1)), tf.float32)
+
+ # (B, N, D)
+ t = tf.math.l2_normalize(tf.einsum("bhwd,bnhw->bnd", g, m), axis=-1)
+ inst_dist_logits = tf.einsum("bhwd,bid->bhwi", g, t) / tau # (B, H, W, N)
+ inst_dist_logits = inst_dist_logits - 100. * tf.reshape(is_void, (b, 1, 1, n))
+ mask_id = tf.cast(
+ tf.einsum("bnhw,n->bhw", m, tf.range(n, dtype=tf.float32)), tf.int32)
+ loss_map = tf.nn.sparse_softmax_cross_entropy_with_logits(
+ labels=mask_id, logits=inst_dist_logits) # B, H, W
+ valid_mask = tf.reduce_sum(m, axis=1)
+ loss_inst_dist = (
+ (tf.reduce_sum(loss_map * valid_mask, axis=[1, 2]) + EPSILON) /
+ (tf.reduce_sum(valid_mask, axis=[1, 2]) + EPSILON))
+ loss_dict["loss_inst_dist"] = tf.reduce_mean(loss_inst_dist)
+
+
+@gin.configurable
+def _paragraph_grouping_loss(
+ loss_dict: Dict[str, Any],
+ labels: Dict[str, Any],
+ outputs: Dict[str, Any],
+ tau: float = gin.REQUIRED,
+ loss_mode="vanilla",
+ fl_alpha: float = 0.25,
+ fl_gamma: float = 2.,
+):
+ """Instance discrimination loss.
+
+ This method adds the para discrimination loss term to loss_dict directly.
+
+ Args:
+ loss_dict: A dictionary for the loss. The values are loss scalars.
+ labels: The label dictionary.
+ outputs: The output dictionary.
+ tau: The temperature term in the loss
+ loss_mode: The type of loss.
+ fl_alpha: alpha value in focal loss
+ fl_gamma: gamma value in focal loss
+ """
+ if "paragraph_labels" not in labels:
+ loss_dict["loss_para"] = 0.
+ return
+ # step 1:
+ # obtain the paragraph labels for each prediction
+ # (batch, pred, gt)
+ matched_matrix = outputs["instance_output"]["matched_mask"] # B, N, N
+ para_label_gt = labels["paragraph_labels"]["paragraph_ids"] # B, N
+ has_para_label_gt = (
+ labels["paragraph_labels"]["has_para_ids"][:, tf.newaxis, tf.newaxis])
+ # '0' means no paragraph labels
+ pred_label_gt = tf.einsum("bij,bj->bi", matched_matrix,
+ tf.cast(para_label_gt + 1, tf.float32))
+ pred_label_gt_pad_col = tf.expand_dims(pred_label_gt, -1) # b,n,1
+ pred_label_gt_pad_row = tf.expand_dims(pred_label_gt, 1) # b,1,n
+ gt_affinity = tf.cast(
+ tf.equal(pred_label_gt_pad_col, pred_label_gt_pad_row), tf.float32)
+ gt_affinity_mask = (
+ has_para_label_gt * pred_label_gt_pad_col * pred_label_gt_pad_row)
+ gt_affinity_mask = tf.cast(tf.not_equal(gt_affinity_mask, 0.), tf.float32)
+
+ # step 2:
+ # get affinity matrix
+ affinity = outputs["para_affinity"]
+
+ # step 3:
+ # compute loss
+ loss_fn = tf.keras.losses.BinaryCrossentropy(
+ from_logits=True,
+ label_smoothing=0,
+ axis=-1,
+ reduction=tf.keras.losses.Reduction.NONE,
+ name="para_dist")
+ affinity = tf.reshape(affinity, (-1, 1)) # (b*n*n, 1)
+ gt_affinity = tf.reshape(gt_affinity, (-1, 1)) # (b*n*n, 1)
+ gt_affinity_mask = tf.reshape(gt_affinity_mask, (-1,)) # (b*n*n,)
+ pointwise_loss = loss_fn(gt_affinity, affinity / tau) # (b*n*n,)
+
+ if loss_mode == "vanilla":
+ loss = (
+ tf.reduce_sum(pointwise_loss * gt_affinity_mask) /
+ (tf.reduce_sum(gt_affinity_mask) + EPSILON))
+ elif loss_mode == "balanced":
+ # pos
+ pos_mask = gt_affinity_mask * gt_affinity[:, 0]
+ pos_loss = (
+ tf.reduce_sum(pointwise_loss * pos_mask) /
+ (tf.reduce_sum(pos_mask) + EPSILON))
+ # neg
+ neg_mask = gt_affinity_mask * (1. - gt_affinity[:, 0])
+ neg_loss = (
+ tf.reduce_sum(pointwise_loss * neg_mask) /
+ (tf.reduce_sum(neg_mask) + EPSILON))
+ loss = 0.25 * pos_loss + 0.75 * neg_loss
+ elif loss_mode == "focal":
+ alpha_wt = fl_alpha * gt_affinity + (1. - fl_alpha) * (1. - gt_affinity)
+ prob_pos = tf.math.sigmoid(affinity / tau)
+ pt = prob_pos * gt_affinity + (1. - prob_pos) * (1. - gt_affinity)
+ fl_loss_pw = tf.stop_gradient(
+ alpha_wt * tf.pow(1. - pt, fl_gamma))[:, 0] * pointwise_loss
+ loss = (
+ tf.reduce_sum(fl_loss_pw * gt_affinity_mask) /
+ (tf.reduce_sum(gt_affinity_mask) + EPSILON))
+ else:
+ raise ValueError(f"Not supported loss mode: {loss_mode}")
+
+ loss_dict["loss_para"] = loss
+
+
+def _mask_id_xent_loss(loss_dict: Dict[str, Any], labels: Dict[str, Any],
+ outputs: Dict[str, Any]):
+ """Mask ID loss.
+
+ This method adds the mask ID loss term to loss_dict directly.
+
+ Args:
+ loss_dict: A dictionary for the loss. The values are loss scalars.
+ labels: The label dictionary.
+ outputs: The output dictionary.
+ """
+ # (B, N, H, W)
+ mask_gt = labels["masks"]
+ # B, H, W, N
+ mask_id_logits = outputs["instance_output"]["mask_id_logits"]
+ # B, N, N
+ matched_matrix = outputs["instance_output"]["matched_mask"]
+ # B, N
+ gt_to_pred_id = tf.cast(tf.math.argmax(matched_matrix, axis=1), tf.float32)
+ # B, H, W
+ mask_id_labels = tf.cast(
+ tf.einsum("bnhw,bn->bhw", mask_gt, gt_to_pred_id), tf.int32)
+ loss_map = tf.nn.sparse_softmax_cross_entropy_with_logits(
+ labels=mask_id_labels, logits=mask_id_logits)
+ valid_mask = tf.reduce_sum(mask_gt, axis=1)
+ loss_mask_id = (
+ (tf.reduce_sum(loss_map * valid_mask, axis=[1, 2]) + EPSILON) /
+ (tf.reduce_sum(valid_mask, axis=[1, 2]) + EPSILON))
+ loss_dict["loss_mask_id"] = tf.reduce_mean(loss_mask_id)
diff --git a/official/projects/unified_detector/registry_imports.py b/official/projects/unified_detector/registry_imports.py
new file mode 100644
index 0000000000000000000000000000000000000000..93eebcca58e586c42379014d7d74f81e603c473e
--- /dev/null
+++ b/official/projects/unified_detector/registry_imports.py
@@ -0,0 +1,21 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""All necessary imports for registration."""
+
+# pylint: disable=unused-import
+from official.projects.unified_detector import external_configurables
+from official.projects.unified_detector.configs import ocr_config
+from official.projects.unified_detector.tasks import ocr_task
+from official.vision import registry_imports
diff --git a/official/projects/unified_detector/requirements.txt b/official/projects/unified_detector/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..081993d5d7486bced189dc115828ce23865d9099
--- /dev/null
+++ b/official/projects/unified_detector/requirements.txt
@@ -0,0 +1,8 @@
+tf-nightly
+gin-config
+opencv-python==4.2.0.32
+absl-py>=1.0.0
+shapely>=1.8.1
+apache_beam>=2.37.0
+matplotlib>=3.5.1
+notebook>=6.4.10
diff --git a/official/projects/unified_detector/run_inference.py b/official/projects/unified_detector/run_inference.py
new file mode 100644
index 0000000000000000000000000000000000000000..13a0c67c7ec4f81f18f1cb1acfadb685eb767316
--- /dev/null
+++ b/official/projects/unified_detector/run_inference.py
@@ -0,0 +1,222 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+r"""A binary to run unified detector."""
+
+import json
+import os
+from typing import Any, Dict, Sequence, Union
+
+from absl import app
+from absl import flags
+from absl import logging
+
+import cv2
+import gin
+import numpy as np
+import tensorflow as tf
+import tqdm
+
+from official.projects.unified_detector import external_configurables # pylint: disable=unused-import
+from official.projects.unified_detector.modeling import universal_detector
+from official.projects.unified_detector.utils import utilities
+
+
+# group two lines into a paragraph if affinity score higher than this
+_PARA_GROUP_THR = 0.5
+
+
+# MODEL spec
+_GIN_FILE = flags.DEFINE_string(
+ 'gin_file', None, 'Path to the Gin file that defines the model.')
+_CKPT_PATH = flags.DEFINE_string(
+ 'ckpt_path', None, 'Path to the checkpoint directory.')
+_IMG_SIZE = flags.DEFINE_integer(
+ 'img_size', 1024, 'Size of the image fed to the model.')
+
+# Input & Output
+# Note that, all images specified by `img_file` and `img_dir` will be processed.
+_IMG_FILE = flags.DEFINE_multi_string('img_file', [], 'Paths to the images.')
+_IMG_DIR = flags.DEFINE_multi_string(
+ 'img_dir', [], 'Paths to the image directories.')
+_OUTPUT_PATH = flags.DEFINE_string('output_path', None, 'Path for the output.')
+_VIS_DIR = flags.DEFINE_string(
+ 'vis_dir', None, 'Path for the visualization output.')
+
+
+def _preprocess(raw_image: np.ndarray) -> Union[np.ndarray, float]:
+ """Convert a raw image to properly resized, padded, and normalized ndarray."""
+ # (1) convert to tf.Tensor and float32.
+ img_tensor = tf.convert_to_tensor(raw_image, dtype=tf.float32)
+
+ # (2) pad to square.
+ height, width = img_tensor.shape[:2]
+ maximum_side = tf.maximum(height, width)
+ height_pad = maximum_side - height
+ width_pad = maximum_side - width
+ img_tensor = tf.pad(
+ img_tensor, [[0, height_pad], [0, width_pad], [0, 0]],
+ constant_values=127)
+ ratio = maximum_side / _IMG_SIZE.value
+ # (3) resize long side to the maximum length.
+ img_tensor = tf.image.resize(
+ img_tensor, (_IMG_SIZE.value, _IMG_SIZE.value))
+ img_tensor = tf.cast(img_tensor, tf.uint8)
+
+ # (4) normalize
+ img_tensor = utilities.normalize_image_to_range(img_tensor)
+
+ # (5) Add batch dimension and return as numpy array.
+ return tf.expand_dims(img_tensor, 0).numpy(), float(ratio)
+
+
+def load_model() -> tf.keras.layers.Layer:
+ gin.parse_config_file(_GIN_FILE.value)
+ model = universal_detector.UniversalDetector()
+ ckpt = tf.train.Checkpoint(model=model)
+ ckpt_path = _CKPT_PATH.value
+ logging.info('Load ckpt from: %s', ckpt_path)
+ ckpt.restore(ckpt_path).expect_partial()
+ return model
+
+
+def inference(img_file: str, model: tf.keras.layers.Layer) -> Dict[str, Any]:
+ """Inference step."""
+ img = cv2.cvtColor(cv2.imread(img_file), cv2.COLOR_BGR2RGB)
+ img_ndarray, ratio = _preprocess(img)
+
+ output_dict = model.serve(img_ndarray)
+ class_tensor = output_dict['classes'].numpy()
+ mask_tensor = output_dict['masks'].numpy()
+ group_tensor = output_dict['groups'].numpy()
+
+ indices = np.where(class_tensor[0])[0].tolist() # indices of positive slots.
+ mask_list = [
+ mask_tensor[0, :, :, index] for index in indices] # List of mask ndarray.
+
+ # Form lines and words
+ lines = []
+ line_indices = []
+ for index, mask in tqdm.tqdm(zip(indices, mask_list)):
+ line = {
+ 'words': [],
+ 'text': '',
+ }
+
+ contours, _ = cv2.findContours(
+ (mask > 0.).astype(np.uint8),
+ cv2.RETR_TREE,
+ cv2.CHAIN_APPROX_SIMPLE)[-2:]
+ for contour in contours:
+ if (isinstance(contour, np.ndarray) and
+ len(contour.shape) == 3 and
+ contour.shape[0] > 2 and
+ contour.shape[1] == 1 and
+ contour.shape[2] == 2):
+ cnt_list = (contour[:, 0] * ratio).astype(np.int32).tolist()
+ line['words'].append({'text': '', 'vertices': cnt_list})
+ else:
+ logging.error('Invalid contour: %s, discarded', str(contour))
+ if line['words']:
+ lines.append(line)
+ line_indices.append(index)
+
+ # Form paragraphs
+ line_grouping = utilities.DisjointSet(len(line_indices))
+ affinity = group_tensor[0][line_indices][:, line_indices]
+ for i1, i2 in zip(*np.where(affinity > _PARA_GROUP_THR)):
+ line_grouping.union(i1, i2)
+
+ line_groups = line_grouping.to_group()
+ paragraphs = []
+ for line_group in line_groups:
+ paragraph = {'lines': []}
+ for id_ in line_group:
+ paragraph['lines'].append(lines[id_])
+ if paragraph:
+ paragraphs.append(paragraph)
+
+ return paragraphs
+
+
+def main(argv: Sequence[str]) -> None:
+ if len(argv) > 1:
+ raise app.UsageError('Too many command-line arguments.')
+
+ # Get list of images
+ img_lists = []
+ img_lists.extend(_IMG_FILE.value)
+ for img_dir in _IMG_DIR.value:
+ img_lists.extend(tf.io.gfile.glob(os.path.join(img_dir, '*')))
+
+ logging.info('Total number of input images: %d', len(img_lists))
+
+ model = load_model()
+
+ vis_dis = _VIS_DIR.value
+
+ output = {'annotations': []}
+ for img_file in tqdm.tqdm(img_lists):
+ output['annotations'].append({
+ 'image_id': img_file.split('/')[-1].split('.')[0],
+ 'paragraphs': inference(img_file, model),
+ })
+
+ if vis_dis:
+ key = output['annotations'][-1]['image_id']
+ paragraphs = output['annotations'][-1]['paragraphs']
+ img = cv2.cvtColor(cv2.imread(img_file), cv2.COLOR_BGR2RGB)
+ word_bnds = []
+ line_bnds = []
+ para_bnds = []
+ for paragraph in paragraphs:
+ paragraph_points_list = []
+ for line in paragraph['lines']:
+ line_points_list = []
+ for word in line['words']:
+ word_bnds.append(
+ np.array(word['vertices'], np.int32).reshape((-1, 1, 2)))
+ line_points_list.extend(word['vertices'])
+ paragraph_points_list.extend(line_points_list)
+
+ line_points = np.array(line_points_list, np.int32) # (N,2)
+ left = int(np.min(line_points[:, 0]))
+ top = int(np.min(line_points[:, 1]))
+ right = int(np.max(line_points[:, 0]))
+ bottom = int(np.max(line_points[:, 1]))
+ line_bnds.append(
+ np.array([[[left, top]], [[right, top]], [[right, bottom]],
+ [[left, bottom]]], np.int32))
+ para_points = np.array(paragraph_points_list, np.int32) # (N,2)
+ left = int(np.min(para_points[:, 0]))
+ top = int(np.min(para_points[:, 1]))
+ right = int(np.max(para_points[:, 0]))
+ bottom = int(np.max(para_points[:, 1]))
+ para_bnds.append(
+ np.array([[[left, top]], [[right, top]], [[right, bottom]],
+ [[left, bottom]]], np.int32))
+
+ for name, bnds in zip(['paragraph', 'line', 'word'],
+ [para_bnds, line_bnds, word_bnds]):
+ vis = cv2.polylines(img, bnds, True, (0, 0, 255), 2)
+ cv2.imwrite(os.path.join(vis_dis, f'{key}-{name}.jpg'),
+ cv2.cvtColor(vis, cv2.COLOR_RGB2BGR))
+
+ with tf.io.gfile.GFile(_OUTPUT_PATH.value, mode='w') as f:
+ f.write(json.dumps(output, ensure_ascii=False, indent=2))
+
+
+if __name__ == '__main__':
+ flags.mark_flags_as_required(['gin_file', 'ckpt_path', 'output_path'])
+ app.run(main)
diff --git a/official/projects/unified_detector/tasks/all_models.py b/official/projects/unified_detector/tasks/all_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..cc75f37956cca273a64a399647fd101ed13178e4
--- /dev/null
+++ b/official/projects/unified_detector/tasks/all_models.py
@@ -0,0 +1,23 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Import all models.
+
+All model files are imported here so that they can be referenced in Gin. Also,
+importing here avoids making ocr_task.py too messy.
+"""
+
+# pylint: disable=unused-import
+
+from official.projects.unified_detector.modeling import universal_detector
diff --git a/official/projects/unified_detector/tasks/ocr_task.py b/official/projects/unified_detector/tasks/ocr_task.py
new file mode 100644
index 0000000000000000000000000000000000000000..8462fd4284ccf1fdec5ad80889a2c5292aea1d1d
--- /dev/null
+++ b/official/projects/unified_detector/tasks/ocr_task.py
@@ -0,0 +1,108 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Task definition for ocr."""
+
+from typing import Callable, Dict, Optional, Sequence, Tuple, Union
+
+import gin
+import tensorflow as tf
+
+from official.core import base_task
+from official.core import config_definitions as cfg
+from official.core import task_factory
+from official.projects.unified_detector.configs import ocr_config
+from official.projects.unified_detector.data_loaders import input_reader
+from official.projects.unified_detector.tasks import all_models # pylint: disable=unused-import
+from official.projects.unified_detector.utils import typing
+
+NestedTensorDict = typing.NestedTensorDict
+ModelType = Union[tf.keras.layers.Layer, tf.keras.Model]
+
+
+@task_factory.register_task_cls(ocr_config.OcrTaskConfig)
+@gin.configurable
+class OcrTask(base_task.Task):
+ """Defining the OCR training task."""
+
+ _loss_items = []
+
+ def __init__(self,
+ params: cfg.TaskConfig,
+ logging_dir: Optional[str] = None,
+ name: Optional[str] = None,
+ model_fn: Callable[..., ModelType] = gin.REQUIRED):
+ super().__init__(params, logging_dir, name)
+ self._modef_fn = model_fn
+
+ def build_model(self) -> ModelType:
+ """Build and return the model, record the loss items as well."""
+ model = self._modef_fn()
+ self._loss_items.extend(model.loss_items)
+ return model
+
+ def build_inputs(
+ self,
+ params: cfg.DataConfig,
+ input_context: Optional[tf.distribute.InputContext] = None
+ ) -> tf.data.Dataset:
+ """Build the tf.data.Dataset instance."""
+ return input_reader.InputFn(is_training=params.is_training)({},
+ input_context)
+
+ def build_metrics(self,
+ training: bool = True) -> Sequence[tf.keras.metrics.Metric]:
+ """Build the metrics (currently, only for loss summaries in TensorBoard)."""
+ del training
+ metrics = []
+ # Add loss items
+ for name in self._loss_items:
+ metrics.append(tf.keras.metrics.Mean(name, dtype=tf.float32))
+ # TODO(longshangbang): add evaluation metrics
+ return metrics
+
+ def train_step(
+ self,
+ inputs: Tuple[NestedTensorDict, NestedTensorDict],
+ model: ModelType,
+ optimizer: tf.keras.optimizers.Optimizer,
+ metrics: Optional[Sequence[tf.keras.metrics.Metric]] = None
+ ) -> Dict[str, tf.Tensor]:
+ features, labels = inputs
+ input_dict = {"features": features}
+ if self.task_config.model_call_needs_labels:
+ input_dict["labels"] = labels
+
+ is_mixed_precision = isinstance(optimizer,
+ tf.keras.mixed_precision.LossScaleOptimizer)
+
+ with tf.GradientTape() as tape:
+ outputs = model(**input_dict, training=True)
+ loss, loss_dict = model.compute_losses(labels=labels, outputs=outputs)
+ loss = loss / tf.distribute.get_strategy().num_replicas_in_sync
+ if is_mixed_precision:
+ loss = optimizer.get_scaled_loss(loss)
+
+ tvars = model.trainable_variables
+ grads = tape.gradient(loss, tvars)
+ if is_mixed_precision:
+ grads = optimizer.get_unscaled_gradients(grads)
+
+ optimizer.apply_gradients(list(zip(grads, tvars)))
+
+ logs = {"loss": loss}
+ if metrics:
+ for m in metrics:
+ m.update_state(loss_dict[m.name])
+ return logs
diff --git a/official/projects/unified_detector/train.py b/official/projects/unified_detector/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..03ce0e2a18ab907a0d8ff427c3a8ab3eef498206
--- /dev/null
+++ b/official/projects/unified_detector/train.py
@@ -0,0 +1,70 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver."""
+
+from absl import app
+from absl import flags
+import gin
+
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+# pylint: disable=unused-import
+from official.projects.unified_detector import registry_imports
+# pylint: enable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ flags.mark_flags_as_required(['experiment', 'mode', 'model_dir'])
+ app.run(main)
diff --git a/official/projects/unified_detector/utils/typing.py b/official/projects/unified_detector/utils/typing.py
new file mode 100644
index 0000000000000000000000000000000000000000..00bcb50e95610f9d0d055e3effd7f1076ca74c54
--- /dev/null
+++ b/official/projects/unified_detector/utils/typing.py
@@ -0,0 +1,28 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Typing extension."""
+
+from typing import Dict, Union
+
+import numpy as np
+import tensorflow as tf
+
+NpDict = Dict[str, np.ndarray]
+FeaturesAndLabelsType = Dict[str, Dict[str, tf.Tensor]]
+TensorDict = Dict[Union[str, int], tf.Tensor]
+NestedTensorDict = Dict[
+ Union[str, int],
+ Union[tf.Tensor,
+ TensorDict]]
diff --git a/official/projects/unified_detector/utils/utilities.py b/official/projects/unified_detector/utils/utilities.py
new file mode 100644
index 0000000000000000000000000000000000000000..2a8c20a8711a28a9e4e30fa76b2d3605665c9103
--- /dev/null
+++ b/official/projects/unified_detector/utils/utilities.py
@@ -0,0 +1,235 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Utility functions."""
+
+import collections
+from typing import List, Optional, Union
+
+import tensorflow as tf
+
+
+def resolve_shape(
+ tensor: tf.Tensor,
+ resolve_batch_size: bool = True) -> List[Union[tf.Tensor, int]]:
+ """Fully resolves the shape of the tensor.
+
+ Args:
+ tensor: The tensor for which to resolve the shape.
+ resolve_batch_size: If True, fully resolve the batch size. If False,
+ return the batch size if it is statically known and -1 otherwise. This
+ can be more efficient when converting a model to TFLite.
+
+ Returns:
+ A list containing the static dimension where possible and the dynamic
+ dimension otherwise.
+ """
+ with tf.name_scope('resolve_shape'):
+ shape = tensor.get_shape().as_list()
+ if None in shape:
+ shape_dynamic = tf.shape(tensor)
+ if shape[0] is None:
+ shape[0] = shape_dynamic[0] if resolve_batch_size else -1
+ for i in range(1, len(shape)):
+ if shape[i] is None:
+ shape[i] = shape_dynamic[i]
+ return shape
+
+
+def set_shape_dim(tensor: tf.Tensor, index: int, size: int) -> None:
+ """Set value of index-th element of tensor shape to size."""
+ shape = tensor.get_shape().as_list()
+ if len(shape) <= index:
+ raise ValueError(
+ 'Tensor rank must be at least %d. Got %d' % (index + 1, len(shape)))
+ shape[index] = size
+ tensor.set_shape(shape)
+
+
+def truncate_or_pad(input_tensor: tf.Tensor,
+ new_size: int,
+ axis: int = 1,
+ constant_value: Union[int, float] = 0) -> tf.Tensor:
+ """Truncate or zeros pad the axis of input tensor to new size."""
+ rank = len(input_tensor.shape)
+
+ if rank <= axis:
+ raise ValueError(
+ 'Tensor rank must be at least %d. Got %d' % (axis + 1, rank))
+
+ orig_size = tf.shape(input_tensor)[axis]
+
+ def _new_size(dim):
+ if dim == axis:
+ return new_size
+ n = tf.shape(input_tensor)[dim]
+ return -1 if n is None else n
+
+ def _truncate():
+ begin = [0] * rank
+ size = [_new_size(dim) for dim in range(rank)]
+ return tf.slice(input_tensor, begin, size)
+
+ def _pad():
+ padding = [[0, 0] for _ in range(rank)]
+ padding[axis][1] = new_size - orig_size
+ return tf.pad(input_tensor, padding, constant_values=constant_value)
+
+ output = tf.cond(orig_size >= new_size, _truncate, _pad)
+ if isinstance(new_size, int):
+ set_shape_dim(output, axis, new_size)
+ return output
+
+
+def rotate_rboxes90(rboxes: tf.Tensor,
+ image_width: int,
+ image_height: int,
+ rotation_count: int = 1) -> tf.Tensor:
+ """Rotate oriented rectangles counter-clockwise by multiples of 90 degrees."""
+ image_width = tf.cast(image_width, dtype=tf.float32)
+ image_height = tf.cast(image_height, dtype=tf.float32)
+
+ rotation_count = rotation_count % 4
+ x, y, w, h, angle = tf.split(rboxes, 5, axis=1)
+
+ if rotation_count == 0:
+ return rboxes
+ elif rotation_count == 1:
+ angle = tf.where(angle < -90.0, angle + 270, angle - 90)
+ return tf.concat([y, image_width - x - 1, w, h, angle], axis=1)
+ elif rotation_count == 2:
+ angle = tf.where(angle < 0.0, angle + 180, angle - 180)
+ return tf.concat([image_width - x - 1, image_height - y - 1, w, h, angle],
+ axis=1)
+ else:
+ angle = tf.where(angle > 90.0, angle - 270, angle + 90)
+ return tf.concat([image_height - y - 1, x, w, h, angle], axis=1)
+
+
+def normalize_image_to_range(image: tf.Tensor,
+ original_minval: int = 0,
+ original_maxval: int = 255,
+ target_minval: float = -1.0,
+ target_maxval: float = 1.0) -> tf.Tensor:
+ """Normalizes pixel values in the image.
+
+ Moves the pixel values from the current [original_minval, original_maxval]
+ range to the [target_minval, target_maxval] range.
+
+ Args:
+ image: A tensor of shape [height, width, channels]. Input will be converted
+ to float32 type before normalization.
+ original_minval: current image minimum value.
+ original_maxval: current image maximum value.
+ target_minval: target image minimum value.
+ target_maxval: target image maximum value.
+
+ Returns:
+ A float tensor with the same shape as the input image.
+ """
+ if image.dtype is not tf.float32:
+ image = tf.cast(image, dtype=tf.float32)
+
+ original_minval = float(original_minval)
+ original_maxval = float(original_maxval)
+ target_minval = float(target_minval)
+ target_maxval = float(target_maxval)
+ image = tf.cast(image, dtype=tf.float32)
+ image = tf.subtract(image, original_minval)
+ image = tf.multiply(image, (target_maxval - target_minval) /
+ (original_maxval - original_minval))
+ image = tf.add(image, target_minval)
+
+ return image
+
+
+def get_padding_mask_from_valid_lengths(
+ valid_lengths: tf.Tensor,
+ max_length: Optional[int] = None,
+ dtype: tf.dtypes.DType = tf.bool) -> tf.Tensor:
+ """Gets a 2D mask of the padded region from valid lengths.
+
+ Args:
+ valid_lengths: A 1D int tensor containing the valid length of each row.
+ max_length: (optional, int) The maximum length of each row. If `None`, the
+ maximum value in `valid_lengths` will be used.
+ dtype: The output dtype.
+
+ Returns:
+ 2D padded region mask.
+ """
+ with tf.name_scope('get_padding_mask_from_valid_lengths'):
+ if max_length is None:
+ max_length = tf.reduce_max(valid_lengths)
+ padding_mask = tf.logical_not(tf.sequence_mask(valid_lengths, max_length))
+
+ return tf.cast(padding_mask, dtype=dtype)
+
+
+def get_transformer_attention_bias(padding_mask: tf.Tensor) -> tf.Tensor:
+ """Gets attention bias.
+
+ Bias tensor that is added to the pre-softmax multi-headed attention logits,
+ which has shape [batch_size, num_attention_heads, max_length, max_length].
+ The tensor is zero at non-padded locations, and -1e9 (negative infinity) at
+ padded locations.
+
+ Args:
+ padding_mask: A [batch_size, max_length] float tensor, the padding mask.
+
+ Returns:
+ Attention bias tensor of shape [batch_size, 1, 1, max_length].
+ """
+ with tf.name_scope('attention_bias'):
+ # Uses -1e9 to represent -infinity. We do not actually use -Inf, since we
+ # want to be able to multiply these values by zero to get zero.
+ # (-Inf * 0 = NaN)
+ attention_bias = padding_mask * -1e9
+ attention_bias = tf.expand_dims(
+ tf.expand_dims(attention_bias, axis=1), axis=1)
+
+ return attention_bias
+
+
+class DisjointSet:
+ """A disjoint set implementation."""
+
+ def __init__(self, num_elements: int):
+ self._num_elements = num_elements
+ self._parent = list(range(num_elements))
+
+ def find(self, item: int) -> int:
+ if self._parent[item] == item:
+ return item
+ else:
+ self._parent[item] = self.find(self._parent[item])
+ return self._parent[item]
+
+ def union(self, i1: int, i2: int) -> None:
+ r1 = self.find(i1)
+ r2 = self.find(i2)
+ self._parent[r1] = r2
+
+ def to_group(self) -> List[List[int]]:
+ """Return the grouping results.
+
+ Returns:
+ A list of integer lists. Each list represents the IDs belonging to the
+ same group.
+ """
+ groups = collections.defaultdict(list)
+ for i in range(self._num_elements):
+ r = self.find(i)
+ groups[r].append(i)
+ return list(groups.values())
diff --git a/official/projects/video_ssl/README.md b/official/projects/video_ssl/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..86b00d819cc046818857aca6d9532cf25cef5baa
--- /dev/null
+++ b/official/projects/video_ssl/README.md
@@ -0,0 +1,59 @@
+# Spatiotemporal Contrastive Video Representation Learning
+
+[](https://arxiv.org/abs/2008.03800)
+
+This repository is the official TF2 implementation of [Spatiotemporal Contrastive Video Representation Learning](https://arxiv.org/abs/2008.03800).
+
+
+
+
+
+## Description
+
+We present a self-supervised Contrastive Video Representation Learning (CVRL)
+method to learn spatiotemporal visual representations from unlabeled videos. Our
+representations are learned using a contrastive loss, where two augmented clips
+from the same short video are pulled together in the embedding space, while
+clips from different videos are pushed away. CVRL significantly closes the gap
+between unsupervised and supervised video representation learning.
+
+Here we release the code and pre-trained models.
+
+
+## Experimental Results
+
+### Kinetics-600 top-1 linear classification accuracy
+
+
+
+
+
+
+## Pre-trained Model Checkpoints
+
+We provide model checkpoints pre-trained on unlabeled RGB videos from
+Kinetics-400 and Kinetics-600. All models are trained from scratch with random
+initialization.
+
+We also provide a baseline model checkpoint of "ImageNet inflated" we used in
+the paper. The model has the same architecture as 3D-ResNet-50 (R3D-50), with
+model weights inflated from a 2D ResNet-50 pre-trained on ImageNet.
+
+| Model | Parameters | Dataset | Epochs | K400 Linear Eval. | K600 Linear Eval. | Checkpoint |
+| :--------------: | :----: | :--: | :--: |:-----------: | :----------: | :----------: |
+| R3D-50 (1x) | 31.7M | ImageNet | - | 53.5% | 54.7% | [ckpt (127 MB)](https://storage.googleapis.com/tf_model_garden/vision/cvrl/imagenet.tar.gz) |
+| R3D-50 (1x) | 31.7M | Kinetics-400 | 200 | 63.8% | - | [ckpt (127 MB)](https://storage.googleapis.com/tf_model_garden/vision/cvrl/r3d_1x_k400_200ep.tar.gz) |
+| R3D-50 (1x) | 31.7M | Kinetics-400 | 800 | 66.1% | - | [ckpt (127 MB)](https://storage.googleapis.com/tf_model_garden/vision/cvrl/r3d_1x_k400_800ep.tar.gz) |
+| R3D-50 (1x) | 31.7M | Kinetics-600 | 800 | 68.5% | 70.4% | [ckpt (127 MB)](https://storage.googleapis.com/tf_model_garden/vision/cvrl/r3d_1x_k600_800ep.tar.gz) |
+
+
+## Citation
+
+```
+@inproceedings{qian2021spatiotemporal,
+ title={Spatiotemporal contrastive video representation learning},
+ author={Qian, Rui and Meng, Tianjian and Gong, Boqing and Yang, Ming-Hsuan and Wang, Huisheng and Belongie, Serge and Cui, Yin},
+ booktitle={CVPR},
+ year={2021}
+}
+```
diff --git a/official/projects/video_ssl/configs/__init__.py b/official/projects/video_ssl/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..976989d6c849e215702132b12c2c88f290d62646
--- /dev/null
+++ b/official/projects/video_ssl/configs/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
+
+from official.projects.video_ssl.configs import video_ssl
diff --git a/official/vision/beta/projects/video_ssl/configs/experiments/cvrl_linear_eval_k600.yaml b/official/projects/video_ssl/configs/experiments/cvrl_linear_eval_k600.yaml
similarity index 100%
rename from official/vision/beta/projects/video_ssl/configs/experiments/cvrl_linear_eval_k600.yaml
rename to official/projects/video_ssl/configs/experiments/cvrl_linear_eval_k600.yaml
diff --git a/official/vision/beta/projects/video_ssl/configs/experiments/cvrl_pretrain_k600_200ep.yaml b/official/projects/video_ssl/configs/experiments/cvrl_pretrain_k600_200ep.yaml
similarity index 100%
rename from official/vision/beta/projects/video_ssl/configs/experiments/cvrl_pretrain_k600_200ep.yaml
rename to official/projects/video_ssl/configs/experiments/cvrl_pretrain_k600_200ep.yaml
diff --git a/official/vision/beta/projects/video_ssl/configs/video_ssl.py b/official/projects/video_ssl/configs/video_ssl.py
similarity index 96%
rename from official/vision/beta/projects/video_ssl/configs/video_ssl.py
rename to official/projects/video_ssl/configs/video_ssl.py
index b2dcb22cef59ad3ddc3a484c3d787f53dc687df0..80bf506d7f77cd489a37dc4973e27cfc426c4774 100644
--- a/official/vision/beta/projects/video_ssl/configs/video_ssl.py
+++ b/official/projects/video_ssl/configs/video_ssl.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Video classification configuration definition."""
@@ -20,8 +19,8 @@ import dataclasses
from official.core import config_definitions as cfg
from official.core import exp_factory
-from official.vision.beta.configs import common
-from official.vision.beta.configs import video_classification
+from official.vision.configs import common
+from official.vision.configs import video_classification
Losses = video_classification.Losses
diff --git a/official/vision/beta/projects/video_ssl/configs/video_ssl_test.py b/official/projects/video_ssl/configs/video_ssl_test.py
similarity index 91%
rename from official/vision/beta/projects/video_ssl/configs/video_ssl_test.py
rename to official/projects/video_ssl/configs/video_ssl_test.py
index d6e3eeac2f8849a4d2a92bac97cd2c05949f0da4..3b11ddec1302c115d03a6425ba80535ae2e23562 100644
--- a/official/vision/beta/projects/video_ssl/configs/video_ssl_test.py
+++ b/official/projects/video_ssl/configs/video_ssl_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,16 +12,15 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
# pylint: disable=unused-import
from absl.testing import parameterized
import tensorflow as tf
+from official import vision
from official.core import config_definitions as cfg
from official.core import exp_factory
-from official.vision import beta
-from official.vision.beta.projects.video_ssl.configs import video_ssl as exp_cfg
+from official.projects.video_ssl.configs import video_ssl as exp_cfg
class VideoClassificationConfigTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input.py b/official/projects/video_ssl/dataloaders/video_ssl_input.py
similarity index 94%
rename from official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input.py
rename to official/projects/video_ssl/dataloaders/video_ssl_input.py
index dc7bd88ed7a13caf0d67c6fe6d6a58e5bb1b3837..f49f712342b419d8380d792653f658a22f11d6b5 100644
--- a/official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input.py
+++ b/official/projects/video_ssl/dataloaders/video_ssl_input.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,18 +12,16 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Parser for video and label datasets."""
from typing import Dict, Optional, Tuple
from absl import logging
import tensorflow as tf
-
-from official.vision.beta.dataloaders import video_input
-from official.vision.beta.ops import preprocess_ops_3d
-from official.vision.beta.projects.video_ssl.configs import video_ssl as exp_cfg
-from official.vision.beta.projects.video_ssl.ops import video_ssl_preprocess_ops
+from official.projects.video_ssl.configs import video_ssl as exp_cfg
+from official.projects.video_ssl.ops import video_ssl_preprocess_ops
+from official.vision.dataloaders import video_input
+from official.vision.ops import preprocess_ops_3d
IMAGE_KEY = 'image/encoded'
LABEL_KEY = 'clip/label/index'
@@ -130,6 +128,9 @@ def _process_image(image: tf.Tensor,
# Self-supervised pre-training augmentations.
if is_training and is_ssl:
+ if zero_centering_image:
+ image_1 = 0.5 * (image_1 + 1.0)
+ image_2 = 0.5 * (image_2 + 1.0)
# Temporally consistent color jittering.
image_1 = video_ssl_preprocess_ops.random_color_jitter_3d(image_1)
image_2 = video_ssl_preprocess_ops.random_color_jitter_3d(image_2)
@@ -141,6 +142,8 @@ def _process_image(image: tf.Tensor,
image_2 = video_ssl_preprocess_ops.random_solarization(image_2)
image = tf.concat([image_1, image_2], axis=0)
image = tf.clip_by_value(image, 0., 1.)
+ if zero_centering_image:
+ image = 2 * (image - 0.5)
return image
@@ -235,7 +238,8 @@ class Parser(video_input.Parser):
stride=self._stride,
num_test_clips=self._num_test_clips,
min_resize=self._min_resize,
- crop_size=self._crop_size)
+ crop_size=self._crop_size,
+ zero_centering_image=self._zero_centering_image)
image = tf.cast(image, dtype=self._dtype)
features = {'image': image}
@@ -257,7 +261,8 @@ class Parser(video_input.Parser):
num_test_clips=self._num_test_clips,
min_resize=self._min_resize,
crop_size=self._crop_size,
- num_crops=self._num_crops)
+ num_crops=self._num_crops,
+ zero_centering_image=self._zero_centering_image)
image = tf.cast(image, dtype=self._dtype)
features = {'image': image}
diff --git a/official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input_test.py b/official/projects/video_ssl/dataloaders/video_ssl_input_test.py
similarity index 93%
rename from official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input_test.py
rename to official/projects/video_ssl/dataloaders/video_ssl_input_test.py
index abf6478968b0ac5d28caa691f57ac38407709f03..951f5bd0ec3fcef25fd4a7f06125d27330462463 100644
--- a/official/vision/beta/projects/video_ssl/dataloaders/video_ssl_input_test.py
+++ b/official/projects/video_ssl/dataloaders/video_ssl_input_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
import io
@@ -21,8 +20,8 @@ import numpy as np
from PIL import Image
import tensorflow as tf
-from official.vision.beta.projects.video_ssl.configs import video_ssl as exp_cfg
-from official.vision.beta.projects.video_ssl.dataloaders import video_ssl_input
+from official.projects.video_ssl.configs import video_ssl as exp_cfg
+from official.projects.video_ssl.dataloaders import video_ssl_input
AUDIO_KEY = 'features/audio'
diff --git a/official/projects/video_ssl/losses/losses.py b/official/projects/video_ssl/losses/losses.py
new file mode 100644
index 0000000000000000000000000000000000000000..2aa2085b80e4392d055230505b5ccc2852562e0d
--- /dev/null
+++ b/official/projects/video_ssl/losses/losses.py
@@ -0,0 +1,135 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Define losses."""
+
+# Import libraries
+import tensorflow as tf
+from tensorflow.compiler.tf2xla.python import xla
+
+
+def contrastive_loss(hidden,
+ num_replicas,
+ normalize_hidden,
+ temperature,
+ model,
+ weight_decay):
+ """Computes contrastive loss.
+
+ Args:
+ hidden: embedding of video clips after projection head.
+ num_replicas: number of distributed replicas.
+ normalize_hidden: whether or not to l2 normalize the hidden vector.
+ temperature: temperature in the InfoNCE contrastive loss.
+ model: keras model for calculating weight decay.
+ weight_decay: weight decay parameter.
+
+ Returns:
+ A loss scalar.
+ The logits for contrastive prediction task.
+ The labels for contrastive prediction task.
+ """
+ large_num = 1e9
+
+ hidden1, hidden2 = tf.split(hidden, num_or_size_splits=2, axis=0)
+ if normalize_hidden:
+ hidden1 = tf.math.l2_normalize(hidden1, -1)
+ hidden2 = tf.math.l2_normalize(hidden2, -1)
+ batch_size = tf.shape(hidden1)[0]
+
+ if num_replicas == 1:
+ # This is the local version
+ hidden1_large = hidden1
+ hidden2_large = hidden2
+ labels = tf.one_hot(tf.range(batch_size), batch_size * 2)
+ masks = tf.one_hot(tf.range(batch_size), batch_size)
+
+ else:
+ # This is the cross-tpu version.
+ hidden1_large = tpu_cross_replica_concat(hidden1, num_replicas)
+ hidden2_large = tpu_cross_replica_concat(hidden2, num_replicas)
+ enlarged_batch_size = tf.shape(hidden1_large)[0]
+ replica_id = tf.cast(tf.cast(xla.replica_id(), tf.uint32), tf.int32)
+ labels_idx = tf.range(batch_size) + replica_id * batch_size
+ labels = tf.one_hot(labels_idx, enlarged_batch_size * 2)
+ masks = tf.one_hot(labels_idx, enlarged_batch_size)
+
+ logits_aa = tf.matmul(hidden1, hidden1_large, transpose_b=True) / temperature
+ logits_aa = logits_aa - tf.cast(masks, logits_aa.dtype) * large_num
+ logits_bb = tf.matmul(hidden2, hidden2_large, transpose_b=True) / temperature
+ logits_bb = logits_bb - tf.cast(masks, logits_bb.dtype) * large_num
+ logits_ab = tf.matmul(hidden1, hidden2_large, transpose_b=True) / temperature
+ logits_ba = tf.matmul(hidden2, hidden1_large, transpose_b=True) / temperature
+
+ loss_a = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
+ labels, tf.concat([logits_ab, logits_aa], 1)))
+ loss_b = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(
+ labels, tf.concat([logits_ba, logits_bb], 1)))
+ loss = loss_a + loss_b
+
+ l2_loss = weight_decay * tf.add_n([
+ tf.nn.l2_loss(v)
+ for v in model.trainable_variables
+ if 'kernel' in v.name
+ ])
+
+ total_loss = loss + tf.cast(l2_loss, loss.dtype)
+
+ contrast_prob = tf.nn.softmax(logits_ab)
+ contrast_entropy = - tf.reduce_mean(
+ tf.reduce_sum(contrast_prob * tf.math.log(contrast_prob + 1e-8), -1))
+
+ contrast_acc = tf.equal(tf.argmax(labels, 1), tf.argmax(logits_ab, axis=1))
+ contrast_acc = tf.reduce_mean(tf.cast(contrast_acc, tf.float32))
+
+ return {
+ 'total_loss': total_loss,
+ 'contrastive_loss': loss,
+ 'reg_loss': l2_loss,
+ 'contrast_acc': contrast_acc,
+ 'contrast_entropy': contrast_entropy,
+ }
+
+
+def tpu_cross_replica_concat(tensor, num_replicas):
+ """Reduce a concatenation of the `tensor` across TPU cores.
+
+ Args:
+ tensor: tensor to concatenate.
+ num_replicas: number of TPU device replicas.
+
+ Returns:
+ Tensor of the same rank as `tensor` with first dimension `num_replicas`
+ times larger.
+ """
+ with tf.name_scope('tpu_cross_replica_concat'):
+ # This creates a tensor that is like the input tensor but has an added
+ # replica dimension as the outermost dimension. On each replica it will
+ # contain the local values and zeros for all other values that need to be
+ # fetched from other replicas.
+ ext_tensor = tf.scatter_nd(
+ indices=[[xla.replica_id()]],
+ updates=[tensor],
+ shape=[num_replicas] + tensor.shape.as_list())
+
+ # As every value is only present on one replica and 0 in all others, adding
+ # them all together will result in the full tensor on all replicas.
+ replica_context = tf.distribute.get_replica_context()
+ ext_tensor = replica_context.all_reduce(tf.distribute.ReduceOp.SUM,
+ ext_tensor)
+
+ # Flatten the replica dimension.
+ # The first dimension size will be: tensor.shape[0] * num_replicas
+ # Using [-1] trick to support also scalar input.
+ return tf.reshape(ext_tensor, [-1] + ext_tensor.shape.as_list()[2:])
diff --git a/official/vision/beta/projects/video_ssl/modeling/video_ssl_model.py b/official/projects/video_ssl/modeling/video_ssl_model.py
similarity index 94%
rename from official/vision/beta/projects/video_ssl/modeling/video_ssl_model.py
rename to official/projects/video_ssl/modeling/video_ssl_model.py
index 01a604d9192d1a5ca224b1eaa0cfac75ce22a725..7faf9e6a289b3eb376b4efbb19693869236ea9c5 100644
--- a/official/vision/beta/projects/video_ssl/modeling/video_ssl_model.py
+++ b/official/projects/video_ssl/modeling/video_ssl_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,9 +20,9 @@ from typing import Mapping, Optional
import tensorflow as tf
from official.modeling import tf_utils
-from official.vision.beta.modeling import backbones
-from official.vision.beta.modeling import factory_3d as model_factory
-from official.vision.beta.projects.video_ssl.configs import video_ssl as video_ssl_cfg
+from official.projects.video_ssl.configs import video_ssl as video_ssl_cfg
+from official.vision.modeling import backbones
+from official.vision.modeling import factory_3d as model_factory
layers = tf.keras.layers
@@ -53,7 +53,7 @@ class VideoSSLModel(tf.keras.Model):
hidden_dim: `int` number of hidden units in MLP.
hidden_layer_num: `int` number of hidden layers in MLP.
hidden_norm_args: `dict` for batchnorm arguments in MLP.
- projection_dim: `int` number of ouput dimension for MLP.
+ projection_dim: `int` number of output dimension for MLP.
input_specs: `tf.keras.layers.InputSpec` specs of the input tensor.
dropout_rate: `float` rate for dropout regularization.
aggregate_endpoints: `bool` aggregate all end ponits or only use the
diff --git a/official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops.py b/official/projects/video_ssl/ops/video_ssl_preprocess_ops.py
similarity index 99%
rename from official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops.py
rename to official/projects/video_ssl/ops/video_ssl_preprocess_ops.py
index 253798e856b580fa0edd94443dd994c662d31843..f6a2ef3aa311a7e7596a22e95baa62b974d91982 100644
--- a/official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops.py
+++ b/official/projects/video_ssl/ops/video_ssl_preprocess_ops.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Utils for customed ops for video ssl."""
import functools
diff --git a/official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py b/official/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py
similarity index 88%
rename from official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py
rename to official/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py
index d7292ffc482446527f4bace7e615a72247fc70cb..7e1b61465a9caa753a74a31e8c4d6dc098cbd1bb 100644
--- a/official/vision/beta/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py
+++ b/official/projects/video_ssl/ops/video_ssl_preprocess_ops_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,10 +12,9 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-
import tensorflow as tf
-from official.vision.beta.ops import preprocess_ops_3d
-from official.vision.beta.projects.video_ssl.ops import video_ssl_preprocess_ops
+from official.projects.video_ssl.ops import video_ssl_preprocess_ops
+from official.vision.ops import preprocess_ops_3d
class VideoSslPreprocessOpsTest(tf.test.TestCase):
diff --git a/official/projects/video_ssl/tasks/__init__.py b/official/projects/video_ssl/tasks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..cb7092512589db9a854ac1127a0694f9ffd61eed
--- /dev/null
+++ b/official/projects/video_ssl/tasks/__init__.py
@@ -0,0 +1,18 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tasks package definition."""
+
+from official.projects.video_ssl.tasks import linear_eval
+from official.projects.video_ssl.tasks import pretrain
diff --git a/official/vision/beta/projects/video_ssl/tasks/linear_eval.py b/official/projects/video_ssl/tasks/linear_eval.py
similarity index 88%
rename from official/vision/beta/projects/video_ssl/tasks/linear_eval.py
rename to official/projects/video_ssl/tasks/linear_eval.py
index dc245e44cf161db98ab97c1e6febbce2895376d7..5d7849422c765b8832b764b07128054962cde64f 100644
--- a/official/vision/beta/projects/video_ssl/tasks/linear_eval.py
+++ b/official/projects/video_ssl/tasks/linear_eval.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Video ssl linear evaluation task definition."""
from typing import Any, Optional, List, Tuple
from absl import logging
@@ -20,9 +19,9 @@ import tensorflow as tf
# pylint: disable=unused-import
from official.core import task_factory
-from official.vision.beta.projects.video_ssl.configs import video_ssl as exp_cfg
-from official.vision.beta.projects.video_ssl.modeling import video_ssl_model
-from official.vision.beta.tasks import video_classification
+from official.projects.video_ssl.configs import video_ssl as exp_cfg
+from official.projects.video_ssl.modeling import video_ssl_model
+from official.vision.tasks import video_classification
@task_factory.register_task_cls(exp_cfg.VideoSSLEvalTask)
diff --git a/official/vision/beta/projects/video_ssl/tasks/pretrain.py b/official/projects/video_ssl/tasks/pretrain.py
similarity index 92%
rename from official/vision/beta/projects/video_ssl/tasks/pretrain.py
rename to official/projects/video_ssl/tasks/pretrain.py
index b82b2624ab3026e8c2bb4fc3eb590b2188fad633..f58db11ce5836ef0ca0912bf13eea928bb97f200 100644
--- a/official/vision/beta/projects/video_ssl/tasks/pretrain.py
+++ b/official/projects/video_ssl/tasks/pretrain.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Video ssl pretrain task definition."""
from absl import logging
import tensorflow as tf
@@ -20,12 +19,13 @@ import tensorflow as tf
# pylint: disable=unused-import
from official.core import input_reader
from official.core import task_factory
-from official.vision.beta.modeling import factory_3d
-from official.vision.beta.projects.video_ssl.configs import video_ssl as exp_cfg
-from official.vision.beta.projects.video_ssl.dataloaders import video_ssl_input
-from official.vision.beta.projects.video_ssl.losses import losses
-from official.vision.beta.projects.video_ssl.modeling import video_ssl_model
-from official.vision.beta.tasks import video_classification
+from official.projects.video_ssl.configs import video_ssl as exp_cfg
+from official.projects.video_ssl.dataloaders import video_ssl_input
+from official.projects.video_ssl.losses import losses
+from official.projects.video_ssl.modeling import video_ssl_model
+from official.vision.modeling import factory_3d
+from official.vision.tasks import video_classification
+# pylint: enable=unused-import
@task_factory.register_task_cls(exp_cfg.VideoSSLPretrainTask)
diff --git a/official/vision/beta/projects/video_ssl/tasks/pretrain_test.py b/official/projects/video_ssl/tasks/pretrain_test.py
similarity index 91%
rename from official/vision/beta/projects/video_ssl/tasks/pretrain_test.py
rename to official/projects/video_ssl/tasks/pretrain_test.py
index e6ec40d577e0c73a22e77ed827106d0a76cfaac5..5f0bdbbb38fe5b8f799d6e8cf60d0c53cd83d028 100644
--- a/official/vision/beta/projects/video_ssl/tasks/pretrain_test.py
+++ b/official/projects/video_ssl/tasks/pretrain_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
import functools
import os
@@ -22,12 +21,13 @@ import orbit
import tensorflow as tf
# pylint: disable=unused-import
+from official import vision
from official.core import exp_factory
from official.core import task_factory
from official.modeling import optimization
-from official.vision import beta
-from official.vision.beta.dataloaders import tfexample_utils
-from official.vision.beta.projects.video_ssl.tasks import pretrain
+from official.projects.video_ssl.tasks import pretrain
+from official.vision.dataloaders import tfexample_utils
+# pylint: enable=unused-import
class VideoClassificationTaskTest(tf.test.TestCase):
diff --git a/official/projects/video_ssl/train.py b/official/projects/video_ssl/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5d1f4e8f58ffabd58ec4ce152626bc583f184042
--- /dev/null
+++ b/official/projects/video_ssl/train.py
@@ -0,0 +1,77 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Training driver."""
+
+from absl import app
+from absl import flags
+import gin
+
+# pylint: disable=unused-import
+from official.common import distribute_utils
+from official.common import flags as tfm_flags
+from official.core import task_factory
+from official.core import train_lib
+from official.core import train_utils
+from official.modeling import performance
+from official.projects.video_ssl.modeling import video_ssl_model
+from official.projects.video_ssl.tasks import linear_eval
+from official.projects.video_ssl.tasks import pretrain
+from official.vision import registry_imports
+# pylint: disable=unused-import
+
+FLAGS = flags.FLAGS
+
+
+def main(_):
+ gin.parse_config_files_and_bindings(FLAGS.gin_file, FLAGS.gin_params)
+ params = train_utils.parse_configuration(FLAGS)
+ model_dir = FLAGS.model_dir
+ if 'train' in FLAGS.mode:
+ # Pure eval modes do not output yaml files. Otherwise continuous eval job
+ # may race against the train job for writing the same file.
+ train_utils.serialize_config(params, model_dir)
+
+ if 'train_and_eval' in FLAGS.mode:
+ assert (params.task.train_data.feature_shape ==
+ params.task.validation_data.feature_shape), (
+ f'train {params.task.train_data.feature_shape} != validate '
+ f'{params.task.validation_data.feature_shape}')
+
+ # Sets mixed_precision policy. Using 'mixed_float16' or 'mixed_bfloat16'
+ # can have significant impact on model speeds by utilizing float16 in case of
+ # GPUs, and bfloat16 in the case of TPUs. loss_scale takes effect only when
+ # dtype is float16
+ if params.runtime.mixed_precision_dtype:
+ performance.set_mixed_precision_policy(params.runtime.mixed_precision_dtype)
+ distribution_strategy = distribute_utils.get_distribution_strategy(
+ distribution_strategy=params.runtime.distribution_strategy,
+ all_reduce_alg=params.runtime.all_reduce_alg,
+ num_gpus=params.runtime.num_gpus,
+ tpu_address=params.runtime.tpu)
+ with distribution_strategy.scope():
+ task = task_factory.get_task(params.task, logging_dir=model_dir)
+
+ train_lib.run_experiment(
+ distribution_strategy=distribution_strategy,
+ task=task,
+ mode=FLAGS.mode,
+ params=params,
+ model_dir=model_dir)
+
+ train_utils.save_gin_config(FLAGS.mode, model_dir)
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(main)
diff --git a/official/vision/beta/projects/vit/README.md b/official/projects/vit/README.md
similarity index 100%
rename from official/vision/beta/projects/vit/README.md
rename to official/projects/vit/README.md
diff --git a/official/projects/vit/configs/__init__.py b/official/projects/vit/configs/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..fa295acb873151f754c8e345b7d8de3191060cf3
--- /dev/null
+++ b/official/projects/vit/configs/__init__.py
@@ -0,0 +1,17 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Configs package definition."""
+
+from official.projects.vit.configs import image_classification
diff --git a/official/projects/vit/configs/backbones.py b/official/projects/vit/configs/backbones.py
new file mode 100644
index 0000000000000000000000000000000000000000..a9169d58303939eda3f13611c0423ec058e51114
--- /dev/null
+++ b/official/projects/vit/configs/backbones.py
@@ -0,0 +1,57 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Backbones configurations."""
+import dataclasses
+from typing import Optional, Tuple
+
+from official.modeling import hyperparams
+
+
+@dataclasses.dataclass
+class Transformer(hyperparams.Config):
+ """Transformer config."""
+ mlp_dim: int = 1
+ num_heads: int = 1
+ num_layers: int = 1
+ attention_dropout_rate: float = 0.0
+ dropout_rate: float = 0.1
+
+
+@dataclasses.dataclass
+class VisionTransformer(hyperparams.Config):
+ """VisionTransformer config."""
+ model_name: str = 'vit-b16'
+ # pylint: disable=line-too-long
+ pooler: str = 'token' # 'token', 'gap' or 'none'. If set to 'token', an extra classification token is added to sequence.
+ # pylint: enable=line-too-long
+ representation_size: int = 0
+ hidden_size: int = 1
+ patch_size: int = 16
+ transformer: Transformer = Transformer()
+ init_stochastic_depth_rate: float = 0.0
+ original_init: bool = True
+ pos_embed_shape: Optional[Tuple[int, int]] = None
+
+
+@dataclasses.dataclass
+class Backbone(hyperparams.OneOfConfig):
+ """Configuration for backbones.
+
+ Attributes:
+ type: 'str', type of backbone be used, one the of fields below.
+ vit: vit backbone config.
+ """
+ type: Optional[str] = None
+ vit: VisionTransformer = VisionTransformer()
diff --git a/official/projects/vit/configs/image_classification.py b/official/projects/vit/configs/image_classification.py
new file mode 100644
index 0000000000000000000000000000000000000000..950fe92c4325f465f22445a283910c052d5be064
--- /dev/null
+++ b/official/projects/vit/configs/image_classification.py
@@ -0,0 +1,274 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Image classification configuration definition."""
+import dataclasses
+import os
+from typing import Optional
+
+from official.core import config_definitions as cfg
+from official.core import exp_factory
+from official.core import task_factory
+from official.modeling import hyperparams
+from official.modeling import optimization
+from official.projects.vit.configs import backbones
+from official.vision.configs import common
+from official.vision.configs import image_classification as img_cls_cfg
+from official.vision.tasks import image_classification
+
+# pytype: disable=wrong-keyword-args
+
+DataConfig = img_cls_cfg.DataConfig
+
+
+@dataclasses.dataclass
+class ImageClassificationModel(img_cls_cfg.ImageClassificationModel):
+ """The model config."""
+ backbone: backbones.Backbone = backbones.Backbone(
+ type='vit', vit=backbones.VisionTransformer())
+
+
+@dataclasses.dataclass
+class Losses(hyperparams.Config):
+ loss_weight: float = 1.0
+ one_hot: bool = True
+ label_smoothing: float = 0.0
+ l2_weight_decay: float = 0.0
+ soft_labels: bool = False
+
+
+@dataclasses.dataclass
+class Evaluation(hyperparams.Config):
+ top_k: int = 5
+
+
+@dataclasses.dataclass
+class ImageClassificationTask(cfg.TaskConfig):
+ """The task config. Same as the classification task for convnets."""
+ model: ImageClassificationModel = ImageClassificationModel()
+ train_data: DataConfig = DataConfig(is_training=True)
+ validation_data: DataConfig = DataConfig(is_training=False)
+ losses: Losses = Losses()
+ evaluation: Evaluation = Evaluation()
+ init_checkpoint: Optional[str] = None
+ init_checkpoint_modules: str = 'all' # all or backbone
+ freeze_backbone: bool = False
+
+
+IMAGENET_TRAIN_EXAMPLES = 1281167
+IMAGENET_VAL_EXAMPLES = 50000
+IMAGENET_INPUT_PATH_BASE = 'imagenet-2012-tfrecord'
+
+# TODO(b/177942984): integrate the experiments to TF-vision.
+task_factory.register_task_cls(ImageClassificationTask)(
+ image_classification.ImageClassificationTask)
+
+
+@exp_factory.register_config_factory('legacy_deit_imagenet_pretrain')
+def image_classification_imagenet_deit_pretrain() -> cfg.ExperimentConfig:
+ """Image classification on imagenet with vision transformer."""
+ train_batch_size = 4096 # originally was 1024 but 4096 better for tpu v3-32
+ eval_batch_size = 4096 # originally was 1024 but 4096 better for tpu v3-32
+ num_classes = 1001
+ label_smoothing = 0.1
+ steps_per_epoch = IMAGENET_TRAIN_EXAMPLES // train_batch_size
+ config = cfg.ExperimentConfig(
+ task=ImageClassificationTask(
+ model=ImageClassificationModel(
+ num_classes=num_classes,
+ input_size=[224, 224, 3],
+ kernel_initializer='zeros',
+ backbone=backbones.Backbone(
+ type='vit',
+ vit=backbones.VisionTransformer(
+ model_name='vit-b16',
+ representation_size=768,
+ init_stochastic_depth_rate=0.1,
+ original_init=False,
+ transformer=backbones.Transformer(
+ dropout_rate=0.0, attention_dropout_rate=0.0)))),
+ losses=Losses(
+ l2_weight_decay=0.0,
+ label_smoothing=label_smoothing,
+ one_hot=False,
+ soft_labels=True),
+ train_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size,
+ aug_type=common.Augmentation(
+ type='randaug',
+ randaug=common.RandAugment(
+ magnitude=9, exclude_ops=['Cutout'])),
+ mixup_and_cutmix=common.MixupAndCutmix(
+ label_smoothing=label_smoothing)),
+ validation_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'valid*'),
+ is_training=False,
+ global_batch_size=eval_batch_size)),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=300 * steps_per_epoch,
+ validation_steps=IMAGENET_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate': 0.05,
+ 'include_in_weight_decay': r'.*(kernel|weight):0$',
+ 'gradient_clip_norm': 0.0
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ 'initial_learning_rate': 0.0005 * train_batch_size / 512,
+ 'decay_steps': 300 * steps_per_epoch,
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 5 * steps_per_epoch,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
+
+
+@exp_factory.register_config_factory('legacy_vit_imagenet_pretrain')
+def image_classification_imagenet_vit_pretrain() -> cfg.ExperimentConfig:
+ """Image classification on imagenet with vision transformer."""
+ train_batch_size = 4096
+ eval_batch_size = 4096
+ steps_per_epoch = IMAGENET_TRAIN_EXAMPLES // train_batch_size
+ config = cfg.ExperimentConfig(
+ task=ImageClassificationTask(
+ model=ImageClassificationModel(
+ num_classes=1001,
+ input_size=[224, 224, 3],
+ kernel_initializer='zeros',
+ backbone=backbones.Backbone(
+ type='vit',
+ vit=backbones.VisionTransformer(
+ model_name='vit-b16', representation_size=768))),
+ losses=Losses(l2_weight_decay=0.0),
+ train_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size),
+ validation_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'valid*'),
+ is_training=False,
+ global_batch_size=eval_batch_size)),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=300 * steps_per_epoch,
+ validation_steps=IMAGENET_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'adamw',
+ 'adamw': {
+ 'weight_decay_rate': 0.3,
+ 'include_in_weight_decay': r'.*(kernel|weight):0$',
+ 'gradient_clip_norm': 0.0
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ 'initial_learning_rate': 0.003 * train_batch_size / 4096,
+ 'decay_steps': 300 * steps_per_epoch,
+ }
+ },
+ 'warmup': {
+ 'type': 'linear',
+ 'linear': {
+ 'warmup_steps': 10000,
+ 'warmup_learning_rate': 0
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
+
+
+@exp_factory.register_config_factory('legacy_vit_imagenet_finetune')
+def image_classification_imagenet_vit_finetune() -> cfg.ExperimentConfig:
+ """Image classification on imagenet with vision transformer."""
+ train_batch_size = 512
+ eval_batch_size = 512
+ steps_per_epoch = IMAGENET_TRAIN_EXAMPLES // train_batch_size
+ config = cfg.ExperimentConfig(
+ task=ImageClassificationTask(
+ model=ImageClassificationModel(
+ num_classes=1001,
+ input_size=[384, 384, 3],
+ backbone=backbones.Backbone(
+ type='vit',
+ vit=backbones.VisionTransformer(model_name='vit-b16'))),
+ losses=Losses(l2_weight_decay=0.0),
+ train_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'train*'),
+ is_training=True,
+ global_batch_size=train_batch_size),
+ validation_data=DataConfig(
+ input_path=os.path.join(IMAGENET_INPUT_PATH_BASE, 'valid*'),
+ is_training=False,
+ global_batch_size=eval_batch_size)),
+ trainer=cfg.TrainerConfig(
+ steps_per_loop=steps_per_epoch,
+ summary_interval=steps_per_epoch,
+ checkpoint_interval=steps_per_epoch,
+ train_steps=20000,
+ validation_steps=IMAGENET_VAL_EXAMPLES // eval_batch_size,
+ validation_interval=steps_per_epoch,
+ optimizer_config=optimization.OptimizationConfig({
+ 'optimizer': {
+ 'type': 'sgd',
+ 'sgd': {
+ 'momentum': 0.9,
+ 'global_clipnorm': 1.0,
+ }
+ },
+ 'learning_rate': {
+ 'type': 'cosine',
+ 'cosine': {
+ 'initial_learning_rate': 0.003,
+ 'decay_steps': 20000,
+ }
+ }
+ })),
+ restrictions=[
+ 'task.train_data.is_training != None',
+ 'task.validation_data.is_training != None'
+ ])
+
+ return config
diff --git a/official/projects/vit/modeling/nn_blocks.py b/official/projects/vit/modeling/nn_blocks.py
new file mode 100644
index 0000000000000000000000000000000000000000..891c9ac2426baab96ccfa26ce93407108b472ce5
--- /dev/null
+++ b/official/projects/vit/modeling/nn_blocks.py
@@ -0,0 +1,119 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Keras-based TransformerEncoder block layer."""
+import tensorflow as tf
+
+from official.nlp import modeling
+from official.vision.modeling.layers.nn_layers import StochasticDepth
+
+
+class TransformerEncoderBlock(modeling.layers.TransformerEncoderBlock):
+ """TransformerEncoderBlock layer with stochastic depth."""
+
+ def __init__(self,
+ *args,
+ stochastic_depth_drop_rate=0.0,
+ return_attention=False,
+ **kwargs):
+ """Initializes TransformerEncoderBlock."""
+ super().__init__(*args, **kwargs)
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._return_attention = return_attention
+
+ def build(self, input_shape):
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = StochasticDepth(self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = lambda x, *args, **kwargs: tf.identity(x)
+
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {"stochastic_depth_drop_rate": self._stochastic_depth_drop_rate}
+ base_config = super().get_config()
+ return dict(list(base_config.items()) + list(config.items()))
+
+ def call(self, inputs, training=None):
+ """Transformer self-attention encoder block call."""
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError("Unexpected inputs to %s with length at %d" %
+ (self.__class__, len(inputs)))
+ else:
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ if self._output_range:
+ if self._norm_first:
+ source_tensor = input_tensor[:, 0:self._output_range, :]
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor[:, 0:self._output_range, :]
+ if attention_mask is not None:
+ attention_mask = attention_mask[:, 0:self._output_range, :]
+ else:
+ if self._norm_first:
+ source_tensor = input_tensor
+ input_tensor = self._attention_layer_norm(input_tensor)
+ if key_value is not None:
+ key_value = self._attention_layer_norm(key_value)
+ target_tensor = input_tensor
+
+ if key_value is None:
+ key_value = input_tensor
+ attention_output, attention_scores = self._attention_layer(
+ query=target_tensor, value=key_value, attention_mask=attention_mask,
+ return_attention_scores=True)
+ attention_output = self._attention_dropout(attention_output)
+
+ if self._norm_first:
+ attention_output = source_tensor + self._stochastic_depth(
+ attention_output, training=training)
+ else:
+ attention_output = self._attention_layer_norm(
+ target_tensor +
+ self._stochastic_depth(attention_output, training=training))
+
+ if self._norm_first:
+ source_attention_output = attention_output
+ attention_output = self._output_layer_norm(attention_output)
+ inner_output = self._intermediate_dense(attention_output)
+ inner_output = self._intermediate_activation_layer(inner_output)
+ inner_output = self._inner_dropout_layer(inner_output)
+ layer_output = self._output_dense(inner_output)
+ layer_output = self._output_dropout(layer_output)
+
+ if self._norm_first:
+ if self._return_attention:
+ return source_attention_output + self._stochastic_depth(
+ layer_output, training=training), attention_scores
+ else:
+ return source_attention_output + self._stochastic_depth(
+ layer_output, training=training)
+
+ # During mixed precision training, layer norm output is always fp32 for now.
+ # Casts fp32 for the subsequent add.
+ layer_output = tf.cast(layer_output, tf.float32)
+ if self._return_attention:
+ return self._output_layer_norm(layer_output + self._stochastic_depth(
+ attention_output, training=training)), attention_scores
+ else:
+ return self._output_layer_norm(layer_output + self._stochastic_depth(
+ attention_output, training=training))
diff --git a/official/projects/vit/modeling/transformer_scaffold.py b/official/projects/vit/modeling/transformer_scaffold.py
new file mode 100644
index 0000000000000000000000000000000000000000..edf13a6235ef3c4e29e6f429c8eea86b0ea3ae54
--- /dev/null
+++ b/official/projects/vit/modeling/transformer_scaffold.py
@@ -0,0 +1,161 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Keras-based Scaffold TransformerEncoder block for vision models.
+
+This implementation is subclassed from NLP TransformerScaffold to support
+customized `attention_layer` and `feedforward_layer`. In addition, this
+implementation has a few features to better support vision use cases:
+1. `stochastic_depth_drop_rate` to supress model overfitting.
+2. `return_attention_scores`, optionally returns the attention output.
+3. `ffn_has_residual_connection`, clearly define whether feedforward network has
+ residual connection or not to avoid ambiguity.
+"""
+from typing import List, Optional, Tuple, Union
+
+import gin
+import tensorflow as tf
+
+from official.nlp import modeling
+from official.vision.modeling.layers.nn_layers import StochasticDepth
+
+
+@tf.keras.utils.register_keras_serializable(package="Vision")
+@gin.configurable
+class TransformerScaffold(modeling.layers.TransformerScaffold):
+ """TransformerScaffold layer for vision applications.
+
+ This layer is a subclass of NLP TransformerScaffold:
+
+ Attributes:
+ stochastic_depth_drop_rate: Drop rate for the residual connections.
+ return_attention_scores: Optionally return the attention output.
+ ffn_has_residual_connection: Whether the feedforward network has internal
+ residual connection and layer norm. If False, the residual connection and
+ the layer norm op are called inside TransformerScaffold.
+ """
+
+ def __init__(self,
+ *args,
+ stochastic_depth_drop_rate: float = 0.0,
+ return_attention_scores: bool = False,
+ ffn_has_residual_connection: bool = False,
+ **kwargs):
+ """Initializes TransformerEncoderBlock."""
+ super().__init__(*args, **kwargs)
+ self._stochastic_depth_drop_rate = stochastic_depth_drop_rate
+ self._return_attention_scores = return_attention_scores
+ self._ffn_has_residual_connection = ffn_has_residual_connection
+
+ def build(self, input_shape: Union[tf.TensorShape, List[int]]):
+ if self._stochastic_depth_drop_rate:
+ self._stochastic_depth = StochasticDepth(self._stochastic_depth_drop_rate)
+ else:
+ self._stochastic_depth = lambda x, *args, **kwargs: tf.identity(x)
+
+ super().build(input_shape)
+
+ def get_config(self):
+ config = {"stochastic_depth_drop_rate": self._stochastic_depth_drop_rate,
+ "return_attention_scores": self._return_attention_scores,
+ "ffn_has_residual_connection": self._ffn_has_residual_connection}
+ base_config = super().get_config()
+ base_config.update(config)
+ return base_config
+
+ def call(
+ self,
+ inputs: tf.Tensor,
+ training: Optional[bool] = None
+ ) -> Union[tf.Tensor, Tuple[tf.Tensor, tf.Tensor]]:
+ """Transformer self-attention encoder block call."""
+ if isinstance(inputs, (list, tuple)):
+ if len(inputs) == 2:
+ input_tensor, attention_mask = inputs
+ key_value = None
+ elif len(inputs) == 3:
+ input_tensor, key_value, attention_mask = inputs
+ else:
+ raise ValueError("Unexpected inputs to %s with length at %d" %
+ (self.__class__, len(inputs)))
+ else:
+ input_tensor, key_value, attention_mask = (inputs, None, None)
+
+ if key_value is None:
+ key_value = input_tensor
+
+ if self._norm_first:
+ source_tensor = input_tensor
+ input_tensor = self._attention_layer_norm(input_tensor, training=training)
+
+ attention_layer_output = self._attention_layer(
+ query=input_tensor,
+ value=key_value,
+ attention_mask=attention_mask,
+ training=training,
+ return_attention_scores=self._return_attention_scores)
+ if isinstance(attention_layer_output, tuple):
+ # `attention_layer_output` contains two tensors when
+ # `return_attention_scores` is True.
+ attention_output, attention_scores = attention_layer_output
+ else:
+ attention_output = attention_layer_output
+ attention_output = self._attention_dropout(attention_output,
+ training=training)
+
+ if self._norm_first:
+ source_attention_output = source_tensor + self._stochastic_depth(
+ attention_output, training=training)
+ attention_output = self._output_layer_norm(source_attention_output,
+ training=training)
+ else:
+ attention_output = self._attention_layer_norm(
+ input_tensor +
+ self._stochastic_depth(attention_output, training=training),
+ training=training)
+
+ if self._feedforward_block is None:
+ intermediate_output = self._intermediate_dense(attention_output)
+ intermediate_output = self._intermediate_activation_layer(
+ intermediate_output)
+ layer_output = self._output_dense(intermediate_output, training=training)
+ layer_output = self._output_dropout(layer_output, training=training)
+ else:
+ layer_output = self._feedforward_block(attention_output,
+ training=training)
+
+ # During mixed precision training, layer norm output is always fp32 for now.
+ # Casts fp32 for the subsequent add.
+ layer_output = tf.cast(layer_output, tf.float32)
+
+ if self._norm_first:
+ if self._ffn_has_residual_connection:
+ raise ValueError(
+ "In the case of `norm_first`, the residual connection should be"
+ "done in the TransformerScaffold call function, not FFN's"
+ "call function.")
+ output = source_attention_output + self._stochastic_depth(
+ layer_output, training=training)
+ else:
+ if self._ffn_has_residual_connection:
+ output = self._stochastic_depth(layer_output, training=training)
+ else:
+ output = self._output_layer_norm(
+ attention_output + self._stochastic_depth(
+ layer_output, training=training))
+
+ if self._return_attention_scores:
+ return output, attention_scores
+ else:
+ return output
diff --git a/official/projects/vit/modeling/transformer_scaffold_test.py b/official/projects/vit/modeling/transformer_scaffold_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..632918b06ec6790252ae1496a8efe80f9cdffc3f
--- /dev/null
+++ b/official/projects/vit/modeling/transformer_scaffold_test.py
@@ -0,0 +1,518 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for Keras-based transformer block layer."""
+
+import numpy as np
+import tensorflow as tf
+
+from tensorflow.python.keras import keras_parameterized # pylint: disable=g-direct-tensorflow-import
+from official.nlp import modeling
+from official.projects.vit.modeling import transformer_scaffold
+
+TransformerScaffold = transformer_scaffold.TransformerScaffold
+
+
+# Test class that wraps a standard attention layer. If this layer is called
+# at any point, the list passed to the config object will be filled with a
+# boolean 'True'. We register this class as a Keras serializable so we can
+# test serialization below.
+@tf.keras.utils.register_keras_serializable(package='TestOnlyAttention')
+class ValidatedAttentionLayer(modeling.layers.attention.MultiHeadAttention):
+
+ def __init__(self, call_list, **kwargs):
+ super(ValidatedAttentionLayer, self).__init__(**kwargs)
+ self.list = call_list
+
+ def call(self,
+ query,
+ value,
+ attention_mask=None,
+ return_attention_scores=False,):
+ self.list.append(True)
+ return super(ValidatedAttentionLayer, self).call(
+ query,
+ value,
+ attention_mask=attention_mask,
+ return_attention_scores=return_attention_scores)
+
+ def get_config(self):
+ config = super(ValidatedAttentionLayer, self).get_config()
+ config['call_list'] = []
+ return config
+
+
+# Test class implements a simple feedforward layer. If this layer is called
+# at any point, the list passed to the config object will be filled with a
+# boolean 'True'. We register this class as a Keras serializable so we can
+# test serialization below.
+@tf.keras.utils.register_keras_serializable(package='TestOnlyFeedforward')
+class ValidatedFeedforwardLayer(tf.keras.layers.Layer):
+
+ def __init__(self, call_list, activation, **kwargs):
+ super(ValidatedFeedforwardLayer, self).__init__(**kwargs)
+ self.list = call_list
+ self.activation = activation
+
+ def build(self, input_shape):
+ hidden_size = input_shape.as_list()[-1]
+ self._feedforward_dense = tf.keras.layers.EinsumDense(
+ '...x,xy->...y',
+ output_shape=hidden_size,
+ bias_axes='y',
+ activation=self.activation,
+ name='feedforward')
+
+ def call(self, inputs):
+ self.list.append(True)
+ return self._feedforward_dense(inputs)
+
+ def get_config(self):
+ config = super(ValidatedFeedforwardLayer, self).get_config()
+ config['call_list'] = []
+ config['activation'] = self.activation
+ return config
+
+
+# This decorator runs the test in V1, V2-Eager, and V2-Functional mode. It
+# guarantees forward compatibility of this code for the V2 switchover.
+@keras_parameterized.run_all_keras_modes
+class TransformerLayerTest(keras_parameterized.TestCase):
+
+ def tearDown(self):
+ super(TransformerLayerTest, self).tearDown()
+ tf.keras.mixed_precision.set_global_policy('float32')
+
+ def test_layer_creation(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+ # The default output of a transformer layer should be the same as the input.
+ self.assertEqual(data_tensor.shape.as_list(), output_tensor.shape.as_list())
+
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+
+ def test_layer_creation_with_feedforward_cls(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ feedforward_call_list = []
+ feedforward_layer_cfg = {
+ 'activation': 'relu',
+ 'call_list': feedforward_call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ feedforward_cls=ValidatedFeedforwardLayer,
+ feedforward_cfg=feedforward_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=None,
+ inner_activation=None)
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+ # The default output of a transformer layer should be the same as the input.
+ self.assertEqual(data_tensor.shape.as_list(), output_tensor.shape.as_list())
+
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+ self.assertNotEmpty(feedforward_call_list)
+ self.assertTrue(feedforward_call_list[0],
+ "The passed layer class wasn't instantiated.")
+
+ def test_layer_creation_with_mask(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+ # The default output of a transformer layer should be the same as the input.
+ self.assertEqual(data_tensor.shape.as_list(), output_tensor.shape.as_list())
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+
+ def test_layer_invocation(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output_tensor = test_layer(data_tensor)
+
+ # Create a model from the test layer.
+ model = tf.keras.Model(data_tensor, output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ _ = model.predict(input_data)
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+
+ def test_layer_invocation_with_feedforward_cls(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ feedforward_call_list = []
+ feedforward_layer_cfg = {
+ 'activation': 'relu',
+ 'call_list': feedforward_call_list,
+ }
+ feedforward_layer = ValidatedFeedforwardLayer(**feedforward_layer_cfg)
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ feedforward_cls=feedforward_layer,
+ num_attention_heads=10,
+ inner_dim=None,
+ inner_activation=None)
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+
+ # Create a model from the test layer.
+ model = tf.keras.Model([data_tensor, mask_tensor], output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ # The attention mask should be of shape (batch, from_seq_len, to_seq_len),
+ # which here is (batch, sequence_length, sequence_length)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length, sequence_length))
+ _ = model.predict([input_data, mask_data])
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+ self.assertNotEmpty(feedforward_call_list)
+ self.assertTrue(feedforward_call_list[0],
+ "The passed layer class wasn't instantiated.")
+
+ def test_layer_invocation_with_mask(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+
+ # Create a model from the test layer.
+ model = tf.keras.Model([data_tensor, mask_tensor], output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ # The attention mask should be of shape (batch, from_seq_len, to_seq_len),
+ # which here is (batch, sequence_length, sequence_length)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length, sequence_length))
+ _ = model.predict([input_data, mask_data])
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+
+ def test_layer_invocation_with_float16_dtype(self):
+ tf.keras.mixed_precision.set_global_policy('mixed_float16')
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+
+ # Create a model from the test layer.
+ model = tf.keras.Model([data_tensor, mask_tensor], output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = (10 * np.random.random_sample(
+ (batch_size, sequence_length, width)))
+ # The attention mask should be of shape (batch, from_seq_len, to_seq_len),
+ # which here is (batch, sequence_length, sequence_length)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length, sequence_length))
+ _ = model.predict([input_data, mask_data])
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0], "The passed layer class wasn't instantiated.")
+
+ def test_transform_with_initializer(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu',
+ kernel_initializer=tf.keras.initializers.TruncatedNormal(stddev=0.02))
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ output = test_layer(data_tensor)
+ # The default output of a transformer layer should be the same as the input.
+ self.assertEqual(data_tensor.shape.as_list(), output.shape.as_list())
+ # If call_list[0] exists and is True, the passed layer class was
+ # instantiated from the given config properly.
+ self.assertNotEmpty(call_list)
+ self.assertTrue(call_list[0])
+
+ def test_layer_restoration_from_config(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ 'name': 'test_layer',
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=2048,
+ inner_activation='relu')
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+
+ # Create a model from the test layer.
+ model = tf.keras.Model([data_tensor, mask_tensor], output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ # The attention mask should be of shape (batch, from_seq_len, to_seq_len),
+ # which here is (batch, sequence_length, sequence_length)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length, sequence_length))
+ pre_serialization_output = model.predict([input_data, mask_data])
+
+ # Serialize the model config. Pass the serialized data through json to
+ # ensure that we can serialize this layer to disk.
+ serialized_data = model.get_config()
+
+ # Create a new model from the old config, and copy the weights. These models
+ # should have identical outputs.
+ new_model = tf.keras.Model.from_config(serialized_data)
+ new_model.set_weights(model.get_weights())
+ output = new_model.predict([input_data, mask_data])
+
+ self.assertAllClose(pre_serialization_output, output)
+
+ # If the layer was configured correctly, it should have a list attribute
+ # (since it should have the custom class and config passed to it).
+ new_model.summary()
+ new_call_list = new_model.get_layer(
+ name='transformer_scaffold')._attention_layer.list
+ self.assertNotEmpty(new_call_list)
+ self.assertTrue(new_call_list[0],
+ "The passed layer class wasn't instantiated.")
+
+ def test_layer_with_feedforward_cls_restoration_from_config(self):
+ sequence_length = 21
+ width = 80
+
+ call_list = []
+ attention_layer_cfg = {
+ 'num_heads': 10,
+ 'key_dim': 8,
+ 'call_list': call_list,
+ 'name': 'test_layer',
+ }
+ feedforward_call_list = []
+ feedforward_layer_cfg = {
+ 'activation': 'relu',
+ 'call_list': feedforward_call_list,
+ }
+ test_layer = TransformerScaffold(
+ attention_cls=ValidatedAttentionLayer,
+ attention_cfg=attention_layer_cfg,
+ feedforward_cls=ValidatedFeedforwardLayer,
+ feedforward_cfg=feedforward_layer_cfg,
+ num_attention_heads=10,
+ inner_dim=None,
+ inner_activation=None)
+
+ # Create a 3-dimensional input (the first dimension is implicit).
+ data_tensor = tf.keras.Input(shape=(sequence_length, width))
+ # Create a 2-dimensional input (the first dimension is implicit).
+ mask_tensor = tf.keras.Input(shape=(sequence_length, sequence_length))
+ output_tensor = test_layer([data_tensor, mask_tensor])
+
+ # Create a model from the test layer.
+ model = tf.keras.Model([data_tensor, mask_tensor], output_tensor)
+
+ # Invoke the model on test data. We can't validate the output data itself
+ # (the NN is too complex) but this will rule out structural runtime errors.
+ batch_size = 6
+ input_data = 10 * np.random.random_sample(
+ (batch_size, sequence_length, width))
+ # The attention mask should be of shape (batch, from_seq_len, to_seq_len),
+ # which here is (batch, sequence_length, sequence_length)
+ mask_data = np.random.randint(
+ 2, size=(batch_size, sequence_length, sequence_length))
+ pre_serialization_output = model.predict([input_data, mask_data])
+
+ serialized_data = model.get_config()
+ # Create a new model from the old config, and copy the weights. These models
+ # should have identical outputs.
+ new_model = tf.keras.Model.from_config(serialized_data)
+ new_model.set_weights(model.get_weights())
+ output = new_model.predict([input_data, mask_data])
+
+ self.assertAllClose(pre_serialization_output, output)
+
+ # If the layer was configured correctly, it should have a list attribute
+ # (since it should have the custom class and config passed to it).
+ new_model.summary()
+ new_call_list = new_model.get_layer(
+ name='transformer_scaffold')._attention_layer.list
+ self.assertNotEmpty(new_call_list)
+ self.assertTrue(new_call_list[0],
+ "The passed layer class wasn't instantiated.")
+ new_feedforward_call_list = new_model.get_layer(
+ name='transformer_scaffold')._feedforward_block.list
+ self.assertNotEmpty(new_feedforward_call_list)
+ self.assertTrue(new_feedforward_call_list[0],
+ "The passed layer class wasn't instantiated.")
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/vit/modeling/vit.py b/official/projects/vit/modeling/vit.py
new file mode 100644
index 0000000000000000000000000000000000000000..4245711dc921a1c6d4adc5f4c18d782767a1d502
--- /dev/null
+++ b/official/projects/vit/modeling/vit.py
@@ -0,0 +1,323 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""VisionTransformer models."""
+from typing import Optional, Tuple
+
+from absl import logging
+
+# import immutabledict
+import tensorflow as tf
+
+from official.modeling import activations
+from official.projects.vit.modeling import nn_blocks
+from official.projects.vit.modeling.vit_specs import VIT_SPECS
+from official.vision.modeling.backbones import factory
+from official.vision.modeling.layers import nn_layers
+
+layers = tf.keras.layers
+
+
+class AddPositionEmbs(tf.keras.layers.Layer):
+ """Adds (optionally learned) positional embeddings to the inputs."""
+
+ def __init__(self,
+ posemb_init: Optional[tf.keras.initializers.Initializer] = None,
+ posemb_origin_shape: Optional[Tuple[int, int]] = None,
+ posemb_target_shape: Optional[Tuple[int, int]] = None,
+ **kwargs):
+ """Constructs Postional Embedding module.
+
+ The logic of this module is: the learnable positional embeddings length will
+ be determined by the inputs_shape or posemb_origin_shape (if provided)
+ during the construction. If the posemb_target_shape is provided and is
+ different from the positional embeddings length, the embeddings will be
+ interpolated during the forward call.
+
+ Args:
+ posemb_init: The positional embedding initializer.
+ posemb_origin_shape: The intended positional embedding shape.
+ posemb_target_shape: The potential target shape positional embedding may
+ be interpolated to.
+ **kwargs: other args.
+ """
+ super().__init__(**kwargs)
+ self.posemb_init = posemb_init
+ self.posemb_origin_shape = posemb_origin_shape
+ self.posemb_target_shape = posemb_target_shape
+
+ def build(self, inputs_shape):
+ if self.posemb_origin_shape is not None:
+ pos_emb_length = self.posemb_origin_shape[0] * self.posemb_origin_shape[1]
+ else:
+ pos_emb_length = inputs_shape[1]
+ pos_emb_shape = (1, pos_emb_length, inputs_shape[2])
+ self.pos_embedding = self.add_weight(
+ 'pos_embedding', pos_emb_shape, initializer=self.posemb_init)
+
+ def _interpolate(self, pos_embedding: tf.Tensor, from_shape: Tuple[int, int],
+ to_shape: Tuple[int, int]) -> tf.Tensor:
+ """Interpolates the positional embeddings."""
+ logging.info('Interpolating postional embedding from length: %d to %d',
+ from_shape, to_shape)
+ grid_emb = tf.reshape(pos_embedding, [1] + list(from_shape) + [-1])
+ # NOTE: Using BILINEAR interpolation by default.
+ grid_emb = tf.image.resize(grid_emb, to_shape)
+ return tf.reshape(grid_emb, [1, to_shape[0] * to_shape[1], -1])
+
+ def call(self, inputs, inputs_positions=None):
+ del inputs_positions
+ pos_embedding = self.pos_embedding
+ # inputs.shape is (batch_size, seq_len, emb_dim).
+ if inputs.shape[1] != pos_embedding.shape[1]:
+ pos_embedding = self._interpolate(
+ pos_embedding,
+ from_shape=self.posemb_origin_shape,
+ to_shape=self.posemb_target_shape)
+ pos_embedding = tf.cast(pos_embedding, inputs.dtype)
+
+ return inputs + pos_embedding
+
+
+class TokenLayer(tf.keras.layers.Layer):
+ """A simple layer to wrap token parameters."""
+
+ def build(self, inputs_shape):
+ self.cls = self.add_weight(
+ 'cls', (1, 1, inputs_shape[-1]), initializer='zeros')
+
+ def call(self, inputs):
+ cls = tf.cast(self.cls, inputs.dtype)
+ cls = cls + tf.zeros_like(inputs[:, 0:1]) # A hacky way to tile.
+ x = tf.concat([cls, inputs], axis=1)
+ return x
+
+
+class Encoder(tf.keras.layers.Layer):
+ """Transformer Encoder."""
+
+ def __init__(self,
+ num_layers,
+ mlp_dim,
+ num_heads,
+ dropout_rate=0.1,
+ attention_dropout_rate=0.1,
+ kernel_regularizer=None,
+ inputs_positions=None,
+ init_stochastic_depth_rate=0.0,
+ kernel_initializer='glorot_uniform',
+ add_pos_embed=True,
+ pos_embed_origin_shape=None,
+ pos_embed_target_shape=None,
+ **kwargs):
+ super().__init__(**kwargs)
+ self._num_layers = num_layers
+ self._mlp_dim = mlp_dim
+ self._num_heads = num_heads
+ self._dropout_rate = dropout_rate
+ self._attention_dropout_rate = attention_dropout_rate
+ self._kernel_regularizer = kernel_regularizer
+ self._inputs_positions = inputs_positions
+ self._init_stochastic_depth_rate = init_stochastic_depth_rate
+ self._kernel_initializer = kernel_initializer
+ self._add_pos_embed = add_pos_embed
+ self._pos_embed_origin_shape = pos_embed_origin_shape
+ self._pos_embed_target_shape = pos_embed_target_shape
+
+ def build(self, input_shape):
+ if self._add_pos_embed:
+ self._pos_embed = AddPositionEmbs(
+ posemb_init=tf.keras.initializers.RandomNormal(stddev=0.02),
+ posemb_origin_shape=self._pos_embed_origin_shape,
+ posemb_target_shape=self._pos_embed_target_shape,
+ name='posembed_input')
+ self._dropout = layers.Dropout(rate=self._dropout_rate)
+
+ self._encoder_layers = []
+ # Set layer norm epsilons to 1e-6 to be consistent with JAX implementation.
+ # https://flax.readthedocs.io/en/latest/_autosummary/flax.deprecated.nn.LayerNorm.html
+ for i in range(self._num_layers):
+ encoder_layer = nn_blocks.TransformerEncoderBlock(
+ inner_activation=activations.gelu,
+ num_attention_heads=self._num_heads,
+ inner_dim=self._mlp_dim,
+ output_dropout=self._dropout_rate,
+ attention_dropout=self._attention_dropout_rate,
+ kernel_regularizer=self._kernel_regularizer,
+ kernel_initializer=self._kernel_initializer,
+ norm_first=True,
+ stochastic_depth_drop_rate=nn_layers.get_stochastic_depth_rate(
+ self._init_stochastic_depth_rate, i + 1, self._num_layers),
+ norm_epsilon=1e-6)
+ self._encoder_layers.append(encoder_layer)
+ self._norm = layers.LayerNormalization(epsilon=1e-6)
+ super().build(input_shape)
+
+ def call(self, inputs, training=None):
+ x = inputs
+ if self._add_pos_embed:
+ x = self._pos_embed(x, inputs_positions=self._inputs_positions)
+ x = self._dropout(x, training=training)
+
+ for encoder_layer in self._encoder_layers:
+ x = encoder_layer(x, training=training)
+ x = self._norm(x)
+ return x
+
+ def get_config(self):
+ config = super().get_config()
+ updates = {
+ 'num_layers': self._num_layers,
+ 'mlp_dim': self._mlp_dim,
+ 'num_heads': self._num_heads,
+ 'dropout_rate': self._dropout_rate,
+ 'attention_dropout_rate': self._attention_dropout_rate,
+ 'kernel_regularizer': self._kernel_regularizer,
+ 'inputs_positions': self._inputs_positions,
+ 'init_stochastic_depth_rate': self._init_stochastic_depth_rate,
+ 'kernel_initializer': self._kernel_initializer,
+ 'add_pos_embed': self._add_pos_embed,
+ 'pos_embed_origin_shape': self._pos_embed_origin_shape,
+ 'pos_embed_target_shape': self._pos_embed_target_shape,
+ }
+ config.update(updates)
+ return config
+
+
+class VisionTransformer(tf.keras.Model):
+ """Class to build VisionTransformer family model."""
+
+ def __init__(self,
+ mlp_dim=3072,
+ num_heads=12,
+ num_layers=12,
+ attention_dropout_rate=0.0,
+ dropout_rate=0.1,
+ init_stochastic_depth_rate=0.0,
+ input_specs=layers.InputSpec(shape=[None, None, None, 3]),
+ patch_size=16,
+ hidden_size=768,
+ representation_size=0,
+ pooler='token',
+ kernel_regularizer=None,
+ original_init: bool = True,
+ pos_embed_shape: Optional[Tuple[int, int]] = None):
+ """VisionTransformer initialization function."""
+ self._mlp_dim = mlp_dim
+ self._num_heads = num_heads
+ self._num_layers = num_layers
+ self._hidden_size = hidden_size
+ self._patch_size = patch_size
+
+ inputs = tf.keras.Input(shape=input_specs.shape[1:])
+
+ x = layers.Conv2D(
+ filters=hidden_size,
+ kernel_size=patch_size,
+ strides=patch_size,
+ padding='valid',
+ kernel_regularizer=kernel_regularizer,
+ kernel_initializer='lecun_normal' if original_init else 'he_uniform')(
+ inputs)
+ if tf.keras.backend.image_data_format() == 'channels_last':
+ rows_axis, cols_axis = (1, 2)
+ else:
+ rows_axis, cols_axis = (2, 3)
+ # The reshape below assumes the data_format is 'channels_last,' so
+ # transpose to that. Once the data is flattened by the reshape, the
+ # data_format is irrelevant, so no need to update
+ # tf.keras.backend.image_data_format.
+ x = tf.transpose(x, perm=[0, 2, 3, 1])
+
+ pos_embed_target_shape = (x.shape[rows_axis], x.shape[cols_axis])
+ seq_len = (input_specs.shape[rows_axis] // patch_size) * (
+ input_specs.shape[cols_axis] // patch_size)
+ x = tf.reshape(x, [-1, seq_len, hidden_size])
+
+ # If we want to add a class token, add it here.
+ if pooler == 'token':
+ x = TokenLayer(name='cls')(x)
+
+ x = Encoder(
+ num_layers=num_layers,
+ mlp_dim=mlp_dim,
+ num_heads=num_heads,
+ dropout_rate=dropout_rate,
+ attention_dropout_rate=attention_dropout_rate,
+ kernel_regularizer=kernel_regularizer,
+ kernel_initializer='glorot_uniform' if original_init else dict(
+ class_name='TruncatedNormal', config=dict(stddev=.02)),
+ init_stochastic_depth_rate=init_stochastic_depth_rate,
+ pos_embed_origin_shape=pos_embed_shape,
+ pos_embed_target_shape=pos_embed_target_shape)(
+ x)
+
+ if pooler == 'token':
+ x = x[:, 0]
+ elif pooler == 'gap':
+ x = tf.reduce_mean(x, axis=1)
+ elif pooler == 'none':
+ x = tf.identity(x, name='encoded_tokens')
+ else:
+ raise ValueError(f'unrecognized pooler type: {pooler}')
+
+ if representation_size:
+ x = tf.keras.layers.Dense(
+ representation_size,
+ kernel_regularizer=kernel_regularizer,
+ name='pre_logits',
+ kernel_initializer='lecun_normal' if original_init else 'he_uniform')(
+ x)
+ x = tf.nn.tanh(x)
+ else:
+ x = tf.identity(x, name='pre_logits')
+
+ if pooler == 'none':
+ endpoints = {'encoded_tokens': x}
+ else:
+ endpoints = {
+ 'pre_logits':
+ tf.reshape(x, [-1, 1, 1, representation_size or hidden_size])
+ }
+ super(VisionTransformer, self).__init__(inputs=inputs, outputs=endpoints)
+
+
+@factory.register_backbone_builder('legacy_vit')
+def build_vit(input_specs,
+ backbone_config,
+ norm_activation_config,
+ l2_regularizer=None):
+ """Build ViT model."""
+ del norm_activation_config
+ backbone_type = backbone_config.type
+ backbone_cfg = backbone_config.get()
+ assert backbone_type == 'legacy_vit', (f'Inconsistent backbone type '
+ f'{backbone_type}')
+ backbone_cfg.override(VIT_SPECS[backbone_cfg.model_name])
+
+ return VisionTransformer(
+ mlp_dim=backbone_cfg.transformer.mlp_dim,
+ num_heads=backbone_cfg.transformer.num_heads,
+ num_layers=backbone_cfg.transformer.num_layers,
+ attention_dropout_rate=backbone_cfg.transformer.attention_dropout_rate,
+ dropout_rate=backbone_cfg.transformer.dropout_rate,
+ init_stochastic_depth_rate=backbone_cfg.init_stochastic_depth_rate,
+ input_specs=input_specs,
+ patch_size=backbone_cfg.patch_size,
+ hidden_size=backbone_cfg.hidden_size,
+ representation_size=backbone_cfg.representation_size,
+ pooler=backbone_cfg.pooler,
+ kernel_regularizer=l2_regularizer,
+ original_init=backbone_cfg.original_init,
+ pos_embed_shape=backbone_cfg.pos_embed_shape)
diff --git a/official/projects/vit/modeling/vit_specs.py b/official/projects/vit/modeling/vit_specs.py
new file mode 100644
index 0000000000000000000000000000000000000000..060bc2d09be50b4dd10b2891a518a6e948d435b1
--- /dev/null
+++ b/official/projects/vit/modeling/vit_specs.py
@@ -0,0 +1,68 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""VisionTransformer backbone specs."""
+import immutabledict
+
+
+VIT_SPECS = immutabledict.immutabledict({
+ 'vit-ti16':
+ dict(
+ hidden_size=192,
+ patch_size=16,
+ transformer=dict(mlp_dim=768, num_heads=3, num_layers=12),
+ ),
+ 'vit-s16':
+ dict(
+ hidden_size=384,
+ patch_size=16,
+ transformer=dict(mlp_dim=1536, num_heads=6, num_layers=12),
+ ),
+ 'vit-b16':
+ dict(
+ hidden_size=768,
+ patch_size=16,
+ transformer=dict(mlp_dim=3072, num_heads=12, num_layers=12),
+ ),
+ 'vit-b32':
+ dict(
+ hidden_size=768,
+ patch_size=32,
+ transformer=dict(mlp_dim=3072, num_heads=12, num_layers=12),
+ ),
+ 'vit-l16':
+ dict(
+ hidden_size=1024,
+ patch_size=16,
+ transformer=dict(mlp_dim=4096, num_heads=16, num_layers=24),
+ ),
+ 'vit-l32':
+ dict(
+ hidden_size=1024,
+ patch_size=32,
+ transformer=dict(mlp_dim=4096, num_heads=16, num_layers=24),
+ ),
+ 'vit-h14':
+ dict(
+ hidden_size=1280,
+ patch_size=14,
+ transformer=dict(mlp_dim=5120, num_heads=16, num_layers=32),
+ ),
+ 'vit-g14':
+ dict(
+ hidden_size=1664,
+ patch_size=14,
+ transformer=dict(mlp_dim=8192, num_heads=16, num_layers=48),
+ ),
+})
diff --git a/official/projects/vit/modeling/vit_test.py b/official/projects/vit/modeling/vit_test.py
new file mode 100644
index 0000000000000000000000000000000000000000..3d1aa8eb065a6f853f890d8f4c7b1f448b9e919b
--- /dev/null
+++ b/official/projects/vit/modeling/vit_test.py
@@ -0,0 +1,73 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Tests for VIT."""
+
+from absl.testing import parameterized
+import tensorflow as tf
+
+from official.projects.vit.modeling import vit
+
+
+class VisionTransformerTest(parameterized.TestCase, tf.test.TestCase):
+
+ @parameterized.parameters(
+ (224, 85798656),
+ (256, 85844736),
+ )
+ def test_network_creation(self, input_size, params_count):
+ """Test creation of VisionTransformer family models."""
+ tf.keras.backend.set_image_data_format('channels_last')
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[2, input_size, input_size, 3])
+ network = vit.VisionTransformer(input_specs=input_specs)
+
+ inputs = tf.keras.Input(shape=(input_size, input_size, 3), batch_size=1)
+ _ = network(inputs)
+ self.assertEqual(network.count_params(), params_count)
+
+ def test_network_none_pooler(self):
+ tf.keras.backend.set_image_data_format('channels_last')
+ input_size = 256
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[2, input_size, input_size, 3])
+ network = vit.VisionTransformer(
+ input_specs=input_specs,
+ patch_size=16,
+ pooler='none',
+ representation_size=128,
+ pos_embed_shape=(14, 14)) # (224 // 16)
+
+ inputs = tf.keras.Input(shape=(input_size, input_size, 3), batch_size=1)
+ output = network(inputs)['encoded_tokens']
+ self.assertEqual(output.shape, [1, 256, 128])
+
+ def test_posembedding_interpolation(self):
+ tf.keras.backend.set_image_data_format('channels_last')
+ input_size = 256
+ input_specs = tf.keras.layers.InputSpec(
+ shape=[2, input_size, input_size, 3])
+ network = vit.VisionTransformer(
+ input_specs=input_specs,
+ patch_size=16,
+ pooler='gap',
+ pos_embed_shape=(14, 14)) # (224 // 16)
+
+ inputs = tf.keras.Input(shape=(input_size, input_size, 3), batch_size=1)
+ output = network(inputs)['pre_logits']
+ self.assertEqual(output.shape, [1, 1, 1, 768])
+
+
+if __name__ == '__main__':
+ tf.test.main()
diff --git a/official/projects/vit/train.py b/official/projects/vit/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..2ef9ebdfff1b1057f13cd4d7fe993134517b3c8c
--- /dev/null
+++ b/official/projects/vit/train.py
@@ -0,0 +1,27 @@
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""TensorFlow Model Garden Vision training driver, including ViT configs.."""
+
+from absl import app
+
+from official.common import flags as tfm_flags
+from official.projects.vit import configs # pylint: disable=unused-import
+from official.projects.vit.modeling import vit # pylint: disable=unused-import
+from official.vision import train
+
+
+if __name__ == '__main__':
+ tfm_flags.define_flags()
+ app.run(train.main)
diff --git a/official/projects/volumetric_models/configs/backbones.py b/official/projects/volumetric_models/configs/backbones.py
index 7fb357d6884995bac0736312765a98e5d21e17ce..faae1882e3af4333b576e201b89cac22268a80da 100644
--- a/official/projects/volumetric_models/configs/backbones.py
+++ b/official/projects/volumetric_models/configs/backbones.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Backbones configurations."""
import dataclasses
from typing import Optional, Sequence
diff --git a/official/projects/volumetric_models/configs/decoders.py b/official/projects/volumetric_models/configs/decoders.py
index b5d0adea7cb8878329283539839fa9dddf25a932..828eaa9898c14953b4067f8c25d7c606d56cfc5f 100644
--- a/official/projects/volumetric_models/configs/decoders.py
+++ b/official/projects/volumetric_models/configs/decoders.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Decoders configurations."""
import dataclasses
from typing import Optional, Sequence
diff --git a/official/projects/volumetric_models/configs/semantic_segmentation_3d.py b/official/projects/volumetric_models/configs/semantic_segmentation_3d.py
index 713f9ea3510ffff64130c511ae7f1afb4a2797d5..3f6987f43bc3d795e25d75d4ab0c4dc6258dc518 100644
--- a/official/projects/volumetric_models/configs/semantic_segmentation_3d.py
+++ b/official/projects/volumetric_models/configs/semantic_segmentation_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Semantic segmentation configuration definition."""
import dataclasses
@@ -23,7 +22,7 @@ from official.modeling import hyperparams
from official.modeling import optimization
from official.projects.volumetric_models.configs import backbones
from official.projects.volumetric_models.configs import decoders
-from official.vision.beta.configs import common
+from official.vision.configs import common
@dataclasses.dataclass
diff --git a/official/projects/volumetric_models/configs/semantic_segmentation_3d_test.py b/official/projects/volumetric_models/configs/semantic_segmentation_3d_test.py
index fd56c2a672350980f4aafa5ac02b620d609a053a..e54b0f98f451688c6a9812a33048f00b990223db 100644
--- a/official/projects/volumetric_models/configs/semantic_segmentation_3d_test.py
+++ b/official/projects/volumetric_models/configs/semantic_segmentation_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for semantic_segmentation."""
# pylint: disable=unused-import
diff --git a/official/projects/volumetric_models/dataloaders/segmentation_input_3d.py b/official/projects/volumetric_models/dataloaders/segmentation_input_3d.py
index 381159684cea6bb523bcc4c872f1ab86e8704848..1d7ba4bfb86c800d5040a4d9520dbc6fa74d7d43 100644
--- a/official/projects/volumetric_models/dataloaders/segmentation_input_3d.py
+++ b/official/projects/volumetric_models/dataloaders/segmentation_input_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -16,8 +16,8 @@
from typing import Any, Dict, Sequence, Tuple
import tensorflow as tf
-from official.vision.beta.dataloaders import decoder
-from official.vision.beta.dataloaders import parser
+from official.vision.dataloaders import decoder
+from official.vision.dataloaders import parser
class Decoder(decoder.Decoder):
diff --git a/official/projects/volumetric_models/dataloaders/segmentation_input_3d_test.py b/official/projects/volumetric_models/dataloaders/segmentation_input_3d_test.py
index 931867f447b4f5cb3c80172984ef135271b6fad0..7a71de141cd360caa899cfd052cd51292572360f 100644
--- a/official/projects/volumetric_models/dataloaders/segmentation_input_3d_test.py
+++ b/official/projects/volumetric_models/dataloaders/segmentation_input_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ from absl.testing import parameterized
import tensorflow as tf
from official.projects.volumetric_models.dataloaders import segmentation_input_3d
-from official.vision.beta.dataloaders import tfexample_utils
+from official.vision.dataloaders import tfexample_utils
class InputReaderTest(parameterized.TestCase, tf.test.TestCase):
diff --git a/official/projects/volumetric_models/evaluation/segmentation_metrics.py b/official/projects/volumetric_models/evaluation/segmentation_metrics.py
index 9d53c7de869a8593baa99898cb7f9d928ae24aad..fc265720f8b2ee75706aadbacf4b1274a40d70d0 100644
--- a/official/projects/volumetric_models/evaluation/segmentation_metrics.py
+++ b/official/projects/volumetric_models/evaluation/segmentation_metrics.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/evaluation/segmentation_metrics_test.py b/official/projects/volumetric_models/evaluation/segmentation_metrics_test.py
index cf93b7556ae5b7ccda23a5e14063291fccc84c8b..1eac720016f06aaaa30af9d618d567e0f8aadd37 100644
--- a/official/projects/volumetric_models/evaluation/segmentation_metrics_test.py
+++ b/official/projects/volumetric_models/evaluation/segmentation_metrics_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/losses/segmentation_losses.py b/official/projects/volumetric_models/losses/segmentation_losses.py
index fad3d695b77c24c752c573754f8ac527a1748ea7..6d422a9243e5f9370f14aadde159be8c5000f627 100644
--- a/official/projects/volumetric_models/losses/segmentation_losses.py
+++ b/official/projects/volumetric_models/losses/segmentation_losses.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/losses/segmentation_losses_test.py b/official/projects/volumetric_models/losses/segmentation_losses_test.py
index ef047f064e5b7190a99a1005609e4ed6baf0883b..f2f444c2b238e51ea336b2c24a2305ce1dca5790 100644
--- a/official/projects/volumetric_models/losses/segmentation_losses_test.py
+++ b/official/projects/volumetric_models/losses/segmentation_losses_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/modeling/backbones/__init__.py b/official/projects/volumetric_models/modeling/backbones/__init__.py
index 08bfc21705e73b63cccd1f1a179757bd6880cf9b..8e220167f1d189e088239c348c991d981b01a2d9 100644
--- a/official/projects/volumetric_models/modeling/backbones/__init__.py
+++ b/official/projects/volumetric_models/modeling/backbones/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Backbones package definition."""
from official.projects.volumetric_models.modeling.backbones.unet_3d import UNet3D
diff --git a/official/projects/volumetric_models/modeling/backbones/unet_3d.py b/official/projects/volumetric_models/modeling/backbones/unet_3d.py
index d5539c9df35a93925338a78f614bb5806c1b0209..c675315aa37b152257cc3d84b886bb13a6e1bd34 100644
--- a/official/projects/volumetric_models/modeling/backbones/unet_3d.py
+++ b/official/projects/volumetric_models/modeling/backbones/unet_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -25,7 +25,7 @@ from typing import Any, Mapping, Sequence
import tensorflow as tf
from official.modeling import hyperparams
from official.projects.volumetric_models.modeling import nn_blocks_3d
-from official.vision.beta.modeling.backbones import factory
+from official.vision.modeling.backbones import factory
layers = tf.keras.layers
diff --git a/official/projects/volumetric_models/modeling/backbones/unet_3d_test.py b/official/projects/volumetric_models/modeling/backbones/unet_3d_test.py
index e42b3d1cbadada1b7489c78c98bd13683a2612ef..01e86a9d1a37e4c98deef399860569351c4bd10a 100644
--- a/official/projects/volumetric_models/modeling/backbones/unet_3d_test.py
+++ b/official/projects/volumetric_models/modeling/backbones/unet_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for 3D UNet backbone."""
# Import libraries
diff --git a/official/projects/volumetric_models/modeling/decoders/__init__.py b/official/projects/volumetric_models/modeling/decoders/__init__.py
index ef86bd5206cd89b31a2187a0484949672412c470..f699cffbcc986c25fabaee28172ee033d32b938e 100644
--- a/official/projects/volumetric_models/modeling/decoders/__init__.py
+++ b/official/projects/volumetric_models/modeling/decoders/__init__.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Decoders package definition."""
from official.projects.volumetric_models.modeling.decoders.unet_3d_decoder import UNet3DDecoder
diff --git a/official/projects/volumetric_models/modeling/decoders/factory.py b/official/projects/volumetric_models/modeling/decoders/factory.py
index 759779caa6a2aae21e0ff8267756a37b4d2f65a1..0e1d17c42996122aea8471abd1e1bd3f1222d1c6 100644
--- a/official/projects/volumetric_models/modeling/decoders/factory.py
+++ b/official/projects/volumetric_models/modeling/decoders/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/modeling/decoders/factory_test.py b/official/projects/volumetric_models/modeling/decoders/factory_test.py
index 50fbd1b2bd76120d506b0f2854040924dc317ddb..bcd4df694507f8d677afaee04e6fc3dc4b19ebb7 100644
--- a/official/projects/volumetric_models/modeling/decoders/factory_test.py
+++ b/official/projects/volumetric_models/modeling/decoders/factory_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder.py b/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder.py
index a83724fe5c5df3a47bb389dc794151a79fec4d87..0f6d43972d568e8329560327807a2e0b03104fd5 100644
--- a/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder.py
+++ b/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -95,7 +95,7 @@ class UNet3DDecoder(tf.keras.Model):
channel_dim = 1
# Build 3D UNet.
- inputs = self._build_input_pyramid(input_specs, model_id)
+ inputs = self._build_input_pyramid(input_specs, model_id) # pytype: disable=wrong-arg-types # dynamic-method-lookup
# Add levels with up-convolution or up-sampling.
x = inputs[str(model_id)]
diff --git a/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder_test.py b/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder_test.py
index 39dea0887d9df4b2cffa03af8cd09afc1d04fb9b..d901a6e46eb18b1caeeca94179dd40a42b825413 100644
--- a/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder_test.py
+++ b/official/projects/volumetric_models/modeling/decoders/unet_3d_decoder_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for 3D UNet decoder."""
# Import libraries
diff --git a/official/projects/volumetric_models/modeling/factory.py b/official/projects/volumetric_models/modeling/factory.py
index caff2e09f97949c5ef0f917380f5db9cb2b797f7..640ba067531606b01997202d7361f476c832486f 100644
--- a/official/projects/volumetric_models/modeling/factory.py
+++ b/official/projects/volumetric_models/modeling/factory.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -13,7 +13,7 @@
# limitations under the License.
"""Factory methods to build models."""
-
+from typing import Sequence, Union
# Import libraries
import tensorflow as tf
@@ -21,14 +21,16 @@ import tensorflow as tf
from official.modeling import hyperparams
from official.projects.volumetric_models.modeling.decoders import factory as decoder_factory
from official.projects.volumetric_models.modeling.heads import segmentation_heads_3d
-from official.vision.beta.modeling import segmentation_model
-from official.vision.beta.modeling.backbones import factory as backbone_factory
+from official.vision.modeling import segmentation_model
+from official.vision.modeling.backbones import factory as backbone_factory
def build_segmentation_model_3d(
- input_specs: tf.keras.layers.InputSpec,
+ input_specs: Union[tf.keras.layers.InputSpec,
+ Sequence[tf.keras.layers.InputSpec]],
model_config: hyperparams.Config,
- l2_regularizer: tf.keras.regularizers.Regularizer = None) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
+ l2_regularizer: tf.keras.regularizers.Regularizer = None
+) -> tf.keras.Model: # pytype: disable=annotation-type-mismatch # typed-keras
"""Builds Segmentation model."""
norm_activation_config = model_config.norm_activation
backbone = backbone_factory.build_backbone(
diff --git a/official/projects/volumetric_models/modeling/factory_test.py b/official/projects/volumetric_models/modeling/factory_test.py
index 86000af99f8a12b64b8d2f0f324c6cb869fb36e8..2de27eeb833a24fe1951a5505ebeabe04fb16421 100644
--- a/official/projects/volumetric_models/modeling/factory_test.py
+++ b/official/projects/volumetric_models/modeling/factory_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d.py b/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d.py
index 3154a271aef61854fedcc3fd0308f84efdf67f76..f2358d64199f32149caa861a0126f931f580cf07 100644
--- a/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d.py
+++ b/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -88,7 +88,7 @@ class SegmentationHead3D(tf.keras.layers.Layer):
self._bn_axis = -1
else:
self._bn_axis = 1
- self._activation = tf_utils.get_activation(activation)
+ self._activation = tf_utils.get_activation(activation, use_keras_layer=True)
def build(self, input_shape: Union[tf.TensorShape, Sequence[tf.TensorShape]]):
"""Creates the variables of the segmentation head."""
diff --git a/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d_test.py b/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d_test.py
index 4dc35fdeb68dc90ab202ead18eb47c7129b0619a..6c3aee1ee92ef302cb0a3d5aa2d80599787d5eda 100644
--- a/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d_test.py
+++ b/official/projects/volumetric_models/modeling/heads/segmentation_heads_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for segmentation_heads.py."""
from absl.testing import parameterized
diff --git a/official/projects/volumetric_models/modeling/nn_blocks_3d.py b/official/projects/volumetric_models/modeling/nn_blocks_3d.py
index b2f6dbd790a2f2ace74f4eb1453c8045cbb38e53..a7c459b0dc18f36b9ee640295cd67b2f51e880f5 100644
--- a/official/projects/volumetric_models/modeling/nn_blocks_3d.py
+++ b/official/projects/volumetric_models/modeling/nn_blocks_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -20,7 +20,7 @@ from typing import Sequence, Union
import tensorflow as tf
from official.modeling import tf_utils
-from official.vision.beta.modeling.layers import nn_layers
+from official.vision.modeling.layers import nn_layers
@tf.keras.utils.register_keras_serializable(package='Vision')
diff --git a/official/projects/volumetric_models/modeling/nn_blocks_3d_test.py b/official/projects/volumetric_models/modeling/nn_blocks_3d_test.py
index 759757ceca4bbd8060af53a90a746e28985634a1..cd18c6b27d04a89205925e6dc9829c578b664d54 100644
--- a/official/projects/volumetric_models/modeling/nn_blocks_3d_test.py
+++ b/official/projects/volumetric_models/modeling/nn_blocks_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for 3D volumeric convoluion blocks."""
# Import libraries
diff --git a/official/projects/volumetric_models/modeling/segmentation_model_test.py b/official/projects/volumetric_models/modeling/segmentation_model_test.py
index 3bfc94882c141cb7bb6f8923d13de3db2d5d158d..f5df0a4241d8d55bc4b65646a28b5d7571aa53d6 100644
--- a/official/projects/volumetric_models/modeling/segmentation_model_test.py
+++ b/official/projects/volumetric_models/modeling/segmentation_model_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for segmentation network."""
from absl.testing import parameterized
@@ -21,7 +20,7 @@ import tensorflow as tf
from official.projects.volumetric_models.modeling import backbones
from official.projects.volumetric_models.modeling import decoders
from official.projects.volumetric_models.modeling.heads import segmentation_heads_3d
-from official.vision.beta.modeling import segmentation_model
+from official.vision.modeling import segmentation_model
class SegmentationNetworkUNet3DTest(parameterized.TestCase, tf.test.TestCase):
diff --git a/official/projects/volumetric_models/registry_imports.py b/official/projects/volumetric_models/registry_imports.py
index 06a551227a0e5838aa8e12852dae11dc96c41490..461a0028f1496ee21a0ca0dba99bdbd846f43d91 100644
--- a/official/projects/volumetric_models/registry_imports.py
+++ b/official/projects/volumetric_models/registry_imports.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -15,8 +15,8 @@
"""All necessary imports for registration."""
# pylint: disable=unused-import
-from official.common import registry_imports
from official.projects.volumetric_models.configs import semantic_segmentation_3d as semantic_segmentation_3d_cfg
from official.projects.volumetric_models.modeling import backbones
from official.projects.volumetric_models.modeling import decoders
from official.projects.volumetric_models.tasks import semantic_segmentation_3d
+from official.vision import registry_imports
diff --git a/official/projects/volumetric_models/serving/export_saved_model.py b/official/projects/volumetric_models/serving/export_saved_model.py
index 1a01003857523ee414ef9fcd8b33c5b7d5839695..0fcf249ef9ec93b2403aa8daf7d24e6473a4503a 100644
--- a/official/projects/volumetric_models/serving/export_saved_model.py
+++ b/official/projects/volumetric_models/serving/export_saved_model.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -43,7 +43,7 @@ from official.common import registry_imports # pylint: disable=unused-import
from official.core import exp_factory
from official.modeling import hyperparams
from official.projects.volumetric_models.serving import semantic_segmentation_3d
-from official.vision.beta.serving import export_saved_model_lib
+from official.vision.serving import export_saved_model_lib
FLAGS = flags.FLAGS
diff --git a/official/projects/volumetric_models/serving/semantic_segmentation_3d.py b/official/projects/volumetric_models/serving/semantic_segmentation_3d.py
index 4d6097095560378b5aee60514a77f61fd96e4a27..a85399c43b6a3c3d6ac0b25a1a0c1010f1fa87f1 100644
--- a/official/projects/volumetric_models/serving/semantic_segmentation_3d.py
+++ b/official/projects/volumetric_models/serving/semantic_segmentation_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -22,7 +22,7 @@ import tensorflow as tf
from official.projects.volumetric_models.modeling import backbones
from official.projects.volumetric_models.modeling import decoders
from official.projects.volumetric_models.modeling import factory
-from official.vision.beta.serving import export_base
+from official.vision.serving import export_base
class SegmentationModule(export_base.ExportModule):
diff --git a/official/projects/volumetric_models/serving/semantic_segmentation_3d_test.py b/official/projects/volumetric_models/serving/semantic_segmentation_3d_test.py
index 11097bf219d90ceafb4a7851065be9e675bb7ee4..4001b829d68fb7296be8f2e479ffd146465e6314 100644
--- a/official/projects/volumetric_models/serving/semantic_segmentation_3d_test.py
+++ b/official/projects/volumetric_models/serving/semantic_segmentation_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
diff --git a/official/projects/volumetric_models/tasks/semantic_segmentation_3d.py b/official/projects/volumetric_models/tasks/semantic_segmentation_3d.py
index a6222ab0d9e0b3c2dd3c2ed73e6e141f731a52ea..928d5d26cbfebf7de84518a2601f94820adfb214 100644
--- a/official/projects/volumetric_models/tasks/semantic_segmentation_3d.py
+++ b/official/projects/volumetric_models/tasks/semantic_segmentation_3d.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Image segmentation task definition."""
from typing import Any, Dict, Mapping, Optional, Sequence, Union
diff --git a/official/projects/volumetric_models/tasks/semantic_segmentation_3d_test.py b/official/projects/volumetric_models/tasks/semantic_segmentation_3d_test.py
index a7fec218d811c49f944bec2c8500047485d5bf1e..08cf0e693d28ee6ef8c7f88c4c35f8ca330b7dd7 100644
--- a/official/projects/volumetric_models/tasks/semantic_segmentation_3d_test.py
+++ b/official/projects/volumetric_models/tasks/semantic_segmentation_3d_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -12,7 +12,6 @@
# See the License for the specific language governing permissions and
# limitations under the License.
-# Lint as: python3
"""Tests for semantic segmentation task."""
# pylint: disable=unused-import
@@ -30,7 +29,7 @@ from official.projects.volumetric_models.evaluation import segmentation_metrics
from official.projects.volumetric_models.modeling import backbones
from official.projects.volumetric_models.modeling import decoders
from official.projects.volumetric_models.tasks import semantic_segmentation_3d as img_seg_task
-from official.vision.beta.dataloaders import tfexample_utils
+from official.vision.dataloaders import tfexample_utils
class SemanticSegmentationTaskTest(tf.test.TestCase, parameterized.TestCase):
diff --git a/official/projects/volumetric_models/train.py b/official/projects/volumetric_models/train.py
index b84569e1b8404f3bfa9f31ae813dac1725f24d61..e04956fb722e122ca40ba65b279e2dfda348ba76 100644
--- a/official/projects/volumetric_models/train.py
+++ b/official/projects/volumetric_models/train.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -19,7 +19,7 @@ import gin # pylint: disable=unused-import
from official.common import flags as tfm_flags
from official.projects.volumetric_models import registry_imports # pylint: disable=unused-import
-from official.vision.beta import train
+from official.vision import train
def main(_):
diff --git a/official/projects/volumetric_models/train_test.py b/official/projects/volumetric_models/train_test.py
index 47a32ec54b86cad29b24afac625f9a0a5ec0441e..50e8fa7e49a9e3812410d5c2ecc90d5ac9af3b3d 100644
--- a/official/projects/volumetric_models/train_test.py
+++ b/official/projects/volumetric_models/train_test.py
@@ -1,4 +1,4 @@
-# Copyright 2021 The TensorFlow Authors. All Rights Reserved.
+# Copyright 2022 The TensorFlow Authors. All Rights Reserved.
#
# Licensed under the Apache License, Version 2.0 (the "License");
# you may not use this file except in compliance with the License.
@@ -21,7 +21,7 @@ from absl import logging
from absl.testing import flagsaver
import tensorflow as tf
from official.projects.volumetric_models import train as train_lib
-from official.vision.beta.dataloaders import tfexample_utils
+from official.vision.dataloaders import tfexample_utils
FLAGS = flags.FLAGS
diff --git a/official/projects/waste_identification_ml/README.md b/official/projects/waste_identification_ml/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..edbe262ca5b5cd3489846a852b9b71759b2fc20e
--- /dev/null
+++ b/official/projects/waste_identification_ml/README.md
@@ -0,0 +1,35 @@
+# CircularNet
+
+Instance segmentation models for identification of recyclables on conveyor
+belts.
+
+Note: These are demo models built on limited datasets. If you’re interested in
+updated versions of the models, or in using models trained on specific
+materials, reach out to waste-innovation-external@google.com
+
+## Overview
+
+CircularNet is built using Mask RCNN, which is a deep learning model for
+instance image segmentation, where the goal is to assign instance level labels
+(e.g. person1, person2, cat) to every pixel in an input image.
+
+Mask RCNN algorithm is available in the TensorFlow Model Garden which is a
+repository with a number of different implementations of state-of-the-art models
+and modeling solutions for TensorFlow users.
+
+## Model Categories
+
+- Material Type - Identifies the high level material type (e.g. plastic, paper
+ etc) of an object
+- Material Form - Categorizes objects based on the form factor (e.g. cup,
+ bottle, bag etc)
+- Plastic Type - Identifies the plastic resin type of the object (e.g. PET,
+ HDPE, LDPE, etc)
+
+## Model paths in GCP buckets
+
+| Model categories | Model backbone | Model type | GCP bucket path |
+| ------ | ------ | ----- | ------ |
+| Material Model | Resnet | saved model & TFLite | [click here](https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_model.zip) |
+| Material Form model | Resnet | saved model & TFLite | [click here](https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_form_model.zip) |
+|Plastic model | Resnet| saved model & TFLite | [click here](https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/plastic_types_model.zip) |
diff --git a/official/projects/waste_identification_ml/model_conversion/checkpoints_to_savedModel_to_tflite.ipynb b/official/projects/waste_identification_ml/model_conversion/checkpoints_to_savedModel_to_tflite.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..9cf5417dd6b5b38ac2f59d0805f4194e55549d10
--- /dev/null
+++ b/official/projects/waste_identification_ml/model_conversion/checkpoints_to_savedModel_to_tflite.ipynb
@@ -0,0 +1,346 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "wm0ezXfhdp2P"
+ },
+ "source": [
+ "# Convert Tensorflow model checkpoints to saved model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "KAy1ciItdrDB"
+ },
+ "source": [
+ "Given the checkpoints exported from Tensorflow model training, our goal is to convert those checkpoints into saved model for inference purpose.\u003cbr\u003e\n",
+ "Checkpoints is a binary file which contains all the values of the weights, biases, gradients and all the other variables saved. This file has an extension .ckpt. Checkpoints do not contain any description of the computation defined by the model and thus are typically only useful when source code that will use the saved parameter values is available.\u003cbr\u003e\n",
+ "A saved model contains a complete tensorflow program, including trained parameters and computation. It does not require the original model building code to run, which makes it useful for sharing or deploying with TFLite, tensorflow.js, Tensorflow Serving or Tensorflow Hub."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Lg4uH43Qds0q"
+ },
+ "source": [
+ "**Note** - We also assume that the script will be used as a Google Colab notebook. But this can be changed according to the needs of users. They can modify this in case they are working on their local workstation, remote server or any other database. This colab notebook can be changed to a regular jupyter notebook running on a local machine according to the need of the users."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "BofYg406d4LV"
+ },
+ "source": [
+ "## Import libraries \u0026 clone the TF model directory"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "oegDgL7yaaAq"
+ },
+ "outputs": [],
+ "source": [
+ "# install model-garden official and RESTART RUNTIME of the colab\n",
+ "!pip install tf-models-official"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "fMROz-xXdx6c"
+ },
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "from google.colab import drive\n",
+ "import yaml\n",
+ "import tensorflow as tf"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "executionInfo": {
+ "elapsed": 1197,
+ "status": "ok",
+ "timestamp": 1659384634603,
+ "user": {
+ "displayName": "Umair Sabir",
+ "userId": "06940594206388957365"
+ },
+ "user_tz": 420
+ },
+ "id": "gz1ajpHgeAJT",
+ "outputId": "1187e44e-82eb-4be1-8adc-1b50f6d7d0ed"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Drive already mounted at /content/gdrive; to attempt to forcibly remount, call drive.mount(\"/content/gdrive\", force_remount=True).\n",
+ "ln: failed to create symbolic link '/mydrive/My Drive': File exists\n",
+ "Successful\n"
+ ]
+ }
+ ],
+ "source": [
+ "# use this if your model and data are stored in the google drive\n",
+ "drive.mount('/content/gdrive')\n",
+ "\n",
+ "try:\n",
+ " !ln -s /content/gdrive/My\\ Drive/ /mydrive\n",
+ " print('Successful')\n",
+ "except Exception as e:\n",
+ " print(e)\n",
+ " print('Not successful')"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "executionInfo": {
+ "elapsed": 290,
+ "status": "ok",
+ "timestamp": 1659384648663,
+ "user": {
+ "displayName": "Umair Sabir",
+ "userId": "06940594206388957365"
+ },
+ "user_tz": 420
+ },
+ "id": "rRGalo90e2my",
+ "outputId": "f0305c8b-cf06-4637-a83c-05f5471313e7"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "fatal: destination path 'models' already exists and is not an empty directory.\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Clone the tensorflow models repository\n",
+ "!git clone --depth 1 https://github.com/tensorflow/models"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "executionInfo": {
+ "elapsed": 189,
+ "status": "ok",
+ "timestamp": 1659384681521,
+ "user": {
+ "displayName": "Umair Sabir",
+ "userId": "06940594206388957365"
+ },
+ "user_tz": 420
+ },
+ "id": "HalXsX7BqdyX",
+ "outputId": "cb5555e4-0b77-4036-9230-1c01fcf1afaf"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "/content/models\n"
+ ]
+ }
+ ],
+ "source": [
+ "%cd models"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "8o7QzpHOsFHS"
+ },
+ "source": [
+ "## **MUST CHANGE** - Define the parameters according to your need"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "xak5WwMXppDF"
+ },
+ "outputs": [],
+ "source": [
+ "# this parameter depends on the backbone you will be using. In our \n",
+ "# case we used resnet backbone\n",
+ "EXPERIMENT_TYPE = 'maskrcnn_resnetfpn_coco' #@param {type:\"string\"}\n",
+ "\n",
+ "# path to the folder where all the files and checkpoints after model training \n",
+ "# are exported to\n",
+ "CHECKPOINT_PATH = '/mydrive/plastics_model/version_1/' #@param {type:\"string\"}\n",
+ "\n",
+ "# path where the saved model will be exported to\n",
+ "EXPORT_DIR_PATH = '/mydrive/plastics_model/experiment/' #@param {type:\"string\"}\n",
+ "\n",
+ "# config files are always stored with the checkpoints\n",
+ "CONFIG_FILE= CHECKPOINT_PATH + 'params.yaml'"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "ddZzH5KhqSAy"
+ },
+ "outputs": [],
+ "source": [
+ "# config files are always stored with the checkpoints\n",
+ "# read the params.yaml file in order to get the height and width of an image\n",
+ "with open(CONFIG_FILE) as f:\n",
+ " my_dict = yaml.safe_load(f)\n",
+ "\n",
+ "HEIGHT = my_dict['task']['model']['input_size'][0]\n",
+ "WIDTH = my_dict['task']['model']['input_size'][1]\n",
+ "print(HEIGHT, WIDTH)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ZWrbqHqJt947"
+ },
+ "source": [
+ "## calling the function to convert checkpoints to saved model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "k3wuYiVte4t_"
+ },
+ "outputs": [],
+ "source": [
+ "# run the conversion command\n",
+ "!python -m official.vision.serving.export_saved_model --experiment=$EXPERIMENT_TYPE \\\n",
+ " --export_dir=$EXPORT_DIR_PATH \\\n",
+ " --checkpoint_path=$CHECKPOINT_PATH \\\n",
+ " --batch_size=1 \\\n",
+ " --input_image_size=$HEIGHT,$WIDTH \\\n",
+ " --input_type=tflite \\\n",
+ " --config_file=$CONFIG_FILE"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "jQb13BbW78bs"
+ },
+ "source": [
+ "# Convert saved model to TF Lite model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "QEKaddZ58Ab6"
+ },
+ "source": [
+ "Given the saved model after Tensorflow model training, our goal is to convert saved model to TFLite for inference purpose on edge devices. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ZXpSX-w_8A1c"
+ },
+ "source": [
+ "Tensorflow Lite is a set of tools that enables on-device machine learning by helping developers run their models on mobile, embedded and edge devices."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "20sV-bx59GRD"
+ },
+ "source": [
+ "## **MUST CHANGE** - Define the parameters according to your need"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "icoDtIin9REv"
+ },
+ "outputs": [],
+ "source": [
+ "# path where the tflite model will be written with its name\n",
+ "TFLITE_PATH = '/mydrive/gtech/MRFs/Recykal/Latest_sharing_by_sanket/Google_Recykal/Taxonomy_version_2/model_version_1/plastics_model/tflite_fan/model.tflite' #@param {type:\"string\"}\n",
+ "\n",
+ "# path where saved model parameters are saved\n",
+ "SAVED_MODEL_DIR = EXPORT_DIR_PATH + '/saved_model/'"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "YE1Z13xs9NtJ"
+ },
+ "source": [
+ "## conversion of saved model to tflite"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "1LY9yoUP6Gr4"
+ },
+ "outputs": [],
+ "source": [
+ "converter = tf.lite.TFLiteConverter.from_saved_model(saved_model_dir=SAVED_MODEL_DIR) \n",
+ "tflite_model = converter.convert() \n",
+ "with open(TFLITE_PATH, 'wb') as f:\n",
+ " f.write(tflite_model)"
+ ]
+ }
+ ],
+ "metadata": {
+ "colab": {
+ "collapsed_sections": [],
+ "name": "checkpoints_to_saved_model_to_tflite.ipynb",
+ "provenance": []
+ },
+ "gpuClass": "standard",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "name": "python"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/official/projects/waste_identification_ml/model_inference/TFHub_saved_model_inference.ipynb b/official/projects/waste_identification_ml/model_inference/TFHub_saved_model_inference.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..fbc8e09a2a1781a874d7724325955fa8923cdb22
--- /dev/null
+++ b/official/projects/waste_identification_ml/model_inference/TFHub_saved_model_inference.ipynb
@@ -0,0 +1,1215 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "rOvvWAVTkMR7"
+ },
+ "source": [
+ "# Welcome to the Waste Identification Colab\n",
+ "\n",
+ "Welcome to the Instance Segmentation Colab! This notebook will take you through the steps of running an \"out-of-the-box\" Mask RCNN Instance Segmentation model on images."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "HVTXSC07QwfG"
+ },
+ "source": [
+ "Given 3 different Mask RCNN models for the material type, material form type and plastic type, your goal is to perform inference with any of the models and visualize the results. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "AQUsAE0TRkmh"
+ },
+ "source": [
+ "To finish this task, a proper path for the saved models and a single image needs to be provided. The path to the labels on which the models are trained is in the waste_identification_ml directory inside the Tensorflow Model Garden repository. The label files are inferred automatically once you select the ML model by which you want to do the inference."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "vPs64QA1Zdov"
+ },
+ "source": [
+ "## Imports and Setup\n",
+ "\n",
+ "Let's start with the base imports."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "yn5_uV1HLvaz"
+ },
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "import pathlib\n",
+ "import cv2\n",
+ "import logging\n",
+ "logging.disable(logging.WARNING)\n",
+ "\n",
+ "import matplotlib\n",
+ "import matplotlib.pyplot as plt\n",
+ "\n",
+ "import numpy as np\n",
+ "from six import BytesIO\n",
+ "from PIL import Image\n",
+ "from six.moves.urllib.request import urlopen\n",
+ "\n",
+ "import tensorflow as tf\n",
+ "import tensorflow_hub as hub\n",
+ "\n",
+ "tf.get_logger().setLevel('ERROR')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "14bNk1gzh0TN"
+ },
+ "source": [
+ "## Visualization tools\n",
+ "\n",
+ "To visualize the images with the proper detected boxes and segmentation masks, we will use the TensorFlow Object Detection API. To install it we will clone the repo."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "oi28cqGGFWnY",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "c2b27919-e013-4d47-be4a-4f62291b8ac6"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Cloning into 'models'...\n",
+ "remote: Enumerating objects: 3451, done.\u001b[K\n",
+ "remote: Counting objects: 100% (3451/3451), done.\u001b[K\n",
+ "remote: Compressing objects: 100% (2891/2891), done.\u001b[K\n",
+ "remote: Total 3451 (delta 896), reused 1476 (delta 503), pack-reused 0\u001b[K\n",
+ "Receiving objects: 100% (3451/3451), 46.92 MiB | 15.79 MiB/s, done.\n",
+ "Resolving deltas: 100% (896/896), done.\n",
+ "Checking out files: 100% (3125/3125), done.\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Clone the tensorflow models repository\n",
+ "!git clone --depth 1 https://github.com/tensorflow/models"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "yX3pb_pXDjYA"
+ },
+ "source": [
+ "Intalling the Object Detection API"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "NwdsBdGhFanc",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "c507dccb-4658-4964-fcce-baed5a817db9"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Reading package lists...\n",
+ "Building dependency tree...\n",
+ "Reading state information...\n",
+ "protobuf-compiler is already the newest version (3.0.0-9.1ubuntu1).\n",
+ "The following package was automatically installed and is no longer required:\n",
+ " libnvidia-common-460\n",
+ "Use 'sudo apt autoremove' to remove it.\n",
+ "0 upgraded, 0 newly installed, 0 to remove and 19 not upgraded.\n",
+ "Looking in indexes: https://pypi.org/simple, https://us-python.pkg.dev/colab-wheels/public/simple/\n",
+ "Processing /content/models/research\n",
+ "Collecting avro-python3\n",
+ " Downloading avro-python3-1.10.2.tar.gz (38 kB)\n",
+ "Collecting apache-beam\n",
+ " Downloading apache_beam-2.40.0-cp37-cp37m-manylinux2010_x86_64.whl (10.9 MB)\n",
+ "Requirement already satisfied: pillow in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (7.1.2)\n",
+ "Requirement already satisfied: lxml in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (4.9.1)\n",
+ "Requirement already satisfied: matplotlib in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (3.2.2)\n",
+ "Requirement already satisfied: Cython in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (0.29.32)\n",
+ "Requirement already satisfied: contextlib2 in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (0.5.5)\n",
+ "Collecting tf-slim\n",
+ " Downloading tf_slim-1.1.0-py2.py3-none-any.whl (352 kB)\n",
+ "Requirement already satisfied: six in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (1.15.0)\n",
+ "Requirement already satisfied: pycocotools in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (2.0.4)\n",
+ "Collecting lvis\n",
+ " Downloading lvis-0.5.3-py3-none-any.whl (14 kB)\n",
+ "Requirement already satisfied: scipy in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (1.7.3)\n",
+ "Requirement already satisfied: pandas in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (1.3.5)\n",
+ "Collecting tf-models-official>=2.5.1\n",
+ " Downloading tf_models_official-2.9.2-py2.py3-none-any.whl (2.1 MB)\n",
+ "Collecting tensorflow_io\n",
+ " Downloading tensorflow_io-0.26.0-cp37-cp37m-manylinux_2_12_x86_64.manylinux2010_x86_64.whl (25.9 MB)\n",
+ "Requirement already satisfied: keras in /usr/local/lib/python3.7/dist-packages (from object-detection==0.1) (2.8.0)\n",
+ "Collecting pyparsing==2.4.7\n",
+ " Downloading pyparsing-2.4.7-py2.py3-none-any.whl (67 kB)\n",
+ "Requirement already satisfied: oauth2client in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (4.1.3)\n",
+ "Requirement already satisfied: opencv-python-headless in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (4.6.0.66)\n",
+ "Collecting sacrebleu\n",
+ " Downloading sacrebleu-2.2.0-py3-none-any.whl (116 kB)\n",
+ "Requirement already satisfied: tensorflow-datasets in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (4.6.0)\n",
+ "Collecting py-cpuinfo>=3.3.0\n",
+ " Downloading py-cpuinfo-8.0.0.tar.gz (99 kB)\n",
+ "Requirement already satisfied: numpy>=1.20 in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (1.21.6)\n",
+ "Requirement already satisfied: gin-config in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (0.5.0)\n",
+ "Collecting pyyaml<6.0,>=5.1\n",
+ " Downloading PyYAML-5.4.1-cp37-cp37m-manylinux1_x86_64.whl (636 kB)\n",
+ "Requirement already satisfied: tensorflow-hub>=0.6.0 in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (0.12.0)\n",
+ "Collecting seqeval\n",
+ " Downloading seqeval-1.2.2.tar.gz (43 kB)\n",
+ "Collecting tensorflow~=2.9.0\n",
+ " Downloading tensorflow-2.9.1-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (511.7 MB)\n",
+ "Collecting tensorflow-text~=2.9.0\n",
+ " Downloading tensorflow_text-2.9.0-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (4.6 MB)\n",
+ "Requirement already satisfied: psutil>=5.4.3 in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (5.4.8)\n",
+ "Requirement already satisfied: google-api-python-client>=1.6.7 in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (1.12.11)\n",
+ "Collecting sentencepiece\n",
+ " Downloading sentencepiece-0.1.97-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (1.3 MB)\n",
+ "Collecting tensorflow-addons\n",
+ " Downloading tensorflow_addons-0.17.1-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (1.1 MB)\n",
+ "Collecting tensorflow-model-optimization>=0.4.1\n",
+ " Downloading tensorflow_model_optimization-0.7.3-py2.py3-none-any.whl (238 kB)\n",
+ "Requirement already satisfied: kaggle>=1.3.9 in /usr/local/lib/python3.7/dist-packages (from tf-models-official>=2.5.1->object-detection==0.1) (1.5.12)\n",
+ "Requirement already satisfied: google-auth<3dev,>=1.16.0 in /usr/local/lib/python3.7/dist-packages (from google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (1.35.0)\n",
+ "Requirement already satisfied: google-auth-httplib2>=0.0.3 in /usr/local/lib/python3.7/dist-packages (from google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (0.0.4)\n",
+ "Requirement already satisfied: httplib2<1dev,>=0.15.0 in /usr/local/lib/python3.7/dist-packages (from google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (0.17.4)\n",
+ "Requirement already satisfied: google-api-core<3dev,>=1.21.0 in /usr/local/lib/python3.7/dist-packages (from google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (1.31.6)\n",
+ "Requirement already satisfied: uritemplate<4dev,>=3.0.0 in /usr/local/lib/python3.7/dist-packages (from google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (3.0.1)\n",
+ "Requirement already satisfied: pytz in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (2022.1)\n",
+ "Requirement already satisfied: requests<3.0.0dev,>=2.18.0 in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (2.23.0)\n",
+ "Requirement already satisfied: setuptools>=40.3.0 in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (57.4.0)\n",
+ "Requirement already satisfied: packaging>=14.3 in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (21.3)\n",
+ "Requirement already satisfied: googleapis-common-protos<2.0dev,>=1.6.0 in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (1.56.4)\n",
+ "Requirement already satisfied: protobuf<4.0.0dev,>=3.12.0 in /usr/local/lib/python3.7/dist-packages (from google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (3.17.3)\n",
+ "Requirement already satisfied: pyasn1-modules>=0.2.1 in /usr/local/lib/python3.7/dist-packages (from google-auth<3dev,>=1.16.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (0.2.8)\n",
+ "Requirement already satisfied: cachetools<5.0,>=2.0.0 in /usr/local/lib/python3.7/dist-packages (from google-auth<3dev,>=1.16.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (4.2.4)\n",
+ "Requirement already satisfied: rsa<5,>=3.1.4 in /usr/local/lib/python3.7/dist-packages (from google-auth<3dev,>=1.16.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (4.9)\n",
+ "Requirement already satisfied: certifi in /usr/local/lib/python3.7/dist-packages (from kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (2022.6.15)\n",
+ "Requirement already satisfied: python-slugify in /usr/local/lib/python3.7/dist-packages (from kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (6.1.2)\n",
+ "Requirement already satisfied: python-dateutil in /usr/local/lib/python3.7/dist-packages (from kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (2.8.2)\n",
+ "Requirement already satisfied: tqdm in /usr/local/lib/python3.7/dist-packages (from kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (4.64.0)\n",
+ "Requirement already satisfied: urllib3 in /usr/local/lib/python3.7/dist-packages (from kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (1.24.3)\n",
+ "Requirement already satisfied: pyasn1<0.5.0,>=0.4.6 in /usr/local/lib/python3.7/dist-packages (from pyasn1-modules>=0.2.1->google-auth<3dev,>=1.16.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (0.4.8)\n",
+ "Requirement already satisfied: chardet<4,>=3.0.2 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0dev,>=2.18.0->google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (3.0.4)\n",
+ "Requirement already satisfied: idna<3,>=2.5 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0dev,>=2.18.0->google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (2.10)\n",
+ "Requirement already satisfied: tensorflow-io-gcs-filesystem>=0.23.1 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (0.26.0)\n",
+ "Requirement already satisfied: h5py>=2.9.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (3.1.0)\n",
+ "Collecting gast<=0.4.0,>=0.2.1\n",
+ " Downloading gast-0.4.0-py3-none-any.whl (9.8 kB)\n",
+ "Requirement already satisfied: google-pasta>=0.1.1 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (0.2.0)\n",
+ "Requirement already satisfied: opt-einsum>=2.3.2 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (3.3.0)\n",
+ "Collecting keras\n",
+ " Downloading keras-2.9.0-py2.py3-none-any.whl (1.6 MB)\n",
+ "Requirement already satisfied: grpcio<2.0,>=1.24.3 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.47.0)\n",
+ "Collecting tensorboard<2.10,>=2.9\n",
+ " Downloading tensorboard-2.9.1-py3-none-any.whl (5.8 MB)\n",
+ "Collecting tensorflow-estimator<2.10.0,>=2.9.0rc0\n",
+ " Downloading tensorflow_estimator-2.9.0-py2.py3-none-any.whl (438 kB)\n",
+ "Requirement already satisfied: keras-preprocessing>=1.1.1 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.1.2)\n",
+ "Collecting flatbuffers<2,>=1.12\n",
+ " Downloading flatbuffers-1.12-py2.py3-none-any.whl (15 kB)\n",
+ "Requirement already satisfied: typing-extensions>=3.6.6 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (4.1.1)\n",
+ "Requirement already satisfied: libclang>=13.0.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (14.0.6)\n",
+ "Requirement already satisfied: termcolor>=1.1.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.1.0)\n",
+ "Requirement already satisfied: absl-py>=1.0.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.2.0)\n",
+ "Requirement already satisfied: wrapt>=1.11.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.14.1)\n",
+ "Requirement already satisfied: astunparse>=1.6.0 in /usr/local/lib/python3.7/dist-packages (from tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.6.3)\n",
+ "Requirement already satisfied: wheel<1.0,>=0.23.0 in /usr/local/lib/python3.7/dist-packages (from astunparse>=1.6.0->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (0.37.1)\n",
+ "Requirement already satisfied: cached-property in /usr/local/lib/python3.7/dist-packages (from h5py>=2.9.0->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.5.2)\n",
+ "Requirement already satisfied: google-auth-oauthlib<0.5,>=0.4.1 in /usr/local/lib/python3.7/dist-packages (from tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (0.4.6)\n",
+ "Requirement already satisfied: werkzeug>=1.0.1 in /usr/local/lib/python3.7/dist-packages (from tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.0.1)\n",
+ "Requirement already satisfied: markdown>=2.6.8 in /usr/local/lib/python3.7/dist-packages (from tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (3.4.1)\n",
+ "Requirement already satisfied: tensorboard-plugin-wit>=1.6.0 in /usr/local/lib/python3.7/dist-packages (from tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.8.1)\n",
+ "Requirement already satisfied: tensorboard-data-server<0.7.0,>=0.6.0 in /usr/local/lib/python3.7/dist-packages (from tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (0.6.1)\n",
+ "Requirement already satisfied: requests-oauthlib>=0.7.0 in /usr/local/lib/python3.7/dist-packages (from google-auth-oauthlib<0.5,>=0.4.1->tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (1.3.1)\n",
+ "Requirement already satisfied: importlib-metadata>=4.4 in /usr/local/lib/python3.7/dist-packages (from markdown>=2.6.8->tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (4.12.0)\n",
+ "Requirement already satisfied: zipp>=0.5 in /usr/local/lib/python3.7/dist-packages (from importlib-metadata>=4.4->markdown>=2.6.8->tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (3.8.1)\n",
+ "Requirement already satisfied: oauthlib>=3.0.0 in /usr/local/lib/python3.7/dist-packages (from requests-oauthlib>=0.7.0->google-auth-oauthlib<0.5,>=0.4.1->tensorboard<2.10,>=2.9->tensorflow~=2.9.0->tf-models-official>=2.5.1->object-detection==0.1) (3.2.0)\n",
+ "Requirement already satisfied: dm-tree~=0.1.1 in /usr/local/lib/python3.7/dist-packages (from tensorflow-model-optimization>=0.4.1->tf-models-official>=2.5.1->object-detection==0.1) (0.1.7)\n",
+ "Collecting cloudpickle<3,>=2.1.0\n",
+ " Downloading cloudpickle-2.1.0-py3-none-any.whl (25 kB)\n",
+ "Collecting fastavro<2,>=0.23.6\n",
+ " Downloading fastavro-1.5.4-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (2.4 MB)\n",
+ "Collecting pymongo<4.0.0,>=3.8.0\n",
+ " Downloading pymongo-3.12.3-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (508 kB)\n",
+ "Collecting proto-plus<2,>=1.7.1\n",
+ " Downloading proto_plus-1.22.0-py3-none-any.whl (47 kB)\n",
+ "Collecting hdfs<3.0.0,>=2.1.0\n",
+ " Downloading hdfs-2.7.0-py3-none-any.whl (34 kB)\n",
+ "Requirement already satisfied: pyarrow<8.0.0,>=0.15.1 in /usr/local/lib/python3.7/dist-packages (from apache-beam->object-detection==0.1) (6.0.1)\n",
+ "Requirement already satisfied: crcmod<2.0,>=1.7 in /usr/local/lib/python3.7/dist-packages (from apache-beam->object-detection==0.1) (1.7)\n",
+ "Requirement already satisfied: pydot<2,>=1.2.0 in /usr/local/lib/python3.7/dist-packages (from apache-beam->object-detection==0.1) (1.3.0)\n",
+ "Collecting requests<3.0.0dev,>=2.18.0\n",
+ " Downloading requests-2.28.1-py3-none-any.whl (62 kB)\n",
+ "Collecting orjson<4.0\n",
+ " Downloading orjson-3.7.11-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (275 kB)\n",
+ "Collecting dill<0.3.2,>=0.3.1.1\n",
+ " Downloading dill-0.3.1.1.tar.gz (151 kB)\n",
+ "Collecting docopt\n",
+ " Downloading docopt-0.6.2.tar.gz (25 kB)\n",
+ "Collecting protobuf<4.0.0dev,>=3.12.0\n",
+ " Downloading protobuf-3.19.4-cp37-cp37m-manylinux_2_17_x86_64.manylinux2014_x86_64.whl (1.1 MB)\n",
+ "Requirement already satisfied: charset-normalizer<3,>=2 in /usr/local/lib/python3.7/dist-packages (from requests<3.0.0dev,>=2.18.0->google-api-core<3dev,>=1.21.0->google-api-python-client>=1.6.7->tf-models-official>=2.5.1->object-detection==0.1) (2.1.0)\n",
+ "Requirement already satisfied: cycler>=0.10.0 in /usr/local/lib/python3.7/dist-packages (from lvis->object-detection==0.1) (0.11.0)\n",
+ "Requirement already satisfied: opencv-python>=4.1.0.25 in /usr/local/lib/python3.7/dist-packages (from lvis->object-detection==0.1) (4.6.0.66)\n",
+ "Requirement already satisfied: kiwisolver>=1.1.0 in /usr/local/lib/python3.7/dist-packages (from lvis->object-detection==0.1) (1.4.4)\n",
+ "Requirement already satisfied: text-unidecode>=1.3 in /usr/local/lib/python3.7/dist-packages (from python-slugify->kaggle>=1.3.9->tf-models-official>=2.5.1->object-detection==0.1) (1.3)\n",
+ "Collecting portalocker\n",
+ " Downloading portalocker-2.5.1-py2.py3-none-any.whl (15 kB)\n",
+ "Requirement already satisfied: tabulate>=0.8.9 in /usr/local/lib/python3.7/dist-packages (from sacrebleu->tf-models-official>=2.5.1->object-detection==0.1) (0.8.10)\n",
+ "Collecting colorama\n",
+ " Downloading colorama-0.4.5-py2.py3-none-any.whl (16 kB)\n",
+ "Requirement already satisfied: regex in /usr/local/lib/python3.7/dist-packages (from sacrebleu->tf-models-official>=2.5.1->object-detection==0.1) (2022.6.2)\n",
+ "Requirement already satisfied: scikit-learn>=0.21.3 in /usr/local/lib/python3.7/dist-packages (from seqeval->tf-models-official>=2.5.1->object-detection==0.1) (1.0.2)\n",
+ "Requirement already satisfied: joblib>=0.11 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval->tf-models-official>=2.5.1->object-detection==0.1) (1.1.0)\n",
+ "Requirement already satisfied: threadpoolctl>=2.0.0 in /usr/local/lib/python3.7/dist-packages (from scikit-learn>=0.21.3->seqeval->tf-models-official>=2.5.1->object-detection==0.1) (3.1.0)\n",
+ "Requirement already satisfied: typeguard>=2.7 in /usr/local/lib/python3.7/dist-packages (from tensorflow-addons->tf-models-official>=2.5.1->object-detection==0.1) (2.7.1)\n",
+ "Requirement already satisfied: tensorflow-metadata in /usr/local/lib/python3.7/dist-packages (from tensorflow-datasets->tf-models-official>=2.5.1->object-detection==0.1) (1.9.0)\n",
+ "Requirement already satisfied: importlib-resources in /usr/local/lib/python3.7/dist-packages (from tensorflow-datasets->tf-models-official>=2.5.1->object-detection==0.1) (5.9.0)\n",
+ "Requirement already satisfied: promise in /usr/local/lib/python3.7/dist-packages (from tensorflow-datasets->tf-models-official>=2.5.1->object-detection==0.1) (2.3)\n",
+ "Requirement already satisfied: toml in /usr/local/lib/python3.7/dist-packages (from tensorflow-datasets->tf-models-official>=2.5.1->object-detection==0.1) (0.10.2)\n",
+ "Requirement already satisfied: etils[epath] in /usr/local/lib/python3.7/dist-packages (from tensorflow-datasets->tf-models-official>=2.5.1->object-detection==0.1) (0.7.1)\n",
+ "Building wheels for collected packages: object-detection, py-cpuinfo, dill, avro-python3, docopt, seqeval\n",
+ " Building wheel for object-detection (setup.py): started\n",
+ " Building wheel for object-detection (setup.py): finished with status 'done'\n",
+ " Created wheel for object-detection: filename=object_detection-0.1-py3-none-any.whl size=1694955 sha256=5b07d9d3f9b50a4e043579877792dcc5f911757c859a40646bfe44b1411c2b0b\n",
+ " Stored in directory: /tmp/pip-ephem-wheel-cache-_e25017f/wheels/fa/a4/d2/e9a5057e414fd46c8e543d2706cd836d64e1fcd9eccceb2329\n",
+ " Building wheel for py-cpuinfo (setup.py): started\n",
+ " Building wheel for py-cpuinfo (setup.py): finished with status 'done'\n",
+ " Created wheel for py-cpuinfo: filename=py_cpuinfo-8.0.0-py3-none-any.whl size=22257 sha256=16043574dd7ea707666388babd039116f8de2bbe60cc7c7bcc35fd39aa978651\n",
+ " Stored in directory: /root/.cache/pip/wheels/d2/f1/1f/041add21dc9c4220157f1bd2bd6afe1f1a49524c3396b94401\n",
+ " Building wheel for dill (setup.py): started\n",
+ " Building wheel for dill (setup.py): finished with status 'done'\n",
+ " Created wheel for dill: filename=dill-0.3.1.1-py3-none-any.whl size=78544 sha256=ed98e6a3a08f7b25f291c3ded9aa4b85fccbf64a0e52816961d5579e44e7594b\n",
+ " Stored in directory: /root/.cache/pip/wheels/a4/61/fd/c57e374e580aa78a45ed78d5859b3a44436af17e22ca53284f\n",
+ " Building wheel for avro-python3 (setup.py): started\n",
+ " Building wheel for avro-python3 (setup.py): finished with status 'done'\n",
+ " Created wheel for avro-python3: filename=avro_python3-1.10.2-py3-none-any.whl size=44010 sha256=6a76a37f9b0865055470da37fca662fff8934ac3a2776a1f01d09fac2703eb34\n",
+ " Stored in directory: /root/.cache/pip/wheels/d6/e5/b1/6b151d9b535ee50aaa6ab27d145a0104b6df02e5636f0376da\n",
+ " Building wheel for docopt (setup.py): started\n",
+ " Building wheel for docopt (setup.py): finished with status 'done'\n",
+ " Created wheel for docopt: filename=docopt-0.6.2-py2.py3-none-any.whl size=13723 sha256=c1fd090fa0616d3d71b524dc465344600ef9cd2cfcff4f9558571a397f0fd7ad\n",
+ " Stored in directory: /root/.cache/pip/wheels/72/b0/3f/1d95f96ff986c7dfffe46ce2be4062f38ebd04b506c77c81b9\n",
+ " Building wheel for seqeval (setup.py): started\n",
+ " Building wheel for seqeval (setup.py): finished with status 'done'\n",
+ " Created wheel for seqeval: filename=seqeval-1.2.2-py3-none-any.whl size=16180 sha256=6a692bf82ea13a55bc0bb10a37d5b444a675ed7f77d72e893fa02a97246e9204\n",
+ " Stored in directory: /root/.cache/pip/wheels/05/96/ee/7cac4e74f3b19e3158dce26a20a1c86b3533c43ec72a549fd7\n",
+ "Successfully built object-detection py-cpuinfo dill avro-python3 docopt seqeval\n",
+ "Installing collected packages: requests, pyparsing, protobuf, tensorflow-estimator, tensorboard, keras, gast, flatbuffers, tensorflow, portalocker, docopt, dill, colorama, tf-slim, tensorflow-text, tensorflow-model-optimization, tensorflow-addons, seqeval, sentencepiece, sacrebleu, pyyaml, pymongo, py-cpuinfo, proto-plus, orjson, hdfs, fastavro, cloudpickle, tf-models-official, tensorflow-io, lvis, avro-python3, apache-beam, object-detection\n",
+ " Attempting uninstall: requests\n",
+ " Found existing installation: requests 2.23.0\n",
+ " Uninstalling requests-2.23.0:\n",
+ " Successfully uninstalled requests-2.23.0\n",
+ " Attempting uninstall: pyparsing\n",
+ " Found existing installation: pyparsing 3.0.9\n",
+ " Uninstalling pyparsing-3.0.9:\n",
+ " Successfully uninstalled pyparsing-3.0.9\n",
+ " Attempting uninstall: protobuf\n",
+ " Found existing installation: protobuf 3.17.3\n",
+ " Uninstalling protobuf-3.17.3:\n",
+ " Successfully uninstalled protobuf-3.17.3\n",
+ " Attempting uninstall: tensorflow-estimator\n",
+ " Found existing installation: tensorflow-estimator 2.8.0\n",
+ " Uninstalling tensorflow-estimator-2.8.0:\n",
+ " Successfully uninstalled tensorflow-estimator-2.8.0\n",
+ " Attempting uninstall: tensorboard\n",
+ " Found existing installation: tensorboard 2.8.0\n",
+ " Uninstalling tensorboard-2.8.0:\n",
+ " Successfully uninstalled tensorboard-2.8.0\n",
+ " Attempting uninstall: keras\n",
+ " Found existing installation: keras 2.8.0\n",
+ " Uninstalling keras-2.8.0:\n",
+ " Successfully uninstalled keras-2.8.0\n",
+ " Attempting uninstall: gast\n",
+ " Found existing installation: gast 0.5.3\n",
+ " Uninstalling gast-0.5.3:\n",
+ " Successfully uninstalled gast-0.5.3\n",
+ " Attempting uninstall: flatbuffers\n",
+ " Found existing installation: flatbuffers 2.0\n",
+ " Uninstalling flatbuffers-2.0:\n",
+ " Successfully uninstalled flatbuffers-2.0\n",
+ " Attempting uninstall: tensorflow\n",
+ " Found existing installation: tensorflow 2.8.2+zzzcolab20220719082949\n",
+ " Uninstalling tensorflow-2.8.2+zzzcolab20220719082949:\n",
+ " Successfully uninstalled tensorflow-2.8.2+zzzcolab20220719082949\n",
+ " Attempting uninstall: dill\n",
+ " Found existing installation: dill 0.3.5.1\n",
+ " Uninstalling dill-0.3.5.1:\n",
+ " Successfully uninstalled dill-0.3.5.1\n",
+ " Attempting uninstall: pyyaml\n",
+ " Found existing installation: PyYAML 3.13\n",
+ " Uninstalling PyYAML-3.13:\n",
+ " Successfully uninstalled PyYAML-3.13\n",
+ " Attempting uninstall: pymongo\n",
+ " Found existing installation: pymongo 4.2.0\n",
+ " Uninstalling pymongo-4.2.0:\n",
+ " Successfully uninstalled pymongo-4.2.0\n",
+ " Attempting uninstall: cloudpickle\n",
+ " Found existing installation: cloudpickle 1.3.0\n",
+ " Uninstalling cloudpickle-1.3.0:\n",
+ " Successfully uninstalled cloudpickle-1.3.0\n",
+ "Successfully installed apache-beam-2.40.0 avro-python3-1.10.2 cloudpickle-2.1.0 colorama-0.4.5 dill-0.3.1.1 docopt-0.6.2 fastavro-1.5.4 flatbuffers-1.12 gast-0.4.0 hdfs-2.7.0 keras-2.9.0 lvis-0.5.3 object-detection-0.1 orjson-3.7.11 portalocker-2.5.1 proto-plus-1.22.0 protobuf-3.19.4 py-cpuinfo-8.0.0 pymongo-3.12.3 pyparsing-2.4.7 pyyaml-5.4.1 requests-2.28.1 sacrebleu-2.2.0 sentencepiece-0.1.97 seqeval-1.2.2 tensorboard-2.9.1 tensorflow-2.9.1 tensorflow-addons-0.17.1 tensorflow-estimator-2.9.0 tensorflow-io-0.26.0 tensorflow-model-optimization-0.7.3 tensorflow-text-2.9.0 tf-models-official-2.9.2 tf-slim-1.1.0\n"
+ ]
+ },
+ {
+ "output_type": "stream",
+ "name": "stderr",
+ "text": [
+ "\n",
+ "WARNING: apt does not have a stable CLI interface. Use with caution in scripts.\n",
+ "\n",
+ " DEPRECATION: A future pip version will change local packages to be built in-place without first copying to a temporary directory. We recommend you use --use-feature=in-tree-build to test your packages with this new behavior before it becomes the default.\n",
+ " pip 21.3 will remove support for this functionality. You can find discussion regarding this at https://github.com/pypa/pip/issues/7555.\n",
+ "ERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.\n",
+ "gym 0.17.3 requires cloudpickle<1.7.0,>=1.2.0, but you have cloudpickle 2.1.0 which is incompatible.\n"
+ ]
+ }
+ ],
+ "source": [
+ "%%bash\n",
+ "sudo apt install -y protobuf-compiler\n",
+ "cd models/research/\n",
+ "protoc object_detection/protos/*.proto --python_out=.\n",
+ "cp object_detection/packages/tf2/setup.py .\n",
+ "python -m pip install ."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "3yDNgIx-kV7X"
+ },
+ "source": [
+ "Now we can import the dependencies we will need later"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "2JCeQU3fkayh"
+ },
+ "outputs": [],
+ "source": [
+ "from object_detection.utils import label_map_util\n",
+ "from object_detection.utils import visualization_utils as viz_utils\n",
+ "from object_detection.utils import ops as utils_ops\n",
+ "\n",
+ "%matplotlib inline"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "XRUr9Aiwuho7"
+ },
+ "source": [
+ "## Import pre-trained models from the Waste Identification project"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "!wget https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_model.zip \n",
+ "!wget https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_form_model.zip \n",
+ "!wget https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/plastic_types_model.zip "
+ ],
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "7AnetxTI6BdR",
+ "outputId": "dfef214d-9c6f-4464-95fa-5f0ccc9a17ba"
+ },
+ "execution_count": null,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "--2022-08-12 22:53:17-- https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_model.zip\n",
+ "Resolving storage.googleapis.com (storage.googleapis.com)... 142.250.103.128, 142.250.159.128, 142.251.120.128, ...\n",
+ "Connecting to storage.googleapis.com (storage.googleapis.com)|142.250.103.128|:443... connected.\n",
+ "HTTP request sent, awaiting response... 200 OK\n",
+ "Length: 521320844 (497M) [application/zip]\n",
+ "Saving to: ‘material_model.zip’\n",
+ "\n",
+ "material_model.zip 100%[===================>] 497.17M 97.0MB/s in 5.4s \n",
+ "\n",
+ "2022-08-12 22:53:23 (92.2 MB/s) - ‘material_model.zip’ saved [521320844/521320844]\n",
+ "\n",
+ "--2022-08-12 22:53:23-- https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/material_form_model.zip\n",
+ "Resolving storage.googleapis.com (storage.googleapis.com)... 142.250.103.128, 142.250.159.128, 142.251.120.128, ...\n",
+ "Connecting to storage.googleapis.com (storage.googleapis.com)|142.250.103.128|:443... connected.\n",
+ "HTTP request sent, awaiting response... 200 OK\n",
+ "Length: 523568744 (499M) [application/zip]\n",
+ "Saving to: ‘material_form_model.zip’\n",
+ "\n",
+ "material_form_model 100%[===================>] 499.31M 147MB/s in 3.4s \n",
+ "\n",
+ "2022-08-12 22:53:27 (146 MB/s) - ‘material_form_model.zip’ saved [523568744/523568744]\n",
+ "\n",
+ "--2022-08-12 22:53:27-- https://storage.googleapis.com/tf_model_garden/vision/waste_identification_ml/plastic_types_model.zip\n",
+ "Resolving storage.googleapis.com (storage.googleapis.com)... 142.250.103.128, 142.250.159.128, 142.251.120.128, ...\n",
+ "Connecting to storage.googleapis.com (storage.googleapis.com)|142.250.103.128|:443... connected.\n",
+ "HTTP request sent, awaiting response... 200 OK\n",
+ "Length: 521268394 (497M) [application/zip]\n",
+ "Saving to: ‘plastic_types_model.zip’\n",
+ "\n",
+ "plastic_types_model 100%[===================>] 497.12M 137MB/s in 4.0s \n",
+ "\n",
+ "2022-08-12 22:53:31 (124 MB/s) - ‘plastic_types_model.zip’ saved [521268394/521268394]\n",
+ "\n"
+ ]
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "source": [
+ "%%bash\n",
+ "mkdir material material_form plastic_type\n",
+ "unzip material_model.zip -d material/\n",
+ "unzip material_form_model.zip -d material_form/\n",
+ "unzip plastic_types_model.zip -d plastic_type/"
+ ],
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "SFFo0fdQtg26",
+ "outputId": "8a8843e2-b251-4d2a-84ed-34bae99e22cb"
+ },
+ "execution_count": null,
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Archive: material_model.zip\n",
+ " creating: material/saved_model/\n",
+ " inflating: material/saved_model/params.yaml \n",
+ " creating: material/saved_model/saved_model/\n",
+ " inflating: material/saved_model/saved_model/saved_model.pb \n",
+ " creating: material/saved_model/saved_model/variables/\n",
+ " inflating: material/saved_model/saved_model/variables/variables.data-00000-of-00001 \n",
+ " inflating: material/saved_model/saved_model/variables/variables.index \n",
+ " creating: material/saved_model/checkpoint/\n",
+ " inflating: material/saved_model/checkpoint/ckpt-1.data-00000-of-00001 \n",
+ " inflating: material/saved_model/checkpoint/checkpoint \n",
+ " inflating: material/saved_model/checkpoint/ckpt-1.index \n",
+ " creating: material/tflite_model/\n",
+ " inflating: material/tflite_model/model.tflite \n",
+ "Archive: material_form_model.zip\n",
+ " creating: material_form/saved_model/\n",
+ " inflating: material_form/saved_model/params.yaml \n",
+ " creating: material_form/saved_model/saved_model/\n",
+ " inflating: material_form/saved_model/saved_model/saved_model.pb \n",
+ " creating: material_form/saved_model/saved_model/variables/\n",
+ " inflating: material_form/saved_model/saved_model/variables/variables.data-00000-of-00001 \n",
+ " inflating: material_form/saved_model/saved_model/variables/variables.index \n",
+ " creating: material_form/saved_model/checkpoint/\n",
+ " inflating: material_form/saved_model/checkpoint/ckpt-1.data-00000-of-00001 \n",
+ " inflating: material_form/saved_model/checkpoint/checkpoint \n",
+ " inflating: material_form/saved_model/checkpoint/ckpt-1.index \n",
+ " creating: material_form/tflite_model/\n",
+ " inflating: material_form/tflite_model/model.tflite \n",
+ "Archive: plastic_types_model.zip\n",
+ " creating: plastic_type/saved_model/\n",
+ " inflating: plastic_type/saved_model/params.yaml \n",
+ " creating: plastic_type/saved_model/saved_model/\n",
+ " inflating: plastic_type/saved_model/saved_model/saved_model.pb \n",
+ " creating: plastic_type/saved_model/saved_model/variables/\n",
+ " inflating: plastic_type/saved_model/saved_model/variables/variables.data-00000-of-00001 \n",
+ " inflating: plastic_type/saved_model/saved_model/variables/variables.index \n",
+ " creating: plastic_type/saved_model/checkpoint/\n",
+ " inflating: plastic_type/saved_model/checkpoint/ckpt-1.data-00000-of-00001 \n",
+ " inflating: plastic_type/saved_model/checkpoint/checkpoint \n",
+ " inflating: plastic_type/saved_model/checkpoint/ckpt-1.index \n",
+ " creating: plastic_type/tflite_model/\n",
+ " inflating: plastic_type/tflite_model/model.tflite \n"
+ ]
+ }
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Ey-8Ij2sKjkD"
+ },
+ "outputs": [],
+ "source": [
+ "ALL_MODELS = {\n",
+ "'material_model' : 'material/saved_model/saved_model/',\n",
+ "'material_form_model' : 'material_form/saved_model/saved_model/',\n",
+ "'plastic_model' : 'plastic_type/saved_model/saved_model/'\n",
+ "}\n",
+ "\n",
+ "# path to an image\n",
+ "IMAGES_FOR_TEST = {\n",
+ " 'Image1' : 'models/official/projects/waste_identification_ml/pre_processing/config/sample_images/image_2.png'\n",
+ "}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "IogyryF2lFBL"
+ },
+ "source": [
+ "## Utilities\n",
+ "\n",
+ "Run the following cell to create some utils that will be needed later:\n",
+ "\n",
+ "- Helper method to load an image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "9XXfEdD9PMKn"
+ },
+ "outputs": [],
+ "source": [
+ "# Inputs to preprocess functions\n",
+ "\n",
+ "def normalize_image(image,\n",
+ " offset=(0.485, 0.456, 0.406),\n",
+ " scale=(0.229, 0.224, 0.225)):\n",
+ " \"\"\"Normalizes the image to zero mean and unit variance.\"\"\"\n",
+ " with tf.name_scope('normalize_image'):\n",
+ " image = tf.image.convert_image_dtype(image, dtype=tf.float32)\n",
+ " offset = tf.constant(offset)\n",
+ " offset = tf.expand_dims(offset, axis=0)\n",
+ " offset = tf.expand_dims(offset, axis=0)\n",
+ " image -= offset\n",
+ "\n",
+ " scale = tf.constant(scale)\n",
+ " scale = tf.expand_dims(scale, axis=0)\n",
+ " scale = tf.expand_dims(scale, axis=0)\n",
+ " image /= scale\n",
+ " return image\n",
+ "\n",
+ " \n",
+ "def load_image_into_numpy_array(path):\n",
+ " \"\"\"Load an image from file into a numpy array.\n",
+ "\n",
+ " Puts image into numpy array to feed into tensorflow graph.\n",
+ " Note that by convention we put it into a numpy array with shape\n",
+ " (height, width, channels), where channels=3 for RGB.\n",
+ "\n",
+ " Args:\n",
+ " path: the file path to the image\n",
+ "\n",
+ " Returns:\n",
+ " uint8 numpy array with shape (1, h, w, 3)\n",
+ " \"\"\"\n",
+ " image = None\n",
+ " if(path.startswith('http')):\n",
+ " response = urlopen(path)\n",
+ " image_data = response.read()\n",
+ " image_data = BytesIO(image_data)\n",
+ " image = Image.open(image_data)\n",
+ " else:\n",
+ " image_data = tf.io.gfile.GFile(path, 'rb').read()\n",
+ " image = Image.open(BytesIO(image_data))\n",
+ "\n",
+ " (im_width, im_height) = image.size\n",
+ " return np.array(image.getdata()).reshape(\n",
+ " (1, im_height, im_width, 3)).astype(np.uint8)\n",
+ "\n",
+ "\n",
+ "def build_inputs_for_segmentation(image):\n",
+ " \"\"\"Builds segmentation model inputs for serving.\"\"\"\n",
+ " # Normalizes image with mean and std pixel values.\n",
+ " image = normalize_image(image)\n",
+ " return image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6917xnUSlp9x"
+ },
+ "source": [
+ "## Build a instance segmentation model and load pre-trained model weights\n",
+ "\n",
+ "Here we will choose which Instance Segmentation model we will use.\n",
+ "If you want to change the model to try other architectures later, just change the next cell and execute following ones. \n",
+ "3 models are available.\n",
+ "1. **material_model** : Identify the highest level of the category of the material like plastic, metal, etc.\n",
+ "2. **material_form_model** : Identify the product or form in which the object is like plate, bottle, etc.\n",
+ "3. **plastic_model** : Identify the types of the plastics like HDPE, PETE, etc."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "HtwrSqvakTNn",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "0a6d2e8b-30a3-4c0d-955a-6a410bdb0b0b"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Selected model:material_form_model\n",
+ "Model Handle at TensorFlow Hub: material_form/saved_model/saved_model/\n"
+ ]
+ }
+ ],
+ "source": [
+ "# @title Model Selection { display-mode: \"form\", run: \"auto\" }\n",
+ "model_display_name = 'material_form_model' # @param ['material_model','material_form_model','plastic_model']\n",
+ "model_handle = ALL_MODELS[model_display_name]\n",
+ "\n",
+ "print('Selected model:'+ model_display_name)\n",
+ "print('Model Handle at TensorFlow Hub: {}'.format(model_handle))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "NKtD0IeclbL5"
+ },
+ "source": [
+ "### Load label map data (for plotting).\n",
+ "\n",
+ "Label maps correspond index numbers to category names, so that when our convolution network predicts `2`, we know that this corresponds to `Bottle`. Here we use internal utility functions, but anything that returns a dictionary mapping integers to appropriate string labels would be fine.\n",
+ "\n",
+ "We are going, for simplicity, to load from the repository that we loaded the Object Detection API code"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "3Kwqa0T1NTUf",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "54b701ab-c936-46b0-c76e-d0cc48e4b87c"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Labels selected for material_form_model\n",
+ "\n",
+ "\n"
+ ]
+ },
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "{1: {'id': 1, 'name': 'Flexibles'},\n",
+ " 2: {'id': 2, 'name': 'Bottle'},\n",
+ " 3: {'id': 3, 'name': 'Jar'},\n",
+ " 4: {'id': 4, 'name': 'Carton'},\n",
+ " 5: {'id': 5, 'name': 'Sachets-&-Pouch'},\n",
+ " 6: {'id': 6, 'name': 'Blister-pack'},\n",
+ " 7: {'id': 7, 'name': 'Tray'},\n",
+ " 8: {'id': 8, 'name': 'Tube'},\n",
+ " 9: {'id': 9, 'name': 'Can'},\n",
+ " 10: {'id': 10, 'name': 'Tub'},\n",
+ " 11: {'id': 11, 'name': 'Cosmetic'},\n",
+ " 12: {'id': 12, 'name': 'Box'},\n",
+ " 13: {'id': 13, 'name': 'Clothes'},\n",
+ " 14: {'id': 14, 'name': 'Bulb'},\n",
+ " 15: {'id': 15, 'name': 'Cup-&-glass'},\n",
+ " 16: {'id': 16, 'name': 'Book-&-magazine'},\n",
+ " 17: {'id': 17, 'name': 'Bag'},\n",
+ " 18: {'id': 18, 'name': 'Lid'},\n",
+ " 19: {'id': 19, 'name': 'Clamshell'},\n",
+ " 20: {'id': 20, 'name': 'Mirror'},\n",
+ " 21: {'id': 21, 'name': 'Tangler'},\n",
+ " 22: {'id': 22, 'name': 'Cutlery'},\n",
+ " 23: {'id': 23, 'name': 'Cassette-&-tape'},\n",
+ " 24: {'id': 24, 'name': 'Electronic-devices'},\n",
+ " 25: {'id': 25, 'name': 'Battery'},\n",
+ " 26: {'id': 26, 'name': 'Pen-&-pencil'},\n",
+ " 27: {'id': 27, 'name': 'Paper-products'},\n",
+ " 28: {'id': 28, 'name': 'Foot-wear'},\n",
+ " 29: {'id': 29, 'name': 'Scissor'},\n",
+ " 30: {'id': 30, 'name': 'Toys'},\n",
+ " 31: {'id': 31, 'name': 'Brush'},\n",
+ " 32: {'id': 32, 'name': 'Pipe'},\n",
+ " 33: {'id': 33, 'name': 'Foil'},\n",
+ " 34: {'id': 34, 'name': 'Hangers'}}"
+ ]
+ },
+ "metadata": {},
+ "execution_count": 11
+ }
+ ],
+ "source": [
+ "# @title Labels for the above model { display-mode: \"form\", run: \"auto\" }\n",
+ "\n",
+ "if model_display_name == 'material_model':\n",
+ " PATH_TO_LABELS = './models/official/projects/waste_identification_ml/pre_processing/config/data/material_labels.pbtxt'\n",
+ "elif model_display_name == 'material_form_model':\n",
+ " PATH_TO_LABELS = './models/official/projects/waste_identification_ml/pre_processing/config/data/material_form_labels.pbtxt'\n",
+ "elif model_display_name == 'plastic_model':\n",
+ " PATH_TO_LABELS = './models/official/projects/waste_identification_ml/pre_processing/config/data/plastic_type_labels.pbtxt'\n",
+ "\n",
+ "print('Labels selected for',model_display_name)\n",
+ "print('\\n')\n",
+ "category_index = label_map_util.create_category_index_from_labelmap(PATH_TO_LABELS, use_display_name=True)\n",
+ "category_index"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "muhUt-wWL582"
+ },
+ "source": [
+ "## Loading the selected model from TensorFlow Hub\n",
+ "\n",
+ "Here we just need the model handle that was selected and use the Tensorflow Hub library to load it to memory.\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "rBuD07fLlcEO",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "6103a711-791a-4ed5-fcf5-96fc6de76976"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "loading model...\n",
+ "model loaded!\n"
+ ]
+ }
+ ],
+ "source": [
+ "print('loading model...')\n",
+ "hub_model = hub.load(model_handle)\n",
+ "print('model loaded!')"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "GIawRDKPPnd4"
+ },
+ "source": [
+ "## Loading an image\n",
+ "\n",
+ "Let's try the model on a simple image. \n",
+ "\n",
+ "Here are some simple things to try out if you are curious:\n",
+ "* Try running inference on your own images, just upload them to colab and load the same way it's done in the cell below.\n",
+ "* Modify some of the input images and see if detection still works. Some simple things to try out here include flipping the image horizontally, or converting to grayscale (note that we still expect the input image to have 3 channels).\n",
+ "\n",
+ "**Be careful:** when using images with an alpha channel, the model expect 3 channels images and the alpha will count as a 4th.\n",
+ "\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "hX-AWUQ1wIEr",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 666
+ },
+ "outputId": "3c0ddf39-c51a-4f46-cad7-8d21ebcaf4f2"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "min: 0 max: 255\n"
+ ]
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABWkAAAMUCAYAAADOgaX6AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOy9za4tS5Im9Jm5e8Raa+/zc7P6Fi0BavE37RE0M2YgZkyBB+gRD8Cz9IAxT9ASA16AQqhBXS36B0R3ZwqylVl17zl77xUR7m7GwMw8Yu17bnUN0M2UCKs6ec/Ze634cTc3N/vsM3NSVZxyyimnnHLKKaeccsopp5xyyimnnHLKKaec8ocR/kM/wCmnnHLKKaeccsopp5xyyimnnHLKKaeccsr/n+UEaU855ZRTTjnllFNOOeWUU0455ZRTTjnllFP+gHKCtKeccsopp5xyyimnnHLKKaeccsopp5xyyil/QDlB2lNOOeWUU0455ZRTTjnllFNOOeWUU0455ZQ/oJwg7SmnnHLKKaeccsopp5xyyimnnHLKKaeccsofUE6Q9pRTTjnllFNOOeWUU0455ZRTTjnllFNOOeUPKL84SEtE/zkR/WMi+mdE9N/+0vc/5ZRTTjnllFNOOeWUU0455ZRTTjnllFNO+WMSUtVf7mZECcA/AfCfAvg1gD8D8F+p6j/6xR7ilFNOOeWUU0455ZRTTjnllFNOOeWUU0455Y9Ifmkm7d8B8M9U9f9U1Q3Afw/gv/iFn+GUU0455ZRTTjnllFNOOeWUU0455ZRTTjnlj0byL3y/fxPAvzz8+9cA/uOf+zBn0lQYOLB9FfF38v8lKAAmQrCCifbf75/134FRyozL5QldABEBEcDMICK7ItktiR6/Tf47wL6n2D+nas9GePySqOzfIwII6NKxrQukVYDsjRiMab7icn3GVjfU9Q6RDmaCiAAPhGeyZyU63EqxbStU2ngPkAL2//Z11cexiSFSQFVBRIfxta+TP3N8WP0aKjHW+zjb8B/m5zgF8V1/dhEBJ7ZPi0KhYOLHQfeB1bg72Vzbj/2nRyY4Hf/iP/fr8eFHStjnyd9BY6DGO9n1Y07H/f1+45nwbmrePYo+fPLwBb+FXR8g4jEH+/d06HcMi767zvj5u4c4vgOgpp9+/cNQgL4xR/GLd7969z6P6xDvfj6e+/BbWyyPY/+tq+lh8e1TuuvfX0divnCYr+PvdPzvcbwPn3l/v4Oq0ftBG/P0fq73fx/HXg7z/HAV1YexiSU0nux4f18DxzX3/po/uYMrkr67v76bl/j3fk/9iT7snzn8VGMt7WPy/6k8DMZR9JvvdRwvhX7j99+wVcOsfPta8bn32r//0LVgbCL7p3728f868u5Zx30PxuGncxK7lu1XEIH2bjaHGEgMSsmv+u4Z43/UvgO39w/rL2zM+0X8cxLPNtZk2D7aX++49sn2CvW99mGsiaBE4JRAzNB3+9Q3JfScCCoK7QJtzZ/n3Xt9w8486oQ+fCW2I/Jx45RBOUNT+tlhoXd75E907icP8Fe8nh5UwfeVn//8owX+9sfeG5/Dd+mogz+ztx3//Y2P7fbyZ1/nYX/71juM//xrF9Xjh35+GGnoJMJn0/37j3vIu5/9zH75IEO39dHWD3/teO34yr7/xHPF3A4/7/AM3x7wxwV6uOS77x72gJ9/Cfxk5sdz7Pd+XEL6jZ8d99h3r/EzCvTeF4hfjzn7lrL8FY7a+7U25iRshH8n/s7DTj14K+MGu8l/b4vezQk9vuPR14j7HAfkIaYYvz9+lx6u83BN7I/CzAj/m4jAbH9CLdkfO0ILHtf6lrenECW0BrSuUBUoEboIpIv9W/qDrR+6fFDHWEHxe31UVb8/g8n8pqMc47V9Y7ZYIvxNu6aAoP79x1Uc8Yx//CfjOwbg+Pa+1omSj+X+OyL29Xl4X/j4KAByz/Ph94f7u27YdXl/FqKHGPd9HLw//0/Xy3sP+Ki1Y5uHALB4dXn7ivryBdAOQIY+q4bd8bGDjr37fcw8nskf7L2/+bBGfF+OmC7GJ8b5OEecExLbnqoq4y1UTb9BOvR7f9HHhyIiJPd7xAKj8XMmHs8Y+sLEYGIQmy8iIvu1mA7Ygb2r/V4hEu9t75IOvtbADPwe435qvlry2Nj0jB06oIOdPtgo7Pr0sBaw77N6eMc91vfr/OxeepjYhyse9G+M0/4cD+ta9BubLT3sZ+Ne7+YonouZfL53Ox9rZI/b7fviunWM0+OZQk90jIP4vQ7vdsAf4hmO/sC47vGx9WDFHnzCff0PXXadIHbryns8Tjj85WALRATEB/umu26pKo624Ccx4MGe/GQWYp8bUynDhjy8B/b4Nq7zaHv9wZUe5lpEHlXnYcj2ePh4zd2G6BiD/fl2ndv9KDzo/b4M1XXT9qJhXH3OFTT2FAXAIPu7Pxc7HvN+DMbY+QASIp73+7/zCfbvvh9rsx0i+z3Wdfudqn7/frx+aZD2XytE9HcB/F0A4EL41b/3AW2rKKWAQdjaipQSxriLDUbTjrnMw1gxMaAWyBERSBRIBAjh6fYd/qO/858h80e8vLwgJ4ZyAueEKWVc5wuUAXQBCBDxa7JpDDOjtY6uiq1tIMoW9EEtYIyJZphRD4VkQtcN/+I3/xz/9B//OZ4vGc/PF3z81a9wvX7A99//Lfzt//A/wf/6D/5n/F//5B+gtzt6q6i1o7eGxAnzXKDK6KLIebJrs2KaMn7/u9/i97/7NbQ3EDOoEEgVTQRdBJkTam+YcgGnBORkjtnBcPVm303MABTdHbDWOqZpAsPer7WGzkC5XJASj41YfBNTEeRShpFPxFAHnInYQFpmgOxeKR0XBQGZIQRI71BRpJRts0kEOGjNvG+otv5ssTDb9ZUUTTqICHNK5vAkRtUOiDt/KUGV9k3OrgiCOZzq12PXAUr28/Bmze+KTcAXqRKAvhs1ZSA2cgJIwtAKugoY5GNBrm+hdx3Jv2ffVXQVAAlECoiAkADqUCE3BR1MyY16NzAGB4OpRyNrhoJI0Xv3sVfY0iEQso01xDYTTui9AvAxiY1GFN3nkwD0LuZUchproYtAVMAMZDeC4o7z7uTtOgQwEicfP0Dc9Tb9MZ06uqFEGaIdXSqYs9/fHath7BU6vm+bDLAneET36+fMfkeCqHjEQpa48PcU36B3PzqMsI1pBB2h1qbjgvDxOPk6IN43ffENgzxxAUIivx+ALrrrvY/5si1IzGBOIFiwFTZwOGcIsH+3T2NeXHOSr0t7Fx16Q6B9HGH3H84BDfwORGn8zsbVgowYc7svH5wjwsNGeHCAUugtHXXV7MH7z4c+PtiPIbG2AOnN7TiPe8d8PzzLIeCI+TQTs39WoCNof3AztY97RKCh7iRxzMThXg/JgHG/Bw/J9IDSGPvkjoCIgsBjz1E6+KtkFigroa8Vb28vWL9+QVvuuF2vKM9PuHz8BJQMEVsDjFgH7rzUBVju6K9vkPsGkW765zaKOXlwFyNA49FVxextrGtfM8OxjH3aH5b8/Y5A5dDR3j0QsPeeUgbNM/DhCeV2BV9uECYICTJPUITzvntEBuQCXZrZkrWj/cUr2g9/Aa0rSLrtY/G8wNij4hniv7G2Yk2ykjuDCmkd0/WCy+fvMH3/PbbLBUoJCY+6PrTzoHvhm8q7zxz3uRFgqdkGOQRgR6UJOxoBaWv94fvw74/3PTrM4cM86CohUfb9wvZSpgQlBoUTr3oIygh8XNu+X8Y7swJgggBuH9jH1e1JvOMIRN7bCxqOeujd8fcxZrb/PSZw3tucPcAGpAtSSuYbjHEHoDLWlvkNtj/EXI09WneQ53gf6WLjm8xmiHSklA+2zceS2Hwlt02iCoH5Tzz2RhrPRw4gKGzextgg7EvY+107WrPk/wiKEAFXetA1UxPyMXSwy90v5gRO5rMwMbrfN/YRzgm1dfTWfT/NPxkTGmtLxnXMZPCYw9Bhxg6gBIClrgO9d/BhDh7sK/gn92VmpFRs/bY+fIXjerGxJHM1XR/jHsdgWFVdXwgpFTAnH+O22zjfO80vY1DKDjSFDbegvbtfW0ox3YD5p4mTB9C2HhK5T6gApwTOdt9Me0IoHfbDlBgpMy6XK5gSUsq4Pd1wu82YC2OrHZSASyLMOSEzcJuBp6ugbQ0qGUj7/pALownwugh+90PH/a64rwte64avrxuW5Q293XH/+pdo2wKo+YcigpTZ1gITRPoguzRpqK2idwWILZ5S8/unaUIu/LDGRQSkii4drXcHNIAuG9atQtT36d6QWAEIem/oXYYeMe3rRFWRcwITo5TJ5pEYRAnTdEGZZxAInArKNIGI0YV9XgS9VfTe3IwI6raitg29bah1M7+FzI6Eb5gTY5pne363K2UqeLo9o9aObanIuSClPQbovZvv3BsEgCghZ9O/2hSCAHRoADwKRe/Nbq9qvp0qIOaPtd7Q+gawovUN/+If/Rl+8z/9j9DXfwXtq9kd98mOa6xLR8r54DfZPVNOaK0Nmzp8b/e/p1LGXhEA1HFfIhBU3s01AEqK51894/nDZ0AVVVYQCmqryMzIuWC6ZUyXyf3SDkDBuQAg5JQxTxPm+QJAcF82rFVwu11xu1yh3az5uqyQ3jGVgqfbzWOajlo33O+vUBVcr0+Y5xmXywVEQGsb3t5e0VtDrRU5ZzzfnjBPEzjziI9EBNu2AQrUdcNWNzCbzSEmlGnGNM2YpjJszVQm0/Xe0bvY2HaLwRXmp3QJjICwbc1j5gQioNY2/NGUkwF9RLYnu0/OHvOH/d/3T0JKtrhqbbjMVxROho+IopQyYoMEQD2WjPlXEfTW0EXMzsPXNwi9dQcdBet6R+sdKaVhF5gTSslj7lJKyO7LMDMul9kB7TTsNrP9iTimdzGcQ+33tTas62r4RW8AFL1tHlsoWrf5Ifb9KBlukRP79WOfMjtq+5p6rKrIqYBSQWt2D+lAl9XsRW1Y7gtEBLlkTOWC1iuYASFGaw21biickXMasU9OGdfrFQHo55TA4OHj1WoxeVWFdEHdKu6b3UdqQ5kLso8Rs/k2mXXonRL7viVIPs4iNo8igupx07Zttre5DTK/mqA+X5f5inmewSlBdI9TBYreml2rNYgqalegG/aBwM1gwHliwlQKUkpIiSHS3vm4BKWEbduGnoXOpJQBFTABta7oBIAqEgTSGVIrVCpaT2CpeNvuWGrFTBNaXff4RBScGIV9HZInX5ogIYE4IfCVlDJADbXBfTaxtZETKBVsdYNKxzxfkLlAuuFxnAu22tG7raM//9//j3+Ob8gvDdL+BsC/ffj3v+U/G6Kqfw/A3wOAcs1qTq9v0EwgtT8QC4jgDuOUEkg8cFEAYg5N14BazGHjkrBud3z58hf4/k8/g0oykILMEAubsbRLPAYq5lApenfnuXcP0GIDts0vjEZhRmdGrdUcAgV67fj09BH/7t/695EYKFNCnidM8xXLtuEf/m//C75++QGX6xPW1QCdMtkzJU4o8xVEbAuGFIw9SfAnf+N7cAK+fv0BxEC+ZFscUDRRZGZcEpA5IecM9Wu23kbWUMUMDghoXZB9g33K2cFXoIvgwgZ2pnmya2wVIEJmB7e6oJSCpgKWgA8VJN2CAQfocs7IpRh41ToU5mAaeCQA7X/PKSElAGqOcHLn2javjjwlD0gbppyhCmQywC7ZBLvxSGOeBA7GiLk17KBsa20ENsbk8uwK/HvuUBOZc0VMkB4OtwU8XQIkdaAqpYPj7HrmqiMI59EMZ4cFriAa2bfI+oTzFcm1LgpQMhiOLPBNRCAkB2d1xG3HJELMpwVfjJzZjd6ewQ6gRdxBj+ACwAAYzYUKI2sAL9OeXZZxfx2bhIoC7pwxHzKfgY7BsvocQZa/W6zFABQjwxiAYUoZnPJw8rX7BuAOaeBJFnA72I40rs3ACMDVwWHyOTDHgSCtDeOsEL9OABA8AiVzfmg4DPDnBvt7um0LgHhk5MWcnUAFujR3dt2JChxELXCakjkKO+xs8xwPEs8PegxYIxkQP+ue0LBMIh6Adz2AreLJkABmEkUQysMGWtBt34nr221l2PIItNTXTMyL6Y19z+y5g6NCw97ZxhloKvZAt/exbgcA4shXsFwoQB1fa/FsgymlBipFYk3E5ydACOaRXEge6EUQIqqe4AKY83Ci+QjSgsxRDdCM94wsxP99AA7G3JM/Q4ArBHdyPEKlmGsBmJGgwNbQlwXb6yuWZcHT0zPK7QmX5yekkqGJxxwPAFwV6A1aK7BVoHV/Z3OgAigAAKHk7BIFuzOvImAAJWcDNQFnmMZjko9TdtBH3AbYvB/32wCGEicY/qeY5yv0coVcbsDtAuEMMCGRTZzNr9tsph0gI0InoNWG/vqG/vVHUK9gB79rrZjnCaIBvuQxt2NdMFv2W91OOGsmEaNLx/V6xeVX34E/fYKUYjYn8OVhF97ZOxxt0p7oPX72kcHwvnLowI5xu3Jkz7TaHETePxtsPdHYx3zuAtDEe8DzCJAdGAMOwATeMQBPqAeB8eo7qEW+R2k39p0qEFazRzI07M4R1Du8s43B+2dypiDbGHQREAL8jTsM1MBsTgAPsHfP6RtAHxGCJULgw15ka0wP70WeyFdRZ8uYncg5uW3z5/F90GbKwNZjQnW8l881ZE9oHplbVn3ENrcjActjvw87d5yD7AnxANQPW+6DrtOwbXIAbXEYH7MFFP4VePgq6hmjCJxVH5Nh4jYiWFg2T2Jj5gGR6p5kjnGx52QgfMNuKGpoxXFszE86JDUP72aVBfqwlmIviLVg1zCQvLVuCVNOzojbEzfxbCIrANvze5fh2wB5EDxUY810kPvbCkCaxRUWd3Rn7iXkVJA4GTjHjJKSJZoOCSRg8bc1kDtlAw8IQE4JvRFyNXC0OSD+urzh9nrFlAuadCARZiY8XS+YS0ZrhA+fM3oDvnxtyGWCiuDl5Y7WgdqBVSqWSlBl1GXF2/2O+7KitQqIoHU1AJiMjCAi2Fa371V8TDDsREkZObmH6/GSiKDXN6xL9XGO5IUFzCJ9pEoEAk6xXSbkPGGa8wAciAi52L2SJzuJMBIWKSXfVBOYM0qZwZwh0lG3zV2bFf1FUGvzSsyGdX1DrXeodveXBXVdB1M5J7+WryfTQbd3fUNvFr+ACK0y1vsrau1QcRDe9dHILMnWGpl/rGD0boCpyK63og7iSeixASDkQJ0BUNl1vtnzkKKw4DIlQN0XZAap2h8HreKKnPZYIgBYHJKxAAYAeyQWDKEdDAzCQshgePseDrFEl8JICK138889QcMMXG8zUrE5FZitSmyAFjNjKgUlZ7StQj3eer7dME0FvTWsy4reGxiEp+sNHz88gwF8fX1FrRuWZcE0FTw93XC5XNF7w7K8YV0WrNsCQHG9XPHhwwfM84wpF0jrWLYF22Ygvoqx+17f7sgl43a94jpfcLvdQExo0h1o3MlQLy+vkNZRazWweKtg7ESGlM3G5mlGSoTr5TrsU/g1ROSxdUIpBbW3kXDurUFax9o3gPeEWsSOrRkYJlAULk4iMVs4l4JymUEA5lzQut2rTA4tUVQ7JVt7I3ZNwGSYS04Jf+NPfoWu4u/Yhh6s64bWKrqYbxrrUKTj7e3VYvXeR1LKgD0joRGREcvE1lBrFrPdblfUbUPOT8iZ0b2aKuLrWus+1q2hwnzR1jbzdbsADtqSRtIvITGQuZhPwWaHLSlmdjxfb/j46RO2dfW1kyDa0doK5ox12wBVtM3u3XWPt758+Yp5nsxO+f1KzpbMY0LOBdl1gp8Z1QlevTVsvY61pYqhi9vaoDBf7IF0BSDnguv1ipzTwCput9vYO3vtWJa7YVscCeSO19dXtNbA2TAmDvKQP3eeL8PGkhp+VVvDtm1YazWSYEpYuiVYoIoyTbafuS/PTMglj/3e1goAEkAJtZo9mwhYPFZn8uvcGNIq1q6g3nHhz+iiSAL0auPUmunw8nZHrw0i1WIbAKwMUfMCOUVs2AA0NDE7bAAvsHVBdtym9Q6qG3jO2Ho3u71uVnGXGDL85p/KLw3S/hmA/4CI/h0YOPtfAviv/6ovjEC5dxCAaZoBAB0d13k2IFUxGKsCKzVMzA7gOlVeBDwlB3AFW1+RSjIGThdMI7NrmVlKjA8fPmCaJry8vOD19dVLefpDxp2IAbHS/ZAIeokNuQ+D23tHSgW/+vQrMAhf3r64QRRsrYG2BdP6is8fnvHhWvD73/8WP7S/gPSGMlvJD0fJRLDDHGjpvaNMBd/9yd9Emibct1f0ZEzXDrEsGYBGPl4pGWhKjEpmdIZTJONFhkPRnUlZW0NvigRTeiUP9HIylmeybA1Y0FRQpaOQOb9NDWjt4oAwAcqErW8WANDuxAo56EYJJB4kec+CARLCALOhK0yDERqxXOLk8ZVCmcCDbgZoM0df0B38Ur+FgEn93SygJTUDAGUPKgOQAigdgDgHZJHMyTYd9AAE49YPgXeUQBH5OzhNPIKGwGCOgTkzIxHQ22NQESGZPxq6Yg902J0mUSDtZVlgY+OJLTjLRMKZzgIoHd5NFaMQzmJHA7qTl94QQEgO0O3sPgPEnL3iztcBIfRg0p6JyRItAaYj3h1HEA8j60rBhjYf0Z07Y3gZQOTMXVX/DINYBp4Yc0Kuj0pmEwAaTiZAYI7geWccMTszRHfmwmD6qHOtBgDrNzowS+HvQxrMQlvXfGCcqlj2VGl3dAMMVJHhoAx2TwA0ujvBoFg3j5uB+BwlTgOEJTImLyUegGwAC6G7PnHmRHsyYQcPPRB3J5F8TViwEcCQgsmeZx9/B08GBBQMX/seHBwbJeXj3Q7gPQcIcgjMXS9Vgq14ALQOdxvAE0xJR+VErCHtzmhjtxNRokZDF1hDkSKpAwddeQBROOh+AOhMCQRj/0eSzNa8VRBY0LID3juAw7aeBshmewOnZMyhuoFaRRLF5XLFdH1CuT1hut7884rmgE2Amdo6dFshb3dgXaGtH96RoD10zkBiNZ9rH1dKMJUgjFK9B32HO24YwGeMnyoNFsVIJLlOlJSBzNBpAuYJPF2gnGEJKtMk0yE+lIeZ7ciJIdpQlNDWhvp2R+kerCUGxBM/PkWjzFR3gGs4mv5uIoLCsEBYjbGTrlfk2xNovkJSgcquowPJdHAg1lZI+Dph50IeWQTjtfb1Lt8oxYp1EsCQy6gyibka+hlALxx4ewRJCWFLaNdZ9nXvijcAyrif62QkotQ3iPHrd3ZrBPvxDnR8K3uXFIkLn4tgY6r4WvAAMJIxoWNjXGJXOPwsnPwjME2HiYnnpliU9q3xbPGsARoLaFReWHWV+VDkdkQtA4RgxthzGjtHPXG4P4cDriQPemiJtIRgk4beHxlpR1t/VCELcvfkY9wnyofDhgOMURmlzpryn49qCr+W4FihgMGc2ZlNu148JBT836rd9xcDhWvdYInjACzCv973xTyxV1p1ZAe9Y74jkZCSWYZg44XOSjM9Owam4cO11qzCigwM6F1AnHz+47llLGlL6Id9BFqzpJXtUdmfN+6jUE/ekwbATM6KtDJn8n2PYf6o2UvTrEg8WaJjX5sAgZLZPUp7MjrGQaBGUpAOUWBbCVNmzCU7a5RGgjtPGevW8f/81oDGrRMEDTkzyjyjLh3r2lA7Y92qgzzN93iAyME0tusBHRwJbvXEBPvO73uWqKDVbgkWBAvO2IuiApFHZiYTI6eEeZ4h6uxECWY5MOWC6+UJZb4g5wnVE1WxIiy5jJEgBYzN23tDl451vVtbum1DqxtqXRBJ2N5j7pM/awOTAcRBTpiuGQHEAgLSzXTOXhmq4iCr6WcuBSVlJAZ6r1BpADFKSSA2X0pUgU5QYh+Pji4EQDzJX5wpbG+UPfax5DyDFJin2UvpCTJIIQ7EJgBCSK5rRABnBgkA6cMfU1VPYj8mycJWBOGgexWkO6IGGilG/EbDF9x9M1FjflvLjF2HFYqUCwiMrh3GuItYErjeJkyTva+qAZcl5zEWZZrAydh3dW24XCdc5wtSnrGuC5blDgbjMk14fnpCyQnrsmC5v4HY7MTHj88ekwHrekfdNgN1GXh+ehp4AQCs64ovX75Aese6rGi9IeeMy+WCUgqenp8xXy7OkrW9bKsV21JR69sYy1abAbcwwHGeZ1zmCy7zPHynnNLYfznvcQ4AZ2HzsBmGhSi2uu3JimS+f3dWZvgI3ZmtgGDdNmPrVgG6xfYEQtsqvvz+92AQSi6Gn7TqY2ZAPrltCYMpusdLcD9imjKePzxjnicA09hLPn3ikfBSUbRabS8JHEBhDHxnMIMItVWw71n3ZQFn8+/qVs3GeZCYEhtwl9Ig1jGzAezOnFdYQXXE7+IgnCab421dDVDdKho6XuubkzPaqHZObHtnysWqlFMCutlHwABRIsanj5+wbSsglvBoYlWO0r3SVQW1VazLCs47psScMM8TSi6Ynd2rzFChEXteLxcHsxNuV6BVY4vXbnhX7FdmcyteX++43xeoCp6fn3xPtL2zZEt2fPr0aeybyZNJy7Lg7X7f56t3SK8WryarUsg5gZP5cqRASQn5esHz8xOi/F96s8TJVqG6s8MHqaWafzHP89DXXMw+TFNU1DeUbmxigrPHxZJUJSkggstU3I/PaK0PooqI4LvvDF/6+uUHIzK2bthZB3LJIFZnZZttNj0xHz/HWnB8LqUETkaIVGKszYk7ZD7MiFe+Ib8oSKuqjYj+GwD/A4wd/9+p6p//7BeIUG7PXm1NGL6nhzHKlhlh/0X30pkwBmQpAvueKBoZAMSSoMVKjzJlVBU0dwKMUdagQrj9yW0o4v1uWYOjQ6agUZIdjn9kFBXAvVas62pBM9lGrACulxlKwGu7W7akN6hUTKngac74/vu/id/+7ndGQ082RcSCnC2Dr8624sQGNGJn+BAX3J4/4+3HBd2L0JqDRUwGQDXtyMoQCJQY83RBc4C6wEpYibzPnwN50pplhMCYygztAlZzJ3vrSIBlRtwZhpfZ5MTIRGitI3nsEsBjThklF9S6+mjapgEPmIw5IiMcYpCVBkE9641RRkmcBshoro+hh4JujE2otbxgApK9OxefnBkAACAASURBVIllBLuzQYmAHoEdJ3MO/ZpDx4Zj7BliYAQ6g/HtDybuhGL81xwSCTBOgVIyVLtvPBGwvAsUUwCAzZkhOnTOnjXYNBIhqLNXD0Dv4XqDCUw0/j6Y4g4sWfAlniGz599L6JxF6EHVeMUIYMLeBMg11ov9CXYkgu3qwZUOUMH8Sj1817Kc+vC8AfTaBuaZNgflNAAbCrYODWM5AC0NVrwgp+xltjLGZg+GDbTVASjtLMcYhyhbTA6yUIAZ6ixB7PNqPquDwQMw2ZMuCXu5nzFqPMvpZUJEFgQPKPMAXoxYPDCmQ3QeDvYDmwjxSJEosLHJATA6OCADKCSodrNDqg6KP5ZXA+/bDzwGw8l7rBCloRSh99GiIhhaERiRHOwr8KBTEfRE0LADCLrPn+4tCB4BmEfm2PG743ndMVfHdtgDX/IAs4lv3nE/Zgc94GW6NvrsAAJzcnaD6z0FAyx7kinmYg+CwuaNcQqEQMkdEH9vf6fWGpb7K2jdQL0hAxawlgkpWzmnMbkE2iwB2sSy+ForaFuRageJ2cSxntQDUQ/uLDHKDiSwBy1ePaCPzLZ49iMAdQTRYsjHd9ympJRgrYsYdL1CbgaEYp4hicDwVhAk5iRxAIe+NrxMDZuiv23gtw1pWcEHJtxI7vmaSB7ACmTstyq7PTI9tiTWRua45ymDnm/A5QKUCeK/B1u5KB9arIQzGgHUu2X7UDKfc/ZSQTwCcOr7HDnL3f8vbM0OvNK45liHGjbdgxNndULh+75bV2c0iQq070D6XgEgD8E2Qhdp529GJcX7VivxTKO/fyS/iQ7r+oAuHt6HfX0lNjgr9Ch0z/QodGtn/6taSZy1ndEYRkQLJnpnP3hUQ8S78jf1dYfVaczRMVnkg+5jqYASSiluS/d1Hu0FgkF+TLbRuzXFzi63u9o+AWYvYw4w/DB+wOiL2J2REs+0JxF3O2lglDGrjrbxOH8U+6GXX4afVHKCgc62tkLzI2lGRJ7ctrEYJdpuK4PNFWug9YbMCdFzMthmTEDD0YbIWFv2g3fAbTy3z/t73ygAASfOjPdmZ6aSxnhgMDQD0IjnNnuz6/vx3IsApM2vNaCSgx2ZCDklZD703extgOBQS6iV5FVtiQLhtOS+eBlqN+XMw88DAAZ7j1gGQXvD8vYC6h2UC+brzcayNSyL4lIy7q8CTgoiYx2W7K3JpmQVindCIkHXDczAfJlBJeG+CLQnMJ4xFca2vaGubfcxQBAldHWbi33vtfVoum7gTbLx6h3jfA+O/VccnJjBXCAeHxAUmQnzNIN9r7tOsT8ZU8pAp4bo1tNaQ6sbpK/o0qwMfQXWulr8c4i5crFxz2yaD4QP38GsBoR7Bcm+5x11kJ2VHWvI6Qnd2LlWAWBM8mVtrluCRIRtq56cImQmEBVQ8oQtAKSCUiaknIZPrwRnTQL3toIldhl7D2sZUaEkIFlRu5V7i69FEttXUyTtmUalVrBpVU2PydfT2Hdoj4+i5YVCH/yC8MvN3toe20QQLZCsmoh2MA0YAJ0x6dSZm4IA1pLbE/OT7F7L2x33t1c83T5gygVEivvbK5btjufbDU+XJxQnK729vmJdF5Sp4Ha9IOfsa2PDtq0Q6cg5WeXMZUa0DNi2imW5436/4/52R+aETx8/ouTs4J+xIbduzNR127C+rajr5nvUzvrmZOzfj7ePzsYuwxb33k0XcwZkT4r1Wkf7jLA9AcwCFl+UkkcPf4IToZhQnIEfc1FrNbZmTnj+8MHik6YgAZpa/JFTwttyR6/mA3XfQ1Ni3JdX3O93e7YuiIqprXVn9NueH3vCj19+xDxPbj8D0Mvj3+x2P2eP38n20KMYOUTHvrPVDVvbALE2G70JlnVxvEMwtxnSDLxEIhz39vkyG4ju9iklA9M5GQniUiakz58NAG4VqoJ1q8ay78b4tfYJC9Z1BYjRpBuY3Tvm6QpmS8al7C1uEmHKxdsQWLJpSmXEBbHerMWB4u3tjtYbSIBtXVHV2oGKx4istke/+RimlOxebODwNF8cI2OI9lEVt64borcy3H4sy4JlXW1NXC6ekPD9kUxXpzJ5ZbQOPVW1VgmxT9bNsLale/9yUpR5wnyxKnHpZj/necbtdosMJbZ1xX1ZnO3aAOaBx7XWsDXbF5iy7aMlo7AAKdteW9yP7ors1ToJBFZ7nlQSUsmm592SQJnsrKhts32gpALt1lam9w1lWfB2X8zuq7ULValgJqSc0bzqfp5DjxLaWiFtsXkAgaiDpOPn5BfvSauqfx/A3//rfJZyBn/48ODIBztpPlDyuxhjKx0dLyJ3Xox6boG+GXGpgsqCVBicGSzm7PUuuK933Lc7Ukr4/e9NCUuZME0zehekkpFzQasVvXVbdKVYv0jde6jV2rD4xGYizLeL9RfijKkkTJeMr28v+OHHv7BAPiVIa/jNb/4lfv3r/9sy1GiY5osdBsaK1qoHkRagi78njaDd3uNSJny6fsYPrz+AtYESYxMFsZWPs4MjrJaxUGD0WByoiXmkdr8R8BlgGs/Q+8HB9WcgmxRYKwbrO6oiyMw+PgZKBCtDWkVJBuJGYE3OJiQ6AoBeBsYRdO2l2tavMRxucxg6wkmW0UfUkOR9w4Jn8427IDsjTWQE+uYsBRjsDpeIs93US/vtmVTU2clRsmYB5wPjgXYgemSU4SU9NOJcBPs2AkHx30X5gKpl1oj2dh32P2mMV4AcAfJYFsoDQmfE2fVpgG2AU/ZVvS+aBSbGJBSAd6ez9Tr6eEUpkr3Dnsml8SAxXTT0Vz1A0e6MgjhEzxmi0RbA9POn7NNgKWX2iUVC61FOaxsMU2xAdu8I31ScTcRWaiDkzrJ6r1w5lCuqA9sH4CPK32FqsffEg9sa2h1zD0PGs4fDAY4+bz5G6iBzsjYdI+gKBVRbExjXhQfY9v5xfwvsZTDi9EHXQuMsSQJgBD/BMjIV9AMjFO58OyD6EPAmtw2eoKBdh6wnloOVB8ecvSpi79PN4HEABO3zih2QIWC0H0geoLoSeIGz+trFuB80SmN9jCgYmns/WgpwiwIWhdufHfA8as1oyaA62iAwk/WIZd6BzPG9MDM0gmgiRsnWa2lbNxsXf2brP7j3+w39iWAL2AESY3exJQUekiseJHWBbhX1voC6gEtBnhJKSZhKtjkhRZQyQwFqAhYrvey1At2Sb1AZNivWXoAxQCRQzZ6Yk8RezrsD7QHSsM/52KPVM9yudWPex3izs9gA4QSeL+DbE3qZgJQsUPW1TZRGiyKBWAMWUkA6uhL6tqEvC9rrK6hbKTwFwzwxZKsok/WCjHdLXlUw5l91MOFDFyACLhn5wwfk54/A5Qrxvl6m454oqP1gE/Ggi+HsRll4bAS2R/b9c0eQCQ6OAsP2YoBC9KDnsUdLaztChbALxk6yLcQTJ2bQdpYumR5E/3ZwzJkF0In3EnJOtlcQG0g3FoLKYJrtYFnotwygJqpXhoxnxdCp7n6fgdhl/NwfdMxNDBk5az8SA+bWRHsSgjHHzM6OBI+vfPF9gJHGXMUc2OFBh9Xuc7eX4NHeb9ztU7Kh8GDY7bO6H0DJQQv7UvLxYWdLiZcUW0uV5P2pbQ+IzwTpdPSNVmPyhN2UYZuBAIPj7w8ANdOwqXR4/mivcHip8er7383Wt9Yh0h6uO2wGPI97AFzMd9KHz9ucqa9p0wdOjN6sTzakW+8591lGL3wwos9K9CmMVkXBxhqpBC+j775mE7KPifXzbM3PxSADYogIXbH3eg4/mQXMk31P9v6nMsBTT0DE3kUM0j4CXXZ172HHRCB9QxAnoo9xvCPUAnz4WGY2f4wTYcrZ9EgtlkquH+wgYc7J+l/OM+bLBbenGbdi3nBisr1iAqYMlAykBPQObB3oPUN6R8pX6NMFIOC+Nrz5gchNK3jKAAq0J3SKhEJUIQZb0hJNmRgp71UECgWrM8uhwBRmiWxeWZHQMJUJKc9IeTIijoOtvXe83d8AGIjRpdr9xHrItlaHzRGxsuYuHaQGthBj2DHAAUKm6BhlwEXbRq/XABNTCsDZfXr1XqIee+Lg50rb/XuNde7+ec7FgAHQvj6ZrR0LIqnmfp+67wVr1yJ9g3QAnIyJ7P1+rerUQWSCt7ozAJzIfBj2aEVLgr6aHykqSDmBUgJ7b+6dwCEjCT5AwbCReiA7+LymnBCHdR39sfhM74Kt14dY1FjtVsW6riumy+Q9Nt3nISuLf3q6WbUkAsQ3f1EJaNVacHz3+TvM88XK2JcVU5nw/efvME0TSIHl9dXaEgD4+HxDKQaQ1XXF/X438D4lPD8/YZ6N2dpaw/1+x7KsqNXAuev1hj/9038Dt8sNObFf0xip67pYcgeC3hWtNkyp4DJncE64zAYOGqCWEPDNtm1YnLkZfn6rDQwYFtGNLd7ao59hbeEYJWdE7/x9Dk3fgk0Lj+3LVOzfbtODPFHyZHFt3gkR02TsSAIPG84EfP78EdGawloIGNtVFNhaQ+sVrdr6EW9ZqEqom7VI2VYnxNFejQMYg/VyvRpTOrHFMR7b2s+coZoSpvKELpc97iEa63EnRLDNXatG0FNgWVfUzXoL60FPkzNtFdZXlplHDJxLxjwbY7v7OujdDlDsrY9zWYwlbW0HxPv1bm+vqN5uLiVrFZCyMeOTV26WyRi3OScU723/+eOnse+Kdu95q6jeNiCxscf3CmNFLgWcvYVO8t7yYJRk+yxxxmWeUGZjNC/3N2fKMuq2oUqHdtP5aD+zJ7QNHLV9yshI1o4hgah4IovN/xId66W3jnXZjHxEAQqvKHNBmQpysraYT06yEsVIhIUNWutm81oX62s7TVCVUWWTutg6L+Txrel418BsbM+2RJAl/JQJPE24TLYBGcHMfIeMK+hywfSho2RG3QTSKqR3NK3YlgUMPxeJGduyIsH81YtaXBm6ZQTMb8sf3cFhD0KEPmcvkbBNPbsj0xF9PRkZVvYMD7pBpsApWca3i5UbcfTTLBn37Q5i65tnFHbB6qU1CkGWhC9fvqB3wdPTzRmPM9ZazTBQQevNyl8TO5tPHXyygO4yW2uGefL+Hilhnq6obUPrgqfLB/z4ww8QdWPEhPv9jsj8GZvN2K4qCkZC1/3QhzAwxBbottYxFQswn+YnbOuGpX61DTnZBtxbtxOnneEXmygOmV9b8F6G4sAqEIzEHSQLkGIH3QLI8Q0aEV9F6XGAMwCwZwyjpDRYLuKlLxQg4yF4PQagQbOHBzjR3yw5o1VE7TAZygdw7gikRFmZO9IeRJr+SLiDiDJAc95hmSeoL+5DIMwB0slwuOO5iAkQB3w8IBJVsO6AxQC7BxgUMY89k2XR+ggAKTyUiE0D6/L7BjBnzpD9LpypYMMFAzGc4QgWKcDBCHzVJsRKz9l6pvpDinZneuwAcADuo02B95czIIv38QjkD8DoHWuRhI9FdP2Lk1H3wD5Ycjs4H+xe+3oMC0AI0kl3BouG5xubk9U2jnIp9nckd5KPWEMAeYkj+78DsHbvCMTiWWO9hFlzBzTmWncHhNgcypztkL6Y4/2QlT4yokdR1Z19E/0nwz4QBpgT99/BIZvTAAfUxzw2omjoHgBVMAYi4OcA7wLAc1vgS9zXdBpsIl+sERoD2AEZY2dY6PzAuqTQJ4wb0bjXDijY6zjTQ/c1FOOzXx9jzfLI7OGn8g4cCvAQwEj0PNiTGFfZP+c/HpuxiGDdVrcXcPA7kk/RT9f0MuYo+i7FgSMAvO0NDQZ+AAqj9UVvwFahzfpOTfOMpw835PkKsGWrUyJUUesjFgBe75C6mX3qfdjgGIgx3/5iI2Ylq0qIeR1zGn8Oa0T3SfGhVyecho7Zrwdrx21ZSl45kydgnl27wxBGcOzr1/tWRt9Yac0SknUF9Q2J7K4BpBFZnytpHSnTIYFiNsYOS9j18niYaCIClYJyuyFfb0DKo/wbokMXY5weVWzsTB58RRL0p7po8Yoe1vhBaQl4WDOHa4fejt/Lvpfawaq7Dlvv4Q5pYj3FsINKUaYookDeWbmiguiIM4Bsf6cjG3wH3ejh+R7AaqJ3a4cO6ravs5QTWP0wGxxBX9sjY92oBoPWnseHcmxrHt+Mz8Qas0SEtywK9T+M7Rh0AMZ+hfsNOp4jxsxu5Gxbvy6nGI+DjRq+wQ7WhDmwQ23Y/5CX+Vprhxi7Vqtfax+PcYDLYawt4UOHdRb9Xw/7RNhz8kR1bILAWG/H99XDGKvbkt76uF4ExmnojIK67mxCIvRmvVqrA6khpUwoaa9c6SKob+vDe7S6QtTA6Kk4oSJlMGd0sZ6yx7WnAjuTwdl/4eOFbx17lUj3d+ronYA47I2MHDBdkpenRgm2V74A0L0TF6S34QsM1iEXtz0G0KYDgxZk5fcGdO1tD+w5OkBRXWO98aKKC6pI2fvBw8AAs0NeDjr0BVYtRgQ7EFbx+rogPU24TBlNBNl73kOAunRsXl7fesa2AOu2QgSYLsbcXLYFRF7q3hq2utq8tIglMN5fVZyFvCegVIHhqBI7GGSgkLIfmiuAdvO9pTUsywrmu/sMBJUNdVtHFV6tBnB3dDvIUAOYP1Skua+USMf6N6JBsLbtADI7Yy5Y3Gm8UCSgc45Da8yvHmQQNzq+Uzt2aZVxEaembMBF9tYTgGIq5cA4dRb+ANbsZ71t6O5Pt7YMH8eYZjR6HxtT1tq9KXmcygmdgL3tlD3vNM3I8wWVrNUBexsNdYD2SAaIff59j3QQQZ3RDT6QrNyXGWcViDig5XuH+Jj6Uk0OIIHUyVh7JUBOZkedtm4+RHqXhKcdzJmvF6SUUVtFbXatp+sN18lKwd/ub2jbisSMp6crcs7GHlyWUfr/8eMHTF5i3XvH169fcb/frVI0JdxuN9xuBu5O2Xq13pfFWYBvaH5YVZA0yjTj83efcZ0vYNgZOtKtxcG6rTY2vWNbN9TW/WBLBh3ORUlsSbSS7RCv6YO1tOCUBtM0WIzm8yYjmdXmDOGKbfRclr1CQDuIgW2tQ99abUg5I7FVDViS1HuP+uHeOfxLtjJ7u0e3FgLup8/zBdWrrjJHLLpjAgH4R2/YmM/RCosJ67ai1TYOxYrS/8HK9jUpIs4a9Z6u/nk79M32tcv1Zvuf7OXurQnWZUVUDtrZN83Ym6xYF6suvt/7qFJKnLzy0Sqnx/kdbO26Yj0LzGYnMgB/qys2PwDM1pGftdMWKAjrumHZlnAhUDJ5H9zibGPDoebLBOmwNjBi/u8VT4aVeNy4bRtUFMuy4H6/my6LYkoMsLV3YFFM1wvKNCGRsUILJcy5QBNDesW2hV6YnxEM121b0furz5O34NHdz7tcLpgmY5+XqQx/TNUYvNnPsljXFct9xcvLi+t2Gofbcc6IA+5TSijThFkvvl7E2mL07jCUomtD3TYsb292eB7ZgXzJbQcxg0RQcjLfn4FONHyH7Ezk6mf2WPuShDQVZJrNK2MBw9rvNHSkacJUMt6WxRi8lKHND4pPljhore690H9G/qhBWgIwyR60EFkfVZAfBkLRa8rgtOhjk9IB2NGO6FHHnNFhjsHb2x3SBfM0u1FquFyN1mybCVkZCQOv9zdnANnkdA1Kv7EAe4/TOR3I8/9eL/MOqIigbRvqVrEsK7oAJV9s0fhz35cNtQsU1RwIBd7ud7y9vqJME66XK56entyQsRslL4d05mHt1uOjlIKPzx+x/bhAYdR4srVvjh2TnWIIWOZJ8bC5mZNnjoo5jQ48vAu2wuE0xxHmjGEvw0SAlF52Qw/B05ElBmcH7MGYsSbsMgyGdC93P4y/OaCuL4rhIDGnsVEE4yAWwjFQjH8PvXG/arBjjwHTCAT34P14DSAOM0vjeeLzxoZiNAgomG9kDGYrVbZgtHoZS5TS2sYRumUBYbAPzNnx8lB5fCcLkHfHKQCP0dNP1VkBAXzH901JyJ/pCBSpB+kROQarXaJ0jw9jRt47Cjv7fbRTcNAgTpGMYJ4AO00zxjh6Nqo9i6gcei3tbRzYy7CY9l558B6rx354O3vFQX63MWTEaWdwRXC9B9QyyqL932QbTna9D0D3MPTj5NQRxMrOMgTDmTe7TnnYaxtQKR74B4i+B45xmuhYM+++b+OxryNLhu96e2Q10FjjGAeVjQDV10yiPN4psu4KZy+Tg5URvwdQJH2sQ2tB4Zuw6Dh44vgs8eR0YIuq/znapBjPdAAh4sbjhPPDWgSiFPkAohO5Tsadd30+yrfApDR0N8DExxYPqjaOfHi2R6DssZ2COTH6AG4E8MzjvY/rEsMWAc4GdFYO2MBAlY76dsf68hV9uYNVkMqE69MV6XqDOoCQwKBuvWeTZ/e1bcBWQZsdkJA0ZtsAJua9D+ewqcBgxg7mhjo4d5iHYM0c52Z8h8gOYNIdbOdk9t6YH3F2vO8r0g1QZvZgzsZsZ9358xH5ScCWSLq/voFe7+DawBA07UjJS6A0SpwMMBGvphhMHy/BsmSql3qGTUkZUib0ZL14pfdh0wnex4wfmdzf0rHx70Nwf7RzR3066q70PQH2fh94BBUDpPOWDjmNhAgQ+5qMa8Thjg/PIvSg78dS/wA8Aygc4CUeVOFh/x9JwyOjKvatw54N3zPs935ICPNgXKliBHjvr3Ncg497v9m89wd1RXIOZBUx0L01TKy/SHDZ94INu7cMCj3cbc9+j9DNI+sswKL9M7vN0MP3uhqzJpytaDdx1Kdj0BP7lniwsoO1u15FGWr8PXTr+K47gM4OauLhnkQEZIKCDXhjY/bUFr1li/eF1nHSfeY02njYM/qBWgcbaX6WgHJGznuiMvb05KBMAAa1NjSuIA9yd98ywB6br5zY+vbZ9oWUymixYEBow+ix6WSA8DftPhVKzZh60etVBJqLWUz3l6KdUuxPFg8Y25dTBqfioEfG1fuF1lbx5fUrulTrm+rxjfrZDCyC3rZR3dPZwOiRGJBiwE3EIzkBWkeLnUj0wplnL9MdOU2ACurnj/ju80doN72fUkIphOvM4CJ4uyvud3unj5+zs8YS1o0h3fqwlpLRyoR1Wxxg2ROU1kasgylhzpeHtW/BanpYG+YXihFbmjH97PClhl5XBwSM4W8s/A3qB6/ZmuvgROiteqIvITtLfe/HfPCl3L+OQ1NDx497l/XuTbYnHMpUw/cx3QRGq6uDjQsiCTzpqGA/rHInw8DBUFWvEMLBtoBQe4V2dTyb3NlkZ+yF3+eVfEzj0Cd7SbOlnKLHstr5GTDgSHoFp4wyzdioQ0jc7wH0kIALsDj8n7BRUY4PGMihahVbtW+jUihKlImsIoKYRxUOEaC87xFxKCWBMM8TptnaV3QxIJNgB84F6xQOCiW2g6MVGNWDKecBhOVSMBeLz19fX72fKXBxVjlB8fb2huZt/p6ennC73ZBKxla3cUBSAIDPz9aP9nq9AgDur6/4y68vxnCtDUyEUjI+f/wEVcV8vaDME7bWrDdoqyAhbLXi5evLSK6R+0YpJe9Fe/FSeAOgE9EgpuQU5xfsuioiiMOPp1L8IDrGpUyIqCEqGaJdnOEn+/k7UB1Aafw7ALnW9gPIpDVjDNbVev9u1Wwr02D7x/5NOXTe2yz4Ia05p6FT2dsvBIZiVQVWlaewtVW36r440LsxV61PaMPq5fGWGNjw8vritsUSb8WTVpYMyrhcvBcu2ED2KaOUNGxJVDEYeGrvVn3+WmuGDdU2DmJv7pdF7Br+3zRNSH4gpLFjjWBzndNoYcFke2MA1arR37W7HVe/t+niNJXBks657AmmZH3ES7GEIIhwuV5BorhcZty2a0QWSGzn4TTp2N6sB/f97c3YuaT49PTBfFsGpin601ul+eVygcVuGC1lojIFRLi/vmFZljGPi89LSlGVY6z3aZpGX+fn52cAirc3W2td1A73E3Hi4d7CIfQl+Z528Wtol6G38d8uYmt4ewkXznoG+/XMx9/JlmUuIDjzv1h8gGbkJuI8kqYNAhYFeR/8y+0KUsLlVgCy+LEt1ru9des3PbNhmc3t0rfkjxqkVbXy8WOprm2EZlyCwn0MHgcAI+IlBmGsHOkWCzqlGTsgzzOKCKaekHuy/jt+r9o7Xpa3ERzkXJBKNkZvzta4vFZ37GHB5ugF5MZEFdu6odVqJxNG8J0mECd8eP6E3/7uBWVizNMMEGFZXvDy8gWtvuF+XyAdYHpCul0MLM4F29a8JM6o0k/zBVszsBjSkRPhuWSsfcX68q8gEqfcEdANPKHekXL2YOinAXSMZwC8Nq6HMrEHoMQMjTFHxR1xGkGeBUB7sHQM1Oz3O+AZWTULCixolShD7PumPQ6nCpB2/NlBS4IDYgG0evl6BGGP7zz+5kAwj0W7O42H9/6Gzql6+wTHfsjjXM4ZpNbrU6IU240TeQAqYn3EiC3DJt5TtsODcAen4ZtbtJ1g0MhWW4mWw+TeRy85Zc/0UbzEcB9DiYcJIA08dDcOfErOqNxdTOuPRhG40R645VTcEXSG7ghE7X0jsLegYqf/aoCE/u+xrtlPPaWMUJNjAOp+JiIgjvk3lpHx7iPL2bo3QFcgWnNZ4Ci+YXirDPWkBolfnwagFCePMxnQG/NxBOxML2wczSk4AIlycKQcgE8+KQo9sLn3YDrmHfDDWNIxyN/B3vdAGPn6jBYLR+AeHgQh25gPh9vnKwKMAGejVD2aq6s7dtYLDCOwAHZ2yQAYH8ZlXy/jtHPy9SiHjz6ARztIM1ap6vGyB4BIH+5zBGnfB1wPIPDDdY/PSEMv6d0YRoa1BzMEeyLi/XPs43MMpKzH55itsGl0rBjoD88+EgbM1lfPQSpWRV9WbF++QtYFyfsoX243pGmGkB1OkZnACmjtxgJrzfax2kCt/wQQg6r1gz2AXGO+9+Efz2f2Z2cTvx+z4zV2ZMpHL9aGV2lYz0rx9bv39Q0AxJgzXuZNQFRAlxLdmgAAIABJREFUmMoxEiu0r8C2gtcGWRuoe8KQ9mRGPFMXAetja5X3tl/1yPRJoNsN/PEj+HbzJgs7g1T9ucJBj+sd9eth7EINQA/PFbo+DnwKdGkAqs6SOXzmuN6+9V8mOyzyuHchdD0YzA9rQ4dORAJBfC/dW4FgJCp2sNGAEBprVB+e7SdrL9ThYNOOejMULxw17Emr4zgfx+5bYO04fPHwc4CcTRKVRY/j9mA/96f2/1VEsiDK+vCO6QtVb5VyZELvCQbTd37cBz2hS0zIiPY9ilHY+84/OVb+2C3lMI8xTju4RLTbeoiBqyVbENY90T1swbCBRwDLgyUvp928BJITIamxnsYhSsEMZfMZwoAcnznG4pgcT2lfO1EOelxHyROm5PpADkbtbS4O86TdyB4iiIOHjblkDESFDgAmfHnyIHIQAFSdPWdBYei5iqAnawNlQbYlgqAJzBnMGGdLZD/gq/cGUsWyOIFkuePr61eINmuNQwQ7rDQZUKA02jLkXKDTDEJDSmX4C+w+JABQtQC2+unVwTBTIjukCoQ0ZwfRncwIRhfCsgqkGeP5OhdjkLWKZduA3qx8lBKWZbFS7rbhfl+c7KJ+ULD3lIx1CTVQAUEY8MOaidBaHcBPDxazeHmyilV69I5OAkhFMMCZAZEKaIcfwwYAKMUAJ2RCqxYfRaWedN+rASfeqIHTwCALwO2sDnNkRB2p0XoOIO+Fvu/x+54RTPJh6ykuaYCYoGPzeVHd16pqVMgcEoVwsF7VkrOepDU7LU5cih7n9unWGtSrZrrrsmm7H+ZkHeURAH9KgE7XAfo/2LiD2bN33cG997bVkmzOhD3Y0HGAoL9ftMkqU0E/AJNxLfsBfN5k9DYNPdpjRb+/RIsXcYIRIQ41WpfVQMFpslhb7awZUuByubiOGlN/21bU2nC7XXGZ5mEL17rhvix4e3tDzgkfP37cDzN3Zu1yv6Oum63PkvH8fMNlvmCejT3YWrfetVtDbRvWdbOKJ41Evh2Il7OBVteLXT+7TQ6Cmh5svvgzm13awdMA+KwE3Zj6tVZLQDu4tQOD7HFoj5AMKSVMOY9D2EabMtrJO0OnaF/fdTO8w9ptyOhxaoQas3lba0jMqOvmzyne91i8X/vuq5di1cijqowBprwfhOexEshA33XbxiFo3StMoix+WRe8vr4MrATM2O4L6rqYj6Vq+m/KiJKjR25BKbYuGLCD36Zp11dfDwoDUJdlsfuqtVhZvJ9q3SqWvu0EBDGinaiiTAYWPt2enUDQhw245J2Jq4jKV0tMWh9eA/utXYSt/b4JXt/uY86GHiRr05RytmohWK0qE+EyX/Dx9oytWbLyOs9YW/NqbOB1vePl5SuICLfbzQHXNPyAeZ4B2F4F6pjmCR+entEdzL77wWLGRpdx+BZgDOvr9YrWjOVdyt6TGCA8Pz2PVleiis0BeQXQts3PhxFL5hAN4hZgfuT1egURYWvGJI8EQ+/dWeK2f8aZRwJAKaojvDUdLBE5iD7EjvkQet2G3SYi62HPgfkw5pvpdfbziaLNyDer51z+qEFaYNjewJB8pzTHK4x4tBo4Gg0LWPoARQ3QtI1exFik0gVT2idxu785MGgL9b6u0GUZxjKDMBfLfEdPFIjg6rT5ZVlw39aRyal323TEe26SGnuFWEDokE64Xp5xmW4gamjtjtevf4mXlx+x1RVEUTJww/PTJ+Q8o8sezIkYyDZPV3z68AkKRq0VL19+tHfOE757/h7L+oov9QsksfdIdedxMAc8uD1sjsdghN3J3cGiyDpjbJAJjARncYh9x4y6Lf7xXez3eAhMY5pVYYyHHcg8ghiEHTTa5zmQOwCHADsCAVGysgIVRIMf8cA/GJS7E++nXaofzCHhNBkz6j0L2ILGHbBpkTjwDU+17y0ZHOzrshv1AQQprOwjHB71nopqkKlzHkFszr6qpS8S5VHaFSywLqY3SAAFE9KOwPHMtActuvfU7HF6KwXoahsBOSjCHhhaCZ0hD8FKTRwbOwPkoKIGiOnBooqBwZTGRnxkMAUr+eh0hLaEM2eH90QwF/pg2eThlEr3bJ33xBQY+1cNPMpEgea4g8lW7uXZTGOZ7Jo6mK8+xkP3YT3FokfNg81yB2o46NiNOfTAMjysr7HWBgDCFiiog/4HdsVYiz43EUFEkDDu6YA7yB0YPYCGABR7L2SCNT2Pg2CSt0TZGyq6k4Od3RcgPgZw5tnbUgbD6+jEvQdEx1pytm0AT3R4zsdEDsUAO1Acz77bk6NE6db7A4seAFoJgHn//u74e+uU0DXay7DGszHbKcoedMRpxqOcTx+rDvZnC2AnbK/bISs3GKDTexArvhs6msgCCyGgvt6x/vgVet+stBOM6XpFKpM3z08oLP8vc+/SY8mSnIl95o+IOI+sqnu7Od0khxyRw5EocDAcQhAFCNBKm1lKO/1EAVwL0Gz02EmApIWgAQQMRz3dJPt9+1ZVZp4TD3c3LezhfrJuz7qzUV11qzJPRHiYm5t99tlnIA0MW5HWYt4KwlHBq0zHjRTR6uFgWdOEbLwLsyFL/PxMso6K4bvHtQ8Dk8YA3abvlDVwCVBpHQaiBr0pRkxTBgdjl0ckEq3AxuQyR349BXjbtoP2FcfzJ8T7HaEVYbtCWy616Gj+yNhOzM0BUEsMRta/gUYcCGGZkc4XNGWHiGSA+ETS+5fxUI92bAH4CDbVUpwZM56P8jOjfqixPeXZDaQa9814to57aTznebgfKyyE0ea0k8bPU71vAawACsa07u/ZGFbj5xhAO+5FvTG3lDF5fwDE39w38CiR4AB77d/3EL8MPmj0E5bcjclgYwFqQgiuwz0WR97uZ/tVq7BHw8C2FFCG9bix9nQ929gfX9ZxeD8N6hMA9cf6rjUOYdTBHsYYRYqNo3b2CAT32KuDPz2GlkSyg8U9aWhVEllpZTdw1E5c+ezWGlgH67o/IPiQKxhb3+LAVsEhegxp7EMDxEwmx55hPw7s2/bgu+33GAUk3PcdRzmQp4zTctbnwHCv5M/GDB+GGWDtrfXhucf9E0JAaTtI40P5JeCgsf/tffUiHWDgDgclijBJC6/GJ8yih59IkrVWhcnEHmtCp1KLPQjDk7omcQCsAGIxir9DWOwAZSybvVaJieMkxWdmUKtImZGss4MIpQJ3AEcBblvD9BJQG7AehNoyyhHx8nyAIcOKattRW7eBFCOYMgLELp0dWVV/sNnQtYLGwnxjVh1MsIMbpPtS5A5ED7GRxMhm2+KLJCaztQC0U40ZrUkMqOGKh1/Mw2Rtoi6JpH6AzOH6/mHXvu3ncD+PpfBXB4aYSF2w67PKvugyIM39dufNj6DmY+wk+vVyJxWyBNXIGkHyO64ib8YQSYAUJjQASfcjAFCUAXXFB2OK9EEMEViumOcnvJB1Wtj6DPdlBVItOL3tprFCKzNj21bYYCo7F+xZzPnbZwQHuPszA6Jr6oPwLBZD6wxa6HlLBC5dxooknAIBmJIMFJLBTQ37vmOKGdfzWRmgB263FbUeAq4+PeF0OqEeB15eXrFuK9btjm3f8f3vfx/v3r3zeEaYtRXtkPbl0/mEy+Usw+u0GLHvYuPHUXBfVxylIKQobdMgzNOEy9MVKYpWpjA9oYPKGLtOtG9VNE7BPW6x+Gdcs6pEKRlmJ/Iam/rmwMJ4ZVZd2yjva1mWh+KUvCcForQQB2bviMsqyZFSwjwvIsgTAmZlRIYgIPBxFNF9ti5g624MAdDnqTYksTXVsD1gjN1t23C73ZyNDQijPYaeU8XcQcLxfGOQ2p/8+/XdFV999QH7sXvcIOsorP/jOAQ4Z5kDRKqjXWvB/d5zBHz6KMS9FFUzVdjAJm2U5wmtsdid2r6f01oIBAuJb9937ApoH4cUusCkgGePQVqT7u8QJcadphk5JyADrUacL2cwk66nFLrut/uD7y3bjhJ6DNoaAyFgihGkMhlzmrTTAzifT5iZHcc5P51BgNxvbShVrsGQPHPf7p6TyjkiQ+YmZauez+eHeO58PgMA7nfFzfS9H8eB201iDSnMZhxH0cKoECym08k7ac129n2XDncARTXGS5GCRc4ywC+pzu2SxVZSSqi7ajprPL5uKwxzkn1AuN9uApifFs87iBJA0l0aorBmKQFojGPfkQJQWWQtANF1jiAn44Efu7Lffv3Og7StWgukNyf7IUyDswaZsqgFofKd0rav6ab+AwepnK7bhvl8RVN2XcoZ2y4aRgwBVEupiupLO1SeMk6zALQ5RUXjG7ZtxeeXZ0l6mVG08stNI31oWwKzTj+WezyrJs5Pf/4j7McLjnJHCCIeToFwWi7IcUFOixhhaTCBTWMM1aNgW3dM84J5WoAn4L7eUUpDCDOezl/j9nEVunwwBmPwhJrss2x17UwOomNLbHxkTdobhNHIFTEkZeMoq8MSDQ4KoAWQtj2LuXdH9QA+ELmzlXsxtmU/dGwasgX6TOTMWAnSNFFDZzKB+gTraPqcTSp2hgCmEFRbQVlCyqKBAaMExDRozOrPxRClAq9BOqvthWApgbBMHEnSBGTUZQMLOCgJsHONtTNPE1b0wEcCUk3qYdN7rXXqzbPZZrAXpwCjQXTWfgZYFdQCUfthu270/Yam73QABEFSIY/O4h2AMSio4v+DD6OJCuj25bGJsvp3es+2l8VR2pAs1blTeQhLqFLozEy3M/1+W03fj+oYrT3b5TLwHaAmCZBooIitjml1WeEAgLcTjq3tJk3SbV6fmMhb6/rBZYmstZKxv0sBdd6ALbp/+GGfCnva/sv2C2swbAGsXwsmpQC3jX5Z9mtbG5atSyDSwXLk53K31Z5kOCDkV1CfIS9X/Xv/t16l7J5pHE5B6PIkBFvD6NekIaHooEpzE/eBbMOZMn5ZIWO0HwcZBuZIKUUYIBqQ+P05XV3LKwrWjUmMrE0Hcqx129mrrQ8bERaz+gzxcEN3g07tLhVUiibeCWHKyKcT8vkMJGnLjawgctUikAb4pOwiGyg2rgpXQzoY6LvefeOoO2rgKrj7brM3GzBo2rNunUSw2XkgqHalDguD/Fvg/k6aCU4rcGpdLMRwgCs0SR5LK6Bjx/F6Q9g24bnq+Rc4OjDczD6tyIsOKsPs0XSZgyQZKSdQjojLAp4mFH2EUqv7fQa8pdOfdUyA3oJ/ChK7Lrml7jysOw+2TZAuCvUSDPY2QvcL3agdAHUAz1BC9HjpAeQc/AyYtHWyP4vFC6PMggNdDL8eDdc1JzGe/3Y/xpiAJlfcvwEOaFvc56xp7qBweBPssgI4D5ar/+R6zhZPmQ3Lvxv7wWV2SHYFs2q06l9ZYca09YmkuMWtgWzAjflQwAE3WTe9L9PQRn9H/rLdA9qN698HGd4JshPdzrdHkFVsDIANQWWzQdP/Mway3ZQAYj5UDABxUFmrop+pg6AIoijG0o5p50NUFnE0VtuD/eo7oTIUKFQiKgi727Tn5GEb9l0mdbOe0SZvYEwYA8usPdZeuu0jv66MdhWAyfyx3oO1Sto5Y4tunUSkezqnbMai789kuNSnWTxKEc008fT8lzg1uP2K3yOQSVyliBwmLaYLQyeGruEZlA0nBQR7d0AIDHBVEkd22SaJa3ogJSAKIVuraAhAqziOFZGyaC4q0MQUUCtQibFtBfu3O3KWyepVGd0pZ8l5SPV8YWByxXFsYC4Iesa0VtQfigxGbYcW30UzPISGxtX3aYqE1ki6Klj8OxNQmAX4tX2hoIfrxLOeScai1vWKoUfUsvdEAiE0KXRCz8am5zVgRXO5BuysIwgwol/NtYPDcG4SQtB3SKL7KYbxtlj0GGOaD7GCju2BcvRhWgbC++wH6vlPzNl9Cyz/ML0p/Qci6JkMGTyYxCeYrVNMwCSdnjGm7q/0GmMXgBfQ0L96AU7vwcFcAeig5BgpikHtW2RQqi38IPMlXXHSks4M1FZ0yJHZuHQqNgaS35/OYQlSHYkxOUhs7E6igGWZQAF4eX12OZBlOWE5iRTCy8sr6r45K/OrD19hXmZv277f73h9fQUzcDqdcHn/3klbBrbVUnHs+me9LpHMqpnmGR8+vEdW+QkOQkCoTdq8iQjb/YbjEKDL4hPzeVOeYAXAaZqcHcvMyHmSjl/NA0ySsDUpJNeBlVxKwX7sWnzWwXcUBFRWdvtRDuyHTK4/VJsWuPlaSnG5X2s5LZimjBAFpCwqnyDdZ1FZnHLvNr8H+LJozWxgYlWGsDGqJRduLMAcdlmT9XaHFXtqbSIpoDEDSPK+nOX6MQbEFJFDNpf+kOeMZCKL245jRzkKSq3YthXlpgU36jNSbH/GmDCptITlS7Ifgg+/m6ZZZEAeugd0iN4uYPGxH84uJQJutztKKSJhkQS4TikhHKaXLfhVjBn5nQDpOSXVVFV2r+rSyrktefRedtTjwM6bkL1iwJRF3iUP7y3FgOv5Kt0zraE8HSJxwMKMdckDJrw87wghYB0YraYHbARIgrBoZb21kLetsI4f06ityiIXQlvQ59aOWRIpoaenxWPaqjbXWsW+79jWFdu6Y1eGufmud09PmPKE0OScOErBPE1wD80ipTHlCY2rMHh1EHCKYjvWxZxyRKsN5+WEeZpAMTq7HQC4MkiH0NZyANzQyiNZcfz6nQdpWUEMQIcWaTBrrBTWpNASaklolcVIPdFsVTUrSdpiiBi31xsu83upaBXyBFKKzpKMpxQwZ6Frny9n0ZUoDWtZ8VI2CdKaVAvv+wZiIE+zsFUBaSuwu2CtOFqSrUnu+w8f8M1vZrS2Yl6eENOEeT6hMkR/rJEOU5Cps9xEJLyojk9jxl52DYqFpr/kCW1iLJcz4kTYyx0fX7/xQAQIDsyxBh9Vy8zBkisoQG4MJ4ra/hY9QQv+nZZMSKIZU0QrVdQOPGBimUSKxwTNqt3RD2X5mdaqap0GD9wUX+v/baCA/n1IEnxYcl1rZ3kZAJaSac8ymhPlLOliT3oA1sE0cGYNWOjuBjI0yKORBsvJtHfs3kJ3/Mz8AAQS5Ae7Bttju7yBUDkpG0MfvgPX0poIgrZ/dAbgyGaxdfLgz3TzNDDtw7lYq9lBUpkwsHuUrYXQWbA9sBRNNwM1gmbnvbreW4C59eeT92hMowqyoSgqTzBy90ROQNbL2/CDJHeGL3sirIn+F6CBB7PQxJ4dtCa1Q9MGC+gMBbt3KIDvtqS/RhBlZH2NjKuxDdHW08AWYaWpRVhuaG1vutfk1YeHd++soJ4VKijRwQ4DLI0lZmxYfwUMmGac3L8CmBUqV8F+/fEzHLiGgbvGElG7bNXt3oN6L9RAB9Eo0BLwnWtnX+KyJAgiEvakfX9tjMpWANOA3fzasP6y9zrIPS6CM8jtmfTejUEyMtLItIrMRxAergPdYwy4/hvePI/ZpINO+u9SNLCTrYJDAJhgw4EAkyohadXU86MBIlOw7Wj7BmhyNV0uwJyAZCzBIkFPayBNmqkWRFQwH4hB9SIf9u7QamwoqCayGM5j2xMpydRvG6TgjCb1P9EKWszePmd26ICY2TtDC5IKBsshhBgDin0PBMxm6H40O0QDUUXhHdRUVxQAdD+BWVi5ShZ3GQkNpC0p7Xvd/KvaSwDilBAvZ4TLCTVGKaBStxGofSRvh+4+4vFM6vY/7jcHQTF8GPBgmwQLuJVJw/08kzUnDzQ77tdtkZqBN5bEy/51KSm/pl1P1riUgmkKjtt3UBEPwIHvQ2Do3GG/mYd7GddCvbL5LguUH30c+TnsayYQn98rQYsrNJwDEFuT+1Ifz02fVQ6Ifl8q10O2NKO9+iMLa9B8DBOIFOisjEiiUwpWtpeeMx2gkbMFrLID9vcIPbaFFRO73qnYina3+P0Ejwm8EO5GwZDgamQ+2xM0MA+SU6wAJxuAaVIaKr2kQ4/YO4aabNVgMRoDqKIjCjvn4sMeYO7dFHEAXYJOchbgU9hXrTakKYEQfADL2ApqEggANAnPIKgGbhN/5YyzFFxfEBB9buvGEz3pBitEWBwVIEOsmHviziyF+qMUHDh8z4ElPneAT88V086z9W9MCFF0EbN2W1UFHRLkHEuugwjVaMy698lBdZN78cGuDGHkq7ZkAGmxgBwgjhR9aIqA3QVHiVj3irQ0TEzKSpVBZED0tvw8ZwQEVC7CnK0VrWqMx9y7njwJE1krk+xqUHCa2P1WU5sJhK5xqTqzrICSnJPmI8zPsz9jYwKoOnjZbIf5vrGoXn7KmdpgLVLKQDIwY8qSXMswx6HY758AWVMWsL9WYW+1IPdInh2wEnyiMvXE7hsLIK1ZoN4U61ppEdHA/NYQQ/KzKaQIB51ACpwZ0UPB85QEaAvS1mwDRiVmssqQzLNwYLRKPMUxoi0TOGS0ehdvbP7aAEKVMbBBXb0w169DRJKPJZFXEv/X51sgAFyUxajMUNZ8+ZHIw4gpOMgodl1hMb4AioQUsspmybkRQ0SrjCmL5qkNBSeGMIxTAojxen9BbQXn84LlJKy+Ugputxu2bcOSM5ZlxnI64Xw6Yd93fHr+/FCUev/+HZZlBiHgvm0o5cB6v2NfN3+P0zLherkiZQGmxIfI2q3KNBWm7Y5ahG2fVG6ASLSLT6cTcs7Y913Zq/NDnmPr1pQcVktREov6upgAFISUISYVsO87zvOCSxCfEodhmQJck7eq9+4CAaREK7qgVWDbVgAsDOV5UrkFwvr8jNbYW+OlwCRMf1LfOilYZ0E1kWjsmlYoUUSKM4igvkDO98q9AA7uhZpWK9btjsYyLL2qVnTZD+yt4aZDZWOIDzrK9q5s4FrO2QuNFALiNOF6ufi1amsioUcyVOq+3iHdARI/rfc7tlWA1hRpuA6hFxkIp5PoHXvMnQLmZcb16aL7RtigFptf6xm3203OtlpRa8NRNv/8WqpfIyY5D0vOPkQv5glpyliCPGvR9RF2bJXO46PrsnMVmRtgd58YgrDAc84yDCxNoBjw9PQORITX11fUJoUYY8cCwLZtWtgQW805q78yTVho0SEjxtn3ObNqzpcuUXDUivu2eSwwTxPyNCGRatUaiMsRc57w7voEkA7z2w9AtZc/f/qEFKUQK9rOQA1huKcAivL5hw7di2mQWYX46doaKgFAw+urDE+z2DDpeYsIFEguFbPge5bTftfX7zRIS3DyitPx3yYaYzVS/0UBDkkqjQETIeyXAEKmDGJgvd+0LVkD/RTBR5XBQDEggXC6XjElcf6vry+4ryuYtd1Ip/5xZVCygEcCrQp2QMyBIz2LY4zC/CLgqAXTvODy7isgA9OSIEwIAtcqk/ZgVWoJuKsOPIkAtm1HmBIONKDsOGdgyQmXr66gOeHj8x1AxHm54r6/4HX/LJORA8MZxgpEsQUxTVtRWJhMtTWEBgRmTOqcJeklcJT1D1BtDWgARJbO9WTMk10NsP0rGAPFWmTkPYYgEgrN3rNpueKxjbqzyhguBgt4AG+2JB8bXFyftNXrAbDRACRqO2xDH7Yl8VuVNnTqsHQgY9oZcEKW67q9GnAQFIyppfrfmxS6mIs9Iw+BSkSMqgfMj+spQCyrjmW/dgwR7TtA39aabqqRmTsEYbqvYohWZng4/AE8sEQf3u3w83b4OKOSqwfLBtw+fL/teQUa9MWO21pthB4GxHjQaaUQIk0UyIN9B+AsV9VhJZEIMFsnTfRJEs5WCgLCA1PbQPSxsjo+69t1Gr8kdhwGLQxAjX2N4Ke9tsZ9P5DdW7NgQoB9xmNL79t7G7/GFlIBNmTHWvLtgPoA0PvnaaJprdUjU9g+i7W6zVRFqsOYzaEPhCMGqqNw/AWA9WAP6MA1uyh7t5VIfZNZQjPiWvxgc49r6z8zvK9xDcf18/dF7kkcnHpMKNBtyZ777bvQjxhBe7k2g1t9AMdNBkL8kqyHsE/kPCj1ALcqgfDtDoK0FcZ5QcgTKMfOmA+EVgU/sZZNqg18VPkFqK/rNjyCydYxITf/CN69tbu3fzbfP663yRyMa2VyA0EB9wrI80Rh7lHDkKD2zx7n9ok/rOD9QNoLeBPphqrv3mw1QEAlsOoD1iqB1PC5XQOss6uIhbmznC4opwU1Jzj/SwsPjW0/jfb15Zq9XaO3tmIgw+MaD/+hLDOZbC57NOlesyK1gZxv9wIroPTwDhmSyJJ8XkNzprzxNYMyRMaizAgu9ycd3s+bZ3PQlx79jPi4Dk2L7fdzjPT5W6tg7YyRzwsP13TWvPtOAU7tsHc74OF9g/yzRu297jPs/Bt8Io9nfE+WAXgbddMigg8TG/yGFdMMBALbBzKMOkgkn2W8ep+ybucxGUBt4D53oJc0LnK76fEyWfjnsQDcZlsVAMl15TWk8eKpdsOYFE+ESD1MOeNQMEUK21EZRdH9iIFL1iYbQhRdvdZU409urtWKbWPUQ2TLAkXVWWUfTCLnR0PVjjtrP2bLAfQ+bXCLsMgijraCFYyPut6+3wc7soSbuYKOAzFOAEs7ddbk/na/ia5sCBLLkqQGOWXtmjLmjPlPPctCQowZKWbvAEoaj4GtqC4soZQ6OBKUheXSU+jadk2lbASsLwpgy4wAi5bBAuxxLajKbIsUZeL4umJZzkhz0q3TEDTfefd01X0HB75rqw6il3LgODY0Fl3fGKI+OVBZNQRVe1L2W9R4poBY2+ARdLjzIwmA0H2Hs7PBw++yF01fzQvXKh8Udd9aitBIhkuVcjiwA7aCR8N+bIic1GZNo1DuxfQTA9vTQc/DAcZlKSYGJSZQSNLGzgNrnS1NCO4rjJE9anJ655TuGdZyUpAJtjidZHiPyEuo39G4OBChFAGqnPRQtAhtIKc6gxCkZRx4j+uHf4SP8wm8Pff94DbU/UUI0h1j78b9/+gLw3heN80T+/tkZs3FZD6GzxMZzqWqg+zsM0MUUkXSOCiFqLJTzf2ADQKd8jTMr4nKJhdW/O12AxHhfL4gc0teAAAgAElEQVR6q/+2yeArQNixp2kSqSVmfPPNN1hVqiDmhOv1ivPphNoa7vcV9/sd+74LO7iKP7ter5jn+aGQ1K9TcGxyLWNKnuYT4vmCQKLdPE+LEmlsvat3EmwKUBljsB7FO2lKMTJNL4ZJS3hFUkBQOuvkbEpWRGLBPwxIFqJR8PhMfgnDOqZF31X02N9kWvZDBpM37j7iermAm4BtzNJ1dLvdsB4H7rcb0pRRi8j1maRG1PjP7MX0g026LyTV6oZ0UqackWLE9b34KzBcPuE4qvqG5r7d8kRmFpC1dqk2wyDskHfJjiiM6xijMDBDwOl8xul86vZqfl7XtDXR0+bWsLfi8jq1Vry8PIMhGsmNG5Z5lq6JlDApYGwDJxMSltMZeZokfgZwHNJKX4uArVWZ0du2oe4bai1Y15vtTjS+OTgtYCZ1H5CyMLtVizlP2f27xYAi73Hgfr/LftDuCxBJQUpB1DxNyNPieWeMUSRESnUGdK3Ccm0ND/t3HAwGQDVqM7Kut+FIRfV/RS6jouybz8tp6lOjPqf9XI4J82USwl6rKkGkchCGzUTSbpB+xrodwgaXSdf7OPiLWTv4SGK7Y5WhhCJJKaQyIulmYQamPOM/9PU7DdICADUDqwAYEPYm0ZbsT4lL3tphoAZ7m4ix4+Tgrfh8+whMAfGYUPYiYsA5YFKWQq1NNV6fZegXSwDQGuF6vSKnqGh4wrxIFaHsRbSTALBNix6AkVJlKqVVcEMIoBTw9fd+gP1XuwbD8vInAvbjpgmfVqI1MNn3DUI9DzpVMSFOQKOG6/sLnt5f8A8//zm+/fgCLg3LfMa7p69wfNpQuXjyAhu6wmzLpl8MaHtWZMLX5ys+LFf86R//R/jlr3+BX3/8iF99+oitrYh5grHRwCytqXXA2BgD6DtMjx5BIP8/8uRB4i7ugQQMpGgO1Mn7VXYr+pAdZz+QbGRJWMWxx2gDpQSo7pJU5IddpKCMAE1GtP39qBVEHcQScWr5FaMlaNzlHdRZmS1yCDIEK43sAHTQA8OasIFyHbIyLV3Nvh4BBLYkVNvqoJpmZvNVWQOWzNne0UTLnCgp0G1J6zE4oLcAw3eBNCP4aBpEGjYjqlakMN2U8YZx0BL3vWMMU13nZmBRewSfxbS67pms05eAQNWAxNZAo38Q2UAFMgRL7ULCWusWNCbvbwNWHoBzdHDN/gzIsCM7sEaQ04G4YMwkY4j5lQC0h/XtgK/anAIP8LUktYW+N1lRBV9vtxu5ZkqPoOMXIMoAutLw/AbiEnoAb/+tL8jvqTPFNLEhePBv77sjH2qnTJqYWkKllhsIsGEavwVgHYEBmwJtX11nlL54lyPU9AhWw32m/d3IEhM/9OW9+FqiJzP2836mOZAh6zPqejbrdCAClBXWjh1l3VDvq+6ZgDhnpPOCOM/gJO+3teYFoFYrqDS0o8pwsVKVZWyMW2Gz6mM+vFt7Ph80hL7nrUgRBxsegS5m0+nsvmtcp3Ff2+pb4ldrRYJqvrKd88Oes/vVNu16HOB9B91EVz400eTmKqycpnbHrb9HZ9oF+uK+JUlmKTA0ICAhTQvKvKCS8THNNA0QtPvn4Yx99Jfj1wja+/c1fviet/6XCWASFhkDru9sK9jUl5H5PGYfFGOiq2+BYdL3Y8MJHbzUdx9N15C+3B8E8iBUZBjp4XnM55lt9eTR3r3qaLq0xpcJu/2cTN62qfAM01I3F9h1sS3JErZq0zWw9ZJ7bcL2CsJqDfzIjv8u365PjscOGD179brSulec0RaCakqGYPX7bu/UGeSC5RljrftM4NFPga3gyfpnK2r7Nutnmz+HuVc7A8dY5eh+oDESrHDSpcOI5Ew05nEgO1Pl+ikrM4mBaVqwLIsnw66Bp1+32031UuX6Ly/PANjZU8bekmGdhMIFrAzEWqszkolk6JR0ywlgDIbHWCABBAhAC8ljRmZGDRZjCmj6xfmnTPycJ+Q84ziqMrCitghLm68RMbQ9pftNZUn70Yag7LaIFLIwkEjOd1Jf0TUZd7lPMKRTKyHHjJaEnV1KRY4TQlZ5l1oEZJBNiRCkEzCEBEQBM1oIKFVYaNbGfZpPoBCwrS9Y79IGPKVZWpPBYB3mIINVRH6CK8BN29AhE6prKw6I78eBdogUAJG1nUqcBmYgCLu0toqGhqizKEABIXYWKGtrc2tmu3I9UkC1H6akRBx0Vqm+EzI7iZ1hVapKEGiuCGJMFLTlWN6XyAI0MKIMxIUyd0lAeiCg1gNIE4TB3xApKrvPlMgDTIqJjJASokh3ESQmMeasFr8661rzANLvof45ZqcxJrWFvvaSUoguY0UFJwHNY0y4TLMOqm1anGT3hQKwbHj//vfw8zTjaOaL4LGYFWz9zMcQEw9xkrBag/u3WgtakXMpJpWeU8manAWco+7W0AsaAkBJmKu+rzXkmHxmgHQtFBAYOSrxhcYcVLoXhHDFqgUsA8CXZUHOGdu2yQC8bcM0TbhcLqK5CmkLf35+FiZ5zvjqwwecTgLSHUfBy+fPuG8rQAIiLtOMZZ7x/v1712i2z7CBXuU4IBrXCafTCcuy4LQsDjYv8wImRjkq1lXAouM4BAROAff15tqjNshcU2fElJ1xKI/f5wCQsiTt8NnWQ8+aPtulNfnMUgrSPD3kKzazJYbg0npJhxaOgBqREKGC2nMKHWg1ZnipBcQkGqK1oBjzVVnFoJ7vm13t++4MW8EUeu6UQnSQL0S5PyMnjTJ0MQ5t8rDzXAZRmbYpAJRyYL+vvqf2bfM88n5fAd0H87wg5uRnvMUzdh9SkMwINMkA62EYMDNj3TbRBJ5n6ewmcvBzW9dezG0yeDLPUngTNjghxYTz+QTKBt4TLteTnJnNtIzFX5ruaymHa9HbHrWOWQGjGfM8Y66zS5QFBVmv14sXkqyosW2bFClU6/dQLWeAfGievbcpZ9RWMV2vLitFIGXKHv4+Wmv4/PkzpJByBvPm7FZ7rwb8mixLijLUy+Q5apV9s66CY8zz5P712Db1/4RpmlBKwemUxCdrB2HRYYE20NkKT7VVBDCOm7DNpyTrEVNEghWmExoEQC6VUVuRuBDAZgMjb3iQEXz79bsP0gI9AUMH8KDOwsSxDchjrQoZmElERvZAZWkfIEXg1/0FYQJOOKOlCqCh1B1FDbeUHdu6qSafVGKrAiX7tmHOVwdwUow4n87YSKtw3ACuXfy7FDnYSGQVJGGsQKvINGGazjidRIj86foBP/xH/xjffPMr/PRnP8JxvALG1fH/Y7RWpK01JZlIDdlk//DzX2D6OCmlewO1hhwDrud3KOXA88tHND76ChtwwNIG0koFNUYOCWiEOUz44dPvIdaGH374Pv7pH/xjpDzhb3/yE/yf/+Z/x4GG+1rQiETMHtAWKZ16Z2AQwQ8RsOo9QRMHdEkDAAD3xLIfNFAwQQ9w7p/bWFqWfABV80xHv59grWviGIseIt2hjiCBaFx1RwtABkVpEtQj7p7YjixJOTTIr1+rXK+a+VYFGTRZcqkCDU4swaxV3jW3foiOoMJDYo3HZ7BFs6T6QRuWenI5YI76WBLEWGLYE+L4AJI6M9fe4ZtkumtXqUbncPjZ39tFbZ/L6xRDaRpwd3aCgsxvEn4wa16kn2M38OZ+QpDhcb1dHhrkG8SvrUK1IcTkmsGWGJOCaOM76Jfq13r7bx3E6gf4W+YrgG676PtkBH86IGD7X3yS5PPNE/ZxorABHwBAoa/fgKPCtY0HcHF8lhEUaD4Yj/oH2O8PoFzsdqXV0a5z2BknQRPoALXnN2sqwb6wCEDk/pPsBaofoPFegAcGYKTgki59oJf8N1F7uJatswE9I4D1AEjrh5hJPLxz38c9WSGQVooHgNbfzeM19EOkIEPD3lU/py9CGGClgO93kBYH5/MJ+XwCnWYgRrEVZqAw0Ah8NLRdGLShAfUQ+QOQvB8Qun+z/Wj39B1g3ujz3Ffq95l/eFvUMKt/YEuhsw+sBY71uQGT7hAfjFIQorb5aZImoD1D54Pi2HaUl1eE1xuigjk2+VUkcMgB2rdgrE89HgAxAfYkBkEIoGVGnSc0yhBNOGntbE0KpdDvlWdQNqSbx7BP+lK7L34sGPSuA2BIjEcUjtntu715R8ZqIdc6fFNMGPypJ3EmbzEAtPLvXftbwCtWQDYMttDv3xjhIzuR7GdZwHzz2f6Lhr8jONtxBLjNrkxSwwAu+Z7kz2eJhX2mn+dE3uptAzw6QMqjw/3CNsb3IIF1l5OR87opKJt0Pa3dWIq7tSiAUqvvcdN7ZWe8VlDT1nC1XfMSik8IK5CErWdJpZ8zb2xA3ktfR2OEWEFb7HCQIrBTOJg+bE8+zX6DsoKZpcWvNQE8WqnSfaQg5LquDlIY60XuA5os7gIGp7EF2HQAC3KaMOVZoDGWvWu+NQQCKd5nLK4KaTekakQEActjiIhkNqzxlvlzeaOgMCPEs0qyWIdHA0fRunz3/gNKbTrZWnVmSfQUS00Q0oX5QNJW+Aiu4tO4mf+uwr+kgH3bdCCagI6k5ABWu9xLQakFtRWkkGRWhdpyY8gMhtz3qxTjJF60Cd4Wv7TWQAkIMcn52yoQJZ6etK2XGAK21oLzdcF1DjjNQEXDcYi/aS1gSSIvFFLGfa/4/HqAwoIUCfum0g9iqEKCCBLPcxV9ToBwNEaLO1rb0ahKkQSMNEglVbXrpPYT1Z8JM7QKa7cZcSH4e6NArk8tMV31c5kJoBgxZUKapKMRbDtM8xUShI90Yry1S7fGWGaRipiSdD0eVVuAQwK4OmAlw49j78hCbxEGbCK9ttLCzp0uuwNAB/OIzyilYK86/6DBY/S27Z7rhBARw6R5rpwngYCURSIkkAAkFjMK+K/78SgIKDhqAyEDLM8HHVIsBBl22ZrRl/ssB6LehaCECIbmYyDkKTnYHojAARobma+TdR+7Fdwlm59lQoAUY+ZpBmJDIxliOqXooHHQuG/bD9euBICjVB3MNWFZhOW3rsKCNTDofD4jpYRj33G733ToUMbT05Pm9OSgq50f18sVl8tFdChJikifP31G2Xds26psRzm/TssJ6XLFPC2Y5lkAMHRZgfv9js+fPoOgk+iVPDRNEwAgTwumPCGfs+/tFBNiiliWBXOe1aeRvxtu4juP44AqL6v2d5f9OFT3u6+9+PeiQ7/snDn2qiCq5UwmscDaDdH1lCkYoKsDF0PUAerKkg2iLZpjwnkRVqL59BiDMxy9yC9uQs4UGz6ouYOAuzqAjIufS/u+yXqQAabJgeScM1prmKeMnBI4dBwhhAvqU9NCHTweFgY+cGhHx74feH55ET3S4Sw+jgMhCjgZiJBiRlZWdooRSQevnU9nOaf0uvu++946yoFaKkqtOPaK1oR9fRw7pmnGuq0gIrw8TzLALCWJm9ceLxk4PeUZmGbHXexcbubfVBe31oZyyDWOXRjR8zyjlILnz88ym+l0wuVy8XWcpgnn89llMwVQP7BtG4Q5vmLbhGl+Ws6uSVx0uHpQNnaMUYfOiX88n8/DELkqbOPWgfsYI+ZpxjxlQP3YlGV21DyfpECkMYitpzGxYwjY1lXiENWDPs0nEBHmeZHhYvMsRSS1QZDigLV5PGMSCBQC2tYQo/lwwnw6YQkTWhU7alW6fGqtKFyxl4IYMn7b1+80SEsaTDOa5mlyOIk+Ze0AriV6BAWCtB3AmW+i7Sp6NKz09YZSVhBXpJBR0LCuG15uz3i9vch0SNL23qQDv1qDidhxazj2XWj/DKz3FXmecVoWEd6noKLXyhgk4Nh3qYJrUlVqEe0TBkKMuJyeUErFH/3hn+CP/uhPcDpf8PHTr/D8soq+q0o+2DS7GMSYk1awUk7IeQLWDffXTbQ6qCCiSSJJEdfTe6z3O47ahCkLCVYtWyQmJApYYsZEE4CAd6cr/uVf/BX+1//lf8bf/M3f4L/6L/8L/Kv/+l/h68tX+PjzHyPOCb/45hO+vb3iU9lQABzeDv3IoqLQ3y0Az1ANtmFjVjp+0YElO6gNqPZElrVNl+sXTtwTNmc5GEDGqtmngdkbkMX0rAjo+nOml6RBHGmS9wCjDQmvg7X63gBGMKDYgFdSTahA3qbU2KDuAOkgqAiJJHmDHLZB2RtymDUP6h4AWv9vSzDJQSJhB6cHoNDu2ZjHIcUvPnNM0u13CxJk6Xpru4F2HsRR13jz9dHvs6QT6Kwe6Bo51qcuACF0bSzJ5OXeKHhBpr/KATxmRqLeohkoIEDbOfUiMrxjXCf0tSMZmjEC92+T97cJvWEpkij19jWbCD2umf2AAwZwXrR/vk0JHYHEoIjGQxADerg2ANUt7EUJ+z67b5NWsMF2b7+s8GCggIMvA6AUDGQhY/iS30MIQRigA4jQwOLbDHAHHu2DhbliQZvft62Rr8XwDjDsWfUf3FgSAgeTHjWAOhME/kxjccB+Z80Y/LlHGJ0A8nXXQVmWGMKSx4Cxk8A/C/qzagMhkLYMFU34BFQi9Q2tVRz7gf31Fdh2JAYoZ8RpQZxmsLY+1lrFzyDKeXRUUANCM8BHknpowCKSBvBnH5//Ecj+UhrC/q7Lv1T9Ox0qqGcNvQHdxs+33431KbdWkfMs96kJbNezNVBEWGhEEmi1bQNvO7gUHXzJDl4ZeGi/qoNV8gxR1xr2vvXdVpZC2XS5AtczypQRUkYi890d4ILaoAXDIANkH4sedq7J875JcgF0HWq5iVrHYhipsht8D6SB3WQglbmA8WjwvfbmnuR8YT+L7J0KZsH+Z2M3gs23wu+zP/fgZ4ggLYadLWzdMG43obf2yjloE94NFDSfUHXoieqHVnIAlkL1e2JmZAV0j+N4WPMW2GOApm1ostYKRxD5ufq26NZaHdgy7PtolNdhPmR1yXwbIDkF6Wd6DA+RC5B/szZ98992RrokFwiwFmoaiyjs4ISvXzMJEUnSxqTG9Nxtf4J6RxIRaTeNSRUB3KpoXxLpmUzY9g2u361FZIYASxQkviAO3koJFoBHpIga9mOVxDWR++qUkxYGjGF2QaCojL+CUnegVS2y9D0NwBMmYcaIvaQkIEaM0Xal+3bZZ1BWc8I8vcM0nVUfl3zYRwwRc044ny9Ytw3TfODY78N1KxhNtT2DxBghg5AQKKIoYxGDb6iVUYqAlRQIXAV0zGlCU4ASQcD7HAKmMCOnjBwSojKBIxHmKSLlGfM0C8AAuN1YTJFjkrZOklZWGywj8T47UBFDwjzNWKYFc064nAPen4DTxJromksJ2FbGeY5IS8C3nysiJWHnJUItQIwFKQYgmORclDilVrQqMSZCAqKwdPUolNkKGv8JqNNtX1jpWpxJAHNFqTtqPdRvCPBjBeQYZeANNOYpx4FjP9SXE1JIiKl3q4hfcrcnhbkQtUAneZ8MKCXPTUNIiHwGE6M18ccCBCXEABAlDeXls4yMQcHIHnoOs2jwUut60tIiXnGUCoTuMxrL/rSOQMrRwd8Y4AUSYQtmPTekvRyNRCZBVt2JCPt+oBwVse04muSpQedMENOQt5lP6gOP9UTxnAukBR71rUFZ8DFFcJP7YysoNMY8ZRy7FGsY2nVpZ5TlUETui0OIIqflA8lYOh9DkOIzoscIAeLHY86IMfg5EEN0cO5+vzt79unpSSa914rPnz+rvj4ctDU9WBvoZCy+aRK92JSiAlOrMC2N2U0BT5cLTqczAEbSVvUQonzeuqHZoKgmbffcGDEk5CXrZwvjVtiDAXxaYIPdoD6jVAHzmHfxo6GfzTYvYFtXye9iRCNGbQe4NUzzJP45dDk7A2Yvl8tD3sDNtKPl2seuGuV6XrN3QMugLeuiAHTwtLKdzf5EAz0g5qTFV9FdzjlrodPa8oPbQgAwxS4XxizAWdUiwKHt/k2JfNysO1oA513BQ5OO+MxNChiht9pLTCG2kpQpG2OCDaWrdfbi2Lv372ASNB282wEDkRk41hX311ccVQh2NiA+UETQAoMxTXOeOgN5lvcoA2ulwLrrADxh3BYFKCuOffW8o9YC19EPwrg9nU8Ad7bzlDNAImkwz7MXem+3V5Raldmt3cPKbG0vjHme8PLy4jFVzln3vviqacq4XM44nRY9S08wQHNbd8HQSsF9W8VPqIb86SQM4JQipkn0bk+nk+a3xoKXPKiU3qFTithSqRXrnVHOJ8VWomvUhiD3tas8Q4gRcUoIKaK2ip0b1u0OMLBvq5znqilus5hM+z2EiPNJgOuddtRWsa4rGMDWDpFNIMK8rjifFsWpBKgniqghIidgmT0s+M6v32mQFgAQrDVZExid0iRApWj7SJCoYKjqjHrwJa4AhSVJRxNDpxxQ+MDz6zMIjNvnzzi2OwpXrf5GsDFiDE/0xFpozy/3G3KeMM8z7uUAQkDT5FijZxHeDqHT2xVTsqCgtYa13DFNE6Z8wrHf8JMf/wQ//Yef4rbesG07UpzBetDGGDCfTqAg1TguFbU0nM/iRLf7TfV0Ggg7cBSQDi5BA1KY8XT5gI/PB0xhqFIFV0YOGYGBry9X/Pkf/Sd4//SH+P3f/yd4/fbvsX78Bb63TPiTv/hz/Onv/wFePn7Ex9/8BvFgfO8y4fT0Hj98+gBcP+D/+dGP8Xn/KH2hzVCkfsDbl2mEisxkgw2XISp9eq0DBjp0jYd2fg3ETcJiBISJxHYkWVFwnTpI5YxGkANLTQMwGOOO4FPjCRI0G3wWiNCKyih4HjrsNEsoIak0cwWFiDYQgMfs2QI1eJBKECaySkSwamCRcUs16CcRuO6XNWM1mFmMzpI/r9QDniST3oeDcOgB/gPr6yGYHRnOj637tckeQiBA2w2rMQgDtHGONSmGtqL1RCags1yqAS9N2psM0OBR281ady2II235JMA1oUnA9YYhG9A93Zr4FdFnkjYSkyyxNxpsmh73NX4LNFnS7Bbu39vX1hiR+rZ8PTsgCfdfDpr4dczG43ABuUmfMK7VYr+FbmiwIX8+bdzsFHBfYGDtaMsOputhb2RJY/R6ZqhXEVabOUEDutjfvwr/wkoh5sO/q8DAGugDPXiHAkYWmJKtBQDW1mBJEh4ZxU2ZBLLevQ3W1sDWi/3j9Owh3RMW9PbXByA6iIIBeAHDtaah7ziRJBTa5QgpnMl1mOD+T/aesoa0fZ0CoXCTtd12tHVDXTcctxWoVc6P0wlxWcA6vNDbnFnattpRgVIQW0NoVQLIWhDs/UKnPesjGOBqdjICItY6NoJ7fuy5f5b17Kxt9eTD9cy2uz+2dyAstcAC4hcI6yZwAXMBSAboBOoDlMCixdXKBt434Dh8be360AKS2TgTAcpaXJYTvBAcZKo5SBhx0DpOWC6g6xNwWgCbpszqZmSZEDn284QMYFVpF+p2HWMHVB0UZz3vWgfcxDeQ7SBdW/kJaVcbzwXyfQrqgBkB2q4lZ1ut1RMRVvBUkrziW9lYTM46ZdHpZjJ2UwMhuZ6v7ZuqjBBj7kQvKLIH2iYPYjqrYIC1Xd3uXxiBJvEBBBtsw32yM9VHZj5RQWPpCIKCnuUoCszB/T6qsFMiactmEzYWMLAQ1b2CJd5jYjT3nXpWDeAn16oFFb2XgOGZbeK4FPzdazVoUiPsH1JGIJEkbuZe7f6NoRv1utLlZR5Q/bb550F/l4d4wOwJTc5qc9/2y1vFNf4ttYrGs+hX4EFSSn1nVNA0hQgkGcDBTFZBBJIM5JimLM9ZCtKUHcBIKWOZF4Q0gcOE2qRzZ0oLYpwUJFRwtK4gNBxll/OcVdZA19bAo5gyQCbXYPszDABCFcAzZEQ21qVovpP5K9sTaCivWtiNCTGfwPVAawVARAwZSZPgy+WCd0/fw+X8AWlazCn6lzGFZc/IOwgUsO8b9l3aXrm2nicwy7NpEqt9I8hxEvArBtHpE88LG9xF0AGA3FC5qkyO6asqy12ibLkfqpgTI0+qkVsZt1tD2QLmCZiygF61AS3IXA1SBh3BgC8C39kLPbU0NCZEoROjMkApa67RUMOM2iK4rAhNpoFPOrjFtB6djcmM/Siow56KcQJI2OtgY883HLXi2AtiBHKWGRMhz5jSrOcxIcQEc5fB4gOLkqiz2lhzkWrD8iD5p3lcK9KlmEDqyxmSxAvLj/3zDNhqTWaLsOq5Btj52jw/YQZyXpCSOKIYZHhUVuDVQDCi2N+52tlRDjkPjx21CZgxxuxNu0UrIOh7AxpFRErIseCr6xOm5YR9PNWHHEDstohvCZrT1tHQ9exE1DhMbBocBLiMOjOisoNnCIScE9Cks7LWJgOoNZioraIVGdjDaP78DFY9Sn7Q6ZQhgcnb8o2daCzKoiA4A7g+PTkD9n6/qwxLxbIsOJ8WZ9I9vzxjWzc0APOU8fROfi6EiHIc+Pjtt9jWTfZnzgLwxIh5mTHrvW3bhu12U3bhhm0TKYOcMlKasJwWfPX117g+XWXwWAJikOvXVlBrUI3Qgq0d6EOZWGOC4mzl2iq2fQc3YJpmnaUDQGPQFJOeR8IwJmO/Uu/aiVHYuQxCTtklDHRcqzA0p1mlD9jzQet4SWr3JnPCml8ZWcFiGGGmVmU2SneBsC0lviilaIs9sCynDqJafJ2izBRgAqWIKc+Y86xAK6l2suRQ5Vj1TBPt5loKGNJFsG2bA9XWMSOdWMH3cYjBY7uUEqIWwnLOPuxxzI/tdwP3rRWfFCN6vd9Ep1dZRknPS9Fzt3hAzvOYorI7EyhEXJ+uGkuw+zFSO1u3zeN2s5Hb/QYbKtuOKsUTSC58Pl3k3UfJzfMk8gxBi5whJbz76gPQBIA+joJ933G/38W36zwfEDBPsw5MbDidTpjzAiLgcr6gvVOiyXHgKBeUWlEZrlErnewN23bH6+ur5rxNh5RdMM/CRp7nCSEmeYfb5rmg7Y+9FuHxaJwYc8Y0iXxDJOkaX+aT7H2YFIQUZwmE+7Zj2zfUlgrlebQAACAASURBVJwFzq2hQGKBGHYZcDZFtAbM6YTr5YoQCM/PL1jXDRQIt3XFfuyQweni53LOIo2gEkK/7et3GqS1oNMqVoAAAyPjylryMLTXhiDTxtEYgrkGb2sPALgyUooIrWF7ecX5ckZt0uKDgA4a6KaUD5aE3qoM0uomtHdro7jfJfExSIJdwF2qoyNw0JS5ZExQS9pSInz6/I0cHlxwlDumHJHmCTEsmOcT3n/4gG8/f8Kvv/k1bi8vWOazaFysm9DrAYQcgRARswQdFQCrZuf1+oS93PHp+VsZIsYkLCxmXAPhr//8X+C//W/+O7z73p/gm7/7iP/3/3rGT376b/FPf/gDzKcFv/f193G/3fB3P/oR3s9XvHx6wcvtjh/84R/jB3/8F3j+BPztz+64Y/PWWc0hNenooBkzhLUB+FozG4jB+vfoIIsnHo+t2Q/gL1lg0QHEATp78314+Bz9IQG9tHVNdAolOTVctf/Mb7dfa/21oM+qmtDnb5qQm74UAAX4rW1dh1qQAlRV70PX00EYDC2d9ryD3fb9YlDKlwCjCb7bc1mL5Lg+ppsy6mXZz9v6+ZpqYDVeI4Tg08TBvXVbvuURFLbA/AEURt8rX4CjDAferNLPkOA7DPYxMknHw8sAm7ct2PZlf//Qbjw+l91P0+TK79HeSWdG9c9m91n++WLsAD8G1d/FPPR7M6DLfeCj/fteIUnbDUwGrAghmzPGNwP9qDP7JJnpRZDOoHhsW+9Txzv47M9h2NHD++gswS4P0lm09sxvfx/3n62r7XO5VD/0/H4GppjdjJqiX2+8xrgfRvt7uH9lB/fi0Hc7hF7skGclIpk7CfisQwNjVBFZXgArO1I11/aXV+C+Oks0aqtiChFzzu6zvMigMiO1HqhlR6gVtRzC3GhVBragg9h2flnw7evCDBr+e9wjBhgOHmF4r2aPg492P99tQ1qHH/cuQWUGYpTEY5OBKrE2hKq6uZT8uwmMchS0u7BoSWMDY9ESLBm2Nn4B89ZjUxmMiBQJTZbdfTFUM7AyoaaMMC8IywKm6CCZPJvsCWt/dDtRkEz2V/E1syKZyzxYwkGEUvueskKBFy3e+Ch7dyFEYRlw7YUN3ac20ZtR9EyS93NYC5e9JUZvy2axn1oZXJThSQ3TbIM7CE0HBNq+apLtd5uBDbthlFZgsWirrBOIgzPy/d1z3zPMwrLh0GSojLxNiSdYStE++FGBDtJ3nZMAyCkGBWRIzzB5V8nZld0sa1PrazIMqwPj5ldMUkDeicirBnCriKot2gs5vTvB/JvpTZoPCKpBae/JmK+kbG6Pb2F+I7h8SqWGra1fnin2MwoGRtWXszPd2m6DabHToP9JBMSMqC29RIRQ2WWBgrJwpQNMZLF8Ej1Ikjpda4ZJvABE/TkDBaQQYHhBINHASykjxISjBgFGtePBirBF/UwpCa0eWi1UgwpNhggxPKklY0cH8riDtMgAFv+SUp8eroapsZ/YbPLPiIDOLorIUnCnCdMcHlp5AQHrWsu4rxWp7noWjmeYnSEyDLFVkjkVTdqV0RghKSGFIXmM5g9xkBbJHovoFHaWBD6koPGVxSwRJnRlLK8QEmxgEKEBxMhJWGLT6YTTaUKKASkA80x4uhJyIhx7Aw5G1rOJG7BMAe+eCNNywro1EBfMMWDLhKPKQBauYiuoFWESYFO6CStKiUBLCCwLbHrhKSWdtM0OzJ7RC+EiHaKqq6Z1zAIYF43RumfrhSzpoiJvw+4FEwFU7SRzxrnaQmsTWDWtY4xIqmUYtTBj52Xw7xcAptQDIOn0YKoACSEhUUDI2vEJBZgHrdmcM6ZpQS8KQXSRtZ1ZwDgZmldqBR8qJwU4691ivaAMyaS/W6Gl1obIhKPs2KmITVRh9S3LgmcywH0o/LcmrD/t6mHua9Zb6+WeQwgeV0tnoJCfrOATlT0oDHrIQC6YHqQyrlneP40McAWxpXTehwSKpEd+mE8QQsC6in6oD51S0C/GiOv1ipQS1nXFt7/5jYNK79+/13io4b6uuK/Sqr0sCy6nE+acwY2xrtrOrdIu8zxjnmdt+5dWd4DxWaURZGhWn09xvQrIdrlchZ2t6/X68llsfyuohaSAgwpuYmvbJmCwMf4FDM5e3DBA0QBG4SppnBw0X9K91hqj3e6QoXUTStldpmbfd9xud+y76GmG0OfsmN8z2yKCdlF02ZYQI/I0WUTrNpmUNTvPWf0QYz82PL3rUhOlFtfdNfDU9E8BOOg5TRPAgqnElN1ebQ3Ge5RBfjIkL1jRlMRnWorOzM7CbYPMg+sJK1PWQH15DxXzLDHAPM0eKyzL8jCkK4SAaZlx5l64ZpZO667HCtgA31ptGKSA+kctuE8LQjR2vcQiKcrcDpEKkL12Pp+FMa2M4RAkBtoPOV+PVTR25fwg0d/l4vnIlCdhDdsaUgBT0wFeGaUULMuCd+/eoQEKRErRpNaKbZXz784yBO8YGKwWJ+WUtLgSEK5P0vVQjKjXsG07dtVQbrXg9vKCG5p2uSf1FYSsOF9Kco5u64qZpFDIRfR4mQj7sSOnCD7kLNy2DS/8gimrVERrCBp3vHtaJHYtRYqnreHQM3fbN8QgBJhahAgwzzP2+x15mnBeZizTrDI24ifKIZ0R2brhG4NK7yj7rq/faZCWMFTuBoPuYJpUgpo57uF7SYOANCWpEDF7JZB1yh5Cw3q/4f2HgHmSSvhWDmmnYqleV9U/dN2jkBDV0CXBEqHjGGXqZlOmrlT4JUgQbSZJDqeYRbBcEwSioNPp5VCTttAGUEFAw5QSchJHPuUJr6/P+NGP/h1+/qtfIKjQ+3I64XW9aT8zg2LS+1NwQFtCbLPGGHFZnnC/3VDqriLyAvxFjvjw7gf4gz/4M/zy1x/xP/2P/z3w8gv8Z3/5L/HLX3+Lf/ujf4e//f9+hHcf3uHp6YJ/9qd/hn//dz/G9djxH/+nf4l/9ud/jRauuB0f8e9/+RPUqGAZi8yEDThx7hVZGzYMbbGX3+3gC1Dn8c8jiGCAAUgnoAZzN9rW/ubnzMG5V1InLcMQpOLXCALExAHcCQHEDaVJ8BXi4/3CgzV4ctOvMwxKYWWlKfDZuGsso7KLorMGhNZuVZWBJUy3weYN1FPbUozBDyIHTsiAGWFaWOA/rokByKPGzmOr/OP76QAxPPC1bxUdtSrDRvQekrf8c2/xHT4rarALNlkDOKA9Fmr+Q2Ce/dnWrgMS/Vo+eTLEL+xOXt8jKGV/Z4npw/eYbAOP4LVyLt744ZHx2gE8N8MvnsPe8wPzVoENgq0N6b6Hr8/4+1tgx8AR+b15YQHUZRMMPLNhUaNkhX3WW7kCW5O3gDKA3u6vbBsfoNHUWG0tyO6T+z3q54I7QBuG92Q+ZdwLvnohPLTaj2sJvGHqvj1rhnc8rqMlA66nzGxZ+OP3DWtB+nAhkABOBIgGdwdj3C82HYJVK3hbwZ+ege1AkHC9y/1AJ56HoDpXwl5slVG2Hce6IaJJe7wOP4QCtPYVQsCh8gAYWLL2b24R1M/lUfLg7fsfTdeLBcM7sf8eLVxCUSlOMZSNpQN/zHdyqaLpGYRxHAIhknY27AXH6w28HaBmA1Tk3dpUaYINdRI7TjGiEckgj8ZIU9YhbDIYVEDaiClN4PmEsCwASeum24MCICA5c6yNrw86pYcCyGhzhOEMMKBx8CuQ3F1lcPSxh8Td7VIDdvmftZQKU/3B9oiARqq9X/Weg9tdiAFcmmHO2llh/te6TnprvyVn8nfd94s+4lDUYkvSxG9SNOCy25FNprZ75cHewHZmRAXebcCenG0paLsgx16QbL3tmUHI2QpRCihTLwJSCEARrbhmHUDudKIyhYL7O38/EUCGJtgRFPuAy6Y2KGw3BX9S1vMnIuWpd/LYXmD5mVaaSguYs2to9YAP1KSuN8duazBUFPYCaxWWuPtpmE3ruk3CyGQGUp6Q8gzTUIXuHTvDvMWarGjVkEKCOeQcpW0eCqZZcaByB3KNkUTmp12hStYnRShYp9O32+GM88YSRzUKiDkjkZ0/CuY2sWkGdJ2gz+aBj/x8rYgQ8CCF4DGSgD2y9w2kMDkKCtLGnnJStDYN0hHaFQQCWkBrhP04sB/S1WZdXjTYGyvIKRIbrC20CTFHLcwJ0IrWHBiMIQj7TZ1lH0IqzCAK3aOb74lEQDDGqyXcye8jhYAcIq7XBafTjGVOOM2E6wxMVHHOwDlFpABMiXGAUSLL/bPo783nhIqIvQCJGc/ThK2csO07SmOU/UDZN2z1kI6IJsOnco5oRZ4nagG9WWxFNkBLi8kxDvtO3xcqStmECMPKkisHDmW/yf4eBiap/qKB9IHIGw+CavuK7YjOIRGQp6zFNQIo4jh0gnrd3QewAtG1NbAWnlII4CQJugzkI5EQSGKHJknQhhxGGLsdCGpthRcZGbjfVwdgWi1qy8oQhJ0bjODvF/5v4N6GbT4cIKy1YS3PeN1/g32/od1X3H/x9zjuryBI3mODRMUh6E5yYgi8W8Nejvm6QITdCt3SMum+XvxAB7itIGV70P2rf6bqOB4FKROQdNp9ShC96j7XYfTPNnzQtFLXdfXhUzkLcPT50yfc1xU5Z3zv/XuXFZNBYiuk02bB9773PR8yVo4Dv/nmNwhBgNin6xUf3r/32Pt2k67W19dXrOtdQTxhQMaYME2zgGgh+HvZ9gP7vqGWglqKFJ1RkcKMmCKmSchXKUZcLhdZR80dmRtClCJRbdX9TSsVy3KSWFnfUtO8wWR6Yox4//5DL9Qb+5l7F8i6boOkDLm8D7MwRP3fdP2JBCfZ9g0pJh80ZTHr6bTABupZMSZNyd9dnmZkTJ5/mMxDKRXbdjzkpALsHajlAPepJNL6ruC5mKQwbVOOOC2LnkGaI8UgTG4v0sg7Gqfl2DXHGS3Mcsbu+4Ztk2sZoA/AwUgpCIr/TYoHxBiViSugpbG8DQj3fFilQEop2FaRB9i2HUTAUaXwvG8yUNPmIDHD7xMA3n/4INq/U5aYjQk8i/yGSKMJkCkM2UM10XeEFoHjQFOtWilMybovy+J2tpyFdW5x4bHtvlYmT2BEhf0QO2ceNK5DwpQzluWEHLs+7fl0QqAE6UYmbOuB2+0zjqPi0EFuYkPRu/RCVHA8Krt6sthM/K3IwJlesbB3j32HDbkDhJwQU8DpvGg3GdD0WadAqDlDZO0ItJywbRsIhGMvWNdNpZwylkVY5pflhJr0TE7CLt93kUloQ27w9ut3GqQFegLyXSAdGjxxFCxO9EyJoJtVGsYpQgI3AkojnfrYsNcDH58/4v3XdwCiFbHuMvEOBHCpjiAyi5bGCNaYXtp9fcUyz2guBp880ayqS0GAB+MypTN4VckRCUg1rXHDvq3guqE1Qm0HfvaLn+F+X/Hy+hHHseN8veK8nLBMM+ZlkWo1mWakTFS1VvCgwGhgiK5mBVKc8XR5j/v9s2jSMAAOuDfgf/u//w2u/8O/xg/eZ/zZH8/45U8jfvLTn2O5POHD19/Hy77iJ3//Y1Bj/PO/+mu8+4N/gqME/Iu/+itQjPjBz77Gf/6X/xz1/3jGP3z6BscAjMEDCUmADMSEHs4EAzM6CGT/NorJjww36aDu7B0MP9e0AhVTxAhyjWxIny6oybXyjDxBZAUSPTCUTEqDqh48WCKesyQHI5Cm1ixtgMO9Ex6TCGGbKlBnoBINCbSm4Lai9jkj09PAKgv+DDi1qcojMCX2Z0wmucdaRWMtBEjrgt0r0cP+ewSd+n4VJgr8XVsiLevfXMvwLaPVviyxsCTdn1MBG0tM7HojUDsWaSBW1O9T/9sANckxOwhifwcMgJ3ZQTdW1b/q92cV07cAN79Za6A9rB9gwLkNyngEXN5+ecA9rJfsd2Ol93c0rmW3wf6+OhtveGi9hth9gE3LtGLAW8b5W4B8HCQ3vgcHdf0iuvb2DgwNsACyNfg3W+ILUv/eb9f0hx8LBwpSf8cCGt7yYCMMAeQU4BF7fGTG/rYCgAP1D+tJX9jiW7DXftYGL7EOy/C2fLU15oqyrwj7AWw76k3+bACl2xJrm/9+IMSsbdfahn4U8FEQWaUMmrQ6Bibfh/YOmCXQAUvTJ422S+QA9Hgm+3NxZ0/78/FoVx1wM5//BUDLw3AuPUslL44IDBysQ2W4gVhaokLTc60xyu2Gcruj3O+IQ+Bp4Mlb3zUWlggERP2zbhVjv1UmcIjI5wvofEYLMvCAtLjqQKJ7KxJQ9Y1NjLbjf9Z4IKa3BaLwxZ/DsObNAPbhHQmeY620zd9JqQKkMNQ3Y/QJ8uytsgScMah8EAurC/DiDLyzXsQ/mBumOGGeZglym05LhwFn4z4TzlMIhJxm2FAfAajkvqsCv/J9EscZ0GRDwAxw8PObug3mpFqdYQKp1h8pkAnq53zOCmJDnkWYVfJ5l8sJKeYHH2BWHELU9ehMWIxnLFjPDdW6bawJxAhGd51YAaulsC973mypF//MBv3XFByMj1HtUNfKJjWbPAVDWUUUkLIN7OmDYnIUpqLIO8m+s6KF2LEL5Oh7NF03AbGtwyKnrH5BrCkr8FJrRQvSF8BRdPS4NtEz1O6yWqrKcOjuUfs6jqpSYQxwQwgKyMSI/5+6d2u27DjSw76sqrXWvpzTF6ABgrchh8OxQiOOYizPWDG2n+xH/0pH+EmPtiMUDkXYDkUoZiSHNSOZHFIkQXJAgQAIDNB9+uy916Wq0g95qdq7m+/0YYBonN6XtWplZWV++eWXHFSDMzZQ0gA4RLj+ZjIwu7d3DREDRUTVhqskgBnE5DH4ecbKkBHJKXFGASGNIMieJZAniRblOOoHKawwGJEGGJgMABQksopj6ApGwv4laCsmZDioPV8QEIkwDtpqSwmm1zgkHQZmdgJ4cWuICSFq8YYErJqmnYoNVQyJ8fzpiOdPR0yBMARgHID9COxSwmFi7AZSPxFQWkMbgIDHc8V5qaggbEzgMmGIA9ZKmLeKdcvIywXzOWKoxdukpQU6A1E1583ndd2G5k8CwWWg/CRX+2mOEg60W7xs8TszhISijDBhpxVPmE1uwAb1VWXMpRibP2SCSCsUAdOydC626eQaY5Iw5JMCgKS5pUkiBAXbRYaioqxri4H9ODUAbXW5I1maNnDRwPkQLbeR4diS8Qi4L+e2LY0lFhpRaZy0IeM/f/JzfPzRv8fy1Rcojxfg8QHzV5+CqNpSAhbnMCngaq3xusZo3YMAfDjUyNIdxCbNo74SGu/mbXNdUHvefSef6ALL/rN29MPdE2zKgtsyK0gse7rW4nvf8gXTk53nGXnbhO2qQ7jmywXn0wnTbof33n0BIlKAdQGznCuiObsD14rXDw84nc6idauatIfDHtMw4nKZdXiVtprXiloFOHv69LmDsgaOmlTBsiy4XGY/7wBgTAMOhz1iYsQwiKTVlFCyeuVOe1tigiIFCsUpvEhYGY/nMyK1odohBu+aspg96Xwcok3PKI0ZVPZht9u7ZEQIQeQi9DuM6WpAuP3eJHG2dUPOG/ImQG5hxrZmVF67/IyQs8o2hKDdFQnjlLw7Qvyy+H8Hc4fBi2UyoFsLXHoNhPbnbdtwOS86YJbxeD5ZdqmxZovnLc8cFGC275Y/Vz/HUxJt4+Px4Ox2u9ZlXXGeL0IAIMKqe71JVJg2bFAtYfaYRe4raTFH/hkneQ7y/XKdWYd95XXDum7uO4RxLHOTgIr5008xjjIsL6jPix0xhZLsk8N4hDC9DegXez2dTpgXAR9Zi13n88m/7+G1AMAhRIwKfh4OR4z6O4vprLhTqxQZtpJl8FYuuJzPQEcCWheZyTFNe6REQCUcdjvshojz5eLDFkXLWTRu52VBLhmPW8a6Lhi1mDqOE2IafEip+QYbxidnRwVYigum9Vte507nXM5bsxOwdAFI14ec8du2KfBa5XxS51hLxrYVkZ5JodsnjJhG/K6f/1+AtC3plYMmhIBaJLDzxIU1OaxiBFFbpFSKVNoVq7W5BKAWpECYzyfRkKlBJl0jopbVpbTaEITQgl+GXwtImE4LMXbDTg7KWjzoi2SHKORNZC25HdBFCkCSOPNnT9/Bq1df4fH1A7786nOc5xOWTSb4xWHC86cvcH/3BAkDeC2gSj4ARNoyC5pwuxieJJuiCUQIiDTgeLgDOOP1/MqHBW2U8dmXH+Pf/tW/wv/43/8lfvCDP8FH90/wf/xffwWuwN3xiHdfvMB6OSEm4OX5gj/6wZ/jcPwafvrhL/DX/+Z/xz4VHKaKP3z/BV4+foVHURaVdiwLPu25htZS74AhtWTS/k6qxwnbtl3ZBiBBbLXAXKurUpE3hqgkMJY0vpEw34AswmaqDih4ggX2YNmCHQNTBIDXqX6wACr59zggXKvbrEWOjUkDYWyDPKGS9xawsY+6a5RLIYBvmD3dzy2A2a+n37OucwwAIyIEVtZI0+rtn1EPVhGRC7NfgVIgZykYOA/HHhUIp9BpDrcf/1wDcWv1a7kGPdtre8DI7KjXeRFbo47Ja8F/fz+dXXELPu1eLFG1Z2jXBtcCM7CUPVA1/bG3PYfmRxqbV8hAjYnwu8Cd2+IVV0YlBlFj7bwdTG/BfY8KtYIFK0AVJGkivasuQXoTeJJ7scD6lrHuTLXePoLtHX7j2V0B1dzvn8ZEeuP+3/gMuVc7SAnXwKGxTnrQy5+n/X33DG6B1jdAStyCxS347W222e7NfdyAyiJPsKHMF+AyA5dFW56gFQVGZAkqAUZdNgREUFjBIWEtEM2tyggsQwu4iIagCOAC0XQFydqSqzOXrq9V0rFia0lvyn74ftE/v9VO1Xn6vuz3PrMOsFQwWN9fuUprccmIFBFKRZ1nUAwIo4APKBXr5YL59SPyMoNzFsBJr9OefT+oyv5dShZ9NS5IUZhNhdvgNg4BJQVMhz3SkyOwn4Co0jcRADcpHZfHMHd34yft3ozV5H78xqf64vh/N9BSEpFOv6p7JqZhGVNC9L+2PcJgVNfEYhYWgex18u+BQHtyJuo5DdW31HKdnEtBWufGMGAaduDESGGFTxzXOM1aeQskaU9xwDBN6hfa5HN7PpUruPP7Q3LaVksoGaBow8SiStoE98nG/EyDAP0xJbVJRtThQvaZxdg/oXYTn7VduTv7bJhJ1bOj6XproU6BPzu3ay3IynBrskEAMxl2oqAad2ebdFeZB4rj4DZibE2ZHC8xg05/EQA8dN0aBOQq8ccwTqCYENQfViUdRJVHEYBaNSuD6txy8M8Diw6wMXCbbELUO5diQC0sOnVcsbjOLSOXrLGTyiXZcw+2/4yuK58fyIYeCdtMzrPiYKQUtyqGKNcd/DO05VkB3atzVu0pxgQBxa2gLbIF9swBaRcN7pKaz87KOhSNSRmoK23WAuDZ/vZWekoe98ekz8Z9vtmpPVfJMxhVEj0dTAwF/wJYWOcUVIJA93RIoo8bQ9OW1PsuWqgjIj9rg4JVNkyNiEEQ8Jw4oqwMSkBIADFhWwsCA/ud6O2VzNg2kVWRMErg1lqF+EGREIkxJMY0BuSNUDeJw8choqQB66LxEAhcRfdWBsJlFNb1ADrmm6zPMEjszxs01gwgJO0GaEVea0u14MGmlhtJQHJHeY8X19dV/GoW0MkAQ5scT48CZrD6whi1gBgCxiFJgZRFcgCAn6Hrtmm+Ip9FIWDNm7vtRFG0OfW9lvG4BIxuZoOqBTgiKUhmyXdCKDB5P2M/Jo0lS9FCiIK8ZvdRC0Qm+VC2DY+//Rhf/N3/g3x6Cb7MiHlBpAoK1YtSdpZLV42sqZ/xCs7mWn1eDGnsWPR3MjiYlXhi8XeTIhS2eBJAS9eo1tqIUjY0Tq9BOgo3MIlfjzrwy5j627qiVB0GRaLRuS4Ldrudg242ef7dFy9EHqcUzMuCy/kMIsLhsMfd3VHWfN3w6tUrXC4zhmnEfn/ANI7KlIs4nwXsXbUVfxxH7KcddvsjxmkEAQ7OCSDbQE6AkQbRrw06EHxICUOMADFqERDRCn95E7Y4+/tlvebl4l0A9ryKAd4sBbWoTE4rLqzrimVdVU4lqnxjh7nUokOsGvBtRYVxHD1H7IFZ6/AwlvG028ne8C4MEq14iH/IWeRa7Ey1lvd1XfB6PV/FMuKvbehldVvoB2KmcZRuZSJnk+52O4zjhCf3z5SYxnj6/Km8phRsi7CBSy3uC7acMSvYZ/mHrKsUg0qpOBwODt7F2O7dhskdjgJ62hkv3dfGLm2yheuyYZ5nzJcZS1nBfFZ/LYDtugnTM+gZtdvvMWiMABCmaY9p2jnDGQCePWMvDIoEwYbT+QJSJinMl+j6ylAxkY+Qzi3COMhws90oxTeR5YzNvkrB6XwWdnNVcHpRbdfttRQ3NB6fphEhqKa32kcckg4LA7LqwZrMRNk2ZGRs64ZxHLDf7STsCcrEh2A+4zBqF434oE1Jmi5rQiTX+PAKx7snzq53tjMRwMUHpw1jwjSNWNcNLo+i0ivG2s45g0vG/rBXO58ASOfFSKMXCJLlVAQklcsxuVSJT8i75N7283sN0vYJngEk1rJtgIuxEqUlzABQZS9oqiJ5XFHmFfm/M1cUymDaACQRPw4VCAW5KuMzkAAnEDq7JA5K3VejGKcJpWTM64wYIlLUwFEZjMb8kGEUBuAIKGcVVRRGSnLFMQS8+uoLfP7Vr7Esj0iJ8OzpPYa4w+H4DoZxFP2kXICRtFVLpwurvIAliQ4ZKOhJQdroEAKGYY/jrmLNjKXOiCRgYE4Vv/zsF/if/7fP8F//F/8Y3/vmt/D02RO8ePE+StlwPs34sx/8Kf72Rz/EZ598hm/84Rl//W//JUZkfOP5hL/5v/8aX3z2G4Aq0kA4DoO0PNWCpW4IKehQluBDo8SJWfClIa3l/8o4y1kmFVowBBYtRiBLriK6BMoENVApSCIPa9OOMI1Btv8pnsh47QAAIABJREFUk0MCWm0TZaWx+/Jp64cmV2KTjWkKqMaaPl5hq7TgylvcqrY/GjitB6WYmoIlZtE6xI653wutRbkNVjFtIdExk+uDJ0o9mGaTrA00cd1F6H+b3XSAlZ6ewqxiSfTbUIWOBaMAhIiOq56kJvzG8rDR3xaAGzh1DdNeJ0g9mG6v7QHnCu7aFdl1pICqDOvqQMMtiH0LvFkg26+bfY8AsAYCS9DEgYyMqDehtsZdAqnrKlOqr4E8K6BcXQcay+8WvLRrMcAVaqc1dOwIbqza23s0rKz2IFK3tgaw2RR5+CuuQVF7NlLNlcPcvts+5g3g/HesuYNb/kuxI0+WFPiJnXbz7TNqa0huX8FZ6woIGBPXkx92W7p93q4J6+Ap+RJdg48O00DaLeUYkgFL8hEB1A2iowYYo/hnw/wd2VmzAcsZuJxRLxtQhDEKPfN8aGIpfh3bsiDWisQMnkawaW7WCi4ryrqpXicDQVvLQ3sWBhhA00XXjAZQmB3QvV4vswF5fbB1USNgvTZL8vqBbYEbwAhSEFAdaPHXBR/MJUNrGFQKaJkRMaLyivlywTbPQC7gRYIfJkJhlrZhDa7M1sx2Zf0YFcV1eQGSYpUypwgjMIyohxF1LwMCuBRJ1HWtyDa/JY8sRbaqw01shUVzMOi2NSZoa82UZ2DA/bWcCBvYx9YubsO62KxYCmvR3oMbm2aAImphb9dMaUBAAwRsz1gLX1V/V1G1JU0SK0kiB9ghY22q1uqfiwxd6ItN3nIcSHXxYgfISWsbgbCuGyoiqurVsgJWwlyQ6eVe7AIUyLOJ7vK7ylmkdYK2uKn0B9DagsXNMJRCKp+lYAR8oIUMKQoxYpom9UMm62BtmwIuMkl7vhW5/DtUMsH1WENQ0Ig8niUSZprck8SAAuSrVIMW8InIz35S1iWDoIKlMuBDbYwqI6URFBKM8SZ7QOwppUnsQWPYqkN57HW5KCPVVo3t7LABJuT3krSDYl03seeo7Oxa3D8012r6rLqnk7CFkurmWlylWwOl2neLrygGZlEUli3M9zcd2qAFBOjwVdtX7drbexjcsYPVTgmQ9js5u2upSJBnaPI8rRA9XCXb9kyDPg+xM7OBdiZraiD3WyzQBbaa5brZBpOQjI+lJjXhw/NQEJlRMpCDMDY1ynefEgJhLRJLChN6QFw2megdAtIowND5ApS1YpmAKQXRN6SCMQLLDKRY/KyIwfybFSsIW65Ala6DnOXMzluVAS5rxrKcscwL5m0T5jJLHF/zhpo3FM7CKi1SWKxayTC5iZQM9GlsQJZ+CcitkoIqG3LJumfs3LHcQAbKVBajIlTkTQpDxHI+VTBKFpuoJJrdgQKq2mzeNlCR/SZs7IiYRlE8GeFxVFVdRtGkzbBuDff7IAwptvPU9rWdIcHsVPyBFKfIwk4tyBlA1xGHSpVOLyJQlIK5ug9AgSQjHAWwDjJmlGUFnxeMdQXiilo3Qes5+d5l/fJKWnzirjtGpasoMEDSJmxdc+Mg0gEyOMreE+DDavUzpMW5+j61wZpFC0FggGtAQEDJUoyJei/E0ikUIEAgWAD4aZqQhsHZnofDQc6/eREghxn39/fY7XY4n884n2Sg1zgMuL87YhiEEThfZtELBfDOu+/gcDwqyCOg17auOJ9P2I0j7p8+lRbtTkYtbwvmedE27xXM1v4u/mqaJux3O4xjlJhEAbXL+dKGeTJj3VbkUlQuUXyQyGLIve2mnXaNQoAvBV7NP1n8GFPEou3m4zTgjo4AS0dNrXb2Wvwube7LJrq+wkAcUHKT5bB5JQCcuSzsQiMCiJ7yOGirvcccsqf3Q+tkG4ex5YgMzMssBcQsLFlhCwueMs8zSq1Ylw2lzgoewvcS0HISOfeuh3z1hYdxN2HkNmjM8vVSC7IyPUGEZZ1RNinu51CwLLPIoVC8ismrFuxCFAmyaRwRkzKiTTtc45GUEp7cReksYRl8eLmcPc6opSAXYSNTFeBRho1tLoMTU8JuJyCjSSYYW5S0+3Oajjgc77BuK8qWYQiHzAsQ8P/xdMI0jiKbEEIjxhl+BmCYTH9fvmt/OOBwsAK57O9SsjB7FXCflw2Pp0e/Vi+cBimO7nVA36DF49Pjo5AxggwWZa5azMrYjVIYySUjlw3bKudfSDJ0cphGGe4XSHx8KXgyDli3DUMaMF8Wt9U1Z2FgV8bpdFYWt1yDaVgbeFtLkdwkiIbwPM/OIj9fZvVbNqxQ9kHJxTuZbF9WFiZyKRV5FSb07/r5vQZpLbCxZKNvpa2dM3fASQMRQym93btrF4dNJtbDZi0LHk8PeHb3nlcHMsMDHiMU5G0V0AwCdNmitqArOpADqPxCxzSKCDaAXq9VElxrJRZAkF22IYaAulXsxz3u7vY4Hp4h0g5x2GHdVKhYE0Sp+GrCphNPWpKmySEpSKWtilvJQIxA3CGlDfO6oaKAibBRBdeM3371Ej/5xS/wwTvv49mzFzg+fYZf/f0v8Yuf/gw/+ME/wve++2189ttP8L/+i/8Jr08n/Ok/+h7C+og/+va7GOoFf/+rX2G8P+Dr772HtVSclwWn5QREwswFlyqsDQRh/wLaZkt0lejImktgysSu4yTJcaukN/DEnoto4AbToyUF8NVGJL1tQ5BEHsLWLEhCpAeFraG1JIuFGVDVgioHdRz0uj4segDUnJy0d9k9sME4Dipa5dha85kVRLAAj1iGMqABRFlZSU2vSO1S+sb0nkKbQA9LuPXSO40U00yzxORqwj0sYDTAr4F9Dooq/uZtWmgADxEULLN9JAFW9QvR51+bfiA6XwAiv4OeFWvJmcTD2tajNtM/D9bNSpa8W2GlNtvzABgdOAdLJgVBMg1QBq5AJZM+SZbY0XU7uAVD/fCgtu7tOq+AWRgQ2voOHaTw17TrvgJXDUBT22x2yv5+6VawhKLfUy3BvQI0qWmTGcBH9CaD1Gz/bWBv2xMKTinASZbNs/i2fghcX/xo16XJGBtjEd17qEFatrbKurkGlEVf3NZETaQBjDdrYAUhBmlFn1AKGkNQ7YptGBzavRVjS5Ex1URnqc6rMGjnFbwZc60ldPY5Zvsg6BTaijCI9lKyQVLbCpTi1XNpgyXjgsH2oa2pmomfq/aM7N99AB+g8gkI4nwq6wDnFhijWytfN92H+pjbXrz6EWdX2aYOK9uJC1IpyPOCXArWWae6KijovClufuO24GI/1vpaanUGUiAFgyGFlXG3R5x2CENCgQE5xnCy86oHtQ3oubZ/ZrPjtvfbHnrzjGj7w6ywAYyBgkzVxnVCxXomWkB49Tm13X/UCcR94crfq9/D6uecSQUgxkFaq/VcJdcCBVp7fEIiwJhqch3CcolBQFVCAGpLhmKSBN0G+VgpMsYgWIHJc3Q2qBYCQJl5MAD1uv1YzqJmt1ULpTLBF14MYq6qA5sbOzeSMleiAuxVWbviJ3o2OaN1TtVaVQdXHl4MphGpLDy3f3Lwg5QZLNgS+Vlr/60mLmdmlevo/bmAXObnCLWuIGqMSqD55HVdvRVPXGzVgpaAXpWt80qLOZp8lCqF/KDgXFDENcSI/SHJkDKWAuW2bShlu/LRcjaYqIn4BmF9tpZtCxhMDiVShBXU7fuAoKCu/KdPXoYBXmKbYMIwSjJuA5CCFeLVDiSub4VGu06gJdwSR1VQJRRk913lymmR3oPsISjIbeuOPv7r97gBvl18FDTJJ0TRHoeXAuV7bA0DHPwjCl0rvAHHJuElvj8UGQw0jDtl4Y4icUIBmQiLDzEht981B2yZEQMwJIaxpwMCtk2uDlUGZbHGWEOKGAphgmgUn8uGOWyyyiTnaagEDlpcYtU9ZnZpCVb7AEUUSEGN1D+LT8x6rbIWMQZUDDDdaNMerKX4eWaSKkQAKzARgg0PivCBVHpG2WAhi/egZ0MIjMyi2diz7YHgAFXU4g6tRsZQH8nW2WNSKE22wsBEI5QIk5zh8wIAGSgHuC1JAUwB2EFtjYAYBu/Q6vNVBhoYGnRIHwKYBQAbAFkH2EyIrjir/qyd22r56u9FT5t0lgsB0JxaASHmXhZLznYZkm2xQfUJ6paC+NDdKx+udkLAEEe3+6T+h0vBqMCKDR8zZqUMIlq99TvGiFevXmFdRUPz+bPnGNMAcMX5fHaQan844Hg8gkja1s+nE5ZlQSkFKSU8f/4cT58+xW7aoeSM8+WCdVmwXES/NkRheN7fP5GJ8ArihBBwuczIZUNZMtY1Y9tkaNW6ikTMbj8ihIjD/qAkGFmPSE3j+rbYW2tFXldUku+wFvpSCgoX7HZT81y658HtmV49V7XXaix1JuQOpDVdT2b2dbVYJ1SRGXj98OAAnEjZBO3mkULeOI1gMKZxwhBlkJz56xgCkg7gMpmIECIOx10XO5Ffi53Ly7L4eWdgcttfrXDqOrAUXBrDupfSEHE8HqQTLQSUelCsoMWzy7IARNh0yNmmshzMKp1SK5aL6BKnNEiEE+SMGqcJ+/1ekm9IEZ1iwDiNch6rf9sd9h7L2j2a/MTlcsayXJCzaC3XykgpakdCYzQD0lkU9Z59HouWhrHbYbffez5q2szWlp9zxpYzLssMi0encVQ5BnlmInnBLkPBLPIOu/3O1998bK0ZZSu4lILHx9cYFMSfpsmHWrdnobF6aUP/oPHjUhesywYFArQQ12IeUvs/7I/Y7Xa4O7Jrzo/KnuZNNGLXLLIRRITLfEEpBdM4YhxHXbcBKSTsdnvs9weRNahFCoRbdtmxbduwrSsYcPsiIoSa3XYkruI3MJX+5/capJVqfANmoYeYTbe1B9ISm2D+QzZPbcmlfJ78SOVUnM2WFzw+vsaLZ9/AMBSsi1SyJYDsgCmQJzbAm6ADoNpnqg8ZQ9QBLT3rSlCwPq6TYK+BMMuyIMaI+7sneOfZB0gDYxyiJjfJHaHVzA1gAKR6C26MM0vebXq4JxVgBBQMXDFOewzhOfhVAdcLMm8oXDERIXLFs7snoqGURB7h8fGEr159hb/9D3+Df/In/xi//eQTzA9fIjDht598BF5e4+6wxwcfvMA8z3j1+ICv7494+u67eH2+4LNPPkaNhFfrgseyYaOIx21Fluku8owKS4bdA1qlIKTYMk0DXdiCA7gsRRuEpcksm44cIC2fVYMv+Q3A4NoSGJtoz2BJRqO0SGm21CU8ysSqbbCWX29vt5299GCF/d5RTGiiyBA2DKFpqko2oclXVZIIOThktYnKKj+Aa71MB6FcL9ZAMfh9gdsgiqtrRFExer0n1kE3wSrWnYOx56H7t9e1tPdcAXQOPLfWiT6A9PXswKEe6EgxSkhvAIUiGrKEEQ4eGmP5LVBQ5da6JYEjHESTpRdgv5cgsDWNMaovUkdbO8BY96dVZA1U6w93bwvr/Ei/PvYcroBlbv4iRvs9fD84pEPXn2G2fe0TtXBhz4MhgyJ0CFAP4PXX1mxZkoQeFLLEub92W6+33dvbiheMpvNsrwMrQ7kDpew9OWcNKCyoZw9mm6yHLMrtPiTg6nvkthsD11YKuHmf2QdfPzPTknYHTPbctbhE5rcBQBhcFAAqDF434DyDTmds5zMEdjBtaqgF2TCiVoCqsKnmAXnNSGEFQIggUNUkqVaVHzHKf1X2S3jrszGDYLT9CVzLOsiz1iIVQ7XA2PePDzN6y08PbuHWLqkVZ329tC2IMlA1iOJadcK8FNBsWEz/TA2gsYJV//3ORNb3RmVvEgIQE2iMGI97xMNda8nWyazGfmrXeT08z1hTt/dyDdAqO0oZCOavzCeY3Vkx+gok1ydsQHHzK22wQ/XvIs++mBujEOhZWxCAQ+2c7Hf6/SGItqkUn6IkslrMdJuw9fd7bp0ishUsEVTWa2WEIsBDjINcT6dt7RtMFtXXO96cbSCSJAoknyMHI1JMGJMkDc3nFu06isroMPkD3Z8KEu0oeMJUsiQpfWHItFntmfSgmxEESqkoNWNIo1xTZSW+qj+BxKNgY8myShsZCC1rV2p3jih4GpmAAC9Wm7/yY5AqYgSotv2UUhKZkyLsEXvuEl/D94JaBhAIiRrrN6isWAw2GZsc+OLKoLyhGNCUc6cl2NiuZo8MndqOxsy98gtsxTEFf7j6Wsk6GeDE0gbObaBqik3PT9bEnkdxcN7ce63NV8h9k/9p0knp8joDnnAVK7U9q6CWngtZ4x2TXOn9LHf7xDTyK1h8jOn9QkK1GKR4HyRE9oQuKgvNBnHKs2w+ybqdUKsANRSQ0ohxnJCmESkGjCNhHIDDjnF/kFQdhRFDwdN7wm5ULgclDEl0alNkl1PZMmFZGZkjmAi5MMY9Yc4BOFXwJQMrYSp7rLUiKZmEmIEk9h0RAWW4ettwiqJ9a8zpIAODuMpZBwZqFYZqTFHlP/RMs9igVlTVjEWwuEuiMAEYrcDCmjuQn3UmkyCLKc/dCiQRwbv1AGhxT89ktu+BfoZ0XYxRCxhFWv/VcGEapHZPvdSBXZsd1yJn1dj1RjgwvUWAQKH6ILFSJNOrnAU0DeI/csniy0p2qQEKJA+6Snwhsnlif9TF3RKCGEnhJmZzya2Wt5gOLaDnZoEXgyiQ6KvauaHOyPxDLll2o8btgZo0jrxOdYS7mHorxXNBhrAwwSygYQDm+QIDEqdpkiFPlwtqlSFIh8MBKSXM5wvmyxk2MMwYdaUUnM9nnE4n1Cqt7sfjUQAclRn47OWnqKUqY5YROOLu7gkOxyOiDXWCyJmUWnC5XHA+n/28ZEQMKSINCbv9HQY92/f7PVJKyGVVP4erQbgGOgFw8FR8njy7Pm5LQ3KguMdPhMV+XUA2e0wp+eusI9DYqDuVMzCQzUBA+z4bkmQ5xfly8evdVhmuuKwLQiCsy4qgdi2evv1YR7IMx5K/jVGAxGnaYZp2PgyOiHB/f998d7dGIjkhtrCoPMW2COCZtw0XBedDDEqcYylOEyEMgzMlDeB1hu5wLXEWQ3AcKOeCeV6wbRmVhWXPCC6BwbVgXRaJSWJwctaYBtEQTkn3AzkAejgcAADPnj1rLfjMzmzeNmFh91q527pi0ZxpGAYHPEcdlCg+KHkMaxI5BvLaHshb9mJiLgUlyzpasQOAM1DNhsZxdODXXmvXa+vQD6BjZrx69crlKuwsrZA1TcOAkAKOd0fsByFb1FqlQKJdDIbd1MqIQTC03W6Hw/Eofj8Kc5bigMPxoLmndOQty0V1hKszm4kkHgQB+90e0zS5LQzKAhfA3/RprVtJc+CsgyQR3Hbfmnvpz+81SNsn4v7foU2Ebq1LkljJTwdUaGIgoKk4/sqbJB4s+iGowLycsC4X144gZb1aIi0HY/QAHZBNb1UdAT9kAIQdJsV0OtWxh6ADw/Qq+6SGqSWMRdtrdvs9nr/4Gi7nB2mj0+otgrCfMix5kVAhhoSgDEnWJMEdqWm4KCgQEXA3BnznxT0++Pq3sHvydfzoZz/Hrz78Cdb8gGU740kccDwO+O43voHD/oBt3jCfH7HNZ/zFf/VnYBBen2Z87dvfxhevH/Hqqwf85sefInHG1957F4fjEYUIr1894Oc/+yn+yyd/gW++9wGwVLx8eIllW7CfDvjWH3wXny8X/M2HP0VmYYx5I0xnuMwQ9rAxBwAHUqoGRrUT3oYBkBZKUYC1KRoLwwJnk2k0sNCn2GuSUEvxQIUABxGvk+1ms8b2eBPQacFEf2CCNYm1wEaLQEFBP1uAnllbFVRoQIGGnpbXo/9OeY2zcbm/XuhAIGjwJUm1A1saP5nuLGtSZYACwZJE+L1C3SjfgFc9uHgF9nUXRLpnrFXIqtS+thoB233Z8BL3DwCI5eBgKjB9QE8Ur4A3uI1426qvl/3DtqDXzwytTblaIumAlAWP1dk9BaxAAfvnNo3ka19nVfCe+XULZjaw1sCh60TTXuvsnN91CLA8Px9apUAA/Pn0TNXrJNDW5PrZy4eym22XLN5cW28H/TVKQiA7N8ToyYjZiYH9VwW8/tl16wDqWsjD9b6zxMOSZb8fkoT/qviAbm9DExJl1VEgX/+oLXuR1U6J3C/Ze91/qW3lUlC2gu18QT6fwZcLQs6I1Rj8AmlcyaawgU5tKFuxZCgIMMvr5slgMDurXUGCRB7Fqua3a/mGqXR7tq2V3FExAMOQPQNr3/IZV+Cp/AG23zxppgZetu9lHeolRVCojx5CdNafMZJboUiWOXSAil+73ku2wlAUYIqYpE44BIyHERgjqrKTGAosWgt5t27V7g8NMLkGT8jvrbEqr884e43fM8LVPrna49D7peZDgp6PYAHSYr/msQfKlF0TbHhI8WEK4OBagfZ8WPdRCoN8bhCAyEAwu3INQRyIsBOq1HpV5DPWfEW9ev8QI6DdICC6Onfsp/ePtiYhiC5nO7dERzKlAeMwIhBcCy6F6AN8QML6YgZCiu7teztFVYasAhliS7KWw9C6CIRpZOxMbwBAjKMzwTlwK7yqTwuIXqiQf4LvDRuMRKpDzZUdlAuQ+KCyEQnghWpn5eq1KtyDrWR9DspIJSseSWG3ltogSgUAK0ilBZoNliqSYFYgtyG6JHpQCJEQ0yRDhkjirJgSuEKHKcnvUggOVEH3lvm05h/s7NbJy0wIMQmYTeS2j2DarFBAPQtLxe6P0UgOZLIhuqf0+Zk994Nb+nio9xs9uNG6TMzme/aw2ncIPhDVfSBUp9HlioKfLUkHngwpastrVTsX3wdPfttake+ktldkCaV4EYcBMQ2IcYCYc8CYgMNIOCZNQAPAVeyESQq2iAmlVMwXRgoy2JUhhILKMqinFGDdgMfHgsvGWDdC3iIulwXrtoIJyrQuQC6evKpkrsqZiS2JLEE7J7msOqixnT1bFWZz5AaMQJmZkbXgEqoUJ3VPGuNSHvj1gKNSG6nG/LDpChaPwayrrw+iqxfwrTOuaCu9/HXFsq1q07LmgDHO1MVo62ugeGM3AoiZNACIEIMOlNPbyKHXVmxnaa14w14LN5JQrQyqwnaPKhNSIXlWMkk0A7SN2KL32279JiaGdlWQUhSK5RbmUy1uEx1rYzEjyPMzcMmL2rXrrmJWPWEGauskCCCMScCmsmUfoldLQaSAOEbEFJxNedjvHaAVpiGpXqnoqz48PGA5XzCOMml+t9uBmbAsMpFeQN2C/V7+zvKTeZ5lANj5jCENrn17d7jHEAdkLQ6WUnA6PWLb5JmlNKAUSAt+GpHCgGFUXdphp2sMbNuKx9NrAdx0D9QOlLMiHNDi7pQSQJumyuTxsA2d6skTJRfkXL1F3kBp85lWQHGwtvNrtv/67hRpXVdgM0RdK4kZpt1OGMpsJBHGtsmzELZvO8eNyCL3mHE6XUA0a/gsMbC4Q9FKtXXv96j5817i4HA4ODgoxbLg5CoHIvMmXDEtxi7riu18Bph9xlHQrrU4DDC29243IaUBu2kCscikhBBxf7yT9QqMdd1ci9r8TN5WsVOukjfUijnL+m86iyCliJQs/mq+xM7nEAL2+0Pb8/o87Xn3nUOrtuwvy+oAuJ3HdjaKBq0wRw2EvzveYcubD99b1hVcGVvenKlcqzDRb3NXK270RVnbR7vdzlmoZnvH41HuX38X/LwWHedxGr2TxuQ97nejAt+My/ns4DipL7ycLwLCJxtoRlq0HPXz5Jx4+vSp24MNk9y2jFrkes7nMy6XC4ZxQBpErmIcBJiOGiuGm30zzzOYpytA+m25kv38XoO09kCvGHWQY8OZCNySu5aAEKTCnz1hFI9iwJ3CgESoEK0PZmELBmIlcJIGKLUl3mQTV6sbvVxngNQcq+tQAbbhq4IU4kxsCIP9NCZdO1CZZGLc8XCHsq1Y11kTVGFophARmF1Th0sFR0mshCIe5RALAdu6ogZt3Wcgsgxd+Oa7z/DB0wnffvEC3/2Tv8AHH3wfH77/TTw8/AavXn6G9++eSNVuC/j3//FH+PLLL3B6/YDL42sMw/fx9Pk7uKyMd158Df/tf/Mc/+av/h0+/PCXeOfZHT7/8hXWT3+LXYr49ne+hecvnuN8eY1/+OxzXNYV58sJAwREuA8RX/vOH+PHP/s5zlQFaKYettMAnAxv6AZ86bOVVkl5ZsLqkkO+2Y4lNrpGhVELXPOIqWcnGVuF/ZCCOgNUlqFsRH5gvQ10FEDpGniyqp8AwcWD0RCMtQ3XsOFg7VjSNnh1IBp4SAoUWFIIHRQHcifW7yNAEj5jFHlYpZcVlEUkzNbq626sOAOwWQMqqxY1sOga/DATvwIfqbUE+7O9uUZfPw0K24RJZTpoBnwF8hogaUlUkISuevAeHfi7BfQY0Gp0dXsif4+AY5aIwp7h7fVqWtZCewFjA5MXewwsws333yZytoa3AG2/F67sH+3+r9ZVf3dbpbNEw8AiGVQn1+3yMMGKBvZZ5otvQKkbwPPqWUdpnzFmEzTI7p9xf53ynMIb92vXX2/2ff+6Wqu3cZEFWmSgIrU9ou1K13Z2AxqyAXt8db2iNUleQBE7bPZDWhSRPVRAiG6PDAFPimq0BbUjwRULQlTQY5tR1xmxZCkOdcweYVQ11qQFQW6LzKBaEYdR938FqkgRSFWYdXiQWCPbNXTPvAfJb+3pluVmQaU92t5DwQCDbl3d0dzYZ590Xxe8Osih+xwr0lg7ExOBUkSo2pqs7+XuY0y6AFTVlqED1yR4zll0qkiLazHKgKiwGxB2BB4g01iD7PXAQdhULGwYi0UIUjwLdvbfngkMj1F8rX1Zrvc6IYiOolbAhPHSm2WTVCCWPUbeWQH9swFFjDYpW8C7FJN+bgJDErRAEUm1ZkupUtTUfSTXw2AqYlqGQqZuP9fGIIUNn9JkRhi9NuRKrt30WwF4+yBAyMsqAS06DUpANXLfZK6a7ycijMMg9l0ZKSZM4yRdJlyVqdiKugzGtmyeEBprr9UaJL4kMjYpKVNcPboW3aq2Emv0ICCc6WgqAAAgAElEQVST3q89j6y+xz7TbNjOc9sKDFg3ORqYb7IkkO8M7VoCyVnlLeDU9pewTjOoA36YhXnGtaDU7OceqRSU+UMBaapenbGt4Ostj64x+oWd2wgL9pyGlPTcF2P3VkfA/ZEMpIHvoajgeQjakcJQoFhXOUSEMLinsPZSroyUDLQVcEcGxkIGf9V2PsUgiW4DKaz1nJSs0bXAhohtayBFb3fCRCffXwTANNotUbPYn/TzRUYj+FkTtavL/EKIpH5ITuZoz8LOP/lyQNfXB76R+HuufA1Gp4QQkrSQb0U1bAsSAXVLWM6MsiasO5kCXquAmYWB1+eCaSCMqQijNkgTvABARo6RGymZsWTC45lxmjPOhTFnxrysWNcFOReZA5IzeJO22Vqkw4NrdmJLLiJDwBS88IWS5WtCK4rYmWNAm2iPC+O6Dc/Rc1t9bNazUOwm6wCZCCL1e8xtXoTHThLdiZ8Ifr+iNyM5GYVuAFa9lhkTMLANoLG9YZPFY5KCkWlHGgDh+aB2/zlLUkFOrgVWIDA7IwMuTV+elPkISFzMxkQTpjcp03e/3yGNI1Z053uQgiUUeAKLf49Jz7pyXTi2HczdZ1gsSapT3SceEqZcv998hwC0G1o3nBb7igwRAlv+FFFqwbwuwsQmINQArkLukLUNuMwXgIFpN2EYR8zLjNPj2VmyAHA6nbxd/u5wwGG/15bxinmeHUDe7w+4uzsKwz0EZ8Kav3jnnXekZX8YtKhWcF4X1zi/XM5Y11UKJOOEcUw4HOS7hC0v9/R4esSyvBQ9y1Ig2R28Dbzk7IzTVlSKfj9Am0ZvbD8D89ssA/Y9xAwZyM7X5Bg7N87ns++J2O0RYsaWswJ1zfaHQaSRWDEQ71QN0uZvs1GkWAxlxwbdF/J3BijaPa7rinlZriRM5nmGAcEG5plEhTFnDUDuB5oJ+N7wmGmaVM+XEIeEcTep34UPDrzMF9hAUQMj87ZhWTcslwZInk4nDMOAw/4AAnTdSaRmUkJlyVmCxl/btmFUkPLu7s7jrpwzrLVz1aJCrRXjmJydDACXywXLsgKwtUr6zMXnGIPV5L1iDNjv9ri7u0OtFY+Pj50UATvLOISIZRH/ernMDjRG+yy2QXEBcRD2d85ZC1Dke4pIusRtUN/5fPZnCjQCWc4Zx+PR2bbjOMLYyiapUWsFKuP169fYSsamvjUlkSMAEShGVGZZ0/1e4riwYqdMawNIAQjblkXveVkXDMvgdmf7Oum17g8HHCDxWa0Vp9MJBsCWknE5XXB6PIEoOBBtNmHrD41xhmHwAlBPdrr9+b0GaQFoRkWtfdz+YQFPRMRfq2p6mNbSkiFPHmwRglSAvTJNEbVcUOsMDpLwUCBUktbQYRgd8Akd0ACgczA69ADCnrPprFEHVhEY1kJniYa9Hwoi+vVpwiGAWsBhd0TeNjBnyKAZ0QoqtShl2nTBGFDdsP3+IFPwuOLh4UFaPEiwt0Ms+M4HH+D9J3u8fvwHxGmHb3zzPbz7wdfx4vm7OD3+Fp99+iHyacaXXz7gs88/xcPphPO64ZILTkvFv/ubH+KP//j7eP+Db2KZV3zy0Yd4/dVvcZgCkDd89OnHGMYJ9/sRu+kZxt2Ir16+AnLGx7/5DV6/foVn794jDk/wo5/8Hc4/+jHKtiBOAHOWhNCzpR4ssFSNPEgjADVLWCC2UOCPWkFMB+OUPSLBpX48EyID6AZgaBSsbYLSTmVgelWdzlotierAic4urCXtKiHXgC7G0EAMQXn8MAApQ8b+ztM4yWwYbeK2cScceCPSQ15aLBwU5L7VnhqApRQGY6eHaG1NdidtyI9snQAbqFY6wKVWGeximm9eSqHuHtm4AA188f1Myi7Uw0/a/6QIEaLYtrQHGajWAR3MLQnXe2Eu6KSTXK9V2istMZbrDyEAxTJbOJBcu0quCbcbi715IXMHyp6r/T01dkvQFxrj7Q2guAcD1XitTdzcjbiKBqT17CN6Y4+Y3V07fiISgXQ/OKoDAwautOJXs+X+p2c59QB5DwgTXdumJam4+Sxpx666j/U9Cp5Qdw0ANT1KW2vdo4XZAUmzPWOY1Fq6bos+QbAHR1cSFgC8gtpAFPPg/sivCgd6vKhd2nVAkk0bMKRBay4FwZ+J3a+0H/G6Ii8zQsmorAkmiRKhF5qU9WZIzi0wbs9D1lp1vmvTmizo9r5hPhrk3z7Pt9nnbQucPMTuNe7Lmq8Rxgbe+Nz27/a6t72mB50MCDfWkz2TUssV2O6PiqUl055xKxBpYzkLkIcBDvLlkoU5udsh7XaY7u7A4x7FWpkb5VyTDOt+kP0a0PaVLrbb8dX1+bqKHfqlqf8PXYINGCv55ox5SzziZ6YWbMUHB41BpOWOuaAEAwsMKItXwz8c5g7WRlwEfM4FnJJIHfj3Vik4eIxGPj2X9boYQLTnDvEz0U9waNRrAGyEaSyaWTVbD+7XFN50W2ZWphgRUBgZBbwssL1iTHovwsaIZVmbb7VzFL1dqqairlFlAqCDZWMEpY6h3bk3AVF1gm8g6VYxLeiQbp5V828gAhduTAwvHkMZsF38WIronacB1Xq02Fh/5scEuASiyvHIi2T9hVxQa2lnFxnDtI9fKrgDa5oGufikWkxHUqMM02inCAqDPEv1qWmIGAbzyco0CVEHdaj2rNptKY30ICw0S7gTQhQtQ2vtHofJnyMBopVsQBCbHzKJoNheR/KMbJBdjNLFQ+gH6rWOFNPHs+sn1e00EJtAGIekMWJRhmITULjyleiLu/L/MUbXOzZfXbkg502B3CQMUxbQENBhKcw6m6J6Asmak4SSESkpgyuAgkgfzHnFOA2gELHkAadtElVplqFWa9HTjzccdwNSDNgfAkKoqHnDkJJ0yGfT3iVsNeK0VjzOG9ZccFkzTpdF2lqrdARuWhirDInPqxa70IgLVWN18sKPFs5BXnwHtQJ0VRKN+eLmWS1WYfcXJk0AkANR1m3l8QLQCkmQIWf2OSDzO+0cE7BKYykFcCRvUGY4XbOeS6kISYYq5XVTxjeBSGw0qTzCthVUbVeXAghUzg6gIXVsuiZfY98hrkWZ9iYF161fCgGVJb5+8uw59vtnWKkNBCYWOa2as+YeGgtVSE7BbTDkLchwVfA1v8balUgdyYoa0Mu1xUbX/zbXJvm+EGuk88H8Z9VCZYXIQgS0+GxbN9TM2O/2GMcRy7JinheRyeiAdbln4On9E9wdj6i1Oju21iaH4LIHl4sAdPOCcRxx2O8xTntJqyr7e1dtozffczjs8e4772AYGmhjw4eWLSOXrADcgpxlUHmtIpMhjEPxS3fHI0b1R8IqlvNcgLjs3U2V5VqituQbkGqkhlorUhSGaRxbd0wPRNZacXd356Ca+OfixYN12wRc5DbcEWofpLMRti3jMl8weOxg8Spf5wYkzOb9fo8tb4hJQEdAcJVhGDCOCfN8wW6/w/0T+V4BmMXv9iQG890ur6Bt9Q8PDwKOjuNVgdykFIaUhAAG1u4hGUI6hAAKMrTc8lSofyLdg1l1TU1SaNrtwAwsi7Bna8m4XM5ewGZm7KcJgUgK5SSkmBQjdtMEBmG/33lcFAIaYMlSvFi3LPamrNZ1Efboss4ui2DrvdtNeK0dHOMgHVTjNGEYJC85HO5k72wy+Mu6G8TXMZZ5Fn9ygYY4Td7CimgGwk4K2B72e8lBqxTqSq1Y5tk1XUsteHx8dNB9miYHoadpwjiOMnRLYziTKzAwmFhyroeHB4kbiHAJwYkIlitEGhCHiGGSrjAEy4EKLpcZUuQzWZiK5XwGYPcjgC0p1iA2ITHTOO4xjpMMy1RyX9EOicoFW67YNnhcHqOREHRY3u/4+b0GaRmsWnHVtRQN0JEXSIJO3DH3oMO3IGwmrvzm+5SVCkA1/zacLl/ixbM7jClhVbFlSW5ks5QioBYF0upEY1BuWfQluBYgSSAkjkKCsgQCcat6yqU3RpRVzgnQ75KDbLefpA3kLHqgRaUaCMJUSxAZgxiTgAulKk3/AV9+9Tnu9vd4+uQJlnUBuGA3DPiDD97FX/6zH+D1Vy9xurvDP/vL/wHf/t638PGnL/FwYbz6EkjDc3z3T9/Hz3/yEX74n36KnF8hF5mwOB2OyKeAn/7sV0gx4tndE/zm1x/iV//5l3j58IhQhTnz8HjGV1zx1Vdf4ue/+hiBEhIFzOuCnFdsX36OtNuQywoe9oi6+YiBmlVeIDKIop/VRDLegZuBKKApSahptUGD3MoyFVYcjLwh6LRAY0daEts/EwNpGPAk4RoQE+aJ/HfHJkADHmSabJ+MQ5MGq5RrwKjsEFAD/oq2OQdjFHPTKPNrqw0EI9D1ILughQENXozZY2C1HY72ldaGWoslGtdAK9Duj/jt+qKlVgSWUHGrFYjiuK3AYdft+9YeIZtUSDecQIMrYVgUFJf7kLZFYmvzb1V7omvgw/Y6oYEHNqAlGIOaK2rJMO1jez2p5qRU5jVZ0om2LJmEB4AAOzPLUi1FjeXTuuCT0diivU3d2ldbW4IPJDObIfJ/9z9ud/ymNEL7e1mnWjug1pJ+/fMVm7EDl+Rzms29TWqgB5EtCfXv7uy3f51Jg1xfI6HWNwEt23uVW1pbwVf3YUyjHtTz9bTPcWCH2764uS6GMSTh9lS1de8aENV78KS/Bwob84krIzCAWoRVC0kCy5rB84Z6OQPLInsoRHBuQLC4KkYliP4qFHgjqL5l1BY4xqDsWwoELh0wrp/RKrttuFT/XG4BWntGFrBfgcJm7+LMmj0QXJvPbM7Wql+7W7u3NNBs/9bHAC1xMGaPgG1BS3duoW57ntCjsXTQXQtrbNFsLIBixLjfg3Y7YDyg0qDnEDvQaACKMLdLAwo70NrAHeD6jHG7RwuaG/OSHGxwaZ8bf+kFB2pAwRuyJsq4NNA+6vBEhACtJSCEqCCXgQvqL0kGkujHwCYwB2oTax3IU/s0DUApkOgHkQGsuqc7FDOp/JIR0xz0YwZrIC+gLeSMpNb2aMXAUhlMUmgPtrZ+/ssGy1WBUZJzoGek1VoRB0n6JaGVImSpklilGFUfHyhg5K0oaCt+vUJBT70/7wSA7SE5x7lK55adUbh6Tm72bU+RtDfXSlfnYlI/02xBnpxrQst/yeldjUUVRO5BB9siyPoVXRfSCfVWJJaiELk9uxa7MfQo6n0FRGWXS8Qg1+6xFUWEOCClCcJoLXr2iE9KMcrgqjT6meZt0Jx9PXKXPFtCY9p44KBAknW9dLEhzG9C9GphTMVe+9aGMwUEisIGchAi+DXlXK5AKPOVIp9lUjFapAkBJs9QAdSSwVvriAKAUrQVXtszh2FAkp5aoDRJhitZD+0KLHXwlvharQV29mvlbgXQfWdA9uLhMEzC1isZucogG8k7pIc+KtO9lB2GFMUOSdrYz0vFbgqgSggRiFHBSQaIIubCeL1UXDaxxG0tyFvWqeQKoGpLrCOpzO43LQomL5ZK3Bai2JXZD0NYcqVK+2sMKjsEuQdmKZ7a8w5oRW/SvdADtHJmGRFB/Zlqe7tUC5FKdtTmi8x5AiovJ2CFDPG0c5Fc8zYEGbZ2GwdueRU7RCs0jHHCfjeCIW34cs5UTxeMsGGAiMRFwfMMK3xG6jTN5QvBpYBrlpyRCyiOmPbvAjQBYdUujgHregGK6vyGAIqDMHiNGNWddV5I0+9osUQ7F51x3M2nCMoUBwlxKpI8O+tWVR4zrHAvkixVrjGINGEtGYiyp6BEgkCyZjUXDGlCDAmXyxk1M6ZxJwUKKBDFAiiOOtV+XhZnY06TaHWaPMX5fMLj6QRAGOfHuyPujncACGXLWHLGw8MDSGfaTNMO4yQDrqZpwjSNAihtG9ZZvruUgsfHkzP/Y4w4TAeku8GJI6xSFlwrECKWnLGUDcQGrKsecdacD4wxJuSaQYFESsg0fpUYJHq1LUYnVFBI/lwNsLRuBR92FiUHHocJh2kvwGNlDGm8Yos7wKnPflkW77ix2MxiunVZZDCs7vN5WYThOxes24aa5fXTOGIwJumywkgbKSZQSAp+Ne3WaZraPlOt3t4/1tr0aQ3EXZcFVWUG5uWCaTc5ljSOwrgdlMWNGDDEAVw3BSqFuHd3HGEzEuw+7+81tywb1nXWeKPJYBQG1pyxbpsCfgWn8ChOJkQMw+h+ZBwHmGRVDBG7XcTd3VHOmCzt+aVWrFnkhUzawZ7rPC+Y59mJFCklLUK0gg4A6f5DwG7XCvPtLFSA2NjNgQSMv8wAhASRYpNlMLZ3GgYMRNjrkDLmNgzNCgj2+vP5jGVZrgrX9m8QYdICSQgilTXtJ5Q1SxGsVCzLisIySI1RMa8XtRXSOCRiyysmGySo5IJtWwV7UX3youDrPM/g0s2z0PWcdoM//+Nx78+cSED7UqToY50225aRkjzauZOcu/35vQZpjWGFyt6SXtm039BAOvTMMmrAj964t4zV2oJJ3TzCnlnx8Pof8M6zr2OcBhQid14WJDuYwC0Msk0tZ7EGFJZwQKr8o2p2eNsGGnhgP3LtLb2spQhVe9xhSCOm6YDLpaDkFeMo1HukhDCOEnymiGW54OXDSzyeXoFZhuhEAp7d32EKCcTAP/+zf4JvffAenj55gvff+QD/79/9Gj/60Uv8+vNP8dHHv8Z6fsST3YT94Wv483/+54hpwv/5r/8VOACBGLs4YggAccLldMIP//aHWM6vcT6/xmVbsDHj7nDA+++8j5evvsI8XxDjQdkqI5B3oAQ8vTsCMeOrhzNK3fDN73wDNB2wMQlLYMhY64x5vaCggimCo7IoOykKMMuUXNXbMeaEPBxhdpZs7XEAFKBiZg8ASqkYhgYSWpCunBWUImvpAvs+MsFajssVEy0EY3039sUVa0rb6gRskqCcyBiMKtquCaxV8W+T/gbwXwNfvU1K4FsdmElkjA/ZPHKdmuA7EASA6Woftes3lkPTP3XAAboX9RmI7pcl/11C2gE/dq3959iPMV8tmSUbdGOJi/ozojf3fgMV3gQSDUgwHZgglBX1K9WTXoA0ma2imVjtcqofBFBQSK63JRSBZMhTQQ8uBggt+xr8sud9uwb9mlsG0N4jdtKDNdefSVevvwVr5e+utTANCIoUxNdCiiPGhuw/2xLtxnblq+9/G3j8NjC62QQZrIAAG2IhlWorpLgUBXB9PZrc+T11AN+ba8kOaFlAbp/3hh1219iun68CF+4+S2zg5jvRyYHAwMAggTtBZSAqeNuAdQW2jFAEKIImvCI9It9NFFvSWu0zhTE+TBP2hz3O5wsqIJNxWVrQrobKoPmHBrSKhfWMvf58u7XNfv2r+zI4qNL2nPzaWzb5BsTHmxIHb7OlvmBhn3lrY2YLPlQO/WfAWZ23RYt+HfzeAmGcBtFvVdkDdgCS7XFcMS/cXk0rNAQP4PTS3ljL2yGK/jyI/HlI14212Bp80d0ymk336yXdCKqvTw0w6n1G0K6AkMT3VWqFN2IgJklgneUkjtWDaWvt5HytXY5akbdFiut6Lkv7uoJ8eh+Z8tVzrFU02GouIl9hUDszCthZGqXkxqaCFSxsHzbwrbW6kxm+A1gNOBfQpZSCuq4oZYP5V9IHF1JQxooV2bUVP0ZUEhAxBQH4AkUpImtMyICsGxdnW9gekTXr/ruza9FXU3acTX2FgZS9ydu+UKA06EA7FrmsGAV8i5REesc/CALaay0xhIAQTVoBgJ+FbV8E1S62QawxJn+mQmbQ6JVUhkF9ZSmbJuRiqyYfVVw64OIm7ImqDoRKafBYw+zfh47cFIvdTrs/98Msbb2uClG1OpuFu4nLRKSD2ppkx1URWZOy3repFQNoUljMaM8jWHG+b/2V/VJKEaCzKx6gA9+HISm6KNItSXVyRd4gu+9TM/efoM9NwLoM4uDgaEoC/Mma2/RuAXfGaUDJG8ZhwG43oWwVp2UFOCOXBMYI4oLdIFPXRaszIw17LBwkXicBCgoHhDhiACOvGxgFMSWMwWYOSDGGwgBS+ZjqQCQhRUKK4gfl2bKvKQNA1ioPJDckZbMFAjJbDgmQtMU52ScGHb5lDh3tDN9y9lhXnTHimNw3COgVUZH9uQQlykhsah12WpiyM0zBMdFrDkquUQ3kIEMMPU5hjZ2787TFGsrO9c8WO5LZAsGZeVKIsX1Mbc1YBnyJbq7c/m5/j/e+9Yd4/OIXKPMr6eZIAwgZl4cvkS+PCLWAgpIV9Pr6E6nF460QUxXc7veOFY8FKI9e2PJzW/MR/1z9f8ubixZFiRtrnADphCCNSygKmy0E1e8E5uUCQIoSIZBPXycSfdJpmrBtG16fHlWKQ/Qwj7s9wMJGtVb6lBLu7+9FIlGL+cuy4Hy+uFTAbje51mbriKmY5wXnx0dtiyY/S1NKOB7vcDjsOr+rLNBasW6iqbtuG0pZsZUNl3VGLnI2x0C4n444TnukCGx5Q4oDpmnEsi6IFJFzEbCKgEqEgZLblXTEFORcsOnr+hiNWVjwAqYVFG1jn0a5zzgk5E18uLW4s+6rIUYM44j94YAIEhmJvlgaI4oWNvqCLREh5xXLLKzikrPILhSRLriczj4AS4orMoirlzCwol4P7tmfTQbAJCJqrdiy7GsbkL2sFy9sgoWlvRbgfJnFf0VCLScEEsJejIOCqJOcq7FpxOayOav+/v6pxFSWZ+l+XzfpMsg5I2+b61sXlvb6VQetpST669M0ic+LAaMO6iKQyyrspsltqeFZhN1u08FdFeuaVZ/2crX2QkARH5p3Oxz2B6zb6s+dAmE/HLAsM/K2YlQ9Yct75fqLSynM8ywdH9zkXux77FnckkLu7++vNGq3bcM6L+ofGZdu/yCSdsLIcMAQI/a7vUo8VWzrho0ryrphWzMunTTDcr5c7cdxFAm0OI5YlxXTKLjMOqyYlw3btvqZtG6rx/y1Vuz3e3kOytK1UH0cJhwP95DYyIoFb8lnup/fa5CWGai5KgDaBoL0Grsy4NaAow4UQwNn5bO4M1Lt7tIW1VoL5m3BeT4jYqdBgGwaO1ws8QrhOkGrysCQL2lJTV8dSHHAuJMK3bps2nLYA2s6lIAVRA4BEeL0U0qYxh2W5YwYBwliwIgkWqw5M7748gt8+fJzlJwxjAnjeECKEWkU8Pbp3RN848X7+Pb738Srf/gSOx7x/e99HbvpS/zyF3+Pd5YBabjDt77/dWB7iV9//DH+l3/5V/joV/8Rz17s8fjygm0JeP7OU9zvn+LJ/XP88sOf46c//g9AZRyGPQIHrFREE3Wa8M1v/wGePzni2fN3cf/uu/j2H/1T/PrvH/Cf/vZfYxcfsJuAL149YJzu8PSd93D39Bn+4Lt/jFwiGBtqPeGjv/8lfvnxJ3h5ueCcV3CQYmmFMOisfTyqE9ETQWxA81qGJH8USY3F9NHkYKMYdECCdv+bbThe05Iqe/6mS0VkMhWt/d7BP5APHLsFzPrPNZq9gTkWTIlt9MNuukDrJjFv+6V9Pmsbo7dY6YbS+SNX7fxsgR468JWMMdkz4uja7u3P1EBtZmEdWXJc3WG/DXi53e/XwFf76YAxurlnva/2qjfXogUaXatc93sbsNcHscwEcIDBVg4YZHamgwNT6MDgjmXbANKrmFMv9xqcsWu+Baqunom9WZMNQ0ZMI0l0dN7UsO2f15WNdL7y9rt8zSxpsPda4kDkjOS3AXm3PrIvLvha9U/Ngn5nNet3cVtvY42Qv0Lt1MAa+7zOlvs14JvfvW3tAQWw+LqYRkSuR9t/9lsBw7esZ/cLgGSyMteCsK7geUGZZ2GskC+3vI5t0EgHVnrCRQBXPNkf8f4HX8Nnn36G14/SzZBVAuDqGm6u2cFkksJS361i5ydsT/zOe7uWQZDfXYMXPUB5ex6/7TP7n9v3vG1v9Lamv3UARfQur/dA/1m3zyjqUB6qFZEDuKidd4bX75H+vX1SZcmmVdINEOlf019D/xm25u1saYU9X5fu/9F9lsQeFbnUqwnIVZAzSeZBaK2lzQ4YkpRECj6MB2xDSTaVfoLGNbMWLtExJcQec1n93kNI7l+hoGQKMqW4v2Yia0OXBDIFGcZRarWxWt266ropkCgSPOHGLgCiVpS0CeD9eocQQLW1dLJKaBhgYB1UOYveaYjGWCeZkhQjagVKBLgU7EZJzE7nk3yOseWIELUTxAb3uV+11tJSkMihTr3u1o1lw68Yto1vi2dadDV3rZODAWGBUGhsOvWEUhiLMmylMb37FnIDxyXhl3XVIYUlCyiidhnVP8o+aWCpg2sMhBgxKHCT89bsFy0OAZG092+bzFwweaMgk5OpBtRV2hBLbkwWSwptSVrCdF0UFdxGgEuCDQQRsMfBVQJyFtZ0VG3xtmdbyz5pECB2Lj6Ta4VVkUm1gqUAb/5IOt9MmsdZ3NVskrp1se/Tgo9uYdbnVEptCb6ekcGASZJktcUJsgahkwux2LD9mZDCiDGMGA47TClhGgnHvTC6tgV49nTA/TFCWMyMcQjA/R45M9YMhIWQeUKgCi7apTDPqByxxc0lK7i2uKUU0UauJSOw7FPvmNDrNQkgC0lEvzYihlbgYNWjtQ6CpEVOkcpqnvPqDDKflJqepXtX61ZDY6UChCEOOpuiDeOBxi4xsAL88h0yYE0GyhDLgCskyUGsS898Wcmyv9dt0z0he6PkDKCIfypF/swVUH/A7hQIFJKw83RNAYYNv2u5gbhqkcuL0iaOgKdf+wb+6J/+d6BtxpgikCLW9YJPfvljfP7RT4D1BLBoBYO1JEZmjxIXpjSAQuvO833j69lmuvSt3i3usOGFwSLkth/0j6azP4yDnJNcMAwJHMX+U4iIWjAyqR/bQynJMMBSRJ+YqA0Ny9uGbZZupuMk2qAAhOGpdjtNE548kXktrMy6bS3eQm9g7zRNWlAqWJYV5/OpaWfreXs8HlVtRAsAACAASURBVG9AxOjv8SHiQbRUL8sMEPnvaikIXDDFiCEScs0Yx4RxjEgJiEPCtB8xhgAaIu6e3KlNWwwo0oxcyBmy0zRCy9HYsnyPDDmSZ9NLH4AZ27ph3VaEELGuG7CJPqiB2ETkbOT9NMlZHqUAm3SgGClganaSUsLe2uJLljNoGDDtdjBt6VpEEoLATZ+3FJxOZ9iAMou3mAVct5++O8Hif4s9jOWpJxJSjCJJkY6yv0GioU2i141SRDIpr6jGXq7C/F7XFVveUFfREs55A7OutTrxGIVgNyg4Ca6IJMVckQgQkDNonlP+P+retFeW7bgSW7GHzKyqc849d3z3zRMnSS25LUvdMtuSW2h/sNEG/KV/qAE3YFgwGm20JYrolmC7RYkiJZKPfPO7w5mqKoc9+ENE7L2z7iX8lS6AfPecU5WVuYfYEStWrMgZIUTRR54L0cySwSRavUd51hxTkTiAqVhDq1/cAqO7nSlnja7TIGC1NlQM84wR4t9nYBlnEIH79cia0sRAOU+cg5VKGpWbmOcZs5zvd3d35b3GmAKW688KmG42m3I+a4NA9iNCufY8z0gms5QJDNzxgLPdGcc1BHjr0XcengB0PfsIEoMcj0dMIq0Q5Pw+TlPxP1JMcN4XX5e1rWtzOiZGGJaYCIEbZWo8KaC87gvfebC7zLrSoNaXe/X1Gw3SApAFXUth9FRS9p+YdTbeKRdt2pwVTMPqcFKWnjpjQAJZICRgmgO2g4E1rGvSvpR+HZvfVweRtWJTjkXTUAOUGBIzYEWH5bTElK9TfsG07Eb3JaUIZw2GrkdKgR1q47CEGc+++QqH44hxCej7Dg/uP8DgOpjMTGFvMx5dnuNf/rf/A5B6PP/yczy/OmAeMx49eoonbz7C7eLx8bffQoDHl5/9Cn/3//wlxuNzZCTsthnf/ugDfP3lOa5e3KDrudHaZ1/8Ete3z3B+scWjywdyUCT43sGebbG7fMCi1H2Py/sPcfHGO/iX//p/wq8+f4Z/a1/Ah2cwKeE9A1w+eBPOb7DbbPDkyTt4+ORd/PyTf8TVN5/BvPkhHG1xddjjy+ff4Ppwg3FcOEgjYfsYAyOl6SDOrCRiJ5YdCMm+Rtb0Ub3iGLVBEjeYc87JgV+Db2UnxMTNLrT0qZYuGi6Nl4CLqAKpKbExN2JUeP1Wh6MG1BHWcWmVBpQ4CSb5JesakFi9sq7USW1fZIwEffKzahrKJjp9f2mUpd+d6wF4ut5f+TkDpUZJviLnBFYIsav36rX5O9clX2XcTxhuBdApjnhz4/I3A1qPmTiGKyC6uVbOHHwTkZTr5dU4qv4uaWdp4ng6CotRG4KlnKEMTtPOsAyvHtqWapm+jF4BUNrAuH3u+ogyX0n1WyXMzpWZD7EV7Zppr6Nsby3TXP99DZgRuOQadap4feu1FEjVTuCEqhnbzG3rfL8OmGqZTxV808Bo/d3Q/SMgltx2ARJLV3nBspj49ypLm+eZXhnvNUjGAVS7Nl8HMP+6/aBORwtOlvmWNWwzYGJEXgLSMrPWZ0qAtVLmrgzxMiTQElxClckhGDx//rwI9KeUQd7JvFQgopyfzavc48laUTiwNGmUa2nJZxlH+fcpy+x1YOqve3/LRnsds/YUkNXX6TXW4JveS20c8Tp7ogFHe98hcmWEBSGLlI0Shtu9Vu6j2RdqY8q/Y2X05ZP3tf8Fmv2SmkQRxL9plrCuT0jljSFbQVAoM9+gssQg5xDKPELWUBb7YUSygYiBUWrGt42RK1hUdZKNISaIGTkzomrRCvCh40UZQAIJy07XnHGuAJYZKHrtOWcujSRCFn+MShLHlIWakZFCQISc0dbByHlafK2cuaFYrnZO110MgZkqnPYVcIPH3BhCXGQNyudiCtL81fO4G8fJFuOw3WzhvcNxPJYu17UJUURKLVAqt9aMaU6xAN9ItUmRNkMF8lpOQ5LDhFpRYHTOKCGmRa6RpMldXeOqocxJDCN7RcWkhNWcuSeDc1a6P8di26DLQsAfBWlBIgMhsyQrEMZ6GOLxTZmlkbQ435Ara1tBGhDrcsKKHbAWav55V/CVtbS8gs/8pdZoI6U6XjFqcI5y/1nOVGU/sV8QANGk1SARSQNYYWeDdZj566jovyKzhiyfSwlkLLommNN+Cylyw9oMTUIqyFxtVNtYpQIKNabxriagipQDMbu1Zb8V5i2UVGCx2WwLW1TlKADAOwtrqXRln8YF2RsMvcHgBgx9hnMRJhssC2GcQgk4MwFLiAiB12axV5CGceDKtyTjXs4JY0VW3sheIrFtplSD6dyuzmokOFsbJ3HgHgtwCCiYS8ipJR/k4qQxs9lAQSgUQLf6abwORJs6BoCyBN4W2eQydjny/bFchDYoZJCecsIyHxGWI9uEjAJQqZ9FRAi6P4vuNq9XQ0CKCwOzWfepxDtQ3yCzk0piW6WqL4ZjSUCp5Ez1spT8lOAvdni8/S46Epk/y3r5yQ24u7vF+OwTIIxQ3Vw2bLl8X85siwH2TZe4NFIqZnWWKDihbEytPtRrSRAkx1VNQun6n6YRfrCiMx5B5DkRpX5f4moCGGCeZsQInJ9foOssloXZos67ope53+8xjSO2/YCL84tSzbA/7HE47tF1Hc7OztD3Pa+DeRHNzwUggu88d4b3nRxn3DzqeDzieDwCADabDba7Hbxz6LxH77syjvPMLFlu4MTA5uFwQIyRdTgzn1ClKZck1lyKcH5gmyf+YEbCEhg8BRGWMZazmzIDc0Z0bbVR2DzPiCHAOT5fY+MzDcNQAMHWPpH8VzVoKzDKK4zIsNQiAJMyM4AzsxkzUgGyliXAe+7ro2vEWq6kYI1W1tIlcHKNdUBRfBznXAHGlSGrSZ4kkklt1YUC6sxqHsv4H4/Hmtw3tq7RHEsjOCfjDyLWkLUWg98WuaWUE0KoAGnXeez3d7I/+F6XmRspLgs378uQ5AZyOUdYHsNwwyplYxo+O7rOY7PpCyvYW26qNc1zwadSZC3jEAJmkZfhUnttis5VFmo7iap8ArPDDTceEz9v1bcCTJ7UyguVqdDAgW2PSMpYh40ArwrCd11XWjuovITqNx+Px9LgTc81/W7nXPm8ym4Mw1BtT0pYckDXTZiPLJWxv5OxJ6AzUhENbnznnCvz1nm+rjamJIIw7XmthLjwfkxJNIJRxkXj237o0W8GWKncAzhW1j3jveeEi9gDfv4oPXh+/es3GqQlNdjNJGhJI2smBZBkZkgYcSiAh5TzmdbgAIjKmFQtTICIGanTPOPeWYcUF1gLdrjSGkBpIzQto+RMJL8npggEPjQ1W6IBR4q5cRKrscvILEQKPTjVGWUmTUqRD4HkcTje4ebuBe4OtyDLmZyLszNcnt/HvbNz+EzYX9/A5ojHZzv88R/9Ef74T76Pf/d//A3s+RP87pvvIk0zDsGDug6PHtzDcUkYzglnDwecnW9xMUTM0wHOGziKONvu8PLlMzx/cYc0TxinI7qe8M/+6J/j8eVbGI97UDxi2t+gv3eOswcPYd2AMHPwYmmLv/rhj3B9uMOjN9/CRfcWzvr7SBRwd9jj+voal+cb3F5d41efv8DNzTUu7+3wvd/5Nt55f4+XL18gxAUxR3z6/Bt8+ew5AiVM84zd2RnG8YDPv/wc0zJzx1JkhGUGKMF1jjX2jAVy7Spdyp0BcZIq0yXnLN00VR9KAqHMGWcNlNm5VEZSC0ysG2wA69JedRbVGCCXb5B5F+bJCsiQbSxMXo65tPQolzW1ApN0feVcm1epNSAFM8s7odo0CkSYxtlvy3cL46SwRjNLTsgZawBpwlJ1h3T/Wuny2oJ1Oj4rwEwBD3kPH5hoDgLTPONqW/JclP26frXgGXcQ5222At5SAlkqmlYKsKv8hAJuaqg1mNDCO/YsG0c213lQ0EshmPY7jWn1lytYpY4DhMWktkY7+ep3lK8uY9uChC04hMLkab+rrJ2CJr06bq8OKOo9NPfbHuoaAJ0ColrVQNrpC83i1MYh4rTpuLYHmtr0mEJx5Mt9/7r7RS5AVRmPOnAFKECq7EJl+CqwkXMzRLmC/i2LuZUi4SfSGecLWGTkcUYcR9aqNZwUSLx05DMEiLwP2xt5riTgT86lu+o4T2XNx5wY5EmJNdvo9ez1Frhd7UWxC9TYSrVZ7WeBmmhp11j7NS1I3/5c35tX1zwFa1vArH1PsWtmDWzwXLRMXlq9V79fnXjImLP9hSQ+pISNCJkq+940e6sC8AkQLUG1V0kCTv25fEajcfVQm/22Al+rmQFRbeJR0PvVJIJBAFn/CjKjfEVzLukaynJfbOzBxpvtthWdRgWwAEjwW1knuvaIamm3Pof3nhOZGizrWUJ6pqzPBSfzp5rrCuboJuOEEs9pO9ftGlRJ+LJGcrWRbbfpdp2qL1l0anPi0vwSxBgBIKgEjnpNThhKsidFJMqs2UkKarrCIDLUgFIpIRsqjX90T3F5HpWzre6JulZV6oCHXpuharlou5YYGg1xAWIowEaUZ1RGBxnDGoWUEMRf1bWSck3ixbSwbnYOAHKpJqp3yM+gQmI83+o3GBjjmFnjHWKKWJYgZdm84sjU5j9ZfJHaNE7PyMY2Z5QEuGvKWFXKyBqShjwOOSkgzU1FTVYCB69PTsQmaWRT9wkH+XXsU0rCYDw5TxofLUMlLpjt2bKWGEwwEpCGQhTIxOAVyd+J1EbxPCtI3PpepZkaQeIekjHjPWlNm7hiti2z4/2q8myeZoSVrATfy7QcERJhCY7HRcgN/eDROYOruwxKC862HZeDZoj+JTAtGcc5YVwy5hBhQBjniGkJSDFwBVxmsDyXoF4S72xoRM5f5Q74Z04wUJkj9W1iZIkK57i81TmWPGDmrYAdIo/B48C+RhY7a8SuKCNZzwMQJA7QecogCyARbDYIomNunTb4ScJ8DCU5nHJCWII0qgFimjCOhwIiE5Hoz9a1rrqy7NNWNnRmRV1wRUWS/anxgBCKROeQUtWaV/cwhqXaFT1mpAE1tAEpZcAaxM5gjMTMSBgY16G7fANnj97GeP0lcpqQYwVRdM/y3qmVVyVSTkqWET+ZMuPgCUKG4rmyJIAhALI1vVPkErL6IOp8yZq3Vkjqug+lObC1fIbnDGMdOt/BWgYCY+SqMy9n3SQyBtvNFruzHYgMjtMo0gUBQ+dxfn4Oay3GcWRA73CAAdD5DtvtDr7rAOL9yeDtrehysrTFbrfDbrtF13cgMNPy7u6OPxO4aRg/bxZtbFNAYd91SDkVliQzWcFNykFYFmaMMpjH7GIYQqQI4zySsAzVR0ghwHoP13HjQ5YQSbjb3zHgllJZlwCwGQZYYcYSUKpD1VYWc5jZX1Hw1FrLDbNShDO2xk/ih4SwICVtvMXzFkLAMgfkzBU9BMIyLTgsR6lC0biUxzWEUMC6RRig2+2uxAYAwVpXqoqISIB2tndMqmOQNsVYGgQiZxwOB4zjhAzCcZxwHKfSP8VYg1vLayiCNf+N0UoIHh8FE7fbrfi1GZvNRnzCVBmr2hBTYurjeJT9BwTLvqX3HiFG7A9H5MyM7q7vmNkJPj+M4/PCOgcDgnce0zyhywOsNZjniX1EkR84HA4Yp4nlOazDOPJ4dt7X8bKV5erkPHPewQ99mXtlLMcQWKIhBLG3CTkFpHRA5z3PvwDk2vBrGAbRfCZ0fVeSzV3XsaxDZtm2SRIi2jjOWscAviRRWVaAz/3dzuFid4Y5LEgxIywLQuYGjJakSmMO3EzParUy4J2Dc14Ac4LvByTvi/+3hMASJcYgBE7YsQRKEMlR3sPKUo4xYrfdSpKUylmutlJ9C67m+f+pJi3AZWCmzSbLAcAMNZTAMeXEh6cGtgZwYrSV6cbOoQj6p8SGwADIBinP2I9XMPQmvO2Q8yJOgDrJApoYpqAjo2x6MmBRd0gmhNrMA6A6jykLGwSaOdfgUhm6YkQNwaCyXzTzkVLC58++xDhN2O3OMPRbpq5bj7DMuHr5Ap3xoBTw1tMH+Fff/6/xe//V93FzE3G7H3HYT3i42+DB06fC2Opx7+IRFnQ4HmYcbkd89NG3EOc9zs52+PQXP8MPf/C/4/rqC8zjLR4+uMTFows8fet3sb04wx//i/8eL5/f4YuvvsHzz3+Owxjx7PqAMXl877tvI/ktDlNCNww4PH8GZ4CP3vttkCU8ePQYjx8+xM31Ff7dn/0ZfvnFDd5++gYeP3yAe/ce4Mmbb8OYDv3mFtvdJY5SLnJx/ghv3r/GtCyICJiWEeN0xDuXbyCBtXvGecTXL77Gl8++wDgfkR0kQLGixyZIizgIZIiZplLPbDKkezMzNCkJkwNc2g+ZE2TVfEJZn7JIxHlZgwn8OSoBEQdV2uguczd2AaGEmFSuW5xTAWeVMU6rwE6BEmleIgdVSrE0zULDaCzZURiAIpaYkaUhhDJIW1BFTuE10KJxoYIzJAAVewotrlOc0FJqmGqpWgverQBBfXb5fg6QTZEVQNnjKILztnEiKpgi3BtlHMlhqhlqArNinWjvFVkUkkBIcQNhpMSM5vfMEOPvDzDwfJjrkIPtjlcnVp9LHFgSR0LXlQKDOhYt4zjruIPLlVrwQI0/z40CJYC65SvANqXVtRknFGBCrq3AkoLUJPdamrmo06Y2uGHEtv9tGdKnQEsNxPU6fF1teKf3yPOXC7hRwFRZgLnZiaVCQr5Tg0EGb2rAn4Sl07IGXgEyIQCeMNFKwy65b6usKiiYqaupsi51TvlnhxyBeHdAurtDnha+fpQO6nJmaLKI2TBajsprLemzyXNoSWvZk2LXUs4M1J7uqfbn5jpVwxHFDgHcO0k9ldZ2tMB0ZYMrILtOcOp3tmtCbUJJwDb3yvNu6z6U/57e/+l8lYQG9GytiQL9XJsQMiBEZdvFVJgDPM+Om9aQlJmXBh1NIkxBATlT1OEjCcQz2E7ElMvaU8mZFqAt962P09yzjlMF6+W6us+MglfcUXy1flvbrfZcgGyW9qmMmARmgRhwqZ8mFDQwaq+npfxZEtVWWB/Vhlb7BpCccQQk5W7xvnXWCVNz4gQrL/46R4bET1vbiAp883g4lVUAWBM8RcTAgHUQgBSoFVEApCFQKP6hbHEgMZMyZ0I2FkbayxKMMGMNkOvcsmROxHE8ousrw4XJBFJFIYCOdZb9QMNjwT5LKIw6ZbfxmtcGtlT0z3hf1X2qQaY21tTmWqdrIAgrKEW2F3Jkc+8FZGEaMns2in/hiq/La1bt0tJUUMidgJxH0abN3BhOn58oYZlHnp+UqwQJqU6gK8Ej2zzVbE3NU1gQmPEz9J7HMbRl+1mA0hoAZTmPK8iKcoblXJNRmgTX5AZXKgRw4zYGXihX1ozaOcoMk7TVQkb7H6AGrwrY8wAqIAvWRRUwmWScnHZgz7rvnaw3kUqRJI42llWjkYXhmxIxGCvMXy5hNUim7uGYCIgLlkWC9mWG73o4a5QrAkOAJ2LN6hRxnAMyemy6Ht5beE/ovIG3HP8cp4xFfGYn8cw8B2hT1ZQBGMuAfeamfwky3zp+NiODmZgpqkene4JlwdSf4bFmeadlWZAs26BIzKDMMSJMc7XtWXXAqeyRLEB2ysyURm7Mr4BrCamwKjMpY5r9k7jMImfBoNEyR2bagsc+xIXnQH0EAZXZppLEq6mAQjEyAKJJsJQSlmlGJgPv2bYWhj4BShzReNYYA8pVkxYlt08gaPMzsTOUQVQZ9jFl5Dkh5IgsDQvznJhhPpzj/Ol7uH72Cywvj8ASxK/hHiLITFBIAn5D9pWxpvGfq9wPgUC2SfbJgWkMYKwvmt7q+4VlkZ4UVAAeGIslAoYya2+miC51yNJa2hi2eZYMvGOWqzbsc87COcv6lPMCooTz3Rm2mzOEOONwvMM0TbDOYbfZFR3scRxZUzNGdL3HMAzY9Fs+ewJLH+yPe8QQ0HmubGXfngE0QxnHm1scpgnTPImuKiexAGAYNthshmIvip9FbAf6vi9AEAigJOAccXOosGRYu8BZh67vmDFrDHo3YNhupKSem7MlEpmihpm/xIi+n4sWqtrWlLh3ApeqT3wGyVxoU64kc6ZzzGPsOMkglSbGGia/JfGqCfBdB+/1zJTzNxsksCYwwYm0o2PJlWXBNM8IUZqoW9YengI3mxzHGbe3e7GjFezXsSyNq5wtNn+z2aDrHHJ26OQZlnnGo8ePBZyrjQ4NEcaJGaulcnGOWNLCGIOt4HYBAVElobxzzMK3HCP4zsOmyhT13uMS97EssSTa9Ow3McJYw9qxSyiyn1r9lJGlWVbE0A9wvoN3FlrB1HU9jGGNbwzM7J4m1naNcvZqVUrMTFBKixpFBaMYJO26jpm2lpvMOevgeh7fGvNxOf8SmG3ujBXd5gP7yjJGKveRkeGdL4xZ1XLtQkDvO6jMhsbs0zQxOUXsnfe+xKTGuDLfznfwwsDmeC8AqfqQ88TM5nmexO+gcj0j1yBin/j84kJOB4MlLDiOI46TaCBLFdkSFpELIZjRYMzjqiqm6zt4b2Gog7WeWfy6r1/z+o0HadsyWaAJEkhYHIAYeoKDKRpQIbHxL7IIxE5o0brJAtomcQZSxuG4R8QC151hTGHVwa18L7gMJ8QggQwkgDCre2uZRcYQoMwdJFjjQI3xAAiIkkEzVipuEoS4zsCTJzhy6P0A73pshi2ILAwMlgAkMiAYzIcRlzuDP/3+H+J73/4t7O9G3GWDe/ce4HB9wOdfP8N+f4WzTY/N7gGuJoMxGcwpYJlGxEjo/QXOLh5gt3uG4+GIwVtc9BfYDQMePH4Tf/Kn/yNuDjM+/XpCihbD5QNMX/4ShwR0mwt8/vk3mCaLx+9/Bz/72ae4u7rCtodkLjmYst7g8sE93I13+OD9j3G2vcTLl9d4+eUtdsMA+vIZ+t7hwcN7ICxYwhEdefQ9O7WffPJLxBywP95h0w148/FTnN27xJIj9uMBTx4+xG7o8POvPsXNtAcyjz3BMkBNTUCfWUfVyrpo15mWw5W4UjE2ADmK3qDEROootWytlo3armMF8IlKxF6C+lVAvQrW2dnTEkoNNiD/LddDy2aTILswZeRZsjrC/H7VVCFh17TYR1suXcs3pZRXwZgkAGZeNwhagbwQRpX8rW3e9P/1YodNGz9UbbWcWWkhI3MAyC5guccVmNOMp36nNYabbyjYpc9I9X5XbDSdhwLUVdC1UCAVTJRx1wFPokdIVKJbtj/NZRV8Sc06bIGo3Px/+Zz82JbZ54b5VsqUZa7reK6Z3rq+CWgqimUshT2iIFH5Hvn+doxW890AzC2Ye/o+AKvnTDm9cs2sbEId4zJ2a1B/DThWIAt6HqCuyyAaX+17T8+aNtHyWkY8oyvIVOenBSRrCT+zGCglzMcDMC8wWfdPlg7Wa/BOn1UZJ/q9CgSRPEeW/cGOctNJHnjtOJ8+WwvsKMjxun35OkC+PHWuTOOq4bee2wrAruUGADTjJHFea4RO7vv0uq/+bg0On96DvpQFpsCkcx1c57iLNajMqTar0s8X+9Y8O4igHb6h3yFglNWqCqp7SlGBas3lnvhLShWH2hLZfCsmK6juh1Zf8tWESR2Rsm8N1fOs8W+I2rFaj9fpGQZx7Nn29GILAEUS2LFOyNJVmvNAOj8MZkyi069rSce5XRsq/cGloFSelcdTSmozMxBT4nJ9ZqvIWkyki6o8A9tFPt9btnSSZ6MGDLbeceVMHUWANBnLZ87xOML7w6r8viYNgJwTxok73acYYa2H6zosAiaXAV8tX127/Hl9S0ocRFTMWVmBnOxXoFObqJCuO+LrhJRgsgUQV/sxCgucq6gMHj98gGWecb2/BZBhHcHBCltapUVqiSnAna0733NgLbaN/eS6L5jB2cG6Wh7sBbxV9jiQi65qhuXmTJIACAt3pw8SAKYUy1ygWdPKlmawGOVs4LXFCzWEhK7roVrHnJjkcdL3GlQ9SJ0TS5rsVXuveyWVoFsDVt3LGutyuS6E3KG+ojSLkYAZyFgWbfyVqqSFMXDwCKlqegJZ9ECF0SvPzO/nvcZ2PSPngBgDQpiYkWREZ5gpvmubY1ijexoDKAUMvsOwcbh3adCZjBQ4uXhExjguIGvRdVKGniOmOYrvrauUYKyD8QlLENYjVdsHoDwnx1RZxpf3gN4jg938nhgDpmnkfQHRFU8cjKsdDKKVaa1D1/mijQk9u8Gg4hICYkjwxuHe+RbOLHh5dYMxbmDIYppnzGEpa0U7qBct0XmGMSyhRtLgKwRmV3OOvknwNf4GJ4liaZDdMhzJEJZ5KWBxWu29GiekZs7X5zTrbbea6ECV4WGfiW2x+h1kKsHCeOD80WOcPX4XL48vkZaRpR0MEzoMqDD1Kak1LLNZ/EO9n9b3W8X3mde/NevGv2hdV4nlKQG0cMM9MhawBvOywBqHvu9gpPGqStFpibuyG6dpxv5wQO97DMMGZA1u97dSRWtxcXGBYRgKOLvf7wGgMP+6voO1BmlJrGc5MiPReoeLy0sMfQ9nubR9SgvG4wFxnJHmBNcNGPotDGVh7rliI9imR2a+EnGTLHkG56tsijVGAKQBWuJPxGXuxT+V8bWOx9r7Dta4Mg+s+az+Pa+hTsCxnGozQT1DaiybEBProyZZ+zFGYRYeuGp4IYSoPl6GNR7WGeS4gMiVsn6SagEvoKo17IOxzZJpN1wdZq2F6zx83wlAWv1sQ2xXliWUuVbbO02TNDtLpfFZ0Ton4MWLa3jH8kWbzVAkdI7jyPr83hXg0BmLvt+AHBuklFLRRwWRVIssq3tYlgVzrnEfEVf/rZK5Mme1nJ8bFTJw68oeCYGf79zYcs4xmM1NOkNkeYODaOdutxssCzNbIYiScz36vivyBgAw7IZyH7o2iKjprbQgZ5aPUBmB/d0d73UjmvbEMg91PbJPjWxKbOo2A3abASmzEcCMAQAAIABJREFU1IM+jybPp3Gqsbm12PRDGSdNOixLQJDx67qu7IlZ5nlZAlKasCwBzjM7FoCAypy8GYYtSyUAuDg7BwCEFHA8HpAzFR9O59cYwrQs0njPo/gAxohEkIPxnIjIOePcuUJCS+LbKhvYHNg/67q+7P++H/DrXr/ZIK0G/0A5hNqDrRxMkMPKGCGCcVmZZhlhuByJmy/kIo9QDhCwNMI0H3AY9zjbbaVPaz3w9MDQMiQtL9K/6+/agF4nORMj75UN1Qa3UpLha5khMzMSs06IQWFvPIaLDhGEZ8+/4UPKMOhjYWGzhUuEnhx+56P38P7TN/D11y8xmyOwBd59+y288+gR/v5vfoCf/+ivgOUGb7z9Md777j9HMlvM4x4pBDx96z3c3u1xe3uNcb6DoYht53C29bh3eYlv/9Yf4un738F7G4uf/uOXePLkIX7645/g/oPHONzd4A/+8A/wo//8I2y2Z/g3/+Zf44f/8e/ww//wQ3z96Y/x2aefY+h6fOvjj3H9/BqX51t8/OFH+ODD7+Lho7dxeX+Dv/jzv8bzrz7F4W5Bb89xuLvF9d0NcgL63sN0PZYlw1mP+e6InRuwG7awMWPjOuyvXuC4v8PFsMW7j9/E3TiBDh1uD1fsLLaAmwAsXJ5NUjwCaGMkQGJso6y9ZmkWpyNKeQ6KHph+rgJ59dWChEkcb5XGyAo2ZRTQRb+rOmNVLqMGsVrexrfdrrMKKNYsupHSTF6fWcqiFAhDvbecy9qOwmhvmW810BV2eLNP2vt+3b/bsViBcw3bsn1u/ht3pdUScHYmSeaKf6/X1z146sS29oPlLervKpsJVeNU7YTak2IHqNEDY4Z/jsr2ZC06ZC7rdRIYZkgTRBmiolFrKpACYKWvq4fXulwcq+d85Zlybt7PoFsWNLWd0/YaACSYXrnXIsOg2ocK4KTVZ9uSpxUAdjq2zasFeto5LvMFEgYIZM8q7lPZtAoEcoy6BgTbIEAZU6/7O1Lz/K+5vzbpcvo3fkbWkWTtvLqm0YxrAXYzWH92nGEzKiNNXjFqaSAz3U4ByaKTLHuebYUA0oaEFVfvsR3b0+doQbxXEgEnNovHQdmarzaKa185Yx1gYT3H7ecU2FkDvrpmX/2umnSoDLrTZ22/9/Q+23soSSljEDMHsjAdyPdA3yH5DrbrQNYimio/016nnCEiO1OCW7l/XbP837rGdH0AVHQp9bnlwcoclYC3AEC0eh79+ZW1cpIcUbao3hjfx8lekO/h7VKfj7W513O4mk+58UUqj0qDDwENKqObNft5LbK+Z2XssOPK11SQlgEstXn1rNMqEGZFWcPlzgzIcaAUszRVEgge2uk8s3ROlskp9lRsSC7rglmU1nBJJLJUpICgmpY6nlo5Ygyw3++xLCw9EmKqWqUCoudcNSxJACrnrOigUrkvZTjljIZVr+uCx1tLPflvuawFHmNel9Yqyx1yH6YkDmPUz6cCgltrxJ/JCHHBcdwX/XU9p9hGZUkk2PJcAMEaB+c7uL5ncHVZAEultLlda0QJOU+sR9qw51JmW6gVQVwVYAQ8B/sahtjPz6ylrMxnEuactezjWMMNV3iNKeO1+t/8b4OUApYllkC7bARZm8go/hozPyW2SJwQiyGVa1tj4H1f9p82AVq9dAOW++KdrsFt3ceyVkplDO8fDiIro94Yw93sI0sDMPNTFxAzsXl+XSmz5ThJ/bgAkDZOI3lPAHmHEJlhP6YFnQtwBhg6i4tBZLcApEyYExCWWUAeC2dcZclmJcUIMyxV7eecY+HMJmJGZi6WT8AcAMYZ5EBYwsIB/rwgi0wJNDtkjIAWKMAeyRxaQ8gpYBqZkVaIyPKdzjmEnDDPESYBH7zzBL//u2/jB//xb/HJVzcwxiJEBrjneUROCwwRFtFV9d6zlmWKxQ+PovmZMrgUPSt7N8PZrti5JJ/RJIKu0eJ7EY+Gsw4RkQHo07NUQDeythIr9NymVGwF2/VcDyix9cz2MkDm9Z2JSS2EDHf5Bp5++E8wz1fYIyDPASlyibgxHn7TI+73YI1FWd7il9SzS8ekNvxju2kkSQ2EyBIlZmUn1rGPJTmzZY+r/w0BECHRu7VGJE+YzbfZbOC958ZLccHZ2RmGYQNjWPLgeJhweXGGvmcgl5tR7UvDH20KxkzLBft5xjxOAkI6bLZbDLsNAIjO5hEhLAiRKzZ673B+vgXIwPU9QhSNOKDocV5fXxdgbLPZ8HlRepqg6K4q/qDjqiXqKQqLO2gDqAnH4wI9pjvRweU1yVrt1nAVYBA94RLjqdZyrucNn1csY7PdMEDWdV3xK2K8VwDbKPeSkWFNB2u4OmSeA+ISy9oMYcEyzThGblTFDHn+7mGzgzGEWeyKSsCgnKm874Zh4BgsZwzDUPyftiR/nucyr6PogsbEEgs5ZYSkSbJQGlEx67X6UgYGm+0WXd9I7eS6Tq2x6HbcJD4JOz8J21+bxvH/KkCpzGkiwt3dHVKK2Gx2ABgDUM1s9QFKwyviWFGB8q73OO93MOYBkMHAKlhDnMd5xrLMrLW8v8PtbVqdN7ovW23fruvgncMw8Hmm63+eJszTUprHzTPL5ygzVm2Ns9wcDZnXle+8JOosetWnzTXW1YZlCqozG5kT/PM811gGgBWdcJVh6LsOMbBkBXKWe0pIMTHr9biHAs/jOEpywGPoe3jfQbWBu65HCAHe+dI8Lcv1DBYsy4yYqx9mAMzjkeUSbA8Y1gm2Ug7te16Ps8z1NE2yl9hnORwOZe+97vWbDdIq0PSaYAtYBxhsCqI4Udy8IGVlx+WSneXkeQ0sNKMIA4Qw4fbmBTb+Hixyce5UyDiJw+1E+Bup6c7asCZOA0H2H5jVkTPBWQVzxbYBwsCBBEUBy7zAkYFxPZyxcMbCEPDg/AFuXl4jpCOXyIJgErNsTXLYbc/we7/7R4C9wNcvn2Fc7rC7NMjnhDjuQeML9OkFnD/g8WXCptvj+jiB4ojOGOR4wHy8wsWDHd59+gAWAbc3N/j4W/8Fnr73Pv74v/tXOMzA1hv4rsM//uMX+OmPfoK83OLm5oA/+9/+PXfoe3GFH/zFX8D3Ozx+NCAcLvDBB+/jyVtv4f6Dx/D9FgEWj54+RZxm/ODP/09sd1u89fZbON8ZXL18jhf7EWYOOL+4RJgi7g4B1mXE7PDg/mPcv7iHN58+wuG4x6effY7w1Zc4jCPmeUScgA4dHp/dh3MGFGbspztorWnKubCkisNgeNGpo6rOnTGGyxuyyk7kUjIxTbMwagkgleXnedR4WoOTluGk6zjlVMqoNHGg36NrSd9bQYgWzKDV31sgsf7NlPWZScuI+ZADKqtE1yIyM5Go0cvS734FVLOmAI+vBCIne7QFCFuQ7hRgbAN/AIU9AMmoZmhDQUgA12Tc6xevsvanoGD5N4sUl+BZm39pmWmK2gyHHVf1HXNjoGXVwAhYn1PDCETWOEkCfGGqIHMJpjzrCgQ8GZfKUmofbw1sAWtg5nSe2vUANMChrneRA8lRQTOs1mwB90pSox7urxvn9qWBRqut1wKEem/VJior9PVAYAunFiuugJKsUQYntKlBLt2v23XA91YD3QK8NPd9eg/tPfMYNtq7wGvfD7DuWEoZJkRMt7eIh0MF4/WZZf8ZqmuyzBlRedY61jUhA6Kip7UCEQuwvgYtT0Fnnuf12LTPwE2FANUGXc2GvJ9Lrk+BPJT1dbo+1oBqFex/HSD+unXTjk/78+kcv/pdci31C4iD6OQc0mYDs9vAbs5AXQeYCjCcfi8Hh+Bu13xB6eZd7p7PEPldyCq9wWdNPXvkvWUNpmJ/+P7ahMvav3jduLzOTiuQ3OSyiok9BeittZJ4qCxEBqRygU1YdqdJhjW2p6HhS6NNFJA3hNQAi4QsTZYUrDeSUNfAScv5+Yup3HMsOBoh5gAkBu+WkBBzlDNBz3oCpSyAcWqeW26zXWM8YcXvVNmQpGBgSZI27y/yI6yTz7rrsiAEKGKtSblpsVU5M8vmdF9DEn05Y3WWJyl5V2AiI2JeWFOV55CfOcaMlAyU5dmC3QzcGem+Xc+RsvcBWNfxOUsZL++YQdv5brVGeA61HL8C0tYA3juEhUsICyBdtrSWmwPH8Q7zMvG6xrq5ZBQJAGu4oau1XanisdYiR4MMrozTsygGLsX0XsEZYTOJb5WzgHMQMNpQ4wcJa1b8CW2kmrNoaSKVMzOpFjCbDnAZMDch9dah7/yqZFm7olfGOTWluGzz2L1x6HsuvW0BXrYD0pCJDFKSvUYK4AE5G6RE6mggWSGRZNlTBMTEOqM8JkwCsaIfyPdm0fW1ycuyzJg8MxJziKCuQ0qEaUq4vonw1MMbIOZaJRRDwjxy87AQEidEgsZfCVGD52UG0CSTqbKSpWlI8U9ijI20E8la5v0Qw8K6rzKvJIvNEFiyyzI4kRM33NLxUokx3kyGG3stMyBJmUzA3/7kH3C4ewFYZnsvgXWZkzTv8oaTcpZY05jEn/ayVwgMOPH8s0SAMU7mW+WY2FdxzgISC/Bn+Rmrnao+atmHaF6JtYpbm1FtlJRDpySphVolUJO+bNcpsfxZRpLGfxkwDr4f8PDNDxDTHT5JGePNNWyYmJV3dh+D73D12c+x3L1ACgFONX0yszt1vaciKdScH1nlXU58f6qatQWyz2CA9HCAO+tw5jcg2Sc5BPSbDiEyOKVgKxlJTGXu/J5Sgndcrp1iwjSOQM64f3mJzdBhWeYibaAg4G63Q9/3WJYFV1dXpeFU3/U4Pz/DZrMFGYP97QExcOn7Mk8gAE8ePcUwdHh0/wKDM7i5u8Xz6wNubkfEuBSbn3IsNsZ7X7Q6c85FVqDITLUszXlmxm3isdVGXkkkUKyzrJU7z4gxwrsO1jHz9pC5FB+Gqh595thEWfqt/84JPT5PWAOU5QL0pQCytQ5WCidSjkgR8N5isznjZBiolMYr+JaTJm4TUl5Yf9s6hBjQm77c//HIzevUPhoBLC3ZIg3mPMsKWGdZgkUkdWKMcM5hd7aTM7P6Sax4uPatCCQA3xHLPIPI4Hg84vb2puBTWXwLLdt3zmGz2QhAzJqqGYoZODhvZZ6CnIfV/8mZwfJpmjFL06pFAGoFeUn8kjaRAQBkapM3AjNPrbPY+A7ctGwH5yyi6KkuC4+ngsW6nrQCh4FKrl6x1mIYepEHYVb2dusQB66eYkmvVM46ZeOGwE0muZx/Qbi5Y+ZoxzIJRfvWcOMyJ2tQGeWQOdJ70+QhMhDkZ51TBZedcwABw0abrzk5o6cChsbEZ9M0jpinqTT14iQE9xWYzSS+Fa+1rvMYhr6c9axvzWs2S5M/9eFijJwoVduUs4ylEX3eKs3kXI+UOvy61280SHsaZGkWuQ0C9X0EwIK7bWojptLwRDZRluxgAgrTTSMfxlIzDre3MPcjeuNwG8dG6FcD8wxnFexlOjpSAqWIRRuRNKAc5CDkjEdEjLlo0ADsdHE1gjgjMXCgzt+GlAMsOS7JlpLyTedxezggZw5Wts7h2x98iDffeAedv8A+7vCf/vYzwCRs3AbH21sc7+7gTMA7772J9950+MF/+F/Rdwbng8fV7YTd0AEp4u76OfY3LzBe/QoX2x4mEbabe/Dbh3h2G/GX/+lHcP4CzhEGd4HpbsRhf4fvfOs93H9wiX/7P/8v2N/c4vxsg5/9/U/xxjtP8eGHb+LJ08c4jBO+/upTfPP8K7zx1ru4d/kYn/zDT/DNF1/gs88+w3gc8U9///fx3d/5bdx79BbQezx8cglnHX76t5/g+tlL3Dvf4OOP3sHf/F//N5599SmGzQbZWfjhGiFmEDlcnF/CWsLNzRXOfQfKA+btGaZ5xJKYYQNihoUGY9oAAtDu9RnKVAghcGmoOHZEGcPAGcl5npBL6dWroEJlv6xLe8saBhVNstJNnVDYvGq49TA6lf/QQ71lymWJalugr+0yvQZMWiAnF0eIDV1NJpRnyrUDuu5JQMG1NXgTE5dhMADVMEHrBuf3xRqoV4dxjbkWoEdIzqSAiARRgAbCMgf0eoBNnY5qZGpwrI4cVuNX7Y+yc9DMMZeRSMdnQpnLgoxlcYtTRhZgRg93agCdFqR+3fpZA7JrIK4CnK+Cmu37YmzKalHXKgeq/CzM4BQpCSiQ2c4dvfY+X/d6HSjcfu609K0CVmvbr07JKQiq61dB9Yp/mGaMWoBgPR4l4SH7ulmZJ/dUQb/XAXUGtamc6jLW+QfHnYbHNEwTjCbviJCClJiKowNSe4Cy/hTUyAareS7jm5WVvX4x0CAsOkkCvrLueAQKSPO6VxlnyuVeWpZCHZs61gpw1HFU2Y/mHhr7s17fr+6H193Tq2vhdJ+smfltoqDVjE8AsjWg3iN1HRbPZegkzCsS25ZprbNrjClJnZx1GQlzT5dVeUKCk31FBXSEPHuqfopUdJQAlhod3IZxv9p3ssZ0NNoqntX4F7letbGv2h/+MzvNBk0prlwPuVY2aRIAUmnS7t8yv1qwlCsTucodVLteri+NUhW8AnIpExasAsY46P5WIDgpuJDTao70RSBE5MKMMKLHV7pey55g1rDMmTHFT1BQA9LNXcFJDSAyeI/xWWzLPZT7oCzNNBm0VuAwxAUxajUC2wLVVNcxyM16UL+yBd9DYLBUwRllC2kQrKwN7fadIU3EmvNa58tZCwtmsyYAUXzTEANSTKt9lDKQpdQzivSTlsGGwD0dYoolkaT6nVp1E4RlxT6CKT0gsgJ1ZLjBjXPghjTa2bxDyswwq0GsQ0ZGSnMBYjSod87DGA6QWcdRz582oc1JKu3Wvt1u5bmC7G22d2FJiIEB+9Ic2LmaVAd/rzFVsqPuRWl2TECMVDRwRQ0NUA0/UpB0KX5HTm2SzJe1r74iB3uu7ME4RTgj1S9CPoiWQTwNqi1JIxhJLscYEUOA6ZRJZaT8PsEPDC50vcF267AdMs7OgG3HTVSGmdfkrbOYQsbhOGNaJmQom9us7BOv0VB8v/ZsMqJFWM4kIlCuUjJOkhIGHYJKQSAjl0oUXVXq+7KiMZEr36XVRUUCQHWSwQ0jIwjO9PjkiyseUzkvIIkX6x0MubJPs4KjWQFpth1WGFUhzkhyf2QEUMoJRNLYzclctb5288poQE0FzVSDW9+gZ6+QMdT/YMKJQ6Yop9XaPpZxp9oHxRjHNitBQM4Iv+nx+K3vwA73MO5v4DPghy3M5h46TLDe4usf/zVyiZnlWuCSX2YdZuTI9jelVNiUCiIbU0vtjUo6iW9aQTXAZMBFoMsGlMDa0J2DgZPrWX7mXMEsbkyWBMwhZsFGJqjstlv03mOaRhyPR8zzjL7rMGw2RY7g9va2gFkXF/ewHbY8l45lcG6vb7CMC4a+w+OHD+AlEXZ+dg+cCM643Y/YjwvuDiPmeUGMC7x36IcO1valklHjq1puPhc70pal69RrX4UooLYVfVMFe6vPBfZREiccjIKEqOe6gsAtcFhjiADWSQ1YllAYoxqjLvMEY2v5vrEG280WDG4mHA57tv8ix2OsZU3hzOdh5xx8Z2AMNxTL2aBLCcNmAMQm8hwwMU4TTBkZy7RgSaGUqmcA+Zgkdl8TFJzKCXhX7JHKhygw7wRUy9jg/Pwc4zjCgO3POIu8SkoIM7MjrbVlnlS7eFkWEOWiK+w71lM3qHOsZfwt2DgMmzLf6lcogKrzojIOGWA26xiwP45iZ4hZ0wD6zqPvBnS9Z7I5LPreo+869ox0o2YeT2WBz/PCSYxpAdGCaZrZXxIw2Fgj85+LRu1pLKra6JuBNetTjLK/OJGhiRC9liH+7zzPUplQ5SBUqoQb7fHZXhqKyR7RMeReP1yR7qwve4E1ghOc7eAcj/84jiCJ0+/2e+z3dywdJL6S2tW+71naI0Q4y+xtfk6Di4sL3gMpYp4X9uHAkg7zPOM4HlnnXwBk6zSuEz+X1iSs9vUbDdLqAaQMCyvBQBvAnQbTbPg5YE9JGVacVQKYCcYbUaMaQXwyH+L76YjrwzV2m4cSWMYS0HNAzs6A8R7aja83FtlYUJoQc+KSlBRL1MQLgA8kC4MQ5qIN0waqGrClII0lrAFSxpIW5BQF7U+4uLjA/nCL43HBrtvhT/7wj/DH/833kYyFMVs8f7bH+PyI996/j0eXlxiPC/b7G/iux9nuAn/97/8ccQrYne8Airj55mt8+PEHuL67wX48YJ73uLt+ia57ig+/+3sYtjuY7gKZLP7ub/8eH7z7Hbz55G2cdRt8cdwj5Yhnz75GigGPLh/BB4vOGlxf3WA8O+DZFy9grMFX33yFZZnwnd/+JzDO4OrlDa6ef4PbqyvcvnyBaRnx+efPAPcrvPOt7+HJ4yd49iLi669eYH89A9Hg9mbBr375NWAcNmf38MtPn2Ecj3D9fXz04Yc47G/xySdfouu2GAYLd7jDjgK+9fR9JGR8efsccQkgy9n2ZAEjjlWCgTec0dbur+LRghsU6QEGHPYTpkkPJMvvkXXmHGsOpxAQs+j56AFJa3aMOl8tWNVmyDSc1UOvOrVrcK7N4qz3BV8nZsmgUy2hYnYwlzSlpJ+N0txESgmB4kjpBVf7gbRJR5IAWlm6zMCKKfBaNw1IXZoX8PNrcLFOiEhDrxrP8+/l5wRufEMgJCOfSZWJkOStzpjSNAYK4IkDm7MwCbScpHwRin0gqkxWBcKYxQJQpgKcRCnNhGEWgoJUyBnZcLOx8iwk2VdjCrPLkLYTRAHpgCp9oDIE2dQsqnbBbZ2o1rlv10IBeUTUg4erNiusTljDisUp0MOBj87/62QplEOmnPLK2H0VQDu13fx3BdwBEma6gQIYTuYtgcihlLaRsOlkrSqotv6eCvYUcFVAGB1DXWjqMOk9t3uVwWIOyrjhjYwjMdBAgJSJcaDHTZMt5rBgGWekKcBGKdmLgTtHE5d5yqKRSpAadRV+vmLK7Zgj4/R41+fjhExl+RpBBFJKhQGun9XEjb60y3B9/np9/Z1mntfAt46jMiXLp8q/C+jcgljNvbeA6+pvgtKVqoOsgZ1ZAYAF0JOX3me7Xsu5K4wt6z2M97Cuh/UDspEZNHVtmEwFaJNHko7pcr8Fec0l8Dx9NkhjF2Xm8nkggTeLa0OZtCWZlLmEGYk7ODNzt+713ACaOXFna50XBT/YOAOAMraz+CWS5FDJHj1bNMgm7bq9rkwoz2TqeWCl2qeeWjzGjM9X1JrtWX2fsmWtAuHgbt9ExKwJ0iqFLECsrGnxB5eFHX4FV9X25pzhvWPmG0ikMdUOxNIcUQPE4g4mvjbDA8052q7NlOqaJt7jKWZpusLJ+rIfxL0jo2wyacxhsh7uhRFCxiCSJFjKHuC9zEA0dz5e7bmckBZOFjOQyTZRmfVBSpCtdH5mVrwwtyI3aEnCeGbdcWUS1z04JpUV4IS2BtbaxVk11oCEcT4gxMg9GwwhIZWzDUWGomxoGGmgZQT4pMY/KLJiORZW8zwze2yeuZyYyKDr+rJWyQirKWtFRkLKVLqI6ysXhKvZqSYDOWEJ3MhD9b25as6Wc8E5x2BYYr1P4xwYaJYmgmkpvlJWW07CaA0RKr9GRMii6+s7D9+xXqMmE+otqv2qIVvZi0Y7cNcKC2sdf1Z8Jt7PWfwTgjUe3nnpRG3lvG3OlZRYi9Fa9oEcwTsLooAwB646CBnUA94l5GRxb2DZjiVkeOOxGYCwBMTcw4aIkBYgLECynGCX8xMCtmgzQxBLjfC+rdUI9bmNyDlYOMvjSgCS1aZdqfh4bLcNklYG6NoTu8nfPQuYyuwupCj+WIbf9sW/roAVYI2vCTQFDo0FYuK+tolJHrz3DJztQS4XHxfENichis2UhljQRGL1RTQZpjrQIH4GT5b3MjW+VGPfCzFJntQgi38sVWKU+H4hcbExnAAAg2tMhjUlBIoJ6LaXeOv8AUvKLAHWGQSKSNMdHrz3Xdx+/SXuvvoMOS0C+iXZy8pML4PP0VXKtYLIGE5wSo+XnPgDpPItKsdFhGlacJwmnJ9tQcjwlhv1JmHX87LicXLOCFjGrFFLhHleMI4TnDc43+1AZHAcjxiPBzjncHnvPjabDUIIGOeZtSoTa1ffv/8Qne+QkXGzv8NyM5bnOjvb4emjh9hsBhhixrw3VrSXDSvu0YzOc1k1j7NgFwRAQMdpmsq6yznjeDwW3KOX5pRqH3e7XbWVqDa7+DpA0bX13gtJrAdXHnM/EUsEUoJbcy2tFE4pCYgm8U4Mhfmsa3QJAfMsuptEMuac8LNyFo7jXPaQ7in1rb0CWFY1agWks4Tj4VD3gzHcnDTF0pCJy/ErQ1KbVCvQPU3TWnYm87mlZ5/2rEiZGY/OO3Ff2BfgxnMCABrA2mqPd7ut2GmSBGVAAlcVMGDMcXYt5xe9/MBnmpNmYgwatvJ2zLAfhgFEVOJkZpuyLEEoZzfP73icMI0jFsEDUoyY56nIBmhsYwR/2mwGbDZbBqtB6HoP5yy2uy2/jwyDsyLTUiUagujvJtzcXGO73Zbr6/phRrjj5pLgBmd+2GAYesTGR2vXeJQEAAE4pCMMFy+tCAS73Rmcd+iGHt3QF83XlLLIJMRCeAwh4nhgnVtOWDBwPeapAPF914lkgsFuMyCmhGVexP/ivXM4HnE8jvxdEBEtMvB9z3PhPTcH1LPKZKQQWf/cGVhvECShHWLCcVq4UbG18OLP/brXbzRIixJaMjCWAPGW10zCGpCuP51FxsAYkjInzshCHBe+jgSnUlqyxAVTmHDZe9B4fMXw5dyAbOAN3EsmxDvHuhOSIVY/gQgCWCUuJ86EZBO0qy13gmNUHZKNZT87wdgq2bAsC5aQcL7b4fLiAW6vv8DTdx7ge9/7CAYWiRzeevdtxHyNb57f4ngHvMwLnPVw3QVu93tsB4NHb7yB+/eAze4SXz17jufPP8O77z2rD0ajAAAgAElEQVQApYjBeWwfPsSbbzyGtx3+2b/4U5yd38e0JBjnseQMJANnO9zsb7C9uIDrN/j0s88x7+9w/fIZvvXtj3D18gXuPbjAsOlx9fIGibhT6INHT3B57xHONzv88tk3MM7g/MEjnE8ZQzzirfc+QMiEH/7lX+HdL78F21n4zuHy3hNYMpiPN/jxP/w95vEKl+dbXD56gmffvER3dh8f/NZvwZDFbH+Gb776BgEjyD9A5yy2XYe3H0UQdbi+ucYUR0yQzs4wkrXVkKyWTuWy1mi1DpBzFZCmhIQgZXESEMo1FJDQ4FtZMSWIVlexAbp4mZOcEfy9yvxCel0p6+vAL71v/p867/o+dWTVmSkAimXHz5jKONH7X18f5RDQAFavW56hGNe82psMYtIK+Wmfu/wsk1ADY3Xm1hq8gGp18rPod4LUEa8lxxqANF9c9jNQ36+sZn5L1Y7S+6rOM0r2W8HUFbBFyjIrXyeBvbAvxQHP8r6oALA4o0meQ9mtDOLxnSpLuR23dj3k9aAjpgjnVPeRx81IYFBsmlGwaw39rcA4VD3R0+/WSWnv61Te4pV7a37PNlP3IUDSSR2gFXidxX7zvEsggSqBYW0TipX9sT4z+Pqy48kUB+n0uQtjQddj86jypgqYgFkiHJAbmMTBEaUMWgLysrBu0hKYHWUIkC7XpXu47tfmnDs9xAtQKuzoCsq9yvQtrAIeHDQbp7xOmfjKDFvZi+a9p7IarX0hQmGprW3aq0mF08oA/c41mKqmgL+jrKcWxEjyjFEqZWx16rSxRfUV6roly2yKaFhnzXnpuB4TshHQqICv9V+A6IFp4JuV/SzrJOsn2vVhGASSckQAtYoiV7dEbUi1pVqJoPrDatPFZ2jWCYO+TXl7ua9qk9oGdOqsF23uNsnNHqqcU2twtl2DOddqhtXfZEBY5UHZbVXSx1rDSQO9jg5uGTtmbs8hwBEKw1QTP2EJyIRSwqYJw5KUIU5E5hVrNJfgspwXjKpUm6BlaikVO8LJ2QBDDDyGKOe9DHstzatVM8yOlWtaw00DyZTf1THi85CPawGCIIA0OHGqoDARIQqABwDOeaSsmoWcYF5m9j/5jNHGLRbzxAGyE1ZJWcfGIEsDppirbSfeVtIXwarLjJwzlkUANDLwvhOg1Zd10vueS03Vw9EkMRqiRZlnA289CEaAKLXR3AyENRl58ZKUckYJPskYbIYN3wPx59kX9yCqzKYkSVRNIhJRqcRpx4Gc5cSZ7HRlxMChSBxpd/gUuPlbylQA+Gpa2bax7UklGWeMQRbWs3gkwgzlwVV2aUYGWY5XiFBiBb33Uxt/+rdiSaSCA+Kj8NlshFnUFea3BozGOgEkFnTe4PLeDt5bDD3QWYPBExwBvQN2A6Fz3IfXmozOExYyCBCZEOI5cDDwfWJNxNkgWsdkBsvJa9XPDMuCkCNLHxDBUC11R/OsAGD7Ac77AgSxz5RBOSEsM/tRslYTEigCCUHkYwS4L/ZV4kAZNatnYVaGYC79GFJsJI7EVhSNUAA5BqScEEQ6I4N9Kmu4vLxtJpdigHGGFxeaRJg0QjSWVv6OnslKGDCG9UH1egyGckyiyXQ+J7lpMpdXyz6S62q1BCB21ErsEJSV7ziJaI0wyIEcOAEEABQTIiIQIsxwD5t7jzDevETcX/OeTzKqzdHRnvl6Nut9GefkLOdYOWdmzGvTwVJxB7a9S0roLMtV8LmpoF8u/pzair7vQYYwziNizBg2G2y3PSijyAZY59APA4y12B8OLM0RI5x12F3sSkL4sN/jMB4xLQs8GWw2GwaNRAIACYiILBmSs8ALBCQgJQa3Uway4UTQEgLmMCPNoZxnCsbq+mr3fUvaGccRKaXyfj1bWoarnps5Z9aKtg7GZGFWOrCcSyhyAWpLlNFMRFLuT7Vs39nqs+YM33WlAiHJd4YQCliq5egq/aJVLKVkXLRbw7JgLw2alPWs5f7Vn+T/KW4yTiO02VYlX9Rnuby8hDGmNIBLYRH8xpbxRla/xBbgM8aAZY64vr6GdZz40vWnpfmb7Rad98xCl7XnvIdzHTaGZXZaf5bE/jCgmOU85cZc85wwTWOJ90OwmKapfJeOn8oAkcSCys7dbTYYug6ZxDeQcZ0EPK/3ASxLwH5/wP5uj67Xs0CblXmkFOFFw9iIL7zZbLDZbKDVM6yfO7A9FemEFCOzXeeprBddx1akQp1zxQ6oTISSQlICVO4t54QgDdFCCDgejnj+/Dn6geUkdlvek1bubxj6si8M2E8jYSFr8mCeZ4zzjJxSeVYr9xkWJkNud9viX8/LhGHT48ztkBZez/PC+u8hcmLxsF+wJG4E7byH6zy7+inBdbyOu041yDMTH9q45yQebl+/4SCtBJYNaNEG3SXwUYekxuUNqCSAROZABLaCECxNy2EDckLIDJK8vHqOJ4/ehnWmoPyrgCcmYJplY9pSiuG9ZwdgzrD9wJ1C5QBKMXJQnjgA0jIq7djJBoezTsZYCaaJDzlj2BEE0MHARcIblw9x++IFvvet97HtPMIy4d7FI+zvAh4+vYeb4xN05HGcZjx4+gjGerz8h1/gbox45+N/irurn+Gv/vqniDTAGML1i+f46INvYX+MuDmM6DY7TIcIawccjgm269D3Z7h3cYGbm2vc3lxhCRHvfvQdWG/xi5/8Z9j5iLNhg+Nxjzc/eBNvPH0Df/fjH6PrNnj85AneeOMpru5GXF0dQfklpjHg8VtP8Z3f/S+RM+Fv/uavYP0WT5+8gT/4/ht47/1LLCniMCX4boOXLwP+4e+PsMMGO0cwvoffbPFweID3v/0h3v74DcRk8Qf9Q/zk7z7Hr37xc1w+/i6Od7+Amb6Bcxvs3DluLm7w7PYZvrj6EnNeECBAvgGQM6KW+Ei0yGuQaWzqKAHE2Tw+1cohzE1M+DpWukHrYWcNZ3sr8BFKgF5Wq/xgjJEO1bL2JGg6BVfaz+i/1yAYHwjr99TPKtPCKAisYFOunWJTSuDu5q8aEnWQ9XMK+BlhuhlibZDT7O7pfb9a+m5qsCrjR42ntwKK1Sac2ABDhEqYr+BsCwRzIF+/u9gVYfC0913YBs0ztGDV6+eC56D8Te8bjYkCb3Utk5bbF7ALKB2OlXJQ1sgJU/ZkbFeOATg4g7I9pTqBp/xVfdtfB6Sun+3VYLF9NgUeVyD4CiAyr/l3uQMBdEjQG2Wzq3g+B/2mWS+89tYOaSttodfWcmAtcQW4AZHeyyvgorI4Vveo54gChcQ4BFFlNsnfESNonpH3d4jHEUaBL+PFrtS5UnDnFNhuX+o08Rp4laXcOoP6Ht7b6/XPwE59/+lnX/0vP7vKY9RkSXt/ddxO7629p3a9tPd4usb09zFGHldDyAKO6itKEiQDDJjSev0q4KO6y3WcmDEEY2G8hxsGuL5DLmuG1x6zTk8acWUGfnSdr54voyQ7GCTQ+4glmSSjLe9X7b3K0letwJq44DMoJwnAJThJjTastbovUFh16i+pY87LU1YsVfmHFoxX4N8SFeZ1ygBZZq/EMg6AJre1qy1am9PuE2Rp7sIDz+lKgAQA0c2Zs4BlUNuHJnlRBk58LjBYaut88XrR507I4gzD5NW6ZJuYEZYFRvoLKNBG0qgipdq5XX1IEi3THCOynAnItYs4ETFzAq5Zg3w/xlY9eCqAch0jK6CVIy6TZttR9T4J4AZsRv0SQhStaNf1pf8BCOgGDnwKUJS5AQqkxN1IjwWVAVDQSoGQdg/mnAtArttTyQ7GOgG1a5JyKLJkqpHLGp6FiZj49wTAGgeCAyLfn3UeCbXMl5MsHs5a+L6HSjaEkLAZzrkk1XLAaqi1IQoC+cIe0oPJiK5wThnWaWUNrdawMbaA8Hq9Yk+lkZztDLzjhirTvGAOLI1iiMdXz9yuaXBCjT0zuq9B5fxpk0lATUzoHji1Qa09VfZVu48YvJP9kADjjQA0PI4xZWFp56JTTAA6r2uC2VSDtxicQW8TvAH4dgnTFOAcy66FSOi8hbMRVpoaG6LSOCkugfdj0oQmj4/rLFzm4DblhHkJxXeIQlrJOUl1Ip8JxnKSxlhX/GgGc8Weyb4IIZS9TckWgLacY7LX2OeNgMgyUAEW69jB5NJwTPU5GZjJbOEyioQagybyHZkBamawUfHjsjQM02Zk1ZeRo0dKj5UVq39TOzZJpUz1dSyMU99F9JNTRAwzuFEjV3fmXKgIQM7wzmOJEXNY/l/q3uTZkuw48/udISLuvW/I93KorKxCVQEEyYaoZpMmdrf0x8q00UILbaRVb6Q2mUxqmkQz0tSCSIEooADUnFmVwxvuvRFxBi3c/UTcV4DW6GuWlVlviOEMftw///xzSSzrlkgp410QBmUIOgdF7X/FeeXoOofP4PsNF+99wP7tK/aHd0pKd6tqFFZr94drOJdC1a7tbZ8Fj7ffrbXFRNH3YkuzVs9ZjwS3JH6z+lKVSjcM0lCtShVDP/R0XS86l7NoRW+3G9HszIX7+3vGURl4w8Dl5SV937Pf77m5uSGPEyF2nG23nG929EPPlBJBfcqUEnf3dxzHI9M0aXULAggnSYalUjmMR1yRhkWh64jet7JsAzXtfF7LH5itsEZEOWf2+33zHYEGhDVbEgLjcWTOCR+DgLQOnFN9coRVK/qhK7+GpTGd7Yii1xemq0gWmISFPb8RY+x5JwXJJIkWcD5qc+BT6TPTSa1V1qCBfOa3m16qrKEltsj5cEJYAFjHAcZElTMlQBGbImtBEmWCy8heMh1l55dnElaugNW1iN7szc0NaRaZC+eUEOglXgkxrli3Ts+rQClJwUnX5so5uLgQ/CBrvH84HMgpa0JNQO/9cU/xMqapqE2Z0MaIglcY2cp65+x2u7Yuuk6SqSVnJgXFSykcjmM7fwzUNM1Yi0uK+kM2liEEOpWMGLqeoM0VTT+2IlW8x8OBiqytcRybxM44SvLk7OysyRb0fS/X1EaWufTqYxXOz86lWinLXri/v2uJYTDd306qaUKQCgl93u1GJDM2w8CZ2VBNAot8xETOpTXx67qerg+gzG3QxImX607jyP3hQNf3lDlzs78TLeci14guME4T7ij+pDGNu64nhHgSvw/9f6qatMjhZyAKxamDZQyShcFjZSxVQQzXjLUYNetoX3I5+VnLfBjgW31lnO5J81Gp1pKFNqdHAJxARRxFcTUku161+tbjSTVrp0XVSSq0gM+clJxnrKtxA8ucZAUBXPZaviULKsTAxnWc91vOLjo2/U/ZhJ5vvnjFo6vCNAH9Ge999AF/9V/8hOMxUF3H+XVk2lcun+z4+rNvuL1xnD3+UzavHM9fvMf3L79nu73kgw/f55/++dfc3d1yvT3j6Xvvc3H1jG9evSRNR94cDtx8+Vvevn3N3e0t7733AeOT57z/4gO+/O1vqHh+9NM/o9ZEiIGbd9+zOb/g8vKKTz75CR/86CN8HPiPf/9z0eEZIi9e/DnP3/+Q337+O2qt3Lx7w9BH5qnwz//vFxzHPdXD+aOnvPjwBU+eXXPzeuBsuOLp4+fETUd/ec7+mHl7W3AkfvLJlhfPP+GXn/Z8+ouXjMd37PzMZuhwRcpfqstM6chh3rPPM3OuLYtY3aIjLEZGNejUeJdizMrSnG6yOivOQ9FMvTdwQEt5LOqEZV02BsYDQHDN7LFgbwVqrJ2eP8xss58RALrWU8abMZjc6npW9uhWBsT2iHtw/4V9uey3ko15ZXtL7iBlSAuAtzCKdG2v9C3tOdQI2E5v72pjst677Wv6bH71Ozae6xL99WcNbuk/sELg9RgE57TD9NJlExZA+WSuVtdt92nAjdkrZ6/YnruB3m1cZNSqljxbOehD4A6DCh0/+L6xcK0b5npcHgIXv29cFlv6Q8ajfRaAypjh8kgPAcOHf8Mps9VK8RoYsAapDPApy78leLbu5M56LOn1Hj7fUp71ELw9SUDoujpB0hWoxSl47GzUbX4WxiHVSf+Woh1yc4ZxEoC2sfocD2dwPS5rYHs9T8bEsa8/ZDQ/3P9LwuSHIH67zx+YG/v5UzuylMH9YAnqxxorWnXLej4f7hOvYybgTdVDmfZM9vxN+0yuojZk2bftUfxpMma5n+osr97bOY+PgdgP0G9wsaOEFYiyXicPgF99jPb19bs9HN85zchK+eHap+kucmJv7BriHAtgYmK2pQjgWYoH1T6stTJNqdmSJZgTNojz5jfZ8BrQLL5QiFLaXEqRpqspCbvYiY5gqZDVEWqjrVNljET88l4Glq7PMmNbGABTStGGqEswV1EGWrZ9KgGggXsKl4nddyzAqq75tYavIsLNdliCtZ0hQBcia4kVnCN0G4L3TPOk69YvjbIao0VAVP9gXVMFLF/vHVOriFoS770jq68HEGJnvyr/Xws+CPJVvQYeeh5b0x2bAqes0WB9DqrHREzavtA91vW9lJCGAE5YvsZgsjXXGVDWWFNeQWK5aTKGXZQgKit8bD5RBWG1OVmbSxLHtEBt5NFgpaPrhjZv3nuSMqqg4IcBj6xd76MkxKswANFXbowxFsa0+fPe0xhfIKDdoOMtjfxOwU1j2srzxlZaCsuZYjIOBh5JxVsh6sHXKzBsc2olzdbgLReRtVh0zJdzcu2jSKJk7a8sFQ6w+Ex2Ptvz1UoLCJtflUXiIsaO2PUCjLPYGecqniIgU5YF673n9uaAFHx4/A4G1eUvQKpCRMhV/KL7Y+E4ZcoMwQlTbyoTdtbNqYgkyJxRNLvpjlIrSUGonEtjgMeuE2mNYg1uJuY0UaZCUPsSdJ/P88Q8jydnJ7A0eTWSRHWU7NQfKK3qcZ6lkY9b2XQtk8J2QKmFaZyELRViA3Va53gFTqNKhhkALv6dNTWV0mbvtImasgrlGZtjocDuDLr2Xa1N0xiUrazXN9bbECFrs9uqIGxOidmYgwaE6Vib7M40T9JTxRlhSPZPyrJGyetEnBBMyIVM1ZjXUUNl9+x9nh3u+eLd99TpTpngDtDGqc1/l72xboQmzEYvDXX1h9aJRK97pspEkMdMvfAUIICwxYPMt4s/7Hlgmp7Ssb5nGkeOxz2xMfKCgp6yZs/Pz0UvNAo4+ObNmyad9Ojqin4YRFe7FN69fcv3797y+OpatEu12mJOM9Mk8oi1ZCKiQ25NRJ13Ig2y3RH7jshpctnKy22fLjHj8jHd2aVPyPLOVtJtf4L35CTgcKmJmhOOSIgiK0B1XF9fN/sv2uOLz2i+w/5wwKQQ5gfyDN5Lc6QQAilnTVjRzn5b310X6fpek2EilzQMPX0/0HUiXyNNwuRXjPW43WxJygq3SgnzM06ZuiutXAWzx3Gk7wc2255aRDpnDTiWUthsNsRYmeaiUgobdrtdu+b5+TlQlRkpZfr7/YE0J23eV5nSzDROMIou91oGQHwJqXYyVj6g8hiBoR+kuoJKF3suLzacnZ21GKyUwn5/4O7uVvZumjU+LExaRVCmCdPNN61382dFhzy0hmB931OB7dkZIfim6ZvS3BqpjePUiGJZKx9MM93eabfd0unZV2tVsF7mdtt3+uxy/olMQ9UqktL0bq1h7H26o++Gtt5jF4kh0nWBvt+IHAViP9I0L888J47HA847xmrxjW8s1kFZu14TGJeXl/RdxzSO0kitZKZxan5aKSJplKusc2cSH06ahOIF8K/OcR4uiOLIMyuTt5TKqH7kPGX6PnDYH9t5ZNIc83+qIC0gmV4FXUDBDbcCWA3E8b6Bn85JF8miTo1vnSblgAnaNExAVHP7HYSKK5CnI9P+FtedtUAGFnDInN9cs3aeF0c8KfBGdWpwNk2TZKozuVQ8UmZBdYzjKIEsEENclbSJ8zN4ycZvhkEcWu8ZQs97z97j6fNr4le/JfYbCIH7w0gYRkjw+W9fkusHfPf6BucHPvbX/OjFhujO2PYf8nf/+y3nlwN/82+f03eFKxU9/vk/f8ar7++odLx7d8P+UHD9OdePL/nu27d899VXxGHD8c337G9ucVfX/F//x/9GLiOH+z0xwJGR6+tr9ndHjrNj2F4Sui13+4lf/vLXXF5d89M/+yn/5b/5z/jimxtKPeM3n/6aX336T7h8ZON7Xn/7JdSXHKcjfdfRDTu+ePkN3/z2tzx//wln2y2PHz/l0eNHfPjxBb/4zSuOh8j+tvDVN2+If5q53EX+q3/9Ie89O+O//+9+wf5wZLeL4AI37+7puoGPn3/M+W7DzfGe796843jMvH73hhomXK8OhFfApdZWnmxAGCylpV71BEFZr0LPBrwaZNF4akFuFT/VnKS8BlRsrdfaDp118L6UUq6kNwz0WLHXzCG0AEl+dFXq1H72FBAyJ7WwMHnNwXsIHguoaKWy4tiF4NpeBCuvda0xUgszfg+oYb+zLuex7spLcqWe7MOTQ3oFgJxgbCtw94Qp6VAAWxn3zqyMvbM6qcqqaRIFJ+xQG9ellGQ9ng1EL8ruNRtVSyvhd/qOAvKhtuv0OmLCaguqFxCnOxk7+ffyrvL+EkCAPsMKFF//3rrs/eFn/fWH66xdpxlnTq75//cxB0meV/eGbo5aJXAwjTYLaBewWkqFvd5bmLRw8gCr54eFrRSU3WCBLatEhJwnS6JAfsq3RNtDIHNpROUUuLOO0TNuHImzrGPRSjb27Slr163WxklyYBWMr9/jIYv1IQB78nULbtr3l2sba/MhAH+S/HCnQOvDtVbK6ZismXDLz7sTW2Nj6+w+bfwWdrzdb/1n/Uw2n63rcT3Vq2/Ah3bsbnOn8+SDx8dI3G5h2DBrYO3qsneAE/CnJXVZxuQhqG57z3Q0qVUTzA/K3lgSNjVnZZZwwhROOemeQEE6r010YFJNzt837/I1bRRZrXhewBUenjeqh5o0KIta5opf6VKvxncdFKHvIGZSxsSSHifJABZ7KGO6zE/X95rQkAXlgpMGnk6YbaXkpsFdyppZdpqAO5FdcKiMw2Ku1yx12d9ebeHSPLTvpMN9R2hninNxsRdmg37PfDtQhpxc24IcsVfKYKwK9DlJuglLjaWxkDJQ8ZE+REXVFeQxFmqztSJD5bySBDRJpP/CGLLOiR9TQNk2RX3gfLJupCRQfrnkQs1mqWjnTox901e3cumAAPmOKgcqZr+W8ZHO9ottED3UqCC8sIRyKSSdz2macMBWdd/mNIm+oZYUFwVFcTJ3stfETmsdQwNoDUTu46L/FqCVsa/yDnKeeE8IA4vcyaL52thtOrbRB7ZbkTAoGpwZO9P8oqV5kcQMRM868WNNyyyIbnas+QenskH2WTPHmp+2kqqx5JfTxIaMvTQNcspIpULNM8eSGTai7+6B7bDFEykZAWIfmG6qsLec+lB9V9mPs7CEivgvpWQKgYrH+V7kACjkPInIqQJQxlQbp0kTNcI47IeB892OLggbzLkznKvc399z2O8bAGu+mey15Yy3z7qCotQMoZKzZ5qK6mtm1VaWfZxykuA8qSa2Dwsj1DlKhqL798T/pJLyzJiOjflra8+q01zfMRfTljQbYslBSZpI071ECLKnhAkrpcQtsRcMmBd2kPdi72rOkmQropc8K4Bh97O1NGchTozzLFQjS8qtGkGEEOQs0vL9xXeX5k8ipVDJpVKj5+LZhzwezrn96gtuvvs1JU/k/EN/ZJ38MYmSnLMk7VTv2srQq05wSsJ4pRTynOmCNC1KqdArEzEYUlBqm691Am3opXP7eDwyjtKcaKel0wL4ZfregMJOGzLNHPeHBvAOw8DQ9RTgOI1MB20w7uA4j03D1cdAKZBw1JRwVHIVybGzTiQVYowMQQCjSdmL634IJsNgDMYQpDzfwEPzPTebjYBttTZ/ce0zGXBZ9azbDAOlRmpJ5OxUmg5Kro2Ba3GLN6kBXTsxRs4vLtoeM8Zx3/dM0yT7WeeuH4ZlDsuiDyu64jP17rDYPUs4asLYe2GDOrcwTZttDAvoaPt6t9s1W7LEx7Wdrc7B8XiU/eotFijLM+eFfb+O2wzgtn9bo69xnJq9Pj+/kHOiyD43bVWqo9TUfJQWP7nQ5luqHRbJqFEbXy5zIKDoMPTsdmfsdju22x1nZzttdHdkSjPUwtnuTMr706ygcmUcj23+bS3JeSZN0IbNIBrkITIMXbuvSAjJ+TX0Q1tTRUFLu56tsfv9vn3fPqKBHJRx2ykjusN5W2NCuJTkXNK1EES7uEjz0dhHDtPYEsUxLomHRXpDmwTuXEsyUyrTPKs/Kuv0qMkFk6kZhoHegFsn5/bQOyU1+BanJ90HlMJhv2fKhbGOhK5jSjNdiKQKVeWwivo3XRfx9mwrLCfl3BosGjP8D33+yEFaYQDY4vUYAKBMxuoaU0A2nlPWq5ad+aALHLoQqAHISTW9UOdLDZlT/a1aqSTevHnJe+//hBICk2qJOoxZUJrzLh3RRejdAoDYaYdKxKBN8wjzTPSR4KTrnpT10BxcV7V7fEn0IXJ5tmXoevp+x0cffcJmM3Bzc8vxcI/ve24PCdftmErBaSfqOWfOzi64Hyuf/uIbvK98++q3/O7XHX/9Vz/i8dUFr98dmeYDt4fAsHnEeNhz/ewxX3z+Fd9+d89me0kXYBz33NweyNXxycfP+Ys/+4j9m+9xYUN8/zkfvnjO48fXzOMtL7/5nmfvvcez957y/fff8uqbVwQfubx4xPb9czabHc9ffMCTx9d89pvPmTN8+/qer755yctX73j39i2OmWdPHlFmx89//v+QxgPeZ6bsmMaJcZ55/uELduGnPHvxI66vrug3ns3W8S9/9j5ffH7HLz/9Hd9+m/jyN694cjXwN//6E97c3HF1dc4+f89hPHJ2eY1/+ZI0j+y6Hc+u3uf9zvNXP7vgRx/9Cf/uf/r3/O3//R+odRQHSdeJMXvM6Hs18nUdVDXwcwEwFlCitv96DZiqghYO6ehsjryAKnegSmUAACAASURBVAZ+GGvXtSDJObvuujuxATwGwCwOvQXMxhixA8CcH7d6Ptt3IAkLAzXEEC+Npuw55ToGWgAUzbi1ELY1I3GteYxrzvU6wLBrNoCxVoxw63TvGzug6u8aSrKWIJDvaYmtBvXSLIbmhC/OpgR1tWozpWqjsbC2LCivzRYtJZs2nyAOMg08apDYApQ6tTh6SFgjJPWu29xKsGDPtp4bY9+swWavQKPNu627pexTp3mZWu+ao2+Aoawvs3K6Lrw/cSweApNrsMtYgLSrOZ2HVZm4BTmrQHNZk6YjqyxW7OecrDu3MGHl1y1xoUFme65TcHb9rKL7aPvFk1Jh0V6VQM6abfkq7Bm/mv8GVOrYwNId+gS4tMBbAbI8T5TjsYEw3ntqyk1njdUe+AHozXpvP2S2noKpDwP40+Dd7I2OmQbCRSUA1vvfptFAcNN6xD1kPRsQdLrmnFvY/WsGtluNo32KCk07J4mDagwTljFdA9lr8HX9nuu/25lel7VoCTEDaiuVruuJw0YA2r4nB/EfAn7pc7Wa68aubp7DYgNPxq6KLm5WtkChCMNgvRdsLekTLpUQsj1byaYCc975dv7glzFYJ+sW/VT5T6lVpQAWWQ/nvWT70Q7z1tHYSwd5K0d0TsvnapWGXjoCdl5IQzwJ1J1Tq2HrpBqotQbLTxMPDejS/WLO9vE4ElbjYyXs3ls3dN+SarZm12XaZneE9W5JNcDJGC7JoKzSGG7BPLQJqFOZooinBFuvAta19eqD3OlkHcq+CjFStGTbOl3XCl3ohN1idhMp5c9Zm3a1ckxaQFz1npbgrKuS76pgkgSGWc5YJ+dZ0xSvmjSOnpQLriRqSSrnpAGjd43l5hzSgV3t7OIrLDbGe9uftHPEOUdwQoDwXu5lM+S09N+YcF4ZPqVCUdmvWhF7bKXOXst9zT4CUetjuq7Dx04rn9rEQxUWoXV1NiRZklGLdEFOswK7nqh+lzHKc5EkqLCOfQOYSi2UvMwLTmgblnwygNAYPb41qBGA1uNbktSSMyBEkZxzA1gExBaAcDzWBixZqW91SujQ+CcowGMfI40ApAYImGyQNqshEbsBHzr6EDDmdU6ZaTrSbQZYrSE5DyvBFYJ3dMERIgydQ3C/Ssqw3Xji0HG7r/i7QogduVQOU8W5AD6Cm6TpShXpFDvTcx4X1p7zet470jSzZ0/0vrH7+r4jxo5+6Bc5ulKIdEBmniZE33IUGxI8AZGvWNsIadbTAZUaAl2sZN0bIYuPmhXwKCVRs/htAgoomFlFxiwoG837QkhwPGaiqo/EGNresuZluSR8EXsTo9qhUgHRKh6nAzWJn+p17YrddNSm4SVVgSE4cnZABvW9zW7iAzVIMBE1ySRD7IkVTYxIgi54T1R7RV3IFQUpC69J5BxClHLfUirBBVyoVF9IFMYEyfWcvfiE+/03zO+OND3k5rtXUtbeCivfxqoUq/r3VjVgAN6oYJqx0OcpcVbAOZGtsQY8pVaxcWhlhfoBtsesI/xm6NlsByjy+yEEQteLJnMp3O/3HI8HShV2/OXlJSEEjscjx8OBUQFZD8Su49H2UqqnioBjecrt/QC6GNgNG9GrdEt105wEk8gly5pTNmoIgbOzMy4uLrDeJoY95JxO2JnjqM2h1KfMKucIi2TANM/M0yTnV3BCpqkV7wKb7aCAnACZ65gTFsa7ERdCkwcDq3Qy0ItaccNAIxioD5cVZDeQ7P7+vgGCVHnvw/7I/f5epEy8lNJj56j6F+qCiZ1+UI5vjMlFcsHrOSvP35skJZlpmuj74cS/bGB2lXMkqZ7x4XBoY31iU9VXFVkdkTpyOLyOT/ABX702sjTfW3yNCwXMuxgbGG8+3eGwFy3leZKKnpI5HA/c3t4RQ2DYbGWscW2tSAJY9tp2s222u16cY8nRaZqU9Sz9LHLOZH1fAdClGadountSTvSqDdz1ViEiSZa+33J+fga4BtinZPIbRWUJMnPSRqpeJCJtHAVsDSpnJEzZ7XaHw3F+dgG1ihZtlj4epYj+8qzvIPOw+I4278PQ06tG/Wa7FYuvFXaz7oFpFlA058wh5yblUaucr5bwF4a5VD50cVDW/Y6KNsUsRaRiDkcykKs0HAsxMk8COBsJxhjb/TDQGdFKqwcfVhKvP3/UIK2DVmYuAWJuWWkDbq2Uj1pa6ZssXKfaOVoyoRvEGzOjqs6aHnxZD+DqCpnEYb7Hu0r0gdlpVldLXoMXELbqc1VrK9wynpbB0YOpQB97ebYKaUpAZtAOhr2P9F2UDrW18uz6isdXF/T9ls32in57Rs4zF5eRLvYkzf6cbS44Hvdsd+cMoWd/GMm3bylxy/5+JKeRy7MtF+fnfPar7/m0vCS4yrar9F3Hqzd33Hz3NWc7h/cDPha6fhA9quLYbTeUPPG7X/2CN19FXr78mkfXz8gl8eq7b/ni80/ZDTtKOvL1V5/x+vXXmoWDq6tznn/wAcNmR+x3nF1c4uPAZnMOOD77zXccDpmPPvqIQOXm7Sum48R2u+OLLz7j9t0rnCuU0NMHz6PzMz55/jMud5V6uOPzX35GGSJvbx/z8UdX/Oc/u4ayZ9p/x/6+MCXHr357w5uX3zAd92zPLwmcM6eJYXPG8e2BPM+8fvuOWh0ffXzBX/3lv2LOHb/+9td8+frXsjZaqaM4JLlodtfAEj0UT4EDY7XaQaaAkl/KOjPCsup8bGC/fawrq0UesskXAKzWpbxbghALWl1z5qQ80AASua4EYu7kUJPSWdkLrZxp9TsLM9XCtFOgyEAVr6CjdFJWyYTiaYeIPmutrgWTNo6wZnAqQFq1tK96vV5V4AjtULv6XQVgGiDll6JFu7YFLtKt2QJeBUYNQLbZc1Cke0Vju9rXvSaCdFvLdRSoM81hAxDkbysfU9CKxWlrF12VYRsIAcYMKe1QW6+vpeTftfUlgPApkLX8btEA3KkjKQGxXztiBhxX5D0esLTtY460OGAsiQezh3Cy5gwAMPB1/f6yXn0L0k/Xg2/rvpZKdWXZFdVKiDgBJJxbHKH1GrH3N0DMuaVk31hPpnO5jL20AVyXw5pj7fTatRQFF1fgKksQTs2UlEUOxb5qQbSydH4IMtKcJtHKMqZuwXQC2/58wK56CPa61fUrNOBd79KAi1PwtAoTxS37QqQ+dP5q++0G8T8EltdrcHm+hUFzck8xCTgFEdfXevhsNhYWrCzAxrrp22IbBbJaYFUBas1HCPiux223lM1AVeDK1cVOyxmwGr/Vv9tc6xo2u2orIMYoIFvJUh7OYnubfZMlRVVgqWl/UjXIdKC/26lenqxHaeTUns0p66kuCbKkmqp2L9O99N6LFmt0CrbaObKcZU4D9bYiq2pYW9dtZ7bKNNhtfYXmo7Vmlw/Ww3rdGhvSaYARg5Tbix1vO6adb7YuGitOG4M55xUvrIsNKwtLtJZKVV1ar6X49ntiC9AzWO2pOvZBKUbyTh6RE5CgvOTcAM1lP1RpAukMfIsCEnkJevBBGtvZXtOxlkv4E1sq/uPCMrOKMu8dTu1/cMr2DZ4QrQnKshdiDPR9h3NWhghEG7vSAgcBY0UnrWSVzdDGIFaWb76FLnzQjvQ555bEtm1XSgLnG3M3+KhsptU5W8W3GacjTgH0Uq3CwVGrXxiRVRredEGg2qLMmzSP0mm61lbe2XpD2LlYBThR3i+lzFTk7Os6kaCY5yT8W11bOWlDKgLORQ3sFzsr9sNsp+wFs0nr9e2dkEWiNx3grGXwusaRsylrIzrn5U8uUm7qqEwzdEUTEQo448Aru9t6YtQqOpx2T9knsqdLRXSJncOFDhc60aUMDoqsT0ol9j1Dv8U7z9Bv2Paiu9kHTwzSJMx58K4SvEPaZzhykvU49Iukyv2hkkvE944pSXlzDBEXbJ0WraIobQyZp+YnbIcNDgOmBGCY55m4AmNE/9dssAFZi08hlQRikS2ZZOeFC5Gh6+jrQEqz2Glt0ledlA8XF+i7gTkn5iTPJuxqiTlP7UjQ9bfBO9HKXaX65ex2mZRmqDDPo4Lsyg40G16yyEiQms9m60pieq2C8bI2vRcgrhTINelzOAXSCiEO6vfKGRu090nnA/jS7Kt3EDVGlqSQ1F6kNIqN9HXlx2iyiqqAOnRIQv3YOXh8jX91Cfc3kmT08h4Omj3RoxIDxyzeMZ/EkqMpJYpfzlcDcUuRhmUCmKMgp8HwEOwkdLRkhmltbjcbNsNAmrVUP0sZexc7qHDz9h3H45G+j2y3Zwx939h4h8MBqYLKDP2gDclEJiSlmXk26QqvGIY0TOqiJBdyquQyk+ZJWJdq47xzTbrAYk5hbcYG4hjrzql9ywq0JQN6c2ZKsu762Inv44VpG4KHTrXOKU0SRWL2JdPlHCvGpcZC+j4pSQMnH8zLWPw1A2o7lSVYx2PmxxZ79pIJUcCvPnbKft1wdn7OE/WrTULBJAjmeeZwEOYtzuHdwvilVu7u7xjHsb2Tw5FSbomHBmQCLlQ9//oGdptfabalVqf2CpLqpZr0hGojKdluavYsH5dEnPlRTv/fO9cAQJzTZEeAOjQ5LwOILy7OleA3kUqhJgH8cxGJlMM0MvSDYgcy/y7QWMGyjkVaoLJUM8YYmz6tgP1iW22fiR+9oeYl4Tgp8Go+5m4YQMfS1qlpw3edsH0NpPWaXDMgvCjYmtNMTon7lFbay9K83Rqudipp0McOVEbh/OxcbLCuxePxyOFwICmb+3A4UktRFmvX5tYY8H3v6fuBc0sc2Ng5x3E8ctgfGKeJNGdNWmR8FHC/6zq2263IBiKx1ND1dKXSh74RKuxdUxJQ2IhV1rgtxEDXq85ulqSDyWj9vs8fNUirOQpwEujjBERNmaZTVIsEVq1DqluAgerF6e067SDpFChLpi1qTJ2MZcTBk0vi9nDPzd0NF7sruhJ0MKUMsIFSK5AMNSbeed04CWMuWUmZ06inC5GLzRlXl1cURLj96uKSR9ePkQ51HdvNhlwjXX/O/f0903wkxo7txTXj4Z40Hjg/2/Lo0SUhRL748gtubu/5V//m3/LRT/+U//gP/0R18Piyx3EkH+4hzRxSZjwmvv8+EaLjbDMQukccp8Tt4YZ3d6+pxXG22bDdjLx58y3ffvkpX/32U54+fcJf//VfcnN7w2e/+AWeyMuvX3J7+5aPfvwxj997we7immE443dffs0XX3/DbntGCB2Prh7z5MlTYj8wzZm7+wN393c4n3n6+DGhZqZpz8tvvuH+/jXFT/TDwOXZGY+2G55cXnAxRJj3HO+P+P6CPD3i3atzfjWO/OM//oJvvv6G6Qglw/jdW159+WtymhhiYOjP+Nmf/wWf/MlTfv6Pv+R/+Z//Pfv773jz9jXvPXufDs9/+1//N/jNhi5omZbzJ4GmaSPb3NdaReOKJfhcAy4La2oJdmUdaJJBmyBZ9ushsFKaZtofBkLW4Ob6vgZIGXjYSmrX1zeQ0vlVl9c1K9ACbBowxaq8a3lemjNtWWC5fl3tEwtoChTXwJj199q9vDJEnDhVntAC4AYmsLD11nO0BO8Li8+AaRnT1N7RnFPRuVqC7aBBuavKLFJ0WN5xkV6xd44K8jVgro2ZzcHCSOQhIGZASFFwWW1SXr1PG2vcD+bZ7mVjuC41WY8rgGnsm6VzpSqzkNNnevCxa5zIRDy49ikYZ+Ow2Edp4lNaQ7ZlruzftLlar6v27C3gX8qAaj0tq17AmwXQWa+LUtY6o46uC82JfFiev34TK8dbz117xpYIWWdDtQlJqXjkgC9hxpWlGV6hQvCUJEDPWi5hzVZdrlubQ77eow/n+yHTdT2v67n7Q79rGWRnSLv9QauYW2m9zu4DW7Tcd7mmfYzF/hBss+dbz8H6HdZA9AIo+ZMSofU+WSewZCnofb3TBJjocw6bLX67ha6jWFBqut0P5qC91yrJELynYI2dVs9hY42CBd6f2Bc7Qxb7iwKuoTHsa9Xx0sDWgDxLwIk8ShXJRBwuWClrkE7cJhPjBDQUNp8+ZS5N8omTLb8C6VdnCwqgSKJsAbIsiHYsDJKu66j5FECX91MwQ+9RFNioZdGerVlhcK8Nserp3D78dzXAAmFQypQL+C7dfQz8QRpcuQAuyngEDx71Gy3gsrlRkMNbUyzrxl5aIyqBJ7T8vxMAMuVEVJ8zbATEFfZk0DWgIAPiyzrnyKMAlE5Z/F4lrnBCQABQyyfVVnp/657d9X1LUBijSUooba0VTUItLKzUJA7cg47PYvdMZ9ECzFyKNCxDwA5jsdjekHm20lMDpFV+AFnr2ecmhwQ0nULzUSyR6lfyGrXWFjh6DzF45jSRqwBszlVynkhpwsXInJL451XkznKSAGmeJ3I6EuMGH72Oq6fWgHPbFQNd3t9KL41o0XUbbfzjVgHpUimA7fNmA5UJqJqywZvQiO0HkbhQ5I6OhUXbxU7KVWvFu42sXbd0yEZ/X86vjbKISgNqbW9IM74lERCcV4Df40IHzrQJnUqLOGLw9F1P10uDtqGP7IaOoYMwAEGStz6Cj5XiISdHSpVcBbTORxgn8cE9lT7CVGFO4kPFLrB1A8cjbd1QM7ETbcLtdBQmn/kY0AgxtZYTiYCWoqq2fgECodviuyJScNqELhfrMaAgYQhUivpZwnzziC7uOB6odaZmSfg473A+ELTBnvkBOrR6X630IeDwxNCRpNBd9rVzVJfxXhqFVclkkOpMCNKt3YdI1wmzrxaHJ7QmRKUl3EqLV7vYi60vmVK1YgwHVao5xX4LKzsoGGvJSo9UCkRtRoRT9qE1Q0aTssqWrXooubBIR7hg62vlF3lJljx69j71/s+Ybu5J6Y3E3gho7nXvSEJK/QmT9fCLxv5D/9JsnFUvpZzJtVDwIoXjHQaai467nA8WgwhDVBi1se8Z54lpnnEOtuc7XHDc3t42m3h9fUWMUlkxHscmRdB1nYBgTuQPSsnMk3zP4+j7gdh1Dex2ykQuJXE4TIJPzEXLwKW51HazlQoMe08nJLO7u3tmrcrAXJpa6XvZLycxo5c9vht6+mHAVZGKKcWabEF3ftbIOE77P6ScGnYRBkvkXmJ6xxXX5AtCjAIGWzKjCqOwaOxhbE1jzXZaSl7twFb7GmMU0M8HrRySxIuVoYc1sKv7P8bI1dWV3EcTd865xlJ9+vQph+OxnU8lV4Ze2JBHBXfned8q+rxzOD9qLC5+h3ML4xGk6jnEBeA0AL0k0WR1TX9eBXY0MTxOouEqjfYW2cDD8ch2u+F4GBknPUeL+Pjb3VZAeecYp6XZWUESxFl9pn7opedRydIIL2mzSRb5G0vET9N0MjdhdY5Zczo7M0zzF0Suous6NtuN+HzIfpMmh5V5XDSLjarh4yI9YO77+fkF3mfVQ464gSVRurKjtWgjPNVwnufUntdAc3veWlVKIES6s3O2g8h+mJ+bUxLMbJqaTMV4PPK2LP0tzCbYnNqY9V3fQPSq2t4pS2Jizpnp9lb0vZ0QCgT875oMia0d7z2bjQDDtLhE1vHxeBRJCyVlpJQ4HA78oc8fN0grSIKyXK2UaikLqVXKZcToK2iiGVVzhL1uIJwEOi5byVzAuaWbdl1pLhVgTDP3457Li2t8qvggjL2qZWVeAxkLytbBpZU1m6i8Uwfb3I5df8aLJ8/55ONPuLm7pesiF+eXEDqO48Q0FXCZi6unDJsL7o6Zbut4dH7O/ThyGA/kmpnTSHSV12/v2B/vqVQO+yO3b/fshi33x7e8fvUF1CwOGp4+dnRnA2Pa0G82PLp+zPPnHzKNB67ee5/jcU+eDvzus9/wm88+5/HVlrOzwIsPHhNI+HJPx8jV+cB7T98n5ImLXeCnP/4x/dk159fP2O4uSDlzPNxpE7ZMLTOUmX57zuWjx1xfXXI87un7yPX7z/n29fd0u3Nuvv6KnBJ9H3n86DFPr5+w2XRcnJ1TfU9xPWPa4+sN0/6e+7s31LhjfzjQbwdyKby7fcNPf/IJ92+kZMz5wjQlbm7vefmyY7d7wovnP+bupqe8nLi7ecPuJx+zG+B3X3/GeLwVIxUHDCwN3sosV8CHWxz73wdvLSAhyp6T8tKarQwVdfiWAJTVWpJAEA2Sl+/bx0ChtbD+snWUBSQXxoCrvCphM4eDYgCjAR0Ls8Ec0Gp4B7UBJI2pUY15aE6SBOZyINgzKcCKg9UhaQasgSy6r6Qk5rSMfAGw6lIG+wCQau+/DjxXwJpTRMRAEwuqLJvYQCCntqIBFVWbhlmHeK8gzPr+i5Lk8vX1My2A9xIUK1Cq33Ttb5t31Z/kVKphLXOwgDcr/VuWrzXgbjUOBvTZM+hSNG8KY4Oux229vh6O+RqAqu1CCro0PNpK7x+ysX/4XKel0suaroitXzrUlx/Or3mzdtcT6Q8D75d5Ws+HbrR2Ljz8LEG5gf6npXkgQR1Znjt2kZI6/KYnl0xAuqomc21WSYyHQNR6f89zXo3ZGqha9kJ759X42Z810GkOg73LD4IhZ1Ihy1BWauvoLliYBsUnY25zdTqv63XR7Nrqe2v22akcwGkSZ72+18zZ0/Wz2MUTvfl2TwFIYj/gNgP0PSVEAZ+dMK3W2vbr69rcnqzLKlx5nCTTSirtOutnc2jZ+speOGil2TaHxgINZt8UsGu+DX6ZDy8BiMT7i36yMRaDMhsLKrWidsJKu21/n6wltYfr9xcmIzq2vjHBgxfw0XTLWiWG7U1ZHo05JWfBwoaXOdfGCy0h6ZmUwfHDNUFbY/JcVQBhDeBkjCrGrpXf12eufmlSpB+Ra1AwVtdLBQH3cqGEQIidAJfzSM6JUBbmm9lON7l2nhrIJ6VyoTFb7I3bPnS+PXOtCj4U8U2HbiusJ1vfOHJJ+hwT/bARH7dCnpd9kPOifbfo6zmmKa1kHqqCPcb0kvVgMhe2jvGLfmWIURhQ6Hm0YrEvZ7cl1ZZzQF0kYcfIgCsYFYhBxtUS38boeci+NgaUVZSETpk5aZSz2FnjDnDB4X1lnkZhRmZjrWZKmZnGQiy9bHU0MVCX+0QfJDng6gKWeNHSi4N0ZJ7WAHWxWELGMShLzQCEqI1ZKk6b3i3sbOec7hOtVjI/sspGj6HDdwuz3fwcrwlscE1ezftIjM3zEN/AiARFutn7Js+BWnYttTStVQDnSepzBN/hYkfoIyGCD9akKjLNmdA55lw4HgrWHb54SBkOU2VKlXGqHEfYHxLjnHEuME+qB68JKFtDot8qQKrtCdyKZV4z1u8gaZDsnJ1louWacyZXR65OACirEMATvMlg1GYvza+CqlqYwmAOcSDPRygJT6ZU6KkED/M8NYbf+hyzdVDMsjplsioblSLsyUoi9jt8mXHaz8L+hNgxDDu1TV2zGtLIOLdmSQbOWSWQw2vzH6ukkv3nQ6DUDueSkjBUssjeW1nr0uQqS5f3ULQyaWmaGbqe6DYnviLOnVYEVPPbAB8IFwPuyZ/w3fBbsr+Bmpr82NJwdzV+q54eZuftHFriksU/xtHOIZzJ/XhymRT4teSwJDVN+9M0RU1ruO/7pplppdSbQRo1dV0kpZn98cB4EKbeZrPByv4lHpRGRcu1hcUvDEkZ85RFu1P2vUpc9IHdZicN6GJgs+k5ThOH44GUsjK71WfV9xOb5bRRpFR1rP2gBtB1yjBl7U8ujHR0naBJRqtUSNU0QY15Kv5DFyNOpSIA3DBQi+oDYxUxCx5i58M8z02ft7ELlZGKc439WzXpeTweF699lSQ/6feg54JVDAzDQEWAyhgC/TDQd6afapWghUcrqQpYEpYtcZkKKU0kZezLfSPjcaKST/WjvVTYUiV26/ue4EVHt+tU317H0KRE7NmnSXRsh82GnKV8vySZw1HL+Mv63EMqKobYiRySD0yYFKBrYxVMUigs59Fms2G73YqUZyns9/uWaDCAdb/fn+IGq/VgCcNaxQ6fn28FdJ5mBY417i9VpQ0SpcwcDyNVgeXjYb/yK/yiTetXTdSUt5FzZuNEwsEak83T3Py/eZ61Kd+iRdyrFJD5CD529N2WzWbTErxpFtZuUtB3nucmnbIwrBdGedeJTfDR48PQfPecRUrHwPWyqryaZ3lGw0Xk7yQSLCwMZ9OOLkkSJ6VkkvNt3f++zx83SCtuXMtwgGjNBy8sWsldZMqcCdr51TttHuC8BJUVPfz1euKNrEAF6bTXSsydI/YdKTlu7m95/2khBkclgJXPqfGV318xYryXWhsrfzX2gbJj+qHn+vKci90F14+f0A0brnuh+kuzhETXb3DOEbuBXAPV9WzOLslp5Oq9F1zWzDQX3qTCm9s7Oj+CK5xfnPPsyXM2feSbL37H/vae+Xhgnvd0nWe72bHpzwj9wJ//5Z/z1Td7huESHyObs3NcDITNwE8e7xi6I3c3r/jqN2+Y7u8oZIZh4L3Hl3jv+Orrb7i/P9B92PPjn35CLp7rp+/TbS7ZnV0SYuDibENO9wzDjrPdBVaCk+YkWRif2QwDx/2Bw/0eF+CffvFzvv78N8x5psxCBe9CR9dt2Zxf8/i9j6l+w83tLfv9LePb1+y//4qxJDZn5zx//Cf0u0dsh8C/+PN/QTomvvrqC15//5LRFb788gu++Pxznj57X7qs55lyPHBz95Z/+Pu/49GjR1w9vuDR/RW8/IqcCyFUona+NGDjBPgCOZxWhs6+Z8ZPDtKKs+yxBtL4JdB/CHIZmCWrtrIGTu22ZrweCsXbofwQoAQaQGqZNNRpNXDmIci1/D+67utC2w8rDSmxOO1AkrFa9kkIEiDK2IQlGKsLIGAGDlfEqdUSD2MNGWwdGqCi47ACUdYM2kXSoWhQW8G6zdaFtSnPIGMhTATXgqgTgAYWfcpaMDbUGvAyUEHG3YZNrrtm3K3fHVxjKlS1TxRhQ/tms6Bqpl6cRGH0FgVF7H1tzh4C+ta065tN/wAAIABJREFUQsAd14IVSzGsgUzvPJlTZuxDMLaBlc0RXH5u/bOVpXxXWAUL07CNTXPAFyB7/TFAzL68ZrKv983yebDmLUGw3lvKRmrrxDrI676Y51lBHGVz/771vloXJ89aBND0XhhyGZhyhpwocxaNNgXBW+dbXQ9r5nmbu2KyPbRxMlAoPtDGtHd8yJJdz+PD66+f3X6G9Tw4ed6ClBlHZXS1MdCgcB18rdfgAvYtDTFO7rV6zz/E1v7968U9mNPlvdq+xyoVALQsvB9g0+PPzgi7HZOyRVANbpFZ4QfXdQ09WAACYwCKHnU4ASAfroumK1kX4Nw5AWTL+n0wRezlIrXSnFkDPKsCoHY+oIx9kyNowPaJv3MKFp7aDEv4yX7JeVlLvoHTxsIRLT18wFormbPcHP0H6+rhWnMUgnMcj3MrY64FYUfp7y+AoGrMsNiekos6yuD9es83K7uwgSqEHJv+rIGoaVpKaItk4ShJGithZ7rz5DQzDD3z7OT/c9amYMsZXHJe7l0lmNvf30vX9WEgl0zGwHFPTeKzUg04lb9TL5px1nW+VtVMjJEQBobNTNdv27nTmxbjCjy1j1cgWq4je6tXMNFO1KCAXQwizWCgN04YNaXWVo4nY7ySMQrW1NBjmrzi00hpptP9FJxHGn51UqLupfFXZWHPPwzG7fllrSrL3IGPvgX7S0LFtzVq5cOWkMahwaYAJMNmi/MdVK/7Xb4enOz7rgHUXp+3o48bSShsYku21CjBX9HgzzRPfRcb0Lrd7kRjcBw5HA90ymBF12kIXsvWRRM26Xhb+WipC/giYKI1sFsSbE4BQQOtogLDxsgu00wps5wvMoAC/GdtdKa2YA6BEBPFB6qTBmND6OmdI2Sp/iqpMmVHKpndVs7JrpO9ZP1AKkW1zn2TpvOaTO06zzxlas1SqaQ/n3NSI5ebrAvOk6uw3b3rNPkif0pOba/ZmWigEU71L52A4qI5rJJO1UDaxd4G71vllvOVXbflkCsu9DgKU5qZx4kZaQQUfCeSUQ9Ca7uXSQIEH3BBxloAAk/Ooo8bwkB05n+pII8PzEX3VbeV71UoZVbweINuMZH5SyrloOvBOa9l5oGcRc+xuoyvsg9NpznlrGW5lTAYoSjjPCotpmwU79vZ33Sea2XpeyEVPiYoVGslCB5NcR0uXlHoRDYsV2kMqrYXd1ohY2dWa8Rte6waEEKbawGf5VqbftC4XECUGJy8Y5pbMkMAwySlyiGQVI8yqt5p1e+XlNlut5yfnTNNE+/evWOeR4btjt1u1xpqTaOUb0+zyG9I46jzBvbIuZV58+adJPaUDeiCY9tvGFTvs9TKNE8cxsK723fUKvqWlmSzkm1hti8l+1lldoqy/e2szDk3R6GUInIP5nvl3HyCUZ/fgCmwpqYSV4zTsb2Lc66999r3r7UwDCLFsI6B2p6Kka7viWufduXT5dVZ1ay9W87irLIKtVqDd33HIiXls+p27/d7QlTtWbWVnYK0ci57HLWxRNeNpkop2vwr6LmRJA6zdeaCNvWUZmf2x+I0IRmpNESGWjPeS3KkNcnynlTVbq/G0HylzWYDq2SDjUvOoh9+nEZKHcklM0/SgDw4qeKR51SgMasNTjKONWc2w0aZnHK/y8tLbTqn8j4rzGKtV1tKEeC4AMEzjjOuVvy9PHN0wtRHxz12gbPzM8oKH0tZKqHkPFNZhVqYVWPXYYmMhZkfNFk/DBuRBwuB3e4M6tJAz2Izi7NNSqHomhj6XuSFdM1uhoGhE71gp4nxcZo4GtNZ/fE0z5Q0M+XM4XBsfrglK6SZYE/Xd8RupQOvyanDQZj2S2wo8c54d0dUzWEbZ1dRMLjDh8BW5R7+0OePGqStpZKLBeVyAGctWe2COGVpngS4sda1ToJiql8cezs8ix4GVcEcF5UhGUQvx0v5REUO3CnNzPNEHzaE4skuNw2QWiW70g89OYkmF6VQnMNr996SBWDuYsd2s+XF+y94dv2INGdwkVQrz54+5fb2lrv7PbGLDJutNDyrcNgfwU9szoR1OmXPk+srPvrEcZzg5m5mGvdcnA30mx1XV4+UJZDIMVEczM4R+57YbyFuOH/vPS6fX/LLL74nhg13d2+4v/ued+/ecXd7y/3dLe/evOTNq9/x/OqcMt1xe3dHKY7rS6SZWIbLq8fsD0devvqGFx/9mHf7e8IklPOhj3TRk1NmuNzwwYcfkzKMoxjet2/fMM2JXOD23vP40TUvP/81f/93/yvTdMB56Sb76s1LdsOG6/geqUbevbsnDI64veRie4XvzgQAurnl9vUtf//Vf6Abtjx9+iH/9A8/5/rZM4L3vHjxIX13RkoHap7oB8/Lr+D8bGDTee6B4/6I84Hzx9e8//RH/OrzzxnLfQPRilG1G7BlwZY5iqy+L/9cwHtjUi2/18p+q2vsLHFyJHtmDor9Rq0WSGuwzQISVBYg0E48V0/BizWgYr+/Bgwb5NkADf1KtS8sLxZjlFLOlJbMZ60N1GqBlnON1WUaqmtQpT2Tc63plpVOyB607qIrZ07L3qn2c3W5fjX5iKrlZavr6v2rW7+vzZ2BMKtSbv25tfMBNAmKk8w+tLlyD8bcgmOcBcoyyDY+hoYFeeHl5u1+62t5GufZSTlUqbUx5B6CISdfM5CzBQZINaTpZqNsuxU49/sAvT90mKx/1ubArdZma87ilK1YV6wMaGtDgnVoi02/B7VJHdDGwIZrAQNtfB9+1gxYe952F6dr3S2rYjDmgAW2q+uczHv5/evBuWW/uBjwmx6oHN68I+KoTs8yhwJpaJLRymXl+U5L/3QN6+uZk2MBaNtb7cY0EEPYfcZk/sOf9g559S763h4o3qmOoNPmanWxOWs7Y2t8BYTbnlrDl04d3QZ+nwTezRI8+Noyfw/Xp9mV1tDNbKle2YWA73tK11GiNlrwvr1TVXB2eSd7UJlT+9byd2k2Yvl7SapJMBq03LG0+akKFlD0fdzy/G5148Vum4yDb0yeUiW5MM+zvp/TRibW234VVClLdAGyHjDIbZy1CiLVpGMg+zVXYxcqEKWAWskNDtIS7uW5je3+sHzVOQVO9LCx6yRl0hkj1Rjv4scZaLuAxtJQy2xhaudG8HLu2NxYL4Pa7i3nlJ/ccjY4h0knlKrdnfFik12h14DetIdxnkxWkCsIKOelPNmaQeRS6II0iy0lI/II2lhE2SVGKMALQNFrMAfgZgkcuyjMk9j1xLghxL6VggJNF86SYsHsr9OEHtL4CedUMqY2YKrUpdmXzHVtaxEa2bPtDYcCX+o3V5XpsX3j1J7NKTFNM6HrZEw9+CqNSGLwOs61aX9755UJq2CB2gwLWEuBVDO1JMbpwHEapaFJ1zcAwNeoFc+e4HtKmluQVfOEcx2x63EuUIsAo7GLJwCFNS5zzkofO2r1emYJwGTMO4hUCne39wujTTCi9pm1u3RFQFgXNIEXHJ0PrXHZNI3a1AuM1a/LqDX+8aol6oqUi8qPqgyKaha7Wpu0BtSWQJK4pFKcx6NyC345S5xDtZOhC1K6erbruLrsuNw6Li4kfpqnCq7SbyJdB48ebVUBp1CSzCHOsdtq2edNITsPh8g0Fykfd5VplGY4LUarogErvbiKNrSqVGeMwKo2oOrasGaClaKVYGYrai6tQZeci7qyTRqpFD13T7uOe+dwRZqFxSg2O5eCj4UQRnKa8KpVK2MqSaKq50AIXrUgxKAHq9DwDh8NSDOwuRAdmvQ36Zrl3PdRm3yViiu+Vd4JcCt7zkeozmlpvyUqAv2wIYbIOE/C8szCPA561ro0M6WMKwGTUrMGcF6BouZXOaAWcp7bWIpfUaxsdeVniB3z3lEI3B5HJN21qnpBYmuLwU/8YSwpd3rO17pUkZlvSa3UlMlzwsVC13fCGMxWOSHzWzLkkrSsPqgfrA0zdT0kbdjUxY5h2HA4HDkc9kBlu92y3Z0RY1CGa6KUzDwLE/fq6rpJ4MzzzP4gIFdWjeDgO/pNz6bf0EdpHCnyG0k10CuHw0EBKAGDQvTCqLYxKgmCZ54kFipZ11/OLWaxscslU9Qf6EJko3q5vZZ0z9Pcps3c5FIrPkpvlKByScLKFlB+mufme5tdPh4PgDRfleSbAG0GSEmST+2ysjut+amtAwHlw3LeAZasG7TEPefSSuEtnp7nGTcdmxdpvz9NE+M0449Tu57Y6SURbfff7rb0XW93le/FxbcXkM+kAwT022w2sj7Vt6RKQjmlxPEwCQnBLfbpeLgH4DgeCd604QW3yuoPhxDpYyf3C9qgTRN+282WTdmS0qZVAYg9rxQy0zjq2eXa+ws2BSgAHWPgOE5sNoNKGbgGWPZ9aOug0+Zdfb9hmkZclevNKjWUpiQMUueIePrN0CQ50jw3XdnYxUWnNgTdG0palCFb4sFcOByPHMeJGAKzntc57xuIbns9BGlKJ7q3ncoeKBN1Ts1W2/zc38vY7+/vZcyd0yS36EN73RON8ZxFJ1eSLzPTnJgmAV4P+0n0Z/u+yUFYVZb1uTIZhVmTg6JTLTZD9ok0xT3s90tQoVUxUnHBH/z8UYO0OAdZGLOSZZcscXCOjkysA4OX0pYYAsEH5pKZS6Umh68zmcqcJkJ0BNfhKAhTzzH4HZ2PbPsOX+HmcAedlNMWVzmOM9Nhz/ZiRwJhQLlKF4JoM4VADJGSK97LZDSxYefoe12sDq4uLvnxj37MeJyY5wMex3g48PrNGzabHU+enAmVPME0jlLeUjeMd/ec+Y4ubjlOcPFoxwc/2jLVnu/vCrevPuPw6jWuvuVwd+RHP3rO5aNL0lxI00TxmX4zEIeOPGdu7gv/w//4t6T9kT99ccfh/h3HOXG4f8fnv/kV+8MB76W52PX5I37+818wTYlh2HC333K2ecInH3/Mzd09d7e3UOFXn/6ay6fPmfNr5jnxwfsv8KFnzonDYU+MWzZn54yv31Cme/phx+WzLd99d894vOHLV1/xf/7935LSns2uY5xmci4c80TC86f/8m/w/RO66DjuD4zTDdV3dNtHPP54y+7uljevviV/8yVvX7+h7mfevvyasIk8ffyUbrfj4uoJ3vX87C8+5sc/fsbt/sg//cNLdn3HTZoYx4kuRtI48/HzD/n00Xt89vJT2FmpiYMgwJ9gWwrANRDBnAjtZlkLhjVJIxF1NqwMqxZyKlSPSGHUosE7DSV7yB6jaqa6lBZMiye/NNKzg7e6H7IM7WBpn1r1PeoqCEHeZVWCK4BoVTxhheJhgIZrbrSxx+1Zmq6dOrPOSbdYYxVXvbY+jgIfC9v1BGSUU1zK99BEi5UTWrMZ55SZZqL3VtyHkCwc1FxaUL52EmsDu7DfOAHfnHO4wqLpVGlMEDQI8A6ddyewSV2VlznViNQXOpkfhzAeGtB1ytb03pO1YCyaoyr1JgogPQB1Vs/e/o3N87psbAnUrISorn7/4Wd9ffuZBtCwKl1fOQ9FG8E5ZWDpE7VnkdJf35rnrYE8C/xlDBzWDboFEejEYnO2et+H6xRvfuPy7CsgklpxjeV0eo26uk5jPNZFh/Zk/A0IsnsVAXxCiKTY4aZZ7IONnT5BLRXpPeKaJuw6mbG+92oCJEHhVixtAxjX44EGUnoda1BSV+/i/el1F+AQLUdFQUe/us/pGlk/2wL+rf9f/22rsRSyk+9FINnazLmx1pcA7VTn2675cE3KfrYYQYCgEDzVR1zs8MNA2O2oXlhxBuBpVzGK2klL5lg5/wrKBLQxWGNhLgAtQMpF58RLg5BSlgSRjrnolS3/31iQ1dhwNEDXwFvno2q3ZmEU5SSJau/bGq5OSpxbItAL2FhB2LFF7FFLIjqtAlL2m7G61eDqtVXHFaf2VsE5tcHRRwFo9GyTruMBEGmcknNjpVhQVauw0cw2ZS3/lTyFsut0DVszyarPldOpdASr92nnkJNg3FeUFatj7R2UQq62F6IGlTJGg+9XjHkpYxViiZTt2/Piq1bYaPmg7rTqFjC9VzCWUui0eVh10h3dabBWaxV9US8M06rM0+iLBscOem2m0Q/4IMHW2v7Y3gvKtjrxHRAtdpnz2nSA27ZpwZOt5bwCS8zG655ANXVDoGoTuzSJNl6tEGJHH4P6JMK6CWEJZLzJHFQwnWKvDUMcrunBr9lTVEkgCngg66MfetFZ1fPL3sd7acrhfRA9XL1vng2wDe2MK9JQgOglmARHKknLTQPed0Qb6yKs5lKLNOBSNlmtjt3ubLWXLBnoWbNdvQtstzuphvFOm+sIMFKKnuX6fHVlh70ybU9sM/a+y/2ssV11MBdJapjvhvqV0njOpJ2sIksYaN5XonN0viP4SIg9pUjDr1wdKQnIG7zs8eAF9PNR1lQuokkbAsTiyLM0yZJGaFBJ5JRFHzgnxjFRrcLMOyqZlGexmwq2Ymeko/lzCmGKHVTLkNG1jfqO3tMHj2nHyF6Q98yaLKlV9q9lIey8cL7KPWNHLpFUMqGAD5E0R5xL1JIQ1mOhVmH7VQKlenx17WJLjy2T5nNaCRWZkwBpNWWkCkBiS2MPZgWKzBdH027S30Sb85qfpF3ErVlTmkfmaZTvlaJgX22kBzCGXzmRopFImnZ2tHJ5ihKg1Fbofc2XKE4Sgp4qvk7wuCTvVqYJivo4bQmb5I5r/7/4czKTUqEqEhmWbDs9I2UlTNPMtu9xripbNLbKxVLk7BGN2MA0Hyml0HU9fRgIwUu5eckqFwF3t/ekNLHZbNjttgKqpsTrt28B2MSeqEBRjIFh6DkcR6Zp5Hg8MuVEH3t22w1nZxdiR5wwWed5ZBwPTNOMqyIj0Pc9l+dn1CqM+9h15JRaw6GaMylPTLU2bWWTphHwEGKUkm+RP5J4iCI9dGSuCh5JzG0vzonxihAlYTbPWfS7i0lgwMZvWtLZzlyrLBuGge12i/e+6fdaBaQBXn3fczweZS0X8YPET80at6qGMGjj0tOqgBjjUm1RSgPG7Hs42lo3H6TWytnuXDXaU0tspXlGJGIkZtvv95RSuL/f8y7fsDQRlXESNueiB7tIyiwl9kt1ppwvG60WxtUmOVRrpWy34hekrDIWSTVTM3hLUhRJ0Kmvs9lsF0IJkswz2+/1fSVhUBb9VNnBeoahQLawxdM8E2PHNM2kZDIHkiw7Ho8CzHad6DvnJHI8yjbGe4I21ur7QexyKSoVAl0fiTnjamaaj8xzav5IUDC66Nmz2ezo+k7+dN3/R92bPVmSJed9v7NExF1yqaqsrau7p7tnGrNAILgYRIIijWbSm/5RmUyvotFMu4kQAYLgYDDADEaYrdfq6tqrMvNuEXHO0YO7n4ib3SO9jq7ZTFbnEstZ/Lh//vnnEhe7TG4bGm1oa80YvNfGtj4w9D25CDEzbQV4bZqGw6EnBAHOu24hfi8SC5v/M/Q9u/2ezW7HkEZII1R/m8pUtzmey6HE2HB6sraly+FwmDXsKxx2B4Yy+c9d01Gc6Dt772kdxMbTNlHkFrwkffuuI+ciOtPq5xwO+///MmkdhZC1i2iR47hxHqcA++3VOe9dXHBx+wGhO6Nr17hY6PsNad+zK4m311f84jc/Z3e4EgDFebpmwbsP3uXde+9ytu549/4dXCm8fPmc5WoJPtAsTtiPDc+ffc2bzRaHJ3tHKdIFNJeEK9J8zDvPyKiOhUbmRZ0YDcZw0KeB3WFXOxCOqg/SqsTB4XCgPyRlIRzI7kCOErgsFytygleXPXfvLvnRHz7g8Yst9Buunl9zdf2WV69f8Itf/T0ffvQ9/uAPfsCdhw+4fvOKrm3AN7zdX/Gf/8P/yM9+8jf8t//NvybcgvMmc/XyKc+//JLzFj5+712+evKY77z3iJevnrPbXvPBdz5kHAutb1isVvjQ8PZ6R2xb7iyXrMeRt7tLzm7dZbnseHt5xaeff8Fum9jtLuEffsPJ6Tu83bxkETruPnqPO48esj7b02/e8JOf/BkvXj6n7QKh62jxkBJD8pxePORf/Jt/w9/89LdcvnpJF6Tb34HI9e6Ac5nl+g73F6dcPHxELont2y3bq2u873nx7AlX28z6RMDw/eHAz37xC3764x/z4vNf05ZrbjWRXd4zXr/lsgSutwMpjeKclkITg2ZFZw11cNqRXECzXKx83krzDWicgIQ5IAkKNKiTXsokW2Blq9aEC3VSgzMQYM5YnYJPY55YJuum1ox978jZAQ2UBVCdymyN6SQ7Eadl6zOQrxQ5+LMCU8eb91gSopbLOEd0YdIwwmzzjOEngyEGWx0358TBFoaiMEFMx3UYR3XmK0xVH2PezGkO5FYwO2ftDnwMvs0lK+ZsNpg0gOdg3xxMrPgnU5Asi+VbmM2YhqGMLRjQOckxJGXky5ryFbyjKDiqY1n0GefZ9XmwPmmXTmuygn7lWAdWveZvAd2Oy9TmP5vPd/YSaDkm9vLk2s/AKgWcrbTXgAELvI8/pX5/kpSY1pcxRqcxnJ55GvNvvs/872/OT10H3wLGVoD3hpNpDQOcjmFGsuapH5Rpnet83WTmMpsX6+g+X4ffBtreBN+dWZnZ74m2qawZe0Zh3k8WaWo2NF9LCmoZa/bGuM3Hdq4nKUHSseTCfC6Us4eB58rTpfXCTmBmr+Ys3EnOhG986vXtmbRqxqElliEKyywGXAw41fzKWSpATI6hRqPOwNRUw1V5s2m9zNfIEQitFQBWTlXtpwbudW/M5rMC0DiGceoKW+VsoK4pAzVtzv1s/diE2nwI+yrjvJWTKyNQ2QpF7WyxNaVMC9HKnIFAWRIuKONUElKOkCEGRygQysQ2lrF3M9ukibMk42kJq1KoJd+T9IBJB0wsbGNwCvPVGpxMtqBpmirXkGEKZjHQTM/IMU0JjCJlo4c0NZTcqk8XgoC2uTg9kydN5BACjY+zvahBlTYds3XkrY+CDkpOulu1K31UYM85Ldl0jiJpPmG32bloRRb+GJQFKrAjfxPrPpnbCfk6k0Io2uHe+zpm9sxCYJmCUcluGsPbi64+CvhqgJ8LwsZSNGaxWOq1TLLB/JyR4gKlDHinjbWU7WQJTueloZH3rUotCFN5GEd5zibq+jcyn9l+CSCDk4ZqOU9nddNKw5E82yKNt3WsYBYi/eBUcz54a7IybS2HrKG+77GeFtIsxEq+J1tgZeEKR9NGA2C18UlnTVkKPi/Ya/MQYULbevLKPr2RLFYg0E5Us6fo3FlKqVTDQQWsnbojMYTafArG2pXdAGvZq3B9NRBcpIt2DmSGMXHwTvM/npRgGBMpZa43ievNQJ8TLnbgFowjHPqRlEb6UcqDXc4MY68ACIzjQEqlBtlyTkxnmtlVoNqrOdgnrKpUdUOlMa+cdUVjsOAEPM250CexRVJGrE0AnYIiuhcteZVL1kZaDmjAFYIfIc4T4VO1zrT/krpns7NBF6Bpptd7x0gJnsPQM/YDJVFlNCTR7wkuatJbmfnKwk2pkPPIYhGBSZfafAdbv9bghpyJVUfakt9SJxFinHoklFKrS+W8TnoGU0HcAhBlFQa103mUxLtTDdSCNP5LyZK9rvonc1tWfexxrD7XfNxsbB1yVoxZkn/jKI2wzYd2NVaSZBFqV0zSxNh7MbZVLuZwOBBCwftOvycg72G7kyRb29I2jcgHucLQ91y+fVt1Pbuu42x9Kg2XWmsAJyCMdJEXCYPYRBov82r3Njbffif6tgYI2Vljv9Pe8DOOiARFmqrHGAlNhKIM1KEwjIXsC/3hQCl7afzHCFnYfHNAdt5gaq7XudR9NSqI3HUd6/X66G/NX719544wMccBY7KKby7n95hGrXZRpr++5ziOXF9fM47S3NTsq/3MEm1t2x6Bp03TVJ/IhcBCf960jbDmdbxarZAbc1J2blH5zEyvuvPCls71XLWS+rmvbvtVdOVljEITtHJaYDWvSbjYtTTLTu1pUs1ykdgw2x5jJKVctZPtf/1Oxs+qfYK3NQO9jof3XlmiQfsQeGIUEHsY+urXmsSCJCb0HiXR92ovSmY8iB/kVU/dJENqc+xcJMlUEv1YaHxDt+xogVJGYYoi/uI4JMYsuvB9n1gslpyc+mpnjGxmVRHRO9brVT1LpUeA2Lq+79lut5MsQz7gfWC7vZb1EAPFeZq2reu0iRGWS7yCwOMwELzIhRgz29jHgILRbZVKMLmeoNIEXSdzGGMk5cK+PzCqdm7OKpmXCymPXF1eij6yAufClI8KgAtga369NSb7XZ/fa5A2uJaQO5x2w5TgKBJL4d5yxX/9J3/K9z/4EaE54dXba/aHQGlbvD/Q5j3r8xNevHrJuNny+OvP6BZL3n34kI8//C5/9IM/5u7d+xx2r/j4u4+4ev6Mx59+ygcffZfF+V3+4bPHvLlOjNsdXVwwhJarvXTk2x12uKiTm7NmEAumT0GWrt7RB9pFS9e1XNy6LeyI2JBiJgYv5UPDyPX1hsvLKw6HnnE0J17LvPOBw/YSn4Vx8HYz8vTFyO17nkcf3uH61V22b5/g/SXr9ZpD3/P0yXMe3n3E+z/6IVdvr7je9iwXga8+/Yy/+Y//jrI/kK4/5qsvBl6+fcNhOPDO3Tu89849VmcrVsvCcrHiq68fS4DuAyena9ana5brE1JxnJ7fplxdicPuR059w2p5QmwWvL3qWd96l7sPVlxev+Ldj97h/Q+/y3/8yy2P3n3AD/7xD3j+IvLm2Sc8//Iz/vbnfwOhQOMZHSzWS9axoSCZkl/8/B/48pPPWIRIvH0bFzva0JLp6fc7tvsCJRCbM+7ev+Dhe57GOfrDFb/95S/4p++/hwsdX3z6hC9++wmfffFzAjt+8N2H9FcvuXeyJhMY4gmfvthzcJHT9TuUr79mGArdQhhLop82gTnkQoh+YialVDF6KZW0Dr7aVCan6ngnZRbNnW+YBVQZgpt+PuGO5nCJUyS/bo6K6uFxAAAgAElEQVTJ1MnUjPBNttEcnIPqxjPxTScgrrIiqxyDaLve/NwEKOYSDFBjBLjxtTgt8y5UJrABGuQy/Vsdda/PGHyQTHEx2RJlz1bQR4OvGZBSFA2oWtIKuAcFwX+X4zMHA2+OpYCGrj6fjfu8tP54bqkgv5+Nfw24yhz8KxX4skFMOROjzPmcdUeZAZpyluPwyvy3Endnt5gCOpsPAy9nYz4HzOuqcMdg5vzdJoajrsVs5Xu5BlkZlHnsaum9vcAEzlpJ8VRadROsPQYp/dH3LVgXgM8xsWznMgnHYKw9heN4Hfy//fsoCTIbiwp85TwlPVKWMsphZDz0lY03T9jMmSL2EaCsHP18bieOMvr+GIDH3mm2x9B5n1/r28DO459PzGU4Bs6PA4SboOzxs1TA0AItZfFUDVWkq3wM9o7H68oAtKmZoT0DNQi2MfB4OY9xU3MF5whNS1gucV1LCZ6xJHxWxpuu+ToPmhSTMly9WZ1uWTNJnV8bk5s2k5yF9e5Vj9o5isv1+W+C3fO9nkuWZp/KqDUg1uEFEJsB4nMtT5OCCcEfz88sOSGlv1k7nKNbv6jZLZIEF+EsYRDq2As72IBCV887AJ+z5qEmQEWkoUYMKC+1OaOXxIU9R4HippDfQCezi5OmpJ1xkw10TsZ6HIV5KyCA/O5YRgXxtPoAs5czu+GcIFFOwEnTrvM1SLUms/pUN/agsdxkrKXSJoZWwNbMpO2nYxtsSRU5O1xlcaBsxKmJhAGhjgmItCUj7x1E502Z+dEkKHJmSpio9a62RUBhIQ44IRJY8KmsJDnPDNSd66tbxU7Qccz0Or+lFEJ0OB/BRdF8BWKIcuhlXWjFUUJQNqqUHyKXmtaTCzg8o5IxhiRrJfhGLqEW2zkhcNh75jxQXBBAomgX9QpyzIA/3Rc+ZKmEKwKUyZwKU9fmzDqY17PWaVdwN93XKn8EoC9Htghdf9i9gzKim0auzWQ3Bfw2H2fyIex0umnX5e9lPct54wQOzhVS07Nfd713RB+RLsgChMcoSYQQG2Js8SFSPAgZpeC8gIKDSS7oWVAK0iSRLICejsPQF5HjWDbstz1ldDg/6WxmQ9btCYuxz1zdzzmPdU/hZA6c2Qcn4KuUtQrbM6gdiz6SY6msuVKKVh0UvDHAAURxn4qR6jkUojVcU/a7E/8heGjbWP1ghzUEHuvcTJ6VUxKP7KP5+TUHs5BdVP2/KREFselwM5bWdA6LjZNy6VS7vdueFvM2JwsYu9ESkLKmYtQ175kAbD0AvQtqn3XtlgJOQOpxHBhT0aSXJgeqHyu+hbfGrk2L75awWFCu1eMs3/QZfB1n6vfsfL3pD8HMN0GAoGFMjCoTIftc1qb0E5HGQl7tnGxXGadx7KEEvG/Zbq+rnVgu18r8h/1uz2ZzjSvQrZaid4knp8S+33N1faXJGs/p6ZKTkxO8F4DncOg57HZsNlvwIgvQNMLQa1Sz2uEqAGjAp30M9PXeK1uwq7bdEvh93+s5WBQQHemHgdhEll1HGjXGzOJreecZRwGoiksaz07ntUnoWM8R8ynML3mjdm3ObLWvBjY7BVFNNzSGoIkEqtyEbzyFDjvMDBQ2yQjTeLUEt72zAJnS7Or6+hpj7drfGpBbdI2DJAaswWQFNINIOiyXS7l+kndYLDvmSbb9bocPQZqOxcjQy7P1gwBuw9ALyDdOcVMuSdaBU/+oSNJC4kyJXRfLRY1rpvhFSuRXq9WU2EeAxcN+V5/J3nVMI360NaCNId3Ui8GAVq+JNKv8SElK782XzimJ5ETw5OI49H1lsYo0xyjSHOMgfqkmz1ORBG2foWlaUil0XctqdSr6u0hiehwHUsns9j2OwH7Xs1otGcswS8hnlSAQ2RYDmCWOEvZ16AJd0ymwnCtBwcDNnCSJlvd7ia+9l0oNk2ZyUyN1Y2HP91LOuWrK5pwrc7YJgRjD8RobxkrQa5pG1niRsyMoEUISYbIvbW+LLZfzedEtaNq2rjfzWb/t83sN0t46vc1HD77Hkxe/guLAd7jsWUfPo9M7/OH3fsTZnfd4/nbH/fdusVzf59m159mzxzA8oX/5ircvXvHDDz7mv/qTP+Gddx5xcecOZ6sV41jYjIlnb69Yf/2Mu2cdH/3gY5puyWdfPeHn//BrPnv8BNcP/OAHf0RYnvHF10859InNbsPmcMk47MnGhvUNwQXu3r7g7sU9+sOBzWbHarng1u1brFcrylhq9qxpGtUNOfD29RsFisA5bW7hEo0LuNQz7BKp30s5UGy5etNw9+Up/WakXSxJNHgCXdNw5+IeV5dX/Kf/8Oc8f/I1m8OWEOGzX/+KT371S/aXV6zighcvXvL09VNuX9yh8bBcLRjLQHEj3/2Dj/j8s6ds9z2L9SkpQ7dcEtqGdrWmW67pi+ft9QYfIu9cvAOx45Mvv2Kxirz/8Y94eblnfzhwujrjwx9+n+9//IjNEPnuh+c0HrYnic+ePOfv/vovuLx+QtvBohNQ+2S54rTtWMSWBQNf/OLviAUePPw+m+zZHRKp7PFFxK1D0zLmwOvLHbvxii5mHlyc8PbNFYQV73/8Pu9/8JDFX3X8xf/691y9eMw792/z4O4tdi1stltWZw+5dfs9VuML3nvnA370j/+Ul//9c57vvyR66R48ajmA6LBpZ3cNJBxoOTdHTofo5k3NVqTbrrEGj8EQ+dOptJdcRL/MqWZVmTuaHP3tPHC0jKP99/wwtc/8fkC9/s2fwxQMl2qkJ1CkPsvsmeTAmjL4c1TlCNwrZcrYe6MKudn13ASglklmIBnYDVU6gpLrQ4gzJtednLoZw+nIwTStVHGZLfsujq8wfGpQ5+eONljQbijOMXtzGof67jMg0wDB2Y+/4ZQK+DBl2Ozg92ospgB3AlwtaJtKf4tey6tWW5owJ30OY3R4YxrYO5RytL7mDtN8rm8CF6WIdIOxoIuVzRavXzWQVcY4hlFX530atm9b49O9FaT34WgvTUGNYjC5YI2FpvmZ7QGbGz2wb95neq/jd62Olo67AdjOOfBOm+5kyqGHbc+43WMMvqyAlo1zXSOzAN9C7fnPbgY5N+fhZgDky7EN+Oa+nUPFx+M/Z4h+GxheSqnlQwFX7WAuRUrfZ5/JKZXfE3ZQIkTPBw8fEoHHz55xud1jXbxv2sWbCYL5Zz5nBjjab7gQKD5SVObALzqy88KaqzYbpNyfmkyzBlpH691gFGfdbSc2tI3LcXJI13owO+NrhUQpMI7fBN+ddwRCdfyne+t6mI3BfL6NIeAdGsxPzyHl3wp4aLA89L0G+u5oTZi9Tap5ZyBtdjbOAqw6LyWWOCdSLEmChaB21PTIxjFpUy1lyM5AZdPyLuNQHVyzixXYLsKyMy1DeVYBHvp+YuDUhIXZvKqvp3qnbgrYZNw8TSPdoSW4DsSmVaBC5yMXMlkD1dkc6c9DmcA9r81RXZg1lkC1Re1di64pqICQYN8yjrno+CIub3Gqk+qmTvGVaaKmw/tA8FK254CmOWb0icZvxsegTF40YFVmR4gCwGdba5kQjE0iQbZIgIg9j7GtNndZCugaatuGos/lVK9W2F2DAP8540PUYO/YlxHwzeNjIMZOK20EPLSEKhSVTVLW1tgzO36JTSCEprKynQZS+lLfSFoL/2CaV2NCyztPZ73so6lxmsiuylqSs0XG5WaVkpA3pwRNCL6CtAkPRRv95KL65IrSuaAs9mLDgkNA3GmPZp3/STtSzpOsa1HZ2r5ghF6v17XkoXNF30XGFids5nXX0ERH40fOVp5FsyD6QhMSvibqNWWuzM6cpaGzWxYOY6ZsMs5HkV3LI6vOkXrPMGTVgjT712JlwuN4wwapH4YmBxwOk6wyUDynkTH1akMnkNwCb2FdFhyTRnWMIpXQZutlYDZ4WjOyzywZDo6gCVgq8O5cmrQT0XHMmZyGWvprdjszaSzLM1niSGy6MfiCJsC8K5rAUvvoIISGUmQdppwY0qDAmjTmErNt5Axf33fypyag1AFjEgau2SSRQ0qEKFIhTu1c9FCy2PBa9eY0SeBcBZW8l6quUSFb3zQ4lREIPqgG8SyZaWfaLNGMcyKFdtOvzLkmJq0KKJdMKoVeJSNKBufl3kHjA5OUKrkQY1uBUAHyE5vN1cwmtFLdOgi4cnl5SdM03Do7xzWRYRzZ7TaUXAht5Oz8lgI3Mie5ZPa7rYJLYpRW6xWLpZRkm23o+4E0DIzDcASILhaLynac+7IWA4QQjph/0zqXOU1ZmoMlbX5kiZ62cbTKiFws5asAikL8ynkihMyvbeCxgaj2MwOIrWP9kQyAXscaEoLEbROL303yNs5hTeEl4Vm0R5Awd12Zfm7M4qZpaoMraYIlMh/GrnbAbrcj6+/3RUr758Cn9yK3EJX5aFrOjim5bQx2jwCrHsdyuay6pIXCQQH2kg3oG4/iJh8attst+91BzxtZ77vtVqqs8jy29JWZe5Mh3LXNcfLf4o+V7JP94SCVV5poOByEEWzzM3+nyc8UcFUyO1nnP0plSyuNu4IPok/rRBd+6AcckNLAMGbymHHFcdgfGFNhE4ICtStaBbVzEfb4qlsx6jUOYSDnfR138KSxED2MQyKNe2FAa4KJ4tlvtxX4d84RW/EtlwtZH2kYSGXqRZG0OWJ/6CmIrxtjpImNDJ+OuzFnbW3ZGB0OB3a7ncTZeu4mZc2WrPtOnYjgA01oNFlJnccYI31/IMZJiqaUwjiMSuxUGTDnuREuHX1+r0Haron8sx/8iJ+x5WqzxfmO85M1Z4s1Zydn3H/3A77z8Uesn+9Yn51w8XDF+avM7j9fcfXF57ic+NF/8YfcOV3TdZHdrmdzvaPzgddv3vLly1e8fv2SF08e88d/9H0e3L/Drz75lF/+8nOef/WS0yaQVyvuvvs+i9UtdtuBYTiwP+m43rfsdxvG7Z7DODAAZyen/OB736eLHSll7j58yNOnT3n7+hXX2wPeBYrT8iio2cJxTMQYaLuWUgLDMLLb7ujDgIuD6FKFlkQhu8C+WdLvE8umocPjm0jxgTEXdocDV9sNV9tL/vqnf4UnM+43wJ7Tc0dixbpdU5rEbnfNh6tHfPrJp6RDzz/54x+yPwwslvDyxVtImXW3EGeYkd22Z78/QOh49fotTrtZn9++4OsXL3nx8jX/6J/+Gxbn93iy+ZrcRVp/h81uxW8+73n5ume92vCPPjxn+W7k0yef8uryGetVQxcK56s1J2e3aNqWgGT9A4k2i6bHixcvGGKDb88YkpRdNb7j1vltFt2ar55ec7l9SwoHnmxfU3Yie/GX//6n/Ln/Mb/+h59Rdi/5L//kn1GGwOOvX7LqFrDsSPE2p3fe41997wfcefCI7Zst/82f/kv+h//5v6PfHYhtiysNKJjpioFEUkrsnJQ1W8miQwJsjzS6ck7n24vDOarOCr8LRCmlHlAwaa6ZnIL9rv3tMQNvYut+E9g6BrvssC5FWKUWNt0MaAxYOAbm0GeawK7pMwMqNcCqnUmP3qlQvHQL9rNAymQeDKwyIE+cOzn8szry5oDOQUpmLORaKqdPZizWUQ1kxjKREuTYwMzBVleDVDTgEebI/D3mnzoWBlrqoTtnOBsAMQdtbZ5kbCdnVZyYfAQI1jgGmDu1ZXZPc7bkngZefDvQZ1+Pwebp+voX31xDs9+xT7bADymRdkVL6nA1yBZ98Anos/Uco87vt7Ao7BlvPrfdf3Jm/Dee0di6N+dMtPomIPE4OJ+xhmf3uXlfQEvaRK+poAmNlPBjwY956qhqetFFgfcZcGqON7haDj7NzTfH+9ueo75/oTqMR79fJCmSv2UevwEYOveN+9pcVMb4/N5uCm7na2p+zZwFeHI4ThYtf/TRB1ycrvmrnzl+9skXhKarGXtfy7uPQUnbB/P5nj+DsepjbKQMu21p1mt812BKpwFPmSXAjtf2BK4YKKCYrY7h9C7z5IUXlFfkE2bjm1KW5NwM/ElpxJjB83erEg/eSsGsydy0L0IINVl1c+6tIZ3ZbGFnlgngLAVrRBG4sZd0n08gYqBkYWlqbkjAtGCAlKzhYECXluU5Zyy9qAFMqnuqmHSP3svb4YixgvPR+kITSBa0hBAoqnMopb+Qm1TfwVtiyAdh/TrRsKxNv6A2/wix0SSo6Kk65wkqx+MtOFQAw57Deav8KIzaUEfmQPZoygIeRH0Xq3oREFDXEALYZee0EVUj6zYJg9rZeGPJSW2Gg8Bjluxxvqln3KRTeTNhCCFqB/jo6zp1LhKDAK6t7qqURnIZiaHR8ZKgMRkgGaLotBZITpqyOTsPZ3NftOw+a4WZgLtexjtG0eN3kRCbqqMbnNdA2c5ihw/CsEGrMtIodiFEYfmMClCannmMjQLB+UjrsIkTyGCVJI0GxLYn3YxR5Ny0J60fhoyzJWlk/O2+tj7lWoq9ZmWqOYfzhaOGYAq044qwckLU64pP6LFEl9ogpvOdYpUxEvS3GgDKTnF1bxg5wFf7pSBIiLgQaHxguVoRG08m0bQtd8467t/pCL6w7hpOV55AIQZHGwPRCWAxjAISD6pvCHA4ZBKFtZfmwbvesdtDnwqrknElsz/YCo5k5xlHYYELC76pjLecMsM4SmNC59SfU1ug7PbGBwqZvpfqGUkcpJpcyp7qb8xlwsREZxoHxWVpTu0mlljVBC5O+0UUrQBSH8DOxKJj7bQ7/DjiGBnGQZvYFAFWMca0BPnjMOIc9LgKEJivm1Rz1ql/lFT2ZkwjITS19LsfDgxpUCBG7YsTMMwY5FmrQLwTP8uSOoCysBXcVysrmq6QCcoyFtZzVtmXkqczykCQmpQAXNFmajnROMe68SxcYWPoGU4sthlKBWp/18eAOWzMoZ4ZOYu2uem0mhyYD2b7oW0EeJOPsFuNuSayMIkQXG385ZzohY4qwXF2dlb1Vzf9XuKFnKXT+2KBNXxOyNwLmKoNipTlueg6HK4mEU0bFE0WLJdLlRiJR80gDRw1ht/833NfQzQ0Zf83NBoryVgFJ2zcVpN28xguNJJkC170Sk1eD6ay+CMfWUHQb/goTtjABqBZtWPKicN+r35mrr5xKTD0I+NwUAZlkKZmBlJaiX0Zqi9mjNlSSm1K1nXd0fPKHhJ7OY6jsB2RM9i2s4DXIjc5xQoT4zWpvr/ZfNuXpkHsvbAgm7YhqVa9AJ127sg8OiVoNE3D+e1zxjGx3+8Yc9KEnCZrNGFgiVSbW7lerO9cStKzdarMiWGSy+jalm6xoCB+2jiu6liZDq01s00psd9rk8q8ETsaG7yXJFBKiU51Uw+a/MpJ5iQsWrEHOVP8yMBAHqWCKpWRPCZS2pFTpms7hl72mw89Xbuw9m0c9gd14EVvOOmzDfstwVN9x65riU2g0WZkV1dXMufO0XaLGuM6BLsIzcR2NT9cWNMB1isZA91HO10DlrSxdd22LcvlEoD1ei0V7+oHGCM2J5n7zOQjjONARnx+Yde7yn4PQRjswcu6XS2XZK1MseverBadf36vQVqc4/2H73LWBVyRxgx3712wWJ7z/NWGV1fwbmjZpS3/07/7K/CRN2+vSddPWebnnK4a8v0LcB2ff/45L15ecrndg3P0w4jznlXbsB0Kf/mffsbJwrEfM0+/fk5DJqTEcnnGxe1zcnfGPidKSSyaliacs2+XsC4c+h0+es5P73J26z5vXr9itegoDr56/BhS5mS9xjUe5xtlRgiQ0sSGsU10Xcty0QEB4oK3lytev3hCORyEmdEsWbiGLlyzbAIu7wTRH3oe3HuHjz54n+u3r9hev+Us7bl18gEPHzzi7eun9PtLtrtLvvj8M4oLvPfuI5pVw+b1hteb17TrhsvNWy6vNxzGA30P+92O/fWOfb/j7of3CDEQYsuya9hevWU87Hj4zjvkAtfbKz75/FOevX7Dj//2Jzx475p7D75DIbJoVziWvH624fmXX7FyD9i/f8b/8e//nOuvf8nF7ZbSL7i1XnNxfptFu6Lvhc4enDB09uMe7xv66+ccXMNi5ejO32EIjkcPLvjTP37A3fOOzx/f5q//fs2Ytrz68qdsXn/CyXLFIke++OILzkLPd77/A97/8DsMY+Hzzz4l4Ll9/x3+8T//F1w8useLN3t+9csnfPrLn3Pr9hmLbsn28pLF+gRCh3OjZGEdGiip7rAhZhZwO9HwgwlQ0MLjiTWBOWdMwT+Stca5GYCgQKMzKBKsyYtYvnmpuZUES1dG78URlqDBMncTGymlUQ4xDQQM1CkK3urNkFIvbYxmcJ06W9URKlM5sgCuaUJGcaRk3RuVjmCC7TPQteh1y6xxkAGv4zg9j/3MgjmDLx2Ixz1jDWAgrs6JAQBB38kh3d2zlfNiU1PquxQk8DYIQ/k8tfHHMUAqB6pJMYCWxZYCqk8qcyWMAGEnTA6rgaxzvWH908rEMQ1kOXwnYXx7Zzn4rSPvNM4mx2FAlgXGBmAao8OcMHMExUGZWL1TUDjNj5Uleu81YeG0KmBiK2bVJJNM+vQs5jTJfUtd03MQDm00YxebyksnzVLnfN0jN4EeV9fBsXaqqwAg1fGzkq5p9U7g8E3WoeZaZH9V4F6YT2nMlKEnHQ5QcgVOQ5H9kTiWAtChrPcxQN3W8RxU/TZW8/HcSAJkSlLoWmLWgEuDx28De6288+ias/82xn8yVKDMtvuNdQIOY56ZBIHznsNh4C/+9u8IzvPy1VtiCBosW6LBEhiyTozVL0CXqyB3Vl1nY34CJNUmjU2kO1mRmoas9mks8uw1YWFGGgkAp1K0os/iSLijNWCd6efJslQyGWOnT6CoMAPNph6zk2+uKwlMBMyQQgG5f/GqN6es3KpjoTbKHM4YJNhBrZWdSXZ+BB+lARWOMUtgkCr7R6258zo+gdAoQ7zuBBAYKVOcNVQqxKAdkb009/DBGppIQxSKAG3SVE9BD2dAkmdMyuBUnUXZKrnOaS6FtmlZLBaUXDgcDpAGHTspJ7V5CzEqkOpUb1jPZydyEU0UPyyZPm6RZm/CMnQKVoCLqvntrRRbgQnn8A6iUh2zIapIIyoJFuT+Mq+hzpUlA8eUazMWYQMJSOOJTI2iZmeg2ThmjbicNSgslTErTBIt09ezuwYu6P+UvRuizkv1W8C5QEpa/eASacwarDbCFlaGaPS+av/amrXGNrFpKhhKmWExToKm0kotTHATuGnAoyNjXe+NRuqCVq8oQBebSM6eVv0ua/opHbDR0kMF82IU8Ky35IQ8f9u2AjZrstZhZzbYQWmgqMerduvkg5g/ImeZdI8vOAhi50UKS/bdHPDwuLruxLfQtalGSJrFCCiZxlGuNWOfhxCUHTuV8E5JZmdqAspCyhXUd8FV1l/TdKKN17bgRPpg0TXEWDg9g1Xr8Lmw6ATMzMNIySIU0LQCgu+HLOWgHvaHkVKEFZ7GQhcCgys0AcaxQILlohOWdC7KsBV/JhcF7IoyCIuTpEKI1SYBR7Y2p8xGGWOWAHJu0ICfqvto9Sg5ZXIaQTjMahu1sgfTwJat7rJtVUumpupnYY24jdGaTMdcgfmk5dOo7TFShbk0xpovpTbpqc1HkcYzcpMiyQIvibSEY0gDOY+qXZlIOdE0LevVsoITqUwsMoolGETXMavvkeqZNkJRrW3natVBLpMMh/h0xlIsCrOaL8HMHxNMtzjo88iiJFi0xEWLaxtK3ytY5iq4W6pRkOeakwrmJAI7e9KoiT7nyHgS0PeJ/lCIPgpYm2fJ7ixjFKNT2yryJg6rKHDCvA9Rx0NWS2xalX5JDGlk3I8cxp4CLLqOECOuFPa7gzyXAq5dK1q21qdj7AeuLq8YRtVmLY6u7cRHjoFusWKtIHBGtH+Hw4GUco3ZpNqhqedOCEWAZdU/ncdBU88JRxODEokS+8NQz0/zRbz3wr5MU6n8MAyksdcy98SYEsFFmlabHPpJgsHWm9gSSejJPszVZrrzU0xax84nqzwYx6Rs2GHWX0XnOYlsQ0pJExpeS/InGyj2TXyUEBXIC6LF6+zMdWiFJiwWC4ZxYLFcqY33laFcEH3uYRzZbjd4J7IL4gMUhn3Pfr+p1XY+CBPYtGctno5NlLM/yPgMYdSzN9K1Czmr1Ece08jQpMrypUjFTozCOB8H+d7hcGBIifHQy1nhnOoN65nnoG2iJmFdnZflciVnkh8oOeEbX21B10ZhrCZlSudMQTRx9/uefhgloZGNKEbVK29iQz/0Cpw3DCR8Fr148S+kuXXK4KNIYOSSOQySpLDkPoqfbLa9MOBdoJQR5zJd19CPA0MaaJso4+xQ/y7J+tSYumj1mAPcQXxXi1ntDAxFm9vGSOg6nHO0i0W1NQaQj+PIfr9nv99XQpmt8RilIbzz0g/HF2XMaoJUGsJldrsd+700AsujzD9azZFSz37bg3M0sSHlUcB2UR/6nZ/fa5A2xJbF+R1Wi0jeJ87OWz784cd8/WpkN1xy9fKaz3/1hL/9+y/YvnhL06y41bZcp57Nq1fs33rO17fpmo7L7Z6kwfT+0DP00q1wEeSgzilx+/weuVnw4tUVh+s3rBee6AvXb1/Q3moYhz3kgYBsxmXbkaN0ceu6BScnpywWC27dusWr58/49LNPOex2nJ6c0rQtLkhpRNtGQvTsrjeSAQ5eMi1DT9N0nN464eLuBW2EV69eIKVE4mz64Dns9wzJkZdifE7O3yF4aZqQx4FI5uzshIuLBxSXuHxdePLkCWkURsHZrXNevnyurIbAw0fv8PknX/Dr3/6W7333A1K+xLtMygOL5ZKTk1MKjuXqlJwLl5dvOVktabzj6fPnnK5Pef70K/bba75+/GsWTcuje3f58vETCg2r1Sn9bsf1m9c875b823/7kr/58Z9z0W1wroPlHe5d3OVsfQsSXKYNwY8Eb7p2g+rGZJwbKWXD+UnD3fv3+OkiFgEAACAASURBVIOPb/HoQUdMhc3rx7x4/Fuefv2U4fVj/tHHF7zz8ILd/pI23ObNm2vWC0ceNjRNwzvvXDAcEpfbDf/w68d8/Rd/z6ef/pacNtxZR95ePkcAOTGIQdmv5loUdbQs8JqYSHoYaomOlYuKWzCVscA3JQ/kEKMGWHNwSKPWaYMoO2D6WCnkBI6Ic+WQGtcJ5M32sxCqI+wqW8eJqLy8ZX1X+++JEaUlWXMgqDpXczBYA6wKTthrzMBde4P52Oj1gwailqmqgJzeb+6cVDBidpjLOAvwY4GX/L5Ej95ZVnWaHwPErBzXHIjaqEIxktoJnQkUtGvXMdJ3NDCxlnvV4GwOZtlza6nQrMTRWDb2bMMwVL09C6ptHASsmLPzHFnHfXp/V+e7lEkrc84kxaEJCF3rFazRZ9J58F5KYote0yNLro4RSA8iN8E8c0ccmFglSMx2cz04c/JvzO18HG1dSVfp471QVGbEQLdpbI1pg47VFFB/A7ycA+lIPqCW7TooZFIW8DuMiXwYGHd7yuGgf5eP1reBnXYv+bef7Rt9DmXwHcth3CwPnf49MQvmz6ffm78HZTa+385Qnl9zbquOnk8BmcnuzOfJEFBXQQn73UMu7C43Uk2iAJ1zkhmfSk2pe6/OjSJr0tXczUBjtb/eQQy4toPFgkETa9U+o7rdTEx7AGviaAw4eXlZtLWc3esbOkcI09hIcDsFEDVpAxXwPU4yHMsiGMBY93ERjVlrqifBlLD6fHC672Tt5nGsAIz3QdiE83mjkEuarZMiHcatnHZesuqobHZXtMGc/h42n5pUaoJqGGrDn6LBfhObCpSuVmthdBRHzmO1AbIclcUaotpIVwN2O1dK3a/K6PACtC3jklFLDKWEUp45OEdNDCGOe4h6TnsF/jBgUcYz50wXp2qHOVOonhW2hr0miIo1sCmSUC1SMtg0Utpacq66l5a8smtJ2TXKuO2IoSGRcIhGnCTFJh+jzpqeo1HHVpibSRMLQc5dAx+8VDr5oHvbgKYiYJ5JN3nnleTpCEX3CbP1j/xeUMavrGVJBJs9q4ztuX8iqxGz2Y2yXKVpS6nAT9XElKi6Plf1WVIiWJ5Px7Vka+zijhN+uvVt7YOANXkcqnSF7FUpaYSJsWcBWXbIGqlnqTIt7ZVKkf1QrJRcy52z6mxrJD4/p0pBmXfyzrJvjOc5H2umZykC6E62QRnqWlZuv1v9ziI2MulZlpNKe6hNCgSaZrIx6NrFF3wRFuFm43n5MpNPPI137HcjqR/YboT9tOga1ktH9I5hHIkhs1y07A+FwzjSdC1pEMZcSYq9lgxZWYfJklPqbzl5x+AcWZNOdbtVe8P0HjN/KhdPLpJkrv6VD5JsR+bQOaRU3kMpQfwVXbPWedzsa03wHW82PQ8KqFyTr/7ZZB8MPAxtV5v3TUfwxPRt284uXpMntu6MLVmB6CIJ7aJn5jjsGYcBKxOW67WaDJJkVsbR94MCBArCU+j7Q10vY86gsgDgoQRKSbrfDDAW30DKnfWdLenthRE+9AOFVNdayaIDHiksQqbkge70XCxnzpCTVmeoLdJzzs76pHqi9pz2MRan+QboHjIyB0ljqHBcNWSMyHGUTupdt8A7IYk4Z/IoxgK3suRO52sQoLQX/6BT4DZ4D7lIA/D+QNNIzxnRm5VGUcNByvFLElZxn4Us0TVTkzIhPjhpKjaOHEa5n1RlBtUNFSagaWIaSClJ1bFq4hf1g8Yk8lo4SIOrPpitLTvTTMvWzjGv501Ko54RwhjcbLZaUTH5a2dnZ9XOTxUPYkckSTv1ZbCfxyZUBjhMVQch3qLkQj8MUMqRHbb33O8P5JSV7TvFnrW5V5LGz8Y8HrcbXTVakeBVdzUEZdFPpBOrzDFt79g0nN+6jUOSY7rwZe0pqLvb7WqVjZuts/1+z2F/YKt61LKuA2OSRIoBeT54Zd16kRnS+8iaaGqVdQiJ6D2r1QljlkSdK9JUd0hj1doeRpHNSDp2crYVtptdLct3jgqyN01D07QsOs8wjIyjjOH+INrKbbtgt98zDKnq+XsmABK3Z+h7FqslwXn6Xmy9dw0oiz5lRxmLqmIlFl2rvrskeEXCSeRxKKU2cizI+dUPUr3kQ+DQ9wypr+u81USIGeYYvK6DhA+RfhjpVapgvgZNbmD691RR1DQtJycnwsCeNY0z4FZY8gr8OiHOCPY6sZ6zkyRot+yIXVObzplEoZ0TYosye00QmM9qTcm+7fN7DdI67+lWt0QMu0u8950PODl7SNi95c6DE24vOn74w0c8fv6SMl7z6NE73H94j2ePA5fPO378k7/nt7/9lFevXvPu+/c5PYtVs40uklNis7nk3r0L/uU//1MoicdPX9C1HQcXOTm/4Oz8hOWq5aPvvsMvfr5k82ZLPxxomo5ufULJ8OrVlRgRPN1qiSuFcRgoKUkW3xUWyw4HrE/PuX37Fi9fPucqJfphENB16AnBsVwklusDi1Xk9q1bUCSr4fyCtomMZYAhs2xb0njAec/V27e8ff2McX9Nv7sijz377Zbnz56zubpid33JbrtjuWhZrE8Z+4Hdtsd76QT65Vdf8dmXj9nfu+CDD94nppFhPNAtWr738cfEpuPOxT18bHj95hXgWCxavv7qMcvFgrt3btOEwumyENNbti++4JOfF1wTabtT3JDZX11ycWtNDAPPvvwNd9cwHFYkBs7O7vDw3nt07ZqhH3HlBYdhSwheyoUypLGnbTpa74mLyD/5p+/w/oM7fPLFaz7Pex7/+gn/+//2t7y4esWiKRy2Oz759DPeXj3j4s4Zd2/fJhaPj56z0wXXmw3LZaQ/HPj008/5yU9/w5OnX1N4w6KBx03gxfaSzW6Ha6M6FUkcFI0pJHso6WPnhf1jzow5IB4DdIyV8e1gyPTfuvjLBD4UBQat/H0qLVTMBesCaqWzU9CfEcfLdBYJk4amgY9Fu7xmfUYDLgxQOAJlbwBrdkgX6/5s7l0RsICj7+XKOrXAzTs/RT/6rkGfIeBqQxnTpGN+xRvAlD3PHDCyw77+1Rx8Uj1K611bmwxpkPVtH+8miYpi/W0tkND3veko2r/lkJhfbRYEl/mjuRt/803AzBw4jmez3v84WJ7AcY1wJPhj+t50n1APjBBEx1KaPCWZE3XosjnG9qy6Hi2AMjaBxLm25grMSmLtM9crhWldypjO9T7nYzuN1/S+E2hpoF0Fm5mAMpuyCWi060mZjYE23wBqNBjO9nwaxNvPigYaOWfGvtAdRtJmRxnGqpPqmBIzU3Mfjp6bIqxvK1GSgD0jrJcpELmZ4Lm5Tm5e18ZjvqaO9o05eTMmywR+TveuQWRli7qjOTyeG6oTbx8L2pyTku8QArFx2ojG5lPvmbXBlBNWSLFAUQyM8BPLNA5jSvgYcNETFx1+dYJbLklBbJ+sQVmvBdFNtO6vAgIKGOBnpfFoMBtqyf8seE9JQCLvVcOvjriuPfn33BbNx/R4/c8kVxSMK1mYA0HBUEABQWFqOw8hwIinbXQOQ6OAnYI1JTMOveiCKrB2OOwqiOOclOelJEB5Komht0aNMolm252bAGgBhb3ojzovzYUaT8QTfcShrFYfcTEoM8OST9bgSPZE8MYeNfB51kCr6DypXqNzEijnkmm8ZX6MSSRXmM4lbX6m4F3JDoKAlPY+ZpfnQNi0TwxQkhEwAEaGxeZcz38NCg0kCz5qtYariVfnhNHlfGDRLWpgYDJAzqk0hjJhs4LkIQZhiKrBHlU6xVWwVEtDQ1B21JToGYYDKWe6biH6+gVFMidwta7PunenhmLGqCmzJIOd5TjqujcPICVL8CpT0YFzArA756WzudW+FNPPlDLQaurEUoIXmZhU2TsdwUf6Qy/l24D0iiuqsegqe8rYRUPf47Q8dbJpxo60sbLD0ZqjCWAMUyVNyWK3is6JNMkxn059CAUdiytQJj9E4/3pLKoVAnNJH1ddglKKrNlZIk7KiVFAshzNHVgFE6Dg7/y8CIo0y99NfkcGjVEEQAixYRwL/VAowYkeIp5m0eK8SA0kVKuxCeAL275QiDgvLNJF1zAMmeAzbSPMMjcUdto53PxhnLHq8kyqQ0Bcjz4vkx/lnKv+Bc7KsicWpGhyZ5qGqodstlbOIS3vL1rWX46Ts3O/lNl90eQ61n6saNLIqn1mfrk1orW1YImv47VmezMfaWXax4L5XDJkSfriHMu2U1PnpInXKJ3fhyFVVmBsGrIBVuMocaUXdmyVQPBTL4CSncYvhZSEvYn5v5bkN5uNsFmz2qiiVXz1+YujePnvjc+82GzYbg+UseDSZENtqU/n0zR/cwd5ngCu/iOofBbam0Hv74TNRykVhLO5p0zJN2u2FqxbvY51SqKdWSWrKAqQRhofVFO4aJm4VJ90bVflCkCIXvtdz367q3IHvmlYd6e0TVuv3x96AR73G8ZeGLopi3+9bBesVitdj+piQgVXp+qpovNPBfYEONJnVNth4K6BVN6LjIPZE3v3UqBp1jimeOn27Ttqi1NtgGTXdE51WItUMeVMZYSKdEnGqgNjDCwWi9ledLhCbfpV1AYVJI6cJ6UWi46SHcsl9f7yM5RRPuC8aNbnnKcGa6lIkzSVHeh7OT+GcdJqNeC4JjN0/3ZtW98ttioxEgPr9ZqmbRhzxlffX86x9cmafuhJWW1cFgmOccxsNzv2e2lCFrw0Vcul1L1v6zCodmkTJ3YmRSorog8KEmqTNoT9a/IoOZvmtsWBMtbS3Gwv0lgeSdQPmeQ8u92ecZTKEwFphWUewoKmFU1ZW3u2rkKMONdwdbWhbVrxj4rD0sgFL80Fk4qKFRi0H0jWMXUO0jBAGbSxXNRzXBj8waGJ3Ey7CFrlKiSrwzDgNnKuNrHhZL0SLWedD+c8bdMcNeEzOY5edWlFAmJignsvAHfbBv3a0jTStD56r31Pi4L0Mpaj7hEjSuWcaZpW7ayck+h+tP3ivVcphVLPJ1vD282G3/X5vQZpySOr2HBy5x7Oj3zy9Wue//w3nN+7zfvf+SMOm8DTy8zi7D7Lq56ziwviYsWXzy8pvWNxtuLVs2eEkPD5Lqum4fTRfdYnpzQxsNlsuLy84t79ezx+8hUxNLx+9Zrd9Uaybt0JcXHG9b7w2Vdvubza4TUjOLqRJme6dsHt23fY7nZsrq4oznHv7l3yODLsD6zWa5bLpWyoMfH6xXNevXjKOA7stjuurjaiedKJHs12t6d5+0oCC+fYbq5ZLZcUMsN+Q1+0HMNlUtPjmyWb60uuX7+k377B5ZG+3zP0B1zJfP7Z52y3l8Qwcv/BBR9+8CFtt+Srr56w3V3z9OtnbK43nJyekotjKIVxs+XQH7j34D6rEylZuH//PtvtjusoB83Tp89YdAs++OBDuuWKBw8e4F95PvrgA85P7rFYnhEWS1KBw+GaO7da1uvIJ7/9KWm/4c6tln7IDLnj4tYFd27fw4WOvj9QfGG3X0gZbSmMQ2LMPcnBYnHOflzy5VevefL4KT/+62ccNnsuXzzhMG54+N1T/vW/+BP+85/9hF/87K9p75zz0b3vcefsnOK/4sWrF3z+5Vd8+tknvHj1hq+ePOf55Ruev77kMGxpFiPeR1xsObiCI0GfSL7glpGqkFiUIeVddZqdn4BNK1e9CUDNP/PAfV7KMf/6bR/TQqqAycwhFJ9SHKs0+77T6/sb93dOgnwpeZ4YqVLOO5Xyz593/vdZA28DueYgzvydj66bjX1j7zx/KJM9KOaL16Zi4vuqk3x0beqzlynKnDk0E/iVikkUyB8aMFAwh0iCBKf/XVC2kZ9cRWM76t2ZO59zluzcUZTvT5nv+Xga+CK/F47+fv4e87+b7nMMCk/jTwW65KD4FiCvHAN99rPq5Gr5KqVIcxvna/MGc7QKpQbFzkEojuKVUYskK/BOGl94Bz5XkNueOfowAbjzdXbjnZ1j9s7yAnNm4vz/rQTm5sfrWrVxlX2XZs9DBa3nY2vPOoHP+vvO4bTjL2Oi0T0z9D3D9Z60P2CguoAVvpbYWMm8BZxJ30101Y5lMXCTzMjN5/pdtmI+3/N//3/9vrAqZhqfc2CtlPpvCxbs70z+wL7KGM9B4XljPh1ndb4c0tpPxiSRi9gjCUp1vN00w9geoFCKSFyUIGXWsW3wXUNYLSntmrheSxWNdXrVJk8OGCUjUJlr+lh1H07DbMkf/Q0NDF2QtesAX0plChkY7/Ud5nvTALmmaSQhpkxCrywmofLJO8fYAAboC+g4nSnT/HddW59OgMJsvrpJC0qyM0320gByCrRewEcJdOV+TYyVHTM9n2yQorbKFe3cHBvRF41tBWdliJwOV66S3sCkp1sEXMu9lP6JTp6AZFkblNlZIAtmlnDJmaCBbClopVEkV8azF6AqJ2H5F2FQulJw2vnYQBkJOvONvSEg+6RlPbGGBESzag55vxgiOQEhqW2dgVLFALkpUZfyWBkbKQmDNjYR75qj/RpCxBfzPAzGdpQsNtaZNIUQ3PC1giIxDAdevHzGZrvlwf2H3Dq/XcEox6TTOwFSx5Ic9j0BYx39eMDpOi040fwFYfskAZXCzMkw21FyYrvd4xwMwyhg3rKbzkUFV9Mw1rPa5mFM0rTIGnE0jVYcmXSCns8+Tyw954SdGfQZnQtVO7XKy+Rc2XFF9ytFG2DNzkN9+ck4IAFy0CDfElZOg7Jse88+hZndmABYmwew6pWs5ZR2ns6qSHTGTE8/+FB7FlSQNpeacHJMYHSt/An+KGCsWuxFPKBhEKBvf3A0zhFCBtdQssf5qQrIORhGkerp2iB7JGnTHb13jI6mwLBPDEOmaBn6OCY9wwUkH3Mhj6aHqSQHtfkOlWf6HeeVNNuTr8Jug+LN1kJB5ROsw7uWdZciTGyPMLrmV6zAHlRb7V2kZNG4LFl9RylQr3uklMJYIHuruEoVmCjVbsyTpLJXxzkDLufqGxjQK6xxJgZqKQz9gX44MKZBwEYvpe3yNxvxVY1MkDO9OmfD0DOMo0pmqd3NFoMMgCThcSKDZg1zivP40KjeOAzjqN3VEzkNsndlt9czO/rEuLmG/iAMWttCZapGs+1VYynd9+b3WaMlZ/vO2RcHuk9C06k8QSAGp/Z6SiqP40gTBXQR+24yNBNzE2C1WtN1DYfDUPeHab2WIkzbMYkObhdb2jbgFcgZhkGYlIcDKSVO1ieslksWXSf6o0VAm2EYOOwOosnppeLj5PREbbAXORLvcQRNIgmIY02y5kleqx6YNz0Cqu2olQ2WDJ7FlU4nI/gwgZq69oz155wT+YAQyWWcbPEozcZkeU3+4jiaRnGu2rwC7EoTvXnTp5wzeUzs9/tp5znVZ9ZxmjdP80jVh7Ee5dyT9eCDE3/FNwQvGrcxRoJv6tqSalw5Y4Sdu69nrryTlLnnkgk+sN/tAJGxKF7O35KSVMc1jTQdC6Il75wwLFOS0vVG2dRZY6+UMst2Ud/T9veo+tfGIt5sN/T7A3nMDH7AgDzZp6nKAvkgMVgMXjT/pQQGr/6MySYZcLhYLCis6PuD2jWR7cuD2OLdtgcXGAeRgxE7YFWs4m7FGIR0WCRJE7ywgM0/djX+lo3q3NQ/xRE47KdmdzlniiuMKODvAk2cxeEFlRESCcm+z4qNOZw2mPROtNB3+y2X1xuWC0mWGHnNwHcjxsQYWa/Xen/RiS96Dsu6twqGUG2/7J8gRMMooLhvAjG09Xya78mUktjHIsBtGUWX2YdADpYkKsKK95HYhhrDD8PwO7Ee+D0HaUtJNG6gH3q+ev6UV1cb0jjSthGGA/t8wp/95f/NqpNusMPQs+8P/OJXv+bJZ7+kcz0ff/Qef/yHf8Tueku/h9sX55yfnpGGA6s7dzg/v8V2v+P5yzd4F/jys88pqaftVgxj4uXLS84fBF49f8Nhv2UZIcQIXpgjsYWLu/e4KIXf/vY3XF9d4p0Y9f3mmqYJFJZsdxu++vJLyiiLYrO95p2Hj8jDSFQdm76Xbo9vcyKnkdV6jSsj0Rd2+x27w0iIHcFD5zvuP7zg5PYFf/WXX7PbH/BFFsGqOcGf3eJk1dF0DdeXr0jDnpwSr19dcnKasS6Ym+stF3fu8PDhuxz6kX0/wDiwWp1y995drBTi9euXvH79mqvrDZvdnrPzW7z/nQ9JzrM8vcX3f/DHvD/seffBPdJY2Owzo7hJtMWzu95yPew5XL8l5x3D4hzcAu/2bK57Pj88YSyJ7X7H0B9QWfta7u6DJxTH+taKNiz4yz/7O7aXX3PYZnIZ2W2ekXzh4t6/4rvf/5Df/PJTTr68zd1HH7H3Jzy9HtkReL7Z8X/9n/8LX335Ca9ev2Gz60WEf5Du0VYOVxz4Vcvpvbskl+j7QgktTZiYEPjJ2TKPQ5wjEfqOYeo6byXfhhDNQZY5W7AeZEVi9eqmaABQnX8npQ/WUVU+uQJPwqDVX3XUYLMULTmCes9Qo6opaLCSYQtkhCUsDId5B1BxrKaA4iYwVL7lfY/AXCYGrwVbtTmAMiGKBj1H4PXs3hagFD25axDqpvvKnDphORcLBJyO8U0AUN/XmHzOKWeiaEMOAQEEOPKz8efI2N78tzGb5j+bB8hm8M14z0Hmb9pGmLMzTXZjWlNaHoir952AhnI0lnPnqc5N1tJtZ0wcFUq3FaKP5YuyuJ3HZdFozLkQYpQGGhTSmImNMF5wE1htQK8+JaanWJDAagpqvDojczkJe/MpeIFpCEqxcq5Jo0yY6FP5rWVSbc1YebC94HztzMfH23qu95XgIuSCT4ly6OHQk2dNHiaQMqtz6TWwmp7baYBaCkdNb+xj8gg3AWSbS8kSH+sGH4Pc7hvXvMmQ/bak0rf9/Oa4zPe9AbTT2pbgSNaiq7bEAlcLzOVekhTIWibrcBSv2XqVMijMgBacMuFlX7omwmKBW3TEkxNy7KCNtE2kZDc5k1m73iLApOhPTUw7XMFHr42KkH1QgRUJJKseNfMAaLY3goEHqiEtRgcfA2UUDToAyzOMZQKoDBA2QG5MJqWQMMZ+LSGb2VJzVA0ALTrHPgRcDMSCShG0CnS5yuqb1ovJ7jjVPpVEhDO8Tqsmcim6Jr1o1/opQLCI2vTR5+vI9p+MjQQaBUmglVIo1nhHWVIlS1mfc9qRWMEPciE4YbVZMsB7r8C53Nv8l4LH+5YQo9iXnEnJHa3/KUlpa9Ewg2nfWEkySElk0XXjYmSwJFxyyuzU62I+g6+6yaUU0ligeNarkxo0hBgQOQJLfIiEQlR2ja03W6vH/oSx2qb9G2JkvT5RPwH2+wNt09U1bnPtnAUtqYLp0/ltrE9LKGoC9WbSRh5Ebbk+F06DoqzAdeHe3buUXHj95g2jU+3YIGW32HVm/lIInhiXlVFe7+kCxtY123LEoMMkQowRDbVsxxU8gWMZigngU6+gbmbxmeSsL87RNaJp7BQAsKacc9a1+W2urqVS3QW7hz2nMbqcs+TCZOu9XnoO2JotQf0Xk4ZKg+n5mi1VzX3Upy1TIrk4qTzACShYHPiQGVNguwPvMz5kfHZ0jTZYzQpCSi6HNIKPrsoaiT/hoGQWXSRTOIyAD3StaKbmnHE+kUboDwnXeA1Uxd8txVRTwZr6jeWYceqd+N9S+p3rXgVNMuT5erVnM2Ztmp1lMqYTS+/43BNGncSiuYwUIofDQGEgzECqul+y2Mdi5btpFF++cLTGZD6P/cOjBJG5OEWSOcJwE19f1rnDJwdZSn6llDvigvoozlVtzWHswRUteXZ4BSwP/UBUtnkuU8WA+NuxxgUFr5UMWvkWArFkhmFPIdekjvjJktiKQ0+32+L317JIyuw9LcaY7zmm1zaf2/ZBraaxuQ8BFxoIAd+0ON9AtrqPqcTZfBUfJkb8/8PcmzXJshx3fj+PiMysql7OelesBEmQHHJGM0aNZFoeZJKZPtw86SvITJ9ANpKN9CDJZCOTqAE4AAcicAng7uu5Z+nT3bVkZix6cI/I7D6X7ygY7PbprsrKjMXD/e9//3vVC60sxr5XCQLnFFQ8ncbWnLKCMNM0Mc2z2tLzc3ZWATGnyDfPvmlEhq7rubh8wOXFBQBzLhz2B+Z5IpqUQOc7qxwKJp2gttJbc685zuSoDcrV1qlNqM3FmiSLybdVG5GqNqf5gckA5VKK7nF71XJuESUVdaEHFJQvhRazTtNk1wgMm5q08ibLE/GiyemlGZmz5oeqKeqd4/zsXLV5YzQmpNqr4INKNRTVZq2l6cMwMPSDNh0bR208Jio3GLzqfUfzqU/TuNj1UhOsBUTPS2ds6cYitnXmvGe73bLb7drYjdOkjNu+JydlDRcD1zPq980xMUfFZ5QYsDRMXJMYlj0sdH3Xzr8qA1EKuODZOi3Z3xmB78mjRyplYjatrb04cxpPFGXJ6L3mTAjVZ3PtzAXYbLfEODf9eOeF4J2dwdZHoNQYWmWRkrGgJYMklZ+oTbmD1yatQQLWlUELXGRVUVTPOT1AcDhbqxoLTrM2GGunqQgB1Q7WnoYqt6O8qaphXCVMILhA6HuCF7pgfgrqAx4Oe07HI66U5hMdD4cG2tbqk5wSfd8TS9H1YLrLKv2xbtzMkjT3ntT1HDm1s7YUlQILfqmI2Gw2ytTGkglHrabylmQTWfbdPM/NNocQWnXPEou++fqDBmlP48jzm6/5wTvvUXjMPE3krfDVF5+y3T7kx3/+L/n0q5nLiyecD56vP/+COc589uGHfP7pR/zVj97hX/zFn/HHP/1TPvvyBWmaQTY8/+aazheevPWYL7/+muubG3CBX/3674njiUeXZ4Q+sN/f4F1PHEdyFHadZlCGYUMuHt8P5BiZxhNnuzMuLi+Y5onpdOLs/IyLP/1jvvzqC148e8btzZ7Xr1/z6PKCfgiMp5Gbmz3vvvsu4zxSnHC5vVAjPrlUVQAAIABJREFUEKv2aeby4gwR8F5Fw12JuBK5uDjn/PIB4j1//S//Y7557y0+/M1/IM8nttsd3dBTSuK9H/wAl99HcuLLzz7m+uYlKR7ppfDwnbe43d9ye3vD69dX/OCHP2bTBYIXtpuBvus5Hk5cXV3x+w9/xzSNnG0vefT0CRcXlxwPB7rNGW+//31e7o+8vnrJ118/49XLK+bK3kHow8DL56+4vnrN1998TMozIh3TeCSlyPGkWeFMZs4Rhx5K3XZjzBJHFwIXZ+e8fHnLwwfv8OzZV6TpCk9GOnj8cMvTt/+Yw/PIf/ev/ns+/+gDHpwPfPLRp/xq/wHXt6/Z75/zwa9+we8++HtS1JIHTF8NyRBrICzWzXUinkbcWQcUcpw5HmdC39FtBmrJZEWaRKz0qf68yt7VoHYNUEJ17JShVwP0ivvU9wpYhhMDGgEcRWogSAMxY5xbJn0ddGpAbP8ulfu1LkPWQ7g5RQY4ZH2oxpatjkH9TDF2CKVQ3P0g9y6404JdljCmXoUilhWtjmJpJccKoKb6kO3AbZ+XxclrwWdZvmUNhLIKPBsLyf4uFdguuTGk9Zbt/RpT08BhG/gKqLX5XAXO646qOnZ3dQkr2IPQ9LJy1rIPQe4EkPUh14xt0PIvV0HOGhViYaZYsMaaGVTa/VRHY5GEoK3X+rlCIfS9NmYo0OMJCnvQBU9OES+OII7dsCG4AM4zjSNX457bovrf2TpZk2u23sBjW58giPc1NtFD3kCuCgxAdYoWMF7vs2p52vPZ50pZA5FLAF81qu6Ci5V17BtgfB8UrYLyYvsiU1Tof5qIxxE5TcgUoWQt6QHd3yJvMNS8OTRQS2rbKmpgsbi6j3Mbl7trf9lJtcRnHTSuX3cB4+XzS3KlrmENXtuykwq4Cb6CHTbOy1csSZFiALk6P/6NcawJiGKNmupzLokW8KLMYg0gl8SBWKCaU6bCmKHv8H0PoUNChwwbwtkWvxlAPDjtVu1w1kxDod5oe9M7b2uomHagU9YtC0igzuVd1vAawKubribNiiExYk6xE98YfrXJhjaFGA2c0ENDRAjijenp8I0ttmgoN+aRWwBWm45qipdA1VaTDK7ZGK0C8PggZiMW5nqdXB+kzYfqnKLnABizyuGsdL8UDZyzLha7F70ZLaeMJCvtqoA1BtZomWEdx3ouiWoc2nO1I6oU0mxacUXPPiMdN+YGMeKLBtjTNBO6oE00XGWnFmIpy5i32TU2tYhJLyzawI3VlTNxlTxLxvotskhDLLbE01fdWKeSEBRZ7YVl0jrTWGv7s64Flv1SijJ7dL4cKarOpvca7Nyt7liATi89Dy6f8OhhZfyYPFMNHqWuGXXYRDRBlOo5W9cHFai0Jmyiay+YpuHa3mhZvzetSWvI6TWgFBwPHz0gzpEXr16x3ShI4g2ETinjbXwqU0lBPT0PCjVx6pZEjlutY1uzi72pAF5NFC33iK37NZtR507s2uoPeDuTnFE110niWkbp67VtXdTvqsn5ykhXUK+CCmo3FjtioGKh+SV6DiebjyU55py0ZolOlkZyGW0S5VxQ1o8FihSdE62SCWZrtCrP+06l5XrPsHH0AbxoVYwTCJ00HUHXoXICUZiTBa4UDaa9UJKu05hMFEGU3ThPaEGI2QhEGAZHiiYd4DzTNOO9Nh/TM8GWdFG7lVFGtThtGqW2oSZf1XaUkt+QINEqnTb1aosFmn55Ae8U4FnOQ9r81LPGizK6hq5jnqt+5sLsz7kgRYEM5+s6MWkBszfVNW3XL7qvsoFCTV5FDFR0Hhd8azZcRJMWHR31ZNJmQ+qpOVEwaJ4ncknWiEz9lGzl52K2brOpTVoLZGuulavUTmlNAAsJV4wlLvWcVzDWiT2I7TGcQyQzjQfG2yvyeDSpGTF7bgmhvFRJ3LUdYnIMjpwdfR/s3DeSBQoE+X4D3tP1mnx0taGgX2SAipjEiajchPPqB4jt+aHfWPVDZjyOTHGmC12relXpgxnnHWfnZ+x2O7zzTPPM4XiwswE2w4bz8zNtbOQDp3HkeDw13eycFfAZBmssJtrYsrI6U0rkw6FpEKu+ugJoqlO6AEKCzsNcMqNJWaS4sG6rb0VRuZc6rqqFiyX7HON4MBuSSVEZl7KEMTivZfnH4y23+2yfdwTfabm401VVY7TqfyiLddFYFictEdyFji4EEkmBae8ZwlrDWWOp3gXOz86U5BFTY1kuPqWjP56UhQqNcYrQWLslL80yY0ykFM2X1uV6dnahQKsBuCDMcabrOnb9WSNT5Fy05N2+ZzR5itrfosZNOauuq649bwBlJs6RXExOqiUOxRouBqtu0IZy3hi5yo5Xv3/jdpznc7NBmmhTQH4mxZn94UA0XdiCMfMRjpzIUX2WEBTg3m4Gi0fV8MxzJpksBKUmr8CHjoA0G7TE8FiSsTSFwuCVOVxjwyCOHAtTmpvExnK+SWOQN+lGhPk0kURIFgf0XWg+suAMmAfpl0ajvQ8U5xgePGAcBiiFbtg04lK1XTUhE2PkcDjgnCN0HbvdeYvLh2EwBvpyluTqryKWpJla0ud0iovskShWpQ3rUPmTzUAoi1ylE+F0OrW1W+UjclGCSDsT/5HXHzRIuz+d+NkHv+bJk0v+9I/e43Lb8eHnX/AiJr78+msev/OMn/zwPV68umboA/N0y83Vt5TpGlcip/2er756xn/6X/03XKeB25cvcXiyK/gAY4aPPvuS892Ojz/+HR99/DF//tM/4cHjh2Qy4+tb5jQzjgfG+QA5sT/sEYTQ7xi6Tkv00szxuKev/846GQ8fPuTb518znyYeXl5ycbGDrE7lu++9S9dt2e427F/e4sRzdj4wdBfGLtHyrMP+wDhOK6YIOA+vb2548Q+/pe83XJxvmeaR0PWqiVIy8+mkxqAbrOMgfPrsK14+/4Kf/tGPeXx5xjtvv8NnX37Jp198zuubW16+fMk//8u/5MFbT3BBiFE9qxAC77/3Lo8fP2aeCx9/+gnzPPMnP/kznrz7Hr/69e/4+S9+wd/82/+d8ea16RbpoZmSBkuTZcC8Q3Vm0CyRNlNzbDdbet8zZNVCifNITKMufufY9QNuN1Dic7758guub24YNj1jnsknz6tXL/nggy94/mLm6uaanG7ZBM/Pfy68unrB8XTLOB5I4143f2XYrEA7xFt5iAaBcdLDezjrtbuwRKaYyB5cMQo8zg4PdeSK6YFVgGgNKN4BJmtgjIFusnqfgXYVTCIn02lFAWCjuniTC8jGoMkpq2abd6Q7+IwxeygtKKvgrPeBhemkh2eVZyuZxh5rz7ECJZosAAswCQs4W3+u/13fUgVgnFTDL1TtL82aywIEsTLy0ECyZf4qO4YFNL431vXl2hXrnNQGDQuLtwK1udSAOSHFt8ON9nyuHVbtGVfjsC67upsp0+9vIEC9owqUlQqm3L1/KViDFwVKaqa8gWusQZwlO1hL0Othub6vBliXhc2rzDMFl2rQMs8TZOHx2UMeyMAmF1z2BOfpgtB32jCElNltt/TdwMEdtGvqfEt2BeeKdjQPoVJLTD5BuVcVL9HnVVDel7vrqTIhF83NZSyXsaUlPRQHr8E3LSBcr4ml87na1/o96zVcD1v7o7ITUqYkbdaYxkmTgNNMnzKpRL2nCvoZK7Qu1Op0rzW66rotsuhCg2o8NsbOaj+tX2vbsYCudw/++8+z/KzjtrCL3pTy0H1Zll/bzxWYE7m7z+paWgO0jQVnQZ1YaeLdPWuOjBQtt7QGRwsrUcy5Vsc+OI8fehgG2O6g2+E6j+sDGKNiQbcrWCN3np9izNWVPqFr9qcCcHWX2u/Er57RxqO4OiDt+8QaWNSpr4wgker8jS04KcUAu7Y+l07tQlGpJTA1TwMb2r7Wd6ltdKRYyzaX0n/V1az3q6BeVYdZ7KveeEo1UaOjgVQQQGV0KIVOHB6129rOFwNKLPFSE3NOGRMN0Miqs9a5gXUDhvqcWsWhX+5sbcWoC0a8a+sgOD2z9ZbrGZjw3sovC8Q5cSwnikwI6pMUA7CHrm9svJwq4FwYhq2VxxlLs+4nOzzr/uj6vjFjdU0YE090brQEVaGUEHqqhMYdBpka/gaUliJ0XhnJBSvR1lNq2XNJS68dHq1X0nuv8yxlAbLrivVewboGsKJrIyaz/zVxwpIEq+Ws2hhtSRIYimhAsJVjS62Eca0CKue8BNCpEIwt9vnnX+Cc5/z8jKabaIBa00HGEneWPBFEO7KXRExaLl9Pc8kViDNwVLRqowbkeqaKae/r9XMW1snd9RospUon2fo3recGzptEBePYbFwuSc+OtaaH2N4p6NptOrQL634tv6P7eElAiu0tcR5HufM355w2TarvM5tqaq64oF3hRXS9qL3VUssizq5p1q1KNpTCPEVIIL3X5oEGLpYMU9JgXkoiSGUw6zjhqt8hHMfC4RjpNgIuMMfCHJPKZxVNknTe0fWOPgrHUyI7IUkhxXkBBuyxvCxJB8kZkaVSzAdPnpNVXymjrBgw70OVZxG6zjXfptljG38pEOeRQgJxRGv4hO2R4hI50tZU33n6bl3SrPqJ3uvaqHr9QPORneQW2De/xUge9b6k2DPjECl6rXZwZVJJTTs8p0iyhjq5zBQUoGrs15U/h8MAr9ySkhj4mnNS3872dsrFbKc9Q4HWwE/NvjJZHVAiaVUxUIqQCnhm5ptXfPXlJxxvbnTuvGsasuKEZGB207V2Vl4cPCH0iGwp4hHJKhtgtdcudOpDGmjYhULfe7pewS5fckuYFMltjKFAVrJLKVnBWNO2VmKLY+gGrUJM2YBPlVg5vzhns9kwjiO3+xsOhwMhBC4vL7l4et7GOaXMeDpwOOwZx5GLi4vWaKs204qzVolMx6PaV2dAfAHvBjofECdNMzelpZmRar7qfjjFEd958jy3M0ljjLXmsZkhWaqs+l4bnF2cn2slkc1rZeI6IyFsQ+Dhw4cqtbAqx9Yx75VQQzEgV5mwztfElLKUK7DVdZogndzEMAyNpRxjbMnkrlMd/YjKJvR9j/MepVra3nPawCrFxMXlpcnfTG9ou+acmcbIfr+3sQioDG0hZdVpnufYKiGcc5CXmGnYbGjsUNFEpA9B5Z9aU7TOpAUWRvPZWe2BYb6l6arGVCuCqnyFyS24gouQ8sSNsU/nONNb8zoXOmNsqu2v+1YToNoUt+8H06TOIMnIOhDTTJwK02lkHE/k5Djuj2ZLYNh0lOJIqTBNM85tWgyKaFNIDMcIVbfXGoDlnJBiCR00Ttaxk6YpLKKM2AqkY35SKdbY0uxgzIovJQMsnfMU23fOaYWWavjXe/L0QcjWsHAetQq66zrVEO46taUxGjFGz/iu6whdx83NDTjH8XhsMXlMUX2LlNqzlupuORg2A8NmaKxbMU3glFQmY5wmXE64UhhPp7amQwhNhsR73xqeVZ+973umkzaD9PdBi9XrDxqknXLhV5+94OZ/+T/4L/7pX/HWw4ccTwd+9OMf8vxm5Fe//iXvPH2P0zFxI9BvEtKf+P5PfsD2wQPy6cDf/PYz3vvgEzbdlhQn8nwCMqnr+PsP/j9eXV/z9K23OL+8RNzA44dvs9sEjuMtm82GOOskbzc9jx895NtvDkyno3LWnJaqdV1PQRs39ZaV3u/3fP3Nt8TsOHvwiPe/9z32+z2ffPghQ+e5OD+n6wam6cRgk7cJgcuLLafDiSdPn/D+937IB7/5Hd9++y3zHCmih+3W7eh8YRoPHI97xquMEzjbbdjniUxh6HuGEDQg8YGPPv4dv/7dRzw63/Dtqyseng34ly8Zuh3bYUuWzOFwy8cffcijBxds+61G0VGNlwB/+Vd/yThlfvvxhxxPI8+eP+ff/ruf8a//zf/JR59+yjzf4NKoTqGoJ1S7DovzOBH6LtiBX5q+Siu3VPeS8aSBayGbnlSh84Gnjx8hzFy9viGmQkxaipIsW1mKx/stmYigHQ8X1pGOUdVSWZcorDU/GwsNFChNmsWl8zU2QcjkNFsWNuEl1HMESlmYWfdAkQaArYEWOwjuhqkL4JGziZSvgvz77L7qiGj5rpCSMhbvlMuLlTHZbdYyMNXqKQsAhRU91Tly7l4AcxeMfeN56jXy3RLolm2tT1nHxgLENbik81ID02Vc6ufqob++rtjP2TzJO3+/D2DpzX7nM7QwtCysFpskarMh51fModXzrcepAlL3pSzqz2sHZe1cVIB+DbSVCorJMrbAnfuoQHVzOlbjfB+wWzMtRZbvWICrbBlwp9pjwDhNPOrP+f7uEdtJ8DmZY+/JpxmOM85AEqQw7g/EMuPFI6k2KgNvoE9rENBwP3Oki7F/G2vIGMLO6WGaF93e+qxGSDbwdmHBaCnrehzurb0Kvjp9ztpUZ7131y9BWkOPlLTUOU8T+TjiYyZPswZT5NWcL9epTSveAEulskyWBVgB2jXQuQY+189xf46/az+u18N3/W09Fv/YZ7/rOrKCLpe/vfn+tdaTsmgs023ldTkZcwGUMVX03PF2PpDRNVnAdT30HX7oGYYN4gOlD7DZUrqNshkwXnmNM83prvdageEGCNDi9sZG0bFYmknVRoOyeuqml8vCHn4DBF7jNvb76rR1Fow1CRBU76ug1QO+VXrYX5utqjIj69LORbvWO2VYFllrdVfdXWfsrdLYfXfnXAGset6BMoZcBap8Ba1Ks7uF+h00yaBsLA4v7o7m+rpE0iEkFokOGgNN7YGWMye60Lczq96rMo7URqu2YlLtRAddv6Hvt+Ysd2QRvCgzKaHAQjDWWgFOreyt0x4Cqw7tVF32GizamNYKDKyCQeUrgrLygBTFghrQrvZ+xVxdlfFGtTn1zDwhq8TRag9ZYBNqN+6SkewMoNV5K6mQc6RK3FR7SVams1iA55xoh3Br5rFOOOTiLSCswIxFK6ztoj53tQBSFuaoiG/ADRXkTrU0VudJ7YGYLQeRqFq8mnJWhn1cgGlXsoLXBnh6K3+twZ7iXsZqsbJSEfVvFAyp+4+2V50oMFY1/o+mRdikB5yHXO7oKWoTGQ2b1pUJzjmCE8Q7XDI2rxOdc7ckdFQr3RK0SCvF1sFefLu7CUjXdJrXzUlrMoSygHIKTpnmtmjDqFRM69JrMKzAul43U8iuIK4wTpFZEn7b0QWh84UQTKrFK4Cei3ZT907P8uCNbRswZlCh6zw72RILjGMyu6mf6/GQClKEHIsxmwSpUjQ5NVBKrYOz+dbFmKKOuXdem7PlhO8UPEgpU7wjRlo5aSk6fznPBg7NTeO4sJL6yIkcJ02Q2b5T+9UxjyfG4237TF3XyYCz5usidMGrNAuL/16KJiJjmpnGIzlHquauan5ajCWr5Ajq09XmUA2sNcZtjBOUmTklPTux5GXoVnu22HoOjU0mq2xwSVrCnXKiH3r6YbBu7/UsgskaMxXzn4ptomVrK6GiJvmKgMuR/avnXD37gny8RsQ0ie0MmycdH6n7vFgSy3v89gGbzZYunJkdmdHoSPWnQ9cp0xZs7894A7a70FHmWe/czm8xgLszvyPGiO+0MhPTzuwHJbbM02wSa87K4jdKuiqF169fc3t728DZ7XZLbw2mpmliv983n957z+PHj9jtdk1Go+qeppQM81ZGdN8paKqSC8vZrg2fJiu9zq3CR4CIMoU7HxBPY+mqzV6aCa5jyGp7mh2aU5PkqMm7mCLiYouvkoFWvTEiK4Bd7Yr3rkkH1GcH2vle19z9SgURZS+GEBjHcQGgzUETEQ6H40oqKt3xrUopnE5T29/1eWs81fc9ZzsFyGvperXVXa/A7ly1sYs2xKrncUyR8XiyBKPZmhBaVWzVLxdRfdyuC+1MSSXTdVa+7jQejznhgwLbfa/N48XYz/v9aD5LISXtY5FyYpxGle5KiUmEkiey4QrYXnPmN2rlgfpLPgQctfLE0/eassunhOBJqRLlgmmD18ox883yksQSZ014RRNGzkgTHmFMJj0VvJmkbP7EIvWT0xKUOa/gOrL4iFBZq2rjREy/O2cmazp2cXGGNjHr2O16rSQXS7TYfs6spAJE2nyXUhi6rvlaNUHx5MkTTTpbYkJBYwOMp8gxntoa1b1sJLyscf8wDHjz48ZJk7RzjArImnRMXfPTNDGOo/kbNcGq5Lqz3Q6HStU4FhmT73r9QYO0KWdux5lXh5nPvn3JlBJZCucPLvj81WvS6cjD844nj99iLo5nz1/xzdWBvQx0b7+H5JH9nPkf/sd/w0/ffYc/f+uSP3nnEW+/+w7d2Y7PPvuMP/nRj3Gu570f/gmfP3tNdhskBMp4oqSJi4sLdtuB01R48OCC880f8dkXX2g5kCsIWp6VkrIivHOtoUCcJvrdOf35OdsHb/Hg6Q/57JPPORyv8Q6e336L7zrOLy/pw0AXBiiOs+0Zm36rDRZy4XQa1enoNXPTBc/QBXKBOJ4QAwWGviNtBmKc6YbAo8dv8eDpu7y8esn8D7/mrYdPKNORkmDOmS+efc3Dh2+zO7vgNN4iJXNzfcXVqxdsdt/n5vaW2+tbdrst1ze3fPzxJzx89JTt9ozTceJf/0//M//Pz/8dL15dU5yAJIqqUFL17pTFl5og+TwfqZpQCqpoh1gFEF3TtVNjbN0+DaS6evECSgTRbtLq2mSC7zRDKwU44EiUrFklRJrmKSXfcawXx1Zfd342w9sCKQMKgg9QCvF0wvWDGrNSSz6ysb6SOSH6qt93l620AogR61JeGsiUV6DenaC/Yln3AdB672tAcvX99sPqu/VectGgqDTDeRdQXuvPVjHy9XcvOq5vgqHrV/3dGyXXZXHUWlAMCoZWx281L/evW+rn7fnWIvEFWnZ4DUSswa7akOEuu9S+xzzRCpJKC37kzvezmof1ddadwCsIu15n63VYs9/LszZerK3rBWRcf9f62vcdofWz3rnfO/Ol/78PzonD2AtLQ4vLYcu563AlMaYZcKQ4WQAdyDkx5sjp9grnHCcSV+XElGacC5YUX3UMX9dXrUBiZY9henka6Nb5bTCbjftdEEFLJ5f5kbaecsoWqC/j4+ocs5S1L8Apb4xfI0mVQpkn0jyTTyNpf1JilzV+qfZtvd7ustNqaU1pCRG73SX4Xq2lf+z1Bti7mmPd/8t4tQRGHex2jeVa6z19f5/xjyRTyoLktecsBnTfX4PVWXfm6Kr2nUZ+3qmzWaSyo+YakyKCghleSwC7YUvpO8qmJ3c9vguaQQ89KWvJbxvXOg6rAPON/WDrYG37ljExPUf7XS7ZKhmUOVTHSydvkRW5D5yLOawVDA7mqNXgOsbYki5SjY7R5qs90rNBZZC+C2xfr7NqL8Qti6sCDG0tlqoNvZLFaeCZrp3lFGH1PTS7HXP9nDJKkmkkOh+MleAXbdlSQRErsy2RbM/fxsheSwWCgbkr+7S2lxpQ0pp+1Y7cNdiuc6jq+IKUwpStqaA965y0adnQ94SuY+g31HMnxmjr0BprsjxHBQqUKaWMiZQmcrLzMnRtjZQC3ndNP7mOmZ5fshoboYjKihQDRVNK5FhLoP2iiecCtWlY/TwIfT+szrhqh5Kx1cAHR04GAImQc2zvr3rCSnap4G/B+Q7IaFyrTLhSVJutJJNFApBlfRrUpLY3q43OObf5j0mDyS71eBfAwHphxQoWtTveSRvzLujz4Qy+EWfN4IQ5xSYr41zVOq2gqK6bLnQtuHJOm5dk83Oc6RlrmbgGsFU/craeEZUdU89GKZVBXCjG4AZl/oawyJ+0UmSKBnR+2XdVFmOxPevzJyGlJiRX9qTu/3Ykmv8k1pCyLJJjGa1YqXQIvUMDqM04ZkvGpGysL2ac75lnZdA6Z41jfKAPThNm3uyzFAYvdD7TuaLas0WYN55xglgcMQrHEY5TMZBJiMkxR8hFGCfHOHumyTfpnmIggN6iru8KQmQL8B1WAj6nxpSjqB6zc8I8R07jaCX3xfQ3s+p/JgU4UpopWUui615WgonTbuPTkRQTMc3G6KLpbVa7A4vMTJXIyGXpTB7jzHg6kPKMSgoFapVNfbZ1hVBKkRTnas5pjWCLNXhy+ruUF/Ct6nyLrM/0TMkzWAOolKMSW6KOQUyZ03ii6zu6vrtj651TPzTFJYlUFKVCqODDokHtnSeVyP7mNWk6gjO7tj4La2WGE2026TqGzY7QDXTDA7wPDP2Z+Ycz4hc/VMQpOUBqQkrognZ0LzkTuqoTbX6bBpmtwMX3HS441TiOUdnWYkzjotq/qn3ZUQQOpyO3t7etmdWjR484P1f27OFw4Hg4MI2a4Ov7nouLC4ZBNb/HceR4PFqDLH327XarYJfzJiGgv6+9BKIxpatGLIhdzzVmXnCeaR5bI0B7tKbrXFiSz1V+aZ4j0QD5nBQcc0bqKdRmypoiWwOnfd9rM6x6HjtlOsekza2qTm69j1JqVUhpOEhX2Y0rn2ieZ3a7Hdvttj17SnF1Piizt+QCWUlP1RbknLm5ubnjs67JRJpkC2z6jUlC0exuLh3eBzabrtndSuaqhLF6ZszThIijD6HFknU+S8mMVgYvFjurxrP2F/K+xpUaw4Qw4d3Jkkfe9lpPSjPeQ98Hzs52XOZLqzquVWYQ55nD4ajFShYrp1nveRY4HSdNcgRtlkkpJCLBDcYkdVYBpYBrztXHFNWWNVtDynSrBGfwToFVtNlYbW7qghG8ctLkjVv8xNmSSt4a2vngmKfJ5keBeI391JZM06gMVWyORH1jEcf1dWZ/OHB+ucH5Sy4vtupveE8Wk6KwtZkt2VzxipQSt+PY4ngnwulw0PXc9xQW2aJKANFGgfUamlQbx6jiYBVDqElvXe3tGmKaw+qT9gbSjuRcWtJjNNZvTImXV9dcXpyz22zVHyj/eJz3hw3SpsjV8ZbAxEdfBy4fbdjsev72lz/nZ7/8ezbbDYef/oRJv910AAAgAElEQVS/+ot/wuXFU559/TklFa5eX7GfI76DfnNOno68fp7p3r7gxz/5Ae//8Y/527/7JWPMvPv99/nos68pHn74458wx4mUOsaTGo733nmXvusYpxMX5zv85WOevXhNt/Fs+sAQBDERbEE3z9D1bLpeF37RhmCHw5Hzp09APDc3N7x++S37myOEwOOnb/PowWMuznfkdMbjh4+5uTnw+48+4fX1NcfjkQePHtFvt5CX0oTtdsftfOC0vyHGyO78ks1my+moen9FHG+9+x7fvHxBKZHH5+d8+tkzdmcdj58+IObCnEbefvsp47jjdNpzudly3B/4/NNPubq+5vLyEbvdU97//g+IRfi7//Brfv/hp/zyF7/kN7/5NYf5SBe0C2sqheBV6LvpCBbtLF+ZdOQlS6EBrTkpxjpQhhVAWRxIWcpPszX+0SysLZQSqRpy4mqjF2NgIdabxzJ18Aaotj481uAKucCUmoORiqp/BpFWpqglNNk0rhYwxN8DLqCCH+vyVH3lUksmViDd6k01sPfek8qiV6oHi2sBxspfp4JX9fCqhyRouN46VpeFAYbcZZnWjOh3gX1tLFfjuAaU7n93C0ZW71nuy+bEdHGUUaHlShXYrmPzxn2sQM76vWtQ/E4p7erf6/es79Xu3sa1ApZi+7vx8xbn4N44rLPYa72iNViz7rDc7t2CkDV4qvNTP1sDTaiN39ZjEO4AvNxZz/fBvPUYrDucr9dIBXA0KNCD5tnNSyQWzsIG74UuOx5dPuBsGIjjREyJOB45TCOHPHKbRo6SkFD1cq1hQxvlCn6sgDT1xJSRtApiK8AmlligAp1AA3vvSUTkKjFQKthWDGRZxk0KFtTTEkkahLy51rTcM0OK5NNEOh4oU8TnTJNmazWy7aZR53A1DzaXwqIJeR8c5N7v1s+1BtTeBE0VrpZax27AFDVYa/fx3etj/f0N3LBbWDBqGxdZ/5bVNdbjdjeZ0BIKRQOJZEmIkgvigwKufY/faIa7VmCIE1xwhL6H0CN9j99ukdCZ3dU5U4CIZkNknS6z+22SB00GxBIiDWha9nGVrdF1kxqTQidA11/bz1aa9V0g9xvfgTnKdq8+VJarBeNWTpzbnBiL1xUt716BOevEmQILQRtLOHWy28OLVQPY81c96rVdVadeg981yF+Klik7A39zykRoGoUpK0NQVUxWtpW7Nqeu2/r8dwHxN/cA0JorrG3Um59TfU3nVL8RrLQbY7JiDKaSmZOWwrmiQF+oEgpW/rl07V2t46JanxU4XJgjSzOxep/BbFOaZwUtnbJYVCvUtaO9GPhLqTqmiw0sObZpK2XRmvM+kLBO2EJrsgaW8Ea02Z3ctffJmNreRwNpFKCZo5ZKL01pHPM8GtPGpAaMWSbGzgRRsYGVH1MbkynI5ZsGZW0CCqZLacFnsqR86DoKybpxmx55Taab1mxKiWDBj4i0oK4GgiKCmA0PIRCprNeOinBp6Wz1kRwUQckEBrJ3WgFXGwLltk8Sc1TN9WzNRBb7J7butUt31ees2rEF4TRO+syCnmu2Z0dxiyZ0JRNUX5RMsevWOazM+ztNGc2+Vf9QmgSBKLvKkpK1qY+el+u0i+qKdqFWCKDrVbQHxnbjcL4weE/XmV5oEjY9bDpwyeyTK3Sdw2OBfckqS+A9XdHS25IC4oXZF3oHc8wgmaF3+KAgbdc5ykEY56iMSTs/c8rENGm5/2zSbz1UJmwy5lXKiWmaLe5i2Z9ZAVLdp1FJFFJdbF0L3nslYrCcqympFIB3qC6lL3gJ2p18jmq3rVlNDdwr67omIlNatCu11PwB43ikSjLU+9fGZImUClCrTARWcmqlaAWSa9ijMo2lq8kjs6kGdIlT5l9Ms7Luvco/9KGjdJl5GjXx7AvilTE6TZMlIaRVUyng5sgGppVcmt+bit4vFbgtkLNjmqtqcGX9qT3KKauUXz/g+w2bzY6u37LdnuOkw/teE21usOU7Iz4tPlqpfkGxpr8dWIl8Ia+aHmLz4G1co1bYrKogsDkuRdmwznm224GcM+M04pxwPB4QkQa+dlYyrWtjxiGcnZ21RlTOOQ6HAwDH45HRJFF2ux273U6rZovqbaeU7zA967mjwGbPMPR34olSVAKjyrZUJnet6NCz3ZprYY0tjQFYQWTvaqNOHZN2DUt4ehz9oEmw29tbQJugr31C7yacXxrwVXtUD4Pqj9Q134Wu+TrVV1Kd2GP7dwP/0XhUxK8wgru+VAiBkjWRpmOi66M2mJ6midPxwDzNjOOJEKyxngiIa0SbO89kPSpUO1eT/mdnZ0viXPTMffDwAdM8qy6v6H7PJRO8SgcdTzrfTjcKzncmCXGiJtQEjMG9BZRcpmx09V2983hjlos4un7DmfOtikDXbFwaubrI4XBCAmaDA3Me6TvBFU1Y5KT6rs5rKX8uixSIApxWUUh1TjI40101e+haM2ebB6fJ3qql7Z1jzgq0e/HM09E0drWSImcj7zl9htPpxH6/Z5pUciQDfT8ofrbZIuIYTycKM7tdz3bTMU96LkaLw2s/mH5QOYJ1sqAycyuDPaWke1OErt+w3W7bOa7gsGsN+qrf5LdbO1t1jc7zzDROWp21amZ5Op1I80xnzPgqO9Z1rlXm1OvOc2ScI9vtVs/kXO74x/dff9ggrTheiOd0nDl+/iWzz/zn/+yfstluuT1cc337glKuOdw+54fv/ojp+gVvP3kLvveIT59dEYtuot47fvTe2/zg+9/Hnz/mNx99yf/2f/2M8VBw37zi/NHbTPOBlGa+ff4V5Rh4dfWSR5dbdkPPO2895XD6gtubW1yAywePKWVi6B3ONME2mw2b7YaYIn3vkRIY/A7SgevDnuuX3zDvD0DheDyRxgPzPDMejwybDX3wnMYLQhC++EqbiRzGA/M0EjpPypGcI323RZzD+47Hjx9z9eo51zdXhNDRzyPjaeJ0vCU4xzxmXl0f+fyrT3FS+MEPv8f16Yqb054Xr6642G0oKeKdZ3d2jnNweX7B+fk5MSU679jutowpMyXhw3/4mP/3b/6Gn/3tv+err74EKfhOjHGxBLTeeQsyaqkPS3MNMedCLFgBNICsbLlaQll9NHNBS6kQC1hjBMUaVoFo+4wdxFRmmzncxlJ1K+O8BucWUMbuoUCeJkpMCKE1wsACrRiTimOXos2SioE1inTeCfaX76hl2sYgkgqO1hJaO/RWDYUcNOPM6t6ro+7a4ZgMqCpULSzgjUMODJwzI2+PTGUJte7h9wzHXbyoMiF1Ep0xnsTuDTsE7R3Gdq3sozWIaKXsszrQ3gIGTbZXNtgyR9/FUuMemNWa5pRyB9BcA7htvqkMEn2OYtpEeY4GlCwNjVxjJRlLqR78RdeXjqtbga01eK4sWAOj3DL/CiLW/65H982fFx5MBdkqKzW1pgr1QMkl33nOem9VL7uNWwUKy92S9LbnimWbSUwBvjxeEZKCHWe5ozzInL31Li7Dxnec3MQcZ/blxBSK6cqVtifEqbRABREK4EyLrbGgEYK3AP8e4NXAKlk1/coVVK9yETVwlbaua/lvZfIuF1R7lc3JzzY/dU4qQJdL4XQ6IjnjUyIdj5TTrAz4VGz8oSiNrn3/fWCu2HqoW30Bqsoip+FWjMrVCliviTXLftEZ5c76oI6PrdF2PbOB98fo/uv+fq/7rM3bmgnNal/AAm6Wem9rDWndawq2a7E4orpRpe+R7cAwDAb4WQY/ePo+4Pue5DzignZ3bmcDgHYsr3Psmn1EWXd1Da7shTqM9eeaAFzsUg2kqcC6mJOdNVnWZGJKbex0fwzvguHFqMFLwkw/7KUy2orppNbgx3S8UmxniU6FPpsOcj1bauBujn9RTbSavEhFKzYSix2s+7vai5JyY3s651pytY5nBd1KKUYcVmaTMhlrU4jlJKtnPsZY8QYUVHuznF3Luaj39WYlgFZ21IoZnbvK+ElZwRjnPDGrlnvKVsYZVS80J9WJTikxl9zKQ/X7jUnjPYKBtLY/tSqoPncNSJf9VsEePTsFnDFXkurESU5WYp3xwWuzDQt4crLzpixAB22dmS3L+sxaTm771wU67y2RRVsr4hwl1TNm0cvUc1Ta/VYfIGUNZJRtFDmdDspCy4vNUdCuswDXdH3FbLY9e5Vc6JyHnK05mzYm0a8Ta65Rny9bLBiZxgOgIHA29nBeleZShCEENKA1bVfnDQCx1Zqz9RPwBN8z9FumcVa2TRcgempzSu8NgBtHco50oTP9Uo0XZmN0Yfp+3nm8PWcIgdCF1qG8AjMpJipLyTuV9KoBbSmWzDBwpuuC+jpJA7gUJxAsCC8G4JXWeMs70W5dxsgRCs4FMO3lanOqX41IKwkXpK1rh+AXZ4ggiuMGO4vFCeKFrhNCEGu6pHakRM+cM0GEPCuxIASv9ytaTdg5MbYXkEwuYNDmTuMhqU8nmoAN4pThWITjcWScQaTnOM6cxlH1dKtvbyw6wdixBeai+rVxnigp0Xd9AxenSbVhKwPfuUKcVQZOk8I0P8k510BEqh9oIUfXBebZyu1LaiCnlw7vu7aPKuOtlIIzKaRo9jrlClYWZptf5zuzfeBCoUyFNNt6Kxkhm1a4AXZBmYTzPIMlh5YEyoqkUCDGaTmHkjDmbElMA6GKnRviCNYhTpL6jyknpAQ0nFP7LuYjIkKpvpdnqX6LsQGodW9GCciwocQExs6sVUzOd1xePKDfXHJ2+RTEGyDX44yk4y0hpHqmvY6DJW6cZDonxKxxdzFpl1K0C3yrZtFDX58FweORXMgp4hy4oSfmyljNeB84Pz+39TMZcCp0Xc9ut6ULHSknrl9fM8/akNJ7z+X5BbvdjpQSNzc35JwbWNT3PWdnZ2w2m2aLY0rEeVYfJS9Ja7AmfrVhqPeIyX3EeVbmqgGSImJArQKWwZis2jwtNFJJ6TuziWqzd7udgc+OELQpmzhhPFl5f9G5DkHt9IPLB6SciPNkkiFaGRC8NvuscjlVLgCWWC1nXa+3N7cKgrrAbrdVeY+cySVacqXKcVgSMgRynkgpakVIzuAqcKljMsfIpt+YLe7afo3zrLrEBuKeTqM20MuzJZ/Vr8i5sujTwlaNEyAcj8cmlQJCvxlaXxxNkppNEYcPyph1OGNxOx5szg0gjCZNAuf+jDhHbRJlPpbqXquPMc8nShFimtT/F4/30+KRS+3h4ui8rrsiju12Q9cNDLsHHPYnbm9fE+NIyqNqtpZRG/CmRM5KBHAixKLyYt4HA5k1qV0oJOOYeK8+sHdihAqN+Wo1ERnFPcSzJJyiNvsMHu90PpTxH5rUiJ7pzhi0I95X1nG1ibquK8D/8OElvoOz3U5B0kmTYJGsTGdoTO5S1GYL2iDPe4/vVL6qVj0cj0cOxqitazRlrbaNlmiu0h1935NFQebgdXxU1qAzQL9XHwS0p0HOlGnidDotyRXnGKdRfYwG1jqGboPqjpv8kWnsftfrDxqkzSWzH0eKD8TTkfzhJzw4O+fhsOPi4TlXz7/i2aff8mjj+f5/9M/4b//Lv6bEI59/e8snz0ZOU+H56xPH415RfzfwyVd7fvPbzxj6t0nTNXM88vTBj7jZd5ylwse3R9JYmMaReSo4yThJfP/99zgeJs7OHhKnia+/+YLIyDyPDL3nwaNHbHcPeXX1gtP+NUNXePj0MbkI+8OROI4cU+HR5TnX5xe8Gke0r4SjxIk0nRgPNwxdx7C95DRHfN+1bNg0nZCgmc2YEzJ1XL14yfOvvyLnESeF/fUrDtc3WsbVBdJ0xfj5x3R9z/tvv0fJMy9Pez78/W+43d+oLMBcOOxHzs62BCekbWG72XC4uaF3nm+ePeP//vn/yrfPrrh5fcvr62+Z4kxGSx9yovEGSilNY1A9srKSGiitVL8yfgDWYe1d1piV8KXKLsAcVm8BZS3HtxKH4Be9H1c3Ok3zcgGs7N5YgbIVfKtlehWbtCYgOQN5KT9PKYLTUoEKJOH1EPD6Ze07c0xq5Fe/q0GqavKtAZgKcoiBlK4Z+trMrGZM75RB5xpEVxq+mO7RfabwwpjQLufZWMJmeEsdnzVAU2HWBcBeymUrCKTheIWmamAJdmg3huIi56Dd3M3oF3AWuBZSAxtqUKW2YAFE7rML77OqBGvs5NaskbvrAGiO030g5e6rgqHmFK80RhVky7Y2C7ULehFlwyxj1m607Q/Fjeoz1oZuFVwv5igLda0i9iwFapf4toYM4MnGXtG4Vu+s2Bzo168Yxm229Pu9V5bBAuJqCWkRa/IgHqFQnOqUESfmeKLbBx7stmyyI3R9W5/brsd1cFtmddKzarU22L8iHmDN9iqAWcvlS1vvNgAGknkqCI4B6Aq+WvKlBVsLQOZkAbXr/FYdRjHHpAIvtStrro3NGigMpEyeR1yM5NOoBdTNnimo53E6XjXoXQGbjYGdba9Bc6LXJYGyWs/1+av9u896rfzgNWBakyRrRmcFT9cAk6FQjS2j8czCsr/PWqzAW7VvRcTw3+V+9bqapXcG5Oj3aiOBWvqumo8Ol4tJ5SjwEjZb3G5LGJZSwKQGgc7KuL1h3LoXc9vzRf15aypjSSIvkHWcMqYJ6RYJgwVE1rnw3hv4YWy+tjKrzSwGBGlGvJ4KC4t1sbHfNWfVrlW2ic69nUWUBioXFDgssjAX1rZkXXpfzW41lzEVe9bSAnJEGSJ1za3XV662zya5iFgpcWkN+ACTkBDV8bRzKQs4FAAoZgu9BE4p0nU9fdczWyOa2NZjaaWM4oPNQ2WqViaivq+C1dQAooLXTih4YhpboCsSDfgTJARlE6VkmmN5Wf/23xjjMoZAmTXAw60YxhbkO7+wZ2uSpTawLFlaYF2KY57rnEmbn1yyBhjeAsCqc1bPKtGnzqXggqcLWiJacrGSZ13TKSmYG3xHap20K/tf95xi4jURXpouIkWsjN81prYRY4lpRtDmQyXpd6n2qoHVOakenFMWXf1fTFFZhUUTcKXv8M6SzmUBhAGKNUBsHG1xRFRDsuYbKrO1VcZktW+entH8NAWak5XErxPttWIi4C4KJQlTnLQJYdjQdRu1dV4saJwpoiDlnGZinJmmmXmOdtaojZKuR3AaeJYEyYErRGNNIkKcI5TCsNmSlDZLTMn8VD07nZ3VIqH93okgwexQsPPXutHD8ky1OqIGc0VsrzhbawVyFlzQHhTee2XoIARx5gdXu2g2WQX+KLaOPRpce++YYiFMsHWOrisMAaYI4ynTRcducAw9iBdS9srgcoXeC513HF3mFAselTXYbgLqqtt4JWkgxGZQACzmwrBxnCbHPOrzZyJSEq6IytiUgrbMC4jPSFZm+TTPLQHmBG1CliIxqn333kHxhLBt2ow1KQQLs18BGPOrvKfveks2zMzW5LGW1GIyFFmcJmFQQFQrwqL6TFKBuGLMwwpCCqUoWFfL3pVplo0JXKtNijZkFcE7jTdccXiUHYyxQ7GzSZMiYjGDoyDWrFXtam8A1jhPONfbPZjepBNcUSZ0MekUkaq1rSxpJzUiUMDLeSEl2+dZY+Uinu58iyaWUvPjXNezOXvA5aMfsN0+xHdbS1TVhmaCF0t+eh0vXPWlMxLU9XAUSswqwWDkCC+6drNJdFUbUc2P2AEp4owVXxjHCe+Fftiw6bXD+8lK/UVM39rrOTFPEynq+b4xPVXnlXl/e3vbSuG1wlUbT3prwrXWqIzRdOAL9KZvvd1umw1zVuqfc1JWojULE8XETXIutbOxym3gHM6SCd4rIFf9GXFOdXOPBph6zzQnDidj9Nr5MAyDMrtnbc7onMY3iDQJhyp5Fy3eDCEQtouuspNVT4yijNlxUomArgsmPydsh107Y+McyV4TEZqASMQ4M89aJt/1wfagnl05FW7zDaELDMPQ/CHvhJSEXgpd6NjtBuboSXloGEST76MoaF+KxQKq+7s735Fi5ng46rzNyfauNiyr0gwuKDu563tdW9Zczwdtina+3amedZqJ44jL4LqO0A+4XOjsnpVhumtn8/F0ZJpmQjeg0kHCOI3W+E0lhhwd/faMi7NL+mFDwfHW08B4uuXV1TMO+9dM05HaqFAB/HoMq+RRjDDHycB+387z9hkXrFmrtIqWenbnUii1QaGdu4j6zCRNiKeSOZ6OpDTTlc6Ys6OB34U4zXS+I5GRYWjrvu86k8BS/yoEz9mZSm70faDrAs555jwrcLrypQFmkwspB5Wk6LqOs/MzatM95z0PHz1mtztDRDidTpwsSQHZ5BoUG5nnqQHLIXhLUDiGftCEn9mD3XariRs7vxdZo3WcUpjn2vdAZSfW7PLRZCK+6/UHDdKSMvPrA/vOMaYj8zHx73/zD/z4yRPee/yQ+OoZyQ/8kz/+Ke8/eczlruP2+pq/+ouf8PidmV998BVz7NiFDieFb1+/5r/+z/4TXpxGLvYXzMcDN7fXfPz73zIMA9sh4LtzDocrLnY7+u2Wr755zudfvyRsztn0W773VuTxo573/sX3+fyblzx/+RovPZvdObuLS77+9hk3+z0Xuy1ROiT0DMPA0Ae8d5xtHrC/eczp9poar4sUYjxyff0SpHBWIPRbdeqG2lUuM+733Lx4blq12plPiISgYN88HknWiOzswSWpFN568pSLiws+/+ITvvrmOU7g6aOnpDjRhZ6Hjy7YbQa8U3mJblDNnmmOfPn5N/zsF3/Hbz78kCkVkghetPQFc/oKGGhaJ81CNQv+vavvMpA1qN7UfVBs/XPNcK+ZnJUunpJ1MLTDprGyGthh7JwCiDcgS4C7JflrVmWVEND3oIGqE6QL+PMNKWjDGi9iBkSDNy1HWoAvLbmRdv9A0x2rbEbtVm6s0mLAa3USRTcvVP3I3LSF9FUDsLvPsmao3S1L0cyq4mHGJGal2wrGcGZlPKSNWc1mN/BTFsBiCYqkrQVYylsr62p9fw5RcXLzOGJWUXH9uAGPNv8Vnq2lOiGE5uytgaP1awHg8gKArdi999dac8bcqjQNkKYLtlzzvpSDWLBTwbkGWttQrJueNaCOBWgxyMyCwYX5WkFypAJC5gAb8Nbuq8Kr9XpWen1HdqIJGNsebCjb8p0VwKzArFWF6ttybkBjcJ45nShkpngkzxMBT9j0XD56yPF6z5QjzgfOw4Z+t+GKkcPpNdGc5GSyII39aYxV3QPSxvQuc3ZhmqpjWst2TfON8maTPCoweBdwvwPm21hle/61vmjOlfmhSSAt88uEnIlzpMwRX2zdr645T1PTJbIpbABbW3s2P2ubCBVgXvbTfWarCNa84+46vr+W18+4lhm5ew939+VSZqtrZP25O0zGNXNWGlb7xhjX8a3PVcwRbmO/uv/2HQBeO41L11O6Drxrg+icI0kFfypglfBUEN616+esjFrEQOyVxnkpGQyEwpzrWhq4PpNKVlDRudSu7ajM21oO3VIxyn6WQsxJ7VwpDZCuNlVZBXbmWMdaIncaa9SAC7tuqSVp99Z3KenOeVmXS2Wi59W6q6xgpT/oldV2paZd2VigQCkGBlJwoowSWLFdxYDvBrgVBeZrwigXVAXWcbE953A6ti6/df8quKXnUgVLQYEJBVeW0vIlsZnbvYjoOq6SNDUJUlBNsyQKUFSAQc8Vx7r7eX3umrwpFNJcEG8VBAbGusoONfZLUmulyXIRKK7JBdRmLzrGfmHFWzVPiktSuRTtbqxL30r0qx8RkwH0hWJzoewQPQe9D6rLmdV/bE2HzB+S1XhpF+r6PfUzlthLS5LIiaMPPalYI9YY7RmWpIYT19ZQBVXHcVSAchiIMTEXkywqyvitHZezzXVO2lBOrEFebXyCLA3TKivUWXmu2N6r6zBG1R5VyY7l7HDB0/UbpHNI0Aqf8XSgJJXicqFHijInN5YI6rqO2/2tMtxE2TjeB5CqUy4U078NdkBO02il97lpQe52O2qHa2W0OgNo1N/1Xaf+jsleVN+u6wdySpxOU7MrULWOA5thWDG5NQGWa7+GahOyAsglFW3ExbqyCQPinDa2KUvCbn1OqMn0tlsSISj4p+1iNKHZhaJgWFZAMM0z3gXmBBiIliWDeAUuY2KcEkUcLmhSru8zecw2D0LoBfC8upnxrufRxRmnLrM/jCpTbIlZZXtlVIpF91cIgnMZJ9HmwWx8KcZ+zMwxUnC4MOCDo2erzb2KsigVECgKtJRCRsHIYsl0wYHXMvU5TuRsGq0GomLZCMlF7WKxpjZm61IudpYoAy61BHyHYWCEThmGJYN3iZx0D6ZsjXGkVuMJ4iB0CU9RGQOzfE6EPpwZoFulSVTbfzbAYhOUnbhJ0SoLM3McmZOx0lCGb12HYgnUjEk+iNlMVxNgpf0/F7VrLkbGkvFB57zrBoZhy+7iEdvdY/rwEO+3eOnoevMVRFDZo6kB5wo+q+SREkFUBkS1WDMuCQSPNjUyDe+Vn9HGy8672iA5SyZOypbfbDYE7xWsGU/kXOiHvulIxpiaRmnnw0oWBuIcmbIy50JQwHC73WoZM8rKPxwOlFI4nU70/YBzKmXQh05Zh7Z/U0oNYKpndpXIGvotoVM9WgVKNTVfz0mV2vFNzxZo5f/KFFz7IaW9b7ayDEE13RWQ1iadw7AxcPVICD3bjZaGK3AWcJ3XqpvaeEqgH3q8aEVUNCY7RRj6od17axrqFnmn3TY0O5QMtJ+mCewZRXQd5qT+UIyJ0zhxPB44HPY4tzRUrFI5w7Ch7weilblXgo9iEEGbfjnfxlJE2HXWWDHD2fl5i1OSNdnqjD293+91jJMSisTK92NJxJiIc+bl8Uqbyw1DwyNOx5HDabS4quB9Z6B2Ifge33X0xX7vOoZhw9APSqBxnjhrwib4nn5zxrbfMGx3FBcYQgc84cnTtzkerjjcvOLl82dcX12pnwCGG0XE5F2i6adr8zHdK/oQJH4AACAASURBVBVyKUWM2a6xrO86a56m5Dt1Q4qCiwXV/HaOcdTK75xmRsOtpjhRXylFw4WU+DRsBqIR4Lzv2e3O9NzI2rRynI70M/gAPljTcBQP6E0bXvGYCharFFey5pMxJa5vbsyHwp47mm9iUgnWtA+rpAStkg5Bm8xN1lQ2pdzmvGEbIozWOEz9S0xmSaURiohylNNCyiilWCK42qilevm7Xn/YIC2Q88i0n5jTyDgd+TjNBEn8xbtPOR86sof333qLL7/8lOvrFzx+/Ih4tee99/6IsHmX3/zmI37/wW/pHl6wP4589sUzLi4eksZIv4G//ud/xs9+/vf89rcfUSh03Y799Irh8Y733vse4/HInDLDZsfZ0CHzkccPz3nvj97h2evXrdnJ1esbbvazalNkmGPhen8ipsxmCGyHTkthBc7PdgxD1zRSYpwJzqvRP03sdlm7vxmIcTgcGE8H9vs9h9tbWAWeOOi7HV3nuTzbcfbOOzx5+23OHz/ksy+/4OvPvuDD3/8DL1+/5Pa0pxDZnl+wv75ld/mIR289Is+6aD/9+EN+8fcfkOaJ16+uuHpxxc3r66a3msk4H1qAKSIWfBSqJls2OlMNjr33zTlvYJRbguFcgS0Wp3GdHVkHpvUAqou7Hmi4BdStB2g1+HcBHxYnQz0D/T0OLNOCKDvIbwP9wzO6ix2y6+zA1IDIvF5SmelEmRHquNTAs3FK74AktRkLpDu/13tbAWuWja9o2fq936VDuf53Yw86DQYWJizaZCF4sl27ibGXZYzulCSzGLI16+wOQAuWsdVgvjEgWQC2Bj6IGbesOkmiud8GplaQKFOMzcAdEKk6c/VVwZrvAuMU6/BNM2cZ5+X9688p60/e+Pk+KHx/TRawxoELmCP33rceg5xrQ5sKeNVrV+aTSQ4I2r14dd8KU9q+sVuoje1YAWOAst0MTKmZ0Mo6oKizWnVU1+uqJjkq6ycpzU8DRumYppksDjpPyo7XaeT3V99wvD3Q+54HwxkPHz3Ce+Hl7XEB6EppOs7O2/g2BLPGOQrsYKW9xZ5pWYMLMFVZBzXY1ItYxFPUSb3fMXMNaNYyp0WvdVm3BnFoyVLRMuk8jeTjiXQ8kWLUzuOlfnd54zv050VCQsz46K0uoMLazpW29mgM3TvXdev1soBz99faes+2tbOyDet/331fxZ2XPdfWE6isRLXdagL/f+re61mS7Ejz+x0VkeKW6uoGGg01AHb0jM3aPpE00oyv/GP5zFfaGJdjRu7a7gwwAzEQ22hRqO4ueUVmRBzBB3c/EXmrZp/BNCurqisyI04c4f7559+3SoVs5qn9Vm+Z1jnggutgT7/n7doKnjAMoo/nzEysqkTGugc0HdwgPdoseTXAsnZ65/xqVuJk7qxSFE7ABz3DKGo06YVV0s8jbH3JzTYcOa8GFqY76BxdQ3RlaGvxz8ZZf9BVu4emWmF0sOZyv1Cm/eb5vO+1TfLWQlJD9HKFDea902LXqocuwERZDSOr7EGAnGNqGCPzwOYg8sS1QKF4I9VtXecFjCMKoBecJ/nUQYt1zskeZyYmxpaS8ZKvzbMkkduz5937971t0fTO3LDDmsjkqLbiYxUTJH155yR41rNMjB5XprX8HtCU3ant+JboeidFxODTxZozwNXeR9qYi8R4atJlYKft8cLaUsNEHSszSLZ5RBVjHO+lJbkuqxGftCeaju66V8rz1oK3Q81cBNC1ThJry69Ir/rSSj/jU1LjFyfjuTW3Akn2dvsdNHrSZETDELwU/Z3nPM9SFNB+yqAFwWwyCUPURHRtU7c4pq8rNWGpqmsekxhDVVovXNecwU1UBVDnrO3zznGKAw6RKmhVWZkaY5Sc+/1UBGDd7Q4d0DaWvN+c4agBU9O92hK1Jee+76/guLXeF7RO0PeQkktvHW4WXtpmzEqCKNoF5kCLE21lZSLxXFCmdvAbTUcQcoWHIQX5XQsvN/Gl7WVDdByPnhQl3p3niq/STh1SJY1ArPgUoIoMmAvCYPUePJ6lAi5QcZTqmEsjDbKHxuSJxXE+ywUspXJeGpVIq7I7ptERF8mjarWik3QdiESIAHZWwC3FWKQy/3OB83wGnUudAV8s9nLk2uTz9MxdE2+PmOPJ2jfpDUkAorKVlfDgG60UEgra1KLF74APQZiKDWUmqsYrVYEz2/vXAkRwjlyWNbZBnoHpTTfbn5GxFNOwgm8qmaMyIt6FHtzV2jgtCyEG9mmUwoHmolkL0BKbV0LNPb+R4RDwtWongg/mKyD7dS7QnJduCX2f891bvnj2Dcu5sDs+4dHVY3aHK9J4BDcQ3Ij3ajjl/SrDQuuSEq0VopM7Lk3e21FprmD6vGlI5I1xk50V9qq16PqQ88WDvFeVMtt+vyfEwHSetNsgsNslQoy9CFRK7uCrFatoKyNzHEeurq663mQphWmamKapn8nDMLDf74nRJDLWfMpYtgamurDqYnpkv47eS5FGgfWiwFouizw/Z5JNK4vPuvUs1uwSCs7YsI1xlOI0loM7kTEJPnJ19YAl77i5CcyzsCCtzV/2j6JSB5VpumXKM0MaOOzHC5BW5qEAnHI5MifnRbXQvdcz1EthwTs1SJN/5+w0vmoY+zCEwPE40kDZybnvA4COZ1bdWKfFVT13fKBxloKCgYV9XQLeiYyQPjeQtekcvcB7PB5w3knxx8gmNueaxJ7n89RjTJqjUrRboJLnmUZmHPe0Bqe7Gx5cPSYNO7kuP3I4HBmHvRjrpYAPIw/igRSS+t04UoikYaQ4xxAipRUBp2NkDInBCZB+c74VbCkvuCYSVsU6hJzHNL23ZuVy3tnelCgFLeA5cl5E098LdiVs8mtiHDhPEzFeeuu0mrtevxVgQ4zkJUtnkZfOoHFMPH7ymGEcpNidxWBxKQv1lJmWE+O4kz3Tc4H1mISU9x4/mAyhMGvP00TNpT/Lm5tbluUaWM2+ZF1Yjk43B7W1aAzgoLFUtq4HjRvyki/wKbsuvHbS+DVGt7XYpbpK6XHC+15/1CCt8xDjTEWYCRXHq9sTv/nmG672A36/41u7Bzw67ri+ueE3n37G7774midPbnnw7MTjD7/H3/3d3+AbfPWHZ9ze3PLT//xPfOe7PyJ5x+s3b/jlz94SWuYv//wnnKeZ58+/4cU3XxIPj/izv/pbnv3+c169fsV+NxJcZS6Fcw48e/6W//bZH5hvGyl6cj4z7gVkyVmEnF++ucY1SKFR5jtubu84HA8c9gOPHj2Qw6FU9vs9TkSchB0UArthFKdN37h6eOT1i5ecbq5VN8iTUpAWlhD4+Dvf5tsff4snj58QiLx49Yrf/PbX/OJXv+Drr77uGmUgOMY47Hj0vSc8vLriy6++5Bf/8gt++9vfcXt7Q61ZWqBUL9XrZiZJZKMhh7vrIJ+BhtIaFmLoE65rAWrr6AWzawuUdaZT6yDDFhy7D3LZz9jhk0um3AMnqrany/8lQJLL2oIPCk4YeTE4aoD9gyPDB1e0Q6R6h/NCbV+wcVCGpzOgUIIYYfjqPbem8GjT1kL7zHvgsyaRW7ClVfs5Y1q7fs/b133A0F6WWMvhturYSsuXshGdVZgtFHwXkNwy7eT/G6ZZ34NXMXPvV+Ytm/dZmXqbUb8Ax9ZxVORnfZ8uv7CaL9mzv88e7PNJ376WokY37xrO2M/299n8bi8cuMtxuf/v7cYqAJLbAMLr/LY5XJVNYUnzO4B4XFnF6/e4eAagrMstyGbPZ2MEZEmeVYNXdqFmgeVdMA9M28zWDz2pwDl8i+yGxG7Y01qmVcd1WfjVyy9lj6mNp+MVH+4fsiwzb8tEi9q+XawVcdXikk9sWkdo0k7uGtYqXw2l0GzSAKX1OdUOFpppgPz6u8/HnkUHTb2wXZomAttk1TnU+TiLaP40wTTBkolgagXQdbE37EAEFNkG4501iBkzrSZBlnDhhEG3MmMuQVq94Q4MNgPi3jM3/y1Q7x3Q9z1z2n7uPnPcxkWCrtrBmq1bvVxiE0Mm1tY4+93tPO5rT591GBLVe6qH5ATYCg1gXZ/oeljnvjH3wZjQpQg71AdJyMpGn7b0fc8Yuq4zMWXaC0vNMpYuQ6FSMy40WqHrw/Z9sTMR5Bk1fdZ2VtjGdlHoCR5XKxHX515/ds72RLSdlQ6s9XG+d54Km8T2Mwv6Kk2DwqYJgukvA51JZcyaGKKyY60bQtdIM6amyg8435+B6R8Gr1pdgDgCr/p/wTdwYl5lbdd2hjSqaqLZPq/c5NY60GjmhnbfFwVEwelp3nWpki7PonGJJBblXleKjrlX1V2nTHLnMDBbQLDYJZVszlrLo517tLWzB/TM9V4M3gAxqFLTDAfOVWG0bPaJCxZUB8WrMqwWUhzkPX2g4ZR1VdU4o3SDGmGZqGlaa30OtybztB+wXMZTPWmoqifLCuKVkkWP0q1O2ADjuAdnzJCFXLIYFS0yPnEQh/QtcBFD7MzeenvD6TyRUmIYdsJUga4F3RoMagaHttY6LNmxVl1LdCx2jsAZWt7M80ALuk23heYGWi2qASngSu5dUR7XPCEODOOOFAemeeZ0vuvPPKYkDt1+T4qxm0f1vcWbuZgkkjHEXjDqW4yzFvhGqQt5WVjliDZxbLU9UwBBOasMfA/CKnXSAp5SYtztidaCi4EbILJtxtDLykrTPUrduUNDda49QkrUYr8Xo5YxOmrx3J1hDoFSGjLlK9TGmGB0gVwqUxbZlVIdywLTAvPcmJeMc5FSHCWLwdmU4e3twu0sZ2KKHh8c4z4Rxygg0UnMl4MXkF3Thq7X3GKkRSvkQ9lllR9QwL8TETZJciuSO+S1oOFVIzHofhq8AJ4xyF7jfT+dRcZJAcWSG9O5yL7uXQd/V7BcpwhrHNtU2ip4TytV93gpL3kfVqZj33Ncn1elVpbaKDWT5wmqmiF62ccMoC+lMi8z+2UG77kad32fA7g73XVjqEaDIt1Cw5AYhoFSK9M0d6JNQ6QTpOuhUZvJVyw4V3n75mt+/7OfcvP5HzgePuDhceCwe0BMOznrQxRpAs1FXPcg0VyAoPNZgclW8W6hNjXmiwJK56qaompMVErWIrYUMky2Swqkchb6GGm1ME0Lg7bvFwU5U1Jdat3TT6cTzjmGYWC33ymYtepkpxjZ7WT9i1a4gLrTWeQSZE+TLloD+0qRr59OJ/K89Dg/hCAmRigoG4IWDCW4nc9nJu1EMeCsoaC6D5qPy7qwPEfW/v2uvA0ArLGrc6J8K7IMC9YVFHwgpj3H46rtbXmvjIPl1CIbMSlYV3NmUlalozEvM7UVzhNrPKjzpSrjXdZ87M9jC5zJGIjJmrS8C4ge3aDjJHIkkiugzFsBWMVwsKjckibTuq/mUiiLyJ7Utmr+T+eZU8cvWicfwWpgKlqlFR+ly4Oicb4TYlAMkd1+R2so+A54z363I8QBSmFazpQiRllXuwc4F/FeOjv2+wOH4wM5m0KgucDx+JhhPDCmAddEm9lpVa066XUIOOYlg4u4MJB2Bz748ENOfziznE56FosJphWJc54xY+iSrau3KZM16l4VcK31YkJrjfM8E4Ln7du3YoRocXkVJrHpxHqvZ2Y01ris8xg8wQ0WieEcpHEgjYlxn9jtE6VlLQqIqaL3De9TL6Zb15LFMCnGzho/Hg7EEBnGHeO4o6XW18Pjx0OP4WCNKa3zYZqWLhFlZ2Q3UfeR3W5kcHSMhybvcZru5ByHHh/Xop4abgVmLc4ax1H0kzcdYu97/VGDtME7nn7wkJILp5szZ0ZCSty0wKevbnnS4MePP4C5EBi4unqI8yONxvXbl1yfCuclc/XwCt8+5quvn3H9+iW1VT753sfkWvnN756Ta+HB44f8+Ic/4cHVjrd3r2C44h//5bdcv3rFtz78gIePP2KMnhATr289X33xJddvs1YrGsMhcXV14PXrr7UNSgK75CMtNGqdac1xurtlNw5cHQ/aTqZtiE0MHGqZMVk05x3NQ0yJw3EnGiJ1YUx7Pnr6hCcfPODB4yc8+eApS174w/NnfPbpF3z5/Dlvbm64ubnm5u6kwYJqTM6Z7Gbyaebn//RT/uVffsrt7TW0okGHmX8IeNi0HVSW1zppu+aGJnBRxbXFzS+qzo22PNW6ats5t4JM+vtoEgz0zXmbQNjnbAFcY812kEuBUpqCi9Uqaw2hsa9AwfYeWhM2mAuO/ZWwZtOjI3U/sGimHIrIBuDFOdGpUZC5UMq1SHLvvGm9rTqV1cClZu2jwsQwQN4ODzuUOgjq7lVleH8r8gqibECo/mx6xifBZW3dWb0piCeg0yao0RTtPptO3qb2xNeuQf5ek1c5oLm4rgYidSDIVG+LtU+zlwFEHcJr7wMTL1/3vy7Jt4EA8j0b63fvZwVVOjCKts6+5/PuFxBszM1cxqGbt3/3urwmn0WrlHJ9wop1tV48y/ut0u9cs81jrN378vPuFznka30RCIOxWpJv7ymt0k73i63hnmnn6ifJmnWeFALOS+a55MzLdmaaRb+pumZ4AN5LS2Fr7uIa7Wyy95Xr2Opaabau+0bZBFrO/q/vYa31trewAQQNqOv/ryu8KLP9XQDfg+iQ5YLXVpeSs7Jvfd+37Frsms3Z0555L1A4Zbhs798KRRsAqTUD6drm57j8/ua+3ve1noC7Fdza7q3ba+h7qryBBDOtCSi0nVNYUrz5DK9rW7dwhySQQVt9O9iz2ZvsVVuV1lKr6Dv53cELA6HU1a3ZPh/L5RRBWkHf1ezQKwAPiLGIybZoRFWrnE1UJxqTrMm9zB1JQnVE9WurTt/WkbhQWWper0n15rwgI30eZEsUBBte92O3Mo/7s1HzBJphxgbyCgArLahyL6Z5KONvLWuiw+pdoJXMnDMaLcuYaetVLxxUC0QzBW0pa5VKUd7e5pxpDbMX73OmSUIjqgBF3hPPUmbm+axJULGb7GCRJKiRaVIWsrGRFVTEip79ocu/1zPNQQGKno9VzGNck7PGklnnHME6Nbi3Nxpg0aoS8V0fHwNobXy2rfiW6OHdRfKesxa5i7X83y+kyhncvKz9tU1zs8nrXiXMcEcyVl5MxBClsBCSMh3lvZdlYl5mNeFAjWbW/cKWXs4TpnW3Bbt7ct8QMxBXiUFYktGHi3PaKahhJpAhxD520MTMxcn7zrMwWoeU1MQkQxUAv5TMGMWUw9Nwahpa+mISABFX8T719ZG814TK9Tb65qQI6YN0PbVSCcnjYyTEBC0grt6eGAOlLORc8a0x7kaiT2j4SHROZSXQ1tqFaVkwE9chRWr1FAJXTx9wPB6Z50xeFs7qEh9C7Gd3LVVjPOk4CtFY22YKWLQQIcCa97EXxL0mdzG6vibAnKID3YhWQdo0RH3mxjKVue+RBHqZJ2GYdZZ3A/PPawKOUT15lgS0VmEB1wZLljVSq+M0V0px+CBtqL4BwZEQVmoIXp4dnpA8ycm6TgyUDMtctD3fC3jISBgdy1RFE7nIOhiT5+pRxD0cOZ925LmquVLTsdL14hGppibxrPONKIoVsm/iKNnmlYBdwcimrYmeIpCGoHuU6LSmICamXkNeO+skMdc9O8A0NU53ldy8yBtkiWNckznsN3u2hjMU1LS1FvKcBbB1wuCqrZHiqK3WBaNfz4uy0opnaVnXWxDZHz2zbc+JMcrehZwNUthVGYsg17YbBDSa86KgqbsAlVtnZgoTsDYj/Ci4arJPZeH27jW//cV/5Yt//RlHVzk8eMRuGEhxB06AP+9kvUtu6aSTRM97kWZzdL1G1ISvRprO36J5stzKuu+Kzmsz1RSNDdBzRuZeCA1HUIB2ZQQ7JzIwNIlJTI5vv98xqsHY3fnUtVuHYSCmhPOO03RWUtYdZuJ8OBwYx/Eib7m7u8NaqadpZr/bkUKSLgXvOwDokP3ifHdSXdaMhh3EKOZ/KSWC5gzhAph1ug60QInEQ7msHWjWvm17fiml5wDQj0IKaninEhErW1SKCVmlcGL0jOMVixXAtYh9fX2N6C1HmpPCoeQrMrerFhCyngcpyvlWc+k6vtM8c3d3ItfMuBMGZZqF1XgKiaBg7Da/aVQF2c9S2HQr4cfGKaVETKrZXYtIHPTcXDpQ725vKWXR2GXVPXfOqVmU7KGWa9RSlGTTxPDQy/4sDQUe3xzjMOBqE0B1PJKSGH8NaWBIB2Iccd6TYiLGgZRGKRx4Twg7ORfkodKC4jmapwvcse75zkeKD+QGXuOJnLPEpoiUQFazy6gSPEOKYqCma2o6zzjvJWaojbu7W4mNgKWIRFUthVJmMeekMKgkwW63I6ssmNf9RLRxg7x/bSL5BORFNL+n6cw0jYQAIakPAKq/X+VMGcc94Kktd8Z21u63nAu1KYh8OjPPM2kQIFRCc99lN+zvHsvlTCkLIQTGcd9B2nmZabUyTSJpFJzENLvDjhACi/ogtdbYHw76LGonNyw5q2GtxIm1FE6TFF0ePnggHcX3crL7rz9qkLYBYTeSvCc7x+zOVBo5z/y353e8cpWPP3jCTz//gm9/+JgHj0Zi2uHCwN2cIb/hu09/yK9fPud4dcUP9j8Q1003cvvimhBkg454WGYOVwPD4Vv8j//D/8xnv/+U893M1aPv8M2bO07zV3z0wSOOV57Fzzz54NukYcfrV9csFfxuYJoX8pyJPnI6XXM+3bEEaRvyWkGNIbA0qUIOgyM1EelvJGoV/aJaZpKvYqTkG61lrq72fPLJtzjfXnG4uuKjb33E8Xjkm29e8PKbr3n2hz/w+u0NL1+95fp8FrODkMj5FoeTymOWYCDnSSb1Iq0NrS6Ik6hTxpsINNemrCRvSaJp29H1Orz3ONUONPkB+7tqe2lw0lJQS+vtMhfamRhLk41b8ZpAwGVitQVEWpMWhmxMPa1i9wOhC+AbiAF437XqJEdrDE+uSB8+xo2B6p16Q2zacFolEkkx4ILoPA1KgXfeXB+dbKBUnOogB++YZznAQnQKgIfuDCxApQQlXZfU7v09QOG2srP9v71WINqiFftToXnMPVk4GQq8aKBigvRrVVv+turt1sTFwAG/0bhbr0HBhw2Y6BUkaI1eSfJOHUydAVMyDg4DqSyubR1ka6wg5Tp3LrU1AZyobsg8ZG0LXNsVt7q+VTVyJPF737hj16nVNuf9ej14nGdt61cQwp5PHxOUsadUzNoM1F41x7agmhl5raoH69zYrg178Nv1sX0WW4DFIeyODgZrYNkRDZstGxDTNwnGi+oXyrTw3aijNUnkwjAAjuwgK8jV2Tt2LZuWeb9qWvRAQ5g92nrrJBWwtWzSDbQtWN4n/cUzszHbApb26s+EzRzDQBlhvNEqoYEvhbLMlHmmzHmzBsBbYLoZ+3WfWltfzFHWeSsSSMJhmp4NBZWwdql3AVmb3/aewoprNG9z1fW9o+v+9jkFLthOpgCYmnq4jZara62DsN7mng6vXsTFXJYvbfZRZPXghBFt1yWyFe+CyObATRpkjQpEsAE7nc5ZbXdGNeUwJhJdn9wYNN6va1f2IRTkWc+LGFbALuieYOBh35u8BpNmfokAEbWW3hkhlfRLNnHvTtA1YwCnYiCdRWVyHVZosTPNdLFrXQFPc2zPZcY53zs/zPCrg9/93NQCpLc93VOW1vf8XsxAAWH07NWxWxbRg7N15pxbWdwKKm2Lhw1hokwzBBdoCoY3JwlKIwOiobjOnxV4bmZi6TxdU5K+rOVebT3pWBm71XuvPl9Nz1hpOa/FCgKyQ5vkS19TtlaamHeZbIJN+FqbdqGotuem+6E03Zuaw1cPTtutq2rUOY8Zitq5V0vRs02/Vqpo2JWzsm+CtFF7Tyuyf8LKgKq10rIap9g8QgDDkqXF2orODr/ZK9bun9yNduo6FjTG3U51+XWMvEgqeNVf9GqIJkWZRoye3W6Hw/dEbzpLe6LoNVeRQUHkAARwGgScrsJwX5aFlKJqnVdCK/LsvBStxfhGTGW8C8ShEpqAA4VKiqmPQRoGjocRcXAWdiQtSVKXRt2VAj4OwuTzjlayJthOHeSF+ZPUYT0vq4zBg/2e5h4L4987hhiE3QNcHY/s9wfaqC213uFS2pzZa2xTDaBDQIkhRpHU4YC0REZCSLoupSCQQsS3CkHmQ86i8xpTwoedFIa1kKrMDlk0rdGqGsX1s15+tzXETEyZ1UWBed+gLDNv31Zu7xwpNMbo8a5SCeCKmEepedHdEBiDx5GJyXETGjfRHKuTOGa3ynwuTLOnEpjmwlIqK2NSVnXyjpgc1faY1jrhwdNI0bE7Jtq+Hw+i/esdQY8jwbkFnJtmyZ+Cxq40aGoE34oBRYXdIDFoCSppERxRAdwgWKaMe7HuKpXzaDLcwTfI8ngCsKhOZyu2n0nxqGjXS4MOeIkRGlrUmSllUqmNVTIEtJhucRZQs5jmXI2BJYMYgImbekFAPe8D1XkKjTgk/DJhhACcw9WmbfSOpIz3XEQ2oTV6nBBDYjc6lkXYtK4WQpR92itq3WjMN7d8+fN/5uuf/ordGXZXD3Ap4OOI88KGF18JiS3Acj09h1qDZrGlnlUqZxHiIGRtJD/NdVFd3ohzFefWbg+H7wafwTnV45T9sTRxjw8ObfGOCpBKseM8TSx5IcbIfj+qzuvM+TzjcAwpkaIAUN45lSE8M08zPgQePXykRlYy5xZtga6zyAFYrLgfR/YKFDsFz0Qjdukg4Kz+BuMwsBvFOCkqk9Tauq3F2jn6eVgrlDJjniD2t7VWG/GplMo8LzrDUGBtuMjznEPXss5DpGOiE4ZUQsmAuCGNiAFWYVmqmhBqgVSLpimpidScaS1z2I0Mww5bEa7Rzc6gcT5PnM4npvNEaUoq0RhlbjDNondqJm2WV9u9GiAHolVvhAkfvQLcq7RbVamj/W7Hk6dPxbQ8iHxNy5mm22uZF3IRlrDk/AJmL8vCaALGXQAAIABJREFU7elOzg5l7DfnIXhSSLLH1yZ6xF7AwMP+IeNwYBwOhGFkSIkhJlyMndi2aIxStcvOZOhak8KknTW1Ni1OV1pb9O+qGrdQmhQQq3dCLHDW1Sc62aUWas0syoY2rwCn5nK9CO0ca9csEAIhDQxpFFmfEOS6QiQF1zv+aqnkXInREx3MeWZIO3ZJCC9jMpBeCBWtNpqLZKwrxinZwWSwIATpHqGue+syLzJPY2Kep97FSUNxsEpMg3ZNiJwTer1BiyZplDgg5aGv0VaqakAXbk5vOewPuAZZJTeYHGlM2p3TRAYnOHwaGYfRQlSWJTPPEzkvlEVY/f+/lTto3vO2wtA8xIHDlaM2j6+eFs6c5hP/8KtP+fmnz/jw0ZGPnlzx7acf8eM/+RHHqyNvbr7hm9cf8fghfP3Nc3ZXH3G8ekIMgV//8p94eBz40x//gK9f3PLk6QMePX7E19+8JfrI9z/5Li9evuL2NPPmzRv+8MVbPh8CuEra7/nbv/tbHj18QNofuDocePnN1+Rp7i26LgRiSgQRYtTED3b7gdubE5VGHAZyLoxeKPveRwmTS+EwBOLOMez3uKDmC3Hkq2ef8fbtW17862vOdydqrvz1X/8F03Rimc4E7znsDtxNE+ez6OKURZx78zyrI7WYN6T9jm9/73tc37yk1lmqLLo5Wiv/ljXU2goKWlJZayV5YVWwAZmMDead14qKijL7TeLH6pBcNJAstvDbJRgAl+3LFyCvAjsGQqCgQNsAKvJjUlGnCfBVAsSrET9Ghg8fU4+Dgh5V9aiE/dq0Ct4QDRKh8gvL2IJMcY9eN65a5cCpZqKBBK/NrwDzVrphC74ZKHWfGbnKDqyMuAtW5Wa8pNvK2qzl382iTOht+Z1NgYExCiAE3xPnqi624PBW6dexLcVYXJfMTafXuQVEt4m93bsM86Ww/do27vrf7wMe+zzTr23Hdfu6GO/Ne6xgqpr8mF6ku/wcAzEurgkBaqsF3vbzvPu6f70XwBdcsBPXMbsEYDHGqAbF23u3Z2nV+IvP2oyhXff9/1srk42RsEM2n98v1LSKVpkGCRykFdDmbG0KzqjGXg/CWYGgS6D0PutT1okYD9hHS5ErdH3J9blbsu7scwycu3ev25cx8XtCC8J+0wC7lEqdF1wptCWTp1kTZ2Xvmyb4BnST+/PvmZsbQL2BGCGs9+FZn9F21Ldr276/jpPMFdPdWvdd+pyQObopOGzGed1bjNkj9+L7M1iNGG0vft/1tLaZ+83mMgoG+otrWtnzOhecZ1BGXnOr631W7TXWGaJjs54799f95ZxHgb8tKNgun4t+rc8MnV/9/DMgr61gX0a7NWrBt0Brl5rqPQnvby9n4LYjBH2PhoBVrq57vzEyt4xsOYMRRKAZW9iYptaW7y7mgI25fM9kgVCDvfWkscKo/dvGSgoqMg7SRajPrO9T61zCChVN3MZTRJyMaxMAXccOtz6b3oqKFWcqpZqJyfaZreOoT7DHEQb0mkmQ3ZN07YgkAA2VQOiDsT4HizNwWLeZ00stuWiC4KQoq/t/c23tFtG9oyqQ670jhnX/XYvC6zx2bsOyxjOkQAhy7dJuG1WOolycj2sRQbTckvPUKG7rMQZKlD15HMY+D2z9DsNISsPFeqBJEbcUSbyG3Y5uIofHEdaWU5srm5hvHHeir1hXxlvZZ86nkwC11TSGEZDQCcM1qgagFfrVshSnCS0I+y/EgRDVGFLPwuh1bFplKQLoDmb64mVflmTT4tRKCp4UB6Iy9HyMeDVeo1ZpYXeus9FoEIdB1n1tK+DfC4sy5sG7XqAVAMBxvjtxPk+EEBl2o61CdsPqLL6Uyu3pxPnujlaz6j86bcsc8SqxEHxkVuZ98oEUPBVhl40pUrK2k8YIbd0DxHHcr4CNq0I0aKvZoa115xBwNzhgIVeNf1ql1pnSCrv9jqrJJV67BWjEWGmtQAWfPK00JHdv3FVla7lGSBW85/a2cJoyKQ3CXMtVTYA3UW9/ZsIuLYhmrDG3svOdUWj5QW3QSmVW8A0qbQaapxYnbN3g1ACtssqmOPJSOc0z0xTYjUn3gUDNFe8b4xCEtKLFtKWYbrF2w3gHWYBAlL1brWTXUFC3IkxEle+wLF19EuQskWKQo+KaJzdzBrdrpcuflarmNa1Czn0dWbdi1pb1Hj86KbqY1mLf31SOpPqVHWu6x7VVaUWvxuYVox7nnALewoSlCcs/u8r1m5d89q8/5Ztf/JJ4nok+kkJUhr3Hh6QPOeCdaTdLPtX3c4t8NmCL0321UXE+Kmmm6H4RKK2JnI8WDfBBY0+nZ3cTCZbe7SVTuGinhBXMSi6cpxO1VnYHMf6qCljlnIkhsB/3pCF1MHW+E9A1+MCjR484Hq/wPnRWrZFovPcMaWB/PIgpqhPQkkZ/r602pZ0Xx+Oxg0dejZ9yrVQ1MXK6FteYRs6aXOxca71A5pzr7ecrY9dx2Ok5bBJRqgnrnBo74ljcTFa5GnQ/xsmzkYJuZp5n3ZNEy9cKoqXKniXaqYPkzMjeVZqjtszJ3TGOB3Y7MciqRc5q51epkMcPHzPtJgFLW9sAsNallMEJaB+J/ew6nU5q4ol23Wo0WSvzaSHnW6ApM9/rvGnc3Yg+bgyRECPFV1zVwlEMeJ2jaUg4RM7ROcfu6sDx+IBcKqfzQi2NYdyxMwMwpAtmiAMuSiv+MOzZ7a4Yhx1uEBKYPe/m6YVjp0BtKWLUJdJ1l6bkUqBo+FYJVFyecSUrUzZT6wJNuim8nek08J6K70XceRGg9nw+dwKCEbIM1Ha1yXkeAs1HhjAw+NU0uRbT5pdccJ5nctX9rzUKhYYn7qJ2vQgxMA0ju92ONEjRrOnvmF67deZ4jSNyEdkD2eeCGBc6x26343g4Ao1csxjSVdGsL0GIGL27C3rMZEUIY7dnxXu87jPHw5UUmfMs+0qTkY9x4DxP5LlCrFIwy0XPywhNcDmRPDizP0aWZVFzMVbZu/e8/qhB2hAjxycfUs+NGBd8XajVE5sj7Wdev/yaF9eZF/PMb2/OxC9esPef8ckvfsvH337Ktz98yjQX/te/+xv+l//pb/jZr55z/fYtx6sDgYW3z7/m3//tf2DxL8nO8fSTj3l1qiz1RPCeYX/D7emO1jKvXr0ieCcV+9sz/9ff/0c++OAJP/mzP+Nv/+4v+U8vnvPm5prp7o4helKMtCFJBbJIUBKDiJ3HNJPGgVrl8FiWCUflwdWRBw8e8r1PPuGTTz5mf9xxXjIvX7/l9e0t//Lzn/Pm1TfSDlAK+Tzx4QcfMk0TwTvOpztubyZup4W3t3dc31xLBaQWqgmhz7MEDto2d3X1iCdPP+LVi2cKyklFshRzY15bBUwn5z6TcZ4XQtwk9dAreFvwTSqBgwQSDUyM3iEJe7E2FgPGNFHZirLD2p7X37sK0NZhp7ZpZe4JkwTVtQGl4qNjeLDDP9rjDjvKGKkeSs3iZduE2i5yaOp4Wy3RXVuHDbxGGSKi7RdoVRgATvVfapPKtWmM3Wf2bYHLS9ClXdzzNpG3n71gkG6AWEMD70NU99/fO/pGD1p9rauubzczYgUITdv0vwegruO/BeC2YJaxupTt4NZnbtdtjKQLVHPzug+IbYHJSzBJ5+KGUdf01HYaaNt9d9DF2EgbYNEuw0BzqYZzcc+mA2jg0hZE3/5tD6lXd+3rra1GSRugyL5nT1R+T57Itpiyvb/tdW0BugvQ3K0MZRsPu07T0RGww/iAl895C8Z7H7tOY/CSHAbvN+2w7wdN5ev6vWpry37WcSGZgoUkqNP6JVi3nXP3tTu342Efakm0fF9bU2ul5Jlye8IvWSrZ9jyrJmdcjvH98d7eq13TFhizV7PsgXvFp3tjdX8+S2u1JiW1KnPC92doOCFtfcbrxqiftwEFffCaLF/OVfvM91V7vYJK9jnGgLCnZHOWJu9faF03OGoSQojCPktRTKgsm9wUkN63zm0evPtcV5b1ug7kPW3NOC7vx9bEqFp1lji5IG3BueaLAk9uleDCRuvQpCwu2VKAmqNVO0LWZ67/Mkbt9tlv90lw3RxrC+LKtfh7P8tmv9hIU2AFUK9KJWb05Xri45xTaZN1gmyWxgqGOiuA2hzxvWWyFNFq08WrRSynTJdVx86ehTB9bY0amK0o/3afswCfRkoCkLdWFeBwvV2VgjJAZR3EEDHZls2N9LGzhFPcwV03YpQ2NDGkaDq25jxtsjFSfJX9adjtLvcfBRxLLeRlkZZHvxaderKO6DTCKqegDosXc1OOYidJiI+bYoe4Qe92e01ERZZD2g+1cyEELuRAVP7DOyetx3bdWNHVKQDYenHQdLSHYa/zXPSjTa85qJEPTZidXs8NMRSC6sXcxGIGnLQ603ScNszoQU3UYAXpohM5nQCEFAScbcry0sS+ImxhRxCgrxTqUmEYcT5QqjCB87LQShazMqdJ52ZmBI03g84Bh6yLVZYAbfeFIaZuxFNK4Xwu3N06RmXitPmk2n4wL4VlXqh5oQaHSwJEUwvT+YSPhbxkYkzMypKTZFoByNaIcejP0c7sqnHxMIz4ONJ0/2tCxxegQUGgqBq6sjytc6FBK5Qm1jC1CoDugIcPE60slAauiqHLGL2040ZP8o40DBQqNUtbc4yBsgjrqNCY58K8SGv5w4cHDs2xzEjc55swSnVeUg3glPZ9p88mZ2VXNtnXRNJUuv9KVm15Bb+c89K1ZuNTG1J8kCC2FgEm8APzUplz1vOgCJBAY7dLpCgAnhkalWKF9HV9ejFQECZ9cyylCnhYrXPBAZoTYBrEK5GjliwDjhhjGUBrcZ8Ap1K4LgruNo0Pc8lS5tCcwDlp+S0Kblg8JdIOoedQBnQ4J8WmqudjrU2MjfQ8yFVlEHS/sl6GpQh5J3rH7Zuv+d3P/5FnP/8Z8eZWmOYpSau2OMXpnJXz0juHN61jPV+k9Vr2o6L3Z7JQTfMDY/ZCwrVZd91GrYton+tZU7VoESwmleySGAZaExBbcCkFektWdlzjeHUkDkl1N0X3OqVEDImkeevd6cTp7sTxeBAgNYosioypMHSnaWJZFo7HI7vdjsO4A4eM57xwXjLGQI1abNm2X1sLv+yfmVnBHpCOlVIFNGylEpMUr0TqJJGS6IDSGlnfj/fmZEgnQxIt+Q5o+9SBqtYau91ej+PGNE2cTqf1PZD4bzfutYNhIQ4bT5oq7M/zMpOb6PE6tAVcI+rcGtOUefsWoJLS0O+/ZOkkGodRGbJrEUTiGCmemWRQl1RwjnEcu5RE7zpVfEHYk4ElL0znqUt6ND13lyVzPp01bBVJKyleb8ggrhBCkoJEHBmHPXmRe0zjwMOrgxQWnIKxaWBUDfTgg4C9Kmtj8jhNi3/WGSFFUPEF8iAGWqWIL4KzGEUK0a3pMei8FiLB5J9aqbSlUnMVoL8UaFJSaq2ShpGmHbHzNDEvmXnOnM7nftbEGBlHGeeknSKlFGVQJ3keCuwXNSV0CujmZel7mrC6HdF70KJGDLF3AlnYLOtAWKmlrpjHtpBh5KTr67eUJfd1IDIvEoPIORylAFALc4U4SEHzfm5ljHYz/bPvb7twUxRw1kftLHVenrOHvX4uNLwW1KZ55vZ0YjifmSYx13PeSTd2bcQk3adbwPj+648bpPWe3bDnbppxURa4q4X55i3n69fcvX1LbVGrCo7h8AhC4POXJ37zxa/485/8BNce8PS3n/EXf/VX/PAHH/EP//CPHI/f53vf+QG//udXfP77T/mLv/r3/P3/8098+sVLxgdXfPP6hunuRCmZYYx8/7sfsx8Sn/7+99zd3hDiQD05nl3fcrU/8tP/PPD25Ssomf1uh3Oq3VQC8yxVwuPhyNXxyOFqYJkLd7cnYpRA4MkHj/jg6SM+/vYnXF09JATPy+s33H39nLubW053J25u73j++e+ZltwXcM2V093EV1+/AOCr59/w+s0NU2kstUr1PEsSVMpCrYXgHLVmTUQSwQd+8L3vM59uuL55oxv6JaBzARBC1wt0usHYgbJ9mYblmshpO2fOvRXR48BrmwLqTq2bfymrc7Ewxla90/ufJSCL/sdAgQ5u2eEuwZ33npY88cGO3YePqPtIiUGqsGXR4F/bNptWLJ06mzbd6LVSd8kODV18HLQt1gCZDpi0DgrdPzTvg3db9tX7AJItWLFt5ZXxrt0hXjDr2j/Xfm4LwvjmVvfbTWJsGsQ0PZhapTppr+ntDjhauzTyuljDmqzZ9W7FsyXErR2wEHzZwCRj2a7fuw/yXd77JSC8BTS2beL9Gu0PwipCD+QVHOyTCzDdVzW/ucf0vQ/ObVvit8/wPjgu19NUk3PDSvQB2ub5I0GqMareAaIVjLKN3oopW3H07fXeB9YND7HryffYsiEEDWRrZ8L299DkdH0W6/x3zgmbrtSLOfo+8Hz7ecCGBd/6AdnnQ0/0fediocmqtQNJ0HWfXbiOW5fI0HlmleVWta14nijnMzUvUKoYiAXpFtgCtCIZcFmEMLDlUpJkCxQb+GWglxQppHreqyH9dWnAdckQ9brOW+tp6Mry1fEL9sw6oLmCe83RV6D6VWmF/R4g2hoG+omIvzAh7TnZZ9oe1/r+DxijX78XYqQ0qD7QgiceRvy4pw2ROIzgxOjKudChWtvjt/uB3N1acNgWUrbzSYwlVlBOVRQwTUebq845qcpre7vcX+3zxIbUiojVBr7Pp+3+5+zC8a2JHE9bWcQNaFXaafv+d+9csNc8LwKMdmmC9edB2k/lC7WPe4gOmrCQ5AIDrkrrekpJNTcFIC4lM8+Ljo8ywPSesPW5loY6UNWaSrXICtAzQ85s06W/ub7Ga0txcNIpFIKyaZ2D5DpL0+n5Ix0ozcIHeabGrHdA28QmoEVcA7obXv/vFQTtc1Hlmpy3z4Dm5VkbGC7JhHWrrH8wKSBUD7UJmNeN50LABQEhajYZFN27x6Y6q6isDrom6bGQmR3S6O2Xa1xlLDaHc5IIVRytlb5NmE58rYiOtEpL5VqEbR+NLdiornXmbatVnLAXSbicMtdKloSplaYAiZzXy1ww46pcs8gk6ByJUQyWopNiHUh7ojDeHLNz2o6p8aMT3T5LrEQ33uOpLLMx33R9b9aincdNkz50LQsDyePDgENAnxQ807KIya6XuV6LSHBNi8YyzgmpQteDOUEvc1YgwtY2/Qwyo8Acc5/3siak22o63SFAr7CZm3NMS8FoCbkBsyPqXl9qI9dbwDEMO2Ia9DnMuNYYt6C7C8zzxLxMDLs9ISRp8ZxviWPFx0H2lSqO9gawp5Q6GETzYs4UPGLIAtFDSp7aBoYU2afCh48qD65G3l5X5lPDX0X2O2Ofe5JrDBGqF0kVYaE6anXMubFkNXRB5CjGnewbWcmoksx7ml5pzo15adJRUaVNWgB6MR/TSJzDDoak+2wLLIuAu7loIczimQZ5EVZ8UYOfkqsYmhVHwxjxkNXBvLXKfCNmWlnbvX1U53DnEe1skS5z2llRSyVXmeeue2UIEI1rKvEg+cSyZOkcaLaupLCyGsIBzkACPb9Ub1PkeIoW3aDlGXIGxDBxmRdqqQJ8q8HTGkXSCzm5mDSLMMmlK0xMxnLOEkt5iTxFzs73gpvpbte7t3z60//Ki89+hz9NpDRAbKqlmcAFxhT17JA1O6SksXTrcb5dm8g6SOuznC2x509eTfKGUQzVar0TrU2Nn4MyYr1HmI3Ba77WWMqyMvNLVWZxUDBW1sbxeEWKkXmZWZYZ5+Bw2AON8zRxc3vbC7f7w56Hjx7hvWc6n2XMFZQxgPDBgwcd3JnVeG0uwjrNs0gqpHEgjkNnftYis9tAdPm8esEgd04KazFZC73moZtOGGjdkd72Wnu/nKWrtbRKLnc9x/Waa6du2uWVmJFVB7hpO7wYjLaLPERM/kZ2gOq8alFot9vjnMgCSixv5q5SoEELKJKrNDnfVDuUYTUCK0thWc5rkbtWkQjya1ep6LHLdd3dnRiUvWtsyOhDz1WWMjOMA4erg3bUiY67aLBKUakWkVtYcqG5xhgDeZ45LxM1LwzJCdiKUxbsjnHYE4PIbsY04r200KeU2I0ioRFC6IQT61iSYpsaIXvJMyxvqMg4rXJGuidscqRKYymZOU+URTRPz1mKTqJ1mygFYTyruWPVAux0fSKMO5oakC7LwrxYYUAKPIfDgZSSSFwqMGsSdRVhHlfnVDe66VrLXbKsNRQ8ldwwhEjFcT7PpJg5XB36vDmfz8xL7eMT1RD7cDiwxYTSIEXDx48f4yqcTifFqBpLXlhOd9ydTHhcsaNSOOz2QmxUrdxR5QZMS9c514HaZVnWfHpZuL29lWtQPwBbu1GlL9FYIsXAbjdwqPsex9Us+3L0EWojIEVJ70SP+d96/VGDtKU1ppzJZFpu0BxlmphvbgnzAmnAZSTbURHqcYjsj1dEP/J6nnm+zPyX3z/jBz/9GX/5pz/hO999ynR7w8PDnu/+6Ad8/vkXfOuTH3N08PyzL/jgW08ITLx68ZzkKleHA+PDR+zGkbvpjq+efc40nxmHPcfjgbLMfPXsDzx5/IDXr99IIDIOOCcV6HZb2Y17Pnz6Efv9nrfXLznfnnn04BHf/vZTHJ6PP/4WUHn1+ppf/fI37A97nnz4hN04cnN9w6sXr3j2/Cvu7s6kEJVd4MhL5sWLV9zc3XJ9e8MXz55znmbR1lB3w1ILtYj2BW6ttgC4Kq554zDw5MlTET9vK6DiFJiyfxu7QNoTV1ZrY00wLTk2UMXAPKBr7ji3Aklb040tiNTFz53rjoL3ZQIupRhWQEGCUGG8COilCXdrNCr+4Z725Mi0Uy3Q1miLVGerM4AS1a2CVopopOmeWGulOAkAohpEWDLVapXKWzQR8kpt6vjaVvaDve5f//1EfQuWb19WFd8yeu3avOq5iL2008RQE757mo329e3Yt9Z089DEA9R4RcBCWsM338FD2wS3YJJe5cVz8d6zlaDoWqgbkOv+td0HZu21As3yOfYzFoxIAdn/m+93+fvb97WEt3aAaNOU955n0fr1r+9vgM77WbT2+QK8eg3QFYARdOyCibf93C0rVD7BgLEVAN26j9ucuBi/9u54WkLcf28DtnUwcVN06QUHrxqNzdwxt+6ytg9cFhm2c97GZFu5vD9W22djAGZrTc13+tPv49buXbutIb9ZB/29NaDAOTUGW8jTBOcJltIB0IaAba2uY83m/+s1qpunBpDrs9re5/qzeGEbmDSAJZZuc/82NhfP3W/n8LuM9u3X7u8d2+6I0tbZLaYgvj+7d9azoE4XTE50vdj1gO6nzlhQ6301BXfjMMh+4jyMEbcfqVFay3DiUosCH/2ZV1Ymc7sE9bf3bmu6y3bo/7eapLZe1z+X5k1O21M9wuxxTlhZ9rviOL3ufdv3smvw6rps60ZYJLLGclFIIrpuOvDfu68QUjdEWeeurm1QUDT0dWpn71Y8w+k57X0Q4xNtQa1qiDcMqiPfJJnKpRAVULTkUAw/6Vp3ToHDVtcuANecAhpyvp/PZ+rU1GhzI/Ghv+sbpFHFIvW5ey+tzfLM5HmskkArIGzXYZpzpUjR0Clbd537Au52oF3P9+j8BTi6Gn3RzyV0/8KpmRQQCXr2B4qygL3zVLfqytsaQoFaIbvLHh82kkcF7bYJ0qpbtNC0XcPoeAUf5V5wAsy7iBlMoj9n7XeSwK1md72IogXb0kRDT5g9iRpNY9BpYow4MSk4mnMhRB2WVqVV30m3UEPaB10Rg6/WizLaoitBDwIwy2sFxdvmDwpYmuSO66TiWgrehw7miHatJrUuYOeSsPoXaVVvjubEDrfNZ9S2VMZH16bTPW1R7dYQPIueEd6tAL7Eq1YoFPDNh4gLqV+Tsf0aiH6ik3nCIma6KQ0YbIr+bKapZt6KWroQIQhLP6ZBZRtM7kHOnJAGdjGSxh0+DMRUoWTCMNKcsNSc9MviHQpYhB43D4OQSUQP2ZNC4WoP+4MUxoYBdkNgCDJqh53jMHiGVNnvHHl2zEvjOHhSEjasa138S9a3T+TquT1VXHScz0BQaYCdgKK5rrIreWnEAfGvAGGMZV2+reGqQ4injSkjhl7BqXu6EFJzbV0qQg6lwJybym4g8iU+MOfMvEh3RDebc8Jsq6Uyz9o5YWt5KTJeKn+Bc+A9XnVaRQ9TO+yyOMobEUE+Qxn7TgGALEZhcm5Wamm0Zgrnth7k4CvVQFo9A1phKVosmSbcMtPITFm0TK24uGQBHBsW05oGu1fWaen7pVNNz5oXzclUDx2RU2hIUcqHyDRN3L15xfVnv+P2yz8Q5plk69XL84zaQh6UAYn3yrIWiZJiZnp65qYoBTwfFBAxQk0ThrLr9yB61KUlpulMo7KUTEg7iQt131mKFFhaE9kSOTeFEej82qkSY2IcB5Zl4XQ+E5ITRroenfM8c3NzS2uyho7HI1dXVwgQeMfd7S1iFnaFU8kmO4+s1b5MC6fpzJwXUkoM48DxcNAOTbnGaRJGZ14WZdObBItcv1ffkxijjJVftX1NtkZiT2HpZs21Syl6hrEWnJWhKz8roFmrUmSbvSPFtJIqdJyMIWiGSiiAbqFl6IDpCjpa0aHpvuo1RozRk4WaTxqCgIhO1oGdEUXz6WEYcM6LBAVrjkMVpm0pWbV/15zH9jiRe5QOYmHfB+lqTpGUfAdMU9TCFQLux5CkKJakw8bHRHWO5Ad8C7gY8YheOk3in914YLc/sNvtGYcdu/2BEJIUbvXc8mE97yRHFfmAVmVPk4YQ2QuyxZhOPBRrqdYwogUyLcI40eedponzdM2ynHFNurPvztfM04mb2xvO81mNXBec7jM1ixnmeV7YubWD7XA4MlbRd5e9onYgcxzHrgscfCA6JxiDi8zzpExguqmaTvC+x3tvBfXcVmcEAAAgAElEQVSC84GUnJ4XnpSUWRxESoUmONDpdIdJEVjeElMinCcaTXTbQbRdFZ+Iaiomc1f0gzt+VSu3t7f6mYnz+dxjaLvP1hq73U7MwEphGAZqLgoEN9G2LYVlFuM025u9lzkTg3RzSQdVYIieFm1PB/OCkMNN//wbrz9ukDZX3r6+lpvJleiE3j0eHhD3B/x8x+2rF+LoGRNznimnzJAGkvNMpxMvXr2g3CT+9//j7/kPXzwnzzO//9Wn/OWP/x0//tGf4PzI7/71lyTgn//T/81f/NWf40JkvnnL9370faL3/PznP+fBo0c8enTFsjzlzds7aInDg8fsDntigKvDgXkpvHn7Bh90I30Ax6srDvsjjx484Mtnn/OHZ1/w0dMP+e53P+HJB4/5/Isv+PW//poX37zk1c0dQxz4wff3HMeBaT7x7Msv+eab17x+cyNnWrKk2hN9Ylkmvv7qNdd3d8xLFk0aCm2ZlZolOhzW3mItKzKX5SCrNfCdT37INM1cv33JvMwddARr7XIXSXsKQkOnoaL2VUzINLmVBblx9evMU68b59IrfVu25fbf72gNattOaVKNcAbYKLtNw2QNLjTJUoMdWmM4jowfPcI9OpKHwEmDC0sgPfKj0s4g7bnBeapW/4IyZYLqdfb2RPR3PLS6GtEoTM3WRcIAIbun+wC1Aa/yY2syZz9vX9+2cYsO8hZA1Cpo0c2xms6vBa6Xn7vVP20GUrr1eyVnZZspw6xJ4uNDwLXVOGcLCtl8M1DeTJIMrLKEWJLHe+PTjLl2CTxtx2H9urU1r+MTVKNq+6v3Qfz74I4kWfZoTOLB9fFtagIkyd+WLSvMo+1cleO+sfZuKPDGJfhi4KosR2MM+c40cE6YYSs2uTKrqrZPW5tfB+GxltZVmsBakTtcqECMgW7Sfr49UD1V27ilqFs0+L5cjwbMBASsVSyjy49sTdruFyP689a2N2skWkEStPVa2mdxdMDBADI5kOlACN5hrK/W6C237/vcdb5q2CQPFVcLvhVJoqTsS9e9bCswJNfniUEYHE6vydoztwWUy3nLJaDIJXPO5lPTZ7GdxOLIre9VW1+3lwxOnXJbgFjbBTtEudl/bK7pN3Ss1o81hhsOCL5DDPasDCjv8wIUvGTTaWGAR8CPA021vsBRhogbkgIewkbU7beDaQIu2rM1bazQJXneV9i6XxwRAHNld1tSsC1MvANouwuYsyd9HWBq6xrv4+/AoW3SXtvb3Vq8wTliWlu1bNlt5Wv6e+M6MCmJfsSkJZw3Mys570xrTp7Fek3O5oqyTHBOK/dDb5O2uQUOVyWJGRJaPKqaZKxnhrC3jdHgehTZVEMyBEmKc8uSWOhnmPbb/XmKAq+NJppqPii7Vq9ZN+auQ2d7TZN91iy5rCunZbrUgLqY0VoVBlDTfcR7YTPoIxIFg7bu3U1iCGc63wRh/zgblyYMG40/qrevs9GYVg6Zs/lTxe1dn7EPnpikzbBh+6jIIAjQunZTxBC0jVHAR9tHaguqp95wQWUfbA22SlDNVIcC+VFYQ16d1hsiTzGGQSevp4YBBwxp6K3yy3xH8CqDAArwoIYmZR1X56Tl0gdKESkGYRMq4Kt7gd8UfcXNOmEa+LLPrUUAAFfXArfbrFdhdWu7ZxHdzlrXfVhYP6aBqbq+QdyeTR7GIS2jDtlnioLpPZ/CEbX1UpLuJO29tfYzwHpInJ4LpmUawobRr5/dE7JmI9BwLuKUfbzqiaokhcmHAMk6gxpSEAiREAZqqNQSiSkwDoMku07NpIo16srLQDhU9qI6R/EaP9dGDE0kGXygucS0CNC720OKZoArIOlugCGq+U6TU2apKMjlcKURQ+U0Z5pP3N4V0ER2KcKcbbVQmydnPddV8kBcv8EFabGfpsbtWXKZGB1D9OxGYWcJKNyYpkLJjVwb0zxRssjqVCRRTyl2rcGqRjC5nCSmbQbjtzWeshjcQa+UKQh4XsSUxmEFahATMGXGrgeCPk/Z17MxOBFQqmHEEwTA6vrQ1RAZrNDdkFhons7M8xlXCp7GvEyczncseboX9+px4rQYoMiaFYtNugUn+5G0QheZl7VQS+aUM755MYYKntPrN9x8+SU3X37BIAGMGB0FTxoTh7TH9NGSi8osFsmSquCgyTIlZZAFK3aoGWFg1fGVbSXQCNJRwEJeTFYHSs4secaHSM4LzsGif6cYtCuHniPlPEvHhQ/EISl7eCamxP6wQ4gOC7e3N9KiPI588OSDfoafTmfmeSL6wIPjFeMwMgwJENb+3e0ti5pyjeMozLrhAYP+myYmTUteRM9VTWRzLpQla9FP9ngpqAyYnIp3lVM+yY7ug5w9dlY5KxzTn7HkzaIjnFIilyLan2nQ3609rrF0OaqBruWfVd9rUQawxQsNyS1zySxzpuGUISpneim16+Ia+cuKYhIXFhbvCX7p87BDV14Kl+dz64xY6/Y0kG63k3Mq58yigGJDOkhSEAB0WmbysrB0hrgEJNP5zCkXjetFoiQEMTrDBUJIhDjgvCeNO8bDI8bdI5wbSeOeB7uR4CCE2DXwTfPXJGWcnvH9/HfoPiGTUSRLlKRWpMNFHbMoykilOrJ3JOco2hHdcqaWCedFhmuaz9ze3jBP15Q802plujvx5vVrlnnm+votb6+vmRXMLVXOlAac70Ta83ye2B927I8HwJO0k1jijaJ4jtd91vUcrzZZu7WKkaDlJb6b+EpsJJJSCfMjWPEAGcN5yVSqjPUwcjyKRIh3jt1eiiiliMbxsiwimaHdyqLjLwaoRv7z3jOodFlrlTTKujO05oPxA1prylqXuT/NM7d3JykIO8+4G9nvdoQomrogJqWjl4608+nciyWVStHrKqUwzes+VGsVYoSXgoAPEjNZ4VaKVgv/1uuPGqRtVWQD0iA3NqiGRyty0B0ePsTFRJkm8jzjceSyMC8LuEA+N14+e86LJfOrc+Y//pef8uCYKDdnPv3sGf+bi/z4+z/h2bM/cH26ZkyF//cf/k9++KM/Jc+Zl18/59/96E/Y70Rb9rg74J9+yIdPHec7cb6LQZx5W9H2/xhZimi7xhjY7448efyUkkWQ+fDgwJ//9V/w+eef88vf/oa3N7fM5xPDMOK0dcl5z+8//YyXr17w1dcvuL2dKUrHrrpxOjxXVwf2hw948/oVy7OZ2zunLZGVVjR/NEMOp+ANyjAAcOgGXEkh8fF3f8hSMqcXX8lmZc+hrUGLAany68ZO0wqYJoVbsAjooKIkWZdA4zYpfh9oaS9L1gy8w6kbqS50kWxb2wcM3JKgNuN2CffkSLkaiClQWiEGR2gGnkg049R91Js2nx6A4zgyeGGMRXUeFgaR76w3711nKUsfth2A2o5bW9d2Ncq+jVFnQm2A2C1ocMHA3IyZ1zalbbtLBwI7AKZtEt69M94XDL4tS8uJxu4W7Kut6BjLiBtOuQVD1muXhNWSCWk1aKrTK8GOJUUSjK1Jkb3n9n62n3N/vtj7rQfg2lr/DtDvLllvQK8wG2ups2gV/BSg21hjlvD49Xo3z2R9nva8dP4iYyGju4Jm26AKp9CjVpPXcVTQWgZkBeU247UFQ/v4vbOOlGmHjbmOsXebe9UChJfgpygY01mx98BOY1uv2cCaCFS285aL53nxXJ1ThreaFrWeC+kepfuIAjomURCcpbiX12ZV3A4q+XU+2DVcMi8VhG8Iu0N1J60dszlnWI+yCW2uoACZmhJo1dlkA+y1LShsP9+S7S5HoO/ndS3YHLFOAAOruHdP273i4vnbnNsERNs1YYCHxucYKFppXbO0lhWAFpaRAGmSyNILVqYdLUFyJCbRgRTDQl0xMRD2e2oMwkJCdaxM88nc7Q2U39yPaNXphHDCFDQwcjuv7KZXtulmDdiS8fROEPveJdNbA+u26sV2wMathbNSpX2py8LoGELrhRFjdcpnyLdDFJfftrm2DlY6e2Zr90ft763gYgdpXV9/Ygxi2nKl72W2fxmT1mkyCBJE1lZwUZ5FLQL0OafnChVxYXcKOq3AgyRKUe9dGTrYPt+bEju4YcDTtnBhoBu4XiQS8xJ5SKa15oPX9n7tMHDrGq9lNdjagrlLNg3OVXvXWKetQcArgCznsrHZa/3/qHuzZlmy5Drv8z1EZOY55w41dvVQjR4ANCnQjBRolET8BP1V/QWZ3iVKNIAAm2g00I1GT1V1xzNlDHvQg/veEXmqWnptZlnZvfcMmRE79uC+fPlayvAS5/DBa5uh/U61hE5HQJP8zthNW9t7tufptGprsVc7q3W9uYomZrjeTQFWFKjF3JtrT4g0kdC2aUFjO+/UbloLyaqX2woDup4bgyfgXKAAwUXbX00qxZg89HWg2vk6pxxDDMwlEZzr+6+Isq2afq9UjYWwZMyFwdbNpsFdxENVXVI1Aou2rra9uCW4bV/dgFinrFTddXYxUO2GMKVsQBZUnElrOCBE153kGztW2nvaHhN6TLut876JW7yj4+g1iY+Vg4F3ri1NkR4vNZAZOxZL1bZdby2f+rYWt6AglGoUanEhpxWqAjFNlqW1uPb9BDH5iNTjO2dF+JwqqVbWpC3OVDOnM7BjmmdiPOCqMj6XrGuqZJUROA6RJUNeKzE6rNmAlLQlXVvXrVgARFEV20TV55xBnD6bcfQkYF0q+MDDY2Y0b7VSKmmt5FI5T0nHeDcXHyaNWFT+AFJyzEulipDyjHczhyEwREf0jvM02T3DPK+sOXM4HjmejoDj9vYB7ehoeuIKiMzTo+qVQt/PmjTEui4mTeMsRKjM68oy3Xe2pJ6FnkoxJ3BlN3pnOZnX1taSszH7FDjM2Trziq6NGCIuDHZ2gu9RgEOkmnajzo/5fMeyzKoFLQpCL6uaIYkVRbG5XjUQh6oMejV4qp10osQGMWB77XtMM+QShLqulPPC/MXvWb/8ihHPED3iRYsDMapcEwUXzKyvSRbVipeg7b4GYInXLpF2Vrc9Vuya1pxAWqy7MUVLmUhpJuXFTLGreolE1cnV4lwhBpUNW3MimB7qNC+s68o4HgCY5wnnhGEclElqxlzLMlMKyio8HEGctmEvysgbjDE7DiPBe9KcmJeFx2nqANQ4DAwhdjKSZu3Csi48PD7QpIiCmXrpe8WtiGBSGCmnLh8wTcmAVWGMgwGCnhbrOCf9a43w1AFXsQ5VgGaA2xiblt8r21OIg/Rik4gCYSmtdsYIPkTteGhnq7ET53krElxZi/ycVqZp0nln5IVqBdeUK+f5cTvjdjF7kykYh4P6JaB7oIKhA87BOEY9T13Q4ppAqipZFqPqY2uR7qAGe6mq7Ak35HVlmdWQbE4JRIE+PUKEWh21CKV4gozE4YrxcMU4HDlG7UBo4wxbDFcsDm5Emn6EVMvTDNzWkkvta1O7tqDmRMoLNWncsdTEUlRqsJRMTSspzUzLmXmeyDUxTWfSOpEWXdt3b295uH8kzTMPj2fmrDIvaa1U76kJUtVzMmDGnOJpLSbOJKlwWFxZOkah95gsd9Xcrelsi+X5inVUOzd1XPTodCZpBBQt6OOk/98kNUoxyS6pHA6tCNLi9AZwr6zzzLqq/Mw0TeaHouzzpj1cpeLFcDp9tEYY0MKFxqEaH+aUFbj2W/5TSiIXZbsHk3mIFquUXHExMoRAdkKI4YJwkUvi4fGBZZoRHxBR/X4Fb88qEQP//cod+BB4/vHHOOe1alFhUWEiDqcrfPQcrm44391y/+YVrAs1rdSSWfPKowucz4+klKnOqcD4G23TevPuLd/98EN++J0fknLmH3/23/jJv/pz/uY//QOffPiS5x98xrok7u8f+P7nnyP+wBiu+eU//5xcFk6fHDiervnudz/nyy9+x3l+IEjm+jjy+vVbDuPARy8OPL8+8NGHH7CkwvHLG7549Tv+z//7P/Hqy9ecrp/z7vbM3e1bbq4PuOFAkoX/+vM3BKe0+8PhmlImQlx7gtUqEVfXR374w89Z1m9THby/v6fOjQYvqhFSTZu2ND3B2pMRTWxBRAXjqx85PvuQ29tbSlLR6Jb87hme+3bhPWioh4EG5w38gK0NvguC24ETY+yHQ/u5tkE35mp7tYOu7q7JLoBUlZGgRl/NBKPggunP+Uj48Ib07ECNjlp1gxEnqv+AWKLUNFYb+Gcac6LAbPTGaMgafNGAEbsOil4nosWCfjAaKOeDZ89p2AMsfc73jXB7PQVg9q92ILRKanPu1Z93F++BXJq5tWfkjLF0YQxXagd1O6Blm3FpwOWOwXepmXl5jWKgSvv8zo8TC/Itw94HaXvjuTYnngLB+7m3Jf+Nxb03otlatKXN2d3fL77f37flrbIDg6QnTHtzlw3oMxDGdL+c4Wp7iYcOHEFvtc1WudvfA2wu5v25PwHh+vo1QKO9ao8MLudLG/fmJunaZRUQAwaKgQ+QrfDUGLKbsV3/nN2z6C3Q9v/erbat86fyHG090+ebx0E3rdGkVIPC4EwMv2ItbSqoX9iDrV9fT0/BzPa1PndEAfiSE+RMXe2+K10jLVsw/TWQt+9xosQ8tmchuz1y//lP53CXFGnPuj0rC/Qv9gIDDp8WHZ6y7Z9+7v7Pp/exH4f23iIGvMg2R8VpMSoEr2eLtZb3IgPgQ9SimAuE8QoXIhkQB8NhwAWhOMEFDYycc4SGnO729sbWb/fWrtEbo6zNKy9imph849jqn61tT9vNKnSNTOedOUbvxryfsV8vmrW50z5nK7IJnR1n67cxyRpopGZzQX+0iukFYkwL6QBuY8aqLLUyPAxxoyRtG/QhUFGd21akVMfqlf4whEtN5FT6+NaqJkaasClI6W2d19KYpKZj1+WPqpGGNYjPVGpKuHbWwFZIwjonrHDbtKorWvj0fX62M6CZAyUMe0WZfvS2Rpx2dKxWrK7e9zZPbXXUAqvhtH3cU9piFmuGIARlfpRakSyd9dafqxWmmvRAK6fBtreXWruuY2xs26qgcepj1qa27jHtwTRmXhDfJRS0G0a/npv+rSXHpRZCqEi2Ap6oTEQuq8KQ/XioYJpzUC2ZiEihA8eg8jS+rY28aYlXK+Jn02guZWWeFHyoqJsztYFVpiNqoHOTgwoh4kTN1jbXbG3TT+vSl0lOqknrfVDZiKzFjpJtT3VibBxnwH3o0jMKeir7pBbpgJaIxwft8HGmk+/FIVIQtxVu+rNxm+O3eC28515gkL4ft9JmKQrIlprtLDbJp7Z35oqQNAbddXBosc/+PS363rt9rdDafA3QUnRMGaPejIBK6ftzycVYcoVhHPsccs6zGqBWigKZjYEnAn5drX1YwZpBGovSZD+8pzr7fCuGFGAxGYFSVxwLox/xwVSqDZ3PFVaTpOgGKo0wnDJXB2VtP5wTy5xZM8RBmXdhCLgK52Xh/FhwEm2fLix5xfkIxSMeDldCcY7prDraKSXuqRzGgeNhJOfCw+Mjy1qoVd2/39/eE71jHAfGw0A1A64QtCX2/u5O92MK5/MDzWjr9vadOrhXIa9NN7ZqsTF4ypqoOfc1nmY1WEs5IShbeam6ltVUT/eUUpIROqCSyXWlllVlULRcRq0OZ/rTVpUDlOXoR5X6OA4j8zyBUyPktC48zk6lEIrGe8777gRP1UKwC4lgYL+TipBVO9bmWbY9Rwv9VmwSyPNMffeO9Oo1kldCNHM8MSZsl4tRvdTc4l4RsKK/BK8MfVFCixjw3bSWq+h4lJx0nUlB065EkYmUJqbpLbVOJsuixohQqWk1Vn/Gu0opalrrHBdMtdPphBNHSivRR+IQrPZZWRZ1XPfec3V1ZXNk5e72lmVZOIwHrq+uiEOg5My8zEy5kJJKDIzDyOl0UvannSFrSt2UqP3vgiOY6WCXCnBqxjitc/+5SkGswBeHwOhiPzqdaMv+Pt4rpYHZjbBSzchaY5CWpCzzYjFC6nJ4tVbq2ro0rUhgZKIklegjEqpJAHhii/saLmDrKmctuqwlU5LG89fPbnaF8MbE3IpuOau0mEe6dEgpaqTofOgxkIi3XKcwTTPn8wOlwOPDhBfH4XhQIBDLg0VZo85Zbl7N8CkEDscTp5vniDjFP7CzzAXGODLE0YDzgRCOXN+8IAwjPmgxYE/u0XVtrPddHL3J711KrbUuQdX7LdScWNaVpWQomVSTnocpcZ7uyMtCsjXhqTxOt9ze3/L4+EDKKmtCLaZJDWnNnJdkz2SLi4c4smQ706oQfaSmQnQDQQIeiy8tT9+6UoSa7WwVITmNqbyxrp14SlWGvHokaKw6DIOdl1rICXFQbXSTN/HiwOJycSoFta4L9w9FY0BgGLRzxRs7ehj0zHNOOI4H28fUhCyX3AtnqsGsMWyi8JjOiitYEatpGudcCMPIYNr4N89ujJ1bADXEc5ZjdFm+uhW7WuGmscybtBC1EscDMQ7kKyUUtnkiIfb1Uqtqt/+h1x81SBuHgY8/+w4pZ9ZpYp3P5GVGXOVwdSA4z+qEyhXzwx3T+UxeVH+EWphzoqjIKLrTQa6OpWb8OvHlV19QysIHH77kow8+5v2rV0haefPlF4g/8OKjT3h/d4sfR14+/5jBX3N89jF3t694nM/EMfL+/XtySUzLLeeHe159+ZaHu4m/+Iuf8Bc/+QEP05nf/vYXvHpzyy//5Zf8/re/Ia+ZcTzy8UffIqfK6y9/z+vzHVhCMMSB58+eIwcNhkJsh49S/1vShKssaeY8Tdw/PPB4PmvykVdqzl0fx3VgDOtDaswWBTycCOu8kMXz/NlL5ue3vP7yt6Z7pr/SKlujlcBrVRZDtkSltXVpELwHL7bPU6An9d9tm1dLjvegQYzxwvGu/Vwquf9uT8Qxjb9aKasBTdFTBke5OnB4eYM7jSwOqHKREAkOLdhoQpawSrqGJnbQJrKxCr20ap8eGOhbAhsoLjZoAp1dBhbcN2AKvnbPDZjef+2SIUbf+Nuf+583PjGt3eRrwG7VxGyH6fRK3958R8EzHYFsbQya3uwBIWPI7J7hBmhU+2mxJLyxyXR+PwWs2lPUREs6aLQHUZ8C15ftwV//fktyn/5Mnzt8M3DWwJcO1NqdXyTCNGBmY1ReDKYF1VsbEn08igHRGCtNnLWMloKr7Z424PgpoPa1690x8rbxFANWL++rWmW0XU1JK3leIVdl9tVCBua0EkIkxED1mXhgYwU9mbcbGHZ5fS042Y/703nSf7/uWEgdtNcgvlKRom09rZW3XX8b6z+0VtprP7fb5/bASb+ARjYJX6tWgnMzdIOyW0P7osQG7OsVUY1t+gSgffp7T8euA0JPfmc/rtv8ugTp2x6wny9PCxhPwcanY7UHti+eITu2pwhxGJEQSCiQ5Z3uDz6YOH+1hCkEqldtyjhEfAy44HoXge6NBmygYE7bB7ZratIq+u/OiHRO2Uml9gS57ufSbqw3OYjaQRH7EE3EZScfsZsT+4D66fm0Hy+VFbGd0ViE2m5dtmC8P1LdNzQ4VzNPRBMa/TwdwpxVWiQXK/zs15UFlMX2n5wyxVht+6JrdezGs3SmqA79xoYINRL9aHuDtazXputZmOfJxrv9TptP0BDPaMwbvUZb687MR0xcyXs1iDJe+HZGGtiWqpqW1VIgVcgrqkiwnWNAB0mWsvbYo99zbcVnK9DafjWbmae378UQFehviaHth3smtXdBW8CN7VPs3NSW/NyZiVosKuS0dSHsQdpspkNioFy/F536BOcY42AxW5P4cd3hvIFpOobKOA/xYHulGbBgWrztfCqVIURlH5fMKBDdCCVrZ0w24M45UjWDGYtxtn0hq5FVXm1uFLKBkQpSAknniGoCK0u31EpJ2aIxOlOFDMuqGm5twarmdSQyAlqUW9ZixQYDZ02DUSTjmMHOCB+iGeoULVQ4lTmo1SQMvGcIgyaBTrtRnGznRItbcJ7glV1aGgsrGVu1yQmxydvkpvWO62Pv49DB415Us9hX3y/Z82NbX3nbx3E6h8RY0VoganFWNVkBz+i9Fak2qSWHyhk4a12lKlDinYKucTgQx5E1Z6L3pt3YZBg8ObV7dIynA6eDIxwccaj4WJVpamu01MroHYMfqFU2trXTfT1ZZ4Ov2oXjvDPZiGo6qJVDhMHBcRx4WArrY8G72sGg083IeIR1Uh+HaVYwaTxGYhBwhTiCj444eup7h8z6zFIzrHGe4/Ea5zPTvHAYIkPwyjxdlH05joO10ydCcFxfnZSBu862/yuQd3V1Uj+MDNWKZimnfi4Ox5GBUQHvGG3NGLi0TEAmFwVKVOdUweuSEpVCdRjzuVCLAbs4SvVU8aoXjZiMk/QcS2zPd3JFqVnN5VxhWWfcvTI1sXnuWodSpe8RMo7kopqS6zJT0mLakoXjMChjsnrtyKgoSJ1W0vzI9OYVaTkj0dNMIzXWdIgEqMqCW5PpnbZOLJNeiVE1KbvWdC29y6NSyQVtM6+ZvM6kZabWBerMmiZqXVnXe2o1/UtnBX2ysZGr5RHt1G3xhK6/GFVvdZlnSs4cDweCD9oOn1eSFTKurq60I2NdujTfzc0Nh0Gfd0rKiE5r6m3MV6cT4zC2gKKbdKWULNZ3DLZWWx7dYj8FmHQet5fKeqjMhHdBwcbWoVd0PqqknRYOxc6FUlSuQVjtHG6B+y5uFmcGbInU40MF8zXO0fdLqbGuFRDz3lO8R09znVSrFY1ybvKJqnk7ryvrshB9tPs1sg3CeBhpFVVxjth0W3cxVkrJJMu0EHuezgxDsPUWcO5Kv/64aGeG5UK1om3nKSPek7wxUEvicDhqfCKBshSqc8ThwHGISIhUH4jOM0SVprg6nIh+MOkD3+PPfedii8FTUj1gUHPAfRzapUp0w0UKpLKSa1bcIq3Mk2pV15JZykotkNeZZb5nOU9M80QpGVcr8/LI4+MD86Jfo9p8zJlaFBFZ1xWHSkNUB3NuoHdkyUnMoNsAACAASURBVCtqZpcZfCRR8VRiDGYKr2dISXp9tbaO0gq+yQxJz1+rFUfEOWWwIziv0jhBlFUfojLbRSrDqCzzGKNiIq6Rabd4V2U3k0rSpMTj4yOguGCMA+L0bFEpBY05BzP/KtYNmUthWVeNLQ1TykVNUs+PZy1ciWNNmTNwOKiz5WAMV6oWVLyPqr1usWgyIDiEwLquzPOsutIWU7XYbRzHTrxL1lntrDDdisYK3P53CtKKPTTdt6z1zTaa8917JKkDtHgheniYZ8RuVlzED4ESbTOcz5BWC9g8o4N5Xclk3rx5xfl85me//BljdEyP97x985W26UwnajiS3BWffXbF1csPeTifeXz3jle/+w0p/Q3zdI/wwItnJx7ezxyOLzgehRC0zelXv/on3t+dOT++J60LJRUe5pnz4y0ffvCC16+OPNyt5DVRgCSOx8cz05pwbkugnIR+AJUCd3cP/PTvf86b16/5xS9+xTyrboZ3Jj3gtFLmXEtYTSusagW3VHV5LBWKVGpJBO/41re/yzJP3N+/60lsY8R04XAuE+OmNdIC0Q1M0A2rtaXtf7clwkAHN1pS0oCd9jPtoOitn/YJylLRKlguKLX9OBBvjsQPbshXAzV4lYtwas4hhrEVGiALUrdKWjvhNaA21gTS9Ug7mGKAUpWmk7mBYdJ64BqKIPSgt41RS+zaZ+k4bsDAhWmPvZ4Ctm2sq4H42++ZeU0fKdNBlNrvoSfy7fsXbNjaNYfb7ZaSN6MV5Mk17MYF6RVSjQ8uQbJvatUW93X5i28C3dr4NL2lr2v2NgBxe/+e8D5hcV4wKnef1xL+WmzMOjixA0NbWFm1ZWQrWOj46i8YsGMad0KbL7bZ7wAcdZyV7hb+Ta9vGo9KG+Ovg21fA+ksQcwOPIW8LORpIRRBKlpdD8owJGfrfBHWpTIcBjYn7W8GjPfPYhiGCybfnql8MWecgz/A0HXObW3QooyNBrK1HUaUJnEBcO7/3vaR9vV9VbsB2lp4SVBW8rRQlhWMVf+HXs5tAJ9WcvVZlFxwVcw4S772zL6puNIO9r0Wt77vpYljqTt5CbiYw/viTdujt7316/vJNxU49tepIIbKu7hgLbd+gGHAR9XHdBqvUaxqTkUr7dGTKCCeMAwUSmd1iWVLInrmYNZDF/uRaag2Hex2be3+GkCwmT59fc3U2hKzvhj1v6IM7OiCnhtPnlFnQ1g83daWAr2X5lnSP1oBDdXI0ngE6tfGGymsU6I50Lazoe1XLZFsGleNxdlYn82QJKWdGUjTjhbf9wLnTXZDNsaKxgzZzKd0XafFkd2ZTQPTANS2jC0JXFOyZEqBSwr9d1Z3WbBpYJeIucmb6ZmTNr5PjPvEGDil9P0ZMearAW9Ik3hSsN2JY1m2sS3mVKxz3kAf08U19EwLjeJY50ljhZQ0oYhqwpLNHEdjCpU7Ss10peqFClqMqO1rNr9qLh1UdLufr7v77GdK096rleo963IG6KBZ0yytVddAWpPJNqhLdM7ZWGe6B64p99JgKxqkGGk1tZwLJ4EYTdetudX3wpCOVVsmFWtx7msuK3AqToEmG0eAWjIxKht4WVaojdWmH95aH0FIZmhTStICoAsmqbIlfNVi0Vxcl5/oCY8oY74B/TR1bLE5uRsDRIGN4LzFzuZyb8wfQfdIMU04J9I7u3IuzMbQ1GKLxkHK8jGJEUusVCbIjLbiqM+tqBSbsrc8zayu6YkLmlC2jjjvhUq2DiyNU7G9ppZsLdOB7PQZ1irWyqls5bUk6rqa/p7u+dk66fABX0ecV8BPRLrGeM4FH9ExqkJNC9F5ohOiF4Ieq+SsRWMBShYkeGXhi+ZcGKCtOpbgqxZuWmzeuh0ywuBRRq1zLKXqcwqedcmkVDk/zFQJxOA4jcLNTeDq+oZ5FqZJyMkxz5m1ZGXOfhxJuTCdUyMak1NWCbrTqG7k66pnEgcqCmQ2MyHvdI8KMfB8fMYyz6rbmbRodDgcOBysMyhl5vOZkYFUFayFQDYgyQ8jUbQLQwRyjKxpIaWVGppJkBrIyGiFMCqCziktiOn5nnJR5rigBBvvLAgXjSmNdRmDMsvWJSj4gaccVwOlc59zbc2U0gzUhCHqXhV8RVUerMhWPOKD6eZWcHoGlGXGzRNpOkMtnS1fSsFHgxGs6FmrmlojjiAeFwJDDAS3dRI674wJax1vVGst1ge5rmdSeqCUmSU9kvOZWpWJ771KDW0t8Dtig63lKlu8vQnLa6w1TRM5JQ7jiHOOx8dHG38hjsqCm2c1YfPeczweGWK0lv+k5kFFz4/T4cThcOA0HBCnJtfzNNF8IWIM/T11vW8SBKqHWXZ5g45NMJkNb2erQys80zTpGFU1QGvFFn2PQoyhM/iajF0DTHU7CAxDpHmm6J5Re/y0mrm4E9WD3XJrZQ2WnKBmKA7nRpOMcYSDxvrzrTGA12TnqwKsD9M993d3Jo9kOXCp2hpucYSaypmRVq09vhYRfNCxG0eVEymlsCwrzjs1Pf/gOU4C65I5nydtTT/PMGCa5Fpchco4DMQwqFxCiLgQGeKBMR44HE4UK5wGe95dHsLOw5rUyVAsvm4x+x7LkDYH7Xk28BypFlcsqke8zmq2ZWzaZU2UnEhpYUozJVfm85n7+3es08w0L9qlsawdC1kXBZ87QNszTRjCoECvVvZ0fjghVS10zmnVcxk9H7XjOtheYRIZftsbRCzORzuJhzjoWRWtC9kHJWX4aBhIZRwjcYyonI9jmZN146oO+ZpRI7dhMAmnpiUfOHFShrDofGhr0jmVtdnreo/DAfFCPZdeiClVC1Eq82MM4HVV5n+IXJ+uTOM2UcV13dvz46MWu4cBQSVAnPdbTCnCGMcuK1IOleNB1042+a1srN60JKZ85nw+97nog8qE+RDMeF517f/Q648apF1T5s2btyqrSlFdm+pJ08T5/VvEGF9zXlkf7xlixA0DYgzS4eaG5eY5Ja3w+kuWh0dYFo658HwcOR5u+Pv/9jN1MvaO4yFyOh25en7Fu9u3fJEXxsNz4s2nXH0cuHn5gt998U/85le/4Nc//2vu333FZ599zCE4PvvkhufPDjw/3fAnf/Y/cHp24j//zd+SS+Xx4czD3R0P728VjJTKvE58+eXviIfI9bMrSk4s00SqlSWtuGVG8gqiycsQBhN71mM3RM/DwyO3d7f8y7/8mvN5Up0/kb4hYRWRFgw38GxdV9N0yuou7JzpEKpGyng68PmPfsyv/vEfuL9733X1VCPmcjJt1aItYd0jk7qJFQv2NtOtPSCQcwMt9MCigU1PwLOW12oAoolAyqvS5auC0oyO8PKam299yDI6UtWAVHLRdrT+vsqwqP1S9f2C91qdcajBDJXBDwxDoIN1GGNDrP2xbAnePnnvxhSWeELti/iCjdWC/y4voIniHnjpoJZpU7X7b2ChJjtNxuISMNsYaRvbqYNVxnbA7kyB3WachSUL2z09Zfs16YMNHG1AHh2QbvqK2AzEfqeBw1QNVi+kHmrVQKzNL5u7wdpN2+dhoW6bJ98EGncZgR1Q9fRnnwKJtZktyQZ6i1jLdJM/MPHRWnVttNRRWZg65mOIGkxJUP2jdaY6PRS9F/zgqd6DacWpzs32DNucAtXHiaaJgwWhPkZS2ubUU/Bt/2+VSFTwJxdrhY2NvVYZYuTq2Q0ffvIR0Wtp836ZeX3/jmJFCnbvdwEm2viyWwd7uZKtIGBjDxv6L9Ln3aVER2NQ6n1ZOaUXQxBlu7Z2rQZatmt6yoBs11z3IK9YW03OpGmCNSFJ221b8afPJQO6u+Ztf4/tvnky5/ZB3F7OZX99DcxpoPZeNqKNW3/rJ+/V5CDaHtbAv/0ew+4ens6R7cK3v+vPbc7zIo44jhBH6hBxR02Ay6rGS4WyPUsnZKloq7u2Vou0FlDXnWGp6nNehL7Ot3Y8jJVh63sPHufc9dSk/Y7s9iW53ItatboUbZ+lZl4+e86f/uhH/OKffsHbB9XwS3krPvbx3jEmnLssgJRszuDSAKZKY602zff+jBEKhbVm0rrSJGp64aSBTO39i+0rbZ7ba55cb2Mcx1HBTANyN7NKNT5qc0qZj+3aMtnaSxuQtnoF6dhyNTCd1L4/ihjoy65IKm2yfK1Q5LwZIDlHY4YKm9t2f5a7tdH23L7nlcYusIKh7b/eO3U7Lgp8tDWqQykGUgdKWbuhphNtx6bq2BVrpy+1aFG/gcH9fEvkZGeruL4eal2hamvk3n3ah83Vupg5Ty0b66Ldj3h9Pm1OindmMKGtzfqeGRHdB1qb4jIv5OyJtVDqYnuCPjA1tFCGqWhAolqONq/WsLAsM8+fv+RsnVZqdILNlZ0khsUJuTQd0+0eqoB79LZ+da6WnPFOW8qXeVGNxlENPxr4pAwmLLlWf4TgNTlpO9vlGeWMRW66dF6dkotJWijL1mPBCbg2pr6f8SAsy8I4jNSsreWyi21WW7s1mYGTAcotsas6w/DB4Wsl4LteoPceMTA5WFunXns2OZhorc4qVSH2nuK9xZeBw3BQWQUDl5RhpTFyj/eoiOh7DT4wWKHbBTNZdB6HPp8CDMMB5xyH8dgZneqarl0MClSgjM+cSDkxjJHBB46HgXGEF9dwGIV5KpQA2oUIcVCd2s6kcjp3Q6gqwWKiKynr3FpNe1W8rv1UCmvRPRgrahyisOTEMJg2eRIQz2Iaug9pZRwi0Qn+oIWYdTVTweKoWRCvxlBy8ORizTCysi6rMcod3g/qdF8r4oM5yyvDrxZlreUEboicDgeOxwPLsiqz3OafOEc4RJwTpnlidIFQIyUVsjH0tathky86HE8c5Yp1Xch5pZRkcbT+TAgNhFIW12Cu4kMIRNOnDN4ATMGYsE0Wx/aFNXWmrHomRMbxBcJM9anH3NXOt1pUOkILB0ZYcR4fB6CaWdFMprLWlZRthbpKSQvnN2+YHu45uAAFqssEH4ixGd5J77rLdsbH8cAwDtuZioL2zvKUZijVjNJKXliWiWm+RdwCkqjlTGUxyRLLYaQZjLY4ZwNsnZ07UjVfSGSa9nZbA25ULdl5npmmSdfZMOCCxm4NEB2GyGEcWZeFaZ06620YdW0eDgdEhPvHB2qtHaT13nN9dbWBnfa9ZVlUrqTkC1JKA4NbIS+l3AHJ1fbNbuDsHHnVzgcFeRSALQiuimkp00GgFoNlY7wqW3zrXGzx5jA0WbLUn6c4jxfHaGBw2eWCWrzT8R4PBz6KkfN0Zk1Fx3VeOB4PXSM/pWxxisXrCI+PD+SsBlo+OYKXvje2uEUlLZQF3c7SWlXqAgSpHu8HgowcxhMhRE7PTgpkxwHBMQyBEJuhmCeEAxKCGS9qMXnwQwfPSgMbLG9XhrN21mgXVzJcI9PIQbQ0v+Urxix2ThQQTbO286eZdZlZ0mz7QtJ/zzM1J6bpkdUm6937Ox7PD0it1glhbfNmklFqti4R18/AYjENVSNPHzyDc2bgNah0jeWaU4HoPB7NXVuROZhJbTP9M4oD4lrsJYxjND1rLXT76Prac04BYe+FOESG8UCtkFaVdRBRHXgl4C0seaEkld5Y15Xr6xu8Dxv5wzlOV1dcXV1Ta+V0Sqxp26exrt9SCtP9/RZT2NoLPhizdbBca+6xexwUlHfuiloqz25uVKZkWSgls6wz07RQ64TznhgHpjzj3ELzhhCE4/FANFU+qnY65bRqDBMi4rQ4rIXyovrXpezi7m9+/VGDtNUOCwes06z6ZPMZv2aCsZWWeWKeZoYQuPnkQ8bTFT6OFjA4hvEKOVaWtDClzLBWXtTM5598zL//d/+B4zjo50wLa0lMwIvjwLPiSUYbv3rxIf70gn/8xVf8/Gc/5fe/+gc+fHbFn/7o+yzTmYMTPvrwBZ9++ozr5x8Tr54z15W7x4mvvnrNMq8s5weCVNVEzWrOcHd7y/nhkWfXz5gfZ2XuLRNBgFpIS9YWFw/FV8RXvFOND5FCLiuvvvqK6TwT4qALnmTgUWsFNKZsVXOcWmtniJSq7UGCUt3Fqd5LBU5XN3zyyWc83r8jl0StWrXSAHL3jOoGZDVcsMXbzYl6l8FpdSEnA6KUEt4cg0UCjaOoQ5AvPsccFnoWXalW3chdOzK+vGH45AXL4FmKVtjl4oLZMbCkZ6bNzR4Lel01Zkw7zKiWBFqChSbkWUw3yEBSGjjb36tVeJ1S+uslSP1U47AZROxZofsx0ARrC74ae6KdKJpo0X93/z5Ce98G1ppeYt2AmWrzRlB9rLpjSPuuw7oD0mjAdGNvWQDIxi6sHdhqOq0ZqZpgI0JGYA+S2LVo686mj9TaCZvx1YYGbyBNN3bZAVIdmHvCTH7aev6U4dWmbQf+atmxixWSTUUNdVyFPM2E4nAZQjxSKnz8/GPyQ+F7n32fu4cH3j285au3v2daHzhPZ7wDGT3h6kCNQjgEqtvNgV3g33TzutmbrakGTl7cg9R+nR0YrJXoNJlPpRBE23OXPHM8DHz+re8weM8YImleyEGQVBhiZHVZmeBl+7z2au3W++fQABl58nya8VYHpPr32qpv39oDzDpfXW3PXRkmIMZik65N+xSg72xUm4P6a1YIqZU1LdRlhnklLxnWhCvQMqNkrTEONLh8Ahr2FldRgKjFdW1u76+lzaV9cL4HbbcEffvZBtJ2sGQ3H+nvoR9abW4ahrKBuE/2kD3Y2MeaDQQvGHBhrcXD4YD4QI0eNwxUrxpl4j0ZbdWtmMuwjbMmaZuZEtC1LvfXgjMWgq2vNoYtkH+6ZhGxpGMDpPfPotRtvBXQNFkf2zOcwDQ/8ubta5a00Ha0auBmA+D7/uGUKVwqukfZgK9pxTvXE926PTUdS5sTzWQtGVPTuwA1kYomQojpqLdnLNYVQQNu+8zRoNWYhW0skNbKX2zO6dJ3qG5pa1Vu66kYA6idd3nN+JxZ19YuqSCrd41hulGKdZ2ZcZGxeKRu5TdN6trT1sIVVoD1IXYmdZvXzWSp63nvig0Kjm6Fp03vrc1rA7hKA+ubHl6GaOOIgUXtWm2fUnMJZUeoJFpbk9s52vajZiDapBbU6quBerpX7td0xlzTnevxyzgMzOtk+7gyQIM5R3ufjeG22hZSDHDhsg2u75/V5r2CpM60Q5thjEpuFNKiLX7zmvC1cHPzXAFkD3NaQDzBivrtvVrxIAZlmU+Tmuo0Ew5ECDGqKVVKbYZqG+9R24b9EPrzKk1b12kRLjplNDkUbHdh0PnfR3sb721vs3nrPYImO86Znl0ctH3f+U0fs1ZU2VCZO3GI6h9QUtd/LDmrznE/6h0hDiSLj6+99DhOmV867zZjqbaezFyyYGxVjwsD3g94A4VFgrL67PvBQF5sbrbiR/CqkbmuCrq382ocj6p5bPGRiJr2DMMBaiYVFT+Jh5O2DLugEiJNZsEpS83HQY0BnecQIymvCq4GgaDzZ10T42jkAXQ9eg/HAxxH1FTXpGYHX3HO1kE/o4W1VPV5yDZXRUwCRkjZgavEUFjWiquOecqIaXU7a511YVC2a4IYtdB7iBBdpXphzTBNFUpLwK1r0AESdS83YyyKo/qIUCyeVIZZcE6LNhWSMfMWKoMPROdwqERCzavqJIfAeBh74W4QmOqMSKTJw+RcqE4ZgWqK5Skm5aH5iQJrpapckPTEZGPcNVZ482TQpMHR5LEqOrzVANFUCiWplIlqaJe+H7TYv4ogRUkw1KJ6sKU2jyCqq1ASy/xghotnZVUWCDkjObHcPXD3+jWuZhLazVJLIovgTbt7rYsx7/QcOY4j4xA0b7eulW70p7fd4/hiLf/zMpFWZc3CQskzLlgeWGqfZ8KghV+nuRlsUj6tYNrWe0qp518qdeY643aeZ32ew0jOSd3dS2YcR549uyHEwLrMPDw80ApZ43jgdDrhvRqNnc/n3r3kndMOkhhxrQW+VJOgaJ9vAGoMF7F7rapRui5LZ+Cva+qm4XEYtWgg7NiKuvbUS0KB/1xWiycyKS0tgLD9XYsZ2rma6ZqjLSa0M0CcFuRaXNo6BUspUIQwaPyVUuI8T/BwxziMm0nhEFSepccFWojUdvxCWhUsPh0PVozQ/bBpbZdSmKeJSmVeJh17RQtN1iizLBPeB8ZwQGohRI8vnsEPjMOJOB5xcSDEA3EIHA4Dwxi10Oj0TAthUMA55R7z5ZxVqKlWJdyIM+hBemeFflvP+k6CsviiFX+oylrPWVjXiXU5I2SW6ZGc162dP6/M85npfGaZZx7nqRdJl2nuOWctunAK+mcuFfFCsnisiskTWrwrJqnlBf25qrGwEzXWOkbFW0ouyhz2evYqoBlwxSQmsxZjnPk4IEKMXvWu0Y44jYWLyYEEtLMpdIAyhIDgiWHgdIJUtm6/3nEZItM8gQjn8+OWI7HhJMfjyd7PMY4jOftOIFRjTy2ctO7rppGcsko4rckIjJZfl6LSBuMwoiYtTUqjcjgcqLVwOl0xzyvO65me1sx5emBZtWCS1kSMgWWdexF8GPR3lVjmOJyOW4yYNC9pa+ubOqb3rz9ukHZNzL/7ksFHakrc3t/jBKI4fNW20iCeD65f8OLFM/zpCENkSRmZF+q64B5vAcezq2fIuvJxOPKX3/s+f/Uf/4offPdPFCgBXr35HT/91d/x7tUrnp9eEMM1Vx9/i2996wd8+L0fs4jj8f1bXl6NnP70z/hXP/lzvnr7jrevvuR6HBifD3zy7U8A4d3jPf/063/h7/72p4SgIsmqu1ZI85m8qv7QPK3c373nBx//gLQsfDFlKCvBtZYz3YBrVUH7lBY+eDngXeDVmzf8+re/56vXbym5MIpopXEHc+phZVkbYkHmBqJoFUDHurWptWqHq/DRBy9ZHz/kqzdfcZ4zWKA5TTOgehwX7bg7QGDPTIRdi7uAlGJ6gi0DbVUajRocps23y8C7TmAD4Wo7UDSYlMFz88FL5MMrynFgLmoA1Ho3XdMfrJdAzlMdx8aYa4LpGhBUrEuxV4qb3W3TAhI7RNRsyNhxfgOV9mDh00W5B2zadX1TdUWDuO0Z6uHZmD47h3G297u4N6RrGzcmnrJ4Lp+fXt82N3K+lGDoZLiqIEnH2CqWQNZuBuYxLcqqAbsG/8pM2aQTLscBUcCmgRYK+DYAfAO+6i5R2jMTacDBNvhfG8enreRPn8NOgnWrPoseCNVcdjVgzjw83OMXiItjYKBOmRJnhvHAw6/fMD/OhBR49tG3+Pw7f8GaB+7ufsv7h4Vnxxfc3t0SfeDVV6948elLwqhaeepg2doqd+Z27T5pQNQGktbajEJs7ff7tcRSoGZdZK0l2nlPovLl+zeqgVY1EHFDgCEQxoFSFmquHaRsB2tLLlqy1tiBT8d1z6TdS5rsQdzGAtf72YKmdrg1reX2/psrbTU2/fac90zS/vfaQHzBVWuvOy/UeWF9OIMZhrU501pai7GPS9uj+DrAv/9s2vp/Akjv132be3vd7bYm2//fJFNwwQRnA8N11HRNtOC6fc7TsbgYJ+haXoiyC2sW1XiqDsmONSmD3FsS6aunpI0ZqY+sPnn/bS01Y7xaKtU9+TkTz98KDrt9oGzz6Oke/XTcW7LXwV37frakTPcUAfE8Tgv/8ItfIogyS9t8so3tKcOl7TWlmJFX2d0fsC+oYBp7/R5p+4l2JijoKd3kSgNQLZRKwygN/Ny7Nlcbn21XauvLdSCvAV3inXaDIBRrW+1sLOdYc7HEDNPDps+Pxn5FLuemnpV2nW4zREM2EF7/uZkf7gF56qXsSH+GVUwKo3RWNH3ZbHvDnpXf/t3MRlSGwbTxrRUc2Ri+ueTdnqOFgBC0xU6nWTsPG0Df2tRt7VRjq5vcAfbMWozVjCr6XC2b2aH3nvFwUNmWalIV1jWi8ZOxO9tzsvQql1bEdta+B43J064rxkiNoWvse6esPyj4MTLEkSKeq+fPGYaReZ71uZbVEq5INNCEEFlL7nIIh8OBcRxwPQ7yypLPBWrq8gC6Ptp81+ff9KM18y7WRltQ8x4r7pSC1EyIQeOl3b7nnSOEwVoRV02Mq3Bo+m76LuRciXHsQIh4A8jM5Mv7gJOmZR1pms4pFUt2lYcenBEngsm4oMB38M1xWcGwxS3UZjjXg0kF+bWVOXRGrhOnMkhhJFexZyd9HVFb4VGJAM6AtRg3t/sYo+ogl0otEUQN2oZ4JMYDjmycAUcMA168mjVJJYRNY9j7QAyR4irjEK0DTIwtpgZw85JxFYahsdZEO88qlFRJQBDVmx2jp2ZYiwK3BW1BH6LvYEKtkOaMi55ohqB5VYMc7x2Hg2OwdlfzBaSmirLIvZm6aDu+c/r/umiwKbUisTIvtZtbqt2WhvtuCNqCWzMlaQddzSrfs50VghD0vCuVZVZWdfK5n59tPy4lU9bUDaV6XkWT5NG4sJStA2BZUj87NHbzHXzqMYsoa7v/my0mEwGVV7F9Fc2d1JROz0ttbHJUJ0hWsLIXXuuOXIDq7IpsHWHbWQsilXldSMvKkmfIM7IWPBFfKvP7d8xffEFMyZ6LR6pTneVSKOuqAByZGCJxHIghMIYBKQoW6p7pKDmbXFE1spG6si/rYvq6M1TVUw1O25Jbt0217odaNpa9djEWOzaadBL9DMaZDq1Xhp6OqzLaEIhD5CqeSGnl8fzAuq6M42B7m+pNTo9nUlo5Hk9cXz/DOceyLMxF8+C2lzc5Im9x+mpdM112B+nAcTPkbfHZsiw0s7D2GoaB4ANjVNmXEALOb0CzBIshy6rFDS7ju7MB0E9z8kZ8aJrvKS30oqnoeDW9//ZaFv2ZknV9zg/3Zpy5adg346SOMbSuOGvNF5Os7J1vdh4vs66JELyem94rwDfoOrySE84pkKpt6AcOcSTGgBPBu4jDIzJSq7a+H4/X+GHExwEfg7WZN9Ox2veCFhOJb7mBLjYvVpylstWnRAAAIABJREFU0uR/cgOc5esxdWlAak3UvJKTnhW11K79W9LK4+MtDw93SFVDqjWtLMvMPE/azr+uCn7nrPruHZOwi606f31wJoXi+55SxVHXVSUohqidLl5jFS1WNAZ3VXKFwPVJzRYdQhy8nkO1MojgYtR8z6mMQTNlW9NKiIFhHC5yE++FaDIc1bprSy3a2bOA89vZJkH3zDiO3YBOSuXZ82ebFIith2z3tywL9/f3gDAM4QLgFZHObG97tIKsbDKTpXKeTMPXNfkpnVdt/wHHOjtqXUFUnmCMo7F+V5yH0/HIeNjMsFvs1nCC8/nMPC8W22ks6Kep7xXeea6uTn1N/v+9/qhBWimVfHvHhCgCXisuOFyw9vDqOJxOnK6fM5wOrK6qWPXjTF0Tpag4eBGPpMh3Dif+1//5f+J/+Yt/y0effsrD/USoQrp7x/u3r3nz7i2nYcDHa773w3/N1Uff5uUHn3E3JX71659zfvsVz06ez//kc47PXxLnlZsXH+BKYjwewQ1UCr/89W/4v/6fv+Hu1WtePnvO9bNrnBfWJZPXhbQsKoacKw8Pt6x54XB1ZDgcmVMipYnVdJGCFxWSnmdKSqSbmaVUfve73/Hm9VvEeQbv8R040/bdPbtDvDf9HwMV2TZJcY0lsFXqRTxLyuDg40+/xd3jPUs6UzPM69IPgn0VYA+89Oe3T6bte01kv2segTpZI1ZhgC0RvWxH70lfC+jRwFaOkfGD54wfPGOJeoiVXHClKpYq0hP+i/klu1ZtA5caaLW12cMGh+xA4wa8VNly59Y6KRpQ7ch0F8DW0/HZ37NeymUy3sa3MVOgBd/b73W9x/Zu3wRM1ktWXa/ilifsQGnA2qZnqK1EXHxWZ7PZ2LS/gTl+7oJSRMGDXIq6gjc21ROgFLD2hY1d0EDwFlD262wB5ze9at104CxxbuOyB+f3AE0DxLxrRj7SvweYxHChmlu0MvsXJAmfvPiUjw8f8s8//Tnnu0fCsLC4M49F202+dHD64FP+x7/8j3z/hz/mf/8//jfeffUFt+9uiYPn5emGCORz4f7dg7brjBHQ6rMLOp690psb8LDpNO9BTXbzDnTsqt1DY9cpM0nbpVLOvH241WQzeFyMBKcJeZmytjW1dmK3KwiIgiy1aBK06UBettV38KLN+T1oaI+sMbZhS9gvQcsN/Nm/r/4GW0LzZI7397AfLCUhpbBMMyyJMq1I0nFq6yFZa5kXM5pzTTbm8n3lyQRswOylluzXwcb9XHz69afruDMgajG38m3cnrKY94Wx/Xvs95qLz8eCTmNkdWkS2dZfcVC8Bs/UJjmg7CWbXQj79n76WCNt3dSvj5lNyL1ZxF7Ko4F1XZqlbgWCdpbALhnYGd20Edyza3S/coiL2xmyG5PLIpW+9oZuFS22b+Dp9tliTIKiWf1WlNzvq0W7AHAOZWAp6GaZo95ju48d8Nn/UlV/q+maapKjP+msWlaKami1tlonosYgFpRLpbM/MVgfxMA4a4E1vBnvO2DYdMFakF3jxrJVNrmyaFX7Uu/dO21lbglvG8/9uLS4YD/uexMFEQ1smoO3xgR2Ftm4LQ0kFY1nmu4h6JpxXlkf+ksKYuasDGLxyoK+NO7b1kebG+3jmqZn31N353ovfDZpDGvJL1UIfjC5KOlJk3OqFZpzIZkunIgzrWYFv0JQwLj2gqw9tVL6+Fc02ChocqndP8rAG+LI8XDS9mRbu+qUrMlJk+XBeY1X2OatAk/NACVreGOM5f1L92ZjsVYFWJ1zOFSfdVnVIEX15tpaqiwpsSYtajfWVU4Z5wK1OsAR/EhxFSmCDwPOKTgrqHajOqRH+0zTYzRPhuBDBw6cV8A7p6wstKrrCSpBAsM44ny05+w6EKJD43G+qllJ30ctrqm6pkOIqhnbETXwLiJuNAPMZOcfKiVk5zJUazduq0H69TuTJslJTaaqgQvSpCJcJPjWXqrgde7PS0G0dr744CiLtsDrnPIdXFVtWYwVVAgeitOvCxAkE3EEUW3g4zBQ8opU67cS8LUwiFPgrGoM2yTIKsJCJRw0tphyYV2VKYvpbUp1xOAIQcgZYlRwY10w7UoxUBCiFw6DNFI6VUAlkQ18MhargmmFh1SZlkWBsGLaybKt1yUt5JzIJZFLIIRIA+Bb6qA5khrVNZApBNVy1vZwh3PVijAmxVKh6Vs71BBvIxPsi7ZaHNO9X2O3toMFM5oSi9kq0s/bHrv2mQRrTkYY0XMw5ab/uIvx7VxWgCEhFEpaqTnBsuBKwhsDeJ0nzm9ek27fWYdni6USYsy8JRk4GwfCEHHBg3Nb8a2qT4oTOgtRpQ3MuGqZyGm1Qpv6sMQ44ryC9sXkd3Jd1XVdMqWYOZqOnhFNuJDjU/NIO6NkixurgenisP2hkPJCCJ7T6dglDOZ5JpfEMA5cX19zdXVFzoVpmnsMcjweuzmQiIK/yzyr4daqnbDe9Kk7aF8VbE8pMRvhaTMY9H3uDta52oqn87qwnhclkBSL9URQIEjXXgNqm/7tPpZsX2vYQPv+6XSymKO1z7e/2yxse6hzNl8c67owLzMijrSuSihZ864r1mRASmHNJvFUNB5zziRH5kk1U61LYByUISmi+ueNdU3Uwus4ROJwJMQDYzxyOh6JMSgz3keiGax5H3X9idOqkp1pjV1eij6XlCwmEoudUpPg0PO2sdoFekepxqRmCFqhmQmu66wyBmlCaqLkBXIhrcn2MZU9OZ8fmKYzeZ1IBtCWqp1ZKWvRrVDNsAsFakVjn8HYrG39huBNQgIFRavKtjR5TL1PK/iIYxyCkuyWhSWvusX5iGB5b9A1WzOseWFwQbuNoplWOpXZOhyPhDHYflVtnwoq3+cch/FgRVTtmp4XkwnJ1Qro8Hj3gIh0g75ciknyaFx/GEeaZ0SLD+d5Jpv/QDZT0z2hov29+aE0U/sQourniuowz8uk7NbDARGn52sp5JrIGduXCqWoAd15mtW0WgpucXi/EoOtU/Ecj4PNLZ0vx6OuJzXfnWnyJeuygsXk87z2dfpNOdv+9ccN0gKhirnUQXSO4JQlQq4EFzi9eMn48iUP50dySpzvHynnCUmJQiJXEBbc9MBf/bv/wL/5wY/5/Rdf8uZ+IlfPP//mlyxf/pbf/urveT5e8aMf/Rk/+df/nk+/8yP8eM15WvnNL3/G73/9j3z28cd897vfZU2VL1+9ppbEeBp5ef2SP//R9/jiy3/hr//mP/Nffvr33N7f89GLG959+YqUVq4/eK7tI+KZkzK2vAjT+cz58YHj1TNefHADLvP69QPrmgheKE2XqKjz+vn8yNt373nz5i3OCceDtgbVLmavWhfDMGxGFbQNSoHDlgzUqkCT5okN4MlQC1U8sziG8Zqrl9/i/f2vKWsmFQ30LqrEO9Cmv0/VVuEWJDeWCMDheKQWFUIXEdKaLeDegOXGgmmvDmXW2ts4cQJj5PjJC8KLKx69bcAldEdCjKHTKo22YwFbi0N7KftBnUdLrkTvjd1boBgoYD/edHY28NPu0fLrXtHmMtlrf+6BgPa7+rObztkeWNl0UTeH1+3rTwHfy9f+608Bm5LzBYCtz7JV2be5Q6/Sboddu59SizKi7Lm5qq1ULU9tbOaWwLpdIrgHai9epe7A8/b8K3uxjQaetRbnpwWCpy34e7DmmwDz3o5QysXc21+7GGAtuZIeV5a7iT/5/Af85U/+kl/8l5/DunBzpTpOMVorDxk/BAKV+/ev+OLXv+DNb37LSeB8/47Xbx748je/5NNPv8393QMhRN6/u+fZJy+Iz68oFvDUkjsYVms1Zke4aPHu6/HiBjR5qYbo9Opv1QKFeBUul6gHKCLUIKySCSI9n6xV5Tb247UHwPcak+zmbTuIUtkSWy7m9Xb9uj9VK0BsYOy2x1hr9BNA8+kcf/q8BUsQjAWNJczF2GMeTf4bk817T/PF9SGY3AEXgOv+z4t5sgdE3WYwtv/eN4GmW1X+UrKjf5/LvVY1pb/OCP9Df/+mMbq4jzY/sBbJGJBjxB9GZBwgBIILykBzykRrMhNu94xaclrFZCnanDEAvycBTp/3ZUHB9o1+v5csOy4+Z2NXK+Dcfms/3zXTllpBiiWWosxGAy0vts3deO+fSZtD2/NQsK/db9v7WwK0/93291Iv2dHeR5q5YKHafLQUfLe3bg9NaJ0bVFRmoe7PoY392dpJ1ZFYmeDe6Ybc2iKVdaxM/FYgcbSg3qQBmkRF3UCjWguuBsSFDgz3rbpWun6vGFjIJWt8A/NNs3T3XGnXZQmec03XvRXOdLbVdubaOOqeYVqE7Xy/0LfXY1zBAnsGFVwxmLmtK808tjlg1yLGwN1Ys+18pt/TZeeQqKYsjYWqPgIVLaykkik1EcKgjEZjX4qBm6Vue5fuq3puOh81GTMJILsS7Kp3etZeW1aHUVvgc2IcR5ZlZhxHQoiM8aCgR9X21tjWZtUit8KCdQMsRajdqEcsttO1IOIQvIGmSgpwooXAY62sxZyxcabVqmMDYlquoc9Bccr8dGbKBQ5EGbJI6yBSxs4wHqCqJms758QJJaNjW7QltVU0fGgFHWiSQA4xyRJtIXXSCsvW0ZMxyYatE6rJUnlxVEtyl0XlUxCn8kdecFGZxkjpsUyuyfY7HePWJt3WTttTinV9bJIXavyZ1kR2OseO7tABKsRMdvoa0D0lBE+M6lAtAiEqGJTWwhArh1ELsMeDcIgwRuF0VE3F4Bw31yMHh4HulTFAdY3IIHiBKEIwiL9agcGwBACiE6asar84Rz4Jhyo8nrXYUFBGf7VNuVI5Xjnev11Z50CIOsvXVFnXgvOVdYU1a0kmV0dKylTXfVaxJZVacda11c5W3SdzLQTviQREKilBTq07S3oc36YLGOaHAgG1FMYxkhLM84xzruuz6jmggO2+y6ntFdTa11K1ea17put7Sq2ZNW35gQLAot0cgBhY2yTZ+v7V54+dw0XzQu2uqrb2ajeCWtaJsihw5Jas1y3gqjC9fcPtV18gJm1Qg6DmUSh70YoKuIw4jQjwovILVjSl2JmAAv8pnSlV14seE4UYwBd0nQsMgyd4IaWZnFH5GB+orrKuM1mUCRucw3l0fxahel0DtTTWp66LlBpJSWekarpX04SsjMOoeY79bFv/4zjq90S4vb3j8fFMrZXr62vrNlBj8tvb2x6TtFZrp0ES3pmDPZpv1VpN01SjdO89JwN6qQ3832LY2diV1KYXC5RNJgGnrOpNSk//j2HQM9GKdq14Jzaf29k7xLHvMcLGzGy5Vt6xZBuuMB4GjvmgWswWohS7n1WrLzT5nCt/MnBYuz6WVXVXhyHiRQv/8zyT1oVlSmreVwv+MJghoWM8PuP66jlhvEKGA4d4VFMq73QNB9UBd1IVqA2BYjFR65Bphomlqv5323tTUqNIZQ/v5aFMg9c2MZVA0XnmXTWAuTJN9yzrI3cPtyzLI7UseFsjaUnM06Rmdca6nOZJwd209jGr7XNF13fNqhUbfKBZyGJ5j67fJkOh54MXoYhpE5dMKhkfHMMhsqZkIPeIc94KKY5lXVjmhXVJRPEUgcPVFWMcoaIGmEMwJitUV0mopIEzLKR14bkQ7Dno9bZ1FYJnHG5oI9gkM46Hg+2nxbSWC+eUerHcOUcM+hyjgbcaI2jx+Hgce8dDA2STMVkvCAACc1q5Pz/qHK7oPlicxWzeJMgqPqhmreazqqXfZBJyyhT0OtOy8PiYet7bDMTi4GmavM14TD1kKvM8c311QwOb2z5RigK5/1+vP2qQtoI6R4qaE+AUqfdOqKni8IzPbuB0ZH54oKRESdkMDYRBApTIUBb+7ONrfvL597h/+5qHNfH808/44NPv8NNf/YqHKfH8xcd8e/yE7//Jjzker3n75pYPvvWCvEy8vDrx/Mc/JBUYxmc4D9P8QHAQhpHT1RV//bf/lb//2d/xm9/+krKe+faHz4gh8BCEFy+eI3FkfVBdsjEOrCnR9C3u3t1xGq/48Nk1V6Pn4d1b0v9L3Zs1S7Ic54Gfx5JZVWfr7e4XuABIADIMyYFM1INmTE+aHz1mYzZmY5LpgaRIaWYEECSx3Yu79N59lqrKjAj3eXD3yKzTDT1jCnbR3edUZWXG4uH++eefQ7NPXqKhmhsB3z57huubO1RWB7GVSTNVIpa9qwZGAEPK94JvZbe0FdNuAUE8MCFroiJgithzw9mTj3Axzbh++rWFwAtjyx12zwT2TSLSNeLCKrtJpADIbrfDbNltbQCiv2/V72MJzJVV0CN5dWKIEDcDzj98jPHqDMfI4AA9CMQ0YY0tBIhp4HrWwrqwG3ggTdk2mpGN5vgEuyfLtgFdyzcE1UXU7IodePByVQM9ggdwstw33OE6LUPGou62ACpWVt/3ggX4MBBXs5LhBBTwv6+DxTVY5N7fKcAqK4VZwBk060Y5flAtYImuEwdlHRTp2AbpeOhBTwu4JTDZg9O1t55nf3WQ14wqiGw+7PkFgAcKwiefvw9ArV8OnHTgxd7j3Zzfy4CzIJ8ZltkjSAXm64rYEo43N/jF3/8D2ptb/Nu//DGuLhMenJ/j4sEHGDcjhCtev51xV3f48p/+b7x6+S0ejRn/+ud/jefPvsF//Ju/w6EUfPOH30MaQExAEEzHAz75yQ8QNwlT0+YBXOsJa921ptfP1UuR1+vJnsNIWsq4go1v1MHW1ngG9Dgznxnel7oDX+95nRyMIieHJXCPkbgCH9YgoTrszgvByffpn6tmRn1+16Hg++casGCbVs2PZEkGsTDQ2OZYbUFrCuSGZEG28Mm9rJ/x/j2JgR3L8/v+eHe93//7/cTMGqj14PskyePjh3f30f1k0Pp14szYZ2IHC4M2nRlHNGuukNOAZtpTBHXYenLAAJD1WtO9f7rH+97ye+qmcVknMUbTpl3Az/U9ngB6ovZ2+R37UddtOItXPagrrMRMD28tsFvZCbEETV8n9+bbk5gna2z1zBAvbbx3z7KMhSYL7Wxa/ayfDyqCqudRP7sJfLLOLJj3c4a0zFKDzIZAZhuZMeRBr+34VFPGbwC6jqc0vxULFBxIMBvjna1jSghBgYgYVHt4zYD3M9Y7T7vi6LLXCV4NcR90B9DlFtg0BdWxdsa3jrMuo2j33vo6ceeeSMvuGguO09HKOAMQ9P6iBateDn/iywBw8IwBBFLdQVDwUKnvQdf4d1bSwjReMaT7fktwqQWd9gUEBFHv6N1MYzt2e6tz7X5TykP/t0Cs6kRB5mgsJUHQRlU2F1OZkSlYk7OIEQKIyveAArw+QIFzS1KTgbQiqllKmszTANdK6c1Hcr3BnEekmLouIbN0fbYIZQyLadURxRXTTpRR230OAqx8m1nZnnrm+aFE4Kb6jSFoAHo8Tn0fKPhAAA62d5f9KiLGaA1gMHJKGPKAoSmgEKLbe52j1qqBYz4PwAL06R4IFBCqy4SobEYMSiohYW2UtPKTKnu1idl3VV/oa4ptL/r5putTGcw5BgWaHQDrzTO1hFTZPbY+jAGfUkDKen7U2sBctZEOCOe7gBxVymDcCM53QdmyGwAcwUWDxABBCgoItdqQQtTxYdV8VtBnqZrThmbSySgO5B4FmI4NZVbGuDaeUcb9XJylHVAYEBTsziLqrOxeCQGVgTKpmWUQ5tIwlQaRCAoDalNJi8YVoAZl+kZtDJMSMrs8iKA1b1qsTP9x3KDOpccyuhQ12cJN+vkyz/r7i/Mdjscjck7KCLXGyg6y1eqVZNx5EJ7caK2Cm55FCGtf1c8qT1g7a981s/XccKB3YS67nQmddKGrRlncuqAZbpY0gSXGZJ2M2TejFT0jWQQDM+LhgDjNmqhK5scYC1YkIOURQ85aTh4BAiOSkmWCWTGQNgSj4OCtNnezohkQMVK2shwoE3wzms5901hCe6wIGleEsJJ580IUa/QrxtYPkeBlIS6J4/Y9ZAWTWi0KgNHiP8+rONZ/Pk8Tyjyj1AoRdMBSAb7ay7C9us0B3GxVF8yMUnV91LkgECGPI2KyxFVWxmIIAVyt1HtFePA4KsagevExYhxGTbCxGHseVkmg1T7K4ptXkoQLKaXLoZlNmg5zr6QNK8LWcngRyjSrBJo1bWSwyU0IPAkLUr/KPx9DVAKEAW5EEZQI2VixOn8ByYCylBJKmTU+pggiBXYRMi52F7i4eICYzyB5gzFGY4aKVZfBdNWrJlrAaPaEgTwuMt11ZrQujaHa6a01lWEU009GW8VRWp3hc0kxwBs+tdrQeMbhcI39/i3m6YBa9uAyAU1QJmPRVi3bV3a7Aoq1qu3UmENPCPVFLZHpWAvZMxioqHJCRniK2mskxYjSxOz9iJi0GWDKEWzEq6lWpAhbb4QxbqAVALXP3xAzznfnWhUiWt1Tmq77EFVneBg23TdmKMg6Hya0HHG3v1Nbqxtb9dTJQf6AzTAoa5ZGNFbQesjJJGemjmGo/awrDEz9n3kuqLVhtx3RjBneCYPug9my3Xq1GGkjwOPxCK/Uq1w79pQtmavVYspUzzkg5xGZAjIAZDI7qglw3/eekNF7rRaP6/r1+waoS0ARUZdkcH+kJ4X+yOtPGqQNAMYQtYGNLVKUqg0TIqFEYF8m3D47YAwDKGeUpHU63AQzGkIAtqXhk8sH2A4j3rw6glLEMAZ8/vlD/Nuf/yV+lwVyeI5p2qNKwKMPHuN6T7i7uUNKCQ+ffIzp+BZv3r7C4w8eIqctvvr97zFPe5xtMn7xy1/gm6+/xKvnfwDqAU+uLnG2O8Pzl08x7DJamyD72TIGukkqAWAFVl+/eoHNEPHpZ9/HXEgBEmoY8qCdIC1bPNWGF2/eqmGGNTLgpo29mBEhmlJjQp1Vm2QYtEGFao1ZKR3B6N2sotKkbA9fwCHpYi9Vg5OcAj753qeYjjc4vnn7jubhPFlG9AQ0VPZJIHWKUho6g8KbdpyUvFvWKpjjCXHHRA8B1TRsWpqfAmg7YvjoEfDwAsfAqCKdBUtEaI5h2OWWbtXNyhZEs1AG6Gs5qNZTqeMNyIr9AFFCGBkg4Vk7/Y4VINX/hGmtLT8OHkCwZsMCaQmVHoyxZzddRw0rHTNnD8G1YmVhWWmH1Njv4T5IGSyYJlKJkBOwY8VOIVKncdG3PQWeTv9uAfkKKOtgBhmAo8cOuDno612wFQyExlvvBbq8C7w4qijLdxNRj1GU5QNzEHSgHba7r8e0Bq+WgBrKqhSY06OObAzOBjEPmAQVDTEmDGGDiWccpiMeDDt8fvkY54j46U9/gB98/gFqnXC522Fmxgcff4zz84f4xa++xmd/9ld49OQxpsMr/PL/+Xu0wwFXuwG/+/2XeHU74cXra8QgYKk4zDPq8zd4OzzD+QcPQbsAjkC1zGWycVR5WepA+jLGi9H3v4UQ0OqiVSf2fKEFbR6xSjCAXedLrxCCBrUKGC3r3VkXCmjonNXWMNgB6rpcPu5r58/LDRdmpLE9XJvSXksQ2FaA8XodaqsYLwMXEUig3ljBNbMczuTWEIogzkC7m1UWBQBEEwHVNNQoeKtO239YbN5aC8lH2ZMXWv5t49RWAGx8V9agMwJP9u4SnJ8kC3wryOnc+or3nLw7duv7W0K/U1BM9Z6pD3cgDRwkCloUTXwRrPlAgBgrE9DsPQzu7OOuqNJy/TUA6n+u/RF9+P7PBcw/BbaXt1sQYIHIskjNdnRmqZ0tZL4D1lUIKp1EFBCsBBXdVhMQ1KFPfX4CHIg++S5yu6Qglvi6hIUtKwAX0GSYMmW5g47N0FE1MeQX6/PlSS4CEPtZsk4yGSuR7fwLXupL4KbgatSJXeYh+LlFprcazMcwpo9GfAoKko976E2a9HLK+qTO9lvtcdFS897gUBSCXmw89XJPBz3XID4Z6NhtNC1j4KOpjEiBcDRfxkvHIlIcAQhSAnbm14SYum309XFqj1agqH8PO2tfwWDQ4ke4JA7o1Bdy/4cM1KWgzWEaGAzVP+XGeu4KA1xtjqlfNwZje3fQ28M1K1m1a4oArZfd635gS94mWwsiAqkF1exjZ/WRaVkaaKTSBha0tnbSIFPXW+tz4frmZu4RBKAUrGv1DAL1gDmleGJ/CbqOiGDa7lB/ECYnQxpQtiZdK9/Pf9Cy7tmQTA3oFKg3vNp2YLTAjuDsOQe2fG1Fir2ktnki2kBnt2MI0fw+9XWUxUSdkd3tn417TBkUomrtmswGs1ZiCRSkV7fN5jpGk1kIYCgBwAFdgp7F+rd4kgwABevsHtHMfgfWkmJRmiOAZLX6Clo3JqRACGhIJNieaTOuFBVEjVHnvDXgcBCkAOQUlEkEOwNS7nrCG2giqLUGicl8cB3HIGLaowvDLgXCLkc0IYQkuDkAkIAcBHPxs93BkYgyaXVdHoCcbOwGwjxrE5wxA5ttRm0Jcwk4HoNKUUXCNm9x3M+6VpmU+U8Kylc01DopsMOM4+EIlqpapMMAFpeNMN1uAYI0A02VASdoyEeNr25vbw1w1LgTwTSuDQhrBtQS0JnuQAID4ObiLCaLxHTSMV4/1ywesvjD1jJDNIYzP6oxAHYwqqn3zc2aVpp9DkAVZRN2BiFrMydpADcCNQZiwKE0HO5uwG1GFe0voVr0xpWWiCFvMOSAlBRojyFAWtWKm+oMXjJ5FkFrs8Z6rRnjMVgCq1pMZFUSUOBJUkRAgjCBg0rYxSDIKaKdNMcW8xF17bsfo8kPZfSzKOHAy+2bgWNOYFG97ZV/GiK4CtqkwPHF7gw5Z5SqpdvH/QFlnhFiwPl2B5crSgaWNtMxZiu7JhFsN1q9EGLoQI2+t6DJUo3WZQRT1IQbgCaCbMQrlcCpWCfrStPk2OKHa6k5ADCpfzCkbAxysyohqsyEE4JYz+ZgiVJdmlr5oeXm1ojTJSdJwURmMRsjBl5WM4pAOyzVdmL+5nYz4vy1y7iPAAAgAElEQVTsHCkmSCOM4xl255egmHVdGBtWm0TCZBJHpDQaUK0M2q65ZQ2zWCpCJGMpWgKXHOxW4kVrrYPJzmbU54JJLgpiAJirPb4GqoFcu7ZqIsjkOkrZo9QJhArIhMP+Dnc3N2b3GVHUorfGaOZjcjObLgAQIax+XPTYzeMia1xGEF2rMSIPCcOo46M6lzpNjQUxayJ3uztHKRrrndtzzdMRgBLnqighKW83CIOgzKbrnpI2YERDGlRmZpDBbIeR3AgYLVGhifusGEQMYF5XyTIOh2klP2ayWhQRkmrIkmijMpiebUqp+xwOXjbTR6YQTLKm4nBc5M5itCqbsGAiRHqOBgrIMWC33WEcx+4DdJDZJF+8B0BtM6bDETGQyrfkuFRoQf1agdrc3XbbbYcmmjWRMc+znXsVwirhNE0LBqE9BlwGLGK72Vgvgfe//qRBWgAKhAXBJkbUpiURDF3sRAHTYYaEgAITM766BM8V090B8+EOY5uRpeJys8OQNmi4A8+C599dA/Q7bIeEzXZAxRnupoqKDfbHgJzPMNUZ+2lGpIC5AR989AmOU8Xd/hoMwcXVFV6/eoYXz77D02++wrNvfocPHz/AlDNev3iFNGbMhwm//u6fECjgwdVDxHGj2c2QkMcB5XDE/nDEq1evcXZxhe+evkApFbuzM+y2WxwPE47ThAZGmytCSiAGYhPLcCg7wYFRzSykHrxP86yLr1Z1xi04ZXNWfdMGE87OOaFUNUBl1gxqEMHmbMT3f/AjfP3P/4y725sFUIMFZlYO1jXncAqqucMfLFCubZFN8I1ouJ2yqQBItK7qoiUXgEAGwvjgAunBGdLVGWYpEOsgrY3CVplRL9sQZ0Gpk+NM4/5nawhJtenUEJEFZBYkQ0E7EHo5GrACAdfA5zqQjqdsQX/5gd0sQ6oMGy9LMV1BB1fMAHujKgdhHKxxwHGtDwwfw9XPegMkMRBOTkGzU/BVA9b7OrdrwNOzp3oPC+PRpRHCCntZWLlkDFv071mCwHtM2JOmQY7lOJjmRt/BER9UA0Xujcv95wSWZmBEZCWLp8CLroV1qaGWf0mt4CiQMuPJbot/97O/xI8//RQ3r17ibATAe2xzxP54wLA9x+uXb5HjDtuc8egs49PH5+BK2LSf4O76Gpe7AZvdgK++foZ/+K//Hb/7w9dgC+JaZbz67gVYBOMHl4gXA8Qa1ixzG06aMRFZyaSX7tvzuq7hqTSJP5oXNjkgamxaWYJaNvb9HwPvgwXm6vidAhf+us9S7nIJK6fUPQ4H/jx50EvFfTJWrw6kAejdacXunz1xE6xJVYOUinookEOBFGNGyun99HEz4IIMKIIFA13CoWt5h5M7uw80O9CwXvPuUC/ALPreCOF0vfpmOmHe+rjaZ5uL5wWGnOzP0z1ykrxQqumJ3p1qEg9A1PUWrVMx0XI/dO/6979r/ZwO7tBq7t02rE3jia3BAuquf3ffTsn6nlaAoga4svo83rFnOtJswSGtvo9Oxn/9fOuEkjLvqX+x2uxTmyM2rhZJWPC+jAtBGZbshx8vDOS4Xit0qimuDCpaxjv4wbOyYWswv0mvaPEzTd9n9jUoO4SCao+R/QcsoH5MCcroiav58/19eu31PK8d9A7kezAZ9L3uByzzuAL9oYHSmtnsa0SvQSDr9K7BVlv2BilL1dm/+jx6/z6Hft6d3recfD964kvHy9c4y3KOrZPO7AzTEIy572f9kkRUqYHW1whz64H+ch+sQLA3r0RDKW0VzGvQ7OwuImNNhqhNnUT9xKDGuwN9DQ0mHYnJQAhlBCqY2EteyWUq/HwPfX+RWPMNVu1Zsu9XbWO1w7VVuO60jrIG8+JjQgZuxqQAD4xNJPrsISSztYsfAAOIW22YeLKSYx03Z6nHYIxY23ceFHnDs2B+hfgziLOS3QrCgAUnEZgtWK1vtkBXJW2WMzEZycGJCOofAzDwqcx6lnrTNYBAIarmu1UraPMtlZHSbUL2Pc6uwsl+qlWJAyzawCWR6g8KAkIUcCFIqzi/StiMCZGAzbD4NxSgjXgSQYr7aMrqnZiBLMjRZH9EMETSBA4FFBFE6PeS78uwOgstkeNYe2XB/lhBlJETMKSIPDLiLGgtocxA1awvPDPZ2Co4SM+5uztjywZGGhJqbdjvZzRoQypp2Xw81XEcd5oUu7uryqgPGh+EGBA4oE6qNboZ9X1w+S4bhxgTQuDePIwb4+7urmsk1tosvmJMpSKJ+ixzqdZ/QxvcegNjZesZqGVxhzeldN8ueqMdW3v6POabgfteWBh5Wq7tZ4XrKkK02RYFQBpQW9VS61qA2hCseqRJQAgMQkRsFfPbZzi8fQ7mWZnRVddiNFtHvSeC7nsi1x1ntDrr9cFgIxGFoOsiEiGnCEJFjrHHnrCoVR9B7ymniIikzxEDmtneJto4nII2Q65VbX5IwZrjKiCbcuoJPIh6Ra2pvJU5lmCT/EkxYbTmVWTnkrBgPNshBtN1FtXDPB4nBXCSNlXKyZoMkvqRtcy9sVakoO8xcMbPnVIW1nYIobNe10AViCyuhcpGiIK/Uzv0mNv96s6GJX3uRBkBuk/Ikn85RuSYe9WC296Uksv3QizRArPXBGUPbzYbFCtJ174WMBuKVTWSrk9yPVw9FPDtN0/h0k4AMA4Z04OCx48f4+L8CudnF0h5CwqqoZ5S1saWebAkhdoaZdgGO6NMg5gAIZXoEVnOq9b8/FbijTJhm1UlR0uStB5XCjOcmuNgrYPKMEY7RJsf7ve3mMsEkCgDvaqswWF/wOvXrzEdDjqXIUIoQkxmKhkRaBwGVIvH2NjIIUabl4V8xKSsf+aKQBGVq8rfQZBiQBpHPZMEGNSdA4WEEAMudlfqV8EkclpR3MWSprV5zw31AeZ5RkxJ/cq4aOG7T7N05NCR8ZiQLN+cUlIZGNHyfgKAwarGOy4TcDzOuHl7rT5ujBiGQZ8/oCch3T9OOWE0fdrWGna7HcbNaIkBB9c9Gc0oZe5JVsdA9P5Tr8zyPSMiSDkjpoRRxu5zne/OwK3hcDigzAVHtkapaez4TEqpa1H7uU+BkGPuYLB+B6GW2u/lsN93hq1KsBCmuB7Zd1//PwBpyQ4zdS7HMaEJo4QIxKGX7rMAtRGAhLTdIg7nyOMWm9sbPIwBf/69P8ejRx/j7e2E/d0Rt29vcJwKHjy4wGb7AK8OEz747DOcXzxAaQnjkPDTn3yK589u8fb1G3z/gx/h6vIcf/jqN3j+9DvkHLDJI7767a/x1W9/hS9/92t89PgBcgh49vQpYsp4fHEGaQ3P93e6aFvB1YcfIW+2eHT5GE8++gjXtzd4/eIFGrNq5b5+i1JL71JMNJsO7BK0dkFwAxZUnzVCoFokHoRwa9BmABW1NWTX+3CqNTc0BxdI9XdKKSYErgzTEBLGnMGl4uHVA5SPPsHv9wfTHLMsFqkzoxo0+lJQxUAzFqREJvEQOruN2RziDvCpA+PX0VIFMlF3zfCkyxEXnz4BbzNqAKiaziAWZl6nj4uXSbqDb0wIXpqXqJO+AmiC9E3YgSv/f7Kgzll6Hmz34G1x1NcdIJeADxaUWFBowRkZMEOsjN5I2sxJnC7qwXtYSijdWKwBLzdM3txk/f3uPhOWwHR9v2vZBAfGXPduHbj2piQerMoCngbXT+6gE53eJy0yBj4+63vwV5+X4AytU83jdz7TAQ/4xU/Gxq/pf7oTrEmDU5BwYXOhZ9fWnwcCaquIgfDjL76HT68u8fIPf8A//fpf8Gc/+SGOXPDtV9/gq2+eYthcYH9zhx98/wuIRPzv/8f/iUePH+DifMTd7TUePniATz7+CBfnW/zszz7H4eYtvn36FEJadhUpoM4F189f4dGYMZ5vICmg2doJYWEU+xzUUpWNQwv43IGS+8CNBckacIrNn5fqO7i/rGN97wLG+SEESAcrFBxYrNV9UOx0LPFH1wDWAB/Qg/wFwDldC+vrOHDgAZF30mUWkJCWIc4FqNpkw41rWM31ffBRbdKpxvZqA/QAnt3meHYJ7upJtxnLWvVSPrJlS8bq16DlBNC9N3Z9/a7GTc2EwBfF2vb4mK6DBAV97FfBSu+GDMqDgrR5QBwH5FH1HoXae+dqDcYuc0DvvE9W/9Y4+PQabivW/16/Tv+tY7aAq7oO7wPG70sy3b9nXderZJqdrf2qq2u9z/4srPzF5p2eBejBfgixVzX4Ga4x2HL/ndd8sjeg54ydITqvmtzzG+12lxepBh8Lhpi6wzIvPQh0Jzwma3K0sqfASt1BTq7rLM+Tc470HPPv9fGALM251meNX66fz/Tu3u4DAFgSBn1fkwFo3ecR6XZbz/toz6janC4T4R2b749HX38+bu7TkJY9G6QGBwXvX8cnQ0Q1HztjxwaxepPOEOEFjYLlvAqmEevP3pgROPSB0sqqxf56IxZvZqeBj7OGdX8E1sCdV+MPQMuPDbBJKWMcMpq436B7gnmR+fDxiDHAm9IpdqA2L4ZoDVO1CUevXhABkSUjnGVMzsTyjuc+jwqRuh4rQF0/MJqNEjHdwbgE031/mG8xDArMOwDv+0XlAJZEj7KUzX/xBKgF5IE8+a3XrUyre2i6b0lB2dSZ2aJAGrjLinQfV3ztmjyYCCgqcBRMi1M1oSOEqruIllzySjFChIHGgp5I0TJeLfMOMdk9KiiWzM6nIWE7EMYMcHNpMQFFXTe1CiAV21HfnyMQwNYQRscsEik4AGX2C4CB9P3rULNbDyL9fgGqmhBAdC8REdrcEBNjM0RtDg0AOSAwEJI2BFOJSwIFxu3+iNt9xWHKaKwSZCzOXFLAsLWGiYuBT0GrFQJhu3G95LYkAsDIWfUsp2lGKRWbzRYUKlo16Tjct5Oxj/l+f+i23+3WGjzvPpFXwMGl19SPzkSm9awSJ9wYiAbisr5fbN/H6NdtHQRf4gytinO2b4oBTMqgZJMCYEtgN27aeMfLc2Hng6LIIBqR2w0Ob59h2r/ReyBa2I0iCqKlbOeOgSUpotSi+0WU6akNvtj2RbIEA2mJszRAVPuRSNnGOSrwqXtU48UKArM+QwgK2IdISKJsT6GINIzKbLRzoYkmY4SsorG5PbE9ZqA7G7EnBEIeBrf8fR3HQb+bwSjzjOM09c7teRi6PzjX0j9ztE7uDrjmaLqazCaZIL1zvQNG90Fa2PmjshR6XYH2oWi1obRiAKpJrsSInFOX2kgxq70YTB7Sq+NYq8xgSQqV8Wiqteq7lgimHn0ik+fPJKIN6UptqKUqExJqF4Yhg4WQ46gl+lB25+aHP8Jhf8Q0FWOuN7x+e425VByuJjAIDy5HjDnh/PwcMeTeMI4o9dhFhOByfArSzX2twBjkrVU7mz2h4ecmm9xLQylTB2C7DyBaVaBNBDWxwq1qMz545YygtoLXb1/hcDwApLjG69evcThcm9xBUeKcMBpr1Y+enZpEgFWnZTun2WJ7YdFEmZ3PKUbEnNTGU7OqEwDB5GZiUukc8/kaN2uyyDgcD6jWRycYLsKWoMxp2+MhTSgwUmZs2g5Eeh3qkYHuS5ce0DVKmGddx/M865psDZvNBhvTmgWWGCBYgsAbfeY8YNxkHI/HFVagev/zilToWNWQs8llaMLdJX1KKb15Y4wJBOn6tQ4gqxSBslvdp7oP1vo96p9aWUQpYrPZoHG1NcUIVk3mz+xgq+Muocsy6SulhHGzRYoJw6jNVIdhWCXYucfbf0yWDviTB2kJoXdiVm2TOGSEISKkwRgAAnBFKwxOA2Ic1OkbIjaIuKKEH5+f4fNPfoBxvMCnn/8Z3rx6ibu7WwxZmSwPH3+OL/78J5imhBcvXuAwT7g73GKuB1ycXyDHgNvra3z1+98g8h5nG0FOgr//2/+M//fv/wbPnv4B/+qnP8HjBw+1oVfM2JydIdhExxBwdn4GDkCKhKvzCzx6+AibYQBvRrTLC5S5Yr8/4u52jyZAq3vVMWnNFkfBPM0KzAp3J0hL2jQIUjBClViEoGAOV2UvkqBKM8abOhCNGSFlbDdbSGuo89wBLgDIY8YYBzPcSjV/9MGHuL3b4/nT74xJsIAoNmWdsdfZZk1QWtPyLLiT2rpjvm7itDA4CGRlLCkmxCFhPN9i+PASOBsxtRnqP3E/U10fBPYd6yBdE8qCsAIonckDzxeuAISuEdjvTCBNS0PBFlyJgEz43L9fs4cWcGMBVRZGoYKOgJdERji3plnpcweUaCn/8bIOWTkQ94ENvwfVWlmMj5aqO1LnYNc9AOfey8G49V5cwAZnGJy+n5v04MBBqBOwazWe90Gd9TPpn+vvPQXj3gfeiCwMpTV70wGN9fuItOTA79tBNgdvnf20Bsv6YUIqMbAZByAHfPXsKfhY8auvn+FX3z1HShltFisbfo0hDXj25leAZMRhAL78GtdvX4PrjN12g6urc1ydRfz0h9/H69ev8IMffYEPPvoY//E//WfcHSZNUswzXn33FHIWMD55ACYFG3t3IF5YpjGpJuDS5KxPmkmJrMdSA0iW1hmJXiLL/tEe+HrIvAZTfO70c8FBqKYNM9bvW2tsref5XdB4DZ6tWNYrtpLPxfvWTk+IQO1QNGYaBBoE1qaNB1k6w3bd0Gjd/XZJZqD77v6zNZjY14Y4y30Bv5ffL02j1s99IjfSEwSLLbq/R9egkj3WAhIb4AFjna3tgjvf6+s4SKjfF5CGAewN5LKWUlEMVnFwyhZbv9Z7s3/Xet/ftwEioLDI66zn+v74nAKtq/sPQfWtT1eAffZ0PdwPmu//vINq3KwxnpzYKV9/J2vV1orw6fnlu+Q+qOt7kbl1LV9PrIiBr3526r5bP48l8Nj3oa1zVmZ4dzZtPIFlnfWyyRBMkuTddUVECxDpa4ZwwhLtfGCBJUE9CI19P/iY+nf35ikr+/HuebM6Yfv+8sTx6owyACa4JI2BG+w17sA9AJksiazzoaxGZ9A6y0Hvy+/ZE5t9vROgZY6wB/D9siQ5FICVfmb0PUXGfCTd+6ozbONuNlXNt/txAdJOmSHr/epz6XMVjV0KLNVTzsoRUUZJjBEhBaQc0ebamVbMrEwZ0+hrXIEquLktfZ0uwZNez/U4fQ0LMUA6pi7dFLNpJDYPbFQLU9nm1v5EsIBMNs9elkpEkGoJLREESidyGhOLBXl5GY+g4Ps0zZiNzZiSXtMrxpwN1P0W0YDdx9eb5SVjipei4NU4DHDGTrdxkTHE0e5X93WtBSDVVuUGcFULwjLD5aOio2pimojcjA0YTAtee1QIrMqHaNHuhqAYuEkgDI0xjCN6l/GQEERtPwVdG+ofNBAqxiFiHLL6tNJQZgZJBEVCSOie7jQzKhECE1IUxMzIgzL6A6lPQympxizg3QHQxe09Y/zO7tb1kSAIwkgk2CQtHS7uVgmAaiXBDNQG8Azs7yr2h4a8STg/T9iMA0SKljWHjCEOiCkokBwFxyOjFMY0V8ylwDUfj8eC46EihEG7wHNEwUHHcxjAbbAYp6AyYxg3mOSocYPwKsG0ML2850Y/d1ce7kkidBjNN9A4lqh2v1Kb23FP5tTSwNK03wi0mo2hyVxfx126QIy1GDyq0p+VOkOk9n3VhFFZJUyYG0rV7vPUigKQouXPHALEHuO4v8XbN88xzwdQYC3NtXLslAbkIUOC9jchsNmSirkWYyQKAhqAGSGoLnIMgiFrg6EQNEFOxghOOdg+AYDWpUAA7WrPEsDSQEGlLaookUgTj9oUD2lQ8FAaKBJSiKh2xoaUejPEcRz7/hdha1CpgGA13dFo2s9eVVamGaXMYGGcn59jHDfdfk7TdBJzeRnzogcLVFZmnvumKaj0QLJGc7C1VErpIK+vnwZtmpSTxs95jNilM9A6Tgwux6VrkJtgrtqQKJpuKbMghwhK3kTMePkGfMKSaiyMuRTzW/QcYvNhKCg4dpwLatUq3oLZWLjK5o9xUKA9KamoHRV4U2mMHYa8xTRPKPMR03HGG36tuuBpAwoZd3c3ODu7RMqjVRSgO3VetVlqsT2mewrcQHZONa5mmUI/w9j0T93PY7FGcrT4yoSmBLWqa0sZsgWtTpjmoradGwQNb69vcHN3h9Yajpbc8aQHRBOl7gO7RERrRasPgjZJjMn18JX4hRAw14JxHEEhYNhtsNlukYYBmuTwJLM25QymaUykcpalao+fWrV83zWUvQIDpsHuFR7meJjkivrkRIQhZbgHyg2dFd3BSLtn/7efjcfjsY8xxBute5Nc7UMUo96TazevCQ4KBKsP5izzyk2brtleaqz7NTqQvZZdyAmUsv1OY7GN+S+WS9c9zMoi9iawi4++NPH0SpieDDdPYcgZm+3W5JxMw7hXj+uf8zz3vTxNRYfyBn0MxGK9GKNKuoicgLv3X3/iIK0A0KzgdnemgXMAtudXoM0GL1+8RJsmUAqgkDptn1uFtIKhNlxuRvz0z3+MV29e43Z/xIeffYFHj59AhHFxdQVGwlwrPvzsMf7pH1/hdn/Ao6sRr94+x7On3wAiuDg/w/F4g1aO+PSjD3FxeY6vv/4KX375JebpiL/6i3+Fn/7kJ/gvf/dfoULwCdNcgZsjpFSk4QyUEx4+eYyf/5t/A26Ep89e42b/BlUKANV9Sinh/PISL56/wl05YJqOGIYBwzhiGAeUmxscjwd4EwrV14CWbECAxrZQTINKVmXExtCqrXUt1caqSVvLjJwyHNV39k9tBdIUBEo5K1sgZXz42Wc4HA+4fvNKAVlSdiEFUv25VbZZzAF2JicgJrAfUYMKpWv50ML8dNkEL8BFCkgXIzaPzoGzLeZWAVZG7DogXLNEtGmKA21m4A1gdTG1HiyTdEcnBNe60eXnEgQkUE1GrAAaLGCgH6j60I5SvrueRU7BM+amOjcWCAMwlrLro5quUvDI/V1QdR1krksF+rd6YIh3wTENgpd48D5Qdv+5XFeNjHWyzoQ5a8W7gPu93mdE3Qdo74M5fgisf3f/ed73LOugPhhbG1iNt93P/bL7cO85l+uhP6PuDb1ENKba09dv8fT6gOtnbxDGLa4eXGIYBrQiaIUhFBBJMKYBIhtQGpFyxLB9gMPdNVo54rvnb/D1N7f49utvcXOY8fmPfozPP3mCP/vBF/jtV3+AiGAcB7QokLkgsjpCDnn19SSinakD3RsHK6MTP4Sx0jxzxhK6cxaMtSy0NKrqY2vj6VqT6zmzRtnwMh2s7uE+iLd+3b9XX2fr3xMRWBGsvt68lHUBXFZr3hAhYVHtJQNip3lGQoBUC25JlF2Ahen2vsRFd4bdFqzszHL/rmkt7zT9u/+c99f+6bpfHn8tS/DHEhMOfPXPiEC3qIPQC5PRA8f1vhEDaV3oP7jOVQgIWbXTtPc21jHo8ix41yK97xnJQAfvCA4DyVV2513m++k9rpqOGRCgjmDHuFaffde+3QfU19cUk09S/IQsOeGg6vJqPXhbypv0/F3qenvp8ntsFXz8YPvInwcKAoidSdIBWllGluxIubfv9Ff0zrzadJ98t8haqsdt/sJclQUZXvb06jl0DS3X973HrPPZAYkQMOTh5Foe9Cpn8dQWvA9AXz9jn8deueL2h/rPfLT08xqAxhhV8gQE9aEZInW1Lp3xdtp9vZSCBkFvVmVB9fI9tglcBzHErj/s558Cu86I7wOhTDcXlobu70Rqn72crzvrRCfj4XIUIlopoAGQ7+mGaVIwM0Zvkw6wVKAqQBCwyEo5s4bsvlJw27o83327If3ZQ793iqHvkwaBtIJp1ua13nREgWQFq1OMiF4WLL6GfI61vFvLtLUZGKBgKiHCtZAVAOYVKAbctTvUqsEbDPQ5HgWCg60kHRvfE8H9lrDwogEglNKDSg3kNMmg/QdsXpjBKfc5dJDOpQ9qrTruCIAEiChtinNWJqQB9JpjtWQugGh+tIK75r/K0iDJiRgAEDgik+tSaul2TFkDVvN7A/Txri4zLh8EHCagTg0kosCr+RA5B1t7Opp5IMSMJaHCGtzHQEhkO1gEPYmhqxO+9P3sv/8iWzlDJGQSRClgYWQDjBoE4xjQJq3oyVnHKA8ZCIzKFceDgOKAFEcIF1DUUvJN1jCWmzZlCgaAuZSDlpwKFPwrCgAmwlw8FjGGkwgoZNSqLClxUH+1X9cvBW9rt70pabJkLeFG5HABwK2CW7EEAgOkup3BbYiV/Fr1fbeztjEBaKOw2pqtBZ0bxYWsFkOptNbczxJ0zrYFUFoDagFa1WwCE8S0TIkImQhoB7y5eYHru2skaBPpYRwQ89I7oNaCkJNV4ACVZ7Sp9qRICgDLDKIGUENMGTkSYlIAN0Ygm86oNjSz86vLnAliUE11YfVtmTSxFGNQrVjRPixEmuBydd8cE6rUPm8kS3NkQgAYqjdPSmrQ0n3p8020nJVuXwNUM3OM2tCKWDAfraTbwM9xswHFRZdc14tpgDpLnFSzVuUiFMQUsyOttZ6o81LunDO22y3ISQX2v0iaeGRa/N/aTEbQEoKHg7K8g/lzRMDsMiLQxuKKmYjZR1Z5iZSxzWqLa7VEh90TM1BKxeFuryvWtLnZWLXSGkRnRVnOgTDNTUvBkzag1UqMiBQyQBV1nvHm1UucnV0gpAzXfz87u9T4RtaVN2zz5IxYBfZUEoHVnw9L4qwnrEn1kJcKNd/LS/O3WvYo80HP9lax3+9xPOy7/z8dZxwOezSuKIVxOE46v9LU/kcHQx1LAIacFUPpzUShVR4IqkXOgmiyDiFnHKdJz4McUSGoYBCpjEltfsYrYBtSQh5H7HZnJqPQcHt3i9u7Wzjt1tIgFpc0HZdqyR0KgMmKaBWlxcsIxrJWvXzGIqvhbFr3D5w5W4o2A5S+3lXihJk7trPf760hGRZA1JLnKQ32b/2e7XYLT5hz495LBUQdCxERY+Oi7y+vHs15gHDDMA6d/VoLSDoAACAASURBVBtDxDgM8GatvseW/2r3B0WU7DabvE1rmiBKMapsCajff++tEhVDG4ahS2uUopUC1WRCHMTWhGrouu0OGL/v9ScN0ooI9nd7hJQxCnAsExoCShiAw4QyTahlQpKEs8st0maLUjXwjmJFHMJ4+PASQ0g4HG7x3dNvEPMGlLdgRLx89RoUIl69+AgvXjzDZrvD5dUl/vDV71GOB7BMaOUNqBUEanj5rOKXv3yKb5/+Abf7t3jw+DH+8n/+a/zLP/8Kky1+BqOVijfXr1CPE3a7LT773vfx7//Df8DPf/5X+Lu//S/48tvnOE4zNlvNpIIFOUY8vLpCLQ0vX73AZhzw0ZMPcTgc8fquQEAmSlwQRBsM1XnGPFekPKgAuHlKHguLwMqpvBkC4I2mxlG7/eaQkHNSofEywfXfSABG1QxkAEAJremB/f0//xF+/asZh5sbAF46aw0ZUjY2inpuAiulhoADQUgbStBs2VFwD7ZJYIeManMNux3i5YjNB1eoOam+mnWWjUEAz7CeOIZeMuqB7AL+eOMHJaY60ED9YO6dAoM2U+iHtx2uXWtSToEYWoFjfgeAA50GkpE5VVL750IKINcxxAJ4xah6VYq4MAjGaOvfF+yawQ6jBaxdB7c+LsEC5PeBQ10zDAtQpDgK++Ix1pv0Z13CNgdAlkBfnOlNayBAbI7fZcK6Zh+gelZrQDoEF6Vfgvg1mLoGTk7lGjRg97GIxi7s40fOVCGtGPayXXfIbUxc81BZawbUQsGcb1++xKYAT558qA5PCJjnI1prSGnUhBEIefcIH3/vZxh3F7h9+wovvvkSIgHEB2x2G0zTDje31zhwwG9++xtcv32Ox1cf42y3w+XVBUIgvN7fIGZl9rjemTJrbBbcIax6ALWijo42hTFAQeZezuEHhTOGIaJJjQggxQ7w+brSMY09aHfAhWLQtcXS94azcZeyZp83sTIgBZzEwTFzzt0ZAgVjFC5McQb3pmHrxmiqNemJAV9b+j3edEXtKyNRBB9nUGFwqUCrWrQcBFKtBMUCIi8/Wl7qwPt6WwMqC0DsAayBasbiXQBVWQJY8nW2JMaYWbO3ZsOXJmn3wL6Tu0LfV/ZG2x/2OZaTz9LquxzoJNNxQ4ogA2k5MChIb55Itu7F97ez4Po3rV739vcaRLxvH9VqLJlvQNdP9HXLS2lQsAy5DWpHI2X1nR1QeofpfArSAl61YeucrCO0gY/AKbN3DSL7dfSeDCwMy5r0tQK4tA2t5gmIlBbwEdIDbC+GXo+GmB10wAwLlgpPMK6fYb1MBFq6FlYl3l2ny68tVmK/SvC8O510YqNP3sMCRDInn+Bsv5SVlegNyZRx59Ug1Peag0F9H/hzoT/8yX3oGR6sdN9At67raWX0MSFEBYq1tFlQWdk2Oed+ba/4YQMnhUVLxUWsKRNps78O9iw2LgTVn1ySCdSd9X7/tCQAY6SlOaWtXz9b0NhY0jZH9vk1SKtBQLTEmfpYcNaQqJ5sjAOGYUCIZOXSGtixB/cWnJvJQ0+C27329WVjo/dgDXf62jJGJRmLjpoBq9a4jQhsGm7ecAXMiFl159w3UO3bxb4Fr3ggWDJcULlowjoEjCa9pWddhUhdaTcygmkyc6uY12Aa6bNr3wbpTXGIgjYksjJ0Pc+cwey+lCdSPHljZ6cztFxPWARDHuwzWPmIxsAUC+aSahMKqf/p/pyDL253vKmcMCu40oNBbcY3DgNSyqCwAINBM/0IUICMzOM7HhvwmrUZsDDGIWEzEkppePHyBg8ebbEdR9TCCNQwDITNEDFEwSZHZLI9ToRNMtaviBE9zM++Z5vetSC2/6EMwvNtQMwRDYLKhGr7P0XCZgT2UwWgzWUEhLOzDfYHQZkJd3eEFAcMSTCVCgkRzAnNdGFZIubCaNXZ2bBS8AyBaoW2OkMTcRor3t0dMM8Vm+0GDx7s8PL5a+z3s7nECvpnO496iTpp471oiYrWGg6HGVeXV8gx2drWxlGEZhIDFcIFYozWmDNImoJoBEAKiBKIFKiiICDzu1V7VavttCrQGhwZIcKZ9DQQChOkmq9kmyCmjDYfUOYjapkQSJMhpcH2IpQAIBU3L7/By69/A25HhEwwJRWkFDXhRQIEVqozSEuCJYIoaUMkaQAzcmKMWYG8HAU5Vmyy7rGUgN02YbPJ3d9prIBGMw3LZix/PdpYK2e4IQagUcQQTdPb/KrgMUawZDN0vYLUH0jJpbiMrBRMu9rISgwgbMhA9IWNH2NEDEBlPeMO0xHZGujlnJCj2wUtfa/Hg8kOJm0ihkX6QMH8AQ7wa4xB7gpZJYACwVoZwvCGZ2zAJAurvIJQtzl+FpZaFUhK2ZiKEaUVHwRIWBiQGgM3tYFQyQchjWtTSkADIqI9/2iSGyqr4MezWCWLZIGMjDYXzHPFXBqOhwksQKnS5V1C1OqbzWaLi/MzTVyFgOl4wN31NRJlUKsgVnZ2HnYA7LyHKLXTwLvGliRpFYQGkRnzfLSYQwlOOW303IxBIU+u6idZszxujFImHKYZh8MtSlHweZqOuH7zFnf7OwQrKxQRTPNkhDBNwIVIIBKrBNCkgrL1FXDcjBtEb2QmjJSzniMxowHYbHaKLcQMxITLqJIhtc7WVC9gmo8Wt2WEEFGZtU/R7R1CDDg7O8N2s9Wqt1qRYoYkAKLVy0xKPKOgW1cbg64INQBICKUVlFrQuCInrRKr1uxsPuwtYRkwz5OtOcJ2u9XPh4BhO/b4nJm1GZmB6r2biAHVrRW0UvH27gYgwsXZRfexx9H1YdWvzCkipY36yCscQETXVSmaeHOgVlgwTUe0xjhME7whoceCw5AxjKPJ4qkPP2626BJ/NiilFIQwIaeE43Q0wFlle5ZksUqZQICUdc9qFUBGziNy9goiOZFyOB6PyDmjml/d7iUA168/aZCWYGUKAtzeHlDQMDPjrhQNDLJmpNo0Qd68xdmDiJRGDTyhBRdTnXGzv8VmPMNcKi6HAYUJ13dHHI4TKgNlBn71j98gZsLn3/sQZxt1MMdxxDBEvHn5DG9fvcLh9hbUCIiMIUV89tknePLgCT78+DM0AX72l3+NPIz45T/+AqUUnF8+wPNvv8M4DPjZX/0FPv70Uzx78QohZ/zgh1/gN7/9bZ/o4exMjWQc8NEnH2G3G7AdBlxdPMDT+Zk6t8EAVhsfBxWFCpp1x+xdaiGLlhwtHYmjHV7apVKNjWuJclPDCFLnw7VddVOYS82MMhecn1/g+1/8CL/7539GmY+qZ2dgUCTdtJ7pX8BDQMCIKWLc7BBpxPWbN2htMparlcFaude43WD78CHaWcBE2mhLiMGVIFDHfB1wMzMGM4LmM1oQ4t9vgAN8IxrIKWKgizZUAHSchagbI2dWdFbXyhNdAv8FEFgDFaqqsDDvHLRal5aGSD0w9/KhQKEHRIYBLUH/ijnlz++GawHVliZBIWgDpQ6Grz57CrxQvyey53fgw+/bwysPgEBkzo8GX8t7lgCzs4w62COnv/NJEdizoa+ZEzbnvc+tf7ZmZen7HTgRJ+b2x+ufBy3as2sMzQK7ZrpYfn3X7qIQcHl5iXNJ4NuG6+sboAmO8wQhwm5s2G3PsDl/hI++/1P863/3v+FHP/kZuBzx3/7mP+G//e3/hadf/QohRDx48AgffPgxnj5/irevX+A4Ma5v79BqxWaz0bLE+YDSGkaYU01roIn7gdvL8gA9ZEuxIE4ZVWSMqhR1bFKMYJ8/c1TZy33Z3TfR3wdjmDMv82gs/r6WZdl7PmdkUh0g7kCqj73Y3MQUVuWd1IO9zmYQhjem8MPUWYGMhcV3skZMF4oUrUIoFVIqZJrA8wwiZWP4+g5xtX9lBZo4+HLSoO19yRCBNzrx0iGfI2ft6bAtWsj24e58uJaSMmJw8lp/53qv+3MC6MyT9Rq/n7A5BW0VSErjCCZjP4C6FpY3MzrZq7D9ugxVv5YhYCeb7T5Au55DDZTdxlG/npcQ+Xq+P95eRuxg1n0Qcd0tdf259TgCbk/X93NqU/yZPbGxvg8FluSeTdHndv1Af0bfJzDpmvUecWafVRYaCGL7SJxtLPfGegW4hbWNXJJskQi80qx1Z3HdcKyDpauz4v5rnZRZVxw4o56grKRgwGPzsnphk2Yy5iv8jARAwQk9GrzJ6d5yMPak2aG/p59pvl/UdjOLlT1n9X/gwPVic9Z6r84Y8ff4tZKxg0SM/YolobFoLS/j6Wt3acLkCUJNAjArW1XAqNWTT9r9HaQ2db1HgzcB62tYA+yYtOu1JsRaZ1xpQxqtkihlBlXShl3Qskpuxn5xKRtj1KztwZIQsWYsQP+Mss8WphlzRYgZgQVVSrflft4vdthYcyGCKBvLv9k21SYpEDE/1le3+q3NAAk/azSB7VNNcHYnkcppEZEC4Q6syqrrfVMGaQyaiEkp691SADPZZzWRwTYernvXWcvmz3berSHK/qyLvp30taIv1X3kWiDGEhJm9WVX36NAqCeBV/bK7EKkYGWo1NebCNAqg6QpqzQlDFGlBUqtHcgb8oAcAoaBkDOhMSAIOLvY9bMvpoBhzBgHszmVIVEAS77o3jANaqzX/poO8T94qaFGE9VUbq1hboTKAYeq66qUAonAOIw4HJSRV6p+jsCYZgEb+ytlQpGIeW4oN5OeVxQRg+rQCgjs7Cv4+ocy/Vrp9jfmrNqatWF/t8fFGeHhox2Oh7eorAxPv3cKhASXR+K+R3wPHY5HzMcj0i6YPI7GG7VVtDqhN8diMcY1QIkg0IZAqpMREGKy5J/Jr5guppdiK8Ncwd5IASkPyOMIYQfzAwo5aUH3VGsVd3c3GqsFhrSGY1PGd2sNLQhCbah3e7z47ivI8S22CaanSlq6Dtd8BJzJSAwwT5CQAUoIGJAikIJgyIRIjO1mQAqC3ahzk5IShFKMCJG75SAocVssSInBJWmk+7cETfJr5SdpIodb9zvSkFBLU7ttNsA1gAMUsG+tqq0I6t3GoD1AilVmxuDVDAb+UgQBqFNV+60noSV7FiJEqcqUCyJIRNaUzrmIUGJVY8xljyaCUmZshrGvoWB+htrDpECaeFWCKAsS6utFilZa770XlGUd4ogcop6NItqwjAZlM1pyILkuc9+aypD10uvpOKOt1jUzo5ED5wrgnZ3trGmeJuiU1CWQIUHujmAhbEbCfn/UJJ2dvWWewVUBwBQJm21CjjrP83TA4e4tYmiIEZiOysgNMUFa01jYNEJrU5yitYZ52qPVGa3uFaQVwTgm5DwgBbV3rQBzmcBcwAzUOmE+FpR5RmkT5qpg/93dtTYF3O8xz5OetaUa8SaBSCzhaslPJp0jU+SurExZCgExqfRYzBk5quY/yP0oXcthSBg2G6vUCAgpInMGsIGgWSy/7X5wSgnzPGGei/quAuzv7nRcSVAOE4xRhhQIu+0GjQk1wOK+aKQC1X4Wa/YMsl5HgQA0ZbkPoya/WCC3gjrNEAMZ/Yxi1gZ4Xlnj52EyaSmKKseyHTdaoWz+AUtA2GyQh4xj0VjM3L4O1pbSMM+TJkJMQqRjGSsfXZuPZcD9TFni0WqJNYLGVNM04XA8qq60+T8uOxCMFeuJ3JxHTdpb9/Y8DOCqGFetJivRBPOkPZPmSe976iSxU7ZxSqlLNWmzNPTx+B+9/qRB2hADQgbqzEg5IQ9bZDCqCMSyPt6t73iYkCjh6vKBbuyUQCGDC+N33z7F5qNPsRvPkYcdgkQ8fDTguL8DmuCLH38fN3cFV+cXePH8Lf7hN/8d0o54+OgSN2++w831G6RAGFPE4ycfYXdxht3VgJgjri4u8eTJEzx8/EQz7JTwL7/7Em/uXuD29UucXz0EIeDXv/0av/nqG0ym40LScNgfzPmOyDkqiBoy8pDx4MEV2jzj26ff4fXbG0xthkCzSQSd2JxH1BBxLLpBFViUHiwAVlpBhCFbOZRoYzEWLXcQaGbFG1qkkIFwWjoPKMNRpIA4QgLh5uYODx89xvzZhG+++xIxEqRZmY0HmjAnDwpURtISvSFvkcI5Hn5wjloKrt8coawENVwxqeOxe/QAdLHBnBoaqezFbGxh77zrAFCOCQ1tCRZWYIYHQR00ETFdEHSAMYTYywlVqJuW68OCX/UYesCqAeNpcOkbrgMTvLBKgQVc6KAx9Mh31p+ILE0NGN1JAdTILyCB/c7K3Z0h5YZhYTH698q9vzsIsQRl2iXW3mOi74t0AToG1cFbe3ZnYxKWsXhnHGQBFp0x0oEFd147eLCgpfcBE7+mS2KstVzWAJa/b/2Sfp82fyukRMSbiNDJOK7HjdklOAJiFYyUMN3s0a6LBZ6E46Eg5IiDHFBLRWkR5Tf/gpAu8ey7bzDkhLdvXmGz3SFvRrz87hmkVXzw4Ue4unwArupMv73ZIwhwKBPibocv/uKn+ObFsw6o6DrWBeKlSD5HYutZ/8nGmiIMMSEPgzmBZIcMI8Rkq9BsCwz0ggI95LqPdh1PGpAtIBFBNhBrDXYs4D4vgFpQvTxpDARr/MJAiMo6XuC9FddSlkzs/deitSz9f40ZKSbTntVmCVwa2uEAnmbIPOuaM9Zu153s2+J0zZ10EJXTA3j9Wta+P4c7EacyBu9bqyfXkmWNrgEm/9z6M+7QEN5dr+v3ve93zrgV3+PO0svaFEQMvKA+9/dY8LRm+0rfO+JoI1Ysz9X40GqeIVC2oizP1qzh5fre74+zLnfp9lITKOhMmfsvB2zel9xZvzr4ugIN12N5YkffGct3r9UHCugMSW9qJ3iXobseJ/tHBww9kbS2Wa7N5UClA+j+fj8XlutqFY2ATsbhdJ0tsMv9deoOMkFJoBqCYvmZ1v73RhOqp67nnsiyi73KAf3fdj+BILwk3GKMi878ag7WmrJeKaBOegNVZcuw6dmtkwyL1AvgJY8+Bl1jzBtu3AP6782uBcJLInO9TpcGmvpqxgByFrMGJeszWjrQ1yVBoMkeEUGOWQMsAIVL77ANW0PT5DqGNj5WSut2myV0zfD7z3LqvyxrMFoTn2JsZJ3zgCjmhcq6ZDF1n2NZ0/psAearw9hjot+TyAEMPVNFqgKarOPHzEgxI6cBwRrpMsMYKYJAKt3FvFo/ZNUYq2DNGe998QnQrDLDS1QdvBdbm95grlQFZkIMykriBgTfB6f2yfeKGGCkv4tWvp/7OFcrr2QAKZmmqDPZ4d2+F/veVQyY+/z5f00EJHrebcYBMQSUWZmb203CxXlCilD5DlsStTBECOfbAUINMWg9VGPGVICU1P+93s8Yc8JAhEjqHVReJZD+yJn8vldP2LOx2mNEqYwqhKlUIESElDHNFVEUrOMmuN1XEFln7sxoxNiGAIQBlIAYG+bKtgYiAhkQa2tQGXy2nRqwGQakMVvzl2lJTrM2mPn2uxkPH1zh8QdXuL6+xVy0kVCZjgqM2txqw73WtUdzzthuNjju7/Dm7YSYFVCf59lYe838dMJcJp3/WlEmBZiblWpbAIKUY48vpnnGNE2o8wG1HBFIWdZMDGIAISAeEoao38mijfvmMkPAqLPai1YmiDQwKXAhMfZEfOGGcryDTDdIckCgCWNUPVsKA4ig8ZyolN48a8yWDMQMUD8noGEcFHhLUTCkhCEBY47YbTOGrKxmBSYtiHHgMQiENWHTmtkOq4ALMUKaalJDPLaCMm2hzHRhk8/zz9h5s0gQtH7NGLXhUMPKfxLp8sosTRnRfv5ZNUEMQIqjnlNR71VEtBqiMjIF5TIEdBsSUsTxeMQsql2rzcp03w8uMxhUsqGWonMkwDCMCCYL4caLAqwheOq6p+uElJ/D3BTIrFyRhlHPQ/OXJitF7w6p2Ti1L7pd/JzPWfEAiJ6ubOx+mP5tiLSy+4JaTe+zzmDW9V6M/DXN2uDPNcshBbUO2GwG0xU/ICZBHoGcI457tUPj5gyAQHiGa503qWAWHKcJh7tbcJvBdYK4ba0Bc0w43h3BxjouZUapE2oVNCjjdzpOOEy3akPAqHXudrqUoiQVS4SuE9kpBkCinlMUNTFMpKAkCHGTtCIkECqAISbdb3ZGRSLzVpS4UlrRZmnVfSbdFzq3qZ8HgK6LnHNfz/2sCEAOCYf9oZ8z19c3WuxksjnqaKu8lj6HNoYHtNdKTMH0pzU2iDFgCBHnZ2eYjxMgXvHY+rxP09QZra1oYqw42AqtFp4Ox671Om42yFkbs6c0YBMTIpZ4wZ8nWIX3NB1xPB67L+hzsJYeS0Y+vN8UbLQEil/4bKfJhVJKPyOYGdM8oxgJz+dar2F+TgzIgFU+KdN8HEcQaRLIfct1rOh+0H6/P5knBfu1wkDJH++tR+yvP2mQFgQgRzW8KSFvRqVhE4GSln/XUnA87MEo2KaAUGcNQIQR0oAWMp5f3+F/+mKLmLZ4/eoaFRGb7U5FyKcjNrsBGEYcru/w1e9+C0LDo8cPME1HvHrxArtxwOX5Dj/64c/xyUdf4DgXTOWAKsp02x8OWqIQFTj6X/7Xfw8hwtwm7DbnuLvZ4+2bazQpuD1OOOz3duDOaHXqWi6RCAMiJEbkGFAk4O3dhOtjAUMBjWjjEkiNTrMMt7pBwRhyupZCUMQ+YGHOQVTMOYgfhGTDHNRdNieTAT18U1ycXBBaUOZhLYy744Qnn34K5ICvv/oSUhuGcWOsN23sEoj+P+rerEeWLLvS+85k5u4RcafMZGbNVSRBQQ9Cg4IgQv9A0L8UoDcB3egHDQ/SQ6MBCS12gaTAri6R6GKNzKzMvGOEh5vZGbYe9j5m5pHZVD+WnCjeezM83M2OnWHvtddeS2WtnGqw6KcMxHTi5vYlp9s3nM8fOJ2OzNNMrYXb588Y726op5EcPdmZW2POEFhZm4bNrADCVaLsNtDTsUuyLLFUkzXRw6fru9mmWG0R7rVwOnMBFFAqpVhAv2fTWMs1WxuKoKfe0wS8J49rgNAM4HHgRQ9UZbLtGU7XQE1PTj3XiXb/nm/TWNX3bMzfvfbS/vp6+7lq1XXm4wa69mRuvR46sH1dGdp/7sqc3G1Izp6HPkPsEHAWKHUgfmPU7kHf7c8tWd2S/+vr67/fAWrH9r1+fR+UnljuPv9q7nh1V44F6nnCNdUdmpbFHCQbyyXDEKk+4xvcv3vDF7/9BdbIiDghLxdqvUDLLNPM129ecziduL295e7ZSx4eHlguF87LzLObl7xrMzkIyRrMe3WwtY1p6GzsdV1szMoOrje0GuocXEp39oU0jtq2E3Wuenueh5CITRnYzWlxoyL4FNQxuQe9zoJh580ZdAPJdR+xuesVnK2zVrCVWVagwY2cVOPMWSZZ6zqf9sDZUzDMi18N/Rwm+u40UPRAy4VQBZkW5DJBKbjaOnaxzc3dnNqvsQ142ViS1+t4E33fMxE7mLv/rLXbuF3/7OnraTGiTz5N8q5Blqeg47f9e7vHbT/rID4+EMYRYiSMA5ICzlrCnXd61j4Bl6+AZUXRr9j7mx5nf/ZytVf2/dJGdd1X99e7gUb+6r89lTJZn5HIBtA+eY77Z7wv3OxBtW8bw6fP5Bv75Pq7189xD57vi2WtbmMvuiF9c4/5lnHe3784i9/7GjOQQaoVGIOeH/qzjXHe59Kq5YwlxKZHuo5ZL5TJ9ZggsoLKnXHTnLX7osDY1vmxmUx1sM75oNdo+704sWSV9Vp7cLzfkOtuv9+S7C3hXp+ToM7GO/atB+16wK17XQf29XevTc9WYDuGNah/+lyu2cZbotC7dZ6Cduvvmau0NzONFYR1XdtsK8DitXXdoYVt57XAthoYgcYvtaAk10pvkfHezI1CXOfnym6JEcStAMgG/F8bvvV7E7Hn6tXzYZMP2lolU1REwulBfjU+Wke3hNCLmlkB2k3llZ1q8pq9YLjOcVDzn8PIMJwQe36tydpmTL+O3bXrVDVzmLYrttFjFAN8TKLE+Q446j071EhK91mHS9qB5pwyALu2XGdJ97imUtc13djiQbys17ffCzRBVtYjlkTHZKBQ3pzft3vaMJX9cwoxEKOC9/M840z2wHmvHTgeHKZb62CIgZortTokRTZssKGMOh2z8aiM7QAckrWNt2YsI+iz/uk++fTffVRxsnoreNFCxHEMiPMKl1t+0SRwWSpYZ9mcYZkz4yGYM7oC2gBj0vN+yNpSrQVfnaO15JVBKdaZJtKYLmUFCS+XxryouVIpWduAS+DN2/c8f3bDi+fP+Prrt1Q9vMhZjaqlqf7mtOR1fd3e3uq8Sepa/nj/gdRNXNHxVaBEgbtaG7lmalbphSbC4NVsSRCWxbQOW6NUA1YotDpB7xxyDhHVx5yzIGmE5ilSyTVT6kJthcfHC4jovtbNpURwiOYaLdIqhLngz28ZlzNzudCcpznHPBfG4UjJRYs9thdJK1TncF6IzjMElazwFKJ3pAApOlJwHMfIzXFUcEaUcNMZ86CFSJW+23IVwKSlAO8py6JmS84rA9BtZnm1VMuzLB6TTsbR1R+8V5AZoSldFxHNi3uRsUmxvEcN0pydFd7iyjCMZmqXLc7VnwkQ0kAIoueNqIZyNkLW5f5R4+yYiMNASoOCxFXPvK5H3lo140TtcJ2nio/QQiJ1oWjLolpVRnX0BuG0ZgZQBqaKmHyE4zLd61ukmcleIIWw6myLCAFHzY2yA4yCt/XmnbXJK0CrhuR1zb97nl1q5Xy58Dg9UqsycmmClEzNGde2PbP7wiyzmtxpEU0YxsByWbhwISZorRcXtTBQy2K4R6Y2NTibLqod2/JMyWriBdXO0EjA0iEHOc/MU6Z6JbPVWpnLxFyUHR+Czj/vPN7OBe1U2c734ANiMiXOJ6ByOJwYjyPDcLD9tOKtq6c5NXqMybpgpFHtHKui9+Bx1NJ6ZGaxgrcL33KfTQfVX+VCvcA9nA7cnm4oiO4txvjVKaKdFa1U3XdbjcMpHgAAIABJREFUY54mWtE98TKrMV6KqsMefCSEBMa8Tj6sxev+v8PhwPPnz03u5aJdBra2Sq5My8KUJ/KyUCzWKqVQRfX4RQebgwHP+1xPWaeRw2HEe7+ZiZXNW6AXYbXoVtf53DvfAE6nk8aWgkl3eNLpaM9R31Nr4fz4qATFrh9Nl1NYVra8W3NdjVli6Axe7bzfdzD3zpqSFwRWrd5luaz5UI8J/n9rHCY4JI6QClkaeZ5wWR/sUrJpowhjTLgQqTVzPi9I1Qp2GE8wHHhdzvz28y/4Z3/2z3i8NNOEg5wbKY387rcfuL+/cP/219wkz2EYqHlhuTwwP95z9/yOTz/9jGcvXxJvAzxMvH3zlnmeGYeR12/e8IMf/IA6PTJNF+5unrEsC3fPbpA24UPm+YsjrR3wKTKOgdP4MSk6pssjv/7Nb4gtEIfAvKgWSauOqWQupbA03ZTLZYKWEee0/aXqRhOsCuec0syHpDo/ztinrRY8emAEa2NQIXaMpWPt5dJp4lphaSJItQqiC3bEGTvOabA0LwsvXn1CngtvvvxyZWsEH5BawQSifYjc3N4R4oAPiWE4QYi4eMCfbhhfvSCUjNA43d1SPCxeqPb7zdikvusFYu2hrDjtE5BCAQJp2prS2X+a0KxZoG0oKADntsSpVHUYfao9uf9zDxD43tJtAZ290YKPXvk1tuIO5Oi/r9e93UeTTaB71cm1q+6/390TZX1uG7CzBzeuwY6220h6m/FemL0DSjtJh8bV53RNTkO810Slv+cpkLOBo2xJ0ZrI9TbGnsB1lvJ2+Pf2J9gA4D2AdS31wJZE7kGyDkrtgZwdSN7ftzKkZffefl8YwLI0lvsFHjOSG/N5otTMs2d3vHx+y83xyN3dM06HAwFHFmFpqhv2eP+eD29e8z4/cp8vXKYJDxwO2tLy5VdfkkLgs08/5ewdl/MjL+bCuSzrday6PBhLCVbtK2xNdAmCnE38vaqxiuqqabV2HAfGw4HQgVEbi4Dj6Ec+uXnFKJ7gInEcePv4nod8IQdhrlW7Gaq18Fvw0eGHHvj2hmgRYZkz+XFCpqxMWrdpwE6PF+JhJAzqsrxvhVZn7G8Cc+sctkRXWltZ6BhoRWnkx4l6mRWcFWV+iFOzm/163r/20hl6kEqPka/mcz9k9wHTJmPypJiwm0v2UVdA9DpXd/e3B0b626/X167F9sl192KFc/2aNp1F71T3tYagiZYzkD5pp0QaBjOeFDbN6x0429egzZ1qhTzZry9YwaP92PU9di2YrH/f7SFcj8t+bL4NjN6/WmvrnHm6Z/e/Py1g7f++D7K+DTzd2v03Zqyyxft+zvq81/Xhr1mtoPPVh3D1XU/v55tAu9vG1DkL6Pve6lcwFQzQXwFk1fIEZQf0q6gqXc1e9qF3e/jdWMvuTKvGbPXe9JODAlmrQLF0UHiT/OhAr3fGBGxlK8qhwL5HE8OGBcq7s5G1SAKwHx+u1ouelXF3dtih7AzQtvXwjQLKjrkdnf/GvHl6lmrQvgfg4hXQuT+bls7c73PduRU86K9+FoPGCZ0p3AEMb6wuDYMc1IKjJ3EG1LftvmotOL8lVOu8sqBpKxADzl3pAbNbV8r4FGIazJS3mbGpJav2Pm1nVQ07DCBwWLzZGl6UkSi1qraeoC2aTf/dYxjpc1GqzVVtPWxWVWuWvHVwU+z86HrKCqBua6e3fHcmUTDweq9X38FVaRDTiBrzsj4H58JO/zavc0os6fNhM27V+LrHOAoI96KGJmibzm7vPqml4mOiS+KAUFuhF8db80Ba935Q8kVP+rWdvhqrW9uZt7MDhsGzLALikFFbcqfS8FXHLkTwXjgdAtG71UgxRY+rlcE7BqfFH7erofynMmlt5eiYGasp2Pm7sutKIRjDKAbP41worSmQ5ITL3CiPKvmh3lemdRgcx6MnZAWYL1MzRjJgXQN4j0h3C29M84VxPBBiIE8L83xRpqsVc2JK3N9fePli4PnzOz7cP+CDOqhP0yPBOXXpdhfO50ecc5zPZw6HA+N4YJoULI8hKqOxGLgrbgWLm1QF+8pCqbPO/TgwcNCJY2zZFYyl4V1Tk2HxVKwN3wOSQcTMm6OtAWMT14rHmPWySdtgQlZVClXAlRk+fM3jF78g37/WXFC0YOUDiBRq9SbXEmzsPcFpUTx5x+C1EC2tEV3ESSOFwM3tgeMhEQctfvkYDfhGC1JssVuIAaqCZXquqelgzlkLUuyMQLs5kq2JaAWj4LWY4lGA0cegRmd2NgcfKGZM3XUpV91tPXJMP7rhneooC0ArOBeUXWxza4havHJ48IE5Z6QWXNOxCSkwpMGAJiNMeDXanqaZaqZIm7SKsfudVzauV6ITvhOINhOyNonFx9HOoEDwiWj5fxwH02KHmBJdMhE7J8XyX3Acb068OBwptbAss+4nreuZm6yHoUXSjSgNKC8Wy/voGI4jInC+P1PKwjIvNDMf6+fnlrtggHNFRLVOz+cHUhgIPiFmSvpmUS+N1go5K5FrXh4N2BYe7u+ZzmcClZIX06YuZjoZCdGh3jUN54SShWYgrs4BIUW/SkU6UWM55/xOInKL60UfIlV0brjgCWkgjQdcCHjxIN68FQYOg+n4+l74bERp2orflFUbXVi1yr3N32WZmZcFZ2d4N1x/eHgAY4DHGNeiYnNQXGYcBgo6b6IPOCsANzuTuxGfD4Fjz//AOhkmfSatUvJMYyFX3YucCOMwrnm2dnMnhmGgg8Q+dpkgR4yN4TByakda2VimwzAw54U8KbO8KiXeSE4bwOpNMiFZV0GMkcPhcJXr9KIpwPl8ARyl5DWu6+Dx+3fvSdYZJFhR1CQfOvB8c3Njn1lN2kMLJ/3zFPcQA4stH2dBrDNoD6Jja2YYEike12supax6yhtAvHV3fdvrDxukdY4aIm5UMICgB1Oe8/pgnDRccIzDSK7FDGEEJ0pDns8zVSr/rhb+i//8z/nks0/58s0HhuFAzYXT7R1TLXx4/yXPb2/5+MULHh/ecjpE3n71K96//T03oyemkX/xL/9n/uGLX1Dzwny+4Bp89tl3+cGPfsRP/vQn3A4j8mZhfvzA119/zfO7n9AQfvnLn/Pu3QP394+8fveW7rBbTVtlXjKHceTV8YXJEjjm+cL58Z7cslYYVZlaD2LnaeJoVdRB3iuoGmMP/HbmDE0ZZcF5xFuLgldnXI+nSl2Bs7V10oJM2pZGrAvDAvsmgpQKvuF85NNPv0fLjbdvvlbpAwfOBcKQGI9HhvFAGo8453Uz85GlVcLhRHz2And7w2EILGVhDo6lFRbTNPOKMvSCxVptVQ1bNEHZhYx7gG+f8PckAHMA1g1Bq4pLVfq7S3qQO2dMJCsXdpZsTwx6kqMt532MuubmdXN2/y5NBtbZvSYHDVEjhaZAOt7a/5CVYdB/t393d47tH+i9shj3yaF+955BZoy2Dj441etxrln7jx4+a/KysmaNqW3gpYKeO6D7yRzZEsI9E5F10+zV537d23PZ3qef0aGEnlhfj+n6rLvzMtdsNzXEMUd5G7+ejEq/XmEHnHdwuD/Lp4BOQ2xfqZcZuV+Yl8wwJr77ne/x6ScfcXc8MPrAeLjRRCp4ploJt3f8+X/1F/zsr/+KL/7h7/D8kA+XC2/evufD2zd8+foNuajhxTzN/Oa3v+PjP/qYY4E3v/wdw8fPiHej7ns90GlPxt5ZS7XYvBFNpHUtZCQDYpp8TtkH82XScY7KeA/eMw5Hvnf7Cc+HE8/TDdLgYb7w9pJxUlUfit6S47rMJsFp8FlFFDjFqrdex6ztqqwBrcx755Rl1/R6XGhq4GQPqQMH4jr8uwf09X/OjL6bKBDVqjIi2rzAUpBphkXXd2cZNHGavLXNgGg/V/fz6OnPnhZjvgHqdXDrinV3DTKu63T9Dq7eu63fb2F0X72eJsob+LQBPfaTPYhq9xxShBiR6Cmu6zZ6pnlWwwW/gUNb8cLWzH5fQszo8BrEFtGAxzZUHet9omUAuDLz/G7tb+OyH3i3mwd7NtseyFZ5iW0P6j9Y2+J3Qd6+qLTKdPQ2qKt9Xmyrc3STLVl3EtbiRC+69R8ppraNE2x6uwBStJXS0RmpT/ZC71bwcz/ebLexBtn6XV26Rp22fegM5z7HxMAfrr5HZA/Cb+2Le3BF7Dn2gFW/UxnM27zq0hkKyikDMRlwvq0XPcPatlddPR+7VvvvXd93XyToDIo+OH1Y9F7N2Vs2YLwZGq1AjDG5nd7rvlD6lFG6FWFU87Wvc01y227e1TUW6AVZvdg1glrnr3POis5bIbnrHwbrSdcOCF0v/ZpKNbMUqWQDX+jspJWNa09FxIbGU3KhG3DqGei3c7yf0aJMqLXgZHRWH8LK7O1yFdGkF9TESFeBOs6jyYuYCZy15iJ2rs0XRBqL0zUfnHXkDMNKDhCgLjquaRiRnMltokhVc6sQiTGtcg/eWRxsc3KaJry1i9NjM2mI17ncalEdV7xKONie5n0whpvFIz2JEjEAXZNaHaqqZ4yZjnmn7MVaC0vOa2EkmLYoeHWTR409vfcMxrrJOVNypqRCrlnXZ23GMldjMESBjGogDiLM00SuQTUDl8yQ1DQu5wmks40dc/A83C9AJEa4vyiLK42+e7pRijAOjseHheMhkMZAXirDaO7TtSG+t55rsQ+nz0pjpes45OqsfPJymMGTgLYgw5LtHNJPJjg4HQKPk57lISRCSNSLULKjVGXY4dWDoyEspbIsVVvejZmUjb3nop5jMTpayUyLMrvG45GUErVm5kk1ClsRLpcLp+OJd2/f8+qj53z00SsezhdiTJRamR4fSEmNmdRdXI1qSsl8/NFHvP7qK6Q1DodntifpGait2nuncm0F9qJA17LMCDpvnPc01wxkCfTYvdkZpPmIAkFOhNB3c1uzzgnRe0r1xlgT01IstvZNRsdVhEKZ3pFf/4r84Ws8VYtCzhNE55fWalVOIedMSIlaQaInpkQMXb5Ajeuid4zjyIvnzzgeIyHsiiH2f51hrVuV5vHeBbqEXZZCa9t50c+eriUp0ohewVAJulbF9Gt7UaUTEpxT87fgw8rI6/lIjFG7Q2vFYXIFNqdD8GreJlXZpK0QvScGXdepnwsVpDoGBiByOkRiGhmH0UAmT84Ly5JVT1QCfkjK2N3twVoiKQiN5ipVZmrL5LxpGnfPiB4zE3WfS2kkRpWmCCFSgSGN3BzvKDUrEK04MfM82zPQGHSeJ0otqzklQVnaKumjYygNxJjKKniwdcpgv3cIgSqOkAvH2pBWtRO2qTa3oAzVaOdTy70DSIu/9w/3BBcpSyXGR1yIhHRQzwrR1vqcF5b5TC2VXDKP9x+oOWuByToL9QyD2rJ6cbhAlyCq1Yr4dlZ70yeOBph2pjainSIxRWNsWywQdN91Bo5XqcRh0PVp+Uw/y0rrnRGOkILllz239yTvSSFd/Tfn4HC4QeRGmf7eGbBq+ZJTIPJyedzi09poHqYyKSPUcrngnYG8rm8Pqg3r1DA1hWTYkuM0jNzc3Zh+cbP2fbvf2rg8PmoHZNt5xrDFmo1OFBMFf0NUAiFyBYYeTycOcqSd9LzMrZK8Xxm/zubnPC/GcG3rearETJWb8LsidAiecdQ4Yhi0SK+dA5ZPNI1BlKhkjNZ5vjqzYkykYSDF1A82QvD2byvOB+FwOFCKSU7VTQ6veySUohq9l8vjqnW/N6SPMfLs+R3TvKzr75+qd/5Bg7RNtNoaRnVO1APOEdNIc7DkiTGonk/2MPgTuZzxQRAxlH1ZeNMWfnb5wF//3c/57/7b/4zJR/7xV5+TnOOj0zPu376l1kIcTjwuDZ9OvHv7BZTCn/3ZnzDPM//XT/+S/+On/4bz5Ux0lTEK3/3O90iHxN//4hcwBJ7f3vHu9Wu+/v1XpCHy4XJPHAZ+9vO/4/7xkSqNQCGEgfOUebg8spj7rj9Dy47nNycOR53cL2/veHgozFRK67qz3QlZqxUqbKx8utgNwFq1Fi00QLWx9F4lGbzzyjisatjRkxxTT10TyxiViaM6IKZR6zTJqRbUS4PCwhAHPv3+92kOpstZWzuitv+Mx5M22Xgz9Ag6WV0MuNORNo9k55HoyU6oLdOc6iF504dt6MFZRbW1VrMnNjMiTdAsXDEw4QowtQDBQgIztJC1JSnEsCXjsrXR6/j1JGtr610TZqc6TZoEarKxJsaYQYgFKN6JXWPRZ9N6EoxufsFrIO82cHlvkOOcXr04ZYeqRpDbgGt77QGhlVXqNgYVrruZO914DZzVgvsGVupn9bYxbXXZM3Bga6+FbeNWljZ0d/k9U6y3FAmsQGNwvS3Vgq1VRqbPyC0w275agYRVjsFt7KO1NdQ5U7XoLuBb6+8GfLn1fhVwsIqpIS/dOMYBzivL5fHhgXpeuHn+jO//4Lv8+Hvf56Nnz5FSqDkjfjRdQE3wyrLgRTW6DocjMTnS6cirFy/hj3/I7373W37569/wxe/f0pq2+H315dd89zuf0SQjpWow38cHA2dEIFpVG20V1Uqv24xmaiOMnhhMp62prk9fGcukTsbNadtaujtx8gdkqjxOZ8DxOF3UaBAhNUdzwXI1t7JXB+cJzjGLasyp/iWIM3ZmCjAM5GEmX2Z8hjSMxHE0TEUFIaQ2NdQoWuUWV8HHHdtbWzMdTtdQNcAFaKXQLPF1OdMuE6E2MEABA0hEUHDMmGV7NvUeuNtAGGf76Q6Wa2Kk/G8HUp+y9WT7wVpJvVoXttY3FFhfe/bl/vPsp+t/6+01zkCCvbZh/+82CkiMhBhtX1Y9K/y2DtQNfK2LKRjT19ZGmVxB0Os2cNb9SteRfe5ui9IfdTDL0YMp/YVmZRxnwCR27fbcdqyMvp7pzwRBZDNjuobIti/f9vQNeNsgSb7x934RW4HAGeBvb7QkuIMxKxbsoPZ/uN4V0Fl4e6auvdnpTGzrLOvtb08B/t7R0o0/u26znUPBsywL5VKsPS6wyR3o/azPYzd3r86L9Zl4VIuwn3vb2AF4y9N0L+jjvt1XP0/6521Fw34pu/m8W0PehXV9dabkdaHCZqZ0CYmmhWW3/dg5bS1utViQ7PF9pBQBVUCug4SW7PR5vWfZ7tm2nf1QDcz2zgATF9TUpfWW+LYG/D0e85Ywbtforf0e2wcBp6BvKUL2mcukumbV7iM4b1IxxeZSQIKuNelrxzuk6s+168qSKDH2std25g7g5pWV0vB4ZQfHSBzs3gB8UOCudQBT255LyapDWIsmujEqGdbiVWl11fvz3vplxCFEa/lc1sS5tkpMA6AGaLm3CDYhxATDAdCitK4XNQz2Hm0DdsJkJkvOaTJHFgPwlE0bgrc4OuDwhDQqA83BMj0yzzO9PbSzcDv455pKLHgXcDng0NbhEDxLVnbwkvMqTRO8Z0iJWpX1dry5obbKclE2ncbWOudiUEO11LX1ms7PpSwcgieGgVJUS7HROBwOesaLUGtvm61UER7OmfO5kJeZmCJjOhCCmscMo74veC2SOO8ZY+Lm5DgkGGKfk9by7Cwv6Ocgfd/7/37t3xaCN8k2x+CE21OkTZo8H1LECdRZC8CvXgZCgHfvG7np2CwVOhu8gxP3DxemacG7qPmJgXTH45HaFnIpCnziKJYbNSlIK6TxRPBHvKssU0acZ54mfG28fPmCr7/6io8/+YTT6UgFxps7NZ+5XDidDowpsiwLIXimxwcOn37E9z77iF/++rfM8wWP08K5ZuPUUteYGKdB8ng8EkKi5LwCDmK5TZFGRMA1EI+ap1aL3e2ZeJV2ca4zA6F5Aztbg6BgWRWVm2n995wSdpyAKwvl8kHPwhgRqev3d9mcUiZKczgXFfCMg+4FIRoQHhhSJEXP6ZC4OR04HgaCbya310+zTQZpi1F0r9Cz32JB55Q53Fj1oFvT4lRD8NGj3BM7P9xmIrsvuEmrDJaPdnb8kNIKujmBMSbGmKgixnQPQJdiUF1Vh+aE0QAdH5LKbbWGDyPj8IwUDyQfSWEgxUEBO+teq64hCdpJ5283KOo5e8kqo5DrQpGF4ieKTOAWHs/3SNPCV7V5EMJAsBipFT1norcIrWZqE/IszH7RPMQLrkLOenZFr3tNk0otheVyMRAp6RnVrNvMt7UVv0lVDVaHdU8p0aGZkVmtlUstVCfgVTbFL5k6KSBVnSOKEKMWF6Q5Co3kILoILfJwnpiXqmz3EPBeQcdStX0+50yeJzMBXGhVCXOldbJEsO6D3iHqUB3xqJIPJq0RnEkpSCSiJLZockEuDjT0DO+mUmkYGQ8H1Z0NQRUVgEoh+aRSEA4ETzTgszZBqMw145oygr0EpnzROWxdx4FAHJLiM8BlntfYw4egRSwDl+9iJOdsxvZaAB/joLk5kHNhulwQgSWXNc7Uwm2zzhQBYxl7DyGoFEeMUfcQHOl4JBrQnlJU8NNyPensT4tvteCoUhStFeZloptinu/PiCi46b1nnmeVnLF4KoSg63PU9VlLIcZIjLNqpde2asZ3/5VlXtbxWdnZbivWBu9pzauus3VTpNWsq8cfJncxayfDvBTqbOxli4tiiEaM1O8ahoExRlRPNtHqpgcdos63GAK5ZM7nR/KS144RjVOVDDUtmYZ1/e2kqb7t9QcN0uqm4Aiieh3TvACOwXsOIUHTh+lipA1HwvFOQYjLmeQctMxSCzjhcpn4X//1v+LVx9/jL/7ivyHFgel8RoaBZ68+opSZECEMI+9ev+ftV1/xnVcvePnyRK4z//J/+l+4TA989uoVz1/c4UfPd7//Q/7+73/Fv/vZ/8O///WvefH8Octl5uuvvkKkcfi3PwUH7z684+HhHnGQPKQwKiW/ZXVaFQUn/uTHf8ann3zMED3jEPHJcamVSqHkBWpjNN1G5wO1iNGzzZDBDziaiblrHB36JuBNf8vvNE6dsiJK6QwNOzAF63A1kzNL8J03vo8LVGEFbhE1czgcDnz/Bz/mfD7b7zlwGnB0QDcdErlWovd4ta3l5u6GePCEQZ2hW244a1ntgEOv3GDJOpaoqiZvZ7oY4CF7Fqa+1hYLWw2aVytbIeAIMSFO8GKsYzbG4sYQZY+dGPNKD0UX/QpeXIEyBvppddiuvyeorrc9OqRqVatV06Dyzgx1tmey3gvaHqEf4bf2996mKawspH1SbOn2BgiJVZLNET56Bci6a+TWoG2Jd6va4ggbGxd2z8itY+sMgOkgT/+MfiOdtaZJagdjVlh6BQH6ZyrzquyAgv5zv2MWb/fcNWQ6MNuT//117gESZcexBY2mJby1C9szzwVXGtN04Xg88un3PuPTV6+4u7lhnhfO9w9aZZUzzjUEbWM9jDf87V/+W95//Zr5/MgSIY4DwUd+9OOfcHt7y83tLa9efcV/+MWvmB619ePr11/zR9/9lKktDFVwrVERXAwUqTqlevJdFeQXSyJXQDqoPl1Kug59tdYZCyJKqbSSiSnyJ9/9Ea9Oz5Fc1Ek52SGVPK+GFzqW3lH99hzPy0STxmk8kGvhPl/IDgVXbawbWnHGe9xBn4+0pkm3FT6kFG2l9tCK4JqntkKpGecjvokZfei8abZ+ffDKgnAa+LEU2mVWofeqB/v6/CywEGOVuXVRX8+JK5bZk9ceFOzraT8Hn7LHd/9Y5/Ie1OxrV793vRS9RwNzu1zLtzGVns7pb/u3dx7fFCRoXkzqwOOGCMHjB5W0cN2BtSdUBjB6W8/Cfl912zUJ69q8Wp+aTdP3xd2vrpqkzvX07XoNr+zajhDYGG6f/QQM7t9nSHpPBldW89UzkTXgVDbjJlmxFnDAWiFlZeDvRn0dm/7dV5qT2B5pCbkzRopqTQaeaoGvSTtc6VF6O/OevrfrY8FO7gUrMNmeOo7jlQHW1VmwgnnXn72fU12PVO9H0Kbzrh8p674dfTdmEcUS7HP3Ws29Zde5uFsj7WquboyEf1qKon/mdt3VxrPac1MgRBlSBedYdTtbFZxrdHmCdbkZ67zPHw96/trz11hnb2Km761W8Gpsa7iYW7iugy4t1AvJ/QwLBvIqiNpaYxxHRDT2yN0vwNsemDXBkx3TuuS8Mz4K5LLYuau/6w0YUTbUxnZdk7+uKeM2k7XaVC7A4/CuKkPP6Tmb+xltc0N0FdCZaqqBJ2DMaWexTu/o2uvE9Zf3qgdaSt4AY2m05qnVcblUpmmGltURWTJTy3qftm86orp45wosLGXiw4d3tFIYx5FxPBLiiKY7KqXTarFuE6FWfb7LJdDKwjRdmKeLtXoHlqzzspkWrUNZeboGIt4PHMYTQqTVgjRRDeG+J4gC4Dq+wgGVhVCNat1Tc9kc6KVqHBTMKK6bY4pzLCVr8SVngrXgi1fdxNpkiwUETQxNWqH5G5YKh9hUj7Y1hqRzPgZlBmoOK8pILY7TGMhN2ZwKeWxMfbc7p/4p5iywGsZixPcmjnMp5vztuT0EpqUyzYu23ptJ1HTRduVhDEwPC6U10hCRrHH6vAhNPHE4MLoO6jeW6ULNmeM48PzZM0qtvL9/pGTVM+xrqCfpWrBRbVJtW3V8ePjA7bMTz17c8PXr19w9e4mIrAZh9+9fE6Pn5cuXvHnzmtaEeZr5D7/4Bc+ev+Dm5k61n61gsZRFDfjQjkBpDmdFAxFIaSCl0WSgTEvYbZ1rfZ9cYwdYY44t50DXtwGLPb5Zz2Ppx6iCVtXA31IfefPmH2E5M/geXjkrEimrLnhPCAnvHWk44IOapQ0xchhHTuNIDIExDYxD5HQcGZNXlmKP79f1apNHWPdgdvu57itYd4CyFgmCFJ3YrTRrDVfWouvxux4pa/zf5WN6t4VzqpkegqNWv563a4zkPa7pWa0SJZXSlIDjwkB04FuF1rgdb3hx94ox3eIISEmM6RlDGogukkJCjOXhm84vATM1CmZ22oFqJRHMy8JlzmqKRUX9bplVAAAgAElEQVR8praZIpnL6UzJM1VUxzQ43YOcc4gV4GrNzHWiSSW3GcpsAFOfd9rhFlqDkHCiOU4ICQkOKCrDIbZY/T6XVY+ZnBc7/DzBR7wBZ96Z7EFeONVCrIVLmViWB5CCUCki5FogjCCV1oydb/PtMs2EuIFnl+lRAXiLE3CqE15qNTMwwUld48smDRcEcUbcQmjOWJgGIjuvhaLaHCkGI2o5sq2paPmItK2rTHzCp0E7znwkjQdwKnOgwHgluAgm7yE4XDOZRO9xmESIU8mAkpt1oXQTUSUSlVKQCjVv3X26f2JSGGEnZdPNskxyxzvwgTQM3DpPvbvbxvFytrNW49o8q8Fa3zdKKZTcuFy0YKhyGcrID/tYb/e/MSbVkKWb7QmHcbQz1QrBth+lkLhcLus5MS8zuWhB8eF8ZjgcmIPKQTivBei+10YbzyvJJljJXTnnNZ6tNTPP8xVDNqZZ57eBt30PPZhERAwBfwjWSWweKW7rxnPO83D/wOVyoZTCMAzUkxY19mZyKi2j8pMNTwoDz+9UYqRRrTCiZ/N0mZgfz8Rosk2mn/4fe/2Bg7RQQCtRoizKZpVqMa0icQ1SoMSBZTwixxvy+UxwjeoENwTTe0r89ovP+R//xT9nypX/+r/8c2iJ12+/ts0z8cMffxfnPccR7g6FX/zdX/HlW5C2MMTIn/74T/ijjz/iUi589fiBf/XTv+SXv/gt81z56vyI9/+Iw62bZ5m1lbi2QsZRc0Z7dRakFDV+qM0AIeGX/peIbzw73dBKgUG1zpZ5pi2zVSawin/gfH5UwCbowlARdlm1wpxVgJoxUjsbYk28vFf2RFNmbE8WvFOKdjPtJAHVi/KBUpTB5g2k0Rb9TAxJg/uYuL17iUMoOTMveQVofXD41nWRGk0WfNMqWhBtgU54StVNoTpgp7mwT4r7JqbAniZD6podroDB/qq1rtpgHbB1oACt70AeNFHHYI0hVmSgowHsAR3QloIOSF6BFsGvAZfDb4ClAS4iBhR1Vo+oLlcTrXDqJckKeHagsd9ZZ/ZigRy2efbKrN7OFtytifEu0e8/65tcDwB1w9gYelsQvt1324Gie6BkZUn57Xdc/xxjRXfWSKu7MYOr61id0C247EBRl2PonyytIf6bYNoVS5Fvvq4Zjx3A3WQd6OBSE5PuMDfnJshSaEvmk0++y8ubW0tyAvfnCw+PF3Ce6KC0Qu0useWRy/k31JIpeWG5LAzlwGEY+fKr1+Rcub27449PR549v+Vv/++f8+H+kSqFglbil8cJ0V4yXFR5jGatpL29C9nkMLy15GIBssoQ9MDR2FC14aogVffSx8uEy7ouDocDcxCm6UIrjRgDQTowrgxq7wJDulEn1OJxxfPCn2hS+FAnHl0h10JyEfHKgGjSaA69B6d7gQZWvS276bjXpsyo1ltU1/Bd78n+ZrUScw6HNi/E3KzbICig7LgCa51zOsU7e20XqD8FxJy159q2+YT9ujnGXzMd2f2+PpeetPd13deNfp9SADu7o0/aa8CVq+/ZA8JrgnP1flmvVxMzZ394pArDYaAElTrQrDDQ4dktsVs3328ALB2ovBq7ngCvWuC2g/WAn86Y13vshpT91TW8NRF1+2/Sf+3WPrCyJp3bAKz+XGy7sXHrLVr6aZ1hQ1dN3u0f6/OgM4D7GbPbM/SXrgLHb76asRm3s6vfw/459k8UMdahgTmAteoZAOvdVnSy8ylsU40OrMIGkPZ2/32Q+m1FhGugtrPHNwYv0gskpm0iHXypysgbRoLX87N/Xt2xPHUsNfF1ziQIOqBkf26meNva6mBfPzOvf89gQhEteO/PJAGRai3nJqnR14MxWUtntXXhPb1lelvp+hTb/pr2wIcmdr0VcX2eK6t2A9q160XW5+z9vvW4d3eoppw4PU9iGnCuUWqmlJ5Y7c5aS6BERI04ulOwXtTaVu0sBnH077S5GFTrtmmbFd5rW6MzdnY322m10MyRPpdM8IFujtUH2zlHK2V3Tcpw7nuj7J7bNl8brSrwuModVJ3n1lqkTuHLhSFGbdMEXbdOQeZqoEupM7mofty8XIwN59b7cALDoHGzd97Wl+j3NDV1krqwtGLJXTLjEmtZFVkBShwmt1AIwTEeEl2+A+eIQySaaVSzdbPGmymZlwCmOQlONqNZ5xyn44lk+r847ZbDR/WrsLMlJh2L2ooC8KbhLE1BWWdMnzAODKYzHlzj1fOB58+EIernzFNjybZfZwcHPQrUC0JZjSEIyeK3Hjuv+y7/8dd6hgKYtESw/XApwjznlSHfcOTmbP9rlvoHlkWf491d4nypLKWo1FvzTLPqc4o4LeL6gKfSBPK8KOuqFk63I+OYOD/cM13OdF3cUjJ5yTbutjabmjk1aXz5+jXPX/4IEdW9VGBLOJ6OzI8D796+43g4cnt7x/39PbkU7h8W5twYxuOqP6gGRTqX6bD7VTyr9xC8tplrMU/XSl1/x1iMbWvZdm7XVea0ELPmSmDFmp4vuU06B2w/8HipzB/e8eHLL7iryrasUtazpBN3UlAH+ybKLkvDQPTKqD0Mg/45Jg7DoGs1ei1yeNPU7TGLfXvX8tY9XfWUYddB0mXe2KRTxOs+FtKg68c+rbZqbfjKkFQ2soK0tVaF68T2+ZV1nLbsbncO++A0F02eXLPGrag2rXfahTGExB89+yNenD4huhO0QOCA96PFV47kk5KjUmIrjOkcxZmJrHSA1uJBAz81H6k0yVbAapTcJVYUeAze6ZoyQKzkSi4LWRbm5UJpE7iC80LygaVlLnlmbgtzyTwsD2pe3HR9uRDx4YAgusZQKY7SFFhMfiA6x2k8Uhv4hnXhWtzuk4KQwIKnnTzvayH6Rm4LZfT4GY7ugJDUfBkDqoPTJ12bfV/D+2rPUkCs+GhEJ33qposelCEbfNIO1GCEBrr+eF8rlqOLqDRHTJpnBwU2nZFGdOF0jVGdd6XWVU7IG/u2ExN0sbk1PQ/Rmxa8kR1CIngDmE1OTCIMaaBSN4JVU1PmpSzEEFa98iaNYnkNoizvHjcsy0yMQWVufIAYeXy8KPDou7mXI40DiIH63uNvb/Wym1cCjGsUM7lTreRplY4rPQZ2btWMzTlzSIMaqoUApsfqcBzG0UzNwtpd9OzZM+7u7sg5rzEuTslwuVaq5YTTtKi5l51xOedV3iWEQIhKNlQvBC14dBNI7z05K0O375HzNAHXxrBdw/bBbcZnKUaazKSo/y2lwf7Uom70QXV+ezxlm24fj96J10S7VGJUwqCC57qX6VxSDfnT7YlWDjY3q8lY7AL5J68/bJBWoDptR/DeK3BpOkOZwnB7XA+j5jxTcMSbW+T9O6VUDyNDTOQGy1xoUfj16y/47//5/8Df/O2/4Y+/8yM++/Q7DOPIzeGWy/RIbgu/++IX/Prv/5bf/frveG5aqcfTLQ+XB/7qb3/GP/zjL3koE0WgFmVuhtioiuZQW2U8jICnLFYxlmgAaYSqrezSLLlH9dI+vPua3/1OSD/6MWM6kJesG5SoaHxwgSJiYGlVxllrxBC17cFhepPOkpPOGAgGkO1y7ga5FpalsKJkThm9wXtSiEpdFz04krWYtbZokFkcc12UmdUUOG4iLCUTQ2QYR5yHpSyUvBCHqId1bXinTIOQIu/P97SmrWHRRaZa8IK233s1MRFj9KLnkgUfO201REmxaBWmm331hK4nVWuQJD1gNNq/NDyR3iaI33TqFAQSA1s7Q3cDP9S4TQONXpXroK7+vbcgG5sG/TOE3sZrD0VXvtH029pKAux0b9UoYWW09Wt02/WCAaW7JPMKuOE6sN7Anp4sbongHnDqlfpr4OcpiLQBW/3r9z9z1hrTJ6L3Ot+q6hGsAO0KvO9A2x6srviCrP9v/d6ngMkKMsmWHF/fsz7PK/mKFZDfknEPJvOgGEURIZ0OvHz5kkNITFPm9es3CnylREiR46ibcG8MD8LayrIsmgwuy8I8Zz7//Eucg5RUq+4H3/s+Qxz56U//hvt5onnHOBx59+Edw3GkRU++XAgprtrWHsfxeKBmOzjQ/UKcgikKjlhw0XWmclFJARwhOJaa+eXnv+EYRkJUc4Xbm1uOceDZ4YbcHMlHpGjQMqaRw2EEJ5zSqEzXQ8DFAHUhzh8o5V5F5ooOqnOs+k61u3RaoNrbXQXMEbYhJWtbHrrG9Pe1bUmaAq96KOozX6YFyYUkXW/WnIO7/mV/7vZ8e/KIAUF9fnwr0GoT7+k828ClbQ7u148CN25N1tffXQHHDlR5G1tWFqPuGwomflshov/5dK0+fZ/zWvQKThMk8YGKp8VAtep3csbAoZsMuA0MZRu7p2DLU+Bvk6Xo16f31u+99r3B+5U1tu4/bOxrYdsXDPrBG8DXr8dL/x5hfWKug507UPXJHgXaRnVldrbup/2vXZfV4nCTVVkZs2JlvN3z3uaBAieruePadeHWvVEZmLv5ZIzyKhuLF5u/0tSVd/892nqt17uNuaUwZjKxZ23vz8M+FvsA9j9W6Loq7rW2sh0RBQ6ccwYm92KABtFOWMEG34tIaDFlY4i7dSz2P++6vT0A3ktc6PWus83YcFYIQLSdsQm1LMYKcSy5rHGRwyExmfv1NnbbOG7gu3ed2bvNKZFr+QUFsvvsc8Z4FXoWV/FdchYEqhQOhyMvX77gq6++whkAkPNiDt1CioM61Ld94tohDlm16wRn92+MczSxrKX2kI4OfWh8ZFIrFgd1/wJt/40sknGmw6aJkDIMtVCW1eQmWSJle3HXyWvdAdkK68owkat11FniyphRjdguRdGfb08wnXPUkjUZG9THoO6AfctbjXWooFs1c58YE0NMHMYTwbQ0OztmM2/S64wpMAwJRD0ivI+MgyZqrYoycWrRPcc05hTkdwxp0BimtrU7yBFYijmWWzu29+rFMI6HVY+262LqPWPzM3A6qBu1so/smlewWw2R+vojOb129JmXvDAcDure7j2n00gIwqtXTgHNpbEsjQ9vZ5p4cq4Mw8BxhDY0xuNAKUJyQovKAqvFUVXdCOvf+sZesd8znr62d+p6TwGeHQYurbFUOF8yYmeSlIpI4HKp3Jwix5vA/Vnn/vEYKefC/JhZsjJnL48T85JJaWQ8nBCM6ek9NS9cJm1fxXtUE7biRMwILDNdZrx3xBQZxgPRBQWHjpF379/z9ZszYxi0+y/pPj5dLqQUicPIV6/fcHt7S22wZDXsqi7j46grVXRtp5BMl1Zbgdc4yHXzGy3et9roKUQTNX4VUTkMb3J2tW4aqyl4shUBtZCpm0yrCtqthw2se7hKyCn40O5n8u8/J00PRKd6170LsjTBxUhajZMVhIkh4XGMMTIOI9F7hhQYh8QQPSHAkOJ6prtgps2WR/nVVb2TR9jAejtPtKi77fVewI/DWuzYd+J1oCMENdtSyTSN6bzo/iW9owzLwbE40s4hlcjQ3LlKVa3gojJBTazwIZG743Ne3r3i1eljju4F3h0ILkB11OaQANGZaVgMeAP2NK0MNNsXnZ190XfgqcefHhHt/tU29Z4zmymbNDUDcx7vokqb1J0RkXdoR1Kjy2KIKGHkcX7kMZ95nO95/eZ35OWBZbqQpZHigBTMZM00cTWz1vizetMXrwgmk2AGkulwA0GlcUIQxAdojiyNuS6q1+0COXs8B5bmIFclqXlowWKqksl1IueJZTlT6oxIpolqkyrIqjPaxxFvZhQxOoZ0JMUR5wz4KtWAMS36Y7XL4IycEkeG4cAwDCb3pXFWjAqua3yl7Mx+3qxm2WgRvXt7LHWxdedx4gl+wEtR4LNCrdYlFrTzhmpz06ncojiNJ2rTotW1PNX1Pttao5VKqVZY3HWWStNC0GLt+8XOoOGgZ9niNQ/y3pOGhPcDoHiMD5EweG7TDctyvNrLeyzWpQrO57N2YdbKMA4sRYFdj2N6fFxjz24otnV06T0NKZj0p+Ojjz/iMs8k5zka6aj3buWczWizMl0ua1ywP2v0jDspw1X0PI2mfzuOI918rK/zUgqP/RqjEhjPj2ctslvheRgG1YJHcbI0DKpZPCSSGXxClwFta0xzmSdyKUzLvMUzFi/GlKzY5BkGYyA7bzJEkdPp5lvPU/gDB2md06Ag4PCtMVoSH5wjHKz6IWY0M3iKgxI8zXnyUhjTkTwtXBbVtUo3Ay0OfHl5y//2f/7vfO/ZR/zwO9/jJz/5CZ999F1++td/yVIv/P53P+ft57/ixU0iusLjRfjN51/wy19/xes3r2lOgzm8JonOg7QFHyM4TTKWpeoBN6pG2RATy7RQlsk2N2jemMDiDGRsvP7i90Qf+PGP/5QxDZT5okGvHerShDJncsl6GAwRBIYQzcFTF3mMEZyQrdXeGailIuBbe5smg3ZgirJwU1TNrphOmpiGSByPauyzJunC4XDSYKLtDFZapQXHnCdOhwNpDKSzmWJVc2sNjmEcmfKshl2+MR6PiBOmebYKrLINcjGauD13qc1ApbAm6hVtH3BopQnbQPpC2F5i19twYi0tGFhgP8NpSuN2GoAboNdZsFsi3tMmbwmittWGtULWx2Rzbm7a5uF6sq6Bi2AJsdc2ipwXBdOatbUaiCt2fK5mKyJr60stG6OPVfdq115t19rF36G3mMpacQTWAOp6LW7MoP6e1hkoT4BRDbY2lu7689o2+QAbR+kArQ3oFdBr39s/w4cO8j4Bw7CWZXbg8fa42Sfd30wi3JbMduzMgJSeyHaglqZtdjfP73hx95x0c6J5z+l0w7PbO/J0YRwSKUVNaHwgxEQphVwWBVXxtHaLOKglk+eZD+dHlnlmmjNLyRzGgZcvX/Cnf/oT/ubf/1ylCwTOHx4geEQCzbSUcQ4XveqZOWdC8Qq21VZNTsAgLifrs/VOjSckgE+B4+HE0qu0WcjG4HVD4Ic/+CGpKnA0DtrOtZRCdAFfG6UsxBD5zqtPOB1PfHg88+7hLTey8MJXLhRKEtrayqoHm9RKK0U1aJ3uSb31q+WZOleCmBbWSuCzdiYBhzfGrRoetJwJReiFHdfXjLWwudbZ5B3462ztDqXrq8/pPStP55W2Au/naCeMr+ZY9Fxoa93br5enRY4tADJHB9sL+vruP9twxF3RYwdsXK2/zl7Zg2+C7mnRmeTEQI5e2SlBGTy7VUwHt7tqjA3lCohuADRX17MHsPfXdwWE9oJHH58OXrJ9l46znY0WxHZmAX2pysZ4bU+eVwdc5cn392XeK+IdjN6DrbAVxrZAdWPWPtXfdcaO3v67vreD97IDw64gC2k72Ri3zpEibdWr8lppxQ6uDfQHM+PTJKKzZDvztbaum7l+3RXT9ClY+xRkf3qPfcxFwFnxA+doonOgLGau5L0yR3bPv1bTgezyJ7J9//67l2WxxOSaob1PErbCxfb7XdIFNkaq/l3IixVpBTsTmwI22YqtzmEaDet50bsmtHCjAJqOq73JhG8byl671ox3V+wxpDPStzZ0EVEX6hxxmC690xjBux6UVVox4M6SB7+bx8H2Cz3/tRAQfFjPVaICHp3R2udzFTV97G23iLY1ppDAR4rXsUwpkedZW1mDtrqq63Xft4qxNZU12s/faZp281vWJNL7LdbomXZfh30vTAZaYaB833eVseOpKDFBrBNDxFkHl8p9lVqYZ2X8Siu4QY3AMCC9S1XonwI+EJxfDcMu08RSqjJpGNUVG4dYUSHEsDHgZDMXm5eLmeIIw3AgkVaZE29zpMeIui668/OgmnjTREzBkktrSc3FAAb1fjD+Fq1W5mVRx2kHtzeqHexY9PrsecQQzaHeMU+Zd2808S85MxdBamAYlf22FGEcHS55hqRssOMQuE2ORGDwjggkx1oI2/Ss+cZrWRZqU/kONY7ZfkmkEUzyIQbHFDy5JOaqQFwujdwC06UyTQs3z04478gLlKbzYVkKl6lxujnSbo4KMPioOuY+QFTD1hY8rag7+rTMiKDGzEH1g1tLLHPVYo0VRoYQeZwuDMcj/uGRy+PC8fmBgKxF31oLApxubliWmcfLhW7SWIrqJXo/kaLKcHjniAZsqYv9RCuVEEHMFFpjYu0IwCnpRRuANN632pHGGbYP7rvNxOZYZ57WquY4Mez7CjWG72CkL5nl3deUrz5nXM4QqrIaLY/UmMYr8B10vxjSqGsyJG6OR2KKxhaTlRkeo2pyd0OmfiY5Z1rxrKGOFr7QsevFWHZXLLCx4a2LRBCixfQlF3yK+Kos+h5Q9PjJx0hYP18LWX7d18N6rtBTHnE0lN0Xh0RDCAwM8cCz00d89OwzTumWm3jHwd2hQuC9sOtxPmle7r1pn0LqhBxbz+vZ6JTp3wkIyv/xuCDGTlSTJK8sILrGueZMptmLMjdxmscH51bGX6uqa968mhkd3ZEX8UAOI5+5EfJMq1kZgKh8QZFin9tjKwWFy1JNHzxTMfa368Wahk8HGAb8IdHiSEpHCFHXYxOWVpHaqLmxiJhUj55FJTp8SNYJlcl1Zl4emKZ7zo8fKHVhmi9m+pg1B/Q22RCaFByJXFRKJCSIPS5fWdV6zPt+xoduFBnVd0dnIQ695hD0LE7Hk56ruDUWLlX1nceoviPiKq2oDrD3ntIEa1RA/UoLpWr+VZusXRzNbTq/3jkep0fdN4dRzflszvYuyS7DgfMMY+D27kaZ1rnQSkUMGAVU2qWWtYOl68AiwrJkJW0U3etDQPWNvQfryOnfGYI3XEkldcZx5NndMzBAuNTCaOBjy4V5npjnWVm0Tn2k7u8fjBDRZcSEOESO46hkHUQZx1G1eYeYaE04Ho+AFhdXDwDb10optKra74/nMzln4mAdW/38dDCOBw6HI70AOgwD4ziuMWWP1y6XC8uiRfEmcH5UTV9EaOeHNU4ZhpEYg7GdtTgao3pIDcMz7bCx/FYNypqRbFSyFVeZTU+379vjeGC+LN88SO31Bw3SAmry4lR7iboNfKMheSGNI/E4skQI86S6J14rz+dp4jAos6uzKObze/L0Hi73/Ob8lt+/+TV//6ufcTOemPKMa43l8QMpwf1y4B9ef827D++YzxPLeQFpDGkgxMRirSy2A6NtsZU2L5TLjLu9wY8RotO2g2Gg1YXmVOcnpoHaVAZBpIGJpH/5+9+ThoEf//hH6sZYVQM2l4uywpyY6HhYdce2RLU3IGDBpLZoFNPz1KSma4YYLdv3VrdNv00reapXo4F/JsWE1EFbyQ4qnp2LasI46fII4Koy3C7yaJWNhK96f0NIhCHgXODN+3fUtnA6RWKC++nMtDwyhgOezr4QNabqLXDOQNUOwAhrEKxNUl1vD0uMZI0IXAcDLOEJrrdXmeGL6OGnwrVWlXZu1XhT/nMPesTGvKm2z/o+8L5tTCGvLcStQQjOkimr9lrQ4Cw46E7P3qGurhj/zIAqQ0kMeNZEvAP8fRODnRSC2D0YIEHX/zGgHuwj7T6d31o/RTCDBTETA9Pf7OCTsCbDHQS90tns3wl0R3ER2YAZA7TFd7kJW+8dyHLgrPWrmx0458CqnCuw6hzBKqzO5jy7YG+HPBmrVH/W9j/uZnNuB7AZAO/FIUUBv9FFPrp7wXde/RGheWiqwfXZxx9zc3vii8//kXJ5ZARC8hRRTVrvG8k3vBScN91P13h29xzvI8+mwv2HMx8u73mc3vN40YRrfHZDPEY+vHtDdInlvBBPlZiijYEBm1UdN1sunE4n1RYVkygxNbmeXCAgrepyilpZDVHbssYUiU0dp5esAOp5mfj8/jXn+3taq9wMyhxYauVFOnFsgcN44JAc7x/uaQjT4wNv3n7Fl5f3XBI81kUBAgM+VNi/siwacLXaVjatqw1aRXKm5Wrr1BtA5UxEvtiz07WztEZMcW1Lrzsgr0lZE8m19Xtd21hluScMOn+LgUq4Dqp6WiuahLhe4OrgUgeBtyq1c9qCtxWuDGyzwFxEVqa8sss7YNRx3l5A203e/8SXdIRzFwR0M0UfHM0HWojEcUSSaWZ18MsGTXbro49JX9NioJSzMRQ2cPLbGLzYupXW1rXXx66Dht1RfdtH+l6mn69grC1OJ/QG0P+Xujd7kuRI0vx+ambuHkdmVaEANLqnrzl2KMKXfdv//5GPu0IKlzPLGU53TzfQB4BC5RER7m4HH1TV3DOBbo4I+dAMEaCqMiPC3e1QU/30009Dn4fteg5IY6Cow6IbqLvdk98LwsZ0xKdiZ8/sPQ6wOVAbonVe7zqlDlLzwilV0+KsBzrIo2NaoYUX9xH8ms7YtbOv2y0HP9nYw2vVbvM+BRoslK5d7olVLwHdj9f3WHHGtGqtsda9hEDbxrT551oHC4LJH7SqZ/SWBGmspiwhTb8h7NBjv499ybeOMdu4WslYTzKFLZHiYHiIUfXobdZDF6BXcKLVZpUvdq7A7sy2PeJleiIv9q/Pa7RO61oV0zac1z6jJ6/OnQbpTWV9WtOkWdDKh3kp2lhox5YRQQGS/i0Fb3zamjLQ/WSrJu+k+ypoCaeEzg7TxGwk51VLdal2loqBLYOCe2J6dgIiVrFF6KyPPYNegrFijTVa66qBUkgmwaX+VIyR83iglsLldmOpGkRqAr1a4Kkss1xqH2+Jqg2X0tBLL3UrbCWrKmFjupZNF8my5s4cmufZyvIx38qZw1Crv091SA+jVrfVsjCXhfk2k2sGMkJgnE6seSWb3xnNV/IzYTBGLGhDMxEL3NwmWZIrhEGbqbXANIwcJmV6HqYDeV5YrjeO05EYI0NMxJhsL1uy0eyeeSTEYVSNxAbjdFRphbKq3mKIJCA2ZzPreXWbM2nQDuSHQXXIBRhTYzoId/eR89Q4DsLQAlMSUmgcRDh0k6P7/Qdw2Rev221mWVfGYaS7y74PEWJslGUxW1RVRzZbQ7eUWG6VwzFxnRsfPi4mPwBrbWwc2yYAACAASURBVJQmTNOBpTRahMN5MCZTUjauyRLlDCGpPIFKdCTGYaRGlfAItj9bWqEokL4YMSLESKuF+7sz67Ly3cN3nE+6nst62yp0mkpAreuq6xotd5XBdCi1nknXQ1B5gWz7oLZM2LGp3R+XmGwvBovHate9F8Cb2alEnmq+BqkWzxkoHRXYyeuMZnqMPVsVRDxMEyPw/OEb/vi7f+Ly9BVjm81ngBhGCBbvSGOIUYkHok0DpzRwmg4cRmUShiFyOB4ZppFkAGOpWt2IaENrwnYOpUHsvA32TOxsoCWO+lmqiydYM6DtsNf/gsl+ZDKRRFckEem2S2Mu78tihCVvGGtng9EwaDhwVlnqqjq708Qh3vPjt7/kk/PnDJIYZCKiDP1ecSERUfgYmvqtfg5ml8TaA8aW3FVJDLVXKSREtrgRqYSmyZZaGopPWjJONJ4ja9MiwBpVhQ7+lVq0EXdedC0NA+f0hrvpCGVFJBNpDFETO25lqFruLq1pQqy0LkeQq65tCYnaNAHX0sBNIsSRKroXSYnGAK1ScBus8mwlr7QAK4WcGnNZVQ6SRo1CazN5nbkuC5XCfHvk+vSkzc3aojGpNe7KVGKIrGvtdq21ss1xU/yjVoVhSy1KcoFNJqXVLsukMbhV/fneCRE8EZcOuHRFbVUlFw6JVlZqLQxNQWIRrQ6oRRnypVRyzNQEjZXWIOeZNd8ouTLEkRh1BnJWMK82d0ybVq0gXf7D5Qy0mtoSvOjP26CVG/t+BDT3G5S1W0rRJmzrSpDSffl5nnusBCpb5YC2iCZGg/ldIgrexhRhGDgcD+rX+3VR6ZllUS111bnOrOuqSd+UWPPKtV2IoonEaRxp9jsnH7j+6z5574znWrVpmR8zCqgqYe/x8YnHx6fO6o0xUkrhME649FwaEnenM/XoSbhCa8fu6685c7nctAJ2WbhdK0OKnSG8rquNS0IiTONB7RiFYdgqnR1UDkEruEvW8c9l4UXToVevv26QVoAYSXGgAPODGs3nql3GW63cn88cDkfKogBdiAboBT2w2nRiGAdiKchyoV4eqLcHpM5cl5mlRJ6ePgBqyN8ejsRWeXi68GVWp831d9LxSLGFhoGRiPWAbFXBHICswENKC2uGdhhI00BLAkOkLuo01FYY7k7I9UZdFgVPmtBK4fdffsnpfOBvvviCuhbaXIkhIRUKxYy4Ro7DkPoh31pjXVZjNlipgjRSUj1ZNxatwTgmQlRq97IuxCjWcc8OE1FjoZrOql1W0cCNsDkMiFhXYWHNmXXVUoOyFLzMGgP38nigLZWPDw8srRBTYCkr+bnwNF+0+2ormNySab0pPLixWjbgoFrw39Dgax+I64Dsgne2AFCaB+au47oLRnCnQTrwsjHHvOx/C1oVtCkv2Kk+F9j9b2X8XqroDkijdvx1r9vWoL4ENVqtnU0jQddrbTonuWxAgYLNxjz1cTCtuNi2QMOfUawc0xk/5td056MZU8jZZz6f/RnZxrZvXdGSQNgYUP5cWp75muW8fc7HQlkorYNCqill824lBq1WzY7+ANjwfYZvv20cjRJQEXJfH/pmc9agmnbXu7t3/PSzH3M/HBlrIDThix99wU9+/GNaXnl4ekSkaYlqSiTRrrnzfKOsKw/ffcuYBs53bzm+OWuiJY1M0x33bybevas8z1eero9cPj5xvX3kTUr88pd/x9fffM3z8xM07bRZqzYCcFYAQBxHYoOaC9d643gYLcimg/XBdJdaa9o1PenPZDCNwRBIgwUZNbOuQibz2w9fqampmYerZkWXUvjd0jgz8sX7z5nGkX9//IOVxjUero/cWmbJrYOzqyg4Gc0ljghIpIgllmohiTq4uehapZQu/r+uWwImGHBD04Z3eV76Gn3hzNvPvsegFnXGNsDG2aEbaOH7yG2XmJMT4/Dqe20fWZm1szi6TXm1vr9nj5z9bfe4dzZe7ynYlQzLK6Y64G05evk7zTSbIQwJ0ogM2onWZSc8ZqE2PVv87MDZfwqiu1P0gpXa2vfuc/8sfo+YLbFf+hTg9oBt93X7igXTnqLCn8ucqyBQXtmeF+B529sod97ClkDb3c8GaAsvzgGbj9e2xO/Fn3rvQPrrezIqr8fFy8AFr9lGJBLtnMDONtfnLUX3x8vvtLLPDYrGmZ1Fs7F+ZQM5Xzase+HE9/uzYKbkjYHan9NWu82dz2m/hp+l/TtbPytdmmk7k8MLWSL/+3Z27PaJfr2eVa/WfWfUevMFu/4e/K15c+4phT3I2+xMxIAon//XGrfVmLhb0y1BjNX/Yr59TWsbe91naKKh1rrTlvV97x2pt7O/mDyLSz10v0ViX6s0lWBIg7rx67p2XVofUx/70M9NvUbJGaKWPXogVEoxLTzpHY9t1qlVgzkJQftDZO2A7vbLx6qaz5NrMdafMkg0QahrVudW5XRqbca8070QgjbAEdFgSlEITdAFY5numdU5b0mwlCKtDV3u6nA42L1nWhNyy7tngoKuuaVaM65SGYaJYRg1qNuxAAEFuAmWMNCu28qwHaz0Ntifvo70PPUzJSXV8NStXXl+emKeZw6HgwKaqG5uaxnVx6fvo2qEkIaC7NM42bmhTTN9/EspHI8nEGV0VSkWRlWEwjjAaSys88LdKXIcVddxOgijQJDKlAKH4G3W9kfplvT4S6/7+ztaY2MO2/8bINKITeU1CsIhwLjCrTaWtRqBRJgmSOOBh4dspeEqL3G9VNYVCAO1KJHgfHdgXRvLqjFJLt5nAyUwVAXCnD0porqKrVbWWnr8kEuh3W62blDW2tCY5xu1ZoY0knNhzQWx5oTX+QaiYiMpJrxcGbMhKSpwLA3GaWINwjwduV6fWNasjOi2A75FG7mteWWer6zrTEoDh2m0/exVDG3HtixmX1TCbq16ZlezbXqgVhrZgMlGXRY+fPnvPPzpD8iyEEaVhSE004dVZmyICgQjlTQl0gjjFBjGqMSjITEdRk6nCURIdsaUWlTn1Oxcq16RJrZHrMIBIRiJqpmNFBv7zSa2zecT67lhkjK+xmIShtG1ME0OxG15MEZg9wu2mE5tR+wxWq2lF/qHqo193p0+483hPZ/cfU5smhxZjYHqev+NYMnN4owSaouWYLGSewHXwKYFtOKyGINUgfcilThYs7FgZ1PRhrprVrAvWDIu7GS+1ln1wAXZJBBKptSVlcUYsyu0TKIxIgzDiKDVNg3FMZyxK9Dl+6IECI0wBm0wXhu5rRAStcE0TcgwcoiJhUQjUYFcK5VB7ZSWFuLVAKVkCpm5ZkpsxLoyzxfWkrXR+FII48D5kChkjnfvuHu7KlCcZ/I8c3t6UpsUFX+htp7kdEmbBsRhwv0jEVHW5KqNxzprNOi6csxDBCSolKFzt5UwV3s/JBEbo1AIVHIFkWQsaqv2k0gcJmRwkNR7zzhIO1DbpI2pWrZGdV7pOrGsi0nwGGZQKosxSbWRduskBz33NGHqBmWaRjsbk4GeiWEaiPHYwUU/N6itf49XpMQglCzcrjPrqnreXcog6nrYWLex+xIxRu7v7ym5MB4mpuOx+2LzfNsaOFZtEHadb9SsuNrzeiGlpBIKhh24hEJKKvEnMRCjXru2BikSLM5trXU9eZVMWPqzzvPM7XbjNk5dWtLBVrcLaRgYUrJkisodxDh0Ilwtta+d2+3Wge0QEiE2ruHWzxk9wEPXCY5D4nA47HzPxu12+358unv9dYO0gBTlhZZclKKtHjVpSNokoDVOVqLfckXWTMiq6XJIiZK1eU+dnwnzhbjMpKKbIQ6JIQ2st1kNLnA63/P2zR2Pzw9cbk/clplhHJQBiuriLteZ5w8PmpWnEgYtLaola0BTWzd0eV0pUoijNo44TBNTHJmvV3UcayOkCHljVIlEyrryu999yds373hzOimVnmTi4rFnBJwtoI2c9HCLQYXVc6nk1Rd3ZBwSS2vd2XYdIA2uNAvswsuCGr6yrERGbfpTVbxcgJqrdaw158sOFEe+VOC/GqBUqFUNy8PlmRAqcUjcHc88XR/59ptvqBSm+zum8UBA2RLKFPVSdulO/sZYah1ooFkZdP+M5rb9896NOCUNhoN33uwOpwZGvStoq5bhVUcYy0Bt8ES3g3izFOBFEKBzZE5Gd66kB0o9QHbA03QHoxk9z6J5FszLfVwqodrfa4O0A21qqx14VZ0+PYTFDyrcX3Dm2Q60aH6cte0BzYB0htd+f3aAYAcQ7373UvMQHPDSDOBWzroHcnvzoLI5cvh3exmhj0v988bte6/dIzkLUMAabDVz2jaHuQJjmvjR28/5hx//kklGnj8+sNTCeZr49P0nfPbpe/7X//Zfeb4+8/T0RDMG/0rbhM1DZDqeOJ7ekKYT17UioXE0R1gEhhR4e3jH+c17LucL33z4isNy4e5/vqeFym9//3v+9//+35klU/JCSMYqQhkhBhlQLSAhTDbv6vy5JrVEK+lpbdP8TRpUEEQdVNPDCnE0oFohu0g0B7Mx1EScQOLId3KjXp/6eIoI4/FAq0IoFZXTUD+tWDfWrRyfnjDxUqSaCy1nLc9HuhPb+v63cLFujXuSMeH6HpQNVNnvta4/yQ6I3a3VbU33RUyHWY3NtF/T+3XvdimEoECMg0WwgeM7cHAfnL0GGdvunl4DoPufu27pvkFUf7+AuE62iDrhoow1SckQt12J4StQk+1rDKR6CfC1qgyeH7pHf+2B5z141+/TPuffsSWAtrJ9p4t2oM6w82Zl56+/w+fczKePWr/uD2n37u9/P5ebXWxdz9MlCjbwM35vDPa2cFs/0u+p7Wy7iJZ8lbIl8EKzNS4K3Aoq9+Ov8OJaOFxrY2fNP7U2fHc/29nk6xjYAgAHNR2sjsmkRZz5vdn/H1q3HvTux9ClkJRJbp/soLgG0nuHdf/nJuGwv+8N4HXQeQ++9zXUWvcLNmzph+fYz6TWQEUMXs7hBni6Fu1+/bg2rAPU23VKKcoKdd+l0fUefd50/Lc9VS1I3pf3gTJJogWSrWENP5T1F2PEZRW0mYUn0Lf14WvRwYlo8lj7uffzzzXgHQzN+WUC2M+NaVJAszZY1/yCFbwaQ3DNri+svku0IDqEZOPqOstuo7UhR7JSQv9ZjIlpGnu5o841FgxFAzddfsm0coM2FIlRCQpbMsg6YpvfrOWTeo8xJFIaCWngcrmYbFbt+qHN/bBgXafjiEhQRpkEClp94/taglNJpY9vqypZcLtqsOpdugEDxwulVKbp0EsqQ9S5RiJB9B4bKuEgwDAk3r//hBaiNkCJEakVRMH0w+lAK40UCinAeIDP3keOU2CZq8lXVP3uAIcgKOzc+vr9czZ+/9r21P6HL/8hbMmcSOM06rNd58qtCMvFiAsB7k4DEhpLhuusNijnVTvJNzG2bCCGzDQKJQdoCgLmvFBZIFRcCL1LmQSdA0Mt+35uKDNMG9GsBCt9djs/iu7FZSnEMJAGteNDZ0HvKvZ871UQVFbDmxfHELnOF0LQOFbXZEDESq1DRiRxmBrDOKjOdNEKKLdzKQ06t2JkjdqQKCzrSgqBw+mO0IrpJRdgpRI4DBPXhwcev/mSsFxIohJTwqCSXiHaM6iswGEHWhwPE3fHI4IwjJHj4cA4qqyDgnpVpT+ELvWgvOLWJaFaseQT25kg4nItmO65d2KP3a/c22maJw7Njw+BcVSGY4qxJ1L0UwY8tq3KMISoPll0m2g20o4LZ/unFJnCgdNwIhChafKj5UpuGUErAWOIXVZLTa3HWrL5TkGZ8dWaZ7rfUM3WRvvZoAI3KqdTV20QXK0SoUIQbXYVW9gYxzQkW7M3Lw9Hz9hCxpvOBRrzujKXK62txKCMWa9mK3k1/9z8EDYfsZP5RSUhWlDQL94i4+HION2DHChU1e5OiRgHJA09rnAZsiEGpASKBEpdkRwUZ4hJ45emzx1DIIUR4sA4qi9UW6GWhXJ/Ja8za1mgaFVHHOLO92pa6Uu0Sge1T6fzOwX9gmsUq8RgNna/24jaMqUsGo8SVEquNXJD8Rjx5o2LxaQWXWsQo+e5nV3uemlPCCVGqd60xlQpJdZ5xUkmrTXGceJ8OpEtsV7zy147DqYuy6IEl2QST6uKN9RaDQCsprOq8eg4HkgpmKRC7Pqtvr9Op5P9m74G5mXhdruS12y4k1nzKL3i9vn5uSdM53nmer12sNT3ol9rGMdOIGitcbo704puPscD5nnWM7NV2mpSmOtKiAHnVfme00S4qJ3aXetwOHA6nTpruNbK6Xh6EY+11rher2bvdexTUjB108qm+0vjOHafU6JqNQ/T2JNPCuTqutCmkSur+SFAbzjW8Y5OYPvh1181SKtMMWPLhcDxdIKsxn46TlQR4nRQUerQCGTK9YkwXyEvqu0mkdYyQ5mJrVJDpFQhWvF2aYFKsqBLxeDv3n/COsKP7r7gq69+r4YiBg7TQK3C88cnYhq43Rau60K1ACSWpGU80wStEk4nBgJrnqlLJoXE6XgkxsRzDKzLTQFdgeX5CSkwjZo9aTHw/N1H/vn/+Gf+5qc/4YvPPyE0LWXAGp4EA6HXosxiLR3SjrLNMl5D8s0ZGYeRaRp1g2bt5FlrJjQtwXc9LC0nK1AL0irLckMkkItQTDrBNfp8bjpAUlY8K51RIXqxw6KZQH+IlVYzv//yN1yXC1BJh5EUImkaVe/XgpkYEuxYwt7w5zUTqpaiHW/DLtirWioULEuqz6fZIbHEpjNxkU3Xzw28IgKmv6NP1+9DzCB35tGrwF9ErJTp5c9f6vfa51w/FkhBdUtbtaIVY1E5cOPAUm8mFFVXzQ/rYqCca8TJTtbA9Z9eB6vBkI/WnAXYwMpS3ZhsTsxr5tzLsqTt/ds4vHbauzZNaz1DtpVX0IN3PTT03w7IOjgS7DBt4SW49Ppe/hJ4pAdAI8umN9nEsust8Ob8hp9+8TN+/OZzDmvgerkRQ+L+7sTz40e++uor/v03v2FdV6Zp4v7+neqPJS1H0vkrhEPg0+OZdHrLz37+j5yOJ/7bf/1fWOcbU4osZeXx4ZEaDwzHd4zHI5/Ij7k+PZDzldIKv/zFPcc37/ndH37HH777A0/LxTi+zQUNVOe2VeKUtJFPNZ0pG+NaSy8NFgPr9nMiEbI1EoxoKQ8WrJXqTo1gF9TvqFpWRdR70P3UeF5nBVGrAhgxJd7fveF4OPDNhw88367GttrWSquVZV4hayM0L0fxdZacWdF0fTZ0TXsSBpRBop/Ts0OC6lEpeL32NbkHIoOEzuR7DaT6+0MIXeNRdqUp+/ftmXCqd9ZersXdny5z4GDsfr/sX3sQjD3A2HeI/bljbW7P5jZDiy8lJuJh0gY/YMB2s+ffGnZ5ALTfy3vQ0p/VAdcXgCEupfMSdPb7wezy6985GNOfdT8G3f5LT6ikIHz27lMeL1cu16ua6n4dsxm7s0CBO/neM722Gf4dHgh7MkltYrOS52ZllRs78uW8+azsBqXJtpRNuiHYdzX7WQhul4y9bEmLqAPUmwfRNjAXB6Kbw2B2XUtU9DVY/bIbe9TPSFeSeIWmWPzs5ZweDvvX+lrfAda+Fmy8HUjrc+pjZdfy4NV/v63d2s9iB2v377FIsQdFLqPh69B1/3zAc9HydXn1fP7SfY9WjNSXlR8i8iKJuJUnvzxjjBO2jbe9lOEYwOQGqu0tT26qDXBpBh2/CqbHZiNsCevW6qYRLS4Pse0f2ZeW+5jj5+3LMXW9t4Z0tskeWFyMeRL23+8+Rb/2NkZuO2trhFJZ7axutVoTHdO2YwOla9VmPSkNnvtTbdm8knNhGLbmS9/D/UTUh5XGNJ5IaeQ2XyhVAbCUEk/PTwxp4HA4UcrCbb4xjqMmwYOx+4BI5DAkUpqI4wQhWkXYYnqnCtoFth4GpRrTkkjJuotLywrwmeaniEnvNAzAG7TksSkw43bDmTjKHNayecSaucmB1rSx0DCOhJBoVazyBG1Gaoz0hrJ1CSt5WRnGxJs3A/NTQYrJLiX1Mc9HIQbtGl+yyjOl1ChlITcBKy/1gf+PALT/Ty8/rxBPBMEhQA6FFCvTIHzzvCrLtgRKFTThpOv+MAnjGDgeRn7/pyspTgyhcj4L1/nG8wXef3rHPAeuC1yukWUJSjZhNcas7oshRBrOADc7G7byXXA7omCpzlVgmAbexU+Y5yvjeFCfqyhrfC/XogBMNdCvmY8eiFVJIMMwMN4OPSnje6pUTWwIyqjVfW2ybJ6Ap1qCYVVfzcZS97n2X2lYf4JadL0UY9IGIbbMh+d/5fr0DbHNDEkLOWLTxpzShCSBNChwekyJu7t7GnCaztwf70FgOCRtziMQg1V1NT2IQlVfmqCNuOClvVIQdWMcb4Qh6dIITirBzxLzcV06ypOAXvMSTCplz+jzWK2v3qYJx3Vdu70upXZw2PWJVeItEmWktsy8XJAykOSIyKh9FFDgshaokiwOXg3U8fiCTr4qtagPiX5QAhSrbsXsVpBATJpQ14ZTmdKaruFaEYkK0i7R1tw+XpXuB+q6EgvlCnNZqG0lLzfyulDKldpmoNJCo1U9J2/zYvvdfWgxDVxrdoYnA5rZxaRyF+ORczozygkZD8RpJB4OpOmEMGhzLhT8kgihRaY0MIhw0kuptIw0ruvMsjyxzBfWWro0o85f1WqGYUJiJK8jt/VK7GHrPraFsRQjRUkHygezzw7U2QMzDkf9brFKspo7y7gRoGoDv9qcGW4HrtgcSmPN2apJFsVicGknnR8RkCyUPNu5p3IUQYK+pTRL0FYui+pTN9nK/d2ORmPHns8nAG0WZhU5a1aAO1uCdNk1siql8Pj4wLoqu/R8vmMYEpfLVdmeIgbsauLP92gTYToemY7mU9iSC0acbMD5fMKT2tfrVTEq87Xnee5nnOuxpxB7XyCCqq4fd/qxh8NBfXgR7t686XiBxufqP6zrqs+5rpRSec56Bju7t7VmDcRCB6nV2dvOtJ5Ytu9y2SQHdUWE1ZrZiohWvozT1o/H5mdII2kQ1iWz5sIhDoZfqP3tfYRq48OHb3kJBv95oPavGqRtwFIqVzvwQmlM48hk5UEiwnQ4seTK9fJMe36G5wvt+QnJGRkmDazqTMhXoqjkQIsN1kwpMJwnhvPAOi8gQi4Lp9PAt08z92/fsea3fPj6gXWtpDEq5X0IDG/OpPOZ4TbzcLkQx0kJP612cG0YJ9ZcyZdK1siLp+uFlAaKNMa7IxIi5ZpYLs+wWMdZO+yjRB4+fKRSePfuzLv7N6xz1tK90hDZmFjZgp2NASFEiRymqRuk2pRhsWlaGtjX1EAsxXSk0MzBJa9AIpsjU1ukihbBFrHMaFBheTEQIzfV3SA05rLsmBCqm5bzysPjt1yfH+0QqRCFYRwZxtEAU+0WDXZY7Azw6wC+GUgzpJ0IvJXFO4gE6sRqAwztcm6CSb1sfm/EtNzZgNhWuuPV76NVlEFj5tuCtLx6l+I9MNPD8O6ktta00VetL7rOY+8qfug6uGAAq7kw6uRaM6HWmmWW9DNVoJlho1nRvnh4/f0yUA189c7ESjscDXYnyQN6B2/24IYYAMYO/NXAe2M1dZhN6MCvf9Z1Zzz4ZffeDaDdAFy/bxvgV9fc1oRfW35gzfirgzXNWVSqpRWa8O70jr/76d9xP56o15XHq5Zrns5HPj58ZBqTGvFSOd+95fHxgelw4Hx34nq9gQWmeZn527//e37z2y/5u7/9R6bxjm+++SNPHz/wXBaevnumtUZZZ9LpHadwpDRIYeDu7i1rOVJKJs4L8f3E3eGO9+/f8z9+9yseHh9IURsNhME6vcdAtOZlIkGdztbI2fTSfP7YAXxN7UDcJcRa2BiEWsy1G0cDhHR96bhV+7evWVlL1wAupXIYBo73d+S8sqJM+roaIBo1WFI9w6BM2tasGaABZU0Bby8D3pdGl7axOd3Rdw1DfZ+D/b6uvOHXVj4nSNfn3a8ZZ/yqg2fldU1egAZ7NloI7vjnDi75uvU/a7WSNzYg5fXv92DIvqy+v//VZ6sxPH8oISKWxZVhpIWoDXHiVrK9B+gUT+yo3QsA8vvAFJ1hSHtd+r797vU+dMdm/wz+2v69ObVm9Pp9qUWHMQ2EOGuic5co8+eure6/uduxH3omH8fmyKglbnQe9ne43cPuk6/mcZvLFwDwD4CEroWrcIQGoQ09ngIGHNI6QLu/757EaPpFxnvpc9DLFiV0rWLxofW/G/gsTRMxet5sSbT9M6kmdLGPGNhrvsGWmLNEcv/cNg4eAKndDn1cv58U2fbN95MmG5PVg/vX++BF8PVnXs0CDHfma4WQIrVsJXNeIriu64tGE99jrNt99fMUBQLA9w9IMEmXbjx17JtJXrS6A4Z3VTGgibdaSmeH9fPXkmbVgfYKrvct2+C+mEtnyV6vF2IckRB7OaBqfxby3LbkF9s5QWs9CG6tsa6LjovE7d73exy6xpwHyb6fvMxY5RnYfefKsmgAO02H3Z5RMHlvH0QCh8OZ+7t3yua1hmCCgmSgY1LW0hk+MUamwUFUbcxDa6Q0IqLapy6xgKB67SFuclCoFE+pzRitWvbtCfkQ9b5BAWevbEJ2FSuobzkMyeZ4Z4ualsXHIAY4pQ5gt2Ysr7glugSrkhtHnXcab84jFJ2f0yQcWuT+PjBNmjicknA6VlJQMzdMkSVr8mSMiUDVwLtVbYIUf4Ad+2c31l/4nYNlBlwqDCacUuSSCyFG7g+BvELWvAaryhgTo3A+6fCdpkiUM8uqa+ruWPnR50c+fAcpKdjLsyCMjClR1pUV0XLrELrMRoiRVirRKtVbQ5skFQXSvJItxoTSH7Q6cRxHDofJ/KvKbAmOgMUtTZA4qO9fNU6j6WcFIaaBKQhpOGoJuycERVhyJqbc/617TgEMnwK1RYUiiWpz1GMBAikOVhmqerUkkGGrYf+LqAAAIABJREFUdGz50crs0cRDNeZji31/xhgYkso1TIfA6RxJw4E0HDidzxpXhtrPWG+cLBZHhMHiE5r6VIiVoisTVMJWdfTiLPZzSsS5Odv3ty0RF02/uhq4qd+1MefTjlGn19SzsZSC5KyMQANNfW3SvOpR2Xsum7CWzJxnWnlkYCXKAGxM09CEKoFYtVmjSxs0A1a1KZhXg1UIzUMsBWlzoRUDaREkqn1R3oE2ScTHpqpMwiIGjIdAJ9iIdNvVgJqhVpV5ubaVNc+UVTXCIeO6rc0osqVWcjDvys9EUZA2oCxFbVzVtLlas2qCFC3ertzkGSkraUnEdiMuV2QaqIYVpDgwpEEb/QX9XIgDIUWGEEkRZBSOx0itZ9ZSWPLCMiurlbYqeN2cjJSYprOCYHbOuc9cW2MYJ0Rab+jkU61ykUZYCdIDTgXKTXe+uT8VaZIIFLTW0OZeO/9B0MrV1iprXtQetKSSDs2rfaphKCa1ZBiPyuroeb2UleV57nNZS7VGbcr0BE0Mjgbuqq57YBpHtU9V4yoJyfy90QDfU/dfVFc2WEXKijdrblWbr+fmGq+abIiG39RWDbQ10ps1H09WYVLt+cZxZBgGjseD7Vu1A8fjsX+vnuOWhKhayXKdb6QQeU7Pfe/2ZEwMig+lpJU7lqga48h9ulf/Ja+K7eRqz6XXcnDY7YL7jNF8FmUWG5Y4TR0MdzzCyT9rWZnnG62VLlHjtsuT+Nd6QzFttUVqwyNDGmHQc8+Tbe/ff9r9nX3M8EOvv2qQVmgMCYYQoQbm24IqSVVyg0+mM0ESt/JEfX5g+fYD4TqTLBg7xMhtuVGWleW2EuJWqlUqtBhVbD4kiKr1eMs3/v23vybXmZwXfvazX/LtN//M7XYlxBtp0DKPkirrooy7T07vuc4rNWfuz3cMw6DdCytWjqQLRzWuVs0YrTOtJU7nO87v3jI/fCS3m2blciYUobZMI/H0eOVff/1bfvmzn/F2OhOaNibJUqFsB0syzUnMeQ/iWdkGVGoVlrwQQjQhcwMmm2aJa21c58UOv8KSq1L5u3dFry4VYxukqI7Celuo0ni8PnOdL1SpSAq8ffuWEAK3+crt8SPL9cJ8fSam2Eu2mqimpkRhqSZP0Rx0sfIW0TIZb/bl9+MsT4kRh4xiUrZVBG0+ZdpFqmOp5QUa16qepTM7fG3QNFMUgCpqmgONWBQEdQCzWnmqgji5g7GeVd9AINRBFdWqQcyBd3BQBBcX7aW0Aloao5sazHnaBahiHm/XXwLNutdNs8mHShsHqIOk5T8ONgteP+wAsti9ggUHO4D09Z/aIEfLdPYafoGk6xLN0gabt2LOjwf9P8Rc3AIxpwa99Pw3QM7YO9Suj+Msre3/+1fbXS90cIIWaJYFHULis3ef8nc/+VsSievTldBgiiPn05HDGPibH/+cy+3G9ZZZcqbcrvzkZ7/g3/7tV3z6+Rf8/vd/ogKfffIJHz8+8fHjI48P3/H1H35HzcK//tv/4DAJh9M9Q9Rxoh1pwx1rrlzmZ6bpxPF44s3de2peiR//xBiEk+nlpeHAb776LQ9PH1nCzKZBDcfhyDCoNlXDmGIdTBPT0pKOWur6NfArJAO9bE05smnrxNdHLc0SA4Jybd1i6+OISZY0AyYulyv/9utf83y5aJfQccKbLjqbJAQhtYAMA+vsoIh9X7PAXqTvEffBXdfTu5A607G1aoHRnt1pa8ASLK5LXVpR8ftXa1CTIx5E/AVpAHZA1Q60coCq65ftPteBFt1wL8AUoAdPDqobdLCta7czr/ePJY48eaZatImWIi0GwmB7jw3sdeDndYz9IplTNtbgdpvS7acDHu60ubO8f70ASHm5R3UYNkBgj7M5AFj9+jR++/uv1DaLdNmQbf9LZwiLsxR+4PXC9hhw2djYObJ7To+SRbYMepN9AmAPJL4eSA3U1VHf2KybTZIeZNDHwCQKXq2nLSCj31MwjXrfx4pJBLzLfJeAYDs7m32H2M/2kkX7ig8s+Gv7+/Y1KdvfEdl09FrrzdPUWdWgxHVKvXmls4d9gsSCWx/jnmzra8QqHn5gQvuewnHo5jO32zMOJKvdWFaT7CjVAjoXPNjK3IwQ92ptbvvX93YF02ytYMBebap77TzbjUmrzNeyZr1WsGcU1VV0B99lDzQkdVDT5tSC8ZJ1/fj7/T19reIAAaY52IwlAimpNFZICWLc+MYxWJdwt7cKf+oadvBjt15s37u8UinFNPT1eRpbQ1AFQdS+bw1PW/9zGrRxUSmrMuwI1Oalvg70Bw7HM+fzW5qontzheCaviVYKa14Zkgbcfk7d378hxITERJJAbQrYNYEWBhCtYiq1gASVXGhCLvqMISRr3CPEoDY2iWo7rkGf8zBNGjQH4XrVs+3u7k4TSsEAX9PojNF1C9W/nlojtEaKOuYpTQzjQXUGTdOuSyOIqC1skRiFd+9GPv80Uhf1kQVo5cApQboX7k8K/qgZ01hAQlRfO1cScExazn9MkWTztNYGtTG65Mx/FKz9D7zcVhWEUoV5raxZrPpNm7+IVIaka3G5FY7HgdM9CJWPTyo5cHkuXK6AJJ6fM/PcKGU0f15JIC3YHo8D5+OBXArrsq/IE9NJbBpSqdfcqx0kxt4wby0ocGpxpNtkZWEaLaNWYkqEFAwkyuR1k3oiqDRCE9FY0UKsGAJBBpsnoeTc7aE3DCZoOa3OR+txgB7DAYWfzFuwRB2+JlpBGHn/o5/z4af/yNPvC3L9mjavEAeC6PqaphNv391xOp05niaOp6NJriSmcWRIkZytYqg7EpWQtBS4N1u2sU1p7Gvdy5Nf+1D7RPc+LlAGrfFe+3dEJA4MQzCbZMzcpuC7MniNcGDxX85FG7flslUmNExCQolNVZTw1FCpQgmBFBKsT+RyYwqjgvCivXI0hmhqmxC71sbGbK2x5sXOcfNhaOSmjF1qoyy5xyFBAqVlZQxHk7fB/ZdqM2tSLVUlZkI0ObPa7Jy2hEJu1Kpx0ZXMtao0QGvV5Clc61zB+Wbxtpf8BzGChgHcSlgwclNrVDIhJNaSqRWWoWkipK6EAmEVGon1IWslUFNbnkxPN0jQ8y5GKqhES9Dqt3FIDCERh4EQA2OKECcgUUplvl1ptTAMidia7e9C14wfFBVrKDDaSSvGrBWEFjZ9X6+6CmLNYNvmaYtJ27h+b2lGBjMAVhvIgshAiokhHahlpdRMqaYhWzKtruoLjLFX0bmcSooqgRFD4nK7kMusAKJMFosFlkV/JjRC1aTkcp15qHq/h+OReVmNaEL3w0QCQzJJzqo4UTiovIGCtaUz1b3vhCcYXXKyGDD59Phktjt3uRVfgzQYp7H7ouO42bE0qF1Iw8jBbGBT40mtleOysC6asFpzhuIeuDKs1zVzPB45nZQ5HKJiK0vUZnMqbxRICU7h2O1Hzrl/ryDKFr/eyEH1fOuzxp0xpg5IiwjDOHA4HkkmKzqGgWkYu7+rDbt1D7uk5fV6Y1lUvqiURil6xs23Dwb+Bs7nszq5AYaQeqJ2L8X0+vVXDtLCEHWTkgstFSKNkcbd6Z50+pRGpcxPtLUQ8oqsNw1M00hdnpifVScylMy83pSyLoHj6czSoKFduWvOjFGQGLncbsQkfPXln/h6uCg4EE3DI7nuUKSmxpIrp9PE5XJhXRc+flw5n09W+ps5ThPjcObpetFMxRrJ64IIzLeZcZy4uztz/9mnPH7zQXVVgtDmTM2rlhUMke++e6Tk3/A//cPfE1szvSUtC65Ny4m11FrLm7FFuppAdgggQVsBZOvSKBJNJDtofsh0wtY8U0z0ozYNPIjJHG8NgkrVDbZkFTV/fHom10xuK5JgGAJzWblcH6nLwuXyTF5Wzf5MWqrgpci0hlinRNescaOpTdr0AHrhIDZM2NmaOHhdAmhJj4QeYItlAu1SWmoVttI/K1IEXNAAqmUYm5X9VxohKlDselk9WBH0oLOO7goiWPmh32y/xga6ImoU/VDflxCro2OZKP98rRSc+Qs901O3wFtwBrCBoRuqpA5L8fd61jH6A/TSLy1h7WGzAgu17ph3W4C8n5Ne8lhden8LbKt7Qy3073gd9L5muW0stJegR/+5Rc/duesBpMNZe1DWv3P/eb+2znqKibfnd/zsR78gtMCHj9/RSmWKA3f3J6bDxGGK/Kd/+Fv+t3/6JyQl5svCx6dHpsORjw8P/PrXv+bh8cFA8sLt8ZF/+ad/prXMl/lXzMtKio3T8cT5OCFo6eSyNGo4IsM9p2EixREGYa7w/HThermo0xQS58MbPify9u49v/36d/z6D/8X83ztaycQOUwHHuaH7rT4YkxpYFnmF6DSNh7aZENAu6S3Bp5kANNECkoyElGxfnyNia+Wvl4dQIxRWVDrsjDGgXGYDHj18mADUnNhLYWwqtyJr4tcXO9Qn8GZbCkpi7+D/Z7MYMtY+/OFvk42UOg1kOo7dZ+U2AO7HlzDSwb3PthwpmAHwnbruu/BtjHZEWcJ7+QW9vvq1V7z7w9gjHs6KMUuqNHA6KBdwGMiDAM1xS4JYwhSV+CU3Ry+fh4f29f2l9349Pcj/R76M+6ex/UtXzAC5fV1+d61nNXvY9DUw7UGvp6gwiRRtrPAu93vX69Zls2dxj4Cfll58Z7OMm/b/Vc8+Ho536+v5SWtPk/doNmh5IztGCA3H+AXN6NnOg46ygZIiiYMmzH2sCVY8sa+Fbuuv6cJys7EpIqk2FLbWHr0YHuzkX3ecbC0W3oc1Nw/u2p9WlMdNnZzNe1DnwovHdwzFPylQbSxqRyEhv5darv0p6VUc+BfzYE0vPO749SeQNSGienV2aN+klbibOeEg799Hdok+n0jJstSiprGutM+0y/u0kS0jf0eU9qBwZGNRqbv7ZIPfi+gvonvBbsvWyZ2TwbO4sG7PosHLL1pnduyJlp+6MCp2/4+BG63NEASIlTtDxGTVlx5mS8WIGljj9rBGWXRaOlfigMxxK7JqWyXjS3nHbRbs+ooxUJQvWXhMN0R4mhrH2oNIFqCOyQNvKP5T7HCdDhrJUFIjHHQajcb4xAS4zghSO/ALBJZ10X1H1NiHE7qv7RCY+U4Tbgcijd3SyEyWPA6jKrrN46jsh3VmWYYJkpWGbHaaq8mimnYysZFpYqisXyGqLqgYMSPEEij6rHSdN1fr5VTFIZo4EoUhgFSaKRRq4SWpbEsKm1zGCBFIcVGjAoyrjWyZmEarWdFgFa8qdufL8nsr/8AhrvtYLOfbk/dVwsKNYYC4xBIoXE8D9AiZQGZhHEQpmSNa2LiNleQgISROBTVqWSgidKFG6p3WkqhDRrM1zVQtXGDroEEo9lhBS5KX4u2pXrzumXJSgapm151a3ovErShnZ730uMrZa0VY+vpGaxSBlV7ZIiBNlaV6KQHMX+i0fT7RWjK59NrptgBKm9C6s1QgwwGOpltlUCpA28+/Qn/6T//F/54l7j84f/k9t23RBk43d0zTBNffPFjPv3sc+vc3ohRpexiUGZ1sYbUzeND920Qi+H0DE7G3HMN8RBCB7t/aD3t7Xb31xzsNV9Dwbxoe347M1wLZl4XQgmbjS6FlaXb4ZKL2VRPeBWkqZ3QqgavlAjUvHKVC5lo/+k55ud27w0EFjxuSXNl46qEjrMpc1lZSyG3rHMokZYrZEzWSRu1NTtbq7F7PQbTprWBaGAiaCWaGIDaqp5zuRRy1QReaXAtKzfJ1KDNh2nZPSrTTFVJDk8OamxqLPrWenMtPV9NNjBGmigYvMbKbS3kRZCYoK1oE7agWroirNlIFo0tKdkgxoGYBlIaGYaJMQ2Mw9j1cENseFM0Nx3elKm6/FCtHWQDP0OM3R3tu+zDqWu4ly5bkOImeQbQmmrZehK2YxSmC23eA16562d/jAMijSyaQEs0JFXqbbYxrayl6hiVHikBLk25chgai1Rr2BeQEAlhMC3UwroujIcDxxi53W4ma6Dra10z65q7buq6bkx9rxoqpXSyVDJpAG2AtsUmCmrr/huPB6phSm/evjE27IwT+zzmB7heb8YsTf27YlAg3tmxynQPxmDV8/zu7q7vedePXddV/YN1pRR9roeHj3gFjpN7VtMXHozFGyX0Z53GkeF46uSeWivLcekAtMsOxSjktXAzjd80Djw+PW2M/Nq6jMqe6evXCSFwd3//QjJhn2y63q4IajclBNayMsat4dpfSn7+VYO0oNnishZYCyFOHE/3fHL3CW/e/4RrmLh+/Ib5krk8XikfP3JoC3E80GpkvtyQstKqduMUtLzhME60WplvN4Skvw9wvDtrp9yWWZbMujZyuZoTpU7WumbGw8DxfGIyY/789ECQwpjUIM/X2RZqYRoHUoqc787asTMshADrNZNiZL7N/OmPf6TmhRqE0/072l3h6esPyGIMhGVmmRc+VvjVn/7IF2/fMRrDANtsjY2lsW0abWATLVM1L5nc9BlEVAi7iRrfajqwDQv6sCAgRIiRbBmhaZrIq3ZgXJaFeZ4teGzaiG0YOJ0nLtcHHj/8kZuVnYUYSBIJadDyCSutbqLFGaVn6HZdielnIdC0cZsF8L7ZexCMA5TOAN0BBuLsr9qDOQ8kYrJMHHofPfD2oIqqXeZBpQR6fG0OVtXsW2uVQDSQik1knQ0Ec6On/oaxzPZYxA48aDvAcQ+gyO47fRzqLpvvYVx3LtvmxDiDcp+53t/Axv79vs6ig2Rt1yRNv1sPzD0Q4sGrB8IbiGcH5Svgaa/Ntt2XjfErAOflM3lm167WoLWsQa60F+/dwBOPaPfOYCO0wP3pDT//4ufcn+757sO3XG4XhqjZ0du6cP32G8py48vf/46lFMbDHU+PV0KAr7/5mpiE2lZCFMbpqOLptyvTOHC73igIa7FGADSeHp8Z0kCTgSYHfvSLnzLcfaaaWbeZ2m48Pn7Nx4dvuV2eKetKGgbu3txxGk8MJfO3X/wCiY1/++2vuC0zKUTe3L3h7v7M48OzObjWlFC0Mcl+PW7am/uy+rabt2JltSB4hnYLrNiBBD7f6jBvYIYnjwY70NwZWNfVsvSBUnYgr4OczZlWFe+y/RLY28AYf5aeQS25l7HsX5tz/lIewwOGkjMxmg52Bz9sL7Zt372UV+BFA5g9i8ITFP6ZF7ps8pJJ7n8Hc8j9kLebqA1LpsmL9SyiAa5fJzhrISZt2hACpGQO0R6o1v3jzpbapW2/fX9PeuLIOiz3xh/2e096GPjzOhBzYM7HdBtb2d2PBbs2ltu+t+e0pKpe04MI2+emT7cHSl/bpdeA7es10MF+8THfnRds4wYWCIs3Dvs+UOuB6t7Ge7DpZxrGLml2MDig2ud+X2bfNvBbRHqiVEm6rQeHffOwrVeqSyFV093299atCamEDQTYOd79vOjrfwuGagdot6DYbb2CztGaNMWNmcvWCfj1+n85hmYPLHFENSDXbUEf2Nb3m7OpxEAQNSWa1BBPrIp9f4gg7nDHLpHiQEx/xrrdU19bfQ9vv8P2jwPn3sRUaC+kmvo5FDTY1mff7Eqx5/PTXMc70iU8mtqXEBNpSAZ8WkArSjQQIJdd0si+bUiJGn1u+8gwTIkUk66aMHSw17s3R9vqff5FDFQwSRmbL2rWOQ+6llKMxBStmQm2VpSF5o2x/EyKKZLXonNowZs25rJyaft8jCpDcTidCUGZVd6sd1sSCjiHqLatFDgcjqrhP4wch4nWlKXj63lIetbnYmWgTZlGwzByOB7RhptiVVAr0zjsLIgmIrrcGRqwd4ZOa5Yn1aC1YEC1JGt6Yp3pjW0bozdPzcSk1Tb9jLZ5brlQq8q01Vl4koF0jKTYzMYLNTfmmomDNhgttZFLIyUFbaMBPBJUoqM0YW3CUlV/OyIMcS+k8v/dSwJEW7dVGmuDYYA5Z3KutBaoVSjmY8ZQKUSuz5mQAsdDolYFokvVwP44DZymyPmYeXhciPVAGzVOmmdNEKj+svuF0GSrKlRQNVqzraqAsaB6nLszNwQhBYuTqmzfBYzWeMyl59y+uPY17t+gcl9rVKkqlawRxnGi1AyyQimwO0N9J6uMkdq6FCMleDM93WUaK+3ijqoVb60WRBJxOnH/xU+JofB8f+L64SuGCPdv7hnSkXdvPuNwOAIZ2kytK4SBQoUeRokdNdXOZne7jUQSTIJgB0I4WcPjVKD7CH4Gbn4Tti+8asMJOV69WF58HuisNH9v90HZaeeLx0fOQja7WzK5LsAmn1Vro60oW59IxlivVEKkS4SVNeP9FTwRrUdyRdoGKJVWqKKVBK1VqEJdgQKhqe51CK45bTrmQXVLdd8PiJVQV2umrntJ7XwzXyAX1TovpbGUxnNeWMnkplIPjYWctclkCJGqOUXGpA0XQYzYpd9farV5xKQx9ORP00Q6TKhmSKRKYMmVKFoeXxFCNX9YzB8QPdOp2piutZVaArQDUQpVRm7rBU/MN2l2BoTuR0gKti22tfSana0VXUpscUUDZR9jbPXNj9h8041N7BiB5rWdOetnd7+yMWnt/MHjnci6lm7jT6fIOjekVWPOaqyherGeyFDpi5K1Ifxym8m1dUKYS0RpvK2J1GmaOByOelabjIv3HnFgVlnk3sBTY5VlUSnKeV6gNU6nszVM1MSkNy+NMXESa0xue+14PHI8TmYjN5/G1743NHOCG1Wfa6nLdopHMcbv1mx1u18FcI9HZcQmA4wFiwfZKss6BmWvUgprXrotqKWQYuJ0OnWA1ff2OA7EcLDTWuOrUzkzL3NParktyTV3MFiNzssqxmSyCX4PwzD0OZimifN6tvGp1ti7mbpK69VPf+711w3SimaVJUKQI+PxE95/9lPef/ITlrXx9Kdf8/j1H5gvMynYaVqgrI26LrSykGvRzEkVqIFkek7z7UbvNtk0azGMoxq2JiCJvGojLkRIoTGkgXGMDCkSgzANE+mTwDdff8vd9IaYBi7PVy7PVwteAs9PV2hVdV2DZvXyfKNcZmXvThM3684nUZlBIY1MpzPxLiCh8fztd8peSwPffnjg9nTjszf3vL2/sxKLqplOB1YMJAkEMk27UVbVnLvc1KmbpkkNeWuoTLky3vTg1VKHVrVEKMRIioHbUnm6PrMsSw8IKpVx0qYIDcht5dsPf+TxwzewrqpVY45xiJEwaClYq1WZXKVAUseX3Lr+DWGnc4l148UyyKKPqMYo7DJAfnh7M7PmFSYdHBGBZo3XpEE/nVqzUiPRTJdEnMRbROcyNAG8EQhboNNelvAGB4/kJUj4/YD0JTDjWSQ9cHRMXgM6Dkz1INbBEOilhvo4+8PKmZINF+W3DWbXcEdnY+G+BsS2+wzbNcPre9kBPBZvBwcqdvek0/tK99CCl57Jxr/Tr4fdmwf5qTsxrqkkwQECDZR8RqTPwwvjgoXACMJhOPCTT37M28M91+crT8+PrBYg1QBrM3kKEeasCYvClUZmGCfiEBhqIpfKMmcO00DJCzENVIHnZSHH2PXQcpuR2hjiwnQYeff+Uw5377jmwjxfuD09UssTt+tH1vmJWleu6wUpkTSpo7rON6Zp5Bef/4IURv7lV/9CC3A63XN/vifKH2h1VWfOnFEN9Epfa1qaUXANJwUxw06ryxlZ+3GzDLXvzz6vxkqvtZfI+qvvP/py6IGMMuxa/+4YB0rxDpgRTDrDnWYPlGotxoh3+YPN2R/CBtBtwW20vbExXzoj0IAYCWkLpNhJGOxee/DqdZKh77VdkgAPGIB9WYvryEa7v/1e2wOKDtK+wN92oM+mC2dAcymkYUQGoUSQMVKDlmBXlDGBhJf3u7+nXYCj07rtf7ere8BAg3wBD1Z5+Tm3Cw4G/hCDeQ9+I76+nK1o4OsrABYMEO7wzU4q5tV62F9n/6f/fZ/U0nOtWQDzF76jg5HO8rSfCi/GVdmfuz1jZwOEjgB6gkwbobQuvePJtR+69xdrcx/g+ngaW8XZp6VYWZVskgtRFLzpAAIKSND3CHatPTPagcM+gru5FAPXgsoBiQHSgiWKPNjY1tSLM7tt4LDbC3eE204nuGuMmg3Z1lDo878xiQ2QNd+GZv5EiDQHl0NUjU6fHxzoAtDy9xcAcA/m9D0uHxViAq+ICQF22uyIEFEN+c70qcbGx8666vtHvZ2QLGCOA8M4dJ06aRCHQVmeQ+3Bj0tMqOZ90c7hVXWE1Y9L5t8Z0OosuJh6qaPfj+vPppR6o131pfSemmhpsFcPjZ68w5MmdUuojHaWFgWhx2FkOhwRAuNUbT4Cy7xqksz82CFOQKQ6HmRLfc/sEqI2AxOtoFBt8WTyFaGDF878WnOBciWGCZFBfQ9b/7d57us5Bi1dDdbBWai27pVN1UpToNrWqdoqYS4roEzYFlTbMcrG6l/WpWv4xej7w9ZuiDQR1uod6TVZN0xDt0N7RlQMgkQYj5HjGECsyZ+IVk3RCCky3wqiXTxJKXC+iySjqPv8SVOfV+IW8KeUusu4t5n/b1/dB7CxW4ranHEITDVSauO2NlrNxEFLo1McSKcCobIsQcHZkhnGhDDwfMncnfWsSMPAJ2/hqz8UmgTGNHJ5Fm7XdZNSCm6RpQfkrWmSwBNsJReIwcAZ6fZEbXV++VBOvACmabLkQGVdl76+YzS2LeB9L4Zh0EZUov5lbpaoCbbrXvkDCmBqkjREb9r8ykfpz6PyFzStvBEJ4Cy3wxvuP/85YxJ+9OMvGGNB1SEGhMhKRshIdck8QVqwCp6ANzvELVbYGhZ7UqFJMPa7zbvbz7bZ8E4OEOnciRfsWS+3781Y9T17zX+fPx+fffyyT4x7hYP2AtmaASm4lGlN51S8j4GIJmaoEApr85imsi6ZFKyHQq0mRWcSFXZPt9uNXIrGtzTNM0asoWCjKamV9bYSQ0J2DZvdj1prJudF10lToDZGhW60zNxjHYsTEq7bAAAgAElEQVShlG6kGvcVncVWya0wrwu1FURU61WT7mrPS1lZivrf+uy21t2vnOum34oxS5dH6hO9WWKMiQJIsyaIcWAKas+16ZtWtaUhkUQBzDEOSINcZ5Z8JZkurKDJ5BidkKY2OabBqqXDllgUyIWeMFe8oxJDBFY2mSMnosz6WFVlbFKKuzWznUc6xqmvrX28qqBstcbMCW8wkEKC4nvSKiNi0J4QZaVavJnXYpKU9Od8//5Tnp4eeb4UbrcrHx8eWcoCTUvlh0FB/NttfuGL6djHrSojxt5AaxgSDi77c3jsNc835nlhHEdNDtTK7XbVeNCaCV9uVw7T1CuAdAwqORdroGWJ+KANtKZp4nw+s+as8kFr7j5sLaXH7LW6rY29een1eqW11rVt9/fr/qc/2zRNvcHqatUvNZcOfM7zzHy70Wrjcrls8Uiwvj+ifsQ0TcQoDHFkOh60r4vFKjGp7vCyaDxas0oc1J2ferlcWJ+ecGbtfux9rZRStLn43dlIicXYyX7W/v9Y7mCSkePpDfd3P+KLn/8DLR745psHvv3Tl1y+/ZLb07c0GvfnN3x8+KBlKkVFpofgsbI5z9JY15mnhwdabQyns+rOIFZ6r5nbWtXQAcQ0KagUI4fjRIpKl08SyPPCYRpNMxcuj49A4HAYuF4y65LJ+UbJqjuGQF4XWs5IXlUrN6vUQi2VeJi43pZe9jMdRuJh4vnxWbsX0lifr3y3PFCWmfPbO+7GI9k6+/nh14N91KDW1pQJu67kqg6sGnB3Viy7X51VVToDJi8L8+2ZuWRuy9w1WVVAPCBJCEm43p5Zy8ptfrasK0gcVHrgcOBwd991Z3JrlHWxcd2AxYADeh5s2tHTMIDUyh6CH8K6TrZgb3NinIGHZWliFWP0vHQ09TAy59823WAaPWODYxOe6sIctfOqBtD/N3Xv9mtLkpz3/SIzq2qtffbpc7p7ZnrYJIdjkqZJyLZswI+GngXYhmHAf6YNG4YhPfnJD7Is0hYoSBZFibch59o9fTl777VWVWaGHyIiq9bppq0HGRivmTOzL2vXqspLZMQXX3zhmb1xD34oajNtopJpTZEcJSlHEFSGQ2Lg4244I9AGXIYCD6CCqbUbySPIMYJcxKtt9qA+AtbYUaqMw18kdpnreqLjPR0FbWNN+aV9PMNhd2AFC0ijOc0OKsl4nmhuIoahDmBpn3cd31vQcnAA/TPvAWM7bJMDigHk7PN677R+6yvWRi589OZj3jy+Yb2u3G4X0xcTZXWmTUIgZ1qt9CTU1ji/mrheLoB1gDWwMKHMTA8f8rJ1er2xte7NDhdEKvNpMeeoW5f6XApN4d27J9YOt+cvuVy+RtuN2/WJtpmGliUuOs/Xi62d1inzwpJO/Pav/ZA5T/zJn/0r6lpZV2MAda0jmZCya1U70HZ8BUiYShlgRPw8nOkBrg1AYM8ABvgmKcqWbe5Cr7EFo38AuDtAHwmWXCZEN9S7E8cajq2hB9tmP3NHV3eAxxwmd64OIFYkKVIOR9/E/oNBOoA+2dfu+wDmNwKlA8gZSQdbVqZDGZ97x6A77HFVNY3IA+j2PvPzuI9EjD35/twJLsciO3tRxFJveZpgmlxlxO2BP604gODWj2Py6TjfEegcnbRg1A6s7v254R5MjaTVsevyGIO4xBj3PaFm7EYHlLi3fapqSSe1tTDAsB23/QawcASG7bnEsSdbHzm7NIsDr+GoRwMoc7pdpiIA5Qh+RQ6yEO89O7sN22dN9mZoB7ua0NExNwb3aG+PzzGSk30HXodUkAeOsa5GWdVhiHLKo1mC4Bqs2kcp6FGe4v1EAjD2cjSCGuM1SqQzO6Arx+X/LZUT8VwG5GZnQYbe9pA1gVGmtuu/H22FJZpC8zOeBw+4wUDZKPFLB0avkWF8jbm/kbxJTVxLdJdYsbJiYc6mu1hKidPVVoDGmap+3R2QiLOtu98VrBIVdvkNZ/6WvHi5npKbJdWHdq3iY2WVYpKM1bQHqOJ2P5sma7J+AKl4A5HN7O0RJHd308fGOA6h6R+yWXGuGNvNwe9kQMu23ixOzXZ2lmzBS0sdaYrkQi4LtTZSLkzzTGudaSkxZASglKSgvY4EnWAAvLWQ9/cdWPvhH3aXbxp+X4DuPmdKZ5qjG3xyNt2+Dm3/yzgTQsc8p31/R3k5Pl+5WFNGIZHLTFQgFcHuW0ILU5ln06lrHeYyM83LCP6M4ZoQFU4nYy7Vep9Aa9qRlFmWzDybRMHDBMviMkRdOD/Y/cc9366meTslmCdvdmUiq5xOiSKdJVszpFys9JoBTv+7e7kb6B3jhSiUpytFhGXOdLGmU8k1WEt2FnAubJpGdQDNgBZBeHm+8XCe+frLlZ6tqdpXTytlKkxT5vJy81JUk6YwW+lMP1UvGzZAPQCwsOljz/ddw3Gff08Oub9Ua3VmlVCrJXQMLIny9d3WBsgWicioeBAxeao29nsaTZPMDja3Z2ZXatsb5wUTzpqumr3vgWapE5F6YpoeeHzzHeSayX1FWqXVjd5vZKmAAdcMv8+Bp7RX0SCYlEyZTJbOARBj/Pv5NliA94nEPVY1+2I9APK+SOIjRvVG+Er3yewAbMNvgT3hfKyw0uZNktqG9noXOwZhJZiTSWwPJYz5unZLCmg10lWr3rzJ9eQlJbZtdSJGY9uMsbj1CmJsb7X2Omzd5AZEBW1QbyYbWL3PSxoxrrCu1kzRqigsYVCcrW3jyC6h070qVYwpD+lAXlGrXI1Ejq+Hrd087ra4NtnUmW5u75Q0+XxHQzXfN9KGLWubsSTzvJgPHuwoXVkVGq7dqb7HS2EqM1MqlFEa7xU37v9NZTK/mu4Nvq1p1jwvzPM85HVEhHmercljMRwnJat66E1IyZjFFusZJoFag0C6NYDctpDrk8FSxW1Cnia69iFNmHN2f8SZuwq5WUP20EMOSTiG5JAxZSWbvUm5oKvFjHvzzIKizKeFqme2tvFhLqx15enpxX2nfd2bxnLler3Z8+cyYp/YCzlnFm8ef2ScBwj98PCK8/lhPG/vjWX5LtEgqytcbxt0Y7DulY196NnGdaPBpPlf5puYhm4aPo1IZinzOFej2iSuF42+hhZ/Nz+y9s3jPBvznLMxYctkEk3arfmc/xxmlmWmnk+gti/x+2+98e7ygmA4iwG8ZsNzKjhBm5IyZZ6HrOY8z9Rs8WWtxpYNcHhdd1kJERlyDURSB9jWlavLXuDxVMlBZrqPU46vX22QVuCjt5/wwavf5Dd+83f5j/6zP+B/+gf/C3/yL/8pUp/Q2zNZGnOZOJ8eeJof2W43er8iqVl5oAiSXHtiW7m9e0ffVlKZLOOVC8UZCdfbRs556GYViWBT+e6vf8SrhwV6NY2m1mm1cu0drZ3L84W1VjvYUVrb2NarsTYlDT1X7WqaX91L7T0LYUbPGaUKva4UnSjTK84ffkh9utC1UXpnrTeevm785V/9Bb/+a9/nzeMHsFXUy2tqb16S4l0isazScJpzjrMa8MAD1+4Sc17XunK93Xi5XrjcrshcrNTWMzO5FKaS2Z4v/OLzz6jbjVSysV2SWrOaaWJeTg4KJeq2kdUBhZSJupmujcmdLFy7K7qug3dX9aBd8q6JRu/WRC2Ml0GoO8OyexDuAMQOduwgBVFKmcypnyRxUuGchE9PC5+khZ+9vONnNL5S5QnoHoiY764u71j9EEgmiI3s5Y4BAkWQlxJRwm3l3h6EeiY+J6F7h2sBbxjQB5hwD265Xp3EVSCCP8Y4R1ZWXN9zIBgGvg6AyaN33Vm6Ot62O1cRrNphY/em/ndgWf4ArobpSX5/7lQeASBxJy/+k1PyrphhCHAnQoZBCzmP5Gyl8fJ7EC861HAYiXXgzDcxoLg25bw88uHbj+lNWbcbW9tGkF5bJYkweQmnaT/DlITz6cxXX3xBKQZOzktmvXS+/8mn/Bf/7X/D//A//Pd89fNntFcmo36TER6XE9NUePv6kc8++wXnN29J05m2dR4fHrh8udF047Ze2LaGamKrfWjs9W6MHxFhmt2RyvB7v/U7fPb5Z/z4b/6G72w31571OekVre5Q5ABpDYRxd2Q4kmmU7wWrSl2iwV+9Igi328rS1RsU2e93oKQNcK8ddKNgd56Hk93afg2LXBDxxMEBlBoffzgMA+AIRzzne9H8I0Aazt8R6Aq/ZQcmHUhid4iO/+IVjMQI1MJBDmcoALnoEMxYwkdmZuy7e6ZMrNZvJDk0AqADUBfP4fvdnK8CeYJsXXVzLqh1trAGi7HvBtPPgtI3b96wrisvz88j8x2OXszfAGZSPNBhnFxfMNbSeBYPwvD5blFV4uBkBBjHTHcElHJ4/iOLN6758OoVp3nh66+/ZtvWUR1zvC/7Otg0x0oLIGn09BqACu68RxMs86nyuK6GbZIIGKOMVUZ5oKNMRHw0zKu6ldOD/rPsesu4jbRkgoz7CPC5+xofkgw47p+EHI64rzk5zI/4PNrc7WDnkUGMiCVE2R3hdABndpZqJGI8OJcoSfWzWnfmuFn9OCtjzzkrFXFW/+F3ktBsf5G9IUeMy9h73c7C6lUtktK4z6gSQISS58MaMN8iQGN1cE+8AUXy862n0Gs1lkwAg7H14+8TYXuyg/vW9APJQx4mfAPE2aV0tIcfwmBPBEgczbdyPt7nDoYbOCKD+di6gQUpZZdCsWuNs1r8mXOyqiWFXq1qLKUOde9enJLpPNI7U5mseYfbG7WRGGvN7sQTbqgxShmw5egtYA050hi/3oPRWjifXpnueiTYuuy+klhna2ua6E1buu0FxEr0rbGJzXNOSjClgmG2rqudu/Ps661YwAQgdpZPk/WXOJ1mS76q+17D/wkAzPZ2LOTqCQlJpvsaCY2uJh4xT4uxICWR8+RgTB+BZwSvBkAaMFHyNIgTuXhQOM3OYMrcVieTOJAV+9U0n9XAh2J9hF8uVqW2zAY60Duby5kkrxDrm7LWxulk2rTSG0Vgks6cM8nFu3Yv9N/9K86urga6nVLhctvYqgX6e0VBdiui9JZ5etc9QZ15OC9cr51aTV93q4WXq9J14euvN1btSCpcL9bcCFHKxNiD4rYywAezRR3txpLU3rltN0y32ua0VaVuG6VMdGfRietlm6b+hhBn9g76KIqkKFW25+7eoEc0WJ5p3A9uQ0rOtF49rjG7YX589uY01YDHuhl7bWjeEmEDJAP2RMwf601BJlQ3SlmgnEhVEK1o6mjfkG7scfNrPGmF4D2C9h0v5g9onH9RhSGOhw3pqIMtdh8hfBEDviCkXKyBlFkVO1+PUib7adC1E7q+OWe35+ZT2r3hlQSuj+5AbW+N2rYBuJGEnCbQNmxd642kCtXY71u3rvG9xvgnek/WZNrn7fl2oTYDZ2urDjCpH+WNSkeTsGkbfm9vnbpV6rZxW2/D5ipQJNNp1G1l2zZrVMfuk+F7JEXo1ro3wHW5CEneRE73pLInKIzRHX6Rnb1XPLZOiVQykhNbW23thB8idl1LSGafYwfAtgvixIeujZIWJ801QhFKGySUtVUoMz0VX9fqkg/7fE65GOtSlSknXjAMJWFkEvFESpm8iZv7PybbFEzrZmezg5LzcvZq19Ax2uWmSppN8tJ98rpVtmslCGBRvRMSDLEoU0rk1ZpzWc8Naya+1RWSGhbVTT7FqqUSy3Li0ivX5xuCNaTXrtaQK2ckZwpCmQ1ojQZVOYufP+YHmA5qu/Oht20b2q7X6/WOiRp+d5BsSsmknFlm+7q1Sil5yMWdlrPjUjaB5kd2tq1xvV653W5G1vG9pl2HVu7pdGbyZJVVPgpyM784p0SZXEfWAfBXr17x+Phoe6c2ogdIgNE7QUvYbiuXl5dhg1IxP3AqZa8CkQBUC4uzfrsq59N54EQAtW48Xa+stxcjTDqImool6PMhrriTrMPA29PpNMhIgGuERwzSR9yjHrsr9vwv3pBtKkfppPvXrzRIC7Cx8ZPPf8y728pLfcef/+k/o61fkNuNOYOkCSmZTRvzwyu2p196xj+6e1rHVG0bt3dP6G0dm0sFlmXyEjVlk87LbaVVc3xzzpQM2drKcr1dadsNbZ31Zhujbp26bj7IybPbZsSi3MMmxMS52+06AnRxZ5Rkm1a7oF7yX2ZjPPTamZaZ9fkFrZVeV0Q7er3xxU9+Rt0qv/nDH/LqdLJAoFqNfkgZqMC6raNj5a1ap8Xk2Y0IpGpvbOvGtr6j1j4cmKYNsnW7K9NkJbSt0vrGyy9/yeXlBZ0SMru8gGegRePA8JI0baSElzxGYAhdhXbb4BFwzdlRhBQBB/ghp6SmPpYehIo5krHZWrO5spJLQWs02vLAyVnCotZoKmF6jqkrC4kPGnyPzO8ur/jt85lHzfyyJ/5yu/GXbeXPdOOdmsJxVqy5mKHHowzG9AStAcwegDLAwnBw7Dzx/HSX/eAfQEVkRHdQA45A2KEREcZ2ifLfozFWxTTxAPHMjXal5ETKLjkxAF0PltxLSAN8svEPHR/Awbs2MucHOzYAisi04usswJUj6LVpp/jh0unmpAR7FSvTyik5oO7O5w5He1fSvfGagf/BrooD2Becl81YPYolJ16fH9HWuak1MLEyWXMSMlhZXFKSBFuxmwO/rUwIeNlIbZ1266yXZ/7h//jf8eM/+9d88vFbei988cUXPL5+ywcfvCYpxna9Xena2MgseaLMtnes8q+RipCZoCdUGmttJhki2cvwhLWa5rZ2oCm/+1u/wz/543/MV1//0oGGmK9IfuwMwCPwEWtTkrDV9S5LHzIPkWRQ7Uw5WxdrZC9h5x6AjbUa7LEA6pJLLBhzpaHV1lBCqFGW5JqARawU7QhI7oDtzqY/ArdHRv0RkI3NcKdLGuBUgIHtAKge9lp8xjiIxUASSd1BjAOrveloYjC6mqsagGMreGfl0Mwi7B94uLUjc9zBlIMjhnb73LADMdclIXNBpoRmQfHxkzTYEwa66h1IF5pKLy8vFA8CghW0A6MyPufIXld2IIkR7O7DjDv3BozKPubjLPRrhJ2KUnJHUK1K/Z7Rpb1zu1ysEqXvGf1Yzse5s8SUaWofbWYimw0TcYaguIZkG2dj2OzeZVxrPJua7R/2/TA/99CGug3eqykk6ViC40wMhlaMT6xHVe/Oayy76jewMxTsn4FUOiovYuyTV5XEmZFz9m7kjH2IOAiYy7D/UsK22hkxWMMxLnKw6+oOLGkHCXRnzKacxjqKeQxQcWc9QZ7KroF52L/h9EJHuwOAzloc8h1pAulDYsIOJgdlCdZCAJNpjNGYF82+9gTTios52tn1Ziedqdrb3T4Vfw7ksHIUOzf9YFUMKGi9mxxO3/WkiQQ0ltgOP+w4ZnE/SRLztAcO2+br2HWbJR2TVGmAu6GlhnYH9jNzKZxOJ1prrtm5P6sSWolRPZT3a7p/EPrwEfjksM0ax7X6OklMZebh9MC2NaacnVG4g8Uk65dgoL3LUiBIq8ZWSsK6xlrOzNM8AlBLSCVag0YAXd0AgzyBZLu35P5Lazw/P9ugOphiDXN2pmByHyzs8LZtVo6ZZgOmAqRB6R1vOAc56WB709Wv4RJdkq1qT5WUlCheiWSXkKitsrVCb1ZyPs8zkrMlKXwNqOzO5eWm3DZlTpklq3ewz2yb7ZcyGyg/F2hNaXSWVphmOM/FGLRA9n+F417/5ut9f/Tf9jXeH2CUmH5yU2UuhZfr5g3BzB9tFSubV2MB9g5rVaQoliNJ1Np59crApesFahUezgW9WvMkUdjWSsLkHloTZ9K1YVMYzWYNNBvrVqC3FU2zgbW50GpzqZWoCDP/0Bj71mBoXTdntumQHPEBcJuY/RNBaXdM+GMT0dhDkpRM9qB/39tZEpoEzZ2kLkMGoGnoiNveUgRr/CTF1q464z2qFrJaJaBqQgKk9DglGmohZdiRURKevOO574UkOygYFT7fshAsrutxFru/HgCuLZLRmjISOt19RasM27VIAwAOgBOMvdlMU2YwoI9XjUovFa+EdL9IXVbGqlG8qmTdhv+bkmLyId3tl8sc9GrAezPQ1So/LbG41s0YuKrc2r6+jLSU2FqlZ7FKAzGguao1eWpto9MGSzM6y2sccepznqMSwuxnqx2V6APgIKYae743q/CNRAD+frB4cZpnluWMSuLmTESThsycTzN5Xkg5M2UxpnTJpFGZhklj1DrISgmo3crdc1NKnpzRHD1oTHc/IWxtJWmi92lU59nnixkMVUqxk0lE2DZjAzdt1G66wVYtMtlJmgoqncvta0pZPNEYBIv9XAtG6sAd1PeGxw1TKWxd0Wz716Qi7I0qLpGTZ9vvKIiJT+zVonYoJumUMvP89MTl+mJ2pBuBSpKV7ffaWW8ra7uO9S0inM9nq/BxZH6eZ07L3pxrZ9ruTPFjRaR9r9xuN3prXC6bNxKDZfIELeavzfPsjb/Md7DEua2veZ5ZTqexnbe6hatDrZXL5eI4WsjzCLfblXU1+ZciiS4XIyuKsYgnx4+6wFImsx2Oh71elgEIZye6rasRMy7XC7WZZN+6boa/1DrA69ZnlzIykHmejHkdqn4Prx5ZXr0iJDhD+kZ7VIV16rbx8vJi9zkv/OJnP+fN2zdWaTUV67kkNn+Ty390dfZ5SszOaM6Txe+tW3Vx3aqdRX/L61capK1142d/8xdsa+LH25/yV3/+xzy+esX86hG9FqgrmhJNzEHtyUoJ2uWZiYxO3pyqN/r1Rl9XSsruuolRMJt1/G3dqPPtZtoTLVVaFTZz+fjTf/UX9F6Z5jwAo2WamXI25mqCNCVoZsiyWLYnytBNKywjp4WaDEztrTOfZvvcunn4m5A8k6eFRoZijkGnm8almNxCrRuiwu1y4a/+zb/m8c0bvvvd75GKZcGlVW6uHVu9+y0iLMtMyqGx41nkbaNuG12VpxdjUU1lYpln8pQoTiF//OCRy+Udz09fsW2Vtt7I0+TdJRksLWu8Y05FdBmNRZgH87IzygqXiUpn8sweA/aI49bLYdwoDSBIApx1gXfZS5ytnMMOpTSMvDnUtObwgrGPpHfeduEH04kflInvUfg0Tby5NQqdfr3yVG9QCrc08RdaecZlJHIALBaUWJliJ2r798YzBnzvzCr7+brerCwuW3lXi6CmdZLcl5YCo7TnfTatsDP2xs8PzrWM93onS7xB2wHwjHHdnXKN/94FojvTxAKdAO/iwLdLWFnO8N8PYNgIaO/GJ250B0AC1AuAOjKswZo6Mu8sNA0o0I5YgaHtOBi77OOWyEzLmTwX1u3G4/RoTfIAzQZiZ7FsnCTIs3CeZ7767Au+/OJrfrE2Ls8v/LV23r08cT4viCZeni+0P/ojkiR+ejqzbo0ynfj0N2aev95Yr1e6dKZiB8ar7cxHH79mnm7IPPHhh2/4ix/9lK1eqFuFLrReUVznsXQDIpplE3PJdE28XCu/9ukP+PQXP+Hzd58hOcCVKKcdQwxYU4dgHDg0St36WKOx/Yrr5GW1BoLJS3rFAZrkWn8cwMT4/zgkj2t1MHR1d5Kl7SBQwkTl17VbycjhdmLex//rDnDcAZoObsTnAAZuvwci8y3765hxPgKUx38IpmMVMXISP0vS3Rrbx1zGGAdYZve0gywjKDu8jmMV1xmAclck2xi0rkzzybpZpwJJmJaJFprd4292Rw24C3B++tOfgupgaRzHZQdRdkmGkWDytxlQE3tTY8sPwPLb5i/AN2KWfU2hKSC2Hfhk70ofCahwRI9jOK4VwJukw1zszH+Ro81LXupq51f2BgMRLPZDsHt3v/j9HuQtjs+4Mxp3PWUbw0OCTe7X3gAOlTune1+XMqoh7sd0/yeHZJplR42lYfbArpGTsVT2ZJ9dMQLw3XQbe3HY5THfXqSswZBMNm9xvun+/KHXBZ5Ipe8MWGU0jBjNJgim+W6vOOi7TtPk56ix0o5r1RJ598CRBGJINPA7BK4DqLXE6a45vf/tPbgso7Ebcn8Wx/4irijije287FH3s7a3NvwE2HVyDYiQMS/2M3+yw7rqijFzvETbdPiaVXZIsE0NtDl2IR5NS/06Yeeenp7ufm4PH2zvfQzC+IeNyIeKgNjr4kyU921+SsW1Fa2JTuy5IC3U1kiKlbp6I604q6JEMhJ8ENUwq60PFZDVwdc+7Ihq9yY53WQjvCS0qxjI4gGsdmuSlvx5gzkWn9d7Hwyl2G+9d7SVMec2PsagFO+wrWqg55BMibJQrOfD0A5NxdeIPWftHfpqTXcTI2k5fNyQqxFha8pazac4PxT38ZW1wZSLMcQTtJsiU7PmprkYCUU8YW8oh5NMjhb73/1rT9zbesk5IbVDVZZs+sLPtxuCN77pVhlJ92RUMiC+dqV1Yd0q3BIPr4SHc+JyUTrGmjL/VTgx0bVa6fq6IRSrMPSqLDMD/d5P7Z3ChLA3VCxTpqvrDXqlXtj2kq3kFq/oIRLUDV9PXvXj9jnlRK8bqonkMnRH2aFInhkjEiPBJGua1FrYLwNecxFnN1qSW1zzvBQrVZ+myZrYPr+AbGzbBdoNtO17FmtW3VKGkBET9+PFmOLJ5UPuwflIyuxrZthBX0p3Z6PY2SEilHI/3jnlcZ6+/xl6dw6HNv4eQ0T5cdvqTgTo1vAnpHvUyRzHBIQkIVNotZKkUPsG6r4GBqjGGdkOidMOnqRKrK1yuV6HPZeUvEmQ28lker5Ju2EDirFOI77JM5nuAHcjJyxJ25WSZqzdIE62ADwJp7L7YnHGxfiHzYmScvXnTsXXpq/H5oSOdIgtt9pBGvP8wDzN9vtkjdCVTnd2t27dNGlTNkDJbaMiI6GEJ7FyRGmq1Lq532B66BEztmZs5l4t0WiSP4oXDaAdcjHmLM2eR3ukO+xcsSaJYskUFJHiwHwDvdg5I9k03XNxmSMbv0gmjsSmCFuLD1ceTm7T/P0AACAASURBVGfmZTJJQwfAt7qRS2GeF07z2cZbTcu5uVyIhSWWgKzaeHp64uXyzLa9kPNEShZ/1V5ZXcc65wIt+Vgpt9vKu3fPPJxfeVVn4BuCiNmB8KWOfnb4X7vP3TmfF1Q7m+us1q1RV2MNd7Xqi61ezZ74Hknuo9MauWTXvDUW6LIso7HW6XTy5lnFdIqbxaG9v/LqTYXa7YyqG9JNK35z/K1q4/HhFUkM2FdVpmlGxIBjxNbLfLJK4TfnM9u6Wp+naaJW88OiSdrRZ4hEaxuYlLGSp3kaTU+XZSElyGL66Pg58vj6kW2rSBJO82x7h8bW22gieIwtxa//+Pi4k40kkebEJJnuSZ72/1eQFoW6vpBInOcJaZ3LLfO7v/936ZcLf/J//iEpN1bxkv71Rm8b1I1cjJJ+u91ME/a2OpDlYBFi2bVaEWcQrZcXF3D3eg5Pb9fa0KRMpzPdgaVlyjw8PjJPhZeXZwNEwUrGFPJyItUXem3cnKY9Lws9CVLK0HOpopR5QqbCVjvl9Vu+++s/JEvis7/+MyRZ17jl9WsufUOqLZhcJh4eH7htG0+//IKXr7+mq/Lx977PPJkQd9FuHelcbyuXQsOyQWUqVK1cny989cvPuL48c37zhnQqRkSks/WVMs8sUpCsfPnF5zx9/UvW2xVKJk0ZmY31McobDw45zmr1qM0lHTzw7XgUaoeMJsuSazBXWpT5RFaxg2tkdbXM+NDRdTPS295MJLDHlAOcEv+cRG7mwGqGx6p8R+G3ysTv5plPmvLYV14pLDnTk2nApcuNc6r88HRC88Sf15VbhqVCz2LMJmdiGFC7M1EABxflzlAcwSCNkm9ckyx9870RHBwDn3h117bCASQDbrzJmWCZZ4IVpTtj18dkd652EEoDfyYcLBmGJ94LMb1xyt0Hx6ah5Q6AB1l71nuci3bLsn8fz2DsIkuKvJ+NDzAuSiIC0AnHBbwBEDujJSX3/9QApQ9eveVxOcNmnTK33ugZrlvjlBJLmrk+vfDVFz8zUA7hJ3/zY/qtsl1XppJRL2v57ne/wzTPVtZRrLRsXVdQ04D77Gc/oTVL3pTl5OUYK0+Xn/Pl58+U8pd8+PHH5Cnx9S+/Zlkyf/Dv/w637cLnv/yMtVpDCbIwLTN96wPc76Xw+OEnvPrgQ773/d/lF1/+gjIlUurGADwMrjEFgaa0tXLbVipWXlok8+p05qzGOLImU+JsBKGlxEanSVQAHNZjgP26MzThvgmVYl1NB3ilitYdwDBnLRxGuF5XL4uZBmhznP/dUd+BwwCbjvvkDtg92Knjz+AAlh6uvb9PQayr71HDGWx9JjEWRhd1dqsH+t2dVtfzil0VAN03mEi6g7Ui8o2kzPHVe/OqgQy5mLM8Z9JS0JysYYEHVcfnugf9DvaFHWx6//NsPBjawsc9mCSCXA8yde80fZQaeM88AInophvP7oPiuS+3KSKjDD+NYNec8hinI3idXGvwbqyONi7tNi2JGwX1yoqQLPD3xLk25nCAcIdAdZhH2W0mFqjpmOsdfB1A5nEk0i6FcVy792vwCFyO+NeO0iOTeLzBfJ06GJ8uh+DJgjR0KwIsvp/v+6TazpoCvGQWgrVjgvVR7bDLd7yfGLCzoHi1iP0s7IXZBActk5XA7o0kd8atrVdvSHEA+fZ9fV9aO3yA9/bRvvf2ypO7eQ0gTo2JFc1bNJoLSQScFdRYqeS8w+Vj+dqeeD9Bgpc9H0GJADts7qcRVKk2QHz/eZVM8+fqDNZKdDBOKXmn4+Ocwt44cbed8f2eKIjA3/0EFLpruTrg0jzoz/6c4QM2VTJKPdib8F2myYCLbduIsm1bz2XIcWybdSBPKTuwb0nXoVMXOogajW8jSW1rKzRokzeKjH2xrRsbzYIxL2M0KbC2N5lzv8h8oz6eNZ7h6Ltob67dqExMo0TSQLvGujoY35VlnohkTcqmXeiWZb9+r+alOXjUe6OL6dYlseZlLaVBPBBfV7nYZ4b9llQoxaXOOtx68yovYSpKW4X5pOTUTIZJ1cSh1EDg4cV9w1bfv75xbh321f/Tew7v9v8Y27KUxCwC2bq+b73RGkMyY2sdTSZr0DuWhFYlZ2VeTLvTWOEGhEwJdBZjlHcDBm+r+YHzlOkZtq1CM8knY2wbo1XEEgWteSO6JGhv3l9k3zdDOoz9PDVAJBhnxffJOkDCeG/OiaTJASAzAbtsS3c/zcDWjrqt8yA/WZl5AG/aDQCYvEKCnNzX8OSpAJJpamdB3a5IvaD1ArqirUK3Z1W/ZsrFys/FwzjfS9bszdCyo93Y53tfA+K+5nEZxJo4Jjbe/5lnRd2XNIZd7PXYiynf+2ph+1trpj3r9jwq7EI2IeVikoNq/SCWeeb8+hUpZWM2Pj0hYnsxpWwa8W1vvqtqMUc0bVPU9GS9oswYcuLJIGfajvG02LcU90e6AVW2B+13Qpxpu46o9rrvliSeaj6Mt/th2QbU/6ZTUmY6JOhqa1Yu7zI9IRvnd+i2eNcmb63R6kp1LW3rj5IoU6GvumuwaqXXTk9Wbi4pfLWdFS4SVaEmCdhcgiVn0561feCEFE+Q39bqMZ3tkdYaos4azYlSpgGymVEw4lFULaHJqog1OfvZANveK02AVtm6xxWqDrIlbyh1soqM3tjC9rfG9fLEcp7JafJreZPHnFm3K3Vbh/60JQfNPxm9IloFcbmA2wWoJrERhL4eZ+XENM2cdB7jt64rLy/GvNXe6ElpW43Ia+wlk+zUuz0W0prWJA2Wk5X/z8uEqjJPEzwcfFXBJDhcWq83073uzaQztXVu25X1enMJIq9a1mOT4GzyDSm5/1Rcg9djiXlCBbKP4/VyYb1ZPDqXic0BVqvwqQP4TVkHgadrY1ksiRC+QQDVp9OJqAYMHyRs9z6WDemd63oje8V1zsnvdSKq6lWhTFZRnnPmg8fXtke0U7tpWqsa8W7bNksQZEGrjgS4JaUs8dgwGzBPs50Xf8vrVxqktQ1cyIIdPlWQMvHpb/+Ay7sXnv/JP+JEpYnlSPp2cz2UDGWC3qA2A6em2ZycupJKsaZORNmAcH54Tc6Fp3fv3EHubpw7aZ55eHw0Efde6W2jA+9errx6OJNOZ1rr1K1hXFBrRCBzod/WoaEVeiTWSTeRpml0m0zLzOuPPubDT3/AJ7/+A9Z3X/HFj/8c6Y3L0416u0HznEZSyjKbRMHtao0ZVPjiZz9nu6189NHHnJcz82likWU4xKadZPpxzy9P/OLnP+Xpqy/d2excXhKvP/zIMyIGNm/VmrCtF9PL0b6ST5OFYilZwXiO4oE9EE4peUdeD7iVPescJTkeMGo3KQRJOJAIrYtleLoOxk04zMAA3tQdajDGXzA9jCYf7FsPaDCntQML8KkUfq/M/HYufKc3PtwqS6umA5MKxuYSzvPCJ/OJ10053W5MeUKK8hOt3LqyiR+YiIMzeCm0Z/K7sT+thPvQ0dTHJUsc0JZxyxJcIoahjcZLx8B5fG+b5S5AjXLTMLajXMOD9sjGRuCxO5s7K+A+6B270vema6O5BybsrLA+FC0OwahfNwzlPUjmGHHE1AOgTePrcELCSRsvdRdDPQvspVNd1csdvXw6f7NsL8vEeXrFq/JgXVdTotcr/Xbh8sUXfHFZ2V4616+e6S8vLDlT5sxpmji9PnP67ls++ugtbx8fmKbChx9+yHe++wmaMuRESZlX85mH0wKivHu+sN5Ml/DFdYRarTxfXritK9fLyvXpJwb41xuvX7/hv/77f488Kf/7H/0fbA3++ic/5+dfveNWK714eZ7Aqw9e83u//wfk+cyPfvI31M1AMklWkmVMOst+b9XKuSTmuRoAcT4tPM4PvMkPnFNGOhRJ5JLZaqPlzpWNZ1ldJyrs9A5UWSWSFfjs6+ke8Duu/6lYxlm3iognWnR33AMYRxgMyiPAeLQ3d0AdOwgR++zbgNlvru8Aatu+Jw7M7VG6nZzdjzXOG2jMYHrrWNPx+WaD9k7sYwn751u5djpsiPv3fBuA3N1xTtNMnjK9CN0IjSbkn+09xbVC3x//95trHO/n20DsAECPf3vYig6mwQ4fJgd62mBoHcFKNAAsGWMm6Qh0HhJL+wx5oHoAdz14GuDVYfgCOLV/UQqYDtpvMS4ug0SAszKkVGLcWpO7iLM7G2UHBPe1cGT86GFN71/vv1MNoPQY9DOuY8+zA+oxdgH0mICRw1XCANNsT+5rMR3kbr4dPzmAsu/9/G5d7IL24DMTQGqcRffrZteMjiYvdp1+ODts3SeJPRNSIYwkzp1UidsanJ2zJ2uOgOeAnHwMI3CxsyiXMsZ1B9LvE6ExP/H5vVuXXxHZA3UNXf89yDFdYE/c0BxUO46qjdXQO4skZrcSZhtWm99Y1+kA5qoEAO7asoL3G4g5sMYcRz29nVUud/MS83G0MfEM6nbNGr/sfx964LEGI5iq2nCC/wB8zAezxEmSYlp/XrKby0wWT0w5otHV2F1d2wBhr94gNyUvocb2f1ebE9MF3qumrKxxYnI2j+nbxjkR+x16SpSyM4WjQ7NiFXCD6ZozoRkc75umidDmjc/vaoy35rp00zwzL8sIxJZlAaxSsJQ0ykFVXW7HgRcraWWwyVLaNZp3HxDmkiiiyDSZ1h/KMguqZezhnISlwHlRtBZOZzgVmBMsxZi6Wo3FuO+YHW77f8Frv/E67p+x2t8zOB1bD5VOVdi6ct0al7WheaKUaSTMpmKVPNeb2eUcoFRKdFEeHiamzaoIl9majJlPaI2HTmfh9mSxnob2ZYGcZ1q3PiTmI/u9tU5VK981lpPbmJzYthvHRpXHxNGQTdBgt8ExKWL7MPwX84tbLrRtdfvkvlKAnm6zxt+7DQmgK/a+gYY2Vll2aSLEE3IItXa2deV2vUC9UtoF1ZWsDdQAWnqcj6YHbWyaPprnoBZrCxan3IOzh/US/pUtBkaDtcPv7xN3+NiE3rpXPLgAbgDcwyazVzyExEpxJnrypD6+BheZHZDc449ULMaP7u6vzq+sdLsrz199NcqdhYiN0mDfBevehtUSZLfN9IAt0SPW0R57bnHGpVWNmcRFImQTDLxSj1lJu8ybegl6d1vaQxzDSWSieJPqNshJyZl5IGPvHP277P5g+KX2c6sK2xNg7r/4Pri2C+uWWOaZ6+065lXKxLwsnOYJ3QQk0XOi9YllPtl9SEi6BKs4mU74cbFgCffaLcady5m1VQMzncTVm9vsnLhd17HOCd14jXWhzqQV01UuhYyalq9LDSXJFnMIXLfb8BdLDvVemNOZopNX+lgMVWs1aT/gct0Qyaar7gPSauO2Zrb1OmQBQjcqtMdjTTa1xvIqnVpvJp3ZNt9jiZytQWJtHfIuJ3Q+n3j16hXbdvPmgnGO2/oOtuY0TVyv17tKuagYCf3tl+vV7YbZoZwTDw8nwOMuyZxOC1PJ9weB4rGr9UMJHKD7Xo+GZva5G71fvEoIXp6tgX0phWWakZsB7vNk1cTzvNiZilIkU6eJM+dhg+263TVyPf7tjeenJ/MdgfW2jbM9zukjnhFNHed55uHhwWyL28n1eqNuG7VuXol0dZbzHtPZ9cxPsWpzA12zLKgqU55IrwzzA8Z4jMICEdbblev1RkqZW77tjPNvef1Kg7QgSJ7MmcmFh/Mjecn84T/+3/j6ciM/TIhat9K63ujbCq1TTme6CvO8IA9CcuOsomibrbFTts5tqnC53EjzieX8ittto28bra5otxIRTTj9ewNfHE1N06n1zrRMKHC7XumSWaaMJmFeHpAmaGnWnVHwrLcdgr1Z18dSCg+Pr3n8+HvM88xf/Is/5vO//kseFoENLl99SbvdDLzIiTwnTqcz7778ysTNHSjQbePLn/6Ul88/582HH5KXMx+8+cAzF5bVeXm58MVnn/H07it63QhdMsmZfuu8fP3CctrLyIKtQBIkA2WiTLMHad452rVAxIFbiAxvw/SLsPKrAOiyHyDdS6ssj+96TgYgqUDT0GhtHrAIre2gTO3OLInPdCZtsHIiEw3u93aFWmlT4qO08J/Iwn+omU964dyFpBubJrp6IwvpJBUevTx0EiFNkKsJqU+S+NN2pbqsQyrRaTwaLnkwnExeIvmBvpfrmvMUGVILrHbAJuXd0ExlGkGwHSr3m1rGQ9rX946jx4Apjb8dQJEEOBLdKncM4hi83TnY6g7SAE0D2oh7sYDMHLFjgHwP0oTzFoY+Oq0nLMsUl9TIEOrhXB/3F2xE1wp158OCfZv/cBIQtfOWTgJO88IynyBNSFJu65Wf/ehH/NWf/gkvl6+41kbOZz7+4CO++91P+fTjt3z6a9/lk+9/wtsP31BKsgOlVbRah2zNkzd9uzKXwnmZWZaJskz84PQJ5+mB+XSmnGc+ePPI6bRQpgVBWLfOT372M/7yR3/DF1/8FGrj4w/gs89/Qe4XPvnk+3z5xWf8r//oX7K8+oDf+MGvk7Tz9PTCdr3yh//kHzEtM8/vfs5pmdnahZxNt0kR2tbotbHdKlobjw+PfOfth1ZRIMIyn3hMC6WZnSopj8xiesg8by9IfeHaNirGfAnQPErv1fdkNM8JvSftOkqrkZ0hIAjSLUOdwNgI7Iyu2UtKRKLhoNnPrp1wZ++AES97CtDmmAiINRNOia/84zZw7/OwCWAEZFFWtwcK6lq9vo97MLscaPTvQ382H575LjiRe4Dk7jMOe28Hcz1Yw0AYieRUVsidcppgsqZh8Uxd1Z1aiATPEfASkXu925Rc/P79e+jDBt8BtBKgmw+mAK7/HGBKdIkm7UAJYw78Rg9BGMMG+B4PW3MX/Mt7dkDuxm7cpwgHjlg8tNkJT+DoGFcZwVa8TQj5lvtgc1zqkDBAvzk+x/k73r96QHVYfMMGhxMedjTWn/2FjL+IIUcY4FXvVkqfsmk5GrBlZcTHJFxOeTjtcY92JsuuH//+eTCScH4nEgDiPjbfxqi7X8e+TyLgjDEJQNafMaQJWq1eNRMA6r6OW+t3a3kHQ/IYT9X3O9R7cNN0aLcG42U/s/ZkiF/ZOld7c6ruQK8188qxCfaKF+xZJAvttgfwcd/vn9mC7ddoCoRkv1bYkV2GZOgiJ29AJFByMTs/QBH1pLc1vjCAMdg839zbx/8/ntERaPceCT8Dg4/JlgDVLWlhT5QEZPKx6mrrMfmzp8xaN7ZWyQcwjrBDqXBkBj2cHnj9wQc8vzwPZnXX0KDfAX2TIjNpm2maWebzaMoh3tgtnrH1OoATa6ZmvmOwkddt87kyZmSwAu330bMim99JBIOQupKXjJqqK/Oy8HA++5qwhFnvjRbAg4NApWR6jsDTGaZObLDzTIZ0jfoc5ywOmClzsaZOie6MPIEeXaTh1YPweM7UzcC4KRXojVYBZy3fpbL1+M2/3WskeN6zfe9/D+6Oq4FOVTtbhy6Z51s1oCUXSlYk2342aYzYKeJxgtknbd0YdklJWVlOwm2taDOyxeWy0aoBYm27IU1Jk7P5vRQ3zqdImvRBKMAB+0pJLjfXuyeCx7IFjL2s28Z2W8eaHprnbrMGQcXnsDgBCfcpjk7uaPak8VkOzLh0jTWjaV4d5jGYk18iuawOFggJ6kbqK+hKkYYmSBrQsPkJqtbvQ7AkPWLAoni1Xj/0oWDsQLF+Ev7dsQ/BMckpBx/k7ihODna7bWlepk+cj35WjzPQf2dyBKAN066crNu72UpjJlszI9ORzc5EzyJDdx/gcrny/HLh6d2X1nC3twECjQRYEmp1m+821Jikbg9bG/J7Vrrv0lnZ1kZvbQdqO2SsulE92T58Rywm7/SxJjrGYCVHyiqq1bxJlpORJJnWZ5J0GHv3v9DhH7fmzeZaMx9brRJE1Xx/A/67n+uZbd1Yb7cDg9/wBu3dJBq8+VdLQnY9ZnE7Gmdc7x3Jpm9bMN8jEl/ajcxT60YWA5xzmpBiZ1vvph8NhdNy2pN1aScACaZRX3tDutIkiAzNpd9srdRmMgQRU5jcg+81l+CJJnPLdLIzKyWaiBPajKmacmPzRu/qqPmUZ7IwbLs1AbUGj+pr184/G+daze5s28p1vZpOfSooFbqyrh2VzuzSOTlnXj08IIJrx4qX5hs5zCp9lPP5zOvXrw/7xHVVWzVwFQMrq2624hwj6+3i8ptt+C/WdGu28yFnlySxKr08FcRZ7eavwul0RntI1Zk9Ktkakl29J9O6bojiPZwSV7mytcaUstkClNk1aafFQNLJtefjnMr55FKHdp9fv3syHWh1PdpWqes24s3smr0pJeu7UWx9nv1slpw5zQvaO5fLxU2O379XJ5mm7sa23hDgermYnIkI2U/PlAx7jMroZVmc6RuNchPzfCLliyWiu5L/diLtrzZIqyglwfL4AW/efh965t2Xn/P01efUVjkXRbtpwfRtIwHzqwdYr1AbW20mgu4Zx3lZ2KrRtRUrB7fAuHO5XZDzA68++IDL8zP9olAbDTNe2+1m+pRJaW0zIwxU7VTUQM5UjOHWKsvsJQY507OSih/srQ9NH6OOZqbzA7V3fvGzH7H9qEHvLEtG2Pjq85+i6+pNuAp5nqArL8/PaG12iGYhTcW6VlZrAPbLX/yCtMx8/e5LOzj8s3tt1OvNMqYaZYJWcqAk+lZ53t4RHQQkmnOIlYb05IdzV3CaN2pZLfvRMfi0Q7Bq9+59VjoSCEMT139Kme5lf63W4bQKxRlUgnQLerpnPzNWcmhZzQj4LLBM0+TOhQd83bVe1cojJoTXmvmIwhsVHsR0uzQJTeqgsKc+QYZFzYm8auU8ZWqfabfK9xG+KoWf9MpFzNlRf3jxsUiHIFG7HewxFs3LqsbhlDM7W8r0oQjnK1lGr49MpwKdnOeR2Y3A6Rggj681ylAdvHJWL4fA1ZrvlG/8/fGafjt7R3R3TiNwHCG2+t/6f8LxvLu/cN7kyNq1PL2gWNm7qxS7U3wMJHdgIRy/fLjBtAfAwdI53rjCVDJTtpLQnDNPX77jz/6vf8P61TPn12d+85PX/N5v/5Df+c0f8uHr18zFMrfvXi781Z//OT/72Vc8Pr7lur7w2Wc/5d3ThU0za9/Y6o3TfGLOizmMJTOXE3MuvHo48/j2LR9/9y1v3zzwve99n+//+vf5/qff59NPv8O/91u/Rimden3h5XLh5Xrlux+/Zc6dL37+N/zrf/HHvPneb/DDH/4W81RY10qtK7Uql6vw9Pw1rx5mnq8XOspt3dAKtG7SAt3Kjd++esv3PviYXquVy2riYZ6Zs5UMpnmysqpqzufWC1NNFBKaPcPvmnilWGnJV19/NZyamKckmarh9BrLZARzQK+bae05mGSZ8XsGbnOAQ93BNCaZI1MBzB/W17d/b+VQBuwEsGeB81jyytgn4eRK7KMD+DeSIL7Muprjk3J2x0HZeiPAyrG2FQdwbd2PjqfvASXxGsCzROmfDboSTRZhSsWaX4qxhrpYtYbgZbvj/r9ZEn8nFZEOoPd7SZ543WvA7aCj4dqRbVZi5yORMLKtF7riA4mUsE8WUAUT0q+02w6Jzxt3aPYnZQ9Ydwal3VMaoHeS0LK2Eu0UZ9WdPYk/fw9wHMBh9/JCnyO/7T6WoCcn3LE7jk8ESeJjEfpT4h8aAT7u5EVpXwRD9nf34Fk0BotmahbztyEPJHRqV7omY4sOsGFfU5E84QBou2JBqD94slFHnOwXGAFoJPtSiufc18rx7HhfSz2AvBiHI6gebDfxNbm1jdGBnYM2eUpkwruVu8+0wK3tPycAyb0EuHvwktiZ+LG2djB0rPzxHHZdLJGMkJoczrCEjOSMs4f63viwI9YWyqURotRVMHCvYxpxJCWnPfF9HMdY1zllkgYzC/eBXJJC7J725lmxxvxpkjE9vpkY2terrU3xdYZ1Ddc0rhK9rVPKNEOMmctkTWzeGz/1ZA0qiFdHTMsJ8W70sT9iDK0awdlhKVG3RsrWt4Bssj/qoJGdD74S1fzJeT6Ty2x2M9iB3uzHJJjsfs2mgmYxkEKsbVar6meBrf2c9/m14G4mSLtW6WUJ7t4aQodUyNnmGlVvWmLar7VuY7+goLUOexXuS1izpAaOSfjc3oDOmv4KvScqBprlXChJUBK3mz3rVIxR+XxbjWnYlTlhsgJdrdlpM3tSkvJYrGdB2LD3zP+/1evbANlveReKcquNjQ4pU6uimjjNmVu1SqDaFG0VSZmtmg4rGCFDxBokRyKqqdJr5/LFymmZud0S755XrjXx7mnjdt1GQx/twsNcKDnRtg3RTgaTQdM9kYJP0+l84nbpaK+mmZ98x4UfnLPPfdAVwt7EeXFM9uxno+0fS/ZvzqZNHhMEoNuaySSJGImld5N96N0Z5ZH0TLZ+kxtwY8K2kSCR3qGtzKnRxWxjSpOTlmYMbVSyOvBGH2BsUyMD7WzAYOC7zx/9RcaJYD9PyJAuMInc7mBJ9NAQN17iiU68cTBO4Dj6WnYItVaHjUl+LS026vM8+T6yPiimWa7GUHXbgPsKq2txBth9u124XV5QggGZSAFK+9GQU6KlXXsyGgoeS5m3urkUhaKHsyAhTCnT1BoPN23+e/ePfNhGstj3fAKTIjudx/k32LYYczFLNvITcWZHhYfHtloZgK/HwvY3xVmmMsatN68a8PPR/DZrdDiexX1/3So6TUwn0wgVP1cRaN58TwJ4046u1rDs6jrqy7JwOp08RrZBbmLlruIkq+asYznYY0uqJFrbvLLBKyp7ZSqJglWUdJTo2ZfEpBy7j7NEhbPMBjAmQLM3nFq5XDtdN6Yye5xgeNB6W2m9kjzp6U4upITmhmjzpGlGNqKH9agEW9KCqfd2lE4pEw8PhWku3LaQRyguvbmy1sbl8sT1ujLPM7fb9T4mFxm6xPM8DyxgnmezL9kA8dPDQm+OqYTv6fPSWme93VzfvtMnXiCAZwAAIABJREFUIyBWx7PWFWeRN8cwrHmipMRcivkbJQ2fMqXMPJ+8sas1We+lMJ0Wk2lotji776/oKdS6UteVrspWN27Xq4P5BpIuy8L5dDa5IjX2b5JESYnHx9ds2+b7SLhdr9S1IsJInNdujfi0dW63Gzlnnp+fdxZvKe5bBy5mazJnA15Pp4m6Na6Xy+4zq+krby7tWLfOWqsTuBqX62X47iHDkFIil8SSJ+Zltkbgf8vrVxqktYz4A8urjzi9/oCvPvsFv/z8p8ZKbY1Ookw2WetXX1O0Mp8nKkqe4eXpGa2VebKFq9MMOUFrbNcbmpy5WMxRva03lmId61JO3J6e6HVFmpf9l4l5KtS18vD4aPqV6ozJZtmODtTbFbk1yyK1Pg7vJMZ4te+9JENcP6Qp13VFe+c0z7RtZb0+026XEXoau79zu61oNco44Xyrlwo7UNmb0q+mxzvKM3oIg3v5mzsCMhV0LiyPr2jZyjpSMc2sCKyMbZDoWOZoD+4NQNxZPhG02QGLZy1Ryyirl/Sl/a0DlIx7wgPDwTbxLLKglJQp3lxEtXtxkXpQcsiQhoOg5kAkRxSLJj5h5te08CjCkjITofGTvVmUZZWqB3AF4XFauNaVCjyUmb7C97uVaV1a40W8iV1rVNc9spPMM6L+nMWF/y0bm8bXqvfMqXDa99+bowWhCWnOZAAgVt56zx57n51n5VA7Q0pI4yBUtcMe9sA27mWUNcf1/UDYmb3fUjorOLPMnTWxAPJ9htXOvttBXcAPGl9jugeQ38bQGozkCPLfB5YHCOAgkYgfgELKwvX6wjyfebm8UFvno7ff4e/953+X3/md77FtT3z5+df86c+/5ssvnvnRj/6Cd89f0xqcl4948/bG3/8v/yvefOct/+yf/3P+4T/4n7nd3rE8vqbpiasWsmSTB+g3er0CT/T8BSnDMgmPjw88vv6A128eSalzPk187zuv+U//4/+A3/2d36K3ztsPHhHJ/N2/8/s8/fJLfvL5V2wvX3PJkyVKfD5SKdycoaSYoP26NrS6jIBa0KaSeLld+MVnn3MuEzkV6m1jnQqvzifqnKmXZ9NvyxN4We9aK6s2mgaQYkFJa9U7be56eb51TXeQY3Micb/d11DOw6Gbppl19TKc5IBA799Y2wF6Gttut0fBYBvAJHvQGODYnYh8j3VwWJuHJTZ+n3ZmwtBeOq4xxEunvVlbgjdv3/L09O5uzYqvc3OIw459c50ydk7cyA6uxf5sCllsX0vJaC5o7miKxm7JA/w09sUdwHx4lsi037Mh9/Lq3vsoG9oD0HuQd5+jPYAABzw9QFDd5y+cS71jSO5g27H0OsU4yWFePcH6TYbqPegdY6Hahl64/Tf5mO7AXG9RGr5Ly/hAjHMokgtmknddVcJ+yT7f+9x306f6xlzfl82+/3dHxq0e14CzXiQp1sBDxvztQLp1rNYaAbyGqwCY3lhUsQzAWp3dkK10X5I4q8LmyBieuO57GH0bF5NUMnBtB5P73df7Puhjno5avN983w74iQewwX6Js8GuE2fJYXwP88hYD+N//HPT3V5WVWfs7WW88Vl39+djlXxNdBHXzbbp12bVVuqgXR3nmDNwO6h0tl5R3UvyEGfr9AbSycVarYiXXEpKaLUqESkygnnBfKo0gFYGOBl70Z6tHcZ1T6TZ35gXFI2roiHJYHjJkQ29f64IY19Z9YolixzBtPVC6IgmUjJdOVKjlGXss9AVjkTOAKabrZXa2nivlSpPhK0pfo8pF1Bx1k2mtubgjkLvo8rKABYDR80WxLmhg9V2TF51VabskgNEiXVovTLYeup708jWMmQP8lQoObN1Cxrtn5VAd7EmfrAd1nuwI/FntJLJIguKAQ0ZZ02LN3pZlUwhzw52dUWTcj4lXp0yU1amJDwuidmTi1WEnCxBOmX/OtbFGN3/L15KBpaSqU2NReurdZlN1/n5giWZ8uQsJvOrt8po/tY24bYKkY9JKZPTwm2FrcLt1nm5VVrtXnJq+76FTzz0Bm32U/JmR2G2wzfetrvBkGTai0g00/Fkip8lGg333MaPxIDsPnxynyE+uxS3HyJkt40991E6HA2UWqu2ACaxHilOYIiblkgAiIOE3pSattG3Z6RdkVZ9E9sz5DIhJTMpaNsoovS2kbTT6oZ29RLySvY9aLrNu++vGqQNxlmCQJmKnds+78Zgt3Wm4qXqw2tj7NnhB6UjiUMNfPKvoxnlDqon39tuIxWqeBNq912qawsrdmZt6+rPY31BOsmBz3R3hih9t0HHhDZ92C3TJnfJBQ4+FxEOGquyJdCSDeRUI/XgUlJ5KiMZmOfMLFZSP5VioGVrbF7W3nsnFb8vPDkXetsOIDeP302CTygCks2n2qo3RXOGZLyiKrF406ddymUvbxdxHzZ8wr77ESKheWpxcI/5SCDTwt7U0mKCeV7G2RTnrOmQrlSvqFXHUuDojybXfw3ChdA3Y2GKCJKNgVl7p3ebbxVhyl4hOE2IZKs4FEvG4Wtr2wwA3hPwFh8n02Ozte7JCmOOVlYRtrUYSJuMjFc9cT77Xn95eQGRIXuTkvXaydPEKe++E10ReSBPIQ9ljO9dSsCbWdbKVk2Kwxigu18V/WAm11GNhFDxcyyXMiSw5nn2ShJ73+Y2L+KezStLrtcraGJjHeOEKqkml4OpjCa5U+E0L8y+DkLybPIKG9UdY8LXTa1tVHfp4+sxtpfLhW3bXL5zT1Yv80JJ1ngxl2yNzFQ5LQuynO78lqbGkhbVMY4vLy/0Zr2jWmlD0iTuIedoJOYyRzmzLMtBWzc5CGzPcTkAuDoZMeR6NZmQ63UdMcW8zLRUuV6vd3HX+69faZA258L59BEpnfnRX/0V7z77MfXyYqzQ5wu33qnFFli/Xqi9c2Pm8fE1yzyzrZWGZVtRuF5vESUjxUp9IlBtdbWFhm0eFahLodcbfd0gZzQltJswdpSZmFNtJYJRtg2dWjv0xsPpTFPrTNhaRxpeauAHuyTrqAoktWxOXV/YLs9IdT2upM4y8nLRXnevPJw4tcOsVze0agFNtpS7ARm5YIBZ2rXURMjLTHlYYLblUPJiBy7cdXtUEpKsdC4pps2r3YAAlVFy0dU0sHKxLOfW6wAk7DrqJZiZKJ0JwekoYQtNWQ5ZxShX6OLsh9CL8QDNC8QY7CuF3F34viszwtuy8Jt94tfJLGAyBESXdgN3JRvA2LQZ8Y/EkgqvC1zWFQQe3JBJyqySuNXKF9uGloJiJWkWROrQmTwCEEe2QTj+sAdCvXcqlUT2EkIZQdER9AkA3YKrA7rEEdTZgSqOny02G0eHJwK09/8+guQop40/D5Ah3hOv7s8drlcwStK3vPc4FgPAkuiGfmT+7QCD+rofjtx7Y7sH9vfamQYmdGjNjHueuG438lyQriTd+Dt/8Pv82nfe8k//8I/4yx/9mOfnif+buTf7kWXLzvt+e4rIzKo64z19b4+XTbI5U5ZpkRbNAaIlWZAM2C/6H/zsN/87niDLsExZNiQZhiEJBm3TgiSa5iC2utXNHu7Qfc9clZkRsfdeflhr74is2/QASEQnwb7nnKrMjNixh7W+9a3v+42/9Nf5jV/+s/yt//ZvcnIf8PTmIY8efIb3f+Qr/Ppf+qt89Rvf4i/9tZ+BsOd/+h//DlcPn/CLv/jLvPfssxx2e4J3nJeFu9sTp5PKBRzPJ+bzHeKUZV2lcnv3hg8+fsUff+cTvviFH+EnvzLw6vkLrg47bh4+ZL8b+Yt/8Tf4+OUt/+Sff53j6Q5xqo334MFD4n7Hdz/8FsfzmSoZjyd5TcZqVYF0UHH6V29fk+OZ9x4/YxjU2facZ1jgXNUsLIgWl8KQmEvmmGfOTls1fbUWelt/TWBeJ0A1MMUCxx4wQGNIis0TnMMPkbosNJ0uZ9IhDtN37iDLKpvSn7fXAHszqS/AsO08a8HN9t/b5JIGUrqVKSibz/L3DLOaZEB7nw+eWkzr0nnu7m5XoKEVRtq8ZGtiuc79fs1d83OzDr0mhx6vpgdtkw5ADLhxICbfmTXrZ4kyCHzt50MLcLbg0/3109ZLA463GljtdztYtlm7YvvvBejag/ctc98YM6Y3fh8QuBgP5y6eve6p7XmvgOb9Ys56b43hC83wrgGWK0jl1oRMVtYiYLjr/b2rZ540feSVuXw5Z/XzLudgvzeM/dK/wwBJ2YKWCpn07zZgabtXt2ttz1SMOaTadisYsAW5twA10FnHffGh6ys4M3Bq8VNPzrbnGDQ2zPYet0B+Gz9dP/7T51Mb2e38ZX1GbW5qWx99nbT5rO2CynDZqENY7LH+r8pXQHPWvigciDL62li2sW2Jvf5AthA1Lg767HXyUYsCgMHp6efronGOFSqHkIjOMXrMzCNah81qCNXGVplL+kyXXMmi7EecQ3xsA6bFt47V6JU2LceWCG0LNOuY63d2R3inc0dqA2oFQePdFUpp69b2Nm+tzG51QPfe9eJGtbgwhcHiS5XT6Rrmm2e73SP786j6fbYVaELmE961llnX50h7Rtni57ks1qqpe04VjHG+6phfJknS5zBgeofrXqHzQtl1ldpBTd1Q2l63KcB4303FmnZkFe2yaMdWlUJdNJ9Qt2yhmX0qqViQbsKqAEN0ynpNUUFX79REK0ZhHIAijEPlau95fO2hKhlhP3hGr6dwiQ6qgrfJuz+1hFBjfBWEGENgmdVIJ5pBy+k4cXeseOtEAmFeKnmaAe0c0fFXcHzJonFQdKTokaI52fXNHjcIftI9tJrO57LMPZneFm1bnN3OkLaX52U14FPQwiNV5xd+c1aJgqO6ddbOpJTWtdbOIFHwrAF5TVtai2wt0LW/W/s/Fo80s1gx9lUHzRoDWgQamFYWXMk4mSnLEcoZt5ErcLb3+5ZDmkFXsc6gYvtc04ZuY6DrcGULt7Wxnn/2cyyPY9Vub+QgzW3anmRsN7sf37rjLJYJftXC3uqad6DSN+ktnV3Bhc4CrF6vsRaV+yold5LGymR1RO+pMXA+K/hUESvS61O/f263eMQ7Z6B/Y8upvEr1xvbOuX9Otbix2F4aY0SKnrspJpP7wp619I7QNsjLojrJVIs1fGS/S2v80QAmY1PmnDtA7aXJ32gRyAnWJWsxvLFm7+7uKKVY10JY4wksd69V27Pt3+Z5pgrEkChlpoje1xxm7VxNY8c6KioB0IB23btDf6adPWt68eLAVyvWO/WwADoIuM0RG1xQq5jWrJCrspYJ3nALhzhHWehrMlixL3jIWnlR8NLW4jZ3GeNAqisA3udDdERphnS2/lsnqFcSSLHi67IUY6maXIYTREpnmbdcfIjJ9gklUsQ4sNvtgG28U6zYoHH4+XxmGIYNISVzPB45nycaOKpSA9LHtBmJB6datLvdvsfyPqi/kg+B0QDPlIYeJ+dZAVMFPEvXpW/54HI6cgqBw7DDxbCyx6uCwjHGPhdg1X0fh8E6HtdunwcPHtg9KXjfNKJLLdScWU4nZdj6oPiTxVNtvEJQg+WUtENUz1lsTJ2R1HQ/XpaF0+lECHoW51zwXvewvKgsxHYvcg6cMX5DDCqx5DD9Y2G/OyigvtG1rtZF0s6IP+n1Qw7SBp49eY/Xb1/y8uMPcNNb8jyRCISqRlxYK0xMkXw+UrPn9u0b3mYVF/Z4nDNmZoqmX9ZAHmUSJmNsOu9ZsgqAX11f8+DRE96YY6EUbdeVksF5lmkiDQMhJZwxFJeyKAgVI2XWakNeZhwwjAlfPFOZkBr65hhDYDmfUaZN0EV8PiuDcxhUEcGr3EJZsrGnLPh1LSD0WP9TD4obM8xVZdC1yrEGFQpEVO25hWAmVO2w7SyZjdEVtExVc34LmhHpzIdeDfHmuuo1HUpNxDl4KhqIgmjlUByuVenq2vbhvLpkbk1GfAgsJdPM6nMt0PQenba+BBe0VRpYjEWWgEfO88Vhz7s+8ZniufIOVxde5YWDF65a5U20klu9g6LBeHFCzjOHNPBoEF6XjAzBUj3Yuz3i4Z+XO75HRUyPSIHnJqhNBzdhTapbkLMFIBT8NafkjWlFY3h4v76/1ksgwG+CmftgVP+7tEBTg4ta8qZd8xJIaJ+p72/S9VY9d/c+996fkZWJt82Y/ySg7DIA8p+6dg2CLoGG9Wfre7eH530wuFZ1Yo3NOVocKYxc7a95WSufeXrDj7z/lN/67X/MV7/6DXb7d3nv8z9JiQ8ZH32G/+g//k949fIT3v/iF9mNB87nhZtnj3n4+pb33/8CT995wjCMjGnk4YOH/MIv/RKPHj7i6eMHfPVrX+Mnf+Ir/LN/9kfcPH3Mj/zoF/j4u8+pFL7zx9/iH/2jf0SIe4QTMR347Ge/hPee4+mOh48ecHd7y9/6zb/Di1vh81/+CvOSVQ/IB8YQqLlyvtUiVjFHYnIlVF3Pi4EIzjnEWmCqdxzLhMyOpWjV+m4+twFjFyK1VOZJm33OdVbHZNN7alO6BcrK3rKYsgXy9ry8a4mPFTGaaWIMyjiLHsm2PXjVuhZjeoq1t1b5NPDeQC275Pa07z33FQzqwA8tHV8Bxgvmuv3MbT5ju8baZ2oAoO6teZkvft6q0luQCpE1uXf8gLVwCX7pdygbu+lSOlRfLe0SkiIlBiT43lomlild7DPY5rpZf43l2oJjfZaX+0f78wpcuIt1th3fDihuwNh1XbeqolMQCLpmt988lwYctrH+gUCyXQeygqnrmr8E/TrA5y9ZcyJt7hhIZefX5fvaPKgd8FzvQey8rZv51WbN9rVqS94Hwdvrcj5frqd2LW1OaHJpZ627ZJFfAuyaZGtYoICs1G2RzrVwgRV8bcn2amyp121nDjaGFyxMXZutTfgC3N6O4WZ/b4W4BrBtn29bh+09DXDWoNtg1nvzs41zisMq1dHBk2aYZUBNEVywzorQ5twli/z+y4lpvt47Y3HaIu28w1VHsmRHnFcfhXFkCI5dFBIQ8PgQeXDzgMGYUVhxQPceNaxtR5pgoEYtzHlmrsJxXjjNM+fiOGc45Uz1DnEqedI5oTYvnXP9vG8vvY/QQY22N4jFbfq8N5IHshbQ18N/bfcUnEpW5camMgkDAtV0/mJK5ojtLRxoBmBtTq0a9tvYIjiPBL8xALH5UR1DGtZimWi8qswlCF5/f4hRzYKdwyrwOBd64radc1tWtbYm6hgpo8b0Exug3OB+5wgOvX+XiSkw7kYwEMpZF5qzeLhpnQqCMrF0nFUvU59b6Gdr25M1ltXW3la4V3Z19I5xCMTgCE6gFgKB/SExRkf0QingRJinzBiTgr5V2zi9BYRBYo+v/r+87hea/v+8Z/MPRDy7GMB7bUHPjv1uJKTCMptkho+MY+TNMXM6Veqi3TxXB8/VHm7vCtPsWEohBNV7XE4L+Ng1x2OMTNOJYntmu+ztGSPUC8Y1zpGatN1SOjjfzvVt8aAVK/R9xtxDARlBFNQ1oLI4Yy0Hjyur+VcmA8bEjFHJMGLF7J4reFtfasaZQtDzSQSpq2Gz6vY7HJWyTJR8JqIGrQ1YdmZa7J2DqvIc4vzK1hXwNLNQqEXHyHZn+/+1oKSdHQqEr2sJbJbRiji1CrksHWRqe6l3vs++ZtoZrZ0a6KCIsuvbXFUjR/Eq46Uu6+oU3z6XDoaoXqnU0tvyxViWOJPRsO8vRopSYHMtfq5nDzTvAZWdcIRmJIWy9kABy2XJnJfFumhhCAomLcuCH0ZwMKTE4LwB6GZI28zCwdi4nrwsBNvHYkrsD/seF+ZFx1SN8CBJpeaNbqq9almUZEZbAyr24VDwqpTCvMy4ZT1nvfedKr0sRf0QRExmZFEGZZm1OOa8SVEYKBaC6XBGagi4cVRPC2Mf5pxX0sImtkxpIJFs/c3dHLyYbCSiY+C9JzpvEmiwzDNv3rwheq/7YooqMYR2EM4l9zMwJe160QJrpVTtfGhSGk3nNZs0TzPxWmMPZ5JJKvmg57/OmeCCEsGMVetEC5ilFTVqtm4lmKZJda8N5I8mizktDWAd+nOOKdKKIqEBj95zfX3dc5gWXz1+/IRlWZhMUxg9cfWeSuV0PjNPE3MuTNNMKdKBV5yz/VPX8zAMfW9KSY3VmvlewyWa2WatwpzVAC4I2k2U9d+k0hmk7b/Kyl8LLbXCkAJpiP28bve52+3Y7/frXlCFpSzKvJ4XEDidThe5gYiobEgMJOtobiah3nvSoPfjnOPq6orr6+sOdjeAtdZqUjs6xsvS5JrQfdcC6tDYtkGJacGr58tgwHAuVixi7W76k14/1CCt857z3R0vPvg2HN/gJRNd6Hqkuc44L8QwqKNazQZkaVIlHmuV0ErkQoEQbPO01iVLVHxt5k9RUfTzmUc3D3jwzlPm84np9o75dFaWaPQ9AGZZCESVLkgJ8Q4vgUUKLhem05k0DPYEHbvdjnlSzQ2pathTpFDzgls0WI/DSF1mXAjkPINAzmpiJbXaYRDIVasMLnhiGJhORwVcfbS2AG3dqSZw7rynWpuELj4Fi32KFK+tAVrAt5Ynq96aKp0GGFWZHAFnovce7DCrWUyDhJUxyRrE1Vp6S4mOvTG0WMNCgwCAVTKhHfbFKteq+tCqVeZe6r21/OjmE6Uqe9Y5HvrA+2HgZ8KBxykxoLrCtXjmGnjBRKXwIB4YalhdC6u2yWSpSM7sU+I6BM4UMsIuDYRFiLXyZb+jAMd6y21QUyMxPaGmstq09C6AANZDsLXutHvoYFIHpdYWRP0daE7DjeV2kWxu421Zj2jvQz9cW+KgwXOlafbdB3nbYbQ1LOufdy9I7ywY0VYmBfBbOCXrs70XsK/zpF58v0j7gDVB317j/e/+NIC7HU9j+IoGZEteqL5CEI7zHc/ee4of4IOXL4gPnxDHR/zcn/vz/Ppf/vd4+s5DDvuBTz55znh4yMuXL/mjr/5zsv8z/P7v/QGH0fP3/97fJucjUZ7wk1/5ccbdwHc/+pB/8jv/lO986xu89967/MN/+D/zV//Dv8L+ECiu8K1vfpt//Nu/hWNW4w+XOFzt2e93nM93zMuZYbfj+Scv+Ph7L/jmR69hfMizd98hDYEpC8fzmVQdTz7zDOlVwUydZlyNyoqyhBIRS5IrGXhxfM0unjRACaL7o3cE51kYAGFxMLuCeANhi4CLPbhtz20L6Lc2KXcB/BuAuwE5GgOsyW/UpbUGbhLAe0BmC5A+DdBttd8u58AW+GngZBX51FzrgJWz8WoA6z0gaTuvtPg3t6vr6+RiPm4SvwbySS2q9bi91k/lsav0Q2M0uBDwKUIaIEVqsmTUrZIeOLrrrbc9v+0DFzCwcxvwRX+wBZUby2cFaNf73oKI6xrT77pYmyum2gN+ETFmxdpu2i7DuVWCYTvO94GmVQP9PjC6zh0FU916n80J2PZTWd/Qz55PF5KU7dC3IdvUdGvasokuQeJW+GqvLXjZxrbduwgWYOfN7ze2yL37cibTcA8oaf/1TtkjkmtnWjjntOWs3SPKpHCdfUV/b9P7bH/XNdHu5bKAZlelrYHyacbRFkBu/yYbAOoHgT3bAoh++grstp9vn29naFvivI7V2qIuVeUNWgHFbcDtTzN918JAS07t9On7ksPYXwKuVvZx4NHhmuvDyDDu2A3qfB2BXfTsY1TA0ZvDtVdJiaYB2MDAdUw0flODl8zevu96WShSmZfMOWdul8Kb08zdlLVDKUaNLw1odJbMNh06ZQe1sXOmd7kmnJdxxrqOewujV9C7jYgy4xIm893Xhz7iCgFqUM1UNYe1BDbEzbmgoMu2aOQsqdXuhi1bVplOAS2Mbc8A5zwuOHJeAGEcBtWGk1ascKbBeFkM6CCtc4hTvV8xoFo/97KYIFLs3/SZVdOx1K63FulYzOZAKJRFC3NNEqgVOzy+j4X3ql2p4LHgLInLRXXfvVeJN90iKrVkltlxvdckmVKIQU3EdtGTgrCcZ16eYRwi59OMONgnR3SFw35QppSsDEhlgt5f3//qXxUF3INzRARfFJDPODyVB4dAuokcT0W7JotjP0ZqUVD2tFQG86fwTs14pDjujpndXoGVu9sZcQOn0xHntHNP2fZDN3+rVdvF2x33fQUF8MSKa8qkX0kVjdiihArbg/SxKegqgA8aK0nLTjRgklq7AZzOJ13vakZWLZ7XFt665B56tLO3/SXESOshrCUjxlb0XiznrF13soqjKLMJzJzKwgRdW95BXnCSoS5IVbkDZwCWByuOiuVlVmzdnHfBAJ3GDtM2eSVDlLrmpFJVA1Nb4WsHYABCSqRh2LBsXf8sQNmkSpnsMYtzDkqh1kmZncZ09Jg8XCnqJYN0SUAfQi/IizPwpRVMLG5t+p2lFHAe76PtNdlmsOCjdcO6jfQR4PEmj1AV+NRkGO8cixVi1AsFpArJzgN9s0m1OJULU/+coP4DyVH8WsSes5qitXM1F/VgCTGqsfqQdG1X20tyJoURRMFMBbUh+AAGPo7jSNP63zI8GymqPw/nWPJC70yqi965V+YytULUfVoljtQQEBFKEXKejJymgCEG9CnJS88ANaDSedrA1WwMZh8CYrmzUh8EnwLXD284XB84TidqWTReFi3qDXlHdEEBPdMOdV5tn/IycZ7UxEpZobAs2hWjIJ3KQPjgGYbUY77oQi8qFND8KUScr+S64FwmhUiKiZQGRFT6IS92/pg2793xjqalH71XMDY4a/PPLMupF25h1VpNZiyWNszUNj8aCBlMp7aTx6qw8ybTdn2tZzdrTHo+nzU/3sR0pRTO5/Omw0iBZGW+un6OhqD7b0qR/X7H6AOzkXJKXihl7WDoko2mnz1Ns7KNc2WZHWFqBnGu7xENL9nv9+s9xsCYBup+lcdr87d1TTSzR9UdznaN+hxDSgxp6AUxbO+IG+Z+Skrmoyporx31FmMj5CUrAQdHzVlJEl6B+dObT2MlAAAgAElEQVTp2PfukKLFy3SQ9096/VCDtLkUvvXBNzi9+oRQHRFt2V2KEEXwtaquWvWMhyvcMHKaTtRF3RljGM3pEXx1PSkJYQQb1rzMWn2UhoJXhiFRc+bV29fs9wPXT5/iQiQvswXlGtyXvGhbblamqgteW/wF9g8eQKm8efGCMquYcUXYpStq0XYbh5hovUCppqmqOmQiAzhVQ4mYRpG3QNkLldI1O0NxLMupI2HK6rC2iuIMFI0KFqYI5lzofSAcDoT9QRM6aRVVi7ZNewXn1HTIjNY0CrG2FJy1kGXbOIIFn6YDW1vFEUuoG+iqf+/a8d73tuaeNFkroOubB5ArkoxJEFVbqvpAddqeV6lEHAcJPA2ed3zi3bjjmQQelcLeO2ypUpzjVCvHMpNC4qrCYb+jSKVMytDG2v6kCnlaiDFwJVHdaHMhRk+pjoeL48sMnMvI1+rMK7I6XXqv1XBjFG6BCNUd8+YwvWmxtuewdYXdJkstUJMGFNSC2yS8Ihibrvbv7ExZr23sYkmqlC3IAtAAh1bI8PZvGpA1do0aHhmo3/T7OgABLcxXx1xNbqsxNhpYuqLIm2fOJYBbbU63O1nr7JcA2Pa9DWQT+96OPkgDy5XBHocBEUd0gVIzt6dbvvITX+Z4zjx99iX+3L/97/L2NvP67Uu8z7x8+Zz/7bf+iNu7Ezc3jyhZNaSn88ywH7k7vmQ5vWXwiTxPvPjkE24eP+Xdd59Q68Td2xfk+cSHH32b2ze3/Pb/+ju8vT3y4z/6Bf7u//AJtZwZhz1jSuyGSPSF129e4mJi3O95e5pZauAwXPHZZ8/YXe24PZ2QZaJW1URM46juxYjKgbhALhlkdRNvSYeIrsOQPMM+gVdWWJHKVDMSArPXOVZsDjQPS/0ob8QkXauqF6nzQYPjREWw2g/eR2UwWIHFO69z0UwDRTTID0MiLws1axDscMby/zQAe1El7Un8p8HUzgSg6W1p8S74YvPVug2sALUFv6rNHWFN5rtOZa3q+iqaUDedVGyO16b/vXFm70CfAV+XRYUNeMoGoN1MY+cAYwv5GCjG2lPTG00WW1t1K4T1l2sgKn19iIW3LUhjM1bbMd8msW29aZK7Lay0/araJ0tf5lXWr28UodConNL2QL1maFrbdl1+Ozj6yU5Wxv3lM2/r356hb63gbS59urjTBr9dr+gEXe96mxzjDLdv8+QSkHV932m7m308qGahb2es/UzWRBkRlVUygKiNpc65npP28WiQe/seJ+18qL2NUmWB7H19//U2xm5zAQ1aU1BKQfCmR26AnfMGQm27QLCz195rupatrauNTRsJTezXxG+7bhv42c4ETLuwJbeAFZy8uee2uKLf4uaMsPOxZFxYDRvAr8w0qWj5VLRbCmX66xoRkz2q+KLPrSDarZM9CeEmBvaHAzfX11zvDlwfrkgx4H1kiANDDIxDInhvbsUw5UV1EUslxcTb09s+FhoDCC4kfBxI44hzqgvugHk+M50n8Il5OpHLxMOl8OxGuDvPvHz7llfnCR8GNVYVLe73ce0tyOYw3uIC5zroAtIB2QZItX1gK1eiUljNHMva8Df7Wlt7ANHWUn9eolrKzYXcW8xQTSahsUuCj1r892vcCFCykjBKrUQfDdDRjaKazEc0pqJq/Np9ICAFYWX5NUBHu8Ya69VbXKtKqcGYh97WlpI/1mt3zus9ihAstgPRZ6BaMxpve89+N9r3iYLQTlnizq8FcgVGLNaSgveatHun2rFqghSN0eQI0RGp7HaR3egYAgxD5XrnyUPg7qznwjAe9JqDJ8WkOYVUvO2tTWnT9c3pT359ulDz//5aCyv2dzQJFec414yvnuRU7zFPC8POsRscZapUlLE8DEKaHecpczzCNDmWkilFmZSewHwuXB0GcqksxdPM6a5vbpjnhVoUZPQ2X12tloeEHtt6H6ydtpp2sJ0fdrYMabD5Y94YUoz8UPvNaUxkDMwei7SYVZjnue+jWqA1GopTuY5obbMKegJVzYZESmfZFgN2fak4MwRDPK4uKklXSo/bQZnswVdczdoZSjPYKgSpKv1XZ1SdtUKby2I5jJ3xXYSnz4Om562dnLp/rLrxzg47qVkZpErhxftIiJE0jMQQbe5pLt5iLe9WMLeWVfOyGSCLsfwlZ5u/2iGIEZOKVEpZ8DiVimpBnzPQVnwvZOv6bd1HqicMajodmsa5OLwzczLbEtVQaY0FqgiDjz2P82FgzrqveJqre2TOc9f0dh4Wa0en7btBY1Pt5tGuWeXSeHKpyKKyg8Gr5FaWYm3fHsxMrIFazqnGvAdqzuRhYJ4XLQaXgvcwNLd7pRpRlqUDmqUou7I0Ny6UIdlIOS3vqz3vt891TtnOZkDnRr2+picrrXjsxLp/hbqU3tlcc7FCmGIhWczc2+lz8aG16yuIdnp7hyAM46g5n5GF5kUJcn6I3Nxc6fXnpgsfcFc7bnhILvrd7SxcloUYb4xROTOdVc+/ywihGv85q26r+ulMpnGs0o8LmRCXXgBUkFv3/+g1Jt8fDix50b25Pbdh4MqKptN5YpqmzqQFp7ICeaFk9Vqa09yLDC2n1zhMOhM9Bh2nEFW6IVg3ukglBgV6d/u9Pr8NUWIlpagHye3tHSCczyctGMyLfU/sAKjzKm0Ukz4nZdnHC53ctn/oOqrM82JSTTqPtOglxjZWAH0Yhq71qt0svmsn632qDnwYBnbjTosJ/fypxvhVxvCyTDgrWhxPpx4rNim73U6lHk4nZf0OSbtsmg9BMU3oZCa9PdcwwpOzGDXnzJwXOBs4bjF3Y4D/oNcPN0i7LNy9ec0gjuASFFTIvKh4MGUmpEHBQW/dGUXb+0XQAygGUtxRloVSVatlSAF1Yy2UXMhlZhx3ZmACUpXJsiwztS7gAi5G9tc35OMtS1kgaGBYqh46ZZpNsNvjpSDB9Vb3UjLLKRNS5Iz+niueXLTiV61tvxrgJoa+R+xBtusSIYymdyOrIVkuC1RF5/Xg0qCiLDNDGqlV+qbqo7a4h5Rw40DY7dQ9sdQuZo8FoorFWnBgf29ttA1IbELezYBEO2ncmoy6TSLpLZBFA5ui7hlAUDZJjOaWaWwetNri7bu882rIIELycQV4W6tSSCTgMyJ8adjzbtrxRByPamCswkgl1KIQrXMsi/DydmKeMtdPPAcPexubZILymnhoJTmXBVcX9mFgDk61OWljAQ994KfTA87La841c27MZBsL50TNW9iY1QT7r2XJlwln2xQbH1dfPXFuSYc+AK2EYq03HdCQDsSod4b+fqvE4dAkaJOQ6QG7ZUNVmhFNS2wak0YsKd9CHvpzCzJaMGUJ8/1XA4O3reTrz8Q2sQ5B0Kpj95m491l27UJW8JkOtDRwaj/sudlfs5wzy3nCLZnHN484377lp37q5/mFf+uXef3qyLe+8U1u9jtyrTx5/JAYA+9/8T3+s//0P+d7H3/E17/2L/juBx/yuw8Sp+OJ4Hac72Z+87/52/zUn/l5vvxjP8rDJw/56h99le/+8bf55te/xn/9X/wNfumXf4U3t2/43d/53ynVk0vi9PaWFALvvveYBw/2fOc73ySNA947PvjOd3nz8i3vPPkcN1fXLHUyoxKrGoq15BUzJ/GBdIjkmClzpeRMoXQZEkSZVof9nmE/kKWSUtSkZD51GB1nv2/60FuGobdQ7nDYU6VyOs4rkoSzpDJ04wwNYBqQDlSHFA2UGyPep0iwVj2K7tF08IaLyv4PAum380H6HLhkZQhquoVTkxsPPVD01jYlXLK625xrlf2+Pmw9NcZbu7c+Rps5vTVL0M9s1BsDU00SoF13A2j7vdq61383cNVYXj5604TbgtW673hrS9Z1VvtabvsQThlkipZjqIn0sdQb5uL5N1AW5OJeVYu77VH6nu24a9B12d7fAEplOG5+bgDtqnVK/z6xxHoFlDYsj+0+srl+Eds//Spf4dr8bs87+AsUQcGZrYyM7ZW+jXf/Ihv7e8Cjnakb+NHalX1PLm2ZXfx+26tks29vkRPXluT2A6rr8+QSGHA4K1Sv12NgZZsvBlDreBiY1xnUK+Cmj2DDitcno5/rlf14Ae4b4rMa2K3X/IP27TZ/9Tp/ACu+/cyGpLES+znRioZ2n4AmvcYoc9Cfpz5Te6dX8F0wwBI9n2qxgkCp7JLnahy4Hg482l/x4OrA4XBgZ0yYaB1LzmnrYykLt3d3qk+NY5ln7o63nE3jcoyJqRnhSlV2n3P4OFCtgDOEwGF/zW6/Y7cbGXd7xt2OYRypkplPZ86nE9cPB252if3bO24n4XZeLAGAVWrExsVACce20LXu230tGDjSnoWaVOm8ymXWT/Pa1qqAh+/sfcvG1m4oez5tXyulQFjBd2eTRdnPtS9BHyIhpJ44Oed627WyqtTzIKRkm4UyK4Nfz5pgcZhZwBBiJEZtTVZSRI+ksFWsxUjTtksp9Bi8FR90nwnEqGazbbuj7+MOLWa0cwjTQ136fNbiuTL9NCFck9YGeDV5hxgUuMpLxgdPTJ7gHSlCnhfG0TG066StT8cQPIx6LykGvFSCK+yCV9Nc53qXjWub/J/Cy1kCLqhc2W5I+OogF8oipJhYss7BFDy5eKIZoZVSiSGxZCGLYz+ONs/AiTcfEMGFwHTWYkgphRgSfhc5n8+IVNPsbMeqs9jIW7HZmFhZn3cDehwOioI31XKtECNBzAG9NGOfujJxN6PaYlIR1SttBd8mE9AAPqmy+Sw7C5yOW7V9qdaqXZughJgggILLNc8gtrdUIYREdJB8xLlMmawTU6rFWTMimZIXkIyrCuZ5xOqKaz7SZAOcD12KqpFA+innQ2+dbjEqDnOQ147UEBPjuMObLqiCJxly6XuWoOsZB/OyKDkKNfBpQE4pWcHADkhZ3i1C9E67aoMz+QAsJrHrbEVti8Oc6be3HDWE1pJs+5kYwz0veO9ZytJjDofKHPT4xSlwY1kfQmTOi+bHtVIM2BdbB06UfaidWZsz1SsDOS+163TGEEhDohfEHMSk7O5k3jFLLQai6hmQUsQNA5ILCxgzP9E7gwFkY+ZU1exawTw1M2udxo3F2SSrVHO2QqWzj6VW090+kdIAqOFUrlXN6rwCqyFEvbYeg6NhcR0VYJ8z4oyss+meElQWQMDwBCg5Mzdd1NNEMuOtBlCWUji+vUUs/9EuBg9eWcsN0F4BTQXk1j9r/D7P2jnXc1En5LywzDM1l840xiv4eT4fydP8KUJRu45pnnpeHsJs/225sWq4phC5ublhHNVobZnnrtPbpKOUSV775wKm4ToBWgQ4Lqcu49BlFoMamGmOtp630XKHmEwawDli3LHfX3Fz87DH4VKFeVIt4GmalPEuQs2VQuF0nrQw6x05K7s8pdQB0NWkXrWA9/udShOkRIsbWrGgmZiJaKHreDz2e2460VfX1/15e5ufjRUbnMpHXF/vqLUwTSdi1IL41dWVSRkszPOZnMvFmCJwNMB7GAbmee76utUY+t7GEzEz1OC4Gne2X2SWrLrYd8c75lpYNp1c918/1CCtlIw/39lmZ0H/UlUwXWrf1HxKFDRR1sS+Us9HTbSzTfZxh3OefJ7IVdjvIt4lBWnnSbdPb21h5rJJrSynI29evmR/dc3VgwdMMVGPR+ZlJkBPXHdWHQdbqNNCnTMUFeMuWbVHlnpWinbADMMMNIuR6AOV0lkeBcBEts/nSSu0ZQ2AW2u6SNEEXc8QJemY2HM2wXcxmQEEwm7A73f43UBxtVfwS8kKVFikKWKBYrtG+67ONrLNKWBte/a/iLZs2W+iZCmjx7PRXrWA3IWId2Fl1gEpRXLVakpFN+L2Hl+dJgLejDlkweO58ZEvhMjPP3jMF3dXhHPmkBc4TnZIKYu04piLVkjHcU+tke8fJxKFvYfDMBLTQF7smZVZgxW7L1dm1Z3BMTUDEue4joG9T/xEEo7HyreWiRwMZEHZgni/susuQJx20Lq+qWjy2SrIBoZA11Zsvy8ilCy45ijcS9y2jljZRa3NZ03DLVgRS1aMIbZl/dk3GZZULq6XflXKIFDzOPvxBZizglw6Z7dg36fBrP7ZG1BmY5q+AgctifwUQHvJyO1X6nUOJufZuciD/RVnt/Dy5fd4enjAOzeP+dbrE9dPnnCaFj7+8AP+5Vf/kL8/n/jcl94nF+H27o4PvvsBH3/wbf7wD/+A83zm/S98iSFU/v3/4K8z7K65Gq4QgfMy87/8w3/A3ekWV4Wf/smf4S/82q9TBb77nW/x9u6WN3dv+dVf/Ss8eecJf/fv/ffcvX1DFXhzN3OaYDceQCpvnr9gvj3C44p3omwQp2zvZVnIS+4HXmlgk/ek3cAwagHp7ninkieWEOQ88/au8PYMxQn762stIsVgoH7twKKzVqS40VmVrIyfFAKn82IMft+lSXBaPXQGhjawqgfKXtdzhs6gEqkQTE1to9ezBV3vtydvA572b2vV9BJsbFpyayGjgUWWhGct5PTWW+c62NUA0u3cEwPq1kD20wfudg20a1LwTX/um8pbxUAeA59NvmcFoiy4i1o4FK96jQSVvXG1dIBvHZs2DpcAqz2CzhTu17n5+3b9NLXLLfDdrvNiLAzIrAbqN1bNxfto48HFMxVLThvo15InNbRyW+x4xVE34Kz3vgO0+nwNEGe9TmdoyXa+bDa6Dv71+94ATHBpMtQ5AG0qbebdBQjNev/tM0XaWtgCsA1AbZ+7gsDtexuzqDnLtyfZlWjc+jm691tBrbUx3wPHt8UOBcYbyHlvDIzR2r5Dt3iLw7aAtGzfsxb22iduZRH6Pd67JlhBYXqU1K7vcq9f1/m9i5ZWFDBDG4urVA860DL11ezGWBuCuYNDqLDzA/uUeHg48PjBDYdh4Opw4Gq352q/Zxw09nMCx9ORl29fc3c8kUthLpklzxq/6sIk50VlPrynaMRHGmNncdZcVHu/VqiFMe64u33J7a3uDUXg+uqGx4+fcnV1zdXh0DtvKo53fODh4nj19o7np1vmjYlVbSC8GEi22Tc7KGoJTTubQzDmXG0FkLCaFbnNmnPGQtUecEuixdgz+ty2e/L2md/fr9efafLWks3tnKn2vFytYMmt81jrftMhNrdqa28FiEklEKQXXnS/VY10jckdBvihDKsUYx8D772ZElUcxe637a8KhpjWGmsg1opO2iYZQrB9LfY9N4Sg7CXUxXtbqEOUsdb9HWjAou7vhxQJUqi5ot3ljnmB81TZRQVSYhA8QvBVu/Kt2Bld39n7mN8Pp/6Vv9o425lUoYM8FYcLMGdsQLUryHsFfKSCqctRauTlq8IyV2JypKjXPh8rBUf1jiyFaVqMEWfroBgDswF1OAPlLP/yrpuANlZgybmfR855zueTvtebbqpfpWoac60l9ffPvxZj60voptAGPpZatGBUC/E+IQGnTveS1aioLhZyO4pkEGc6pAWRbOdw6B0muGrAbUEJGLUTgTBzo5oXVLnAOvpCM5lkY+IltP+jxUibIL2Dz1nHEDuHYwwcrq41bkypu6QLTn0WaGdpI26Evk83xrx32FhbN1NWvchSm3GT6+dHsSKTOIi232E1K4cCtLXlGO09Pe7U+Rei0hEQMea9FtRUm7XJ6awmsl36y+JdEJx4gldtc+d8NytPUYkRKUQtDzgPRhSblkV1jW0eFlG2eDI9c6mV4JMCaM4Rg92LqNyAiJqPiehzmBYjEaBx7ipJFoy5ry3bbQxKKUguFocbDhACPhqQbF1jtctfAOK0nb2q/ADB4UugylnvuwRcieAnm9CO3bgnpESIq+apgqUJh45NkcpSC9GiZed9Bxo1ZsRi6trz6GLzvBXrtoQNNaBa8L72OZGtKOKcWw2tqus5QJPzaOdjSqlrlXoPMemzcf0sDSqXKMI4rqBoAxkvrkkqt3d3fc9vYKSGfZrBp5gYhsE0YH0nrLS9ZBxHbm5uFAw0I2ZwHA57u+9mKCZ9vZRcTNZACRxtronA6XjqXbiCFhyGcdT7944YVI92GAbNC3f6u4fDgQagAn2cSsnUWjidpm6i1bRyi/mPbElYMQb2+71JRIiNx8psbd91dXWljOuqz7STIBBmk6loeeiQkhL/fLv2ZNel+3jT2NU5pPtnk0ao1nlc7PPmee4SEG2PbvN32/mDQI5Jx8hY32EcGVLSNf7/cN7+UIO0TiqxKKNrcWoiI8sCy4KgIMSqK7eCnR49xct0JkhiOZ0J1TEcrtiN6o4nFXwKXF3fUPKOZZk3znwazFbv8ONIKTBVYZ8Su6cP8Dczy/Et09tXUCshRnKeGWJCSqGWBWohWctfsWqtLIWQPBHTs5gmnTAGELhaSD6Q2+FnCXopWp1yVXDBWcC9cbuMwbRZMLBAWRw6KUERK5NIGAfCfuBwcyDXynRWIzNlY5lbe21OlJVQq7Wk+M7QLI3VIwq6RNF2jFpVK62Iv9BF2er0bEEC57SiMvjmfqiBQq0F7wd1u8yrBg1gQHM7sNW5NDjP+9cP+OmbB3w+DHz+5gkPd9fc1ufU4y1SVasphwguUWumuEoaPNfRsR8i5/NbXpzPPN0N+Dloa1nwnbUqUgz9TiwRhup4KIHsYPLCKI5gAdB7YeDnbp5y+/IjXlGZh6iLsErXcjJclKUUUki06vSaNPgeeHmrxGkA0QBb3TSLbcINoFhBIukt6M4i+i6LIGVN2mqFqokUJuvQig39OqzdqbVMbSv7Xf7CrTCGoV398y80jbgMWC8SbC6BjbZR59bKZInw9vVp4MsSvA1Q1b/D1pRDK6K7cc8QR3KonI93PH5wIOK4uXnKj/3Yz/D08VOe7z4gz0c+/O53qGHHT//sn+Wv/LV/k/0Yee+zz/j9P8j86q//Bn/1L/9Ffu/3fp8f+8qPc3s8E9zCy+fP+bmf+gpf/YN/xh//i2/wxS/+CL/+K/8Ocdjz+fe/jKRRk6nTHW+PE1/5qS9z/fDAH/3B13n5yXf5m3/rH3D35kM+97lHfP/j7/PNb36bw+FApXKez9ruaYyDUovpVjlru1J2zgJEH3j27lNubm745je+QV0UTBWryGekG/KV81FbKM2socpG09IeVNmM/VIK1XlevHlt8gTemFs6v5sUQgPadU9TPb8+x0wjsWRt7ZKCAo6ium3eANuWVHYw7z64BD1gvg8atuttP1tBVzShts/vIJwUWkV9NRVZ52XTU9r+eXs922uqm8B9vYbVgECkd7+3FaTvszFroGMwRoZPkTCMECMMEZcG3EbXtUpVY4l2e9Kq5f5yDGydaKvdBjC7D4qxgow4d7FGV4zzEpxczYGApltH6DhAB3vZJq72s6oFSL2dFRRsrIJuLhT0yrZAdK06Xxso1ApGzZBE7N+79I5N1IbvdX1twyxUv042uOBm7zKQT6QZzazn2v05cP/P23FqUCo01uKqlYxds5M1/43Gvi42/5rRZ2fbupbvW2LJqgHcf2H7ANs42/Oln042zMakaPfcQArBkt91svS9eAvQNpC2ZE0CWqfP+lnrvLkcGzvnpIGzWyB9PXOUyWHXVlvJUFbAXASoSNmguN4EdJrZmSgTyjunhSa0WHu4Hnny8AnPHjzm5nDNYbdnvz8oo4qM1JkXr1/z5tUr7u5uOZ2O5FrUqCpE1TeNaoJYRRl9yniH/X7Pbthxe/vWkmWd38NuJNbGvitc7QfePH+B94EKfPTRh7zz+AnlfMublHj06B32Vw9xcWSMO8Yroc6VR4cD128SH798zW0tVB8QnGnHWtHcQI/GVNc1tBrKtVijASm5lB7/9f3NnMIVNLDCfYwKdYqY4RqXz68/xnsxAW4FX53rc68lcKBMvFqVSXuh79q0dkWfcowBH8wMxHuSW/XRndNxqCLGIDVtXYTgVKLHOW0NloK1utN/p5liBqcxWSnOgCp10EY0NtsWKNY4xWI0a3Ft8Gi1pHY1iW17c1ueOieKxefa3KZjnhchxEZerpTqcFKYJpAMSwmECqVoK/UuRWazyriO2rW3smg36+Rf0+vi050WmJZSWLKwZEG8au9qEVPIIoToYLFKVM3cHRdyHTidhTkLu11kmnSsbu8mpqUSxj37Q+R8mnAExKTqKppwq36rR3DkpZCl0M2SjXXpY5O1SJv9EmNBOqJPJjHXyBfa5eKcdIBmW0jWW+7Rcs/RNLLSgkHw+oBrzco4rPb7tsd6m0NCxVucFJwyq5WltXR9ZDEALriMr1kL/FKQvOh3SsZLA2wXnd9mrKXbrJDrKoXRGbUmD+J8yx3ABRA7K2pV+YPFtGCDrdPd4cA4jgSXFDwDclWGLAZ05lK6nI0TBUViUAmTMCTKMvfug5Jz7yizFYHbzDDvQgeZW9FGWM8ovBo+YsBmK7KvxfZ23reZK9bxWvrnqAwAXYKwfXaRSmTNZVJQyYQiqoGbc7EzyxkruCqRx6QOfYq4Cs2wMKLM/iyFLJlaRJ/fovuSE0G8GLN+R3WQ/NoFsC38bGPlBvQpOInJ8BXT7lxYltk0mcF5ITQgrRQWYy4iQhCHM6KP2VOtxQ8jdCyy4LOuuRjU1PEsd6QyUplYyRPKQPTeq+50DAr6tmJBjIQlqNyBcyaV4QlhBVjneaZ1NrX4uwGcImLeHS2nXb0X5mVeN2anco5lrtxNk8VbnpQGsoHE+nmV01FlJxrI3NvfbQy8hyFGdrtdzx1aQSCmyLjbdb3UNo9i9MbmXJhOZ3LOnE6nC3BWAU2F85qp1/aexnE0JrOZjoU1j2nvb8UiHSeNzfa7PdN0viBOZANb52XuZ3ZKiaurK1Ia+me2NaDfnYz9q0Dq4epGsZ3a5FFCZ1/XWo35m/t5mPO6LhubNpr+bmP8DiFSnefm0RUtli6l8MC+qxOARHWG52nh9u0dpWYtRPvYY8o0DOzG0bAad7FWUhyUsS6q29uwjZadROEAACAASURBVGVZND5aVKJDRMxYUAshp/NZyRVeuwz2467vK9vOv/uvH26QtlbkeCRLwSevDNll0UPQO5pGS8kZF3Sj9c519qW3SVlLJp9PSPCknVaqaylI0QHbNeq4bZhVqmm6BNJ+wKHuctO0EIm4FDk8ekwaR05v31BLJoVEzUWjnuqJMSB1Yc4zu92emCKn85m8TNzdFZZ5uXgwZbIq/zAqy0dHQBH4huLnivNa1VwZBa0ztSoAaCy3ZZ5MUtYhXg/WkALpoG6Qh5T00I2jArq1cH110BYUrwtsHMYOhEfTdMq5Ms2TVsmsEuOJlDzxyYvv8eY8wbAjlwUvcVN5NkDQSWdzipirogeHarFVpyLoOc8QjT226ekUCxJ8CAxSeBI97x4e8pOPnvITD57A3ZkyV/JhwMUrcnlJchEsQQlRpRVqXrTtxsCZIQ0c7yae5wXxwrULxDgwnY/UVr4XZeHUGgniuAo6Bm+9I+tpjaOyr47PhwM/ff2M37/9Pi9LpSatjou1UzmgacDp5i2boGBtu21BvrLKdL7W2qrXmqA2ZpVzStVf5pklL/jobe5sQm8DHS7z9BWYBQN7yf1X1vbs7epswIgBumY+Y4XVri+5rRQCJtzdgih73yZRb/feq9OWPN8jB18cTv2zO6Aupr3YHL03ewqrxmEulXmaKXnizfEtuIllmbja33Bz81D1+tDA4ld+7df4+V/481w9eMSb16+5o/Di+9/HiyM6z83Vnuubaz744AMeHA78y29/jd0w8Pz73+fzn32Pb/3xY8QJz959h8Phmul0y+2rF0AT6Vdw5ke//GWePX2P490twcHzj7/Fd775+/zmb/4dvvfRh/z8L/wir05njsuZ3W6PBkPaAhWi53y+o1RzQfWBSgYnPH/+CS9ePtd54QSf1vbQwXuSs9ahcWBeFsVVW5tUS6S9zlsF3ttcWdmvVVQ2RaqQolemRvSmN2igjoGu+twasOpVr4tqrCT93pwnS3ybdnKbo5fJfS2l64yurbuXQEJ//g09tkyrVeFtQWIpRgc0m0GB8767cvfvvQcCr+vXXfx3Nd3i3jw352rdhSwh8n3tSwfdjOHRQGPnEOfVGCKq6UHLHZsNluV9m3RFLtbZlj3n2nc416+jXfN63X3oO8Da/nYfmBQDPpre3/bfPw3m3mcY2f7h1ip0AxzvF3baGJZSe9LRkj6zaTTwZtW1Q7ZtmwbotASsXUebHZtr0uvyfQA00VEta33/KmGxnWv93jaDdzknt8Zg65l+OR7OUh5noEztY4wBjdUCwlJbcc31J9/20hV4FepW33Z7n/0c4PI5sWHRiu452/u8KLwZoNzv0iansj31n3xjH25Gosc0tHuzNSVOE6VaTdKHVcZBL6DfnXZKrFjKxV3LvVOkgSchWHFax3bvAg9urvncZ57xmSdPGdOO66uHfPFLX+Lm4SNevHzFN77+dT768NvM+YS2+cN5OSG+Mh52xDgQQiTnhVLVuTrF1trnmeZF2Z3TeS2I1YyTSpDCOAyarNdsa1OZOG4Y+dznP8c+JcbgkJJ59eo5r9685frRO+yuHuB8xA2VjPDZJw9J3vPtl6+5K5WMMu6rYK3BbQ+y8XfKI8XOSdXlt3Um1YCbdU4LdNkt71U/VSpaCHRN19PauDd783Ydt86qdV3o3NDkK2ziD+mAQgiOam7kK5NVi4RtDi25kFzER4v9UrCJoeun1qLAllvnvjettFqVKZuXrPp6pTCkZGQEkzpwqASB8wieglicqYVHV9bzpS+dzfp1eNPVbZI+gSXnXnBqxde2J9E0k50jZ4dUZTlLdcigxJJx1PtPyZs+aqGgTMRcPd4nkjfQwaTGOgjcdox/vfisjcP6qGuFXIWliGlvCucpUyQzDANlEU7zRBwCtXimOVtr7kDOjkylusBp0nxwGD3jYQdnoaDx7m6fmCcU0M6l7aSqNRnUfKvFpmDFvhZ7O28Fa2PZ9rNa512ppTPGmmSe6oO2LO5yzvdODNGYKIYEUtXQzjoT2MTQOS80PwgRjMHoTMZHwVL9Ho0DvNi8tEfpguBkWWGzMkNZCBQ8leCsMyurRq2URWUfnGjBvHVsOsyDpLXyt+4fjaV0napcXStAaPErbBzgPbvdCNYBVoqZM+eipjvmWaBSKAZCOS1K5GXWp1TbGiod5HKdJbzRjcYMf0T3nuCwnFgZ202mrRUae9G1HatgZ4udb1WN+lobv4aMXsH67Xnt/WaNW1cCzti/xboQaift1OY9AsTkkcZsd1ZcliYt57i9O0LVPLQ04Eoc1RWkqBRkNn1anALa+NgBPW0Ft6K/W8HE9jMR6a3b3nmytayfz2dyXuw8K4QUNCavys71OKiFpWakKGYRnOUAokaO7XQHjS9DUDJELZDiiEcLa8XGeMnZ5pyezc47XIwMIXZzSJWJsWJEaAVB4c4YqRpL0kkSQM9lfZOqCYptlNKYp8r8HIahGziezxOtuKZrsklhrFIKtRYDIVVGpebCbV7MWLOdc7bvBQVSW9wqIuSalV0+JIbBOmu84lm7XWQcBuZpZp7nnuc4p5q0CvDDmzdv8N5zfX1t96xMYh0PXYeHw0G7LKGfp41Ak1JkGMauKeuuXZdLAbH1pqaDuWROJ50XLSc8Ho8KrHrfMaIQQgdx+/0bsSANyQqtGm80Y67dbmfftRBj7MzfNj8LlbvTkddv3jDuVMvao1JCev2ecdz1fcE5lfUIwStwXp1Jp2heOS8TpZoHQSkcj0dOp5Pu3VW6BIKaEN6RhtjZsrXWbtCaasUdDn1fKlJMhgVi1DUroBrqxzscWnRd++U+/fqhBmmlCvU0a+I5rwl4cRlMJ8WHaJU8Qbw6xk62gUrwZFEWqoBWCf0Oh1ezgWptAehEmkSUler08IjOsx92OJ94e3tHmU4qKO8GFgJuPDD4xPxGjR/C4MjnE4MIzlVyKIw31wxxZJ6nrqlS56knIaW1EdiCKlIRq8oHIDpPzjO12ERwXg1ixKp5Jkzsm/aCVPK00IXUq5DGxNNnz7i6PnDz+JrHNw/Z+YExDiZQDlhSHaJVBQsMadDW56AtKTgoWdvCVN+3ga8CdeH47jNe3L3l5enE89evOM4z2aaY94AJrVeB6LQi09gWzrXDit7eskwq9K4sjk2QTiXVzOfGkX/jM5/hy9dPeJiuSXhOqZIFZgfu+ob5+UAwR8kyZ+IyU4w17VxQUN0Ow+oHPjoekXEgpB0PfCT4SCZTnQbupRZCjfg0Er3nQRECiZdOmERZxTvnGWLk52/e4ygLr4+fUJ1t5H4FV8UCm9ZG2F7Ogq9SMiEMmjwE06BsiawB3c41drE5P19fI1V48fITHfeWdIkYOHlZ1VeAYwVEGxAxpNGkLlY9xPactuYhDdRprKoW7Pc1vAFg1taydlCbBg2XruDbpF8Bq9A1ihrLbB0nnfci0ltRxEA451Ygzn5Nx6DqAXt7PkN9wy55zsuZh1c6xnkRTm/f4krmow++w+MnT8B77u5e8uLlB3z8wUc8PNzwI194nz/+2tf5v/7pP2Zg4vnrV3z44Ue8+t5zXr99xWffe5fPvfdZvvPdDzmdJ47zc/7Gf/Vf8uzpO8zzwuvXrxkPB+Yq/OzP/SJC4Xf+z9/hZ3/25xh3V6TDFT/1Z/4c3gu3d/8d58UpMyQM4NQ0wAdPKI4hJfb7vVbyijKbglNtRA2+CnVpFf4GsbgOzvkQcN4xxKT63WWVR1m1JBvIsY65UDWxFBhC5PrqmsEFPMq+IDriEFiyaqcVyboHGGvVBQO7irah5ums+me5al2kiga9yitVZo1T59Smr+o2Acv9Ku5F4NznYAMMtSOhSXQ0s4ZmVrcFDsRAvrJh8W5bdBpou2UPOktA9XdVoH+7zjGQBFmF9nv1VRR8dM6x5DNX11emmVkgJQ3gYgQDdfFegbGtHkCb9BbgtzmhiXG9SEIaiNthsnuAYwNwPv1agdWmveiNqaJJChdrms0aX5/D+ozW31+/QYG/S3apzd4NO8lYe0kNF2IIJOc4G7WqJWItAQvGwBNZ95PWxtmvz0DcxmBzwWR8au1t4tv9Znu99//sNvvQlmmjP15bSUETmNy6eix5ExFledVihjKRGEO/vmbG15JNH4IWdZ1fzwwDdvW5y+YZtedvf/d2Pm3a05sz9/oc3cUzauOmYLixd52zIvrKVtGjyMBAqRdzym1+p1ZRZ/Gtbq4lnhrmrB0Tm4swPf9742/32FrKgjE72/xR9hYEER5eX/OVL7zPO+88YYiBIQzcXD3g5vEzTsvC7/4fv833Pv4YXyZSVC3uFCO3b18jTthd7QgxaRJXqxr/LEByDGmE4piySledjmdef/I9rvcDOS8M407bdoEUIvOSyVKJQyLWYt4BhTEm6jJzmjPjMJKiZ5rPvH7+AefjW9559gVCjJxOmjQ+urliqvDd589ZRKjVgM/aGKtbXefQ4fdgSUi2ZEb3t62USOvqsiKErXdnTBFBmWVN084eo5rWyLYoLbaG9CzQx2rs61I6UKZ7LNaZ4TZgfmt3FTN284DHeaGWhSyCoMmvD8H0XappRbaCLqrJLZq0ldwAfL3HXDOuqBt7sHb0Mt0ximPcH8jhwFwDOVeWqh0kWjAzPV9zY29SIrpeK3NVbeJaqp1rqa95Ze3qvQfvjWFlBkHOI1nY7QfSMBCTJ0VwXojRMwyOWjyHISBG8kAqMQr70THGiEcYg7LGHa7rsP8pYLT21O2bnLJoFdtTY6gQPXd3qtEYYiCJ6RJ61WbMVdvC0+A4GECbF3W6r2SurgOH6DkdhfNcW4qlRkudLRvwbmWS+eBxYe3+WotdmodVrzIoCmo3EFJB1ZwXnZOmx9n2zeiDGae6CyZtLovmIDa3lUW/WIxTe3u20IqK+lyqqC4oroIU646zfZICBY0nNjFJ8BpPeScgCzXPSJlwkhHJBjxOarAoVQHaVpwRsYKYgSRu022yeYbtuxoTLy/6LIc4MowDwzjq+wz8FJM/UP1bfSZ5mcl5UTZqKczFdCctL2xxTYvXSsm6ft32GFkZ+c11XbvKGntE9wvvVqPqWpXIolItxqwPEedbhxRWwAHYxgiiAZ59Vm+5Z/XNaHFyO+vzspCr7ifaubW2dqsnjJ5JczY9V6fg3TSpedfS5Qk0FgzGZI4pEa2NWgzwqrUqYBtMHs9hhlO+g08tJvHOE1MkG3txmicFy3M2nMH2d+8ILlAtkHI+qH56zpTsGIdIwHdN0mU2oKoq8KlA5lZmQfXBSwikYUCqFgiur28IMahs0KJAbxXzk0FwFaK3eylVfWRiIsZArcJiUgHZ5AK2nT222UPLF0RIw9A7mtvZtuSsJlrjjmHYKXnF6dq6vh4663PLvHZuIGcldpRYGerQc45melVrpSxnlnkidENTvb+ZBuxrvON90C5imZinqUsLbPOM1uXivePm5tr+HDrA7L3jeDxyPJ6oJTNNUy9QaLe1mbrZ70qtxDgoqOk9IWrnKdh5HlUucZcG9vurnkstxiBF1ANpntSEC1Qz/U1+DU7zmpzVnFE1lZXdHHxQwzR7RluZtnEcL0hYV9fXFAOJcSohkkuGyXN7d6dF8dNJ8SS3dnuN48g4JJxorBFDJMbEuGtF8TWOrVXjrWKM8mAykfMycZ5OHaDvWvnmSzIMowG4xk5PSbWdxQpyzpGrFlVq1fy5d3b+gNcPNUjrXS/IKfXekrfgnVWbQt/8pnnGDQM4xzDuWM53trmbu+RSmacTfkzs91fkueDNHRHnulB8LmuyMsY9h4eP1Y337RvKrJNwl3a4/5u59/qVJcvO/H7bRUS6464v29XdRbLJph3OgMAMIQF6l170d+phCAgjgRJHQ0oUxRZBisM2bMeuLnftsZkZEdvpYe0dEedWUXqQZtAJXFTde/JkRuzYZq1vfev7tCWQ0a6h22yJIZCcQuuEPQbieMC5Fu0snW5pdctg9+zv9qV6JvpGIYaiu1JNZOqkkuTRKiV6LFqCtqyReqgCo0tFsQSoWmeyD7TW0O5W7DYbHp6dsT7Zst6uWbcdaNHBMlp0U0LwBB/xPqBI4EWLyWpH9EeUEw2SmCzGQbvq0CkyjJ4QIWeP1gEVFLt1i1llHqstx9sVv3x9zZe3I3eHHkxNCDM5a5KKhQ0h+mahiH5nLdqDKYhhmDEONYGDYFJkTeJJ2/Ct9YqP3Ypn3Y5oGo7DQNtaRLohcfLgDDU84/jqC3TRUh3GkX4YSVqDToRYgxLY7Db0w5GX/UhnG7rkaYzBay0mBFkyhJgTKnlcFm0TqxKNFTatItGuGqKNjMOBJ6plnTR9TORawa3OoRLt3QMnJjZgSihEO8ooJd+toAIp4sYZ0IvNM6XE3d0dFTjPpOKWrEtCxb3vEeODrwKvurRzGCMH1Ry2z9IKNfCowEku95JS1RycWYc1YJkMzVgANonSGlaDPab1N4HJBVzJFVBcgA73f+c+u0sCpCV7SlrldU0wjcGuVhidGfuRkydPZDyVhLz94Y7b2zsyipvra773f/wl43Dk5z/9KY/On3C625DSyPf++j/wN//n/0KIkSdP3uG/+a//Wx49ekTjLP3xwMuXz/nw/fdJGr748nN++cknAsBpRT/0pJT4+U9/xuZkS4qJn/3gP7LZnfDBt7/Nd3/39/nv//Tf8erlS5zt+Lu//yEffOubnJydk3Um4rHJor1luz0jKRi9gFVoqnqTjInREzAXYsIavXhGERLsx1H+TYuu1JQIl2SlAoj1wExZArkYEt2m5WS9pU2KLmvGKEwemwzZWF77Gw4lmWHSYE2EWABJmXWQEhaDNopRFV0rJfltKsGsLRpHsizut6XV1z2QsTBjmOZrXgCaxbSsro+SNNcqtrXVcVhN62Mpd3Bv3eb7SYNStQLMPO/LmhAgXFpj/QSg1wp31ZrSOA1d06CtZsiJWECwmEA3Zronuc8sAIkq6zHOUiGih1RA+9KdIDrBJXNaru1760tuKEcpCN5nTsq4w31t6CUQOz2LKSGYE7v763V+qcXvTQHp8ud1L4CpLVOKPolQdLeMsYVdWkFCNQGuujAuE0xM8bz47Hq9ucjO5CxzwtiG87MT9ne3Aj7msi6m8ZjH5u3C23JMZKzq3+c1pbX+ShFq/qw8AV9ZgS8MxcpoEsMkNbemlaQ4lko/WQBmXcGFXDQeswA71G8oSI3EKeneXJeiokKp+VnX9XC/GJeJSSHO4Xl6X54ebikITGMkK68CEaJVKeBWUuIyLYZUaQJ/J9RvGuOydhFWYZW0EDOSAkZXoKCA22KOk1k3Dd94+ox3Hj3mYnuBNtC0Dmsb9oeBH/74L7nZ35KBbtWx6hzO6qKp1pOUgHU5R8ZBdMy0Aa2tFAQkiAUSVmXpZsiZJvSsg7TvaUYur94AkXcePyIcrnn94gVnDx/S+0Tbbfjg299hHD39sCeGEasSKkVsigSl2N/2RD/wznsfstlu2N9B01ienVmiP/LZ9R37KG3VNSmtUigT86is5crOEaBHtDLlmQg7LOWMKSnEPK/ztG9RxjwWls1kilqfeTmvl3JFtbsoZ9ENTyri/TjNkaozq1QhFSjpjqqAizWWUGSaphZj5zC2JSdNWqy/OgdqnpFyRHiwzAUEpYqMgkarTM5xAlLvrj7n9uXPWa1XdI8/xp4+I40ZTENStQCdRfqidiakRW9DgqTSNEdNSRipxmtlmDQy9hhFjr78GxjnaFcrrFWoHLEKAeuSAPBDn/DHgV3npC1aZYYh0hpLLC31KSOFgAIQ/ed6VZ5/3XmruY9LEhuMwGoFWmcaR3GBBz1mxqgIg7T2pwQrp4gBwiixih8ytynQrUSyzGhNDBJEGqOEkJzAaEuzcTLXYyD6svcU4INakFPFV6KcqeQ86X7mvCy6yb2k6UygAN/FAb6AfZUBKobPImdWW5wVpuzhlUEtbPZw7Bn8AeNaUBFNRCcBVuRoiKQazmTpOJB5LdIGSiWIgRwGku9JYUSlEatAGuvT4g/kJDmDMkxasOLDkesuXcbTkkhT63I9PJx1Am45B1r8USQBKTq1sZh2B0+KXmKLnIA4sWRrHpNimrpO61muC8gyn9pz/G+UKeutjrfEPtXvpMay9TeXJrRiKC7AZsqLrrHJSHk24UpZ9kddpaWUEL7q9lbPdpGcoBTd62dKnKKNEMbIeZI48FEKdTEJmDX4njEEyZFlitE0Lc60UOahMCAbjNEEL74EKmtMeXZkiGnO5aoufGUnugIqQYlNU5LxUnKeV73del9VXqJ2dYZiyK2TaEBXEoWvmAazHFOVzQuhyO4FTyhFSIWQCQ77O2E/N64wcrVIEJBIpuYuWgpyWvaMyko2xqJtx2q9xo/jRGZbxmcxVQajzG+qJGW5v1jAS609+6PkaKXPTFi2NU+CRdwvZ5cxVuRFrOTVlSm92WzLGQDe9yVJEEawUomcXWnlr24+iaCCxGxoDocDKOncTDlPLOgKQBuj5+JOrjJAQjxcr9ecnOxQ6CKxEUnAGAIqgx/GUgDKQjdHEb1n8IEQpatEGy1gqjGT1FiNCUU33tEWb6aUEm3XsdntZP6XTsiUpSPHF0awkEUyQ3+cxm6SlyvYX9e2rFarae5V9q9zjpPdblpPq7blbHfCXbdmHIcCLMscDd7T9z3D/oDvNbns8SpLPmKtlVJXAbebppFCl5Z7lnxI1sF6tWLw4z2ZuxgjcZSC68GLsaGxZiKmaW2Eyb8SUN5qgy5ynta5RRz81devNEhbN1TZHKWqkFWaNlHK5mqsQQcBPLUCt1qRSfjDoRwoclgnX3RFU6Z1LTkkqcynymCSCR5CQCvRAgzDKNR8bcjWyTmSRP9JaYVBEVqDbjTbzYZx7NlLA44wxHSmjxGTEw2WI4jRi6oVCzsxIjNK2v+VHDiKzDgGVMwoJaypHD3YAuxl0TvLPrFqLA8e7Hh4umW3XeG6Btus2K7WxJwL2y2KU7ExU6uFWrTRKFW006Iiaw1Wk+2GkTUru2O1akolp8UMI9c316ThBqMi1Wm3KRT99dkF2905D6/v+OkXn/H68oYULcqCaooQfAqg52qxKkBedbuMKUAo7K+cWDvNQzTfffqYcxLm7og9esyZQWuLzyNttyJqhbIGtKK9OGH/5kvCfsQp+d6maQhZDkTrLCrHsplZNB2+H7gNgV1OYrCUB1SSqq4p15qCx6coujhAawxBS9CdcsApS5Phvd1Dvn0c+FH/mutVJBtHomgEJSYzHMhFeyUIU8pIlbK6Xco6kGClur2bIuGg9GzGdnd3x6TbqAGtJm3L+lpKCUxgR2kprJWkyki8x0acgE+m358/p7aT1GrkLD+wTMLuAzf3wVRVnvMC2pgYP/WzM/e/e3rn2yBPru+pgGAJsAog1bmWBoMBhv6ICvDg9Ankhu1ux+npCa9evqDvj3zyyS9ZrTb83r/4Q/7L/+KP+ME//JA/+5/+jB//+PsM4x5lK3NB8+ThBb/33e9wenYGwPMXL/nXf/zHbHdbzi/O2O/v6A891Rn+iy8+Y397i2tW/MMPvs9PfvwjOu35+Bsbfvnjv+Av/uy/45Nf/ASjBkJMpMGWQlRDUpnbw3EKILqmZT8O+DHSbIUxW1vRaruwBIm1WALC4mMBGFXwYgHS2dJ6r+eW/jnRVljliIzc7fd8Fjwr7WhNh0qajW3otg0eYTVGXcDS5T6fhJ0vbayivywXJXPEaHFrnudWXvwBYcTHKchUFXxczA1JmGVOkSW5r+fK2wxNmNv9azFB2LVq8fP7Ke2SdbsEK+/r0Mn3V8BL7r20eZTkpoJxcwBk0Fa0zbI2uHYla9RospFkrrZ4yacXhmIF5heAaEwJ1NweWEa0MHTzlNDce75UIKPwwmK8xyJdvqf+01K2ZfoZ99f/vSKMektzMt0Hb5bX8zYAWgsI5V3kLMC0jyNDHmSulYQlF1YLZSzU4jqWIGp6awzqHNBAKrFB1zT0UcCjtLier7v/+m/35FjUzPrOed4LY4rlbEz35g4gJqTUTpP6rGXvLMsTirlJLgmAnDPiCk35DilIlGeCxFMhpCmor1NwTqpmAL6CW7WYUNu9ltdZW+PePjvenlPL31OqFC0R8JJcr8OUa5R9yihFUqpIJJX2VS3Jk4+xgLzFibuAjjlWOaBCw4yBXGQynLO8/+gJ33znPZ6cnqNypnEWbTI31294/uIF17d3OOdYbza0XYdSmf5wh+8jd8cDg8+sNluSH8nRExHprc7ArnWSLJT1Y7QYUSltiX7k6WbFptH4mDiOkdPzR/jhwGazY3vymD5odusVKcHu7AHPnjzhxfMv8bcjm84Qc0+jEtFkbntPY9f4wxu++MTz/kcfY3ZbvE+sGnjn0QPGrOmv9mRlyKbK14hWXm1r1kakvpbPXVXwvswxXdzDJQmatbanYoYpiXhpr40pfGWdLYsbk+kM855V3aHnGKXKdiRSUmSVxRU5qIkhbkwUtgoCPrdNh1IiJ5XLWshZtNyrPnLOCWeFXVyNg+T6yrUpJYSBHMFAHAf6yxfsP/8xL//pb/H+gD35v3j/W7+H3T6kffgerjsjRLmmGoXUOc90/5pcQFrZ6xQx1G4Mpv04Z0N1mTdW1GONcWhnSQgJRTTlDQkBLL2Sc1ZpiYOd0jSNRFCtkxxbJZF10/98fvif5ZWSkDRSkV0DxdDLfY9eNP4E8DBErzn2AR8NKUf6PpKVQ6MxWrroIoowSi5lLSijcdbhi56tVrbIlQvDeipEqXkfltrXLPFS57jWImuhylmSSmfg1JVRWFc1np809Kl5eCwFskwKuay9hB+95JlKSAmaaixJATRHbq+v2OxOMEakoOT7PKpqHKtAQYIJseyPCtmTfE+MAzoNZD+SwohVAgYSR0ihHESq5Bws7lvYuAVylLVYyE+VZZbK3ltNjZyzUiQtnUoVcBPyiwAAIABJREFUwI0pFt8WkYhQ9SyqhbPCsEs+zHFZFlA8Jelg0SVmWRbbtFLkQkqYuqZK1d0aIyy7e7nHvBdNsYeEgxMDjlgK7mWm1PcK03EutgD3wLIUwhS7TOeiEpkvm60QwkJZ81qjUpXamDuclJn1sxvXCHlE66l4oAo+Eb2YJKUx0PswyT+mMheFYevkWWRdTKJCkbMQVqQ1bp5zuuhvKqlczYzCOV4CCoNbru9wOAqzVkncnoo0oNYOo6MU9RCWeY55ml8xVcZzZux7WtdgivSHH0Xf0zaOxjq8ly5ja41oyztDimCi5O7WeEbr2G7XKJWmoljXdQhUZCaDL4nx1NR1GFPtTihiOaVroQK1OWcwZuqi88OAHwaGYZj2BAFMZe3VDtFZLxVATNDk47UYpJWYQGuLKQXd1SpN8pYyh5OEdDGj+yN3+zvGoZ8k4ypBylrD8ShyFFpLq3/TtCREEzpn0UNuG8FvbLnfrhBQVm1XCtyFvFULHtrQDz37uzvZD5Az9Hg4TutoOf9Xq9W0DmqBVBmDKRia1prWWPSmxMSlcyWEQJxM7eRn/dhTpU8Oh8P0fSknRu9FQmG9pmkaUko4bUkqsmpatqt1yXnnOLMatqUsHiy12JCjjLkPsr8YY4SBraS4QtnfTYl1u66j1e39WEYpqqdQ3/eM4yhxeZKiXUoeozLDMOKMozq7GC0M8rfSqXuvX2mQtgYpcgCk2llALo6yKQuTlJhomoaxHyZGbLPekFH445GcpaVHp0y82ZN1Q3uyYcCXIEpMdzICalQEPRnDmEoridVkJ0BwjIGVWwkbMyZst0Ybi2vX0G7QzYb9q5fk0KNVJISe/eGOJieSH1GFfh9zqNEbGTW1ecAiAUuZGIVmL5o8RRIAzXbb8vDhBQ9OT9lt1rStYePKphYTx+DZ9z1KKdF8McVDXBXB6ATGOtZtS9sm0aNVBm1ks3TtBrs6Q5sVm/WG7WaLcS1KWZI2vHzxBXevPyUMr1BtQ3+8ofdHCFIVc8bwzsUJplN8P/+SNy/u0F0jTJfSnqmV6I8kqoaPJFXGQOMcRlmSD2y05jcfPuHj9YqHKZCurzCNVDiSFmbyq1evOT874fzBBarp8DGyuTgjv/s+r/7xJ5BlHqERVk5Mwk7AleROGKspjlxe3XKy3aJUpsmJtrSXi2aWOO3mEMCPaGOxqWXVOgYyYwqk1OFMyyOr+JdPnnH9xYEX/R2aRFCGVePQSYB4FFP75tJgqOr5SmdQaUOlAgsyS1hsknXDkMMfFlnVAlSbAS5j5MCvwdaybVt+Ljo79VMmRlsBm2qLZNm6JybgdG3ke5vYvetAWmyyUtOBUPsOcwWtakAAVAMTle+DYMt7/DpQoLJ6poMPYWm11nHSrVg1DS+vXmJC4mJ3Rn8MRH/gpz/7GVYr7m5u+Tf/+t/wO7/7+9zcHvir//3vuDjbst+/4a/+6j+w2qxxbiV81Rh5cPqAD995lzGOfP8H32fwgQ8+eJ/Xl5es1xseXJzxxRef8sMf/ohutebp0yf4B+d89NG3efHyOX/7N5d8/K//gP/qj3+HH/3kR5xvM3/8Lz/kz//9/8oPfvQ5p6dndI1jPB7kQA0BH0RXzRrD4bCn9z0qWJFAqSAUFdBiGheogNI8lrV15h6okhbJdZ0HlJaqnHCNw2jFYei5Ox4IxhLazFq3/Nqv/QY6Jz5784q8MJWohx4pk4yAkWRJWuaEn6KfWITsFyDfMpCRLU0zt+zORknL+6iGNDMYKvdc24tKhjaNS03WlgnaEtT7uvn2NhBR5/y8Bu4XSxKxgGdzYCNnQypnHaAVPkdUtKK/VXTGsirFwwVAUosaVEBgWj+yl1R31DrASikp1OVaKJH1NzExy72lnEpR0txLduZ7v78Gs7rPfM3Ach+4N8aLP/Wa7xdzyvNjBtene14k1iF4KWwpNe2nuQC3Ahrq6VqW3798RjnnUiRU0xjV8cjl76/fvEFc1d303V8dj/tA7/2WuPk518LJZARa5mJa7O3TM63zdtp3F6xtteiUQAJppav5pPxdFxa0FBzqXC0zMmcopgq1fWn5TJaFtlykDpb/Vu+7ng9yu/N1/nPjDZS2y1RA1cKkJE/XrxFmyNSGXzXqUmGRGmlbWydpkZOWPDsVVqo+X4yRkCIKjbYas7I8fvSIjz/4kG3TlVZTy2F/y4tXz7m6eoW2mq4xoDLHw54YPJvNmuF4JPqRkIWZ3ChhozlnWa1kf350doLWhvPzByjjiAmO/RGlDU2z4s3lFUkZDiSSNdBYuvU5Jwb60XN32PPgg1/HIYaQzeqEL697ktthTxLjeCD6nk3ruPz8F1y9vuTddz7gbvDc3rzkuUl8+K3vckhi7LprW56cbLk79NyEgE8CYMyAu0Ipg3MLPd1qtlakg4StbSBXACtPhaGMaAGmFDg7O4OsJUFRamKrLdtDJSmuunt1js17QZUvqvPGWmnMT6kma3luE9QSG8zsOmFnGlvlXYIU8qwuIEIkRTHCIUmRwmlLNDKHrKlmO2VOaWEfpzHQXz8nXf4TW3XN+tkOZ7YcQ+blj/+Sj77zR6zSEzkzlBRS8xTj3wdsqxnszB4GbYpBYtE2VApSFJaXMULoAI2xjqY1dE7ROcN21dG2iCFoTrgmQ1DC+DaKoY+0raExSpK+SNGiX2jy/id+3St61TEoYzKGSB8DSWuGAPs+kRHDpxgzvg/oIhU2ROkiyFozxCK7ZjTKGowWbdsqGZcy+FH8RkKIxJil3beCUCWH9OMoBQVdjaUUFAmG5bwVBh/SrqsKyzpLIVk6AgPjOMh7rWhAmiLXFqKfjs6cC1iVi5kbGT8GtBN94yTiJqQCOnZtgzrZSoeTHxiH/VQM00qKP0JMKGBrkWfz0QuglgJGRWIcUCoWFmgGxHhLl05FpcW0TgEkkRrRaj5P6itlcYjPOUphq22xxtC1XWn1nbtDcqxneianiB8HIQNVY+uUUCqRYyiAdJjjgFI4pHhDVDIJMBddEVxAzoU5hpiKrknO8JpDzGSS+7GiAF/ynkzpXEWjlSGEQYoqxXRUqzmPWsY1VYez/iyRRUNVz3mZdVJ0DwXgViXGUEUH1hhDzKIrbW29FrlvH2Ue9yWvn/RxVd3/qnQNUGL0pikSKkqTnaVDnhWLM7g+U0ocXtmRSUtuiEa0PAuYXJne1lqsazkcDsSiVzv0vRDQnCGrtuiUC4MUW7xovGjWVgk/XbAX5RQ5KTGAV4qxeKr4UNnNibbpcM7ivXwXKhNtwsbETSkGatsIrpCieOwUzKPqzOaSvxqtxbxdL/02Equum2QFakfJEkD03nN7e4v30tkg4LloAh+Pome6Wq3oCrNU5onkKDK2pdA5gfF1b5Qc2jmLc43sP0pBTHTrFWfnZxCSFD3LNcUkhdBhGOj7YwEIy+ehUEmM5I7DAa0169Vank0B6sliZmaslfnaNDjjJqbobrdjt9tNBRmA3ckOkDys7/vpHut7lFITKB6DaBavV2uME6O4nCR+dE1lrraYtqPGihnYKpFuFMPZeQ8OIaCNgOT7wwHvvYDwVGkOkZY4OT2hsa4QG/QEIksYU/JIL5KaYnBYDSPjNBfGIpsxxa45c+z7KQ+uWttVJ79pWrqum56BGOQaxtETkxfT1Tybmh2GAT30y7TwK69fbZAWSMkzOUGoTHXeFNFpmSTD8YBpGlrXkGIm+IF2vaJbrbm7uiZFOZBi3+MPe+5SICpwqzXZSIuDSYZQKlMCGAjdf/QjSQmTKztLDhEfPbeHPabp6OyatlmRrSNoQ+MMJycP6IeA9reY8QD9kT57hnEkDT2ZhOsayJJ0Rh9RVqQMaiBc6qCy4aiMazVh8NjGcXbxgCdPHvNgt+LsZEfrDJlY2s80WTmUzbTWEAGVRGsSY6ilgWwzRjc412FsV4IJg9EOhQC1tlnRNVsJMpTGuhbT7UTguWlkU40j414R/R0xSRs1yRf2plTqnp6d0b8bub36adGEKkE6crjqMkNrEiYtLZqNaXhgLFvX8O2nz/j4/BHN/pZ0eYm1a5KRqvZ4vGN78Rizanj+5g3tdsu23XD95g392PHkg29w6EfuvvgMEwYqwKhz0XwByAgTZhxwOeHHgc+vAudtw8PVikal0iKgiEgbrI+B0XuUGtH9gGk7XNMQnZMKWJNIac/WWb6xO+GTV7fcjR4aRU5S9c5aSZVsUXk1RnSsIjNwkIp27BKgXYIa9XfnADgtkvea/L8NGMmrslgW+Gn5jMzyn94GpiaXdZagxAxCLIGPtwN0YGrDWeqETt/FzE7QujAJM+i81IKcr2OqPC4Cj7eBHq0pILti5TrON1tOLy54/fJzTPaYFHl1ec2Dd8747d/+Lp9/+hkhBL71zY/Y397StisOhzucCdzcvKJpNa6aG2SwtuXqzSV/8id/QghHPv38M/phYLs7QVnD3xjHMBx49vQhOSVevnzOk8ePOT0542c/+yl//3d/h9Nwumsgj8Thlm+995izB6d87y8NQ3+gdZaubYg+iPRJhmH0rJwYJfXDLWPY0+Zd0Y7K03iWaT6xO6ACLRqYQfrl++8/93nMa9JNSVRc17JtnHQeRAF8Bj/ww5/8kBQ9d8HTm0woBTajNCnEogMriYi4EhfQOIuZhKpZHPcn5xLMqwFqBaBTTqgFYLssPOTy2SlXKQ1VJ2O5tzzdfCpsy2kuFeAxv71Q+Oq6Ws69ObiTuby89onBAdP8jaW9DqVEIy9nnLHYtsVbQ1TiGqsLSEeeE0lT2nWEuVYTHXlTDYrr/U5gQanq1uuQ+P7+fdSiodLLPUZ+aV7blcEi7B8We9rbMUgdq1ocetvwrb5nCXZ+Hfg5wx568XvM7A1q0lIc6ykSLcxMmOUzuwcelnVdRyCjpgAvIawgw1LG5evB5a+bD8s/sn/Oz79KVGjk+3NM09ysXRSqPqhcZEKKlmjV1wNQSdZV1dKdjRQLu4BadJmZjRX1fbvYMD+bOVF5+77u39/8fOb3zBp9yyQiJwFcZp1UPY2JBnTMxCRmhibBpm3YtB2NUZxu1pxud2w3W7brddE0k84prWaDVT2BhLno6Uuxe71a0bhGNMe04vWrl3z2xRcoBavVajKGQynW3Yqc4XB7i04ZYx1nqwajpZ327MlT2mbNuoHLV89xVnEcA5c3NyjtyMqCaRiPibS/RemGEcNwPHD0I9oknIGnTx4wHvYcbm7wPrJdrVAJ+iGJ4Y9WWLPGrBqaNby8esUnn37J/otPeOyMaOatt1x++mM61/DknY+4GQMpwcPdlmPf4y9v8SGXVVA7TeSPHz1DHFDaTOyXTCAnJcws14nuXmXbKmF55gwnO01O41SEl5bD2UVaK4Oxc9oh/gZFxmZBvDCFASrzSVrb5+kp3yWa63MBSO4mQ0oc+ztWXccYA852YjisFZbEy5evSGFkd3Y+Fa9IqsgUij5g/WCtMqqYFYWcUcMN7u4TbH5Ou/LobkMKgQftinXjaNI1brwkNVuSaQiFDJALSDOdw2Ut1V0rJTExhRFjVAFlq1GUku5yEtCgjWLwHnTG6WI+5jMeJfIlMXDoe5lfgyauHCkoxjEXxpYwvRutikTCV/fnt/ewr1vn/19ec/FKWLRKa/wYECm3TNuK7mXKiozBONkTxiCxt7IG74VYcjwMONUSvYC9NT5OUfIdazVi1l7boRXj6EEZtEm0bUPf9yJfY42MkVKyzxegIiWJ/7NexBMpY51ogztn6fsRhbSexwL4ai1ndYxikOS9mAMpiolU9MQwMo4e7z0xrFitOkBAZKWVnKNZTwXIkFOR+aideEqAqJyKi3kgJ2mhTmEkpShZS44QR3SRN6i6yZXYlELxR8kFNCqFPV20mmvHzVL+BkTncVXc6p11JR6pQKnk6zEGgvdAnqURCpOdorObc0IZWdexmE9Jy7MANU3TkklyfpfgV7ooEsHXTgw9FXtIcl4mNeuk1zhWaXm+NRaWIj/UbgIQbX1nLSolGDL9cZSVou6vi7eLzXV8YowYJ943JDFcUkmiLXn2AvbZEv+mxZhkrVFGivI+BrIXFl4IER+FJj21ZrcNVf+WVHOihZFqiTkVCxIQEmOGyiJWRW+5gmA1xtQaH3wB1xW1WCbaqnECMVMW7VkfhISWMsQi0WeNJUXBU8QYCoIx+NFPZloCxPpSIy7xVM6lFb0UElWVIDJlb1Q0jUHpjDGFbUzC+8DxcKAfBEzTqgLMAt7JcytyCaZqtzLJBwD0fY/WmpOTkyk2Xb66BYg7DMNUUGsa0aq9u7vF+7EAsXWewTiOkyZrSr6wa3MxLaudgfJsa5c1SmNQwnJ2BhVFK13MCTWNkutuGkfblljGuNKZ63HWoLoCRBaDQwE8IWVhfY/DQIihYDYz8Cj3YGhc1YqVOe+cjGfTWLquKWt9LtzHgvMMw0B/7ImjJ6UIUbrYxsFLPmTk3LbG0LZN6eARNrIqhdLGNdNzqTnqRckXY4xFT7fs71mkDUwyDMPI0Pdlf6zmaKVj3speVcFY1zickpixArCxFOmq1m4uMYz3nsvLS3IWLd3D4VDSJYld27ZBKc16vZa9VCu6tgXdSk6nRBFgHMfCGA//j2flrzRIKxtpKnlBnJIHFByPR6oCTkoRax0npzuGYeRmGEgxc7bd0WDYj0eOoSeXYDKSudtf05LYbXc460Q0XBui9azW66madbi+JcSIckaYY7roEWmNNo7Ts0c423F13HP0nsY2GO1YnZ9wuDpw9+IN+e6WdDyShwEVAsZJy1IslGi0iOPLZpfQajGhjLA7N9s1F+8/5um777LbnbFuGkzoaXQFDkTYvhqhoRSNs2Q0Vmla2+CzRikrrYJaY+0aZzuycrL4qCwWMRwKMRLGIypZknL4JkOTgUAYC2tkfYJJgWNWaDvQtEWUvhqTkFlrx7eevsOLV9f88uVrcs44Y8g+4Bo7BaoxiaNn1ooxJVzSfOgc37m44On2jOPrK4IfaXSLVlGMO7qWjdPkIJWTV9c3/NMXX/DxZkcKgeeffsH67AGPfuPXuTvcMly+xJQktXFOBOWTJ4cIPpD6AZWk9eqNHznEBK5jmxOWqiul6L1n8LLhx5xwMdIOidgEVLciRYVPkdiu0Mrw0WbH1f6Evz5ecVRynynPYGStUOoSCIWYpKpegExjZbOu5kD3GHwwmRXMyS9Fw68k9OQShEyr695/7gOclQ1Vgo9SPFiywt4GNKZrmQK0mmzPB0/9nqnqXIyRkprZZPJNM6i1BKFqa7Z8TmVlfRXYgRnSk2p7mqq1KSUMFmccq6bFGcPLFy843W1onOHm+prf/6MPubu75X/7iz/n7uaam6tr3n3vA568+w77/S1/9mf/I0+fPOSXF2fkpNnuTolBjGCev/ycP/2f/wdSDPT9kRAD2+2W27tb3lze8PDhA1ISgwS05Xt/9T3Ozs7JJN68eE5jFNvOcHXzhucvvuT9dz/g7uqG51+8kqCka0TgvyQMobRfUYLZod+T0gBsqazVJZxVBm8aL2HYLXfdPI2bjGd9Zm+NbwG+ulVLIpJLm+aji4d86/1v8ONf/Iz9oefFeCDlSNCKpCqrSQ5wXYpUIAcrC4CVXJncWVqtlCrpxAJYW8RN98CxVFqECmCoq95iFS8FDAXYRQJKpSgsJTlPYBaur686H78OcHt7btc5PwNb83v0Yo6qkpTeczjXBcA1Gm0N2lk5M4zFOidyLhXcW7KctS5tfeXaClAp7YayG0/ribqelnqQevHc7zNS5FrlfFjuBct7nMamAuCL/QhV2bpf3TOUUhNIswRM395nJuZV2dNEHmcG3qsuYEppaiWj7KnVJENpJYBleSKV2fA2QEz9TuSN9XdyARVRtb1af2X/STFN2oZ1/Jb/Xf6/qvNgApnk/03R0wphBl1r65XoIVYGY9EcLFp4Vbdb9uGIsbPe1bJYIaiP6AxK8mYmQDq9ta7uP7NZGmf5Wu7xM5On/Iz5DFrOFXLR/yzfEUMQra5c2uBCoNGaXdvRth2nuxMe7E54eHLKo5NTVmtp6TNOzBiUMyhlUMlMBcB6D0ZVpqgk99rKc/PjSNYCIoZhwJwlrNXcHQ4MQy8ank3LGALHw60Y0hnN4yePeHh2Rqczn3/2U2zT8OTZe2S9IfQ3rE8T/fGG3fkpX7x6zfXtKy4evsO773/A3d2Rw/6KzWbFNmfG1Za7w5GUIl1juL2849gfON+dEYJodmcVCSlhMuTgSbEn58ghKqJe8e43f4vPb2+5/PILHj4+56TdsNGa6xefcLLd4VanpCFyttsx+pGrvqc/iBGNT2KQQhbgebNe0TYtPsztoBoNRhJ324jepICYxfzFmJJ0WJRqSVliyMZ1ooOd52QcwBhZR+M4MBTWiVLM2uEUQveklVs7zcquORX3Jc5QyLqgdGEdD3e8ef2Ck905Z6cPUMDxIL97e3OJIrPZbsC6cn7maS8LKWNyxqi6lWpC1GgDp83AdjuQewF2k1d88vlzLi4e8J2PvwXtlt70XMcrtHIYvSKqCoVVVnya9qaYpHimtEgdUMGUwiK2xtA2YppViQ+ihykAHVqjrBJmKYrGKbpGY51hKPLvMYp2fd/Dau1ESivLM51LWf//grCyJ/y/A7xLcKvrLIMXfezWyh47BtgfRxqnyRh8Pd4StEZhGkVrG0JMDFkzDIHtpiUUozutNMYqYivSCdZanOtA7SkkOIS55orkUnV7L3EwiHFPORl9abOVuSLmc66pIIWwQavbuTAjBaBTSTq4mFqsg/wJIzF6hn4ENN3KUJElpXVZC7kYlimqFnRG9m4UU6uwzoEw9oxDDzmgdRIvi1z8LVIQaTeSFMmjsHVjAcSqiZLgd+KFoZUml0JV3w8FfBY9yKZphHVnTTETglqUq0XHlCN+GMkplQJiEmPqlISkU2KGUCSvlJE1AaCtxGPGGHKRPqlnk0j1lc64+s2xdBuW+6mgkjzk+3MO1JQPqQJyKQOuaXGuKcacwrIcj0eGoYeyUsRQt3YS6gmYylk40NXkaBgGuU4j4Lx06grbtl5T0zRzZ0w5V1OWmDfGkdEHhuDxvsjgOSdyPMVg0RphnFagEUvRRK2GwZRiRybHTErj1LYvy1JNklFLrXchv/VikJijMLWZjR0hT5qitftNiiBhYcAlMagubHhrHdrIftO2DoXmeDxCib3C6NFlTxTso4DX3hcfHYPTRkxkY23H19jGCEirNcZqVp10IrmmKfN6lHFIInskRYNZpqcWECs7uWkachbG/X6/L3PBTve0lPepeWv9+TAMVLmBzWbHlE+VQs9msxFsxXsOxyMpZZrGiT9PSoyjF437DMPgiWmQ/CxBUqUoVHSTtS5aqoVhKt4ds562aLHbGew0ho3albg+lX2kxIspEYZxYgmH0ZO0nNl+GBh7keirrO2sl51hujCUrXRVGiPkO6U5XZ9yen5GGEd5Zkb2r9hH/DgWqbBUijiRZt0WGYnI6AXYtcZM3e3VwKyxosGs6hywdsJB9HpDmORUZI6HInF1OO5lDVtDbOLUcNz3PT6I/Oiq66b1M4H4OQtOpzVdkXORuSPXvsRNgo+EMDL0o+A2WfIGpcWM1RqHdaI9vuq6KR/7516/0iCt1hrdGJS1kBN+8MIkKQI5WlUNqYz3A/t+j3MN2mj2hwPdZkW3XXH76o4UgqDp3QoKIzIMAwdtaLqOjMatNrRrEWYO3uNzxq068tBLgpQURjes2hatLG3bkTW8ev2Sox84PTvlZL1FG2HHHq+vGV+9It/ckEKZbI0jadFLwthSabHU9hplhL4uKVtE6cT733iP3/r4m0QjLo4GMcZShRlojbRd5pSLFISZ2ElOOS62lsePH/Lp8yP9GEFHrGsweoPRDcZZab/wAYpGU/IeZ7U4spekyxyPcqggAG5WVXPEkWzL0KzIKpC8IseBnCLRR2JI2M2WxxdP+Oz1K1LZ8GNOGKfRJov7aM6oFGmMsJO2VrNWCrM/0IvwEyvraK2CHFhZTWMSJg2k0bB1K062W/p+IEXPxfkpfhx5+fmnfPjRBzx89oRfvHlBYzTKaYYUsRqUT8RhwGRYW4OPoM2K5C1jyrzoewar2KiMzZk0ijj0GBM6lQ0mG0adIXpUFMdU3ZyAUTTNBh0avrU94x/9HSOAjyQDLuZiHlEDVmn/S8UcI4VYNIt1OSQr4EA5/KIEYVqSej0FKTNDZgENkBfVVGAymlGLgxVmUGxmk32VJTgHJ/XzJ8iBGeit4NVsrFDfW0EwU99f8uqqdyWBVJp+v7Zw1UAh56qPeB9UogIV1MNRdIuyUsKcTJCNxXUdJmcO13ecdVt8tHz62Wf84Ad/x5s3l3zve3/Nqun40Q+/z2a74fX1a37+859zujth9eic7//gH/md3/l9Tk5P+PLL51y9ueT87Izdesvd7S1XV5fknHj48CFv3rxht3vNH/zhv+Afvv8fefXmNU3T8f7779EYx91xz9nFBTnccXK64fbumrv9EXLi9uqam+tbNu2KXbcubTCZ4+Eo0iBak5QkxfEw4rwEybE4W2ilika2nPYyZjWKmsELSWCstAfGsYBAM9MamPS+VBlnkSYxDCmSxsDDh1v+4De+w88/+bmwObQUhnROBZwsYKsqoI6S1v6khJmikpK5qzQpe1KM6NIiUhP2+68y3wTdKnOnFjckqE9AZUhV9u8EPKkFuFjmi4B58zfUZK8G0RUQlJ/Fe78/r4cZzJzXzQJgrEChYnJ4HYsUgXONdBMLCQ2MBbciONnXjdYTy6wGGcbZkkxS2vGmb5iuJ01rcx4zVXcIXcF8We8zMFq+RU23RGXpy1jNyU5lzUxSRAtwsoLTS1B7NpJSk8zPWxtKGbcFcFs/N2dyOYOUNlM3xvT7qs6OPCUL6h7oXq5RSUAv2GG5LiNMUHGELoUDBNzNleHQx/zNAAAgAElEQVRcxuptjeac5QxWdd9dAIVvg/mqJEbT2kLYfNKW1Ymzci7mHBV0rM+syidQgOO6tyom4DMt5t+9P3V+lvdqU4xTKQm6mqUTlFKLDo4FY6iwDVXdSxbzbN7jyxyakN/FOYeerl72KPmr6MdmOmN4+uQxT8/PefbgAdvdllW3olEOoxRNa0RvE4fovSoIWrqF6kQtjERd57pZ6OcmMZkybWnNBVitOD054anW5Bi4ubnk8uqKu+ORq8trznYrnj15zGa7Zb09Y7Pacbx5xd2P/56HpxdcXr3Bh9eEMGJIGNsRs2W7ucDrlve++R3Ozt7DuiusNRwON8Sxl7Z8I8naerXm9vZaWgJRwvDIimHsCWNlXGjEG0YRUyZicNtz3v34O8TPf0Ls99w9H7kaAtv3v0N/uOPi7BHJH1FkVm3LVieuxiN9MtA0KMSvwYfMsd+zLyZpUBMxYVillFGmoW2FtVyNKWtiG2NGRE4TKkeG6OXsNg7XtHgviaCwStMcvwDVhI+shCmn6tOrRmAOkOQ0RWGmofQk9aONLhrdst8fDkd2u3OZH1oRkYTu8ZMnkClGaKLnLLG0sItygqQV1oi5lhg1JlTOnJ6ecdI9YXh9RGMZ+gOPH10QUuRwvOXByQUGSww35GDw3UNQa6oLilYyb0MKwt4tRQspJomMgbF151Zo4zBu7rpTppqRgDIKawqLUolpMYCxms3KsN3Izawag9UNNgY6CyursNksQOgFmPXW6+3z9p/rDnj79XZBarn/ye9SQH5orQAvOopRckgC0I0h44dE9JnDGPFBiAvKSAyndeL0NDMMsN8r6AynqmO9VfRHMfsNSdZIKmM9jEFMgJXDGGkbTiHirGWsQFWZ8/WZpRgnOQRyJsVcAA4kHzOGvu9JSfRp/eAJcWQ0mpRXWBOl5bucDcDs8h6StIEXy7qqFY/SYqITZc2lUJzkY+Dm5hqtE5uuJaVQTLI9GnEj9/6ISiOds1BBYiCnCIX0VMLgiX06eUJojUpJAE+jC4BW9Ttlfm3WG5pW3N9dYR/KuhVmnLWW4D3Be1JIYgyWRF4kpiDrXYFCF7OiiA8S63WmlZ+VPKdqtFrnhJG6ONMSoJEu11pqyPX8oxhdlpihFlmhxh25GFLJmd60Ild49uAxDy4eEn3k1csvRV+yP+D9SM4SU1WZiVwO+CXBRQgBJbcqjNOQy3sL6xmjUEZLwY0ZJPQLIDqX2ERrTeMs1hWT9OJDMhU4s3SGeD+U+MbQNEx6qcvrqsVlCmCuKP4kWXJOa4yAbEVqgAwxBA79fgLjlnlb27YTGD+OhbAUw8RO1lpk5hKJrAQQy6XgARnbOFpyYZALQS3EULwTFMlLe/iqbYVBWzsLkkhcxhjw44gNDmv8VGyPJWc+OT0T8LBbMRk2ZsEsas5Txygu4s9cQOpYgL5QNIbr9lXShgKOZvp+f49BWiA5UApjLW3bFPMp8eWwRV94s9tOeVglS6w2YuZeryunJCSYlKX4EyL7/R6lhHk6daKVPWgY/fRcrd3LPATBe5wYmqEUbdNgdZH+IZGtxmSHRdGuV9OYVNPkYRin5xuL/4fM1VBknAZS6jGFEWudKca6++m9XdvhjIMUMY10OFRjtZrnt4UVrpSii4HD/iA+BIXYM/qeEANX3hdgXNjEq67DOmHG2sKazmSUtqLBWwD61WYr41tjj8Iel1xwLjxMxYoouF0GnDHEkt/YwjK3xlJlVwRXmYtdxyK1WnGIYfTE41EIGDkXXGeWW/nnXr/SIG0Gmq4lZjDaYa0T2rECZSxN24huVtG2GYdeGElGkoe7/ZEhRmIEvZfWgyH2ZJUxtiGFyHDoyTnRdB1d25FiJg4DMQRW6y26ccQw4kNEKyuVANvS7c7IzvHLNy8Zh5FH52c8Oj+BnHh1c8vQj4TLK+L+QD4OBayQdr4ClaGtm8ClVBMJBTkLSPvgwRkffPQB33jnCU2O7I8DeRzQxtE1K7QzAm4aRfJhaltQ2mDtCqM1J07zmx894/GjC+4uf8KLPjBmI9IFKpPwUsGfwzWcsVJpComoM9iEsYGcDoy9oWk6wJG1EpMG02KVY+U2mBwYxoHD8Q4fejmYjEKPPRe7FV3bcoiQYqbbbrBtA1FBlrHZmRUfdie8061YEbA3t/RhZLdacXG2Y9u25KFHR43K0rIZY0KZSGcSH737DI+0HjVW8fDRQ15dXXL16jVPnj1lf3fN/vKKNHoYPdnPDqs6SUuGMY7RaGLbEQbPm/2eYwo8aB1rCjOhBDJjjJBFF1RpTfaBPBxoYmSzbonaoM0BrQ0PNyf85viIv719zUGDLtokWUtlR8wvJGOoGp21QlqB1RgLQ2CRcGpty6G4bEutrMUCwNTKXwHzFfUQjtOhM7cwzcy8GXRlOkyWrU4TAybXJHwGgmYAta7mOWBf6ocuMwRF/awajOn5d0uMEeN9jaAaKNR/EyAiF00tqbhTgOvKlrRty3p3DqPITjiT8MMNN5cv+Xf/9t/y6J13+a3vfhejDO16zc/+6Z94/uolShm2mw23+yO/+d3fJSbF1fUNjx8/5nR3UgJ6j3GW8wcXUuFLmfV2y++89x7H/oj3gSePn3J9e4NrW7YnJ1x/dkfTGpquYdNpDoc7VEz4vufF81f4IbLZXHB6ckJTW6hUOThk0RNipO8H/BDoytilwmCigOSVhcMEwsl/a4uLUoqgo5gITMzTAuAvQaky8MNQGKBGY53l1fUlf/rn/57L22tAJDuMMQKOl+ckbrgzoF5itsK2SGQf0Up0CmNK2FyS2yyBVJUhqCyGlAtPqYLHZY+dLjSnyQSkBj5aLzQVF5p8WktbELm00mb5nsUqWADVlYXwdvJ6H2d8W4dU5rncdyiawlLxVlMrsNHimow24BzZObRdrLkKpqUiL1AAPWNKkSfNLsNzlUaMSVCU4GyhN6oWMiamFnHqOqwfU5meLBi8FcjTU0V/+VnzOs1lrI2cb3U+llE1BbBdJvNfx0Q1JfC/9yrP//7vzZq80xyZngPUTo9pzyxgYU1opEWxnNUlmaoqRBPLdzm0sAjmVQGM7q+xGdi/byy3lA7IZR0Mhbmgpjk6PysN0g45TbSyn08FunJfzHqsNVCsrMFpXucoLJ/C0FPaMBcQKrCryxqZ9fxkT7g/0ZfjP4P4hbGdEeC6xDdkgd9yAet0jKxdw/npKd989g7vPHrMs0eP6VwjYiwlkY9DL7qJCQEJbYs4cs+dOyEGSeCVmUAVmSZmuq+uW0mrcfaAyK8YY0ubXka7hs3Dxzw6vyCkzOF2T4yB3cmO7dkF50+e8dOf/YLP31xi12dc3hyx/RsaZ3FtQ9M4xn6gP3hCAmtaAWGUJCI5isbby6trTk83WNsIENQk2tWahDDXjDHS2pgsDk0/DgzRE/sjzlqE9K8I2bA+fyZ6ePsvSOPAsD+wOtzx+vNPefT0G5gUuXr5ArvqOO86DquRu5sjPjqCFranJtEPR/wwggJbYlSRKRaWo7GGlLy0GCPxZhrLfpIzRIk/cgG6tFJoG/BBHJ0h03bdtGfVVVSPAq0zSovMQHUkT0mMomIUkIdcGGcZQllXzjmcsQQfOD09YbPdYE0zFQ/q/l1jj0k/EjHiynVf02ZigylV2MMqcLZSnLiB/ZcvePX5Jzy+OGez3rDebLi5vePqzRuMaTh9AGfOwZg4enDNY7y2xNI1YbPoXCZTMoGybkIQHUdr7aSLV/eMpQeHNgbjLM7o4qEgRaVuBetOM46Zccxs1pnTlWWlgKxYNa0UDwrQPfcT/Kd7Lbsg/jlQV5NxAErTWOhDmvZfYzLrjcVGzf6QGXwUhmXZW7xPKGUIITEE0ZtOY6Y1meQT3sMQJR/wFTiMBXBSkHOiH/pi6GeZ6nglVokhSjtzMbuS+KEYBpmZRVkBNlRhIybRcR/HkWwKQ1VV+Y8M1qKUZciJnAwpyz4RfRANU8TVPAYtwIuWYpkw7xpS9Iz9kZwDJGHRGg1ZZVZOugm0KgAMxTS1dtaQi2F0Pesi2ljpJM0ZEihjpr4lrYQtvLIC8og5kEgBGKOLpi3TZw/HI8fjgWoAO/SHOcbKiZxFQzPkYt5XvmcZZ6U4sxWrTFQskm+1426SKlCqyKPkSYbr3rmz0O2Xz5v1r43VoOHpux/wzW/9Jtm13Fy+5PL1p1y9+oLhcIfSUqAUgoxaxAoyf+qESSmRcrxXuNWLWFFCvio1VEks8vdaAHOuLbr7JZvK0FpdjLQzIQmZKoSxdJjpAiqKLmfKkWNp1bdWTIadc2hjaGwrsWIWve5YtVb56h6TCwCllOLEndAPw6TDXGPDGsM559hsNvJZagYq5e+KmCPBC6N66EW7NqUkRabGoYxmGGQfEBBVWJHee4he5CpzIuaILnu1UllMxoCcIkc/TISgWkTxweOaFlVAPJHukY5lFJOfQ2WE12dW4+iU0iRpIHtYNcS8v7/d3d2VzxTiWd0zYkzoEER3l4wtuMrtuJ/ixJp7CahqIYMobmRa56aCSs3FVl1XtLUjMUorQNfKcx2957A/MgyDyDCiiqFYL7jZUYodwXvacq4bK7lYVkr2gHI91lps0wJSUOpW3RRLannI0zj1/VjWOzRNeSZBYrzoI8exx48jNzkLS93JM69xrTCP2yn/7Dphordtw2a9KWujSojI3BJ5hkjwAaM1Qy8dOXUfrs/TuZb1Ig6XfUPWvnMOCoNfa41MJ1XGVqQOKkN36HtiXctKHsoU6xfgtm3b8gxV6TQoGrtKxtCHMBFpvA9TYWDJzP661680SCubnrBFjTHY0lJV235iOTiVQsT1tUZnaQnNRirf/dhLFa/vyaoFBLQx2pTKjGK4O9CYhsY4jDUcQsRqQ9s0wojUlnbdobMBa1hvT2m7HTd3e1a24+HZQ043a25v77g5HtmdnPFwteP2+oZcRYazbMgGaSlLU2ttOYhyJme5H2MN7733Lh9+4z1Ozk4Zg4DGzlh2mzWNaXGNoz8eGClaPmWRicC4tAZlNI8enHB+soY48OG75zx85vjxL98wjEG0dowhklAp4azCGs12veHi4iHohl/84ktSlETR64FwlIRaO00MYLUlGRGbJ0VicThWWdxLnTWQAowDT8/OOF9v6a9upeJY2nhjEhbtw27LH3z0azwNitXVFTp59llNoJJRCa1GUh4p9YuSOCtSGCAn2pUswFdXb9AaHj1+ysOLC4Ifef7lc9AGZcQFUPSvDMoVYCIGCR6SuAZHpQl4fI4ilRH8dEi7mDEJjrFuIFL5C9FjXUO6ucWmhDnZMsZE2u1YdSve73b84PIVNzZjCwaj0cWlWjauegga81X91QnEeCvJv8/ky/dMh4Dicp5LIDQDGLUKvvz8e6wwYOLYVTmCClJMSbkEEzPrVbEMzGcgd3F9qrZD3z/Qp+/Ny3v6Glaenk3OarohOEWpdhMEjFi0FkkYoLCuZbs7p+22DH6PSpnt2tD3VwzDga674Ld/+3d59uxdxmGQhCpnfv3Xfw1rLbfXl/S9CJaP44G7u1uurq7ompY3r15xuNtzOBy4vb2dqoRnZ2f84b/6V3gfGIeRGCJXby75cv0lr9+84cvnX0DIvPtIxNLDMOB0JseRV69eoZTi/OKcdtVxOOw5eC+HYtswel8YI4nDcS9siNomqrUAIoKSLJ7XHGRlJKixtkMpxegDtgA+S0Bs+Tzra9KmBZKC6/7AzeGOpCrToRQGcl6AVgJwyXyJVD0nsrAjFZCjtIYp9GQqWN1+lTFFj7Bog8aI1YUrkZMkI8VZs0xuAWsWc5wyR0VyY76/WuCobfATuKpmFufEhl2AX8u1U0Gq5Zz+ujUx/468t+7fokejMK7BtC25aYu52hwg1nWccwajCpNU8/jhw/+buTf5tSy70vt+uznNbV4b8aLJzMhMZiaLVTRsWCqhBHjkqT3RzGONNDbggfUneKqRgZpZsA14YA88NQx4JnugEkQUyapikSySmZHRvRevu/d0u/FgrX3OfZFkFVGSYF8i+SJe3ObcfXaz1re+9X2M48jl5dV8f2Bp9ZoTFEHZKf+fDxKLGayd29rFxDCxAL/l5wy2HoCrHHzXh+MCBZwvTPnDsZlX+wdj9GGCVV5TmOGlBXgOemJ8sD+W+5UPDOiyEQDpcC8r7AF5Xn5wHfP1KEji1QG5mBrIXJK5XNVLZ0sBdcu1l+9a9CmLzEV5PJBemJ9vKSzlw/uTc8YqULXoD1thgVvwysxCW2QLUDAnj2UsZ03yco8WQKUU38o4lefM4zHPFTd/h5wLc0i/u8Y4uRQHsjKbMlTAuql5dnbOi6dPefHsGRen5zjjyFmMpZzzeA+VD3QK1BkJNximPVHNeqY4akAv+nbFTKpywrQurBBvHcPREau2ZQo9BktdtbRHx9RVTd+PEvx7h7U1JgVWq620BE6Jm+s7QrZ88+3XvLt+z/rojDCJk3RTO3xdMU0TwxS4u7un7weOz58xjT3DcM/NzZW0zDUtVbMi4aibitvbHa4KHJ8c4VxFSreiDaj6b8Yn6tWKOA50iOu9956mbcB6+l3CXXzO4Bx3ly/ZjT1tyLTGcHPznpPTM4ZpoK4c67bm4njD1a7nchjIVS3axTlLO+3BfCzGnlk7CnIKhASJqEwsuRmZD/Yn3X5jhjxO875hjIEhz/pvZV4fxhQ5i27woMkYSIHV5CU+8r6ieAqklOg7mXfOWupagCWDnN227P8K2EpLpi3lBln7SQA/p1qFGIgp4EJgVRvOVomV6enNpOf3FUdZuqWOthtef/2K19+85PMvv+DiyROO6zOm+1vcesSuP6W3FRnRBc9TWVdlXxPvCe+klTwYJIFU9qRR1o1BuqUswlqeojD+nc0cbQ3eRYaQiM6x6yaOV07A9ZSpte3C6GIshma/Czw93L+X+/r7gboPz8LvviYraFVMkxyyDyXAOEsfRZ6qbRzZGcyUGYZESFrsyRPWeqYpI1iUdExVlWiorlthft70gZiWIqT3Vli4GJIpCbcWulTWK85njBoXOpkltavnfX4YBjDLeWQ1/rDe4ytPjKMY5lknjNAcCTGSKmHyhRjnzqIyl43GOzGIGdR6tcb7et6/h37AWcNqtWZ3f03OAY3mdQ2Kxiy2yNgIqJFiUNmENIOLztm5wOi0C28GfkqhNUXxemmbWa9TPASW3DVL6UGNmSb2d3d03R5UViEr867Ed/J5himKwVkxR3bW4tzDOA2YiSvGFPPBJT4osUwBi+QbFuaaDK3o1x6cl1YIMEWywNgM3nJ7d89Pf/IX3Hc7bq/fYFKPCQFiUhJAEh+RLHZuRkHpEv+Ws7/k83Pe8eGaSMv5nVJSYoV06orZZdIOYUtWqZkYBPiMKRNympmn3lotyluaRl6jZGcKycY5h/WyB4YkMkLZgNE81hkB/ovZUwZMCAcAroSjIQTGMczzIAQxwbPWzjqvOcvcLmBbzlnMyF1F5RsFfWGaBkaVgrBWxqJpm3mvKC331iTq2pKi6HXXSEdBsiLlWFVeJL5CJCVpOENf7xST2O3uZJxXaxplW8rUkE6aEAK73e7BPCpjeujd0baiEz2bbCur11rLZrtVcgIM44gxhiOOEMUmNSuX7V7iRu/nAmGZB+W/Em+VVnirnRNOz8oYorb5m7ngU677aHvEdnMkGqrTJPMKaNfr+XwdxhGSFJikg1vn1TSR0jgzc8s9LPe1zF+vzGDv7Hxtvq5Y241IhhqttCJEshgSvusYx+ogr3DCmFY5ga7rCCGI9AWolm6gaRpCCFS1yI/UdU3rvTBrQ9T8e1QjOLn3MUXNu3V8M+yz6D9HlbGDzHqzkT07M+dFOUuHWGHJlu/fNA1hvYYs41TWuxBsRF8758wwDrofCJhfVfV8NpQcpOg8r1erAzPzwxLydx//vwZpc86MIejmI252MQVJZq0VZz/yTL+fhpEwRVabLb6upU2WDJWHozVjCqQxzO0OVV0xdANxiozDyNCNVHVNVTXkFLl+f0m334MXevp2c8TZyTkhI4F3veJ7Lz4FLF+//Jpd35PCRHjzmjc//RHh6gqjJiBGF/gDxNwY8FYNQhJxDNRtzcXFI774/uc0q4oxDNgU8JXjdHPK8Woliz9GPUvF7EvcOUVEOydlNBA5PT/mmzdvubm95od/9ENeHJ/QtCt+/NO/YQxgc0XjYLtpeP7xY168eM7p6QlnZ+dk1/I//4//O+MgIuZkKwGfk6RxHEe2zYq6rUg3iZQD/f6Ocbgnp6Dt0xUxJGyCta15vDnm8vIOU0kC6YzIHXxyfMIfnX3Cp+sz8u0Vw3iDz5l142b6uMlohQhhJHirJiCiO4OZiMNIdC3HjWU/jgz9jsY3TPsdXben33fE0rokGRtEmWsxZ9q2ISQIuz3kwDR2RJvosmi32VzRZiNBfwyMITHlTMyiqxRDoiKRbMDc3rGKgX1/i01PqP1zVpVn1bR4H2EYBUg0iZCzBliSVB8Ck/PhqUBGYb4dAkBLkrM8ryTJJVDJFKCuwK7LNCzJUzko5JBfmL1LQp4fzOEFNCguxQvDrripLsDMQfBly+sX0LC8z8LgYq6gHUorHAIrBQQomFO2Mg5Rwb+cmA0XrLHEKePqlqPtY9p2w7jbk9LE2fGa2/trduPEiy9e8PTpM2GsBtHRyinx7vI1zlp+86u/IUwd26MjnBMX0aZpmMaJq6srrt5dcnx8zPHxMV23p65rLi4uqJuGy/dXbNcbMplh6Nnv7uk6aVW6u9/RfPoMbM3d3R2WwN39Nb95+VI0uzJkY7V9LBCjVLHDFDGaQAxTLy2RmiFb78iT6nmzOFQKqCIAkLVZheZXeh97bWlRrR897JxZ5k25zwXIU6VuYW0XgEwPplnrjFJUyFrUkcKUs4YpBBnrFLFZPycXmQoFoqy0ihZH1CLv4qtq1ljLIUrSYi3GCrg6t27lNAdTRoMTYawX5l+a5+bCtnhYuJh1uzTYXtbUQ4YGf8uh++A9ja6QrC3y1ghTyFVYX5GMn9vx7byuD1p0tD0ypYR3jvu7W3KSefEAzDv4Lg9/CrurBJwfVnQPE2xJ5tDPLmzc74LOlO9z8PvDtQsPP+O3PQ4TsO+M2cGfzcHYFxavfILsJYVRbJRZCoWdL9vsYaBc3rsEqss+dHD/tQjUNC0A+9DN11MC2xnYn8dc5kRhE5Ugr4zlYTGgmI6UZCEWMxcO9+nlusu5kBVIL9NOAOIorChrJbDNUvxCf5YzwXnROZO2b3eI31MKZvq3+e9Zk9ECcB2ul/JcA6qdywx42Qw2iWzQ0WrNZ88+4dOPP+b548ccr1ZSrDTVQQurxBU5RsZp5L7ruLu7IQXRsB3CqC14QcbXGEy5XKuGe2raVLTFck5M4wnnZ+cM/SDuvRHeVjXr9QZjG6q6ZVVtydmQojAeja/wORHCxJuXv6EicnH2iP7+niF0ome2WrPr9kwhUjcrtlhCuMI7S+UsUxh4//4dFxdP2Gw2uI8/gRxp6oq22ZBSxlei5do0K3KUQP7q/RXeelarDVNVwdjx9vIdTV1R+RNWmzV3U6au12w/+SOiP2Z9fE86ekyo1+zHiSfrDduU8JWnuvcQBtYE9tkSEQZIDJGUu4M5XJGTMFZCDLgYNM70YLSN1VaM04ixItHgCivXGIqEwdwCPO/fy75yuE/FlGbCgpbA1DRMAV01YSkIsLVmBmgE1MxiAhXFlKZtnOpcaiHGMGtfC/ivAHEpXGdhWMUo5603kTzu8RbqmPC+5+z8jNZ9xctf/YJ3b9+yWq8I/YQzhm+//kbW0jTgmvf84jcvefb5f8Tqk4pQPyPYNZFERJhGhWBo9Kx1ymT3zpNNMbtc9qSs51nKiRQM9ynhbGK78ez7jNMQsq4kZu9GAXBXSOt/kVeprPlbt+G/jdnz+z5+H0D34HQgk4kZQkaKTN4xjdI9Zo1hvbJUNUxqtNuNkfWmImeD9wkfDVVtqL3h9NRStZk+wn7MpBCoKss0GtpNS0pZzGjJKk8jFxO1U3MuiCVlb6KFJwXmqqpiCpF+GKW9X42RMHIvhQixMCgpEl3GgLPYymM0/ohaPLBOTB5DSths1JSYWUM0xkScghjLFc11I+faTFbKEZOisGjFRQ6Ic/xQpHvma4PFVDFEULNA7xxV21B7T+UdCdVo1vmYVOfWJjHQHPuRYegZh44wjWo2FkkpyE22dpZhSjFpB59RIDXKvuHEvOvwLClGmUn3haKBfThPjSnf3zApEA2CW1sr8g3GoKxIy+I1IKZXJhvev3tNTu9IU0dK05yfFLC6FCqxzB4Jh4WIudBUpFusFQBdc5o5L6LEGAKKeudo2kb2JVdiRwgpiht8TqRJXOZTTCTNscR8zszxZtGkP2QSF23caRJAdExpBrHFTE6LCHGJR2KJr+b4Lc3fKYQorePeE2NQdnN80FUZQmCaptl4ane7F3BMO+mKZq2v6nl9iTRD6XZDZT4S2QvLMVsjkiARkknEIOBcTpGqFrkj7yus7u1ZSSrWWajFw2POTyUppqkbKl8xjqOeFxJ3TdP0cP7pOAgYaMVLBGT96jyMKSkAJyzSEovWVUtd1Xg9v0pBPjeN4FNKsJLCctIiSSCGiWkc2e/3D9ia5XyqvJe8jjIPZQYY4x6wcr33DNO4XF9VcXpyQoqJYRoVQwCRERTplRTTLPFwSCBIKdH3vejcOgcmqbyAkAMLeG+NpWkbuV4EwN1WHgxk7aqRTsU8z51JxcH7vp/HotwLMUFz3Hcd0yRs8aau8UawnxInewWMV+sVq9VK2MTjSFs3s5RazhIb9MNA10m8xtwtCqP6qlSV3McSp8QYhY0ObLdbjBFJCrnuglOk2UAuJelO6/sO8lIQDopl1lUlxXdlHZeund/1+HuDtMaYF8C/BJ4i2/Cf5pz/hTHmHPhfgM+BvwH+q5zzeyN3+3zK6HMAACAASURBVF8A/yWwB/5pzvnP/o7PKH8Q0MA56qYha8USa2bKt/eeaQpzZdjWlQTXU2CaegFau4BBWwdyYpzEXS+nxBRGhrEDC87KwTGMgwhBG8OqadkcnxBC5rbfkcg8enTG3dDx+s07hrGjttD2I3e//CnD61/iSYw5U6jR0gohpgQKH5NTVG018E3F6dkxX371Jet1C1mqlMYa1s2Ko3aDtRVBk1EoraMV3lWaGEeykwN3WznauuKXL+95+/YazM/ZrCouzi/46NGKn397xao2fO+jp3z1/S84Olnz9vItP/o3v+T84jH/6R//8ax7Y/UwdaYmhiCB5jQwkGiqGte02GnHarXBmsA47KRaibQneFvhsuN8e0JrXmF8RbCOHCNP2y3/2ac/4KnbwAhV23JJYtXWmJTZ7YVOf79vscYy9B1hGjjerlm1DftxImbwXlp3TO5pmhVVvcJ5iGPH/fsrdl2nVXRhVhiDmAlZiynVLeMYwijs1xgBFS83niEGbqIEOSFNJAf9mNmHiSiKUCKyPk0MlWUEYhcZh4A1mWmAdHTMuqqJ3e0MBpVE1yjgZWxpqzgIYQ+q+7IBLonN4XqRxEoORDPfu5kLi02yKVS20oP5oDX8g4fEFyXrLz9+G4hTZBbkM8rGlXOZ5YUNFh+AKlCCm7gAw/P7SWAlIu/Lv896docA0Pw6lopwEkkRYTIUoERI3bZqWTenrNcbbi5fYkyibRt+8/KKXYDt+WOsNbz85mu+/eYbVquW7fER7WrN/b6nu9/jHfS7ge1Ry/nZKbe3t3z77bcYY/jhD3+oQfzEu7dv+eyzz+i6jt1eWkK++uorXr18ybOnT/jse9/jF7/6Nc4a9nf3XJwf49LE+8sb7q7vGMfI2/c77nYTm12vbpaAynL0Q880jawbcSGNKYN1VKoZNo0Dziz37eG4C7AjLWQO7+SA23e3ujcpcDUH9zInZiZezlrFFnYPWRywC5hbKtpZWZwY8/D+5BK0R8Io5hI2F5H3qAd7whgpGKDAcnZatHDablVLi9jQD6pJJmwlm4XhkQvwZaww8FJhb2dKAaEwZ3VWU5xfDwOVksiJNmlZDwX4ewjmfXeNLAGfmdfLol2VUNZr0b51luwc1qnm5gcgawHQY4qLhlUSnWIyqs35kL1ZruHwWg4ZrYdrcHkeD14vRTcJpEwqr3v4Hh9+X/mpa/bB3vC7Hx8mYoeV7YfJ/wefaxamdtm/5s8zD1+b4sMOhMPvecjqOLgQimnXOLsE//ZxXd6zJJX5wfvNrFQWmYSyvx3ei5QlOZLzIB0AtLqeZ/AgFwlFZakaLeokcprm55fvYdQ4wmrynI3w3pO2kpdiGZj5/QtIG0JcDOfm8UlqYqGtYzN7QJDlrAl9Yxyn6xVfffwJX3z6Oc+efiLmJ5Ktk1OmbjYYkxm6O/Z3t/T7O/ZDRx8Cd/uOYeyJ0yjgZtOIY7Jek6s8XouKMQfq2rOqayot4mhOQgwDu7sbxjHMyZHpDd3uGms8dbthvz+m8hWVc6y2UlhLQYrU61UrbXkxsneWm9oxpUQ/RMIYiFkKKNZKC2PtK8iWo/UpTx4HMdqxlrPzR/TdThyYcdzcXKtUk1eQ2gjaoKzsaRiwZKZh5N23LzFp4vM//CGTa0hTT8iJl2/fc399x8cff0q9OeLu9p7TMXJ9fUtIkdVqxbpuqazhxdPHmPc73vUDIddkK+2QZd2W/doiyUWIEzijnRYyV7L6Iwiw5sVlOyl0oOCRpTCVRCMuZ2Zmrug9FrSyQLOG0ubsXUWap6WsGZtFnKEwdyxIK3BQbUFTCh7Me0FSDXtp8U6quadxW1RNdCtnlEXbaY0YeT7dJo78SBp3hDBicqRuar7+5tecbLbEmLm4eMrjx4/5m7/5FaujDa6asKHnyNxh93/FFIHVJ0SkMJgVhrZGWcLW61kb55imFFVLsmgKY9NkjMnU3tO0sF6DTYmcHcYnVrVo1W4rQ2MMlUxHbawq55n5u2qJ/8Ee5WPLrhRyIgITltuuB2eJ2TIFQ9+rKdrKM6bINAbpVouBOCUyXr63AZJIINzcJ1brinXtsWSOti3vryKvXt/RmVFcxVOm7/eYjBi5WEvMavCU1RHcWhlXzUEldlHH+oy2NUcFmoC5wOuYC1V6BlVVLV2IGFzdkGMiGIOPjjEmYtJ5nxPdMGiLtBIydK5PKYGVvT7ErLrbAtBktFCZRENasCEr3X9ZchkM8xkmsYjG59ZSNyumaaByTtzrVy3OqJyBqkNZMqhnSowDXd+T48Q0DJAElJWuVjljrLZSz5JjLIXJWZrQLl1NVvObpWuE+dy2v6uwYFgYqnnpFCrM1KIDDKXQKYW6RMIbpwzkADYSXSJkBb0s5CSaqvIxcv5bq9rFeYkVCjjqsuSgzoqJa87StVvOde88vjIz0BtzYtJYN8SkUmAKaDnR2JR9STWMs4CC1miBJ5diedJYb9FW7bUrKCJGcYv2JoRJ9nVTydwqwF5h7FsFkEMMhChSfiku8Y33do7JigboIWjdtu0M6PX9INiMgZTk862p5pjMe8hZpBqMVda0Mg6naZSznswUI8SMdbXswWRCsBjnpLvJOmonEgFTCDgvxJWqrjg+PaVpWwHLUqJ2NU3Tsl6vhSU8TQ86zUp8FkI4kLFa2LUxCGnwMHYrfxbgd8D7PU3TkhBWvMx5LZJM02x4JfIhWji0ZiZBDMMg7PliKp8SOSamEBhjQMAMgzNOQVUZ5xIvF6mGbFCtf0OcAm3TiGmzFYMvkRAC6yuqVUVKia7rHsTAMUbW6zWTkuQO49BpGhlzT0qZynviNEEWqbpC3BJjsWrBKDQ/KWzatm1p23aOA8r4F8C7gLHTNLHb70V+JueZCFjYr10vuripmH55x6pt5zxovV4TUyJonBqnoBkcpJ1oyI7jON/Hcg11XUt3ghEyhlX5mdKpKEzfZmbSA+z3u1la0jpLj0h47KcJYzJ0IqUkviYPZTQOH/8uTNoA/Dc55z8zxhwB/9oY838A/xT4P3PO/50x5p8D/xz4b4H/Avi+/vePgf9ef/7uh1HmoJEKf8hGtVtV58pacvaSxJuir2G14h/BeYxx2FyT+h6MJvzOycR0UlWrDJCDgo6lRSVi6xY/TcretUwYUkhUdcv6aMVtd8+bV6/EHMtl1rbFdTdMV9/ip8CoOiUSeMrE9G1N1vYDQ5yrRzlOtOuGJ88uWB1tSBY8TvRzcRhbk6zDZivtTlZEvlWISDa3FMlZFmlbwfHWQe7ZD/esj7d463n17TvClHlyccHd7pY/+PJLzh8949dff8Obf/2Kvh9JGT56/hGXb95xv9th/RYAG8WBcbCdsmDB4HCV6Bftw0RQ8e8SbHvjZmMHTOLZ2RmNNYwGGlcTpxHfBLZNxTZZUhg5Oj3GP30K9zc4a+iD426cmC5vCdNIClHbfrZUATFgqzzBZNI0UZNJ00iwMs5xjIxDhyuAeJLWXW8ttpWNrO/2ZOfZjyPd0JOJYCLOGZwRR9whDexSlJaDEGh1/qB6SQHxLiFHupTYp8xumkRM/75nGt7w8u1b3rrE2Fqlvhu5DgVvisal925h/RUgIGXVKXrIYPNOxPMLKJoxWgnOB7qiaHuVMhZiWkDhA/CgbMzzQZWyrpuylRUw6iEIAwtQ8V0G3cMW3UNgQ0Cw5XWaUs3V7kW3Zbk2CZSTggtGq/zCdkjK4I4xzKxki6dKNW3VsD7bcHr8EefrDavKEqeOlBPNZs00RY63x7SbDcl7dsNIipmbm/f86te/mtsjXnz6KVVdcXN7y+3ulsvbK+5u72jV8fb91RUXjy9o65bNes2Pf/LnGONZH59RNxtWx+dUN3d8tFrz9MknZFNxefmGS/ctvkp0+z37/Z7tyTk3N++5v97jfIWppFDgogUrpiFDL/q3Vp08p3FgGPZ8/OwJVdvwy1/+Qg6zoqWkJjvzYZjzbCRkjFSxjSnt/qWlWV6HGkwIAKv3rtzHIsCeIeQCSEWSdUtGpgd7TkkNrxZmnzPCbBFdTIOxAkA6q8CRKRVlI8wXbXGXhrtENha/akjBkUIAq8yRIC0u3lUYKxVxPwOcCnrFRJik0OOMVRBLzB0LI1TOHAloJAhys7ZdaaM35jBQLethmesppRm8eggAZyovwFZCwOhsLNlbohdQ2liLNctaijFKYONbrq6uiCmSrQDRpfgnSae4eFt4sO4erNEC4uutLpXnhU0wC1csQWkBGQv5Iy9goRS2yrUWlvCyP8xgeF6YsOW5ZTysGoIW/UgZv4fSACXhyDqPZY9c3J7NQU43662pjnkBKFOa5rmVc8K7CmsluTvUxStsO6uM8VD6CvUzctLAMy9GY/La9GDPLEYJWZPWcu2H7ZHlXkyzZqfsf4sEzAGLR8fcYHSv1oJ2YVrp5xcc3RysxbJfythKe5bBCXOrXAcCNNtyj7VAPOuCF5uWHFUPTOQFsKKTZnLAjoG2rnh0dsqLp8/43sef8fTRM9brIxKVmqhabIqYFAihY7e75+b6kq67Z7+/ZQyBMSb2XY+xwowzOVE5SchjhhSzuJJbZQkZmbUW/TenQJU15BiVFSP3yDmZszFMhDSCiUxhJwmstRxPpzTrI2GLhoC1FdbVOC9GsifpjLdX11xd3YgGv/WMIVDXjqfPP8JXG3K2dMNI8pYhTozdnnEKbLdbYcSPEVs1jMOeYejwzjH0AxZxhc7JMAVxZK9WK56/+IzKZNp2w+5+x3rVMnR3eO84e/KY9ckx769u+MmPf0rdrDg5O+N4u6IyhqppadenrCvPbTdxuduTssc7A8bJfpJl/Tnn8LWnZGfiIi2xhcORYynSZLwRc1vva0yEMSeIAULRahSJMSdwj2pFi6ZiVVXapo0ApC4vhcICeInwsqwl1d62XhLvMUoXhfEK3lrHGAaMM4jpmMEax6E0RwFuZauWfTciUgKVixw1mU+OHU83DpMmxui53+8xYaJua84fPyYNgacXjzk5PePzbPjrn/2Syzfv+eKrrzjZrlnXDptvCN3XYGtYPWWKEps6nZPCvIxkBXBBwJ2SDKcscVgx3XRqGtZ6kQrIE2Qr8zwiAEzrrRZME8OUcN7hXImxyl79XZT23weL9rc9DuPDw78L1iVdepLULkXftpE9ddcNOGepa0M/WqYRvDfsOmF2B61jTCkTLeyvEs+9vP++T5jJEYMky4JIWLL6O+QUZc0aq8xNGMeRqioxkNFin8Qb5bwzRph7wn6WuZQmMcKzzmFz0nsm+77R3SjqcSpxugfjcHkCkxUcE3Auqia6taKZLfIgGZLIAyTVJGYOm7VYojF/MgmbBbAttCCJSwyBIk4i+aMAHhVVU+GyAV+RjZezUdeTt9J1laaeYbcjDPeiLzqNoOCs5BzCyC0FP6vx+iwhpbmFsVAY9wWUcVWRYiqFTdVDz8s8nYuxc6HTzIZrznlh24LGPV61byNTDNioZ5lBvpstO4sWLG2lY5SUmS/nn+LbuGy0EFmksvKyhArj05hZIkbmuUokUDogwfhFwz8lCDGI4bhhzgPna3Pa7YkjjuN8hscDWaakbMlCqpL4u7B8Rd7BVdrCbg3tSjscrBTgjJ7pYsqYtJujpjXN3JouRqryvjlZnBOCRwHIDqBw1TK3tO2KtpUOvcKUDCFgkC6Xw9b3aRyYokjJ5DjiKrm2YEWXeQxRpCrjRDJZtdEzOUYp2pk0m9sBhCjavH2/J6RI267xzjPlhPc13u2wRkwvrXNkisTgdwHoAt5KzCixg3F2NhMM04RznqqqWTUrmqpnHMUML6VEl/eq9y/7RLBuxoastTRVNXd4GKRYWDAu9Ax22uq/NqWwKGOZyUTvNQY2M6Bb/rPWSm44Tdzd3/Hu8pKqqeeWfGtV4iVnmrqW/EvJNWWLqLRgeXxyMu+ZWfOjnBLTFAiTzJ+6roUB66Ww2HV7drsO60TnOKY4YyZSMzSsVyvWq/UD/KEU+2Wvtayads7N+r5XKSSVvpoCMYvRV4mtfVXR7fd6Dw2+kk4ViWdqHZdKOtCAqm5nZrMxZpb6iwrKT+NIDIG+70Vqwsi+7r2Tbk4r3Tmy5iWGsV7zai9jvd/vRc3OyvgaaxmHYWYT/7bH3xukzTl/C3yrf74zxvwU+Bj4J8B/rk/7H4D/CwFp/wnwL7OczP+3MebUGPNc3+e3fwYZ29TCklAB36I/UdoFSsJrNLFJWRwuwzDiG2jqCm8a2aDbhmkyGK8tAVEqUNZasJn97g7nI0fHp/jGs8pWqzITwxAY7necnz7GObi5vqa7usakifWq5aRqONs07NIenyf2McwboNXqqVFtsaQBptMNPicxn2pWa05OtvjKCtiKgICq/y7VEV9puwvsuz02C3ARoqDz1mTayrJuas6Pt4R+xMTA559+wmdPL/j2uOLNm/d82nzGf/yD7+Od5y//8s9Zbzb8w3/wn7DfDfzqV7/m+19+wV/98tfs93vWRyvGsZdDPQack1YKE8Q1NVbiPphCacMuVHlLtpFxioxI6/Wmrjg9PeLr+1va3OCt4eb+ltthz4vTY4IK/D96/oLXP+8wTDhnCMPIbpjIMeCdZ3O0FfMJE5lNkZKw+LwTY6VpHNm9f4/3jZpB6IGZRTcEI5tqypCdZxwmggJ/OYO1nqoVx8M4jvRhYD8F7kPGhcB2SmySxcWkGlcQjcUkcQ3tU+DOGMZs6W46rqZb3sTA5bqh+vgRwpCxoo2Vk95XidqTbppFJgOzMPAOk+0Chj1k1B4GxPN6XVqQQbtPlJGVF1Obh+w3Mx/6meLuuQBF5XmHf3/IcvsuKHt4jcbM+PGDVS/P/fD5ZjkYUmkVlHVgLeIimyWZCRM421L7hirXbNZbPrp4zvOnT3j+9CPq6oij1QmVNXS7OyorLZrn52f8yT96zstf/4rj4zVd11OvWo6qlidPLnDGsO96Lh4/5vL6mpjh8aNHfPPNN1xfX/P86TO6bs/+/p6UHev1hreX17x685bPP/uK09MLbm7uaJotrlrhDWw2x6zvbggnJ6xXNY8fnTANe8Yx8uTxKWkaqa3HO1ht1tKarCzdSQM2Y8TMxWnl2TrL61evSFYOcmvE4dhqUUXup4xtYb+JqL4CSElA2FJ9XH5K9ZiUKUZMhb1QGHPGmNlgo9zOnDNRk1DnHCQB9xZNNiSx0QAWpzIoWSVRvFeXWJkYwsyQQMJ7YZmmLImLsZW+RoDJaCdM9lS+wnhLrhzWqFGQgmQ5JYzT9kMUXFa9c9yyFqS9bGm3W4DOh61v8s9LAnzIZi2/Xd4TsJaqbrDOEY0D5xV49wQDyWRsTqS0AMEpJfb7/bI+9H8Yqc7mlBjVzLDciHJPD7W2yveS0PC3JdH5wfecmdA563sfAJkUQHvZe6JS4DIHLaR5Kdp4K0lYcW4u771IDpT9Rg2dlgxrBna/UySyqjWp4y0urmlmkmRNy1AwEgVq5iLALAnw8H2tArlJmfliwncgp5CXpLHEt+aBSdfD95sLAB/ufrouFuB2mW8yXcxctCo6g/M+WxAnK4Mucy0toG1Zlvq0AozMRkLK2Dxk9FpbYGAzjx8IoGA0EcQuQHYyEo+4FKmt5fHJOX/0xR/w+Scf8+jsDGdrQjZEPLm0w5PZ7W/p7q7Z93vGcWTX7RiHTnRjtaBoXVaAWM7LYdjLeS2Rr7LEDN5WeA/eGpLq1NpWExAN8lPK6lCt45yUha1dT0YTvmEIpBSouk4K/OPIdntGuz4GV4H11HXLs4uWtqq5vb/hvpP2yGEcWLVbqnYtZrVIp9DY7TEYwlT0Ig3GV6xWGyAS+kTOlqbdEqaO/d0Nx0cnGO/ZD4HjkzO6+1tubq45WR8RhxuR32laVuZCWhDrhmfbx5xefCzab+PIOtTYtfxb1Qjb6fzkmJsx8no3yLh6IQOEEOdOiRDDHCMY3dOCAWxepJSytLOmVDMlkZ6JOdEYQ3R2LgaFJASJEsNLm/NSvCItRYsCqFqk2JZikWZxczfRogephlh6JmZEYiPGCWO9AL/ZagKle0vpLFEN3ZwTOcIYJ05rz0fbmkdtwMRJk/PI61ff0hKo1jVfffkVr1++wnpPzJknz57yx//oH7LvOm6uL3n69IJh6Ng2DWt3S5yuGP0JkRaTAyZJ655F9Aq983K2TxOmLmZWkt8YL4BgmAKV1bZW6UFnHEeOThyrNqsbdSIEIQ5YJwYyYBZdd36/x4f707+/R57/P2aIGCY9A9qmEQDeWELMmNaDdUxTMQi1xAzWeFI0xAQxGkKAsVdZvDGzaoUVud8HjXcloZ7lmIyl8hXTFHVfX/TFrXWEKT5g1c1dZDoklfes2hUAk69AO4BEnqCcF8t+GopOvn5v7yzOOAVnLCTxxCAL4zIqK1SMV5HCSE4z8FPOwbL/mihMRYtb4poMJlsFS6WiKuvHYmwiRjkIioSDtY7KSjwpZ7YSSZyltoaxv+f+5pJxf4tJgZwjKYw4OVD1my2F5JSFrXoIfIHMyeUMQ1uMpUBkZnKAzFeneYdVUNUpoJaU4FTY9IDoatsF6DVAbWqRP8uO1eZESV/SjaH1kFlCMSXEoLWg9aDAajkwBazHoKSwJZ4prfRFt/SQiXioS1muLaaoUjtZJXWSMEiVKJBynk2jiomuPA9ijjPgZ62lbVoFaZfPE13WTIhZ9xanYKTGfSUOOejqKXOr7yS/KAzhoLJvZi5yyZ6TVLKjSPCVhHOPFDAKy3GOf7OcuWOcpOuOjKkrfBbjNyLYAFjRjzcebJAcYBgHyKoxb5XkoNKLEpcUoh5ixAtM44g1Rlipw0jlKpIVU2KDaOseHR3reNl5n7Qq+1Qpg1IMoUpcK3quGGgawaUqBfuqqma1Ws1Gavf394zDwDhOYBbfgkL2iJq35BiZUmK33zGOA77y8zzOOUnXoLWkEGdgWbpWLEYxoByDALnuu5JC5T4XBnunbNRK750zia7bc9t3yjL1ui79HPM652ZJr7qu5+5I66VbKamMQVVVrPRzUkqs1iuVkShECzGC7fuRaRR5idsp0HX9gRSRW9jpCtjWVSV5qrOstmua9WrGPkIQjf5SsJjGSfVsK5FwSpFpHPX5st7X680sD1GM38h5XjvCmJW9Z5qkW8BaO2vJlp+x6ErnNO+XUApGFucNZgKD5O7S5WC1E9SwXZ8+wDo+fPx70aQ1xnwO/APg/wGeHgCvrxA5BBAA9zcHL/taf/cApDXG/DPgnwFQ12RkI3K4JXnJS1Wjrmu5AUOv1UZDDoExSuuFyY1qFaoUglZQixGM9xZfVwQTqaM4rBrv8OsVJhi6HFmtjxmioTo5pX16weWrr9nd3tIYR7V2NHXgee1Jec/1/TUmSotEUiHiwgQ2zuBZ9DOMibLYpZjK4yfnbI5WpDAqCVBaESrnaL2nAipnaVcN++4ekwOtN2zWNU27ktekiEvCXjBxIg6G1lZs25pf/s0vePzsjLFbUdtEP05c3e744vNP2Ww3fPziE/7tj/6cpjG0bc2vf/UtdS2ufimJrqU1mWkcqCuplMWY6PqJ1WqNPT4mDpF7Ju7u7uj7PUnHO+eM2zvaZs3x8TG22xGiGLT1OfCby0u+unhOs6nouo7joyeY06fsLr/meL3BG880Tox9pGkrzk62+NoxRQkKwjhRW4ezNc47pmGg74WpMo5ZguGEsoxkMY7DwNCN5CztH6RMjkGqYsbincM5Sz8M3Nzfi26mtewtmKqFNGFSpDYHAIf1jNlAMkzAtTF8S+RV19Ehmj82JVo0pImZMQgQ7b2fWY0S6+QH4KwAI07BVfn3hIJkcwJvZ0ZVaSs6BImMWdrmlqBCE/qDoOIhY03ZB4owHf7bYRArl7QAPYcAbfldeRTQR7/ib30OlGHI2t4n0ggyQmYGBolJ3GyxuGypfMvR9pSL06c82pzz8ZNnfPbpRzx+fMbx8SnX7zturncQI5dv3tJUNXFKNPWK2/uJt6/f8NmLFzjg0bMLLt+95vmjU15+8w2vXr3hfnePqxpOTo5o6ppVu+bq6ppvX76ichLofv3tO23vgNX6mI8//R4vPv2c/me/IMbM1dUljx6fc3N3zdff/Jrd7p7jzZqPn13QmE4cvlMijgPDfod3R5yeneKritJSXNrdY9CWMmsZx0nY52NPMnJ/ggb0JT2wB4FwqealnFjAWJHBmFu9Uz4wWZGilVVmZ9CDuPbSJhNUUL0c4PEAHDMKPAlzQuRTxFWsAElmrpxmI2BbYV74uhaGri1zRqqWQdtenPest1tyTOx392CU0Vhry5hxBDLZe030gKg6ukZc7VNeDnAp3CmgnWSNJZhdSVNYJDh+m5brUsQoScSBJAILAKhotTLkM3iLa8SR1npp1STL0wrL9MMCSQFey+eenZyybhp+9c3X0kLnbIEl5+cf7gcUsFrvxeH6La95yJQ4+PcHrYRaLOPBdvEAmJ6TlXL95fsdAvYcJg/lumWfkGuXe/Dh3rIUBvI89w4LRw81UwuorJpupgDqiwzFvIfp+8/GQ7m8Oh9UmczMCihtxIeFssN98cG1/pZH+TwpoCyJ/XzdB3+VyzbznwuAKo61bkZjhYEnYzzP1yxwdfnuUZOwhYmTPvjMZd5aPaOk9VMSJYzBkoWpaTLPH53z1YvP+fLFDzg/OleJIQvGzWB7nEbGsWO3u+Xu9ooUekIWMCxMIyFOWsRWg0Ei1mbNBzMhi6O7KYm0kVZ4ZzK1r4T5FRetUlNXqtcse07RoFsKAAdJ68F5OE6DFD2QdrcpdPjRUa2OyFZYZ95bnjy6oF21+Js7umniendPdg3YmhDBRcPR0SnXY8S1Fftux9XVFUfHJ6CglHcVfiUgqSUR9j3ryrBd17y7vianianf8+ab3/DkxQua7QmPm60YiVkvbeDZshvAkDg7f0Z/f8sUMv04sZpkfM9Oz3DWME4jj8fEfx/WIAAAIABJREFU3XQtxmyhTLD8IEkp976qKjDC4k5BCm7GeWpf0WCpc4YgEhKTMeBriJmURlzOeDLOZqJZ1q7E8YmCr8yscGVsO2+FBasrr7RaHu5jC0ArhQVh3eqaTsKkNvZwLyiFDXmNrlCSglhnK8vjNlKlgRRFp9IioPCQRo6bY9brNafnZ3R7kR3KKfL9H3zJvuuJMdCspKA6Dj3VqmGVrgnDayZ7RMqW7BpSrsg2zeycBSgs5p+SBwj5ykqOYiOjMZhocQ5SnIjRUbpkjBGnbTdLv2Q1pTzc/x789f+DR2KKiX6Stv8hiEzANAWMs0wxMYVMxjNMSKEXSz9M2KphGAWczXqmhpiYosFVjpATr97t2B5thPEWJAbyviJokT8j4FWKFlLCe4upamm7d4huMGh8ogQKoGi8lnuUUdBfDbgkdpIYyvDhXnrYMSJjYIyhqp2I8apuMGSc9Vq4MOqNEHWeCoswBrmf1njAq1lqXK5BgWKyMMiznl1SkJOj2yEAmLGWVdMwhWLEK+B/Nom2aYnTyO31Nfu7K4b793iTiFkMppyVmCkliHGR5hANSskzDApWU4w+hd1e15XElkblDrSAXArJhUmIKVqlwtItcljl/MvaMSLpkJ5RpXssW6pmxcmj5zx9/hld3/H21a/Iw07OQCV25SyMam+cGGeZMn5ajD7YDzPxQd6TUpxl2az6PHyYCz0oUrOs8br2AiQTyFkNcJFcO+TEOIn0YkxJgAKj3y3nGQAFKVzVVTXnfTlnMQdniX36rmPf97OBkTGFtSs5vleQWxiQ3TxvC3DlnH2wP5XvPYxjWSqy3+g1FCZqpV2GIG38EwGLZRhH6Q40QlozVue3xtnFbNh5T617mFUQ1YbApIaUvqoOCgtLwU/mT5LP0PFZbbegYHZh8eZcTHEd3jtCTCQMoeuEnGbMbBYrDE9wlcdEq+x/qH1NmAJd7kTH1Fds1mvOjk4AmFJkHHqVjlDtdZ1T1sg+1g09t7fX3O/uBe8YR+qqpvLS6j/0gxRVxmEe37mgeVAIOTRAO7yHdV1T1zXbdiWMZQTIzsBq1TKFiX3XSXE2Fya7kCL3+0XL1Ts/z6FDglf5WfIRY1ApDQG/505EDEdrQwiRcRxISfTofSV7XjE/K4z0cRhV51jYuAbJD6W4JGzgpGB30zS0rZhgO42BS8wQYhQfAu2erJxIbg5dxzhNTCGoNIObC1dOv1/5rmIix4N9PcRI3+2lG63E06q9LbFTIidZIylHqsqp3JLH9Huc/91Q7L8zSGuM2QL/K/Bf55xvPwBisjEHWdzv8cg5/ynwpwB2s8lxkEpI40XDRITz7XwQBN0coCQoSAuIBpChz6rDpKYEErWpk7ZoDjWrNc5Cv9vj6orkKoaECI9Xa+p6zfnpY9LxMe/evGZ6d0UzBdq64chGnlWJM+55/f6a4e6aEEZNegFF+Z1zRD2oDBmrlR7rLLap8E1Ns1opU8sK8IaT4Mx4ZebIAdp1e67fv+XzF+c8eXSMjSMxTPTDIGZCrsEi5gAxwnpdc7u/50d/+df8MH/BJ8+e4P1E2HdsNqf8xU9+zvZkzaNnT7nv93zxh1/y07/6C379m29YNUeS0KRExFG1FXUtQvm1l3aYMfZYl9msW+r2lNO25rqq+fpVzziOChhmCqPn/PSc5vI9UxTNDGMdv7i65Mu7G75/dMzY3XHb9zz94it+efMWYzObOhNNxrVH+Kbl+HjD0ekZ0RjGceL+5pax6zEmMuzkgIkh6IgpazoV7R4RgpdAJmOmQBpHnBGZgHYltPdhnHi/67jpO+7HAYyhNp7RGXK2WJOxyTBY1RBLUqF7D9z5zPU0ch0y70MSqQwJ2aiyJSjAarR91NhFj9LYA1AUTSxmfKAwnCTJzPoNH4AqMB8sh0DpEjwdsF8oONlDRqzm8JS245yX9VU+XzbvOAd1ubQzUdqTF9f0D8GJ5Wf58wct2PkAEJivJy0tRYVFoIL0Hk9jHI9PTnh+8TGff/4lHz37hCfHjznebqjbogsN3iSsSVxfX/Kzn/2MdbslpxrLmpvrV9xe3/GTH/+YqjL82Z/dMk0T/ypMjNOetmn59LPP+ZM/+cfc399xe/2OFx9/zKefvCBn2Gy2PH36lH0/0fUT0xh48/olIKLmMY28v3nHOPXUlazzH/zgD/nFz/+S2ogA+9XlHbtu5NnTNTe7PSEntsdrTk9PIGcmrRDKGENUZl9QJ1+Z38xaxDPYEKNoXtlljw4xUhkzA6lFr68wuUvAm2KcHV8lEC46rzL+RccwpSQtlnkBp8ohbvVeH86zOdnWeZtgkYDRiC8pAJTKZevBjxXWlTWGmOFut5frsZaMgFQ5ZzUJzMK2s9Ki5IzBOvlkU5yOjUJtZTw8olmdpb06KbPOIh9NTjwEsgpoa+b1u7S9L/+epCw9SxM470lGjCxt05K93KOYM9araUkxwWRJ4kEChyJ0X9775vqavhJtyexKC5WZA8JD4PIQLCz34PB3C/ulrF/z4P5BCYLmFSn7fEkED8Dd+bsfPFIs7DczA6RwGACV7/mwMDTvG2YBHWfw8QBc/bBQ9HA/tHrdBbwws4ZUYdvOCcwBWCvvwyw/YdTUCA7XHMwGZboe9AoejGsZy8PvdnifD9fP8rzMDAqX90fPg4MC2+G+K8WSMnZ6L4u0h643MWJ4CMb/tkcpXBhrCCRskv+cMayrmucnj/ijL77PD7//FXXdEGNDSIZaY5ycErfX7+m7Ts0Tb5kmMerMZDX4C5qEZwEmUlAdvqhGLpZxFBaqmKhI66n3lSRQBshRO5AMORpev35N7SwXF4+pfUWYjOrrLqzlpXhYdN0qGTOTuXr7Cgucnj+WPTKMmJxYnTTCDBPCNkebM1btKde7e3y1wvgNvmpoVmvW22MwME2RMAx0fYetPKvNEQbY9z11IyyPOoy8//aX/PxH/4pPPvmYqbbcXV9RecubX/yEy1//jC++/D7jELi6es/F+Sm3799z+fYVp4+esDk+5/r2jt1ux6PTE2kHD5JUN3VN027IOXK/33GyyTRXd4xZWkYzqL6rJHxeGSzzecISh2MNrTM8Ao6GjvbuPS45rK8Yjk65rlbcusguJ5GiyVD7FkxYjHZykk6kJHqLwrTT9u15DSXtiDro6EHjyrkAo8m2mpRkBGRZCkKZpqnFGVzXb9nXyWIAa4GLbc3jbcLGHSmrKR2WzfaIL7//A27efYN1ApCs1tKmGSZhXLerDevtlr7vcd4w3d7QdzuOqjVrc4lJexxn7MwpqXkEtlI9E/HJQFd3XYu5jsRYmTRJ0pwS5LGA4MLI9M7S7UX6oK4zdQW1iSLrVWshXVvCS3Hqd/Fp/64i0t/38V1WrrASjRX2e1WJeWEq4KYr0m4WX1uGIOzJJgqemSfZK2KCKYFxmRy02Ocs933i7JFje+S4ei+t1liLt14N8hDwpaqldX4uYMm8KACTsKemB4U3IQ4WAGORgAohMoWockMG4w7PL0POcS7IphhEFsGKKU1yCkZaR8zCqizznqwARhI2eLKO4AMmBimYzGdNwjhl2+Y4r1lyXpi9WrBzrsJWTgyPjN4LJ+skpAnnpWB/fXXL3fsr8rjDMmDzBCnNoJ5XMEjur4DES/uuxFNp1m8V2YeMaPTaSoroSburCrgDAuylJPIlwjpMGGtmKZaHRdeDorOCVaX4vt48YntyzunTj2k3Z5hqT3vznuSMmDQNg4DH2o5OzqKrjehSpKjnbbaYnEksRkSFyVeuO80Yw1Ls+53rIEsnG1E9H3ImZmEcLntXwntDiFKsiVmLr1bY94ckmXEcyPGhJFSMkZCYmbSF/bfvOy0uCOPSe09dLaBb0UqdWeQP8jkUwGqYO4rSUvCcwV/NBcv9KvfMGIO3XnVyM3SdFBaDngdGYqoYAtOUmKLE3gJ8epFkc9JhllRNbYwThFEBXJ2L3s/3xoCSsCImQ7sSA7SqqRnHSeQLrBYzjORFoiWsLHgdtzJeGTWK0u/ljCFVCWccQ9+z35kZfPXO09Q16+1mZgCnJB0rRaZLCnSGZnvEyWbDfr+n6zt29ztZZ3UtZ906EaZANFkJKhIjD4PIweSDgv4hQFvmRLmvRv/dey/MWWeprICSJ5VqwOespm9JOhp0r9NVPT9KAXcaR2KMjMMgHZ9ezthpGpECmZ+BfvT8cc6KXq9zShIwsxRc0PnQdR1N3ch3MkYA3G6cz3RnHa0CzDEKmdDo3D49PaXSTkznRMJj1a5UW9rquT1xdLwlqvGoeBTInO36binABDEQ85WfGe9Wr7dyDrtec9gxIAUGS84CfBsjuVJMgYRld98Bo/gTmP8Acgd64ysEoP2fcs7/m/76tVEZA2PMc+CN/v4b4MXByz/R3/1tn4Bxlrqqsd6p89yAVSryNJWbwozAUyYWYIJscqumlcpcLaLGMnHjnHz140S93uIbiDimBFMXcHiaesXR5oyjkwteXt+wv7yhyYGqDrjU0+xvuGhXpP1IuA64mDFOnG9R4MtkqbStjo6p1xVjRgLbVkDZTt0tbdMKzT87nLcqTG7JCPtrCIFVI9WYvttRVxcw9fz0pz8lBMhWKsONdzR1xXq1ZrNes1554tBRuYZ1veXs7IKYJ1Yby49/+nPeX97w+OIH3N1ds16vca7iR//23+BswCILz2ZJVk2WCljlDJUT6QE3BayDqtlggyVXhhwnrm9WvO1Vi6QSHeAx9mxWDSebFZf7nZi4kbns9vzl61d8dnbK5nhDjD2u2nDxyUfcv/yWla8wcaCpatpVK5IWU8RVK0iRvp+4u99jrSMZGMZIDgnjHFJQXQDaHLO0M5qMxUn7gPNiOuQkgOtDYBcio3HkaoVBQPaIwYSETYFkDZ0ThrO0SE8Ea9hnw8tp5GqK9BkCJUDRBDpnTMzkMUDVPKhQlqTBmHJQ56U8KZASC3rL0hozsyCTAlsKEh0E3EXfFTSAKK/XYkJ5LMCB6nFRgA0JHCT5X5goxYSggCNzQsRDoOCDveM7wMUhuJD1+pXrRZEzISdpdU8Gm8FbR1NtOF4f8/zRI148fcoffP4HPLt4TtO22kKfENEKS0gZlJl1eX3Fu6tLvv/pZ8SYefzsI37y198SYuDq+gprIqcnpzx/9oJqVfP59z7l8fk5z5895+mjR7z+9jd8/Zvf0I0Djx9fYKyjbdcC5q9arF+xatccHx/x7u0bXr95LfMkJT0QDHd3Hfv9PW/evOaLTx+RXc3lzcgYDH2seLuLJL+madesVy19gjhGbFTWoiZeXit4JblwRpygMUb1JBezH52NMxBVAKgi9F/mUWlf8Vaq12lGTmW+5Ji0K2wB44sxycKY5AGjMac8V7sBAY0VYNFJoACsmYHTw/Yt6/zMDskZmkaqmiFHQkqz7MEhM25hJcneYCovAa62V2YLeKtBXNJiQzX/Pal0S+URUXyk2JTCIbCzgOGSEC0BkxiNmWUNF5AMhAHtRdcbJ9dnvWhIhYN1VIBQytgVwPuDdeaspR9H+nEA5/CVUybKAuo+eBSQrryH3gNgduidpqlAixIwer8Ue8rz84fyJ8s6L6DX4Ro/uABAkzSzXNsyp8pvDvehg72CRU7i93kUhne5T0nn6AMwvVzVAeDLwfsvRazynR4C27Jlmvn3OR9+74fMqrn99WB85s9mmVP5wfiWe6+reE6k0jxH5POWfVuS/2V/XbDyMo7y/FIQOQTUSyGumh18Vb8OYdxYLFtf8ez0nB9++RVfffYlx0enWCMFkSmGuQ0shMDd7XuuL98QxoExBVIYyFl0/6V1OVIYwc4ackzEKHq3SQsWWZlNxgA6J8U1F10HBwIeWQCBZ0+fkoI4F4vnhoBbJDnDytlZ5JPK9To1dYoxSHEzJqY4wSjjOKXM9vgRvlqDr4lJxvp41RKmgTGpwUXT0K7XWJM5Pz+n3+1QB48HiduqXYt0TRaTj8Yb9jeXbI4fcfH4OeNww/37bzlp4GjdMlYVq7am+X+Ze7Nly67sPO+bzep2e9psgASQiSqABRRJWTTd0qLC4Sv7AXTncDh8aT+Bn8BXfgPfO3xnXTjCvnNIiqCDpFSkaIuoAquAQpvI5nS7WWvNzhdjzrX3SaBkWhJD3BEIZOY5Z5+115pzzDH+8Y//rw11IzrrOkVhDXUtSmdnc6KwmfPY9eZuI+OWtuJ03aK/fE6I4VB4GomZ1lZUukxlFIaNQhnoNKzHkbPNDZebW+a3V4xXVyQPZjFDP37C+u0f8dX8BKcio074GBmy2SExygQD2UQy6+4fTyeEELJhiRItwaITGKJIJ+R1XMZujRYQoK47jLYCvhhNiodGkcQMpu8HZKw4eOa14sNHM87sFsZs0FLiNZp2vmToF+iQ9c7ripbE3XjDarmkbhuMtmz3O1IQEDeGBCZh9UgXhbnlTY3TZ0JUSEmA46qWBqg+xBalpA0UCps8M9GloFU0TY0xAnJVVtPYiCGgo6LS0BrxjBC93zQVsX+9iPk380r5cLda0dUiXyCGzonGSJ4WgDFEbKXYj1JPhSBTIT5ERif7u2jWN61h23v8KEAXqsWHiDVGJO6CJ4QoI7wWXICkYmalOpLS07htAR4EtDKAAEVyRKlJjzMlxEQolcalgAOyhnOjLjefSu4+5bc5R4ghHFJ8lUeiATVNyEgzyY1ePlcq8Vp8PiR9TznPkK+bPBmk8qROiGHycbCVNFzEXTx7OmQJAa0kRkTvRP6t39P3O5IfMWkkxkGmNEtWHgUsU6Sj/VrOttz416IJKUZFKssqFI3dgzGw1DKS24mOqiVFd1SPcCTfNK0kSr4p6yqbtimLNg2z+ZKzB++yOn9Atzzl6tU1w+aaFAIhKkJUiKygmHDHJDVPmbApLEtgOluIMhlbYsmbbEWKhmuMR9d13NieNkCWS8qmoSkJASVCytrRShsMmtlMJPwG7xhHofxEDkBwqRvLhFe5/9polLKYnNt3XUfdtlkqxZS0agLkivY8kCdO7k9T6Gze69zIOAxoIzIydV2JKVOuMQu7VIhwB/OpiTBCEM+dJCzYGDybzSZPhsp60gUQdeDSKMB3iuK9EyX+E0UG4jiPKZJc4ziilOQtPkWsSiRj2G3v2G032FqIetZWIi+GLssv17PQzRpIWhpumVkZMvM3JgGQjTWYwlafZOIkt3PZlKwfB3ZjT5my8t7j87XXVUVtBfyTfDBO52E362RMn5wLGs2s6lD52Xkv+zou4qQPG5M0SVSO8zEIyDyOI/thpN8JJjPJF+U1KZqqBlNZoLCgZc0WAL88v5KLOucObO5uNt37kMFwOTQN4ziy24lGcNM0GF30niXXslUlUgB5r0zSCkDXtNP5b7TIDQyNg3SUG2hDUl70Y4OAzj4EXl9dTczYkCdQtdbo/CyBLHmVMDkOHJorin7YEVPAO48fZD3FFHFDL/s9f8Yqyx3ZTCZVSuKcTNYqlvM5kM0tVURpy8lqyX63yzX6bz6N/5VBWiVP9n8C/kVK6X88+tI/BP4r4H/I//9fj/79v1NK/c+IYdhN+pfo0YIANIGE8CGjtIkVhOAYnQRkY62k4kdFV0LAC9HwkW6DdApqXIigpDMRSqHkI8MwghUdxL4f8VqzmnecnT9gtTjn0YMHvHj+Gr0bMdrD9hVm9x3vPprRJcWrIeD3gxwsxqJwGGuo64owjsL4qC3JCP0eDUErMOI63DYt8+UJVT1DBykaNDKarLW4f97tR8b+Cud7fFC8+O6a1TsP6EPF4OGD99/hbNVSadhudgzeobXirYcXVLbm8eUjVosFV1fX1F2LMpa2Nfzu77zPT3/nA3be85MPP8SNjv/w3/99Rp8YR01Khm++fcHrqw3eB5oaaquoa03T1rhBur2m1oz7AZ8MdVOzWs65vr0moDC2wtSG3u+pbMPZvOXV9pqoa1RKDEQ++fprPjy/5LdOT0nec3P9isXpKTYkxtevqNKI99LxDi5wfXUFZosbA0MvumO6qlHATNmpMxeD6OSS2bwhd4GVtJPEHTFJVzuVTk1IjBgR50cTxoAHQnIFqiSRcApM1Nz6kf04opRmbw290vQoQu4kq4kBK2CEjsJE0VWx0JD17txI0oq6rjIjMOZDK2sNqaLTGMtGpJy0UyKTr85kJuEb+zYHmjSBfNz/lunrJYFTGSyWLng5w/M151GkEsxT/qvODZB7+zkdAAo5/EvX/P64eJr+X5LwcnBLtxmvqKlYtHMuTs55/OAJbz9+xLN33+bidE1rOyzZ6EQLWz2lJKxIBT56xjDw8tULnBu5OF8RdQSVuLu74Q//3n/MH/6n/wnDbsvl+UPqesZm2LM8WfDzv/yEz375GX/xs5+xXs754tdf8u13r3jr7be4uLzkk09+wQcffsjgEh988DGkwB/90R/x4x89JQTPk3fe4fr6hpTEXOfbb56z3V2x3d4y657gA9xuPV23xHnNi9cjL252XD5pefzoATdb0b6JWpG0QRmLNomqqkkoxlGYSjGmnKCVZyoHRIoHY6NSsBUwPuaEydoKNcr4qFFGZAFSnO7fxKRTUhSkxHTIpAysl0SvrMGYD15UWYM5Oct7SaWcmBgrGoUcCqS6rmT0OZW1LsnKwbEWDGbSo1JAiqWZoaZkz2gBQl0UIfigiiaqEuqdTiSd4aGyjmNEO5Ud4Z0YOBTNxKxvmcL3x8PlV6ujvSJxwKDQOQFPKsmZUzckDdoaktEU66viIBpjlEKoAHiQaZyHQnvaW0nYt4mEVSVmHEbxy/6+f5llkRy/l856lPkLGQQkSYzKEGDWCk3TMy7vXMBHpTKzrZzPMR6aBQUsnS7tPmB5KBAKgFo0Y9X3vu/4pUrsKE0epQ9yEEdSMALW6ny9R+OoE32v/HyOf/l5H+u1ljU/3Yfjiyg3Q+WmIOroc8p1dV3LMA4HoLks23uvVG7fgeWOXHspCEqsPDAPOQKS87hpmu7wBGjJ58o6nTrvbZVHiMszfLPZkRJJgUmRVdPy6PyC33r3GR+885QHZ5fSvNwHlLYoXWGMI7qBF1+/YD8O7PcbhmGL0RC1xuo8rpwLl3KV94vGvH58yAmwxbYNSgnLvbKKyhaGci72lZyb1tisj9dCqiewYmIpToWH3Dvn8whlHp/03mFInKzWEiaMJkWP94kYRLZpHEeqZsl8dYo2NaiEtYb1csHNZod3PdH1NEZhq4o0m6FTYnB9Ht+NuGHEaoOJUhBHFN1izbMPfsKwvWO2PGGbWj7/+f/DF19+ycPLS1CGu9sruq5iv31Nv73mdrNF1a85ffQ2bdfgvaMfeqqmJkaReYKEsi3WSh58ujqR/MfJRFFUBxMerTODxbsMWgtDxgZPd3fD+fOXvH3zmmc4LolUJLyKuH6k/y7watjhT5+g53PumpZdCvi9SEeJFIXHGInT5VwJU6FUQNXMlPcOF3JhmgIuF4UiyVV0yY24xiuDtTVVVeGjY3RemqMpEWJNIuYmr/g8hBhR0XHSWGZpg3JbmcoTiJNismltSzdbEYfNpAFvrOin7/Y7lLU0jWE+X7Lbb6VBoRRJRdCiL1oZaA0UXp6yFVGpbM8o0gZTzFMHs+CUQbrlopUGnI8s5pZZl2hMZD5LLDvDqtG0CkyM1ICylsPpOEW6Kdb8dZtc/6ZfCrAZPPYxYlQ+I6KczTF6TNKMw4iPlv0QGEcYHcSkGFwCNLv9gFI13gnAGCIkDJs7iQ3FYMdoadZbA15HFBay6bLkChI/+mG4BwwaayUXMDprKEsMCSGIUXIGyRSKuqoIuhALin5/lipIh7M6JWk1+QK0AUULNSkmvVilwLtRRo2NNKAkNxLTbKLsAW0UOmVtUJLE83ygaGVQVpro1lagikSB7AFgWt9+HHD7LUSH229R0WN0QpElAIwRIFiVRrzODHfFOOyns0zGrTPzEY22mqYW4CXGdFh/KpvGwcRmVVpLxVSmSguZpPxdxqAyA1cYcNZW1JXB2IaqXlBVM+aLFZiG5ckZDx495tV3L7i7fgFhpMhHGKsILk17q0wFlly31FMxA48FSIJD07sAtonMrC5a7aSjXEj22PGEUAz598SUc1bJcSQ1L/m7yrq0jn4vE53pyCBJZyaz1gaVitSBxO9ynhdZsgn49KGk6Pn6cm2syZMliTgKCa7k9gVMl3xM4q/ve4yx2L2ZciVr7dTsSKK5MQFi0hwHZbXolieZKm7aBrSmH3u5ZyFigbptmEUBf73zjG7Ej9KwrauaqLNWbb6vSavJwDWlNI2wm6rCNMLUd8OI0rDbb0GBqaqje6gzMcFT2Yq6FbZwSlk+xuSGR14bdVXTNg1t01BXDUbpTEqRZ+f9gQXso5xXPohu9uhGXPAMQ09d1dhK2LTejwIKFymBDAyW/am1xuYJuvJ1m03SY5bGLDm2MSIRNGQ9VclnPEPfC8gZQzbIlbxyu92Cls/QNO0kf3Ect7QRbfQCzorEouRts1knzfapiQHrkwXiobGZvCZi8qgMaO+HHj2KnAEqT3xm4zJhXevpnDJKi+yUraSpmTSmtiJxELsMkmcW7H4/xVUfDvqxo5M8pm1bZrOZSGsFL0z5/HnqSmSx6koMxvRMasCUC8P9MOCdm4g8KEg+sN/3cqZZSwwRp0Wuy1gNSTymjCabMGq6uhLJ0+/l/IfXvw6T9g+A/xL450qpn+V/++8RcPZ/UUr9N8DnwD/IX/vfgP8C+BTRlf6v/79/Re6QTWN8ibopQsYBrcksJwl2RV+xdA9UJaDb6N2EbNuqRk4ahU55PLfW2KaRcSAnQFi7WHB6+QBXVfjo+Qf/+R/ibrb8k68+xfYb1MtveDDbcLk6IZmW/maL9w4XHX2UkWOdtDygSoO1RMMh6CmVQb2AUoFFd8rF6RlhEJkDccT0eYEmXEqEIbKNDlKkouH19Z4HF3uePnvCZ7/8klVbsWwNv/5gwLa0AAAgAElEQVTiC169vmO1WvDOo2cE79juttR1zctXXzOOnlNzwXJ9yscffcDDh5dUdcP1ZsP19RfE5Dk7O+Pld9+x3zvee+8pv/vxMxbLU4bR8eWvv+LF81f4ENAE6sbiXY9VgWQSGAFp57OGxbzBR83oIy5T0euUWM9ajFKMUZxqA5GrYcvPfv0Zp/OOJaCjoteK9uwM70a0VcRxxCdN8nBzc8UQAsa2FF06UphcKrWF6GAcBNhq6hkhJElKUtY1SjCOgzgTKgG7Bmu53W0ZtTioBjTOBkalqWjp+54QxaFYqcCV2/Ni6BlTpM6BtNdKgLRY5AiAdOhCeQ1eJ6qUIDNJkkqgI1pZQtbQMhNQW4yVDsnBBCwcFfZTwcmB1XZPCykVt9gMdLwxYjztPDXxkCQ469IEObAmgYPIP4cAdhxv3kz+j/X+yoEvgEO53jglSuR9QizGSUlYW82Sy/kFTx+/w/vvPuOdt95jtepoG7nPOkFUIqyffCIGSRijimgjGtbDsOPu+grlPCfLjhevr7m7czTW8Pu/93dRbuTFt8958e13k87M7e6W69evid4zOMfjRw9YLJZ0mx0+BK6vXmENfP3F5zx69Da//tUn3Gx2vHr5nD/8e3/Ay9cvOD8/B5V48PARF5cPePnqNXqsaNqOi7NTxn7Ltt/QdR1aBbZ3O6zVPHp8wdsPL+heb0g+sR0HRhJKBWqTWHYtwTn22y1VCxg5TA/gj8o6UQeQqSS+0v2uKCYAMdNaUkwkJXpdJFBFsiRLtwizR5KwmIQJEVPKU2IZUANp0FCMENSUEEUUMa9VWxBHfXA/Rhs8kIpAe4x5DC2vlex0XQBSiau5sM2jThMLUimiSsK6y7IHogkiYzc6u+1m0UPZZ7lIQitprBkyMKuzUR2kwMRkLHuyyGoUjcSSKKQorEOtcsvGGKgMXosuOja3flJEJ0mEhBEtI3QlWZ7YwvF+kT2BlaWpocWArRR999ia+c9xAgyP2aFqusfe+wziRWpjWJ+e8fr6amJXHpjzh/ctY7TH7NFSEUwMan1/rF++n8P3T+8XUVMxeABoD/HmANgeF76KwpAFkpjooAQAmZyi0/djnvzhqDl0uJz8/zfHhI+AW1X+Lt98uCZJgE1eF4UBbbSMzWl9DOYf/T4Oa/uYwTCxodNhokGYY1HOGBJM+on5PiUm5FYpWf75KsVlWWmCz47A+fqSKiN7xSAta6uEwNJYHp9f8vH7H/Duk3eYdwsUFdtBGIGLxRKF5ebuhs32jn53x367oR97QpYy8CTZ21qAj2HY47yjqap8ZRleTlKEKKsycJrHDo0i+CigRQoQEj6A1TbrQ2pImUmeR1QnDeIcm2K+jykEYdypvNeRWGG0FvZ9blg4SS4lBoSE1IM9PkIdAtpAPVtjTUPCYivDcq7Y7kf0sCX0d6g0p2lbUkoskyfFxG67pd9taduWq5tr5t2MEHo2d1dcnF3y3RBJdsZ+0/P5r79EtWecv/tTRlWz373g5mrPt19+xvtP3+P3/r3/gJCyi3GIhOimZuUwDLzut5ycrDBVxWLeQVDMFjPqxqJ2UNXCPMoQKUQIGolLCuYGKt8TXj4nffk5+rvvqJPHLhcs1ieI705ER81+11PH57S7nufLC75dnfFZXXFnKvZajHVJkUCUqSYsWkZ8iOlgsFKAiqTJXZEMPmUTGVN0+vPLhUByQ9aF86CCjLgrTXCZca4SYwqkEFnMKnRynHXweAl+2JBszDqJsncUMtcWUWhV4ZOMcipHbrjMxbcgwegcXTvHhcA47Kms5ur6hhgDy9U5plsys4HIQNSBZGuRuko5/iSIUczapOegmXUtRic2d3uRbIsCsFigqxO11hiThPUcAnVtaYwp3JZ7Me57zL43Xn/ToK36XjNqajOhrJEpFS36f4GcQwSRMYKiIe+JQZiQy1XLOCR8VNB0AtaGSFKG0SfcfhRChskGVdFjLQSvZX+kbEDjDrFW9FbzyHJdUbRUU1L45IgqULT0Eyqf6/IZrBbgMQZ/z2T13lmJ6IAfxhoOzdlCBAl+hBQxCpbzjjINqJQi1RVhFNKInORZH9bW1FUtckfRC4CSEpUVh3OVmaIJqGqFQYgszg0k59ltb8H3NCZSmUhILjfLsiSCStOZcryeQghZMsdkprHNubPJ+pEC4AUnkgg+hgnMmqZBkOaK5B9QpAsmNqvWgJkAUaVkHaAgKYMxLd1szWp9icAbiugGnn/5Bc+//pKbq5e4cYNJHqNEQiGlHCOy5ICQvuSeFcZkWbMpRpz3E2NUqYNxFYgZYgxpIoZIBE2TRMuUoxw1YMqaSUnygfJ9Ieute+fZbLdiPmXk/JKcTaQRS04jaa7OdWI2j8uxMpaG5JHxa3kJOzSPzk+xR75WjMRSjJP8RAghn8UyRj6M4k5vdDbB07kxag9TeWW9lIkXU9lDPjY6hsyQLEA1FKKQ5L11XWOrhPWe0Mh0QyjNUSMawjHjPLqwTJ3D1DUmNxzLLqlrAfjKxEipWZWSelalRHReNLGHQTSsgdVqhdF6MvuSFCESnMcNnsoOzLoOa0Sz3VYV2mqSEWKYCWXdJGZdTds1hBQzICuMY8GpOipjRQ6q72XKDqktvPcisxAjTVOjM1hackJrDL1WUyO1TJ37TLLRWmMqy6Je5VxQnk8BfPthYL/bse97qqaS2BayGZdzuOBRPgOpheBSIngSPVhj7aQxH0OC/Q5tFHVTYW03/c4C+nddl02ac02TdWBjFEmJfhiy3F6Yfk5X0vgsRmmSR1sqYyejwWpRZ6O8hMk7MYbI6EbGcZRJKozsnSg54TAM0gBuGtw44rN/T1PXh8+sNaBp6w6bPYIKSWPoh+melOuNCXZbYd6GjFcaLXVE3Uge6I+mnN98/SuDtCmlf8zh7H/z9Z/9wPcn4L/9//lb5NCS6JgDOJQCknw8iVu3sD9UBiNUZuDEKBFHa03UMgJrimO3NURlSMYStMFUNSg4WZwwP79kv9kz9reYJvEP/4//k0+//AWqv2L/4pes3R2PH19SY+iHntBv8XEg6ohLopUWQiCpSFWJYHUIQTTZkmgSKqOwyqItrOZLZqbmzm1RxhKlniIULUKNBFBrxAQLYRS/ennNB8+eUD99wu31S4xZsR8HBj+y2+zZbfc0lWG/3fHNN9/Q9zsZv0oJZWqur++wuYvz6rtXJDQXDx9zefkQrWr+yT/+Y65eXXN5ec5PPv4J773/jHeePOTTX3zGL37+V4QkOk/CqLMo04ANVI3ldLXg5QvY7AdS1ARvZEgjeZbtjKVtuAsBHx1VFpb+5PkXLGeGv/vWu5xWjYwhVTXziwt2L4I4N9uKcXRoU+WOTnU4DFTMnciYQQaHC462bqhqi1WGcXDIDYZh39PvRmzdUHcnfLvb8e1+ILStjL4Yg7YNdCecnpzx7sN3OF+f8LN/9qe8ePkNQ+zZ6VvGMTKmAacVVSwdeZUdCqWQL0BrN5sx6zqcLcfz0RhrKGOrAkKpqpqKEp0LpTdfWmkCYeoCHmshvXkgH5hr3zcIK/9exiRCKMCwnkCEN8eljxP9e2zYY+D26H3f/D75h8NnUujpXigEZEo+YJLFasvD80c8PLnko/c/5Ld//CGnizUKQ4ij6BZqYfeFKMlRCEUjKVFpI6xp54kucPP6GqNs/pyaqmk4PTvl9u6G59++xvmA0QIYDONAN+swJ6f88tO/4na34Z/+6Z+y22xJWuOGkSdvPeHJo3dIwFvvvcf1zQ3/7M/+HGMqbNXw3fNX/PLTX7Lbbfngtz7gZD2nqTUbDJWZ8eDRGabuCXHk9OIB3jv2+2vmreXRxQmzqkKtTtE0XN3dcLW5I0bRtJlVhn7YEBkzQHkkMZCLBKMmrCy75iLAewwo7QhxxNgs3VG0aGPMyUjIMgK5MZaLv+DGnOFIYmSMBoNMFJRnWsy+kuhWFv2lMpydSCStc2JcVKQVIEyHELLkhT4wEY+BsmMg+p75T1n/kF2Gs5b5caNACYCptZ5YKEZrwuizcYgkw9FD9PlzREmCgxunEbjjfVEaHBNInEBp0Qw2Rj5bVMg0R5ZiKR1mbdTk+jklMhlELQwOlSCFmJPy+6Dl9Dthes83Y8AxE7SwJI+ZIbJejpL5DGoGrajbZpI7UEodmqLlfv/A3p/uyRvxYQKwjwDWHwIH3owh0/u88fd7ILW6/7NSGksnu4xjylq5P/Il6yPcww/us2bKpzwuUGWPTIl+BpSUOmw4hYxIog6jTcF7McY5um5lhPF+vP+O78mxoYobR0m883OY7j8558mTDzIql9dBvl/B+6NJIjEwzURp6bFkHTcxqgmQHDUw1zUPTi74yY8/5J2332HZrgWEDpq6bWi6ObWpGIeezfYl19dXjG5gv9/ixiGzSKKwvjgAz0oxuezGUfQfra0ETK4jyQ+5aZ2nQFLMTRTR60wp4mPMsi/5cx+tKzfKVNGxzmTRQE4psd1sWC4W2bwzszd9kLCmYBj2jM7TtOJUrE01aadJNHKMg+KOG5bKomdgjDT3rDUsupr9uGd3d8OqmaF0jbKeqmmJwVOHmrPTNUorRh+YzebsNwG3c1zd7dGzE2y7pI0VH/3uv4uJv8P5xQMcmpMLQwgjq/UJbVWzmC/Z9qPEaSRLbuqaxmqqGBj3e4LvGDZbum4tRasxedIo4SMyAQSQR69jEMBqFiIn21vs1XPM1XNmd9c8qeCdbslaSQMeFD5GNDBPAd0PVPGalkQbRuLpGV90K1xuGCYUKoJKQbQAK5NHpO/tQkD03Ejioq2VkUZHxlSUVlkOJ7PKciwXAElifgwBY4u5jhRwg3N0o2Vm4d2zhpN6wIYRFRLKHt5PhENL4yBJ7qCrDCYpqrpiueowpuLq+poQdzRtS2UFgPjkLz/hxYuX/Ed/8Pd5sHiIYYOnBt3idI0JCXTMOTKE3DFUmR0+OmFHVnWdc0ZIyZOUFIpjAN2D16BbKQKVBOfpLDx+HetH/lt9JWl92fw8xiB6sSFEXEokND44qrrKerQiY+a9IUw6rgnVRjb7LItRGYYYGIaB01PL1SuPczXGBpIyWW4qopQAHEGV+yX/FQOmQ4zPF1ouOSV8cJTph5QitpLrj1nOIisjQH7fY831ex8/xcyKPWoYAgLIisQKSWT9CnsXgOCJfoQ4oDObVwBM0bwOIck+sjKOa3Qe2c9RQbSmIY47+u0t/W6LCk6YucnJ54gOXSTGVGmq5Lh5lH9MEiLaoIzB1jXG2GwWpTMIm7Ud8z07TLfEe+9TDDOPz4bSXIMDoKEU2VlEY4ylm61Yr8+ZLVbEpKcJvDhs2N5d4UMiuFFY0yqJBraP+blkiayjZ3wgqmQubc59i7xFacCW9VAaDdqKF0zJuyHHpqOay+hilHZo7JukDyCoIDl5mkVjbY1SooUZUoYb0yE3KSZLaqrR9EGqByZ2adEPLmuoAH+Qp94QORCt7ZTTxRAm6YPJKCn6DMLqiblotEanQ71R1zLFgFbsdzvcKIbcCslfSwPKe3/Ic5IQAwrrM4aAI8sHTLm0Ivo4/R6tFFFlo++skatNQkWT+63iQaHyNZZ2W2kaQJZky5qlSmuWq0PeLPenMEalMbBcrATT8YGh78V4PETuBjcxT0lSFiUta8x5J6x7FN7kJsQk0SPgXwFq26qmywZVAdnLx8Cm92J8FZM8b+8cKQSilntprMQ4lDRnK1vlRvuhQWatnRjO+/2eolG7WCxYr9e4YqKepyG1FqM3H8QYujQenHPs93ucC8QozOr9rqeua4IP3PlNlk7SWGsOcif6YPBWZPZMfoYlLlTGik57zrH7vp/W5TD0bO7uqKuaoZbnZo2lrhqKoa0yOkta1FKT6kTbdcBBCizERJPSJIHgxlEaCcago2ji7nY7SJJra2PE5Cw3Va21aGto25a6EWkFkTiN014r69u5kd1+L83jGLndbe/VbD/0+tc2DvubfckwUNRyuiSl8shOmjQ6qloOU+/89NAnCjZMbqwxsyK0VujKkNBo26CqFq8tURmUqpmtl8wXa3a7PX7wrBYr1hcP+N//0T9i9/UnhJe/pPF3rNuO0/kpw37H6+vX3Hy3wXkjo3d1RRgixlY084bZrEUbi0sJVVl89PgUSMlgSNRdR7ucs9nv5PgswaiAY1JxAGCSBmQ8rG5m3Ow8v/r8JefrjvlijRs8Tx6/xaNLh8ZQVxo37rm5fc3l5QNOT56x2fZ8++0LQviWk9MLQoz86tOf890339B1c0IKrE9O2O421E3Ne8+e8qMP3iMkz5/8yR8THPRbGSNAG2ylMUkCojE1xjqMiszsCedna7ZffYNKNVJXSeq5Wi7pUOx9JNQCPGulcUR++c0Lni4veHQ5J/Z7NiEwXy4xs7l0tlIUBp612FygpSTvPbGplSKGSN3UaLOYqPEBj7GVJDdBRhhqY3FVx2e3d3yx3dKrhE0aIlTaMjMVs7ZltT4jtjOqk3Pq0wsqAlUFlfOc3Nyy3W14vbuCGAjDjomln8ejtdb4FBiJdEblgK0R1Qt76Krm8R9SIpWueUyU0SXy4VEkBQqz6M2XOvq++2OdR93NstOO901JwCZDpZJAJSkb3gBTjv/+mwBbOYAl3SnmOseAx/TXVNCOSAoKlRSLasVqvubR+SUfPn3K++++y+PzC+Z1jU4RHwVMQGmUNZLEaJEVObjeC5cqEhmjY+/2fP3tN8znC4KLDP3A9c0LLi/Pqa3h1o30w0DXLfj2+TeE6Ln5/I6manny9F32w8DtzQ1La1mdrDldnzPrlsL8iIH5/JzV6gF/Yn/GRx9/zN12y8npKavlAqUS52enONdzfrFmHHu66pTz8zX73Sts1XJ+ccHz777G+ZHVcs356Rn7fqB3lm6+wDSNOFSGhFMiS3B7e0tQ4I/1jeMBAJc/lpG7zALKCbtSju32hrE/yWxbASh1Lo4FGMnsugyGxuzem+kfxCRM9NILL2szOyxl0EdJLE+iVZaUNFIEhK3wrhe2ktboCHWlJ0mC+WrFMEgX9ADu6cMaKsFSqex+y2FsVmsxh+DIOEuXdE0dsVLTNIon90FNOlUQsFaRYsD7IRc9imJMUy4hpURxJFZ5/yigzuNBMUFUmpT1nyIKayShIBfkOjMLgINxYCx7/sBMKH/+oWbJv6z4nvYrByCxjPMBRyYjhyLKe8/z58+lIEPOKR3jFB9KjCvx5TfFBnUUTw4slPvg7veB5cNnmr4e4xSfDrFO3bsfb+YDIcQD2zlC0Qn/oXv2Jjhc2DKT1Mf02fJ1RtBW1l0B7Y8nB8o9SkdTEIWtO5kjhjiBjClv1CkeFxCBNDFcshCD7ANlKJIUKSaR1ZieaZous+xnkjAvYsxmNhOkVzQMsyEmksS+//htPnr/J7z/5ClV3eEDOA9N3bBcLDC24naz5cX1LcO4ZT/ciUlCSNLIDsV8J0KUtW4zmOazoZXRmsYKC8tYS4yeOCK6tiobgZWzERkP14SpiaOVgL+lsVEMgVRucgszkzyyfJgsKW7ARY5D52eHEkbE3d0NPoiZjgqGqgYJfQJuquQpo8obFCmMLFYnNN0Ma2q8GYHE9u4VtqqZnVzix5FhP2CNZtbNoRVDj34UE1i0ZXH2gH5zw8nFQ9rlKVt/xbMPfhtjLdc3V4zbO16+usUHxztPntBYzVe//iWvr655+v4HbHc77m5vMadn1IsVC1OTahjdQNXVaC1+Dk0tuoAJadIVcMIoYQXGJPIGD3Y73nn9irPY8/Ctx8zfe5cV0L54zSI4GbeNGhfBq4QiYFKgDoGTfaJLjtoGzqzir6olL4ylx+DdmHWHE94bqqLJeAxcaQnEMkYtuYHVlZAzgjQdtDZZJ+6w7ospnM9u1haLVgmryEw6+cznqxkPTivM7o7KqknPFn20/60RVjUapSvqtsLWbb4mGceMgG0coxtpTcNiseTu9oaum/P02QnvPP0xdT3HBYfqb4ijRS8u6ENCBy9NukliROczy1BXlqrSaBKVUTS1XFPTCiPSD0II8cHhI7ikICoapbA/ENd+KGc8fv1Qc//f6OsodJZ2mUcRk6YfHV4ZghcmeMyNUpJmGBym0lRWE2sYnGIcJRa5MWBsAfhgHIVRfPmg5dvnAWVEVzYFAcCN0RhlSdlksABvhfBQQJzje6CNolJGzJyUAD2TaZIRZmWYcq10aLKWNGV6r3JWHfJ0uRcKkhet2hDw3uG9mO+U65NGnocwyn9Z9zaVmjEpWaNKQApdVcJWSwmtyp5I3N3dMe5uwPUQRoLbH0wXTb5mdeDqppzDKy15DDHL5UTRSm7aFmMy+JPAB/nEJrNhZU0VACwb3L5RtxfAtzyDAuDI+7ls5FW0Z4UdPV+sOT9/RDdfAwJaaR0JbqQft3IvYyImJ5iAjEARokMMJyEEIJAZ0XqatEwTwzRNo+wpOqaxq/wcQzakfpNIk5CvqXzWHcBfqdtG78Vfp9yDbCpejBSVVnRdk38CfAZW3SisynLvvPf4MOapHQFVbWY1ksFvYwx1XU9GWG/mPmKaFEnJT3lI13Xfy9Fqmvw5FbpqMFqLtmv+bNbaXLNKHrKYz7O2vOQtPgTBSUKia/X38sUDGOnxST5nyAxmpRR4kTAsgL42kv/4wck16TwxpAz9OBCRSWqVomjhjz2oJDIdWVasbhuiVagkEzhaG2GFNlWWBJDaOyJ53Gq5YrlY4pxju9kI0zRLJcUgjOvdfsduf3vflyMlYcOSMhO0otLCNs+mHjS2EuNI6WBRGOxFF1fIX1I7HYgg0giSdRDY7raCgdQysm+1ZbfbMY6iy19A2un5J2lmGmuom0bul1IEfTDHM9bQtI1opGegv6pEj9g5JwzVDPbGGEl1osrrW34v7Pc7jLGHfV2eO9DUNcv5QmqKJFr6xppJ5qFt2yk+ONcx62bTtSWtpqkw7wP7YU9Mwu6ftS1FEsRkIoSsNSNNz1xv1XWd9fuF7WpSomkaWZ9RWM/7/R6VYBzGLJt28F2JMTKfzSeAvTxvYzSz2YzZrGWxEO3eECIxRXzwU33zQ6+/3SBtImsBepStBcDSKbOXmPTlyuL2MUwUewmaXgI5keADI4kmazcKk6mlmq0IHkzVcnJ2QTdb8OLVC4ZhoJktGaPjq8/+ks1XvyS9/AJDz3zWcrk6Zdl17NzI7d3IzW2PtXPaqiNYQ9PKeJyuDdEq9n0P1mCjJHExi7k3xjKrG9q6oR8GbLJUVpfGQcYN8kGfoNbymWWTSvF6c3eLG2559vRtGtuik2M+b4kpMfR39Ps91lhurm/lgIowm83oR3ESjt6xXq7pmoaLiwfEqPkXf/HnfPfqhvnilMdvXbI+WfHFV1/zySd/RXRQ246qbuhmdRZctgKCKIVNlShtqcByfcL86o7xdsAFR+YJQIhcrNe8ev4tVlcZcBDwfe8jn37zLRdtw2Xb4GPk6vUVdhwIMeQDVnRGQgaNyqhGCB6r7KThYrO+q4C2KbsL565NXVHPW/aD4ypqXmlD384Z+j1j7xi8h90Wq65ZrU+5G3t2n37KdrcnAD55fPTMFwu00szXa3odODk75fbVC+rtHZudyGD4KIZDSQGVYRhHkiqFtBhgJJIwd0IUlrXJXb8jZ9QC0h6/jhPo4+5NCb7HQN2bQMgxkHsM3ErCBwVpmpoFHLGypiT+foB5sytUvjcVzThVDuWSrMT8GSUwU5iTPrGoW56cPeLD93+LZ+++y1uXZ8znHZWRJNUnSMqSDFhbS0IZIxqNskxAF3L3UURicvTDlpu7ax6enhFCYjFb8KvPfkHT3rDf3dHvb/jJRx/x4x//BKU0m+0d//TP/ozoA30vaxmt2G/3NEMrcgc311x/9hp04t0h0g+OBw8f8fTZj/AxsVqtsBpevXrFl198zTD21LXFaMVsNWe+mLPbXmFMQ1XN2O9HQrQs5yfU7ZLt6HBeiuqqrjg/PycZy95HrLGHUQulJzDq+Fnr3JkPwd/7mrALPW4cGZ0jRnLxkPUuc3Ifit5VSdxTorJVduZMeY3kUTVR2kNAT4QBEANidmEgacYxonRLCktcMiIPkjyGRApKdItcgNpRtzEnkJKcHa/BwkRHSTysqor5fM44jpLc5QP0sFoFOM6YbI5bea1HZKRWIWN5URh7E2MR6YjHGARgIgOz8QAKlf16KLxyg6IAcYj+LMaijMVWddbFEmZIyKPrx8VLhuLuPc+yt47Z829+7TcBtxOYTDq6zlRQ5SluqJxwlZ8fxjEDCPJsC1P9TZD4Hpj6xv/vNw7ivet8M36UYrYkVW9+lvTG/ShrVxQqjgDgWCQf3oxTh+JwYiipw9dLAjh9Lo4+J6Am5ne+l1FP97QUb9O15iJV9mY2tktM73X4fAc35IP5ioyFoyQRVyo3oLMzryTq+bnnhoMbR2lY5PsbCpMr38uSXxTgF8hu6dKQ0SHSVjVPHr3Fx88+4NnbT5nPl2ismGMZTdNYrFaMY8/u+hV3txu2uy3O94y+l3MkSUGeEMMPnRNwYkLZPGVCyoW1FjakNoToGHYb3H5DDFLUWGuyRM9B902YSbmpmKSxr0qjswAksgjytWR28RGLsBQ+E/PJlLE2aeZ03UwMrmIiJI/WI7bKxjuZOVdZYb2MfQI8VaWp6wprGqCmlujB3cuvCGOPti1VHkMsMe36+prtZkOVJ66quqNaafqg8HsHqmbfb1ksW2LUGFPTNh3z+Tltu8AohfOJ7d7RzhYoU7Pfj9RWps1GF6i0JviBRufJgVwEDf0gQLS2KMSp3lgLSdP6wMWw4f271/wo7Dldzlk1c3GutpbQDITNDTZFTIQqipRNVi7AhEgYNsy84yKOtMERzh5QzU74WldcJU9UMkGEE/0+YVLnYk5oexhbiRt9DlXGClqui2afEl3GkAOtFFeZR19YLVnaIqUg7KroOak1716sac3435gAACAASURBVNJWprFMBmZzES/7Rhi+Vd2hKzElreqWZr4CBX7s2W9vSSTOLh8B0niLMaBrx9vvPOXtJ085v3wL5wS4TmHLy6vnNIuHeHsBupnYVDqDs+pI39QgHpdGJQgRYxOhjwwqS4IQWS4qrBbTGpSY4xn9faD1bwR4/Wu+Shj+3hVMdYAmJE0U6VHaxuKiyJloZUVmCEfdWoYgMaZqKrqZIUZp+ogWcOL2NqF1jbEjWhmZMkDLejuKs4I6Si4EkmaXfVl0F0MMqHjIJeB+Lk0SRhZEAVAyqFQaQtP3ZMCgMLzlGo7YmSmScqPMuyHrNBYZJYlNAWGV2mKUrQ/6qAmk4ZvHzgUYJTeYR2IYCQT8uCPFEYUnhBGdnJwZupyjmkhu2iRpCmttcsMwHe6DktHjtukAmZY6Bh6k8XOEUvPD66/UISXnsFlfUylxYfeh7HOEtKUbVqdnnJxeUlUzQhJm26yqCa5n3O0QRQmfG5YxNzyZ/AyUui/7FDIIVGQipLGejq4vTIB6CAfmq5guhnv5V8mrjo2BJuBeK9FZHQeRY8pMyjhJaDA1NcdxJCYmc1zvPcM+m2CqLAdgDDLGZkRLPIPlpdFgMuhdcsbjmk+Ar2Nj6YT3w/Q53wR0D0xIMdb1CMux5GvWmilv0kZNwFeRCzPqUHuURscxMH8M1CYSaq0Z+4F9vxdDsDrmqQiTAa9A8A5rKoZhZBj30/XpfK6LRJc0sTTCeI8pA6VWGJv1MGazs8zkTQmjJAe2VnRKk9bcbe4Yx4HZbE5TC6BZNRW6MhRpgLaytF1DtdXs97sp59ZaYyuLz6DfbnvDrOkwdQV5nb/c7mibRgy+jMpMe01d1+x3O1KMNG2dJ0ZkoaQgMUAbTaUU8/mcylbYPPGjlDoAjtNzjhMzNTnPdrsleM+oFH0vI/rFPLjEHW00Gk3THEw8S17fNI2Y09U1wyAyGIuFaNKOozRipWY45NTjOEqTIkaGcWS378XMKzc2jDET4UoVvE8pmralbpoDmcVI018rif9VVeGDY3S9YAV52CBO+17ua5ONG0uuX9fikzTGSJXNk60x2degYp4/TwpBZO+imOP2fW4keM9utxPGPaUOg91um9eRyTm5BEOjwFa/+Sz+Ww3SKhQ2KamTR4dSmqACpqloWzkMyF1wpcTwQWkyHRs5nJIk9lGB63sMhnaxYtMPWG2hapl1HevTc+bdnLvNHX2/ky6bH7ndvGTz5V/C1Qua2mFSw8xaHpwtscbRXzlu7yJj1Lz/3vuE4PnFt58TjSKkiG0qQvQEVcY78wh5SuJOj+asmdM6GIYdA4bK1lSmlgMpZtMeKXdIStE2c1rT0uCZzSLr+Zx5VxP8jv2oaSqh8lfaUJkK1WqM7nAh4UaPNnbSxn316gUKw8XlQ+pmzvXNDj96uq7jwx+dsT45xQ1b/viP/i++/Oo7glcikG0slbXE5ElJhJZHNwitnRpHghRpZ0vmsyWbnWffDySlxCzEGlbLBXwnuktaG2HHak2vA7+6fkn3lebfefKETmvG7Z5qcFTZZCSEAFplZ15F9PL7iuNqSmS234FdBVAZi3cHBtYQHF9utlzZjqHpWJ+t2N/c8PybbwgpYLQk8rv9NWm4o9Itbz2+5PHTZyQM//df/HO+fv51ZlEoSJH1fMnMNlycnfOLTz/BhZGvvvyCGAK1UZN4vk2KKFknAOPosLV0cHUS9bPipqm1IWk52EUsXLp1AggI4HkAKkJeazlxS+meQdhx176AAMf/JslZ7pSXbqkiJ1k/MPJbOgqUxsnRHlaH8ReV37skPBPUU8CJmPLYo2Jm5lycrvnR43f46Qc/4dk779G2HW1bo0zChZGQJPk1JkrynZs6JikxDsmdsJjZfjZr11idwI/EYeDhxSVaG1brBbvdno9/+nf46U8/5C/+/GeMY+Tzz3/Ndrvj9etXvHj5AoMiLEbqtqUxFfVyzaxt2W+23N1uePHiG7RJhH7P9XbgybOfEJXm9u6asd8zDnt+/vOfMww9VVXx/rP3SVFzerakqWvG0dN0LTFaXr/e42KFadeoeoWLkkyWz9O1Lednmt0YWXQtYb/DJCCbAgzjeEgOE7hUGHtHYHyCMHpQCe/GSQcphDgZCQHZiLEUrvKeOmuNiQ4WCMtQ5YOpYhoV0wcwVemGGGusaXND7ZTgVjhfZAgyuBtBJ4cfr9ltv6GdD3R5TE3WdkB0uOy0jotZgfeefr+fzpCD/M1RAaPySPqk2yt7SpVx6hJxfUAFT3QelRTeRUgGmxkzYmR02Ec/BFgWQKmY39i6IVYVShuqpkXVDSEl0cxVaioEpnuP/h5IW/aWzolDSZDl3tyXABDgnsyeKcaDR4CnLt8nSyWGArADMaErnZlCAn5JSEhoXYGK0/2HA4P0HgNuAjUP8g/S+7l/v0qxKs9B4tY0ooWaYnrRgZP4luN/ZgaV131JBz0BkcKQLteYryqlaW1P9+To+kNmHUgZV0D44xElYVdILMsFWzi4zhdwXv6WwdEURH9NHdgEUxFUANSYMvsniJ6ikma0aGNJ3DVaiY7ldG/lKqXQlCI7lbU/gdZy/QrEgCRrLhc2rQqBWdXw9O13+PjZh/zk2YfMuxUualF2VZoqSUK8H265ubthdHt8cAzDSPCSnPusQV/kZoyW5Dlz14XZU9a2UpklIdfug8eNe/Z3V8RhJ+wvEjrJGK0cHrKQytGm87oqoHQ5BOV5yhSIVioz+QWwILOFKOdEOTMpTT3RF2zbBQolGqPjKHssyi9VSpyRhXklY2xORe7uhJU8m62xTUddWQwJnTy3L75CVw226cBY0BaMxfuBGHoWsxWvX71m2/d8/uWvWa7PefjWe3SzBW4cuLu+pTYVs0VNW2etQBfY7Aee/egj3v+wpqoaYMPJCTy4mGPxxGBpupbrm2vmS9FhNNYyDqOMoxrJ5WIUwYM669o+6nf81tVrPtq94twm4j6gY2J9coqtWl40HcN+z9JHggWUIYWiBAw+jQzOgeuJmxvUdy+pzC95+8cfYh+/i0exCQqMIZnM7E4RrVLW5q4IIWK1pakaWaequLOT9VxlskJyiAM33FYVGE3wnrqWUV6tNQEBlC+XNb/97oIH9YbN6xfZzFVTGU3RFffKkJQmotGVZb48BT9i6w5dt7loA9sGRtezGz2LxZqqbrM2omOxOiMqy2Y7SHPWGOr5iou4pb/5FfX5nH21JiEss5hHpo02MpqrNVaD1YlZq2kaqCtL8KAIojlqwCox4zJai6TIMaL4Rmz+t/ZK3/+nHI5zDEi4FAlJrn9wYsQcvIxjj14Y14NP9AO4KHInMcjZ4IMwRn1IvHzpqGuLc2VqR/IiFwIxOlLyRwZJ0iwyVoCulHX3ow9ZW9ZPZ2VCZZm3+/msUipPHGn89LV8z5WwvayxR7XJ8aSGAmLulcr1SBFvM3h9GPGW21U02HMPL9cIyhStfWnoBx8Y9j2awNhviKGnqyCFEaIjBtG2zfhHPntFfkfOFdFWjLlZbaydpm0K405rIwa2E2hd8p6DfmsxF53uYf7ewgyEAwBYWLQRJD+i9PYi1lRU9Yz1+pLT80tGl9gPnqYV41nvRnabrRgkxQQhA+4cmrUxKlIUqT5SZhfnuFHY9yk3R8qESvkc91zgy1q+V1+ZKd8TlDhNuYpSTECwjyEb6uq8nhDJAAoLWxi+PiSc8xNIqxHWYdsIi1Xne5XoBIBV5mC4nEG6chaO45iBcLnG0ogouzBkubOUWZmjE3ZkYVAL4UkYlykldtsdIESMkjcdg60yjKApWsqF3KCmiTozgbWluV10Vqfx95SwxopsoakQJrWe1mkM0ih1fqTaD4yuou8HtNI0VoBMmfoTo9IYIy4pMQLNz6qpKiGMFZ1frUjeM4yOYfBYG9B6QOUmTMprpkguWqNpm5a6aqQOCQLaS90uMkoy0ZWoreFkNs8eHlJHpLw/YozMupk0JZwjFeNmDT4DmuPouLvdHGQSlDSLTb6XMee9sW3wmUFdapTCqC57bopfLSxXy2yGGKZrKTl63/dsdztCH6jrihDctA/Kf9ZahmG41wzwxdzTaOq6y/uGac0tFgtSivTDwDAI0UgrLXIfKTEMPcF5SrNdaY2pq3v1glZ5mlsF2rrBVhZbKVrdEcN8mlArgG7K3kUxinZxSmkyjt9tt4zDkKWsYL5YTLJJbQa5vQ8YrahtRVVX1EDXzUTPNuevKUsahCgNhBDCxHIm5+wCwhdM5Ydff6tBWgCXdVtE3/fQ6TLIqF7RbE0hYKxogCU8KYXJ8EKczi31TLM+f5v5g0f4168YIixnS5arU6rZnK+//JLb6ytUJYnY/u4l8dXnxNtv6VpYNRW6d5zVmmUnB3AfxXjqrQcP0Srx8199yuh6TNswm89p5zOUUgztyN6NUzFZWKPaGubdklrXDH6PthqdUp69SDJSF2SMSiTTJTGbdy1r63l4MkfbUUTfs2nG6BzODazns5xMJLSFSufFGcWsrGlqtBJ5hro1LJZrlDbUTUXdVCgVGMfI69c36JR46+FDMJb9bqTfS1DxLsk4cmNIPomotq0F7AiJ+XxO3Wqi8pDpD0ZDCCPdvKZta0YvdG+Tg+cQPbdJ8YtXV3SzGR+cnbGaz6m7xLi9ZdzvZZRaCztENAal4C2O1AmVpQLkzxoxcE8YTFOTYiBGz83thlfbHVd1YB+hYcBay/vvvs16ZVkvEviBpMRA7NnTj1DVHLN4yDcv77g4u+Dq6gVjGMVsI0R+9emndF1H8p6uabC6ol4vBJAFgk244LA5YGvsJCgegyRYMQlTohT5MR7cVMX1WmenyQwCZS1WKEBUYZkVlmAGItJ9MOLNhP3ApFXTz9x/lWAiIvulFX2v05p442eVsFxLopN/LiUBByRJygCvT5zO11wsLvk7H37E7330U85WJ9JRsxZ01hpExAKtlUNecimVk50MaeW/o8rnlCDvx5Fx2FM3lrPzM0iOvh/Zj56vvnuBCz2//uxLTk7PWJ0MzDopwtarBXVds16tUUpzfXXLcr2m7Sr+7M/+gm+++VZG4E3iy6+f45nx9OPf53pzx2a3YXtzzXq15K233uLs7IxxHGjahpevXnCynlOpxPb2jtlsiU+Kq5uRvTPobo5pWnkqSuWxfZuZBJZZA21tMApO1+fchh3OJ1SU5o7IvFhSyoZVSRKmArppA9ZYVITtzR06FUBQ9muSXCgnNAp0ZlkXKQDC5MUkup/STEteNMpClMJRaU1Vn6PUQ6yaQzUjMPt/mXuTX1uy68zvt7uION1tX5/vZZJMksmuSFFiEWUBBgwY7mAYKAseGIbhf8B/iGc1M+C5R4YB24AGhZqpyi4LVSWVSiLFJpnMvnkvX3O700TE7jxYe8c595EUPLBgHiCR993mnIgdu1nrW9/6PpTNhN0FOgZycojjsialHnLCh554pVB5R7vUaFMA2mRknhat8anVHdj2vQBUtw4/QXOMrspjSoCdEoDWaqouiUSKUq1XIaBTEB2sEFGqAgB5+pvXQdHfXFsCFMWyiSuryVra6ihnXMySJFEAkv362Sc2tzRKM8QUUAEBrKZ1nfaFkn0lZAK2anV3agmvP7t1/fs2xODHg8RrD8TmFCZA+HVQ9nVWb857ELUyWVAFuD8AKYW1kiazjozMm6qvKVvHAaiJdCNIHlQ+8+C9KhOj7qN7kLckX0WSJk9FJAHu6vtUFgKF5SQd13kazwl8r3dX2p90WT71fXIxVSGX1iwlbfmJ/Z67Hz+NOkjGUpm3eRoAYckdJuqHz62uW21KsqGUMAutFifaJGyiGsjnDDGMqJxpmhkPzu/xra+9zTfeepu7p/ewaoYPGuNa5l3DMI68evWKnAIpbhn7nk2/ZQyDmHYqgQ6UrmdJLMYNFK39hG0acU4uc8P3pUBhFORIjsKo1yrjWkuKgaEfyIWFUjhRE7BTmRwV4jAFoIXC/ipaz/JM0sFY7ec9Sdhs2pqy5oqumdoXA4wCk4QBJ8O/l1CpxdOcxTAojAObqwt8v+NodUy3WKFcQ2ekO+j6Zk1MAdvOsY0ApU1rWR0/RGOYtTPGfoSoSrHIk6MwfcZRkrsQE9vtTuSclJImBeMwtiWETPQeZxSN0dhRXK5DmQ+pyhMo+PzLF4wx4roOpatJkqbViuP1lq9eX/DOsOV+HFFphODRIZGM4ejxW+g7b/DpX/+EcfOShBSbXcqYYcDjabUiqcTF1TVfXlwyopgdrTjqFMNuw73Hb5O6I0YlReqkxARLzOsTttNFCzuTlZjCKa1pdGUeFlNTRH9RNJUlNmjbOaZrUKG0SuvyGUROGs07D1bcW8Jw/YLke4ydYWwLxpIpklJV2qbsy938eEo298URjXUz2naGLkCy95HGtsxmJyyOR7a7NevNmsePv0JUDc5ozlYdm96zjhu0ktXSaMuQpdjUOj0VqYyB+czQWgHvUpQ14JxCWyFx9AGsBacyTSEyqIN5/v8WpD1kzv1//dpfEVPBjpxLjAHGKposshlSyIJ+0ISUCoMUYlJsd5H1NiA2HWbS+lNoSt2eEDN5lFxA2K2huNzXHVjOIwGFLI3rRBIhi3a3gF2KHIWZHOMojCglbNZ6MOWiuZ8KAGF0AXFTJNXuGqSAZ4yqisMSo+oKIpYibYm/6rkpWt55D+blLF0cxbxMNqksDEotv6O1I2dDDEIGGYatrN00YnTp6ggjqei0qhI7kaqGMYxh3Ou0KjEkMs7RNC1aH3QgxBqjqCkWFImseFBEkb03VuBH6SIZU2V8QB8ocFSgKxQWYO180VrTdgvu3H2D+WLFrvesb3a03YzjowUa2G23hDCASqQ0lnNd8NqcKsgu41tlfcoF7n8m+hr7NaCEeCVfSuGxxhUqg9UGHzOTzrOu8YiaOqR0eR8BLw2NMego7e+xgvAIyQIlnS1Jg2kMWWAQYko4baWAXrs9yiTWypVc0JAK+IT3E+hcgVrvR8QsuHi3SKVHQD5jJnkg6dIphAEt46KyIus8sarbblbmaGRiilo7sSyt1gzjIJ1+WuGsmFrZomkr11JyCwQ0rfIeqRSbyVm8NihFWEPpuBSArsbGMck1WxpclFUkBQuEIJairLUc0aXTUsvSIWaPxeCswbVOuv9iJMZOfl46rYyxoHPpyhA29TDsWHuPVmLOZ20zybIZK3FE1WJVRdogp41o4CpV8lUhejnnWMxm0lI/DoTkS2eAELaqeVgIYdLzBWickzyigIE5S9cf6jYZIhVWatu2whpVCkNGmcKK1QpbCi+Ha3E+n3N0dEQogGMu2FrtpttutwzDUKbZvrugkhaapp2kBmoeUX9uraNzDZ1rJvD4kMThvceP4z6bMwK4brdbvBeJiW7W0TYt15u1dETm4pFCnmS1akHD2lZQ6VQJEYnBh1LgOIgdUyJ6L32hSnE9DGIWFxOZSNfOcNbJfm4slQTSmGZa5znLXMkp4r1HlfkOCu8HxtFP+c5ve/1+g7Qi1kmktAsUN0ZiJo4e55AKhTJoAzErjHPk6MnRl4kgB2XXdQL0NC2bfiBEaGdz7t6/j1WGz59/weXVS1KOzG1HDiPDl5+Qrp7RGUXnHJ3VLJeZe/MGoyPr3UjvB07PT2jmK37x7i/YDDtUa3Blga/Xa7rZjMY5huAJWlgXnW0ZY8LrzKATLiW80jhjicoRQmmHLJUSVHHYiwmjEndWirvzFmtGbjYb0a1pWqL3kD1aiwbXdrdlt9uyXC7pZg3dbEXbzWi7Gc6JsLdprFRcXUno4kBMW7rZAuM0D7sTlGqYzRdYrbheD4yjIdFxsx7wxS1vKDqey1mL00YOGNsxnx+heSGsV5UhSSumdZaZa7gax9IiJJuZVgoPvMye916+ZNG0LM/v4LRi2OairQTKCHgpKzKWIKIcwpLdY4sWUwqeXT9wc33DYnksrfDRsxl3tE7j4sCsdbz1+ISvvP02985OUOxorVRGjk/PeXFxReuOSCy59/hb3HvrLd799ff43/+3/4W/+Xd/S46Wq/UWnMa2Ha9evWK9XqPnjvM7d8FkslVs88gw9tL+bwyKjCqtzkrt08+pEotsNkpOqAlskA1BwE4JRqU6yoSD7sHYWnW8tbz0Xru0tr7Ul5LI+VagXoEiec89/pN0ZbKp4r5cqpYHVdH6N2mqZMkzEsdmDRFa1XDn5Iy3H3+F77/zHb7z9W9KchekrcW1LSF6YijXU6qCSpWK4IExg0qZTBGk5wCwybLBbrc7qYQ1jpcX15yfnst4xMCv332Pe3fv8rW3v8ZPfvITzs/Oubm6YfQDy+Mj2sFzc32D0Zbdruejjz/k2bOn1HhJcOpEN2s4PTtmtVrQGsOD8zNyThwfn+L9yGzW0bQOZzX37p6RgX7wNF1DP3guXl3hbMNytRRn1eJ+mpXCGodSBhUVlETi0cMnfOed7/LR88+42L2SoELJnqELaC5u3Zmq0a20IErWtBh1jN85ciqmPnkPgphycwJmAIUlIUGsJCFKa7KKhJyISWOzwlCu182x9gG2e0zKd4mpIyct7FHdY9yMpDw5FvDKCKBk9AoD6NCxu3kOObI4AlF2LvP7oD1uYjeo4o5bDmZhfLOf09WYKZeJWYEtpQkpEn0obHIpAKYo30sxiT6SjEYBu/fOt4evqXW6BEnKaZRz6KYhO0cu2oOqIHrG1AJDuVD2wQ61ivxa4iyJTGVt7tdF/btD47BDxnxdL7cZv/vPqsH8fj/Yf0Q1JJO/uQ2Ivr6/1HFQqiZjHOwne7D18CVM/gqU1rEx0/5V2RbTdR3sT/s32X9DZV0Hi2rqIIFx0cUlYrWd3lHAazkLnXWTQUINcA/30ZT2us+HnQiH11iZTwqoLrCqXPDhvU/jyeH7p1v7dAhB2Bk5TfDCHjiXc0ErNUk9VfBa5Qw+TXuyNuXaorBijmzLkzt3+MbX3uFrb32D1XwFOBQtupthspg4bjc33Nxcsd3cMIw9JHFV7seeIQw0ZR3uTetkj49KmPer+aycWYlxtym6dBGVghQftUYohJFMomkcJmXGFKhaqbkAcnkaT9kDjC0mHJMmd9mjynmYy1pXZX4rxVTwzFoX7el6Hr4uwVFwkJJEVXYZUyKRRMrBSOEolfWVYmC3WZNC4ChDtzrGGct8PkOpxGa7Zn294eyOuPyO44giY0zD6fldVsdnHJ2e40NAGcvoR2KKknwU6YbLyytWR0txn7YOa5rCJI04rVjM5iycZug93WzO5W6LsY0YxlqDM03pgJBYWeEx3qO1pRsHHrz6gq+tL3mQM0ukYBHiADETUuDTD97n6//Nf0v7g+/ys//5f2W1u2aRR3LaYZSma454+vIpT59+xnbYMT8+5s5qhVUt482adfiQB/MOdd/xaVJo48jGShErVQMmh3UNSUPGTOYgOUdy3D9XVQskNToprPdGa5RxBBHiQhFYOvjKueNONzBcb4k+YEqCrbUtJQAB0WQP0MVR3NPOZihtCxGgrHs0u92IayxH8zlaG7wa6YdedH/bGa11GOtQxXAs6YBS0LaO3fiCebNgsKcMwRCTIkXPYAzOOna7gRAVPmhWM0XbKrJXWJM4WSlyTLSFsUUWproue2HWr+2Pv2evDLLAyqjHEOjHUAyWLSFkxiC/k2LCNRbtYDtEIeA0opEfQsaVZ6VLx0VKcXIbD5tQzBmlsyplJWtOybMWIEEX7epcWqRln4hJwI9xFN1LZQCt8D5MRW+fKhAoTPMcS0txljvLSeKqFPcFbEltJcfLWfwQVWFux5yn4qMU1WS8oveMg5joWGXlnoCmLfeNKtIIAhGqUvCCJOBiStKhAYXkkJCS3qG+fqkMFt1/rTRGGxrbiHO9kus02pa9sL4K80+pSbNxX/RXJderLzUV2VQ5F+o+W9vdVQHqYso07ZzZyXzS+766viZn6OYdR0dLttsbhn5gHEdIocSm6RYIMnUapgTUbkTpgkjF3CzFKJJJVLBGCuhaabIS2Zz9GO1jmtp+XvVYq36/MOIL8zNltJVukmEYix67MO6SHEoS7xVzTYMRDKQATdlQOlJEL72yJKVDMdzSxxRt2N9kUK5WS2EcF6AvJpnjEmPstUblJm9LON3S2y+M3FxiYFO7lAob2lqLNYajo6NJt1nizCx+ME07fT8UndmqGyrjW0HQQXTayzxRPjOOw96AbHoWUiCOIU5M78rsrJIHIKakYjgua1quQc4LVwyvYhD2c1sKESDPNSUBfuU9xBg8Rumg2PVbUtFptk2DHwcxjDUCuColWrdZKTHrUpq2aabxVFpNRl1GC2CcVZ7A1BglFp7P52LMVQoY1Wyt5vHjOLLb7SRGMroY+InJ19XVFX3f03Udq9WKGAKkSNai5aqNLiQwMcM6NFutOYJzthinSj7tnGO1WlGlHg5fFQdbr9e0Reu2Fly8D0jHjJ5M3arhnNYa18p9a2eZd215Bkk8F2aa5XxBSlH0YRGgeta0bDdbYpS5HFJEIXMshig+RVbWVp2jNcYHJl3aOp4V8K73EmPC+yAa+mXe9bVL/GDtgXi0TIxyLQB+ZaBL95iTzqsY+F2v32+QFkrCKId4BqrroOx8mhQlibZaYZsGZW3d90kpFLHujEc0K/sYUT7w4MEbNKsjdiGwuXjJ1dUFikijRszQS+vw9gU69yglCPmw23H/qOH8ZEHvR768WrMZEl234NNPPuXi1SXZQutm5eAvrFJjpCLog1R3owBI0vpqUUbh0whIVS+miCoyD7YAm7lU4xIJ4xLzNmJUoO93hCit81FJy5M2wloUxmzm5HTFnXtnrI5WHB0thZGIgJzKiGlDKO0usbSFaGtRWSo4PojD3253IxTxbFgsT5l1R7z15C7NfIFPmsuLNT/5679h7PvSeqEAzWy+wDUO7XuJmXUmKQkWlss5+eYKnJ2ACHIuLYmZF1dr5cRoyQAAIABJREFU3kvPaNG8cTSj61pM7xn7AYWI/UvwUpNuUElYfzElsvfEEPGjuB0v5h2QGIYR2zrO7pxx8+KSO92MH/7wHzBfNQzphs1lj3OGgczR6oycOjQ7dps119cv2GzWWDfw4HzJ+fkp//4f/5ivvvkmf/uLX/LuR5/z9OkLNus12+2GsE3YmcPNHSf3zri3vMPV5pLtsCNnadPLJQGt7J2UM5F9u0EIHsi4Vg4GYK/ZM1WspJJNqexW1hCAKpysQ8frQ0ba7SW3hwluBWy/ZW1WBpKeQKVDkAKYgKwqeZDE3VUiF9nQoqbTDW+eP+K7X3mHH33vhzx59ACVI+OwA6Vo2lZYQDGWCjal4lYCe1USzBIL6hIoyRWo0gqmCFFaFfZJdmC77VHmhpQS3/z62/zqlx5y5uLVC26ur4g+kEPk4RsPOTo54fL6irabcbRc4ceBpnUluNCHg8NiPsMpTb/ZoJOm6To+//xTLi+vOTo65vT0qIAunuW8K+Cu6Bj2u5Gb6zWNsZysVhhtiVUvrDhlGtego3QVGNNwdnqH733r+3SLJb/67Je8unjB6IWB4XPEKEprjASbqoAWmo7j5WP++Mf/IZ998gG/fO8VIZlStS4Bh3X4FEhZPo/MZCQGFp0kMZGw1qARR03d3MWrh4ztMaN+QMonJDq0jti8xqgA2ZJp0caBlrZlryJat2QspslS3OkDN5cXpORZnDRgSqKRmYKUw/lb2Rm32Kfl37EkSbIP7s0qIhJ45pwhBnECTqm41gq4k2Iq7MY9sHkIyKqDw7oCpdoYYfIZjTIG7ay09upMzuL4qlJt+9onSlU7t0zrW585rd8DOZcJAFUHAOFBcHV4bbfGK9+WO7kFUBUJEwFPX7u+1/aN1//+FlCcBOCpwbMq93cI8E7AbN4zYg/f83BfkTgv7fch2AOqpaVdQOfy+fVvEDZEBWhvi/bXlr6aUO3lYG4zg/NvjPWt95i+V9PTPCWfh2OtSnGAkg/nEuzUcZt0ctnv9xXsPRz3em7UN9PKYJQhG6CYpijU5Mhd9VydcpyfnfEH33iHbz75CqfHdzFW9E6zsuhGYp/r60vGzRYfBkIaGH2PH4eJbS7rMBdmQv6NMRPNyA7nLFbDdn3Nuz/7W+7cu8fZ2SmkhEoCdCYEhE0xSOCewRjFarko6znI/UxjIIlv3ZdqEZfCBlWKqV2tPpV08PzKaSJHUgFwa4F0/xzr7+sJvKmAElk0kGuRyGg3AcFVWqbvt+ibYkTSLWidRdGSwkYSjuyx2qEAP0S88qTcs1otuPr0JfPFEaujFReX12IeoiXJTznx6NFjrK2gpDClr66eowzMbMNR16FigCgmGGpzXYDsRBoHxrjm/PSE+/fv8cGzp9hFh1bQRbi/7fnKcMO9sMaVuMSV1ooYRxhh9+IFv/jX/4av/ef/CV/5r/5LPv5nf8bu0w84bTu09mwxfPLiBdY5vvHkEbOmle3cB14lj9oN9L/+Bc8/+oiLxqHaGcu7b9CcPyC5mehMZnlm2ljQCtdY0UIM0kpoihZdprQzpxr7iCN1TJnGumKsFHDZc29muD/3mOGSFBXWSfIspAhdzgdJqikgXtUlloJl7dJTuKaV39ciU+VDRiuJt242axpnaJqOse+xbobCTMw5iqdDl7bcvHyX9vxbbDGEJPq6/UhhjmbCLuH9QNPM0UHRuCymddGx7AxGSUE2xIw3wlTcM+5/O1D7u/exv8fXwUdN61CWDMYYFjMpKGdrGKNiDBkfQGlbYnvQOrM8Mqy3GWOl+0DwAUn4Y8yMY2DX99K+GwVAkPZyATFDiISYaJsG78PUbitMPnnVfbeCH6po/mutcdqSYk9MSfT8Y8KX1nIjFU3Zj5Q40OecsLq0AScYRmkZrpqcSksxLJNJWUCZnJn2wWkHq2eodljTSTGRhFIDopkqwGsMsXQ1jlgt3UEVtE0hUZW7UYUUUlkG9YwoRTDXNBPIaJ0AXLkWT5UqwIO0DldGao2jJBbj1nkOtbippr0zl4Ij7I2NcymmoRTGNZzdvc+9B4/YbDZ8+fxLclYsFktms4YQR64uX+G9nBtGCyBbz2PZ/zPkKMBZGc1cTHKrXE0FcSWPUkVyKUmuphWkqkNetYWlEw2lxKfEByZz13KvtbKfQ42lUmHXpSKNVM6awv7UqsrpQM7FGFPVIm1lWMseFJP8ojVSaLNGlf3Kyj2WDuMKuk7F01rI0QYfonTCVn1PihdQOT8lJqlnqOSSuXQSpFxMyQ7AW1LCti3kfAvkgn2hswKfAogJuzaEQyB335K/XC7p+14A9CyAeYrzCRAcx1E0VHNmHHrJAScZgDQBtHXOVYOter0pRULQaB3ZbHaTjnPKCWergaC8n7EWqwzJJ0IyQiwzYprXzsREchzlPqwxhHHYM4KRuDSVYnCKcdJ+rbld0rmcbSLDYkvxea8DzH6/eC2HFxAxYq3l7OzslkRKHevT01O89wISa02ylirTlFJmHCqzWU8GYzHGae+sXYtirChdN5WdW80W61yr4189Qqr0Qd1TjbEiT9f3FI9BYZsqAWub4Ccm/ZRLVUC3/NsYMxl16aIfbrWdYsmQBHsLQbqxht2AsXqKwbXyEyFHmOT61nhXs7Za6Mgp07YSh1Yd86axRStaZBSMrrliIIy+gO+SW0iMKHIkUijLE4j+216/1yBtpjITMjHKg7POYFwzJVEgSbZSoominGU39BjrIIJSUokLlAqnNqwWK+aLY67GgZv1NdtXF6QQcHnApi2bi6eYHCD1mKboX4TIsrE8fniPJkeu1wPrPuO9IvRb1lc3pCgatBkkKPDQLTpM1zDuekKONAX8KFLFHHULWuuAjIoRpQPRDzSmlSAieqxSOFH+p+1mLOcNKnm2m6Fo1MgC9eNI0p62a4TK7hyPz++zOlrQdNLC4Kwh5cRu15fNxuHDKPTtFEhZi1ZkOQAUqbBcPApPyFJV3G0T43bDWjU0qyNOzh/x8OEpVxd3ee8Xv0KZGYokydXRivm8Zb2+IRf2Xowj2ipWs1ZairShcY0ENuVA9X7kRe+5vLpiGwfi17/G49mMZgEmKaIfUKXFh8LqizFilCH6UWj5Wajyox8ZxoHVaonWirAbCHFgvjwiq8j9xw8xixnBan76018Sx8yPfvRDhnHHzasrlt7wwfsfiVlDa7j5/COevvyCm23m//oXf85/8Z/9xzx6sOLhgz/kx9t/xJ/+03/O519+xs36FRevnjPsdvS7HXEIPHr0Bqv5nD4O7MaIpbK7NDGVRF2XitEBwAKUwyWW6jRUEECXJKIevuLubUqlJxVAVFNV4n4zid4forXKVYOrQ33HejiQJ1GB0mm9lzqoreMlg2UyTShrWq5HAiCdFYtmyeM7D/nRt7/PH37nB9w9OiUlX4BpuYhYTDAOmb/7XaLgAweHVtVUSkBtBc+oohFzABjHkZACnz19ik+ep18+Y3l8ym675uXLC370D3+EVvD86TPu3b3Dk698lXW/pd/1rC+veO/dX/L0+RcCfOo6XhmwLGZz4tAzjAOzbsFPf/IrlFbc3GyYzxc8e/YlMckBcX58DCkIA9U4Xl3tuLnZ4Izh7PhEbgEFRlpRtBX2BErAlG6x5Op6zfnpfearY4YwQFC8uHiGTx5FQtuqRa0nIMo6h9YNq8U9fvzjP+LkP/pH/I//0wveff9vMVr0pGRy6mmNCZBUgsTyHY1Cq0TMFqMWYOdEe8LgvsfOfI+gV5KkKAvZYPPAghd0+RIIJXmWAFYaSUz5WI3WDTk3KLdCpcTm6iXWKpqlQZVEeDpwD4DG+pp1HQrRtdszHnSZE2lqm7KqGstk0TUMCRXENjrHDDGVdvHCdz1YFxNAc6DzdIuFriCSsFoTcsKUBKdY5QgjQSuUKmfBZMpxACAeAJk1EDsoAN8CYW/vGbeDucO1X9/v9h6wf5967bc/QwtYcfC9w/e5vY/ISytFZF9MowCGvAY4v/5+9d+Hz23//bpv7n/n9u+aWyO4b7HdA7hV71G0hUtQXzZXrfRU6Kmviam9v9ppfOq1HQLjkyHipKh3+xkoxS3jN0nAmLTHc7b1YybwdmIHFaYMtQh1OIao6RwwWVhmIvuiiT7QWM35ySnf+to3+MZXv8mD07tY1ZBNR7KidUfKrDc3XDx/Sb/b4Pst2igigc3mhsqWks7IVApjwuTRB5pkwnKXG/BRZEOssXz1q18TcAWoJi3T88rCdiEUg7DDIc+ZcbfDh8Di+Fg0yoyRM8JKoA2i4VnHWkGR2TiYJ7GMv1ZYXfeyIoPw2vqoSbUkYCMpRWFBhIQ1SQysqja82RvGVI3tEAKb9dXU4tl0y9INoTFk0rhFm45l1xCC4dXVDSEmYthy8eIztusbzs/PmbdFjzVLQut9X+aJjK+xjt32ml/88qecnZ/z1cePmbcK5RNtM0Oh6Nc3qJxwRvPlJx/z4QefcPzoCU8e3OPDTz9l3PR0WmFefsnq5jkn/oYmerQq7NKsaVCMCBjeRc/1v/m3/OR6x/f/uz/B3fnHfPIv/iX95x/w/r/911y8vObR3XPuHy3ocizSH5obIp+HkU+GyHMf2KQvyUra01989j6Lr3yHk2/+IV5pfBiIKcjaQOGHHc42ctaqKt0gyWsIaVp3AmyIvIdxBpUinQncPzI8Poa53pHTQEIKvqoyPJRCGYewKuoaFnDYNW3xA6jzETIabRrmC8sw7BiHnsaJruLx8Qnrmyta19C0M/q+JwPWtqhsStu3xiq4evYRjVccPfkDtnaJsjOsk3Mp7uSsdc0MlGG3C7THsOgcVWvcOQg+oq1mGyJRg3IWk4W48FtR2r/j9fcN3FZWfF0jYZJkAqMz28EzZouPmV3vhS2oDSGAj5kxRukG8IoYNdFLUg4RP0ZhH4eIDxFXdC7JIsUWlQCq2hiMdcQsUmIKAW+rhqbIiUnCXsEHYT5mumLOFIdB5mZK6BgErM8SydTOGF2DxOnsrwxXMQkOKk3noUxCyZ9SUqVTR/Yj8bRQtE4T4jC1SascMFmK8qIlOsieag05BlQKaKT4pXKRwQKmPpyUBDxCzs6MKvct8aU1GnIUbW2jpbW85CnyyFJp4w7cigVeA+T3sUjVmL8lfnG74K11uR5F081oupbdbsenn36CH0dOTk7I0XN58YKcs5CNps4XjdYZ6TRUEwBL6USB8jiK9mhl0haFtOlaK5hYX9poYbdG0eO1xjBrRRKt98NU1GYCmveFXpTECRXEVaruWaU7qQC1ddxCjIQcJwAoFJ1MnYqhlbMlhpDFLaCZgLSK8lmvxQbCdgzTGOSi/RyC6GiCRCvSxSDyaoft+ihF8HHybjjs1oqFEau1JvX9tOaGYbjVrdn3ucQFcqMCvk2ZI1XOxhaDM200s9ls+vsUBQhv25YMHBXzy+urK66vDwroQNseMwwDVd4NKEWYPAFlpb5GioGcJEfRBlRShNHjRzGBMtaig4dR5n3tXtVFl7YClQK6SZG46zqq7nR9hcIwr+zfMPrSySNzz2gxqtrtdnst0xBK3NFNYOxh9141g6uxvZjNSdHSlbzdWksobf3L5XK/DrPcm20arq6uDroL9mC3956+7wnBMwy+APzSVVBjI62Ftdu27a2YvL5XZQRXoF70dUfOzs4IYyhM5WpmJ7J2GsXYD9KZXeZnZRBXpm8IgcY5GtdMQHbbduhcNLRRtI1jOZvJmkpSIPGjn0DlMUh+WMd6HAWsbtv21vhqZUpBonZSFXJNFs1aaIrMAlPXhbyvF5JjlOJZjLFoiGvCdsvvev1eg7Qgk1gr0XuQapwcXjHG8r2yIWclbalaKh2ZVHZgMUZIWeNmC9zZOblbcrnbcbm+Ythe4woAyfaKzeUzYn9J0xqU6wTYVZpWZ+4tWo67DuMHvlxvGDaeOHissgzeo4whaY1xVoAgDViDVxndOmzj8IO08Iw5SVUtaxo346bfSCLlI9FGgpLqqyoJjwGcVtxbHvHw+Igm3aBNxDrFGEWjprWGtlUcHS05O7/LbNGIUYJR7IY1hAIP56KtUzRAY8z4ckgYV9qwMgKk1aA1Z1RS6CjghNYR7RL9sGV3teVmc4W1Hev1K2CAWBejpmlbFoslRr8Ul1kt10GAo65h2c248h6lQ2E4Fa3FGOn9iMmKj1+8wimHeetN7tsG23QQPeSA1hKoa61KG1CAlPDDgFWGHFMROrfEGMSUYBiIybPsFhwfHzGSef/ZS7aj52cfvmR3PfDZRY+2siHdPXvEp59+zvd/8AOevPlVFjoTtz0ff/wrmqzRIfNXf/nX2FZzevfrONfyox//iLYN/PQv/4Jfvfsxr252rF+u+Wz7KXe/ek7bagZdRKaJGCXVX8pGe5vJc1AZjNIaLRpUciBPXta1hVmVltOiS/g6e/a3rbP6qqyz11/1kK2trJU9m5ADSzYm9Rp4BaLhqfZAwyRalThenfCtJ9/mh9/+Ht//5rdptcXHXgJGspjalIpjRjZRpStrbA8ox8KQnQCeVAzyUkZbhzUO4yzJi3nexcUFMQVQiQ8+fI+nL654/PhNHr/5Jt38hPWrF9y9e8rV+hKn4eh0ydNnn/PTn/+cZy+fMww942ZLGD2ua7EWCcizxhiHxvD4ySMePTznZnPF0HsePrrPhx9+wjiOXFy84vT0lOv1FavFkqPlEVdXX6JNy6xbsF6/YH2zZjE/4Wi1wiiNc60kdMh+5odAzJqsM9o1jDHTKsv56T1++L0fo5EW7s+efUzSCWsbYmHDKqVRVtZ6CAOvLp7yV3/11/zxv/dH3Lv7kPc/+RUpexJFCiNDVdEUkkHeP0tlQVkCmmTvodxjgnlI0G+w1W8wmhOE56ameRBRtMoJKJKi6HwK9UE0kbQTFqsXuQrXaEJS6CCt8P36hpR62tV+jQh4mUrwvy9ueO/RVKC/JAi6GoblKaipmlo5ZdIYYLdDjSN4cfGsYOot8LWslxQPEjr1m+st50zTdihnCmAmVfO6zpyR1uPGtqAyu6GfguhDUPUQuKyfd7h+fxuwOZ2jh0wH9knI7wJZJ/CQqv2lJkOvSarggI37+ucefh2SnGd16e/zt99kqf62azssygiAnKeva2Hq9j3cNiQ7ZLZCdVDeX7sxovGWSiJFFgMNcwAE1+s4HL/fOfZA1fWsxSsqYHgA0h6O0xRwK0kcpKp/uDfXQoaaANu9pEGZfwdBey2gCYsWkhdX+4d37/P247f41tvf4NG9x2hlSV5a8rrFArIhhZHLiy+5unxJ3/eFkSBdKW0rpqZaKznLM1N78DCMmMbRNkVbTAaGEDxjSlijSwt2ppsv0Crd0lWT/b3qRSKFoSxttiH4ySQj+MDFyxe4rmM2X+zPy/0EKvO1ML9LQWDSLdYyB3brLcvFAlWS2xLqTEl0TaQri8IYIyBbOZOUkmRCp4g2zZSUa703NFRKdMoVkc3NFSEkzu+1mKbj7PwhKgWGIbDuA03bsiWRs0erDnzAxcj182ek3ZZ5OyMm2Y99lAJ9P46gpD3VaU3TzXjnne+Ss6LrlqIRnD22a3j27Bmh70USIcCrLz5lYUY+ef+n3Pv2H3L35ISXF6/oXzyHX/+M2TIz61oyRZtQw6gUJhlQFpUUre85RXPxk7/hX/6TF3z/v/4Tvv2P/1P+j//hn9A9eMJbDxoeWQ+bS6If2ZB4mSMfxJFPU+KFUdzkEZUDyySgjB/XxJdP6cgkLXummjoZIklHPKGw+wrcVZhp+WBtCCYnUik6R1TuebDSfP1cM8sbsvco40gpoIk0dg7aSBdbZdOmAvjqCb2RZ1v3F1VktyZH9UQcd6yvr7Cu5eTkDsF7hqHn+OiI3W7L1fUrVqsjnFuIbIJKqMbhrGG4+Ax9/pBmNWNAWkJFp1yYlcJEAiL4wbBJEd1lboJiaCSWh8CiNTgSaqGZWUpBQNVtdNoO/39h0h5cQt1cjRaPEUmqM21j6VOCKHJf2ihS+ToE8cLAGE7OMrud7IutgjyUVm9naJKlaZ1IOhUWVPSxxMYwm3UF6C9GX8EXoEDIDLVttXC0S+uqIeWREqHSuBYfRCpDOQuhKTrmUQxrplNe9iKjJH5PKWE1dK2jm3UiZRKqj0YZIzl4ReojRoa+RzUzMcNTgJf5L58lzum+uKh7P0q+YzQ5iO4scYAUpjM0l1w6eS8AlSnFTS1zWWmDcR3KtSIxoRWaWIyahLEt60HczqVDickoSu56fz97HUrIec9yJOdioPNaV43ad7X4vufl06fsdj27vqftWtZXl2gj+qfSIZqKXnApnmYtTMKCROciT1UkxgVU04o+eEIMZT9PlV9Slvrt3EgphVVu/3WR6kOpCaTy3oOSz0ox70HZAv4arQkF2KqF9jHGQmAS0kOoBeGssVpjmoa2XE2OVWrATudTyll8UdJB7FS6wLQW89d9HJhunbk5759NLW7LPlOKYFk0YWtcrZ0lF1avlgcruEsItAft8VpLp6gp2v5ySXUPkxgsRF86IoSBKGCnvMfAXgYg5br+mM52rbUUhYMRwNoaTNPUTEPGocgK1nsSANPi/UgmF0NpKXQYLXJJuuAJKSdc05CSAOZaa0xhkWeVMSTBT7ywoYVc5vGjyAVtgoccy1m0l4LIBSBWSgmgqcWk0lUQM8s9dl03dVSNo0hLVuaxtO8HYfAfdO7VWHK73cr1BM+sm00xTEpJcq0yHk3T0FqDjxG/2UiuctDuX39vPp8XL5WRvt8ihbU9O1kpYTRvyntUUL9q6Nb5VQv3FQRNKQlwrA22cWWOSNdDVjL/mlk3xYkKIQbUvx3HUcztjMZMDPPM5eUl/Sjd28vlAlPlQpR0gCalaOezCTCWz1YT6Ou9n+Z7Ndvz3hPDIKQkI539WquCT+RpPdZ7l3VemOZGk2kg104sgSh3Q/93nr2/1yCtAhFHR0kQVVq0YiptzjmgEU0cXVqUyLVC1xBNLAPd4BYnNCd3sLal3w2EKFWzxmjaFFDDBbvtS0gjpuhGhBiYzZdgEtqPnC7mWK1Zj5HGLVHjBbEPuOM5SWloMs1sLuYYNtGuFnSLRQGxMso1pCGBkgNcgjotvUxJaOliBpDIpiRWaEYyKnhQhuCFjt/nnplTNBlaoGs1p2czTs5mLFdLmrYl5chu3MJIoViLxlEMuSQiEZX01M5sjCOr0mZREhWgbCipCJpLVTgrGEPPxdWao+MjGpNJ2WOMuOkmn0Q0vlDom8bhnEHcVEUeXaeMy46jznLje7QRIxGrgJAY1jvSODJrZ4Qc+OjpM2Y5M3vjDe43LU2cF0YZDD5IxXw34At1Xiqw4Icdu90WZQ2xzzhraQzobgYohgAvXt7w+c0zXl7eiIOssjx9uRH8SWmut8/xfeYn737IR1eRu2dnzFTkYtNz5+F9VidzFsv7/OLdX/FX/+7PuLze8Z1vv4mPG5688QSbWj76/BlbFbm5vOTZh19w9uQeaGFKZ21ISlgARoOmHP4HAIoYY2ip/EoEIq0u9dBScjTFIoRfDwNTAvHDNtT6qt+HeoCV708rcK/hR2YSzq8/rtpLClW+lpdUWatWkDh665JoBRIWy2l3xPeefJs//sMf8dbjx3TWiGZtmYBSYa86nZIf6Sp6W4MwIJXAum7cMWdZW1pakIQZZ1DaEULRf1GaxXxOiCPPX73k5rKnXw188N4HnN0948Nfv8fJ0TGP3rgLLZyenNBvPT//+Z+TMkVLOKJb0ahKHmEJqgQ6ErSinc25c37C0ZHj5as16JEnb70JKM5Ozwg58exvXnF6XMwFdyOzbknTOsbNlhgys3nH0apDzLFEwyzGyKN7b3B0fsrPfvlztGpBO2KGQCTEwMMHjyWFiIFhc8PT6y/ZDTsxjhMHACRQUyiVWG+f83//q/+T997/JV8+/1AMGWvbWjYCpBZGADoRcyRHjVEzdD4m6DvE7g6je5NoHhHUGSEv8GZBVlJVljLxiM4jDknKwaMRHVuhr4omWy6BjXIa5SNZN2AXaBdJPuJ9JO0y2o3YTpPxKC2swiofUlvevfdTe0kN3Cjgldb71ucYC/ASE6HfEfsem3LRN84TyyWXPXRChHKmqtSmmLFFq67qSylj0I0TZpaxKFU0ybRiz9FIEgimEWvctN5gD4hWmZraKiSfXcBRajufnrTm6vr+DRCQ3wQWD6U6pvHJezfaygKpIIhkBnLd+zQsk6rL3MF77994fy81QK0AqxhZFXZL3W8qwDrtR3LGT9cOVDGI14HY6Z6zXFfOyNkmDx6QQqVAhgKAVKkB2UNE1iOVVsI8jUeRvZDT5dY9ToxltTemm0DBWqO6NSYyzjHksuVVtk1x+fXx4HczSsW9pq3amypIsW7//hMTTUmR1SeJN07mLV99/ITvf/t7PLr7BsvZEWlMbNYvUMDy+AwVNlxeXrNe34i0QQz0Q08/7ohFj9TaI2F9U2SnpiuEqBTLrpsSnwpm6gKSpNKuWCZI0REvibg8KXkOilIasMK+VwZryvPIisVyhXGOrptT4OjSOSFj44zdAwKoiRUnrZ0eowzKCIupHiR7lm1pX61rofxUa4mNcmmd7rc7ZvO5dKxkqDI8WbLmMs8L+56EshYfRnZXL1Fac37nAc1sQcbRmIzzFwzrC549u8A0C/CO680lV5cvuLy+YbN+RbM8J+uuSPZUUyONTp75rMM0LcE4ODPoMPJgtcTGLd6KztvlxQu096iZAJPKSavj+vpz9NOPeXzvHuOLL/n8Vz+nefkFd0/fFKmIkMDsdbeVkriCnFAxYPOWU52ZXV/x0Z/+M95/9Zw7D97kP/iT/56f/ek/5fpv/wKTFaOZ8VlMfBY2fBozL1NiG0fW2zVKG6yb4ZqONmc2IeCQVvZUOjlc6VSwCEs2F4eQXHQnVdEiTUrtdyWjQGdMHri7iNyf9bQxYk0iKWHT9ENP4yJdO5de0lGGAAAgAElEQVTflwWPVoZsi1nTwQxNOqNi2RsTk2wLSqNNi7EdQ3/BR+9/xA/+YEHjHNvNjmEINK0AcpvthuPjDpWltda6lnsPHvDs88/58Gd/weMf3gHr8METEsIgJTCMmrOVIbvArIPOUfQ6DWPIxGBwFqwp+tQIU1xXwsW0n+6BjL/P1+vnQD1fSi1sf11a0eiyZxcOiVICmDinYCd7hbEKiomnsaJ9rwi0ncYEhQ/QtU0hJOYJyHFVP7IWH2MgK+Tcz0ghIpXzvRShcnGRF1CzgEw5IJmZJhaGrjOu+CuA0pm4E6JJjV1zVuicpFBgLNY108+VYdrDMVbyoyjzOiUpgIUgDM1hHLCuwUcvXQuxDGQIZD+QfU8Yd+QkzFmTpAvI+wGtpA1dUe4j5vJ7Rc9UKbQ1Ra+6lW7UMi+da1ATICHScdN5l1QxjJTVoYvR2y2d2inPkLO4VsNq95FWTK32+y6EPAG0MSXCuCOMPTEGae3Pvngry3s4C41yZf8uxV+K1mrwBaCNxfC4xAMp0/vSUl3OVVMMqA8ZveVwpWpcK6VxtkV+EBkKyJ1ilLg7U6SAEiHL+Eq3lOR0GY3SdmrfD4m9vEXJr8UwzwhrtnSmqGIMpawAtSklYt5LS6hYWHsTCGSKtY+Z5rG0bu8B5xhE/ktCM+n8MBX4LlIc0s28L1zE6BmVECBCjORk5N5jnDRHK1Ba40jRb62gPMXESbNYLrDWMfS7Mh4ybtpIcbYEifRDj/fSxWKNdHWI4dM4xRrkVKTn5JlJ6/ueYVpJRtYYjO6kiFGKe5T9W85sUEkM3KSJWdM2VqQ+nEMZI/IAtWAXxZy0aZqSt8u197ueVy+eT+xiYzS2GKvX61lfr4vWccY5I+xhpVHKkLVIiVhraduGrnFTTKmtwThLN5tNcgR1voru8Ip+GIRFjOTHdR7txmEy+WqbhjibTV3HOedJs3YyOzuIN9u2ZTab4X0SXyhFMSw0DOPA+maN0bbIPmWsk66mcRjYbbcFzGzKnpqmPcFYi0aJAZrWUw5VJQda18lzRUHeSyDIfA9S1KjdjBpcC2PyDOPI+mZNTiLVUjWXjTEka2W/ykJ4MWXsG2eZdW3BGeQzhWHrxeQvpIKzlHysjME4erRWhUELtQJjS4FDQFyNtnLmaQOdmk8YzG97/V6DtIBs5KVi6YtT7WTO4BPaNjTdnJgTu6oHYRSNdQTdoecNx3fuk5s525i53G3Bj+ikcKaldTvCzUt0uCH7a6niti1+2KFUg5k5TNzxaL7i7p1z1sOOm83Aqjvm6uITtiqxJBX5F4VxwmwzbUN7tITGEL0kV8koaBwxD4LmF21W5zQz3RJyEBBFSUuFVPwk6fYKtGvQbUvMme1mh146ZrOG+3dPuXPviNVJByoQU2l10WImJeGHYhwDOiW0qQskYu1eC0NAvBqOqqLtVhzOtSx+cV9WqJx49eoll5cbzs9OJHhWhuVywWaZ2F6OojduFNZY5vM5bdfhBwg5yKaoRZrgbLni5aaXjU1prNIENDlEGiQIa1yDj4GfffghLkXUo4ecKk1rFL7qTo2esB1JIRIVpU3Ak4NHk9ntNoz9jqN79/C24cX1mng14M7vcTOM9NtAozqyg9VyAVkAPal+G86O7nB2/w1m5w8Z+h0f/PrnfPnlM4xJDH/2z7l/fsLl5Q3vfvQhx8sVTz//iJcXzxm2W4yFJ2/e59LvUE3my8+es73asjhrSSoJ/V6rspkKNV/o8PtEs7o7qnIA5aQK8zhOANQEpJWAiZK0q3rwH4AZewDkoNZfNSKLA+oUiBWUtDJ3y9KcKpVMAEcFV+u/60YqGsEqZxrd8MbZA7771jv88R/8Qx4/uL8HHLSa5DskkNcYW9uOKzArLTi5ohFZdAgjUtkyytC0M6mAZlUOU7mXYRSTu3k342i1IgZhhx0tF/zg+98GPMczw5uP7/Pxx5/z4MEpF5drri6+4NmzFxin0TFjrWI2m2GdojWKzjYoa8AaFoslrlsRxzX/6s//DGMio4chSDGEbPiyv2G967l4/pSvPHybfuxZb3c0jaNrNf3uGp88q+MTlssliUBMihgVQ5D76PstMSeaZg7KimO80cLqSIYnj7+O346k3chu23MzrMEWTVsK26EUtXzecbF+Bk3maneDzgGQeZVUkQVQwJTItAQ6sruHat4k2G8y2jfo9V0SK6Sko8gFKFcKVApkFSF7NCOGEZ29aPvkVP6TQEkhemIaCUwBsB1uDqFX5NEQfGJcRxrAtgmcJmqIPkzgn0zqPYNz3/pfkmuklTr4CDFKe3VKwthFo5IAMuSMn/S6FFALgpV9l2+1n2tZTHtGgxbgAKWwjSOX6rgqgWRWxZxkjPR5mACjvXbpb0oZ1PuryURtOap7udz6b0/AX2dz3vrdvGdW7O93D4xOAcV+eAtwO73T9J4TG2b/69NnVUDxEHStAVu918oQkX2P0sWhDz60/u/2Z5aHI0DLpP9UP/swYE9lzCTRMQUglSupoMb+RoWprQ5+tmf7qvLeNTU9vKx8sDdWkF2Yn/LZMd7WsDssmNUxVbqMYwXmK9sUjSpGYEZpTCkqhBRxKM5nc7765DHf/tY7PDi7z8zOsLoh+MTV9StaI4BDv7lhe/mSbT/Q+1EYGmSG0BNSoHar9P0WXfTxxnEUFoJ16CztXlqrol2/lxWBTChaY/UexSGXwv7dj2E6gMSUFlPTlEx9IsKosY5l201dJ9OA58LEq0ltmXsKNTHBnRUWmraW1WpVgPIg9zCdndy61sqKHvotu+2O+XxOyhTTDD2xJkTaJxBjaeWlTkORb3K2RZG5ePVcdOOcQ9lWujpyIvmeTu8Y+pHr9TWz2Yzzszvcv/+I4CPDzYa2zVxfvqBxmq5pyBaG7Y6xB5Mzu2FkDCPnixmLWYvf9sxmR1xfv8TpjHOW+w8f8OryCh8Sn372GXEcufriE/7B0Tlh7EkXF3zr6Jh7tmNBwlIYZlFYyFgtoL1VUngPEd0Zxpef8Ku//kv00Smnf3TEq/feIzeW7p3vcvHyJZ9fX/DLi2dcGsWAo99s2Q6b0toIvb8hXV8RlQa3FHOOmAh173O1VVyS6AnwL/tlqXCjUqKxnRS7NRzPMo/P55y3PcfOYxFQxBiLnYsprjEiZRBzaRmNEtdXE8Gca2GmsqP1YeQkwE45x6xz3Ll3X7TcQ0I5x/LomJyhna+wTcPTzz/n6Rc/58mbb7FYnQiQYhtevHjOB79+n+XJHc7f/jFrZmhjcJ0VuTfExfvsZMbRLGGyaNzpaqWZDc5EZq0qTM6Iwh3skLe2y793kPbveqmDEZzOUTQ+RYYg0XCItYAqe8ZmJxIWVhuGPnKzyazXkRW6+DhkgrRAFk1FU1iyAWMEoMpkQs5Fwlm8LXKKRVaPAvqz/zqVlvumKRqSIquSUsIXAEaVnCmEkncUAKKOdcpZzF9zYWbFfQcPw4AfPGgtYGfcy5KNIchnKAFsh2HLfDYvYKCAzXHcCUs2lOtPkRwDOlfmaEbXcyUi8fOBfJixlrbpcNaAMpKFKINzLbabYYxFIbIiubDGqGdUzhLXkqbilkgqlIcqm7b8o+YfgmpMAJAYOMpcqHqvlWV7GKvE5LGuyNkUwEMBuuQWShWmvdqz7HKO4rviR5E9KQBwLgVMmXFKQDGZlCXf1dNcSaUTSH7hkIEqZlchSvdmBkIB/qoWa0xxAnlz9Zqx0jIdQiht14PkcAXbiCHKaVe6BnNKjEX+LcRYKAEyv5WRorDRRjpVtKXt2mIIJsaLoiO6B8Brt5cpLOB6vd4PJcYp2p7OCXhm9BSDUgD1mBNJiXRj8qJPbpSaYjSf9jHNbNZRF4IxRjo/y8+GoSdnaNoWVfL2+txrTGutpZt1KCXszb4fSgxlOHKWfhjYbtYE73HWCShmdcHQCyuzzKecMz7to7SQBNgVvWFN9mNhPgqwFioLNGpcjKQMrskYSuFLKVTRODWITnXVa10tFhwtFxMzs+rM1nXnvS+maMLM73tZu1rJbu5DKDlhW8z6ZN67xglpJ0g3yWFReWI7a5GIaGdiSkrpqNJGY4eGxWJBleZyRgxfm6aZrm273TKbzab3BfH+2O22pRNAY638B1IMUDozmwspxzrZy4zS6FYz6zrm89k0vw5B5b7vGf0IWWQ7tVYi9ZgEfxKQeiZsaYS0WQFjY4zkaKrObxmDxbJlNp8xlk7Kuh94JXFtipF+uxNwue/FDM5Z4mZNLmdpBYxns8U0H4TdvPcFqv835Z6qrvlk5qfAB38rn6n7pjZ68hj6Xa/fc5BWNkfXWMbBQ0r7tidtmXUdtpnTzOb0o4cwCHDdtHjXsVyesDy7Q7IzrrZbdn3POAacFRaFiYHdp+/jX37E6s4p1ogmTArC/ENB2F5yb9bw1ukpysBu9KJJGCKb7Y5LFVHpiOw0JoOPHt12tKsFunX4cvgoo2hmM3LuiaPowShtsI2lm7XEoQq579s6tbYiMq+S0Pi7GbZxxLhhsTCcnc54fO+U+3eO0C6jjYA3MWa0LeNUKmDWNWRdK4ANPo+Moye7jLTvyPgaI1UziqmKHKK6bPLFATkkvB9ZzDuOV6fMugatwbUtWinOjhfEITH4gMqOnALzxZLVasV1GCEZUAWE0Um0aE1DUFpKC6WVq3WNuMNnRfAe4xyjafj5F1+gSHzjaMkdY4khM/Y7svfkLFUNlRI2RkIxdsK1WDo4O+FZr/jg+TUfv3jJ0ekZZ7OBqA3zbo5ZNOzGgdPTMy5ePReTBtcy+v+HuTdrkiTJsvM+3czMt1gyI/esrau3mV5mGrMAoAAc4oF84U+gCP8e8Q6hkCLkCAiIAIRwMCAIDGbrxlTXllW5xuLhbotufLiq5h7ZPUI8kGC7SHVXZUa4m5upXr333HPPiVzHPSwm7q9B644HD5+h0Hzz8iv+3Z/9Aq2lOB5DQFv4/MvPud1teXB+hmkbYpjY396yXDWcnm/E6a9kBa1r8ClidTlQlQiIH8aDSsFXDGCUktEZVZIG0XY6BgP0HCBkJF1W1TFAW/4AlDpi4sr1aH2kJwOzllb93QqEHAMq+ejv58+hNKCTjLk02vJoc8HPvvtT/v7v/h0e378PiZLIKOkeGyPrr3TChQlb3724ehfYJ5UEyCdhhXadoe0WtM1SGjlH4IdSMnKTQuTrL77kZGEwShHGyHK94Ee/81NefvNL+u0lr158xqsXX5HCFTEHoGG1XPL3/uCnLBcdi7Zhs15yerLm/GQlo9PW0KyWrNdrrOkg2yK7kFC6YZi8GHnFTPCJb16+ptUPePJwhbKJgOfkZEnbKt5evyLmSLdYobRh6EUOxTRrHj15TMyJr79+QfCJbtnQLZdFID5DhGmKuKbjg+98l+2w5Wq/5Rdf/5xILJqNAraqXEeiIylPjGEiZAPZobJGZU/KYnioAJUbUl6R9Tm0TwiLj5jsJ3j7jElviMqhMORsikmRPDNyQE5xS8ZCrOOnuSTwBXzUpSGhDvm9Mka6jq4lBzCtIitL3AeG3YTTAXQg5gFsYVvW5L6sx9rEmE+WlDDGEb2wH4CiNxvF5VtpsjLEVBMJ0eSKRRNM5bvs1Lre5SDWc2EvYLgSNq21JKXmeqWCN3XssO6bFA8j1lkc744KmFq4ICNSJdmuBcG8L8nzvvzbDMHqawYZ50IozSDx8T6Way6s+fd+l3lPcpBEUAeguTYAj9m8h/t1B8kkw9wxl/tQZBrebzCVIrEyboRVqua3mq9fHa2p9wDueg1whFvkUpgVtE7N9zLPaxKqnl5x6y0mQhw1B44ZzEZLo+kYoE2pOm7f/Z363/O9OypsJaZXyYAKjqtyJkjta3QiBI/VioXWfPLoAX/0B3+Xs7ML4gQqWaxpQGWGoWfne/l93eBjZIqefhS9e9240kzO6HLLYghoJ4Yj1a23fh8fApkyJlfOhNk5t36Xsj5zTkUzHGE1HT+/YnJZpREqm1tpLQ25sp9roZtK7qKMPOeUAmCwpo6n6tkUzGg9O1mrAtwqjg31VFnLaV7TcqYirJS679VdECfGIr0SPN6PTKOnW3R0bSsNNCUmM05ppinw7u1r2naB61agxDCS1ZILHbm66QnRorRmvT6j68SEpbUaFXvevfgFt9tLnj77gJQTu+0NQ9Nycu8BMSQ6Z1k0il0vhl+ua3n32Rt0TnSLBdY6brc7TE5M/Z6cA2p/zdWf/Rvuff0137m44MPTBZsYpSmuMjFHrNZkXUEeRSiApTGK/f6GX37+GZtuw6cX94hf/Ee+/Ju/Jp884NP//r+jve75k//5n/Di218SmYhTwGA4XWyIBnxpZqEVb/uB0WkxWEQXM1iDyiJ/IWx10fw8oOqarLQ0LkvcMNrwcK356L7h6Zkm7W5ZWoOxyyIdINrHNc/NpW0yjiOtkb2fOAJs5j15YKaqIrMRk6zt4Eeu3r1iGgYuHj7GNp2M8WOlIZA82rWcnZzz+uVLLt+9plss0HZBGCfaxnJxb0U7fsvu63/P6tnP2BuD0pnV0pInxTgFbreJlbE0jZynziqMjhijaJ3BZGEhN/8PReD/16/34+3x6+5UV2KMiX2I3A6RiGYImWlSTJM02WxjGKdECArTaBlCLHs/JpnCqRIw0zSViUkwRnQAnav6gIEQKSCnGNTmmAjFsRuSDPaUuK+1EckVH2YmYH0dTHDk76dpPJjHIDFaq4N0QkyJ7c3NfF/85IlKpBHEUBphuCJrzblWRqhDwBiRnAIh0JADKnnJ05LHqET0QcCbkiNYrfFTKEAhc9NKmg1GtJpzEnA2SxxvWoe1LV23Qnet5GBTjx8nVGko1aFjZbRMTebD+Xc45/PcRJX4zQz0zSzElGYmorA6DwB1Srnorcp7SG0iZ09tSB/03zPTNOC9p8ohzblM8DPLtRrFgsYpESNVaFRO+BTKecNcd8n05/E6lfeuoHlMQUCjAtLmOgmoD0xBVTvERWYpR/l5JaMZoveLIpZcUNdpnCzZVix+CEIUyPM0n6mGtEpIFyiwVqOMRhsnDM7SPIgxk9J8aBFjwPtYZK3yzBSsTeBqGDUFmWK2xhZdTkPTyGeLH0QULCEK2D1rd5bnUqUOpinMIGDMzLr6OWf6QYBQWwkZ5fNrPuS9aIdWRqnWB817EN3Q9WpF8CPDMAigZoQVS2HECvgbGfrhyBBLzOV1kHsgEkamgOki01RrUTGAz/iYsJN4h2Tu5rBtW6RPSm5eJQzmZ6VUMdASrdLlconWmr6XRrjSSgxUc8aHTD8M+LGX5jsycZRiJPgssS2m2RNmBgFLzm+MQRuDLsZjKos2bSgguDGGrm1l2o+DJJm1lvVqRcqZcRznXFSpqkvb0/c9zi4YwoRSGec6UgrE6Odn03ULYY7nA3hsyiRh27ZUGYecxRjORzHl1BkBbJWQa/r9fjZYy32ecy6lFPv9fl5Di/UKkjTPuiLvMJvalRxUzxrBhTAhhwDjNB3Yzapqkgu4b414KoiGctFETof8vOu6OVa0bVt+7pC7p5yZ/ISfvDSglBiYj+NI8mII/35ddPz6jQZpazCsD9Iai2sENVcqY5xBt44HHzwn5sRnf/1LtHXE7gR9ep/NvRPeXd0wxUk2Ts4srWHZNvjrN9x+9XN497VIDSSFVo7Q78ko3KKh6TQfNZrfefYBp6slyiRi23B5s+Nyf8nipOPqagdokjPkJMExWYtaLAilyFBZ9K3QCt04CCMaSSSCl7FfU8ZddBGbTlTAVnRScvQsLDg1cbbWfPD4AY8erjhdt+QsB3iKhpRhnEacUjjt5gJWa4PYwNeCHeaDU8nIG1jRpyMQc8SVcQQZCUS+Z45EJGFfrZZo5RiGHehAm0U3arVpuN5axmRRRjoSy9WS9apluFXEQZIclQASTdugW0coGySjGPs9DqhstJQzzhgWqw37/Q1//vU3hP0J3793j1PbopMn+j0ox5Ampv2OpbY0XYNZiubt9Tjwbr/n339zxas+sFqvOT874yZGsi8iziZwfn6P9ekJX774QkCaqFhvznn46GPas6dcb3uu3rxhvHmDmvYsbEPolmQFw7gnk/j2zSvevHvDZrPm0cMnvL285NX1O3ah5/H9B9hzy2W/g8agC/3+2AhIKWZX3hrc531RkoF5bKwojkuOVA9hjro2FcRIRyDGMUsPDkxcEIhCMrpaOB8g2vK75TPm4vn4+nJmdh+lsHITLEzHg5N7/N0f/R3+0R/8A05XK9E0LAFONGWlG5zUQRNwvkgg50PCfyigwbkOlLgsN00r40vacHu7I6bEerPBtQ0pi1bx9vqKp/efM009fhoY+4n/8Z/8T4z9W+6fNTw8a/jtT3/G+mTDYrkkZ0X0sQA9VT8pkYcb3u63pJyxyw6zdbxRmpzAug5tjOjlKMXJ6SnL1ZLVosNtHI8efsD3v3ufk82aR4/O+eUvf86jR4/ZjwPvrm6wTcfp+T0mX3SHUDx/+oAf/+7v8K//5E8ZhhGFxbYLmoWwbbSxaONASTJ6/uQpP7pY8O3NG15vL7nZXc7d35QyRlnRbFIKm3TRr2qJeqBqR6E1CYviBLiPXnwC7QfQPGVU9xj0CV4vwbTkbJhLW1U5+bGML5bnlgcBbXMgp1D+vSKXRwBVGSevoHxWgGlAlXEgMv1t5HK/5X5nsC4BYpJ2YCJW9oaeF5GmjrqLNMZUnH4pgHFKUYD0aSogdmERlz1TWY/vA35Vf0krCCFjnBKQwRqRNRTICpQ+SuwKQJsObBHZt9JNjykWA8zCDtSqNNCALKNuKYqBQtM09H1P1YKDu8nb8fvf2VvcLaSPYdz5d2qj5L1a+9ftffIhaT28b37vvw/v/yvAca6SAmWXK6imKe8DoPW+HwOyEuOK/EoWFtY8jswhYfyVa6nfR4uOWpVaAZneScV5+fALAsQba0hJkYm/wnSu30+YNgejh+pyW8lW9XscX9v792W+1pRmwDGj0LmOCAvjW+nE8wcP+OHHnxJ2PQvXMOwnfJtYNitM4/DRs9vdCsskJiijartxL+dLzChrpEBMUZqkSpGUJPrkPJvo1BxNWEsZZxoBJZTIGShTNNMzpTi5C/4LUArVpE2VAkmVtUSU4lFT2ELOzoD+cXMi5YBOWliYyGfXxrMuhYjSpqxRpCDSJeEvxkuq7FNVQFXKHgXIMbJer+kWLdM4YqwhpoAPirZZzPfAaNEkG/pbcvI0VkZbjbGz1pwxipw8/X6LUmKK0y4XrFZLhmEN+pJ3lzcok9BOMfqe7EdMnAhTj463rF1i//YrkXeJCc0KfyPnzrpZ4nfXxPWas9NzxnFH9BOLtqVbrbjZ3mDJ3F6+pd9eEQwsjCa9fcHHAb5zcUKrEyoIsKGzNNKSUTKeXVRNshLmVoyJX372Szpn+O6TRzTTFh8HcC3fjJZ//I//B/Tj53z1+iV6GOkWjvb+OdPNDnJkMIlRZcYYGXPCrTY8+uQTlouWSIcqxRtaH8lJKO5IkShNzhqjHCiPVpF1q3h47jhzI9bvODlbYkyLx2CSxM6sYIoZU9htb16/5JuvvuAHP/wRrW3JM2h/eFXGTlnAsm4NqKL1GP1EjmJ+6rr1vK6M0uikud3d8O7qmmcffIhx0lA3wDTc8uzZU773w++zaBq+efmG/tVf0X3wY/qo2feRVWPwPjHqyH5QhCB+FUZFrAI/BholZAsfIg2G6ATM1oV88p/79Z/C1q1AeEhBAFfA+0zGEFPEh0zjVBkNN4xeGiMoaLqMaWDYBUKQgjqmjDa2jE9HqZEoJoMpEWJpGCXxbhiGHmVKY7U0ncqFkVHzOHAqEwDVvKe+KjgZQyDnQC4Am+jeS6A/NARFCzOlRBgDVhussdK0y0XnGgr7t5hDag0p4JyABVOYCOOATiM6TyiE/DNPPSnhfBpUMfSSuktYYDIhqLSAoLqsl5Ay2jgW6xNWyw3dYkm7XuGnkXffXpHCVM53jWsc69Waru3Y3V7T72/xUc4A8TI4NFFREt9NaaIc6/bXMzOE0ujkcPZVI6y7+pgi0ZfKuWe1GHZNUVitUCY5UtGn1kqMkYyZc6OEEJm0sYjxYJ5BeV2ey2xWqY6mEKk5QxIT4rIG5rytNOkzqXgOAMWoSBfWrypNdwpYrYuZeEowhZFQDK5yqdvDzBI0tG3RVqXmCUCR81AIU7svIFwiz/cv52LopfSBXUvRsR2nEp8UOddJgcrgLVqtHMDDpCT/aNuGpnXktiO0QQhiocS/IwZsjZXHOafWukjXwTiJ9EsqjY2macp0jp3BRpCmSwXAlDpozMq/yJkv0ijCMkW0zGQKoTBj+74vkmROYrNt6Mxhsmqq+zsXE0GlcY1ILhjjZsDTOJEaSAl0TgzDgPeB3o/ztSuECayONIKNMYWJKU3glATkXSy6MlUmwH1KmU4Z1psNmmICng51R1aZBlVyNbnnNReqYOo0jpL3FvxAVyyp4CzWWEIBj+f7qqshoDybxojOb52YWiwWbDZr+n5PCNA0tsQ3aYhO08Tt7S0+RGIYZJ2nUIgXh/y2fmY1DzPWltpf7m9nLLk0HDarFUqJ+dw0idGYOQLzx3HEe0+/73HOStMrJm5vb0WFLktMd+5g7CY4i8I64UM3bUslY9T4I1MME9M0UiW5qjxGLOxsoDQFitp7PjQXVAG8qwRGLuaCsjeBzXrOmY9rtvdfv9EgbS1itZKbuOg6rHPCqgWSNmTTcD0EYs6EdkG33vD0g+/Sbu5z9fYF+36YA5y1DZvlCeHt12x/8W9h3GJbS9YNIWfarsWPE33fo0LmyeqUH17c5+Fmw+1+4HzTcd3LWNwuDeiug86zC5nsGlI/YFyDXq7wVesuZWwSJm1UYNoGRjkkcxb35JA8zmoCTkDSJFpBSWVybrHasrCaEx14eGb59Pk97p+AayBGT1KZSKKKpE9BWKdKOWJMWKmCOJ0AACAASURBVOPQypSRRdHhks1SnGs1iLlTkOCnohScYikvWqkxYsrhO04e11hihpubLbt+h20WbE6g7RzWtGgL2EZYw4BxiuWyoW00MWiCTyXQajau46xdMO53pBwJUfRWVBkf02WU2zhHYxv60XIbMz+/vGZIiU/XZzxqZLxgP2RyVChjCcYSXcOkLJ/v93z26pJXV1suI6AMy3bJsl0wpUiIE1MY8LkYEhSqemOtjLUbB0pzfnLC2dl9Hl3c5/rNKdevvmZ3E8gsCCR0Ay463l16duPA8NbzFz//Bafnp7y5vgKj2e4GxkE6eS4rJqTjTWGoGF2L/yO9vBI0E4dDbj74EDmGGTjKh/0zB54MVUPxbkJxAK7meeBKF1OHQ3AuhMv7HfIX+fvj95K/FwAhFeBraToenj7k9377d/mHf/h3OTtdk0JCaTsz5LSpbCM7Ax4SMw8lUiqH2B2DHKVo2uKym6AfRvphL82OpNDGFVkPzTSJvEGcPMF7bq57Pnx6wYfPP+bTj59xdv492sZi0o4wDUx+4PbdThL4kmBkBSEkPvzwO1jbsrvd0Y8jjRKWmcqabrmmW2/IGOgHxmHPft+jtebqzSXOGEJOOGe5d3rGV198TRg8rVvw2RevubqZOL/3kPP756BEwycrxeXVDf/if/9TdreXOGXQygoYbB3Givi5MS3aOpqmpTk54cOPH/PbX37J62++of9yT0hjcacU2QjRCjUCISpJ2iNR2M+qI+tTsn5IMh+R7DNi+yHBnePpSKol0AAOsqt1swAHADke1bERlUaafEubrjHxFvKE6AsdMSplZVPZoLLuoGTRJGPIqkHlJW5xztRDGPdsTk6Z0lsgzZIZFeybR6ozJf7pImMgyUtNpoiRHKJ8VJKRppiE/aSQRD+nAqrqA8h3Z1/l0pFvLNpZolJFykSkJlDMyb5MKAiIWxsnqkgwVMZO/Yz3C0L5XocR+pl5oOqYtZpjxTFgeAzY3mGylldllR2/6vulOTgc/m++7hpnfk1BXgu145ghTaACyOa7+/zuz9UpgbsI8fxdYJZNOG40KVVZ+IXNXJKv2ThPHQrEueFVCvLKBiaLxnrjWtLQ3yk06j08LtKO7/NxYUnOoA9/Vz+3NrqOY+fxPa/fSR89r6NbLxB/lnVrUuJktea73/kOv/ejn3K+OCFOon2vVEPXrtFaEdPAdnvN7X7HbppAiylf7z1TKGBCTuhYm3eqJM/gTEk6y2SFL8yymMKsS6hzIgUBJkKM2OyE4RjDUTFY70UBT9XhjBPALRfHbagyCznm0sg7mEMZXdZ7McoMIdO2xRVaqXl01lpkSujo2dWkWh/dezF3SCh9KFTkemUqI4SAa+y8Hvuhh9xjTi1t2+HskpQixhrOz88Zx0nkEVYbrLHz2dk6Ya3lMDHutxTUmKZpsbahaxvWC8cUAvswiK6oddg8ieTX/QtiSKw6h1WZ3ejpJ4/JCRUHXDA409A4MUt6/fIF1mhcu8S0HW++/pqw37O7esNp13K927FOiaeD557WMOyIOmGTFIS6jMVKo6xOAwRIcHlzw7s374gx8tFHz1ioBOGWicTLMfFXfeTLq3e8+4v/izT2LIh0iwWPzx/i3Y7x9pbrPKF0QttImAaG7Y6bVy+5//EN3ckpdfoio4hal56eorL5qp61VM0Smzc28NGZ5vmZ4vUXL3njb/mdn/yYbDqMkuZG1AK2GKOwTYMis+/35DLVhK5j0Ooo5zgUcmUJFbatgixsodY50tjTb7c07VqM6QrUa10j7JvGsTo9xxiD9xGlAvcfPpJzxome34MnLV+9/Apetpx+/GOCEtDGh0zbGvYT7MfIqjOslw5UFE30EjOtKwSLo7D9m/qql2edxaUsUzMGYlJoq8hT4nYXxTgP5Iws/yijChAgoIH0nSz97ZZM5vR0/SsxmjgVKSxpvkeEx0IWGZNYnMQpcaECITM4W87eCjjEGAleGs8iC0CpJQ7GUfUfYwQgHfc7Qs6cbk5wVsy2QhAmbKSaWCV0TqAhZkWIMtkAkIIn+T1a+TLJFwvLXUykoMTVKr2kFTlXF618MP4sbHDbNLTtgvXJGSdn52hlGaeBy9ev6Lc3ED3GNnTLjosHDzjZnLC9vmEYJznitMgpqAKaqfK/YqZoypmb75wDh39SYS3rmZhy5wzlcOamol2qtSF48aTwWcDGw3QTLJdLlusNThuGYc/N7XY2pss5zvmpVgKmHwymNNQmY7kOYNZX9150TGOIApAWELrqkwu4GklJ2LzSDpC1Gkqupo0hpCSa01HiUKgj0iSaon2qzAGmEZ8RpFGbDuCc5BPCCpdzVwzHQxCG6qEpqYvUggBiNkZk8kxYo85ljhtQNcdVSiQpqnZrgsM0izO01tJ2HQphR/Z9P4Os1WjaucWcq9ac0RhDu1iwXG8Y+55p7Od1oZSagbWpyNTNIFeRMzFWWLpDGTF3tso4OGKW5xGDkGQqQDl5Pz8jlJxlxlp0Eg1ojOTaThUDMg3WNrimQdsiLaBBGzE4JWfWy3VpDJRpwBJzY5AGd40ZVTtWF+kJrY2YpsUo7Get0YgBVcKgtMYYMFmmaqypEx2pfLbBtLqwPUVGpSnmY9MkWNYUxZSrdEzmnDKFwH4c7wDq9ag4gJlCLqy5p+SDJYZpS+MaaQqVJve6XbFcLYghYazBTxO+yEXEwoatzeyq0RpCmMFhZx2tK+Zp5bsaXeWrDMvlktVqJY2s8l02mxO5r9EjkyxxZrrGHIs8iBJcTymca8Q7puS2lfmrkEatmLxJ08w5V4DkCoDbEiM01k4zS1wrYeV672d2b1MY1FKS6ZkJLnmC7ImusRLr36u3jl+/0SAtlMNXJxrXStfLWFwn4FVQMpr2+vISryzLB094+PgRXbtid3ON3+9pjcYjB3ajE5ef/TV6+xXnq4DvOvpBOpMxjCw2K+6fPuLLz39JazIXreVkJQ/UGo0fBxZtg3EN3758x34acGdr1LpDGwn6er1ALxqSEm0qRQF1SMSsyCrRrFeMGAiePnpC9CybJZPKZG3RJhP9hFK6mB4oNgvNd56s+MEnZzw877DaM/iBFOXgTbEeAxwCWayZmej6xhwhahRySMtIoccAMXuCjwyhJ8XEOHlUb6G4stfgs+hWXN7csF6tMNYRYpKixWgmP2IbjTWJprW0AelcZWEIN12LtTXwGEIQBp3TkVWjYeuJ2pILBV06gXKgxCz6PyqL4c5uiox+on/7DnxGn625bxzGBPCZZBturWNA8/m3b/mPr97wZt+DykSlsDrJaLw1JC/6TD4GUg5cvnvLbrtljD0T0O8HrN2x7zM325Hlck3WDT4MhMKEk26sR5NYLVpsc8HN7pZ+e8v17Q1By4jHxdk9ximy7wfaztHgSMbgUy4mD5TC4IjFk0V/VZeCVCs9a8em8nuzIym12M13QA/BSApwplTJiKXYyFVFUZWfmwFa+UOlij5xTUT0EdhbxngrMCtvr1BZl45qxmJ4eP6Qn33/J/zRH/4XnJ+dyMhGEnM56dpWwKUwbxHTpWMwVt67JJwl7VEqgdbF7VYYiNUkYrFcoXWLL+YKIfgiTj+JRkxOPLg457/9bz7gfLMiJc/u9op+KLo/tmWzXjKOPbc3NzhrSEG64j5m3l1fMfQj3377Atc2PEyPmbxns1wTU2LwkTFk9v0E2dMMjpubWwBWyzXLxQalDK9eX+N9z/e/90Oud4Gff/aay8uRs3trTk5OaLqO7EUPc7ffoaaAIhFKcdI2LTkmxrHH5oCzkEPiMl9xkz2r3SlPn3zCD777W8Rxz9fffl6MMpD9kA9guY+TFAl+iTIrtDuH9gO8+YRBPcXrU4I+JSLj0pDBKJQWLbNC/kclhcp+Xm85R3S8xsUti/iGNr+FeEXMvq7QAthVoOoAQ1VQEwTsVElGj7ANplmhp8B2u+fexYLGdozT/ojRcABOa2dBzufSvYxZpBfKJ6ZU/t7HMq5dOuDKkrLoUSldNQqL2nMBbExh6SnEnFAXx1TdNDJSZ7SwNGA2qUCpojt2qKBrAvurUgV1D6hidiLJXAX6ttub8j0Lc+XXNGOOWbQzsMrhZ8uOn68lRpHHOIiZlO9bAwb56BqPwK87e1ZALknuyvoov1/jTS7PWBXATZiRc1iS5JKjuHQENOc7a2ReNfMvy8/N74TCFPAbOU9K3BPtNn1gNKBRumpZj4exSg6gfL1Hx8Ds8Z/fAXW1gEpKabTJB/OLzJw855xmcPj4uSithY1KOIxQZgVEDHC2XvPh42d8/9Pv8fD+IzbdRppFq5bFYoVSiu31FW9u3rJaNLhGsXt7y3W/l9ipxYVWdnQxWyzj2ypD27QyAmtsmeRIhCkU1oUSBr4SBtMUZESsdGnE9Kbsm19hM1NA8/Lsy92V9aILkzkZlLKkLKN21fgEpRiD3CtjFFaJNmEKgWRkjNeahqqvpwu4l0pzpBZg9bNrQp2UPsSKLC0ArQ1TnLi6uuTiwQWLblnMptpioiPPumkc0Uu+E2MQgEZWFDkHjG4kdiCTI/1+R0w72mHk3oXFWkfSkcWypTEnXF1t8c6gmgVdK0Xu0A8MQ0M/7oHAZtWxOVljhpEcR/bXb7m6veLs4iHdw0e8evEl7759wcl6TbfouL66QqfMzdU7dA5sWofeG+4PngcRXAwE7SWHVRpl7MEDSBz+RM8zZpKB29stw37P8w+f45xo1SaVeOsDf9n3fGkcXsF52/Hsez/lZtxztb3m7fU1at+D92gLNmta53DKMk2Byxef8+f/6p/ywe/+EYuHH+JRjEliuS7eDanuF8kWBXBQEttPG81HZ5Z7NtE+fYxxFtdtCKMX7wikyK+xTBuD1oonzz7g7PQU2y1FokZrORfUMbtdzXG3xr4aeJxrWSxPGIcRpQ3Re4wWFnUs59JiseTRkyeMw0DnWoLfMwz7oqXfFk+KTLvoeHxxyqvXn6EunkB7wT4ouqXFR0U/Qms13kdudoGTTtEUs/mUEo21olWby947OlYPV8/R9/rP8zp88uFyMkgOnvS8f6wV1rk2BusM211m11c2ZMLHTEolnhcWprWyNppG0e81wzixWFimUZFjKO7sEPxISgnXyH9rK4ZRWsEwCDtLK13YiBITchQpmeA9VeheG13GxA+NZcljgwAEqk60pRKDKnNUQN1q8OrzQee7Mi3ErFAOK6U0yuSiZ5+KhrJjnCI5jYASVl0WnU1dT0RtyFrWucjHyDlktRJwEpnoaNuGzdk9Ts7Oit9Cy831Da+//oI43qJLrmaMY7U+5fTsPuM48ObdG3zwqLIvhUVrRAIgH05dVRrOGoXKAlyH4OdGtFbMAJN8zqHOeB9g11qjE3hfxv8rcKcOAFO3WHKy2bBYbRiGXphvRU7A1LwnRLIq2U1OoG3R/RQwEVWmzbJIYUBtFss9m89vcimr5DzLKRPLyLTRbj7jQED2muOgND5E/BQKc1YXQpA0hyrYVGv6UGV6Ss4ACEM8S85prZC8jD1qzuvCIC71nC55qpgDS1MpEWUEvd5jCss2CMkqJfFHqe8ZoocpE1NAjdLEaJq2TAIrNpv13OSYI0vOc516TGggJTHz3pygTzaFXSjP32iDsZam7bDW4qeJcRoLqCy6uMvVkuVqya5o0g7DwHK5omlb0RhVYoR10+/nRrzSYg6fYpDvXPY6NQ+u37XkrFmJmWyOkLLoxJoCbkvur2naDq10YWwXqaejqSjRslZM04hSlVyR0DrIvg9eJueSNLclnCnZW+rAPpX7Is9J2PdKzMyq9FlhUmutWayWrGrelbJIVZVGhPd+ZnLWhs3cKC/gfyh1vzEC8nof8H4i5ojKmt3OoI0qBq7pztSv0g1t29CWhgTAarWa4yrq4KMhAO7E7nZHGCeatikgeyE0JKl3GtdgncMVM7Vp8mRSMb4XkHm92oiJfPBU2bScEt6H8ixkIjx4jyp5WGUnT/2+EMXK9yh14mq1QmtDjL6A2QmtYLVclKUtJMkav/u+p2kaqg6u1vIcK9u5cXZmL8+Ejb/l9ZsN0iqFaxtCmETndXVGt1iw2+9EK8NYBj/RbBasTi/YnD1k8J6rqxf4MRBDL27aAdLuiu3VN6TLb7k4Efr7rpcive3EmGoJfHJxhtudMU2RTbtgGieupy3LbgMuE9SeL168YMiRZuG4uDhn8/QJn33+Bc6ucWcbktE0tYupFBYtOofGFVaCpbnYEIcdJo6MMbDOCYOGrqNtW27evi7dnkS3UHz8wQk//Pge5ycR2BMRths5o3N1/a4OgmY+SHKKBBKNchgrXfiQZQxre7vFOctyueb1mzeMcWK12qAxbLe3GGtZLk/QRgoL17S0bcPpyQnGOpQynJyc4OOINo6uW2OsGHxYq1Bl06ZJY2xLt1hj3ALv95DKYUEkqQljEyGJnokrgVsbU0ZjshRguXQ7tWLZtAx+og+Br/dbUg48bhsenm6IC8NlP/Jiv+eb62u+eXPN4BOUhNWkLDT3rmGMmevtln4/CiNZi/Ozs5m2BWuXVNZbjJHdduTd6x2300BU1yxUxqWJlBVj75FJ0ICxlvN797l/fo7f91y+u8KHiCujznkMYBX7YQBrZDQmZbFbSgqsBOKqwSfsnsrEKUyiMrqWy4EvCaKWg1OpORmawV7qv0uxULUC74SHAsAc5+y5vMdxogTM5naKqgcpb5BSQT1CpsHw7OFz/s4Pf4d/8LM/4N7JCTlmYgByGddAoWxNHoobawHAoDhtl+8XCuCkrSlMQy3sdVs66pQDxWiMaTC2ARWJOYgxRBjZ7URn1jROPiuOhCAutpvTcyiOkFMQw62x3+PHkZwcy+WSTduxOjnFdQu2t7e41s7meMZYGcewMg4kLq2WzXpB2xiMNUxBxmi0UnTLBY+fPaVrG16+fsc//Rf/J3/8z/6EjMVUA4CY8FOQBA1xCI5kMC2Nhc41BO9pmpblYoFVjqkwRO2kaHrL8uwR3//+T7l985qbt6+5nkaUqwrYFtG71PR7Qz+06OYhevEhqv0Arx6y5wEDnSRscrqStQCMIN3+rI6kCUgoAoqITj06vsX5b3BpSxOu0WkL+AJggMzPFnDEHNiGwvA4JLQqU1BUwDTkBlLn8bcLPvv8JY+fqdlgiQJs5orGlPUm40zCiqggTM6SwKii8aS1FEO5FBBoVVy4y/7QSsC+EuNTkrHZhIwINV1DkNlmtLFkJWu7Mq40MjqujLoDqFZ2JQU0qrE8BD8XJ8ZYnjx5wMuXL2Us0ugZJDClSDje1L92tL9s8JkhUpohMwhJASkpBfX8+wWoyKVhUosTVUb3lTroAR8BwjUEKWoYqvHkELfma54L08P1VIAhVakX3mNez8XgIYYdf88aPwpULAl4Sgdw/BijyOJQzZGWd71XxyDtsY7UXUbQgTFb760wUpSASOXehaKbd/ye9WKUKt//6DtUBoTSyBh/hlXT8uHjp/z2p9/n+cPndO0KlEWZlta1GGPZjyN9v+Xm6h277Q392NEuG27HgTHE0uwx+BRKU0Jie7FHp20b0U5THFg7ZTzLmnIftUEbYbJmFNq5eX+pnMHoUtDmu+tRpaOFUWD/Iq+ghE6OwqK0BR3FyMSYUjwVsCPJavXTyHR7S7s5YaM1WpkyWeDmZP3oib0HAoiWp5iEVtZ9ZaQLq6rrOu6d30crgzGWRbeicWFeZykGYlA4axnHEa3AWcMwDIQwYKwWc1jtihFLKnqGkd2tZ7HoZJTZNRjr0CjWK2FrjSHRNY1E1Qgnpy3LxZo3b74BlXn+5B5Oa/76L3/O1TefyXdNiQcXD/nlf/xLFo04s2sDU79j0Tqub65IOWIyPHQN9+PAshRsKQcwmUmDzVm087Wwb3IUgMXYJZt7F+Q3b/nok09oFg4dA1EZLkPkL273fKsgM4GPfPr7P+PJd3/CH/+zfw7NKX/z5Rcssud03aBVA1PAoLFJs+o6kolcvfmKX/wff8zHv/sP2Dz6gJAbcnLYOTcsUucUjUOKXE0YCVOms0sWrWa5PiPhhNk09WizRLkGmQyXGK3KBMFqc0HbbkBBiEp09ZBpMm0ozTiI1Dini3dC3c8KuzrlvOmkiW7sLKMTQ0DhUMrirOOrV1/wwdOnNI2lHyPDOBBiJDYNjXMYZdisVqSQ+OKv/h3nH/4Mug05KVwrLHCrYNFZppgYQqZtYPSetbNYpbDcbcj953r9uvPm1/4czBqVkSIHIsNs+KLPKWYYGaNzCfZKJB/GQMxKzGUBimycMQpjFeenS7Y7y9X1jrevXrFaLlkt16QoDvUpJrq2FT3GQniQuCKNl7q4fGVrTiPjNJKS1HMpJYhqHl+vcgUK0TVUQFKHRm5l62utiSEV1lci+EBUAs5Utq42SkzPtAynm2IqFcJE9B7trORjOWOy+ByQhQWsix5z9F5yRevIocoeeLR2krqlCd20tM2S++fnPHz8Acv1ipubdwz9njztsXhSHAlxYrFYsjlZ0zSOcZzY3lyRYtWplVpElXuoyjh+LHJuSiuqrnoueuw6J0IQ/xXXHIEjQM7FK+Aol6m5FhSN0TKaH8ufVQOlxXJJt1gx+sDNy1eM40D0I5pEzKlI9ZTxa2WAauqT7pztWlUTwVzHdYpkjSbrdMQKlmsLKcxNv9pcJUacKePvRQpAWL+KXOJH07QoreincS7TYpCzIZYx/Ml7hkkaC1WT3hgzywM4K0zDuvdq3QZFNqucfsIeT0VDW0FOs7RYNdSqeaExmhQClTGqK5O3YAtaCfgepkD0B+NayVUtzlkBFFOan5EwHFN5f0OcPFMSZqWA9MXINctEbMqQfMAH+by2XUh8IJepNcnjFt19+Q6FuUplDS86MYlOYr4mTHWRdEIxszy9DwKIFjg9V0BbCcN56PcYXbwpUmRQh6m5nHPRX813ZB70PNFTpnCco+vaOWeuMmwxRvqxlyo9pwPZAkXwYhxYpVSMbjBaAD7xIKoyWmpma4pecMJPE0aJ9mzbttimmfeinqUXCg6ghOWtlCbHiNFaGMzjKH5ORQbCGtHsrezREDMhbGcAsoKObduy6FppFJqDyZ8s3cOEPAiTuWsXnJ+eyfmX4qFhj5D9pknqch8C3pj5uhVCpPM+0LZNkTuIOOeoEsygZh1ckTKxqKabY3uV6HBFHqQavcUoZ7ZGl4auaIjnnIglbpnC+BXzROi6js1mg7V2Zg5X/Khq/Nbfkfhx+C6/7vUbDdJKMHR0qxWr03ss1ueoCCGNRKNIzkGzYHnvIa5b8e7msuisQasd3mQIAb27Ib39nLi/xBoYQ2LfD8So6JzidNnQGYMbPfl2z6cPHzCNEyTN5U2PZuSxW3Fx/4JXl1tGNPuYWJyfcvHBc759+w76kc3pBmOtuPAZTdICnGYf0VmJuZGWDq5xwgImK276Heu2JWuHjF8ofDY4q+ls4IOLJT/+3hPOloYQruWhFrfWVEZFj9lRzrnSGUjYRroNwzgwjhM3+60EyyJh0NKwMhtsYzBqwdn5CRrLSaGQrzdn+Em0rYwW52irFNM0EMJETogmbdbcv2dou462k2ID5TGuxU8y/rNcnbA5OeWrF99glcEUNyKH6KGtmoYhA4Y7YxapaIA0TUtUIlvhdMLkzDgNXPtE72/51sDZNLJoF1yPI1+8fcvgA9FoMQ6p96gkSeM08er1K8bdwGa9YXNvw+Kso+scnXMoDZ1bsmoXDN4T7EM++a0/wkfFP//f/lem64F27Ak5Mg47hnHA0WCiYxxGhnGgtYbnDx9xenLKL7/8kuvra5xrUQbGccLahGqcFLEaYaHkjM2QtLAkRY8mFgZOnlkHVcRaU9ltd0GFY9AACjBS/ryOwBz/wvtAzvuvY7bdnMhkuY5qKCS4g+iGNRg+eficn/7gJ/z93/l97p/dmxmOoldVn0lhmKCL5px0eas2ksrvAUj50F2OUda5dJ0p4/8yVlUL1fLtAAHm/LRn0cDF+SnrVcvJZsnCwNXlJSGDMcI0a11DcpIktEHA/Lc3O6Yp4H1mux8YRl/ExynAWjEHUZmsHMYtcW2LsdA0cHZ2xun5Ay7uP+CD589Aab788ht+8dkX/Om//XP+8q++pB8S1lmWqwVN00iBkAtTPqdZJzUrGf3VTpov1i5o2g3OtJgkUgYqGnwvov73zh7z+PF3ePH1V+xfv2DKipAFfIyqwXLK08c/ZbP5iK/etbzeb/DmOZNeE3NDLI680p1HQFjtQDVFy5qyTuU6cwrovKOLr1iGryC8E/3tNKBzQORZKBIa5TiunWcqmFlHrjORMkpUdLNkvKzBNQvU8oxxP3B1c8N6bXA6knM1ARAJDZTEy6ikuK9aX1mByYrkIzoWBm0xEajSI/WQrUVCTUbrvpn3B5Q9KmtVkmEZRTPKlLh2aILk2tk/rmGP9mHVLlVzoSpyCL6MbFVQ9Ph3FAfg9/j63t9DICNfFbQWALWgHjUOKFUJQ3OzShKLClgex4vja7j7WXPhpo7Ypn9LvKmd/fqqhYEuRiz1+x1/zwog6/n+Hp7JvP/z4bnUZ3n3xh+BooXleQyev3/v5kLs6O+PY2T9WQHaZSSsgv7vM4PuXkM1KzrE5AwCWKaE1RlnNA9OzvnRd3/EB0+ec7Y+EzOwJAZ1y25JCIntzTX9sMP7kf3UMxaTKX+dRMOvnCY5hjKGJ00Ro4rmnBNALM1aXGF+5labwjDJMmaZDs9s1j+kMmILiFGnRMgzo6euiRhj0VgTZ/JIQudcJA2kEWTLe9eJjmo+mMua7DYb0edWZma5qALrZ6XKGpH1KfVzGTUs0hfjOBCnPd1ihXGtxLdS0CiV6Tph5hqtaZxhnJDmYC4Mt5Rw5qBLprVoqcUg9ycrAaZF40wmQYxRGKXp+1uca1hszkFptGnplsJO3r+9kbtuOlzX4YA49Zz5kdXCEb1nMC636wAAIABJREFU3O+Y9ns2qzXn9+7x7NlTXr/8Bq0V3WpFu+h49eolSme+ffU1PgpjxaE5nybcfo+KUYzisjQWYq4sKrnGykpPKbHbXvLVyxes1wvOH56z327JSnGdE3+93/N62TCljNru0GT+7M/+Df/y3/4ZTz78IT/9h/+In/+HP+OzP/2XjNmTy5irj4o+R2gbNpsOFyJbv+fLv/zXPBi2tPeeYZb3C/ApQLxS8gxIYpqUlYLo+ebVWz478ZycfMratvSTF0DLtYDh9uaGq6srUJrHT57hmrY08QzOLUXrLsrz0rpIZ3Bgw8/GSWVd1fiRtEYrJyGsjHCHcY9SlKLNYoLoPU/jnldvvuXJ02cszYpxEoMj7z1NI+QItOH09IRHaeDq9V/x7Ac/QS86Ghc421imPjBO0pycQjF/UVr8LkxXAsmdME2NpP9/vxKS601BJqumBFFL0yWj8F4z7Epz2hhCKIxSJc2TlEWbVBWwTM+NYwgxYxtHFzVX2+08eWKsYaij0yW21nyyalbL5Iea75PIEJTR2cKsjoXdqPSBpJA0ZbIRImJiqBUlXsl4tAA3hqS9aFxmjdIyWRjLGtNFfkDe9ugsKyBwCJ4YBhaNFfb+OCIN0zxfS85ZpHqsk4ZGCc/WNsJE0wpyw2pzxsWDJ5ys12ht6fcjw35gv71md/0OZSzrs/uM/S1NI1Idzllub96xvXqLyjLZJXq4FaCTeD+bUaVc6tJj8DPiGoexApQqnX7t+Xksv/T+GVxZizUfa5qGpmnYbDakLMZCfT/g/YShgMiAyD8Y5puSC/hYpkIq0JTJMxh8PK0oRq5CtFDGzEAdSaT6ZtZ0OVt8mO7IpSgluphGa9xqSYgCxFmj6AfREg0FFKuu8gJQtqJTXJraonkp0mbWCBmssrlzqrWiZKUpx3ny0lqZHM3Fj8c5JyB6aWInqka3Qbtyj7WZJQPmxnxOs3RaCAcT3ipVF+NholhpVf67srcPgLjUb2KmdPyqTN5pHOcR8rnRYWQ6TSHwcyprpMqCVcA2ZD/LS3RdJ2AzRe4M5rH7mDK3/b5I1tV1OGdjBYcQqQpKg1eVnH+/3+OznEPH8ieVLVnzwLpmrdUCYBtbahQB65qmmrDGIu2kaJrD9OrBjM3OnyF6uJKDWKsLiz3R73r2+z0A+71l0XWyB2HWWNYcpohsmShQ5fyoMhWL5RKl9Qw4Gm2L6VhXANs8A8PjOLLdbtnv9+Sc2fc9/VHOUE10jbGzBryxVtirypTv29B0Xdkpcu8WRc8158w4jIfngMT8cRwJVUZBqVlyI6U4r9UQpDnTNI3EFC2yWMYIWzumND+vrtwraa4e4pLW8j4xi17t8O4aYzTWaroCgB9PQDrnaNv2DjYnxJBUmLmxsK//dij2NxqkzVqhV2usa1lu7hGjYn97CSpg1yt8u2R1/zHBNuyGPX6/IwwDrWtwNpDHG3ZXN7T9llXeExvFMA4Mg8IogzGKpTW0RBZaYXIi9Tu+84NP8FPg2zfXvLu+BWQM2AdPt1zh1mt677GrFS9ev+Srv/kbTu/fxzYKHwYUkTTBhIxs6nQYz9JKur5h7MV9VcO279mvpxJke5xb0LQLQhi4f7rgtz6+4P4GSCNjGNG6oZwHpXBnPtDrYhCdlp7dbs9ut5+7mJkoSP/pCcM4Yp2j6zoePHhAPw70+z1dsyQneHv5jqubHd1iTc4wTZ576w1TmLgdekKKtG1H2zhSkIDalQLPGi1djdwwjZ4YeqxpWW5OSFoxeU/ntPC1FJx1S1ZmK+NLFbQ7EpeXLjIo61iuLNt370gpE9FkrfA5scuZN9s9+Wor42m2wRTdTqM1/TQQI8RQXGSnkTSOfPToET/4/ndZnW6glcCXCpMnTYGnjy+YcmIXz/iv/us/4OnHF6Cuef0LD/stu/6WF29fo98qXr6+xF9llM7EOLINgfF2x3c++YhPPvqQz7/6mt3QY9HF8MPQ5DqmVDpzOeJ9xDoZUzJWmHjJR9H71FIkVh22mmdU3cWU89zZV0d4C/XIvgMKHBXWx2DuEYhQA86xzEF9Ka3KKKRIL5AFiDCq4cmDR/zBj3+PP/zd3+PB+QXRe1DFJb0AxAI+CUiUj0CPqh94SM7ughsxZlCG5aqToFnGQ4wS6Y+YhfXiygi+zuK+PI0jZycb/st/+Pc4Oz2fBceVUSwXHT7Du6uBN1+85epqy6vX73jz9i39OBCDR2eN0Q7rOjICTKrizJoKo8xokaNonKZpAmnrGaaerDxKf0tMP+f09B4fPn+CnwZCgJtdz9vLG0YfMFYKz7OzExnx8RPVrVaT683AKHDO0rUt19s9ORpytqAbNKKdZYzBpIRN0K3X/OC3fsKrV19ztdvzaneLbpaslw95/vy3efr8e/zox7/Hw0cf8M2bkf/lX33GX7zMTNqAcfO4dgw12RRx/mxU0cQ2BZwdIO9w4R1tvKIN7zDhNTnsBDAp42VZyV4XfK2O2lTwQh1AvJwkoa1JUzn0a/GprIPmFJMabnffktMbTlY7lAksXIOfgDKa5n04CNnFWCgLiTR6AWhjKfRTGYOqHX2l5gN8HmcqCVr0oTjJFuCxdNiVsUW0n9moTIyUDhphFSA9HotSBVY6NvxSZd+AGCi8evkatC4AFkc/k+Z9+/5evstsPQIVCnRZ2ap1d8/J/nug5N0YcFw0lXhdrv3u5x4mS47/zugDC7iyB6qUS86SFJ2cnDAMI30/3AFftSkmQkese9EgPjCSM7WgutuMqq+Uf7UoBCBGxGDl8OfHMfH4z47vzfHr+GfTEYBZtcjkzw9O1vP30vUckGJG5cIaipGlMlysz/jBdz7lBx9/yvnpE3wQ3XZjW6xzDNtrLndbJu8ZpxGfRkY/sR8nRh/o/STvrTWq6KemMpZrtGbRONpGwFnvJ8IkhZMAr4exzqyF5VMQZJEyws2sBEM5p5IUaho1a6fV90u57OcURWPSR8LQyzSIkbMdFAmN0o3kMFk03QDsrJWq0NbSWMs4TgR/y+npaWlqpaO1YAsAktAaUlJHTAjL7e2W119/ybPnH7K0jTDVtRHn9VS00FUGhNHbODcX3xoxqKms91qoNo1IRBAjMmpTQFptMMpSTYamYeQmX4FxLDanZC2GdKZrWCwXeC+O7VZb0TdOhtVyQes02+trdMp8+t3vk4HHjx9xe3PFm5cvxOzMWXbX19xevkOlyLcvXtBoQ9d0NBnGdy9pdzf0ZBqjyMaCFo1xlRNj9DhlsUWvLYTAq7ev6JzjbHGP6eYaqxW3VvEXlzf8TYrY1SlrH9iNEykkxt01Fs3Nyy+53o389u//PV789X8gD29FRqZr2ObIXnma9QazWBH9xMqPOCZu3/ySm9sr1g8/ZLE+RyvRiptCJGVVpEoMaMfSKYJZ8uef37DY7PnJpxe0rSXmQAiJ4AXYOb93TogCxLgazUxh1mmFURDjiFaNsJxLXNTGYCkNrGPNUZWJOUt94TQ5BLzvudnesOg6YcZFxeQn9rsdjx49JuZITJm2XdDvB8QhWxfmVYNSVuQbWo2KA7fffs7J8x/QewtkWqOxKbNoElpF9oPm/tpgg+iquqZI4pRG+vuvX9fM+3/j9Z/6fglF1kbILd4zxoRxGmUUoU+zPAEl7xt6j08ZHwSIrbkEgLFVoxh8QMDd/5u592iSJcvu/H5XuQiR6qmqV1q3AhoYwjBYjBl34I4fgCt+OK7INTdccIzKjMOhYQAQDbRAi9JPpoqMCHe/iotzr0fk6x6SRhuYdZqVVb16mZER7tfvPed//sIasaDoFsJKm/yhKM55Bl8OZ6Wem3g9ezOWulQrYpTeQOzrpCap4JZCwDdxkCl1sxKWvTT5ZgbOjHGcnJxKGE2qw1zJojAFfDK6yudFXZZLiKkMq8UrPEBZL0KW0FqTYhA1WQFBVE5ipYewI7WSvA2nDe+88yEXDx/z/LtvGcc7VM4Muy13Nzf0Xc9bT5/SNI7vv/0d037HbvT4uCf4gVD2Pl/OD02UvcyLjUEIcQ48MkbPgT+5kDBAzYq+Ouw4rhvKSiq36v46VQWMqeCXtZblcslisSDEyOZux36/hwyta8reLQCKZIlmqpZMa+ZBalV3zaxA6u8t6yWlMuWDFPI8uNTy18z+sDnPXpnHPZMuvVsN9s5B/Ny990QvPVT0ufRDkrWitQCMuZIkUOisCWVdVcVVynEG1+q1zAgj22pL1rkAkpG+aYihegVLTZ1NmnsumdXXrAPxok8xzjuIDEcONU7TNPP1kWtXe8ZDLdu0zcwsrNe4bTuMsXh/ODcPfy/3pi0/F4LYQMbITCAwWqOVnp/jEMI82E85YcsgDyWDrGrx0DStDPVjJE8jTdOyWi4FKE7H0v1UgFw5IXI5430Is9XA6XpdbIikRu0KyBiCKG2maWKz2RCj4C9t60r41G6+NglmAtlx+NRBGS0szaZxpBRJydM0jrZdFTKSPrIOGGjbVpTOJUTsECKuiEnWba1ptNKwL4N0pTFKwscq+KqUmsl/MQbZd1OmL5+zsqD7vqfrBFAdhoFKKzNFPeSniavra4bdluViSVQR5cO8ZyvkmW7blq7rZsuLlMVSQmsNxmCtoWkbgg8YY1g0De1iQS4gcLUZyFkG78LyZX5f1W93G8K9z2jLXlJre63BGUPbtkV5JaDwNAWMdtze3lKB/Nk6gkP/o7Vmu93O16jey8a5mYUbcyRz6DXe/PqjBmnRhtS2RO0YYhRpiFZgW3TfcXL+kCHB3e0GlSO9a3Ha0qQRtX3N+OorzDjSOplcdO0C1zqmcZJpiRLJYK8bOjIpT2jg9uaWrltiywbQtw1GZaboWa97TE60rmHrA+M48uDttzh7eMEuePx+IBSKedZ1Iio3yypF1mCVojMOnTONljCHkMHmhEqBFIX6T4p0zvDgbEX0A0ZLgFAMucjDtfjOZkpSYypBN5ngPfv9yLAfcU3Dol/gXIM1qlxagzdRvJemS3LObPdb2qajb8Q/JWdJqGy7luCjbPSNoTMNGJFu9IsFi6YhB40xLW3j5gARqxVG2yKFlCAw43q6fsl2upVkciRRvjOWVjlJMFYWVdKYoU6QAeTwb63B58AUxrJhR5GAaiPm3TA3cRRAJJJRjYVJJPIpRnbDntPlBU/fe5dHTx5i24ZsO+5ub7nb7cV6QMGz56/JSuNWD9hPievtHXe3L7ApYpylaVacXJzwg88bvv/+Bd8+f87XX3/FrqRp3m33/POvf8vT997hnXef8uXXX5GyBBTZ4MQT02rxf9FIirgxxAj7/UDXdyhrZiZSRV6rFKdKdoW4keb/Jlfw4AhkKCwDmQqX1yoYx5sg7JtgRGWrQQUgajBBGRRUT9GsOV+e8icf/4CffPZDHp6dS9FYAK/6OqbYN/jkmf17CkuhgsmmyBpkSlskrkom68Y6XNuSmQqbSSQ8U5l8t12HLknkISYmPzKOnq5dYjC0XYt1DX4/8OW33/PlV7/j9fU1l1d3bDYDxrZo7Wi7FU+evkXXtqwWay7OHnByckbT9VjX4Lrqh3MoMGIBHcgwBc922DIFz2635243EENm8BmtWtrO0kfomh0hit+tc04M0isIRgWsK/tPig1XmW4+SvJFrn+l5m9VWexCll2LffI2T55+zG++fM5JvuCDT3/En/7pX/LxJz/FuZ6utTgX+eyDFcvFF4z/wz/wi1eXBP0IdFvWUH0fpeFIAaUnVAIdt5CuMPEVfbyiS1tUHCFNqFwaDV1khaoWDcV/Wcnw7MAVlyareByIb6ySz402EjCopRAzjSFFy7S/Zecdy75F68Bmu0XRYLQuKfUBqzWmLPvoRemAD+gKwtSinFqox3k6XUHaypKj7E0zZlzBVq0LMKtnBt/M3MyHpu7YlL9+VYZo/ToU+DVUQtiAwnC9PzSZn+0jQPWY/XtvwKKqtLM830dNtSrF9fEr32e5HPaCeg8raF1f+xikrF589b3NbNrM7EfNvMfUwEi55tvtllgSbI0Ri53tdkuq4AjCCLgPolbA+zC4zNxXFhx//5tAdt0z67WrMqnjvfAPMWzr9Tm+B4drXd+X/r3fdwg7EVCWwhRVWdgaLivWixM+e+cDvvjkMy5Ozll2C5Rq6HqRx6csHqf73a2EcITAFAOjH5hCZEwJH2MBpsU+yBiNNQqrhc3QNo6m7JkpBmnuOdwXSrOTc7EN4fA5VKZ4U6tZ3SFrVaGU/b1rlHMmp1LT5YxOMO53bK5esVyvQIvkvza9pXIRgDtJU62UwjrZe5US8KNpSjOVIsJkDGJrogzoTMoKq+WcctaSswAr1hgePXzIo9MVYuHiCPkQUuOMBVvYHsaIHjtnWicyNwmVKbtWkTfOrJrCKHPGiVTdyZkRYybG8tTkhB8Hbq5fE6NneXKKtZpBW7p+wd1mJMYNzgl4HKcRrURNJNdds1guaRcLdtPEl19+VWTIieQHvvv6S/qu5fnz5wyTJzuL8p51vySGkRgnJpIMzlJDAmyjsFqTszBIslZklXh1e8vy5ITT9QneONlDneXrNPF19Oy0Ib98Re8czWrJtNmC37Pqe7ab5/xv//1/x+mTt9BNQqmOxeoh6ydP+N2zb1B4zHKN7lfYECDscRhsv2IfM9vnXzLdXrJarlGmEZ9A7UTpoRyYRLYt26AINPzdb15hrOVHH78j5WBO4pMM9P2CjNhxgSTcVybkNBXv2pxJqbCkmwYJp9LFM1uuR53BxBBFHlzYb9aIfcXJ6YUwc8qevdtuGf0tq5MzAeW0YRz2/OoX/8SjJ094++11YYSJh+pmu+Xr3/yKx4/eQtkbLr/5Nau3Pyb6nqSgW0a6JgOiGIkhsm5bchAZr3aiXMtH58p/Wkj2/++XKjYH5QJqi1aJwecyuBVWX0jgvdhZNK0jjpnJTyjjhHjhI57MQrkCmGvGUXI4hFUoIFIswS4SSnOoLw3FjijLsKlmHIDUpGJnUeqFUlfrUmApBFg9lsgrq0VpUM8QXaXIjmkK0hMq8H4CiuIyi3xWpNLlLCCLb2qRqKccZcBUhtopS78gfup5VjMo1Az2GGNIIc/7sXyDRVmxuiNnvv36S64vXzANW7GaSbBYrjh78JAxKu42d4QkMvUYAikEYhjJKcwAshQlMqCLPhS/WCl3XNkj57tezpFZWaf0DNoezsp6thzXQPfP7QpmzcFHSrHdbhnGiXGSYYdRkm+hi01Orc2NrjYHlF5JS+BbrXuO6qtZJXJ0vqdU7Idq7VJ+RvaLo5quDI7r9yqk+ExBFFAhpNmHlXLf5sF7aWStlcyIOgBVhZzlC3OzgsmqMrnLWzVWrMxkLei5LimIrAxWlSYXVqlBzRkjdX/w0wRZLAeEI5JLH8p8n3KGcFQHSp0sQyQJYtIzk7Ke/wc1mprl6ZUdWmsuAeIDfd+hlIRhVfVLzZt1zmG1mUFa74t3cPmcBoUPodiUzM0u4yTPXsqZFOLMbPUhYMrnF6BQmNHGVFWbrElXn/nCMl6tVnNtW+0OANoi6e/7fgY+m8aWGiEyTZ7NZsN+GHCtMNX3ewmprc9NvX673Y6mkVBJWf/uniWKc809y4m+7+n7frZQqV7GeR7+iM2b1UaY1eV6UkJSq+T/eC+JKbHfbbHWMQ4DOef5s9XPX0ktzmhIGde0s7XCxfkFu91ehmXl/taAvZjEomG/2xX7QhkiVFZ40zSyVyhmsLV+1hoyV+3WlssFOWex6pqxDeYspJQy+7xnLCF3xliUkGFnb9mUhOk6Th5tBGR11uCs2Is8eHDONI1SU6RcSDeHMOG6X5EhRMELYwwMe3k2XfE71+o+g/z4648apBU6u2G/3+NDwHU9uunBNZh+yRQyfhjQSSaIUxbZ3vTqO9Tlt+Q00DvQSTNmQ/SZru9ompZh2KLDSKs0HZoV0CwXnKw7sQcYNpyfnfPRJx+Tp8Dr5y/ISSYoq8bxUbfmn1+8wmfF43ffwfYd28tLVsuWOAkYICnEAqaJ8bOm6RqmacQZQ2MsGsVmu6c3juWJQ5MJ456YDKTI9dUld3dvcdJIW2+0JUqVQIERDodvWYQVtGtcQ98tCoLvIMN2dyeTlRAZg5RGp+sT2qbhZO3o2p7Odljl6Pse5zpc0xfvpIhV0ohpJxOFrpFNLCFMlsp+1VqCtGIowiUlrDFjGlbrU7a3d9SgoKzE52TV9ti9x6CJ2gqj4KiJHYeBxlhUY2j6Dh/EvF9bVTzehH0VY0Y3heEShdlbZR7GGZRV+Anx+FRg246QM370TDvPtNuTYmCKk3j4xkxrliij+D//11+wODdcv/iebhoJCsyMTHg+fPcx77/7gM8+fJtf/fq3fPn9c/Y7z370fP/sGZ//8AvOH17w4vvnxL0nJXBtI2yMksiajSLkWGSfmX2ccE0j0xxkGmiMSHXycQFzwE0o1Imj9fH7rDjqhFMfN83l+wr3LNfiY/45kapWL6i5dqprD8PJ8oTPn77PX/3kp7z/1tvkUCU41Y9RoXXxlZNxq/gQxoR9Q9aUUvWPypJkW4oCa4tBe0xFIpZmEAhK4EItKMpEeBj3hVXRYzLc3m35P/79f+CrL58x7iPZKKzTPHnyEV/85Jx3n77LO2+/y8XZKSfrBc2iwzYd1shwJJUDKfogclaYzcmTEulL9EEC+wxsdsLkTsim7WyLVhofRu6urvjq62/5/sUVl5sd07Dn9GQtAWtFLqaseJJVlp3WhlRkedEHWuuwRiORGnJ/DbqA2xCnANnw5O1P+fwHmbfe+Zz3PvkCVVgrbQ+NiRiVyOmO9x81/Jf/+Uf8t//2V3x5c4mPD8kl+Gau9cmo5GG8QYc9Jr5Gp5cs0hWOPYSxeL0lUFU2pgiUyagyBXSXtRlySYBPuUz/RSqdUsJQq+fC/CyFXNe0jDFhtUL5BdO2ZT+MrE4ajA4QFTEF9vsRjcKY8gopEYZRhkdZDth6yJKTgNAFtK2A0FwkqyMQsDx48nOH5ysXD0KMyKNSTsVXu/p6cTRsOTy79Zk8fl7r81s/fS20j0HB8ovngm6+Q6myz+O987WCq8dAYn1PtZj9Q2yoYyBTvv3o52txfwRepsIQEr9ANe8n8zFWn3dVW5kqhZdPW4tuUwaGT5++zfffP+Pm5mYe7hxDDpW9IT99eL9/qNG7f42hdmgZCtMy3fv+2jzUa3mPAVstINShqH4TQJ/31ON9uHxmeZ1EvXUxBIiRle344OlT/uJHP+XDp++jTIMvYZcGh1aSXL3bbpj2d/hxz34YmVISn0ovE34fS5K1UbjSvJIjThe5I8KkTXNadDw0VYdZnrzX4j9dJYP1fFdUqf88zkNlSWyvIShKSVhDTGE+czIZlWEc92zv7liuljROko8LtC22KAi4Wj0E6zmWM3Mz4RrxtIvRk5NBGfGNNLa8+yT+Yao8G7OtDuJpqFSPD8J4iUn8WacplGApXXwd4yyDrT7R4l0qzY/3Yg1RAYQpBl48e8b5g8c0/WIONEnz2VXB/4jfRnZxolGZfn2OUdLU9V3m9auXkmbsZW8Zpz1NJ57s1jkWy47xbsOLF8+EEZsVrnFcXj7HGsXL1694eX0lNZw1tG3D3WaDHXcoJanyU0pEEl3ZH1zTUidRMURuhz3fvXrFx+9/wOL8CR/+1V/x5d/+Hd99/x2/HrbsnCVPkd5qAaGUJvs9aZxITcv5ieNm8y13X72iuzhj+fQxZ++8y8vrWzi9YOFaEh6lHW3n0F5hmhMW6xPOUOyGke12z/71M5Yn53TNCq8VEYO2DdaW4K0MI/DN9S355zvOVy0fvvWQpGQoPmwHJh9Yrk5pTENGo0u9E6InlDUQVCDnxPZuS9NFTk5PSUkYoKXCkn0uyzq2tnrlyZ4nfpGNPENFEdMvDU9cw3J1IsqU6NE5cX52yuNHj2maht0w4sNApyCrQNM2sg4WjptwQ9pdYvt3iCGxG4QZaDQYpcUOAtlvxU7yaEOsp88be/ubTMV/yS+lDnWMNOcZHxN3UyZgiFmz3XlhwyqFj3kWvrjGgMkk1RGSginhh4jCMIwRa0UqPgx+zrTIJURZm4OnZNM0OCugRvZynqU5GFdjXSNnZxnGaiP3tyqmVMpz4940wuqqA7Da16QSvnhgNh6ur9YHdpUpigDrykC5DHwqESKmWF5H2P/aWnktKrAxyJ5bzv966sSUsLkwqEv4kNZlcGYcU/D8+je/JkdPDgNt0/Hk4RO6ricr2I0DN69vmfZ3aL/DqsTdTti2Ssu1BfGWjR4Gvy+fubJkRKngnOQ5hCBnUfDi3Xp/CEwBn+ZVUvbEdO+cPe5n6v5aB+cicU7iX6qNBA1pM8vdMwdvVKslfT5ELyrWWLzQi7WJKoVALlYaYskmX3I+lmc+y7qxxZZOQuQOwBGFZFIfPalJChmlKCOta8QKQEsSfSj+zLLepDdNgA9+lpxXUoi1MlxCCfmqKi1NWQem1LE559k3tECreD+VMNCMc5YUDmca5fP54EvvXsgJpeesKi7nGnKMDKOHMowQqX4oYJ0p/ZiEqVnnpP4rz1EN9fWTFw9ZWzN2pMYyWkhjWsmgvW3bwmau60eG9LZpZqC+Xu8KTFpjQKsCOlaygwxUUoqMowSSDfu91KHaCMuxSOhDkLCwGCtLuva/hzp7Zs4bg0vik1tBROccp6enhzoyR6ZxxDnHen3Co0ePGP3EVIBO4AiQDoQQ59efxglTrrH3cl/3u/38bLumwehKJJEBUk6ZEAOr1aqcCQqVDFh5P421dKYnFiaqUZrFYnEP9Abm9XN6ciprsfgEp5TmZ69+jzGiKm2sYb06Yb/byXNSPGptAaDbYutT7Tb8ajV74QY/0TWt7BdFebgfB6Ccq65h8hPGGHZ5R4wyGF8uFoSgy32S+6OUpm1beSYz5JTou05q4xBmi8269owxDKNgQJvtIEC1s5yerAkxkbKfbRbUBow8AAAgAElEQVSs1aV2VPMeXDc3U/b4ansX/EQOUxkIyhqqjOs/9PXHDdJmcGGCNGICGFaEpmNqGpm4BtkgtJFicHr9grx5Rbr5niZssb0RgC6MxePSslgvcE1LHPYweqxrSOPI+rRn3XbEnPDDBFmz3e94wAlvP3nER4/fZjPuePb6mpPTC7w2vD0FhucvaXTDbrvnbrej6xf0XYNVCvwk05zKaiOz3+04Xa84Wy3Z3GwYvSclkeub4lWWkXT6NCkub7Z8+dX3PD1/D6MhSDS5gHMqH7xTjBYft5zR1uJygzMUSYRnu7kmJ5n6G61ZLRuWWTbqi7NztLJiOK+NbFAWVC6+sSEJEF42JFs82ahTuySyFkNAaSuFS6OwXSTtRrRRZC0eMq4xrFdLLp0Tz+GYSvZQ4KS3NK/EMN9nOSxsAqs1IQVyiDSxQ6GwyiLSohL6oLL41jqRE4JslqaU0TEJgyhSAiZUpulazs+XZAIvXl4WfxhdulGD0Q5Fwo+e7PYM17/l5h92qOTJ04Z99Chi8cfJOOvY7YaS3ggffPA252drfvHPX3O5uSPkxG4acF1Pzgo/BVpXvITknRUZEzJl1hkQypyKoKK8NQ3UpByj60El071ZvpszlICxCnZw9K/5GSvS2rqxpOofpET2EGKdnsoPZ3VgNdWDXpZkJidoTc+n737CX/74J3z03jsI5UkVY/r6W1U5cIVlaC0QBUiPUbzHUOpoMiqyhVQ2XKXzXMBWLzpF9a4s7AhTfZK8PH45YrQAtvvdjru759xstvzs51/x8NHb/MW//hPeffqUZd/w3jtPWK2WuKYpQLZIjZMCP43kMu2t1yaGWIpWK6yGIlXLUQYbq9UKgOvruzJthrbpOT+7YLlccnX9mmW/4MHjt3j/asPtdmR7e8vp6RpSQOco1yxLw5IUZZKuQTeQDSHIc6aUFG+UQiwlYZkao7nd77ndekx7wZ//1V8zBIVXlmXfs99uUNvA4vxcJGBqwqqJn37xiO0U+W/+7Ze89gMC+8q9Swp02uHyS4z/Cre/pOUOzQaVfVlLEnGodENSipwK26IsZqO1FPqpsEVSwmhhqlltUEYX43ZpOOu0NZVkWrKAOw0a1bao88dEldltE00TsHbEakVOAkBpirVIjOQQ0KEyvCkp7VXSXT1Xy9otRaGZJfAZSrCF2Bzo+wyInGnUAcDEmJneX19LZwE1c0bClRD5VgVo4QDo3QciazN9BM7W/5sraKCLF15pLsrzUi0bZuCyNh4ZmAc0h99UrVQKRkPtQI2RyfNU2Agz4Ho01DlmkkrSr4ISrlD3nCSUyPJ51Dx8PLD04QAPSjLuL3/5i7lhKt8tH0Adztn6GbU6+GGZev3vo8PyWY/A7lwKupTy792HY9ZrKj5/en4nlKFTAavLNa7hGvV1jn9fVuKTnFCoLA1FyGLJo3LirfNzfvr5T/j8w895dP4Qo4Q52LTCZplGz/bmmv1wI6EEURLSJxJDCozB4ysDuIDgKUSikXu47nrargWlGKaJafLz+XEA2WNdAserT5qoY7C7nCXoYjERpc3UGlROGKUJWVgGIYV5PekKjOcMWtOtVhjnEBJ9eR9VQYIuZ2QqFgkFwtUiDc2UxO8MyhpSmLBHjFgdNeM4ofIKlKTCK62Iidmy5Pb2mtubW85OL7i4uEBpS9daFHI+ZRRGZYyqTXuCLOnXyijSFMk5YJ3BGmHMNMay6FvG/QZrFUMS5ce429P0PV2/IJdBikZ8UcXPMQrI0Cga25JCx83Nhv04sVotObs4BwTsXSwXTMOO7775Ld4PqBxoW8fN5Uv22y3jMPLq9SWuaUkZdtuBm6srVvs7Hk17ckoEIj5LNUIE4xXWgDINOuRic/AcZxNaJ/zdyOU+smtP+Kfdr3mlMn4YMSnz5J0P+Orb77i7viR6jyHjd7dM0x7dnXFysqI9P+fzP/sLkjG83O9ZLR7gB09IYnVhmxblevrFinYhDOeug+XKc725ZrvZYl2mPbNiy6MMTStBcTpLfeyV4tVd4h9+8TtOe0e/6EkJ+n6J96K8yloLoC9PMT5MovBRYHVDypHTs1OxRig0tXmPPAI154EbB6scEFB/miYy4JoWZYQBX4dzUSl0s+Dt9z4qP2vRyjNOO8Y4sV4s6D/+iBQF9DizsBsuGW5aFmdnUAEbbRh95G7KtFnTWzmTqqDyXx5+/f/+pZB6JiuFMcWSRiW8V/hE8YJWxJDpnPjnTzkSVJKBnVNon8EVy4JkymsomlYTUmS/jyi01K3ld81ntJK9JOUkLPEk7D7vg9SfBVBrSqicjoHUCgjnvdT+1kporMr5sEUVsDeRj5jLUl87V5mCwg7OSuwIrG5BWyiSXqV8sU2BmAIxjTTWSP1UiBI5TcQg+wiq9D31sxU2ZUSBslhXgN/iZWmtgFZDCMScsEZzdvEW773/CeenF/TdgtdXr/nNb/+ZaT+wu73C5LGsTFFmGStBuKkGXJUaWVcrF1tYxtpwenbG6dkpm82Gu5ubotLIQidQgayTWFUcDX8rqUNqgUPjotTR0AEZ+kMZ0pFRWdG3HcY48eQ1ghHEErIaynkWiq+/RhXPcA85kUKtiSoEKL2U1FYHT1VJdFcFlDbEVGsYPdcvooYJ5GIDUZl+dTBntIDHBIWymThJMNwUI7HUCnEelMrntIUdm7P4xipNAd6lVzSlV6heYklV5m88+LWWBs4HL365OROSE7zkuF4xCq0syuV5CJvkERIfUWNAF+/aWuPBbGuhKDZlWRdliyJ6UahmVQIps4CnIQaxhzTiv3sItQ0zMaIORO7VsVBk7mauwedwUiUqoZgzJWcdrcXqsq4lpSTo94SVMEsL0Cdl4sEvNATPNI0zaKtKPVID7rb7LftpwhQFxXK5FAb0XvqaxjkBTHPGKC3PLqBtwFnZY5qmOQz6rdTK+uh5qAztamWXYmTc72fCSqawrxXkENlOAiI6bZgKqNo5R1SiujbWEnNi2u9o2k4GCsjaqcOPrutmfKBaSZjSA+922wN7NEvwoTFGbONiJMXEpBSb3XbGIvzmTtZwqc+1Mdg6XCis8BgjxjmMFYJjv1zM4Kr3QRQF5d67EsQWQ2S33zFOJYSukrtSnpnExhj6vp+ZtTbbGXytXufy6Mt17tp2toaQZ6fUtdUCotzPFBKjHw81/7x2IwFwTTOvpbZt5TmK0ssG70Ef+rg3v/6oQdqUIemG9mRBuzhhM2WStmKDkBIpRIxpJVDq7pb29jV5eI1PA33b4yy0RjNmGKeB1aJlvVqiQ2Y7TFit0cHT6YZV07HqLLfbDa+e3XD1ekvScPnyFTfvvc/Z+gzTGC4enNCtWp69eI158oCTi3NuSVxebejahkXTsm57Lh6tcUax2e3YllAE1zTopkEruLm+ZjvuxaheKW5ub/GnC5zSRYqhSI1iGDS//OYln31ywbsP1ug88+TKRE7+S2nZsCc/MexGNptbckqsl6cyfe8XONsC8gC0XVcmZVX2UdghSTyslDIlRF3YzCpTJAEOhS62AnJIial/IqeJFBUhGFyzYL1ac3l1JQ+4MeQo4Muy77FGEUOiilUpAELTNkQUbd8xbndlAi5hSbJxRlIKwgZqTDEy0QLuKUPKEWsl1S+UJjJET8oC/uJlY390/oBP3vmQ9x8/pek6xnFCayOTPmNJSOJmpjB+ANfAxUNHGBM3lxGfZFOaonjkjV4SnWMKTNOI0YqLsxWfffIev/rya15eXfH919+RlSYM41wERKWYtCIoATGyUrNPZE2IRIGPqch6i3dKkftSV8MbzXWdrMP8q+59VRZSBVYqa7BOu2QiKiySyk7TSBJvBTcq0GPQuGz58NFT/uIHf8KPP/8CO1sXSOUq77JIQfHoHMklREyXarZKa40xxQBcZKL1kBYWm2ccB5S2GFOSskvittHFBxQIYSLFCZ9lqjn5wOXVDX//s1/R2sDZgwv++q//mj/787/g4uyMzlmcUTgr3qX+XnJmBaUp1zMXqYh4NBlrChBVrksSMKQmWBpjxQKEhNYWpy0qaUgWPykUIjfu2g5tLGerZWke6hQzQy5cslyuZhLQ08fIWHwjq7RPI81kJKM83Ewjz6+uCOaMzdRw0i/pT3tevXpJBM5OTpn2WzZ3A6frFSprvN/z+sufcZEj/+aHZ/yPP9uwyxm0lZYvBxr/Pf30G7rpG5p4g2EiqUTKDkVAxaFIxVYk26GdBBkKOyGhcxLfvzChYsCQsMqisbIf5YifPIU7V4CMjDIiXwuVHaqkiGnaFf0JjBsvbNo24BHPN10P2CR7WfIFZK0+WwXEkkt8kHxV0PMe+3JerUW2Va1HtJ4HH+SMblRJtq/PmwRLCBuvyr8Km7VI8mcwrE77dWWlcA9gPf4yRsLj6ldVUxirIRZWgjrI8I8/y7FfamXx1oL/eK2j1czIuM/WfXNPOYCgVZLYtu0cJlD+4h6QeWCX6rJTyLWon6Neozqlr0wsY0ohW0JZDu+/Aqu1MNdUJuyxlO5Ndu1xSFm9E7O9gdYlt6X+TbGfSXm+rlrrWd2QszA8dFlTqbArZksMpYQ5Tin2IuSQcSlx1q/4/MOP+fFnX/Do4glO9+TYkHXxV8tSIO93G2KaGKY9wzjhfWLvhUEWy3s3Sp4eqQzlurfWiS+WObCCKUB2nerPXqsF7Y8lzfkYrj1ej4d1qmYAtgLmPkiQn/f+oJ5AFQC7WkBEmlaYDVk7AaspazUhw5yMNBFZo5SV4LC6arS8l+1my912x5PHj3G2Q2mLSsJ7jNHTWIMBYVMOA+NuFLVTSphFz6LrpROtn6N81mF7R44e2y0w3QKjG1QFm8u1Dt7jJ/H8bVpRGakon09bK8nFpdi/ff2aX//jP/HknXf47Ec/lnmsFubYOO3ZbG7AtjTdCl2Yv6dnF6R4I/ZdnTQhSmVO1kuGcc9Xv/sNw37LNO7QKuMny9XVNV1j2Y8j2loJ6kBzdfOK59/8jidJcZo0gxLPTavEZsMT2SdP9pq+sP+vt7fshz1vP3kkHq5hy6/+3f/C7+4GnqnMNifCfkuL5rsXz9gMW2EBagHcdUyErFg9WtM9esiTTz7FdQv+5v/6O+gcpnEM4x7XN+LDny3dYkW/PkW7tgxxM03TctYuaBYjL1++ZPvyO1Yn53RLjYqOpBpSEqsGqyFFxZevB86/es2fffE+bdOSrCXlQVjVBbyTO61oGpGoamNJSYaiShs0kVTsqQ6sv3RQWMgLUE6QufIRxfNB3YMSckOqe0kGbR227Xj56gWPWkkBn4Ytm5trtDUslyvx248BDXRqy+bqG7SxrJYL8UOeQLvE5BNei+WYs0ZYb0dPbn2bx3/+l2bQvqniygXIVkr2UG0U1inwBXBRsOyM5A9YmJTCNIa9VwSPWKXESOskxGYcJLBW2GDQtbZ4D1umKZCilQTzkAuwKXt8rmBs04rPpFEzW68Ggwl4UGtQU2TmhSCiDRHpZaqlUM5B7nwpLITlJn1WrYdjzAIO54RzRkgLSYZaKDlbZF0l8R5FfEw1mpgDxIkUBgxJ9o5Uva71LI23BYQxxVIqU9mWlhQDGsViseR0ueBkveTq1UvGzcj7H3zKcnFC6xp5fvyAIhRfxoyyipQDKibpjwrwKKHWlfxB6evaEmxV7M18EIA0RTLCiEvIdLKGAdX1Uv1RD3++ry6Cg4Rfht/QNFJDO9cK+GP0rNZCG6x2MjQJo+Q9xADFGqcCwrn0OFI3HQ1n82EwCZTrYeZnP6uDbRwUL/kpCQhbB7rKMoeoZghTYJrkzB59kCFZkvPWVH/YGnCkqyKrKFYRJqjI0yUot1rrSI0m11AY22oGAcWGUdGum7lvTLEEJCoKB0iRDbNv71yj5dJ3lttQwdOTk7WAZUXqPQ95o+xxzpVgpQwhBwEilSHFjNUNhkbUrakO9A91qEZAwckHpiEW1eDBguy4T4Oi5ikeogZTFCuilNFa1AVzvVbrSBTOOow5hJPJVq3mflj8YFPJQan2B1J/99MoNgVluO9KSKEPInPfbrdzaBWx1KBakcbx92p9bWQAYo0p6khZ6841NI2jMsob51h0HScnZzN7OCRZi1YJMOuDZ9qPmCgeqOkIuL/b3LHd7zCIj65x4itccQG5VoLfCAhefKCVAMrWWKqdaioYRAVpZ2/ifCBMoDTbuy2jP/g0H/cAMwhc7UvIqBxmr2G5F46T5YnsJUX1pbUu9pu9KNDyYS8xxjAMw9x/7Pf7GYCemeXFTqHru6OeQ7AxW/Z8qwQUN2U9VH/cxVGAW33/x564KUXydivqhLL7O2fKsEALEJ3/42fvHzdIqzWcP2RxdobPCn+7FwAiiwm2NZ4LPdD5gaT2eJfYY9ibnjZrKaATdO2Spl9htCH4xLDZkfzIyiY+ffKAs6YhTgNfvb5jGiOahouLBdu7gZurgV/5rwnht7z3wbucnspUoVGK80ePeag0L3ZbdIpstlsWyyV918u0EWiNgq5jO4zs9jvi9g4fBDSYgYbR4xXcbPecLw1kL/I8A0NOfPXijl9+c83TJ6fI+JU5cCOmyOQHfPRstkInV9aKbEZplsulNFkI05Mki94oSxWl5ARKVylPRKfqAyKbqCkpmNlYSVi2jjgk9sOIySN917Md5AEwfsLYlm6xYuGWWHvHuBdPG6M1BujbhrZ13E1blC5SjSwZilkpppzRToofUjwAjCkLcFY9Y1Lx/ihgiSTuCpCrVaZ1hpPTE65fvWaKnouzB/TdiouLBzx59BYL20NIZGVoFmKKbowthVsmloexbddIiI0hTnt0ziwWHTEr9jVZsTB1U4rEUD6vMkDg4mLF++ltrm9uuXl1JaBIFBZWVnKPJ5UJZUItYKAcnKaskZjneB9yEm9BU0AlVQGAIzAH7hfFxwX4PXYYB7Ckyk7qZnks9Z2LjpBqD1L+rhQmWfPw5AE//OhT/vSzT1l3fUn61FRPUYWwW2KKTKWIOAao5veVAjFVL6qDvETM3humSby8VLnG2gpIlkqyatO0klY+RbHcSBFlW4ZxYr8ficnwwUef82d/9iPOLy7EE2ocyiReS8EU7l+7+b1V4CalwqZQRWKjUUp8m+Ew/Q4p8fq1hNylKFK8prEYC+N0x263kcmtdXNQkDDH5TPHLMBITpCIUCSsOWWSkaJxmnaEsCcTBGRJEZ0i+yGw89Ctzun6JXQNP/v5d6TmguX+is/e73j69rs8e/E1jdOslws219c0znC+svio2d1t2F7d8eGjH3Hmdky7PVlb2aP8Nf34FWv/LYvwHOfviGSiNmQMhgnld/ioCGgwDSgB7ExSBC/AYS2Mi6pQQHujSMnPcqWYpMBNCrRxZJSkyqvaCJV7ow1tf0pKgWlzjc8ere4ICJNLFWCdEFBJ/KRUYpa6/B5oWA7POiSYn59M8W2tkvYDUAciC1KmhKEVYE7q24RGBhCSJCxNmwC/vz9JuQ9+HZ7dKrk/rMtcmgc9A6W1eK7gpjGVpaPmn03Hn7Wud2rhdHgPpsjF6p4QYzVA/n9v7mvRfmC2FsATxRx+qHTZeyhrYu4A5vdQP3f983HDVkOa6t/Vwl0Vq6HaZB3f3zfftyoMmCpnF/C6AGwKUZKoeg2KL+sMSh9+b0bOsTrESkefIaQER35VYMhEsvGo5HG64cN33uNf/ejPee/JuyzaHiF2FQkbicnv2d7dMk57UhLP2bvtFh8ldXb0gUIuQqtqbSAsAa0VjXNlDQRJKy9nR/UGrsODWqySsgxi5+t1tPkfrdPD/i0p6TVILxWfwuBDAcAroJ7L8wMgHuNtb3FNV5gLgZR02e/SHJooJB0phOfGNQb8ONI4h2ta9DiyG0eMa9hPAad1STSX4tw5keD2zZLdbsvt7SXfffNbHj085+LibVYPHpG1KVCbhIy9fPU9r559w4effkHfteSjwBtVwOtcmuK2cSW9WMJayGByRvmADyLrfPz4ETpFFqs1SgmIrJU0WSl6dtsMynJyZmiXDmUsru1ZrT3OqRnkapxlGnc8++YbpmHHNO4JQZh4V5eXKDR5vWJ9fo7tenwI3N7eslyteff9j9C3G3b7ketpwkTFSpsy5AtMSmOSw/iRrDXXuztOVivWbY9KiW0eeHU98sqd0Dx8i5e//Qfe++x9PvzRT/h3/9P/LIO3mEhOkycBElaPH/D00w9pnjzFLJf83c/+niF6nGpEPulalLXIYEzTLlZ03ZqgdGHnZSIREzLW9Jys19xeveD29pYhRDpAL05BN3MYntWKaDu+fLHho6cDTx9fMHhPt3A41877fKoAjbJIuazYF5aR0wad1FxrCCAh+2rda+v6T6moNShSW6VpSk0kgI4qAWWy1xjbYKxhsVrzuAT5hbJfTZPn5vqKlBLjNHH9+opFv+Dx40d0KLZX33Jy8pTHZ+sCvkCvNG0jrD1TgmDuaySO973/tODsPTD2//k7mc18ldRMKcqgKAYZWKEyXQvoxDRkhsEzRQPZUUh8qBwlHMhpfMqESAE1Dc5ZQkoYawheo3WxQVNa9pEid1baFham2MEslgtSiLSt4/pmA9TzUNEvFnRdS0oViC0+ozryZs2tyr4qCeA1wCjJrScTkyeOnhhlsGOcQyFWT1jNNA2FfSt7v8zbIiqVfSRnCSKtXv5VNZEP3vmKA0CrlFgCgKzLvhXV5zDsuLl+RRi2nK0fcX5+QsgTt5dfc/3qa1SaxE4DuW4xTKAp6qhi6aCQ/qmQFTISbmtUJvqJ7faO7WbDOOzIMQCiPkjRY5QE6VQg3BQFglzj+0AOHGwiUjoA45WRZwqRSJQNAtaJN6uhbXu6ruHy1QtCAWijn0SVIY/2vIYVtS481HgyaInlvh/bB0hNcAjtYvZO9VEsvFLO+BSo1ocoIbyEGAkpMowTAnULCast53SihC0nCbVNWXpWIQaEMuQ5DFQVzPe+qpDMDPQxn/FK6VkWnxU4Y0s9Vp4DpcV2j0o8KSpe7tscTYW5KH+GQ+Bq9Qwu+yECIislwCkIvqDK9RX5uoQEVom9PEOFmVvqZ/E6zmWgcRh4V2n+NE0zg13X2qe8Vh0SKyWesk3Tsh8GpnES9WUBXCt4q5WmLUzSQ5+iASFOaS2q0BgFX2lO3GFPy8K+tV3HarlEodgPe7QSL3zvfbkuIrePIci+H4Wh76epWGeI5V9K4skqIVaFsBTEErFpGgFFlfQlqoD5bdPQtC3r5Up6SjJEWYdOG1hrzmOQYO3STyHlLNvtjnESZbD8TjNfwxzkOe37/mA/UcDcnCSzSRdVwLxmUsIaR3PeSF7CNM3PdR2Iee9nH9yURE2mtWEYR7EWCIGmaen6TqwLrC11q4Zi21XZrfUfay2r1WoOPqskhJlwkzPjMBK9Z9wPs6dtrF7bWc1+vKYEv1K8hY8HMmLnEuZnX4YAyOdPGV9IQftxYLeL8x7tnJuD5v7Q1x81SKtcQ//OB1xvbxnGkar0aHuH8hO7V99wNbzmTGdO2gVdoxiCwhlLm+sBaehWKwY/4YeB28tbxu2Gx73ho2XHhVNEP3C3m7i8HRmGSEqDeFeaFeuTE56/eiEb2tWGb169YBgn3n//Y1bdgt4aHjUWSyZdPCBruN3tGaaRoDSBxN6P7MY9oSw86xo5hPwkTVQJDrgdBvrG0BnxhpEFlhm84Re/u+JPfvgWDxcdYfD4OBFyYtjuUFH8qqyx2LZhsVwDEIOXApRUmk7Z7CRRWJgDcnALS8U5KyyBcjCFKIs0kolh4m53x91+4PRUgqBu7zbcbPZ8+tnnfP3sOdYalss1i96wVkbkJlYCMsIU5/y65bJnsejY3N6idQ1TEFuD6omnrUE3kt6rBBGhtUUuUHxtWtcw4QkzEywDIjdPMWC0YtH25PUprWv5yQ9/wmp5Il5TgA8BrwKoChaKgbrSCgsYZ2USqwR0qmER1lj6xQr0AsyOvN0z7HcYk4uHVQMpEKLCuY7lwrH2MuUJ11tho5YDxjQyiQpyKspnKN4s1UtJaTkEUMy+fPKAHDaZWhC/yRI7LhqPgdxjdhjc92esflIppYNH7QxYqfl3y/RcWCa9W/DB2+/zo08/Z71wpDhCKQ7Lvi/rLRQkJhfjfZXmaaUyNWW0AqNyKMdYjb5T2cDlzzlLM5uTEUuNLGveayX+tcXTt4ZUxRho24YvfvAFX3z+GQ/OH5LixLgbyDmQrSZpW/yXmQ+ZylanMr+QcD5Tii2t5ztS2A8VlNIYrcRQPEWa8iymBMRATHVoWXyfcpn4a8iE8twWIKhI7uv1yilBGFDZo/FEv0Nrh24a4n5iPyam1LC+eEi/Pmd9eo7b7fmBPuff//1vce2SL3/3PT/64n0uHjzk1euXNM1D+uVSZFauo+1XNA8cz77+Jf/h7/+W2ysH9oQMmHRLO33DYvqWjmu6fEdj9jIlR2xmSB5tEpN27DXFbznJNHsSECBrTUKTjSXnworAoEPET7vyPBiyEoa0LpNZKntaM7P1RM8kB7ZrFiR1ym53w6K1WBvQWWTQqcjAtBIblZQiOousst7rWpTL0CcfrYMjQKr61GZpUioIaEyLNRAVxbe4JNDnDEdNQB0s1Wf0TeDw937fvMYEYPLei3VDFrnNcUpyfd7rc940DU3r5uHL/Hr58P3z79WHEI8DWMo95sQ9VvEb4Hb9enPveXOvymUoRGkkZ6e0o587BlSPw7WOX+94Tzve2w773eG9VlbE4fuPf1cNESlMjizsLvKRvLFctNnypTZzSt0DysmHtVSvY875XvMhLGCFAUyMXKzX/OTzH/P5B5/z8PQJCkcqNh3KCLN9t7slxpHd7g7vJ4bJM/mJMXh5z0pLM18GD7b8I2EHVfBckn2LkiHBbGUkz1/Zn8nFbyzXpTKvv+PrXtfZvI7mdaJLyynSX3RtlvTcCEhooNjeZGqTJGEqZHn2xNpCXosyDNdUfHgAACAASURBVHXOobRD68KQTQEvj79IyVenjCGQtzussjRGs+5bTNtQAZeYMtZZzs4u6LuWF8+/5hc//4ZPPwk8fe9jlCqNVPAsOsejRw+4evE1wY8YlSQhfG6G5bzStiUZU5WmR+usDmsMWheWddfw5MMPSFnCLpUSJh3zOgwMu1usM7i2QateGB2Nw/syrDaK/faW169eEoPn4uyUjU7shy3ffvuKbtGTI9im5fp2Q9919M6hFGy2Dq07nrz3Gen6FVf/+I+o2w0pZ04UGMSb1pc0+7vdnpgT56enYjMRI7dj4re7zOXZKX7ckXTko7/8Kf/Ff/Vf87NvfsfN3/yM1lqsM+SsSMbhzk45efoWq3fe4Ve/+Zr9tMP1HT56UKYEdmq5f0qDNoQkYJQx1UvYs1o4ptGz6lsetIa70xN+++133F1+x5k19IvTAgoonFIYa9iPif/9b3/OW+drPvnkA9brVfElzKUQRtZjMvPzaqzFWCcgYoHGSVEG5/kgz56DT2P1UZZ/5rBHVZvYea6D0jCFRA4RrQsBxHUkHRn3O7Iy9Mslk/dCCAiB65sbxu2O0/VZkTZ5Xn4Ny+5tHj9ewxg4Oe1QOeKMmW0OCpQoFeR/Wlx2/nrzDDgepP0h0DbV/be8M610GeR5nFE0VtF3CnRmuw0oo2i0IUS53rZIgsdJWHbawKLX7AcYpkTbGvKUSFrYz1pJuHBOVYFT9hwr99tQbY9kb5omAXVilMAsXyT1IQRyCjMgpbWWY0MDKpN1BbKK16LK8yfNOeBDmP9bSBsiDUZB0oqoICcJ7klZrHWmMAkIm8RqKwSxVVEplpZBo42aPRArUzCVIGetxKc7JckD8NOISh5PZLu5wpJ56+FDHj444+bqBb/81T9w+fwrot/Rt1ZIJzkRc0ATIZtyNgoBRwBMSq1egUkYhx3jtCdr8KOAISqLrZUusv2U0xy8qLR4u1Js1A4tx/2BrYAc0rcdg3XCZnNCQFLlvWVh2LZty3a34fr6NdO4QxVLLijy6VIPaaPJscjyM0gNwf3aSVUo+mDHcFx3zZLqRsLsLMX2SR+GQVrL+Wucw5T1R7UkkKVUhqMSbjUNowwgrJtrSGuFbdm1HVaLH7wpXslyneq6i28EGskeJvcrF4A0lXoA0JmQooSRF+zi+Nm+Z7WVa50j26hrGmFchihM/vJeYpHBk6XnkcGkEJGIiRqYqst7TlFAaWUtShemq9NoazgO58xZAqIE1IZhFPLUarlCo2fwsIK4FUxrmoamE5AxFtbpcZ5DDZAaxlH6hBkzKSo+Rfn/cr60bSPvsQSfG2NE5ZPBWUNu2vn127aV2p2MLWQUXfqJRC7gd49SAvrd3W3L2lbEWAYZMTHuC0u04CRoaNsOW5RlPgacERWBNobWWFEmFlaoMwZnXFmXzMP60/WKkCJ32+08tBflVSqBlJ6hkNSqgqwehqrU9nOtaOo+KT7RuoCex2dDZbcuFgugEF0QVUUoKu5xGPEhcHl1Rds0LHsZmGmlGcaRyU/YEqbdOEfOsNvvaYtFRt2r4RBcV5V+CiUqqHRQxkxhAhQ+Rcbg0V5qe6vNwZqCehbZGXitzGtTsLQYE0rJHtO2TSFIhNnSarfb8R/7+qMGabPWXAWR7uScsDnKlPXyBen518Sr7xmZ2DYtu6xwzqKdoclgrJNFow2b7Za73ZawH2h94Omy49OzhlOXGG433G0Tr3cDl8MOZxsyiqurG0Le4G5fMI0TKMOvry9BZVanZ+xXN7xMoIm4rhHKvjKluExsx0kk0MDgPTGDMY6mMyQFu90gD4jWmLYhpsx2GtgNmXbRo4jobCBrgtI8v9rwT795xr/500+ZYuDy5lqCjrTmZLXi4uycFDPBJ5wTJsowF4eaSGnCyCSVUFqm9zEmRj/g/cg4egExNXz17XeMUWSKTdNwe3fDYtFh3IKvf/lL1icrHj5+xM2rS759/ZxBBXRSPDx9yPffXbO5e87HH69n/6NUNgzbtDR5ZL1ecvXaobKkoOeUaUxNqp8IGWzbkkMq3kGJmBOuMMgqgBlDIFY/jywsTcglcElxdbPlpz/+V7z71nv0TYefRu7uNlhnWK/X7MeBzi04OTnj+bNn3N7eCFMjJUwU7xqZoIivUQC07jDKoJSjaSxKLbB2QQwjYdoR44hz4o+2WKxZny95fTeQq19ZCXtSRknTqEAZoHj0VDlCTolpGkGVwstamVZVn5wj/9gqb5LLcDhI77PwjgJ1ZqDpTYBWVXxC/NU0cj3LtJwZ1yiTTKDVDe89fMq//pP/jE/efRf8gDIOSjp7PgJbUpQQMV1eF8G6pNTxqU4MUDAbkgsD1czFhMiOSkWcEmkKZBPR1kLyhCnI74kJnc1cSPkw0baORw/OefDgDKNgHAZSCBhbLCQygKaG/oVSTFNSJpXSmMKWDTEW71uZmFabiJwrUFtYeDrR6IaubbGukdC+KRFilXZn8brLGZ8mASJKcZKzgMFVPk+JE0gpotJAmHYMd3cMe/EeGvwle69pTx5y/vghDx48QKnMOGw5Xy2w7xuitvzN332JefiAn3/5jB9/9h6rVWSa4L2nb+FD5JffbfjVb57xy++2GLemu2johmcM4zXOGE6aLXb3jHZ6hlETOe3QNkpYDaByICCy5sa2JN2isy/vW4EfaHIiZCA78aLSxVsaIEeUOnhyUWTAKWWUs4U9LfeDGMiqyLmRQs8qQzSn+HQmxX8OoEKxO0jFf7X8SCmK5sfmyIhVfJDNXLg455j8JP5c6tAs1GdtBkq1xVhF1FXSyTywmJ/Nwg5QuQCQR03I8YT2+Ks+p9vtVhqxgvsmdSh06s/WYqM2FmORVd1jhxeCxT0GcarX8vB3ZGb/2Mz9hvsew/jo/725H73ZZFUPrePPW9mVx983XxNV/MeO/rvuYeJ/fJCv1c+5XC6FgTbW9NRqgVBf+2B/kOrrHjVqc3JyCbe6v7eagnkepvbyPuo1rkO1Gjp3JOdUcnYrMsu+47N3P+HHH3/Ouw/exxqHjyVQzyiMtkzjwG57w932hhQn9vs9kw+MqfgzZz2zrJriR4iCtineaEoYEENhIyglhfMcUlecdX2RaIm1wMFuIpd/S4PFvZCF4/tah3mx/H4JBqrbqgyb5K/qYECa7OrumnOW6UZU4iOt3P/N3Hs923FlaX6/7TLzuGuAC0OABrTFYlVXV/uWRi/6cxUxCulhXqQXSRMaKTQaqU1Vk1VFFi0If3HNcZm5nR7W3nkuqWqFRmop6kQgSAAXx+TZufda3/oMqOIHpg1to7FKvOdF/ugZQoHOTMuYQEUNOEiRYTeinIbOMfhEjD1GQdNF2rkmsEObOUfHp3zy8S94/N3vubh4zuLoiNO7b+NoME0jQKlzfPzLv6ZpZ2IlEz3GtdM9Uc8tpdSUFXC4r5UA8qaynDLr9RZbfOpCTOgSrCeDpkwMogJZX0eMdRwd3UNZh20aVsZwdXnB9fUlL549Zex7Hr3zFlopQtjz9Nlj2rbh6OgYyVfoUdrQdFIbamvJ2rA4vs3Zw0dcdAt8H/Gvz3n+3TcSWKerXYXHh8T55pqTxYrGOVL0bFE8GwPPdGK7ec7Y75g7y3/4t/8Tn/72MRdfP2PZzSW4d9wzhoRbLGlvn2FOTnh5fYV2mocP3+DV+gofE43TBRwd6boly9VtjJ2BcehmhradSNv9QGMMP/3Jm8yI/K///X/LV1/+luMH99ls95w//pzT03usTu+hnHjtWUDZlosxsn56TbaPefTwPrdPbk01ckbAe9AY15DGUmNpGeBnCrtHqeKNl1HKMgwDTdMUebKc+zV4ZrLOUQe7g1QC6axzxOQZB8+sm5EzpKBQytJ2c0Y/4NoZbduhrGG2sDTaMW73ZKNIcUBFReSKJ48zy9U7nM4dKQVcI3ZVDfqwj/9/hc7eePzHMHO11uiUZT/xQWpKA/M5eC+Bo1oZhlGYf7OZI6RM7hGpeAG9tDMMm5FVJ9YORoNSsh93c8N+70kknG1KPoUw8lKUPXnWzdjuduQEs/lClEsx0Pd7/Dgylvo35zxZloisvC++jbOpRpa6Qqy+vB+BWqdLorcAQoUMk9RkA4CRWne326FyAYRyYhgFmMhhRMVYBmoRnQJk+ZWT9MZV2WWtFTJDKbBTHIkhUv0sU6nz+xDR2QNBamyVePbiW77//huuLp4zUwKypRAJaJR1QGLWOnKubMgDwB6SvD/xdpfPHaoNmC7stFT8PMsQT2eRf8ccwP5Qfi7ZJ7KebhJQql/8IZCtSLPLGs85Mw4DMQTa2axYoSnGYc/rl8/p99eQo/ihl1BbuTdKWjxZMl+oQFMNXT2c/xW4FACm+BDnOqg3E6s2RfmMKSWMEj9ZrcSP36BonROf60YGUyqrEhSnhCglp+m0l1Q/0hAihdMpgdLT3iIS60MYkS5AXzic0bpaP0m9pbUhxFAk3Jq2BI0brXHGTn3kwYuV6fpbY0QtUxSe49AzhmGq72pYYrWjygkCSfqDJNc6+VGYwldxkvmLTZyQU0bvC6Gon+rTCozV9zUMA2gBKatyxzpHY1ux4FASLubaVs6YcZTPrMS/1M7nU883DGMB6DO2aWi9F2uMHCd/U2fE9iTniI+J680epRVt005knrZt5TOqg6rNVP9VLV6ouZIHSvi5zuLv2rZtUWbWWnYpAGkZDOaccZ2jbVrZj5JYZFDWhyp1Whgj477Hl+Fv51psI5lAfrstw3yp/5rG0bbF7sE1tM7CfCH7WObAQp6LHdB8MYey7nIJjcspMfQSwhYLQJnr2sqB7W4/WQLcvCb1kVLCWYdrHFqJv2/TtCyWS8hiEeOj2EpF73HWMZ/N0Eazf70vN6colSu7eLNeF9DU4Bo3Aam+MGKdc8y72cEmzhhyLvVAAaTl3qm9vgwIJtJFQe9vAsDigaskGK2cu64Ry49WdVOvdbDA+sOPP2qQlpxgGLBKoSx0fk9+9YLx+TPM/po2jzil0V5uguD3GJQYxmvoSirtru/JWeGy5t2zIz46O8LsXzNse65f71lvAlfDyOt+i3OWWbfAp8zF+Wtc13B6dgufA8lSwjV2rJ9/x2p7gdMypbHW0RpLIjOMI4vZjFXXcf7qnO2+l+AypTBJFoRWCqPEsFy3lpzF0+JZ9LTtjIaD955SiX4f+PLrDb94P9C0jqYxzBZH4s2CKrQtbhxWBhUgF4mBRouhOJnNuGc3jNhuhTaa508fc7Ra8N2TJ5ydPWSxOOLpq5esbt/m8cvnvHH3NkYpri53fPzJI/qdl+LPNXSuYdXNuLU8ZbsdMEpzvFqxnJ8CibZN7E0GZUm6HEamYTZfYpxlHAI5O/E40QKUZTKRhHYW27UyYY7i3RO1pCySizeXMehYEmJDJPQ9zhpW3Yx7dx/w3nsfc//em+SY6Pue9WZNzon50YqUoXUNTbfkzv2HnF9e4y8vMWQGP7K93uKsZTaf085TSQeFVWvRdo5tZ8xay8w4xt2W3foa72bEsIXshb2pWy4utvT9yL7vy41ZWEjKQNOQnZVQqCzS2MLNIk6gaGFnpYQzjsYV6VOd8qrqB1PAFpg2DGGEHoCHVMB66usoyCpXgp94W8WDH6fch1KE5dKcEIWZqpUUH4vZio/ffY9P3n+bTkMaswSoUILwsrCOSAWwoPqA1VdIE/ibSsEOkJSeJENKi5+SLgVDjEFSO4skNRVaqjaFkZcTKor/aw20CaPHGst8NkeR8SVhkZwwqkHM/w/TYlUKAaW0+D1pVVgICuMsprAxatNFYVrHlAhRUkRt15F8JMeAmzUsVisWzQkhL0ghcXJsuHy95tn3r9F2IPgdMRaQqQD6wQd8GFHa0Hazwl5IjH3PxcUlXs8ZUstidY9mcY/d1Za/+/QJ7703w7RHnBw7XCNevqerOY8eaMZ+5POvXrKaPeDV+RU///kbxH3g68cv+NUXz3h8ZbncJYZxjksjM+dZdZZ+d8GHD2/xi7fv8/i3j/nyC5FgKTIYS8jCjPNoUhpROaDSmsYmGrR4xkUPIRLVnCE5hD+gC7AkTUUsElCljLDLVPFrNaUwU5qQwWhhnkyeYymLFEgZ1OqIMZyx85lZAqciKkqypla2sDUOCfa5TMmLmVr57uVmqh5c2VcGTpp+tsrHtFJYZyWYwie0cuQJ4AVXZHcV9Kv+p0nliaT+YzbooRE5FOBwmFDXdTKxFktBOLFobjBOqcBYfQ0q4Fn9ditYW7cIuc8PW4MqbJkKVsqgRN0YBB3YqbUwn16O2ixMvzN18HIYNiktXn0pxQMTRC7ND65zebEJCFOKArDK/iIJ52LhEUIQiSXqB9e3+qvWgloLNeYA3EdfZJAVXBGZ7PRZUyJrVaTERS6WU7HwqftdaRrLOjVFwRLLunvrzhl/8tEnfPTW+8zdEq0aEtWaQIaNm801u92GEHqGYc++hCOEnIiFfanI6CzgRErCOrDW4qyltZbgg1jVpCRkL6WnWYQqB0aKqaT1HnbmmmwtAFVZa+Tye/lu/k9MZqUY/EhM1TJH0TWOaltD8Teti0FcJTQplHDIEpApzFtNozTZeKyGzjUYlRn9wDAmfCqssXJPppRRWSxNNJpsNMY5tHPE6Hny+6+5en3O4njOow8/5OT2XXZJWCm37z6gaTuevviWy8s17WzL6vQWWhWpKQqPorOWYT/iR8/CNiijp5ChTC7MHTnfajim1oro0wTeA1xfvGa1WmGXR+JrXPYAUe5poirWSSS26zWz7pSumWFQJBXolktevX6O0vDw4Vs0zZzt7pJnT56QE9y//wDvpTlab3cEP7K9voQMu2FgsTzlg4//nKvLNc+v1thZx9lHP2WH4tWXX6E1dCqLt7zWGNMwX62IShi2r7PiaYgM1hDHHcoPjGjis0v2TzdYpbFtI1602tAuDHfef4f3fvEXnK97vnzymDv37zN4AeA706C11OvKzOjmJ3SLE6zrUNbRLVcsju7hh4Fw9YJsFLtxzz/96u95cfmaO/cfcvuNh4wx8OrlMy5ePyUHz617b6JtC6o0XsYw5oaX1wN3bvec5gFtWzRW1o9RNZe17NWylm42YtIUx6m2qv6i1krtXVlCMco+YmxhnWepDVSR4Iofuqbr5ihTmDlaBieN7dDmFhfn55BiSUk3dLM5Cov3cToPtYGw2fC7z77ll798n3mrywBUbJJiNjIYqRtcLRx/BKj+mAX7H/v4Q//mDz9PPlxjKU5JZYghgJIiqswYE2EAH8HHjE+JwcM4ivPbxdXAfqAMnDJpnVEqMvrM4OPEUE8h4sfAuL8uvYPn6vISlOb45AQfDCFIsFuKkTEmcowEnwqbNYmqroz8jTFE3xPCQEy6DPTcVNtK2FfEj73ImMu5KIGbuoBbmrax02AwJVlvoQ7o1Q37jQRW2/J9ZQFr40j1RVbKYpwjZwVahj6kYmuEePsLgzWTdAGftFiR5RRQcWS/63ly9YqcPHHYsGxkn5fBnME2LZoaWuSIuUjr9WFP00kYwSn6EqarIMfKc0ClEjysi4+ryihbioSYAVvUVaWWL2u1ZmLAwcs5TYCVEFd8CuQstR8Uax0lTOKmcazDQL8f2G+vIIUplPIQmKzLwD5MakYZmEGV6dew2JuDF6nbZGXU+sza4mVtDCl4fKggsJzBRiuxqUARsvSbQtJIDNFPKkWdi78+oK2jUWaqyQToMwXMLxks1VuXg8JlIjQVGb1YHrWga+1XSCWphuwJ1ilXoJATrENrPQGQk8JFibI0Z6lhF0YTwlwGqOMo/sNJGNJNYwooJ8pQrez0HkxVqrUCsBprS21hSKVGy2UQEJH3KkzLw/Ar+MgYpMfe7/dkpdjvejQlD6js1W3byj1E/W41USuisQLKG03rLFUdlXKmsY6j1QqyMIBHLwo8pUsGRUzs93tSToUMIXYKrhF28jiOZK0YRk8ehwLUKtRQhpIhYE25DpUJrw3KM0n+KQMYlKxrCRYDbY0Me2sdVtZhresb10j9kqJ4bqOxzgFM39GYQRlFHzxuHIVVvRUwNRT2tb4BpoZBwhtVAel1qXFryFrbdRyfHItX69ADpbdX4ne/2W3xXoK1q++05AIJKB90YOgHETqU12iLn68xhrZztJ0TQlZOZKOYL5YSwFqA9FxstoScNhMVYZQaMRaiQ7WTAMVyvpyGQM65SUnbuAbd6uncT8lNgxCl5uWcl307psQ4DKLQDJEYA75tmXUzYsmOsVasdXIWy5nK/P3nHn/cIC2ZrDwLEvriNZtnn9Pu1tzWmsCI1pmuc6QxSNGiIIweRSYOA5fbDZA5UoY3jo44u3/G2cLS9ju2r7e8fr1h0yv2Y+Rqt2VIkYxmGNdgHLNZh69hWl3DMOxp2zkexZgS59ebgvI3NG3CKo8vC8MtFjx59Yqrq2sUmjFGKdZHjzUjroQVjCESsngo+ajZ7kZurzK3Oi3TVDTZBzCWJ99f8tnvv+dPf/Ymt89kwmyxMkxNGaMNUYuRO2Xz1EoaHWECaq7X13z/8hmr27f53edfsB/3nB4t+eDjn/D09TVfPn6K0S9onIGUuHVyzFv332A1W/DkyQuWRvPJu+8Ixd0o3n94X1i8OYifrhpY3rYYtyfnQNeNwIBxM8ZBQGOtjTADkOTPMRY5QGvpWgfbiDKWiPyZCw3DZovKsNsNsjE2dpq6pgwhJbQ1LFcrThYrPv7gJ9y7/yaumRO8Z7fdFKNvuS7n5+c8fOshi6Zls5d5wHotP9N0DTYbZiVcLYbEsB9pOknl26ctZmFo7DHt4jamWXHnXsN6fcH5xSu21xuG60uMupbpmDXcWh2zbFoudgPaFmnkwqHmlqSqf608pC6RInoqQiiNso5UCbZMr6Wq1ROg+8M7SN9gPAkmW8GTUjBQG2UJuclF9peKxLS+B5DmOyD1S8piX3HUrvjowbv8xU9/ztGsYxz7YjbPtPkVVyyyypN0lvIZ5PeH0B1drkMFdybWn9a4pqF6UE0eimVaVqe1qfp0KqYkX21K4FDMWNugdfWmSdN0t07Kbkp6jNXo6ktYwgqdE587VSaGSot5fwW8vB9JKRcf4QNrL8bI+mrDdp9xRxq9OOGTn7zFX/z8Nq/PN/yb/+bvOD9/AVhUKTBzjgQvzLdEplESOph0R0gdo50zXz7AzO/RNIqnlyNv377Dg5O32OnbfPb5l8yPjmlnRxzPZoQ4knPk7KhDPbqD0ZJ0/c6jJd9894p//NUTfvNkR5g94Hpoubh6jgvndH7NzHhuHS95ME/Mrn7HA/2Q24+O2LxouHxxgbOKmCzJzAgZxnGP8plGBVozoolYo0kKRmXo9VzsQnRTvB0LA6ks4ZAyGIdzDSbL/pZzPIDmSUAj8c3WZSWXJrSsYdvNaY/OGDaJ3S4wyxtskm6o9wMpJ4yuDWKWgpzCmiqzDBlyyDtLKRJzXaeFeVlYKdULMCuxOBDPsRJuVSffZZBEARRV2ffr8ygEZFbl3x5CSG5K9w9Nr1IKVRieIqmUAq2yMG7K7lAC3hWLsnKty/sqMYUpHX62nr8ouUcmA+26rygtxa5SDMM43bPURkWVV0iHgUfOwi6v+08MvhRoFTgtr0U63PelKa2J2D9mbwpjzUxgrdiNFBVAhmfPnh+GPlkGLaoMvlKWMzPnalmBIGQTCC2eX3oK68qAeKTXcBZRfRbwJxef3lS9cEtLX9aByknWdc4czTp++eFP+OmHn3Dn5AwbJbk7FwuEnCP9biPhYP2e0ff0455xEJ8ycXiT4YXsQeIJ2FiROzrrpsZss15PDG9T5JUHprOs/1iva/FPvbnGbtoZyLDu0NyqIjusP1v3uuptZ63YHhV0S1jjWUHxYpamW4ZguUoulYxpFXLPWJNp21aGEEFUB0PQJFqcBa0SKcsgTE/nm0EXvzLjBEh1tuHo+IgvPvuM54/34AO/+NsTktZstxtymrM6uYWddTz//gkvnj+lnc9YLo/kHEyO3b4nKUvXOTbbc+L6muXRUs7RrEszVexyTPWgrB6Acg2ttex2G4ZxzyI2qBxk6JMTqYAM09AJAY36/TWbzUtMY3DtjJwzXRlEmyzf92a74cWLF0Tg7v37su7DyHw55yQuSFEspi6urpkvj/mzv/xbdHPK77/6jvV+QAX4q1/+DeHt9/nNf/WvcVcvuEPGYUUy2bSMIbLViqAtT0PgVc70IeHH4aCiCNApwMCY5dxvT8+YPbjHm7/8JXtr+PWvPyVbg3/2nGH0tF1H23Ukn0gxcHxyzNndB8RsmS1WWNeRlWEctlxebrg4P0cb2FxdsTy5zUe37wiIZBuSSty78waPv/093z/+lpffXXNy9yEsbpF0R1aOMXjC5cjp6zW3j+d0ZJybC3M+V9sq2eOCh1j3Jq2KfQdTynhl9VUWX0rVs1IVQK4pTHDZ09u2LQwehw8BYxxtO5N7GalRqjzeuY7V8Qnrywv2e89q5WjaDrEJk0G7dU4k4sCw7fnf/+4LfvqzR9w7WdBoQ5+g1UVKXXHZWi7+aD/9/+shVV9mTMITHMaRvQfbWHRK9KNHaUsISI+E5vVlzxAd+zGx3Sesadn2itFntM40jWXbR7FKQeF9LLYCZaCWEsPQY4xmHAeuLi+wTcvJyQnDIN6LSimiFxWkSkkCGfs9Wis0jqHvD16vCiCVZPpI03QcLVf44EuIzDjV2zUoKhXv05vKDRkwyllmrSHuRQKLKWtIK7LRqCSMxaqe0VXJg4D/2pjS7ylCYc2mYp9CiuQQCjgpfVBQRbKePIx7iAOWXAbrnlSsoIyx09mec8Sarqj5JEhIztwgZ1Px2aQQOuLoCzFE3msdGt/8lbIEX2mlSUrhSl83scsKaA9M362ARSWTJAs788CwtBhdGbkSkDaOokzwo1hEkCOq9BLyfusA+hCwWq0sRA1XFD7GluFwFkuKUuPXc70Oz4VxLnRN3gAAIABJREFUqief1JizhBBGYeKTdQFxMkPwjDFIHkvxsD2oGhUqFWUMEpQkBIEKIlMGEfV6Frm1c1gntlVWC1FA/GFlkJ1VteFQaGVRWWzmch0UpIQx8vepBKcRSy2UmcgsMUV08OX98sMhVohQyGnDMEiGhyz+sq7LfSRNEkrrKVjrZsBrBc6mQCljCdVOI8k1bJxgCm2xJ9BaArsmQkLOjD7iRwHncs4TMCxs3KJeieFgFaKKhL3U9+ONcGZd3kfOmeAj1hhWqyP5/SwUJrnYTigSJ0fHsj8PQwmUkiGEKcOKfb8njCMhy/fXl7rZWgMxClu7XIsaIlcH8ZOFhTowm7XWJJ2LzYK8T4ejaysDWYDG1XJBzgIwjyGU26CA8sBY9s/KytZB+riaqxSjMPgb6yRHqFzPiWSkMk3b0rYl9FMJMbGbSw0zDgd/WO/DpNTqdzvpyckYJ8/X933JDdLTsGHCJmKUQZUWpatzDVpT7C0CbduyWCykNi2AqrDghTQzjgObzYZqJXdz/7lpk3BTrehcJYwltJY8HKCQMOWAvcm01WhCDPTDMGUutG3LTM2Lz/IffvxRg7QqZ9L6FeHFS3j6Hao/Z3W0ZNVYtFthY8RqzeWwZx8Htj4Rgkw9QkjoHFl1jg9PT3n37IR2aeg3a/Yvt2xf7nl9sWOdNaMCn4UNMYYidVeGxekRvkw10yjeQRqZPKmsiShilNChWQ7M2o6ATCxenL8CVVoNuVtF0qvUxLbLSiZ4YRxIQFSG9W7L5cUVp2+cYpRC51Qmfoq9j/zmq5e8884DjmcaqzMmQab67snGHstmapSleh7W5vvJ+Wv2IfPW7Tvop8+ZNS1+6Hn29Clt2/LWm0ekOHK8nDNvZ4BiNe+wWnH/bIVNEqJAm4lxYOYUWl+iCcIAUFKUGj3i2lam4y6iQ0ceTYVR0ErTNR1bL1OWqCXcYN5ZDIGQwBrxn2kWnVgg9L5MUaU4TVqaS0+xB8iwWB7x4fsf8eDBW2jb4b1nv5eCSRegZLff43MkJ9ju9sy6Y7q2Zb2+EplUTjirMabDaCvJ8NYwny+IITGOgV2fwAz0YU3Ie9548Ij7b/+Cu48M50/O+e7Lz9i8/i05CxOm6zp+9uFH/O6LLzi/viRrmC06TKNvSK0PvocVpKQAjfU7rY/K/hJ56YGJRv1vBVqVHNRy8EUkgVXfeP4ypeUGi6Ic+LmCIhPGKwAGOkNSqGS4d+sev/zwZzy8fbdIPHMBaFIBvQR0yTGLJ2kFnSdvNnn/xjh5rweE6ACWGls2vDBtlPIDTIdCLJMtOdQNSSvx78pR3q4PIoM3xS+1FDn1I6cqqVHFO87K/RKzgEM1Kdfowlwziq6YqceUCCmKvGoKujNkZQhRCp6URPar+h1eX6FtwLQt1mRu31ny8IO3eXV9jR4aQt6Qo1z3VKZ/2rYkGjwduj1lfnSL27feYdPDxXrg7tvv8mr/gu+eveKD997mnUd32Y+Kv//0W5ZHP0Erw2ohqbbLWcvs/hK3bPni66f82//5Gc8uLJt8h4s2cbVz9Os9TQ64vKbTVyjf4/drFjPDcL3m5YunvPfomA/eXvHp5feEMaN0y+hFnse4Y2Yz80ajsiclGa64BCGvGO0xg5pLI5KEkam1NCEZhbYNyjRgnEw/VQkOqkOJAjrFFMWL29gCTIYpYTdhcN0S7wdGH3FxIIeBOGwmMFga7B812bGmBRd2ZqqsVjMVl2XRyH2hZR0aJanJhRg8MYQoYQ4xJvHaKvvWJPMpQTK5yu4LS1G7g4RN5QN7seKaOafpvd5Ak0vTUYvTcqOU3xxA0+KhenPPyDIImjy56q2Yq/3BTXauZhh6cpKGxBbmgynN5xRIloqHcmHG1Km5FL3+APb9ACSozNQ0sXQrE4B6TUtRXwGReg+bwk6pLHz5ix9fCzV9vKTE1qDK8GTWk6Ccpbl+zar6+x0CyeqTlDoMyu6VCpCfkLM+a0mCJwYa3fDw/pv8+Sc/5ydvPsKZGQSFHwNd16Fdw3a7ZRj2bHcbhrGn93t2/V686ApjRUDBjCrAtFESjDWfzSaZdWUYSzMVbkjlKlhQ98Ake2Vt/W6C9JR1lg5ewnKv6MM9UIADeS0BQ0AKclPO9RCLc19tBrOmUkdjSMQgqoeYxPdQKQsxYbVCq0AMnpyVBAppB7ZDxs8BRcTgBcSY7p1OgBGK12MCDNy6f5e/+c/+lrjdSohbCoShJ3gp2hNwtDrm5HTg66+/4PzlM45Wt1DaEpXh6PisyIph5UfG/prk+7ImLLZdsN5vycB8tpBBn1EyvE+RxnXiIegst05PaZ0rLC55aFWHjlK0VxDB+y3r9Sua2QzbyH5HhsXimH6xYbO+4vrqkuPjWyyWp+z3G1CBrDP9sKdrG9q2Y7E44vQs8fa773Ny6zafffZ7DJHVcsX1do87e8Aut4zvfMTFY4u5fsWxSvSbLQvbAJk+Z7ZoXmRYa02IWXxuo3h+m3L+ZhTJe5QxvP/Jzzl6732eXl/x/ZPfY5xhFxOby0sW8wVvvfmQ9XrNi1evsN2S1dEpRydnDL6kxCNrpu83vPPObYweyEHRzWagM23bCesxJbpZx3JxQvCZMA5cXbzg6sVj0hk0x3cJ2RCAq33iy8fnvHn3mIezlhgGEgJ2au3K3q7RVjyArZVhQx0Gad0UEFaGCBWgqftDlWKLP2RJdCcV65CasM40XJvOmVzqM6rKwLJYHXN1dUE/eBbzBdq4MotUZZAse0JDYr/1fPpPT8kfn3H3dMEQFTgBC9rGldv6D4OyB9XFP/84DGz+BR75xtlqhJGcQsSVfAAGGULu+8wQLEN0bPqRkB0pGVGt6MR84Rj2wnAz1hFDKoN5Gf5QFAYheIahgiorjDE0zjKMYVJoicxVgnlj9AgY+ENwMQRfgFE9BRpGKRgKSFHCbmtTX0BFPQG8cv0yxaqoDP6sa9A+YMrQrQ7+KrhWviUyWizFsvhDRh8IdsSaChIK4ShR7sfgISVU9Ggl+3OOwq41OmNULKMHsVLISVQkdZhpjQWtRRGqxQbKoMvZA/v9jtH7osQQwMvH4m8OPxjkVTbeTcAWChs6C+sQCtO09C+ZXAKsZb0HfwguFfsIATbFWziSUh2YBKxtCH4oYcMalJx3mgMYWN9bnWBMVlS11qjr/eaAo34v0x//sHepLsSSkVIALSPKsKoai1nsM7Q2+CigpqYAmVlyWiCLL2whotSmTWrKcJDOW4trhDWpjSly8eL2n/ME5tUg8ZSyvGaWIC6ls/RpUb7DGAuTFCbQVUHZ8+y0fifZdqj7f62N1MRcrLZ1voC7dcAlMn/xi00p4YudwjQI0cUaIuWppkkxoawo62qGR0wSKOpaR9OJImEcx/Ie8o/u3VB6wwPzOaU66M2TNVYIQZjDxk77oqxN6LqO5XIp4OIw4JGMm1Tq2RoqlWKQYLRYvhNtcN1MiBQFm7Fa0zVtyQ0qtVYlZGgle1jO7HaHGrDve5RSk79uBcyn5zRGgkuVLhY8TMCu1BSh1IGq+MDOaFIu31eka0WO381UAZH7OhaQekprHFVpIvtfilHWdBCv1bEfMNbQzWeFpCCA/DAOaCM2mM7ZQnhJExg66zr6/YLNZiMEyaaA0WUANAw9vhBDKjt667f4cp3atqXrZrL/GvGb3+12E8jftTParp3ClOuZHv3hHlXqEESXUmK73U73dQ1RAwkzj7GQt6wu54mbhnN1r5NBl2Y+r6GWefJnDiHi7D8Pxf5Rg7TEQPzmC/yrp3RRvCdsVOgANma6IdINe4604rv9lgFNxmJjYmYtt7uOt24d8+B0QdfAfrPm/Mkl/fnI1cs1ax9YN4o+RUKCpGVSbmxD3w/Y1mEaV8ykM2Y2A6MlsbJY5eSy4akk0jSReIsUJxslBtdRDjqRYhdZZIoIzFu96xJjDiQ8z16/5Pik42Q+w1TfS60ZUubb5xt+/81r/uzjM1LcIRbQB7lhlbwemukabiMBTLOTJedPrnn+7HveuneLe7fv0O/EL/XWm8coE1F5YDZrSGlk7Hus9ZCh7SQBUdkRVMA0QTA750BbcgbjFPPuiFlzh832mpj2pBxQaoZxcl201iyXK1ZHx2y3Y3Eu0pAyjdFUF1Gd5abXTrM8XrHJ14z7QMxR2DZZQJasBBC5e3yLv/zTv+LOrTP8GNjt9+KJpxKubSAlxrHHNhalLE+eP4WQaN0VX379BTn7AiwnjHViZVF8VU3jSDlz6/47PHr0U/7h3/9v7Nc7TCNNyOVFR7QLPvrpz/jP/9XPefb9I/71f+FJ/TNSusIoxVuP3uX0/n3+4bNf8/jZY0YtsnWf0nTQlnpPCr4JXAHUwQw+pzRtahV0Qd1kRx0AzpsFtbrBWJzMKAHKmr0J9CYKu7YEK+ScIYFRhRWUDcfLW3z07ke8987bOFvkSyiUeBsI6FaafxRTOI1WSiS1haGolJ3AhAIhTUCB1rZMTqUIcM7RNM20eeZcGylDjTTPUz2VyMkTcsaPEligs3jMbDd7rBFvXNc0BUAS8G+32xJLOnaMcvHDKP5eKWVC8CWJ1GKdo+tmNG1LN58zDJ4M+DEQo1gqBO8Zh714UCkwusUO1+zWWy4uFbvdludPvyOGDTmM5d9si0eUwboFiRYW95jffUTMHRdXe9ZXkbN7D7ncfMOz5y/44MNHfPG73/Hk+294+533+JOfvckYt/zDr7/kb//6Y2YYjpcN++D54tuX/Hf/yze83lpyc5uLcMSrITKGhPIBawJNNDg1J+U9Gc+4ucYFzazp+OzrJ3St5+6dO8RPMv/w95+R4kiKA6tW0TTC4mptBm0IUcDtbDRBGUZtGZV4M4q3p6TVakQumpWwNKqMGC1y6Hp/iMwvoa0twWoSIuFcJ/5JCbRtmDdtAdsd27WnNXt0fk1nIzF6KZgLACeV9qHwr8zVm7YBlSVQC756B2WlUGI4CSaTVUJZM61FuQ8KMz6BMuIRal25h2UWw+nJCeM4cHF5IZLBG/J6ygDuB8MYmN6LDGEOzU+992MKZahT77eblgV52mKm56ovl5mAztp0KF19lCMhSEMtAZ1lGp5ueGNx2JMyoJMA3MKTPDRuoVgbVDaAFa341OjWPS6lKo8SkDAFX5qqA7CQYrVoqIGEFIZNARYnUED98P9Lm5WLvPHQuE1LAmfbySdavos8SQ+LeFnOQ6Wl7yn7hdIWpeH+rVN+/uin/OKjP+VoeQoxE/eyP2pt2Q97hs0VQ98zjD37oWcYBwYv8ikooF0Jr6Gwppw1dE2DAYIfJ9D4JgtlSqH+McCSRc5d14Ka/v5wHyhFaexKraO4cb1lMHbTCsFZffBIT1lYi8Vzmyw1WspFjhcjcfTSgBuISMOnSFhNYd4KOJ6SFORGtxjdCVCRAyQvw1AtgG2OJf5Ey71mVETnYuXgLKcP7mFS8TA2RkK4siRC+yANiVGKrmnYry9ROWJMR8oRrR3aCnCgFFyfP2fWGLa7PVfrnnc/+Cnz1ZKUalNkBWRMxY/dinR41jWEQTz3U5DvUitZ9ynHcv5VNmaRzA49Y78nzoIAhkrhXIuxLdvdjpNbt2jaBettj02R/e4ShERX5HSG23fucuvsPk3T8bvffUbYrbGMPLh3n/H5OU9fXXC+2RPf+xnx5B5Xn/8KdfEMZbdS5xnoSVxpxYXSrP2IzfJZZ9Yxmy9Y73v6VHzCY6ZzDdfjns3TZ1ztepx2jFmGohlh0Dz5/iljCDTzOe18RVKGbe8BsckY/BajF5ycHvO3/8lP+Oxoxqe/+q4AF4oxKYzrIAWwFp9hdnKPM++xzYKcB87Xl4xK0a3OAEPWDRc7z3fPLnlw5xaNs/RDEBuLZYNATOKPGPf9NFCamF3FN1PrArCmCDbhnCFnYfIf2Hgi5xzHAVv2fsiSnTHV78UeiuIxqcS6TQLqHKe3zri8PGfb92LZVIZHlRkvticwt+D7Dd9+l5i3b3F72RFAmpbDTs8/9/i/A8D+vwFqb1riNNpgFaiYudyP+JCYdRJisx8SY1SELGCWaxq260zw4DrZcY1NzFrxsm9aQ8gZ22iUimw2InVWWvZ+ZYRl1u92RK2w1tE0jhTFDscHOV+sNVKDpcLeSjVdXc6EKuVOUTZarTXGNrhmBgqRut4gW1gtoUKow9m73+/JugQqZQltNlqTQ7Fwy8Kqjl4GNhVsTpQhsapy8EzyAWNlSB1DKLAa0xBZSn0hAxF6sopYq0R5kARIbozGh0QMAzkFIQchtZmEHUqAstalpijha2GUM3q73QrZQlsqu9jog4d89WO/GTZ5UxmkqPZNtW4QMkWmZlhoOavK0DqW/VeerMDWhZhBGbzK30WCHwlRQteUrud+QpsfBgmllAp7WawDlKo9WWXVlQpKUazPfmifVMGe+plyPoDSflo70teJlYX0KrZthMCRUmEASzGYihem1nI9tDI4K/L52i8qrXFlDUm4oZyzKYnsGhSNNVNNk8oAVWwuYlnLorxtnEUrI4iCkTdotHg8q1QAsZTIPpN0WadKCYtfSe8aC/Bbzy8ZcIiKGCPqXO8ljK8pgKEfx+m+uFqvi1erK4BiGWTlA5MxpRpvRlmXdWicRHlbVESqerMaPe1XWmta10xrp7Kec22AtYDMGlVCdg8KswrSVnZk9SFfLBYopeiHgd1+LyFeKdGUwV1TrG6G7a4Ef4kXrbMWrQvrlSi1k3Powq7VVmwwdePoujmL5ci+3wscoNTEovVe7Cf96KeatobSppTohz0hBObz+dRDS/hYvJHVIOF1Euxl2SexOqDsnY0tgH/pf1pz8AOOUYhQIcnaVsDQD3RNy2a7YRiGyUqs3mcx9WX4YcoAU3qLDOzL9ZvNOoxzUw+hC6B/tFpNrNtqg6G0kEZCiOz3e3a7LU3TsNttBU+JcfrsbdvRNG5aT0rJ3tQ1s+m16n3rnEMZTTebTexbhTpYfkRf7qEtygpbVq7Twb9ZlTrNlXVnTLFQqCzq3f7/4rT8Iwdp07DHvn6BJhMbRz8Gct8T+p4lMAuRT1anfLi6w98/fcr/uH3BCxOYN4Z3jo54++SI1cpiVGC3GXn5aseTp9eMa08/ePZaMaIYckLbwtiKifmsZe6sMP9IBAXNYk60pYGtkxHZPVFGFe/MgZCTyNe1AGKta8nRS6Mj4LtMbIq0Q9gwiqw1MEIeuR4i356/xuo7HBlNq43IILX413z35BU/f/8OxiSyzlO9dbPpVgUIy6WZy0po4g/OTjjqGlLyHB+1tDqgO4VuQNtrkrpC64i2DpSnswnrRMLd4AlJk5KEIyltUcph3AzrZuQcsa5lvrjL0fINdsMIeiyHlDRxqUwf58sl8+WSpF6hjSMUC/RZ29JaKbbIGU8koXCdoTlZkJodwSRGHQk5MaaIT5H7t8/460/+jDfvP+B6t6dPAuRqazBW0RhHv90x+JGu60qYGVinSGFEmcTyaCmArGrIWfy+KsC+vr4mxMzi6CHvffghT779jqfffo5RhlnbMQzX7M9fcPzsHn/58Yq/+Yt3+c1nf8ZXn/8jsTf0/SWjSdxenfBXR0esvvgt3zz7ToCnlDFWCcsul4YXkfhTwRZE+qDKdNKag/E7Zb1lyuTtnyFCHKbxN+XTh0L7prwERO6fUzmYyyEWCmvK5o5Hd9/hF+99yOnRfBoGqKx5+vQ5bdtwevuWMJGzHPAibxFfmgyT9FsYcdJsiYxAJqHeBxTCQlFGvJ7rAVnZgtWfsk4w69/lmFDJo5WEVZG9MGhzZn29ZmwbjpZzlsdLnDNsdzvOX51zfv6a3W6La4T1pxA5wzB4Ntstm+22bLqWmGKRUSx56823ePjmmzSNZd/v8SERYmLfD2JwHjwhB8gG4y9g/2v+3eUT/vE/NAz7NZuN+BiHcU/wgTFnAhZnTlmePuDo7CGjPmEzWrrZirkeeHW5Rm92PPrgIz7/4nPOX77gk48/4J/+6VNevnrJnft3+NlH7/L1V99hzMimN3z6xTP+6feXfPVyYKfvso6OzTrjGUjGooLFhD0NPUZ5UJGoRix7vB/Y+YHV7ZbRB/7dv/8n/tO//iUP3nqXJ8+3fP3dE2YzePftN+is5tnjb4jjpqTKW3IOUIKAst+irSNrN633WtSCrOdYJrMT4KjFZL8CeMaaEmyXcMbQOIO20kzkrIlKY7RiuVjig2Y77NG8pm3nqLSZvDChMsYPxdjEdLlxM/2YdVGB3YwwgFAJnaV81FrsOWzjpEBX4nlaG/3oi+9ZLuqK8jNXF1fEYutwU8Yvr2l+IAW7+b6yPNEP2Bw3fWvl7iry+z+wQcjAI00F04FxmX7wfNSQl8r6rQOS4k9V5YfT0KUwNyZQLx+e76bUdrr+0x7FJJuv1g0/DA6Jh3VRCTDyrMKw1HZqBqoPWgUfK2tNmDMUYFWK/ypD08UDGSp2n4hhJKsKlOtJLlgZKsIMkUAgAWgFZGyt4cNHH/Cv/vRveOP0HgZH9BWAVGij6P3A1fWFSGSVNPGD9wwhlEGFFJMKkbZXQ8caeqFyJoyjfP4SaJbjgcVcmfniJ3uQdEINPYly3W7cbzcfWh/WwoG9LFLVeukr0zmVwXUIHnIgRoWPWRQwqYSYpNJkZmGyatMIOGXkbBZ2bCJE8Kkhk0sDm9DakXVLRhhrqJEcNcoEUvIoHchJWFQyEASjykC3yIizER/rmBXGWrEkQQJ2xgAazWw2ww9bxnHHar4Q1knxAByDJ6fA9nqNWc04OTlGt0toHEqZ4r9nC/CaccZhOjnnRj8iSpPMbr+lpVgyHHBwbp7Lcq4q8ZTdXOPcjOMjB8aSNcxXS+7cv0fTdJyfr9ns1kS/x/s949Cjs8Iul1hrOT09xWr46ovf8Pz7rzk+Pca1jvnRKUe9Am253g2cB2hv3ebspz/n6us5+Ytrlk3LvG3ZhpEXMXKVI2NOoA2pMbTdAmtbVAiYkPHDiG4bmrunbMceu1+zun2P881A7Ld0nZL6J2bW255uteL9n/wE4zoudorZckEcM8QRlRrGcWR9vebf/Q+/JiRFt+iolkrJe5IKKKDfjGJJECPL4zsY22JcZrG55NvvvufyasfJnbeYL45pLHz36pq73z3lg3ce0jiDH3qC91jXFWAT5vMFN+1W6kCHch4J02fker1jsVyWOkqk0bl4zMQkTb5qZAAZU8RkV9hihXlf1EDGCqMcZF8Ra5bM8ckpl5cXGDNiTDOx1qRG6QHNbN5gc+L6fMM/rD/nb/76Y7rGMu280xD7/xnI+i/xqPtSIjOGxG4I+JQwrWXTj+z2gahaLneBmMUPuWkyXZMIIzgnmE9jHUkZNhvP0HsSihDGiWHmrJteMJMhJZw1JePA0c1m9H3PdrPGNk0hFmQRCMRECLGwrZgssaSBtzKY1EKoMLahcS1KKbY7AWNs9Su/ARpW1mcIgaRSAYISqBnZZKIv56f8NClJQFmKAaPUpBhSCkJhXJsmoVOYLJ/EllQCUpVCgMswytDLyLqKPmAKIKozhVUrYJWM/gSxMsYWKw4ZAlhj5N9qTUheLCLIiPpB/Jfr70WBIiOHm4BsPSsryJNSIYNQfV3rXh+n+61K9FPM4llbahozDapv7Jg5k6L0wlprQpUcI8CjVjJQ/0NDBqkJhB2vtQBd87lIwjfrNYdasb7UoeJSN87OXAguqaxxVfDjGDxt14ifa/nsk3N9HRzXWocSEl1s14xxwsTWB//bm4MDyUwRUD/VAXcGP1ACuApDGBkuC1jUMlssiwxc1KWqYBogQXfKWIyVnzdaQFWpUcvQtBBcpIRTVIZqvV90RwEcC2OxDPGHYShDZlkL4jXaTcFcICBxZVuGct/EEBkrYDZ9/xptFRE3XRelFDkmuhIcmVIkVfuTLD1jCH6yXUgqTYqa1jXiKeuknwCpf4+PjlFa/cC2oPYCq+WSxXzOMI7sdjtikOFJtXCICSj2ev0wMAZfhqeVZCHnV0zS+66OVrRtQyQzbK4F0HVCaNIc+pRKXLIrR/BhqiEmK7Ecp8GSfAcRrS1t26G1ZRxHhmFkCHtRAhTFcyjK1aqIcgUwtdbiC7Gi/pnRtoScASmzWCwwxnB0fCTnUmGriMVARAU1Aaep2NOFwlJOUYDWZQG/bWFd5wpwN41YPRTwvdpWuMYSQ5xsDYy2LBcLMplhGFmv1wKshkjQh9fPWbyandlNFhJ1b8pALrYErnHTMNQai9S4lfwggWJ17eYsHuYojfcB73cotcMYWZ+mEBusEdsGW8+pP/D4owZpVQo4C0m1hOjROuMSzGLgvmt5f3WLvzh5g/uxhYXm8bCla/a8cbzgvbMTlo1hjCPrqysuX+95+qLncuPZ7PfEDFlZktY425GQwApyZn68JGnDZr1mTBE977DLGd73qJjFz6MU0hmhiGulxM9DW/HHsFZ+GSO2DSmWRqv4FdZNXkZEaKMw0ZRJBVxsdlzOt9w6voXTDtU0kgKn4PmLC85fXfH2PVcYl9JEKUxpxEQmEYzGB4/OSYBXBVZpzCqR1UA3G4W92gS0VWTtcXpdpoQBP+yJITEzisurq5LQ19E1K5RqMFZ8kfwQCWHENQ2tPcaP1dPUoHWgaQx9FtA6K414qsJsthApSiysAwMOjXWSJqpMJiWPV5C0Rc81XbcQ3kGGbj5H+cjMz/nzP/kzHt5/m+DrBg22aRCpZmESAa5txE/GuRL6onGLjnEc2Q8jzjistiXBT6RTCs248Zyd3efbLz/n3/zX/yWr+YzV6QnaiBzCKpk4X18lvnkinsW4GbPlXbKJzNqGy+tLUoicdCv+8me/5P7ZXT7/7itebS7kkC6MUTJgi4ymTImdM8wbJ0VbFOAapYTJVCj31cS8nPUTUALlv1MlcwCglBKwQAFKVxmSQDohlmJxAliKj2NWPLzzBj9//ye8+8YDGl0NNyBmRdvNaZuDtYXNHl9XAAAgAElEQVQCjEriT6hKuFZMKFOes3BWcnkfukyTtSkfBFW8iES2670vzXdNSS0A7ySBF4mJvK4kpCvtGcPIxcUls27G0dGS5XIBaH7/5be8fPWCoUiKu9kMZTpyhvVmy267Y7fruVpfM3qPc5amlUnvGPZcXG148eqCX336WxaLJWdnZ7RtU0DlUMDow/eQ8ojKFygyF2NL9HvSuCGEgd4nUmqJ7hbHZ29w58FH2PaYo5MzrofI+eOXbK723Ll7j6Wasdn29EeJ9z94n08//QzXtLz97gd8/c3XHJ8cce9sztHqTX7z5XM+/+o1FzvDq3HOVThmExxBN9BYVAkfQgeykb1QE7G5R8UBE/YEemIaeL323Ll1m+cvX/LNs1f87MNHHJ2uGL/saZqWdrninTfv4Icrnj++RtPgjITYhTSS0x7NDJMyMWmSSje+99J0F9Ay5SrzF5aGNQVYQ9NYAcpJnjzuSalFMcMqTVQS4hhjICmNamdk0xCVQ5uOFPYkJaoIlVVhqYyEqLDVQxMpWFNN9i2gWG3Tp8FAFm9Ta60oLawUudpolCnBDkqWQC7gVc5SaAUv0r5c7q1YALScD36yR0dHJGBzvaHabmitJ4+vCpoZbZjNZwzDMEnTDoEbaWoebtzSBeA8sEdD8NP+cQBZKzD8Q1Zx9TRNMZBrkrRS0iD+qGGp17I+bgKudTpfWQ0SHvBDlqvi4NF7Eziu91T9WWmaFDkJ05Us7ExdwF5jDTEI49igRF5YgBYlkgwZGtR9smxgSvSyRbJfGT8ajOy5OcgPJrIMpXKmUZoHd97gZz/9U376wc84m90ijAJGWGOxShHDjnEMjOOeFEeC7wkpSggKpdEqn78GnVUpW2UtKKSwLVztKeROGBqZ4MO0nurH0hPzJaE1E0B78/ua1v90vevfl2abXKwiMpX1rFCkIOB6isKu8D4RC6NY3poUsTFmGHf47cC6HzFty/HZHVRraax8uoQiZsvu+jWzztItjohZ4/d72m5ZTg5FVg6VYL25xBhYLFYEPwrGpj0+jWQvgR1Rt4Qokr+mgdZZtFFF2SEiYaMNum0Jfs/5q2eEMPL8+UveePCQ46MTkoJuNuP2/QeM/Y5udcLpg1tgWwlASwk/etpW2E9+3DKOgzCVTGk4/VBqmUCOkJUp96WZ2N9kprUY/Mhue8lifiQybCUAkWulec8x0jWWV/2O3fYSjRcf5DHgfUOII+urc4b9nouXL2TfajpmzYzr7cDJyQnOKBbW8TKOXKpMOjqhPbvN7reBJS2LxrLXibXPRCTNvW0dqW25Cgk77klkCTlqQK0W9I1lt90w71qUcxy/+QB1dc76+hVhGFExyV7cLfjq+1e0iznN7Dbb7ZaT5TFjLxLPplGMY8/L55mmawpIK2f8OA6MfpysTWKxl7BNw9m9B4yhp+sWWLvgV5/9hhePv+L+m5nm5DbbPvPpF18zri94cO8ubjYjRo8pwcOjl5BSbcpeqlQBcMq9UraJRKLt2h+wbVWGlMXGaT5bMJ/NiH5gu7kijAPNkZW6fRo+CrijUuLJ4y+JKbA8OpNAFDLWdZyc3GZ9fYUf9xwdrQQcSxlnJKhGafHJnZnEOIz86tff8OEHD1mezkhZo3Op1tQP9+R/icePhzt/EAiTDZWEFpuqHKX/iJpt74lRkUxHiBpnM04bxiA+z0cLQ44j3UwTUma3DyQNwxDpe5Gv+hDoewGsU6kpa3q5L+FJ1pUEeWsZe0miVzCFMDkj/Zv0D2linnnvRdLaNIApEv2ID6kESMu+LmRIAea1ylOtkLMMaTJMLDpnNaaETaYcSVH+jaLYBUVPSiMhZrRxNE0rgF3MEvpVQNsYAqowXHMKqByp9hqqSH8zGmIhCCGDPy3BDjI4En8lqmw6I/V0Kcsgy96dtCnBaALS1utT6/CbA/f/g7o3+5Usy9K8fns6g5nd0adwj/DwmHKIzMjMyiqgWw2NkHhBIBAvPPP/8Y5EC7XUQDdUFU1VV1VOlZkRGaOPd7TpDHviYe1z7EZ0lRDqFirsJcIj/No1O+fsvdf61jfId9VzDzJJrlV55iEUKXvEWC2fMyfipKKRJkSGIoD4SZVaLJcA11wIwwWg0gaY66l5PE1BIQsYm+f+It/ZZ+V6Gipb8dZbT3DO8uLFc7F6KM+0JLLnGZhEqeLTKu+Bkt5HvNYlcyQpYe9GX9ZeUSD54EGLoiBlqU2UEe9RZyzO6nlAn7PIpUMM5b0FDAoh0I8DFPbvVLdN3RWFDTpLufOB2VxZh24qYsqEMcgzpyhe/qIiVDmTAowgahsjXsRCUJj8PaXemoBHV+yt0lTHqVK7FPsPYX+OTHdHF7/uyTJrAuC01oXdawSoD4Gu7xlHL9ehsCxNsUCIMRN8jzKGyjrIEmjeNA0xxVnllYt9wtAPAmKGkcH3Eu6nDcaIJ/kU2Dddr4m5K76n0oOnAiorDU1d0zZitTjMFngJV1nqusJYyzB2s2/0vHei5FlAzpqu6/BB+s3JbmqcPJ9joqoqub5RshasrVBIiKG1xWaw9HV1XVHXNRNRK6WEs5ajoyPxvB9GCb4qg5EUI6pcr3EQdaePHqMtahzpx2EevMQYaesapWVPdeU6TYxh6yxT7Wgw2GjF2qs8z1P9OHncjmOxpixs92nfnU+SYSh7g4CdlXMslkvBQpSwVquqQitNTLJOjo7Ek1ZA1ImQYuZhxzgOdLuO0Y+07cGOIqVE1/c0dYN1hhCDPB9Kgh+NdSXPRwLp2sWiWH94UXCg6bvJDkvWU4yBkALD0LOPkbZdiFXd3/P6hw3SorBJgY4ov+csac5yw/vtMf/03lPedufoMfDq5jWvLp/zqIJn9x9wfNyiUmBz+YZunbleD1xsO4ZtZD+O7JQiakmRU+NI3dSSfJwjRhtCzASbGaNnjJF60dDlUJLlxYh533UFiBQ5lpokfhmW7QKlNaH8WWlTwDaNKofH5DUoqd5yQhhnJXBoiPiQeb3ZcmoX3Fs50jAUuYFhNyR+8+lXPH3wEZgsRWDKZBVQSvx0RYI1ok3CGA/spDnSDdbtMNWarDeEEGiaJTlXbDcjoesJyaDMkn4/gopYnVCpxtpjnDvCaUeIEXElghQ7yCOoiv1gyanj7OyMpmnZdBHjZJqjAKMtBoUhsVycsGhXDPueyijqylJhcXVNCBsgiU9OTgSK9MJayAmrLKvFkiNteffsbd57+iF9N7DZ74gh0FQVCkU/jLIhGdl0q6aWgta56djGVjW7rqNpWimsvMc6x2bdcXq2YvA9TdPw5O13GMZP2d6+ZtgvqesWZ4RZZrOBccfu+opf/faWP7xSvNkGgq3Z+0T2gZgyez/Q6lrAtLff5+T8Pr/+4m959eoFg/cEPR2ecuhPU+3JD7bMDcl5WtQacmkamKaZeS7c5yI5TwXGJOEuyemlsf52M34H9MwZVAFGpBOhrVd89OwDfvjhRyzaGmIorCSBE05OzjGmyBeykFHEplM2XT03I9KMTqxp8eaNDEMvxbWe/J/BJKgqRy5bVioFSipMFaM1uUiJKIW/+HoZFIkQI7t9hw+BhydHLI+OWO97Lt68Ybvd4eqWpDJ+v2O93TLerEkps91s2G93DOOI0pp2sZSD25ZDP0ZcrXGuxhrHbj/Qff2cuq3v+KQepG/FfAyFoq4ObMCYNNGs0IszVsePaY4fcnr/Ee3qlH3f08VAu2x4551H/P4Pz3n+8iWP336H/W7Hm4sLnr7zkB98/wd8+cVX/PGf/IBHb32f63XPn//l7/jtFxsuxhX7fMp6SKxDRdBLcklsRYPSqZivJ8iGMWuqOIDfo+KeSA+Inct1lzE7xdtPf8AXX37Der3l+volq9MlPip+//U1T95+zLMP3qffrbm93GBdLqw4CRdLuiGpicldWKkFkcgwF7vS6IjkSw5eYZ1nZbBAjiPJ76lyRMVIHsG5WtjZsXhVk3FthV0e4ccTevuAHDwmJ3QSSRgZssryjKXi18p3AMGyTysODPdUiktjnYSNOEs2YCpH1tKEyiCvTHyZQMBJjpdBCShEKvLyiQ2fpVkYRinKR+9xhXEwSZ0m5tXEHr93do/dbsv19fXspyvgm+IgJTzY40zNGEBVtWit2O12M8v+ruWDFFQH9oLWGpXTHWB5Yp9Q1rMUm4oD+Pdv/Xy5jpN3E4jnlbrDaDbGTH3PDOTOdIFpx0p3r2suhXieB1dyf8WY1FhdQF8rns/THlhSevOEjJXzufSIKGWxhT6lSkjS7CcoHxGdNdbA2WrFD59+wM8//jn3z54AFV0fSN7jGkfvB7rNhhwGlILRjwx9R8qiEIkTSIdM8in7q9U1i+VSwAg/ik/XHca5UsUzWx/29OlZViUARDExSSJzOnjO89WcAPTpuZiGZmq6EOXap3gIbBH2lPjZCVCMPLchCzCgJva1KiwraR52ux1+L4wbcS4YUE7R94qsKpR2aKO5vbrk88sLPvz4jzg6bdnvbqldK1JGpchZAPx2eSTnVTZo7VAqE7NcJ+139ClhwgJMK4OHMKKawsyoyrmYggDXlUVZx363pm0cfliz37TUzhCzoqpaHr39Ltv1DWhHTAqdJKAGYFeCa9u2ZRx7bq4uOT4+plIVMYz4cZTGKmdIkeRlYB/8WLwrC2hbpItKQQ6eMAzE4OVaIkGoBsXFy+ecn55QK7i4vaWutEhYnSvBSYHt5oJuu2MYBharezx8/AFffPWSzz/7lHuP7qNMoO9Hmraico43L77h61/8a9TtJf2wZW8fYlYrhlhYNiUMYx8iVmnJJgCccehFC8dL1n1A6cjN6wtOq3N++v7PWDQ1XbdjHGMJuanZ+ywDsYXDJLi+vGTsRuqqJqvMarXCe0sIieBHVnpVLJ8S2mpUJxYo4jU8SXVdkbErRq84O3/MH/204rPf/pKvPvsL7r/1jGdvv0fKFeMYWS4bVOXwUZp5XeS23o/gM1XVHAZH0wwZuecx+sICZ97D5/WGgiJZDnlgu95IzQyc3n80N892CqRJgW+++owMfHz+FsaKzUnOYExF0yzpdpes19csFjU5JirbYpWZZvxEhKW23+z5xd/8AfPxU549OsbmKdjwAKr+vwFr/5/+7netEP6u31HmhvL8WoPLirwPhGTY94mkMiEGVgvZ+HWQvVVrRbOwDGNivVEMY8A0lm4YBUgkMA49xmqWi5WAD2GU4FcUYwg4DSokNGIPQxm4pEKIkPAoOZuqyhaJOjPbb5btq2L8kwwhSn8mcmpH9gMxM9u+pPKcWCf9jXGJEAQoECahE+WYKuBXkkGDwKqZfT/Q9wPn5/dnmbvNVoaa0zAgpUJOyDMfI8c479ji3y9yTms1KQ6QYqkLEmhR+xDVDH6mnA4WPynLgZfj7E8rQT6T92hEKSOy31Iv6ALOGWtLbaNL6CYEHwoQHQvTMJD8BIKpkvcQy3U1xV9y4qYCKQrpYz65DnUFyOee1upMUtFilZDRmKI0VcVbV5WQJ3kngx8DX3/1NVkJE2/qF1MW/9EYphpDSeBhEuDIWosPouRUSlI5Rh/K55TnRobeEo6HBmWUBCcmPw96J4bnNBS+6z/qvT8ERpW1JfuokSwXYwsgm2CykiDNvZfKmRwyPo6MqUdbuY5GWzRKsnjIGOQ+5jIEDikU5aeeAWtdQFWpiWEYp+ev9D75bmhZuVclO2DqaRVyTeVZlvwSYy21dSTAlf1Mcn2E4bt0FWP0DMFD6f1iyqiYRMWhDbrRVFqGsN2uk7qo7Ol1VVG7ChbFgmTsCTHQdX3xC8303YDRHkjFSuJgudY2LVVhXuaUxLGRDLHYhEzPcVGSqQzeD6TCzGyaQx0+vVI6eOUeyAcZa0pAFZKDZLWQoLRShJSIPjL0Q7FOEhuUab8KYfJTV/PnMlYzegFbjTESkmkcWk9e/vIZjBMioPcj4xiYPmqzFKyk67pCcBvKGjcyLCrPuNJKbP6MWKbUVYVRYhVyGHjVopYl37ETKxYFsXgdFyKJ9wXYzxDHKJYrAfpuj8qSc4He0batqB10Ae3D5Dkua6Zp5ByPBUNwVc35+X38KCqMlHNhQBvadsG+29P3vdgsZhmeVcZQdgCMkh6kaRrqqiIrJZaZVrJrQN2pycUOJOXEbreX54S//0z9Bw3SJhRRZRZ9x8Mx85Ft+eTkXX50/22e1MdcX2349OJrnu+fs247Tu4tqZcOqyJvrl7T3+y4fj1ytVfslEIH8UFTxoi9QJJiL+17KZC0JobE5mZNdbrCKENdOzIKW9Vi7lWCgEQaonDouXnRzuCqCuPEu44QsNoUQ+2JxSINE4LVkGLEalum9AptLcpGrDJsNwNfpWsW7ZKlKswZlfHG8emra/54veft++ckIwcceFAeZWKxHk0YO1K3W3AvUHpLDg273YhNin7YsN0ETu9njk5aum7N7auetj2jWSmsqbC1J6YtOUfa9oTF4h5jtyXmHlRAm0oCsXUE5RlHOD56AkSyGrFVw6Jx7CtbwDPxpTHK0DQtTbNAbwdMVZX/1tBULazXoBPKFOPrmIlZJrURyBpihGPX8PTJU3KCfTew6weRogNplERJZ+ycpkvZoEKSQ6+qKnbdjvVmw/17D0Rm2vcYa+mGAbvbkhFj6HEQGZ1xThi22rLfjzQuo20ixQ49Ki4vWr7/5IegK7a7Lft+zebmJaRIJBFzZqE0VeU4alb86P0fctIc8bsvPmPHKLLQAGRFJqKMIvgsKb1NhbOGECOHRNI8b4hzqvgdUORuME9msggo/ol6Yobd9WA8HBq6GN2rrEpBaHlw+oiP3vsBD+89EBaQdoXxJGCNsVqKA5WL1DTjFJJeGtLM+k0xHkI21OTBJo2/TJkLUJDT7Osoc2GF0lMQTWL2Spp8fHPCqIRReSKoiOwMOD05papaNrueuml559mHXF++Zr2+5vrmkpubG9brLT6K9LuuKhaLhfj4WEdV17P8TSlVAkOkGZx8Z8axl+9gTZnmF3a3RmwYhMNXmr6KrBdc7zWpOWe5eod2+Q6pXtHFmtbW2Dqz221ZGsvpyZL33nnIl9+8otvdcHZ2zotvduzWez766CGPH7ds+5G/+utv+Pxlx9ovWMcHvNyNbIMmmQW4BkoIVi5eTnK/ImI+lTEpYhjI4RbSFugxKhIBj+bV9S2Le0fsfebmmwv+0Z/8mJwTf/Obz3l5M/DXv/2a/+DH7/KjT37Cr/7yL7m8vCVVS3q1YqvO8OaYrCUsROc7ntp5sq2Y2A0yzXbOYGyFIhVvbwUxYJLHhC2VyiTvGccO1y5pFsdo4xgjmGxQSTE2LRu1ojcPqFYK1p4c9qQiySNPg46D1/HBA7UwVrMELEzyLqMtxlnQhmw0GCXnQF3LGp2YHRMgWRghtjR7GfEKnwYouqTzTl1WKGm1hyTob0vRrdW0bUPXDeScef7867lwBvGKnAO0OKzt6Tqrb71nnot7OHiaTn//rgXE4T7pufC7+55TCJPsN8KoiCkcmjctjJmZmTx/pVyGToc1Nn0PVVgLOX3neqaMsgcvqQkwzuk7FiiZIo2aPrMGWzNJwEBhbAErC6g4ITEHfFKGR0qpMlSa2HQRFSIGxdNHT/jZxz/jgycfsqqP8EMiJDkLq9ZydXPBzc0lOiesE0/UfhikYTQHpvYke1WIpLCpa5qmhizsj5zSt57NQ7GXZ4B+ClSZZgK5MIeUYpZlaa0xU8E/78lqvv6H522y0pHrNYwj1uq5vMwpCVgVkoDKPpCzqIRAQGFiQimDM0YsGJSiOVrSthXWGFaLJSHCOEqDYI3D2cyTp+9zeu9tzs4f4+qanCuUa4QhpiyJUbzwqBn7DnLPsi3IeXaQDc7W9Nst1+tLTs4eoDXsvWfYQ7tYUNUNxornrFENSomCZfJte/r0KUoZxnEoNhUGayvO7j0khChNZMoM/a6EGSrJKQgWhfgc+hCwzqG0puv3rJaajCmDCbE16Ldr6rqRYCBtDwPUnPDjyHZ7y9HJOU1Vwq2UyFY1kd3mAt/dknxHNg1jTljjSsL5jq4bGPuErk55//s/o1kd8fyb/4vN5WuOV5aN9lCfMHaJ3dVz/vb//F/YvfwClxO/3Hdsr254Vi/Y58wQhck/ek+2HmuUNPNZmIs2KmxMqLph2Hfs91u4eMPvfvlvMBryOKK0pT4+4/j8IUOCIUb5vCmRdaLvO/qup26FCSTSQZFIXl684fT4mLqu5/2qXa6AzO1mW8A1aQZHP0LWDKOnaha88/Q9FgvHV88/5YvummdvvcPLbHm8fcDZ6RmVc8XKM891yCEAquyDShov8b0cGPsdI4rVUbEjkfn5NHucmX9KG07PzhmHPdo6jK3IFCsoFEmBq2t+8vP/iL7vaBdLAXbioYGtmwUPHjjW6yvGfmR9e83RciVgbhnYq+IZGXNmGAJ/+zuxjnv66Ain1Pw9/r98ldmrXB4FZE0fArf7QMQyeuGyx+BpGod10HUJghVdvs4oDLfrkW6QfilEsYAZSrhg3bQ458oQPUGOZCX2WqenZ4z9nrHbo5UWn2Af5uGw9FhTTZ0LKH443+5KYSWJPDN6PwcKjeVZSykKM76cEb7UgCFFqiKbdUZhrMI6LXW4l8R6rZXYihVY0BhHVS8wtmWxPC5+kxAY0EY+Q84JtEAGwUswktjyIZ6iSsJrjFVy4VMgh/IMKCPD3hJGKGCv2MTEGPF5xBo7q0FFMV/UcymijIQfTlYRcWIrWzMDQOk79QPIeSEg6TT8PYR93lXZTODstwQ0d+qYqca/e/Z/96GbJOtlXjn3OfNnUkjIE7mAy1OdUywuysA3hBJEmSXPQogw8rOoYuCREzkHmAO9ITN56ArgqpQApeRI01S4qpL9qe/oxmEOe8oxEZChZghxDmm9O9QGITAoPT3DELwEv02y6pTTt+T+YqEkn8GPnpCCeG+6hqaq5roHJUqkqnH4GFClf5+k+66Ar6as6ziB6OVnldbk8O3h/DiOEqYMxQqtsN2tLQqTQC5i416VIWzwgtkoI2QfZ2YPU4yRjioLA742jqNqQfCeo+XRDKamGBm9/G6FxlqHKQHROQnbNCtFPIqEGAk+0A89EkQXsVmG/94LWDn0PTGEwmhVcg1VIRBlqcsmCyz5mIIFdX2PHQRjAOYwwbsquek976q2qkr6zTARC8p5sqhX5JyIo2fsfXlOhhJgKLdRfGvTAfw1qhDehNhgncUpLQNfY8SrOyV0AZ+trTCmOtS7CHN08rndbrfyHDpH7aoCympu12t23b6o8DKUof7dXI+6DqUm/zZxY/49lZ09mN3RipgSYwiisCybguAEisVywb7rZtsBpabhmmBA4zjOe5wQ9WSQZssQqXKOEALVtM9nhalMUcYWi4uygKxWhJTZdR1+GMq1FosptC5e3hqnxTZG9n1d9kp5Ho5KfsE0CPy7Xv+gQdoqwU9Hx/fcMT998Ijv33vIEQ25i1x++YKvbl7xnDcM54rFyRFt6xi2PVdXPZfXG/rbRLcf0VlYShudGUq4i9IalYQa7vsBPcsrIY4eJQlX4sdS1fiYylRSijavCkk/CutSGY2yYp/QFSaFUhCVsLnS1OUVRu2EvGtlUcrIlERpsFrsD2LGGcO6G7je7FieHGGUeCUFHLcefvn5NQ/OH1FXkeQDSkXQO3S1I7sB40RWqVTPZveSYbjGd5qhd1R1y2K1YNWesr0dOT5p0Qwcr1ZkDDGM1M2CqnFkPE3bUNcNrhZGVg4dySS0qgRURKbF0Y9sbi3rmzURw2J5xtHqiG2TIA6E5EXybIy8f71A63VpvCusaWhsK5MxG1HGYMqOHXMWiTQQVMYrRb04RjWOPg745EVSUJgjm92Opq6xlWO76fEhYJwrU2GZHMec2e93KC0yqc1mQ8qZk6bBVRU+SMDQ2el99ruOYQicnx1xevKQ73//R3z22afstjd0Q892u6VtVoQUuby6ZX+7RsUgflExMIx9OSyDRNypBcu6oXVHnH/wfVbNks9fvRRfrZRZ724Yw1bAMx3IKMKY5s1VziWRQMHk7TRN4abAlwON3hT5a065eA7JlEkfKCHzpIwC2ohPsxQzdVWzcEd8772Pee+d96iqunhUluKuFEBaGymmlUzoVVkMkrLYk7OwYkXekNAqYScJVJzSj6eGRj7nFIg3gcmFRFRkflPBIgdazhIgkzL4AvQN/UDfdaAs+76XglRbvv7mOV99+Xv2+51IEL0nxsRyseLo+Hgu+hZaE3y8w/AThpQUFsLAnxKe60aCyOq6RmWRt3k/kmMurDMtDUlecrN3vNo61qHm3Q+fcv/8MY/ffYYPnvXtDfo68uD+fWrjiDnidObpk3uQPc9f38DJgp/8+BHWJd7cXvJXv7rmd1/cslct63DCyzV0PpN1i67bwiyUojEbARdTFiuCrDMqB7QOuHSBDhcQ18Q0lJpNwNFUCsib/Y6HT97mq89+w9ef/4Gf//Rj/tHPP+Z//dO/5tOvrjg+Osb1V6z3HWPWDKmhMyd0+oxRObG7SFF8Gzkw+A7/bjBG7GGUhqqyaJXvWA4EUtpTqz11jnRDxpiGOmaMPcLUDfiMHxMGaBYNfrEkrIXBZpot3l8DobBP9KSGQ03gpgJjBVCdPJ1EtqNk0lqV0IRSTCakcUyTZB+Ru2qtig+YxWQlxWAZKFCK60n+p7WcS5P8y49ehhPl/0vC6VCK3jz7NB+ayW+Da1NxeABvv+27O7O5C0D3d4G0UNa3YrabYQrqQNb8BPQemLEFEESKVYebB0eoqTSfZPwHf6fv+vHObJECEtoSuCCgOXOx65yaE4CBEhxhCyApoTwHH26FUrYwQMQz7bu/qyia5f4kGWRISzlJ/IX1ARGVM+fLEz753sd8/N4PuX/8EKjZ94msDYujBSbD61fPeX35EmOEVRWSZ9fv8YUtUKjfs/WAMYqmaWVvKV+mulUAACAASURBVGDsMA7is5cPib1aS4MEsrcrikpnkrB+B5CZ7tHUTBg9DZQk+C0FYW2HNHnOCvtYF3GF1pq6cjLkThI+NnUEY/Aza0gZCcWQRSVrTJOY/HXvnZ+WgWemqVosDeM+gfKgR0LoSEPi5OwRy9MlpjkiKYW1GbLBpkzOI11/ydXNayDh19ek0GHfOqFtrKRb60b8r2uDweOTwWm517v9jsnf3bpEu6gYhx3OWiqr6LY969trzs7vo1SSZkNpfPIzi0MYcm0BcjTWiPxQGqQerXXxNpSny1rH+fm9w3NPInq5/sN+Q06BulmgLeLjizBxVM503Zrd7hZTO5R1BUgSz7+6bvjxTz5hsVzw6tVLfBjF008b+l3P1c0Fbz3+gLff+2OWp0+4uHxBv7vF5D0u9yyaU26N5fLicz7/q39J//prbIyElLlV8PvdDtV3tLX44RpniT7Qe49Rwty1aJJP7Lsdq2WFNpak5Zzv1he8eSFD7mwr7r3zjOX5A4xuMEnhUkLlSaYsayRFSXxfr28xRsC3tl2w7XreXN7w4P59XNswEggxSnajNfgYBFgAchzIGEy14PzeQ37285/iry/5n/7H/4HPv/ot+6uvMcqw6274z/6Tf8JbD1bC4imyx6quBJyZ98vJWkX+3DQtRslQZB5mZMhlzVBAkYzCuob6tOHN62+IWRcwT5r1VPYvnxTN8hRXr4qXc5rZnQqpg+p2wb3Ksdlc0bQ9/bAn316yOj47NIPGkLw0tNud4W9+8wI/Bj54ek6lZKj/7/v1XabtXdn7tPeknBlT4mrX06PZ+ohHYSuLqxTO1uz2iWEIhKCJIWJrQ0rgk2bfwe3Oo3QtYYMUhpyadjqRjwurXnorU85TlROpsPZSue7iAzlilJqH8CkdmIoppXmvFVugMHtu+uAPw7IYiNOfy3eNOYniRpf/loRoYLWEPlpTPIetFhCjBPC6qpGaRBusq2cgUytT6oGS3xDFBmyyQENbsSorShxlLNZACiODj5hSQ2nriEGID6BR2kk9rxJQzmIlIFrwYbLvJ6ZIKEPjaYCh7vxTFcBsOleUKVZB6eAVKkzFhNGTXdPhdVdGbUso1tR75/L/Jz9HmKwk5O9pdQAqp/rorlUA5ENPMRV75Z4wDzDLoNMopowQ8XtWhVgi/dzsnV/k2nI+qrmOjeVMoVgBpXJeowQAt1pqCVssEUMIjMEX1Z6Z60wB6sXnfEqWn2q6u8GuUy0TfJgWGj4NhChXTnzn5bqokjbfNEJCieU6Oj15fyqcrUTFSKa2joVR6MpitdjW+RDv1I0yPNOVWAXkJHY/PnhM++0hftuKisUH2Zun4ZPWmmAtNkuYr9SaSva9YjUTs+yxfT/OAzOlLZVxtLbl7OQejx885GjRSs/Xd/TdnthLPbM8OkNbjdYVKWd8GNj1O6YpvORmZKwF5yqqxsr6DcVWZB5mF/JEymKdmKE2tYRNE0h52kfE49k5JzJ+hK3uB48f5RkK07Nj9Ldq7sOgYmKSF6uKopwSa0NTng/L8qShutcwjCPjsJc1ljKmEruBBjX3AXM/UN5v7AbGLH6tSjEHYyulZl92VZSPUzZO13VoLXuieLaLhYLVQoKw1nLv3j2OwwkpJVF9pUOo8TiO9H1PjF3pF9L8XB8s1XKp4WWvUVrL8KfS2NI3TkQUYwVDWC6XdH3P4D05xlkVJuB3zWazoVYCgps7YYbjIESXMA0yyjpOxQJClBUyYJNIiESlLU3bCjGASbUX5XcXokLvPTHui0XOgek/kUW+O3D57usfNEh7bir++6c/4V13xH1To0LPq8uveXl7w+W4Z1cHqpMGtYBsApv1Da9f79l2ik0HYw9ZK6LOdEnRVQ6PNDMqQfRBmFxOYXVV2KhqNoNXbS2T7rYhqAxJmGeSVCgbrHYVzWIBOjPmTErCHhHZkjAEkyrTEmAKi8mptIpKaP6umC5r51BqLKxTCDny4vqSVWU4bl0p2BO6WvK757d88oMtT1uDznuU2WPdFmWvwewZh8jttcdqw9AF+r3Fj5nlckFdt5yfvcV+nxi2tygaQlCMocNWmuXRgsVqmkBWKFWhTMLHHZnSUGZLiCJBSDmTIqQQ8HmDMQllTun3Bj8KC0pbTRqkMIpklHXYpsEnYRfaLJtnbRsWtiXo4vGTywSmTODFs0Ym7suzc7IuNHejcE6ki/vtlm2/xzU1224vqa9aizy1sKASMgEdis+oWBIKu9FYy9HxMSF4bm624qOkDW3Vsqgb9tsdn336e8ahFw+oEElRY5uGP/qjZyxOWr783Y6x25JCvMMwk9+7HweZjvqIcYZFs+DdR09Zrc7FzP1oxeXmipcvv+by6hW7/QaTCyM0i8woF3lVQWWYyuADAHNgBUwSmVl2EiewUxgad4tKkGst06kDiGO05a2zt3jv8VPOjk/kgEmGyTpWcQg9IyNME6WEYRQzIdzxSsyH4l1sQ4RB4LtBJloFUJzcbsVrKN75btOhX9h1+QDQkj3jBC4oxeXlDc+fvyajiSmy3W3ou47nz5+z3mzo+j0hjMToWbVL8Z+xMnlNWYqJmBLO1TTFBL6qHEdHRywWC25ubgnhIFMx5XlMOVM7V5IkgSyF8JgdF7eaLy41r9YVN/6Yo7N7/Oc//Sd88uGJsJ78gGVkv+vY3N6yOj7Cj571+oblsuHRozOa1Ypm2fDi4pZPP7/mq6s910PN7XDK5T6wC4lkF+CM3BWtsSZjtQBWSRmykhI9alPkdZEqdTTxAh1vSGkoE3+RWwvbT0KA1n3gZAUn9x+w729ZrY6pwsDbD4/5/fMtf/2br/noYc33PvljPvvyFV9cBrxZEU2F1O0CWE/3VCRuYvURQkRrUDrTDztMgKPVAp2l8BdWR8THgdRJsmZrK7JTGJXwwx5VrairGtJAjiNtpUjHp6y7gaHfs6rvo/prVLxF64A1jpw15ESzWLDf76XwqKq5MJpDqPQ0yZcDWwY+pQAu0vRE2btKwJSaJgtT4EKRTEqNcEj1nYIjJuBWl9CHycsPDmtSmCsH+xJVFBd3ZXDTRB+KNQH/NqvlbhE9/XkqGGORTE7SwOnfBasyc7CggMgKiR0v8Kw6MGtnyLYwgWSLKmCHEkB+BnEL0DGxdOWzypk7rf9Zxleu+9T4SaeuSkOZmKxgUAe53HRdJnbylNo6vSaPQtnDmBlx4ps9vZew/i2Ktx884U8++TkfvPMBjW7IQRFIGGdRVtMNe7r1muAH6soBEgjT+57RDwVo1kXuJWvVGEVdVTR1VYD5cZaSTb5zMRb2ldLSOFKkhuV+ii+WYlIZqLkZmfzzpvOi3LHpe0XKQEcX8Hhq3g9NtNYIsJiCyCgLwKamMLHJ67AUotKMCsivESDNaQdZiR96hiFllK7RFlIaSP0OPXrM0RlmcYbXLdE6jBXmRAiZHCwhXROz5urymi9+8ZecnS65f77CazBa5K05K5Q7oq2VyHzxGKs4OWshlZTklNDKS4PlbEkw7+m7HTGczM1zosjXtCIlTxgCplhhTF59uTTpsv4cyxLQQlkXddMWIEiRfRBXg5xpFst58ABpvp5SL2ZC6On7HctwhsYQkiepTDaO43uP+cf/9D/lox+94n/7F/+c3/7qr/FDR20d2lTEAM/e+5APPvmEv/3sJa/fvGTs1jQmUIv1Hv1uw1e//ku6y2+oVCSUALacM12M7HViWTfipU4q4EIijZ7KOY7aBW3b0JgKP/QC71stMkANMQygHQ+fvMt//d/9t7y53vHLv/g1TlmS0gUEyTI01LkMLhJd31G5xHK5ZBwH3nr8hIs3F+z7jncenlM7zW5zy+Z2Q0ISumMKNM6RjCMpzaNHjzi7f8KLr7/kr/7sz9hseu6dnJMZSUnz6vUrLi5ec35yQoqGiCWbGmNlzU4DHqb9oAwjqmZJXTfkHIlJ/FazAp1F7pzKEDClyaJJcXxyXsASw2RLUuBBCllPnlvS/HvVPFCXuko7x9m9ByyXDVcXr7i9ucKPA6en50RBfgVU6PckO1LZM/7205dYZ3j26Ezsur4Dqv67vP7O95pRs8MfU86EnBkTUFtqbTExi6AlgSYTbCKiqVcWH0VGPY6aTZ8IZdAdBpCcRF1AG2ELCICais1HmodtIp3VWFuh9RTyeQCR+2Ggber5u0yALTDX0HeHtd57fJSAoJzF+qiqKsLQgZZ7p7P4c8oQw1C7SgDOsl+EAkBaLQzsjKaqGpqmIg0dfr8jxFF6zyTBlDnL4FlIA1qYZYWdGLMQN7SyVM5RGU1OgTElcpC+QWZFBm0ypADFWmU6G/P0nOWJWapK6v2BQZzL2aqYGJQKZw5MY6NdsUTwc3DaBDJJOFsS70vunil3VXFS25tyfybQNoMA8qWXnu9e+awT8CrL9KB0nf7yNFyR/1qa8XmH5TDkvQPQT76ZMkiWv6/LNUvRy9CpDElzWd8xll6qBNGhD2HEagLKjYMkQUmjjwKY5zwHm95lGk8ext/yMS2g0lSjGWfLkFfP6iFtTAGPBSBUShVloti01ZXDNY6qaVBJsbm5ZVdAJyW/XNSPyqKSyO4jcQ4rm/u4KOGqtkjNqZi/w2zJVeo7bQx1AeCn4TBKoVIsgcLFcizKPlE7ue8hJ5LX2CzBUCiD0RUWw1F7zP3Th5yd3GPVtpgzAfRIgX6/Z7vdMow9292OkAIhR4axp/d7GSRrsSTr+0GUMTHOw58pu8CUYU9VWypnSQmUmUKmMlVVk60r1iuU51t+drVakYqaJgSxVJlAIMkvGWeSwYGgkOb1okr/oZXUZTOIqoSMFAYwupuB3bqupefNE1DJTCjSRdEtZAcBI8fRs9/tmWyxtBZQdPAjw1D6clejZt/jhPdhBhmNc1TWHiwgck9ClK5NVaPdIRwrpVRCt5dS18ZUvg/zMyIKGAnO1RRMIiW63pMHCTBPhVRSVTXWykC1UweCygH4PgC6y8UCH/z8zGXukBbuXPsQwgyMyxqTWtsYGVJoBYmIsVbwowLiOyeBlGjJvwijnwd68wlYzvyum+7X/089ac9sw8/UMd1m4FV3yUX/iovxDZsK1qcK3VZkpfFDZDdseHnxiueXgW0vjXTjxPy9s4Ydmr33+CBBLYRMCgm7rGlPVqDA5iwyAaMIFpqTFSjDqDIhRazW5BgIQLNcik2BLUnKOeGsLvJhkbNO8nNTZKw5ZwEnVRY6fzFFzwjbbmraBSwsG7423PqOi3FL1R7htIWwRSnHdTfy2fMv+eDdR+j0hphuibln2O9QytAPET9KmvFuMxCDpl22JD1SLxZcXr9mux85Ol6iVGR13GJOW2ylSDqB7olhSYoVKWlC7DAE2ej1ipgMadTkbLGuQaVM9gnjGkxuUWkFfoEfM0PYM8SxeDhakmyLGFejXQXWkrXD2JpF1bJaLLge12X6J9PZRLl+MyCgaaqG5DNj5/E+YStH1hafJFAjKfDFWywiUzhjioerkkVllGa5WJbGqRZpBMgkG01VtVR1Q9953nr0iNVywfX1hpvrV1hrqK3hwVvv0B4/ZpdWPH50wunDitVJzeU3A303SLGtNc60KGMIOdOFRN0YPvzgBwxdRz2O2Kql3+05a1qePv4E/96PePP6FW/evORmc8nF5hW7rkMRC9AqLOas7tTCaqpT1DxhlWYQdCmurDFzwujUmBcUhUkyC8BcqMh9e//J+7z75KmENsVBWLSl+TcHygiZjB8DiXJARJFyWlcf5K8pU7ki9SzSDQoD2OjCLKFI25nsQuahZ/muqkxjozAkogcl08CYM19//YJf/M2vsK6ZTb67bsflmzfsthtQhUmg4K1Hb9E0C0h5lj1sths2u+0smZiMzVMKpLSSwJJhFH/LJAfvfrcjhMRiucQPHctFy2J5xnobubhOXO5qNukBn98aXu8doTrn5jbwZ3/1OR8+/YRFFTEh8fDBPV7GCzbbPTjF8fER3bY4cGnF7774it9/ecltt0AtHvHNtebFzSim53YBrkbZAhBiUNZijKLS5foAMXkyMGLl+SSySHua1BPjKJJ1pYT9JvN4TJYBjY+GF1cbThYtw37gz/7N73jy1gnjOECGcYD7j57x5J0jBnfGZ+vP8chBrYttRdYCHuaccU4OOzl0i60FAhDXlZl/JiUJxFAq0zYLKn1KoxJRGYashf3d78F1uKUlqoAykSor6gePIStuvniNz8csTz6ku/kVqD1Ka+IoAYt91wEyUR6HoYB+Ewt9WmOFSVJAUOsMQRVv5RSFXZpK+IVV09JgkrzKNDujK5ERVa6iaVvWm7WAjXEC1oSpq9Shgfi25UBZGOWfU9N5N/l3AuImEHl6j8mbcNo4ZF+UdS+NVJyHIQcf67L/TsXQnX8KeF4AZX2wWdFGpJDzZy3F6QQ2Tp+F+aMcmrq7DNcY7w680vx+xhi8P4C7THtg2dtESs7cQCXprspnnzziJnAZyhRplj1SfF7LlStAgqJpar7/7H3+w09+yr3VOcGLF2vTNCyKROrVy9d4P0pjLsUCKSfCODD6ft4zS7Ic1ojtjzHSFHvviwddKkUkc6BGLsySNDVBE+OaA2AyNaWTNDOXfX1iweTSKKkyyDF3/OPmYlcJ0JtSYS0hnnopBqawpuk9bVkrWpsSABIxszWURueMVWKJY7WETHmfGFMEa6jqGhUtOTnc0nBz/Xuuv4k8/PCUbCQwaLO5lnNscSLrZnnGahzZbgJHZw949v67tMv7kHvQA1ZDnjwElRav+6iIGFFRK0RdouR6pyTDGkWSkLac8eMoZ4jOAuYsllhlSUFsmXIUS5uUFTkHJla794EYe6piTzCBKdM6soUNK8+2xTUL+dmUZgmu2B5oVMqQRV5PlqYypUDWmXqxwrYrdiHz7HvfQ2uDHzteP/8DCgl3vX9+zun5GVVbse83XL15wdjdYBG7gu3NFV/94Ru2L77GhiLT1hkw6CwxNK+vbjlvT7G2Ztf3ZKWp65bey8BbG097dIyyijj2jD6QVSXNobaMY2C1XNCszrnee37yk495dnbG//6nv+S686SQ0SoWhrY8x6P3M1u46zq0gqvrC959923WV5dcvviCtrKc1I4q1+y6gZClajDKcXx6znJ1zBgG/tU//5/ZvH7O6njBhz/4mDz2bDevGPxA09S8fP2K48UKrQznD57IfVMTQJKLdFuXwWvxpk66DBoiSsXity97vXDHZeCrjEYlOddc3c6DOGkQJ7hJgKM8+UFOa3MCQ8qa11amR7vtFpKnXRwxDgPrm2v80HN8ckbdLIhB9pp+fUUOPUdnD/nFb14y7vd89OwxlbOHim/Gt/79AbdM713qwkxh/WfZP4diiWLIRJXQThFD4mRlGSOMSTHEzO3G0/WGzmsSDm2k30Bpmkbjo6idYhYrlq5LBeCTvUtrW5RxYpmUsrBCUbLn1ZWw1ScprpBZaoZxmBPHYwlsEmmyALIqSt8m4KXskcPoqZcVzjWMgzAjKysqP1OIFTLkm4aMMtzRWYCFyjkWbS1KsBgxQYalKQZh/Go9A26RLN7qSTIFjKtwVuw6nNXkKFLnWNZDEeEzWRUJ1plQKaOx8mypKbxpYr4J4DeBq5pi34EoSrQ2kjcx9Rx31DLKHIKg5DtMBBE9Hx2T3VD0oag/5b+lDBQWpQAxktsynWEKNae7y96b53s9eT/msu5yTuSiCswF3NLzszlNjZkHyHdZf4fPWOquAphP/vi5KGumn9FGoaKeATbnquItzgzgKSQ3IeeMyhpnNDF5bNMyBnkGrdb4YvM32eWQc7G7y6W2kUGM3FEZHE6ArrVyXyRXJAqTUytiknuTY6TrAvt+T+JG2NdZ8IcwCEEj5UzUlq4fGEIJZ9R5BslTkjMy+EBKsN5uxS5G63kfOQTwlQpKFdso7oDi5TugMmOQ+lkCTUuugRJ7MWcVJiFhrVmCoh6ePuDp43e4f+8+bdNgjZ4bRWcMZ2dnxOC5vrrmmxcveH15xbbbkAgkFSQYy3vGMRY2aak/tUJZVchhirEfSm2j0Fb8fynBYjLLFhDUFvanMRo7ER/KXiggZlWui2Aaxlj0ainPcAEoU5GmGiOM2f1uL2BfsfHzo5fPUtbHptuSM1jjsNaUIZ+sC1GnidzeGC0qGK3RWoaDrtgqLVdLphBAuReK5dGKEALDMDJVwKYMU3rVM45y7UyMRGMIxWu2H/qiMhD/32nNT4pT6QmkZq+bGmctlNp28qPuh0HsJSghcuVnYkwyPAiB/V7yoZyriVF+xpbnT/baSZVpZhIQCNiaytpWlMA7I5alqSjKJgKKnP1yXYIPoqgInowuVgwStJ5TYrlYFNsysZ1x9sBKlrZJzgvvPXXTzKScv+/1DxqkjdHz2YtPeb655Sbu6Zcjfjlga0u2in0c6DtLP8DNduDlleJ6UFBZnLFsdGLUli5HAoj3YMpYY0g6YpYVdlGTtWzYqsghVVPhjlfYtibEJMnLubCIlMhZMQK6JdkZZ2P4yZsllwOMHIU9kAElk1U1wR1aodG4qjSSUbznjBsFbMoKkw3JZK7GDSfJshozpspkDIvViq9fvmJgSdNeMN5esdmMYuAcnIQdpEQ/DixXNdYZTh4ciQeSMfhRs1gtca7Fj4mmWaC0lcCdYSRmQ44npHEBWaR1JAGfnTXomPEpEULE2pWEM20vUXZEGcP9M4sz4hEcw0iIoHBkXeRCMaGdw9WtsPSUISYx3h+7DZgMJMY0haFN/oURH0aO65pFXROHkaSKzDN6VBKP33v37tPUC8YhkGOk7/ek4umTyVgctWlY6AVZCSvPWgkcIVnIFqMVy9U5zfKY7e6Sxeq0HPpS9IClqs6oz97m3e/9jDeXPa6t+PQPGzbrQFsvcfGYTdcLwKUNWUOKGacsx23L04cPuLx6zRgcThnWYySNAR0U908f8ODkPvsn73J1e8WXb15wtb7han3JvlszjDtplosXUtRyHWY7AFW8E5lS1MsGX/wIJYnZzA3jZJMgh7UApFJ0GY5Xj3j37e9xtrpHigajarQuU+icBTgu7ykMP1VWhJ5N9AVMhcpalBKQ2FW1MAhyFDmaLgBDTlJAiplraY7kewm4ZEFHVEyFLSBJlMoI4Pfy5QW/+OXv2O099x6coI3i+vKKiwthm2jrMBqWzrFYLFitjgA1T3pVhqEkdCqtCNGT9rGw6xL73Zo3rzZstiPn5/dpGmHFp6RoKkfTLBh85GqjeHFr+ObKEptznn3vYz558oynb0b+2b/8BRddhWfBn//mmnunf+C//KfvsnCWROatx2fcXHdUTU1T14x95heffs1vvrjh89dbtD1jyBUv39yyGw1ZH4ET03IMYFQJp3AldVMazoRH56EUiRaXJaRPBVDRI3HjQZ4DxGNwYjwLGy7hSeyGRG3g/N49/vDmgt9+9YbWZk6WFX7X89tf/w21fZ+j1TkPzk75+rIn6opYprECGpmiqMlEP2JNhS7NjM6Zyi1IyUvBZworOImVC67FWk30A4EksvUogwuGLcrJ1DNph8qJurbos3t0r+4To0c3Fa55ybALoAIxeyySlC4NuBKbCqYJq8jLjNEYLUVcKoM1yHPQVGUcbz16zHa75/rmChUz3JmWThPbiblijaO1NU1Vc50yyhSh2x2W6jyHLX++6990aCjS/AzfZap/mzF7F8jj0IRQWDNlcHUATwXYnQCF6aWUKhL78kpRlAoyeSxYryrgbebOF5gL8kwx0S/N6t3P+d3XwUbh2y8p2u6EaEwDnfK75J8TK//wXiGF+d/n4DoOtg7TMEiXhi7FhJnAep85Wh7x8x/9mJ99/8ccuSWbmw1jCKyOT0Ep1jc3bPcbYujl/EvF+yp7Rj8UObZIW5MSxoE1hratsUaYDWOcQgakYM/E0hhljNE4o4pP3sRIKt9+ugDlfoovcP4WYDtfG8QvdWLpfZeFXe42MQnTxyRFCiNh7MiTtNKIBDdEL+ectSI7zwUkQZpEZyzRRxIjxkiytDEasnhC98FjKk1lnDB/YkddRfrrr9i+OUPdswxB8eLz33N99YYf/tE/pr3/jKxqVqbl2ckj3v3gI6xSpDyS/RUqXkCUoK2UgSghnjFmjBY2vy432xiFkF01JgtbxRkBcf3QFUnpxACSOibEQIoS9GKrqoAZafY5Sykw9B1aiR1CyGK1BRS1gBEv0ZxJUewjxnEUy4O6JiWPqxqMsuRyZsYozI5aKayr0FZUErvr17z66lP2N8csl0v+i//qv+Ev/vX/we9//UuOG0vVtFC8OI/aCsYdR61CZUcYt3zz1Vd8+ZvPcXT4PELMUoOmwyB4fbvmS/uct87OUW1DzjX7ELjutig0brHEazg+PkaFJdtdhw8jubK0dUMyDltbut2Wf/HP/hQXKv7jnzxlfTvyyy9uuLh4g/J7yIn9vkNZkdY6ZbHOsd5scM6QtOabb55zVBvatOV7bz3maLViGEY+++ILrjd7sllwdu8+7370Eb/+9Wf8+Z/+K1LY8/DBQx48esLR0Sl59Lz4smHfbXj87jucnJ5ytRlobOAkDVS57OvGEr0op2y9ELAlTzJuIRNoNdmpIB70aJLS5MLMsq4oygrYm3NCpRKopIR9O5+zSlRnKc2KU1nQJUTIpoi1iqs3z9neXPD48ROOj05wxrLdrLm5vuTeA4N2lkikco719Wuq2nB0+pjff/mGrhv54QfvsFxIOJus9Dubx/z6dwBt77ydyEQzvU+Mqjz7IZAQ4sI4JoxVOCuN77iP3O4zHkMkkZUmjIld58FYrAWlIu0C9ADeZwmw1QYJOHLFS1hRVQ37fU9UAW0tw+CpqvYAPGpp0IdhYNG01K0w31OmWFZ5pgyEybvdGIOti4WaVAugDbZZUjkZtE2WMgfgqpBwVBYLJCvKQNDYwoIjBYZ9IPgBZWXAQfDSg8YsIAlelApZ4nQTN/sFaQAAIABJREFUuShFLNhW9uPkyRmGKOer0baAPgo/lmFAVmhtxa4jCtEoEQrpoOze5d9zeSaykrpH9jAB1ZVKjDmjirw+InJ9lbSoh2JhzpbvmJWwfyfgJaeIms6LjAw6yOiS2YKWcO3ZXqFkZVCAD5WkX9RaAnsVGpWl/6H0MxSAlXK/Jrh66mGymh5SUWzlnAWsUROjNpW6JaELeCf2AgLAGFNYeD5hzORJahmGUAI9KWHhiO9y1ZK1kAFCyuRsCEBUYnsw5S9kBFjOkyKPMmDIYo0lrH0K2CyLLaVAjJP9lBYbmRQoam4mi4oYI4MfiSlhECbgBKAqpahsqQVDkLMzymDDWscUCG6VkT05K7puz363ExJO5crA2cyydLEICQeLiVJ3TDVujpGkyjNZNr5xVMWiD6yTHt0oefaWdctbD97i2TvPWB0taZYNTdNKSKMP+LEnxIHYb1mtGu7d/7+pe68nSbLszO93lbuHTF2qu1r3SAxmCLUEQO6SfOIfy2c+LG1pK0AQgBGcxQxGdk/rri6ROiPCxVV8ONc9shqzNJhxH8Aw667q7MwMDxf3nvOdTzzAuBnPz59xefuSlAMhJIY+EUIWdU70IvmvLMZKr2KNDG76rmUYvGAYIeJcVSwHEz7IMN7L4i9ZAlWFtU6GsEoLXpSSBM+NZbGRnJysZLhtSshWLtdRa8N6fTidv6wKKzlGXOUE/Jw1k1Q/50zf9+SccBhyTPRDOwGUmNfzKGKKkyXMaDdmjIST5RK6NZ/PynOCkA5TppnV5CTWBfFeSamVYm7nJBJt1zOkVO7xBCHgXEW/3bHbtYUMIQFbrtgeWlci05WW5/8e4aNyFabZ9yer1XpiGuecmYfA0It/rDYGH4Txy/TEy/mpq0qez5HwkPYZD7mQUPY2KrrYg+VpyGS0wKchRsGvsqyxmxIGhoIUongfO4txBqclzExpTcxyTvZ92+9//YsGaW98y384/xg9q1mcLggzQ7aa3eDp+kA/ZM5ftezaSOcHrvvEHQpXVeyAwSgCmZQskmOk9/RuazBVVdh6QJaQGFzF8ugYM2/QzlLNLGGX8SlSmwpdUrVNCVSCXPyEhA0xBh6lJCEik61BYpJWqnu1j0Hvm1YlzaKranwfsAXEUMoSo8YHjTbimdsPA4dHMy6uX/L5F1/yBz+UTTJ4TwgV5JKqVyWySjx68gbaJiID4IiDQ+caZVakYU4avfCMI6WRpu+AA1SWz5YGBdpye3tHXSmMcYSQ2HUDyimUrvnk2TkRODt9xPGhfJYqBLISUFMV82jZIMC6hhQhINJwrME0DUMBNaQQViMtSh7WnMkxMWuKjDwBSjEMA8aJNLlylTAZkqaZrTk6OuHi/BV3N5fUTuwplHGcPXgXlSzPvvoY0jWVlaCNkGSiU1c1C6XIvWfdNPiuZdd3aK1wymA1zBYzlF3x4qLl6HTNp5+33NxtMBqaWUVUDbtBvMHGYYCzjrlxzJzi4tmvmDULGlfRHNU0bslmN3D96gV5iLzx9G2Wi0ZSU13Dk9OOm5srzq9fcH17QTf0dENHn3qGPDCkIKCoViU8p0h0UyYXC4l8jzYhILt5fXKsys9kWVSrXPPWk6c8ePAmVb0kxDxNyFGShKxG1qtGhg/KCIBQQCFjLdYqkWuNhRWQc5Foo0CnUi+Va57HSaxcjwkMS6BULmBiLKbeks6ps+LFq1f83U9/xtffnOOMA3PN4ckhbT+AMcxXSxFup0D0Casd1lh22x2b7VYmZsGL5L1MJCmBTxKKk3j21Uv60MuQ5/KGeeNRRnF4fMz66JQhzfjmYsuLG8Pn146bsOR7P/w+Z+/8AKe2vPXQ8a//1bv827/5nE04YuMP+Pd//4yTs4b/+S+eokmQNW7e8OLllr/963/kq2/u8EkT1YLT41N0NePwdEb67TlfXSmiMViXQCeyAVM5qroRVqeGaKQZNEljvMFmRUyaqCMme3TqiXlHir340xYQcWTAZARwy4iEJxrLZgicKM18fsAmwk/+8D2ePDrhk0++4KPffszXLzv+5I+O+f77ieu7j7j0PZGKEDyL+bKAfyVEIEd22y3L9XqSfKEkpTr2W0wpIFMM5bG37ELA2BnKKpxrMFkRY2AzBOIwcPTwEXfbns2mZ2h39D7B4pC0eYUPGW0fEuMLjIqoLMntqMIsL453U/Gh5fqPSczWWJFMKimkVSkuU85cXF0KW93IZ7gfZDVNUcj0Q4+xmaEfGK7PyVoxm4nHU8wlrOxbxvIjsHgfSJVnOUzfM/7/+3+//zPflthMsv8iZZJlQE2yp1warPH97gPBwuqgWDOI5YC8twRFFdzzW2BxnooT+bu69/f9Jvk6CJ2nr91ne44eW3um8Pg79uvH2GB+Wy747c8yHlcubNrRpiIVRouOmaP5AX/24z/lg3c+oLIztn0k25rlbIExhpubG7a7O0lP9lIwxihBYakcbxqDwZQEcNR1LdJEpaYmgHLmVB69FcsxlqcxjV7643HHXJrAEYRXUwjJt89n5vXzOILu3743BLwVe4IcpcGKw1D8vgqQq6QBNSUIRJf9QyyKii+bdjjjiJWi3W6wusaYGpVhPnfctQP90LJenpF1g1IzTICDwwdc3l6yufyc07OneF3x4Xe/A/r72OVDUjYELYGqm7sds+qArDLJb9F2SWV7+t0LYuipnBVPRS8S/iEEcKaAQpbRIy4VT9QR3I7JM5gBqwxKJ/EXK4PEVZExZph8qMf7bLy/66aRc6nvsSMVCCCRJuBiBHavr68xWnyvx2TvujaluY+FZSbAiVYOrQzWOm4un3N23cCwoN/MOD19zE/++F8Biq8+/QhlGw6PjjlaL4jtNRVbHp4u2e42xLTl4vwbhm433VtaMbHGcvERzilxfnHBZrMhFwm5DxK24owVG6vFDBeXNM2cha7I7YakLLaqiRRGPgGdPD/96ce8fHHLX/7r79E8eMI//PwTrs4vib6j7S/JkQImRZEVpqqcb81u1+ESfPj4iLffOKTd3tHfXfLO4yUHM9jsMv31C37+d1d8/MkXED1nZ2e89fa7zJYHxKjo/A7THHKyPmU2P0JVa27bC7LLtCFihy3N4oCIgHOxeEy2XUtl3dRAjjYock0gJwlZyuXY/VDY9Fbq2skCIWdhMWohgYz9xWhTM63jRb6PstR1Q4gDfT+wmM9pbw0xZmxlWB6sWR2sefHiBc+ef8OTN5+wWMxRWTFfznn14hshq9iG331yS46BH33/Pbm/xs14386Wu/n/3Tfvn/saATFtNSpGrAZlFDEnTJB9dtcGrBMwsveawSd2fSArGV5VlWehRW6ulWbbBchgrcFVwhKs6xl2nlktKowVsLvrBKxKRgJI61rTNA193xdAI06+s1Vhe7VtK2F1IRa/xMxsNmf0HpVHWNhqyggwk2JGm0FAtTxaOBWf9fEsqGK/Vgg+RmmxBiinPwaxGSElAXop9TxJahOZbApxIHgJUkpOatqRNZoCZFHcyb5SYVXG6jHtXKTgoMipyPMLeyyVwZ/WWtjNShQM43Y/7kMCGpUha4gklbHFkkiUAeUzl6ZjHKiKDPn+3i4rgraWWIDGUabsnCuS/b1X52SXlve1hLDPQxkoKyEdoDDFVzcz9hZl6D7dkSO/WMBXyho31gPGKggCuMXoJ/ZdjEz779hTyc8YRmZ0zqJWg7IflHNSdm9CHOQIlJ7WghDG+iSX4CqFdY7KCqATQyJrjVLy36NSkjIcVKUmGod9MebJR3QCyPPrIXi1aaTeSemfDMKNMUXtUbFcLgXg90EY6ZoJ0NNa/I+P1QmjFchmsxGyhRLwFwSQ7r2n3e2EtX3vusYYwVoGHxiGflr/1LfqZ6MURlvWqxUnxydYpdje3YKSc6q1YrU8YN40aCUepZsEt2lb9k6Fq+bU9ZK22zL0AzEWf9Pk0UbC2JytUUqUpwpw2rE4XMixhjgpPIwdg6Hk2R09esnys6MKI4Qo9heFES81ki65LzIMCjFgrMPZgYkhLn4ZNHUjz0MJmQz3/LBNsXocsx3G6+KKFYsvhKOU9wG/8mjKetCHfvraOGQe9yGQIbQwcW1RWzGRLZRxuMLSHd/f2hptNE29KNYoetpajIHKGSpnRb1e7t3RSkZpGUSTR6BWM5/PMcZMIY1KCYt+PptN4LUxRjyPFwsZoBd/2/E1eE+IcQp9G1n4pIS/T/YopKTKVeW5j9Mabo3BlmNKpS6PUdbZ+z2KUoq+6wgh0vu+ED3BGSGFAdxtdzjrqJvqv7Rl/ssGaTsiu8eah2crdDLk3rDbJe42A5ttYNP2XN8NhKRIJuErRyThVUI5SxiDPoIs4DEJ088aIwCgKhNNI8nTUWWa9QJ3MMeTSSoznzXUMWLKpEEmi0XmMd5wpTEZJ9Epp5HzAoyNq7CMxugRci5hYmVTUMhENUQJG9Mi17ZWkbQiYNn2igMVySrSbwPb24Dr5/zsH1/ywftPMHomDc9yRT0PzBZLMgN9rwi+InUKzAqjDgheEQM4ewx5WdhiYKghRoIfuO16utjR7a5past2u4Os6fseV8l014fAg5MTmToqg5st6XdbHj58REqw3W7J2RaGahKvRtGwYI0RjxNjIQVhpBlDvViDcqUo3QMLZpQ9kHFWs2oq+ZpS9P1OFngnQEU39OQIKWqUyfzkj95ntT7ilz//GXU9B61oVg84ffwT5gdHXAfD9vpLXLzB5VCkeQ5nDNebDX3wWGMY2g3OlOAYnXEIUB13PV5d8xf/01tc32TufnuBUonFasGgauqdY9dJUSMijoizhoXLGHZYDUZvWc8b3n37Hfo455f/+Fs21+d86j2ro0OscZweHRF7z9FixZtPnrBt77i5uOR2e8t1e8O2v2PbbdjuNuQEffRg1TS9ZWTRCeVNZPpxTHNVpUjXZaJd6vUEp+tj3n38Dgfrw1K3S7hZqQmF7VE2MqH/y6SYaUKlUboSjyByMeMO0zRYht0jKAeUAm4snmS6BTnH4s85+hsFQtcSo6eqHDO35PLmlp//+lOeX9zSLA/QGTa7Dl3vWK4PyFq8BnMUI3NrFPNmxuZ2w9X1tdgZ5FBka0MpAAWESxn6dkuMgdb3pBypXU2feto2g1vx/Nbjv+65i3NebB9wPTg6fUC2M37+6Q2HJ9/wpz84o1ED3316ytWd5z/99BVenXDeLfhf/+or3n5yxHtvLXn+4oZffPyc33z8kravgAUpKs5Olnx9/g1NteCP/vxHxNjx4j/foKuGmdVE7UEp6trhGhkuJZUJ2oqZfNSY7MSTNmd0DjRDiwu3+HhHjjs0RbJbvCVjAQ1TATHFmwhCgufnt5werOjw3Nxc8+HbZwzDLR7Dq+vAxeUNTx6s+fDpCX//0QuCKqGJORFzoqkrKicS0aZeoa34+cQUqawwYW5fPcM5YYMlQLsaqw2qntEOOxrtQAsDL9mK9XKNm83JCKsv5IG+3eKjQS8PGTYX3G57jtaPcbtPCe1zXFVPrBbUKHkzRSKWChNIgLWUKM2Alk2dPPlFJQXd0E1ynr3UpUjz4wimCggn3kvCRj9ZH3C37fEhloRupkHeODG+L/e/L29/XZ63B9xeZ0W+DoSOctpcnt1cHnwJ9SjfU35Xfa95fQ3YZASq98czhopI87QHpYW9kfZFOeMavweFRaq4B2HHc/ftY7//2e9/blWGeq8zckWidd9iAT0Oiu6DlQVMznlvd0DG6Awp8/D4If/tj/6MH7z7PaJXtH3ENQvWRzN2N9e8uhB7g973RUY3lGAwyLp4XU+1iMVax3K5ImcJhItFTpuzSNnGe0cXUE9BGVTGaXgwnXO9944GGbamAhSlFLnvM6zG749hAqZT2vvHjX9KMWyKDE8KZwlCSRPQTClUXSVArNZiO1Jcm3BW1E3Oim9hZdbCpuhb2s2G5XrJ4uAUPWuIyhAxBKVx1ZJ2EKud5XJJ3+7Y9ANHp48xzRLvFSQBWBLig8iw4e72Cq0Vy1VF20bOX1wyayz1UYXRCYyAPH2KoiYYQ+IAq0aZHPR9jzZijVVVzTSASKmED712juyU4m5Gdtg4JFH3FBrlOWZ6hv9pYMiDBw/o+/becxDLPyPIIPeE+IiLusAazdBtuHz+hQBKOdHurnj0xgf88A9/TLvbsesGrGvo21u2V1/TGI+dVTgzZ9sP7DY7gu+LC6raAxpCABKZrBLjmbuukzWvgJNGG0JKnF9f4ZUAnIv5iocPHrFuGrZtDwVMttZiMIVROvDsesvnzzt+8P2HRPc9fvfrC+5uz3G3NX23ox02EgQahmJdBTFmqspADrIPxEilFToHlrMZh0+O2ewCPhq2AY7cQz79ImDnFevZDGcdr25v6bpOvKONwvsBWxmePv4eN1ev+PSzL3lyNOfx0++ga4exhhgVpFiUKfsAFxCrDG2kkYUsA9ysxX+5sABzjCMyhxAPSq4DTGDUJJvWewZPiBOPEW0MFktXrtXR8QkHhyd0IdANA/PZnDff+S4XF6/YbjpmjcXUNSQZkPzqm7/l4OCYg+MHfPFMfCY/fPdNjo6W7Eeyaqq/uL+M/n94jT2TtUZUXko811VMzGtDH2Np1xQxKEJS+ChMuggYnZnPDHPjaHcQogyhYswMIaCNFgacMTQVzGcSALltEyFI9oQ1hs3tjbDXyzpsjGYYYgkXkwFy36t7g05RHcbgqasKpWC33e73zFIHj3unQgYbuiqABuOwIxaN/Rh+OuGtZZhWLIbY/65UQAvu2eONwFwcbcyMA60lhMgUF+QsKgyUSJ2ts6gUiEEGhmSREMcQyx4I0cci3Zfrn1IhY1As/GSnL0MTqf9jyZrIRLlG4z5V9tPg/WvgT06ZmIMkzJf7XfbcPegtUn0ZXI4MwZGFy3TeNKg0HSsUFjHjyZP6bOrExxqMPK1tUAbeRrI5ppoPpgyPWNRTWgsxZOxRFLnk2BQmfDkOsUWSwUN5AyikBvQeMHbOospeOoQBsTeJAoDeq/NGNh9JrA2cFSuHGPcAlCog1/3B73ifBL8H7UYQeQxAGsHaWV1YhUmsFHLOExiW82gBNNqSObSxKF1Ul7rUwEqGybZYW1WzGc4YAUCL5zuUVPvlkvlsVkhlYQriG4cky1XFUGyefBBLNjPmE2TZDyvrOFoueHh8wMF6TW2VWHv4zO1Npt1sZYhmFLudZ3N1w27b0Q+e280tV9dX+OJ/TkKCoZUEfzZNw6xZopSjcroQ7ITw1FQNdSWAqNTXo3WDmuo1YWuL0iamOFmkKKXxwdMNbQEQM23bMcRAXcu6EnaBvu9o2x1N3Ux+zsMwsNvu5F40st8bK36s41BE7lM9WbaMmQI5Z+qmEXn9VFPvcydGD9ZxYCWet25ij/fdQBcG8Wkt4G0uz8j4vVIzScbGfRBYGyOEt7qWawgoIk1VcXJ4RNd1dH1PKlkMYpWSGQaxOhh6uUe6rptA6IlRnBI34/ubMZdDnpvFYjGB/OO9awvJh9VKwneVmr5fKQlD6/seX/r+UJTXk1ewVhg0s7qePpt1Viwa7D4YeQS4m1oCH9uuLbaBsg+IBYIjhkAMgaH7/ymTtpk53nnrhF17x3bI3NzAZhvZbSNXNy1DDvQqE0xmILHToOuaqDNDHERqUW7InBJZRbQ107QupIjBiHQkZ3TjUKuGTgtwobLIl2ezOXfbu7JZSmAMZTHMSgKzjDWy05IZqbKhTEFDLBNGW4yJyxRdfMlks1Ral0CVhKksUUMOMtWMWeNjIqRMzAabLWoXibvAcn7Is5cv+eKZ562HDVUdWR5kTH1HYiDHGhUX+HZNHFYo3aDdmjQIY221PsBoh8oFNEiycXRdz0effkOfMzkFTg7XVK5hXs8wrmaxWIJSPHv+DSEGKqPwKXF8dMxquWBeiWQ4hp66cdTOssMTs0xsZSOx1HWFq2q6LuGLtKiuZlS2waetFBa5NKgpSjGcM07DsrJURsv5N5a6kUVhfLDqWc1msyV7zy//8Wf4PuFsRdIwX6ypmiOcm3FydsrbH/6ILz6bk7bn1PGOSg0E39G2Hb3v6YMnBmGKHK0PUCV9PatM123J6Y5Hpw/YbUEeq73MvFfSENauphuGKTyFHNA6YbVFqQ5nMotqzsOzB+j5Ce3mgpvzxPPrS55/dc6snlHN58xnS2bzGYnMcn3A2cEZ13c3XG4uuL65pN/dsWnuaH3Pdui47bf4JKmV5HESLfcmaQ+QTKweKIVmCdrRjrPjJ5wdPaKxrjDqSgBf+WwSnFCa/CIn8hEyppjUG2JSpKBK4ejIWHJ5EkaLAylnRrBHCtKRkTVVXgpSLGAFxWIgBtYHhwwRfvu7L/j1x18QVMamjt3trUwTNZydnVFXDUMB0HKGEAMvz18KkKIVVV0Rx+AcY+i6nu12R4iRWd0QS0ERMtJE+ITPgXp1RjN7gy4s+fJ6yWU4ZqePSEaLvISK1if+7h++5GBd8eEbc168fMbj0xXrxSsufAtuxbOrHf/Lv/2MNx9kzq823IUVO3/M3U1LDB0//v5j3nv3kPPrCx4/fMDz51c8+/oVy8Wc66GDeoHWcylGtUEj7InxnBolk2isodcGHyM2JGpajL9ED9fE3BUmrZNE1RSJcjMUFolcCpPFsqTzGp8SZ6cnvDy/4urykuNlw+OzFc9eXvDpl3P+zV/8mD/9b75Pnw2//PISZSuc0VhtsFqVtOXC3iLj6hKwoTIh9FS2ot3e4axhNpvLnaKV+LvuPLthIFaBZGqag1Oq+ZpsjKR0ew/JS2gaYh6f50fsho5d1DSHT2n9BnI/ASfjzTbZA5QBxp5tJMCttuLxxAhS5jwF7ehS9KewD75w98DGshAK4Ksyy7rihx+8z+dffM0Xz1+hjEHkknIsY4/ybaD29zFMx++DvS/ttyfoe5B1/3dVep49S2TPzOi6ToIVjZnYqxPr9TXANE0+16PFj9bi/bcv+Jk+131AdQy5uv/eE+NF8KCp8Bpf32aE3n+NX1OowkB5HczO/NPXeFiKTCysS60UDw7P+Ms//gs+ePMDcnLif1XXrA4OefHN17x68TVaRUIUtUssYV4jyDFJ/EozI2wNAW7F63psfrOEO6Qg1hdFeSJztvvNqppA5an4Ls4NuYC13o/MA/mJsfCOMYpvaGn2Jr+438NoToVhZYwpbN0CdKcoxwPkmDA4fD9gii9euSOIMbDbbJjNG1arNdbWpRkdRAKuMkpZjF0Qk+zxlQGTEn3fsTp9xPz4EXcx0TjN0N4SdjtCMFibxR7FZ5TfsHn5ER//4ue8/cEPOD58jzZ6ZpUTFhlgK0eymrYTAN01VWm05PlorOwtbbvjxYuvOT07xBk3JXuLP10k6QAYYZ2lRD2TBnwEacemdGyE7t9nSbFP2i7rBgV0HW19rHMMfVGpKE0IvnjTynvE8flUeQqtCWHg6uqKru1oZpaj0zW+v2ZWH/Le+x/wi199xOXVNfbmmuvzZ8ShpW40R0dH7J69wLc9U5BOotj+iLRRBrIi387jQGoC80pDhjDOb26viWSevDHjtms5PXsIbkbXdljjRKY6XzBERdcNrNean/79lwyd4cHTY86enMrwXme4rcha0fddYTwK615bx8nJKQs9pkY7rIX1+pgYeoxRnJ6sCEnxyBjefrDiyWHFVy8vuX3+GfXsCB0g9S059aSoefzkbd597y2effOSv/2rv4X2nOonH3LyoGU+W4OW5rGqJEhW1impeyZgdWSuGz3d/1o7nMu0ux2brmW1XIJ2QtYY12ptpOmrKgkINGNugniODt1O1GJF6aCVhNwmL820dTWLZkkVZLDYzBoe13MuXj3j5volVVNxsD7g7OyMm4tnvHzxCV23kYFCTGw2HT/83js8enD4Xw2UlYVkXL3lc0Yy7eAZUiaXvV9pg1GKymWqpOi8/Ew/REBjnYGkcA6cUfis8DHS94rByyAhJpGepphIOeAWFT5khjbRD5m2HWQoZmDwHSaNNWuc9vgQo/R3yO8yxlA3c5TqSAmsq8XLdmSPhzAxomfz2cSMc1WFLf6H+yAsCugKWWmGGF87R9Kj5v1erC0jgzynvfoBRosj9qGhoz3ZqADJcW9ZRBmUFuR3HIxS9vSUSo2dsli4ZY219X6fmcAchUJ8smX2Kp8bhJgkLrny/qkoaEhyPUagadz7KOfMFOXIOBQYZcUjS87oUa1XeoCprpH938gmTRpRbdkMy/nJGKWIxcJAld4nM+7D9/fN/YAW8gRy3VcUSblhpr0ihAI62n2YU0yxgKXjZ6QEdI2WcllIBIz7fCLEUO65e4oeJb6fWjy1GNmEqZAlxKdegqaU3tc9o3RbFLkScsx8b383DsDHnm8cDLdDL2xXY6c9aQSmJu/78t8hBAn3ApQq4XFKEX2EWLyWszBmR3JDKEPhDPQ3N1zd3FBV1d5Grbzf+D4uyWDfGDOFWE/M6XKvzpoZjXMyVEoepR21M9SNKKRjCNxc35UckYzvenZty83tLXebW0IYCH6AnKmtJg1Sn84XjTCX3Yy6nrNa1NR1VQBYJi/o8dm6rzwahw45C1vWuUrQADUQg3y+ylYTCYUMTT2n7TtijlP2yQiwj31xKlZZIQRRWcVIiBkdNF0/CFCo9GtKuvG4JpLbxHje2xnEGCflhrUW5xyz2Wyq7aVf0Mxnka7rJyA4loHRCGB67/FZns/x+dVaAtFi6Yfqcj/K+8vPdj6UAZGa3s85h7Ga2awhBvGfHQHTECTvYfLBLe81HsOe+CEA8n7QofdrmTHiC+z2oOp47RaLxd6WoawTWst59cNA13fiFz32PCA+8+XZGd9zNpuVz6lRGmbzRryhc8IZx2K+ZD6fs16vub29ZWTw/77Xv2iQFjTXV5GLy567XcvmLnLb9yREepE0RA1tjrTG0FtdWE3SyJSxI6oEE9l6Ni2aVmmUMwwp4kNEO0ebKERzAAAgAElEQVS9OiBWNUMBAlVO9D5QVwJCiT/RXgY2IfBMuCwjLR+EkaGzTEJzEk8Xa0Q+Z5SwDuSnJalTJ5GK1E2DqQdiv6VqDMloUvDstlu2aI5nFSYE4u6G3MzoVcWvPup47+kZh0cOrTy+PST7I/CPiL5BZ4dSFf0gNgrGWGQYkNC6pFeSSFlusnlT8fbDB+TKUlWGWluW8zVVU9F1gSFEjLMcrOeEoSdkKZLW60OGdsPVy5c0zQHr5TGLWYUzBpJHKYtzwkiJUXww67phO0igm0FT25ra1myHLYpinJ0prA1IKBpjWda1qOO1sHI774n3GtY2BfGli56vvvgdB+sT1qsjTDNjuX6DxeKMH/7gjDceW95+4z3+z0rx0a+8SIt9IMVEGLzQ+G2FcZqYEsOuY7FeUblG5BDWoRYGrxJffd3hFuKt66xl6ALeR4ZB2B4LV8nnyNA0FRlPipHdpuW2z8zeeJv5+g02wxXL5obFWct6bbm4GLi6eMX5lcdUC2YHZ9TzJavVIdV6yeF8RXVwyNHBQ/xuy/XNNdfbG3wOtL7l6uaKtt+xG1pS8FKgqBF82ntblvpAZE8Fl6qaBY8ev8PJ8WOccuichTUzDEQtgJ9CCdMjSbBUNkjoVwG20khVyiV4RmsoycVK+wJkFF+2IvvK5emYlOHEaRqtsrAOja5ZzBLn5y+42+64vGn5+OMviVlzfnOF1pnTw0MenJyglGboy8JNkbcaS+9bUhb5aF2JL44PMlCxVortq+tb+rClGzoMmpwcQ54RdUN2j1CzJxy994ccnTxgtTpCf9Hx8lffkHIF4vQEThhPV97yN798hTZnXL284q6/4eTsmN21oks1UVn+r0/v+OrK8v4H3+HTXz/nrktot8JUmY2qma8afvidt7m82/HF1zv+7Mdv0Szm/G9//YwXMbGzNVYrnDPg5HpkLVNOmySgwqNIRgp8kzIqdaR0jY63oCIQyLl4XqYA2oosiwKUKWlIYtJEEq92nvffOCN3PT/72a/58ffe4K0/+R4/+/gVn33xnKNffcQf/8F3+f67j3lxvWEXy7pKKmEHamrgc85TZByqTGPnCxqj0ZUVxogum6+VpPTc9fTdgFpUaGfZ7O4IMVI3NaRApTw4RYUmZos5fszQB3bxkqZ6gnIvSf6bCfQST7QCHpZBGoyWB7xWqKUsfnmjFQuY0vgJW4WkME5PE2jUGJwxhnpJGNPBfMGD1ZIXKmGyhKuMkW2jHx7sQdkp4Xg8lrFYvwdCvg7A5fIZ7j/zI1BbimFGFu7eJmFkAI9A7f3Xa0BtFoWJNCx7lotGTwzREYi8f7xj07YHBiee0fSZuQckj97Z91/TMfzer+2/ec+0Hb3tRjaoFJOjTQzk6XitsTw+fshf/tGf8913v0vwmt0QmR+sWcznfPy7j7i+OS/PTMAPfSnYpB5RSpgPY2PUOEfd1JPXIdlPxaVCmrnxGunimR9TLr7bIkurqppRUjnZWLx2jRUgRat4/+mJLTGyArLPr50n8dAzr1/T8b7QGp3LACNpYoCxvRaAFnJhBoQMTdMU1g+07Zbzi1ec6TOWq7Xs5KqidhofN5y/fMmT1UOUtVhtMRmC3xDDLfXMUM2WdEnRdrcYsyP0mRAVISp6PJVpUMqC3+J3L5mbjqOlxmpP4zJVk1G5RyWN0XNCzMQo9Zi1htETXSlNtooUIipHzr/+mu35c56++z7NbAXGoQyEIL78foh8+fkXPHjwEFfPMNqiq306cAiBxWIh17/IDjMKnQpriyx7mVZQnhlyFraKsvRdAUiNKMGscdMeLfP90c9MrvEwBELa4bKjb3v8bkceWhINJ8eHPH3rLe7uNuw211xdv0CHHXVq6Lodu82GOHgBWvL9NURqMNCEUMJ4CkCr2IOMsq5J3RxD5vrmmnq5olosWHrPanVITAIkWCsBRUoZvL8mt2tutjf85teWQMXZowPmK8flK8eXnzybGjnvW3kPYCiBTjebK04XFT4PGJUwKvPNi2/IGR4+eZOUNU1lqbXm7ceHvPHkhE0Pd9vIN5cbupd3RK04Pn3AroP/8B//hs9+9wti22EVfP7sgrNHVyyOHorFT4ykqDFWF5BPBhKmWCGNQJD8KffSMAxEP5BzIKeO66sNi/UpdTMnk4lBgqmaxRLtqntAQKLvesKwY7vZoFXGVE72mDK8STnTzBdsdi3VTNPMF9zebkl0OCtN87yZM4Qdfbvl9OwB7e4dvvrsV2xuLvBnj9GHJ1xtW372i8/I8R3OHhwgSugC2P9XQm1z2fyUMQwxkkLGq0TlHG0XiEHRd5FtKwxx7yU/ISFM4lljip2MZ9PB0Am7eyQdWKWJcaCaO243LTlZchapekowxEi2BmsbUdcEv1/jrS3A68iEF8Zv09QwgVSybqQYyMqAFsA2k3BRLAxM8dI0miJtTvt08qLGJCUiSoDQUvukOIKp+30uZQGF9s+6QmlHjp6cFCmNIKqRwVkMUqslYYdqJaF1TNvz3rpJ3RvEhugl+Fk78VrMAVfJz8cYsVaToidHUcGocVCi9gohlOxFAt6J2pD7QFYBmyQ0SOOseF6OQWHkTC7PzhQAliImjnYiegJb4xg+po0oUtOYvCEgpoRujqoGCSQaAZlxyGX0nnkn9imyB5BzGVDpCQyXoaPDOTUFeOZkqVxVFLbyrMY4CGA+UU2E/Z3i3oM6Z10UhOJrqbUEVWttcFaRhmFSkaWc0Vb8TlMefweEJMSvVNZCbXRRf+rX/pF9x5RzI8zfPO7h5X6w1uJjxA+egH/d7kCBymr62lgDxlCOrYTwjEOYXOCmEANt302em+gx4E3qraHv5c9SWwOv1YZtYd9qLV7EWmkJjishXSlm+l4GS3XTYbST5yFGhigBvETo25a2a/FB8gRiKjZSKVG78vuSJ2RNtahIaCwOS4XB0FSO+WxG09S4SgBsbRQ5SWZA8EMJH2QCAFMcg6DKOU5R7vGyfwoLes+eN8Yxn1liDvR9i7Ou1CNJfLgL8Nk0TXm4ZM0J3t8LsRRwEwWbzYZhGCZwd6wl79sJ3AcmR6WG0aaso6MfLWhtp/qyrit59tWe6AHSg4xsbbE9HAkXmXrWsG07vB/YdR1j9sM4WNB6AwqcdTSumuwHtJZ7XCvDrJkJCFrYshlotGG5XAlrO0a8H8raoqbPJ0F2aQKjU0r0g6jaTCGMaKXE2qYMhUYvZl0Idgrp33LZvHKWumO0NM0FlxqGnt1uN7GQx5cA9bYEF4qyzVlH2/XM2p2w2BdzCbr7L7z+RYO0ISSen3fc3iT6AW6HyDZHSbN0clN7q9mlTJcCSlWk5Kdmz4ehSOSL3EyJCYHTMgXy0YtkvXKYeYVb1UQ9UnWE3h6IEHu0UXgfYdzwxpNeKOylywMpcfcXljK9GpevVDYqpYTNBoASa01dvKmUYr5YcHfXEjqZ8Nu6out7tsaybpwkxvqeYadolgd89vkd7e4RC3VKv9F4b1BpBXlNigLWJAVD31FVGVcZqtzI5q8skf3OrZWhcpqnjx4VeZdMXmNKJB/xvWeIiTgM7Pod/bDlVb4kJ03fB44PDnl58Yqnb9Y085q61njfElEoZWWaSCn/dEVVzahsV9JCJcXTuRqGAroz+uyJlDNGD/Wcuj5CEjITg4/EJA93irFItAX2Tbp4fDlLshbn1sxWRyxXR5yeznjzzLLYQFX3VDMLWyUyiFL4OSVSEI0iZKiNLNzRWLyu0LahMeIle3pmOTw13F3JZxzTTLWiPKyGXb8lZ13Yg57bmy3eD8xnByQzw7gZ51/8I932ipkbWM0bDhcH5DcOuLzrePbqlueXX/LqlWG2OOLo5CFHpw+YzQ/QJ4Y0eJbX16w2N+jkCWHHy/Pn3Nxd0w0dd5trbrYXDENHtpJ0nQrdYQKiRtZDhtlixYOHT1jPF+g04Iwjx4Aukk3GfbYUaDFFxFZpb9SvSoGZEc8wtDBoEwmn90CB/DozsS5QqkzipMhOymAApQfCsEVbw3y+oq7veHV+zqdfPmfTd+jaUlcVq+WKd995F2Og73pubs7ZbW44WMq9Uzc1xmT84FFdj0WjIzgtzPChG/A+CKaMYfCS4Kv1Gm8f4eszNu4tQjpjad7mg7ee4kLHj37wgG2Cn/7qGZg1yjh0XZVpseWrlzv+4bcX/OS773Lx6dfUixkfHB/wyeev6IIlzQ/wNqNtTTOfsUmR7Jb4KvCbZ4HHBwMPmsibDw+w1YzT44r53PCT757wVx8l+VljcTOHNYVJW2SVOueyjmUcCqMiRgVIEXwLcYtNLSkFoi6S63TPBwymplnYAB6VM32ClxdXPDo64tUnX7O5O+CNp09xFjof+OzLV3znvXd48uiYdx8d88uvbvA4YhIvvZGFlAsbIxJEoaAktEi5mtpajEq07VYM2bUhpaKY8AMkqGxFjJkw9Gx3O5RaY6uK2byBIMqEbe8xtaaaGdrLTEiOqj6mHy7QeZDGKWtG4aFFLAym5OByf+rSgKSY0USUtdNaPwViIPIkBaTCcpzsBVRhSqAx2XBzd8fX56/YDR5lHfF+c6z2bKSRQTmyQe5Ldr4NVt63O7j//77NOB2LZVGK7NkB0+8uhV2610T+k98zfraMMC6zsFiwemqO7ksfx9+9ZweNTZSc91FORjl2Y4t3WwG5mI5FTezl1z9Sng7sPvg7gsGTp+q9702F9TQOWK2Cx8cn/NmP/5j3n36H6BV9N2CwOK346svPuLx8gTIZn4SdMTJcxlGTNbLe55zRtkJpKdgH70uqrZomvaN3ntLF+0+V8x4GQvAlMVdTVY4xcG26H/aXQdjZUmGXr6lS/O99eH0YqOuayoos977f330QX1izI5A/hrQJhUnnPcDfFy9drQ3ex9KEKubzJU/fnJWUW41ShtoZlKoJccDUtUigjZKwKpUl7CMG1GKNN5bBD0TfYVUlCKUfMGmEkAbqZk7fb1mu1pz+wY9YHc1J4YahveLu/Gtq3bKcPQJVgbY4Y3BG2Fo5emIK1NWcWGxMZos5y/USv7uVq5IjbddhXYVzldyjMZN8FOuJEFG1JWddml+3Z1MoGXaBmlhlUhfogpbI4L8uknhjBACOUVYTGUZryFoY1t8esJQGQGvNcrYqaiVh3fTdHVUz49GjU4YUOL/uWCxq3nzrPb75/Nf0IRL6xK4b1S96Sm+Whut1j2q523KpeUvoWmaystJKY2tDVIq7zS3N9RWL5SH1bMnq6BDjKupZQ9u1cs9qy+biG3YhgIXqcwfG8OiNFU19wtV5S9du0cahgoShUMKKvvj0Y46XgcXs3cI4zvjQS1CcrbAlo6DvO7RVvHz+NSFpnr73XY4OD3n69tt8cLvjs88/4+XFNX/3f/8UHwMHS0t1uKTbtVzf7vibv/97moNjTo8fkGIgZoMZ2YIAJfAFZV6rh/bglVwzax0DcPHyOVU9p2lmIvWMkc3dLbN5g8qWwrMmhp7t5prKag6PjuQz5ijheznLM2YbqvmCrpdapUqJu80d83lD7RZ0rSdGqN2cu9sN11fXPHr4hMoori7OscZQNzXt4Nl2O375my95fLvj/fceUFcFyJqQvelf/+zXZL0CRBJDhiFJc5+iZrMN1E3i+XXPptMYZ4XAkg3aZUKf6UPCakW7y7TDwG0X8d4VH0GxTKq0eABjRuZnpm4su9az7Vqs1eRUmGHLOSkGdtc7QFFVroCHjrZtp2dQFCGhAHBegIggIYRi41OWwQIw+SSBNIoRFIyFCVrAidGrVGlMDMiKIAOQcUNX9/YopQsomSTbQRuLMhaVKlTVELa3ZQ/M5DRIbawgm5GsRCE/yOKtpUqRe6uoIIS9KkxBsgATKkUoVlgYkdeDWIzkiaS097wflR7SG4+sSIovb9lvFKgyFFNlT9dGFzVUGTZnqS/Ex1RL2BhRPMCN2AGkECW4CMBQlH25YGLFOiGJz64qD2MqoWU5i1yfvPemH0PjNCXgO1NAJMr1EvDJaCOAZ86AZjYbmXgF6A6jHY3cFKPFDYzgbCrBzVFCvgqoLTN/qTX6IeJ9ErZ1UmJNRrFWUWXtN4pqPt8zaJHg8RDCdNw55xJ0l+mRcLOqctP10nG05jIoZWicI9pK9uJyXcX6SuxsqsKC3Cu37nmuT6A3mMpMQ27vPUqbiY04sqVr50TNkkuIesrT3jUpM1Ii+Uw3DMWSqvSKtsFaUwDFwGa3ZXiRuLvbcLheMJvPqOsG6wzdMND3vihQhBSxudvRdT0Zg0bUCK6u8NoQYi7nPdLU4kttSs+ujCkDRiUqzjx6FOuiGJPz6r30VbGAncLeHoFQVXCpgBk8vpBfcuwFDCRRWY3KRrCpnIuHsQCCQ/Ez1lrT9x0oReUq2YOyDNiN3Q/YBbeRoYJC+jjv/WRjcZ/12/cDQ99OoVhKCUAre5rcX+PwUfq00UpBfg+F9W61HIO1xTLLWJartdStQyFj5XFOJaHzu92OIfTo4oWjtHDyQ/DkBLu7FqXF11+C9MAW+62gxYalaiqsFlZ+CLEwqaOEQ5dhjE+JOiaClxpdj8GAg0e7ipATfdtOZExjjCjHzbguyyAkA652YnuEqG3n8xneiyUDKb8WkpeyQsX9QDDGxOAHum4nvcE9q4bf9/oXDdIOfuD5y+eQtEzYtCIEiE3FHZmoLIP3KKMxzkxePCmW0K1KPF6dczK5AZwrfrIpihTVGVLtcIsl2QlLUKRcwv4hSQp0ZR2uhMTElDHOoZWi27WgpYA32hS/TGFNhFHOohitZycZRFaqhEiOG6ZsIqZ4yUQSqTH0d1tMtmjniMBm6PBqJTR/o0hJMwyW22vPF59nPnzyiOAh+IxVNUYJmC0yCUlpN1kYqz4FlLLorCEmQgpC9Uam105ruu2Oq7sbNn1HVAqnrDBpfWKInk17h3OZxWxOXc05PjpivVxxffGSuqrwfmB7tyl6FIX47pSiBDDGcXJyxLbdlIgekb7P5zPUrhQBYgxYwBBhU85nSyrb4IzD9zvabicbagIKTDKyMkfav2x3lqwNPhi6VvPs2ZbaKu58JCKG3MOwIw0tKQSMqzg+PaXtB4a2pyJQu4qIIpmaYFZUzRmzw0c0i0OeP+/46KMXXLx8SfStyLadpW5q+sGTo6R8L5qapqmoqx04wxA1WMfhg4fc3N7y1Wef0F4+Y9HA4fEZpjZYHXl0pHh4ckYfLS8vt7y6vOXm5Tnby0+p12/zxts/5k//zQ/AZP73f/d33F5fUsWBJ9Wao90tXbflbnPDXXfFzeacXXdDH71IaKLIN4vdPikIi+Lh2SOePDgtFhZyb+osqYsKRQ7yNbIA/DJlVZOMSlGku+XKpJxk0zSFQWDKJBqRd6Qo4FwuU8JRDiqFoMietNLsdi1tTqwPDlFVw9effMYvP/odfc7UTcX7p+8xq2asViu22w3GOQKZLvQ0wbNYriQQwfd0nXjxBGupqooQMn0vTXJISZ53Gnxe0ekDgntMZ5+yUyfc5UNCdNx99IrjBwe8fTYjhw1/8Sfv8eLyludXmWyVTOfRJK1IasYX53fY6pKTxZz3Hs154+mS/6Sf859/c4O2J2wGxavrW95595ibj14RlCTUt1Hzy89vef/Pj3m4rvDJcLHZ8tnzHT47VtVANo6kNdZo6krjlCKi8FnYHTIQkkTqrAUIUsMG/E4SS3NEkVAxAE4Ys1km6NrIdFyKHIUeg2AUtH1PHwymmfHRl694+sH3WS+XrA9WXG92/OaTZ/zww7d5crrik28u2KZQZIGjqbxsYO2uZTZrqFVVJqJRZEJZE3xH3SxQRjOEQAoB73tUCLhqjs+KMPQALBcLWWlSxlYVPnYySVeFgbua025qet8zd0covST7C0ZQL49NqZYyESV/joWxRtb8yjnGsDGlNJW1VHVNjJFd2xYptSGHVDybjXhtKcg6lbVRMWTNLz7+TAp+Y4rXWZKmqTwDcrKZpurja/KgKq/Xmaqvv34f63RUhVAAuG8zKfcNmfy++8Fk35bIjcdyn92Zy8+Mv+/b4PHY7OzfQ00fcrQ8keagtLaleJTvvw9g8xogvf/8efre8l3lOjN9HpDAAsUIOkXWzZw//oMf8503P0AHzeADVV1jTcXLl99wt73FWk3nW0Iq/m/jZyv7kLXSCFlr2e62bDYblBI23mgbMx7/xBxWUqiKjAt82BfYVWVKkNgoud5fs1gap70XV5oaOvEHl7DI0TPrfjhRLjLD0Qt1vKbk/dmN3pNjeM1KSmR4g9gA6RE0RwaqaKyZUVUzrJF1MORe7KiMY7E6xFZzpKfw0uTEQPSe4AOh2ENprZk1xTtPgTWKFITtvz5Y8N/993/JX//1/8Hnn32Jto52d8WQOnbXz+i7W5YHEt4VQ8Aaw/xgxna3ZfBbxgfKOMPJ6SkvvvmGqBQffv/7hHbDbLnCNQ03m06S4xE2V101vPPee8JsSQGVrOyLShUJoXxv3w/sdrvCqtV7AK+sI5QBlTaW6IWNnIqsVZu9xYwp9akAPuV6ZGHqiSVPZnF4xnbXcXq4wloJUglhy8WrQUJpVGKIA2++8z6bu2tePv+c3g94rWlDnEBFXY5PlkBd2IjqnhRYHqGRJaig+NVpTO2kvs6Zu7sbzi9fCujtDnHWobUlFr/mnA1D1zOkCCQurJVQWv+Ah4/XvP/dU7KK3N1UEFdYI8E15y9fsbm94tFqyaMHpwLsDy2+7xjaW5Sx9JsrvA989cUXqNDx9ee/4+jklMYp1mdvUS01BzPDDz98k+9+8BYHi4rf/e4jQhDGolk6um7Hi+fP+Y///t/xP/7r/4HlrMbVDYlc7tkCxKo9qWCyjEDKV2sd2RhyMtTNgsdvPKXb3hUJqDBtuq7DDz21dRT/HPww0O52JGc5ODxh120JPmBdRdfuCCEwWyxw9Rzt5P7WxvLo8aNyGIHF+gCd5/hhh7GKTz/5mI9/8yvmVvHk8QPa3ZbLq3NmyyVtuyOFQBt6Lm9v+cF33uLoYC4g2L01c//3f94rI3VHTIkhRNo+EzBkk8kabraJrCthHAXFcmFIXrw75zNwGQ5WlotziEGj0cXuQTMMiaGP9FkRg6epHYOnMOsyMWa8F/VCLMMWHwYJcza2AHeVJM7nwiwsfqQiqxXgVGtd8goylXEMgxdWXCr799SqZAFLckJbqZE1Y3077oupDNm4t0fG8iDp1wBE8QyXumGslazSzJqG2XrF0A/4vqNrrzEGUrYikybLWp1GtY+wM0MOjPocax21q0rQ3VBsABIpDJAiuXjnp3LZRdortnyaYtOU0x68QzxNtdbYYok0MiydtmDyvf1NGGspC2Q2nZ9yX0lQWvE4jaP6poRVIuDYaFUxqoUUWoDeGPe2IylPnvqjdPm+77qs5UGGadNtvR8cKyjhT0I0Gf1cR2Be/H/LPxJVvq+NlIDaaTRnHx8GlQuInckpyOA/RWKQe2pkSYL4WEbEmmi8P8f6avRsBfB+IKRAjPI5x319PNfpfj2kMrDf41HQ1BUxWwmAG601lLz/GAYFTL6x3gu4LUojU7xCAyoVqz9Xye+5J7mX4bqitm4a9ueU6AuoL8xNAdIrY5lVDSFlum7H0A54EuvVgtOTIx4cHWK1wQ8J3+149eJGfnfV4OqaBPSlfuq9gL05QI6KmOWsGhIKYek6ZFiuVKKZVbi6omoaGfSlMusuJDpV/J6ttShrpoCqVCwqk0bYurYqPayAtcIITlR1ADSDb2k7UVKkoFFZY+oaNfSinLFCSvt/mHuvJsuy687vt90x16Up39UO3bAkhhjQDUfDGAUnQh9AX1PSu0IR86DgiCMMOAwRaIIE0QC6urq6ulxWmmuO2U4Pa59zs0AyFHrjjc7o7sqsvObss/da//U33g/0w4BCspRG36OUxlcBKR80aRfntTld/+l631ZK1ZOfqj6GfElAqazNcfRzZsGUJeGDpx+GEqCl5gAtYy1d1xFTwhVPVufENkHC6uIt0gUliEusMAXIlKHWMAzSF1kBjtu6oesODN0gQ7hiBzYBw13pCac1rot9gnVCYDQlgNUUGx2tDZGIcxW6bdEqzSFu41AC2srf0UV9Fn1kVCPWaoahIxfFDAoOXVcsG+oyyJY93Fqx55zu05mVrBQpVbfuv8kDt2fshmNf9888/lWDtALKeWLSDD7itYG6IrQVnR+JOWFrRxwCyQdq18gFUtNmW+QaIc7SoxwTvmyKlXF451CrNalqZZaREzrnaag5A0S+sCAAKmPYNEsymcPNFowWw/LSsIjE78hAMcbMwSHCmqAsoMnPJ8+TxTyxUrTCLETCq7KaEhsYQiYqJQxX7wkqEIKi2xt++5vAJ/fvQe5ReURpC8qgVCIWD6+6EVAmkVFWJD3b/sBut+Vmd8353buElLm5vOGj99/HVJbFes0XL74hKcX98ztoA/fPzuWgi/eIoaNtW5p6SWUrhn7g/GRDY135TDSLxRqu92SlQFt0SSZu2yVt24nMI6Tig5SoqtI4amRSPBWEGXQ2nC5PsAWElea1p6oblDJlsh7mCbUxBmccTdViTC1SZ21ZLS1Pv7rkydcvGXJguz+gyPjo0RlCytRtRbNYseuvSNpQaUUA8QoU41KWJ6c8/uhjVusWTSaOG97mb3A64aN4vCktA4WcPMY6Tk7PWG8MteuxusFQc37vEc2i5s2rLxj2F+QY8T28efESaxWrhWPR1iyXG9q65eyDmu88vsN+N/D1mwNPX3/Jr//+wOu3z7nz4D6uaji98x4qJ7ZvX7Js1/T9ns36Lrv+ijvDGfvuguvtFcMwsj0cGEIgTbVEjNSu5aOH3+Lu+g6Nqck5YRCDcEsBTYq3zszCzQqdFb54twqQIPdPKoWLMkrWnwacFaahGPWK128qoE7Z0GQAJxubNGNSPGptUZVjSPD5k6958faS5ckajWbR1nSHjhcvhbEigEgAACAASURBVEVhq4r1ekNlYLVYcXl5iTWQ+o5uv6MbRpmlKFmLxmhQhpgrsl0R7BkH/RFbPqZTZ3QsGVNTig0BL5+/uOG9+xtOzh3twvFHf/At/vNPnnLwBUQqB0bOikNv+fL5Df/xf/4hdxvNcLPlz3//Q16/+JznPpGqDS+vB+7dP+H990756sWI1Y5sK77xI3/5iwv+4sd3ef3mkt9+dY21mg+/dZ8//uGKz76EPlmwBmuSyJSTImVDyBmtEpWODDHjE+i4Rw0XZL8TOxlTkyd5X06oHGhVoj05YTsKY27avwR8OwY+XVzd8Pjh++y2O548e81Hj+9zGDr+7tfP+Pkvv+Du6ZpPPnrIxX7kZ795gy6pqCAsqJwzbVPN7I3a1TJ2KT5J3idW6xXaOsZhpBu3YFtOTu6hbM1QWK/Be3IUKaWJGa0cShmGbk/IBm0a6sWG+mRkuHjNorpLvX7I7uICk5I0KdoQlcFYSWlOKZX0ZtldQgwkjSRVWz17c2Tk+WOR28h5IiNkrRUnpyd0h45+7BmDF9masqANXZRhlvhWpnLvCBtnZs3esj24bXVwm/06gaW/C1be9nK9/efv/sy7gOftn/ldWT0wAzdACRCYkqqLFC4JW38qWG5/HWVuR5lUeWZpjMr/zUBieV7n3AwKzx/6rdc8YdjT9P53QYWJvZNzOjYQSEBFTFIELquaH//ej/juR99FRc3u5ppmtWGzXHPx5jVdvyeEkXHsi/+sFLezbEuBNZa2qTFaFSaDL4X0MTTlXSBdWLGTPC2EiNKZnCWkxFqHMYoYveyjpamf7BKy4haQlt9ZC1IcHj3BUMdGdQ4h0cIg82Mor00X8LYwwUrDl0uDOm3RwqrQxa9ToVRgGDw5K5atpdKSJp2VIkUvLN7FCQlLzIi3ZO5QOIIPzFIzWxXvQkvTim2OFOglhC2KB/Dr18/Zbd8Qwx6fK0w0aD1SWeiVAtvy+mJPdolvffopf/rHf8ivP/8VP//sZ2Q0dbOg91HC24pU1xnHYfToccQ2mcViQVW3pJiIShh8GbHessZIfXMLQJ2AWFsaAJHfZVH8TMs2T+tUz96yU91YVdUc7JZSIFEBUv9pI/uNUUoUTsFjqobN3Ud8fOchrYWLb37DYT9i7Mhuf4Oq1jTtGlct6Xc1TXvKxcXP6cYDIWnGW+D8BMTeHuccGYbyoqe7NZcaVsBZTdKiEHB1jasq+mHP6zcvQBtCUoSQxcNtGNG2Jseew/4GkyPbnBm6ke12h1Lf4v0PT3n0wXus10tM9qzbhv3hwGG753CVWCxaVouW2N3QbXd0O5H1d92WbnvNhx99h7NlxZPfPGG9bDk9WRPTSE4DOXWEIK9/tdzwpz/+N3z86IyXry55dXHDvh94tr3m5mqHsa94e3XBeBj49ne+hzG2yDt1ue5qhlSmDUmV9TGFsHS9p16sMFrx+sULyJk79x+xOwzcu/9ASBJjT1YGaxxt23B2do4i03cHvnzyBd6PfOfT78n6qGu0ETWKMq4A6wI+aqUIQyxstihSezQffvAhd0/P+Puf/w0/+9vn/PBHP+bZk99wcnZKrSzuTJPNkleXA93f/oYf/uAxD++fz2eYlGMFSOP/+6HmvVkYmMZojMl0Q6YfI9ZphoNnDAZnNdFnmhqGlNkdElXtWNZGCBwqY7WhqTVZe4JPuIWw2mMACaazhbGo2O5Grq62VFVNtXT0w1iyMgJGW5qmvSWHne47ARmcE1YtyHkre5tiHAdhwhqHKh7zKSY2q80MZmsj6h6lMlS39laY/dwnO6SY0zw8kzNBiT1G8YtEZalFc1F5JMBJrdC0S1zV0BuND3uSDxhj0SXfxHtPCNLT+nFApYEYB0hJLP+MKsFnhfFV/G21tYRhZAorVAh7VYhQ8lryDJzKe45ikEu+dc5PbD2nSxp8OXMnZuUElE5ne5jqJWRIqrVkukyA6zRsnBjKt9Uvk1JGUYDwcj1TjtzexY71z8Q2PHrrToCaPG7VW7fO53n/yxOUe0t1UK7xFDA5/YFYg8m5HmOSrIFUCBNK8j0EGBMVSV1Yr9JTHe0LYoz0wzB/3pO/v7yviLZ6Zm7WdT0DdvPnlJIM0oDJp1gk7JnQdRhn0Uj9EsoAQkRNky1GJASPLcFH07WgDHYpAFWMYjPxuwSBuR7VWkhpE5uTqZecQP5S12khyllj8SmSg5DwKqNorKZtalKrycuaFD273Y5uf83z5/uiRBNyRqL4TaNx2gn+gbw/ayVMytmq3PeKqiqAYWXn9XQkE0Rh7CMDFfFOtnINCaUOlDrSGFu+TFEJFqC9yoCWTAJnJbCrG9HaF4pZFgKigsWyZREz+xLWK96wkruTE2VYJN7Vfd/Na0Vr6dOVMojD4NGfdfKllftPakLrxFNfOwup1M3pWEX7ErSVyoAmI/1PXdfFI9nP63IYxnlvsNbMQOtyubxlpXAMC67runh7q3mdt21L27RibTLBAOUcyTkz9P3R6zgJYzj4nsPhqIRwzontqNbzsMAohXV2PiuNm8IGM21dY5d2XscTtcw5S4pCmogpFm/8gLNC+IlRavpYBlS1c1RVXX7tRL6QNWTK8M8aw2q1LEznf/kk/VcN0pIyaQx0xnBwhtw29FozaE3qEiqVTWYc0c7OPjXCUs2FgVCAICXLymDIOWLrCoyh3pwQ25akDZoimQwJjFzIlIRJl0txkkhUuuJOu+DQdyJBjIUFoUQWoBCmX84KHzySYFvADPmmPAfzqpsbyVzeN0CzaAn9iB+GeZM8pMjNfs9ZY3FokofkPSpqvnm249Bn2kpjvCoTnSTNcpbgoqwTgVw8Sj0hZvZ9R4gjh/2edrOh7wdh6SqojONkUfO9Dz/FNTWrZYMfPRpNUzeQM0N3EEadcWhlcLViXTcYXWFsQ92ekImMPojfllJEsoQ5IV4+em6Y5aDVGpGZO1u2g6OXSaUWrBenKFSRsWSMtlhbUdtKrB6iL6bz4itVu7okPVoW7R1+9KNPeP+9hv/yV7/lzesLxtDjKsNm2RJ2S2IepfA2hpubLdZYTCNrqFms6HZXJN9jjKd2hjt3Ftx7oFi28FS3XL6sCQbGGEjRQw44q2UtAatlQ3e4YIxvaesGZ04I0bDd3/D29RPaOtAdMn4YqVuR51xfH9jvHfvDwNnZOc4Z6spytsms2hMe3YOX1x1fPf8H/v7Xn3EIieX6nM3pWfHFEUZHVVVUlaEbLJvFktP2nL7v6YaevkzsOt+x3+84Xd/j8b1PWNV3MDiMzuTinTVdryIOJoVcvIal2CBnSaydwlC0Kebp4o/otC3s80kGPBnfixQ0hEhIAWud3CN5ClSAEH2ZnCu22y3Pvv6GXd/j6hpjDcYo9oc90ctUumnKAawN6/Nz3r55xU9/8l/YbNb84JNP2WzWpJsd+64X36Doycqg3SnJPSS699nbh1zyiH26S0Amlk3luH9a8ejBmscPNiyayNX1a07vPMCHjs1C8+Dc8fTlSHZubmhzDqgQSQF++tMv+IsfP2b36hWPPn2f//FPPuB//a/XeGA/KL56fuD+ww0320u6qBkqy961/Oqm5vonNzw+jfy7f/ce95YN3SHhleH6EHm7jSRrGaIMmSo9eX+VxikOhHFADT3cfE3q3pBjDyj6ALVzGDKp33FnVXHa1PQ+8Pb6Ah811eoEQdajAPfSZTDEjG1OeLC5wz98/kvunS/4kx99lyFZPv/tN/z6qTDE37u75tmrK66HEaNqamfEyzjLVH8YR0KKoCxWaZIqEnIlQ7u2WlItF5jFppjBN8SsaIgQPT4p+r4rkuGAi466qoWpMYy4Rc1ujCi7IJqGnR84WTzAHF4RujdUqnjJFfDQGicsFC3luFGGpKWoUVaT1NSsBMbOl8JCYV0l+zfFq5XM1fZGzoZyqCsmhq6ZBwUiMU2iriiT2rnIVTB5P90G4qaC/XZAGEzStHfB2n+JYfu71ggzGCsV1dyI3AZhdamg1C12LCkRf+c5bwO7t8HlSQY6AZRTITY1XcenfxeQVkqJD9TUEOXCKkDO/FwY/qgj8DyD2VlOlSPjtChoiqTJZMV33v+UH333D1g2J+yuOw6HHdY53rz8huurS3zqCGkEVRgWWGBquhV127BYLKRhLo33VChOUedT8MbtzyUUz7GJ9SPvWZXmqJqv99RgTfK2lBKYY7rv9L6cK2x1MliFVa4811HydptVNBXcKBmeqQIkZCQ9XFwJxPpFKY3M2qwEWJgSBpSkaVfG4cqfS40mZ/449lztOs7ufQymIcZMSgMp9aI60AZrKkwSZQcUaWwWdhIalLXgR3o/8tkv/oExwnqzIY8JoxJ1XbMLC7pBsz3AMA4ok7i53PJX/9d/Y+i3hBA47D05SkP2ou8EWDOKlCVZ+vrmBuMamtXpvHbkfovlvjbMm2sBaVWRk4LCOc1qtSr3xnRPlJ8t95xWmWw0CmGYgPj69kNHzkdPQm0kFKpuRfqptaHrPTnD6dkd7t1/j+XqBJMCpt6I1Yg75+TM0HmIuqGqNHkIjIeRm7fX7IcbfDLHM5Z3wdlEOfO1mr0VJzRDF5WFKrJH5SYw3tIul1RVRdd37J8/IyTFe+8JgzCYipQtf/qnf8bV5SV/9Zd/SS5WIYGMriyvvlmRQqZdL7l3/0z8Goeei4vX4g1nNMvlku3NjssXz6itJaJx9ZK60myvd/jhgLOGx+9/wPm9e6i6JemKfXcgmSuUaUlB4fsRbR337j5gvdnw6L0Db9/uWFU1X9iK5dkJ3Zj41a9+y3J9yuMPH+OyZfRRPpoyXEYV5lAKJAW+MC6bdsHl5RXLRY3TmuV6LYO/whxr2pah3+P9gK1b/DiwXCxZLdd03Z7+0FEZTQzifdguN8ImnGqwGKW3KPs0qtTWZLa77VyDKu149MFHnN855cvf/Irz83P6MfDy2VdyjVVmfXYX5xYcugN/8/PP+d6nH/CtDx+Kr3ZZG//M8fEvP1QBz5TCKY01EeMSuVf4CFXt2PeJw41nGAfG0bNcbHCV9FEpQt8nDoMHXYssWFt6EsPoqawmKkXOBleabu8libxtF9SNZGvkbIhBMY69hOIpjatk2KONYSgJ4seAnbG8gUxWkg5urQyVjSmhq85RWUdT1SQi3sswTRVwTqvJs/HWQKzcyyhmr3ZlZH+ewM0wEXtynkOzQkrk6Om7nqE74OMo1yOM9H2HUQGjHCBnSIoRlQLJj6joJQw2yV6urQDaqYCVMURxJlJZ/JOjWGtIdSI9mUoCNsYkhJrbAVu6WBnknMhFDecqGaSjShDUxCo0R9/m6cybFSgUUJOprpgslnJZnnmuAeaaBkVd1YA+eq7nSWmT51rsWNNMPf0EQt32aZ1qjel3T5uhNOgTS3eauxut8ansiQVQFUJKKqA8RBVF5m4kVDorGfSbEgymlQGnMVaRlIDkMUUO+46xsB1lYCvJ9rrYEGaFAOdZMk6ONdRU/0314dF/2I+eWOqqacCbUqIfB5RWNKW+yCA5FrdqTG0NY98Rkuw7E9Au55fI1GNMhJAYx24+S6Z7ag4JK3VJjJHsS0ZKQkh5wZf7wostVMyEHIlZ4bShqgzOgMpRGN/aYgzU1lFXG7q2IibD25s9B38gdQe0Kb1XTKKy1gmVCwEkS36Q9I3gjKGuHboMlI+hcvJebg8NYAJCxZ7DNRUa8b4WiwCDMiXLo5DWJqZlzsI2V42hcplF7QlxYAwD7OUeETKfLXkGcq5UrmazWopFQfDUdUMkzlPfiR0rtbkCNDGVwLFwBHene2IK6zOugLYFu5KAYF2QF7lXp4DwqSaX+13qlFCCFG+TQeaQwgJ0S57FLc/tYo80KQyMMVjn8JliE6VngBuKN7QST+umqubnyYUUSc6slyvGYeTQdWL3VAIEtSvWPSkTc6ZpairnZtb/xNafWOxV5bC2IiOEBu0sKcs9FmMoDOckeJiWdX/b3zwmUbCl4Ol6CSqvqoq6rjCqXK5yVB/X0z99/KsGaSOZrrL0Vc1YOXS9IIySroaWbj7liG0aQOQgKJllT1XElEhMORStsViVCVaRly12vZbmWhXpb5YFpZRYAKQYMVoxzUGdlqn1y+tLvPfCUC1pcZUrzI5UDnRbobWwaI/+PepY4JZCXuUkPEOlUGlCUBTKaJqTNd1VwOdEowxewWW3475fiHyq3EExwYs3e755c8m33t8wJcfmjEwSc8JSoxT4EHj18hXYCh8TOQUev/8YP46gRNLT1gsJdtAOazUn6xNQCptNYdBGsbVMIL6wpUk1BqMElE5JArSMW7DrXhFipnK6FPlykE0QdUpyAIvp+nFqaHCouUzIZAzOLVjUawntwpKSxrmWtlnT2Iq6KhukknTB4Ae0Ev/I2lbcu3uPDx6v2SwzKe3xYYfvtuQ+0VjDwmoGV8nGYS1hFJ+epABtWZw8ZN8nUuhRVnzIbq4OtO2CoYuMHqqmlglXjJBEVlEVj8F60bBoDYebwHDw7DrP3dM73Hv0CdXqnOtff0Z3/ZbGQFtXMuFSir7rudld0vUDMci8bblsWSwq6qph6eD9M82dZc3uYLjajnzz6nNefD7idUNUFU27oqlrlm3Lwq1IpuF0/YAYA123Zxg6vB8Yc+Rw2LFa3OHu+hFON1D8kHKevPIK/pHL5DiJbEMOgpIkiayJaVKas3j/lfEXBkMMnjF6Mom6bVCVk59FDqWJjZuVwlgIYUS8pyWArx8Cl5cXkCNNXeGHgaZaMgwdZJkQHg57rrdXPHr0kH4c+L9/+lccxi27l9dc31xyenKOqyRQRilD1W6o2lN67rDnA270J3T5nF6t8GoFaE5PDd/77l0+vt+yUJlGjyxWNb/+7cgv/u4Zm9UaoxL/6U8+5P/866d8ebEl65aUFTDg7ICOgc+/2LI2B7736SNe7yOXNz33VorLYeDgE69uRprVyPuPz3nysqczNdlaRlvzNjc8aBPDUFFtNC8uO/ps2JjMnQeOZCM3Q+J6b9mPmhxh1KoU4D0mbqkOr7Hdc1Q6EEjoHFnWlv/pz39MrQd+8ct/5Or6wFfPX3A4bPE5YWxL9hZbLdFGYXVhOWiLcS3Xvee9kwW5avjy1Q137z9m6Wq00zx5/hKXDvzge9/mzsZxuPCzjMVVppjyDzMvab/bsVyuaBcL/DiwWC5xzZKsLdo2VEYVGw1DioGURlSaGI3F05bMYeipdYNrG3IeCEQUIyoOaFsxxsTAOfXqO8RxIIYrioCOMI6E0UtjN7GGs8h7Y8oQElVdvEUn438KcwEBngUYl0C+mDMqH4d7sw0A5e8pZtmfnv2ykjRKpRi5DaJMj9uslt9l1sKRRXIbxP0nYCzz7PAIHr7zvdvNy/F1TJPpnNIM1hrkvd5m/E7Pf/v1lGd75+cmJt/8M7fAzAnInN5jznmWlMpTTK/l+D6MmZJfj/63lNpA/kppQLMiZ82Dszv8ye//EXc29wkekg+s1i3dsKfzgZgHen/AB/Evn6SaE+jcNI0MG7pOmD+TJDRPidp6HgDcZrtO4V7Be0k8r6oCbh6BaSmmj8yI6T2O4zhbHExA3+R3FYtVUHmrt+qRI3NzKtJNAa6lKU3z0G0CgYe+R+UpWK34rpfhhTD2E5ZM7RzK1lRNjcpZzsSgQUk41mmzwriKHLUAXSkTwyCDueLzGZPsDdbIAA8y1zdbnNM0bY3SYKu6sE425DrQ7bZUesAoUU09fvwJKXuGeMGrV8+5e/ecoRuAgbqyvH11SRwCTm+wi5qcM/tuQCPnt1JaWPOl8Tgmt5chQk7FBBgywiKSdTkhWXmuaVJWhQljSCGyvdmyXK1w9ULk3trNIIIx4r83xkjOEZMjCgFTUxaLKpuz2CPkTFXVpGHE2wM+R+7cfx9MTcQKO1xnKJZEwzCScqKuLUMwvLnaij+4vW2ZMt1LxyERIA3s7MWXMM5gKieNkNEYV+GqBdZVdH1flGia129esVxuWK0io3FkvWLbd/z5X/w5v/zFL7l49QW2drSbczZLw6p11LrBZoVJYLVjFzqcqzm/exdnAovlipRF1t5slqybO9jacXj7HNd5+uhZbjbQtIwYQuc59DvGfqRtr4koQh8xruLeo0fUyw0KxdnpHU42d3lw/yGr9ZInz1/xs//n79HJ87O//WtC7Pjgw0/IKZRGTiS2E2NuuofHsWe/2/LRtz7h8XsP6fZ7FIH1yRnL9QldP1I3LdYYbrqOm+0l7XJFu1zTHQ4oJYwgQ+a9hw/IWqO0EeYsWfwbk4Th5JQLOCckiBRGhm6PziLn1lpRrVra5Ql+7MhZMYziHXn33l3evnnBk99+zmJ1zuk9DToTUsNnn33JsO/57nc/pKod//8e+TjIK4tKKU0OwlDaHRKKhGHAmcDjjxYsly3eayJw8XZkt3MMoyHmADrhR6k3mlpAAq0zWjtCEAh5knY7Z9mcyNC+bhTBJ7pxlCBgU95HsV+rqqa8vDyH/Glj5tfd9z3L5YJF2zIMPWMYcKqRkBkjvpAxSMCfABlH4CD6UCT1Zt5DhmFkisj1UWTyKk4KhQlsERWF0rKmRDovyfFdONANB+mTVIY0YKxCKwnlG/qeFHrxqtVJ9ogooWJkGcaFoEjJl34i4ooPf/Qy6NaUIbJKElaXptK92OgUBNMVK5/5XJ6GrDkV8FCYrUarsn8aYj4yzKddRog78vttsaKYhrXTPlROMCabg2mfVFoxDsLos+aYayEztRl5LQD7UX5/23Zpuv7vDLLzLQsiVAHY47xHSw1iJEBqBqDK9dfTMPbIWJXzW86UKTxNgCeH0orOe4YgAUdj74nE2UKiLvZEsfghT4zlEIotRQpyDOXJkza9U2MJ+JqFXaiOYK4rasZY9nQBdRM5KTBH+x6lFCcnJ3MNclSHFP9VZWgaXaxC5FrE4pU7DT7IiK3kZBuUQvGbNWStCSqRgpgfjt2ekMBnCVCr64pFbamr46CEIp+XgZV4KaM1aINxlpxFaYMyaJ1JKmAQANVaI9gDCm0QFq3TIt1XRsJaS02Z81FNnXIJMc+x1FfHz1JrTXULkFXWFFB/ojdMtbwwSQ0G6zTZOHJuqJPHmIrR96QcGYdewFlboVCMXvYNV87WMYwzKQKY9y4AY6wMuq2ah+9yTd7NsQghkEOaA2+NMfjBzmBs4lj3T3XqYrEQ5UeMiIOTfPbGuPkzgTz/9xSmKs/n5/tpsjKY6nnp99WM2YUgdlt1XbFZLuWz14h1QfGVVcXNGC0Wf85VLNdrvKRKio+8ypBkcLLbi62fUhIAG0tOUs6ZoTDVQwwYI6/FmEIsLJkBuqjNnDOCVxlQ01kx9Ue3avq2bcV2YxgYynB5ClGcMI5/6fGvGqQNWnG1qAhKQFI1HM2UIaOsEiZpkkCRabOdaczGMcYBSvNkSxMRokxlsIqkRYIzM42yQIcpZjxy0YwSNmdO0mD3MTL0gbEf0M7QNG3xzynWs0pu7JCC5AgUHxNdkni1UlDMiAvUVYDlkpxXpnApBrRTmLbC9wOjHwk6s4uWqzBy3zTkFDGmImnL9WHkxcs3fPujOwRVZCpaQSwycZ1JSUGCVbvi7M453dAz9j0PN+f03tP5wOnJHVIMqCRThZgTh35AKYdpWrSCYRzRWhKIU56YF+IbKFcnCwsvStBOu1hi9FYWJhPrtgSz2BpJlKZMpSyVawqqJ4bhRulSjIqB9ObklMpVjN4TlWZ9do+z03vYbMgx4P2BcewI+70EnblIyImla2hbKTpevNjSdz1+6EmhY/R7hnGkaRq0grEfWCydSNos6JQYxkBtxI/HVRVt25D7S968ecr67FOuv7nh8uUrrq+vSWEghy2kPdpEtBFa/3rZkuLIoq1w7R1CVCi3pDp5QLI1N7sb1DjS44lB0aqauqpZLBckImPfcRk8JycnjMPIOA54f4E1hnaxwljHaQub1vHw7A5vd5FXNyNPX7zl6tVz9m5FuPOQ1XKD1tCPMq1br+5wsk6k5CV8QSlqu8IPA28uXrFpHetFK1I6KrkXkwefiUmGDlYrrJVJrMpa/EqzJmspmZw1pBxJWYYiRQ0mybIK7CjBgNlonFE4ZcQ+Qcv6CCTGJFJZjTB7uq7n5nrH4dARcsLVMr0PPsh0PUsxcHZ6xnLR8ou/+xWXV29xtQWr2HU7rrtrQm5p6ru8//BjHn3rh2zufcibXcPTJ5GrcIKyJyQt1g3KGPZj5h/+8Wu2ly3fur9kbUZ8qFmfrbm66KjrhvcfLmhqRz9+wM1//ZyrIYBp5GA2NcbV9LvEZ79+yaVXVJvIwjr++AcP+Ow3NzztDHGx5DoYNpXj/p2Mv84krWgqMLni65uB4R+v+eKrkVVtaZqG739U4yrH1U4RLyJXPhOyIiiK3Z0UjOKZo9DZk6OXwpLE3fWGj+4vcCrz2c/3fPnsBSiHqmpWJrNoKrLJBAaysjIUKgFHUWl2/cD19sDZnQc8efaay4st60XD+bLizcWeXZ84OVnzrfd6uuGSi74jKkcWDGgunlBGwvucMExDVphqwWK9AW3xYxRglkhMXg5k74lhnItHim/WGAK5H6iqiuQTYxSJsnOQnOzCMTq0XZO1BABNAXcmS5igtHNmZn0rBTpmVJRiQlsDKYKWAimTibmklFYNox9kaJdlGpzypAaIs9dmLDYqqjBspVnUEPMMjE5Nz8Sc+l1Z2+0/uy3vkwTnMhy7VUxMYOftgv6d31eYF5McW4pSbj3X5AMV3wFWpYA6PqbGaGqsbn1n/pJeavKzVTBPmd8Fe6f3570vrJY8sxljaYJmhcrsyzq9PzX/6/bziaIj0rqKH33/Bzy+dw+TM7v9geRHFsuWbX+FT56Qx1tSQPGtV8hn2DQtVVUxDkMp+qRBpbxmpyiqgUmWWSwXsrClYmFo1dYWFqx87pONkvh9TYyMXOSe4ueuKeya8nlODWnOKgk7RAAAIABJREFUxboEkYcK0yIxuQDOTNx8ZBeXj7MMJQqbKQvri5SIQRFHT7+7IefI2f1HZA0p5nntu0qhCHg/MoaMci0ZS+0WVO2arG7Z3WTEa95VDKMXlotzVJWmqgwqB0gjw8KTs6FylqQtMciarNoV1jqsgdYYYuhRtsZoR9/dEPMgdgxVLZ7dyqGjp13UqJDZX73GqQ3G1ZA8GGgXS+q6xbhaGEAhSkgFurBABIwdx5HG6LmpVeILQcoJH8XvVt5j5PLiJWdnZzhb0TQVOSVG39M07QyGvjNQCYocMzrLOspErq7fovWe2lgJH1GRxWqB0okYxcst54pEIOk0J1HXTQM54ZoK2zrq1ZJWBdTlQe6yueHTcy2rsoAVM0iShVWHUiirsJVFaYM2Dpylalq0MRy6A9F7tHWy1xrN1eUbUggs1iegM//9r/8b69UZ3/v+7/PTt1+Xhqzl008/ZXN6Rt8dyKEmJIs1cHLWULfvszo9QX3wgCpe431ifXZO1JrV6pTzqub67VsBno1lfXaffj9gDLRNS9O0dNsd2/0BV1dYEwlxJMWOFBusXaF0BVrTrht+9Id/zLd/z/P0y694/eJrXn3zJb/4+c9Z1jWbsztydinpADIaYyyL5QofRtJWJMZSg1sJf8pgqkZIDcYS/AhJkqAX7YIw9ERr8XngZrtns1lxslqTnDoO/MojkckpEoaeYehKYGUm5ZpKg9NQL1v8OJJRnJ3dISXFxasr+n6kGwa0q9nd3LBYNIyXN/ziZz/hvY8/5e6DDzk5uc+YMr/6zXN2h57vfe8jTk+WpX+ZILOZW3J7nndr358GQ4ohRLo+MYbMmBOjD6zXlmbRyrmgp/1YEbwEg3YDDGPGR433kaH3WFfAa2XQjuLhKGvSBzlHfIwYpeSMz4HBJ8CglACJRilSFhDMFT/lgsgQQ3iXCZtSYfELQDcOo6gaUPgo++noBVyT/R4UCWKUzz5J3RaSSJm7MrxzVvzpfRgxGarKIdZGiRAjJudyzYuknERMPSr25NCTYyCpElxKLTVcChBHIUIYDTHOntLTNcsoYhRputjGyOvWJAgjhBGlIxJen8RPPAt4obLUAyEFGRggfsBKiZXcVDMI6eaW9RIy2E6k2bJJBs9Z3nMJ3UlqAoKPuRRMAGcJ9lFlsYnXcWAbtrJulEQST2suzutvet9AKmqHYv0nKpjpMQG20wC09OnS3BcQXtbXpOBRs8Kg9NyoWV4evahppwR3WeOTqq0MFHSGJGzmvuvovQRLoSCqggtohbHC+LTGHX1QJ1/jkhmR5nLqWB9O9+A05JcqX16/sRZrLE45uX8Lo1Ds/CafWBkA6cKsVcVrc7JcmGqvEH05FxLaaiy2DBiOdgFz6SVTh2KbIOzMmAJWG6JJsz9rPwapfZUpPs6RbuhpnaVuWtartQyriPh+z2G/o+t7+tETlaiilUrSH2g9v/6qalDGkZTgFsYoqspiq4qshIQRUoICaEvtWOraJF67AtpHjJYQY60KiaO8x6L/Zc7YLiC5MqbYcEAue502lhQ8KEvTrKiqhpQioxnwfmQKou36jsFLTUmrUD346PFJMKnKiX2DHNkJCBJ2Rma1WBBjYBgC5FyyXyDnipylX2qaUmM6hx+9MEvLdZ4sWIwxDMNQhiOaWDKeMmBdJbXRpEbQ032kcK4q/Zwth4Wa750U49H7OGfJp0mJ3W4vQ4g+0Tsn3rRGY9Qg+2NRRBgnYPjEMF80C7l2WqOdxSjpAyrjWC5W5Jzoh16sX6wtSgY1e5JPBMvBjzhjSFkxDLL/CKgvr98Ui5gUBRdQpZdSKAmeAwmTXCzo+wEfPCFJCNy0xzn3Lw8+/1WDtFkpbkwBUaPHp4gfermwpiRvxigFtRIQdUpKm7xDlCkfZhJ5ntEGU1c0Jyt8o4nZk5LCoGaUfwJ61S2D8qkhUuVLEotbUIWtlSXoTCST0gSlIlVUShhh0iQeWQqKMokrhwTT/qVkcicbmma5XNErw+h35NHTWc3BB1JTDiMCUWkOfuCLL7/hz378A7RWjCmgs8FoS87ieyNNouXu+X3atqGta/J6jQLC4DFWGp+312/p9nuW9ZKqlWlnYw1OGbIOaBUhC6PZFqak1rowwzQhSzGhgBwzTd1Su5oxKbI+mpqbnHFVTVXV+DAU4KMEREWYgqxkmCpA7YN791i1DWEc6MeRarnkz/79f+Djjz7hb376c14//5qb6y2H7obge5q6papb6uWCxXpBComnT3Z8881z8dZUhpgoTNDAYb8DYNkuaOqWUWuayqFyYrza8ezp53z19DfUC8vy7WtaLDQnvPzyt1ijiWNP8j3OH4jxQEiyLpypMEZ8T64vL/H9W9at5sG9x3z8/T/iOz/4fX76139Fv3/DxoLVMhzoDh191+GqiuVyxfqegPMxJK7eXpAR9lOIiTMMp6c1sZj/W2W4t1KcLSs+uv+Im33g5ZXHa0WiK42wQ9kVjz/4mP3+mq7bYV2N1QZra3KKvH79itd9x6I2LDenbNZ3WdYtjTHiMZwyOjlMrmSdaYVNiipnTDhuxEzlQWF3GxQLwKRGChWfGHImWqiclUR0lcSTUUOXE2+DJw4j2QjTed9HhqDIyuDDwNiJ9NNYSV/3OVHVDSen5xz2HU++eDKnNGY02i6pmxa3fsj69BOcvY+vf0B1/l0enK54bDzbpx1jdGRt0FkmvmME32d+tXuNRvNvv32fIVxjKwGYwziQ84qr6y1N5bl77rh6mcGIV3QyKwarsc09+nDFr94o3m8a/uO/f8SjU4OqIy9+2ZPamqArDoeRB2cVOXtGo7AtOK0gNuyC48urS/7s9xrutjXXVwN+7HlxGbgYKw7BgM6YEKjCCHGUAUxpDogjxIEUR2LwvHj1Ff/L//YEw8jFTY9RFm00tav5H/7wBzy6e8LLN9f84jfP2I7SmAoglzGuIevMxfWe+6crTs/u4L3nx3/0bzlsL/nJ33zGfoQuKL7/7U9Ybbb85LMv2HkYfCCoyLJtqWrLzXbLMAwsl0vZa+oWa2v6wRNiV5qpiLEykQzFQymlTBgjzkmZFEOkPwyMxuNONzLFjyKFN0ZT2UwcJbhBG0VVbxj2b2XI5ATEClEYk7WqpIDUhmxEnqa0FqmyMVIYF9aLVoqsBZh8/Pg99vsd37x8KaxNEJCjTIFTAmWO3reTj+WxYZDAJwl1KFNwmItl+XXHVmOSk83hEUkkyUkVpUdSEyz6TyTvUlAef8/M3ixMiOkxy9dKgze9BqWOkvuJ8WmrSmT8hfUBRyBYXmdpYIxDGKZ5Lv4ncPAdOfYtNGB+H2Vq3R06eU1KikOg+MQJKDmDvVEYfvNvyhkTPZ8+fp8ffvwRrcn4YUf2A+2i5ma/Zbe/YYyeMYSSaKsxGJwVRY21C/FJH4rVRhIJcSprU5VhrDBDNVPKbS7eW9Zo7GJRAirSO0FNE3NJa1XSpI+fgdLIQEsJI1gwcFXAOml2U0pzPaNUZr/fEn3g9PT0WP8UUHtiRM9Mo1JwQxaJcIDoR3RVQe1QWVM5Q8jC/jZKGjSjNcGP3FxfY+uFDMfUEuWW+AQqJfFudg5tjDDcNFSthaSpnWG50DgX0NETxo7Vo5ptp7h37yEpV9zcjNxcXrG/usCojNMjd+8syXnB25uO4CMqWVaLhtX9R4QyrE8BsnJsTjeYOBD6kf5whauX6MpR1U6GyNqS0RK8lcdyNlZlvC7AR5xksEqAtykJvO872TvrFpUzb16+oNvecHayxpgFVSXqJhksMNtdpVTYWFIMi5VQ8CxPNpyendOu76KyJvQ911eXLFct9x88lMCWKFYYV1cXaO1wzVrateAF3FDCPt6cn9PHyKETSy2lhE01M0Im8GJaZ8UrPpNLMEnG1k6S252lWa6omgZQdN1AGkdhGlr5IkVuri/Zbfc8eKhYtA2HceA//x//Ox9/8BHn9x6wHw5kMl3XYewNwUeGcU9VrViua+7eX3HYKwKaw1WPHwIptLTtCZfXVzRDxNmaT77zQ9brFePQ0a7OybrBj30Bihybs1UBzl0Z8oHWFSlrQlbEEMA4MnL2bTYLfvhvTrh87yH/+A81z599wS8/+zk//NGP2Nz/gFhAe8pARFtDWy1LIIrF1S3j6NHGyvUMIyCD++fPnqF1plm0tO2Cy+0Ob3rq1YKzsxW77Q3D7obN6RnKOXIacEqJL3eYPK5LWjvi05uVZuz3eH+gsS3WGXnulLi+umHfdbz34Qe4qsLYltAPPPvilzx6dJ9uGHj2xedY7Vgvl5jKEGh5eTlw8de/5PvfeZ+P3r+PtdP+o28fC+88pOITVlkAUrHHMFZTK0M/hlkWOwyBpl1w2EE/BsZRcbX1vLkeaNoWbTVVNiiV6fuE0R4iovjTAsYOPtIFCUrOWcBcsma76xmDWMZorXCVQWVNNwzYqqgtg3iRS+iR2HZ5H2b2Wu9HSV4nE1MmjSMoX7I0CtN/mnHEJLZZYST5URLpU2bwI4d+IPrCKkvFfztlSGIlF8Io4GEWe7FQCoQURsgeP+zld6cotkilcQwhoVSA5AlhIKWAVkKCcNqQlSHnILdzSgTkM9A6Y3UldXkcySlS3GdRSVj8WRUwIpR9KicqJxYSgkJlbLEdnKTWSpu5vpgKC+sc08AxhmILYaQvVdzyVs8T209W0ZRTkQugI2f6cQgsz5hxRs/nblYC+E9nO4rZ1nBiMyoQawREdjxZBkwD3TzvhcwgrMqT5U041g1KI+IVGd5POKnSGgtEBUrbWZ6tJ8xBC8ATx2GuWTSZuhYrlNrW8zkakwzbiIrtblcGeZMUXNafsk5CORErLt2ombCQszDtpQaSWs37wvxWJYwzM1tHkimgVMnW8b6oho5KqBl8lX9w1uKDsPtF4RCY2MSzBUMZ/uYY5XWW/0/FiiN4YXyLqkcBBtcsJHxyLUSxvh9I8ZphjFRGUztNZTWrxZLTM0tuRi6vXjP6Yn9RCHCqsK5RAiS6ygpTMgTQjYT9aUsKASagvXifwuQ3P7FQjz6z6ALK6aPlRUyRXLx6p/eulLB7TTkHFBBCKv2F3BfypVDKUTmDszUZAZqVogTTe2yyOGPp+gPOWJHy+0CIAyFnAQOVAI/zv6d3kjPKH6+Lto6mXcwYmFIKayw0DbGQKmKM9H3POyosMsM4QkoM40CMonDVRoDPMPaQhQRQVbXs46YAt8XCISuFcxI2N92DqvQDy+Xynft8sVrKdfGpWHUGoh9IIzSVBECGlBj74g+spEeyRkJ2rXW0xa/ZaIUqFiS2DNfF0zyWcieTQ5QhegySb6UUgw+YbI6EkaRKjoXsTXVdi7ogTmCukHYWbUtKdemn5N7QxjIFIP9zj3/VIC0ZqiSNhVUalRW+sGvU/ME7keNpYc1MDR8wT7xS1mirC+sTzKImtRXYqWmSovOfSB5mV4IiaytUWYWwGnLxrPF4+d7UeGv5mQloneQzwNzoSuN2ZEwojjfxfEMrTYyCstcNpCFIMR9TCSLTpKmT1prg4emL17y+3nL3pCH7sUynhGZurEzxHQatxRxZJwNWPhcfApfXl6xOVhijGIeBNGbu1Gc4lcjDBbvxBnQmq0Sy8tqMniQrx6l6cRaaky3vnN/hq2cXDAeZUGg1GWkXhtaEUGcB23UpKFJZ3BPbSCvDul3ilMKXjaxdtnz99Cue/vYrXn7zgqayOKOprfjQhpgI5QAZxz0hdtQN3L274WZ/wzgOHHaZNCTiGAn+QNcfWC43WOdYNA2PHt5ne33N1fWW3e4NMV6z30ay72mqBbWK7J9t6fs9MSXauqYx4pusVY2KHsJIXTucSvR5pOs6ri97fGj55Pda+n3P25dPqUwghQFfQAlrywQxJjwj3ksQRFVV3H9wn8N+z/XNjcj96hpQpVjI5DTg4wjZ4pKldZnH55ZAZtuN7FKkD4oUOogeZys6anKyAnr6TAwjJ82S09UpOUeu+z1vt1+xsg2Pzs85ac9ps6HxS1xc4UmoYGgitDlQx4hJwl5GiYTK6ojSgUwgHwZMP5J0hOwF+GqBWpEsuJOWmCDVDqtgnzN5DPRamPBvrzsOvSdr2Pd7jK3kgFCKUIoHpzW7rqPf37Dd74hKk4Nhsznnu9/5t2xOHnHROb6+8GwPKy6eefKJ4sF5w8cf3Wenb/jNkytQBkWE5GWSqhXrO3e5GRWDNjSm4s3FlkMfWJ61vL4a2R86nnz9DRdv3qDiCmUcuV4RbUu2FcFZjLmPyombPPDliy0PFitOK8u9xrK3Wjx2vaEd4e7aMSZFLzaNaBJVY1lu7jLi6YbMbicTvWrp0FnTkCDsGYYt4zgyjprx0BG6V4S3X0D3ChMOBD+SciDR8/pt4HxZ8fH7D9ntB168vqGqa07XNWm44QefPOBqu+XvnrzFuiKbssJ69lnAxC5kNqsNL58+5clXT/n2+/f4zqcf89O/+y3//bNf8x/+8PucbtbcPWlJ18K08+PINolkuF0sWa030hDlVMKOmAvomAKvXzzHZDg5v0PQFuMcISpGH1HKYCtNTkGsbqyTNZ2F/eLHgTiOsv9qYbb2wdI0D0n6G1T0WBTJZEw2c6GTC2iVgKzBVHLQphSpbC3Ds0JpMFmglqdffjkfxvn2hB7mxj5O3nXGMI7j3Hzflv6nsj/+Llj5u5YG0/dmOaGimOhDyKWBQc3n5m3rgHf83qYi/NZzTX8+h2jwu2FVR9ZIzuJVG+d0WHmO2xKfCZSemaGzxQHFx7p44hU2FvCO/9X0ekIIt5pI+fyF/SHBMzlNXnFSQ+hcmGjlZ+PoOV8t+YPv/oB1s0SlTH/YY7RjDCMXb9/gYyCVZtAZi7WaFEUcUzvxkoveS4eWokAUpYnVxkioy9R85oRW0tgUm1iJiiusrZkDXQCziZksRfwt1nPxLJub4fJzk+c7pbk0WpHy0crAGUttBdTLaYLfjv7FepLZltcp57sm51jYFtKUr07v4qywxER9k6mahspVZBTb7Z4vvnhC06y4+1CzPl1JYKQuvnTl+k0SwJxkeJujFO+VUxgjYU/d4Q337p3jXI01AahwTUNMkee//jnd5SuW6wVvvl7x0SefQoKvnvyWFEequqZtasYS9NeVcM6cB5wbaWwjg9puz8Kt0aoS9nEUSbYyxYeNqWbM5b7P1HUjISHWzY2WcxXOZZQSD7z9docfB87PzmnqFgrD6HA4UFcVeSHNsshp4y2CQCLmSD/23KkbXLVCU2EsjDmxP+ypq4rl+oRxEA807z3X11fEBKt1pmoWKDRjH9BaYRrHZn3Oen3GbnstJIJS03KrCZtqumkTyQj7Sxn5DDIZtKFZrVhtNqSQGPpBml4KeFCAjjEM+ADKwNX1Fc6eo/AYbXn2daCuLf8vc+/1ZFl2nfn9tjnuuvTlqz1BAOSAhEYxnAhS1MM8KPTf6knSgyYkRTA0jDE0oAEJEA10d/lKe905Z1s9rH1uZoOcd2ZEdlRVp7n3uLXWtz4zXx5hq4rNZo02LcZUhagRGfrIq1dbbN1S2wx1Jo/qIAM+Pj4j5cToEjdXd5xcfMp8viBiqNUOzI6x39APDqMi2trCQpefIf53EuoTUyhKMBkEcgoYU3F+ccHp2Z/y9tUn/N1f/1f+6R9/zh/MjzCz45KM7amqmuADtq7ouhldYfWA3IfjfsSYmhCkzjVdS86B+WJOcoHtbk82hna5pOs69tsNtYG7q490q2OqpmPY72i6VryMsxK7DGUgOdq6JuTI+8u3hH7NmX0q15AbccNIiJluNaedtxwfnZGjwu92nF084fbujq5rqXTkV//4dyzmcxanFyjbYqoZWlt+9o/v2O8dv/fD5xweOVB81O+fyRS2XAZiyvgkta1pLG6MaJWYNQpbyTOwri03G0dKhozBefGKnc8bmtqQkmZwka62qJg4PokYpVnfeYy1YDLjKAndtQFtK7rOsN0MuCFTWSODOQ1KJ9x+xI0j8+WC/WbL0O+4t8bxpXYpqqYsGGPA+bJMqyxaaVIKDM5BBmtlSTOFw/oQSd6TvSdbWUZ5N5DKssQU8M1ojaorVDKgEs6NhS06Sas1OiesTsSxJ7k9MQdR2BRGWkypzIcGre4ZiylTrAOC+J0Wj3yjZEmtMhJEHbx4gStdou/yod7oQ881qWtyscQJpe6YQ5+izb0Njy7PiykA+N6eR+Y+KUNl8ZwlVHGq/9OSegJrwwPS08Ol8cOehCSvU3Fv6WSUJk15NUnOp873y8cYxU83xkTW95ZCWlcHgI5ibSPIYqndqky6ZUltrBKrnySL34kpbApA5pyb9m+HvsVOS/2cMaZGqZrI1FsKyKbgsHTzwQvzmUIWm0DP8pA2poRXHsbpRFa/HRQlhIaYJql+xvnxYJGVs4Sa34ON5VjmjDJaQqELe3YC7ibmoCqEqpxBwvsmUP231VNKgn1TxqCIOYvHuBQ/hv2OnCJVZXEx4gPF3HeGGx0z3YESW45d2DGqzNUwSO9BYkiGmJFQwlFAtpg8KWqM6bB1IyGgdcdivhL1LJm2acXjNQmHQwDmQsRj6pHlfhB/4QLSlh4tpoRRCqVKroHRYt1USHJy/emyGDEHy4mmFea8945hGPC+EPiKzymq3AdojKmplcEmi/MOWxQAMUUWszn9bs++37MbB6qDmkyOcQqRHCWnhZwP4W5KQUw9qZwj+ZnT6ytM1ySeqrPZ7B70Lv+vaQO1tQxuZHSOxtZUTQtkQpix2+3o9z0uOMI2MIUpC3FBl2WwzESVrSRHqL1nl1ptygLfHHA2bTPzhRABkg9iI6CE5BKz2GemLORJhSWUpYz3nu1+RwpRvP2LVUtVLBimOciUXt1WgpXVpkUh80jvZTEq4KuozMZRrCJSjOz6HuscRkl+TtfOSAl8cHRdR2XF2iTEhA7xnhHzL3z8qwZps4KhHFirFcpq8LLBqkrqrdK6+IOBUQIsTgdXCh6AoOUJkXqa1Rxn7+V10/D7UEY5bYWmP8tm0BwGvElieCgYxctlSiqcihCUohfC4XUrhXhllAeYVveFFgqLoYDSGgmvqSoLixlRi9zG+4BVGptVoctnktKsd3u+ffWKZxe/ixvFC2QapLUS/4yUxfTYjSPaQGMloX4YBm5vb7i9u6EqgRTLrmbY3ZDjJZW6k4bZiBQg+hPS7HOqelW8juQBfD9QShMfo0PpCoXIkEwt8mgJZENYbUoTQqSq5fxabTAmo5SHbMtxjLRmzmK2ELp9dsSYuLm6Yn0jyaZPnpzx6SefkoOwl32K3G62wpIwFkVF2yyZdzPurteMY0BrCSrKuWEII00z5+howWK2ZDafc3JywvnpCSo4Lo5PqDe3tM+eklVCZ0NXtdKYETFu4MPHj6j5jNNnT4nMMFmjxwFCz6IVmn7XBPRJi3MVzewY5zU/+8u/4NWv/hrVX+LSSFXV1HVFjJBzzTD0WKuZt7V4UvWRus40TcPjR09w3mOrSjbIMTJRG1KIEKYQn4zBo3WkseBtgrQjxpo33/4NGUvdrDBdS6Xn1M0plTqlpcZkqGaZ7vycqCG7yPuP11y/7fk3z3/Cc3NMiyFERQyZyoN1Ce1Ggtthq4gyDqMzxgZUlYhExuDIcSwNq8LUBt9mQmegregri9OKiGKbMlFLYzOMe8asePX2A7frDevtBqU189lcPNm0EY9nKEmiisVyjq06unrF6ekLfuezH3J29gSoMMsTPvQ7Lsee6DterzW2TuR25GJpuV1VXG0TiZK8akSWtjo75WzZsguBXdb8/E3g/c2O+Zs3HC87tneXJLfhi+ePOTm/4OffXHHj9oymJlaG0DZ4rTEqsqbiZ984Pn+aeXpR8yfK8rNXPZdZk2zFkDKnx4oUErdJ4VTGKlg0ikpHvnk9smkTXz6dY7IianDR8X67xo8DediTxp7oNcrtaYZL4vYNjGthXeSM1ZCxVE3FD3/0kn/30y+4vb7j//y//5LbzcCvfv0dX7284LvvfsNmfYnWMrBrYw+PMZ2FTbDe7Jl3M87OLvhwdcvvfvGC5WrBfLXiw82e1+9v+cGXL3l2vuJu94G2qmXxphS317fFO66WzbOeinTxgAOcg6apiaMT/yelcD5MuXYSPmgNla1oK2Fbu5gYB8fYO8I4kMOILindEUVIFUafoGdHxN2ajCckkQ8ZbYpXkQRETj5rOSYCAQ8Y3ZCZwj+E+aCVLYyE8qEU6uFiSylhnwMpl/R2rQ7gYc73UnetJblXWBGeaasP97Y9/yw4LCdCTty+fcuindEcLUi2+LY9GBz+JWD2oR3C99irU62Ew0BVftL3viYVwDF4f2h+Dv+uphopTAalVJEqSg0hURhN4keZCvPgnr0xVdsyRKbMdrsBxKPSWmGjJO7VMN9vMibgN6IT2Kz44tmnPLt4QfCaYRwIWdO2DbfXl/gSaqGVjEY5BVQ2ZTEog25wXljLGXSW+h1TQBlFZar7ZW6e7BwEyKrrmpQSo3McfGun4ba82PIdcsxL6Mhv9y7TAiN4zxS8kJOwqSaJ6KS/q+vm4C2rKOojeUlF7VJCkHK6H7bLzWWMLewjj0DRipSEEarJ+BypjSpMi4G7m2s26YbgYN6dUS1OwWq0ufe200YGioSojpQWFYauqgLCVFR1RY49YdiyvvlAO39MNXtGDnvy/obWJlaLGS4krm5uCzsjgZbgH6mDGmszdWNJocaNmvWmJyep413bYdW0ZOeQd6CKZcXESHLOiR1D08qgV4LCpv/XdXIcKfZVHy8/kGPg8cUF2tQSjFIAzJxlaZTyxOgrOc+KssRWzFZHNLMlRjeEKKDPMPbs+z2Pnz6lmy9RlcfOOoKP2HbF5m7HftgRsofCQjRWo8yc5dEpq9Upu+2aDx9uD/ci/+w5MKm+AKPFO9IgXtkpYW2NMVYyAEIURg0ZbcWnO8VADJmUwFQd9WxO1LBzA5XbridUAAAgAElEQVS1hP0d2kA3P2G+WpBzELZg8jIwKgozMOG8xlSOp486lifnfPj6hpwHtrvIcnVEjJ7bm1vGweGjYUyVXDezmqpeYKuOYX/HfnuNUgFyEi9RH1G6YlbPsRZ8KmywFMuSBaK2xLrBVi0vv/wBx6cn/OV/+n/5s//4f/Djn/yU+ckFLiRGpUFZOrVAch7E548k57jfb2jblhiEryg2FzJbjMPI2fkjmsWMuumw2rC7vWHIjqPTU4Lr6dqGqDOuX9M0TVnKW3KK7LdbYnAC4PcbKjyVeVA/lKFtW47PLtAaxn1PciOqsjz/7AtuLj9yffWO5XxGZRzffv0LXpiaR0+PUKahqltCjvznn/0Dm+2W3//x58wWbRkmpyfVfSUoe3KSgjEmQhb7HmNlsbSYV1S1Yt8nfFKIBWHGxUBIIsde1VWRHIPWCWsV81bAyKauSV1CV5DQbNexyEgjZMN2MzKOgbqq2G63KG1RusKve+IooY+ZyH4tdaOq66milEyTQqqJsnRQ5dlpa1EdDr1HFdZszJaqFnd0750EsyZRjYWScJ6Cx6iEkDETGEvW8oxRyTKOPWMQBqw1piwnZUmks9hy6Cy5DrrUAyEnBUCRjTAhjdFYU5cFg6jWTGFtagVWJ3IsNSPJHBRGR8KTCaTsUUwLz1BmZYXSseRNTACdeKrmFEgpFJZlPiybJsAH7r3oJQgxoY0tye+BnALeybXxEJSdlDcPl8C/XccP9jBTfkyWBeMUcij1XxVbwrIwzffhXrn4Q6rCgDTFc7x0G6QUy4wvF/QEWt03EWXOKHZQGVkUUBbhh2dpYfiqCYhNiSkIySgJOg3OH4DZ++DP6rAUR57GhVSQCTHhvIfJ0gnK4qmoY4v3q9hrTCxnDsQEW5iqqi6hpLocy2lZ/+C8CftQcJCJDDd9yN/ToWeYgEuDkX7pQU9JUVdE5yFGUpyG1VQW3FIvezcScyYkcMGjVaI6PSHYmpCUeKPpjCey2+65XW/pw0jICp+jWEUgi45pFqyUeMZWpmLWtBwfrWibhimoarKWSKVNYmJcT33YQYkkz+7MBOBPi4Mpg6UwBZSSa5py/aUMheAxqZsmQHexWIiNoXdsNht2m005LNP1rgsAnzG6om1MCSDOpffIWFPRzmYsSgCW2GLkif+HcyOh+K5O51QpxeAcfhgOvYv44Zd8oNKfPbwGJ49hbYyoZ8tixRiL1Vr6eCXv6+hoxWq1kkXAdM1rzVCIG94HYhQr0zEmvNcMw/5wz2oesHsr6aFNFkywqmtUhsVigUbu+ZBzWZgkRgFQhBk9bS+sPtyLPkWiT0Qvy4fpWRJjxFQV866jMhaKbRhl0QMyX2ijaaw9LIqnTAk3DCiVOZ2d4Lxns9nhvMd5IetJXykzYnxAuPjtj3/VIC3AdO/GLGbdlbUUl2L5c7HIqyop4qEEKHBA+pG04zL0VIs5uZIHsE6BkKQ1mvwhYGoEVNkGyQ2qmVgGIpWIE4W9FKQDg4UJ8EUGOC3JegcKOYLwq4npk/Jh6wIPxtsy3FVGJJm2suimZjf2RO8IwygXaZFpiN+cYu8U37295Y/+sJLCWbYlkyRiKnC97/nN61/j44AymtV8hfOBD3cfSUXqcrrsuFjUHM8CTTVQGYdSQYJMMtzt7lhvXlG1j0viaV189+R4yZMs4XzPbh9Esg4oJbIfkeaIh2lVNfiwoU2Sot42HUYJS9BqVS6ExLyu6WYLXNa4mJkv5ry8eMRidszt5Q3GRJq6xTQNzo0Mw4gxDSkFatPR1kvOzjsWi0zbJfzoGbYjY98Thz0hZqISEKHvRzKWGG+4vrpm2O+JUQIllukIazVd26BsS+8iKgbGquHtm/dc39xyenpGVbfMuhnL5Yrl3LK5/gbvBuaNEfuHGp49/5yj03Ouv/4Zabwi9z3Hp0colUgZ9vs9WldkNHVlefT4MZVW7PtePMX2PRnourls9qNcOy5nwt6jrre4mzURMMsF1aLDNal4xoKJA26/pl9/AGWpqjm+W/Hk2Y85X76grT+jyw0z7YnqkkHtCCbRnnRUVcfHry9Zu5HzJlEDsfg1ZpVINZgqwTLitCcrh1IRtCepQNaJNDNEPSNpqFLGVZmxSaRa44xiJIlELmVu+z2961FVxXF3QsTQ92tC8Fhd0dSW2awljLHYkUgjVtUVPkGOFY9f/IRdbgi54+9/veET13F6fIZdHvH45XMu4weG1PGbG88Q1vz4h0f88Y/OmdUtf/Y37/B0EjJYmp9vXt/xRn3kHxhxIeFzB9UZu7HiMlbUWvHFyxP+7R++YG4hjnv+9tWWWEVUV2PampwiFouxNVuT+dtXO/6HlzNenkDUDX/1LpFsxFQaXSdOTzX5DnaCv+P7xOzE0BzPOJsHlrUnRUN0iadd5jrvGTJUdcswjoRwhx4vseMHsh7xKhCK55cwJ2p8HtnsdvS7HVYFZnXCdTXfvbpkOZvz7MmSLz9/QX695s3tSEKSknOmeLmJJOfy6oaT1Yyb7ZZffnvJbnvHotN429B78QV6+fwRHzeOzYc9jakBRftsgTYabSxGFQmgc4hFhS0gkuX45Fy8kooiwSpFtAodtCQt98XTnEhCMThphJPzZD+I92SGjPhJZsA0NfOL3+HWbUh5gy4A19RY29J0aiVLuByTnBsrjY3IfOJhOTY1u/dMEhkMYp6CLQtLNotPFOQHjVmpgcUzVGsJpXLOyXCT75/rU525B+wmoE/YNMvVSmRRpiwwH/yKh2BsXawJnHOHxvqekau+9/UP//7bP2dSkWQkLGIKn5hkRfwLzcnDf8kKiqoapWSguJfvCyD528zffGiq4/cYHw8tHSbT/kyCYkGkUmLVtPzw86+YNx2bux0xRmbzGYMfubq9ImdJcjdGxpyYElSKtmtlKbh3B0/FKTAjuMB2fcdyOaeadYfvE7mlvT9nKYp6pQxIUy1NuYCkORXp33RspnMtQ/jUXD781BoqLec7xXTwFSsHSiwWmH5+JAZhORj7QBpZmpXJvzYG8WZWRlKHu1r6qcFBUAofPDfrO7LRNCzEo05XnD9+xPbyGjdsMTUkAjlaJgVRiAm0yIZT1mhdlabbi+SvbvBDTXCJu+v31NYwMw1NnanrRBX35Og4Oj3DxUjdtZydHHO3WfPy05eklGiXJ3SzEzabHXfrSzbbPbOqJfqWj5c7Qsh0taV5vEArQ/AOW1km9nZ5OhJTJg4Dr1+/5vzigpeffHIY8CBhjPSPu92GtmtpmxZb17x4+YL9bkfSArBPw9nx0ZIYI8GPJT19GoDl98YU0bZhsTqn6ZZFhgmQ2e13oBXPX35CN1+iq5HJCmw+m/P4/BG927Jeb7m5FvsYFRLGKrrZjOPjU25vroipgBNGgFy5zx7cjIWphdY0bUvSAqAFNGMImH6gSwKuZTJtK0FMwfviy5gwTUfdtei6IgDbmIQV6Txqe0c7a+j8SFV5wrhn2K2pjCxnQuoxxmOyYd973njL6VxT1xaSY7e+xbmB87MztnfXHK2OqKzi+vojq5NzKttg6jlV3WLrjhQy15ffUtlMZWuiG3jz3SVUb/ns8x/RzubSr2dZHEXvycCw31C3M4LrMFrz1Q9+wP/1v/9v/NV/2/E//vv/mdOLF7iYyLoSXz8fCjAHKXhcv6WpFCo7YoS67sRDNYm0XhtNO1/QdB3WWvbrW/7+r/4CUzv+w//yv+KC5t2r33By8YicI3//i7/h5PiE0/NHzGYrwqCJfqRpWpazlss371E5szo5xTZz6ralaY/QppUQxHEg+xHbzQBFs/Ack/j45luic5ycWa4+vMEaw2J1SvYdt5fv2e9v+cd/Clzvev7NH/wuz08XTHExU22RuUSsAVyGMUYyhtGNBC+hiADXNzv2owZdyUIzi4entRBT8XFUWZiHWQtQUilUrslJ0zYZjGI3gguRjKZqDN5lQtDYSnNy3NDvdyUARjH0kbquUEYRgsOW67mqLeQoDGWVJQuk2JHUVSOgi5Veh/JsNkr8KzXCtHfjSBz36DAcQD3pAeQZrlJmGPcFgBB/7Fzm1tGNAsSSIYutXy7etpQeiANrcWK2R7ExyuJRakptMEaE71kFkndF2ZELVqGRbAIJvw5BfBJDUuQ0hZoiDLc89S72Hrgp89s9gCWAqrDzpD4B5JTEEkrde9OmnEqtUeQ8MWllAXgAjh8sch8qbaY+ZPJxfFj7J6/aXMBLAAr4KiFe09cJaw8FphIJuLGSsfLQginzQL2k7nuP+/5DrADk1+jvM1tzOUtqeo3yjxNoWpoleT8JUklzicWbM0z9ni2p9OVYT8FhPohP8nRuYkzFGkNUvxqFT0IdCEVdZEvfXBkrHqpaU1UVdV3Tti0nJyfMuhnOOT5efmQcR+mrp16vvM9prooPyEBU1SE0D0CrJB3DIXB66s8EYNaIpVH2geBEsUZKuJTIxlBbgxtGcpDgbhc9N9c3aB/wfc/RcsGsmVG3C7QqoHTKuATOj+z6PSFnuralKt7fbdUwa2c0dVNsLYQHK88WK57qGSIKkzImlhNJsboEIdCV5lQVe5vD8qCA6pO1VSqzUE4QJ4KBNveLlYmnkTNjP7DZeLSW56IoLDrGfl+u64msEQ91WSmNVRYqSJQcIxJKGZqmI+ZEHD0hRgbnyCpTVw2zpjlc19O1NV8scN4zDAMTg1wrRWWFmToWQDUUe52DKg55/y4kcjnPRmlMVQkLtQDXdV0fAlcVYt22mM9FBQYEJ9dpLCG0Ocv8FFIswYvSE41uxPlArS2mltlCpYytK9q6xRhNSBP7eVqsg60rVCEatKZDq1xY74rgPEYrqlqydpxzokCPgf1+z3KxIAbpy6Pz+BICeWDbFvtO78Yyg4LtRN0Vs+QXLZaaxXJZjl+58pLCmMQUdPkvffzrBmmzwmQpODokYT3WkjiXy9Vd2QpragKBvu+lIEyIv85ls1Y2Fa3Fdg2BsiKJ+cCKUBMDTKnDDRDTxHy6ZwSYwmyZhvMQw8F7cEJYFepw8qe98vSanC//qorPHhMbSJVNxzToynJOTZs5nyQYqqrZbPd45xm9p7Y1PobycDSk3PDNq1s2GwE3J+nHobAAKEki7+Y1V+/eYDvF9u6S9+9ueXd5S9e1/OiLz/jisxXPV1fo8E4WVli0bbAmkjRiwq0dN5uPZHUiSc763qNNPGkT3ves11uUksKayxucpDrG1Ghdo7WlHwZWqxXW1GSfChtaaP45Zera0rQt+9GTlIboufzwjqt0RfIJbRLGtBwfP6KuDKenZ1zYmhQSbT3Dzs548vicdlZxdHLED3/0Q3zv2d295+rDt8LA8BKeNfjAdljLIOId0Xu6tkEPtbDejGK3j3SzhrZb4eNAt3zMVz/8A26uPzIMns8/+ZzZ0QlN1xHjlvXtL9AmYrUY7B8fn/LZlz9mvlyy31wzbyyVPcFazTDuCSFitCX4QMyR2WxF29RU1nB1fcN8vsAYy83tXWEZFuw/ZXxMpDFwtB54PHrW2zvc7TVjtyDNjtB2js2y+dHBk92elDx+B9sby/pqzcfzyPNnmovVE2azhkW3oLGGUY+YquX4kwtOnr1gvBn51c0181SDHYl2j8ZhyZCjNGw6o7RHkzAqkokkEk5ZeokGpVGGfZXJJlNbRTKJkEQ+rbXibtihyVR1K2BWhLaxzGcdY+xJOFJM1E2DreqSYA1u77i6C2z3mrVbcjNmxggNBnu5pY8zzHjNvq5ZPvqM/Z1hF1terT0nN47f+x3NV5+t+MWbS95c92Q7A5NRSYOe4VWFTwtUMalXdY2ua2y7IHnLdthwu420q8jzJ2f85iayVopsFU2tsMnQmoSuFUbNWPeGu17z9KjmLMHFZmDrNSlqtn2mqyJV0pggyadb7/C3mlVOqMsrYus4PT1jf7dltmhYzFvuRsew79nstgR3jdm8Qu+vxDO5bI6nwAq0wjQtX397yXB3w+//7kt++pMf8I9ff+Db12tu7kZevrjg8dmMb7+9BOfQqsKoRtKBi++ZMYr9sGO1aDk+e8TPf/Udf/Dj3+GHP1zxy6+/4/X7jzy+WLJadMLkCJ7koWobAXq1hCSRwcVECF6UA8Mgz5okT9yQYlkuyVbSeUcK4tucsyYr+dqYEm7cE12PTQmTMkobYbnmWAYTaZ5Wx1/RX39guPt7rJGmPpUwhZQkxVkZXYIntHgX5YCqJfAjemGsqNKsp4MEMRdWCGh1L0FTBYjMqVj2HAatiWXpDg1gXdfsdrsDcyOlh4PDvYcslATgLA2wXXRkrXBkdC6ruwfA7gQU+92OXN7XwwCjhwyWlCZJfT78jEPxSmWBKQjyobmf2DDTx/1qk8P3fs/CQBePqBCJUZKLJxZDLqETKYlMbLKEOLB1pYqTsz6Aw/nwemRg06YArSljteazZ894enaG2+/Z77Z0sw6lMpvNHSG4+2FV2UNgQVUZYUoFYfxqq9EpQ5bX07UNVXVKXVdYJdcLWmGUAF6pvKapKc5TH6AKOHE4LnK0psCQnLMMFaW+U5p4le89+6ZjMYWDeSFElSWyfF1KsUiW5YiplNAYUghcXl7y+NFjbCUDbc7Qu5EUI3VV0TQVi0ZTWY3VsNlDN1sRksbYhpgMfgzoquPi6QuWbUc3W7FazUhaQAbKcKuTgOptO8eaCh8kVKduaoZhjxv3mOTQKeGHNbN5I4Os27PZfsf28jWz+Zxnn37Gu7fvuLm85KsvP2Mxa7B1h6lqoqoZQ+LV2/d8883XEBJH8xnEkcX8BG2AFEWa5iMu9DSdxtj2sJzPaLKW9/zixXOquma9XmNNxeroGJQM5FVlUSqJf3wWq426aWTRU1hSRsliCCbpqgTHTed8Wt5AwlY1bbeiaRcHJsfQj+y2W7Q23NzesVk7vBsYhz0xik9cZSztckVTzzlaaa6ur8mIdHtmWs7OH/Hdt79BGSsehkYXEEOuCaVUkWcW4kJK+BhoFyccPX7K2YunvH//nuvXr9httygUR8cn2KqiH3qRdmfEC9RIHx0K6ytqQ7I1i2ZGGnpub+/AtqImMBUUf98UDMokVkcr/JhY363h6IRdUpx1lpxHrFF4J0wgTeb2+oNIJmMihUH6RS3y57qZ8+jiKWHYMAw35OB59e23hBw5ffyUy/ffcHL+mNniBIqKR2WF63s+vH/HxeNnVATu1lvImT/5n/6EN+/e8vbNK2JUVN2cxfHZgcGjAZUFvNdkbj5+YLZoWSyPMUahKD7cOmMazdBLMO8kI7c68/HyDd++/jWff/773Nxc0XvHo4tzjIb17Uf8uOf04hnGVqzvtmidyDGxvr1hs7nl9ZtXPH/5JedPOtq5+Evu9nsSUNUN7eIICthTVYZKKb75+pe8ffuKH5yd8e71L7Ef5jx7+gk6jKjoCHHgw9WWP/+LX/P7Xz3ii2enVLVFF0BC1IbynNWJwsAWBloiYk3Gp4zStnhVG3ScLE4zMyNMNbkfZW7rWkldj0lCrZKKoDPDCOt1IKNoGoOpNTFk6lrYdjlnFosF/RjIOVBZg1WmgGNlTouRFIX5nsv+yvvxMNvlnKi7lrpuMZWl73ckij0JgZxlVghjTxh2hHFLVTUkZUrCfEIlz7jZsNveoJSmbupC1ClMZ6MxUfICXE7if+7kHqqMoTaitMlaH8KHErmE90w1F7Q1B+/VPN3PhxmVA1NQrs+ENZqcxQpP20bOYfZy3Vor82oCkEV00l78XY0tYKQilnM8AbGmpK8fJPFqsjww4g+UFTkVW7yiSgIO0vvJJlDqufRPVV3RtR2TTcxD0NSUWjgpnA5EqALQppTEe1JrTAnyMtaW11k4sKXf+R5jN3P4/VMPMIFzZaCVRbSSkC1V2MUHgA9ZxkkPdK9K0IoDQHP4b2HrGT2BgfJapnCz4Lyc7yAYQExSMyg4xkQesNpidYUxxYe5gPExBiGZpPt+0Y0ONzqG/VCuR0UM8UA8TMWTNcRY7Jqkt6hL/5ULuzwhQWkxUKws7j8mdZRCHXoUlZUs7wuukpTcYwJuycJvsgXr6hZra0jw8fqay8tLyIrl8oi2qWmtvK4QJaRU/HNhyD3RVCwXFavlitV8JR7UWmqL9JaRZHPx45+A+XzoedSD9zAtlXNhYoeUqGx9sCYSexLK9VsdAsaMLn1eiEyqpKnOp7KAz1o/sDxw91jStF8ofeCh70Zm48rWZJXAVPdLhpQIKZJ1w9D3uOxxXnI1vE5iN1Gu8aoSpbnWmq7r7ueBiSmfoW3bw71cPEKBorRS4p19t10zjo6uaejHQYBZbQ6BYLncO9aaAnLaQsQR+0trK9p2CiCe/KqFYODGURbTSmEqqeuj9/RDT0wBgqKPe5Q2+BAJXkINMfL7ptA7qacVKAl3JIuiTPo1eU/dbCa9dowHcD5FIRAEvGB/xTc5Fx/gsfQetoC2VV3LwhsFUUijdV1TVTVih2IAgw+Zqmr473386wZpFXLySSRj0FY83UxhLGSjxbesXCxVU6NR9LudXENKAN5MRlUVzWpJKL4sOUMsm0YTw2FwcX6UB6I2WG0KySaVBM0iI0CBMtgSCJPLtl1mr5ImVx7QkqYsA05MEvIloRolHEupw2ZzGsxkc1negOJwQ6qcqeuKuq0ZfGDtPGd1h0pBiiWyHd2ud6y3A2fH0rwK89hDMmL3oA2Vqfj8+Rc0dcbOtrg8cLu9o1nP6azhfJV5tNyBv4a8lU0vNaSRZBoUhrZKtCuH0kuubjTN0UqSEjOFaRyxdoYioXXxnTPlPWktKaY543yNMR0pKWLcS1BUkSSY0mDEjCRKzhtsVZF8JlvIRIILpDjKVtB2nJ8d8+jRI2rboZSEFWQMddWBtWzXAe8NN7eZ2XzO8tGcNKw4P+q4u73GFal2bTLHJ0fMFnNubzdcX12RfA+qpZsvaDtNbU84OTvh6XnD+uqOD+8HxmGg7QKb9Qcao9C2wVQV2+0OVKRtIhbD4DXV7BHHTz7FuYGq9hwvH7PbfcDhJaTKGkhKGIE509Udzo3EIEyjlDV121E3A7YWQ/6ARykJIsjjwMms5clqzvpW48fAdrDcXves/Z6sAkMDuoFaiRShH0e0UYyu5zc3r3n1m/8Pq055dPyMLz7/jJOnF6zOz6hUSzOvOVl2rBd73ozfsd4HKqtBOQQ8igWEkHu5MplKZTQChPmscMGTVKZuKtZafOCU0gwpCYO9fK/Kcr4qJU2Xj5HgBpp6Rmv3aK0IGdpmgVY1zkWgYr44ZrNN/Prb11zuPEZZrLZ0bc2qPcK2lnfbhO/3jHZLXD4mdTO0ywwx809vBv5gm3hyXvMf/ugz/uN//pY3tyNZzYsTRyajwRoxIVeKZEAr2X4mVbELDVfbyLPTit5FuvmK49QxaE0DVLX4O5oqQtJ41fDd1cDLi5q5Caxy4nazY6crPC06G+a1/Py+z7Rtw+h7ctdi5o8wamD0AbuoqRYV8x6G7RWbzR397go13pJdTwqOUAIPpfmIcs0pMBliNtz1QRqhVrGaa5SJfFxvePXuI4+OWj777FM+jq/JukEDIY4s2prHZ0d8+dknvHv/gW9eveXli2c4t6Pf9SyfnnCyrLlca/7mV6+xSvPpiyc86x3fvNvSmRlXl++5ub7k08++RKmK4DzjKH561pQE4SxFXCqAyBZTScmtjUFn6J0jFDgw7Efc5oqu8uRsUaYhxcnw3QsjNidZEOkjTs6e8urul6jsIQnzY/JBD84X5oU0RFOa7zBK+uj096nBz2UDPoVF6SIbmwaECZtMmVLApaHxPhLCcPg7ZD58eF/kq2nCQQ8DxW8zWg/2B1mAYi3Kb2nE870f+gT8TS9E0qjv5ZQHa5+UZOmihMGZsjTWAgZyAHvtA0aKngBb7l9neZGH13hY3j0Ag1XWRXExgcRTWFaBYGNk8rVKJWgi5ogfxyIVlWNLzthyvA9jU/kxppyfxio+f/mUtm7Y7wJVXTFbzhgGz+gDla0eSPzk+xurqbUmjF78sJiGrlyWCxmjLMa0pYEvk0th1/gkiMQkkUvF8y9OgzUPr6GHQwIHWbwMoOUYIfZHdZFHQpmFCwPC58LCiOIrL3LWdLgu66oETGgZgCudqTRUtSGS8X0ge48besaUaB8/wueKYfAMHqKusLbiSNdYI+xgYy217Vidn7H65JzLb79h++rnVEefUh8/KUOMgJqzZsFstpLQIB8lgM0bUhgZd1d0dk9dRc6OnvD+1be8u/zI6dOa4W7k7dc/R1UVTmmOHz9nvdnhhkC3OGbwie26525zCdoymzX89A9/yqxtcWPPuNsT3R6lBnLekHxmfXvHMPaApa48upoW6YmcDUbXLGYdMSU+fHjHxaPHhDSiMCgln9Y2AsyQMNqSUvGsNEUeHFPxn1W4EPDeY0sTzwSiB09lLMvFEbP5CbaaS4iL8/SbW3y/5fGzF6hs6HdbxmHP6HpiKFLrmLi6+kDTrlidXHB+fsJ6e4srQ+z5oye03ZyQIlRGglVURNv7xZFSAvpk5D6uuo7Z6oSkDDQNn/zkR+yHHbe//A1tLaFLISl8DPgg4azVfIFtWgHikGGzVoaumdHNFzQnltvrO67XOzKaECO+kBuu373n7fsP/PGf/qlI2jcbFrOO2rREt+W2X6OriqZt8CHy/NMvef/uO/Z9z9n5M0KA/XCHrQzbzZroPc8fX9AuV3y8fE1/+068oXXNzFp8f8cv/u4NLz/9ASdnT4RZZSvqpmG1mEH2aKs5OzlmfXvN7PwRZ4+eEnzmb//6bzi6eMz546f4pIqqTxikSlna2ZJh/I5+uOb47DGjT+KjrwwxegFNC4vWaIOuGs6fXrA605gQub285OnL54wuYuslP/7Jv2e9/sjt5SUfP17y7OVzuq5l2O1xbqTqKsgJN0ZIAe92bDe3eJ9ouxm5riXkVFW0bcdi9Qg3zjhaPWK5Oucv/4h5W7MAACAASURBVOuf8bO/+C988cVn3N5+zYdXv+EnP/0jvvjih+zHkaxqWlPzX/7il7x+s+CnP/ldlvOOpiz5IiK1b434n8YMjVXUWqw8IpIhoazGJehdxkfN6BPBJ5Q2RA0pKmGraoX3iWHweK/IWtSV601g5yLaWOq6IoRAXU0e34ZxkHAc5QJpjKicSFoTgiw7BLQSyX9VFYm+LoQcxMvbakVlJPQxhSjWNs6jnEOFkZwgjHuS63G7O0IcqKojogv4/g43bsj7Hanfk2MvHvSlttnKiCxfG2EkFx9qnTOdqSXIuBUbk5iEMTypLlRWmJzQpsIqi1YGq4AsYagpSS3VqvoeYBuRPpUUpIbpJLLeylJbsQw0JejXuQGlpValaTGrjYBSRfVhrEJbc1gypwl6fCCVFrBWwEbpDUxZgHkxCdD3frETE/sArtQV89kMMmw26+JrL+DxQWZ/WFL/Vi+BOrBYbWHBSY3UpJAPy3L4vrw/p3vG8oTWpRIUJ36ahcmcJeBY3nJGwqFkkSu9TQnujGniFhxAq8mnd/L8FX9w/WAZK71EzhQimvS44kubRW2q5DjqyspSTBtRO2RhFU42hdZU5VqfAGiZxUY3st3tSi8pMxiqKF4KYK5Qxb9X3r8xhqapD5ZK02vXVnJRpqwaOcylL9W6+IaP+GEsCyxFdI4cPLnYH/gwSgB5qZcqZxZdh0HTGAEMh77n3eV7gGKVZggxEmIWG4CUqLsZiSjWNVlszSpTg9bMZnOWq2MJuNMGnyhLf/leVcgTEws+F/qZLD/yoT/zwTGOYlFoExjTMJvPOT4/R3dzfBTiiN/vcLsdfpCQuBQ91gjhKxJRRCHEKY3RApaPYz6AnJM1QkGBObDpkwB9pjI0TUtTmLLOefq+Z1bPsFXNvt8T3MBuFI9YW4kNW4yBpPJBla2y3E+TlU7OihzuLUG0lkA3nRVoeW5pLeoC58USbApSzUnU3OM4Mo6DME6jP9wb96OAKtdTA5mDp/2s6ySfpOsO11IGMELmabtW5rcUy+801Amc84QU8SESoyIEsd4EeV7qsgGZlIldWxNjFCJhzlilCaV/BZkzc8rMFot7jLrcm26URV5d35+jjCKW3j6lRPAju92eHCUfRTdztFkAc5yq+e99/KsGaXMW6WdO4mlW2VoUCkr82JKWDURTVRzNFnjnJfRht5OQGW0IKHJlqZYLUvEjm4ZCYwxNXTMOqTBfxb8zZ9C2bJ2AST4hL+peRqKT/D8KKwUmm4SH2zgJBhCQlcOGT01snvL9ss0tg6yarKiLzrMMkbF4a5ipkCjxSkpAJJOUsILW/cj7yyvOTh6hEMNotAYNWgugrJLICZ4+fsrN/jUfrq64OFvSKc35quPTpx2t3YPz5BxIXjxQUoYwbU8toD2LVcXdJpLSnhQtSlVoId2TYsbamm7WkvL6MGCnlFCRQ+qgVuKVZGxJ20QJmydnUgajJCxrtVjIBryzeBfY7bbEGLDFT2YxX7FcnEC2B7+0XEynycIo6/ueYZQC4VRGBUcad8QYmM/ndFrM162BpuuYzxfMFyvOzk4Zt3fc7bYoc8R8seL80QmfvVyxbBPvbOR6nchWk1XP6vgcg8i5nR8Yhx1WZawy6JzISWP1EYvjFb/4xT/hwi3tzDCOhnHo0UpJs+nlAbiYz7l4dIa1GTeMzGYdMUmDOUlXQghleayw3mP3A08eP+bi9IjhtWGuLO79mhMTOdp75rd31JuBHY6tCuxri+o6crZUOhLCLdGvccHwzc3f8fr1Mc3qiEfPv+Di6Wc8+/x3ePTsBY+fHrE4Vdz6LcmIX6YqZW1i/2UyIxlTPrOGkCVspqorvNHCwEQK7mTInQT5QWWN0RUhR1JsJOU075nNLJGAMjXzes6iO2E/RJQW76fdPlF3RwzxDUFbjpYrThZLjo4vmNVL1s5xfWe5TecETlFOk+pa7hUMTld897GnyZmzueUnX51y9Zfv6NNMwBWTIWvQlqRN8S/MRCIpOjAWZxb85iZz0++5uttyfHzK86rmwz6j6owxClH+CXNkiImbu56+16zmilW94WTRYajFV3WIVDlhEuR+QHctJ+cz1BD45ptv4djw1YtHjG7Lx/cf+Xg5Ev0Ov/sI+w/osEYVH+Ck730tJ7N4TZJnodLc9YH/9Fc/58dfPWG17Hj+9Ih3l3c8fvoIgufn//AtQzLoHFi2ih9/9oSXL18w9I43r9/y/mZNHzPXdxu6+RE//9U3dDUcHS84XTjefLzj8fkZZ6s567srPjaQg2McevHMBFJwDIM0kSkKk7RpO7G48a6AZyVVN0swRFt3JB1KWKAnKWgqQ8wRN4woK8OJCoM0IWYGpsakEVJgs9twevYp5rsnhP4NxsRiVaMnOqewvLKw5fQkqS/PYT0dT1OCKwo4Afcb3ZBiAX3uATax65Fy85BVOv394ONavMS0Voem+R6Uffh1+mB9M4Go01Z+AgwPAC33A9XEylRl0HkY4pFSGRyMRqV8APmAsn3XB1+nyV9u8qJVcPiZmX/+8RAQnqZJa4vs81BbBayOMfE95kuRfMI9C6Y4Wh2OzSQNPLyecuxPj4558uip+PdpzfFyhTWGzXgHKZTfnw62SrZpJNAxRbGYMeYw3Ezsi8lTS5QAGU0JWsuQVSqg12Q5IICOEHwU915n8hyV6wORbyqFivHgc6iYLB2EnQRizWEeAOXehXJNIsvvwiLT2h6GMK0V2sD6+pKPb9/yuz/4HZIW9i5K4V0ow3lh6BqNT5regfMSspRCECmrtmw2t7T1DKMM427L8izizI7bzQ1ZW/TiSNocJX2eTlK7IpYorn4M/R7j13z3zdcs2sDtq3/iy5fn7PYjSi+I2bAd9mSr6eYLUZc0HfuxZ58M/Yc1+2HAWIWxDafn5ywWK4y1eDfQj3simVfv3nFyPOP09IjkPfXY47MnoyXdWGUUkRwCmIrgIlf7LWjN2fk53awrDBBhaMQoSgBVvA1TAVUOklitCDEU70WZ2MdxBGuZJJgCoCdss+Dk/Dnz1Sna1OScGPZrduv3GB1YrRbMFgu0GZkvl8xmLZv1Df3mjmG7JceRlHturl8zWxxxfLRiu/MobTk5O+fR46c0dQvcCfvjez2mgGm6aZgtl0KMSOCcY9w43n6bOYmPOT465ga5Vvqhx6aqDFoC3NRNgzatLCK0RpsKbRuUaUm6YXZyju2O+fj+NdthAKNJ+RKtMvvNHe/efs3rVy+IGWbdAu+37PuRyjp0yszqlqZuuLu54vGTpzx78Snv3r5lv9vLczUG+l3P7eV7QnScHrXUlWU1X/I3f/7/oLKjbmesbz7y7OUnKDS3tx+KtH3GYnmCqSvOLx4RtYTt5pjQVYULAzFFnjx5yR/8uzm9k4RpAWdErSG7kUTdzvjqh7/Hfr8BXWOs+OwpY8BDHIVwkLI8uZqm4+XLL9msW6y2bNd3nD5+iq0MTTsDZZnPTlm8POHDh/eMLuCT4vj0guPjJVo53r35lpeffcnnX/2I9XbHbn2DTwnbWgFqUxSSRNLU3QJlDb7fszx7yk/+7R/z3/78z/j7n/0dz58/w6jMm7dveNHMmc/naNPhg6iXrm8cf/m3v+b3fvwpj1YzKsBOVmtAcwibUzTaEkuvM0bxDXcehjHjgrh6xqTIEXxEQrhSIvSZfZ+43UptMlYzukg/ZLKSZ32aVJIoRjdZ/sgyVXjp9wSCECMxelSOcl1isZWAEDEhC0lbyXO3eJx7PzIMA+N+S9xuqch01hDxqBwYN9fgehqTGTeXbNc37K8+MNzdoL0j+ZEhDZicsST53SkQkqgUjBKmVd126Lqimc1wa4vXwqCNOQsIBmhtS00w0FT4uoGqIamGSlnwvkiOpR6gJ4n2VEU51GWUwVZKZkUV0Vlhibix+ENSUtAfVO6HgZ+TRc60GJ7q/sMgsAlYjpM14TQHP6j/00dKSdiVKdO2C+q2Ec/HfsT7WAAqqZcp3vvZ6t/qaYGDDYP8eQo8VYee6NArlc/pfRysCpU6ZB08BJdiTN/rYx6qmQ4L83IHpDRZX0zL9XwIRFKFRZqzPH/H0QtbPGcI4WBVoJWi1jVtuY5DKlZfEzFMCWtdXlvAxUhyQj5TpgRzRlkOT579intQ+hCYV6wwrLEoM80G4p/rswTfkSD5hCnsamvvbRWDsYze4R/0puT7ILXaVjhb4foBPzqxYRtHqX1Z7nfnHSgB560VRamuBGS21jCbzeQ9xEgqXqCjc6Skih+qsBqbtqMp/vu51GAJNhXm6dRThZQOvdBDz12xFIHJ9zVODR5iWwWgjcIF9+AZk6jahjobktJYW7M8W6COE/1uw3Z9y7ZY9PRhLGHC99fu9Dkpp6bjOi0WJqrCFOAloHklM2mCtulo2xlN00JKLE9O6Ps9++2W7X5D22zIWST9gxsK2STgnC9EKcUwjJCLam66lrUs1CpTArWaRo51mWuslTCvuq5RKGG0KsVisTjYbSViuf7l+A4l6NR7X5Qw6nBt3m03h3tpsufQFGuvsgicfISbpkUUbJnZbI62BucDfT8Um4EaEKvHGDy+zI7/P3Vv9mtHlp35/fYUEWe+Iy+ZZDJrdJWqIXW7GxLcnvrBgAE/+//0mwG/2Q03rFZLaktV6ipVVVaOZJK88xlj2JMf1o5zmTL0Lt1EIpPk4b1xTuzYe61vfUPbtlBUCV3XSZ02ArFa1r5zruSMBPmZWlE5h7EGR03d1Mc9rus66RNSlMFBApQlaUXvA14pVKio3SnKLsn2nymTVinKRikyeecqUEVamkXGGoOnC+Ho5TZ4SfkcFwjWoBZTcl0TVPEK+YiNMnQDKTylRDb1hIwwcCVVD5HljzrLLJNOysSF/NQM6pFllPLxwR3lGloVkNSOMswymcsJGYsYAYCRydi4gsfNX2vZEI2WEBOdnwy9VSrJy6X4Tz5xd3uH+vlzcnyi1I/vKxYWjR8C225L2x/wh56cPC9fnbF/vEWb11TNnL6/ozsIGF65DudqtI7E1KNzjVIV1sxxdkoYIsZEjDXFFFsJBV/LFEokeunYNI4HubFyKIUQih+j7H9aeHEikQMq67g8vxRZTjL0sSNnaOoZkOj7nrZteXx8oKpn0kwKBUs2luKVq7JsKElr2n7P7rAhDgecFg8/VSYsKmVySPi2I5PxbYvVNacnU5JZcv7ijGZquLkf+GL9wO31Nb4fUDmhU2Ba1cxnM9pwg2ssC3UGb4RNYyvFanHGi89+gtaGb7/4Nd36PZXLEi6Wa/pB2HPT6YTKVSyXcyaTBq0z++1BpK4qsd/vaZrJ04auFCkm6v1A03n6/Z772pHqOauLZ7hTT3+/5XB9izM9k/sBHzKPhwPfPQ7oekqHwVQN2hg6DYNxROUZUmDY7UjfdGyvr7l/8y1XP/4x+V/9CYdDTzYaX5gT47oTVnkshaVI15L4Z5BVxmqHMnKPjJLUQ2O0NC2FTQtAzgzBs20DSl9ikoYoXj739x+wswV1fcJ+a4jKkTV0/cC3331AVwfOLl7QfbjDGfGKqyczbL1gNquZZ83jdk40CzKW7DO6riHBvhv4v/7qC25ezfjTn13x6tmUn//klL/9/QGyeFFiK7LRhWFIsfDIKKclqMI5bnxmw5RPf7Dis6XmdKH51dc9uxhQTmQ8MchzH2LmcedZd5nn5xUXz1Y8ftsytDvWmwTGolxkvqp5dmrxWnyt+tbT7vfcqoa2fU/Xr8k+sD54to93+N01VbjHpH2ZLGe0ssL2UpCi3BO0wjgrkrGYsK5BJ8O8cfz8pxfcrv+O//CffolW4LPmk4vnvH71kh+8vGLo9vyX3/6O9x8eiLlC1TXaOW7XW148e0Y9m3O3G/jpT6+IMfP+5oHbuzse7ieczedMzZa7zS2TykEzZb8/4PuekMVnKSTxXRt8wDlbtkpZI8GXibfK7A8tIcTCGItQjPCn0xm+VySj2W/voX2gqqeo2QRFQuWAIrDePjKfv2a6/AHb3Q3ays8dk2q1LlJ5ralqhx4t0jMl8OjjYisynU6lEIyBUIBRrSl7oyapjLVlOv0RiwLG1+ojS+PYbTB6oEtxfHV1BcDNzTXAsUE5gqt5BFplwJdHiuZHX+O+rItMa2x0npi6ugDER4xXvNPHBkjro+3QKOlSRbpnx+spP2dkK4z+dUdLAkZ27xPgLGnB+qNfx+P7+rgpkqbCEotk8FjQpSdA9/vslYhF8/LiBYvpCdFnnHbCcA6J0Hck30MWSShZvBGnTY1SGe9j+TzS8baMVh2UYZXK4vMut0+GR4zgbVkzKUmgUzrWB8KWjQWMTRlSlPUdy9oQf8OnJO1SVQDCRAh59AHOOKcLW1D21JA1vbdPzaoqbCKV0Smyub3m4WRJmyLz5Qnz2YK6csKgKKBbRNF1npRNCQCVQh1rMM7STCfopNBo+v2Bu/DA2emKfXdLU8HD3QdSNef84gWz+ZLtrqVtW7SbyhmQEvPpnIWt2G3O2K7fsdsMfPdui5vPmS/PMW7GZBV5+aMfsZitqFyFJ5Gs4/Ovv2M2WXB5dUFVO+pmWvyYLcZUtMOO9e0tm4cHNo8bFvM59eQKrw+cXdas4kBM4qGfU6Tf70T14mqWqzOcs7imoa6FCRFjQnwVxYJj0tRUViSwIiMXCXsIQaw6omcYOmkk65qMBFaNHsTybBvOLj9lfvIcbRuRMfqW+/tr9vsNp6cnzBcLPnn1mru7Ndvdhj7D9OSc2fKE7775hmlyOGe5u7/n/rbDdz3L00uRHU5n/OCHP+GTT15x/XhHtrqkwXNUslhjUc6StaYfBtrNjr7di+T7sCe2rYCkdY2KQdg5waAwGD0ORHRhk2qyyiSrUI3DVBXKGPohcHp2iY+emw/fMaoPVPJUyvDjH33G0O9ZLs+4vf7A1dUL2rbn9MTQNBXX797g+5Z3b9/wd7bmX/3pv+Xl6x+y3RxoDxtmzop3Yb8XyXzoaPctL66e8dOf/JS/+ov/k5x6Hu+/I/kdV69+RPYT7m7ekjw0syXPnr1gsVjSZ0XvBzQi0bSVpWqm+KSYn56zMJZD24tKJUWykkBXHyPKWmwzY9XM8SFgVCQUAoazjnrMx9DifZzRLM+eE0PH3fU7tBv4wY9/Sh8g54F923Hz4ZZn5+e8fPUZ9+s1D5stVTVl+3DD7rBnuTzl1Wc/4W5zYLt5pLGOSTWlqRcS6muy7JlZ0flEU8+o6xk5es6bGf/d/3TGl7/9W373m7/h1SvLtILbD9+yPDlnujhBuwmr1YKM4XFz4D/9v5/zL376KZ9eLpk4IZsoElaNbEFFBEIWewIfAyFbYtaEAH0fwQgbMueMD1nO7CTqD5Q06wKcJOpGP3nBh0TOY+iUeB9OJ4nZRLFeKypVM6gOTy45JBnrDDnIwKpuppK+rRSZgKsaIQog7DwF7PZb9vsWHTryYY22CjdxAtzu9wz7DaE74PsDu90D+/trwnpNHFphMCqFR/oE7QdIg4C7sRMWWVbgnAz9UyT5DgW0Xc9Q7AfqqkZpy2J1iqsblDbCotSOerrCTObML65wlUONVJ5UgmFzxqq6AOapDPQsuvjPamNROYMy+GHAFv9xKGdqVigVjpYBHwNKHytuVAFtxj8bez87DkhLzzqex6JKLfhXmSFrZQCxumrXnQyNUjoCsuLVWfIIyn07qk1GJiciCZe7KAPRY+BZfhp+KwVjSFiMI4gsxKlcCENHZijjwLvYJWa+V7t8bDklwL4/glJSO8oA2yiIZV2NtYwuEv+UnwDlkV08hjUZRNovPYfUaiODcZR7+2LZOAyD3IMkA3RnCuCLALfO1jhT/NT1TKxo4pO/6lM9KF9WW7EuySPWoYplRXh6jTE4OyWmSAhiIXSUyxt5Xk9OTghTz2G/x1pL17Z0+z0hDPSD/Ot9URe4ijBEzk5OjjgBudhC5CyKnPL55fLZV1WNqypWqyXGQC4KX6kjTSE3mWPdno71JB8xrUUNHYrlQwYJZY5iW2CU2Eo6a8khkFWm71vJxGlbtP2AsTXNdE5VVwVUFFWVMCwHwjAIkaSsDzXWjx+RC2TdjAxzyTMYP4OP2eeh2LwFH6XG1AqDSPq1EZtFpR3OTQhxIKaIjwPe9/gw0OYD0aQj+TCmfAzv8+VaUTBojVWGoR/wUXIKdBngayPeySoLG9cYsdc5ZkMoK7hA6Q8W8zkxpZK/I6SWuviVj9kbIUQiYi86dj8+RAFEtag/J00jpMgMSvXEnLBOgGvnHNZKX+WsE4uN8gz5YaByT+z6nLOwnYv3c4zxCNoflYIFZ5TwMIO2WsgcQfIA5PfHPWfA1hXGnFAvKqKeYSfPwcxJZiKKpH/k6580SAtapKUpHycEaJn5pChU7pwztavYbzfCPTWWSVkUIQSaaU2sHUGJdwRlmjOCoCmHMhDJR2/ZEIJMvKtaHhbKw6/KBp8g5iheucqQc3l4i4eJLr+vigfN92SoRpeAmzIBQAC1sbPSpWk7NnzlkMhZmh+VM85abFWXDllLkl7OhJwga0xWHLZ7mfJrBakAZrnkb5lMe9hwu77hzYffk+0ObRPN1LI6tbx5e8+Xb+e8vPwZuXok+0wOLVl1GBvQdiBkRVYOMAyDJdOUX8vmR1aEkCRwR2nxchuJw+UJG8FQYYxWxwmSHFIiwwmIHNAozWQy5WR5hs5GDLFjeGrYA8SYCSFSVbX8HcQjN5cflsq0uK5rmqbBdpp+kELKKgG6pYl+MkPv9y39bo/sARlUg64dpsosV5b1tuX+ZsAPlmxOqdwDKooEx1hLPZkTH26ZThoW00qmXdZiraOanfD6xz8k+RYT9vS7R+5Cx3xSMZ8tWa1WeO857Hf4nFk/Br5zcHa6oq6ngCZm2fiaZiLvrarZ9y0peULuyDpw//4dj+/eYasZbx977LRBozj55JLzT865+e4N/eMj1Z3GPe7Z7T0733KIW/ZK0zlLmC7JE4dqOvkcdY91A8E/koZ7Qn9Aq1qYmSkIyxolz5USqRoRTBYWhUyiADVKSAqgU6aTMvGMpVCU5y+U0AmtKnKekZJl/fieFCyL1SWbZLhZg42J2bwi5sC+zfjkuH1/x09+9nNeXWjubm9Yo5ksIU9nBDWlmWlcp+iBrBWTxrJ8vmS9jewfMwNz3h7gFybz6rzmX5oT3t+3fHj04p/sHNEWXzmlUNZhncaZUeUTS1hMYKI1L07gtFF0V4q/fx/okyUWaoStNHgFbs7nHxKff3fHd29vqVTmxYuX+LYjxIyqHFZrZvOGvVe0bWb/eKDvBh6TZq0ksIEust2uif2GigFLgOiPu+xYBIyydTIkhfh/G4vSYtlw8clnfPPlF7z/9lumkwW7fuD1D19zdXnOJxeX7A4H/upvfsnN3SOHZNGmoaonGGeJvmN/aLm/ueVsteDhccvt/ZpJranNwOOm57dfwqx2LJ1m+eKU33/9niGCylqC42IJ1ZIJECFCzGIDolHHYsJYTY6BLkRiFBAtk7BY2qEnR1B2InuEqVH1AuMqUgroHFFISnEYAofDnno6ZecsKXXlAFdHs3hAbCpsCeGgsER5CpNs6pq+75nPpmijWW83WDS+BHVY6/AxMIat5dLEfcxOGVksYyjW8d4x7qmyd+73ezlH9FMq8sfA52h2770nj88nfPQ6+Yaj5+vIVh2LlxGcjQXo1VZTCUVMAh8K6DsqVcb1NYaNjA3HmKKaKY3UyFTh+966+hiy8XRtT5LE7zOAv8++BaNFrXIMEOUfMnQp1wqTquL181esZqfiT5w0OSmGfo9GnmFbGNE5JZQRNlXw8el7jo1mlrNCCLElCbh4YWbk2XpiIkmTBOMcWJfAglj2SVX8ACO9l/Rk8TONJXhMpLejgqcUN6VI5fg+c05Yo3BGsZxorDFsDp4hqON1SAiKsAOtNjx7diX1lXEMXYt3hmdXV/Qhcv+wIVOkzNbilDkyOirjiGRhIJJ4/HCPXU1omhlt2HO9h+vNwPrNr+nsKfXJC+rJnJylpqutQgcwUa4pRcs+Cjuw6yPz82cEY/DBMHcNiYp6foJxNY2tyNFzc3vD0Pe8fv2K8/NLsoL1ZoMOHt8PuHoqEs+uFx/ToefVy095/uIl9eSU5fKCt99+TggDrz97zXa7JoeW1m85bB+YTGekxQxjhXEXwiBsk2LHJYqlIoulDLvyOFwItO2BGD19t8e56vhc5JwFlCns7IhltjxleXpJzBrvPVWlOXR7hm5H9C3RN9zfvWOImcXihMWiOdY9KWiycTw+fGA5m5Vrg/XDNcPQcXJ5RVU3nF5c8Mnrz/jPv/mVDFn4aE2X9RH9INftAyplVJTmRYXMwSc6BTn48rQW8y2lSEjY0zF8zRgBd6qKqmmw1lBZK/LzEDg7u2Toe9YPNwIi5EQ0Fa5qaA8dv/ijT7l5f8fD3SPufMpkespEe0Lo0WnC+uGGD9cf+PD2KxarM1anJ9S1Zvd4Txh6fAqkToK8usOWfjvwk1/8gm/f/IHvvv57fL/m5rvfsX74wNnVDzh//hrrKnahw2RPDhe46VKGm1mYVWNg6zB00Pe4uha7Fy0kj5AENKytwVgnz64yGCNst67rqOoGnD4yD3MW5idKYyczJotTmu1GwkljZrNZ8/a7t1w8e85iPuHD9VuGoWN19ozpfAk58eHdF+wPHVeXz4tHdM/Z2TkE8Sq0tiEbRz0p+5axDH3H0EUW8xXWTcFNmJ1P+eM/O2UyX/CXf/5/s15v+fHPfo4zisoZKi1rX2mR28aY+PXv3/P+3S2/+NEnXJzOypoCsoCtQ44cfE+yDdlaQtZkNEoVVYIqpE/AJAkl1MW/uTLCVPdDKl6tmrqW/JGkhZ2YUPggoV6LmWU5V7T7RBwUzli8kbNPxQDGElPE2MJEy6okdQujyvcHfIjU1qFzZP3ha/q2o8kDsX3kELsSrAPJe/x+2ipy+gAAIABJREFUx2H7yGG/geHANA+4GMgmoZzYYnkUeC2DWSzOQDYLcs50Q6CNkT5lUpAhbAwCEoRhYLfdkEqQXdNMRepcktUnVc18tqI5vaBvN1TTJcvFStiIWvzS5awYMEpqKg0YJYFzsfjuZyisXtm7xvNSIeeNzt8ffn6sUB2/PrYN+Ph14wD3GKI6nvnltVC8Pct+aZQWoPHpRCPn4nOrZTg2qnP+IUBstLAwRyafgMVyhoryRmorYa/Ho/pn9Pwcg0ZHwGxU5cj2WMLZtD6COON/j8BzllrAGlvCzArgytPf/7jOq40oSHMl50IoVlLH4LQYoXyW3ntCDMQ8MnqjWBoqOeNVwQaaWSX4RS7MXcRz1loZQJJS8ULPYMpwP40szafh9vj+tFIMfgx1G5nBmTgO/QvANwadkUeFk2ARAnoJqY4saklTOVyK5JjoU0KpQe6rKtYiKvD4+EgYPHVdYavCyC1s2GMGg7VFgSQ9v3Hitb6YT5lNapazFa5qyvmmj+BsjP7Ya0qt+MRQzTkXsE/6DKU09KOCL6KQkDalR2BX6tW+bcl0KG05bNcipddI/zKIf3zRWBTA8qkuHMFxpSj36fuhdUelXLHCUMfrHm3I1NF72GcZTCitca5mNhMcom33xBSonKMreBR1IZ8gXtujGlaVAcAYJqyOz7diYiYC4AaxN4qDXGvlBKQc+5Kxrh9zNsZ6PudcyFkSMEYZVFhjmNTNUZU3PpuxvF8XBaeTIURmGAK60MhTysQcodPFBxZRkSH+uarQIZxzYqUwKuXKmq1dJXZbH1tNZFEAjMzfYfBUVUVVVfg+EVMgR1GhVq6CbKXW0RFlFbqeYuszqFZ4dwK6IirNkP+ZgrQKhdJOJh+FbToSRn3wdG3LpJnRDwMhJyrrUFlMfFVJ27bOlExvjUORRj+dsrHosZAsi24Eb8eGOIkRbWHJyp9nJezOPPq6qe9ftzBcRwbhSBUvCzSm8i6AVACqMlXRo3dNHhvQ730SxwfDGkNVKWIIx4RNeZkwXEyybPcHUoy4Ml1SSiSvCTh0G7797gvW+weS6hliYL254Ycnr/BJoc2c333+LT//4WdcLD7BmprY3aOjwmoNTHF2gjIzMjV+SGKfq3QBdSpqU5MIQE2Kmn3b4f1YHEjzfaTPq1HOmgu1X9J2jXJAQNJ1FU0zw+mG4CN+EInS6FMIEWctZ2cXTCYLjKrLerE422Bcw6yZSyKsEhAlBE8YOnL0ksyOLgezIha/HjFkj6gkAQjCAohUFoIPGCQZtGoMySpC2KL0gM+ZaTXF1AKebu5u+Obzv0fjcTphqZlPnuHclK+++TXRPzKbTthvBh62B6ZejPrrqub87KwUjJ6H+zVDP9Due1xVUU9cOcAl/CgmKVpVVqjZnCFado87zGFAbzvyw1u8ktfMZ1OaaUNIicnpKcwa0vyO/P6GqoNpG5l0Htf17NtMaBJxURFnc0y9J+YZXXacnMypG8thLV6244SblEoBJUWRdaaw90A5IyEtZFJUxODJUZKNFRkfokzvy7rwQRKiK2dZNoq2vyfqDGbNQMX9zvGHm45DCLx6vsBlw6SZkFTDpM/ofeDD9TU/fP4JfduxPgQ224Q+WRKrlbD0VgabJ1TOsVhMUQykFNGTCp0rbncd//GX1/yv/+5TfnrV8OWLKduuo8eAdeh6Xp59UNaSNTiXqU1Gm0x2GkfF4yHzzW0mzDrOF4bVGh6Dos+Zvk9EnaiMIc9mvGkjNmjMDF6fa148mzOguN9rjKs49IE+enxIbHc7YtfhjKPdbfDUeD1guz0mbKl1L0FXQSG0TwHVhMWsSrhLJZNGbSSZXmmSMny3ifzv//6vaDf3pBC4uHrOv/7jn3OymtHt9/zlX/5nHofEIWqinjIa7+scqG2NtXNatUOlQG0qrtsDv/7N73l5NeXHn73kt1+84/3jnn/7X/8xnyxrdn3P++t7HlpNRBGSYvBeZFwfSadSEIsAERokshHJjiFhtCP6iMni2N23XqRISXymrDJUkxVUUxm0hR6TxJtJI15eh+0jjQtgMsmP+3IJOijMp8VqBc7QdrvjVF780dJxWJhz5vbuXoIEEPAmxsxsOiMr8FGke6Os6MjiGIsR5xDpkD/umcLUHb3RpNhp2/bop3cceOkjF/2jRglhfBfp2fi6FCNJlYGgln0llpTh0ZtpbMSUMoQUWc6WECO3u42wKPNT4MdYgI0/9+Np9McN2ogqKqXQRh2BXsjfY/GOrx8L1RE8PjYROT95heUn4FkpacCeGDP6eFhrpVktljy/vKJyDX0SH3dtLe3mgZhFEaP8IIM8rXBWvC0nk7oEbYzXlQo4yxGg1VrOTWt0Abz19+weJPk3IbJo+Sg0xb9WqeLrKN8v5UiI/qkgL43kCETnmI/1R86lDtFagOGsqKzGqCA2H8XH62iHMTKkg0c5y+WrF8W7z3F3+4HNpuXsfEE/JHQZSGkLFoVK0scnrcEIexmjcFVDH6I0kaZi6xucsRy85v7uhtlZgz+s2Txcs3uApqk5XTakdGB9d4e2jtn0Cl01nKyeEfcb6tWSGAKb7YbD0OOiomrmKG3Y7zbcXX8LNvP8/BndoaXvN4RESflV2MoKCJ7B1g1XL15wcX6OdTOmy5WU7rri9PyKEDYoFTjst3xydc7F0qLCgRAzcehRyrHf7+iGyMnpGU0zIZIIgSd5b35KKB+G4biOrTF4DUYrrNG0bS/hg9HjfU/MhunyhPnJFaiKtu2gG5hONbvNLcPhnm57zVc3XzF59yXT5TlVNeHk4hmrs0tcPaWqJpyezhn2js32QYb4GhQtm/WOmDznz19STye8fP0Z0/mSvttzTH0vz2jne4L3pCAJ5NZYxql2Cr4o2DRKZamjxKAQrST/QBknwyQjTZFtZtSzBZWdoaPGYHB1TcwJneDi4hmkxHZzK6oxF+m9RztpyBbLBZv1PY0bSPkUZStOL65wruL06iV/+M1f8+G7LwnDwOnVS+bzJYvVgq7SLIZzcvB0h56H2xu2uwd+8rOf8Wf/4//M//G/3bC7/5ZKJZI/8K7d07U7zp6/ZDo7Yb8NGAbmsadZXoKxBC8eiiH1kOVs2XcHZsuV+HoajbKGw6Hl4e6Wk7MLbFURQ6Bv92itmDYNaEs/+NLYjoqBMnShop7MuXr+ku1+R11NaGzHyWKBIXN6csLm4YZ3332Jqx3z1SVD73l28ZJGS78UYsRqhR96ukOLrQby7oHp6gLj6qPHZe0MfdvR7fdQfHitNvTZ8Yt/8z9wcnbFX//5v+cv//w/8JP/6uecPrtisjrl/PIzOU+TePwNGW42gb/422/4k59fcXlxQlXk0JI1IvvDULwvh66EX2lFVRkJFCt91zBk0AGlIQ2JnC1VrXBOl/0P/CA2I7YSlVZIYI3Itn1w3D14et8R8jgwMYgLo0YV7ZciEcJAiJkQNcF7uv2e/rAR1pyxvL1+w937PxDbDaY70O0fiTkTQqZqJgKOpUilE83JHFhQaYvOCZ+CgDy6JIOniFOgchQP71JzmiFg+o4pqniHZ2HnDz2d7/FDT+z2rNcbfAFNQt+Tbcu2e2To15jtNZP7FfVsRttMmJ+cMlusMK4BbaTHcg7X1DhtyHGQ+6IpdmyifrRK6naFQSvxN1VHMLSAlzyBkiNIp4t68WMLhI/BpX8IOOWRuFRqiFTO87HBTjGhrCk96MeGC7KXZp6UQyOrUCwNJ5ydnaGN5v7u/uhjSxmWalUCp0IQT1n4XtDZsbYo74nisTkCkxKG/RRYLrWPKj2/7IVSwxmKKJQQ/DEkTRVQaAQxgeOQ1hhD9gMxBOmdxoCuKMFPQ/FdDSP4aopVX5GkZ6UgyaBolGtn4LA/oI3cy6QyMYg6R7IVYlE4jSDg0zkwfha+1IQjbiFWARKkO+K0KSVyyOD7Y83lnANjyTGWoDvkffiBXCT2mWJb8hFIWtcGV1WQstjsDB1aK5q6Jk8mJRhKat6YUmEBw2QykZAprainDZPZlMVigbUNGI2rqrI+BTRGpSfyhXXl/lRo40pOhAScJiJVNSks2B5SxCaDSgFVLOtIGWpNzCUYLwbaOCD2ZqPFVSYXO6RjpkNZ96Na7GOl2NH2QIEdn5WxCsyJnBU5S05BTJ6Q1PH9MA5nlKKeTqinDc2kIfoOP3RU1tG5hs609CX/I+dMQoiMo99zVddQ/MWFbKWF2KSmRC9/j2LBZrSmrhq6TkK1+r5HIRykvu/R2shwrOByI4FkxOCstWQkrwAQuw6kd1Moqvqp1xkGTyo9mdgYBBKZfgjleR5t2mSgklNgv9+jlGI2ncrzWb5XjKJ8U9pS15Pj5y9YBkwms6OS7zhcUWLjlImErDBZE5QGM6VpTnGzC7xbErLF2JreJ7JqiRgCE/6xr3/SIG0ik1TCVoYYEil7nLbiWVbYjt4PaCNFbqUsRmu87xk0zCZLWUSJJwBUKQH1VC6z/lI5qlGWmKltJcUnoCKyARvxz1Q5Hxt1OUxK456f6PFj89UHX8Bd2bXquiqpy4VxRGHZ5XEzLw+a0ZBVkUcWuSfIz0YV6WQ+Sk1QAlQYKw959J5N2zHkJJ5EWaaNKQUe1re8efdb1tu3KJepZzPC0ICa0DQrfv13n3N/s6fbH/jVb77m5bNzVlPF2XRCUyu07slmAdUVkQVxMMQ0o5rMUBR/FzQZi2umnD97TT1Zso/3vL3+juA9xiS0SoAAiz6GMhkR4E6pMRmZshEImF03K2y9JCZdPLRyeZ342daTCck49l3HpJnijND6tbE455gtp0wayxCyhChkSL5HITJmTTp66uiMpLFTpotZobKWaaTSqGyobGR+OiMNifVazMC996gs972ZzYk6EULP+u4NNx9+x2ya6UwmJceFO2G/23F//TWbhzvmxnJ2ekbXH7BICNgweNabSFVZVosFJ8sVzln2+zd8uL5mOplweXVZJl5RmOEFmOiVop1O2CSNqSLWZ9S+hW5DNXQM20dSHzA6UtcVbjJhsVhhZzMOux31NsHtjvC4oTKZPuxRBzFlV2aCrjoun7/mx68+JfpE8qk0b2LDkFQx8tDFngRINombjkoSkqBkjcfkZZKmHWQYuo7tYcfJ6Qpla0wWZrXK8rj6/oHff/GWv/n1b/n9Nx84dIHV2RVLU9H2gThfYKqGbnvHdj+Q0Ox3LZs2cPr8h+RDZKgv8eYMOzvDOaidwg+aylQ8PG7oome6OKFuavHAyhW3h4G//s0df/azBT99ueL+EPj8uieqGVpDZY28Ny2gtLYKW0FlEq7KOCPereuQYJ+4+apjz5RUg09Kkp6D7DdZKULSTKuKZ8tTLk4Sq0ZxNa3ZPDzSDRmfBlQcUKondR0qyc6p84AhoUJE5z2kFpP3pNQCAzHJwWu0JisnSfOlyLaIbClTgJeU2ftIDj1nqxVXJzNevLjiZrvlV7/5HVo77PQUXVVUKdN2nhQ7ghevqUkzAWOwruYQBu52PcvFktv7Wz55ccLV5TkPjwe2bz7w9VdfMf/sBSGLJI4SajQ2NiAeR1pJENbIGvRk2SwE65L0ZwLBh8JeAJkJP6WyymegSNkikThSYKrC4FMq0/dbdNwLEwxDTAmbgfy01+/WG2jE7sIqjc4UjzAlTIfyuYYQj+9BKY02in17OJI6Za6Rii+3EhlVkdnlJMidNk/G/aPNgRRo+f9XSJvCOpInTB3Pq+O0vRxAOY9BBUqYYcpAliRyabxMsYsZ2ZoKIjKsVPC430szRXlNkc2P0qZYADEo/nFKzt1cgDNr5TMBCqAlTbuwg58CPY5nawFsn+SSHIsrsSBCpuJJfA5FllFYAv9wogo0xnB1csp8PqMbBvZtUejUjiH0ArI6gxkk0bVyFq31cYKulTqGzhgtjT7lnllrxLdKC3PF6JJyXwLNYgzEwt6hTOljqS20zJKJOUjacQjEGI7NsBpDNeNY9EOKAWer4o8rn7usB1kbPkTWpeHzoQC6hXmhtcIZV1LDpfS3OlEZ2G1v8N2O55enJD0lJ2EnqNGDv4DAWilyjMKqyyIxPT+/AKXpup7BZ6aVZXn1mmo6p2pWPBw6UtxzujylVgk7PKBsTdNozi+vmMzmpOg5Ob1EJQ9xx9C3aFeTkpciDc1mK0NMZyyLWUMKHTF6fGdFuq1gMp3SNFO260d2h8PRO+z88gXaVWhT0fcth36P0pn5tGZ9+x3vvvw963eOT1+dY01ku37EWckzmMxXLGdL6kr8En3fobXFzecFaIMYPV3XUtXN0dpA5UiOFdv9FuemJSylJYdOBkFVw2Rxxvz0BdZNSH1P3/U83uzYP94Q2gc0A01j0QyE7p7tQ8/6/g3aNDTTBSfnz6ibCTl1xLAlpUzZ2ZlNF8TQc/vuHdVyyer8jLPTC7795pGmceKtHSMpBnLIqCxWItJAaYwCY+WZSDmLlFJZIQWlhMoypNXOoSpLVdeYpsbWDbPlGc10KeoNRPqulATWpThgjebVy8/4pmvZPN4QKgmSbZXiP/7F/4Oymtl0Rr0J9EOgUhqjxCrssOtQpuH8SjxZbz98zdCeEMMFs/mCT1//kMf1I7vNA313IIXA7c0d52cXzE6uOKzv2DweWKwWnJ1NCf2abj+XrSMveIwJrSvmp1eYShp4sSuIKBI5ynX4vkPbSoLgim+5M4p2v6ZJU7q2JedM04hPL8W65GPygoBfmhSg2x/Y3HzHV998CSqz3my4ev4Jtp4xDAPLk3PUbs0QAsMQSRmq6YpTY7m7e8ft/Q0xiu9j6D2rkxPa7R3NZI6pZ8QwIKywRBgGGlcRUsb7jGsarHMMPjJbnvKn/81/zx9+/0u+ffMNN/c3vP7Rj/BDwLkZ5+eXWHtK1weaekFWFX/9yze8eLHlZz/5hOmkknDHnGkj7EPiMEDIGp9EETfKol0lXVoMiaEfMK6mbRNKJ6YTS8FRZKgYM0OQMKyU4NBLYIwxhrYNeB+IHiEDaE1VaYZQngctFh/WVcQMIXTkoWW7XrPftRAHYrfm5uGa+7dfQbdDDS0592Jvpirx3nY12lqqpkZpsa/JxmFMTVXVRYYuzDsJ5UwS/FzWLoh/bOUDVRgE/E0FVIyR/W7LNAahkwTP0nv2+w1haNmtb8nDoWQ2HLD0hM2B/U6Ay8nNnNliyXK1QlcTJstnmGqC0UtsbSAN2DwIqHg8A2S4mREVTcrFBi6LV2pGzihRgahiLST3RECaEiJNUXWWXpRiTyBfsh9RBu+MQ+MCQI2AsFglPdkByM4hyRdKC4A8DqZdYVc655jOZ6SceXx4oO1b6ZOSDJoS+RjmqRTF/uJpuDwOQ4UaWn5fld9Pqgz+KHWNOV67fI8RMH76vZzK8KoEjo3DXa0UaBlGD4MXVmA/SAjX08UdX5uQgDBDxipFhVgpJlXyBvITiJ0QP/qu79FGButxkIR6Vwa8qfyjjNgwxDK8tXYcrgkQJ2GYFmIU39WcZECbswCeKZVSrlg/UggJQYIorR4BULGLstax2+5FhRBbgvd43xGzhE9VzkldV7IGtJYzKARf/F+lfpo0DZWrCtAs69Vay7SZYE0tIGzOhKQJyVK5Cusc1kow1niflH5ihyplQBtUNcHVS1CV1N5xIMZWrBNUhbYNKQZ0Tse1EIInxUBMCYMVz2tx7i0gdJTzJMlQX+xtTKETyprPOVAg60I+KDOLYn05Bg6OPZB4pJfhQ8GUhAynjxYCeazLrcU5w6SuyHFGCANDP3DoOrpGQFU/9OzbPb2Xe9h2HZGxr1dHwpWsEXk+FQrnKgHjAVMG9lUZEKQY6fsBX4gGqQwdMgK+j7604/OeEJuU/SGRsi65H0ZUbSkXlZnGWrH00lpjKglr90Fq3qqEqMneIABsZRwp6fK8DcegOGPSU+YTmUBf+pGSBZU5+jprJfY62mhUjPjsmboGqzU+aoY0Qds5ul6hm1NyPSVRQ9L0fqDzHqMzQwrEf652B0ppyBptKqw1dH1Le2iJKeGHkh6fEyQxoRZ/N42ra9ykQk8mMgMo9BSVcwE/VXkUKJtl4bbmJF47GHTWWC+LyNMR6MkqYxCzZHEWGGXasvhG+UXOsniIgViYX6ZIJp4kiRS2Tfmf9NF75ok1K/LP0a5AibxQBsFPoTSFteaHXqaJKXBoB8KQMbUEcMQU6LoDN/fXPG4ewGaqSc1seUp7t0ZFy9tvH1g/BjbbgRQ1b693bA+e6Deczjyvria8urqkqc/JLPB+Rd9OSKmWByoW38AcCKHHZ5EnvFyc8/rVD/nmTc/68Q3ae0CJNL4AddZYXF1Lw2WsyAaQ8IyUAzk7JpOV+LAkdTRKz6XZ18YW6wlhB4GEClR1RUQx+IHNdoP3dfFDKcAD6snIPYnnnzUlaEwpCQTSuvxMwDhUPSVES3ewuCWslordusOkAVIkDglT15AV282eYejZbDYMvqe9adHa8vzFlGpywh/+8Hser99xvpqgemE/L6YzGicby3q3x1hDTIFDt8cYRYiGpmm4uChgQTnIRnA2p0wfMvuux1QNg5NkYuUjpmpQbcSsA/Qd+BbVHWiI5EETdUOYKILOKNVgJhPmxpFrSxsDKlm67Bj6RB0Tv/jsFctpxXfrDSGM0lxIyAamAGUyOUqAiMoKlcUfS4OcOsmjiOJHm8UXVSnxTBqGAZOKIbm2bA+e//L5l/zNr77iy28fuVl3nF2+4AefntDUmrv7NQ+3a/6w65hOKtbrNe0gLABU4na75+r0B1TNJW/ve7b3W4bbxG6A3s1Q1RRPYOgtZlJRVxZHJFeZoCyDmvLl9YFPTy3TOvFv/uicTbfnNoJxCUOSQJ5aYywoq8BmtNPiaZoTPmluN4n3baI/ZEzl0dmgnUEZBV5YE7r4U/ZDZBMia+15fbrg+UJzXQ2sd4peOXJUVCkxdY7N/R29P+CSJycP0WPSDpV7VOzIoWUMQUpZipJM8Ww2WoC94oOXAZUDS5u4PJ3xL37+L5lNa7758nO++OoNm9QwuFPqyZRcNYQUCCmQtKGaTGkasRZJmRLmqDCA33Q8O11gqil//8U7vvn2HdPKcjJt2G93RKVZnSxQfE2KgWRqtKnxcSispZHVLsqEI+tCyXAlJEldPhYuWYBmtDTQUqwEGc6Qy6BMmuwYAioFEl6Arxhp/R6R6o6y+bJxF+DQe4+uRMJYCBpHIG0ET7/vDcuRyYp6Ct44yvT4KJV4rLTL2TU2CzHEI6D5MatUJEFPPq4f2xaMX7GEXOmishDGbkJlJdI67Z5sf9L37RU+nuojuywhp5IGO9r7iLJiZOCqj97wGLwwfp+UIuiP/M6SSHxd8ZFKKRwbl/JBAE9N1PiZyl1RVMYWVrKweY2V0M6276WYLOeG1uKbGwur+OzkVGRTIdANA3VdMwy9eBDmiC1SZZUSdWWLzcCEI+5b7utT60gJDJM/EwatOnrmyXVL05EUjMoDo+WszgWoVSOoXpaLOzaW+alpzJlh6I9sAWMdKqej3YWsW2GY9z6UIYdFa4stAwF4ktJZWxMipVlP9KEjY2iaOY93a9zcEZRDm0TjpuIn74MMw60ojIxtqJ2l2z1wunAc2p7t0OHqBjedc7I8wTw7J1vFZH1Pu7umfdxQz+fkYLl8/pz5meNhfeCLX33O8xcvmc2nZK0Y2o6u26O1YTmf4QdPO7TUszOez1covyYPLVl5Ts4mpCHycPOWLiQUkfnkJd3hgT/87vMSQuho9ztOL56hjEWrTE6Bw25DYzxD75lPa7p2y+OjZbaY8ckPztkfAmGQe2GdBI0MXhQfdSM1pVYyXI8hUFWurGvZeaIXhsfm8ZHZLIsHciqsDzthvnqGdkvqySlZZSqVGNotu/UN3e6W0O9xozQ2JXzXYVTC5J7YDzxs79k/XoucWcHJ6QnEjLY11lVoLRYYAH/4/W+havjFL/6E6/t79ttHjE7osomKcPKJ8TYKM5/2BxmKaKvJBsRaXfwWbaUxlSZbRXIKPXXYSV1CfCPWZhReGkVtZG1ax3Q258/+9F9z0kScCuzXWz7cbrk/7FGmJno47BI5edqDAFcte8IwsDq9QKvEarni4XHPZDYlp8SH9x94diXAPymwODlF74x4PcfMfL4iXr7g4foth67Hv3/H4DOvzJTVyTkpZ9ph4Kuvv6KL8Oqzn7BYXdL7KKAriWQUzoxsYmFGhyTXuZhNJLR2aCXopJqUDeTJK+9pGDXaoCViv2e7vmO3feTZxTnZB67ffs3VxTlRGfaDB6VYrc5Yri5A15ATTsGkmVJPZ+x2dzzcrFnffCD2Hfv1I5PVM05WV8KujEHmbyGyeXzADy0nF5c4Zwje0+8feP/mC26u3/PZ69f8t//uf+Hh7oHPf/d3fPPV17jqLS9e/ACVerr9A5tDz+r0BWfPPoGq4Ys3D7y5fuCP/ugzLp+dEBPsh54uWXwU5rDTwtwLAVKf6UsYFCSxlUoyjFNJ6sRQWHDWgnEKouLQerLR9D4Tk0IZI+GiQcC58XxVRjOMZ6HKJfE907Z7DpsH4vaG7c0H2v2Wbr9m6DYcHq7RfmDiHPV0hq4Xxc+1wU2WhHqJqSdMZ1OMswx+KGGyFjebQgikMMgwLXtUiujsyaEnxYEcnTDWs6H1iZAjWVVCUFAJM4XYteScMK7GTMFOJ5AGTs5POeweGLo9bbsleS9DyiDWAt1uQ+ha+v2GZjojk2imSzapIzZTKp0RuE6OWY0EmkE8nmMUYDaXQbRYcuSj//5oB4DiaOOnzWh5AEoZsc+KUUCw8r3Ghnj8X2XELzSWgR8fgabCBuSYVTGSm8ZzfawJxrNxs94UX8tIKXmEwRk9I8tVFQ/YY6lSvseTldJHNV2pU4wdfePTscbT2n6kGCo1GEIMU7owKo/X9uSpH2M8+qGO/r0xRumX1KjElWAuawwxC4lDf0QMCzEcyzzx85Zfxih8RDt4AAAgAElEQVR5LSOb2ThLUzc4a4+1SFWL9LyuKgE5c0ZbUYGRS+BZjMfBu7Ui21dKY0sPHbKEkY3vPxd8glxY0NoIQzilYg8hSiGRmmdUjPQhHGsqVQgiGTkbBcopn6kxmFwIPUMixpbpBAbv8T6QgHouILB1VvxoCyCdycXaQRScjDZUY8OgIkYXZnM2VG6GcRLQaKyhUhU5T4jeHxnOKQRyCmKhkcBYUfqOijl4GgAIG3qU+BdyXll4qlyHKmtvBGhzuQdjCazLszGu05H5LcQ9UcHlLFiGBMJqsnn6dS42GEoltJXhlDMe6+pCaqvouw7nHIMX39rK1rRDRzd09EOHQnqEQQlTGiXnhKucDKGVKABdUcPi5df1pMZGW9Z9wkepU8frDCEwDIMQR2xRgGexrRv6gapqCAjYq5SRnrp4Lo9Wls654wDEFFB17DtUqXidczRNU7yiJe9GF5bgOFgnZ3zoAUUswH+K0ucSMklpGU6jMSYTjCPZKclOUPqEanpFMguickSlAFFIZx0JDMTkhahBzz/29U8cpBXT4ctnz9jvW9rugDZGZK/GYJwhBaFKG21wxsrBYQx6MiHXjTSBufhPpCSgrB5NtjUoWyanAZcNKlgaM+PZ6RWvLl4Qkufb91/z/vEtxkYwg0x5dCybYEZF2ehCiCLhHhe/MiJN1EpM8MvEQ5rV0vCmp0ZzlFLIQoKn1OfSpuUsc+4UsWUnE5ly+fmjp0rMBJ9IPhaP0Eg/tDyu72m7LbPpksXJc5ancx53G/p2R+0su8cDRjWcnjfsDjs+//YNq8WK2axi3Sve7wceB83rFwu00njfAo66WqKzE39INbKEAzl51g/vMVrTxaVMkrT93mEnBumSTi0DIgHejdFFhis+UaSKxXSFzk9MZR8kedkZdwSViInFbIZ1NVkrqknNajXn+mZN1x5EBmIUQ/LEnGimc/r9ULgcSabEiBfTmGjtKifAhdYMESplsU7x7sOB3SHjzJMNhcplHViYzCse3twQQkfXdyyWC0yoOBxgvrji/OKKw3d/4PH6HXW+Z9FUTGdLrIWubVk/PnL7+MjVi+coA5PpBGUUd/d37A8t1hqunl0WlpsUCyFlUlbc3jzy4eaeT3/4I9ablvl8inIarw19dKSmJocBlQecmVINnrTb42JEb0UmEDHEpJnMFzhXkxpLruagpmAazp+d8Ys/+gH3w4FuCGgzF7niCPppAeJziihlKbpeAdiyFICKBDohts8FvDWaSWWZT8/Q2hAivH9/x5ff3vDL37/lZjdgmwu6ShPqAzQrqJe0qadLhr1PtIces+vFlsQkag1GJZKquN0FTl89x3Qbbh46vJ2S7QSlGnLS9Dmhq5qkA74/MKlqXCWyiz5ZurohTh2ajs37W66WFSE4ei2M/KQN2oIxmdqBsyUcuDA1RSrrcLXDqh0EhTMGYzVD71E5YZIwFrQWI/hH7/lq13LaGJ7N4Ccvl9x/sWV3GNClsXUGmtoyDNIckiL4HU4dULkjp172LkBrS0jFH1iPNh887U/WoEl8cnHOL37wnJOJ4frmji+/+hprDaeXL2nUhG/utiQ7IStNzgEfAj4I41kD/x9z7/VjS5ad+f22iYgTx6bP6+8t11Vtp8khORIEAXoRBMz/KggQJEEPEgYYjAYkh66b7Kmq7uoy19+bNzNPHhdmOz2sHSezOOA786GrqzvzmIgde6/1rc/Q97k4kb1M/v+eGx15eO+M1y9e8fTjR/z8Jw/53Zff8bs//MC3b95zsLacHi94v3rPrmmJqiR0LjOWZFuMeQqttULZHEgTAimqzIjr82CM3DQIA39gMxADIiT3pNSTokMnhws9IXkpFJHnSdua4CW0oncOW0vIj/cOlafG5OZkqPKHPX1gvQ6yoyFcQ+f9eyhA9yETQzGWz8C7ScTywuQmSu+bmrv2Cjp7tYqfV/6THKKllAKTbQ9SEjYIhsl4zGQ64uLich9kdRcIlTNo30LdNkt3wGapJ2+buP0sMjcTWb3PrYxNke4wx/YhH5lBUxTiRx9k0klZWsbjMTc3y9u/z5/PqNyy5fcytsAoTTWqODw65ocXz/PXuH0/gMJaTILDxRE6aVwQq5WyFJC5axuMjpRWGqSUxI5FDTZFiPRQZ3scpU1muIoyR45waQTLsmCQ76YU9uvAR2HIxpgorcUoTcznqKh75LoV1srfIIOulIeMiUjrvQwUbSUsjuxDLwB5ZulmD8N6PGG12jAel2grDLTIrR1EPZngYhK5WzSU5ZRPf/qn9NsbQu/ROdyx6zusKinrGmsSSXkJFTMF4/GMUgfayxuM6Tg9OAA1pR4fM5+MGKsdvr2kGEVG1vFy/QH8DKUqqvEUHyWx/eLDBZeXVzx89DEhaoqyYmzn3HhH2zlcr8HWTOZH2NFYBjk7keZrY8AY1rsrXjz/QZoRW+C7ju+/+47NcsVkPKFd71glYeCMp3OqUYE1WkLGYk+ik9DJZoqpCky9oJ4dYCeBuncYI3LXvu+IMVHVI0Z54Ox9S4ydgG/aEHwHRqNiEM9VFUVK7VrqeopPoMspJ+dPmR0/wdTH2GqK9w3Re/p2RXQbfL8hJUdK6s4wQ1Z4NJqDw0NSSFxdX6GTJihNs1G4AKf3HzOZLnj37hKtI/ODCaUtWK23fPLJZ1z38I//8DesLl5Rpv5Wgqxy87/fgAabsETKtZqOEpRJ0sQoWQPlpIKyQNcFdlygx5ZgE/iIIQ/1XYdCLFTKcsTxdMKzB6d88mDOtHJYoFSGH56/5Pcv3vL87QXtesNH9z/j8GBG6Bq63U4S0AuxrzEKIiXn9x5TVJYYE8cnp3S9RwePKUccnd/n9Pwe47rm1fffE33AVmMmsznGJvrO4Zst129fc3Z8RB8AXdJ1jq7bsdnc8PTjn3J0+pDRqKLr3e3Ghwygve8BJQzS3hP6hmgUk9kxpqjwIcnwaE8wyPSMmJVGMbNwiwJjC05PjxmNF3zxxc8ATVWNMdUEpTQ+grEjXJJm05QjfNeBrTk8fsRkPMfqEb7ZstmIVL7vtmybBmtLxuMZVTlmPKnxoSP6TrzGfc/68iVvfviK0XTO0fkDQjnj7NEZ08Up1e/+kr/+q/+A0QWTuuLDq2+JSB2n0hHOJTbbHcu3ay5uNvz8F5/w+NEpWIsOFhOyB6iKhDyolzNDeiQZQBr6PlJYUTYoLWCucxrBeyJ9lPF/SrfhlsMAbahtklL4EOm6lpA02haEPl/73Ybt1VsuXn3L9atvCZsPrD68J3Q948MFo7qkGI8ZT+aMj+5RjKegRb46nh3R25qiqhlPJpCgaSXDwQXPrlnTpoBLSuym0KAcsXO4zoHv0TGSnIMgA+XgQz5rFL7vJHjMdcJut0Z6QQ0pacpijJqJWqBuKjarpTAmtUittVVgxDqMZof68BY/2WGLmjSdUpUF5ajMZ22BUQlSBjJz/0kGZAeASGqPXLOkJBQ+BFTSRuUBsd4PTckqpnxbsjURe3CJPIA0GbAdQEhh5ZofDXPvWicMsvBhKDz8nvce50JOmJfPOfh8DnYF4ukZpIdMw/83gLO3tcIA2t726nILjTb5TNd7FvFQ64nFoUfvJfQ2s/aCwA8Mw+rM8ku3daA1RoDPO4CzsErFF3WwgxjCRZ33+Ch+wsYUgNSYhbHokWR63BIBfkwk8N4LQ9W57FtayD3TRgbnKqJ09t52nh6PssJsjEEG60nLEFlrCdlKuaZVmV8ge9sAhsr3bdoWgiJ6h3ey1qwRKzav8tAoJFzoxdbPIOqvXMsNOEGMid2ukWBcBUVRUeW+TRjtRa6lZSDtYoDgZU1lpqTKTh0hRmLyuOApy2zhIywEuaZaLBJUOcLaHNZtRDFrkwz9Y4zo4IBADD3ayPApBA/ek/JQnIFAkuu8YeAQhTqT12TgTksgYV7J79/nlvQgdgcynL+1SQAoy5JqVAmD2FpCVLlODPt+xQXpdUBjbEVZSraSNSVawaQa07qebbtj09yIMiEMFmIChG5DoOs7fFZ8yT0zdwYTwgQXkFQ8l+MdAsmQmVHYMl8fucejoiSNoO06OQ/KgvF4uh8M7XZNzigS3/62bWUvyWq24VqUZSngMkJosNbuPaVtrg+Hc1cXZg+Aex/EFiUpjCEPTyLOB1TuKb0zFNWUZE9J5RRlp6hCgjkT+d4jBKEUWnxsaJsb+uaGrtvxL/38qwZpITGe1MxmY1bLG5kyZJ8LhTS3qrLDjF9kFVYzms1IhcXlhlHt2QC38oJhAYjvLJhkGOsxj88f8ssv/pSffv4Ljo9P6NuWd+/f87e/+Vu++eFr3tx8g6OBQopUbfIGDQwspz0bNrMwQ4yEvpeGfZiuKWEUDT+33nn586nhIZWpIfvpizSsWql8HUSyjLVUo1JYVKqg90K/TtrjQsd6fcVmfUNhFA/vf8zx8SmXy3dcXXyHNWB1QWVKHp6f4XXkxdvv2W5aml0g+JbxpCQx52ZbcbWsqIsprg+MxiOMqYg+yzzzNVYkjPIo1dG3S242LehZlnrKtRqmGpnxTowepQPBNRQmobVsYjoqCm04Gk9QMRJi9uy5M/Z0PmLLgnFVUWXQxPU91x8u8X1HCorkI9vNGltJAqBWsnmpUJN8R6FiTibOKaRdK5KCVJGKiMLuH7SPPz3hw2XAOUWMhsSIttvQ9wEXE4VRzBYV7ruWqjSMxxM2vmI8rpgu5jx48oSyLmk2V6ggnm7v1yva7iUH8wXHR0ccnRzjFbx4/pyHD++zurlhNpsJAKG9MCVKmRgFH/Nmp3Ah8OLVW7aNo3j7gTdv3nF2dsJms8baEltVkCyhGhFVBBtJu4g9LJi5lmqlSY2TCZLS9FGj+h5nNNWiIE1qilHJRx8/5uBgwh+/eU/vR9SLWtZ1ppQlRN4tAwaZTsXgIHm0ink2JYCZMYpEYLvbUdcTDAWYmqt1y29+8zX/5e++5OVFw+z8CcfnjzHFiHV/ybubDV5rPqxarq4uWa6W9BlkTSlLCHUiWgO6wqsDtlvQuzWPnjym//4DLllUWYK1eWpP9lWUQr/PIEZdKFxwrHvFf/lmy5nZ8vNPT3k4rvmrb3perAOhKEmFolKJQkOlI4VWFFoJY1MnkpdhS1JQz8akXqGsDFdMBroEVPGIKYvYhyxdwYvryOFYMbKJB3PYbm7oXS5Ik2Y6HeN8j+ocPnlc2JDYoJIT5gAgHAnZY1SmFohpuwRPpBiJBJ49POeTRydcXrzn62+v2Ow8tqz46P4Dnj48Z9f2XN9cs+03pGKEAkZlidKR3km4ges6drtNlv84out58ugBJwdz6qLg/tkppTXcLJdMxiVFWfH1d6/55MGcZ0+f8frDhjcvVtgqe4HlZsH7IP2AEnk9Q+q9C1kuKWxsVMgprMJwvm2AvQBd0RFjh8IRQ5+9pxU6e8gRPVYbdFERdlKX20LsaFQG5XX2ujRZ1SB+teyl4C77yBZFwXg8pmkagvfSHOisChgGhwONIA3fQe6LyszWu96sIOeCFrQQY0SyidJSQPmepG69WuWhTJydnNL2HTc3N8KajuJdfnZ8ws3Vkj4IAJiSDDIHIEZz27TsveRyU3XXikCAQSn2VPYWG1K04bYJGY5MfcdHbrBH0PtGUM6JIeCibTusrRgaQVnNA3x9+58xStG9Wq1pmjY3Z7fNm5y5cj3qcsThbIFGyzpNwv7pO4/3DrQ0/8YaqqrIoPHAjkj0XYc1Cqtz+KWPt2B9SmhdUJZ2D5jDwHJNMnSQZSwBYKjsAywAbyCzjvL0P4W4nwVolVm3KVJYg9YiKQt7+abOLHFhGpgM6re7rXjjaQ8UArvlIUAIka5tSQlsUcnVNAqfHMlO0cqjbEGpEr3vadoVprSMSovvvRS9WKLzdH6D9lvGBWgCs+kBk8mU84MSt3nH9eollkBoPXVdcHjyhMniHFVNWa49XVD0HrxXbDYthQuMbE1pwPsrQirQ5QG6nBCw0mgrRbIjko1EFeliIpiag7NHKMD5xGa95fXrd5ydnvHo8ROa3YbNbkPT7Dg5O6XrWkbVTM4QX5AilGpCMZpJoIYeofUETUNlZACVYgcZUIpJ/OCSd6QodWoKPu+1mqoqqYxmu76iadbMpzUxRpq+Qdkx52fPWJw9o5ycoGwtDOi2YXl5QbO+JrgtMfSIZZBII53PrB6lCD14H5lOZhhrxAopBlbrFUmXdL3Drdb4oHj88CltnzDaUlgNRnF8/oDPf/3f8fVv/or1m+8odEKr2zBVRWacIQ2yMWoPRLnkUSkxPTjAVBXz4wPGizF9UYiNl1EYC1F5SlNgkpGANOcwqSNqxWxW8ZN7B8x0Q9o5tn2i2zasP3zg+uoDn3/6KWfHC37zu6/5+Nlj8QE2VoZzWsAI78CUJZiC8czQthu6zlFWY2H4obBGMRqNScHx4uVL/uFv/prQr5nOpoxLzYcPb2majqooiO2K19//HrSlaRxN03P2+AkpdWx3a5599nNOTh9ii1Ia6zwkCzFKdoG2xODw/Y7LN88pp+JdOj04FesTdLYoEYuWmBlaQ/NuzIj5gQRBrbY7vK44vvdUwgTLmqKeCTM+RBKynzZtQ2WlsUxAwKKrA44ffc64KumaazbbLb3vcSHR9R1lVTOqa45OzmnbDc55XL/BNUvWV28Az73zB5SjOZ1zxFQQ7YgvfvFvOTg85O3rVyyvPjAuLavNlhfPv2F+dAxmQug3TMcW13b83d98xYf3Wz792ROqaaIPgW4njXEM5NAhUEasi8AQfMIYqGpJ73Y+4HzCeVBRRmcuRAE0ckifhHlGylJULn0fxHc9JrzzEvkTA67b0e/WbC5e8f7VH1i++D3t29ekbo1V8OTpJ4zP7tGEDluUVNMjRsfPGB+cUtZTjFGYohYmvpHw577vmZY1KUXWq2ti30LXUClhBsYkbPqu6Qi9I4WA77dSl2SbkUCS4Dzvia4l9Dts8sTgSB4Z+qgMbhqNDx3etWzXW4hkSX8k6SRe81r8yX0MNOst7bZhVI/wuwprDQcnp5SjmqgifQroFDGaOyFeUXop8tmm1J75p9Tgw/pjtY3WipCVGTEPagf2otK3w9Vb+0D9IwCRJOkiEtQtZ3YcxkWDNVCuF4wxLBYLiqJgt9uJdBqyX/YtqJWGgXK6HabL54u3zMOUfuTtf/d7pT1qpvavSa6PBmXU8Lu6uPPvRmOVSK2HPvPuMPxWjSTD4uSlXgD2w3oJFpULuQeOM/BqlfQ84imbM3wG+XbOmRhA2eADScc9wN7lAXCMUbIr8tBf7etS9koPpRKuEXawSWrf83VIdsQgxR/un7xvrmK0vJ6PUl9FJ37KfdsR8jk2DAGMEZ9u5z0Jn4PC7C3gmYwMPVFyvSAHUxpsId7z1miqeoQxJUbbLGeXc0IyFKIQJcgAbRDiUIqJvt9hdldiB1VMKaspwaX9Ole6oKpKWXtlAdl+agiRDKGD3D9YrcA5qb3SbV0egthZxWyzllSAJBaQ4qCg9uvrlgBy+5zd/Rl6hH3vYIW46L0XT1jT5TUmuMFQD4dMTvMhoK0h+VzX66yuTAmtJfeJ0Vg8w72na7NvbZKhQVlWJGJWA8S8hrQ4fue9omtbSAnnpF5UGXSPMdI0jTCRjRXy0UAydI3YhiiFMkOvavZEzrqekJLfP8O3eRyGzWYrPrlA37vbHiAlQtOQYsQWBZW1OJ1xOqXQRuw2tDF7ImAIsr4SI4wJTKcVSpeUxZhkJ6jyEF/MccoSk5H15VuUUZk44/G+pe9WNJsrmt2K4La40PIv/fyrBmkVinbT8PzbH9huhV6dvITaSMKgNCsmg30heMq6JFlF0DKdGZobNUwIMuPQJC3+T2gqW/P0/hN+9fkv+Pzjn3F69gRb1rRtQzSRj57+hNOTR7y7fMFf//av+O2Xf8+y/UCyTh6qbGZ8K7UA14sx+OC5F2IUeYLW+w3hn2/84s+R8jeXAuM28iWDuEkLM0d4B1jEj7ZzsghtISmlfQi00dEFkfmvVhtKW/P44UccHR9zvbzm++fPCVGxmN3jcH7EwVRSjb979QPv372nmlXMz464d3KPs5NzRqMpMQbqcoZVJb7wMrHLw3+dpZohiDzU5Hmo7xtIQi1XSsB0k1IGNXJQWFEIszJ2rK/esljMqSoLjaLSJbOy4nhSQQiEIEErQxHgnSNhKMqKSZZOEAVUCNGzul5RVSMAXC9SSVtWFFoRXZbBZHBZD9NN7ymRhlgj4C25SAje8ebVlqKacXBY0TaB1kXcrqOyBXV9gLIWrcWQfbtpUYyZHzzGhUQ1OuDkySeEQhNix3wxZ3W5ZNOs0WViuVmzXG0pSsvh0TF/8ef/jsV0wnq1xEfPxfsrNpuGe/dOkSIh7QsXpS27ZovznuPDY7774/fYoubiYsWm2VEUHtdfUxYF08WEpjXEPqJMgZ3M2IUKVSTitsO7BhsiMzXGxCRS8k2HiyvOH57z8S9+QjCJbd9AUVFUMBlXaCVJl03rMkBlRFqP3HMVDUQpNEMQRjMo2sax2zlSWnB5veJ333zJl9/8QB8sy92YvpqyOD5Da0i+Z3F0SHp7zQ+vrlGxw7utTDwTBOOxupA1WNRQHdPpKU6XeDMmrBL1ccW9Jw/ZvLwiKLIvlCZaJPSGArRmlwI6Rh4dTSBEPmwCl27CaGRRdUnqHce2YUlPZwuwCmsVhsSoUFgrNUwYDk+rqCbke6bwJNyugxAwMVAWGjsdETqDa+X5DnQELN+8uqa9WnP/aM6jown9Zs13b65I2tCGhK4rDqc16/6KpBxRibwuxEBUhqCkSMck8azNPlMCPhbZ7yqhk2bbev7y77+i7VqqekzQY3zrmG9aztoWE1q+eHzMVz+8YxcsfVQkH/bFeooB37WkvqOymqOTU6xWjKqCxXzGcnnNeDzin77+il98/jHnp4ccHdTcvNhyenwfesfhbEppN/SuEyuaLFcahldiSSDnQoyDxE7tw4gBMCLhlIlnD6FFJZftb4TBpBVEJX8nTUckhZ4UOoLuIPZ3wFiRnLsQJGBNaXyIROdF2pNBjLt2B3BbVMUoEqOBk2ZywJDPRbvlx96rQ8F6t4EYJHGSz5PD+tDCTNXD2ZJ9XIn7Ishay2q1wuepc0iiXnh3dcnF8r1Id+yIWynW0HxkG4OUXbNUbtSG4n2YkN9ht9xlo/yo6eK2MboD1/6osbkr77rLJg5DuEQuQgdf+bQveuWsjGIMhskSO2MNpS2yAqTfA60KmIzH1KN6X+gPoLk0fZroe2E8pLRnw8pnldpCa7G8sDmZ1lq9t86RFFvxF1dqkALKe4cYJH08N2bimy+KH2ssSkPnPaJIV1kiKtddKylsjdGSQJ6lbsJqAucchS3wnadt1uzWSxazOZPZAaENDKFPt0NSnUHgxGazQWmLtmW+QhptDdQa71p89BjnUF1HrCpZD4j/bAjiq6aMeITZ7G26XLaYsafUS0Kzhu6Kg+lELJpSyfzoHpODR9SzI262gdWmwVYTOu958PgJi+MjbFWxW13x9noJ4wMqo4lFTaCQUVbMTbseU04ksBOjGU3Pqec3tM2G2PcE3/PJZ58xmS6gmlAXFfXigOOTI8qq4rs/XLKYHVKNRgQvfvYpOmwKtLsNbdPQ7d7QrJasry+ZzCac3DuX4LXMAPGhR4UAxqBMQeedXGNjuLx4x2Ja0+42rG6WTO8Jg7aeHjI7fsLk6Cnl5ByvCpL3JN9yffmG3eYDfXvJzfI1KTYYCyZbdfnoxOdNZ0uR6GmbXQYvotjGRE8kcPH2JUVRMzs8Q5lEPauZbKasdhuc60Erxqf3Of/kC24uXpJSzyDPlAZdmihRS+jsNefxIXB0fsj8/oJ6McGrSLTQFI5kQRlh26bYy96rIkkVRGWIzpOc597pnH/z+Uc8Ol3w9vnv6csZh8cP0Fg+vHxJ6DbUtmd+/5DDw/+e+w8fZW9lizKVsGEqTZ+bsqS0DKp0wfxgCvmMKApREl1cvOWHF9+zmE+oKs2r129YXkWO5kccHNxDUbJeXlKUlq7bkaKi2/W41vHdl7/lbH3N4fmK3W7N6b3HPPv4C4piTO8CZVXjvXj428LQuY7Lt6+5fveKRVxQlyW+GqFHc5K2UtMbhfN+zzZT2WPSVhUwZ3p0Rog9o9EMignet6gcONk1DT4EJjNpLMW3T8LA1GBngqEeLzBWoWMkbFr6VuSqXefYFCXzgyNMNWGkC/p+y6i03Oyuubh4z+zgkPOHj+T9uo5yPqH1PS9+eMHDs/sYU/Di+294+/6a+w/usW47/vjNf+Xzn/0pHz15TO8118slf/jjH7h485Y3b97y83/7GUdnR9gKmtajMyhQWGHIDue9NomiFKC2ayGlLIfXSixXQspKEoUPea/tO3a7hsl0ks9NsVoLMWJMgSHidje467dc/PB7fvjDl7x7/jvS+j0zXXF8+oD7n31O/eBjXDVm7DrG9Yjx7Bg1PsbWx0zmczSOKHNpuWdZSh+8MNGT95ACEhogBJ5+J+q+GERJ0e4afL8j+B6rBJQcwiNd36KjKP66diu1W+xI3olkNnuiRiJdt9uzVUMaUtJlX4pBhrKRhC41VkWSa2UIpw0boxlNpqTxdM+mVNm2Q8IX5TqLP21gCA4bmHzDf/+RCge1lxwPvzcMLP85U3X42dskyS/JAIPsb5tJBfI3g2VRoqoqjg4Pqeua5XKZE99/DLAOHp7CslP72kbum8bkkKy7Sp1/PpgG9nZJtzwrlV/nbkUz1Dm333GfEO8CKfec+SuKIiJJPdH30hcPqqJ/zuy1WZadcu0VY8SkW62TCyH7CqdbYC9GnBNygJIPl5U+aX+9h9oi5jrI50DbgYEo1h5iP2Ki9PL7oNasoCwyaLn/zilmi7IcoqgU2tq9ArjLVk3OO/pWQqyi93lILtaFKQ+0B9DS5KGM1grnk1Dv84kuUOgAACAASURBVG9qpbIVRLagMKLO0Jm9rtQQHJVwMUkvZIQWLUxO2TcjkLxje3NFs2sx1ZTx+JCExtiSoipRCAOzrEoiJSGCDgK8Ygr6vpD6kR5FjU5B6nRiZomDTSkDmo6u3eD6LToitmt3+oBh3cqQ4b9dm3fB2UFZ5zJYigLf5JyPvI6GIDlRq0lw2sB2RslgI2TLEgnL02hbUYxKFFOc62mLnqZphEDhGrwPGCuBbiRhDyfI+QxiYeinQazEnFjSCXY2eIe3eBfEG9bYgeuBD4Gm2eVzzTId77ksdJ3LFhx6/xwVRbG3/1osFplRP1imsb8GXdex3W7xIRByppPMETTWKlothMgQFUVZo1UhgxOlCamE6pBidkaoDrLFwRi0zTY2SQb3KhJ9R+ha+n5Ls71mt7mk65cCwKaILvkXf/5Vg7SktG+cUALCWmsIvctec1lqgEYXRujPSrxDdWHA5KCtLG9NKQk4GMFEzciMOT68zy9/8W/4+U++4PjwFGtGGTCVCUy0GqUiMfbMJ3P+5//xf+Hx/Sf83//h/+D96gWqjkhSaU5IVxIuJXY7t36ncLeJlU0tJWTKboYk1zw1SZlaCnklqoEkhE4iU01aNhujhe0kU64onrAI8bZ1gW2z4/L6A3U95d7ZOeW4ZLVe8u0Pf8BHz9nZIx7fe8q0ysBrCvStYzwaM5tO+cmzLzhZnFOoEm0sfd/lpjBhSwl56F3KjMm0P+AkYMvsAU9bVKg4xSeNInvl3Z4fMuVTCrJ3T8zxFjElUoBxVVOVFpT4AkKS7x5BqYJJPaW0paTmRgkIkqmZXPPhn2JM3kFyuaGSpkNpS0KaVzGll2mS0kNACySVxMMtwm4dOBxpjE5UVrHVSl5DQfCeyWREdJHkA23jCB7qqsaUUyaLM6bHR7x7+5aua6mqgoPDI+pa0fsVm3UvRYPWdO2Od29fkU6O0dowmU44OTmibd5QllaM+pPADTGJTGNi4OdPHlLrOf2yoZpM6RNsNy12XBBdz/PvnjOeTHOgnHzv+XSGVRZlFWleAmOKmNDeYqJINMfFBOZT5s/ucfb5A948/0DTtmjVs7r+wMiesThakHRBaSPrdUfnAZUwCBMyAj4gbEsDpa0JKVJOJlztGv7zf/yS333zFqcqTs6fclRXvPzyG5arFU/CE8am5P3VFc/fr2n7jpQMhVEUqpR1kSDplK0ORgR7gC/OcHpKshZsRYhzPmwST58ectJF3q/Ex0wKQJFsGqUJKqAMPD4yPDt01OWIf/jjDTtbcdVo/u7LG/78kwWfPz7ATBzfrwK7DJyJjUpgNjH0Dro+ZYlUoneevhcJZFSekMTPtioMR9OK1ioap2n7LUmXQECnDtc5brTh48WY0vaobkNwDV5byhBp3Y7x4gClwLVrTGoBkR4lDCH5HPIDI2uyL3Si9TJ91KagKEQ+++7qhhTB2gl9lMm0UoaX7z9wMrf8u199weTDJd++vmDrFDFK4eqDJ7mW5D0xP/vj0YjDw2NGo5Jvvvma+XxCWVVcXd2wc/DNi/c8fHifZ4/u8eLlBV9+/S0/++JjlNJUWrPb9dlH1YqnrCIzZgAv/rrC2NYiHR/wQwWJiEGh8ajkSThQ7g4D87bYEVZoBnyyHYix4hkUQ48tzf5500rAt5Cy5/HAnNAKlzxG6R/Z2QyT4iE5VFCxHwO6KoNv5NcZzpB8GOwLd5V9wTy5kLuFYsXXOXq5ycOZwm2J13ZdLtx0/uwyOba2hOzFLarFtAdfUwayhysWs59qGvbxXBgP7FT5Creg9PCZITNDs93N3UZokOINf8udTz2wWrwffOTy+9xpTIYfYZneNos6rxVxU0iApigsWml831HVFdoaQpKBiADCUZQdeajrvBjApDTcq+zFqaAsC6IRkDTlxGJjNFHlM4ockiIdFfuAA5KASFlKorQwdLS69fpLWYYv9ymSUzpADbJMtWcUoJB05WwRYZSHGNhtthRFSVVXoAQwisqIh3uUNYOW66KNIWaWrzJgtEVHYX1FJTs4CEvHRamlZGiOFD3KUhQVk8kIm8b0aUp7vaIeHTI/PiL0z7nZXGApqEaHhNQynk3R5Tm7XhMaz9Xyht6XHM0PePj0KZPRlLIas9pu2fWB+uCMqtQ434OyiMSvk0DVBEqXwrSw5d4beTS16GKEa3ek0DJfHDKZLGhaL2Fdqaf34ut5eLigsAqtEgGRSnqvcO0WrbQEcYUWVwhLQ0J3hLmtVYToCC4nsnsHRWa0RbF+KUvYbTckEkdHRyQMtpxxcPoJB+cfMz64j7YjtPf0/ZblzVvaZokxjr65ptleU1ViJxCjpBhLiakoTCXNO4kQHKWpMIWw+1zvwEd8tyO6XtLOJ1PG02NC7IhE2rYhJU3AUM2PUUVNbFp08ASt8cpSVmNct6PQAfJQwKfI/S+ecu+njwllwEUnrKuUCMnhBysjEipqOu/odYM1NTaUTE3JR+f3+bNf/oTTozFtc8X5o3uMqjnj+hiM5eD0HO8bPlxcsTg0PHr2c0bTA1onzPuilibLGoMta4L39F3Lh6slELk/OyLFROocISWu3r3j4u1LCD3TyQlGGw4Ojri4eMvL1y84PDhkNB5xvZTQ4NB7ml0nz7CGEYnLN895//Yd959+hm9aUtez3nTYasyf/7v/gaAhGtmPR2XJvXv3ePX9H3jz+gWzxRHt6oqJslTjo8x1uPUw10ZjlMhSlQJVVUwOjiElynKCLUaMdblnFA7/jFkaPh7VxCAM6lFdYVB0fUtQihQLwDCeLFBkP90gg6DdbkNZVECkKksKZVkGsWk5PT9HG8tms6ZzgdkiMBpX3H/0mLqWUD4foNltefvmDUYl7j+Ycf3hkn4KtpoxWxzwxU+/YNs2XF22/H//z2/54tef8vizB8ymhq6L9EQ6J8BcSgqtAkWlSUqzXHvanQDvISaREt85h2IC76HtAt4lUlTsdv0epJShU8G4tqR2y9sXr/jw3T/x9T/8R96+/B63WfLs/jknZ484/uRXzJ9+jquPKHRJmQLTbKcmQTZawIN0V/YbCN4J6Or6HGSq0KYiuU6ArRjoux19u83AZ8D5nugEeFXG4kMkednzQ/YbVSGz5XCY1BNCS9c2hJDk/NKQUmBAD5MWNpfKNUKIgbKw8v7RIYZR2RojKUzXg2ogaVxZStBtpVFZyRnjkGhuhuN3b9032KIMwEs+pvb9r/yO3KPBNmEP7CJF6fCawla9A9SmQRQt+lJUrmqUxuosia5GNE3Der3eA7QyqL4FuYbWOqVb5VMaCqN9f66zSiXs67k9EHoniCklsbsanj24ZbsOYafyfWJmxaus6h1qJxnexxju1H85YDaTHGKUgFvx2FR7kE28M3W2D/P7wX3KdV1hrZBCsuLUe0cIgbbtcp2oKayhHlWiGsuvPai2BjZiTFGGH9njVCmNsVZIKEUOcgtR1m7M1kx3rLfIA1sJJhWyWvCBqAS7KYuC4HoUBa7XMvhLit6Jf3BhDXgojKGwJquK5DkWj18B1CIyqEwItmOtFVWJkjVPktDGlGspYYJHnHf4rPYaArX2nztjKtHn4NuU2PoebUrKqoZUo5Qlpkq82FVJUVSoUiywfPAYW0ESsFmAd9CmIGUmsFz3bNkQHF2zpNst8b3sDRhF8C06r93MG8uFbh4yDMzQAfhB7oE1opISOw4BW1NWkZgckN62LXpPGuQWr0p3rTkzOzvIZy3KkhhzAK4pCDHSt52QJVPEOwH3Q0oyNFaiJrLGEnzI698wGpk8mEj5+VaMRiNheKccQKilZg4pZgvKkO0tAt4LUUVUdvIsQqIsq2yVlsOPMxFpIEfCrQ2dMYaqqqVnzANoyL0wkBDwWkVD7J1YqZY1SlVEM8ZXZwR7hi4WKFuik8KoSMLvz4SmW9NtLujbFdvtkq7f4kNDQIB8a0uivcsq+vHPv2qQNpGIKeQEP0dSSSaDhRgbKzSuF4BJmYLjswdcLa/kYFQeq3PaZMhAZ4wYDCMz4uz4Pj/7/E/41S//jOOTeyjMvvmLCTL3JTfFEmzUty2z2Yy/+PWfU49K/q//93/n1dUPhBTAZp+6bL2QBrYPeTqlB88Q9omj1hgBCozQ2ZWRhyjmQ8smAT4HsvstbitgUkhpL80UH5UgbA4FVVnR7TxXYcNiPuXe+WOUSux2a77/4XuC83zy9DPO7z/AxgLfJaJWLNc3bLdbHt57wEePP2VaHuA7R0gNthjhfdgffjK5FTNqY83emF9rKV6CTyQv1zAVlkiJMiUEOUBj3nEElJUH0aREaUuuLi9pdztsglFUHNVTvOuJ7Ag+b86mwNoCU0yIyP8WgiRXJhuhzBNXpbFVRVWNiGElvjs+EGO7lycPDWvKBuBKsfcRUtoITq5lAphMQTUaMaosKWSvmegwhcJ1Pd51nI4PuVmuCX2DVYqQJ6/aaOYHh4ynJRcX12x3nhGKrndURcnB/D6Pzguc69ncbChthSkTLno26xvSlUwTP/r4CZPphL7vsrWAlmZ6tYUPKyarLbQtT+yInYGXlxfoZgulZj6b8p2L+NWOs3sn1IXl+xevCF5xfnxM37YoI4FkISauTcIqQ11Oqean1PMFZ58/xlWJl5c3YEcYbenajg8frrNkQoBxrTRKG4xOmBgIvaf3Hb1vpYCKlh0FTV/w7Ysl/+mvf8fvvrvC2zk//fkvqecFdeF59Cyy+upbXrzfsPv+DZuuwQfLwXQCCjY3N2Bqkh1JQaE0QVlSOcEXC3p7RFAVZlSjbEVINR/WPZN1zyefHtD/YcUqFARToAo5gCxyRhilOJsoPnsgxcZyZfnuRhOLOUu/Yh1hmhz3D0fcOE/fOqLS9C5RKCDJ2mpbj+/h6LBgstA0O0dZSsiImY/oNy3nc8XpOPJP335guYJeWTQJo0WirzEsG8d//tsvmaslZ4cHPH54wh9fX9JutwTlSEYxqjQ9DmKL2EtYkb+RiMlR6MCT0zM+evqIddPwT7//njb2WYqUJ8oZ7EaJh5vWMg1PuuTisuGbb18zKgvunz/kw/fvcb3DarE9CSEQnTQWISbWTcvu+QuIiUoptstLxlaTuh33zk55/sMbXry45NOPHvLs6Xv+6+9fsPr7r6ms5hcfP+Cv//EPNJ1B65LsQZI7AWELJKX3oFZSSRreJME3KsYcgtGiU0/CC8goozUigeglYTlG8YsKvkOFLcYECmsIKLTJzJahyAMpQFMOdhJEWIp7nVmOTjyDrbX7IC0QpqMprEiVe7dnrSpuWSQp7QmPQPac9oHkegYe656tayzO93vWbkzDa6QfsTv6nBQ9JNhaYxhXY44PDnl/8ZZeThqZ9Sdhz98tH+7aENx2YrcgcEwCiA+Suj2zVskpZoyRJi3/7KHYOyyaWzbuXeZAzGwhtfc43l/3O6+RGCSNeg+iit2F+LiZ/NpDqJZOEkxjy0KaGsQrKwVZX2qYuGbWRwhSYBptMzguxZwwnNWelaKRc3iQa2kl/rtaKcgSSjI47hCZeiLhfE8Kbi+N9zHSux4fZBAwhJ2ZbOmjEDBH65gboChAYllmVaHi5ORs33yGaNBGZZA3I2x6YDkZkinQSWw4dNLii4g0gtKkGeqqwChQpgBl0LbK1ilQV2PGozFWRUIbuHh/hV9vefKTp8wXC7pmjiorlJrgoyalDeiKYnxM32pcNIzqGZNiirElWhU0nfg5KgVHR6eZlRUFOMwe18VIGCtKB4geMDKsNyanOBfUoxk7u8R1KwgO5wNFVdB5kcNZZRjZEYvFnLZt2OzWWG0xtiBF8UUsy4qyqtntVuiR44s/+RPmswqjLZvtTkJXvMtNqayZshix225Y3ywZlYXY75DoXY8tF5TzU+bHz1icf0o9PwVT0e427DZXNLtL1jcfSKFhc/OKi4vnqOTpnEIFgSxUHuYoJFBm2IdQirbvsieb+DQ71xO9JyRPGy7pfGQ6W7Lregygo8H1ARcU9eSAxdkjbp7vgMTo+JSnH33O8dEZ3375Wy5f/AEbBUA8/ewJj//kMy79km3XopOAG4M3vQQ1yX4RHSTTsoktGkPRwcOjp/zFn37Ko5ND2m1LqUvG9SGmmKKKGhM89x5/wngy5eLdG4rRDFRJUhXaIr6PRovkNbMFQTGZHUj6NoFqshBwppqgUs96eUVZlUzHhpsPF8SQ+PyLX/Poox0X71/x7s1LlAsUtmC5XDEe18KQjglrJQTOAterNd9++Vv63QZcw64LzA/PSaFhVNbooHCux/eRUT3jF3/yF4TQYWzJ1eUHri4/8ODjn1HUU9mTs8e6SPJ7FBBcYNcIoKeNIWKI2U9czjwlNWktbDadgaiEohyNMEWBiYmySLTOkXwgOIctRiiVqE3JZEoG8hLNdsN2swICo0JzcfGOxXyBtSOWNyvKYs5ivmCz3lHVIyaTA1JMFOOaw3uW88ry9NNf8dXvfsPV9ZZHsxO22yt2V+85PD7j8OScI1Py0dOK3a5nebXlq9++5vGzE8rRVPqBmBUuPqG1ZdtGNk3L1ZVjVJVUdcRYRUzCnPVehgW7VuwonAsokCY8epx3GDQxOKyNpN2Kr/7uP/H9P/4lr//4O96/+BptFB89+4xnH39BdXDO4ulP0fNzTDlGKQl9CQhxryhELbferEgxyH3LZJAUxW+z73qMFmuN8XQBWtPuVvR9i3cO0m24plbZ/iYl+iBkEu0DRkUJIQoB121JfkP0DanfEaOn9730L0nnID9FUZZCfMlHtBxfEho1qBAHFUUfhMVXWEhNl22hNCZ4nC0obI3N9aMQkgBlssd9zGfvEEhK7qUQMgBCztif50rmjGIJSO6LpT8XsPIOJJH3MiUH737Iq1D7wfFw/nvnaWLzo5rjVsE0AMUCbqY8iB/8L4HsjT8Md+8QoPLrC5HH5L+xDEofsT0XIPUua/cWNE3DF9kzGmWINgyzBTAVkFpnAD+DRFpJwJUaPHnl9wZAHCWs1qCE8OLzHuiDyxmzKp/tUcIjszeogJTiw9q7XoAsJX0sUcKTxDNXY5XBZABpYGvG5HEO+rbNVlV5sDSAhsNdiSlbeoTM2BQ7BaM1PnjxYc5Mf62grArabf7MWsD4wmpMWQgjNERMVZIxPakJg3jhDtfHeY8tNIUxqCQ5DEVpMjYjKGeIEmK9Z56iiEqDVxgvTFpjrFRXWqN1IkZHDIoUPRRi60PyErioEk2KoEuqSvyAlTYUeoSxJaRAiIkyRMqq5tGjh4wmJdt1y/t3N2JtkzwhOibjGWlxQttu2K4v2a0u2QVP7xqZoyclXz4P6fcNwkD42A8GBFcxKtfHubxWWbF1q/ITQHoPymc2bYwhP2dCNkgD4GqEqGOtAKzGlhRFSQiOttmy3qxZbzY0bYcLYjVnrKYsy8w1zCF5UcgCJhMMxVbjjvWekprFB9nDLZbq6FRwrxDY7baU5Yi6HpRskb6XczbGgHNpT1xwfSAFWZnWDvfX3Okz5HoUxpJy1oSoWvR+4ECMhKhR9pjx4jF6dEBUBdGMCKoiRk1O2yVrYyF4XLuhuXzJdvUS19+w63eyhyqwZc2oKoXw8N9QTW5//lWDtCC+PmEw+NY6syQTOkUKJRuDyqbjl5cfCDHLA4NDeylUrC5JHgwF94/u85NPvuBXv/hTHj78iKqaElOBDwoJ+0ooLd4xOkHfeWLyFIUc0Lt2hy0LfvnTX6O15n/7P/9XXt+8gHEg5XGuQgg7KW/Oe7fBOw8IsJcv/kgequ/8+4/EoPk5Uxl0LApMYTFFeXtNjM0p0nI499uOo+MjDg9nJBRd03B9eUWhLQ+ePGKxOET5Au/E47GPHcvlFUfzI548fsKiXhAchNjvD/nhMyit82ae2bOovX9P1/e5ySxENppKRpMDml2WiKg8sVFKgqa0+GOmPPGsqpKrqxbXtahKY5NiUVZ06yXJVigzhQSmGGGtLPKBpb9Pl4wegwWsNOpJYasxi8OSlCJ9t82gfUIjgV8qRvGhDZ0kp2bZ1SDnMNqALsFYrE3YIjKaWJpthOSIzYpue0NEM51OcM2OIiUqrehSwsUIvsf5jjev3rG8vkHbKW3Tstx4+uaGg8mU05OC+XjC4fRIJAtxx3q7kimoD/tJ06geiTTGOTZdx4SK8OaG6Q7GdsZNv2GcSt65wEf1BI9lN6lZxkhhNKcnx8wP5+Ac5agiKsPlckPX7JhORxR2vJfTtG2L9wl9pKhPZ4zvH/L6+pqVM5hiQlLi52psiQsqhx5IYIY2YLWi8z2Xy0u6bkdV1ag05vW7G66jJXLKxdWYrTqlKwpmR+dMFucUtqfplzSuJI3v8XpnSekINVJ8+vgRnz054Obmii+//JrLjSfoObGYErQlYVG6JjIi6hpT1uhyStQVGI1H8/qi4+G55cm9kq9edgLyFkrCvtBYbbEqcbXc8cMLOBonPro3ZWth6TRFHPPdh46zMlCXiaf3KvoPCqcMcSwgV9/nYY8BrABEh3PFycEY5xJWg2sSVW35+IHm2Hp2N5bltqNJIyl6oodgULqgi4GmrfjiJ59xOnH0dsLrd5es3A6rWtx1y3g+YmQT3skuErL5fFVoPnn8iHvHE+6fHJCipzKGk3nF1TYQtIBFKaW9t1YULRghJCI9Gs3FpeN43vHTT485Cxr7/Wua3VZYJkpBUeKChJ/ZwoiZe+epjOLP/+wXfPLgkIlJPH/9ht+/uqQqRvzww1s+/egJTx495G9++0dW28S//59+zWIKL1+X/OHFBlvaPL2OqMFTPEU5I4aAmwQqCmuWGFBxGLz0YoGjhM2okiYF2d9jkKDDFD3aKJSOxNTkJqqQPUANAyhhq4TksEnCXMIdgFUbtS+sh339rpTfZnuDmM+AwQJHMzBWda7lB0+vgRFLZpvEO6nq/AiMFSCpzEnxIpvvY5/ZmuwB05QLWK01VVlTVrUwhPPvDZPB288te3aM/kfvqwWZ3YOnWmmROKlbeeHAzEjc8dC6A9Tuz7d/BtTebXRSTg6+JdbIe6UksjG/BxFvz9LB3kEA8kTfdyhb7JkxQxNo9/5XAm6EzEpUSSR8JksLtc7BkC5k9cvg2ztM5uU518MZqW69r4Zrro3Bak3f91grzawPMghKMUrQYtI5ANLn/d7TdwLA+xAxthAA2MiQcM8CQgLUtNIU2fNQFWrPcBGAN+OyVrPXkiWpe8pSU1UVvQsSttJHMIABXWiRGCaxbyisoRxNiEkY2CmKrYouPVZDYUrM6IDx4j6tvobC0rtAUFOwM7RaoGyFslu0KTD1AYtJhQseU3oSJT4pUVx0gbKUxN6k5Nr0zpGCJ4QOZTT1ZEq32+F6J2FvNgIOtKEa1RSmxLmO5XJDZQKFVqxvVhyfnrCYHbBBU49q5rMDdrtVZr60tAlmswOUivjoUNFilGE6O8JoxWJeMZ9ZUvSYSnF9vcK7HBCRNEVR4rM36XazwanIbDajCYGgSmbHjzm6/wXToyeMpicYU9I7L03a5hLfrFC+Y3n1glcvvyK6jcgUkwAGKkmgnjSVkozc9R5rS5bLFV3X8uyjZxQ2M7MVHByfYMqadtfQtw3vN9+RlGE0P6eqKvSuo2kb0JbTJ58yridMZjPGx6fUBycUtuLZr6c4D9cvv+L842Pu/eoJl3FN63oB+lIU/7Yonoxaa2xpJDHcRQmE8oHUB4qx4eNPH7KYTsAnkaYWE1Kq6X1BUVfs2iU6wNHZY1I+v3sHIyMWJm3rqCpLNRqRQs/q+oK+6zh/8Ij58b0cmmMzeF6iiUyPd7x//ZwPb1+zWV2jlebN+/c8/v+pe69mybLrzu+33Tkn7bV1y1e1R8MQAAHQBSkNJzQyL9KTYt71qA+lbzAxUihCCkkhxozECU0QJAFaoBtt0K78dWmP2U4Pa2feC/ALcLKjH7r6Vt7Mc87ee63/+pt33uG7P/oJX37xa65fPePi5TdcXb1mMqlYLa7otz0KTT/IsM9ZQ+wHLl58yXpxTjM/Yjob8atf/pz58QOmB8doZ4hJgbFMDu6gSCyvL9BKcXDQ0K1es1leUY8mDDFTjyZyzu32eaWxtkapXGyJLCmKF3GIgaYZASI/9v1AVUmyuTCLHDpmPv/VxzSjmrOHD4R9bPS+x/LeozUFfK6xSth1m82CtmvZbtbcPTvh8OCUrVes1ivmrsJWE0b1lL7vuL5+xXR6QDU5ADKutrz/Oz/hqy8/4dWrlwzthoPDQ1YXnhh6qvqI07v3OTw9xI3GvH59wS//7gVHZ8c8futQFAweBq/wfWa9jPgsBJSqdtROJLhtD12f2HaRhGGx7Ir3oCqy5VzAWfHaJAdMGPjl3/w7Pv6L/4uXn/yc68sLNJZ33v0Ob334Q2Z33+bo8bucPHiXN9drkjIYU4mdTJb097quGLx4xyoyvg/F27+AeVoUG00jZ05MCl01RAWdbzGVk1C5wjSVQCcj3rTZS7elIzEOJN8y9Gt8tyKVQd7QrYXEFCPWugKSVlSm2p+BoiLUe2s5smSY5AKA7xCdVCTgSol3pTZB7J+yYr3tMEiYVF3JmSsK1518uJCgVAlBUoXBemt4rdSN1F/dOuuV2tUvO0WRKoDvDbuU/XtIYfLbtkm7IfTtv3Pb4zXvrfFuVDvaSEqUsOnc3tt2V3fs7AdjjPs5tHM1o9FIFExB1kwI5RnLMjiGG8/9ff2y/6f0vRT1YmY/2AVhX2Z2lh2lxir2ALdfO7XV7nvlAmzlCEMQBar4W1PA5hv7hqpuxM83IUqHENiFpaUknq4hBHbhYruCSwbB8rl8GBi6geBl/zMFvK6bBm30Xu2lS94CWUhIsVgGphiLRYV4LQc/kGOg7zqGXYCYEn9YUi4+zyXcqcjzdbnOxsiztrOc0krqNWctlaskPMxWwhYudXYMAYo1hVIlVAqpLWMMck6IGTBRKbSWXAGxK1GQJeiv71tcPcLYJCsoZQAAIABJREFUSgbWpiGnTDOao7GlD9DkbGVvNZDQhJyYTDTHRwdMZ2M228h207PZtnQbK5YCVU3jLJUCSKyWgZjC3gNaZ/ESNmV4ckOEUDuEVlQDZe2JZZhcp12QloQxyvvsAfjSQ6gduaEA2aJ0BpCa1xgt9WsWmxEFhPGUw4Njlqsli+WCTbtlvV2TcxT7rtIH7LJz2rYX0Fsp+mEgBlFuaCM1pVamELwKu1kJZqSV+NBqXRXhnxAFm7rCB79fv0IoCTgb6Psgvc2OHFgImQIYlzVrBONxRkD9lAa0thIaX1Xo8Qlu/A52/hTVzHBK4+NAHgYB/kMiZ88QekIcSH5LWL9he/2c4BdkWqwN+BAxqhKmbgxi1bVn+//T1z9vkDbLpr8DCdJeIiGgYibhijxXuzIFKkEuOUbICp00FYZpPeODdz/kJz/6Ix49fkozmgK2HFKyIE2RLFIaZevkxr98ecGdOyfUrqL1HcPQUbmK737wOwxdz//8f/wbzrsXstiNSAF3EwjZ6G4mhzuUnnwj09RlEqIo0w2kaePWjVMUvzUkhdlYmZxT0hfn8zlD39OlgZwD1hge3bvHndM5MQzEIbJdrTFY3nrrPSpXC8MYI2ypHBiGgcP5AbP5vPjLlcNQaUmBtuIdFkPEWjlU1su1mHv3PZOJ+D5dX11hq4rp7AQ0RNVwfHqX7ctBmu0scocEoOW7peBlCuiFZXJ4cMR8POMqdmQ08+mMvNnixlGYmrkiJ2EU2BCxWCrnxC+lstha/FbQmoQhZBiKdx/WoIJGJS8RSikKKK8iPg1431IbjTW7YBZQOqOzmItap2lGFuck6S+nDH7Ab1dcvznn8PQujbNcPr8ih47D+QRjLavNkn5o+fWvPuLTT36JVQYSZD3C6xmXbctXr1eYLy44nMF7T+/z8N4hZycn3AmHnF8suVosaLcth8fHoDVhEI/ajz7+hPvTY+5Gx7GpMdZysVnTNIeY0QSXI03coi4XDAp+5/4Zxjn6oWXlJVyuGY9ZXC2IwXN8NJMDdzMw22ZstsTaooZMczpjdHbKq5drhsFSO4cqEhvhk8vUNGZFjB4TPNkaNu2WN5dXhC5iqoZVgD//69fk6V3eejzh4OyQd4xjpa55uQh8/rLHpC2LxTWXnSKZx1g7IqqE1YnZ2VscnjqMq/ju98b89O8/Y+FHZHOAMhalLUk5spJhhq0rsnZkbclGoUzFQMWXLwPvPam5WHvWKeFqh7KyBrUWiUe0IzZ1orEavzU0jWJsFbmz0iS7DpUDI2MZ64o2y/YyeJHeZRR15WgaRaUTfgtDl4hKYTRsNxkbYLnqqVjz8Kjh9VaxuTAF3IqYLHKSSI03B0Qz4vSOIybL2/dP+NX2HIYOG7cM6w1WeZKWxM99Op9CJCndlvn4hFfPX2Gi5t7xEZv+mh5HSECZKN74gmpiSCgtYGiXMr9+8ZzKtRxO53z4zgPWf/8p0SeMqwDxvtJGijIBqaCu4IP3H/DRz/+Cs4MjrB3z5tUFp3cfslot+OTL53zx68+x2oE2GBN5cHbIh28/5PMv/xatJmSti62LSGJujP5F9qtShH4NRNASggYBkZmLV6iwOUuhGKMc2qVQIyVUEoazNTINjYOEKbGzpdGZED0mKiy3fEopXqqqFDb6xvJgx9q4zWzdFS4h3ICf+wm/3lnXCKCYdrLBLIwPZ52wx/xNAIX41N40R7v/3svpdqeJugFgl6slq9VKkoELOruzrrmR7hlQae/rtCtsjw4O6QfPerspLIu0L/Z332X/PcvvM7tAiz2QeWOJUI7LWyyUm+ukitySLF7tKcXfYCfffu0K02EYmE6nWFtxft6SYqAqzLqcs8iTtIDisdQMEEnJS3OcB5TKGAXGyfCpTPTkRwuGnlJJQi7MohAjRosUT+UylJWbj9XCdM050w8dirS/TwYF1hKHAT8M9F0v/ppxp5IxGAW1dbi62SfsxpSwxTJIIZLJ9WqDqytG0zHRD6zXGzJQ1w2qSL9SFimro2OkeuY20ypFbxS9z9h6hA+7QiUCFm0cSjsqJw1g37U4BS9fv+br9ef84Ee/T1XVaD3j7MH7+GHJeDzDMyIZjdIV2BnYCtucQo5kLfYEqm/JSkBYdIUxFfPjE7J2eN/jQ0vfLolDi7MwdC31aIwaj1FKzsNhiNgsQ+6UPTFmqrrGDwPNaERlHKSAc5lnX37Ng0ePuHPnHtvtli7E8oyK5ceoGQlgFgeuL7asloGph9PDOcvLV/itwm9rZtOG6WhE6EZcdp5S80tT4AdyVrjKoulJVjGeP+Dswfuc3HuL5uAhUY8IWROHgW67YrN8TeyXqNyzvn7N57/6R2LcYF1pxpQhBAH1rRPGsyLTdQMvX78hxIyzFaNRw+BDab4TKMP86ARMRcYQw5LYb0laGIJHp2es7MBX11+THRycPeL47AHNuGHbBwnZ1JbJyX2+80f/ks8/GnH//TEb69n2HVYbTCzS5AI+EBNRRwgCWtumFlaV96SYuTc748m9J2yut7jplOnRIVmNiLkiK0MAhpjxfaQaO07uP+H6+op112O7jmY8Q1tb1pwVCXBMjCczlKlJyqFMRUwZX+TaRjnGs/scnT5lc/GalDMHh1O2XcurNy95+v63ePLet5kfnTA7PqX+6nNyatlstyQ1YLUm7r2tDXHILLYb9GqLXVwydBvWq2sOTx7w9J0PefzW++hK7EYSIl+fzw+wFtara65efImtxvjxAZ2PTA6Omc5P9sQHlGI0nuz7iBgTPnRorRjX4720er8H3KJPaTTtask//Ow/8ujJXWYHFbY6KuGQO1bWrvEVizLrKpzVKCJ9m1BGsd5sWG9aRgd3sM2MwXu0i0W5GPn15x9zenqPJ299wHq9BQXj8YQHD99l+eYZiyFyfX7B1WLJd3/4YxSimGsmQZjG3RsaN2X96jVfdtecPb6HbUb4FNm0gRgTzagM7/BobfE+s9kGtl1i23p8ynS9F1msVoUFJ/JdXbJMHJ5f/M3/x1/9+3/L5vO/p716RbIT3v/JH/Pt3/0TqoOHNEf3OXr8BONqWHR77CMj4FtdNxgNIbTCZgyeEHqqSgCLvAc7RFFmtHiHBx9wpqKuJ/ggwVYxeKIfyDGidJaQryBgQg4JHSK+axm6FSl0RC8S+1jUAmLrooRRnoUdG2Mu96+cw6kwUHfs0GJzpbWoNYwSQC2HgBkGtKsgJoxFrGy0ZsdHNNaJa1eRr++YfLuwtx17VCl+I1Pl5nDeP5o3tYS6YePu/yzvhrI376HUDfj8G3//twbCt/+8iEVu6otyjspw1ezrI7kuIp3XBfiUwbmspdn8gLquZe35gPehsA4FtN6VK7eH8rtroct3NomiRpXpqpCcxK9DKdB5B64WJdPOBrAs5x2uvvujsGcnyWXSxfccxEIjF13u7iWqImkHcozFUkJTVTV1ZakryW4Zhn5P+BLrpRvvX60yrlaglXjcWru37FAp7+0Cdndf6cLSLfYOsQyeyZnoPaEb8H3PZrshDJ4cU+EWK8mhKJYGu3u/i1zfAc/GFJCZLKBvTqw2G0xVMU6RihIErOTapsLclXuTfmOgvvsdO+a11L5gTEaliLFpb52oyQzdWvozNFk5gh+I3jOeHaN0DYUstCPgxRj58quXPHtuqWpHMxpjbIOpxkxcRfBbNosV6+UVOSxJMVLVM6YHEIPHDwNdt5bnRglhZVdDy16+w5ViGb4YjLJFISG9YM5+v072ir29mkqua4w34W17C5OcyyDPlrW2s+mUfaVytYCirmE6PaAferbtirbd4IPfe62LZ38SwL3sE8ZZUrgJOMsFHJJW6uacipl99oKzkdGoIuVICH0hUqpbxA5Ze9ZaZtOSs5HjrXsLSQtQ3fcDWYk6RWvxEI8hgtEkozDukKp6jJo8JFYzFE7AXq3F8il6dA6kYcX162f4YUOOGwgrtAo4B+gROtUYm1FGEcq6lDv2nypIq4r00Hs5DEAku1qWqdKKrDOu2j2EkZAytXWY7LDJMXUT3n74Dt///o9574PvMJ4dEzMMETk8EZ8cazJKpWLWL2wsbQwH8ylGP6CqRHq3fvklfgjEOmGs5Qff+xFtv+V//7P/hav2Aj0qTa5KKE1huIjpgWyiphQM4psSdmbGZQOWn1F7Bvtvv4yiIPAeVQBG2G1YMnkgBsaTitnhRPwhUyLFTOVqmskMo4Vxm7PGGoXSJeCkbqjruXgphkTUAaMU69U1zWhMjprF5RWbzYY7p2fMZwdcn1+gjaFpGr758ktOTk6ojOHo6IiYHV3wKNcwmc9xF68kuG3HNspRAOcsJssGYVdsL64JvefYznHeMmJKHR1huWJqGpTpwIhUdz47hOQIHsajsQS3OMcumZxcJKYh0G83wkYdeixJmpPk5SixBqUjOgdJMyaQQip+OYqsHUPssWlgiD3kiAoHdNcW33l0bBnXlntnd2jmYyaVZXO9YOi31CPLbDLBarhcrGi3myI5jCRtCNkT1Qw7Mkysp10v+Pz5N3zx7Je88/gu3/3gPgdjx3g04dF0Lt8hyWYTU2I8mfLhh9/Gr3ucqnj98gIur4gpsXAZnJODOQYmgyLHgTr1DP2WHDVNVfNoPGV9fUXjPe5gTu0qwrpHL3umvmY2ndDpET4pTk4PyKlifZ0EKM+BHER6lnMgRpFUp6zIytD3Hb2Hra+I7pSrTeKnf/GMo0cfkk6+zbY3zE7OODtQTA6PWbmBb/7yEz5/uUETcNUReTwh6zHJNfI7yLxYZM5ODdbNmR2Pufcwsnm1wesGlCFrke8q16BcA9qJNYWyEtRhDRjDstOsO3j3yZwvv9mStCE7vS8uKquwlWMdE8M2U1UKYzNVjLQpivxtXGFMzfK6l4Rlr2lbcUM12kLZa5zN5G6griqGvue6y7Q4+kHLRG51wZ10zfEoc2inTGJNa6Zl/xBvq5zleXzx5oq3jg45mls+eHLCdnOXzz+7IoUNOUJdW2EuFd8vkkjbPvr1c06nlvfeesLZ3Xt88/w1IQa6fsCX8BtQ+wmrTINlch8Hj7IQNaz7gHFjwrBFtRsaEtud51MhV8iBLH/mc2axbXnx6pLHTz9Ap4FvvnnOfDIipci67fmLv/xr/vDH3+Ps/l1++vN/5NMvXnB98YahDzy+O+V8scUnjQ8Jst4HKca+RStJI1Yx4NQggRzBS0iKVuL3FkthTvEqT1HkeAS0EtaKWFxESJ6+lyT1HH0BXW2RzN10bTlllC0AOMhk2Uqy6nbT7RvtG5+uXYGo9pv8XilyS11xU0QVoDOD0oa6qRkGj7PFjzDLGbLzWYpFMrl735vmZP/L5F9tIKU9wwOVC8PmFhvlVu0g0qgb8/2YItvtVpQMiH+nEEulIbztz6aUwuqbIaQMKqVR2J15urAbdpK8XdMFlKn/Tt6obl1D9tc151wYYcKO2f2/1WpFSjtAXBiS4r0mrJFhGKSgjemmE0cCKSWZXb5XDjKBTzFK+qyMTgkhEn3AjETWqoqUcH+gZxmu5gJGxxBw1uK9x/thz34hZ0J5DuTZHUTySgYt0/akcrlWqviTKfENLMX5jkGTlWJ2cFBqJoWk+erSqJv9Nc0po1PGmkjyay5evmZ8cMywWPPsy+fMjh5w+OAdorH7Z0Abh7KVsH1D4up6wXwy5fDoLlpbmvFMfNAHj84Gpx0RRaIh64qcHdZNyMaisXi/ASQox6fExcVrlHLMDu9g6wbcWFyls+zJxndUFoZ2Q0zCuFmt1qSUGGLAugZjMlkJg8PoCpTBVSMqZ8m5J0ePpUFtei4XG+6OpjJIXS1wSuSHk1FNPZ7h6gmaCcennq7vsK7izeuXXJ2/JE4qLl/1WKd58OgJ2oyx9YQQekgekufqzSUJQzOeYOtjZsePOHv0PeZHj3HjGSEXxUJs6TYL2sUl7eYNKg4QB16++oK2XdPU4r3WtZ52M6A1NKMK52R/1zoTUkK7CqMyVd3g6oa2G+gHASetrTk/v8A2DX7o8LEvzCZF1/c0ZLR1wrYp/v4JS63rMnCKEnrkNdPjO7z/49/lvPuY1XaNqR0p5P3wQimxsZJgU0mFT73BuSIv1I7ZeMqf/vhfcG9ywvPPn3N69g56dIQPCmdHJWep4u69J8QiAQ86U03AaEeMAsrZqmHoe0LfsV2vsPWY2fEdlHHEIGyhfuj3ioesDVUz573v/QHjScPHH/2c+eEYvbrm4uKKn/70Zzx8/JSjw1PWmx7lzhnXh0zXPcvFlk23pa4FGB76gRAi3id0lP2gay7ZXtWE7ZK4XZCGDY/e+ZBqcoyzjhzFKKWZHHFxfsmvP/2Ud99/j9OTh+Jdb11h+wjgEXOEaLBu50mpqeqK4HsG3xf2tmE6ne73TNlLRbY8nk158vQtlos3vHnxmodPD2X9Jgnt1UoV9qmEyyxXK7zvaRrLyekJzyYz/LBFOY2yFbPxEddXVzhX0XYb/LDl7PQObbtmaDdyRmotQbnjQ04fjjm595jL85cE94yqGTOajBn8wOrqEgio1OOUYlLN6FYtH/31J9x5fA83OcBaS1PBfK5ZrRVXC08/JLoBui4TMmAsKfTk4peulBImXWUJXUelNSG2fPq3/y///t/8T6xe/QLbbfC24f0//q/4vf/yX2OaI+rRMc14DspyfX1dhryqDHRzAfzA9wKsGg0hFoKQkr696zoJk7SWthMgtvcDfddC9qQQCVmTsmEYOvpuKN6m5Q209EJx6NGhk70uBOIgrMMMoDTGOshyFmstZICUALcLqRagC/JvnKc7r/mdV+VunTotwY87YA6EnCNAYlGyqrQ/I/dz1Lw7ewQEVGkXDlbkw/oGNKUMmYV4FdhJjlX5vbeH2QJS7gBP6Vl3SpjbXva3Fam71202rQSrSvVgtBUI0dh9rbMDolCq9Muy9oyRNZdikpCh7UbWWi7hUNwGZG9+72+op5D7QhY1Qyy+oCgB00VKLmDU7c8eQtzbH+yYgVbfsGy5XSdqLUGheWeQWIb6+ea67wNoyVJLKcTyS2WssVjrRIVlDU0jYLS1Epzpg2e1WtF1HbnsPaLk1Pt76gcJ5dsPlhAGrviSZrTVohzLFhX8Pszy5tqJEmCvzCoPVkwBa6yAa78F7t+up3cEuBACq9WqDK8zvQ84ZQQXqrQokG49O9y6VzsrJQE+d2tFEUIi5wiDZzA9KC2KD2MFoE3iud4u30j4X+4ZTU6om7l40O7ez2iI8hxst55tuyRzTc5FRdV3hCBWTP22Jfstu5AjW1m0rsVgK8t3NVrJOSFbRiFDyPMbS+ibSruLlqR+TL9l+aWN+Mvqm9pwR16Ra2z39aJz1f5nbl4SvLfvGxCf16pucM4yGY0JIdC1Heu1ePEHnUgmFYVnWfO78CyV999Z/G47rB2Bgm3XE4InhEyKMviGxGazvdlrylrZhelK7yAZIUrtb6vYG2S5v87VdEGGVU01wkzGKDclm1qIXe4AqlP5M5WFWJACKXSkYUv2Hb6/xK9fMSxfMgwtSm2pbEYZw7hpxPJCVfLZLPgMOQhAm/6TZdJCkVeqMq3ImOITao1mMhqXyVDZ9CgeKrmi0RWPz57wo9/5Xb717neYH5+R64YhSnBK3TRYbeVhL4eGDJ9TkQEARlPVNbPZBIVh1Iy5Wl7TD0PxP01YW/OHP/5jNqsF/9uf/6/C8NU3vha75ru8ufiqlE1sGHbegrnYAuySCSmN3S2qTvmGpIRRiaYysigR+YovqZe7TdI5g7GZmAZI0jg29YigFJRZVE5JJtIKSQIuFPPVYoFCLB82qw19u0EnTa4V08mUvutZLxccTmY0Vc16tZbk6NGYzWLF/GCOVpqhJK5TfIY0aQ/SqlwOwxSJSNiKVRC2PdvlmqEPHNBw143ZbgO//puPmDQVJmiawxEHRw1HJ3epZkes2h5tE9aJL26/7dGjClW8kcajqUiSg+fO8YzlpaffrMUSIwYcEZ0NWiV0ikUSIUEiOYiULIVAPwwM7RJVrdgsz1m/abBVhcKgc8Y6AU5zann9/BsWF6+5XrxhNB0znRwxGY2pxyPM9YKLN6/xQ0fXZfoY6YYEqsLZjGrGDLM7DP3Atpvyq08XLBbPGI0ND8+OOTs9ZjKu2XmR2ZHjcDQiHShyF8UMarVkrjTnxtIPHWy3NCkTosIOkVll6EPAthEzBMZaMVUwjBuYz0Rysuw4UiMODo+op3Pxdjs+5O69M9rrjtjJpi6T5CxhUeW50cYQkyYlwxBrLhYdyy6T6/v0Y8e1DTz/esUPf/xjPv/yG6I2XK48H31xxU8/vaJTBzB1ZJUIKoIRyYp4LVly1rxeDXxx3vL+vRlGdTx5+oiFf8nLhZcJpjZgKjANysgmn7QWFq2tij2DAgLnl4anZ4r7xzUXbWIosnZnobHgchYZv1HgFFWZWs9mBmsySy/szKapuVtn1CrTr4tcxsmZk4DYB0zbcTjWdH7L5TbQ2xPaPhOGyPNVwjjDjz48ZTKb8OzyBds2S4EcRRpncFRW0XpYbBPTkWezvODeySlffzFm6FY4HfB6l8IrfpwiuwVDxcU68DcffcGdecXLl895drEkRcf86JDFVvaEXUDWrtDUSoG+mayv+8TXL5d8+PSUHDc0zrHuI93QFV9SsTMZkswM2+DxWfFn/+4vee/BKe88PuIHP/iQpD7j57/4mun8mBcXzzHGc3RgmY4dP/+7X/P+Ww/4k9//gN57Li++wSdIye0lSCm0pGFFJkiTpECsayLGFKVCiKgowT0qGpJKqLz7F+GI5ECtPNZCCq2Yu/dbAXo1JBwG8VjWVkIJdoCiUUpYNKVRiDEyDCVUohQNu31faV3Cs3a2CLcnv5S9WSasNyFWuZxVivlszmq9oe860DchFaqwa0Pwe09aOTjKPSz+VbFI7ZQSmwitpPBPhYGVS3G2lxSmJIyNQtq4/VnbrsNW1V5WeMPWvSl8tdbFKuHmffOt/08uwUrFs80YU2T8NwxksfDJwpQb+j3zOJaGVWm1L0wBtJaAil2Yp7CmxWdrGAbqKu/tbLq2E4ZVuVw79oqoA2qUimXf0SLTTjKE0M6ICkMJwJgBHyIK8THeA/m3vjOFUexLONcwDKzWK+q6IYQgthdG7BD8MBD9TlbpaeoabesSzjDgg4CQKGGTJzLGCXAVUqJpalaLFW3XMZ1Omc2OCGkH6O0CUAbQIpOMwBAyfrWhjgG1uOT1xRLTzJme3ce5CmMcrh5TVc2ewX169oDJaMxsMuXq4jUxK0IMKC1MH+8Txmqyzhhdo1SFNjUU37fsISN2AOfnr+naLfODE2LKECm1gtRTzWjKfDxmtbpksR6YTKdUo0qAjZwYjacwtGy2C9p+oG7KelW29MUSfpZVwqrA/CxDSvgQcFqzaVuS8bSbJePRGJcEmMHWuPExZhSoneVoWnE61/TbNctVS8yJPljxInYNViuyFy+77XqFG0+ZHt5lfuct5qdPmB49wY0OQVtMCgzbazarc7arK/z2mhjWRO/puw3r7ZLxZERVWSEiDJIS74On7zzOBpSRJOaqrjk8PKTd9vuwl34YqCrJE4h52CudQuhJ3pNjlhAh19H3HdttGeikna+bpg+RVOw/vBeW4hACy/aSdb+mmdVUszGbthUgRyec1uQoTZg2GWWL9VRJjDZB8eTOEz689y3S1ZKzs0c00yOynqCcIqJLLoBFGY3RFVlXRN9T1U7Wf1LEIaKsYlRyC1b+gpig7Qeq2sicJCa8HzBWAky00gwZsq44evxtfnByH6MCybe0my1XF5ekFPnss6959eIZcZDBzINH77BaXvPim8+xblbAD4+tLLGE0N6/e4+Hj+5R146+79hcfM3f/vQ16/WCd7/zEw5PHpKCIaSMNRX3H76F77ak7Nmsrun6xMFJzdC3ZO2wVYONACX9Xd2wyLSRGlcsUAQ03gWxaG1QRvoJVVl+9Af/GevlgkgipFDABwF3q7piF7Dkw0DbtSiVGIbIZp2oqpqkIm40YnZwiGLEwYERZU1KKDfi6ZN3+Yd//DsuLy85OXuIz6CL/VWiwjYNJ4+mjI/usF4vyKanqUflfFPU9VRCtsKAU5GJ1azfXBOve8aHx9R1JSQaFN4bNl6Y4ar45+9CZaajmtGoKowry3o7kFFCknjxKT//s39L+/Xf49jSo3jn9/8Fv/vf/Pcc3P8WQxeYjObUVc3l5Tkhiku7LoO3HdjYdi2+74WtWCyXTLG8yWkXFCVdW8wKn6H3PZGAShFnLck1BLPZMzmVq/ABAUnDIAE7aSAOa3LspVZhzz0hY8qZBNXe81OyTkyRcVPqiMI7Yk8ZyuIP6rQha2HfmlvuPJkdOCN1XFa6gLBpV6KwhwN3jNV4Y0ektBCT1B4avRmuGrNTz8iV3fW2GfZ1zA1L0hR7id3g+DfBV/n1N56a/2QgXcDRVLzkBZDe2SOkPZizA2h1yWSw1pU+2pFyoO87hqEXZW/O+wAv+RyKlHYBnjfD4F2QV8qiMNopjfLOgkBrYWhSAC6SgD8U+4sotgNxN6xPqQSSCzs45yyK1JRKYJ5c0xD9nptnCrh5I/+O5MIuVOysJ+S8DtuB7XZDXVVYazFGM/iOvJH6U+wtkgyis3xmzc56IqOrqgwJ0t4qLSYBmim/HwWx76Rey7JOhmGg7zuxatmxcZ2FLFaWpXor5aBgJYWje+ueZ5wx5cyTazP0Pdv1Bm0do8qhyITxhKk2+7NRawHrd8/M7Rq83N1i30Cp0xPBewkqi5GqHhVpviywlAb61uOjZxgCs3mmGYk1Y1byXVzTMB6NMRZC7NmuW/ou4Iee6AchlmmHsTWKwC5US6HBaqp6vLdgFKsVXxak/IwCYs5438tAJ0cBmPeYkny//XOVFVrLMyf7l6JyVWGT79aGDF21MYVQsLMmKRkRShOKv3am+M7mKGt3lS97AAAgAElEQVTJVML6TYroI0Pf40MQsDVJHkOIvmTZlBBj48g504waxqO6BMWJpUYIEgwdQy71r2I2m5NzLACu9AQ7Vv6urk45ALH0CpEcu2LXJaQulRS2rsnVFMb3qKaPMc0crCErS4h2T6aIZLIPhHZNaq8J7YIwPCe0FzjVo1wkq4BFLDVN7iX8jyhDEa3FB7n0Lek350u/8fpnDdLm8qAZVxVWqi5pyBLMUjcOHyW1VgM1hkqPeOvBO7z79H1++P0fc3h8QsbQZ8iDBHAMXUtT2b13z44efbMY5YHWWdFnMTN3laKuKu7fu8vXz57TDVusc0BDU0/4z//4X/HNm1f87KOfokw5FFMuU8BY6NtqX/QqJeEGudgz6LIp7H2CkMlaynF/wCkEUK614nA8omkadDAybVM7PyCLtonT+YTGWHT2+CjNrbbiYeaMIwwD6+sFzlqU1Vydv+FgPkc1jvVqRewGzu6fsVws0Ak616KspOZOD2dsLi9Zba+pRjV3mhq05t7Dh3z5yWfswte00mRlIYu/r4rSEJUVLxIgL82zJlNbQ9sG8jYwtxVJaUYYpng2m4FRUFx/+gJdO8bHG958fU6cNsyPjjk4PKaNG4w6ZTp2wg6JgcqOaJoptqrRNvDeuwd8/YXl/GUm5QG6gCWg0gAqk+JACAPHp3fo+5718gpFpt+uSb7DuRE59GIKnaHFisl5lM2lHjliZ/hqeUlTZabzOSEh8ruRY+Y013bNEAJWOxyRNgjjr223XF2di4SxqpgejHn/W+/x1oNTfvqzn/HzX/ySX3zxNSfTZ5xMLWcnR5zdvSfNCZGsIslm/NwRRxNysuhOk7oFSWVi7djGLbbzaC8ptLMSSLVNgco4kta0CZYhwqA5vfuQ6XRONpZsKuqjUyo3Y33RoVWNUoZhiHiyJD8qRe4DUcF6iHz9asUvPn3F8/PI+OCM3/vJBygXee/db/Hps3POlxtO793j//6PH/H6MrDyY5Qbk1UjoSNWQsDQYi0BYqOgVKYNkddLxfee1kzHMB5nfH9IZM1VWwIelIKYcGpAa8dgKlTlqEwx07cGR2TwHatrxZ2jBghcRUA5dITaZg6rxMFE0YWIrTWjSuODgLAxCwMslkLqwdxyVIHBcxGNFOhFAl8r+NajMSN/SagjS5O42G4J0dINiS7UuDhwsTVMDioeHyuuv1qw7WVNiXNpD3jerLf8Pxdv+PbTGR+8dR/LmrOZ41Uvh2eKGa0M49GE9bbD5kztJJ01Jc+vn18Qhhn37pxxcNgwPbzDr58tuV72ROtIWUtxkKMU+ylLs5LBkNmGxKvVgHqx5OL5BaPJjFHsuFhtS8ES9un29++dMd60XL664J13H/POwwOmVvPNV8+5uL6mahoBGjD89Oe/4A/+8Pu89fgez755Q+sD//DxJ/zq48/pWsDVkDXZZ4g9OSyxykOiNBbCfDFWfNHk4PbYYheAkoNTXgmlpHipncGpAd9eEbs129WyNFuZrGUKLv5UpUkuQ8OIJIumVlgS2lmaUS2eSiYXeaSAJ2/Oz4W1EkGlTF1X6AK4pCgyOG2MaAyVpPLuEoiVksLw/OKNyIZS2hfhKYK2qrA+irw5Bims8k3TkslYJyFmIQ7lGsTfaI5uA7xKiVol55IDXVgIFPA+a/FO3QWE5Ft/dwe6plLEZxB2fb5Rf8iZCBEBjk2xyFDF5khlTVPXpRZoiQoBWzWlqUkFEFRUdc1kPJEG2g8lkEJYMLlcr/F4TIpSKJISOWbaVn6+bkaFSZPZbjcF6CgMVS1+VVFlFMLuIQUJHrM7lk75nnnH7JApqnxOOfOET7FrocA5zahy1JVjUBCA3g8lnTqigeXiihgDzenZfgBBlsFmGDzGOZRWxJCJEbS2VFYTQ+Ti8g3NqEaZBNpgTV28m0tggzJk1RP7CUrPaI5k8BH6DdXZA3wXcE2NNQ5nK5qmAdOglWFaK/G4dRUheLbtmvFkTFUZKLZG1iVSVqCEyUsWMCumgcq5PYNru1oTBk9TTTh4cErUjpDFS1gP/V7S66MMrOrpMXeaAyql8bEl5YCOLVMbcY0mdYE3l+fE6SGTwwalxGIjqYzSVtgnOTMeTXAqsl4vGXRmNJ2glSf5gDEVyloykZi8MCqSYduuiZtrdLaYyRmHU1eaFWHgauTc8lnT9y2T44cc33ubOw++w8G9tzHjMdbNMG6MD1tWq0tWVy8Ztleyn6UB37cM3ZZtuybERDOaoBBLC/IgDUrxLN12HcY6lLXMRmPqlBjaAT/0YGFUzZkfHhNSYrFa0foe7Qeij4XVIfLxmAPdEBl8pnLCwpVAE2HpjRoZAAzJowisN2+4WHxFagaq8RmHx6fU/ZZru2DTbQglNCaEyGQyQimHnCBKQqsGOK1G5OWaNEQmB0dkZdDG4lRNRsmAOWWUqfCDMMsra4qcPeF9jzKezbJnNB7L2aYcNkfa5RW+7qmnB8QUcVWN0Yau61Aq4EYiOUxqTDOboIik4KnnioOHCaMyq8tLRrOPefXNLzk/f07jMvPT+yhtaDcLfO8xUIK+NPfOjvn2d77NaDxicX3NYnWJMwavDL/4q//Aq2fP+Z0f/zFHdx6SbENMGldXvPX+tzh/9YzXL18wOzgi+ZYYB6LS1I1GY8kYYpFram3Yrltc5WiaCaCIIeKDL4MpaRYyGqL0OMo5xifHMgDqxZtd/C9lYONctQ+4zCnjtKLrWj795BM219c8/dZ3Gc0folRNGga27YKmcjTNiJDH2Mrw8PFbXFxckkhU1UjOLZ0xmKLkyYwmx9SjGf1mQdttqeqaqqmJXWK7WmJdxXR+yNhmSQ9XifWbZ6yS4/TxPbK22FGNUV4YgFoxDAHfJWrTMBrD6R0Z+l1fS8CP1YrLNy/5hz//P7n89G/Bb/Eq8s6P/5T/+l//j9jDx2RV09QjbFUzhIHeewE8oRBoCsyptAQZ5QJ8hShS6hJsLWAcRa2hUMZiYqK2DVFbElssgdHBEVX25NgxDBo/SA3tByBUKOQMSKEFHRmGQQJQtSgmdZK6RJNlsGoMqqgUJZRapOAxRQmnlmmmnMfalAApAU1VAWxSKuBZ+fwZRQg7EpPs66rktpBu56ewtyzQSlj9ZAprMe1ZfyntZNnyfCp21hwlqKiAsXsVDjfXUyn9G/XFbTuk21ZRqpzhpUgoYWDST+fdIFZpdsLwnYeqfBbDdDZlPB7TdT3b7YYwiNpAyJ5KdjC189mV9zNaAn5FsgPKyHX1wWPKdVcZUfdZqY0yaQ/u7YbaO6WMWA2UoLRbYHRG7P6EdSrXR5Rq0l+kwjpTBWTf+ebftq7a1b3ClBQLkBC84Coo+k788pumxg9e8BB149U7+EGGoqWPV/ta7p/aVMkQSEColJO8n/cSMh4SwUcZRsdIjgmnDcaJn3Mqwzyrb7x9d46mYhNx4yFsnYCzVlux8bDyvZTJxNDTthtc7cAYjK4Z1bU89+U7UJ5iCY2T4FTRPnLDZAYZ0ueEVYqcIn27IRoJB3aulnpbKXLo2CxeEro11eiUZnpEM5pSjSbMDqccnxzQ1BpNpu8G1suWbdexWW/p2oGQDTn0KJFL7YkD+9pSG1CVKCzSAOUZ0FmC2EIG6wai34gSICfiIIMeyuBAXjfDECUPKLEA2M5V7Pybd0ptEHxsZ2GHguSLzyvCOI5lcGW0wpmabMTGwNaambVsNhtUZ9i2Ldlnei/s4UAm9HL2iHWRoWprtBVQXStD5RwKUaE3tQMloPDOZzcjw7qh74kpEXwvQ3aEsKh1JntRKfi+I/pE1p3kI7g5VX0He/gAPXlIsjNUZSDLcDQbIQLkmPChJbQr2Fyht8/Q/TNcXEiekdUYDFlVOAK2kDiMln46F6az7HMSVpaGG4Xib7/+WYO0IEEb5OL3BqhsycrgY2SxFdmioaKm4t7hPb73rR/ww+//HscnZ2jrCGWzlqRZg3VKQi+q4lm6Ywtl0EoW434iGrwcKkQq5xj6jtGo4fDggOVyDdmiCBhjmE5P+S/+9L/j/HrNV68+Ro8C2BLohRImB5qs1R6NT2UyCsUM+taGIazZ0ujJyoQsUjLrGsajI1COjCQcxpjk4dWyqR0eHAiDye/eTL5nt92w9h6jNddXFxweHHA0OmKFlsSUEJhNJlx3Ay9evGTwA7PxhDD0xNaSfOBgfsDoUGPtiNEooHykGjVUznL34QOxUwipIM6ledWAkrCdrGS7tc6QcIReJKfKR3RMKOO4f+8h/dWG7tWSua04cFOIiS5HfBtYfv2Ky687/Mhw5+EdZt/5DpU5plaSRptSZgjg/UDnL6hHDYcnEy6v1sSYCL144ehhSy7yxpwCKfZoEpvlFV03oLIs5mHo0dFjK0fGEokCBOgKQw1Zkbwn6Ex2DqUttRuJz1gUmWHwkat+y3K9kUKlyJoCEl5krWFUj/F9z+J6zardcHW94NnTxyg15tGTb7PcrFheX/DF519Rm3Nm0+fcu3eXBw8Pmc1gNrEoAykYtlEA4GQcaXbApd/irWLqFa4dUMYyqEj0GaxG0sNlLteHTG1qTD2m96CyIRqDthXnXy85nBzjsCgrg4jgA9ve46KlUo4vXiz4m8+u+Iev1lysLdnMOU5j7r3J3L8z5ezUoEczfvbLz3j73beZHp7y2YsX5KoCWxUvHy0sbCOggpRJFmUVVgW0bpjMjni1zOQGJo3j4cmMdafoXm5Yd2B0Zj7X3Dme4KoJLzewUZbGapSF4KDSihGafsh0KTIeGdre0BU/ommtuX+QOagVQzYMFrJR+JB3tqdYFLs6eNtlTBiYmsx52+NVTYhZ/I914vWra57OBhoicfWGtF0ycIxRilkVcDnxqy8XzCdj3r07ZVQ3/IdfXtJnh1EenbcQN7g4kOPAF19e8/RshuWaJw/GrJaWvhdJSD903LlzSl05FsuNJLzqjNHw9uNH/O6HT7l+8yVn9X2UG2HNmGfnH7H0GaWqsnyTyFhLcRAzspfaitfnl6TU8/0P3+Nw0vDLT77mxavXdMowcoa3Hz1hvbhi2HSMtMUYePH8NSe25dGH73CF5uDwhI+++JgmZu7ee0S7ueD44BTlYVrB+auXLK81MSqePrxD1DWfffUCH8WjV+eA0akwpgbZQjUliDCjskcTQO28wYLYxOQiT1QaqzNWefrtFdvVhQB4xQtwp3bQWYBqcmmKtIQtGCVFTfitIMiqqkhJfFy7ruPNmzeFeZMLG1Phh6E0goV9EaRY3YOkqVjf6FIM7wp2pHj0/YApBbNSisPDQ16+fAmInCfsPFvzLtxKGpcU0z64UgiLoRS8Zs94VYiE0RgZENyWGKZ0w5iNIcjnKmzR3UBRqxu2g/zkDVhrdrL8FNHWFtsDCcHwKe0HpQl5hlOMJRxM7rM1hkzGqJLbGwLVaMTZ6QmrzZqXL1+IzOtWKrQms1ktRMEREtEYlNHkHESuagzWKPrQY7TGVhXbzTXOmcIc0KQsQD2F7SIhdJSGQVQyWpny3Xd+Z6qwOOUaagrrN0hogqvq0ihFuqEXFnYvrG/nHEeHR6VorguzUIKEQKR7WluMdWTlpbkuTXwImePTOyJnNlqYkErYZWkn96Mk2FqxplGuFraEmzK5p6lTojk8IOSIBVw9Ipuapm4wJK4v3uCqmul0jLUGkjCBytIRGZ2SYNaMpDqnnFC1I/gt2+2Wtm2x1jKZTwr7TyR9Lou0PuZWniljRVEA1NWEulGk4MneEH3H+vIblldfcjKuOKpn9AdS18gekUhK759ObSztdk1Yv2YyrsVqwUsy9Gg6w6lyjYwToClFnNIkrRnQJFWjbI1ppgLWADF0hL5FKwHlMw43nnH69kNO7r3NeP6I8fyMIfoSirRmcfWC5eUrhnaBzj3J91xfvSGGDlJkGHoqV6OU+CA2tUNRFUluLJYZfs8yWVxfoZSwntbrNfW44fTOjHo8pTGGbAzr5ZK23aJyEslfsuX5EBalMjVRRVLuSN2KbrUipp5RPcJWDUlrmqZhs7mmXy+pRkUqGSIHzRh9bGABoW1RNko4SUikoRNf86bBGs39+SkPDo5Fit5M0dWEbEaFaODE77jfMAwd1tlSv1fyfJa9U1sHKLFFy9IvHN85xZL47NOPWSzXfPt7P8TYuoBokeVygfcDd+7dF3BbiyWQyoqkbJGmZjZdSz095js/+iPefv8DXrz4ir5d0K+v6LdL3nzzOV9/9o9cL79G+YGmrjg8OMBZy2wyJafM86+fcd2uCnNMcX1xyeX5G37vT/4VD97+NnUzInjP9fk5X3z6KX23YegHuiFyevcROiTWr14xOjjAuDExFaAnq7LPFHAq3WJCAbuE+pRvGGKSxq4kUdvZckbJ31+vl2iVmM3m9H2PsY623TIeT7j74DHx3iMePH0L24zo257sPdvFFYNOTI+OqUZzvA/cufuI+dFdsnb0xXfSGEtOIn02WGLKKGVpJodsN0uur68Zj8eMmwnu8FhAWNfgGk1G42OgMZlhu+D55xua4wfY6oT5uNqrYDSaNK2JIaONYtsqrq83dB004zHboeVXv/wZn/zir9gs35Bz5PSdH/In/+3/wPT0HTZbCQx1VYXvB/q+pSmMwhADOYQCwkHOoQRWq3LupeJxL2SaXeCOLiGsKss5WjcjYgoMyYvyIoOrGqpqLAPxBCr2YCLC+YokJVVvDmKZI31kJmctPxFC8c5u8FEkuDJUFQVPTLcGpXHnxSh+qMaY/5+5N2u25Lru/H57yswz37kmoDASJEhwaoqSaEndCrXU3XY4ot/6K/gz+RP4zW8O2yFLockaSIkSJQIkQBAooOY7D2fIzD35Ye08t6Bwv+tEAChEVNU9mblz77X+6z8URqV8P7mAEvgUPQoBplUZZOccxec2x2KLdKvQGWCuRBmEobZsSaCERJc6alifqG3/vSUwcbteRaGnt2sc2CqSvqo8ko8AuLmci6U6KVLvVOofowe/VAkMjSltf09d10xnM1LOrJerMrz1pa4ZTJp0GbyW71y+mja36qisFCkImKjLMHSQgg+5AhIAdQtyynoxaDShDMWk1JPh3+01lnZeUZQEwjJOeYhjGvxFlQRt5tswqK/aZ+VtbTb8v0AMwkjuhp5cfdWCYssGfkVVNXxufYTVv/q1ofcdq9VKFFCllkxB6pyhPkxkQk7kJGQECXJ9tX6U+lc8jPP2/+V26FLfC5fUGUtAl/dMlGkqK2xW0HmylVwS1GBHUayctLBFrXVbAHtQg4UQygBLvlsq60uYm+K5KnZQ0icro1ivrlhtVtjVNePpHrP5gQyoek9G01SK8bRiOqtIacZmlbi8lNBOciR2lYCLRmrQ6NOW2JcRqX+KCpTY1FidyTER+168fHUm5kAOXnzhcyQnJf/Nt7YAg7fvcIbKPpG3AK6wjWXNDIGUKWVRLof+FTLJYEuSX/nzuvRClpQrCVPtx8z6ToZhXctqvaQNsfiJB9CBEBObrkd5ee9yYb6HKGrE8XhK07hCEpFsJQGbi40pmqzExskZR+0cyUepeRXU9YRoQemKpBxm/hr17CF2fIdgpmCKLWeSFz6rgMqR6L3kDLQ3aH9J8OfkvMbaRKXLHghgFGPXSLaJqwkp4fsggcSvDEdASDz/vc+/aZBWJBdO/GGy+LGEnEka6mZE5WoqDPuzA773/r/jN7/3Wxwc3EfXY7qYRG6aM03TyAJUxZvVOpErlE3Ebjf9YVOXTUjkiYIvaqWIKdB1Pfs7C0KfaLtOXlaXIMCbD77Gf/79/8r/9r//r2z8CabSGDOIPjRKWWJOUKaJRonHGoV1KnR0AIUaduNhE5TBJClFajNnVM0gJWHRFs9JrUAZ8cXb253LH1PCmLy8PgelSH3H+fkZ77z9NrPJCFUYOXXT0AXPpt3gKks1HtH1PUd37tI0FZWtJExHg+07amWgHmFtIIYl4eqcqdljNhmzbHtS32NHjTT9ShcWVSQXyjnIlNlZS4qazfqGsFnicqTbbDh9/gLTZ8ajChUHD76MzQ4fA30XiH3kZrOmXa3plz2Lozu8950K14wxlUYFi7PiKVpXmsODCbs7hna5wtU1jgU6GmwKSGLjks1SNsQcM5U1pJCxtmI2c4RuQ9QGV48kMV576smCZjRjtrdLMx7z5ReP8asVMXmUduIXqIUR3vmepGXCeufwiK7t0FWmyYnnz5/j+05CbpqGZjpm0k04OT/nb/7+p0xHMybzBdoqqtEedhLovOfqYs2j489wHyUO9sfcOZxx52iHo/07hNAT/YYrH+mVRY/nLIPBzyrquieS8OuWPnToKGCHbxy9ylQ5MrGW1cUZo/GcoDKTu/u89u++SaIh9VYKVaXQpkZ5WK02nNys+PXLK375eE1vJhw9/BaLOOIXj664Snv85KPH/NYHR+wvKu4cTqk/c3z6yWO++4MPOL7oeX6a0c6inLBMlDZo50gqQYyy8WvIVqGU5YsLz9PTS95aJL7/3j6u0dRVBBVRumJca+7tOu7vGeZTx/4m8ujK09FgHezsRo5mlnGuuVp23HSa2dgx1aB6Se6dNo57O5oqBrRznLVwsSoedBqcLiCf02RvOL5qWZhEo8CGQBcUm5AZuwAu8+LFOdUy8ebRmG+9sUt9Dp+cnPHum/d5/8EuZy/O+ZePPuPRjmOvbpkaS5O8pIvriE49NrWYvEabTA4dy7PnvP/mmN1mwupsziePlygUy5sllTW89uA+N9cr2U6yJkXF6ek519cHTCcLTp8/IZlrpvM5B1PFxcsO60oQXEqFQWvI2dAHTywSm5ig33hC3+JGkXcfzDg7n/Lx02uSytwsV5xeXLPetHzvG+9wehI5fnlKvD/n408/5x8+/JJHT08ICUbNitfv3SV3mb/923/m4199wvn5FW+/8ZAffOd9lG5RyQMVZ8dfcnETyAX9yllYBtvmtCQuW51JoYcUSwELOQU0EWsUWveEfkO/7lm3K/rumhS6bcMghXiZjpfadvBbTWrw/NKYITHVmjLrz1svpBA8ZIRt7pyE6wxFn/ekIHYQApzJZj/4s8YCMubyc4ZCSXzLi50OiCwvJZ4+fUYYGEDOkpOI53Z2d4khsF6t8KEvLNzBgiFvA8FSCMhcMBVWKeKPl7OcW4hHWE4ZY8327EpFYjQwTLY+uoDKxQ9NCdi8mM3pvadtOxRgMltmsPd+W+BpLWm+oWvl70rD/RaWtvcelTNWCTvPrzc8f/IYHwOp92K5gch/s5JnH2MkhyhBFGQqW9NUNZtNh1oYlBLrFpAGupnMIXt0eZ5DMaq3NgqxVCryzAT0L+d3howEfg1WBwPw3/f9NkU5hEDXdXRdR9tuRFaX0tbaqW5GpVEo4VpGhlhiPSKy6boMoIVXJc2xNo7JdCGrMYnPmjEVqTTHikSOEW0qnKnk3bEGlDQZu/dGCHs7s15tWK/WdD4xW+ywt7vL6uaG6XSCrertMELa34zSRW6Npm03GOOk8QGsc6TU8+LlCcZY5otdqmZCygVIxlA7R785I6cVJjkwoM2EbISlUIlxNBsfCpPCMh/XnD2/5sXLC47uvM58cUQU7hm9Fx85bYUdq5AcAh9a2k0UiwJbk3Pg4vSU2PfUo4ZZMyIlz2a9ZDqbk2PGGEVVWJtZV6QITV1Bp7lZ3WC1B2UYL444vPc1Jnv3mezsg2ros8Y6y/XlM9ZXp2xW5yTfolNHt7ri9PQFPnomTU3KgRC6Isk0TJsp5EygB69RRop7pRVNLcqTzvcoI6BBM2pY7Owym87ofRQPTUQR5tsN3rf0XcRZJz6+boPvz+ijZRlOWHcr0mZFd32DCsIgSSqjKotRGt8tCaxQl46VMfiuY76/Sz0aM5nNaLWiR4Fz+G5J6jM5Skr1pJ7yzbfe5q39+8RVYnJ4QLBzuh5MLSEvikRTO3IMhL7DutI4o1C2wSJ2J0aLN2dKmeATylmwjtcfvsvBZlOYu6EkdcN8NhW/wuBBKYxyCE6jQJstO+7qaolvNxzs79HMDnlj5w6KBMFDjFxevODTD/+OX/zTX/D8i48J3ZrNZs3pyQkxdMV2xouPsobdyYimGfPxJz/j5OVzvv7d3+b3//C/cHW14vz0BKsy1ajhwb27HF9eU1mN73s+/+xXzPZ3Obr3OrgxtpoRQqRpKtk72g2D7yaK4m1aFB9DL5Uim4349o1GI9pNJ2ykZgRA33vazZLBf17StDUxK3YP7jLfOcDVFReX55yfvGRkFaFb06eePgV2DjQqaVZtRzWakLSAIsbKGZRLkKwu502MUle7ZgwkYvCsVkumkxHGicBZhiRiMWONYm8+wufEZnVOXHW48RSqKdFatIM6J4JWdJ1n00KIFVXtiDnx6MvPePrlx1yfP6dLmd077/IH/+1/4cG3f5dVZ9F6hTMGsiKGhLUVGFs8mG97QPIAXrCVvMciXYfif4rCFOnLMFQ0WlSMJIVxNQZD7NeEvqOyltCXA8paQhTgzhlDVErqPpVFZp7EWkHOL42yEuhlCtCirQBzvfc4KyC+tQKwKH3LbLTWiF+tugVYtxYnZHKQAMOmaTC1wmorvMLt8K3YXkWxzRhAOfHtV7zqGzsMX0Hev1QySBS3tgYDUPjqkFsXEoss4FcHxOn2+/JKrVF+xiB/V0oJI1IBeWCCiqGwsImLbL78DGMdfR9Yb9bbvntguuUsqpuMWB0pRPJv9ADaFi/u4lRvjCs2CLZYJIj65Sufgg5+Fdgs9RS3wKjKqQDr8qysdaKKVRqTIj4EYt8J4aewYeEVu6pXGLRDzbG9vwg4mQe2L4P6tzAmByuOUutYJ9YzcBvS9mo2wJbZau0rAVOZmZoxGo1YLpdsVmsG+pYxplgwIgur/FznHNZa+rbDbp/b7bPWBbMZBhBigSDv2UAUMEpk7QpFVVXkUq0FpTDl7x/k+9LHyncWGwonTHgd5B6U5/EI3KsAACAASURBVGMLuUB6n6IkKzVciB6lxGrCOI8xUcBNI+dfp40EP+fMxdU1dT2irg2jpmLcOEaNYjpxxIXDXVbM9w9QSVQgOSWWyxVa+8IYDTIYTmIpgE1iN4AGlVAWAWOThtCDMdIrJk/OUsOidGG2C0EjRlUsYnR5V2Vfy0DX9aW3Kj2/EmVZUplQwjhjDFvCgrBk0vadlDXhSn8zQueED73YbATPzfKGTdez3rT0IdAW1buo8eSZd21L1/dyP2Jms9F4r+R6MTAMhMoAExRVbXGqorKOuhI7zOAjWtc0kwV2tIuyE7QdEdwBxu2QtGAPYuWhhbxAIoaO6MV/NncrlD/DphtS7uX9Lwzl3vvtPpG8orKOJlsZJBeA/1X7O7Zvw///5980SKsAlcAomaYJiytiKse4HjO2E77+xnt871u/wbtvfYPZbIesNJsYaEPAKSliB/+VnG4XDBlSiKU5lpubi9xUKSWyqspR1TVaWaL3VK6SRMfo2d+bc3p2QYih+JlZnHJ8++vf5qdvvc/PPjmV6aext4tWFX/ElLaNnEqUhqpMMfIrV18avaFxJ0u41nyyoDYOH9cMCZW6zPoAmkqzvzdnMGDOWRrqk5NT5pMxo9GITduitSGGQO97xvMZMXqqUrj5rqchszNqqKcTji+uiAFGJE4eP2JntsNiPicZQ1ivWT39gl0y4/173IQozMwyLUxJpB4xpTJR1OVgN8VsXw4Hq8AaR+NG0IpXWi6m5TEkprMJVim0VzR6hCXCOtKtMk8eHXN8uuT0asMHP/R8/4e/y3iyR+gTxlRUroLkODltOT45g+xlbWSFS4EUN8TQYVyDcxVVXbNe36CsYTTbxYcIyorXoLGEboNPntwnUu2YNjNG+7vMV4HOnHB9c0ZUicYZQtuy3qy4Wa8ZTaYsZnOMtpymK8bTKd/50Y9Qf/on/L9/+ad0vsWNGsbWsZhNmUynbFZLkUSsVsROknCzSuhaM5vMSGnG5dkFL84yj548YzI/54/+6Gvc3Z+z7p/Sa1kn7fqKVXT0OmFqmaRZNUEbR50yySRaJxYBWnek3LFeXYosanLInbfvs/P265x8fkofBjlozbIPfPG841ePrhkfvsdHL8952U34z3/0m3zjnV3Wq8hN+ys+e3LF/Xd3OLq3z07juO4zB3t7/OTpC44vrvnGNx9y/dOnrLSkVmJBm2obQqWMAqXJVqGN+PIlY/BmzDJ7WjViUWeOjjKvxTHH52uInvbmgo3dsFMn7s3G1KOG487Re8/DXc3RQqF8wlSKJ6eZqCKTkQBEMUEKcHqVuDO16JhRXcRmg9WWrDK2Ah9g4xM6G1bZMao8TY6M2cC6p2KE9p75XBNGmudnl7x+/5C9keFed8nycsMdu2IfxcZf0mjP5599xv533mF1c8PCefxyDQgTxqQs0iqT0dlzevKC9cEhmp75SGFTRzYVu7s7uMoRQmA0arherqWQT5rj8xu+fHnCa/sVrraMdxZcXF/y3jfe5dH5Z7InokrC5tDABlTYkPuWSOKNhw8JmzUffvQr9n7wDciJ2aTBpguSV3zx5WOchbffuMe8ydyd1zz54pQ//4sfk3NHNVlw9+iQd999m9PjYy5OzjDK8OOf/DPRGPYOjnjn9UNOn/yC+Y5js77h3v13ONidcrM8pWrGxKzou7ZMgSUYQnbQBEmY8SmFYtuQsSqyMx9TOcXJyQu61SXtalNqgXS7327LXeFhVnUlvtelcUMj4IiTqfwti0EKjyFAT0ArkeClGPB9f5sC/UoBPbBXpWAScFFBCYvLEtiBFLF2W8BD7CM59pQ8aKy11E48G3NKWK3ZrNcCCBepUs4idROQQuFLKMO2cC9ArcpAkd1n1PbPphQJbbdlHwxJr3LelMI/JVmjMaGG4UrM4oPZeyiepiFEOaOVouv91m9LGQnvGhg7sTCMhybMKinWYx/wsSdsmyWFzpkUApQgNKVkX1NZbIwMCqct93YOGZsRy4sV+bBYD0mvijaWZjyl29ygctg2U+K3NsgGyzE7fLfy3XNZS8K0KGtKyRqIKeH7XkAvBCDvuo7NekXftcBtAFzX91jn0EaYhBQQVhoIC0aeYUhR1oW1yG0v3wPxbNSmNMRlACmBIUZYrYU1bLScw+REUykaZ3FGEyL4kaWPinWf+PKzX1EbqcdU8qISMI4YZa0aLbYsWksQiLGa0UjCiUIQ/7HLq2tImfneDnUzIVP8vsrzTdFzcfqccR1xbkEOHdnKPVBKk5OAcyqLRZGrDHYyx80Omc12qOZzWt/TREUwFL/diEORlFihaK05u7xhZ3eXUVMTycS+49mXX+Lbjtcevs5iZ5fgO64uT4FISopq1NC2G8bT2TYMT9a8xdgaWzUsdu6wd/CQ8c5dkm7o28horGjbG66XFywvntFtLsi5RRNZXl1wfXFKjJ66KYC5ynTdkr5v0VmDEl89FLjKYZ3Z7jkKzfnFBahMMx1LgFhhwd9cX5Ftx2qzZrVeMqprSaNPia5vaTIoV5OU52r1hKftmjUdvfGoUcDahPEykPEqom0Gn4hhLdK/VcdZd4Jerjm/vGFnZ8F0b45uxqik6FY3DP7akUTygVndcHeyz/X5FbPRHarxLn2vWK9XTGez7XVmlIRzra6ZLxYFRJQ6wLhazrIYC7ggfoGhj6jJmKqZYiuxNxnyD4IXKaa1kjtgjUY7Sx7yahBFnUaxt1jQ1dLcrzth2iul0EkSs5vd1/ngh1Pee+8bPPr4H/nVz/+B2F5zudyw2axZXl9weXlJzorxaMT4cJ9R07C3GNPFJR/+5M9oXOKD7/2Q6bTm9EVH37W4quLenbuk4Jkv5hwcHXB9c8HlxUtG80O0rem7DkW8DXfSlQwhtIBdWt022iBrcz6bc3V1QfC+hI4FBr/znZ0FflwTU8JVsv4mszkpRfoQ8TFAD8vra1QStttkPqduarlvObM8f86Tx484vPcas70jposjEkYs04gCpBfGnniIaup6TFPV+G4tgYHZU9XCDL++umA0mZKVYTIaYytHSjDJIpXdrFvx93MzkrGoKBBZDPI+oMSy4vr6krMnj7g5fky3WeHmd/nef/xv3P36b+CT+K5q6zDO0vkg9W8B8mIuWQJlQJsK61IrYenJeS/XNTDStLW4qir7d1vOVQVZ/CJdPULHFkLxX7RGerKUiElsR2KKmCiqC6uFJZiVAGim0CyVEj9ZoqxXbUsodTnvBqCUAr5uKxmjcdZKCFVhyvHKIHUYNKboydEQ/YbsNLqSsWeKqYRPDyBeyYvRMhATMDtvSUcDwCVl1WB4Us7xV8BXtb2fQ4iTKF2KQT+D3Bq+Csx+BdSl9LylAhxCuI3WxeJAahStDBmxehFGaWa53pS/51baH1MqNVguw2qpCI22hdUpt1fp0ttHCTRSOpdhr4LC9A4pI05WsXjKlj/7FXAZBk+G4d0dSFiDL+1go7ENXFJiQeBj2nrzOldvh/yv3rPhXg/Xl8twaiAADKos52SvE/WS1JSyH7P9LkprWZuv/N231pFpy8SV52ioqxFMNMQs+4k2AnQrJQSmtt1K6Zu6Lt62psDeAytZ1hpILTUEhg0VOwOPgcKq1JpR08jaTImQxE80BFGuqqHmMEMda6hcLeuQwT4tFUKfRpli2ZEy1soPFo/UITdCgPwYPCEgYL1TWAOVNRgDxiaU8vR9InhNu4JLEjl6OaeUZRMUlbVURqOrok1TldhFhFiGjB3OaOazCcpGum4txIecUUETAwRUuScaTBJFnKKE/0mtFwtDeCBnDF7UwsTmlgyidVFsS8iv1oqEDOcF9C1DAQYLT7N9R2/XSKnF0WhTS4aUcYChqjrqekTXdaw3rTCvsygMlQbTNNSVDKFkKGZAnibi1z4EPCraVsI8YzRUtqKPMtyompHkiVAR7YJo9tBuStXMQNVoW5F1xOSESYZMIMeeGD0ptMRuhQkbXFqiTC97r1K3Q94s7GJRJQVh2DeGlHvqJBYlkAtZcegl8lf6iX/9+TcN0mqlqaxDa4OPCR8TtqmpXcPe5IDf+OA3+dEPf4/xaAdlLG2UNNOUMsp7bD2SyYBSEj5RJi+5bLwppxJiIF5AWxaJgrqSKcuwMEPwWFvRuIq229A0lr2DOecXN+KbFhNWBxrX8Lu/9ft89vhDrsM5OGEPUWQjW1kSg8+PFBYq5SLdubU4GM7VlBIqCoDrtGN3vmBUOXwbSnNoSuMs1zWbjtjbXZRpoEgyJpMxXb+D1Yq9g32SD4zL5jUaTWXgEnr6q2vOzy7lpbi+YH3yjOb+fcbaMdo7oDGK9acf0dSOxihCFvp507XcfPGI3cmC6ajBa7beRimpUuQIlKwKs1ZkTxqjHc42GCyhTdTeMXYjooloNJW2mEpBEHN1i6FRlt3plNF8QvCJ65sl7arj8uUZn374MTt7D3j/OwdUTUOIii5orm4yXRtIAaoc0P0GFXs8kZhauebKoV1F1hZMhbGKbCTxcjaeM53tstxsuHj6jL27D5jv7LPuEs8eH3P85TE5e45Pv6T3LfPZDgpH2wV8jBweHdF1PfPZguOTM9o+0+VMZ6ZssiFkuLm5JFz0aGWxbkTTTNhZzJjvjWnmibTquL6+5PT0mJvrGybjKdpWBJ9ZrZdkDA37vDjuWa8v8D2MZw/YPzjglx/9I4pAr8RQPGVpWpVTbIQagEeAmTSuaTPUvqYajRm/dp/dN9/i6qajXXUs7JQ+V3zxeMXf/fwJHz9esWaPb+8c8PXfeJP1P32K1ppJbalRfPebR5xcfExGsekUVycnvDi7RmXLG28f8uTRc77/wbu8db/iFy96QrKS1luK+qxyYRpUaBRj27GYWNoE3lfMZmNiNnS9Z1Y3vHW3pjKJs/Mrotf0QRGyxeSaRimmuWVF5OqqYeQzOfcsN4lGN2hgXIElE5JYlHzy5IJPu0t+61sPWcw0ocusNhLy0PlE6xXLZQCt2Ww0eM29UWKuW16bN1yvL/nWOzvsqhVxf4cf/7Lj549e8nvfe53X7+8Q+sTHP/uYvR+8w9H9A75lRxw/fcLBbMbrd3Zw7gV//TeP6IKHypIRUDFT0/c9L06WPD8ac7Az4uBwh3fbB3z6+Ck+GfrCrGwmY9JVMZO3jmQsv/j8S0b2ATNXs2o1//zRc5b9KV0ndiUhyyGbSGQTmY0N3333IRWBk7ML3nr3AX/3jz/j8ctL/vzHH9E4w9PTS7Q2hBQZVZYfffdrPNhpMPT8++/9Af/X//3/8OmvnvH229/kt3/0bfq+4+TsGL1X0a8tVTWjPj/j3v27fOe9h7z84l9w1nPyZI2xhr/+4u94cV5CCcIGkhYvJoJISzT4JMBl6NaksMZoqC04DcZGQnvK2fNT1qtraVTyAITenj+yFxd5ndIY50DLHpQQP1pttMikbSVFSw5bewHf99uiOUaRpQ1sVF/YtSlLwFVKCWOkqdBG2EdDASmNlwBeg+fVkMzqCkvGdx1JiT2A0VrkmaVIzSHS+80tKJxTYRQnfOqLrGxonG/tDJyTtN+u64YZ4bYR0mXyq3IukrJE9IkYA9o4XFXJtRb2a0EOySlz3Z6XBscIS06Sb+SmpyHIzZB8t01QvgU+kUa1sDn61IsiIUvziZXpfwqR7EUlkvVgDyBNjtYGbTW70wUH4z0MlvXNGu8DxlqcM/g+SkNX2AZmADuMtJhbySgSphJDFMm00ygkWEm9UrShbhukYdgaCkAtKcQSXiWSLlDbbqMU/qVJjGWwO/gMi+Qx0W7WhBCZzqa3zCZKWq8y2wYrxVyaOCsqFm3pfSD0ATeqmdQ1lQ40tmNSiz8qxnF5FZhOjhgFhSWyvDxF2xpnrYQzaQGEU8rUVSXrCymuR+OaujL4PuB9Yr3paOqGyaTBVmN6n+l8R9OMxB+1sGmMcyQith4TckVKCpXUNgwpZaisWBVoo3Hzu9x/b0wIa7r2gotPf8HxZ5+hmxF7b76NGc0hiVzNKI1zjr3DezTjKePpnHazJoWeyXyP2HiUG7HuPDlEdnYPqKqqSGTFU3p9s2Yy1qAsISVyViwWRxzeeZ3F3l1MPSs+axtWN6ekMGa9umF1dUFYX9H3Szb9htB35OgL26QqTZEMKCQsMhC8Fq+zwmAxxddQF3ZRTJmqqSVkz9bi09m1XFycU9UbFos9agvXvmPle2azOePxFFdXWOtYp8TLuOHZ+oqViXinMBocFo0kyCudZOAVEn7ZYUYynQxJwm3y5Zr1+Yr25IJq3jDdmbPY2yGNJvQqEDaZQIYQeW3nPnvNAhMrZjtHKDdBh15S7H1PiqJci8ljXEVcLjk/fcmdew9IZbgUC3Cj7MAAFA/0GD1tuyZUlZx92gpzUBmygrbtgSyNdN8zXxiMrkgxEKKE8cnAo8LORMmXCpnC+xZnFF3b4ruW69Pn9Dfn3HvtfR7cf4PjZ5/z61/8Cxcnj8l9YjaZE0Oi9y0vT87QRthE9w53OLu85q/+5P/g8vqK3/7dP+AHP/wBFxeXGFuxvtmwXPVM39rh/lsP0U8ym37DwahBIaGYoW9xdY0xtcST5AK0GL4C9GhdPEetwTlbbG40TTMqvU0Qf0alJXDYWLwPbDYbxmMJrGu7lk0Ls9kOej7Hdy2JRN00aGVplxecPPuM8+efYXUPRCbTuQS25sTl+QmjyYSmGaO03TLzctKkpAhRMZ3NcEZIHO36hpuz51y/7IgoDu89YOfgLhGLyolRBXVtQS9pV0vaXKHdLjo7jAJrxUt1eX3NydMv2Zw8IVweo2Lg69//97zxwe+y8g3TTnqMpCyREsSWlaj+ChClrZM9P0NClC3K6G1viXPCqstDTydqTwHBKiF4kLeAeka8tWPKZGOFJasdLiRSaHEakrUoKmKsqZuJAKM5ymBGFWsapchGAm6HMMu0JfncApkxJoZAVeckEEppsJURv08ftzXBAGy64kMpFg8B71uiNyVMy25Zk1XlCnAtiKPlNkiKctbmlCX0zOit7H9gGN8qloZf30qsByCwzGvI+aty+ltW7S1zt3TTW1Bu6KGzErsdrc32WeUYiwWE2vakFLkypT/PClQawgstlbEYY6mqmqqqYWDQRY8EF/USLBXF43Xw70+l15UaAqlRCvjM9poA0hYQk7pR9lYyolzaStFFr0VG/OszZRAlv9f726ESCEgdyhB3uNdSQ+pbkHMgZaTb77C1yBrqT8TGQgK+EkNobX4FkN9aVShF8AGPL8GrqoCjjqwg5lBUNRGdZGDgdFnbOaEGK4d0WzttfYpTlCetS4RYef6hfJ/BanHL6jWGyjgqFLN6hNUDE3dgjnJLNCAXVVux2jDyLGRhyDAQ9VWChbWWEMr7naV2zIVhS+7AhrLODFU1Yr67EGZpghQ9KXb4NrPZdITYlbAtsdpI0UkwsWuobS2ZCn5N17bkGNmZj3jt7QeE4Dm/XHF1fklcX7HZ3NB2HV4bYt+hk5ArUKDLWlVZrjX1ggfEKAGZxpiyrjKDdYYQMkq9mxJKi0JJbEYo7/Owlijv1JDNoLZDiWFAIe+O+GBrU9E08h5XxlIbh0mJTdfRprhd20ZTQkSH7+PICOFMleFK1wdUgh7pCQW7c4TosMyp57ukekHSNUmPybqiTwbjanyStZNIxLghtTfCZPfyjHRocUTB8pQiaNDWoKOoZZyrsa4mJk3vA8v1mrbrymBGgi2TNuXaM31/q8z7733+TYO0smVEIgpvDFo5nKo4mB7wh7/3R/zge/+BuhrhgxhTazIqyoHTdj2Vq2WRlw0DrUghSBiZltAgNGUqYLYp0q/6rAyHwEDn1lZTqYqYPJPGkecTblZd8TPVWJN56613+Pq7H/DTf/krsELHts5gsiZpSCrJJlOAy0LFKdMSxKumXH8Oxf9HZ1TOVNoyH02IfcJ7iN6jtTTsMWYckaPFgqapUVnkpKowRw4P94t0SADSuFxikscZQ2rGXF5fcP3ppxzcfY35/TcwOzPOfv5PnD/6mMW735QJjBHzZnwrUlOj6Mnsv/EW58+fcP3iOerwiNw4lBqJJFjLJFH81GRjNKYwrTSSAB9asXJIlokyNNkSEemwqbUYiitJEOyDZ6QtMxTjymGmBkvm+PqKbrnixeeP+En8M5aXa37rd36PnYO7skb6ntx5XJkgx2KirV4x1hb5kdDSrZOJklJgrKXzCUKi2bnHveaAozu7LOZjXrw4pd/ckNslSkWs1nRJcXV1zenpGcY5jLXMFezMplhraFcrptMd3HiPzz//ko8/+Zh129E4w2bj8f0SxTWguDifMp5MGE+mGKOZ7i2Y7+3Qd57rqyVXV1dsuo4+yNofjxsm05pVu6LrEjG3rJ8ds4kO9JiYe0LaCMCfS5GnCgqThTHpTYZG0Y2m2MMjJvePULM9ro43JF/z8ZNrPvz8Kb982nPRTljmQzZ6wc9+veG/vvcaD+/f5W9/+mvmc8P9+YS378749tfu8U+/fM4f92sWNvH9b7/JvXt7LGPg7//xOS+PT3n9jTt8eXXCVRtRyt4yaLVFKYc2iVoH3n0w5eGdmpOLjucvPeu258PPVxxMLA8P57g6Mp9MaG9aYb9rg5c3jC5LYW21JWXN0kcqZ2gmDbEb7oMwv29WgarSRFMT1YTrjWKuFP0mAI6QFN0m0/aw7g1rH/Axc3WTuTzveTCpebhT8+HpOU8ftdQ7MGsqdiYNT44vefTsmoOJZjwGT+SzZ9f8zt19HuwFUjvlp//8S0K0PD5+wmjSUPuObnkqIREqiWl8itx0K/767/+F77//Fvf3p7z92i7Lmwseny/J2rJatWLzEtZcnl8x2r+HGzdses+L857VuOKzDz/l+DKTtEZXtQTeJZnE5xTAB6bG8r1vvEPuLjjam3G+bnn69BwfLOeXHe+9ccT7b815eXrF549f8vV33+WNg5q//uM/5s03Xsdpw/Wyow+K0WjGZ79+xLRR0K9457V7jKqGX3/xkr39OW/cm+PSFbWBuppiqzkX12sePz+hz65IXCV0UOtMjhmbenTuIURy34kthI5onalNhOy5PrtgeX0BObFYzDg8POTpk2e0RVYvbBIB9QC0kfAsrWRiK7JS9UpCrC4BTqZMeCUtd71elwI3FysaGfhlMsEP4Kje+trFkNDOFTucWBgfAgpL21OYrQGs0ZLS3fdbOZ0q3rYqio/6JnhsYSso6SC3bBalLMZaNus1lbXUdUPOidVqWTzOMqRcJNJSkGoUUZfGRanirRpJRgrp1HspXLKX9ZKzBDBpg1UCUIderts4h1KJHMRbMxHKvZGPMRL4NQDCAljnEnqXRL4cAn3vpfnRihzBZot1FV2Q35MK80QbYebmEPFoajvnaPeISo+YLeYkA21omVY7ROsgeGFLVBVoCdNKwZenICCyUqn4TGuiingfGDy4BIjNoDJdu8F3LdY6XF0JcIpClNO+SL7k+gffWGV0sTsovoZCyNkWwkpuR0mwTdicqLXGRLGjQBtG4xloy3K5xMdA8EECTpzBWoNVlmDg+tmXmLpmPLqHtRnaU2zekMKartvQRoNpDvH9krqaMKktlxfX1BNNTJYQAJXQRtGMRjLYLFRz56Qg3bQdq+UKHxRaN9h6gtZuO8Ctmwm2GgsDKUfWmyWXF9fsLqZo46hcRVLN4D65Hbz7KL7xlRuJPNhY/DKi7IzxYpeqiVR6yVh7glb0MZIzOGqMG7F757ViVWIxSd63PdsQ+w11Y6lHU148f8xmecXbD+9zuDfj5PxKwNEY8P2aiKaqJozHC8bjKbOD16in+yg3RoUNKfew2nB5ds5qeUWKPZWF9uqaTz75iK7v+OBb3yImAfB96Ag5EGPLZDzCaOh8RGctz81JWGf2EbRImo1V2MmEmBJJGbRVQEUmCzOlXWObip3FnBhgvrOPdQLQequ5vDnn6fqarhZPOhtkLUZdKvBCIICMUQbTTBi5Me16Lazw0kjHHMEKk2X57AXHz19QjWpcJawZskbriocP3mbiRmAqqtkCZWtcramapgAeMsAAGUCslldUTc2m2+CqCTl5khJZsUJCm1CSZ2C1FTuUvi+gNqAVOpWQtFr8roO2tKsbtIJmtotSmthv0M7iY8RgxNswp63diTYNzpSwpn7F/sEe68rwN3/5ZyxmNf/D7/wWd15/l4/++cd8+fFPqbLHWceqvaGyNW3nabuO3V1h9BkSX37yc5bLS37nP/wX3n7v22jraP0zjh9/iVKRew/f5ODOPYxrGE/3WHeBLnTMplOqpqHrM71H0B/EI5zSOAteYfFevP/yIHvuOupqRO83eB/KntfTVJUwsQoAN1j2aOVIOTMej9hsVmz6lvlsIaxBA8+efMHV+TFaJR6++Qaq3qFtV6Aj09kElRecnZ6Sgmdn9wBlnAyclMjfjbXEXNP7jsppXFXRjBraqxt2piO69SVPH12hbcV4uoOrJowmC4zVkpexuqCq19R2TMojfJagvW51wfLymBR6ui6we/99vvEbf0QzPcTZMQmN0qIq0NgCoCWCT5CEFatiQClL7z1Gy3pShbGstIaQioIiD4pbdKkfVZa+LRZLo5zFSkBHT/KteNFjyMljdKYyGUciW03SFcmPiFqyR1Lyogah2OpQwpWUJhKLXz6gRG0gTEQZCgj2JKCXKyFBGkpvWTLhM6gsKhSVxA/dKCUWJV2mRdGMxuWdE4uvnKXvFn/OVMA4sYIQYwX5TkkxCDvL4Fl+3gDimEKIGgBeY27RnpwHn2VhyeVUws62F1bKti1CJEP0rPIrbNdBrVpS58t9HJixufwcYwpKG4fArQrlLMZNGc33me/sUldTYZsbhV+3tOsLfHtJ6Fti0oQkZ7lKcWttuL3kLSgrapPBS5bh3wPAvWUKZ/ENz5LLM3jJD7ZJOcYCbhpSCOhUAOksNlBlzkxKbAHWwU4qlTrzVcsCke7jRwAAIABJREFUUzIJBk9Ycv4K2OuqaltDDv9sra70MLp/FTuh7OWiODZOMka0cresQgUpB4wGbS0+CPFMm8K0NamEpZVqqLxbWWlUGtZK3qq3FANNWd7TFAM5w7iucc4Qc0+lrIB8SrzuYxbSB0HARGtdIddRhmIyYBzwFIolxNaqI8s+m7MwgwW5EuxJWwGKtUKylUIme8msmM5GOJOxeFJMbHrPzXLFuu0ZQN2Y7Xa4n7OoX1SEjCKkwMXVJfOrBffu77N3uMvqZp/U91xdLDk5O+f87ITN6gZlGrRpSakjZRnup9gh1jK3qoyUUrFYE6A6Ab0Xm0rnRCGgAGVkPQ7BfMPDV6/U61syB4IxDGpAreQ9Hmp8GfBY0BnjIrWrGDc1m7bjer1itV6z7jaiGAuSHaS02e4TQ59lrSFT/MJNRmWFszW2nqGqBWp0BzM+RDdTlJLBf9bCSk+qlkFnCES/wfsVhCVkv801UGL0i7D1NTkbKJ62MXtSZGtTNp3UjCdjwR+SWKaghfCThr0tFULKq+ygf/X5Nw/SRjQxZoKGcTOj1lPuHbzFD777Q2bTBZu+R9sKqzU6J4IKaCMyaaflhfPebydzWisqJxImY8z2AE1l6vKv0wn/tTyAYtoMmpwijTPk2tKGMpnQllEz5jvf/B7//PO/gRBRQu2S4ANlJTwL8edKZXopi1rM4ykvfkwJnRQqazk8yRzu7TCbj1heXhNTEPp9adbKsuHe0R7OCsA7jAVzzjhrCN2K5fMTXOPIOnPy+a9J1xccvPU1VErMjg6Y3z2k1RrXzJjsHnB98hyTwGuDzwrtKrp2CT4Ie0prJnfu0MfI1ctTajTV/Xt4K1PZuqmoDeTQUxy8i8xGkwtACkBMVNrRuErkkioXw3dpnoZQFmMNKgS6sOH52QXnmyWj+RTnnLCSNi3Hjz5nc71iWjf86D/+j0zGY1K/Iasen8RsX5UJoc6K4MXD2BcJrtEWq4RNXbmGrCzOKZrxjKM7B3S9IYaO4xentMslVkG2cmge7O6y2NlhtVpzcnqKs5bReCxgQ4azy3O8iuxMRhzuH/DTf/wJ1y9fYGIgk6lthduy7gSIX10v2aw23Nxc0veeyXjGfLHDbDpjd3efw8N7vDx+yeXlNclHnj17zs7ugqw1q75Fa08zHZOTw1U163UDOeDbDeQeo2SS7kuAT1QWPXKk8S7pziHu4UM21YKnL4/55JcXfPxozVk3Y8ldgpsSck1SFedXkV9/fsk77z/gV49f8rOfv+De773LfFrxwXv3+NWjY04uMstK8dpNz/3XEuuzlum84ePPntPsznjrrUM+/NU5wTiwRbatFJpIpSIjk5jVhplV2JnDrx3HN4nOKzY+EZRFp0ylNKOmIhtFpyyXbWRiI8kYnNVklcWXq5EiuO0iIWsqZVh1EJKE6iid2D+cYNNY3tecmI0sqzVcbhLnm0TrNW1StEERk8EkRfaBw6lm4gyvHe3z6NFT3tzdZ7GY8KBXXK9v+OiXn/O73/8a08UO9x6+yfHxGV88PeXuwZiHrx/yxd/+nMurxKhyvHl/wfWF59nNRSl885ZdmNC0PvLo8TPm9evMFxWHBwuenF0Djqw1fZAGqF1fMds/gFSRsuOXX7xE50zAEtyErMWXLWUF28Nc3B3Pz2748Je/xtHz4ce/5vllC87x5oO73JydMh5NuLM35ejggKvLJSpFTk5eslxfs+5a/vKv/oLLa4+1lh//0885OBjzP/+nH3Hy/Esuzs/xXcASOVxMeProc1Zjx3q1xMcrzq82dD5R2QkqCktCJsPFM6zIWVPwpBRxKjEeGYg93WbJ6fkpMfSSTFoYp33vefnyWBJry0cVJKxEOgwZTVIQOAXOkI1MiTvfYWqRmsZchoRJGoKBRSv7lsIoizJSHM+m4vntrDTQAWG0SzEDIMUcWQQ9mSzhdDlT5UTTeRoQ5koSwY+PEa8UnkyvwGrAB/FV02I5k1ISr9aQxI4hZXzvaZoRddXQbtYolBQGkjojoZl9X5p3uUNkpPhNkTCwDrIAijFlCZqLAvRmHQkpQJDnlJSwDlEFUC6y24GxEQqjVCEp8BLEIJLM1PWFQS0sFZvL2VmKPaU1PgjDYOthWxjIGWkoEprZdEZTj0iqYpMS7fKai8tzZuNZaQAtWiXquoJ5JKyWdJ0w8IbQs4EVNcgjX5X8qUGSWoAtH+Q5xFh8yqDYOuRbuZk2ZKKwIrXF2qp4crFl2uSUCL5HFc8tlQ0xB3zXsWk7xgwsLAl4ubq8QhlLXY0w9FQmYhuFrQyushjfU9eWejxlPBrj6Lg8fcp1f0oOG6azHarpASqLVK9fX0EMTOZjVN0gqjlp6oxxWF0VywMBb7wPLJdrgo8YO2I0neKDIuQKohTWVTNCOwmMSjkWUMFy98GbTCcTQlKg6yJdF1aXVw5nNb5d40NbwpAqQuhIGNAjxjtHTA/ucnP2jEyidkUVRSKrmqQldC3nROcTIQuLXVcjYuhY3lzj/YaTZ49ZXz3nzqxjMb2Hs5Zx0xCTYrm+wQfF6w/vc/TaW1TjKc1kH20bGcb0K5aXJ6wuT0Wp1K+BKEEZmxucgfFOUT1pCD4Qo/jG5RTEkskY6li8ELXCGEUIPdkOmQdgtHTjOmlSsmQyzjiyUphQwmDajsViQeVGBG3ooueqX/EybHgZVvRNRtUGrRUGWF6tcVVN5RybrpOmNSXiJmCSQSUIwUtTkkTCmpWmGjlGYxn6BO/pi9/oUP/eGe+wO5sRe0/fJnLWqGywRrPY3RdWnNJYK6ykuqo5OjpiPJ3gk6ZtO7SSPTE7cLbasuW0kVoZoO87eQedIwfFxfFL6koz2V3Qx8Rk5Gh0wvcdoV1iXcXZyyd0mxUHh3eZL3ZBBdqrK0Jome8eisVIjJw/f8bf//Wf8s7X3+OHv/kjfOf58z/5Pxl99Anf+OA7fPDb/xPGTPnFP/wJJl1SV475dIpzLTfrJZ9/+aT46yVuLo9Zbi7ZrJf8Yep57/3vcHiw4OZyyqPPPsWHxP3XXmOzXGGUsJpTt2a9SfTtmlXbMp7s4MyYmAI+tihkH92sE1XdoIC+bwV0DQFXWZTOrK/P6bsN+0d3WPkNXXsNyrB3cBczmbBZb4gRqpEt+7ciJRiNZzjXlH1IQO+ryytyFg/JGAP9+hptPVZrprNdAfeUJpd6riAgZAUhBpyxrNYruq5jb2+H6c4+Z8fP0bbHL9ekDK6uUDEw3h9JAFEIjGpLXU0J0dOFK6r+BhPHoDVPr5+zWV+w6VcEV/H++7/Jzp03qEfiVyhe5ZoYIsYIk90ApIQvfsJEtQ2qtEoYYjEPANxtUM5gLaAYFBLFImdbSQxqR2GERSeS3dQXxh0SVOhsTex7jHIY3bDJpvgXaiEV6eJRn1OR8+dbf9yUijekEEOECamKF6IRgFlJXxaDBGIbXYB4DVapbWhnTpngI5U1EAMah8oelcRTn1zuXR7Op1ugIeVb9qMp/rWZW695uYb0Sl9emLt68Gm81a2/mg+ghwllYafmV3724EV6C6DpoTgGVWy7tIIkYKXKpefmNuAqRpHYJ/4/6t6jybYsu+/7bXfMdemfN+Wru9oBDTaEZksioaAUpMb6DPocGGigmT6ExorQQBEiGZQgihRbCBANsAF0d1VXVVfV8y99XnPMdhqsfe97RZGaisyIqnwmX+a95+yz91r/9TeaenLEfO82bjajbhfcvfeQB+/co53VvH55zdOvnjCsAqH4wocYC1zNzgJkWy+9wRQUWov6KRZrxS3akYoaQ29rlVzqlvwG7CTngl1IaJjSwl7WReHFCFmLHZIu+Ed8K+it6/vycyCEN0G3W0A1qrhjloYQ5F6VV7gN8spZ1tu25jEFrEPJuUH5ntvQra0lQ0ySoeMLYKuN2BY1TU07aejWG8Lo0cNILLXiNvxJrB2khtUgjOIs3shKyzPogwTyoQT8rkpgqtqSCXKSnA1d1kF53yYXH+CUCsAeC1Cbd+9xq47bEhZk63oDEKact2p/tjaP2mjqpmEyP6ad7jGZTKgrg9WBMHb0WmFUxrQOU1ma2jCbz2jbhvOLS0JIxeZKwF9VVN0pR6KvqOsZ1kRCzLx8ecXh4YJGGQmhclC3t5genIi0Pz8nho4chImbtCMrgx+XxFQq2TQIkJoVMQRZp0r2wozGaEUopA1lRZ2hC8Fku7bf8NDVW/shu9cv10+M2Sh7RN61GkYY/tahUFT1hGaSWewdselWLNdLLi7OWK1XdEMv2E0ZDPjgdxkqOYHSwnbXSjFZ3MJO75HcHrneJ1QzrG3k3hlT2PLiv761NfDDCpMGVPKy5+1wv+2gQIYk2jhisMSk6YYeaw0uC8boC2nOGmHAb58HdMmvsEbWUHzDsv93ffwHDdKCIieN0Za99hDn3mV/7yGHRw9IcYpSBlvV5GxR2ZODHFpaK1zl0IjfhhhhvzG13k6GspKgFGD3IG43qN0rKJuoHGxaGtssHkA5C0AwrcEZxXIIhLjG5ZZ37j1if7LPzeaaxjUQM9ZYrHZl6jkwhg0+D2RXJom8meopFC4Zmf5rSwoJQmCvnaELu8E1IvWLIaGCJ/mBysCDe8cYHYUpWhhMFNbo+vyM4eqSu9/7DtSGyfKa62cvUMd3mU8X5L19QlULMKwcqWkYlCyUFBMRcNMpw+qCsFmzGSK2qemqivbuA7p1R/Ce1liGDClqjJIDw1mZWmdSCRYBihwhjAGVFAZL7VpySgy+LxNEYXykAlxT5J4mKqa2ZmwyKWuctqy6EeUUYbMk+YF/9b/9U0w14yc/+xlNDSpssCmgSvu884rSmrad0k6mwkDCiNdM2XDFq6YiZ00/ip/W8mqJCh06BCoN2Wj6IJ46xhjm8xlN2+zCd7QxbIaebtMBhn4c+f7j2/ziz9YQBiork8+cwBqLdroMVWVdpJQJ3YgfPOerU149e0ndtswWB+wfHHB4cMjtW7cJ3rNZb5hOW07PXrNaLzk+PmQynbG/d8SsvcsYPJtuyfL6nNB3GE2RXMLgAypFtHUkVzNZHHJw/F1+/UXgn/6T37Eaj9no9+irOSMy8Ng2RlnBLz+75tadBT/7w+9w+Xrg9eWKWwcthDV3b8347EXmmopffLlmE684mlXcOt7n9dXIF1+d8/0fPOb8pObZFcV/VjOrHJM60hhLDiM3y44rGzhaVNw/mRNszeXVEldpll1ExcR8b4Fta86vl3TR0o+ZykcqK4dsUhqfofMZpwBtd6m76zGglWKxqNA642Oi9wmLJQ5ScJ9eDZz1sEoTuqgYciaE7XDEs/GBW93I+85wMM28biteXY6sV884PFzw3uO7/PzPP+O3X79G5544RqaV5smzU95//F1M9nz8wWP++rMX/OjjRzw6cpy9rhhXHZfLS2Kk+FRKSry2NWeXS755fsrvHb1DWysqAzfrDXox43K9ptGO2/fvgzGEpAloggKNEesSBYog3qGIlD8jjAsUdGPiT3/+t1CkzNPFIcPVFd1qyfnVkl/+5it+7+PHnF1csrpZ8emvl/S3a26dHHL/0R0++dEnXF9u+Ou//ZpffvGSi2XkT//PX7CYWqLf8Ae//weslx0X11dcXS559mSDT4FYiofKtThXFRZHKIFTEXIgxAE/erROtA4ciX55Rb++Yhg2iA8QAtyV82XoB3r6b+31sp4Lc1XLVBajwEDWWZQBrgRkOLtjj2wl8SpntmmzosCIZfoq7M7ZbM6tk1s8efqEoet211ak6ZT9GtHPpEydMjYkptpxiOEgwX5UzFNmamuMFYuWjVYsSVxHz2m34SKNXJjMKnmMslild2weciaWAiJnuLm8xDm7Oz8VWgDwDDlGcgjiRRjE+y7FKHLGDLmweXQWOb5WhUkUYmGNCAtApYwhlaZVmqqcxKNyG0QmAKjY+0hKaxY5eJACTyuFNcIg2hV/ZR9PKZMGL/6AqMJoyGKhoFSRGCrapuFgf6/srZ71amD0Pc/aCXdu3aUyNcFWhODxgxcropJwm1LAVU2RIoocLOVMBAm52TaiScJSEqVgbFoJQdS2vF9hVFOaBRTUTb1bl9ZWxfP1jWSPLDJZcmIYeqqcCYOEcIzrNVeXV+Q4sjg+JnrPsPSE3nN05yHKWEzuOF5oxtAR04ixFp8zd+7eo1kci3/68gaVPSjLmCpuOsP+bEGMLSQwYcSpgJlN8cVLLOeKiGUMMHqpvTKB8/Mzum6gbRfUkwOayRSlHXmI+LCVVKrCLDDlnNMYNFUzx5i5eOgGUK5GWYdVEg7Vdyu80hhEvtd3S6Kvipy3JhmNNxNmtx5iTaatNH64wWSLshada1Sudt6TfhzwYaS1IiutF1Ouz6958eQp5y+eMrEjv/o3v+DJNwve+fj3cZMHODulXZywWJxwcvcxdrZHMhZnWzbrFdeXL+mun7O5foEfNmgDwQ+cn5/Rr1fUteXRwwdo6yREYxtwqAJ9t8Y5AVi0s2grJisC8mSauiKrqnjBbWtUSnK2KuuwNKKVwiiDtkXqTCIHz8p3nKU1L/XAuGdRthKf5FRCd0NiDCO6kXsAkHyiX3boVHynEVsXSj1t2wrbVJhKGO9WCaNIqUTIoIPi0d5dDid7jNcd42gLk16esbpuSlq2KoBKpu97pk1FSuKN6EPxlXUGioRTIeyytL0OxqK1eHumlEjjml/+xb/kzq0jvveTn5KSJgSxd/EhosaBuqrYm895dfGK4eI1vlKYpmF9fUZMA4u9fXLWRN/xzad/w+XLb2h+8AnK1fzkP/vPefT+Rzx/8TU3g2Zv/w7f+ck/xFYtn//t/8XV6XM265coHUsGhi7DOGGO2zRw/uxz/tf/6X/k+r/4hzz+8IdM51MePniIdYbN6hrvPS+uT8mJQkhQrHNk9COz1glpIgT80KG1ZTKZ4325PsZQ1RU5RoboCVGA8xx6Gu3ZXD6nmcwYU+Li4hJjnQC1xjAGqS+mszkSRFXL3mUrmS3kxJ07d7l5dY++u6FtJlzerHn9+py9YhOCcUy2IYaFCScgkvgJOyuy+NliwTD0+JBxzYLj+++xP5/Qb9as11csV5cYa+i6S0wtXt25qFssCWszeei4Ov+Gupmi+zN8d03XdRzffcz99z/EtTVtXaPN1jJDmKhbmx9hIFu0ErVjysL23ZJFBHA1KBV3QOSOxJl3xYUAjjljdEapSPC+gG8JP/ZyPqJ2nqMGRUxQGUM0ApRksz1DHMYmchLgV5eME/mhJbFdCaBmnfg25hiwriqHpLxGpbdjQ1WYuBmUAM7aWkLwMgwsoKEpPqzWiS3DNoBbQqZUuVa6sDffkJreJje9HSj1Btjm2+QnioJkJzln1wtTQNS3e/Jvh4Wx+z1qC87mN0BxlqZK6YxBmPZ6q/4pYJrSVpiQSmOqhmq6x8MPf8D9dz9Guwmr5Qbfe569WGGbgdevXnL++oLQrcBvJEyQrfxd/DijEr9Mk9m9x+3g/v9t87C9BsJ6FRf1b7NRt/9uy4TdfggInwRIMlvGbhKWYH7D000xEr1k0Egtk3e1xTao6+17tcVDtiDu9muTvLBim+TYMqFTErxFVGKmrCWpu5wxVHXNMA7bF12ep1xA1CnT2UjXbRj7Ed8PjF2PH0exSiz1nS0NslYSlJjZPguKyol/rNaKum7QWmGtsIGzLNQ3n7XahYSh2GEu2zXj/bgLwlJIAKLUsZQe/Q1BZnuBlS51rjIoZWjqltn0gHZ6IIBj46gri6sVuIhRIylA1w34XmEtMjxTlklTMY5jGSDEQr8DtGHSNNROQs6GfmTwgZAyfb/h8NjRTh1jV3N2GvE+s7c4IIXA8vqCQE/MPVQTKi2Bx14bot7gVcSXgNWcM9FHWU85g0oIQz/v1qNia9MmNft2n3mzluWeyZ/l3bMva4JiJVPsL4PYpGG2frN5d2+dVtRty9HREbeOjjg7P+PV9TXr9YqUZLg2UROCj4yjJ8ayvlxNszjC7b+Dau+iqznGOqmFtCpYlCIVMgxxA6EH32Nzj1ERrWJRxknQstivFUZ6UljXkOKAcS0mNWJLoxzW1GK3FyM+hfI6S39DJsQRaQu34Y7/kYK0mUyXE5N6j2bvI5r5j5gcfEDnHJebitmeEmPxmCEHYh6LEbt4iCafih8QCNfIguHb9gdlkVltvrVxbj/ePgRCCgLMlskpOaFzJBNprHjs9WHApMDUZu4ujqmjZt7Omc1nzKYzKivFwXTWgsv8+a/+gqeXz4tXT9kQ0OgMNYrGtEwnM05Ojsmj56Bu0clhXIMZhakgw45ITpH5YsJiPiUH8cTZtsMikVHUTcvk/n28cZgAzWyfs/SC7BNWO1bdmjYrJlVFzJ5xHNGuJjtHSIGqnjBM5wRX4XMkpYCqa7oM1WTG9NE7DMHjjSVGjfeGdQc+ZroxEkOW5MHC6tJlsttUFQeLPdTZFdlLMa5sSw5lE066GHTnXSPbNg25rqjjhC5Gor8hjCOd79FG0fqei5dP+Os/+5fMJg3f/cHHVMZAJRKeMSHsrJSF5VEJawVVEs/DWDZGjTLyOkI/cnmxommnchAGj+/WIm21CjUisjJlcJUwvH2WNPFhHNj0Et6To6Jp51yt1jx5+kIYL00tDAg/onISaYRSWOMwxrFZrWmqGqNMmRZK6uLzp084O33FdDbj8eNH3Lt3j5QTm/WatqrQTOjWK1bLJb73xP1jXFNTt1Oc0ZAUfhQvJeMqKVicYdI4bKroVop/9r/8Ob95PeFqfEBy9+jVPkEVQEUlVFZlHmC4XEd+8+k5f/+n97h48TnPniuGzhPGnp/8wSP0p2t++fXA63XFdKn4wSczWhIhHfP0Xw88fb3k/r09TtfXjDrSNoaTmcLpIIw5Y1gOIxedZTGHxmn2W8PYOzo/Eq+XLKYtk6alrRzzpBmvOipjqJ0cACFFYQtbhbHiZKXLerRa4VSJN4gQIgxRM0TFZoTXg0KHAVVF9qeW7nwgjzJNzzFiUiYrkXs/u1jzwZ2GxmWO9iqePL/g44/ucn6z4ndPLqic4ey644++/4C7Ry2vL9b85ounXJwtmVSKw8Wcaf2M3335GabbY3/W8vjRQ5a/vsEAjx/fo6kyX375GcvVmhgiT1+d8oPvvUNbO6Z15vRqBakmROiN5dbdR5xfLolZ4YsnnUqJpJ3I5rMnJysS6VCKw5wYgZwcPsM4bjjZq3h4vMeUkW+efEM7WXBxec0//1f/GqMUk+mc66sLZov7/Ke//1NOL1/w7OlX7M/2uXNrymdPIYSM946Dw7tMJ4bffPpbzk7PWG56usGTbQW5Lqz6iCcRvEh0KGb7Jid0GqjyiNIBZxVhXHN1c43vN+KriTRfbxdWKae3igp2nxWUr5Uvruoa19ZkU7zmaod2YhdgqoqkpOlBqcLShW0IgbWlWAVu3Trm7PyM5fKKrlvLZLUAslkpVJDBmlJKAjJRTNGcZMdeTNwJFe/ompME+yhaBTaJhDhnw2ANg1F0TrE2+3zVr/iFv+TrPDDgBYAvTKqmrpk2UzarDT54UQ0GAbxsXZFzpus6AZ6dRcWIjkJjyDt/3cJ3yaIgyF4YCMUoUxKuKRc9S5CG1rKPa4rnZvHjlSAfAdyV1lLoG5k05xh3frwCfOaictwyQDLbUBbhlL9pZJTaNnUJHSV0bzaZYY3DDwM2D1KUjyMvn71g/cGK6WELtWWdCkibBfSxriZlDUWKF3MkxfRGepjl529ZPTHLf1kZnGsKEC+WSymKT6345oklQ0qJqq7kfZF3gUcxyV4uQVAVSWliDlTOsb4+58nXT3n/ww+5e+c2F6ev6VdX1O2UxckdZm2LM5rJxNCYjMvXLK9Osa6inc2xtkXrhtpmDvcavJ3iN8dMmvtc3WxYdRk3vycDm2GJij1jd8lea7FVxZAlfEN8+DKmmhKzYrPuUaZlOl9gXAvaMUaJelBGAr9yfKuhf4s1pZTBVK3YNmBAC0sl+pEUenII5H5FRJLFQ8igNYPWzGaL4hlYUZl9cjfjar3hfLNkyI7ZrfsoPaXSMGsrck7EqNCqoR9Ap+IDm3qatmI2m7GcLpg6jVGe1aZjPTju3D5icXCH2eKIul4wWxxg2oab5Q2XZ8+5uTplWJ/TrU7ZLM8gemKOdEPHMKzRBqrKFX/bQAweUgQ8wa9ZrS6YzyaMqpK1Qd55E6rSYGaQ4VW5dpT1h35Llpk1xlQCrOWMKyyj9ThwFjcs60RuK8xUgqSImXFIxCGhgyaFRIgDugAd2ScqU6MracC891J/K2nGrDbELA1ZVdVgMilBSFIntNrx+NYj7p/c56x/hq1aTF2V9yeeshlN2lp7ZM04jOiU6IaeTe+5dfsBm81AJlK7GqMgbPMNjDQ7EpijiodeJqWOfrzCxwnbUL2EgqqlMhXJj/iUse2UZjrni9/+ivnrJ3znRz/m5NYJ/dhTNxOsrVm+uuD01TMOj484uXOXzkfUkGn3TrijLVeXlwzeszi+ww//7n/Nww8/4a/+1T/js7/6OX64EosODNZp6qqhMoYQe3T2bG4u+Bf/+z/m9dklf/jTv8fh4V0iluvLM5wThvwwjDRNS1XNSBlCTuQY6bprqnZCZSzL9QZnK/EzLcB90oZ1v8QYS9M0DJs1WU04e/Gay7MXLPb3efzuR7iTY7559hTramaLfWzSDN0aUsZZhx97UKIwEVl9wMfEvcfv40ymaiYsn70khZHgN4z9GoJImZWSQMSqsvRdJyBrhqpuSogTVFUtZ6Yx3Hv0PpVz5JTpuhvy88/xY8dyc0WfRmo3ZTo9QOWKzXoNyVNZzbxWOJfZqzTfeXyf23tzri6uaOpI6yJqzFAJS1u7qjAGhf0XMxJIZkQqH6OwnUTdKIxUCTD8tupS9i9ZW8YUSWvxoLemxmhN7PvCmXkTEm1LiNUWz5BwIek3kxXrA7xBZbGzIKVyBqqdd1tSAAAgAElEQVQtHCLnD8WXHYipKDwUMiwuIWTl5ZXXWmyNSk5IjAltqt15rYs9ibEV2loSBh8SlZUArrf9R7dMVWO+He61tYPa/p6c3wJmS+2Q39Rb3wK7d+dBAXvyt8Haf9fHFuRNeVsjsPPFV4Vtqk3xgy2SdzRo67C2QRuHbRbMDu5w+/47HN055ux0zfLmhuwTMTQMl5cM3ZqmdozBMo6QsyFGQ+/F910rUGm3M+9emzHs7AjETuENYzgWFdb2umhtUCrsAO3ttd4CoqoAl7FYJlhTkbKiH0eM2YLeCrMFK1HUdY33XqwGCvj6bwPGbxPTtp+37OeUkuzvWQbs3nt57eXeCbgfC2Artdx6s0EpvfPDBcBolLUkVTxZUyqDpFZUZxqcNWzWCh8iUUCOgvWAtVpsF3kDZCttSAhYrbTUaImMj0WLpkSVZgpAaKzdrdsCI765zjHIcVxQWZvSLtx2CzznLGzzssogv8kAqOqWZrJgNt+naaa4pqWuHJWzuKaWGshklI6lRhVylh8FlNUq48oggcJCDjFJrZNh0jr2inXRZhhZdR0vXy45PR2ZzRoODxzzvYqjOxYVD3j+BH75V1f4QQhESYF2FVZNZS83kFXaBSSS2eUDJCWgZMyyFrd5C9v3vuthtIDYUv8WjKfsAZRtZwv2G60gb+kapjCiCwZXGjVhh2dZ51FTVZa6nTLbO2LvZsWLF89JKTL6gRBGYgV1o0A7lK6o6glMTlCTe6hqD2yFcxVOi+dxyKI6CH4gDAMhrMhpwOQRS4AcSwiiKueAKDDFcqQ828pQ1zPqSpNDQ/IjKXqxJnX1zhpvGLrdvubHAW3FG9uHWHIy/iMFaTWWpnrM3sEfYg9+zDh7j9NqHz8ueXqVuP+gwqqRWAKpKH5uWhmMtqQ07phDxpiSXvz2wpHNx1lH7cT35W0JALDbmN7YIMRdmrPeJctFFIap1dQqEPOGUa/545/8Hh998BHHx8dMJhOapsE5B2i0tVysrrlZXvH81QsMlknVsNdMuX14zPHBEY/v3+fR3QccHx9z985tXj9/xr/85/+CEAur0o/4YUQpkXY5lTnYO2DWTiEvUbutp8gwc2JydCDpgIjnStCWYB160hDywPk3X+Ji5u7D9xhzJAbF4Tsf0U8XBF2jlUMd3uZwMiFN95jMNSMlEEJrzMEdGiKD94RRs+4UoTKsY+Z6k8jKyPSsgNIxZiDhrGZxeMDrz85I0UDx43OmjAaVLib2maAyKz8wkghIMWED7LczNtGzvjojoTHWMSezefIVf/ZP/wlPv/yc7/3gEz54/zG+H4tP05bJpAu3q2ibkWmdqRzGVYQkZvRbX8GQAr3vYOxQ0ZN0QOmMaxyqL2DNdpKL4Bbj0NOvPT6ObKLjO4/fYd11rDcJbSegB3JKWGXJWczWjTE0bUsIIhPRWRq0lEWGbF3NZi1hXuMY2Ds4YH7QUbuKup3Sak0TPF3X048dN+sN4/AS4wxVU5NDwLUNdV1h7ISUNPVkwWR2yMiUb14PPH+14irW3KQ7bPQJIU/JpjTPUv1ANkXGrIGK3z7vOfm848G7dzk7XRKwfPTxA6pKpndPX7/mdDB8/XrNr7/QfO/xPvcPNL/34SF/+dWGutYc7TW8uIno0HNr7qgwxNGwHhPnyXHtLV1S1CgOagjzlsvOkeOAj4lNL9Nt42qqJoBKZCTsLisjIVJGCg6DbPC2VugEMWviKLKgmzFxPWrWEfoQsSFxt8784N4EkzN2s+I3lz1Kz6RhzpEqe3xMXAyJX3x6yn/1B/f5TjvFaMUvf/07rMr84Y8+Ym8+4y//6lN6H1h2PTkHhn7Dn/78r/nw3Qfc2m9o4orXp2ecusjRwQMO9icc7c+ZTSt++PE9hs0VFy8VV5cbyHB+ecMXv/uKdx7c4nsfPWSIv+NytSarliFmvKpoZzM25xfioRVBq0Qo3k06S0BGiMLGygUHizkJsIIUfj/68C4/fHzA/h99yO+en3F1vebPfv4X9L3mk+99DCbz9KXjr379GZrId9875u6tWxiV+eCdO3zz4oxnr5Y8eHDCy9OXXJ69RpHpVmK2nrJIfDVAUohBfBG1KRjGDqsSRmcsHTr3jP2S627N6HsJk8lZ/Eplm4HCFN1Oz+ENRLs7d3SREWdhudhK5Ehj9CW9uISJ7Fi0RXqbv13ASQHMLjTs1atT+mEQ0CUjk2kjrAeV2fnWaaWoU+IoGN6xLR9VM47InKA4iplai9edyxoTIeRIColpiCStCChGYzmp99h3Nf/H1TN+nVYk6yAEyOBTT+gGKYZyLmwHxTgMJSEWdFEEMIp1QM5pF0amUpIGNGWyEuC1Nk7k0N4LaFP2vm0Zm1BEP5ZmbduQSMEjbKJEimCL7N0ZYQvEIFYUOUdSAW23LBsf4k6SVrbxYuuQd/gwqnjulddcV3VRb4gUWxX6St9d8/rlVxzOamxVo016M+A0DhU8opWTYtxkS0iRhDCOCzeYnOSeKCXeXVuGtEIaG5J4tK26DbGEMGyv0tYT31ipO3z0DMPA1cUle4s92okw5ivnsFpTt1M2/Yh2LaZtMK7Fry8YRs/k4ARnIpdPP+dyvOFooYih49nL53z4ncek/pzKzElxSloNjHqPzeaGSMPaO56dnnO17KFd4pyj3yw5nDfY2TGqmoOdwJgZ/YBWmlntGLprrvpUpGr7ZKWIqRSgUeGsZTpr2XQdfd+J36FWaCsgvClMl21hrLTCEFFxJGXPOPakYUCPS6z2BNXidAUGhp1lSaCuHFbVbBQMN5fEHDh+/DF2ccg6KULM9F1HN2wkLds2uFoskS5efo3OHYtFy2RxwO2HltfPnkPWfPjJj3n0nR8xPbxLVU2omgWmbulTZDx7wdXZK1ZXLxiHNTGs8f01y+U1OQ5yT3OiqWvqWqR4aFNCexTDsEGlET+uSLEjJs0werSy4j27lZhS1AOqyH+RIUQRY4o1jVY447C1ALQp6+LXp7jolny+PGczq/HWCuvEJ8LaE4bIZtkTlh41JozSJD/KsF5b5nv7uGlDn4vtyLqjW63JIWGNFoDASqK1ziLrrWyLUw6TBma25eToDslbrNvn4NZD6skBEUPfb7BKkZUtjDgBrA4ODulWN1Supp3tgcq4yrK8uSLVgXaixe1EC8N0K0NVVSX7uVJU0wUffe8HTCYTjKvI44aUFbYS2aMKuXhqVhzefcyT3/2Grz79GybTGd/9T/4+VchY22Az/Pbz35JI/ORnf4/p/hF9PxJDJ+CFqpgu9gg50g+eupqzf/9j/u4/ukVV7/E3//pP6a6eo/EYI4E2s9mUnNyOZeZXl/z5P//HLC9O+eHf+Rn33/uE/f0jRt/j6pZ2ajGmkuBdDLWRwU4/nqOUZrE4xFYtIWYJTqsqNFaUD8bhrCWGwGKxT8yRF8+esF5e8+Wnf8OTb77m9/7OT7l9u9hOZEXlalII9OslXc6Mw4bpbEoYMzlLUKdxDc38UBRZpsFWLc0kcnR8zBgD12fP0LZCGcvN9SWziUj6ta3YO7iFm07RpmIce/w4MPQ9TTshJINGgoZcc8z7H+wzdtecvn7JGHomTRmC5oyzidOXr7h9/yHz6THrmxUfv/+IvaMTYs48/eobvvj6CRM1YFgxxhqVHVYb8eAPosLI3jOG8IZVmoSYI0PDcs6X/TrzbSBiG+SXKWQgbVGAVeLlnLKmj5KRkGNRXgDKaTIWVENMHUkrkoKoEO9NLZYgRkFMoQCQxXrnLVZlSqImrZ0EXKWSYk+xJ0hlCMrWpgD1RoWSRQXmrOwz2hUfzTJU23ZG35Z1vwFTzbfA1zfg7LaH3p5xbweDvf01bzNw3/687dXZDVzffJ+09dTdgRxvGKm771EGNUqL96N46srnlDUYYUoaW2FdA0YTU+Cbr55yfjUwme1z+959rHHEIbNZXjNpalKOXJwaqtqQwwGVcSxvzjh/8QVksfZTSkLaVHmPIUS0ESuSt1//VukrwCrlGkrtMAa/ey9syZzKlL/Xu6+VCithtMNo+xZYFnbEA601TdNI2GNRTWyxjbcHDttg2u29efs+ZmRQv5Vv+/K8aKPZ3obt94qj1EwhCAPcOSd9dGVLuNrWl5Sd5UbOkgWgtaKmQY+RPEAYA9uEBhmuxl29JD7/ki1U105Y0bCr9X0IdH2PMvIs+CqWQYfeMTeUUoVNK4Pz7TVRStP3fekLDM5JMK5Tb+wxU8qI4EBL0Pb0gGayoGmn1M6Kx3bTYp1DuYbKOLG3UqoQ1d4MWnNOuzDUVEKKUYkxevzoGb0nDIYwjLiqAW2oXI01QsRZrQOnz8/E035Rc+fuAVZXONdg7EDMQQY+OWNMVRisVhjA2pU+pNSqIQgBC9jZGpTncftcbgPro2wooj5UUmMVd2i2ShezDXgLCWcNRr8hxaFE5S4M5q2Nkwx9rGvYFgVVM+XE7bM3P2a9WXF9fcn1zTWjadCuwVZTlGmoqpaRKSMNmkiMPblqyWZKyoEQFYGRkANDuEYHj1UJmyMqBcmxUNJ3xMI6T1tbtiQ9U3HYRStHNnNSGsl0+NjhrMZRQaYMn2WtWGMk42gcGfxY1Nr8ez/+gwZps3LMbv0R5vZ/ydLcZ232AINPmWc3K4KytE6CY3zQOGV2B4US2ookrylNXVW7DQnkgbRWPEuMKQEdIezCYLJShc+ylUwIQLv1flUkSAHyKNObEo5FHFGxZ2YSP/z4Me9/8JiqmkjaoooiIUuBNGTOnz3j6sVzfvzBJ9y/94CHd+/zzr0HPLr3gL3FnKrSkDykRGUdr0KgrlqUHsELI3PLyDFGQdTszee0dQOhQ6kEOb6RewBpSGwuLzg8OaSezLhZr5ns75GmDVZpTm7dZnNzwWrs0K7i8P0PyHVLT5HeK42bzaCp8bpCW41OIzkplKkJSbFZjVycr7nuejqm3D2ZE7Ji1YvnUww9VArtND6O9N2a9c0N51++QPUjVE2ZDiqytsK62RYUKJx2WDxBFT/bkLBoxm7D2PdywJSpjMnQEOguX/LVZ4HGVTy+fyK+MHhCjrIBaEMcu3IIJtCKup1i6wkohUmgrCuG2+CaioPDfTYXPUPoZfJZQKG2rtn0I/0wMJ1O0VpCfmKKpBCIGYI2XK86/uYXf4nv18zaCSkb/NCBSnh0OcCl+Ry6gXHoBUbW4kPZ9z3OtUym89LYJZarJb/97WdoY5nNJtRVTTOZUVcVB9MprqoJ3cDgN6xurhm6jqQU7bSlrhusndLFKS9XjmfrmqtunyHep88tnT0g6DlZS8o9unRGShXmiy4VhGWTFL/6/Jz3//guq5uen//lb6lnn/D+nQUPb0355N0ZP/9Nx2S2RzAVSSUOJ4qPH8741VcbXr5cMd+fMTSBHNeQIntzaOaaq+vEOmj6AK8uRu4e1ThnaZpEoxw6V7jsC+tBjOqNk1CIkBLalIm9ylRWUdeKWieMVQQlWJ7JUDvF2Hu6TWTla66TpvcKGyEuE3V/waNF4IO7Cz5/fkrcBPZmlntHM66vep6eLhmj4nfPV3x1+4r7+4aTkwV//dk3TBcL7t7eZ311RV1r/uJXX/L9Dx/w8GTBdz94zC/+5ndcXF/z/qNDPvnwESYHnj17zp07B0wmLffunvDi2e/46stfibn5uJIm2Wesq/nm+Sv29yZE33GyP+XF+SXZ1mQFy6trbh/vc3WWGH1Ca1cYjUH8rTMkveVopDKNFsA6pwxpxKUNJ3PLxHnOX3/JqydPMNnwzt0Zv/n8FJUD02nNBx884OvffcHZ5Ybr5chm+Zp3H98HlTna3+P6asMXn/8t6/W6sPEkeK+uNJ2XhOWw9XktB6bV4rdps8ekkdRvWPc3hHFNDP2O2SiT5sRqvd5NyUWip96wzygFZSE0OCsMWYUAhzkmuuWKigm6sjR1i64dytgimxLwTRcfNF32SSGmBvphEGZsCCgCWE02WuTzWZFUQkfEl8goXE7MQuSuqnjPNryrG951C/YXU9qxJ11foErog84Cupgic5Q/k+KmyglN4ON6wmZxm4tXa07DwOgsBo2KsZxjxcstie9wHkd0YdFYrcg+iVRnm0iaIsYKoEwpvLbXFiNM8hwDyrwp6KW/kvJalWYr7lKVt2wfKd60EvZeZauioAC9ZezLLUJrhzGazWaNKWwRVSb4ugSSmLIV5fK/WMBpFCKfMpY+SyqyNRqnNdGPvHj+NQ/v3eaovU3tiuw0lTAlVxP68Bajx+xYB/K0IDYhqvy+dFvWChMspUBIka7bEEPg+uaGkCOL+QJbGGUUxkflDAqNHwdqZznY30Mpi7YO10wENDYVtprz8L2PyNqy6T3tYp/JpOXq5pphGDg4OODVV5/ir1+xrDLt3pzJ4oCYMuvVEqsGAh1Jiyzah8xmhNOLU85v1kynC149f8Zm08t9un+bo4MDPHs4NaWyHcmPaGVZbTZcXI9EDFOlqJqJADNqB5uRkdBS61paLJtuKfYwVtY/6k36tFWWHD39ZkVljTQzSAK6iiM5BWzVAiOKvLN/qpyhqgw5RMZe2N1dP5DQNJMZKomVxenZK67Oz9g7OGR6cJusNDnIgDl6j6trrKkwbsbR3Ue8/8EHvPvx9zHtAuUmGFeTMvTDms3ykuXFK3x3QxpXpLDh+vIlEBmHDcvVDUdHh1grwXHixy/3W5UBkrDwI7ay1G1T6lVh1271Q1pbrP12yE4qQ4mtbBqlcFVVpk8igbXaEIMiKsX1suMyduhmIgFFYyB2iqvXVwQvfsBpDDgt4NjY9/hhBB1wMy8ee7MG1zhCGDh98Yrl5ZI0eJSraCYTjLGEKPJXWxpSm2HPLlhMZvTdyGzvmGZ6QC5WF8YIs1mXJs8oTQwebSzVZEoMntY6yaHQmdmkZnlzjdaaqhEGd4iS+o3Su9CYlGUw+87730cbXdLdE+M4yrpCEZ2oSCbtFDef8N0f/phfDRtePH/Kw5tL6vkRKMPl+Rlnr1/xBz/9KbcevMumD6xWN9y9c18CuEIg+oF2OsUHz2q95mZ1xWI+42f/6L/h5N59/u8//Z8Zr5/TtKYE1Gq6IZHV1nYjY7Xlm9/+NRmYzObM907wUdZ4TgqyQRtwVYuxDaP3uHoqHnlkmsmcGBObboMOEVeLLc4EIRAEH0jZoIHLiwuWN9eQer74zV9x+85dPvn9nxHNlJxh6DrGflMYTZEYPGPfMd2bMPQjMWequuLp62copTg8vkfb7uH9wHSxoI6Wq+Uaax2Hh8e0tePm6gzf9wx+VZ4hz8HRLXKSxOvRB7QR5R5ZvI/DGLBG0zT7zPYSIfY4a+lWa5ZDz/7enMpZNt2Gw/k+7rACH/HrazyRw/0Wox9wdnmDCYH+eoMP4jM8hFis8Qq4EBN+6BHlpIA8ddtSWbHdiEphlVy/mL2EVAkUVxisciYljFyvIP7tWmkq25Bsjfcd4zAUCS0leMmgjANdoXWSYGfrGI1DRGBBVF8aTAnhyWQ5T1UJFNPbYC35nLKoPYT5Ks/V1ik3k4lFqWxK/S4WUkVdthv6bK1FAnEcJCvCOUBhtH2LOfdGIk/Z87fS/C2ouANUlaiN5Hn/trQf2IUR5vJ+5ex4Q6JSSuGq4u9eGMu7gbtC3qPW6Cx7rTD1NFkLUEipB3XxTJWA4pI10G/IyxuynjGdHTGdTbBWcxM2jKmnGwZiSExme9RHh7R1zWw24+rsBaurV8RuAFMV5WcuQ2upLyW8LJFCLPdCCBBaicfqdsCfUyKncqfKwFmpbV0h91EZjUGUBJT7XSkrwVrb+gcB/oSoVb43ws7cgoz/tqfw24xoRS51eEBnsdMw1khdTqZyDheC+DSXU80asU9QO2WDsG5jTORcvJCNLWtegL5h6PF+kNeeRLla1w3GRBmGJ7HMoviZJpk6gNGiilCydp0gHYURKyreRPH41aL47KxFKWjrCdbKkGs7XNn+Wmq4ck4Xy8zoU/GMF/a/0rY8gxFtNXUzoZ3MmbRzqnqKse2O2GCsWGapwlzfelVr3lieZIT1vfM/1Yqt+L+yEkpWG83Qj6yuB0K2aFeLhZNxWOuoa0NuHcvrjovTDefnPdZofBgwOtBYS8yOGAthQhm0cSQjCm1XKWIYCGNffIO3BIQ3Q5LM1kJUgHkZGMp6iyHurF5Qb+6LQhWGuLzrlDLayF7pip+sLrjNrhaWTxJQiTB6U4gobambGWiLtjXNZEFyDVEZIi2ehj5alKoxpfZWIbDxhmpeo5TFZ0OsFmQ7pzKOsLrADxeF3RwlMwEJmA8kTM5CIigKbAkOA6MMIRoKLw+IpDQShx5NRJEkJ6vUbmJFIlZzRtVybf4/mLTmT/7kT/69f/n/98d/99//D39y/Pv/La8nP+bCHDCoKTEjXhHhmuO54mQqMrQUQ2EEGZSVKZMPwlpqqmpX1G4PAudkoqwL5T+RIHqaxrK/t0CRGb0EkIifq/ge5hQLODuQYi/0aBVQyqOKv5Is3kylYW/vgJQVMUXGsWf0njEIg0llzfe/+z3+wR//A376+3/EJx98zL0791hM52XK4BnGNdF3hBh4/voVQwjkPDIMYrCfs2zsUpxGfvjJA955cIAPS1AjioRKGqMi1iTy6obTrz+nX12TsmW9vOL43kPyYsqAxVQN7eEB9cEtbDslmopQQDl56DTagE8C0BmjUAmGXnN5PfD10+d89eSU15eJIS8wkyMWR8e4yvHNV9/Qr84he5H6ZYjBM3TiixteXzNLjtlkgXU1CvEjloNta7YswRDOOLR1XNxc8+rsjKqdYOqKfhwhQwXs11OmriGFkZgC4zDSrVYs9ibs788IXoIUjk/uEEKk32xkMqc0KYoPlyoywRgTrm6oJ/to12CMIw492Q+EcYQUiGGUCak2wtZAE1IiK4VPievrFZeXVzIdjZovf/cNX//218SwYTppIcukSWtQVpdDzOBTpNts8JuuFF8y6fXB430ijJ44wmTa0swkBAuluLq+4vLynNV6xeXlJcN6xcH+Pq62TBdzVquOFFUJDtD46Og45Cw84En3Di/Gh9ykO4z6mC7P8WaKcg5VDh3UlohcaC/aoq0V+ottpXn0PY8f7fHl0xsurjWP782YTCzKWV6cb/C5IvSBMK45PG55eTHw4nygS5nF1HDnyDAOgYznnXstt+YWraEfEmNWeAXTSoCXlJV4EzuH0+JJGVNmjKCMsD8JHqMAa8BpKqdpG/FLHoLiZgPLLtMPGZc8le8IMXN6HbkaFIOPDGOgGyLj5oZ3HizIfcfqcuDRyZSffH+C7c65Pj1j6EdCslgU4+oCaxTL5Yrj4wMuzs64e7zH/qxi3fVcLjcQEt957wGLWYVTiRdPv+TWwZT9aY1WidfnZ2hjOD6YU+nA65dPaSrN3sSIpN9YVt2AUZkxJNq24uG9I5TSnF5uWI9SuKUw0FrZD5erDWEUhixZQha9lyl5irK2VJGa+eApSC1pWPH6q0/Jw4pJW/HR+x/wzuNH3HQbvvz6jMvraz746F2chuXFNWen59SV5b333uPq6oZ/87efcnbZEVNkeXPFZr0mI55nWoHK4oEUi5xLKXb+RIYRS49NHb67ol+dM3YrUpLwjS0V4eDggIPDA66uLnesjS3D4u0gB2stVV1JSEgB2HZS+Yz43TUVunLYSthpSQmpUopOYYlorairWvyskgSHhK2HkdKSOKqVBG6FADHumMk2ZxYx8WDM/J6Z8RMz4xNV7A1MTVPVVJMF4yYSx0Am7gpKobeo0lIhcrrSsKgMk3qCNYbL1ZI1Zd+OGYKXgK6MvBYfyEFADpW2rE/xAFfbCiwLi2IbRLFly5Jzaf7jt2SYb/xnEd9JteUg6Z3EdFuuqowwG1KGLABwGD1baZVM7MWLrK5rlJZJu9oySrb/HsqvC/Mkv/HBA2iahv29gxI4VBq5Uh+sNitm0wknJ7fRyhGiBCIpreWcHT1aZfFZVIocPSF4IO1S0YUdTGlKhEWtiyxYkYk57rzcQkrCsNiylwq7zhrQSuS4IUiDMgwjVe2YzmZo4whJiuPZfEY/SI0wnU5J2tCNI6ZqOTi6RVO3zCcN3WbN0e37vPPhxzhn2axW+FwzmR8TdcPlzUCkAuXQtmJ+IF7nyXucM8zmc5q6oapb8eAyllrM6jl9fc7ZxYpsWuqqxllpwox2ckiQdyB9AlLSuLoVwD5FKtegVEVWZtcMWGMJ3vP61UtsVWFsJUqnFFheXRCjqCQuz5+jwpr5Yg/bzDHOkVTxG9SGnAPaOhYHR+wfHNNO51jrCOPA6vqGuqqpmgnr5ZIcR9pmgqsmxJxp2gl37j7kkx/+mDuP3qeaHeOaBU0zhZxZLS+5OnvO8vIlfnOBygPBd6yW57x+9YyuXxebqYbJdCZew2orcZVnTOVEiiMh9YQ8FGaYNCspihwyRU9MgZw8OUeCH4jBE71YZ+TS5BtjsK7ahazGGNFA09TM5wuS0/zmxRPWLqMmtQCWY2TceDYXa2IXsVlJIJ+WQZMuIIEnMb91xMGDOzQH+1SLltnBPpP9PdxkQkARMjTtlFk7o25axgxD8GhTYY3joJ7x3buPmbmGZnqATwbnagkvKewh/RZgIAN3jXWW9c0VkIuyyBP9yHQy4ebmBpSQJ0iloY9biW7Ze6KnH2UvBhjHkdPXp4ybNX7swCiGcUSLASnT6Qw0nJ6/Zhh7ZvN9rG3IKTFpHTEnfJLnfb1asn8gg4+YItbYHcMrxECKmWH0tLN9Tu7eZzadCHlCgx82BD+yWfd03cim6yAnDvcWpOBZXl1x+uo5KQcms31cM8PYCu99kWwbXFXTtA1aW0IMBO/ZKkZ810tQmKtliF5Wniny0sZq1tfnfPXFpygiB8fHHJzc5+juu2DaAqRlYgxMJlOcqyQk0NZMpvPdANJYjTGOW7dvQy7BiipRNVPa6T7tbI+6nUFWTP8f6t5s1/EQO/EAACAASURBVLIkve/7xbDGPZ45p5qrurrZJFsiZZKyLAkSDPsR/DoNCLIF+A184Tu9gQHf6cYQYFKCRUrd7KmmrMzKzDPts8c1R4Qvvlj7ZBPWPX2AQmbWOZl777ViRXzf//sPkxmL5ZLlfMHgYTpbkJdTwOADpEnKbDYnTTOSJKFrag67DU0rQLE2Vhhq+YwkzUiMoW0O7HdrkiRhMl1gbMIwNNxev2G3vseaIASI4Nk+3GMYOF2UJEZk066raKstxiS03SCezH2LjmBP23WixhxL3egDOgw9TV2Lf6yX8FJrhWknQVQB53pc38bwTRmouqFFuY6uPQh4i7Bch7YmuA6in7NysbfoOwLyjKuYb6FHJv0ILmlRAxptjr6O4vktW7DRkZEbQRCj3udohXj+jiGnikRrrJF9WMehkkmS+FyZ2IuM1E45e0f7uvFLmKQRjIrPMUp6G23EC3UEYsJ7nqs6qil4r34Y+4wQwlHVaJMkniF+LOfGTyO9atxHtTExi8ZgEhmya2Pj+7NonUhAExqtcvJixmS+ZHFyzsnZGVmhmU6h63ra1qN1htGW6VRIONXhwGazYbt+oHq4xyqFTnOCkXMrSWZoW8j1szlBxRA3od1E0O7x/btIwPLOPwKz74GpOtYUY+aB856ua6VGH8GtOKQL4XEvHYHZwYvN2Sg/fx9Yf//PibVoEyG6IGtr9AsXew1DYhLpuZIEawxJkkZASnr3xIq9yqScMJtOKMscm1iMkbVkrdgTTWZTsiKTvvfIMh73EnVUkfDe+aCNiWQ7ixprKK0E/IvDPuckDKxtG7q2oe87OtfLcC8OGo72OpE4MAZDgZZeRI81LcccAimHlfT7JmE6WTBbnDGfLVlMT8jLKWkxIU0LkixBx6BSsUuRayhf/jhcONaq0UJARWKMCoHUajJjKbOMfAwrdoHD4cBuv6Wu9rJPRJ92VKAoE9JMPqPUX7KGXBBioXMO1ztc20aAXDA0Agzi9wDR/1o+9xgMxnEthsfFdlyjoxd8bBmOBBkZ0IxrWO6dbKgmsqF5by1GxbgT/GWIgW7ycya+nJwHSZqJRYY2oCwuWA6tp+oc/dDStxWH3YHrzZ5NN4jqhZS+OMMV56TZkpAt6JymqQ40TUfbNfgw0HQ9qBRt0/i543WM/rJSp4FX8dkgCPvW9bhBQmC7vpG+2ksfPTjiOWrj2jZ889uv3/785z//3/g7X3+vQdr/+d/8rz8/+cn/xI39mF4prEK8P4Onbw6EvuKTy5JZMqCDTNiCSaW57zr6vqMsy8hSCXRdh3PSIP3+tC9Ikdw1PH96iVKe9fohNl+R/xFGcHYQdqvrCKEl+A5Fj8WjCVgjfkRdWxOGjpPTi7iRDjLt8yKh0Sohy2dMp0u0MnR1y3azZXV/z+3dHfvNBoMjSSyJTWi7jvvNA03f4IaGvqnp2zaaGssBlyaef/hHH/Lsco4fGpxrMLTo0GHNnsRWpFlDWfTYQqPKOXa+ROUzem0YtAKd4nXKoDUeTeckqTooYfgELX6xRlsImq7tub3Z8+23t3z76obVpkXZGZdPPqeYPGEInurQ8t3vXrO6/QbclkS3BFqGvsG7A4fNPfs3d5h1y9TkWJtJgJhKyUwqj7+L0z8CqbFoFIPzHNqG3ntWDw+44JkVJefFhKXNOckmZAgwZ33AOk/dVGRFzosXH5ClqVgUpAXVds3QNdI8G/FE7PoBYzNpFoce5xRZPiefTFFKUW939NUO11V418qEVIHXBmVSeu952KzBGLp+4GG14t31NX0/kKYZs0lO6PYUZYJCs98d2O33KBUwiTk28v3QS0PdtiSJidP+QaZVXtEdOrq2ZX4yIy0TTs9P+ef//F8yn8959+5dlGl5+r7mfnVLPiv54MPPefnda4ahI00Kgj2nsR+w0Z9y4z/jwV+w9wUdGV5pgjWQ2ijRkKIiImdygEXQHKNlk09TBpOx2zc8uUqYL6fstj0vnpXMp5a2gapXvL1p2RwCt1thxb59u+KTDxdMZznb7YGz8xLXw/YgE8BlrtDK4wdN5zWkhtNSk1t9BFzel2YFbfFann/lHYlWpFmOT6xABiHQdnBo4GYXeLcP3FWBh32PdQNfXk44nWd89+qOTR0By6En9R126EiM4cPznD/4qEQddly/ekMB/PjjU55cnvLq9bUUN9Zzspxw+/YVP/7iY9b7mvuHLSfzKc+fnJJYy/3NNctpxtDvmWWGdz+8Zr/dUk4KQnDsq4rbm3dcnhQY1xAG2QsSespc8/TZUza7A1XV0QyKQ73j+dNz5pOSxXTBDzcrehclJEEkc5vtnsHrOEiCvo/gXzxgXd9zOp/y7PyEutpJI+KEaeyqA59+8IwXzy7Z7bes1isObUvvNbf3D3z80XPKXMJ51ts988WCu9Wa3379krfXK3Z1TV0f6HuxbDERRFWxaFKKyD5xqDCQ4ElUD/2OoVlx2NxQH9biAaQ5epCN+/rhcGC320Uvocfvve+1pSKwkWUpSZo8Sr8Ix6Gespp0NsGWGdmkIBjNELykmQcJvFJIMvuY0ilYo0z6VRBgypjoc+ylpMnShERbEq9Y9J6fkPPnZsE/1FM+cZoLp5h4UH0vyaGTM06ffcrtZkNwNYbYtCiOWWNjiFlQYIIiDZoEwywtqLuWd/UOR2TtuQF8ZLVGb8zHonC0mQjRNkJY6N6P1yV2Zup9qaGclvAYwvn+5P0I20ZAWevI6nlPZjc2aD4Wmt6Hx2CCyBjSRnNysiSxNnrCyt8f2R+/J5Xk0cdufJ2u60mTlOVySV4WtG0X/b4cXd/T9x3Pn31Alk7xXjPEAAkTG/Ouq4/+ZPhHWewxOC7KF9frNUbrGDg51gAStmGMQWmLzXJJXHcDJspS5Ro5NpsVw+CxNpPCNDhC33B2Msd5qDoJDXJuwA2OJM1Q2lK3LcYkpFlBOZ1zcnrGzbu3vHnzmjSf8PGnn5NmKUYbapeSz07J8zky5k1QGNzgxJ7JGNare4pyQl5OMElKmudkRYH3A5uHNauHNU070DsZlOVpHj1TTZRxCVPJaGmQA9LUWJtED9EACFgHkYmsxY948I68mIgHvJKzR+voa5lldH3Lr/7zf2CaBJ4/e4bOS4S/JvcszQqKciIgL4rt6o5m6CmmcwwGnSQURU5iNUNXE4YerS1ZVnJ+8YSLJx9w8fQjllcvyKZnaFsQAlT1ls3DNZv7NzTVA8rXWDXQ1ls2m2vu7t7Rd40oWfIisksTRo/UcT0LQOEIoaXrdzjXYBOxQ1BR/id+yAlplsnnMOY4KDU6+u+maWyIkyOjKnjxzFcR+MqLjMr1/OLVS4ZJjjOavh3Yr3fsVzt8K6x+7WRP81FSapXGzktOPnjK1ecfYRYlzojaQhlDUpSUsznt4GidY7k8pUhKCYmzli6ASTISnXGaTvjR5ROmyQRrp9w9bCgnC5SKrHRi8xufYak1TQRlG7QOZIVcy92uopzOSK3h7vYdyrdkqXncABVHJhdxLx+9aq215FlG11bc3b7mcNgyKaf88PI1d3e35EXB6cUFdVPT1jVnJ5ckWY5JLIvlksGNYFyCc46u7SNQkZHEezey9PKiwCaWbhDmUV6WXFw9RXl49+p7Qt9KgGM8wCZlznI+YzaZ4Ieear/hzdvXzGenXF49x6QZQUt4Y9d1+CGQJKIU3KwfGPpOWDpGi99e38nwfDyYEMbj0LdkiSGxmkk54fTsih//9I+5evExJpviEaZbklgm5URAYC+Di6KcRA9VLT5/NmMymaOt4f5hjU1z0iwDZcmyGUU5wxjDbr8TVnVSoJSmmEwp50vSfCLDIS1DhlGaThxodPUBa40kdmt7ZJuCFsJH33O/ukNpxcnpBWlaYK2mrXfstismRcp+v2N32DGdzfAh8OKD51ycLpnnhpOpYVGKXc9+t6Xe79DBCftNCynC2ESCpiNxxztH1zTs93vc4GK2iUjn236gbluG6Dft3YD3YsvghwHnOgmrVQ6tw/Hf830jieIIMch1Dfo9kFYYnwalLCB75AgYjbWHjmDsozXUyAx8DyTh0SKIke0ZpNc1RpMmFmu0/JcIA8x5fwQ7xXoFIq0sgr8cgSziPj1aEegYmin5GnIfJ9MpRVEQInAhz/2Y96KOn+dodxDrC6nXBMAfhiF6ufI4qFYKpQxJtMwTQNlGVZ0VGzttEdvBqKT1CYoEm+acnD3n/OpDrj74kLOrSw51z9u3t6zXFYPT5NmENCtk+OMHuqZmv9uyWd2zXd2ifS+WL2nJdHHO+dVnLC8+YX72IfOzZ0yXTyjKBUkiA0QX/U+VPxomyTPqH31e3/eFPQYQBbEKECa1o207umgnpSDekxFQl3V8rNeUrBdr7dF64shgDuG4/6o4CHBjMFQE73QcrrqR8cu4fUfbNB/oo/d+37UM/UDXtrLGvYs2GSqCsWK94JyAyChROSuZhghhCqmvxmG6tQIC2ySJQLvGRhsCrTU2DgCUkt+PzNRhGGibhrZtpC8zVsB+Kz8jbM/HdTjagYzXUqYRMewq1sEaS5GXLJbnzBcnTGYLimJKlhUkWU6SF6SZWB1oK+vwfYDzyHJ2otQOMefgaEXhIgkEhYngc2INeZaSZanYOxBwQ0Pb1GIlkCScXZ7w5Ok5k3KKTSXLQNsMbXIYfbB9ILiB4ETxZ6LqRXyBVcxBsI8DzzCSUsb+SR9B2vdmM8ca51j3j4SXCMqPa/nInP29nuxxz/I+4AZ/BMbFksEc78VRmTe4WE8FmrajbmQo1vmBfuhom477g+PtvmPbtuA1aTLBF6d02RLyc9T8gmR6iTczOp+w2Ww47Pc0VUNTVbRVRdNUtK08Y0lmhSzjgwQwRmxSK0gsEpKsRB01srS7OChxTvKy+sExOMehrnn78vX/J0j799ruwBNoVcAr8ZBxkQoOCVtO+OXbO370suKf/GhCqiW9UcmokSRNSbNIuQfCIBvZ++bPj1+KPC3YNS2vXr5GG00fD2I5LH28GX1kFo3fizI+LxOVxIJyPa6vOazekpelTGGQzTx4kfA5H6jaHqcUvRvou5q2qembBt/3tFWFCp7b14FkknF1ec7yZElXN2gGEhNQ0cdwGGTBGAW5zZgWKdo1pHpHyF6RpWtS25GYNm5UgcmkwYcpLXMOzQl4g8JEeY5MRo2STTpJNFpFKn6QZt07zXpb8fr1NXf3O+raAwkmLSmTjCydEvqW3fYbtoctXecY+gOKAVKDYWBw4uTr+orNZk3f7qDpaJUluIZ5ljNJp1hr2ddbKUKOxYVMtzJtebo842Jxzu36gfVhy1k+RWuofUXovciRg8V4hQmOXVvx3d/+ikU54bMvP+P86TldV4NvsGbAhR4VPM61OKfw3hGCkcm60iRtR2gbRp/BwIDHjT1BnPpJM4lS5JMpXoncsqpqwHM47Gl7R54XnMwLDi2R+n6FwrM9rDEKYQM5j/cyMVJKQjnMkR0GfSem63mekGUW5wY22w1//Td/TbXfkeWpMGu0wqpA0An7g+eH729iKMhAH+ZU5lMe1MccwiWVX9IGQ9Bi7h4iwyUokcILIvY41ZTroIXBTmSmJQk+wK4t+M9f1fx3/+iM+nDg+7d78hQKa/ji6Yy7+4ZvVz1bV6J2jv/2p1d8dplRtfDvd3vutx1Pnxb4t4qbHZxO4DSHPIEZClNobKrxWny/0lhsytEgRWwMSo3+PtAOjsYbCc4Knm5wtF5x1yk2g6HXEsjk6opL23J5mnJeen7YrAl6xgTLSea5OFvwzfc/8OnJM5Les9uuUCHwxcdPuL97x9XygsRtaUJJNVgmiyUfnP0BrhtYbWrWVUNWlvw3Xz7hYl6wnpX8zS9+zR9++YIykTTUH24eCGnOF5+9YDafcPvuFW7oOD2dEvwp33//Lcl8zrRMyKYFV8sTVrcVHg02Yd8qcptQpo5Ce7Ztz9BDW3U8uTzh8uqKH27WDNHOAGPxeHQITMqEZKJZlI4PnhQsZ0/57e9es6p7QOH1hIe9YrVr2W9uuLg85YOnc1zvefP2LS+/eUlZZKzXW9Is4369oalrtts9VdWihMxMEtnhIaaXC9hu0NqhXINyLVqDHlqa/Y6u2dE1+8hAkeFRzKr6/fMjsgWOB37wkaX1KLnz0Wu167vjmeCDnDOjPMwRIDXoPAUb5XmDx/UyCb26vCLPU15+9x2SiGzwLmCVZppPmE1nPBwqsVZRioEBF20k8n7gtIOf6II/1gUfB8uyc2Q4DMIGVNqgXWD3cMPiy59wOfljrv/q/yJ1Q7TZjXK+mGxLnOaqWCjlfuDCWv70/BnX3YHfVlsORqqmUdQWxvZKje1QiH7hkXWsHkFOFQMCvPMYo6J1AZEBAcPgfg94lUJfgLXx3UmHI/duBMZHUDfW5jgn7997dXwfSin6tuPm+ka83vxjQTeC6n83DMNHJra8qKY61Lx8+R1JYjk/f0KeZbRNzxB6DJb7+wdevvqeL79coq2Ah8MgA15hDHuGriXNMpySppFY0KOk0RqGgeBE0qRihRri+aCCJgQvPmW2lEFFN8RrKs1I1zYSVuItZxdPQSsmRY7rDlS7Nb2Z0PWaal+BcwzDQJI6kgwOVY0OA11V0VQHJrOcbXugCYGXr17z/M07TOJxQ08+OcMkJThHgsPphLYPaJOQJhlu6Lm4vETbFK+MgK/KsF4/0BwqsaMwBpum2ODwaJxvqaoOk/Yk2ZRUG4xKILJwALEWUFrsELqWoZf3Lrp//ShNNJYkMhNV8KJyUZrFxXPaw5r7t68ps5Rq+8Ddm2+ZP5Wh5uuvf8t0ec6TDz8nKMOgclIdWN1+T+ocs+UFaZqzPDml6yvC0GDVQI9nPp9zcnbBfHlOPplRTk5Jigld1zG0DU39wGbzA3W9w3c9KgyoMLDbr9ltV6wfbui6lrKcMp3Po/+0AAPjYzH6VQtjxuFcyzC09L5HRasFHSSQxWoTZXLxGRREJga3dNhUmjSRsjp639O7IM2eAz802ERCMleHA/umxYSS0Dv6fcvh4YBvHdppST7XlvERNWlCNp1QPr8kW0wZigTnhN2eKEvXi81TlgqrNslzzpYnuH1N3fYYn5Api/UO03mKtKAs5jiXkeYzrooTAfNIaGMtcwwQiT2AhIdYAQNT8c4z2rA4Ocd5J9d4qLm/fYeiZzK/kIT7o72KxgFpXsjQDAlhy8sS5XvcUGESgzWa6aykbSuarmW6WPDTP/4L7q/fSBARjs458izn5PQJ+90DWhsmkwkBi7EJSSqDhu16JcB4Xsg9TBOGITD0PcnknOnilEm54P7mjtdf/yeM6cgSzcXVU/wAXilOLy6Zzlq+f/WGm+vv+D/e/VvuVjf8+T/9H5jMn9ITh2Z+YL/dkOU5i/lM9nGJ5UZr6LuazBWoJCEgAMcwDHRdw/VujVWaT370hzjX8+7dK9xmx8XkTLz9e+iCp5hMqJsmymlzGeAGKazECkdFwMizOD0TCa8X9n5dV0xsFpmPqViGBS0+yUoCqQiS0xGCj8xLhVHRsixJODk9I8SzxQcvQKmWfdiqQDld8NkXP8X7Du+C7IvKc3n1AaenlzTNgTwkNH7Hi48/YWRzJlqR6wBGMc1TCtORhpQ721O3vViiebHk0UYTgqJqapLICBWZtdSSPiguLs4ZXODlD29jboR4AY/n0hDaGGQlZ2pWTtCdpT7s8a5DwmoQz9gISGJEoaZJCMFhI+AmmSTuaE3go0zcRs9TIsAUggyMjTlCqHIW+YFIEjwOy5SKtn2RxhdiXeWjJ6MoGtVj7YQw26T3eRyIjqDvyHoUz1qLSRKKckKSJJRliQKaRhShIn0nWl8+DlbfZ1AS651h8LihizYHCm3NsUcdAUylbLRfMHFPE2sTYSFHchMG7y1ZOiEv55x/8BEnZx8STMZsOUMZxebhlrpuKLJTlvMSqw1N6+haTdsNx5CnIk9RfU4wU2yaUC7PODm/4OlHHzNbTmgqxfqu5u76DYf19yjf0zd72rbBOJncu6DQyqKilUXfj4FFj+SDEDzBR+WQ1kfbQ7G0sI91VAS6j8BXtHUQwspYj4Sjt+z71gcgrzv0PVorvIbgPEbJ9e7aDj+GJ2EIKrqnuiEODYT93EZQbxikRknTlCxPhSiHDBqtEc/afhjEok6JRYd3Ej7m43v0MQTeWivPkFwUed0gtlWEKCOPNUPfdce+4hH4E2uFh9W9BAL6QDmdU6Q5mc2FOHBcx6IkELZznBlFD2ejE9K0pCxmFOUUm5QonYlViUnENs0a8XY2MhQYYfjxK4yWRiMgGwkHI3PaBQ/GYMN47yUPQhOtHYxiOc1EKdVNWW92HKqB4AfKIuX8YkKWa7phxsPmhMO+pesamqrl/m7NbvNAExzBt9iQMdpiBtcyDAKQ64i+EQacS3BDTz/I8zhamRDAh8fQ5JFY4SLZZ0xF1Eofn8FRdRZQEWMb96ARuHcMg4t+2uINPDJxnO9JrI1+z7K39H3MosgN3guLVRNogsEUc2ZZjp8rlMkIIWc9GMpW6tQqnZImE2w2QRUL8sVTSOZUP/wt+9vfMOxeYUNDkhbYbEk3PyN4SPMErYRRHuJwwqMwSNZVonL6QRTSzgexxFSCTYy2J4P3ZMl/HYr9e82k/Vf/+t/8vPjsX9CXH4OPbM740EszoWm3D3x0teBkpqIZv4mbHNHIWnxqjdakaSoPeGzoxgnSOE3p2oZ+6I5SkRGMJQwiQUGKcRUNulX8N0RFXVMftlS7e27ffEtXbyinM87OnhIQ5iPB0HtN7wJOuB60zYH13TtWN++4efua7cMdh+2Kw/6BQ7Xj7bu3XL99C0PP/c07GDq8F1ZdG6cHKPEQOplO+NmP55zPbymz75iUXzHJX5El11hzi9EbrL0nzbeYpEGbFO9bSTPVE4xKGA3MTaT6ayUyJqVSmsZxfbvht797y9ffveXmbkfvU7Qp0DEBNPhA3zRs1zdst+/oujucu6HINpyeBM4uPVdPO84vHVdPUy4uB86uPMP+wPXX9xhVspyccDE9Z5JJwXloDpJ0yqMcxweR12TKkpuM0+mcMknAi1S768RSQkJ5jBxYWjaSpqp5/f1r7lcPfPLlj7GZZXP3A31bYbISozRtdcAkKVle0DQNXdeRlSXzixPKhUiihrZlaHdxzQi44IOHuN6EeSxSnKFrqfc7mq4hBE1dVXz33Vfs9ltmi/lxalqWBdamDIPIjI2xHKqaw64iMUKNTyNLYRg8+23F4BV5mZBPMjrf0fc9m+2Gw2EnG5W2pGlGlmYok5FmS6zOaAdLa59TZT/ils9Z8SGHMKcPhoHInjWaoMUgW1h6huNpFYtJZQXMRScEYwWgjrYN3igOnWaWK56clPzmd9cYbXl6njHLDWfLhHcPLU1IUUZztTCclQl2cFij6CrHtLQUZYobNHlmyFJNlkKWG0xq6Ly0clqDTRTKSvEcIj7rAB2E6d51PW3X0zmPIWCdY3OoODSOQ69pvRQ9AUXXK3xTMS8UqR/oBsXqocZ3HR+eap6daR5WN1zMJ3z87JSryxM2mx1VXfHk8pzr6zvQCYeqo+0896sV64ctr1+95fJiSVEUXN+sOF/MOFmUHOqWr799yazIOFtMsVpz9/DAoa749MOnlBZC3/Hqh9d4AkNbsVwu+N3X3/DsyRP6uqaYlNytH9hXLb1X7A81qbEkRnF7c8tqvWMIwkDpu5bl6ZJ9VdHUYvAfkMmq8p5SD/yTf/Apf/j5Jalu2D6847uvvwOdy3rwgd12x8XpjC8//4TgB7LEYjHc3q3YrCu6XrFvWtq2Z/1wz3a7eWS2ehk4pEkM0Ii+aYAkSLuaTHeYUOO6HfuHd1T7FX1fx30vTrbD+2UPjBD9yD44filEZmXFX1WI4OrI+hRwLUpqRuYBgXI55cUXnxKs5lDXsuYjQyTPcw77PauHVfRpjZJ7BUWRc7E4YTGdc7/ZSO8coItJ7lnneOE0f5HO+MdmwgcOZm4g8x4bP4NDrAfwwnbZVhVZUmKx9F2DRopSHVkwijiNRq6t1wFvNEbBJEkps5KH7Z5VkCJbxXRlqcwit0+NhvgCpkE0to8A0egVJ8xVkfiKx1sM2XQOPUoh378rkQEBkqL9/vePzd8IuHoBnMaCbbytIpGy49YDxMIvNpDDMET2jihanHe/z1yM4W5937I/bFFaszw5wdpEBnKId9mhPrBYzplMJjivZFIeBtq64u7mmsNhT1nkKD2GgDzaPgQnthtFnpPnmQQQIJ9HK/EkI7L8NIGhq9mu7+jamjzLgJF9EtA6Z7ffsVrds99uubm5pu4G0BlV1fLdV7+i2jxQ73bc3d4yXywJwfPVr39JQqCqKxyOn/7RT8mLEoLi9OQCZS1KW0wyo2p6mmpL3zbsqgFlE5GlRnZWUU4BHdkthqbp6OqGoWuZzU9QMVUaVGSwWGFAeEjSEmWiD6u10Z8tNi1jCJtRMUk8AuoBsdQIHmMtSZJhVHweY0CI857qsGe/XWOU5uH2hhA8i5MTDrs1b77+NUPXks2X5OWCyXSJShJMljE/uQA7BZORpjltJ3K4Iis5OX/K0xcfcHr+lMn8hHwyx9icqjrQVBsOm7ccNm9pqgd0VFXtHu64u3lLtd/g+o627ymKCZPpHGNSPIokyVBKiRQ9iPWDBEl4hq6maQ7UTUXTNAxBPDAF240SQCNDT8lLEE9Jj4C4/TBEa42Bpmuo+4au64XdZy3G6GgV0XBf7bmuWwarMSjabYNyilSluG4QtpKVQEQVhC3rMkt5eY7KM1rF49DWyVDII+wqkyZMF3PyosQWU+anV1xdfsSTsxfkwZJ6z0Kn/Mnnf8p0conJJth8AjoTsC48AjHjLn78NYIWxmYEnQlQmxixkAmessxRCl5//xL8wKSYRj9f8UcUMEk9Mq/UmM4tdiNBiS/ucrlkNpujlaKqoH/2dAAAIABJREFUe2xakKYZVdthtKaqGmyaoxXcr+7wLjCdLignU5RJRY3SNdxdv0UHsSvZVzVJkso9i36nddMRVMLF+QW7w56mrfFDB25g6CSorW17siyjbRs2mzWH3Z6vv/od+92Wp1dP6PpWWKROVFpZJiCoiRYpbfcYKqxNZLymwvIV5l3NenXPu+tr8nJCNp3QO48yCZPpkqAMTVOzO+yYlJOoTBTLA1ASinVkO3qcFyWJqASEwdhWe5p6J0FAypCleQQ4PcbYKK/Vx3tCHKKO6ezSmAt7Ci0AvUjhxXMdL0xKYajJzwUPm80D7969ZjqbM5mdUEwXlNM5y9NTKT28QweD1vJZ+r5DOQdDzbRMeHK25GKeM80luLBtW/GRR0d/cwmAskYAKucdaZby5PKU7X7PelfFYcIY7hcIXqTIwbt4HvQok+GCEal6t8P7Do1ncD2Dd1gtVYAL0tegNKlJkNBRqU+GvuV9yTQKYXJG1j5IH0EI79VDARvZcfY44Q7CBB6ZtFYfGZiJtfE5VEdZsjoy4eTsH6W+R6BWj6oZYh9pKcoJi8WSJBElx2az4VAdjhP2caD7yOyMLDw1yqWFUEQc94575CidN6MX6viMA8akIquOnbu1SbRFsgQzJSnPuHj6MR9++gUnV8/Z7Fs2+z273Z7dw54QQ1ETA7uHe67f3HJ3fUe1XzN0FUMvFmNJmuK9IkkzJstzTi5fkJVz0kVJNsvoPbSHjv36jv3DD+zX1zTVGuf6I4FgBFi1VpEh7H9PYi51DhGAVcf9Uhst0mng0WIi/kwgys8dLqbJizWLj/ZmEk4aX4AhhoIdgVMntk2JtegYzpWkCTYVIDQx9mjBYbUhSSxZlpOlKWmaiQ1flpNl8uxbK/XqGOBqI1PTqEfAGU8cJHXHdeud+Ij/fnCcKKuOtWcQMNfFz3AcXPb9MbxM6kkBAfuup2lbmrbBDR6rZf3IbE9FfEfY6lqLlYPShjwtKfIp+WTOZH5GOTshL6YkeYEyCVZbbLQdkfpPx/U6Ms/VceBPBGdHwPboRxyVLOOgQ49/Z8x6IBzbcGsMaZZTFAVpKpZKddWyuq9YrRu6wTGbZ5xf5Dx7NuHyckZZTmg7AEuazrHZBJuU0Y7DYtJMmLdJLkP6EGLQmY3PVIa1KUmaY3QiLHltj2SF8Us8rUVRNg6Yjt8f7clUpG/8nb8H+rgPjEOYkXksFhyPfttaI5icVmRpQpZaUqUo0pzFNOdslnBycs7pk88pr35EsniKzQqxbbG5gOoKlE5QdkKWnWDSnBBafH2Pr1f0bYMbAsFp3CBkBqVt7Ftk6CgMZVEqhqHDqkcWulZyZiitoy1mEq32NC9/9+3//+wO/tW//l9+bp7/Ecw/IqhplDGADkFYmMEwtBVm2PHRVUZhOlRkHYI8sFrJTUusFSp5nA4CR0ZVwNO2NcH3kuqNE9/A6BemgouArUPRo5U/boCJNQTfUB9WbFbvOOwfIHQYq8jyKacXz/Boeh8IXjPohC5SnQ/7HXfXb6jXdxRpwtXlKefnS9LU0HYV727esV6vCKGnryu65kDfibSyaluqpiXPszjqNCxKw89+ark4/Z40+ZbEXKPCARUZZzYYjHO4pqba7Kg3GxaLjtY7fJiDykd4Qw49mxCUoe09r9+u+PqbN3z/9oF97Y7MAWEFabzykQpec6g2HKoVSlcsTz0ffTLh0y/O+PDTjPMnFZP5imK2JykqsuJAWnRcv7zh/mXDLDmnUBNKnZOaDNB0XYvz4iMixUJM41Q6TqCiXy0SaDO4ISZAyqcJXh0tG0ZDfT8MHJqW848+4vLJGX21J7Ep2WQui8N78umcbLJgcPHfsAlnz845vZhy/1DRVj34TkIDZPzE4AcG77FWClUXJ5MPd/fc3dzQ9B1gabuWX/3tL/nVb35FWZZMyild16IUTCYz5rM5RVGQ5+I1Vlc1bSOWClI0SYJlXXU0fUM5K8mnJa3rsdHX03v5WYVMooy2KJOhs5KgLBWnbJM/ZGU+YsMZTZjilMVrDUqa+NExUuZfEIyKRbMUz9pYVPTORcvvMQLSKuUlmMQmDPuBF5c5Wg1cv9tQGsNHz3LKqeV667g7eJHCti3ni4TTRcKL85RFkbCpeuYnFusHskRTTjRFAa1ztAOoRApLq0eWlhQtSmv8eMChwAdcL97V3veoriIznm3T0g0O5xV4R+I63ODoOvBdw8XM8HyWMc0y3rx9w+VZyj/9kyec5gOpFr+yz17MuX/zHXmW8/KHa54+fRLZmYGmOdD2jsZZ2nbgZ3/wAf/szz5lnpW8fnXPenfg6nzB5mHNw8Oa6WTK1emUoTswn0344YfvmSSapxcnLOYz3t7csd7uOTuZC/i6WhOiJ/XyZErQgeu7LU3nWa13EAJPn14ynRQ459nuO3Sa0g09aWrJjGW3PcRCArwbMMHz4jTjn/3pjwn9htnU8sGLF7z87h27yr+XOKyotmsOmzvKyYTOw6vX16zWG9pOUTWOzX5PU9cw9ALcByfvdzxYNRABNrGLgUQ7UtUTmi3b9Q2H7QND10oDooXJbYylKIroCzvKY0cpDI8MDvPInJUCRkWm2CiLf2worDUx6ddEdq7HljnzqzPaYaDr2jjBVRhrmBQlbdvSxSLX2hQVoK5r2ral3h948+YtVSc+tV3T0TYNMwxnDfzp9JSfJRNeNJ7SDRjv0LFhCih8fH/GGoxSGK9JkxknF09kMuscJkiKqkaYsUpBEIM5gtL0wyAMssExK0p6Ai+3K+Qda4KJz4d5D7BFrtH7jQDhPYP79/7/0QMvTv/HxuzICiCy67XIjCVV2B2BWfM+mBuLmZFxqNV7+098aTM278KhOTZ0wtYxKMWR3Rp4ZOoS35MPAtb3fce+OmCTRCSwMfxQa01dV4TguLp6IudQ0LhBWFBu6GPwkz+GHY1hAPI9+UzjQFiYwdFv00iDOcQkY6MUXVNze/2ah/sbUiuetH3X0bSOtnGsNmtZO21LkmZcPX1OXs6krmh23L19y+27G9YPa5ZnJzx5dsF+u0ZrTTGbYpKMYjLl26+/YXP/IICzNsyXZ6hkQjCJrHtt0emEJMtxQZoFY5OjVLptWpq2x2qN72q+/+Ybzi6uxONPW0nO1uNwQ2GTHGNzjM0kOdvYONzTaB2Bhnht+mE4NooKCQo6VPsoTU1io0K0QeAonVssFsJiMYbFYkk+mdE5R2ozTDohW5yTFTPa1tMHcCYhLeYEZaOUz2A1TMsJF09ecHr5AeV8SV7MSLIUYw1Nc+CwuaU53NHXKxnmKrGC2a1X1PsHDpt7Xn33DYv5jGI6pyymJKkEiymt6NuWpm6P60Gai1gvuJbAwOGwl2d1ZJKMzVhkqRzXWJQ/Ds7Ru4FukMTnum2pWznLwGCNJUvFPsqrwP5Q8f31PfddB2lKYhL6xhEGUekEILHpUS6tgHboaIIjny8YEEVBlmd0TUddVaRFji0ygtbkRUlZTMmLOfPlOdPZGZldcJKf8uL0gkIHttd3fPHsc87OnpBkE4JO6Z0S1n4YedbqqFSS5lj2IgkgS3BezneCp652DEMLAeaLU5RWfP/t1zT1AWvigEcb8Sjtx2CbcBwyG2OwNiPNc5QxEqKEDLWqumZ/qJjMprjgOey2cSAkQETbdhgrnss6Ao5CxvC0MexOjaqj2ORrbcRzOrHYJGVxckpZTsmznK5uaQ9bpqV43/nBkWUpN7fv6LoOY1KGfuDm+i2r1Q3LsxOeP39OmhXHJrdpxS5DKbl+Arb0EbDWZFGmLV7FIWYUZFRNRTmdoLQlzadkxQyTZNg0E59Jo2mbhqIo0NFqYfT8dN7jw3AMvzFjQJPr2W5uCb4jzTL6pidNM7x3HA6bmEA/ntM2evzxnqWOj8QAAddCgODFYuCw27Bfr2jqPV1XE4KkcYv6QxEYMMbTNi2rhzU2SVitVmw3a9rmQBh6MpseQV8B8+SMUUqkqr7bM0mhzFNub26ptyu6asPoHJEZxHorDibPTpcYpVit1jh09IwNUUbtJdTUxVwTBKgVcEnOFj8c8ENLiCBtGCTnZBi6GDwqQ2WtBMBO0oSh7/C9/LsCSsrw1AUeJe6oGBr2ntIkHuEjs9xYAdiKIiVLU6k14hBWPNLlNb33x6BtFWuw35PGjxs4o4dnrMFsSpKmTKdzUJq+76nrisPh8KgqiIPUo88to3XD+Ouj1FnpkSwiPYgx0QM9ElmCEgWSNWn0X5bBs9IJRiconVLMT7n6+AuefPQFH332Iy6fPaE61KxWK7zr8F1L6HtCqHFDz367o6r2BN8CYn2olOwnkushbEA9BjAVU7rOc3ez4/tv3/Dq6294/e2veHj3NbuHV3TVCt+3R/m/VqP3rtQ/I8NVQgMevTpDCLFeHQHdONw4np5yb7zzjK5UwQfZnwZ3HOD0fSce1u8BsscvNQ4XHsu9EehWSh0DzbTWJBFkFW9ZsZNIEgHCVQCrNalNyZKRQSsYzUhw03Gwk2UZRZ5HCwaN0e+r3h5ryTGfZpxKaCX3N0kT9Dg0j+SDrhOLkYBkBMjeL2fyGH7Vdh37ak9b1SgvHtLWaOkpk2jtGMlq2qYkWcZiumQ+W1BMFjLIzSYkSSaKlZgrMHqrq/gMEs9yeQ7HoyjmPgTxMQ0jMTAWwRotNlFaEidUINb4j+HHgm3oIy6S5Rl5npEkKc7BZlNzf7fm7mbHdtXS1A5rHd5rvLcsFqdcXD5nvjwjyQq8spIvk6TYrCAtJtgsRycpmASVpCQml4GJEZa6jkMhY5NIcDFHpreOPZh575qMTNrjLqHEg/qYPaF0PFeixYF6JH1IW/G4R7jBiSVECKIK0OZoCSGKa0hVQ6lq0qTE56fU5SXJ5Jw8WmElOpHAagXRCJFgUjqdoHWKHRyurhnaLuZ4DPFZL7DpFG1LXDLFmylK5wSdYzTY0KFVT9/VkdwSHyYVlRgjeKs13/5XPGn/XtsdBOXx279Br59gTv5HBn0i4AriodhiuTMX/NWrWy4Xe/7lTwtS1TH4A9pHabOHTd2xPD3HoY/phhJaEplEbsD3LcH1KBVDwmIatJc4BAklCwgVCklVtBpcu+ewu2W7vqWt9+RJglxWhVUSLtJ5zeAzsjTFOaHar1c37LYrZtOSP/2jv+Di9IQ8MwQvk63dbs///Vf/gV/88hf4YaBpG9AG3w+EviX0A4VNMYnFDYEuVORZy3K+J7Fv0GGNQUOY0rtGfJAOLet1Bb5nms24v71leT6hLO7Z7n4gmJIQMlCOblC0dcXb63vevH1gvx9QKkWZVKQ4wYvFQg7nV094d3NLVe3xVGSl48VlyemZ5vyy5PQiB12D6hl8TecOeBpcb/BkaCVsVatTSpNzPj1De4UyikW+IDUJN5t3bA5b6rZBKUVqMzGT9kEk+P2A6yEMAR3EjzF4HQsSh1FKPNK8Ax0kiKPt2O22GKPJslLCyLKcw2GHSlJMPiMkM9LJlN7vsFlB26c8bAJpPqdJHMbO8I2CvsUrIr1fJAoh+hB3XS9Atgu0bS/BD86z2j6wXa/RWnF5fsWbt29Zb+8ZnMLajOlswmw+ZzpbcnHxjPv7FfvtPff3b6k2DygSUI7JLOGzn3xB5xVT19E1e/quo20kpbrvG1QIDDYhTaHziqY7Z68+4JbP2IUZjgjsKGQDkd2OsWrw0UYEpWQKqI3IV7VI1cQ/CPk7susIry+icA/O882bnj/54ozrPGF2OWfT9/zHX2/5YWcIkxkoSx0O3G0aniwMiXecTDTvdgpfDyxnhubQ4/uEVTvQDHJ4eS+BBdbKAYhT+NHiTvzT5cDuO7a7jaTH5ylZotltdjS7Dqctmp4kelsNKmPAchg8m0PP50t4sTD82ac5g+7YPOz47a+/RtmU29Ut7X7Nn/3hh5wWBdd3a/7ml1/jvePLzz/giw+f83/++19zvR2Yzyd8+PyUzWbFty9vOTQd+67hYVfzybNzQlPxux+ucf7ARxcz0sxgrOE3X31FkngSDUVq+c13b1kuJjy7mILN+S9ffc9PP/uQbrjm4ydPePnygd+9uceT8ruX1yzOFsxzzY8+fc67m1/QDBaH5eb2gcvTJVmW0HQOH6SptNrx4uqE6vDAV998y0cfPeU3v/1b2nqP6xOwUgg3SvNu0/CP/+xnPFQb/tN//AVN1eNRbPc7Dk0PRmG1AK8+hmuIb4/Gq0A3OIwfsPTYAFliqQ8bbq6/x7cVo4l/kA2ZcKzZHGWR0XftkTXlfTge/sYYjNXHibSOcuOAQ5kx5GsgHFmdUZITgWMXBOhsu5bX37/C5hnGGJFdaQkkGA4NfvDYIIBAYiJb7tCjjaZRDqUNiQfVDpLu7AxPG8WfTc75R8kJJ22HctFXfQQoQ8Cb6BWnpdlz3oFzck38jPNnn3NrC7r1Namv6foDruvpq4p6qBjwPHv2Ceu3t9T1HpOlUOV8mVleZzn/T3NgZzzeWBJlJUNeCWtXGIsR2IzKk5hnGlkAUUbpPE5L0rWEpliEdDrEeyYsHgFl/Xus1njGj3vFe17AAtDIAEBeXySw8Q84NxybwjE1GaRwtcbgg3i1SrFnMDEsJHiHSiJTJHhQCUPb8d03X4H3nJ5ckNgEhaWuB169esWHH3zCR8+/QAWDHyyDTpgtzui7hrLMsEkBKLpuELmXEn9IF72niJL90eNYa43yAw8PtyRpwsliiXcBExQmeFzXwDAjzWfkIaPpD8yXV8yXC7796rfU+4oPbY5NJzSbNa/f3bM7VHRtx/MXn7A8PWU2y/nTP/9jsiyl6wf2h5a2PqCA5cmcZ88vObm8QiUizVPa4lwOdORA5wJaGXrX45SjyAv2+5q6bsmnE/LUcti3nM6ELZPkOW0vhbX3HqM81iiUBU8vjNOQCoDio42B8hgioyeCFd3Q0+23MkjR4ommEO/MsS63iUUpWYNJVqCyDJtNIIANLftW4XxCef4h6Aylc+7u7tmsVlw9fcp0foliwDc7mn3FZL7g9HTGdLogKZZ4mx2ZNG17oD7sqPZb2mZH6GtAgqn223vaekPXt9T7NYfdmiTJSLMJ2kiZ7wYfw/cc99dvcF7z5PkTZHCs8YPD4zBJQt3t6ZzD2vSYBq20nL8jgGlsbPZUOJ7DfggMweNUoANpopRH6RSbZngFzeC4vV3x3df3fP3DLeVnZyRJRtcamsMg3tapIl/MCF1gGFqUFU+/tFO4tmdoWmZncwYFfugJrkMbCURVIZBlGdNiziQ7wWQzsjTDd548WTINlmdFyh98+BH/9rf/O//uL/8d//0/Sfj4xc/QNkUUDBKIFoxCGWG7aqXwfc8wxPotDjiS9wCJvmlwQ0t+ekEwBU8+/BJjLb/8679C0fLsxaf4ropJ1RnaZPgwRMBDyAVSy1uMTdkd9hACbduQmECiNHXTkue5WApkgb6tyLKMq2fPaRsJn0sRaWjX9SxmM5JsgtfQh0BiDYe6xppB7BCUSBzzNMGTcPrBT5jMT7l6/gm/+y9/ybvvf0WRgfKe7XYX6zJhB1oz4IY9v/qbv+Tm5g1De+CLP/gHTCcnVE1P29RkeYlNc1SAw34vcuwkgzAwdDXOBw67PSE40vkJT559SN+3NIcdBI02EkqjjSG3CSbA/c07docNk8mEqj7Qdi0np1fSR2kb9/aBpquYlLOoZhSgo6n3WDzX9++oqh3lZBatOAYZqKPwfhAQREUJd/CiFIkggIpAlR8Ghq6h2j6wXV+Tpob5Ys7D7YqynDOZLCAODNIsBwd1XbF5uCV4SJSirg74xDCbnzC4ml21IaAoipI0Swm9sJmVVuR5ivWKRdgTtq9Yni6YnZXUXrygD11LV1dMbELqW+5WDb3zFIlmGHr6vmb4f6l7ky7LsvM879l7n/62ETcyIrLPrEJVoQCQMCmR1vKyZEsamGOP9HM4sGj/Fw899oCytSwtkZBEEgSBarLPyMxobtz2dLvx4NvnRlLLnouxFlBAVlZWxLnn7PM17/u8wUn/1baR3ynvszxJKfMiqtZ32EbjtcJGKzt9J1kXXoYGSRwWgSyIdWLI0o6WlTwjMURJVPgOpUUxbZRhYNCKcEPhvfDgdZx1Ke9IM1GcJlqLylYJ5uFOgavIEhPZmCaGdoYDiz14j+hBpEceVHDyvSYoo2m7BrvbC2c0iAjKDO9yPQSeqkHYGxcpSbwnkLpgWA64YXEzDNqHusQhM1wT701ZnigjAxeTjhlNFzz5+qd8/ctvaRxcf9rww4v3bFdL2qZhYOw6ZclVQpoYnLU0+w7vLXlZUBQVaSI8cHHaekya09Ytna3x7S1Xlzdsbm9odje4fgN2D87jbY3x4qgCj9YxuyD4g4VcqSCOBS/4BmH1ew5s1LjgsNF1Ya2Nw75wcCUoxJ3iYm1rkgTlPJlRdF1LcIi7wIgIYPjn78IbZRSYpSnO2jioJb6bxBkgGEpZmB8C3IKoO1Wsy5y16MTE8LIQXU8SxuesxyswiXyuQXmC8qLUTQxt28cFfZBFb1Ao7+mjcMtJ0AZ5moKSADPfCetTFn2yPMqLEkEX+ENeRN/3KBqyLGVtG3abK4okp8hLpkdHnJyeMR7PKYuINMhL0qJkVJTkeSUBqvkYx8D9Ha5j/Pd6hXISEhnigtoL4wvwBCtLmxC8iOmCi1d8QC6IWpQwDDQPTwgHbFhQwvFXkocNijwOi93IMak02x1s9g2XH3a8feMPooEsyxhPxpQljMYVWZ7jgyHLS3rbHHjAsjjxON9juwbXNbh+S9dsCNZLXlO8PzEJJnhxsMTMhoCN114+Rylh7ji/PgT6TjKgPAGUlUuEisF1n80Fh84hKpEDDmtl2ZQkCV4FULJ0mpYpYOiDJbieLNxi2jdYnbILFvIppAWJ6yWUEXHOo6ExUFdHdNNnFOcdZW9x/j/h21u8b2jqFUkyQaUzkmJOP/kSlYyY00rv2L0kq1/gmre0uyXOQpaUaBdDAhHHqtDjPluQ/Bdf/1Uraf/1n/3Zn947nYk+qHxESI7wXoOXIYw0aaIUXN9cclzC+UmJCXu087IJsx22b6WwJ6CDsKV0ELuziqouYbpYVHB43xJChwodhF4+tCHtJW5bNQ7Xbrm5esvt1Qd815GoEFmukCY5i5PHTI7OcSpHpTkeuF0vufz4Btus+PLpI37x7bcsjo7QBvbNlqZtSNOMvMx59Oghp6cn7PYNXW8p8oKAwvqetm9xHgYAtO12LOYd/+j3YJp+QLUNfu3YX9WsP96SU9LVGhMymk3HeHSMC5rxcS7WCl9hkic4n7Ore168ecuPL99zebWmtwptCmnRQ0zZc44kCcyPC7HRXb0nLxoeP0359hdjfvLTnMWDQFbVmKTGh1p4UTg8O5TuIBgUwqb5/j9esH+bMTenPJg/JaVAqZRROUVpze36hn29E5tsTIt21gqzBNmwOyuqkta1uNjsOy9blqCGTbm8sBQaGwKTo2MePXssyukgiX2u77FdJ81fIkrWAJSTKfl0jPUJddsRbCeb72irCTKRIDWZWIWShN5a1usNfduy220JWuwCddNwefmJqqr4Z//jv+Bnv/8HPPziGWf3T9lt99yuNqx3O/abPX1vSfOSyWzOdDZjOpuhTSbbT98yP17w8NFjqlHFdDrn5Pg+j86fsDg+xSQ5vZUiT6sEnS9w+WM2+htueMQmLLAhJ5BCDN7BEDfVOjbHg3pWFLPKSMEV9FBcie0QHZkxcaCrYohYUJJsb3vLbByYTwq+e7HmP3y/4ndLw9aM0VlOnkNSpNB6cu+ZFAZwbFvLtrZxUJOSJhqTpbSdIiSKfS8vsiJTkoquFU4Fei9DPfqe0nXsV9fc3CzZ1i3rumW92bLbblFGGizbdWjv0N7TqBwbAsq1NKslutvz5P6cXPe8eHnBr39YcrvxzKuMxcmUl28+MR6NOD2uSIucDx9v+dnPnvL80Qmh7fjwaclq09A7xauLa/7uhwvaznE0zRkVGbvdLfdPJ2jfc3l1w+3Vexazkqow1PWO5fU1Acfx0QTlLTfLG25uV1zdLHEq4IA0STg+mnM8O2LbNrx6f0mvishJ7Xn2cE5q4OLqhtW+Q6mEvm0pc7Fl73bbqKZNSKxlMcvI8sDV1Sd2yxVVWXByfs6H66VgO5SoFNMk0DZbXr/7yO26Z7Nu2dY1bRdV5hqx9ARpHozWsYALUR3iSWjIqWk3l2xuPrK5vQTXodVQsJrDYO7zQImmaT6zxUULazwfklQf0AYuOIxRlGXGeDJiUGz4uK2N9X1UcA4Frvw5JktJ84w0yUi1ESV2HxlZ1sftdlSrOE/XdoIf0CoOUwxBQWYMSWc5svDLas5/O15w3jnKrsP4XpjJAWR9KAFKwu00hyZGabE9b63Hj2ccf/UtNsDq6gMfP73n4vKS/WovAZPeSxp332K7BuXFZK29I00Nm2bLygVaJUstH7f3B6VxRN8clBNhKNbuVLJSNAYGDhWIgmdQyhoj9rw7m9lwjdXh+v89hUj8IIbi/nNG2ufD3UFJEKKyIjEmcviIYH5HCHdhG2lk0Q8NzDAwNUa4413XUxQFWZozoGuk2Q2cn52T5RkuFpbou2TpJCkIweJdi9ZBmsZh4+/9AZsxMMSHsI4hAT5LEvquEzRNCJTjI9LxlHQ8J8lGbHZbLj5e8OrVj7z87nsuL285ufeQarqg7QNVkXN0MmO+mPPo+VPOHzxgv7mkq28oMs/t8iOnp2d0vae3nvnRjNP7p2RlhQsKF1JcECVS8JG9Fl0T3sm9vd/t2aw3JGlGXlaURU5b7wkoitkck5UEDIlR7DY3dJsbCeU0GQEN3qLNXfCcj81owGN7h3WisDda0/edKBBMgkFCo5Ko4JIeXZQXwYnS1KGw3pMmBusc+9YeAjKcTnDxvTWdTigKSZVOFChnSRPD0ckZo+mCbDQnzStMkmLQuL5nvby/QwR9AAAgAElEQVRks76k69ZY32Bdx36z5frTR24+XbDfLtlul6QmYzw64mhxjE6NqJV6YUU6a1neXPPh4gPT6ZyiFLeSDxC8JVVyH1xfXxMIjMZjsiKTYLeouDSJQafxHEiE/T4symWpJNek7XrSrCDojKYNZNmI21XNb797y1/96hWvX9zQ1pZ0VJBORwQlfGelRU1fjEZkoxJyh09EweVcwIZAMhkxP4+DfQUmgXJckBaFnAHOk+uSRJcEU4DOMaHg/tEjzqoZYbXl6dOn/Pl/+He8fPFrrq8/cnJ8n+PZgkzk1BK4qtNDkzsoTIK/SzgXJd/dM2W0WEiLcoxOUpx3jMoRi9Nzbjcb3r97z6QqKPOCzbbGpCloZEmgRG0WgqjE0jSLVmhR4Q/BNMYYMgEmQ0CGoEmKNoJosq6nKHKUzg7f03g6l58lSbC9DHDwgSxLcK5HE89Wbdi3HWlZcfLgCfPFQ4IuaPqeNFU424HzKJ3SWXk+tQLtLdvNitXNJZmGxeIoBjqlgsvqHU0nCeZpmlHkI+r9jhA6+q4lyzLKYoTSKQPWbLPZYHRCUY3EiqkNidbYvqftGhYnC/K8YLPdsdltmEzmEV8jyxdnbQxljoFNKmD7hkBgNpvT21bs/IZDEGH/Wf0eb+Phv2BwviGLT28tCnfI5dB4yqrAJCZyq1X8GW1UUibkRcloJEr74X9b27Hd7qhG04MqdMD37Hc7Nus1VVlJ2FvXsd9tqcYpjx+f85Mvf8J8OuV4XnG6mHF6PGNSQpn27G5veHtxQdvs6Zs9+92arq0P/YR1Hc73QLTlR2ax0pq2rXF9A7aTJYwX4ZDvG7y3B6WB0sLoTTMJZO27lr4VpadSEW8QOWs+ENWdsazX+pB0r4JwVJMoVjJakybmEHzNkAQf37U6qmaH5YaK7+zhnT/UYwMjUpSSCaPRhNFoFK3E+jCADAFcDNITtZwMa2TnGg413hB6dfj7w5DaJAyoQpPEvkSpA880SZKD60cpExEKhiQbUU3POH3wnOPTRyT5mOWy5ubqhr6p6VoJUFosjoWZq8QurZRGefnzJ+MJJ2f3mR6dSC5MU2PbHVkq7xON58Ob71l++JH65gJX3+C7Fdgt2ncE1xKClQV8CIcBmybWi+rzWvaglzz82lA7fc5YlWCl6LYYlClShQiKQCvAi6ssOst8nITrOORWUVF+p1iU4CbFXV6APKtRjX0IkorM2IgaHO4RWRpIwNeBQaoOT/dn1n5wwdM0NV0r2J7hfgpDPRm/9wNiA4TFPqAdlAzVpf5z4pr0MrOJd44ofBNDkmiyNJUlA3EwHcUjXddRNw2b3ZbVZs16s2KzvMH2NVVZUI2mjMdHFOMxaS6OgyQtuQvzNAdXrwbh6MdrJgtb4Wm7qKj33h4EDHymcNdqYAoPMy5kLDs8e3Epced0k/tbDe8HIE8SxlXBdDqiGkltmyU5zjrarsf2geATvBMkzr7paFqZ0RiTkKYV2hQoU6DTnCQryYsJeT4lKUuSoiDRORoJQDYRxyALdhlYB+6CA1VEdciP6rBuEN8gYhkgKHUI1tLDM681Qw7G36v/XXSwfSYi8VExLr9HzjeTiMtWnA8OoyyF21H5NQFDpwrp34C46olnqCyyVNeincVYh2+uafZXcq29Js8m6NEUNV3QTb7AFieofETIRhil0CrDmJQsDQQlwjatdQSmCn9/6D9f/vDqHyDu4H/91386e3hKsArrE9LRKbkpSZVsb1Kl6Z3HBkVd79jdXnJ2r+TeNCdxfRyWJhRVidEaj4SpqJjABvJgemejBbfF2wZ8F8MghhdVOGz1lALXd9SbJdcXr6nXV6ISM1qGuQAqYTxZMDt+hDcjdDbCOs/q9pqL19+RhJo/+uVPefrkvmyK+pZ9vRUFVtxw+BBIU8O9xQlJXrJcbTiaTtGJorUd292OzkmAj9EGozxHE88f/Cyj9Ndc/PCe5maP3zr6jSVPKnwXmIxz0jyjOhozOZujKwg6p+5GXC2nvHyz5u++e8dyvcO6yO0hwQWNdR5jAtPRCILDui3b+opd+56Hz1J+/gcTnn+tmC726GxFUDswnWxR4vY3sAcl1iujU4xxdJ3nN3/xnvpDxUgtOJ09Zj4+JUmEz6p0wn6/xbqOPCswRuOJB10QK6CEqPWSuC5n1iF5Umsd7aUKkyaEMAw7FOvNlvm9BUeLOb2TTU7fdrRtS+8DNog1te86+t5isiLCsx0q9Limw7s4yA9B0lC14AW22y1d70iTDNf17LdbvLVMRiMe3H/A0fSI+XRGmueQ5fzRf/ePef7FY969eEPvPPVuT3Ce2/VWVBJtx7be4oGiHDM/WnByb8FkOqNpG9qulZRQMrKk5MGDJ/zi9/+Qb37xh3hT0jClqb5lk/ycS/WYtZrRU0jTYu622Uqbu4FtbKCIL0iS7GCjPqhqY7jY3e9X0kjKL2BQZErQA7ULnJ+mXN94PtmKdjTBlDmFUZSJ8GTnZcoo12gVCEGabI8jSyFJDTWKBs3eeoLWtL0FZ6kyKSL7AN4rdN8zDg0TGipj2Wy3fFru2DU9rbVge54/Oufe0YTcKOrtlr6z9A76IJ8xzmPrDtd1lKnheJoyPzrmu1fX3D894U/+6dd8/eyEy9uW5XLN8bQiMZqLTxveX1zR1CuKLHC0OOF63bLae9adwoeCn3/5iJ89n9NuN7x49ZZMGY4nFc7uufx4Qbdf85Nnj8gSQ9/3XN3ccH5+wmJW0XYNL95e8PDJI37vm6d0bc2bN++Yz09wfeDiZs2HqxWtlSZnWqb89NlDqjylGk149/GKXW1xFvCBB+f32O/kflUYgmv4ePmJzX7PT758zpdPH3J+fkQ5Krm4vGK53JKmFWUxYjIds9/vubndsmv6g1VL0kFB64AJAcLQHKi4JHMY3+KbG2x9Sb29ZL+9pW9F7Q/SnAsvdHjx3nGLDgVrVFkeeEZxMCwKTCkwnXfyZ2WGclRiI6MqieiCz/lphz9b3RXNJk3QRpQpwQcSnYidzA32JBnqDums+LsCQrhTYHd7iqbneVbwT45OeapSyv2exPei8FcKEzQJSrbBelCPRduQ0YfvZ7Q4YXT/Abep4S/+8ldcvH7D2ChOZmPu3VswPzpiOjsSt0OaUhUFaVYS0kQKlszQ68D7umEXl1ZEi7P8OwDuBqtSXw/XSJqwgxsuDuvNYFdl4GsNcphBHhwbOaU/+xxVTPaVazgU+MPX0CAeatHPvnSUPFvnyNKMxWLBZruNQ2FI0zSmw8c/LxZ5orBODmxbFPS9nPlVVcmgK2jQKev1jjTNOD87BcRG6j2RSyxsLud7nBMuYIT3xs9q+HnvFgveO8EKGPm+vLfx3JXiUpucYjTGpAVd2+LaPdvNDaubS9r9jr4PLE7OmUznTKZT7j8458HDB0znC87O7lNUOV1XM5uOSbTYG43OcZH/Wo5Ksqo4MAv7GOCptMI5GSCMxyV4y4cPFzRNjXP27npFm6n3gXI0xumEEAwgad/r5SWbq49MJzNMXlHXNTefPlCNimi1lSFCUHf3woHTRmT8J1LgD5ZFDwfGsRT+4cBwc1GJ4m0nLLxqjIlsfEE2uJiEnEvnQiBLDNPZhKOjBaPpMWk1xWQlKLBdzX57zWZ1SddswHXgLW1bs96suL78QL1dgurZbTesrtfM5gthmuVTSCck+YTFvUec3n/G+cPnPHzyFf/9P/+fMMURHy8/0rU1IXQY7cmynMvrJe8+XKDSjHI8RmepsNLSDJOKc6m3ogr3HjorLjGLweoUj8FZjW0hWMPq1vL6h4+8eXnJf/6PP/Dm5TX7jSVYETjoRDG/N0NlUj933qHzhOr4iPHJCRSGPkjStA8K6xXppKA6muOThKADSaYwWXIYvhiJygCVENIUozNKVfDFyVO+PTuldND1Lf/3f/q33DZvudl+4t3rdxwVIxajEwldGZ7HeO54Fy3ecXo3hImIa2JoWAXRMJgUu66naa0oU+8/Yrtd8/LH70g0nJ2fCrPVZBKc4x3G6Gj3leGCicxso/Xh/B7wUllWYGNOQPASVNPut7x+9T3eWUZlRb3f450jH40l8EnHRo+oknPSV3gX8R5ak5clWTUmJCOqozOefPEt1eSEm+WS2+U1RkORJtRtjY38Qu8t4/GER/cf8P33v2O1XjM7nlONJpgkB5WQlSNGkxnj8QyN5vbmA97WZKkMnbM8pbc9XXSiZKkmSWWxkmW5DLyco2lq5kdz8iInz8XmWpaFKFUR7ETUrxzUZDJAGriKgXI8I80zGViHQFmOCMhAral3dF1DomRA58PwrhEbuUahQ4gDxECzl5CtgEebIWMEqrJkvb7BJIa8qISnmIh7pm1a2q6jrAom0xlFUWIdB+5tlmUURSHszugksK6n6zrBhuQF1XiErVv++i9/Rb1bcnp2zCjPyJKO2UhxMjviaFwQui3bzS22b+n7Dm/FTZClmlFVDgWGBP91DZvtmqbZEpz0neDxtsfVEmgYXI+OQ5w8FQWv2MmVMHm7Pa5vhZXo72zyotpVWOs+q2+GZSvkRsf7E7knkgSTiIMhBAm7uWOk6gM2Kok4qBAC1rsD63OovXRkxFbVmMl0SpJmnw1b5YU7KIp9cKKw+2wBOwzNh6HkwfI+KEgZMFYDt9hAPBsTkx6GkEqLgClJM/JiRFnNqaZnnD35ii9/9hXFaMT1zZb1rSi9g+tQBE5PT7l3ckxd71FAnuegFFmeM55OmB8fkeYZfd+zvv7E6uo9XX3LfnvLp4u3XL1/xfb2At8uCd0OFeTzV8HKADK6rkKIQaTx5z3gCYb3sZehE2rAKQnrfriGw9dQw4a4RFcYQQAoeasOYbmS4xIDKOGwXP+8HnMRe/D54Et9XrvFhQ7xnXwX9jqcz4PyUn49SVPysqCsStJUVK6HMNX4vheesIpYFlF7D/fUYI03icEN7wUfovpQFrVGG4KK73trabtOlOvWYr3MHlyIDF5nsd4JCzsWlVqboWwbZnN0rseFyKzdN+x2K25XS7a7bRSGJeR5RV5O0FkOA785DlQFcYK4Q7wsuwk+igFjUFj8HvGxbjzUiiqef4M6XJ4PrTzaO3l/hKg6jwPaMHD+FXcDTS3iNJUkFGVGNSoZTysm05K8EmxkbxXWRTcyssgRbnCOUjIj8ZHNkCSaIs+oqpIyLynLEWU5Ras0OtNNXPIjs4KoZJfFvIQxSzshgWjDuW2dYJ96JwFzIQbgDIvYAQlwQJaB5HQcTos4yB6QKFHoIWGHERWn04iKCRgcRWiowo6EHk9CTSVBeMGLMymAU2CUCDJVMASbgG3Y1yt2+w1FkpAlJen8mHR2hs7vYZMRNhljkhGYEZ0aoVRGpRHmuXYEHZX+OuLjtMbhefX9y3+AuAMUnQZnP6LW/4Fycp9n35yydzm/fr8jWDm8+qBZ9XP+9rrF/PtP/Kt/9oSHVYKLrCqDRynZ+HpcnMJLIzcofoJ3sSDvIfSxeZOQCmlQnRTr9Y7teslueYVtNhS5IU1MvBEDJslJixnl7IyOFNt5lK/ZbW/4+PYHCt3yy59/zdnRhKbZ0HiwTm7CxAjw2fYxkVxrUmM4Ol5wfHKPnBZTGHSas933tLtbafJAuG2AdRKOYXQKvudkccJ6vUWRYJTFOZGkO+Mwo5yGjNXmmB9eww+vXrKrS7wXy5kcDo6giRwlhCOlO1BrZseeo3tTzh4fMzvqUcmSwIY+eJTXUYkpW5Q8H6EwdNtb8FrUCho8NalRuE6SRtGBpMgwWUG/b9g3LaOqYrE4Z7tfYRJJ7gvW0gP94dCTh9bHBz4kKm6rIjMqyM+e+JQsLbAqIfGeerXjxW9f8PyLJ/gAXd/T2o7OWXTfkfZ7VK9o9jUoQ54bSHYEpQi+EZuL66JtRWGDJ8HTtS03yzUYQ55lcvg4H6mf8rJ++vQ5x0fHfLq54Td//Rtu1yueP7vPx08fefHjS7744ivhvWz29NZQr7dc3VziXEuWZJRFxbjKManG9cJKqbuarvHYtqNp9rz58JHjh19z/tU/5dJccbU8ZhUeUFNI1ID2oOO2Vg0BDSaqlnQ8AKPdQCuCHoZXMjz6fFgbkNA0bTQxG0cA8UaJwtykrHvNq089j56M2X7oSZSCNJA4hYnDmrRQUMDKKhKrIAlUk4q27djUFqdz+Ywjh+y4NEwKTZXAamdZ14EyMYwJjI2j72teX3zi+qYWa0m0zwajWC+XuFFOWY45no9FfYrgKbRPCVrTKc3FyvKr333kp08THp0vOJ8Fvng4YjZJqHd7ytTwu5cf+fhgzrP7x/TNnutNx/Mvn7DtWq5vLrh3lPPxeo0mo9ltubzouVdMyXTHvWnB99/9wPni9/jmJw/Idcv7Vz/y6f074eCennK5/MRut2eUVUxGOVWWsrq5JXl2xk+/fE677/jz/+cvKdOSxdk9vnhyzt9+/5bOKi6vHS/f3vLVs3OOJo6HJxOuL9+i0wmb1ZrtasqkHLG6vSQYaRJwio+XDd9//5ZJ/pgZGZ8+XtI2LaNqQllN6dqam+tbnK0xgFGeQIc2jhATxpUKkYstXG/fyjkbfEffrOnqlZzVQg2TwilWTCHIZvX/c0CHFIpZntK2Ym9HxUIjSw4Fo0fwFsSmYrVaxQEEpKlw8aT5j7gEBiWBWHm10pjYJPnoJOi8DI9lYeRRaGmerY/bfVHR6fj3RA2gGVvH46TiTGWovahkVCw8DSq+a2ST7qOyROlB2wg6S+h9z+vvf8ObX/2K6vFz/uhP/gWb3zxgevse367x2y2tb2m9o6PDK0+vYBugVRrrPTY1nEwXnPaeq91KCiAvRXmIe5nPrzNqKDpDLAQH9as/DGglQEsSsP2hYRCrnFI6hlDc8YNFHe0PIWLDv0tJXSrWJe8PYWD/ZdBYgHhvKDrbc728kXdUHGzL9xU5fTohyzM22x1918VBoBS1ovYN7HZr3r57xeNHT8mLMRqDJ/Djjz9w//yM05P7wkv0xAWhNAlJVuBsSbCKvt/ig6NMy/i5yveXJiZy4HoSnaBREtjX1kxGJdPZjBCEQbtfbxiplMwExqXi5998SZkafrQOnRTkZQI48tTERrIh1YEQLMbkPHr2FdiG5ce33FxuWN1a7p3fZ1SKBV6phFFVUGQZV2snikWBvGKSjLZrWW0k7EfoF7FZjEqbpu3A5DKEUkm0oUrzX4xmJEpDWhwa0cl0hNz9Vt45QaExMShueN6kKRQlHnRNzX6zIctLVCjQRhRnLnLWQZ4LsdMJjioohTESSFN3Pc52BAW9d/TKU5QZRV4yGo0YjUQNGVQq/D7bUO9WNPsNbbuWIYWCrqtZ3lyz2W5o+4ZEg85Ttk1gcvIlT768x/FiwfTomPNHTwjBsN91LI5P2G9bmr7j3v17nD+YsbN/wcerazLdYpstXbfi5eu3/Nt/9x8JOqCNIssSxtMRVVVS5JmcT1phgjTbXd/Tdi3WOZou0PQ9Xd3QNx3trqdrO+qmp60lOCxeKHmgYpZCs9yx/3BN+WBOphWdk2fQZCnPvvmGF69/YLPfoVNZPOdZSlYkKO0waRA1iDGglVhK41KiDz2JstDvCWiKaiRM35BgMbz57d8wti1r5yENvF1+z//x5/87l1ef+P1v/wmLe/fRWgQBg3L6LqAwDhGc1FmDkgslLgUXFDoQA6QSegdBJTz9ybeMJ1N+/N1vWO82PHnyE0bjBUon3K6X5LmEw/bWsV6vyPIiMscNSVpgrWV1u6LJG46OTwRN0TYE52iaLYkG2/Vcf7pkMp5C8LStJdltMUlC14pqNY33bNPsSGNQcVAB29d4V5MXY6wXrn9mKh59/Y+Yzad89zf3+PTmdyw/vsVzE11/Aec1WV7y+Olz0k+f+Nu//s9Ya/nDP/6nnNx/htYlzgZa27GzljIGqew3S8ajEV27Ew4qGkVC19roAjR0tiVJDEmayxAkzeisZXu7ZjyaSgBYVFT7KHK5/PiBybgiz0tMqobVHNrkmNQRkHfleAzr2yVdsyctRhiDKE+jUxBv4+A/3DXlQezPEoZkSLOS1luSvIpBNfLOb7uaAORlyWg0xZPQ256+68mKCtW3dH2P856ymlBqE9/7gbqu2e13HB0dSaBO3dJHhECRCc5BWc9v/+ov+Pj6B4r8a96/ecHi6Jyb649kZcrJvUc8PHvIz768z8v3V7x8f8nbj9cQAloFmm5PSDW2ranrJgZah8gb36NcjY6ZE6IglvojUUQGqKi8BkZsexjeWvBSb/koKhkUW0ZLn3XA7ShRpiUayVpxniRNoqpWkRtzl9kSezdRW6r4bpVQnAFTRFRwqhDiEFX+mWo0Is1LXIjODD0oFh0uoois7Q41xN1fh1DXz8LDRGJ3OMv0gUerUUoWpcpkpMmw/HPxPSGoo6wsKEdzqvEZ2eiIfDRjs+9o2g3XV7eSQ0GgrXdYZ1kvA+ubS7a7rZw/qSDdtIkDzuDo+pp2v8Vub/HNDryl60UoI8zKjsbF+YMRRqZcK3WoLw8hSITDYnlwM+E51LPOOg7b5DjEHeqWYVirGZS1HIK1ZdBlZMCHIjWSB9A1nfRPBFyIeKlYN5nIhR0cSINSdhCqDUpmcabeBdMpL7W0c+awTHPO0Ud1PQkUeR4XXJ7eWupmJ5zYYPBKcD6CjbKfiQPkeuW5OH47bXC9x/etKE+1Bk9kAg9c7KgAjtgOQWmp+Gvy8+vDYDqqXqNggIiGaGxP6gMgC9LW9WyblqvbW95dvGMxO+f8wWPOHz3l9OFTxrMFWVoelvEhSGB1CLJgkmXEQQIS1b0RL3YQm8hzj4qLqsj0VcGD66GPwhUCSicRN5gQTIZKC8lg0lqeOWMkV8W1qNZijCLNxJlzfDzh5N6E9b2Wt++W3Cwl/NyjxXGoc9LMkGWGoshomoS26TBoiqxkNMqF2d40NLoikJHkKfW2JJgtrtvSd3u8DigTUN6ieunXlYr1ZBBGsNaySJJlhHwe4m7gcB2V/izcOQw5E3cIlgFNckBAqHifxmvo44JDq0EdGwj0aGDqLvF9xl5NaFUps3Kigxglzue8IBQdyXSG778kbzfCQfcd1tb07Y4xAetrrAGXTQhaUacjMBVNMIKNUFua+pIQWlI99FEpPmiCT/n/+/qvWkn7v/xvf/an8wcLtAfnGlRfM6lm7GzOVW0I3ojKQjQYdGbEzaan2+w5PykYJR0quKiIJQayOBQO53tRQHrBHIQg/+Ez9WxQg1QblO/p6g3Ly9dsV59QtiY1njSRjtYH0GmKTiuO7j3l+N4TTDUBlVLvdnx48x25avj5L54zn47om5r9ZgshMmkQIPwQhKK0KE21Vqx2Nav1mpQOk5ZMpmdAznJ1i7UtaWqoqjGzccJXz1um408UqbDkur5HGUM5mVBv19ihyUkyuuSc719rfvWfAq/ejajdGHRJCD0+BFGLRlWV9z1KWZK0YTzteP5VwVc/Kzh94hhNtmi9Bb9DYaP1V5QVmgKlKpLsCGPGdO0WHyRQKSgLWEJj+Kv/6zX+Zs698QMenj5nNlqgleLq5prxeEpZFFx8eEOeZQxgfes91t3ZckIQ24T1Dh8Zjj7E7Z4KEc5uQKVgMkgyemtZrtccny6YHE3obE9dN6JkznNManD9Htvu6Jsd9eaa/W5FXW/p6i06tPFFpnHI9sUOliLkZbnd7diuV2w2Gxye1W7Ndz/+yM1yw/x4wbQ6Ik0q8Iq2qUlNztHinLyYU4eER9/+km9+/kckFJyeHHN9c0nb7mnbBsXdkHW4d5yz9H1LXe9xQXNdp/z6bceH7YRbd0KdzAg+jUPIWFzFoLAwsB8jc4iopFUREh40sUBK5NeVoA/QgjfQRpOkmtRAYoRpleagCk2eKcpUoRzcmyrSXONdfEkaT54o8kQxKT3j1GOMoiWw97BtFMudxXrF6SLh8bEnR5ElisfHmsVI0W5amsbT9g6/25C6ju16zfVyzbZxlGWF71rq3ZoQHH3vWG8l1KusKgiB5e2tDGDoD9B2r3sUinpf85PnCx6dFiwmE169fMOLl2/59e9e8f7jkvF0wv3TOQ9Pxjx58ohd73jx5hM3n5Y8PDvh7N6c3WbD+nYJbodrNzx5dEaiHJnuePHqe8aTgkdnU/a7JdeXHxjlCYnxNP2Ot+8/0FvL8WxMVZRcXS95+/4TaVYwGVXkxYjvXnzg3tlD/pufPeXh6YTl5pqPN2uaXvH24hNZpnl6f87J8ZT37z/SNr2khPeW6XjK6vaW3vaEIOwnbXvuL2aUecoP37/id9+9ZrMPoAqa/RrXbwjI86yCF6ZSaPGuEUJM0MIdC5ZU9eBq+noJ/Zpuf0XXrohpjwfFxKCcGpY8kobMwToOdwWs1oo8T6mqEmt7JMHbMKqErxTHjgCHICcJSxjsNKK2HY3GMdRksOTfpYcqJSzMxEiucIoUTzpy9bzz6KBEneXiWeQ9BC9s7N7T1w3GWp7lI/7x7IzzNpDVcbkzFMqDavezgeQQhqURxWmrNe8+fGB1fcX54ogvf+8PePzHf8iH5QXrNy8JfaANmo133Hh4Y2tedg0v+5bXoePCW967lk/eUpuENsu4dR1eaeIlvcOYDI+6uhta85nK1SSytZZBypD0rRiYgkZr8iyjiKmzbdsxELUGtQzIoP1gm1QcCmg5hjSfD2eHa6K0DMXDZ8pqwTuIBW4Yjg6qI6X14ddj9cYgltZaYYx8313bst2tSFPD8dEx+EDX1XTNnrPT+2RpJud6HGijQrTRCfMx+FbO46GB9Z6+62PCuthPi7zAecu+3gsj0BgIPfvtmtc/vqBpeqpqAljq/S2TyRHT+Rmj+ZzZYsHseEHbWmazOeNpge2uGRWWNEmopidkZcnHi/dcvnvP9nZFYgLjcUFRlGRZhQ+wWl5R79aoZILSKX1nKbOCum5EPZyXTMZzkjQnIAV/IGpSc7sAACAASURBVFAUop7ziJ3YRPzGEOpiTE45nZPmI5SS5iorKuGqumhb11rCxHT8XExUnyhwtgfXsl1+5Orja6oyPygwDsoSJTZXjY7IlbhMRkGSyrLFOZq2xnoJX5qOS+azMUfzOdV4TFAJKsmkQbAN9eaaZnNNsLX8Wc6yub3h7ZuXrJZXEOsmaztC0CzOvuFP/ud/xdd/8MeUR0+YLh6x3bU0TUPXtyikCWm6hqzIccD79x/o24bJeMHzL3+f3XbHv/03/4bvfveG7bpldbPn9mrDp/dL3r+65M2Lj7z6/oJX37/n5Q8f+DH+9c3LT7x9ecmHN5dcvbvh+uMtt1dbdpuOpnE4J+dJkpjYsMgwfHi+lPckiRaXQZqAMSSpIS0rHj77gs45mnqDogN6iklBOR2TTwvK2QidiIp8UCF2XSfsxIjeMii0h1E+QqUzTFER6pZ0f81ZmcBWAji60HPT3vDq4js+vn/NuJgwPzolSdO4/HGHs3hQ0iv1OaMy/kwiFyJJk/g8ysCHWJNP5scczRd8fP+G969fkZiENE/xvmOzXgt7N88OA3CtQmyYBYGglGZfb0nShPF0KmeyCiRpQlmOmM8XnN1/SJrnJGms2W+u8bajrEb0fnifDao0qa1DcHjbcPH2taglkcBedIYPDhdazu4/4MHDn2CyEX3X4dqOdlsf1KqPnz3nJ19/jW0bfvztr1lefyTLUhSeLEnRSLgaOMZVQWpEBJLleVxAysA4S3P6tmF9e0OaJGR5ISpVpUWhFZdzRVGilabtWjnrjcH1jtVyKfzWJDuoW8VZYmXQOSrl2EVJcFfoMLG5LvKcvCwpipIkSeNZIOfnYEd22BikpwQ1Y1JMkmHSHGvjPRHdC9VoikOyOkSBJngascOKi8+5ePjHrzRNReDhIrYhE9aohCt15FXF7c0tb1/8mqPjEfefPpeQHp2wvLqhb1uyVHpF5xzzyZjTe8fcvzfn4fkxVZFwc7vi+uqaptmBb9HBo+lw/R7X7zGx7wKET+96DA7rOkJwd2HE0R6uvUX5Htvs6NsaPPSDM0MuttRS8V2XxKAmpRRlnpFpwQRVZUGeCos2rkYO4W/aJHKOIIMV29vDYDvE36v1HQ7BaEOaZaR5/Cx1EpFTCm+lF+u7LiolZWgitu1hEQPR8nBQFRLrBRVFJOKQySKeJCPNKrKsoBxNyPKKJMsxWUaSFYwnc6rJmLyak09PycdH2ODZbBvWqwZvO7At/X6LcuKY2G7W7Hcb2npP2+xp93sSrSizlCJLSJRntXzP8vIF9e1Hut0tfbPDuRZjHIlSBN/j+lbmb0NIXAx31UoUxMEHbG9FaBTPhbvFxF2orVYG70WwQDRlayUM1+FMDISDKGGoaQfxsdFxqBtpdInRUVQz1FNRLa10XBxI6GQWla8mkSCwATExBJV57xgCXGVmr+IQ3zOooJ2zbOsdq9UtNzfXbNcb6qam73sRQSgVbe+DmjqGTCUmBoiJ48gkgkgrClHlGq0ld8A5jBIbvXCJ5VxWRBSHUhRpLnVgksqZQ8AoA4NoKgozZPGX0DsnC+uI7LOINT8ERd9Lbx36PZvlBZcfXrG5vkL3wn7WSXLnKPNqODb/3oCWELMd4v0t6nQJAsyyTMK4IlJQifwDE3qMa0hdg7F7jK3RfQ19Q7BdVObeBd4Pn6v3IS5wHK639I3Fto7QO5T3ZImizDV5pjEq0HUdXdthXc9sVnH/0RFHixFlNSJJpYYsqpy0SAkmw5Nhkly44tFppojvtuj60EZcEcPq7hAM5kTRrCMGwX3WFwznwBAEaCLyyjpRJmtCXNKou74pKrQP941JUEo8PiYub5SK195aWYBoQwiaXlf0uiIEWQQqpSXbSGtSPIXfk/k1hBZCwHRL0hga32tDkk5QxZiQT1DJmNKANQleJXR6ROMhtNck3RJb7+m6hr61uF7jbYKzmrevvv8HiDv4sz/709GD0wMdx/dbdruGXi3o1BTrlDA1QgBlcErjk4zNesfq6oZnZ1PGlUGpJsrYFbKr8ofFnI6sveAt3slkf5DYayWNadfV3F6+5/r9j9S7T2QqkMYUaaXuCpmimDOe3Wfx4Et0NScow26z4uO7F6Sh5ve+ecZslNO3Ld7JTaxCiDFj8hIU3IEEoASl6VHCnry4wHZ7dJpRjY85ffgFP756Q7vfkqRgMs0o6/nykeZo2qKLmrxSbG5b2m1Pv+9QRlEcT0kmp3y4PeYv/ibh198n3O4XoI9QJGKVUSqW2gqlHUoHJnPFw6fw1TeBn/1exfHpnry8QasVsANlGYDuigRUjtd53GBpAhmBhN7vgA1edaAtKkC7S/j3/+cPpNtzTqovmU3uMR5PybMC3zvZBhvPm4uXsgkmogzUod3HeYt1VpiLWtMHz75r6bzFhiFFWZIeTZIyOV5QzefUbcNus2PXNjz+8hlpkWHbGhOMwOaDpW96iPMJ5y1tv40vNSMMFYjLTVG+SfiypETu9luaek/b1TRtTdCa7b7h/cUFOs159s0v+R/+5T8nq0b4oKg3e5QyFOMZvc/wZsbs7DF5NeH68hqjLJvtSoYKShRQzgVBZcTNTJaPxI5jUxo/ZxnO+RQesgzntHosRRscsBAoEweud0raYTg7vOllEJvc/f/44ldGQaLBKFSiSBJFaoQNa1JQiYJUYTLIM88oR5jSXnE8M0yLGCKlYJrD/SN4tNAUiWZdB5ZtwAdDbhTTQvP8VHM+98y0pxpndJ1nksDt9ZZm2zAfF+jQcnO9ZrfaMhvnjEYjHjy4x8nRFEPPZrNmX0tBbL2jjunWPkgaqO178EI/S9KcSZpQmZ4y85zNSgoV2NYtq53lt9+/4uGDM779ySN++e0XXF5fc72r+cvfvOL7V5ekynB2NOPZkxM66/j46Yqr62sUntx4FtMRl5/e8f7iA3lWcfHmFVqLbefB6QPeXbzjcnXDjy/ek6UlEFitNrz48Q3WS4DV7W3Dwwdz6Pd8eH/Fh6tLqiKQ0ZFmGa/fXaF1Qdc7Eh345tkpmW548uSMtm35dH1L6zUmzUizlLrey2eMw9sagmeza3j3acOmNuzqjqZZEXwcaASP73u0t+BbjPJoL4EQSfAkdKjQoOwNrr6h399i260sfqJidvgaFBtDwX4YEn7WUIlCT9hHWS5JsOWoJMkMWZkebFdt18bBohS9QyBPbINQSoD1LsgwQGki12vgh94pFqpChkWhl4JHowgu4DpBYfRNQ+gtJoDrWpzrcV2P7e1BQWICPM0zfpoVzKwjsT0osbANQ2pRBklBP2z6ffCsNkvevHvHZmdZzI549uCU4+mEZrXl1W9/YHzvPrtixOvNkhf1mh+d45WG1zrwySiuSLhScKMDSxXY5znT+0+49+ghwTuyNKVvW+ygkvnsuouV7U5FAXdKEB9Zv7LI86LAMkaQD9Jf0/V9dCj0skxSmhCVUsoQmWn6EFwYYtE/2DaHgYyPbeFBUWn0YagOxMCpiKQIsnlPMgnF6KylaTqxuR2aDXWwdBKVI1me4r1jVzeMZzN0omXQsdujk4x7p+eIhdRGF4uJzKlC3ukRezCgOHQMV6m3a7IspmXHZltrRZJoCA6tA/t9w6fLS0bTipPFPVEQ0GJ7R5ZOOHvwhMXpfcpqwvLmEvyeyWyMNpqiOqaanIPOaeoaAsyOZgRtSLOK0WjKdDQl0TJw7R2YbEQ1OpJz0FnqpsUDeVGQmEQajiRF2JopKEmxJ/78ojQQNa3yAx9Ui3rJBMoEciOBbfvtEmM0DoPXsWbSA+tZhkDb9QrfN9hmh7WWajQjzyqGblLS32VAm2gVr1u01ZkMHUNNgkKW8G3N8WTC+dkJZ2enFFVBkmVonRG8xdmaenfLavmBrl6hfEtwLfV2x/L6istPH0RRaxKUAdf3JErz7PlzHjz8inK0YN86iiJlOs65/nDDKIfTxYjFvEL7mof3pthuxe72CqUUx4v7jMs5aZoxnUz47W//jtevXqGNQidGFLVKxabbCzPVOqwNuN7jrDu4IwnSdKvEkFcjjs/vcfr4nOPTc0bzMWmVMZpNObl/zng+phhHpEBUiVbTKUmRokuFNwGrDNXsmKPT+yzXN/S+pQsd1dGUpCohNeTjShRKSkecjTybiYqogsgd9x68NYzyCX3XEeoVWV3z1b0H/OKnv+RnX/8BWVaw3t1w013zYXXBm9cv8W3H0XzOeDSSOs+6g2JqUHcNZ5BXUel1EFr4iLpwYv8e0D1KUY4qHj3+ApNk/N3f/BXdbsnZyZyubbE+kFcVgSA83MgE15qYWJ6SJil935EYQZSsdxtG1QjiksBH1ZXre5r9RsJoi5K8rJCgY2Hei2sArGsJrhPVZteyur4kL1LSopSz0LWEvsN1PbP5MQ8efclssaAsKvCe8XzEbH7Eyfkpk9mUxfwY5zwf3r/j6sN70ixhOpuS5QkaT6oUXbtnNK7QRuFsT2oCwSSEtEKnBVlWoLzF215Yklkhy3sjnNksH3jKjrZt0TrFaMGgHB0fkaXp4aYMSqNUwLY7umZHXo5kGRet2U3ditNEabJ8DCTstysS5bm++kSSiurLe4t3Hbbd0dZ7vO0wiTC006zAh0DX92RFIUuiNGc0nknPESBJDEaD6xtc39G3LXme4byjabq/p9pKkoT9biVhwmlGCJ52t6NvW8aTKVprppMp984fMTq6J8iGOECyfcNqecV+W7NdrwhOmMLz6Zjj6ZhxmZGnKVmRSy2tNNoHfNfgXUNnW9q+pu/EXdP3XcTxeGzXor1HRfGFhB7Lz+P7GtvVNHWD6z1W2DDEFysYERAlxpAaQ5aY/5e6N9u1bDmv9L5oZrfa3XfZn44UJVESpKqyfeEbv5gAW2U/jgHDQMGAoUKVSy6hSrQkUqRInjYzd+bO3a1+9hHhiz/myiTrCZQAwYPM3axuxowY/xjfEASS1eQ6MMpScis8SRHt48ANSJI0sjRlbyKDOvnjnMMYEe6I/NkkiZ9fk5CkGSYOTAOKrutompq+78QNH4aBHXEv8d+mpWAQt6Sczlq5DhMrgpvNcmw2Ic0KdJoRbCpO0PFUHPFZTjGdU0yPGE/PyEbz6DvRpGlBYhJc3dL3NVW1ZVdu2ZYrXFvS1Ru6bkvoahSSyqjrks3yng/X33L75re02wd825KPciaz6T7SH7yjb7s4vNSRUx9j2IrYfyL7JTFEhE+e8Ed37Ees12BKECfowJYdMF8+Yn9EOI+7R09ko0pqVYRXSZJkaUaSy39b/RGhpeLeCgVN21BWJWVdiUDZR+5sEBOCjwPx6XhClooIquN+WdZoEV27rqPqaqqqZLvbsixXbDZLNrsdddPQtg1VW9I2NU1d4qJUN3y/mCV8HHi7PWJMyib76DDXuIhnIIgAq6N7WVAJCR4fzQB6/1g/8s7V/v4ivQSWLE0xQ3mmkTh/kqQYKxi8vu9o+47dtmS1WrB4vJFSZe9w+PiaS7xeD1xaFVB4tHJY4rWmQFuzx0/FN0E+8xC1KoXpapJmQ9rvSFyJDh2J70mHYlaxa8n663t86CL3PqCClHJ+5AZ3VHUtLmYFiVXkmWaUG7LU4J2nrBrKpkUnivlxwuFRwmyeMp5aPB1973G9pFzyIicvhN/ctRWda+SR972IpDbDmDjsj5/RhERek+AIXomZJ543dDSMSEJr4EzL++2JZpHBRKOGkkG5ztI0I0nSaBb7yKXWRsWiQ3HDeyXnEtd7nE/BazozJaiUoGTYa1TAKEkYpDZ2AuBRvsa0C6i21H2g0mLSMMkUZ8aYJGMUzZtgaVTOVlmUh6nxaL+jbyrauqftNFUDzik+vPsXKNL+L//bX/3l5OoU4scV39P3O5zOUdkpSlk0RBeMwQSZJLimZvl4j2seOD+dMk6kJEDHjaRsJpFFj4CJjqkQgds6irSu79iuHlneX7O6f0vfrDHak1grTJQoACRJTppPGM8vOTx7RTY5oeuh3G35cP09rlrw48+fMsosfdfsEQuDjZvoBHXeM0C8QdG4QNl0rNYl3377DY+PtxwcnmKyKZ//5Cdc396yfLjBxsdvlePFsxEnxxWYa4L2JGaENiNGh0fMLi5Yhxl/+49b/vPfdyzKS7w5JzCWiWZk9Sol009lGqYzeP5qwo//MOfFF4750Q5llnhWuFCh6BEOiUErGyeHmoAwTyQ7m6L1CK1zCB2u30X3p0d5Rb1J+bu/fk1WXXI6e8HB/BitEpzXImB7h2tL7u/eRzFULlAXYyGu70SgjXFklGAHatfS9a0ID0GE+UQnZPmE6eEJVy+e07QN9bZivV1xenHGk+dPsEaEnrouJTLQ1hibYE2G0YZt01HM50wPL/BIJHe4QREklmWULMJlU9G0wqbq2w7vFLuypu8Dh0dnPH/5FX/+P/wZD9uSh+Wa2w93rFY7nFJgLH/6F3/Ok+eXHB+MeP3N11y//k7KGJwUMGmtcEFKWXrfS4TbWop8RqePWHPFvXrKinMaPRU8AdEZGw+4Q0mYiLFmf6MWJqaOmz4p/5KvQ/7OGLBmP0E1RkQPq+SfghI3rTVA35GEQKrl6/MsMMo9Z0eW03lgkrVcnmiypGexbFjWmtpZQnTrHBWBqyPN+dyQ+gAdXC97fv5dy/fXS95f3zMzgQOroG0hKVgsN1ycn7BeLSkSQ2I01zfveXdzS9n2NL1sCQad52A2ZVJk+LamqxtCcGTW8+r8gD/64pTDacq33/7AdldzfHxM5z1l3fLnf/bHdH3Nrt7x3ZsP/PzX77hbtoyLES+fnfH25ppfffMNr9/ec7/Ysus8zkuR2nr5yMXJiKODCRenx7x9844kG/Hi2ROmkxG3H2747TffMh7l/OiLFyjgl7/8NS9eveS//+/+gtTAD9//wJPTQ86PxhSp5frtNU3Z8OL5FVmq2ZUVj4stQSWsFwsuTsa09Yo8s1RVw4ebB9o+0HXRLebkYJwYzXw2JUkSttuS1XbLtq6JpDOJ2gWHCo5Eg9EBa8QpEFwHvsOqlkTX9M0j9fYe39f4vifgI1hd7XmTwMf41CdO0mHaPMRddDwYaa320chdVUcHdMBY4SD1TqalHuKUXBZ+KYfRtG0n4ojR0jobB2fClpL4vh7EvCjsBR/o4rS5bduP1/7ggIjMpbZr6bsO53wsV4FMaV6kY17oglkwGCeOfz+IsQqJdcZ7lAP6AMvVmpsPt4zzEU8urjiejrAE2l5TGcN2VJD/6Me0F+f8w7vX3NJRTUbU1tApT4gT8qqLrDGlcEpjioJcKdbX73kynjOyllVdsnNdPFwRz9yDu5n9e/Gp42PgyX3qQh4Kxj4t0eL3kAXy80SIcT5G+gLxYPHxELL/2igKDX+Gyfmn71uICZDUCo82oPbJhoGLl6ZS8GNtshdMh8+Zja6RvneUVYW1iaQ3QmC92XJ4KIUidd3QNDUET5ql5FkaWWoVUjYqbgGlFUliSBODUuIsSRJx/Yl7QjBMWgsSwlrL0dExh0fHjEYZ2jge7xfcvL+jbCqmswMmY3G2G+2ZzY8ZjY6YjC+xyZRu2MAGRMxIUurWoVVgt7jDtxWu7bHJiPnhJTrNcc5TljVBGcbjCcEPfHURZ4yye6eOc17amEVHx/sQHSpqsIyggcR4VLcjCS2pqklCR6IsbSdulTTNpXzO9wTf09Ylb7//hkkhTkRlDMVogjF2H100Rt7P4eAfvFzrWsf28BhfVn1PagPnZ0dcXlxwcHRAMZoQIurD9R1NtaEulzTVBhM8Rntc1/Du+i1v317Tdo1cgfHz2XUdeVbw/NkL/vRP/yRyYOWwldDTbpeMk57Ls5TNYsHd7TtWj3c4V7PerXn//hFFQrUryRLNk2dPOD6/ZL3b8bO//6+Y1DKajbCZYTydUUynjGZzZkcnTA+PKeZTJvM5R2dnHJ6ecnh2xsHpCUcXZ5w9veLixQuOry7IZyOCVfR0IvgWlsnxjIPjY2bHB4xmU4rpmGScExJNpxxmkuAzTZ8YSAv+4l/9T7S9Z7F6BAPZZBJTNBqVJuxi+7k2en+tK6U+Fp0AWluSvKBsdrx+9xser7/hyBhmOmU2OeXy8ku++OKnPH/2JUFZHtdLHrcPvH77Nbfv33F++oyz40tsWuBw0V2v958xGeS4mISTNJqLjv7gOoJr9/t6YS2LM2s6nbBc3bEpl3z/29+y3W5ouwbf9hwenaAzEZlQcQjnnJgm0oQsS+maFpwDJ46gtmllzQlO+KNeGMltLwk2iRvH0troAE/SjMRmZPmIoBOm07m4u3WCMhIJVoh9XCkRuIrJnMPTC0bjOUUx4vj0iMurp+TjCT+8/p77+3s+++Jzjg8O+OUv/pEPH96RpIbJZEySJuT5iOAdq9VCRL6+lY4EH4Qtqy1pNsJoTd3UYBK0zVBG1iUdD8uDoGFtitZWXKpGBk27siR4h7VW3FhNTVuVPNzdMp0fYKKbNQRNUcjjkQJkWbu96+iaiq5tBEHjOppyA31N6KQA2hgtLtcsl/VfKybjSUxLWLJ8RJKkDENYpWG7W7N4uCGEljSV+4dNMkbjCVma4r0X0VkpguupqorpbC4OPSd76s4rUIbDwyPSfEwxOQAjg29cT7vb8vjhHa5r0MHh+kZEAW2x0dWeZTnPnlzx7OqC85NDCtvj6g1GeQgtrtug+pZRnglru+9QfY/rGlToacoty8W9FIq1DX0niJa+aeidp+1cTBJZArLm28SA78lSS54YUqPQ9GRWkxlNaofzizgsJUIvTtoh8jvcY4fBIwxakgiCe06tMXv+LHtUmuBAhuI3hqHK7zhGI8Pz9/Z8+70Dcg4ZBoXKxmsoLUjzMdokwnhPpGxREQuLbIoyOTafc3B0RVZMUVoMUGmSCOd5u2a7eaSptjS7nexR6w2hK/FdRWgrdptHVot7Vo+3bBa3NNtHQlehlPBqrU0IAeq6pq4qmqrG9X3EYUV8hNJ7A4Dw36VTZUj8yJpp9s9/eF2GUq4BBzE4EQd3oawvQypJS2G2+lhkPaQo5EfLWqiUMEGd9zF9KuKm/6Rkbm+EQBA7fdsJsk8rbCzCTbKM6WzGZDohyzPSLCPJMvJCkEKj8Xj/OBIzOEwDGi2YquG5xnVaK0PXB0lc+UBdt6AkQeZ9wPWxaMqLYNe2La5zUcuJe2g/CLuSnLXWYrXG6ugiD5K8Hp6oMWaPzIofSIy1FHkua0rck6VJio2irXBWVSxADbRdQ92WbFaPgszoG1KlSFQQs5ICQ8DgSXCkyPX20YFu4rBIypW978Xp5XqMb0m6HbbZkrRbdF8R+gZ8j4qsa61D7DlIUMaKohXAeE2EEsYSM3l+KppGpE8Duc8EcaeavWs1UJU7Vo9blvcl1aYitYbx2DKbJ0zGUg58e7Oi3NXx+u7oOkfvIpIgRHSasVibxn4huY+nNiG+CEDYfx503NcBe5avd46u737nPRIBXwpmB1zWx9dTfXJmGdYSvT9f+BDoEcyo6xqavqftoTc5QSd0OpXh28BWBzGo2Yy+6wiuk0LHpqRqpFB2mo+w+ZTa5HhbkNqUkKV0OpFieRfQuiANW1R7K0WRDlqnab2m6wKL22//BYq0/+tf/eX86gyi5VvrDu1XuHZNoizTbEKwGZ0KApLvKny3w7c1rWt5/+6aarPk4mDCOBNmjdGDtX8wZw0FBJFtoTXKKvq+ZfXwgcebH+i3t2i/xaiexH48oCqjsPmIYnTIwfFTZqevyCZneG+oyx13t28plzd89vSIaWEid5G9ODtMfj46J8SNqtB4pXFoWqfZVj2/+MXPuX7/hhfPX6KSgqvPPqd2ntubD/hWYPNN15FlnpcvIE3egdOoVJHMjqjMJf/0g+Pf/YcP/NM3lt6+IpteoHUq4ioypbPWkaQVx2eBl1/m/OiPMp6+bBhNPxB4R+cqAn10PGlCsKAMUh6i44RDRdFXbhzGFKTpnCSdEXxH125ABdlIoNk8KH7271+Tt1dcHr7i+dMvOL94xbasaJodVb1hvV2wWD3INCzeeNquFZHWi0jb98KkkdZnH6M/7KcuVltGWYE2Kb02lG0rMPG6YlduaX3P1csX2NGExsFofAAmpXaOXdOBKrD5GJ1PSEYnvPr8KdPJlL73EmdVAW0REGvwpKlA7LteYnXlbhe5sQ3FeMZoNKeYHLBpEv7hF9+w2VRk1hCUo+0Dj6uS2/sFi8cHPrx9y3a5JE8kOpDYhNSmeN/Tu5au7+j7jrIs2axqyC5ZqBfc6Zcs9BU1M4JOowP2U3E2Hr60QZkhTkrEF0h8cfhv2U3xUaBNbDyIgLZSEiUZAXHVKk101gaM75gWhiJVZJkmz0SAD62irQJN6ah2sN4qyj6hjRE7EyHe0xGcTTWhc7y5Kfn19Y7fXK8oe8u27Xn5dM6r8xkGWO22vHn/ntVyiU0088NDVotH3v7wPb1rOb844+hwynK7pm57gpMY8ihPORjnnMxzmnpD124IfUloN5xPEtb3N9w+rrl73PHiyRVdt6Ppex4eV9zcbfjlr3+gcQnZ9IyuD/ybn37G+UnC2w/3XN9t6dWEy+dfsNhsxUXiPMr3HB+OOBgnJKpntVrx/ev3jAphSKeJ5e2ba778/DnPnhySWsvrt+8xqebp+SGu2XF7e8tuU/H08og88xT5mIe7Bc+eX5Jb+T2v3z3gVIrzLVmi+PzFU5qqJM9HvL2+pW5FbDyYFBzMxuSJZZQneNexWq9Y77YiAGlisEW4UIn2JFYGKbg2xrxK+uoR32ywoaatHml3C8bjlOPDOWW5kwJHFXmh9mOhBHyMu+9LCfYb+LjxSg0mgvpVPLR/LA8TZppTIuZqo9FW7yN7WkuBi01EODVWi5vxE/eCtfZ3NsVKQZ7n+02lNeIe8n2g69roiLTxgBCj8MOEHk3XdhgUuTK8SAqufMLEa2xs8BhaSFWctJt4+NnVDfeLBbuyeWJyYAAAIABJREFU4uz8gquLM/IENB2lVdzblGtteRsC35QV3y/vWOweSFVP2nn0psJudiRlTdI4dNNiW4fpHNVmw+PdB+rHBXNlmAaYFWO2rmPVysFZq3i/BNncEBgKIvZCLB9FGlCRNef2G6bhPRzEdR2/R/A+iiECpYlYh08OaEmS7O+1Wsd7NvI9A4ONEIszB/yBl/upsRKLRMnwc3C1gjhujRGG2UcnjyRqvHf4Tg5FbdPQd93+kL3Z7qjriqurK4kEW0uWJiSpiWKhlOh0bbV3bkuDr5PNr1YslwsUkKYJm80KpYfDmSbNMoqROOSyPEdpT1Wueff6mjffv+HN69eMsoQsMfzmV78Cbzg9f4q1BdpIpD7E68EmKWlWSBN9mpMZw/bhVpAyaUofNMpmtHXD4vERhWIyHkeRK0SWvrB33797zWK5IE1zQBGUwto0Xj8Ga2I8HUmpYFIUgc3iDuUr+mqBDoHeKbZVg8kykmyE1kZeq/hZK/KUNLGRy6ZJkwyllIhGiOtiKBRpu07uW1FQU3gsPYnyzHPNfJZxcDBjPJmR5VO5zyHvb1WuqHcLQl9htQffcX/7gffvrqUoKJHBjw/S9tz3HfP5IV9+8WNmswO01hRFSpF6aB/ZPb5m83jN4RgOpglvvn/DYrEgzXMW65K6C6T5lD/80Y/58uVTNps1Kim4X2xYb5a8e/8Wm1imsxnT2ZTDk3POLp9w9uQ5s9NLTp4+5/DilMnhAdPDI/LZjGwyJZtJy3I6GoPN6IIwSOtqR1UKe7lpG6quoW4aGtcRNJhEE6yi7Du2XYWZGPQkIZkU9D7w6sWPOT455/7hns7VewG8I2BHBZPDA9o+povUR3EhBEFMOdfJfiQ41psbfv1P/4ny5g0vpwdkjWO33GHTA/LilOODp3z56o/46vOfMD86Yl2uef3mW371zz9nt11zdHjIZDpHKy3Cggt7UVRFEULQVBJ/rnY7mnIdC4ClvNL1LV0raBkVPIdHc8aTCe/evCGf5kynOct3HyjyMeP5AeDwXUfb1Kwe79ltVrRtg/Ji0GibRlBgcX3r+y66dmRYlySWx8UjSZqSFyPqSuK9aZpjbEqSFBiTo5IMZTLARATDGGUTuraT+H1g7wQr6wpjcw5OrrDFjMYLuit4T7ndUG7XbJdLHm7vub/9QLlecvv+mrZpOD45jTzNnnfXP6AJwiA1lq6VdJkPBmUzXFCSqMlGGJuKuOQ9rhesl0bECRGgYlGNEtGkLAUJkSRpTBo40jSNIlYgSVKcV3SdoxiNybIc5z0ez3Q6x2hL3bYcHh1TFCPaKPJW2xXVbkXXtqTRqdk0HW3XxgP9xzUpy4qPopUK9M5htcR5tZYzR99BkU8FU+fEFVzXNd57JuMRKENRjMnSjLaucN5Ttx2rx0eKrKB3nrKqCQh3vq1L2qaiLjeU2xWrxR3l9pFxkVMUM2FHorBGM8oy5qOCs8MpZ8cTTg7mfPbiJV989pwffXbFH796zuXxEevFktViQVXv0KpH+w7tO9p6R1ttcY04aEPf0XUdLiDFOxERoiCWtCak1pBHUTIzmswapkVOEs/A4jZWEPz+Xmoi0zEqYPsiqU/HpmmekaaZCGGDaK+lyEtFF18XI+l928oEO95nBwzDXpiNP/P3BVriQ9DG7IsrbZKSJjlpNsYkRTSWWLRJ46FekgLT+QnzowuS0Zzx/ACb5PJ1wHa7Zr1aUtcVaW6ZTce4tqHd3uKrDX1b0TcVTbmjbUqCFwyP1Z5Eh6gvSaFvuauoSrnGgxd3obwmkTOpdSxKEmOXiwzw3ylCCgNb8/ddtENZlvDE5f0S7vbgMpb36ePrprWO+w3BFwQVzQNK4Z2naVrqtotl2J0MGoh7PS0iXVEUFEURRWiLUbEYy+i9gK+1ou86qqqi7/q4xzMRkyiJmt6JEzsZyvfyEbPJjNFkTJok4sLNUvn5VsT9oehV649YKyAOg2UQ33RDKkGef+d6OScESWL1kYm7f/1CoIuIjd7Fnhr/sYti+OPiAEGE0+EzN+gZsfhKnvzHAKCW39/WFdvNgs36UfAZ9JHtmpFoTaIUaZA9fuATAxRxABnEza68pOxsX5N0G5LqEdvv0L7+yJ/2LuINpHRYBTDIcFSZBCIiLW6R90LmcKYZ0nvyOjh61+F6GaRoo8gSQ5El5NbjW0mlbh5LtuuerpGUd5pJOrp3gaZ2tF2gDwaQ4kprxJEve2sxu6gggrG1GUlWoHRCQOMiMk6roeiOKMaKgBsknizFX1qTJpLAUjFNI/+m9ueOeEVIIvwTrnbvXOThBrpWeiGq3uF0QYOlUyldOsPpJIJFhtfL4oLBO4fy0NU1XVfTtVsIFVmSUkyP8dkBPj0gzSYEG5Mm3mO8xwaFqZeo5pG+qukbh8cAUtR2f/Prf5ki7eTyWBYnDVp52Wi5HZQrUgWtHbHtwHdexMq+QXlhw4U+sFqsaOqag8Mj8jxB6eFQOQzlDSpuNmTK42nqLQ9379g8vEO5ChNaCJ18j5KbkE0ykmJKWhxycPKcg5Nn6HRO1wc26yWbxR2bx/d88dkVz65OMHqYgPFJbEvefhfLV0AOVy4I8wtlqFrHelvxdz/7OxaLW37yB18SSHBkZPmU9WLNer0GKwtW09Q8OR9xfBDAB3qd8GFd8O//35r/9F967heHjKevmB9eyiHYibjb9SWTSeD03PL5lwWf/9hyelWR5O9xvMWFlbBOYix8aKGU5j0R/jwwsM9kAYtFPiZH2xHOKVxXEcKWEHqCktjw6s7xD//xDeP+itP5C64uv2I8PqMLHU63fPvma1a7JW1XSzwjBDzi6OnbTlAHXRfbMWVKKELjEF+D4OV3pTYThkpeEBKDlF0pWtexKUsOL6549qMfodIxOpuQjY6YHj1jdnLJ7OSUYnqEpyBPMzbLLdvVlr4pCa4RFyESU3RtR9c2dLHFd/H4SFNXeN+za2qCTtBJjiNwt/jAaJwxGRXQO6xNZe6mDLttyW615Pr1a5aLR7brJX3fY7REvkTgCqQmEV6imZCMX1DlX3KrXrDQFzRqBsSIMQOuIIrrSgYTH9EGCmWHoUUUZlH7fxcx18afMbhqJU6A3n8U5Ho1CmMhTRSjzFCkJjKZFEkCiRGJZuscjTc4leKNIdggWm9dcn6g8b1nsQncLnt+/XrL12/X1N7y7HLMV0/HrB9L5iNFuX7k+x/eUsxHXFyecnY05+Hulvc3t8wPpjy/uiLPpDzjD3/0iofHex4Wa7lfEUDB4XzEfGRp2g1ltZU2Z5Xy5OSAz56dM53Pub55IEsNZydH5MWIH97e8uGhxvWWxKaoxFBul/zo5SnHU8NmU3L7sKFsFJvdFt/uSFVPaHfsyh3vb26ZjgqeXZ1wMB/x9s331OWOSZFweDBlu11xe3vDk8sz8L3EELXm6cUp0yzBZAm//udvGI8yTk9nTCZz7h7u2Ww3XJ6fUu1K7h5LqroDDX3fcTKbM0pTehf49TevaVwUyVzL4XTEbrdms35ku13jvEzfdRRole8wGnxbYuhQ3tG3Fco1aF9hfI2rH+ibDV2zwTUlUgQiB6KhSTsuIbEt9RMHJsgGJv47wACH10bHFEPYuyqHjVjveqyRgZNNLdOJcDFNdHrYyLkaNrpKySaNQTgcHJUQBT75TFhr90UIQ8wrz3Pato9C37DGhP2Gb8/QygopcvAeQ+CpsTxBMwISpQQJgSJRUg4mXEJN0zluHx7oup7LizOO5zOMkue5BV67wPfe8T5PacYjur6lfrjBPHwgXy3IdxVF5yj6QI4h1wm50eSJZT6bkVgDfUdwUpqREDBpQq0UD+WOHh8PAxHWH100H8Xw2EjsB3baIKoL/+93NkufOmTkDduLt0MJyvA+DkNU4aT9vjv34yEO2DPwhLUnjdHDpnB4r5wfRN6h9CMID21wT8SDqoqiMSHsg2bD5yPE522sZrVekacpx4fHTMbTSH+RkrfgBQegjaauG3HJBkdTbtmuV1FkDiRpijGKxeMj1kbkAY7ZbEoxGuHc8Jx7Hu5ucW3Lw+09q4cVm+UDvqt5uHtAhQSbGsq6EqyM8hidRjZmKnFkk5CkwtXM00zWbp1gcllDtpstfdtS5MKjzdIMHbmu8tp5mrZEa81keoDS0vyeZYWgOYyKZ28ZzvqgZBhoUrxS0q6uEzA5TuX4ZESwyT7REYJI9MZYbJLQdT11VcWyh0Bd15E3KQiN4HpxUAaJRQYFKjgy7ciNY5Yb5tMcnUBejDAmQwVN31f0fYvrG6rdAtfuSDRsNyvevHnN3f3dfl0QZnVH17WEIBzO07NLxpMZpydHnJ+fUlVbXn/7NWfHI7747IppkfPuzXu+//59LLfMSYsTTDLl8PSc1nuaqmY+PsBjSfIMrTw/+9u/4eb6B5qqwugEm+ToLCdJxd3otaFH0XY9TSvFYOvNmtVmRVVWVLuKpmlpmpZtuWW5fmS7WdKUFa7u5DULsp7lRU5Tl7R1hUksLQ5vHHZsSaYJNssI3vHh5h1eGTrXsto+gtYkWU6wgjv44quvqMqS9WqJ94E8LwYtB+fF9eK8w4WObrtg9fZbbFVxQMrMKR5v70gnM6YHZ3RtgC5hPjrjixc/4YtXf8D0YM6H22/5zW//jrc/fM80n3F+fopWej+IV/H6Hy5gaw1Wg2tLNC19W+OdJysKlFa0dYkKMqCxOuH1D2/40U9+wvPPX3L74QO3b6+pdyUXl6d8uHnD7c17LAoxifZslkvevbtG4TCJmARGRRH5uVK4lWYZ292Otm0ZjyfMpjOSJCWJBVy99yidxL1X5DrGW5wiYJKUNM3iITbdn01656l3GzYrKUYsZgfMj85QfWDz+Ei5XZMlmndvr7l5+466rEUY63tu727jfRPaekdR5BhtaJqW2fyQLC9AWXSSg0pETLRpTKOI69H1rexdg0cbI5Hn6DADcWV1XSP70CzHIXgKZeJaURRR4LH798poRdtKZ0SajkgTKSvK8gK0OOaTLEcbQ5pYkjRlPJuRjyZS6Obi/UgNGAxxPbVty2azxvueNLWRSZ6RJBlZmhOCpu8VeTGRs1d0/hZFQZ7nkamaUTUiPlU7EZ7zPONXP/9H7u7vGU8mtE0NvkWrwHgyFkfhfEaaZXz//ddUuxVPrq44ODyNDjcZLxIkZeT7FqNglKZMJyMmecJYO9rFHZuHR6qy4fHxgbreSDFx29A1JeVug1LxbOddxGwoSdIRWdRmiLdbsjQjM4bcWhFqbUJqDAZx+WkNeBkMa5BhcbxHOzd0BahYRhWia1YchmmeRbE+iaKhjiYj4v1LBCAZWMseexh0D9xoPQRjwvA17PdQQ2mUAqweRLNBFLb0QRBsOjJAMVLirXVCko/IJ3OwY3mMiVxL9fC6tiUqsRwenXBxdU6RW5a371kvP+DaVoSrGK8fHq8aEl9iE4R41lNKXNJFLsLmqBiRpTJg7CN6yTspjh7Oyz6mO4c/JhrEPv0z6NTDHkgENfn+IXErP4+4txmEKbUvy1JouY8PImBk//Yxdeo9ws/no7NzX8obXZ6jPCdPM0mtGflciaYf8M7RtjLMbqqaummoSxGtd3FQOPivBxe+7OM0Awc2IGgNYwzoIMzcqNEEvBRqWits02gJ9UEG8sTBujDpP6bw9mYCAK0ixmvg8MreVZJubm/MsPYjZ11eX0nm9L3/xFQnzt6+b6Rsy8tnoOskSVHWFVVVUm43LJePNH2L81Lwl2pDmopw74nluiEyUp2U7xnvsK4l6xuSfkfSb9GuQoUeFT4K+8rI+V/HgTYo9NDdoeUMH0zEzuhoAoycWL+/LkMs8fLS3+N8PH/IQCkxhsQqUmNkRxxq+r6k6zp6L4iapDCMJxlFnsqeJg4njDLxZ5n9Pq9va9p6F9MmGmVSrC3keh/wHPGz5wZHdOQWy9lT1ihiYmYo5FNKkipilhmS6HHfrwZG8sdhk1KGXdmx2lYsNi2VS6lDSktKTU5rJiibklobHdDRVDL0hmhouooymjGMtZh0QjE9h+KUkJ+SZVMSa8iDh14MBEW/w1aPWL/DdCW+q2WxC3IWvL35zb9Ekfbf/uXk6jRe3EZalQnCh9k+UO2uIbFoPUU7LYtg34BvCaqTTb7TvH+seX+/YTyeMx7nsjnyXZxoCJjdNRWuKanW93y4/i27x3dkpsdqLxZnFEkq3KY0G6OTnKQ45PD0JccXXxDsiKZtWS/vub/5gWp9x1efPeX58yuSzO4PvMPCLhsgWbQD0DmZzOejKeiUoA2EwHJTsStb/p//9B+4vX3Dn/3Jn5DonPWqJM0LAoH16hGre6xOKevAw2LH5eULVDLnV781/Pv/WPHPX09o/DlpccLxyQlaedqmoWq2mLTm6oXhD36a8+Izz8n5DpO9x/kP+LCRMhSlgNgoiHBQrUkJPjZSEg9qcbGUtUSmaHXb0vWQZjl9t8P7FUE5PD0axf3bhl/8zQ1j/5SD8QVXl18yHp/S0rJuF/ziV39Pu9syinFWH+OrAZnQSFS5398EUMTG9ajxBL+PPKRW+ECkSYwCD7ByEZ+LyYwnr77A5hO63lH3jiSf8+TVBS+/mKGNoto0+KahqTe07RbfVWjfQl/LhKXp6ZqWzvWRu1OzXokTAKWovScbHzIaH3F4ckKSJGTZGKMsZVni4sE1S0fM5nMSrXj25Cn3i0cWiwdxqbhA1zt0LAfxPWiTY8ZPqZKvuPMvWOhLGnMIpHLDE4Adv4s4UBBjw4O9fCgCg0FtjRgEJaDZwdloFIKjCNENp2WzYbWIT4mFREOiApklOgTl4JNYsAn0DgKWYDVdgNYF0hTmBYxxPDtMUD28X3R8v2yp0fzxywlPjnPqbcs//eaO7252vH634e7hA3/605eMU8t3r+9IreWrz56wXjwyKiwf3n3g7Zu3HMzHzHLLP/7TL9lUHdEAR+8cfVfRlSsmhUSct6XHJhmfPzvFNWsel2s+LNZUrcMFzWq942FVUveK85MZr54ccXw05e7ugfV6yZevrphkKWme8ebde5Qr+R//4o+YpHBz+57GB/qgSW3K0Swn0w3l+hE8PHtyiVItTV/y7XfXNI3jxfMLmqbm7fU9d7e3TAvL4bzg7m5BWe548uQU5zvW25pvv77mxYuXjOcFWhvev7kDk1GWDbvFgrOjOfP5lLKquVuWaG0JzrHbbVlvVjjXY62KG3kXi8E6CEOrcE1wJcHVJLojVQ2ueqTZPdDXO9lYIFHUQMC7QNdJuYGKiAythsgsDGUDIYQY2YsO+HhDFiaXtMgqhWyiozOBKLANDcZaw6gocF0HIZAaQz4SZ8BQZgIIp1oN0XlkxRjWsSAb1SSRjdUAr0/TFKWkSM4k5hNRjchvi025kUdmIkJEEbjA8UQFEWl9LIDQChsPAihF07a8v71Fac2Tq0vmowITHC2K+zTja2V4U0zoj4/Rowy/2xCWj/jNkkJpRjYlixw0gjTfjosJkyLHKUPjZVgzyQpILKFryR2oJKEZFXyotrjgorAZ9v8bhPN9oYVW+9fo9zEG+/K3TzbOH6PR8jqrKOoM2ILBMTKI+EMBwyDqEu8rWmtBW8SfNzhWPnX4Dj8zQCzmgqCkSGwymf7OZlV+hY/8YOF+igikIv82sNmVWCvYgs1my+H8iNPjM0AKonZVTV11dH1gPJqKezc4cA3NbsPj3R0BGI0Ltts149EIazRaBU5OZqQZwrxb7UhSEbld1wufUQWODmd88dWPUSqlaTsw4hQryxW9U8wPTkizTLBOg9AdHXo2kdJHneV0yuJMSlAilCZpTlqMyIoxaTEiH48xSeR+RRdCURRMZ3OyYiSlMCaVA4YRF4tzgeCh650gimwqDDKTY/Ix6eiEfHoC6QSvC4l/Bdn4Jkks8+u7yJyLLhH/qbgvJU7Wmr2D32pIdMCEmkmhmU1yJqOEcZEJcy/NsEmG9466WlDtHumqHVkqRaCur1ktV/zm179mvV6TFwVpnu3RGD66cIxOmEzmHB+fk48KxuOU9XrJ/YdbrA78xb/+KWfnF6yWFW/evWO9a8kPr5gcPePsyVdcPL3kyx89o+kD6+WWw4Mjbh9KvvrqnMS1/B//+/9JVa6Zzaf0PtD2Hc6ryJ/1sY8BcTU3PU0pjr2m2tI1JV1b0nQljWvQSSCdaPLDjNOzUxKbcHB0xNHpCXkxYrvd8Ph4K9eOllIn39ZkYwsjiyryuBftOL16idOBx80twSAlTWmKyYRTuVutMFqz3e4oqzJev3Lok4Knnj70VOs13XKFMTAKCc/mJ+Q6wWYTDo4v8V7HdmOLwnI0PeOLlz/mxz/+MaPpmMXjLf/8y79nt95yfnZOkY/QyuyFE0LAdS31bsXju9fcvP2OLNGMRgVJVoBNCMbigscmgizYbjfc3t1w9eQ5SZIxnU1p+oZ3717jfYOxhuOjU+YHR4zGE45OTyiyjMRqnGt5uL/B9RV5Md7HOIXPmdP3cl6YzQ/wThzfWscBRN/L4d+IICPiTU9VbmirbWQtDgKMFZZfIuVYKEW9vqVc3+Gc4/DglOl0zna1oGl2zI+mvHr5ilkxYvFwR+t6vBLTyeL+BuclBXhweMh0OifNRyiTYLMRJh2JSyiIEz4occg1dYV3HcYoQuhwfb8XNIaBnPc9XdvQdrUIekbhI0cYLxgXbU3k1ErMu6lLmrqi7RqJFhdTvA+s1/eEIGKBsZa2bVFak43G5OMZST7CJBnaJBibkab5XtwZbj/GQF3teHy4E8RAkgOGpnfihkOTpImsiTG5MRRXai0xbB9AWSk1zIuMtMgZjSdcnJ/J77cZTdMwnR3QduKy7XpH8HB4dMpkOiaxgffvrlE6YVRIyWrf1SQG+npHuVnRNhWh29E3S0y/o374wPWb71lvdqzWWxb3d3S7FdV2SbXb0Fa7iHASgScoQ2JTnI/XXBwqJ4klzxKs0tFFa8isxuBQvieJ+zmrP56PBgebiWlI+R0eY83eWUgQhE6WpeJ+tBEzEAWt3x3KhlgMJfeSIFnrvdtS7tNRAP4YaxVh8ZOoMsj3q4i08YMDREXxR8nvVcZErryIMFkxxmYTdDJmlI9xfcdysaRtaw4OR/zkj59zdHyMCob3b3/g1z//zyxuvqMuN+A6vJfhu7WW1CQRVcC+ZGq4N1mTcHh4xOHRIaPRiKIoSNMU7/x+GOz7WOYUomMWGfJ43N4lKqaY33cRy/9/yuYf/j4gA0oxOqhYki3Cfeec7LrDsPMOg/+GYfjslbwPkkGRn4GX/ZXEy+VM3Xc9LqLAur4XQ5kTDFDb9THdIM7gpmuo24q2b2kjgrCLPTHBO1rX0rpW8EF9H/nqnq7v8b0UyrVdL7pVFJ29D3Iu8QrX+0+MENFhGyKrlpjyGoxa3tMOBd6xI0ZFjFaWZqSJ3Q/qB1yHuP4taZ7FojQjfFMdRdDoiJfnK4WwTV3TdQ1t19D3HXUtbN2+3rHdrvhw+4714y1dtQMn+LQklYi+Cj3at1jXYF1D2lXYfot1Jbqv0L5E+QYlPjJQKg5DzJ51rPXAvtWY4AiuJUSkBUEQnygVcQeSQgtiId4zfkPUojT2Y/qNKNJH00WWpmSJ/FtTeapK0iSjIuXwIOHkRHN0kDCfZ2RFgrUZyuSgU5RN8UFJ2XvXCn4oDAgyS55ljIox4/GUYjTGxPemi2mMoQhNqxAReWIIlI9sRJSaoeNhEG7j6DP4vdDbe9nT7hrHw65mWW5pesOuViw3G/rW4b2l0xnBWIxJMSYVsVnJ+cEbS6cyGjOlNROMHZFnGXY0YzQ9JpldkEyvKNKcPPGkVu4nOI/pSuhuMX5B5msS7UD1aBVIjeLd9b9AkfZ//rd/9ZejqyNx7Q0OQKvpmxa3XhLqFa7vSZMclY5xQWDE4ozpMcoTlMWrgk3Z8/72gUQZpuOMIvE43+L7GtfuqNePLG9/4OHmO5rdAqMcuZUL1CQJSSKbAqUtaItJR5xdveLw7BXYCb0LbDZL1o8f2D7e8PnzCz7/4gVDa6EP4kwJQWOTNH4QHS6WqaSpuF+CSkAne2fftu55WO/4v/7vf0dZrfhXf/rnjIsJ280GowJZlnN/d0ff1Uj5mGZXgTNn1N1T/sPfLLi5HeHDIUYXJGnKrlyyWt2SZhUXTzU//bMpf/CHGQcnK2yywPGI92tQLhoVZPIvkzqID419NH5YUYfClOi6CijwnsVygfeK6eSQvtvi/BqlakKQVvi335X8839ZcWBeMLKHnF99jiMn6MD98gOrrQheM53GgziEAZbuhiiItFfKzS/QxSKxwT2llMZgSIxFpQkhEd6puK1k8Q9O4Z3i8ukTjk6ndH1N1/Z0nSGojOW25e7dgnr1SLNd0Xa1RNK8j6gNEaP72ByrIu+m61vKMk6gug6bF8wOTygmR7x4+SVd21HXDWVZ0/cOFyBLUubzGfP5FFRgtVqy2+2iKzCLj7mjLVc0VUXjLcHOafwRD90pK3VGZw+EcwZxk2yiEBsds9pEjEGMW8Q7ubZWvn54o4fYSXStDA60/QdhEHu1Eg5tFHATs+8UIzGDOBMd68OmwEPAsat7GqepG0/bQOoV7a7n8abEtT2kCdd3K86PCr46s/zN3/7AP3y74P22p2RC5RQn84J/8ydP+Ou//lv+6ZsbttuKP/3JM66v3/GrX/2GZ0+f8uVXn2Pw/P3/9wvevL8nG+ciCgQlB4Ruy9nxARfHB3gH98stHsV6t+P6/QfuHtZoU9B1gdV6C77n5GBKoOfl1RGzwvL1b7/jcbNjW7ZYFXj+5IhEB5qqxtcb/tUff44OJY+rJdtNieplV/Ls7IDc9EymOffLFXj47W/+mfc371FK87hccnJ4yJOLI5xz/OLnv+HoYMpsnJCnCd/9cMOuajk9nrHbNly/f2C93XJ2esB8nPPhbkFZ9figaeqSy4sTyqrimx/esytYWIhZAAAgAElEQVQ7jE4/mV4KON2qgOtrgmtQvsUER6IC2reEbgdui/El9DuCKym3j7iu/uiYMESnSi7uHBcYjQvyIiMEcd4MBQEwsMmIrgkdm8SlsM/j9hEoOUAJN8p1wzoln0uTyPRY4lRpjF/JZ69parq23RfCyLT94wFiOERIGYaJbfZDcQORXyvxMOdkAm2siagDWRNlur23g0QvCOADBzjOE8vYQaYMSYym4YkcXcfdwwOgeH51RZFnBN9TqcCNNrwZjbkZzejGY1rXkCphPRuvSW3G5PAcn+XsuoZgU0I+whlLcB6bFOy6nhoINnI8U4tFk6LQRYo6nPF2+UDbtfsDw8BqNXtkRHQ1649ICtncDSmRIXY3NADLVf/f8mhlI/WpGCyOZXFiycY7uhr4NMb08b0OIZCkCUGB73uMUns3rdI6ulaTvQhsrCWLn726qhgKSwbRWRYoeVxJmkqxkjE0VUNTV4yi07VpOs5Oz0lsKiULZStCQBTa0zTHuw7f7wi+Z71ecnYmPNuq2pJmVmJw1pJZ+bqmcVRVDwHyLGGzXPHDb7/m7uYtOrHkkwPOL59JXLEsOTk5iqzMKSdnV5FBazCJNKwLxsnEdV7hEHSMsQnaJgQiMzFNMUnOaDRGo6Q12YNNbURHWJLEAg5r5L7Q+8g27qJTKEiM2cXnbk2KR9N0AR+EL9/HQVjXNCjERaWMRQrc5KBtkzQ2Sqf7MrA0SUizHKs9u/s3bB7ekBnPyeEBx4dzZrMRRZGQWCvN3jZDa0PXlGw39+w29/h2h+9brIHtdsXd7QeWiwW9k0h2XuR7od55KWkx2pDnE66ePOX89JTbDx8ic2/E5eUFTduyWu/IRyeMD85JRzNW25qvfvpnHJ2d8+7dPXULr28+8Pr7N1RlzfX7O8qq5uWrCxbLFb/81dc8Lpd4o8nGIhQHbekacbmjYmtCCLhWhDPXd3g8XvXoUeDk+TGnX1yQXY45fHrAq3/9B4xGBW++e0253LFZr1neP+CaRgQH5+U1V5q+achyg50X9KkmyTMm8yMmR6d4FVhvH9FWXguTWExqqKuSuiwZjackacZ6uZJDYppKiaoL+LYj1QZXlTS7nayTrefVyROOijl9FxhN5iTZGK/EkBBckGGzN0zGBzx78hlffPEVs9mU777/gd9+/UtU8BwfnlMUhYj7bUu929A3JW2zYzabSIkQWhIng+iTCq7GeU8TsVCXpxc8LBasNluePH1OlmVkWcbFxVOSJLpkFZRVzXq9YDQacXF5SZYXaG1l8N51FMUIpRNQhrwYkecF1ogoW9XVXkTwrqepG1zvybIsXgMSH97tRHSXgZ7Bu5gIQ64/KbQx9K6j2u1IrKFXSgqllGNbl9zePfD+7TX3dzdAFFTw9F1DVe7Isox0NGF6eMpkehTLlBNMMsIrI0gHJSLdbreJZysRK4w1aAQ3kRcTuZcHibO3TQVAmqUysI/MzK7rYuleHPAPJpW+o2/EHZZnGTZJaNuam/dvKXLZgxTZiLqs2G6W4nBN88g6FIFuGMKhRODyIQ7dnKwrWZ7StPWeVe6j8Jimws3UkVeOMnK+ITrnfEfdNOI8zzJxK3oZ9CVJxuHxCcVkGpOZY5IkR6Fpmoa2qei6ljzLaOsdfdfSdTWPDx94uH+P9z3WKMrVI025pMgMfbOm3y3ot0vurt/R9j0PyzX/9Wc/4/rND2wWd2y3S0Fq2LhWm5TESJljEhmw2ujI2pQCR+E+WkZZSmINynt06DFxnzT0R4gAoSU05JHKvNDHch4tuI3I6Fd6aKDPMAPuQovzcHBoKvUx3bQXSKJzcUAdEWIZVBQZhyNj4BN+5H5/IOcLcUpbtLEilnj5ezO45owItsZocU5nI7DyPic2JU3zvVt6NEooMst3X3/3/1P3Xs2VZVl+32+bY66FBxKZicwsX91d09M9TbZEDseIfKAUCukz6UGK0NeRYwSDTpRoZloz3dNmyldWeiQ8rj1uGz2sfS6yGeL7CFGorEAhgXvP2Wfvtf7rb/j8N3/F0y9/yfzyJb5Zono2oVYMRyOm0y2MNTIwUFLfECWITWvNcDhkZ2eXEGJaAy2L+YL5fJ6scpwASXJ1Uq0RNrWRLMuk7FV3wPS7bNB++PwuqCge4GyGYz3YK5frzr6LKMBWTD9LS6kploDeJzF3CmFKAG2veApebPyapqFru01ug+pVtD0w3HWSu+I6us6Jd+07A3mV3qsMdO8YxaF/DUFY/3Xd4FIvHhLxIXgZmvdryrk70LgPEVMKCIGmbjZetV0Khep9xcXH1ouioRXwzxi9UddlmQxuskzWe2azzWsEURAAyUdf6nqp24OwwFO4mQJc19BWa+quYb5esZovWd5e0FQ3ON8SlEabjCLTWDqK0DAILbpbo9wS5WsBdGMHiK1Q7GthI1YXvR+3AF59Dd4rxCN0DuU7TOwSwzb17wkwFCIKSSwoAxOUSkzid2v0ADiMVZtQYO9dUgrXQGQwyNnbtUynmvFYMx5lDIZihaJtLiGMWuOcXCthp2pUZtFWgPDRZMp4ustgvMVka5vRaAwRNBJ2qHWQQUnCHFTqB7TpbTUlkLf3+hXbs2SFoPoo5oSnzWpmbWDdtFRVYLlqmFe3qLrFdA3OKFQxRmvJICLZ1zkCUVs8GpeJH/aoLBiPtykmx5SjXfRwFzPYkkGZkaBu09twRI8JS4yfkbUrFBVoT6YVZW549uzL/0+Q1v6nX/i79CFbeZDUcMCblJJar8hcQx4d1c23+GjQR56R/YCaLZzKJcVNl2jtQUcalfNstuLmP3zPb7/u+JM/2GFvFHDNLfXiGuNa8GtU7BgNRL6RFbkwWoJMSYMMJ7DZiKMHP2Dn8IQ25hCFkdXVC9bzCx7c2+WHP/xI2AqthG3ECJ0LEkCVjN17rKuqKoqipGs7chMwJuCjo3MB37bMFrdczG4YmpA8ECN5BsE1jCY7lOWUxfwGaCmLEm0GrOoHOPUBs9UbnJqzrpfAilEI7OwZ3v/skE8+3WFrr6YYXBK4onMrmdIASr8DtAK9MiMGl76WvHlTiAek5hkN0SamZoYPnslkKinSPiZPU8RHBQFE2joQoiYfFwy3dnnw+DHECa9ef89gMMDHSNCQ5TneOfEVCZG6kiKs9zqMkFidAp5IpJm8D/FsEe8TFSOua8kHAxyKGJwcDj4wv7zki1/+gu2DAmwmG4sV3x6PRsWczGiilemTsUoKJleggsboHBd6jxx9Z1beWwloxeXbt+zEjL2jKc+fPSfElqurG7yH0WiM1oqm7fDzBWE+p+k6GucZDIeE6KmqVnw5o6ZqV7StIQx3aMM2SzdimQ9pVJaAx7RJRSlI6Vlsup9IpwAQ+oIX8dvpDefS2R9TIJoU9rJRxgSS3KVSCgbcRvnTw6aQaCLokAhgCRbrNORWETtP3UWi1nivWLaBZu04GBQo3zAsLfuFYkvVfPvFgtdft7ydRbyZ4LUhtBFDh3Et2rc8fHiMC9d88v5DFI7Ty1t8Jiyw3/76b3j5/AVH+3v81//kz3g7W/Kr332NTx7JXdeyWCwJO1PGo5LJMKdynsvbJTvjAR/94AGnb86oVgHwfPzJ+7TrJQ+O93j+9ClnnWd7us3RvXssFiu++/op96aGpp6xM/C8vDrj9fNvOdgt+cGDHeqba26WLfNZy+9+9wV//vNPODy4xzdPX/Dv/uIXPLx/jz/94z+h62r+xb/6Pzl9fcmT+0c8vLfHXynN9y+vefjgiPvHR3z3/C2v397y3pMT7h8fsVh3/O3vvuB4b5tHj47YmWqub9fEWFK7yF/9+mvatqJqJEjIdymVUwW0ChijwHfEdo1SHoUUcKHriG6NCjWxW9E0cymWCMTofw/YkzpGWAUqgfnjsYDay/mKGGTv6A38e1ld8G6zXu/dv8d6tWaxmN81ZanAi4lBEmMKINPisWYzKSbKYkQcCADYNi3rZU2WCyjQ1BI2Rip8+3Ap8UCKlGUmILBPRXYKGBPPqxRKluRKvezVOxFV9axY0veGENHec6siNwoOg8NHRzQFKEOXZFvXN1coFO8dPyTPDBWRtc04I3AxLFhNR7QYVhfnqHrN1v1D9g7vs1i0BAwPPvqIfDzmy7/5FV1Vo4ymVIH64i2XyxXr6KnpcJA8+QI2y2mNZ1WvOH+9oKnEJ1QZvWEU9GC2SgFRCpJ0qPeo5U6KtWkw+sLxrpD6vfM9RjkMuAuHENakHDghgM6M7Olp0JZnyf80qFS4qtS8wGA0JDeWrmlpuo6gJfDHaINzae2mxGGd3rsIVpJlg1JyHxHmZlYWZMOS4CNq3dC6hovLc3a2Dzg7P+WLr/+Wzz79Q5QySIvs0caIyqFrMcpyfXPDwAYODndxvgVGDEcDqvWa0ThDxcDt7YLgW9YVmHxIkRQyq9VMQivNgGKwxXT3gL2DI25uroh+wu72NpeLFZOtCRFPVJ6IxQdhDSqkmQwxUDVr6qqmrZtN2IlPlgat87jYYG2Ga1s6J02JTmxdRd8kRKxRCeyKwhpsGoICjZWZbrp3Pjg653GdxypDFwNNAjHWqyXEwN7+PiGdk0bbDVPLx4DNxVstJsYXeNpmQVvdsDvNefjggMneFtlwSkwezllWUGQF69Ut89k19WpG164wOhCcNMyv3zxPXsMtishgMJCBlNa0rQx9UTIEDkHxgx/9IfdPTjg/fc1ke4f7jz6gqipWXcd474ib2YKvXlxx//GI7eNHxO/OOD1fEcMNr589ZzKZosohOsJ0a4eb2YLlasE//ze/JMTAP/gn/5S9e0f85ne/ZLm+ZmswYmJy2tbR+RanFdGWWG3JByOK8ZTWNzhdg11TbmmKvZIbV3Pjak52j/nm7StOf/U1vm0ZeCuBTF1Nva4pbIYuMpxpsbZEaUO97piG1JzZSLY1YO6XrCu5t1ZB0AGvPK5ey7MUIufnZyg0w1xeX0z7fKg7fFUTbI1JDWEIgUu/5Nv5Wx48eYCfVTTza8rRHsbm78iCIw6NjqD1iO3JY3784/t8/PHf59n3X/LN11/z+vUFH3/yMQf3DslMxmhckpkhcW9HhuIp2wFtk2S7Q2cao4URV9UteMVsfoPzHTvbu2jfYY1h/+iIyXSbq5s5s9ktw2HJYr2maxqsscyXFYPRNqPJPsNqjXOOpm1BiT1MXgwl7M5LCHCe5xsWW24t+IbgG1zbYHNhkWuTs7WzL6wppfFBCqeubWlCQ14UFJlluHVEOZwIKN1K2FlDxv7jz3hv6+/xq7/4D3z+y6+JwRK1F4B5WbE1HtGsFzz77iuG022ybMST9ycopViv1wzUgCwfYYaWpu2om/VG+h8jhOSX2TYt67rF5gOKQuwJcmMgyzcDrq6r0+BLFHf9sF8lAHEzgC1KYnTYLE/7v6fMSwaDETbLcZ1Da2iqNU1dYDIZaCmTSchMFDKGnNm9GkfqVudkHY2GE6qqRqmawXAk/UwUCxVrxJ5CkSy9YiQqOcfL5HPey8N7pVXnHMp5YehH6OqGzGaMRhOMjuhRztX5G3xwnJ/dslrMGJRLjFZ89NEn+NjyN7/4j2yNR+zvbTG7XOO6inYx5/tvvuPq+pZX5xd89/wl59c3UstoCQDLy5LheAJB9kiFovNOQH7rsT4jt33IsUUjLFoFhM4RQ5es/sBq23d1pLFyOoUDzikiAZ0l66KUVdGHEvXBwiaxCvv8gLszvTfwkDqNBCTdSfDjpgqIKtkQJcsklZqIvo7oPxQ6BQg55KTRGCs9ZPROZN0xYBDrHU0K5PYtoV2z9uJn2jZrLi5ec3n5GhUcs6tLquUFsVuRpT4ms/K8ijVXS5MAPZ/6TKU0IlCSwVXbtJy+eUOMUfydf88eqmfJ8nvvS2kjTF3MBrS9+/7+U97TnUorbv7sAW+VWIXGKqKR+tF7T902m2tnEhkGrYRVSdiA5zEEfICAxyXbhjSflnoIhcmyzfPbD777DU2CWVN4WqrfYwgS6JXsprQyDMvhJtRV9ohOwsiCRynxq1Ux0vk0zNqA0j7Zm9lN2Kv3Ht9JiJlzEtJIsjLUSuMJKdBXFMtZJsS9tmkSVmAITgY5g3JAXuTkeZbyD9zm7I9a/JlDUmxFZAAkKgHxlRV7KZKlULpP+OQsYahah28DruloVtes5uecvX3Bwb2v2Tt+wqMHjznePWB3kKN9g0XWrI5R8CsiUYf0DKj0774HT1CKtfgolpm9R65WEaV8ymdaiu95LhJ+bIaOKYsmrU+dgF6vobcFkP20z+TQaJX2SRWZjBWjEGmDomsaXr+44vY6Y7pVMt7KGY0t944NB4clq0XG+dmA588swSkao3B1SehaXHSoGAgxI+gRZGPGwwHlICe6lu2dY5azGU11y2x+yXx+I+oLFci1bC26xzKSMqt/RnpVJu98zXtP27TyeAVH13Q0TaDuHHXXQH1J165wBjJTopFwszIrCFHhY0Q5R4ZiZA1mNCEr7mPVIYGM2K7xOicYDYTUFwRyPDpTOAaEuIcJx5RuRcOMQIfSBUY7/nMff6eZtP/j//w//Q/jB3tpEuRxJIPjuqYMIqNWpsN1M0J3w1hFTD6kMxmZkvRwq5JhMIEudHivuTx9zRd/+W/45je/4ObsFYX2TIcZk3HB1nRIntKXtU0pqzH586DJRtscP/ohe0efsHYGnximy9k112+fMy4Vf/SzH5MVuUyg+oYwgQo9lVwlUCAGAQ9kE/GJ+dXhg0zcV8uGL79/yr//q//A3mTMz3/yE6bjqfhLZjlbe0fczOdcX73FuzVKyQY3n8353d9+zs3NNc43FIXn0ZMdfv7zI37+D3f45DMY71yi7VtiXBLogIA1GfL4w91xqjafG9aZSjKWGNJXffpeDRi0ytAqRyUTd2OnoEbiVRZWEFsBTnXG898uefN5xV75iMPdT/nRz/6QTgVurq5Yr25Y3F7CumKk5VBru46mkXTNPBdWVIgBHwNN6HAx0AaPI6ARMAEfKbIMnRm8QtLNywEk6ZaPHqMg+I7VesbB8TGT3UNUOUQVI7TJCb5jvZ4RfCUFj7XCXjJGGFwJjAgJEGi7jvVSCurlQoAsqzV/+R9/wbffPOXD9z9kPBlTloPEzhNwADRN23J+dUXrPZPplNlsTlVXGKvxHlwjMn2sIR8eU5kDLtspC73P2h7Q6hEqGxATC5r+cE3Jq/Knujt0rRI7BK0kkEX1QG46HLRBZyJdC8l3ePP3492tN1oRdQJygajvzMt9EJsMlcB/h6IFYrAELHUL81pxW8G8ElN0HSoWsyseHW6zOyz47tUtZ+sClw+lmYmRLd2yXzb82c8OuXr5lqODHX70yT22Roq/+MVvuF1HTt57j6uzU/7wh5/w6ccfsX9vj2cvnvPd188EEA+BYOTn1as1g0JkIm0j8ozoOzSBzAhje1QWNPWSvf1dzt685ORgzOXFKVc3N4xLw+7AcLQ34vz0DavFkpOHe6jYMBqOOXv9mv1xzu4oYzQe8OrtBV3XUc9u6VZzDJ7pZMTp5QyTWT55/yG5dswXc158/4p7h4co42mD4tnLc8ajAbtbQx48OObZy1dcXs24d7jHcFRyfn7N8b1HbO9OGA5L3r69Yl13aKWpm46uFZuVoKR4ir6D0KHwYhvjaqKvUDhMbMCvwS0JzRzXzNBBWHEii5RdYzAoGA4HSboeNiCehIkIkOuDpN82bZtYFD0DQP4Mm0JdrA98kMFLXhSMx2NJkG5b6rreSHRMZikHBTYzwkCNUVKiY/Is6i0I0uS8HzBo0yflCghLTLKpIIWm8y7JIPtALGGU9iEDPRBpU+hSCKlQSxN35+XvGasgGkbGcKg0pTNYZVAWfARbFtzOF+xub1NkGV1umZcFr4zlbT5gPZnSaujqNbZt2R6OyIoBdrhFPtlhdHjIreuIxZjR9gGXsznRWrQK3F6+JdaN7Ifey34TIy4EmuBZR8cidsx8y6Lr0EaYrD2DQ06BO484GWirzRnRfw+waZrftUF4N3Ds97yH09dFGuiTX6EwGrIi23iEbe5bLgFBxloJkjCZ2GFkGVkhMnfvPTbPxJdLaLf0tgh5UZDZTFKY61qsWYwmJqDeZJkw1KxlMBxRDqeEGFmvl6l5i8xmM2FUdy2DYsDO9rawUELviQvOifWR1Q4VWra3J7hkaeR94Pr6BmNsCnoxGC1AhLGWPBNWnraWqqo5vPeA9z76IXvHJ7ioWC3nlIVlNBnTKc3W7gFZWYCSib+PYZNu671jMb8lOLdhNEcgKi3p19qitLDinO+kMXjXx5c+REPYTFlqaJR3EoQaNa4NdHVL9J7xdIJWcHN9RQwk9lKRGk4v6faZsF6NMSl1WSVVjJfhXpBzPc+0NArREVzNMDc8eXLCw0dPGO8cYMoBOsmfrRUm7HJxy+z6Jc16hootOnpU6FgtF1xdXrCY3+K69p2E8TsGfT+ECN7TtR2ojJNHH/Dg0XvkRY4LnuW6ZXf/kNdvTsmLEY8/+hHPXt1wel0xW7QslzV5PsZ3Nd3iljKTwKjWNSyXK2w+4NEH79E4z+X1LW3XkBnF0dE+WhsePnjCYLzLcOeAraNjyukWRTllMNmhGI8pJlOKvW3YgmZcsy5bFnFO5StpvFYNq9Nr/KzBKMvuvQNCFtGZWA+pukXFgM8NdlRirZZQqvGA8f4Wy2ZNPp1Qbu1wu56zXi/EM1kbolJ0bYtvO1RIbJgIBpG4N1WDazti2+LrlugcKnhiK2tjHR1t63iyc5+JKWnWNShFMZoSjN1UmomcBNEQgyF4jbUDTk4e8/DkMVobbmYXXF2eMZ/dslytqNsOpS15KWEkJvnmm2RvpaLIZm1espxdc3NxSjbUbO/skUXN1dvvITqisui8JKJp6zWrxS2j0ZDhaEJZDnEB8sEYTI7JBhKyZTO8a1ivboUtmexxZLgnnnXC1oybAYaoQkS6iurtWTTz+YI8LxKQ0zf/kaZtadtGSKraslq1G8l+tDlbe8c8fu9TjM55+eI5navJM0P0Tqy+jKatV2yNhpT5kKb1DAcj8kyGhCHegTA2u0vijiBsSTTBOQbDMXlZ0DZrLJBZeZ3CanNUVSWp2FoCc0zaQ4IXWwQVxcNSG00+GJOXQzrvIQbxQMwLYoQqBbNkuQQdxij3sidnxBAwfV/lxDZNAj2zTb06HI42Sh3zTjhocC2L22tyrch6hhz9OaFlWEjPEGVjjbQJZjKiMLApu2G1XnFxfsp6NWe9nnN4dMzx/RO2t7e4unrLejEDJ8Opna0pD+8fMRqV4uPrPf/8//hn/It/+a/5zVff8s33L7i6nYO1otCxwhieTrYoB8OkNBCrAWUzWX/Jc9wYQ5GJpVueZVJlx4COHosnV5GBNWQ6kierHY0AebEfkFqbwlaTz2wCZbWWALuE4AmzVSelBr2H/O/L9SV3QCzpSOei7lV8CZRVUSToPQiF2uiONnVF//MEeJNaKkvek8bk8gwog7E5eTlkOJwyme5grMU1NW2zYjm/5OX3n/Pqu9+wun7F9ekz3PqWjA5LZFgWjIcjrBX2nfMCBMa+8lF37xEQKxqXQoic2Nr1loxK94CsSkSdPqw8DT16i4O01voGqmcfy3/31k1sGLa95ZMAnnd1Vj8g3zBNvefdj3d+A2JHKFN239stRgFr+/VOYgz3wYiibElrPst+7/72P19rLUz9LCPP882nTeFOMq+Ra2B6b08FWQoiCyGI7UiyHRgOh/J737HS6F9LnuebNSTXyW96iP463l0v7kLv0uuISChoVNKTGGsoykJIBwng905+ZvBebBs6twGeRQHt8Z2EihKDWKipnu0prM3Q5/Qk/2EVPNpX1PNX3F58z+rmLfPLM/FpjQ5jFJlR2BQnpfVdxa3T+tP986Hueo68KMjLEpPldL6v1SNaBXQMKO9QbUVsF8QusXSRgbs8/3d2IT2N9j/NfujZ2UorslzWg6iWBsRoWK3W3F6vuD6vubpoWK9kODseaYpMcXvT0XZKgGIzFOskZcReBYvKhmTFgKwUmyKTDxgMtxhN9ygnU4rBEGtLtDJoJedZ70lLTFkW1shQIQopLSJrRqwy5H7FIGQ9g0eD2MXESO0aopMARrIcFWLKUBiAsRsPYU3ARI8Jgi9qrcGUdFqwFmOzZC+jUhhjTITERJYzGaoosSiiEX9yEzuC6vjum8///8ek1UAWIpGWQZkTmpaBNsSspPUropLQpCys8OsXdC3gYLL3MXk2JsZMwqqigliBP2Nx9pRw+gWD4pInP37ADz4+YX9nKmnzuSEvBSQNXph9WhuCtjjA5mOOH/2Qg/sfMl+JLF1jqJZLbs7fomPgD/7gMwbDEVVTbwDaO+88mZw3TSN+P8aQ5SXb2zltW9G5ltVyTuc6bG6wxRbeOc7O3hDaCqO22NneZjQa8fr0nGGWY03k8OCA01djmnVNW9U07S3DQUnXtIyKwMFhzpP3h3z6wy2O7tfYYoYPc5yrUEbSyVWa3ss0SSc6fOjHgEDa/NIJ+s48FPpJuWxNAhTjibETIA2DD5oiH+GjIroblKrkZhEJXSD3GZM4ZJIP0dsaPfDUdc3N1S3vP3jMV6fntE1DVEhiaIiyWZM8CmMUD5r0ypSS4kNHhSHijQRZRaPStCw1ZkphyyG7Wzs01ZqbqwvqZcPzp284/ujHjCZTnBnh2kgIDrJIDIboC8RSOtKFRtgf2qJxKO03B6yxmtiK5KdZV7Rtw2w2E6PpwQBNoK0rBoUEvbSdSBw/+PBDOh/49rvvuJ0vuJ3NaeuKTCva2kG6TyEb49yIm3bEzB7g9C4+jFEqge39xqvUhjnbF153E+10wpm7TZoNwPJuwSGm2Um5gnh8yUYfCNio0T4maY3CJflHl+wZNRGTfryP4Ns00XUR76FD03jNqhGz7Wa+oDzMKTxUiwVH4xGPdgxXrxyGwHbZYbuG/4/D8MkAACAASURBVO7PPuT8xRtO9gf8+vmKv/6bb/jw8QM++uCIDz864bPJhPOLOX/7Ys6gyLi9ueB//7f/Nxc3a56cvMePHj/ky6+/5vXtjGgkuO/txRWjcY0mkisBFatVw4vnLY8envDw3pTJIPLm1Rs+fnKfiW34ycf3+ff/zzkfPdojzzTadOztDPjmm5eMxxk//PQRtzdfc3H5lu9yx3sPD5kMLAMbiZ2Yz5+en/PppydYq7h/tMMXX33LX/4i8t7DHZ6cHPPqxSnPX7/hJ3/0MZ9+csL19ZwXL9/w+HgXpTyTUcGrN1fMF2vKYcbR0SHPXp6RDSzfvzhluW7l9ipIsXlS4LhWPJJUwBIJroMo09jo1mjtCa4iuAZXrwhevt9kGUZrfFpDSivyQjxj+yKpH6SASMZCdBwfHaHQfP/sNRJWIs1BL4Xq2a4xBBbzOdGIRM+Fjs41RKAcFtjc4DphTolUXomagAjBs16viDFirU0e7RHv3mXfSEhLHwzW+1CJ91UvUxWguSiyNI1Xm2Yhz0t6/9SuEbbecDhgNB5wc3MrHlQ2k31TR9ZR8aJueFxaJgpyt8I3mrZT5N2AvZ19SptRxcA6z7geDHgdAky2KG1OO7vi4e4O+dYeb0/P2No7Yvf+CW9v56yqNW0IBHPLB+99wNuzl9yevWV2fc719SWDsqTIS7o64o2mMwjbLELloImeqqrxMWx8rjaBCci9tQlM2fi/cseoBd5hzd4Vy977dzzZ2Xxvfy5qDXkuacXifddLu4wAHlFYODYFz/S+jSoxoGyRC2PWGOq6JhqNSf65PsbUPAV64/+maxOYoOl9a2MEZcTzzmjI84xyPMHkI0wIZJmItBSKarXk7fkb8iLji69+x3A0Yn//WEAsJ4CDzSyD4ZjQRXTIaV1HOZhIYawNR0f3cK5luZixNd1mMJrSdg3LtaR3F8NdynKHT3/4E4aDHFuMUOUYlXnunTxidnnGYDrl/u6QvBwTCLSuIbiGonRYA76TIVPXNclLuaAshikAJMPHXiqpwVXkGeTWUFUdLgQ6J3LA3vOx92YT/Z0H34HOKMuMoAOr9QriBIVBK4/WPQjqsFbjvawBU5YQAs45urYjhLQnZRbnJF1eqwC+w6pAVliKyRbT8YjRcJiAIwFttLb4GKnWM1aLK7p6QexWcjJHz2o5p06MR5CiuHMtWmfYvEghd+Jx3EsbXQKjtrf3qJs1n//t51SrGePJiNHWmNnNjNV8xXrVMBjfI5DRNuCaFV3tePLTQ3y9xfzsHKuFHZMVY7JcY03O/sERJit5/t23tGEN3RqbKU4ef8Bi2aKNYpgVmCJnS4FysGpqbudXVN2C2i+Y+ytaU6NyLSFsWuqs+WJNoCMMNKGE/Z+dsPi2wq8gNIaCLdbnt7JfKmFfu+ipFguG1ZTV8obp9ozpByWzpaELHbpTjLMC3zp0COiQQofSINYqWUcmBuymIowbBq02Bow0mbNmycubU45O9mhub3nz4nc8yDMm++8RdCb7LskirB92xQBB0bQBbQY8evIBRr+H75zkVMTE9VKaEA02FzCpl8waLWuB5LGH8xgN9+4dY8yQizdvWK6WjCZD8iKnbTuKYsTDhw+5On/Lum7Y3p6QFyW5Eg/yGDxaZ2iTi49l8EzGI2bzOcvVioODe/RSZJvCe5qqRuGxmSHGQNe0SBC3eKEqNFXrKMpAbsRiJLMmDbgDwXU0XRAll7Gsm4rF7EZCO1Xk8N4Jf/SP/xu8gb/+N/8bq5tXFIXD+46209y7d0BwLcvbS4wteeM7jh++R1mUVN0aZQqUsuKjayRxuh/Naa3Ii1Ka6Czj5dNvuTh7zSc/+BGD0QQfHKvFAu8dg+FgI8eNPSswOFxb0UUndbLNhZ2pjXi1Wku5vSOASOvIixytA7PbJd6vmW4NN+fKYj4ns5bt3R0U4rku54sE5pCCyTrXoYmUmaZt14QooVIQuL2+ZL245Oj4hMFoF61zAoYQOgHAjDT4Id4NFvv9L4QUjKaFaVsUAirdXs2xeUm0GflgxJaFH5U/5dV3XzG7vmTvYJ+d7SEXF2+4vDxjdjPj4uyMb7/5irZrqDsvPuFZBs4JsagNDIsM5x1t25FlCFCmDZm1Iul1rRxgRtOum0190usgYxCbmkFmKawhMzptFymrIkA0yarIGKIGbSx5NiCqSBI7CYya2JubPjAECaOkB3b6dkOlYV8Ka4p3YOPvcX9SHXB3tqTerP9diVEqM2DpR33X4rQmL4SxHjPNoBwynGxRjqcMBhNsOaBbL5ldnzG7PWMxu2Z2dY6v15SZYZIbUd7kuXhp+0BVtzT1ElRM914RoktAo9qsg96CIISA6lVEvDPooB+8SK+p0/vvladS30jGgjFigQgIGUT0h+9cICEB9JyFnvD1bn3VPxcSaOXorQv6Ok2rRLxJrGaltfRjSpNZg48adJB1EMKdd2kMaaBLGrZAbxirkHuDkrXWOslh6V96P3wvioI+XDbESPQ9USMkCXjERYdzjizLJBfEuc2AX+s+7EmwhxCcgHJGo/IcRWTtug1A7bz4fmfZHXO373VDyq5QCIDmvbAXe6WYtVLfGxQuuFQTyPkYlbBV1ea2yD3wriNEycbQMVlBQbLMEKDVKMuwNAxzQ6kdRVgwqi8JFxdcL76lvj3m7fQ+2zuH3Ds8Ym+yzagsyXSGRuwIe0yj/whp+OG9R9ssEdAGKJXRNJUAw5trDTp4cu/wbYtTHapo0YMhwRQEU9Ilz/B3P/pnPXK3AQhBRYLHM62xMSPPDHmh6LqGumqZ3ay4ubpNA31L0zjaTqwm7WDCYFAS2gJfZbTVgs47UKIcqhsrYKsxWK3ReUGR7ZIVA4pizGAwplrf0LVrIR4kSDzGIEQLTLLwEJDZOWH2OydBenlWUBQ5Ez1mayuyXLcMhmuC8sz9CmUKshgw9Qy9ukSPxngdoJzIkEUg/oRxeHTCu0JaGFYJXmAVgOApITGQM2Nw+YTGZ6y8wmMpfCCLa3zDf/bj7zRIG2KEruPx3h4ff/iYv/j1r1nP1sR5i3YBrEFHRakUXVwT6+f48yWx+hY7fkI+PCKoAbWHavEKd/M5xfwFP/7giD/7oz/n5ME2RZmBb1G0Sc6t8SiiChL0FCNR59jhHkcPP2Lv/gc03tD4DqsjzWLOzdvXtOsrfvqHP2J3b4+6XtLUtWwkSryZevNv2XZlOpHnORotU+EowSzeyWEswVMl86bh9cvn5L4jN4rxdIvxeEyZW7p6QbO4Jvoa17W4pqNr1vhuBsWS7W3FJ5/s88FHQx6cQJ7P6PQprV8gPis5WlvQXuCaqN+5+hqtfWpg707V/kEWGXtPgevBPIDeRw1CbEHnhGjBgzEDdDTEJgcsWlliVLQNKJ9R6IJBZhOAZLFK8/DwPoXq0E7hlBcJoOvI8wKQSZhKlYFPbNoIwq5S4lEhac2O2aolGxbYciTYs1IoYylGhxwdP+D89CWXV1d0Vcvp6RnKyPsKIRB1TEmwGaGzuHRNgndpapZhMOQqJGp8wEe/SVSs64rVckGzXrOqav7gD35GPhrL9/pGJj/B03YtnfO8fPGSwWhCkRdcX1+TZzmZNrTVGowiy0p0MWFe5VytNfN4QGvv49RAwGOVCuRU/GhjCKr3oFViaZC8kuhVAXfqgDt2YwJ3I0iwjpMCllQ8qVSMK4WAGVHhFHgDnVJEL89xQGHTZLEJEhimvcJXDtoOFw1OZ3K9Okf0jmVreHPl+PGDfeaLOZM84wcPp7y5eEkg8t/+yWfMXj/jw53Izx6/x+ffnfPqusZby/GjQ6z1hIXj8eNdiqBZPTzhf/1n/5LpuODxgyfcLp9xOV/ySW7507//U/6Xf/6vqY0iaksdFEM0MTRMhyXer6m6QOsDbVdxb+8eBRVffP4Ftrvg4AcPGGWO2Fzz9OnnjIYjhgU8eTDl7K3m+++/5/H9bR4eDmiWe3zxzTOm22P2pyV/9OkJXz894+yyYlZ3vDo/54OHh3z24X1mV5d88/Q19w52KDORdP/mi2/Y2p+yt13ykx+9x1/85V/z3fevONgf8+jhMa9fn/P0xQtOHtyjaiqen97w4s0p62oljGilEeN2Bxiij6DEAylT0my33ZK2rdChBr/G+RrXrAWhVz17XsIDjFHJsymK3NsFUG5T2PZ7H0qm88ZY6qpmuVqT5RadWWLPkrBa5O0qUhjLZDKm6mqa4GRwFgKL5ZIss5tgqahlwSotYJ5rJbQvyzIGZYkyhtVymZJ49aYgzDIJwfOp6J1MJhuZVFAie+4L9BACe3s7zOdz1uuK3kd1MBgkMCJuCvGmaQihlf+nxcM2quSvpRVXIfBt27CrDLkXiXXTekbBsT/Zpostt8pwpmFZFLSZZag1zeKG3Hmuzy/pAkx39tm595A6KnYOD7i5PGN5c83tm5ecffs5USmKzKJGY7LpNrfVArV2DAZDRlsjKhVZ1WuyvMS1Da6zGO9QVbUJIuk9/egbLxLLQyEWPa5Dvdu0bBgndx61SolFgUmSWKXvwN932Tf9Z4xgk2+g0gKaS1CkT6ydO/9fm1uysti8ttb5xA414guVZQLQpZCJKIfGptlSRZ5CfaQ5MtoyyAeMd3Ypdw/JhrvE6zOK9ZIik2J+sVhSNRUvX7/AtR0YzX/5X/wp0+keYVXhXEeMgWIwkUl8bFkvzqjnl2QWtqZTxuOCtlmgQmRYBqxtWcyv+P6rp7iu48GTH7F3b4wtMm7nt2ztDsgQNcNk55DxdIusKDDZgHXdsqrWiY1WEF2gWq/RSgYYTVPjQyBLQVpV3bB7cIQKSI0DDDOFYY1qPJka0EWF6xxlOUBpWK9WSeLcy/ASk8o1WBUYb3nKrGVdn9OpktwUKMRWyOmItfK8uXTtjRZ2rkshLTbvfYM9yje4pmaQG6bDMeVggC0KbF4QTJHOn4D3HfVqwWo9o6nn6Cg+bK5tqZqaqlrhuiYx4v2GkdtWFTYvsSkUJEY520MINE2DMYbxcIJrW1bzG/YPRrS15+XNGSdPRpytLunajqLUPP/+W7yeEG1OnmtuV3Nub+fsH27j8zFOBwbFiP2DQ/Z3x1xcznn27BQZTldkcc3jB7uMtsb88vOnrOuaigxNjk570nRvmwfDMRD59Rf/jtNXX+KzJdmkwJeaddNx/PgJe8f3+eX/9e/Q3sAgw7cV3158jRu2/PC//3O+/epLTrb2efWXn7M6W1Al4N3kGZ1fUhYZ2VKzvr1htbhFGwnpVTEnUwZFFKZJetaUEi/hiNiNqBCJ3hOT92ZfMwQiJtPgFTWB354/5+TwIUfjMX6+5Pb0W4p8RDHclxAxlQJiYyB2YrOSGUtwGqVyuq6ibqpNOJyKkvYc05AwRGEcSY0j/sIKKyzO1ZxqPmO6NSU3JS7CcGtCVe8RQktZ5uJli2a1rIkYtrYPJKxPO0BUCDbLCVlIdjCappUzJM9z1lVNXa8YDqdCFEnASFmWaJWG2BHwQbxZrUnenxlHR8diZRCEhdszp4zNUZklBCdBxlqRmSH7h/dxbUUMim+++YbBcMrf+5N/ysmDE/7q3/8rzl5+zWp2xng84sOPP6UYlNRNB27Jeu55/qzj8MFjBpMDDMI+7uo1IYLJSvJiIKEvJHmplsHIZDThVV0xXyyY7BxgM6jXtTSuWm9At5iKybZtuL25RBHY3TtAoVivV6KIAzAFPoj/sjLCvNU6YzTaoWka6qZhkOUYm7N7sC8MMK3BpGFqcAmABWs0XduwnF0zvz6jqhbovGDn4AHT7QOyrODk8SOefvclN7c3mGyIzRSeDuda2qZFD4Ul2rYV3nvyXLzp3wXMlBaGW14UHB8fMxllROchGprWMZ8tGBcjUJaqbVjMb4kucPb2jPV6ju9aBqXhH/zDn3Fzu+RqsWI42eLk5BFN0/Dq9Wu+/e4pb07fcH3tqZuaPM8pipKsKBmNt7BaEdoOFaRm7o0MQlIRKmJKrlfkuSU3kBtRpbTei7JN90xhUVcYK4o6CYYUj/TeA3jDEg1RQpe1IjiXFJgJSIsycIhRwCSthAEqIVDqrk7g9y2L7pqQ/uOdwS8BFSV81XcNXmtCHoThvrXLZGcPmw/x0W2C6WY357x++gWL6zNC6FDBU1jFdDxhNBqBjiwWi42XqfdOck0SFGOMJfbvIwWM9opYxd06SPA1MaoEosZNyrzWGvWO732MUYhKaV+ytiBGOZ/e9abtQc3gPSF6jOmBWVAqpN/jN9enfw1ZFvBt885wPYUBBtlPc2tofZCgzig1lA93wLDSgkd0rtvUfW3bAHpjKxVClECpzN4N3IPAk30QOv0A3qRwvnQ9BEyNBCevrW3bBAxDhxJANEaqqtoM7SWfQqAq76U/dHIx6TqxPvQh4JKtZN+b9uoEk2Wb3x1ClD1bIWHjKLGfjBLySKKbic2ZEwZk0KKaS2ec1ppoDS54YfN7R4wBF0GpFMCoIqXRFGVJrmFn5DgcwQBHoRxD1aB1Q3QrutmCy8Ub5hcTrt/eY2fvEQdHx+zvHjAdTsn7zJgNiKqF7JQY2W3X0vmOrHAYm1PEXAYZQfzKxfJHoWIk+haCI7oa5xvUcJvY80qtFQVKv6r7iUuP1PeBfX3IHUK8yrOMUTEgxpaucaxWLcvVmqpas1isiTrncH/KzvaYLNOsq4qb62u6wrAuS1aNPK9d3eG7JZ1zZIVlWJZkeYFCEZQhK8aMJl7UxG5I29S4rhEcI4QUVKiSIlLs01CatnNJOSaBpTabgMnJVUbRVBSrBboYcprd4LtAR0C7JYP2LXGhcaEmKIXJJ7J+CTJITp7eykcCtTDmk1e7cB5F7ZEVOUoFMq3pfESbIe3omGgMuVqSd2do2/Gf+/g7DdJGFRlkms+ePGFgDGNtyKdbvLl+gzIRZZJnSQSrIzEsMb6im12ynr2mNVNUMaXxGjc75eG44U/+qx/xRz/+lIOtAc5XeN+ljUZjM/HxDAF85wWU0hlFOeHo4cdM90+oapEsZtayml1xe/aSenXNJ5+8z73jfZq2oklFltZ6Q5PfSOo2LCNwXijTIUSCMhgrk+xyKJP6ZdXx9u0b3rx+Sa5hWJaMh1OsyRmWJbeLOV/97lc8ffmCqllhlcfaivG44fF7Y37w2THvfzSgGNwSww0+NESWIj3QZaKEdxA1mixhrRGUsGCFBSWHY+9F+u4xqnoDG+RYS0NCUCEBgEoYN0SEqnv3c+UfhVYZbd2hdQlW0XU1zasGk4/ZHm9Da5hfvd6Ahj6BL73niPOBzjd4Uhrghukb5DNETGaF9h+SvBmFUcKKyoqC0dYB5fSAwXpNPhqznF0zu51xcXHB6ECzaubkRS6BLwRUYkuBlw1PGUKaEHdBEjaVNaggKbnONWgtyd43l+eYXPPeB++LPNfkdLP6ztTcOZQ2zOdzrm9nOO9puw6FsCm0tRRZQVaMqfUOF7PAzAxxHBLimBgVwYQEzoqXjNw7LUWXVpvrQwKqN6PuKJYe/RWUdRo3AIhKh1/PQgZk8r6ZtUlBQ5ANLARZMz5GvAKHgiD8ad95rAvYLqI7CcnoQpum0y7xtSyXtysup5FsAM9eveHx8SF/+tP3+dXvvmB5dcM/+vsfMruc8VdffMFff/mGnfvvcXJywHx+y/2dY/T2gIuLC371y9/y1dNTbuYV461dfvLRJ3z19TOu53NePn/OTz/7Abk1OGUJaIKyTLd38c0KrQ3Xq7Ucwlpxc3vN29OCYQbvP9rl7PULXm4FRrlhZzrh/OwNn/3gM06Oprx585KdceT5qwtW8xkDtWR3rAmu5ssvvuYf//FPGWae0MyI3rFyLb/+7ZfsjS0mNhztTXj5+pK68dw/OODD99/jbz5/yqtX59zb+4iybMlM5M3pW8bj91gul+xsb3FxPaNrPS9fvaVqQUUJnOhDAmIKAIhpHRvtUbHDty0htAS3wjULdGwIXUUIIpMlTenT3ZdJYRTpq95YBviUCB3T9hBlIJKe2bb1XFzNNhN2dEggoFxfk7jZo+mIBw/u8/2rF7hVTfQqkb0VXevwOiTAJikVjKEopQDLi5zlaoWPkenWNnlebKb0vX9sCCH57omErCgKjLEiZ0/y+ry488IaT6bUdcNqXQl7VyuKsmS9XgGQlzlFWdLUFQQpsA39DEuhTSqUyoJrD5feM4oQWinEhzRU3S0+K3lpCk5DS6EV7WKBWteUuYSdBJszPDhgsL/HxWpJ5wJZbjh9+i1Xp69ZLVcMxmMGO7uorGQ0mfL44A+5vblgNZtjjMVMBnS+xbdrXNeAUpTFkKNBSe06rmbX5LlFJzaI0WI/gALvpamabk1wzrFarTZnnITMZIlwIXu/tfnmbJGQKZEekxo4lZg5d6EhSqScRQ5avAN91+GCSw2f2uxLthTwoiwHtHWDzjJsUQiwkVmyoqTrumTl4cmMoWsbCTJK91hrJYV7VpAVJUU5xRYj8vEOW/ceU9cNJhuIBVHnyIsCaTAazq/O0Tbjm++/5A9+9BOy3BK8IgZFQJpea0cMhyPevu64vnxBWWQYnaPwHOxPGJQl19cXRL+UIMg2cnF2StCaPI/U65rp9hFaSbBclg/IslHyBzao2uHaFmtF1hVtRqFzQvJmtFnJsMjJ84JqXdG0jqbthFGrDVZplA/cXJ6zuL1h6/B9VD7eNI3r9Zq6rohAng8ECENTDsdkekm1vKZTLTo6CmNYdy0mK0WOtjlD5P6WKTk5uACtS8ywXEKIXIu1mnFuGA0GbI1HFEUhzLs8JxorvYKCrq1YLW9o1yu8rzHKU1hD5xSLqqaqBbTWVtPVjYDRoaNtKqr1kmlRojXJLzoxZjpH0zRMp1uEAGVRsLe9TVevmYwnVE6xs/+A07PfoAkMjGE2v8YODMMip7CBMlNUy5bB+yXZeIxrWnQ25tHJPQ73c0aTgvlXb5nN5mztTMiDpsg1VkWGhaWpZ1wvPYOxZzjdonUlK+fIVMHDhw/44uWvqOIKk6eU6AGUW3vkj+7x8R//MU+vX3Pxb79gWJSoQc7o5Ij57JplEfEm8NV//Ava0wXKDDHDAjvMybIhN+enzBcLotFUTcXV5Sl6OCIzhmq5YjAYYjKLSgVWVDE9Q1K/qqjEMzJt+SHd7xAjLgasMqA8nYVzt+D7i1MePP6MrYmENV2dPUWZc7QdsX3wQBKhgwAfXdeBBWN7mTTUVcWqWjOajPEukmU51mYYRJoZ+gpG9TVsoK2WnL38jtvrc44ePmC1alk3FVluOX7wmDevn/H9d884efQhWT7k7Zs3jMYjjnYPWK6WrJarFESYhkTeExSUZUlmLdV6hbElW1slIUaqekVmC0J6zTp5LBOT7Fv7dKayAdS0MYQsIzqXhko9y1CnMBSD1pHMlgzLEpOL56JvazA3LGYzVoOcg0cf8Y8mO5w++4qrl9+gVUU5LLGZYbG+5OLiDVvbh3giF6eKk3LMcLRF5xVbWxOUzliuG1zXJLm/xgVF3UiQ0NbODj//+T9E56UoFZVmPJ7SdRldUrZIyJKA7EZHjPJopSQEK4tE11I3YpHSD+dIwEyXAj5HowmD0QTn2sSQy/FRZMjr9XITxoZSDEdjiuGQwlrqasXTL37L/8vcm/VYdmX5fb89nPHeG/OQI5NTFovJKhZZVa3uVsOAG3oxYNiCBL/42f4S/kYGbMmGYUtqSy20WlZ1yerqKnaRLDKZJHPOmCPueKY9+GHtG5kFq9/7JggwMzJu5D1nn73X+q//8Ozb3zHaqPjgk58zGo1S+CXUky0+ePAT+t7jY8Sk0GOtVPKxFEl017VcXFxycHCDIi+EjZcsWogCSMr+MYhNStdjjAwlc5vz6sUT5vMFZVlQZsL8G9U1dWnRVsBP1/Xin1nm3P/wA27cuMlivqIuM0JwvHz5nNl0xmIxl+DLsiLPC0bjGVVRUGQZudZkSZUSnBMRcZYRvMPqFIobZViWJ/sa5wauA4mSdVBMILRGBhxK6Isk+Jz4BlEnxIiOUa5pYnura+RSNHZriXaIqdVIrNnrviK+IUVPffGbQK1CXYMv4nUszwFKUeQFk80Nyo0xIXoW8ytCt8APoqB69fIJ7fQC5QZMAszqUU1ZVDRtx2o5T2Bg6nsTGw9IoUPpM2oBJtfApzZGxCQxpvpB1pS1ouaJwZPlGXZNiEl7xTplPubxuj9VStbyMPTX10TYiwkvsBHvpS+SMLcoJJywBmoTU1LLUDzLc3wM9MNATMC3DwFlbbo3cj3d4JON19r+6I0+PtVja39Y6T+FiWtS/oiy5npQp5QQd9ag3lqFtrZIUAjIvc5qyDP5c+8TcOqdAMUJXPBvDvC1BNZKffl6ZfVDJ/k0g8cPjrV+4/UrqTgS6K6U/Gyj9boFJi8Kok/DgTVuEGQAEVRMIXoRHcXeQiUwWauYLP+iEMp0AjCDwjmPNhl5XjIqNOM8Ms5hq1hxUGhGuSYzBhUzvIe+BxNbtGtR4YpFP2U+u+D86pSNzUNuH97h5t4hZVlQ5An3ILEzScSDEPBBMfglSi1TeK5gLkohz38KDlNaGL9KG5ySvQIt3sAx4TnXntPr3i28Jmutn0pYq609xJ7MGoqyQm3AaNwzaXLapma6XND2nkx3TEY5+4cjlN5gvihoV4HZ0nF+ueD8+IJmuhLFQNcR8aJbU0klYTJ0FijqEVmhGIYK26zoVktiGFL4dwLs1/kTQTAhFyNZVqFsBrbGmZJBjwCD15qiNtSDYtJE2sWMoVnK+61OUEpUEz6rsDrDqywxs1O4XbLQUNqiVMSj6WWSgtEKqxKbWivh+GpAG7IqJxYb7IzfZ7zpiOGYv+v19xqkNVFxuL/D+HCTX/7yP1JujTEtuOjJtEZFj0lm0XgxDo7KkYUVIazoe4VbZJRZzSc/uMuf/tEf8/7dPYz2+LBC4VDRyaQ9+ViF4AlpQ8hsSTHZlr/2ugAAIABJREFU5+Duh4y279I7jSLgXcv04oyzk+e4ZsaDD9/n3Xfv4foW5wYBH7VlGNx147pmkfhE0VbJh0cQfvEZDSGCcVhd0A89V9MLnj3+mtOT53g0h/u3GI13iINHG/FOe/HsO7rFBUVh2Nww7O5XPPjxPvfeNYwmDZ6X9G4GBAEm1wddYrxyPdXzMhnWGVpZ8SxMXhpReyBDRZMO0zQp0GlTX8taYpKPrh2skQdbUj0HlqtzkQxE0MoBHUprhr7B+LEkM3ZLrp6cs7lbsW0rzi/PaOZT+tihXSSkTUqYFuCJLENP54dr5vI6Idx7SSlVmRVmgNIpkECmmFobJhublOMSWxrqrQ2qyaZMek6mfPmbr/gv/ttbXF5dEhqEdbYxweQZRCuHS0yHVhSmlwtpEpNkeGixPBCVgOayXaJtZDIqMQqil0liTNerzCzv3v8Q5wOff/k5Lh14Q9cSkhzK2gqyGxwvxhx3EMwYHysgpsJKUrvRSXK2NvBX4Zos/abnTNTx+naJZQXI5qwSWzpRbNPBEN/wnwxOjPuV1jitCTpJPbwUN8JsAdd5hhgRhYlC+0BwnYSaOIVDpvoy/E1XI0acjzx8esbk7Q1sN9BHyI2j7Rz//q++4dXTF9w+KHjr1m3+q9vvUk0mPHv6hG8fHaG94uLikpPzU27u77E1qbh99y65NYzGJR//+EOOZi0f/uAuZ+dnUkTEgEPRtB3Hp2fsbW9wNZszXTYElYH3XLQdz19e8JMPDvjw3g5jf8nRqycEr/Au8tH9ezz57ne0VyP2dze5//Ztzi5mfPabz/j0wW1y5XnncItvv3vJ+cWMPNP84N1bzD/7mt4FhtXAk+8fc/PGFmWRURc5v/vdt9zaG/P+vUOePzvh8aPH3DrYZWNieOvuTZ49O+L7pydoUzBdek5PrziKV0CShdOx9ugJfkDFgE2hiIQB4zoIA75fUGTCilu2C7pueX3/4+8VQaDUG55ZUQ4tFWWtJWVRssiQr+s0WVdaCwsDf33wG2PpQocbBvI8xznHyekFF5czhuBAKzIjKcJmzX4NoEzyFI2vZWg3btxgZ3PCd0+e0LQd5xeXWGPIckMI6trryvuBYejxCSyeTqcYI156VVnRe8/gB9zQ0/c9T589T362OaYQyeqqWTEER57l8jOspaiFzUiQ6xPcgIsRmyUpY4Rz63kyKEZBsUOGNZpCa3qtOMs0L7XiMjiy82OakzNuTbYJPicrCyabe6jRNv0gAQFd3/Ld199w/uQJZZ6hlGdnXzwtn59fEKqSyeEh5f4NhrbDu4HGrQjNlNa3rOaLJOuKlFXJ7cNbdH6g65sU3CBeTyChBTq3RO+ZN0tJOc6MhLethzOEZDsjTaGy6dzQspdkOoGycR1CJYFtOk2hVRT2Q7QGbY14fytFcGIrYRPLoe8HhhiJPtD3Ekxn80LWd2oOhuAwmcitNZrMai4uzsizTEJR0q88y9F5js5yTF2RT8bkVUlelUy2d1iclAwpUE3CxQLKB3yMvDp9QfxswPuen//0jzEUtE2P83IlAhpd1ty+94BxldM2J5yenoFvGSYZTbZiMTtnPr/i1u0ttC4JpmI8sjx7+oSziynVZJfdvKQoRmiTQQBrFPNmxXw6p5nNqMY5dVUSlci7jFZkhaXvByQItUxDaLkWIfnX1lXF6cuGZ6+m3Lp1B5VV0lwbRdc2xOjJiiwxx2DoOparFZubO2zvbxOVJgxLqrHBdI7eS1MW3YDO5OcNbqDIS/KyJM8L+qYleA/aXss388wyHpXsbI+YjDfJ8poQUgO4lhq7jtXVFavFBSH0CA4kQOt8uaJvRVVE8OIbr0QyqY2AiW2zYjGfsbmzjzZGrJO8S75hSoAvpSmygk9+8lMuZxfMplNGG4bNvX2qzV3KasxqdoYbhKFy69YtXNdx/vIbcpNxeXrBV59X5OUOtowsmxXH50va4OmdsIS6VUdUNc+OnvLomxfsbk748OOfUtY1R9PIy9MF04sLkVFmNau65/Nvfs0X3/81akORbY2oN8fEWpEXI05nCxYucvOHH/Hyrx/RdIFyskE22sQdn/K7P/v3qKbDRMX4zg0WJzOCa6EoKTa3YbZgMVuSb5X0fc/xo4eY8ZjtnT2mywbfN2R2lEoDkZYOMWBUiVJWAo2QABuCSVYIgSyX4EWXJOI6RoYQ+fr0GR/cvMedyQGGDG01zi3puo5uWVJvHhK1ljpNZRISFYYEjkXyopSaNipR38SQwhxV8p/VydNP9pKhE1VcMSrZNnsYU5BXFUMI9F1HrjPKcoPj43OGoacoKuazC3Z3tuiHgabtqMfj5NeamPcRnBtwLmBtTj2212wz51rOT48Zj8aMx5som+OdqIV9GK4ZSyHKtqgihGEAbfCDxztHlq3tXSAGL3LoKIz48aQiakUfxKJH54rJtkYTWcynoDaoN3f46Gf/kLPbb3H84hva5SXeNRidMZue06wainrM/s3As++/ZO9wye7h3XS9xU+671qMiSiTEWLKI4heasu8FhuGoRdGpe+E9KJtqsGFvWesMFsNQTxEldQAo1HNEDx5keO9gGRKiUd8VZRcnJ6B0mxsbtKslrhBatIQpM5tmxWZVrhuhbYWGEGE46Mjnn/3NXWVs7O7ST0Zs727L+BO12KtYTWIb3de5kmKs45+FAZhiBCdl2CwusYNPUVWJMudVA0FkcN732NwGKMJmUrqE8vG1jbGOFAtF6+eghJrktHmBjCACmTKcLY8R9ucT3/0Me+8f5/ZdM6//Ms/569/8xsW3QoXfNrnPH3n6dsepTSzq3OKsmZjPGF7PCIf1UmuLYxDb7R4rofA0K0IusSqHKNiAhDSkDITf1uUERn12nogyhA1t1r6gASESbhd8vBOg3mV1HbEIdWGJg0V1uDPG972ai1Ffi1rD+seKD27cg3l56gYhb2HSdZTimbZofUcW5/hGVguGqaXM9rpGe1qhRt6QiJ7ZHlGkefUZYXrPCfTc9pmJZYlVnwtJX9mPVhGQK0gvYp34RogXmcc5EV2zfRcM4PruqYoSyTaIqbnO4rfejqHvHcoK0pLlTxB3TCwDsNdW7TIYCYplGIaCgSuwUqpu1/3u2sgWykloLkb5Jol0HdIis4QJSMhpPpsfT/XDaCC631TQVJw2jfsotZHQArHRdSkKkJZVWIpGKHvAwQvn9ualPkiQK9NknnQ2BBxidELkdxYqqIQT30j/v1CMhICkVaamIuyYLVcoFxPVO4698F7sSNTCWTPcyter5mVtZ7WmosBnaozIRO9MSBQAhxH7xj6nphwg5gCygA8HjcI4YAQiS7go1zvTGcMHnQc2CsU21XgxtizWXrxs9aWEA3dIINW7x3BdcTY0/UNrp9xNj/hzG7y8vEWNw7f4uatu9y8dZtxPSE35TUoLkHNkRhtomp7nI9vDEtIe6pF2RKzJpSlLAKvcrzJiVYTtUl/LhkNGP1aMa1AeLPp/q9Z3DHSdw2D72i7nLoqqOuMjUlG8HDTb7JadSwvZ8xOLnBNy8buhPFmyc6u4q6FoR9z9Gqbl0+vODm9oOkTy1tbfALNtTaYoiDLFSqWBD/Q5UuWGIZumWxq1qppzxACTe9Ze7ijc1RW43WFMmO8rSWM1eY0K0MXWtoB5m1Ds1qytrKstEWZHIWWnqY+wFNhtb8Gw6UujmTpmYwKXIz0AZyKlEZRWStgMoCPWB0wOsOWN9ja32SraID/if/c6+83SKsMP7z/gKPpnG9PjiAzKAkGRmeZgKnIxhkQM2cVFTpIYIFSkbt7I37+0QP+6Gcfs7lZovyANmnzDMKIFBcSjet7Yfqg8doymRxyePt9TLlH2wYwEELD/PKco2dP6Jo5Dx7c5+137tH3Pcvlgpj899a72Zqub4xMg5QRX6z1JrJmWQnAmGQVEVbNgsvlGRfzM4a+w6qcW4d3ycsRSzel9x15oRlNSvJ6zGg08MMfTXj3/ZKt3RYXzmi7hqhXKN3L9CeBLUoNcgaHTKYrDEQCQRsGF7g8HqjtNuNJhspXRN0RnU+MWvlc60GOVpqgBDCGkMzBvTAtWAtaBHwLntebQAyEKM3V0PcSOBU8OgRGeQFNQzkMFNHTN0t630qTrRU+OEknN5qgAiFNOvXadwckYTIIQ88NvVDQo8hVnGopMmEtg8Ua8WnNqpq8GpFlOX3bcvLqOcZ35EaxmM/SAR1Q2grgnvx201Elk8/gidEzeEcztCz9wHS+oO0jIWgur2bs7B0w2RzTNEthoASQqVwgzwxXl1OZfvrAztYmXVXy/Plz+qG/TltfNo7T8xWD2wYsURm0zYjegbLpPqUD3yT7g2smtEr3ANaeYeuJ7/UrJKPrmFjQShPXLFsZ3cr/psRVYVTKaWejksTIIJu7jjENIYIoNGICdJwUDj6kJMYoqdFJvU5wLdH1LBvHxbzn7u42/+ovP8NhgBxtFY+P5vzpn3zI6ekL6syzW+3g9/Y5Pl7yqy++5OefPMAQ+JM//hmz6YwXR5d89sXnfPXQ8d7dt7jZR86OnnL66iX/4Cc/5qunJxxdLvEqcjmbMZ9NiS6QKzEPX/UrApHvX7wki+e8e3tCZjyuG3j//vu8evmKqig5Oj3hxsEPef7ynJPzBX3TkuWGxaIhzxQ3b+7x/NkrHj16yEcP3mFvu+TnP36P7x6/5OzsjK4D5w2b2xNs/oyzyymff/WIjz+8x1s39njx/BWPv3/Ozz5+j41qzNAFjk+u6LxisVgBhRR6KgKeEJ1c36ixKohnJB6NQ8eWLLYoFYi2p7CBzQ3NRTCctiFNzCNvnPtpGaxZEEo8jEmAGwLIyf722jPLJNZiTMzaPMuxmTS2o9GIMPf0Xop8rU0Kk4oYLetZrUF/H64977SWYBEfvIB2g+Ply1c0y4U8x4OjaUU6dXf/gNl0Rtd78rJkuRLpmk3BICFKkdyuVqgoXqfBeWKUwAOd2LZVWRJjpGtbQFFkUjRFpfDI2eS1F/aEF0uQXOvkayXPyorIqdZcBNjsI0XUtN6wUhXPTM6F1XRhYHl1zkZmscrgnGZUbxJzCWKqTI5rl5yfnYGxvPXhR9y+cYOj01PaADffu8/kXiBmuQDnbiDbjIR2iWoMeRbZBqzJmM0u8YMjuIAKmq3JDtPVHIc0qkYZghHf0KzMGfoB77yw5xSoLEnqvMiMJFglw2QCsAhoKsCfTT7GIh10aGsEzE1FIShsUeCQAl1lBm00Q/CQmL3K6GsJnbEy3VZKlBHBW/qulfdKEkuthf0yn81plktyk71m6USF+MMJawOr0UWOzgzVqGDYHBG0Sv5gEq6plMhMfYwMveP5i5dcXi7IbcknH/+cLBh8K8PC6DzBG8gyNnbvMpx62ukFs7OnLGc541FFXUuIoLEFWhUU9S7R5hIAVIifcrNsaZI0U8LKMrquZzweMRkXeN+DsgJiEEBlKfTQQWIOF1nOYMWKRBuDNvIsnl3OuFoOvDPaS3uGsES8H0BFrLFktiC3munllbACo8JTUIwP6JopIXQ4PxcQKwhTKwQJrjBFic0qvJPCte9fB8XZXFNXGYUVAKSoKnReEshSeEnE9Uua1Yy+XYm827dYq+jajma5lHrCr4P8khRaSZiRURqV5XRuwJicnd0DRiMJMQ1RGE6yxwkD0xpFlsH5xTGPvn+Mx+CUwecKXQgLQs01Mcq5qqLDd3MIgzSkfYMbera39ilLxdMnT/E6cnQ1ML8a6FaatllQjMesnOLhw0f88L0b/PbXv2SyfZd7b93nvQ/2eP7qmMfPn3B5cUyw8M3T/0irX1DtZZjNiqGwRAKua1k1LZ/95peErsMWOa4ciJnULSrPiFdzrC3IbmzjlaIcF9ioaPqO9uIEbcXve3u8x+xqSugHmstLbu0fEqqKftWIxBgBBUZlgQvCAhPwdc2KS1oclfzrQpA9OwUb6RgZnOd5e8LfvvqWgwc32VDCaDJW9sngV+A7QjQC6CVyASpJpFUEZZnNzqmqktF4A20yfCDJeh0eGcZpJY2azXOqapcQOposhyhNazXOsF2PMYrxxi637gTGkw2yzHLv3XexeUnb9ViTU1XCxAwhUBaZgJDBJ7/jBKyk8J0iyyE4zo+ew84KXY4oyo3EMhvQyR8yeIdSlhgS20yMIYX5GPS1zFchTD0fAkFJVobrOpp2SVXmXJ0fs701YuiWwoifX7C/f4DLcg7vvM/OwVucnjzi+aNfs7O1w+3dfWbzC56+fMloNEabjO8efgbBs7P/loBVSljs/TBQZgqrrfh4R/G0HCJE3+G7FdoKQ20d5AeyH5sUZugGj3fC9NMmFy9hFcnzkhj1tWVBpsFoiy0rDm7cZHA9Z6dHeOcZT7aklkfyKJQ2KKMZjcfCzlUB5TvKQjMe11hdsrX7CdV4Ql5t0jkPQ4OmwHs4vzpFa0NV1ZRVLQogK2zddZ2aZTk7OzuJHJGzDm9aM2ij9xgfUMiQYHCOzBaUVYHCY20ugTdaBmvCeXACAino3UA0hk9+/ofce+d9jDZ8/uuvePb8iFDkFIWhqGtc18ln95IWL+n2Eb9cMjQt2nUURkAqgoCBldFkBnQMROeIbiA5uOGCS+HYGVgrsc9qraRT1yFKcoRKTa50YneuWZxpwCk1YOojeG1Z9Np7/jXr801bo/Wfaa1f14rInsKadau4tkcaXC9EjiCA7XLZcjGdUY5KVssVXdOB66SXRlPkOZPJBpONMX3fJ6uqFc7LjRAGsPSMOtV/QkDRuChWYDr9O/K8uLa+ug7TMvoaKF0//+uua01cMFoTtf79WjnVt2tgWiE+/EZpsZgJ/lrKzhuha6/toBK8uvamTUCrBJcGoo/Ssin5OzGRqa4DzENAW3M90HI+SlCs98KUTbU9axWCUpgUGPamIvj6jivxdO+7DpOtiVzCsHXeCSvVpMRl1iCxnLVi6SBKDAFlHQEZqkqvsA40NEBa38hne+1bq7GY32PgrvN/tJaBa17kKF77z5rEQDYqMDgvNonqDS6ukkwV7z0xETX8up4neYQHnWDuiPea3nvKQgb44zJnUivqcmBn3LIxCpRW+mylLL2PonwKUcBQJdad3vdE30BwuG5B2x5x1B0znR5zMZ9zcHCLw70DNuqJWIwYSRZRifEbg0rnRxqKKCUkCWuJeUk0BcoWEmoWIaoMEJuDmKzwrp/PRMoQ1u66j0vs3Wu0Vq6Z78G5QNf0okrMDVWVkReGus7wbUaz6FjNFrRNRz7boqpLRmNFPdLcvlMxGudsvNrg9KynaXqcb4RQB2L5oQAE5NZKo8tI6FrwHYPz6BghGhSWwTmGAH3nhOGqe/KsxGQFUdcoXRCNkEByZRn7nHmvuFyu6GOLCpHeBVTXkutLqS39gIsZoTKYQvaCTEm9iNJkSixgYox0bmDROlzvyG1gXFu2R2Os0QQd0UH8j7tgOFk62mD4u15/r0FapRQqKr7+/Ctyk9HjZbKmTZqYJC8naxlS0RMdZEqxMRrxzu1Dfvajj/jBvbeoJxU9jrQbC0AVNWiZoOoUK6xiTl1tsrl7i9H2AS4UtIMhKo/vVlxevuD4+VNyAp9+/BG337olptl9Qsm1MD2N1tc+PhFo2zZN+rWwepI0QDaW5LWnheHSdB3n58f03Zyz4yPcquVw74B3br9HoWsWcUrTLNGu5/bNCcVY8/4HIw5uL1D6lG64JNBgtCQpBxzEgRhcOkwFWFRrBmWUps6ojNOjOX/+z79DNxts7U/Yf3vM/Z/cZrQB2ji8Bx+cABK+IISKoS2R8NQlRaHRVoHxiYYujAq5NFaYM15jdIYKFdFVeKfx0aMzAXCsUaym52S+YzG7ZLmc4sOAMgIqr0Ee54MEERhDriTxsSgKCY9RUcBbH/AmST60AI0+eLqhIxt6XD/QdR1jpemDZjUEfJrYPXv0hL/4V/8PDz79mCIvGLxnPp9Ls7FmooYoCZUZgKJ1PfPljH5oubyaMl8t6JYNxilwiNw0Rs4uTrh9e4R3clgNXopUgubw4IBRVaKGhs71qOAYhh4XIuNiDGbC1SzS+QxMTlA5ymQClCkpuoJKDEa1NiNIUhR0KoBehzqs14A8dFz/3fWXZBteCwgTSB8RxQOgQrheQwSZ+AaV/IGUEpYEIhlhbZUQQ2JaJIlJdKgkW4jpsFFpzXpv+P7ZBYfb71DVu+we1Pz849s8fPiK//Q333J6uuLm4Q2CC3z18BHfPnrMdDmQW8Pu9hYf3L3Fxfk5v/ntQ77+5gXd4Dl+dc7nv/ktIXRsjUv+6A9/RlCKz37zlCxURDNByB2Ozbrknbu3GHzg4ePHrJqeVeuZLzxKTwhE2s7x5Okr9vd3+eKrR3hv+Pzz7+jbjlXbs7u7wXJ2xRdfzvn00wdsb1r2dzZ4+fQpd29ssjmu2dsuOLvIeXbk+O7VGdl4xPTyJWFoKTLLd4+P2NkYUVcZG9sTrq4aPv/8KWdXV8wWgxT8a3lZCu1RJC8wJT5GKkY0XoCFoSP6BhMbrO5RytO7FcZoJllFHFdcXs4ZwtqK/fcFRf+5/Xq9hpwTqft1YqxsjWidirQYiSpiorDZlst1oFdiAxiLN0lCr4XJaa2sU5G8yXsK0BeuhzR5nqOV4vzyCpvleOJ1wmxVFuztvsMXX3yNd566ruU9rsEdnewaxHBfrEcU1mRYm2HzLAGxyc/UGnZ390DBfDGnS0GROhPwJCqDziwmJkA7ydi8C/ioudCKoyywmUW0i8wVHA893/UBX9T4ZknetxSjTWIIjLc2oCjpcRi/4uLsglfPnrG1u88HP/qYcryBsZrCBVTvKMab2KLCoRmi+B/Ol3NUOaJIVicG2Teiilycn6MRIG9zMiEbVVyuZng3gIasLNDWsLO3y3w6Yz6doXVywYtQlJK+3XWdbB/WikdTKvSt1mhjGbxnSMVuORqlwaj0JTbPrif5Wol1Rj8MlHlOVogPedQKgniJWZvShpXIME2eE7pWmHvWStK40jjvsVoz9L0Us94J2JGam3XAkbGWIs/ItGZ+dsbF6TmLy3NW8yll9AQnkt2oDEF5aRasrMPp7Ip/+xf/hqLI+ejDHxOipmvEL2voO7HrMCUHt3/AeGT5evqS2fSC3Z0JVVWTRyUDwKAgg3FtuXdnl74PjCvIbSRoxTB4iJF2uSIzImeTAbCVdHoFUWlEbamI3tAPjsVSmM8YCRIBk743sL27y3hzTFmX4vnnpWZQ6WhQGGHURAkIOzi8xXhjImdlMcaS0c4usJlB6xzlDW3riFEa6jyXwKHgA+2wwrkeqyObVU5Z5WRFRl2PsbYkZDmKjOgig2tZrea0qxnB9YBH4RLD3TGbSgG9TvqNweMiEorl1wCsWFM459nd30cpCXgLUe5fTGeeMhkb9Yh7d+9AjDx/8ZTFcoHOKs7Oz9i9u0VR5XT9IOwwnTHaKNE6UFcZDQUmGsabI96/v8/F3FDVBbuH+3iTg9ds7Si8K3n49Qm7eyW7uwU3bu7yT//Jf8/nX37DysP5dInpCu7ce5+b997l6PyYxy++4+Xx79AHDRQjYpkRMkN0nq6TIfzZ0ycsT8+xgyOWGcW4xIwKqnIPXZbE3qHRDH6g3tmBCAcmp5suaC5nOBxN9NiqpO1alBXyQ1YXTE+m+OipJxNyo3nw9rssmoaHL55jcnvNrFI6AQMxXrOgtNGytysBzmMGA57fnXzP23tv8ZPD+1gfiUgTHGgw0dO0LV5BWdaI3D8x+Y2lqGoq1xKjx/mAVaKUkrUq+7MM1g11XQuY7QCVoW1J20ronXeRqMSfMysqRuNNrqZTilwYs8umpU7ZDSF4yqxMKd/xmr0jFj79daWktKKwmt2dHZ5dHnNxMme0vUduLT4mn9zgMMbSNC3drKUsS0npNgqPSzYSjhjXShg597IsSwPzgA4tYXXFMIDqpwzLltDOsaHD+J52cc5lG+i7wM7+Te6+/SMe/vrXPHv8iFIFrs4vODm74PTJOdt7B+ii4Orkind/+DHb+7fIR1u8Or+iGknonaLj9PiI4HvuvPMemSoJXlhEOjqCl7FvkWm0sqnO9AxDx/TylOgHqo0JxmipZ72orLyP5EWB0orVakFV1hibkRclV9NLmtWc/YObZDanG/rk+e6pykryKcoa2obL83PW9k1FmVHVNXv7B6AzVq0QQpazKVVZM5rsMJlM0lmlcK6nbTuxVzFG1A8x5aIkRvjrMnntte+Ig8OmWuZ1HURiU3tsXqJMSVltkGsHMdA3PX7oMUXF7uEhP77zDts7+8QQ+e7RV3z+xRdkZc3+xqaEqEbSGbICJz7Z52dnUvd4j3MD51dTOheT3B5GRSH2SN4Ja3BNqggBWxR4FSBKyM56jw8xoq0RReeaeAGgDEFp8MI+FvDs94f0a7//a/JRUm29/rq/vj7ra7d+YNY+pmvv2pgA4rVPa3TCIB2GlEsQZeDrXRTCTjuj73sU4lFss4yNjS329w+o6zHTq0uurqYsV8tEUFHXYVLrmtV7L96oWidsQQDXLMvI8zz5+gpcsiZdrT1o1yD02s5LrcG+CAp1jQOEEBiGwDrLxWojoKT3iZUqEK/0zK+vrdUGF1Pugaw+CSU3UusLliFs3xCEVRtSjxxCEKaufRMEkn+g0TrR0wQs1uY1QPsmiO6DSP11snmRkMPX3sJrLKPpOoaFe20fZazUz8pQ5yXbW9sUWSZAZxRCx3y+YNmsGNxA23esks1JlmVkeS7DvsReBk3w4pfrnZzvayurgLDXRaGwlsmbRIIT0F6te9Eo2QNSS0p/HBMb2TsnPqPpmTDaQugJaY0QYQhBgq8TECp+9ilISmVUNrBdOHYqRWUddW6l9xKegNzHmOwCfMAaTS86A4wVT27jA9Y3+BAZ2obgO05iz2JxxsXsLjdv3mVne58yz1NAuhHCYUQIMj7IWleA9wQfxaLDWrSEiXpWAAAgAElEQVQp0XkuAxZPGoSuOcJCoFJm7QsPXgHJ91WtyWiJ3LD+LnmMJNcoOEXTa9pFKxa2Wv4NJv0d1y2ZHXcsbM5ZZtF5Rj3eJC8t9aTmMKvp20jXScBv26xELcNaBR7xg2foOkIYUEqGpV7BEKPs3SrDxEjfruh8Q+4dtcmoMlE5RyUhwUobTFmwYTcI+QhV1py9fMIwn6KUJ6JwQ08cTlGuRSkrLF59A7KcTEFhtQD9fmBwnr5r6Jo5TdPSLFoinrywnJabbO7doBhVFCqQKUvve17Ne9nb/47X32uQFgW//eoLrq5mjPMxWWGYdUtmqwWyiUl4RFSyaWggN4p3bh3y4N17fPD2bXa3t8kLRe87hmsQKSS2icUoy7rjDyYjyyfs7N9jY+cGTUSYUSgWyylnp684OXnO3vYGf/DJx+zt7tANvTT5QTZktMJYizU2TVgcIfmUiplw8vBSXCdQh7CWR8h/84Uw+IZVw/GrI5SDG3s3eO+dDwhBgLamaXjx7Rf8+Ge3ef/BiO39BhdfyBSGZOGgLDpOsGaM91OCHoRVqzO8G+MGizYDed6gdIeJhsJvY4c9Xj6OPP92we5TTTftuXG3JCjHfNHQ+znv3X+bvi24vNA8//6cyahCq4at3ZLtmzn7d0uMXkhoQjp/bGZQtqLrxdzfxAw3ZHRNIAZFbi34gdnpK+azFf1iyeX0DNZAC7LJ6TRBz4yhawLeDdcy/sE5XPDCHPXxdTEBySgdmXq3K9T8imxjA7NcEYLm5p13mV6c45YLgnOsVi2PvviKH/zwA8qNEdYPDG6QzR/Z0FECLAXvWc6nHL14ynxxxWq5YLVc0XYdZVGSa8tiNWc2n3F0cc4//2f/Mz/55Ke8d+8Bo/EmuS3wRFbLOY+//R1GadpmxmK15OxqTggwGm+hyk1O5pYXi5wVE5Sp0TonaHN9DdZWwWt5ukrTsN+zOFh/Yf279WELrOe7rHm3b35PmrCuMdy195yYv0vz4NYbeTrpYmKzqcSeJYRUTEciYlsSXQ+hBx9EjkEKkAoypZqvHF9/84SP3t/n6vQpy/OK1dUpcRj4d//vV/zw/ZtcHD/nxsEGb917i4MbB0ynS7768iGrvuWbJ8dMF4HcFmzXFcoF+mbG9lbBn/zsAWXegYr8wUe3+ea449HxCo/BKHm2D/dKmtWCt29s8v33r+h9z6qDxSLQd46Dw0O+/PJbPvvbr/jJTz7iJwf7fPnbL1ksW3YP9vj0k/usri746199xjePnvKDd29y/907jOuSbx495f4H74Bf8OLlC3yAq1nDrz97yLt3bvAPf/4p57MZX339mHmr2T7cYu+g5esvH3F0dCZpvMnaQhNBecBDlOLPmICKHhU8xEECdkJHhsdmjlwFKhtFqhgcdVFgojBU8zxjaHsBJa6tMNL2nAq59WtdtIUE2r9mTMg6uk7FTVPrEDx9F9JE8bWcrG878RO1Imv3weP7gHdgrUEsWiTUK/jAcrkiz3NQ8Rqs8kHRNh3Gige1955H3z2hrmp6H4iDI/Td7zUR4tGpyHKZhgcSmzZKoZ3lr/1pI7IufVIoaGspUpFb1zUTNWE6n+FDxBqDUSJxC4BhAJPRu8gr7cg1dI1ipeFMexqtiEOLm6+oE6PY24Cqcgal0DHSLedcnJ5Tjbe48+4HjHYOcJniu+8e8er5UyKGvYtzNm/eQeU5OgZ8u6JdteRaY01BzCNBKQoVqL2n7cTfT86mDAPJUzFKU5cYEeeXlwxdJxLTa0aFsBWV86hM2HMmLzDWEgaHD46yrlkHaa4ZDd4HrneCFEZFklsqwBBSYe7FoiBLE+i2FZA5/T6oNftDQFyT5+RlmULohDWaZTmZzWVgoVMISfDkNktAPhADzWzKcjYHLRL/dnpJ6FYMWqESS8GlRGFlTBo4BdCKs8tT/uxf/ws2NsbcufU20QeR6RLwgSThtFSTW9x+51N89xybB1Zti9Y5W9sb2Kqk6yOZGdjdyPBBkVUQs4hXBh9LvHdY7cjVgDWO06s5qy4y2twjz3LKLOK6Kd515HaED4F2cYUxAlDWlfgvu67F2Iz9/W0WswvOj58xmWyIzYQKSdWQAFAFCsvhjbuU1VjQaUBHTZ5XUG+jknyw7wZ0pmWvV+JXNh7XDO1KGpOqoq5KJrWwrbXNwWR4bbEqh+hZNhe0qxkx+WEbFYjR0fUrmuUyeaCmAZLi9d5CwGipvVbLOdF72q5L/oLqWjIqz7tOa1GalaKaMNnag9Dx/ZPHYk+lpfHcGI3oFiuaxZIsL6k3t9neO+DgxjZ+OePs2SmbkzHbO7t88+UTysked28eMCk3eXU5IHY6De++fcCzR1tcnn7P0dHXjOuc/+P//Bd8++yU0c4ud36wiYkLulcv2Du4yb23f8Dx5WM61aIzyS8uiBRFjiotg5qjFwNbN7bx3jF/OcMWGb42ZKOSWolPNCHg2oa4TGBBZskmI/Fp3Bgxm89YDo66LOnblYCIfsBWFfm4Jqx6cAGT5zx8+FDkytZirbArJUBQBghEkR6CMNZClOfD2px21ZBZw8Iv+ezx33J3c5+DYgu3kuARlQV8u8Qg92VwXQq5Tb6liVW2ubUjgGkCq5SRpiHGSJbJQGGxWKCNZlxM8L1YpNT1iOnVqVhJpGbUdT1D8lEcemEjjccTbOElWMg3okZRKoVIpWTtNBhcM5eGoScGhQ+ashpRlAWzi5eMJjVGOUxWsVi2LOcz6qqmzHP6tmE2u0JrzebGpvisKy2s+uRHi5JzMnqXznXZHyaVom8XKNfw9NsnNMuG2zdvsLk1EfmtjjSrKVdnnunxKd/8zW95+fXf0LZLQlB4rzD5lGdPz9CZxdbf8tvffMmtu/f46Kd/QL29w6gYE5o5v/3lX/Fv/tf/BWsC/93/+D/w4B/8lzitWA1O5JumSgo1sbzpm1Yk59FJg55ZYawGjxs8WV7QtS1D1wAjqnqCM5mck33H2dkp3jvu3H2biAynbFZch+JqrSmrGqUto6LGZAUXxy8Z+hV5LkynzgV8GOgHYZ5ak1PVYyKKqh4xGk/Sco2UZXXdrHgvaeDOOVarJeOJoiikPtFpqKOVpkuyf6MUmSnwWkKEBtdDhCyr2Nw+YDG9IIYVzXLBYjGjyDJ2d/e5efc+4+0Dota8evk9v/jFL3h1fk6wBcYUGGUprREv/riN6xtMlqNsztD2uL5lvljgQmS+WiX7P4ULkVFuKQuFi5JRMawDhJRYGL3umk2qyZQQE1Jtxxp0TPWd1mkYet0DqFTfS1AYipRTIoOKN23R1Lo+XPs5h9ekjxBgHVC6rq/WLEnJT5D7E1IwVIwQ1+FZbri2I4gK6mrMweEh4/EGi+WS56+O6VYrhsGlECudFH8p1AsJ+lIg3vka8jxZOGAoy5KiLK/rWbkOWoBi+fhSt7yxJte1sQyspP+xNhO2dwJ6BbtwvM6oSUCTH95gHMfr6yHEAZcGRGsrPwl3894nH2Tog2PwDoxmePP9iQlkU0kxJvv0OgB3/XLeJbsLCRUNXnpppRQMw/U1AGH2q/RZsyyFkCNKH+fkjC3LMgHBisxaJqOx+D4rsQF0+zu0g2OxWvLy5BiXzgvnPctmJT2NMVhjUBj6fhCLmUGsI8OwJp7JoEzuBakPEYbw4AapAXUyt1LgPckX1wvB7lrZlXxN+54wDOgY0c7jhkGG41pjbI6PkTgIqI8fsFoA1iqD3XHGwShwMFaMMk1uDdaIYtkoMQJzIRKcQ3nJeFBK4YKQyPLMEIys6SHZeoXulOaiYzo94uz8mPOrUw4P7rK3d8DmZINRMZI1qAW4V+K5ce1DHBHbtUgrxMQ8I88yTGbxKTYovLHG13V9jBG1PneC9JQq1VgKmXArvcYV3DXgG2MaqqbESUUQoDf1n3po6VbQeIXTFpM3bO7ssr9fs78vYPpyWbBaaKZXkeVqYPAO53tUHDDOic3CIOeyItB0A4ML9L2s776XLJVh6Fm1S5Zty0avGW2ISl+XI1HRp8FKVZZs7N1iiBl9eUS3OMf7IANY36PcBWH4GtuvcK4jjvbJxxN8UHR9T79a0PUO381QiyPU5Qv8bEbbBxprmdcbLFYPKHbfYjQesVVWmBhYhYo+5vxdr7/XIG2MkdOrK1xWsLe7z8Fkk+fuGV0zgBcfQB8CRmlM1Iw3R3zw9l0+ef8tbmyNqUbiBdUjyamVEZPvtl0RXJ9M+EW2YLKMvN6iHu+Sl5u0IRKipe2WXF2dc3L0gr5d8v577/HhD++zOamTnyEE6V6uQSznBdqVTVe8Xo3JMEqlKaBIBOA10CHArUzIZtMpRmu6fuDyaooxGe+9/wP2bt6g847WDSyahr/57Ffs3F3x0egHDP4c1EqkfsrgnOXzz15xdvKUm7f2+ODDbfJyIMaBi9MF33x5Srfcx3PG2+8F7t/f4+zkkl/8u1c8+NF/zR/94X3+/P/6Z5y/OubL5oi//cWSDz76Ibfe+wm/+sX/zvz4BYc7t/nVL7+jby1dN1BkFYv2kj/403tgx2zspemj0sK+jY7MWjJrED6aQ+lAO2/JoqXUlkob/GpOWK6Y2JJse5fu/AqIaROxskE6YVK7EOiDTFkAVPC44KRRN5o0m5Wvpam9BNE7Vssp5uqccuc2YNjY2uPWnbdpL09o5lM0nunZKS+efc/hvTup0S/IrDBDVu2crl1BdCybJScnR5y8fM5sPsVYg0EOiiLLCVnkdHHB5fyKqCLnp6/4q7/4tzza+h03bt/k1t232d+7QZUVNFcviMowOEfbdnjnKcsRZb3H2WrC8yvDZdilV6lRXoOrwUs9b+Rgi6moUjr5H4f4OhdszZglvgZeSaxbJcXbmgkbrwm08RpwF3uHN8HbkN7N41QCY5HjQSGSlnXW2rqxlipHvIsIThi5av1dkRhk2qhCx6iqpbDpB7bKEYvzGR//6D5Fvc1/+OuveXz8LX/04AZv3dzgL//Df2L5K8cnP/qQ23fv8r/9679iNpQEDXt7E/7RH/+Q3RoefvUVMXisCsyuznF9w2q6AFdgfENA5BDLRUvfrNjeyMnNDhcvzzhp5pycLvnaOz59cJusyLk6X7CYLrlz8waFWXD//Rv86tcPqUqLMVEGIoXh9PSU++/ss71d8upk4NnxGXYy5sbOhL2dHVbLK1aD2LC0jRxMTTulcysevzjh22dPaRYDPnrIjMjZ0i+dikWzZiX4HqUcih7tW0wcMAwYHDr2+G7A49A11KXlYHuHPPkdWTx5YVh1r03luQb+X0uv3pS1CbguLMf///6WwP0o4KaKOjFlJdQuBJFVW5sRVUyiB/FtcmuG9RvvKUwPYRj0fU9VlYQQaIeWvvdkZY41YuiuQqQdBtp+kTwFxXPKpxRYSeCUz5FlVqbjabhhMotWBhdlWr+WUhEjnXeShKvFxoYYybThcP9Qnt++I7MZOkYskc4PZEVOPh7R9j3TbuB5LkXGCpjrQGYVoe1QvcPWI5yX6f2q74m6wCqx3zg4vMn+W++RjSZ0SpNllnFVUZc5o+09ynEFWQKSVaQaFWwPm/RLCcwM2oAxFPVYJMx9T+CSLnjKrBYvu6gITtEz4LR4W8lFUuJBmQq2GBXeakk8TXuMeHdLoWxscV3MVXUlbGqJw6WuqtTYSwM0eCdrOSY5tZJ08XXTZxIYblPDl2c5aOiHAUmSz9BeghhtYsdG71k2DWdnpwxJEr5OkJDEaU/TNPSLFcFJmndZjbAaTOhxwcnZ8Uahb4yEL6zVBTJ01ZycHvFn//e/5B//N/+U7Y1d8WZLe1sIA8MQMLrk5r2P8W2NG84I/Yqd7R02Nke0bc/p6RWzy0uGboXJa2EeKQ+ZpqoKwrBiNj/FxpaiGlNkhawNa9DKkUXP4vI5L14+E+buxh7RN8yvrlgsV2zUJa61XE2v2N8/BBWYXZ5xfnTGqKrJcyvMEp88CP2AC4YiG1HVWwQUXZ/CPrzcq6zI5forhUUxBJcsImTAE1xPkUWKUU6RjyjKCpNbwEDU6TjwrOaXdN2C+dUJuYFRVaGioutamtWMrlml/UTk4MMwXCdUu+DB91ycn/P8yROCd+xs71BvTvDB4xwMbiCzFmtE1ktMITdak+UF51crxrUR/77BEWN7zax7/PA7XNuzd/sWZb1BPxiaweIHzWRji59++gG7h1s8fHzK6aVmwyjybcvp6SXkI549vuKnP9rgD3/+gL/51cC333zOKsz59rtfQb7F7fEWlxfn1Jse1TbCzLea6fKERgt7qrSKQgdmsyv6QTH0DUMbmPqBW3/yU572keZ0BqMMXVjsoAiZpLbrwjBow3I10PWO+WwuAW3jmlormmXL7XvvUNcVL0+OUNpy9513edL2LJeXrGZLTO1Q0ZNri9XZdZjfeoquk/+0Col5qJXYlGRG1AUpAMpk8PTqFV8+e8jkvU9RRoJNuvaK46Mn3HzrAwpbsuodw9BhrQRnie9NBCXNe9OvaJoldV39f9S96ZOk2XXe97vLu+RSe1VX9/Q23bMBs2EjSECkANI0IUqygvafYH/w3+XwEgqFRDsUFkWHQoJMMrAQALENZqane3qm962WrMrtXe7mD+dm9iBEfacrAgGgY6qnKvPNe895znN+D9bYXOMJmgYUi8UcraEqJPipsIVgdlYsR6KE8nkvzHFbcHr0HJSlHm2uUV5t16CNRdbzZb3TmNUQUp5FGcJ4UoIQYTQe084L5uenlINt6rHkWgwGtfDzGs9wOGBnZ5u2ben7lhgjZT2gKASrE5GG3aAI3nM+OaIoEoPKEkNPVVcYvQlKUV2pOTg4YDadChaIyMZwRDs54S/+zf/B41/9FNMt6JOm14myHhHLimhLglKk1nH+7AXzkwn3P/uUq6+/znf/5Hvs7xywuH8P8+Aew9rwwb//t9y8+SZ685IwqVkFSwmDE8SdGoKnMLC9tSsogXJIv3QEn6hKTdtOibEl9BrqcQ6wUiynZ5wePefGG29iy5rgJdU7KU1h5N7plw3aFkQFZVFQj7fYcR2z85yHoCTlWzazInWZHWTa0AdPkVYuxDxoVXmbUa9EIekfxmNJ9RaHWeb4I0MdU5YYJUgBpaCKmYucn1GlNVvbe8y395ieLHlxckS3nHPxwgX2LlykHu2AGdG7JXfu3Obho6d0SROtFU4xERflWVdREyjR5RbD7VqeS99SDyacn50QU6T3Ho+m6Xuarmd7OBL+aOb9xiShlgFQ2qyqOfn7lZH161zkv9wuMiKcJ9a81VUbsRZy9GodOm9OZZctX+iJdUYuabVa/4+55nopkH1xpX7lxJVWQQYXKQbUSmjNP71oRZIDU+iC2dmMyckZs/k8O9wFp1QWhfRFUdb6dcYVGC0CotSBNgd3ZcSVFpeluGE1Lzmu8uysclDkx8j1qBe00OpuSXmIJEFhai3IpjzwXRnOJJQ5D7myALzCeK0csiLY5hCyRBaYpH4JMeJCkDtQZbezymLkykCRt8ZiHjTH2LPC3636SFmy0hgraCrpLWN2iv62A1kbEUW10lRVxXg8WofIpihDcBc89C2Tswlt01JYS5nXxY0tsgO2ZFSPsTtWzkXnabtW7vZcoxtdMKhq2XYLgfOzMxZutu4LVl9lWa7F8pQkuDJ5J/kJWtY//QoVkXMFhDEds8s3kdmIRO8JWaCVrU8kaygPOgyySVsVBRsbQwYl7Axgp+4Ym8DGwDKqFAMrz67Woh00QVj4BIhJ45PCp1UfJKG6ZrWVQsKrwGJxQhfPKNol7fyc6dFzTg5e4eDCIYcXXmEw3KQqSkprRRPLn92UpLYW929H6KKYowYjimFBXdZEZeicI6aM6FqdifnZFJesR0UZjK9MWiRQMYeSx7y9m21e2R+PCmr9PIvjWJOil8Az5/HR4DvDwgw42CsZjyxFqdjYUiznluFozHyemC88s/k5XdsR/Yo5nVEzzpG8J/SST7FoGmbtjLZvWMxbus7DbEbXOlznqYOhVnIfxSC9tO87fNCocoypxqjlhNA0tIsWtGx4404pNego3NxWJXQckJAclqZribNzqrMnqBe3cCdPWC5kiKI2R5ja4OyYJlVopdisB2DzkOu/8vUPWqSNJKgU2gdc7DiZn+NUIhYJY8XZ4OeBjcEWVy8c8jtffYedzRKVOigU0VbUgx22Ny8wGG1RDwcMqwFNs6BzDSgwWIwuCMrilXA5Qgh0TbOeWpxPZ+zv7PPWV77O5cv7JAWtS6QgEzXywWryJZIidKGXhxqx1q9XRNa/3YrrIRMzazRaJdrljH4+hT5wdHLC0fSczY0D3nn/G1CWzNuO+XTKyckRnz19yKK5Ism5sUanITr1QMTqgmYJn/xqwf0PNYsTxY0vDdjfqfjl9z+j797mO3/8P/Lhb37A//t//2va7xTMz2Y8+zTwO2++SjU4oK5HJB/xrace7XD96rvcePVdfvSXP+DXf/WQr33zABNL/vC7/5hqNOZf/i//ktg1zB70/N30Ia9/4xob25rRIGCKhmCfEsMxupujlAFV0reJvvOUScIDUnDM2zNsqRmMDF2n6Ql0fUddD/OaWbahN47e9/JnKjNRVcR7EfMEAiVrtinmQ4okva7NIujZjMX8jBBn2MpjRxW7ly9xfPyEpm2Ibc+vf/YzNu9/io9yiZZVSVEavHd0fYfREHxPSoH5YsHJ2YSqrqitrF73CCbidHJKiImiKmU9D8XJ+VOW7YQ79z5BKcPB9g6HF/YZ71xgOL5AUCNSsYXWW8z6DZ5Ma07CFh2boCzKGQnuKhDmj7EoW0pKKwnBXCgwlgxYWj1+qwpLLmcfCUrJDb1KJU0rLlUWwEEapCzkin1JLjRJK5VQPLk1cxBdQgQTL6EXqAyfzys9cnIHQSSsrcCySpG8h+jYGCr+9DuvcTi2fPiLX1HXBWioNbxxZcTDBzWfPpiSQs+f/6t/zfNFYrx9SFSwMbZYFTjc3uDKpYtsDmFUeB7f+4zLly7y//yH/8xHtETXszseMtrcYlwp3n/tkE8evKDB4JLlJ7+8w3tvXmFnCLuDlvOTBb03PHl+wvYI3njjKm+9foHz40f8/Ed/y9d/51WuXhrTzA/58PZdbl4dcenCBs8Oxty//4TJ6Smjeo/xsGZQwPmzY964epnyFctiuqRdzvAxMJnPeHo8wEeDouD0+DSP75W8/2o18InyckZyIJNbO1pCuyDFJZYFtXKMCo3WkS50LF1L4xylLdnY2qIslDC/laIgMjQwJ+F+qwzKb9MXJvAvXbMZa7B6PljV/BEXI9ZayrJA5yKp73tMURCiBCqYyggqITvjbGkoy4KNasz0fAYxi9BF5mCnyGhcZ56cZj5dUFQVptCkJDxZ1o2YrHgJIzsQVcJmvpFCnkttcuAe4tQPiFvBKo1LnqgiWgtDUJPQVsv5vnKQpMSsWRCOn6GtQisrvKuYBJOgFcpY+hTxKtFW4sIoBhGaDucCSRe4pqNOgaQiPZrGGEzwnE9O2BiPUXWBHlSE0pAI4DsImr2r19m5fAVbVuhqiM/Nje889InxeJO2KFk2M/rGczaZEbxnMKygqtGjMWUKOMDExGYcUwXLtJ+z9B192+a1uERICNsMmd5ra6UI7qWxEdSKiLQkCbOSj35anz1KdqCwRYGP4jb1PlCs1vNSknVAlPC3ksgBZV2v+dwrF1sK2aGvZN2u73vKspTQM6XolkuUgqK0KAOJiE4WoiF6hOma73GVHN1yQuM9w+EIoyE6abrroqTKfMjGOQk0Wq+Ayq92+85t/u1f/F/82T//79kZb9F3AR+gd144sKWlCwUx7VFWsLnTUheG4BNKGbTVnE0n4BybWzUp9qAcRkcqE1Cpx8UlXQCjKkw1YkMXRCViSegbjHIUBoJrcN0C1zX0yznDssQ3U3yA2iRie0zneggdb7xxk/HmNiEuCaEDr3BJtlK0NwTjKYysiYtb35ESeKVzKIZmuWxpl3O2xiOSd7TNkjpVlArqesBoY4uyGmSxzchnMT9b7VK2WFQKmOTQaNqlbKY0zWLdvIvTa8WSzauxiDvlk1u3+c3Pf07sG95++202trdJRmPyNkBZDNZsUZ0U2lh8UuiypBptcXD1NWKMzNwt+pA43NvG1AMJNX12xnh7j2q4iTLicj87OWFnf5fBwTab+2OKQrGzucHJ6USaiBA4ffEUqkOsLohuzu+8fY1LO2OadsntO7/m2hs1XhnsYIvT0xOmywW7uxfxo4bJ+RM+e/QRvTrD6jG6qiiGA46ePGY2a1CqpBoNmMzPCNMXbH3rHdzPf41x8jp55TAmUmIxpqbeqNBmiZ7P0CnSd04GudqIw6as2N7Z5+mLY5bzJWVVUVRDvvL+NZrZjPtHT3BJy1lmNSrFzBYUVVYXwgckCVPSpUBQiSIlrIqYQYGtJIAxasfPnn7MsB7xxvZVNsqS0J7z9Pktdi9eo6i2KG2k6wLtcsZguCFuvaSJmVdMCIS2IZWWPkgDHaOgvgaDAc73knvAy5T7JNIs2grbNaHy515RWEPCc/fOb/jSO19juLFFjG69Et00C6wpcK4jBEVVVyKiBITNagz4QOxbYu/YGG0yGI7RWtEuz0hJM9o6EPE1JnG0JoMpawKK0HUQA10zp6iG6KLCqAJFpCg041FJ9EthPWsR2Jply4NPb1Nag1veIGLY2t5me3PM5OiIf/e//m98+uMfYHxLNBY93uZgf5+iLiUlvelYzid0MVEUBSoYnG948Os5/+eD+7x69RrNoyfsGsU4JE4/vM2dv/spN7/zJ/J6xczY7HtCXkuV7QTBWLgcShOiCKjlsMSHhmUzxSgoq0jnO9AiCj26/xmDusIWiuliSnAhM4ZXwcCe5bJhc2sbwWsGQoBqYwdT1XTdEqU0RTWQ+58Waws0Cuc6CezNjmhxhHnavkUpTVXVIjwZTcgbF9ZoCUDzHSFk5ZUAACAASURBVN55jNYUVUWBcCR9SkQMwdQiZAQPyeM7Qd1sb+0R2inWGA6u3+Daq29iqi2CqikwPHr8nJ99/CkT5+kUaCUbZRI8JevuChExKWtsWRJ9j4kVdTWgKCuePXuIysNt7zpCqqmMloGZC+iY6PqWYlCgi3KNGNLZ9aoUeQOUtXj9UlQU0Uj6VRlGKvXy/4sJJEoIcb4DtdYkHySnwKjM/0556JHv9pQ3dFi1El4cmUlQGCvOtYRDJjH8hJd8aqVko0olyQM5Pz8lIGvqCoW1wg0vSyODx5gEaaFEmF3dJatw77Ks1vXJatgsjNmMFoj5d84hWjHJnbOqh+V7JZATVgFgUre8lEBziFdciaa5bkmg0fj8uyotoWUxGwFCXq1XiIs75L/TAr3r8SkQfY8PPiMTdN6CSmusYwgO8iAVY2Xdf/0+ZCwA0l6stvOM0S/7xLTi0Sp88II5RNj1IQjCZW3gQOoyTcK1HZOm50ydAxLopbSI50UhA9KYVEaCaUxZMiwMfd9nsToSg7y+KQdJjcdjCmuZnk/XWTDiNtYUxXCNogBy31Gt3c9llE2PPgg2ITgnGCjEuUx0ED0x9ETviHi0LglB41QiaahMwUap2a4tm+OCC9sDqtRRqwVbg4ZRaRhUA+pSo4koJUPDZCM1JYWFplsS+iDvHybjFaJkuqzei8JgXCQ6j3OReXOKOV8yOztlcvyI50/2eHxwhZ2DS1w6uMje1i4bo00U4ow3WlPoAqtKfNL0MREz0sp1rfDShxsUhaF3MniIIaJTyFiKCEG0jzUzPefepBQFt7DSDlTKJ2rG46VIVKIhhBRxQTLtnIc+RHySzboYjon9Kff8NpOzC4y3xmxsFgwGilc2CoJXtMuSZ8/g+XPPZHpMSi6LyDpzaiMg9bh3HbHriM2S0DuWy57eefpOsEeVC9h2TjXao0ShYs+ya1k4zaL3JDen8w2hXaB8R9DQRyNn6/IYYyzFYB8VB4CiMiP0cEwfIoszxXzW4M7PaeZHMJtjMTQLRdreYTQ4INmKtrRYW+bMj+6/6K9XX/+gRVq5HDy97zmdHGGzlboe1MS5IywU1w7f5Dv/6Lu8/do1nDtnMnlK7x3lcIvNvWvs7l2iHm4TlRw4TmuKYYFVmyil6Z2kkLoQCcnQtz3L2SmzyQlHx8eYwvDO2+/x6vUbDAcFKckaS4iZS7h2kuV1ci0peVZrvGd9oMW/53eDrHnlCyEFz3wurtG+7zk6OiEGw2uvvctrb7xPShXOzTk/O+Ozu5/TLWVyYGNidtowmR1z7bUdbC2Nx6XLVxiUlvfe/kN0POE//pv/xOULm5w+MVy/fpVHnzwlLUr68xG//PFTXrk6JoWCh3fvMDn9NcfPnrGYzwmh5+Kg4uzZc+6cR04fzjg79/z4rz/g0qVXGA13KQc1OxsbdElz+mhJ86ylHIAplzTL59x44wLVpgRwuJlienrK9u6AYTmmbxJVQlYxXct8cUZ0kcnsFD2o6FxP8BGtDEGLW2/F7ZH3YGUQzTQZrelCQNs8sV3xaDPvIMREoXSeavUsJqc8vXeHG29e5uqrQ46PEnuHF1keHZP6wPz5CSkFKBUuynRPW3njFIq6rigLizaK0WjMom0JyVOUJXVVynw19ETXUdcVsTCoIOKkAgIR3wteYfL8GffuWYpywHDjAls7N3nlzd8nDbY5XlRMXYULJcoWuSiKYESESEqti5f0xYsy+MyrNdnx/YXRY3bFvhyNIYdwdhatUk1XbiilVmsOsLLYpjwmUyrJIZ7ZNcZFknP46GRgoQyoIjumpKhSsH5f1tjblESUiJlhi2ZxtsAMhuzvbHJ2ckJZWH7+y1tUg5rTs2OsirRdy8233uNL9YjLr7zK3m7NX//tT2iXM9669irf+eaXmJ0fcXr0gl/+5g77++eMNsZsbx6yu7OJCS03b97krPF8/MnnxHYGekwIMF1M+exOw9tvvsLV6wc413L38+e02vL06TGHe0MGZWR/u+bWrQecPN9geGmbKxf3uHf/ESfPX3B5f8TFg20eP3zC2XTK/sEmFy7t8dbiVT7+6DMeP3omE2YjPKUYhO/59Nkx8/mc5bLFZLfOyrmQYsiC2Col1wEe4zuiiig6ijijcHPq2FCrSBEV1UZNVRcUOkIqKEuFzgEfKYGpSspaJuNniw7XvyysV+fXF/EZwLooWjte5Z8UB7zRqHxmxiROJ+dern+tRFlBCaR1OJg4KwN+sQDIwQHpJVohF2F1XVGWJUvdvDyHs3hHdutqpNiMPojbfOXGTRLgopW8tlGJ0KC0JMyawmBMdtOGlAvoHIyjNNbo7PaQLQlrDJ334rYsLD4EQgooNKNhLUzLELG5CAuFZa4idYpUnSK0HSokrC2JSmNtQZ8CR+cnWGOpzRa62qLeu8DCJ6ySKL3Y9ZKwW5Y0MVEbYVX7vJJZ1AN2dvc4mZziSPTBU1VDcSPkVauUxD1UaYWOAVtWFAF0oenmE/rsABG3hfovngNJGpc11lVDseKyWSOv98odIB91WaP3OTAiRKHkBe/FsZDFfO+d/DMxUg/NWpxt23a9KpkfN3kesjt3NBrhvaeua+aTCYUxmIxBcN6DiqzCLU1u1kJ2jaxcvCH4zNKOSNhkyu5b8H0v7GLF+nkTpmHg1q2PGQ9H/NM/+SeM6zH0ggJYbTV0XSSFMVZD1085Pz9lvjhjOZ/Q947KVhRlxbJrKLFUusRYg42W6fkRhVVU432iHqB1KXdgSrhuxqd3PkCHJZcuvoIdDMAkUlWytbOH94n5fEk5qKnLGgUordncHGFp6JYJbSMq9lSFRQVN5wOtcxAVxgj/3RiD60VoUlaEAW0srm+JvmdQbVOOa/T2mPHmFsaWmKLGFkOSKnLD3uH6lm45x3VLSIHKGElzVonFYoprl+sQspfJ3znsLwT6vpNwVWN4+vQJv/jJT7n56jVu3HyVoixwwQl7LTf1zWLJbDZlc2uLwWgkTms01lYoDK99+S0++vAWXeuZnc/QWnP1xusE32EKuPTKVRZLR4ll92DM2dkUWyiSsoQIvQs0bkE91iyDxwwKbt68yqf35/Su5/MHZ1zY2WTeBy5cfZ3x7iYnz+7x8MkTulhAVbHoek7Pj3HRsxnGtG4Gyonoq8Q9Xlc1Z8fnVFWBDhG6wPRsQvHWPmm3pj3rwSSKXmOVOIpIGmsN1aAmZs5cDDJUBSis5eTkBN+1ItYlmE7OWM7nTIsa37X0fU9RDajqAXU1zI2SDPL8ijmvXpYYL++C1WezZmdvm94HzpcT7p8/4ocfe7beqxjtXMaWNePNiC0SSgWStpjMiV6d+QmwCZaLBSk6RuMxtqxoe3Eo9d0MkIyCjY0NvHeolBE5MdC1Df2yZWdnmy4kklLEVBKDg+DY3t4TR3DwEMT9Vw0qQkiEKInxITq874ECkrjkVRD8Q6JnNjvh+bMnbI1H7Owd4HTJdDYH39OePUeVFcpU2KKWDagkwlGRnYh3bn/CpStX2b9wSQSW6EnRr2gweNdlIXrIsDrk5Pljnj15SPvJB2ituXztOlU85MO/+Svu/uyn6K6j05rh4SX+0R//Ka9/+R1G4w26RcvJ40f89Mff5+Fnn9DPzym0ojIWXy7pFwv6yTljXTDa2UUtzgnNnHu3f8PN3/99rB5KICZkBqVdD461ltXilGQYCyJ+WmvpgqOqhlKfmgJtC+pqwPNHj5ien/PqzjXm0ynVYJzr90Dnes4mZ5RlKWeKsfR9R1JJUAhenJZlOSAl6FqXxSKIvZNNnaJEGUXXiTt7xbFMUVawdeaSKhXWbs/1Snt2cMaM2lNA3wv6piwLggr45EU0dI7Q9/gQ2BqPGYx32D24zLXr1zi8dI3eW5RVTI6f84uf/C2Pnr3AO3H1y3amuDlXrFeltdR6QPCyOYApKIuSncIwnU+Znp/K3aRWA8OE1UpQIzlLY1WriOapXq45KxmSroKf1mv3XwyT4ovhVXkzaj2MF8FW2KgiIObWmBWuwGSHZwghO3xz75sPCa1WAdoJ14ug+BIJ8PLfAToP7BQ5jY2VU1VrnZFGElYl2K6SGMCUNm8WCm92NehdibU2r/+v+Npaa8LKBZgdhiuHb4L1tuyqThFG6wqrE8U8oLXkvyi9NgysT0aV1u5W8U17kgrr1xcV8cnhYp9/RjKuYfXeRXzMzN4gqD+fEQtKiTCmc88nnrDskFayoRHIgVMKktYZx5iRTiHIcNbBS9dzrvsUgmDwch/Lb6OIsftCbZ5yryKmjRX9wjsPC6mHldIokyiLEm3E6bzCOchiWhKTkTxNhJDoXQdJ7n1Sxul4EV3D6v1IshmxyrSQ7w1YY7PIKGGSKAkIS2415Be1JqWUhX8JumTFxc2mL1sYdkclF8ZwZadgo4ahabFxTmFatoeGQWVBdTIsMp7CWGJAOP7RkDDUoWQ+b9Btou1zLwwQk+T0aHGiGsg5MAXOW2ZtR+wDVdez7ByzZc/z5095snfAhUs3uHzxCoc7OwzLiqgsqIixCrTN21aWoBQuSvBoCEmCx7X0n/KoqvVAZbWxuPKMJ8jPtc5IPb221ur8WZWAz1W4oAxhnJP8JhcCvQ84L4jK4Bpc2zFfTnhxMmE03mNrc5ONrQ0G44pyIMNTFOA8qlugYp/DzQxlUYHStK4nhI4YZVjRek/Xd3RNw6LrWMwXLKcz7Pkpg91TNjYvUlcVqMhy0XC26DlfLgnzKb5dYkJAWQWqICQEW9q01FUi9IG674jVgK6oUOMh4+EW4+EAX0eO/ITaLwi+wTULfGNpnz9kb+MuxfCAngu0EQo0tar4r339gxZpSVBSYK0Gn9ChAFtR2QGbO0O+9vpX+Kff+zOu37hBjEuaxTE7F/fR2lJWI8rhNsaU+EgeDSHqf0y0C0fbO/q8BuL7nradMT875eT5MwpluXrtGq9/6UtsbO4RoyfSU1hL27Qy1UsZqK1X04eXfB25UEx+nBWrlEbgt5g72QoiDcl8Qt8tMEYzXy55cXzM4cEl/uSf/Au2dg9JWCazc27ducWvPvgA7yNloUD1coj4HR7fNVTDwN6B5end+xwMx7x54zVCuMQH3/8hP/y7++zs7jM0j3j+dMrJ8SNOnh6xsbPNO+/f5O6HP+NHP/hPlHqEb2ZcvLTF13/vfe5++oBPbt8hpTt42zI+GLGzt8my89y7fY/Ydzy//4IUNSFZ9q9e5Otv/zMGw5of/s2/48OffMwffO8rHL7yZSZH8IP/8K+4sO946/WLmDDGakUMHq965rNTYoCFa5gsZjx+/owQ5OJOZKi5AWtK4dbkxphMM41RwlSUXl2KAFJgxSSHceccRI3WJf35MU/vwLPXr/Llb77BvJly4603uH/rQ9y8ofdLQq0Z7A+IqUObuJ64WWtJKFmf9nLgG1OikiSFay0iTnQd/XKBLUpSYTBlZrQmhFvYtxA1Spf0faBvzjmftEyX2+y8vs35fJMnU8u0L4l6CEEJzsDKpA0tqwbJGLmOlYTvrCIrVV6BWY8S4aXTMcnnY3WxEhPKSKNFLhZXF7zOlZdwqPJngFUogXBrdJIwvDCbQ+9gVKKVwaJx0a9T11ep2mtXbf5vlae10jgmFuczPr014bX9d6hrzeHFfU4n5xydnnNy+jnvvv0WfeO5fecTXr12wOt728wXRzx5cs7RsxO26iHd4pgnD+5gdeLpg/tcu/QK126+yrMXL3j08Alf/eqrzM6e8avf/JLz85atrR3eu3mZX956TFKy0vbi6XOGpeedd17l5vUL3P/8EV3QTKcN55MJm4cjLl7Y5OhozEcff8ru9tcY1iV7OyOOXpxydzDkk1uf0Cw9d2/fR6XA5ct77O+O2d7a4OmTI7b3dtG2klCAGOhax2knTr3ClqzWiDQZb5HEQZaSFGyGDp1alD+jTIGLWwPGY8v0+Yy+a6mtpVCKSleoYU09KOV9kz1VwRBoQzLCJT24sEfjPd3zc0nF/Xu+vli8rfnauVE3VlbqJIRLBhsus61W620+BIrK5KIouySMxhSW0hbrUBbfSZO1SsZd8aO6vl/zTU1hc9BAXDcHJPmsmuz4WDFytRIsQ4gpDzjkqEYr4TsbKIfVOpU2xiw2a5kcF0WB0Ya+c6QY5T3LmBFt5EwoMrNUFZbCyvTZFAURKfZNEmev94Gy02y0id452gjoROs8w3rAbDlnPp/x2s03qTf3Gb1yg69/53d5fvyUu3fuMDZFdlx4hsMx6IJoSpLShOTQhaRqL12gGIypU6KsBwzrEc1iTtvNaX2PiwnvJKDJalmLtES0C1TVAN81RHJAgVLojLiIeQVUa82gqiEhjqUkn+lEQllDYSV51Ttx75miIKaE1XJWhtjnkaY0LdqotVtS5QA5WK3frZqdl41PSnK/jsblukmq6wGnJ8fMZ1Pm8xnjopC1CjGjy3NqND6vt8U1L09EHQ3ynhYiwKwEQ0n79egUX65IFsL+TBociV/+6ucUWvG9P/4eWxs7NK2XAMUkDWnbK+4/PmWj9hwfH6Nsy8HWiJ29ktPJC7lP9IBmcU5yDk1PA5y8eMzO3gUSRpwnRjYPumZOs5xSVCUpKBoPetkS6LKDdYg2gc679V1qjKG2Gq8a7t36AKUNG5sbFEWkrAwhjBiMDnDKoFJH9A31YIy1Ctd2LBZLRqMNYYN6x6BUbI62GQwqhvUwsz2HhDxcjSQIjq5rWC5OCa4juh5DwJBoW8dsMWXezCkLmxnKhvCFYcBqJdY5R99J07ZYzvnpj37IhZ0dvvq1r2LqkqZt8E1LcD0hRmazGST45c9/wd7BAe9/85toY6mHsqVz78EdLn16l+OjE25cv8Gt8xPatuX8/ARUxcb2Ie++d5nPHpzx6Mmcy9cv0LXICjaK1kfaGBhvD1FlZD5vsaVlY3OM88ecz85J/ZguwJMXz3l4/wH4U4qk+NbXvkExPuDje59z58FDjFZ0bcPRizmL2RleN7AoWZ5ZQu/p2gblA9oESmvwhUKXNcP9XeLX3+Ls8wd0Rw3VpKUOmq2NDUnB9p5oNYPBEO1lyE0CHxMdPX1mEQ4GA+qyZHp8QoqR48kJxy+es72/x3i8gcZQodgb1uxub3Eym/PkZEJQaj3gkIFuRKNzYI+isBIe07Y9y75lFhZ88uJTdm+NOPzdPYaDEcWi4/TJ52weKMxwn4CWPkC/FJkEc7fijA5lBdXWKGL+7Asf1HuHNoaqKFmtN49GQ+7fvc3wy1/Cx4gLvZxnGsq65vzslHowxrueGGdEH5k6R1GWKGtpl4rheExZjQFNUchz6VzD9OwU/ILZ5IjeNdTjSwQ7BltRjixufsazh5+RUmC8tcPW3iH1eBevLUkFYnQYWzAcDjk7OWZ/Z5eQh0XBt8KXTwGlEn3f0rYto+GQqzdusOyWzE+OIDmWizP+7pPb/Ojf/wV+eYYqLRvXrvFn/9P/zNd/9x8TlNSuRdD04cfUe9vcHH+Jw909mpMJn/7iA6bPnlMNaux2hx5uMt7fxQxL/PELTo6eEfsWXQ2IWlBiwTlsUeThq879jhdhJwuAVVXkIClFWQ1BKcp6hLYlzaLj448+Yns8QBkt9UAeRscoYpjWUFj92wxTg6jBgIS8iXsrpoDOvEjvHD44lBYR2RpDUZhcT2gGw0EWYyV00TmpK8qyIkZZD9daCaIluz7JoqDJzPOu7/E+UmQ+clGUDEYlGIuuNynHF9g6uIouNzA60S6X3ProAz66/TFd6zEqC6JRnsXVen0MQYbcmfMcQ8yccA3GEJxiOBgT+o5l5zGFRhlZ6S+SoUgFmpRDjiIqRMIqLCiLKazMEynwRRyfDPFenrsq/7mEvJIFwbQWxla1lUry866o9WbV78IXpjarn0kub583IyFnLOiVLKTyIqA4s0E2dCQQ0EmwqylkiGothTYYbQgpUZUldVXl5yJmZ6z6rUCwVS++EkJXw0AUBJdDznIYWowxuwhZC7pRqZc1SN6akjpFTGAp+fwrC+vdh1UNvKpj/fq9Tlk1IEo4FdqgTZHrRCe1qrx0+TsQbECuvwulcL0w2KXMeSlyGqtlUwURWlOMYiLIv5PJAnSIeWU9pXWo1ur30zpvC6SUm8fV8yCmBp+dxYSQNzQy73Q1XdKCuopRPreSVeLREZRz+TmL67973cMrRQwioi6bhrZtUKtnbrXNmVJ23y5YMZONNsTgqesBYSUURi85FlIwYpWElxOkNjPakLTcYaYwxBQyVx3GdcnusOJwrDkYO/YGno0qMTKBqnRoE2XAXmhQnhgVOjkR7/OzWSTBSSkVqW1J2yZOZ4H50stWAl5e/ygbaCmKm98i4aidhy4EFu2ctkvUndSqZ4s5j5+/4MnhI25cusorBxfZ3NpmMBiBFve11iVal9k0JYiyED3JJaLyKGMl8NgocTejAYvJwawxu2fNin+b33sxncX1uf8FH9d6OJCvbXyEznm6ztF3PSk06CBon74/ppstmB/XmGqELjcx5QBrFfQz2tkLQjdFaw9akslMWWG1MMMTHgh4H5k1PUfTOU3r6YMIxNOupWom2NMTxhtP2djeRZcFzWzOZHKOj4EigtIFRTnCDIbY8R7JbqJtDSrh9Ih5qNF9pAoJp0qirihMwWDrgM0abAmn423mj4f0T27DoqOfz5ifPqPcmdE1gUInbKmoiv+f4g5Q4NXLN16rgkptsLN/wHe++W2+87vfZn/vAou+pw0BVQ2oBxUGK9Z0ZdaHjQhDKk+gPbO5sAmtViwXc+bTMyaTJyxmZ+xvXeBLb77L9uEFlLU47/IF7VBJ0Tsn3LuU3YnZlZOCl4cWciGZW83sAFkLs1/4EjFXDqz5bIJ3S/q+5Xw6Y75Y8s1vfpv33/86urTMmxmPn97n17/5BYPaMiyGFCiWM8/zowmPPjvlxtWvc+eXHxD8p/Snif2NA84e3WW+bFiceyKJy69e4N6jD2kXNVVZcuXydV69vs/m9g7/3f/wR9z76BTtx1R2TDGE/cvbXL1xjRgG2JFBlzVlWbOYzLj14UPOFg2P737KdDEn+ETULVdfu8Tzhw+ZTZd8/tETgmp58XnD8uSUk+OOxYnnZD7j1ukjbNgQkPNqlSV2FLrE+Yb54gznunzB+pfFQnZ0FVqhks4Xu7AXAay268M9JOFkueBJWuD1PkrKZgo9he8wneP53WcEEsdPnvHGtZtsXdzn/q1jnIO0mHNwfRvnAst2mYsZWWViDebPF5aGInf/Oq/beB9pli3aWKJWsHLypkR0DhUtpba0vpMVJBRlfZHrb/0Bs3TIk/OCaV8RKIkRcfdZQyySoA0y/+q35wHqpTk2ictVJfWFQ3MlRug8iV4/kFm/XTFi0/ovTUrlpm41JZMJ2yqxWBFJ3hOTw1pBOsQ84fRRuDZRYtxRysghnlbk8rguJ1AJlXJIBo75fMnZbElUlkDD5/fvcvXqdW7evMK3v/kWT59N+eCjj/j40xfoVOLdlPfeucl777zOZNpw79ER3//Bz3j3rVf5yvvvsLc55JO7d7l7+yPqesQP/vpv6Po5u3ubvPX6TU5PTtgfWzbLwNFiCcagkuL4xRlPNh6zOajY293i+aSj945Hj4/QcUldWm68epkf/u0v+OTT+7z12mU2RhUP7j3h8dMTRqMh16/f4PT4mHufPuJgb5etDRFpnzyb0LU9p6cTSezWCqtF2BPqm8prb3m1NAYSIb9FHSb1lGmO8XN0mDJMkSu2woaeSGBKQGOwyhB9ROf1TFXYtfs0eJm+Cx9WUZeWCwdbTCZzZs3LhN7fOqaz0JNSzBPV7G7IYUMxRvlMFMKPXD0vRWEpq5K2k+T1PLESYS4m+ralT60UU0jhtEoJXol/RVGgrGa5bFDAcDRer4mRxMlKjKQoQWBpFeSlNbYoqAdDWK2OGREBYsrBV8WK2ZaLd61RxpKSojAWkqSRG6NzOIc8t7awBBRWi5PLWotLEhzpvYQ6aG2kUIZ1gUkOfitjJGTnX0yRZbfEtR0qBYIumOdp/+XXr/Det77Mi//9jLiYo0ksl3NUVVGOB7jsWnbOU1alsLtDQBuLLSqUsTmoT5OsYRw8SRuWyzlER7uYEwFb1hQhUqWWoCwueQmnRVoKo182ATGI870aDHDeifPLCNvZx4BVwvtFK0bDESgtk+51cS7riDFkNhY5edloBmVFURTrP7dFkQPApPkqCstgYJkv5vL82oLFYinhZFE4kNMs7GkU2soGQgiBpFg7LpQhiwEiEsjdL+dtSongndz3KUqglYaXfDkpXGOSVcvgA7/+4FdsDIf8t3/4PayxeJ9WPTHDumRZlLx4fkK71Gzt7jEa7TDeMCyWDZOTp1S1wdiKqByRhunZOcbkVVUgRo8PmuSdNIPasHPwCkrJvz9FuadOT0/ZGG0yHm+ie53dMB2VtRRWYUvDweE+XdNgdaIqtAinasnhrsHpmmUfaJoJyS05OTkWwU0ZqCusKSmrAcNRnUNFLLYcoO2AmKTU9L7F9Uu6biHhC6FHpUShpH5q2yWLxQzX91itxI2W8Ttf5GA75/J7EdBKHLX3P/+MQVXy3lffpagKWh8kSKLruHjxEGMLjk5OGA+HTCfn/PSnv+CXH95ltLVFPR5QV5bCVsxmDW+++Q6HF/Z4OB6iLQwGA/Z290imQBeGy9cv0ETFsxdLfL/g88/O6BdLPntyhrYlrxxuMqgcdYgY57l//4RmmTjcH+MXHdNpQ10O2agt3axjdvyC/a0Rh1evc/+xRqdIVQ/EQECHTYa4DMS5x5mW0Hqc77FBYVLi4qVDTm3H02cnlE9fMHrtMlubQ85+8iHu6Tnbg23qwYBCGZplI4E7KUGIlNaS8eYoVeJjpLCaopJVvNA7xqMRg7qkCx3GGEpbUqLYrUt+/90vY43hZ7du8zQJM9F5L0zaXGusFmmNNTjXc3bW0TQeOVzC3gAAIABJREFUt/RoU9Bbz4ePPuWVrQN+761vYHTkzq9/xv7lKW99/Q+ZLRsR86oaY2Ubh6RESPVyfkheQIlSEWsFpTObnYOC8cYmvfM452iayMH+Lg8+/5ST46dsbG+t7x7nAsVgyPbeodTzRLpmgVsueXH8gr39fVCKxXLJcGuHy5evY4syV1s5cbqf0c7PaZslO/sXKMfbNF5DCpiipto5wKrEs3u3mJ8do62hqEdgDTHE7Jy0XLl6lflshnedDFCDI0WHyS7zSMy8yUDXe3b3LvCV39nhxdOH+L5hb3Ob23/7AYuzE7xJuM0x3/3n/4Kvfvu79MFISGQSZNvj+w+Zn51RDBKX33qdb773FT7+4c/4yz//cx5+fhfXLxhsNlj2GZUVemefzklquFYS5qlNTiY3mS+dxIFqjEVru/7sCrIsC3m2oCgrjCmIzjM5naBUwcHFS5iyRBv7hTtf7ofxeIPhcIgpShFAlIQcmdqI6FxURCW1gi0KYoq4rs+3bURCbeTeNtpkN2fe8sj3mFKRtm3oupa9vYO1u3Al9jrXMxiOZcBV2xxA1ONyGGlKSK0QJQne+UA12ubmW9sUdUUfE8u+5dHd+/zqw99wslzIqngUEXI1hErJS6+gZLsk5F40pUhVlqAsy2VDNz9HJ9gYjfBxSUr5XkNTlVaMHEHu7ZU3Lma3rGa1eQQkk521KbtiRYhT8IUar1w7SVMSIXKFTIg5c0Xqgy9g0rKTdr19Q178j4m+63BuJRyKwUQhyALZhCILqPl7taABQYar2hSUZZ27HQ1WY01BaQoCUBU2u1/lLDJZVF/9Z92TK3DB5fc/4+KUmEZMZvHHlYGEVXBa7q3WIm1GB6yHxtLbx4w+JCWUTl94f18OmiXUDFaZHSLeSk0VI/gQ8xwirX82CSoXJ79KidIY+uiRIkaCg7U2IsimnA2SyPnpMT9TmWObjWYrEXgd3rYS3LNDVmcB31gZdKz0DdlIYe1OljtacAcy+JaetzQDlBqIsYREiG7tjl73q2SEW/5enR3UqtCsgqhTlEAva7KIuhrk5ZqR1TOb3zcf5V5yTgbU3jlIiV4srPK0Zm+S63t8L9iZFRM8IpsOw1KxV0X2Cs+GCVgcNkUGBdS1RtuKGFZol4ROUbINlAxWlNbYpGXrUTVUlaFICRc0IRb0rWgUMQZiFI1AA6VVRGNwSbFoEgZ5Xpq+Y9afYXXBqGkYDs6hW+CmM+azOZdeOWRv75DNbYsui9/qJ8XlmgSvkrJHNsj5oIyi0JkFrQVH6LxCxZA/Q2rtKs/yO9mHTExCi10PHCB/plgP7FIIeNfi2iXRN9lIBgWVsOndErpzoj5G21JEYt+AX1LoSFBirglazqykc6Bf1MSoQBt8UMz7yMJHkhe+t9OgQ8Q3c1znmM+nUBbEbknfOdBQFgPhWG/UqPE2ZvMVGL5CvXGBoioJSTNMhhLp5yKrUOxA0opYbzK8+CaYmrLQFDFw+uw+rl9ycnqC2nyMVrtsXLhEs71Fv7KZ/z1f/7BFWhT0FhWgigP2Rhf56vvf4Bu/97u89tprFFozdw19EIgwURq2ZGSKq8Jq8pOt8j6y6Fp8iJh6QPSe2WTC+eQFZ5MjiqLiy1/6GhdfucJgOBbCpnd55UkeZGGdZnt3VJiErEiRJ0xKWFerpkKs3/LJXwm1q2ncS3ZLpG0WnJ+f4LqG5XLBdLpkb/cKf/q9P2Nn95DW9Tx99oDz08ds1RV/+kffoZ8/pz+N/Pz7nzHcKnhl8wrvvvE+x/dO+MEPPiR2LU/Hc549OcL7SBuWXH3rTb79x9/ly6dTPv71A6JzlOPE7c/u8PD0NnVRQExMpx2+MehksR/1bO+VdD6gdcV45wqjjYvgNG9+5Utsbx4yf/Eu0z96xuOnjzk5PWJ+fsKdX/2Uk+MZDz+9S2LJfzz9Ad/+bs0f/Df/jH6y4Cf/+a+w85aB2pKAEeTC2RqMSA6GoWR/d5um6/PKg6zmSVCcom07YbdkqH1SUjj44CVcLErBm5RcSiE7abWya/ExeMdiNkfbIadPHvH0xWOa5hzlPW+//WUe3b5N6AOq6Sn6ntH2FmiFc+K4Ei6mou0cUcuzZnMCrFbCc3EJJudz+rBaK1qVi8j/1irD5fM6eIxoPeLa69+i3n+He9NSBNooooKyiaSFXYgWl9c6nEPpHAjwBZd2FkCTyoJsFnPzqQpKScCS0etJs84ibUirTkt4SSqvm8ulIyKSYzX1BxUC0XVy4OJxyzNS36IKcfrhWpIpscNNkqkISPOSx4asAgVQAUOHipKKPVs6/ubHv2Fzc0AzO0LHiAo9m3XF3/3kN3z+6ISIIUbH4YUt3n7rXVTyzM/PuP3RJxzNlrz+xk2Wyzl/8+MfceXSLm+/8QaGwKPHz7n9yedcun6F6XTGL579lO3NTRkA+CkpWEKqJXxovoRuh1QbdnfHLJaeydmSzx91TCaGL795ldGwYDCwPH7wgHffvMLF/U1ODndZtpF33n0TFXsK67n/cMmiCQwH4iBomwV9H+l6QUNkeqqsYsbVNF8mDykFFEFe5xSx9FRxzsCfU/kFGoeNkdOjh6iU6GMWHjWydh4i9HnKWwmPSxzqgeBlNacwhnqgGQy3OH5+xqLp1wXcymGRclGqogj7eu261msBbFVoOeezSyU/eCoLcKycC3m9MAd2OBcYDoe8+eabPHn8mNP+DIDgZcpclqUIfklWaFei52pFJ8RIoTRFVeCdo8/uzXJQZbSyxsVAWVk53418NlKEqirY2Nxk0bfiOsw4CRkk5GY6xfXPUpQyEFRaC6MwF9l1WQpDz/d0XSciqZKtAKUUZVWJm6LUnNcJWseoMZR9TzKKqBI+9KAiyhrmvoVmwvyp4i+//1Pe+b1vwMYuk+NTapVoXYe3JfvDLZIydM7TtB1Ra+q6xhYlZVWiUmI+PaMLCZcAWzLa2sFUJebc0i9mxL4Xx0FRSdJ6cBTa0CVHlzw+RWJwuZiXA8BkJ0VZVtJ08jLxOAHzZimFeiXFog8+N9/53DMSCiF2F2mg6rJia2tLnFDeE6I4PdCKfPXK+l4l55f3gdlsxmAwWIdIDAZDku9kKIHGGJvN3isOWcYUZBeItRJKttrF9L7H9QltxIm4ahCksVqFhSrIH61Vo67zYOEnP/0JOmm+9a0/oB5sZMc5JJMYbGwwn52j+khUIxZ+TOorUnGNPi7pm47DV3Y4vHhIWRX0XcNkckrTn7NfHKIKS996ovcYWzMclJIenDR1KS4OSPS9o21n9H0jzhxloUroVJH6QFCaerxNWW9mNmCiLC3LxQmTswfYaoukx+A1s+kxT+7eZXt7l8vXbrIxrLH1JsPxFoPBBvx/zL1Zj2Vpdp73fMMezhxjRkZmVlZlVnV1Vw9VPZlNsmlKlCwJlGVAsg3Dl/4pfSP4zpe+EPwLDNiwBVu0LIji0CSbFJvNbnbNVVk5RsY8nmHv/U2+WN8+WS2A12YADVRnVUacOGfvb6/1rnc9r5bQHmUMqrAE72hWc2FtuwZyIq9BBOSb+TWr5RxrhPW+vLnh5uKKwXjEaGMqTslcMznnvhQyIyLs8eEBXdPwve99h/HGhqzxdZL+PJlMGI0mFHXNG299ha2NLR7ef4s7e/f4P/6vf8PTTx+RFJRGszmZMqXk9Vu7HLc3hORlfTsZOtegUsnTZ3OiMdx/fZdHj67o2o7zoxOuLy6oByNGI8v2tGJ/e0ip4eR8yWefPGM43uDX3ntAu1jwH3/xBRQ1i5VDh8B0UHL45FNOTg/pVMnubMBVu2A43qAsa0blGHWhKDqLWQHRQxT3kW87nj9+jB8Yyipx9eQxemtC0BY7mZDUWXbhRZLWDAdDOu9o4lLOaVNglMYHT6EKjPfE4MX5FhNd11KWlsZ1rLpWHJHI2ufWeMS33voKJ8fH3FzPCUlY4DEFGWQhgWuSYSpCibaCA3MmUBcGypqlW3AZl/z4w59QKcM37n+N2aRAxxtce4nG4n0kauHkaWOFh2uk0XSuJfp2vbZZ14O1W84UmVmnRSR+/vwZb7zxkNnGjNVqyWxrE2KiLGu0kSbaaAkl9t0KHSOWyN7dO1SlBN0kIpenL5mfn2JtnYdEmq5bYJRcezs7b7B1+y5BFTRNS2yXaGsIxqLKEXe/8h6d77i+ueHy6orprBC+b255jS0Zjcfr52KKAZBnCUFS7YuiZDgb4wIELEU1YPe1txjUBUcfPeLgi2cQHTFZbn/1HX7jd/4JMVq6zomIoEREjCQmk01sIfzqWCq+8r2vk3TLf/i9f8v7P/slzp1RxICfzqgmm6y85/TijL3ZLUwOh4khZSxNZlrmz713K6q+99EaW8gZ7HPQWLNYcX56wZ179xnNpnmBJdeyJIhp7W6tayBvSsznC4bDSkpaDSmvCSc0EXEwFkazaBfMb67Z3Niiqmoury4YjqYisiuN1j1DVOFDpCxLBgMJb5Ow0EjbNFxdXVKVBcOBcB+VgmW7omtbkncYK9dkRGrxkFEiVT2iLA2oSNes+OyTz/nJT/6Sw9MzInYt7sn6uyCSjMnhqmTcQ9vguk7up64hFBbXrPCLOSZ4isJS2X5AJcGoa7eQUXTBY4KjjJZgyPWWPOtkyyGu0Q4xo4cUPeqhX/GPa+GlZ6n2q9labJO53wBUzCgAhdJSBwbniVkwSwl856RmU7KtopU0J73o2YcYx+zE1srIgNZaiqLOLHQx5QAoawVrYXIouOlheOIANTa7QBPrfkvEW8EdhCDiZsobMmSRUmoBEdpiShm9Fb8UQKjWTu8UXzlPyW7b3uvyK8iEFDNDVoSv/vslEr7rcthl94p925tplJLAK6VFePR+XZs773JdKu7YEGKW5EFps15Rl8JbDBaRvun7kghrJCTMZLH2y6Fu6225/OWck4GpyQ73EKQ/RH2Ja6vXW8TGaFIATZJQpZ5Jux52p//EzS11Vh8uPBpVVJVgtVbLJb5z9P5lncW6PrA4KTEXRRTKKIySPAFhsjo6J+HcKSWC8+iUMERCFplFOLeYQgwXhdZoVhgipTaUJjGqI1Up12eMBpTJvRZo5YCAtZIFgvbyXkcNlGgVKQqHqgq0MtykROc6rNG4EEH5/D5ktrEtGA4Tyqv877OukCKLxZy2NSyXLfPFivPrM54ebrG/f5+7995kc/sO061dqkoqcplNpbWdS86BIAagLslLNAZrLVVZMh4NCXmrIIScQdOL+PlaiEkRUsZI9IMLFV9hxKLcNykFkutIvsV3c7nWjEF3Uhf3KFCrDMrngUESp37K+MaEmPti9DlAVkEsib4Vt7XrSD6iWjE0lYANSbaydCCGJc41BKUp5PRDW0tKjuhXhOaauh6ikxczU1Whx1N0McVIk0mIab0BoZP8/p2u0YM9yq2CcR6mp2LG2fFjllcvUc/+iimeYmoIbkxKhr/ty/zoRz/6W//l/99f//Jf/o8/urV7j+1ii2+++U3+2T/6Z/znv/3b7N7axQex6bsYCD7k1Dkp3oyVYJNebeqnkDeLBT4qbDGg84HLi1NePv2Cy4sz9u7s8a1vvcet3dvYsiZZWWdJSVa4B3WFLa2IgSThkmiFRh6o2miKoshNWsSKLSE/FF7BtNEWWTPMKdUKtApcnB4wvzgk+RU38xWLZeTd7/0WX3/3ByRdcXN1waNP38fECwq94OLoMaurc85PTphfzqEJfPudd3jy4QccPX3J8eE5O3d3+fXf+Q0Ojp+iDdx5cJ+d+xs8evERX7x4xOHJM3buOL723TFf+fYeX/3WPd751i73Xx+xsVUw3S7Y2KnY2TNs7Ca0XRJDQ9tecnN1wNXVCZ9/9j4f/uJnPH/2KS4u2Lq1xXs/+D7f+NY3MSlxenbK+dkZ15eXzEYz3nr9IVU55OOff8ijX3zB1VVHmWrGZsy4njGuJ5RFTbNcsWyWLFzD+c21OJd7+SZPb5UWhmEX5BDrV577SZuIRjrPcxQ+c/VWvhNLu5EEVe88PjqabsmqW9E54Wfdufcajz79HLdcEVxLMayY7MwYDIcMh0PqspRJrgZre6u9MICMsRRlSVlajIHTk0MOj1++ErAw66lS7IS96r2A92NKTGYPePDO3+c6jjhrRnSxFi+KUXLyG00y4uzDmgyy1xIQ1l9r+eGWejespARkbnK2ciEP7qK0aC28I20kbIv0KqVTRl8epQJGJUoZWKNSH94CpEBwLfgO3a1Iiyvi4gqrE0VlSHGFii06elIQx4E2ZW7Yw3qNT0IXWkguC7cRZSzz1nF2ds63v/4mf++H73J5ecZ83vDhJ58zmW3zzle/wuLqlIMXLyjKkk8//oQPP/6Yjd1tCjw/+Pa3+OCD9+li5O7rr3Hw/CV//Zc/p10t2Nza4dnTF8zGQ958cAeS4/DoOVtbm6SkmS8WJDqIHdq3WA03V5d03YqVc6QoFoV7d/eoKpkyX5ycoYDbd/eYTSdcnZ9z+OIZTXPN7Ts7hOA5PDziyeNnvHhxDLqQzwWykJ8ddzFhMrAdFdDJY0io1KG1o2BJneaM4g3DMKeKHUUG6be+Y9HJGntpDMNBTVFXiIYv2A5byBkVs+NUAVVRU9clVVUwqAcEF3l5fLF2DWitGA5rqrrMzsZEUiIEK5PTPhWvnBNarVfJ5M+FTRdioCj68Ke0LoBTSuugkMViwXw+J+kkq0cxUlelJHRHud/qqsoDmJ4nptc/ry/EQ0xYaxgOBxIiZvOwRud3Qg5llNEUZcHd/X2m4wmXFxfZzSLFX/KB6DzRhbWjoW9bkkbuL5VXe1Ki807e7z5kL+U0+XyPxgRYgy9kUKVdpEpQ5GC0qDXDyZTp5i7FeEjUkag0i1YzXzmGwwGX5xe4xRIfA+Wglnt6MKIeDBlNJhS1NLEpJbq2wzlH23Z0IeVArkRhLVVVUZUFRU5i9pnvpVCSoF0NsKagy0WtMuJkKmyRXWwaZQq0KRkO6jVjyxSlpMUqjS1KjCnoVi0uyHqsUiY3PZmJFlnjEJSWRiRkYbt31/Zp3EVh0dmhZwtLXddUtkQhYniIAWU1VsHqZkFoHMYUr9YG8/kVnAidwWenbXb0pCiOTZcxB7n7RGUuat+4rhvL+OpM1PlnxBR58fw5VxeXvHb3PoNqKO+NguFgwGA0ZTTdpBqOUXZAUhXWjhlPthnPNrhZdhwenRFCYDoZYVWFUSVltQFqQBdkwFlWFUUpooM48hLgGQ5rytLQtgu0SpR1jbGKelAwKMFaRRcgqRJURULjY6Bp5pyePAMczgeWyxaFpWsik/GMW3t32Nm7y2TzNoPJJtVgAtrmhshgtKJr5txcnbKYn5Nih1WRQid0DCyurzg9OaJpliRkUKK14frigqOXL7i1d4t6OCIirj3vhZsdk/BZvetou4bgHRubG0wmU3wKdM6v15P3dve5+/rr7N+7y3A0QZtS2J86oZLj8OCI4AJDWzEuKspS89ZX3qRzLScnL0nRUxUljddMJlt8863XIBg+eP85V2dztmabXJye4UPDV7/2gIcPbjMdlVxfXmNtxfF5w/Ojho3NbY6OTphuzWhDwfHpFTdXFyg63nrzbb773W/x2eef0y6X3Lu/z9MXL5jfLKmGA7puyfHZc3QlZ1hKsqIfE1ITJHG/DkZDktHMlyvq2QSaAMc3FHMHeRAhDxVxEVZ1RTGoMHWBD8LQjDFilaEqS9rO0XQNNzeXKK1o247JYMJsNGY6HFMrzfLmmo++eMRnhyd0xpJ03rZRgijp6zAJbVRYW3Brts2dW3tc31zRhhWtb8Q93zkuji/YGmzwxv3XSdqQUsn27fuozOeU1y/f11g5l0PXcnF6yNMvPqYwislkLKvuxqCwaFNAinRdAymxvb3LxnSDTz76CFLAOQmosUZzfXHOfD5nMByCNhhbcHV9xdX1DVvbu2hrqYcjRqMxVVnhg+fs9IjOrUjJo23J5vY+s63bBAoR65KEC/eDvITCDjYYTXcYjWeoPnBHWyL9uZJD8nR2HiWHSg4to21xMxUVw9GMwpYi1sRAaSoqM+Snf/jHPPrZX9DMLwjViN/+b/97vvber7FatFyfnRO9Y1hVlLrk8viUi+Nn1Cbw2r277GxvM7+6xLmG6B0Hj57ju4521ZBCQOnEPHl8VbH/xkNsWTFf3GSxV8TLGCM+SuCRRrjiKXp85wRvYxRKGdpmRVlYDg9PaF3H9tYMlKIsK3Hk5yGfIM16oSjinccagy0so9Eo80wVzoe1i2ttREBEY2GJC9ey61YMh8O1cCzCVeL89ITlciFnRFFkN3CBUon5fI73jtlsJpiE5AlB0CNaQ1WWFEUpmRVKo00pmzvGYIsKozW+bXj86HN+/OOf8OjwJV0earRekux9kOsxBi8DjxBwzYrgO0LXoKNDJ493Db5ZENoVBZHCaIKXMCS0ojKKzdGAIm989ANwlbSI33m42kuxOiPSev5tf6+l3FfLtWv6pkH+fJ1XkeubpKCvwXoHZRKGrnMe13Y0TYtzXR66ygBR6V4ElEGcyfVWWUiPZa3gJIyRz6SsKsoyh4daizFFXlHXlFWJzkFgxti8IZM/f5OHr339lXsw1rWAWouCvcNaGQ1GshGSuK1E4+1xddkVnnozTBamIOuY2uR6Xq+F25D5+iFEXNeJmSHXyl1+b3qOb0hRMg10b4pIa3yYUkpwLV7ObR8Cznek7EKVTTbB8qEEv9EjHkwW33Te6hQHfPYj61emsx4jKL6dmLdYpbalr2FjFB6u73+vkIc18lqDE8duCHLfeidInRCDYJJClMFRFmljf73mHr/nkIszPREJJJWIKchwBMEa6H6oYUx2emYcidb5uSnvoTHCX7dao5I4Z1OQjCFNWjOGnU/roLKyrCgLTaUD48oxrUuGJYwGLZOqozCvAtiMLgTJohPGKIz1GBWwVuX/afn5Vkl4VNFRaEehDKVRMoQlQRR0WwB81IRkSJmrTcZLaNXrIiHTGmTrIviO1nfMl0vOz49ZLRqaJt9vhSYUQ7SpsbxyfucVCBElk+TLkCQbIoSAMobC9kMteX8NWR4Igt0LiOs2kPEI0cugwAe8k89c+YhzjsVyQbOaE7smG7Wy012DVpJtIwFmHSG2ck4lQ0oqD0vln50PdF3HarWibVqWq4bzy0uulgtWy3a9dqaSMJhDynpL3pSLSTYKbFEKyiHKhjLBE5sloW3AtxjlUDoQTAWmwpcFqTTY7Eo2eVIYlSUkQ1AFmIKgNU5XpNiRFscQ50yGlnq0RaomDIGDH/9PL3/0ox/9K/6Tr7/TTlqtNG+/8TY//N5v8PZbb7Ozu00yisVyLgcEiIMlyUUa+5XWPKny3snKaohcXc5JpqCoZZVyfn7K2cELSgXvvPcd9vb3QclhVxoLmS3bNm0WJIYC6c7MEjksxAmitazYKKVomojScoP3zCTIsO+YxDGqpDmLZGHRLZlfnRK6Od57XDDcf/ObvPPub2B0yco3fPrZB/z0pz9hZ9zQ3DyiNDf803/+j/j4ow/44pOP+PTjK1wT0CZxc71kMBrx2sP7jHanzO5scXl6Qhgsme0r3tq/TV0XWN2wudlQjSJzt6BxVzTdnOvFJZc3C5qmRiVZb20WLd4nyspSqmV+sHVEX0oSrOu4Wh5z/OlTfvHRn1MNLDtbd/jBP3iP/+w3vsXP/+JnHD094vjlCSF8yid/85T5DYymhmgVyWrKoiIRWTUrebAUFrf01MOK5JHpmFKZUwU+RgkVy+ybFHonXha4sjtTkfKkUkJ9Fs1CCnKgKiTddnEugnA5nRKt4eCLJ+xu7bJ9a5fL0yOC63h5eMTo9pjRbIrVBlNUeXUbjE2UWWiSoCQJIRKnr2O1vCYqh1LVeglAZ5fY5bwBhNXmXaAod7j1xndZ6h0uGkOXcgHQC0kJ1hyYXEwlcjJmno6qpAD9JX5Rnk7m9SXyPZJVQLxvZNkkiaiRiPJ+IkWbJmKz+BtDIAA6B0RYHMEFlHMC2lYJrWSVoRpUMkFvL8GtxAGTwPlGVtGpCbGTiXwMeY0pkKIn0rMbFQ4NymKUkYZ8UjMZFXz66Ii79+6hVGI2jnztq/f54z/7BT//m0/5zjv3MbHl3XfeJjY3uPkBdBcUZsTh4wMuTk94+OABr712l88+f0q7aEmt4+mjT5htzPj2e+8yX7S8OPglJkogFcFzdLLg6uyY2XTIwGgKA10b6JzjyRdP+crDPbY3J/h7+zx+/ITNnRlWafZubfDppydsbt7h6dPnHBycsFw6NBZTjElaCuaUp6IijWkRsPNk2aqISQ0meRINig6bHJVqqVlhk/BEvc8DrCwUgqz326pEVyVt1xBTpLQl1ggXtA/hkiAFtea+GW3Y3dlkOCi4WXZyHQKT2ZjReMSLFwe4zr0aRkF2JupXg4D1rHZ9uMt56j1lKZzRfkWpfw0hBIw2LJsVi6ZBWwU5XCWmSHT5tSR+xf2QIctrt0LIhbNSIgL1P8dHmW6HICF/Sb1yfPoUefHiBQoJhxKMbeoVOSnQs/tWK7N2KPgkz4XkU3YOq3Uzs07/RefatkeOSCiFDoFFcFAbinJE1XQ43xGUYuU8w40SXVhkqcDTzk9ZHI/Ynj7k9t07vPz8EdYU6KJAGY3PrgyCp3USeFnYQkJHUsIWBbPRmLIsOT87wrULGfAnhYsIR68opZFSiaKsKY3B+JqoNOfzC3x2wbvOURQioJaVpSgLeTYaQxB7AypKerQ2et1oRBVZLhZyxhhDoaXo6gdtdV3J6rTqnRFxvYUiXPhAMobCSLPftQ0KLYJxEmHAxcCwGGHKmsl0g8t5i2s7irpYN3DkUITCWtq2zYiATgavyGfe/+wUZQjX1xopIWJCdo6HFNZbHH3xm4CkFR989AExJH74W3+fvdu3hYGbFOPxjPF0c30fCs4kURQ7MvQ5fcmjz37J5cUx27MajWY23QHXBYn2AAAgAElEQVQrgqi2BeWwwPY3WX7uCRIFYpQCcndnA4XGeWnE3XLOxXVDWQ9R5ZTo1fpxEXLzpHWF85ZhMSGFCm2HTLemjCcbbG3tUg0nRFMJBzmCJOxG2ralbZb4bgXRobK4FENgtVrQrBYsrq+IKVEN6vXQUivD9s4OW5sbaFMIIoX+/RTVJXrHyjUEL6zK8URWjzGG5DKTNHqskbT2zz/9jPF4wHA8JiTN1cU5l6cvOT07oUiRiS2pBwOSSqxWS1yzYhU7unbOoNwg+Q7Xttza3eb1/SnLZeTiRHPsVowqxfbWDhM/4OK8paobnjdz9vdGnC4ajs7nDGqoq8jVFSRt6VrP7s6Y1WqT8xNPGG0R6m1+97/6F5weH/Bvfv//ZVQX3MwXnB0+R8dAZUqcWxE7OW+s1r0mQli22LLEesPgGmJaYGZz2ssltSmoSk3bNpiqIhmNUUaGdVEGbM45Otfg2xZrSnE/J7nO7+1tcXZxTFkPCUFhyhIXPJ13zFXkLz75mKv5DSsSUQuvDq3F7Z6C1EDKkCJEnVg0Dccnp8wmExJg64KqK0lNSwAO23P+6P0/p6gNIzvF2EsRJo0Gw5dq6iTNVITjoxMqq9jd3mA0UCgvgqKPQQZGtkQZzXA8FgxJTLItF+S5Oh6PsKUwRc/PTrm6WTAYDLFVjdYiutpySNK1BNKGQDUeMpoZZjGwu38HoxVNs8D7wHA0g6LEdZ4YPVVVYYpK7qsoWxHKVPigQFUUpWzLaG1yYnq/Jp3y4EtDDi1WuS7QRp6Tq5U4yZQVjnt0cHZ+yfs/+480N1e0wTPcn/C1b7yLokQXgeFkJO6foiSpmtsPvsLL5x9T6mv2dm9xfnTEwfNnbI5GfPHJ5wytYm93m/OLC26uL+mSJ/oJP/79f8d09zZ377zOX/zkz6hGA37rt/8hOzt35V6OSrZ+8rPu/PySwWAk52VSmMJK2O7NDcdn59x77Q7D8YCmafJ7Je+DD57oI2VVUVVlFrUk98FkrnyMEaNNHgYgDrMkzHuFCI2j8VQwY94RomfVNAxHgiXwMVIUBVVdyUZMVa17vbaV+q+uB4zHYzn/gydEj/c+byLJWjpaoZOW4W0CH2T7pyhktf/TTz7lL/78zzk6OyUpRZed0TGjaVL0IurHQHAZq6MQB3UM6FzLGxImBXnOokghoEnURlaOB4UVwUmpvAkkWoWwveX3Qr9aDzdKRJZ8+0owVYgYA951aFOshU3yc0qZ/E0huxZlcyppnZ3f8tWsmvUGRC+yy8/pMUK5tyCv1BvBZAgqI6/sJ9b4jKIoZRBvC+ljkjzPbMZYSTiYPH9V7odiihD4FcSB1nqtJYC4U2UoLeJhiGHN3YwpQdJI9lTKIq3UhCEjH8hO2S9jDMSUYLPwF9bbPillHm0SYc3nLcWQe0hSyk5UK8P96MUBGpMg+7xHJ7nWdR+cGiKFNRmPEPJApQ8VjjjXyemRP/e1KzoPM1R+Bvc8V6m1IOHXAqxwWnuEhGwQ2cJi+pXvKL9TyFtSpFebw1prwQ3kcDWb8WE91znleh6VtZ1euF9vH2u6rsNHcWNLP5uH8SmsnbhaC4sayMNqEQ9fDW1iRqqtCJ0TNE8fAKfkfghRrmPvI0aBToFSKQoVSL7FFgVVHShti1FRhoFaBuOF0ZgcpC1bkWB0RKcOowJGW6xOBBWFP60U2MRooLA6YkzF9dKToqXjFYPaEoiplR0BZeS+ztsDcm1JL0GIrFYd7nqJLSxlZWjbjvOLC44On7C5f5fNu1/h9q17zAY1xlYi+hLyFnBEC7wZohKcREx0NILM0Pl3yj1eChBQMlCA3tOcz325d6K0HSLIt3mzMAU5J3JYoTG21/2RgZzkO0igHVkncHgSqZXzAC3XRLtc4JuG0DWkIFkFq8VCzD/GiJFG9T1hAHTOKZHrvKiHFKMpRTGgspY2BIJv0d2ceLnEzY8Il08pZvukra9gtx+SRruYekjKgxhZ3s+bozERtEYPNgnT+7RdifaJQddycf6Uq7NHMNhkaoak8TZ/29ffaZF2NJrwX/83/wO7m7ukBOerSMLnRkCaNOcFbG11ZvAkR13VFNbiQ8Q6D74joRlUU1xouD4/5vDZM4bDEW9/7S2mszE6RRY316SkKI08oAtTggmyJu/zxZQB3yHkaQ4RW+S00szWsTZP/OlToPPKR4pEL6uraJ0fPJHVckG7vCEGR+sUw9l93njnN6nGe7TecfTyMb/8+Y/5q7/4Q16blfzzf/wOG7PAe++9TejmPPv4UxwD9l//dZ4ePCbUJ9x7Y8JVc8Fff/An3Hs44Qf/+Kts3x5SVg0ueJyfE/0FN90pL585mnZIPdjExAFHBxdcnltCK3JnWVqxiAWZOsXkSUpca1ZDTJdQLNGVR6sKnOdsdc2TTz7hL9//U+7tvMaDtx7w+pt3eP7kjL/593/AF58fUlYlt/d3SVfiJksx4VYrQuioi5KBLahswbCoaaPDOSfuZPKDMEZs5kH2IHaVckgNgBKBxseIJ4JRlLZgYoasVk12o8j3jSHiFguMNai65vrkmIuzY3bu3uKzzy2p7VhdXbO8WlLWA4IJqCgr2TH0KAuVuW5SJBmjUcFxenrK6fkpyRh0KjA6MqhLpqMp+7fu8sH7f8OVWxJIGFuwc+cbzO5+hxerbS7jAKdL1hwkLYEAqZd6+5Av/Wo1RB66Kje0eWeg/xtKgkKMFY5Pr6KVmfOUUsJHLwJhYWQylAJVYSmNzpNcmxNFI8E7iA2m82gnk/+QHM477HCMNhq3vCJcX2KsJ8aC6Du0sRRa+Fkq+jzpD/l1imArbs8ML4/yJIgx8vmLU94+3GNrc4Pbuysulx03l6fc2jC8dneHW7e2uDg7pKzu8f3vfZ2L0wMOnn7EzcVTbk6eszG7wzfee4vhN1/jw48+5I/+w++jtOW9d9/hxcETtrYnxJi4ODvjyZOnRHdNpTw+KkLIASs6Cs+xsAxShzGOznecHq3YHBneeLhH/doeVxdnnByecHf/LsGJg+AXf/0hHkWMGluO0GiSKujRJz2bS2PyPCeRtM/nnKPScwbGEUODSh6joSKgkoPkJRiGfJ1kkUbm4Rn54V1eGQ/YWppAYwyqKAmuoy5LilKLMxZxbm1uTtnd2WTx7AhlZIXv7PyCs/MLvA9r5ld//WklU6ggsepr4bd3IoqTVL63sKtYF45aKZm6xoCPLWVVMhwPif3WhH4lfvXXfAghF99SzFkr7pW2bVH0P99QVQUxN41aZVdFEhpWQtjVyih8F1l2cja4EKRIK4pcnEdhcSKFtOscVikiHhcCrnMkyI2EwmT+rFJp7e7wXlwHtizwIVApzfL0guXFFcuiZFUUjAYFpZ0QvMemxJKWURqJE4aICgv84oKLowN29u+w+9p9los5g/EUOxjQdJ6m7Ujes1rNmUynFONizSIzxpBi5Ob6iouLC4Z1ZlDGxPV8Lg1a77AOHmsLEYVQlEbO5Xnb4YJgJDonQr0wpjrIq3kxKVzrMHk12fuAsgZdF/iuE54vkRIp+ApjcC4L6V7wQuIqCWuXdVWJMzj4nKCdEpvTGYv5Im+zSHK9z6uDy+VK7gtJnCR0jpoic/ReBWhprQWjkYV8l1m59WCAXy3XzYYP/kuNQ78aypqV2jdvMrCQa7b14iD76S//ipdnh/yD3/kHvHXvAUobus5RVAPKakhRGJQycgQqWdHb3B7yIA2wtqNtLzk7PuJ6pRlaB8ZQlxWF0bhO3AbSHMm5733k+vIK3y1RasWdO/eEq9sFzo+ecfD8GRubuxJOqmsm07GE9lBRDcfUwx2UMgzGm0zrDcrBJqPJFmU1ROlCqNjKoNGE4OiaOW27om0aEkEcGcmRQid8f9fStS3npye4dsXW9ra4wPJKvk8xh0CVmfMljZ/RPZNPGqmubek6R1kW2Y2ts5NFQv2UUYxHIxKJZrEkdg0fvf8hTw8OuTg/py4Mn37wOfdu3+X1Bw85OD7kiy++4Pr6ik8/+5jt2zuQPGVpWSznVHZCyPXC9kbND79/nz/4o18yvz5h/94mTbtN0yyZTEuencO8SWjl2ZhWPLz3Gk+enHJwdc77v2w5PTnj9Tf2+cY33+P9jz7gja++yRcfP+frb+1za9/wve//gLPFnOuzBR8/esyL0yNc19IVjtBpbFERtTTHMSW88ygHNIlaKWyC8OkxRdswVgWjjQn+5kbYy8bIYMVJOnZVVDTLFamL+EWHKhXBFNSjiqqumdQjjtvI2fKcnb3bkODo/IybqmBYVyzmS2nCjKLMTrzU10EZZ4MWhnRVlVyen/H09EAGblVJNSiZTbdw3ZyuuWFROj5rXpJ+/if82mvvYdWEdn5FskNUUYkLzUv+Q5fk3N/c2s5ojw1Wy2suTl+yahu2dnbwKgq+Q1m0tdiq5noxZ2M6Y+/OXWxVMd3YkfRm7xhOppTD8Zr1GGOkKAdsbQ9ICK9dWTm3gwetDOVgJsnhqsaHjpgMKmmquqZz4kI3Vhx+ZSHCREpJuMAoUsor5SSSzo27KUUkTIK3sioQmk7qpJhFkGwWXd7MMYWhHlSUFTx/8jHXLx8zqwsuV4rprSl1EfE3FyhTUI7GqCQJ311IbOzd5vs//Hsszz/n2eMnXN2c8fDth3RnC44fvWBgNJujmr2th3zy/CXHV0vCckWVFJdHzzj49EOOnzzB1pY/cUv+i9/97xhNb+F8wLddNhMYtrZ3sbakbZrs9pT3+PDknJgSm5ublGWRXa/SuMcgfEitM2pCyRaMyW7dGIMkxkshmwNtsmEC8L6TAVxRiJgTxBE6HE15eXBAUZSkCE3bMhgMiCkxHY1kiNX5vNouCCpr82uIgm+KSYSktSHHiKgcmkbEhrJAFxZSYnlzzdOnj/njP/0zDo6O8VHqZN91JNcQXUSrSApOcE9ddi2nLJxk55qYKSImJAwKK+tC0oPkgbdVmipvj/RRWzKQTDjy819ros9Cakqybp/AWgSZFl8N7Y2VQX7+SAhZMBS276stGLQ89zonjr0+TCx4vw6UEoG0FxclCDblZ5ZgMYQpa22VneRm7djVSlOWVc4meeV+7WtHqRm8/D3kGvLB542S/r/R+fPMyIFsOuhFxB7P0IeWkdLa6apz7amVbIqE4DOzNOWh8SvBt98gEya+OCNVxjr1r9M5t66LnZc1+N4t2yOg+gDGkLLIHuL63khRRHhxxCoR/ZKiCSIy9wWu/JwcepYHGj1zNvQ9wpc2i/rPyRi5ZuKvfM6CBSjLHjlRiDCaBbuQt/FCb2ZIau2o7eurqHrHcb/1ZqhLGaz3Bg3vO/nsTAFoisLkWt3gQifoD5dD55Qi+B4nqHNwpFv/Tr/K/pXtL+8crnOyQZUFWgkhlB7G+UDSGl1YhoOSaVUyLmGgIpNSMzSOUZGorIIkq/dKlxhTZZFb3M86b58WWqFUQBMglZnAKwgiUsBqQzQRY1qKAupS4ctE6xNNRncaoCChaSmo6JKRoXt0uOiIytL6AFHRuYhPitSuYBlYtYnLixsW1+ecnL5g9OIpR7dfY//2a+zuPWA4GlPakqqwKCXGIJJBKUtfzKbM3k4Z6RhCDs4DfEKChxFTYkyikfiYCCmzlb08P110YkDxklmhVCFueCubjPk0yc596YeTioLx8oE2+nyN+LXjfHFzTbOYC5Lm+orlakXXOUw2D8imipj8ZANQo4JoG4PRlPF0g3Jjn3Jyi7oaZOzWNc31Kc31IbE5JS7npJsz7PyUtDolzL5Gt/GAVT2kKEpKpSkzlshFjVcWbcesyj3mwxq7rbH+BpbHLBdnxINfMC5HtN0+f9vX32mRdjiaUU3ucd4krC0FRp5vpBBkPaVtO1aLOaVRKFWQUmS+Sijl0NozHmgm45p6oFCpY3l5yfnxKZu7++zde51qPODq5IDzzz7k7JOPCauOcjxmY2eX3a++zd4b9zHTMR5o27BOKg1ErJGJgV6PaHIBjFofZmKglRFCimKnVxqU1eTxDfPLc5rVihAspthg/+G7jLb2CMlwfvSULz7+S5589Of460OSHTPWif2NKU8+ep+bs1MgMZqN+MZ336XYHPHLj/4fip057733Gvfe3KQYdCzbK+bdJWl1Q0oapSOuveb64oLFlcJ1kaqA0FouTj3LFRQqUpbCipT3W4u4lIQnE/JD1/lldrUqmm5OFyJKF4zGGu8Vp8vnHH/8HMuEh7e/wQ9++9vs3nnCyckx6BWGIdEFVssFhYmUugRt8UmCRK4uZG1QilqZJMqDNLuU8kOhTw+UNfEvMY2MCJY+81CKshQOj/N4BE1hrcWnBM6RtGIJvDg5ZP/hfeyoJrmG5BXXpyumO5rWNcRciCgr7mifG9BBJbb21bJlPp/z8aNHzNsWWw2ILRRlwWg8IkaPsTCejrm6XhJ9YjTe4tbDr7HQE5ZxTOtNFp0TurQEa9ZJ42hBHkgCZ1yv35Kni6/4t1m0RkRso6KksscEeSJm89QvrQsQizUCGDdAYRNVmYuJGGlcJLiO6FbE0JJ8wiSZ6EWCTFqTHNDJ1lSzHcLyjNS1KCLROZy6JpSQdMprSEqGAdkt1Xsv05qJq4i65ODS8bMPHvMPv/eQrz+8w09++ZjJcMKTz57wne9M+e43H/Dv/+AlP/7zX/D09i2Ub3j97oyt4T3ics6Dh2/w/MljlB3w/Mkx33jnTTZ3JlzczPmbD085vFB89xsP8gQ+MCpFgLict7IejiH6xKqLzKZD3hgPGc8mPP78GSdHpzSNTFkVstrZNImDg1OePHlM24ExFVYros0hIckSUoaq5/dQJZXdyxFFRwwLoluAahmPNbuzCd3KcDO/xsSE8pKYigewUhxoMhYhYbU4V6IXd6W1BqMtKq+Vay24FlsVQofW5PdfCsSyKrmzt8XBy1NclD/3PqwL21c+2bWVD6UUVlnoh/y+Z0aRr1dZuWVdC79iXfUBESFGvHNURZE5oeIkl7CAV46FNVYhR5WnKEFdphd+tWBJ6B03hc1hYoBSrFarXJRaWTFSSc6D/n7wEfDrNbXCaBkQuUTyAV3KPafX958I3/0KZsqONZQMSJQSdquLAe86FueX+Is5sXMsnGOhwSgjrOiYmA5qhjoy1PI7aaOwBqJbcXZ8yPbtO9x78CbHRy+xRUlCo1RkY3PKcj7Hte0rhwRpLUIqEyjLgu2tbWkkUmQ8nnKWHcymUNic8hqSrCsRI7UtUKMRIXb47AYhRiy5kPNeAn60ZljXrJpGmmalcd7Jc7B3a2YrR9sJ87YYFmuR1nkRSYeDIa5zqCRBFH3/ZHLTFGOksJZBXeNiJIQkjXzwea0uom1BMRhQTycsLj1dLhB7hIfK14HWOqeTk5uvKLgNxavGIhf/fcPVu7Z/5TrO8zGtsqtQi5MwGXh68IT/+/f+Nb/79/4Rb3/1HYIHpQyg0d4K0zevKCprKOyI8WwXoxO39h5we79lMb+h666JSQrO4MF3cd3ohSguPnnm1QwGBdaMWSxWLJaOpmlZxUSqxiRbspjPmW3WDMYbJFVS1ENGoylVKWu62lbYaoyygtPw8VWidYwdwXf4donLoWCahNWKzju8WxFdl+8fKfSNMVTTiTjhgqTxpiToEHl/xf0Uvaz+KiNBaH2vXVU1g4EMb0STDiLKx4TOQS9Xl1csb1ru3L1Pip7LDz5jd3OP2XCbdnHDt7894lvffo/v/fqv8fjxM/6X//lfcXL6gtPTM2a7m0ymU6wtiVFTlYabq2tOz66YDCvqsmJzc5uT+Yp6NGLlWi6uLqnLfb79jVscn1yiSDy8t8WkNtRKc3necDy/IoTA4cERX/3mDvu3ZnzwN59TmZqPP3vCuNZsbd3n6cufkzrHUMNsPGbabnDUHWfHj4QCTccjcZHklc8QAiYkyi4SLhushqqosIMBNocaZcgeq+USlaCelmilqOohi5NLCgzDWUlZlJycHPPs889xzrO3f4f7+3c4OHjJ9fyKFGua1VKC45KS0CNbEI3CIe4XknCRyqEYJ9qbOSePn6J8YDTbIPpA03bogcXWFa5c4TpPMIGnV8fU/iOqeoP7fomxg3Vd47pOeNN5hXgym5Kih2AZjS1XF0cslxcM2xGT2YY4V5EwIlMZnO+YLxfs7t3i2dOn3Ln3OkmBNgXjsXBKxfWT0FYGJSkP5FarFcPhIDev4KOnmS8YDcfYcohhQOc8nQ8YxE0ZU5LVUW1y8ynOIFKObzFWhtPIMywpcepJYynPEWsiFxdHJLdgMJAm37kWDRRG+LJWgSFgY8N0kPArT9Kau6+/jm8uOV/MqTf2CMUGthiAsSg8ipaq0jw/P+H6/IR7d28zG0341//bvyV2ATuqWSwdnpLNW3d4tnpGIPDdd9/j9fv3ia2jOT8nJU9YrVjeXFOONnHJEREBwtgibxxqfBGxhUWjWC5brm6WTCZTqqoixb6ukGGVqlQeeArSy8de7NOCaWk9y8UNNjskfZKwt+A6BqMxZVHhwysnn2SEKIpqyK2921RVIdev0XlDAnEvIk7elF381oqgGHMNIVsWBSE4QEuwDZGrywuuT0/Y2dlmPBA2+7Jt+ODD9/npX/0VL0/PcUlcmskHVMj9YXCklLfIshvPR2FDF0avnYNGS/1glUKFmFdsI8NBTVlXlLbAty3tckHSJdqUa3xPTHI2CgZAgp4EOSVc6kgvVsr520tbr9zQkocQQ5BaTEUychdFXhtPr7I1QpRtDAWkHlqZQ44LW2AKm3EW8rP6NXylZBsmJSXbd9lZtw5wVa/MTwIdFMOJDOjterMqRjFRiUtPZ8EwZi01ra8FlYXSnpkqYWE9P1khOUSymRhzTodwZ+OXaoHeDpEdf5DxVq/qBFJc82p71nEfSid1WUaGZbNByKz7mEIvJWdHYc9dJjtJRcBSRq1ZxDFntKj4qi7phfr+M/oy8uE/rWXketdf+txFh/HeZ7OCzuz5LNQl0FZjVXZHR9nW7F2g8iLy9WW1DNN9yEJrjzaQzZgiD/RA4UNH17mMZZBefaBq0mjCcrnM5jiXz8ksOufXG7OLXgaG+X3ve+IEwWV+7xpDlrK+lDLqCybDmtlowE5tGZmOkYHN2YC9Tc2oWFEWBqMSuihRuhYdSmcEHBGlHErJxpnJLnYxxthcG1oUBUpHrEmkKuIDOK8YVBHXRhoULpncJ2rACWaxsDgvImZIXvptZYlKhPqUm68Y4fxiQWhFL9l0c7puSbe84ub8mPOzM7b27rK5scNsMmU8rAQ5Armnytc1kkPhZWZBT01MSeNjwkXRxCT0TrYNO9/hnJiMggusXMticUPbNesBGsqSlISk9eYGBbLRnn/jEMFlREFIwj5vmwbvZAg0X9ywXCy4vDzn4uaKeevoYkRrqQ8FwyABw0ThDRur2NzYYHPnNqPZDnayjx7vU1VDSIlux7G4PmZ1OmJ18ZLl5QXziwUDP4eupVtFFl6RNl6jHc6oSktMhiImFDYzahNUE+zEoPw5ZjimHm7QnS3x80vmp58yjdf8bV9/p0Xaqq7Z2rsDyrwSoOBLh7OwZptVk/luSpw5zqONxqpAEVrKQmOsp53fcH1xyWy2zbvf+QHL+YpHf/oH/PLf/u+4x59gT08oUQSleVFVsLPJ7je/zrf+6T9h551voHVBmTmIIGIheb2+ax0KtU41DCFke/crhqP4tpX8vRAxMeBWl1yfnxA96HKb23ffZbb3Bm1ynBw95bMPfsLLx3/Je1+/xfe//jqnL57w45/8lDuPpoxmU44ubqCcsbW3z+/9u/+Veqb5nf/ya7zzrRpTLFk0p5ycX8p75GE8LrCFxXvF9XnBxVFFs7IYOyR0kW65onEQbE2I0HoB76tkcV5wDzHmMKAQSd7hgsMHRUyWEIVFksdbRBUIxoOG5bLhrz77E25PHvL2177G/fv7fPaL5wQi6MQqNAytMIXPV5d0XcuLgwN8VNQDEPFFilqjMjtHibi0alZoo7PzsAeQyzQnkgUGMtsnr/RElbkjaFRMFEmRgsO3AeccFydnvP3Nr7N/a4/D+ZLGeY5fHjPd38TUChUC1hb4lHBdS2k1zjW0zQ3tasXJ2Sk3zZLL1VKSXn3mfVayWnd6eoJ//jnD2ZhwGAjasv/GezC9x9JVJAN0DSoAZU0sLWSmXNQqc2Xz/kYWZuWE692zvTM1IZwo0EZRqIRRiaDEt2m1ptC5iVCynmGLRG2TiLcg6mF0dF2HC5qu8xIQ5lpSRo642DNUgRRI0UH0aOUQEHeHjg5lFaFtoV2iy6FwmlM/O8txWeup7q86a5WxRN9y+uyA7ivbDAewU3nO5nOqQvHki0+oJjMe3N/ik4++wET4F7/7Q3T7gvl54NatXQ7PzvjZLx7z8MFXefudr3Nz8YzV8wOeH7xkf3fG0emStos8f/KMs6OX3L17i+3tCZcfPULn4oyYuLlu2J7BZKQpUgOuI3p4/vKEzVsb1EVB6+HwxQlGK1S0FOUwNxshu9ElqIrQF8JRVjpR6Nhi4w3RXdItL/B+BRaG2/cYDoYkYEhieXFJu2pQzlEoCa6LIVIPBjgvYkyR18qUtmgtU++8kCDrmLZEa0n6LrKIKIUcOCfBHg9fu8PTJ0c8P7kSzBZK3L5ZNJHBFNlZq+hDElXsC1thRYV+WJKssFtzA7x2QyiFscJXiyEyHo3ZmkxZpY5lk7l42d3wSpzth2R5bSq9Kiz7VUvv5f8bY6R41uQVyTzTjsL87dcYVcaBGGNQMRHa7CxRmtB4Wu9xwYsrPBRoK0UiWn5edOIgMvbVYzbESLNqKIpSgg98i7+e017N5Vq3CqUR8RZonIRKtLFluhgxKacUpsqilKzwqBBYXM+5ffcNupcvOD48ZGdnj8Ia7t2/S9t2fPHJgsFgsBYZ+/WyLjuNy6LCeYVzHeVgzN033uT4sML5hq5raBdLXNBaT/4AACAASURBVGhQWmFR4ozCsDGd0viORdeIqy87OFKErgsM6prtnQkbr93l+PiEm8WC1rcsLq6ZlQPuTMY4DRfLFT4J069pW5p2JWy/vMa4XC1pliuKoqAoCnE8Zwd17/jovMcUltVyJb+jNRhn8FGSvIP3UGhmt29hioL52RkqCYtXDpdX/OJ+JbJfz4wpCUZGZfdKvl5870jOYmXPQV4fyySUAR1FbEkKCmsobMHV5RV/+Md/iC1L3nrrq6ACxJbgO5qupRrU2LIUBI6xTCYb0lxqTT0YUw028b5BVvckmdmPWkJ0xBRwOaDLO0cMHq3kHPU+Mp4lRrPALMLe6yWz8QbDqqIejCiHm0RlUaaksFXm0gnCJyKJwspLs55SQ+scTbMiekf0LSoFCp2IoWPpWpZNS0pRBlO5sU3AaDIFZL1Tyn8ZYPctewyB6B3JN+LMcV4a55RYo2DUKxdV/zqMtlTaCKNsueKdtx/w+oM3uTg75bvf+z4/+M3fZmtnj8ePPufx5x8x25ox2t7iBw/e5ic/fZ9//3v/J4tVx5NnLxiMBnSdZTrZpGsaFjcLfvaLT0nKUg6HmMmUgS64vHBMNyuub2a0HWzV8ODOBkpraiWM1t2dCQ/ubcCpYjh2nJ1fcnF5zcmLQx4/+owf/ub/x9x7/Vp2Z3d+n1/Y4cSbK1cxdDWboZOyNIZGsC2MpbHHMISB/eT/yK9+sGAYfrGhsQYW5CDNjAVZDaWW1Gp1s0k2Q5EssnLdfNIOv+SH9dvnsuGZd12AIFnh3nPO3vu31vqub/hV7ty7x1/9xV/R9xqVxqwWz9mdj2jVPqlQXH65FPsVH/EqklyQoCCjCL4jpBKPpUJRBI0PCVNaotJMpjOaxYL1com1WclQFnTRQ2k5Pj4lFgZHAOc4ffSI1reMdye4zrM7neIXS9zlJbiOtvmqv1vAFIUsVQqDLgtsBB0TSVvquqIsCh5/+ikpSB0eT6ds+p6l61i2Gw5nM3xbw1lL0oGVjXxw8ZDmo8T1197i6187wvkgdmRVmcGygFZm60nnu45xXTE/vE0934UIy8UCU/bUowkqB0SN6hEXpyfMZzM0Gt97irpk07bymdnBIxNh0vmcYG4Kqkr+32qR8kffElxLu4kiG7UVtqgxRbbhMQZRZQ6SXjJ7LQcKqcyOzH2rSqJ2igy2KdJURb+hLjTK1owmI2JEvIIJ+LahsAXT3R1M0rRnZ7z51qs8/tjB+TmvfePbVKMxZy9OmOweoHVA2SjS3X7D489+zNPPf4KKa7793W8xG435g9/71/zob3/AwWiKM5qLpqVdN6jJlOuv3uOt736X7/yTX+Po1h2aVcv+3QuqquAb3/wmxWhE16y2NmNDmA/KoK2lzAvYFCKnZxf0PnFrb08A+CyrFt9BQOkMYitC8AKsREfUGu/Em9oqIRMYIl2/4eLlU05PXnLr7ivcuH0PrQuxNErgg4B02pbUo0izvMBYS1WPZbmpZcYTsNags1Q9RgjBZVa/3nq5a22355BJntFojDrcYzwdY4CzF095990f86P33uPk4gKfW3StFaU29ErhVA7xybY7wQdsWciyTil0SlgdUTGgU7YUCR4TE5ZEVZZUxhB7J9L3FHCuIxWWFCJJS3C2LUuUFQ93Yy1ohaGQ95NJRAJEZ4XJcGbne1aZfDpn9DaFAQBUsnT2XopfUhnQTCIcRV0xVxMUtqQajbCFzQxydQWYKnW1sDSDzYHe1uSBjCNWBQKODmCiVmwVQDr3dSRReYXcC8YUs4o1bcFBrcyWaSrf52oBSZSwalm0Z+B6sCoIw4Iw2+pl28Xh9Qz1bhuMGwfrrRzYFePWTkErvbV425KMklgwbMFSAkVlM/goywNjbVZFJlzXEzJrdxvyBdkHW75vWVXEKMF4zrm80I1bViL5zw39vFzftO3ni6KQn6+z1D1FUCbbSQzsaZf7Ir2t08PixRqDj247y1tjZLHuhZUcYxSiS8YCUsoBXggZKeZsB6U0VVFKJ6ANSvXZtuMKcJaA2MFqMmyVCSomtBIrt4gEv4Xotypd57OaVEt+jEEzKg3X9+ZMrKWuGuoiUGgEPxhG8yRWGQZHYQJlkdn32TKQ6FFWnivkMdkuQpRCFgpKUVhFaSOx8IyqhGmgSz4vWHVeugSMchi0nA+mpA9yLXwKtJn9bVW2X0Gx2LRsXMvZpaIqK/YPVswWS05OXjB/dsT+wQ2uX7/NrZu32Z0dUBZCKBLu1BBlLa9ZSDpyLcTJ1xDzfeNDzD7Entb1uTb3tJsNy2ZD0zXE6ISIZKwsPEPAoImEfL8MVrIGpRIuBpwXoNfFjr4Vr9nkHd1mI1kSStP1Hb3rRJOqBBMS20ay3aKEuqWYPZG1hqKinB1SzQ5Q9RxTTyhtxQjFbL5LN6lYjmrOjOb07CWb5lLOvmzjlVLCc5fEjpD2stVKUlpC60uDYUTVjpnUe7D/CmdtQ7864+L8SzwN/6Gvf9QgrdaK0URCLIY7WQ7EK2m31iWzvTHZJl4uboKuD7hNg2rXFCag8PjuAqtrvvXWt+nXG/7h3/wxD/6v36f4/ENu9j3j2KNjJCQFy4bucsni9Jy/evKUt3/rt3jtn/wa1f4RrXdbeYeQLwPBCys2pZDp9JaQBNwA2eIMMg/xSkqoFFhdnLJZLonBcu32fQ5vfQOnLafPP+HLj37M0wf/wF4d+U9/8z/mzmtv8ke//4f8wb/+v/n408+4fjhj98YN5kd7dOGSd757j699e8Jkf8W6O8a3GzSKST2lWzkW52vazYYQFdEXLM56/GaODyWdViQczsHGe4JWeD+w2uTAS1FtmyKjxJza+04M1ZNGjGNV3ryIZCtJ1DUk2QansefFxWNOj8955eg1Dg9ucnx2QTkusaWhnNWs1huatoWQGE1GpCQpwTEGGeSQhiHkRkIAlRw4NBwhw8ZSRaIS+4Eo+lEZ8FE5NilLzJJck5TllCZp+rNLXn76iJ3JHmflc5r1ktA7ms2S/dkhISn61rHq1lwsTkkqsFxe0CxXclAl8CmgtTRKZOsFkmzpQvCcnL5k0jYoY9g5uMl8/3WetWMunaJ1HZBkQ280ITeGypitfyZqCOnIjGJj0LlwSv+fWbUIUGEUmGxTIWFISv47egorjMjCaowSZnWRpZGd87S9p+scvU+4XsAjEhjEciLlJkSTCKkn+A06SKpx6taY6MEWRAXFpELXU1xhiNogqvhIEg5O9pQS03CJcE/Id1YUvsF2Gx789H3eePt17t3YI3YbXjx9zPNHl3zrF36FN+7c4PGnj4gugg9cnpzxN9//B568WBLtLh0lH332OWdnj3j76zcJfeLazi4Xi57V2VP+5uVjCmP49lv3uXY0BWVYt7f4/ItntBuRFEcfefzF59TldUozYVQJ8NZ7z5ePnuO6jnXjsGUtrzwz3obUVJW3nMomjBLvMu8dpVFZ0nlBu3lG354TQy/AULKsVxsWl1+wbpbcODykHo9YdWt00ugUBfjM7FYhTMoGWhuLLgQYRYMysrxQCsrSoEjY0lIYmwcZYQ6pzCKYTafcunHI0+MLCWA0YoCflMi8Y0yURZGBxqFBFYmLYJd5G5s3+wyFOP5s0zw01wqwWti248mE1UVLDH7LmNFfAWoFqJFnX+sMujH8mMzE1umKIZkZGNpeJRmLyX3+OwxMCTJzLVEUVd6yB8pSLEgyt5e+bbBlmZsuaeSTl5+ngsqyNxm8QGTZ1lr8ZUt7sRSVoNXCMNYSuCS+/fLZOddzsViyN94wGk8xmYllbUk1nbHetBy/PIGkePHiOWVRMN3Z4fHjL+i6lmpcAZr1as3F+RnTyYSmSZycnDAaj7h16xY6WtCBpmsIumDv+m36fsPl6Qm984S2w+TXE4KjbVtMWXC0d0B//ILeBTBQFzU70zmr5YKCRKUUB+MRsa7wlxeUZcFsVKM2Gw72Z9TTHYoA567FB8em7XA+os1gYQFlWaKS2jKZpSbpPKAJo+Dk9ITgA6YoGdWjLUt7CJJTVkuTB+xeO2Q0HhP7nm5zSfJOWHPGQIpXNgtRBiEJBsnXA5FubaXjfIUpk+8erQXMHVKfB9B2UHzEENHK8vz4JX/7d3/LbDqlrmqMtUymOwQHKXqKvgZbYMYGqyWUyRgjTDsSdlTnZ8VgbUXbbvC+xRjouiaHWOoMNHkJj9KaoirQNqGURdkpmhKSwhQlyojlBXmBlFCZTahJ3hNCT+g7fN/iXZMDQqT3ScFL8nzy9H2z9dwTe524PRO01fkcGML9/BbcTjmARD6vRFUUuBByzbxiw5CQpVmu78Za6tGEqqhYb1pOTxfcuH6dGzeuk0KH0RCVYtW2pOUl9c6Mo7t3MSoSIvQx8S/+6/+Gg905P/yHv2c8ntO7jsXFilfuvs5i1bJeXrKez/j+Pzzgzuuvs1itqcqaSV3x8YdfEmPkctExRnHjoMoLrEjbe9ZrxxdfPmIZPLPDuwRVMdvZpWvWbC6fcPriIfNZzc7eNW7cvs3FxRnPCs/+UUn3ww/oo2OmJ5z1G1IPBsXy+ISYz3NvFcY5bAoEFVAxEfuAHsu0IwnWOU29T+LnWFnKUUU5HYu6oO0J65Zmveb82QvMtOYbb7/F4nKFjYrLk1POT0/F9zMnG4cYWDcbUGJ5Uo0syluKqIh9Tyos8/1d6tGUorCo6ZijOzdZrpf4zjGZjqnqEe/c/wbv/+DvWa4uKbXB+cRGBT69/IJ/+xd/zHiyz9HOHZIpJflap6ysk4VNVZRUtpD7yBaMygl9u+Hk7AVF6SjLWro9o7YgyWa9Yr4z5dGjL7j36qt0XUvwPaORhBL1vfQ4wQWilro1rsYMrDfvpa8T0oB0lOJPmqNElIUUc29KrktJltYx/kxA03b6jVe9KtHTbC4J/RodOzSB0XgsQWgqSR3yLUVdsVou6fuOUVmxubxEpUTjOoqq4uDWHQ5vvILrBUTamVQkbVieHvPg3R9w/PinjOrEN966T2Ur/tX/8nv88Ht/zdSW6LqgSYmLrKKK7Zr/8l/+V/zmv/gdLlctCc3Nu7fYv/46RWEo6pIQod1suDw75fLyktuv3KceVyidPcpRFMayXi9YrFtme0dMphNJsh+CiXLqvSy1hU0pDEJwXc+nn3+GLSx3bt+mrsosA5d6PBqPuPfKK0xmc/E817Lcdy5gS1l+xShWdovFOVYbDm5Icvkgv495ISZSewnw8VmdoBH7GmNM7gUEUGg3DcYYdnb3KI3m5dNn/PjHf8eHn3zCpu2xVSWLpyhgvDg5RvGgzQFNmiuP82GhbDLwmhwURgBaqzQxOlKQpPXleokxBb5vSTpRFIYQHWBFGWfFYz4qQ1RawtUy02vITFGIjYbWZtvDeTxG2VyzRBmhuPI0dc5tpfBfvadTyu7JSmY3rS3aSDBQUVXCKtdmC+DFOACL+TkwV0SN4R9ZzufAW3MVKpeH/8xmVtlrUoDckGuzYMBZbZlE0aW1yYFoVyCkvJ5cl4Is5eXvCGkhZXXXtpdVwpCUoLocIhaHPA8YLBVifm9i+ZRJAPnRJ8AWAo5sl5Up97UhXFlrxLx0HsDPFAIhDv6vEs5KShlwFGajUVAWhQBiiIftYBvi41e8a7c4S8p9Xsi9s84gbvaGz88iA/gujq8MTGWxZ4gEpWX+iGJDonQgIcCpz5613nl8GOzNfJ5bIr3r8vWXnyPX7EpNF4OA3T4rpYbfj3GwyvLbfkKTQfYgYLCAe4GctMXg8y3XCVK+L0PUbPrAcuM4iY7SVtiZkMU22mBGEwyB0mjQLluVSKh8XUZ290ZoPUalEZqeREtKnpikVqY0zIJ2ayWmVInVkdImnA6iNNU5m0ST7SoUKWpc6AmpkOscFegC7xTrVkJFUWkbBgiyoOi8x3vNsllzse4pnr/k4GiXG90Fq8VLVhfP2Vy+5Nbt+8x3jpjuzqjqESrblSk0Kp8F5BMsIedJjAORbqjNYv/WtR1907BarWh66fNj8hlQ9zmAXckZqKw8J1r67JDP/N572qYjBbEadM7J60gRqxMqBlTy1IVhUtf4BMGJNamL+aFPQpQxVoKDvXcsFgtseU4xPSKNHLUVgoKydVawWFQMxKTwSpEKw/ryjNpGTDrDNl+Smn2WtsBrRVtPxdoCsTNKagDeS6rxPnp6G+YXpOaYEJZs/IpuM0D1//+vf9QgbUoQ8oBPBmqHsA6VPRBzvc/FAPCB9XLFcrliYmFET1WWxKTxfc/YaC4efsn3/vj/oPnR37H/2cfsLC6oQNhugFGyOTRtRJ8s6PpP+GS1gb7j7d/+z9FlicfI5kflQSEkdBIKvanEtygEcsMhfjXiwagFZCAQ+5aLs2N80Oxde52ju+/glOXZs4e896Pv8/TTdzn58l0O798lLk/5/L3vc3z8BDueoOuK+996k43vMRPPP/1n73Dtzohi9wIXzzH0KCN09c1qxaOHz3jy5YqyUkzHO2jdE72jaxVN42mdwGMBuamS6oU6HzyJSPSdFL/k0UqzcT0x9qSUt3YxM1KJpKAEKIlJmFDD9kpBUAFdrnGp4afPzjnYvMpcX0fHROg6lIaub1FaAJj5zoxm4+g6t/VRCjm0QpIgyZ6G8hCGKHJ7lSfiSKKPIgPw3mUmoRT24CUlGlNglc4MKQFRdWFQXcPlk+fUO/tYU1BoWDVLHj96yOMXT1gvVnkgDbShwRsJt5CCIME82g+SC4UPKaeUatbLBc1qhUoJpzvm431u3XkbNb7F4mLC2he4qElKY2wk2URQStZ1mSmI0qgkUgejVAaIRDqlMyBgtLBog3dYU2IUWNkTUGjxf7FaDtzCiJeV1XLopehxQTwlfQDXdZLQ2TspdiE3LYnMLhUmaELum4FNrVNm7I4mpMJibUWkoJcHF3yDztIZKcYWjUOHhiK02Ay0ezQhaUJoOVmu+PDhilhajg5n1BUsT7+kX2/46d99H0ZTUtxwvljx7/70L/Crc54de7pQUQDjSYExkf2Da1T1mCcvnzEuaq4d7LL3q9/i8y+eMKprrh3tcXF+wnojCY/zsaVbb4gekYEHSR2vRhOmu4Fq2WKSpVu3+CjyIPHiREBUlYgqotHSAWaJnFERcFjTU+iO9fKc9fIlyS9QyuemWECTs/ML2r5jMqrZme9mENETV0tsCPSuYzafEn3E2gJdlCQX5J5BYa0h6oSuLD3SHEkYgzTNQeewDekI8jkbSQpu3Tyk/ugzll0kGfl1uQfEf9sPXl8xbp+zbWOtRR4jzbSk7xalDJsxXTX7LntXTScT2rZlsV6xfLhCa0U9Esnr4G81+JOKL5bIRfvebdkVw88HtkwJYMuWGGRYwqbIUsh0VVOkyctskfyPUoq+7wHxudOACglCQBXSYBATegjV0Ckb/AsLUBkgBhbnC5YnpwIsGg1Rzrc0NPxIirZWYi9ztlhycNAw7jdM7SgzL8XHuvGeZ89fsH+wy1tvvY1CE5Pm2RefY4zm8PqtPHyumU7GTKcT2t5xdP2agApaZ/9gjbUFve/pg6JtPaDZ3T+gO+7pN2vKvATQxuCdZz6bwpHisyePcEFRA6/dus3u5Gt0bUO7WbNXlqi6po1w++5d9vdmLI5fsn/9EOcss9Gcj19+yfFyhTI5IA2V2VYJkmawoZMZZGBJiy9c02zE68wEjK0IKXJ2cb4dogECEVOIz6mpSq4dHNA0LcszRXdxjl87kTxnUFaGkmwbkhkkbd9tP6vtsoGhvl2xt4MQW4hRegBrLUPAikjrIj4J0Pvw0Rd88N67fOvtt3j/44/Y3b/G229/R1hh7RqsIYYOZ0tsWVHWY3kfmRUNMnSZ0hI2UJQjuS+tMKfLQrwwo/f0TcNmvaKcTEhGy2ety7wIHSJoTK6DWaaY5Ox3rqFvN/TdRj7N4Bkk2hCJwQu4HYVBMQzOKsmyFxAbkRx4IouWKM9/cOJvrhKoSOgdJLE1IYFLYl+i8uA/XE+VbSR0VgC4xvHxZ0948MkDZpMp33z7Wzx/9hhrNJ2LLFYdP/3wYw6uHXHt2hHT6Zze9yhbsFgsuH7jiO/+2q/zJ//vn6FMZHd/Tte33Lh+i7Jas1iccf+bbxJVyRdfPOXo+h6Ly3Nu362oS1hcrhiNDH3sgQKCMLjee+8BTZdYNZGXpyfY8Q6j6QH1uKSsKq4f3OD4xQvWTjHdvcsrX7vL9KXmgx83YHoOb95m4QLzep+z1QmqR5jRKOLwbxeIrYfSEbJyp4iaQmffWu9EOmgtm8sFRSFgzHQ6Ba0oKyvgVNScPT8lhIRykePHzzi6dh3XtHz57BGb9ZqyqlG2IAJaW+qqzrYWHTE6lDH0QfphFSKrxSX7O3MO5nOenJzy9PFjOt/jY+D6fMpsNKJbr7hcLgkqEZRYzkQb6KPjJ5//Ld0frPnn//R3eOXu21CWmKrGp0T0XnpMPYRFKqKTOmSLMddu3M4+sSEzaOQQmdRjLi9OqUpL02w4Pz1lOp1wuVnSdS1KSX8kjE59FUyJ1LqkRCWijSE4YYZZoyT8NC/r5Csv8rpOEseNBO7IsiZtF0DDaaKzjyVRgpD6dgndGh+bHOwoYAYh4rs1wTV0TYvzHU8ffUrau4VrWj788U85OzujribU4yllOWNv94jz02eseMZqteDxJ+9z+vgzJtOC19+4T3SJ//l3/0c++dFPGGGoclBliyHWI7T37Bwe8M1f/XXUeIfURJIPsjwqC5KyEkqIwhQj5rsHTHf2mO/som1JyIs1oy1WwWLdYMcT5jv71LXIUEkpL7MEnHFdj9FFZpoJA9RpTaESlRWmGsagrCYmhSlqdg5vYuViZ19xj2sbLs4vGE3n7OwfghI2s1EakxU2gaxUS9KzpwRRZYshpUg64JPovWwpHopyfiXx342BUVFQGMOzp4/4qz//Mz778jNcKkgUVIVwxbzXoprQHk0Qy6rclwdFBhvlntBGANPghtcahJXnO1RwpKzoIXqqscaEXnySxxVFVVIWg1JEiQImkyKiEkA1BemvyRNcSClTImTG7p1HZ7AuZqbsVk4eJaRRGOoZSFN5MZ5nKmOMWFsYsVcoCvEyHfwmByVFSkMfeaXkkgVeZuwh/qYpJfl+VmeQWRbuKQUUBWhRiekYcdkKx2R2sNby/c0WAAZrjcxqg2drEruRAVxwIZOO0pW9VpQbNFukCBAsC/VhGXP1nkIM+RoKcDzYbKkBIM//nxA7P6Mkq0YZCcbTUTx1Q5RFvx6WwEllD1dNQjzdtRFgUeVgroBYnpFJSM4J2SOlhPY6W0ENxKa0/awGpqHWGm0s1khYr3c+A+7ZU3jYrKK2y3CbyQbbnpur3kjFlMNS01cAYIVVhhTEu9Q5qf0C4spZYIzFKEsKAnhLix0FxMvWkjH3V8OyIGSrK++EiRt6v1XgxpBInYcUCHpgySdiGgIqlRAw8v29XHf4RrIN+n3L/tRTGU1RQm1yYGBSGKMoCkNZFtQTw2hqmYxGkMZo1YGqCN7Ru8i6gaatSNEQk9vWBLAY6yiDwtkkgec2oZ3GJ0vr5V7uMKyaiFOKqAwBhU+K1vWS1ZQSKoqd2MZLiOpg/0a28mh8Txt6uuctrlmyt7dL317SrY85PX7K3rV7XL99l/3DI6azfbQZo00lz4eS/lvqYr6+JAaBb1BfUTbGSOccTd8J2S7PiVkAT4wu54iU22efNHgxR1zvaLuWvm3EptJ1bLoOHSJ4R1CiFiM5RrVFmSm6iBgSTRdYNpnslcTrPXjx+06uo/UdG2W4KAp0UZPsHBcLtBaLvZQSupoz2tUYqygLw8iUpH5JSh30x9jVZ1ijOdcKp+7gqhGlkTNiy8TXina0R7P3KvQrdvpLjNvQtsdoWjz//q9/1CAt5AE7SeMulyxLqvPmMmSyagSIQUJL+oa9aUFsNlIAMyKfUuDzv/9L3v3wI/TihP3FS/ziBSaDSEMYZVJ5AEChWkWFw3+Z+OL/+VNm1+9w85d/iT5LHslgmTFCQtckYpIXFFMetlOirmuM0fS+IyZFaQxNt2Gx2DDbv8v1179Npyw//dFf8/TRB7w8ecwH771PWj7h9k7Bsy/2sFVFt16xP6+4du8Nnq4aHj19yH/2X3yXvbuWat4y373G85dnJL3CO4VrexbnG85PI6uVZhLGJGdIKUiabw+N8zRe4RK4KKbKJjNAQnBb5qnICnI6pXN5iEtoPRS0XMyi+JOJF5HO53+CZMRXRAV6BBxFCxNOmEmJ3jl61zGdzohFIMSORCDGbKuwTZ/OXl4alL8alhVAkEg3jBIWbUxb0CkmkeLKNlETXZaWJdlikwdopRyhW3F+8pzDqmIyrmnWJcrB2clLWiKbTUNdFyirCSp/0+jlcFdawg5k74T3Io2Z78xycNCSorBC2VeK/d1Ddg5e44tmTO9HMsRGL2mHOQVSkFc1YJ/yOeT7dDBAVApUTBiTpaNaS8hGElaS0VJIjILCgDGJwhiMTmIYjjC8m3YjTEErskLfewHsXS9gVMiSETQh5rFZk0E9L98n+2mqqgQVCNGJbDxVRJVD9EKH9a00xXZMMmMCDkOH6S/BrUAlrK0xuqRPGq8CFzHRX7S0733OL377Na4fzvn6N+7z5NFTzpeO6cTyc7/wDi+Pz/nkvYfYCOPZdWrfcu/mEQeHuxyfnfLxhx/zxWcF3/j6HToX+Oj9z7h+e4+377/Kn3/vezz58kvGoxk3ru/yyu0jRuUFKiheHl8Sk6Ioai7OWlz3krOzC0iaspBNqEW8PFEC6KqUfc6GMy2lLQPapA3TEdy8tse0Urx41vHRg47GR8BSmIKolMhuCvG860Lki2fPaddLpqXlaDYlbhrquuLWjWs06zUvT8/AyhZ8sL0IKoHVpNJglKEP4s9pyoI+eHzrWC1W1EXF/u4u47qU5s85duYzDvd3WT07zY2QPHUDG2JgpQ7gp9Z66/Ml7NK9/AAAIABJREFUTWuEDIANnl8M4JsSr9UtAzfGK3l7CJJinRm7zjmqqto21iGjYkVhEQ8oOYu2NYQBJ1JbSZsSqsCWaau0nHExRfHqzQxdXcgw4ELAGoMpS9o2S7C3oWniyUxMV96lufeNMaJC3uTmdHK3blgenxFaSdtVCZFWkj2YlLAavesHCgibtuXk4oyd6Q5lltmsuw2z0uJIrLqGw+KIV27e5/nzl6wW5yzOjhmNphS3CnRRMJrMYDwmhoA2MKtqYhR7l+Dl/ZVmglaWjV6zPD9l0zZc3ztg3u1w3nV432OVoq7HON+TfGBvNmd/voP3iYktoeso6oL9vX3s4SGjwnLw2pSj/T0Siv39XVQMVGXFJx9/zO7hPt98/S4PHz/j8dmCLrP+SWkrFbwK6FD51/OzNYRX5C1+jH4rjx2GRPHIkus++N4VhWXdRMxoyt54h+ZyxeXJCck7rC2wtsDlgDDvHKnPryUNgaBpe39deaDzM/fccO8qpYjqiimutd0OfS4GPnrwEePKsjud8MPv/znNasF3fuFXCEmjoiH0Da3SlFWNbdcSgGTlmhpjUdUI73qUVpT1SB6pzGjRpkDYvRpTQFFL+KNKBq1rwOZnzwgjp5cAyBh6Ce9wnuBaQtcIQyh5AZvyIjTEQN93eQC8kmte+d+JbUnMA5f9ind6Cj2bzVokxEbngVe8n1OUnkGRwe4ECmFX+/zMB6VIXjMqJjx/cc7HDz7nk88f0zUrfuXnb3Hv3h12piXz2YyPPv6MepTYtBvOjk945d6rGGs5Pj2hc3B6esb+vuHVr7/BzTt3+Mvv/TteeeU2r99/h8WmRZuC3YMdXv36a2zanvfff8jdu1+j3Uy4XDbMd0pOjxtS6hiPxlglgEXnEkU14rWvXefZ8Q/pWpetRRKLdcflcsXe0S12DvfR430Wy57lxZJ7d25xcP1VTk+e8+Yv/gp373+LJ6cveX75kOgTqfLbYYkIqQuEtSPoVpjkRYkuxcNeaTCFIUbLtevXWY4nnJ0eQ/KEriM6LcykCJvVktVqyd58R1iR65ZPfvIer735db72jft8+A8/YXl6SjmfU40nlFVJParofU+MkU3Tik+3sRRWgN9uuWZ/Oqe8fZfTp885OzlFGdjd28MAq+Ulzx895nK5BLSwDCOiLEgJbxs+efou/+ef9PzOb/+33Lz5NUwhfp8uRKLOwEnuf4aao7Wwx0iO4DpsWW8lsKooGE2mLC4v2ZnOOD8+YT6dUdcTTCFMv4FpmLJ3uLV2uyRX2gqxQyscgfPzM4pNTTWeM50fgioYhpUhQ6Hveqq6FNbiwLCLYcvW14NVjzKiikExmu5Qzsak0KBiwJiCruvouw0ajzaKnf09bGE5PnnJ8YvnXJyfiTdx1PRJk3C8fP6E80dPePjgXZJxVLWGruPw+i63790jdI4//F9/nwc/+oCRshRaE1Ogcz3eFJSlxdYFX3vrbW7cu0/vE9rWNH3DYrWhqiayKMt11tiaqhptATvphVQOwYLL5YrVxjOZTJlNNDoFNpsmh0ddAYFt22G0p6pLNptWFCghcevea1SjEUoZ1k0DWlPVpXhlJum9+r4R5qvW2MJQjSqWy3NG45pqvEtMkYPD6/JZR3KAodTDorCUtsiyWSU2LsrSbBbEmJjs70lwTq5Pish0MsYQefbFQ77//b/kkwcf02U/UY3Bu5YYeqKLxNjQd5Jt4V0PMVAaURxKWyXWC3JbR2oDZVLQ9Kh+A31LkUkrWmmq8RRrFcaKb2dV1SJtJ4LR9EHuNVntybRqBiZ3Bv5iSFuLIfLyAEUGYq+k9wOgOrB9BwbsYEkgjFQjYc1f8VcfvLFikjkjZOsJ8tJcxuWY2a8pM1rVtkeTHq/ILF95J8K8FOaqtQJ2DvaHMHiAyqIFpF/4qu2T0lcz5bZPTGn7byGOXP384SvkfmKo7z8T2qwgZrk5Kquy4gDypp95P1f9p8bmxY+wkeWuET9lC2kgKV0pTVAGa7MFQe8YdqYDMUymPrGA8L0Ek8kMnPBZiZoyc98a6aMUSJaEFsDWWostJJDOGwFpSdncYWuLlnWpSWyJZDbPS/avvEcfsn2iFtaqnN9elLFBZvHcVlAYO7S+V4zlgemcVVLeh8zm9lib1WpWFBDDJxxRWUWScE5+vozSnkSgCy6TPqwwlGNPqY2oqlTCmIKZVujQoTVsGs9OFTExUkRHqQwxWYwqmNQV47Ghri2jUc1oXFCPbL6PNdbUEq7a9WBkGdf6lqQ6tsHZKqCN9JjaarSFolToVsgKpBHrvqMJms5pfFZKggDrYvnZX7HBY8h2e3kVEKSX1loxmYwpy4rxaMyo0JRFLdiNa1hdPGK9PuXy4hn7B9fZO7zFweFtpvNDUlXK+cQVGDGAsxpE5m/lF0oLValJkwrvSro+kZImRrZEmq/aVn3Vvi7lZ1fqoyzHmmZN123onKNvW3zfY0uDKQwHe3vM45T1ZoO9XKNDgU6BrukgBXoXiP0GwlqWIVHO4tWlg1JT13Oq8SFdUaN7S63q7TkUbA3lHrpeYyYNm9DjXYdrzzHqIdqOqMwOTXmdSzthUhhZviWx2XTK0poSX+1QTm8xbZZY13B2Hohxw3/o6x85SJsgdvjsc6Kz3FsO5lyIfZL0uAiua8C37E8LrOpZpwZTGNAKHRVGJZoXjznoF8xsj0sNFzrQxGxsn4R1oFIQarWSrZbuPFWjWX3xkOc/eY8773ybopaLlwzbw1eSsGUzZbWmKEvI2yuVpR3aJNq1I1nFi5NLkt7h9mvfgXqH4+PnfPHZT3j44fexo5LXXnudzfOOx0+ecXx+SUig7Yhbd17h05NzHrw8xypFEzowkWbT4n2kW2hisnR9T7NxXJ45NmsICS6bFja9bMWCJwaNixGXFD7KgRZdyPKbtA3lIsnWzOiUvSLlKiQliZKySZMNZgpJNrIRYRUkLf68MeKCou8VwRuUV+KhkhTWWMbjiRSTnMittSJEL2Cmc/hG2KApXTGqhyKcokgWRUopaYRd8LgUc7qg/Fkp5RmkGeptxk9sWYhs20fqImGSx3crWrdGT0pYV5jOoEKHLTSq0PQ4kpOiI0BMtsHQUcDbJHIUFXOafJYReR/xLtK1Habomc5vsApzni8UrQ8UZcKaXK10CbpE6YK4tTnYXhQpWCltmWbCyoxYo9EIE8Vq8dSxNgO1KjKuNFYPQoVEoQZWtBepGcIE7F2ky0nxPlt9DN6EYks0DBryfSRwS8JEtBbmByWoVJF8REdF6leo5izzaRXRr6nqObrwOK1R0UFoSaHL/rQGcenM/m3K0seSTbTU0zk+aS43gWp+wNdu73F+ccHEQpUC+J6dg11++ZfexijP6clLvnz4EVrB0d4IbQz7+1P+5N/+KSlpbry6x4vTYza94ubRdX7xF94Gf8nl2Ut2JpYzE6lKQ8oG+etNS7NpUVqScW0h719l/zmSMGxAPAKT7yUkIrTEpmV3XPHGG3e5e+8G43FF6hqu7Vti6nj/wwcYXbIz32U0maBS4mA6wz3+kvPlAu8uiK6nmI/zJyOMqbOTY6w2TCcjMBqXWdi2LtGjgjY6XBQ/1S54XpydM2oanJdgFNc3HO7tc2T3KAotQEuEwlp2ZhPM89MrL0Jjtv5aIMwEnz1DvxrKNODSMdundJ2ETKSQMIXBlhYTtXhK1iVN01CW5RZU22zWdF2HGkK5MnOq769SXJUa/L+ugkKGjf3wfXz2vNNZyrjlVERJkk9BmKIxyqYeZOsbiNv3pYdDQ7Nl1foYsHWVdXRK5FRWmG5CKhQZ3nw64/PHz4ibLv/sgRWaMnNTb5tesYGIOO9IGk4uz9nfO8DaEU0Ef35BsJaDW6/QNC0nZ2dM5ztUk4rLC0ddWy4vTri4PGe+f4QpamFleEdSLpPXpeG2hSQ4G1tQa4spCxbnJ5yd9JyfnVOXEtTUbkQmao2hUCXROULbc2P/CFuUVNoQXMe43OP0xQvu3LkjYR4x8MrX74sstOu49vp9eteye3fJaFRw9/Y13v76mzw9a/mbd9/nxekxLnl0JR7FotaQphOtiMFTluLPtrgUmakZ7gdtqKoK7z2b1Xo7mMn90ufwPCvp2slgy5rxfiH3SAj0TctyeYnJdhtFZej6fht4t03mTV8duNje68OzMHggX4GzV0OnWPWIPcnFesW777/Pt77xBikGTo+fc3ryjNnOwdYmxXlPt1lQViMZclRmz9iC6XSH+e4+VTUiOkfXd5kproVNlFkJxhrGk3F+jYHQrrcskIj4ssUgIK33DV23YQg81SDgrCb7jvnt+5TBLeS5WG2H9S0zKbN0UhKGrsp1ZnF5xsX5OUdHR/J3kJTrYek3eFlrMqsleiKWEBNFWaNtyWLV89EHD/ngoy9YbRwuFmBKbt+5zauv3KFbXfLZp59yeXHOO+98ixfH5zQ9NOsGj2W9iVRlgesS58fHjEZjbGEJPtA2LTu7+5ytLrk42/DdX/hPqHZ2eHb2EkzJyUXLrDasly3WBNx6wff+7AfsjKf8/Fuv8ub9mwRgujsmGsuyCdSzPWZ7O9y9f41usYHY0XSGfbvD82entF2Da69j7S7X7r3O3o1XuDhfcvvWEb/87V/i8YsPOfGnwoy1cq6TEOlm70mtR7UOOzJEDd716KQlENIWuN6RUqIuSuK6YdE4TFlSViNc07I+OUOuRBCV0Lrn9OSc87/+e+7d/xpf/7mf49OPP+H82XN0jKhQU4xKJuMRUY5R+qZBD0sq51ienXHy9Jkw1sY1k7pgPBujjOJ8vaRdNfjGkRA7BqOtAL19IEbFhkBdwsdPf8Lv/e+/y2/8yj/j53/+N6jHc7FrMhavyPd5wir7M/WnMCUqKtarNZtmze7uLkVZUZQ1RdlASozGYx4/fsKr919Hm8xUD0JUEGunRHA9wQn7qygqgnNE7yhLy3Q6ZrFcE1HU45kE1g7ne0jZbiPh+p5MUJeGLX9QAzM+JWHeKJOBpGJC0kF+bvBUVY0pR8LyjR3Wanbmu4QUuTebUwXDi59+Qr28zafNkvPNkiefvs9Z/TntyQlueULUChOmHNy8zZ3X7tO3DX/4r/4nHvz4J1RGFiNeKVyS3AmfNEUpvetkPhHVix1jjGK+M6PvW1HUwDbgK+acApLIsYXwaiFJF35xuaB1nppAaQZ//pSBlqslVlFI0NVX63lVVUDCJ/HgL+vRFhBHabz/qpInh9hoy3xnh67vuLw447CaEkPg4vSMy8tzZjsH3Lx9jxgkxFhPxlTjmqSUhDS2G6qq4OT4GW7T8vW9HTZNx3g8kRCxqPHB8eDBR3zvT/4Nn33+Cat2Q1CQENWA7zZo4tWCL4i/rcoLLB8lUE3l0E1RYIiM16Se2DT0FxeY0FGpgC4KmSmMksRyq6nHNdVohLZ5bhIdm8hukyj7yqrE2DInq1+BoFqL1U+MkZgX50pJbRhAze15/pXnC8UWfDN66M0kaG2wskpkn/FhcRqlViiyrUMaMNy0ta4bArKuautwTQef44G1K0SRlECZzHD/Sh8o701/pU8cfj/9DKg51OhBASsqp2yRhYDMwmYfIpnIKtlB36Eyk3MgH12FWoOAjCkl1NCPIFZhw1JTVFNJaqSS4GXSQADT28+alBWLWwKUsKDRgz9+lKDgrGCLPtCHgYFs88Iubuu3z69BGfmMY4bySYnk3M+C8DmHQkLOhFYAYgkz2A2GGLP/tswISg9My8y+1UN2RLYtjMJu9RkPiDFtiRdaZ6JX9EJUyUo9AbJl3lAq206GkO0MBPA1Spb9ISFELTK4jkLEvorQGVyIFFj58zqidRT7nLKkLMbMSkWpFbsTzeG05GhuubnrmdZrdAG6qDCmpKgKRtOKSQnTcWA0IhNHNFoVKJXED1qLUkKFDVYtcK3Cx4KQsuVajCgdKQxUxlBoIV45l1i5yLLXrBw48hyK2M5Zq6lLyWxISiyyQq73IYPrxhiqsmY6HbG3N6eqSmaTGXVlGVUjjNZUpc4KdEW3POOk6+jbJX1zxs7eDcZ7NymqSbYEsDkgOWNFCpJOWKvk+qlAWWqgIM2ntG1B0xm6rsvBebl3NjqHN2Y1Q5bpKqUkdDJW+K4HNOtmQ9+1uF48mHXQ7BQzylIsr3Z3d9jb2XBxueT0/BIVPSdnl3Rdi+s36LSR0LbQy/MUOtrLgvVojj24ga5ryqJG25qUme0RS09JtGNiMaJLCudifhYvsPohtZkyrvdpC4NX05xTErFJ7vEyWZKucONrNPuKIhXMizEundP8hH/v1z9ukDYldBJWBSmhMBRGEv+GBFCrEzonRCvds3s44fz5Yx5//oD9Wcnu3XsU2mRJWKQILWZxxig6ymhYZu/YQmlGxRibDCp6lE54xMvEAFWA0HouPvmM1bOXlK+9jlc5zEgLwm+sJTpAJ3KmYG5aLM5F+t6TVMCHjsVyxcuzhluvvEMoppw+f8Kzxx/Sb465e3OXn/+l7/LWt3+Z/+13/zs++ODHfPjFMQfXbvLON9/kkycv+fDkjEYpRlbx/PSY05d7jMtA0uecnZ1xdnqGiz2r5ZLNxtE5AetCZnaJ4breHuiy6VMCrCVB/2MKGWwDUhRTbwkAl02Vys5ESg7vPiSqyhCyx8yQlRZ8QiUtrNeQKPwY3ZeEGOmiJKjaIjODckE2RhN9oGlaYjSZFm8y2Mr2IVaZjRiS+KPFvPXtgxOvury2V4kc2iJFWFIl+1ykEvV4RFGV+GUAL16cIUWK0nN2cYKdjTGVpa5G9BthvxpraHyHRUsQnCnQyhCIeYsqfq0pQpGZStoU9J0AtG3Tk4Li6PAuZnyX55sJTue06uCz54smaU0yJUrb3Mjkja0WNvBQtCFQWIPJjFmU+KXVNlKVmmktYGFK8vulSViVt9Yp0XdZxpcChUq0TjZ+nc8ez7lYK1S2V8ghcqJpZAAtNGwboJgMSZegCpEvpg5ch+4WmH5JqXqSUlQqUIRLun5BPZoTbUWwlpRGiDQYYWlFJ9IYxCdsuVrygx++yxuv3+bNt7/JptlwfnpM6Bf86PufMhnvcPP6jPPFKc36HK0cP/7RD/jOm29x89o+RV3wwU9/yurignfeeZPJZIwLHaerc27dvcfi7JIf/M33aTcnXDvcpyxmKGVyAUNSSkGCt4w8I8KIGcB0nQnGjhhaXNuy3ixQsedgd8y3v/0Nfvnnv8Xe7pjO9Wzalr6t0brjjfuBzarn9OyCndmMddOyWi2prTDUxlXN3duv8PDLL4QdngQ8NLkx1sYyKgxRIVv20mAnFanQ4KMw32LPpu2ITcuqa7YLjlRZmtCTCgEZQ3Do3Dgf7e9Ql5a1k3vcB0mx3oYUfAW0GgBS8q/L0yvhLcOSxZRZphqFVahNJGz8lqUKAoRaayjLiiFdOWSrCa2kXR5SfZXSW4DuZ0CxDJR9NRzBZgBNggYFRY5pcL5O2/cg1nCZHTssR/KSamg+hcmZPXVTZoR4j9HFdpjxTcfp5YrV6YUw3rXOksMgz3qeNIwWDz5TFLRdS1FVKK3pveP0/JTd6R5FqFit13z8wbu82ntG+9fZLC9ZLy7ZOTzAHV6jazeMZ3N5VlHUk5mwgI2mQNH3naQ9W0M5mgAK13WkGLDJsre7y8unmsX5BdPZlKquxTcweKyyJJNZLCFRW4NKiqosGNtSvKrbnovzC956803KqsbUJVprKh/ptKJLnjuzHZ4/f8jT1ZqvvXKPf/lb/5zf+O0NP/j7H/A3P/w+n3/5MWenL6iqkrquMFYTg5NnS1tiSMxmc4qi5OL8lLIqaZpue+2dc7nRF3UBMbFp15RlhXNZrWA0Pjr0ZMSsGnH68iU2jLPHag7wScOgJ8DnlkfwFdbXV7+uUpuvwFthc7gr1g5yni5Dz3rdcL5YcefGEa+/8Q0O9g7wPm7v/eA8bdtxGU6ZzXeoypK+bQgJTArUVUFhNKfHL3Cuz1KzK7Aq5lo5LCh93+NDT1lKoy1/xucBCkLsxc7HOVKCoixRSYZAnxPJBxZSpjwIkyIvFlIa7J7C9rFRSgLFUvA4J0zd8WREWRV5kIi54ZezQhhDeVDLW0ifEpiajTd89tkTHnz2hFUTWTUBZUVOWBrNG/df4+zkhC8//4wXL485OtxnOrKYa3Mar/nww3ehmDMaz/HOc7S/w8HOmAcPPmA2LinLkr3dQ/b29hiPxzQrYRH5ALt7u3TrhmbZc+twl8XlOc3mjJ35GF1V9LHk0YuOW9c2zOY1Dz99yOniE2YH+7z52k0++uQ5t27PuL5bcXSwy4PPX7D+9BN2d/apCw12xPMzx7Wbuzz49CUnT5+SNqfMyx1u77/CybNT1EShdSHKiNyHKSXDbrtY4rsOVZYEFylHEhhrtaFZrumbDhM13aan69bYqkRNA6vLS0LXMZmMwRrWbYvrHOPJDK0Uj794xKJteP2dt/lSR06fP6MYFYyqmuASy/Ua5x06J6I45+i7DhccP/zh3zPd3YGqYFbPSEROTk/wm57UeUxS4DzGS5OZXKRb98So6IlEGym14rPnH3L6R885uzjh1/+j32R394gYSzlnhd/NNmdgCyRpTFEQu46m7ZiGSG0KQojYoqLrWuYHe3z404/oftpz/+tvYAqR2Buj6XoBam1R4L3D9SEzu0VO750wPOc7uyhbSh2K4qU/hKIKyUGLLHNgzTKwFAXU8MFLQB4KU8jrd2i63kNUKJ9QOGyhmc732GwuaZs1kyBhoMZWlLZkNt/Bl6UEdHUNi5ePqK/vo9WG8XxGqnY4vPEat++/RV3W/NH/8N/zwz//G0oVMIUFrelCICmRnpfaYE1BFxsePHiPj979a77zS7+BnU3p+5wEnyXWaLVVJqYEm/UGHzw7O7vYwtC1Lav1irOTU4KyTMf7okCMiXo8lmu/ZWymLVMzxLBdzoIsRWNMROe3SfTSFwdMAQrP/8fcmz1ZdmXnfb89nXPumFNl1ggUqjF2o4Gem2RLJEVKJEXK4VCEw9aDw6G/wX+I3x12+MGKsGwrLFoiRVEkQyFSnAexG2wAjcZUhSrUkFU53fkMe/DD2udmgSbfmS8IFKoSlfeeu/da3/rW79MpsFoucc5hh2OCVuzsHsjgs11jTcnO3i5JJabTCRApCktROJbLJd5HJtMpVVXK2qZK7O3vU5crnHVMpoO8AePpupoP3nuXX/3X/xcfffSuCJ5JzjNChzFJXqMk52VA3IIqhysZLcaHANvVZJNixiF0xOWMOF+gmg1WJYbDAlsaorIkI0PuwXjAcDgkKSXGiq6lS2C1RWlF6UrKosrsddmyEME1G1yU4BW6mM0Tocuiliblzb6QBYeteJoFOG0MVveuXHnv+pT3mERUi31vkF+XPpSyd5gKJspkRiXZ+GC2YmRfN27rOZXNAaZfu5YaLmUHyd8kzPb1wBZLpBI213kpXd7TOjtxfezzPbKAmSLaWNhuxqStUEoM0v9k9mvS6dJdS8ZJhJa267IG+nx9IE7I3oXaRbl3jZX61lgRK71X6JjkvYsRUpfrCI1RYngQYjk0rSckL5Q8bbFGBtFoCeXrRVoR01U2CmTRPr/mPe9VapdAr8hbI8OYFCX8MyXJrOmzYrSRrbmUIiZjRFK2xoaeMf/cMLv/tb5u8l1H5zuMFZ6ys1bwl1mcFne03Q5uQubtm6Kg8Z3kv8RI8p7oOwhenOBZ9JNwSMvh/hG7kz1ShPnFBev1Gu8F22NTYqgMuuuYjhXXdxQ3jgr2d0sOdwzDaoqtjAywjLjRh7ZkZCPDcoO1kl8i5hEnz2928AbXooYtFsO80SRl8+cwbre6lVWYUmPWMZ8JinWzZrFOrLymBSIR6woK6zBGMRoNZKNBCIQ0WrQKbTVF4RiPx+xNJuzsDLIY65iMdyiKgtIK7105RWlH6Dyoi8EADcuL+3Sbc8arcwbTQ8rxFWwxxGqH0tmgpSQ7RgR0RVEYwEIEbyzRCme2f98v70cjMoY1+f7uh0dStyZl6ZKlU47ay1aK9zVaK8qc47Fcbag7j3OOajDixnjC4dUjjq5c4b33P+aTe/dJGS0Rga6rBf8XGjbLZ8zOHep4ylhp0CXBFJhiKLNU5zDlCOf3qDZzGAp2sO08Xe3xnGPMp+wMd9BG06qCTssmiU5gU8LiqaxiVU7pomht5XCIZcXf9vV3WqRVSlGYgkFRScKlkiR6Cd1KxOCJPhIsrLuOwVBzsDfA+T2e3tM0x0+prt/CofFK5ymPx9crklJU5RDtCjpfC5OxGlLaSoS/Tth7XQg0bUtICouhnc3ZzOYMtEGjiUoOKKWg8zIFKcoKbSztZiXNiiKvNwEq0nRzHh8/xBRDBnsHnFyc8eDT9/ngnd8ndXO+/uZLDF3g/PhHFHbF3sGQgzDi1Te+yt3HT/j46Tkba/Da06qOVbNhuV5Rr5eczR5yfjFjcdGR+qlo0EJpVUgwlpwE+cOEcOHy5KxvpsShmjnA+YPkfSB2CGvXy+8VVyaQWTmhSUQvjacWGyWxjTKhKjRtB2kzZHEK8/UaM9bowm0bs5giw+EQUBhboJBiwiiz/fv1k8n+8g3RS+GQi8OUMRMhiiNuOBzS+cBivZKgitGIqpL12DZEXFFQDgesNmvqrsniskwlYwiEzUbcA9qw0RaLxufXZcuZzA27TKBzeFPIa9hRUAWTKifyzpe0dUfoIqUdUBZ7LJsJi25E55UwqzoRioyNW1FKHiA5wPpmWwqsiFVJCgStKYx8+LWR9WmiYlBpBk5cxBEt/BctYUlN22z5igpxfnebjRQ0bSRERQpgEtsiJcaARX72oKRQEXNvnzyZV5NBRNooAoA2GpMUg2FJUY1plmeYWFNgxDnrPaGTJiEliElncH9CRy98WqK431JE+Y6uiTiVsLrF0vL0wX0O9ndZXZzzzW++yclswR/88Tl//Cc/5K03X+KgD7fYAAAgAElEQVSbX32b67tTfvCDv0QNJOH+7if3qCrHnZdusjOeUh3tc8oZiydrLp4lrt+6SdN1HB+fsG5AmbI3TEqRbh1aycqb1nJZyvRNxJDNakGzPCV1G27cOOK73/42X33jS0wmA0Y7YxFbgApBEBB2uXEUia9tePf99zg/fcJi7bl27RrTnQmPnj6h1JZxOcgMKUNVlowHBaTApm0JMdI2IpB0PqALYU35vMIYQsDHLEhqkGRjWbFL2rLpIvPVmuAdhYVCC3tsMh4xmY5Znc7yOZG2BXBf1JE/C+J8yBbaLFRppbI7RlM30gwkIIW4Zf91bZdXyi+Frr4p+EJybhY1Y7zk1Pbro70g1jd2KSXatt2eGzFGmkbCCS5Zg7qvp2W4ozJiRytxyvdppvnzL4WtNN99WrVyopZolQPbeueAtazOZ8yOT+TSLgok9V4GGkrLGe19wGUemTS84sCwRtJTV5sVs/mMo8MJpbM0m5bl+SmD6T6xa5mdnbF7cMTh1ReYzRZcnD+jSIp6U+PKIYPxhNViDsmgrJNzwgozLcSIsobYCV7GOsfuzi7Pnq1p6hYxSRlZQQ4BpQLRR1KQwMyydJTG8ezxQ2YPHrK3s0dlK1JS7Bxeo1ORLgRUUnQhUrc1bTmAnT3uPfgMLubcWNfsXX2B7/7MIW+89RN8+vEH/Kff/U0++OQHLJdryspSFJZEZL1ZYZRlPJ5QVQPm8wuqspJnOl2Ko/2Xz+ieoiiZTCY0Z56mFme7KzU+wjJ6hlf2GF/ZJdQN8/Mz6sUyN9F9aBl5Y6AvNC8d471D5fk76nIFVG2fQ2nwyGvAmmhg1rRcNY7p3gGFq+jqhZzrygiWZlCxqWtC2xA1OB0ptIXQ0tUrFt6zuHhGih3eBwbDgXCeW9meiYgoJIalhE+BqhpSlUNxwGkFMQdChZb1asV8Pmdvfx9rEz56SSvOQZ0xBGIK+X5SeQ3Vb18D7/32tZLmORB8K07uJMxsiIQY8F1usvrVvYQMPWMQ17BSBKVZ1oGz2YLPHp3y+fGcpskrs1pBEgzIwf4OVw72ePfdH9JuGto2sDOdYnSkqjRdHYmxZjTcZzodohWMRw7NhqH1fOubX+OdH7zD9Ru3qOua2cmccVGynD3i3kfHvPbqEYMbU959/yk3rw0pKsvDJ0u++daXeeXFq/zR9x+wu7+PK2RtPKwin318n90Xb/OVnZcYWPjxX93lez/1Gi+/9jpLP+XNt6/x9P4c4wp+9MkjqsGA7/3EHZ48esSniwteufMGVg+4tnebBxf3OfVPUMaCFeREioLp0iR851EpokLC4kAn2rYhJYXRDgt0ITIYjAmq4WJ+Tt3UElZXFiJQao3qPKW2VKMBtnDsG8PTp095ai1f/3vf5d6nH3L29JzxdIrG0nXZTU0gJknJjlG2itqu5fT0FKxl4AoZFK7XhKbDaUdhCwISTkMXoU2YpCh1QaEiXdPglSWaxEl7xu/83m/w+OF9vv3N7/HVt76LrabCo9T9Cu4lXkTuOMtoPGU4HsmWkdYMBkPKQUnT1myahtt3XuLH7/0I5wrufOlLImjkVeembRkOBygibYp0ocUohXFuK1Ip68BYYpI6rhehYiKvGffuoCRBnlnU2p4RScQYyQwQRIU824noDShD19ZEnyjcDsEHfNOwml1QVY6m3mDH+4JTu1hiOqi0w5lcO5dTDm/eZufmywwmhxTVDovPj/n4z36EiyIIaEN2Z6eMdLAUphenNGdPH/N7v/1vqYYj7rz6DapqF99FTp4+xhjNZHePqPrwNBiOxJ1ljCH4lk8//ICH9+8z2r3GC698ielkROqCPLta6r3+/BCRL2xFmf4o71esrbXZGa7zEps4Gn1oWF6cEr1nUDoJ95I2BbTFGk30LfPlmp3dXfb2dzHayn2uFePJWIanMRJ8wNmCYlqIQ8w4dqZ7WOtI2krd30Y+u3uX3/oP/4GPP/0Er6KIYG1ApSju2exWTEoCtHpRW/ehPsh6eVKCfTFKQ9uhQ4tfzQjzc8pOhKPJwDEZDUhK06WEqxyuKigGgtXrfKBtapq2RRUV2pYMRiOcKwTzlsSt2flGzuYgQqpOkvERM1OtH6vL8ykIBFLOf7n8L2w941sBNQ9IYiLpeNlXboXJKHfednCehRrTZwWY7ecjPieYpiQu9p7bnHSfYyE23JQiRDEq9G5fleu7lHrOfMpbnQGlzBfqwl587oeEIvzK0IckgliM8ZLtqS5fgaTYhjT1YmQfICobJAg6UCtMbyjI30Bn4TKGkNPuJTPE9GxeoPNtHu70CCMR92MeTVmrc3+nABGWnU10sd2GPGlt5IyM4uD2Ud4H6y5d5/1PZIzFFYVsjSot2zOdiO4++G2trI2h6HWZcoCPkS54Ou+zkC01gLxmSbAKOovfOYi3rx+0uRRzTUqy0dy22NiHgyWpsbfPXkO/pae0xhqH937LCJb0XS+bizEgrF8R2BMKbSq+9e2f4ed++h+ibeLugyd88MFDTp49o559gp99SKhPRfwOkSJphjYxKMDaAUUpd/+gSgwGEgptk/CyrfJoFdEqiUhrcg+fAkkN0HYDnQYsym1QoRGQKzJwiz5DqgsNVjaYdIqU8q8k7/ER2qjRXaQ1nYQKIkHMhRtgByUTt4NzFlfIFtXu7g67w4LBwGINMtQb7eGcDPVcqYkOrBJsVhc9sTPE1BBji9Ee488JjaLWULJLspW4rEOerJBrSSWbEDEmOi14C2MSJhlSk7NKkgR59TXfF7bTsrEAFMo6bDlGF51sF0sVS/AtEWibFmUcbQTjwXuy2aDDWMPh4SGLdc35TNHUGWGWe96UIpv6nHjiKc2AAQVNMUA7R2ET2lViNNMWygkMdih39jB0hMWCuusouxa1PsbOPmFkxjRun66Q1yVmrVDj0ToxKguMGVGNr5KaAfW64W/7+jst0lql2CsN2jeExRy/mLN4dsrm2Rl+NaednRM3ntoYJm+9zas/8xPo0nDr5jWG8eu891v/Dpst7smAKSqicmyaQKcMpXMMd/ZZdIFhsUM1HGF2r7P7la9z/N4PUKefMdHQoGg1tOWYNnNKgo1yAXuk2SGitayQdAFi20AQtinE7G5TLFdLHjy4x9mzc1760ldo1hfc/eh9Pv7Bn1LPP0cZz/27a8pwhfX5EEPDzmCPt15/gfsnJ/zgwT18OcrOSkOXHOd14GK9YHP+iOVySUtNMNJsRZ3wqSFF0FHYWSImitMyJUUXQ161Ik9189pvAhUThEgXoO0MKkZSm/ChYNMFnA0MLDgrhy5eeFoSuGBQURN8oo2abmV4/KTl2ZNT1guDrxPXXispr1iZEip5DUejkazGtFDpAU3TSOJi71baOoPidloWELelQmO1EVeUSuyPJ5TDAXcfP8JYLWzPGGlizCm0ckGsN2vmq+Vzrh1xSXa+IwZxljldoJXB2ALPBlTARiWp2ymh8tRUJXLqcbflIGmtcYUjhI4YWiqjUeWY2y+9yc3b3+LHJ3ssukqYwFqToqVyMJ1WLKKlUyJWK53B/Vkc0zoK5DyKW9bqQKEAoyidJvmIMjAoNZXV28Y6tB3BSBMVuhwKkEHrTb0hth5lDBIbZLBK0SHuWRFjRdDVClnjy1XYpZssN/FRQtzk9yaiNqSiom09bbMiBoMtJgSl6LqWohzJ9+k2lG5AKIRZVBApuiUmLmlMQdClrFM5w8n5BR980PHZhzWL5YLz5YZXbMHBwVUefP6E0WQHo+D89Jy6vsr1W3vce3CfuvNslhe8/vrLDK1lOV8wKgvOzo4xRlE5y/7BPscn5xyfzGibDVpZ4dWpSM/j0gZibFHGYozD5TCJetOyXl6wnp1iVeDOrUN+8id+lrffeoPJpEQrj1bQdkt0Utjs+tZuBEOFmnjczSN8e8Hv/um7NEGzmC2ZDAoSBp8SIbYYJc53oxJds6ZpGjY5nV4pm9eYIzoEUlOTSkvQCu0qrA9oGyiKYjvF7rqWjW9RCT4/O+PoYJcJ4rZ0DnZ2Rxxc2eH4bEaKUlB8QYzKoS/bi1apbUAFSUIpwIijQUFInsIVl2svSknDZFReh8n/Ab1tHvqvnnErznpPH472PHd2u/aGiGp9wdpT60VYgj6RmPz7Uoy56M4Fu8lFBLLgFfOwUCmVE4I1fSJy0oaoEoaIIjtMYsy8rsSwqAR7QpA1JC0IF5sbE2Nke6Ct6+wkAp8kP3y2XvJsfsqVazcoywGhlrO9Kh11vWI5Lzg7OeHo+lWu37zJfL5gs9oABWkcOLx1B8wpzewUa4O4XJQIaColCudQRFkvKyqObr5A3a7YrFa4aogrK1bLOaGt5T1RhmSkMdssV8TlDN1uKEZT7rz+BleOjqimU7qYUGVJMIlVVGysZuHGnJPYjBri3oYPz59x8ke/zWsvfY2b+zc4PLzGt6+/yJtvf4f/8uf/md/5j7/B/YcfiuMTQS4ElXj4+GFGWbSEJFwyaTpVbjC67JRJGTmjefj4iQyifItShtJV2BRp6hplQFtDORlxbf8Kj+/dZ336lOgjeBFdgpJ/yoThi4KsPJv/fxdtfxf0iBBrrQwXlITtaKV58Ogx77z3HsPvjrBO47SjLEo2mxqtNdPJhBACi8VChjNDCdxZzp5lRpsk0tfrJcYEhoOBMMoDENq8dSF3vY4SriDu1r4JlSY2ti2zixld22KviDMnhAhGzn3ftXS+u/z5Yv6z/d3ctQTvcVnw6Zs12b4ArS0mRkBvmZ3ee1nP1W6b/NuliG8THZb5xvHwpOPRs5rV2oE9oNItMdTEWJM6GU4VznJ6+oy6afABJjt7vPDSHaphxXpdc/zkPiTFl1/9CoPhPq60zC8e8xd/9vtc2dnnJ//eL/DeR8fU82O0sjRNTVmAjzXt4oKTR5KWvX8w5f6TDcO9farHFwwHYw53J+wNDdcOLaNxQdtG3LBCURKbhnbTcefOdR4+OGe9abl+dMBnjy549eXbNOc/5sEnH3F8ccqN21/m84eHhOh4+Y0v8+qXX+XHH9znxs0vc6c95/zzBc5pXKFo24Cng6QpnaXUWlYeU0ej1gQvrE1rC0yFOFbz693WtdSyWjZUjFZ0PhK6lq7zpJBYnV0A0nAFHzh79ITTK3u8/vpXuevu8vTzJ7TrhmQ0Psk2TTQa7RweT+zkniBE2s1CXhMlDPxCGQpTMHSaalDRtY7VfM0mBIIJvPrGHW5evcHv/NZvScgRBbjIIp7xFx/+PnfvvcOzJ/f43s/8E0Z719HakZKw/GPIriSVtvcEUeHbjqACzhVEBa6oSDGyahtuvniT02envPjiS6CTCEHGoY048IpqiHJyEYSuJZEYDCYo+rXufiZp8udeHJExh9q27YrkPePpRLjBOUCpd6g1oRXhzkeaZkFbr1BJ6ihrZCOrLC2T3X0ZkHWBpCVU1Xs4e/qY488fcHF8ju3EBekDuN3r3Lr+MpOdm2wY0SZwjWZxPsPPzinLgmg8bRDutDNWxHpr8Ii4MKpG+JR49OO7/Kv/9X/m7e/8FG987ZtU5Yj3v/8Os8WM26+/zqtf/SaD8UE2WGiiAt9saJYz3vnTP+KjH73Pz/zSr3D94BtyrhiNyWveMfXNei/GynliemZ8P1hG5cAucXgmFdHaZjFW0hq00ShXYIdTVqsVKYXMNIXlYsnTp08pC3EXnp4cU45W7B0cYc2AQamYXTxjkzoaI2iAptlAbNmZTiFLZF3TcHr8mD/4T7/Ho+PH7Fy/JkzJGKjXSwge7T0qSp6DzSiDHgemkYDsLiSiSrikMG1EqYBqG8JmQTOfYXzAas3OXsloOJCgJmspnBXMklLSr8TAcrVgvqox5ZDhZEI5GePKkhBiHpxIHZYiWOsyAipBFFdy2tZQcl2YzIDdckj7z1PvgCMhyJxc/0Wpq7QRc1TKom22n8uvqZRXm7Pwmusu1QvEOoo5JAfvoi6HnCGI4CX5IYKtEhOAzcFbSTYukEEkCKqP3Luk/HfQGpQxgg1C3g9yfZpi2gaqicaaoP87p0uzEOnSQNDXpinJXei78EXhSZtsVPEYK59X40Q0Dcbi0yUmzCgrW3i5Fu23eFSuJVUSXcPqSsTS/Gb1ruQ6KayODLTLAmfPiO2FZNn+lLcl1wR5K81oy3g44srhAVVlhZWbg55iJzjIpm1pm5a6rsVJG6O4nrNY3XatPGshSAgYz/GHjaKwBWWuzbuuy7iCbRNASomqGuG7Bh8FsVVoQzmUkGClFW3naZtuK94mHfNW2EACDzcbuii4g5CNW9oqorGgLMkrPr37MS+/eoevvP0W//Drv8hP/RJsNmvWTx7wyfd/i/f++NeJFydMRwZbGcoqUgwSqoxgI4UNWLvBKY3TFdo4kc5TkhrH2PxYmIyRFHNciJaEIynJhyh0R1KeFkXAodHY2FCQJACwijifKIaWomuwrRjAOu9JviMkTeEMhVWUrkDHQGEcB3tHjKaa8diyP91lPJwwGGgGQys8Y1vg7AClrPQAvTHEFPJZ8JCMIUZFio6qqhiOpuhyQDKggicayaixRkvPmfLoJg8bk9F0paHSFT50EBLaCQJNa8ltQIm7fouUU4qIGEJU9BQ49HQXU5Y4G1ifF8wvTlgsV1ysa86bwHjTMRqOMK7CDySss96sSKGjqgxfeukm680+y/kFJ0+fcTELRDxJaxwWmyLd8hnP7nfUfsHO+pThwcuUwwMGzqGz29vR0RkDboAyDc53oCPKt7TnD6jUgD1dsTYtqZoQ7ZCUZPgq2UAdZakYqiGjyqFHHZ/wN3/9nRZp/XLJ/X/zb6iPH9GdHtNcnBFWc2zboWO++ExJOrrGjZ/+HtPBgKXUEqzOF2xOzzDB06UkzBFTMhod0NgB+BZU5OjqVUqtKaKhdAPMaMr1r73N5tEjmvOHlFaDdXidSEWFne4xOTiQQiH4rVuHJNwgkoijKXj5KCaFUQ5rDIv5GR9/+D5Pnx0znRxQFgUP733MvQ++T6xPGRSGpql58OmnnN7/kGgMgcDO7ks8Pt/w/c+OudAaqxIOhY5yOZ2d1Xz+8Iyxq4VpoiNedSgk+CQgzs6cxbCdDAZfy8UaVQ7Tkimjzrxf8oHpvWGxiNRdQGNQ8QqmPCTYDZvZ5+gKKK24J5UkDC7rjqb1dBtHvdacn3vqumW9ioROMAmVE85oSDELIdnFmV02KWg6Im0KdFEcFn1ibgyRmNf8+oM/JhGbN74jELAoXFVxPpuB1jgnBUGIEZdXKKSZ3dDVm7wCYnJgSZI1CQW+htViji1LolY46xjEDm9K1rEGLnmXRVHgvWexXqJtnqQqKIYDkjaSCk7CuAlHeze4dftN0GNhlaoOqxUqaKLRqNLS6gKvCpS1RBVk8qPIBXuiKAwJjyNSWSlsDMLsKpwmaAkh0Mbge45RFpV8FyB5VBQQvff9+onCOocrSxrvaVtPTEJh1MIVyS5sWV9SSVZ8xA0on90+6VSpzErKSfQqBqChC2sUAe0KkhNxGlfQZYewSZLG2aGJGoIxtEqjfSKmLjMPE84o1k3g7sOnWDpZsShHrBrF0ZUpn316j/XyM65f2WNYwDs/+EsW54cQ4MrVI1588WscP3zEcrHm8eMnLJZzXn3jVSaTIXfvPma2WNF1iabzuKKUglIJB1hrlYOWDMKzEgdx1y2pl0tm5yd09YxrRzv8/D/4+/zkd77F/t4UbSJds6Zr2+zCAa00RkW6lLKAo7FWMRgUXL96yLX9PeonFyyW5xw/FfHDKiWXlxaMR9u1NM2Gum7pQh86ByCNTreqIUbK/bG8fsbK5yjGbY8ogSuK0gqfdL5cszuZCnXKJBId2hhu3Njl43uf0zSeGOU5778icbuiGGOUZPlevM9F7pZZy+VaY0qy2gay4mWMpigKmra9dOFqs0UoPC8Cay1Jtflfty4bY3pXnjTsvTC2DRtT4tZ73gn8vKAWYwStvhA8ZYzdOs97Z/827VYbGUnEiDKZh26kgdBIeIVzRQ5jNFnkv/z/9j9XP5Aqy3IrLrrCyVmtFZumZrlaMJlcYby3Q9Sa1nsRFVJkdn5OOSjZ3dtjb3eH9WLBeDREG+EyOusIrqBt1vQOYknc7QTbYqwI1skwGe9z+6XXOX78ELTi6rUjHj38jNnFKTF2aJfZ5UaGerPjc2jW7E53xX5fFTAcsggN7UbR2AFrZahVYkMglbvEZGHP0KzP+Wx2yvlHP+Ro74QXjm5xfWef2/tX+Jmf/SVuvvASv/Zr/zd/9cM/JqY1upJhoyLIUFAJkzZ3gpfDx/z8GGO376PNqInhYEDIrMe6rjN6Igc0YqiGQ6aHB1TjAZvZnPNnJzJ4inIOy1bDJVajf+77567ns/bvI0igWC/oWGu3oWdJQes73nn/XUajId9466sUWgaLrijouo6iLFFaMZvPOD05YX9/D/tcenQfrjEej4nRM58viN7TbFYopdjZ3UVbR0qaIv+5EMIlB1BeOEKMXL1xPSeY52dUI0U2l41dysM4EVr7gUrCaoVxEtLUr0wqpdDWZdE2Yk1JjJG2kTOtbWuccwxHjq5ds6kbNrFgFixrX3AyS5zPSuqoSbZDsUErOZdIGpE85Bn//MFDhkWBNiW7e/so42jaxPHTGctF5OrhbdbrNZ8/PmZvb4/FcsGDx3P2D26itKOtA8dPTvjmt79HGzrJPAgeX5/z43dPcGXBd3/uWzSZf7g8W3Nx0XGxrlmtFtz77BGuvIVKluGVa9jRCdYVqOjZ35+iMeyPBjAIhHbGD//qEz679ylNfcq1G3u8+dU3ufvJQ9579/v8N//tP8Ynzyf3HnHzxbcZXr3Gp7/9kEX3mHLkgEBsxMkf6ppUDklBEB/a9m5E2WYJNLSbGkXPxu/k/ei8NNfI0DF0HqUMOgnTMCURdeW8inz4/o/5/LMHvPKVN7j+0ov82e//AYuTM+HHuZKqGksN4z0avw0bNfn1UkHWsAtrUEqE9el0zPlsTjUZsO5muLLk88enHD86EZEgBoySDYpgJeT2tD7lt//zb7LuIj/38/81ewfXmS/mGOewhbgNVYqZiypbFbP5ivVmzf6VQ4x1xBgYlCO6LlAUHusK7t+/zyuvvQYkCWGylpSfL6VFopNhtAwKQw5YdYUTDFLM53ie5Oi8CqqKgi4Gus0G3zQkoKgGuMJJ85480QeaZsXFyRMKC+NRSUTjhlPuvPwaaMXZ6RkxRA6PruKjYEGsdjz66AMeP3lIvVkwMIZSl0z2bnN4/cuUw31qX1ArjSESnBKcTopEo2iswTce7zsGlSPpRBeEEby3uyOrqErTzmecP33M7/7Wr/P+D7/Pm2+9zZ07d7jSjNnUa1bn54yHB+LqU7Jd1a4u+Oidd/jTP/g9XnnjFb7+jbfQKtC0PqO8slCE+sKAFaCtW85mFxwdHaK1wWfOdiTiMiatF6e6TpjkO3tX8G2dMS8WZSQjRBlHTFAUA27ceAFXFKQoGwHOKJzuWZcSyrVaNwyqhEuW1WLG40cPeeWVL7F3MELrgvV8xkc/eo9nFxfsH90kWjGT2RTE9Rxakm+JXS0bMrle9LGjq9d0mw1WCbovqIQDjG+xBOgamvUK5Tsqa2UDrhgStRgBqqpCOwmz8/l+WW1WzJYrTDVgerDPcG+PgNR2XScOx140lc90uKzViM+F7untwE3JJSfmmS/USEmCy/rtB9L2n6rvNZWSvKNcJ/W1XI/KUTzPpb0UcWOUzSqpjXoCrDgNVR78k6QXEZScgcj2fu+rM6UNMfhLTnHSkpWi2Q7v2dZ/lyaA5+ux/g5X6vlaN20DqS75rpd3v1Jyz/du3edrO2HThm3tl8jouLZ5bsibxWqlaNsWo13+2aWHYzt3yn+nJIYAlIjYhSvpQiffO+XePtepNnOeve+kb6avwS8Zvk3XMJvN2dSW0ghf2DiHVRpnJYzUaEMIidS2+BSo61ayGZzD5p+9y27XEKX37XtNbWxGW5jta5zS8wgG2R4bVBJK2flOtpeDDHudLaiqMWkMTd1mLId8WeeYTnaZz2e0myV1XdO1HdZZdnZ2KcsxREXXRs6On/Kr/8e/5Df+3QHXX3qdV1+9zUsv3eKFw6v80i//M27ujXjw3n9k5C7Y21Fcu1IwGhmcjRSmo3Se0iSMiujk0QFkozLlDWFDylRCFSMJT8q9KuQtDGzu1SXwUAL6PEEHuhRROlGVil3laKIhdSUqObp5IFiovaewReYWJ1xVMNkZc+XggGtHh7gyMRo59nenTIYjhoOCauAyVsSilUOrghA8bdfgQ8yGFUFmGVegtMbZktFwF10MUa5E6ZKEpcl3XMoDEfVcX6SVwVQObKDzgp9oY0vXejy9+Q7ZjifkPi7300YMSZiKpEoiDltaxldeINoJa3OEq+bE1QWr5Snn8xXLZY02siknHyRxWGttmYxHjMf7jIZTynJMMSg4v3iGj4I3TUbCq+lqFo/vktYXdKePccMDmuGEYAraCNavCH4lSI7g8UnhtLzvyq+Is3u45BmGE+LOl1gNX6TVAxwGlweuqEBMLd6IC/5v+/o7LdK2J8fM/p//nUkITJNHE9A6SIp2SmzWa9R0D7vzEuPJlDaIG4mk2FzMKTYNum7xocvsqYL9qy9wXzm09myaDZUZsXtln262pE4b0vlDfvgv/wV+fc7YIgeiVtRaUQ8HvPStbzE8OmLuu8yX6iSlNQh/ENNtVyxkSirw5qdPHvHxJ++xPD9GJ0m2v/vR+9y/9ynUM6Y7I27ffg3rLL/3O7/O+x8+ZFZHvvmdrzNLQ/7s3qd83na4cYXJHL6iMERVcDJr+fPvn/Ctr0wYVIpEQ9JSdGgtr0dIWg72mN1keTIujbgUv1p4DAjnD1CW5Sqy3iSWy0SIFcZepTavofQhe4OG1UXg8bPHlIWwJNEFmwYeP4nML2C9aIhBCllbaEYjJ78vBU+CacIAACAASURBVIzrG8R8IFst8PEoDEzfwWw1ZzAaUQSNWq1k0ib1rzjQuDRIKG3ofMeirdHWMHIlF6sVq7YVp0GQVTyfpyHDfCmHmJM3QdaLkwSNhbqmCwGdKprViiYK8053La4zVBhaxDEnF4okiuu8DqRQpJAoq5LBYEQMlrZrAcPhtde58cK38UpCR2JXomKL0w5FwitNGx1NV+BtmVlNEpijtcJZRVkojAqAp1RQWXEfGmUpCoXCo3TIaaASENdPwmNOF44x4eta1oDkiAHEEaiMJraXBUe/lCXFliIkWSsHWXXRWRCUOiuikzgyYvDi2EoJk1pSXNG1c2Jbi6stp1AmLZ7bmN0UKgUCghAxSRNwdNFhUsQgjVrsgky7bUWnKnzn0Q3cfXgin+/BGDrNG6+8wKOHHfVMXIevv/YG89kZP37/XZyBN996g4OjK5xfXNC0kXf/5B3OL9aQKqyrchEqonPPQdJG1sF651oKgfV6zemzR5iw4frVfb77E/+I11+9xfWrUw72LJoNKUVKB6UtaTuPMVpCARU4Z4gRnFN0NmGcZjoe8/Ybr1J3P+bps2cYNGNXonViWDheuXWTRGB+8ZR6uaDrAk4nnJE1G5MZtioqYiPuf1u6/P80tF1HSCmLMQptrbDsYqQNntWmYbcYYo04ULROXD/a42h/h88fnYH54kp5z5fqAx1S/jXZTMuMQH0p0F6KklGaNcC3nqZpSPRr1FJcXhbAaisAy1T60jlrnxeItd4KxsRE0zR0XXd5yWglgTrPCaNfcAUjTcbzyaOky8CG3k2R8rqW7zpMWWS3Qv7585/X5J/DKMbjHVCKzXq1LSz/uuPy+dALwS4ocbcnYT8+fPw5r453uH79GtZNmF/M2dnZwWlFW6+ZnV2ws7vH1WtX+f6jB2AKro8nKBXZ3d3ltNvgO0GdeC/puDF6VmuB6zf1hhgSSRuuHN5gMtnn7t1PeHD/EVppRsMdurChZU30LZHIYFAyfeEFFqcnPD15yujJQ8bXbjIqJ3RJsYyKlXI0xol7PqxJlMKUqwJ+vcEMNH7omLEhPbvP6ZMH2Jdf58bhLW7dfoN//s//R/7wD9/id37nV1nWT0i0uNJlt5zLKA1p+Pq1x54DWxQFne/vG7t9fX3X0badsA2tzYMogzGOZydn+Bgop1OGO7sU4ymr8zOWF+dbTbJfo3Q5BRn4YqP7HP7gr+MQ+qZXmczx1orz5YI/+PM/pSoLvvHlNyUArW7wnQcFw+GAK4dXmI5GMpQIXmoN62QQq8SBRBR8QBc6fCP3ItnZ1H+2gu8yq03TB5ZorTGVcJC9knVKrbIrOUohLe4rYadLs9sX6tm1nv9dBNyQz3oln588SEl5WCL3eqIaOEpX0HY1Z/MV843mIpRs3AGrUHHedLTKE8yaEBaojKEK2TGdtMIaxe50R4bygxE3b3+JK4f7KG15cvyMZ6dnlIMRb7z+Ze7d/5TjB/c4eTLEp4rB6JBkS+aLOYe7ezz8MDId79Kkjs0CCqPZLGf4NrBcRN79yw/ZPbzKuvGcX6z4fPGU8/mGi/OWi8Up490ddg/3cfsTUlVIDRY8oampTOLKqKLuOvYHAz56531imGELx3TnKqA4P3kM3ZI//7P3OTufM97d5ebLX2KnucU33vxZ/vN7v0oYilvSaifhcqs1vgXjSsrSUhhD2/nMIa5p/ToPVfP6bXZq+TqAkVVr8kZBP0iQ1VjhlQ6GAzarNUYZZsdn/Jenf8i3fuHv892f+2l++Cd/xsmzE3AKWzmKqmQ5VyQnQ/8UkjD8U8THkJEplkpFvv21b3P/7j2877h16wYmOV67802+951/wP/2v/xPckZpQTilXId4lQiloutO+Pe//6+5+/Aj/tFP/1e89srX0EGxmZ1BH0orRkHQmvF4wmA4pChLtJUhSFKK6WQPqy1aGR4/fsyDzz7jxs2bWKWIxpC27ac85yGvhqucVj1bzIXxN51uxUZhOMvWiFaCGjEKfL2RTaYUKZqawXiIJmJ8Q7NccP7sMQrP3o2r7B8e0bSR+XzFcj7P7P0nFFqjGVIMhgyqMReLYxbnc5y1rL1nVAyYlkOuXH2Jw+uvMV96IiJqqRDyMNdQVSXtSsQEVxakroMU6doOrxJ26JgvF2AMO3u7FM7im0TqWp7d/5Q/PX9Ks/k23/3eP+ClV96ijQXWOUKSOqKwigcPH/Dvf+1fo1zkF//pL3Pl6h4XsxkJEdM3mxpnHYUrtndez5nXSlFvNiwuZkx3d7cCVTYfb4cQnW+zA6/KiK2cn5A0zlaSs5Er2eFomh2Pcqb2Q63VcsFgNEFrxY0bN7i4OGW9PGe52XD7zmtcv3ZLGMHCheDRo8f88P0P6FxFWQ5kiJUCToOrxuKg7lrqeo1zVgaa0WNCTdclog4o02ERbJlTgSoGwmZJs1yg24ZhKSFGVmuiNkRtMU4cam1KxK4jkmjrhuW6ZrCzx97RVZJxbJomI/kyCzTfVf1rLGJbRm9kdN/l9tJlHSL1lNTrPf9VZXNMllmBuN1K2rJfFZj+ru3FUCAllRmWgi5QKXNX81ZJb/rQuYbscQu981zlN3/LT80OpMttPoC8Mr6tsjLOSgmGAAUxBOl5e5csEmRtrcu9Se5PsoDZY0tCzBs1IeKcQ6eYxe9LkVHQDD3v9fLujzFsebi96Gy0xqW+h+rvUhmGPm826LdOUu7WjJI+U+uc+6IUWssJqaORMz67Z/rv1RtBWiXZNCFGOVH15b3ctZ6z9lyQYUlt8VtWaTGpZFFVpf6eFwxC03X4lYS1ohTeSziTNuY5E0+gbsR8cVkPqa3h6vlBt1JpOwjTiNB5idJZYvJ7Za0Er8nwWH7/eDImDEsmEZqmxlrHtWvX2ZkcMSikX5zNF7TLGWcXSz7+/l/w4Tt/jCsMt65c480v3eD6nuOFW/tcHcPuxDKdVFRVh0q1BPrhcUaLaUZ5oJNPg9Jo7UBZRJkS97cioLWENisjWpTRnmgCSkvIn8qiZ/AQO0vy+XlDU5YV4+mEzkQa7dHrhrLtUMpSFCWj6ZArV6+ws7vH/t4eu3sTlFJMpyOm44rRUOqisnT5829k4NUj42wf4Ph86LPKIZsTrN1BD3ZwVYXNSI6OTu5zH2lbQS8RexONJoMP0Qom49EWG7NQG9pW/iyQ2cbZpq6MDFfRRCyoAmMHhATJ7qK4BS7huhbqM/zsMavTJ7SrC7TfEBcLCVELgfGw+EKfVhYD9nd3KWxgWDmWmyWrzlG5gSC4YkSnNWlZE1jTzB5QFwN0MaTJOLpIIiZN5SqODq7hlJxhbQjEtmEz/zGsPkMtnuB3F/jqOpQV0Sjh79Pgw4aVurQ2/E1ff6dFWhc7rm9OGChDUVh8kqmCrFWIoFGbxHBvTGcVhMwONKBSpFutaGZz1LWI04qoYbA7JZaObrnEpsR6scBVJdGUEFpis8bULUUR8UYExIWCWeW49a1v8PVf+gXqqiSFZrsC0AYvKYopoFUEYwFZA9Eq8uTJAz54/z026wtM7GjbDZvNCt8GlF9w9XCXwXDAa298maNrh9z96Ec8Pj7jYG+XncNX+JMPP+A4rImFHEaFdThlSFkcjHHC/Ucr6vUZd+4orl114mrVEecKfOtRKUloWF7PkPNCmDYqu8nwmpQ0rVc0naetFbO5Y+MBO8S5azTmZU71bTwDEVKLBZ/ef0LqZDIUQo0PGu81KsoqinMqX9Q56CJ4UuwojGNYjjFaLsOycKiikKIraGo60Imjq4c8e3JMiD6rhUbWPfpGD7aNrlaaQBLguLHQNgQS2hkR+rwINL7raHQOEPNeCsoYtmFFbXfpDDI+0q1rysGIQVnSrFeyxpBkIt1EL01nSthohJmTFD5EiqJiOByDssRUobXDVgaqF3nW7uHRdCpyHgx1chhTELSEtyTlCMhavzIKZw3aygTGGo3V/Tp1YlA4CiOvs3CbY14lj7RNxl0AMXkUlpDXUGIMsguSwe5a9anjiXq5FpdzysKRlgJOwMbCvgtRmIpKiUiZkjTkAtAX5m0MrYQ7aLCpodnMSJsliijNZJ6yey9TOHH75klcvrA7MYrg7ZCUJ786RVTMwQYKwXL4DmKgXne0qwu+8qUXGRTw2UfvM51YDsZDHt77nPXFiqMrUyqr2dkfczY7Z9123L3/hK57iO8S1g5RyqAMoIMk12Z3qlKS1uwKS+db4cLNL1gvzjk6mPKzP/kdvv2tr3Hj1lUUDcGv0cnn/q4v1KQQjSHRNJ62bSjLUi5FlYcWTjMcj3nxRcPx6TnL+QXXj47Q5NTSes18ds75YkZo15lFbNExYXTCamG1aSPCu06KuKoxlKjCgpFAldRzVlGkIBwlQqQ0htIaKR60JDZbY5g6xyu3X+DJ8QU+9a4HEYB6Ebvp2syY4tJyCuKgUOKGd4UkmvYM69a3svJvNEYZ6qalKC+btr5h6B2KiV5gjegMyJdvfpnuWhgrg5nYbUXh/vvx3PeC58IwcjMh5wriiiWHS8RLMVecs3HrDgkxkLzHltVz7p7sJlEKWxasm5oUE6OqAtiKyemvNRj9r/XBCGr7ew3JwGw5Yzk7p9k9QtkRzlqB7iVP1zYiAETF7v4h127cwnsRC5pmw3AseJ+2XuO7yHo+J4WaqnKsZqfEWLNczInRUpQjdvb3GE0H3H7pDp989D7r9YqitOxND3jatKCCNE9KYwYFB7duUa9mnJ4uODlbcOft6zgz5Oz8lPPNWgZeylI3sj0wrCqSmhJTSxsT48mUiUlM2o4hhtXilGOlmAwO2D24xi//yj9jf/8a//bX/wVPT++SV0Hy6yZlTdd5sHzBPd11LSonvxtjMNoSgqcqK3HDGysYMFvibJm3OiTYUqFAW8b7+5SlI0XPerHs28UvOGX79+z597B/r/vnr3/mtl9KXNIi+ERmqyV/8pd/wdHBPreu3aAIcrbG6JnNLlBK4XKYSMw8clmlugwK08iwOBnLZLqzdarLGW5ysrRwsI3WdJ0nqohWFqWNCLiBzONV9GEpKUrwZlOvqMoyu4vys9s3mqTsYMrra/SMx2477ICE0oFiWEhRjqYNgZPVhkezgmU3pDYHBLVDMCXRbuiauTQ6CmFmElHKEj2YqPAq8OzZMfPZBV9/6yu8+Y23OX52zKPjp1ycnrJcL9jZG3P87CmhrRlXloDi6rXbjA86RtMdQmi4/fIr/NV/+SNckTCFxShJ/LV2wM7+hK5dEdtnXN17kb967zFG1VjnuXK0z0uvHdIt1nz5zhGLLhKwlJMhxipK54hdZHGxJtzc4Uc/+ozjR2dsFmccHE65cv0F1hvNe++8y/e+8yaPblzh/vE5B7tTDm+8iNIFm82Kl2+8wfff3WF28Rg9luCsDk8MCYXHGUdbN6jkUU5C/XRMpCAu6a4VbrGIJhptRbAZDcdYZ1nMF/hOWI3GGnwrHMNxNWD+9BQXoLDS4Pzhv/lNXvzqq/zEL/489z+5yycffEQxLDk6OqJeLwjRU+1WLM6XrOZztAokA8EHQmYyH105Yvb0nHufP+Txg0c0s467P/qY5bOWzWazdcql3j2WXXTKgS4VzWbF9z/6Q54++Zy/951/zE9956eZ7u3RhRZSKSFDuVGLMbHZbOROT9C1LVoha6JKUZYFN29e58nDx6gUuHr9GmhD0pec8hAC0Wcmc5LzZjqZbD8j/WBNVHDJToBI7Fq6pmUwGFAqCSYzhRU3c9sS1gtSs0KrwOG1I3auHFGO99FNSwgwPz/h7PQpPqyhKKjrhQiOg8jnn3zEen7GsCqYpcRkOGKwCmyWC5I2eJ2DdEINMWF0SdOuqE2g1ol111EOSgaFI3Ui4iongTY+eqwxzGZzuuBJge02UWg6/uQP/pjPHjzlV/5p4qvf+inRMDcNzXLJjz98n//3X/2fbPyK/+5/+O+5/eorbNqNnFcmb9ZVgy+ckUopvO+4uDindJarRwc0dU3wDSozOZ0ttkPYtm1R/x9zb/JsWXad9/12c7rbvjbbyuoAFHoQIEASpmSCIhWWHG4GDkXIIVsKTz2w/waO7Kk99sQTWTIjZFu0LSmCslqqo0gCRBWqgKqsyq6ye/na255zdufB2ue+BC2OzRuRkZHx8t3m3H32XutbXwOMRiOUUqw2613oUIpDRoPOYB+QhAmJEpCybiyb1YrF4oqyGRFjpK4rRpMxTz77gKuTF9y5/Qbj/buw6eT82q74+NPPWPgIRUVIwiE12qCV2OAlNFGV2MqK3ytOwrC9InqxC1LKYVSkJGCSQ3Vr0mqB6XuqqhQ/cqtRmTFqiwJtE0E+htTrXcdms8bWIyZ7h0RlcSFlG6u0Y8IPfdNueI0oaFKGWQem6M8DudeKCflnDonLh24IHkzKJ2H2l9XXVlEpqzSG2k3thvOvMVOVwoUgthaKHM51PewEGfINXNcBYB48SVP4eTDzusbjWvkkco7hlhSmYwZSrbVUVYXJ9nXa2F2AqwwSr4etO2C70K+F2dkM5l6f90PNptT1EH54jwolCsIBoslHolJyjg8kAK0VySID00w0SjFic3DYQBh5vdZISUDa5D2qUKQsLtIMbGLJmElR7LYGxnQIYj0QY8zEICuD2RBwnccFR2ksKEM9aqirilFdUxaiAvAx0Pc9IUS2m43YL+UgUZIEiGst6uQQoc+vJX+GEEWVc3AyS1u4ZQykCZ0SSUt9E7zYB9j8Pl8nOYjyVsg/Rlui1rgE54slXWcYNzWz+Yz5/oTxjRlvOc9nj1/w6OkTuu2KdpFYvrpiojzHxzCtCvYbxWS0ReaM0k8VWuW8FgmAlFpUC8tUD57jKtdF2T93YEHrhCnAWiGmGS32dRGxwogR8dMNls7XXG1KFm3NNhU4HbClYqagnNdUpQzrZvv7HN44Zm++z2w2pShk3zg4mNNUBYVVWFuS0jUTXWw0EraQLAzxTle7dZsoMEWNKSZo00BZYquGcTOisoqoPZGAd4nVsmW9aiVcM0pmTkiyD4WQiH3AKlFr+lIG/ikZog95LzBgLNqWMlBTlqgrtCrok2HjNSun2ThLW4wJpYXmGFvepB5d0i9eEpdPsf45xI4QA5vNCq0aqrEoV9EKVWhG9Qi9J0rUpq8lA8cK8GyNKJFSdBRWySAsbmTYXFZoU6O1pakUN/dnHOzNUCmxdpG+9ZxdnrJYbvEXH9Osn5Pqm/jRFzCjI1T0JOXx0WV1An/q4880SCsBXh6vIjHI4aKsTNms0lS2JChNVVm0ThKSYEXePTs8wvU9Fycn7H3pPZq6JBSgxppyPmL96jkjaykTpORxJIJr6U2i0IltCvgQ0RguAtRvvcvX/6P/GDefsM1m6ylIYE2MmYFqjHh5KLVrFM9OX/Lxz95nu1lA9PRdx3Z9hTGJuqgYz2oILWHjePbxB1w9KbChoyxKbrz5NvdPTnl8fkrEY22dTdUhaWFC6gxaBjPj/gvHR08uuH2oeeNmwcHBmNomSh2xBrwXKYKK4hnkugBRpO948BvNdqtYrB2LtcfFgtTcRE1uEcsjvNpnkQ5Zun16bZncvse9m+9x/8efcnnxgKLQ1FVJ8E68SbQleie+J2WFMoqEFCMJUCFhEjnxUqaLGpl8RyVgTl0WrK6u2KxXUjCagqG1FQZd2B3WMcfJlsayjZHWB4KSlG8TFXVd0SXZMIYDuYtdltZkOb4Wc/nOe7quxxA4KBspSLE0oymrzYLOiw8PmZXaeYc1EoBi0JhS5KRFPSIaS5c09fiIg8kNSjvjIhxy1k2gmKKsxU57qs0Gv70Uo20zJxLRKmJ1QBtFURiaQjyEycy8sjBYYyh02kl4jI4SKBAC7bbNacHDhiO+aD5PI9ESZDBMijVK5AaZQSONvyLFLOuLAY08D8FhlKZPcu3F/kP+3smklFgXJBwpePq4wXUbSPI8Sif6bkNK2ZIhxF0DrxKo7HEUlXjskWR+HCPgezFbNxYdHPgWi4DJzjvazZbHDz/m3q09Xr18xqS+w40bB7x4ec5qs+Gbt7/Een3J8xdXPHj8jHUbJLhN15hS5emzGoLLczGX2alGo7M/b7dZsDw/pSkCf+nXv8Vv/OD73L01pxk1+NCTYqIoKlCJkEN1Qggij/TgnQArZVXI/CHkQzx74QUfqUcNX3z3Dc5evWB5cUqpNevVkq7f0geHJ1HoAXQcgG71WjEcUUYYz2w6QnDo+RhblxRWCixtZM2kGLFoxlXN/t6M48M9dPKE0BKDIaaCUhtuHx8yHTdcrDevMU3ZSaf1UIy+XjhlFp/SrxWrSlEUxe66iJQNkjI7K4IhWGBoLLQxu7CumAYmu8lMCinji0LAOOfEoqGu65+b0F8PeK5ZjX+yMRlajpCBJmAXtCEeXYM0x2ZmsNkVYUOCcSLRe0dRGIpRxWg6prtaiUew4jpZebiGXPM+/iS7lxxGphBA+9XpCZP5MfvVBGNHOAIXq0tsMWEUE8t1S1QjymaK7jqIkXa7YbG8YjqdoJTn5PlzfPR06yuuzpcsLi/EwiMFqmbOfO+AqAxtu+VqcUkiUJRGAF9nhS1gRUodk6LzgdIabt99B1U1nC7X/Oj+z9i79y4bW7C1Yza9Z1rXvHE4xbgNCc+mtqgQ6SipK4O6fIbeLLlz711S7Dk/+ZziCIoE08mcX/33fo3D/WP+1m//Tzx+9iHNyMiAQClQopwZzhWzk5mKb5oktyvKoiBoQ08nthYxEn1kNtrj9s07PPn8iQwQlKzdkARk3K7XhL77OVB2WJvDGrPW7n4G7F5/eBijCV7UDYMHscvTKFtYtFWcXJzx//zzf8oPvv/neOuNNzNwIcDner1mOh0LCK0NwxIZ7q/8D9ptLwMYZWWg4r1YjYWAMpqqbkgovAv0fYstxfMteZGZmsIivYffBacpJYGhVWERP+Oh0cysF1K2MRD7CK0NfW66FAL6GW1JSmdljGK9jXTO8GoZOFkYlu4QXYzRZkJC0W5WuL4lBYdNhhRksGiU+F0H10vGRmGIfct4VHHv3i1Oz57yox//iHbdY5VlNG64+8a7xFTTuUjdTEhmyo07b3F3NhWVUuH54fsf0lLiVYNYywf2D25y9+032ThFU9zj/v33uf/TB3RXC+rCsm07itJz79YBcV4zqaAIik0PTT1lVMsQScfEs+cXVKMRHz+9YB06mvmcwxvvUFZjytLzwz/6I57eqDg8vsuLswVv3Nnj5cUpvtW8fPECNop3D9/h9z9/QN2U3HnjDZ48eUy36UH34ldqNJ0v0KMCqzWFMkzGY5zradte9it1bcki+2JCK8NoNBJ7Ku9QSfbewlhOX5yQtj26KFGVpdQ1wWlWyw2f/uxTbt66yfruBrRidjRnf3PI6vKClDSjGweEyjIiYUNkfbGgMAZl4Xf+/t9DOYPzie36Ct0l3Ooxp+fPMCZS1gV+K3uMFkmHMJOROkxZja8ST1fP+L/+8W/zwYe/z1/4tb/ML37336cuC3xU+KgzEJLoth1d2zHf2xPADpFhXl0tqeqK6XREfzjn0cNPaUYl+8c36XxmIsYg2Qeuo+tbbFHhup4iDxgHFuG1hY5c3r7t0Cly4/iIejwRNo6XMJHgA6m0hMowP9jjjrmHLisCmuViCylSFiXbfsu4qdi2QhKI0XF59pyXy/tcvHgM7gpFD8mLP6GJnD17gvcdAYWKgbRd4pOjD5qffvSHvNiekkrPzdv3iDGyulrg4paoFboURpy1hhs3jzh5dYZzfQ4MVMJuVpoiaT7/7BN++2//z1xtl3zlq9/ixaeP+cPf+9f88A//kGpa85//jb/Gd7//q7io6V2bfWYNRCWgXJKw4wHM8t5LavfqkqqwbLcrlqsrjo5vYcvRa3vhhqapabdbKiM2bymD5yFlFYq+BvVgCIvKAco5bLgZTwlJQuKMKQhRURQjmnLEy9WKdrOinDlsYTAxcPb0M05ePUNVFcaLn6NLEUUkhkhAAotICrSAziF0hNgTYk8iyHtIjjI5Ring2iXdxTmm94yqGpuDPU0ha6ssjchjFQQvYFzverabLbaq2L9xA11WuJjwMYrMfzfgHs4eswMDh8VplEJIoJEh/CrjkT/H5pQzTOe+N9dBef83xkhvnITdr42wSYV0MaiLBsByCIC9PjOH92JtgTJGSBK5DmdgnOX3FPK5AoOt0TXzb6hFh+1hqKhiStg8gJeaQHyXy7K69uJNSQLJQ8CHRDkMNjPYNtiW6KzSIQ0hqj9vi3Bduw3M5eznm1JWVRmC0lxXxgK8xqx4HD5PQgg30agd8UnYpVnVFaWPI+dDDDXHYAsm/y3JQImYfYJzWKcPhOjp+16UMYNvbJL3apWiKKqdbVGtJVjdeelJZ7MJ89lMcjhQuwwHlWSI1XY9V4sVl1eX9K7LbF9FoS3NaCyMWOfzfRFxLuzq+SFIzQdHJAOfUZQIysqaCEGGjSEKlfp1tQ95341eALGUFEpFlt0Fq7TEGIUtrXjLj2vq8RRVWWG5ph7vVvQOjC/xLuIceAeudSQtFgVKaaL2SD6MfNdKiSJQlu01SJswiGewQSmxj9BGSC3Yms71RHLYGomQFC5q2hBpe826LVi1lsulo4sOjyUFaMqC/fmI+f4N6tmcsq4YTRpm84r92YimqjGlZjSqr3ukjMGkJANHpeTMV1qCXDN3XQICkwU9omwmmHIkFqNlTd2MqesxTVmgy8x+DTCfeLabLcvlgm3b0bYO33uC8zgfiM7jQ8T3TrCGAaRXsq9oW2LKMRFDUiUps5F7F7naek63ieWqZ7Xe0CcLuhTbrqLE2SldnW0Ztx2qPyMlR+8CfecYNxJSFpLCqJIqQd8HqmqK0aLcTTpRlxWlEkatLcSL2UdQuqCxGm0bkqmIVtjrF1cX6EozrWuayZhmUmInNbx4xvpygV9dUV6+pKhfUExvQDnKViEB3/eE/jV15594ai1nggAAIABJREFU/JkGaVM1YnXrHdzFgrrvaFSLdh0FBWiNTQmrCkpdUlkJnkkq4qJidusYNZ3z6vyEm74lqkZkO82I5ugY99NPcuqewvd50ShJk1UqEQJsQqBFUb1zjy/8hR+gj/ZYbBbi+xpFuhVTIGR2qhmaIwOYgs224/mzF2xX54RuTb/t6LZrmpFlOm0giYfh+mrBswefsb6sibHlk4+fMq4PSKbko0f32YSQQ4UiVtsMvAiTT6Y2UoyHYspmBQ8ftjx71FKVHaMaxo1hMhbfr6pMqGRyUmMkeEW7dXQdbNaG5cLRO8Vouk9z9CaxeZc1c1w4oA8K5yr6aooZ3UXf+DZfeueQ/vQZ//Bv/49Y3RFSoiiyx6OSyTFaJCwhBIwSsDMohMrvQReGuhFpJV6kkkZbZntjTk4XXJyds922uCjG+YRB7uDytdcMOoqkkvjYaJFk9F1HPWqI3uN6tfNI8dFTFJb1agPZAwaV6fZKEZWmqGuIPUEn+r4lbpeUsxFRKwIJowyltnR+i0gGIODQymBtSTUao6oRRXPEaPwGs9nblOWcbQftJWxdRT07gmqfogmsn/wE6CmMI+gRvVwsrI4UVYHVSsK9YkCbEq2hzqFtynuKQhPUNVOmD4HOOUkgxmc2R8InR0oKlJHGJSQZ2RFkTUXPcODKdFfkWll7IUVFBmmldjIZaA+k6He/T54SD9YaOnlhk1p5Te9EFqKMsFSjj/l3hok8eBdJWoYeCpUBOC/T1OjkfyUPaYtKQRr/0KHyYbddb9muamaTQ2KQAvfg8IDnL0754Qef0nUbLi4W+EQGwGTTJSZScrImlaUwhlKbHDyVINs4XC6uiN2Cb33lLr/5g1/hW19/l8nIslhe0LY9ZdngohN2dZ4Qex/EdwiLKorsmyiMUxe8GOgnoK9RRUfoe4LyHB7s8cW37vFvf//fMgQExCiFic4MA5SEChRaQHm0WHeopLAJmnFDYQy9dzjn6ZFADp0DmJqiYFbV3D48ZFw1VIVGa5FmiU2AgDQuwGQ24fbNQy4/3ewKR+TSCVPDmsxMB0h/wpfWUlUlxhopspxc67IosiRFPod405qdBEs+osZona0O5DkrKwEIwcnaM9b8HOj5uk3CUEALg2zwjRKW3+7nXMvTFOInOww7tdYYK/dFSnbHmFJaZzam3nnSajsAUWJpUZQlB0dHnPUefMjM9bi7bsPzqzzFHgBkee+ZdZ5yWBuWq/UV55evKJoZk1lB0JrlYsGoESuFl8+fc3jjBvtHt1lenhJSwrU9bXzFV796iLY3ePDgE4xONHXJxemaUTNiPtujGk/ZP77FZtNydnZCu7lkdXUBKVLZkvXG4TpH04zwTtN3G3zX06uELyrWLlJXkq768vOH9IXC3niX0WyfOmmOp2MOYoe7imy3KzadBBaW4zHoxOnVJSfPngCB4xs3KeyY7fo5/eoV3eYGBzfe4mvf+kX+evPf8ju/87/y8cd/hEo9yiaG4YpItyKuF8nd4ElbKrEBiD7ifU+Kkb6TtWqMpt0Io2rw0gOFtoa+b1ldnLO5uCB0Eq4XY8wJtnHHiv6T1hVDw/b6EMD7sFtV3gsAGqIoFxQmD04sn5+c8M//9b9i9IOag6MjlJYG0RhDDA4fI0Utr9/3PdqI9F0a0VIGFbk4Bui3W1zfoZWmHI2J3slEP0kwlMpM3OBFfmdf8+ATtYTI9gqrKIqaGMR7McUhvEP2UO87UvL44FmenRATjOdz6qoCIjEF2q3jchPYYHh56bhYWla+IJUTbLNPXTc5fDOSvCM6B0ox9KVGG2LIoTspopE9PKTEw8ef8/5PPuJqveBqtWJUT4GCu298iWTHRCre/OovUo8LVotI28KyuyA1Dfduznl6vqbeP+Ltr3yTelzz0fs/wY6OGc1n3Dva48fvP0QVDbbUuLjAXXZEF7g4u+R80vCVtw/QQLvZ8NGHn0MIXC1aHjyz3Dk84O692zx+ds7VcsP+4T4f/eRDNtstt+/e4etf/SLjkeEn73/E3sEplA1vf/ELdA9f8ujZc1Rc8+r0BdPxEWPfsH21ZjNbUxYlfQCT2c5EMNETSHhrsKUm2sh6u5GcAuQeQZO9J6F1LdoqmlFN37cCrMdENZIGfX1+QWEMtqkpZ2PG45Jlt2FyeEhC8eMf/4RvfOdbaKNZX12yf3iMRXN5eUXXbdCVIZmCuNlKmKvSpJC46tZ0XY+NEdV5dBTwtjSypyssQYmKR6F3zK+EokgarUu09XgFq7Dio5OPePK/Pedn9+/z63/+L/PWW+9BMihbUVc1R0f7wtQy4g+ZoiIGODg4oOt7lNISymQUn3z0U74znWNLsaeIwaGKEhDppLHX9Unwcu2TNsTMciP19O2Gi7MzpqMR7E3pnKOq6zzckaAorWvK+R4gwXsxJQmkMYFuvWS9WXL26hWzSc1oNKNzW6bNnOX5OZ8/eR+3OmEyqdg/GnHWCBNxXlkuHz4hdh2jakrSgZQKlmdnvP/jP+b3f+936UxP2VjmR3Padcvl5QUuRaISQkyKkfl4zi99+1v85MMPefjoGV4JICmWYIpR1YAynDx9zN/9O/8L/2zvd3l6/xGzYsKv/4Xf4Pu/+WvceOMm7XqDSnJdex/QxqOMAA5ydov3ZsyA1Gy2z3azYdO2NIXlybMHAj6Mxgxs29XyktHoFlVZcHV+AipRT2bYzIyO4eepSl3XcXl+znQ2FYsaJYxnpTQ6QQoBZbNMOWnuvPklSmNpJvNcg8LL55/zw/c/oIuDvUu2uVMyefUp4nyuiYLP7EA5z0Nkx2IzWgZWheso+gVheYXpnfQQZY22RmxcigJtDcWoyaFJkloe+o71tiUay/zGLcrplN6lXEs6YkzXCooMMoYgQIzUPzk7I2XQJgf/SO0/DLARj478WyFbC2h9reKQD0omCsi5aZS8ZopJgLX8OkpJfSq97HCeiUe8sTKcz7BuZttqElLnhp3/ZdrVb0OlJ6HXw3uX1xZQWM5km319h4BWpYXkIgCtqLtCELWS1NZyHcmgqlZitmK0zgHRQ/aB3Z2Lcl6p3N9Ijx9iJIaAMQLMKC3PIyHRcm6iBmbyADTHfP3jrv5NMWW7QiEomcwKj0msv5QahgFegrucw/lACJ4QBUDEy7DZB2HG986xbdsdqWCwbCpsIbVEaSm09CfGigoz0ZFSYLlasW23ApxqeS9GCwGqKLKi2GQfXGtzPkUUMFIojbneFts8FJD39QHwRilMVt8JKC4gtnyXBSmCdx7vfA4j1qCKnP9gZfjs+50XrtRhAZ8SXYS21zhncRfnhKhEQk+FV5o2Jny3ZLuInMRE7GA+ttimoaoThe4pdEtpBUxTyohlm5Zwuev6XrrkRCBREJUFFVDKSRCr2EpjbMDkIaAP0DvwTtF2ibaDthOLoL4PhGSoy5r5tOHG/iGjg0PGB3vUo4ZmVDNqGuq6ZjKaUJQF6GuP45RvkIGRrneDKrEysQPxVxuUHWPKPap6SllJPo6yFbYUa4BkxCLM2gKtFKNxYjqP7B8dsdysubpYslxs8IsrXL8hJsW2c3TthnbTsvWBxbZDJ4/RFeVohEqaZCSPp6Vm3QmYerFxnK0cq4srlhfP2a5OcT5iqj1UM6GoK4yt0akCpli/gJCoUsJ3Pd22oxxZISYlYe6O0yyT1tagZGiNEqKdJoliNUaMHfYpsalQhSUZA6aA2HN5fkpbWIwp0aYEY6jLgq0OmH6J2bak7SsqzjDjG5AMIWi0d5Jn9ac8/kyDtKPjY77zX/83nN9/zOmHH7F4/Anb8yfMvWLfFGg8sXdsVitmWtNpCDqBVxSjEUdf+jIvH3wEmxVqNKEwlvH+DSZ37vGyMLgkviBEhYmITYGSdFqnNEEr1HTK27/8HezxIYtuQ1GPRBqS0u6gGQzvU0qkoOi7gIqe7brl7OSMbrMl+S0qeubjkvG4piws286zacGZKRfbyIM//hDntjhfceveOzy7WLH2iWhK2Vyjwmoxh045gEqpgYpl0MpTFwU2aXSoSZ1htY2sLnrOjBShErLRkxA5vfORzlc4V9J2NT5WjGZHMLnBUh/Qbg7oTQm2hGIf1RygD9/CTu9wutrjxWrCu9/+D5j/o99hffIR1kgDlSKUVmMLSdl2we08b2PIm0Vm/xkDdV1gtDi3uL6jnkypJxOaUUO7aokhYfLkN2YvIWMMKYSdB9+QWlkaDc6JD+7gFWOKLMMQqfxoPBK/Kx8kdKUwuBDEtgJJnyQC2tB2jmAt9A4fAuPRjH67ISVF9AlX9qzbVp5HabQZMx7tYUd71Pv3UNVNKA5Zhgn9QoNfkVyL855i7ybRWHo9xx6+S9v3VHqF1gFTkJn/CmsVKgPydWUp6prCQmNEBh1iJHlwwaFiZlNGARIjEa0LVBQPlRBjHhCQw4K8HJFqKCL9riAQv9lI8j2EnpT87vAhiul8Stl0IeUE7+h3bMCd93H0cvi6/rWQmuxVJSp5WTfD6DsllBF/VinycrFIkusQuxxblgi+RyexdIgxopNDpUAi0gfFi9Ml7755ZzfV9yHQ+cjj5+cZJJGi6nWJklYpW0YoiIFCi71ESD5P/jzt9orD/YYf/Pnf4BtfeYdbhzMILV0H7WbNpu24efP2jlVMSKAsyYwoqilNPaEoK6pKgJQYBKSJUYLFVotzrs5eoq1ltVpCUNx74x7PHj3h8vySoiq4Wi3powAnKYrnT2kt42bEKFsJ9D4w+E6PxiP25nPOXr2ibzcor6gqCYqqyprJqKEoDFUC5QN96LEFGFNQlXYXEqG1FAhv3rnFZ4+e4aMUqNqIl+efZKcqhbBBMtOC/N0VGchNSYYrgDAotEYnzeDz2XU5UCGrB8RPVBisPqssAGxZCLNuYDSGmN9Tlt3JUxCTFNO70LQUs8xnYK1eWyu8/hhYD8Yo8ZOLUSbhAyUWdknDvM7MTZmRmxKmqijrBrdeS6heEjWBNkVOO5Whx9CkkhsppQcWsLxWUInWbVmszjnob1LYY7FtUQpjNc73lL5ldXXOfnWTZjZldXnObDYnacXzx0+5Wq9YLa4YFZa+9Rwc3WQymTGZzilKC9FzefqUl08es1hKAjgpUY8abh5PUFoYtb5vWa8U7Tbhoqd1PS9PTikuLtBVgV6tWW3WNOdLzN5N9vaPOJgaJiX045rCKFb9FmsKNn1PDD2Mavyk4V/+8b/l7v4ed++9w+MUSbHgy+99j8LdokiKt9/5In/lP/sb/N3/Q/PBB/+CVAR0qWRgVxiCkyCJsixwvcc5jzGD/2xB367RxrDZbrGFpmlqXPQ8e/kMTxL3oihhbO1yQbu4wrfdYCeHUtcg7FAHXKc9y2NgwMK1zYFIJ4Osn/x/hgZvqC8GxsyTly/4F3/w+/zyd7/H/mSGVmC1hHSCNGkxeFzvRLWiNMoosbXJg5yqLOjaLev1mroqsFbjXZuBabOTow0hZLYYrBGGAUsk+D4HMFlSkGJWoq/lj9aKRMC7ntXVOdpoaaCCp5lMpMhHZO6bznN2lbhsS86d5nQFvbeoqqEsRmALsEV2H4Wqbmh9krAlnQRsyhZFMQqgbazBt5G+cyw2W05OL/DRMxnP2Jvu4TtomrHI18sZmBpSYDZpOd4vCTrwowcXfPj+OQ8+uc9oNCVZy8HtY45P3+HW7X02vSeedSijIHrOTl6wuLykiAmMobSavb0RIQSW245gEovlAl2M5D62mtG+5o3ZPi5t6d0BX/jiHR4+/AxwnL74nH/24gkk+Op7X+NqtebDjx/xe6bianGOVonj+QGb/T0W2wUTc5PN+glXn59QzMosf5XBdUQGu2SwaOPWrDcbbFEwGk+EETlYyDCoZ6B3HTFJKncIAWUMVVMRM/sWq0m1RU0qOpPoXeJ0ccFaJ8zhlI9PX3L3+Ca2qFkvzkEZSiX3mO8dfQDrPEUStt/QzE7HDb/6C99mUpT89MNP+Pz5cwqLsMC8zh7hsmcXRcH+ZEZMkdNXr7CmlPemNehAtJFVf8W//KN/xIPHn/FL3/gl3nrzPW6/+S6zvSOqppAm2HtRLBmdB/DQefG6n+0fcLhe8+zJY+5//DO+/PVvUZcV3usMtkXKshL/9JQoS5uzEvKgwzm0T7SbC2Lw3HvjLlVZCiiJgIVN3QiQk0eB2414sVs7yJ5jHgQZRk3N875jvewl0HC2x3z/iOQh0lPWoCvDwfwmZn+fthpz5+1b/PjsirhaM757zMnpS/7gH/7fPPzpH/P4049ZLi8wlVjVPHr8iBQSnetpJiOskYZWrHMc77z1BpNRwYvPP6dHrJRCJAdgGlRQ1MZA2/Hw45/hu8Bf/y//Bt//wV8kFhXr9Qq33WBMgTEF6/WGoopUTUHCMQBzSl37hqeYOD6+SYwdynUcHh6Lx6qWw9wYw40bNzAanN/i3ZqyqrGmwJqSGIKw23ZMcWELNo347JNEpm2zJ793nuDFqzcajTIFs4Nj9vb3iVh8lPv+ybPP+fzkjD4KMzFlJRMkfPR43wtLlEQkSnZJGrwpc+NPoEgBGx2639BdLgnrDquVAF2lyXZe4rNeNY0QXlISBWVMLFZrWh84unOTejLdWRx47/DB5wyK688fhlpaSz0dc5CN8FTyZ9iRFgbQcAi4ek3Vk39nuKZaaXQhgE8kh30Nc/lcwwtZJ2KN/bnAqN1QcwB10zBYlxrIGMPOp1aR1UTD20gZOlY4nwNzM/ArvqkKW9gc4sVuiJp5OcQkrGoy2KuV2dWZw3saPicojBFWdopJQKp8BisMVl/XfEOY7aAK1emacZwYvDflekdS7j35ORIBEpUlZxyKUotq0bm4G+RK9Sh/A0IIyYD2QAy5ttSSwYvRmqKQAVFRiJ9r37ud+jFmhZo1JoOyQX5mTLaLESst55ZyD2orCl/YWUsMoLjz2WZKK3RKOUAs5vUpnaLLZ3jf++GS4H3aXYeYA9mVus6DcL3H9ZKLouI1eSEGICax2QueQc4varu0CwxGKZQV/+EQBYyzJmLGDVoVmOgIKdK5VlR91kjQk4uYoqbdrInFFl1CGHAYMQyRNUJCRY9SFpXyPZWxGqGBDPtSAO2wNmFMyOTBPAyPBhUsvjdsWk/Xa1wAS2JSK/b2G+Z7B8z2btDMZ4wnI8azKePplMIWWG1kX8s2AoPH/DC0ELasyeMlUZLpTARBWZrxIXZyRNK1rDej0bZAqwIVVa69glg12DyUYOixZODTjCcoVWabDVgs13TthsViQd8nlm3PsncEtyEmy6iHpu4JyhDthF4nNt7S9Y7NcsXm8orl2VPW55+zvXhMt92gq32mt7+ALe+BmZBSia+PCW0L3QXRL+itZus7xtsFVTESqwljKYxlMmpIscNHLzhECLJ2jBKlbq7x5TszKB3Q9GhdobSwvek7NmvpL0DReVExtNs17fqKvu8IQYLv5mgKO8JTSg8hE8p/5+PPNEhLWTD67leovv1V7qx/g+2LF3zyz/4J6f7nLB89oe2W9KrHn5xyuFyQ9nsMlSx/bbn9C9/m5PljXjx6xI39PUamgKObTN96m0/GNfV6SQrCxlBWE4zCx8g2gVeKTivGd46pb91g5TwTY8l4khSzw26yMxQP+GQoqjFVM+XZg0dcnJ2iY6QuSt75wtt07ZLl5RnRRToHenTAf/qf/BX+zb/6J/zTf/B3mI4mHN56g4+fPufh6TNaBdEU2VvO7A4LrTRDTZCSUNWrjOpZpTCFEuNnSiRBUOS6ASPMwxDytKkSxis1dv8LjI6+SRwfsehaQt8JqKQrzPwNJrd/EW9m9LrAJ7jabPn45St+5e5bvP3VX+WDl5+hokz/tS1R2uJ6mfxooyisxSOhV9ZYCkrG45mYVKdAUgVo6IMjtBs6Fbm8uKDrZAo2hO8M+51WCqPlgrgY8uRHjitjZCIuBvY9ZVVT2IKiKLFFyfxgj9PTV/R9L6npafBYEsm3LD9L1wngGLwnblu6TWA8OWRlVjgX0NFifEltooR2VTMmsze4eetLOOak5hZtGLPsCjpqNJGZO6PefsJqHWA8QR+8Ac0RZVWLlPb8YwptKBHZNylIanBRYC00dUFRCMBVGYRFlFl8IWbpaRKmat+uxUMV8WEjQsgQavQCEpQE8asNYqHhQxAmwQA2xQB9T4qegDDIlUI8iX0vXm1KZyagWCIkJfK46KSp10BIUjjGID5gRV1RWCuT3lwAogaP5KHwGwokDSmgUiCGLSrI5C1HDEgYXxw+Y49JUkT0aFzrefDsJbNG03Ubzq/WJFOitICJZgeyDNLkoV3ltWI2kJTHmkRyWwo83/nFL/H9X/kmt2/tUZqAVY6Ix/ceoxN1Yei7LUoXuKiwuqIZ7zOZHlOM93ap0iFlL0sd0cHnlEvFZK4Zjccc3rjB2dkpl69O0Mby5a9+nQ9+9MdS7NqSrl1RW0tdVUyaEYd7+5TG4NoNy/UKnwdJ3gfWyyXdesNqJb5ytiwok2JvNGNsG1IficERQsJUoCuN0YUASzFLRaJ43RZGcet4n/m45nS5EaaEIgP3yC6pYPAdCz5kdpLZNTNd1+8kocMfrTXeOQG1ErnJkqJz+E6G4p2UsJn1MDQPPoW8N5ODktjtGUopTKExCBCVPOLtra4l6ZDZwD7s2L+vhz4NxbDKTD6jMu87sQOSk4LCWilq875kjCUgieTFuMFvtqQQKMty99xaLmBmnKTdeyoKi7Ga7XbL4IlWFIX4WS8uON6uUApu3r7D1dWS6WxGM92n7xzBtWzXVxzeuc35xXM+/tkf47vA5t5dLq423Dg4orQNYbYv6xt5rfOzZzx9dJ9+u2I2nTIal1RltWOEkAK9E4shraBtC5Q2pCCFiguBka4ZGwkaWl1d4B58RjKWsm74dL7H4dExd994m9n+IXVlmTBisWnZdKLKiPMx6xPDp48ecnK5Yn5wwP7RHZ5cXbDSDxhXBXcP7nD7zh3+2l/9r/h74zH/6g/+MdE7ikrv2NeJnGQfw26f7J0ntE4sc4zcayhhpIQU6Z3H1gVNU7O8umRxeoZbrTDBo2PuP/N3/+8C9F9/DD8XD/lrVvewloZ/m6z0GJ5bJvka5x0ffPop223Ln/vud7l14wZaJ+zA/t/50ytc32bmiWIXBJIQW5yiYDweZ+ZvYLVeo4yhrCqUtvl1BSj+efsPAWh3Cp4oIZYxyJ6cgoSIkRIq9rSbNeurczlnEuhCQqRIsO08J2dbnp13rNMh3u7TqpKeJeggTJnQo2OPCio3cwGVoFAel3p0cmgCyXeQnLD1Q75uMTAeNXzlK1/m9p1bvP+T9znUmvmtKaGKbDcrvNvSthFszc2DMXdujams4sHTM57f/5ifvP8jFs8/wJqan7z/U7oQuDi/pCodzWSPV68WXF2e0bdr+s2S1LeooiKlyHK5oigLvFIsth3jLH/btGKf9dn9lyRvuHUDLhaObQcvTxaMxmMWl68otEws33zzXapmTNEnqqLjs5/+Hm5zzo3jWyQNf+nXv88Hnx3y5PEfsOhO2J4v6PuaYlxhLLswnkhCZbsWHyWbwNgKrTRNXdN2ndhg5ZoqxYgPkZDBKmsttqlQmUUy2ZsTTaJTAedbvFLQFKi65p1v/wLvfP0X+PzZI86fPkGtVri+R0UB5pUL1CHhXSD1jj5GnBIPuMIWHI6nHFYlb9y6SWzX3Lm7z+npCQ8+fUm37SAaacS1KEfefvseR/sz/v7f/wf4mCirMUaBKjQhRTCRQMeTq084/RcPOHz/mK++9x2++t4v8oUvfoP9/Ru8PHtBHzoOjo4I2fdyNJnm+xVu3r2L1pEXL064//FPeeudL0rDmnqxV4ueIQxJGWnAkxQw4kvqWoieyXjM3sE+xooNi/demOdR7E0k5FAABNd3FKZAG4GfvO/xPlHWFZPZlBefPyQ823Dj9i3qwmBST1XKfdu5Dntrxv43v8Gjj5/wX/zmb/D4//xHLF68oDq+zR/97j/kH//vfxNjtngF5VjjU8S7QFVWeDx9DNzZP+DNO3c4OXnFq4szFuslnz26z2/+xq9x8uop/+Zf/5DQA7bMA0YBgmxQVFFxNJ3xsj3jJz97n5tffIv9w9vMZ/uoyZjORVTUjJLNvqoZvMyAYIwpMzWlTuid+HAfzGfcevMLBF4bimpNWZYSCtptJVS3qrKPvLBGQ3CABEcO/vXT2RStdQ7bW6NULbZLRmpnCYcS6NzrkhBzqJSG5y+f88FPP+ZiuYSyFqAu+5uSNK7td/711x0juZgVubEyCZ06KrfEri9Qy0vCtmVUWaqmIRUVUSXKpsSUFfV0AsbIvZpEUr5YLblcrTi4dYvJ3j5Jafquo3NiGaFy7aeQWsjvzp7rs0nlWlsh/qcmnz8SCqnzW74O4cwljtRPgyIpCWguLFGzq9FCSAwGnPJ+RM1irHgwo6+HQxkykgF0vFYQWZtZrbuaSIB0o4cAsqyG0kaYgLrAFqUw+/T10JOkMrib67VB+RWjAC/qGrxKQy2H9IHSAw6hmoNn7mBfdO2r+/NhuLmTGIZgWuwkQg6uvu4xQGXm5bA+Xic3yPObXe2QEsjlS1nWL1+iiFYVUSlKa6irGkhs+o6rxZVYcyWFT4HS2h07FRRlIS8dcn2ktQzNBLxWWK3pnaPtOrFDs4amaRhUZCmzYo2W4bD3nr53bDZSrxZlyWANUViLDy6zgiUALMXBs1RYv6Is0Lvhl83v12TCRed6XC/PUZZ13jfSjkBChJQ8XSdg52B3YrQSK0bEXkUXRsBsBJwvilxr65ISz14TqUY19Rjme4q98opR6amqTohzSrIzYhT1p3cx9wGaqLwMllRksL8cvlux+oOgkviz6yT4gRG2tsITfI/3Gh9L+hjpuoB3kUJFDmYlx4dzqskx9fwu1XyfyaxmNptSNg2TcUNVVrKclNCZBlvOXRCe3P0oLQShGGWYFJALF9SuAAAgAElEQVR7pazG3H3rC8xu36Vzke26Z3G5xTkhX8ln7gm+J6asilW5f0GBNkQtFoZd29G2K5xv2W43PH/xjKdPz9g6Q0iaPnrafo2PoPU5pTVoU6BsQ6pmeN2IDeXiFf3VCetXz1iePyWuXqJCTznaxzaBNJ1j529TFSNqPYfxjNbC5kwR2xW23bK+PENbuU/QJeN6hFFRwj2NxiiVrTa82IF6v2OX++DZth0hLqjqGozsOQwkK+/o2hbnApu+J3jyPSJrkJTYLC4oTYGdHaLsVIBetZsC/X8e5rd+67f+1B/+//34H/67//63/sMvfwNTWvR4RHG4z/ydt7n7rV+gunmLq5jY9AFX1pTvvI0rK4ItsboUNlFZEbYbNpsV4+MDQBO0JvQ9n73/I7i8pMoHOToRlQAZnkSXIpcmcfPb36S4eQOvLcd3bjOkvL/uFah0bgKDxtYTprMD+q7j4f2fcHX2nP29Ob/8S9/jYG/EwwefEIKg9c38kGp6gG1GnJ+fcnl5xcnZCkYTnlye8Xy9INq0m8QpBUU5bFS8xnCRhyIR2w4T5NCKJjMqBeElKUNQEaKGaHCpxqkbrMr3UHd+k/HX/irFu7+OPvoGavYeafYu+1/8FvbobXz9Lnp+C19U9KlEq4KULG3fczApmOs1Dz/4N6jk0NpibAMovE9MZ0ccHN5hNr/J3v5t9vdvYsspBTXv3XmDkTISwpYU3iW6XjxTQ4icn54TIjgv3o+CYWTJUJDpXgCiyonRxN3hJyBK9m4Kgbquaeoa5wMXl5csFguZ9sJrv5W9gayhaWq2fYtPgYAn2YQk0Y7YtGtc2Ii/rbHYqqEcHTPdf49q8g6muMGyrVl5i4+GLjY4PafAMOpP0YvHpHZL52s4+CLV8R2KsRXWqutJQTOuJxhj8SpA6qlrTdOUVEZn8l8geYcj4jKoEELARUefmQ8pOPGEjUF8+1KQMLDo0clh6DF+A75F+R58j00xh3558L2waH2Hil7WbvCkIIcIScIwUgqolFAxoAg7Bm30juidALzesTOQVxI4IRNZnydw4o2jojBboutIvhcpQHSo0KNij4odKbQYIiRPih4VhKkLEZOiXEcgafG09c6x2nSsWo8LiNG+SthB8qll8ikRKuRwMDnQrNGUNhJji+9WHE4rvvvNL/O973yF6digYkddGEpr81QSabqUoW07EpaimbN3/Cbj/TsUoz20raSBDjIhJwgoKJlskT4ImK2z5Elrg60qBluPi8sLPn/2FEViVJbsjccczOfMpmOK0og02DuZugdhRistQKB3Pc47gYdCoLGW23uH9NuWq/NzYThpTVlWFHWJLqQICUFA08G/S6lEVRSsVhs+f3kmERnWoIzO4Q9iO6BQWU4m9693jrrODVFMu6LhdZm4Vpq+E2sNa0T+du23de3zmavpnf/ftXdrbgrMNdikrJEgkaLY7Zsqe2QNE+YBHIu56ZD9XV0zPV7f9zNANtgUJKTpEJ9nkScqrbFlsRs+oA2BiAFcJ/fFEFAmgyedge0hmEznv+XckWGVeLUZI4EAMSSsskynB9SjfbSpqKqaL773dc7OztmsN2ht+fLXv8B6dcXTR49IzrNZtxwd3uZrX/8a+0fHbLYdMXiCc2w3C9bLSyaTMW+88SaHh8dMJ6NcaAv7bAjKcq6n7ba07Qbne2KEGBVJa6pxQz0e0UwmNFVNQaIkYmKgXS05P3nGowef8vDhp5xenJBswlY13juc74iFlf2q95ycnbLabNj0La+WZ7xcn3B68ZzJuGbSjJmP5rz15pe4Wq54/PihgOdKUnHbXtK1Q4xMplMOD45o6iazaeS8NFoK9EKLvC8psYZZrq5YXlzQXS0wMVAMxejARBgY+K99X9e+eNesmtfZtUNz+3rjSW78ht/VWV5pjN0NwRbLBX3XcnCwLyyXEHcgRcqsMtlXhSE1eMBBlkkqLQE0WpLqi7Jm1IyxtsJksEX93OcBpUStsLi6wGqVbQby4C84vG+JviMGkYETOlzXcnZ6Se8CpigZj8f4AK/O1zx4esn9ZxueLw2dPcBnj+J2vSD2Swie5OXf2+UF66tztotz2uU5/WaB6zakfo0OHQSHwiNuMRGVHAU9773zJvvThna75ZOffczyasU3vvY1Do8OqWsBqLvNGh0Co0Izn1Qoa/jhh5/x2c8+Yn32jJMnD+m7NUVRMp+PwW+wugBKHj64T1EoTAFnZy+pTcloNqftO3wqaaYz9vZHLDdbHJbTCwnp8n5D121otx2rVcAFh09Lzs/PxKPY9dy9fZuyrJjOhSV5en7BV7/yNUalpV9dUFnD5arF2JpxMyF2S84un3O1uSJZaTR9DrPVaUi7Bq0turAYW4iixLmdpH63pyGgRcyqIq0UTdNgqlJAR3L9WWi0NfJ8dUU5n3L41j2+9+d/k4P5m/RxxdX5M65evqRQlr3ZlM1ySV1WVGVJt92KpRDkvU9Ciw6nM45HDfduHPKNr3yZ73zvFzg5e8mDBy8IXpN8onctXd/ROs/Z2RneiTR8s+l369doA0ZlkDOiTCCYnlVc8fmLJzz67D5PHz5hbzplfz6iqArGsznCNtpNYAABiVQKWGu5vLhgvVqzt7dPIoMJWss1HcJrtDSYxhjxsww9e7MZs+lM/EG1DCmT9wTfEaPHOfELl/rKYXN9772cgSpGVotLqrrixq3bhBi4PH2Ja68obOTy9CUXz59D6mn9lrtvvYup9/mDP/ghJkba0wVtZXl1dsrv/q2/yWbznGpm0eMSVRpc5/BdVgjm9HfnnHxPIYiSBYWPHb/8q9/jl3/1V3h4/xNenZ6hjOwbQyARSQZLprC0XctHH33Io4efYnXgcG/CeDxDFzNiFCWVNiVK2czG02zbli6Ha6r/l7k3iZE1u/L7fvfeb4o5Ml/myzfVXMViVZFsqsmmqG7RarWF7rZlQxsBMgx4Y8NrA154Z6M3XnglLwzY8M7DQgY8wG3DgmHBbbVFdrO7SRbHqmJVvaHelC+nyIzpG+7kxblf5Gta0kZeOAqFzMTLjPgi4sa95/zPf0i9T9PUPH/2jNFkSjEYYrKCPlypVygI8wyqakhRjTBFRcDjnQA6Pg1Ed0GcSsnjJz/xl6Xw2Uv7MCRALsrzM8rz2f3P+NHPf0HQmQQjKVI4ay69oHVJGibAo9QOPZCXwnLahrLbUKwvKDYrTLtFG8VgJJJiZzJ0nmS1mcbGgFdxR2ho6prL1YrhfMb+0ZH4xltL0zZEn8A+SOoMKW7C7txJhJdwPaBOUJUMv+kHdWb32vZEhpfroP5s251r4Zr5CioFt+XXbNk+iyAqjMkFmE2WB4rev/Nl0oTZPZ4wQq+H5vSkDq0xmTBly3Ig73F6X+U59CWhful7tTuvpbY0mEzWgPqVwak2YjHY12ZZ8lPXiSKiU71KvCbAKKV3e0g/xNnViPQAa9r/emVpz3xNgPTumhOw/LLfvSISVcRkQioR1j1keUGe52ldJ5swJUC5MGLT652gcZtAJecc1tmXArv8DoBW6X31IfVUXqwSdl77OmMwGDCZTJhMxozHYyaTKbPZjNFoJCFtSammjSZPeTCDSuTyeZYnxrywd/M8l+eQ9qHdYDu9LVmWYTKV5OcSBu6cpbUtPvTenpEYHd5buq7DWvk/JJ9bsVyIO/fVEKHzYt3i0RTZgEGWcXM2ZD7JuLE/ZG9cMC0UVZVRlR2DCopC2Pqk/bq3cfIuSC8XIxLv50G59FVUmkpJFk6IAeUjPjQy9LSBtgu0XWTbZKy9ZmMtdaOILnAw0xzMS2bzA6Z7rzDZv001r7ixN2U+m1INpbfq1yT9sF1dg/29B33vEX293oHE3O5cxMcMUwwphwPm8wnj8YByUAozvcjwrqPerHDdFmc72nrLenXFarkUK4y2oW0tbdPRdR2b7ZbL5YqT8yvuPzzmwaPnnF1ecbG6Yrvdslpvqbc1m+WS7aZmeXXF6mrB6vKS9eKM+uwLuvMv6DYnuO0lWWikh4/yWsZqgh4cUFVjyvEeen5Ivv8Kxeg2hS5Q3YquXdHYLet6SWtbts2WTSPK10Af5sduSOGdSwOMQNdZ2q5lu93S2o6mqdluNmzrmrppaJqarmuxTmzIfJQBUFQGdI7W0gv2THIbIlGLh/Lx/e89/4M/+IP/kl+5/f8apP37/+F/9AdfffSYL77/fU4/+ZTVyXMJTzrcZ/qlt7j1ta8xfOcNJu+9ySLz6HJMqEZkeUmMInEvhhWreoOLgWJQoQthA5wfP+fi/gOMjgSlsVHThsjWOrbBs1KR+a+9x61f/xon6xVKKe6+8QpaZb/ScImHqY+GrJgyHM7Z1hu+ePRLnjz6hJsHc37zN3+T/b05n/ziJ5ydPhdTdF2y2WwZViXRbXn86D4PHjzm5HJBZzKeL65YOvEGIwXo5JmWglFdH7pyTiY0PwSUDUTLriDoN1kBWJJkPmS0asa6fJd6/m2qL/2rTN/7Pbr9L7PMpjRUoIeMB5G3Dg1fvTfBXq5wncapAheUhBDlGV4r5hW8sV/x4Bc/RKMY5CMG1Q3m8yPu3HmLW0evM50colSJt4rt2rHewsCU/Nrbr1K5llzpJK2QYIaiLAk+sDi9xPmIRaZpPnhhuqZO0UcJ5Qkxpo03vTRRAp6U0ckQW7PZbNnWW+qmEUZoP7+NUYia/eRSKbbNmk2zEhaizhLYp4gGTDGlixobNCrfQ1U3iYPbxOo1TPU6zo1otg2d66jbNW57RoZjNJqS5ZE8ruiahm0YsKKiU2OG+0dUw4JBlTGfT9iuLjC+kbC1QjMoM4aDgkwrVBQZkwsBFwSktE42E+WdGK0na4HoWgFTSTVDDEl65TGhJXQbom3wViTGwXV438rh4QNt2xBcJ2mEwdG2NdG7BGjK/cQYpBGMyOTee3YS2OSNp9KkkxiT9COBuN6ighUfW28hyDXTbQjtBhWSX4tvUb7FYGUQEEOyZxCv28SZkJ9JZvpKgUrAq9KgjEgwjErMK78DZDVglHhaaQIqWExwlJkmUx67PaetL7l7e5/33jritbv7jCtNnisGg4Ii17uG1wePD/IZNFlFNpixf/Qa5fhAvIgQ9r34C4uHcHDS8PUS6OAt0XUE12K7JgHispaLSuxPzk6OGVYF+/M5pTES9pRCjZqmxrvEfE6HsTGaMs+pioKgBCDWia3cth2XFxd0qzWVkkClcjjAlDnRgEZsCpQWn1VpngK5kYL+s4dPJWQkl0JWpGaaXuznUphcjJHhaIhKg5O27XYhKz2LVfyyPc56qrISsFNpiiIX8FcnuwOuJ89ZllGUhZBrtN75Y+2AtATQ9tKvHUtQp8K5B3V7Vm/4y8xeuGZWvPy9S/YIWS7gb1YWUtAbAatRiiwvMJl4Y+nkQWaMxhFoNvVfmmpnuYDZ/eP2csAYQ0pmFofcPM/T7xhUCNi6ZjqdY4qSPC9ZrpZYHzA6S2ncnhfHJzx++IhCaWbTKYe37zKb7zGaT9m/tUfdWE5fnNJsLwnBcvvuK4ync9q2Y3V5xWZ1Sb2tsf11KINzDYvLM9quhl3h76VRdR5rO1nrTsrhrPedywvK0YiiLOV9cR0Xp885ffYMt1phQkduFLooUFkuRa326GFFrHIuuzVbv2HVbdhslmyuLpiOJ+ztHfLqq29ycXrB8fEzAWmjDCjE/1EsjUKMXF5d0Tayx+rUVLrgkp2ORmVgbctmsaC7WqOdSwPZkGxiwvVZ/NLtV8PeXv76cnL5NVtGmr1eBaL6UzutR5l3yd95BWeLS84uFuzvi2908DJcFtCcBFzY9Hgen0LGvE0hmz3jCyjKgsxIMJB1LvUaImeU55rSn4NYWmSZFg90FYnBsd1eUm+XtO2G9XrFer3GdR2bbcNiuWU2P2Q4mbHedjx+fsUnTxY8Pm256kqsGuOCpt6uCN0GfIfyKcyk63BtjW9rXFvj6hVue4VrNiKtUwpvW4KtEe/w1Nz7jlGleP31V9ibz9nfO2A83OPmzSNsZxlPKmazioMbU7ZXC7rNksvlFVfbLadXG77/gx+zXp0xnw15/vQFy+WCe3eOePOtN0UBEALDScXl8pyju3d5/f3X+fjjj9mfHpAPx2RFBipjvQ0c3jog4Nm0imfPL7G2JTNA8DR1C0Ree+OQg4MRv/j5x0TfEoPj3u27DKqSzfKKp48fQLCAJUY5IzWKh48e8+LFJYezQ4Zxha1XvDg9oXYdsWd8eYXyJK/HDFOWDEYjAd3bNsn59Et7r9oBtaQ1XJYlZVnibEdMoK3UVAoCYtk0GKCHA/Zfucv05i1CgBfHj7k6PWH57IR6cYVxnvFwwNnFOa2zhFaYJbYPfhUjc2xr2S62HI3nfOODr9N1juenJ1xsNxwfn3Cwv8df/+vfphhkrOoN1XhE7ZwQMlIIDuqan96P3rySUBCnPA5L57ecnj/ls89+xsP7H3F5fkKGYTwYk/fPTwk4IRwHAUHmsykXFxes1htG4wExeGFkaXnfUQbxtRM5d7CWrt6wN9+/9sEU1gC2XUNKjm7rNbbdUq8v+fgnP+TZg8+grVHeElyXgKCINgXlaMrBzdvMxyM0MBwOuTg9ZXn+HMKWzWbJvdfe5rXX3uXZp/eZE9kfTPmLH/2YP/uLf8Lp8X1iGbAEvNZkJqdZb3BerFeM0ZhcqHXOWm7s7WGynE3T0NkObzu+81u/Rbddcv/BozSS18IORfYzHwNZAlps03Dy7Amf/fxnPLn/Kc12zeHRTUxRJBVL2pNSnV7XcsYQw87HMi8K9qYzslz2Kp3AN6UkGHTHtssLTJaTVSNUXuFthyIyGAwpimIX7giJ+JL6AxkEq2vfe6V3A9vkUE+ZafLQ0TUrPvn8M754cSbeylokzv2ZKHZ4LhEXABV3fs/aSMCmty1Zt6JqrxjWCyrXUJiALuX6PRGMACFaq11NkVwkCSFwuVyiioybd+6RFQNa6+msFal38jAVlYvenQu9+jOkdS3XFXeATn8CvVzrSADmNbuzD+v6p/muK/qBuYCmRVHszrH+rJPQ1yzZ/OhdTdSfpdePrXY+79cNTCJOJGVGlpcUZUVRlhRlKQCqkSGIDzJE1mmP01olIL0HhiX7JM/y3c/0A1NIXr1a6jhUslHor2xXCXINh7MbsPfD7N4fPfSAfbrPRCqltwQw2nBNVrgGJ7PMyHUnQkCeCwPZBwmp2/2nZFBEYhc771lt1qy3a+pms+steoYvGnwMCUyS7JLwEntZ3vcE+BrNoKwYjiSktMgLqqraefH2Z0XTNMK8pe83DKPRiPFwJOvCSFibAKt+N1yuqoqyLGV9q36gKMOSsqqYzmZMJhPyQq5FJ0VQWRZU1YCyrBiU4t0cYDfsMWk9BS8EL+8cvuuwbYvtRKnnrPjUhhAIzuO6lqbpCB6GWrE/LpkOMmbTjHEF49yTlYGijBR5gTEVxhTJAk/s/mKU15Lg0z4QEzP45SpR7YD2mN5D52VI13WWrvM0LdQNbBpF2+V0TjIebsxKZtMpw+kR1fw21XzCbH/K/t4eo/GYLM/lc2Wy9FnqiTAvET7U9ee3tzrS+hqgV0p8i1erFWcvzjl+fs560wJQjUqmexXDccnl4oJtGpx711LXa5p6w2az5uzinNPTc548OeHh58fc/+wJj7445uTsiuW6wXeexfk5y82C2q2xXY23LX5nZQhRg3Vrmu2SzWpBc3XK9uo5BCFwmWRpaZ0j+E6GbcUINZjjxoeYySGzvSMm030ms5moTaLDBE+Ra/AeFxSrrQScCUs21ehRLOqcD2ybhm3d0lmfws1FoeF8EFZ82jeEEBtTqKGoAkLCkNAyAIoqw6PxPtI0aUhSb7g4/vE/FaT9F7Y7UDJq+wvgaYzxX1NKvQH8A+AG8APg34oxdkqpEvivgW8A58DfizE+/Ofd9zA3fCk66i+esH3yguMf/JCTO3fY/8oH3PrWN7nzV77CvV/7G7Rtw9mHP2XlGqq2JqsGlFrSIUc3bzFcXbJZXjBT4juSDwfc/tK7PPnu/816c0XQhm0IrFyHj55sNuLur73HvV//Oq3JWNXnNK7j4f1PuHP3TfK8koJMa7yVlHaTD9GmYrna8Pz4AY/uf8rNGzN+4xt/heloyOe//BlnF6cMqooYNbfv3qJuLD/64Y8IEZ6dnvH0+Rl7R0dEPBfrFdEoAUeUJstyBrnBaAm5ihG0l8mxzgo8ImNDCWuuUHI4Ch4mfpgRjXYVWzOnnb5L8ervMrn316hu3MUYzdR4jrxjkHW8e6fktcmY9vgRr92c816V8WDh+N7TBRdqhsZAsyC6Bc+3K7L4lKNX34HljDxKURQIbNYbnj29wNoGcLimEcm7UoTZkOXinAGgcpmMm0zYDyF4nLUiaVFOPF4SMw+VmK9RJoQqSTuF/db7JCUj9iDzskgvxQ6yeZksJfa5nYxapJzisWhDi1IRZSZ0akrQY2JUrGuFtWO82acrPFkxQ1cTKXhT0qDbnpO5NVQVXb2lCA1FkTHKN7h8D5e/hpm8wtBnZFnJcttx9eSXvHrja+TDGeXeGF+fc/7wUwZZzng8lo3Ud+Llpo3Q7NNhbZAGR0dhNkXfAiqBr1uBonMptAieTCli6HCuQfkO52T6qCD5e8qkJwQlDUKMuGRgH51PUuzeWysSdi2R+GlGAtaKt1DvJUtMwG26Re8Jyklj6hph4CqRDYWugWjFS1hi1a8nZeG68QpR5DIq9v65EbwTZqo8CjoxAEIUGZfRMRVS4gsWYQf4SsqurAHtLdHX+O0FnWvp2iXoyP78dUZDRZ51QEdmBpR5hVERGz3EFIJmI5ic4fgG4/kRppphfXqNlIA73nvxBw7X4QAhyL/rKD43tutom1YKvCBM5bLKuffGK7x78iU++snPWG7X7I2GHOzvMRoOWW82yaPSC7MrhOQTHTF9DVZk1DFgvEjVV9sVk3IgQSkRtJMwEK1NSoFPgVhRwNW+gVIK5rMJ8+mIF1crQtA7cPalEjIxVaS4H4/HNE0NCEur65J320ugqMdTDSuqQbnzrA3eCSskFdN9iAOoXRHUy/BBQPK+KAaVwMHsuhCNSvZ7I7LA6GMq6IRZjRKpSw9aoESO3vuigazXohIPULGwFrmMeLIhw6zEHulUl55DRkAx2pvTrlaEuiPX4nk1HA1x1rHdbuQ+oyc3GYNqxGq1SmFOCu+kEAxCc8ATWCxeMJkfUuYVyhgW5yfce/0tqmbAerXG2YbpZEJ0HpMVEroULc+ePWEwqzg42uPpA8O2a5hMp9RtQ73dcnV6JiCZr2V9GiNKigCd7dAqYjJhGhnAGAk+0EiicLepCa3DlCKrjwlF0UZjqpIcCF1Hlhm2XUv74imrkycUB/vMX32V0XTG2lnWlwvUaIiazckCECJOBY4XT3CLC9669RqzyQF7Nw75vd/7O1wsTnl6/BF5VRC1kj0nFdB109K0Eoo0NAOU1qk4E6GJC56u3rC8uKC5XGJ8H1SSPP1Ss9yvv39KXbT7+jJg+5ftDq4Hg7smsQfJ+vtMLBSVGn00ZHnJF8fH1P/ku3znG9/i3p072K7F2Q5lJJl8vV5zeHhEWeQ412HbjpgjQXzyLtG2XbqO3rIjnadK9hpvux2zghCoyjwNxuTCvO+o15c0TSt+c0bSsTvrOT1fsN62zKPi8bMznp+dc7lVbLoh3kyIZkBeVMTgcFYCpLwPwjFPAZmkMyYEj2824Bui0gzKG5SDIV0dMcpJAnRnQQVMjHQu8vjxE165fZvX33ibb/7GXS4XZ3z60U/52U9+ytHtOe+88xZ5ljOeDhnNJ5xcXPLki6csLpZ455lPJhzc2uP58ye0dUuz2dJaYQ/VrqYscrrW8vDBFxiTcfPOXa42DUc3bmCKCQ+fnPHL+yeMRoYYhyyurshNZDwYSMNtOqzb8OLFFbfv3mY6O+T46Sc09YrOvcFbb32JB5/fZ1Nvme9NOTi6QQwwHY5Znp9QFacMKo12C77y5i32Jr/B4xfPqM+f4KwnZNLg5FnOYDTl8PY9oobnJ0+ISuwpejZdWZZErWjaVs7vEEArdIhkRYHzgdA5INLiiEq8BQMe6zxF44nbjovTU378o++RB8Pq6op2uaTrPKZtOV89YzafURQF66V4hvquwziHFjEORLAhcN42fPcHP+Pp01NioRne2uP23Tvc/+QhPlqsbzk8uoEl0nnFYDzj3u273P/4Y548eoRGBg4Y8a0lGAGBldifRBVoVUfILE+u1jw7u88nn/2cn3z4Ib/9nd/ng6/+FSZ7h9RW7JmK0YBqOGJUDogxUpRD7j94wGq14ujmEbZz+K7BRkVeDqQhQxGVZrPdEpoWoqhkjBE2pu1aCI4iM+RAVok0tZyOUPZVVhdnLM+eMR+XlKbC25phWdHFwGJxwXQ05sbhXbK8xLmGqB4RlCVTHcNBSXCOi7NT8hhZHr8gm97CrFbQLaB0OKXQXcD5ho6G4ANlWZFlojJRIWC0xjnHVb0FbWhDIG47vv/9D9mb/A989b23eP+Dd/jBTz7FOZIEXYbgYqUVGY9GXF1c4I3BN5ZHP/uYs0ePOXv+lHe/+W1e/9L7RF1CzFGUAkKXJdWgEsuBBPrFEIlZgSSo9wCI+I4OhkMksC35WWY6MR8NVTFARYePEBPxQKGuw8JIo8XY5zQkz/xkJ4BK3p5odPTUqws+/vQTPn/4EJOXQt6IPagZIJUfSoMxYi8SghAWJFjUi6IsdBTRYtwGbWsIHSqTPs+6HpxW4oeuxQcSLeGjne1YbzZ4rTg8uoUpSuquw7pU+SqxGoupphZlhIBQ6iX2Zw/QxnjthdqfaT1ztvcx1Urv/EpBpNNZr0JVPTM0pBCuXIBNLfaB/f2aLEvD8NSLpXPQexLwmx471atS2ogMnETSQWmKspIsi/Q3AmgmMCRGSPLyLDPXwVyxB4HjDh7ObjMAACAASURBVEAMAQmJfukM34FZkOTxch7F0DOiYlKkXatfpP5Mfr1R1JsCWMstzyQMt7ftCuH6Gvrn5ZzFIDVUX18KWIaQr7QMAGKQDBXrdBqqaAIBopZBbow78LVuatqulc8M1zkM8hzlfcnzQkgNSu3UUeGl11xsLPpg00jvO09aDyjAaGzq1+smst5udwB3ZgxlXuJ69mp6DXtGcNd19HYXLr0+MYQEnMrr13YtWQLIq6rCOktZFEwnc4wuRCnVdIzahrqtWa83WNuhg4cgYdhaKYzSBAdt06Ji/5mwROMJ2pAZpD9A49oGW0VcKOXnaIharB8hoELPiRaWpDYlOkRi6IjRE73FxohyYPSIrCDtjRqdCGEx+RRnRhPznCIfYzMwmSbGluCjnL0+QFSUhaYsYDaZM5rdopgdMpyPGe9VzPb2qKqhqHF2OLtCGZJ9icaFVLsptSMxybA9XOMkoWerS+5Gpj1Qo3zF+vySbuPITpYMZobxYECzWUHwFMm6z2mxu2tdy8XlJZerms0Kzp5vePTsmG23ARWpbY2Ogdau0FrUtCHIPhGdwlcDTFYwGFQUoxu0VrPd1HS5xhvPtlmgnCdGGYjlRhHjFrd6hF8eEWe3aJq7ZCNLqTXjUUnM71EVOdX4kPWTH9FcPEL7E7IYiRhaK2u/rh2uW5MpsbDMc7HuFOKjYBx5lsugy2iyRNos8hyjSDlA0FqxXGyl8UcRcEETlEZFjU4WnaF14qP8z7j9f+FJ++8BHwHT9PN/Avz9GOM/UEr9F8C/A/zn6esixvi2UurfSL/39/6595zndNWIcuMZx8gNH/DrDYP1Jfu3SrJpy/rqEU+fX6BQBBXZXJ7LvjHaQ+cFypTcfOVNXjyFs4szptMpOsu58dprDN55k7Of/oSstWzR6NmQw1s3eeOrHzB741U6o1lcXHB1cU41yHn4i5/Srjcc3XmN0fQIT4klI6sGBFVwdXnFxdljnj/9nP3JiL/66+8xqAqePXvIo4cfofHoqsLojKPbR1gf+cnPPuXDP/uQbFTy+7//eyzXW/7oRz+kDS0xl/Ty/jBSMTKkIM+HFMMRR5M9VNQsVxs2zZaVbbCFxhcZqlNkpkrSWoXJJcFOmT32bn2L+Orv4I5+ja0pGIVLbsUV798c8N4b+9ycVkzMhoFp2Yw8g+qK4q0jruKM4o+/4H/+3s/Yrixh/QjlLnjUXnJsF7y6l5HpgnW9Zm0XNPUW2wizA1fTtgu6ei0NXWZYr9ZsFnvke/sURZl8L6EoS9q2o+0aglHgkhl12mSU1hgURI+OAq71xGEfrkGWkA57k2ny3NA5z3A0xoVI2zlQRoDCBP6h5cD2wWPyEnDEfAb738JmdwhK4fKCxWiKKSusbeg6z3S+T2trqFdoX4uJ+OAQvXcHva3J23OywYBGGZp8QjO8SSzHlOUQwgZ9/pB6eUG9voQbR2wbjR7tY7Um9y1DZdFZjvUhJXV6lDepsRdw3tlWQj6ChBGYGLBdTXSNTNa8JSCBdlmIhNjRdVsELhL2kgZU8kgLKsN7wLoduB1CxPTAt+4l31L8RvGawCth3MrfyPGrVSR6CwngkQKwA2+JXuwLDD4FHCgMLk31wku4rniBAVJcJb839VICKjFi0hQ3qhQ3s5N7kDyZPEbJ10Dy4Qt25/FM6CSl061wzRVNc4nCQ4zYGDg/fsr7b97epT4bpKjwHrIsx6fBiTIZZjijnByispGY4Kue1QMixRH/JRVjYuZ5CE7kMrbB2QbvHM6HnW1HTNYSWVny+jtfZrnY8OjBp9S5ZrFasW066mYjctcgshXx58qSbEpAH6MMZVHg6hqjNbPhkNfuvQKd4+rsjDxqaYSCsKciHqMFmPPeExGZfRscRZFzdGPO6WIpTU689u0KqcCU1Hj528Xigt7HLMuulQk+eZ1ep13LfRRlngB6KeryPL8OA4syAd6FP5hrZkfPTBQmhxHWrJbi0iTvKpUKe2ctWsv6CT1TP4oURcVraR1KYXbyGuFR2K4jy4SdrHySZSXWsclynA9Y3+58NVWImCLHAOVoTN0sxJfbO9arVRoqhOTtK5+Dpml2XtPeWWF/pDJRGg3FydkL5vt3mYz3GY3G0LUMyoKbt26xWd8nzzPee/9Nnjx9yunxBXfv3aQoImeLMx78UlONp0z2ZgwrzWa94OT4MfhApkHlOVmudsFmVVlS1zXeeYbVAEVk23V0bUv0wiBQyevXBbFXyaLGdRavhcnu2gaCpyxLgoJ8UDEoMirrqJuay+fP2S5X3Lx3j8Mb+6yGYy5sg8kzRsMZQ2Vw9RJjN8xGI1QUwC9oxZ1X3uBv/a1/nf/mv31IW28YjoeYvKBLha/zHcZoqmpE1zYYrSnLUhgqgG0bLk/PqC8v02AjeXlpYY6HXVEb5HOlrm0OXmYWvczE7m8mednFl+63HyQIo+za9283ktLJCiOxQkye8WJxzv/x3T/mr/76b/D+O19CG4PzHWVZslqtWa3WmPlMbEvmGXlRpOuSbbEsK5n8h4gyijIXJnoM4pcnA4pAlinQGlNUONfRdSLR3qwvOT05g6gYjYboStgvIUb2D29z4+6Ax88vePT0FKs0UUsgWKskHTcvSmzb0Gy3bH2dLIamVOWY3AiY6VVERY/dZmy3V/gYyPOCoqiwbYsiQ0ex8SGK32GmLNvlktIoitxgfcfe4Q3urO9x8vwxz55f8OlnD1HR886X3+Hm0R3qNmK7DLq1WIFsW/b3DhkOBigDznXU2y2D4YhoAwrLyeMHrLeXDIxmvDfH4lC5xkXP/o0Z7abh8nzL7VfucXV+QZkZ9l/fo9YNCsf+jQPyYsR6W/PG22/x7PkjdNnw7tc+oMrm7B1GBvM5b7z5BsWwwjnN5YtzLi43fPu3/ibrbctolDGdz3j09Ix/+bf+FZb/+B/yYPkFtnEUhSarpOmsGy+S2NBb3ni0ERaISmCG7ToZWhph32V5lvw8RQnTWStrNRMPejMoKTPFanlFoR32LKfbdtw+vMmNwZCTq0vq1ZKy9aigaJqO8XCEry1d48jLHJzYMDlnZRASLEvbsF6teHj8nDzTOCOWJYN8SNM6PvzxLxiMKqJRBHJGOmezbblYLGQkGBXlsGS4NyAq8A34usM5T9t1gE7hNQqKCAasu2BzseV/+ocn/Ohn3+Odd77G7duvc3TzNovFWao7oqg68ozZeMCLp0+5OT/ANS1Bid9jUGCKEuGkSFM3HubE0JCXQ2IU6wDvO5GcpsDCtq5Baw4Ob3Ln9bdp9vc4f/qUohow2z/g+PgxrtnQ+kDrLKqZMhqNGU4mLM42KByZjnTbmmAKBtMpBwevcvveHT79R3/E0BRMK5jGjAuVLB00YlsVBEgaj0agNU3XJnmxAHyL5XIX7NN0jst1wx//yZ8zGo0IMfnldlIjypBUht3eWsosp8xzbLul0HA4HGI6x5/8L3/Iz3/8A772nd/mjXc/4M6d1xnPj6SOjIGiGKATSGy7lqZtUaZglIlEPmbJUgkt4HsE6z06apx3VENFphWdF6fbgNRaWmU7lvQ1IBnT1qt3tkKhr5NQ5Il9udqs+PGPf8xPPvoll16hdAEqeXsm9Y0P8pkiKmIUhnGIYqFFhBgU+EjuA1VoKVwL1qFzkbX76K8Zd1HCyHQuHqvKGHCOzfKKpmvZv3mbvBqytRbf++dKEMc1aSGq3nVB/PET2zXGmGLqAPTu93oAScomuRDnHFkCo6EHD+VvehapNobcqMSUNKDN7n1RWu2IMpKqLhfUg75S70mtmJnE9PMie9dag46pfpX/s6JA62wX8noN5poEGKeXL1GDX4Jgd9YGUemkqNN/yWJIWMN9nxF22QDhZSZkVCmqS1S0KvaP0w9Y5axWqQfSCcxURthzYmcg9ee17ZEQXgyaYMUnXxsja+Cl5+is5LMESccSVh/QWbdjibddjY+BOkmvtZLhrFLi9WtMP5QVwDhPbFi5z2ThFRxRCSCrkHBHbzv5bIS+z74GrK/vV0gKJpNrccHj6i0hSJhejCkvRiuxrnFiR6C1JihF03UEF2g7UceoEGlakYwL8BtQBBgMmd6ecOPgFuPxnNV6w+ryirZrWCwXHB8/pVktCc6l8DCwtkuhgBGPo1BGSGFIjeF9lOwInafw6UxAa5XTeU2IBswArTvEu1lUqYEs7ZVpgBQDPlix/YpIv6kCWWaTDZ8CJaxKk7zLPZE8l+z6vMjRWS5DUN/QOGH95qZgNhkzmc6oZkcM9o6Y7u0xmg4py4KoBKCNMZGb6L2VhaBnTPJJVjoFVSV2d+z7497STuo9hUq2WBF8Q6Y9VSEWYm7dsVhu8G2Twt9lr7NWBgBaG7JiwKbb8ORizdPTS863G5RyRN/R2I2QzlSHi5FMyZqKXsgdTiuKYkiZGYrJTXRxQBUCdvGM5uoQszqjvjqlXT1DhS3Gi6pvs3yBOnnIoLiLLmaQBWJxiBoWmKwgjo8gGGK9pYiG1ja47YKyyCkGI5yPuE7677ptUMoT6xp0htY5w8GQTElgrzI5KLHsqaoBVZFhFIJL6IzWeVob2dpAU6cQO2RPdCFK9ov2GB0x2TWD/Vdv/0IgrVLqHvC3gf8Y+PeV7HS/A/yb6Vf+K+APEJD276TvAf574D9TSqn4Mr/+V27eeiZ7NymKIcuzZ5B79j94lTv/9t8me+M2oV6yPT7hoz/8Rwxmd7n1wTdYKMfyRU2cbRjPD8nKEboaMdk74P7Hj4laMb9xg9HtIz743d/lwcEM3XqapmV8OObW66+QT+csmg7Xbnj24hnRtlTDEuqWsy8es77ccvNVxeTwFQbjPZoA54tLzh7dZ3X2mFfv7vHGG6+Q5Rnn58/49Jcfsl1eMCpzOWTygoefP+T45Ixv/dZvQlbw0ce/oBoMeHR8xmLTSNOam8RUFEDKBseonPDbv/k7fPmDr3MwmaOi4XKxYL26ZNO1dM2Gtu3YbDxlOWEym6GDTI89gWwwoZy/zspNcWrL8bOPOfn8I/T2lHI54Ojgr3E0OmJ59oKH50+5e3QTHTNcfcJ8HPi7Xx/wxQ8/5Psf/oQq0wwrBaHBGI1dK1abUzbbBXlmCN7hmprYWkK3JtgrXOjIdEbXQN2VdK29BpGUpN2KVDyIn6dP/iAhAIYYVEqSl0PRJ9/0/gTtk0xDb++ASLet87i2Y39/j3Xd7CbI1jky2falSCAdVlHjVYmtjthOv8amfBtnIOQF0VQUOqDVCU6dUWcVVGNcgNwHsvld2vIm6+IOZqApto/YxDVtHNOqOSGbCuU9KBQV5f5rxOyC0ycnHAz26bynMiUUI7rYgLKJdiWee9aFlI4r0/DoPa5rcCHiAsKUCQ7jk8esjqImjAijIwZC6NJBFOi6VjbmNAiQF6NBsFYjE1g8mYqSJh4jeGnsXSsFImlCLxtDmpYmpEFAVA/RElyTikCR0CrcznrAe3mP9UvTaSGXJaZCz5BOLEUZtSZXoR2qIfYGMfbrBkIUVovYHgSUc8kzN4Ly5LpB+QycJ9c1rrlAuxZsS+5risygTEbrYHl2jreWvBQpkEZhfYcpS2lkElicVxNGk0Pyag9UlqbCYXfdvRytHxdLSnmD8i0ES+gasVzAUmjxBw6J6YfS5GXFbH+ft995m8XJM9bbLdYpcr0lhk5CBbX4WZo827FjeoatePXJZNcHAf+7rqNAilZPpNnW5FVGNiwgJHN537/X0DQtdb3BOdibThgOStoYEpOWHegKJCbsX5Z6v3zr5V09sNWDtUAKOUppui8V1DswjGSloa490+Q+M7TJ+sNKkpq1ItOZ+FGp1KZEKLTCW0eIbreXoKQJ8cQEVCeLiCQpE7aOSlK1xESMEWNygu4Bt8Qa8ZLGK8C3Jy9KlNYUoxFd19FtanSImOgwicnRy9Ocu5ZMkaRvUUNC1FLxHdm0W16cP2d+cMRwPCI3cPrsKbWLjMcTMg1//Eff5WJxzptvvInW0G7X1KtLms5x540xb33pHT7/6CNWy8e4pqMwmTBD8oJMjcjy5CtWZKBztk8fonEMR0OR5SUGcjSSaOs7i+8sMZPQuRAtQSvxfHUdvmmI1uIBU5boXP7PixKd56zXa774ix+ynM+ppmP2hyLvH0e4PRpRjIasLi7oGseDRx8xHe2R5QqtK77ytW/yjW/8S/zJn/7vROcImU7nQiQzubA0vdCe6rYVALAoAM9qeUm3XgurPDGBeu/gXWMpNGZhvphrT+WXZYO/us5fXu/9udaza3vGUUw8XaOzHashpLBGrYwEmCCA8cVmxR/9yXd5dvycr3/lAw725+QpNKTrOmLw0nkDdV0znkx3n7EQE4PBeTrXJH8+nfZv2bNl2Ik0bUHRtRZr12zWK548for1DdVggskjretQKud0scZGxbZb8ej5KaaYgRJqZ8SKT7OKZFF27zLTOCQIczKcUAwHZNqQ55WErcRIVw4px1Os7whBJ3Z97yuXhrQBVID9vRnvvv0W3/nO71I3Wy7OT9k/2Gc0HTBt5sw4QuvAT3/0p3z0ox9zeviMe6++zvKqRncrRuN9tM5o24C1nhhaVqtznI+YFgZlQdt0rNcrhqOSohxw6+YBsGG5vABlONqf8P67t7n/8ITG1gS7JS+n7N84YNtaWuuwTgbMV82SvRtzUBle5WSDjMP9gtu3XufjX1b86Z99ynBvzOHNI375818SWvjyV95jW2+4d3fO5eWWV748YLh4wcH3v8ezVUbTCahmlcM2C5bLJVmZk2eSem0QAM7pSNNuUUrLZ8QHYRUlTzsfOjnXjQYn+QadFQb23q1D3n7/HT7/6CecnL7gS2+/x3f+5t/mcnPJ5dljrp4+gW0N0eBURr1pGBQlhwc3eH78gs5ZdJHho8PZCM6iPQQnvtg+1yinyKPsJ1rnZErAovWqlr8Lke22YVFWtNutnKdivsz0YAoFbBYbTDHBWQ+rtbCuIXlOB6IO+DwQTGTbbXj2yyf8xad/wdHsDl9756u8fuceRlm6eo11joM7r5CP55w/fsJ9pbnz2psMxiNiVHQ+4DpHVlTkUWOCw9slWIPHkZmMQnnIAqYqybKcYZWj5hMhB+iI61qC9+wf3KAYDNmuV+RaBgVVbqiKjFx3GOPpmg0vHn/G4uQ5RMNq49FF5PjFGdsm43x5gRkq7rw65ry7xDQKZTVBux04ViQfyxjFjqbI8+RX7ARMScVjWZZApLUdp4tL/rv/8X+laTdEBPTRyvR9fxpAN2QmoxqUNI1GB2EZ3ZzNuby84viLx5z/b3/Ig49/yje/9W3e+uo3me7dYVCOUw0uqrGrq0tijMz3x0DEerkG7wN13bFa1yhlyPMC10lKejmeMKw8xiiIBh0lUKqvv6L3XIf59MPvBEopTaYEvHCdJXrHs+MX/OBnP+fRwyd4VaFykxQzMhQIyH7krCNYCWYOzl+HTUWQCbcld5bCNYy6Dco1MvTOJTMk+qQwyTKyMpdhSBp4i7Ig4pxnvrfPeDrBpgAq5yS4J4aIjqneipGQ1KMa0pBZ2KIYIRf0NVdfT/VevS+DlX3t07MfQViBgT6TRe2G7RJkaRKwKOCsgJ3XNlK9XUJ/psZ0vSo9jtKGssjIk6+qvDfp99MQVOrn+JfOUZEV6109FmIkuECmTbK6SHYjPQN4x55NmQmJ/dr7d/b32wPb/Uohvgxkp+MyhXCp/ldi3L1m/S9Kb+rZ5RgkZr+P0iuFkLxKE3gq6/HaIzxGT9PKAMU6Obt9CGhlCDEpfILYBQZIw18jbEOErRzS2neeXUZFSIQRm8DhGDUxDQuCD5g8I88KclMg3rYR7aX3zPJMAPcgYLMxOtkApPyIVMvq1Iu44HBeWLe+HwSpFNRExGQZ0TuKQSl/E69D36y11HUD0WPbjk9/+QkPH3zBaDRl/8Y+4/GEohwzmg7JjeLBZ5/SdXKmxehpaovtvOxTWpSnSkn/o41BRUWuFJnqKJXG+JzQebat5+LSUthAfiOS7SkoCsCRidaZoBXeZERv8DvQE7yPRFqUlkolLxwFlXgmp8+I1ppgPCoEsow0RDDYfk17R2UUs70Zkxv7TOa3KOc3GMznjKYzyipPFWMEZG1FFRP+IaBt+iZ9jkI/nxIAVu9aZ/rwdJVC6lUKg0Vl6AQ2y7pIqsOYasPU8yslpMK8UIxHAybTPeoTy3kIdDqj0omdqgyuS6Hdsvmgg5ecmSBWQJ0GO5sTszHd+A5FOaLcewXqDebymOLsIc3xgO35E5zb4KMiUwp7uWBl7jMej4mDjHqgKPMZgyKnyA1xtIc7eBOHZeRXtN5Rb7bgOkKyMehsIAQZOAYl+whYgrLkJoKSMLGqrMhihnPQRUeRG4pSgqBNnlGkoLpBlaVhhsIGsD5DBQnbtbYD98+m0v6LMmn/U+A/ACbp5xvAZYzRpZ+fAHfT93eBx/J+RKeUukq/f/bPuvOiKNB5xoVrieMRg9mM8b17EDWXH36KWl2RRc/+8YLznz9jW06o3n2TZdtyeiweYJP9W2TlgOF4RDUcorTBdZZAYH7nFq+Gr+CbLbZx5OUANR6y9RZray4vTumaNbPREGMMXhliB5NswnB0g7KaYZ3i+PgxTx9/hl9e8OW37vHGa7fwdGzXV3z6y59ycfKUIoLvIM+UNJEE7t3a54P33mB1+YKnDz/ih3/+52yyCZdtoCsMuc4TfCgMw6iEHfvuW+/z1mtfwjUWbwOHRwNu37lLU9eEriErSqrJPiobyKGlFCaCiylgygWyvKRdrXlaX/HT+JjpYcGX37/HsLRASzms2A97+OA4ffqC/Rs3qUzO3WnJv/t3v41afMZHn3xBGceUKlBvtiw2l8SwpDAK3wSado1rG1RQqOiIGgIZPu52CAmNUrKZW9uKybcLu6ltSHIhn2RKPnr6qseHgIteCu10QvYfeCCxopSkvlpLboxIr+j9pmJKb9U75pzzTozOfSCoimj26PIx9XBORy5AkApYf8VYbZlVlsydY9WIbDKgyKdYP6JThzTZHiZzlNkW7Ud0g5u4ah/KAT50ZFExGs4w2ZSqGnPxxRe0FwvMaEgMhvFkn/rqKdF1IjEODu0s2jpwFq/lOUQvHivCsg1o7dNhbyG2ONehjEuZDhKi08tIVfK2DSGKjUI/dg8CKvkYUYjMPnibJu8iqwouSuEZnEyotfiEWtfJ4YscAjH9jooiPyEKkKpkhxeJSHAoQTrk7VPXAMfOS4tentWHFiSQUwtYtfv3INOsfvqjEwNVvVREKYIwdpUjxxLjlhC22HqFtSsqk1EYRSQFWmQ5WgdWywWf3/+MwzszRuMBwSjazjHdP2D/xgH3P/ucIsuphntk+QTnk9cZyaO3f028gM1S2wUCDhUtwbfgO3T0GCUsZ7RMZqMKZCbgg0zOzxcnPHrygKatJRjDwng4QEWZZBqdYYre1F6mnSFA9E6UeVpjygrlPZvtlodfPKZMTNjBeEzeBth6ggngQets528mfrI1m80WomY6HjGbDHl+cYUuc9DswiLkbfY79uvLEvC+UfCuB3QF6OwZElqBTZP23i/uOuU27ti6OoVo9eEDOrFifIw76R2ZgPUSLKNxLq3FBHL2IQ0ojYoiuZLGoi8m+49GYmkjRU9WaJHMqSRLTI8Rldr5meHF53M0GnD75iGXl0uuliswhtH+Pkt3SrfcMMgyotm5Zcs+5v/fB/huMJVkd1GB85aTs2fcufsaVVnx9Oo5h4dbhvNDRtOKxekz6tUls+GQ/ekc7wLr9ZZMw6DKyJXn7PSM1WpFDNBsa3Q1wJQVKEVrG9Alw2pEXpSUQaT3hMigGqBcvvPmMun9azZirO9coN60YERejZWG07uOTdNRjYZkgyFOaTyRrCyY5oZSG4rWcf7oCcO9PQ7eeYXMlMzykhtRCg9z4zaLsxPWZy/oNiuyyRgfFIUZ8O1v/TYf/+JDrtbPyCsjjGxEBoZSEv6hrxlE3na0dc12eYX2gSwB8lH1XBx2+wpp/ZLW4PWavA4T+9Xby6Bt3xC/9K9pv+pD8EQa55xNQLBKSoHeGkETM00THB9+/BGPnj3l195/n699+V2mwxFVUcqATIGLPsno4vXzUcJm8p14kPV+lOGlgMieGdfWNZnJaZsaa9e8ePYMHRRHN29yedVyfL5iNJ1zcnHB2XJLXpY0rSUaI+wX7ZPcs0JTiCLD1zsLk7wYCoPFZPRBfp212MTg8d7JHqmU+Hl2S3y3xocOo5N9RBAQ61vf/Gu8886XUfmc6egGJ4uPuPjsAXduztBKcX5+zsH+mN///d/h9ddeQQOPHz9hPK65dTjls6cnfPrJY3wbGRYZ2IZZGcjygvPFJbUxjGY3aNqWTGcUesp4UPL1DyY8/Dzw6MkVV5cbvjg+Y11bPvn5x1R54OBoD4tiPD/A6ILxqOTZ8xN86BhPxqigadeW05OWenmCCh17N8aMJobX37zNF4+f8/T4AWWMPPriIUdHhyIPH5cY6/jouz/h7Ts3Ods85IvLLa0OeKsovaZzDd5pKDJMZiiLEmdAKUkaNzrsfD599KhoiCltO89zsQlCWK+3bx7iQyAvNKdPH9MsN6jOc/roEX/+R/+IB8cP8PUSv7oiF1mB1Fzes1gsODo6Yu/GHqcnpwIMoqDIiEKEYxgUt6sDnp2e0ASFyYdiR9JZbLAJRNHCXIqeUsPm6pJopXYLzmE7hbMwnk64DFtCcBSDir1ByfnpGa6zGJWRRU0f1OO1ALYxRhq/5tnmIYsfP+XDj0ccTea8fucOs/GEko43bx+SOceffu8fszw55f1vfIvxzTtoreicRWEw0UOzptucYXNHMBkuAUjWtWByyqoS+XLX0tYNznuss6ggXt6jyVQG7N6y2a4ZVgVZZli3NeEEAY7rS+7cuUvX7TO/fYtms2F9csn/+Yf/Fw9++jO+/toR5qDglr7DJ/Y1TwAAIABJREFUp1f/D2tv9mNZlp33/fZwzrlzTBmRQ2VWVdbY1d1kszlKzRZFSoYlCoRMwxJgwQ9+MfQXGDD07kfDsA0LtgXIgiXAEkxBtCjahgRKbDUpUWTP3TVXzpVTZMx3OsOe/LD2uZFtUzYsOYBGV2bGdO899+y1vvWt37ekqkYs1musljtZ2W9IRAVObnBVUeK8o+tajDaZBZsE7ZNKOh9xzmHMYNPcK3oWbYkaSAZEXa9EpFOWpDXnTQtmRRqMhEW9WHH86CGfKM385JyDN97h1u33GE33scVMtgGjRhGwQEiJ9dpxcrYkjaZ0vmIVhC2qvSHqIYOi4O6TmiuTjt2xZlRZsD0rWJrvGK24T0Mk+WwGSIKs0lpjtITPrtZL7j14yLc/eJ+LVY1SpdyXVY5e6g+DXB+7rs5bY9KA9z7OEEKufz3GN5TNkrKdg2+zW1MRoww5JRhJSxBykFpe523B2nUMpxNmu7tiPEkypJKathcZs/CoTa8dvlRNkMWavLlFdsFthNK+vosbV6xsGqZN7dWLmP0516N6+hCu3sEnRom89m7LfK5dCqQy0CQ/5j5rJX/vvImktISMbc5WnUjeo5QMKl+uB+ndoeQgraRQxlDacoM+uPzZLw9GxS1MykHT+fk0vXDKpfM49rXsS3VsL0jG/Ny+nHkg39/IfTWHfIYQswjrc1BXxpxpcE5ck6k3keTeq+laCRpyjqSEld8HQgbpLqRHyoOGFHsOqlynzkmIcP97JfJGT4qbf+u3+Xp0mPxuAVsW2UQlZgijFVAISsDa7I7NTt0gg53e1WvNZeiZc92mz+5Zqb0ZI4RAFzzoSKEsKRsqRsWAnekUa0s67zm9OOXs4pToPeu2wS2WPHn2hOrzkoOr16iGY8GBZVRKkjKJrnWs1+uMr5Bepg8glxAtwQKoGCkLjcWjo6OtO54dRQobWQw95/OGa0vNtZ0BV2cVk8pTFo5CJTGElANwnhQ0yUUCjpjWOJdQWegMSqFM1jhU3vIzEYJB61KuYWMINhLoKEvNZDRma3eH4fYVRttXqWbbVJMh1XCA0ZqA3MMl9wXE5X7JkZawtFzzatkajfm6g5Sd0THzm4WxLtdpJCUvBqtQ47uSRAtJ5/eM3Bd8aPGuoXNOeqKckTIbVOxPJxxPRsybGhv6sDbBd6gkPbAmyiTLC5rQOYdiRXtxjJ6eoKrrUG6hBlcwg33UYJdiOKRSJSoMWZx+AARU0Ki4oqkfYC+uokZ7LIcjpuMBVaHRJqGHBjfZwXUH2OYaYb3ApBPZYE1QxEgIHZ2TekcXJal3viuTebJRAtpDom59xpHI5T0oLcOqREW5zpK2aDNkMrtKmtygthMWaoBtF6jmgtA4QtDw4f/yx/YM/8YirVLq14AXKaXvKKV++d/0+/wx3/evAn8V4NpwyLKtuXLjFWmmByNO7z3j/n//G1ys5yRX45sVae4wxRaPfvADrm1XFFvbtM5zeviQi7NjJttXmE3H7O7t4p2DlKhsidreZ3lxSkOSMAxdEAI0qyVnJ8+YX5wyGVYoDcvWUSjN27ff4+33foo03OZiVXNy9IzP73+CVQ1f+cqbXL92IAy4ruP+Zx/w8O7HlCQ8BUYFZmVJNSi5d/cu777+Ko8++janzx9QAkU54KRTNBFsUVAoSwyyYmBtiUoRUw0pyzExGBrfitBlLU4pdDXE+0hSBSEJTxEtjZ1G3AUWi9ZgUouyHa/fvsr1a3+W4XDAZLpFVGLFnpQTtne2OX7+iMlkRmkrvGvRheULb7zGX/kPfo3/8q//Tc4XKzyJEJYYU+NDS4yamDymiOiioCgqyqpAG0hRsbyYUy9WhCSHkjWWsizoosdaS0whi7NymBRFiXMeCYOzskoQZG08Zmecz7yb/sahtPBljCkuxb7Yg+k1nXOsu0am0MgNM8out0hmMeBjh29qQmjRwwJlpqjoKOIZdv2CVD/nbHVGc/qM/dfe5PqXfo4LN2HZjKnNNtiKYDqaeJ1hadHFFMyYLhWgSoI2rH1gPV+wMymxA8vZvY/Zf/UtotGMqhFd1ITGUxSyVpaCwwAhOLnxxkChEopAkQKKiPYSliArHJL0asoIUdZdZMVNGnEd02atJAYvk8/U2/H7glXn1WuPUiG7P7OYlgKWgMKgkkyLdBQXc58UCrlATSGLSmymxAq/CVUQEezlVd9cUiWZMJPiZuVbpbxC1hcz/USbJA1XFBh8Py8vixKjkjCIVEeBQ4caGzqUX9G1C3xYC5IhJapyiAFckKlhiJ1cE8nz8YcfcuOVXba3Z5gUUElzdDrn3S//NBcXLcvzC6pqRkJCJEBc7ML2ApWbYWLK5ZU8FqsUUWWwf4p5TSqBkcfofYdrVjSto+k6JpMxB9cOOHvxjHh8iomR2LY0XU2VFKq0RCsTbI1mMBhQViWT4RibEutYUw1KtiZTnjx7Qu0cdepQCbqk2VIWio5YGgpTEmOiywFgWmsJprIFhSkogmJnNuHZ6Tk9U2vjalWgkHCasizpuu7SUUvvVMxNhtIbdm0f5KCU2vC8etFoUwgjgx6jrDSZKl81Ssv9AXEMkFEPWvcNgCBXUmaNbtba8msTEyijMcmA7Qv37CBN/Rp7DqhAmsfheEhSCp+dF1op6rqRNi3/rqYwvP3OWzx7/JS667h24xUODw/p1jXLZZ1RI0hlKZdBDohgU3TBpctW69yaZfxHWy84PnzCYDCmTZEmNEyN4urVq/iuo3OO3d09tnYkDdqzJoQ1y7NjHn/+OW0XUBH2traJk+kGlzE/ueDs7JT9q/uMplOUtVSjMaPpFutFoO48RTWgGEQGmX81Ho2oy5oYoV7XqADEyEW9wGdxzgefV6s01XBMUkFwIMZQaGH0zaZbqC5w/uKUsxh4Yzjh7Vs7TIzGdA2zyYx3ruyyOr+gPnpGSUU12aFpHHs7+3zpiz/NP//mE7SJKGNy8FnCFoaiqujWaxTSlNXnF9QXc2g7afeUNHQ9CzukywYspYTR8u7tm9zeGfvyglDvsO2v6f5rhQlXvNTsWULP+tt8HpRlhdYeFwMhWzRi7AdyCnIY2/l6xTe/9YfcffiIt159lVevHbC/t8toNMaWA2EippjZjNJ8lWWJ69q8CpwvuDy4UEY45lppRsMR3rV0boXzgd2DG5TVkNY72vMLTlZLDptzVm2HKip0NSB5T1UVQETwNdldlcA1C5rYCYwpiZXDK0/bnOO9IflA0zp8DoJUmRkevSf4KMKv8iJgpLyO2rXs7x3w2s2bvP3O25wuVuyU29y4+TrnJ8+IJOouMZ5N2D/Y5earrzCvW+7ducOL54cMR0N29na5+8mP+ODDT+nqwKQcsD0Z8mf+1C+wWM75jX/wv7NYrrlRVNLY2RJTDlnVAVsGbr/+Ck+fnXL04py68ywXc3x9mgNiHavVikE5YjAZ8PorO8yPnnLeOEbjMdPJlLPTp2gVOLi+y9HRmtPzgGthfnLCg89+wIsnHzM2JfeT4+jJjHufjHn19pu8/+H3wDX8wld/juuvXOG3f/93uHP2lM63eGXRVob1AVkdNdWAsiqo2wZSu2no0cjGiRG2eGmtNLGk7FRsGeavPT4/Z3nYYn1ilAzro+fcPT+jHFWCW4rZWalFvAvISumiWbM928LoUxlWA6PxkN2dbebnx/zJr/wEf/KLX+Hv/4Pf5NMHj+W94MTl2fkW7wODwZiiqtBWDA/Rd8hmgdwp3drz2Y/ugBXuX2kU09mM0XgioorN54V07PKeyE170oqkE65oCXR0tMwvLvj06C6VLbny4fe5/eF32dk+wNqGD3/4TWJccP3tL3PzjfcYlyUhdTSnzwmrQyq1Zn1Ro/NoWgQRj9GGtqpIRFaLBfVyxXS2hS2tDCdjYH62wGbHZwodi7OO5DzaapIWJM5gkNfuhyXaF/zwB+/z3W9+hyePX1BZzcHemMdNy9YrV1E/us/29hbP5s/RVlGWRe4TwBpNRIS7kM94ay3OB1x0EBKd7xiUFTrJYDJlqUzenwqS1I/7V/Ypi3POzs6o6zrrXppWJU6a9UYQauqOrnScPHnOowdPMN/7Pu/+5E/x3k98lWs33mAw3MG7xHQ6pm3WPD1ZsvJDvNkjqoqORGs9ha1QRpOMpXMBd/KUT779A5rDO4yKyGQykuBhE6GccP3VL7FqHd4rIhYfI61v8SLFEd2aerVguVhxtlhTBycc29Tf2z0yXhfnVQo+r+oGfHSysh7y56iMjgoOrQI6NJS+BtcQvcMYS1GUBCdmgry+IWeHvCWFOZ4UbdMy290lxUTTuU3dol96HRJK6sw8Vfbe/xgeqq8fekdr2Gw49c7LPmjIEEI+CyRljEs01eVWVC/YivinshlCZYyAvjzLetGzF3eNxmqTt6Pk80L0eQiqcD4APc+xd4LKZqkEyP6YbrDBVchqvzjadF7Bj1FcjWxqqEuBVvqRbARJl/2JhHamzeOM2XEpCDANWn6u7gOZ8v96tmvvRhaTUc5VEJsj0YswShbVxAEbZbOF3jkrvUHyjhi8uFz7EDqtiC6LtBlFlxcIMFZvcGeCjFO4LtBtvHOI+1LLdpvWGmMNzndYZfEu9x0p5SwJuT+qLGZaq0WEVGmDY9P5uerNNc4JIkNZsvkpSLhTD5pV4ILffH7/HEUXiD4RfRaRlcPagvFkwnZRcv3GdeaLOev1knrd8OLFC06Oj5ifnbBazinKAVbLdaVSwmpNyA7f4WgkOK6MO7NGQuRTErav0QqrxE1nK4sLLatmRaHG+LLk3BY0c8XzdWD4eM3BJHLrQHH9ClydKgpToFPE2iEqies4xjUpOFJQhM6iiQTlUDaAGtAHWqMEm2U1lGWBKhVBO4rBiMG0YjQcsbW7x3B7DzuYoquSpCKr1QKNyUefygMTfbklYOxGlCclQkgSvJ77or5KFQOMImrpw+R1NjgPwXuib6jrc6nb7QCtSlKSIMOUIsvVirae42MgJk1SJQqYFXB7y+B3Cx62iot5InpDCGrTE2oAHwj5ddBGo7EYpdGxw5/cQ+mKLim6yQG6HGKqKUyuUe1Fpp0jpTPWL9a5l/P45hn6+AFKj/CTim5rlzAoGVVQJIiDgna0TZzewC/O8G4t+URGgrG3trao1ysuLhbULsgwvqwwmUGLUhv3ehM9XRdovWgdRkVGRcEwmx6UKbCFo9FjRlsVbnyNbnib0kYG/lQee4jwu/yxH/82TtpfBP6iUuovAAOESftfA9tKKZvdtDeBJ/nznwC3gMdKKQtsIQFiP/aRUvobwN8A+MkrB2lkKk6OTmm9p9zZxWMZT7YJ3Ri8JijL1js3KA5ucIjnxWcPOfjqFkZpXFfTNWvq1QXz4XDjnmy1YXu2TTGcMpjus5yv6XyDV2tiV3Nx8oL54ozCKorSEkOiqEa8+vq73HzrPcqtXY7nS45ePObw8T22JyVfeO+LTLcqWi/szfPTU549eSAOxKhwKTKZjplOZtx+7z0++OADfv+b/5zxeMjDZ2c8fnzCq+9cE5FRJVSS1cHe3KiIFFYTk5KbaMrg8+izc9BirKUYjrKDLMPh4+WkNcaIUyJceR9QtmQwGDHZ2sorAAWuaVkuL9DaMB2NmYyGNCkQkmNZO4YqohrLl26/xq//hT/D3/m7/yuniwuM9ZjkCVHcGqqwVOUYY+WAHo0HJALRJUzqqApN5SVwRkQ1KZCtLUAZQoibQ04pEZp6uLMLCWXMZvU0qXxo5qmkUeKOKgcVZSGpkdZY1ssG1zpJj+5dcirRBC+NLuQiNeGSJ6SA92eEEBhs7VFub4FbU85PqUKLNgXz6oCuXbI+OqZdrGmqXdrhhLYaoIsKo4YkNSVaaU4DBd4nSJ46QGwTKZRcrGQNINbPmT/3jA9uoUKgGo6kuMkMMZ9kApYyFzMpYVGpKGtZOgVwdZ6IB1RwEjLkPD7b83SerOmU0PJLZSE0oSIygRb+Azr2q7mRREAWU2Pm0KY8kXNAkAY6r+fqPBxQiIOQJHxDyCIrEuSjSCLW5snfZnqcC0wpPLNYF9kc8r1roF+tjyFkATcSkeAfUtysekW3Fi4mDu8biDXarVC+htBikpdCWskB5dtG2MI97DhFNIlSadxixaM793jnnbeoyiHWVqzXa77//R8wKAfYspICNwmjSJzEm/vbRrTLf0EiTzG1RtzL+bmgZ7squqZlcXFGClomzYViUg3Z+vKYyije//a3cIuapu6E51UWmKJk7V0u4jxNjFRVyc0bNyiU5sXxEefn57jKiaCeV8Fc1wnYfQU6tMxG+6gyYaKiaRvm8wWTyYThoGIwrKhsifeJm9evcu/xM9q+aOvDtF5yXUhIghSLRhu5NnJR3183l7Xz5SRYqcsVcR+E66eNpqpyYnP/JX2hYszGyaqLAlAZKas2r4NWmqjza6M1MSThMDoZbqkItioprKXrGpyPkq4LwkPThs45lusV1WAo61s5fVZZy87OHm3XUtdr4dTpgrr1/Ms/+EPadYMuh5DDT0aTCWG4RHUuF9nCY1b5ZyWlNm7Pl10aKjcg2YCC1YqL02Nm2wfM9g+wg4K2a0kJ9q7dpHEOj2b76hWu3dzl2/9qwepYHOTL9YqqGmNUSb1as2obScWuBuxfOWAy2RaMQjkgoSgHBfsHV3m4moMyKGMYDCfovJI8Gg9FYDSWtm1p65Z6vQKiDD6CMMpsoXFNR7daY4cVKrszkotEJ3yn0XBCqGqe3/8cg+LW1h5bV/fQuqDrGlSbKJyjXr9ggWU4nFDaAdYM+Pmf+0W+94N/xXJ9SDHYtLMUtmQ4GGXWZiR2Le1iRbdYUhUFqniZHUt+P+qXnvvckKqe/XWJ8fhxJ83lv/UrtTH27pPLMJMe85FeanyJSVYb+2FF/mVCCHIvR+XAUIUqLME5Hp8cczq/4NM7Ffu7O9y+/SbXrl1jNpnIACSfA4IYyUiRVBC8k0GQc4TgmIwnpJiEI5gLeDMccHJ0wbp22DLQhci8SXTJ4BNy7ptCGiRjkZZb0s+tkQT4UK9Zr5YoWpQyWD0AYwjR08V+wCjnQ+8T6hvhFGSIkPrVQJABXvCMCsW7r99if2fEyfFjzlc1rltAiKzqJaddy9tf/gqHh094fPiCgObB48ecHZ1w+/XXmMxmHB8f88kn93n48BGzyYzSKpbrOS+OnnH44gjnOpruhM/vRkazGZPJmK0rU87XHQ+eLnj95oy2aUjdBWEZcMsLSgOv3dhHDRRbe5qr+2NGVOzPRpw8mfH+50eyzaIhJM8nH91ltU4cXD3g+OSQk+Nn3Lv7XY4OP2daGn75a3+C1UXHJ5/eYV3XNPNztsYlZucKq2Xi5tV3+ZWf8Uw++w7PmhNeHJ9I3RiQcBMbGRiL0gVWB4KKRBU2q7VWyzDJFkXGJCVSMtJL2sST5y8ocsBK9BB9J2GESjEoLEM7Qlclp+sjopatHaVTpt/D6cUFXd3J65gSbQy41qOOHJPC8u6b7/Dme+/y9T/7pzj6zd9mOW9I3mzucT2r0vsga+QE4WsmEUBSv3llEtPRgOQcPngWZ+csLxZyRieFzzVM0W9cpASZo00WQ1LSdARCAdFqFt5xfPI590+eMjVTtkczTIq8srrC7MWAp/WaW29+AVMEmovPKc2a0gaC9zgvgYVVVTIejzDakJS46YbjitHQYqw8NgPYzPPGi5PcdQ3PPn/C2fExr7x2i9nOVm7ONcE1nJ0e8e1v/yHf+8PvsDytSVZRp8CDwyOK9z/lzbc8k+mQEDq2JlNa3+A6R1mWEnqSV1y7rqXthG29tbuN84Gziwup1dC4zmMwKJMHWPm+BhJmFGNiUJWMrl4Vh3DbSJ3jPVFFvE8or7DI6n5SmsZ1Itwulnzrm9/g7sc/4u0v/QS33/gi2owZTIacX8y5SLuk6RtEU6KcBAh55HcotIG65sWDT/jsW/+E88/+gHJxRAUUxqBIeB0YX3mVL/0n7zGd7HHn4TNcYXFFybwLNM6joqdbr+jajhQtsRyhO3H9p4SIroBKspURnEeC4bIJIRscNlsuGmLGx4C4aXENXduhQqK0Vs76vC0hOKUkrk6tMQmM0qxWS5TIF7LGjeADZNCda4VNbdkbJHK1/JJQ09eWibRB3KQk8zkRzUSEANBGbVbWldn8AKw1aCVYhsTl0FjZXnS7HKSjEaNQ3hCRUC+72TLqg9pE4xPBrnN+w5zVSowiSptNXoDKNb9WKnPhJaRKZeHtZcxWyCFJl1gH6NEeP35eX2aaoNi4h0n8GNJBFSIgxVxvmvxz4ktiNYgBSQRLtxm4gtpkUUDYDJX6IZFzHX0InvNOfl6MG3dtH77V1xsxD4aNzmJc3mQSTUCjrcY7MRRsahKtNn82xhDyfbV3ESt1uQ4fk4RMeiI25V4d2TLzm9CvTTqCBFdlwTj4gLGG0hQZI3XZ53ddR+fbjG2IlGVJQhyvXesISbSBWmmaroOkscayPZ0yKEuqsmRnf5et0YxYNzTzOe1iQatXlNqwNduiLCqwiq6//mO+fzkJEKzXNUYbjFEEFyhKCWYXMT3gSSyWZ4xCy+7+dYpqQjHYpW46zlZnnC0dp0vPoo50VxL7W1qyN5LNeoUi+ESMnQzyo8L7DmMAZ1HKIFKY9BLaSN9UlhZTGIqqpBoNGQ4V1XDIYDqjHJTYElQh4crORYRIIMY0pWUQqNBoaymrCv3SsCDmAUJwnWSdWCv9ihYxUeV6UBudXcdGwsuiZzk/QynZxBhNtiirCbYY4APY1uCtwTWe1glOSKMpTOBg2+LaCYv2nEXb4H12nystG7Z5AF+VhfCRleSnpBCpihIVatLyEDe+RhjuYoOn0oZkx6RhhZ1NGNSvYM7mNN05JkZScviLh/gIbmvCYvsa48mA6aBioDWMKoqwTddcoRjsEswRbbdCRyiIFMYwHc0wpqTtAi4K/9lqTY+YU1rLSDMz/BVe7j9KNrtjShQ+QsYgLk5O8Oku5qqi1leg2odyQNQF5WUH+3/7+DcWaVNKfw34a/kG98vAf5pS+o+UUr8B/CXg7wH/MfAP85f8Vv7zH+R//2f/TzxagK5uOHv6DD0eoLemvPGrX8fcvk25vcvhd96nbDzdekFRGPR4G7ds+PTD71PsbGGuXwcghBbvalarBU3bMh2X7G3t56Aox87ONueHhyzXK1xqqBfnrJbnWCVIgJhga/sq7375axzcegdPwfHZOU+ePeT5o88woePdL/8Us1mJi7Iisjo749Mffo/58RHDwVCm/VpBYVk0Hffu3hXmkyn5zvsPGM0O+NN/7teoveGz9+8zKIYkKxO1pLVwIDWkLAqcrubc1v1hKKvUQTkgs0ptSVJm09AlwKeUi9w8bss3aR9lumJsXhRRMBwMCK6jXi+x1lIMxqyWF6zXSx7f+5jxaMTW9h6/+iu/wMX5IX/7f/67NG7IzVtvszg7xLtTTKFxIRC1ojQGHxK1D/imxStFtTVkpyixg4KIONFEnIpYq4UDCkQtzBNrNT7mP6MkRdUYVusVwQVGo0pSzRX4piPGgLGK8XSMi4l13QhzcDgk1A7bgU6eEJ04urKLrypKWQ0MHSRDqo9QfsFoLzF+TaPmltYaiEO6Mw/TV6nsPuvP/pDl088Z/OTb1GpCrKZYBTZGQrQ0QW78LZA8JC+8txQCNkr69jDBgJrV3W9jrcaOrhAri4uOwgVUF0k+i6QJiA5ig0MTvQPXQFhTqMuUxhgEg5CUNDJG9W4q5BBJCqMkGCokSa0kODFw5munczn8JgnvSGVbf0wBHxM6g8pTDncSaPylY6tHEfRiJL2gkcjsG50P+8vjnhg3DkIVuXQv0vOx+mAlEZuJIa9aRyQcTJquQmUfa/JY5VDdBbqdE5ykTAbAR9nxk8fYH1AyKfM6OxjF0igD5gh37zzi3Tv32f3yCDuUSeb50WNee/0tRpMrNN5hEI4emZcqAVTSzPQPU23eoXmFXoNVEYeTcLdmzsmLRzx+8AmrVcOb7/wU5WCLZrGCqqQYFNx8/TWaesm9jz9Glx1TLLOdHYajEUfHJyzmc2wpscPNesnz4yPKomJer2lcy/OjtRR6SgIRdCHp1E4lShKpaSnGFboLFGjGwwGz8Ziy6oH5hmGluX3zgI8+nfL4eEEyeUqfww9J4LzHOEfIDu0NaiQX/jFKWIQUipdCV18cl6Wlc5KCq4PJU/4CMh9NhFObU5ItMa/iaW3wqmc99c97Tug1kqKcvHCoSaALBcoiqORI4wNJWWwl4QaJRNK5cDcV48JSloMcqIM4sVRitV5uXJRSEMNkPKZer1mHgOlq7t2/QzkaEFRi1dYMA2xNtlg39UbMVv01H5O4O/LzEmI/yMqTcWXwMXK2PGbw4iHVYIqearp6zZOH97n6ymvMZtvEFLlYXnB+75wnTx4Qlkt8vQICVTXkjbd+gq/+7Bf47nc+4PHjp5hhxWg6YeRFGGzbFovFYNk/eJWLiwvWyxNcu8aYEmMqrJVBqEIzqMacnp+T1BpTVYzyezR4T9fJep81Frd2uHVH6zsCUNiS0HmS6xgUBZPtLabrJY8/vsP3bcX4V/40V3YmKJdo6iUXzx8TW8/N6R7JdTilKYYlr7/1Dr/4y7/Kb/+jv0OzqBmODEpFus7R+nNhe3tPvVzSrJf46FFeUeoCo6y44DfOpEvhtV+7frmMeblJk/qjZ9DlQEsl3v5+3VJm2WnjQirLQWbm5cYvJVy4DC1RSuGil0CZ/B7q07dTTMI605ZgDOdRcX50xp2T7zOqSm5c2eHW1Rtc29thWBXY0mCKAu88yTt81+G7Fp+E2a28x4VE42DeOo7PTlmc97igip2dcd6WkecLpdBRY4siB7lYSiVBbaIoR/A1NmkqI4NSgBTXKFNQGoVJrax7K2kyTf+8E6RpiIFABtFHTTKShl3GwNuv3uQv/+W/SFCaZ+cLSJp+3KmTAAAgAElEQVSn9x+wtbuPMRXFcMArb73D8ckSbQLv/eQvMNp/g3/8j/4hg9l1bn3pK/z+3/67HJ0seevWa4QYWdQtdx884Pd+/19iBxNMOSJ1ia6uqYoKqwumW2OuXRtz/8FDzp7ewy2PiMlzdjrHpMSNgy12ZwplE/PjJxwnx25RUKwbbr92ncMm8vDeJxw/v8tkNOKVV1/De83H73/E4ZN7PHn2EYv5EYM05mu/8Ev8e7/673Lng7ukBnyhqOsTrl69BoeBkxfHbG2/zi/8zK9gi5LnF494P37Ix0+fQqFFSDcwaCO3X3+T4DvuP/pUuKwEonM5GT7h6pqY3YKq1FirMVHq0bYL2FI44l1UhGhRXaRTcpYoq0nJ4/ES7hp1FgHArxtWFy3DoiQFGTxrBYVWHOzs8v733+eVvWsUoeTales8qB8ToiJ2HqNlMwuk/pBFFIXVJU43G4xQMdLcuvUKv/rn/h2+9Uf/krv3H9G1ka71NG3HsKioiiK/fxXaZPRVzoAQoS2RjPy7IwfjGE2yJS7CeVhxvl6Bg/r73+JrGN55zXB4f01RJIxaY1TEt5AIeNcQuzV6uIMuJLI1ZfcZGLAGTxadSEQn9WEMng75b+cbRrMRSiXWqxWT7W0ScP/BI77xjd/lo7t3CcEznhVMQkm97jhb1ezvjnhtu0JNLZ+eLRiPpqxP67ypF5G8LAUh0jQ1nRdziZ6v+cKXv8jtCr73re/inSRSu5SoqlLW8AW4SkieEBwhaRbnZ3z5y1+gqgzL769YLteAmA10jFSFsPxS9DS+IXWZ9a0UyXvufPQBH77/IYPJLmYwIbgGErz21T/PF3/pBjvXbtI0K1wbSAYSHe3pEZ/87j/m0Q//Od35Hao4JwEt4krWWkNQnD+9xz/8H/8bfvprv8xkuI/Z3+JElA9iWqHaTlxTtpDh/3pOW/cuRMEgAETnxHGZ68cUPKSOGDtilEBYRZSwviS1b/AipJngUD6homzBxCTnuta9G06Jww+NionONbiuxY7GxFybmszT7Ld0RFlUWcwT5JCscvdbbTGfPSoHBuqNaNcjDHyKkCTHg+y06zeDesG1/3lJCRpFa7P5914C7jGYSoujtizKzc/W+tKgABBc7meU/F3Pqd18jlYEEuSzVKns4EM2W4wu6PfaN7iGKAYcoy6RRJcqc8qENBE9tboUxqO6dNgq3ddtZoMv2iAZtELnwKyYa1d5l8e85RJy6GLcOM6Jgjnr+6CYDSk+h1slxDwVY8R30sOGPMDdcO6TrOW76KWu8P2AKqMljKA4qrLcOCZ1UkKZU3IdSa0gtXHM+LmeYSq8+4w9yLxb5+QUCD4IgqjraLsObfsaXDB3thBxfFBZqrIiZXHZB4dD3j/JyGuDSVgtCBTvOtqYJCCwbgiZG+u7jjoG5osLjC1IwNELuwkzHlQjqqJktZiLruA6IrKePl8sGIwCg2rIeDJlUGzT1TVN61iuW84Xc5z31PWaQSnsYx3keVBG2PtRKYxOKNdwGjvmF0Mm0ynD0QhrRgQSrao4nDsa1/BiadnbaplWjq1KY01EDQs6VdI1NT41qADWG9AWrVqMcoJhQ4wkGENUCWuGDCYWXVoK67BlRbIFiQqtCxmY5mu0U16MBrnGFPSjMP0V4hxNGze3IAJV8iTnaNtWxFlr0ZViWAwpqhJbWBQFlTUoDN571jSCpFw1ON8ynXlGZpfBYMRw9AoxXKPrOuaLJcvlCuccXYoUpmLnYIerF3MWZ2u6dU1IhmgqodAhxkSjNUZLFgMU4hZXFh01Oi7QYU5MDYpBDjsdw+waioIywk7bcHF8h64+JblEt36Big2D4y2qnS3aUSIOrmKqIZOBwaYRK7dLWd9Aree06/ukdk3RyvKqKcUtrnXCJgnD895vhHC/MaVpqQUHU6KuKLUiKoNxDaGTLT2dItCwnj/FN0tY1KSDt1jOXqOd7WCrkn/dx78tk/aP+/jPgL+nlPrPge8BfzP//d8E/o5S6g5wCvyH/2/fqBwN2f/iewz2tuDqFuOf/wnC9oDH3/kR7ekL9EXH+nTOfLmk0AV1G6iPnvDAaq5WM9IAmfaaCqMVIy1sVKMThVE4oBqO2D3Y52R+yOnxc9zqAk3CliNsUbG3c5133vsZrt18G6cLlhdnnJy84Nn9D1B+zcG16+KAdLKCUS/P+fT973H4+B7ONQyritF4RFEVDKcTUIZ/9o9/h6Q8b773JXavv8bh4Tlvf+FLfPTZM4wZyg1WeYHdK0MgUGDQicw5yrwgY/DeQZJD3dr8BlZyEW2UIC6ZMXIA9iJeTqdWERUj/faIUkoarTx1taUhqSXOJU6Pz6iuFpydnLCtNX/2l77GN3/vX/DJvSMGw20GVcWjx2eIlFqKGKgldMh3spZsSkkADFHWT1US+L4UxrJSYm0hQQ/ZEYzW4rxSEZsUg6LisF5w5+Qpy9BwY2uX23vXKFV2PiBNYiSxbhvazqE1glzQCaWjrKp2HhcBa/G+IyqFD7KqVCiNTWsK9zmL+9/j/NmIYvWMEacUfslyrjG3voIZ7JJ2nnFy9JxbNjIbVCwQLioh0YWIC+KoDM6Rd2+EXeU7lFtSpRqVloyGFXV9yuLhR+y++RVhXMVAmyLOt6huLaueyMpM1y7ypFoCQWLX0AUvdX9OGFUp5uIAERxyMddPUzVKwkT6hlhBUl5CZ/KUNeXXJsVchvUiWhTAvO+EeaO0FmdBf22RV1XlwiJtXAgvudEgO8U0PbdVviDRU1xJWSiNma2DFDyKSEjuEoMA8v4IXQ5LAJVqSj8H3xBdTfJrbGbwiXlG3NdFLsgKbTBIQJ3pjZbKEjKGI5FYXKz57vc+4NrV61zZN+iqIsbIi8Mjrt3clu8dA4m8FsXlapW8N7JbDtAxEpIXt5EKxORo1mccHz3h8aNPaOZHxHYFyfLiyT2u33qXrm2Fs4UiGcUbX3gbVOD97/6Q4WjCaCIcv8l0LHwuorA21zVPnz7NhbWwgctCOJAhBHzwWFtgtGU4GDIcDvHOU69qjFaYQcF0PJEGwWVHbKWwZUlRDrh67YDHp3OZ5KqcEJodf73At+F19u4O2KzRWWuFG/rSWnn//6v1OhfOhtFoJM6blMQ5L/t49MEQyipZCU0I66gPdtDiCrlkuWY3ggKVxQkfAwZFF0QY0nlQ1nNJE2nTfIiQJOwzdA7yy81Ikx9rv9aujaGuazrnNo9XIcKfc26zin98dnbpdFRKmFMx0jvN/6+hVL27vGdc+RA4OTnl+o1OGHjasDg7Ymt7C6uh6Rx3PvmE9XqBW8zBi5BibMl4NKWLgcdHNVdvvk3tNCp12DKg2j5kwdInNw+qit3tHY4OPxceMiIUJqVpmo7SFuxt7bFarFmGOdFLMrTCUI0rtKppEXGgblb4IGuAg+GI8WhAtJHoC1SKRKM4uH6dkCKfP3zED7/3A7743jtc3Zry4sGnvHj8kLff/Srj2TY+BVrXslzX7O1f4U/9ia/z9P4nfPt7fyDiXh4IArjO060W1BcXxLbFZOG1DwTr36dh0yReIgte5tD2Hy+7c+R1yfcvlQto+DFuG6rnDutceeeGLw+dBBXQD2Xj5V0k/+zLQBdpnhVRiliTG9qYWNY1H9+b8/DpC6aDivGgZFAUDAYV1khIS98c9s71tmtYNC3zxtPlld6t6YTp1oyULHY4YlAE5vPFRryWzQdZS3fO5RVQEalDDisZDg1FWbFcOgmMQoaJ4/Eou46cNE35Bq5UdmrpjBvpMnfaKFCBpBzGRq6/ss/WlRnPnz+mC4kvfPXr3P/sPnt7OyQVqZ3i29+5Tz1fY1TH3Xt3OFs5Dm7cok4Vy9qwf+MNvvozf5o33rjKnU9+yO/97jfY25rhnCVpxWg8pWGN95pkKq6//jbzdeLkZEm9nBNX51g8hTGkImHxXN2fUupIWy+pLxzPnjxnNqgoiYz3Drhx6xYP/+A+7eqUiKSWHx8/49MPv8PZi6e07SnDccG1/RuMyimqg+tXb3Dr9pJnZ4ccHp3SdjOMbXj69GN8XHHz9XeYqhm62OfWT32NMv0RHz+7T2vAN4F2vWQ2m3J6fILzAVMqhqMRqmlRQLtaUC8XlMORbCVQUowqilLwHMK/l3Ak0Z+U5CJpj6dhOJjw1rvvcv/OPXTn8a0ntF7cgp3gpZwOeSCYr988aDg5POQf/eZvobXFtZJqnVQQwThFQvByvxc+B/1q9WAwINiADx3DWUHdLfjWd77F6dkFk9kObt1xNH9B0oFYWcrpGK3sxuFmUqCwlnZVU69W9KUHvSSU1Sdt5L0VtCfqiNLwbP2M3/oXv8XNj27wyvY1rl/Z5dqVGbPphNFojLLC/hxPZ1SDAQEJewr5jFFKsEqb93YKNPU6DyvlbCpswRvvvE1VDriYz2mj5mzluPvoAb/zu7/LwwcPUJXBlJqzdcOgLCmqEW7Zcu/OM6bLlut7V3lSXDCpRjxzIhcRExVa3ntBBKXCyoZKXbd8/OHH3H77NcaDMYsz4ajLvdBB6tfVM9/aBdp2zYvkiepNfvqrX+Txwwe0qybnGwgvs/MdpihwbaBZN1hbMJlMMoM0UpUF7arl7PSYwCmFFmfWj77zDeJsn5/9pW1KVYlG33RcHN7l8be+wdMffZP27HNK02BMkIJfq+zkljqs6+Z88tm3ODx6yJe/8ov84u1X8I3npAs411JpKBA2fwCs7pE08cfCtrzvMp9UBvB9vZcwKB0lwCv6jNASs4LynYTS+jYPxoWHvsEyIc517xyVGWzCaZfLhq6pGc625C6fLnFwicxPTbm2VMIOTaQcxntZa2aTLYUxG2GRKPUXMQn6A1kT752vKYt2fT3ivc+aqNpsevV2gxACyhh0DnLrh+igNs8b/XmVVGZiZlZsNjHEaH7sDE1ZOJZwIjkfYwqoPOBX9OIpmbvaD0NN/lp5rrS5PI/7ulTcyoK+AjJap/+83PskhXOhvxmIbqyFYRuCBDTKw4qgpGfyIWBNFrpjyoxYsiDKhifbn9+iv8bNc5zMpaAcU0BbJf6WQEao9V93KcxppfPavtnUqEpLYG6IQda5szDbORkMON9vsiVa5wgp5JwYqSR0Nh2YHOI2KAtMWaC7YvP6CI8/oKPU1tZayqqEBGXMzNskgjVRXhtrBL/Ui6+dc6zrNSkFmiTB36nvk/M2ZiLShUToHOBRSbSDrlkLyqsTt3HqIstVQzg5pSxKJpMZezs7zMYjdrbGTMaBstR0bSMYNaLcX1TLZDKi0AWxrokx4KJkhbh5B0vLxekZg9EEbSzbW7syyNcD2mBZO8+8admeFFybKXaHYJXD2AHGJNrWQ0gEbVCqIVASzAitRBAlKTAOZSODaoutyZDGBwINWhcyzEwRmwJ0HRJWaIhBwgHl3pkkgDCrOcEHUqzlWkqI4U+xMU6FEAjeoZwEZ2sspbFgUmZSF5hhIW5aVaBUuwmZW8wXOAfVsGM8mWKsZTQaMRyO2d5uubiY09QrFss53nfsTCzTccnZ0tN2glQySmGTBxwpCWoyyaqUvEfJHOVmDusT1OCIQhvp1WyFGu9iKShCB64mhoaaxDrO6bo1vlmiTh4zvv46q/N9FuMZZWWodEE1HNGmq1TNgr35U+JiwGK+onUdRIXxkl0RQBAOGEI/RE0Blc0xpphQjvdoBgdoOxE6nrbYboWrF6TmDNOeyzXsFii/pPA1Jlyw7DRrvSMGmH/Nx/8vIm1K6RvAN/J/3wN+/o/5nAb4y/+fvnFZkt68ys7P/yTVF9/g6N5Dvv8//R8cfvI5Za0wLURbYYZjtiYzRrt73NoZsTrY4unjZ7jKMBhX7OxdESu10kSv6FyX17GlMZnu7uGComs6pqNKkk7tiL0rr/DOuz/FlYPXcTFxcnbE4bMHHD17QOEv2J6NmE0rTFGgbUnwDQ/v3eHw8HOqoWG2dYXxaMRoMkEVhvPliqPn51TFmINrM776tZ9lZ2eL/+6/+G/5337zN5jsvsXWbAtzmolHGlzoskMQcYmlRFWK6u6DrEFqpJAo7BD66fzmbZqbQuQg8V4Sm42olSirMjIhbtaW2rZlNKxyoIQcXpPZDj4kZtNtjCm4uDhnMB5y7coV/spf+nX+h7/191kuFly7cY3wucUkR5EUNinw4lpKrgOlhbsTHTWKtanlRuICvhNXUeMadKUJmU9jrKbzjjYEWi+J46PZhNXpc0IIjMuKYTVAayWHGcIX6lzHIJ+0RVWik0yCR9MhkcB6vqa0OXEyiUDloqwkxZTwSmENDN1jlg/+GU3tKbojgl4zHI7QgzcEdL7zGmP3E6w+/B1Whw/ZfecmyzoKzsAjrCHvhYfqc5hAVOgYUb5B16cYPwfbocoh29dvcnZ0xOr5R1Bpoo/o4YgueLSvSbHLaz6B6FeErsZqhUopi7U91ykLBCFsio+Ub37SVNu8OprQOXk4ZOEzJeH9xZSy+TVhFUQlNxMpsnIDEQMqhKyr9imewlImX3faZJditjL2bjERLvriMfZcechYDilSxB2j6JNIhSm0EWbzNxER12FUwuIwqUOFNaG5wLk5diMiyMqxVlIcWlNilaKyVh5LjJQalJWVptDzepDnIcZE1JbV6TkP7t5ne3tb3J5G1o2buqYoh8IyLkAlLWstolRngTa/NRMkZdEInH21Pub06QOOHt3j+PgxKq6YFaAKQ9s6msPPmesBr7z1BZZtx3w+R2uEs3jtgJ29HZRXGXGS8rpMhe8aCq1ZLdby3Gq9Kfatld8ttjWukzCAPnlUGshI6DqGswnlcEQxqLKLT4oinR+7QnHjYI/P7j9i5QLjyRhbFiyXC3nUWmFtQZGRB72oIwFK8lpLUI0Itf26XB+wpHPAhe6t3ImNAyTBpnmWCbgVRICVtSIt1u+8WqdlcJDFWwlu6N3hCV3YXHBDSNIcJsOGp6YyKzWkKPdplZuDzDcE8vDrZSyBygFlIa/lydkTYiR2Do2sNAUETaCQ9TltDGVVUa+kgN1YTPL3vAwVU5ufo7Rm3aw5PTtkb/cK1ewKKbR8fu9T2hA5uHZV7sVLWe031jCezhgMBmgbODm8y/HRY37261/njfdu8eH3P0OnvAJMxJYSnhKVwrmO2dY2uzv7eNcJKF9pWh/w8xWD0lLXLVU15PrBdZaLmvligY+ObrmWjZIurzylRPJBeNM+0i6X4ohJEmCltGKyPeOt8YjT01OWF3MOn70gzi9ozs442LvCO1/8CmEwZtU5iuEQa8E1DTvTHf79X/8rdD7yo4++TVSRcqgwKpF8S2gacB2lQpjAObiiF3L75/dlQXYTWPLSvfZlJ60MTi9LLCWrA/TpznJNpHxuCb6of137hjbmBOv+PdC/T3ohtf85PSd6c+JnQWHTBAKprOiM5TxE5os1NiVxE3ctSgmXTudQHJAV3YDCoajKinFec1PGUmjLYFCik4i6xshqdu8QluAHNrVIiPIaVsMBhS3xLlKWipPjBUopBoMCpeT+npLP95/0kriQmbZaYwtNH26SO0xKa5lubfGHf/Rt9KDAjq6xWLTs3bhFGz1vvXWdZgX3PvqQNjYMbODpw7vM2yHTyT737z/iYuF49713+XN//utErfhbf/2/gvB7nL04RqWSECy7e1usijknJwvaztF0nsn2Dk8+PyZEgykLVISiKtjZ2abQnqJUlJUlOkeVaiba06zPeTFfcGMyYrQ+586nP6JbnYEacO+TD0hace3aDtuTEuxrHB8dsXXlCo+ffs7vf0NTDGd8+ug+Tw/vc3H2BG07urrm+tU9iB0vnjyg0obdgxvsH+yzuFizWi95tH5BR2Bxcsw//Se/TVkOKIclShXcfv1tQtI8e/YIXRgGswnziwtQwrsO0mGjMw4BJ+dMdAKlEJCIDA41imo84Ss//3N89EffJTaB0HmUT+iQMl5KHF8JRds1zNuGk+WCSTngxePHFMpSL1uapsvuwZgdLAFtEqWtCF5YjcZAWZWEIuKb7v9k7s1+LMuuM7/fns45d4wpI+esyppYLFaREkmVBqottbrlbrfa/SAPsAEDfvCTAf9LBuwHPzRsuG00ZLRbrbFFSaQ4qEiqWMUas6pyjjnudM7Zkx/WPjeTcuvNBhREAcFA5L1x7z1n77W/9a3fx7f+o19jsVjww++/w6iaUI/nqEbjZhN8t+H6nev4GFmvOmk8FTEqbB1kz9Y7VZo2IQr3ttLVdj9BZ6KRibFNaHn/+EM+fPgRYyzz2jGZjJnMdpnP5hxM58xHU3bnu8x3dmjqGq0VTTNCay3jzUpLYLIxONsQk4xAt5cbYhQX8PHZKQ+ePuHo/JL7T55wujinDZ40n4g4qDPaGtqUScrSWMuDswX7RL75+ut88fiM87ZhZzzneHVGYnDLyfZibI0polUG2tWa93/0XjnXK6ICtNzvOSD7lJKzRfAZH+ByveGDTz/hH/6j3+K111/l6PicEGStCqqXCYkobrrkI+OqYTab07Yb1j5AEISJ1RatxUCiU2Z19jnv/Mn/xsg6vvr1X0P5wOfv/oAPvvPv8A/ew+UL6srjjDR8lZWpKB1l6hAFGE/wGy4vW3743Qv67pJ/8J/+17TW0aYMugJrSWEtfOBgZRw7FcxXEc+cc+SsicGDooRmQa21BGB6GQdXShBjKgZoV8TlAt92mMJWDTFKSBaQS/NzaIRaW6GhcPw1zpbaRCpjEfaU4RldUsTCYbqCUjlrLWPNMZXGimJb/w6BWsOUEUh9b5ygDIaNJsa43Q2NsWX/yxgzZAUUM4LS20AorXVh/z/bF0MMpCz4KfmROCcH4VSER2m8PxNryyvOGVP2PFWE32FflInTIhxjSDGQokzsoTRJpe2+veXiFgE5l8cczrvCSA1b92rKSRr1PMNMScO8TDXFVBoX4qrNOZGdLSJ5EVuTYB9y2dO3iAg1iN0l4yDJ55q7In6aZ4zZlJMwa8ukYUoDIkyEeVPe+2E9ywDG0oeebtOBAmvsFp01TKnFFDEpobPCGrXlKVttJHOiIGYUiqZqYCyv14dA8H5by242G7quY7VaoZUWd62SYN5cGl3SpPG0fYvWlmYkzYjpeCJGrXAuNiuTaftlCb0SdEQKMu2hzWAq08SQ8MWNHZOsY32K9D6wShsuFyuOnh4xHY+5fnjIZDJhOh7jpmOcc1idyX6J1Z7Z1DIfV+Res+kjizaRYi+fc9L4COtVTzUOJDpav8a0NZs+s2kjp5eRprGczi27rmfiJHC6MSM0DSpvSMFK7gJyXnEotEpoxJRn0MwagzaGk2WkjRalrRh/osf7lZi9lEUpB8M7UXAfSVxFsp5EwRukKDWZ1aZcLxIA56wRxGG5l1eLJcF7JtMJ47HGOFcyjiLWjEiVQ4dIYEPKmXbT0vaBzVrCYsfjCcbIJOZo1KBIeL/Bt4lpY5nUDc5GtBfzn1MBm4vorgJa5YKVG8uakyWDwHdr3MUDalPjtIVqF20LXmK6Q8g3qWNisg6oLqP1MZfLY4Lv8esl5w8eU7lrzOe7jMcV1VhwjG40wu5epVndZq+7xPuO8/YEjCMkMEqc3yHLfTmsf1YnDBlnDM6Nqee3WI9fJbldgnFE7VCpk0yg9gS7uIdb3mdz/khY2rGF0x4dDMZ7wnifv+vr/w8n7f9nX77raA73cW/c4eOfvcuP/uX/jTqGV3feYnL3gOrqHtX161RXb1DNZvRWEZ98wAvX54QPPuZv3vuUfHJG34vYuLszI4bA0ydnNPWMnb0DtEqMR1Nefu1NSB4VLtBKM929wStf/hoH11+k7TMnJ495+ugeTx58TKU9e9MKnQKVqxlNd1Bacfz4Mev1BXtXrkDeZ39nj5xlgw1k+mgwzZTL9RNumpqn9z7gwcc9Orcszy6Y7b3A6dkZm3aNnWlhzZELLDySs0Znh0qWHMAZSwye2HsEFK2KQ0g2BfWcIKRKB0Br2eifecLk90IYGEISEqJUYrNeUdciWhtjuXrtOoc7c7xvGV9M2T/YR2vLG6/d5je+9TX+7R+9x0frlhgzVmV0jMT1hkig9x2h6+mR0R9tFKmuUKVj1vc9CeHfpSSj95WzmMF7VFg4SWeCyVx2K64fHnL98BpVJYVL221og4RfCXNmzc7OPpPJmOW6FTEAJaPsSridXV9GJ0uHVw/tZpWJiLBS0TL1j3GxJzuwGGKUkYX1ZsnOCyN27R3CZzOWH/+QgztvkeIefa/wfQLfo2IPJZxFxukGsHliVIEJgUwg6THNlbvsuBEXp/eZznYIOdEmT8wG0hqDF+aqohxoE8kHBmdkLp3WgfOpgnRQtdHE0sXWCnTZiKUDkFHey2hMHqD1CpXKGH4uwPoypqNK8SKTgZIqqZFNUljBQ4+f7bW2/V6suaU4pHS+s7SJk4yTqRTQg7G2iBUpeVROWCXoBSfW8lJIRRw9OnfYHFD0JL8gd+dkv5EnKUIiGBFelaRQjm2DNZrQd/i+xxrFeNTgjHSdUzZlpKnwoJLwVCtj+fSDD3nhxTtcvXUL4zQ5BTari/LvFDF01E0jKcgUtldBfikyUWWUFU7jyePPePjF+yxOv8Bmj9Mt9D2qz9iQCScXdEdnnJ9ueOHmLep6gnVui6WwVcV8d4/2coNPIkKKAGRpzIjZeIrvxKmplaJyltl0TN/3dG2LVopR3QAQfEfQCt9p6knDeDKhrhvSML5WOZJyZMT5HoHsPdO6Znc0YtFd4r2XTnRx04WS/DqwN03p/A7jb1IY+3Lt/AdEr7IvhJxQg+G6FLVoKZy1NkVgM4iT3KKNwziDIREH84gXB4E8tylctkwmbL83eWC+KVQUfApKHK7WOVSK+L4v70clgn6MUATZ50W9UEITtoJ4EfdMCdDQVcXO3j5ds5HiVhu01VTGsLlcEGKUKYAixg33zvCl1OD8UBI8RaYPS0Lqyv2pubx4SkaTNpVs2U0AACAASURBVBNWl5esl0vG0wnT2Q7j8YxmVOHTkqcPPsAZx+riNSY7h7TtCu0VzbgRZ2ZxfrRtz+nJEXWluX3nFb64/znaGPqc6GJmXI2ppw1d57FNzbh2+HhEulyQUqbb9KDEpZFKqKC894G+a+n6XjA4vpf1RRsIU6zR1FVF7DyXZwt26jHV7Crz/V3cdB+lJxjPlmkXY2S1WjOZ7fK7v/tfkYi8+/73MTYxacZsNi1EcW0YK2tDThKIUVfikA8xbt066m99ts8+g58XaPXf+oyGi3jgfKaUyyE9lCaDsLjk8J+2B7kQwrZxBeJgMs8Js2ng0GXBYWiltrzxLaez/DtVggxUOfBG9DasMBuZodNG3NtDU60pDR1jxTWXQk89Ujgbadf9s3s4SvjQYC3aitlZYXURgTUYEyUMp8sYIzy6ZmQLQ1+Jo4S4FayHpmKMHqst1kqdIyEsckSZzXdQtqGe7vPil97g888e8873/4q3vvE1lq3mww/v89Zrt/itb71Bv7jJn//pH6F1w5Wbr9CtlhBb2ovHhE1Nrm/y0SeP+Oo3fp1pCvz1d78torO2bFrPetOJG74OnBw95PqNPfbnN6maXdaXT6C/wGiPyp7V4oLHvWK9uGS1XHByckzb9rja0Ux3OTg4BGPplpfgNzTNiHZxjqlHLFYLlHb80//kt/nhd/+aR5/9jO7smJPjT3n1jW9Qjy1OexqrWJyfQ1S8+PIrNE3F+eKCzrccXrvBm197G1M3zA6v8C//4F/xuD0VpEG3JuSIsRm6SNd5Dq7c4ujkiHFlGM9G5COLtRIw1kUJKhK3lgZryM6BzqSNNAU8EeMD69ML7n9yj72rV+naHt92UMKGbFXJ+LKCHCSQzMdI8j3nizWtTeisWS3XrM9XTMcT3GREt2nRldQcIRaUEhQmueAKVGGL3/v4c37hF3+R+DXDkydPiAF2rlzh1Tde5y/+5I/IKmOVIWw6uR/LvRkTIh6agjkpTXU58EpN1PcdCnHzihNSuPhoR6oSYQRLn7lsL0knx+STBxAVE9UwVhWVEpb6bDwpLnaHGxLUKQ77ske0Xct6tWa5WtJ2HZerFSvf4clgFUln3KjGTAw6a3wvr8c1DaaEkhmjUSrS3D7AXU0c7kc++uKE3cZxfBmJwbDuW3ThIGqlyQjeQmoBT9/2cq9pSyaC0WRlZd8PSa4nJZBoZSAT+OzeA374wx8zme1w5coBZ+crmWgzBpxi020gyUh68IEQAl3biWiAhHoqK3t9VhLQ5XIgPP2Id/7N/8Tm6Xv0FyccffQ36PUZYx1onMboZvvZkJIIY3kQ4xKTUY1WIshvwiU/fufbdH3L2//4d1npmgs1IuDQbgQErKsYjaeE4EnbujRhjJVrwRhSCOKMLs3lECWHIZdaOkWPaxeoxRF1WAs/V1lpPpVAX+MqjHPFuSU2G20Nvu3xPjAaj9HGEorbWchHZlsXPRMNh73oub1KsWUwU6Y4pOaSgig/V2AZZwWPF6V2o/yXs7jfZN3Nsl8P03jbqTyNNrb8f9mbYp+2vONUXKwpBgkOM44Bc6aK61REVHhm8sjbv1Uruc9NWYcG/m15OagMKQZ8ztI0L8Kr0hI+68qEqN3+jQNKSmq7kMK2sdn3veyt8Rlz9/madAhYC+HZOhRj+Tu1lqCyLCi5nAVTIGdMTS6O561Qq0055xchM2dpgqS4zT9QZa2xRpGsTJ/U9cDpFRetKzxeNeAbisu1qip88IQkNa8uuC6tZCIXVVjewdP1Ld73Ykoo11Xfds+9ZtmPh2lcH/zWNKOtvMbNZrMtTCV4WhrUIEF2PkhwtQ8BvZCfW2Pp2o7QJ6x1WKOppobgPeu14FLIEPoejy/ICvAhoo3FmEzst1eTTHSFVBr9kXXXs2pbUgrUTY2rDVp5ZjPLfBrZn1jqCqxpUbkjREcbx/Sx4WwZOL70tJuOymZGqhY3ZezJQYOx+JgIqqINhtVGgc/k4Bm5Cftjze5MMRsJIsQlx0gpXOrK5+fQqkYli1aG2iSCitS1pttI+1NlBPfkWyIBkaklq0crTdamCP3i+hzMKzlLY8b3gTg0Toygroy2W9OA0ZaYNbnsO1o7HBXGSV1qKlvWrVBQHQqjK1ASxB6irIHWFnQDWhi4Xn5/Mpmyt5vZW1Ys2mP8psdWMIScGa2oKoOzkLNF2xISrxVWZ1xeoTZPiPWMMLqOUwpbK5nsaKbEyS7V/jX86hExXVBVct7WOpCzp+svCGFJ3zXEyuI0VErhXIWeX2O0OWV8cc56sWQTkuQ6peEe1mKokBUJlTWZiFW5XAOBrCtUs0+sdlnrMV6LWznFlji9yeT8p1QpE9an5LAibRQj9T4VHW3/wv/7rFC+/l6LtDjLwa/8Mp99cspHPzvnhV/95xzs38aMDsjNmIWKPPWKdavw68hyveLsuOfLe4lsDZcXC+7cOuTo/kNWbcQ0Y2bzGWdPHtC3nl/9lV+naWq0zRxev8bFxYucPf2cK/uH3H35Ter5nC5lzpenPHl8j5PH95i6xGw8xuiENhWT+T5KOVaLM46fPCCFDmNH7O4dcO36IQ/uP0BlGZ+ezRpGk8iknnL8+COCPyNlzdMnF8Jk0ZlNWNPHDZYJKllxXJKwWGpdM3YzdHLkgHS5tEY7Q1UNIVvPHRp5vgvJdvOLwW83uFwWS57beGIsfJMcIFu0cixWK8bjMbau0Dox3d2RuIasuXFwi9/45bf57Isjvvs372N0oFKO5fkZYXWJc5qUA8pLui8qo5x0f5uyaChj0IgD4GD3KlZpzo7Otx0fo7SkPpKJOdK3LTKckmi7HqWRBT4Ecb4h40ab1QrV1EUAkGJCq8IZshaTKkyOxcUghUdK0tkPSaGcpmrGzMdXCOOEqStyWECGTe5Ynz/mcNpy5YVb6PNf4v6//1fce+cvMS+/jQ4OFbUIbVlSc7MCdOmukzA6gLPkqiKGFbGXhNm+HhE1LE6OqfZmIhx4yGGJMjJCpQq6QmsLRhH9hpx8seKXMVxkgcvJC4eoHODZOmTlOtFKcAZKSUhYiiJWSVExsKakQzxA4cUYpredfXEaikCkskiSWusSSqa2XXmtxIGjSsiXLt+rQsBLKQjnK8ph36ALz0lYTpLGqdBElBo4ty2qv8TEFY4eH1tCaIlJDpbWmKJiFaFLKZxSVDlTpYDKYE3GTGqcM4zqBoui9y05g8/IqEMpfGbNCGMsi4sFn937jPnBAVXj0CqSc0/KPTHC5eUpOzt7TCfSiZaiSKM1eN/Tby7ZXDzk+OE9FhdPCf6S2nTE9owxnrzq0Oct+XJDveq5HhKbBw9ZffoJe19/Gx8zy82KzWaDHY1IxuBGI7RxUpykhO89m+UlftVydnpB20lhMJ3scniwz8X5Of1mjbFOnE1ZCrucAu1mhXKZUapJwaI0gjlwTgIviqtPK82y7VhtloynNflMitxYxrHEMZW3TlAJPUio/CxgYkCyDOsQPCvQoVxzxkBpnmx/R7ZQEiWwrqSRa5k3BIbkXDmgOOswVUXsuq0zdwAv1FUjTa3iZFRISIZRmr7vt2EQIScB86uCMrDuWeiELgiR4iJ8/rUMI+p930uoQlXhKkcMUcTkSq4TWw68OUXyai3hI6kA93l2aBjW9e2Kr8QFoTS0/YrFeoFzc2aTKdNpg86a2K7RZMbTEaPZFDcaoWyDNiNCtyRnx/7hTT7/8D5teIxVCVPJWNoQANF1LW3X04wnjEcNdW2xR8eEFJmOZ+xemTNtZkCLv7ikaxVhEzg5X5I1+E0PyWAqCSTKQQppbTQJ2Q/qukGh6DayT6kMm8WSrMTFFPvAydEJ167d4eU33uTTTz7kJz/7hLfe+iX8Yo0zFKd0OWTGwO3rt/jP/sXvYvOGz754DxUzfdfTbVpxzA0cu/Jeeu8x1m4Pu88Lsc+7aIfP9+fHNJ999lsxNWcRHIqzZHCXDY0KVRmMccQo+3KWyS85ZCJserH6ImtZyj9/neVcBH2DYsDVGMTkndEpYUwuHGfEaZbtM1d6GX1VuRysMltBeHsdpyRibI6s1ithJ2uRQCoro3HWWhmRLYdArRTGOvlZI2zpnCJNbdA6k2JXcCIBCVtE3NvDnqHLgTYPDivZR4XtF5nPphxevcbFquWjjz8ipYqv/cJXOTtb0G4S3liWhzvcfnGX85Vm3SXseMYLr7zKS9fHPHnwmG//wV+Qukve+c73ODpekrsT/pv/9j/nzvUdHh2d4cyIyjW0neQFHFzZx1rN++9/SOgdr73+i5i4y/nymPXmKWFzwacffMDp8RHteo0ycPOF27z51W9yeO06T08uyNHw6PEZpozEHu5d4c7dV7DNlM8/v0dKmdl0xv7unJ99/ym3r+7zwisvMduvWT9+yptfeoXx6FV+8u5P6LpAjB17s112xlVB4lgePnzI8cWGl299iW9++ev86+/9Pra26Aixj3S0mAyffPRTLi+WGG2ISgIXb790l81mQzg5hxiIOov7x1mylaRj10bMck1oO3zXEloP3Yb2bMGpT/jLDSplcuFNZa3LZZzpcsAkS20q8AndJWLr8TGSE4ynE+bzOcpZurYtbiBZI4vO+6ze1SUARtfc//QxZ8d/zrprQUem4zmriwX9co2J8OTpEbWu6DcdA1Mzk0q3q0zZpGeTCzJGPTj7Cj9UZSrnsNrQh4hPceuci1YTawPJFqFL05YkdFIi95G8eCINwyh7gnNOnHQlCd5oI2sAlJAl8NmTHKBlpFjpYY2TZOzsLKHzWGUY78yhNmBgNJtx1J8TDyf8s//yP+aD9/4XdNXwdFlx0QUyhpyQ0D8tzXyCjOjHgiCThngkBSXidJKDtcqQvdSFzlgsSgTWLvD9736fq1cOmTQ1F3lN7D1WK6wzhGjRxX15cnTMqm8Z1yO0sphshFePEoBAVkSjcdmgc8CsPuPJD87IfUcdexoDrtIYlSF6aVqVz5VYvGY5k5V4vof091ZBx5r3f/odsg7c/uq3mO/e5ULNCGhiH9m0nt7LJICg0hQheWzdEFIi+ExSmaylbuqDh1KDk0MxRLQ03QW2PWWiA5WGLghSa5gQQBVjTqmDpKGn8CGRlMbVjYTEZaQJb6zsWRIwUZoIsscMIVDD2ptiYgiJTDmjZERo2zRXw4ailCBJoGRYFLG34JlkDc6olNFWfmaMNHIEzWS3YVYxPkM/JTXwXwvagLKvpLitWzRqu7XJflMCaJ87x24n7cpel4ujdGgKyr+RPJaty7js2zwnispjqnK/inFGxMMW7wURFWJp0Ci7bfg+Qw4Ngq3ePqbWYu5RWpzG8pSKlMxQnZHCIPZSBNThnFYcu2Udk8eX16JLzStO4Lzdp5UxqCQu5KzAFddqXcukWyJvQ8ravsUYwc0NdYhBF4ewvJ0xRmLy9DHIVK2Sv8enRAgehdSW3sv0wiDSDiiMylkqhbjOrTxeHwJenDkloFWc413bQYaYgkxDhNJ0S8IYrqtaMiWUBDtOxmO00jKpqDSrNtP3Ml0k1Av5TIwra4pSqJLlg7SViAp8jug+YsrkaGNhbi235x3X55l6NCGhMUZG7Tu/YbGWKbk2ObQ2VCjGTjO1kPsVbegwboTSYpTRNLQ+slpC38HEJRYrw6Ifsb83psswdhtiXlGpDqsMyUzE1JMTUWmymuGjpU89IUkTQWnK9G1HiGu5LhHHvbEWCeoR1KXkFg7TJ+KkVVmCYp1zwrhFzB5Ky/6ktEZjsM7inJMmfgoohDvtjKNq6sJQnhBDRhuHNWKySFHyJYL3ZOQ+8d2GGDvByTnLdDbhYN/y+GJF6BMheXSOxbyWSX1AGQcYul643lpLCLZRkc5f0HUn5O4YbysqN8egicqTXAOjKW46J/YN467B2zFM9nDTCaqZE6iIZR82dozNmamBPJmwnE7Ync5Q0ynHiwXrGOU+SAmlxFigskz9pQzKZHy3Bh/xeoRtbmKafZLaJdoGXE1WhhB62mQI2bKvLfXph/QXH+NjQLWnjHTAxDP+rq+/1yJts7+Pv/ESj48+oX7517lQNcfZcrZsuTw9YeMjy1Vmd/eAqrbU9QHN1cyffufPYH3CnTsv4FSmGs3YuTpHYViu1ugMX3z8M+7evMadl17BVJbpaMS1w5s0bsKrr7zKaDxl0V5yfvyIB/fvsXj6BTujyKSgBrSbcHjtBWazfdrlOQ8+e5/N6gyjLU0z5+atuwQiZEftDBjL3duvcPXmLUK34a///Pf50Xf/mHv3vkCZmq+//TZtclSjhmayIwVXBKMyTTOhUlPm9QHTah+iHKAkoKNB1Uou7CyjoVK9yiaVcyKFKOxaJEm068RdZY104ZQWccJoi4+B0HfoFDEIzNtaw2a9IPg11hi6do0GXFXjJnMaN+WNl+7yT37jm3zyxac8OQ64qy/ChaXrzsih2/KAjJNuqfeebCucq6hHjYwPh0DwAZTm2o2bPH16Snr0GKtsCRaTm8bHSIiRECR8xDoroH8jCYoy3mLwvadfd7issdpST6asN2uij+SYCL3fpmWKgVYOf9bWTEYTupDx9YSoG+bXX6Y3YxQZ1z6gvTjHd5n05CfYs5d56atf5+4/eZvfe/fPuPjwuxw0jvHuKxAbLAGdO5Jvybom12O0M5jk0b0Iy1FBUpUIwyHSd8LQjX6NX2TMxBJjRveXGDdwWaUwIssRQ5XiZdjwK1uVUZSM1aYk6UogmLxeGS/Og6M1yYKus1w/qYhOOZcBxiGsC3HsymavMANTSwHFWZmTcHJQErrzjMsoYyNSRIprNjPwugJGZVLZuEHGH2IUt0FRKDAkGq1QBHLsMWFB9JfE7oIcfbnvkrwOLYwmlUW018UhXFlHBbicIHbMxiN2duZoY0hKhIjQSvp4VgrvA6FojNoaqKQQnNma80ePefLkPvX4JaypyKEn9zLC39TiWh+Czow12ErR92vOTu7z5IuP6S4fktIGm3oaG0lREReJ+GiJfbrBrAMmZTQNKWo2vuf+t79HHu3Q3L7DEsWm81ycntFuOkauLknDSZyaKGL0LC8vCX1PU4rqxcWK++EhOQYa19DUIyjsp1t37hC7locPHhNWhlC1uGjksO0UWVXELC63lCKEFqMzKMNoOsOYY7rNRlymTU1TN4XfJu+tHAjk/ayq6ucEzL8tdA3VuS5OZG31ttAdWGxRJQymFLxlVDwK1iIXcXZAEfRBmM3iXBSR1yhxUIYcpHOahLcrI5NO1hqVyWZAK1gpXJUcZGLw1E1DiCKMZeQAv39wwNGRpMKL6zeW8a1YXo/wuK2x+OgF1wB4FYW3qxVuOkItLaqEShhjtg6HQcIWAa1wqFJEKcNm07NYLWnjI67ZG8zrhkZblM6Y2pFCpKnHGDsi2xrtGg6u3MI1Y06fPuXzT3/AtRs3uHLzNtVIeOoKQ04B6yzznR15DUqK2mayw9PjI0azEVevv4iyFWdHj7D1nJsv3CaTefDgc5bnG2L0jEcjCRlUkXo0xqJZrRb0qkWpLNfiIIwUZ36IGWskybsa1/Rtx/0vvqBqxjw5OuXo6IhKJW6+8DpV5eiSLofWSA6Bdrlgp3b842/9Kt/9fsdfv/tjFqen6MKbFfC7iI0pJbpeED3Cj33mTEpljR2cP887bAbRfLh2yxKNMlrc2XJxlwOevK7hyyiDVrY0liLDJExKCWdccV3I9RW8cMPzlpWbIUeMLTgk38tjaotGnBNam+fEWIVVGu0qxHSWymF0OMKWmZwsvEVtXHmOhDUW4yp6H4rgPNyzuXCFQxnNVQXtIIdDrQ0pyR5eNRYfwPctweeClUE4oYgDhOKKUcUfI4Emart+aK2preHk8QO+8+//lFff/Dpvv/omdTPDNbu8dfcWjx8f8+67n6LUHXwf+NH7n3K+VoytYrFeUtWy7tezEYuzE87Xmdhabt65QTaG6d4Be3rMrbuvcXnZEeJTXnrlJb729i9z66W7PH74iB//6F0+/+QdLo+PMFxw+vhTjo8ec3J8ijWGg2vXuX7rFndevMutF15nNL/Oef8p63VPu7xkf2eH5Rpe+erbvPXNtzg6WfHZ/WO+8Y2XCD7z+N4n9Jslr3/1t7lx90X++gc/5MOf/ojf+e3f5IU7h/z0vR/w1huvcLh7yJP7T8k+cGW+x7je4acffsL5akPIia9/5Zf5ycfv8sXlI/oqgQGnFGkNq3hB335MPa2JTnF88YS6qalHIyajCR5IKqErzeTqPvPDfbpuw8mjI9yoQm88y5Nzugi6HnGws8vpwyfExVIOSUpqiVxqDchl7NoUsc6SY08u9VmKUq+EmFivL8UlqxQhlfticPRRmhXhOTRBSKyXa0L0hOgLLkDWzspUxJVnncNWeJDGfmmoKF2Cj2RdBmlCxuF5KY3BwrOMKpeAEYUte1RKYExFzhJ0E0lkAyFlOUhn8DlBzKhK09QSGBhjxJcQrYym68TNaCpxlPkyjeGqwsUtwayhC1TWMp1P6WeW3itaY5leP2B86wrJWu5/HPjXf/KX/O5rX+GK06TOcHP3ChePHhKtpJzrGLcTfFL/yXtsirieihszZU0IHSFntJY084HvaZ3D6ApDpt14lssN686X/IxEzqa4RUvorFH0MTCOkdpB73s6v5HR5aixymBzxBKoncUoMCpguwuZDKw07jn0jDR8La6IW1ZpTBLeYciZjQ8obXFGUAIhSX323ns/pO8Sb/7GDtX+Lk/WmsV6KWuotSgiCoNPiewDXQ6EXtAsWStpLiYjCLUcxBSRS4OxD+jNgipvmJbrax2lttU5kVykRnBQgVymG0REjMljTeFMKhFVdPkdwcKIIKusfD4qpy0aKkQvDk4lghxFyBzqhcGdqYp4Gos79vkpEKWkkSATDSL0KW0w1pWg1zLyn4trL0sSOqU+1EaVBpzaBnDqwk1NxZGc+XlO6xb5Q0IhQquz8nsql206hq3wPKB2jLOEUl8OryvD9owXChM/hPZZLkvO20mnQQTVWvaeGCPapJKVULBnaZhyCSg1hNo6aWYoCRhKxb1ZAGsilqWE0rLKpFjCvLJMj2zRSWXdUWjG41lxS6vCah/MMDI5E2MRbEtNnWJAV7VMy2gR27UW52pOYbu/xyiZC2gxC/gyqZPKGWUImBoaR6kExg6zucYYYdeKwiBNZ7IE5mpxNhpjcLVG9eLITTnTWCeO8ZyxRmoOYyQ4zPc93XpD6AMpiXNX5WfYjaaWYF6jTUFtZFZ5jasqsqqLqK+JQeoy6yVXJtpEyCLCa6XoNz3GOmyVmbiOm/OKm/uG67uZK7OAqwPaVDhToRT4CL1X3LjmOFlqFmuFUhIORZZQvXXf0fpE73XJ9ehpfWCxukDpSG1HJBSBmo3XNMFhsKxzxsRMiBZlGgKBrBwhNoTYkkICv2bTJvpYS/ZFLvdTAkHoGYy1xOzkVB7lXm19KK5uVRrospQ764i5oVEGQsZYME5jnEwhVs6hnStu7IxREVfeO6OFG2+dIzmNUo66GuEqSybg25bNpqf3Ee8DxI7oe0KA4Isb1UDTOK4c7HBymun7VVkbBAeiCHKPlr85xoQPK3LaYHLC1D2VvU/XXCHYHbKb0NhEZTWpnhCmV3B7t8j9EpKh1jV59zZ5/yXGk10aE3Emo3IQNCKKkQFdG9xsQrU3hcuGkAKxDbRRmsmaILiaFElaDGM6ikib84JGdZjxdXSzT6p2cXYCakwyiiprcjVlwy1WJOYoJnpNWF7Q+YzqN7h0xN/19fdapO2S4p1PV7x7hACmtcFqTVYTgopUY0cdl4xGjtqKTVuP5ozm1zA2k3PHZNzQZ0fXbphPpswai7eJuDrn9Ogee/sz5ntX0LZmZ2cXlMPWI2JOrNdLvvjkfVbnR+w0msZqyB2Ymtn+Ffau3QCdOXr8OavLYxQZ60bcfvFVdvYP+fz+PRnxI2ObBldP6Mum++IrL3H88B7Hp0uuXb3O1976Kj/52cdYbajdmBBaKu2Yz67QjHYwaYzLYzQNo9FIks7xwg1KkZQ8KVJcsZSRnFJoZemEGa3wWQKylMpoC73fCCtSgyqAfGs1oW1ZLheEcgitjGG9EAdp164hw7UbN0ApTi9OcWR+6zd+kw8+O+J//7c/YHTzW+y/1PDuH/2PhPZztA5FNJP2XFaQohQEo+kE37ay4MfIar2mj8KU6boOW4+Km0ZDjFsWT0oJ5yx1VTGEDvU503edOD6VCHSh9/jYsVgsyDlTuwqjNNPZlPXFuXQsS0dfFQGk7/tSUCswDWZ6AzW6Bn4tozUbhQ4e3R9xfu9DDv/5L3BwY8xP777Mj7/9e8STfXBTqvpQAqmUJ+d14XJWZL0hhTWhX6FjJvpM17MNE6OVZoI1mrg8FqSBqdH9ktCuSClimzHK1KAdRmty6sSBWphO1o6IRZDKpTs+SJ05y8ZrhjTjoXOaRdhSoqyKg7eMqkhTMm5HaQZ/rVEanXJxosm/00PLe1sQUoRTRYqZ0CecK84Hgoyw9B2pdIBVis/CxZI4skDYeDb1ON8Lj9evxf2XVljktQ6ptkobYklvTcVNMR6NpWANAZczI1sxHY3Ym08Z1xUhRtZdx6br5HAVEwnpkm+Jjzmz6Vpi6DFAG9bY3Yar164ydhNi8CTXYZyjcjUgTjFrFConzp4+4P4XH7G+eIqOPbWVpkWNxy42dE9P0Q8uuBocauOJPuMzeJUw2rJTj1l1Pe//5V9x9esdcWdOt1pz9OgJvg9IiMszJplGMCJ1U5F8ZDbb4cqVKzx8+ID1YiFhMCjatsOojFLl8OoDGsVm1RJ84GAvMjU7NGaCLcpTRkZPKSN+A8vVVbXA9XfnhQEubDiy4DNU2Zgzwquu6+rn2JuDc8+UEeyBQUsR/AWLIGNiETloJSOPbcilm64BXcbLCrOsCL7yN1A+URF8lNZyvzOE2Ml123VS0GtjcVoxm80A422fbwAAIABJREFUxcX5OTFnfAjiiHWOzWYj4gJy+OnaVhoO5V72PmybHzEEutzS9/12z9s6NYqLIWvheiWtqKxFlfH3YcR2G8YB1HVNVVVcXl7KNbpa03UbmvGMEDqiMSRrsM7grMVWCqsFBeFGBm0zISoOrtxkb3eX7/3Ztzk5PmZ2cJPDG4es15sSLJXEBaPEBQlSpB8cXmfVRqyb4BNYZYjZEmLPpu154cVb7B9eJfYrdA6kvi2uD2n6zGe7bLoNOSgIkdB7QKNSAN+RY49TFnwmxp6mnuCsIbVrzo+ecP3ggPd//AM+tI7X3/hFstGSlh4ji8UF88kMlRNhvWavafitX/lVxrXmD//wD1h3rYRdKNmvB54rOZeG0bPGwRCENbidhp9vHTvPfZbA1pW9/b5gh5TS2yZBLge/XIRIERokbC73ckhUSpGNIUVh04lIrLGuYgjaK0+8bYjFEDC6OIERESUX15LKhS04/G6MZJ1LgyM+u0dL46+pKgb8QNM0KG1EMCuvb3tAXZd7eFguUyIV/qRzMmZqrCN6L00U8va+Fp6esOeK/PZMHC97SSrCvd66ghK7ewe89qVXuHX7Flev3CLEnu/85Z9z95XroA2NC2wuTnkYl9SjEeOdXerRlAcPHxDbBadPL/DWsV52wIgXXrzL62+9zv2HP+WLJyfsHtxGmSmjyYT9gxtYO+bhg2O63tBYxaw2fP7h97iyO+PLX3mV/+vDH5PsjJfefJWr+1e4crBHM6pwTqHtiHo04+qtFwWbZE9RFsbTfR4+ueDaxRKcpaodB3szNhcXPLj/CNPMaVPDTz/4nE8/u0+Iifc/eJ/PPnuP1arlo08fYl7d5yu/8DZ91zN2NQcHh7zwlTe46BJ/8c77qKrjF159nYc/eEifMzp5FAaNlUklLwxY7wsXM3gZ2ZzsoLQTpvC0ZvfwOvu3rvLRxx9w2bWMzBACJKzglAKPHzxgdXxGZStGozGb1VqETuvQxlJXBa8RIXcRHWT0MZV9XGUZtX/y5CnNuOaVV1/j6OiE5eUlOitC7GW6ohxeYxSeeu+74hgqDvGy9ztjn7ni2S71w66+/V4ECvleF3EpkbeNGmPkuqurahsmaawp3FFxkA0sa2WK4Fuci+Kmk4kj6xS5BLQoYxAfZC7OObbihsz0Pmv6yLpvtuKNQhqSm7aXxvHt2xzefoHrr97lNC24rGHhA/Obh/zNtz/hhaN3+drLr/LjT464yIqpHbGIvTB6NxuMc4WlnctjFyeWVtvgzb7rMcWJOUyNxOLEytrhbAU5sVpv6DrPYrEkl0Cw4MVkIMGioI2mrp3UBj6IaFPyNiwyZeWQ96kqzz8YKoweGmgFsaK1OL6qClMml5w2GAUh9nS9JyRJbi8XKspoQsx43/PxR++iq4Zv/NP/Aj+ak8KIDV6YsDmL2w3hh+bQYbfWTko+iEwoyLW0bSujcsSmQPQdQTcS7lP4+KVTQVKCWNKmVNYx0m029G0rr1mrMg5fMHVKMGHD/4Y1P5UJuaK1l2tX6nuZbpADotTGpvAo5ZeVNlI7b+uz4bqjPKdMbQouQUb65VgmAVrC3S91WGlwZJ7hJtQg6PpYxP2BkTnskc/ts1qL25eh8VLwC1mRdS7cZF3eEzlPUI6YsbxP3nsxVaiy36LpYy9uv/SsOfr8vr1tZPLMPSuCXdgG6imNBBgpSoBlQpth7xzEU6khUx4QCM+ai1kpjK3FFJTz9vmSEsRKXTegcrlEn6EWuq4vAnoipaHRK2HiKcrrHciZw+tvu6X8PIXizpXPNsQoYWyabU0Riou/vBFiBiviKEpR1TUAIXgx/cRcXLgeY+X9DzIehFJ62+yG4qyNabufU9b4UdXQGEetLavVRv5WH7bicUwd5EyTa5yV834INVMrSA1d1nStBZHS9R61Lk0eRNx3Tmp3R8KpxP5Mc+NAc/vAcOPAsLczYW8ma1FG44xcKymDRgw61/cMITX4ZElJEWKm95rL1YZNH1n3NSeXkS4GzheXLNcLRrUl1DXKWDJi9ulasI0ipoZlm8mXYnsiO1kTtSPpjpg8Z4sFJ4tEmxKuUuikyTiMkvwHhTRKxmOLMZBDFHxdX0JZkyZruS8rawVJk+R+lIkJcLaiasYo68Sdr/WWr52CJ7DGOktOPSlpUBZTjUWTy9JMVSZt6zipVcGXJigI1sRqwYgpMtN6RNtEUgA1oCvoJEyu4BoUkGMghB5SL9OnbYs/XhFbh0sKrQN2MsOaBsYzMWH5FXWO7O1dB1WRd2/id65wdTrmyqRm7Go5iyYxBJIC2XtM1Ghdk02F0hW1lXuriz3kQAo9OfWE0EHwYpbo18Tc06c1Sf0IpyxGTzC6pndTonbyeuwInxRnugV9wdXRDXQX0LlFqVQQlf/hr7/XIm0fFV+cZFJ9SNVM8V1LNonptMF1mb5LzK/tF7ddRySwWXc4V5OTJ3SXTA4cj+8fsV541iRC7Li21zA92CX7Mx5//gEKGO1doxk1JDTHp6d0fcejBz9jdfoZN/fGNBZQFlSNG+9x7fbL2PGY06ePWS+OcCSqeszhjbtcuX4HHz1934GKZJ2YzHdpxjM23ZrN6owPPvgJVZP57/+H/44/+9Nv83/8n/8rN26+zO5oTnPSghmxv38TV++QlNjUyRY3mlI3E3HMStuEGKQbZoyTDQ+KQBZoV0v5XmXq8XgbCpRJpYgV5+JmtSBlxc7+gRy6rKEZNYyaiQTKxECfNZvNhovzSw6vXWO+s4d2jpCEHzuezPgX/+x3+MGnmdPmFfa/8g1unJ3wxXf/Z1Q8JmPJKmG1gSSdvtCLa4KcyWXsK4VIu9ngfS9dG6RcjEGSdFMSJqo4daSQ1eQSKmLpug0DSN+nwLrtCv/PCM/UJGJOLNZr2r7F970UdEWgVWT6bkMbA6aeokJi4Sv6nesYtcQAqfHMq5bz0yec3PsZ9z68pH1pj7hzlW65Qh9/Th5dxe5Z1GgPrWuaSoF2+LAmdZ7Yt/Ttmhh6Och2ntivUXmDChs5aFQ1ZnOfvFpjx1cweExsqVJHVYIrfCqODN8zOI4Sic36shQtStABRQxIeQhQogi40s1WWtH7WPhBqjANpXsmHW0RhUJOwmstHVSjFMpK514O5gWRkMoBo/ynckYn6e7rFLYubp1Bh04cBVGg5oNQpkKiURGTepLwHojdirZfkOMaiNTaoZQ4V/PQOcwJYsKixLGX2Torur6nMYr5aMRsMsG6SsZ3VQm1Cwnf+cKtLV3pWJAMSpi9vhOR0MfA+nzNp+9/xCt3X2JnPMfGihQNxkywpsZajc6tOO4f3+fi9CGKlpGJXLt2yEt3X+DTj3/MF997h3jvlPFpx66quHXtOvdXTzjuzggxEU1GO0efMovLNaebNfMXb2FqzfGDR3z+8efsTOdobaTLnaVYFdSEOFZcJcLaZnFBrTJVXZGNxvuW1kvzZTSq+PTjT6mMKQf1CDGJ2zAmcsjCn3SlIE8FlZEUTivGleHW4S7jyRSfEkfHJ3JvDyFJRZABaQANLoLBTSuNIrs9HMgHK3vCIJyB/CikRDUacev6TdZdy9niAlXcRvG5QlsrRdU4qrpm1a5BCUIl9H54aARtIFtiGFzkJZVXoYlBeGVn5+eCXynCVEKK4YsLcfYoLb8bQuD09JQBmyBuFHmegX0dSrrs8KW1ZjwaMWoaIrBar+j7nno+J55dEjpfxvERLuDwlxdxVwJGBk3bc3H6hNl4gmNPCh4CVWOoXM1quaYzLTvzGaYgURaXl0Q9Z393xt7hVa5cvc7elZuMpldZd2dYtwYMKXmZZsiZ1XrDYrHE1RVXr9+h7SRd93Cyi6sm+C5ycnTCo4eP0FXDjZdf5c0vv8Yf/5vfE8dNCKQUSOkc5SMTZVDZk/qW5D3Jd+DX0PdkLwcZrxJZORQWPZmjNkv0rds09Zg/+dM/ZnZwwC996x/iRjv4GBk1Y5rJnNCupIkUAnPb8Fu//GvsjSb8/r/7fY7OTjCVwxQu+vPBhCpTxorzNiV5GIEcnD/PIyi2jtvioNl+KbUVduBZ0IWMu5b7yXtcuQ6994JcMHaLRKAIpao4uHRpRsjz5SLeyPUHoE2EqLBFRJBDlYxHW2efNQYoIX7FZTOMXZMzTsuh2SiFq0eMR1NxxQ6BkUXEqquanBfP3ddyj4ckDp1hHC6EwHKxKFM+4ogyJSU+5yGy7JnYkJHHU2UNyFn2OK0NRMWt23f5+tffZtN6Pv/wPbRRrC4+594Ha8Z7u+zvTtgsL/CryMXKc+fObZ48foBfX/LR6UOuHL5IMBVucsDETfFKc7Lc8NJXvsG7731GSJnL5YK2bZnMHFdvzAlpw3f//A8J7ZrFxVOu7s+YNXtsVh0vfumb3H75F6lHu+Tg8etzNGtiXvP06JRmdoW7r9ziwaNLPr//mCdHF1y/fZezZcfywvPinSk39ke881ff4+jhY77y5Tc4vHmT4wtBGLSLBRdnp0zfeg1CS9Nc5+D2W9jdu7zw8mtMxpVMLIVA2weePD4jRM3cTXnj5a/yk0/f55Pj+2ChJ6GiOGhccS0FkwujsKff9IQ+gqmZ6H3cfMLF6YIvHj0l58BsNCdu1vgcadcrch/QATZ+g2tGTMZTVIB+sUEbzXQ2lxHXrqxV2ZK7SOozJutSb4QiUiiSz2yWLfc+voetRIAr2gJ9Ca4DtpzNuqq3zatcxrPFDW8ZQoMGN3kubq2qMoU/mcr9VSSqLOLY0ECMMWCsKdgXto3s4X7XAw+yBJppqzAYbDbkEEl9Kk49g6vs9nkG08HAiVRZFWeV3LMysWG2dZrgHmRagxKu6E0mVZqbb32Jgze/zFFYcbZWLFLEO8Nof0q4eYN3P37Cb768x60HxzzdZA5mO5wfP5JxU6WweZhoEZwBWv/cumZLgnyKfuibbseedR54nKmId4nlagEx4oy4ikPy2xCukEoYJYp2tWHiaoJPhCBYiIrMxBhGVgLEZMpFhD+FiBIpIeul0lhjqeuauqokoLMsILo0OUPeEDtfGu+5TEKA1RrloI8rPvrpd2hGli/9g9+hNRNaLUIQXkv9meTsNRhhIAknNA0MSHD/D3Xv2WtZlt73/Vba4cQbKnZVd9d093QPOeQkDSkOaUomLBoGIUGCYb1wEKRP5QQBNiDAgGxYgmBDlEWRkoakSIgz9MSezl2hK9940k4r+MWz9rk1EvievkB35Tqn9tl7rWf9Y17zBLTzuBRQYZA5Umn6KLONUogqSxmsNfvukfFeJgZC7kkwGTg1WkrbzCv3ZQrjeqkEIB+3G31FwKHzCzIKKa4UsyMQKWrNK9Jtn9uaM9JJeb4JQZSiSu9VpjELGlLeo8a4tBjIcaQpK0zJikiT35sQO6+SnCk/VzFEjM5K9jDOi2b/zMeUS7SUziBunveMBaKoTYGkAtYW4vIIY7ZqVs3mc5+xVtwp6Srr3RiDNtmxUZaYnJ8pKQwpO2FeyfaNkbjvR9D5uRXQay8+iIGxmDdx5Rwbhj4rJEVkgZaYlavx4dXnMJ+3UgatIySV6PsOE63EEeTYsuDDz+2k5P+PWbHOGYpSCB89aFHtqqsIjBjFOYNSOaZLZnOnr9T8VpMjmuJ+NlGZ8B3XYR/8XsihXwHsBx/x3UDXtvR9J0rQpsnqYQi+J6ZI4RxlWbGYzzHWMpnO9tiA0kK4jL0CaE3Xy6xcu8CsNCwnBfM6MikGjhclrx8a7h5GDheBejqVuAhtSEqjkzh1YwQfVFaGR6z2VIVDOY1RBu8V86rBx4GTizXbjWcTnLj4UBgiVktxX0qRYQDvSjoK2miISjMEQ9NoQujzHuCEQFSKTdOxHqDrLart0dGj/BarOjSdYEJFybYeKKzGKjmPJS15vNF7IZWIUBQCAAeIaJwrKeoZ9XQuAK0ewe4xZkru67bZEbeBEOV5MrbElguKosaYgqIssc4Qos8Fd7JehCiqemcNVSVn7aqcU9UbrJXSOO0KdtsNystZQgoFjejnVcSVJa5wmFQQQkfyItbwuwdUmxImhmhfJ5UF1mmK+RJlvwSzOVVocDah6zlxuuDmdM68zAVsWsBkoxIGRxwsTSjwqiYUE1TRUfYtMfbi7ok9Xb+F5Om7LfQNfZRoQ2siPiiIP5K1Xs0gGoKe4usDkhLxRzIG747Z2TPWTCmtwsQ+x+TwF379pQZplTEkbTlYVhjnUFPL0HccHE1JPvL82QU65WEhbGi2Z7Ttjs3pffzpQ4bdhs3pE+bTmhu35zgrg9HERRQ7+qBouh2bzQZVzMTWNSlAKy4uzthuzlnOHKWV4jFVTqgmNzi8dpfJ9JjzyxNOT57gfYvShuXRDW7cfoOkFevVCj80YpUwjnIyRVuDjYZmu4bUcevmjMUsoe3A85cvmS9ew+jr3L59g02zI3ktrLRR0hg/WXJ8+y1mh9fFlt01bDYrdps1RVkxnx9gXZltg1KmU5Y1ilFl5ZACzNHGBNoUDH1H33ZU9UQ2K2PogoSdxxTZbjesLi4ZFbk3b9/m4OgYnxLDbidDcBTrxHtf+TL/+e/8Nv/w37zki7XjtW//l5zf/z7t438tQJoZM/1SBisUQ9cTuh68BLvHYWC73ki2k5HCsN77DD5oAb7VOBhGkgZTOAKBLgwkrZlOarbbHbumISnJ6bE5H3XXNWyHnjaIdV9p9XNDqEZlhZFs3FF5+tgzGAu9IiZpXJ+SKNBszx/x8MOfcel+hW11HVXWdKefUi0OZWB0imBqopEMqs1my9A3pDAQhx41dKI0UsLDyyaeh1gfUaEldqeUWnKoZMYK+HaDKsA4AavG1lOS5BiPlm01qgMRTYjKtp0x+8gAKuXNPOQYjNE6BgL5KgGqSHnogPznZYAZFVOKq+HKao1CVN4qCYNvUiKFjoTYsoiJEBXJd1LohpKBNrPIVg241DPszvH9Rg7mKQIDSgVRUuT8XWscyShi9FQ5m8gaw6QssEozdMLOTp1luZixnE1RStGHQOsH2pw52vUdg5e20pD8lQpOqZzbA2jNwcEB1miePn9Kv97y8KOPufvaHUzpMNrgdIFSHSn1PHh8n6dPPqE0gcODKYUztJsd50+fcMMZvv3Wu9zbwAcf/BsWQYrM1ieXDL1n1XZsfUcXpEjJD4FGad587yu88947POtanj58zPnTU9Jy4PB4SVlVMhBntjwOYu0YUqLdbfGqQadIWdcUdUVRLOians26YVbXlK5gNq3ZNS2660XJohLeD6S+J/YlLsHQtbRdR4gJqx0panzvmRVQmMhqdSEKK+MEmMyDumShXTHq4RUGf1+qZc1eFYi6arIdM7VAwC0V4fXXXmfTt2w/aQhxkKwxo3Mmkwylg/dyEPWynvs4CDmU95sRYB1td0rntt+sDkhZwZ9ipI85ay4zzkqJurDLCuwR+NofgvSrlrYr9c0IOo0lUWNJVdO1KCVFAAnFdLmgDVFyvSI4bbMl9+r9jwVTYgGUfOfN6pzVxTk3jm4SlaMbOhYHjn4INNsdk8kMowuSN1yuznl+8gh1ankxPebO6/eYHRyKoyAmbt+8zeryJevVmTgdwoAfAut1S9t6zi9WvP76Gzx7/gyyg+H58xNSGlhMaw6WS4pizrPnj9i2HcpYut0FB/OJDMO7LYshwNk5utmQBimhlEN9L7bNoOjbBhUlI23b93TuFL3bsjGa1+69zePnD/ln//QfYZznl77+HZSdU9WHohSJA227ZWi2zCpLVdX8+re/g7WOf/Vvfo9Hjx9l0FQUqzar5+TGTHu+4NWsZPKPX1XjjD+3JxdIWV1y9dnHLHka4zasFduwNXLI2qtV8kFJK5dfX7LDTS4OHfwYd3B1H+8PRyllwCS/FzVaUDUmx4bkY3tWQ8k+EoZBSj2MZJgpFTMpCkUlMUWg90WRcmAU506IMRNiozIcSBLPMPT9/rWGftiXP5GfBrmuWe2TQe7/8JruIz/yrzssStV89NEjrIZbr0tJxcG0ppzO+dq3voFWgTLseOvuNV6edTx5+ozvfOttQr/id//l79F1a3R1jVt33mW3admFwKAVD0927Hq4uSxRKkIauHH9gDfu3ubPf/ADHj38kLoo+PJbr5H6HaSBH/3wx7zztd/gxp17hCR2zqiB3qBCoGs6LtfnvFHdYDnTnJ+ccn6649f++nt0akJ3ueaz9Qmq3/CzH/4ZKQwczd9ldf6Cbhv59NHHvHbjmLNnH/Gz99/n7/5Xf5eOBWr6Js9enPOjHz3k5kHFbrfli5MVZ9vARb9Fp4Z2q7l+9DZ/72/9PX7vj/4v/uyDHzOoyBB7GDyEQDs0RBsxpaMoJSIj9C2JwPo80aUefbkRW2uOv9AJCmWJ2460k0JdrS3KOYbB015cEDatEDn1kkdfPGJzfo5GURSSlV2aQgoZ00hYSFiiqE89u82WejrZx+P83LP3SjX92EIevCflsjLvvWTBjxEBjMCKPJ1tm0ufQsTYUeGn93/feC9frbMjiJEJlvzlnKNwjiF6fAiEFASYyFmU2miiz8q6HJOfstoxR2fvSydV0lSTWkQNGSweZ1WldCY+yXZkxWS+YPHWa6jrUz7fveTMbwVQVIaycIQ2Ed+8zc8+fcQf/vvvcxQdVdty82jJ4+0FjR/2pZnee5yzcpZICZuvufceNUIsSqP1mCWfASStcdlyPXYcCGAmVnzf91mZKwrogMRSjS3a26ajzUq6msTSaJZ1KQAG8epaZTBIK0VpLZUr94VrriiktV4picTIykWlZAZomw6fxHarMwAprefIXh9bPv7p95jOj5i88ytUzuFVKXOsTujQY9B4r4kq5HuMLJBgTyCJQy0RCISuZZIiDmkGjwn6EFBBis0UCasUUWuCElB5zAuNIaCsJvgB5b08d69E6qisqoV09e8dycV8lwqQaXIurOSD5ze936cktij/PQlQo6Iu7sHdlBJ+GPYEHJmg3kcmpPH15fkVB9zohhBgUWcAc7/qj/f7K0TnPuYqn/NiilnB/vPP3LgfiEo0O0O0kXiweLV3p5ToM2CrtcGaq2ItY+V+1tnlOOb+p5TkPtLkdSMKGJr3O1J2aSW5ZlorybTPYpBxjxoB6JTVyllULPdHuvo3pBHhl63w5/bwV69ReoVEyRTPngw2SuF9n0FaEdmIWDDS911Wnb4izlESsSGbcgQdUdZksleuvZVWkHx7JXzbintOrlq+f4RsjSnty3O7Toj8oCQjfxRUyXqd3WIh0needrvDdx06Rzm0rbj3QErTAbbDQLNrGLoOYx1HR8dUkzpHb1hSGAhRSHSnNBhLYQ3zWrOsDMcTxY0Dw2IK148c1xea46lnOdXosgSsiDES0tGqIv3g6QfFNrsJxaHRYuspVVljVGIyGYteE31QDE8GdjpSOlhONDeXlvlUUZeaolrgymNSOSPpGh8LQllgpjVKlyRtpYg5ebxPmDZRtoGw2dFtNzi/RvlPiN0lPnUoZSFCHAZ6m3AmO7J0QQiJ4AMhabSOmCgCo5BiVnI7XFFhy0qi6zJJLkNmzlYPiaGL9IOUyXkfMabFFB3GFALSFpUorI0odBPZ4eSHTPRBWRjm0zmHB5p6umY+33Bw1rI8nXByVrJZt+z6ghAHhtiRlL+Kb0wxB7oYEgarHaiAas9R3ZpQDVgbqewg8+10TnSa0JxCf4rrLyiqGqstuqykYyOJu8AoRTIlRXGEtY6yLjCVRT2+zyp0DH0LvqfvdiQV6PuG0HcE30ncCRJLVxUGFxrS5jFcfIaqrlNM7qDcDGUdTiuwkAqHKyfEYYFtHI5IH3M041/w9ZcapPUhcHl6wvHxESEaXFkDiZPnz6DdYLvA+ctnPHv+GX1zSWECgQZLx7yKTJdH2LKiLKB0CmUrnDKYNGDdjNJOmCxusFgccXF5QYyeyXzOfFISjg9heI3YvsTHAeMWzA9vc/POl5hM51ycX3Dy5Amha0FrbDXl5t0v4aoJwzCw25yjwpaUPMbUlEWFUl5yPb3n5MULptcqHnz0AZ9/8oCzs46LW4Z2cZPF67/Mo48+pFs9Z6kMdYxgF6jlO8xvvUexuEYXzwSk7DuMiqgkuTMaJwxf5rjn85lsniP3nERxqLWm6zoZBkKkdCWTekaKiT54do3IsGNKdH2PLizXjm6w3qyxRUkxmZKUIfoOP3S024E+BK7dfI3/4td+iR/d/wF/9uQLjt97i3f/+t/nJ//3F4TVp/uhO0VZCVOUDNMmBrQVC5DYrrZ43+OjJw6NlJE4segoNEMY9orNYfAUbiAp6LuO+XTGwWJB27T4oRWGJiYKbel9z8Vuw6AUQeesH3LOKEjQPgmnHVE7bDUlWMeQmSHbb0jb56TtI9zUYXTPsH3Cg/f/mGvLewwUuOvH9M8eoU4+o6ymDFHTFMc0xqKjgGRD14LvUKHHpoiPCWs1Jm6JDIAXGX5KmLJEDWfo9VPU9CBHpMvBRdFiUqLIbfYpiUVjr14d6fqsrDQKlBIzXoqSCRaSRE+MqhP5NuzvG5S0e485Vlpl638GUnWSPDiShOZL/muAoYMY0LFHRZ+tHBoVWkZLocr2YpV6dBKlVBUaJnFAERliS9NvafutKNiQnKTC2AwvIxZohGGPMRJIFM4yrSeiMvEBo6CeznFFQV1Z6lJKbGIIMHjapmXbdpKRmSTTc76Yc+3mdbRWrC8vef70KcTRhgvr1aWAgRGKpHn+6Ase3P+Ee5VDRfBtw67dstlcsFmfoOmpqynddo1HoTY7mufn/OQPv8fDsuCtg9dYDJZme4lO0IUVJ7sdq0ZYu6jFsmacKNiO37iDO1ry9IcPefL4GZVyxG3DyjfMJnMmkxnaKGIY0MFLy7p1HC4OmNQVfmgJPlAWJVVtmRYVDNJ6PakqnFaUzlDYGhsCNkXCIE3dg5VBN/iePnjaLtK2W56vVjw+PWG7XWOLAmUsRVUTYs5K3utz2+WtAAAgAElEQVTjeGXovPrxPt/TXClVUWpPppD/tMngUSDR+4Gf/vR9qAuGdKVWJReHDL0QN0lB13XMplOWsznri0uOrh0xPVjw2eef0w19VvvKkG6tFeBMG7quZdc1aCUt9TEDWmVV5XU1cXR0xMuXL2n9qBIXRS1a8px9JCucI9ZJ+c3QD/I8mStgre1aVA9ai93dWgcG9GwC6y2xHdDZak4e2mEEE0Z5jlzTEDwXZ6cMd3omruLg4JDpbMH55QpnC2azBShFu9uxXq1YLg6ZHywo3QRdFLQhElNLYRre+9IBT58UfHDRE/qBkCRjUBtYLKcoPaB14Mbxkgf3P2dzfsri2k2+/Svf5s27B/zg+x/w6KMPWT9+xMp33LIGNaswzZrN2RntdkdqtujNGpcS84NrzO6+jTu+zvLGdaaLBZPC8ZN//QdU2xXXr19n6ztWq0tOzs4J51uWbyj+01/9df7H/+V/4H/9n/97vvGt/5ff+ht/m+u332K6OILUcXH+ktSumU2OscZSTyd865t/hYPDQ373X/xzPvz4Y5TJdv+M8Eue3H+sngVR5Fzd1zkqg6uD8h4KGpU0mRjQxkiGpVLZImakdTor/mKM6GwjE4WHnK5Uzs+0rsBYu9/DFAIgjQV2Y6HHqFJPZFVvthmLIi3u358ZrcQpsndkRE+ICmuUxB0ksEbUxt3QocgZnnFAaYf3HpsBLjnE5+c7KcTaG7PzJauLzNVhFK7u473iMfgMyuoM7opCT7JxxQprXcWte+/x1b/6HarSsFu/5OnjhzTtmjYkUhiwVcHDzx/y+Yc/oBugrhzLyXUuzl5y/vwJxS5w481DnK1AKyZTxxtfus2fff8zzs8vMLsLJssF77x9D3zHJz97nwcff8TBbMq3vvlN7t6c0a5f8vLkktlsznQyz5n3mslshjKW3YUl7FqUHjg7O2O7abEmkULLwaLixbPH3HjzF1heO+Lk6X2O5zO+fO9L/Pmff5eHjwK7NqHVFKc9g5uzDZH3P/2Mn3z8Ke+8921Onj3i5Pkznq0vmFvHYrlglxRRF9Begu7oUgmx4PbiTf7B3/n7bP/R/8SD9Qmr1NL2Hd3gUZ2jOpozKScMsafreqyyOKPx7Y7NqajpJ/WSYjLFlo4OKKsps/qAzekJVT2hunHA2e6S3baRwiilSbuOBz/7mBAjczdlOp1nQCKyurhEqQl1VeccuIDvI8EnjHEopYkhgwAZMBy/9gQYZIu55O8NIUo+XiYEXwU8UDH/mchkWmGd4fmz54xsh5B2ar8XjK83grQjzJReAVAUCqyVAi1riAR2jZf8WTIoq2CMCoIMOsoL5u9JZFcIKUeb5TLPlK7IixixZY0fBsKuZTqfoMqCs92aot+w8gMdMkNZoKpqSrcgRIX/6tt873tP+DVXc6gSO++5vTjiwflLlBEwTSzwQZx5WoPWmHGNUCa7cyT7tKxqCidxP0MIewJ1iELsmLLENy2DFzX9ECTHtXSFiCpywWDwnu1GiuumWjOrHIu6xJlEsgVJSQdC1/eibAsyjypjKOo6rxsCS9oMGvowZFCCfZTa4D39kJW6pezxiYDR0nofQ2CzOuMHf/r7vLHacOMXfxVXHbIJ0MWE1RUm+Ry7IhFfwUvOLTqijJC3RkGKParticOOrhtQMTspVMizTQYs9VXMEUjeqjEWTaIsDH3MYFsWxOBUBjBGEA+ZejKwNs5RMe9bQC7CQkoBk2SJqj1RLq+flMRjCQD+ipsJmZ0UMkfFfH1HYhnIJLwSReroikwpxwGoHBkl4OX436vuk/H7rzo78hOWlbQSp2KMRaVECE1W3V05WaL32KLMpEGOxdEqRzGAsm6/RowAKvn7Wmuw5j8iOff7U7raqwTYTBlwvlLJjm6X8e2PgKq4P9mD5gr2mdqjMGh0OKqksdYx+DHaQAjb8fspBUL0pBRI6SrCQACyV+IwtMwN3st6aayo8FMWLsQggoCu7/fXzwe/L37b/1sY3QJCyvogRdsoTQqyDhs9zkKapHMxau4vSYFcIjfGdEhxsqi1NYVzBOMYQpvJaZ8VwBJvMa4jzjn84Gm6gdC0RKWo2wmT2VSeFSPXUN6vJww9AUNlFxzPC24fRF47ShzMNIu5ZjbVTCYzSleiXJkJARErhZjwPtD1kYuLwPn5jkSgKmvKImCGjqEKFDbhbELpkqo0vH4TattyfbElpYrpxLGcK+oiUNcWO1/SFq8z2JukNMEOjjaVKDtHVzO0K2R/QBFDQdkZ6j5S7y5pNiviaoVe3aBdf0rfPiLFFcMg76dwimCESFJmKvdfCCis3DchkUIJKYjCNl/nYfAkLY5lneMzghe3U9+LmjlGiaEJIdK2DTQbtLa4oqKqZgxDjTbSe4CSThpCoDAWr3MJfRhw2nL9sKJyisNZzXJSUmh4Eh1FfSBuXr9l112wXb+k2VwS+jVGeXoiTikqDTiHVWuoV6hiLY5VNwVd4ilIupCZ2Xtiu6EfPGfbFbvFnGlZUjpHWVXiEtcapWuWB4bptKCsa2x9SEgF6/Yj/GbDEDyJwDAE4hDRuqCsamKQUvgwiLtYDVtUeIkezlDbC5KeoSYGU1i0AV84wuQa2/g2k/YE27cM3QV9v+Ev+vpLDdKGoePB+3/McOM6lBP6GCF62u0Fw+UZRRwI7TkmNUy04mg2wVUJpZw0xjqHdjXT2ZSytETtKJ3Irg8Oj+mTJemSuizpupb1xQVKa8qJYjabko5usVsbJpXj5u03cPUBk8WE1cU5jx59StesAU0xOeDazdeZLI8k26tpaDZn+KEVuX09oZpMSUoWj+msxtmC7/7x94k+8snDFbuwgOW7xOomL3aBZ2qOn0ZiXbPxnqI4YH7wHtXBdVxh8I3HR8/BkdjpTs/OUCoQYp8fKmGjJpMJpNGKII3twXtc4dhut1RViQJcWQonlzfyajKRvCZlKMqaqp6gi4r50uBjtk9nQMNoQ0gDQ9Pw7MGntL7mv/7Nd3nyzz/g2ePnvPvGb3D963+Hx//uH0K6QEXJ03F1LiwBiqrEGWHwhqahaVv6rgElYf99DKBzoQhJBq8oi7yKkWa7gaRQKbHdrOmaHW3bQkIiDmKgj5EueLoU6GNCI6zryLRr1L7QStrWxWIaUoShRw0tKnSkfkO3PqU3FUYHpmYgPvsZ+slPKOMUW2r6rqF79gkdEXfboKeJPllUsoR+QPkOExqC3xEQ63zySeIM4sAQepJvSDGgbIktJ9i+o28ucdUUlGRHpdgS2y2mnJBMLWUFxNz0qvNwlFUcjKy73o8KioQfBV9ZDUDoyb6bPOBlG09E1LlWFAsyKA34IDkzom6QT0inIHliiG04hV7U30jgvkXAzSF5ChJF6lD9gIuR5dCyiJ7BRF7Ehsbv6JMoDeZlxWJSkbwAEYP3RD+grSaGntI6qnpCXU8BRds21GXJcjZjNpmLvT8ONM2Opm04PDjk5tExm13D548eCdPvSlShmC8WzKdT6rKk1IYXT5/uLYkxRdpWPreicBJc7hPPHz/j2o2brNNLzi/OafuOupbMIK09F6enqD5ih4B5eUH64iXXNwNJO364/YLTixVGJ147OkahKLShMgUtrTSXAkTZ8K/ducnFdsNHH31Gs9kxdzUTV6JVZHu5wrcdRSEquOA9VlumixnXrh3jrFhsdputqFRCQusC7Qx93+FDmW1aWcmhFbaQXPC+j+wud7Qp0IWe08sVp+cr1tuW7RCIVnKLbFGJWmZk/kn7gXlUgsSsVtgP2fn6wtWhOt+qMiTrK5tUjAmVh+pd1xCGDuWuDpVjXhWQB0dxNUQfmRc19758mycvntGut5RFAUbvFb1C/gxYK63iUi6j9vbu0jliTHRtm22A8Pjx4/37NUYzLQvmsxkXqzVtbjxNKDko5AKEoLPnVim0s5Jnm69XWRYYbWn7Du+jWNvLgtD2UgplxI5YuAqtDX22xmtyyQgCaAxDDykwrWvqySQrRwKL5ZIvvfULPH7+mPOTU2bTiunyIFvPpfDJDwPWwHymuHmkuLG4Trdb87NPHqNST1FojC4YfMRZhUqBo8UMe+9Nhhi58dobEAKffPA5zx99wnD5gnuzmvr8lN2zJ7TbM/r1JVMUC6MlemNS0uxajm7f5a/9d/+A4o23eb665OnmhOmN63ylmvHg3/4Rt964i3UW7Qf6fsd6u+F012CmR9y5dpeffvo+F5s/4PHjZ/zyL32bv/Hbf5PZfMLRfI6aGrQSsk81LQfzJV//5W8wref8i9/953zvh98XAspJVqQKon7SxjHCKyM4Ph4ER/XPqC4Z72P5Pa8At9mqrPJ9sicttexrKko2oHOFDNE+Er3YU62VtueQD/RKGQrj8l6thDT0UjSjqkpeM44W5EBMXVYLmb36VRRwAqLK4ZGsYr1SWYk6W0CBGALbzYY+9Fl0JcoiZyxKG4nqiKMSQ74dfcd7gCzGXLaic7HJFaCdRmCclJVRo5KLbJuVXyOTkSkpXvvSG7zzzV/g/Z9+yN17b/Ps7CVN17N++Tn/9H//3zhYzEjNJb5bUU0rbFFwdnrEYnHMdPk6r3/pPUx9xGq94fbr7+AOKta7lh/98Cf4dgel4fphie8uePr4C05OTqlLy+tv3GO3OuOzyy+YVZbz0zNm1++w25xwcHTMxWpLWd3i6HhOGDy7boWxPSGrEf3Qo/DcvnXMH/3B/8PhzQ/4tb/2WxA6YuvYNjt22x2nF+eEaDiYOnwf+ca3/yqd0fzpn/4Bf/LDH2Dn1whNor08pahK9HSGrxRxaGl2p6Ruxy56ijqxW63pHVy7OeM3vvEb+J/+CcdV5KJdsd5s2KwbmtMVygeKRcl0uWD98pQu7FCVw0xLUUANCbqB2XwmJJK2TCdzOrvDmIpiMqU2kaFpKeuK5BuxiLYDk0mNtk4O8zFRFpbpZEJZTzg8Oubl0y+wRY3WkRB2BJ/tozpHjyCgig/ipiIrUFOUREattai5rWXohwzcieIzke3Mg5AYs/mSb33r69RVwe//3u/TdB6dyzWN/nnV30geWGulyGvwQjxnRV3wYjEWyy0Sd6A0YYyXMmCiZugjfd5TxnubKOpLHwWcmM4mkuuZ51NyRm2MHlM6lHMsFge88+0vcfrsC063ay7jlt16hVneyPE6V2p6O5mKE+ndNzk5Szx4cMZb1rDsOt44PGZXGZ48e4JLkWgiOmqM0VSVgIhamQxUicPMOLMXfKQY8cNAl5Wy2hopWcl7mQ+epm1RIe7ViTE7oEQplQsolebafMqktDirMxAVsc5irGG3a+lTyoo3AXxrpdE2l8NqMCoX06YgCiafWO12NH0P2gh50bT0XUvbeAF5S0vtHFYrSm1JKrDdnPP5j/8dBM/tb/wnFOWCU18SvAQUJSUEZfDDOPVmt4QZR2+wVhrB+x2X2wbtZAYIPjLkfaMwFpN7NRIyV5OiFKSh8Upq7ZyxRGPxKrsfFNnifZWfvt9n9uup2kc2WWMlkmIkG/XVfDWS4Rr5LCR3VXKmU85f30N2MedPq1fUunk51nZUVb+iCBXZKGMEwLgPjsrEEEMm365iHkYCdAQ7ferlvKIM4FFR7f9sSkJ4xgz6jTtESAFrHGRH1J7wHkkYpfZxQ/InyM/LK06qMepNKayTYuoRxM0xrXtVuPx83Ef87IFmNc4K4yuN52ed4/uyc8wYVBqLN8P+7w4hK0p/7nkSF8pIyKasYB2v37hfS4yKrM1FVlInJetISALADd4Tk8SVhKxwtUYAWa2vxBKSuy2xMWOGcMhqcbmPRkHFmEcszyIp5b9X7d1eJJmjNRJDYiYTdJRzSts0dAggKFEUEoETY9rHMykDbdcQUqILA0obAd0KyX+tKkVlDYUJHC0S148S1w9guYgcLzTTumAyLZhPp0yKKUkpYhyE9IoDXsu1bjvP2WrLpulQCnwaSKakjj1918t9Ha30+ViH04nrR4Ybx/Ns8y/zWgRFUaJnC5rFdTrzOjHMGYKjDBVDcYyuD/J5xWNUzG7GEnRkt92yutywPm1YP3ud9cUvoE4/Yrv6mG73DNW8IAxbQpHQ1mJCjzOgk8SiWKOEPFcJ0oD3LW2jiEpToSmqGSlKSZZSmpiMKGfHKMokubnWyp6QyIRSEkesiglT6H0/s5R8Jjmv7Yvx5J5WJOpSQ6povWK5bnn6bMPqbEtZOYyDytSocobfnjP0O7q+p42eFAdsVKALri1h6p6hVEmMLcZex+g5Sk0JKVAkURKnbke3PmGbLElbSm2YzKaUkynzwxvMD64zmS9xRqMpqKZHzHrL/GbHs4tL4nqHC5EQG2ozpcuEYlJG1rsoz6KPkBgYLu8T9ZIUr2PMlGCneGspjAUT6eoDuvQms/4EPawl/tL8/zWTdrei2H5E+/Q+QRUEPMYYKmOZlRGjEsXcktKMEAJlpShLafhTqmSyPGK6OOLw4AaTeoJyiqQd0+mc3g90G7HqD7uGzkcuLtcC0CjDtJpQlFP84Llx+ybHN2/hk4Bvz548pmvWKBXRruLg+C7zw7tEVeCsptls6LZrVAxYUzKfHVBUE9phwIfEarvhW7/y6zx9esLDTz8n2inX7n6FgztfRe223D95SF/O8fURJxSU1SGH0zeYHV7ntZsz6M9JfouVZBE23YBzBc4afOiFOUmJ4HuabWTME/JdL2VNOmGUDAFWGXzsiApiFCWmtY56MpONR5k984YyUlQ2RGHzfI/ve7z3TOopoWt4cfKEi9XA3Xev8617ln/2J/d5UC+49c3f4fyzP6F9/D2i7akWC0xRSNi+khbduqpkkMrKJT8Eybu0mqAFIBzVSDFmZlNl04USy733gwzKJHyMsikjjcBjKyI2b4Y+ij3LyMY95j7FdBXIrvDo1BOHBpV6BhUptKbtIyFm22fwVLuXpM++y+TGO9y5dsgXzw4xacfQPGW4vI8yE5Q9pPfC1Nk0oGKHoif6nRzYrUUTUHEHYUcMnbQQqoApamnC3F5gncKaKTL+9GjV7luvlZ6KLVWJlSbuwdZxcJP/ZNiX5uSY7XQgClpSL9ZelAxkSkBJKdBJEIz89uDzop8P4MFjUkRn5tskIQVIERUHqqRRSRPCQI0s2L1SVKFD95cUoaeKUGf2fx08G98wpEilLfOi4vrBASn0NMPAkNlOlcBqS1k5ltMZdeGk4CEEJsuC5WJBWVik/LynbVvarmXwEn+AhqKU56fte5KXAa3ZbjjNgEez26FQGCe2HYNkz+mcw1gUjrIqefLwKevVlnqmOTics1gsSH3LdhhIaaBft6h1i9vuqJ+tqS49bbKchh1PdltMUrxzfI1CGXzwGBSlsdAHLrqWSVVTaE0xKVEaXrw44YuHzxBqwRNUgTUObaT8br1aYzQ4Z5lPplhrslJ9Q79d02cgkl0gKilZcNFKcZ7Pse9arDCXIdLvWl48P+Nl03DWtbQpSLOuFWWrc05a7I2S9WgQ1l9lFaBRZg+0gAxpe6Xff2D5GAd1srKDrPgQUEjhfaBwDuMkxmU8KWhjJADfCIPpikI2VcRauygnHC2PkCw5QzcMhJT2RQNZNw6ISjcR5RCFk4ElZ3QZbbB+kGcpBIqi2g/LKXoOFwu+86u/yg9+/BM+/PxzCusECE4RozSH0zmdKzII64kqx6vk9l2f1TSlK+ijpyoKzDKx6z26H/ZNyfP5Yp/3ZXOzsGIv1KAoSuaLOUkpds2OFyfP6bqeN7/0S0TtODg8ZnW2YTJF8pNNgTKKqiwhZ+s9PTmh+ixQW8vZ6oLV5pKoOjoCy4MbDF2HIlI6gy0KpotDfvb+D7n/6YfMyin/zd/9m/zOt9/mu//4d3nygx/TvHxOvTqnSgPBOJQaFRma5CqsDTx5/AUPnn7BvXe+zL//6Ef80Yd/yltvvsnf+MpfQX16g+//4Pu8c/MuhVFsuw1Ds8NOS1wb+O1f/+t88fwJq7bh409/QrO95PrRgm987Zvo4BmGHoNFK8O2WdO3HYc3jvnKO19m9rf+Nsf1hB/9+ffZDg2NMwSjRRmFAASkmFtefx6MZX/P5mUx/5JYYPMP830eg9+rTEWhnQ9GRshGCazICtyYYfdxuWU01yoh8tBi53J6T3joMBaeJSmDMWPhiDyP2pg9OYdS+ddVziTPKEMWuKYgaq3B90zNHFc42l0rBxCVKIwo6eQAN2C12lsulQYdxdo8EiBkwiaEbN1WV4Uigkel3Kxtrt6fuioLyxcbiGgFN28uMann048/5Ju/+Nv81d/4Dv/HJw/ZrDu6iyfQzrl1vKCaHdJ2DSppFkd3OLr5DifbKcXiBinlgqvmku//9Id89uhzDmpNcbSEuGazOufs9DnOOax1HBwdMPQDL58+4De+8w0uL85ouo4D43j57Bm3br2OUwO71QWz+QRbGIJ2YEpSDFysNjgrbeR93zKfVjz57H0eXpvx3ntfkSIqHbh+6ya/+LVvUFc13/93f0q7SyQc3/rmr9G1G3760Q/58LMPuHt8Rw5RGkLq2WwaAUZQRKu5OL+EtZAib997g37XcG1xzL3rr3ESVyyPl3zx/Cl954lK0V5uaVYrilVN8GJzVs1AOSRM6dC6Z9gNrJotRT2FsqbbNSyPj/nq17/O4805frehqmeo1OGbHh3l4NS2HbaM6DAQh0i/U9jCElPkYnXJarNlOVlgXEE5gTh4UZmNsx6iituX/2RSQI1xODEwDPJaRAUE2l1DWZUYJ3FEXg3yOVyc8t3vfpflYs5kMmEyNbSdFAtZY0hB4p7Gr1GhqI3BxJjzBvOjkhJt16F6mSGsk32xdJqggqhBQ8Ra6WUYenmdlK3jymiMtVRVmYFgnxeNV8CwCEMMpDJxdPcWR2+/ycPz+7RNi/KezdkZs9vX8jqVwBrspGRQETUt2PUlxd0lnz18xlsHC4rVBvoVd+7ewB7UfP7+x6imxyUhzWLsqYIhoIXIMQXJIYp8BYFO8lJjpOu9gOC9POPN0IuQQmlRdSX5fIIP0gaftAAdgkVjgYO6YFLk2TSBcg5lDMRIGnpC12USUhH6KPNaVJSFwxgFUWG1lt+vFG3n2a62rNoOYyzzaU1VOayGuijpY2TbbHEobFlQlxpjFa2H0K949NM/QanEa1//TbZmToyG5AzJCzAs6kBxyEhkgBFSNaYMikne6NZ7FiVoI0pf7yM2k3ajBV76FOQHIxmg/ZhdfHUTJiTb1BiJmNqrnpXad3uMytoxLieOSvAQsErjsip2vKeVkt6GGDTRR5KWZ2fsrxCccUwDvso/H+M3JKJD7lOr8uelRoJSXc1G+VsyUBzTlXvi575eIQBVBjq1Mng/yLOlFNpADPKPkJgCAbpTnqXY//1qv6eZvO+NebTj7DlGX+yjO0iZ/NH7f2d4xUnjfY4VBEiiDo1J7WMgYkz7/Wz89+1LbHPRsrhgcv5z/syj1oTgJaosylkbVC4Eu8p4DXl/H2P/gOyUUXvVzSh8GLN7Y5LPI+ZCURSYQjKFvQl4RMSVsvMtRbFzW2OzCAd0EmJBKQg20g1jWWIGvvNnrBIygxu9j5BQJr+Wl+tMlOvkg0cZjYqGsqjoi4G+H3I8B+go4DJJjeMTSil83+3nFYXBacdyVnM4qVhWltp5rk17jheK5QKmc0c9UUxqy7QuKUuDth7Q2BRQuicomaf6zkpkQPCEYcjXVz5jTQmlzXb5APTEKLnUSimcsUyqkvlsImQ7cvb1uuRgdo2uukbHEdEsqJKloybZCuMUzsCkiszqwLWlprSGFJf4fs7lKvLixW3OTt7hycO3Ob/8ZV4+/Sm7x39Gd/kxXdOgjacqFK6yGKPQOmBckaPcEkl5UhoIQTP0DbYrUcKykrTD2AK0xVUT9CBuuTHaRp6jiNFgjMPoiqKc4lxJVFek/yuUDjEIBhV8kF6MEGnalm0j5GFRwfLIsukuaZtz6MVtEAbBtwwWHz1pCPgQccUSbQxdiPjTx9ihI4YNtW4owyG6XBBxELak2MFwiWrOiVEhJpxIc2nFAV8fUcxvcXjrDtevXcMUFh8USlfUs0OWN++xXm/wQ4P1PaYoKOup3LspEH1L22wY+oYuSkZz2Z9RrX+MNjXDpGJr5/SFwZmCwoqDm2pOM3uL4Lc43zFz5/xFX3+pQVqjAsdVy7RKJBPBJIyRhcAYsZnEFHOIvRw6nDUUznF8fJeDu19Gu5KqnGBQRCUfsk+a9bYnJGH9Tk9e8uLFKSYZbFGxWa1xCQmar2acXLZEs2YyrXn88HMuL05kGKBkeXSLw6M7KFOTjGHbb3h58hgVPCEmgimw5ZJuMLSdx2N4frqC3RnJlLz55h1+51e/zmeP1/zkg3/CtdtvMdeOaSxpfGIwBxy99hUOD++w3T5nUg04tWO1PkFFxWK+5PmTJ1RVQS63pK6n+H4QMNZKSHvwYo1o24R1GucM0+kEox2b9cBus6aqa7GpoDi6dp1iMt8ztFJaYBiGjqTkmoeuQcdAt13RriNHB3NOzxSzRc18nnh9seVwGnh28oLFL7zDu7/53/Lh751jiqeoyuGHgnXb0A89pTEMvbSoCtgqeawRtX8PI9vrY8ilVmRFUlYjJbFixiiLQCQhRLqE5g9xbK/MuV9j8U6K0gJrHcl7ur6j73tRDZ6dYdxaQv9jZLNZkZoLyQscIsWkJmpPf/kFFx+vcBePKesps6UhDRGldjTNp6RNSSrfglSikME3xhZih1YDRAj9QIo7DDt03OJSXtzCgFcRZ6EoNd7nwixnIQ4kJE6gcGKb1qoES1ZPKqwbwSU50CcCUSd8GnWveQMKMQ/SCZ3EHj8G8acQiH7AGBlO9D7bNmCVg+CxBCwSLWAS2BSIvsu5YYprzrHUhq5tqZUc3nf9gG+3qLCjSJKfc6kilyGyTQLwLqzjYDpnWk6wGDoPJlmM0UyKCZUrmExrnLVE7+nbDmU09WTCYlpPsbsAACAASURBVD6jKhzBD7mQrmUYhgw8BF6+eM7JyxcCdw9dttHlXF7t2Xo5JHV+oJjUuUxB71nhMZtNWQeuYHW6pu8jr1dH2BRp1qfSwGw0KiS6ky3t4xdMup6oHOvOs93uaOIA2nDn4JgDW6NDhCDFQp0Xe2BIiU3fUxUWq0qePX3BDz+5z+XFGpsUIcKukeD9SVmymM9Yry5pdlsMitVmzflqRVkWOK2wJKp6wsHyEKsi660w00ob2t6zHTp6EfAQfeBl27EJgSYEvAIMKGcwZUlRlQJWKllvpJRhHK7JRWCBPgjRVhSFlAh5D4H9ECyK28zIp6s8LvkaSwkyWKYMVut92YLWBuNEYT6WPHW7lt3lGmKinNQUtsDHwKNnj3n+4hld8NSzKcrJQdtqgzW5tV6JOsMVhfx8jkQJPuAHAbqKokRrRdM0zGYzibppGrR2rLYNv/9v/5BN22ZlpESSMERKo5lXVV7HkhzaslU0jVZCMiCQxjxDw2yxwG8buv4SleQZPzs/2wPc40GRrDqLITGbzZnPD9DKst2uuDg7Zbk8xtUTLtcrnNPMDhas1s85rGucFTJOshx7Bt9x//4lH3/8CUolNtuOru0xsUVrxWRywHRaY3Riu71g9fQRF2dn+MtLap+4VS8Ynr7gwfM1u08/5ZaHldKcao2KDm8Vm6GhCx6HWCxN6Wj7DT/4g3/J8o17vHb3DgfPZnz++AGf332Xd3/rP+PPPv6Yl2cn3Dk8xKIwpqDtAvFix1fvvsWvf/Wb/Kvv/zE+eO4/ecA//Wf/mH6z4hfeeZuiNDKYJil10MqQes+sqrmzPOJX79zj6GLFJ08e8tn6grMY0caJQhuuFJ8IKBDG+zQmtM7qpBzZkX+XKKQgq23ZA49KC8Aqh0pNTCFnIeeDNhqlRwti3rPyg5VStrcCQxzGk3Q+kIqaRspFyGV3ZHWUHHyKspDvI8+QJBKIHEL2e1m7InI4Sdn+PJtO6YZmTy4obdB5Tez6DmfHhnghi3jlPfusRldkACArLbyXiJ2xEXrM/zO5KCYharBXswsJgAr8+ff+lIvNBZ99/GP+9R8fYiy88fZrHF+/jnMz4tDQ707Y7c7ZbHZEB29WC2a37nG4trTDmkJ5Hn32Pj/74Kc8evqCt9/5MseH12i6gZdPn3L6PPD2l79M1/VUk5rJZMLlxTmvv36He/fucf8hTOZndO1AwnJx+hJlDYSe85cFWpU4rcGV4Dvuf/6IxXJGNzQ8/PxDbFLcOjrkt37tG9TTGc9evuTWjWu8eP6Ay4sL3vzaG3zz29/kwWdPSCHQ9x2LyYSysDx79pjbx7fQVjGbaJTasl13NI3n1q07FEXJ2fkFIXpu3Tjia7/0NvcffEbYbfjau7/IH/743/PBZ59y1qxlbrJWcmVJ+HWPF+EcZhCXTOwSsRcHC0psocm0hG5gNl1QTBfcPjiiWh6xefGcx/c/FY2eleJQnxKHyyU3btzkg/c/JAWFI9G0LRpwStRvzpUkrfBIwatOr4CkGdRxzhGGId8zEgtg8r0YvCjRlL66D8tRpZcC3/j6V/nqV97ln/yf/4Rmu+P42nU2mzWLxVwy7PtuDyqN7fKvqv2KstiDVAKKhP09LkpBjXJZgaQMfexJKuw5EOMM0SexyGspoXRFgdZWrJUj0JMLoEYVsTKWa2/eRs9L7p89Z+Ul77lSima9ZqYCFiEyvRoY+l6szX6gU54bv/wlnDdcvFxzIx3y+P5jNrsN3/nNX+f2V9/hR//q36K2HWjFGzdv8Evv3OPRo4dsVlsm00OZXbYbuq6n6bqr0isR1hEycWmMpiydZNEOA8oVeW+FlKQgRimHT2LK1UmarlU0aAWucMSU6HtP1+3odg3JS8xCUoqyKOm7gdXFmqOjJWVR5DVF5stm19DsGvp+AC9268EHMKJcXMzmvPH6Xf78/2PuTX4su/I7v88Z7vDGmCNnJpkcimRVkTWphpa61a3BRruBNtDy0vZ/YMDwxisDtTcMGPZOgGG4AXshbeyWuiF1aahWqwqqqlapBpLFIckkc46M8Y13OoMXv3NfZMmttfU2ZEa8iLj3vnvP+f2+v+/w059TN2uC7ygLs8ke0FoR23MeffAjpldvMrz+OZTNqBvovDDIekBLCa0u+eB7dL9ReCGMrFygDcmODMiTNRiERIR5LngrXUOnFLooBJh3gWic2MLFiNcq1Qvy17vgURtWpwyavfcoY9GZpWkaActUssDa+C6rxHiVbIsoKGJirpsNs5TEQieBYsKMk7pk80yk882sBJr1mj3UJWAY070hgWP9YL7PHHjOXgBShgkb0Odyji91EaFn18pxWJ1jbCaMy7RXQAq9NJcWEAIyh+e+3wOb/eEqnvesTjyUzfFrozd9J8SUkRI3IYO/vE6I4utv2zrEzd8X4MhHD0pyX0T9JCApqrckSiSbfi0g5Sf0N0xMHrTp3NJEmICj7bpLH1ktgzutLCaXYGOfPhsXXeptO0L0Auj3frIhJHBdCXs2AcaXQHBMCja1IVE1Tb1Ro/bgeX99Sf2Bbxxt14rVgpcQWW0gKyzeC7gXEhnLeckh6QH2opSwdxAA3SjDKMvYHkSu7hi2hxm7ZcZoGBhODaNBYDyCYaZlqKP751F8+7VRlMbSRUWlQCuxxutSsKSxJg1Yema2onMBQktUhhgkmFkT8TEDbdE6F4u0kEIT1w1b0wK9d4AbbhG0gIc+RDofiV6TW0NRGFovv6s0ikGpmQw1165kuHbMxRenPDq9zl99f8gTlbHOx6xOP0S7C8RqQlEUhvHAoDOD0RZjM5TKiCojInuMWy5gXaFtTlYMKYYTbF6CtthcKCtFMaAcDEj52tLfBVm7bSYB81mRBvXWpiGCp2kb1tWarq5pQiOfp/fShyyOWdYdjVeMr8D1KTTznOgsnYOL00DbDmndiCIvIE7IsoLdyTWG4wKUYlmtCUpDe0E1t+AqbDFH50PxT1bgg0fh0UEINT5EulZU+dVySXt2xvHpUy6uv8pkb4+iGGKiweRTDq7cxq0WHK9PWM0vcHXHeDyhGJYMBiXeNVTrAYv5jPWqlmFZCOj6lHz1Lnq2i7MHLEvFSk8pKIU9b0vOBy+AM2w5TVZ9xt/1Mt/+9rf/zm/+//36n/+n//Hbv/b1zwMalZLghG6tREqUin6jEpXbWEyWs3d4nVsvvsZguIOPYG0mSfQa0JGmaWg7TzEYMV8sePL4EavZgtffeJODq9eYLWYsljPKMiMrB6ANVV0zW5xzdvKIzDhQiuHwkIOrL2OKEdoo8lyzOHvK7NlnKFejtGJr/yY7h7e5qCFkUy7Wlvd+9iGfvPvXPL5/n91pxj/957/B9lbBz3/wPUZFhhlscTZvGWrH1uQa3/ryF7m6P+TsdME3Xx1zdRKYXZzhfWC6NRWw1RjW65VM/7UhyyzFoBSz9eQ/kheS+uldx+npKevVGlFNSpGRFwXGWIbDEeVwTNQ2SbkMaJFHNl2L9x2KSOha2mpFkRkMgbapmS3mXL9xnb29XbZ39/jsouTuwwt0ucWt2zcJZsGz0/cJoWMSC/b1gBf2DyitAIlN26S00sj52QW162gRH700i5NC3KdtK/TSDln9LyeeHpV8Wn2adnc+iC9WBFIhg1boxL4T9rFLjbX8Pm0z8ukVwvQ2dv9FqtUFZVzhl+fktmC8c0AzmxHWczLjWLUL1utjVFxgVYuODSY2RB8xqpTiNDiIDSa2EDoMHgNE14KvwK9QwSfBssgMxIagxlBhbMS5JUUBmQEfWqAmhDXeV3RuSdvOcH5JlkWsFvDGqECmWoxqMbSY4NExoJUTUDZ4omsx0WGC2C7g2/Q1L76y0ZH5jjJ0lKFlED0j5ZmawLYN7OYw9jWj5oI9XXNYwG5uOBxk7GeRPeMZh5phvcAuz8mrFVNgYjOs1lQKnnjPeegICgZZzrQYMMoKDIpMS/p0WQ4YD4eMh+JhZ42lWq1oW7FV2NreYmd7m7IoiDHg2paqqlg1NS4K07rtOqq6oelaOuewyffIaPE5i0SU1ZAZgpGQCqN6f68UdKVIU8eS1jtWVcVkPGEyGtB1jbB2q0i1ijx+eMb9T485O1kTXeTFqzdwqxpT1xREDgYjro62GJWZbGYhMK9rVq7DZtI41M5RBU+dGZbK8ou7n4FPidAodIiMypLRcAhE1tWK8WjEeDyiahqc9yLrSEVikReMhwOInqbzVE3Lcr3m4XLNo9WaZ3XD0brirGpYhkhrNK1S6NySZZbhcCjes6nQleIPjEmBCcSNPKyvgkOUsIk+AOh5T9r+1Q9ndGJPqdRIbHxC01v7gJeXX32V/YNDqrrCdx3r1Zr5xYzlfE69WIMLYDRZUeC8ZzKZ4FXEK3ozNWka0nWPOn20IbI/2eHqzh4Xi/nGl9B7nzz2+sYDuq6j61LYjZJVtXEuNQ2ZNDmpUo0RFvMVjWvFQyvGxAhQG+bGBt5L61UPXgfvaNbVhonSgxV9SFq6VDI8wHDr5h2uXX0BbQxt21LmBVvb+5hyyLrqyIoRo8lEinclqoYQAvP5OXW9xhrFYn7B+ekJrm2lmQyeXCsGwxHj8YSubXn66DH37n7A8uSUW1s7vLK1zWA+R52cUj18xPndu0zryMBLQ9M5R+c7uuhpgnhgESNZkipbrVgvlpDlfOHr3+TWCy9xff8mN6++zM7uAbprOb/3MZMiIx8UMk1A0dU1mYb9/V0+/OQutQ/oPKdarbg4OeNwb5fdnV2MLTe+vqAocwuLBR98/4eo8xkvXb/GdDRkvVixqNZUwV0ygxJr4Hm27PP38AZc/48FpKQf6Yc9l9QQnZpSlRpCaar6UJZ+SEn/s+l7kv942eyhLpPse7+8Xo4N/e10Kc+M6Ti1En/650P8YgLDjFYMk31CWZTs7uzSNGvm8/nm9+V5QSRQ1U06hmTN8JxPZUzH3u+xgb5hFYBKawl36pFwGcZc+neqxDbqz0SrwKDIGQ2HWKV49uQxX/vWP+LpkxN2Jlt87vVfYTTZYTzdIarI8dFTqjpgB1s8OZ1T14a9rV3m50f84p0f88ndd1jMzjE6cLi3R7VaMRoXlEXGoCgZDIecnp6ytbUtadzRUa0WdF2NC5FyMOXZ8Yw8KxlPp3S+pWtlMGiT7FBr4Xu5rqVtGu5+8B6ffPgehTbsjCY8fvwJ7777LkfPngEwm82YLxbUTcNgOOLqlRtUTcfO/j43b93kfDbji29+iasH1zk7OWV/d0xTXRC6juHAcH76jKdPn2KMYW9nj9LmzM4vsFaxs7dFXuZUqyU/eeentNGJsiYIsysfFmTbY/LBQO6NdZ0k+hrfOtqqEcaLFyVNpjUhKigG5IMxRVYyzOQZcusamxhxwXtu336B0WjEgwePUsNuBAgOUvGIQabI3LWWNbIPkDVab9aLfj3umZOqH6SkgV/XCUtLP/fsOO9wTcP2eMQ3v/JlNDCfr5hu7+Kj5+DKVbKi4OLigq5rNwy6vx3g0/++PM8laMs5UXLFX/am7nmQPoWpkEDAnr2uU72BUpvhRg+KSBCacPgVCOs8U+hRRk7GC7sv8NrVV3h271OsUayMJ7u2hR6M8J0nBAmiJEnKO+8YTybkWUZ1fsLOqKRaN5yerdAHO0zeeIFVtWY1P2dvMuK/+he/w3/z3/23fPlrX+L82RP2tseMxiV5YfDO0dQtksVmUICxmtxaUQdoCxFWiyUuRLwSoCUQaTq38RmVc47gPdvDkuGgkEGVUtR1TdO2GzabSvkDUYtXtQaCb+nahq6rZZijxQe+Wq2YLZd0sQd2wfsugZcCOu7t7OCamqZt0pAsgjJ4pOZTOtC6hhgVo+keqhyycmJJBsK0U6r33EeCjtLnH11HWM9pzo9ZrddsWcVuYbEIyGt8TIxQJcx5LtniCoPOMjCWxbrGR5GRm2Qxp20mQ6uYAD/EC7cfGCj0BpDsuW1Gi6WEAgEUrVhWyAC6v8dN2p/SMLKXvYeIbGcpDFL1DFaD0QLUamuE8ZhCtCSsMyQFSNw8L32/1f//5b75y+/r1U3P7bD9xrD5p9GXPu55VpBlOcaIgjL+0s89V19GfinwTphx6WtSxW7YriFJknq2qtYm2SfI/m2NBdXXYvb/wwiWAEQ261QIPRAdRP6foHkJ3XQbT9YYe6sg2ev6tcT3TPQgrPz+eijic1Yw8vnrNA3qOi/XScv5be4B1TNT++KgV1kKgxZETSvqkXRuUfyNnevwIYjaLEZ6C6KebGGM2Gp4LxkNvgf76XVqYpF3ackRxDokKSGUEVau971XcX9/SKhwZnPyoiSiMVYUdWU5YGAVA1MxKTuGhWdraplONdOJYTIwDC0UeYbNcrSy6XkRrEApCZs2lMSQiy2i0WTWkucFWVaQ5QWRQnLWNKImVYYQhQHtQ4PNJbtCwirFGgNVEGJGXS9oF3Oq2uF1QTEsGAwN45FiOFBY62X27xRNG1k3jnUVWFWBxcpR1SL7H40M29MhdV2ybDJ0McK1Na5aCKM6GqwR1Y+EYRZYO0CZEmVKQsqv6XsY8ahN5JqoN4+ZeGjLwFQbizIaa3OsLbC2wFjJzoga8jJjMBkxmIwox0PKQUmWVId93dc2LVU1Z+Ge0WQVoXBk44rdK5ErV4dcuz7mys2S/WsFk71AMVHYwR6D7ZtcvXWHw6svMNm/ynj3KpPdK0y2dplMtinKYSILRIieiMEheIsKnhg78dsNIWU3tDjnqZ2nahtmrRN7Ny9q4Cp6gnCmcdWMtp5TN3OEVRTJc2GTZ1mW1D2CTTVVTfCB4Bu0ztDlLr7YxpkBwYyxFmwEpzJanwuwrwbM7/4/T7797W//Ln/r9febSathUGi0EmDGKSWWBdGjSInYXWqydIbNh4x3dzier3nnz77LG6+/xc7hASY3aG3oXECryHpdUQ6nhABn5xecn5/z2ot32No9oAV2rt3g2cNPeXp8xN7OAaPhFI/mYr4CNCFo8mLMwfU7ZJMtOt+Q60BXNawuLgjRCUvX5JTbNzhux9xdZDyqC/7mZ0c0n+V0dx8z1Z7bN67x4MOfcv/hE44efUK3qnjpy9f4qJ3TZIfs7+5wZ2fM42drrm0PGQ0HtO2c3d2DxK4LlMMRw9EEe2E5PT3BaEvJQDyuvBNJRdoUYpKxT0ZjiqIkzwpC9NSNYTAcYbMClBUTfNg0SCE4CGA1rOuK5bxilJUoZWi7NeenJwyKAS+9cIejs2Peeefn3H7tK3zlzg3efbTm6NExk/E1Dr/2O5zO7zH/+IeQiDBt52l1R2YzlHCegQSYAigjsoLO4UgO8BsGjrA9jZaFuvdZ0pmibsXHyCBMIKMU0XkpX2ISiyZpKcFL6FAQBpS1Gc53KKsJvgPfUeQ5o50Dysbh58c0SrG18wLZ9jmhrlHqnMwtcb5D64DSEVQgjxHdPMYRMcNbKDPBB0NwHVmajjrXQmhQoZL0QS1HbdMmWihNYcXKw8WOVs1ZN0tUkDTSfKBYri9QcQEhMcxNRrfMsGaAJJEqdGiIwdNWLdHL1RH9ucgxlBKmi4mBrp+uer+RJA2sYZxptqxmoA1bo7FI771DdS3NYo7vVozywMgoBmVOBNbLC/HHcy0DbchCS6k80SicbqmiZeYdz7oKFxWlzZlOxkzKAVZp8iJHI2ET9HKl4PGuE19QJd5G5XTCdGdKmRfEKAEcXVvT1jXrumZVr1FKYZMnqBiHq02j1Sect50US51rJbjjOfB/AypquVNHkwEhBNbrNUVRoEzGch0wmeL0fIEmJ0TN02cLCjVgZ3ePnYMpo2HBUM/YLifUsRYgwGpUhNa1NG2Dix06UxRGY3SgMRlHQGcy7t67z2y5JjcZPoJP/m21axmrsQAv2nAxm2GMpnOezJgE0mqi0nQxcjabUbuW86rldNVQNS0XURoqjLDnTEqFjQpyY7G5TFm1lSK2KMR+oW/AAyLJ0lyGr8TYF9gx3XMxhSXI5h0S6L1pd/q39iP3qDaF1NZ0ImBqjDRNy9HREflwRLOucF3LeDjEJisEYyS11eFZ1VWSzHlJZhY0TOSa/TAnMa7ydA+dnpywms05nZ1RDoebYkOaxUgIKhXW8oxYoykyS905XIgoE5EQPwmG8giTUVmDtoqqWosvbwrSsFaapOhd6oPkegjQC9loSFaWuPV6w9Ygva8HLZQB33kyUzAdb2N0Rte2PH5yxP7eIXlRcHb6GG23eeHFN3j5jSt88nHB6eOHdF1N01W0bYM1hraucU1Ds1pCkzGcjBkMB2TGkFvDZ5+8y/xsRqwDh2XJP/zaV/nwhz/iyb1PGTUtI2XI6xXT8RZ7422ySU5HoKxXNK7BhsCkGFIog/eSzGutpQkOV1e8/+//nJt3XubqG2+Q52MWn97l44szRlHSVRezC/bHVwWENxYVG1ZHRxxcO+A3v/p1/u2Pf8gsdLjouffoU/7Vv/0Dfm3xq7z91lcxmTCndbDE+ZpPf/4zOD/jS5//ArPZnNlyydff+DyTB5/y44efsnAdnY3SFKIJaVi8CWlB2KH/sVC854cQl9Ye4h0u8skOYsQa4DnvPpHQqs3XOidD4p6xExOgJZYKcdN49swh8AkMEf+6vhEl+g1r1ntHDHojH++ZQK731rMWH2Py2hRw1yiNzgy+c/SSTd2zuKLYV4hdwXPXR0khK8z6KOspAW0NhSlQWpQyfYiNSucV1S/LTgXslmewHAwZ51vYJse2A0KjGGY54+GE6e4Os3rBw/tnvPG5t5kv1lwvxmA1n9z/hONH93j66UcYVfHs6CE7WxNu3brOxx8/5OTZEQcH24yHu2xfvcloWLJaXYA2DMqCJ08es5jNuHKwy/7hVZ4cHXN8uuDk7IK2jVy5cZN8OKCuVjTrY6xqGI62aWOL9y25luspQ/EhQTlW1Yzdw6scXDuk7jxHz55gjKJ1HWeLBbsHNzCDMc35jLZrsUXB21/8VZQyHD27YN103L33GbevHZLpwBtvvsCf/vkPcXpIOZxSB0NRlMyWJ9TnC3YP9zl6dsZX33ibH//8x/zsyceyDnlPFyOKjHKUi4fb/oTmYs7q9IJYrcjzksFoSjSaZrWmi46sHDAYZjy89xHdvY/Z3trn5o3bfONXfp0Hn7zPJx++A0iq/fvvfojzHm2SRY8QEWVNC4F6XROi5mBrn7pRSVgck8es2gANWmtUnj3H1BMwShtD45rnAopkmRRprkiEP/jgY/6X//V3cd5RjsZkqwU7e7sslgua1klgSOxVIZd+lKlD2YDB/cAxzwu8q8RL1Dvq1qF1R57nAuQpJEip92NN0QHiEao3Sp3n2YSboEElVih5mdHqjtWDJ7z2xgv8sy//JjcPXmJ86vj+T77Dxeocf3rO6PAqISi6ao0LnqgNJioGKuPo9JSlhaeDjvXRp7y2v83NquX973+fLf11Xv3mN9na3qb68CMGBdx/9CFf/PqvMBwP+ON/84f89c9/wvninMY5bJaDCyhzyY7TWUZWDFguFiyXSzrnRJ7atMIMyzLKzLBVSkaDc01KNe9onVyUpusSi7bb2EtoY9E+0oWIkSJws14F71ksGvHvHiOM76QMGxU5LkSi1dgIoWpRLoIPnJ2doWLgYHeHqgtU9RrvAybLJHU7KGyInNz7BV5n3PnWb+OLknndiU+mMgJEBpWshgT0id6jggEn0nQHtF5Cp3QIhNZjjU6MVpMsjsSWTfxSI1FpivEEXTUslmuGeUHsxIKLkOoCYzBa0bkWtdlLBEgwxm4YmyrdV0JCkIGf7AtpJ0pgrHilSjBcDAKES60l5+ejkvMLQeytUBu5e3AurdU9C1x6DGXtZv/bKEKSbU0PFoZkHfJ8eFgAfPIa7oOs+uewt4MQMD8NI3luSLqpG395z+2fraB6D9nLewjnNsOVECMmsWalZO3ZsRKsF3kOvFYm/UwQywfVh5/J9Q4hbgIHez9XAWVF0k+yEnDeyV78HKlBmLG9ekSslvprIP2KfNabvTuKFF2OMVLkQ0zUm1q7c6JQ7D2FZX0xdKEj+IhrRZIe+1o8ras9GK8zQ0RCxgSM7WtQhdFyv+k0FMsTq9J5nwYgyY4hMWOlXtWEItA0FWWW09a1EOtCIC9KsayJSWmQVEACGBthfxohk+k8I88tVitGpaXIFcYqtG4ZZpFppii0gF6StyGZO72/NDGKUkM5YiwwRclgAl0QW5bVcs3FbEXjOkLssFbjXIRRho0AYiOglKfrNMsAzkV86BirqShh1Zrojlmefczxo484/ZsXCKMbbN96mf0rB+zvb5MNC9rOUK0DbRuou0DrIq7z4BvoKtpmSegcBsPFecPZ7Ji2DeTFNmayT7U6J2hNQOEcNG3Ah5bWV9guCiNfWwIqkUgKGbB4RVOL1Yy1BXmek5f5JSFBuh6MztKe1geWB7rOs1zKM5vlufi1AjbPGE/GsmYpTV3VoDzS/7VJgdGSGctkDGUOuiiwgwGfC1ep60POzsacXGQ4Zwh1Rt0IRhWjRmwbfbIbEcsWrTReZTSdo7FasMPgib6ja2qCC9RdR9V2VO1KbH3WS/z8mHzvCnpvnzgYY9BMRyXq2m2iWxGVo67m+GVHZlSy0xQF93AwJTOWxhraekVdn8PFO5SDEYNsgIqKlgKnS9m7NOjhlNbf5MKU/F2vv9cgbb8IKzE1E/BMZyjy9KArvJY4pOFklys3bvPw+Ijf/Zf/ks/uP+Gll1/ltdff5O0vvM3rr73JZLolnixkuA6eHj3j5PiMwytXuH77Jk3w+KgwtuD6zRd5+MkHzM4vGNiCfDBkf+8Kw8wyvzhl7+AGw+kWC7fmfHbM/PQMX7WEZk5bebo2Ix/d5Jm9zbsPDH96t+KdE4ePL/DSNHD7lcec3fspP/ms4Wj1hPOHn9HMHMf1nLcyw+Gw5RdOk4WC+xeBWy+MuJoV5KqmadaErkEjADeQdAAAIABJREFUi7S2nsFggMlkYcvyjLZtqJta0uwHw7RpeKLym2urknQyL0pMlhEl6QDQaUIX0Mim2bYNeSbm9qPhkNwYcIpynLFYdCyWa7yL7OzsUeYF1WLO/bvv8NpL17m2M+CoHXLv3jn6pX1eeeuf8/OnD3H1EePtqRxfD5oqRdU05MYK8OQDISW29iFWkqiZMnGjSpuWTHmNleK4LCXdr0kFvY8hAUFSrNvEvhU7o2TcnozcfQjoTGEw2NzSqUAXOpRRhLygbgfEckLbrVmT43evQ/OEenaE1rVMcSNEnTYUBTau8d0DQhUwxVXQQzHcTsVE9A3EFq09WkUJj6GjsFHSeWlQ3YJVu8JFh9IOHz3BO8pMQvUcEWMUW6MhbVvTdC2Nq6i7eSocg7BqXWA9X+KrJg1pBfzSiburlE+pr7LJx8T8y4xmUubc2DtgO3TE9Yx9BcvlBdVqhfWRQQhMhwMMgWY5Z71YYpXZTKdUVGQxkGcG76EOnvPgOXWep8Gx1opJOWE8mTKdTrHW0rlLbyKVCp5I7z/ckWvDdDxmMp2gM4PDUzc1vvN0bUNbV8R+WNHJOqJUpMhyVJYnsF4LkytGJpMpAMfPjiEocm3R1hI1m+TT3udJASbPCXVNpg0qz3FKsXKKxfmMk7MZRS4pkt7Aq69/gf/8n/4LXtod8dnv/59k2YBCF1y0EuCmjUVnGY1rab0wR6xS6OjJtIQHVSHybL3m6arZNHBdAjIyDeerpRQ4WUZbryFJqTJtyYzZPGe196yqmnbesWgaLlrPGqR41dLoSpGXYayhDcJcGpQ5Jjc4HfAqElUk6j51u2+GU7MZorCbE/tD/VKT2yfS9rit3qxNYSOxUxvFRM8MUFpT5mUKymohBE5PTwhn5wQnoTTFsMTEAhciLog0SpPAVCI+WKZbE+bzmcgyU3PS+hYfPMF5YZTGyKqueXZ+QpblG2ag9x6b5ShjqFarDTPQGoPVGdH7TVFZVQ1WK7FTIeJdl2wlFK4OKeBFJ59CCJ2Ax8pohoMhWZ7z7ORE2GNIIIbJM0J96afWy8hCaqpikLUxsxlFUeBdoK4bhqMxO/v7XMwuOJufcnhtRIwOtBeVSbemq1bih6uTj2mEohiQD8eEuiE6h6tWrLuO48f3OTt+yuHOPq9cu00RHB/95Xd49otfMOgCWT5E2QF1U5GbDDXdYf9wl0U9J7CLUpGqWdK0K/HQTaElMqSK2MwQ13N+/Ed/SPbjH/D4+Jj67CnMznn71qu8sLfHk48/ZXtvB6M1eT6gjeL3GlY1X3jpDp8eP+LH9z6iRaSCD44e8if/7jtoY3j1zstMx1vk2jJ78IjzT+7x+isvM1vMOX52yqt3Pkewnq1Bjutq3j19xmlMTA/dN2YRQtyEZPSvRIzeADl9mjGKDaNWwP6Y+EHSuDkUOugN0/b58C6lQCW2t9IKE5Pksu9FNywWs7kfILFXw6X382WIg8a7ZD+grfgoJgbvphFM3t06MYZiFBnxYjYTUElpfBAwpecJ902m67rUjF82yJsQmtSM92x4kMa7a/2mod+wHzfs/9gvHcLUCxbDgGuHt/hPf+s3uX7tIx7e+4wr1yZsb+2wbtZ88a2X0WbA1t4+r37hq4wGUx49+pT1+h329xTnJ8fUi3NG+ZjF2Rp85MrhNh98+DF7W1sYH3n48BHXbtxke7rDlStXePzoM05OTgjOceP6Td5884s8evJdjk8vyMqS45Njxg/u8/kvvU0IDufXuG5O10rISExqjtwaiuGQyc4eV3Yn6OC4/+gzsmHJjVu3OTo+ktAP5xiORoy39jk7vuDk5BmNbwnRcPulzxGU5q2vfp5nTx7yvT/9Dk+PZ+yOx3z24CnKTPlH/+y3mWxP+Zsf/IQr0wEXJ1AdO54cLyBmjPMRb732Ou8/ukvTddhygBkWUhr4QJeByjOGwz3K7TGrkwvWZzPC3LF7eJVynHN8dCTD5rjGFC0xKlYBnqLZ37nK6299jQbH/bvvkkXN+mwuAadZoPOOrH9oktTddQ7vlzx70oknuNEMhiOMafDpvvLeo4Iiy2TItWFuhbC5X4wx4OOGqaqUEsuaEFFRc75qyHKD8o7jkxNOz88kAK3twMnQEZTUAD14khpWlYaGLg11NyqIeBmqG2JIAYw62ciwGUBGwFoBAeReV8k/sqcxpWR0JWE+TVuhtCYrNa9cu8M3Xv8yV3ZusjO6yje+8Kv45TMWH32XiydHTF/7HHZQgOvoWmmKXXQCauUZSzzZCweMpyPe2rlBt31K/Ju71Ocd1755i3o5p332hD/8kz/ixx/9mN9p1vzjX/9t1rHj3/yHv2ReNeCt1K8KYmxxnUdri9EyqF2s16ybFq8QWW9SYRd5zpWdLQ5Glmqx4NnFCqVyohHAs+k8VV3LNU7MRfGoEt6hCgGxqjGoKLJ8FSOZEdAwOFnrvI8SIKcAFSkGJS8eXGPQBB6fHFNFz/JiJnXkoKTMMxQF8+VcAAYrn3tAEULN6f33ONi7wa2Xv8wjoIpKlHkhMZ9DFPZyJ4q86Bz1es2yrnGAA7ogahFxFE3BxDGt3T0pJoqNQZcAyuHODlWELgTauiZX6VwT21L83BOBqe9pBNmX+iINz0IQmw+bQpj7sKmNj6gS8kPPXFSQwkzZrM+9xL9fz513G5s517XSN6S3ZHmOSiFSOvVv4qmarJ1CCqtOAGKWFB8x1Wwq6atFOCJ9SB/2LAdwWTtqlYDIKHU8iR3bszxjWl98Op8uea/GdGzPM0A3bFR9+b2edeqDl3mnUA5lr0qfv4DbvQet2jzjiTdKCJ4QXLo3Xfp3SDV5z+7N6DrEyzOdqACaOtXY8r6QWPYoAbx1soJUQGalfnDBE0NHlmlc14GCIjM4IXungZHcB4XNaXGELICGzndyDeIlwG2tSY5K+cb/u01h430GQs+mVVISC5CenkEXw4YZ2/cuct6aIisJSkhUmfViz5FlyULqOV1p6itCVESlycshLkZMZiisZWc64nDPsDVs2B5rpmVNqSqK6Mi1BEIqnUF0ovpQSacQAzFWdK6jaxTLyrFaVayrmtWqZrlqmC0r5osVShXkZUbwkkmTFx5rNVmmJFvAyb3dGcWqkmybolih6VC+IfeBoX/EerXg6fF9Pv3oHq0dM9rZYWf/GvtXblMMtjG2wKOpg6LuIqFRqCrQVZ71qqJZz5mfHnFx/oTYzbDNOTpGOjKUtrQRjG9xdYe1Aa08yojSKSLrsc0KxpOpED9iTGQ8Q9CCgSgk2FOsRK0A5KrPAUrkA6WIHkIH63mFsV0qftP+6QO+7WibFmMNxSBj0AyJncJ3K06rNYuFZ5bN2drawQ4m2LFhMsgYFgXZdc/kMLBeB9ZnGWfHJd5pfDR4ZalbR7NqAMOwLNiZjtkaTQl6wHqyS3UxZWkszWlL55a4Zk1Td6ybwHyxhNBRDCfU6wVn7ZzYnqGH2+hyRFACxo4nu6zrc4yJhK7Z1LUxKfi0dZSZxtoCHR2hawjrp6jlu4wHL6LtiJAN6cwhnbU4DWQWM5rgjOPvev29BmkBTHr4lBEf1czIBYk6w+Ql02LAZHuHrf0bXNSO3/vj/50fvvfXZGXJ+d13eOfTT/nz7/2I29du8tqLt/mNf/RPuHrtOlXjOF9VzJcz3vzcbbRVhCgeOjEqTFZy48VXOD96yGxxwkTtYIsJ08keNh9zsV7zV9/51/zi3l3uP3zIg08fslis2dne4oUX3+Dw5ttk8QXefeR571wzd7s4hhRFzjNr6Ma/hXr9G6xp+flHf8746D3ycoDOcmazE27vD/jwoWcdJzw8hddvKQ6tJ+/OWVcVhY5p+hPoOkfwLd5HJuMJMcpk2hotfoq5hKEpIl1bEUIkL0pA07aOIssJrt2kdobQkVkNQdO1tWx0PmDLnBA01g7JTE5wAi7s5gWZHWCsZjwasHWwx3A85q9/9B/Yswv+s2/d4f73zjl+orn/oOFXvvyPufnG+xz/6P8gSEuKsTIh9N6xriuO25pZt8IlZpCLwsyLWstDH8WrRWvxphRJhfgw6giEQJFLgFrXdfjOizdqbmWSSExBFFIM9QmWSomkXqwQZOMNvqKMK1RXk0WPi0A5IQsr2voMqzQ2n1ApDyYk9bRsID4ggRGxI8YGmgfoYHDZHlFrWQJ9h44SkibgRIfVgVEeGectk9ywXRZYxtw/mjGrLVXMWFQrjA00bUDHXvqqaX238f1S6RyiEo8p58UOYzAaM9zaY2s8QluDawPLxZrZ7Iyuq0BHQhBTdoMlU4bdQckbN2+xVyjcw4fo5Zp6uUQVOdOioBzmhLolrBZoPLqtMV68paNOsqAQMUrkzrWLzLziSYycRYcrCw63dtjb2sE5T+c66q4losh0JrYDifFYZBZroDOGyWjM/u4eRmsa13Ixm1M1NdEFfNcJqIUUGGZYSuOkkECKEJK1gDQVgzznYHePteu4WC3IjJUQBCuFp/gmCnDqmxZrxSDeG4MLkdZkBFvilGbtFXY4kWM6P2OSGw6mY1698wqre/d4+vCIG8pR6b5Qc3TtCuXEQ7f1UkSoKH+7AVyMNK1j7hwO+YCbADEprLokn7tYrcm0IlfIM2GEWecU1E2H61rOnOc8BLok+Y4A1qQUZ2nqtDXoPMPHQFYWsiFrI3KxYFEGggp0dStyryT7EMlJYi2la5wNe3Y+Gz8zY6ywPkiSuNSkChuRzTMvfvUBE4UFvzo7ow094BoIncKWJcPxBGUNFxfnRNJkX1va2KKMSj6hgc61HB8fp2cebJbTti3BCYs9mkjdpo1YwXA0AlQKz0uNi/FEzy8FHMUY6FyH80nW2XuwKWEGxa7dMK82FwNhwTjvUlMhhY02RkDlKB6Hy8ptWIpmNMBVLc16iU2sMZ8aoD5YmRAx2pKXOU45ojEcHO4zGGQ8ffKA5WLFS3cKjp/d4+x7D3HdCt81OOfpmcyu6yS0RcPW1hQ/aGiXS47uPSQrDIdb24wi7BQFi0/fJ7Ow+OwBg0XFuMixGiLCFGlcx9HFGV6Jb3VpC8ajqdiC+IhvO9DgY7J3IZKbjCmBxScfUn/wDt47JihoO+b2Ibdf38JYxdnjIw6vXhMmamHJQo4JinHI+ebrb/Pw2TMeLM7AaDQZx2cXfOcv/ozgG95+7W3q8xXPfv4z9kYl2nc8fvSUO2+8iSozPvrg55TW8mtf+xrDe/f4i/feY60h5H3ACKB7OwqdmrE0+MOI6iOx+0jXtf/oRdp6Keg02oh8TAtbRas+CKYHhBTWJkCg80TzHJMFUNoksCBs2Dx9Q7fBl/wlKEBaF4TpHUmzvHR8asN4zTLLYFhIeCcBozWZtpAALOcDJqUrxRDQ1qYGvwcIZCgaY9z4HQqGkOSkmA3jfsOyeg7w7m1mxPMoJpueJLONhtc+9yJvvvUS+RD+1R9+hyNX8vTJU26++BbFuKQNLR9+8Aus1gxHY5bLC/CO8XjM7iuvo1aOa/sHfPLgM37y7l/x8udf5M6dV8htyWI+59nJKavFmq9+7ctgC+5++oDVes2v/9o3uHHjKu/8/D1OThe8cPsVtrd3+bM//g4PHzzgxku3mWxNcIsmhRit0GqA61phAukcbTIGwwnew3q9YrkUD7fre7u8eP0a7773LtvTKboYMMgMfphTHG6zamomWwesXMd4e5dlp2jjmFt3vsSDD9/h1pXrFPku1+/cYTDY47OPn3K4fZXTo095/PiE6c4B588eoVhhS/jKN9/mB49+xqPVku1r18mKAXVd0bQ1sfKoYUE0mriVkw1Ldvd2WT484uT+fWw+gE6YiY1fomxAZxYbZGD58Tvvcef1L3D7xbeZX8yZ+0cMpuDXNV3d0niH0zDILZ0T4MN1jjy3mKihbSAvKacTtM2oFhf4JJc3SObCZsgnN5EAGloYcD6I1zpak5cFqtN0oUIZxWA0IIZIXXdAFNsbt8B7AVd7gIEorDJJrk/PvpLwwH6d75+bfrBitMZEhdEQAngfsVZjjRKlCmKp04f/+RAJPoEXvWQ5NxTTgqgDs4cnbOsxv/KFr/DmK1/kK1/8FuPBDo8fPqYoRnz+zhswOOO7D99Bn54yuHGVxg0F6A1e1Gk6iGw1Ktz2hM/OLvh33/shrzPh5nDEX/38ZzzQNdmNKde/9VUG5zXvv/NTfv/3fp8n9+8Ts4J1FaXubDvEplKhEcsCFeWcqrpiVbe0CCtT+0BhLNd2d9gd5mQKus7j0VJPpeF34ztcV6N0QDlNUBLYKsN5j+9q+dtJ3RNCCymjwChNdC0xiC2ADx0kqwydgfMNBsXrt1/D5Jp7R0e0wZPlfXCOIVot/q9di7ORciBhOkYbtHI8eP9vmAymXL9+i0drz8xVON9AWwMR33Qo78RKrVvjV2fUThi5MWi6YDDWUGqPco2oEgIoo7BoCVeLEZQo+3znKQZDtnY0s7NzkVS7jDxJwp0PqCBAk1Ya1zlClHDTGCJZss/wyV+0Z2qH2DNBxfJGa40QCkVurfQl+zUm79wQVALM5TOXr+vEhuuJM5fMcx8kv0LYqGHzPu+9WDPozXaY7HZE/SjDfJKuMhJDerazNMhIvRJR44LkdViTgU3+8hGiisJojyEpNpBnKz2n/WA+hoBRNjFVU3jspv70dAmEVElxCOB8m/x95dpkJllQaHl+NZfP8fM1QYg+lQAxrf8K0poi3xNLAWMsTaOSwqVL5yq1qEny/EjEBAMhJyK/I2GuUj0pKT28F0Zp5NIaK8vzzbC4Z1MrrRkqyeZo2pq2a+i8ZHkYLX1Xl/IxejViUMLW7LxLxAD540knl4JQTf9lofnGQPCX4H9fQgUfUy+WVL+xD6tWdF0Uv1utKGwmqgJt0LogKrn/VJQaIy80KENRWHamju2BZTwYUBSt2LDp7LJOUSH9W0DaEMB10DYtbV2zvDhjPl8yWzYsloHV2lO3DSp0BAYUhUVHTWYj+dBSlhlaxxSgavHBs66RnjpWKBxaOSCjdXNivcDWBjc/4mwROPINqAmmfJFycotyuk8+GWNLg9IWqxSZilSnp5w/e0xTndI1x7juHBUqom9wbUORF4SoWbvAujMYnZObiFEek4LDYwRlDFo7fFAMPWSFIR8UGDwZyXM7FY7Ps9kTxEJq96TmTDZdPnR0Tdu/K4U2y/MQYiDPcranu5jMUNVLpm6FrTyn62fMmwsuTi4wdojOIlvjjMnwAFts4XUC1bMCrXcgDlnXNWeLluOTBcfzOQTPVmE5PDzgcP82g8kuwRgmox2saqibC8J8xcXyAlcvhXFcr6WOjUuirqntmgsWZIsprhijTcFQiTLD6kCnIyYXr/xiMEjEBUdVOYI3RGUoBgV1hLZzZPPH7A7/mixXuHJKpSf4cowuS4yO2MEQlxf8Xa+/1yBtBKIVXx6TGbIilzRuF2iC3Gzj7TFMxzyuK/7vP/wD/uTf/ylmXDAZ79A4j/MV580R649PqE+f8uvf/Ic4r3Fo0Jrj8zO+890/Ybw1JiqFzXKszSQpWcFyds5AK958xbJnLMHmFIOc2rUcPz3ij/7gX3P07AxrMsrxIZXZ52T9JiP/ZaonVzi1O9TlSLxTUbQ2cOy3qcyXsaZgXGiuTbYYc8zX3/4GtV/y8Qc/49Uv/AbXjj3HDDmtIn7WsX+lY3X0AKJnsLVFJOJ13PhRZsagh0NcJ9Kh4WgsrA0UMSRZTFbi2xZtMjKbo7VLTB8BcYN3uK4hOPDBiScgAqZ07Zrd3T0poL1DaYuxOUU+wpQlMYrHqVKRne09XnzxRUrT8uYVxbViyenwgDpajs8MN1/9Nbq736etGtb1imI8oeta6q6R9PMso0sei2LH0EKy9sltJotF7AuIS9lGSIWCQhrAssjJswwqxbprN5IPtEoSM9Xnq2x+LirxcRKvGQlYgprYnaG7BsIaK/GGLJZnzNYNw+CEpe08NpcCQlkDwUHwidWh0DS49qkAydkWPk3SY/RYYGRzSqMo7YqDiWdsPeNBRqYhtyOm45eonOJiNePpaca68qxCpGlrYSH5Vjwp6IuKKBN2L3/DGMPh/i43D26yNRiTW7k36rrDtYHTkxM++PA9VsulNMDKUxjD3vaEmweHHAwHrJ8+xtYdk9EUW+ZoK8VYu17TrSuMi2JRgJVEUqWF9WA0XnV00eCi5sR1nPnIKjMUQ2E+DYqSxgcWixVt11EUBePxiNyY5P8TQEfG4yEuCCBWDAas6oqubmjbmuVqBsaggrAWEwVXJPspSb0JHat1JQElVqwPMiMszbML8ULWxm7YDOIdlfyoUnCDLnO2plMOdvdYrFecLObYzGCMwnUdZVGQF7ncc2aJiZEf/OSn3P3kv+dm63htvaRTomL2Cdhfryu87rCpKO1USIMMxEeXQBXFl7ZNgwDxooVcazIDhdbJMkOlTVbAz4umZRkClRd/5gpopeYVRkAEnQpBDdgiw+YZor9OvmkasuxSjmmMwSiThltxwyDqqzUJhwiUWS5gjLpkDPSNrY8eY2yaxso9qhHbB2n4QJHS7YMEcmgUoXMy6FAWm+SVwRpa71nVUuyXA0NfIoYoDXXPjBBrAkkLXiwWm2AYpSSdOIKEFCpxKRM/pUa8i62lbRpq75NvNxvLhuC9MEjUZVF86ZXdsybSNQyRvMw3XqCXKcCJpdC2cjx5hkJY/pGIyixqWOCrZZJkBqK+ZAWgNJ4gn2GZExSUwwE2M5xdnHAxnzEeT7DGUa1O8CuFMRGclwYjRoITiVpmxE83M1CZwOnsiLq64MredcrYUJ8/4+n9h5jlisHVq9zYPeRk9VgGfnhCaFHOol3BYrlCK0msJcp1zLOSYTHF+UgwHmWNhEtFJYnbWpNbTakiXQt0HVErjo4eQ4i8fuc1Hn/6iExrBsMB5+dnNKs11TIw3B7z0v4BX3n5Fc5++iNqTQKPMo6PT/juX/wFI6e51oE/PmLrcy/x+LP7bF27ijKOj975BZOrB1x581XCoGTy8AlPWvjJR+8TXEDbKPuQsvIMJ6VK77nX1zEbBlHaq3RqQklArTBZe487GcooUvCIVhvQ93nmqVfSxOk+SESpzb3Tv/omXGmN0imMC1LAksY8d2/KKnF5bOa5hj7PLGWRE5ywXqzVFGUOKkNk3BGUT8ejGJQlzrkU1vTLx08vR/NeVA26X4TYsIq0McS0f/2yJyGXX1ORqBtateYXH3/E+C/HPHlwlxeuZsyWC+YrB13k4vQCt5qxvjilT8be2t7l+q1XMfmUq1eu8I2373B1t+Tpo8/z4//hB6ybhhdevEVpLdeu7aI/znnvvXtcP13xuSv7EDyf/9yr/Ce//Vvcu/eQdz58n+nBTd7+2tdZL+YUg4LT4yNc69jauYrrNIv5GUpVEATMUdrQtiVdW7OYX3D7jZf56BdP2dvdZ393j0f3H7J/sC9rhM6p12uefPoRrhPVjc1KLk6O+OZbnycrx/zor95lcXZKkXn2D2/xjX/wDzjY3+O9T9Y8+Ow+3ewRKtacPLrLcrWkdp2k0BvFTz76iNtfus1/8V//l/xvv/d/EZVDh5ZpmXPSLGgv5hg/Qo+HBGtRw5zh1hQ7LKg/fUr9dIZxEpBjGqAL0EWyHHZGIy6On/B+23L9pTu8cuct7kfNWbgvkEcA1QUIgbbpknJHWGfbu1MZup2fMRjDQVHQdZV4mWuDoBJJQiw3mDTz6Y7yznHlyiGz2Zzlckk5KMnzXJQm6b8hebWaZLPigqOtW7JcvPxsSijv2rDxVibJjqO/HO7/v8y92ZOcWXre9zvbt2RmZW0oAAU0gF7ZPT09Mz1kc4YiTcoSw7JsWVaEbTn8z8gxN/oDfOtLRzjssCJ8IcqySWlEipJJimPODHuWnt4bO1BbVlYu33YWX7wnExhaujYzAoEIFFDI+vL7znnP+z7P79kO3l56pmSPtNR1TUww+J60qRVTVtJnfmeI0tiz5IaWBlVDsWexY0grz43pLr/59q/zN97/HbQd0zfw+OoRVlWMd65x/9EZb916A12W/PHjC8zuHsZWDK6i7RpUlP1JRdBoVkXJ3p17fPaLE64++5Tf+eY3eaVZ8P1/9xfc+U/+BvHOMX5vQvd8n//nZ5/x4KPHoA2hC+yPdhhiy9p3dHmvsFoLJ1Ubmq7LB3TB/OyNLEe7U8aFwyGJ6gqN2zTwohzm103PUFgwm1mSJnqxSXsfGPpA2wzYIolSODcHtBKVX9KKrvOoosDoAqNVVnjK9T47u6A7epVrR7e4HBJniwt8GASnphI+gDEVXdtBTHjlUU4xHk+kduwuePjJn3O8O+Hu6IDz2Yr5coH1ElRscshcAFxIWb0qKkAfRd2rU25shQGjrKARMkZGtgHh/Q5tg3EWD1TjMQDtaplDskwOi8yD7ZAIyD1qs2tnK4fN9UsIHqtsPu+wdQVBHihY/Uv37nbN3qpotSByFGyUoby0PqeUtsKQjdMTDDF5abDnYDNFRgNkJI/WEsIUt/VZrqmiNIZ0HmbKGUr2RLQ4B40xJAK976RONIB5wZLVasM8DQgtb8Pizc1eozf0rW3T8mXXiUrIvqYMWsvQUlsZKqYg592gFdF7lJdzZ5b3Sh0Hcv7J/28CCUE0Rmz9IWRupqxlIci/lQFpROsCpWTPjbkZmxBUzjAM+d5X28G2UhvWO/S9hD2/QFm8hJLIjXnSC5UzCcnxURqyI7RXKaMrEtZmtEVMOZdhIKbNn8XteyGLLbRCsCUxZk5xbroHfvkaK4XvB8hNwU32Q4xRAsSj9AKsk+tfOWmOgogqRoUwrHdHIwrtRMmaSnxw9DESkgzLlZL7NcVEUAGUzX+Wz//KYIyg6qTsTXifaFtP10KKlhQcMfVo7bDGsbvruHY4oR7t5HtpE/+n8UExBE3fdvh+oBt6vEiR6X3HYpW4mMOiGaGjw0VP4oJuOWP5/GO6VJBrrayyAAAgAElEQVSqirIsBEdFlqh3gW69IAwLUrhCqbXUiUnOSqNaxEiiFE84HSmMp7BgVEIhAjZtI0WBOKX7EuNqYpI6DpcFPrmGjNHjB345cDDkwOMYtu4PEdaml+4FWUc0OfTOKJybMhpV9P2UZlgzDTvM2kMu12fM13NaH1j1K2aXCy7P1yh28SSitsQ4prkcWM8Ds8uGi/nAbHbJVdfjnEKPRvRdx+Wsg3qEKmsmWqNY0odEHxWrzrO8PMH3ZxiVcKqg71q08cBACAPjiUUnRUxruqQYuhVpyOKI4FHKsFYWVzhc6ahLje8HBi8hvloVRAa6do6//AVVeUBZ36FTFcm8QqocUTkGpUkZm/Dve/21btKiNG6yTzWe4JXnqm15+OgpDx4/47MHj7i4XGKcxdUToq358quPaenZOzykqneJ6wbfNXS6QyUJtxpXNfVoQvTSQLiYXfD9f/HPGHxL4QqssWKz0JqQEmEYuH10xH/9n/4dvvvNb2AnO2g1ZmdS87d++7c5O5/xB3/4xxxdu86dN3+D8533uT/9gOfldVZRmjwGsZFENMlDlyzB7KOAYeh5bfeQX3nrLf7m33yLYj/yP/zjf8zZw4/52uH7nK3PiLsHrGYN+qAn+LUobpUWlQBiyWibDqslLXOxXEnD1Dimu2N8FBWOdQ6CwjcdZPh+UWhRkOUNLQZP3zfEMBBDYHW1ZDwec3p6zsXljPfff5/JzoToA8pAoUqC0iRXQAgMfYtOkfnViuvHt5lMdijCgl9/bcSp2+VqcDx4fkJ5/Ziv/eo/wP34+yQkqXXwnq5v0dZilFh7VLY2aGPp2iazZ8qtNWez4JKbncSQiw27bdQqElVRglZ0mZ0ECeMcrrCAou97Uopi2dQa56RI6AZPGlpSNye159D36L6jIDIE8O0lvmkZ+hUxeFnUlWxIKhdPWr8A2GsC0Z+jVIXSFdo4VPIYBmqbOKwTlemZVj3XJ4pKJaAhBlkUSxJ1aZm4HfbLksurjmVouVzNWLQtKy+Jiigj+AuS+FB8YFzV3HvlFndu3mJa7BD7gRgHjKlQFjyBV27doF1f8vFnnxGip7IF1/YPOb52jWlZMKzWWB+Y1jV1UdAOPcOylYl6jJRJUTibp5KBZCASMRh0CKAVlzFx2nVcBmi0xdY1ph7RND3rq3VmwBp2dnckNV7J+w9+YEgejdzPVVWgB5lmV3WNNZrxuGJ3Z0zSsFouubicycQ/iprCZ+C+J2GdzUB8I00RIw21xkti8RDCtsb1SgDhrnDS9GczIIDLyzkPT59zdjVnDOiuzQo2x7oV5EhRlgQfOFuvuXg0owyKr9U1IXi65KWRaiBoTdAScDVKiqHv6YFew1InrkJiHqGNEHIx7JTGakWlNSNjKLTCR88QoY+JAfBDpImBdUwMSZMwRDmpycaKbK4Cec/Be9YQFFJAZvRBTNBnJprKk22T1XuKX7aNbUMZkIOWykOXTeNno9KwzqGUqP2s0eh8z2YD9PY5JgzSEE4SDDIejcTarjRKGxIKnyKpsOxNb1CWJYsrsdQalATB5/9Tlo5cgHgJSdgGPmwwFrmxP3hhdW14b6Ef8j2VG3Jqw6J7qRmbm/q89PNu0oLl0CaKDescN67f4OLigqZpgLRdi9kUOJvpdRBGHEYRlaKYTOjXK8K62Rb4WqmthT4ZjXKZCYooZIbe8+DBA3wMjCdjmvWcstpB22KbzG3QWJ1oug5hNTtK5/DDQFituXl0yN6dm5x89DH3P/0Yf35G1feMTIled5R7hr29XS7Oz1g0K1xRybUYDEWILJcRNZpQlyPMYClNhRk5dvcPWfULVusFrW+IJGKWBWtrCMoQiUQVpKkNzNcLlFXcuHmd+199ydvvfZ2yKJiHwPzygqurGTfLu3zj3mt88fgrvlrM6KxGJ0OR4OT8jD//0/+b7x5c543RiOXJGUopjqYTPv/op4wPr/H6B79Kt7vDaggcvDbid//Lv8/i9xKffP4JofcYXeT9na3ScyNnTptFImWbJC+UdnJwkWdIhhkysNmw51Le35TaWCdfNHpfDBpyaMz2e+bOr7Q3toddUaawVc9shgHbw4+1+Ysv/q4xDpWVNTF4sdamRIzCSg7ZSrnBPqSYg1NM2loc+14wM1qpF9cCthZpsXHK8GJz1t88L8borRJX0pxf+rnyxY0EtPbMzk752Yc/4te+eZe3v3aP7//LP+VsPvDk2RPMZWQ6LfCq5/XX32K5bJhftRT1lPc+eJfDgyl/8cmnLE8e8uiLc2ZXM8wJXL9xjE+eG7dvY8sR3juePX7Od77zHh/86jeZjhwhJr588IRVp3j37W9w1Xh++uFPGe1MmM/OefDFl4x3bzLdPxJXiG+Y1CXOGM5OL0iDxyS4PD+nXd6EIXL7tdvcvXOPy4sL7n/1Fa4qWSwuBa2ylMDLuh7z9uuvootdZicz3npnl5FbsU7nnJxcslNf5/6jcxbLlsVlzyuHJa+89y5GDfzB6gx/qjGjCYdlgY8NqvQ0a8vdW2+yX044XV9RH45wtoA+0Z1dkGYL0o1r1Ie7xNqxih5VOsqbhzhXsXw+o1+0hBhxhUYFw/pqwc5kRW0LFrOnPNWat9/5Jm+/8z6fqMD5k4e4GFGtJw5e1tYgTRjjLEVV0Q892lia9YqnTx5RlQ5rjIRQeS9K14zESnlQprXUu5vwupQSRSH3s7hhxNnjo2fohsymF+Vh6D1aawkntZau71BRlMH90DP4AVfIfuj9prm2We3zFpJeDhqTw27tHKtVj4+JYfAQBSFidIXRlj4NZNAIMQXK3Rqz66CI+L7jWrXPtz/4Or/+1m/w3te+w7IJnFwsqHYKFos1z+cLdvde4fThT7lzdJP/aHzA50vP+VjTlDVd8gTfyXaSxD0zhMTVqGbnvTdZLVt+7e/8BtNPHvLjf/L7PPvJp6j9EVe2Ix1U2PU1Pv/4Ebb1HE6n7FQlalqg4xy/XkIIKGvpQ0/nBxbrNUZDpeF4p+LW4RSVIsPQifVeKYiB6L2oCZHhkNjmA4V10mxT+e3CNqCqsBHrREixUXOSJGhUwqURBS2SK6AURB9IeBZhzsnyjD5F7r7xKrfsXT786YfSmLeaohyzu7PHcj5ndnFO9JE+DdQ1jEYFSrdczb7g059WfPOD/5ivHU35weUpTRvQKjIkTyTik4bk6aKEZ2mgDUm4tEpS4lufGGIgJC9ChJwCr7S4FWIYGLoONxqjjGa8s8O4rgkhsG47UBtFqQgSfBah9Pm5SGmjrkzEXHuozf7y0j0re8MLDvpmD9ngDdSGpyQqFl4CCGxfG0bqBqsglv6ADxLmtmGoSw0kzbUNHkcrg8JIE0e9zKfNw8skzU6lNq5HnXnlm/3RkrzUBkMCo1xGcMj+orMDUwI4RT0bUma8oraIlM3Pv3l+QwgvhupKeOkpJWxS+L6jcA6VB45GG6wtZD1Km3CsFwNQnYeRSgEOUHJ2l7rY5Kb2sL321uZAXvJnkw8jIUjDW5TdJgcoSljvRhiRUi7q8/fcfDabBqvOSKxNJkN6ae0cvMf7kDnL0kAXDFLKYl4tw/cU6b0nkvfvJPxdFChnMJvGfoiiVFQI5ksJhutlAYPWWsIFu16cryGQfGTDzdiUwn3XofwAsaCsssOOSGEUO+OavZ2acW0pK1Hd98HQeehDIEZ531qRQ8zE4aqy01TqZ0A5UembxGh8jWKlcGuNcT1DaAWNo2tG9S6H+wcc39Ds70/QusrheRHwwpNt5HMW7jD0QeGDQhGIGHzX0i4WhLZDq4qi0ETj0WWkVD0jVeLDDDUoCJYBwc6Fvif6Xp5tHQg+EYasXtWKdpX7HNqBNmg8Bs+4clSF2zb1TRB3qLMS0OmKgqqqsIXLA5AMQQyevm0IeT+VAYMMYIIXXNEGA6gzu1krcNYKWiXnfQhyE5wtcNpSmpJRNWEa99mrrzGvT7mon7H0C1a+YtmuGXpNu2pYLxuuWsO6aWjmKxbnS87PFywXAVKPVw5cBHdAdBXLxSXdakGHxvaBdXuJC0vS/Iz18gSGBh2lD5CCoLmWV5cY7dDGYl1FqST/QT63nqjS1uFIgtVijTaO0WSMKyxJR7QrwHtMHGPCQPSR+eWcyn5OYW8wDpbGQRgVDHpX3Bt/VYfw0uuvdZO2HI+5+c77/Pzjn/ODH/4Zn372BfcfnXK5aghKo6yV6RiymBa1ZnrtEFeNUWVB5RyqcyyHFp8STehZX12Av4NKmr3JiLu3bmGNYzG/JOiBFAMmh2QoLfam+6sl//Sf/zOa9RUf/PoH7ADWVEwnE/7b/+Yf8sq9NxkGKA6/xp+d7+LjiEFZ0MIr8knnhoPwPSMJT8AB9fqEUfiU2/twcf8zPvuTjzh5cs7j+x/yrd/6GvuLB5jFLtfqGwQ/48atY5F8bw4qeaoZjIydjZZQnMl4hNaGru8xttpujlVVbw9rbdvIhU5ihTJa0/UdwzDQ9y2xD1lRaenajrKoWC9XcoMqKIqKOHhGu3sUZSHcVyTl3BjHZGcswUthwVG6ZCdUrN0xV4w59RXT0WtU1Q5lIaFQIQx4PyChZfJ+jTb0eUJTuhJXuBdqJKMlcTNbTWMI2V4hqooQI84YQgw4Z+ijwiRJhow+UDkn0yYSVVXjg8dlRqYobBM+SkqfGhq0b7EYsf95sfK7dkHVr7BxzaCkQNlYa4zSKGuIGxC8tigSMXUo1ri0xqUKQ8+NazV3buzSLk9p1qfc2NtlryhIQ6LPU3ZJPIa+aUBpau0wO44DVXBYa1aDZzkkzhZzLlcruq4nKlEi7pYj3r73Om/cvUOlDSZoqAzoghgdJilWfo2Pnhs3bjCfzVkuLjmcStjPri6xqw6zWDIJUA6e1HfYEBi8x24bUYGoosj4lWAB8mmcIUYuhp7HPjBDYcZjlCowZYk1BYU12ErjKofJvM/BD3RtDzGQMlN5XI5YrXuWywsuZhccXtvn2+9/W4q+GLBEUhqYz+dcXs3p/YDNPFMydsFlto4CSRH1klYaVW6sbBVkBYW1mMJRjmqZqg+ibPXBs2ha5qs1V+uWPhloekZ1RdN2aOM5v5gxnU5BKZq2QfUD+xGu65LCB0LfAdKoHJISbltWApVY9o1iGRVPUs9ZDJzGxEWIBGNxeWJpErhc8HQx0PhIFxM9sA6BLiU5/GlF0mIb3KhU86kwa1qE5ZXdnDKNRxT4lZMEz0jcDkXspnhTG6blRk30V5VFG0Wp+isHAyksQkpoI9e5UBGnJezPiq9b3oOzKCpCtulYbbBOVE5Ja4qyxJYF66Gj6XsKH1F6IOXNdLNeBi/r+/YA0ffohPzKRTkpbQNjNs2jTdGR+22Qm9DyZ7nxlFUb5Kbt5hCzCUx62RIrfz9ilebqarENlWCz8iVplm2s8tIEz83bSM4DTmhXMMRG7Gi5ptUvBTnYQgIkdJIgzsvZJYv5nHuvvcp0dyc3v+XgLAnoomCMoSdGYYwuL1ecnpxQ1TV3Dva5c/OYiy8+5dMPf4o5O2FilTzrGhZXc05dwdHRNa5WK2aLOabr2ZvsEL0m2kSzbtHBs1NPmIx2CL3YEYtalNtWO7r1UwlstEpso1pho5J9WbQ0GCWhax99/BHf/favc3FxwU9+9CPuvfo6d+/epTs64tnJM2IbOZjs8v69tzn/6IeZ5wrRaEzheDI7535SXNc3UOeR49fv8eyrh6QUufutr9PVBat1i1KGnarmg69/g3vXjvjwxz/kz3/8Qz67/xWrriVZC0hidMz5GHKjq3xA+6sNVLN9DmJIaJsZdlEYz0ppnHVA5snpHEy2+cYpq8vT5lDM9mC+uUdTbhIBkka9eSI3TdP8xZAHUihxyWitGXwvybXZdSJIEwiDWBKtc7K5IOtqQGEQZcp6LWF4dV2jlMqKn/RiMJKfCSCjecTi+nKQTUovGtqbRvPLa0dKoJNiWo0YF5bDvSmJwIOHD1is1tx77U3e/NbX+fKrh9x79RqLo2s8ffic6OFq0aHdiPv3T3n8pOP8yZL7n35Gs7hi92CXJ0+eYHTB9cMDvvzqOj4GvvObv8bPfvIxP/nRh4zLnr3bR5yczViuA6PxPve/fMCDRw8Y1gvKqsI5y9mzZzz84nO+9Z3f4MbNVzk/eYotJAjXVR5TjDB2xNXVgvlsRmELbh0fo1Ji6Du0hsJpOgbqqmZ3b5/da8ckDFW5QwiRkbN88bMvoWmhXzEuwXPBo9MHuOo1bhzvErolTddTl5Z7r7/DPD6CUqNTz+7kDiF5fvHlL/jZD3/CXiqZK1GpRkBHzdhWDO1A/+SMogu4G/sMI8fgBSlgd2uKwdO1PbEZiF1A+0CIa06ePWVnMkVbx+XJY76yJW++/Q6vvvZ1hrZnkU4JukW14FTE91JHlKWoXsuqoqpKnLMsl0u6pqXIWRVb3mRKOOdyM98ITz3f/7PZpYQFVzUhpNy0EKTPxgHie4/LyrWh7wUTZizWWZquFVdBVECkKhRlqVl3L9i3W/VhRnmEKM+IUooweIZG1ugEJGXogwIsVo8Y796iHO1JrF9Wwnvt2X3lgGrkMJ1n30z5jV/5Nt+68w126+t0g6Fvrjg4OuTsfMbF+YLjm8doH7j/6U/o4oK3fuUWd492+XE78Gkzw6ueBT2kmBt3ERUjywG4c51qfpf/6Y++z2vj67x6dMSPHpxw+fkTzDfuYq7t8Mq9t0lvv8OHv/+HLB894fr0gIPxRNSjiBZAiWyQ1WqFSoG9ynJtVHN3t4bYsuoDKqfMD35g8J7oB1QSpaMERcleLAxNK84Hq7ZralFYtHYS8BMHjJHaJQWfHVEK6wTRY50mrj0JJYGcKoGJfHX+AG0cv/bumxzeucmsX/LZzz6RmsJWFNbh9qFrV9sgsYv5CoyiHhcY0/LFk49p/qTjt/723+PqaJef33/KkAJGS4MoBiUqY2TInIi0JK6GgevUWCVNPB9AGWHVmphEuZ0bOzY3lCprhIkcxcmQuh5nLZ33EpqjDMYJfkawGgGrpI7c1mFRXAQRcUVtAi43atWXA/BEwWmlWZaRBJtgKmOs1B5682+zuT03MDcqyLTh4qo8yM+fzyYkb7P+G2NzwNnLtNsXXOeYtylrDUlvGsbyK0YwSef8uBfNUJ3P3jordaPKw+5c17JRN6cN/1zei9aGF2FimzBOxFVJft/IXmWVBOqKgclssUNKv9iPZf/KbqvNT7ZR8m7QfUoLhosAUWcloibEIBkVakOtl8ZaFBG/WPyV3Q52BWcAbAazUZBA4GVIkLJYIqMdTQ52CnnA4ZOoa0PIzdeNCy/KdXHWSi1sDSH67ecRye8VJFtGvzhDaxTG6W3D28cgLilEWbwNSYyRyWSM2ZnQdwPtek2zWtO3HYnsZMzIjRQig1fo4HBOsAeKRGkilQtUTjOqEnWVGJWOogBrtSxOG1VwPi+F4IlDTwgDMWlQIsDxSRFiyeATxo4wNqGNhIE7Z0jKUtclk5FhMrYURRb8OIPWch1ThGAtQ4wMIeKThAK6lM8+aKyJTMYt6MAQBoIuMW6PpCuK0R51PUaHNdpY2ha6APPlkjYpClPkJmqB1rUMdPo+B70JSsKHQc5sCZQp6L1iCAFrEs5k52VZ4TLOxWiFdZaqKhmNZEgr6AaN94Mw5zfnIe1A2Xy+FxXvZhDkw5DPW5HSZZFiCgx9T4iRwcgQLmlPUgmrSkY6EO0ENd5jrDXeONowxafE7OoMex7on/dcLTqaxjP0He1qTvQKoxKWiI6B5moGyTHdG+OqiQRra0+vDP080a9O6JoGlzRGVcSYuecYwQ2lQIwdq9U56AFXVPJzOiioGGKHCRBzoFxI0PcBHzLOJQRisiRToVRNILL0Dc3lL6iiodz1xNDRJ4eeaPqkCbHnP/T6a92k7UPif/k//xX/6vt/wPNnX0HUxKiwdUW9M8aUhoiX5mAIVFVBXY+xtsKToFAUpmIUHFF3LNsVX3zxEbdffR1TjNkbV3zw/vs8fvK3+YN/8c/pViux6hhRfVllwcpU86vnj/inf/h90PDBt7/Dzu4hSlWMxxN++zd/h8fPZzy8SlwfKyZXLTOdP8QglUV8SWmjooJkCEOHuXpAET7nwdkvMJ3j6YMHdCvHYhm5OJ/z9vVTZvMfcLzzu4TVFauksbUE92wW4RQDZVkSg1irDg+uUZTSiOiGAZRDWUU/DHTDIBuesazbRhRxRGLwWO22CgKjFeXUsTMZYbRld2+Xye6Uoii5uDgn+oHFumG9WlPt7HLz9i2ZSCVPDAPPnz2hLu/g40Cz6hj1p/zqK2/xx+eJy2rCwkf68T0GvUfXdNRGFloNoI2oaHnR9CEziIZhkERRY8SSi0xVnbPooMVmFCPRi80yZVvbJmiFPJDURqGUFOwpbST8inpUorXBp4gPvbBVU8CmxDAkegxBa3zKqo9mRZVatBlIToGPVEaKUB+jWGBizIeGFwf38cjyX/xnv8udw9s8e/Q577x5zNDO+d//yf/M89P7jLjFwd3XKet9bAzChozSbKPXaAzKGCoNhbUcDFLkq6IiWMXTywu+ePKYq+UC7SO/8so9Xj1+hXFRUm4KOqPpkwRsVUqBrlg3A+Pa8sr+TVYBRsYxDR47P8cvFxRKY1Ok7dZ47yl0gVEap0y2L5ls2xVestaWxgdWcWAeep57z8oWXLv1Crdvv8KTJyeAYjQakwax6ASdKEpHs265vJpL8ZYAI2Fh6/UVnM7xvdzLo3KMQjYSW1icSoQ+UTgJaLHWMioqSGR2krCShuDBCzJBaYW2hqKuREGrNQfjPW4e3cAlmM0vGYyEDQQi0UuxMW/WNMax9GuUKrGuIqLoBplSjsd7GO1Yr1YM64ZXrOHrheGu77Fe5SaKNGdICZM0JpGDFTwOi00aVGLhPc+6gTUaqy0OQViEHLawDpE+RYaseAtkjEJWo6ckRbvQLuPWhCIPgKxPgShMTCXXwzrDuKq4c/2Ys8tTOt9vi2khzJutBXQzPNlYq/RLTZeX02o3L5nse4bBU49KnHGUOjB2hpEWxpzWL5S4Kx/oU5JQEET9Z61YK+uqYjSqOWICQXhWzxdXDGj6zJxWSlE6hyslrbRpGqzOSb0h0bcdGwh+30eGXhQx1jlQRgL7lHqhCNl24V6oLxJZjZoTkV+2l2mtqeuarpNBmAwJFF3Xb5WRL66joBiSYotISEnQJTFffYViNB6LY6QRIL/WJrNPEz5suF35gBAi88sZVVFwuH9AShHve1QyxLSx36vtnoJK+KHl9MkjLk9OODg4wNeaj/71h1z8+C+ZNmuK0YjkJa3dIsrC2fwSV9XYogK1kGfXDxDl7xETXWzp1h1HN29hlGXdLDi9OEVZx73X3kIXhvsPviBmJmTyeWCWm9dKaYwyRJ24mM94fPKUu6/d4/OPPmX2/Bnnp8+ZTHbQQRGbwGhc8PadN/nk5BnLs8d5PxZExNJHPp2dsxsi79+8Tde2PLo4453vfodqus8yRCpj6JZLlk8WhGWHCwMfHN/jvcPr/OTjn/HnH3/IFycnXHUDFKXMTnODVOUAEbUZUihyMKPcQ5u7KGYWm9JZRa5ltCthRJuE6Zfuk/wUp1z0b3AdglrI+ybCDpQE7LQ9aP+Smnez/gjVODdS5evishFW23rVMBpVckhMCutKUjLbwBBhlkV8M+QDcMI5TVmW2+d989ocaNfrNSltmLVsD3OwaRxkpU1WCUmSdk7MTolh6DnY2+edt94kKvjhT75gvTwjBsOd/cDOtMBpxb/74z+hHk/RSoJIbhwf00fN7NlT6nrgg2+9ym996xb/6//2z/Fdw850h4uLGZ/+4iP2j464du0W1c6Iv/G7v8m//bf/jp3RiL71fPTZz1kuPdpaHn31JaFvBCGR1Z3z2QXzs2fc//TnTHb2OX7lNofXd+mDZ3LjiMWix+0cEI3jwePH3Ng7oGnWFMUNhqHDGNjf22E27zmYTihcwdnJCcYVLC8viATu3XmTvl1Ru47KGZpmSb03JamC+4+f0Xz2Cc3qiv39Q8rCErzn9r27zObnfPnJl/Q7LfWkIiwbpmXJa3fvcP7VgkIlDJEYelxVUAVH27asHj7DDD3jd14l6CDM8CANNlU5dEzEriP1Hh9bemNorKasJsQUOH1+H+tqbt66zfGtt4TfrS5IomhAF5HQR7q+Y3ZxIXiZqmI0KqiKgtPnJ0x2diidoygL+mEg5fs0AePRSNirMeJTom06iqLEOfdLVmarDYN0FYkhiMsqhm1j62o+x9XCYXdFSQxS2/3at98l+sCf/MVfbocvZVluGbbEJKE/aQPtk+fIuQJbVmAqblw/ppjscXznTfaPbrN/dMz0YJ+ryzmoxNlwwdp2mC7wanmNX7/7TW6ND9kvpszOV8yXLaPpNZ49ecbssuX4+C6zi3OUnfD6r3zA2cWPmZ2dcmNnn3/w7u/wh5//lB+cf4bXgRDExo9RBCVKuqWx7Lx5h//n3/wFZ88b6umINxZ7fPTDz/ju7/xNrt19k6uLM+bmhJvf+YC5/YRHn91n6AdcbggZ7TBonFF0EcZVwfVJxW5h8V2b69MR3ge6dkWICoLPtb2E2JB3thSlcblRbG5r5w3uSCdi3Kj3c+MMk2scSf0mKnE5aLetdYzRFKOCwShGdcn08IByMuX1d97lyf0z2sUS33WsQ4NSAWUcRpV437NetWidKKsjCjfGh477z75i54d/ymtvvsd6b8rD2ZyOhA4RP8CQHEnZrTCmT7DygTYIT18GIZouBqoo4QI6fzYbjishEpoeXdYoZbYq1ZRVntEH+jDIGimCQHEgpU0t8YINblRunGWnxi85msxGMRlfDPa0JqmM+dgMzJDGosrOHQkfE0XeZm+W/UAai1pJU2+jYt00hzdhX3k6mJuySNNSmxdiHKVIIWG2ylmZliuzCUPzqFznkAclYueXmqfOsZMAACAASURBVCHl4aM1Ir6KGWElNZXY6V84wHJoH4kNLk5LOAmKHGC2qfEyMmHrZsnDzEh4gUTTguCQxmXaDt+lLgCVtCBIYv5/lZaGcoq5iStriEqKEKJ8xkqjjMEaTdQGlwPDYw6NUwrSBuFiLCpzcKN6IZJIIW6bpJvhls0u0+SjBCEmLz2MyJYruxl+GaRZXihDSAifPqUtIlByIgJDCMQsitjUG5sgRnHpbe6/HKrqLMYoqqqSmq8P6Dhs//1WBT0MpEICrk1K2JQoVKJWkWmp2K8ju3Vip4xUpaFwCYU4XZW226a3Ti8U5SlaYnJEPOtuRdM39N7Q+0AIihQzA5eConLsHlTUI8FNaSVoH2MEC5GCBMQ1TWTdJxaLlqFbY42CJGKjFKEsDNPJLlpH2lDQpxGeGrSjUIGSgbJ0RGuEn46jKg3DEEnI/RG8J4SBIQRMMYhDI4njqetaul6QFN4PJKNk7UzgfYLCARLiHTcCgZhVxXpTu8r9nVKQ7JYYsljAkpTN66qIE7QxWzyQ3OcRHwdSCvgw0PcdMQasdgyDgUJyFQpVY5WiLsZYbWipadMVVTUQjKfasVTTCfWow5olBZaVtqyuLhmGFkOVsSgW3/T0+hLqA+q9m1Q7+6hUYoZAmF6n05JREFZP0dGTkvS+QpCws8F3qEFTGMGumSDXwLmCwkFnOqLJDpk8etHO4LQlhgEfRIBjVIkxI8kXCQozJIbLB/jlwLA4o100pL05yY3QSvA4/76X+d73vvcf+NL//69/9N//o+/99JPPuTi/oprUlFXF0fF16oMJsQBdKmyhcaWjqmtc6dBOYOToDaQ7c4IUMlmN8Orde+zv7WBtYjTe4Y033mFv7xrPTy8IUTY74xxFVVLUpVhGjSVgWCz6rKLdoS4rSSWsaqbTKUYlwnrg+drwlF18ZsrpXHSgAirK5qYAlhfsX33IOzvnzB7+JT/70Q95/PA5ZbXLvXtfQ2nHbt1zb9/yq+++SrueUZSasirFsj14wjDw7OkTuqbJhWiBdkYCdeQ8SBx6/NAhQHhJvA9eQjNiTCyvrtA6ssGMHBwcUBYFi6sZzhRY52i6NZ3v6NqOUVlR2EIO8Wmga9YoIlfzGVfnZ9RVyf7hAcYWPPzyU+rSUpZjxrvX+LMvF6zLA4YO1NCyN/uUW7ZjUliGvqEdPFYbPImLyxnDIE3XpJQsNCFP4o3OQPmYA8Rkk7ba5M1XrntRSBMx+CCWTQPkpnThrFitlCxIBjloOqMorUxGffCkZBjcLnNqzhZLVLsmrhZ07QUDDUNSkFoK1RGGRji9ZUXXrvG+Z5MyPATP4DtiGvj6u+/x3/1X/5BXrh9y/doOYTjn5x/+GX/5ox9RuJrZcs3aS8Py6PoB164dUdc7VKMxo/EOO3v7HB4dMRrvMBlP2N07YDSaUlcjdkY7HE4PuHV0g6PdKceHB9w8PGA6GjOuKqrCMhpZlA7EMORiLoKBshyhvSEuOpqLU0bRY9YNrNfUyVMNAwwDKuRCR2cbE1KUKS0Ll1GJdYKLpHk+RM6AdT1C7+6zd3iNN37lDUbjWgJnjFh9hxAZYqIaj7h1/RarqxWz2aVAyDPwXxlL1yW61otuyxgODvc5OjqENIjwDg06sm7XnJycSBqlEfvtdDxm8J6rqwUqFzHG2vysjyjqiqSFUWWdZf9gH1sXnM3OaJs1wyDXy2pNO7ScXc24uLrCB5GfNs2K1brhxo3rTPemJESZ06xW7DvDu+Mxb9iCwotlqtKZtYs0I6zVGK3RBEyMxKS40omLyvJF33DSezCWysqQplOKJkGbEk2MdCQ8ELXwav+/Noq8KKC2BabJP6+xBls6OZDXlVhV8qbbdi1N32GMRSPXbaPYTCkHTOWGp4S5KDA6T+tVDgmQAIIYIipB6QpqV+CsFgaSipJKixT8TTcwBGiGwOVqyeWqo2lFebtcr7larGibnvWqYegaUtdTJhhrg/IBF2FiS8Z1hbUwrWsOdqYUhZOB1brDrzp8O7CaL1heLbBFka1jYpe1xrJTjpjYkovZBc5ZCuu264zKBx6beXxqU3TqDaZBbRVaANcODymKgrbvqKoKo3UuXOK2Ib0pdDY23c332bS4FS+4f0VRMgRP0zZSMGwOJbmhtTfd586d14lo1l3DxdlzSmeYXjtA1KhGuKAqK9WjKJtSPsg45zh99pyD8YTb0ynnH/6Yyw9/wrUIE2Vw2bZpjGWTbB5jzDiFCTpjKwJS6ERnMK5ER8Ok2mE83aeqKpZXVwxDz7pf8ez0KdYZyqqmadutUicFYUGBwliHtQ6DqKOv5le8du9V8JGzk2corWh7Ufl17ZrZ6XMKBQe7uzw+P2EdBsjJ4F2KdP1AGDzXypp+taLcm3D87ttEV0AKnH36CR//3v/B4+//Ky5/8AMuP/xLrn7yY/znn3HQtbx3/ZjX96/j0DLhT0H2Xy3KZL1hSSjkucz3Tn4ic6J7kOIW0FoUChtkSMoH4q04d6Pe3ipo5RoNQ49W+iV0x+bfveDRwQssSYyC0Ah+8/m/CJEx5pdn+FXhKEqHsYbpZIwlcXF5SVIQg8KZkmSSDL3y9942xWKQcla9aCh77+XgmW22MSeMv2Ay5+4vZKu6SLpESaWFW60Shwf7fPPb32H3xmvUB6/gigmKgpPHz3n6+IT3v/1Nbt855v6XT9nfu87VquX1t+7x7OlD1ss5R4eHvP3mTVCJn3/6GavVnHVzxZ/+0b/k+eMTfvU3/hZ37r7Gct0w3dvj4vwcq2Fn95CvHp/R94G+azF5DdVKg9GURcn8YoY2msNruxAGZpdzVDFGm5qEpW16Hj14zOtvv8EXD78gDJHJZMq4rFjP51jnePsb3+Rq3ePbjuvXb1Hu3aDxmt39Q47vvsbFxYzz08cMw8B075hX773F7t51VvM1amhp2zkpBubnM6xKhLhiNb/ApR7fL5juTkEZFqsZN17Zx6eWPrYEFG0baRdrKldgClHVtCFS3Txk9/ZNhn5AtwO6DfSrnjgErDVYFKx7UteTtDDvjJGEaI3BqJK6GDGqarqcsu6MQqtIOSrEctuITb3cHdGFTtK+tWG9WlHXJcoaXFmKYicEYgiYzQBDJab1COUjTdfinBNFe24eOeskVyCJos4PAe/DNu1+o0Qz2mC1k0HWEGnXK85m5wRlCWjeevdtOgaKusJ3Ym2MQRAWRWbSpwSmGnPz7mtMbxwzPb7D7u17xLJm78ZdDm7eY1CW3ib6QtEZ8CaxHjp2zZTfeuO7HJgDqjTi2dMLLudLDvYPePjwKVfLNUdHN3h+ckaIimvXb7B/sIdvroCGbt1y+8Y9vvHudxlWgdl8Rqc8Q/J5PqsJORAtOUO9s8PFgwe8f+eY18Y7PPrkIcqU1DcPWSbY2Tvk4Ogao3HNfH7F/PRcnF5GPtfKaXZ0Yt9qDkYOl6LsjWWJLUv8IKGlIjAhOwyh7wX51IVI4Szj0uXn3JByE0eahC8QLrKWSKOSPMA0Stap0hmGoWcIkUDY2sqNEqWYrUumu/vcvvcaeiRiG6csp8/OuTid0yzWhKHL4UsivhiGSJ/vb1dYkpK9fjabMa5qXrt9i6Fp8UGwXCoM1MnTLa9oVousYoVaa/asiER8yAgZH1BKArJDDJmzmourkCSPpa7ZDNWHzF/1MTCEPMCMmQ1qZL9w2d04hEEUbpvhrhE01MaQb7TOSuaNJV92J1HjRXmPbAIe1bbZSx5Kp4yHCl4ELxsV32af2fwu+8mLgnSTM6WNODE2H6rwaS1FUWTXhQyMtyrWl2pZm8U16uU9byPuyQri4MUdFUMghbgd0mz2m00dvAlQSymHXamN+0QUs2pj4865FJtwMQUZweGkfs0/itUarZPs40kcapsALqctBkPKzi2jRQ2slKgZZQhtpamHedFwzRkURVbYCvMzD621zmrIPJhPubbPjd0QYxZjyKe/QYe8UDSb7S9tNT4H8zpXvLi+SprF3vfimszvPyQRu4TgafuOoR9o2o4YxY3WNi3DIIKMEGQAl0LMoqrMuB0G2rYRdmvbEkPA+yE3+MURu2miRx8w1lGUNVZrJqVjUlkmdcHuqGBvBybVwG4dGJUdletxNqFVAarcDgJEUQ7CphUsV1SBVRtYrwNt37NqB5brjm7oQSmKsmL/cJejwxF7U8veXk1ZO5yRzy4qwbU0Tc/sasnFxZzziwWXl2sWV2uWq55VGxh6QWCiCgo7QbuSqEQ0F0IHeW3ww8AwBOGp+iD3hU5UpSD/RqMd6vGYqh5TVzVVOSZoCS0LfUcYWmlAJkSAAYDDOcd0Z8yoLqnriqKsUM7iyiK7HcQR1vW99GbaNavVkrZtWK8blusV66ZhtVrTdR1d1+OHAa2iDHLCQIjSmF2vl6xXS9brJX7oscqBTjlvJYl7UilKV1OoCpecDH11QtkALmFLQ+EUlZVntvE9TR/oGk/0KbtQEqiewXcEwLsCu3MdXb+CntxgvHvE7uExuhyh0BQqEvpOekbkdQ2NKhzajSnKsfQP7IZpLOvQ4AdS8oQ8QHBK4wqFNtLYVlox+MAQE0PvZVijHUSF1QmlAtG3hPUc087Qi2eEp//y6fe+973/kb/y+mutpF2tVhjr2DncY3o0Epl1UYAVW0jIB5KkkjQmxedBSBFrtmlQGDRRukd8dfqMf/ODP+E/39/jYH+f3gf2dnb5e3/373N4cMC//qPf5/HDhwxRoaxGZej/4d4eNw+vodE8OZlxcHgO2rG/GymjwlVjbl7bpe1W3Fq2/HRxTq+ukZKTzTwpUrQit1cKE2XDuIoTPj2Be/Uxr7w+5vnjr7h+dMjf/Xt/m6Go+b3f+794894dbFjiisR4Os6cGC0PRtOyMx7j+56hbSTBNUWMzfgDFOhE27SkYLBB0zUtxhZMp2PqccVyJcpKsTp4mvWarmmYX8zZP7hGPSqxXUtVlDRtR583gvFkQlmXaBS7e3ucnZ/y6PQZMfUUlWXkKl45OkJhmYWG9752wM2PTjhbrgl1xWVb0ASXN99IypYS72VzsMYyaOFJJq0lodAJV4wNWymKnmhj0zHWbhk4NjdawyDqSYXCqgx+VxaikklmbujKpqryQTBRFAW2a6Vwjw397CGoEclA2y1QaY3RXlJlU2ZrpRxqokWl0EcvvMe0CRaK7Iwq3rh7zPmz+6xnM5rVJYvZQz77xc9JQ0IVlsP9KfvTPQhwcXrO3r1dTFngVKLrOsqyoizEAqiQjcuVDu9FOTr4KIXXaI9VuqK2hRSvhcNZYeJI64QtPiP4AR8jpnTYkWHo1oQ+krBYFam0QmdJuDGFYAKIRGVk0qxk+juExOAjF94z04mmcNT7e+zuTcWujuL56RnrpsEPikIXolQMid4PrE8vWM3XrBYLFDJVPT4+RmlFUTkePXrM3HeAlbTcpuXq/JxRbdHO4VMi2UQ79DKs6Ad8iFy/do3jmzeoLi+ZL68YjUfUo5EUH1rU7j4GsSsFUZ5//tWXW4A/xubCL4miI2l00gw+UBQ1ZVGyXnUQI91qRWE1zhjWMXPrYuRy1fDcBw6TYlRUwqyOcrhMJgeeRAmRSwrWJjLs7nCpFU/OOxol91WIA10IdHGjNdnEBryw8kC22WVLaK6rAWENiT0zbTeeDQJCUmtfSrhNibbv2SS0+xAktCuljCGQgJYUE2VZiFWPJIy6JKFmoetBJWwtYUWyPgnXNXpRrfo+EJqBRQy0bU/fB6rRCG00/dCTQIoJBaumpW37nDSsqArDsnS0O7tMR2OKosDZAqUiVWGZ1mNKKw34Z5cXzJ4+ZT6bE/rMjlVQjkeCQHFWVAxIGrexhuMbx/Qm0Pte1K3Z1sVL9i6Qz3CDPAC2GANjDEMInJ6c5k1c46zF+/BLwTN6oy4hN602atwccAGbg4/KhwjL9PCQtmkYFmtUjFgNylis0XIoNXKPNl3DMPTEPvHl/S8obc3uaMq1oyNReW5UzwSqskR5z3tvv8dBYbj47DPmP/8Z7Zdfsg+YFOh9ZMs3NSaH4QgyY2ga0o7naP+A84tz+igFt+o7xm7EaDRCOcvzizPwntgHLIbCFgQfaJZrhjAwqmq877cBbsKRFPtWinJdq9rQdT0///gj3rz9KvPLitu373Dr7uush44vv/qCSVbR7RrLGwe3WD77ks6qzBaORBN5Fjr+8uIZb4Up33znHr1K6L7j8rMH/Oz3fo/y5Ck3lGakLDElCqMxV5r+QhFOTrk9GrG7O+Hd3Qk/XVzyi4sLZn2LcmVWJ2dFWEYZxFyfiNAnP28bZVNKoFLGEOhsz47bQ+XLbNqNSt05SSkOeb0xRtbljXpW0rQNyWwCO17GB7ywyG2GLSo38IXn50UVk9liIQZcZnnHzLDd2F0392/Ksq6NcmmD/9igRrZhJsjBT9RLm8P/drHKz0JEfDOy35usckopcna+4MHDU3777W/z6tEuf/T7T3H1iENrWKzmzOYXoDzBL2nXlxwdHVK4ChUthRtzcnLOH//bFXXtOL59i2cPP2e6M6VrWppFx/n/S92bNVmWXfd9vz2d4c45Z83VIxoNtDGQEGkzaJFy2BRNB+3wix7scIS/CSNEW1/E4Re/WA490aZsUQTFAQABqAECaFR3VVdVTpXTHc+0Bz/sfW4WFPwA1O2o6KiqzMrMc85de63/+g/nl1TvrPnxj3/A5ZsPGI1HbDYVn7++Bl0ilEfjooRUCoQxZHnBveMHDIdTzk5PGGSG2aTk1dkt1e2CaVFw8voVL1684NXzn/HJP/o1fv8P/xnf/dP/G8yAnz17wc4w43DviNt5zWx6xOLynKAM3/rOd/ibv/k0yi1Hu7x88ZrVpmM4HPPkyQd87aMnWAJ//Vffx7cN946mNNWK3dGYybAgH2nOzs558uQxL052+PyLE5TKkCFwc3lLsI69YkTXrLmq1uDiIOslCC1RuUHlOeuqwrYtorN0XZse5CjrlkqhMoNvAsWgREjBejmnMBlSevZ2Jvz+7/8Bf/U3f4U4fcl4NMIZSaUUttkAC8ajgm986xu0MvDs8y/o6oa8VLEvy3J8ApC0MZG0sJXoxnqsjUHpLi50jMF1btufCaISQwiBrwJOOkSIPrOdddGPT0Z5iZKaZlNRDguCUpy+OceUI3IjWN3egIf5fE51u6DMi8gkVJBNxphBiagbWucIeY43BdlgwKJZUdUt/uIlax8YTCcQFLXskFKjtURow8PDBxzt7NFdVKy6NfWmxZicXz77nKYNzKa7fPnyS0bDETs7M0ajCYqMw8V7vP7iisXNFX/7F9/l18tj/uBbv4vtLP/u5AecyhbrLUGIdJ55Vh7M7ojhk3u8eHXKe23BN3Z3+MG//nPOlld88t/9N2Sy5PXlG/LZlO/84T/lZ//Pn3Hyk5+hhSDTkkwISh8BKms7lDEMxyOEkmyqii5J4fsAJiFj/UAKvI1VQ0gIMhImrO8iM5a+j4GeVisSgNor2cHTdY5Ntcb6jB5By7LIchYhIH0gWIEMGu8Ey9WKbGcEUvDoySN+8dPPWD9/jUGATQFNKt5PF2Ko0+XNLR0dxTADAk1r+dGn3yMrNA93R4jrmu62jXY8ztM5B/jtwry2jk3nGJveWzsyJDtrEW20JepU6pMkECyhrZDegs5oo+cBvouhYdDPFnHmgai+sc7RUytjnyQJIdZwfAzxiedCH8rVnzc9UJvUHknOTroWMby095MNkTiT7D369Pf+c/uwsZ6lugVvlUQKnd6L8QzWSYH49oKvtwboe1u2oGo8o7YBfM5hiUA3vZWAD9B7mieAvD9R+iWnlCp5ufZnsNqei1LGwDuh7wBgKWLv3NsA9QCn0Sqe3dyFxcYexUcbKpIVAb0lFrEfNhpruwSAarzvMx62CHa0r0g+2ltrhhCZmF2w23uM6H13EzM52TWK1J+pNMcIcWe/8LbPfW+V1CvATGYiwJvuDyJK1gMx4DCGqkV7P+d9BHWt315Lk2X0VkhC+zvv7gDGaEzy7nWJiIDzeBefp74meVJAWeu2C14foh2UCw7btQxMgQ6WTHg0Fi8cNkR7k9w0FNqiRbcFz2N7Er1zpQhxblUCiycIie0MIVi8d9jO0TWW4ARKFXhpKYcl08mY8ahkMpZkOWgtIgAfU/NIDRHOdTRdsyWdEJIthVLkmSfDo0yBMQETDLnQECKG40MVF4cCQlvgRI4LAkMkcDgv0CaQFTmj4RAtDb6L1gpmsWApAjpYXLeha2oEESNTeQx71VpF9fmgYDSOIK8wWQyu9Z5qvUHJBo+n69oIqNvIhu5cVFd5YthfZz1aR1JLnmuKzGBUXGxYZ2maJtZA7yjyAklBJgyZisv2/r0kBMgg8Q4cjlY3OFEj6DDSMxxpur2ctnbRB7cukJuG28uKtrNoZaLKioBvF7jlOWH9CKscGIkY7CCGe0yNoRhNWb0c4qSkW52BTaqx1pL5QJ4ZhsMRw/EYZQYobdhs1rBZoRuHa+OZ4gLUrcVLmdSdBoUjyxXoDCkzbNfgSMp3JVGywvhrglWwWdx5fv89r3/QTNp//sd//EcHDw8Z7Q9RA4HT0OHpiPIyCeR5ThARcpJSJyAuApQ+gW8yCJTUaKGorOfs8gpc4GB3n+lkHJmYOFy7Zloq7h0ccLh3xO7sHh999dv89m//Ho8fvIvysF4vycohOwf3sC5gm4pce7QWmDxnZ1jQWssvz665aXOcGBJkl5hyvVZCoIInNI5gxozzjH01x4Q1k1Lz0Vee8vWvf8De/QnPPvuc99/7GjobILTYpsXXdY21lsFwyLAsWC8WzOdzRAj4LjI6XdsgXEe9WrJZL2nqDa5psG30mqvqhrzfoMiYJiqJnpvL+YLhYMRoPI7pure35CYjz3OE1ORlyXgyIXjL5dkpVxdndHVFaRSurTh99TkXJy+pFkuapuP+oyeMdmdcrlp++mJDGE6ZZI6D1z/gibhmmMF6NWfTVEipqG3HYrWKRvRCRaaWjNtCUlEPEfmMm8/UcNvY6aXFezzs15tNAkN6OUw8KHxivakErGit0Upv/fJMlsetuO0IStLahjLUFGEJzRXGLsncBtksUe0Cug14j9QmHiCuw4UQpUXR2AclJff2d/jkg/dx1YJ2dUmzfsPNm1PWizWbVc18sWA+v2JxsyBYGI/HTKYzxuMRYKnWK8oiiwXfJy9V30UZgRYYI7G2pescUmZ0TcdkNGA0LLb+XaSNpJCaqq6xdYtE0jQtAUG3WLB89QWDZCWinaMQJOAHVGoYpJDIENCADYK589wEmCNYFwXs7DE6vocejmm6aEhfN13cutkAQWNbWKw2rFYb2iZKZZGws7fL06dPGI6GHBwdMhwNUUpTFANubhZJVgGaLoJxhSErNKt6wembC5abDetNFQcRAkWZxQAiH322lNF0XUcXHHXb0bkuMbVlMg43KbQggQQuLgfazZJ2uaJd12yqltuqRckooQ/eYaQkT5vtEKCqI8BphaD2ljzAPZWzKxQZYHCJjRgZIiqAIaWgHswovvYV/uTz5zxfrlgHqL2ncY4uhC07om9a+9fbQM7273uW0VvgRyKoRHBWRyZHfD+w/bz+/z4kufFW85UC+hL7T6eESiFkDGWAGPhWNUgX7li7JAZAiGEX3rroFWg9Mgi0zggS6s6xqRrWm4amjc+5MYY8z1mva9ou1oZ+m1/kBVpomrpjXVcoqRgNhijv2Nze4lYV0/QcXs9vGQwGHBwfMjvYZXawx3AyIsvzuNjxdxI/6x3LzQqlY2Pn+yYspOv3Fr8j2jykRr+/zv1wSQQxgcRGiI1g/3qb1fAfBtGYLNuC6j0ALISgCx5d5JF52LSYBMz2ksbZdIeH9x+Bl7S24/bqkq6uqG1Hva5pNhX7e3tIKZIZvqftGiSOy7Pz2GxUS07/6q/RZ2dMXUCnRUU/9LztgxpZNjKx4wPD4Yi8KLldzYGQQFyJ0hlra9GDgodHx9h1hQxQDIaMZmOUUVzdXMbUbWJAT2TX3EnnnY2BVMgINFSrDTuzKbs7B5ydvmF3dz9u7m0HHgZ5ye54SqkNN8s5S99AFlOyARahY97UaCU4PDxmtHdI2LR89id/SvbZF+xLQ25d8pb3GBPZLhmSvHUM6pbxcsOe9dwbDzmcTam7lmXb0vVvtHR9IMTlLXeD1zZoT+kEQrz1nhZ3HCTx1v2HFMKSwFSlFM7dLS3je42t0iQOwZIeA/XeJZm2TXYJJA9gtX2mA5FNUZQZk8mYtu0YjUeUZc7Zm0uKwSAyl+tNXELb5FGd/lNvB9KEgPP9Wult3+p+APOJx9UPzW+xo1wA7uxTnHO4zjMd7bHZWIbTKU/fe8jZqy/ZrK+oN3OU0qw3Lc9+/jNyEfu01abi5mbJ3u6U3/itb9OFwKvXX9BUK4SXrBZzDg/2OXv9mrPTcwiB3d0Rl+evuL2+5PjoHu9/9RvczFdR8SBisreUisFownRvn+PDx4xnh5SzGc1mw97OhOP7h9xcLxiVY3ZGimZ1xsWrL2hshZMl3/zObzOZ7XJ9ecVgVCK0ZjTZxVpFXTeU5ZAXZ2e8fnPN82ef8+b0hFcvn3P++iUPjw8YDEZMZzscH+7QtS3L+Q33D3e4f7SL98s4qPoNy+U1h0e73FydMcwNRTHgyxfPubq+omprVqsbJmXBvYfHvDw9pV7X8VlLw1vnLPnOhE2wdE2LbB20lpCS7G3TEdooiQxKkpUlT56+R14MqJuavChxKBaVZb5ec3N5CnRIo7GpxgXbUpgYevPss1/iG0emTByKeusqkfwpQ5JlJ+mySEy3uq5xLiCNQUmx9ecjDf7xfRJoWxufyeRF2fvMlnmRGO3Q1ht+93d/i3/6e/+Ek5MTApInHzxlvqkwZoRrIdh49nsfMOMxxe4OThtaohxS5wOCMLTO0bQbTKYIWmKlZ6MaFmLFRm7wOKwUWtzwVwAAIABJREFUtE2HW1TsmRFHO4cYoRFOoJWhayzlcMgXz5+DFEynI3Z3ZzHYtCyYTWe0izW35xe8OT8hdIKnT77Ch0++irCC129OY20VMcOhD2MNRlGMhqzeLKhenPPudIddIXn28xcs7IrB/R0ev/8+h/cec7J4QygNWijCYsWQgA4OfIeSIIuMbDhASM1qtaZuWoTSBCFBxmBbKSVt19F2UUXVedBSkCuBjrgiyigyE8+/PpDRpbrReworIdM5GxKIGBBa4/raGmLwq0ghhdrkOK8oypLJ3hiTa24u52xWDc7Gjy1GBYPRiKIsGIwGjGZTxtMx050ZQSjq2uO8oOk8nXWsNmtGg4LhoKCtKmzbsHIdm3pJvV7EBQKgQ2CcaQbJz7RqOyyx7vZBPVrEPlv6kGzpPUEphMlpfMAR8G0MbQpCQGI/ynQ2vh3gmloQep98n2zy+gV8vD7xveuTP3g/b5GW/y5ENqunD5/yyd4gfo61b1k7JYsxuAuovOuP1N25JHsLuJ4RKn6l39yCkm+Bof3HRBD2DvR1Ptydmemc7a3y+kWmC9zZ6si78Kr+nI3fk0Iqg1KaPCvir6KMocFaxxDVPI/EnCTrTt9i/FoxsW7bJ0fWrU4MXBlZ2P1cISQmM2iTVGn9TKWIwDaJqSvesv3pr6e483CPbWh/Vm9h6O05Gbira1ElI+761mSl1F/fPlys65LFgI+kqQj2xp9RK4UxmjzPt+xan76yUoosz1JYchZZ68aQZVlcrmlNlmcIKaMiTce/NybDKEWWmbvnJUTbGK3kFmCMzO2YtaC0ocwHTIcD9iZjDnfHHOxqDncFOyPPtKyZDWuMalEqEB2IUn+sFFoZpAhIYZHSIYTFO4+1irYL1I2jbgTrRlI3BmTBoMw53B9zeDBkZyIp80BhMvK8jCC4EPhgsW1LU1mWq4aqtrS1p20snQ0EMqRQaJ3sAUVBliu0hswoylwzLDMK49G0KN+CW+GdIGAQMt1lqUAqsrJkOI39WFEahuMBw/GIrIh2dVFJlcJ2fWScxufKU+SG3PTPp9ouLm3b0XXRLsHWNavlkuVyyfX1Lbe3S9arDev1huDiciUzGik1bdsyv11wezNnsdqwXKxYrlbUVU1dN7RNR9M6rIsEAJNp8l65mSkQMWSx9ZZ5d83C3bK2620Yo1LxuVFSo6SjlIbMakIV6JomEe5AK1CyQ7NGCE8jC6wpIB/ghUZlJUGWeKkJvqWrb2nrBVrGDaHJI8isdEE53mG2e8TO/n129o8ZTXYosxItDG0bQ6et91iXsij696iKOILSBilzMAUqz7dhoU4OQY4QMpI4ujd//fcyaf9Bg7T/y7/4X//o/nvH6IHC4qJfotF3w07ywmhdHwZDZG4ldlUQIENKjhQRrG2BxjkuL665vV4wLEomw4JgG9bza3Icx/s7fPD+B/zOf/57vP/BR4zGOzRtTdNUEByD0ZTRdI8gJG1XY7uK4CPwOcw1u5MxSuU8v2hYNIaQ3gD9tpIQadXK5IhigvI1+/qSoV6xvrngG9/6hM46/uIvv8fO7hPeff+bmGJMORwRgK6zvLm8REvN7u5ebEbToOa6LtLbbUu1XrJZLVnNb1mvVhglyUzO7v4BQiiazmGyAqWjWbaScfukpKYoSsrRIAYnVCukgCzPUlGWjMY7SCVo6g2rmyteff6MkxefU68XTIY509EQ21iWt9cxAO7+U2oHo9kOf/6TW5Zyxm7umJ3+LU/lDdo1rJbzOLopQxs817e3tG23lcU46wj9tpPo6xO3bmILFPSm7tG83SUgJBp5CyGi5CkxBG3XxTR5GSWKzlq0it46OtH9N/WG4B2dbQntBl3f4NcXGDdHtXPkZoGql4RqiWvqGGym40azT61VEP2UiN41X3//A957cJ+uWuG6ivXylizPePfdd3jw+AFIy8WbC46O7zGZTvnJTz7l5csvOTg44P69Q8ajIcboBLT6u82n0THV1nuqpmLTNPFadh07sxGjYR7lACH62Ght6NqOz37xM57/8hkKze50H9FJNuentG9OyYnNTWweHVIRZR2CLRtTiRh6EJmzmnY0Q4ynMJ7gsxznRfQX6ixdGzeT3np8B03lWK+jFHI8GTMcjXjyzrs8ePKAg4M9xqMxm/UGk+cs12sW8xVXlyucExzf2+fRkwMePX1APihYdxWmzHAy8PL1CVXTYfKMYjBgOBohpOT69oZNVRGkYL5YUrdt9KCW0XOmB4IykzaBAYK1tFWNq1tc00Db0K3X2Lbj4OiQq8UCQQzCMEoyyAtMkuyuNpvkOaoRSqFCYB/BE6k4BEzwSBkS6B0bJ+njNrnDUzx5xGpvnz/59O+Yd10Uh7zVfPdQyGAQZRld173V0LJl3r39e7hjOZCYt32zFd//AvCRHcBdEx09rMRdE5yAphA3UFufyUAM9lIBbN2iQvSC9T2rz0PXWpq6S2EE8dnQUhFcDJ3LtCTTmuA9xmgGRQyCHJZlDDisG4KLTaSSguFgwHg4xGgTbVGCp+0s6/UmhvRozcXVJV+enGEzw+jwgGxYIjINWkd1g9E4onRrMBhhu+il1EvgVKQSRKlVur/RLT8JiJTags8iMT0FkRkRko+cSCCVD73/ttjKbPth4m3gqn/1i6O+nrnedy2xGvGebr0hWBsZA1JhW8toOOLhgycgorfW4uY6ehILwd5sh0f3HpDnPQAcrTluLy+5Ojvn3sEeYrnk8+/+BcXVLRNtKBL4Gq3WkzVHGnQgBj0673GCCOALxXQ2o3OOuo0pz8EmeV46T1zdYAKMy1H0Qy8yruZXXN1esWnW22CpXp7nnU/SfLcdCoWI3nzL2zlHR/fQOuP1yy/B1bTrBav5LcvFnLapmI3GKK25atY0IX6vHugI1NZRtxacYH/nEHm95M0Pf8i+jUEsnXC0UtBJRQcxOEOIGBIUwHhPbi2DzjJVhsPdfZwIXK/mMc08yeHVW4vzt4NLogpDbhnvbCWevwrMvv3aMmdC2A5xcZFwN9j1CdhxaBXbod05f5fcHHrvRxkHx8TCdy6en0ZJdqcT6qphNBgwHA44u7gkKwoeP7wPwUbZeNfFKpAYvnf8pTg4J5fpCKi4yN41SSHT16t+SNsumRJDMy5JwDpB10mclRwfHjOdDBBa0jSB9fwM3JrbqzcIFMFKsI4nD+4lplC0N7r/YJfZ7pjb5Qqtck5evmQxv+TBw4c8fvSAy4tzvvj8M26v3zAZlXjb8OUXz3j18hWtdWgp6DZzdiZjpJRk2QClS0w5YWf3Hlk55uL8jFfPP2cwnXLv6VO8MExHY9brS4LbcHr2CoxBFTu898EnHN27x89/+ilSBJ4+fkRAgSy5XSxwwbJaryB03F6esVlc4to1m9UtwtfM57e8PrlisXL86Eef8uLFF+zsjbk4e8mTJ4/YmU64OL/g9cklg+EOJis4fvgO5WDKD3/wA25vb9jd2eP87JRmXdO2DWcXp7R1HftrYt0OAoZHu9hMIZxHNh2i89jW0lpL6BzCpRqYFixZPgQhmS8WFMWAyc4++XjC2cUJTb1AyBhcI5QhMxmDsqRuG95cXcalj4zPY103hODJinzrpRjPqPjM102zXVoIEc/KuqrxrtvW1QhwQB/Yo1RioMnEEgyQmSzBJLE/7LqG1XzN1dmC5bKNPV5Z8I//y98nhJzbq1s26xXSeZqmo9zfoZhOtsGTeVHgXdrtBUeQHpMrsvEAMS7oMvB5iCy1tDghBHzbcnN5iTaa470DZIAsXaOT01PKsmA8HrIzm5FlMdjHZBmT8YTri2suTl5xsDPk9PwVt+s1Tx69z5P776Kt4OL6DRvf4XTYSsYRAptp8tmM1es3hNdv+Hj3CNHB85evefDND5Gjgh//5Kc8v3zJ8Yfv8NWvfYKrG5avTxHJymA0HFIMCoKA9XqDbTsSnh7ntwQ0tU1DXTdpKQo+xECm3CjyzJDnBePRhOFoQDko6Zn5zkV7hF7t49+qE7HPiX8m0+IY0mI+hWI11qF1/P46b1kt17x6fkLbdJTlKBEjxgyHQwaDAZPRmPFkymxnj4ODY77y0df46sff4unTDzk4eIjJhqzWHRfnb5hNpgy1Yb2Yx8yUbsNmsdh+jwYolWKUZyA8m6bFEuMwtYxzWJZ6L1Jf6JPNDybHJZVPDL8igbtx/qGvobAFMiOwHfsMpXogsWe2xjodfLSY8r0SQkRTvrhwT+fCW0u1HjiUiem5JQEk4FcmVmwPUPY2ImyXkiloLvWhfb5A+JUz645dtz3rekZ1f06kZWPPwBXJ85bA1r/dJzKDTHOhFDGEzWQZOgG1/fJSm2hVNxiUlOUAo3VSN6nU64it579Ud2qzSCC6A5kjbp6sAyRJ1Sm3KjXRWyUkELa3K5IRoSUQiWUyAaPAFugFiKKn3lc+ed+GuMQI9GdoeiWiTUgWED0Q35/Db/dvvZdvn4OwJeIoHa+BjnVYaZlmFpnek/5X54R0n3/lfvbPDZGsoGDrgdorsMKWABE9w1WaSbSONktBCqTKMFmRrP0GTEvD3qxgf7/kYA+OxxX3pi2zQUuZNSjlksrWEO0kFIgeBA8IYVEiIKVFiFj/uy5Q1471xrFsA62LRJQi9xztDdibaQalJdeBPCvRukDKQBBRIWQ7R9sFmlZQ15audtg2UDee1qro9RsCWhXobEiR5QxKyXQs2Z1m7M8Kdsaaw4nmeNQxGSyQ0iDEBB8kUmVoPcBkI3RWbMMOldFIk1MUI7IiBm+WxSAqT1C0NtDaNi4oICnVHG1jaZ2n7TrW6w3Vpqaqa+qqoaoamsbSNo7VsmY+X7Fe1VSbhuVyHcPdUmZQWQzITIHUOUU5RqqMGJArCUES1a8Cm2zQBD71dpGRbV1D1zpsF1hWCy5vbri6WnM9r3BWMVAjMp8hjaDMFcYrjMuxbUddtzRNm+wxLVJZgq/Ad6BLfLlHXkwpCCgRQXqlFEbFc7ZezfE2WW+4NgH2Ahsk49kBeTlhNN1jMtuN9pLDCZ1PVh9tS9vW6Z6KZNflECJEux8VCVB9/Qgyo5MlrSjpdIEVmnDxl//x2R0gAwwSCECUf5BMi3vD6RgIE/1cJAmcgyTDi4Uh4aJJZqporediveAvfvgjXr8+49uffMSH732ACQathkhlGU2HjHeGjGXGxAYOdj9k/fSQq8srlusah6LtWlor2FxvqNYtIRjEbmBnpPj9j6dkWeB//94Jz+cTQr6PN4YgowGllSHKMgLcNJafLxtOljVju8NffXrO2Jwzv93wX//3v0mxM8OFGIpkbfR+LIqS6XSG94GsHKByg286XNfQ1ivenJ+wWM6RQTAoBhipmE0nDCYTrGuYLzeMprtY26KUZDVfoLSISbrDGLL0i5/9e6RtcW2DyXOGDx+ilWJVR5nU7XzO7dUlCI/JJJPJkMlsSFUt8V2HrRuaagnBszub4GsYac9/9sku//Zc4CpL3VnIFUZBUZSxUCQ2hDSa0EYZnehNhaXAE0GK4D2kkDfoZ8K0SgEQ0Xw/kxlFUcRmxAWatkHg6KRDKbNt9glsmbqQ2Dw+gAso31BQYYVAY6PHrY/yJ0KIafRCxqTREGi8o0kSK9d1kT2goyTs/sEBMsRk3WrTUNU19+8fMxoPKArFdPwtnjx+wMHhEYcH+1xevMeXL16RqXhgaq3xbUx3VdogbYfvLFJGRo9WktFgQFGOuL5dYlRgmOdoEZmc3lmCd7x8dcJPf/YZpxdnrBcbrucVg+EuEzOgurkBYvBGpvMIJklJkAZnIpu7cw4voEUghwWdlASTQTagctB2AazDSGi8xfqO5WIZARqlUMqwu3dEnhfsHewQ8GR5TjEY4oj+svPrOYvbJa9en+NDx2g44P6DI2azGXkO1q44efOa9aaCIGi8ZTabMNndZVM1EWgU0deqahqqJBHTRmOyIm1yFdZaiqJAa0XbtNSrFZvVMgKHNjY4KgD4GKYDHDw65PjRI85urqm9ognRl6ttOoKCTVtjA3gXE0GlUQhvEbZFKU8G6ABWRhmVTwxnax2Nd4iiQJYjVs6zspFt0bPMwpZUEreqVV29xZq4A2Lffr39578qyXKEIHlb/ryVVqc3Qj8w9Gw3xx0gFHwKt7CekLyKXQgIl+SF3uOEoF7XOAfjyYj1qqJpW9oyshKCS+mf1uKcoMwzgo+MbaUlRWlQyqCU2Hpq9zJvIWLYQN1UoOLX6xm+zsPVzYLRcABScXF9ibCOCUcInYIQhIhDH5HN0DQNtnPR7yxd8+A9m2qD0joyO3oQICSJeIhyxu1SqGf6yDu7CZ9qTNyCJ8BqO3DEz33bS5R0n3ppeO+lFpyPMjg8MsR6ZVIgWrWp4vWQEhccq/WKpqnJitiQjAZDqmVkzAogz0z8Wi5Kx16/eskgz3n34QP2tOTsez/EvD5lnJeUmcZ3UX7lRfJ613oLxsmezeQ90kt0EPi6o5lvuDfbR/lA2zYIa6FtUG3NummpLOwOJuxMdsAq6rpicb2IzUliWmhltuw3IaLPrxAheY3Ha2qMwrmON5dnfPj+x9xcXeBdzv0HjwHNotqwaWuEDRxlQ+7JkmW9oVaRXZBnkaV03Vp+ePIlg5/8kG+WE/KuJZMeKy2bXLL7/occvvM+4/19yiJDVh2L0zPmL79k8/IVuQuM64Cya0wb2Nk95jDL+HevX7IgEHTRny4kJCveciK47pPlSs+AQYgYkvIWI7Ufit5+xpKzdRr6ogVJJBz2AC1p4I3SSyF8GlRSIrGPDFsl45C1/RppcPc+JitrqZL3mCAzGYvbOcNM887jh1SV5fMXX3JzewukgDDZM4XVlt3k0/skhuGprfWBEQabvHEFd6Ctc0khIyEgqRuPjTbWLJcb9j/epVosqOcbnjx+l65Z0NWB5W3F5KCkLGcUZcb1ckVZ7qCk4ur1l1TzBYOdKXJnxoPf+R2WyznPPvs5l9fXHN2/x+7+Dpenr/jpj3/AcDhiU6+5vbnm8vyM46P7TIYjHjy8z2xvD11O8QK0GaBHJavFnNcvnnH++gX33n3E3v37eDng+tXn5MpydnbGsmmZHj2lI+fi9BStNWWRc/Hll7xztIfOR9x7/IivzD7iu3/2b3n66ClKdizOXqLHGcPxhHv3Djg/fcVwss/Dxw9pmwohYNl2ZDuHvLy4Yf7pCb/5nW9S5wuKowPE4BgvBK8uHc8++4x13TIZjmjXDXvjh3z8ycc8e/l3tOffQxXRU7xn+pFY1kZrgmi3vZLJDK11iMygvCBgCc7iq4bTFy+RuUEIz2p+SUBy+PARgzJDi31GowHras16taBq5hwcPeD+u+/xi09/THV1Tecs1jUoKWPuQgIA+tpJSCwpqWJwm/cUgxLnPJ2WjMbDOEi9FdLYh/gpLSkKE5mBmG0f6JxHiYBtLMEbrheaT37t1xHjK/72x/8fl6sXXJ39S96cRsuWYZkhbBzIhrszZKbwtcX7jq6Ng19WBEAjhEHmCkYauVMgjSFIsL6lsi3CWgwKJXNet47N8+8jjOQb9z5idb5C55LHj+5TNzVlUUbgwYPUMQ/g9ctT8p1DHn/0Cc9++G9o2yWvfvoD/qz2fOcf/1f8wTd/F0Pg//q7/5dbUWFVyn1wgVXwmN0Re7/xMSe33+Po8pp3JzPenKz58f/2rzj6nW+zmOZ0Q8eL2zN8ecT4177OwfEBr/7sz5lJhSb+vE3dgk0LSGKP04cHdd5ta1T8Fcgk6GjpTGYMeZbTqw2EEIxGo2QhFGMORQJ0vHW4ziY//8g89c6hQ1QJ+eRtK1BkJo98fAX1puXk+Xkyxo2et5LIpowAqY6ImLeJ+68RTlGvLYGGohxw7/4jDo4fIqXh9uYa29aUmWJRb7i9ukDLng0bAaouBJadoxOCLAHW1gYyEcErKSWtsxHcExIZRFRWbSoo1jCMoa4uy5A2Wg34EJDKUHft9ixxyXNV9QomI2K4VKrrb58hfZiVT79EWiJ33vXWrinEqgeNSfXbvdVLpoV/Ulb1yqC3iQJbix5I3unJEz/50mqpt+Bi36/azm29Yfs+oz/z+uVM8DZ9bwEjMwIeJXsPXPGrwK/UkeGpE+ErsYmVkuRpcayURqQeN4LQ/VntEcmzvb8WiMgu7ZVz22BTmRQr/u7njpch/ly9VVcPlutElgJJ13qCT17bpDk3zaYhEAPEgsf5LtlWhJTBI7b/5ttz7B1zNqoPZAJYe5uDO/WojoF9MtA2MXxKpdCzt+0m+hyT4NzWLhAfYpgziU2tTGK+xl727eDQzjuET0GmMjGpvb/reUIMCI6XQyC0wOgCXRY4H0HlcZGxOzTcmzqOxyv2i5aplgy1Y5AHMm3RgjgTCAHCJMAwLun6HiPacXi0UOgMjA4RxJUFJmsxt5ZrFYMliyKGg+EsRgbK3CSbA4cIHcJbJAGlDSY36EKRFS1SW4TydMFyu2npOtAisLubsZ85hiInVxk7Q8V4rCiMBjRaBETw1E3gUVVyu/GcXze8Wbe01uOqhs4b1nZDqzQqN6ByMlUQiI3xcDhE5Tm6mDEc37BeXqc6ExcNPgTWm4pN11GUMbDNhwAp90JpjdFye9ZmRtM0kbjineP66pLVcs5oPGa2u8t0tsfedJfReIrSKiqK0wzdtXFZ6rqG4BzNpgEvqDYdbddh7RqFIdiM66rhZt5ys6qZb+ZIJbnaqdnf22F0XJIJzVhZ9K7A33e4Doxas6obgrAoJQjC4pol+eol2XKPkE9wo6MYRlpKQpgi7EOmdUO9nLO+ekHoljjfUW9qvF+RD9Z0VY23HtsFTF6SjQbM9Jj7IqMoh1yheXN1Ep/bLlp4IFTKwhFIEQmDwUmkNHRBEj3ELQjXU/H/3tc/aCbtP/8Xf/xHg6czvFJbtmTPHOsliqEv2kEm1iyIEA9TiH60/VYQYhJ5imLBW4FbbfBtx6N3vsKDxx/hVUlro6FzkBqBQ4vAoCwYjoccHd3j/sPH7B8esDOdMhwPGQxGKCGpN2usaygzwSSXHO9kjEYFJxdLbiuJlzoViQhqxHHD081f4pefs7c75eHDdzk/O+PZz7/gwYN3+Phbv4Yqc4QSGC1pmxofHMYYdAoPIslSSAW3baNkvtqskUjKvETqeBB23iJklAsUxTCyY4XGmIw8z2i7ls5GbyPvOqr5DdK1OBdl6G3bYooBo8mE01cvOD95TddUeNuQZYKr63Nuby5Z3V7TVmt817KpGjrv+OmnP2G+duw8eZfPLjoUjp3Xf8uHecUol+A7Whd9xoIU3Cxvabpuy3LsN6Fp0bs1chciQVVCoLXB+SjX6CEtpRSj0QiZglCcjyw7QTS+yrLkxZkO4shGjA2/s47MxLR76yw2xG2k6tF/nw7tEFC+bwaiV2sXPF54ZrMp02LELB9xb7rDx++/j7UNy9WS9XzJ8dE+x0f7FEbHQC4f2N/fYXdnggiW/d0JTx9FJkw0rE9HcTp9hWfLrivLAqMzyrJECMnl5RumkyHjUQlYgo8p6+enp/zpv/43fPHyjMZ6gjRYH5iOhrhqw+L0Fcp3BB+9gaPnZCAESRMEKw8rIekGQ+xwhC2HdFlJMDnJEjjaGQBt27JuaprOMRiO2N074MmTJxwfH3P/4QOsbZjOJigpub2dc3l+xRfPnnPy+oTVaklRFjx49Ih333nC0dEMqTzXNxdcXV3QNDUudNHjpygBgW06uj4ERMeExrbrQEi0MpSDIaPxmHJQxga+c9TrDVIIuqZhs1xTrWNhxlq0CGgERsZGomk7Bjsjvvmb32ZVrXn95Sl15+lcSmf3EEJH55OcJUiMNBRSstN2fCjgiYIRIfrQyig3BBJTLBqOhyynfOddnofAn3/2i+hFtkVM+/sfX38fMHvHRBBv/b4HdeKzQ9qoi+QxpXRcAmRGRf+cQJKipX9TyiT9yujqBmyH7Cx0DuHiL+kCXd2yXtbUdZRNNU1LVcWE37Ioog+Xit+Hd2Fr9dvvWaqmxSZ/q2gdEpciVVWzXm/wLjYMgshSyLPIfNIqmsfLpLKAZODeddSut9LQ5KPhtmZYa1FKURYltuvwzpOZPC5YrMOn4Amk3MqBem+9HnANIdB2XRpC75rRnokYQqw7d+FI0Y/LpwFBhGRP4XtPz+hdFvwd2wXYDjg9ezSGcycWA9DVVRoiVFoiOY4OjpmOZyAERmnqugLpKbOSyWgSgzKFoF5XrNcr9mYT9rOMs+9/H/3qhLGP46UgAe7eJiVD2MpkQSamtWZYjBjmQ4wwaC/QCAZ5SalzcpOlZRbkUiNDZKoT3DYora43tE2NwJNlBq1UYoKExNToGSW9dDMOSZmOfl6rxZzd/QMOju7z6uUrvA/U1lOMxgynU7z1MXgDuFksWHYNVoXEhIEWqLuOxe0VM9uw19ZktqHRkuN/9Gv8p//j/8S97/wGYjJjMd9QzdfkSDIEi8trshDtSqQLKOvIWsvDvT3K3V0u5itqG8+3ENyWWSbT8JQq+lu+sDLZD8i7gQeRJIvxfdsPrHcsntQrpaVAL7PsP6+vCdZ2NE2F83brNSvo2fRyy3/tlyGZVoyKEhWgLAZMZrssN2uqqmI5n7O8nbMz2+O9996hqioWi0VU6QSB61w8P61PCcEJzN9aY7it755JAVOjckAIMXghFR+sl1irsFbhfQxIHQ9Kvv3Jx+ztTDg9fc0Xn7/g5NUpl2eXmCxj//CAX//OtwDB7WLDvQfvQPDkJlCtFkiR8+rVGR98+BhpFFeXl9GH+viYTAsWt9fUdU1AcXh4xIP7xwhX8+r5Fzx/9gXL1Tym+Zosyj3NABR88ezv+OWn3+f1l884fXNL2ynq1YLN8hLbVvz433/KzXKDU4a6qhkUQ/YPjjk+2GV++Yrv/+V3uTh7w4sXz3lzccbnv/gZ9/enHOyM8d5yO5+zqWpIYSDGlBR5wcnLn1MONKPxCC/qHpg3AAAgAElEQVQU7330dYIZQzHkbGlppeGnv/g5Xz7/glevT6jqNUWhyRTUVY0QGe999ZssbxecnnzBcDrgerlAaIOUitZ2+FGBz7MYGrtpoLGxZ0ZEYCwxlfAQGkuom8ScstGjr23YNA2j6YyyHECsLnjX0XY1k9kB070DuqYl2JbgA13dkJkMYzTOOrq23YJR0Kd/34Xo1XVNU7fJk/ZOzaC0phwO2HqcSrmV5KoEtiihUlhprHydhf/iv/0f+MN/9j9Tjnf5wV9/F+M61jcLQtcyKjO0EnRti1WS8mhK0IL57S1dHa2oTGnIyhwnAj5TqP0JO08eIYfDKHd3cSxwIQa6uq5FCEWQCic9l2+u8Nbx7uOH7IzGaAT7+3sEQEtNZjKUlrw5P6etGophifeWy7MzNqsb5teXDIc5+0eHHB0+4unhI+gcF1cXVL4CFRmD1jka79GzMWVRcPPsJabqmJqCq/NzLi4uKZ4eIKYZTVfx+N5jsvGUVsJoNqG1LYurK2xdb5dHUihCYipb62KPn9izhGhf4UWsU8MsI1NJGbZdtvrE+GrZbDZkWYaQagsKyrcsmoSIAcIBYqCrNphiSFGO0HlBVgzIiwE6i4FI1gakMGipQRp61D8kIgXbQMVYq8uiQElF5zrW6zWr9Zq6bqKnbJaze3TIcDZl9/iI1gfWqznr5YK6c2n2jM/hQEXWsArxWuiU7SCTZ73zfa2XqCRJN1m+nYeDUoiUISBTP9dZu2XskkhM/WK/Z7aTwLG7XjD2F1LGoNk+PKwH8e5Yqz2r9Q5YFDJZ2ujeRkdsZych7hb/IrFVe6ZoD/6oxFTt7RXSCbZdoPjU8/oQtvYEoV/e0Xvx3i20tY6Wh7Gv7RUkKXU+fb0sy7bhWr1lQWYMRt/Jw6EHUROLtGfRqt53MlrwqcSSk9trk/rl1JzGvqxXGSVrhN6qJYGTUkVAV/cM3bfsopxzMaulb4z7++QdzndY20KwONel/ILUx6RvISonw52NSzr/AyIqVNN9jPYGfuvD2n+8T0oykZZZ8X7G0LWu66iqirppaNo2qXKihYyzvS1G/Bnquo6kjK7F9oFgzsaFbIhqsM5GoK73Iw6kxUBIdUKqyMBXOTormQ1y7u9qnuzBw93A8SQwzhx5FsgKiRQeiUUrm+p6hsLQc4yDSItqEb+GFBIhA0pDlhvGw5LD/TH3j/Y4Phyzv5Oxv1cwKiVF5ilLRVFGHCb+myl4N4D1kraVrKvIqLVO0npBZeF6UVOtwXkFSiCUQxkYZiWjUjMcBCZDxTBXaOVQJpCbjPHAsDcN3N+THB9NubefcbgbmJYbhH3DZv6aNxdnXFxcc/3mitubc+a3V2zW66TmlAzLgtlkRDkcILXEeRtnK+fxztNaS9NZutSnRX92nRQngsxoijwjL3II8Rnw3uG62L8prShGBdpEFrk2imJYsrOzw2Q6YzqbMhoNGQ3LWMOT8j14Qdd0zBe3LFZrVquK89NLrs6u2dzW2Lmnu/Eszmuuzzasb1vcShA2EjqJbTtc52OGiJEUA0OWGbIyI8sNUlhEsLRygNUTyjKjyCJpTktNphRFJmnrFU2zBOkRTkTVSpFTjvfIBjOyYkBRlihTok2BMhlSCowN2LaKoZgi4EUEY4XMUDLOjFFBqbBOYjG4kCFkTlkOKJShPv+PkUkrRGwMYyRh0kekVMXETuoZtci0AgwOmYKQAhJCksbjI6sLSfAaI0bMxoavPXrER+98hcnOLrP7jxkcPGKzuKJa3nB9s+D2+orxIMMUJabMKMsJQRm0luxNR+xNh4Tgca1lvbjh7PUveXPecXSsmOSO37o3pPtPBvwfP1rxotY4L5A6MCkds/3IrrtZeHZdycP7+3TzN/zdsy/Yy3K+8vVvY7IBSsaAmbpqUiG+k/mklRbr5ZoQHKPBAJ0NePL0fer6GIOgWq9ZLBfMl3PGxI3UcDymaS1KB/KBIXjHer3A2RjGVq1bCqPJM8Xt8pa6bpBSUQ6nPHyyh20ars9OuH94iPQtF5sFzz77GXWzYpCXjIpBBDPahsmBoaqW/OSH32N0tKbIvsqunvBycYXoHBQyJiI6S9vWeB/DidqmRogEvhqTQJzI5DMmI8tMvP8SmraJg6CPxvg9gAuCpmm5ubmhHAxiyFiIRv7IuH103hFIkmap0FlG13YpHOgtI3ARAxGi3NJGGw0po7dXAjJCZ3EiIA3Q1pRlzkE+5jCbMvCavdmUwkluug11s2Y0yLh3eEBZFFGKkllc19F2Leu5oygHOCni1kvaCKhnGVJEEFQrcDKmXFsCUkdWqFEFm2qJcx2TyQgpo/zQS3DBsrszYTwecn67RqjojaWCJ9eC1WaOVBGoalygw+M8WOtZqdgICGPQ5QCXZZGB4SWdE1uGbdt2dF00fx8MC+4fHrBaV3zl46/Qdi0H+/tsNhuMiYz0m5trzs8uWK9qBvmQo/37HBzOKAYKH1qW8wUnJ5c422xlQ4Myi72QVZhBhkh+jHXbYlNCvXex0RyUI/I8NnkubWgjcLihWlQ451jMlzHxGRjmBVaAsJZMaZqmY9PFBMtWwCcffchwOkbPF6Al9aoCk0fPXiUIvvcHiyEq3nfouuG+9zzWil0JWYAmLRxCktEjEvAnICtLVDlkMb9NDfvbwOwdqNvbqPSN9NuA7a96m25hF/o0W5Bx2BEShE/ASZIkkUBdYmBTD0Ye7O/jOs8vTt8gXEdhdARNZTRbl1LQtZZNbXGkxGYZpad5kYMI0a7Deaq6iYO9TkwXIbDOYwOYxHKwLoaLNXX0zuxN7/tm2FtPXcW040a3DMoSJWMQWfQc7KibBowgNwXCB9bLJWpQoE2U2AUX6Jo2st69i2zzEK1leraBQhL6IAoXgdC+d/Y+Woj8imeY6CXocSkoEXSJMejTx4YtkfLOZzv4gDZR1u+DT1Y26lfuo0xLokBAGRU9gLUmKwrseg0ufh3rOparWw7tfbrO0bn4XF2fXiCdpjuwZLmmB4WPZjOOioLLn/wUd3JB3nTRizKB0NFWxaCDTg25TxYHASEVg3JALktMSqoOKeDRbWoG5ZBMKTqZ0dQtw2KIEDKxwD3Xixv2D+8xzsZUzRopofIVVbOma9sI6guVAGiBJNZgZeKAI4KndRLnLM8+/yXf+OZvsL+3z9XFGaYcUgxLpASpJJNiwtenY66bissvf55CI+KZobXDe8mbesMXb845NkVkZOzOePAbv0k32eXy5IIf/J//ksVP/o6ybSnxKDwZghaxlVdm3hPWG7Jz+PXHj9EfTvhXn/6Ipe6SRVOfkB1S4J4nJF1wPzwL4qDTA66R3dpLPf32Pf4fLmpUWmQ751LQSbQ4gCSdVCoxV/pQkvhsbSWthP+fuvdqjjRL7zt/x70mHTKRcOWrumrajDecEY1EiqTMShsrRUih/Ty8kNZ8iL3eq90LabWWK4mxFLkkZzS2u6enXVWXAQpAAUj7umP24pxMoEfceykjEIWuBirzffPkOc/zf/4meT/Gddwkn7JMKpqmwbvAoF8yu4QgNYtVzbNnz8BbCi23+1KwYcu8kRJivua1H7wQAZlksUpphsMB1XodGcPOp4ZS4qzABghBbocUUgreXL7mlx/9nCcPH3F8coq3nrLIt6yfDz76hFnVMB4NmV3NmEyXEUgZ9vj0Vx8jURxMx/zoRz9DICh1H4vFKMlkvM/v/+Hf5/j1c6p1Rb/ssZjNePr0kxgCGCTnl684OX3Jt79b8eTJu2jg/PwLfvnBT3n5xSdU6wXzZ5/w4Y/+nH/yT/8Jzmo+/+wjLi6ukEWP16+P0SrHe8Vgss8w6zEd73I2GtDUC06fv+Hzj36M1gLJOzx8cIfBoETnGR9//BmL2QUER1NVvDl9Tdcuefnqcx49fIvq6oqzL55z7/Hb/Ns//imT/SN6hQa7ZtCXfPHsKUe3j9jZmxDaAoHg9HJJ09ZILennJaO9MSeXFzTWYQpDV1u0i2dbGzwmeISPDHuRWEooiY9myJEdbi1u1aCGJcoYyl6GbxaEZk7bGa7mCzrbYm2DJNA2FcurGSEEBpMxg/EOy/MLZheXtF0XBz0qAh9KGyweoWMTb5uW0MXG3FoHMnqGaiWhI3r4hyyGoKUhiBIS33VoNh7nyb3WxyF9cC1KK/7N//NX/Lv/63/Duzo2fiJgdJQ6267DecdgMkRnki5YBNDWDTrTjPpjhIl74vBgytHb72KGE+arNcLW+C42+YGodNIiKjts8HQEGhN4//hTyiLjNx5+ncGkz3KxRmmFk4G2s8zOLslMTlb2+LM/+WMO96bcf/wdTo5fcOvOXYyouDr5jIvxIZUT/OHX/zZSaf7VR3/MGypE5tAKOhdYyEDx+Ij6Ow/41Q8/4RE9HpUDPnlxxfn/+kPGf/A1sls7vDx+Tj+bsrM7Ye9on3o64fPLS8zFAu2vW7fOudSokth8mpilEBDIFMaoyPMcb5toXSEhkwJsYhW2HcvFGu8cedGjcy7hYSn4SPiYQyI1wcV09k5rip2o0LIhIJRCk2T8LgJ91vlI4hDJlkylftJdByxG5mDHarVArFZ4aUBITF6gsyKSJTrL66rCmDgkee/JOxyMBhRC8PNffcKq7fBAFeBsWZOP+kwHPcxqSeNAq+uASWsjcOKVw2Q5GhB1RaY1XqkotU1WWdKo6H2sRLRlin4eUUEhAsHaa4ajlOACSW6aYOM07JAinRGB4ONQPZ4z7ks15U15e0jD7Og1GwGrCAhes2ZDiD64W+AyAaSbIbVP3rvO2wTQRb9WpXSqr8KWpbqpEzdK2oidXyuSNsCxuDFoVAkUlirmjmxet96Cr2pb68ZhZ9y3NgPhCEJHUC9act1g88pUt3EjOCxcn8MbhS8b7FawPfOv1SIxtNBvhvRCEHQMG+989JUVm1rBReB0A2iGBL76BDZuw99CIIRrwBViPQseIXW0zAjgkypt0+ZaF+icT2GeUQETWZP+ujkh9nattXTO4sImoFRs7SFi8JoBkfI/nMN6G+XtzkZwW0q0zlKN4ei6lrautzdJJBuWGB4Yz3/nPCqT5JmmNJ4iE+SZocg1Zd6R5bFld0LQEZDeoUWLoN4OEkK4tl8gxJBUTyAEHcMihcdkHcpIhO7Y3dV0XQQmbQoUlFJGWztpCc7jgyRIhUzvvQtxeCjRSJkjVUDSooPEJQufEDTBGrARlEcSAU4jIbiIWwUSbgXONmS6407WIEaxppNSsu4CF/M+n54YPjsreHMVs3gWyzn1ckGeZcnCo2S0M8JkJdoEOgvWVvjW4W1LFzxBRmVjtAuSNEXLYGdAr1fSKzOMMvgQ82m8t6xsR+cDxgtWqxVmdkHdNixnS/Kyx3hvF6UMvTJieVlP05nYD1rnaZqGrm1xztI5T+NbrKuwrsa3jm7VoqXCqIzgAtoKuktL1dY0ooo2GF1HJqFfZlgRqH1DkAJkZCSHINHKYtwc0V5hbEaesETf71O5CVo8xLdLgl9S11ewblmvVpAvWa4WlFVF0dr4juoMEaAcjrFdi6gtdbWGAMt6Qetj3SFDCoZO/ZjWaZBlcpTI0MWA0c4Uowuu+Osf/0kzaf/5f//f/NH44X6ccKTGBK7ZJCLEzdB7Ep0dEEm2gcCmjQriB8j7gsCUfvaYH3z17/Ottx7y5P4Bea6YLVYIU9If76PKAb3xLlVV8cH7P2Q5P2Exu6Cuai4ulxyfnOG6DqxDh7i4pQj0exn9QUldrVnOrigyxShTPNgf0O8bTi9nzJuKWwclv/2NHu8eae701tiT99kV55jmkp//v/+e5vwN//gf/EP+3t//L2hs9ABbrRe0VRU3OM+2oYFohK+0ZjTcwZiC0XBMXvbi4ZMOiqIsmexOCS5weTmjPxgilWK1XNHUa6ytOT09YXZ5wa3DQ9p1xYc/+wlvTl8w6BnWyzmhC0x2Dzm8fYf/8KMf4uqGb371PX7+479gdn4SU+mVREmD0jleCGoXuFpVzFYNdWuRClZthuwd8ezpxwy/+FO+OpbkRlCtZ9GA2UNrHW9mM6wHhKJX9mOwVdtt0zK7NoZ1CCkimJLM2o0x9Ps9ijxPIEgsKrIsw7r0c0olL5R4jGttUqNokInJ07kISngffVw6b9EiDgjwqYDyjkA0jpYqBhxooF4u8E3HNBtzZMbcLsaMRYbyAT0saGmYjPrce3CHctCPacImTnml1jgXmE73GQyGcUNIBu+xOU+T2eT71Pk4wcoyAyoCXlIKnn7+CUrA0f40Mn0l1PUC7x3j8QhjDCenbwgBRr2Sr7/zhMf373Ly4hmm6+ibjEVV0waBBbzKWEsDeU4wOSLL8FLSWs9q3bKsGhbrKjZzZY/b9+8zne7x+PFbHB0ccnk1Yzye8ObNBd47rq4uOTs7Y7WsaZqGye6It956wJ17hzGgpqt5c/ma+fwC7y0mmfb3Bj16ZUmW6SRhrKmbhqqJPnohePr96Nu7md5LKZFaUjUVs9mM5WyGXa3plktoW4wgfQl6meHxvbsUWrOcz6nrlsvLOeuqpgPuPX6EygzL1ZI8z3n58hjnk0xdhHhoCMBHCTvCMwG+rjXf1zl3A/REZIAiFQ623kyEWGAGJRGjAflbb/HhbMZPnz29AdT+/4OyNx//8d/fZNZ+mR0hZWTZKa2iT2yIQXvyxu8oKbGd5ez0nJPjE2zTpRA5hdH5do9e1y3LtsP6+LxGSUb9PkWmkSom8XoEq6qh6+K0Pfopx+K+sy5OcpN1QpRjJdmbEBiTArZuNAlN21I1Heu6pbWWqqmjBYaIe8ZyGQ9Qk+Xk/QGLuokewTIGR/ngcV27DcOIwPF1iOAmmOY6kX7DYJVbNuO1B9l1EEP884YccHvP5bZwJkSA1CSgagPMbUCmDbN28+992WN4EwIiUUQ/O5cass1zGpNzeHgH7wLVKkqh18slShp2p1P6idkcvGOiFJfv/4L22VOGtiMjJHuHVCyLCNgbZRBIlMkYDqcYHQuoQT5AC42IunRi8Q0g0dLQ6/XJ85w8L2JIY/As1ktkZrh9/yFf/ca3qZY1ovPJX9jTutgIdLaNjXxRYvKctukig9YYJPG6421zrNcVSkoe3n/EelUx7Md99PjkFavVgqaOPth5bpivl8ybiqAUoBLD1eGEh84yEZoBiuGtQx7+4G+wahw/+V/+D+b//s+4HeBw0GNQZBR5ZOggNYjIxlMEpHNo5wlNx+F0j/7BhM9PXtI5tv5osGHgXIeFbdZL2HzuUyLxht2UiOD/0eNmWMvNgcF1CFd8RH/YFPCX2EgqnYuIJGdNP+t8BEwnO0PK3NA2FcNBj/FgwGI2S6stfn7Pzk45PTuNDdZmLZPkkmKzz8S92RhDWRaJ/QgQWDcVy/WK1Xod/cyFpnUS6+JaUiKgZSDTYEwAW3M0nfJ7f+v3ePToMedvzlFS0rYdv/zoY/aODvhbv/d7/OynP+X18St6oyFf+dp7HL8+4+z0BCla9naHvHrxnAzFaJiTF4oXL76gWVdMJofsHeyRZxrbrtkd9Xj7na8w2tlhsZhRV2vOXp/wxbNPyTIYjfq8//OfcPzyKbatEnulT5HnfOWr3yTrj/jpT3/CdHeXhw8e4dsueckVDPtj3rx8zqcf/JhMWPLcUJSGyXSX0WjIoN9jdnWJkpK8yJnu7fKVR3d59yv3qasls9kFe9M93nryBCXgu197m4Oh4dnnv2J2ccKbs1coEXj7yRMmkzEYyeHRIYMiY9wfUJYDimLA6cUlDx7c4qMPf4a3nkVdUTtL1iuZLZcUwwFBK2zXotoO6T2etO7S4CD4OPwKTRdDxboYEqlNDI9q1gtss0aIQN1UtNUaOkdXt7iuJXhL17UoZRBFhskL6qbDOo/3gtZZBqMddg+OQBcMdg84vH0f21qqDYszRNZXHAwmCXsCV1Smorw3nX2BqBSrqhopJEYbhJLoLENKxY9/8uf88oM/p1kd0y/i57VrW4rN8NdZhBaU4z5mkCfAELqmpRj16e306BTs3L3Pu9//m4x37yBcAU4jvQKvCB1IK8jpkYmS4IgDUi9RJscpwYvTY6quY7o3ZaAzpPMEJZktl0gn6PWHHJ+cUF1ecfbqjMn+LR4/ecLi8pRCWWaXb/j5T9+nrTyT0R7v3n+HLEiennxB59dIFSIjTwjaTCNv7bNwLfOTU3aUoRSK5cWC8+cnDCa7vPON7/L22+8RhOOjTz9i1TYcHB1hl2va5RJDDJYNiMijQUW1o4jp586D99GGbjzqozXYtiHg4uDde7rORhDcxbqgbpo0tBMRPCLmSBilIQis9wijKUdDBuMxeS+qrFxSL4RNiE4gDfqiz69QSVmnRLRREyExHRVaZ0hlCCl8zHYWb2OgaXBxsOuSJCh4GzNBVgv6vZI7t48Y9nusFkvapsEHaJJceDLokSlBa7v4vIK0xuOXFhJJwAiBxKFl9K51HhSR3Wa0osjjAGTj/S82/ochJFuJ2O+EEKJVyeYcuVFTsrXOSSeO+PKZ8es1DGzODLEN2b1ZL27qoug367e9CwhC8iWUItY80UIuAoNKq/Q5jedQDCIjAbIJYEvnVkg1yabO3wSB+XDNqFVKIZKvNTE6GWMUxmTR2iBdz+bsTOXXNcM3EUOuB6ckq0U2rwSRWLciMXelVmijESoxhjfZNElGHrb34Pq+bmrCyDSNIa6dbeOaSiCmcx11vabrWqxtCT4yUzvb4oLHuWQllAhNzsZ16ZyladsYEKriNUZbo00eQrzDsd/tku+zT0oedT3MveGnq7fDVbX1FRZCkGXZdm3c/MqyLCnxbtbJ1/2ISfZWeZbHOrEs0hAsgqjxeSOwvttXHA0Ek55nWGr6eUaRK6CNPqQB8JHBaJ2kcypWOykkTIiwDZ6MYVyagLl+PTLaRgnvUIDWAp1sWIpck5ssStlDh6BJ+FO0Vuk6Sd061nVN1bSsU4jY1WzBbB5BPFMYsjwj15pBWTAa9BgONP2epMhAypgBo6RJ55PHuZYQOgQOhEPSIUONoCMLgcLkFP0+MuuBMAQXqNZzcC1KxHuc5X2y/hhlhgiVE6SK4LCWtHVDu1rTLtbUdUPdtGmPS32a1HHIIwJSQZZrijLiXmWRYfKY6WKyHIVGm4wsLzAq5t+slkuWyxhC1jQNzjqq9Zrz8wvevLnk5OR1DBtbLGjWVVSndy0Ej04M8V5Z0C/6ZLlBZwqhBTJTBB9DumsbaGygdgHrFd7LtJdGDMGYZAEqsqi8NEAKpiwzgxYeb1tyHclHnbOYsqTsD+kPJuRFH6F19Ns1GUiNdzH/yrkYtgYKIzUeERnmCITOUaogzyMwO909ZHfngP1JVOV/+vN/+Z8hk5Y4fU2oXJxyCRk/aBtFRxBokRrBG4dLBHAF0gaCy+nkFKfvIMdfpz/5Cg9+49s86Z3w5osf0dkzjO549fQDCJK9Ow8JGup6yfGrF5z7FXk24uC2YbQ35fjklM8+PeNwf8D+JGdYaoa9gv5gQF4MuHW/z/HzTzm/eMN0qhmWgT94a5edbMCffjgjn7Tc72doqTg/O6NYv4L6Dc+efszlyy/47sOv8Ie/+/uIFNYgfNxMTJbR6/WjdKBpY6iW90itKMoeWV4wny0wJqfXL+m8pKlbpFD0+iVZUdDULcPRgLatQXY0dY0PBcOdPfYPb/HZp5+yrlvG013uPnjA6+OALMDL6A1pjMT7Futa9g8O+NUnv2K+mDG/uuTW/pTecMDzF6/Iyz77d+4yX1V8/OlTMqH5W3/wB2T9Ec/mfdazN+xoS7/Q0U8oyK3heGZ0Yo/KZCYeWK/XSCG3wUjab+RtkrZzWxZbnueQ0jVb29A17WZJREmGjeyGjfeTJoYtWOcw0tAl6bPRBp1+V4mAFZJORCadJJCZjKppcEg6kULqiMe/7droUaYzxrrHgJzQeHSvZN3FDeno0R4PHt5GZbEB3gIvIiaf7+0fYky+LYRs16YD24IUZFkExZx35CJEGamzFFlG0e9RLVdI4dmb7iJ9PLSt7/BdLBCd7Xhw7w7/6L/cZbao6fVKdgd9ussrsvmSLIDUGl30aG1scDyStunABhQWWwWU0qyrLoLpJqM/GbJ/65CD/X2G/SEnr47RRmJd9Pl8+tkJby5e8/rkNVJ6ptMJX/nKWxSloWmWrKsrjl9f4rwgywzGRDPyIi/xBJo2ArKx+fc0KYxIG43SkTmWGY3WEuegbZpYTIcANTRth61qRNugvaUggBFIEdm1XdOwWs54aVtAMrua07TRB9rkObce3ef+40f86Ic/ZHdvh29++xvRsF04yl4f52MhVORRpof3DLzn67nhO0XBA+spg8AqSevT5i1ESlYXWzYlUtFqiS0Na9tuAbubAK28UVBv/nsDKm4Bnhssuw1bYMOMuwZrUyprpuP3WkXGuAtbBqeUEt855lfzmNJMINeGzEiM1ulz56mamqaLIKFRcW8eD/v08oIgYgLyct2gM0NZxIC2um7S9D8yMqVSlCaLMngiywYiy1goGROiUxW98aZ2kAKBJKt1jZZQ5FlMEA2K/b1dbGdj0ndZIGzHJhTGb1mLkZnliYXgrzcx3l+/B0qpJNf0bJNnbzQhNz3YIsuD9HWNqkXrG9gcZjZZKCgZfX43AySR/E3kjfWxAael2vh5RtaVLgpkVtEmUDoEx+XskmW1IjM9lNbYquXhg8cxUTfLqOoK27bkAS4++5zm2TPGguiXlzZPlaTMUkZ5kJIaRRxo6aAwStErNHmIEkFH2LJeNsCzc45+v0/nHe1yycXFJfN6AQJyAtVyydnxCc1yRWkKgnNQ7qRQFFg1UdronEPLOBDDuziIlB5kTNt2tIhgeX38gqO9Q6b7+5y/Pufh22/jM8F6vaJeVVTVioGSvLW7y1U959TVdNEMEY3Des+F8DxrWvZNTr9rcLZlNj/l9JOPOBCWQhc0bQNKkKz47hkAACAASURBVOcF0miEDzjbxcEdAXSU0eXVivDsOd9/7y1W73yNf/3++wRknA6JTUO5+cz6yGBxMewF75MPnUxMogjQE77s+felP5VMU3xxPVxIjWAMt0hhSqmx3khqN+t2895feypHBYk2faxt6bqG0d6UQmu8dbQhsm9MpumLPt6HbXNtfVRjxLUc/cg3sscQPE0T03+VVNjkOS+iuyjWB5yPww4tA0r4LZAUggUJxycn9HoD9o/ucHx+wfNnz3h46w7L1ZL15RlPP/gJzfyKu3cfILXh/Z/+govTE2aXX/C6XrL3N3+HR/emXFysCJT4ILl9+yH3bj1K0s2WvJhQVR2jgeTo1gHf/Na3+MH3v8tHH37Iy5cvefr8Of/uT/6Y2eWK6d4e++MdvO/TKzOapuHizRk/+8X7/KN/+k/Z27/F+ctPmL95TW5yRjsTsv6AUX/Ax89+AXgODg6RSnJxNePszQVaG1arluX8BaevTvn+b/4Gt7/6LtK3OFeBe8Te7hSlB9x++IjXp8fMVldMxyVvTp7ivUTrHsNeTgiC1xdL9m+/xfzNMZ9/+GMGWSQAVI3g1qN3+c43v8Pxi0/5N3/yv+Mai3XxHLJdR1c3aCXIG4uy0T/QB4/3samNfo4xJT4gwUbWYuhavKxobQxsWdiWoojWW0jITYEyBhccrmsigKAzvA+YrODWvQc0TYMUsFjOKXeGzOqK/mCMyvqIrEfWH2HWa0JXo9AxyC7Vi9oYAlFeG4LAuZQgrjXDnTFKreL+VXcRvPFRQi6Fpp9JfDeLtbbpY9tAlpKx4wAigTd1i1utET2NLjXjowlSCNrgkJNddt9+h1U+ZN0GClNytDeNyjMyDAKNZ75YcXZ5zvn8FC/aOMBRijpYGuP4i6c/p+kq/u57P6BpK4TOOdqfcnV2wdMXzyiKIXtHD1H6mP3799gb9dgZ5Pz0r/5Pzs6f0YWC8c4+L559yoF9wO88+QG1q/mTT/6Uc7PGmYADOsAOM0a/9XXWPvD8x5/zcDLim0cTfvbyhPN/+wuq228zNwWff/EBJ/NXPLr1gKPxLS6d5/VqQXtxxUAYCiFpbIdLQyAhAk6CFYIukCTx0Y8WJVCZpnM+niYu+kcqISl6OYt5R1XXlL3e1qrJWhcJDgKCVvRGQ3rDIWhFZyOhorOOENrIdpOGTGiQ16Ge2ujoL4rCC4H1CSi0UXId3NadkyBdrD+sx/pAZzt8XcXkeSUxRtPv96jXK4QQPLn/hIOdPT745S/45OlTLlvLrHOczVccjXIyIxGphgkhssy0kgQpsUFS+YDuHHpdRS/aAQTvsdIj8gwtMoqyTNZQ6xQuGm1mNgRIITaZG7++z7MNGgupItHyy0qsX/9+Ux5s6pDtuRM2/vSAj6zkcPPvSLZJiMQEvLbq2dRJzjl8AtBvPreUkflOqs1C+iUfPMHF2kDqyHCOjDeNMga5ARKV3oKJKqV33gz7Ehv/dBnB3Y2vr5QisrDTUb2xWAjpmhOHFoHZ1vEqsZAjCUJ96WyOQbGC1rbYzqbw2WiV1XUdzkUPy+VyRUiXrJINRbTT8oDDe8tGaeNDUuOk2jEEET1HAedjCv0mvM8nW4Jca4wxiQjhkkLXgpJ0XVRiWbcJ3o6M2psEDykEuckwOqTwv5A8owObPAVCfH4hBC75U2+A6eushXh9Sm0A/hT2TsAHjXVuS14I3iKcSqQEBcHSNg1t1tGpFq3WWGEJQtHiQViEKBFCYTJP3m/JjUUKgxQ5Qpjrtbfp46VCCIV3ItXp0fNbSE0MSfJITHw/sHgsIdhIGPQa76LCzznPoqpZVh1VXVE3FVqLCM6WCmMUWW9APhigyxKTG4yyaGFREoRKivC0PqzVkWGfhvW4yLJuLdRtR2gvKOwC1Upcp1m1K1pajBKI3FDsTNg5uEd/eoDzESep1jOWizN8vQCTIa+uqP0yrlEFzjWsVx4hQSvIMpGYzVEZNRoNIslNRFBSaUOvP2LQ22E0HtMfDsmSOrmqAk3jtmvDdh1VVbNcLLk4v2S+mKG0SPcypDCu2N/IEOtBbzt8sHghwYDMJLky7EhF6z1rO2NeR3Z37PEEUnp8s8Avn5OrDq8D3eAdvNlDeImROZQ70Kzp7dzGNRUL/wWDUYuQCiOANuBah2tbKHKEyLa9kMhzRL8gHw0xi4J23WzVtAGByDIG4z2yoo8xPfJySL8cIWVGluVJbfnXP/7TZtL+t//8jyYPpvFCvU98pOgJCjENMG6piYWGTJR9TXAGYXOE36NVT6iH30Md/T7y1t+hHjxmd6/kN746JrMqBmwJjwg1y9kF3nZ09RWnzz/i8uQFTVVTDA/Yv/cNasZczlo6l3OxaHhztQQ0J6/PuJo3nFy2tE6SK5hfnOM7i8kCOWvu9R1fPTAcFpY7ox59WVGdPWd5/Dmzk6e0x68R1ZJ/9l/9Y37nD3+Xq/Uca230XDQZeRYZJ85aOmvJsoxeLzbeeVFgsjxKhEIEBSLbqGI2u8IFT1EOyLICkxcpdVNTlAXaZJS9AaPhmPHOmM62XFycs7Mz4eHjdyj6Ay7fXFAtllxdvMHScefuXfplny++eMrd+3fpOkuRGTyB1WrF7bsP+fbf+F0u1w17h3f5/b/993j89nvkOyPIDJ33fPj+h4zevODxKEOFBtfVLKsKpTNcgNl6EU2rs4yua+OBlAAlrSXaKEwWWQydtSl1M8rJOttFGwLSIZoOAr/Z7DchLLBdTyF5SXrvojzP2eQV6KmbGicCiMQSEVHu4QMEFYtH21mChHm7YtFVKG3YG+0wzHpINDuTXdDRN7JXFpT9uClLGUG61apiMV8wm83o9QeoLNtOZpWO16pNlGQl0mK6HxpJPCx7ZYmQitfnZ+SZZm+6E43O8XRNhQgOL2RK1a3Z3d3j9t27jMdDcJY3z19x8fQFeUwFYtU65tbikFRtR+OjX+OqaWldoHWevcMj7j14yGi8y3A0Yv9gn8V8xmq5Zr6Yc3p6wssXL2i7uGbfenSfx08ecu/eLbSRNPWSy4tTLmfntF1DWRaMdoYURZ78niRt27JYLaibGtt1hLQPaK3I+yW9QS++/87im4b1YkG9WtLVa9qqwrUdPSF5MJ2SA6prMd4h02Sa5AvWJunFYrFkPl/iAmR5TlnklDtD3vrWuzw/PebVy1e8++7bTA8mvHrxksVsxXi4g20aMiEY9QsGvR4s1jxWht/oFdxyNQMCQiusSOCpFIgU5iYEUe4sBcJkrPoZxbtv85MXr/jV8xfRjPzG41oyfF0g3/werll1N39+8/ebP7WSZEaTZ1myktjAIxupUWSezC5nMZiKOBxTKRxBSMHVfMWqrrd+RgJQQdAvM4pC0zRtZEN6HwdvAfYmI3aGfbquxiZpVdd5rItTbKNVSn2XWB9B9OhLLTe7fmxIUkFotMQoRZaSdL33+M6m1xmtZayWrFLgnTIak5noIRQCLrjkcxcTkL2LQWabglPKKPWHCKhGL0QR2aj9AYvFEjYn0o17nfgfX2I1bt6j6J92/WMx+DKBCES7lQ1cexNA24L6G7EIGx/TeN9s1SRLFkHTWfrDMYP+DkoqrmZzdqd7TCbjuPd0HdIH1OWc5tnnjEXABBW9gqXaBjn54GLyetGjMH3KvMfOYBT94JH0iwJc9GRWEIFUrSl0Rp78wGVKOF2tVnjnWSznSOJgZb1ccfLyZfQ+Lcv4nJ1LTOHIQomSUwvOoZMPrkhdpRQpRVVEz7amqqhay53btzk9fkVjW+4/ekxZ9rFdi8RztLdHhqRrGi5Wc1rp8am5kgHqLhCcZSihr3NuP3lCqFuOf/IzplKSqZQe7hx6Y7MUKT6xcUwDvCBAdwHddARruf/4CYss58XpaUQlZLyHxFlBLNo2jYzzW5+8GASjUmr8dWG3Gdhs/Ah9ssi4OWTQNwJCrLVJfeK263sz5N6AHrHHjo1U5xw+MUqGvT7Oxtd0eHDAYrlgvpyzrtYMBn3u37/Lg/v3yZQkN5q8yKJvm4z+e9Y5mralrusYkth0SVpJaq4VKrHDndukvrsYJqQl0fE9MmFIw4p6VXFy/JreYIBPrKjj42OODvZ4750nfP7xhxy/fMnXvvVdxtMJwTmODvYYDgv+6s/+lLKIoVbr1YLFqkVIQ68s+N3f/i4/+N473H/yiNHhfYrBkHo1Y3n1hsXsiixGyLI7GSCkZF01vPjiOfVqzp07d9jdmyIkzJcrFvMFy+WKXm/A808+oEfN9771HsNhydH+HlZoHn31HS5np1SLGZOdyIj87NPPKYoeZa8X2eq9Hj2TsZzP+MUvPmRVd4ynBzgfk6TPZxWnF5dcXl1xfnbGYLTDp58/5dnzE3YP7tEFw6Jq0VkPrXMGZc75yQtWyznSGEDhRMbr0xOCq3nvyVd49voVi/kM21mqqqUc9CLY6RwqJYd3NjILIWCExNYd3aohVC1u3UQQLgjcqokEihBYLxd45xiNdqL9hhSMJuO0Xyq6LnpVS0T0QEcwnIy5c+9e9CdfLGiqisPDI4Q2nF1e0NoaaxuMEpgUSqe1IsszlNFRueJiMKTvYq0X5dCKLM8B6NpuO/iUIrKvtJbgHVpFhlXbtmgdQ2f9ZpcO0baoaSssjtZZ2rpl3azIpxNGTx6yKgsu6zWLekbXVLi6JhOK4WDCwf4tRoMx3kKWRe9chGRnNEILxWq1oPI1lW85vjyh6Toe3H/AwJRUyzqqilYVF2dz5osFT957m97OgJ3dKU0Nn3zyOV3bMOwZjl8+53J+yoO37rO3s897999hVO7w6YuXdMERdMAKjzASV2ry/V28d2g63ro1YWQE67MZv/r5hzz77GNMX1DuFVSuZV5ZpntH3Ll1m9nFBXa1RotosWLZqFViPd056HxgvNNj1M9xST6tTIZLMvc2eWZu9rzolRmTtWWyCFBS4QiQafqTMf2dHaTSccjjLG2dLBRs0nXLNJQNHmM0ZVHQK3r0i5JR0SMzBm0MSsbAobazieG6qRcCzm++HBv4VhKiKqep8TbaQRmT4ZynV/Z5+/Fb7I1HnF1csqpqRPD0tCSTImZdiA37L66pTbhplKfHXgbvUUKghUKVWfSpTQM8mUBAl8LUtvY16d8w+jqc67qWjGeWTAzHmz3S5nFz+L8ZnN6sZ0KI4VcyDZUj8Be2BCqRzqlY80iiaiWw8aSNRN5NjZQsBzZg4A110gYkF4G4N6ho8ebSoCih0Wgd3z+TmxgUZAxGm61iScmNH+4GpJUJ9GNLipBJKRU2z7z1Lo2kpc1wPITNNZGuMwKkIoGrgthXNm0EZdvOUlcNbdttM1Tato3swuTh2jbNFuDdoNfRzz3a8/kQma6RLetSLZgAVLnx1t0Eb7rtOlDpPZZSpSyMkHpqFdWHSm/Zqj64CD7fANkF4ZrAkIbmPgFuXWdxzqcBbAx6ddameqPbft+2TfLBja85+tc6mrqh7ZrkdVtTVVX0sE7s9cisFtHKoI0s4kDMjZBhjZZzCA2u62jahrquWFcrVsua9apjVa3ougoRYniulD6B9TJdn4OQaouwwZU29zRCspEFLdP77AnBpn1KYa2ntR3ruma1qpjNKxaLDtd1aOUZ9goOJlOmkz7TaZ+93TG3DqbsT3L2xhmTYWBQNBTaIoRCyCx9Fny6TxsF1PVe4FzHumlZr1tW8xmr5YLTq4anx3OOX19g247SSPq9gn4/DjMdMvoz54aiLNif7jMcTCj7fdbVirZt8AQ2MxGR1rlUMVzOZBlG65hpJDVa5QhlYlhfiEG1vV6PLM8oyoI8yymLgjxXlGVOUZTp7IT5fMHV1VV6P64JBdZ20Zoo9R+E637WBk/QoIosXocpUELSK0ukykBkNLZDAHlRkOUGIxWZFGjhMGqA6I0x/QmZycl1htES13X4psa3a7puRV4Y+sMxvcEe5fAAU47Iez2yIuJoUTUYyQuN91jb4tqOrnOUeY9Bb8Du7gEHtx8xvfWAyf4ddiaHDEa7FFmP0hik8Cjl+eBH/+qvZdL+Jw3S/ov/7l/80fjBNH4YiIXVZhKkNlL1EH1pLJ7gBaBwvqCyfVpxHz/6Lu7w93G3fpdu/C4rPWCFQgrPd5/k3JtOkCqjXq3xviK4hvnsjPnla3y1oK3WrNZLDh88YefOV6iCQek+O+PbtKHgau65++Bt+uM9lnXgV5+dsVy2vPziGZ21VK3FAv3RAB0gkxVd9YqRUdzeLTkcag6GhswHdN0w6pf8s//6nzHY3+H8zVnyV9xIF/XWa7Uoywiwak2e5WhjYtPTxVTQzjZkWZ6kiQ1FUXJ4cAtpDG1rkdqgTIZIk4DgArazdG1D1655/uwZSmbsTPbpOs/84gKcYz2/5Oz1Mbdu3WE82UMohReOnZ0h569f89HHH6Oygsn0gMnBHQ7v3Of+vYdopfnoo18ymexxcOs21i/5l//T/8Do8jnvHk3pZYamWtJ0DkT0FrtYXOHx2wMD4gGTmXgfokl88s1LDaZLMulob2AYTyYI4rVF9ln8sG/8FGMT61IxzpYpEh8ieiTZmOxqg4sAigAHtN7FILGkRrbeU2GZdWtqPEpp9ncmjPIB050pu7tT6npJt1rz+vSEl6fHOO/o92IQwWbK2+v1yfI8FScqTW7jxhxlN7G42chgJfF1GxWLkNnskvOzU6Z7E4yUOBf9XrzbeA9Gr7b5fE6WFxT9AU3d0K0qXnz2jMXVPMmuFOvOc1W31N7hgoAsxwuFDYKdyT5WKPZvHbIzHmOMITcZs8tLPv34My4vrnC2QynF7Tt3ePDgHgdHY0wmubw85+T1MW1bQbBoI+OaLorISBOSpm6o1hVtW9M0a0LwKKPIC5MMv6Oc1uGoqnVs2FZr6tWK0DQEa5HWRX+64DkoMgbOUi0WVNWato4FUxciI6LuLDaEKH+TBp3lDEY7mDxHKsXtt+5z6+0HnM7OmU6nPHrrAYvVJW2z5PLskjIrEN6yU+T0Co1tWna85ElechtH0dZRQqEVWpvUQFq8beNBJMAJkJkmGMO6VzD86rv85cef8PnxSWJ4XrMbfh18vSmXgmtQb/P4sj/tBtSVN8IQ5HYIIjdeUOlX6qqirpr07xCloETbtrpz1G137TmXCpgiSWGCCKzrOk56A+R5znQ6YWfQp+viUGkTDOJc2A5TNp9RTwyNQMotmLPx5N4IKAa9HuPxiMnOkH6vjNYfwHA4pN/vR3mjEPjCYLWIydAp2dSmfcAFfwP8jGElQgh6/T6j0Qh7g1UhZGRhIQS9Xp+iKBJIy7U0L4GnGwZqbEq50aCS+gmRGBzXAJkLLvpw32xS0vt2HeoQtlZAEbhObDGlorS4s2zIK8pkTPcPUUpxeTljMBjQH/Qj41lrTGeZffQJg6Zmr9fDNg4hNYPxDr2dEcsUSJbLjF7RZ9AbJslQlKF1zrKuVrgQKFTOTjlkkPfpZQWaJKtzjuVyQbVeA4Lvfvc7+M5x+voYoyRCQttFeVWZ5xHgMxll2cOYPA4yQkxcVyFtu0EkKaoCovdp9BGPzUzdNBACh/u7vDo+pm0ti9mSxXzGm9NjurpjWAwYDYe8WS24bFZ4JFYmBrcPBBxaeAovKXZ2mI6mvProE4rgMFKCDFuJdxccIbjodScEwbtojyMSQ0cEfGsRwXDrrSd8en7CVbVG6OS/l3hMm/fzOiRNpGYwrgHnfQrL+TJze/P/hLzhuRaX4dZPebt+vEfJlMKdmuBtsFgC/O0mACQBz67rGA8GSCGxPjDd26VtO1arJaPRkP29CYPRgN3JGNt2LJcLnI8s+LZptp/vDYum69y2kfchNsrpWMN2NjFq42sySiJTvsBGtiuQeOexraPIMu7eu4Nta4bDAcfHx+R5xg9+8/vcu3+P+WzGj3/8V/QHBWfnF1EiP97lL//8L7i6uKAsCsoip9/rc+vWIWevThj3evT7JWsPtdDcf3SXrlrRLGZ8+uEHvP7iU85PnrGYX3BxOScvehweTiE4fv7+BzRdx2q95OrqKnp3tzXHz5/Sl46+hu997ztkhUZpSScUdx8/YjKZ8vmvPqZaXNE2a27du8ft27dxrmNnZ8jdW0c8efQAAfzlj9+nNz7g4M59Tk8vOLrzkOPzK67mS6pVjRKafn+EKfq887Vv05HhlaGxjtbGoct4NGC1mDOZ7FG3DqULvvbNb3H+5oQf/ujPESJjtphTraNUMQjF3tEheljicoXSMtaiWQwGNCYjtI5u3SAaj+hisyv0xspFXKd6J4Cm85687IGWUbbrPFLo2Cin97ttYmhkluWMx7u8/uIFlycnrOdXMdhNSIQSDIYFbV2RG5UC2SMjESmidYuUW9aWkpI8y/ApuBAZAdpYT8U6y3oX/e0QWOupmxbbRR907yObzeSavJdFGXvb0rY1Mo8A7mq5JN/pc/DeY9phwdLWtO2Spp7TVguaas7xyTM+/vxDPnn1lPeffsTz489Y1XM6W9N0LYPk0zxfzajsGisCwShmywVN3XL34IhCFTSrFro4yLp9/4i9wymTnR2ePj/m5PUV+wd36JU5L559TCYdu5MyMueCIlN93rn/NpnIOD89wYYGr6Lk30tolGB0ax8rG4xbc7DTw7SOgci5enrC/PyS/jBjcnDIW+9+k9YJLtYrBnu7sFwTqpZCChABRQwKaztLVXdoqdkdlZSZiR6F1sagoES8cd5tw5k2jEilE3Dnk6enD4hMMznYjwxaqRJo5GibCJRsmJwSgdBim0EglSTThsIUlKYgU4YiyynzkjyPgELX2QSGRQ9LpVQaEMY1vRmqEWKYcPCeYDt829E0NXkvxxQ5bRc42L/D0cE+F1dXVPMFJnh6uSE4F5lybIa4kWChVdqfRVQBahH9MLXSqLKHyDKCiPZBIQ3o8CHK44lhed55Mm0SyBuu91AR/UCV+rKlgEz9xwaQ20jWNzXoJozyZv0p5fXP+HRftsSANEC9aUkQ+65rsHNT022s/Db2UZt6J+K7cgvabKzsQjo7QqrdopVRQVkUUeKcANvMmASuyu25uKknZbqGNDpP138NDrPxQRdxsB4E6Sc3YGgM6hJJlu6DxbmWrm1p6gg4Vqs11XpNVdW0rSUEl+w6IKQgplinhwQ4Ryae8y491ybwDZzvUhCt2/bHQlyH225suLRSaXgttmDvpvj0zrIJirPW0jRxkNHaNqptttZZqbZKU+QQHbsT0zgC0G3TJha33w6at5ZLiYwQ64/IBN4Mkq8twiKgHX3oN3WyiMo5Hwc1LgRaa2lDDINeNy1N47CNRwYLocNZRdsq2kZSN562hraFpvE0FbS1wjuNCFlkyQqRfKDjurKuxXY1ro2EHWtjTRp8ZMtGM82AEA7vGyCBxd5gHVjfxRC0tgEcg8IwHRv2Jprbh0NuH025d3fEg/s73L095vZej8NdwWTgGJYtZVYhZSDIHGSOJOIWEdewBNchvUiDqpamWbFuVrTrmrZqma8Fzy4VT09aZrOWUhuGvYxhmZFpE2006hrbVHTrBbZa45o2DnnbirPXx7TVGq0igcdkGb3BDqPxLoPhgLIs6fVKirJkNBwzGo4piyE6K9EmR4oYuB6Ith1duo9x343DfR9iLRsSiB+8x8mA1DKRZzLiLujjsb2xEFGb8MGoeJQq2UB6SfAKFwTBx5C4um3wCLTJUg8Wa2xtCoIY4lWGyUqMKVFZRmZkVAx2LaGrCKFhMJgw3r3NcHeP4fSAbLhHMdqNIG1Wok0WGfNK4ZK9RJHFs2M0HDEcTxmO9xjs7jMY7zHoj8kygzKRCOWti8Cw9/zyJ//6Pz+7gyAEHdfNp5LRI1B68MLHoIIQEM5HbxGb4cWYtbpPPXyE3v0bhJ0n2GKXVvUiuOQcAsurleN4JnhwVHDr4buMdsYcP3+f1ewFoVtBlw4Jk1OWQ/Z2dxGyw0nF5y/OkGJN5zRG7HO29Nw5GiF0xc54l3I45dPXKyhHFIMRF1fnZOGU6f4eDk9fWUJ1ilt27BYF9779Nr/5jXd48cVv8fL5F5S7Y9bzJcHG6ZTWGm3iJHDTgG023dlshpISU2TMLq/oFX2ca1iuLnHtkjzLMJmibda8Pn6JyOM9zE25PfRMluN9bLSFVigKsv6QwWTMxeyc2eU573z9G7x5/Yof/4cTwrzjJ3/xl/zW3/2H3Hv8Dudnz/jJv/+/efb0c775vd/mwVtv8fzZp/yr//l/ZLx7wHg8QQXPhx98wDe/9bv89j/4h9wZG8bylIwlEo/WefwgKRGZhAi0FHRdbFslCiXYMoWi15JHJNlxnDSxBS6ANJF2kTkRKbNxQgbJhNtFAFyLNJEE23YQBFlWIERgtY4+P0IIMhGlVPjEdpQKGSSFBBs8KzyLtsaGyPo2KhrPL+s1vnvFbH7GbHlBbTu8DCxfLvngJz/n3qNbfPf73+PW3dvkvTwyBolf23PV35DjbAoJHw+q6A+jCVrSuobz1y/pZYLSRNZ1CCKqYxB4ofFYyv6AIDTDwQgtDLl2XC5WvHr5CukcNR4d4sRKmOjHVeZ9ytGYtmmZzRYcHd3h+OSYpmpYZSuOXx3Hpj4Ejm4dcevWHv1BgdY58/mKi6s31PUygnzG0OsVCOHRGSBVDKdDEPyK1naAQDhPZjS9soihBsEhXPSsw8Y4ZBvilDa4QC8rKMo+3nbYugbnkJlhPBxSdpbuas56PmNt23hPPbQhyqdtAKljIr1SGlPkeB0DGZzU3H/7CXv7Y76qvoJROfOzC55++jmP7h1y+uqc2es37JkeRyaQdS2tNIwmPSZtg7IgTYHXJrI9vCXzAukj4B9EnA57IUAoroLjqvMc6Cwli28Kwi8DtTf/vMl0+PWfu/YRu8k8jAWUyTWZia5xGw8z6zaFK6g0RVY6FoBdm1ikCgjRewkiG7Iocqq6QQrJeGcH29VIJLk2SCxCCqY7I3q9kq7taOqO3vlNXwAAIABJREFUXjFInr41vV7yivaRJdt2HV1rUblECbCQrBFI4LJEaclOv4fOc0yWYZsG21Xsjcfkw2EMLGg6rBIIYxAi4FKx48XGFzQV3xuWbghbuwofPHXbxMJRxMJDyE3QGbx5c7b1TduwbEJiw8TylghKiNRYiOv3JJ5zCbzdcEREiMmnQmyLVZEagi3QLq491LyPCdQbpowNgU54ggrIEBuHi9lrzmenHE3vpLC0CBx6AhmwOn0NV2/IhGA5W+LaFiEE66UnG4649/Y7nD3/AtEqenpIpnJCZ2k7RyccV+s56+WKwWCHaVH8f9S92Y+lyXnm94vl286ee2atXcVqFslusklKohZqaI1mNIZhGYYFGPCVb/1vGRjYF74yxgMYtgyMaEkUtVAkm+xudnd115r7cvbzbbH4IuKcLHLAezmBQqHWzPyWiDee93l/D9uDfY52j6iqipOr1yzawMK2xrKqG1RmqduWbq9PnhWBdyUUWkKzXDKfThiOtkhlCsZhyxJf1yjrUTLBinBY1gQnFMJhZQg6EMahVYrMNcYaTk5eMRq+x+7eNuPz1xwcPkDtbtPtZri6YTq+QSp43N/mcjXlzFYh5RfwClYWjltH7uYUP/sFR/1D8l6X5nJMkybB0RsxGRs3qvdhVNUEB4gUbuNuyb1ncXpKv5Py59/6Nv/LP/yI67KBXCJkcOqsxwqJblGpA9vOx2crOMzfctDGhsLa5aTWbih/+3diF/Kt9SGI3FLKwHATsOYOh9A5i5RhLNzFsBKDwjhHnmXoRDKbTEgTzc7WFv1elyLPqeuSpinjYViHe6tEaLKj0ElKlmtgibE+CLesXRLhEratCVzJ+PVkSpHnGXVdBf5XdEtb02KMwzvL6/PXvD7+nF5/wOs3z2nrkjzb4ez0hMFgwL/+N/8F//7f/8+U02uMSXjx+afk+bfp94esqhVpNkCrjIuTE6aLKzpJn5/97J/59MVL3nn/G6RFly9+9QLTOi7PTxhfHfO7v/Ntrm6umC6WfO/pfWbzkvPLK5IkR1xOefniOXfvHWGiy7RXWMobw03dQR/s8vMPP8I5y3g+wyRd5vOaorPF9miEyD3VasbewX2WiyWvXryk3dshk5qz49PgtFcJn376Gednx4y2Rsikw+uXrxlsbfP9H/wpi/mEajmj6O2i0gLLgvPLS7Ksx/7eEf1hn5PLMU/e/wMyJfj8009YlSuqxjEabfGrL17RO3zKk3d/l8v5gjeTG0QuUT6EESnR0nqLcYFbHaaaWlpno9MnPL9Kq+iyFQEJAtiyQXcylMxZLhtUUdLpCqrVijwrkE6gpQ7BgrbFuZbhsIdUkqurG2rbkg0yRmkH6TQpnvlyhrI5WmZ4DF5bnJRYEUN52hDmooQn0VnAvxhHeNsD4sd7ECoEWTlp8SLWUD4KUUqBDKxS01oQhq2DHv29LaaTJfVZRdHpkhUFjbCM9odsP7xDmwrqukLFw5wX0LqKuZsH51dZ8Wb8GQhFL++QpwLpQcmcs+sOtvV46REKOqpHIjUr2/IPzz/EtZZ//Y0/oDfqYVvLg8cPwj7S0Tz7/CXPvzxhtLvL7ug+Qikelitke0Gvm3D+7BM+/eXH3Hn8TZ68/13+5L0/oDvo8L/+5H+nEjOMCusCHc0sh/43n/Dm1TGf/9OnHGp4dDTC24bjkxmX/+cvmXx8xepbC7bvHXJwdx8/6qPmLVZ9gbk4YdTrsFgYpvMV89JhWiiSkJ9hTBDnvWti5kQwJSCSjZvPO0h0DsLg2jAZ5zzk3Q47h4f0R0OapmVVBtHCR4Fp7aYQIjSXdTRtSAlNU7GK0yCJHtApOkgtsCgSC8It2OpapINVU2MIAkGYMJFhb3PBxNEYF1ixSuOVwssW7w3VRCGdQKiE6/GEotvjv/yTP+HDf/wHLl+/oGwsRZJgqio0xaQKYYHRGYkIeV+CgO0S3lM5i9YKJTQuS4Kr14TGYJam4HssyhWmDftK4PqHehNu9wYRr4WQtwGlAodizXe93WM2f+p+3Ukrothl8ZsmehBdAzc/IHPCFFX4dz6IwCI40QWxieJu65y1CEisvXACESexdJwgFFIjEDFPJAi+aZqTZzlZmkMUWtfTGUFUNLGmCiJPMCcHdz28JdgKYuW9dvfefl04sIQm45oD7H2omZ0zOBeaPV7JMABsAzcZH78HHbIWsAHvs5ZO1w5OIQhhdn79aS2CGGorbBCERXA7roVqGRvL69rfRROTwAdkkgjBYAGV4IJI7Ezg7ToXhS02Rifv17XpRs/GYQPLlxgCKMI9UtqADc+WR4TARbhl2EbBf+0WXruoRWw+C8LUappmGyODIO7zLoj8xhqkbLE21Na1g5NJQ1UK2rZlWVn6hUBhyJRHY8LaQYKPwWpSCG4W0CsgzQ1ZUdIrEjpZC9LhMQhnA2rRgtehLi2yJDDMlUTpnETnSAlCWrwDR6ihtNQU2qF6ilF/jQgDRTDFCanROkElCV5qBC6Il75G0cZGQagBpTMIEXQO5ySpdkjvaFuBcy1N3VIuFWWb0zaWZVkyWRiu54bzac101eKkpieCOai1FbKeoaUD47FWUpmGcZxmmM8mLOcLRGwSKCEQUTdJ04R+r0+nyFBpaMwGU1UXIZMgXTsfn/0YMC4E1rRU5YJEC2SRo5Mk9N+wIC1FJ2UwGuKVpKyWLJcrTNtSZClZEs6r1rShOeotQjiUaHHWY1tJqxweCULTWg/KkSYt3Tylak2obYEWH559b8n8JYgEmw6wSYH3EpNIVHeHYs9DIkn7PbS3dIqcTrdDZ2sPn22T97bpZglS+KhBadK8R9+LEDA86jPpXeCtRyUFKuuQ9vroNAuBmV6CcTjZ4qVh1VZBz/gtH//inbTDh7uBBUhE0Tgbzi0ujHc4JNgM7DaleETT+UPcwZ+h7v4xfuc9mnSHSiWY9WHOBY4b1vFoy/D1uwnCSLJuh+2dbYSwLGZX4NqY8Km4vpjQNBa8xTSC16dzdPcuN+OKLNcc7PfppKEEWK4alrUD1cF7zcP7d8jSlOm8om6hyBMSJWmNZVmuMHWFipb7bq9Lp9+laWusCyNY64Usz/OYVmtu2YVKhRGJpiVNUtI0CWOjqwWnZyd4C/1Oh/HNJZObK2azKYvphHK5JFGhs1qWFQhPnuWxGxkK6r39A/rdDuVizJeff8JsNubozl2KLKEqF9xMluzsv8N8PuMff/zX+LYiVykHB3dZLFfMb65pV1Ouz19xc/GKy+PXrCYTdgbbJEmX3YNdPvr47ylfHvPk8C6ZlqyWc1pncT6IB/PVIgRFuPXoiYhgdHt7kDQmdNicjU7R4Fiz3oXESQAhMNZs7PIAb6djG2s2IxfCr7vL0MYRprWYEVxuNvZ31qmwYbP0QlA7w9I2GO8Ci7PXJxGa0/MThPJkicDakso0zMuSujG41nF9fc2b18ccH5+RZgWd3iA4FYVAxjRA5y2b+siHFFi1GV+VFJ2CTpExHV9ydXXK/v5udA379T8JIieOLMvYGu0w2tolSTu0WKSxvPrkM65fHZMKQSbDBiLTnN2dA7Z39tBFDlLR6XQYj8eMxxPKcsmynFOuSra3t7hz9w7feO8bfPP9r9If5Dz/8jmvXr7G2hpETZ5n9LqhG9e2oePovaNpAvtI6TB2mKcBqO5tKCpNRAK0iyXNdIpdzHF1iWsbhAflPJ1E8/DogO1ul6YqKedzTNOwPRrylUePKKczysWCxjuMAiM8jTWhsPPBVSqjqwxp4liYZlFXDA93ePrtpwy2OlSrBbPxhLOLMx5/5SGPHz5gOp2RTlZ8d7TLAy3YbWreTXPuAyPX0hEuMKV0cB7igoCGdQFjEAMUPBKhEmbSUw2GbL33Pn/74S85uRnH+3jLow2P9q8Lsr/JpvzNsKD1R/BohINmliXhugsFIggmoZklbh3sUuOcQSJD0JZzSKnjCFJwunayhE4ROr/We0b9HnW5pJul9IqUPC8o8oxOnlFHPpMgNER8HGHudDL2dkfoTLEO7VjXqK1ZB3MQv6Yw2p8nKTs7O2xvbdPrdFFCIVXgcc+XCxoTmF+tllgcayUoVenaNgJEJMo6wE285TwWoQBs2zAiRXTfCqkwTbM5vGxcF57NnhWu9fqHCJu0DKFSYT2KXZhoyF//PR1dZ2ycKFHwWBezIj6rhDXsbZd0kiRIIamWZXBxIoJrQwl2dw4wTVgD0kQhjCFZlcw/+4J+3aIIARXShcAdYw3L1QonJAd3HlGtWvI037j3S98yni+4ni9RRcHB1h67SZcsLUjTgra1rOoyJreajQNDKUm/12XvYJtqWdKuWoq0E7jjpqFtahKtKNI0oGCqJc4blAy8VyEFWVqQJMF9aq2Njk1xG8YVr1HTBv7w/s4ep8cnbG/t8uDJE5JOh85oQKfXRyvNYrWkNDWTckkrJS4e3qxQVF5gW0e2aBmohJ1+h2ZyhRIeUCDDNVfRBevjXhUOKeuk6PDcSUAai6lqDh89xnUKPjt+g10/D1EsDQ+DiAgOvQkUu323bw/Uv/5usxGT5FtcQRfTl992JwEYYzcby28iOXzc48KfBkbcsNthbzTER+e89T4GowiyLGVVLplOpnQ6PcKYcANCUDcty7IOOJP4OdYJ0t4H0UMnIXQuuHHExim+dtG9zbG7vecKgY+BcBU7W1vUVc356TkgGG5vM50tmEynPHr8hDt332Fr54C9/SM6WcH56Qn7B/f48//2L3j05Iir01f0B1u8+5WvUZuGRmrOT64YX15RZAkXb77k45/8DYUWfO9f/YD3fvd7CKHRDu7dO6Lf3+Lly1foRPPBB9/h4cNHnJ+ekSQJi9mc6+trbiYTtvePuPfOY54+/TqHh/uYpuH1l89pqxXDnSGdfofZdMrL58+pVkuuLy/5u7/7R9LuiC/fnPDDH/6Q2fiG/qBP3hsyX1ZcnB1zdXJMkWmGgw6ffPxLnn/5BfPFjNZJfv8Pv89sabh79x2+/cF77OwN6Q5G9Id9Lk5eszXqs2gMnz9/xvb+Fl+8fMN3fu8H7B/e4Sc/+yc6hWQ5n5ClCU6GMXLdhvWwihgSZy1mVWOqGt9YvLHx98M0kHcBCeCNxbcelGTn6IBiMMB4z/bWDlIqmqqmLivqsox1e7j3o9GIPM8pm5L+qM+dozskUnN1cc1ytUTJkIgudBgTtW2o70xrsK1hjX/TcWS7aRqUDMgf4QNexLZhAkjLyMGzYelPkoS93W2Gg25ohmhJr1/QG3XQnRTjLTIRFIMCOglq2OXw0X0Goz5X8xkuOgcTITBNSbVcYJo6CDqE8VtnK6wtqZs5jSmZL6csywlSgUwUSZpRpB0UgnpVobyiWiyZTa/Z2R2RJjrsJU4xuVnx/MUxRafH9u4eZxcXDEdDvvu7v0NeFBy/eMX08hJbLzk+fsF0ec39w0NGoz4/PfmIRdoEByISi6WVFpsqTDdHD7oBgyIESaLJATk3zI9vOP/sSxZn59TXEy5fnWDallSnzCcTmtowni5YLAPuJNGSfq9DloZwqbVDsa6q8MyIUJt5gsiSKI0UIuITNKDIOj3uPXyH/vaIxgZerY2sT+csjoDrWTed1dqZGut/533AXnjY2tpi7/AOnf4QkoI075CkIVTMWEPdNngcRjiccHG6MzZnvcPZUKta06K1xPlwXmtaR1mtwnQHgtY0JGnK/tE+dV0zvbmJ6AVF2wRUjmTNXg3Cp3UGSRC0hQ/vkfIgfZj8Qd5OVEkRAhqDJ2DteHQhiI7oyn27bgmbSvgp7lXrnIf1XuN9yKdYnxVdZOhumOcyrMWbySCxXsPDOUatw7OE3ITzhRHp+P95F12DIazImGZjTpARTaFUwGDJiAnSOiFJUtI82+DxsiIPTOm185dg7FnXyeH+r2s8sRmjDvuki27PiAGSMvJWw57TRtxgXbc0TUtVhcDZsmyom8A9bm0Y+7cevDNRu3CxnovXN5jU0SIyR8PiGGr8dVYC65oviN0h7IrI1PZxHzRxGiU0otY4o7quAjok5rPUJiDHjA0ago/fo/dRdBbx+sbAXB+vhY3J9L9ZZTh3W9k6tz5nxr2ddf3gWPvB14aFt88v62dqbUFRUpKnKWmaBpe4kpuGM9GxKwhCaAjN9rQejIeqMTStYl4JJivJeOEZzx2TOYznMJ455qVivpJMl5bZAq4mhrNxxXzlmC2WrFY1q1VK06Q0bQycVCFMSikX30EwVmBaokDv8U7iXAiCE3jSVFIUmn43pd/RdDs5ed4hzzOy1JImBiXr8IMlUs6RooyC4hqTJcID4jdXHGgRtHiC27muPG2Zsiwl10vD5bjhaiJ4dQnPT2fMlhV1U+JtnJJuK7xvkFiKLA/vSaIiViAgRBVBaLWmwdvgpi7LOpzVbcQZpQVpmscguDS+i4IsTciLjKKTURQBE5jlacANJJok0QF9JQiBdibgBps6TBtUdXSZVw1KSVKt0SpBqoBVCNpuxEwig8itMhA5IbtKIkWKc9BYh7GOxhlK0yIiUqNsy+iM9jgp8WmHVvdovcILjUxSVJrTHR7S2T4gH+5R9Hfo9nfodLvkeRom5cJXEI00AqUydJKT5B1Ic3R3i3ywR2e0Q1IMkDoDL3Fe0tQNrg1ms3KxwFQlLz//4f//nLR4QuswvgihqSUAhfAS4SSt26J2h7j8CWr7O6jt9zGdO9QqDV0k4kIHKC0YjBSm9tQr+PysZu4L+gIcCTod0OltheRLZxBYet2EopNw8vIZl+dvkN0DqmmfcmoYDjsU2YBnz1+QPL5Lv9ulN7LcjOcM+j22Bl2ca2kRVOmQ04sJNYKj7YIsbfCtQTjPctpyXZ2h04ymNWilWExXaC3p93pY66iqCq0D97RpGsooVKqYUD6fzVEaer0+DtjZ3adX9JBSU2QFTbqgblrOT99Q5B0SCW1ku0h1EJhOOoQ8yERibINrLHmSsrezTZEH8Ha/t8O3vjPixasLdnd2OD59xqvnn/Du/bvsHO7yi5//A5dXNyg8eSbQiSPPc9CCabPi4vKYR1VJR2ru7Oww9bDm6iACen0tYilkTAgNTCfvDbSBA1mWJRCK5k2YWEyYXIu3SmqwHil9CIBo2ghfD92ZsKlFCLsLbtP1iElAHKwdb0TB3GGEBBfDxwhdTOMdrWlDASWC4zZVml7epzJxZEx7DIZFVTJvWlY2jJFIARrN9GrG5cWY4zfnvPv1p7z/wXvcvX9IhIOCt1gX8QeERUEQRseNMWgpqMsF4/EVh4f76ETS1CYUREqihSTXnfhrFbuaMmIQDM18ztWr16TOk6UJWapBKKRMKHHUbShKqnpFUzehqdDN2Tt4wGDUp5Pn4KEqKy4uTsmyAHhP04ynX3vC/sGQi8tTJuMFTVNhjKeuG0KKcBAl+r0wNr7mTpu6orYGW6+5NBZhWlRTo5xFKoFOw7iBcQbqmvH5GalUXF5eBMenMVzfhK7udDKmqlY03seQk5CuK/AB/UEY0bLSUQnBfLmiquc00nO008dqqOqSbp4ysQ33H9xl/84+DTAajljKl/S058gnDLp9Mh/5vd4GZ4VUYZTHhkLDeofF0xK7z0LSrpsEKLq9IciE1gTx6W0R9reGBcWPX3c9sPnzdUDWrcUzFBrWOrxcG/cC6mLtOrA+OGyVlOHgZIIDQQqJi4KZlEGgCT10vynwOnlGvxtG1ysrcB7KqmK5XJClGV4IVuWSRVlSty2LRcN4vMI4S5JosixlNOpirWVZVfgqjEwbaxDSh6ZGv0dvOETG5lfjLLUNQUZlE8YcB90+KtcggkNWZgUChamquKVEES2OZvtwkYPzNYpcWZph2pp1lNlwtIWzlvH4OlwrRzgkAWs4QTgg+M09y9IsCEvx11rrkHBtb52QYs0o8LfpymvO+OYjHsZCIEfkRcnw/Dofvh8vZIT9J+AsN5MLrieXJKrDOsjDtzWz0xN0uaRQGqSDRALtxsIvhWA5ndEMdxnub3FxfkEhJZ00wytJbRsm9ZJ3D/bpdTKcMSzKKat6FcZ/TYUVwbEkHUEIbmumF+cUGWwP+1STBbassQoSJVDCUa2W0OmzvTVk784hz18/4+bmCu3XQR3xEODj+BnB8Wnioy2j+yAvusyWC1preOcrjzk7PaH2goWA0re4uib3gl6nz+PkDktv+dXkEiuDcG61onKOK+t4Xi0Yfv4R3713JySWO49RkUnpgwAgpQpNPOc36BAcSOtxIjTKtHfoxZTy02f8q+98nc/OTvjo+A3O58jo2Fs/NwE3YJDCE+E2m/u37gT85yF3keH8Fg7h7eVAxsNtOGiFd5U4cvj230l0DF6KDRuFZzKbstPvo4WkLOswOSKhrD1NU1PkKbPZAi0X6CQlzzOstfQHAyaLEts0G5f5JjREqRgKZzDWbw7z+LVji00gifcea1zsYcS/g0ColNcnFxzsnPGVx1/hJh1zfXODaS39UZ8f/qe/Ymd7myzvcv/hE+49fEBVr7j/6DGrsuEXH33CvSPNo8cP2L/3FJkOOR1fkrYNbVVyfVMy1ilXl2PyfMT+qMP1ZEVxVLB/912+/NUnTFc1WZZwsL+DuLrk+vKY68szmrrCWcPRnSOurq44Pz/nsy+e8fjJVzH3HZ1unwcPHjCeLJgvrnn9/Jo0yWOjzLCzu8PB9ndZzGvenF7w53/xF8yWS+rJBefHb8h7W2ztbXN98Zq2mjC5hP/7Pz4n73a5d+8+xVYfrxNevL5gNBxRLaf86K9/xNV4yp2HD0iE4XCgqZcLlotrdnZ32d4+YDjYYTadMJ0aVtMZeVdy//AuN4slVjjIFAkS4z3OtjjjsY3BVDXYYGzwkWu4xkl5Y6JAEcSJZl7iaku/2+X16SlZklEUOW3TYFuDJjQ60iKntYabyQ1ZUaK0otftYVvH2ckJzaomy3PqZcX3/82/pfUtH3/4E+qyxZkQxiO9RbUCoSVtaxAishSbBmcDM389fqy1Jk0SRFljbUMQUUX8OWC+kjyhNyxIOikkinzUQXXCPm7zjGRrQLKzzf7eHjdvXjMPgGV0piivlywWC3q9HkmSxsmU9Tvr0DryCJ0lSfNwKNYpCQplBa42bOkev/vuBySt58NPfgaZ5Afv/xEZBaqS5NbzlccPubq84fz4JVvbWxwdHpB0MnbvfY13luD4OZdnn/POXspg0PDD//d/4yevX/K5PKd4tE93e5dGO1zbRieTYqkT7L1d8tGQNx89p1mNeefOkK1en+zkillZYp8fc/zFCSLNOE0F1JZe05JZiyU0dvM8JVGKLNW01gY+qIA0TanKmkVZkzpPtxveBaVExLyEAsbjSToZ2/t7dLf6VE3NcrmkrZuNSOt9cNuq0HkNQk8UPomYM0fADEwmY66HY+4+fMru4UMaJ0KwsW1ZLZf0hpdk5ydMJjesqgVWSIyyVG10J7ZhhF1KgZLBHCKEDO+CMvjWYNsWayy9wSA0GKXi6fvvI5zl7M1LZK7wMjTPpJBhCsGDtUGgNNaC9DiC01q2DX45x7sWYzqoPENKSdUGoaPIc5QQLJYLnHe0tg31XJQYgpElNu693zQDiWIfUoU64C3XrRC3Nabb1DMOIUI2zNtNwF9rNHuiwHtbp4LfGI/WTdywlwVsgZSBFeuj+LdmzXpvQ3NMJ6hEQ8QgWHwMoA2fyzh7i0yIE08+CupBYLSb2mtTK8tbB3Fb1xGbEcRN523EQBD3MDbfnxS3eL4QWgRJnPpcv9fr85vzoJMksPuzDJlEcVTIIKw2FWW5jPV0EDudC6GxgvCeBBze+rqHax2a1uHrDeFFgV/rbHtb68frLpWKY+3B6azQ0ailQ1SsEZt9N1Yam7yHtdgNQVtxCIRfv5trQ5XbGCvWCIzb5yb8H8a426aClFRVFT5TZK8qGQRh4WJuTNQLPPEc5cAKwaJOSZKc2ouAccKibINwAemQ6oSEhCxJwDQYmZFrTaoblBZIWcY6PCVRmiRXdHuSTAu0MqSpRKoE7xOskEGYjY2S8N0noQmvCAGnMiIfZErrExB51AxKcCtsU0ZcjsP5Crwk0QVSpptm/drNug4cDs9ZuN/rk0bdWpaLltWy4Xq84nyRcbOM06W+ZdU0HJ+vWExThr1wHtsZjTCtYLgjQpiyUChhSdOUdLiFloKFM7RNFaZFcMwnY9pqRblasKoMwsvA7dZtxLEEPJsUKprIZJgIlGKDNPEQsaQCHfEDa8xKW1tm0wU34xtsa8g0JIlEoJFaI6VAZ8FYI1QOKiHJ+6ikQKgkHFtIECgS1dLKFCcK/KLCVAtywNuWGkPdrmjdJVYorMhRroca7CN1QtEpyLs5iXckyiClRYuA21KaoFkQ9ul1mCTEhowMuUyd/g6BuS1uJ25sizNNQE1UFbQtq8WC5fKSphnz2z7+ZYu0EA+rYWHiLXaZdZrKDVnobyL2/hC9/12a4i5GZhhBYFPAxo2CdGR9weGBYDXxvF4anl16zhaCQRYaGFVjGM9mtM6ivKJ1gt2dfe7YnKvph4iqxtRvWF55ltUL8id3MKbPq7OSs7Njdre6qMRim5Z7Bw/4/PNTlnf67B+MEGlOqQQfXVQ0wvCVHc9OnrCsTRj1UiqM8+ADny/NaZqa0WCEw3F9dUmWZfS7XUg0VkrqtkZKxWA45OT0GKWzMEbeG3FwdBec5c2XzymylN2DQ0CSFSnSQ5ZnbPf7lE1Iwm7qkn4+QukULwRVVeG8IdMJnU4PU9V8+atPef3yNd/6zvv8wff/mKvLG378139JOb3k08U10oWxFtFaDAKXdhBe0NYNSiY0puH5q89I//nvOHhwxOP7X+Ez/0PSJInjgB7vRORdhhcD6/AilBJrJmRAFOjNxis27BtFnuebQsI2LbPxJPCLvUclSRhhRoSOZSymwihbFIllcFJKEcYz3Vvd6ZAg7zbJ694GodDaGOSDIwGkShmtep06AAAgAElEQVT1d9jfu8erV19gQpsYayzL2lA2DV6Bx9KaBu1Dl1ohmVzd8OO//lue/epz3vvg63zjg6+zsz9CaYVW6aa6Wae0SinJVEi4HF9f0et0SNKENvI/gxtJk2VJGMEUQaiyRB4gHmkdJy9ec3VyziDNo6MTfNOAhGlZcTavkEKR5wn9bo+dnR0GwwHGWa5urikXS9IIpB8M+tzchAAOhCDLM/I8RSrB5fUVzoDWGVmWkaUp1lT0el2yvMC0NYvphOVqAdaQOo/yFh1HdiRBTw88K0VbG9qywUT0w3Q8DmWKFGEcSiSsyoqXr17HkKlATA0pngKVJKE3GV1dy0XgCU8bi3eeTpHx5OkjvvLuI4bDHoIGW0kODw+xSrKsK84vbnizXHKeeD5vZ2jRQ8ei78oZrk3DtlVsvcWO8j4UkkaAkQCS1jlKPMa3tDZBpCnLOoz9seZT+Vux9W0W2G9+vC3mrn/tNuzmW8H3bTF3zaDCg9YKJ996V0wUfWIYRJIk6DShdSE52BpDWddorZiXTXRgeAbDAXs7W0wmY5arJXXTUkbngZCasg5hY2Vj4thzCAbyeMq6QS5r8rxiazRkZ2tIVTXUVUNVBcZRrlOGgyFpkVMtl0ynM2arBW3bAoGbuaoqpE7odPuhYFYak6XBcQlBtF1frzgS5uPIuffhgUvSlP29Pc7PTzGmAQTlqgzFNzLgdogiN7fX/jfF9DtHR9zc3DCfzzeOh3CIWTsLwni8tQHF4rExDC4cSoUQ9Pt9rHMsV8vwLMcHw3uBis7S8N6lSGNIEo01jrauePXqCw537rE3GKHRJF5zeX3DlgpIE+MMMpGopINbzPFNKOy7acHkekyTZizQpA6YzuhoTesMc1+zsEs+Pr4mdYJ7O3dIrUQ5F5LaCY0KZy0iNlyuT09w9ZKtw0N6/ZzleIFwgBJhnE6AaVtcY+gNC/ZGR9iyZe48DSbw9nw4IEqCC8PGonfdWHO2Jc8yqtWKL55/zgcffBfrHIvVnK/+4Ac0WlNVNbasWI2vcdenvJvknM4XTKoFRoeDo1JQasFLZ2BygW+WvKs0o7xAC48XIW22RaHc2vtNZGuqcLiUKji6tEA56Ang5hp5fMaff/e7XF1fc24anMzivuNjUX/rYhLCgY8CZnwmfhvihOjEWTts4nJ8O8YYn7c1RzAcmNrgiljbN4jObXxwQUjJoqp5cXzC/f0jpC3xONIsiQcKxf7ekKpqubq+YW9vjyIvWK1WZEnGaDji8nqMsC4G70nWaeZSCNo2OG1lDHYJeCMfAzIM64N+uOMBH2KcjRMtCVVtOT695v69d9je2mY2nYK1ZAoS5Tg7OaYsQ6Jwp5/x+vycz58d82//3Z9x9+iAy5Nn4B3LN+fIbEVjWsxiDNbR1Et82+Hw/lO63QHl8ppa9ri4bpFywKP3fp/ZaoKrV3zjOyM+0IKTNy+ZzSboRPHixWuqqqRTdCjynPHVFR99+CF7uzscn7xmVZXopEOn26fT6VOkPcpqxcnNOYNBh8RIvvX+u/ztP/+cV8fH/Lv/5r/jh//Xf0CYhpef/oLd0e/wzfe+xvn5G7549jnlqgSpcbbl/d0/5PD+Y0orOTl7wWJyirOWq/GMxlzxx9/7PfaHHf7jf/hLTJKxrASz6wmFThkWih/93V+xmJ6DzPnqt96nef4lL89PyXYGuDQNLkTrMI3B1Q3CeKQLtZHYPI5h/0YEJw3eh+CuecXll69oTcuqqWiWSwaDYXiuPeg0xStBp9dDpzmL1SqMeyM4O7ukXi4wVUWmFd5a0iLl7tEDlm3Nk69ZXj9/zmJyhSkXCNNCdIAXOqSat63FmhDwJSPywBqLT2MzUIHSwemN90wnk2AY0JqiKDDWUtY1zluyfgdyhUxSkkEXm+VcLuZ4rSm6g5AbISWL1QqhNIPhVhShdKi5JAFP1rakeQ+tNKl1gA6hZa1BrlqENdzde4fvf/BHPBzsM59M+OknP+eXb75gVbf86Xe+T8dnWFoOj0aUixlaFty/s41O4Pz8kqax5HuPeJAMuPf0KdKc8fGrn/A3n/wTr8oJs8wizl6SD0bo7QFZr0Pe7aCSNNTeWjIvNL33HtN9cIfB2Qx9OuZANOTXktmqJkMgTTjUtjaM6kopSDtdBqM+wrmAwfBBzLHeoaLLsPWS0nhq34IQdIosEKkFUSiyGDydXkFv1KNtGxbzOatF2BeJmDKtFdYYUAJn/WYi01sPQsf9MzSma9NyMx9zPZsw3L1HtztAYJFa0h/uMto54ujeI2bjK07evOLi+oJF5Jg77zFthXMGpMB6ibNhVFvrBGFtxGgIWmA+NXSHQ3SeYaXi8TfeozQVy+tLUimxraVpHKSSVEWBTgWR0lmLVHLDg5d1iZQhrNWahqTXJVeSpm1xIjDbsyxD1HWoIZ3HicA1FzIIhj68nKEWjPdhLYUjiFxUjzF+0xwMblTCWswtImAtSq6bhN6Hmn3t5g0LgI0uTbURa50LbNwwSRjWCRk50oG3H5y3a6FzLRgKE2yp1nuUF3hlQWqUFqGRxxqFJzaj9rdfa8DrhPCnNW7IR+EwpNA3TRP385hfEtEub098ROQ1WsrY3F7vUkm4OlKiVBIbyDHULE0ospw0SVFJgkTSRmfrfHKF8I6mrkK/izgGz1rk/PXg4LXjVcqwVikfTCHOBkcoUeQUQkTEVqj/27a9xUoIF13rYTrJGLMRt9cfTVPH+x/qiqZtgugrbydj1kaHt88nYeq32Thp18FR63PHJmfFO9q2xhoT6g4Vw8ykirkRbbyXoU5IhApoSKmY1o6y9WgZXJi50ujEo6QHleBEAkKSpR10oen0NP2OY6vvyZIMhKVTFPQK6OYNRRbqeyV1MBDJFOs0iQhNeBPZvesaXEhA2I0Zpmk9TRscnahoGrSCtlpRlxNM00RHgUOplF6h6RQKnZjA3JYCLxzeS0AjZYpSCc5ohGtxrqE1NZPZkumkYTy3nExqLiaWtm3AtQhl8UjmpaFpHMuVoW08jgLvJHmvj0q7aJ2QZVkw7KnQcFjOJ6zsCi1iwJ41VOWK1pzTlEum4yG94ZCdvQM63QEizYkRh5tnUqGw3E5yGR9q9LKsA67Rh1o9ZDisQ+lCQGNVW6T0KNsihCTJOuzuH7G7e0RWdFFJDyeTsD5ZR9N46taGuq3YQ3UasuWSfDHBVSucbeiIkI3R1gZVjUmW54h0n7rYIkk7ZGnOME3IXI2MzZTNWmfjc+5tnAwUGCdorQ8BlQ68Vwjh8Wb9brU01QpsS9ssqJYLbLlCmZrF/JLL019xdfklv+3jX7ZI60H4sDCJtfXbpDifYMUOJv8m6vDPYPdb1HpIQ4Lzwa0TTnsevGIdAGKqliJJIfd44blcSE5vHF+9L3EGKmuYVQsWbc3ick5jMnbvfMA3f+/7rOwWs4vPWc0njJqSq9mUjz5f4GyDpkAuz2iuM4qeZjqZ8sWHP8fqgtdXQ959Z48s6zKuNMcLxfXFG7J3BY+P9umkHZzPwsizEnTyLMDdM0ddKlbLJd7bIBjaEGqT6hSnHLP5nLY1dPIuUnqsbfHAYDBisVpQl0vSvKCuF+zsjnBCcZDlaCFpqhDYo1USu9eh7dg0LUWnQ7fX4ebqjLYV9AYDfvbJjzl//Yrt3V3quuGzzz/j45//jPHlBb28oK2Ds9WZCizomJanCPejbRsSJXDtkmZ+TjW7YXe0S1akeAGrZc1qVWO9JxEOrRRFlmMnMywGLwLkXymFaQJcfc2rUlpvDuXr1PW1ABVcES5wUKSM7sD1yKS/dXd4v+le2RgI5uL4bFsbvIgd5uhgkt7FBZmNwCK8RyPIkpyn775HkmQ07TO8JaSUa4FzhgTAS4y3wb0UmX94F7Zga7k+v+Rvfzjh1ZsXfOs73+DJu0/odPsx8C3C/wlfu1CC2XQGzrM13ArYAGmwzqJU6FZJlbBhWHqHbcNi1jaOarrg+bMvwvexHrOxEuMsOhF0jOPeqEdntIPOC5aLBVdXl5xfnIVxoyyhyFO6RYFWCmMarm+u8DjqqqE1hvFkzGR6hVKabqdDluWRq+gZX07CYamqqMsV5WIWeEvWhnvuLVKG4sc0DQ5L01rqZRkERdfilQyjhDqkxCZCoLxApxonBD6OSIAi0wmVC53lBsHpsmblKoxzmDY48SzQyRIef+MrfOuDpzy4s4cWUNZhYS66HSrrOL444YvrK2ohqZKMY+9Y2hKP5ECnnLYNYwFCWHIR2IoyzEChopynRLDsNc5jhaORkoUIaaC+XIZmTPyawi2/FV7fxhz8WjDY+vfiL9cuiFtpZs2ADI6isBXcuvGsc2BMGDUiFD1CapyPuBUhOLx7RH9YcXVxw6KpmC9LpNK0xpGL9fhywmS+ZDxdsKzqiLRIEEqzLGvq1kZ3ITjJ2pYQxuUc4f0zlvl8xcAkZCqh1xsg+iqEcSSaVCiaxYrldE5bViRCkRUpRV4gheLs8pLpbEHrG7pJhk000EdkeXDoi+g/8B6hFDi3rmlvR8ON5eT0FO9sGC3EBzd/LPzXDljx1v3xG78nm6Lt9PSUNoLiE62jb+Ste0koVK2zoRCNrLDgigx/XpYliDBFYGI6sBQSLzy2DQV8oiRJmtA0VZhE8RbnYD67oV908fYe3ayLn5S00zkocMJjW4txlqLboxiOqBZLfNtSO4/sjvjan/4Z+4+fIh0cP/sVn/7VXzJ585KbZsVH12+oF0tkA1dty1dHB4xQONPghcesw0gIh3ZTV6yuBb3RkNFOD1uuqCqDFJpUa1Kdkqd5CDSqDYPuFm6roa0rvCupTROKuTgSFgp/jQyVfwhQkQLhgkDdloZXr15w7949zl+84drWiJ1tZkVLfpiT3b3L4eI+3cklrxdLfvnZL6l8i1WCBIXRUHrJm7alqCp6Okf5hgEelUoQCSYy0rVfC6LBuaIjTiQRCW1kkGkZit7Ji1fc3f82v/fkXf6PD3+KVzrw9zbmFb95LzajqWsnU9T21wep/xx/sh5lDQVyONjdNmjWTR8pxW3aMuFZWzd1tFJ425JExI5xnnllqFvHINM4Y3Ba41xAyBjjONg/4PLimul0ysHRAdYYlsuareEWdW0pywovAurFR2QPhGDQum3C+qPF5gBvbWiCusj9C2OGbL5/IDKiNeeXEy4ux2wPu0g8dbmkyHb46pOH/Kf/56/pD7apllNwNfWqpm01j58+IU9DWOcXz77ALk/p5FOQoIsBWUeT9bf5+FevUOkWf/Rf/ddhNG/Zcn1+Qblasru/y5Ajit6A2XTK+0+fcPLmc3720x+BtXz19Ixf/uIjnj/7ksVswd7+IW9Ozri8usF5z3Q8ZjiQbN15wiA6ft+cvMHKnOM3b/j6w0f80e9/m6v5NX//47/hv/8f/kfe+fp7jF8/Z376gme/+Ed+//f/J4p+TlWXXJ6f4TxcXZ3xxcc/Z7VqOXz0NXZ293Fty7c++ICffvghx69eUmQFz5+/YTqrqWlovWQ8/pjDgz2WswUff/LPdAYZ9x+9w8OHD3l1+hrVGExlqUyFaC1e+oATaD3SgDMeYcN6JgjTAd6ta/qwOiql8c7SThdMXp9BJ8GYGts05EUXKTV13VL0UraHQ5K0S6JzxtMJQjvSwlNVNWXb0lCjdEahFL/8+UdsHx7xve/9gKI74qOf/T3CG+zK4KwHqTAxnEwKjY5BYlGPIokBS04EFntv0GU5X2LN2vGVBCZl2dB4h7ACowM2TRU5Pk9xeYZIE4SD+WJO01haGZz53trABl/vDTJOX+gEJyAVIEWC8AlCmCBsG4lZNuzkW/zRN7/HVx6+y/nZJf/87CXvf/0b9Dpdxn7By8kr/uqn8Cfv/zHdImW1arj74B5NuUIpx+XVGYsS6sbjTMuDJ485uPNNfvXFzzHza3aOxly9/iWlrXGVo12eU55cMJUCrdOAhcp1MB4sa1InGI56LJBovyIpEkynCI5oB6ZqQEBRaCBkayRZD51qbF2Bie5JFwIzWwd12TJf1TRehPNEY0iyFKllcCzZcB9QmiTvIlXKcrGiXJSIODq+xjmt1xZrTBTpwjppjaFs6pACrhMSFUJOT69PEJ/8nKaB7d6QrEjobW2T5j1AkeYF2/tHUHTRwxHjmwtm8xuur85pCHutbR3NGoMUcXJKERzkUoEB7w2LqWOkdhEIjBQ8+dpTnv2ioo5ZI8452saHfys8Qgb+ohYS4QTGWXANuZBoY1A0tCZMIyZ5jhaCBo9BkGc5WiqqsgxNL+9xXqESFZt5t0iZ32zgr4VXhNg441VkpIdSLQaCsW7KxPOUC1zUILbKTV3k4pqwXt83TlRJdA2uQ8YiX12sm9/idkIFoqjjIAb/pUlwgq6btt56Qv5gsPC6twwO6/3U2uD4dM5h1s1x6zZnzFsEUHTIRtNO+KaiQUgFB6EQijY2iXUMQyPp0+n145kni45CAUIitSKJSIbGtGAdbQzrDOdTuakrQxDbem+/FU5v+bHhnlr31jlA+DAk6m2c2nMh8DaGoOHXyAoVWLcEnIO1dvNj/Xk8PhhfJHhiQzyi6oJAKbDWhOdChvP4uvkrhKAoCrI83yAUvAcp/cZY5XzYz60x6FrRtg1tXRNSZRTOtKEuip4qF/mnMlHhvkqPtTXOC6SL9yFPEGiE9FihEUJj8KRORme0x5FQNpbGSmSS4qoMgSVRJmAJEoHSGYgMT4oXanMv1s5/70PDec1ydSaEUBtjWJWOtlK0vqFqHYtVh6ZeUc6X1KsSiUIoQVZUbI0qtrc6DHoFRdFBpwXhAQaBCq5SkYUAVREzdoTDOcn1Es5nislcM5uWtMYgtUB6FfY754MW4yTTqkaPr0kkOAz5MOg1zoPQmrTo4GzA8HgT3LwyPu/ee7xtWc2ntM2Kqq7wXpAVCwb9AXmegQjBgt1Ol7wooqlMxmZNaMZXdQU+nLaLImG43cX4ETqR1KuWtqlCA0oqlGsRQiPTHj4boofb9IZDBoMDis4AnQgM0BrBqrSMZyVq1tJpPcO6ZDgfs1xOaaol3hpktmAym2GFYWU9pixx5YIszTEmx6cCL2wMWSSKiqE2cMZQx2kIkFgvsT64vb1QOAHeBdxIU9aUyzl1ucQ0S1qzpK1K7HxCOX7JavKGcnqOX9zw2z7+ZYu0UUCTPg0MNxQNe9TZ1zDb30VvvYfvPKEWHayII/Ne4HwbOgGJCC60OBqAkSjr2RpIpJLMy5ZnZxXfv98Li4StaZqgfGudcTNxzBYpD58ecPToKf2dIdIZ7i8l/PINX7x6hTAr8sTh7IxePkR4QyIFta1x1rG8MVzoGqUcKyN58XLOT48/ZfKow5//ye9z/8kTOsMd5vMlOIX1BiuIgV996rIG70jTBC00dVmRpKEbpJOUNMupGkOad3DGcH15RZZ36PR62DQnUQqTShrrUcoHnqCUWOspV2VMV0wBxWK5QCjJcDRCyQTTr9DS00kVWapIU8XRnX26WYcf/fhvub58ydHRHqPBkBdffkknS6iXU+qqRgmFqVsaTEy9D9NceTfn3v0HHNy5x6St6QyG1E0TEn2dRSUah6OXpRRp4Jj4MDtKGw/eguAmS5KEuqowzoZOKx68JU11HKUXwW6/Zhp7j8fGxHOLkFEsUwLvgyhpTRMOguF/24wXAFhnaIzBOIsTfuPidSJ2oa0jEZq90T2ePnifk5OXJA5Kb5lVSw6zDqM0Y0UVHLnWY6TAq5B2KLxAewFSYT20ZcOzT77g4vSUTx5/ytc/+P+Ye68nva88ve9zwi+8sXMAGmgQieSQxHDIGU7SBmvDjNdarWSVpNpSlcp/k1W+8oVdvre9dlmy7NnaoKndnchhjgCRu4HO/cZfOMkX57wNaku+32ahQDbJRvcbzvmG5/k8b3Dzxkv0yx4toDNFFqCpWpr5lMFwSBAaoUK00BC3yIvkbmNbrBdokdPWDlu3tNWM/fsPGT0/olBxA+xsLOoyqQimZV0JWqU4PDvjZPaMoKDX0ZRFSXewRKcsUnHmsbahNS3tpEGJqLwSOGbVlG6vT9npEFygmk2pQ8C0NW01xdUVKgTwjkImxawPaC3j3zsTA6Cso2kcdRu5YJKAzHJC2jqSLDIiqQe6ZY4NntoYpIiqmZF3HEznnMwrKudpSBvOkAr6AGWh+c6b3+Bbb9xm59pOVPVVc/b2n7E8HEIRuH90wCd7+xwdnpA3ik7WQYbAOHiOdMlpsDzpSWQdWHYWrXQqZAImFbcqcXUCFuliAzt3MA6CntY0bc2sbdOIhVQtk5YD6Zj8+wPaxecgDWuT9SwhMhaFOLF8JoQ4uJdiEfgguRDjJXtV8JHV17YW4zxBes7OzynKgqJTMJlXOB+/YqxeMnwQzGY1TdNyfDJFK0m3W6ILRWscwkalkg1JIS8ELm34lVQEFuECGhcCs9ahhGc4yOl3I+/IWstkNsXNHN44bJwwJc6XJ+8UvPLKbUaTCQdnR7Te4hpHe1QTlKQ3XKEoO8lFnja4wceCSETuG87jeRFu4ePDmprEKMUIaRAW69lksSSkQlRCUttGVXSITYCIV1PwkXO9gCUucBiRWRxrNNJiyYXoKMizqASOTOeoirm4NCU4CUEpKhsQdZ1CDCXBW44ODzhe2eDq6gb2/DkFlmCgpUYisK2lCpNYkGc5gRy/vs3v/Jt/S//6S1ROIHXOq9d36Cx1+V/+h/8etbzGGR7X7/CjH/8T7r77ER8fHfGt9QElDhFSgroU6ODQgC5LgpTMj49Z295Arq9weHiGMx6MwzBnPD5jdX0N00ZFaicpT6qqRkiNdJYg4hmeiaiqsM7S4pLyB1rTILXEWsH+86cM+z2WBwM++pu/4faP/4i602PmBFpovCjQvRW+/Z3f4Xze8smTj2OjIxXoqHI+x/OVcyhrsMD1zLKsCix5Wr64qAhKDXkIkXdokgLGJU6bljlaBLqTKfbxHr/3+ht8cLDPV6cnCNlBOYlQPjENJToQA4fwIOPyINoKXrzv//454AmJS7x4XQasjWEzUooYRCNkCrtLfId48cVBrYx3nApZbJ6lQmswrmXv7Ij17ZvgwJn4M5vgOD4+YffqLrdu3mJ/f4/T0zP6vR7GOGrryMuMaVVjQ1y8GmsxrV1osb42iF4oktMAGgg+4g9CiI0qPp5XWuXx/5aC2ilOpzM2N1cZLq1h24Yi02yuLVFklmu7l+n0l/nsw8+Y1HD50jYyy+mvDhgMetQhZ3Syj5md0yn6CNXhxvVd5tMKr5fY3HmJ1e1Nuh3Ngy/2ePTZJzjbMO8N6C0P2b19k4NHj9l//IhCeF7a2ub45IhvvfEaN3Z3OT4542e/eJcPP/qIyjkePt7j5s3rFJ2G5Y1dLl97jfWruzw/mZHPAlLnuDDn1quvsLtzmSfPnvL06U/59c/+hre+/z2knbFSWOazMZ2u5tbaNUw14uqlDeZVS2Mc1gqePX7M8tYuN26/xKzx9Fd2mDfvcnhyxPtffEU7HeOFZWV5HZ9lHBwcILOcB3tfUiyVbO1e47vf+S492UNWgY6UMZgpVyiSYqgNqMYSTAr4TYOVi3sEfxGcGDlHpKFFwNU1eVfjvGNeTTF1Ra83wEmBHdU8+eouWXdAyEusM0gC3TKnt7lOVebMRmNkEFTjEe/95u/Y3rnNN157m9/7w3/GweFT9r84RfhYGwjAtCYGSjoX2Zg6i/W39xRZji4yEAadCbJiwHQ6xbiWYa+PzqAZx0CmtjGomUf0M4QWlJsrjKyLZlzjIg+yrqnHMzqDAeVwiSYAqdZ3Lp53ZVESPVoeqXNaZ8FZgg0U5FzqbvDWN17nW6+8jvKeX//mF/zq8/dYWd7izp1vstbtM6kqXK757OQR89+0/O4bP+C1ras0s5a6Dcyqlsm4wlhJbQyXL6+xvD3ki6M9jjPFWz/6I67u3WH9/Xd577NfcjzZow0jLAZtHapqCS7Qhsh5zYJi3rZMnz9n31qWdYcbww0KpXBOgbPIdo4L0FQNKsvRZQebXC5N22DGU/pFdIkFu2BOQpnrOChKDbB3IWVveoxz5GXOxuYmG9vbOOeop/P4/KKjulGKFJxraZsaUzf4NmYgqEyjMkVTN0xnM7yQFP0+Mi+RruX07Ij9x1/yaF4xHp8zGC6xtrLK6voag9UNlle3yGREQYm8iDVETGlEZDqqfE0UXIjgcb6mKOLrXqqofszICUYwOTui0+1ijSMvutx+7Q0+f/99bIg/j7OBpo6WbeEdQUuCzGIf4yWN9QjhsKFB5CEGTBL7JZGXeBkHgp6ItOuWESVirLsYmAZJFKIEmWrEeBfEEziGeb3YiIkL8RQh4qFEqh8Xq2lCyjWQIv1zHFwvktnj238hjlmo57hwyC2QBYu6xaVBrkpIHud86uMCOnEupVTorMB5j/UeTINSLtZQCT3gE6PYOZ/wCOnn/5orzdm4XBeKOEglS1z4WP3FwDIi71ZmsW9Bgi4wsoPUiuHSkMFglZW1PquX1+mUQ6qpY3x+xrye01ZzbFNh25bKWUhuThHAC4UzHucXy8jkfAmOIFwMRbZtYuTaC57oIrMgLJSdYpGbYhNXPoaINcbirWHhzlvkKEglL4a/zlmqtr4QFMRaGDKtKYoCqWIeBEKiUw3sXAxpfPGHxwqE5GrMdByg+xCoTUvwISoNg0fJiF0IIpBLSZErnClolWJaxSBp42LAsxKSTCoijk9euMdUQgFqCSp4BHFREpSiq4rEF499nnGBaQ3TpuFoVKNUSP2UQylLllmGnZrtFcH2imJpKBmUjrKoKXKJEAofFvcZSRgQecRt6/AuLjNM2zIZe0ZjyfmsYlq3TOcV56Oa+XiEbT1CarodwbA348q2AjeMPQKSnog/bxAGUv0OgSBtxNOJflrEN9hgGVWC40lFE0wMRPeORNCO2CCl0FkcmrZGYJxEiCKGprkxdYkAACAASURBVDuQwZMR0EKgVUZZdNErybafsIIeB9aCd3gvOR+fYZ2h013C2pZeN2IdMq1p5nOULpAqLkKF0ngZF7MxJNKjhCfPc7Y3N1hbW2VWRcHedDzl6HTEdDKhm0kGwyHDzR0Gm5fpra7R63Qpiy7dIqfb6UIRv7ZwUFUtR2eGk7lgVHmKaU23aaJlPjjWG8tkMmc0OWI6q2iNhOoEssAscwhbsNRRqGCRIaADkTXufXQluiiiWbzMffA4r3Ai4FyLnc+o5nE46+ZjnGs5nZwzO3qMqE84P33G7PwZph0jQ2Sh//99/IMe0gYEzqtoLULSso5d/T5i7R/jl95krro4JxN3ViGUpSgV+EB3KFhfgwd3W1zIoiw5QDUT9NYEvZ5k3AqeHsxoXY9Ci3i5u0CuMmbNDGcldRNoLeTdJdrxOZ1SsTpc5tKkiyt3cNYgQ001P2K42aVTCtq955xOTjDWULSSpmpY6mQwnRIOH8FkzN27Ez7bOWBt+wo+nLDUH2K9oHWgdE50F3t0nkFQtK1HFyVVNQUpyMoOK2traB1RAUHEsIPxaIzKCgKQ6Zw2DR3xAusMVdsghaBuGpwxiKKgrirKTpfV5T6nZ6c8uvsFmcpp6jHnZ8cEW3PybB/XVOw/ecT0fMagUDRlgfISrbpcu/ENnGvZe/oQnGbn6i6tm/PwwVdkOkMGgRMKQcbB6RgvFb2lHllf4bEXfWa02UCnU6JkKmZ0lNo3po4HvtQXalghJT6hBhYMvbZtads2WrSJw7DI8/EEG4skHzy4aEkx5gWTSCarig0pAGahUEoBRlJLZCBZSOImOwa+KGRwyBADIU5Pn3F8uocP0f40nU+Rww2Wsj4iCKq2xskYkpaWulEVqnQMDPA+WUKhGlV8+dFdnj474MHrL/PqzVvsbG3FEDfvcW1Lv99HaY1bFB0IhNbJMpQ2r8ERnKe2kWvsvaWaTNl/9JhMSDKZLqqFCllwoTSup1O8zugWGhsC3SKyY9tmjkx6QGMaQgh0ugVFUeKto8hyJHHbaprI4LGtpa0bZPAEZ8kEZHhypSPLRgSqJiYetsGB9zgblVw+WeJ0ntPrdXBtg5ZZZHiZlrY1eBEQ2mLRjBrLuDFMrGfWWiZVTeUclQ80cMG5ugjjAbQSvHrrKm+8eoN+L6aYOzyz2YzJbMY0RG7nFwfPGLWWXtHDTefkUhOCw0lJdWmVspsxe3aAPJyQSYnzgrP5nMpYhFSsdfvR5qEkzgDB0jjHJHiaPKODxNQN1ro0i1lYfcOFjWyRO7V4zuBrA1rS58OCX7Q4V+NfrXVJER7fX0EmC1eIjdBie68SI8t5H59pFV/3Z6MxZRPtMak+jHwvGa0ypq0pijwiXLSkW5bkuYqKPRuXWYIQE7XT61+EF0ytkLbV3rk0/I3JwbPpFNu2KKUxbUvTRq6sbQzGA0rSLQrKsohKUmHpFRlba2vM2pa5M+iQQo9sTVPbiJtJr4E4BIo8RScXqq/Fm3Sh5vCJx5WYZmkQIVKheMEpEyIucIJHBEl3WDIY9Hm2/4y6alnMxYQQF4pQLpZEMXU3IhLj0CzTid1ZxXNdAuHrrDjiYFAIhQ45PQ3WthToeGbVlmY25ln+gE3RZ3kyY1D2ydoW4UUcbEpwbUq6lZpWlXzn9/+ApVvXeXiwD16xtn2JRivUxhqTPOP73/keo2rO/f0Dvv8n/5Lr3/oh//u/+3c8Hs14edhHpebBOYdOjLlB2aNflMxcg5nN2VhfR1o4PT7DuZogFOfnFV9+UbG2tsVwEIPh1pbXqdo6WkmlxOmACRYlxcWyj0CyKsagDKV1Ssh1PHn4mOXVLfoIxg8fsXbnDlUQhEwjVB9pStaLPm+/80MenTxmXJ3iZUBIDQKslIzw3DctvrXJpaAockOmbDy3CRgTVSWDvIv0KXjEprtGKpwPaJ3RCY7R4QmD7cv8wdvf5fiv/5zKNDiZIVRcVizCN0gcPZHsYIulkko8drcI+fqauv4CC5Tut7Zt4+cjDDwOaNPZIWVSTISQCk+XFEcLPnIKWVGS2XxOO69ZX9/k7PSM1hu8AV1rxqMxw36ffq/HZD5laTCg3+3QjEaUmaYsCh4/2aM/6CJllhrFlEQt4hYqLL6HZLuMy6LFEilc/JzyQsEef5lgeX58yA++9x02Xt7g7OQ5Dx/v8ezJPYTMuPOt7yKzPg8e3ieomno+4d4ndxmsrJHJkq2dNdpmGtPfrWFtdYmsKDh6+ozvfO8tJo3i5LRlLM748N2f8vzhR2yurZOJLYTzfPzrD/n43Z/xxq1LLPWhLBy9boGpa54+fkin2+O//ed/zPalDf7qr/4T9+7d5epL19m6ep3+0hbF0gZORFQCtmZ9uEx9PmNlY5Xtq5tcvbrJzuUNnj56yPWXX+f6K2/z5W8mFL7l8/ff4+pLu3SLkjuvf5NPPv2Cp3t7IAuclXSyAVe21rn31XMOn5/gg2L3+k3uvP1tnj2+Tzdv6PcG7J+ccO3aNYQueX7/hNXtHfJul+PjKfeePuLa5RsYZziYjRg1bWwqjUc4YiCY9xcIGO/ToiC9JuNV9IKFufjNNS1+3iApkQJa2yJERdbrIozh+PCI3qqlXF6LwZBNg5PRkaJ1yXBJMx2d07QVQpecHR3y/ru/4Z3+b3Pr+qvUR0cczh4BDtc2cd0mwBoLSXXvvYtM3SBxwVN0FGVRUnZzNrZWmUymaJWxtb3K4dPnPNs/pshLnHfoomS4s0W5tQSzitk82nttYtz2+326nS5WKJrgET4F5cmAaVrahA4KPtDUDVnQ9EPJ5eVt7tx6ix/cfptlWfLp/c/4+Wfvczg5pC4sMsyoMKysrPDV2R4TV2NV4N7oKe17P2X4/T9gZ3WLjWLI3qPnZGXB/HzKzes70BF89vQex82EiorR0Zg3Xv4m3379e3z/7u/y+b33effzn/No/pD5fEQzniEqG22ffqG2j4nVEs24MjyRU8qg6XZLpMhAZUid0ZcZWR4HJTpolpYG9Ht93v/LX3D65JClLEeoiCeIDGONMgYvZcQkzRuEi8FaiEChUg+UaSaTMVVdJU63jPVO2qaatqGp5rimjbZoa/BVoOiUtAssmIC6aciFop8ptDC07TlloShLz/nJUybHT9i/L9F5l/7SBnIw5OnhIfNqxrBX4M2MMovDDeslTktM0xJcrDGdcynsNzrDIHJHjW0wbUO3P8QYQ2+4zOXdl7j/6Wf0ZYbXnsZ6MhXDakTwsUdJqu4gPE1bk4UM6R1Ka5QoYh/gAjrP8TqLHPA0KFGlIlQ1rWnJVHZh6SUtlYO/eIcmJuYisPbrdWSsLwMh3VPxLollzwtX0YXqdPFmDy+EAosaauH0iiG6UcAiZOrZlLpg0wpBDARLyAGIaK48L9JZk+7KEOtEQhxMRXZrOmdcCt7WejGnjP+sojgm3oOSTObRlVl6pAzx9SgzlBTxbhACpzRBlqi8S7m0xMbly1y6vM5wacDScgep4XhUc3xYMT2taGcznKtwpk7MWBtfD0Khs2jr17qI6sxBztmhpaqnF4xZ5xvwDucTczYF2Xrv8NbFF3L6sMmN5ZzFGIvHY1LQtnex5164UUNSwqrklgkCClF8zXETa/HFoHXRh8Ci34hDbf21QLYQYu4G6TG/cH8uXgneR9yJs4CnaVzi9Uc7uQgRvxRcYD6f0xoTB9AuUGhNtxcD/XKt4vC40yXPC0otKDOFCILWJhcsXPT0CGicxzYv6kQg5oUkDCIECiV41ofdbcvmWsXWasHqUDDotXGJJ4v4NYUDGpyDtg3UjaVpGibjisnUcjKRzGYZ5zPHuLKcj2um0xbXOJwN+GAYDjQbTtEpINc1UkyS2jzQkVGoEkSs+2TaXceAvvgrctZ07G+Su46EvsBHtbUS8X7TOqO/tMLasM/K6gr94RCyiJJRMi5cYuBbFKKIpFoOKr5HMqVReQkuEJSgNpbZdIZpI4qi6nco8pyy06FqDIhZfP0EF0VBahEWKOmWBVkm6ZQZZXeF1eESSA1IrPEcnpxwcHSAMLEuGa5t0llapRgO6JZdyiwnkzoJCqJTT0hHr4Sw0oFcIAsJWReReialYEkIttHM6zGj0Yjzs4ZZ22KDwVYz5rZB2YxOoSM2zXuCV3gUrW0QKTbMB0kQktY5rAtYF4Vv9XTEeHZKMztHzM4RtmI+PeP48ScwO6I1MwQuPt4y5uFQWf5LH/+gh7QEgfIDnAAjO9jBO8irf0JbvExFvISEJzI7hKDsK65sQlNB1bRcWeowW5U8O/MEn4F1jOeOjU3FWl8xGcHzkedg7rjaFRwcTTg7mZLbgNYlvZ5GKMG8CZSDJezzDOs1yns6vR7TuiLvbtI0c8qlVbavbbKz2eHq7jlP9k+4/2iP1aWS9SVFOz3k3t2POXu2T7fb4+1vf5ff+/E/YWUIx8f7TO0pZbdHLjUiGITUWGeItg9QeUZjDUEKamMIOqM/GERctZI0TU1W5Gxub8Uhr/VYY6IA3zlq25JnGtPWqbER6CIjU5LWWZw3jM5P2H94DyxIr3j48C4+uLjNb1t6RY8iH/L8+XOkMAhgNp3iRc7K5iZXrt4kG3R5fPcBb7z9DvuHD/n8y3vYpBLoDYbcfvWbTBvFyekxWgEqDmhkssJ+vamUSiVAuEjpquIiibo15muDqXBhgfHe0zQN1li0jJdzcO5FY7AYKDkfJykqWlIWhYREJl5puuRsChJyDicClhBTuwWY4FjcVTIJCKUUjMeH/O3P/5zWzJE6ADYWnQF6WR8vNMgM6SpcNSEQLVyReeuiVUdplBDYIPEu2vDPDsa8777g8wePuL17mVeuXmN7a4t+t4P3cSggZUpulfKiMPIh0O112eiv8fjhA1rTxg2/CxzvPeN47zmZiYMMn7a5i/CoQFQ49joFtQg0jaOdt8zirp6ya9EioPOMbq9DWRbxMlcKEzymqagmDW3TgohpsQJJL8+QySKiVEzqxTjaeYUK7sLSrQBnY/pyhPbHwuD67lW21jZ4+vQxZ+dnEU9oIvS9CpEvJ5Rn3BqO5w0jG9WrgaRsTEyz+LS/sKorPBtrA9588xV6w5LhUh+tBFleYNoRRsBhNeHoeMzEtKxsbjJ7/DymvgZP7QwhKwgvX6Oe1cinxyxnJV0FTVVxXld4qchVhs80aI0FZq1nbAzn3lPraJ8Yj8bkl2wsrL9eFCEu7M+LYihqBZII7mtYg/hviA1yKrtfMAJjQ2jbmD6rtUzb+Dgw9NbEQikVBBJ5EYzUGkvrDKax8XwSL0L/RIDQGup5RTcp9jpFjhKBQmcUOrvgE2Uq52w6wzh3MUheFP9CgBaCXEXLW0YcYrraUrcBoT3D4YBMlzTGoHUgQxJ0jtIS8hzynMppnMrp9dbpruRMvcGl71ktVPVCETxIGS/lqFSMwYBSpLTiENloSsamQEqFSYytaANTqZHRIPTXhqaSPC8TZy0qZ7dWb9IpO5RlBy3jNazyuKSICzWLdw1FofEotCpiEmg9p+x0Y9Fa16ylJrWua/r9PmVZMp1WSDLWVpeRCJqqZmk4wDvD6bOnvPvLv2Y+OeXw0QMy2WEJBWi88Fhik6VVfDwa6ykvr3HptVeZe0db18zGczYv7+ADjKsxVnq2r+1ypddnJD5ADZe4/r1dvvMvn/PB//w/st1zbHZLTFWjkkqtrzus9ZfZGixxMj3lfDZD9BtWBz1mo1HkETtPphSunTOfnKKkZLiywfblq8g848HDuxjh8BpUUDSmiciSZBPUi3R3t2jmMrwTifdY8M0bt/nVvQfcPzigHQwZty050Fcd1ldW2VjZ4vXb3+SXH/wNIdgYApIprAnUXnKkYGYstnIQFLsOdAZe6NiUEzna3tiomL9oTGOoglKSTBdkWcBWDeOPv+CtH77DwZvf4j/+4pfYIkMEgUoMWpG2eTHhOVwoqGVi0gkhIkIjDTsXn/s6sxYWmBPxn/H5gFTEv2i8TBOL/UWQiM6ixRm5WE4Enu49p9PtU3a7VOMWYw2tdYynM5SWDJYGTOsJITg219ei7dJNGPS69Lo9QJJlGYuhbNM0aXEWHyvrbGLTCfCLZj5udF40ixcnW/rlODh8znQ+pdftMZrPmE5PCDaws3uDZ8dnvPatm/zWzZt89P4H/PVf/ITLl5e5+drrnFctw9VvsLy8zOOjY5yZcbXcZDo5Yu/JfY6OTjg4nvPhRx9g5scsZQ07Kx1EU1GdPca3Y+pqzM4aDDqO6fmM8/MxSyvLjOszzo4PeDAaYduaO6/e4Pj5HksrQ1A5r7/5bVorCVJydnxIPTmgm2k213f46vQZhycnvPLKS+zuXmHn0hZ7h/f58MNP+Kf/4k+5/I0pf/ln/xO7V66wtryM8Yr/4z/8BWVvyOFZRZ5ZvO9DyMiEoJ7OmHDEle0tbFjl/uPnOCsZtRDEjJXlJa689Cpbl3fYOz/k8PgheMv+3iHj4wlv3HmF56fPGZuas3oeOcJWkCemYlTaxcVVurEQgrQwDGm7GAst4dOd5KE5nyDrBtkpUYWOLilnKIuc1hjapqVrLYPeMAb6WIP1AW8MSkhkkSNtjkIjneHJg88QRWDn0hY3Xn6DujGY+ZRmMsI1M8o8xwiJ9xZn4lmeqRipFHnhOi3wWr7x+i2KTo+PP/qE7Z1tOt2Sw+NTgvAsX1pj/fXrMOgyTUF7eZHhCOjg8DJyBWfBkknIvGTettjWREyLDajG4YQiCx0ul5u8eeUV3th5mZuXrxOE5JN7n/N/fv4ee9NDpoVEdB1KKOa24XR2xqXNbdTdTwjSYoTF+MDdk4f8bz/7j/zhO7/NrcEWZUfRdRlrG1cZbnZ5//GnnNkatKKZ1HS0YmtzA2kkO5du8+add7j5yTf5sw//jFM/oqahOR9TnZ1jawuNg6QqCnXLy7sv8/br3+Ls9JTjs1Nu3LqBaQydcplLW5d4fvCE2fSMXpbx8O5nVMHx+o9/h72ffcTZJ1/RSWzqGOzrKVR0LwQtMK2nbaKaSehAbzhAac1kPGF8PmIxCwwJi2JNi20bbDPHmTYO/4hOO0KgrSsaF2iDoLUOhWLQl/QLjcQyrya4LINMIgpNW9WE4GjqEUejMyYBZJ6jJZyfnIJ09AaDuBw2Ub2opY584xDvfeuii8G5cNFbKBEdU2Ei6PV7zKqK1cuXGI0nHD98Qi/XZKoFbwk+BtoJXuQLSOJjJYRGBBfFJ0bgQgynDtaiii4qz6OgKdWTnU4HqeLikXSfCLk4W18IRy70tF8LoYwL+bhQC2lJyNdQckp6xMLtQVLjCpn6NJkW+VGhFyAO7NISUSDJiwIhVAzUI9WCWrNAICzyArIsSwGYIfVAMUTauciDtDbyOIWUMV1eLUQr7sXSKA02rfegdAyrvvheM7Ksj9aaQkdmLDIuWb3S5L0VNrausb6zxWCtw/JaQXCC0xPH470Z86pmftbimhYVanSYI4Mjy3KckkDkgOqUheK8pzVxgGqCp7XRPbhg7RPiz+YT/mcRriW8j5zlqAhggTYLYfH5xOElRARUEBeK4gusQ0J7GWeRSpKJ7KJmWOAi5GKgntTN3iUUUXrdhKSsXrB8Y/0g01BxMbxNw3jvk5MugI9IhqRRoDUNztgYHt00uDYu0qyxSWxlaE1DpywhOGSvS3COTEgKnZFnGikkSvs433CW1lmMj4sN6yLqz7Q2fc1FOJtBa41WBQqJswqhZERUibjI09kcSYvOXGSYL5otGRXVIUDTNIzGhrOR5nDimMwaJnOoTMZk7jFOY6yKghCgMprKdTidtmSqRWUVKMkCZ1AURcRIAITkoAKEtCCjytaEktoFHA4hDCpTLPX7WONpqgZvYxZI3TQMhULqPIlKAirN0JSKIseIX4xLnqqKqnupFEWRkecZQudITQyAzHTsE9uGyahlNonYwSwvY/CmWiAS2ugsVDmrw1X6SyuUnQ666FD0likHK/RXVllaXiErIqrumrVRST2b4016vQpAKzIZw6wjpTEG6Dlnoto4eDItGWYe2Rp0odDOM28jI8urqIwf6AFa5+ispphVVE3KU3KOeeXwPifLVHQJJNaGJUfJqHS2HqwLtDYuBOr5FDuZ0MwmTM6PqMaPsWf7ZK5mMjmjPd8jl45Mgg5RjY0XqAAV/+WPf9BDWhkkQ7VFb/0KSy/d4St5h315m9p0ooVBBrxe3MyBLIdCgcwEk3NPLh1ra4qD8zptUyQn04YdSla7in0lOWwkd0eO9dxzNmrwvuTspGZ1ZRnjPYh4sXd7HaTWWOPRtAw6gpWBJO+VlJ1VDg+e8+W9fVZ6N5DkjMc1q6tX2d3dRGdzPnn2gCcHz+kNBvzwB9/jv/u3/wqpDXM7Z3V7h7OTI85OjyhyTZYXZGUXhEbpOIwmBJTM8C4mmOvErHGp6K3rqDwUUrCyuoFSiqauEM5QFDnONHEr0+lcJGnGsJ8ahMDVFaOzIw6eP+H6zlUKlbOxvkrVtuxcvUZdtRAUr3/rHe7d/YLR6Dlnp8+YjEecTE6oQoNThm6nQGrJ4709Whe4ffsO7eiY+WRM6+Dxw/s0ocsHv/4VL79+ExmSnSV4vI9JqNbYi1RIkdQ7VR2fw0UIWJZn5EVOPa8uGlBrLS4VDMEHcp0jPMS4kbjVi4SDcDGMXWwIX9hd0vYJkcKNUuMXPfdIqbDGx2Fh2jaLICiLAm0lPlm+rZ3hfIskw3lPb9iPyYmipJdn5HSZ1iPqto4JoukxWEDrRVIM42KRARJjDLOzKRNvOPv8S6bTin+6dSlawxeAPhmb8Hj4xkFtDAbwjEYjWmPxPqoMJqdnPPz8S2gaMhkbk0WIBQktEYOENN62id8FOimf8qygUDnKx2YhzxJHqG4Q1kZ+rHe4tkUjKDuRQysR0VahJMZEVRcqp20bmqZCsEhsT2ypLHKTpYyaXeccrqo5Pz7lbDRh0lYEoWltYNI4TkzDxBk8YJyLScsh2WKzVKR5R6mi8iwkrhTBUeSCN+/cpjcomVRzRPBc6XaxteX4/JyzuuJces6rORsbmwTjmNdz8kFBbVqk0mxsXGJ1uMXh2R6tFagii0NVqxgMBuiyi5GSiRDMfKBuDUfzipqAVQqpMnyWIcuCrFOwtr6OsTE9O8jFazUNGVUK1wlcoAp8WKS3vlCHL7ipsVzmBetLRhuczhRZpsizPA4qF8FZid9WFjndMgYaVXUbLaKZvvgzRVKvRKvqDK00S8MB3bJIvKtoreuUicsl4uvZOIOxDu+SBVyrNGuJwywtdbT2q4jOKHQBIkPmHWTZYWVtHaVzessrqEwiOx1kOUgLnIBWOXneQeuMTCp0J8dnktr4hGBxNPMpTdPS7w/j2UFUo+aJmex9HBQRIMtzALwL0UpmLUovhraxwQjpMUFEzme06KmkmhZY0zKdziIzVxeUeRGLXREbIRUgiMBkdIqUsLSyFm2N9ZyqqukPByipmE0m5FpxcnJCp9NhZWUF5yzTyQzv42MdvGM8GtEf9BHSs3P1GmD58jd/R3s+wklQRQcRMqwxuIthOyAkjbdsXd6iFR47HoGpmUxOkHm0648nM5zM6K5tsrZzlcunc4TUHJ+dcueH3+fzP/+/eHr6nBs3dlnykvNHjyilplAZoQ00jcXVFjerODb79DY30J0cM5siLdApEMFS1XNkfo7Ic4Zlh8vXX2biAk/37kdcjalxNkDQKAU+2QEXimbv49IyeIsTkkfPnjC4vMPLV6/w80cPWd3cRJUlqg2oFk6fH6OE59r2dfYPHvH04EFsYnQ8W5sANlgmWca94MiqCmkDO4WioyS5iksfBNSVIUiVwh9VYnHHxtO4FiGg8IHyfMz08y/4r7/9Jo+fH/He0z1EViCCTFws4vtXphlXGkyGVAsgFFkek4GlTMy65KoALhrqRWCd1urisRFpYLsY6i4CQ/7zcMKoHgoLnp2UPB+NKA8OePnmTfRkTAhxgTOtK9RUsra2xNLqEo2p6fY63Bq8hLv3kNpO2L60zdloFJO4RTzX4znsL4av3i6GyDItlbhYrGmdked5DBxMTbpzHkJ0IOw/ecLv/OAdru4s85tf/5rbt14BlTOq4Gx8ytH5EV89uEeRKbZW1illSdbv859+8v/QK0vOTg5ZGXZ5qA1ffXGPxw+f8Pz4hDtv/5D58R63b+7SzTJ6mUBoSa/MyMSM8eiY8eiUv/zkfeazKZ2yQ1YUQKDfyVgZbHG0/5BcXuH6lU0+vvuA4dolNrauMlhaQo6f4WzN67ev8ejhg1jbdnp88vk9vvedtyiKkrXVZbY3l3h88IiHjx7xW//4R5wfP+Hjz97jbDLn+qt3sGRsXLnF1rXX+PTDX1G1LV5GJ03VzBiNDwhYsrJLJxuws/MSm0sD9h5/SrfXY3t7l8/vP+Xl22/SUYGllRLjPJ/Zu0ybeA5xuo9MwwTlFJlIwgkf0rJXgo8N9mLBihAvfksDHxGIyeDeI1oT6yqRI3KJ8hYfNKiI+zref8r5UcHy1kYc8HuP7hTUVY1wiizvY6oWTc3Z4UNOxs/5pOzTySRlrxenwhhaYekPB8xmE6wVFxkDSueRUasFaEHdtqysrvD8YI/d6zdZWRlS5grXzRE6EHLJ1qvX0ZvLnJsY8qOFQOYZmhxRV9C2BKGwFjJbsExJO64RCIadIev5Mmv9Va7v3OTla69weX2TTGUcnZ3zqw8/4u7dD7k/OWDctYSuRIto8dUO6mrGs8N9vnvzW+QhOst0QkbJMuPB6ID/8Iu/4L9567d5efsqA7dMHSw/+finfLD/BWubm1zpbfP9b7zJdDrhZ7/+Jef1mLPxlD/5gz/m1dvf5NKj9zmuH+JXJHpnm25dY6sKHZIgIOUFXHnpG/SG2zz6bM5JURJkxbWdXbYuvc7RyQn10hr0ch4+fshcaTZ6S/R6K/yjf/PP+Pj//mvu/eo9itZST5uGTgAAIABJREFUShWdPUIS2haJp5vHYZyxjiIv6PR7uOCZTic0pkUTgxmV0jR1w+jsFNvUSCIORy7YpqkmCsYwry2zIGOPYBs62ZQyE5GX34xjxomWOBuYVxVCOLIiQ8gsqjlDi/QOV0dF7LJ1DJdXkCn4SgbwxGAlKdN5lhStzhpEEn5IJWhNTdYoVJHTeMfVl29wfHTCtK5Y7ZT4pl6MSxEu8eN48ZayzsbBFArpTVTpWQsp7ErpyEu0iV+qhCLTApcWZM57jIvil8WgEkEM1IKLgDGIateoMIs1i3OgZXovy3RWL+6nNASM3+cLZAJCpNiBeLeIxH9dJL5HF6C8WCpGBm6aDagYTGtMDEMyxrxQ/4ZYIy+4py4JfhQLvE/6GgRQyZWRePZFUaKzDK0ypIq1p86Ki55K6ZJOMSTr9uisrbN7Y4fdaz2ChKOTwLMnLacnY2bTBu8tZdFnOOzHpbe1zOfnVPUc4RqkabGmpTJNrE9aQ9tGgRHBU1cTptPzVI0l9i5AWDymCc/gLc7b9Hj7i3s7xVsnBaxK7tHYOwQlcD4ppsOiRoo1ulmEhQV3IdrxaZq4OMOljsrOOOh1BBv/zIVqVaYBvU6BX1LE5Yu1MdPC+pjBElJ/GlF1IrpefUA5hQ0m9g0+fg/BWLyxCKUwzqEIkSddzaOoJADO0c4FRZ6noXfsAW0KfzPW0tR1auej4lVevBdVHJYHj9I5eE877CBkgVAZGYoMSa4FomtQQpBlBYqMEDRSBvJM4IxECZ1EY6CY4doK1yhcK8mER0qHUkTerhTkClqjmdSCbjejmANZ1JBp1SKDgNzjU8i4aS1VZWiNorEBEzJqA21w6ByWS0lWlmysryOcxFhDPZ/irKeaG/b3HzM6KRmtLrE06LOyukzZ68XAOSlpm4jomU2mjCcTCBKtFFXd0u2W9AY6ISeSxyvNLrx3GGdoZlO8hywtH4KSlFlGp+xR9DooFYOcy8EyWXdI3lmJLHcVBWxKF+SdLqWS9P0aeDB1Qz2f0lRTqroCZ2itvRDDeG+xLuBSVkVLSW0UxoCgiOdvOnOUa8DH88tbS6agyLMosPDxzPMhpAWCR6elchACJzQ2xGUKAqp5zbyqCM7g5hPq83Ps9Bw5OaTa/4L5+VOEq6ma5PiUOY2POS8R6WdRXwtb+/sf/6CHtJ2yz5/80b9m+8Zr7Jkhn37imblobfZyoY5UyW4TIu+vkShf09aGDz7zSOV56bJkNBWcnLUYLziZBDJn6fRyJhPDwzPPb+0U5J0+56MWO/WsrHqqpuXBg8eUy5e48couw36P86MjtNB0M803bq1yOg6cjc6w1rI0WAFyPBVBGl66usrSMOP9Dz/m3V/+nJ7S/Oi3f8if/um/YH1ridPpKcZLpBP0ekv4tmFyfsbK+npkD7mUNps2sJ1OBkmtJTyYtkXKqH5s6ppuWTCbzqIVWGdRgRgMLlims/HXLjsVLzkpUEKhdYbSiulYMp9PuHfvC67uvMTLr7/GV0+ece31t+j0VmlNQOUFt7+zhmsr6mpE04z54qNf8NF77+JNjQyeejzn4YNHXL31Kv/Vj7/HX/z7/5UwnyA9jM5GrO1scHR0yEv1DjpTF0rVhYXYtC39Xg95ekIQ8YJQQhMWYIvU6BpjaFPIyNcB71KIGCCTQo+EjAOhiDII4JMKRyy2f/HiNq2JViGl4sA4/fdCpu0paZMoIldUEpU8UsiYQiw0Xio8ESotpCYEQaYLVpZWogVAF+gEXdc+MM8mVKahyCTehrgplzIeyiEOmoP3NNZgXTyohFb4XsmktnFjby1Sq5QGzwVsXkqV0mQdVTVPbCKFaQ31vObZkyfUoxG5jFupPNNRQRiiItKFaMeVQqCloFtk6EKTS43TUQ2jnMd5QwTOm9jct5Zcxksw05pup6SXFSitCDoOgKvZjMa2EOIhi2pj6BFRJaaVikWBdygVC6h+f8B4NqGpKw6PDmmUYn82ZWottXGRiRegIg5lpRRxYCYlKiSeFcT6UKXYrrThBSAEup0Ot27uUnYyRufjyNlxNSdnU06rGWMTGVLDvMRPppjWsrqyxKWdHWbtjHo85aVLL+Fbz9rKFkvvLLPsGtT0nJNP76IHS/Su30D3engZLTnOtqxbl4JvRFRQFxkMB5hOyY9+93eZTKPlSRdZHFJbi7OG5ZWVFHL1YpjSti0uhevF9Neo/iQNdrwP5FlOUZQgZXyeM0mWx+1zVKu49F6CPNmThRSYlMieZWnDqF4wqOIyyTGZjiM/tNt5MeAJPqqmhIIgCc7Rtg2LMAqlVHpv+sVIKdmuZLK3RVV3kZXkRQ+V97AyoxgMaa2iN1yGYBBZAfkQmRWUZRmxLY1JlXkaFDhLJ8uSOs+RD4Z0u44sz9LiqkEiMTYC+7Osh5QOa1tak4ZVqXGxTtIYR9M6IAZEQVKMiaiCj+ElHoiKZWNbvBN4Z2ltTVNX9Pt9vBSRXVrX1PWcpeGAsuwwGo1jGISPB9VsXkW2m5RM5i1e5lgU55MqKt/zErxn1hqcbRFZzrxuGZ0f4UzN+uWr3P84p3Y142rOQAtKlUU7j4vnThCSoCAIQbffwbUz/von/y9P735Ob7DEcGnAa2++Aw6CzMiGSxitCUrTmJZPP/2Yt954g5WXdjg/f87qtRtc3r7MR+Mp5nxEG1oqqQnWU7uWuTVRoX90RHdlmW6/S1XNaH2DUpCFlqaeUZRTZvMJ2co6b//ojxE//SsOj54wq1JKLtHyt7DExyVcHIgu7IVKaaypefboAa9+8y02tOLoy/uUu1exKkN2IyO6nsxRueDOq3cYT46ZmBoyEBrKTkFVxaCRMYrPg8X6iqYt2NWKYYAcl8JwFK1w6KDpZiUCUnOQkCVIhMzoIqgePyLfWOKf/+CHHPzkJxxNJ+iivHBFLKycHn/RbC5C6RYKKaS4YAsurHtCJNs5C3WthwV3+UKRn1RQKi4UvFIXyhmZFoHh4sxcqFrh8OSE9bUVlNa0rcUbj20MjZzTdDJWBwPOzs44H51y62Yccp3ODZaM0XSKMU1sQ30MqHALRf3i+RNiocUEIaJqApIFNia3R65gckVojbQ5v/r1u1zaWuXHf/j7LC+vcHByzK1brzNcX+HRk32e7j9CC8HSyoBnz59wNDrhpRu7VKd7PDs7I881mVvm06PnzMZTJudnvPrKLW7cuE63u8zbb79N1XgGA8XZ6R73P/0A2Yz56u5nPHv2nNu3bvOPfvgWxsw4OR0xHp2D8cgQGPaik2b38gZ3H+zx+UcfkmddXnnlFru7VwlBUA67vHnnZb749CMOjgVP9p/y6edfsLk65OaNqzzZ3+PZs2fc/+g9Ll2+xG///p/w7w+eMp5NmIzPuHL5EgLJ9ZvfoJ7XfHH3PpUL7B3NWd+5TKFgOpowm885PTzg5qU13v72N6lfv44KgadHFTtbG9y4ucv54QNu7F7h2cEhr736Bk/3HnDntTeAhqN3f4FooiPKpsRF7/yFmpaFgvZiRisX1208K5POQiSGs/cB0Xq8NOg8RyqHdRVkBUFF5bWXELxgdXmV8/NzBAqlCrJM4K3AW4+1NdQGW88QvQbjomoq7+T0ezltLRhVM/qDPisrS0xnE8azKa13OAFZpiN/TyreuPNNfvmbX/J3f/s3vHrrFXa2NvDrK7z3yacU25uwNeQ8tBgb7y6RyRgy6QN+XNOORqz0Vrm2fo3tpStsDLfIyoLOYMjy0hprgzX6nSF4ycn5CZ/c/ZQPv/qMx8/2aOuGV7Ze4vde/h3+7uEH7JkThPaJwRiT2p+dHpC/UbC6tMKT41NMBgUZWmtUpjmupvzk/Z+j3inY3tjkJ7/8W37z/DOmecP5yVPeunmHG1evcHw85qfv/4zPJ/dR3YzVz37GtlhGN4AJtI3FZTIKSJARu0KIIY7C88GjL/i4/YLGGnwWODtvmFUerZbZ3t7Bn3m+/OwxlzZ36WzuknvL8fOnDFf63Pi9d5jhePjzDwnWk+Uq9jFt5AIOhl2apmU0ndPROSrPqeqa6WyGsw6ZKbQQNE3NfD7HGoNPyfWqW8Y7TUKQL1SSXnpmjccCBPv/MfeezZId553nL80xZa+37RsNR4CAKIBGpDjSSsMJzY5CO7PuxexE7DfYz7URuzPa0K5WbmQoiUOKViAAsuHbobtvX1f2uHT7IrOqwR19ABXiRt9GV/c9VXUy83n+z99wPl3Smo66c7RWQFLnZXmU4LZdS5ZrhoMRPRXDaTGG0HZ0puXs5ITlYs5oa5u86K3DkwCcTQFZIaTgrgSOEQfGUmW0XUOZSbz1ZFnGjRvX+ODdu9TSMCpyOucS8JNyAtZAaLKi8rHmtgm80HlJcAazmEeLsTJa4cU+JoEsWscpiRQQIvgZVuFSiAgmJHazT2Dzan9eW8QhIsNPPCfWhPUiT2FtKVyMpDZa2ecQIE/D71W9utonVsGXEbSNvfDqvLPOUNct1vroVywknuSd6dz6PJBSo13AkCwnZDo78pLBaAgiMnd1nliCieDiXYjrR2uczMiGW+wdHnL1aJ+s6BGykuG4ZL6Mvq1SaLJc0x+M2NwaQ4gB2INBoJ4bJs8WLKfnVPUE08ywTY21bQQiA9Fv3scaOKR8D3wEck2S+qfxeaoDfAJmV4G/kQ0a0iBXQCRvqMS+DdHej1WfqMT6fZMrwE1JpLN4H20AfYggqU/3Ez4C7oWU0QdYS3JdPAdrWd0jSa2jNCqL+1CmYm9tjKHumjUZywaHtymcLMTzMSSiiUry/K7pqBZLXFLMKiFjgG/n6EKHlhk+d3S2IXhBZxu8D7SdZdl0OOvWCltnLVpFog6sSF0xkC+XcV+LZngWbxusHxD8BtI6ZHAxuDtIlHQMiCQmgUgjogYto2o5z0FmXQw6FB5joW08JrSRICIUyIDM40CiaSJJTc4VXmV4Il7QywKZimQRG2IP421H28GyCSyqwOXMcnbR0pqo+uwrjcoKtMzoF0UcpIyGtE3LpVwwnc+ZLBf44LmYzzm5vKTfLxgNhxCgbRpMZzHORVs8Ecl0WkpaF/2ue3ke85GkiPOixJjWSmAxWNPSBUnZHzIYbbG7t8/21j7bu8eUwyFZUVAOIpM2zzciZiMkbWOwtkabtNdIiRCaNY4ZHLaraet6XWd45zDe4nyyMxGCLvSxIcch8TKgZUaeiWiJ58HYOKRrOxc9j7uWYCOZU/j040Q//uy4lPA+rsC261gu5hHvqivq5ZLMLLHNhMXFGfX0FDu9z/L8AU0zQ8ho5SF9huscWggUK3JVBLAbFvxTj3/WIO3O9h7f+c6/ppKKz++es6gMolCgQLh44EqfzoYAtovI9Ks3B8xnU5wKfPXNAaL1/Oxu4FKoGDzRwXCYMTSexVzx6DzQiUBvkDMYbVHVmwiRMxhmNJ0hVzGIZn97m+npY1BxctzM5jy4f8p465D9vSGX51MePw1cvTrmlS/dotSCf/zR3/I3f/H/0gs1v/XWl/mDf/VVNoZgbENelECcFIsscHj1BvPJgNlsijOOzfEAT2THZiqyb3QWfYcClqapyLLo3UoIbG/vUuS96DtnWoQMKKmpZgsuz8/Y2BxjnKOpW8ajTbY2t2i7hsViyc7uLlev3uTk8SNOnzziYnJJubnL/pVbZMMdjOpH/xFnQSpUb8xgMGYkHFs7Y5p6wd2f/YQcSa/c4atvf5s3f/NbvPfzn/Ds/IzdwZCNzT3Ih/z2v/63DLe26boZKpNRNp0kYqSDlRCNp3WafggRm+3om5L8yJyL74f1eOeQAooso6oqvHU0tqXXK6OHVfIfw6XmdbVAhIwyByHIEit77XcbV1AC81KwTAj4IOiSZcSKpVhojfOCzgWiP7JGpMNOSM2g1ycrc6RQDFSGaS0hK+nrIv784BB5ufZQzKRCkUiFSsYjQGg662iXHW3nsJspYXDFXEHG5jxJiMQq+MfZ9CWwJmC9YHYx4f6HH1GEQF5kCJ+SmVXApIbKpim5BCwq+TSJGIxXVzTekaEJKiA6SV7mKCnRRNm5zDJ0lkXPIBXDFNq6Ah892ILtiL4smta0iCCSYsSDl9FD0kWD8o7ApTEsmpaF6ait46xpOe8MLSIFFIQ12zaOc+MQQsYuMT1nNQ0W65Cr6L8T74vN8YidjTH9QY50no3hAGMagnZMzILOA/OWV+7c5ks3r/DBhx/w6emEZ9MJQUT/3H4x5nD3GkVe0rRLZNfgl0tEPgQhmGxsEgZ9fDr4hIpyhygBI4YgqSg1yqxlMBxE2acQFEUewQv/PCFVrRhxyfvOeYdiBWykh4j//opJEn+ViQkBkAIKfIgDnNQ4px4gPSd5FfsEoKT/IlCbmL7BM94YpwFKu2ZRlEVOECT5U0AoKAdFlEmugPKIKgExsCuIyOZwQiCExwVLZzyFylCyQOQ5XWPQZU5j42cYrIOuQmhPW3cxgMWYeP8LkeRNXQSdlaSpKvIso+yVcdJuOmzydatcLALKsh+ZMCr64zrnn3t3pUu21hICaR+L3kzGWMqyJM8L2qahazqyTKOzLL0P8bn4jraeJ8mOIFMBWUb2etd4XOWiRD8vUDoe2c46urZhMNxAa0lVzSJwprLU2BCLDh/llVpKemWfkOeU4x63X/wSP3t0n4v5OYM8Y3ewvYLBolRUsLY/8Qo+ufsLHv3sxwzaJa9eOeZ7f/gfOXv0iNFgSC49vUxTL5Z88sE7XHztNarLU6RQ5ONNTmXG52cXPHj0FL+oGAtBEFDTEYLDykArApVpCdMOUWh2j/c4O5ME00XbG2+pF4vISC2HzM5PCTrn+PAKi/mUeTZDiA6ZEolJTBPpJU5EVrnONN6uACHHs8cPGW2OefPFF/j+T9+lZzqq4QArNGWuyXs5i/mEQbHJ7Ruv8N6H70UZmFbRnyvT+MTUOZVQO0dlOuYq8FI/Y4dAGQJOeIK3CB/wWfSQt86uh0YuSLJSo6Rg03om737AtW98jf/xt36b//0v/px51yDLHj6lB+Pi4DCKPFLIFqRh4nPJaWS2iPQzXFrM8ewL4XkzBax/XVkfCCnIshj2FhvdOBTwPjWBSiKCQiKZLxZ8du8+146PYyGWGDvegusC470N+v1hZKuEwN7ONpdzg5At4+EWp+0ZXduQaUWQcThHiHuRTmvMB0leDMiyHK1VlEHWTQx/sj5Z/UQZbQgBoTPOJgu+94OfsrdzQL1s6WxFZ1sOD7epOsXO3jF7e30+f/CQRw8+ws0nODfDVDOkb9jfPmb/4JCzswv293bY3d2jah2PHz1GiowPP/iY3eNb/MabL1HoO/x4Y4Pv/un/w+buVfqjQ1585RWu3N4HN+e47jg7PeOnP/kRw9GA3d0tFvMpIhheuHbMex8+oZ5esJhNmUxHDIebnJ1ecny4zesv36aqTvjFhx/ygx/9kP/1P/x7/uW/+h0uJhdMTs/56Of/AELynd//PV5/67dQzWNG/T7PJs/QvTHPnn7Ojdsv8mRi2D7aBZnzza++zvvvfszMzdnc2mG8m3F6NuHRgyd86fZVnp1MeOdH7yI3e7jgCEFwdHyDyaTh7i8/4cO77/L2m/+WV1/4A0al4s/+5u9Zdg1ORNVACBK/Rl4ToJ/UHeELZ9L6EVb3MkgvovKkDVAZjA3IQhHKAJlE5YrBYMgLd17nYOeAn73zY9quil6bQD8NxYQTBGfwnWU+eUYWQIgMco0xDl3kNHXL1t4BN29eZ7mc8tmDe8yqBV29xHeRoT6fLfiP/+n/phz3MUFw/9EjFrMZw40xW9evwN4WlfJRsWMdwsJy2UaGFFkMUqn7fPOlt/mfvv377I2PQfZou4ZpteCiqnj8+DGPT37Cpw8/4f6zzzl3M1paSpHzm298m3/ztf+WrWKENIE/ee9v6MYCdPS513nG5+dPmTdLbh5f4f3HH1ALIChs29IvFTLP+Hwx4f/4u//M7u42DxZPaIeKIHJs7TiZnHE2XfLR3U+pm45Qai7tlCfnj3nztZf4zewbPHlngrWXeBXVbrlRbJabdFhOmnOkVgThaTLweUZoG/o62vnUszMeNBVn55fcPHyRjV4PnYNZXtCvp3z44EOO9o75nf/l3/HBlSv87E+/i1jWDDINOkcFR4agTXY2QipUllPVNZ1JSfEuenMuZlOaqkYhyPMC0zbJkzHWSiBi4JeU9IoMbToaGwegViq8zLDB0QbDoFewtbXFk5NnaCXY2NvDW0fb1HjhyJSiFIFMQlDRoq6rl0ytpdcf0h+NETqyghHJKcaFKEGXKQDLxbMEJMY7fLDkRUHdtRzu7XGx+4zzZ6c4IRj0ekgfB8ICl4ZtacBmoxLBJLl8r1eurRCCaQnW4m0XzwghCDqHlYRaJbl7JpKEPQZ1Om9TbyGesyhFtq79VkNQKXUahiZLnCAiS1OENMzzSC0S0BgVfyv59spvXSQANxDto56rOqI3aXyWw5rIimy6NvbPyFSTSWwALXWqa9W6pgZBVhT0+gV5rinKHqONMYPBECV17NdESLYC4LxA5Zosy1G6oBhts3F0yCuvHXO8V0AITGbQtCGSGHrQdI7LSUu1XDK9qKnmLcFLMuXp6gpTT/F2QnA1xiwJ3kQrnxCSf3dSwmHxzsQvbwiJCb5iQItkv7UaYsa/J1bHe8qpCEixhnAjQzn4GFBNwIV4B8XaQf7KV5aVaOURQmFdCilLSjIhImgvZawrcp2RFZFI5KzBumhJYK2NoJ0P0arAeYT2eKURItpUqCCw+FijSRNtTaRA2JWiU0Lyy1Wpd0OAt1ElmekMQpTct1WNxOP7OWLQj7k1EoSO5KNl20aSRWciwcJHNnZwsZ5aTQmt62INErm2tB1cThqwGnyUwgc5ILgCJTukNPRl93ydpc9KKU+mPYOeQswyvMhw+AQGRhspJRVKRwJNCBIRAl3TMkeiZIYWimjhXdO6lmG/j5KaIByd89SNZL6UnM8Vjy4sz6YdzmWxH5OaXtGnUAVllkUFsBV45eiVOYh+HHC1NdJKlm1Dv86pqibm4qSQEU8MLoyNucdnCuegWdb41qJzRV5kFHlkv0qpwBukUgx6Q/JiwPbBMUfXb7J7dJXx5g6DwRaq10crhdYi2ZDkhCDXAxhjOpqmjv1HCCAkWoI3DYvpJdOLE5aLBc6Ydc0qM41UBcgMobPIeFUCQ4ZzFi90GjAJjHU0Tcu88tTG01UzusUFbdsgpMKiyMpBYoArhI5gtLEe5wJNY6iqJdgOt1zgqiliecZi8oTF9Amz6VPM/BRnlvhgkXyBOCLi3jkuSjbLHB0MG8M+Z4tz/qnHP2uQVmqFF4KiyNjc6CFDFRe8zkl25VGyLsAFhUpMxL1ScjAMPJ1UtCeKMmRsDQTPFtB00LUBvRHQWTRgn8w8ywb29vpMD69yYiYo1VEWDV27ZDY5wZpDdnZHPH7Yj5LQrEDnkS25s7vFYnmJFp4s0xSFRmSKjz64y4//y3fZzgTf+Rff5K03b7JcPuSzzy7YPbrFYGMPmZUEneNsi5We3uY2znsunz2lXkwZbIzY2NklqBwfwNtELVcyNkpJyq60wjgfiwIpCM0S7+PB2e+NGA038MaQFRllXjLojZBSkuc5QUFlOsajMYfXXsaFgp2tLYYbe4z3roEoiQ4J8T33LuBxmCCQMgAFnQPbtfSKIdbnXLn5CqeTC/7zX/8Z4PAoZq3jYH+L3niT/aMr3L8/JwhB3bbgIgMqJlYHzk7PWMwWdE2LEXEih4zeeAjBaDSCEG0eGtfGeyEE6qaObE5j6ZUlOlexaZep+VTiuVxEEMMiQmwgMp3FoJIVeyeFGIUEHokU1KNTcx1kZAQqpehlRSx8rMWZ6Ltk2pTyTQYmQJFkHcGRF5rGxSCgzCdZT3C0wUOIsuh4eKcDVwkyFLnL8ckbUnUdwhgUEFIA2dqXVEhQGqkLhMoTqFNH2U9nePLgAWZZs1GUKJI/VipeuxRa5oWORYGTtDiqxrLwHhkknTEUox6j8QaNaTBdiwqCQmmEChF0FALnLLO6opE6poESsCYe5EqAFAovZDSMR4CHrrMRpJWRHSAkLLsI0F5UDRNjWAYwcZeIYKsLZFlkgFkXG/Y4ySel2kYAzKWJ8MoYHdI1hDi1293dRklJtajwAZrOUFcVJ4sZ55czfMi509vk1cGYvabhpK1pZ0tOL2b0+xnDrCTLRmxtHWDqBVXTcn5xgRCCwbWrkbkqYrqodRaCQTm5nsZKIVAevI+v7nkCa0xgr9sGkjRNyhioYEkhLfI5cyARsRNgEyfcMvbI8b1xLg4HUqEWwdcUkmfTZJ3nbAlgzVRfp82SQL2EsiqtCEGtmQ8hfAH8YeV3G6fkPgS8T16S4v/vmxnWPzvqmyFEyiYAxvvI9LUWEQwqi3wSF+JAxXcNy8mEIGHn8Ao+RJBJAHmeJY+hWJcVeWSKhxQEGAumyObOlMJ4T9PMY4EqI6ge762YZrumM66vW8TwOh8BWq0j83kVArD23E7fx9CDfpJpxz8TOqYVG9vRdhHo9i5+3rPJFAJcXl7SmZZXXx1HW5HEJtSZoMiyyIIJnrZtkKLACY3KckQQLOdLdg+vU/THnD97yulizrAcM9Qa4aMkMgQZ91QElsDeaIORg+2s4GA8Jr/3Oe/82Z8wPjoC27KYz1GDDZ7c/4yf/v1fsbl3jSIvIMBgNObWiy9hJjM++vhjgoghllJ7jNCYdH9CbBAnlxfIIkNmOTQdq1lB27W08xn90ZLR0FCfPEVnml6eURYFravwPkrtyOL6ionMktDFkI0Qkl2Kc7hg+OSDX7J3cIUXrl/lgydP2L96nXmQ0aJFSspgMabl+tWXefTkMefLM1bexFmRR2C+qgnATEg+kVB7y9IEXpSKK17TEyJKbkUELVGpKXMeco3MM2SRRysYa9loDfOf/5I3v/E2i699gz/8+7+lsS567IbnIZa28s9IAAAgAElEQVSRKRTWDVog+qgDOB9NfuIfxXvUfkEaFpm1/lfW3RdZteu1n9at5/mad/Z5sm3wAZTi9OKcjeGQXpah8jLJTCWtVXgxZHd/zNaowHc1k7NThr2CuvMMBj0W9WAd0BmCRKroH2yaDkT8PkhFfzBmNNqkbZaYpoUQG9qViiakULXgYtiY1BnWw3Q6Y3O0wcUkMnimiwuenp3zzW9/nTt3DnHkdF1NDnTtkkcPH0EwbGxtMzeeW6++wbPHj5gsnjCdXLIrDYqC5XTB7sFVcunRAmSmkHmJkJLja4e8/e1/wcX5E57cf4qpJzy8dx+lS8rBJpu7e+S9nA/ufkjTdhwf7XI5O+PxyQYXkwnXb9xgNN7F+X1GW1u8/cZXmEwWPDk95/1f/IK33/gyr770Evc/ecCnH3/Oo49/zicfvsC3fuu3Ud0jmrMnnJycY+qayeUZuhywvX+V/YMRhRPsZBKzOGM6mbDVG7Kze43P7z/mp+89or6s+fCDz/j5++/zdHaCtQ3jnZI/b5d01tHvl+xub/P04RO+/htf46tvf5uP7z3l/Q8/wXjS3qrWQI6QAlQKSE2H8uqeW4EMqxs6bvkhpWV7fNWgZB9Z5nQhMs5a69nMCl568VWuHF3lo08/gNohlIxgv8gwzTLe/6qkaedgbUwll5pe2SNIT5EXdLXDW8XZ6QVaOW5du8a0mnHv/r3oo+/jdV/O5uwM+1y/eYsnDx/x/qf3efHXXiff32UhHJkLSOfice0Ci8kMZwxbm1toqSmLkuPdY+zC8Nc/+Us+m55jQ8vF5ILzZsml61h2S5x2dH2BDQ5dB14/eJH/7q3f40BvI7rAW9df5p1f/Ij7tsZlHpssvM6XEx6fP+X68RXGQbO0hiDj2d/6DttF9VZdTZmed8iRwBCDXIQWPDh9QHvnK7zx+kvkuzl/8f53qdyAMT2u7h1xtLPNP3z6j5wuZixbg64Dr117mdvHN3j/018wrS5p6wZVlqAVjTHkXvPNN36DnWybd7/3fcrRBm+88hVevvYi7919j7OLU1w1BSHZOjzCSsVSGl781le4vDzjw+/+CF3V5FrGgaGL95VSitE49i/WuZgOj8B0HV3dspwvY46GVCitKcs8naOeTAhItRRAL5OM8ngee0EMchOKTBcE6ynyHlvb+zy7mKAyzWh3j2vHV7l39xe4uqJXFIhmCaZDCYXIYg0ng2Axm9N0hs2dHUSq572LTEEl1VoNIdLrUCH5ggswSqKExATH0eEBz84ueFIZRkGwW+Zx4BBCUhraVPsnD8tUU5kElIU0ZdcyqUlcrGWM89FEHRAqX58JUgiCVAkUk+v/v5qh+5XdjY9s7hV6FkKIlhOCdY8lktpiFUa2ZhKnAeIqsDUybONzo8d0PL+cc5g0ACeFuXoH1nqCWFl6ZXjA2hYRNEEJyrygLHvkZUleFIw3xvQHfXqDXgrri8oxgUKE5/YMmS4JQuFFhpQFRTlgc2ePzf09xrt9xuMcKSIgO5/XXJzVNE1kaM5nDZeXNc60eBP9i6WSBOuxXYMIDTJUSGERoSP4yBCPXJGUQxCiwip4l15vsgEkkSlWdXcCV6VIdhTpM5DJ7syH6OOeZgLAKpQ6JMVbZF2vxrYrooZEpjrek2U5rWlxTmNVDJ4VSsY1pOT63++MWfeqsLoXEgHKx2ArZ2yyLmjiqaDiGvEuEhq8i3kjQbD221950rd1zXJRJTsOR641Hk9nLVpKrO2SjYIB+uRZiSziXpFnOlrDOJeGxyurwtj7rKwFV2GlkaziABdtEIKg7ToWVcXTS0NjJaBRIUeqSK6SwVBqIisWCVqT54ZBHzobGC8WVBXYQUboLLPORMxDakpRkocV/SwCoVJovBfURnA6N0zriuLcsTGEQQF5LrA4qtoyazNO5orzpsfSO6SMAyATYoi4ILHRA0k1nZNlLSFolBpQt12yy3NRIWxj+DnE4HkhBIVO5Jf0vjljY4BWiHVg13bYXkbZY62Mzoo+mxt7jHf22Tm6wsHBMYOtHcreiGE5IOuX5CqPg73YHaZhewx2dKbDdR3GuKgecB2mWVJXC6rFlGpxSV3VaRgQ1VVF2SMvxqh8EPdCbQhO41AYOjprqVuojKNuGnxnmM9apouKbn5GvTjFNHW02esNKTcOEEKTZQVeCRAZxjmqumFZLejaCtEuCMsZfnnB/PIe02f3WcwfY7oZwnmE8FHhHJL6WiqEzCiKnJ3tba5s9RmVgjzT/ODeR/xTj3/WIK0QxI1UCrZ6ORuZ5aReIOQmQiV/oRCp5IhoWu2cYDYNbBU9TloYlT2ONiQn9+ZY7/F6wGyhqEaOvjIM+orLqePeiePbL/U5ebzHRx87NpRjs5/RVXO6aoZ3jt5WyWBjh66zZCrn6uE2zu/xyf0znp3OOdg9pqo9WuV8/NE7/Ph7f8vrt494/YUjbt3cJMvreEPXE6qqYu/oFlu7xxR5iZWCulogvGAw2qIsepyfPeHHP/ohr7z0IjduvUTV1mTlEB/HYOg8RwgZJTK9kiwvUDpL/jGStmko8wHD0Q6LxYLZ7BnNYsne7h6dbfj4sw/YO9znyrUbXEymkGleeO0Nbr70a/R7wxjaITU2xE0spI0tBtv4KF9AMJ3WXJxPkSgCmhsvvsrhrZv81d/+Cc1yzku373D2bMZXv/k7HN+6ysn5GeVwFEOGpI4SChEZsjiXgkTSZCrEaaBSCuMdro1N+/RyQvSmzbHOpeFtpKJ7ArrIKQd9OtPinaXIsmjAngoMIYhyvHRASq3TIRip894/9wgxXQTMtFYUeYZrbGL3xIKmKAryvMCRvH+0oqlqjA8oFNuDDbZ7m+ShRHpwrkPnBTrLohdSliEJhKiswzjW/i4r0JUgyIRmI8vomQ5tO7K2Rdgo55IhesGE5N2a9Qb0hxvkRY+qqiD46EtjJ5w+fcLJvfv0s5y8yFHBI3UsXNumQ3YSR/T3JQEM0gWCtbQmed8mgFuYDmFiorlwnrZpk69onJobY/DW4bUjeI3AYbuY9OkFyXfYoTTgwBhBFzQOqI1hYQw2eBbWsLAWEyROSrxYzeCjbEBpuZZd6cQ2XHm3rsBK0n30KyDESuoLlL2M23eu43BMplN0r6TD0gTP6cUcV0PpLFu5oH7wiE/dgqZtEV5QZnkEHomBQEF6jIv7RJGXiFyTjYaEINBIlHfYtsE7E43VIYUduCgr+cJ1wnOAFCHpuljoiBQeFjN/AytfydXmuQIDV7Ydq2GDW7HsQuITf4FRJ0Qs5KsqHlZlWa6ZeV9k3a1/nxjLa4A1Nd2rAdAK0PQrz6ovvPchrABav5ZZP/9c5Bpojpcdi1If0pBECrSO6zaulRhUEa8PpudPubycsLe7x6C3gTMpDZewLkxxHp2kdTalz8ZbPgI9WguKXNO1nizPIjOM57Yqa4lZeP56YpKuYTAYru/DyIBWqH5v3bjI5C2lRLQFCYLkJRxZij75POs8ho3JFILYK3t479nd3SbPM0y3ZDKdUhZD+r1BbMSbBVKElHhcRDa/C3i6GN7WH6L3rrJxcJMP7t+HrkNfPuXOzgGZkqkRi++UJrC8uODKbUE53mB+fooVkgxLPptwdnGBCJ7PH3zCl7/2m5RC81d/8hf8wb//D0gdWJydxeFLWdAGS2UaCmJzpr3C6zj5j8qGWJSH2lHPlwxGG8ycx7RL8jwDHT1cm2aJFIFSx1CWjbyHH2/RtUucbAmspH0SL1ZexxltZxFS0e+PaJuGulrQVEs+fP/nvPbm2zw+Pefhz39OcXwVi0SGgCQyKHr9Ma+8+mX+4R9/QGUqdKaQIjZQce8UWBGYBsHSOi6d5ZlXfFkV3FA9RkpHSMR58tXZBhRSkRU9RJ6tm4dSBNzFJcsf/oTffusN+Nq3+KOf/ojatlHFQhzieZ4PPeJNbNI6WPn+xfUV++k0oUlAwRfX4Wo9r7xpvxg2tn6eDyn0iahK8HHA7RIjrO0sT05OuH10hVwX6XyE2aLl8bMFu3tXGPRK5u2Sql6QDffZ2upxNpkxGo1QQtC1HUFmBOnJtCbLPW1rEFKwubHF7v4RddPSNtW6effRUTGtYYdY2R6kg3M6uUQQuHHjOkW/4N133uXgypyDay8xWzacTFu8KpgtPAPVoqTiy19+i66pmNWG0fiYbHBM1Z1Qt47j6y/yL377t5Eq4969Z0yWSx6ezdk/GOBVRtvFoJRZZQi9IdnGASeTnxOaBSrP+fVff4vRaMDF/JzN3UP2jhqq7ikv33qJ2sLlfMnjR0+ZT8957fVf45MPl5yNNLn23Lp1h+4jeOcf73Lz6Aq3b9zk6OiQg+MNfv7uXf7+L/+SF19/iy+/+Ta/PP0uotim1x/TkOGC5urxNQql6WuJloqDvX2KzZvsXjvi5OmUl1+7ysef3OeH9084nZ8yvLHLddtnONQ8ffiIZ6fndM6zNRrzW9/8HbRwPDlp2dx7nZdf/JR7D0+YLGt8anC/OJSTIu7V3kRmtk8MPCCyZhM4GwLIEP8k+EAwDlu39MZj9o4OuVjOqduWy/Mz/viP/5DxeJNFvWA4GvPCnVe4ODvl9Ok9yt4AUzd0rSHXBT0t2OwPEsMmWmpIFEpGb7zpYsLJyQNuXD/i4HCP+XLBsqqjh6ixlK6PzGIo687uHvnuFjt3bnBWzTDzCdXZJXmWpNHW0lManZcIG8hyxbA/5tb+dXY3dnjn4/+TH59+ys7hDq1pWOJoS0WbR49ShEB3gi9d/RL/wzf/HQdqF18HBJ5rG0d886W3OP34+yxVWoMhsDBLPnrwMa997Ttc3Trm2dmnhDKe0d52eGLwqkLS1DGYVW1o+ttjrAicNhM+PrvPr994meODHb4yfZU3X3ud+nyBXXZM2gkBR/AO0VnevP4qX7/zBtP5BWcnJ7imo17OMU1FORwzzga88cobHI6ucPHknOs3bvHirS+xPTxAWcmtO7f5x4+mfPDZPe5cP+b6/otMnj7m88vHNLMF1W7G4ddeY/bePdx0SYGmw4JW9IY9NsYbOOewnQHrIlDl41CSVd1HVO7oTNLr92jaGJyjs8gkJUSm/vawZOBgXlVkAjpjWbYdPkgaAwTJC7dexAnBrRdfYTFfcHDtFsJY9ne2OH3wKYuzE6RzlL0iXUcMoWvrmsnZGZubW9G6I9dxryXW01LJ9f7tvItApfdgHFJL6qZlOB4iyozJsmFStRjgyniA7AzOdRCe5zUE71IAMzRNh3MhDidW4KiPDNlgI9vWWwveooIDpRA6gtQy1QC5ktGXUcWwtRg0Jte1FCtGZ2yk8D7GZUaDUBml+0TmpA/xQ/EhpFDn5+oNayPA1HUmDqyJih6fwt5WVj3xU82idQUh/VuCoigR0tMrh4wGQ/a2t9Fakhc5vVGfXr8PQrEKMFMyMnWlzoBUg4gAqkTqApn12No5oOxFD8281ITQ8vnDGXfnNWfPFlSLFls1YBu8aLHeIIxDhA7pO1ywWBMiiyx4hLAILM51hGCI3usuDVgTg3k9zHfEwGkHYeXhGuL+kGrsaCsR36tINEmkASHWqrkQiH1mejgXg/5ksjRekT+E8CgVMxhWBBYhIJMChEaG2Kut+r6Q6oDO2pgnk/zkPSFZKwRECuzWUtG2CUg1kWUpJGu1n2MVhBqZviqw/vy7xtC0DU3dRAKFEOsAaaWjVduqb7HGs5w34Gb0+wN6vR55nqOVRPaHZFJT6Diw8c7hgS6kXnRldh+Sp65I5DcUnkBtLX6RYZwkzzpEqBB5AUQW8c7YUBQm5k6EgiLPGQwAZQkiowiGM+npy4wi68NE0XZR2eGdiC4jIkT1qBBRNeslpvYEBnjrUSctRdZR5AUST+M8c2t4dOF5fNnRhkiesx60yFA6kggCIGQMG1QqoFN9pn2gyHusWNeFigB5nueRsOail7NxAaEigLt6s0WWRwJHCHRdC0rg/SwqC8o+g80txgdX2D66wt7REcPRJr3+iEKXa/A+iIC3cY1bY2lNS1UvsaYm2A5TLWJuibWYrqZrl3FAb1qqqqYzDoRGyRwfVLS08BXKgbAWL6LVZ+s1rVBUJrBYdtR1y6ya46spk+mEi8tLmmqKNTUKjxKS0fYRRmuEilYRWTnECY3xkrquqJZzZDXHXT7GzU+YTz7n4uRTbD1DhCYqu2OiDj6I2PcrRZEXFGXO7vYmxztbHG732N0qyTIJ3+WffPyzBmkRUforBWyXmqtjeFAv6MIQH3LW9JH0CFJzWXueLqDfLxkODVIZZhcOW/s45VaaqjUM+4qXtgd4Z3n0cMnPnxq+8ZqiGOZs7exj5g8pC8mgDDy6d5e94yscHLzK7t4+k8mcMssRos/jswuOrx2we7yL9AWhO+XJoxMeffaI//73/iXf/vqXmE0e8uzJx7R1FUXVIdCaC57cb2mqKUdXbpIVfYosx4dof1/2+vRHQ5bLJZ2xXJydElBUdc1ovBUBZ5tM7BEQJC5WurEIcJbJ5YSDgyHFYMjW7j69fs5yPkcpwWx6gcAzn85odw39csx8XqELEBTIQhBEDOXwacoiRYjeiEQQUQoQzjA5P0X4aKKclwO+8vZbPHr4gF/+7GdQ11w8u2AwPGAw2qG/scEvP3oPDwyHGoxHBYXOMiw1wXm89JCBMTaxSOOBLkPABUdTtWt/WWtcNLmXcUlEti0RXPJRBqEQZP0C8HghomzZP29AVww476PcZZVo7VeG+QnwGgwHHB/vM5tXnH/0ES7EJGCfGKheiLXkVCpJpnJGOufVK9c4GI0JC5O8fVZee1DkObiA9S6FChly0jTdr2Z7keWqEATpCMKRC4FtDNaIRDaM1y6koyh6DDa2yHr9+JoIeKkYjLdZTJfc++hTFpcXHO1uI3VK98wFeI9sXMojiP5FqyTMmOQZg9OkUhjbRrnBbI4NHpVFEGIF2PV6JcFabGfIUgCEVArXmWRh4PGpaMqS91UTPJWHmbFMupaF7eh8NIR3QuBXiTlp2iqIbOjo+bnyuwpJ6pT8G4kDgAhSyPV+sfrsV/LdEAT9UY+bL1zj+Gif4WYfVxumzYKFcuxdOeT8bEZbNfz4yS+5sbfF9SsHeJHjszmIeNCb4LHB4DzIrEfe12zmfcgkWmX4+FHGYjbvYU1L8B2m7TBdF69TerwkstiAhNKxChsSUq79lOA5A271MMYkpkAeC1shUuH+nMGkVGSYN3WFd5Z+v78GR5US1PWMoigYDAZ0XUfXddGvSzwPgnie8gshsZzkSm6cxurWdGu26YqNsbrmNcjpv7CJp4cXIZGIn6/DKJ3VhKAADSFDCr2WRq3afiklg0Jz7+Ipp08ecvvlLWrLGrwjxP1xxejlC69JJlALHyf9Qsjo3bZigyTOBSEyE1b+R6T3Ns9zyrKXXvJKhiYIMv09QmJKxGvprE1pzWLNmrfOxvUnZWLHiHVhkxd5lFo6h7WC6eSSLCvo90q0jmEoi/k0glw6S/50DiUTs4bIl1DlkO0rN+mKH7JUlsf1jGKmuDLcJdMysjxFIBeCxbMz9vd2ufbmG/z8u3/HrLE4Y6LZvrGo1nDv/ff5b77ze/zuv/k9/uSP/i90UdK1LdV0wp2DQxpn+fSzT6hNQ18rlI+SKuEjKBNIg9a0N9q2Qww9o9GQs7Nn+MaQD3oI55jXc57Nzjg+GlLKjAzY6A2ohht472hMlZgnmsZYEIor128z2NxmOBqwubHNs6dP+Ifv/zUq1zx6/JDt3X1euXmDf7j7IaWtMUWJdSCUQgUNwXK4f5XrV+5w99P3QEf/N7EaDiX2JlLS6sBlgI+DY+EWnHnHrZBzmClkCOigYrgSAukFwXg80TNdxC6WMlj85Tndz97lN998g+Wbb/KnP/sBJmSgdLSGWXmskxrMtI+uvT9XQFnaN+LWKZPM1v0KELvaQ1bMpl/xg02/V19gPz7ffeL6R0jmVU3TWfaH42j34Sy4lrPLMy4mR9y4ssti2eFsoFtUDLeP2N+7wqKqIxO6qbBBUBmLCIJMSgIGHwL94UZk58b5dLJJSVLfL+wn1sW/K1NKca4ydre3WSwuadsFu5tbjPp9bl67wvbREY1TbB1cZ7TzmMnJJ1y9esQrbxwQmor33vsFP/nhj7h+Z0k1b+hsyaxe8L0ffp/rt1/n+isvcPfDz3n3g6d8ZfACp5c1y2VDP5O0fsFnnz3ljV9/mf3rN5k+9ty++QKXZ0+QFQQvuThbUGYDDvb2mZ6fkQ9GmGrG7taAi4szHn72S67fuM2zZxV5obhx8xZHRzd4cO9jHjx8yrXjA8r+gIMrRww/e8wH77/DH//hf+Lgyv/G/ouv8+HnJ/RkTr+3TX+wzbIyPHyw5NrVLWohaIOgax0f3f2E05Mzvv6t1+gPBswmC2ZtxaDMuH7lGkpZTh4+pNff5KWbrzA5O+WTTx/y5pdfQqkxRbZBoUt6WjETsfmNg4DnTEFEHBTxRfCWFYtMriapUQoeRJIpiyg9rjq6eY3yKrKizJLl9BIRAlI50AVC9zm+8gqb42ucnlzQtBXOgQ2BjZ1tNreiRUq9rKjbyHDr9XMGm5t8/dvfYrq84L/8wPDpw8dMF0vK4ZCNok/XNnhraY2h9YbPT56ysbVFub3Ns8tL5vUyqpoQCBXPMiEE/cEgDW4FtrX41qGspltULBeXBNVQ+Yat/Q26xYyFibzWTCqkgZ7N+NarX+fa1jG+Mkk5A4XO+MbrX+Od84d8MH2Al9GF0lnLvYf3qL7ccPvwOr98/AmNNJBJpI+gnCKuKVu3CDzWVfS3dnH9nHqx5E/f+TvuPvyIgS5QPjKTDm7v8Pnnj/mj7/85n04eM+wV3N454u2XXkc7zcOHj/FBMdjYgX4JwTDQA9566evcOXiRD+9+wGwx4807X8J2Niqu+oIf//Kn/ODTn/LMnvD03jm/Nl9yY3OTp5fPmEwm3P7SbcYvay62t7j7Vz+CRU2uMowQFIMeQiu61mBas05+N9Ymf+p43smkNJQqyuizLMP6WGsrpSOzMDi0dBQqkImChQ0smobaeoSKcu95VaPLHsfXbrKoWz5//ITN0Yh+2SdIjRWB1hlymdEr+wgRySN109I0DV3dMPGXbO/v0httUA76zOdz2vki5WKQAFQXy5pVQjuJuJLl7B4ecP/TB7QEnjUdSgr2yiISY6yLynIXQS5JXG9Sxbq3bZuYWJ9l0YaG5woKKSXYZNMkJaIoQKioSlIyBmutDg/A2EQMSGSQeN0BHywhDURDqr21irUGq/pbRKsJmX5dKVrSy08BUVGhFO2lUk8nfKoRU86E9wQvyPKcfq/PaLTN9s42vX5OPizo9UrKTCNXYXEyBbpGtAqtMvJ8EElOSuK8xvkcqTIoMnqDARtbmxTlkNm8ZnJ6gTOWrq5o2yWdjaxQTItoG4RrcaHFhw7lPXibrIhWPr4unc1J1bYiSXgfSUE+AbXeped4QrCpToxArSCFWKdtMpacqT6V0TvXObEmTwhW0m5+5Txfnd9a6HhviWgVEXuKyHoN+DVRyVhD5x1YRxBR3YyIdTLEIUfXxRrYWRv3fp8ICyEq04SUFGVJKeMg1hiDDWb9mcf+BJwL2HQtglX/Bm1EM7HOYXxUDqzuKSFCsnskBYVFH9osM9EaSUUbDIEg0xqKIr7u4KmNwdk0nJbRj9cZm4DNOOTvjCFyPxzGSxzQWzhCaJGFiPpPIZDKs6Wg0KvBt0BnjjIExr0c9j1S1PH+JUdozfllRdM2dL4lHxT0ypyy1ORFTp7nMYdDgPcaYwNd6Fi2Ld62VK2nNnCxbDhbGs6rOvVhiTnv8phrZC0YicgUudQEGWiFilYQQiYXSIGQgTx5MpdFSaZ1JLaEQObBdQZDCtQSAecjaU0KKMs+WSYRIqkRVc54c4fR9i6b2ztsjjbJizIOzQjRx9xYrInX4JzDNDWmW9DUC9p2QVcvaGYTnO9A+AgQrwD0QFKRSgJZ/Aoy9k2+AWsJUtOR0/olywYWjWbeeebzGdVsynw5w1QXLJeXtLaJAHlwlDrufdX8DBMEy7ph2Fbk5QaWDIekahq6ao5YnGMvH1Fdfspk8piqnoA1SBH9xh1xGG2dRytNv8zZ3Bgw7hcc7gzZ2e6xsVVQbmiKMv+veuDV4581SCtTUaE0XN3NeO24x73OcS5hWqd0Qx/hK+Kwisul4dnC8+phzsZGoG0arh/2OXKC9581GAcGz/nMs6UKqmXN0re8cwJniz4H+2M+UWNqV7JsKpTO6Jpznjy4y7WjbbY3t6MEW0iUzDk8HDL95Cmj/phmueTGtRGlv+B//v3f5bVXrxOo0b2AzjUXn9+jWkyQBDIdcN2c8ycV1eyM/YNrbO1dQZf9RMuuUUFy59Vfo5pPOT35nFwLmvmU0WiIJIseb0qSKU3XdCxmM/qDAaZraOslG6MRg1Gf1jaI5JnaG/RZLi6ZTs9wnadqA6YJbB/tU1iPl9FTzAWPDzJKCILHekdZxg3OrzdWw8MHH/LB+z/l9OQpQmgODm8wHAz587/8M6rzM3o6R+iCN77yFnt7u2Qq584LL7C9u8PHH7xLfT6nGG7TuchWFT4QXARKV7J1nRKrvfFr300poj9vnAKJNUhb5nk8BNbFmopAavBrL5DViFEqiXCJSbQ6MACtNcavENKV3DzabhSFQi4FSmq8BBcCtTXYqiIvcoKWeGOQAYZ5ySuHV3jlYB+zaKiFw4sEcBML7l6eE4wlmLjBhVUquI8LOzJRIlwXrAEXmToBqJuW4GN4ge8saPAio9cbkOUldV3T1Q1d00SplbF89P5dHn32Gb0ywwdL3cWpdoZG6wzbh7mpqYkgmUdgULhyQD7us1vkqbgFMoE0BpTG2Djxsp1BCEGnFaZbEt10ieEw3oK1qACSOKHzQtIRmNctF8uG2sLSGboAfpUWK4gHbcRnIUTz+LV8fFU0qhQGJ/0KZf0AACAASURBVPiv2J9ffKz+/wooj9Nk2NrZYPdgm6yXU8ohl80lHz56gtgbsrezS20r2taxcAE/q1kWU5QS5KJBty1eaLzPifVuSVaUNNIivCfLkqwrxHtGeI/wBqlbfFOl5HdP52s8Hr9KOk1ekIiVX09kHSwWM8bjjV8BWYyJhc/KgJ3V61+BNkn6smKuhnTYrQrDlZWBlIqtra31+5XnOVrrJCV/DgavGJdR/rYCYp8PILz3NE2z9m/t2hadvv8ii8J5t/4eVkxdIri5ZqoSp8TOYsOcMijqxpCXjpEuEMqtfTSlCJSDkhAsP/7h99BFn/F4G2OiFxQJPFBq9X7EKadMIR9SQFs3TCdT8qJIAWYqFszJN63tTGQKJ1+sL8p3nYsBAF/8bLzzeNdBiD5yIQVgeB+QokzgWHwvV/vNurD2UcZuncW5aL+xXCzZ2toi1z2ctSzml8njzbMxHiMQtG0bPaK1xnuDSCCelBIvFMVoA3JFKx0+0zyopgihuTLYWg8CtAvMT59x7+OPefUrb3N4fJNn9+5jaw8OrHGURcnTp0/5yU9+yO/+3nfIBn22D6+yXFQs5jMO7txhNBzjmi6FkEQDnNq20eZEPLfIECHKndquYTafsrmzQ9WUTCaX2IVFyAxZNFSmYracsd0bM+j3CY1nZ3OHebWkNQ3WGwbjLb701tf/P+beo8uyLD3Pe7Y57vrwEWmrMstk+epCd4NwBAGKoghQgqSFJQ4wkUYccaxp/wppSQMtcaCBtKglEQsixQUJjSZMd6O7y3RVZZk0lSYyMnzEtcdto8HeNyIbAMfCnaSJzDDnnrP3t7/vfZ832O9lwur6OlWz4ODghEXjAz/TWxLpePLwa979zjZXV0c8evqYnXfe4by1nM8WiNbg6hqpFNd2brN3uMeiOo4sZoEVhOFfbHJKGZwmYwELHOe2Zq9pue00N3TCdVI6SDJUQBjVbRhmdTKMsAhjUU6QO0N1cMj840/4zbdex77xFt+/e5faNAidxENaQMiIUDBdqmpj80vARWHrfLS7xgfKxXX0xWfvr/96+axfWhAvn9GQUNuaFonEOMvTowNuvvY6WZ5Tj0MqcNNUPHj0iI31EcanzOeGvB+wG1tbW4iTU7SWTGWwBzppscZhGnOBKmmalrqe4qWgrkNKs2eJUwnfSxjSqWBRdwItNTjB5HxKt5OwOhjiu4LD0xM++smP2TgYs3btVfK8oNPvIeUOv/7bv8F0OuGP//D/ZHY65rXXXuPd736bzZ0hH334c372Vz+ibsJhdnN7xF/86Cecnp9zdWuNT376c6p6xrXrdxj019GkjMclv/Ibv8EnP0442NslH2zTuJa9R89ZX1tDKM9sfkBZ1ax1OtimJi06dDuKn3/0Q5TwbN64zfl0gdw7Ctz3vMPh6Zij4yMm85o33vqArLvJ//Gv/oiffv+P+OCD7/K7/9Xvcudbv8Lp4THXb91B6pyTs13S2vL0aIIqBqhujwd376GEoawanj2Z4RoY9rtsrO0gXM2zJ7ugPM8Px3QHKf3uFuujq3w6W7B/WrHqDI++/hRtPIn0CFuDTC/uMR9dUkDgU2oVa7zoGoAL1W0UiEXe4jKmFaRzlKcT9h48Qg06JM7h2hrfyTC2QucZp9MzPvn0E1ZHGyR5DwNUpsZ7y6KtcVPBZDylWVQgU7SXVLVFJC0f/vynTMoxad5n+8YbrK+t8PzZQ5pmQa/XIxuOODw6oG0M+bCDWOvTaBnYp3WFIAzbpQoWdu8szgtm7RytM0zV0k4Es+MJj/fPOfjmG9qipUoy0s1VBp0OZ0cnMQlb4Yzn5dXrvH/1DdJGBueVFGF4altmTcWo10Odg/IC3xratuLp0TMe7D3m7Ttv8OHXH/FoegYiRWnFfFEidIpQPjhIREo78xzdO2R0bZW0WzAuS35+/jCIRGTO8x+MWc17nJ8ecn/yhGI04IOXb1N4yenzEzY2trh28xai32dKxcf3foaTktbB0dER4gy2RhvsbGzy5OFjrmxtsfAV+8+O+OMv/4x53sBGj2lr+On+V9y9W7K9MuStd99DS830bMzmt19DaMkn/9e/p2kNvaJLfzjAS8F8XlIvgpNpOlkwW8xRElLlWQYqIxStsUilkTpBeRedcQ6tAgYrSzRpkjBt4PzojMpZjBAIE6zVq2srpL0B4+k5+08fI5qayXxMf/MK0iSImDSfJ5pcJ+gsRbcNSutwLxiLtS3z8Zhur0O/16XTKXhetzRNE5wJPpxMjImDDRtzMpKM2juuXr3K188PaRYlC+fZn9cY5xnmCd2sCDgHF87MjfEkKjooIuKH6EoMrqpY+2qFxwVVbRw0t9UChwqYNK9wTmL90j0XRChCqqCqxEUGeggMC24fjRM+1J/eIxXx/4Q1migoqqo61n7u4vzmnA9W63hGct7HZmEIdPaEGiHvFgwGq6xvrNPvD8jyLv1eH5mAUy6uKQrvCTiQeKZdNqS0ligdDObWCpApw401RmtDWoLSTWDZ23vOdDLFmUUI+G1MCPoywX6NXYCrAxrOtoAJTWkXnJ3LhirOBiQFy/15OVD14dp6F1XDMa9BBNSBVg6cBWkRS1HJUqDsQ/4OUaAkvA0CGRNdoEukXxQeIIJDNEIiEYTGJFFYgwi4nmXgdhMxW2Et8/FMElx3IoaMSRU4/14HlJizlsaa0HRr2qD+lQLlHVrr6DhNQ56Mt+ACP7lp2yig8BdhYuHjEemmNU1tL95/JQTIoAjXUiFEPM+JMIARRrCoIiqjySmKPNbnocmvVPBfFlrhHbQi4KECtzpk1ATGswk1lfUImeB8S1l7jk8FrVE43WCdCIgNNIiUPPEownWzUSznhccriS5yeib0LjwVdVmCa0mSjGE/D24xGc6wjfVUtkUQ9BIOgRcJjZWUleV8bhjPSmalpzQRdeJDuLH3BG54leAUmCQqjb2hNSGI24qERMQBj/dYb1Ba0+0N6Ha74XMYR2tbaNpo01fUTYsQBEeyMXgpyRJNkaUUnZxOr0+nO6QzGCKFR3sHrQFpwjBWBZWSt47W1FhjWFQzmvkMWy9YlHOadoFtK2xdohQ4XFgjY4i01pokK7BOUNYO66OTzcQQMedYNAumdcXMKaZzw3xSM65rJuNz6umUytY4V4Nv0SIMh5QMoiKtEqrZKeV8jM56NKdPUbqHzjo4IWlti7CG6uyY+elDyukeTT3DuiqMFbwCFQOyTUCo9DsdRr2czbUuq4OcjdUB/UGPwSgj76jISv/bX3+nm7RBdg5gSaTk9atD/ujuQxYMkXIQAcfB3i4EoAXOSVoLWkCuEk6OF9zaTljpS1a6FYvJAq8zDiaW7Z5jdT3lsISDiefJbssH1zRXrrzEkWiYT79GuoRBr8A3Yx58+Tnv/8qvUeSaxgab6vbWkDQNDJet9W3WOhVd2SORnrKZYk2NFBlrmy/RyQbsPv6C2fgY70wIxXKO2ekB5XTMopyzsXMTkeRhMXagdUbeW6FbLVhMTpDSMj4/oj/cRKCwpkUKyWQypjo94fqNa9SLGcK7YLHRktaGSWtedJiOD5lOzqnLOaeHZ+xs36LXH4VgqLRAEK2PBCWEEuC8ZTYb0+1sAgIbGeO2XfD00Re4esFouEIqEm6/+gbPd59yuPsYSbC+GKGQ8SE+3j/i+GzC2tYGR8eHlOcTksEGVsW0SOdROsG4sLAv1WlCKqqqjkEiodjo9nsIoCwr2iYmKhY50/mccrEIU54iwyNonMW4S8h+mHIGNY61gIgHAhEs4jpu8ku7uLWWuqrZ3z/i+GSMB1rrwvX1HmdaamPwOhxaQZKSsJLmbPW7PJ9OA/cq9n4b51GpDrgElYZrbkKDM9ihw3lTEjbb1gbgufIpxlUID1VZcrD3jLXVHtYJUAbtNIvZnHnVhEl+WSO9Q0vBk/sP+OTHPwbvGKysoEXgpCgHWhekvR7VomZawhwV1N2dPkW3j+70SbMCnQgwwTLbCodpGpJMU1U1TdWEZpSzKCx5r8QtZjSTU+qqjA1biXCWpjWU1lF7mHvLxFkqD0tLklIybmYh8Ztlg5Zo/Y9oA9O2pMumg/OX/y5uymJphV9aLFxo1LsI4Q/dunDv3X71FlmaMp8vmNU1X+0+Z+zBLyq8PKK0FdYIOoMV6qbkbDHjpZ1Vfvtbb3N8NuUHP7mLSXMkOd4JvEyRWRHUAK7BtDUgIpheoXxUJesYVJB5pAihgMuGik6DKcjFAlMKSNOMbq8XE3HjARfHyckxi7Li6tUrJIkOA4mo7Alq0WCDi58JJQU6L3CxMRZplbRtg448ohfVdC+qaP96E+cXgof8sqkTeJLLjyVJGp+/JeZC/MLnuWBeWhvvg5C4GtS6QVG/KGecPT9ia+cGvcEI69KA+7AOFW6JcCAQgtHqCqur6yxmpyTCk+Y9EJ7ZYo6zhpXhECFUZMBeIjKatqUxJXWzwNNSFMUF3xtkCHCwFm8FKBWZQ/7i/gzFrIElFkIsBwxBLSrxNLahqWuyooMQLmpsw30spIyHDB+YS1EjbGxAm+RZTpokocGmkzDMEY6H33xNp+hy/drNYP2pSspyQa/fi5xIETixgpDiq0ND0UkwQrFwsD8+oyMkK93ehQI+RfDwi8/ZvnWblz54j7OyZNoYChv4cTsvvcwv/87v8KNPPyPv9fmtf/CP8EnB80dPmc7meG+ZnhwxPz5B23AAZsng8iDSGBIROot47ygXM8q2QiSCoptxPg2FdJHnAUExn/F8+hC/eY3BcEBXdUlcihPw+PAp85N9amvIBwNU0ef0fMr+8TFeOLqDAf0io5OmlNMzFDAuD3l4/3Nuv/0+ez8/Y3x4TOf6y7RZDzcvQdeU1YJcd7h1/RW+uD/BmwotNUaA9W1o2DoTDPhSYT00Dko8p8qxXy/YM5pZ7riqNasCvFUk0tO0hmx1yM7tl3j4xVdkVVjXut4jD0+o/Ff8xis38V7wp19/Td02yCy9uDfw4mLvCMMTR2ssWgXVko+DBBXTyq2xF8/fcmi1RPxcDrAun//lx31UQLp46Mf7oCIUArRmPJ+xd/Ccd99+j9msDgomITk5O+P+4yes9Tqsblxj58pV7t57QH9lhdXVISfeUtcN83KGs562NRgTBpdFp8tgMELohLPTU/BEZUU4tC7vbaVUCFXTOjSorWO+qDg7OSPPNKPRCld3djgdnweEhm7x1Tln5yckwpMNN5jMGhrjaYwkKQZsXb1F6zs83J3w7ne/RVnV7D/aY34+5a/+/GdIW3J++Ix/86++4i//7Af0MsPf/09+j/FZi0gTnj09ZOXNG9y8fZtHT57xnQ/+PntPHvLnP/gz9vf3kElK09S8960P6PVHIDTlYobyFm8afvLjH/IfbV4h73Q5PDllZbVPbzigtfDs8TMa69jZ2OCd97f57Oefcfz4KT/+f/4t65vr3H7jbcbHCybzmiT15EWH0WqHWV3y+NEBbVuxaKd0MoXKBZtXutz76pDHjx6ztr1Bt6s5OTskSzLeePMD3nn7fZ7vn/F8b8Zv/NbvsLnR5U/+7Q84PTjm9vVX2fz9P+Bf/q//C8/PprEZYcOOsuxYxInBxT0X9+i/4bDAX+zfbonYai3lyTmJM6hMoKTHVA3TyYRhkeOFY+/ga7LcIbQhKSSNgSWz3rWOtbVN0q2E3b19JvMFg6SDK2d8/vnP8RqytM/v/d4/Y3VlxP/8P31OU0+RWkOakXQKepkiW+szF4a6skitMfiIkgFvLa01CGNIdAyHRKOkIhWanfUtctPQ7XXJWDAfT3l47x66m6NteO6MMcgW3rzxKqOkh6s8KIVWkidHT/nzLz/kq/3HPG9PqJQJTjdnSbKUqjZ89uBLfunWHe7cfIVHH/4Qo1sSlZMkOUtLtY/BNImXVIuaw0eHDK4MyNcLKltSti1zN+fo/CGJAWVbeisDfvmtb3NldYvToyPmLPjq63sYCd4rXtq6ylHnCXvzIxpreLD7gKt3tnn12i26ac5Jd52PvvqIzw/uc+zmnGYlIpGkMqXNJWpDcmv7Or1FCMZVvYSVK1s8e/AQ1nPe+se/zu5HX5I0niQL+Q+mNmDAt57FPKj481zhvXihFozpJTJglbz36DTFWENrW3pFl1E/BwSlt1Stp7ECJwNvM0tSMu/w8wlHT3fJqzlJ06J1xbgxzI4SaEt6OiVFhPXHhialiP/f+AZhDfVizvjohCLPUWkaG1RNYNQKgccGVrmwCClJfRqaVV7RLTpcWV2hrCoq75k7MGXD3FjW84yVoodwFlNWCBmbk7gQBRXrDyVjXkFUbRprY23mIz4suE2lFuAizoDAxl2em0IdbUEEV6P0IXArtL1CRoyU0ZXoARMcgt74cMby4FVoFro4XPTORa6qwIok4rfCvqOSlE5ekGcpnW6H4WjIxuYOvV6fJNUx+0BFvI0NGKnQA8ULGW3eof5UWlyc/ZwAJ0DIgs5gla3rG6SFYm+/5fTshHI2oS5neG8RbRuulylxrkE40DbcV1aEa7d0TC2VxM6b0Bi3QVgUVsBw+HM+qPacM7HqC03e4HYLQx4Rh/3Ox/ovYlC44M++IAwg7INChiAmG882IXMiKiaXEzBP/BomfN1YO6RpSpomaJ2glaLfDc66utulbhqaqma2mNNaG8JzXQjNuxS6CBSKRAT1rBQKa0LD1Zjgsls6HKVUaJmE5qcLX99ZQ21qTNvg26DItW2DNS1KqcChbQLmQEJE6sk43HAX1yTUNoYacMbS1KHOzossKKuXgwYgkZJOJ6fEUzUWhUS5ENC2FDOE+9MjnLq4povKgjIIHdZ86TJwElzCSg8UNSqCF403kZudBieogqwQDF2GdZ5et8Ajw36BuFAIe9cGPrGDqoVF21J5QWskZWUw1lN5SSNNEH35FONrsCGjhrqi9DY0PquCTOckOiAKvNbU1mOlJ9cpwgf2dmc4QhUFPglhY9YalLWIqgooKqFJVELTGpxpw76kNXmeMOgPGK6uMlhZZbSxQbc3IMuy0MT3oSfg6wrpgjCrpcXWTUQHjLFNiW1b2rbBxzyNZQByqvQlak+FMGmPxFiwtBT9Ab3hFcrKspgH/FvTTJmWNfuTiul4hq3OKU1FvShx1iAVSC1RpMi2RnqL8BbvDNa0eBeU7M3kACcShEjRSUD/eRGCG+vFgmpxhrNVzCuKqmqZhEGXStGJpFsUrPQ7jDqKrbUum5tDOt2MwaDPoF+Qp2Fw/R96/Z1u0oYmCwgfEvNe2i7Y6GoeHTTInsW70EgTcboUDvmSeWsZVx4rNLtjS/rI8PoNyatXFM9OF4gkZ14qzmaO1oStojSWL58seOdqnzde3+T1Wx0eflFx/PwAOZuyv/eU8fmMqy/fJCl61LOWqgwWxdV+l343o58tyEQFrqKq22Ctieq2TtGhGK7x8qvvsbf7kJOjR3hXhwLPtZiqYu/x59TlmO1rr5AVQ1rrqMsF3hoG/RHdImNv9wGHB89Ik5zh2jZOaqqmptvNGeiEtqxwNjQ4kzzDWEdTNygfJqaL+YKmNSBVUMf2OrTOICOnTolLxpsUChWna8f7T5mdJ6SpBhUOoPPZEeX5MeX4jFvXb3Hv3gM+u/sxR0fHpJnmnQ++hRSa/to6z48PmX3UMBgOWd/eobKGrJOT5kkopuLipBMdNtClYgeoqwpjA7BaqjB1yPKMbr/H6fl5BMiHZMSxOQ+KvUSTpvoCQi5iGiX+Un3JEjsb7RvLRstS4SFkQC64eI/NZzWzecmirnGEqZ1pHZkU6DQPqaNlQ22DNTxVCYXWJKnCeBMmLNHGbJyjaerwcFpHqlSYWgH4ZfCSj3aZwP+1MqF2Dd5ZEqEw1vL11/fY3tlAdzOsUKS5wHFA3bbMy5ZF1ZJphVtM+eqjDxF1w+b6Nq/evoVSCWfnc6rTU1wiOaklNl1j++VtXJ7j0g5CpwE1EKe9lbM4HxLuW+NovUAsHN7nkOZhcmsN1llkMUIWCwYra5TnJ+w/36Ou5uA9C2upYhkRPj+hkUicCEsR1Zhh9quiytHaYA/3S/aiVzgXrGHeR+tGLJiUiv9uOVVG4KXAuBDoFmjqkmyQ0x0UbF9Zp5NmVNZTzmacTUt8kXD9yhrvvHaDev+QB58dc/Xl6zz+4nMKo7izvskVqbj10jWe7p7w6d4EITROKBCKNOmgpaAux1R1g0oStErxMjSghRckqcPGw6l2FmiDgtQRlINCxcl8CFgSUpNm3VBgWYeM13E0HNLtdUnShIugrouVdEk3/kUbMwKE9ywWJQhBt9NBuGVjOxSBLwaGLRVrQi1t+EF52jaxiZV3L2yES8XssrkjlWLZpF0GxvgXvp/Lhm1U/wpA+MAyQ6FUxupql6KzSm+4Tn8wIs17CJ0SWfeEUL2GXm/IB9/9VaxpuPfFXfaffM2Va6+wurFJp8g5OjoOzc6McP2cgYgWsMbgrLvgWi2LNWt9/LkEzgkW5YKM8Oxzgc2InEDTXtyzy0bDpdo2rFeBqddEdYe+sP6EwlNijaFtG9q6IkmSC3vRUlXuo8OhKAq0VvR6I9IsoWpqlAgc8cFgEN+HcO2XdiXpDNV8jvSgXLBGkmiqquTw/JBEw2raAyHpJJrJs8fc//xjXh/8GjoPaBNnDDKqf1965XVWbr7Gv/+T79PWkl/9rX9IOT2nn+UMs4SDx/dJ24ZAxgrDJxe5rK33mOWgQICSAcXhmoaTowM2rl5htLbObDxBaoVta8r5IVoWaJXSOsPKaEgmUzpFj15vQDo5pS7n/OzHf0ExWOPVt96lNxyGfWsyZj5esLN9nRMlOTs9xvmaZ4/usn39Om/cuMGXh2e89J0b+NV1mrpFWsvs/JDz00OyXsbp+JS951+FkCtEUBcRQjSCHc/FwK2gsp3jMdoz9w3npeH1tOAVDVekZKQlAkfdWDrbL5Htj9GLKZl3KO9IrEONJ/DwKb9+ZQv/quUv7t+jbA0+dXgSJJeHtoAMF4iY9bDEpCzXAyFCOFewmkaFTmzQLhtoy+f9xV8v1ox4XhRKYC1oLTGti4p4z6NvHvHu2+9x48Y1Do9OqKKF8PnzfcTWDp3hBvvHZwgpMHXN+voGVV1jrGNR1kzOFzStJUszdJKh0oy69ThTB2yIs2ipMNbFYdjlcEgpHe+usG8YC6enY65f3WZRVjzd36esGpJul63NHQ6PjklUihZw9eo2n374M57tPmFtOEDKhJWVPolqefjgCeujhG+9/ybfP5lRFAPyQpMKOHl6ny8//YSDg33O04S6ati+cRsjDQePHzI7foy3E9a7igef/5TWtgyGPa6sr2Ks5e7duzx5ssu33t/k9PA5J0eHXLt2jURq7t97yJ/9yR/zj//pf44ehO+pnFecTxeovIs5O8OWFcONDd56/VWe2YbDhz/jX//Lmv/6X/y3bG9scni4i/IG7zXP2hKroF5MOdx/ytl4zPUP3sf6jLbVFMWA0aCH8DW7u0fkxQbShVDVzz/+mOFwxNb6KrtPDllfu8PtN9/l9it3uLE15JUbQ7xY509/+hMePvqCo/1vkCLsBWH/Wg6h4hIfRWWhsRG77S/uBX45XIybQWMR8xqlOvhE4VvH5OQEUklnOKRqKh5/U5EmKaOVIUVPUy/mYAL30GpFNurTreaQC67evIEXcHx8gBQWnXh+9Jd/QoJEC0GNYDab46REDzN0lmMyRd02GGtDAJEnhMWa6Fqxgtb4YEFGYRc1qczpdPrkoxHzsyPsoEsiFZmxrPdWmNgFppyTiqAa6sseL23fQjoF3qK04snRE/63H/xrHi+OmCpHqYLqznuPl7HekfD4+SMOT09559X3+OFnn3FYL3BJQE9JC1InWBkYk0JIcqGxpWf6aEpeFCTdPLCehcGlgYq5sXqV777+LTZ7Q+7f/wKkYHW4yVpdIjsZroFMSt567S0mn/2U4WiFN6+9jp44zo6OyTY38alid37C8/aUMvOgNUhPG104xknodrmytoafzKkRfPn1PXxTc+fVm+QvC6z2HH/ygEa6kFA+WwQ1ngnNxoZwPyVSUeg0OhbDsNpGdqZQwSaLE0wXFUWekSUJVVmxmM5oTQimCucPD66inp2yd3BEmiT82tvvcmWwihUapxSdwRDTlOw+vs/z/WdI7xBti1Yi4JC0AhdUUsJYzo9PMMbQ6fcxrQ1KcwnSh4wGScDmKJWBD03WMIRz3L66RTWdsDuZUwoovcc0lrpd0FrLWielNwiomaapYj3sL/Yhay3OyujaCauk8tB6G9WvOqSQ+zBQ9qGjeDn4hoC1C1VcbADHw5EMYVXOg0RHZWNwNHDRjhVoJViGFHnnwIEXFo/CuRAOnWYZUnpWVgZ0ugVpIej3C9ZW1sOekGexOFyy1d1FKI+La8UynyJugLEIjs4RkWC9DC5EBWVZ8vCbQ1SWI7yirUpcUyFMgzU1mArhg/BECw/CYWMdF6oqCdKF4YBtf2FgH2rzyIr1BBRP/IixxEF1CJODoJxV+MiJFVGkExrKnnCvxMMSwdoeGr8+ZjjEPl9cW5cneYH/BV6tQsehRRu5sTiPbduAYVIOp2PIqglnJYuLaubYkI112hKn4awj0SHcvGkaTEQVhj59c3GOSJLkYhj1YpDzEn3hjcHb2Ly2JgaEQpFnKCVoWhOQMGqJsXgBXehDz0IiEC4Im5y04dnyLUWRoXQaxMli2dgNwgUvAv+WOMy4yIPxMfgpfh0pBC6xzOsFfqzwLr+o3b2z1EaQK08mE2QiA1XYeForMU5gASsVRceznWbMFnOms3moha1H+MCLD2AAT2Uti8pyNDOclg6kjqRTQYOg8SAwYA2tDUK0XIfME1dHjKIxeFkjdApK0giFTxNMltEqS6okJBlGZyjdoegN0DpBeYPGI2uLKEva6RmyadBohIZEaoosJytS8k5BmmYkeUqnmzMYdMnTTNRz2wAAIABJREFUAkSCThMi3wtrK1pjqJsFbdNSlXNMWwVlurPgguvg0rkVrvnSgamUBg+NqfE23Ju626N/5U26akDbNnQnY+TzZ1S7T+mKc6azlsV8GljQpsXREtKUlo13i/ctzlSEzm+DaauA5bpwVItLx3V4UsPgRBq8FFjh4tPuA8ojtDPQmSYpNN1+yuooY3WUMehpsq6k6ECeCRIlLurvv+2lvve97/0HP/j/9+u/++//h+/9/h/883ggDSFi+5OWLx6dUcsODh2sFrH5gAgKscY6SARzZzi3krL2XBklZFrx6FmNdRrjDJVVXN/RqFZyMm4xleH1qwXXeiLAsRUspmOELZmNT6nrGu8kqVQIb+hkjs21nGHXkYgFNBNsO8c2gXVijaGOXKK8KPBSkOcdev0BIKjLBaat8K7GmwZTl8wmZ8wnE1Kt6Ha6F7YI4T15nmOInEdnGfYHUT0jQsJ3jHEUkQvatg2LxSIsiHgWsxmplgyHK5jWoXXKYGWNvD8EneIJk6nlniYFoAPj9dGDr7n70c8Yn+yTpzl5mtKUEw6e3uNwdxflLc/3nnB4dEhvuEJa9JjN52xv73D7tdeYzBfs7x9w8+VXGa1vodOE08N9Hvz4Yza7IxrTUpUVWkqQQem1qCqmZRnYHjagC4QIPM00Hoa8c5Ex4yOn0ZBmKVmaBGvtsqnkuQgnC82luGFB5Nvbi4IkNIaCDdvHzVEQFLKVNTTW0TqHIYQxaa0C1Nz6OEF2CByrnS5v37rF2qjP8ckJxokw3Y2qTykVSnjKeoERjlZYatOGafpFI+tCgBJQE97Seo9XitZ7zucVTqT4rOB8XjGflZyfnLK/t8fRwR6z0wPOnz/lyddfBSWA1qSdAVbnTMqWaW1JBxt0t3bINzbJV9bJ+wN00UOlQYXcIlkYGFeWaaWZNB0OppqzusOs7TFpupybLmOTc1YKZiXMasmiFbReYoQiyXNIC47LivOmosTRILHEKXicwCt1Gcy0tOJqHYqBNE3CoSVUKsu6JwwXIncsHPCWrYfwurSNhwaEdQ6dKIp+h3zQJRmkrK0N+fu//G16Wcp4MuOb3T2OTs8ZjXrcfmmb9WHG/XvfMJ06JrM57XzOIM3Rdct0b4/Z+RlH4xmPD0559c53uHbzVRwSrYIN0jrLoixxCFSS44UMoVdSIhONlxJnHIlUpEkWVcuhCaVUGu4vLtEAS3XSi2ntSZKQ53lAErzAXF5a75evy5AwcVHAhqCvJF7bUJyZyDBdvhdLTMKL/0/IMESbTM45OT6i2+mQxhC1FxEAl0rbX2wEAX9jg3qRFR1WdoFUCUma0ykGdLpDsrxDXvTI8y4ySZBSxwaN5/TkBGMcw8FatOk4ymrM4eEeeVHQ6Y3o9IbkRUFd1zRNYFzbyOGScmmLUjE11oRitK05PdpHOkeRd5iXc3SiQ4BeVEPYtsFZQzmf07YNaRqKKudMPACF4hPvydMMrXQ4FPvL9xKCisA7ixLExqy6eB9evK5lWWKtZT4P+INOt8OTx084Oz1lfX394tqHaxPU2QDCOSbHh3z+5ccgbUgw84JUCNyiRBpLkRexgHY0VcPZbMr+/Bw8zPb3KSdnZKngfD5h7/yUN97/gNfvvM3PP/qE/aePmR484+zel/zmd75DkaTsf/UVyjZhCMOyWU1I9w1ezcBXBJRWJFmKF4JFWTEcrpCkCYvZgqZuEUmG7HYgT9BFB6lzmtZQ1RW1rfAyBIrUi5JqHvZk50ALQTkbMz4/Iy06vPbGuwxXVzk8OMA0DVVZ8dqtV1icTxlPp4x2rlO7YMtEK3rdPiujEd2i4NnjJ7S2QarAMwtKNRFnDDEwScYaTwpaoaiThImEk6ZlYhwJlkxJMilo65ajkzFXtm6wvnYFSNFCk0pJike3LWI2Y300YLAy4vD0jLJtcULilQBvQhoIUfMtLtdSIcULz6GPaid4caW8aPJG5ezl+vGLzGsfJ+NL7JFbrq+xBqvqiqY2vHHnHcoyIEacM0wnU4y1XLl2FS8lx2en7D0/wHroj1bC8Fhp5rMKG4ckeVFgjCPPCxblgrapaMqStqpDEGh8Zo0JaKSLnzcOf7CWXHvefucOnX6f6XzBZFZSNZJ+f41yfsL2Zp/ne3tsba+z++whvmxJk4KXbr/G+tYqX9z9kLwn2dra5Oyk5PxszM72FUDSzCccPrnH0d5jzk+PkdLTOsftl2/RzzJ6iUO6KYf7j3n5+g7CNjhvaaqSRCr6RZdOkfLF55/y/MkjPvvop+A8N27eZDqfsvt0F9+2lLOSV169Q39tm2cHJ9R1w2g4RDpPIiFNNcNOyjd3P0G3M77+7BMaJ/h7v/lbPHv6kN2Hn7My6LBYLHjtzTcp+iMO9/Y4PXrK+fiE85M5zmgSrdncXOHbv/Q2WuV0uiusb20yOz8nS1Leee9bnI+nHO49YWVQUFUteT5id/eQ+0+PWd1+hVfe/C5bL9/iwVefU09mEVoQBs6SgAgJidMRyLFUhiEuDvaXKyEXqlphLbYJ9lGnVAgriUo2rxRCBtWOTAQ6C+nuUmoGoxUm8wlGeIr+gFk1Z7S6wo1br3P9xm0WVcl8PqFpa44PDpmcnnJlZzvYZb0P4TLdBJ8qKmdCwJKQGGtRCLQIDGTrHd44pAz8T3M2Z/H0mGzh2O6s891f+hWeHO7y0wcfMU89o/4av/9b/wXttOH+o3u4RJGolOu9K/z6G79Gj05IkvcL/vjD/5cPn99l1vXU2uOkv2hkh4aMRzmPm1esd0e8f+c95udznjx5jBVhGBwyiEKYrfJgK0c9aRA1CCtZTBa4xlD0O3jt0Uh6quBX3vouG8UKn93/jI/vfYL1hkLlbGxskkjFvJry5OQZR+MJo2zEP3jnV/n2y+/w6rWXOTk9Zvf8gJ8+/IwKQ9YrIrKoRRKQP9ZCITq8eu02d27col7UfP3wG7avXOG11+8wm82oXEMx6iG9o3UGV2iaeUk1K5ksZkGx5j2L1qK1ZtgvyNJgkfcQk+W5aDJJqagry3hSorTgfDZn/2zGtLVYQgMzlZBLiyS46BLjuT5Y4+3bb7Jz5Sa3X3mT6zfuMBptMugPmS8WzCcTvIk/lw8uGi2DG0pJhW3b4DgzNiIALEoIUh1UiYELquJwXuKlJMlzHB5lPaasQ5PDmsjnFhgPtbWUxlKkCiUkSgicMSwDt0SYhlzY5S0uHndiDSaWmQcqKtVCE1AIzRKrE/j9UZ0qQj0ainfi/wn7iYoW+6WCNMakxc0jhm1KgmPCtAgVAlLzTpfBsMPm5go3X7rKjRtX2dhYZbTSp9frkWcZIoqLjLGAusAaELFVLxizQmM47lsq4tCECEgGEW3tSirSLKc/WA1NyLYKTlTTgGmwbY10DcK3CG/A2eCi8tFNEjmywZHZBIWqN4joJAAb/87GP4eaYMmpDapZC9LHxnhQqfoXamIfUQO8sM9eDl9FHKTGc4Hngnl7ubaGwdgSVRbqQRUELNZFlEK8D/wl1sBaS91UYShlDHVdB0GMCEM1GXsMPjZZTRsbhdbSmJZlsKmKzVTTGryzNE3g0jZNGHY1dU3TtDRNTds2WBOcli6e2YKUMKzzOg2ut2UdvPy99wGl46Pi2MPF2b1tmvD3cV+ROg7XRKiBfLTSB8SjZZmPICQoLQNuQoJUCTrRJEmKkh7pJdZInFWx8SsCU79WLNoeU9Nl1hTM2y6zKqFqwBtLokQYzOgQMi2kIk1zlMywXuCFxskUS4pXGa3UyLxAZQUqCQN2icRFREiiFFoIlPckOqiZOwg6KAYqoScUwjiEafAxaFESmM9KClKdgE7Jix7DlTVGK+v0h2vkvRFJd0DWHZJ1OnjborEoHKkQ5FlKf9ih6HUDg3bYp9vvkmdpQJj4F3NHWkwbMJz1IrJnywXeWnAGvI1oExNxlRXeByYzcWgR9gpL3dSUVUlV18zajM7mq6SrV3FpH5F2SDsjOv1N1rdeZuvKNYR3jE+eUZZTWlOBMLHNY8M1qRe4ekFTzXBNjWsbXFtj2/B9CQxK+Oh4cJf3dGg+IFzIGVk+o1pIhAnBxv08Y23QZ2t1xNbaiPW1HoNByqCXUWSBASxVqBf+8N/9xfPvfe97/yN/7fV3WkkbbMkWHZUgmYAPbg74wYfP+cqU+LTHMixGEIuVMHDn+cTTcZKNXp/5eMFpaVkvEq7t9DhpHMengrIxFL2MtRXB0xN4PBd8vl/z+moHLxSj1S3mG0e00+Ngeyn6rHRS1vop/WEfnQgELbZtoxIrNFSrqmY+myO8ICsKOt1uYPcIaKwFmbK2cZ08TXi+e4/TowmJ8CgcbTVjIeDRg4ob3rO6to7zMJtVGFKGK5vkWc7J/h7P957QX9kg7w0Y9nssyiZsTBJa01LXIUlRCkHdNjjvGQ5WSNMcawVa50EFJpeLvMWpZRGtLhrg1hqqxTmP7n+M27lBgubpfcHVKyvMzsfUiyl7izF56rmyeZNf/+3/lNWtHb66+ylnkxOapmFn5wp148iKHiH4RzKbLqLNBYRQwUasQ0c+USokgjoXNrAXlH/OOUzbkqTywhbiY1iA0po0z8KGZmOoGCKkhnu33IsuG0QiNLWV0JGL5i6sUkmSgDNBfYbHS0ndhs2nJaoAkCyamsZEDpAQOCUpihSpCYqqWDlYZ2LRE5tPMdUwWKybwOiIqlWJvFD/xiEUSkCeSBqvsd6RZxnJYB2TbdDk26A8ZVNTTSZMTyfMzw/wzQK7WFAvQspxZ7BOd20HOv2QfJrkyLyDLrKg5ioXeB8aM631TFvNwVywP1csXBelR1jVo+kqkryDFCnOS1pCMSFNhW5LhHB4O0eZCW52SM9P6XX6bF3vc3hwj7Pzw/BW+MCoCYPv8JxrrQLMPqoGAYQMHMALizbLMALQibpUZnp/MU0Xv7BZX/JT0YJi0Kcz6NEqaEXN6mhEN8s5Oj5lOm/46sE31NSsqoLZ4oyPPttl7/kJZiGo2gaFYlrWTI1DWM+zB3t8czzFWIkQjiTv4kQb2HtCkGQdVta2aE0NKrCUlZTYtsUjSfIEhUa0NQIbVYYiKDSjfV4ohal9XGcu+cwgowo+FqzuUi2+VKT/bViBy9+LiCIIxeOl4u5ywhca4b8YKrQ8JEoB/X4PCM1y7+0vWKaFjIOJ2Jx9kYO5bNS9qKYN31646b2MIRQ6QagEZGjWShVsbFIGxbKLhwU8JIkmzcKhQsiU7Z2b5HmGNQ1Kd8L95QVgyYuU+XSOICSZLg8zy5//RSWwdWENaeuKZCgZjoahBrZBDdDUFU1d0et2SRNFVde0dY1OkmDPFgJjGup6QV0tcMbRH65iPdGmvrwGLvKIQ9heQhItZi80yf/ae5IkwZFgreXKlR1sa0iShOl0SpqGQ+myz9aawLrq9XoBIdG0JCollZJWa1SaMq4qOqenbHVXggXOgTk94/CzL+i99x7X3rjNXz15wE7eZ9Dvcf/HP+QPG8s/+Wd/wD/6nX/Cj/70B3z4gx+wKSWNc+w+eUZVL0gvrIEBo+NtSCdXQodQIO/DQhcn5zhHbQznp+cMVkY4XaE7Pa69/DqTsqW0lp0b19m6eZuvP/uc4aCPOQfjDHMHjagp64r52QnXb73Gg3tf8fjJN2RZzsbGFi7rceXl1zg7PeGbu58xPTli9+FD7ty8zY+/vs8Xf/mn5FevM60qTN2ivSdJYTRa49atN/j0qw8Rsgl7hg1D4ovkriUOW4RDshYa6QSVh2MtqZylqismzvF+p8u6BMZn1P1z8pUNtMpAtSjXkGUpyntS5+ifzllZX2f45oD/++u7PK/KcHgWhCAywaWaR1x8CwgZ1SbRjhr4d38TXfJiU/byEPg3lfXLV3vxsTAEtTgePPyGG9fvs7G5zXg2JvCwFdPZjOPTMzZ3tilOT3nw4AmV8bw9WqPbHdBYwfrGBvv7+zjnyLKMpjHMZlPchRXNhYZf5EPjfVBt+UsedogKCUPUo8OjENSDYzKfM52NWdvo8smHP6TfzXjl5nXyLOHg4IDNjW3myYKiO2L96k1Ox2co7+inilx6nj16jG09Xmm63YRHf/mE1Y1t/pt//i/4/p//JSdn55zufcO9T77P22++yfz8hLffucNkfMTHH31GlqXcfuNNZPqczz79hEGR0u8VnB0e8pM/+xG9bk6iM6yxvPf+u2gtOTuZ4Ko5n374Ib/5u/8lN196ha8+/xiFZ6UoaNsKU1dkWtLrZqygmfcEP/2Tf8Ov/sf/Gddv3Gb32UMWdRkOq87QHwzo9Htsbm/ipWRRTSnrM1QypKoVn32+R7+/Qt6dsbY5QhjPqN8lKTpcvX6Vk8M9jo+mTKqKLK/xHqpZSeoV6Jyt3k1+7Vf/Kd//d/87bXmIdyJkES5vynjAeZFzLPhFbM7lfRnqvqC+A1u2yCRBZ4osS7CtZX4+gaEiTTXWt8yqOgSMWM9w1CUtuhjrufHKa4xncxbVnMl0QV6M2N65xtnZPm01x5qWeWt5+mwPnacYKUi7XawQVGWJEw6pE4TQF6rfpcLMtPH+bFvsXGImM9ayHHl4Tl5UdJGMJ+fMmpJSCq6vjHh963V6b3V4svsNB2aCbATra0P6uoO0HqEcZ5MTnux9g888RjqckygraEPvm9iOwgFGWO5+8yXffuMDvn3nXb6+f48H4z2Sbj+cj2wcHFkfDqEW0iRFKcX8fM74fEKapxRbBU40rKQ9fFvz2ZOPuHt4n7onGexscPXqDcy8YTw+5/HhYx6f77OzssOvvvv36LaaybNjVjfXaZXjwy8+JlvtcPPqNaRSHEwP+ejhRyycQXnBWmeNX3rtW9wcrPHFk284PHzGS6+9wmjQp55NWV3dpK1KynTOxnffYfH0OeNv9kI6vbUIH9AZqZIYFPOqoTYenYbBq41cTU+opU1r0VrQ63WZTOc8OzhHp5KFCevIsg4Y5ppumlHPa4o0xdaWL+/fY5B1efPNb5EWKySJpluss7Ulef1Oi2stB7uPw7D3opkCJNAIQ5KmuOic00rSWg/OYQwXdT8isDKtcXhlIu5LYBXIRLLeLVBK8my2oPVghGDhPG1jEeMFXSUZpppOlgbkXGtjAwri4xWCH33EdMS10zqLUEEdulSgOmfwMWDIx4Gxj+IVqaKTdTkUlAEt4m1geQYlZ0R1xZ+hdZYk0Thr0UqTd0d0h11W19cYDIYk2lMUBVmWXeZJxOFbqHMvkV34Fz53HP57IS8az8vH40JT4EVgE8fPq5QiTRISpcMwL+vQGWYIa5ibEOjkXEhqF97FDuglbsBH5mj4SmFY6NrQiDU+2lhwodETxSPWelDRRuBDKFho5L4QFuaXTNnwE/hljoJSyHgWDOjecEZwPuJifHCzeL/EHCzfx/CHpSpULs9BuCAwEGHYJWO4rRTBWdaa2DCzNuSN2DbW7h5rPYkm5MI4h40IC+vCfZH+tYGvAFSyFApYFJpmGZRMOHc4H2pBlu8bcbjsQiM5i8HF0oevcxkeCkmi4nsdcE8mDiiyJMWrwFCumrBPpVKiwy0d3jPvsLYNaImlMpxlfo0kkZI0y9A6QydByJIlikxl4NMgIrKe8SQg0PI8IU08aS5QaRZqXaswTXBXhHrFI5REiZRCdnFOoJxAGIdBYJygtZAIzQaSVZ3SImnbNgSs1i2LqmExmZO3DtUapnbGrF6ghWAgNV00SXxGGhHcJA6HE562rRFzKIQiTQRGp0hdUBR9er0h3aKDVFE970O+RaEl05MD6skE19SoRJD3CmSakXd6FN0uSokwiGkbautBKKjmQUhoQp/Mx8F6wHCE9QTnsMZR123k6obhhcNjm3pZmAZnrXc419K0libJGKxeobsywHuJNZ6qkpB0KEZdRlsrzMYnPH+0ijML7FlFY1oaW6O8h7ahXczAWZq2DoMNa0E4pNAgAhZOsBT1hWGbEeG98BdCvQTjmvCcuzAa7GYJ68OcnY0OG2sF66sdBgNBllm6WYrSOq5bxF7b3/76O92kBcC0eKECgFpJ3rjS49uv9Pn6k3NEPsJFVZ0LauPwADSW0sPGFU3PGaxvOB87tnpdNnuW3QczaDu0U8ujB5Apw0Y/4Wz3mC/unTN96QY9X5O6lq21Ebq9zp3X3mB1ZY28SAPjyte41mHbwITVSYLUMZ3ZR/aTh27v/2PuzWIty9I7r98a9nTGO98bETfmHCIyMiunyipXlctlW65uXLRpukFq0QhoHpB4aZ54QCAhixceeaJBLQQSQsJt3BbQbrtl2mN14crKrMoxcoiMebhx5zOfPa2Bh7XPiSiDn/F5iBs3ruLcc87ea63v+3//oUOSBY9Z6xzGWpx1KJ2yunUenaborM3kZB87n9BuJwgdUVYz7tz6iNHWNuubO3T6G0gZ7As63VWyrMVoOOTo+JA161jf2CJNW8zzgqquQ3JhXeAIBYy1nihKiNJOAKk6LfYeP6SoPP0NB5FrmrhnLDalJEp4TFFydmOFz1SBmQ+ZD5/y0Ycfc25rDWenaBwSg1AxXiSItMfKzi5nZ2PufD5kOp2zefYS/fVtorS7/BwODvexjYRbRREyijDNIROnCZFqApBk8GzBOoytQ/OmI9qtFk/39tCRRqsAaEgIlg8+bOxxFAGEZEeeTWMWh4PSGtUELeV5jnXPQC3fyJSVaGTypqZy4brWOCpcAKRckIWJRpxkcQFwJgA71nl0lOLmMzwW5RyVCwd2XhXU3iOchNqRqJjKGGzQHDUy1mbi3TQ4Rijaq6v0t8+x/eIb7L70NVZ2dkA6jvYeMB+N2bxQMj58xIMvPuX05DH99TO88Mqr7OyeR2RtnAoAZpgTgak9g8GIYRFzmntG85patCnVGkWyQb2yilVtrOpj0TjlqXREq7WGSmO0UFjrsWUBdRGaQTNH+Dl+esJ0skd++oDI3GFtR2GNYzo9RapQDC5YUHiWbEbnHFGksc6ihVoCBaZJhJWNlLzhcC2Lsub2XU67FwWilR6ZxbS6HZJWGyMltXBEKuHKuYvEUuGV5ss7X2CUI2ppLlw7x87ZDe599YiT4yFRnuGMJYtCmvPR9Bix2kdmCVaO2Ox26agQqDP3AhmnKCmpxznDwZD1rS2E0pRVDd6gVBRcN6RAxBpkDM16woV70NsavEISI6KY2XSMtxXtrEddl6HAcB5h3dK2Q2m5UEU1pdyzwvXnHk3BG6Qfdln4Lli0C0D15+TQTYEnZHBeQoThRKvTCRYTDavCP/crnjFYwuH2DPh59lIW19c3bOeFtCXc+mF9C6ERUuO8oSpLoqTTFKE0wJ8nSdNGGlUiZPCsnRWCXnsNpKQoC+IkBecZnJ4wHg3Z3NzCE4pOpfQStLbWLl93O8uI5RqRihCRJpES6yx1WWHxFEXegGEiMJqVpqwqkGFi7qzF2JqimFPXJVVZsbK2QZJkS7mXbKiXUsilv6gI+nX2nj5BK8X6+vqS+ZskCUmSkOd5UBXoxiNXh0FAlmUopbFNc56kCR6IGzDaIxnlc1paQBQCFkwSYS0k8zltNNub20GG5BzbUUbHwyxLsGlCbqHjJLtJyp2f/JjfMZZ/8J/8p3z/B7/OeO8+5t5t1tfWOUkf4b3DC4exDulDmKNb+Ik5kD5cY0VY48bUzcUPjTeF5crrb2HTjJNZTby6wttvf51cCKa9jJe++22S0xnyM4uZl2irKPKK2lq2d7bYPneGwXzK916+xtmdHaSH6Tzn/Z/8iPXNHQ67T5iOj/nq1k1WNza4dnaTT57epndmDdKUWgicsczyEbWv2Nm9zN7RPocnd5Ga4LUWQbVgKy+AdwdeeKyvQxiLEMwUFFpQWsmkKikRvNpWnE1i5qMjtHdEQqG8DYoNY1FATymU8WSjGd/a3ubC9/4Gf/D5x7z34A4uUjilmxokNBkBlw0S1gW7dwHMPm97smCLCxFSkB3PBieL+/J5MPcvg7deCIRSgWUkJMbX/OzDd7l65UVUlKJ0FIpSBJPJlJV1w4Xzl9l7tM9gMOTk4ITt3d0QeqNjyqLkdDDEGU+WtqjLIuyRDXvHWhvkuiqcGVIsGtMGMhDuWYikgFarBUrz9jtvMRqc8O67P0HrFGl63PrqEeeuXuH9n/4Fo6Mjbrz5JhWGaTEnitvMp5bH9z/jyf09Nte30P0Wva6m10vp97o8eXRK/+xV/uF/9gMePbzP7/wP/w1aFHx58z3W+quUlSHrbpOtRvTX1+mdeYlrqksctXn86B53Ht8PXm6rx1TGkXQ6jKdzjLBcuHyOo+MT7ty9RX3nLi/deJWXb3yN0cEaxWxGtNLC4oiSlLrO6W9vw8hy3lkef3qf3/+n/yP/8L/8r9i5+CJPHz8gEpr9x/tcut5DJxmzEt548y3iFO589Yh+t0cUK2bzOUnWAxPx4NZjtKtY213n3oN7jOclq6sbfPNbX2M4L/jwo7t0VxLqY8Pp8ZALF3f5m7/4Lf7tf/0b/NdpxJ/+0T/h6GgfbyyokDoulMAhA9tOPDc49KFJFiKw0/HBW1A0+yHO4WuHnxRYKZEqwtkKISTlbEKaaKJEc/7iZTpxiwd3vmI0HiE9RCpGEXHuzC5ffPYRR3tPGJ+eErcUrVZGbg0+Aq/BOAKY1mshMk1ta2wT7CPxKC2wSxuixVAkNFr5fEoUp6xurdHzCdXUoByYac7hwVOKqiAvDZuX1+ioFpdXz/Mr17/D//XhnzKpS2KpSCOJLENgS1GUzKoKF0usFDgrAysWh3AuNJaBOk8tPQ+P9rj51af88hvf4/vf+RWO/vnvMJrNg8TbSurChJpSSbSMcSaAMpGNYZxz9OEhG69skZ3JSHTC8f4Tnhw/xMQGIySfP7zP4HjIa1euUyjLw9EBriO49PIVVtZWSAvB9GjAT299xMcPPmPz4ibTYkJZzLi08wKyllRbL/HF3l16rTbfe+u77G6c55ObP+UYZIPMAAAgAElEQVQvbn1AXVeoWFHMpmy02shWTO09cbfF4fFTDqoRqa9w0lLVxdI73QroJBGTqWHvZESvFdOKJMKH0GDR7Bd1HViorTSi08mo6sC0y9KEfFZSWUMWSa6e2eZbb32LW7dv46VlNB4xOz3mvU/exbia116NMUbSW1lDiYgzO5cCSScvGA0PcC6cX1rIRpbo0UlEVVaBsFFVS29vJ0CqYPUWQDMHKOrSYo1FxxEyidCJJp45zvU7GO85nM6pvA9+lt5zWFoiYZgaS1fBSjum02kF4MQGD+PKhPs4QMiNuqIZ6nlvQiBTFGH8QtniljW6dxYa1chCArwMCbSN8lA0QA2NZ6kMAzqBIoo0rVZGp52ytr5G0ukRt2La7YwkikE855PbADnWgG5CXhcWKGEEp5aDnyUo2ZxbUgambAAwQ+hRUKVplI7DkF/IRvU0Yj4vSNodvBBMhydU+ZiqnOB91dh/NfsSBKDYNeBpQJmCQqnJH7C2CYf1jXWgexYkK5zFOhogNdTR3htMXTZgcvCxDbkbAmc9WgWP+xDg5Zv3/2ywFUp439TQ9rlhaqM08H4Z4BhsURVlWRJFCa2VPp1Om7IYM5uMYOGm6oOFmnSLzIvGrqzJbEGEAGPZ2CYgAqAayxD4VlfVs7q+qUWsDWC0awgqIdC2ITE19YOOYnxVU1RFUMdojaybArEZFLC41v5Z57foG8Jb90SRDuzcugxBZxaE1JR1jVdV6H9FOH+0CCBcJCOUVOAduskpUVKGrBudkKYpnU6bdjtFiZpUB69ShCJLJJF0wf5DSXykMUJgrST48gt83Mbin10rHCiPiCTSSZS1JM6TSo1D4ZrBtvcClIaGka+loK4qZrMp5WCIHs+I8oJjITmxHukNHaGIUSgpMAJqDw5LjaO0FltbbGWpnUB4idUxpizJp1PKdko7kuA1kdJEUUocJbSzlE6aMooPmc9GIchYRngvnw0snEY2DPGwOizOLLCQGuEa9rggALhLYpXFWhPwEmOpqxJn6iYM+1nQdbifHN7UlGVF1Uopa4lzinYbskwzmTiyUjT3SrgXVvsrUMwxec7pYE5RzEE6bDHHlAVFnmO8Q8so7InCk6RJIMo0+JC1IYCyqg3GBUsGU9dL5rp1Ye9stzukcUy7lbK22matH7Gxrul1JVkqiCOHVgYhPNbWCEK/9Vc9/lqDtAKaqY/FOYn0gpZWvP7yGf73T+5T1HNIwyQHIYhiQTcDNa3I65p80GVVFewmFfpkQtz1XOsLZm3LU3tM5RL8wZDdrYRXUgUXYrbaBcPHB3RXDZPxEZPpCd1+m+317eCPWlfU1iw3Qy0kUkt0rFjEH6goodWWWNv4xTSHjRIyWHXLxlNQarorZ2l3Vzjau8venS/B182UzOLKKfuPpgyOj7j+2tfp9VIAagcizuhvJPjjI46Pj3DOs7V9ljiOmuG6w9UFWgVfT2dBJylOKpQS6Fiyc2YLaAEhGV7L4JVprSeITitsZfnyo48Y7N+mnOcM631OTvepZifs3dsnaUWBAu4c1gp2zl7m3KUXmRQVf/H+TxgdPGQ2r9g+nfPi9WtI78JG5RzD0SnOmRCCQ2hqTV0hvKeqKqqqQiuFkZJIKYRSjYdvWK0nh0fYupGWSBGAQh9kGs4Hxp7TQf6zkHEsfE2ECJKVJE2Jk5S6rJGygjqAxjQFSQBqJfgAUngHXgYVRuUsxlt6cUakNN6GhthYQ5GX1DoAPWVRYU1Irlx46RhTM6uKJTMjdopuElNaw8jmjT+tByFDwqEJh1stImS7w/ruJfo7F9i99ha7L12n1e0xn42ZTGfsXrlGr9vhyw/fR7fWuPaOYOPcLtlKL3hHAcJ5ZtOc0bjkycmE48Oco0HNUPaY93YRvVVk0kNmaxid4bUkTQQpjtl4xjwfgoupiLBVinOhccBXeDdHoZEOaiJ86ww6apH0NrGHLeYn0F6bUFQGY8ZLwplzbhl0AyGUaCHjWUxjg1VFAK2WAMH/i4W5ePhlky6lpNXtEa+0iVsp3guqqsZLQbfV5uzGBv12xkE+5nh4RNSOEJnmZDRHJwPeeesGd392i5s/vs2lixe5cnaD17/2CsqXbG30Ed7w0adfUNNlLU0RzZAGFRNFmq8e3Ofzz27y/V//W7SzFsbO8BakDp6rTgp8pJEqCgebCwbqGoKkxgQPKE1KEqc4U4Gr0VozmQxRSjMej9nf22N7Z5v1zQ28baQFzecgnvtsnmfKLZmxTbET2Jnx8vNdAJVACNhasCqkACSmCX3wyIYJ0uxvDYAuCAMqmsHH4vkC8OuXMix8KFwWxZz3QRK09NgUNJ5yIVRMSdmszwBkBn9c1QRdEOSAzuAFtLs9oiRlPB5Rm4qNLCORGcKdAo7ZbILWUQBahWRr+8xyoLPw1i2LOaeDAWsbmygbmmNTG2pTE8ehiIvjkGxuvUdHUfDNkjKEldRBJhTHaTCvl+Hvxj3HGlsASyxAMtkAYJqdnZ0AxC5tQHTDMAyekYdHByRJTLvVCoyJhvHovViunUgrhNKkUhDFEXlRUBtLZQySkKKMiiCGQVHQtnM69YwsblFbRztJKAYjinzG5sY21WBIXubUpqSVxLz96ut02y1MXTOdzejFEaaYcfjoPgjbrMeFx3XTzAhwXlCbCmEVsrE3CQGWAi8l62e2OPfyDebWcnQ64bVvfRcTpeidHeYHTzl8eJ81GSMPR7R0xmprDeEkk2xG4QzH4wFzW3H5+nWM8Rydjjh9+gShBEJ6oiTlxquv89P3foipxtz84F3Onr+MOXhMfXKF829+m2lZYCtLt+pSe8NsknMtnzF87ym1mS998IRrmki/mDCEr16E/GevwjqTCCol2JOKyhRMppa3BFwROqgm4jSEwkmNUCDyGdI4fASZcMT7go6L2Hz726x2Ovzw5kfMKXGxbsJiFjtrY9/T3MuLsclf3jufZ8cu1ioLVu1zjHwhFgz9sP6FcM/2koZR63Ecnz7FecO3v/2rVJVjPptS1xXD0wFaJ7zwwktcvXKVTz6+ycnRCZvbZ+l1+wxOT1hZWWH/4JDxeEwcx1hTo2O1tCHRkX7muS2eva6FDcyCQeVFYI6PRgMuvPAC6+vreFPz0pWrPN0/QmlJhSXtrTIczPDlnLV2yjifcefWZ1x54RVee/ObfPrRe6z0Omyvr/FH//Jf8PnNn7C9cwYlHWd3dzkZTvD3H/D00SNqYvYOxtSF5cy56zzYH6I7a2y1Nti5cInRfMZgVrJx5iJXrr3Bn//xH/DjP/k9km5G0YAucdpiOh1T2TkqjZCRoJ7O+L1/+r9iihlnd3Y48J4oadFKY3Qcg0q4+tpbzAcX8Le+4FoO+3c+4fNPfsbliy+yf/cWylecPN3n4rWr9FZ6PNl/RPJ5i3e+/jZHe4c8vX+bl6/fwArJ6fExq70+05N9hLD8ZP8OkY7IjaB2MBnNOXd+g7r2PLj/kPFkwtvvvIE1NU/un1DmE3ZXL/J3/ta/xwcf/wnvvfcexlRNMKIMLLgF83xxNi0Sx5vvpQwDcu+fDfswDm8qaiEQWuOz0OBqKUKAa1HhnCDSKa20haFkpbNBUVo++tn7aOlRzuCqCUaaoIJqmDNpIhE+eMvpOEJGmlq4oIAL2D+uqlDWI+OoGRxKcCEkTauI9spqWC9pihUJ+sIOne1zVMIynI5wAtoiZq3VC3Y21vOLN77FcHLCn938CbPZNOwnlSQio5V1yJIEXw1ROgr3t/No45DNuYoO4IL1imk154ObH/DWtbd55doN3rp9iz/65F1qIZEiDooMIHKgvQAhMcaijKJlelRHOYcfHrLGDl/7heuseMeDR19RyRLV6TIupxyePmFYTVntrkGqye2UH33yE+7F9/nX3v4lnoz3+dlXH9M9t8rU5dx8dJtO1GZn4zLnty+RxhFKpcQK+nGH9z/8gJ8+/JAxJd1Wi90Ll+h6zcHdB3Qc9LdX+eCrT7j76A74MZ2+IRkp6hhsUQZCSRw820WsGBY1Re7Z0RmJXORNBAl4sBMQOFcFNiWKytRkkaKXaERZ04sFmTdsdVZ48dd+g3k94WDvER//9EfksxGf3f6Y1d42Z2Wwg5Na46xgZWOHF6/f4MFdwXhywmw6BRtUfomUVC7YfpgyWLUJrRqlUdg3F3WRlzRfJaUpQYf+UQHW1rSjhCvrK5i65qisg+dys9dbD8eVYSZhajwrqWelnZAmKdrLhq1pcG7hDe9Zhku5AEJKFAGbDUpMQeibzAIseb5u9As6GLjGV9oLAitShICmwFzusL6+RrfbotPLSFstnIhAg5IebyuQHodqFvrC2knivQpXT4QaM4DZoeZb9Au+AW8X+RkLowUhnlmELViWmAAIOSvwXoHU1GaCw1Llc1xVImyNtybYVLgw2AjszedYrn5hQxCyCJyrMbbGexMAV+8Cm9kuXyYSEZjNeFgEiHnXDFCD1aJs6kAhwlnmGmXZgsjSxGWFz8CFfbKubQi+9n/ZSx4WkRSiAUulF7RaK2yevcpsPqWqRjS05CWH1JgQbBeOfk8UqcYewC0H0MbY5WChweYR3i/JIotAF+89GBtALaAWoZ9ZVByy6fGTJIHMoKs4DOeso6pryvk8KK+8o7aNJSA0toHNvSh4dla4EJ4nPGh8sKZRYZBe1TX4GKVVCGbXMVlLkGhNIiPiSBNFmkiFTB6hFWnaZq2/TrvVDqFlyhI15ZVQEcI7nJujdQBlxYIw6EIvsPBfXyg9FzYsYdrW2C7YGinCaxSu8YYW4Szyrrk8MgDlKlF04ph2HCGzBDEZgwqAns3niKomjFgk2gVHMyGDh63HgxPMJcyrgnoGWkgqNCNX4OsJ9eoGKmmh44xebx2ZpERao5OEOEspXI2oDbbBwLw1eFPjrcAuyRXNPcGC/erCehLP6k+QIH2wXVj0joThhK0tlbHkpQEPxgQrjbIo8bWhzCvEes7jvQED06PdbtPpaCIFaaLo9UBFijhSrPZX6McxiYqQ3nF4UmGrnDKfURR5QxgJww8hgyVGUMx4vDFEaYqWAdRPIkU9LwM5ExEyU5wgFgohFJFQZElClsbEUchxktKgtUdJRaRTvI8QPpAKsQ2m8Vc8/lqDtGGNLzYO1wzZJTfOdfnGec2/enpM0uqRjywCS09KXukpzvTn1NNDxGxMNTigp2Gj30HddayvrvP3r2+ioggn4PGjp4h6hq5yXn/la6z12ohqgCnmRMqiJbSSOMiUG48NV9cUZUEraxNnCeAxpm5YT+FCxYlqWG5BZqJVI5tVYWPyDaNWCohUyva5yyRZi/1H95gNDnBVQVmGpM7S1nz8/o84t3uF9a0dVJyhdAfrodftYuuCw4OHeF+ytrVDFMfEWjE3OUokCCRVXWOmI4hj0jRDeEW70weR4uVCJmaxTiNtxeef/pQin9JNIp4+uM3egy9pJ1HwRxuN6USCui4oy5I8L0l0xuqZM7z6ze+S9fo8+OwDZtNTts9sBU8lKVBxFDYbHMYZ7j9+BNYjpcaZmlgorJfUzuKNo7YNICFE4wPkoPHQmU8neOfQKvg8lnmJ1aox8RYIF+bESjSyWQRS+iXgUjcedjrS2Dpci067y4zZMxmGUOEAcr5R5UuMDBT8ha9TIRyRr6lr28irJbGWWFdTmRDgc+7iLsejEXLgqKqCXAQGLUoArgm+CwVGEkXoqkR61QA1jb5FCoSKiKOYOooRaYfuyjbtfg+pHFWVU1U1rc4qWXedo5Njot46L31zl1aSIZSCSCKpGIzGPHp4xK0nY+6Oepy4LUTaR17oUOsY2e6QRBHttIVudRjOZ0wmE3xtKcshLTdlRc+JooT1zRVanZgkTdBxAl6gXIVtJAtFXTKbV0ynFl9rjHqROtOUOqJd1YwOv2wYZh5BKAKkaCb3KhQMS7DJNde/ARN+jtnlQfgQQBYOwWbE7j1REtHaWEN1E9AKpRsbDWvQUrK+0mNzo4en5nQ4womYuhJMB2OOHhzS60e89B9d4crLL3M6nPH177yOqOa8+c4F1lqCo9EJw+MBL1zaYFZ08TpM3ludVaSiSb2VnDlznv7KOkJpEhcCA4V3gTELOOnwrmEHe9n4WknQMbKUqMVEXmuG0xHDwQE7Z3bo9Ncx1mMGY1qtNt3+WpjcsgCLmmKxKfBCMWUbcFQ069GitGjwJLf076rrGmsdSZKGSXpTyy+9f/2ClUFTIIb1EpTIYjnpd84tw42Wa7AJVZSEIphF0W8XHlwWIUJQl7cWbywyDhNIqRN0lCGjwJLwIngUSikROkJ4TzEdczo4ZX19g1Ya1Az9fp+6LDk5OmZlZZV2t0On0wpMKWtptzPyfM6XX35Av7/B9uYZlAzM8bbKqKseOMiLedPYWObTCarbI4oCezWKIoytl8BoXVWB1WAa8EipZogUihIpfeOtpYEmMLBhk/mmEBdCknRXlgyC+XyGtYZWlmJNTZykuNqQW8f58xdBwHQyCdevDhNppRXT6RhbVyTScXp6RBzFeCMoCoNLQuGY6YQ41Sgb7ovxaEDal3gdU9Y1ZjTh+OkTkgjmtmRa1MyN55f+9t/lO9//dWpT84e/97t89u7/zQ/eeJOjvX3MZIRwFagkMCn8Qo4f1rK1IWhLKY+34T6onKC3tcML117DIPjZpx9y8cYbnHv5FZ6cHNNdX+Hw05/RiuDxhx8yrhXbWZ/+1lm2NzYwpiTr9Il9xXAw4PNPP+L81Zd4cP8JK602HkiTjKs33kSUFRP5lDPnr7D/4Dbl+JR80OXG+Rd5/913OZqVJDu7zGwI+dRCIiLF+QtXODp6nc+++AkqCg2dkAllWTbecr5Zc01QoAxqm6WUD0HhBQcyDHXNdExuPNe8ZztrY+IEvbLJlZeu8vT2l5STGaohZkWmQj/dIyor/sGNb3Klt8Vvf/BjjvMctIRIhXMXjXAhOVy45zw/BUuGjW4kgXi/9HddrNsF+Lr4eV3XS+/wwGJVaOka1lTA4gG8lAyHQ44O9nnxhWsce8d0WjObjinygk7WYvfsGU5Phjx69Ijjw312L19lkraI5xW72+c4OjqgKKa0O13Sdjs0mEIhdYwSIvjzL+vFBZAcgCdEGI5rrRFobJVz99anPHmyT7fTo9NO6K5tcuX6S9x7eI9uu8fFK1fRcYSuLRu9Lk8ePubVN2/wje/9Mg+/+oLf/u3/ib/4kz/m+iuvIsyLnLv0Ejfe+A4Hxyf87IP3+f73v8fb33qL+/cPGJ4OWT23RauV4ZVmbbPPw4d73L99my8+/DG+mnP9lbf4N/7O3ydNJP/in/0W02nBk4d7XL38Ai+8dJXBZMDB8RBrCzqdNjc/+ZStzTN8/wc/QGnJcDwg1oqiqiiKGisz9k4K7j06IspS2k7xf/7P/4T/+L/4z7n+yjXe/1c/JEpXcEXJ9vYqNrd8/O6POHhwD7zk9dde4bVXX+HOgyesb7RYX+mzp2qKyZB5Nabf76CKMcfDnD/74Y+5/MIL1EXO4zu3qSso5jVVnjMqLJaCSy/dYDRo018XTOuCo5NDjp48xc0qlEgbUCa4gIJYhiYGdliITxFagVnUVw3g5j2uqLFFTdJu4esQuOiUpyhnPLj3BcPOKrGSKCRZ3OP8+U1+/N6PmU8nREmE9RZTz4izjNXeDlMx5vDpU9pZG5lJdNbUxKXDWBPyGZQM9t3O4q0kiJ0tzhi0WgQXSWrrGE6mVFE4O7sXLiJ7XSZlDqkiJmZ7dQclYloJxEmXX/vmr7J3fEQ9LynKnH6yhpSSzZUV3nnxdU4//FNOzBwjFNrGpD4hUoraBY/SwtVYIahR3Hr6hJ9+/jG//PYv8f1v/yr7h0/5/NEdTCKxThLZwNIyeLQC3XzmMpIom6AHEafvD7mtHnLplTPUWZu4UZC0+x184hnYGYPBjDoGYTQzO+Wr4YTxj05JnWTr8jYHs1PuHTygu9rl61feYb29RV1UrHc3iCPF4eEef/7un3Pn9AmlNpxb2eHX3vxFVkTKbDzm4otXebL3kJsff8Xd0R42NkT9FmUUsyo9sXJUnz/CTyq0UCgZbAqc88wrx+GsZK0Vk0UhhE1KBV4gZGDaC+GRShIJhStrNjsRnUQRRQLhDad7x+yuXiHRjujCOXL/Crc++4TJyZAPbv6I3BVccJZOb5UoTUlczPkzL6CjhMHokJPHDxkeHZBX87BnIoNs3dswsEAhdLBuUk4EchkgUGGY2ZA7kiyclSLRFLZCzWe005jz623mB2MmttnXffhaE1S7hXWMTclRaciUpJvG9LM0DOKjYGuGtUgJRlqkC8GLCIHUwVgr1H0B2A4Aow/3ugu1azjCRTMI9AgZ6pgkSel0W/T7PTqdNp1+lzRLiJNgzeSEQ4i6AWWaQNEGXIWm95PimZWNXADZoah0jsbftVHTObckGtjGD14GNhR1abBm3tSsPnhdCkKdLcLgWtmQNeMav/MFocBJ0wCwoS6zJvhnPq8AWFjueWfx3jZetQGZW9h6uabmcd43thEGa4JN4jNWaHOW4cN5LUQYgrrQUwphkTJYrSwILIiwe6pmv1QNsGdt8B1FLMgtITtBCNBaoJOM7vYlMu+ZzHPq6RxFgTE5lRUUpqIuLcY3dagMANqCPevwgRTR1BO2ITLVxjTAHI2FYGMcICVRnGCMoa6q0PdJgdIBE4miiChSKBkwisXQoqpKXFUym06ZTCfNZyvC2eEaRd/CK9eEXsdbFxj2DUlC0dRMWpJlLZJOlzhOSKKUTGe00hZZkpBoHbxWuy3iWBOnKTpu0W53aHdXaLXagAxsaBv8sS3B5qIuphg7D9fUL4KWK7QIMv1Qu8ild2mYTQY8Q3qHXgS5et8MY5r3YhrYXPolgUMKgVIxvrOCERIrPKkUnFFgTj2Vd02gZMPEVhJbW8raoT3kKii8ZsUM73KM9BTOIW3N1Fumszlx1iVNOoyHY5JEoXXwWy2NQ6iMTDf5BsIiVAirVlIjhF72h6EBfObV6pUOo32x6GuarIRmou51CLi3WlEIT+kNtTUIIxnlNbNZhckrqirHW8v6VodZbpidDGnP5owGwaomjhT9Xgg1m+Y53dVt5EpJlCW02hmtRwn7Tx+RT6dIaRDeLnXQUZQEspgP/sFCgFz04giKyjSDWahqS1lVaBnILdYEm5NYRfQ6KXHq0bEjTSBSNdGibhaNLzWiwTUdf9XjrzVIu2CA+Ab9FziUdazHkl95fYfPjvYY5TOUs2zGhtf7jvXpQ6a3f8xuX3Fhe5UHB7fZbK/y2ktfw0uFVhX97iAwsbTm7X4HaGOdoZg/gYnEU3MyHbK6tsXOzpnA5qwtzgusq5hOx4zHE/S2JssSnHfUeYWHwHLDNlOuMOVZyAWdd2HiLsJI3tnAIgoHAHR6a5w9D/vOsPfwHt5ZIgHOVRTTU+58NWc2H3DhysusdtYZDkdYb+j0ulRVweH+U8q6ZmNzh1g2zM20Q1XWzPM5rnAUeY5UEUkUoYSkuxoCihBxKF7wKFkzHe0xOjhkHgnq2Zg0EmRZm+lowvrmBloJTk6PcbZGak934wznX3qVsxcvk8/H7N2/w9duvMHFixfQRAiVIlUSmr3SMrdTHu8/4nzje1J7R2nr5vAU1KYOAQPGIKII33j8PM/ss0svvGdsvIUMWDWy4NlshrU2eDbCcsKoGr9HZx1FXjSJ4o3BvBTL5rVBSpf/VynJrCoovGl8hxy5qVmkokZCk8qQti2loHSGzd0zbB4dMjg6ZTIcU3uLl6CECqnYPjBmiRug0dqmWGk8bln8foVzgqKqwkbpJWWeMx1Pqe20kTorTo5PcN6wtbtL2moHq4eyYDIY8Pn9x3x494ivDh1l+yzF6nXK1hZJ0qIdC9ZbknllEcaQFxOqg1MENbvtlPVWynbvHFsdR0uN8LZibb1LknSoKhf8sTxQeepl2reirlOqWuIQjEdtJqMO407CkayZz04op/vNtQ2H0IL/KRsJzfNeiAuKlGjYscsCLTjBN76z4bniLCFqpbT6PWglVDQHeXPIS63BWbbWV+n1OszmUw6PBhwcDuitr3D10mUe7d3BasdJMaOOa9LNmM/v32RDacrZZWbUjEcDRqMCS4KXNYiSKI2wQgGOGsnlazeQDrJun7ysULFD1GEPcIv3pxRehumadDHeWoQUYGtk4olF8Lyryhn7Tx9z594dks4Kq+tb2KLmzPkrRCowGKypQvNomzCCJfs/jJkDAzX42CJlCKcSgv2ne5wcHXFmZ5tWu41zgXGRJDHGOKI4Xu5nywCy5/6kYUb6ZYH5LLBIK7VMcw2MU54VtAJsMxXXMgr3g1JESQutU6IoQyXJMpl4Idk2pkY6UPGCUSEQIgTsOTy9lZAQXFeW2XxGPp+ztbFBGidMJmOiKKKVpUwHU6oiZzoa0MoSttfWEAIefvUZ49GYF65dI+u0iSNJkU/DNLspOLSSTVpuOLCXjVJV4r2nnM+oZtPQ4GtFnGVoAXVRUosihAEaE4oDnaJUFNZ+8zw0w0qlAlvKmJrBYEASR0gdGqfjkyOkEgxGQ0bjESAYDYfBqsWH+8BZi5aScl5gXEWsY7qtDrjAMAre2CawDyJFkkpG8xxdO5I6JVIRvrEhmYyGTIopwjh0lvLijRt8+/t/AxdLfviHv8+f/tZvcUFGnO322d3d5V47pTwGXAhnCB6lAchbWMuYZlqufYyMW5y7cpnz128wnBTcuX2bo4NjvvYr21z/+lvcu3uHvTu3uPvRx1STIf04ZWX9HCRdprMJK90ecZrREuuk0hGbir3bt1ntrZDiWOl0yDotRNZiHkWcHBxz93jE2QtXGAyPqafHTEanXLz8Eq+ev8T9w1PStS0qJSgs1FVOZXO8Euzunufk9D6nw8cgXFBVxBHGBLY+NM2ceDZ0E42fqmnYEkYIDn3w3xrPAkiaWE8rDZ6Ax1aLw0kAACAASURBVEd9eptn8Z0SjKHKp1CXtLwhOj5hnNd8e+cMK7/wfX7/i4+4eXALqzTKdfDSggpDK2tDUwOB0bP0rxXB5iDIthoGvFiwIZ6tcCElSuum9l6wcMNPl2F7uCYgU1DXjq9uf8XFi1fp9PrkRYGQFiUjHj1+xMrqCldfuMp8njMcnLK9e4F+f50qL9ncXENJz5PDfaSUmMqAVwgiBDWVqaiKYhmE8nPM4Gao7z102h16/RV63S4P7t9BWsn1l68xHJ3y8adfMDo+IhERr772GmmcobOIfPCAuh5z5ux5EJKj4z3+5R/8Lj/6w99npdfm/IVN9h/fJU063Gnd5u7DPVSU8uXtPa5cvcDVl6/jAYXl8YO73PnyFqtrXfCGrz5+j88/eh/vCvLZlPWNdb77N/82Dvizf/7PuHfrNjc//IjNtVWSNOLc5g6P7z5ERoKNjRXu3PmSV/bfoHAwHA1Idczm+nrw2TOe0dGAw6f7ZKlEdtYoBo/47f/uH/Hv/vv/AVcunOXxk9vMBkf0z26zvrHGp/c+wZkxWnc4ObfD/v4hpiiwVcmdowMGgyE72xvU1IyM4NKLNyjv3KWYlTy+d4tzZ3a4eGGDO/efkJcjnh4cgbW89to1vIfJ+IDtjct885vf4ou7N0mTFg8+u4Oz1ZItiAflg8zQ/pw/93O1VxRskoLvXWiS7XiK7qeIOAn2KHkBWjA83cdWOau9LsVsztMnT4jva7QSlN6iowQvJXkZ6sN+ssLO1nl0nDKZnkAsMLIBXI0NNZol1O2EhpMmQCjwDAMIIqWmNiVSamxdUPoSJSM210KI46yYPetuvAj2QBhc5VnL1vn2a7/A+x9/RFnWxP0MUxgSofjua99ECcH94z2E1vTaK6z21un3emGo+PAun967xXE+weCZm5off/hTXr7wEpe2zvGDX/w1Bv/HEXuzcHZ5E+EwCCmpq4YA4RXCaZSPkE6hZjU3/+xzJqMJ3Ve2kDonNzk4S6KzEDgkQAuNExqEwxqLjT3bZ8/x9GCPe0ePqYTj6y++xkvnrjB8NGBzY4vjwRhpFWe3zzMqZjydnZBlgu+980vc2HmJ08cH2NTxdPiY9x9+wX5+io8lRJpaB1af0Z4oz2hfXKc+mOAHgZ2qJfTaCbUvmZY1zns2ey0yAXVI+AmhwqFTbvoHRRQ5BHVgQCUxXkhGwwnzWUm61iIRjvO7l6nKnNv15xyPT7n55UfoKOWsu0K7txqYZkmLjbVzgCBB0E5iHj+5z+lsiIvjAPKbwMy2NgSdsVQgBGDJOh9kwlI0jX/oQ2TjuVmVFS0pWWt32F2D+4MJufl5zawj3LJz75lXNRo4LUt6ZUk3S+klCalUJJEOmQfe4yUIrYOyq1FMeQFKNX2IaMLHgrtlo2oTS8uuWGuStEOrs0Kv32dltU8UR0SRRiURKgqkm+BB+ozhqoRs6puGRSAWQGUDAi/2AtkAmQIQNrBaCerKkF+iUDowqnG+Ydd6ahNY089Cahs7OxmCxLyrEVZhTYWta0wdLIusC/3Zwus8yLoty6DMZg3gfcNQDoQxQUieF55lGNUCrPXeYdzCOiEQtZ5/LJ5byKb/bH4eep4AkIrmPvECYhXAzTzPw2u29pm9wfOMZ7EgVYARnkk+YT6vuPjy67iq5lE5YTJ4FN6/YWlFtcj+wDdWZ96jdUSkQnCbUrph3dZ4Xy8Dd4UQCB08ZJUMjGypFN7FOJ9iahP8YE2o1WMdkSRJQ1aQSzWQ6AqErZi1O7TbXcrZhMqUVA1JzNgQJul947EMJFkCwpNECXGUkcYpSRxYsmtrq6SdLlonRDoiiVI67R5JkhHpiG63Q5YmRGlMnGbESZc0a6N1DFLRzN0DI956hNLU84p8esJsfoQpckzVWFmIBpCUQWcoBCgVYZtB+BKc9yHp5jnKbQDbrYVILJmodqG6a/YDj0QmGaQVqq5JshrR7WB0wJtipellGSrSmNqSlzWT2jAua/bnBXNXU9oaM5kQGYsTFiMg7Sq0LDHAtMzJtQUM0gviOEOnWQhnjxR4QxQFhZZ8LthYNsMBLwOmopbkKhcm+c17CMrnoN52zmBtjakMdWEopxXzaUE1rzkYTalKizAe6yqyTpvd85c4s7NNIZOG9KioygJvHRMkp6dj6jwnjYN9ZhJFZGlGuxPT6bRJ04T9vUeMR4OlZ7dz4boZW+IdRHG8VMMba0NYnrfYKjDtJR5No0b0PjCilUfFIeQtUpI4itE6Rqu0sbY2yz0faBRo/98P9Zu/+Zt/5Q///378t//oH//m3/17/+FyowrsaIfwjpXVFsfDGXfuHbIVl/yb1yJ++eyQa70xb11d460Xdtjqp/Tbihev7tLttRhPh1TVnEgL6joPDVUzDfDeojR4YSjqiso4WmmKXjQu3mONoSzmgCdNY7I0RjVIez7PmU4moSF2deNHFKTyAaC1OGtCSmRjFB5YKp6yLJqGPkhYpdJNWFCNcxYlg9e4NTlFvvgdFusMSgvKqiCfznG2xtQV8+mYSArKyrCyskGSZgzHI2pTEknJwf4ep8fHSKVZWdtEJRnOh9APLUG4nOPDR8wnE1ItsNUcWzeSIgRSQVkVVFUJHqK4wxtf/x5f++av0Oqv8MWnH7B//w4bm1tk3TWmowHj0RDV6ofJFBEnw0P+t9/5Xzir21xaP4uQMBoOEM6FAso58iKnsvbZRMnaMM2kOYAIkgma7xcsWilE8+8sLQ5k85y2MUO3jTfKsyTNhg3dUPMFCyP8xh+xAZGdsZTeUcng+5nFmkRJUi0RwmNcsF+Q3rHTX+P82hb9Vpt8lnN6esJ0Psc4Bw04XdZ1815C+I+zjqJumhdcYPI2DHKlVTj04oxWtkKvtU7UWyHr95A6hCV1OxmdXod2q81Kbw3rFfef7PHBh5/yxz/8Ge89zHkiLjLdeBu3dYNo+yLp5grtLCUqpxTDfYrxGFMW9GK4vN3jtSsbfOPaWb52cZXzK5aNpKLtJ7QoiExBXeUIVwfpi7Xgg48MNBNnHyQ8mjpYJrS6pJ0e7W5G1lIMDh7j6iD18A0wuwTG5TOwrxnY/zxwsPRKDExb39iPZL027Y0+0WoX2UrwugkRa4Ao2xRbwjveefVlLp7ZxpQVD/eO2D+dsrq1zpvffI2XXrvMzoUtWv02Kxtdzl0+i7SOycM9Xr1yliwzuArwfapKUVUWa1N621ewRGGaLoIXaCtrYRxBAk8I3FJKEkUxURQhZUgPDWwdjVoGHEi0dOSzIbdu3eT25x+x9/AulYHrN94gy9roKKRZe++ZTUbYukBJQSQlkVZ4Z6irnHw65nD/KfPZmOloyHhwyvDkFGcqiumEvUcPoK5pZS2KfE5VBduFNEsaMPdZkBY0QA7PDpgFsAOhWKT5zK212Mb3cvG9MXXjhWlZSqIIcjUvAuNUSA0qQUVJM61tZG9K4pHLwAEvmuLABwmU9cGfNYo0tbGUZUld1YzHI4aDIUrJcA94R2WqUICamtPjI5x1dLtdJuNTbn/5KYPjQ1ZXVqms4fDwgOHgFGvqELDQhIaVZYGpK2xtsM5i64qymCOxFPMJ08mQssyX17OuKlwdXlfVWLwIEQLSQC49zBcFshCCsgjqiqqqmEzGrPb7mIXtjtZUVYnSmizLmE6moWgXQWbY7nRotVqkrRbdTkhLds7x8YfvMxydohK9lMSBp3ImMGYQYbLtHEJGdPp9dBxxfHpCWQTJT3t9nV/8jd9g7fwuH//sPX73H//3nPWOy70+x8fH5Kbi5PEjRD4LQIxq7hgZBKg0wxnrPbV1ZJ11rr3+DXo7u3x6+z6tjU3e/M53mBcG1e1T1BVffPgep3e/oD54RNfVtEQ4v1QkSCLNSneVVq/P6rkLnLl0hSePnzIdnmKNZffMOe7cf0itItYvv0DeXWH90oucu3iZWCiO9x8xPz2imOUUZcX1l65z8PSEbK3H1Ruv01rbpLvSp9PJUCrCu3Dmj0anOFc3rIeGpe6eJVsvnOTCfiaXzejC0sIqQSEFUxEGcdoYVuKYxDmK6QznJEpFwWstz6GuEc6gvEPZGj+Zstnq8ObLrxBFir3jQ0xtgrS3YbbQFMzNOGPZyC3W6WJd/1xQ2HNrerEPC55nrjbc3GYbWIR/SB0a8rwoKcqaLOs0hbBCRVFjHWXZOXOOJE44PjomSlK2ds5RlgXT6ZBerxMGfrUhjmJwinwyw5mK2pRL+4/nrRqevS5wxvDi5fN861tfp9NN6WYpOEftKuJUc3hwwIM7Dzje2+fp3mNOR0N2Llzi+msvMhzM0AhGxyf88E//iPd/+Mf0s5R/69/5e1x58QofvPsTVnsrzGdzOmnEy1cvcbD3iId3vgxKBQG3Pv2Ix1/dZKsfo2zOSidjY32Ns7sXefsb3+Le3bvsPX6MUzFJ1qIVSUw15/HjxxwdHgQvXSTj8Yyqrji/ewahoHSCC1euoGNNZYJtz9bWFvl8zq1PPkK4nFbWIkliVjuKe599xJ3bX/HO2zew9YCks87mucscHOxRz0aYosR6iJIM5xzlbMTRwRPGwyHWeb77vXc4e/4MT44nCNkniVpcvriLliCFoSoLhoMZTx4dYG3F4Hifnc01tBbMZlNarR5pJ8MoT+0Fb37jOyidcbi3jxShrgRwMtAxFveabIA0vRzmNOvIN6zBqv5/qHuzHkmv9M7vd7Z3iT0i98rKyiqyWCSrubS62Wqy273YI8m2DMvWXBjwwJZ8MYa/hr7DGIahG3uMkYEBBrBHHsmWPeNWS+puspvNnSySxdr33CJjfddzji/OG5nsMXwvB1CoQmZWZES87znnef7Pf8EraG+N8JGkLHKStIWzIeBxOZuQLWdMZifMJmNEHfzQu8MBg8015osp46cHGAz9wSaXr16lsHMWxZKqyvEQchKcRYlgueTqEEirlQbbALarXlsIsjxHy6bmrC2JN/x73/x3UM7yiw9+xsQucJXFLRzP7+3TMTG+rLBVzdponfl8ga89O5vbYAnBVSbhyoXneOXSy3xj70Ve3n2O/Y1dNpI+z2/u8fzuZYbtPgdPD5hnGQ7JfJ6hnODa5StsDUYoKfjq1i2qwkGtsKWFymNLh68smsA4F86gnCJSCdobxkcTVCsm6bewKihylJDUdXlGlBDOI71gc7DBpYuXeXzwhAeHj6hMsHdZTBY8ffyQMi/odToYL1jrr1NlBTvbm6RpzMnpCRQw0F02hmuMywl/d+MXHJVjZBoFKzMJRitia/GTOdXJJLyeVoq0Hqrg3a2lODtflmWNEIq2iUM4kKYxZloBfg3RY8WEFhJtFBpB4mMuXXqetZ0LWOuwdUVv0ENIwWx+ynI5I8uXtDttpDJU3oPQGB0jpWKRT0ES/G6zOVmeB0UCIgA+oYj9jXpKKn225wZ/2CgkygtBtlgyPjkNZwsei8ckEVIpsqKi9l8HMc/rs3NfckFVe/KyJqtK8jKAkVEch75TBAsRqaPGlghQKgB8bkWV8lS1xTuBFwqpDc4LoiRlOOwxHAwYjgZ0+12MCTVYkBArrK1DWPIKLF0pTQj5B0qKcw/bRkEX8mj0mR8pzYnqCXZWYjX8pAF0G+sBvG2sEmsCXB367cBcDd9fhWR5W1MVGWWxxNsaa0tcXeFsGUgTwgXw1Qf8IRCwaNi64VNxdYmgDv1P0/+vSAjgmjqhboA4zvqZ1ds663PE17x+m/e0+rjCMSdXFxeQKB0UllKppq4On4lU537BzacFTRI93uKLCiVTti69hBSakyf3yeYH1FWOE4Hh7V0zqG2Gyr6x6zBGE0cxxhgiYwIJQ4dQNmNCWr0QAq1kkMmbkC+hm9A0pULYVxLHwXIwionimFXmhNYGpQ1ax0RRQhw1f8cJkY6ITfjdJkowKiYyMUnSotXu0e106fcG9Lrhz9pwg/XRJmvDNYb9AVvrIzbXN1kbrTEcDhmNRgxHQzqdLq1WB6UMQkegI5zQOK+p6lCbVrWlrj2VC6B0XVcsl0uWszmzyQlFsWhY06vbuyHjOY+tHc4GCwTfrG+3Ip41KpFwb68GFU3z31w+51YBcatvizO/XyEkxjl0XaFtjbA13lVEUpFqQ6IVRkmSJKGbpnRMjJCKSokA1HpHURWUNgSjSy/QymCilLjVJjYRURQhhAphxkYRGxOurVZoIYiMJEki4jgijmN0ZBpLidCD6gaHEfL8vvY+5AzlRU5VlWR5xmK6ZDZZMh4vGJ9MOD4ec3h8zNHpmPligdKK1qBPe22T1976HS5ceYnhoMfWRotWIpDCEWkdAs8WM/LZGOUqpAwZRHGSkqStADZrg3VhP6usa1RXIVNGNQpRrc0Kccb6oKpZ4TYI2QxjPE6E7JF+p0On3SZNDINui27L0Gkbkjg6C+cDHZjDrulXK8tf/vTXT/7kT/7kT/m3Hn/vmbSs/M6aaQPWI51gXUv+41dHnN6+y9VLF3i184h4/BWX9naobESVLzk8ndJdG6FbCaXN6ffTQM9XimWWU80LjNLBtFcIIqOJtaJtIly7Q+UDGzVMioLZu1aKNEmIIhMmALYKC6gucLbAWUVskmaDdEgZNvDwDoK5srPNRM05KmvJ8nk4tDyBpj1co9/vcfT0Ho/v3yGbTyjLJbUtyLMZ9/OMk8ND1rd26Q6HKKU4PXlGK2lxYe8Cz548YVqXRFEHrQ3dwYgKwZPH9zHK0O/3mE5nKBlkJ5GGxXLKPM8w0oAvuXbtdb71rbe4+fF7fPb+IVYotDQknYinTx4xm56GjcEkRKaHaa3R6o44OTri5o3PMEJgooRnh8dMTh5jrWO09zxSKnwEjx4+ZHayoNoSVFWNVGFDl7UgIkindWMNEVLqXXOwhwPDuzCdEyIUH45V4JQ8O/SqqgoMnDrISqy1Z6ddZWukOrdHUM2h2G63GY1GHB0cBslqkeOMocRhS0c77fL8teeIRi2UcbSkpxNHRFrz9OSArx484OjglGyaM5svePzoKb9alKRphHSOTmQ4XQQ/0loQQrFkcxDbirIoMUpSe0/tVpPmUE5WQiJMjBAxigSlYvpr62zubNIbDUhig5ES5w2T2ZKPP7vDrz+5xYef3+VkZkk3X6Xeu47uDhmuDUjaLYqyZjxeMF3kpH7JxWGXy5t9hj1D7AtaypFoSOwCVQiUC74zyBihXGP0PUaIJVE0xJNQWYdwAiNBaYGzUNchPdRKQGrUYEQrukq75VBVzucf/JxifhwGGI0/S5ADh8cKZP8NQOFrX6/rGicEMtIk3TatURcX67OANGwoVuq6bgaXAfRPk5i1fp/pZIrCo0xM2m5jpSPuGi6/cImTkxPKMqc/GhAnfa6M+rx/fBxAFScoKsdsueDZ4YQk6bDITlnOJkEKPj9lfesC8zynyDK8EJgoDYwIV7GSRNnaUZZBdmZtEQYReJQO3klFNuHT99/li88+JFucUhcZw41d8iwjjmOqsgYhmU1OeHzvFrgCYyKEF2gtca4+k+BLH8IAi7zAVlVg2i8meDxJpOl1usFTdLnEAcsiY5Et2Ni8gJWNZ6z3DfOhYcoqRZLEwYusmYzSrMmz0DHOC9G6rs9AoXBYN8DViiEgJQ6J9TL4o4kIIQ1CBRDTr5hLyqBNjGsm3IjzIkhK1fwcmEgQxTFRHFHkOf3+IICpLnijZtWcdrfPaLSGACpXE7XaXH/9dVzt6Q5HVNbT7nTZ3r5AWRZURUGnOwhrs2pY/0JSlQVVlVHkOWvDEUpLWu02abuLjgxJ2mI+W2BiTTsehGbSO2TDIFgVeKs1EJoV2YAPNVJAt9cD70i73QAEVjVaa6I4CgEMOqLT6Zw9j3MgdCNh94ATJJ0BWhlUI4MPQFuwucDD0npOfPDXanlPWS1Yzk8YJFu0k5hlFuHKgsIWlKpmPDniJ//b/4o/Ombv0mUS7zlaFrz99vv0swVriSIWjctLIx+ShCLUeo/1guHWRV545dtMK8nsZMYL3/gtXBLBaMDrv/c7HNy7z0//+f9MffyEaxc3qNqafLakrCwWiXMlsrL0kx7t0TZaRgw2ttje3qfbalFVBfk8o9PtkYzWUDvb3Lxzl80o5dqVy5w+vkfuJBcvv4SvLfce3Gb98S32L6xz894dehcvY9Z3qJEkQmHiLt1OjziKmZzOuHP/M6Sp0QKUVmA1ZR0GjcFDr/Fibnz/PBYlPCZs9HilWAjP51iKYk49FfxWd8hQCNzshCLPgp9dlaO8xVlPRYFIDD1Xkd+fo6bH/MMr3+Di2iZ/9dHbfDU+gShFa4XlnF20KizPqq0VSCvOvRFX/sc031sNWVZDzFWoSHj5QXa4+j+rkDKlBHfvfEVsYl57/ZscH58G1g2KJ0+e0e2tMej1aLdaPLx/nytXX2ZtbcRsckS2WLK7s8PR0XEIH2vAz4DAEgJF4TfOhd94iHAGXXvxOaIE+u1r/PQnPyXP55ycHlKWBZGISTVUwrKcn3Dv3l2uvXSBql7y13/zVzy6fYO17T3+6I/+G+7fv8OlF19F25JsnnN88ITnBx2mzx7z6bMv8EqytbWFyR5z873PeXT/ATtrA/JJxSLLiJSg0+3y1vV/l/5ok/Gs4sN3/oZ3f/ZToliz3mvx7be+y2hjwO2vvuLvfvZzHILhcIjRiidPH7FYZkyzkitXrnBhb5dDKTgen3JwcsRiMaWOYfPqS+TLAuoCo0qSKOdnP/0Lel3BP/ov/wuOas98VtLtDSmdpNsZ0R2M8Dhu3/6SVhJR24qt7T32L1/low+eMNjscmn/IvfuPMZlFS9e22M46vOLv/sVi/kUYxytGJKWJtYpt768xeXL+3z/ze/y3ief8vCx43d/9x8Ttd9hf+9F9p+7x7PDGcf3b4CvQOlwhq/8Mb3nPJzonPHNioUmQ+hJMV6QHZ7Su7zNYjqlkDnXX/0m2hg++ug94kTT7qbMT6csshnGJUxnpxSuRHiwdcXDB7eRaYtpNWOeL4OKq6qgDuFOshmseh8YQQqJb3znXWOt5J1AKkkcp7jKBh9p0XjVWcuvP/oV49kYG3sk8PmDz/iLv/lz/tMf/D4j0wsqLJPw5qvf5sNPPmQ6PWHQXkdpHfxGS4esRQARAFd5qqygLB3dJOH7199AIvizv/yXTKxnYQt+9sGveP7SJV6/fJW33vguk9mcv/rJ37LIMvAh5BMfwoCsdQi9aqAFSiQYUqrMcPz+mNlkwfor6+iWZ1FVjU1ZjbAeZRX7W7tsjDb58quvOJ6dINMILYKu8Cg/4uj4KbudjN3di1wZbTGf5gy7fZRxTJM+O60hjx7f4+H6Bkf5M3715Qcc1RNcS6KiGFNKZF4gTmcsHx1hDuYkhcembXxHo3e6Yfh6PCcRkl4kkCFhjXmWY7ynn2q0DbWoF+f72orcgQqevVVRYCNBUU45Pn7C5Zevg1DB6zQTvPTCK5SLKbfu3uWoOOL20S3G1ZJ2PCSKOyRxiyTWJK0eeV3Rjgy7WIp79zhdLJvcEUKIpqjP/PUhZKusBhIN7SpY0HiNdQInJIUApxWzsiRG0GunLPKSapZjV/uxb3z8V1WmgNqH/b92jqLyLGtHJaDSim4rITWtwLR0wdHSeYKyzwf/V4EgMgYjJJFOMVEU0s+lot1p0++nGGPQsUEq20BO4Ywpq7IZEAb5t/ABcMcHT0olw4YtaNaUCwzJ4G9as7JhoAGMg3UFjTKOpo6sWRENadatawBc25xZ5weew1ZNxokPHqzhp1YkERnYf35lZbhiAYYB0YoF6P1KNeiRXwOFv+7X6xvSTdi+Vi8Qwla3AlLP6+NzJcEKx26GV7451IRi5XUfaunzIeWKMeycP+ubz963bwAlwNqMg6c3+PSTASbukTXhslEUYWRC4QMjV9N46HoXLCqa13mugAoepMI3NmdeNPcKwfpAiMAcFqIZeDnwwRJBEeOFBqHx6OZ5JKBwLtT5tqzRwiG8wpgU2YYoSkltF9cMC4QUGKOQygRSlgAlQvhXlMR02l3iyKCUp91OMDpGNSHB5z7fDkd4z1VZIYoy1ORuemZjI0QYcltvwVmqugy2htZSV4ExrZRo8jEE+BrcOeFCCkFtA0M+zB8aNZMLIxcpBbhGSYJv7hV3likQBuvhLAoZZQKLAmVwUUylYzAlwpTEjT2k8xZbhwXiqJFIUuFYiyVTFzNxKfM6w9Wh16smT/FVGdSHJQxkRL/XIYpMsF3xjiSSxCZCaRPYwTiMUWht0FqSthL4Wuj0alTknMXaQKgKZ6xlOc+YTqYsspzZbMZssiDPLAcHEybzKdPlNBDXAC0Upj2id+ECSX+bOmqxzHKSyDHsGoadNpvDFsEmw3Lz5hhJY9lF6DOljEhaI4brCqki4qRFq9Pn4f1bzGdjJGF4o5uMCesdrrQ40XgHCxBKN6pdh9AaLSVCaDqthEF/QCdp04vbtHSLxDSsc2FBWFaGYytCjA9JLPx/Pf5eM2n/2//uv/+TP/zP/gi/mnwRJN7e13gcvVbMblew33eIxV1cMeXk+JTPb3xBEhkWi4xWKw3ee0pilCDWpmnxLVWW04rj1UCKBgpGqhBeIrXCGINAUNuKqiqRCLTSeO/Il0uEEMznM8qiCL477TZam7BIm+dasU6kDJOVkARpsXVBmS/AlWFjbxZxp9sJskCh2NjYYDw+4fjoSWBi1Q5vPa0kRUrB8eEBRgW2UyttMZ/PGY/HeGeD1D1uU1totTpoHQ75eTbHWsfO1h5HxyesjUZo4fj0k19zfBR8Co2JODh4zLtv/xxXF6xtbKLjFsKEpPBYxUgVs7l7ma2LL/D8y9+kt7HNfDml02nx0vXr9IcbpO0WnUGPOO3QaQ8wJiZ3Gf/6X/8bPv7lh1wabLC3toGQcHj4jFhJdHNoZVVFXlXhJIMGSOWMEbmaONa2PjuIVh40Ehqv2fM/Z8whGZpl0yQNSxEKBYGg3WrjnSVbe/QWWwAAIABJREFULMLBKyW1deR1SeYd3Z0LbO7v8dvf+y6XL26g64wk0qyt9TmdnSCk59LFi5RZwXI+I0kiFosp2XTCTr9HS0JdLMnyJXVdNMWHJ9JBildVBVVdUjcFZHgnikJCpiJM7yKjq9d5/tvf5dXf/i6vfv8NLuxfIGl3qeuaxWzJ3XtP+Vc/+YB/9d4jbi4GlJ3n0VvX6L7wKsP9S7RHQxal4/DxkvlkSVtrru62+NYLQ65fGLLR1vRiT+xyjMsQPqeqgjQzzzOKGqyK8DqidJLFbMZkOiVudajRODRCqCYQaOVHLwEZTNGFoCoyoma6Nuh1qPIFB0/vo7Vs5Ephg1RKnAEHYU/7ekhY411Z1zgJSb+H7ndI1vqIyGCbWktyHhiwug8UAqxjYzTih298iyrPWGYZd+4/4mg6p/YVmzsj+oMh+dKSLQvyLOPp/fswX/D43iM2tveYLh1f3X3Ep19+xcOHh/RHF8iqNqOdaywKT10sUVozGY9ZjA+ZjA8oyxIBnJ6OOR0fY6scXJB8CeEoigUSS7ack6YdTBQjvEN5RxzHjDY2KeuavLRc3L9C0mpT15bSBRlgt2VotTqkrQ4mStE6IopT0rRLrzuk1x8y6K8xGq0zHK0z2tyiMxjQ7vVpt7vEaQuTpLS6HYajEUma0Gl3UMY0oEsT3uU9T548ZT5f0Ov1SJKYlY8qnAMnKzmy1vo3El2NiTBRUyipCCVN4wdkQlMWJ0RRmzTtY6IWUZoQRQnaxGHqLBQmSlBRMLhXWjUTT4UQoeBbhV4IEbyITRQ3e2GEMhFS6yC104ZWp4NQiqwoiZNQxEVRi8FoC5N2UNqQJi0iE3NwcMhymTMYjpBKk7bapK0O2gSPci0lSkfErQ5pd0B3sEa7M0Aog0M0LF7C6zfxGVOBhkFyZifRMMmVUngZVBZKa2QTgKi0QUndJKJWwUaCMHQKtg8eE0dorfDOUxYVAomWGm89n33wDodHTxBGgQr7qms6A1t7cmqkcIy0oiWCtKfX63FyOmVZVMRRzCLPOF0uuXzlebbW17l/6xbZ+JhYGrZeepWX3/weX37yMYn0dJLw+ay8UZ3zASz3sH7xMpevv8bDo1NmWvNbv/s7jHb3UElMkS/5mz//F3zx9l/jDh7QUzX9botWJ2E8W+DSHte+/RYm7XB8dEJkYohSWps7tIdDpIC6yJmOjzk6fMpoc5PN567Q371E1E4xRcatX73Nk88+5pWrV3nhxets7V3h7q3PmYwfM9pcYzqZkA6GfOsHP2Jte4fNzW3WN9fp9roM+kO0injw6A55Ng1e6U1BHXzZQqH+9SZxpfAITJWgNkAIvIRSSZZCUFQVCZZepIgJQT/CO6QtUbZANuFrdV2j6grlKigWqMmS3Vafq1eeI/eWg+OTEMTIKniz8Yv+GkMWOBuorHzAtT6f438dAJXN/XXWHIrfbIAD41Y24AeAJV8u2dm6wHCwRl6UZyzFsrQMB32Uktx/8Ii02+HC7kVsbZlNZ9RliXCeoiiJY818MqbIloF9wm+eB+ePUNQJPNIXPHdlj8Goj/WOJ88OefDgIWVR0G53Ga1t4YTm2iuv8Z0f/IAP3/uMD9/9NZ/9+m2KyZRL+/vsXbnMzu4+adrm8YM73PryE+7dvUO700ErOD06wJYl3lUo6Xn27CGz6Rgan/S8LkFA1tieVE6yLBxb21uM1kZ8+vGH3PzkfSbHB1x+bh/hLGlswMP9B4+pqwIdGbr9PpPxKUePn2HLgucu7xPFCVmRNx6Ego3dfd768R+Srl1i7+pVLuxf4for13nw4AE3P7/DN775JusXn+d4VpF0Yn75y59y5/ZNlDC8dP0VysqC1kRpB+sUw/4aL1y/wrIouXx5i3yZYyvN7u42dV3zySdfsra9g4kNhwdHrO9eYvPyZZ4dzxl026SJ4vB0wqOnR6SdNZa548OPPmA6OWRvf5tnh49YZgtW7Bpx5p0eKGRngZd+RSxqQuKaoRIWyvkSLwlWFbMZ+/vXeO75l7n38D6n0yNMpEmShDhJQArysqDKM7z1KGmwrkDGgqXNyeqMqlEDSQSuYdD4lT+mDACxawbFq+Cl0Dfo4NtZ26DQqB1rUY83r3+Hm3e+4ItHNymjEApo4ojT0zEtk7B/4RKRSrCVI44MdZVzenLE2midKE7D63B1UGrJUEvh6iD/bpRHRgiGvS4Pnjzh8cERTkjyMmc6O+HyhR22R9vs714im865d/suzgm8+1rwklN4J1FovNd4ESN1myQaoH3C+GCMsDWj9SFVFCTKSiikE1xc32anv87t27c4WYxxxmMNOBHAX1dYdnqbfP+b32fQ6XHn7lcM19ZxwnH39i2SyLC+s0XcTfjy3hd8+uhLjpjjokBYEJGmFWnE02Oq288QR3P00iKsOAPyhQ51XjZZ4vNwbkktMVqSFxV5VZMg6KjgJe+AlVf/ypIJFYba1lpcbWmLlMR06I+2GY02ieOUuipDL9k2HC+X5EJyMp0yn0wYtLu0em0WVcZiPsNog9KarCwgiqiVIcsLuq0UbWLqZlCslW4AoJWNVAAyPcGLVZrgdzhfLBhPpgjV2H+omNr58JqdY1nUZ96nUgiMbKT/omGZrhjGDaiwqqttk1aexElg9hICpK0LalBjIqSURMaQtkJ6ea/Tot9r0+226bRTOp2UJA21jDYNiChogpoDSQmxCqY9V8fJM8BKnjGIz0Ivw+VtCBlfU9AJGqVZUMGK5gwNteWKvRoALu+CLZ1veu+6rBr7L9f0jkGZGsCwcwsGRJOH0XCWweF8HewLVmFfrj5jx4pAd2yIW/7s3D/bvDxnrO0QmBi+LptrdUYwamroc+ue8FPOBzgH5HkwG+efh/OOsiqD7FsGkthqr5RhgYfa3DucqynLkiLPmRw/4fTwPovJAcqXKBlAepQiiVKkCnubkiqolaRsnjcwE1e1QV1X2EYdV1XN381njQuEthDGFpRjRhsiE6NVTG1Djxh8f9XZjG4FknlrQQi0MWglMFFM2gk9SrvTC9kSvQ6ttEWn1aLX6dDrdhj0enS7HeLEECeGpNVCmQSa9bbCalbRL86veOfhvnJ1hbVlE4xVYquCusyo8wXlckFd5jhbItyKiBd8+b1rQF9XNcM9e8b2XoXNrX6P8A3LmXBPr2wWpaCx0PANsO1xNtwvDh9Uz82wJ5IaoXSwXnOeWEpiIYmloqUU6cqX13mU9YBlbmsOrGMsBIUDhMTKUJO7PGQCZbYK5p22pq5zbF1gjKCTxkRGN9klEGlFEmuiSKGUDMx5FZilZ6RgfKOeLCmLJWVeMJ/OOTo44fjglAcPnvDwwVOePjvm6bMx958ccTpfsCwLqmbKZKRhNFijM1gn6m6xduEFtGlhbU2eOYrcUzbh7yZWHBweMJ9NUcI3ijKJQOG8pV4x7BtWvPI1+XLRhDqH/grB1wYeYT9cEfxo9oxISwbdLnGS0u+06bTSs/uv00rpdiLaqQl4k9CAQvpAyPFI8AqJ5i//+oP//zFpBR7pqoat3zBAXDB0R1piV3Jp4FlOT1hqi+6NaHW7ZHnNZLKg0+sihWM5n9BtJw1yrYmTBENCqxP8GAGEq6ltM0WLonDzNdPNsgybrlH6TEZPsymFzd2TJDHdbvds8iWlbCbpjdG4Cwi6dXWzMIMpcdRKyTMPlAgv8Lbm6OAwHCZFRredsntxH1zBwdOHCO9ZzKZN8FjJeDZjNj2kzEsuX36BznAdLxVxu8d0uUSlC3RdE1UJve4aKmqhEs2zRw8pimU4gGzBsycPmR4/o7YVifEYdYFnTx7jFWxtXeRHP/wHoBLe/vU76FafTpLS72+wd/k51jYvIkyb0/mcKI65ePk5qqLi0ZNnOO9Y21pDlmGSmtQV8/kxX315g1QmpCbFS8+yyHg8OWan02OgI4BmctTINlyza8tzCWmsGzkMq4OsaSTdypvGIZRGrkgZMhyPQAMWyrMiISizPc+ePg0AklKU1jGrK2ZFxrwq8GnCS996lUpX3Ll/g1EEd29/waX9K+i4mdqXFqEd3VbEqH2Bf/iP/nOWTx7yyz//C0zV4cXdIdd2NMeLJQ8PJzw9GbMooCbHlQJtBanwtGQSijoklW7j0z47177Bmz/6Pa6/9Tq99TUibZguCianGcvlkpu37vDOLz/h/Q/vskh2sRffIB7u0R8ktNqG3DmOD05ZTAraqeHaTo+drQGjtmJgIKlKjK+ofYGvciIVZH219VTWg9AICVYaLBLhY5AJi/KEB7e/Iooi0sFemIquJsirgLxGDuO8I/YOFSVgLe32AK/3Sd76McvZCfdu30BY11geBK9mv0qrcrYpHkNhixQ4AbqbkHa7JL0O1igqfAjKCccjXq6CiWiYAPpM7La1fYE0bjM/PuGrr+7z7OCU2tYYqbj9xW3KbMnB6Sn9tQ5xKthII65f2aBbLBgfTxnPNIenEar1HFu9PsQXMSZFSEWn3cJoSbfdI01bsLlBXRVEaRshFKN6jZPjA+JYMxxtIaSmzDNaRYK1JVGc0usPsQ2ocunKdUYbF8jLOS9/45vMplOGw3U8OkwupQwFQxKF9eIatqJSKOGpyiKAOY3Xla2rUHAK2+x9gVVqqxLv6mZABVGahqalUemFZRiKwKIsqYoq2CLMQgiH1hpna7Q2IbAOztZsYEd7yrIgjn3wn2181qRWaBWH9yvD1DyOU7RO8DoOIGVkkFLhvEDICKEThI5CUS8DIzQkdMrGJoVzkDNQOIParaFeSClAezSesixBCuI0RUpIdJtaWmonUF4Qxa1QKDnL7sVLLBdLhNRIrREqvC6EJUmTUEg5qJ0LvlXS4LxsPIZrlI4BqJzDNUFMATVrQnSaQl00E1dr3Urj1DBtm4RqGwo4E8VEkcHZYE0glULp8ByRiajKkrLIwhuXQYZelhWtKMhE66pEqig8Z1U14F0oLk+d40BIEu/R2ZiimlP64O3XHwwpZmNaUvPBL3/F9Vdf5w//63/MX/3ZP+OLB08Ynz7jyvM/Rj9/hUdffMRaJyXyYd2uPE2lMWzu7NG7eIk74xOufONVrr3xJhMhOT444vFnn3Lz3Z+T3/+KUQw6FtSu4tnJMf2dCzz/1g/p7DzP3rVXyGdzyl++w8k8oyscETXzxw/pao1xYdBRZ3M+++BX3Lh3h+SdXyHTlGG7TdtWXN/eRCnBLFvw+MF9HI7FfMZH773NJLccL2ZEiUamPWxlsaImSSLa3Q6//eo3yE+f8W/+7i+oXR76MSUwkQFhcVV1ZiPgnKOqSlZem17Js9RfqQIrb6YFt6iQi1NKHK87z2ZsSaRGiBCOgSSwyF2QayEMqRdQn1Au51xcW+OPX/42r2zt8Zcfvce9xQRnIrwX2KaJDk8CwWc5/HPVMK6GmmcsRsK68U0TKtW5J+1Z3dawDl0DfKx8BZfFknfefYcf/eh3GA5HnIwn5HXN8ckx9+OIy/uXuLR/kTu3vmR/7yK729ssT0958vAhIJhNxpRG4WxBVa+CX1aNu2/uV9cAw7JhyklmkwX3bj+mLGuiVLO2fYHZIuf0ODBp49QymYz58P0PSXprXNho8Yu//RWb/RYvvfYar7/5LR4+fRz8UKVi1Ovzz//pn3Lz5m1OxnNGawN6vR5bG1ugNHfufsUiW7C5tYM2HWazCd/+7g95/uoLfPn5x8RpxNqwj9SKw/Gcy1ev8r3vfZ/PjOOTj97jzq27dDsp/fVNeqN1TqdTjNasj0aMNtY5fPqMVlRx78sbfPnpPq+88QaDXiuEXjpLr7+BStf48R98j50dw6Mv77A4fsT3n0z4s//hf+Jf/i//O398+Zu4qGb30jadwYD59IRHz+7T+vh9orjHxt4+O3sXeXj/Hr94+xcUvuLKpX2U9UifsrG9zuOHSz547316/TW+853f4u23f8mlqy/x2z/4DtMljNZ3yU5P+eTGEy5de46j4xm/+MlPkWmL0SBma22TOt/k070r2Egg8iXzg+PQEAsQXrNSX6wsRBxwZjzY7FFKCmxRM7t/SP+5LTqdmBuff8xkkbGxsU3pFixnY9K0HaTuKqQy27pmPjsliWKG2+tEbUMlS5x0uDo0cb6ywYNZyRWpMQx8XQj/Ec43TWkA/JwLtmbQeEAi6XYHJGnM6fSUZVUgXYqITAh8cYbTbMmTo2fsrV9iPlsgRcn+7i6ffn6Du4/uce3qy9RVEZ7TWlQUNYHKTYATQbrtK08/SnnrG6/x5Z1bnDoLUnPn9j1++e67XBjt0Elb/OF/9B9CWfHXv3ifrMwRJg3nFyAaZaBSBmeDosUjkaJN111gfnPCI8b0Xk9Rokbi2NvcY73T5aPPP2JSLRCRpBYV1lfgQ2r31a0r/INXvk83avO3v/o5Dw8eEQ/6ZOMpAos2gtt3b3KYjWl1I+a1R2tBrTWxUVDlLO8+JPv4Fq2lxMiE0oXBROmKcM/EEU575KCNOw12bFo6UiVZ67WYLAomywKDJ4mDdDs04gqPo14BWkoSiYg6yzlZTFlbTpnNT+lmQ/prm6Akh8d3SQfb9HcmHNx5wHI5YZY/RmvFC70Ek3TIi4JYtWm3O0xPZyzrAtUbEudL/GwGypOmCXmR4bAYZYIPaDCnwRPO8RD+JJA6+CmfFhUtFSOEomwGvtSWTr/PBobT6Yy8qpGAbvZqhQcR7NtWtNPQWymsgIX1VHmJlwv63Q6J0cFOxNrgQy5D4n0UGUykiSNNK9boqAlhUwKl3BlA5ZxtagiHlRVGBXITTf8ctuxz6xwpw9A/LKoAFNEAO1KEHAkkSKnPiB4BNPWNZUEZWJW/gYWu2HPuHPBsbM7kSqW3IrTxNWZj8xWPp3buzK/fNp6z3jdhT9AAtKHmXBFIhOSMGRu+3KiBxcpPNjDXBWEY9XU/yhU46124XkElej5YxeswGA20XpwIYKcQkiJfNgxlfwYGK0HIvPA+sIKdwBKAHycVvq5hcYzPBDog38HCQjTBgrZmZZXhbBMK5jy1q0LodvN+gh+sP8sYsD6Eg1sfpP6wYuuE1yGAQW+N3touOh1inaa2NbPZhDxfUlY0RXqJsAW4GkEA1IXkzAZPK00UxRi9CvvzTeiTx0hFFEeB1dvYbUilG9JIcx/JANYKcX4dVqoN19gg+qaPXAGNYINC2ghAB7wHmqExZ4Dq+cjYNqV7qJXCvX7ujey8Cz1Z8+yCYIm2Cne2HqRqmIQ+hPlKGVjxoiENSiHxKgmWjmUJrqajFO2qRpclshlWWC+pcNim9Ku1pLCEz0UJqB0l4XfUxRQoKMsJy3FDQFSK4WiE29qm1+mEXidMVrG1pyqbe8WBzAPDeqUUtHXJIl8wn02p5jPKvGQ+KTmdFBwcj3l8fMzR6SnWWcqiYrbMiCJNEhlEkAGAcAgUlRWsdYYMByNio/DOUhUF+SKj9hYZGZSWTCbL8H+aIGbZ5H+tBj8IgTSA9rTahk7LsJznoUa3GhVFIcNBiZCZInwzxJLoJARFx5Gm2+1iPSTGkCYJrXYLE8eYNMbEGi8dTiiUUM1eEW60MyXp1+6Wf/vx9xqkDaONJvnQNxdaOGTjrVLVFYvsGO8z0nZCO04QWrK+OQDrUVGENobdi3tEJsJaqG1F5HTD/CDQ21f7qbeNtDT4trgqjO7LokA13o6I8BxSQLvdpqoqBBprLWVZhYTvZuFJuWJ4WKwNDZn42ibvm4COsF0rlNZEUcTpeEwSG6bjGbPpKWlsGK1tk2dLqjKEEuAcpycH5GVJlk04Pjym3+/z/MvXubh/jbywHJ0cMR0fMxwNsaVFJS1aaRo8EhdLkqTFxuYOWZnx7OAJRimEK7j1xSdMjk/o9Xu89tpv8ejBfY4mc7b2NnjjzR9gjETriDwLRc7poqC2OVGckCZhqlHVGXEnoZW2EaLxupKSyubcuXmDe3duYpQk1hrnQviSk403n1+FdjWNYTNltHWNI3hNehuAJSkDE2slq9ZKNQCSR2mNMhpXhoZuxVCjAXxXiZDQTEtsYAeUtiavK2o8p0XBpFiSWcu1F1/iD/6T3+fG7Y/58sb75E5x6coem1sbHDx9Sjkv6cYt1jb71NWM1PRIWwbZ9gxaDpEdMuoktBPHno15cfcCx5Muj08WHC0yyrykn3TpDjdAtyhlwoQW+WCf7gvXeePf/xFXrl/EacN8FnxRcI6DwzF/9ZO3+fWHXzEtY9zaq+jBRYa7l9CDPllV8ejJKcvpglRbrl0cce3ikPWuxHh71mxUVdEUQpK6KJnPT2g3YU2rogERAHRnaZphTX+0TbZxyuef3WDnkmV7/zqgsTZIkrwiFA3SE2IxQ0iNaHJBddxCjrZ5480fgnM8uHsDW5doJQLjD3F2fVesaowmarfQSYxpRajIUBNkYas02BUIH8Bi1wyzg9QLH7waB8Mezlt6vQ6mCbYara+x+9IOnQSGoy5RNwJTEsWCnbURsS64cqnDjdsFz+28wQvxCEWEIKXILbPJlCzLafW6KN3DI4LpfBTjlUGq4EFrXU5/sEZVFUyXOVEch/fpIStqlI7C/F4IvNT4qE3aU3TViKrKGG34YLBelWEqrFTDZE7xvsJT4RAYFaGNDr/bh6lnmBj60KDYxl8Hj5AKESmKbEZtXWC1Ko1zNVI1QCvnLLtLe3ssZksEkGVZ8PCOXfCgEvwGwy28N4/UKgCK7jwU0jfVevCEU0hpUDpGymDWjwqSKKF0YMCikDJG6rgZvPhQAyJDseFtw6wIRfLK3zcUQudos7WWsiiQwlNXFSaOA2MjGCST5UuU0sQisMBXx5JUOnhoKR1CYqw7C4myNhR9VVWdTeuDdMmykgtqpQFPlucslks67XaYFzYetCuJIKzq7SbNtykuVsWctVUIY5Mi7ImN72+cNCC1c5yOx2jVWD8oidISYwxpHAU/seZ3KC+pa4uoLEJrahf2l3lZ8sR6+mlE6jxFWZMVJUhIOm3Ecsb6+hpXX36JX/36Xb717Tf4gz/+r/in/+SfMKlybt6/y8bLL/HejQ/ZKSq2Y3lmWaOBza0taqUolOabP3gL3xty6mqm41M++cXPaOcF63HMgVFE3iOspFaGrcsvsffa62xff42ns4KPbt/m5eeu0F1f4/T0AWWe8/DTj2mZFsQxoqgxSLSWXOiP6G1eZHThIq1+H2trnt27xf37t3n25CHLbM5sEqRPSmt8kdMVEvvsHr/8Z3+KQ6C9CJ7lSqK6HTpbO7T6fXZHmzweP8aqFQitQFSUtsZWTTKs9w17wwa1QLPOw7dCE1MLONWCu14gi4xYG5QQrBmFFhLjJE4ofNJBSMlyekKUFxjlcSp4M3ZPZ0j7hO+uj9j+7g/5v+7c4Oe3v6KUIEw4lwNXqPH85JwRu/Lil2f76dfCAAksuVWLG5rcc+sT54J33yqILDBI4ODwGTc+/4Q3v/tDyjLYxHjvOTg6ZvvCDpf29zl6/wNu3viM77zxBr1ul3Eak5c5SaI4PToC54hNFFQa3p6xf8H/hpefFI0PYu0pipq10QYPnz5gtLnDiy+9yN/8m3ssspx2Z8DVK7vcufeQL95/m85gwJvf+z5XL1/h7u3PmU4PeXzvJlp2uPbiN3h4b8ZwtI739/jOW9/jxZde4uHdWzx+8hCjIxSBMb6YnRIlFV4YrKvp9HuMtra5e+ceu3stvIPZ8TP+7H/8Fzy9fxtRLumPBmRFyUsvv8jG1hpZlnF6Muazz75gNr8HzX6itcKWJTc++ohXf+t1Rt0up+MpSmmKbM6trz4m7nY5OtAc3DtEuCWXrr7G5eef49fvvcs3332Xb/3w93h07y6Lecayqtnb3+X9D3/JaLjFa7/9PdLOkGX+GbWdcuvzr3j1+X0ujmJuuCVf3XpIp9Wi1YtJWjFPD+b0eltIJXn3ndtYm/DiS7sMdjocP53w7OED+glstRTb+5d54eXrrG93uffoIfeeHfLpZ79gexRx74sbPLpzB4ogb0WwEiA3g8cwaD2n1xI6ZCfwWc3iyZhkt0ctJ9x/cJMLly9z+bkr3LuVN2oFQsiMDGqLssyQ0tOJ+xTONgFIYchgaxtAKkCJplVyvrHfaeZdjbor7PUCX4caZyVJ9dYz6o4w2jCZz7Ba4x3kRYXS0OsP2Nu9xM3bXzLsjmj3OkxODqg97D93hU9ufI7DcenCJWKTkEQtkJKiKvFEYcgoQn3jrUNYz/7GGptJRD6ZU3uBzWreeec99nYu8ea3v4OJNL//H/weUsb8n//3z6nLAq8ETjUfpa1xTiNVm9rXqCicyYlZY9jeYfr0KdO4YOuFEVsbAy4O+/gqZ9gbMRnnWFutOELgBeu9Nd586XWMF/zdL/+WW4/vMFhb4+nTx8Qo9ne2uHv3c7785H18IlBGcvjwIa2re6hRG+kd0wdPEQ+PaMuIuB0jSkEtBLgaV9dYbyCJqYxAdjWSBD+2GAdGSoSW1LFhWtec2pqhiEJit3NNpqIIgLdowFsEaZqwnJXcO3rMhfFD8gg6yyVOCOal5GQpWZaa/mgHRcT4WcadZ/fxnS690Q5l5ZCdAWmnQ9TtkZ3MOZ7Pka0W0loW0wlGStJOUE46F5jarvH9d943gVr6bFhWO4tFUEtDqSJKB044tDDESZt+2sFFGk4nUFuU58z3VqrAkPWEIQPSUzlLTQAn87LCyxwXG9bjKAwSnUMJgdaBdNBqpXg8aWKQWPQKO1LBQmKVWM4KJ8SHgaK3BJxVnq3dQHhyZ2w1ZUwAL30TGCxDL6eCD8KZ56mUgWVcVeWZ9dZKSXnGQJXBX/jMaqux3jmrnvzKvzYwOL0Ma1s04Inj3KLL+hVhpPG1bYC6QESpm/MmSLrDAN03A8qw/qUSZ/kMq5r4HB0+P3fDy2lqZX8emub8SjUoEEKzYsd6L4ijmNFojZPjMVUZLARk00crJaAhCqimhqQ5z62QWBxO2OZaBGUCDmg4AAAgAElEQVRpOPNXw7AVRiFDQG8Dcpd1DYT9xkPjP7saMod+XAiBrBW6qYGCPYRjdQe2uynXvvEavc1riHgNL00YSHjPYjHlZLwkW2bU2Qmz8VPmJ4/xNsOLirJehf9ppBFIEwVfYOcxWgbLBcJ9EnyIJUZFZ7ZhUgTV4spWJwzFaexFVld91bN8zc6p6TQCYZCzXtSwsrByTSZLuBdWdYiTsDJUDnDGirnfAPhfG0pg/WpOAd4393y4jk56rKipK/C+Bhn8YQNZKawbJwVOSQoCszoMOTym8Qy3Tc0tnKMD9BW0dcMwdQJlHaWyCBUs8nzlKF3oKiMpqYXk1Huk1NRFwWDYo5XG1A5yL6mrIgCcEKxw4EzpURQFWZ4xnU05PjhgOZtT5pKTScl4seBwuWBeZgjviZRARgovLdY7IhWDtzgZUeKxUiN06KP7nYQkDozobF4yz5dktmB+OqdczhrFSfgMz1i9HoST4Bx1VYYwQFcTKx+sNWwzTHBhaGmiBKcEUkUgJLUPa0ZrSRQFhShKoAmM89hoTOPFG4a4vhkuNLadDe4km3r/vI7+fz/+foO0eFxtV3y48BVncb5CanA2ZzE9bHy3FL4OvhV4i9KCNNW42iGJSKI2VV1T5AuqQpCmgcbvbZDTu+agDkBN2PylIARvCPDW4qVHqAjvPVVdkzTBYqsgqqoqWSXOi9VUqmlQgk+KoK5XqcP+7GchJM1rE4KD1tY3wFvKYkhV1rRaCWbYJ01b3L13C+vn2LKgKLIwwalL8uWU+3ducfHyC1y42GXQ6aKE41l9SDab0u8P0KIiMh3KtEWv22e0vkF/tMbd218ync0wJiKOBGVeooXn6aOHdPt9Nja2abfbHB8fMB/P6PZHbGzvYZIwxX947wuEh+evXWOxCMbZi2xJXmR0u33qymF0TGxiHAUffvIRJ6cTOioNDZwIsgCJI9IR0smzBR4OvmC+LQKK04De9kw2fVbQqCY5tNksV7Ls2jfykzqAfLI5UOqqAiGIjWGZ5yzLnMJairqiqitK78l8Te5qKhS7l56jso7x0ZhXXn6VK5e2ePDgDrPJhMcPn5LNC7YvXuDi/g7DCyMOn4759NN3iQ4e0Y8sdT1mno3odnoYEQCXvY0+OzsbwWvKVjgnWLouhegz0yNGl77B5R//gMuv7tEZxCwyz3jiqTPHnfuP+T9+8gs+vn3Ew/oCWe/HtFspw8010l6XZZ7x8O5DiiqhFRsu7454YVvR90vswUe4RRvZHZDEfaq6QtiCqqwxSuKKjGy+II2iQNNf0VdEAD+xzYqUEh31uPD8axQ1TE7GbOzWmDg5P9ya5j08ZGjuGzagkglg0XGX/4e692yy9DjPNK/MfO1xdcq7rvaNRsMRAAUSokRRJCUNNZrZlcatidiI/Sn6EzP7C2ZjZnZHblejleGIEiWBoEAChGt0A4225auOP+e1mbkfMs+p5obmu7YigO7ocse8b+aT93M/1729e4Nf+pWQvzE1Tx597sc9DEa64DwEWCWQUUjcaRN3OojQCfbad1al/z2LJFVfNEgp/WKn0MYJGKtLLfY2VqirGTLQ3HzhEg8OnnHa67PJGulyh08+v093uUuQ1kQZhJtXOR8POXw85Kcfn3Dt5kusrq1RzzIqOyMvS2yh2Vu7RNJso41AV7nftAxR5FypRVGhvcMyCCUiCMizDF0VYCpU1KDZbIHnz8VhQpFNKY2FIKLRaVOXJcgcK6Yu2drgNxGDFcEiYV1GDQgVQkaYqqQyFhUkNNshRusFW7uqSsoypyxrzs+HpGlKu+2CzMIoQoUBVV1R5BlFWTEdT4jjhDRNGPQHRHFMGPpCOoh8N7JeMCqF8MWqxY0cLYpNl1ospAvJMEZgpcISYEWIkKFHAiiQEUI6F4mQoROZvVvB4J2x8y72wjHiq57nmj4XQR1+pzHGd68NQgYo32FvtTpord3z94cFKQV15dZ/qdzI4HwtWgRNLri9vvS22h9brXt+vqANg8A1QeZlupxv3nIhcD8/xm3Mxb8ZY8nzKVrXpElCWZXkeebxEZI8y9F1xWQyZnNri6TRdM0KoCoyDvcfM51OnfvCCKo8xwhQvmFl8fzhWjPQGUc+Lbc7NdjKUuoSGglWBbz7zrtsXbvOV9/6Bf7u3b/n+tXL2HabjZ1doqRB3RKUq+s8nY5oBSlN92ywImRYaHZv36R99SY5AWcPHiGq+9z95GNuv3KHay+8QHbe490/6DE7PKaVdrn9xi+w97W3iborfHF0zrVr15gcHPJn/8e/px6OuLl5jfFoSDdtkaaKTqONbW8x7A0YqzHXbtxANjuMh2c8fXSfp08eM+2fIPIJ0riU3VasnONUQ6WM4zsbQ2pqNwnjC7myMphyTNE7JUsSVmPBJIwYyBqBcN3zxO31M+MPd3PuNtKldyuLCjzz0Nk6sAhyITiNFJW22JlLbn+j1WRZKkxtKHREa3OJyy+9yoOf/D163KNSkqDRJAwaKALkNCcuj3mx2+byK1/j8uoa//X+p5yMx1ShK+wXwTLigiF2kQr9/P0ifu7afD6wC9z447z+mbsgAYdrEQIjLffvfUKaNHn55TfIq5x+v880y3j8dJ9XX3mFne0NDvafMb59h83dS/RnI8xwyLWNLcZr53z52eeovEYJixaSunYTF8/f93OPlgWMFKxtrfGVN17DfigQVnH/7if85Z//Gbu7e7z00h1eeuU6SSp4/OSAqgx56ZXXGQ3HVHXFs4cPOXn2lPPTAc8e3ePmrausri1z/eYNlldXefjoIeVs4sbno4TxeMj1W9dY3VxnY/sKVqac9Xv8/u//73zy4UccHRzztz/4PtlsynBwyrMnX2DKDGvh2q3bXL91k3d//C7f/c632L10iddef5MPfvYpZ6cDWktddvau8vknd7m0u0u3u8zHH37EtRdeRhI4l4dVjPpP+PxjwfbuDcKkxuoW6fomv/bb/4Lf/w//iR/82e+zfXmPh8f7hJEgaQUsraS8/fZr3P3wHgFTvvHVt6gnz/j0/VMUBR98cBerDVILxoMTznsZadIm7ewQRAl7V6/x+OFDGmnClRs7PPrikLw34vO771FlI1SsOTl4ipxWbDQ3yMeatctX+Z//l/+V//jvNZPpIUs3Cug0OLv3hHpUgnD1t9A+LIx5/N7c4+SrCi/AVP0p1mqSPUFua54+KWi0mhhtWFtddrxwXaGlO5RGjRAVBxgstTZUleO+SuGS6q13ZdVaI8zFGLEwChWF3s1+MZ5srEZagRX+gFxYLi1vUGcFw9kUGgkmEMzyEqEzmqsRlzY2+fFnD3jvk5/yrbe/TbuzRJXPsKZgeanJn/75H7G0ska7uczu1h5rqxtEUcI0myGVYnlpmaVmy7moTEU7iViJQo7y0jXDpGI8mfHH/+XPWe9ucufmLaJY889+6zeJopQf/OU7DGY5lUoW65WSzrRitYU6QAYSKRJMkdKUO0y/OOa0P+SV33yBjVab2azHnUu30FIyyM+xtuJkcIoOBbMs48nhMz7uD3l6vM/69ibb3U12ljYIZcjp0SHXrt2iLGccnj3ibHCKSgKCWDjM1v4p4WGPm+u7mBXDwy+eokczV88bh38TaAIkOlIULbASojqhHpdOlLCaWAnSKGCp0ySOJKquqWtNXVWOs2oFenFeFoSNFNVMKcOInx18QWc2oNM5ZW/3OruXb7ER32FUSg57T2mvLzOjop+NODA1/ekIjKA8PaLQljBQFK0ms8kQXVREwlJay2w2o7vcdROg48yxO7Ul8DkoyngOowocGqaoFqaDPKtRSUqcJgRRSCkCVDtlrd1CqQOywQBb1y4EDIgih1coq8rVfcY79IRzjBprGOQFudY04oRWFLvgKO9WTeOQNFLIwImhQeAMSRdNbyfGIuYpLIGvfay/Rx2GSaqLCUi8qOnYsU5oc05Hh6DyccH+fF04dMacSe3rx7nLymizuA/tQpzF15mAvRAk8S5E4dEO7p4Vi691DVQnlFprPDKChZFnHjonpfLO+QtD1rxGnK8HwojFmeT5P93fzcJhab04+POff36fdaLj/NNKKTqdDp1O201KVQV5kXsnrXf82eddnU6k1cZPCWCxwuVhOFSYdPgXFfhvDwhCH24lLVVVE4WKIFA+MNeJnnjBX/o9XwUBSihMeMGwxzi3qNW1D+8u6Q37kIxIuksEjZRGp0sSRaxsX+J2c4U4TrDljN7pET/6qz/h2RfvU+Q9pHSM1VrWHrumwToe6txB7TBnjqPspprFc8KY9K+hv7bmArpdXEp+nzFIYdHm4j2Zi+nMLzthnaPVuia08dfV/H201sy7JIv3dE42c41t9/itx3EIhP95jg/skFjzpF3HP3XXwpyPqxY6kjZuahWLn4Bwj0NaTaot0t8TgRFkwonZE2uYBApUTF5rkCGRLpBaY4Sl9nWhxLnZZSCp85zh6SF6NqCctUmbKanH1s3v19yfRZyZrqYqa6qiRJc1eZ5zPpkw6A0ZDAuyyoWJZlZjFMRKYY0gCkIEFQLXPHUhgi5YzuFBQoaDEdl0RhwLGs0lAhmSthp0kw6nhyW9IkPYGm0kVincwKX179/c5e3ua11V1IXLbVFqjl5x50KlLKGMCaKEIEzcte91iSBwLvzaaAKpvDAOgYRIOl6v8vWAsXI+vD/v6Pi1VPHf+vjHLdJaPK/DPWlrnANVMB9Xh9l4xFIjYTKaOFaEgJ2dHSbTCbWuaSQpVVY7kdXzh6qyIFCSLMsIw5BGs4U2oI0baZjDwKWQVGVOkqT+AGV8V9AuRhbBLaRRFKGkS6/EcjGKuuiqGN+hB+W7YMCiU1LXpU+9dJ37oshJk5Q0Vc7dpEJaS+usruesrDq+2/6Th1hdIHRFXVakcczJwQFFDpd2LhOmMd2lJYyxnJ6dIVXE5m6XlWCZy9UV5/wFRr0ejTTl6pXL9M6OkSJkb+cy54M+3c01zk9O+NEPf0Dv7IwkbrC1d5MwaDDKcprtJuvr6xRlyWQyZTqd0Go2mAxHrKyturFyU5EmIUEkGU6mPPjyIcvLW4QThZAxSJdKWRUldVWhhUuLxDpGi5CKqqwWgSHGXGzOxjghYX7l6/mmYC15WfgDqGcPaVwCX+Be07woaDSblLpmXGTMPAu20BWV1ZSmprJu/ChUMTvbu+R5RURCGnXIckGjuc6gP2Y0mVHXmqTdJmiusbnc4fILktHnn1Me79NdWWVyfs5xb8ba6pYTleadXOv4LjYWzGxKadcQ69d48Y2vcv0XXmbpUodcwLC0TDM4Ohnyl+98yF//7BGPxi1qdQe9tM3K0jLtCEokXz45pzI17UbMa1eX2VgOSWRGXJxzeO+ndAJLnF4lpEVChRQVMjBEaUQoFSbq0oxjJywJRa1zJ2JZN7qhvNMQa9EiJmikXHvxdXSRg4qo5gwdPAum9hwe6dEFQei6S9Y5S4LALYrrMuLtb/46eVlxvP8QGXr4vVCIMCBuN4mbTcJmig3dOKT0jCspBKH196Wwcy+H226tueieYpGmZqPTYaPtDnD9854bVYgjbFbTPx+ytb3MYDjm4Nkxt168TGNlmZP+jPcfPyQ7LalmKYef36cYC8qsoqIiL3MacYcr6mVX9EkXYDWejDg5O2N3dxfjESpGu8ZCEsfudRKCKIpRMiEIU6wQ5EVFnHi3qHCijrUSo11X3Y3DBYQqWAikdV2jjEHZ2HXxwtifO0pXIJUFpiqJAsd4ssozcvxoXRTH1LpiOp24osDfn1GYYIViPBpRFgVBELk1LgBtDSp042xChm5kyjuS/CLpxFsVLYRZ44tpZV1nUQgFKKQMnKtehhgZokVAIANEEPr1wgm2wrUmFwX73BHq6nIvdBkf4OTdVwuIvRebJArCmtkkQynn0HDBC5YwlBei87yw88WVxSJVQFGWAC7N1BdQc4F2zvOc7ycLYe7nmhZub3NuQ7V4bBfBEfMuvvBTH2YRdub2I79GChe82G413T1Zl6RpSKhSHKrXhWA6TrobpYrjkLwqqXRNXbgnF6YRYRC44ARrEQYsgspYjmY57ajFel6wstzl5PEDcl05Xp3R7D99yqaSfOPtt/j+//PnnDw7ohU2eenNtxicjkjW1hmO++RW0xQGKZxTZ+/KTV7+5e/weDjk/PiQ/tNHjAdjXn31K6zduEGvyGm2UhqbO4TtFV559Q2aGzsMa0HbKoremPc//RPOvviU04OHbG/vYYRmVmbuYIBBItnduUQZKPIHlqOnJ0yLRxyfHJEVE6yuSJRFJQGmsm5qwwq0EYhAEgiFrQoExiWHGydkSGFRdU2n20CkKb3+CFFKOigmukILJ9goKWk1U1ezzGZo6yYKFgWbtU4YF+6w6EarXRVYAH0En2OppwMaEl5Km7TCgEDEDHsnpPtPWNveJW91CDCIIHT3dG0JdEVkDcVZD5mV/LPrL/DCzg3+8O/f4acHX1DHFhTMg/vm44h45wxz9+x8b33u43ke7PN78vw5zZ25c1xRoATalHz00QcsLa2xd/Uata4pezWHB4eseAZ2lk357N5dvvq1t1jf2qGWTZY6q1y6fJuz3oSDw5/QTF2idaAEGhdQKYXjSsp5Mg+Kqq74/T/6Q4p6Squ9TLPVpqpqNtY2efzgC+5+8gGNZsh4NOb61S2OTobc/+R9nj095OaVXVbaLZI7L9PfHvGT936EMDPK2RgpKspiitAFaZISCiiKEilDVlc3KEtNrz9i59IKP/uLP+UHf/l9ZuMZZV7x8Xs1rXaTRhrSCCwyTDAE2FrTaTXZ2tzmw48/4+GTA/LJlKvXrjKcfEYQpWxt7xIKxfrqClZaxhOXGm+FoKgKN5WlIhqhgqqg0Vyl0VknXbIgAy5f/ynvvfsOP3vvXb773/823/zON3n3xz8k0FNu7mzy5o2bhFmfk/sfExdjwqqgLgZIYfjROx+AknzllZforrV58OAZUoXc+/QeV6/u8u1ffZXhNOPz+08pRmc8+uwDHt79lBdfvsO121c4O9jn/PAJpwdfUJ2vUEeKlZ0WL179Citbv8Qffv8PaDfW+KWv/xanT57w7l/938z6AzABCuUDXC7EFL84MufMC2sx4xLTz1AKSltTTzOSOKa/f0Ze5LS6bZKVFlGsCCNFUVQenyER2qBLjQgDlBeOEHNGoUX6w72wYGvjA6Au+JnSjyj7bgehkWx11zg7OWRSTbGJL1UNUGoSqehEDTqtDu+8/w7rW+u8duk2tlQ0whZZq83VS9u89/mnnA+GaCuI4yaNRhtd1wQyYGN5g9/87q9zZXsHazUycLWQqWu0cJOC2goOjk75z7/3f/E//qt/ybXLl5DS8E+/9y2WGg3+5M//jsNe7qZXCDClxcoahPGCjbNk1khMnRCJNYpDzb0fPWWleZtGd4kwbnJHBmgqVGD40Yc/4jTrU8uKnzz4hNjC9StXWG6scXnzMqoqODo8Yn19A6lgdXOP/ckxZwk0d684U8txHzXICS0cHB2x2lpGFjVlXaFwwaUGh8fSlSZJQogkQgaEMkKJjGI4Rhp3nmsnEakKCP36YIwDDChj0BrnNrNQS0ElBPHqEqrR4el4TD0aEMlnPDzc5xfqt9m9dJ1CKPbHQ5Z2V4hv3yIyBp20qPIKRmNmVUZvPGKp2aKME8o0pTI5UZBAPmY8mlL2S5a7XWQEprLkuiRRMVZahwXCoqQkywtmnuVdFAXUNY04otlqo01NXubYkQuRS5IE22hQFDMnOMjAGSqQyDAgtC7RXGtDVVWuSSfVIulca0OaJkQoF5IkQAmD8vzG2s6ZqO6sO6/nnEDh6hEBboLs+Ua8uBAsn+fSzsObw9Bj6IRAV+VCILOw2EOMPwNKJZwbd+4ONcahIXwDXHgmuatg5pkW7lZV8oJpPQ+Qc7ZV9yWGi3MkVjsmpXFTStZPO7nHb33N7dGHczl0LvaJOQ7Iu2LnDUz/GJ2o7Nav/+/e6hzBPtBuLmjPnbq+Bpz5XBwVKBrNhgtjKgv3pT40TPmfIZkHibnXQ6kQrJvuFUi09s5NFRLIC8OTxOV5BMpjmYwB77o189dNCKq6do5bqbzTuVpM5dSV49Aq6TAzVIZHn9/l5OSM9upVGkvbpO1V4jh161trSLu9RCuJSRvLXLnyIucHXzLOz50QKQBvepBSECivrHNRu1ww8uev7YUI7qZo5eLvUoqFYGctfkLBYZOUdPgp937LxfumhHRYD2sXa5C08oJh6oPKzXPXupQCqQJ3WS3qJN9Q9o0SsA7tZ8QimNVbTRYIKXCsZ38huinhwEIUIOIUledgc5QxpNaSegyGFIJIuMdZG8s2klwGlLXkVFlMGLBUh1BkZLYC5QKZq6pyU9wCl9sxnWKKgmF/SKldFkYUJwSe5ZrXJVXlOPyVrijynCrPKYsCow2jvGI6LSjdpeDCz6whQBJgiYSEuiYIBIH0uAMhCYPYTdh46/N0OkMnCXUtyCuXARAEIWkSko+HmLpACLMIEJ+zmZ0FxWKE8QHSmlmeUVtDe2mJTrPlxG/mE7gSS4gLuJOuvpbCCbTSnQiFcdNxKHcvCSNdILN157R5zoPwE2hz1zvWUOuK/9bHP+rgsH/7b//d7/7O7/wbt7xaP2ogLAhNjSErcyaDAUtNl1w8HA+5/9lnbG9vEsYh0/GMJI6YTQdMJ2OEFD4BO6asXBc1ThLCMPZ2fU1Z5IBjuQghCEIX1lLXrls2rwydYHVxw4Rh6Aoj7bqJ7oZyHZo5f8RtVHNTl1m4upxwUpJnM4o8I8umTMcjwsgll4dRhDaW6WyGUop2Z5nVjW2SRpNKu3HJbJqx3F2m2+0yHg7IJiOyfEoapQghyPOcyXBMIJ2LOG2kZNkMozUnx/tMJ1Ou37jFxvYOSkVcvfYCo/GEp48fcPLsEbPeGeia7lKHy1eu0+ou8eTZE/JZxvalyxghOe+dUxUZymoOnzxmudOhd3pGlmd0ljrIQPCzT37Cf/693yNQTWIbs9FI2V1fZjIecTrosdxoEStFECqm2YzSGEo/xivxm40Qiy6qBr+JXWxqeOamMWaRIm+0S+cTQlB7t6wWIMOAStdkdcW0LpnVJZXWaGkpbe2SUq1lZWWFW3duU2Qzbl67wtr6Oq3OMo2kxeGzZ3z55TM2dq/z3/0P/xOvvv0NLl27xdb6Om1TEQ1HLMVNkmYbJQOWOmtEaYdapWjVRMZtCtFiEmwzbNwkufUar//Wr3HprVvUzYjKQlHC0XHG3/34Pv/xj/+OH37SYyAvo1bv0N66ysrWOghN7+SQ8WDISrfJV27v8vJem51mzZoytCxIkxEreOHmddqdLlIEGDSBNCSBJMTxknVdghHIIMQgqSu9EG6UdM4/XTsofG0qxoMeYRgRpY7N4rL+rN/wnEhWVpUTVH33Twjpx8VdEMZ8U2p32jSaKU+ePKSoCkhiklaLtNOi0W2TthuI0MlWSliUNCjpCy9hPIsLAukKv0C5hHG3vWrHMRKS7W6XW3uX0FXJcDCmkaREacqorhlXOXk55cXbLzA46jE+HdDpLHPeG7D/+BlX1m7QNpLh0SHn51NOzk45Odnn9PiIMGnzwkuvgwwp8hKrK4ypnhuPdEWWlE4EFAJ07QQ0NwKm8EBrtDE+GV4QhW7DDLy7VhtXFIElimKCIHQjMDIgVBLqAl0VBGHoOK+ucsNaKKuK2kIQJWgrXFCAUARhTJI0SVsdlpbXaC+tosLETRCgyLKcWTZ1znwZUdUGAknabJK22qTNJnHSIIzThUAzL4aVjBzGQIauG+r/E0JhkWgjsDZ07lQVIIIUFXgubRQjghgZRARBivCHDt+yY+GWZV7wshBXQbiCMZgzqOWiaHIFb81sNiGKXCc+CCMHos8z5yIOQ+929esMrgibr/1z5u28cef2Cn4u5d7ai0LLGkNZFIvOuTvMKOZsL+s6N24/8R12uCgm/LaxEJqVD0C0xk0H1LVzwwss08mY3tkpy92u4/gCRZ5RFhlJGHLvs4958vRLkP7ZCevcDp4lbbXG1u751sairKURK5aXmwynY5pLK9jKBXV87Zff5i/+7M/YXd/gza+8zheffcbJwTPWt7cRQcxkOGZ8vM9mM6ElJYGBEtfYOjg/Y3Nnk/0vPmc2GvHmN7/FtdfeJG4ukY+HPP7iPrUIef1Xvk0RNSCOiCPJg49+wv0ffp/zzz4mlRXUBbY0NDvLGJzIaRXoqmR1a5vl7SsMxzm90xOmw1OELQmtQemaAOcic2OTbj+Zpza7N84FYAhlnZtIWwLpnNRhIyVstyg8s00EiswYauUOgYGSfjQqxFhcM3dRT/jDJmLhlDa471HzHoeEXFimRlNqTSIlK2lKgMGWGZP+CKlSkmYXoRzaqcpLx/IzmkDi3stJhh2MWY4Sbl+9hsBy3nfCeSBAKe92Eo6fLBALTNDc9X0R3uIeuxASNWe8e/Y4QF3rC7be4qK1IKEsDGfnA3Yv7dBstdC6pihLRuMRy0tdRsMBZyfHrK2ts7S8hlANlEpY6nbptJsM+ycehyMv9iQvxBic6xk7x6fAYNhnPB3TaDUd5mltg3ba4LPPPmE87TEaDBkORnzlzdf57NOfcXL0lP3HDxj2zhiM+mxeukQQBKwsL9Nutth/9ox7n92lmSasdjsIL6Sc93pcu36DOGnQ6w9JkoR79+7y6ItPWGqn3HnxNnfu3EYIzcnpIaEStFtNNLhrrapRUvHyK28goiYffPwJX35+n7XVLr1+n8F4yur6Go1GzK1bNwBLq92m1e4ioxgrLJGMiKIGUgqyLOd8MGV9a5MXX97hk599yI++/8cMz4744MOf8eTRIbduf4XXX3uL0ckpvYOn2HLEwYOH/OgHP2A66BFFkqzKaXcapIliNuuR5ZK6DojCyLmntaV/3mc0nNE7z3lw/0sm52cYXVAG8LNPPuDBw03hcYEAACAASURBVAdMBn2GvTO0Mbz11jfZu7JLtxnw8O5jTB2wurrB+HTInRd/gRdvv8zX33yZyXmfw4NjNyr9cwxiLgxKTulx94q2mEITe355OSud202D1TVhEhI2G8gwpBZuHNiWFbbW7lClDcbXmy68zDvBEH7ddePEjo1ufq6WZy46WdC1YUk2+advf5fDwwN++ugTisiN0ksk0sKVpS3euPYygVK8d/enPD56xFp3mXbUgBr6vR43bl4jKzJOeicUlFRKM9UZlSnRpqZ33mO50+HFm9eQEsazCe/+5CecTwqKyjUvjDWYGoaDEUcHh+zsbNFpNYmU4NrVy2xubHJyeMRoOEHIFGsbYFOESAHHnrRWYa2rQcIgJCLh7KjPeDRh78oujuBjsZUhIuDqzmVMVnFpbZt8PGVvdYO1xiqduE0ShvRPT+l2lkgaMYf9Q+4+vctxOUC3YnRVU54OCWYlqQZbVUynGbOTEWZaOmKZcWJdrR3uJwzcATpWCqkENYZGkmJmBaJybPiqdIJkrQ2jWcmkdPz1UAlkXTsclwrpbm1TRiFDbamMZTgYcd4bctw746zfc+gKJbh78oxJKhCrK/SSFufNJqUI0XlJXZYYKcmNpZYB57biLJ9S1jkt5UJijdZMsyl1VRMGIVqoBbfVmRcC0jQliiLGRcHR6SllrV2DW0naK8sgYZrNGE+nhGHoBEOPEcjL0uGaUpeTIJQkiNw9K4RrrjtZyK3lUgXOzdhu0YwiwtCLu0rRiAOiULk9VUqMZ6NK6VyYF7W9YsGO9WcFKRWBcvkD83O4q10cZiIMQ18jOjNUVZYURelzFNy0l9aaBc7Am7asqf2o8lyA84KIr6vmGC87x7oJuzD7WB+6qesK42vpsiy80co3wn3IlsQu/p15U9JeNOBd839u3HKBmhcC7cXHPzQdNa/5nm/OM28G4Q0I0jlD5/RHV7+6M25RFEynU2b5jKouPYbAuzit8WgAuXADz8O1Q79Ph2HoDQbuPBaEoTtL+A9nXjOOyekFWONZxfMwpaJyDsm8KJllOXlRUGtNXWtnAtC1xyC6+rQoS/LZhPHgjNnojNH5Af3jfWaDHuPzE86PDhgeHzI43ufo8BHT/jGj8ycU+bnLvlNu1L+RpLTShptye64OmNfGwtfh89pE+uvLLvQBJ44Z48PmvKg2RztYo12gnRTud/paZu5gnb8X84wbcMi9esHMZ3Hec0F1c0FYMGfhPl9PORSmuz4FLBANxr/xCzbuovbybQiBuy+tQGkI85x2WdKqa1JjCI0lMpYQUHb+wAShMUTW1biVgCJQBEjHARcKLQIqf9/hrzlXwzkR3hhDXpYMh2OGg6H7czRmNJnQ6w/o9/v0hwOm0xnj6cz1JmvNrKqc4OnKQ6RxIYdRoNw+a/TCYTxfKwDCqEm7vc7S6h63X/kqndU1lz9iDEUxc0YUpdC6ZHB6SJmN8c4UENLFhikB2q0xdTEjn42YTIZM++dMhwPCKGR1ZZWlbpel5RVWVtdJGi6gToUhSRrTaMZEkfL8Y/fezvErUirSOKbdbBAmiiC2RLE7IwZzF7A3r1l/rYWB4o++/5N/MDjsH7lI+7/97m//zr9GCLtQqytdUNYZlS4QWEaDPuenJ6RpwmjcZzzq8XT/KaPphLrQVFnGeNgnTiLiKKYyxo3lRhFWCJI0dSOqxilLlQ/WkVItkgudzdrdhGohxjq7v/TMIKWk74KYBU1wLlC4pEnnoDVGUxT54sbXRjMa9KnKHAFMxyOE1RRFhvCPr7PURUjFaDQCa4mTBiqMWVlZY219ExAcHxxxee8yy90u/fMzDp49oioz4jBhbWWNdruFEpLjg32qsqDT6ZA2WpR1ycH+E8qq4NLlGzTbXQ4OT6k0TKcjHt79EFVmNJsxWliCMMQIxz25cfs2naVVB8kvSw72n9E7PSGwNabKGI96DHpnCBnS7C6Tlzl/9cM/5f0PfkqWWWKTsNVM2VlfYjoacTbo000bhFLQbrWYzGZMi4KqnlPJ8KnoF6MHFvwB0YXrzNOytd9gke7mMOD4S1pTW0tl3djKZDZjVhRkVUn+HJOsoiazpRs/koI7r77ClRtXyGdjLu1us7G5SaPZ5OTohC/u3ac/KPjO936br/zSL6Kazrl49OgLzu59SNgfMhvM2NzbY31jE6taqPYyOl2Cxgo6XWYUbVKt32H3F7/By7/xVZYud5nkJc8OBwRxxM8+fsR/+D//mv/yN59yWK9RdW/R2LjE+vYyEs3J8TGDXo/VpQYvXl7jlb0VLjclLZODrRwuQNcEgWJtdY1Oy3WKlPSjedYQCuE75ZY4ikjSFCEl48mYKImcuJQXBIsRi5rRaMB0OiYb9anKkihtOkejveBfuaIs9DgKt8E6gcK5dF1H1v27s/1rmq0WjXaD81EPlCSMY4I4RMbKMeWsdgGCdYXQ2ncea9e59Buu9P0vMU+2nSMbagmV5s7VK2ysLKF1RZImpElId7nLIJthY8XppEddVohpje7PmAwnmNrQQlCPR3RixdMvH/Hlw2MOe2dMx30CKdncu8L1m3cwRjGZjjG1wy2oIFjwGR3T1RUade0KTemLJHyhLqUkCkIQOPdqWboudxCDdOuNsYYgUJ4LpdDa3RvZZMCP/vr73Pv0Iza3d4gbTReOJxVCRaStJUQYUyMRMiSMEqIw9veZIAgbBEEKIiAIEqK4gRSS6WyCrmu6nS66tu7nBQGt9hJRlDjebpwigwhjJc1GkzBQbvTFKpqtJeeKliFCucesPKc3CCLn5AkiUCFB1ECFESqICMIIGURI5b8POcc8LR7z/K/O2SR8gfOcoCT4Ob6mBUxdYeqKuiqpqgqlAoJQMRqP/MiUZTgaOLE/DP1olAuDnONULkbR3Ify17FLCHWfd3gW7Z3/tQ9FFIvH5x76fA7Kj+Dguvzz7/Xtdxyf2zWuoiBcFIxzFneeZ4ArQE+Pj3n8+DEbGxuuoBACFQYoKVACHj+4zxdf3MVbxPxhvva/ynomPP5zuG66rVjttlFBiBIRzTjm5PSYO195hXsff8yH7/6Y3ct7jEcjTg6e0Wi3Wd7ZZTIYcfT4IRvNBi0VoLw75ex4n9Ojp8yyGbVW/Opv/QvE0iq98ZTPP/yQ+++/R3epw9e/8z1smBBGEaEu+a9/8J/44m++T2s6pGErgkCx3F5mNsoRQUycNDCmJi9mhACFodVco7t9icF0wGh6BsKlgDs+mxP8F0ww76mZ581ZEVy4foSTWoyuQECdF+i8RiYJjVYTFYaU1pCZGuN/oEundgeFeeE+L7DdVNy8EHbsYORF49FKMMI5vKZGo8uCVaVYiizKaqyWSALCIKQGtNVUZYbVrrFW+eZzKCUNYxDjMWE+4/reVS7t7XE2GjEYDTG2BpR7vvMxPzEXRMzF+OL8FXreMTSveaRDkDiR1lzch881FyBgNnPjmZsbG3SW2gglGI0nGG3Y2trA6pLpdMqVqy/QanUJlKLIM6JA0IoVS80G7U6LMEwIVLDY8w0u+EnX87VWgrScnJ6wsb3B9s4OwioaaYtn+49IGiE3rt1ge2cPFYf0zw/47O7H/Piddzg4eEYQR9z//DN0XbK2suHQTUnqnBzDHuPhgI21NVbX1hmMhvT654wnE2azjHa7RbMRsbO7zot3XmFjZ49f/OY3ePW1l4ljd/jI8oxGu0GRz3j95Ze4fGmPqNHhV37tn3B0esa9Tz4ijSOyPGM8m1Frze1bN/nqG69zeLDvnRoKGUQ0mk2MlajQBap0OstYARtbu1gq3vvbv+Pg/ocoU9HvnfL4y8/5+KO7pFHKtb0tZtNTZpMek94p2aSHCiRpu0tWZdTGcGnvBqPRjM8f7HN82uPjux/z4OGXWCOZTSuePjkgmxWkcUzv7JjW2jpf+43vUQvNk4dfIqsptq4Y9DJms5rjwz4RTWbDCS++cJnvffcXaQYNrl++zuXdba5dvoqSDT69e4/ZeOTLBm+QYNHjWAhNwt+2NjdUeYGSjrlc1DlCKZJmQnOljUoCylo712BVuzhz7cb7daXRtXeX1a7pJrx7T1t3PavQHfYDGZA2Gh635Q6d2mhqbRAabqxf5huvfp2PP/uIz0+foEPprENGoCxcXt7hqzdfo9tZ4qB/wEcPPmE2nbKzukG72aGz1KaRJrTilDR2iea10WR54dbmyhBaydtvvsnVnR2ktTx6+pS/effvmVQWYxQY6dyQGmzlWKhVkXH1ymWazSZBKLl8aYure7uc90YcHQ2BBpYYYyRVZXx4qQITYLQhkgG2DhA64OjwnNPzHmsbHaKGoChzEhWhKsH1rT3u7F6jqSWRCNhc2yKbTOn3TnjlpdcAw6ODh3zw5U85KQ6RjYC8N6DYPyEtLbGVhJVFaIMyElFCYBVWQ5FlHmXlxDAlJYXH84BBSwikxE5LZOGEmWlRk9WazFj6ecWsrFECGmFAbFxI1PLKGjdeepnm2iph2qCRxs4AIEPCOKa7tkZrfQ3dStnXGcHqMjs3b/N0POWkmDkxZpaTVQWm1WT9ynW29q4wU4JBlQMVgS6o8ulCoKzKAmElQkV+Ctatr2EY+VBYGM9mPD04AbxrNYpJ2m2yImc6nlBpg4wjN2frufPFLFvUIRZX/7npDoEKJLW1lHXt125FmkTESUQaRbSShDAMsFIRSEkjCghD5Y0bXtgVwouz0q/9gccZ+Ka2FRcuMhmggoBGs+XqIlxDcD5FUtdueqsqqwWSYZHb4t2081oEHIJB+PoenwEj5kKtvDDvCH7etevyR2qsqd0Eq6ncpKUP/ZtjB4wXipg3ar2wd/Fh3b7oHYpzt66Y52ZY3+T0j8mJpm7TlAshdv6j7KLJ6D4hfG/YO+8WTlD3nKT0OS3aCYJVVTox25iFaFzVlXtNvEA7LzWtNx7NTWauXg38exn4Ws96gdoJi5UXHmvtAtYtbj00FqwPYau1ay5r4yZXq6qm1q7eddOO7t2IkoQgChxeMQip8xnD3iHj3gGz/hGj82cMTh8xPH3I+OwJw8Ezzo8fMuo/o64mCJzQF6iQbrtNs9FA4pppLnvCLq4vd925TWIuKLuwXV/bWO/HNRcWDOtFS+NzLS6a6PNpugs2v7vmWNQ47toyi5poURtZN/Hr8jLAWv+9CyHf+vpIzIlnfqTfC8HzJWEegLU42wjm6rtQyuULFAVxVdGua5pVTWINgYXQWEIrvMjt1ktVVoSmJJSuhshlgAkCdKSQoZtyLn0IoHU2VKq6Zlbn1LUPhvNYhnkotBNF3dfWdYmuCsqyoqos06yiqJ0zVRA59zsSJSKHePHn4CiMieKYKI7cpKACoQRh1CRN11jZvM2VF1+hvbJCs9Om2+0ShaFnWQvqumDaP8NqFwaNDLwr2mMFjEYXGWU2psjGZOMBs8E5xWxCWWRURUEgA5LWEksr6yyvrrG0vEzSbJCmMY1U0Wom6NrldlRlSaVLyrp0BhsFURgSJQEEkCQhYaAuesp27sa/yID4/6lI++9+93f+5b9Cm4q6yql0QVHMyGdTqCsCCbPpjMdPnjIejNl//ISV9RU++OQj3nnnx5wfn5OEIVd2L7G6supYKT7wJYoTqtp115QKFi43N5IbUNU1ZVl6JkjgEvSkQoXuhbZ6zqlx36OEXIhBFje6K33gkuvQGAIlkUHg+BrKLd51XZGEIXEYkcSxGzGJI5Ik8aMRCm0MSdJAqBAsNFttsrwgKwpa7SU217c5OT5BSZc0WBY5o8E5aZIiVUh/MKAoK65cvYmKQp4+e4jVhpXuGkmcgHSH8lZzGYtiMByxvbtDmkpODx4jlaS91CUKI7JZRpbnDMdTmp1V0nYXZOhHriVSGpJQUuuMssyIpGRlY5fmyip5NeHZ44dUpUDriKbqsJHEbK2kZLOZGwuKU0IsdVkymo6pBFS17y7Ng6D84mTxY8K+G1x5MVwLQaWd86zGLpyzlbBU1pCVJVlZkZcVldYUxgm3gBO/8C5a4VxwQZLwzW99h42tbfZ2dtjc2nKO3LqmrGtWl9cZDDPe+uVvkK6kTLMRoZA0Vc30y8+woxlWK+JWm7XldbQMUEkXEy4xsgkj2aV58w3ufPfr3PjqDnErYjy1HJyO+ejuI/72Rx/ze3/819x7MqaINkhXb7Jx9QpRM+Lw8Ixnp33iUPLSlTVe2m6yFc1oiAKl3IZsce44KZ0Lrp2G2KoE6+hKmJpAyUUH2mjXnTXGpVkfnxwTeFt+I03ddSUUKgzdKLCKaHe6hGHs3Gc+iT4M5+P4rntlrNuw55B/V6w876x1m1TkRd2V1XXnMqoLVlaW6Cy1SHzYURAqojAmVC5MRwqFqa1z8Houj65rBP4wZ11BGKuYJGiw0urw0s1rLLUbTsiPJFEc0my0efLwGWEcQ6PJ8fmYKreYcc7sdMazx4cU/YyT3pBLe3s8uP+Io8OCWa6RomZlaZnLl/fY2buOJqK2FUpFiMA9T3f5Sj+CphYddSEkMggdDgLh05vdJTl/b8qy8E5P56S1VjtnbRA7R6pUBGFAEIQU2YTPPniXo/1HhM02G9tX3ESAtkRJkyhtYaxAhRFR5DZEIST93hlGa39fK2TgwrqsUCgpGA2HKKWI45RaW1bWNmkvrRCGsUMZyIg4cQJes9H0o+EVp8eH3Pv8Sy7tXSWKmy7wSLqfi4pQKsFKBUEEKiaMm4RRQhBEhFGCCiKMCJ1jQ86d9PO1wCfLPi8eges8+3t4MTb2nKjkmLluTC0MI4Ig8IK5RQhFGDiO+MnxAWWRucaed9CGPuRCa+0dDa6wc51zs3BL1LW+GIn6uQJfLFAK88c9dy76B+iKemOfY3LjpzEEWZaRZW6MV/oO99zRlc2mGKPpdrusra+zubWF1obRsI/yruBIKfrnJzz+4h5ffnkfiwtjkLhRXlM/N+Y+d45IS+V5tUvNJu1Gm3w8ZXWly8npGbs3b5KNphze+5T9B19wdnCMEpalVptWd5nJdML+k8e0AkUnkITGoHB7Z1lVrO1c5e3f+OcE3WVGoxGf/uR9jh894K2vfY2os0zS6lBMh3z63rt8+sO/YvLgLquBIAYwUNSa5uoat157jfWNLU5Ojjg92oe6dGK2gVhFdK9fw8Yx+48eu2kXo9HWHT6kd2A7NrJzy0gp54g3kP4g4F+b2mg3polE16VjUoYKGYdYAdMsJzeGWrjxUG1cgeZyDJzby2nD8/E871bALhqOVoD3F2CkawMXVY3VNa3YEsuQwLp1QSl3jQpbY3SFwocjlFOMcQVrEiZu5K0okNMZa60uN26+SFVX7B/vU1rtHU9y0QgFFgfSxfXJnMVpLvYZ4Q9vHsVhmbt5WDRQ5kdnqQLywnB+esb1a1dZXV32Lpua1ZUVVteWndDZXWNre4+00SKKI0bDASfPHlNmU0QgUWFMHMXEkSRpRKRpgzgKCRz5AGM1UeBey9svvsKtF15ESYcX2D94zGAwwIiIV19/C6UkH7//Pn/zw3dRKmVtbROrNWXhwv1qbTk9OaHMxqyudEmSmF7vlGfP9tEILl/dY7mzyiybMp3MGAzGDHp9zk5PuXX7Da7feYOyLgiMphE12Nrc5smTx/QGZ2ztbPNPfv23uHLtFiiBCJ2r6ejJY6bjMdMiIytzhoMxO5tbLhk+m9E/P+fo6JDhaEScNFywioAwTFlZ3aG0kihd5qw34/GDzxicPabTco676WxG//SALz/5kBeu7/BLv/I6Uah58vgZZakRgXNZtbsdZnnJq2++Rdjo0h+NeP2rr/Hl44ccHh0QqYj1jQ00FVHo1zGhsarF8vYuX3n7NYSJGA2GKOHxF2bK/qMHHDx+zGR0zvH+IdWoIhuMmEwrtne2aS+vcPOVV7l68xU+/fhjhv1jHwIyDwZ1zV7XA7gQM6R3dJpKE8YJxh8itbAEzZQgkAyHI6R1QSpuWkEu6hK88GDsXCi64M5K4Vz0+WyKUJJOZ4lZllF7Z5Fr/mmC3PCLt7/K7asv8MOf/DWHszOssVxa2aYdJeTjKZeWt3nzhddIRIjF8NG9Tzk+O6KRJNx54TaRCgiEoNNucfXKVS7v7fD4yWNOzgbowmBnObf29vjet79NK4zB1Pz9++/z/iefU6Mw2oWZ6aJAVDWXt7b4tV/9Vb79rV9hdb3rG0JQ14VvqoR88OFnaBv6AFLHnFQiwFjHtQ+DGF37Wi1OEKQMejNOjg/Y2lljZa1Jv3/G1sYmgRCcHDxjNp0SJi7oTFrLyvI6o8mE/bMD7p885LgaYCMoh2OmT49oiYiGCSj6U6rhjGqUEaqQREWYyjHRa106tNPcRe/Velu74Bsr3DSJLWrUpKAVKIJIkZc1s9pQWWf+iUNFGioCC7EKuXb9Bks7m5h2yvLuBlG3RR5KBqMJ22tbbG9sUrYa9OOQoa2Z1jXTvKA/HJKV2WLtG9Y5Mor4+tu/yvrWZdqr64zqnMlkwHh6jqozsG7yIrROCBdWIJTb55WUBHFImERoDL3BiN75CGEcs9IGAXEjRgaSJEloNJuoML7oXGjDdDgh9PWK9epMbR1nXHgxxSW7u1qnkTiEjEKRypAkjpxQpWvSQBFGIUJJ1xjxa7r069R8T5AqWDg9hW9QBkFImiYkaYM4ScAY8tnUTfWUBXmeOWdbXTiH65zdbi6wWPjJIyX9+2pd43rBYPUmqTnKwDlm56xP93lr5q5cF4Rl/Nl8HpLljoBztI9ZuCnnzcmFoOb/7+o3V4NawaJewjtt8XW6FB4R51cSL6st7AWC5+qM56pYKYU/38jnhGC7CIi9MOQ6R7nxKAYnwpqFOcViXZPer3VzJNfzKK85Us293nYRWFbryvG6dYkVbi10WRNOdA+UJI5iAhUShBFJEtNIG8RxQhzPg6Y9bk65rIwwjAiDkEBFePkTaWvQOWXWZzo5ZjraZzJ+xvD8KdPREVWREYjQTVxaXDBqI6XVaDpXr3av+VzodE5VZ5JQKljwYr02eyHcL+q5C+PX/F2Y3xtO53FOfafvzKfx5OL7rb24bh3H1IeXWXdNhT4weB5+Nw+zE97oZ7kI1BXCmfrmbmDsxTWBEH6a1Qv1zuHkHnWtEVVBrCuSuibVLkMh0PNEDEvgJ08D4fYpd0X6OlhIxiokD2NsGCACibaGyngXtM8CqrTFCuld1tqFjvuLN0pigsA1n6JQkUQRQRBSloZKS7JSY428WKfcBeumuJS7B4JQoZQgCqSfiLWowNU0Klji9e98l1e//hphGlJZA9Yh+cIwIGmkRGHA8OwAXRbuupaKQLog2doKrK4oqzHZbEQ2HTIenTMd98myMVU5Q+saFUYsrW6wvLHJyto6rU6bRiOl2UxImwlhFCOMoCgKirqkqgqKwonXUiriqEmY+PU5DYmC+XXJYg1wjnuH7fujv3jvHxRp/1EzaY3RZLMRZZmhTQEY6qxE1449pAtBpxFy5/YNjg9OGY8LZvUpk0nGcDAkKAMaQcibr73meCpCoIKIqqqI49R1xqylrEonzFa+8ySsty27wJzQs1uwoF39ixGWqnbsJSkdjmCO58Z397QufdFmncuvMs4VNh89wKJkANTOYVuWnldZUNeVQyhIgdGa2WxKq9lACosMA1Y3Nuj1zsmLiqiR0F1d58rernPmTkZ0lpZYXVmh0QyZ5hPKKiLLp3SWl+n2uxw8fUin1eL/pe49niXNzjO/3zGfSXfzelPedrW3ABpAA2gYksMhhxOU30haaTOhpf4BbbSWIhShlRQxm1kMNdSQhEiBAEGCQDe60d6iqsv7a/PmTfu5Y7Q4X+YtxIz2VEV3R8etqnszv/y+c97zvM/7e5bW1zmxeZIiCwuzwuNtiS0LpuOMzsJiGNf2HqE8nc4iSXOB9vIm46MR1u4QtxdJmi1EFNPuLhMLgxeGJI0pK0HcaiEEfPbpZ/ztT3/DaCSR0QIllokpcV6GbEylKG1JJ0kR3gXXbp7XtvBahGDmkg2uBg+h6JACQxhP9QSIs7MuBL/5sBk7ETo+eZn/zkLthccS/jXOhfGMGXtYSpYWl1laXqLdafP8yy/TSFMODnsAXHrqaQ72dzl3cMjiZhfrSnp7Oyy12ozuP+Bo+4hmpWl1OlgRc5QbSuNRkcZ31skWltl4+hLPv3GZqKOZljAZCfb7Gf/47h3e/vAmQ9cii59DrVi2ti5CY4Wd3SP6gyMaccRzqy1ObS6xtRzjprtkRw+RzS5CeqROqGsd0jiimShwBmdN4DhZQ1knMioZhIA8zxkNDjkaDLn87Auc2toCPL2DAyohiZI0iBDWkSRdtAzj084FhpmUKoRPCI9UITEeEYqNrCgx1rDQWcA4G1y8SuO9xHpNJFOmxZBINYgTuHzpVdZX13ju2VNsnVqntAbjTOgoOiiLkrLKMFUovkxV4HxJVVb0Dnqc2NhERzFCRcRpQpLGpEmDfDjk7tUvKYsSnca1uCAZDSfsPN6msbROfzpkbAuKGBY7Cbe+vI03ltVzZ6mkZ1QIVs+d44sbH1P5CC1ihof7DHrb2KpEpZI0TollQmULjHBQOyv/Q9EuFIm+3piDW9/WYQaSpA7lqqqANwhg85CqGhwSct6Jdc7SWVjkpdde5+OPJaNJTpw2ULqJ1IG16ZwIYH7m/iOkiGh2lkOXT6VEiULrsLVnWRj9X17bZDIZYYVgcXWDOEmDoacsUErQarax3nPUe0hsCtYWWmSTEe+99xsePT7i7NkrPP38S1TTrA6r8EgvkSpCChfmEEQUHMRKI2WEjBqgonmH+Umu1yzR99iQWq/DnvAcG0Mcx3Vto54ohMN6rqOEOI4IzgmHjqp5l9pZQxxpNjc258FsQoV9SWsNTgYRSgiUjrDW1OOvsxbScUFszCzkIHx9NoIVzCYBwyGgDpwR88NHUeRMp1M67fact22cIWkkpI0UhJgLZ0VVUpUli8tL4D3TcTyXBgAAIABJREFULMe5wJbr9/vEWgWneVWR24o0iUnTBtTrpnJ1srQ1odPPsVArAGc9DsGgNNx6vEvj0gJxGmG9IWmk7O0ccOLMOe588hGtMqMaDFlqN1nWguHRAYUtMVpiYkUpQjPNeUh1QrOs6O/sUNoJxcjz0S9/iS0rvvG9N1g7fYHe0ZgvP/6AnWtXaactnrl8hS9ufkYDh/GSqL3EhWeeZ/XcGbLRmFvXvmA6GuKdIROWUdwk8oL0KKJTXeLCc6+wfW+Xe9tfUmX72MMdynKEE/VBTUjiJKWYjbxpMRf9hbcI7zHehOBCBMIJZGlwWUHpHOnqMicaC0iZcLW/z8AZrA6lmasdM61GE1EKsjwP94Gvxwm9PXYBiRmzj/kBIZfwWFmUrVCDCa+kEed0jLKGqCgR2iGlA1NSVQZchcSClVQ2I7eeKI5JpKA5LhnefoRfWuC/uPgcZ5eX+OnnH7CbTfGNBgaFmjmDxLyF8B8cWJ9YxuaO25lLx9c10DzhuG5qm9LRXlhi8+QZfvrTf+B7b36Hc6fPs3/YI8tLVlY20XGL3sEhm1sVS6tr6EmE2TxNM07o7T7k4HCH4XCElBO0ajLNwzimT2JEu4m1ll6/Tyw9zmi+/Pi3nNg4w8bmCXZ2diiqCulj3njzj3nma9/mk/d/waeffsUb3/4Rl596hsN+H6kkq+sdvvji03AQdAZsyfnz50kaCc88+wxxlPDg4UM2NjZ59OARB70hUdTi2tWbbGwuMZ4Meffd93iphGZLY7IJDx4+ZHNjjW++/k2uXb/KxsYpzl58hsI4dGXAVmwsd/nOd7/Dz37yt+gootloUOaWG9dvcu/WLZ6+dIFWq8Hh6ABnDXv34PTFZ3H1lIqVipWtU9y5e5u0kXL69BlufNTk9OktXnrpNf7vH/+E2/ce0t+7z62rn/Kv/tV/y+mTFzgaxrz/4cdILaic45lTJ7l+7xHOVsTNBhNrWT99kpPnTrO785ijox6dxZcRqcKVBU541tZPUFWSw4e7XLlwmTd/8Hssdta49slvOHh8g6PBA6SNeTTcxWFoNNtM9+8igcPM8v/8xV9y/sJFnn/5Fc6fvsJ/99//D/wf/9v/xP2bN0CKEBRZ12/M3Ie1cUIQglLstKA8HNNYW8BqKIZTRnKfcqmNtY5JlpE2EpIoDmu3Dc55UduXJMdJ53LGIzQWLx1YmPSHmKJEJxGWIBxLpVBOkBjJmbUTDI8Oedzfw+JRheAHz3+LjcUV/uKv/4KsPybPCxqx5plTl3jx3BV+fe0jfvHlB1y+/CxPb5whdp44CW7Gz+/e5+6tO5iioiVTLp+9xJ/+4R+xstgFaxkMBnzxyVVEKdFC4KoSm5ecWFnhW19/je9/701ObJ0O3HhvwAsODw754P1P+PXbH3Lv/piqbKCiGCkU1AGk3iuEU4GZaiqEkLhGRD4uiFRMzBJ71w/4x+o6b/7JZVY3lyirjP3HOwhKnn7uOfqjAYe9Qy6eu8Ioz/ji5hd8+fgGh2KEiyVuWGB7U9aiBRoqYbzXJzsakRhBt9GgsEE4arRatHSTJFEMhoM63LnmB9euvaqqkIATijSJiCKJLAwtHeEbCbJ21KZpTCQ806IEIem0F9k6f4FxI2F7MqDRbtFzcNtUZI2EZaUYFyVibYWVtRXSsk1vOGRaVWQ+vD4jLI1WkyQWZLtHHPYPuHrttxwMewzJKaiQWYWuHJEh1D8EHmxpKxpJHEQ2Ql1RGYfxlnFVUglfT2ZB2oxJ201kkoZ9A48pw1i5sBYRem0YH0KAHKGpGGQ2GUQgpUh1FJLdgWiuEIZUdyuOHYbWhTOZ0AF5EUwex9NAszOatRZdPweewEAtywwpBUWRc3gQjBrOzaaJZntKyHxx9jizxdc1mqhr4nCWrt2g4gluv6d28h2/BueO96YZw3UmSgqYi5oByXO8fswCn8LU1Mwf6wMu6sm60/va+RdMVzN35jyc1oX1JORwMG8qBR7q3FM3Nx65uUg8c+LOhJzj9zmrH+bbbS2khkDeWmKsRWJV1274YLaRQuBlCEKdMeaDoDTDdmmk0HUDOXSlrbVo6XFCIpSkMHnQwuufMQv0NqYM+AsXkJRaaZSQVJXHRzFemBCQWgvuRV7V1yfspQEjBR6LFA7pgzs4G2bgHXHcIk7bKKWJ4hipNE5AVhQgBe1Wh9FoTJnnRFLXe0MtBP7OZzYz4/1uUNPclVqv+TAzJ4SzUv0RMkObIWYu6fozIBjqvH9yD6rNN/PnY8bDdfPXMxeK63Of8yHrws+y+OrXF6ZPXW1KqwOEqRFJs8+5rhC1DGu/V5KRFkivWXQO7TxeBm0qxgfcHR4tBMI70ipHC08lBJWkRsgoFpsNmokOk8jGhM/cBe6/qcoQ3ugsJRUeT1lVxHFEHCcBu1YLpMILosyhS0tpS7wvw54qQg/f+eCODui10PCsiFBSEUcKqXwIgNOSc1fOceFym6YGZwWTYcnO45IiV2SlpawCUsJYS5mXRIkjajRwBpzxuLKAGudWFQW2KimKjPF0jPAmNKKkZzI6oH8QEycxi4vLLLca2CrFWstoNKEYTVHKE8cCYVOKLMfbkDmTFSWVDXtQ5UK4baAYhtqFGROZMAX+//Xrn7RIa01FOe4F9qULqWvCWpSzmCwPYHkTiqq1jWVeePEpeoeHDA826Ys+y3GTTpSCMeHQmk8piyGNRgvd6ZLGMR5Hnmc1zNmhdUSkJa1WE+8dEk9VFcQqANBxnqoqqco8bIYixVBDuAnOWCWpu10lczscUFW2Bow7Iq3RWmOrEmcrokhjy7rL5zxS6+Biqx2G1lTkOURJKCbTZkq1W1FZh3AVzkNnaRVjLZPSkkQp7YWFOomzZDDY5969m2ydu8y5i5exVcWDR/eJ2k1a7SXa7RH7+3vkxYTR0SH25Em0jkkaC3QXu2R5zmFvH60TRNRiZeM0SbtLYSyVtcjKkDaa+FiTjY8orKDZ6tBKFmgudDHW8Ntr19jvZ7Tb5xGRIi/3yb2v+UaeaTalkBKSBOsdtg76CWJ6CJmR9cSIrYPYZsmiwWgrgpuSMKIRCpKwyVrnsThUvcGFcZhQSFQuuKgyU1L5IBx5GYoSJTTra5t4H4TfrMx5uP2Y27fv0O12ORqOiNOIKy89TWe5RVZNQpK1y7lz9XOapWex2UWJCBHF5AX084iJUGxeOsPzX3uOtQuryFQxzi2HQ8+NW3u88/Ftrj/KWLr8Mi9ePMvRkSerHP1C8tXtfYyFl6+c46mTDWRRUBQZTW8YZGPG4wxXOdLK0mh3SeNGGPVTAi08vg4LCE5BiHUtpBIwH51Oi2YcQnG8KREiOMnX19YYF5bHez2azZSNlVWssGQuNBSsCIdxISHPJrjKBGeyE6SNZt1Nb5LnWV1UOPKiCFxoLcnLEHijGwuU+YBILaAihdYT8lwQyYSVlWXitD5gWCiLENaVJilJFFEVExoNza3rX3FubYWtrS0a7Q5Ox3ilKIoQ/rNjpvSPeuw+mnD5mct0u4vcu32X6XhKVUzYu3uDiVBsXTrJ1tll1rViePsh46Mhl84s0V5fZf3kOg5HYzVlsj/FywbjyZTptMB5CTYUMjOcwSw5fVZUJUkyFzRmo+/zxkH99cB3nDUpgrhnTBXuc18jImoES1EWUDv7tNScv/I8K5snkGmTRquDdTGRDCEA49GAJNVEOrhrrbHEUcLi6glEjQKZTsYURUa306bMMryvaLQC/3DGXQovw2Hq0MUIj9QRlYWrn3xKf/sBD3d3uHdwiLeK995/j/NXniVtdgL7zwf3iCIw2oKDLw71ktIoHQfEjIpqEfp4f5izX2vu2axggrqIdy6MskZRKCgJJbF6Qijnic0SAUkjJFybqjoWKEVIkJc149jXP3s+ll6/KKU1vt5rJMfctdnn7X3gOM0agEIEx7SoO/PWuCBq1aqcn/HEotpBXDemZuNAwJxVhRAkcYM4SkIwg/dIqQGHUjGra3VYoXehm2wr0labOA1OGe+C20EI5oUTT1xPCPeac47CW/anU/YGfba6XbIyZ2V9neFRn9e/9W0Oth9x89dvsdlp0ZGS9aTJ7alhMhiGbrYMnWPrPVpYEI5IQ3/7Pu/+zV8iF5ZI4w6vfvdNlk5scTQYcfDoPr3tR5w9e4ZnXnqNae+AT/4mpvCOtbPnuPDCS1TOc/WjTzBFRqoEDVlRYUAYsqriMJuQDHsM795htbXB5UvPMjjaZ1AWNNoVlQdp89AY9Z5IJ+A9ZZGHNR2HM6rGQYRRSCVCMJ2vgwJwFlGVlL0jXNpgubvAqcUlsv4umQsYAiFsnSFn5wfyvChqN3h9zcVxAT+7n504DkApE82u9dwwlqSYhoAioZAyJvIarRzCuBD8VjtdrSnRUlKFHbR2iUQ0jMH29vFlxg8vn+fk2gZ/+f47fLm7g4pBSBumAGZNBT9zjsv6Hgws23C/HD+f4ZA88wzVroG6CR4ePclgVHG+scLh4HN++atf8v0fvsnm5jpHR0NG45xutwsiZnfnEZWzxGnKQneRVqPB4vIKm9Mz9A93Gfe2ccWUIrfBxToZY01Flk3pLjSIhccZmI4H3Lr5FQbLYb9Pq70EpWNt6wTX797i3//4zzl97gJv/uiH3Lv3gMNhn++/+T2efeYSX3vtZYZHhzx6cJf+wS5/8M9+n92DAffvP6DZaGC848qVK7zz7m8YDDPa7QZLyyu88cY3mRYlpdU8ePCIOJYkmtDsVJput8srz7/IZJzx5WefsrCyhI4U60stbLdBM3mZoiz57dUvuH37DqoTsbS4xHQ85NTZs1y+fJHfvP8Oa5vrfHX9Fvmoz9LWeaK0SaPdZu3ESQ529xkN+3Rrp9wkK/BesbK+xv29fWxh+PXbH/Dv/6+f8Y3f+yPOvfh9qtYWLuuhq4xGknDu5Bb9g11K1WEw6DOd9PnON5/n7vUvyUYZKoo5e/IM5XTA4/v3WVlfY/vhYyZHQ669b7lw4Rw//OYLnF2M+c2HMffuSHbuPQBriFU4PAlRoqOU4mibVCv27l/nvf4Y2VCcfWqF77zxbf7sxg2s9XgdHIG1hBIO1/N7S9SOV4cZZVRS0j61SqwVGoU3x2PyWTalzPMgUHiCcCDC+LdQ9cjpTASsRRCBCBM9SuGr2gAQyXrcV6AcLLdX2Vrb5NHuQ0b5BCEFbdXg3PIpnj59if0Xdvj4k0/p9fusnV5CW8l3X/k21x/d4XH/kF+9/y7n/vkJkmYD4w15PuXzz78gURF/8qM3ObNyglOr6zSShPFwQCNN+fiTj9jd3iYmosorYuH55tdf40dvfpsLF06TJAmCAoFmNJrwwfsf8c6vP+LmzV2mIwGyg1ItsEEoECGbKzSJrMHaHCciRC3ARdLiqgqUJpbrHN4f8M7PbvLdP7pIazGICCdPrHF01OP+g4e0W20ebT+iVJ6RLJgmYRpNTHPM3ohk6lFGkpUTyC2xULVJJEwUVMZgS0PLR3TabcqqZGIDIsU5F8QMFZjBeI+XIJIIqwTGOWI8jSQEpCZlyWy6vDKWCY7GcoelEyuMsynTytCfFhx4Ry8zmHHGQDfIlMRmYzpZyoWNk7z+/EtMgM8f3OOzG9copEA3m8jCczTo89Zv/pGsLCBS2EYEzhNZSeUI+4axxD7gbEpToZ0hiZIQRO0CfqjAkwuB1cEotLK2wsb506i0wbCoGGUZSoQDfaQ0RV4wPDwEEbi2VWWQSgZHmwuVkNSBjxjAPSCcJ6ob3FoIrA9icOhShKAuoUVIjrd2vj95f9w4FzKcKYQkOFABvAkmihlG6XfcjsehTqEequp9JDBYhZA4KZE+pLNbGxy1ddZSzU8PYpit6xdTVUH8sLX7NehX8710Jg7PfiZPvAbmIugTnsr690O75nfrubrSxNnj0frQhA1ICaECMz3gzlRg7vrZpOLxZjm7LrNfc5emCPuoOLblPrG/HgfI1r8ZDBbhXcyxMHhfu7NdjdmqURAqNO1ngiQEYTvwg2V9NUJtGEUKrQXWS5wAa4/H8MNZLmSOiFrkrvJyblpwzhLpiGaniZQyuDF9TLPZIp+O6fd28c6RaIkpXBAobQTGIWyM9RbnFNaGUD+JDbgYFbImnA9cdqUi9nZ2QiaDiPCyfgez+t75ea0+E76Pw8VmX5vpuqK+B8OUZmhYzd5zuM8FYboUXPhndu0QWHccBBXQgG5+FngSg/A7NZ53IQxMOvAh3JfaiBY8fTXLXIq5SCtEED9xYVpplsljvKdQglJDZBVtIYkxwbUcxsaRUpDEHlOVdISnRJEYEYKcvQnRKAg0wTEde0cpKoxy5FXQTCobmM6REjVqL4j0kZYhqM5ZoAqCbyzQBpQBYVVYD2pBP0w5BqyQVBIpAysZWe+zMoTOCiFJ0gaNhSbgSaVAa+iuxiy2VxAesspy/96AG587qspQlkXAkrkQficRwYhYBf60r8XafDINe5mzWKEp84LhQY8qq8imnoXlIUsrXaIoNLeskEzzkvFoSl5kTMcF03EBSqE1OKcoKyhtEPttjTuZTctSr0FSiHn9/B/79U8ad/C//i//8//4g2+9RlnjDYQ12KrAmwrvKvAWb229GFg67RQlPcIKLp68wGsvP8vXvv4yq2vLOB+EO5wjjiJm3JmymFJVJVJJGkmMrQrybArOUhU5k/GQyXiE0iGQIvCpDVJ4okgHjmI9YjzrWtmqpKoyqiIPNn5Zc0CkDE4/U2FrVtzsgGZsReBU1myYmq0SrOSm/t7hgfLeMhkNGfYPsUWBwnHU77GwtMry5kkWFhdDV7I+hGmlqKqSo36P4bBPq9liff0EB0cDSuPpLCySpGEBHY2HaK1YW9+g0WpzNByzsnUGJxssr21x8sJlljfOELcX0Y026HAN5GyUwQdYfRQnKBVjpSaOU3b39vh3f/ljikqTNpaCmNU/YEkaLp1YYTw45PHONivtDlGkKa1hnGWU1iGkCgnQNmz6ToTiy+KprJ0nTM7GTsL1NEEUEwE34Xw45PoaeD4LinPeYbyjcJbMGawUNWOnHj2SEa++8jpLK6tUzpDlYw4Pe1RlyXSa8Ytf/ILe4YBLT1+g1U0Zj0coDytpRPb4Ec1xQTtOUVGD3MUc2Bizfp7z3/0Bz//wFbpbC/RGFZNM8GBvyl//4jP+4qcfMxEbbD79NXR3mZWVJlJpekMYjAzNNOJrL67z7NmUjWaEqoO/uu0GrViz2l1genTI7qMHbKyu0O20SJQgVZKoDqNxzoSNXISNXaswthIO027OI4rjBOvAiYgobTPIHY8OpvR6RyhX0mk3iXTY6HTdeFAqCp0xF3AKOkpqkW3mJAsd6JkwZlxwZgQ3aOj4TvMMoWKipE1eVJR5SbvTYmmlA8LiXBk4okVJVWQkWiJdyd7jh+TjCaYs2Xn4kKXuAmkzxWs57zZrrTg82Gd/ZxtXFWgJX127zqcffsLK4iIrq10eDnroTkIjNlw6s87dq19RTQueffYizz11hsW1JayKEFIxKoZ46bl49hxCGBZW1jl18QVU0sE4Q1lWWBe4X9aG7vVoNKLVas0LLFG7GnQUgP3WhoJHPhHUgw+BhWGkS6KVDoWekOF5py6+BOTZFOsVTiiitIF1EiciXM3EFEqhtJqPNFsvwsiMVOFAiuSof4SUgnarCc4yHg8ZjkZ0OosIqSmNqTu8wUkQxwlITZSkdLpLjMZjPvjwQ/rDMUHt8RwNBiwur3L63IUa5q6OR7lEnQBcM9Sk0kgdRqgC/zW4IELIQSjQyqIgTZL5wfnYoeDqESM951RZZ+esMudt3f2eFb/hz3vrQrOoyJ9wBCqajUZdgNehHXXl5O2xG0RJWYfN8EThdVzoz7rwgR8s52N1guB6UHImwbl5ay/SkjRJaud0SMeNtJoH5QVeqqvF+TpdWYVRKaXCiJWrw8aUVnUKrsGaHC8ct679lmvXvsBh506P4OJh/rrr/6v/G9Za6x3Wl6yvLwUH9sIC+/t7nDx7hrUL5ymNZ//BI7o6YnHjJIMo5t7dO5SDIZvNJktaIZ0nkjOXgkPg6G8/ZmFxiWe/+QZHRUUxzfnyw/d4dP8mX3/9myxubvHVrTtEOHrbe5x7+lmuvPwKN2/f5MuP3sccHKBMTrsZEytBVkxBx0StDuPKIlWKdjEuN6yePoMzntHgiCiNkEriKoMxxTyRN9JRcNrU7ujZ4atCUtXIjkpKJpWhAFwUQxQzNZZhUVB6z/L6KtM8pz8e1e7p+tAlAts20iEpWdSzUB5CoVrfDap2yTtCorAmHDytV0yFZ+gN0ocE36ZwCGHBV0g7a1H6MLVgDVrMmiomjJICwhtSIC0Nvj+i22zy/AsvUDrY3+uRmzKM3/tj9IWrQ3tma9KTqJH69MDskOtMWOOU0jVzL4gpKmoyLiJyo1hZW2J//wGH40MajZTl5VW0jpmMJ6Rpgo40h4c9Hj68x707t7l18ya3b95kf2+Hvd0d+gd7lFlIuo5iTWehQ3e5S6vVDFxFwhieigReGDY2N7h48TKj0ZhGElPZgn/9r/93fvvp55w9/zQyiplOx5w5c4qV1UXu371DrASXLp1ldXWRZqPBYDwhrzzDcU6r3WZ3bxutFbfv3qcykmmWUxQTjCm48sxzrG6c5OKV5ymNo9/bY211mcP+Eb3eIVVRsrOzz97hgOZil9Wtk6ysrLL3+CH7+3ucOH2aS09d5LdffolCcuLECZaWulx46jJCS+7ev8vpM6eYTMdMpxUvv/otstLQWejSbnex+ZjD3h7CFjy4eZU0icmLgjd+8D1WNlfZ2X1Mr9fn1p1tVk48hW6tYtAsdZqsLy4QeUuiIw72dinyHGcLlhdSTmyucu/uHfYPDjh19hLLa1ucv7AMwhMlC0ynBeV4wnRU8NyFdV64sMbmygpTlzLwjv2jHjt729jKMBpMWeiu8eYf/BEbJzZ46YUr9A4ectB7wNKCpJj0uXjuNDdvfcXh4QCh5byhFUQfcfwczQ7TSLwDm5dgHe1um6idYISlcsGx3mk0yCYTirIMrb7alBaQQ0+u46FemdWbUsgav1cHPtahSd4DleeV8y/yna+9ztsfvM2t3Xt4CeutVX7v1e+ylHbYXNugf9jHVIYLZ8+Dk3RaXRSS7UePyMZTuq0Oly5ewAu4dvM6f/fWWwil+dEb3+XK+XM0dISWkihN+ejjT/jpz35Onhu89Wytr/Av/+gP+M/+9F+wvtFF4NAy5uBgzNtvf8Kf/du/4ud//zYPHw7BLYNYxIsUfIR3CucEdiYK1WqmIIzHK62JpUCYjHx6RJpGJI0WWrbo7494/HCHCxfPc+L0Orv9Xd7/5H1Kb9k4ucXu+IDfPr7JwI6JEknR62G3D/G9CTL3FMOMYpLBpMBXBmxwiAol8ZWF0lJNc4yrjqdqHOg4CnWRjuZN21BHyCDi5gXSeYwMBgRmgjxhHNl6j48UJy6eodCKGzv73BpN2M8yst0DGI/Jqinbhz1GCB7uPOTml7/l8f37CCE4sbXFyuoGnaVVGp0OZjIm39/Hp5o8n5DEEadOnEKUjnKa4cs8IJMMCOHJS8u0rPBao+MYoSOsFBR4DsZj+uMxVVHQWuhw6vJFkoUO+/0hhXMBg2NKfFmRTzOK6ZR8MkHpsL9IwvurrEXpgO4LoZh1XSIA65DeIX0Izo6UoNtshjFpY2jEmiRN6jAwUe9XQUj0zJyC4Xl0M1yAr8O13BPBR/ggNomwO4UMiYAWCCLjsXtXMHu+j5vwM3yBnNcmvsYYVDUGwM4Z6uGPzEKYavPDXJB9oqk/u81nX/N+fgb/XUGvvq+0Rusw4TZjusZJcNxFkQ4rjzwW4aIkmLx0HExWthZHRY1XnI08I0Sdz6HnMnGSRMdTKcwE6Vr3qGtUV2fqSOlrUbheC2sm8CwHYbb//u57D69l9rqss6G5IaCsymAKqU1KZVVQWVsHgIXzuFIS4455tAHzVdVhYcEh22w2aDYaNFtt2gsLLK6s8/Irr3HlmefYOnmGpNGi0WyysbGO8zAcTYKw5STOx0idInWC0lGN1pAh5BVPpDVxkuK9J8+y8LProPcoio+FWDFz0Iq5YApPcoaPBfAZziDoCrJe7+tJvNpg4Wsx31qLsSEPxVoTguCrgAYIn1OtNvnZvuLnvNlZzSSlRNbnsVluQdhLZo3H+lmoERfzc0X9WnFB23DO4Y1BVQasxTpDYg0ta9GEZzDyAnSEqvFtAos3JVhFYSKmQjHEMhWO0s5dcdQwtKAHIKlM3QypswDKosKYimYzDZk3IkwCKCWR9VnEIyhLg7MBqxapMKkVa40UlkiHkEKlwjkvTLJrFHUwpGzQWT7Fy9/9/WBKQaBUuLBOQBQJmg3PeFBy6/o9ptMR3uZITB0yWOCqCUUxZjwdMp5MyLOMbDLi8GCXfJox4187BFXlMJXDVo7pZML+4QH7vX329/fZfrzL9oPHHB0ecTQY0B8OmUxDboC10EjbtNstokTS7TZIdTjzCaXDWlg3YmQ9qfZXf/fe//9wBwiBKUsm0wnNZoyONFUVCqtg6hA4B0VlyIoKYwIf54XXnqWpGwwHh5AKdvt7NBttIhmBsGTZGC9BaoX3Njg7bAleY6sCVwXlPxsNscDq2hooQVlllEUdh+Q8zfYCUqdh9Kpe/JXSKOHIphnSOUT90CAlQgY3i7FVgCQbT6Q0US0gqRrAHsdx2FwE5EURcDuEjsVkUgfaCEEkBVVR4COwpmQynXKqtcDayTNMJmOkdZRlCS4wCKfFEYPdATtJwtrmOU6fOs3+7gH7+/usb51kwS/gZWDNNJpNJtMJ3ZU1uiubdJYVpiwx3uCJ8DKmMuCFIlYa7wVFUSKEoNFoY8ocayviJMGYil/+6m36g5x2c4l8MiYfHqGKHDseYqsJwhliEQJxCufDqLKz6Chcp8qGkR9RdzodQaSrV+JQAAAgAElEQVS1NghWzoUQiFhrnCRwa3DzrqZUoUhxKjBWvAusndA/hMIZbO3LBerVVNBMW1y69BTWO4yxFEVBu93CO89kNGE6HtPv9UMAF5Zmq4l1gp3797GjAm2hV07wkSLTTZLzz3Pu+29w5pmTaK3YG3v2BnD16k1+8f5X3DhwNLrPknRPUeqYcmq588DQ6x0hZcqZ9ZSTq00WYxG4XFVFjCFuRAjhQmpxOyWWjlYrZWGhQaTCOEYQgerCwzmQniKfMp1MabbaczaslBKhE1qdINpOJhMyWxK1JZ9cf8jIxFw+fYHOkmQ4GZBPJ7QagQOD1CAkaT2iZKzHOskkyymKcs56CguxmHcmZRKHIpkgrOu4RWmrwC9qrzIaGG7c2mdhqcXaRgtjA/sriiPiSGLKMXGsKbMpv/7FR7z67W9y6vxFDvsDKudpLi5ROkuaNGmmCxTjnFbS4MTZJQ57Pe7dukcsU8ppiY89VkqaSwu8+NxFmgKmE8fiiZO88Qc/ZDPpcDTJGRYly3GHl158hjMnRyynXXr7Gqcr8rIklSKEa4lQvMgaFi9lRLfbnR8wZgXYjJ8EzBm93gXMyKwjbExZd9dtzXuyddLq7DwZNvVGMzBno2YL76ta/Jk5VSVJmmCqAikFOkrQLjjHBQQBUCjWTpwmkoDN8SIE0YSwAocXci4yS6XnPL5Gs40QGu8NL7z2Ovcf3udX//Bz0khhpSHLR3z44Xucv3SF1Y2AZ3EqHGwlBIFWJ8xZg16Cl/NJBe8tRV5gXXAiNxuNOUtsVlDXV2Fe2IQQAeZCGzXLbCYkzQoN5UPh1mykOBJwnjiKcdZSVRVChg1z5qJw1gaOkqzZty6ETkZSzw/3bhYWET7V8PGIsG+5OugOb+qDQc0TcwE9M2sqzNi1xplwvRC1Gzf8jNkIlFRhHZy5RmYCnbX1PQI4W1GVOZPRgKosmYwH83HhJwPVjpfBmcgcjAiKcECJEkXhK7YP9+lEBXo0pre3xwcfvoNttfj6d79NLDT33nmHTjll9fQG8lrYz72x2CRi4i0CBS506xMF1lVMxmPa3RZmnPObn/+U1ZUV3vj+D1BJi8FgTGRKPvvVr3nxtZfBW97/9VuM9x7TNCVSBp55lSUsrazQzyZkeUbZ3ydtr9HeOE1na5NiOiBdSLj46ov0R7uMBzskkWInmzLJxwhcMMILXzcuwj2P9KDT2d2G0JK8KtgbZ0jj6bYTiCPGsqSoDCKv8IOME4sbDAvLoCowmDqEQYFwaClppCmltWG/rx1+juNi3tsQsDAniwnwUpGj2LeGa8oh3ZSogk0paOsYvEVLcMJhsMQ6hHc4DHiJs4JIaIwMh3LtoJNPSe7eJy1z/pvXvsWljVP82dt/z950jG40gOAeVzocdkxZMYMgzBxSs4m/uWgrnjiwEsTaOE1RcZtyKDno91hZO0NnaZnKC+7cvUNZOl54/hWUlGxvP6TVXqTZatFKJY2oSacRU2QxZZmBM2RHlns7j6jKCustcSOhsxAY5q20Qau7EhrxZkocKdZXl1leXGJ96yQrnYt02xHn17do+zYvvfYmJ7bW2dpY5MT6Et4UXL/6Je+9+zY3r33GiVObvPTqa+Sl55dvfcDyygaTLEMI+OijT5jmOYtLy2HSoIpot9tMp1Mmg5x4YYO1rTMc7NzHWcMzzz7Lta9uMOgf8cI3v8uFZ1/imedfZDytmB4dcHg0CcLMouDk2hYvvfA8v/qHX/H40X1UpLhx8wavv/4Nmu0Foijma6++xs9/8Rt2d3eJWguMjw5YaC/R0IJuK+bh3RsMBwNi0eH8xStcuvwCTz//It1Wg3d/+Q4P7t3k7//6r/jn/+l/zfb+Dme3Otzcvk/R36GRJrQ6HdJOTKxWyA8PuPnZhDMnttjb22dv/yF3H/d4+umzPH35PI8fj9Fpk/bCAmU+5fbdhzx1ZpXxsOTyM8/gVjsUNtTTUZ6RHY149PgBDx484vKVyxz1dpjmFV5BkvggOslNXvn2N9jrHzHOJiGMSCl87aScN8fEzDilENKB8WS9IboT01zUSELY3/rqKpdOn+Xe/Xs86h2EKQR0aJBKGcI2bR1KJMIorJASLYKjrC6jkDIwW3EKhUVawemNkzjjuPf4HkaE2nJ5aYlWkuLyisWkw7df+QYffvQhg/6Axc4yWgm++9r3aMUpj7YfUUwzXFnhPXz+26scTjN8XvLOu79h618ssb64Qpo2uXbzDj/9u7/nwcM9tGzw7HPP8Kf/yR9z9uxJqrLAokEkfPLJTf76b97i6tUHFIVE6TZaJ1jfwPooNIjELLzG4YUL+4o/rkuoG6nOV3hb0Yg1sbQICowVaN/l4G6Pn/z5b/jaD8+TRRmy3WH5xBYHxZSbvW12yz6qKrHjIdWDPZKpwXpNrGKclhSlRZThzONrkbYcZ8F9ZQlTSpkljmOU1GHctDYZNFtNPI4sy/ECchyqHaMGGsYlXioSpVhotShKw2Q6RSiwAnb2j/jZW++x8ewVdoZDqqUlIiEpiiI4CW2FdZAVObKhKWO4sf+AW29vs3ptncWTpxhWns1LF1lcWme/uYDTEdI5Lp+7wGsvf4MvP/2cTw8OsbZE2YrKZ9jpBNVu0moLkJCrGK9i4jShrAoG0ynWe9JGStppM/We/mGfo+GIEmh1GigfDABVUWDyYh66Y2pxFCVDY1wHQ4Ssa0oIZx0pApJMOYiFQglBXDcVjQotQ1tVQegSx9OL81rHhqAlU1X1PRNGt0X9e1LVaDljQZjfET7D/uFAzAJ1FDATG2uTjXni+SZwRqmb4zOMwMwNOxtfn+1JwLxOPEYHHKO+6vJwnjkwe0+hHq5xADWuKooiGo1GmGCr0QmhDq4DtIwhz3JMWdbIhOAA9z7U2HZmLGJ2HqtNQVIgCD9jbn6oX1lwY86Yqm5elx2/n9qkQWDfO+fmTVWkm79Ba8MU0KzJGkTEMGnjaqOGkAJbBl3E+XDGLwuLxWG9wPowri1kcKwbF6Zag1HriUZZCbjAhxxNp5SlIYoLdBwRpYavbn5Ft7sIzqPihLSzRCPVNAqL6g9xRYEQJZEMn7WuTSCiDm1VMriUi7zAFmXt4pa1o1XWBreK2YR0UL/DpZgJszOHK4JQi8645LUgOePP4sAJi5ZRnW8BXob7ZYZbCw5jS1kjAawz4U6dNRHl7HvX16WuhWZBczOeuayNM/UmRIA/+/nnLuquiKsn8qq8BC9qB6/FVAaKCldURNZRWEMuLEI6tIQYQRziVYmiEAgeKUOSOBYrwRqObWsYOomXgkrnSJWglUb4gFUprUcLRWELMBZjK4oyGL+Gg6AJpHGDKIqJtUZHgSnbaTTQIiYrC0xVYaqQh6O1xPlwxkREYULGO0Ska41AgtJUXpB2FmhELYyRFM6iHVBJCgNpJGikimxicKYCX9YmmJo57z22yhhPR0yLktF4QjbNmGYFeRVMelJqDDCcZujYkdvwd9NiipVhGs4UBUVpcKVlmmUMswm5CTk+1nl0FDEc9qnKRbxRWOOxUQiGRIBXzNdeZ33trv2P//qnLdLOojV8xWBSkOgEvKPRaFKUgZvnZjehqRDGh/Rv7djpP+Jgv8fydBGlIsaTilgmJGFyFNJGLZxqtNRoEYKIbGzqPSMwOtO0Qae7xHQywRUZ1hS4ylBWFTqKabcWKKuSosyxVegGpmkYv7WuQliPq4KQEQJ/gnATRxqPIC9L8L5OcZf1QxpYkJWpE1wBV4UNypQFtqxoNNs0O21c2mA66iNwpGnEtJxSAZ2FFVaXlhlnI25d/5zhwS7CGBbXVqmqMdevfsjlp15kbW2F/aMBrU4HIT3NZgNrHb3eHjjH2soSrszxqoETGlMYjLfI2NdJkAKEosjH9A52iXSCjhOiJCaKIyIleLz9gM+vXUfoRXIDWT6iqS1GhiRU6UBJTSoV4zwLgVReUNgKF4ngcq0qQt5uEMMr7zD1kVXMxBnhqWwVRoiDIQxZLyrh8wjirhSCylZYwAtZh4TVXTV/PHKq0XQXV1hab3P77g2WojW+/Pwrdh49ZrHTIUk0ppiy1G3TXVnEKkEzaZJPSw4Ox8hSkC6t8LCXk0ernPvmd3j6219j4USXo6knG3vubg/52Vtf8fZnj5hEW+jlLVY3VumsJvSHGZOjiqWFmESWXDjdoSk91eCQkbe02l2EVMFGbw2mLMLhWUh0o836qcALLasKXTNWXN2x1krjXRlEXi3DAh7FQVSUEhXFlIVhb3ef3iRHNReYHmbc2Z/gEkHaGxOpFpe31jgwOXsHu8RKsbayjlKavKoCY9mH+0MIRbMZUriDWByeMS8E1liUjkFWeFcE4b+xQDkdgdS0Frew1rE/3OX9jx/w+ivnWVlKKcQEHwm0U3gjqSrL2YuX6PVHxHHK2bOnGA0OKLIpR9uP6XS7/PbLa1grQ0o9CiUjdBLz6msvcXJri+k0x0vFoyRhohwXTj2FnGa01nY5yIb0SsPyQhdZpSTkeBxnTl1ibWHMZJTjBn2mmSFVCZFSVFIjVEkIEtRhEZ+Pu894sgohwsFQAFIGKLt3tStSzrrdDuNLxkc9Dnd2OX/xKZLmArZ290g1Wz/qAxWA91gbxPc5GKQOy1IqPAthrMaHUe26WJE1TkSq0E203tFeWAiOBe+pyoIsM7TbLRY7XarKU5hp7dJoUpYTjBO88Z3vs7v9mDs3vwpcLG+5feMq77z1C374B3+CTBKEc8Q1Ywoc0hbh1UuB9xX5NEfSIdGaqiqwZUGW5ahWKyAGrAm1jPNhfHAmptWHdls3j2TdkfEWqAsra4NrHFzgEOGCe6guiKZZ+H7OhvUlJADPRvdCinAIa5i5CIMoH75FjbaoCzKcCZqsI4QweFND6i22qiiKCWGMXlDmRRjlci4EDmiNdaZmEgc0wWwdM6ZCqTBS5ebJuw7pwmh+Xk6ZMW+rKoRhRkqzt7PH/QePEM7MaldmPN+ZY/Z3cAcysIN9bQCovGR3MMa0BWa0h3Se7YcPGJYVPrN84+tf587VzznyhkurG8SxxriSrMwoGgGJIXTtgLMuOFOihOnhAe/85MeIpMOpU+c4c/EiR6Mxi7qJsDmH+9tcefoK+/fuc//6FzQiQSvWWOlCYI+XTMdTZBTRarQZHfZBxXS6HXSzgVcSpSqqR/fxUpIaR+klmSmwJlwfVztDjJcQa1wSARJDnTZtg3u5wDKuLKbZwOYV2pQgLENnqDzEXrE/OKKxushSd5Hp4X4YNxXB8eJ1mNyQHlKlkCJhUlQBeVS7BP0sVX42TVOHHAnpMb5iIgR3ncELR1ROKZ3gVNqkK+rRLgGqvt9V2kFjcZMxyArnYgJ6IhxKpHd0LET3d7GDgu89dYkT//K/5N++9XOuPXoASQxROLBKr5CJmB8cn/RAhcI4hHXEURzEFm/RcYxOm4g0IWo2aCo4enjI9mPJykIHLy1OJzzY3WWSv8PZU6dYXVthMsrYe9wPjVudstDt0llq0WhsoIRg/0GLB9IynYwZFwWD0YhH94cUeYEQIdgkaSQ0OynNRsqDh494/OAxy4vLIe3Ze4yrWN7ahCSms7qFSiL2DnaZHu5QFpMgkDRbtDtL3Lm3w9Fggq0Cx78qc5rtNnfu3mcyzTBln5dffoULT51nMuzz4MFjrPF8Ocn40//8v2JttcPf/vjfcfpMQrPRIitK7ty5RVHm3L91lSRe4N7166wtpmye3WAyHjEZ9MmnA7zLGQ8H6Cji048/YWlpE2MUN67f5vd/+CZPXTzNj//Pf8P3//CPKb2jHB4SRYoWlsnBNkom9HpDNlZH4CTLiye5cPJphpf7tNo7fPTez2k0Ei489RRvXX2Xk5urHO3tsri8xpt/8qeMCsvj7R737t4m8YKltZNsnDyi13/IYFyhZcHzzz+N0jlSJhwMR3TaTW7dG/Hjn1zFVBWNtTXOnj+L+tEf0mxobn76AcZ4jvb7fPDurzk66hFF4VB96vRJ2t0Ou/u3uXv7AWc3L7K5scmtu3fCnifDOi5rYcY6G0J7fHCsy9rVZq1l/KhHJQ2NzQ5xpOmmLVZbHfTaSUxl2J2Mwt9RwSU7c44jZiEu4f6urA2GNB94jSpoayhr8XlJy8RsNprcvP45j/cfoCOF95okSTF4SuOQrmR9cYVLZ87x1Y2vePGFV9FKE0nNc+eeYqPZxNiC+3dv4KXms+s3qEQ4KH/w+Q1On77MH35/ky+/us6/+fO/4vadR7TSJj/47nd4/RuvcunyGSA44O89OORnP32Xt9/5nKN+hVYd4ijBo/E+xntVP8ehoe+kC1k00uMxeB+BVzgJ0ht8JTCyHnnXCaYUFNNDhI5JFpfRImHy6Ij3f3KXp7+3zKULz1DElpv3bjA0E6ypqPYPyR/3aLuUNImwicNkOVaHM5oVkMiIfDLGFmUQG0UYNQawxlK6Ah3H4XVbSxRrukuBT2mcDccnqUhaMTqSRHFEp9XmxNISy+un6K6c4sbd21y79RlJpBl4z+3JhO3tPfpZTjF9DP8vc2/WY1l2X/n99nCGO8acMWRmZGXWPLE4SRxENkWpCUndLbu7JTfcbdgwbMD+BH7wgwG92/4MBmzDgAG3YbWolkRRnCmyWEWy5qqsrJwiMmOe7nTGPfhh7xtZMiy/WgEkKguJzIh77zln773+a/1WW2J392g7Azrb15BeYKUn7XQQrcW3E5I0YVJWnN67G2K/iWSYdXELA1y/w/q1G/jukHc/fJ+D00MarSjzDsPuGr/19VfRZxOWN1YYRAH//skh09GYylv29h/QpoJut083zXEyYdYaLoqKxrdoqXB1Q6KgMYayDHieTpIhRSieNdZgjEVlc4ReiE4L4dFSBeSCUqQIQqoIsBaBC8zKWHIbflmMc6H01QX+uVIBc+BcSISaiLKSUbxzzoEL7tC5KChVFKmiE12GfyCsV2o+IA7lf3gd98siODh9KCOTMuAQwv7nSTeBEHOBd44NkH8ntRZQAFEQlvM1SwR0UcQQzHnqc1FaRmdlp9Mhz7LL93FeIm2NoapKmralbQKr07UBnSKsuPwZvA0SoI/iuf07P5e4dOYH/drTtnH/iMBaR13VmLg/dS6mbMUcozbn6bqYGPOBTUx4XKVpYBxbazBNG4Ra52P3RSj1CzZaeWmSCtgxgYssarBBIPcC4VUUtgn7mSh8SxkMZ9iwJ6vrmkk75jItrDV7yU5wwSbRlGYdWaKpm4ZOt08o6lIoBVolJDq9REYkaUqmFQqPlOE6y/OMqpzRNOHFKi2DwUKCt+GzMzboO0oGxq6PgzyJBhFfR0T0CRlYL0JEt7eNYnkbkGNzZJnWQdw1RmJ1YLyapolmMBOQWDK4Y0PRbChh1jr0Uvg4DJxfjxAwMfMCMSFV7MXzgMJH4V94ATYONJwLQ7PGII3FGIu2BhpDbQ2nrkE5z1AqMuFICcgSD+hEk8ouyhuk9qTGsdg6CuephSRFspDn5MMlrJTUTYkoCiYTj20taEdVFzgXyvhaE7zyCEtjKgolyBKJs+BoESq6RwVIHe7btq3ABzRdkgdZUsVkX+PCPlhJSMkZDK9grWRWWDo5dDoaR5g9gaOs4PyspC0qqEO/k0wD19Z7Ede8cL1JPHVVMZqMkdaSK42J5zThwt7WCc9oOqN2LjjiEYAOBcDSB5OmdzgvohlLI6zGGsdock53QVPVQ7IkIdWaTDqUcJcmLOLz6e/7+gct0hprmFUzdBLcNq1pkASGVHDoucjmkIjWYZqaoppyOhnR7Q7YuLrBQj5gcjEF62Os0mMjG63T7eKFJMs6aK0ppmOsbQFDVRYoFRxnAk+eJkziDZ5kKXXTMhqNWFi5wmx8zsXpEYP+YnAbicCZc7alNs1lhLltgh09USKIocZhpKWuK2LmBYiTMSdp6jK0eDofEAJagw/u2E7Xhyim1BzszfAoUp3gTEtdlNjWMFhYob+0TDEbcbBzj0G3gxQS05SYpmbnwSdcvX4L4VrG58esrm+idcLZ2RmPH+3Q63TYzHIa02JoECpDCIuOop6QPggvWGw74/jwEUpnLC6vsZStYHGUtuVX73/A8ekY33psY0mVA18yrk4pk+DgTJRkaTAIJWDOIZ1Do7iYzigaQ1G3eKUu7fHWBlFFRUD33HXk4mHWRVfgfF7pP3V8tC7wQdGKqjXR2h4XacHl5FlKz9bGFkmaYXEUxZSHD+4zGU+4urHJ2fkJQile/uyzDJf61MKjREbbOAYLS8wGY8rK0332Ctde+AxPf+lzZEsdjirHwWHD2x8+4t9+713uTzV+4SVUb43tjR5JR7K7P8HVFTc3F3juek5KgkQwnYwxVY1xlm7Xkeed8KApZmEqBpcsSm9CDEM4FxEOYI25bBkNTtQwbZc6NDBWdcHh1DJqW45GI8ppyWKacW2wAJMxz24tI/MVrq8PGfQ8k+KMYX9Arzvg7if3GI0e0O/k9AeDyLwixFV1EhjLQmCNoYkCrk5TdKKCOC4C80iKFJkqEjFfxCDtDnC+YVzMeOudHb721Vv0Bws0psW5FodApwkySXn5M69gmhZrary3dDsdfvXGLxkOF/ib7/+QNO2yfW2bajYh2bxClmRc27qKc47b775H1utzbX2TibcM81UaM+Pa9nOc3X2PpnW4uMFKddh0NmVDqjKMqnBtRTlpKacXdIfL0T2rQaigO8ow7ddahyi6B2MiXyg6LT0gdXCO4kwQnpQAKcjTBJuG1l0lAvsoTVOmsxnKK3Sa4L2naYIAHz0OdDqd0HTpwn3StjVpmmC8p2la5rEwJwTjsqDf66PTFGMt0/E5pqlIB110oukkCa7z5OA6K2eY1lCUI8qyYNBfprUVpq7o9zK+9tUvc3r4mPFkDEJQ1yVv/uKnXFld5dkXXqQ1DaWzVE1N3TZgfNwwSaxztK0l7/TpZXl4XRFdo0RwbXhnmZdIOBs2zM7bS5fA3IkAgY+Fmw9ibBTNHU0biimJcHwIhwQXRdeAW0jCAcOH721ji6T71FNmfgCxkT1+yZ51gWHqTJh0O9vincG6JsbSHMZUKCXJuwOEzJhDB6LfNwjkzmHaliwNTNpQlBhj+G7ueg3N11hBNSsZT89AOFKdY61heXmZjfUtUt/S1mVID4jgFPNzcZYgMs8xHPOhvtQelSik8OhEYgQ0OJI8Qbng/t6+epViNuEHP/4Bs7aici0LSwtkUpAmmuNygk4lMiLbuypFC7Bti05TUm/55Jdv8JU/+ENe+0df4nxSMlRw/91fU47PWM0UH73xc6Z7+/QSgUahdDg0yOjAMbFEZ2F1lf7ikNOy5KI4o/j4Pdx2ycZwifsfvk8+HNLrZEzHYEsTnCNaU7cttXeINKczGOIltNZRmxYR70ljmsDL9wEfMBeM8C7EoFXY6DfWoE3L4uKQSVtSTWu8fMIUg+iyUAKdpOg0ZVaUkV8cYlxzht9cMGLulhGaVggm3vHIO1IM+ApZe7xI6eaSTEgUHqtCYkQRDg4GT+lqGimx3oBxdLVmUeRk1jM8u6B450Neeek5bvzLf83/8fOf8b23f0XTGEhb0C4wIyMHT2uNDQtQmETM44ReYHUSDlw6Icm7yE6XJE3p5A6dXDCbThj2llHao7LgpD8ZnbN3eMCwN+Dm9k2WFxeoq4bxqOD09BSEQenganLliLKuWFwcspxlATVQNUwmU8bjCW1dU0ymHB8cBcdY4/jCFz5P01bsfvwQ207ROqE2DR+8+y6vvfwSBwdHHO/fJsOQa8Hm+hVu3dzmyvoWv3rnAy7GU7Jc05qKpq1o24bprGBpcZGjgzPu3dthuHyFugqH3Y2NJXrDVdq65OrGJs898xzvvfMuVV3T7WTUWlBPR+QC3vr4F1wcHdBubnL95javvPIyuzsP0cmQ3nAFrTRN60jyRf72zbdYXOyxvjpg7+CQV15+Dpzg8YM7ZIMV6rJmaalHL0sY9FP6g5zHu4d88P7bPLi/w5WtazRtxahseOXVl8nSD/n1D/8dJx9fZTyb0r74Es+/dIsrG5uMTk65mNV08yFXt28isw7v3d7BecFodEF/mFLPDrk4OkNYydHhDq2bQjZgPB7x/oczenmLO7iP/2SBz3/1Ff7lH/0xv9i4yk/+4tsc7DzivXfe4PD0MV//R19lcXGRwXCBG9dvoUWH2x99wIN377D/+DHetbjGBre7CwN3LiOEwTkYljURh08Sakv56ALdeq5+5mkGWc6jnYf0sj5bK+tM65o6xqF93DfC3HEWOHlKaJqmiVH6IF5ZY8CElIMvG9YWlhgmgjfefZOyKdHZAOsd93Ye8N4nH/FbL/wmvjFooXjx2ed456MP2H18n6eu3whxZRSD3gLWlZyeHvHuJ3fZPzrGpR2UTJnVDX/xvb/h8e5DPnz/I0ZTw9LiOn/4+7/DN3/r8xTjM8qLM4pa8NOfvMV3/+ZNHj0eg+yTJEOEzxAyARTOyYh38SgUPhZZKaERMsGhAofUEw7SEQ1kjaVpGrzWpKkiywd0hkN6C6vUtcFlSxSTh/zkL37JrT+4gusJatOSOOgUFm8kvc6QzOtQsNQ21LXDBHwgdduCtSGlMx8+ColrLWmaXMZE5+ujjMmYyWRKVdYhcRgdZy6R+H7GUtLnM1ef4drKGitPPc32C5/lldMTvvfTVfaqU3Jbcmc0YmpKrLTYo1P8ZBJSkYkM/45QCKXRWY+8I+l1ApalrWp8qkK6ohqxOehx8/oWx8WYwja8e/sjOs5SlzOK8QRlDDeffZp/9k//iMPbd5iUI/Z2dxgMl/nm7/+HHD7cRQ4SPrn/IT/6zl9imxrd62N8cF+pPEHLlF6akXqBKadoKel2OgF/FNOWNpYne2vwxiCSBC9CUiSNOCitgqfTWUcSY/XI0N6eqCjeWYfyAuHCgNGKgEuY9yfAE4fivEulNebSiermEX8xP3+IwLon7H0AACAASURBVIrkiUtby1Dw7eZuQQfGNUhjo7s03N8qcj6fcGbnblwuXe9z16FzHqWeOGrnEWNH+O8cPRVcjSIEXKIoq+Z7HyUv/36SJDFNojHGUMxmVGUVC78/hRWIQ/qQCptH7AkGrLYNrlYE1vlLLIePKaro6w2vxQeH5pz/673DGhP7DDx+Xu4W/2yOhDAunKWViucr72kaFxKkHpyMp+KIRggoCEiiwCoVCC3BhBSmV0G89FJifWylkxKEo27a2NMQTA1BtA5YhLZtmc5m2FhWPTeUCBE+72DmUmilqaNW4l1IJeedDgFLFsRMlSRhqC0CEk3haJuG4+ND8rxL3VQYaxF46qYmJZhcWj8Xj4PwF3VtnPPBZStkFOsl3sdysHgeIzpgg0u2vbyuEp3EcncV05CQZR28d0wmY1QbXJzJvCzKg4jmDs8TDnK4f8K3CmeYYJoR81NFxIbIuBdHzsuS4zXvYvndfL3ysT/CelzraWrPebiRQCqWhYq4lyfdAEmWo71HJo6uMazXElfVTLxneXmV1c0Neqvr6F4Ha1tGkynHZyOOj0+ZnJ+hvONsfBFL3S3Gm3Aej1g+IcJAxjQm/rygtSLNQmLRuRZnoa5rvAiGxrCfDkOCcH0oDF36y5sUtaA4aWkbSVuBwNDvJfQ7Eqzl/GJEVZeUdU3VVhiXBsSfSvBCoXWOUgGBYJo6aCUSTCxHFiqhsQrjHKZtyIUgdQ6NZGFh8RKv0TYN02JKcpoxmZaU5Qxjwj3YmIaiKqmqmrpuqDR0EkKBMyr4tOcO+f9Hkd2nv/5Bi7Tee2pTk6Q5QitM29IaS9NMSXQa7OXeY+OEZFZNOBuPODw5py5bbl2/xje+9DVWl1ax3rO4sID34SGa5zkiRgSyVDOdzth7/AjhLbiWpi5pDfSamrqtqcqSYjKh2+2xvr6BQ7J/cMiV9SkXJ4eMTo9YGS7E6G+N9yH+UFfx8B+jRGGDo8KCm4RWTu9cgGPbIOB472mdxTV1LHjSIR4uJXme0+/0Lh8aSki6nS7Hhwfs7j6kN52yEJ2/56MJSZ6gVcbLL3+Wpiw5On6MtQatM5p6wv7ju6g0JVEO2y6hsy5pkpBozd7+PsZYVtbWaV2DUC2dPGM6u6AoG7rdILBmiSJTkKeKPOuwNByEhcUJzmYTPr7/mLJwuLLB25qqOmM62qOtLnCdPEQmhafbyWia0AyqYmEDPkwdVYRhexncx401aJkS+0OfHAg/vVkQ4Hzkx/jgJLPRaWtwWBy1bcMEV3AZk1DxUJwKxebGOg8e7LCyssYzt54mzTPytIMWkkd7jxguDlnZWMYJgfA6WtcFTktmKsUMF7n+1W+ydGObWqRcHLUcXsz4d9/7NX/z62NO1DZucZ3ecJn1tR7GFnzyYELHS157ZsjLtzoMpcC3ktFkFJxO/R7OhElonn8a2C8up83BStKQJyltW8coRVwUfHitTRs+T6UU1kiEE8zKmruPZ5yalL1xia0LVpodFtKGldUr6ESxt/eAzuI6CY7i4gjfX2HWOFavXEXhOT3YpdfrMOgvUNUNQrjg9hNhkouS6EQFCL13NE2FVHmYvCoJKJwIwqb0FukNWXeI1IqmGHN0fsRb7zzgN75wCykS7j24z9b6Mp3+gLZ1dLo9LspjrNFYY5EKut0uN2/d4taDBzS1YTYek+kEKRSbm+tYZ7DO89KrrzCaFbjBkBvLayz2l5hYxdriKpvDFRbzPkpolM7RwepGWTiMq0iUJk81RXHKvTtvY31LZ7CM1hmJzkNkOvJGbdti2wIQwUHqxTxvFa/oEBMTzgZ0SFuTZAk6kdimZDjs0rZTpqNjwDGbFeSdnG4nFB4aEzYvNvKvEYQJrA+fxXQ6oZNn0XX7xGnUti1lWSKlJOt0471kkd7y6EERFnStw4alaSJj1+JMS1NPcLYhTTo4b3DWkCUJpqroas9UxI248ozOjvjpD/6K4727KCw0JU1bhuiUF0gVvm8QUcPGL016qCQlydJo/HXUVUnThGesUposzcNmwJrIJwtikXUWaxqaugoIGDxaqcjRlYEfLrhcH4SQQYxUYQPW6XZJss6Tiaf3fwdR8yRe56NgDFoANkadACkdVrQ4U0DbhnblJCBerDFoYZBC0tUemYrLsVLcSSFFKO5q6pBa9NH1MI/nufj5CiEh6eItJA686WJNRaeTUBQNHR3KF5xtKOuKOX97LtDCHLcRfq8SHeNacZBiLUqHyLtUiklR0EHQT3oIJ7i6ucXyxiY//cFP2D3cZ3lrgzwPG3GB4HA2YWJbFnWfREiWsyygbqwBY1ASusJz+OgBjS3AG9783vfoK0tKy/u/fAdGYwZa0c06ZHmKMRbv5SV3XDqBNY7JxZjB+hqjtqacnpH6nIuzfRIMHdFl0Ftn68YNLtoGVYyQvT5eZIwmlnE5I1MSH3nzNS0WD3WLilx0JwRKpwz6w9Be6y3Ch2LQylmUSjBCINOETr/HOlcYN1NqGzaj8/U+bA08SE8iod9JKCU0bXTNijCKfGLYjpiOKN42QjISlt0EBCEiLIVgo25QUmOlR3hC+ZZwdFRKKzV+eZWtL36R7Oom7ek54w/vcPF4j6GEjgBdzZi+/z75xTn/yW9+ldXVZf70pz9kVE0QHYcVDkd0r8dhk0TH50r4f6VCSU0YeCikSpEiwXlNlngG3YTz0ymPHKyudxkshcNIp9cnSTIuLqa8++57LA563Lhxi063g1ACY2rqpqGZTHFVxc7jAzqZDoe+NCXRKYNBn4WFBbx31HXL5GJGMZ1wcXaBkIIvfunL/PKXv+CNn/2E3/j8Fzg6HbN/eMbO/Yc4DNYrFteucG1jkY21BQ4P9tg/PCLNu5SnU25cf4q2qZhcnFNOZ5i65vrV65yfjFlZXQ7t6Z0ON268yOHBHt084+LoEaY4Z2t9jfPDfZYXl3jxpefxwvNwZ5dqVvLNb/wG7/ziR5wcPOLo0S5ZfxG84mtf+23OT865d/8OrbUkpsfScIA1Dc7CvXt7KJXxtW98mb/86x/hVMKN517j4cdv0SSehUGfq1sb3Lq5zWw84u5Hn/Durx9z/dmneeHlFylHFyx0cs59wfHuB1RVzUNXk2pHMS7oZR2WNzYDk3ZxmYX1bba2n0Kpiv/pf/1fsKJC0vDmG6+zsHSF5Ss9ZrOa+zv3GHT6WDEJEX4cs8NdBpnla9/4Ejc3rqG/8XtkSO7eucOLr7xKUVS89ctfsbS8TFM1YS0SgrzX45nnnwvPWSWZTGfoJGU6m7D36FE4YFuHuNwWeiwhJSLR+MpS7E0oVkdsb6xzVk45Gx2SD3q0xiDT5FOHkBis82E9sjwxAFjsZUzRW4cSKuAPrOSlm0+TeMP9B3dBR+eOd0zKKX/ztz9ka3GDW+vXoQmurJs3tnnvow9IUsmN6zcY6iWkdNRFKI46ODoOlJ4mLCxaphyfT/nuj36Bqyy3bj3Nv/qjf8GrL95gNj3mdP8R7394l3fe3+Ph7piySsmSRSw51oIUGu+j4Djno4dlJlJ34gv/VJLCR6EUE4aN3gtwEutioRApxmmayiGNxbopZ5ND5DVNqSxJktIWLZPjM9JZhagcpnGQKqz3VLMarESJFEmFRGJMTZokNC6kW5ROMHJuDfTz4ErEwgRBriwqBJDqhHmbupIK1+/Q1J6lzgL9rE81aRmfTOjKHp957vP4w49pzRkdY6lUinWOZGmBNvIrTZoGoTjVyKSDShMWE0U9O6WYniFUH+UVftwwqyr2z0ckQoai6bxHM56QKwWTEt1YFtOUr7zwCkd7B3z3Jz8i6So6aZel3gKJ6tFdWOGNt1/n+PQRs6qmKAps0mFldZWFbg8vBXU5JReaejzmoirDvkmacA6JwpSSEmcMaZIEkceG5I/UwdEnCZx7PXeu+hCFl0pQtC1ShNJWiw/Fo/NrwvlYgBmMF/HyCfdLFFDnIql3DqlCfF7GSH2Ia+vLz2i+/iEljWmDAcf7sG+O3zOkN6ORaf7ZXjoixeXaOP+vlP5S3JwXOM3F3SDAhn1MlqbhXvZBkJ0PQXUUaS+NP3GYHc6LlrqqKGYz6roO5WzzhFz8+4lOCIVQ8TkRBTcXzQBChgGJbeyli9JZdykOi7ifCaVo4XWEfXoT930+3gf+8mEVDAE+FsCKcN/6yLG34X12sYDWzs/OLgi/QoAhIK2cDwJ8QMmExJ0UoKUI6RPn8d6Evb4xRMx+GGA3kRcdRfkszfAkl/sW0zYIb9CJRhLQDPNE7HzvOXcWB7Nh4I8bF8VhxKUQ7lwwrjVNdC2LUDxF/Psh9TSPlIez/hyFJiIeQQtx6SAW8ZkYXox/go3w4hJfES4Cc4m4zLIcHaP5Ugp6XpDZaCBxgZMs4rU6N4rMRVmBuLzGnQkpy0uE2zx1KkRIVxLTgTH9OO8gCRMWEX5+Fe4xmSTR0OURsT/gwhhOktBp0fXhWjUiuHKlVCjt6OSaBa2YCUULTJsaXRRkeBaHQxaGPXCO0azg5GzEyf4h+w8G3Ht4j7Pzs4AIEoKibEikpN9PSNMMJROENKFUTUica0m0QMnQY+N9itI6PJ4iOxgVUqaZ1GipIOuxdGUNlYfzWZJ5iqqlLB2zQlP2Arp0cjHGmCowlJsWa1rwnoXhIlfWNki7XcpmEoa9XlGWJaVraKoZtiyx3lFUFYlPSJIOxlhm0wKsp9vtMRgO6HQ7odxMwLXiKmen51xcjDgfTXA2XLfTScXRwTndvEuqhrR5gk1kcKZHLcBhLw02/29f/6BFWoEgUZpyNkNoTVNVtK3B42ldaAVtgcI2HJyesr+3z4OdR+zvHaKs4L3eAmf7F/z+P/4W/cU+4/oCYSzSC5SWzM4LWtNSTJep6pZulgemXVvS63ZoW0fa7QHw+PFjZuMJX/zCF0EqJpMZvV6f6eSCTppgOzmz8TmdXg+QtHWB8PHBBYCnKspLsH0jqxBpjIJC04SoZZokKCmCE6sNrfCVMXQ6HbI8p55MAM/G5gbjYgYuLLBpIpC0jE8OybVm0O8yOj+mtYbx6TGdRLG4usHH9z6mmk3Z2tzA2Yrdh/tkeYJ0Fb08Z7iyxaDbYXPzKpNJwcX5BcvLq2Q6RWiBa2vODx+zv7dPnnfI8m742W3gWy73Fzk7PODkfMLi2gY/f+tNfvXLd/CNRDtLMT1kPN7HtVO0D6wwZ30oudGKpnFoIZHSXQokm+urjKYzDk5PsVZGJoqhrFqUF/Ty/HLhNC6wVuKTDUQoHvOWEBmVAWPhncDi0FqFzUcUdb33sSVYM1xc4ebTT7F3ske3v861rS1efvllzs8u+Pff/nNm1ZQvvPA50ryDbaDbHyCdZaIT9i5miKVNNl/4Avm1bUqjOT0444NPdvjOz27z80NNtfwq+cIG60tdBrlndHJCPal5er3Pq7f6bK9lZM7TVoaiqpkWJb1uDgJaa5jOpvSHvRCJMQbhg7M23O8CrVLwbXAFz0umXOQZ4jHGUtY1edahqgpSJVlZWuaF7iYfPT7FqQ6p6NMvC44O7vPoZEzb2aDT7dAgaWYtpoDhSpfVYTc4xq2hn2vOzk7Y2d1la+sqOkmp6pZyOmFhOARACoWIUy3jJRZ1OeFWUjGrW+pW4VqHBpTskqUZ2iucF9x/tMds9iGf/+xzSNkl6wyZlC3vv/ceC50Oti641XuKpeVVdh4+ZHFlhc2rW/ze73+LX/3iTV7/2a+5unkNhOTjO3e5f+8TXv3sZ1haWWZ59QozRHiQX1xwuHcAruXWyg02Bpvkqo/qQV2X4CztdMxsNCLvZAwWV8m7Uz5473VODh6g8wFOJiip4tSbGGMRocgQh0yCuO9tcGAGjqgP7Zg2As+NRaexTdqaUF7UNtimxdmGub4mAH/5+1DKVFdlWNzjgj+bTXHOoLW6LP0RkQeNkPHAo6mNYTormc1mTCaTsKkkxtNdQATkWY4UsLjQI0tkdNp4VJLgbHj+eWNJsfRzxaRq4xRZsLe3i2+nrPRSusphTBFasqUizRLSLMU6T1PUGOvJljZQ4snhIwihBktDVZUYIcj0IjrJ0QqcEhgTxdQoJmmhydLwfBUCtArDtE6aI3C0raepW3rdnCRNMd6HsgIt0Ym4jMKHSbb+1IZPXG4Q/84aFg8Tl0wqPEYLdJaTJ1ngy7aOyWRKkqRknZys2790cc1FhvBphgm5/BSDcf6c8z64s8NiH5wEKI02iiSRpEkoH0sShbEt06Jg1hjq1s5HN+GAMj+EEJ6bxN+HyF94bVLqGDvTKCHxwlNbS2YNpg1Cc5KlfO3rX2fnww+ZjKe8/rc/5WI8QeUdvG9wacbS1jan+4csWZBJGLhpH3jIuRbsfvAOb37n27ga8skpRTNmZ2+XDhatQ9uyw9AYLifSLlgOwrtnTeDLW8fKcJG6dgjTcHL4iIvRCWvrN0j0U9x85hYLQnGvqSiUw2Qem6dUxwf0BkOETkPrqw9uZm8srq1pTUPjYjmizsIm3jfQtvi6wbUttaiopMDUgq5t0Z0ua4srHI/OqFuDE3M3kI8CiUfiSJREdnIkLa11l2JE2Eo82dDF1Q6JwOAZWc+OFrTSgK0QtcJIQ6oFuXNho6sUUyFpNtZ57b/6L+k89TwHp+f46Yjrn/ki+6+/ztHPXmfVGjIcw7Jgdvce9WzKf/TVL3JjeYX/7a//ivune9jMgQ4isBWh5VgaQ6JVOEDKwJR2kW3oCQ3dtnEoHFLAsJtRjg3FrEKyQi8dUJYzkiwh62QoEsrRmJOjcw723gTpWN+4wvb1a/S6XWoD5DkLS6ucHh0gRHXJjU6SJN5XGf3+kJW1NdbWVhmNTnn/9h1e+Oznuba9zc9/ElxbTVNRlxOaeszK+hWUNDghOS8aZo8PqWbTwFzUCiMEt174DOX4nLqYUp5fcLJ3xOrqBivLi3hf8/ZbP2U6GnN1awuH5OH9Rzx9c5vecMDZaMzKxgbT0Yh7D3ZJ8hwnU9JBwurWAr/xpc9z7+MHtLbh5PCQqiy4ODmmKaeh8FIJzo93qabnobAG6OXLnF5YtkTCF776m7z13gGLy9f43t0/58O3/pYXnr1J1uuzurbGwsoKv/sHNxhfjHi4v8/RwT5ne/vMRhPWr15lcZhyenjA8cE+H7ztOTs5I9Ga61XB0uoGs+MLxqcNW9c3Wdtc4PraNjvHu+i8w+PjexhdcfXpzzHeGTNtL/jSN36DvQentOWU3/zSq3z0yw957vqAm8sJOx83pGmXf/rP/w1/9u0/5alnX+Kjd3+NVhmJSpGpJO8NeO3qVfYP97CuIUsEq6tr9AaLXNna5Pj8mP/uv/1vGB0foqQKmsU8DUCMN/swjLat5eDDHRaynCtPX2XvfIfjchrwf9aFUk3xqUM5oeQPG1jkXsYiPWERUezBB67zcneRz730Ocqq5Gw6xSQS2RIwaRJ2jh/xZz/+S/71H/wxm4NlZhdjEpXxzM2n+eXbv2JczHjm1jO0SvDR/Xvcv3+Hk7MR2IRUZggX7nbpNNYJbtzY4D/7N3/Ma6+9iGsLqgvPnTt7/F//5/cZFZLNzWfo9YZMp5K6VXhsGBjaWE0oJFpoHAou8WAEDJA1OAROhAZ3rItsTACNIIi9bWtp2xmTiaXbb+l3S86rj0muFWx+aYM2mdCWFePDQ3xtGOQDnDZYbahnFWVZU5UNyhOLocOzIRi9QnJgzt6UMsTVVewCUUohnAhpOqmiAy3sI5RQeOPoqIw6h8PzQ27f/ojkuRfptJp9e4fOwpBcpTy9fhNzCpNlx4cnhxgc/a3rbH1hi7KcUpyd4z00ScJgeZVyf4/VpSGr3ZQPjxoeFReYpIMtS/xszMHBPliPWl+mt57R6/ewRYmxLamUfPWV13jqyhp/+p0/Z/fwMc+++iKvfP7LvHD9GXY+usv6U1u80rzKd//6Ab3+kBvPvcjK2hWYC3V1RVPMOD8/Y3x8iqtLEi/J0pTucEA1K2irKrjYtAqOyejAm/N7nbXIRF1i49x8PxEZvbWzSAMahzOOpKnJYkJk7ogTc4wa8+1IdLfO1ygfo/cuCKLeO5yds+/nwmeM/Ap3KWrK6DW5rBFzAcUhtIzXRyxa9e5JOeylQDsXS8P+KYijMpRXShmLY4MjW2sVOnMll9dY2IMHfn9IY4nIc/WXg/l5qslHkVTrJ3KKadswGHAWIdRlYbCUwWU6/yVVvN9ipDs4WmMfwVygNW3cd4U9TnCsRgHT2Phcc/HeiHs0wDsTi6HiucC5UAAq/JOBEh7TtEGsj05N53zQHvy8ztVjLbGM24WhTGswpkXIBBE7GeZpLKmCmQwRBGfdKvI0DQJ5LKT2nXBmVzK4h42xAUEYGbaXDF4pkOgQ7Y869PxZ66xHy9jzIaDT7SGVjiaLIJbKOERQsYB5Ls575jzaWAbmA69ZyQRiIR6ELhvhQh+BF+FZOU/YfRovobWLZq9grtBJjk5z2rbBmxZsi7UVc7MFmsshmIiCs8fixBOExXzPF84OCofFupDKs86H9BmxS8SH+yAwohVGKYROcFpCAmkrkNYz9YZ7tmKiO2yqHC0lrfDk1lMrgSOgTAqpqboJpbHMqprzvX1GZctkUnD1xiYbq0usLA0ZDvqsDfosZSmdJOHu3bscnV5QNfF+lY6zixm9vqPXkSwtDslSgTFtYLa2RTBBSIXWin6/G+5RldCagLX0XqGsRwpPr9dhaWmRpqnRTtEoR9ZL0KlGJAIjPZOTKcX0HGtKnHUE8UdQFQUL/QX6/SGr17bRuebpFz7P6LVjDnbv8+DBXXYf3GF/5xPaqmB5GXqdPkJI6rqhrisa67gYj0NPjFoh7+cM+n2WlhdYX1+hrg0X51OOjk84O53gWs90UnJ2OqGX5eQ6JdUpWZrEARIIaWmalr/v6x+0SOudo5xMKZsap4KLqGqa0O7tYVLMOLw44cHeHg929jg7mzIpQkmO8o5mNOFHP/8FCsmXv/I5un2NchJnPGUxZTqZBseY0uR5nyTJKcsZadoly1LsZMry0gqTomBxuIRygfmz0utxZWOD4WDA/bt32FpfI1GK+3c/QWvNxsZ6eEgrwsHOOlrXUlU1mU7QUuOdo21qvKijE83graMxZWjxjhEFpRRFUbC6tkav3+f07JTzixGrqyt08pxHu4/4+P13ENQMhzmDwQqdLKO1Lb6q8Uhwltm0QSU5vf4ieZYhlcK0NUJappMxp4eeVChSndJd3qA3GLKxscWHH7zP2ekZW1tXqZqG2rYgPZ2OQkpDpyuYji+YXJzQNDX7j3ZZ39xmPK14++13eP3X79DOJmRJQlUVTCeHwUkmA4S8FpKA144lBTF2IAWkMsC+Q1lOEFmlD5svh6dsalKdkMYiIA/hdfs4KdShIVEJiRMC411wvMYiCB25l3WcHocNfYwnk3Dj1gusb25weLbP6eEJ3//u9/nCV36T2WTC0ckBXhi2b26htOT+/Qe89NJnMM6xd3BOkyyxdeN50pUt6sozHo/50a8+4N//5DY77Qaz5afR/VW2NzuYtub+wykZns89vcAXnx6w0AFhLNaEoYH1ll5vQJoEzk7W6ZCmmryj0D5gCto6RGjiKA2pNE0xQxAiOnVrkM6hksDwElKF1lsPZ+fHDLpdlrt9FjtwfSljdejpZR0W09cophUzk0I6oGoMuwcjtJK8euspdBKuJ2/qgO5QisXlFabTafxZNEJ6oKVtTeDhEkQrg+Ks1JRlQ5oK+rlicZBTThp++Ot7jNuETDq6FDx/bYHVnmd395hcaKZFTW9wxKsvb9PpZpTNlO2bz1BdjCGRGOcQMmFW1GTdHhbPypUVynrG0dEhZdkiU8niwgLXrm3TVjUff/ARw4UlNravc3F2zsGoZmP7Ga5s3kR4FdpCgdbWTC8+4eHH77H/ybuoJOfpF1+l3x+wvnaF/b0jHj38mKJoGFc1bVPiY8xIyiCONk1Dv98nzTvgBYlKIwNLkKWSJAkRbu8Dfw3pQ/zPWGSmQ7FDjCbNWcNKKqqyBOHDxksKmrrCWkOaZXS7XdriAmcNTgqyLAchsDZsMueMsKY1HB8dc3RyTuCAmchSCpN/JQXdTodBt0uWKDqdsOjY1lPXFaYNgycJZFlGp5MhkgTrHOPGYkX4fE5HMxY6OTpXOK9QiUKrBO0bFA6UIu90UTqj2+uGw0HsmlCJIpEd0lQFHlKM7QWWeXDfOwGWgCjwhA1kkiZI1cFbS9MGN4PWGu8tOm52m6aMkbY0TNgJgqSau0Pm7kFBdK3Pp+J8CgIfhda4GVRKBwE6xoAk4VknhCTv90Ha0LjqVXREBMbsE6EgOg2EQMQG4UuXh3WXkbVQSh5ci6rfxbua8cUpdVMHB6i1VFXFdFZc8tDmXyH+pQJrSTwRmYPrA5ACHaNm1huwCotFCs+4qejWFafjMfl0ylp/hc9+5nN88N67jE7P+do3f4d333qLux+8i7ZwZWuLh5OSO6fnlIs9ctvS85Ih0JGCTtvwyY9/yOJwCW0tRTFhmEiECU5n50P7sPaOLM+j62HOK7fh8NPU+PGIpavXkB1J1YKpKsrJBVWS0h7vcP8NRefqMySvfZGLt2E8OqCztEXfehIhaNqapizDIU0ElIFKQqmL8pHPPKtoGoOXFgUkCDIfSt2cDMU7F6cXiKRA9zKWB8scnp0GV0EsriC6sOeuICUEWaqhbkOJmY9cwCioCyFQcegW3DCKuvWMAZ0qbmOQruJ5MlZisYTyUDWOMQnbn3mNdOsZXv/eT3nre39Fahuee/kLfPFbv0sjBI9+9mPWakPWGnpphj46ov7x63z1c1/g6n/8n/I///W3+flH70DmEWkoy5PRihfc7x5BPBCF+SBSQlu3YGW4biQkUjPo9CimI3rpkKe2n+X2xx8E1IO3tM5QO4tF0zQlo/NDdj5+n3vLy2w/9RTdhVWWhn2WBwNsMaFsLFYFsveLTgAAIABJREFU7l7btlRVw3g64/x0hBaCXreLTjWPD4/4+RtvcG0zNEr/6ldvsbq+xvraBrdv32azmDEZjVlfWebKxiukCVSzKcI3jM+OceWYD9/6BU0xZTY+oa0LRhdneBy9Xoe9Rw948OABTVmxNBhw87kXODk65mDvgEHVojo9trZvcLS3zwfvfcjmjRu8/Oqr7O0+4Ndv38YX53z1G/8Eky/z7T/9M4StmFycha4DL9EiYW1pSBsPpWVTs39yyPL6OogBk/E5s8mY3Z077Ow85O4ndxlfHHP1+jZ1W9Pr9jg+OuaZZ27xe6++xnQ85ddv/IJ3Dt6kKA1K9Vi5cgUhMw7Pjth5WHNyds5gYYFnn32eZ595HqmP8dNz6tE6Nzau0V9e4dHRY5iNWBgOyNIuVVXS6w3Zfuo6RwcFn3vtea6s9XijqLj3cMxguMTmzZe4e/wW7310B4Rn9/EjDo6PuX7rFnmnh1c91rZu8ewLz9P56Db37t9l0FXUhWX72gZZMuSVV7b5g//gX/DdP/u3nJ6coJSOHZE+PqJjSiAOQ9qJ4eNf3mFWlGy+cB3XVeyfHDCaFaFMJUniwD5itHwYhjgfBqp4h4WwZyU42HQN19e3WFra4M1fvk5hQCQ5pnL0sy5FVVApzzsP3mPtZyv8q2/9c5KI8bm6eZ3JdMZ3f/A9fvSTH2Fcy+PHOwz7Aww6lrekoMDYBltXrK9e4Q//ybfYWBti6inTyYS/+s6P+f53fs75RNPtL9GJ62dRuMBWj8/5OYPR+bmopXDoOMRX4DVclhVGgZvgtPVxKKl0El2tLRJFa6YU9oRR8YiFl6H/UgfXnyJsgb2YoCclWZKGoVaaYmxF1c5wjUVJjXQtdVMFlqOSeKlwbR0HPOE5F3oXIFFJdLhFHJGMzEkd1upUJeFZnWn6KkUKx80XPsPgQnJ2OGbV5EhrGddjVp9+hqu9NVot2RmPac/PQlJkcYVnnn+J2w/ucnJ8TD9JUTgmR4eY8TkjM2V7bQHlW1ZXNuluP8XORx9RHR+DMeE8UTXoqgZSTGuhadnc2OQbv/27PNzdoSimfP3Lv0W+ssrS6jrZ0oBfv/MG8pOMb33zH/Nf/Of/NT/8yQ84nY05vTjj7OyA8+MjmqLAmhpsLM8Rwfmvsy6Ly0uce0ddlyE52smZl1tb7xDWI2V0yFqD8eE6Zi4++eDwcvNiMBfuI1M3oT8lEVEcnCd6ngyq58g576PQT0i7ahXEtfBt5om++ZBSRpFXXe6JmItU0nPZ+EQYVz8ZfD+p/poPz8NejMs92bywSaknkWKtk1BgmYRUVttYlAZj2kvclSDsu0P5lKdt24gsmOOy4jfxPjhlHXgREy52vueMXjkTeiCkmou0QVwVceATBD/H3BAL4LwN78qnnMHWzhEKAV0XPq+I9BIBS+H8XJT18Vw852r70McgAgc/RNNdRF/M0S4BNRG6FHx424WIpdqe1rQ4L2icoXWORMpgRLt0Cof3Yl5A67xBp2kwcs3ft0tRPhhVfBT48UR3objs7hBeBkNPvDYJLyOcd6IQn6cpidasrq4ilWY6nVI3NYKoo1ySl2LBb7x2EOLyc/RRPBVxjy5iwtATeb3eIYRC+SevM+72w/XoCO9XMN9entukSHBSIL0kSQPew9oW5oK6C3YM8akzxFxon38PEQVjpZMwSY54Gh8FyMt0VXyhDoHXCpMoRJpgZh5pPcIJGmOZuhaju9QSFpKEREHpHSUETFTTMPVw3noKa3AuaFNn44rZyRkXo0OKWzdYXl5mcWGR5cUe2m2ghAr9TukuO0enNC6ULLZtS2VaLsZTZsWYK2uLLA0X6K5vYI2lqmqapghFXKOgyWmdkXWHKJkiVYKKGIqsuxiG4IsDksQz6FrqsmE6cfQGlixPqMoS1xRYUwVcnrUkOjj2L8YT1ONHFG1FZ2GVxeV1Vq9cZW1lka0b17l3bZN33tSc7T8mQdLtdpE6nLGLoqRu6iCKiyAiF5VBJ4Zhr0fWyRmQsLrq2NxcYXfnMUdHp1jnKGZjzs413VyzMOxGZE54NkghSf4/mLTqT/7kT/7eP/z/++t//B/++z/5ymdfo67Dg7KuCi5mF5xPz3h0+Jj3P7nDex/e4f7Dx4zGFR6N8zIw9JTCKk9rGnZ3H7Nzb5c8VSwu9nHe4kyFsDU4i1YpW1ev0u32qFrPo73HWNOgk5xOt0ddtwgpuL69TVWUlEXB4dEebTvj5PiA9Y0tut0ed25/xPnJPmsrK+gkoWlbTLwIp5Mp49EFdV2ztLQUxMGmwtqWpg5lYIGsPHeQClwsimnjwjGdjpmOpxRlhfGend1denmHYjahqWb0el2GC0sMF5eZjMacHh0icSjhqZuGrNPj6vWnWN/cZFrMKIqScjbD1EWAe89qhr0Fsv4CMushpGB/f5fD/cckSUK31yNJQ/RTK4VrG6TwnJ8eMRuPwvTgbMzhwTGv//xNPr79SWTElDT1mPHFIbaZ4CPJ3CPRKuG5p66TWkNTFBhjSQNWnVldc1GWnE6mjIoZKtEkOsTAdaLxct7syeUGYW4nNPOyHgIzUsR2ae8jHkEGR66LU7HgNg1uMedBqpxvfPP36A+6PNq7T10VeAvHhwc8fLjDgwf3Md7w29/8OpNywkfvfcTq4hXu3n3E8XnB5o3nSYZrtNZy75Nd/ve/fIM/feuAi/Q5iuEN1LDP6mKX0fE5hwdTrq5lfOXFZV691megghjnjMc5qGtLbVuECCLcvOU9zxIG/Tw4PtqwoXDOBm6Pj9B0UwfXgU6ZN3dKneIihyZNOwgkk/GYpg4HN6Uk3VyxOuzQyxVpkqPTLk1reHD/HmcnF+S9BVavrNDNE/I0CFxSEDYr3sd7UCJ1glYpIg4crI2LuNI0IuWtO4/5/q8ecjwtODsfsXN0jCVnaW2ViRWclSnPv/w0T29dYZB6FA0X4xGjWYPxmllRsffgPoNBn62tdfqDAYuLC7RNQ1WU9Ho9bjx1izRNePTwIadHx9y+fZumtXzzd77J9vZ11tfXWVle4c6d2xwfHTIejUmkZHNlk+ubN8nyRSZTy3BhA9saTh7c490f/JC3f/ITJucnrCwvcnX7GbLOEIwkcZLWGoRwgEXYlraaQNtAY+noDGkdwtX0OinS/9/MvdmTncl55vfL/Paz1qlTVSgUCnsDaAC9sbvJJkVSpERKI1HSTIwnPI4YxUQ4JsK3vvedLib8H/jG9lzJYY+lIe2xNNbCISWKbLJJdjd7QaOxoxbUvpz9fGtm+iLzHEBj/QGqiAoE0I2DU3m+L783n/d5f48m9D18KQg9SaMWstCIbWqyL12wk3LfmiSJSOIQiXZjZcxDGDBQ5ilRYEMhjLEMbM/ziCMbmmO0fR1bshoHNLfiaFkqTnpDNrf3GA6neCIkCiKMY3YlcUyr2aTdarGw0KZZqxGGHmVlU97jMMZDgieI4xgpfcIgoF6rE/oREsk0tSEgGkGuCqpSsdhqEvjOTWhs8rBG2uAmLyKqNQmjGkgPg7QFH8yZUJXWCCwnTAhphVJpma1K2ZOBVjbwIAxD4igiCEP8wMfzJX5gx6SFc6pKL7ABiEGMH0b4Qej4Zba4E9Kl3ANSGMvn9q1LX86+PTlnMgWBHfkJwoA4Tgij2L52ENqmoufZQ6ELwZDO/WKFc4nvefjOCev7PlEYEMexG1e0214QeLZxE8eEYUgQWHZxs9mweB+gXo9JajGZMhz2RgxHk3njYNY8mDHKZqcf4VnXCJI5O00I4/AQVhJX2lAUFQJDs1Gj3W6jK6hHdfb2D/id3/sDLl27ikEzOj1metqjWa/R6S5y/+kThlnOpKqIAkmMQWpF7Ad4WlOlU6RWJFFIgEAog6mUK4/dnl5ZN40nQTlRLzeQlYq0KMDzOHfpJUoNaVWRahhg2Br0+cW9BzzsDVl46Tqr169wcDQkPT3Am6Zk4wFplqFMSRAGeEFoE2exe1lVVpRFQVUUVFVhXSrSs+zKwLeTHb6PF4aEQUhlT50kcYIfhIwmY6Tg+QjpzKPmmNVSSALPivZlpdHGsenQTpy1f8s23eTz8C5hyKRhgiZQhshofCfsKiTTqMZL3/kOW4d9fvQXf8Y7r9/mwoUL3P34U1Zv3uDSr38NkdQ5ONihGAyo+TGJFyKnU0Z7+yy1F/nqV79GKQQ7u7tk+RTjYxsPnnW92IBPg8JHejWiuEVS71BvLBKGDUBaJ1KpCT0o8pTDvSMEAUYrynKKrqxAnqYFeVbYxpRnufqnB0ccHPfZ2Nzn2eYzhr0TtCppthpW3DaAsde0J320UlSqICty+sMRo0nK+YsXrBtPCK5cvsytV27TWjpDFPp0Wk2iqM5oknHz1iskic/hwRbpeEw6GiO1ItA5Swsx7UZCvz/g4OiIK9deYvXMCv3TU9Lx1I4e+z7GaCZpwcq5K3zla9/k5Zevsb3zjObiMtIPCfyEZnuZdDJmPOhh0pTNJxusrF/A930+/+wOzXqMKnKGgwmeFxGGkW2CNRKkZxFY/dMhlZYk9RYXL57n8b3P+ODn71JkU9CGyhiaCyvcuPUFOivneLy1y9HxmMXOItdvXOLcuVWyLOXoeI/JZExSaxMmNdqLi8gwZmNrm88//5ynTx7x6OEdTg+fkU9GdBa6LC2dZXV9lel0zOP7D8mnE05ODjidDpimmlarSytZ4KNffEL/ZJfepMejrSO2Dg4pKk1eTijzjCD0eenV11m+cI0r125zenzKZKxZXL1Ec3UVP4yIg4A0U9Ylqyr29w9YXKijRcnGk4fgAmWEc73OmmjWOWUQSFRRMTjpE8QBYT1klI1ResbzN+AJF/rlRA6BFVeQ9jUdGkD6HtIYEu3xW1/6OueWVvnhe++yMzxFeAK/MvyL3/o9FuM6Ozvb5EZzsHdILYi4euEygW/DczoLLZIw4fPP7nLnwT0GWcnJICfLLGPaIC1aaDplpd3hX//hf8MX33wV34OdZ7v88f/2p/zgbz6iKJtIv44xgrLQTNOKsvTRhEhh0Vh2n6oDNgzFGA/wwY2gW3HWn4cKWveZsM54ZUfiMQZPCHzPgB6A2sdrHdF5WXH2ywuUizlKpRw/fkp+1CMmJIpr+FFgR3DTkqw/QuclVBVKVRRlZoVHJwoWeTFHGSitkZ50jf7nX9rMxrWFxbV5HpEXIJHUwpjV7iLD3oCvvfQlfvPlb7C6cJ44SBB4HA1GjIsCL4wRwrBzesA4HdJt1Mh6ffA8SgnT0RhhLOLCvidDIBSlrEjDmNXrrxI26xw/ekA17CM1SNtd4+z58wRG0fZ93rn9Br/99d+g02rz+OkGX/nq13n5+k1Oj05QSnPt6hV+9MMf8Plnn5BlGa+99ga3br7G55/f44P3f8Z4OmQ6GVGOx5R5Zq9rY/cwoQVRENmMlTSlSHOUUoRhSBTFSN8+SwLHiZS4b1fTIKE0UChNWSl86RF69toWrt40TuyqXADtHAGAsaxSM3O0OiFV2KwPnDFjdlSzzy1nzEHgSxvgJIQ3dxCCc9POx+Btk0U6odd3Z2UcF30WHigE81rPcxOZ0o27z0TEmYvSaJfhUFWUM65sZUf4tVKo0opUulIYZc0QbinsM6V053THZa1KO95eqoqyqsjLnDRNbeZCXlgMmZv0mDUSZ85UVVUYpdxI/N9voNv1elGAZr7udh1xBYFz1Xr298IAUjALQLMGTueQraw72LjPxICrn8VcLPd8m3fjB7N1tKKkNtZcPzMPCDeFZ5ta1g08c+VXjk9bqWr+OZVlYcXWsrSOWmNr6Nk0pQGKrKAoqzkNzg8syigKAjxpjSxRECBlQL21MDeszHEQRlj+Ks/XTHpOsHfubRt2bIOd7blBEPjWcW0kz537zkHtBYH7fy1SIIzjeYi6515jdq0JKZwRYnY/uPfgrnnbX7dpxjN3rnFrJ6V0+oZw96d8fj4RzPMycO5rgZ28nAWduS4I5XSM0dYKVzmEnPRCCgEZmkoIMikYA6M8YwLsZYrjNEOZyuHuDJ62OQyDyYT+eECeZpiqAGWDi2v1hGa7TZg0yUvNZJpRKkPlnOgaqKqMbDIkTwsC36PVqtNqNFhY6FCLG8SJmxQ2GiN9oiBByBA/ShB+zMLaJV5959cIohBfKjotn0bi06iHNBIfX8D+xh5HO1tMxn1rLgoCoqQ2R9vlRcbh/h4HO7vsbG5xuPuM3uERZV6g85R0cIwqUsIwQoY+eJbdnSQxURRa85SrtWaNl2ajThJFhGFAFHs0mzXarSZxFOF5Nk8rzVOiMCAMA5IksNfdLIciiPjun/3nvT/6oz/6n//Le/4ftZN2OBpx/+kmXhCiqUizMXu9Q456xxwPBuSlwegA4cXgl0jPR+rCHZrtYUFrQ4lk8+CIwV//gP3eATcuXWEpiRGmJKw1meZjtrY3qLe6JI0OCwuL7G8/5fYb54mimMPjY1qtFitn14jCiH7/lGfPNtjdrUjCmP3dLco0IxAKmcQ2Cb1WRxlFOp2Q5wVFltugAw1ZPoVKUillOw9SIkLLLtLGcnaLLCNNx1bAWFzk8eNH+L7kwoWX6C6fQfoeZVUBgqJUBEFMmVWMhkNWViULrRYbT+5T5GPq9fp80zT41Bp12p0zpNMcbfoEfoQxHv1Bn6OjPZKlNcKoSRBHLHQXOdjb4eGDezTbC1DYTWM6ntI7PmGaTTg4OWY0Sdl+dkyvNyFNS4zr2kzKCblOmU6GmDJ34Um+cyYI0qqg9NwmnheoSiECjzAKYTLBIFCu8+UhQCvLUJKSxA9c9wjHrnGbsRD4bqzFPpykTePFutx0ZZ+wM/A6TqgFu5UqA/Uk4trL1zg6eMZkMiKfTiimOb1eQNKocXh0zMraGZrtFnfu3GF3a49f/PxDFtcus3bhJiKI6A96PN0+4v/6m0/5fNghbd9ENpfpdLtUGo72TvBLePXKIm9da7IUS8hLplTW8eY6w5M0pVQlcWwFtqIsWFyo02qEJJEkKzS1OCbwfLTQKC3JcyvWJl4LrSqUcdxKA05tsR0825xkcfkc48EJ4zQn9kI02KJRG5qNhOk0pd1o8corN9EmZJhV7O7t0ttX3H7pPEHgod3QlPAknjRoNJ60h5ggDPGBB5sHpEpz6/pFtPLYPp6g6i1ef+cGiwb2ej0+3zikV5bcfOkcRu8xPNriysUz1H3wdcTt69fZOzomDgMWEkExeMLu7oDLl86D1Bjh0+6uUk2HPHn8mKgWM50MeP9n77HUWULKkLNnz9qwliwjyzOkkFy/cQOlKtJpwXA0YvPpDq++dpHQrxHW6gxP9vnZ9/8T6bNndOMmX3/rGyxcPousR1SF4uTwiMxYJ38t8NG1iLycEmWC2PfIXZqqUDZ8L3JsYwP4UuI7NlYY+rZQ8TwqY0UgY7QVEWUAzgEtpWc5TWVpHSMujTaKAqIwpKpKC+kH4iCwaaYIGzYnbBfPGE0Q+AR+yGRasHd0Sm8wRmmbXmzxSZazGXqCWihZaCaEge/6zCVZYRnc2li+d7fbQZlqzqsVQpDECUVR0RY+p8Mp4zRD+vYAeDIcc9irce3CMsaU5KW9bmYlqh/a0SEb2Gb/zBMWnq+0BiEJw/i5y1TYcTzLPppVshLfD91ImAW3SymIg8BON7n/L1DO4SBtkq4nfZeCbeZp3+DemxvLEthRJU/6+EGE8Hx7kmDmRpXPof/ua54ajp0MEL54nsyr3Yi7nv17tpizRYF22BK3+mX5vNh1ztLAD6hcQMFM9C3LgqowyNJQjqYc9kccD8YYaVNuJQLp9oIZXGx2wDIGWxzOGl3aUFWGwLNOK+Z7imGcTTk83qO1nxCuXSVqxDQW22QqZzQeM82mdJa7nOzuMDg94MobF/kssmJkUVnndBQHSKWs4wJbDJWV5e1KXFCJrVJtyI6G2DG5fSFRQuNh8ITFdJVpQTFMmU4Kjk4H7PR7ZBLq9RpKVehIsLDe5OY7q7TqdQ43tvn4/k/xJhPCMCRpxZhCWUePK7CVzqjykspovCDAN4og8VG6IpukgE2TVUYzHU2R9RpRs45nBKVjOq50lpimE0aTIVraa0HOT6/MR/M8YfEgykBZapsaDO5g+jwZ2rjDaakNw1xTxj6VJwlNiVISKuHYY4ap1mR5xfH2A9bPn+ft3//nbDx6iPjlx+iioOwssvZb36HeXeLhn/wJR/sHdIWhZiTeKOXkxz/D393l33zlN7h64Sr/7s++x97kFBMqPDSVAhnELCyd4dLVV7l06QZnVs7RaC4QhAlKa9JsSu/kkGdbmzx5dI9S+TzbOubTDz9j+UyLtXNthGeIghDZCqgihaw0VeyhVU46GqOUjx81GU1SekcnBKJisdun3ojtlFRUo9WuIz1BkdsDX1FUaKGolObxoye0m3XeeO1VXn31dWQQku4fcveX71EPQy5evcZCt83W9hZrZ9uEUUKVZnbkXedcPH+J1bVlHj7cAOHRWV6mXq9z4eJ5fv7ez+h0Oqytr7N27gK9wSlJc4H2YpdaI2Zn+zHpeMjquXXWzi3z8N5DnjwsqTcS1s6skqoeH773Lod7G3zpN/8p3/n9P+Dk4BnFdITv4xrN9pCnMkXNCzCqpKxSyrKgvbBMkoQMTnfJ02OgwvPj56OEBNTbK3zxazdYWljkP/zv/wuD4yfcuHqJt7/yFYrsFg/v32XzyR7ai7l69WVqjSadlWUe3rvPpw8+Q1WKO599SuNv/5brN7/A7be+xJe//U2++ZWv8xPxHg8e3SWtJjQ7XU52dvjiy29RjI8ZneyzuNjmdFTQH43QUcz5C9dZWuty/vJ5Pv75e4RBCxm0WF07y6h3zCefPCKVH/DV3/4yr7/xOsWoz52P7tE/3WdppYOeGp48OeRse51Xbt/m408/QogAXONASqhMNUc+Cc/uraY0bH3ymOT0iPBci6TdoMhL0jS3+7dnXYBamTkLcMaA9Gf7pV8hSsNKa5nrly7TOz1gc+cppS7wc8XZ1gqvXLzGm5eucbi/x6c7G6RRwA9/8kOWGm1ev/kGWTrF6Iqb167Tabb42/d/xt/94n1Oe1OmKHy/wpceOs9ZaMT8s+/8Lm+9dpsglNx9tMuf/PvvcufOUzCLIOt4ssLTGeN+Dy8RhC5vQhuDVgVB4M+nS+zOKtz+BmEQkOVWaDLGpmfPRC1tbO1AlVJU4HkJkVfhhSccjh6wsFajebXFQO+gdcjw6Jhn9x5SkzEXzl8hkD7ZJGN6ekzZHzE9HaBKRSAlVZlDqdB54YIZKyuaC+vIEi6Lw2ZHzCZZrNxhBSQPiSsePLtXT6dTdvKULC/Y2z+hSgKaSZtWskSmC2R8zN74iNHeFkUkWYma3Fq5yDgf0Tvucf+XP8fvrtiaqBlBWeEZ8PyQDNjPDLWFZQaTKXt375CdHBMGPr5XI2m1yUMPqTVmPOHV67d5+5XXuHz5KuPJlJvXrzMeHfPzB5/wdOeQsxev8aXX3sZkJcXomE8++Ql5MeBf/os/5J9/5w/wRclf/uc/R2pDrd2hyDPrplMKYewodKUU06KgFAIRR1TTirQoiJIEaQRlpamUtrlPOFELMz8PFZVCOfG9NAYjpLsOXKp9VSFKaV2P0oa1zs5dVn21JhtXuuBaiviBNdhorS0a4IXAHKO1FZhmD+1ZKBLG5VPNsFy2KSsRjqP8vE6aNeclFgtlJ6Y86xZ3xaTNObBnQSUr8sz+O2qeB+OcqrPzsnPFCp5PK1kMSskMIzkTy4wBlC0MjdHWder+rcqJoVKIv8frndWBM+QDc8HU1bFWNWXGuJ0/619w187EcOPc8bPXNOaF13eyuHsFe7/MmtxCPK873GdhcDWfe784Qd8THqWyvGCn91sECsYxU2dsaPczaoNEEvhWVC3LwmbwKEVeWsyC0Ioqt5NaStlaPQhCZ5by0FVFqSokHtJl9BBq8CRGGpCGUpXsH+zbEHjPd7W7tOFTcxyGQHo+vh/Ynxnn4HZrDjaoTTObZnJrZcT8XDETUpES4UwVc0e39GyDYTZRp+35Rwp3TjM2N0GKwDp0ZxN+s5BVF3Y84x/PvmbcWhRzTInv+NiqMhhluxbaObuVVvbecFPKMrJTBFQVvgjQpSHXpWse2/WRSpMXirysKDyPXBqUm2iehbQ1wgA/iMmkR1EYBoMJSdDHKEWj2aZWq7EYxsiwBl6A5wuOez2G4xF5lgLWQFmpgv54TF5lnA5OSKKYbneFdqNNGMeUWjHNFZWGOKqhtG9PX8KnvtBFJiFezcOXkmlqqIqKKAyoNyAMLVarNAZEjJAVYeATx4mdwHcMHYEhzzJ6gxO2H/Vt3lQUEciKPBsyHo3Q0gNPEIYBKopsY9BY05/SGl2WKFPh+ZJhEhH4C86YYxtBSRzT7XYIwgCODplmKb3BCN+XJLGP7/t2qt4w3+/+oa9/1CJtVpb84Bc/t+nvzrpeVopSa7LcB99DBj5+YPkcGAhC3216Zm4PL5SiMopsUvD9H73L/c8e8vbNG5xfXaYjAyIvIptOqLU6RPWYtfV18tGQ0aBHv99jcalLo9FiY3OTMk9ZP3eON8O3efTgM6QyPPr0U1SR4UcB9dYicWsJP2kyPdon8D0bJOLZDqc2muHgBD+KMUaSY7m7nkuuVFpR5QXNZoPxdESj0aCqKoqiYGfngChscPvVVymrkk6nQ1VWBFHENBthjKF32mNne4MgCFyHXzBJJwhpHRdZOmIy7ZMXhotXblJv1AlMyah3yubGY/b2twi7ZznTXEJIj+7yCp3uEtIYRoNTJtOCeqvGcNzn8PiE3d09Ng+O6U1y8hKqwjgIuCKvUibpKWWVoqvKXpDSw5SlHR0T1m3nBZ4dvdDGdexnD0g951/OggE8KfGER6FtUqTwfCpdzR/O2hh8KdGzkWPXdpyJF0Ywt69jXoC3a8vcsVNskovdZbRK2dx4QBh4lFIBt2k/AAAgAElEQVTQG/W5cuU6jXYD4QcsnVmh3mqSjnPOX7xOd+0i3TNn8YKY496Yd9+/yw8/3mMnukWx/BJRO+bsuSXG/Yr+0Qntus/bry9xcyWhJRUiK6kqQ+k4sgibgCgCn9C37K9Raju2i4s2WCvNbEhA4Al8L0ALwbTQ+FoglO2+aWk3PNvRAiEcr80o271VmkLbJPNhVjBWYwplg98WWgv4PsSRIA4jEi8AL2E4PiQOA1Y6Xcf+cjPo0rMjakiq3IZUaTUiqdWIohoibvDBnUeIeouXr6xz8fxZDh4fUwthvRGx1F4mjiN+8fFDAhny+s2z3Lkz4c79+9y+sMRCVKdW81mVIVsbj0nCFnH3PJsHB4QfPODcuQXOnevghRW+rNFoNwHNyvIyX/3611hYWOT9937B4c4+P/m7H/P6a2/QWVlmPBpTq9cIPEkcaaSMMKaGFzapt5ZQwmP/6ROOHj7hwtIyX/j1b9K5dpUq8EinE6rBhNBPiaOMKKlR8z2KShNGhiKAJA5RaY72NL5X4YUBXhBZN7lbPzuKo9AKCgyhQwsEYQiA9K2gW5YWPRDGkWVACst/tOEMEIeJDWgjnmMQZsXiLHU9CAKMUUwmU4yWnKYT9g9PmRYaIzwCz+JFlNHUw4hz3RWSyLK74iSyo2vY5krshQSBREqD7wnqSYSf2CClmXMgThK0ruj6MWGSUNx7xGCaI6VPhWH3pMfKmSUuXbxIWZZotLvffVtgC9eUcuNbwh0uZsVvEkeuqey4dEKgNTYVVHiUpUWdKFXOXaO2aJ4FNNj1jwILi5oFYjAPDbBjgWAbPcaNDpYuRVkaW4SNTE5/MqU/tuxwsGKvDXPQ8zGumYiqFNbpi/1vYeA7AauYM4CtIC+dK9ixs21zel7M2TAI60yB50X83wvTmDsvndPFFzTOLFEWJVlvYCt4JwhK4UZinWNF+HK+TszGs8Ss4LHnKiMFmVYc9I6p7UecO3eRoJ5QX6yxe7jDN2+/Sl7kDI6O8cKQ/mBA7Aecbbcte3s6QZQlXhJY946GEo0RhrTIKMWs6J4VuIbAWDezrxWhseFUoQyoS4mocrxAUCrwG026r73O54OfU0wzMlkxGfVpBTX8OKSehGw93OP+/V2efPwJjaUujbWz9jAifPpH+1RVShIG+Oj59U8lUUUOnk9R5ta9lKXExkfKGN8PCP2KymhKY4f5yqqiGI2JawlLrQWyPGWqc+dccetpbIGPc1EEkUciNMJIOxbmRvQQrklgHOrCuOwVzycrfUwkeeZXGGGQlUaVOQteyDQrONo5JGm0yPcPefjBx3zw3rsstOtkh8c8/uBD1l59m/gr3+BGo8OT//tPOLp3jxUREocenbIkffKYYVXy9Xe+zOq/+e/5X//jn/LR1iPiTpOLF69y+413uHzlBguL64RhDYOHwD63ENCRkosXb/P6W4rpeMDOxjY/+Zuf8tMf/4TTwyG1OKDejpE1DzxDIIDSjmH6gUcUJ0xGKSLMSeKYVDWpypzj0wmngxFS2pqx0YyJ44BaXKdeaxPWapRVSV6W7G3vcuwbXr19m5ffeB2Z1Kne/whEQKtzBmMkg36P/WfPyG5cIxCGaWqxF4FvGA6PGU9O2dk7BV9y5uxZyqrkgw8+5PDwiNu3b/HKK68SNxZIpxMePHzM3U/f57Vb5zl3bplaq8nW00cstDssL3c57Q3odJrsPN0inh7z+rUzHJ1Muby8QLTQ5alU7O2cAf9ziqIkkrYB5IUei90ueVGRFSnbz56wtLyOQXH95iV6vTf5wV/9HQY1d0n1ez0KBcNxzsnJKYeHh9z79BM2N55wYf0y6+tnef2LX+W1t+HTu4+4//jJXCA5e26NpB6zd7DL6fEpvYMBe0d7fPzhe/zyJz/my7/1z3jzm1/l27/9Lf7sr/6WzadPaJ6tsbIg8Wp1jha7RHGDtdVzTIspZ9auENba1Fsev3rvQ452DjnZ+Qm/+Z1v84VXL/Js8ymLK2vcvnWDRhDw7t++T/9gH8+UkI8YTiQ3b73Ft774BX74/R+QjUc8frrDcDJ0nD6DcM5YrRTzckUI24icVEye9qEU1F5uU3rChpwUlW2KSCv2SGOs0GEMxiibXm/shJJXCV69cp3ldpsf3v2AYdFHRgEiN1xeXmeptkA99Pin3/ptDr/37zkeTdjNS/7jf/4LlrpnWW13QBXgVaytrfLlt9/mw199Sk9NUNKGjeoixdcV3/7db/GlN2+RTvrcu7vNH//xd9l4ekwgFtE6tveZUQgDcSCphMLzDZ5n0KV9FpVlQb2d4GuBUgkgKSqF1tBuNZlMS/qDzHEpmT9njH1c2bBHT+OLKZgTpnKT6OKYM7faVN4R6dGI6kgg0oLlxTa+iSiqEkZDpoMx/f1nlIMRolLU4oRmXOd0PKAajynTCb4QDithJwEBO0knZiKQec6UnDdnbRitRFKUFguidUWWlyA9DkenHE36rHp2gklKn8VkEW1KpvkQoyryowFnu0uIbpeN7Q1Ur4c2AlmvoWKHIkozZORR+gFeGDNIS6aHG4yPThAyoCoKjF/QrdcR2lCNc860l3ntxi1WF9ocPXvCo+0dPn/ygOHBI850m2RlwFF/gZ29A4th8hWZGvPRp79kPBrzO9/+fX7/t/4J/aM9fvzuj8gpCYMIO0Znw48qqUnzHOVLtCfRcYTRFblSaD/A8yVFliGUsbg3h5HwhXUdGifyamPwAxueVlQVgb11HL7Aip3ChY4ZV5PMaihtKqQXOLHPWDei8FxzwHFY9QyVoJ24ZZvkSlkhfj7q7UnXVHlRlHzurH2x2W3/3OYqaFfzWiFrhmBw3HrHO67MLETLOEewdKKv/nuva144N83rLauNuprMNg00UFYuBEg44dkot17PX9e+mLEuyXkzf9YgmXH/pVufeXysK98Mz98AzB2as73MzN6f4wS7N2qMeH5OtvBdy2s2tprGGMf0n2Ud2IwKIWb5C3ZfUEajlKYsKkpt0RkojZEWq+iJmWgp5+9ZCjMPUw1d6LAyisq53y3LXyONwFS2eaC0DSacrfeLWIuqrCg9abUVcJhCh7AQnkWKWBPpfG/QxqJZLJ5FzvUWY2w9L9ya2ADu2d+zU7XChZgLA4Hnri3M3F07x2gI5qgzi5MR8zOEQOLJwNXotn61eofFydizgTVdaIe8k0KiqspN2TmNyLimmlFIJzqW2n0+wrefhbIOcC8I8OMEqRuQAnmJ8HxbC2qPwAtJgoh6HFHkGZky5KWiUCVSSTzl9BdhbMCcF+AnCbUwxniGwAsRwkfKgDiqU2+2iJIaq+sha+tnOX9xhe2dHTY2N9k/OOZ0NLG8XTetVyhDNcmYZiWVlqRZRlJrEtcWiOMFpB8Q1eoYKVFlRak84voipwMItaIVC6KGR6k0VS6sSG0qTnslhfIgiIh8Q+gCjoUQBH6I73nEcUiWZRhdkI0qpqNDDg+GFo2pFHlZUBmN8ARREJJECVFoQ9ZttDdurRVlNbDGP4GdMHU5QWEc0qQJUjDNJnYdjeakNySKQsIgIuxYJI9N1/qHv/5Ri7QGwVhV1plRqblDMggDpDFURgEKIwx+GGCUmR9KpcS5rEDb5w8aiaoMj/f3OR31ubp2ji+/8TovXe2AMTTrMVWZcto7Ic0nbHz4kCCK6CwtcePWbUyZgdLUak0bRuH7bD96wtSMEFKztHSW66++TXP5HAeHuwzGKefOrpDEdU6PD+mdnjAaDvGCkKWVVbwgsiE19Tqeb5V1rSGOEzqLS1SVptVsIYF0knF8eEyz2eT06JCHjx5ybn2d1bV16o0Go9MD6vU6lYbJaIDRilqSEAU1klqdWqNNHEXsHWwg/ZDhMOfqlesstDv8+If/iXR0wng8gv1nNM9cYulcih9FNBstGvUG09GI3Z1toqSGCATbu4d8/NE9eqdDtB8jZB1UjipSdDUhz6fkVUlZpGid481GWFwCoREaz5ckjYi8zImwbkKFFV3SIiOrCkqjbJiDJ1BYV59CW8C9Z4vGwI0MK62ZJXja06rr6hljxxc8SWWBjSjsr8YT5JUi15pKa5QxSAIunL/MzsZTIk8iwwYHxycYIanVa9x/8JBavcGFi5cZjqbUFjqsnLtFe2EVjWDv8IC//ul9fnQvpb/wBtXiVeqtLkudgP7BMb3+mEuri7xzo8uFToCobBgNs4ekS5E0aJsgbuxcSVWWlConiiJKLclKQTqtaNZ9pDPv5RWgsSBxeyc4V5x72EqPGd+pqkpr8S9LxqMBaZ4xnKSESYtOd4kznWV3iMnxZGALLwymyLh8bplzK010YQNMpB+gsAgPzxMMpwV37++x2O1y7mwbRUWlFOfPdXmtFNy5/4wwjHn58hIbBwM+urvJ8luXCYA4isHr8PnmgO5KnXOrqzzdzHnv7j4ND9ZWFlhfTjizeobDw32EH1AXCQ82RgwmKYtLbQLPUKqc7tICIFF5RWO9zf7+Lgf7+9y/d48iywEIo4i4smwf4fkoXTDqZdx+/QuE9Q6ZsZ3dq6+8Rae5wN7GEz549BAe3GexVae+usJCe5GgXqMpl4i8EC8vSI8n+J4dBSyFYxZJD+PZ6w7nRPR93/GTXRmmNcZzBxEpiWt1BIKyKi2D0w+dyGgLEN+3zR0h7b0QBSGeb0+hsyRVqW2Ro5XCKEUUh0DAdJLzZHOXSVpghG9RGNqgBMTSJww8VhcWubB8lij00O460sZNKwiLuAgdx9QW3Vaw84Qk1h7ajzBCkBclwhQsNesst5v0hiMIQoTQ9CdTHmw+Y+3COguLi2ht3FiVRlUKoyGJAual6QuF+Ux8nCXa2prTvCCM2vGuoijtNV9WpGmKEIK8tPdNLanZzvtsrEnMHBZ6Xtga7VlXz6xw1tryvY0NN3iyuc3j3R32T/s2kOv/9x7/frf0uYBqf4C5Q0LMnn6zv2gPoEj7ec7Dy/6LA4ptPBknxD93Asz2QINBGjkXeIUQtFa6KK05KjP0KMXNK7wg8jq+mLEHjSCwI12+L+zRXRhXhArwJEhDbzxGbu9y6cIx7asdVtfOcnpywtHxAfVmg3anQxhGVJMxRZ6x0m6hez0qXzqC6QwTIcnyFOVGtHNTIV0KsAcIY9nzUkhyVc3HYO2VbbmwSgpMGDIOPOrXLrN62Gf/Z32CwCMIrEBfF4JH7/4dd9//mM6FG3z797/FS5e7HO2M+OiXHzI6PkC2W+ipZ1E9usBIjZ8E6MzxKSnBSKS1b1EaUHhEcUSCoPAFqdYoN6857A/RQtBdWKBZbzIZ5vZggeU9K6MRRtuDs7DXh+9Zt32llBOPbCNNq5IgMISBz3J3nUbSIU81oyylKIYMAwVCUcmcoYYrlSYWEx5/9D5f+q//Fb3JiJ9//69YiHxWV5f49Ec/YGJCsu+MWfvqr9F47Q1ebrZ4+L0/5dnHv+KMLmn5IZGQTHb3GXz/B9z6xq/zP/y3/x3/xy/ep3P1MhduvErY7OLjo7V0hxMwLrDE7kXu2SYhbna49doKN268xmtvvcVf/vn/w+NHd2lndVorLfwAfK2RxgaqCE8QxhHj0YR8ekRUaxHVYorMhakIhTICVQl6fQUmR5gxnjzF9z3qDYv9CEMfoys2t55yeHzMyWibOx+/z2uv3OLMyjkePHpCt7PA4GTAwcEJly6so0WfdqeDT4uNzWdM0ymTtGIwSVlaXqHd7lAVFXlR4QcRb73zRT786A5lqeifnNLstBj0Tzl7/ia7J1vc+ew+b7/9FS5cfgXhb3G094y9Z4+Rw12+/MpNeoef891/9z+xcuUGq1euIYRPpaAoSuIoJowCy10LQ7pLq5RKozDcu/chcZywslbj7NoZWq066VRhtGW+eUKQjYdsb24wHffIJqc0koR6o01WGh492WF7d59Lly/wxpuvcPXqJT751adsbT5jcHJKGPksL3aJopjRcMRwMOZosE/vvb/h7t0H/OLdX/J7f/iv+MoXvsm5Mxf45KMP+D//9HssJi3KacXLVxf44ivXWOxGKOGjgE/uPeSjn/2EUIKQip3tfT74aJd793ZZPnOOvZ0jsmxKPilpL62QT3ucDvf58ONPGA9Llt95hSRcJJt6LHXXGE4HIBUzfqGcTWNogyorlyCvbVZFCulGz4aVXlnGjwK79+SKUmh83wXRmFlzSliHVKXAlLTjBd58+RXyPOPOg7soaZ2JnpCsdJcJvQCdF9xYv8Qf/Pq3+e73/4JpXvBkZ4ufvv9L/qt/8rsYLRgVU3wZc//xY45Peyx0uuRKk/aHmLLk7bde47e/9Q2i0OPDDz/ie9/7CzY3T6klKwgCChRZMQZVUQsD4jDEk4HjbabWQWXsgTEMJVlWYlSGFAHSWIEhnYyQInQTXRVCGzwCkAEOeo70LUakKnssX/ZZ+MJ5jjttshYUJwVqUlBpgzSGei3GNzVUVTEejRgdnlL0+gg3Il4YTY6hGI/Jx2OqPMOLIztWrawwNAtmkk5s83w5F+ssSuv5M1c71NPsmSvDAGEk/azHbrpLt163TUktSYsMk1tzSalGVOMJnbOLNBcbrCwscnK4i/E12lNkRYYvfYQqyHs5stEkiBKm0xFFv4/RJV6coCtFUkv46jtf4en9DcJ6jesv3yCphTy59yse3/+Erf4JvaIkrobkvSGq8tgv4enGXc5cOMMgPwPSR2mPjZ0d/uL7f8bXv/gWb776GgeHRzx88hBV5kTCueyMJnDBSdNpRtJq0ukuEpw9y2Q8plazbrLhZIKolBUjlCKUEukQNTNxT1WarMoJPEnmzC2qKpChZ9PxlG2C481ER+y+7FAi2jwPgMKWCODcrpaL/ELd4vAhM2SBk0Bs9sFMmjNWnpyJf7P6aVYHzb9c3SelmRtweMGtapsM9hmsqnLO+9fKCspVWc5e5oX6TLt61JvXYnaqaTb5ZH8epTVl6c4RQjjThT3TGedMNsLMkQxSPN9HrNZqxWjhjEmOiGprsBdqSIkNjJrzX+3qvYCeeO7Snf18Fr02e8XnQveMcS+ed/CdIcDMudXGFib2djH2u9IO1aAUulRoYWsXtJmjJebcYLegsxBPKSW+kchaw7o+lV0jZcHHKKMdB5j5OulKIT3L4TWeR1VUlF5FLAOk7+H7IbWkTqfTRSnDaHRqA4O9EI1FY0nPTiJaAdZ7YdLWCnhhGOGHIQhrnJlNwL1YExtVuZ9N4UuBcza8gCOw16St323Ro51bdubS1rNJqPn1UaF1idKVNeloRVW68DznNJdSIgPXlFDa5fYItPQIowihNFr5lEaiy8LWqUpTiYIgCBHK7aUAQYhvPJIoph5HhMKaWQigjEPQFWcKi+roGUUmDUr6ZP2CuCzwajXqfgB5ySQUJLGPrioENvi72ajTXe5y4cp5hqMhTx4/YWt7l42dQza2NpgO+xR5CQbCKMH3LGZnkqcUxlCJgIYfEfo++PY85yMwQUS92cRUFTpTaCGpQtvIC3yBNILRMGMyTjFG2s9S+vP73yDRyt47ni8J/ZB6nJCHIUkUcjQqyfMCozSetLZ4D4/MhXrnWYbn+XbKwPcJPR88YQXdIsdIQ1mU+MJqidILiJMATzaoyg4CGE2mZGXJ8cmQJLITrZ1Og9AZsf6hr3/UTNp/+z/+2z9qLS+CsLwQ4xw8lbZgc2Nd3vb5MBsNADx308wcV/agaQ/wxlhodlaWHJz0OBmNaCwuENUSDvZ2GZ6ecrq/TzkdkY5OQZcURcbJ8RHDwSlVaaHvaZ5zsL/D1pMn3Hz5NgQhze4yF1+6TaElfuRRryVoDOvrF9ja3OL9D35JMS0I/IgoqVFvNB0bZTaqKC0vMa4xnkxJ04x6rUZnYYEsm3B4cMCF8+uU2ZSdZ5s06g1qtTpSCsbjAfWkRuAHTCYj+r1jlNJcvXYThM9kOmZ/f5OqsAzcer1BECYgBA/u3+X4cJcqSzGVptNZ4czqOjOA92RiAzSSJGF7e5efvv8xH350j34/pSgr8qpCKE0xGVKkI9J8SJpPqFRhH8BCuLRdu0mFcYCJJGEzptZMWKnVaGpQaUZV2WJMGcU4SxlnOSXmufNttjnN5hFmvwrc5+26ltjgh1miqRf4TqhgDkHPtSJXFQWG0ji3gBB4ssa3f+N3wBSMRwM2N7ZJpzmXLl8iiQI+vXOHMEq4dfs1lFY0212WVy+gtMejZyf8hx/d4ydPFeni26jOJVbXF2nVfHae7pNPptx+aYWv3VpmPQkIcyeGIFFG23E8bBEqfUkYeNRiyXiUIrA2+nqjORfpNHYUL0kkgWfZtHZTsl3iGTJBYUdClLJYkLJU5FlhnXxaMi0KjJB0uissLZ2h2XT/BnZdtbbcSaMs1MAPfDfCFIIfczSuuLuxx4NHWzQSy0Y+mpZ89PQQHTZZ7nbI0xHZdMRCo8Ew1TzZ2uHS+hnOrrZ5un3Aw+0hj/cr7j7dZZRrlKk4PT5BCMGlyxcZ9KccHJ/QaDZYaAREgSCIEzafHZGlJfVGm+lkQiMOWGyFFNM+/dNjfN8nz0q00ZwcHbL9dJNGrU6r1Sap16g3667zXhEGIf3+iHwIN15+A6/RRnkBIkgI6026a2usXb7M2sWLdNttpv1TNp48wgsi2t0VqsoglHVz9EYnaJ1jysqOpRhhmameHX0PQx9PCoIwsuMTGDc2Y1e9qCrbyRUSKe3YppQeQRDZbz8kiiLqSY0kqROGPtPJiEF/SG80pT8YMRhNGAzHDIcThsMJo8mUNK9Is4qD41O2dg6ZphVhUqdwTS5fQtOTnPUC1oygMc0QvR7p0SHjvX3GBweM9/cZ7O7S39+nt7vL6fYzjjafcbj1jMONbY6fbHL0dJu9p9s829xie/sZJ/1TjNJ02wsstNsMByMrljpI/3SSUYsjrl29SBxGRL5l8kahZasmSUIcR9RrCUmSUK/VqNVj4jgijkNqSUwS25CyOA7xPUEUhySxZQn5gU8Q+Egp8H3LDQ2jyKYhJwlJbJm9SRRblpBj98VhRBLFRGFIHIVEkeWchaFPI4xRecXG9i4f3r3H4WCIEq7wds8lOSv4HC5g1qWfMdbA4HnCifTgO7ascAcfKWejnE6w5TmKACfgeb7lV9mDkRu/sg9G+17E8/cjXEEt/YDaUoe4WQNTkQ4nvMgWmwcszMfB7LVoObk8t/MiZoQE+3vnBvUMNBpNmo0mO5tbTKZDao06HoKDzS1GpydcWL9IZCryk0MCzwr+QkJe2edKWtlQE6eOzB031vXgwkuEdY7iDjdGKwIZ4MkaQdBGRk0GecWd+w/5tXe+xmJ3iXQywuiKbDqgKnParQWuXLvMK299kZtv3uD81TZBXOPu508ZZzkLi2eoxxFVnlGlY1RZkJeFY2x7zpluKCtFXpW2EAxjlrsrFGVJaQwFoIQNosiKklIrpPTwA580nbpn2QtuGWbcR/db4ZrNxu6NRkC7u8j161f5ypff5AuvvsnNK1+mEbyEKJZp1c4wmgwpzRjlaaaex1B4FFoRCkM16lPi88bXvsbLb3+JM+fX+PyXv6IR17hx7Qab9+4xOD6ge/4i0bl1uhfOk2cZh083SJRl/gVViT/NON19RhxGfPEb32TtpZuIuI0SCTb9nXnui0BQlZZdLKV1Tk0nQ4wyaCMxnmD94gVeee11jo9O2N7cgkoRSIF0nD6lK8qipKgsc10VY4xW+GE8F2s0uOTpCGMkCM82P7W248DTjOFwzGg0ZDqdsn9wQBQG+Bh8lVOLBFkxpTcccPHiJXq9E8Io5vzF80zSIWdXukymE9I8p1Zvcnx4yt7eAevn16klTd772S/onw64dPkyURKxsbXBowePUaXizOpZWgsdGq02u7t7TAZT1s9fob6wwOHxAdmkx/UrFzje22Pv2S4H+7t4nuDy9eukStMfDPnV+x9QVYqza2usrq7SG/TJ8sKF6VlRa3l5EaWnGJmzfm6F3Z19Tk6G+EHC0soqtUaT4aDP4e4Wk8E+zWS2J8bz5pvnSUbDAUeHu0SBz/n181y+conFpQ69wSm9fp8wjKg1LE+uwoYVZdMBW5ubvP/zDxgc7PDKyze4+fItRuOUp1tP6Z0ekE8nNKKEa5dWqQcenqp490cfctA7gTiktXyGS5dvk02t67fVaXBy0uNw/5j186v82jfeIDeGaZbiS0gHBZ9/8ojtgyNqrTqFGbGzt2GbfNi6SHrPnV7G3VvGzS0bAA1qkiOMZb8LaSUQewidmaPsXqTdfogBo+CNq7f42lvvsLn3jHc/fJ/ChS6ZShMFCS9fvkY9DEEplhaWoNI8ebpBVRlacYMvvvEGWT7mz//6L/m7n73Hhx99wnCUY2RoUR1pyuX1c/zrP/yXXLm6zulpn+9+9//lwcNdfK9Fo9FGK0M6nZBO+hb/4tfASxAisKnsymCqillwTVnYyQ5VllRFidKelReUcsKVbex6QhNHIYEbj/V9e22k5Zi+2aX2cgVXpmTtkkpUpL0+eqowSiK0QeUVXhEwPj5hfHhA3htAXros1IosnVLmOQL7e08KizpQ2pkMxJy/7PsW2eAJgR+4wEL5PKxIet7cQQhyPvVhJHhK0w7bnK+vIrXlqhZ5htIVGCiLMb1yyMHkmIPjPTQCLwhQpnT1WWQDGLXCZIV1b/m+PaSnqT2BSA+dF3QWO7x0+TpXz17k1vUbaKM42t9g88H79I+fUIsN9bqhRoHKc0ZZwXg4ZKnp0UkEjShmpXuW9bULrK6eoRF6dHyBVCl5WTBJK/LRhCrPLYNbQKU1YRjhRRGtbpdz6+dpLiygndCV1GpMJxPyNJ2fm2eYLFvn2+mN56FTdnpRGA26tJNmYTCvZWB2/zhx0HMNOffQErPPxTnQnwvpls8pZ/UJti5RxmUsCMA4fIGrZ6SUDl9gHaie58+dp/NRdGafu3ku4mr9fPxe2HO2KkuqMreNi7JEz6QS3SgAACAASURBVDiwbiJFKYXS1XPkgbZro1T1gkBr5hjByvFrMTNjgHPLzH5Wt8MYXMCX46HOjbVOuLWIJxDiBcMZbp2sZsr/R92bPUmW3fd9n3PO3XLPrL26q/dtemZ6NgwAgiCExbRImooQJT0oHAq9+MEv9h+hB+tfcDgcYVvBB1u2FaIcDJEgCBAbOQQGgxnM0rP09N7VXfuS2827nMUP52R2M2y9U9VR0dVdWZWZ9557z+/3/X2XeWCtt9ry31/UQu45e/RFprELx5h57+zm4Vv+lwrnSW3G+rCzea/siSL+Z+e9iAmWWyIK/WGwR3DhJmqMoaq8BVdVlQu/3/lxXNCQw3mNlEIFD/84jhY1nhNuQYpw87UqJUnscy6UUkSxz/KwCKyM6PQGOOH9blUUE0cJcRQTxSlp6pVNUZwQh880SUnSlChkRnibjCSwJiNU4jMvRFCs+FBdiNTch9l6pjCecfsc6/b3Ih/O5lVunnjlyTrOsbgOnHVoE4DasI7mwxLfJyiiKA4ElDl1IwD8gaSwGLC4EII+B/+NQbjaZ5BIQRTHRNE8lyMmixWxs6TCkQpFKgVZXRNXmso5CuHQwmEsOG0wWlPVFU5byqqiDl63/npQCxxLRBEqikmzpg8XW16m0+nSbjeIlaOoHSoK5yFJfMinxJ+jJCFtNMiylieEBEtAIh8e2mn1SWK/9o32e5pEkiSQF2Me3n9KVeYY6xBRipCxt8qzgeSna+oi9yxu669ZJWBWVuE61jhrUFIsMji8sNLbyRhnKUofiq2D/STWUlQlptJEWHDaq+jiiEhComKEkMxmJXlekE+naOuHWrGKiJH8yV/81X9+nrTzDze/+nEwD29x4GwA1kKDOL9puUViYNg8QtiGQHgJiLZIFWMjxRd7e9z99/+OWy/d4K3rN2nJhG6SMRudIJShmWUI6XDllLyqMUXO6cke07Lk8HCHWTklaTf4xmvf4e6jB9x//ICVM5sQWZJ2G20No+mMWaXpD1bYHKwQxTFpnNAKhtPa2BB0JYKlQ+2TpK1hNDrl3pefsfN0G6UEuzvPmE6G9Nptjg8PODg8wpiKyfCUyXBIljWwzlEUE6Kk4vDwkKzR4tGjL2k1FO3mCjJJMEaz/eQeSZzQ7baQZpWdBxPKvGT36ROujU/QkzFG+RvE4ckpd+4+4uOP73A6LTBW+cVMicNROgdGAxUeboJI+jACi/QlrYAkSYjaKaqhiFsJRkoqZ1Ay9dITq6m1v5mo4O/itMVhFhs3OIS1vm+XUAU/TJyfCKoowuqastZ+AxK+0I6jGGEtZVVQCcc0UNqdlCgVY00NFpaXlrn58su88zc/4OT4lFajjTCS/OCUu3u7pIni9ddeZ21lhZX+Ct3+KlVl+PTeY/73H33Gp8U5zPrrZP1Vzm320GXB44c7dJspb792kZfOtsiswejS+7ZaDwZpF6RG1icJx1KilGA8mWG0QcYRjbSFkjHGQOkMcSSorcQYcGgiJbBWMJ3MmE5LQJI2MoTwlhtCJf4QopBRk0oX1ELQWzlLkiiS6Dng4n2D/SbhIoGpNQQZhZExuVE82xuyvf2AJ4fHiChla2mZTm+VLI555eZ5RqrJB3eOkE5y82yHTlJhheTc1gqPdg/YPpzw8vklvvvaDf7sbx9wVFXcuLnFai8jkwI9mfHs6VO2n27z8s3LfClqJIIobgKCNEq5fOkC4+EpcbuPKyW//s1jxicxN6/2iaIIrWuyRkq33WJ00iVNUm5cvUaz1UKlGXEa+7RnXaNU5IOy6hqjwdnae3tZePLoEeX+LsXJEadHR6ws9TFWcvPaTQZntpjVlqKuscLSWlphpTjL9OEJcRTT6Ugv+Tc2MFpq4hjKsuLhg320c+gg3281U269fJNIRJRVhVIJaZaRpQ2arTbtdpskTUnSBnEkUfiwwbrO+eC9X/Hl5/cotAChvPwLiILpvRCgjWFWlpRV5S1IEOSVQaJoKEUmDFsWVqYlvboCoyl1TY7x4EpofESYCAsEUXC40ji08I8yfhHTXR7Q31hh7eIWa6srZFFKkVfoyYxf3f6ckTXoKEVXmjtf3OfyhS2uXTqPrgqcCkxwlC8SQwHq9wWfTq11TVWZRTO3SIsNFhAWS11rzxAO3moLECKOiSJFEvsgLubsW+eYTMfgHI1+P9xHQIkIoSL6/T5lnvPhL3/Ng8fP2BtPGWvjX68fFS0YFf5r31i4hdWU+ztM1+cKEI/EuZAii/MApC/oDM+JJGEQaTRxEi0aIRkGPF6OFaSZ1oWwgbAeLEjnfamttWhnaS8PKCYzipMpwhIkZL5YNib47UbBW8salFN+6BlAY+ccKgyakJKiKnm6+5Q4Frx841XiWPHwwV2kirh05hLLgxVOnzxhNByy2mxQ1z5IoMYxrf3vjIKXeBJJOkkKVeVljyKwOvCMqUxKkiA7M5XGWei0eqz0t4jjHoezKXa4z+hwyCc//xmi00FoQz72fu3tlXVUr42pFffuPmJSWZbXfNja5vkz3HrjTWajEbf/5sdYK9DaYSrjlRfW22gI5yCKiNKEtupQVBVCxcg4odtbIh8eoqscLUHFMe12m1lVMc5ndLttBu0Bw8kpla1DQrQI9YDE2pAubSxCRbS7fc4vDbh6/RovvfRVWllGNa442a25/f6Q492ImDPE2YR+vMn+bMcX23FMHSk0FZWecXmmGf7kzzk4HfG9f/nfUPZWiDbOcuvWqwzHUy5Iwc6nn3Kv0+PGd7/HsCg494d/QKPfZ/cHf0nPFHTjiNRKlqcVw3feIz8Z0voH38FunEc0W9RWLFgjSIcz+OAF64d9w/GQfDpmdWWDsq6QTmKdZrCyxH/73/33/Oj7f8b3//Q/cDIb0uulJDEYp30AhnMkaYQpJbrMcQzJmn2iJMETonxRLVRIORHexkSgEE552abxcsuD/RP+7E/+A//1P/9nNBJBXpZsbm1xOoQ4tfQHfQ4Oj3n45AmRgLJ24Vw0mQxHjMenXDh3jnySs719m3v373Pj2g3OnD3HwcExB/v7lMWEV16+RXdpjazRQ2vB2tIy+fqEH/3ln9MaDOh0U6rpiJeuvM64sDz89GOW203iTp9KSHqrq+jtJ1hbESnlGRjOcXZzk1lZc+bsBrW2FKVjabAEKuP1N26QJYq7t++w9+wQjQcQTk6POdjb42TvKXFc08r6nN06h4rh5OQI4Rz9XscHVbZS1jdWSeMMYyxnz6/y6pvX+fzzO9y+/ZlXgBUxMnYcScPpUY4xhxztHPOX//dnPPnsN/z+P/0XfPsPfo/lP/xtfvSjHzMdz/jyyTZnHywz6PWYDXOubr3EmRs36G92qWzG/U8f8+Gv3mU8HNHrp2xsrJFlLW5cO8/Z5RbRzauM90/47NNP6Xck4+IAbSo2NzdZG24Ryya1cEiFD/3B4aQNCd7h2pqPosP+YbWjeHKCqDTZ1hK0E2oHdVnjrELFIpBERGDiOpbSNm/efB2QfHznc07zGS6NsXg7nE/ufsqf/+QH/JPv/UM6SUonbfMH3/ovONg75Jfvf0griZHO0O91kELy3q/fBxkhRYYuqpAsH/HWW2+xtLzEF19+yQ/+4sd88skj0nQJJTKqqmI8zqlmFZ00o9HsoK3EWC/jdQSGXpATC+tlpNZVnlkmmsypDlKEcF4sVVkBCqzGaC/bjiNJrSty+Yz1r0qatxzTJMdOc6bDIeXJGDexRCpFWsv0ZExPOfK9A6bHh0RWIOOYShtU7HsMISVxEqFNjagFTilMbQMjLjDZwt4295vEBWVHnCCEoKzKF2ZaInjye4DNOsidY2d0RNE3tFyE1gVCWWLAakcjUjSVZX82YlwVaCu5sNRnlYqHxyfkekbUalJbi4xiZBRjtQEr0AbiJEWqGFPVnDm3Rafb4srZS2htePT4S/af3CYfPaKZVgwi0MIhmpJplLFXFYjZMe1yj/XmClkW0VpdJcqa7B0c0G30ubi8xPaz+9j8dMHILKYzsoYPd7UI0l6XwcoqrW6XRrvN8ekpe/t7RM5hTO1B2bBnR0qhtSaW0q8Ra6irCmF9H1XXNWXtB4nCOYqqottIX7Dns74JCyQDLMEO6gUgKhBpXLAcwAaFoAWkCHDWHGD04JeKIgQqMLZ9GBzCD3Cd9T2druuwbnztpEJ9a6wNw8B6IXM22gcgWeO9Yp32QWhz8BRYeM668Hqt8aAlCOZvw9dtL0jaCWBtANaE9K/DWjwpyVd1BMjCP581+IiQ5zYdi6puDvgFsFYG9uzCW1ZKnDWB2OXBVkMIB3P+ueYEchNUZHb+xC/Uzb4vCKAiXkIfMa/3/C+Ys0P9jFwiFNS1IYp8Le6s/xob4Yy35vKgpAe469oDgyoE0dZVvagV5yxWodSCZS3V88GZZ1f66tIf2zk46Wv4wnrg2skYG0lfM+HI8xwhFELFnrmMr7vTNCNJUg+2qiiQXKLFcZkDwFL5EDFh/f3dSt97eG/WeThX7fsorX0mzsJewwawEj9wtv58yChCKIeQQQkQ8Clral/TI1HWgdNePSjnQLjxa1iqxTp73jvM62+Hs74vm+dXSKVwwQvYCH9dq8hbEyggxpA5SI0h0obMWRrO27WlxpFri4sky0lCqWsSHKWIA/lNUEtvyeaURDsotOV4koM6wfhbADOtabRaxHGCEtButzlzdsOHarVTosYOR8cn6LpGCW8LEkcRadYgijN8qHyKsGHIYyUiiZmOJhzuPKU1bZM02zRaXW8RVxnKKmF7e0ReaFzUQIgQxozzvaSe+R6wLrFFTlVMMfWMLIlZ31in0cg4ODxg72CPaTFdKJtVpFgZeJC5LEuG4zGj0YSyrvx9RAmMAT2tGRqLrAuODxTtboelpb4fbGVtsiQiSyLiSDItKg5PjqlqT+LKW03+Ux9/v5m0//p/+FetpW4YH7HwqpkXGi6wifxw2zdKVrjFBWsDE0jI+SRv/rPCT4EigUgijJIc5GOeHR4wq7xP4ngyQZvCT6yQRESYMqcoClbXN7DOMhuPqKqK3mAJqRTjyZgkVkjlGOcnlNMROs9xusbogoaKaDY96Gt0RZ77RaO19mmEQqB1zeHBPmmSIJ0jn4zI8ylxknLz5ddRcczde3e9JNwpxpMh1oTArSim11vipVduEWVttrefcvnKVbI04+mTx7RbTYwzdPsrbGye5dH9u+SjIcVk6BODT4YcnI4oreP6Sy8BDgPUKuLd9z/g1+99RlH4aaPVNY6QRKn9hFE7DUpQmxr3AtgxP2dJHNPodZDNlKTVwMYS5WCr2WHFRZiqpCi9B5ZSMZUxzIxBJDEueFT6fd17tGhrPGgQ7CxE2EgtXq6tnW+gvXeLT0asnGNSlRTOUjmLmzPOwvQJIbh64Srf+vrXuf3JB6RZQlFVnB4fYospSRzx2pu3eOW1N9jYXKPTaaER/PL2I/6Pv/qCB+Yq9cqrtFbOcGa9x+j0lGePDhi0Er731llurKakziK0xmnrp8XBF0ob56XZiz8QcNHAFohIk+C9aS3OWLS2zPIZwjnSWGGtJp8VOOeoKoOQMWmjQayEl61JnxA8yS2jWUXUSOi3MpqpZx56CZ8/b8L6Oe08OdSbkYMl5t7OkF/c2eeDB0PGpWV1pc3bty7y0vk1Wpk/X4mwrPba1BoePH7GeDQCW1PUjjvPhkxqx+Zqn34KrdTLGQ73D1hfSnnl/IClRLDcitgY9Li3fcS40ly5eJbdnT2ciGh0B4AkUzGlNozGp2RZiq4t0/GYzc0lVOwTRYVxvPPXf83f/s0vkU5SzKYcHR7S6Xg7BBXFqKRBs9lnejIlzy1rWxeRrQYy8pL2d/7iT7n74x+ze/sjju98jj4+Yv/xE7SwdJaXORkN0bokjSVpGlEWUw72nmJ1hRAa53xzLCNIEsXa2jJxFLP9ZJ88r5jmBWWlqWpDM0vJshZxktFqtcjCZDFrNGh2OiSNjChLg4RIkTVi0iylzEv29w4oqpJIxf77SUykYqSIwEKRz5iVNUolKJV4f8U4YqXZYitLWMeyVhpaWpNZC85SOhNSeiWRUCROkApoqogURSIkCl9g2DimbKS4bpOly+e5cusmF65eYnnQRzjHyf4hk8NjOlnGcDzieDqlCvVHXVeUVc3li+dIIu/DWhsDRgZ/1CAZsgZr9Qser2bh6eTZD8/ZrL6084yHOoS3efmVIglpm0kaoZTAWo3BIAJjpN1u+QZFCR/oFsfEUYwZF9z78DaffPI5+9OcqbXeLF+F9GDkC8V3GK+HghdYgKpzRu3z8AjfEJjgv+u/FzyqlHzOWCAUusIzGr1/6bwfeu4HNm981JxpASGMAmSsaPQ72DQGEYGQPogkSJHA77EOf96dtRBJv6bmHl5i8UyL5gbnGRBlXeKqkmaa0e0tcbi7h0Jx7sx59h89wY2GNBpNWq0mo919IiGIwiTeWLD44y2xJEKg8DY5dv4GrAdpFYpE+SZOW0mjOWBl6SybqxdY6a8yq2ecFCNmrmT/6BknR0cYB41BF5HG5NMp0+GE8STn6OiIg51dnm3vcHB4TG+pT7c/YHSas//kHq6aUhcTL8czOjRHzoMD1i4802utqeraNzhxzMl0ghY+fCdWEc2sRZwk/jyjSNPUq1xM7YHuwGaqdU2lARHRX13nlde+yre/9bt89c2vc+HsZdrpgIOnOe/+bJc7HysO9lYoqz7CZUgqbHzKuHpGTY3A+0ZX0lE4R+kMXWspDnY42Dlg88p1XvrWN9g/OODDd37BlbV1ZnsHZN02+eiEn/7Z9xmcPcf1b3wTl0QcPX2KnBbEkSJGIitDdXjEcG+PtNMhHgzQKkJEKRLJYr6At3SIpUQlCa1WhyRNPJtEa6rZlGePH9Pr9blx82WslXz2yRfURUWcptQYqmKGLWdIV+OcwlQFTpdIGRjzUfycVWUM0gVAjXmdIMKe6teVQDA8OWRvb5uL51dpZAkXL2yRJjF379ylrjVSRkwmE7CW5aU+g34HU5XcvXOHRpoyWFrh4PCY6XTG1tYZrt24xtLyKtM8p5xOePWVK/zjf/KHlJUmr2rKYspsPGQyGSGl5MyZM1y9fIE7H39IVWs++vW71MNDzm9tEbcGjGvJhRsvc/fefT775Ata7T5lWbG/v8fS0hLGGra2NukPOgyWl+l0W7zx2ktsDHrsPNmmLkse3H9Enlc0232OTw453n9CLA1p6pUIaaKIU0m/16HbaZM2YiIlaXdapEnKwf4hzljWVwecO7vO5cvnefmVG6yuL9PrtlhfXWZtbQWlFEUxC4BCxfD4iLu371COZ7z26husrZ9lVmlqI7nzxTOe3Dvl7MYSFy4uk8SKRhLz+NEh9+/d52B/G6OnDE9O2Ds65pXXX2G526HKS975m/d5/OgRSTQjYUZ+csDOo3ukmeTdd3/O3uEOIpYLQMvhvUxxwg8EtA5DKd9jzEERHJgi+KB2M6/ImjPPLFjnRbASB+Ocb1x5md+69TbDyYQf/eJnHE1HSKmoSsMbL73KUrvL3c/vkEQxF85fQiFJ0pTBUp/9nV3efO0tLl08j5Ca0fiUDz++TWUkggjloC6naJ1zMt7lg49/yc/+5ud8+tEX2Fz4PdymTCY1pa29r6LMECIDwgAPEYzDxcK/Mo4T4khhrPbM1CjDiTjsRfhwWRF8MqMYhKLUUBtLzZQ82qF3y7D+9QZlNsTWM06fPmP07IB66iWppqqZDse4okQZw+x0SOSLXYTyAcECn6YeB/WIrWt/vUaJPw+1B9LnTNnnFgdRGH4qZBT8vuYen+HxIlgJIcBpR6krROm41j9HJmN0XWJjwBpk5Fg+2+Ng8oxpPkVoCVVJPR0iag9CVc7gUgVJhK417W6bWAr0rPAy2DhBCMVSr8vvvPUVzvQHGF3w7ofvcvv2++jyAOyYfqLYakMvSylKy7jUFMWMpq04N2jQjhVSprTaHQ6ePmH34Zdc2tpkqZPy0acfMrKCYTnl5PAYtCNtenmtFZKo2SRpZuSzAlSME5K93aeUxQShLabWVEWOMMEaQAQQNCjlcA5nzJx7SRwrIuX3dWktnSwjkeL5/dzZhe+z75afQ58yBPXMbQ9EOHc2AIueWCWCSkQsyFYeeI8DaPYcJLXOBNYgnviDB7CMdVgTwEf7PAfA6MrbxNU15aygKkt0XXngXwTbqFAb6lr/HU9Xz6b172QuV/d+rc8zU3zImAkByTYwXkOwGfidJTAd5RwInDNgQ+0g8cclcC8XFesizEt4vGPuWf/8AHjF6HOf2/CTgVFs7HNW5XyoH8qzxfUhha8JjPWfVe3Dzees2/m1M2fmGq2JQmi5CAAheMJDHHmWZrAcRQlBHKlFyO9cNWzNnGEcmM4QAsA9qF3XNSIMZJw1WKdxTmCNDoozD8w3opgszoiiBCUkSZygonRO0g3qM8/oVHHkwdk0pdFq0cgaZJlXzDWyjEb4OksS4hfuIfPaVoSaRQlHliZkiWfzxoHR6wdCLOwEHRKzYMM6n9sSJ6goJsm8ei/JEuIk9qC6rSFYhBDucyIwOaMoDsOG+Xnz1p3Wmuc4i9VBReY/MRZhgz1DyPaZg8meXesQtSbSmpaUNC24usbpGqe1z6QRfu9QiSJrZTS7LeJ2m6jTppFKkkZKq92m1WrR6vdpdTo0Wk2yRsMrHJxnlPrX6NdoqaEyCmUkQqUkSebv/XGCdQpsjCNGW4XVHqw26PC3wkUNtPbDRV3V6LqiLGaU5YxJXrC/s0s9GyGlIE4bZFmTLM2IgrpCG48HmLpkNj3l9GSf8WSIBDqdFivLywyWl8maKUpBpCTaOtI0pdvpeFJHu02UpCAhSZNwvI0n/QgL1lKWBUUxpZpNmU3HjEZDhuMhs1lOVZcUVUlRzJhOxp5RLyS/+OA3/79M2r/nIO2//le95V7YLJ5LRSH4ekjnQzKEn+gtDLvxPlDPG/VwoQkfRCOkRDVTZCtGdhJUu4GIEyZVyeFoxMHwlFFVkqYxB3sHNOImS4Ml8iL3E5mshYqb7DzdJRWC8ekph3s7nBwe8vFnn/Ljn/wVh48fkTpHOZmQJhHtVpPpdOzlhyEN3bPaPL3dmgpdVdRlQVnMcKZmPDwBIUizJluXrnL15VucnIzodntcv36DbqfjZS4Waie4dvNVVJSxtn6W9TOb7O/vUc5yRsNTBksrNDsD9vd3mE5zts5d8FMnB9N8igmLd//4lFpLrl29RrMVYUWCiJrcf/iERw+2AzBYU1Yzfx6swQkbjN0tVV1inV5IDq0AafHygW6LqJOQ9JqIVFKHBX2x3WVJKMqqxApBqW2QKnoZvgWMNosNzqfRK+qqhkCFl2F9aGu8X48UiCgCJTHSU/anVcWonDEz9cLywG9abl6Xo2TM1976Gr1ui49uv8d4OmLn4BCk4u2vfo3X33qTl15+hc21szQbDXKt+duPHvK//eWXPI5v4dbeZHltjY2ljKePtxmd5lxaW+LNrSbXVxNioyFMHQX+4nTO++E6F8DmsHnqINPz8uMgj7EhjMtq7+VVluiyRNcwm9RIIej2UtqdBknaIEkSHMoXcEimpWU4rNA1tNsZraYkln4Tmk9w8acFJx0iFkgRIYg97T+SFE7w/r1DPno8ormxwT/8nQu8dW6J5WaLRFhwXsYmcSTCsdpv0mwm5NMRjx/e4+HuAU9PS7Is440bZ+glENUVvX6TXq/NnXvPEMZybjnDlTNMHJOrFrfv7rO2scTZM8vcebLLuHAUs5rDYYE2lmIyZDI8JU0azArDs519ut0MXM2/+Z/+Z77/p99H4Lhw/hz9QQ8cPHrwmO2dPdqdAVHaQtfw4M5D+kvrbJy/gWz0gRhpNA8/u83vfvu7dM5scDyZ8nv/+J+yfP48dz69TaPdp9VfZrC0TKpibF1zeLDDwcEjjJkFOYsGNGkc0e93aDQzJtMZp8OC2vpE3TmwaJxhZWWVJE4CEJsSRzFxGnsQIlEhtTKh1WqSNlKE8kBcns/YfrYTfLS835iUEbOqZDrNKbRGpSki8mmkjSjmYq/NlhCcmdWsF5q2dmROoMKQCwHSSmIhaUhBSykSGRFJBVIySxLGacK42YaVNToXLvDS229z8eZNekvLJEmDSHhmoaktkXb0Bj1ay312Dw8ZTabMZfb5ZEKnnXHx3BYqAFtSCmSkglH/3Is3WvjRxaFgSpK5lMl/3Ww2/WQZP5fXei4xj0mzhCxLSQILJ0tS4jRBCUGiIhpZgzRNiZMEqZRnHSuohmPuvPchn3z2JYdVRQ7eaxQPhs69saM4CiE9/j1ESRQGjSwkZHEyZ4I89wfzE36HUNJPgoPX1fwxcv7/kR9W+UCzUFTPC/GgHJHCg7vzbXAe/AMgk4hGfwnVbBElqVcg1BpbVAtmwQJUdmFfTRRpHBFJCfMGwc1h4/BYvPypDsM7oTWyrhgeHuCE5fyFi+w+2eb06TN6gwHdTovhsx0ffihVeB94oNsnmIG1KOW9xF24b89tHIQDqWJUs0175Qz9lXOkSYuIiLIsGRU5M2eohcbGgrTdQSUJMhIc7+xxsruHM5piNiWNJEmkqYopxWTC6fEJdVVTz2ZEznjLltkUazSmLnA6FMB2znTxcjkZe4ZIFORSlTXYYHMSDCuCdYGhtvUCcM+LEusM2tTMdE3S7HL2wqt8/Zu/xxtf/S6D5cssdVeZHFcc78Dedsr+boM7n1eMRk3qCoQTxBicGVK5Qyb1PrN6gpAGpIFIUsmIqYOSisQZ6mcH7N1/wtLmJuubWxwf7DN98oRYWgatLu+98w7XXnmFV775LXIByWDAyrUb7O48ozw9pSEVSkpSU1IfHnH08BGplLQ6LUSrgwshJQiLlN5T2AlQMiKOIpzx9geNLEMXOadHxzx8/Jhmu8Nrr72OMJLbH33GuLRUcduvM12ikQgZYU2J0TOcrYjiBkmW4KTwPRT8fwAAIABJREFUChTr904Trp05oOACO95ZFozzk+MhEkun06A3aPH2197mk08+5vTohFazQ9ZoMSumjCcTer0+jWaTzz79AikVn31xFxklXL56heXlAUmaMp0VVHXJ2uoS3/n2t2j3OnzyyW2yVsYrL1/jwtYme3u75NOct7/6NZaWBhw+e8zp6ZCzG2tMh8e0mw22Ll7lyc4hqJiPP77N/fvbIGIm0zHNVoNXb73MrTdfZzqbYQzEcUan0+JrX3kdU884Ojxl+/FTqlIzmxWMJmOm0xFZEtFKU+Ikot1usTzosb66zMb6OlVZURfew3t//4C7d+9SFgXnz58jSSRGe/+2r7z1Fq+9+jJLgy5rKwNevv4KX/vKN7h85RwiKtG2otAzxscHPLl7l5ODE5ZXNzizseWPT1VjTwreeG2Llc0Wj+485Wc/+5CDo5yXXn0NmTqOhs8YjfZYX9ug3VljNJry+adfcv/uPeryhCsXB3RbXnaej4f81tfe5N6XH7J/uIMODDsXVA0Sz+i2tQfvnXELdp5fWAE4Mo66qJAIskZMrTzoIa0LWIpDlhUXO0v8o9/+Nv2sxfsf/4Zff/4pRnj/u5ZM+ee/+4/4+qtvcO/uXT7+7FN63R5nNjZx2tDrdGg1W+zv7mKqgkG/Sz6b8ot332OW+6FTocdoRrRWIN7U0J8Ch6w3xlxfFejJIScn2oelKEmz0SFNmlgnAYUjQhpFJGMkynsaehoLxnpvYyljmlkHlWRz0jkoiVCSJIpJ4phagq6gtDOG0TOW3rCsfD2haJ4wOT3h6Okz8uNjEgudpEE9K721Ao5WnFGPp1TD3MtmnUEpRZYmwVrHS2mLWUFdFAtvS137OlcqQdZoemAkSVAhUAq8jNg661Pb53skc1XNc1m6E4JSl+iqZrnZZSXr4rSmNhX5bIqVhte+dpO9o6dU05zMRqROkBiLKDTO4P0wcRRVgbOWZtogJqKelaAka/0BV89d4Xe+8g1unL/E00cP+elf/5wvvvwIUx1jZU0cCy6vLLHVECyJkmJWMascTTPjQlex2RSoekakYvobZ5meHrDaTbh+7TL3733BD//2JzQ3l5AtycnJGCciosSDT61el6yZok3N8HTINJ+RtJqMx0PqPEc5QT3N0WWB8Kmlod7xDE1nvIrPBVsY6yxpGpOkMcJYIqDTSL13fKjNEN7mQEi1CEbynDs5LzoWIM3chtBBAAjnOQBezaik9IBKqF88Hmkw2isMTeh7fPfkmZe69sN6rb3VkdUOqw1V6QFan2ng18ICIAzFivcDnYOvYINPbV3XYWAemiHAKzXD34EZq+Ys0HlQlhB+CDQHQecWVYuBfQDuXLA8WPyMr++ElCi5MIAIQxICVvqi4kr+neec97Ae+PSv11sF2MVQ/rk/7XOwdi6RN8ZL8itrFuqgFySVC0uHqiqpyxJna6zWnm2o7QvHlueAtPLHwjqvgk1iL2tPk5Q08zYDaaNJmqaL9+xf+zz3QQTg3OCzOzwzEqmIEx8umwZgOFYRsfJWBiqKkCrYeCB9/kCSEEUxzWaLLEtJk5Rms0m73aLZbNLIPJCnlLc0mAP/bg4iOwtBkS1DPz63zmHeoy9qfYk1NtQW1gPV4bxG8fPXkyTxIuwsknLBMlPKs2R9TxN5kDac6/mASsrF1eWHGCEQD7zdizXWs5Gl8BZbznpGstZQl8iihKJA1BWxNTSsxdUGtCYyjhiHtNoHZUYRKs3IOh0a/R5Zr0uz1SFtdmi2OwyWlukNlum0O3Q7HZqtFlmWBWsIF7CLBG29zcFobHBa0l85y/rGOQb9FXpdHySqoggrYDrLmUyGzGZT8nxGPitZWt3i3KUbxGmTsqwoioJZUfo9oyzJ8ynT8SlGl0TS91ZJEpOmCVnWIk0yjPZ+x6acUhdjZrMJw9NTppOxx/eyjKXBEkvLy6wOlui0O6hIkSbJ4hr1dm8xSRp685AnEyeRJ1cKQZrEtDsd0qRBpFIQURgiefsgrKOuKmaznPFoyMnJMfefPvvP0+5gfuPx//DMGREJhAkm/i/S44XzoVLWT68i5S9667zBdpqmRI2M2hlELHGRwwjjk8SFwiWSyjp2yyHH5ZhhOWMlyrjWXeL13/omd7+4zXQ6Zn3zDO3eCqPhCcM97xeWJhFKSH7z6/eYTEesJS8T4+UC49GEdrdFd3mFKIk43N1lmk9pCS/r13URZAGKNE3orvQ5OjqimE1ZXh6gXUSSNTDOsb65ydrqKnUx4cn2pxwf7IJQnDl/kTe+8jW++OxLpkWNSGJWVtc4OTpA14avvfQqs8qgH92jHI3IpzmDlVUOqqesra3w6O4xcZwSpRnj8ZSTgyNanRSXJKhGk6whsMyoaz/pMlY/Z2xJsdgodFmjdfVcLussiYzIGhmu00D1EozCg7pS4oyhkhGqs0S/1+d4d59cDymtpqhKz4rVOvjWSLTziZ1lVfrJXpBlWOElXBofmuGEl0DU1jDNc9/aS0kdQpmA/8/EVyJJ0wbnz5/n8HCPq5cv0mo1+fWHtzmzeY6XXr3F2voK/UGfVhZRGM3P3n3En7y7w0H7Fnb1Bhsb67Ri2L73gKouefX6Rb5+fpmV2OCovDeKxyCw+OmhZ1Obv3McQfii07mFrNg57wOjpCAJ3j0CQdZoE0eCZlOwvJrRaAomU41SBmksqUooSsPxyZTaKRqtBmmicKYGG5La/Zn0zy/8dNdJh5NQ1JIHz05pdxpcWmvSkI7Xb53nlF2eHc2YHJakGxnOaIzTRKiQBOs3qYaouXG2x1JccT9/ytrZMxxUGfe2j3i0vcvGjTMIDRmGq5ttanOWj+49JkkTuo2UR8dDHuwVTEvDrKi5vrrE1fOX+OzeE45NhcTQkDMGcUxVWrZ39yl0QTu2dHqWi2sp2w/3sYXj3JnzDJYGSCXopQ2SrMVoVpJkTfrLq7jSkqUNEpXhbIIQWbjFVMgkobG2weraMpuVpXH+MqPPbjOdGZZXz7K6dZGynlGYQ3Z3n/Ls6ROc1YHB6Au8JI7p9wdorb0nazFjeaVPs9tkNB6Dg3arQ3fQJ0nShZTFswvnk8AKY3zgjSCmrCtmpfVebklKnKWhBvU+wtJBqWums9wXlnGKkxJhNQ0ZcaHZ4eysYFBVtIwjdsGPKnAVnLUkCGoFOEPkvCSykIoiiambTcZxjM5S1rfOceHyJVaWVlCxwtgaZ2rPcBCKKFGsrq3i0gZWWW5urXGa5xz87B1qz2ElLys+/OhTrpw7R6/X8jJ254I3lL9mVfAme562614oVv27n3svlWVJWZWYkCzsrKPdbpM1UiIlfahgaBQAyBqUswKpJGmWIaREG9/A2OGYex98zO3P77JX10wEGAFOeomoZ01YpBJhDGRRsQrMkIhaa7TxthoOL/ORUiKFQgSZnpfMqUVxuPCmitRiKxRhMuycv4/KEJQpwxR+zsIQ7oXiN3zPGD9Us1XtC44koTIagyNqNylPR9iiQlpCY/JCISp8EIdPd7bPGbeLfdoPUn3InKDWmqOTE+rRkHKak2QxRTFmdWOVw0bGHN4VwsvgFYFlgy/y555klQUngrzO+RDCAOPiRIxNUlS7R9ReoiTFlIbp6IBmmtIaDIhMgTVjsiSjMobj412yRsZy1qQcDSmnJzQySMWE8cExMuvR7K0zzXP2rUXIiFYkSBsNqlabaT1DSM/6qnQRBoigkoxGs0Wkm0RFDlWNcNDMGpR1TlVWnt2lPGvHs4OdD8qJfNFvEDR7a5xbO8PN196i1VllOjVMJy20yZgNDbJa4ouPdinHhrpKmE3amEKTqoLITiiqnLRX88rbb3PVrfGjn/57ynrsJd5S4VSMixV7ZYWwJUpMEU/u8NM//jd884/+iK/+7ne5/7e/omVq7nz2KVc2N7l66TKHX3zJnffe5/Rwh9/5oz/k8j/7r3jwx/+W6nDoFRuNJstlhTw55PiHPyA6PiT97e8i1jbJpcRKia69CkRF3vbAuWD54VMyKWczpIR2u0VtakpT8/V/8Ns8evyQn/3kHWIDrU6XRjujKmfUjLFqhpAFVk+pZ8cI0QfVJE5buMig68o3/MIznhxz/0DfpC6GplLyy19+Qj6d4JSgPdig2Whz/+gxW2cu0er32TuY8Wz3gI31DaQrsSJimhcY4zh37jytVoPT02N6WYZQkqKsESrjV79+n/FozKxwOFLu33/KjVdu0F1d5+NPv+TjDz+g2W57WXaes7W2TKO/wpP9p4z057i0zej0kEG3gXOWw6Njut0G585vEScRaxtr1M4xOp3QbndopCknR8ckkSSOMpRKaLdarK4MeHZwRKfZIEtSsjgOgLVnb1XFjN3xmP2DI2Z56Qeg1Yw0jVhfW6OZpThrOT0+ZTyekk8mnN3a5I1br3Cwusb/8j/+Md3uJlcuX+al65d48nSPH/78p3zwq99wONrmz//j/8Vkcsr3fu/3yQZ9Vi4scSD2+Olf/4KrTy/x4Mk+6aDBmXNXOD09ZXJ0SGRrIjOjHu6iR4fsT6c8fXSP0+MDuk1oRxucHM1YP3udtXM3ePu3vsLPfv59Pvr8fWwUowX47BzP9NO1DmClWNRdcwmxQCzkopSW4ukJCEO80cVJgat9qJ8xmqZQfPXl1zizssrO7ja/+fDXlGVO1GphjGG53+P80horvS6//73f5d/96f/DX/zwh6z1lrhx6QrGaF65fo2TvV1+89673Lh2BSFitLZUVYGOcxqrhsFqRnslJhs0YHjAuf4Rf/Cds9zcWOX+w5r/9d/u8WBfkaRn6HV6OOul6nVtEKRI4YGBrJEyGo08CBdUJ0Ioz/SSEoFBOo11MdgI66LFsCxCYOohI/uI1TdjBm/EzDonFOWQ/OQYO5t5WbmM0WWFmc1QUtFMU6YnI2aHQ1InMXhv7lR5cFZKSVV5H0vPqPO1rtY1cx23Mb4PUEkS9kDpexDw+7PWlGXpQS3lQXlrg42c8fL6+f43FSUfHn7OZtyjZ5rUVmNcwXg05Sc/+CEVJe20CXWOcoqmSsm1Qhjj10VVkyiwWZu6clTCsL5xjrOb61y/cIFzZy7RTtsc7T3hFx98yMNnj4iY0GtAL2rRa0asdlJ6oqRhDWoQk7qaSkqWujGDzGDQlLokso5Bu825zTZxZvjVwy/ZrUrWhKEdCU+wyBokjQaNTodZOaPMy2CT4+3ykk4LlPJs0srQkIo4Thasu1gGwNt6xZzDLXorbR2lNjRCLW+l9wxGRYhQGyL8MMwzM2QglojndVkY8L4IJspIvqBgdGGg7Oseay1OWCpdBlAMhFDh5h36JVfjpAEXrPSk8sQ9Y9C1Cb2pW4Ck2OdMWBkASKM9Q9tnnNgF48/O16B4XlvKAKTO603wTNHnfa4Lx47Fcy96OReA0UVVTlBPBhvGOdg6f+xz9COA1HOmrH+COehKOM7WzgOzHRbjTWqdQwkwLqCmFn8McAj1wnMI7+lpnAsgd6izRbCsEHM2qPDg+KI/9K87SRpIlWAg2D+B0b5HcdZQVYVXZc7fkbU4aUEKb3MSx74WNp55WdcVdeUZu1prVKR8UFSwEjDWW17MvfoX2QzWonWFwNtjSSW96jaExCVJQhwl3vZtUVf78z23Y4hj5f1NAxBrXUlhK4KZKbXVWDsnCUrPPl8cRocMx8rWfuAkVUyzkdJoNpEy8jW+ECHfwbOLsY5KJZg0JqsiZrOMspyhq/J5nS1k4F/MiYqhT18sFh/cLawH2qUAlcQ4bYmTzPvU1l5BKI3xKt6qQOcFhdWMJGTKM4hjHJGEVAgS6UH2UaQopcAKH7YVRZknOcYe6O622jTaXeJIkWXp871ECO+E4qS3WMP5e2itkWmTa7feptUbUORTiumE0eiUk6MDpkVOnk/YffIlJ0f7KBXRbHZZX9vi/PkrOBkjiKitYziaBNKjw1aVt4mMVTiHADaw4xVCpaikiYwmHi90cya4Rdeak2FBWRSMJ1M63S7tLGNjfZPB8jKz2YyimFHOCrTxlhs2WFJEkUK4NDCmBbGStNotuv0uWdIiTlLfWwqHtjV1VTM+GXJ4coy1lrLIKWcz/lMff/9BWvn8hj+fBBGYSEoIVNg0rHWe3s3zG6pQngUYR8H8WUlc0xck88mCCFI3v3P4Zts5KB0clAX5rOZnn98lOXuVixuX2f7wXbKdQ75+/hrr586gdU4+zXFJTJZEDFod3rh5jY2lDq4uUI0GZTlFzQStTocsTSnygoPdZwyHQ5LYT3iM1gjpvUCGJxP2d56xuraKLipUGlFOhpzsbVNXNceHx0zGJ0zzIYN+l6WlVQZnzjLJc4qqZjgc8ZsPHoMtufXaq2w/fcaz/UPOnrvA5tmL7Dx5zOnwlGa7w8nhIcLk1JXG2gaFyVCpYDyaEcuMQhuGpwc4SrTOmRUeMIqiIGGQEisclam8Ab/xMoi5dEFJQdzJiAZNRL+JTh1zp56qqmmkGTaOyVaX6ffa5FVJfXxCZQxjnVOaCiMcURKjnSHOEi9fMSFUSXqwow4AbSVgZjVaO6paY3G+oQ87qAsDKxE2XicEws7TRC3tdpdur83H779HMRuxvNTl+pWLvPLq62xsrtDrNWn0Ymoj+Y/vfMb/+c6I0/43cWuXWd/aRNUFjx5tk0TwzVfP8/JWl15SIKzF1BKNB6ucdT7Zkjl8JxYyFBm28zmYa5wJQ03PxPLMSIUIXqRSCKJY0OomICzOKt+YdfzEbTg27O4dIWXMcrdDpATOFdS2AhejpFgkUHpZh5cNOSKwkuFkwntfPsElbdQb5zmzlHGuC997bZMfv/uUn//mIfFXtri11aEuHI8OxpT5lItnN0LguyEWhpVWTNHPWG1W9FJIN1KePPiCR2rKlfNXcXVN7EpeOd+nkvD+J0990IVISBsd3njpPBeXOkRVwfmlNu3sOrU1YGsil5OSE1ORTyYcnR4h6pK9E0mVz0g6F+BwQhQ1AEm328cRsbTWYKmsiJKUOG0Rx5J2swNEVBpiJxGRJEszbt58GaklnbTF26+/TX46gULz7e/8l2xdvEJlak52nvDBBz/n8GAbZ0s/7xcRVloSFdPv9pjkebA2qNHGkjUSGq2MVtMjfpcuXGawcgZTa3Z3nqHLEpMaZARVZTBmwnQy8dPoKPFFgIoRAqpSB8l7KE6FYDKbUdcWoWRgQPqgiBg408zYco7lcU5La6yAMmz+c0mw96gySBw1UAgBzTZ5s8E4jhmriOb6KtevX2d1pU8cSTA1tqp9xorAr3kpiWXE9pNH7D95jNY1Wxe2eOPKZba3d/jw/kO08AXHs4Nj3nv/I777nW/6AEBhFw3bix5ecSiU1Aug5Yv2Ac45qroiiiIG/QFVWXNycoqua7J+l06riSAEFOC3ASV9I1/WlTfal5JURUxPJ3zx60+4/dk9duqaCTwPG1SKRKkFY6c2JoSUKSxQlQWxSxZNjfdGhCj2TNq6LEnTZCFRYw56Bias9+Kz/uuFjCoMyEIJHCsfjriQ7OKL2SiKfZrzXK6LZwhIB045ZmVOVXtWhGpkpP0u+f5R8NwCFakA9LrAGPXJs8yDcdwLe/P8fhYaHCNgWmt6WYtOu4ue5hzv76KSiKzTJM1S7w2qNUJ4KxcZQAN/DkpAYIWgqi1NIYhlhJD/L3Nv9mPZdZ15/vZwpjvEjSkjM3LOVA4cxUkSRYmmJMvyVHJVt8t2lw3UQwP93i/9r1QD/VTdKLjRBuwql8twqSzJsAaLlGgNHJJMkUzmHBEZ453PsKd+2OdGpoyqdweQAJkRkfdG3Hv2Wetb3/p9Du8CToKTGp8UuCBRxoPy1KYilZLVE2uIJGU+L8ELUi/Z3dtnMpvTFAnXrj9FQ8Xt7bvM9+Y83LqLEYJTpy/hp3MaqRFmhkwyhk1Fp0jp9vuU0yOG0zEpYKoSKSDr9iBkyLyg0EvUR9CYCU1dUwfHvKyRWrX3HgkuIKxHa0UVHHjF0toml06f4fzFp8izFYrOgPGkZH5UMXMVjVF0k3WasWB3q2K0d0iqQIsELQJ1M6YUY85eOcVXvvkGT332EpP9T7lz52Pev/VDEJIkeHTq8UowSbPIrXQNl/yY9OEt/u5P/z0v/843eeWLb3Drww8Jpye8+Hu/x6c3f8nP/svfsJGnbK4t89b/9//ylT/+X1h/6mn2v/t3rAdH2umSFD1WqPCjQw5/+H2a0ZiV118nPXuOsr/KXGc0Ljrsjgu6xR8R6C0N8B7WNk4QlGR0NGJprcc3f/9fce/WFvfubzGzBVXeIekOyNN18nSAHT2inOzHRm88JssFOi9ogoUFi1bINlwjCkQE114PsXl3TuA81EawceoK+0eWxmi0SvjsCy8wbzyjyZC5ztBJxsb6Cc6cO8f+zhbFaMiZ06fo93scHuyytrpKmubcujWlqmvqqmY2rSAoth/ucjSaoIsuG5vnObW5ybVr12iCQuuMlfVDPr35Hl6mnDh7iaLbZfP8JZIsYTx8xKBfcH/7iMufeYp/+2//mK3th9z+9Dbd3oDl1WX6/S7eWB7cf8iJtWWq2tLtLjEYLNMYz9ajvRhKWqSs9JdiAyo848mY4UFDbUwMOwlxoJPnOWurA9bWVqjrGtMEvDdoJZlP5nx042M++eg2v/zwl/zw+/9Av7/OhzdPsL6xwpVr1/ifv/l7nNk8wQ9+8Bbb93f49rf+nMPD27zxtd/i+rMvcOLMOh+9f4M7d/e49Nlnef2NZ/j0zi5v//yHXN7sUKuAl4K1jiQJh5hywvrJZWblEXsHO/zpf/gzqkrxv/3v/wfPvfJZDg93KX10s6eJRCcpxjq8V7hpGTmigfa8FMdDLxd8K57EwTgBfO2pdqYUMiFd7WAFYB3KOJ57+mmeu/IMLgSOZiMeHe6hExn5n9bR6RQkSYJ3jmsXL/N73/ht/uov/4r//Nf/hT/+gz/k7OnTpMLzuZee452fv8P9O3e5v7PLbG5AOU5e7rN6PcMXEzAl5c4jLvgp//qLqzxzYUShH7Lx8hpCdPi//sMDdqY507EgEO8rnaxL8ElMZHcNjVkMOROEUO1WWooQElPPIx7MtynYIcUTsxKk9khtEWuPuPhMRv6SoOmMqOdj5vv7uMkY5TwyCOajGU09hdKh0xQlktiYKxkDfKSgo2I4WSCQ5WkUqqTAVDUBgVaaIOOasLcW0zTUVRXFMBsZ8mmSYCJ8GkFkROp2a8RDRCC1G4uBWD7IoHDS8bDaZ3t+SJ5mBG+Z10PGkyF+v8ImoLop0jqyAGm3R2YNumzICHSDZ2ItcxeQy0u8+NqvceX8JcrhIZ989AHv//Qd7nx8C2NKRK4JUtHMHKiUk0WfzQEs+SlLRUNHQZHU2NmEkfUsF5pEOvCWxJfs3f6AjbPnWOrn3Nm6x6SZojpdpkfR5ZaJnDRPSYsMh+PgYB9EoN/toELAmQbvPIlKSJQmRaF8IO90yFsBR7S9tXORreaEYVY3hFZwDUJirEeHEPNTrMHrlokfIptSSUkQAteuqUuhj80vx4iDxfA/BBQtZqYVGa21pK1AGwcHC0RVINGtQAvINrB0gQIKQSJka3IRccRr2ms7Dn5VdK95366lt4PtII4dtKFFGBCeQE4RUXSLoffCtX1s7FkIpyxqrfiAov3ck7WobO85C6Et1tZRDI11azvsbt2kTwQXtBs28lfE4fh8/HGY6/HzEcdlXxu6F0VI3To+VctgDUSsRQgC6wUOR9M4bFvbPf4dBFQiUVqjpCTvFKQ6IfhYs3in0GmPJO3GwUsIMcDLWYytqKqSGKxlmU2nTCYTnLEIFVnxxlqMCxGT0PaxEOvNiIHiGAMRAlgbmfyhrYsXGw9R3I8oAt8aQoSMgCWpEpASlWi0fmxsWgjrTV23jNlYZ4sQt3CljHizRTDcYpgVWlMVBIz0bQm8cDxHNUlJSao1aZqT5sXx2r2UycLHQPDRpkUI2KzBNRl1k1B0OtRVSVXOMHWF99H5+dh8IvAepHDHaI5FP6STFIR5/P6Q0ZABraBrDbKp0XUF5RRzGLnW80Qz1o6VTkGRJGQyfn0mA0HAPO/iOwWjPMOJiPMqOj2yTpelbpc8TcnyyPjVqt16FNH0YgMtdqRkOq2ZzxqsbVBZn+7qCfLlkxTrcbtwrZqxMRkyHo8ZHRxQz6so2k7H5Fmffm8NpQpkmqKShK7O6CwN4nDDOw52d6nKKaHdSnucXyLwQWBdwMYGD2cX4XYLDCEoBOVsxnZt2Ts4YNDts7KywvLKCqurPWbTCRNGESMjooBeVWUMqQshOneTgk63YLCyStGJfN00z9vQzRYtZB393oCkKBBSMTqSePO4f/qnH/+sRdrjA729WbjQroK2q+GLgKWw4Hi2QmtUhiTpUgehIjTfOo8DhI7i2CIxMLRqmBAqBuG06ct4DwqMl9yZzPiLH73DqZUdNouUzrBha++Qo8mMmQtsnD1Pmmc0k5Ivv/pFEmUoy0NGR49gkuJcYG/nIZvnz7KxcZbzFy4jQ2A8OsI7h85y5k1D4yqquiRLEoQQzGZzlJqQG4cMjoOd+3ghGSyvUc4nTMaHqN6AvEjZfbTFBx/dYjBY47lnnuXu3U+ZjSbk3QEhOWQ0nbI8m+FFwomTm+zt7XP/57+gPNylqUsm44b9keXh0JBI2D2a4F2cRlljSZOCpo5rEbEEkm2yasB6S93U2KZGyFZAiPcWkiJFr3WRq118IrE+FlVSRLi6wyExGDND6A5ZJ41uaCmwKtAIixcCpeNqpG9fX5locC1nGNB5SlmXzINh1uIMwuICXTCAWlyACMTVZREwrp26tiD18+fOIQjsHxzicZw53+Xlz73EqVOnWR0MWOpkTAP8x2+/z1+8PWF//VXU2gXOnVunmk2492CX9aWULzx9iktrOUuiQZjY7DhTxYJIJDg0nijgRNJu61g7NrWG4+loazqOE18kdVW6fqpoAAAgAElEQVSiiwJJIE9T0lyTZwnOCqYTRzCBLJeoJGIiOrlg89Qy1msaY7Emuma0ajmTQR4XNVLG9RQfLIoUGSSn1ns89cxFvv/eLt+7sc1vvHCG0/2E04XgjRdO8bc/vc93fnaX6fwse4c1d7f36GcNOss5v5IjtcQHQZIXXH7qacrRFvPd+1wabFBUgre/+23Cl+acOH+BTCfkHp5a65I8fYKgcwadLp1E0k0kiW9wrgSpGHRSjNMYG5AUSC8ITtFdStEqR4QS4UoaUXDhuTco65pZZShnJVlWoHKFDNAplpjVjumkppAp41HJhSvXkFl0GHbSjGY658bbb/GLu4+iE1sIEhmQQfDaN36L0eSQn/74R9z/6Gfsje6iszSu9wiFkinWN1hnOBweMitLEAoXYrGjZCBIT56mTIZTDve2WFs7TfAxPC4WEHHtRQgwxmLqisloQpqmLC0to5KMNEvbYlKipMZ6mM3nIOMN3BGnfwqJFrBS5Gx0cvplRdryjQgCRYjXpVQEEUcGxjuclEyTlHJ1Bd8fMBcCkaec2TjJic0zFFlGPZrSYDFZSl500EIjZdZeh57RwShyCV/5PPV8zr2PPmL/3jbXTm2yezBkazhESo2TCb/85DYXzp/jmeefJoiIhIFWNBSxGFJKHxewi+JyIUZWVUzvlVKS5wXzyYzZdEo1L/no5i+5eu0Kzz//LCG0621yMekWJFkW0St1g05zmmnJu2+9zU/fu8F+Y5jEzRe0UHjBYqwSzzalaDFkx8VgkiSxoSG0zolYFPrgcY1tC/knwgGEOHYKPynIIiLKZ5EUK0J0Nhyv/sPjYr399xrTOubb80WKlsmeKJJOEpl8jUNKTZrndE5qQlkx3x8eM1dDOxg9dr78k2ZjsT/nj8MygOAQUtEEOJiXbKQdlPH4sqa/2udoMuLUqTMxUdVHZ1pM300AgVYS6dsbSRAYZ6mNQ7crsl46nAKXpox8oGMsRWpJqOn343rTFE+YT1lZXkWXCcbWdESK6ylI4d7OfXZH+xhbo9HkDoS3mPE+s8N9RJph54egc1ZPbjDoLbN/eEhWFKyurVONxlia6Kyz4JVHdXqcu3KZ6bvvMKvmGBPZ7kIIsjTDmxhW1e12mJdgpaDXX2XjzEVWNi/QX15Di4JyZpnuOfa3LOMj6HS6KL3CrXv7HO0c4k2gozMEltoMaULJ6cvrvPjl13jp1WdYXu0RXEldVzHUrYo1jcPhw4w8lRSqQ+k1O1h8qHDCsXFo+Nmf/znTwwOef+MrnHn1FVy+xO7ONiuy4dzmBqrT4eGnt6nrQFheZ+oMg7KKK6tJn6KXMxABNZ6w+/Zb7A4fsf7VrzF4/vOofIUyh8bGzZLHWm1cmdRJxtqJEyDA2oZOkaBC4Mz5C/yrP/p9/u9/938ynkwxdkBtA2mR0SvO0u2epmsmNOURzeSAenpA8HOCSAlCRbeJ0qggCEG0A32FkAEhn2i6tWU4m+Fljsr6dLp9dJJw/+F9Tpw8S13Hc2hre4vl5YKnrl/nrb1tlBKsLPdJkgx8oJtn7B8c4Z3l4GCMFEkMpcSRJoFEOB58+jHV/CRLvS4HBwd85tmXOLF5lhs/fRMhJY33dNMuV5/5LJtnzjIa7lPNZmyeWGU8LllbXebWJ7+M4rtMyLMOKhGUswkS2N+t2TxxiiTLuXDpMnVtkElO8vHtxTEDwZOk+hgZFoQC0TIXhScER6focPbMZmTw147aWspyTJpqsIKd7V1G4xm7BwdMqhrSKXY/8Gh/h4OjPVZWljh7Yp3f/Nob/PVf/x1HhyN+9OM3uXvnIV9+7XVeeO0N+mt9dnYPOX/lFLoxHHz8Eac6FX0lWEoccwXBzamqfZIkY2XzElanjB51mU8mIOH+7gHzt94jlTVnL1yiOxgwN5Gj6KUA6zC25fUdoxFb55X3SN8yOWX8PCKesWIWqB+MSH0g9DXKe66du8yXX/wC3bRgPCt57+aHlE0NqoO0ARUkd27f53tvvslXv/QqidS8eO0ZZm+M+Ku/+Rv+89/8F/7kD/8NvTyhyBI+c/E83/v+3/HOp/dpakNnLeHy0ydp1ubMK4XYq7kQKv7N66d4+syYTJaEUCKo+fzTZ7j5guQvv/+I8RCCKhAqEKxlqXcSYx2z2ZT5bEqRd6N7VmkEcXXTBxs3dLxDhBgyKbXHBoszltpUmPSQ019KSJ+CUTqhqYbU+0eY3SNsOQMnUY1A1hDmFmECzhsqPyfTCUlfooKMtbd3ONEGIRG3I5VWOBkDLQW0Ico2hpiJGKhs2vtmoiJmKYpcC0dhwGERqNYhJ6OwYmOOhvMeXNyyrINl6mqSPGV/Z5ej4RZNU7abGjFEqU+KV4JeMaDrLP3EUfnA0FaoZsrR8JBu3uHCYMD00Q7v/uJnfHLnQybTCfV4QjdLyESXjdUTXHrlZXI3Z8CIrn+EGB7QGEt/SZJrWFoS2GDpdzRexDCw4PYRruL0+kW27t/jxjs3WBMNui7Z2h4THJQNpIWI9eW0JC9ynDVoAULJFodnUSLioZp5jTWGpoS5nLcOwphbkGjF+uoqhMDd+w+prSW0ol6apiRKQF1Gc0mLpnJP1BnRLataE04U16y1aCnjqrUQ6HagHfno4nGNBMeioveuXVWHxbx54YLVQrR4QH+8zSlkNBIomWCDiQ74VkCuaxMHc97jXHSsKhUDVYNrzUStUP14i7ENIZMsnkHrwJXHWxfA4wFAfILtYRoFoug0bb99YRzjcU0oWyOAd23vt/jk4mb4hMngydo2HH96gTf41Q2yEPgV8e5JB6tQj4vDaN6V8fUNEiEiV9i1QmA0B3mca4cb3pMJjQvROZjmXTqdFZTu40WCC2BDoDIGbEOaFoikIHiLFp406+GCYD4dx00yEYV8IcFYGwcE3uGciW5oazHGRDHXmBjEJWIwrQoBYyxOu2NDg26RAsFbvLMIkbRoNI3UGtnycIUUESGgdBtOtwgWfzw0ioSLWC/rFjcWg/Ki4EirJyxec9G+pxOdkiQxABoUnU6PJMtBR26uVAkL/nK8ROJr75OapvQkmcSYgiRJkVJilKKu6zZEzLecXn9ca8vFP7NwdAGyNa2pLMPLuEEUvELaViCuSuRshp2MkJMpQmh8ntFkGpcEZMseF1KSFikbOsXphFkR/4Q0o+gN6A76JGmBg5ijUJUIAqnS9Po9QvLYVWzqklk5Zf/AM557pnVNP1+Kg1MSpExRKkGqnKXOMksbgnPnGw63H/Lg7k0m4wO01qyd2CRNewQFIonaCTJiIWTbh0QTvIyoHqlgMWxd6IP4lpMff/++zf4IwaNlEgcIITCbz3GNjZk/tYnvAwLeQZqmpN5SViVVXVHOZ8gAg+UB3W6X9Y0TrK2tkiZJ5KW3XG3ZGmqskqSFpL+8grEOhWQ2nvA/+vhnLdICqDY5EinROj7dRUqpbWxM2BQKrSTGGmQiyfpdRKIgj1/vvEfpAM4RiPZ+WjfLIjFREB1/JgS8jEB6ZIbUObq/TpOf4960y/bRmE/3dnjv9jbKHXKiX3Dq1FlWlpeR/WVWVwbc/vgmo9EhrpmhpWVSzhjNJtRVQwgJ66vLdLKMfG2NoDxVNWM2i5Oms+fOglToLKOqGxgPYckhlcfVNU5ollfWME3NdH+L+XTKzv4ew/GUsnTU8xL7zDM8/eLnMHVD1l/h8tWUbrcHPqYdfnDjPT784F1m4zFpyBhNKw5nDQcTiwmaNNR4qemubtBNEux0TFb0cMGA1HFiqVVc0/S2dWS6OMVuBUcpJFmvg17tIZc7WB0ARypk5MEK6KY5/UShQmBeVdTDOaY0UTOUYGuB8bHRtz6uoddNiVISnSXU84rgAt1eQa1hXjfMgsECop3kECIKw1mLlgrbvt4xCXUh8kf+TJoozp5c42BvF6k0V69f5fNf+iwbqyv0Ox2WlruEIPjLv3qbv36/YnLyy+Trlzh3dp3xeMj2g0ecX1vlC9fXubCWkhBF7YCPTNIQUyqDdIvuqEXfLxZhwq/ciL33WOfjdE4JFvDyosjxzlHkabT2y8jinVeBREKSSFzpyDNItUDngiTNGI89+/MaZ3wU30SI4rQTeBUnhdbHAIYkXRx4Fi0CL19epjGCN9/b4vsf7vA7L59loARnVzK+9uJZ/uvP7vLtnx2SpIJnrqxxfbNPlxrjDYnN0Do+/9LUIDRnT58GL2i6GZ1Bnw/vPGQaNFfOnyNJJZkMPH1mLU5/Q1yhEd4h8NTGIhUxMVOEdu0prsIEJ0lCQ5IlOBewAURIWD37FK90NYXbhcTRWEMhYniItY5upw/GMq8b0ryLQ6KTPMLTg2R2NMQ7wZd++3dJej1CktAJhhs/+zGj4ZBHOx9z44M3CW7CyuoStRWMJiN6RRILkiDjoEgElNQgFCrESXlcsVQkUpJmCfOmJO92qBODP0xwNlDOJqRaQhIHFUIlkQ0dPKP5lCwz1DZBCciKgoBkXk5xQKazuKokQQqNCopEQyYDhY+haraF+2fE92uQ0Unrg8dgMArmnR7V6irl8oDKBbr9LkurA1aWV5HAbDxBYdHKowk0QlI62H20z7kLF0m0YPv2XerRAcn1i6xevMDyyhpbD+/Q4HmhucD05xOmNhbJ06rmJ7/4BecunWV9dYBt4vUipYxntowJw1LK1snpjwtWa2OhmmVFXPsbDTGmJkkSVlfXcT7Q6/fxIl771rs26CCFdoChZIGpDLP9Ib/8+Tv87N0bHDSG+bHTPSYEx8pbYdsgiTwvUEnCvJw/FjSJhXLkVi2c8wtXaryGI1s2nl3HQ8i2oF8U4OqfcMiA1k3QNgcyvs9iQvdiWh+/L65ySZJURV5nIiEovAt4JdpUYk+tBJ31VcrDCb4tnrWOfCvfhriFIFqzrDj+Gb0AEeJzde26sG75XBNrUdScCDA5GLK8epKqqUnThHpeQqLRIiboSsBZT+3i+zUOD+Jqq1sIzVJhpMckBS7V1DKKjIfVhKRYZmMwoJqV2NmUXqdL3u9CmuLKGTZAh5pHowOOJlOsb8h0Rp7luMSjvaNuSmamRtsEZ0pQKdvVhE7RZToacbD7gIun1ukvLTE9OKKZlVgCXnom0xGHh0O8VohuXM1KgyAPHtdAYxyogBIpxfIKaX+V1dOXOHP+Gv3+OmUZuPfJNrsPh1QlaFGwVizxyY17eHnAbO5Y6fcopxW1meDkmHNPn+Cl117jxVdfoLfapWnmjMcH1KMhu1tbdLt98qyDsXOCkDQO8ApVtEiTRLOnNZnO6IgcXZbc+Ltvc7h/yBt/9CeInmXrzqecP7XBiTMn+Yd//CnXXvsyJ5++ys0bH+JMhQ0NdpbEkKF+h2IpsmPDcMzoo084rErWEHSffRlfDAg6wzpLcLGgX/SoIfh4b/bELQJjkbkAb3juxc/y8msv8fff+a8IM8P7LpXtY8oOSaLJuqt0Nzfors9pjh5gyiFapegkxbYOLSEETZPQNDHkNYpGoW0Qo3t8Z3/Mn/7Zn/G5l1/gt7/2ZQr5FHc+fo/tB7dRuuD6U8/w6a1PePMf3uYbX3mNF194Ge8CpzZPc3B4iBSae3cftC6+KCrknYThaMTFC+c5sbHGwf4+qRZIWzPe2+Wjd29w88MPOXvpEsEYsryLTnKOhmOM8ZRVQ1AJZ89foqk81lv6/RxjPf3lJbq9AU3d4EtDr7vE7v4BUvUxIbrTu90eQmt0lpOmOa52+Mwzrw04ETluKoovSZqhvUeaQEgEZzZPcO7UJsY6xrMpjWkIzpIVHe5t7fHeezdZW1lnZW2DMxfnPNrbwzcNnSLDmMD2zh5WCBItKTIYCjDO8mD7Hj/40d9TOcvFa9fpr66zd/8eHbOOmO1iZgfc2Bqy1Ovxuc9/Dqs0N+885GBcUVqFcZIvffUb/E9/8Pu8/fZN8rTLZLhPObrPg4d3Kbp95oeHx65ZbwOhCRFZQEy5b7XYtuGWrcghWOwVB+LgOpQO/3BE92SfZ166zpde/gJLWRdrHTv7e9x6eJ/SO4RtsMGSy4xcaP7hrTfJleIrX/gimda8+vLn2T044B/ffovvfvc7/Oavf43EV6ws9zi9uc6Pfvoz+oMML2YYOydPc/YfTdmYjPjDr53mpYslwU0Q1FGYrBVSHvDqK+t8+nDOjz8Y42VBIFDORziXkKUdhGg3O9ozP/7Itg1YjsKPAJSOdd/yap/53DCsJ0zFHoOnErgSmCUTXDmjfHRIMxzTVCXWeBIrUE1AeQFpgteRr6ikxDgLiUcBKsSQT6Ekqr1vBYi/70wRGaRROLPGRlRQrglVIG2DevBxQB6xZhHNFBmnHN8fpZQIH3DtOrME0ALhQCDZGh5wrT8i+ClOWJaWl8mSnLIq8d6RZtHp5GtBlg0ospTgPOV0lzkTrICj/R2+81d/wdRaRrMZVTMB19DNE85vnsLbipOrKbLa52h8SLGWEXygnFZMqiYKilqQJT1OrRckqcAFj1FQmQm2nKKmR6j5PuvZnL4LHOSKj6czprXEozHOI7xEq3a4mackKiCVIpM5k+mQVEk2z26yd3+L0XCItDaGs6nI+cyLlFwr1HKfYmkJsaOpm6odXlgSCbqFFVsf+xkZfDTChDhg9iEi3AKAIwp/CxGzrVR8KxImbZ/jQzi+zoxpjl8756Jo6Nu1dMJCaHkcqBkbJdc6ICHuecWVf90iqiIKILQ9hH0sqNJinwjt+rhssXIhBo1DW3c8sSEU3BNi7MLluRA9F8zQxWkS3boLPU6KJz4fJ94E4R5vhT3+FXGMXmnviYswshAWoWJtf9jqGdHM5uO/2a5gO+eO83sWdWZwof19g5YCpSUy/m90+1sXV+ZdFGh9iHi1eNkIQlNhlCTPunQGXXT3BEW+gtQKh0TIlFk1I7i4wm1MRVNOsGUZg22VJiiJYCFcqePrPrq4Y81uvMM7S3AG5+PmqW9NCIttB9kKqc7Fd5zSMasiOmo9iZARpZAmSJUghUTrmFshlYwbqK1zefHaRYRCrJ29j2cKrZNXPvE+lu17VogoskfRP/YkOolO0yQrSItu3PQVaSvWtX0Lcfs4uBggLiQInaFDilJRIxBCMkPQ+IB0nuAMIrhj97B4YsP8GPnmFypCRJIlWXxMFwK4gOw0yNkUNxli65IMjwgWZyFkKVI4dIh9lNcp6coGYXCCXpqwLC2N8lityIoeqc7IlaLN4KSxNd5Y5iFQW0NWZigRcE7QGMtkOqacB0zjMdUEkxTsPtolP9Ehy7t0e3nEEHmJUhlJnuJ9gpY5utCcPHWOwcYmSXcZkXjSNNDU7dkgNEEJrDet6K4IUrW/h7jB6YPHBXfMpPYi4jq8czH3hIjLVEpHPJnO6feXSJMOLqh4TdgGFdqv9wHlHdJbXFNT1oY8S6htg1OSrNtjqdMlTQqs9xgXc6hMiz8zTU3tLCiFzjN8OeN/9PHPWqRdAMiPh0twnGKdJElMJCQekFmW45Uk7WSoLCUoSd0W5QRB8LFQDfgWZMwTjqD2JiAEWiikbyEIMoXiIrp3DS/O4GWOSQaUZsTO/R063nCrusPW/du89vlXuHL5CidPbfBM/yXe/N6QnY8fsrK0Eie/iaKpZ+xuP6CaHHDr5gec2TyL1ArrLEu9Jeqq4ehgSDkv0YmKwGkVRbmjwyOcgzo4XLCsrq+wfTelNpaTm+d4+vnTbO8eUHuHLjo8/+KLbN+/zfe++20SnbC2doLLV67T7XXYOxozbiSjWlNOK5raUzVQuYiO0AKyvE/RXcEpQZhNqeoKF0xMD9UaEzzCO5xrsE0V6YsitFxSR9Yr0OtLJCtdGunjRE3pGPDSusk6vZxMeEZJ4NHoiIN7W+yNhpSuZqnTR5MzHe4TTCAXjhrTguyzyDTqZdh5xcPhIWPXMPeWkOh4xS0O3MVNVRLDB3QeG4x2ZTfRmqYxCARLec7FM5s83NrhM9cu8errX+DkiSXWul2Wl3oEpfj3f/kT/vx9x3zjN+itX2TzzDKP9g452j3gmfMbvPrMGU52QDmDc5FjQzsFjkO/xwntkYcXn9uC7+ucP57sLYTcOKGOBeii2Mw7OamO073gwYXYbFg8s1mJFI6T6x10TyJVDF0rq4rGNAipIzPWefAx5Ms2hnuHDfcPI1ri4sklNpY1moAO0PGO155epnKGX3xwwA/eP+Irzy3TlYKz6ylfe+kCf/vjB4Ssw7NXTnA2D4hKor3H2hLvEzKlOBrOmEznXLh4FhkcXeP4+m/8BgczG/mYApxpiBEXgmDr6P4MxBVVKWlqQ97NotjQNIQQb+iEyGYyRkTxiQKDpLEVCUsUa9fQTY80myHknDTNqJua+bwhzT2nNwcxjbGc0xhDmqZYFdlnxhqKlTU+84XXmasMjyOb7hA++EeSIuVw9wAjDdZYMpHRX1kj7y8znxzgXWymFlP/JI2H/iL5cxEksMCHKJUyGo1QOgp9xhiSqkQR6C8vAwIRYgCKKSswLh5hSWQ9NfOS2XyGdY40zyKrDRFXxRKBTOIAIXWeMKvZ3LzAyc90uX/zQ8J4SBAC6wNWeDyKRi1h1wf4E+vMpcLlOec2TrGxsRa5pC4GsVgfWtETynmFntYU3R4ry0vYas50NObShfMMtwTvvfkTzly9zuDkOqevXmY2HrJ9f4uNbp/ZcETjYhr7/e1dfvHu+/z6V75MXnRaFimtA2BRL8dipa5rAJqmoSiKmHodPNa6OORIUrJeB2dhdW2VTjeLTSL+GM4fV3Va14IKUJbceOsf+fmNDzloGiqglVJpjfqxGRTiuDF0zmH/iTtjkVz85Mfie+LixmOBOaYGi1/5ukVzsVihe+ysWKRexybVubjqJ9vsZSkl3roYghDiaRIDOAJBKmbTKb6THTN5vY8DjM5yj/7F0/jhlGY+b50FEutsXCP1Hp3IhRXt+Hn6sNgAiOJwfKzI8hv72IRluztsnr/M+to63aU+n9y7RxCBpq6QIWvPPnm83iUQuNZRG2QMLkQkzNKMRkdWYqZSkJKhmeG1xg53yUygm8RrPEtSOrmmcZ68LjmcTnDO0S+69LMBQUBZlSyvraLygp3DPbyIKbnBVvR7BQbL1t1PMa3z5fa9h6ysDFhbXUGkKWY2obYN091t5saQFCl5JyYJN2XDrHF4W2OCQyVdzl5/mQtXn8WSYlyGazI+fGePo/1DtJOYkSVPCqajMWkeGBSKJIEjYZnaIclJwdNXLvDZV67zwheu0enlVGXFfDpmcrTP0aNtEuDitae4+MwFlv52lXffe5PR5ICynNGYBqnmFEUfURS4LMfnHZokZz6Zo0cTPv35W5TjKV//5u/z67/7L3jn77/Dj978CWtXr/LM7/wO5XzG3u2bZDYifYKdRO56sOjegKKzhPcKOZ0xvbPN4V/8J7oHhxSvvo4r+pg2A/u4whOBFusc3Q1KYxtDWZYEUdHr9Pna19/g5o2fMJsdYrylthXB5lRzRTWFyZFAAdJ5RMjQQaKeQBrF2lISRBJRWS5Kda5d5ZU+rtl+8N4v0d7y8jPn2TzR586tIZ988hH95VUunD/H2uoJtIK7D7dZ39jg6lPP4IKk0+9z9uI51tfWyIuc8XTGvXt38S5QNYG5EVx99nMMtrfZ3X6IsyMGy6s8eLDFYKnDudOnKeczDh5t0en1OJiNuHvvLjpNSbMU7zUBzaDXY315hfNnL2K85e6dWzza3mIwWGZl7RSdpVWCSvno7gMGvR7T2RShNOPRiG6Rc3h4gK0UVoIkwSdxu0e0/DjrA0rldHs9it4y97d3mU0m2HZglOddPvp4m3fe+QVCBS4/c4nz5ze5eP0U3/rW95jNDEJp5qai6C2zfOY6l69e5c1f3GLn8AOUMeAtw4MD7t36GCXg5OaE+foypivIE8/R4R4uBC5ceZqXXn2dncMRuxPHx5/8iCwp+PLX/iWNKJjUPV7+/K/xkx9+n56yNOWcu7fvM5vEgNsFEs010cUuhIj33AVTShwftjF45YntDFqRRCDwlaEeznATg6sMtrDMLbzz4QfUzjNYWY+Dn9ry5S99mdde/ALjwzF3PvqIn+qf8/JLL5JmCb/zm9/AmDnf/fvv4m3Db7zxGt1eHjdweoL+pQEnL5/n/vAu85tTmr0Dvnm9z1NnarzZQSuPD6oNkvUoNeXKZ5b49V9b5eatEbOwgWl511VV4yzkeRGdjiEOJGTrLHPeHgsVUiYY2+DsjO68Q0gUo+Ihq88r+i8WlMk+vpwyH05QdUWoa1zjkVaSGIG0Dm9NzJDIohCjgZV+l1TrGLrmBdPxHGdE25MJjK/xSiBQ0PICa2OOV7pVmsY13ABCR0a9wpMXBcY7TNPEIZ5z0UDiPc570jSNdXXtCf5YX6MyNXebLW6P+mwmmk5asJQPyDsdjHU0TYmzjjxLolhnDNrnCJWx1l1hUB/xSEq8ljx4cIdGSFSSkWVJFC2qKXv7+wyWOuw+ekSmAuuDgkJ6mmnE6KnQ0LiE0bTGU5Llgo2TK2S9VVSm6GQVsoSj7dvU4xGDLONgNufapbMM3DKf3B9yOJzReBsH2FJTZJpExy3HTr9P4zxHo22EEAxW18nOaOY7RzGQiRDP7AAugyTNUTpy8/2x80wghGZeGlJnSRw0lcPqQJq2102cRMX6tlVtgg8LU+kxVlAq4pq9CBjvcW29QCuYSKV5rFYCTzhtfetwf7KmWgyvfSvuKfnYmdpY98TX/GrNtWCrCinRLVtXtKKoaPsyWme2WgzYnxBn2784/vvjAUB7fjyJ41p836JOWzxWFE8fPyd4/POEJ9AGgsfB6AvhdYG7Ot4GXph8nhCUj4XHAN5F/v3irFNK4wSYusGHGITnXNzQm8xnSDSto6N9aePQ3clAv9ul2x2Q6SUS1UelSwQlUELHoWIxQOt4z7amxtRz6vkRk+k+JtRU1QylNVmSIpRuQz8dwSfte2aX5isAACAASURBVNHhcfEe5yzBWRSPHduLoHilNEIqjjV3ETN9aLGXeZYh0wyVRGeoJPYTiwCvWHO7Y2OC9z4aEtrXxbm4gdaYGNKtdXKMVJMtYs23D+7abVyFQoSIlcjSDhJNQC2oYBH70bo5Y6kjYkhd03CMPnC2xUZIkqJLR2msG8bX1wNE9OGivhbysVkDQbux99gYIqVEK4HTCq0CqYzbbtoZMEOauiY4R+0cpjWsaSlRMiUvenBiA5WnrKWKTAVMCIgkxUvw1uKsieelbTB13PA8OjyMoeeuDTsPLgZAOkfjAqZydE+fotNZZza31NWI+bREKUiSlKVBjqkrxuNDQKCTDsXKOkYKCI5USnp5gtGQpQGhBNYarG3D/uLaIQsDj1ASQQzDU7Ll1cpoRorbi7EGla3LVihFUeQUnQ5ZXpCkGY0P1GXA1jOCMDRmTlXHewSA84a9vV1MY+ikHdYH6xR5nyRJyQV0fEIdDJ6o8RgPtfW4EAdSi772v/fxz1qkFTKyoghxuuKcO1buvTH4RUOdaEInJQkJKksw7TRLIFu8ywLaHS8qJRfWdR/h3+30TyBQrfNBhAQn19CrL1KsXkfSw9I+djPGJh2mRw85fPARH7z3c27evMXVSxf53Bde5uKlM+S9DmfPnyfXaVypVwm4QJbkVPOS6XTC4eEBaZoxryqkTkh0wng0YX9vj0uXL6K0pNPtUFY19+4/5PBgRNHLmM5L8iylmo6o5hU33/uQFz+3yvWnnuZgfMS9O7cZH73Dpx99wNbdu6yvrEJjONjfZzib8umnDxnNAne3pxgDidRImeCCxTgDWtHrL6OznNpW1FXN0dGIxsUJ3GJFLgSPMTU4hxfx4lfBky71yE6vQT/H6LhCIUJct9FZSlerNvAlruoOpSG1HjkZsv3oES4EamsRqULlCdY7Gh1Ik1hEOi3wUsQplfY0vqGpBA7JyvIydVVRzmbR+u9bp7SQODwySQhBxBACoeMUWSt8Y1hZWuL0yQ1C8Fx59mlOndiglwmWBx0Ga6f4d//P3/Ct9yqak1+ld/oS5zdX2Hq4xeRgzIufOcUrV0+wmoLwTZvQbdti+DFIXgqJQ7QpqK1zg3C8okMrAESPYGwehfB08rSFXMcVDK3UMQcyMp0MIUTxpcgLunlO3QiqBrpZFPVqY0HG71dC4rzB2hqLwzrHzTs7vLer0J1lbu6MOL/W4dLGMhdPDUikoCMDv/bUGrb2vPvJI3QaeOPpVdLgubKaMHthjR/8fJsf/bjmq589xclcQjAYD9vTkkePDtjfeshSR7O6CZ00QaYdlFKcOrEURRjTMB4P6XS76KTlBykV1188BCkYDAZ4oagsNB6cJTbhvkEIj2sqcKB0Eg9rnVCbDGs9jlVyE+glvk18tXHg4zzGGuZlye7uLp2Vs8xmU/TyEuDxAo4O9/n4g/c5cfYCmJp7N/6R+XDC6vMnObox5tHeDr4qkSLjhVdfIcsUP/7hd5mPo8glWTj4NUFEgVaEyABGRDE+ejxUDA0p50gp6HYKfPDs7+3GoLGNk0B0HQrvscZBqKmbhuHBATfefzcKtFnaDgJimqRSCYmQpFLEVHoTKAIshZRTa6eZDQ4YjqY4DCDieZAUuPVNyo0BQyWQac75c+dYX15GqkDdlCTte1gpgXeRNV1WFVu377CxusZzL3yWxls+ufUxQ6V49uplVlZXuHX/PpVtOHPlHPVsznre5eXrTzH76Jc8PBoTZJyg3/jwE65dvcL1q1dwVYlri2mt4414UaM0TSzA8zyLv88QWWd106B1gvW+FfUFwnqsVWRJDHyUixW0tshOhGCyv8/Nt9/hvQ9+yZ5pmAriKs2ic1wUSUC308E5R13X0dngfpWd21Kh4n+LRWDw4+7hVxhnPCHuLtyyAsKiWfnvfP3iaxeNwJPfp9N4Dgbv8UTeH961rgbiz69EPFNCXA12UtA9tYZIEvbvzGKDIB67NpyPrgsl9fHje+/jtkvrpF2EOi7CEhoBR8GjJiNm0ylnzp4jaMHR+IglEQda0kh8gCRNkDFiHETbvAlwQjBxAa+hUQnWW0RjycgIKjJH8Y7C1nTzfov9CCgfoDHkOkM6QTOr0EqhdULe79MZ9Lh97w5lU0U3epoi8NiqprYN5XyEUAXeBborK2xevsy9O/c5HI4JUrI0WEJ6SzMssd5QzkbodBmpNcYZjPd4F0NNddLj2edf59qzX6IqBVsPt9ne2WJ4VFLPLRfPr2HrMR3tGE+GnNw4yf7ONgbHcBI4eekcv/nrz/PcFy+yvLpGbRKMC+wPh7jZHFOVTEYjsl6fkxsb9PodRuMDvvr1P+Bf/8n/yu7+PW7fucmdTz9hd2ubo/EYG1wcVKiMCQHbKSi8pzudc3TrBt/5syFv/MEf8fnf/Rc8+uQWm1evoIs+7/+3b/Ho3Z9yyRtkkBBqfDmOTvwkI+ktU6wWGK3pTI4Q+ztMvvvfyJ1l5fOvkSxv0ghFHcB7QwgW2zZNi6Yc0XKKtcD5ihMbJ7hy+TK3Pp4gNFTW0jRTqnmDLQ2hEhgRFQQhLFaKlu3XhkRB29yFdpDgoiOjjaxTIrowQhDcvbPN/v4Rufa88OIrbJ4d88Ev3+PWJx9w8tRlDg73mY1mNOUSZ85sUrehF3VVMhwespGdIlGa/b09nn76Wb70+vMcjktqp1naOBc3DbYf8tRnLnN0OKGXdTh4tM3uzjbT4UEcDlRdBqt9rly7xHg05wc/+glep+g05YN332U6mbE06HHnzk0uXjzP1SuXqaxmaXUDL3R0w4mEsnGsrq3z87d/xtJSn6PRUbyPAHmakKQZ0scNI+8qjLcEmWC84cHOXnQnETfTTGPY2TrkwfYO3nuefe46X//6V3njK1/i4w8/5Cdv/ZSqPGRWVtiQIfKEtdPXeeX132bjP/0tH71/MzLaXMAFw927txiPh1y5epWNpQJfHqEzFfFeq6uUtuHDT27RW97ghc++iDBTLp67xPTwEcWJK1TzilwFZuMj0q5ibeM0v/lbv8+3vvMf+ej2+ySJxFYxLAUTTRlPNrOL91r4lbNTHA+hgpBtkyxpJjXvvPkOB492ef7F57l6/RpBK1KdcvL0GdJH+4yPRlw5c5Hz6xukJ09zfn2d927c4OYnH/Hcc8/QK3K+8fXfYmtrjzd//DbnNk/zwkvPcffBNtuHu5x6PmdXVITCEyaONef5/OWCerRD5Wp6XUVWxKCvpjEEJUjzEWfWJedO1Hz6aI4L3bZOVsdcxSxPEULHus+76EYN0fEqhMDZQGMrBJbZZJd62XD+ix2KpwSjzhBpptQ7u/SFRmYpPkmohUV5SFygKevI+fMKreK1lmcZg27kWVZlRVnWOExk1GcaEMybCm9sRN1kKV6INqwzvibOu2Px3Lf3Gr8YUPrI/5U6clCdc8eCintS8BK02J/opCtlxdZ8l+VsPQbiqJzZrIoCQ2idii6GUmEsvilROXTTjHXR4U44YG4NdVOR9nqknRQfHI2rYmBxVUcMm2kotKBIJWYO8/GMUFpqD/VRTTnzSO1JCihdw+aZwGAJFAosHOzdYTKzjJNzvPXJNnuzfbqrBuElWSrAxWuyVyQUucZYgxBRaCrnNa6sCc6wu/WQwdIKl56+ymR3l6NH+7EqSeLW4+qpE6A1e/sHTCfTxcUQh24ItEqQ7fA5WEfQESsYMwsUXgRQrfPzeMgahxtCxMr2WGASHAu0YeEabRFOi7PamjZMebE91J7bcuE0Db9aPwX/+P2wCCMTPrL/H09hOB6uL2opKeOZD3GbKbTCs6B1V8rH37twpoI4rofCMZKqFY/b1fhjxy0LNmZ0Bwfv4zbn4vm3Yqt37vhxj8+f9v28eK4LNNTiIyIX5PEAXkmJFEQ2bAjttRKNE2KRy+L/f+be9Nmy6zzv+61hT2e889TzCKAxECQIcBBpUYMpyYoTOxWX/61U5VM+xJVUknIlUiq2FVtSFIsiRRIUCQ4AQTaAbvR4u/v2Hc989t5ryoe1z+mmrD9Ap0g2q3Fxhnv2Xutdz/u8vwdqa1gwCWtrYuCXj+/VWLd0FAtBM9USUKmm3emx0l+naK2wuXMen7bIux0Ikul0hvDxhk1VitJpU7s55tW4qc0Ws7axSSaFRKcJ3loUHmNrEp1QVaaZYIjhTr7JDnLeoQgotag7Wa4Hi+9HNHV8ohdIAxVRXlrHkOC/95WG4JEiNGV9cw00f++cifudtaRpita6Ebxf0pFCQMsYRxpNGxFlt3DmikYAZIH9CPF+DdbjTYmzdazvncPUJcbUuBBwQoBKUEmK8wYhHN43aIjlpSOWZxfRhCm/vK95KRBaYEPAGY3s9Cm2ZdN8yKhHg2go0Rk1EisEaqGdSYXBE6QiTQo6qcIREFmGITCbTamMbZpahrqsmY7HDIenjIZT6lrH+lyADAkqicgTJ7q8tnGVzfPX6EuFlA5bV5wcD5iXQ4ypmY+OqatJdEWnOcXqBpUL1GWNRzOVEhdoHNSRV2yMbbZrGcN5ZdOUeKkJGxtJKgYN0mT7yDillxUFOm2RZF2UalOLDKlyVNYi1D7WRw5EGKNkjTVzhoOzGErtY0DZyekJD+/fJ83bhLQgZBn9NCPTCQRBqQwIg3VgTMBYH8mqizXjH3j8oxZpAxAa92ttFqMBkRmS5mnsGgjIO21IZBQsiJDgyJWN4uyiGI9rYpPuRxyXiY/FOExM6LMqo6RHZ/MtWttvYeQqwkfotkQivCLoKc9PTzg9PkDWhk/uH/Lg/gF/87c/ZG29zbndDV69eoVbN29yae8CrxRtTg6PKNptjC15tP8UkRZY6Xmw/4hZWbO5sUmWJGxsblK02oynIyrjqKpZHIFxFjeomA4nBBEX5Harzf7wIWcnY0SaMinHTGdzRoMJeM/2xgZnZyOmJjCpKj69+4jh2DIzUNYWpTN0JrDWUVcVSaLI8pS8leOFx7ia0XDI8cEx3uvIbvMO70wcOSfayEMIJFLS6vfI9taYtxVOxXAJAL1wf+HIEo0IHgt44ZkDh8ojUo/NIq9o5A2yqlGtmIwXtACtEFJjG0ajC45QKJRJwFZgBPN5SZy1aTYD0YzhNoiDmauQiUTqlOBDPJwSC4Hd8+c5f/EC2+e36fQL2pljpdcntNr8D3/6Pf7kFzDe/Bb98zc4f2mN/c+eMB4O+NrNc3zx5jpZKBG1wIv4O6nr6AIN0i8LYR8sLogImV1qPY08F2KjIFGCPBHo4CjndWTo4BohLHaCvFskU8ZOYFnOkBqKohVFFh+wQTIvI/w9dpZ1XDC1jknyIuCCpTRzgtBsrPWQxxMqndPaXmV/cMadJ0/YXDnklYvrXN5eYa2T8K0vbDNxjp98eoQS8PVX1siBN3dWSL6g+auf3eM7H8E33tpheHDKo/0jDsdzam/Z6nd59cp5iryFUoLWSg7N5wpIbEhptRVaCyDC7I1xpEkWRUDv0CJQGsustNReEMjwSoPKwM6ZjqZsra/Gjq41uCAIuoWzCdYKZi6QhITJbEqiJEqntIoeSms6vR7/5Ld/m6S7QxAxbGM6HmK94+LOFt/5038LpmZFKTa6q7z3279NtrVHe3WTlW6ftd3zvPrW13jljXd5sn8P4yWVsQhbk0jPfF6idEKaZVGAl6JhKIEIsUASwXByckyaZsQcjMgjElIwHAxBaPJWu3FoB7zwlK7i2cEBt2//Cm9r0jTDNo0tQogg+zyP3WRr0LZmXeW8sbLLm6ubVCcD0rJqmgMxqMmlbdz2HpO1NYYqpq1fPHeelZUe3lmsMyQCZPAYWyGFRyhBmhZ019bZ29nh8MEDPnr/B9y4dZNv/vbXOL73iNsffsTGpXO89e6X0EXGZDjg8P4+K60eK3t95m3N4fd+CErhvOD4dMz7P/wp58+dp9VuUVflcocITRFqTOyi5nneODkdPjSC8ayMIz+eBpkTx+aii64JDmoKbCUkCpgen/LL7/2YD3/9GU/qihGLUfvQHDgaV0Qjv86mM0QjBgVeBFAA/8WfLzuA458vj8v9psPiZUZtksSgCdsk38ZnYKFfxgPlcvOM18sC6ROIQRPBL5z58XeXZwUiLyIH3EWcSCIjD9bWhtrVOCUQLhCwSElkkROfy3izFNICNOPr/oU4GxpueMM7q0NgakoOTp/zytUrPNvfj4yyLFm64rXxIJrDBwqR5AgdD+hVkMylorIeYQz9Xpf19R2OJxU3XnuDk+eHjJ49wbia2lkKHZnw0+mUjs7pd3poL5jMp7j6DOfBVjUCwY0bN/jok48J01nEamiNVBoVYhimDBZfTkhCm1TCufMXODs7YTqfYPyANNGkWYabV8wnY7I0QSQZtnGISAStYoNO7zzS7/GdP/+Y4cEpaa7or3cwozO6nS7ezGkXKWeTM/K25nR6xshN2b2xxzffeYev/d7b3Li1QvCO+/dLhmenPHv6iM8//RX9vEO/32f34lV667sYW/PRr3/F08d32Nzpo/MWu7uvcfPGO3HNlY7j0xPu3bnN4f1PqY8OGDx5xMTMKZKUugVrYsrw2V3+6n/9n3j9W9/m1te/gSsyfvH//ice/N//npXRgKwJ4IqjdR5RKcRsjEtyko0t1ro9BgcCdfKc1umAZ3/559iTI1Z/97+i3trB6AQTmjFWF1mGi/FTgkeqhOBjgnTW7vDlr3yTJw8fYMKQohC0CwidJI6mGcd8WjOZzgiiEaI8CKGaNd01olxDg/eAFEglEMIhfOMoUQnjScmf/fnf8N/+899nfaWg3emytbXFwfMnrKys0+8UlLMarVJee/UmrVbGJx//CrG3w+lgzOd3PqdVtHjt5k26nTbD0YC6hsf7j+mubnHu6puMxzWlceg08PDzXzKazGKjtWiRdTvU8zarG2sUrZxP7z7kws3XmZVznp0eM5tOOD7cR7oeu+ttTDnk+Og5a5tXKNI2B8enJGnCzvo6J6fHdDo9EpVQrHc5noxJtMYFGxmzJuBdrIGzVNPf2uHijeuYesaTx/uMBwPmszFVXWJKQ1lajLdcv3mF3//d3+XKhWvc/uhz/uzf/wXj0TwiJsiR+TqvfeFr7J67wUc/v8PTR8/wxqFSgU411nmGsxHTasasnOLqiiDgS+++w9r6Lnvn97h4aY9ZZRkcPsYaQzkaMzg64OHzKYNf3eHr3/oWn/7yI6QvaffP8cUvvcXGar8RRn+Nsw5fWfzMoHwUnV52xoXFwtw8lq625botaGaqIQjM3PDgzmMOjk+48+ghX37vHdqdgrOTU3ZXVrBnE2bHJxw9fkhRpOi0xbvvfokPP/oIrRWvXL/B2uoG//pf/Wv+j//93/Kjv/s5WavN/f0DQpZSScPZ6RG9tI0qLW9urXB9p4UOgnmZ8fRJRdG2dFux6e6Fx7s5N65s8JV3Ex7/xQmzKgOyJuQnMC9LpNK02zkgKMt5vM+kXO4/MSAUKlvxcHSb1Ss5m1f2yFYLispycPcRo/v7vH7rFrVSdNsdRscTwtxh6kBdGnTScPRlYLXfYr3fZ2t9nXpWM508Y16WeBmbrELHKaIskVRCYJ1FpxqpYh3tpQGzGFtvApAasdbaF6gG7zxeOJYBSk1tIKQgTVJ8He95LwRBxtf0OE7qMacUbKsexsasjUzn1CEGShnnSGQCSGo7QZiKIFI6MicLkrmCdr+HyFIsjmo+A+fI8hwfApPKEoIkL3JsZRkOKwpTUVtL8BnV3ICXpEJSG8/ZkxFBO/qtFkol2GAx3vH0pORn44z9ec64DKinx2RSIRKF0ppet8Pm5gqT8ZDaGMrKUc4NZVmTOoudzxmbEiUF3Vab1Wvn2d1eZzyeEFJNu9fBO8uD/X1Ojs8wdRytts6TZnE60gVHcBVC6qYaSprqJ4pnUuulK3Yx8SpUrJGiM9URkZpyWfcsRMnY/P1N8d2H+D0J34iiS2VNROfqwim7+FsfmoHYOAnLsmkdn0tJ2egA8fl846azNmZCLOqpmKnSiMMhNKiB+B6XQmfz3sPC0do4kpFiea0u/pkQjQO4YVKG2AFYPufLIWOLR2zkv2gWvZy18PI1DlGolc0YfDTqxGZjEBLnXRRgA83/CLw1GGtQMiHEFG18EHgvYtCWi9MGwTemNBGF3yBkzPWoZqi8YjQ5wTCi7VbJ8gJrZks3qGgEsCwV+NIxHZ1SjgdR5JeqqZ9DDDgjYiWC91hj4lq9KJJldDT7EJAqhhj6uiRNk3jmiypyE1Ynl9+ZtRblHGlRRMSXTqPIql6wkGP4dmOACCxxmotrKkk0ugme46UaflGTL+p82eDLfIgOTusdwZQgbPysTi/3kMW14iNTAm8rnC2xzmFtTfCe2tSxQbW4NrwleNvg/qLxId5LjWFDCETToHoZjxav59iA8FIStMYZh09yiv4aYlqRC6icIREpQSXUBJSI17KyFuUMmfNxytorAoG6tFTE8FUhFXneaq6r+DsUCGbzOafDmsqaiMJRGTqNZsikkLhWn3mQ6FSRZ5q0l6F0gpKgZODx9AjhG9ds0Wbv8lXyVhsfFNJH7aqyFpWk5KlmNqkxJq5ZIdDwryNaIvjGvWpqqnJKVZdUtaOqLaWpY+BccJS1ZGt7g1de+zJKdKnJ2Lp4IWbJHB4zOT1ifvKU0ek+tTnDB4nSCu00Ak/toyP2ybPH1CFQErjirxPWVpGdLjrJSLRlLkxESXpPsC6G5PnfNN28/PhHLdJKIaMbDDB4rIm2c4QgLYoYIKIUKksobRUdQUSeiEAuOx7NFtCMYshll20xphE7e4GF6dmIHq51je7O1xDZNmXpCF5GRd5XhLqkHh8zO32ENDW5KiBI8IHpfM7oySn3nhzyo198wt7Wj7lx4zrvfvld9nbXERguXr3Ktzd2CNZj6jEyy/j+97/P0ekR3U6H6XzKtZvXEUrx5MlTkiRhMpkwm09RPo7tp1nO3DjqegISxpMp3gsm8wkmBHRSEILk/tNDSgd1GHE2mDKrS7TOQTqyRODMjNLOCSGgpSLPM3orHXb3drA2UM7njM5OOH5+gHc1Imk18GyBULHDbZyJKejdArXVpy4a/or3JCqK26L5PjXR1YWI6elCCYSWlFrgOpq6m6K9aLqbzWivFCgZWU2uCbOAEHkrLgK3u90CP5pTzedoJSKPdrFgLWpsGZ0gy404BETDtmm3O7z6xhuk7RYtmaN0oF208Crnv/833+Wv7qVMtr5BsrLLSr/H40fHjIZTvnrzPF+8shI5vqZCBIUSmtBcZ7GgjAtq5EJaytqQtzWLNyZD45gNMV0y0ZJEReZjnqdNkREXRBEcvhl7cQLKusZb37B2XBwREQYnEixgvWI0DLggSJIcj41hVikI6dA+QboKbz2vnd9kbDJ+9HCIDDlffXuXyWmb+4+P+MHHT/jVwyE3L/TZWW/z7s1tvJd8cOeMJEt493KPTAReO1cwmu/xd58e8hc/PaCajkmF4tzmFhc22qy2BTv9NlrCbDYjzXMCMTUzEIWRTCeECLWKI0xSYIynriusqeh2erTyDKMSfO2RQmOFwAqJci1adYnOUuazGeBiwAAJQefUwXI2z+P4ipd02oHZbMzG5gqShNF4yN2PP+PizZTt3g54T9HKyfJNCv8qr73yJsOjQ8zRERfPXWLzzbc5TDS7V25QTZ5x8/IVNi69SZApVRUZNwtWmgDyPG8EwYZPSniBsRDQabepK4E1cRyxrkqC98xmM7r9VYoipyprTGiCswBU4ODomNuf3Kaqa/JUU5ka5yJLNEk0qdJk1iEwdKznui74ysYub61v0zM1g+EpiZtjsRF3kBT4vfPU21tMvcFUNbt7e6xtrGCtwXiDt45ECgKO09ND2q02nU6XomhRtFq0lGKr12Hw7AlP795lenjMlRvXaa91OBkNkZlmPp+zf/ceuVDoTs7OjYuI7T4f3v2Mx89OESLF1Y57dx/y2ad3ePcrX46jjM7ibM3ZYMDh0QnbW5t0Ou2lo1PKKMZ6H4tP5xzBhYjUUIIsS8nzDKlU49KJfK4iSZmenPLxjz7gF7c/5aCsGYkGtdEcLMTCwdO4JkQzGvZycRQLpsVh5GXna1gWbE2JvtzvfkOUfenvFkiEhaPiZSeFaPawv/8cC9f+4r00ppjle/DORy63cyRNYel9XFuUlNE1l6bku5sIAvXRGWkSD/OC6L6LB4+XXjzEMVrhm9d+oUY3/ago4FlhGMxHHE8HzE1Jt9+lmozAGbwS4CR1ZdFaxrVeqjiBoBPmIWEsE6ywdBNNb3uH7vo2E06obMloeoKTlmldMdEVyig6MkNLjURgKkMSJOtFl4EZ40RgNqs4fnrA7qUYDnlyfEJAMDU2duqTjCRNEEFS15bR6RHD8YS0s45SmnbRZjIaMrU1eSun1+sznowoZ1OkdngBUnjSrEeSnUPn53n0YMDT/WOyJMVXFec6G6yaFhtba4ynEyaV4Xh4TLHW4/pbb/LKG1/g/OWrJO02Ac8nH02opyPG8woRApOTfYI94ujkOXO7ytruLlIoJoMR08kZ21ubbG5sMzwac/DgHq0MOq0W/e11Or0Vvvr2V5Ff+DK4is8/+pAf/PW/w4yOGfmUUNdkxrJzdsSn/8//xdOf/IRMJqjhEVuzkp4XcUSuEVQdCulqxGyECQo6K7TXN+mubzOclUg3YmU6YfTjH3BW16z+3rdpn7sGSmNribUxkdwTU0vigTWKGTSp7+evXmNlfZenB2cIGZtDSgtk0FjpyVzA1TV1HbEvwUc30OKAvTgsqURFZ73UqDSGa4ioNyNFHB385Nef87e9Fq/euIIQktpYOnnB4OyI8xevopTidDDm6cEhW1tdik5C5dqovEtvtaYup7SKlH5/hScHR0xLy+bODpmyjI8O+PmP3+eN1y/TaqeItS7nL12kqh2DsyEb69vIJGNz+wL3HzzhycGA3Vfe5pN7d/jKog3M7AAAIABJREFUt/+Ye7c/JCsHXDi/wbkLO4hE8+ln+zx5dsbb77Qx5Yz5pEZd3iNNNFpqVtfWUe2CDVOTac3+kwfkecLOxSv0emtsd1e4sH2BzsYFLt96lbOTZxw/us10cMjx0VMG40F0XBpPmmV0Wi2OTk74X/7n/41HD/c5Ho5ApIg0Z2P7HF/95rd4972v8/zghJ/96Ac833+I8xblNHo5XeQwtmYwOGuCYhXPnx+hpOJv//N3aGU5RbtFUuRsbm9z8vwQqdt87Z98i//v+x/wy49+yrmtDd750hfZf/6EdqfN53cec/DoOTrEyQacb1imMYTGv+SYXWRT8NLa+puNs8UZghdWvNpTDkvu3r1P6Su+9PbrrG+s8ssPb1POKo6OT3n9xlWOz47YPX+ZXrfNG6+9xgcf/AwlE65eucLe7iZ/+Ef/lKOnRwyHQ+49eoDsZKQ6x5JTzypUNeXWK1soxpTljCJLWN9IsM5Sz6EUnvaqRqWSVE+5dCVF6jOotnEm0GmnVJXFVobJZIpSKWtr60gpmU6nxET3iBiQGiyGSs4orgWSqxVn9SN6Jx36OmVcBzYvXaLVzpmN5uQypfCBaj7HVQJrPEprdJLQ73fY3V7n8oXz9PorPL3/hERJuq0ClWqc82SJboQlx6Ss8aYZzRYBmSbIxvnnbXTWK6WWGRO+EWNk7GTjrY3uKK0wVZwsoxGnlIhuspeFL2cCY2qqHKSKE0aIFBdK6srggiMVIGTEclTWoEWAUGPCHJIEIy0heMqzAQ5BliS02x0SrTg+PWE2nZFkGVZpjudzghC0jaawKVqkqFwj6yie+qAQVvDk0ZSNbsrmagvhBUmQhHLMycE+a70V9vZWqa3Hm0DWzhFJTlkZpuMhw7NTahMQOkfgEKam0AlWpxhnmJ4MmT0/ZXOlz0q/jzWeylkmZxMmgzOG43HDA45OVrSgrGpKpekWKdI0KAPnlgE8C2EoTmzFU3SsDSJKyjVuSEE8fyd6kV2ymGIVMe1eLNxvAi9erpNi7RBCfObQsHAXDtulo/VFefOSGNvUKVEFbn5eLsi5LBz0cVLopUCoRdd5qc42z+le1HfupcYBzcQm4sW0U3S4elhEqdmwrOUWtZhfijNhibpbvOAin+SlXlJzrzacbN+EmIWYDUOIrmDffFQbbMzB8FAb0zxXI2QK2WBFIt80xgMLEikJQcZwxeZ7UKiIx/OGwei0UVNSxtMxLmh80KRFRpJmiKBwwTQCsowu7/mY0fFzzGyMwuOcYIEidL7hU4eAcC6aarwFwRLxoEQMMPc21gM6yWP96hvnnXiBC1NSNdiuBcLAI7RENsxaqRqHv9TN+rAkki/r5mimitqD0irW/i+5dRfNocVrLy8yD9goqhJAKhczGnwzgdaw9401VNagULi6xtZzPJHR7pyJGAFnl0FmxlQxNNkZaDJq/ELsbd6Hc3FMXzbawCK3Y7G2xjcEVgSq4NHOI51H+cjEjWfJCEkLzRSidJFRK4Ih4BuNX8YME+eY1RWeyHxOkhTVVTGokEBpPGUYIqqaclYSvME1yL8kjUioGAApKVKBJtAqMvJMkeWCk6cRVYcV9Nor7O5eoN/rEoIma4YZfRkiA9sFymkZTSbNuhCbsFGkdS6Gz9V1RV3PKcspw9GQ07NTzs7OKLKMItUI7xhPJgQ8/dUe6+cuc/X110AJqvmccjzm8Z073PnkNvfu90nsHfLaYqojpAeNitetrTl8+hiCoJ7UHO5us7O7xbnVNZRKyPKCfrfLZDKmDnEtdU0Y7T/0+Ect0sZ+WArBk6ZtdAY6z9GJAiLTxgkwxkRnlI8AaYSI7gkE4SVOi2gubknsvHgRuxIySkJ4qePiqdfZ2HmXrHUO7xNksFEgFAHv54T5GcMnnzF7egeqCZVQ6CRl5h0OQQgpwQsqb/nswVPuP37OD9//gLW1DtcvXeLtL77FrddeZ211g3EZXV6pzsAKqpnBScvnn95BpxF0PTgbcnJ81tSPEhcEVT2NDA6paXfalNZQGYdMUryxTMoK6zWTWjCaG2pbxYJGK2prMKaOYwTWNRuTIElTsBXXrt1i98IupS05OxswGk6ZTGdNEeSQiUKLKFrLJiW2WOmiNjr4XoqVgI8deZwnTbOmmxgoUoUP0eHnrYuBSt6TpAlBCXymsC6AlATnSHUUOuLt1qABGiZM3PRBasgKTZhEiLixIbpv8TEoYdH1JI65eRc30kSCt4EsKfjaO+/x3rvvkbcUuUpJdM64CvybP/1rvvt5h9n6O7S3L7HaS3n08BFYw3uv7vDOpS5pmOKNJ7gY5qGkx/oAUjVuXolQgtpFR1ZeFDSlQ9PtDcu6f1GE0jiTFknwxH41At+4AD1V03XM8iwmW4ama+w8AUddA6nAegEuOlJHFczqmqBCZA9TkGQeQ02eaL722gVqcchnT0/pavjyjQ1unlvh6WnN7fvH/OTX++ADu+e22D2/ydOp5oe3n5Mq+MKFHjrAu9fWcAE+eXzG9etXePVciy3tKLAoYfDOMp6MGY9O6fe66HyVgKas5+gsIUlTpCcGi5ma46Nj1ta2yIsWE+9IsgyRaHwu8FXgpAyczUK8zmc11amlHh9HZ563YKYkRId1qgUrmcTudlCdVZLZmHbaYTopUcpyPBhRy5y8t4qxNfv3HuNdTZge8csf/Zg/+oN/Ti08P/jR97mw/Yjrc8e53/oGl67cYnb6kNX1dXqbO1gSequrpJlGqYBCI5tDng8v0nAhhlQh4lhgbWAymdDureCtoa5msbBSuhmLaAhU3lLXcbxjNJ3xyd07zOdTEqVxdRwbQgpSlaB1QgZ0bWA7KG6113lrdZtr/RW6OkHNDWllUM5TCslEJ/jdS9jzF5jpgCbjlaubbG6s4byNjNFFgSIFznrSRNFt52RaIr1jMhhwcHZKdXJMGA9Z7bZQ1vL+j97n2tuv88obtzDTOY8+/hXT01Ou3LxJe3eLqatJ8oSvf+VL/Ic//w6z0kGSMKprfvDjn7J3bo/NjVXm5SwynWpDogSddtPNDQGIQPu6KmMSuwctEyAsAwSU0s0e4EkSTS41OtHUwwk//Zvv88tff8qzec2IJuyCuG8s2NFCCoLzMfhPRXG2tmY5Zumb4lw2KcWLIrLxlSwL9ZfdtS/E1xdVefy5JnCwuV6EkIusDSI9Mv69bN5HLNZlc5hhGeohm9R2510UnJXE1DXSxCIM5+OImIrPGZQkSRNWz+8xQMJ0TNJEygoR1+fFcF5o3okUsnFnxKZa/F1EMVsikIlgWlc8Ozuh0+mw2e0iVvuMygnBaxwQVHNocgGEIUiPIeBEH5PkGFR0eaAYzEpe++I1Sq/4+MOf0M1jYu9Mak7cHC8UKtW0hKT2NaYSFCphfXWTp+MzWittDkanlM7y/PFT1la7jAajKGDM50wm89i4VAlSBpSGupwxGw4o6pqi2ycI2XAQBZPZjDyP43i2tvj5BJkkKK0wzjE8POT45IjapaRZQavdx/mKo4NnKO14dvgA1WqxvbvL1//gd7lw/RLt/io2CKbziunpEXZaIZwDUVJOB0yrgFcJNs149c1X6HT67D94gCsDWqdcuX6Tfr9PIlMGZwcMDz9j+vwJ4zTh8EmHNMtptbsU7Q4rq6ucu3yFt9/9OtPTJ5jplOrkmIO7jlaSsFbWzPfvkSHZzDUdBVoJTIhNcdkkkThrsWIS3dyjY1yvTXt9k7qyjF2gmBrSsmTw8/c5qsas/fF/h9i7DLpgWFuCcGihYkgiHuEsbnGV+UCrXbC2tcGDx4ZUxYNphNkCwqFTQd6SSBmoa4sXYH2NkAItE8wifJKIcPLB4htUSXNxRSeS9Zjg+d7ffJeTw33++I//kI31LQ4Pjzg9fkYgsLKyAQJG85KTuwO09AwGY5TuMptZlAjs7O2hkpRtkYKQ9FZXkVJRTeakYcrzJ/t89d23OJhN2N3a5vUvfYOf/eKXfHb7l3jjefz5PX796W1Oho72xnV++1vf5u133uTP/uw/8qP//B95PnFs1J4rF/e4cf0Nfvj+z3j64DZFZ4NybphMZvT7K8xnU9prq6ysb7N75Sa9tU36GxtcuX6e3c1tjp8fc/fjj1lfXeHZ4YDv/sc/Z3W14EtfuMSzJ3Dz+kVanS4Hzw4hzRGJRnqYnQ0iZz3N2NFtBjOHTDr83j/9A3Z2d/jow19QJAW2nDEdDSNuyXl8sCgZnZ4hBOpQUzvHlUvXSTOFkIEH9x5Ql47NnS2u3LhKu9UmyQSfffopK9tX+J3f+Sbtfovv/uV3aQvF5OyE//Anf8JafxVTT2OD3zl8aaIA3zjr/v5auxyfbxbk5dioFFEspBFNiA46AoS5wzHnyWf7zEZzvvTOF3n15k0+/Luf88ntT7l48Tw/++BvWdnY5o/+8J+xtbXL629+gR//3Q8pMsXFS5e5duUKly9cwAfH5ndWeWQOcc3El0KQeM9m3+HqGZmSSBzdlmAy9xibIpVnOo4ouKRbsbWR0M4rng8q+qu77G6v8fn9J0QN2jMcDFBSo7KMvNWmLqs4eit8FHbaMzZeKRA3FdNwRnVWkdQV5y9e4Nx7XyDTCcPBmMo6JjOD9IJgHEplpCIyAFWW0Ot3We312duI98vh8RFWBDr9LmkiKec1WkmKoqCsHDqZoVzc7xpVI/IE0wQlm+Zrk3humr02TqmHuAbNo7iRpOlSoLVVjRM1Sqqlg1LKKPo4JRg6w9N6yKpLKLKcEAzG1Y0D0WFMFIyCj41NFwyl95yFObXwWKLzvGilCDRZkiDzDLpdsm6P+dEJ7d09zoyh2+pSJoH6KCaH93TA1hWyqghK4IJEFxpjBMenjk7HoVQM7u31cy6PDb2OIWnVOF2gkVQq48nEczKagauRMqEyFWY+i9d9XZOrJO6nQSCtZzKcUA4mHOVH1CaaRqLoHQV2JXW8Fxo2eFXW1HmKkCktpdAhrp1SxvonFhnRhSyFIHjTiKlNYUNAoJt6JwpvC2fpgj0fWGASolimRAxXWoiti0aKC1FwD00B9feRJbIRMF9GP/HSz7w8maR4wRVVS+d8lCAXNRli8TM0jTuxrO9E5ArEMrhxYYRmqjROELllPbZ8bfGisR4dkS8Y/i+mr8Rv/PyLn3npuRc1ZnjBWRdSNOFI0UloQ2RfWgSmqdKCD2RJDPOTzcg3omH5Nn861wT3Na+JiAiIIOM9MBoOcMZRFB0gIYiE2VDHg7hIEMJFkTE4gnNgSmw1AiyIgNJyaWKIjdUQJ9pCgyVysZHql0fkRrMh4rWSBh9og6X2Bi8KDAJkgtIpUuuI27KxuaNU0+jxvjFvRTet9831F+3dvMDbvCTwS9AqokMW14QQxKZviJd9aO4VEQJSRqHQuzqe05b826YmdlBWdczFaSYAF4F2gbB00wZnmyA9DzhEk+0gQ6yrXxapvY+s28U5IJoJ4zmxWfEgCIKFYBsh2MV/V6JRTXDw4jYOKuoW3ntkiBxfqRRORkNKIiIPfF4aBuMh1s4pksYUJyDJMvqrK9TA0ekJtY3GC+Fio2Z9vcPmxipZpsm1INMC6aNJSWpIEh/dpSrFKU3ePU/eXiUpMhIJ7TzgrYvOWx2/v+OnJjaDpIxnMBEbGlbIiEos57j5GF9OMdMx07PnjE6P8bWhcgHlcvJcUp6e8uHf/ZBOf5OLr9xi7krWt8/RX12jt77FzXaPjQvXuHI04tnD2/z4r/9P7g5OwLjYPPAOpVKcdZweHXFyckZnfY3N7S0unrvAzs4uKssJAZK8AK3xcnHG/Icf/6hFWgToVoH3nkJJgpZxsZFxMXTOI5puSAggg1gm+MbCL3Yimr7eCwdtrMJwLh6wxQIYLCUhZKyu3WB98yYuxK6J8x4ZwJsaayfMhvuM731ImJ8gVbR916aOm4MI4CtksLSyhP7qNrubm+xsrbG1tcZ6v0WqAo8e3ePB/buYcoQtZ7xy4xrjwQjrQkwpzlLSVsZ8PsfYmnanhfOCVCdkRYGtK+azCVs75zgb1xw9P2Ywq9A6hqxMZ3MQAacK5nUVLx4RMFXVjPs1GwSCLMuiycka+us9vvqVr9LqthhNpxweHnLn7l2Ojo5ABGpTIUPsunsTF8mknZOt9/CdBCea7rUQOGJgQ0IagwREiCPRonGuaB1DdpwFF5bdzuUof2NdjxmcIS40IVrXF4xECOR5RllbklRHJ1cQTfp7s0wJ8aIx2tTmslmQJQlv3XqDf/nHf8TO5jpFJki14KwK/I///sd871GB23qHzsYem2s5jx88IBPw3utXeeNiD10PGl6MjIstAiFd5GYKGX/HShPwmLoi+EDeKpbu9vjWFo6N6GILzkZ30PJGaMZpGmElsi8NiBgqJxsBOrKfYhdJOIf3CbWPYs209jw7HHM8mFK5wKQyTMsaLQXnVxKu7XbRStJLLd96axv162N+fe85iYBv3trg9fMpF1fP8ehojTsHM+4+G2EOHxCSPmPf5ge3j2klCRdXFHkqePfqGlc3exS5oqcsWWjuL5EhVYJ2lk63FxdSW6F13DjrqkQI1XShBYGERKfUtmR1rYfXimEtKavA0WjO48MpDw5mDCeO0jSda2MRIRYN3lmUFWRY8LE7mWGoncevBcZizs56wlaWkCqYzUpWtnfYvnwR6wU7WuKqKZ89/BXKWZ4/vM/nv/45m/2Cb7zzFr+88wkbr99iPDglICiKFsHJCNNPVGQaOUuw8bAOsSCEuHGHEDufWifEUANDkefs7e7y6MHDWEBqHQuPZXErkcE1Dq4hn975nNl8jkriz7gQ6KQ5exfOEYxnejrggk55vd3jtaLP1XaXlTQ6XYWzmLrh0+kUo1LcxgZ+b49ZngKGc5s7bK33EMFSVTWT8Yg8S+M9paNrfWtjEy2jQ8k4y+jgGb3VPnub1wnjMQ9u/5q9y5d599ZNdCunGk+4/8lnnD07oOi0yVe66CLFK0mRZrz+6k3ufL7Pzz76FKEUQWjuP37CBz/7kD/89rfiyJL19Por9NfX8cRu8sKlT3BUpoypmipEYbZxdkgVxSQhY1BkkqakSUI1HPP+X3+Pn374K45ryxioF6JqI05C5FoqpUgSSVCxSPYhHiBpDhoKuXTxSxEDUpx7EXzxG5sci6Lwv9yoF8Vi0iAGFpgDH6IguhR2xW8eQF4EVkS3R2xmCUCBc/H9JRlZkZMXGZU3oGVzcGrWHKmwIpAWGfl6n0k5QzmDCtB06Jq8g6aAbRa1pSDdBImolz5nDH3xPD87xVuP3z2HsjUyiaww4WI4gVdxf0qa351xnlGY43QWAyhFQqpS9rYvMhsNeXTnEzJikF6e55SmoiwNNrGIwmN1Tt6MPmXtnKJoY7zn3uNHqDyhv7rC4ckhRZ6zs7PHncePEFJhrMNOpnSKFt1Ol9obKEvKsqKejXEE0laLotOmEC1GgyHz6SxyDRef2dRYb7FWU1VTjJFYm+JDyqgcxya06bO9vcmVSzvc+sJbXL12C+8l0/mE07NDrIVIJJcoYRhNTijrOavr61x+9Rx5r8fd+w84PN7ng59/RDU1rK1tsbNzAZm2wAeGB0/45BcfIJmxtr7JfDwkmCm1nWLKAbNhyvg4X9ZXWbfH9s4G4vI5dq9dJozH1E+fU+8fkJ0NcU4gk5xAnNQIwaO9RxMdPSY4fD3Fjs8YHGf0rr9K7/VbTK0l2BmqtnTrOce/+jlHOqf/O79PvnONSivmxkR3TYhJ0yLEproI0RHvnWN9YxVvDE56ZKpAqEXeCTJR2MZBkwTduGVFPBSFJhFcxIO1lHGCRTYokSYom+AdUsW9tzKOO3fv8b3vfY/Xb72O1JrDw6dIETg+OKDVbvPKazfp9lcYnB5TtDZ4440vYJ3n8Pk+vdU+o/GEot1ldW2deTXnwYOHmLJi99Ilgqm48/Ev2f/8I3741/+JH73/Y66/+S5Fu4XIJOVkyOhsyJPHR7w+OGZtZYOZK3jr63/AhcvX+clf/jtG4xGTswkyJHz5i28xnnkOT0sqN2U0GbO5uYp3hk6/S5HnvP3eV9i4cJnHTw8xM8H+vWc8uPs51dkxa63A+XWNm464fL5DOzVkKjAbz2i31uh0NljZ2mRazbHTGdmK5Pf/6e9RGk9rbY+su8ZwYkiTnO9+5zvcu/0h7335PbptiSAGt/oQD5KtVhutFfPZFFNX3L9/jwtXXiVLM84mEw6Pjynnlrm3OKXY2tnjwvlLHBz+gl/94sfcvfeIL3/1q0hX8fntn3E2eM7Dh5/zymu3WF0reHKaUs7LJVM2utfC4j/LdXYh0C7+fDmkcVlfhUU4UZSeCAE/j7ifU3fGB+4XfOmtV/mtb36N77//AT/98EOSJOfv3v+AvOjy+7/7bfbO7XLh/Bbf+85/5l/8i39Ft7dC7UqSLOXa1evc/+hJDFyNXUHSAN6MMZUhLaJj0VYOawLDYUW3W5CkmtFZSZYEWlmPTn6GFIaiXeAJWOvQSYagadaPRly6fIm9vU0ePnjEaDTDmpKymHDpt3YwF6eUnRHqLKEcjjkYjimU4vzOJiLLuXb5MjrLuP3pPXrdHpmX0Zk6mZK3E/prPdqtNr1ul4OnB3x2+1OmtSErWnS6XVpZiusBeLI0ZTCZUczmEVFU1Y27Ln5+oRqHc3MeC0CaZLFhbO1S6NBKNwJHM5UlF0Je5GqG8GKvcs5TW0dlLcd6xlDWdMwcgo1MWVtFlnOwGNsIiiHWVrPgGLkKFyyJ0BStgrzdYjI31PM5k/GUbHWdsigQSHynxfj0DC1Tdi9cIGm3mD68Q1dXOBWwLoYV1rVHZ5CmCbOZoaoN7ZajyDNWipqvXu1B0MyFZkJKXZXMK89kZJmWjvFsTiYinzf4gAjRiDKrKkJtKdJ0GWI0n5XMxlMWwXjL35cPMVxYNKE/PqKLlIe0qWlkUHG8HBnF18X5yovGOLRw8S34oI3QpBTe2+beWbhW478rm4AhgnxRH/kozP19gXXRKF+GYy0b4OBsrIvFAo3wkui2FEEXT99cU9C4gwksJjfwMYdiGeQclTb8srEeliJxCCBUfD6/FHibwNSm8pFNto4AQpN664ghXi+/t6ULl+a8uni7L9dZjft3sXipJhxtETgmaT5/iFgQs8D7CLE0J1jvECpiv4SQGBMRA8bY5X+FWAQoWtAa0RimTF0z9QOqaoZOc6TMECIKtFIohPARIyfj+UYoR6LBeh2Zpkq9NIkVXx+lENpja4H1NoYZEidqg4+OW4SKDmHnkAvXrbVYa/Aunn3IAkH4mJFDw5pvmgWuQZstRPjlddbUyQvDwdJEs9SLGleuf4Eik0u1Nl5iUWiNjGYhmvO6d039HZvLPtBgJeLPG2uaeiPqGdZaTFUBIU7EBhcFi+AiLjLETImXA+6cj4GIca1bTLC9wPUIIutYE79715hBvDVxSsB5tJcYYzABZNqKYY5LDUcgQjSayOaMKiGeAdD4oPBeMRpPKasZVRn3Wesc83IeGcR+kS3QpOyIlNpYclFTtFPavdjkC1KgtER7i5nOkMLhdUbaPYd1KbOZoZ2B7gqcVKQB0lw0GKy4Lyzu+yVihZjX422NM3MmozMGpydMJqPIN9YpUsnYmKstLSWpZmPm84qTwZC7d++xsrHH7rnLrKxtknfbpFmBzlvs7FxifXWTJ3lO6aByoRHEY4hhXVVYN8G7kunZMYf7++ydO0dvbYO81SbT8fyWFQVpYzz8hx7/qEVamSjylRbOe+raxC9b0ljBLSEIdMMXcX5RWdO4D6NlOz5eTqpsuiBIwDZrtIywexRC77K++2XINqnmLoo8CqwJWOMoZxNG+59gBg9Qsoag0NhmVELhFaxvrnDp3CY3Ll9lfWWNbitHJ5CkkjSJfLXxrGI2GTObnGKqElvDaDZlPCsx1vHg2TN0KtCJZjIaQ5CkWcH5C1d49dabOOu4++mnTJ1i/3TM04FnMDWIYEmSDKGyJlwqLHkcSjg8tlnQBWmSIYKMwUtKkmjN22+/za3XXgMkk8mU09NTDg6eYWwTyhQsdVXRMCVI2jnpeg/XTbHSvegQNkW4ljE1XIZAkkSeqtIKISW1id3wbLlWxhRLbyxpUTRGvcaRRSNq+cX/90vnqfeBRCesrfY5DSOqeR1HoGhGlJtx8kWRpmUEYwsLN66+wr/8r/8bLpzbJs0UaZYyt45/+xc/4f3HLdzuN+htnuf8Zof9xw/JbM1vvXWdNy50yfw8shxlZDf54NE6jem5zfuMrylAxJCaeA0qIs0+NJ8vFgCZgkwGEhqH82JUuNlEQoBykUCtJEmSNuKwwQfXuMhjp1AQD7LCSU7Gc27ff04dJNcubNBtZ4xKy/3nY+49G3CwP2UeNO9e7ZG7OX3l+eYrm1R1zWcPjuilkncur5DjubzZYWulzbXdFT47POP+sSeRgZkVHI1KdjspqYRMafZ6KgrOocYKgRZpdEILRVp0IwPIW2wg8lND7B4KNGmeRTyFkKyub2Ck4mBgeHo05eHTMftHU8ZTR+USnIi/18VnR3dBdACH1A6n5tQ+IF2Kl4LKzvnkySnKJVzf6JGX4I9GvHppk72tHUalxgSBRVB0e5AmFEWH7fPbqNQwmh7jMs1P737MbOIpp6cMTp5RVyW2DsipQXTk8hp1zkXWazMWtkySbdQ/a2OBKKUjSxN2t7fJs4yyKpnNK7KgiEtaiAEmMm6as7Lk/qPHTOfz2D1s7o8iy7h+8SI7O7ucng3p2cA3Wqu8m/fZsIEixGtMCx15PcHiVTwU1klCWF/D9NvU1rHR67G9sYoIMYwiTROElExnU9ImXAnvODo8RApBkeX4soThKVuX9ujvbuHtOiE4zqZTru9sMh9P+OzXt5mdDTl/8QIrOxsUvQ5BqzhWrhRaJXz9a+/x5OCQw6MBAsGstvzko494863X2NtZZz4ZI1USOZiwLJpjMdN9Zkc2AAAgAElEQVT0ihZ7gQCpNFrGkJwsTeNIoErwPjA+OuEX332fn//sYw5rywioFi720DybEI2DRDb1WXS1KqmaA0PcY36j6G5EUqliUN/SiRVehIL9RlDNYsda/rOIxXAuNjmWkyI+sr8WheRCaFqsjYvPrZSMnKgm1dQTokMRgSgKuit9avXi9RfC8sKN4gLUzqLyDNVp4QYDlA8L4wyLpHR4Ab9/EV4QhYylO8Q3gpuUlNbwfHhKS0g2m4JrUbA7Z5ppSElQEqkSKgMzVyPMnERo1tfWyds5Tx494en+A6QItNqr0TkvHaPxGFNZrK4J1mCLHp2kjUXQ856Oyul0u+xPnyNrxzqa9dYKh09P2XvjOkmaYawlSTOq+RypE9KixXQ0IARBt9vFS0XpPdPJhBCg2+vT760wCgOmfo5zL0I2fV2jlKTVkazvbqHTNlneorXW58L5i7z29he4cO0ivrYYU3F2dsB8ZkjTBPz/z9x7fVl6nWd+vx2+cGLl6qquzkADaAQiEAQlJtEKpDT2WKORr3znf2xu7Ctf2MvSeGktDTWiJQaJFAPQiJ27uqu6cp38pR18sfc51dTY9zpYDWBVn6r6zhf2ft/nfYIJ/lpCcnJ6yrPdXcajEe+89y6vvv0W3Z7m+KhAmJyDF8ds71zlyuUbKK+p6pJ6MGR4esIXH/8TyhV893vfYjw5ZjoekEgfbCW8wTtLU5vQ1AlHogSlV7TbXTrtZUxd0nSWSde2KL56wP7BEd57elqRR/WSs0GirAmhoMJ7qAtmZ2f0Om26H36IGk8ozw7QzYyOd4hqyvknv6RMFf0f9jDdDSqnsI2H6DPo515/3oOzKBw3r10lS1RQOhiPV/H5AxrXYLwNzGwZU321DINrM2+Ew6DGexfBWkgShfNy0QR5H9hD0ksaY/j1rz+hqR2vvnqLm9evc+e1O3z66T2ePH3Cj/72R7xx5x3WVlZZXbnE2tYOItGcTSu+fPCIRAmaxjKbVRRlQTEpWNm8xKsraxw++JLJ7ie0VIleSpB2you9h1y7cZMsSfjb//xXHB8cc+3yNscHT3h0/wkTlmmk48rNN5l9/Zj7P/8bLu+8wv7+M5pmwvH5mMOzCa3+KnUxRfhl0jRhpd/j87ufcHl9ibduX+Gzx5/wxdMTOnk3SBeV4uRghNaCRHrevHMLa0oOhOf4fMTh8QPQLfobl0lFQ13XVGXB6lKX8+ND9h4+4OrN22zuXOfk9IjqZJed1YxMTBgPnuF9hVCCtZU1lvp9lpdX6LTbvNh/xnQ6YjQ+4/mL59zqv8b52ZDltXUeP37C7GCPqqlotzt8/YMP+Ogb32B394iPf/lLjp/v8eabN8g6krOjAbma8ezxJ0wmp6RJih1N8NZdrL3EAbmYw7RuMVQJf+ljQFFUKBAVEdYtQKU5rgMO3ziaYcGQc/6l+oQPv/413vngazz4/CteubxDr7PM3tMDPvntJ3zw3tu89dYb3Pv8S/7q//or/vw//EeSVjDiunXzFvJXP0YUDpUGmXgiFavLq0jOqaopJA5nPInS9HuKuqqDFUvp2X0y5flRgfAttFScHJ9zPpqgVYqSelF3VEXJ8PSYVuaRLqzVE3VO77WU7A3JmR3gZ2PcZIxtaoST7B+ccH52xq1rV1E643wwYDqeIJQnXw5S56SnydKUdp4ivWdwNuRob5/z01OWVtdYWV4G7zk+OSVttUgShc4SpFbk7RZh5YCmNgglw0DGBf9iawTVrEQQvOfrpqapGopihreeRKWLfk5HK7Q5Q81zwVh01mFNUPMZ5zhvCk6yimVfk8QQZGMNOFAi+K4qFyTfQgVrjlldU5gG25IcH5/TbixOaqrKUAiBzFvMmhrRbnP+4gg7nSLW1klnhks2pdBtXD0Na6VUYA25FiROopSgKhvKomG5m5BmKU1zzOXVLlLm3Dut2B9UHMwslcxBZbR8SWEbmnmfi8DUFlPXaMWCrehsCP3zzqFVYD17HwJX55L3MOgOPo0ykphyAWn0BrUOhBOoEOEU0uitRUh9YRHiHIgQWBe8vsM+KBZ1Wuzj4nDMEwJ0Qt8WG6f4nP1rMHbORF2EIzn3O7XUy6Dty2Pv32HdBtToJUZ92A/UHOy1QUr9OxZUPpY88dgCmz7UOqE+i30a8wH5S8Cwmx8f8Vz4yFS9qL1etrryi2MKw28vLzxr5yGA8++bv1nEf5ROw1DCGJwlBHTJoEUNPbaP9ZpYBB45H/ZFM2d1er8A1C9eAToOlgkCYxt8I0gzhfWWAOkFGwEn4gAfF2oyHEpIkiTBRaWb9S7u72GfnzNKpQiZCI0QKC8w8bOFaxXCt6y1WCS2bjB1jU9TvDUoGe9iH+LuvLe4+EdF6btUEukuru0io4G5p28MDvQebxbGGJEgFq91qLpxIuwcxgayhm2irYeI6K0Pwd8i7i/WuaAasQFbck3AtZyzuLrGNQ3gwt/ZJgSceY+VF6xwJUKNLmQcGuKi3VroVcLzHHMhVOhVxHxwoRQ+sr5V7COtMcE2VMQgLS9DXpMIMIWZ24bOB+YiAuuEe6mqG2xlqCpDWRrquol3i0b6JAx1MAgN1ucsrd2gLEpGTw8YnWSsr7dZ6qUkWpKnoFyNqScoEZixq9urbG13UYkgVaC1oChqEBotw+eyTcmCRxPv1DDccAhvYwixZVaMGY7PKGazoJIIFxUlapwR1I1BK0WadhCVoDhtsNNzZkcvEFmHpNejv7oK1jM8eMb54R6p1kzxNKZGK71YcxKd4G1DU8xwTYORksNnzxifD+gsLdNt52gVlPwXd9l/+/o3DdIKIZB5ginDdEE6GwCtRT5gnGx4h5ChjDI+PASW+OFjAQ7hP9bZ+EDOCzQbb+KUghU2tj8iXb7NhJTGNyhfI3AYNBNTUxw8p3r4FZ4pUjoSL9notbi6vc3Olev013usrOYsdRISKWmqBqip65JZ2SCFpDFweHrO8dEhRwf71MbTWElTeyrnMdZF/5pA3VYq+Pwk2nHvxVf8+FePg79eWWJQIPMQwqVznAlp7+U0eNW1Wu3A7BICaxp8ND5XIhybEJIsyfDOceXqNt//3rfpdVqcDwccHx/x4P4Ddnd3F8wgX4dFxDpL2m2Rr/Twyy1KZQIjSAa5fuMsvrGgw9RMa0iUiOzXMPGsijIuIgKdKFwEgJTUKKnodNq4usFWRayFQ5GglFpMyQGQCo2gnQuaTk5dBbmSiIsQdg5ahCJLANIKrly+wl/8xZ9z585t8kyiUsHMWv73//IZ/8+DNmx+g9b6DpubSxzs7+Ibz7fffpVX1luocoBMgg+qFJJgqqCwzoXr5wUyGpvPQQsp0/j/LxUQPjSyEksrScikD9LOuCHNzfK9NSFFVUgSrVASvDNxkw8LdNjE4+Ipw+T2/HzKP335jHavy5u3tugoRyoaOm3J2ivrLLVSfv3ojI/3DTKd8NG1Hso1tJTn99+6QvnJc351/wQlNW9d6ZNSk6WS9kbC5Y113p/Cs9MpjfW8cqlHV5vA4o2LfvASDpYYYQofmnfvPF5oqroGqcmyFmmek+YhGTiYO3icVhydzniwO+HxiylHg5LaalAJiBShUoTU4d3ehA0oNlRZnrG03GZwtMelLKEYnFCILjPRZeoM944ngT2YZjSm5tHuIbPhlI2tWyiXhgYfTdJOeO1r7/M3/8fH/PJnf0O/nbF7VHHv8RHf/eb30RpsNWF4fspkcpnL2xnV4kpEZpcQCBE8Ub33F8FPkcngnGA6nWGMZ3lpE600dWUYjqd0rCDPWqj5nF4qpkXFsxcvGBdFkKcIkNax3ulyZfsyGytL2KpACUuaClQ5hdqHTVgrUJIka1PXFdLa8GymCtptpkkC3tNOUq5vb9HrdijqadjMvGdlZRkhwrM4m4wRCHqrqwjTMN17gRuO6eSSuz//Z1774D1UO2fqLGvbm+w+fcrg8JjZeMrq+jr5co9hVTI4PqK3vkYaWRvCC67ubPPh+1/jb3/0YxAKqRIOTwf8/Je/5t/90R8sAFoXG7m5LC34NXnq2mJtkJKIkJqFzBKckNTOktBghWJ8dMZv/v4f+eKzrzisG4ZITAQ5hQ+BiMj5wIVYhF80+X4B9vjYBIcrP2ds2fnUP/pJWR/W0nnR/TI4+7Kn7L9mf/jFUCoU1vMU67lHmZ/vmVojVPBBVokMAC2SVGlkEqRMDYLOxhoi1+AavGPB8MYH5cjimACVpXQ31hjNpjRlTRIZAxeBCPMmavFBYnDZBSDtCIEJPgZZGAFlUSLbPURUSfi4RuRSoFSO7HVIusskLqGtNVlvmSzvsbm9Q4VjOjhhNJtw9dZr3Nq5yY/++v/ElFOcdRjvmDYFeTullRicKfHCU5qGNd3jxvYVDmcnnJczJmXJzZ3rnH4x5vNPPkV1stA42OC/vry+RoNnXE0ppxOyJKG3uoLwmqKuGE/OGE+GdFrBaytv5XgnFmBAiaZsDJ3c8dF3vsbmzlXSVpduf4Pl5XVUu8O0qmnGBbmynB48odNeQqsudV0xno4YTCY83ntOZ22VWzfuIFttRrOK07Mhp8dDpBRc3b6KSBKWOquoxnK2/5TPPv4nhicH7Fzb4f1v/RDqhOnweVC26ODxSgScbGx0lEpJUg0qh6RHnuc422B8hm2vkLT6jB8+oN59zDaODR9AZKF1bDrm3sWBBSeamqqpad26zurhOxw8f0q9OyOrG7QtyabnnP7yZySbl1j57g8os4yJ97imiY1IDDJxFm8aJJZOJ6eTZ0yK6cUgABYgg0gkwqe4MgSE4n14Lgjrg0D+TlM/Z06GwBcXh/xBKaCEQmFp6oonj3fZ2rrE+zvv4URYS5d6PWbjCeV4wizLOTz+iuNZwYff+ojOxiaTB/dZ7maA4fmzpyRak6UtLm1ssX90RH95ifFuQ12XvP72N7nx+tfZOx4wHQ1ptGQ0HFBVNW+/dYe17custBPk+Jxnjx5ylKUoM+X0fMzn954yGA44Oz3l6vVrzGbPORucUpcFaxvrtNoZlzY2OFx+znR0hCmPWep6HtshiVDBc9MmLHevcGnrEsYMGQ9qTDPDGrBO0DhBv7dGp73EbDClmU3otHI211d48sWv0fWM892C8dED1ja2ubzkeXFSUI7PKKdjUq1ZWbvE5e1LWFNjmpp+b4OlN+9wdPiC58+fMxyecH62xpXLV6iLhvuPHlNWEziHT+/exVrPRx99xLPnz1FySj83PHlwjx/+93/K5Z1L3Pvylzx58pjx4IxiOsFHW6/58uQX/54DDy+tu3F4DpGhNH84hAggkowSZBdBW2L4kXE05zNGZcO//PzXvPf+u7z56m32Hj8hzxKqqsI0ht/+5rd879u/x4e/903+03/639i5ep3vfOf3oDK8fuMGq91lxsczOnkb6xpK63m+V5IuNWxv5XhbRXaSp9ODJHNI6UjzjP19xS9+/pyD/U2EaIFIsU3ca3xowtvtDGscJyfn7B+dsNzrIzoV2WvQ+XqHQ39MY2YU+8fU4xkqydBpFhpJmXJ8Pub53jHlrKCamZgsHiq25dUlsiTBG0s1nXE6qzAeeqtrLK2t0uq2OT0943gwpGcseaYhBjjlrQwtFUo4illFU4U0cBmZjZHGiDOeYlYsgCQZg+DmTDet5yBCCP8SUmKsRzgX96kAcEmtSLVkZGoeTk5Y6+Qs+yRkobRaFGWFMYFN39EiSPB9sPXRInja1rIg67SoXIMwjsYLfNaiMhYpNcIZsryNnZTsNJ6ts3PWJmdMpzOOxgWNbPDCkEclSaokWZrg/IzJcMYk1+SdFC0kxcSBUowGM06OxuzVbcp2m3aqgxTYVpRFhUQu2HZ1UyMj0Nw0TVCaxmfAeB/CtrwPfr0eMC7adAbgXgKJhFQ6UhXXStcgHGA0jSvxEewNdVcojKzzC/VPADLFIjDKGBeRyjlNNCjngqVrXMPnYOBL6/K89vHOL1inL9dQzl3YO82fdf/yf+fvITJUIwN1Trqdq2zj7fE7IPDcOuFikBPrvpfBFR+G6hc1ffR19eHem79UtMAK+2NUe76MLr30u0PNd6GYeplVvAg3XIC78fmIPsCGoL6xIgzbF6CkiBhiXLsidRil1UvWC4FFvKjlBJGJGxViHjwS5wVVVQdLJ2VpfJCtOztn+zqsqbC2wYsIfntLhCEwTXMBsFuLbepoM9IsfrcigIpiXt83BqtjDxh/B+7CWiJcUxVwBK1RKoq+5upWa3FzWbz3i1yFOUDr3NxHOYDXjTUEBUY4X8Y4nA+WYNZd9AVzAs58IDHPVfFzT1sfGO62aTCNWdhXzEl0WIcSPlqTRD9+T7QvvLjuYXAY6v5Ea5QO95q1BilDZpO3DuMtyl/0It6HzBcvJF5ovNAInYFpsB68VJTO4oVEeaI3eAi9xQbLKRkXhblFY11XTGdTismAoqyoqjpiOIpEa7ROyfOcEDVmEb7DK7c/4L13ryNSizCGWdFwejTCeU2SCDQwLWocBqEtnV7GZNSQdxKSviPvJCA03gmyBIpxjS0KoukVi93de5w1NE1JXU4oZmNMPcPVJc1sSj0bU5cNSEmiDWmrQ1nPGOPotAr6yxss9ZbxMsG5AlEb6vMhJ+dPg7fybEov8VS9PmXjmDYjKlejZchhss5i54pgLzDOoz1UdUW7nlELg090fKZeHif97uvfNEgrlSZp96itw5cV+GDubV2ggDsfFg0/l8YQJ3QuBjbZSIEWMfkwMtsCsBsvpPPgBZYO9N8k3/kmM7GMqSbgLM5JjFA0zRRbPGf26CfI8S7dHNbXV3nnjbe5eeUyGyt9+stLTOqCqpnibclkVmGaYNw9GI8Zz8acnU84PQ8Nl7UN0mtGkxqhU7wVOJHgmUsYJIYgnU2THKeCSbc3ErxFyAyDDpNhF/xQsRZvTPAGSVKcCQFEjZknys0lXBIVJRrWW3qdFt/77rfYWF3m9PSYo/Mjnj69x5f37nJ2dhSDcwTEjTBp5WTLfdRKD5N48IZMJ7SSFKSiKmc4fJQbOJRMgnTBu/B58oy6riOzkghuBF/cui6oqzqCBbFRdg4lw5RiAQzEhzLsXw4lBJ12zqwomczqyOzyCwNtAWipSTwsdZf43u9/m3ffepU0c6hMY9D8zT/8lv9yd0K9+h1aazusbi7z4ukTZF3y/p1XuXWpA/WEmatwsoUTCmsCCGNMSC91eHSSLqTO80U6ML0j21OIIOF0BiEEuZak0iOcWRzrfOLqnMU0NUppEq1BmODX5QVKCbwKE+3QYFwUP6UXfPrkmEEJb799ib6scUWDjWBhS0ve2OzSNIJ/eTrj070xuRS8vrOEa0raOuHDNy/z098+5+7jM7K8xRvbWShYawN1QZZmrO704mbqwAp8ZMBK5/BOBI+kuggJlEoBgqapF/YPiQ6gBkqgvaBuBKejmvt7p+wennN4MGI801jZxevlUDXK+YIcJsQXzzWAQmAxVcNoOMFVExKzR8scMJGbWLVFlW8yblLu7heUVvP1V7aYygmlM9RNeIaIm71OBGfTKYOTE06PDxklAlNrLvX7aJkyKyuwlsngnNFkyCUqhEzDJm5MLB5fnsheFJlCRHbVtKQoJ2xtbdPr9NBSYWwI9GiMRasmgF46gGyHpyeMiyJIywgFTjvL2d7YoJfnTGZTvLfUTYM0FXtlxXWtWEpSMuHBWDSSWqhQdDiLTxRe59hM451ha32dfr9DbcMs2zvPdDYjSUMwiDGGdqeDRND3nsnhAQcvXnBra5NrN2/y+MU+D+8/pLOyxPrmBpvrG9z/9DNGp+esra+xfHkT3WmhvccQvJNVyKLAYBEKvvbWG9z99DMODs/Ispyycnz+5UPevP0aN25eoapD6J314JBYL6MfF9RaQaJot3ukaYYkMGRcKklEg3Ql1ek5n/z8l3z82VecVTUjESx15o2hFFGqpuayKxeb+MigiDY5c4YBKnoVLuRzc1leTKmds/hkGO6E+/YlBoWf+xUT3xeTiYUOxTdBHeAFqFQHkDY+70mSoHUIqguhDxZDHJQlKWm3j07DOoxWyF4H45sFMCcWxxGbehc86sLnkugkoeh3aKxBIdA+NDZzdoiKA7dQzPpF+AJceLaFz+hQOsE7x6gpmbmc5TSB2i2YxgiFSHNaG1uky2vgW4g0RbdykjTDKYFSGcuXtmgZw+qlTSo/RSSWalIhpSRRCVIJSAUTX1JbQ64Es6ZgWlW0REJuNM5LDidjlmdT1tfX2X90iBKhmXXOkLZS+qtLGCyb6Sbd/ApnJ8cYb9hYW6a3tEVZ1xwdn9HKWpwPZtEzFiospZT0btzkg7fepJMmtPodGt9QlTPyjmE0GeKGQwTQSlN8JpiMTjk6fE6vtwGkqCTjxiuvsby9TaUEpbGcD87x9UOWVjdY3VgnSzQrSx2G4wFmfMKLZ094dO9zRuNTvv57H3HrtXcYVzKw3pUiTfTiukgZJNF1VZG3WrRaWQiDUAnWWEajMeV0xGQyoJjN8NMZjsD6IpPURcWqT1mSKVJ6rAtASSoVSMXMVbSUh1aCWFlCXbpEMzilOJ2EZsjWpMOa05/+Pb0br9C/epvzKqyrUkUP4sg48dbQ2IqkldDptjgdlkidM+/8AsHbIbUklS1EkuBMFcIYpcPr4I/orMU2dtGYmiaGEEV2VWBexmaSyCJBMRqNmU4mTKcTHjx4xOnpgCRNubpzk6WVNVSS4vyIe19+yvJKn16nHaRtJvjVX925xPOnuxzs7bL34jnTwrC92aO1sh4Gtq11GlKmZcW7773Js8f3WVld4sXhCUXTkCaae3d/Tqe3hrIwLkqcnzEanvEPP/kJy/0VvHfkWZuvf/ANPv3iS46OTxkMh1zafh1nHL1Om3a7DRZMadBKkGQqMJIR3Hr9JnfefIPJaMgvfvKPDEbHdPs9kqyFM5Z2p0tjAhOonWryPMXUM6AmyaHVFcyKc/aejUm1Bd9w8OKAqmjIshytFbu7u2gJa+sbOO+Yjiacnp8zGI65ZAr6rZReZ4k777zPk2e7PH92n+l0SFMb8laLGzdfI+t0uba+xJtvvM5oUqKTFmnWpphWlJOKV2/e5vkvfhI8D+M6JJHB1y/6R16EM4rFvTB/r4iqCSlCiI53F7LZUKPFxS/ID0JzXDRMzgo+/pdPeP32dda31jn8/D7Tac3y0hJPHt/jiy++5NXbt7n96m2KokAgaRrDcn+Jd157i589+DnJukDkCq8l55OaY2NYW0vwtqaYWFptyDKPEgqPpd3VXLmyxO03HL99nONmIZwr0Wk47uiRrrWm3c6pqhxXTDiY7dG+6rj07ia2V2LshMnpOc24RlsdZfCWsqpxRc3odISpa6Sz0EjSNAMt0FIxawpKZkjnaGU5NYY0y2hnGd1ul7oqOTs7AwRaKbqdTvAYjRkMSnnanZxEK8bDaRy0hr7Nxf1bOhFqPBGGuYnSgeH2EuC+YHQSWc+R5DBXs4W9FbwJXcRRMeJMj8hFFxUHsTpR1ASwozCeTpqHPkrFIEIs6/0Wq1sbvJg2nI4rmlQg8wxrLanS2KZmenTGJQO3nGBrOmW5LNlQOf3uNqdmyMnsDC8hSVOyJCVTEmtSbClwJiHXHfKs4sGzIcNihsh7qApqA667yWBWoQanQa0oVJAuVw2YBp2FzBLl5+71guH5MMiyuQAuZSR1XKCFLACn8DMNZV3RwSNMtEbylkynGOEwcViNiy0OfsE69zLYBMzBwHDG53VM6OMW8uQYfDRnvF8ch3iJMXsx+L1gucaB8Zwlz8X7FjWy53eedx+VGfP6TCzqrwsF3HwA7edInJiDlHMswcc+Ye6FG89htF1cyOZfWmNctJDwNgwhFvYJYg6YvgTCxuvxrwHZ8DYXvVUvvibj1x0XSmIf2eNSCTzypdC1oOr0QGyh0DqE8sGFtdYcLJz33QtgnLm9XvhdLuYmzG1snA2etNY0QakswBN6ZCGCz+mceCAI94L1FlfbOHRx1E0dmL7OI6SKQKTCmQaX5S9lLrjo8WuwBrQOQLOMnrCI+XXwC2AUfMQkLnx+m7l9inOLTAUbwdlwOsP9YJwNgHP82twGI7BRw3p5MTeeF76h5lgEHy/ukXnIWR3wG28j+zjewzIQllQEP1mc/XAetVSLZyNYeAQGcQApLSo2x84YhIuf3QcMQCpF4yq8FTEDQNGIaJtQNdAYfGIQLpCv5uqGef6NMZa6sUxnJefDAbOqQkhBr9ujJzukWUp3qUfja4w3NM0a06nk4VcndNcUm6spG5ttltdaOCcpZg2HuwOKYoYQhlwrNlZXKKuCSW0YzhImhaGVCNodSSsRGFeH7BE/fwZkXMo81hnKumA2GVFMh3hTI50BW2GbcfAadhlKgmssaaIQQlMbQbe/yc71t3BJTm0dTV1TTYYIW+HtFNXNcLqPlhZkQmUtRVFijcWZgEM6HyxNVKIx3lPWFTqRGFeRCh2VmRfkxf+v179pkBYpaS31KMoZOk8B4g0dFjBrHaZp0BGFVkqFYKzGUJsQjCWjr2nwIHcviZpC+Fi42VJUdomtV79NtnyLyXCGLItQ88sMhES7Ke2zz+klB2y/vcFb195hdWeLq9euk2QS7S3T6YTJ7JxpMaGelZyfjzgfTDg5HXJwcsbZcERRGlSS0F3qo5OUVHcRukXTGJwTkQElSJIcleQIERbOcNeJaMgdpImJVpimxNnAWLFVFdxNvUdJhalL4KJpRkRJrAtGD0mSIoWl3+/ywx/8IX/w/e9SzAaYacn+3i6/+fgXPN19RG1rQsK2QiQKkSakK33S9SVsJpHS0dUZeRr8AqdlkCRplRBYzqD1xVS0qmtanW5siOYLintpOhk21aaqgvxE8NImFyULUi68aqTUwQbDh2ng0lKfqjnFecvcvyicPUi9ZL27wp98/4/5kz/6Ptcvr2Nlw+nZgJ9/vMv//QaaZekAACAASURBVE971Ku/T7q6xdbmEgf7z2g7xwd3bvLa1S7S1lTCUyMwpQHhsKahaSq8cyRJhpTBuFxgCaURkQGuqI1BKxk2zLiZJQKyRCJjuJqIE775omtMQ5JokiQNC73zSGeo6xorG5J2J/ivehFp/YB3TBt4dDojafXIE4mvC7A1TggaMpSHRMNrl1tMLHy5b/nN7hiP5vp6m8Q7LnUyvvPuZX7x6XPuPtynm2xxba1FKgWaBGsVCRa8CRM8oYKHGIFxHcbjkulohrAGleY4gqw0z1JS3cIpgZGCyggOTgo+u3fAw/0RZzMwsgVsgA5FkvBEUDaAV2HIUuBpQGlAI4Qh+BcrqipImM72nrDBMSqDVn+LRnVAJZR1yVcHA/K8YeWNy2TrLUbVjBcv9pgWM5ZWV1jqZPzqpz9h7/khMzSqqNjsX+L2a2+xefUaKs14sb+PsJbJZMDh4XNWLu0EBpZWqOjdiQiFTygMwlRZKolSmqWlnF4348rlHa5evc5gPF54WtVVg3IekSU4a9k7OuZsNA7eTkIjnSfTCSvdHlLCaDqidC4A/s6CsTxsLOtGsyQELa2Q+OAZKaAR4Wo1qUCkKQ2OdqbZ2FyhiZKnRGpGszFHR0dc2tpEaxUmvEKikYjJCDUZ01We/eePUFpx+2tv01lbx1iLw3H/7iecHR6ysbbB9rUr0GtxcH5Gv78SZFDx3rbCRdmNY7nf5b13v8bf/finYXKatRiNZ/zq15+yvn2VpL2KRKKTFkmW0+r0aXeXUFkPJTNQKVmrS6ITtFJUdYkUBjE55/Czf+FHP/47Prl7l6O6ZiICu1PEfUbGIsv6wC6Z9+OheGbhee3mflZxnw2BDrHpMIYsS7l24xpZmmIbw+BswNHJaZB0zot+/KJoEzKEMIWCMjIgRGAEaR1CPXSiF/YCAQ72yFQjdEKaZcHiQAtUniDThKzToVaKpqkX4IRxzSLJfkEniU2Ai2zfsCJbTB0sffKlPqYoMUWFdEF6JcRF4Tj3wA12NvWikHQu+G1nOsHIILt0QjDDcVBNUVmLnk4QjcEKSSkTut0ustPHyBwp8+BnJgJoYuoKmQhUmpG2MjJt6XcUO9c2eDgZ4b0IwYitBJVpzsfn5D6hlcBQpuTlmM3eMjtr25wcPmHgKr569oRrl7ZZ7a9wOD2j0nFgYBxf3b9H3s/p9ltsX71Ep5dwPhjQbjnabUe332Jt7QrjQcnJyTHTskFmLa68dYd3vv1dPvzud7m0tsw//+jHnL3YI001Dx4/5fzslO2dq3TzNu004fBgl08/+5TPH90labX4wR//Jbduvk2Wd1E6hdEJ//Drn7C7t8e33/8WWaZYW1/CWcFsOOJ47xFHB08YnB2hteP6rSvceu3fkXXXOTuZUk5quu2c8awOnsBYlBQIrdBSkLRzhALTlMymY7RO8S4kD1flmOl0RF3VPPvyIYf3HrG5lLBy4zaJ94z3z7lUOVaVpqUEAofQIgQj9Fr0rm/iNPhM0dvapluVHE4P8EaijKWHY7S/y5O//Wu2/of/ieWlLSY1YQ0LFLgweLcNs8mI2eiM9bVlDo8TpsUMnSZhkCV18NuLz5IWGpUIXJ4iEAufwaaqMXUISSlnMyAwL9w8idwFu5AsSSMjxkMT9t179x7y2uuv8vprrzGblfzd3/8YnbbJexu89+7XcL7i8OArfvOTH/NnP/hjru9ss7f/nCzTJElCMRszGp+yLKEjM5qqYffFOdXZAL00QPeOGc/G5K02v/edb/PZ3bs4fx+dJ0wmY473djmJXtMrK5v0+h0215Y5PT4mSxRVZfnNbz7mtTff4lvf/gM+/+IeT5/ucuPWLZROkCqhLEOYrGkaUg3KG7TKaZqEqgzyxd3HBxzsT3BSkrYkKsnxTOn0epydDsltxdb2OtPZjN/+5hdsXdnm6q3rnB4fsb+/T1OLsD8omE2m6ERx7foOrXabkyPH8tISp4MhP/3ZTynKEtOE9XJzfZWmmnB0+JxJUbN9+RKnx7sU4wHTaYlKWwxmU77/gz9jZb2DRnCwd0xjCn79i3/i8uYW7aRDtrTCJ/ce8Oz5E+YhP3Ofy3ky+gXdLgA6C8DnJSbdnO32O8GRMTzIvQQmhW+AelYzFfDFV/e5ees6N27e4sEXD/n07ie8/8Hb/Pa3v6G/vMI777xNUZSUTc3zZ8/Y2dnme9/8Fp/c/5TJxNLtpuhUk3Q73Li5gnUvwAYlnPQwnShGQ0G37+n2BFmrpr/qmTVFkLbaIGHWOmWeQzHP7JBSYeWI/LohfTthpAZ0S08zOMENx3TTHG01pqzwWETtqEyDayKRwDpGpyO0TlldX8G5mknTkKZhLUl1jvWWxs7otXs4aylmJVmS0W31uHRpk6V+h5OT4+gzHYCkVAkS3cI6R248s2lJUxmEVpgkXagjkyRBJBpTN9S2pjHB8qsqK2wa9iFvHY298KOdy8TDHhcaYCEETgv2ZwNS7eiTBjIKHiM9Tgoaa2iaIFNuVAjr8baiI1MudVNGFsZJF1uVqCTFeoMdTbl85SrF0PPK+YS3jORaOSNpwLuETKd0tSTxjuPJiPF0RtOu6baDVcSobFhb71LXYcgqOg3PjkaUxyXnwxrT7pL3Nyj8OWU5RZoqqM8QJHlGptu02jmpVCjCPYNzTMdTfG0REURVEU1y3iN1sgCQnPNkWYb1nmnjKBtHR1ikDwM9b0Nt4GXoWUP6e6hZlI7+wAvgPBRP1hnm1hPGNqAUKvZIMu7tL4d+hSyOAOjPQUQlZByguqiMjYQHefG8zntG8DH0KT6jsdZyzgV2oBCLEKXA3YqLwRyYjRXW/LkPbMh5XkhkbiLCHkVYMuZMXsSc0e3nS0lcbi6YviImwC7UUP4CJnfhIBbD7peB6vBR/cVAKXr6BoKaRklBnmqUU1BBooJdz8WRB09c7+e9UjgOKWMPrgQSFZVPIXBrbp2FD+FfLvbuMrI5g497uNZKSlDgDCgtsVbjhV8MBKQM0JNQKiq4wvOfJJJSxkXUO6xLAsvbuYVNQ7jN/CJobr6wCzUHPA3W1Vhb42yC96FmVjIGc2sdhhLYherOOYuxlrIuqeqQ22OtiwpiGc87wffaE/Ny5qB8uF8cgS0Z8m7mahwfrQjmoXoWEy0Owpo0txKYA/A+hoLF+p9Yz4hINhNyQagQ81GEeAnEd+F7zZwc5ByKoLL0xiCbOlifAE6JgCFFawxTJ5BmGOFpCYGoDVQNNrHRYiJQBrUAKTKkTkEmOC8xFhoXPJmlCGoTlSb0ekukrRYyDfeLs2u8fuc2KxsreOUoakF1DI3x5Jknb2WoxOPcjKapyJM2S51l8AKpE5KkRVk5qplgOrOMRo7TwylF04RhQrR6DPXafK8Pf6wxOGOwpqEsJ5T1BOcSsrxL3krxOHSakXaWaHfW2XnlPa699jWsSqgjK3dwsI+vpzgzoi6H1GOPEgF30nnC2dmQs7MBxaygcTaq4EOmQp6EYXa3kwXyCBbvwn12wbP/b1//pkHaYHptME2NNYZES3wdWIuJVotAFonDOJBaRhmowQkRJytBYoqU0fdh/idO9bzE+A6djTssb7xK2TS4ZoSyJU4IhBYIU9I1Z1xbEux88Bo7qyntVNKolMpNKQuDKytmwwn7J8e8ODnh7PiM/cNzzgdjirIOMplAy0InOd4mlI1k5hoCYJwhlCLJFK0sJU9ySmsQBKPpYF5tsc4sGl9jfWBTyvD3WqmFF6qz5sLPTYTNDjcvLBOshU63hVKeP/rD7/E//vs/pdVOGU9OmIzHfHH3M+5+8gXjaYmTQYricSiVkK0s4ZdamFSghKedBgBESk1ZVZH56pFCo5VbWIV6Qjqn846T02O8Dx5EhuCZJNyFQXei5uxXGRdnj4tBXBdTTsLGL8JES8YpSpJo+r0u02mBdT7KdwKjNVMZ3/zw9/mTH/4x2zur9Fd6jIoZv/7qiP/8y0PO+m/hu9tc2Vjh6OCA2bjgm29e59Ury0gzW0xKAz3dRWPscM9prRbFgbNzoMYv0s6JUzYpXEhCl2HRT6Unib48iLD0CiGpmjCBVEpHhly4c0OaY5AdVSZI/JOsHQoCIUAG0EggqJzkaFBzMGzo9HKEc4HxGhd45zWdVPH+K11U4rj3dMj9owmdfs5OxyMrw6Vexnu3t/n84QmHx0M2lzKSxJIoj8DQOEPdhElWkqbRr03MB89INGneAWvRaYatS5ytcSqnETlnpeP5syFfPjzmxUnJqFZY0UIoHX+ABmmhqUNREQFPREOWa3p9Tb+T8PjBOV71g6u5SEBYvHCopI3OVxifn1C7hior8FkWfq5u0zjL3acjEpXw3o0lVlqQ9XrIXFOXAx48P0ClKX/5P/8vPLh/l9P793n/G/8d73/vh3RWltndu09R1ZyeHrO6tspGWVDNZsE3OM8IY+p5AepwLnjfFEVJP+mQaEGWSJzPQSZ4nWGZYKyjaQxaBm+vupGcnA85G44QMYVXEBLMe50u7TynbhoaHNO6wVd1uDexDCpLT2u2212WnCX3oIwlAYzWVF5RuYqiqEPIklJ0shSt5pIkQZa3uLy9jc5CEzM8H2CbhtwYjh9/Re48vmpw04rD57vMvOHtj77BYDSiGI443Tugv7LM5s3r6JU+U2fpLK8G+X1dgpQYPMqHwLtAUZBcu3WHy49e8OjhI5TQeAVPD06w+QbvfPR9KiNwaFCBGSCQEWwRqCShLGuGw+CJJ7MEKTWTsym//PFPufvpFxyVFVPAyOD9G0OFX2owwtjIz+c9sSCcT8ojL+d3GLHzrwuhqOsmBC966GQZa+shqfTpk2fgPUkWDPlns2lkmYYJt1SBKSQFpEnwv1IRpJ1L0qROkIlGpQGMbfc6ga2ehEGPzjJqa6hMg7DNgm0vZFSWIF5KNr5obObsEAiFd1hgQeQ5reUl6uo4HIMP6dbzjy6ECoWntcEvKq6XwVnI05gobxPh0XYITpsKvGBHZfQSha8dRgl8lmIai7MzKjNBKBWY3U1DbTypkMg8x2M5OT5k/9GAYjxDJRJrPcoBzmLqCmtrrBRMRcVIVSR2wrLsc2X7Co+O95jakqmtMCi2Nq5xMB3S2BpnPaY2HB0eIoeSVruFLQtSLRmMR5wc1WxvbyJ1zmQ2YTAqMUnKrffe5t1v/iHvf+fbdNfXGAwKfvPP9zh69gItpsyKgqI54WjvGY/3HlDXNZsrq2yvbqEyWLt+CZdokm6LvNNnMq0x5QQPrK6sUtQll69co6Uyhscv2H/8hP2njxgP9kkSweb2FV554136qzvMKsHhYYFE0e922Ht4n+HxMxJdxIYioZW3UUphXBNAysgoLKYTdFQlldMJzlhaWQYKJk2JHBd8cfSC3//mN+ns3ODgi3ucH424pDWdVGIyje/36L3+KvmdV5l6w2h6yuHzh1zPEjqrq4zqMaIuwXu6rubs4ZdMPv4Fy9/5UwoZBpuhLgg+bsJY3GzG4GCfvd3HQTroobY2qFl8TSoliZLoRJEkwbvMI0FoamVxTYVWQKrxLgSQCOERimCj0M5ZXe7Ta7VYX1knb2WYpmEyGHDw4oAXx2f89Ke/4MrVG5RFRT2dsLf7MDCa83fJsoxeJ+Ng7zGff3WPdjfI5tq9Vbx1rK5vs7a5SVFU1LMGiWd4PmKp2+Xa7dtcv3WTsjYUo5pPn39FYRPuvPdNRJZxOhxRVDOEMXSXVtjauUySKsbjdR4/esT29jarm5vsH7zg3ldfsr62xvvvvMVvP/mEvd3HIbxiuc9wMMLjufHqDfYOj7DGIlOLV5Ldh6cMDu9zerKHFRXWV0xmwSMakZC3lxgcviDLDO1uj/395wzPB3z7+99BaegvrTAYFrwYHYUmXkqEcHR6GesbS1RVQ56ldLptbr/1GlVdcXp0yvD0nN1ne/zsZ//M2voKH3z9A8bTGdPxmPXlZWxVMK4dH3znu/zgP/4HjE352tdfYXg+pShTEj1jc2OTfktjjGJ58xo7W7d59mQ3sLt8BEacR87JcXO2U2TiEdfB32WuyQUzbd4Qo2QY3Fn3u2u/93hrKKcWJdvs7R7iLguuX7vM3U8+5sarN3nl1Tt8cf8B169f4/mnn3J0fsY//vSfuP3KLb7x4Yd8482P+Osv/ivLa+t4nbB7OOTDa2sk0gXP/06Yfw9Glr3nljfeTKlqwXBY8/SZ43TYRuaaRKVRfxF6GRsZXnVTMm7O0Ddrlj/sM+7OaJoRp4MJZlqgEThlqazFVDW+CcMSYT3CQF3U1KXBVIJUpQirKIsppjbkqoOQkllR43FY23CeDJkUIbRoaWmZLA3Bo0fHp4xGExCaXjdFKcA5irIm67aQPoR0TgcTqtqS5hlGuiDTF3FIH0ESKSJL2objTLKUxgUQRkZwxc3BnYDIYQhlugSOREVGhXRB5aacp47KQeGC2q7d7mDKEmkkUiQMh1NWej0+2tnk0RQ+e/CQmfe4osKenFHnS9xcXuPt2rFJQ9vWJDawuF1j0RK6vU2W0w5Pzk6oi4qCGWmWYGtDMa4ZD0a4csxKLthY6fD5k4Jh5XFtg3MlaI/KU2TZ4JoK4yV5ltDutsOw24H3lsoFYNZaAyIwhRsbJN2eCPCYC5CQONBqfAiVrZ1DZmArg01SJA4v4jl0LtZHc8DRhf5IJKFOCE9f7IEDwUaiAklKqBD2vPjFwYtZzNmCSkdVg49gmQnvXVi8RfqVCz6hSooIfsY6KXKIiYzKEPA8tzSJVk2RXRiGL7H2jGpdqVmAYZ6ob+eiGJwzOUWsc5wPQxycR8p4DNJHEFqxAIxFBDbngLCMdivzoKXFUIkImofBg7PBY3Puuzofjs8HS0KGfBkpBLZ2ZK2cujF495LtRGSQEq195uhwWYYBDAK8dUSXFOb2P/Pz2ESiVCDmxM8VjzeQBwIBTmmN9O7C+iK+Aps24DNaiJfOGWgpcTHANlMpOrLsKt/QyKBGkxHYlCKgJwHPngeoEfx1mzCAlEpHoFNinEWTxDo3XIu5H7K1JgxjrME0hqZxGONiPxHpClHBqaOt4zx3IuwV4R6ee8wGZnkM/OZi+DA/7+AXbFchAqnNAyoG/M4B14DHC4QL94uIYW8XPswvDxQiICw91jbRNz38DCkCuK2FxChFpXQIe9YgfbiWFhsIX3FAYMqGZCngOw6BlRIRj0koiUxTUAqdt2i7PpltyBJNq9Wh3V0ma/fwSiAzTaoytFxBaktjgnWCShVZqkkbgdLBgmU4KWjKEIyZ5W28CL2M9BKsBXRUz0tMIxgMDdY3MA+lF/Mt4WJo46xbWK/hfPg5IjwLSilExFiSzhKdlU22tq7RWVvFakXazllqtRAC2pmimAypRzmDpmJUNkggb+Vspeu0Wx2SJOHo+JjhcBYD/Nxij0q0pNPKSbIEJTVa6oV9y//f6982SGsdo+MB9azCmxripjz3zvNShFATAV4IKmuj92CYIAdg1mF8MMd3XgRTZCWikbTD+4S8d43+zreZiTXqaoj0Fi8bqtERMstxdsad3jm3V9qsq3VSVVGWU6zznJxOmIxnDA6HPH3yjCdHRxwORhjj8FKhlSbJe+Q6JUsSakJj7b1GiAwrNAaJ1JJMQ78TPJHORyOsgzzPybME24T0P6nVojleyEnnHj3zSVsMWHM+sjIjiwkvMNbjbbAGaKeSP/7B9/nLv/hz+t02Lw52ef78GR//6lf85Gc/4/D4NEwxk3SxGVrlEbmmERYtGrIsDUbLKqFqGuqiomoaPEGKLwQkcXrV1GHa4Yk4m4wm5u5iUxCERRoXptVqjjtKtbiZhXwpBVOEbUrKi+mnUopuuwPWM5lOwo/3miztcOfO2/zpv/8z1raW8dpxOpnx6y93+V//61POu1/HLN/mxo1rjM9PmI7Oeef2Fe5c75O6Gd5UQaaMDRKMhYAoWEsoHVKk52yFsO9ZpBRkWoG3yIwgLZQB+NFChGLHN5E5G763iZ6KaZqhg1v9glWnlAzsoyRFNpaqqTk6myCTnEtbm0jlEB6yJGdrtcfjBwN+9sUJ3bfW2W63EM4GoF4aHJq2Elxak1y+1KclGr58HkC9qxsZvnII49jqdfBXLb1ORp4IJBYZsi6wJpx/YwzG1KTJ/8vcm/1Idt13np+z3C323LOy9mIV950StVmil/bSbrc9BgYDzMv8OfM2L/M0aAwGDfR0owczGA9sQ7bVkiVblmTRlEiK4lLFqmJVZWVW7pmREXHXs8zDuZFZdKPfHQBZZGblcm+ce87v9/19l/is8fE+hJklbYKzcJ7aGyZ5xebxlPt7B9zfqxlPLHUjgBTiDsyLSxsSIoPkugvkpB2NrRqcNbz26iovbMSsDiT/aWubrVmEF+16lTVCRjjf4/Kz32Syv8JenVDLAY6wxpAanwwoTMQ/PTjheDLhnecWiA9Lnn/mEo/vfsDmw4d8+9vvkKUxdnLM2sTxykuvkvT71A7KuiaKE67duMHN55/nyjM32T8cY2wZgn+koCktRVOTpEE+GMdRAA+UR8nWrF5G1FJRCrBWoFSMEAVCKxrg6OSE8XQa/LlkYBRAAMYNnpNZTtU0lE0YCtmmoXYW6x1awJUrlxhvrPJod4++beg5g0xjXC6xtcT7KEh+cWRpiveeJhBxsdahkoQ0klRlgTEN/ayDNWP2nzzi5rPP0esMqI7HfPHxx1y4cpF0ecTDh4+oZjPMdIrWEaO1NfyozwnB31Cgsd7R+MCCVjJDJD3i3jJZf0SnP+KZwZDexgv8r//L/8xsfECiJSfTkg8/e8Qb76ygtKCpA0PUWfCmdQrTgrg2TDe3kFVJ4T3D1VVOHj/k7/7zv+en//B9dsops3B6EgpLWqaHOhuWfKm4IqgW5sMa759u7ufyujYV1wfQ0jnH4eEJznmOgO0n++gsAt36VevQMGS9FCEkUZS00rC6Ld4kcSxBRygdhb1TB5mpT1Jky/ST6imGeZjckXQymnzGHHidv/x8Vslclthew5zicXYI+7P/t94hI013cYHYOI4ebRELhY5oZVjnjBFr3RmY4drhW/i55w3K3O6jxnHclChrqISkiyAhgKN1WWJFRV7MqGqLqXNGy2uIKEHhUKZmd2+L/d1NRFOy0B+wMFygKAqMsRRFTlUW6FhT+4bcFpSqYeIrxk3OpYUV1gaL7O1P8JFif3bKYrdLL+3SlCbUCUJhG0uDY0pNaSULy4vMKsM09+wcVug0xugBt775Di9/5dtcvfUayA6zomTv9j7FdMrBo8cIU4KqmZxOcW7GtDilcZAmCYenx7z60ld4+53f5fF4j0/ufMzu3mO6eoT1CQvDBTrpAm+/9A3M8zn5ySn37vyS/a27NOUUnfS4cvNZLl9/ltULlylq2D+pMEaSRB1Uk7N979dsfv4+UXRKNNLEUY8k7RIlAYR0dm4PFMAR2zTksymT0zFxmtDp9UmTlFdefx1blOzcv8tnX2zS2bjMiy+8TO9rb7L36ecc7uyzXDVcXelz+TfeQN68wdQb7MO7bP3yH5ncfp/BcMTS6hpaCiZ7ESY/RdmGpbJgducTlt54mzjuURjX1tUeYwW+EXgUadKlrgR1YxGxwHqPQCN8g6kanICq9JQ+ZInPJbS1qzF1hSLYoijvGfQTRqMRvX6fXicjTSK0FGRpymg0QuCwjSCLh3S7mtULS+zu7fN//+f/hPeeSMHFS+s8uv8ZP/2HDlevXyfrZnR6PZAhhNIScXIyo5hOwMPSINzLEzWhLkpu3HyRlQvr3HrtO3hTc+1qydHhPn/7o3/kt/7kf6AgYuuzDxgMu3R2hlTjQ155+VWuPHOT3d1tjo8GdPsLXL/1PM89d5Of/PQnPHz4kMl0yptvvY6zJR9/dhvnGrJext7uFuOTU0xTU1Ylg6TfBvfUFM0exf4xUll8XOOMpa5qGmcZLV9nZWOJ7Yf3kfkR166tIlQ4571TbD3cYjQcsLa4QlM2PPv8C5wefJ+93UOUkDzZ3uOZW88yHK5gbMVg0OGrX/0Nht2Mjz74iF/96g7v/eJDTg4P2XuyxerqBSaHh/R7XfrD51i+fI13/uBPuHTpOof7OT//2W1cbRl2etz++EOKWc3VCxt8fPsLHuyPUQIwbj41Ox8StfWUP2PRnkuRz4ZV7V557jXesgCNeerviLM9rT0VwnbrPPmsoLGGWVXwzOVrDEaL/Je//lv+7R/8IcvDBcrJmMdf3ONnQvLgiy0+fP9TvIv4+lvf5Bd3PmTycEy01mHreJ+TSUVvQSIiCc7SVIJIN1y8IPFNw/REcXg85L0PD6maReIkxtu5CYCDKIALdVNx1BygrhlWv7VANZqhjKE5nFJOSqQLbC1nocpLmrxE1IGQIJxEOvC1QKLpdhK89YyPJjS2RnhHUsdoLymqBiE9WgnyyZTRcISSik6WsbiwwMHhPkU+ZTToBw/vlh3YlBVRVCKKElM3dHrpOcOxCsGQ1bQMYJUHb0JWA8qRdrI2VdtiGhs8sUXrx2pCKMw8bNjboFSyPsi1p1h2XU6EZ2AgdgLTihi19zR1je716YiEpa5GD1a4dOMir73+Gnfu3Of0s08QRYEa9ImUZmF9jWR8yPWozwuRZlQXdJw7y0rR3mC9xDaCVGUsrlzg0ObsTI8oZ4Z+PyLTknx8yqzIKU2CICZvLC7WYA3V4S466zG8sMFs+z7Ca6SOuXBxjVvXryEaR1nkNEVJVdUcTydYEc51K+cA4D97NuZsSx/uGzIAZD5LEV4G6yUXVGFRHKNECFPzba3gW0BEShmITue8UZw1SBWdAYpWgDP2Kcn7l/t/qRTGGOYlilAtmOscKo7OBilPs17lGYA1920VTwG851ZSQY7szix/5iGsT7+Cl3MAJ513yJYp2O4MLcAWkNZ5RzhX754xY70/A5VpiSvznxPqRHHmhR5ONtozOABlrv2VzqwSVKhNP0HZLwAAIABJREFUvRPn+VTtLZYygGnOWGrv8T74/fo5GO0CIzCA4LTvSQvwemhME3YwF5RbovVjD2Q4gfQSKRXGB9sC2e4TtvUoDbYH7oy5KDxB1dXe33kdOGcbSyHOgtCMtW0JKoPNkgqWbLh2UOR8GDBYTyMFjTOYub80c3LT/D0DY5oANJoGqVtrBQIbOpL67H4CX2Zht+BpsHsIsU7hmuTZGpKI4Ok8J8adsxTCOm179mD5OD9HztepnAOrLcArRLA1OM+rCWHD3tqzc+ppO56Qy3NuzXP2EmCsaXGCgP1IH/CxBk8kRCB9CYkSIgSlKoWygaxhGksiNMI7vLHBMsVbYmdJEZQ6xnh39r4maUbWH+GVxuuIpqqC337aQekMHWfoOKj6QNLt9kiSBIECJ5hNDaWokCjiVKITTTkpELZGUTNY7BN1O0gdbBK9EzQ2AOtaBX9yWxmUF2d7jRCifQbd2T0PQK3HN7Y9EyWK4G2rkGihQphvNmS4uM5weRUvJZPTE6IyJ09SkiRF6YjhwhITZxjfO+boYBclTGA4q4gs63Dp0gU63Yytxwccn5xgjEFJTVWG8G2pNIPRiCxV6Cg5qzP+W69/0SAt3iGbCo3H+hCuI3lKDkqYDMzZopVtkELhW9q9da0cQwga2yAIbIqmdkSiPdxln9WLryEGl5kUNbLKiTwYBE1ToVzBUlbx4qpg3cfsbJ2wvbfNZJozqyzHk5ztnSeMj8bUpaVBgs7IOl3irB88RD3Y2oDWaBXk3iEVPCJCYb1AKoGyIbxE64h3P/w1jtCAOOdDwmo70X26+YUgVzFtQMlZM+xoE8XbCWF7S7UME7b11SX+uz/9I7717a+RpIqT6TGb25vcuXeHn3/wHlsHe3gJUuh2kyekdGqBU444ieikSUhKjxJsbSmL1ktWQKQ1Ao+WoeCzjW2L3SDV9cbS0tWCp9ZTUzpBmHSoNuRLSfUlSdnTaZ6ylafNZQui3fwkkjSNsSairgzeaS5fuMzv/v7vc/naJSJVYo3hs/u7/MfvfsR+9AJ29AzXr13H1IbjwwkvXbvEazfW6MkK6QI7u25qJpMxUmuitItvg7DChDTIfp3gKbanR+Ho6DkzTaJEe6h4j5qvX9qN1DpMe1DoeWjc/NrnE2ipsCrGC4V0FdtHR/z0kx3QA36vt8jGKMI5Q6I8b1xf4t7ulPv7BX/3yQF/8Poyq70Y6vB8WGExXiG9YT2TfOvVBXYPD9Fe0E0VRkjqGmJrWRloIiWp8yIwW30A2lCaSMcoGbXr8nxCrBXEuvUzVh6vBLno8vH2mF/d3+dgJjF6CDqEqtAe7HjR3kKBr2tkIkEK4gh+41uL6Nry/j99zt0PbrNQX+CZN9f46psXmL2/y6yu0U1DrEZUYoVaCB4WCbW8TN3t4lGIugoTYxVCxxBgJHx+cIxrDnj7OY1UOxRHR+w9eczmF7fZ2drk9It7iO1D3v/r7yIX3qVz6SLZ6hIvPv8itlhASkXd1NS2YXo6xovAHizygiIv6DYx3V5GFEUkSYT3wRZCyiDlUEiaMjD/lHRhSIFgMi04neY4wiY/L/Ksc5SzCdOWZW5btkhwaJ1bqQcZ2/DKGs3KgO39LVaqGYP+AjpJcWiskxB36PT7HLYhO6GAalr5UpAPS0KTpqSkmyWYImcrn4X00CwhjZcYzi7i0i4VkjjtUFcNVkVceuYyZCm1EzidotIUHXfQcYek06UzGJF0BmTdITLt42SMFYEV8MJba7z01R/ysx/8Bd41eAu//Pk/8Rvf+YSbz75A7Q3WVmFo6YMZu6sq6vEpomwYLS7SXxhxePcOf/dn/5Gf/fi77M5OOAWMFKytrTArcibjyVmRDZyxp4yxIJ8KB5Cylf+EYvxpO5bwNecAL1KgoygUiW3zYIUjzmIirc5YF4nO0FqHQZoObAIdRURphE4UkUqJ4hQVxZQmGPRbFTx0w74XhpQCkC40npPxOBSOtE3OU8drkBTOmwHOhkBzyZqQLbDl5pN4QRzFRLEkGlhm6ZimnKGFDOuyBS3mjI8oioK/19yexp8H580914I3mKRqAVrrJSiBEzDNZzSyTf+Wllh6jvd36GQZCyvrVLNTHt+9w/HxAVkvIY5jStMgI0EUR2S9jKKa0U269HpdTqsJKtYkw4xyXHM8HXNz5SLX1zb48OHnmFHCgSvIxxVpnBIXE4wI769yEikjdNphPD1lZ+8xadYh6g6RSxf56m/+K26++BrrF5/B+JjxpKYsZjTlFFMVyHqGr/fRskAq6KRdFnoerTIMgqjTJY76DNcuoVWXg80jTndPSVdHSGXo9xZJ0xhf14yfbLP54FMeP/iMerpHfzjk4vVnWNy4yfqVF9Fxj+OTKXlRkSQpncRzvLfJ1t0Pme4+InInKN/gbXomHQ2e9YGd7Z2jrht8U5OfnHDn9qcUec43vv1tsuGQqqrpDwc89+ILFHtHjCcH3Pn8Lt2lBa5evED2wg3ktQ0m2zt8sH/M3X/8CcPHD0mHC5jxjNknnzIqZkyaMcJXJFFENliEOMZMxzTOUB7uIPYe0dm4wdg6vFe4JsgPbdUwnZxQlDOcCB574QSVCBRSC5w3OIIdUmNtSFE2BnHm7AyxjlhZHDDoZywvDMmyLniJMQ113VCZhiLPmc4mSMCZhlhLlIThoEccae7ee4D30MkShLUo4dh/8phOlrGxfoGDnX1+9IMf8PKbX+PK1esMez2KVFGWgso0bG4+5MGDByysrrG6cZEf/fAfuLd5wGsvPs/W/Q949PAepe3SGS4znTlu3nqVS1c3eLJ9n+PtB6go5c7dz5nOTukOF7hw+SajlSugOjQNod50glk5xbiaF156idULlzg6GDOdVuwenDAYddFJSm+0yKC/wMMH97DqhCQJyg7ZJEhHAO+AxeESsRIIX5PnU/b3Dun3RyytrHH//iNm4xMmR6dnIFoaa7IkDV58jSGJU0bDJaI4oTEF3nnu3/2cjdVltrceceXyGsPBN6maisePH7Gz/YBpXoLq861vfJvLz7zA+tIKOw8esPV4j5PTGSdHh3R0Q376GJxnZ+8Jt+/e5TjPWV5eCH574txjmLbeaiHV8FEvUFqds8a8axtlHwAs/uvAorCjGoQINjdqPqBrf5AzjiqvcdaxvbXN+uoawjb8zV/9Bd/82tv0OwnVyYSf/O0/UJQhLPSv/+r7/PF//ye88dxX+Msf/r+MOquciIgv9mdcWEzANZiiASfQkWDQV0SRQqZ9jh522d1v0NGwDX5pA6Gw+NIirKQQU+QzhuW3+1SDGY4cO51STyukVyivMNOKog4Mb90CFbaxNGWNRuOtxxpL2ZTgBFIHpUmnm6BUkEQLH0AjJUNQcD7L0VpzKif0ej2iJMKcGrrdjOFwEIa1xtLoCEuoxwo8VgiSXhqsvyjD8yxaey1EkNV2u9TWoghhWWVRtV7+EVEcQEHdWh4FMN2hvGjPnzBErL3nWDoGkSazMtjL+wAkCgR1njPNwzXMtOfCzRd57oWXePzkiEhl3LpwiWVTcaQk08aQmYpnXMQLecFaY8mMQbkwBNe0QI1zND6EXqdK0tF9Oj3NkSmIEoH2ipPDnONaUOqUsnCkkaawDlOUZKf72HyGHC0Qr2yQ5DnDbpdvvP4GVy9fJo4jqrri+OCQzcfbVI8tnJ274sxf2bl5OBRnT8i8x/TO4yS4Fgn0CBpjcU61YF5Y7nL+la2nrPAEMPDsWWll+W4erNwCs8zl//NhNy3LTbS9q3jKCqFVCT4FUM2HIwHoPK9t5nJ00X4/KeUZIG+dRfFlC4E56WH+9aoFNxtrcC3DExEsvuZT7jDnbnNV2l/dOcvcAioMqNveuf09zoZE7TqchxMG6Okpb11/Hmj5NNNuTuZR4mmGsPjS5+aAn7EOKwiWY85RVk3oD1qfZqVU2N/a3zWQY4PtovdhgIHwOG9QBKKRCKynlkUarr+qTPuMhZDaxhqsqbGNQUcROgrqsGAd04bT8RRo68IgNoDBYVAwv3Zj7Zm12BmW4QLZzDUmyPhbdmpQogW/23nBG+w72lBpqTDOokxQvsqn1qaQwXpMKYXXEMeCsmrC7ZXnZ0R7o8N76c6BQE+LR7XniZ8D0XPAHc6u1bfXN/eyPfM5FwIrRGCr+tDr6/Y+zEkNc4D2n2ebnD2v7c8QLSCLb4JlBKFPMNahrEP6YPUhhCKSYa3L1kbHOwvOor3DmQZd1whpMLHDK4EStD1sRpzUVM6ReVCyDEpaJF5G7UCmBZaRZFmK0pKiKVFO0UlSPIq69pSNwZ/WHO/tYusZeEV/dJGou4SMMrTSJLGgqAzzzcqWBlPUwV9an/s+C0JPFYgyEq90yxAOw5/SGJyMECLYaVjv6MeKThqFzBXdEiOrCuGCRYKpSrSSVEXOk8277O1uMZ2eAA6hk0Cw1BDHEWtryyRxj83Nx+zv7zK32plNGuqqoqkrsiylyFJ63c4/Gw19+fUvGqQV3iOsR1qJlh289TQ2NOjCBzQ88hLfGCyg2pAVb22AY72ksQ0ogtm88+BrBJ6OzpC6R7L2OosX3+TESShP8cZghcKrDNe7QFo8YV0VFPs7fL73kA8+/Yx720+YFg11ZTGWkPAre/SGfZYHizgfvLuKwmBc2Ax01kpTVdoWcxJjDQgZ/EK8wzjN3buPUTqk70kRzL0bEzwEg+wwhEiZpm5p7WDl/OCjlTEAhEUxP1Cc93gDUitu3bzBn/7bP+Q773yD0hQ82d1if2+Xjz/9iJ+/93M2d7ewOmyYYWoavOCE0kSdjKgbk/R7DLKs3dQlhtAMCSVJkgTvPLGS9HoZSohWThgORdsE829r55PNAFQKpZCRorZlAKNFkMPODzPvJdZb5kl41gZJgfWOSOnzzc77MwlClnVxpiTr9vmt3/o2b771KpEW2Nqwc1LzZz+8zcPqEmrlJdauXEY0U3Ye7XFjY4U3bl1koGuwIf3QWkPV1Gf+PNKHUDTXgq9n4Wo+WBy0ImmUdETCosWcURa8Y8/ZtrQG+rSTuMAg9q6mqW2Q/fsAnvi2kW6cwDSeVEcMhiN8dMLWxPHuvQN+89XLdJVE2Zq1ruQ7L67zg492uLs35ce3Fb/12ipDDU0J1tV4JTgaS+rK0usINkaKQRryubwUKOXBOhIZrBK8NdSmLTSkatdpkN8Za0LRgkRFuvXINXgVMa4cnz485pPPD9jcK6hlD6FSELr9x4EIwTChyHFkkWLQs1y5nEIU8fGHe8TFgK+9uMrV3i1+/N5Dfvbup6TKcv3mRd4s4f0P36Oc7NJUy+iFiFr0OK4jhFwIc2ohWnDWIxOF8A2SGkOK6G1w6Ga8e3cHr5folRU7e5v85f/3CSqvuDpaYX1lEVmV9MqGZjxFrq5w6fIVth8eE3e61I0ljlOSLEFpSdXUjE+nFLklimLqkylx3DAc9FDChsZBhfc+Tfs4l1J7SV41FGWF9zWTaYFxnigOSb/GBsmIcTZ4gXk7J3O2r/aZJ8SojXp9rly8TJLGVMMeX2wdslAvsxytQdqhKaa4JCMeLZB5T+0kRWVQav4tHdIIsC6Ems0KHu895sJwyCAZcPfDT1i8cBEXaSoPUafD7v4ei8vLdBYvIPsrZNduEvf6dPqLpP1lOoMl4s4AoULYoBcK4zXWQuMdtgnPcdNY0qTHO7/9b/j4lz9ndriJkIrDnS/4++//JasbF9BJD9sYnDdE0kFVUOztEztHf9ilM+qzc/8zvv9//Qc+/Ke/40l+xASBaf2Tjo+OwrMZfGnOzqA5mCilOKvPjDVhEkzLUCI0c5wVCMF6p51KIbQnSiVeSpQLPsREwZZBtwWXcQ4rJDpL6Xa6yFijEoWMIox3GFfTOIlMUnqjEbOjw8BGaAHec0P/AKY74VsQ4qnX/Bzw5x5nwWPrKZbJvLAkNG3ByiWcPwqFbyxWeLzW9FZWmOzP97r5zO2cLTBPz50X4nOA9unmSmuN8AHkzZ0lV4pEhiGPcTXOVnTQmNY7VyLY29lmNptyejpldnpKHEd0FwfUpqaqa2TbOHaylKXVReq8Ik4i1hZWGfR6bGxc4osPP+eomLA9PWJj4yIr3SEH1SkmUxSN42KvywqO7fEhtXR4C760lHLKOK+pvOf566/w9ju/y+tff4fLz17ldOI53Mup8lOsCaGQWtRoZahpaOocJQxCShKpWOhmjHqLWBlToRiMVnmysw+N4ZlL69y4vI73MJ2UnO5tsTvNOdrb5nD3EePjJ6SZZrSyyOVbr3Pp2deJs0VOxw353i5pnDBIU0w5YfP+bfZ3buPKHfqZpZpOqWclSQyVngCeKM3w3qIRNLWlHE84Odzn7mef8PlnnzIcDVB4up2MKi9onGHpwjIbt65x+vGEk8MjHj28z9LKAnGa4rVkcOsG0YWco7sP2Hvvl3StpW8sC8bSkQJSTXG0jdUdsigDFSHiDGxJ2pT43W06yxuYvKZGY5qa0+ND8smYphyzv7dFUY9RkcCrOXspNEBxkoY1bxswYdCNNSgkw8GQq9ee4eLaKr4uySdjnDHMxjOMs0F51Q5EMY6macJQXQgaY7BNRRJVCAH9XpfJrCSf1ew9OeDi1StEUcxsmvP553fpd7psTjf5P/+P/53f/p3f4V///m8z6CvW16/w8OFDqrLmlZdeobu0yGxWMJue4OsJxwfbbD56wDPPXOPVr36bX/z0x2zvnbK+1OH9937G6ekei/2MF156ies3nkUnmuODE374o/eIPrnH22++TJJ0ubB+kcmkoGw8Ms5YW71A1unxpNrHGsf+/gEvvfo8jzafkBcN4+MxTd5QRzE+ihCig0z7CMbYumnrMbj7q4+IfYEVgvHJhP5oQLc/xHnF0dGETqIBy6uvv8zW40cY5+j2hhweb/PgiwdMpiVf/fpXWVwa0EkjZpOc9x59gJSSXj9jaXkZHUm++Y2v8Od//l3yquHll19iaWkBRWD2UObMxjt85Y23OT484P5n73LlxgY7T3bZ3dnmwsY6a1pz+9OPECLUTjyljPgyJhRAoVBTBmbf/CwNe7xsB1lP+WW2n5UqDAdCqM3cG3A+5QOcx5SWXBVsN1usri5Rljn/5fs/YGNlhfHhlKoGpWOSJGE8qfmb7/09F9YuoKZ9Du7kpDd7fLI75tlLA1R1gq1gcUGAhCjy6KTDUd7hJ++dcpIvIyKNUo5OloZng+ARrTueZDkmfl5iOxNcUdGUU5q8Rsk4XH/dQO0QZfCijGSEiKKQci5rvPEUsyJYfAmNMxa8DkF+3T7OWySgVRQsyAhhNXmegxBUdU2SJiyuLJJ1eyGJ3oXg46oOw0edREhvEHUAxgQKmSh87pBx+Hyd14GxGSm6wy6iLCimOUoHiVeZF0hl6Io5mzAUSF4EhSUu5BV4F1gS3jkqazkVNSsipW7rASsEzovgTS9DL1NbS6wU3gmsC8HO0/EJJ4e7FMawMFpkzQleqA2XakNmfKt+dGhrUW7OzAi2PFp4am9JnEOgyZIBpSiJpGI2cUxqRTPIOM2PGXQSHA2piLDFKZYCGWmS3gCddbm2tsLqYIgpCkyZhzAmaymKgt2tJ5gy2FfJOYMPcba2v9R/t72MaPc90wJTKDDOIERggfk5uNf2n6L13xRChAFuW6f4+QMnAkDrfVDFuvYZ8bg2Y0S2RKx57SVRLQQ8dxSehz99afjbWl/MWbTzPxEq1D5zOz3vz3rrs2d/DoZyDnYGnGcOmgbpOXIehj23wZqrKcXZuOdLe0BbZ1nb2jcI3w5/VPtx3wZ6tWdOS7YQ7WDgv/K7Zr4HtWBzS8rwPgDB4fosQgWCTWMdDkHTmGB5QEvi8MHyYX6/A0vRhzo8UGTPAmjnVoUe2hCtsLFprfDetr9veJ/mNZ5WOgxFhaSsK5Q1wc/2qWtRLat9brcFAUCb21EE9rI9UzcopZDWtpkP4f0oy5I61RgX/GRF5ImTCKnC9zMm9M/O+bYbD1YNWjmEnYP54YqiKCbFU5QtPUhEBGWse+q+hzpbtNfhxTn32rfhZqIFhuX8v/3518/rbubetbSM4xZsbYM5wkDTWbSUNGfgv/vS93h6TczzLOa1uhCiJei5+aJp59gKpzRWR5RUzG17nLVoD9EcBJfhPJTWoxoHqgZVYyuN0wojCdY5LREvieMQetZ4cBBFmiSOWyA6WE7KSKK1xPgKrTPSTkqnoyiLCoQjUjFVUSBcg7MNOu2R9NewMgMkiQ5hYcjAZo8jwfi0pprN8KK1Ewl87/kMBSU0adrDdBqa2QyihNpbAmc9CpZ4PtD0I+nppjFpnASrVGtoygJThaFGeN49+fSY3Ud3OD05wBqDigKW4EXIRwq5HNDvJ1y6tMZg2CGfFVRVTV2XCOHIixlFPmEaKWadhCiK+G+9/kWDtN6DKQWp6pIoHfz5lD5LRqyNRXiPqYogZ/GW0pUYUyIRdHQHoxMaU6KVopt26SaCxeGAhf4qqrfOdPFrjPUGLi8RtkQIRS0EpglhVm5ywM7DX/L5/h3Ge48Zn86onA+ekEKRdVJGy5eJ0yWUikiTDscnYxwSGdd4W2FdSAyUtSPJQvHn8GgZ/BGtrzEIvAqeriavETphTtcWUhFMtOfTPnc2nfQe6qpuF4Y6m9Q554LHmNZ4HzaBxcVF3vjKW/zxH/1rXn/5BZwt2Tk8YfPhQ+7c/pR3/+kfuXv/LihBt99HSUU5yfHWILVEJIr+6oh0eRG0wliPaUybYG+xLdjqCBtl0tLtnQgJhMFrp525+gBMBrZza4QuRWjwkhrRuFAsz31WCRIP2unSeTKiR6moZdDNJ6eiDb4BISKyTsQ3vv51fvO3vslwkFLmBZNxwZ9970N+tZvQee7rLC9cR0jL3bsPuL66ytdeusBiYrB1EXyXnKe2dWBVqWA67m0NSIRO2olioHSH6WY4+JQUITHQGbT0WEyYXrV+qw4fjOsJpuKRFCgfEjGNsdTGI1SMUglCKjwOJQWVFRgniZGMugnXF2LGZc2HDw/wUvHN51ZZjC2NKXl2vYdWF/mrD7b4YDMHDvn2SwskaJDBh2qSSyorqE4K1hc7rK6keNOgZYyIBMaItkGr8XOngBasdt603r/hfdQ6Cj7Qga7EaWm58+CQX9495tGRx9YKomVazjRBLgT44G3kXYN0jhvP9Riohm+8tEZzcsJotcfpbsp77z7m+SsDrq4nLP/eLf7+Fx3uPS6IF0oOTw7wMqe7kICsmFYPkOoy1nVQArIsAM+zqcOLIA0SXiF0F6QnShQbK+vsbN7h57eP+ebNVV54/Vvcfve/YIVn6eZ1Xn7ta3iZ0uuvY/oDkgw+//jn5KcnrHS7mLpCq5hOljI3ako7CVkW0e33OB0fMTmdoYRAa0u/l9LpdVm/fI0bz32TpfVX+OKLT5l+7+/ZP5mEZ1tHaB2RRDFaKpSzTIo8SHzbwYz3tmUkAMhWxgleSC7feJbVa89BkdN5tmJ/8j6fnO7z1cs3GFxY58HkABfFCN1jZbjIi2+9TqeTMD7coSkmNI0hPzihqCviWFMcHjLq9igag84G6MpiXUQ0XGNxdYXewjIrz3pwitH6BouXrpAuLIDSeBnhREjRtCKs+6oOMqtQDrYm1s6g2nC4Rihu3nyVF158i5//eC8U8WbKrz78KV+5/x2ef/FttIxx1lNPZvjZDNVUeO3Racreo7v81X/4d3zwy59wVE2YqgivISLYkzRVDdCyNc4L43kRJ9Xca60tlowNDBIlSLMUY81Zk6AihWqHAGCJUolONaVpiKUGIcj6AzyhQdFxhBUCnWSoJMZLBTIAra3iCITGS8+sLpnt7eDapGolRWiIW5aIsyGUKyQkz5uNlhH7FI3sDChtp+dKKZq6aQu8IIvDzVkuAlqQ2hiDQ6K0JltewJuG6fFhy7oNjY3UEhxBKklYn9ZYojjC2SDVCo1fE4YIEpCaaVPhfJC1LcsIFDTC41SEJMLTBFmTc+ztPsE07QA0DudBLIPvoMTjFXQGHd762lt8/MGveXD3C0YrQ27eusGlm1d58PAx2yeHZOM94oWYlYVlPt0+pK4lUZLitKbf7aInx0xdTWkNJonoLyzw+huv8NJb3+aVt3+HxaU1ytzzxedHlEUV2A+uQvvW+1e40DApQRwTWGdSglekOoYoRidDTmY12gukq/FNKEKPj4+YTCaUsyP2tx/g6hzratYvXKLXu8T65Zts3HqDtLdMXjomJznKRyz1F3GmZvvBbXYff4ZrDklFjqHEO4MUPjBD65q6yIM/WFGgtaacTnl8f5N7dz6nEyt6aUJXazpacf/zz7gqBXGUIICmqUk6wdomP52yeW+TtfUrXLx2neOTU55MZ6ysLJA+c42TYkY0myGNQQkXBgplg7ZA5KhVFZj73uKcIDGOJC+DdNZZqqqimJww3nnA5PQQqT07O/co6hN02kHFSQASrAlSPlpWsAhJzIlWXFi/xKULF1laWqXTHQXPurggjvpMJxOEsJxOjinrnDSJQp0lAkPceU/tLOVsQpVPWF1eZtDvsZIsE52UPHn8hAcPH9MfLRENSkarCSdHh/SiiCuXL7H5eIuPfvGPvHhrldfeeJnx5AQlI5559jmGiwvMplOK8Ql/9Me/xyuvvs69z++xsLJBko0oZ1OKgy8Q4wmL11/CdlJWFtd5dP8hT57scPHKDRYWFzk8nPDMzWcRccJf/83fQDUhUoKT8QQh3iHLRhzuHXIpTYhVzeHuJsotYsqCjfVlfvi3PyPSHdKsQyUVV599ltpEnByfMitzdCywFvJmipke0tEVKMEsz4nSmDhJGI6WeKKeUBtDVUzJsow0S0k6XYTWzIqKsrEcHhxw/+5nDPovsbxxlcebpzTGsba2Spx0MNZTFDn97oDFhRXywrK0sEBdFtz+9GM8GUsL63SzjN0njzk+2GNx2Of2x+8T65hXjg9ZAAAgAElEQVQoSllfWSPqdPneX/wF7izDAM7b6n8GfjAHTOQ50NI25q71Bj+TrIpzgEdGgVmqhT5Dfb8kRW1rwjyv6HT71I1ARl0cBR9+coc0TlHJAG8cRWmhtkzGj7j/6yd4epw+mfIkc4ySDnc3La9eWsNzitQWKR0qijiZ9vju94746XsxlV/DKYX2Df04YnFthcdPDtibbpMsNyzd6qAXHbmZUZ6eBiJLpPF4mqJA1QbdtExSa6ldg3cSJYI6orZVOEicw9mGKi9Jeh2slkwnUzq9OEhRmxrlgh+hc2DnjNXG4nf2GK4scfO55znYfUJRVQDUTYMPR0+oL6MgU8ZaZKyIs4g4jkmjmFzlNFWNVILJ9BTjw3uslCRLU2wTsjGMMcxTP41ordGkAK3awe55eI91ntOqZOwEURPkwUgFtgWqtEBYS+Utv/z5h3xw+wGnkxmqMbgmRwqHco5BYXitu8Yt5+k7i7TtevGgrEcZzggdQjgQIeAn8iaE7zoZlFbaMxr0ELbD/dJSWksUJSz0NWVtOWlqNA41O6auZ9AdMs5zjsspfdmBpqEqS/aOxtx/8JDDnX18HUAo12ZgzM/8OVj1NHNzzhQVQEgMCqCTawFMSUsCsg6l9BkzEOfx3oJqA79dYGSCQAmBI/RqztjWE1i0mHWwiQrDkrZbVLoFOUOgVWivgg2BjqIz9iCiTaVvyQlSBmWTs62d2HzAcgawii/ZmAQc62mg2reM4NDXWGdbH9hgN+YJXpchKPl8VxHQ2ii0g+5Am20/589YvdBmDLTgm9Zzwott8wIItn+0Evz2DZkP0q13LWjakpaMY552K2UIW/NSB6eXeg4St/fOGfAWXNCW6HYoJVwgvwU/3aCYC32dRKLO7BWEgqZulQaCc8sEaOs7SOJ+uATmwYtt4Jz3ZzWg1m0AbkvWss7RVBVNFZjaok3yPWM7t8DnnP3YCMGsqZDFBKcEOh4xD8wSSuDbGtYYj05aYL4d2szref9U3k9Qx82vQ9DpZGchemfnhQfbhDp7/rEzAHduP+oCthH8kc/Z0K5VNj/N2vbt4GBuxxR8jd1ZptLcL/lpNq13of4X8pw5apxra31aP9tW1Sbmyl0RsBMpKWONiDQu1gijiGzwDo+VbO+Jp6pKtLFoC8pBJEB7R2WC0i8AyhatBNqAV+F7W+dCsGXLwJ5LhZ21zGYTNjfv0x0tMxgN6cYLLI8SsjTDAE8ej6mrAo8kynp0R4s0HmxjSLXEmqBEzlKIIsHYNzRNHWj8T5FkaNdWFCmSOAo9s3DU9ZS8mGCqGXVVUteBKa2lItIpWdoLlnLeUzfBe3w+aMJZ6mLK4f4Wk4NtnKmI0oS0k6GjiDgKZB7nBF44oliQdiKEHtDv90K+hjPUdUVZlzRNhWlKJvkMrc/Xwz9//YsGaZMo5puvvcHV1XUW+xkCT6xT0rSDFGE6ZE2YrFRVzcHREXkxwQtHEndIiZGJxjQTTvcf04kk+WzKcGGReHiBvWaVU7tKYwVSJ0QiMJ2aWYWrG04PH7P//o95tPcR1uah8Nc9OlF4wx2SOFsA2QWRkJcNZZ0Hn1VvA7sTT20dUZSSJsl8uwrm1t7iZADp5iwQJxVeR4GB5dvpv3etFCFsWELMPQDnm3sUmi8ZHq5wgLYm0y5MKa5cu8q/+f0/5Dvf/g6LK4scnR5ysLPFF5v3ef9XH/Hxx59w9/49jPR0hn10GlM3DQ4b7AkSRW99he7aCsQaN/dzcsGcuygLLB5rIdKWTtppGV7hOqU4T9UMIRIh8Vsq0SYQCqSTNK3ncFXmlHVNt9s5sz2gnfjiRDsgajfaMx+9+aw8NMhSREhirl+7xu/89u8yGPUZnx5iG88vP33Ie/fHqCu/SXe0yqAXcf/BNkujEa/eXGMhqjF1EUCPswmzA98gZZBgeOkRInhDSRnDUyC1a6f0WaSJpEd4wzwNs66m7cAhwRIOFB0n4WBEYG3ZMqMlIGnqikY6RJTiRfBPCZYZnoPjE9JYsD6M+MbCEj+9c8wHnz8CV/ObL2+QKEciDC9f6nLarPK3H+zx60dHaAlvXF1kcZDiJNS1ZfOwZFbkvPXiEgs9STkLOiZrobQCaQN4IyOF9pz5RRkTxPUSj1ZhGmy9orLwaGvCB3eO+eJJSW4jnIohmdfMugWDLB6DwOAJ4KkXjpXFLq9dknRdQ3dxkQjHd96+xP/z13f59ef7fPWVDd77ZBOZddgtLFvvHVHMGhQpsY7C/VcR6ULMsN9lqZuxOIrJ64Z3f7HJpG6ZAFiciBHe4Zqa3EhIR+xMGn56+5g3L25w46WvcO9XP+P9Dz7g6DjnpRdfQ3UW6PS7ODMjz6d0ewO63RElYW0LaUE0SE3wlbaO2hRopYOMQjo6vYwbz17m2o1rDIaX0d0hndEy/ZUreJVgnCPRGqVjIiGJpA6FspmzAhzSy7MiIbxaoNMHMCZL+7z21ju88tY77G0/IBcgnqt59MHHXBofcnXjUmBwdnvEUYJXmuHqZW49/zLF+JBHn37A1t37LF/YYOnGZaq6ZOuDj7Anh8hM8/I33kR4wejaTbKNyxilEGlCLCJ0lCB0hMHTWBfkU7YFkNvSfL6PR3EcSKy+leDh2tACj2sqvPCsrC2TZSlN1aCV4Hh/iw/f+zm3XngrTIRzgywM9SwnShWDQYfDRw/4x7/6cz781c84qE7JhcfrMMWfS6FEy2AI24xHSh2exdZfS7YesGVTE4kosGJMQ5ylLK4sMplMWyCgtYVoi0kpI0Ss8JEmzcJhLrRGpRlRnGK8pzG2LXaDz5V1TSjyrGmLrLagR50Va1LIFpA1IKBpE7dVqz10nF9LmCi3W2dYHm3hGE6jSEqyNGPcBjCFfVS0ASsBONcyBmHbawrAsJeCaNDHTSeYpiSRsh200BbWPrCghCfLMpQWqCShrpvATpzLHdt1qqSi9oJTPKn1dJTCSkXhDNqH4aSKFNJ5kigCEZQzs7JEFwXD4QCVxYwnE1xlOR6PGawt8af/0//Iv//f/h27W4/56Fcfk3V7bFy+yJN7TzgoJtxrdqhlaGycbbAi46RpsM4SdTp0swEvvv46t17/Ctdu3uDy9WeIOgNmhePwyT5FXmBdawuiCCoJKZn3WVoJhKuQ0qOEar0vAzsrSjVpktFNh3gEs+mMvS/G7O0/Zvd4B7As9jtksUfEkuHSNV58/TdofJ+ks0ph4fQ0D3WAEEhbMD06YmfrHke7d1FySqQapHBYCbOiotvpkg0HWGNpaoNGIYTBO6hmFceH+4xPd2myDleuvkZezZjNTrj36085PRhz/bnncDg2H9zn/iefMxtPGK0MuXL9CqOVJVbXrtIdXWJyekRxuk/RNDxpDLOqbNlbUGOIakvQPAmUDQGq3oemusTDbEJ+uEvjI+qiYHa8Szk7wtop02nBwd4ulamQZCjaMA/RNsLeYV0DtSERiudv3eD61ctUlcMaR1l6dNplNBgRediVO6hIkfZGTCbHKA35LDQMgmC1Y+oa0w4WyrKm2w1p4wvDPlVRsvl4m/sP7tNoyWA4QmsdZIDdjAsXN9Basr2zi/rIk2VDuqNVRBwzzguOdndQzhJHiq0HD3j88AuW11fZuHqFujEsLA44PtqjEyumztLpDvnKN77K+so6i92MRBlmkwMiBfl0yr1P7nCy9wjvDGsXrrJ/ktMbLHJy8AXrVcm1Sxu8K2F2OuVw74ir1zZYWOowGFyksYKpi1levURtIyaTzVCb6JhO2qEuSqQpULGDOKKqCtJkkbqJONg7wDaerN/l8OiAvf0jnBNknS5SKBaXL/LqW9+hzieUxSkP7j8kUYpOmtLZuEC320OqmOPxCR//+lMeP/guZV4wXFnhyf4hV7JLdLsDsuGQ/uoC77/7E042H3HhwhIvvPQs2w8f8cprr7Gyfpn720/40Y9+yPR0GkA/OZ9RyXYn9GeMG1pARSiB9OocjOWcUYg4T5Wfg7Bz2fXTVghP0WzPmVotkJVPC65evsb4dEw3HRBdVJycnFCWMxYXRrz52otIJTgdT/ni/iNOJxWRTDm5P+X2pGKxhOcubNCNi/D7KM3OoeB7Px7zg5/GTJuroBOaxuDEjOP8kGpPcJIf0gyPWbyVkMe7yFzR2Iq8CCxMZRz1tMTkZcsw1S1pUmCMoyoalFJErapLtD2MwSE7MSIKihDpQx3vrEVIj0ji4JFpHd5brPE0tsYKz+HRETefvc7JZJ8yr4hIEFJT1zVV09A0BbEM9hMQbA06vQ4KSRmXQcI7FdAEFaEiAhn8NjtZQlNWNJU5s30K+ErLZJQCG6rNeWcR/iUcua/Z14plp9BWYI3Dzr+Lk2G4LxT1ac7R3j7GK5IoJlKODMHFrMOrnQFXpGRkXbA0w6FoAkDrBMoL8BIrCH6ubXshlCcSllg5nPKMT3KE1GRJTD0+xreZK7U11N5h6ipwXsoSYS29bp/y5Jjd7U30pTV83bD1+JC7Dx6z+WATU9VnoFGwkD0HJZ/23X/6FUg0gso2IBIiqTF1cyaflgQ1YSwkJS6EGvvwnM2fiwC8hwHtfC3Mn6c5/40WpLM+KGFUW4PhXRvU2tYWLRlHtWSdLzEUfahy5jVTOzduQ4NCTSJ8q6xtQV3Rgp6+JQ7RMl5dW5c8NdNh/hdtS4jwLcsWAoDoPV8a4Ph2mCF1AHZpAV/RWkIEwFKc1fLM12RbP4X7F9YPiJbYFLxvEXPbh3O7P43Ey/+fufdskjQ7z/SuY16TprJ8dXe1757u8Q4DCAQHlgBILLlahiIU+jcKfdEvUeiDVgopaCBxl1jEEgQJNwPMYLzp6a521V0uqyrda47Th3Mya3YJ6TNzomNiarqyKjPf95zn3M/9XHcMG/chnketi0YNpMQ2Tfy6MwvBb/F7yCRaEjEhUifTl3ULR2QMhfb41sXfwycTVRA4J7C2RWtFlmcURUGeZVHRFXGyVyqZalq1EBPtvFBKzlKpFFlWEvw8xK2lrasolvkY8KmQWGOwWlJbh6xjk3ngl6KrVwi8dzTGkGUq4VniFJOQMUx5ERyW0DbzxoEUCqEkztuI7JEpBya5HCRRjGuNRQQR84+IC6JI5iyZgtlc+kzhLOw8OuoT/jHEJr5Kn59QOk4Vi4iT4UuZF9Fl7FBSRE6vsYn3m+7bkOr+kBj81pKRLmySucxanFIIldGUOd7ldJxBGwfWRv5z5tAyQ7SO4AwST4ZGx1eOVZpMSqQwi2vSO4+QgqLMCC5iL3Q2N9YRG3pBstTrsVRm4CuqU8fO7ASUoOz2WN9cwbQtTVUBkBc9lgcryGCRPmI3mybe78bGfsSsaQmKhYt/ftOftZhivVmUBWJtFeevYr1kfX2d6XCf3Uf3qNoKtERqRZ5JcgV4h7MtEVYZP+O2mTIeHXJ09IRJNYnXMyrqbUR0oiOiRpwJKfNcUwpN0B6rLQKNKRRdp7E2x5mCajqKE8j/H49/1SLt5uoa/8MP/oxCSISr8dYmZkvssgYP3sVxo06vT9ta6nqKzjX93gC8ZDSd4doZh7vLTEeH7A8h0znH0y6PwnmGos/xZExQGotjFjQnXiCMwT34FHu0QyYcWaePxERLtxcEmdPtr5J1VnFE5V0JgXeOPCuom5o8yyg7BaORR6l4MUemaEIdEJPypIobhXNxHEFrTds2UbyUESAtbBR+nY8j9vPRqti1dHHTCxGIL6Wg01H4tmWl1+Wll17gL/7dX/D6a69T5F12Huzw3rtvc3j4hI/vfMxb777PtG4pBz06pUJkUUTJkNDpoIoM38vpXFhH5RnG2sQXczR1zfJgAMExms3wLm4QAonwdrFBiiS+mtTVTP2a/2KjccFhgwclYwBS3dDr9aLTrW3iWLg8G5mYj6dYb6No6n3cVKVCSY0iY9Bd4Uc//FNeuHWbaTXCesf9+0f87S8+Z7z8Et3eZcqi5OG9LyiM4Y9ffYZLg4CwI5zzcaNMC4BWEu/TJhXmTjOPkg4RWhBxk44MxgytNLkSSAzRhwohWLyrMG2DECVC52R5gXctD3d22FhZpbu8RJCaQBYLZQHonJmTDEcVFzY30CrgpcBkBbmWnDt/kau9Aaqzzt+9s8dbD2pU55Q/urZGcDW+rnjpXJfmuQ3evTvkvYenPB6OubbRQwsITUW37HJxexUhJMbULC3ntG1gNvURtBvi9a1l3GCdsXjryLISoXKsM6ACVgju7k14784Rdx7PqEOJV31QCWmAItCCj1D0TBq21gVL/Q73dibURhJM4O1fPkG8usJ3XlyhVDAaTnnm8hLPv7DNrz84ZH/S5e7dmnFzig8lZA6pV1laGaDaA+xsn7yAm9vLvH77HGbSYoNg31ouX97m04cjnItFXRzHklRWcn+/RoscynXu14Fmd8w3L7/MlRfg5N5HhOkxv/67H7N9Y4ebb36Tm889SycreLzzMXnRZ/nCCuPZlEyfsUqzTCNFSwiGLAeddVha7fHci7d59vkbQODR7i4rm+dY2bbJCR7HLvO8QOkoIgcCVVVTmwab3AGLYutL7of58JVA0i2XuHD+KuRL0F/j1re+z97GJpOjUz7c3aHs53T6/VjcRL8LR4enXHQClQ+wM8UrL3+Diy++woXnl9nfH/L00mvkIVAOuuA9B3v7dLcu4HsDrGmwwlN7QREyhCMmjXogjUUl6wPzRM6yUy7u6RBIwPw5GzBwfDzk0Z3fMzl8ykq/z1FzHHnZ1vDe2//E937w77hw7gqND7hMUqyvkncyTu9/zn/63/4XPv7wbfarUyo8VsgExQ+xnfMlNxVE10cIlqAFm5sDrl7ewjYtTVDs7O4CAhUkFBqlJbPxGCVF4sk6pFaoPEMWBaosIPG4dBZZX0iF0hlBSsysiiNTqatvrYlhmFpHJvWXRsEELEbTFo+zSGQIYtEMC1/6mgiBrCgW62bbtgvsig8hsjePK3zaayTzaQxHkc9D0Gw6REQHzjzEoejm9NeWaYYG15jEmUtMOiGSqyA5cAM44SA51WzawxAsCl0XAhNryKnReYcOUDc1wgRyIRA6I9M6Bu9Zw7SqCDbui1VdI3V0FOuiYP/wiLfe/i1/9mdbvPnt7/Djv/4bdvcO+O1773H7mWdpVGBqWsaiockC3aUeE1szbabQ75OvbfG11/6c1771LS7euo0J0d36+MkxTf0UKRRZVAXjHifnh1EWacJSxkCG2MxsUNqhpI7CfxD4pmE02aeaNhjTMhqNODk8ZDY7pegVlL0SmRdcvP4MG6vbrG1cArlCNWo52T1A5QV5ljMdjzgeHTA+ecL45IhcB3I1pm3GiDw6s7OypK8Vuc6wpgUlyHVGmHMCZWBjY4Nz3/0uL772Ak+e7nHpyk16a0u8/9tfMd4fMh6OuH/3HtY7RqenBKG4eu0qr371Jda2t1jZ3ObSMy8j8wHVdMx7b/+cpwcfc2oD46ampuVQCTaFYFlCz9ZkdctAlxSZQhUyOhHygpG37O4+oO4NqGYTRuN9JpOIOzgej9h9+iRyw5xF4dFSIr3ChujGy1XJxkaHrbVlttbXKTpLqH4XHzoovcTS8irL3YLQTjg6PiZ4T5516fYcs3pM3Rq89ag8oadERpZ1ybMOSM1sZiny2AwfrCzTPRlz7/5jOoNlup0Ol69eYXllBSEkR6dPOXj6hPObPa5sbVKHljac8MLLL/JPP/sH3nv7Lf7yv/0LdKHZ399HSs+rr7wIOmf30RPK/hp1C/d39vnqt77L1qWL7O09hsxj2hPqvZbxwR53P3mPd3/3Aa41ONugtOTR413u7zzlxjOrNG2gbirKLKdTKo72Dtl98IDrty6ytblMkWvqVnA6nPLzf3ybrQvX6Q+6HOzHa7vb6aaGs4ru9tBSTyoGnT628JjqlPsPHrC1tYmSHcYjgw+O1ZVVOmWHvPBcv/USB3u73PvsfZYbyf7+kIsXNul1+kxGDU8Pn/Lr3/yWJ0/3UEojBTx37Vmuv/R1nnnmGUzTsn3lOh///m0e3/0Q1U44f+4ya+sdzp1b5R9/9lO++cM/Z+PSRSbGoMouYVwvRJDoDEy1Z2ooCZkCYnw4Y2um9XbuyotJ8YmGI86wB3M3YsTgJAFTnI09LyYTgMlkzOeff87NmzepqhqluxSlpdNT/Hf//Z+zeW6L1lQMBktU05bfv/Mxb//6XYbHlq64zONHM/7qP4x57uYSxkwZDj2f3jF8cr9DI68S8iViDoJCeM+0OuFkdoo657n59XOU256sv8rx7ISTo9PoErUCWzcwM2QuNoIzoXHB4IxHqxwRZtimBR1xV5KQBCaJyjJccny1dUs9m6EzidSC3EXEkyKOj4b4ZuMcPH2yzxf3drDecVpN0CLmbjgRw2WzXom3Dp+ah0JJVBmntArVwfl4/jHTBmwSkLTCJP40UiC0TiJHbM5kucYm/rY3jjQvns6UauGYP25rCjp4F7m1IoUg6xD3b4ju2mWZEzIdp0u8YFl4Xhus8FrRYS14sI4mxJ+RE8XJQMCl8f9IxA3JuRitCl5BrqOgM/ESgWb38JTHpxUmK6gbx9gqKgt1KykKWFvqsDzos7QywFvL8cEhEs90MuXuzi5P908wBiBLTXCfnLN/WJgFzhzjgQVKKU4RxbBunwQ2kfASLom5IQlKmc6jaJGck1E59ITFfegW4qk1LUoq5IL5KWJDExkFQGsTSkGxKNfmzs05RimJX/GcNed0+sX/m3t8WDgo0+SZiCLMXFiL78ncvRoW79M8c8CH6JQUSi7qsTk9Yd6fmTtFI04gNu19MiPFKTCXHHuRX5tl8TXgQ8zUCeBTGPM828ClppAUKmoCIk4Ue5/OzcRJB+sDPhiUgspaWmuo6prWmBTOFYVjEc5cvUGqiBskTkfG6dno7BWZOnN1hjhdorVGOM88N8SHdFYmvlZrHNCmIOKQ0FdnDlFw0czGXPcOCasQ3e/BO0SIOkGeZRGx5/0CoUVwWNvQNCEGfOZdjA/U1uDSusTi84+fpTMWF6JY3EhFWRbRUZ0+f5OEsvlZynuR0IqxjiNE4X/eh1NKY038HqUS8zwJzfHvpAZdMlTM94N5fZ3+avx808RlFHglQsaao21NvJaJGkRIDnOXAuCMMWdYsXTFCjlHmQS8iaLuGfNXxCk9pXBaI2T8t9caFUiivovNSiK3OBPp/cPjFVgt0Ok1Z3kWURZFQTWbJlSUiH933kwh3RRS0u0vMRgso7M8id6e2homxzOO9k84PjzEtoZM5qys9Ol1++n6kSljKYbbNi20xjE8HWFsQyYcIjUM/GI5iyK8MZbJZEI9O2FyOqZtWoo8p+x0UkKBw+KxwtGairqaIUQBEryQ8d6ppkxHB1STQ9pmhNKOLFdoJSCZjCpn0wSxAB8DGXW6p3SWU+gMKTxCeLw3mLbBmpZCCUyaJPlDj3/VIq0UAVuNqOoZ3tRR5U/dLq00PkQWjc4yRtUIiIdcOzLMqhHWGKaVoVQKlUkq12Jby6hWPM42OSg3OW0ibxXvadqKU6+ZthaOHmAef0wmZmR5dAaGYAkujtfn5TJFZx0v4liNV44i18zZpMLEFdt5j3XxYDofqambJnKXtEyj8/Px07Do2hRFQdvEWyPEXSGxf2KRo1SOaVvyPItdofjUZFpTNxMyrbl6aYsffe/7fOPNP2btwjkmdcWndz/n448+5NHjHT794lM+2/mCCkO52qXolgglscERvIuA6G6OLHP0Sg8KHTeFlDhobXRElUVBUymCdZR5l26nG+378+5QGjUS6oylshgPSB0gqVT8LFWGEBo7rcmynDzPCcEhRRE3ca0RSmHqxGCZLz7pJg42davS5v/sc8/xta99lV6/j/OG8UzwH//xfU7EOvladP4MhwdMTvd449Ylrq86pJ0kCv68O5qYWS5C4H3q9s2qBik1eScD4sYYgscZgyokRVaghUPiEHici+KPkpa8E11DlbUIWZApQb+bU+bRqTCeVehCY4NEZCV1yHjnzgN2j6d8Z3mNc31NaAxZtoTXELSktprjcUPrPE71effzEaVXvHwtZzo6ZHlpnee3Byz3e3yyN2HWVIxnlkG3x4XtPmv9glxJhseeRgsm2uJ9oGnayH8S8TV5H4Nl8ryg1yuji883lHnOsHb89u4B790/4miicXo5nWoUwkVRDq9Sjebp93O+/saA15/JefLE8PjBCY3MEVJgrOQ37x3TTKf85bcvcSIzfv5PDzmadBjVBe99VhN8hpeKXOdsbPXoDkqyHgy/GDLa3SUrR9xRPXIpyVHsD6fsn844bTOCl7EDB0DkyTiR0bYKI+NnJrI1nrYZv3t8yhvbb3BJlYw/fpuu84RqxujkgJPxBo2zbF24wmDtHFKVtO0Qb6vUDQ1kuUaKWIB47+ku9bhx+xrnL51jahqcNWksiiTqmIi/UBFiHgClFa0xNKaltXEs579mE50V3PMmSGyATKY1suiwfv4qWanZeknTDk/Y/9nPeXR6yLnVLcTplAwLGTwZDnmmMXSQeJmz93SP9ZsVOlvh0cExVVGwPFhh5CxPdnboliW9shNHDgWYuo2FS3JLCiEocp1+3y8t8kJAplERbh1Hi5zDpMThEDzG1PS6JUXR48rNF+gPlvnp3//fuDY2wo72H/Pwi0+5vnmZ4fEpupuxtNRn+OAL/vGv/z2ffvQbDusJM5EOQZAOZvE9mrs9/gsniYBer8uNa5e4ub1JieD+wZD9PQlaR0Y1ILREFcl1oBW51mRFDpmGPMOJODVAACfTz/IB25oY3hHSQSCFNwRYcGrP3qJ4uoh6bEiF45kg7xfcqfh+hbmSkJwgYh6GkApUYPH8HoEWgqzs0qRml3CeXGo63SW8cDRtjQmxOJyLu7GolrQE8n4XV5W0Tbv4rKMZRKQmXOy0z4N1Fn42GYvXdH6aX7EYITi2DR1vyAVx4iKeorHBR861jO4B7mkAACAASURBVMgFlWVUxjCtKybVjDzPuHrzBijB8PiI3739ex4+eMLa6joy7+CN5/GjJxQyp+yWzOqGia5ppMHnEqdyzt+8xte+9S1e/crX2b56Cy80k9mMuj6haWZYOyP4Gg84kcUDmFDg0v2YOvpSZWduEWNQEnKt44RLAHQ8qLduysH+Lk3dcnJyzGwyJu/22bhwlUvXr3P5yg206lJPA+NJhvcVzrUEO8Eaycl4xPHhE+rZCd7O6A66rG+s8fD+EZPZhI7PKMo4gdQpVzg5PiYoRV5kcdpHRna/qRrGxydkeUHZ6XP9xoBM56yurfPsCy/xufuAvd2njE9PEFKw1F/i+vO3uP3Cc5y/fAHjJYO1y3z46Q5lZ40rV67SGVzAqbsYpfAERqEleIcTYIqS87duMjmccv/+HsuNp28VoruEW1lCrK/SiMDjh3fYO4qu2eBimNnB4QGzagZC0dR14lAqpAsQalaWN7h+/TaXts9zerzHyfCUwblrbFy6hcqWUbLD6uombTPj6OldvMoQwRFEAKHwXpLlPWrjqJuWLIV4ZqqDdxHxNJlOsG2WmjI5G+urjMcTHt1/wOrKMsPhEbNqmppQOd5Znjx8zGvPv0CnU/Lk5Ij/9Pd/xy9/9jPMdMaH77/H5WducO/eF7zzq1/xrW++yWBtnaODU1ZvnGf38S5VZVhZO8/5K9fI+32OH30B0tEtS6azhudff42dhw9pplOgy+bWefae7HP3zl1W17fpD1bQWUG33+PqlSscPz1heDRifDJhc3WNybQlywS9rseEhs3VgpdeuoLyYz746HOWZRRNj6Y1zis6SqCygroOIBzT6SlCeQ4O9+j3egipMY2jyHPWVlbZP3YUy+vsHY2wokfZWWNlfZ3xZMaHH9zhzuf3OR5NqJqavOwwWF5m++Ilvv2Dv2Djyk1cUXL14gpbGyt8+lZFPT1B+YrLVy6wvraC847LVy7jm4ZHd+9y/tx5eoNlfvWz/4xzNXNnzVxRifWpWLjx4iRUrP2ETC6hZKSYr7kizN1QIeZPaJVCXZNkIb/EKbRnYb6kfeb09ISdnR1u3LrJdDJF5x36/R4noyH/z9//mNFkyupgjeduv8CrL7/Gqy+9wj//7Bccnoz4yle/zz/8h/+dn/96DyEkLqwQ5DkalnBk0cmKSFgdy8xMkMuKpWcGtEsVBIGdZTw9OKZ2llJ2YWawY0PuBbgoyLRtg2kMwXlylRFSM0QLifDJ/Sgj+6+tozvPtm7RP9S5Rup4kC5Ln4Rqg9IZWVkgtcLUhoc7D9na3qCua6S05HkWG7k6uiTbpsUkZqPSGpuEL9XJI5bBKpxT2MrE3AypQEb+e152EDKKR6S9zzkHIjoMgwfhPcHELI1oyIhdttoahtaCyik6OUqWLC9tkWcdGtNQ2xo7qhBSU5uIPlsn8PzaMi92+2wn/vyRgRkRj0aQdInoujkvVQAypJooROHUC0+QERXk6xbR6bI/GXNYObqZpGpbxq3Cy4ygcqyzFHnG6kqPXi8ny3rcu/+QnfuP0VlGt9+jHNdMTuvkxA0L5/D/r0Cb9q55rWCtAwRKKqwxtI2hW0bHphekEO+zkXof4rQpsBjzdtbGcxrxc0SqiBGJv0zE4oWQJuxCmhqzi7M0SSiF6EiVShE4cylCErNCWGSeiDSCPa+XfUi/lThrvET2KQsnZKwNI8M6xQ4gpSIQMzfmDt30JpJ09sU4vpRnbFmVMIRzHm6W6ShmqrnofOYAjGJdbJ5bF12Wi3VKxpAnqRU+iVEmRMG/tS2mtREXEAJ11eJ9oDJtRKKlOlGQckO8Q6dReZXFKVDr545ZHQVIa9E6itZepLyDRS6KXDSkYxWZ8Apzo0gA01rq1NCZM3hZuFXTz05c2vm1aP1cpI14R5Hcs3MxeX5thiDieyGiOYKELGitobUmmtiUml99kBokIkTMlhdhwciVUiwwDiHMa+uIVVRCn02lJZNSRPaexTLPpyoWNbU/O0/MHzKdbeY5OvF2T/fY3MnrHTJEpvAcrSMFMfMmnE0ALJ5XnDUPAUiNBrwjOI8WMukR0YQ0RyqAAK0JRiG0xiuNz2LWSbyHSdtjnDK1NhqqvDG4to2GoXSNCxkFyKUsRyvFdDSOgXSp5o+2n/haC61wHowLSC3itIYKlDKGvNftjOF+hXNTnKvpr22RZdF9LtJkOWGO9pM0bcN4Osa6Gi1cOveExbU5z0sSQuJcYDarGZ2MmJyOGdsT2tER3sZwU3ygaQwHR0dMZoZ+b0JR9EApnHeMxycMj55QzY4ROHpFiSoVQUgqkyZSINWJCjxYG9e8Ii9QUlIUOd1Ojs5UnKRIGVo6Kxbe3z/0+Fct0pqm4e7HH3JyesR0NmI8muFCcp4mjl6WZagsJysLiiKjyKJjKHiLNw1N7XBty2w24unwgMP9hmZlmfLVm0woqKuTmPKocpA50tR0Jk+Y3vkVsnpCJl2yz0tCKxGyS94Z0B9s0u2vUDVxLKff7bG+thQL3lmzcIgaawkBer0+zlmsNagQyPOcsxHbOAY/TxaEePPlOUgVkz+rmUWqaCNv25a2bSnzjE6nZDazWOMJPgbabG2t8YM/+Q5/8s0/5ur2ZYKQPNnf4979e3z++Qd8dvcLPn+4w8HkFJEpim4/dp1kdCUHE3m/EUAuyXS0qeM8QkQujTWGuqoxxnDv/gOkgE7RodvpkSmFtyaNtEdRwROo00FVpY0ppIUwJJ6NC4GiU1CPZ0gl6fW6i2shLghRlI24hCjWx8XkzDcY5t1UIbhw/jzf/d53WFodMGsbLIr//Kvf89Gxp7x4i83tGzip2N3b5ca5HrcvleRqEpkw87lgAo21CcJNurbi8+daMRffpQRnGryPY6daBHARNSFkFNSUVGA909MxbVuzsXERLQS2qcm6HbYvXSZ4wbhuk7AiICisUFROMKzg0bHgp+/u8P03rrOeKwosOss5njl+98VjPnsyYnNzg+5giZ07T/jlp4/Ji22ePX8ZLz0Sz6UlOL+yghPrSOcpCkGmAu2sAQeCHKniWH1VNdjWxaJFghIyNUbyBLsWKAXTJvD5vUN+e+eQu+Mcm20SSpWcCh4RdCyOgySXgZVeD2hpmzFUjqOdjHObfba3PJ89snjZRSiPoeWduxWHw7tkhebe0yaNAxUIbSk7BRe2V9gcZFzejMiI0aSGfof83GWefHKP2cljjk4GhLwgRp8VsUIPBjG/zhPzSnkZ3etS4uoaQYPKOtw/bTDe8ealr3EpX+H1G+dY3r7IUxyVN2xeu8Xy0hLIyN3z1sYRB2NjwZsSXKWWrAwGXL1+ibXNVeq2QosMZyz9pQ16/T7GWqaT0+hMFrGjiZRYb5nVdWr6sBCD5gfM+WMea+IJKG/pOsN49z5+NqW/uoq3lt7yBZ79k3+Daz33f/mPdFtDRyo6TUUdJM5YTFXRX1nl2a+8znDnCx7fu8/2pQFZnWPzkpmPI0OrV64ihacispsRkizLo4AoodAqdastpycnOGvQKpakOEOwNnXi/VnwHw4lJbNqStNUXLhwga+88RWKN7/J4wef8/77v+Xxvc9xXmLMjLd//hNubV9DZwW5Fjz65AN+/n/9r3zywT+xW48YBbALftP8ceY5jYVScvISIsqm6FAUfUbjGp8VyKwg73Ywic1XFBmqzMmLHJVlZ2FdUmDnq4cnrps+8tTmbC3vfRQZpUxIhfnom0rJumHB3T4LufHpMDD/vNNB56zGTyEdiSk2/yKCuq5xzi0cHot1NcD68hpbGxt8sXOXWWs4t7rB6y+9js67vPvhu5xwjGtrnDVIIcjzgqZpcM6ztrJCFjy2njGdTMBBLuLP9cGjhFi4aoVII3jeLZKdtVQ479NUV3RxuGBpPOzPxqhOl0xINJJMKYy1jKtmIRK4EGjxNE0V99Zas3R6yvbli3SNYTqesffkgN3dPbRQZHmOM5bx6YQgJUNX0TSS/vISz77yLP/2zW/w7OtfpT9YZVq3HI8nmLpFBI8SgW5WIjpL1FJiTRMbvHPhOLlkghfUxtDpCFrj6ZYlWkmKvEBKk0JWokvDCUGQltrUGCfYuniF7QvbnLv0DP3NC+RlSTsyHDw9wruG5aVAcI7h0R6Hh08wbYUxU2w7JfhA2elz9Zmb5J0u93efcv3ZizSzU6rJmKZuWOr18T6GZLgQcKaNh1qfQi2Dx9UNjQvITOOVo1OWbF+9xtJgwMnBEfvDIzySy5cuceHKFiovcBYGg02uXH+J4QefsfvoETeu3eT89lUef/Z+FP+DQ1qDEy3DYJn4mpXS8dyP3kR+sYfbO2Z/eExnc51Zv8fR5Jg9G9gfPqGejWiamrq1nJyecjQ8iTWPFEha7HRKUfZYX13n+uUtrly7hc6XOB1P2Dsa0++v0l/bpr9ygRByyrxkbWMdFzYYT4aU/RXcdBw5ZDqjKPvxENxa6ukp1poUEBX/USojKztknU4MP3KWrpesrS3xdO+Ijz76hKWVAVorPvv0U3rdHt/+9vepx6e8/du3uXT9Oo2PTrdvfP2r+Nqwv7fH/vAIFTyffnKX/+l//J/57g9/gNIZt198nms3rzA8HPHBe7/l4ZMHrK8u01USIRXTpsVlPV75o2/w/p0v+M1P/z4mRCtNt9dFq8Da2oDJ+IjHu0/Z3LjFysoqUkqqyrD7+IBBf4XJ+IDgBV1d0FqHHR3SFZd549XnqdqWqvasrG6ztn6ZtZ7m5qVV8lzjG8fTxztMZnfY3Fzl8uUr7B8cMhyd0LQt2+e2uH79Cu98uEOvu8W57Ss8fnCPk/GUB48cv3/nLQ4PhhDiGqCVpFNobj9zg05viZ1793nmlVfJMs3egx3e+ulHnOw/pNfrMxm1/B//59/Q73WZzmr+9Id/xs4X9/jdP/wzrJzj5iuv886v36KatcxHkwOwsNzMBQARxZq5qDLvjEklF3vsIhQxZT24lJI9F4MEEb8lk1tPqETb/LIpARgeHRKE4/kXXySfViil+P37H3Dv3mOU6nO8P+TenV/y+3c+43vf+wZ//pc/5JNPP8dL2Lr2Bm/94n2ybgehCrToorKIa/PO0qYk7qAdpjNj9eYAuV1zGqYwimzcWWiQPtDUFXZYUUQIbDyIJ1OX9PGwG1E6cQy4bUwMCrOBbqeDD4HZbIZ3cb9WOrpRtYrNSmMamqpByIDSoIWOlYlwBOmp6pqtcxcoe10e3H8Q09RjiirOtpiqiSIDgjyLDMZgPA6P7mVY4fC2xZk4XC9FIMujazM4j8o0pm5jiBHR4Sm0WmyYrjUI4yKTV8kobvjAxvIyz125zPbqKmXWYXjYIGyfembZP7lHbU+wIpqGWuNZsobbq33+aOs8G0LimzbVMhIvBVpDZh1Z8NGNKwLCe3wQOAROBJxwBAWhAKM809ZyUnnqXLHbOKZOoqygnaPjnEErSa4y6qrGO9jaXGFluc8Xd+9wPJxy8dJFbty4xvrqGm+N3uV4WCGS43UhSsOiJpizMxf8VpGcYSFgWhNZ+EohbMS3Ka0h7eVRXIwj2hHb5qJgjk/iyhnuDuLYeOqTx+dc1AjROOVCQEqHkyB1wgQJz5wv7HEwzyYRib8Z4hRLdDMmvui85hBJfVq4ChOWQ8QVwTmPUpGvKpVAyuhWFKk2CcnJqnRq3EQKTpy4dB6tNVKqxUj/3M2ZaR2naJUkEwqVxZF2JeYj9PGcHFL95lL+jBfxrOl8wvkR35vgI0LRe09V1TF01nmsjY2U1nlsa+LEjpIIl9i60Z2AllEUlSIkLIKP57QkDqv0xwSLcjqdh+euV3HGy4Uv1W0q1khZfO+lFOhM431qXs27AsxdqGox9UUKmwPQRKe7awwuzGEcZ9fmXFgNjSc4mUL/opjonMG2Laap8WV3rvGTZRrv4wS08vEshRTYZJKY80DFnKPq4+cxr5UjvjAatISPeIovn7kWnNjwL6cav/z4shFEiih8+8Runk8BxzosBs7jo7gZ4XVnYXLz58qT6SUyeOeO4Gh68Ck7IjZ+5iZBQOr0oc2l6BjiZ4VAeE+h0t63+FlnQb+ZUGRe0piAyDT4gFZlFKmBbhnAWGzbRESljFhGRGwMeARNa5nOakwQFBlg0nS8EuAlLqHQvBcMVjYpun281NHQqGM+RwgCZwPtrMVUE5yZUQPSe6SKZitkdOErGRsBeVbQ7Q1wa3Evmp60+GrCoD/A+hYQeBsYnYwxTeTpxyn2iGc5Hp0wmU5icLwUOAOFC/QGPfJuFythejpiPJsSXEJTOL9AuWRa0+t16JQZWguKIkNKifEuTjCmScc/9PhXLdKORmP+6m9/zN7xHuPZhNmkISBj1y4tmkpn5LkmKyVFqenkPcqyRIjI55tOZjT1DC/g1DgornL91rMEvcZsOsN4hRGSxkumocC4Ec3ex5j9j+hQIUVcYD0BnXcoOsvorIsjIyDjwSN4rI2BHFpFxlrdtqiUnN3t9SJv0cbORlmWOOcwySrvfVxgiqLAOUuW5QveFcElCHlk9Cgl0VpBiIvhbDZjNo3j852O5plnbvCjH/0pf/L9H7DU73H05ClPnjxi7+kOtp7QDp/weOcTTpsZqt8hlzllnsXOt5BRkDOxo+kR6CKn7HXpdjoRgSAUTdPQNs2iO2pCHEnolCX9siQIm4pVgQ8WHf1csTgLcxxA2nScIxMpWCB4at9gbIQ5Wxu7llKJxcLu02Y076AaaxIrJ3a5CLHjOuh2+MpLr3L98tU4+hQCd+4/5ifv7MDm6+TnblAsddnZ2eX6uWX++PkL9HWLaVLXJnV5vXfpeePi6NqG1rSoTFOWXbyLrjFnIwtLEh1UWkoyJdHCYU2DVBqVZ4ggyVTByXiE6Vv6ywNmdZ066BlNGutAgDNt5BjiGWR9vvbidabtF+weTHnr00O+8fx5OjLw5KTiN58dsDdquX3tAi/f3ERJyZIyfPDpLr/46AhUlxe2FL4ZU5uKbm+ZXJcICZmTmLZmMj6hzEpUWdC2llb4KFcpRTbvdgq/AOG3Lo7fH09a3v7imA92a46bLkZ1QRUI4RHeQpCEYIEWHeD12z2+/vISeW74/IuM//zP93grSP7t96/xo29eZvyTXR4fVZHVg8LRY+fERqeT6iG0YnNJculcwdpGj0J52klDqGIglfOCSVinXt9APXcN7TNcthL5z3NEkIoFXbCW3nIfrT0dDSv9HquDDpmSTKerNHVFt1fw8OEjHh/u87td+PqV2/z6YIfl0wmr5y6yfukc5cqAyrR4O0Ng0VrgrKEsynh9OIMXsLK6wovP36K31KFqZ9jW0aW3aEJkeY5Qkul0jDVtuo8AEWIwjk+BeAl18mUnxFmoydyjAQOpuJRn2J17THZ26A36iDLHWY/ornHtze/yzs5n7B+NuLR+gdnkBO1zjsZjnj5+wOraFkH3Wbp8HVA8+mKfBx/8ngu3X0IV52kIoGQcewvp5wqByrJY5JoZ+08ec3r4lEd3P2M8OqbIFUJ4dGoASfxCvDQmil5KidgESIXr8d2c7uoq/dXzKK24dH6D3Tuf0F3pE5zj/se/ZffRm9x+8Ss8vfc5P//rf8977/4zw2bECIGVyfogvuSCEGfv2VlTJn5dSBhNxrz3yaeUHUXR6WI7GdnlC2QyFpg6V9FNK89g+3HNiocBTQyb8CFgcSgrF4eeGC4Wm43SzYMu5IJN+y9TXMOimXX2WZ8VywuHiBBnI4fpWtCCxfeKxcucB1EIRuMxs9k0ivqZ5mQ64v7TRzRNYDqb0uuUzGYjcAGpM5b6/QUyYXVplSJXjMYnZOMJzdEY4UIcAwKET9WgiE0Fb+cDctEFIwMx/IO5Mw1UUFjnmHrPaTNlKS8JKGZeUZsGF+LYYJkXGOtxMrLPhdRkWclwOKR1lrWVNc5tnMOLwLiaYltDd2nA+HjI0+NjysEaa7dv8fxLb/Dsiy9x7upVssESs5ljb/+YuhrHQ5ILlGUnMsiDJss7Ma0WRdPW6X2e+4ABH5EknW6XPM9ROmIrlMhQIvL25ocmIQXL/R4vvPASvf45sqJL01aMxzWj8QOgwVQ1wUGRax4f7TKbnGLbGSG0aC1p2jG2rQlCUFsYDg8QuovOlzh/6RlGJwc4+4DR0R73RjsURb5oAjSmJcs0SghwlrLIwbHAdjhvaVtP0S1ZO3eeleVVzttrND6QZykw04C3DVMm3H/8mGdfeIHf/PMvOR4ds7qxxdLyBvXMoOoGEwzIOIKpWsvvPnwfdW6b1evXsFtXmE2msLLKvScPOTg+ZtJUmOaUIC02RA4jS31K4xnInOlsAtawvtbn9u3nuHTlOnkmCWimVcXJ8ZBO2eHKM7fJl1axVuDamsPdh5hqwrntGyihGHQGTOoZobHx8CYVOispyi7BW4x39JZW2NzYoixLdCZZ31hjaXUdlXU43Ntj9/5nDE9OyU+mOBf46MOPWer3KLIM07QUnS5bWxu00zEb65s0bcO17QtUbcuTh4+RCKppdIO/+OrrBJVx++VX2FgdsHX+PMPDAz6zn4KrmB3tMnt6l+XlJe5Op4zGp+hsmW53k5de/iOefPQR1WjIcHiIMXB7eEjd1FhnGfQLuoMeUls6/YLltWVORiO2NlYRziFty9bKOlZocCMO94fkK6u88OJL7O4eMTo8Rmdd8rVVdFZimpbpSUNTSXqdAUJKXn71NT76+GMODg6ZVRVrK0uAo56N8aNjTNMyWO7jzISD4xGTytIGEZu/eUaRa5bXVtnY2uLw6IT9J48YPn2C8Iann77P/c8+4NLlbV569WUIMDo+pp6NGB4dMZ6dsLLRJe9INrev8dzNr1BkHWoxT0uPDZX5Q37pQK1VrKsXoWGwcNQSztZZ6x0ii24qz1lQI6mXv0iF5+xwLqVcuPsQcHx0wqcffcwLL70Y62hjIwsQjcoKXID9w1P+6m9/wief3+XP/82f0usWdLtLfPLhXRqjwQagiU5QMlpraV0d92Ht6F/vwgXDREZ0QdXWOAnGgDsek880eS3IdBZdYq1DeCJvPMtxwlFXsT7N84JqNotuSARFWUYBxnlmvsJZQ5iLa7mkm/VS/WyRKkMpgZAZkLBntqKdOXaePOaF51/g6HTM4f4BIrHXnWlwrUv8mDO8QmQGezqdLrLIaNrI0/Yzi/CQ5xH1VpkGa0gMSY2QaSQ4Nc2DCKAUvk0TTsKTacGzl6/zyvVbbG+c4+jgEFWUHE8PGQ33aWYNbTuLk04hoCWs5hnXOj3+m4sXubSyRs8G3PiEzLaUBIKQFN7R95ZO8CgJVsRGnQ8BJ6AWnlYabOmwStJaGM4CB6HHnf0pT61AlF1aUVAHTxBxnSqKkuV+h06ucU1FLjzrgx6DTsmRn+DrikGpufr6C3Qyxdtvf8De3iF+kWzvFvXEv5je+a8ec+F2XpdIKanrBt3tgkpjxqk54eauTWvSiH78/iwxNKNI68/uD1iELsXJGYgXIsgQsYCx2ati8LKM4qJSUeiV6feRKeRn7lgMIYCJIqrU8bryxi6YtSKxSM/QCAlD4ee11lm4WDQW+cX1FH93zRy7J0WcEpq/j/NgrOh4j0FPudSpPBRnHM3gkxAeGdBKSZQQ1K3Feo/xDmdtRAC2hrppaI1Nf9p4r8uIf4xYxZhbkmVxwkOqiE8Uafxbpc9WpoAvwXxKIIrZ3sUznkjnoyAidkEpFc/dqe6MrnSRBFdF2SkikkTF0Lss0yhZxjN8cpLGXJroiPyymLmoffEYPDoEZPC0bYuDhVBoTJpAExCCjSKz8wQnCCYgnY+NJhvDzkOIeBavJCqo1GySZ9e6EAjizxUyMYrFfNovHRR8WPy30hHlMD+Daa0XOs4fum8WuIwwF3qjcWG+54Tgo4ZAvP4iNuZLAdAiBlZGLKBe1G3z71/sKyEkcVXircGlxkp0oPrFe+6CS2JwxMlF/Go6G6h073gfMQpaInwKB/QRBxhURLvMecFC6JiraB2IeH2gRJwuSigt72L2klKRT2xdIE9oNh8SBscZmnpGa2oaU9PMZogsS3uyIs81SokYogwQHKFpyL2jcg1BKbRPzPj4xqb7VaKVpttbQucSqR2qkGSlQxGd4sFbvLUYU6d6d4oPTVpPkuZkaiQ+nqVC4HR2wpLsIaeOQg8YZCXlamouGgteMJlMGB4dRZq5Mdi2oikzikzRFsnklp5vkYfyBx7/qkXa49Ep//DWrwgyJBZmHnEHQJ6X8YWJGqEFchJi18AFMpXR63dTUWQQssThGIkel1/8DvmVVzmYVvi2RQSopGIUJE3dIEfH+PufIZpT0AFUjhSaTlZQFF2EKBfFmjVtBA0vdzGt4dGjg8iLwZMLhZaa1gWUgKaqMc6itaQsSpwLODeLqZMIlMppU2JgCIb+0hKNqakrE2HPtcHp6Nhs6hl1NUmdIkWhJNcub/Dd732Lr//Rm9x+9nmE1tx9+ICDB1/w4PMPOD3cZWNlmTdeuMXm+hK/u3eXzw+OcEGTGtcIKWhNdEjFiz2gypyi08EaA1LS2BmtbSMQW0mklzHIpSjIOwVemngDpQUuCPAi0pdk6h764FNiYuweuVQ8RfhqXPRbZ1EidnWsc2itYqpo2pitc9i5eyGAdUl085bQBs5fvcCrL79Ot1tiXUtlPD/+yVtM9Q06m6+Tr27yxc4DlrOS775xi83S4RrPrDUY01DXFTorUCqLC6GApqmppifELbkk7/awgLUtUgjKPF9wdjSGjhaoYDC2pmnAGwN4eksr9AdrBGBW1XFhCwLroDaGqppxOhqzsrpBUSiEd6j2lM085/aWYDTz3Nk9wQbJakdwb+8Eh+bVW1d5+eISXVkjA3zjmQ108Pzu431+8fFDjNvkypKIUS0hgLWAw6m4kHbKTgy18gbjkujmIkOlKDVFN6fQEqylcZ69kee9O7vcfTzm0OSMs3WcKBDBwDwMQUiEiK43fAAAIABJREFUbCkygQwZvppy4+KAsh3y+7fv8LWvv4zgBj/5xVN++qt9/uTNi7z+6han//AJ9WxCt8wIWZdGr2Btn3PnSy6f73NtI6PEI6Tn8MkJk4llOLI8fDphNLM0riDIHFGcRziP9PE16+AoSri4vcLKWpfDJ8dsbC0RvKCpHZmSdLoZwgVUd5nJuGK2fxyLsmLAp8djQha40u1THuzyYmeFC3nOqKpQOsfZGIaXlyVtlZHnUfBWmeTChXPcev4Zlpd7VNUMY1xapNPojioSUN/jXIOxLUIqggq0pqE2bXJKnglxsd6LhXEcy1l4QymDYFvn3BIZnf19Dj55n/6lLUynT7/bQ+uMcu0cz3/nh9z58d/AwSPKbp/2dJ9OlnF4/yHVzRcpsoyjU4unZiWT2Lbls7d+xY2vfRs5WMWLOLYVXCyupVQRTeKnfPbx29x/5zcc7t5lenzI1etXyMiwoSWIQMgz0BmZjO4Wa2bxACizmPwuRFwrRw3jyS6nT++iu122NwesLfcw9Yy8yDieHPLxR++y0R3w1n/8MXc+fouj+oQxHisTcsD7lDKcnFCATwFs884ySiBLhSwUuj8g9JdgqYROFtep5I4QAVofpyxwLhX4ySUgBN1OFyUlw+GQyIlKTi1/1qF3NrLE5zzT2Oxx6cB/JiYLWKzJsd77Uud+7nhJ7tkg5mOJZ5u+TbpECAGRpQIxJFdECIynE5SSlN3ojBrXM97/9MPouNQKfxIdY0HGaYeDg4N4qFOSu4/vxd/VOzqDAUxblDGJqSzAn/m6QcTCjzj5sCiGRUSpeGujA1grtIxs0kkzo8xiCKA3Da1rYzCb0lEMUFH8FCEGllhjmPqAlwpnHVqIWOQLQSk1VdvQu3CRi9ef5ZWvvcmtF1+mu7SMC1GUn9x9GN1lbYNSIjrDfKBtYlNBCJUmTCCTRUq0TocGIISYLr5W9iIzWeVRGEgHvjhFEg9B8ZwXUDLgXGB8MqQ1Q1rXxOtABJSMDdy6ahFITNMwGHSRssUHw6WLF7n3xRRrBAGHDC4O13qojGXSWHrLG0ynE4KwNJMxbV0hhWJ5ZZP9g6fMpjVry0sEBG1V4a1HSEUuJYjYiDNtmw5pmkJInLUxDZjIGbfOMhseMPr9r7CTIXb6lM/fPWVjfR3palaWuoyP6himSHRCeB/YOxjy/ge/4/brJbsnDtftw2jM7vEpxoxxNqJgGmuZtI4TG2iUQq4MWOv2OY9nY2WNK5cvU+QlXggqKxAyTuksrayxurFJVnSYzSaU3VWKIsPnGbcvrWPaU3SjyLorMDtGz6ARiRsZAv3BGs8+9zzrFy5SLC1Hrrr30BqGw30OTiYsrXYoN7bZCJ7T0yPa6ZROtwTncG3NG1//Gvd27vP227/mm29+g9PxmI8/+SyGSbYVjamZTqd0OgNeeeVV8kLz7Auv8cn/y9ybfkt6Xed9vzO871vznW/PAxrobgAEQGLiINKWIkWWYkvLdpx42ctZK2vlP8vnJM6KHFuyYg2UTZGGQBIgMRLoebxzVd2qeqcz5MM+VbcpO/msuxbJJtDdd6h6z9n72c/+PXfu8fjxYxQXWcxlOLF74RKzySkaMN0Bw9GI2DQUWwO6m5scPvucQb9g58oNvvpsitER2825fu0KxkCWZfQLS2YNG5vrDIYFg0FO01Q0dU2RC99yVo4xyrK+O+Jg7wnhcMzecQkmw9UzTk8OCbMj9u45TsdHlLOWza0BTdtyenrK0709ZlUtQYHTKccnR5ycVOxcPM/+rGU6PU53XIvGcv7aLbpNyRvvfYdQLujT0M7nTKZjNjY3+af/4l9x69bLPL7zOXpniBuvsTYc0F/bptvv8crt2+xs7vDDH/6QwXCdo72n9PoDpqdj/viP/g9OZ8coBTYTfqbcnSl4CHHEKZXEgJWDUK9Wo5f8Rqn9U0htwiAIjkzEDp9QYJAGaakeDHG5JpzcYenuPjo64pOPf8Hb772DzkQscE2DLgwKQ4yKpon88hdfc3x4wj/4B7/JO996mze+eZO/+fArusUQYyK1l9V8lTr62izYvDmgc9XishpftizqGtO1WGsJ0xY117Bo0TpL9ThnJgplWPI8fZRBY6Zy2fQzguyZj08xmWxVdbXGZDlFbtk/2EehmM2m8v0bcaj5AJlSRA118HgPXed59OQZ5y9c4vU33+LHf/0T6kUpGAJR/YhadlvqtkZZCUYyGExmGHQKVFRM9ZRZOMU1Hl3LeaqNIkPjGuFtK62xRtF6LynuWmE6GVluGA169Do55zfXeefma2yZLb785UPK6Hhy8DX3Hz6kqWtUVBS5bAlF17JTWL594SJvDNe42ClY6/boZAVHJ8f0fSQj0neeLHiyIL2gQlpLpdTKONB6qBUYrZj5lpMSjlvFXma5W1aE4QhNpE3uVBekDjSdnGsvX2WUReanp9y/fx9rNWvDAaPBjLau+Y8//oArV69x48oVLu1s8eMf/5zj8ZRBv8Pd+09YVO6/cNKuPqJsbnhlaFpZpe+lAbRknwUiDt9CMCaZ9OSbDGq5XK1WNS7LYbLWKX0+bSEuX+somSs6hYKppUIRoXVRarhVhYuIM6mWi+lrCkvXekKLGaXQmhcEMqlHljtTpKpZhOSwEsDkmV7+PifM2rT1Y0wmgp9RwtGNStAEnAneq5+lWjrqtLBro3CO0TJAEMFaROuoAq2H0gWqAGXTMm8ayqrmdDYT1qtK+KiQONjJ+ZjZTD7HCyKgVhoDiYe5rLniSkPJUgBr2wiqyreO0i0kOCmkgOylmSEJpeJ61tIba5UyMzLyosBmcm7oFKIWQsSwXFEXQTFEdzYUSK+VYilWBVRc7qvIu8cHcTNrraUe9Y5ldkXwqY72MiyKXn7tXSt3NUFkheCFB7rKhjlzvcpmmlnxQ6MO6d8llAfymgXX0Ol0aKom/f+E6nrh2Vm9cTjbmkPJ6yBOa6lzQ3hRrNYpEyXiYkj30RIX4tErV6iRGp9fD91dfs5l4JzWckaHxI5WyTSijYiuVos4qtEYJUiI6FpckOfcoFB42tBikgGtjS0htOL0tek5d2Lm0+JMQ9ESQ8TVjWQzBRm6KjRaWbK8I8GQrcM0TeoCAuiIocW5EhU9RkkYdm5yGQik2tonzm+eiToVQou2hk7RgzQ8UUYTVKT1NVXrMXUjLl1jpN8t1kAXKKWpZjV104CvgBoTW3zraZqG1ge0kcGeMYa86JHlRXKFR4Jq5WyMkaqsKYqlPqgoRjndoktVVayvr1HOZtT1guBbVPR4H6greY8qrXHtMiPkv/7xd1qkjQqyrRFaawmFiGkS5j0Wu7oMWi8rOiiIRlgus8rjmioBh6GNlu7Vb3Dx9m8ybjqUXmMxOBRVgMrX2GYMT78gHt2n0IEQhAdqs4JO0cfaAtcIy9CgsMqs3mhNCkbRSlyexlo5XIysAC1mU5oQMa1CQqUyEeeSu2g5jbNWhGXnFzTlhLZpaBdzfD3H2ChrTF6ae2U6rI02+f777/K9777Fd777Hr3egMOjY/YPn3N8+JxHv/ol86Nn+GrGo+Pn+PoiVy5f5pVXb/HF0+c82Tvii/v3OJ7PqJuGupVF3RgDg7URg411mY66gMcxLxdUdZMECWk6O3lGv9OlsBkqtCtuIZz9nKy2tHVLUF7SHBMHZik2odMaoTJkeYdKnU26ZAV5efkiLi6iJMfrs3ROAnil6XT7vP3Ot7l87WWCtqDgj3/4Yz7dh/4rr3PxpVd4NjmkqTzvf/MalzcLwmKCyTSN19RRWETGWjmgfCAvOpCmw8PhgMYF5vMZWeKNaG0lxI60xupbjo6njHrC/dMEFBFtJURIa4vzQRLbU4cgcx8gOZOtkfeCD6B1wPjI1VFGdnubv3kw5VdPnmG1Ymttne+9fomrG5bcV5I6GTxdHfn2zS3qquXTu3t8/FXN+mu7bA8LQhpdywqYS85ACW9qWocPcpioCJ0iw2QZuZWJ9taW4WSume/VzNsOVZFh85zMZzilaUMOeJRzdHKNbTyv3+6zs93nRz885NPP97j521cZDtf56Y9+xXd+8A0ePevyyZ0T/uI/fc5ax2Prr+m2c3TwGNND+Q0qs8V65ya3LxRMnx7h8h6Hc8/hRPHg8QlVMyfQQdsCpTJiSO9lV8LihM1LF7mwu8nORsEwV/hMEeYFh3sHKJWxf7ygdR4VHNFFWq1R7QK1OMFm4LVBdYbcOZhgd3f4wWs3uXB5jafP9/j6wSO++53voZDCqyYQowxlssLy8is3uPHyNbr9jNl8ivOe1vkEpBfnWlWVOOeo6wVVPReuktK41lG3tTw36uxi/jWeWIxpnQkgkgPnVcaNos+uUph6wZOPfsbw0gU2Xv0GutuVS91kbL/6DXAVjz78z7THp7SnB2QoVJbz6MtPeOmtd9m+cAltaqrJKS+98T6urrD9LqXygibgbI0Iq4jG8ezru/zkz/4t7tFXcDpltLvO+nqPykYWlSc2jrzTpfURZXK0MfSGXVrXsmgqVCtulaZaQL1gfXONwhhMiOz2OlzevcCTvTHbm1tUzVP+6s/+lEe/+ISDp/c4WByxUJI63M9zMm2Z1xWtX4atJWeO1bJFkOeC8SgyEWS7lnw4Iuv2iBqquMyhJ13OrFhaS0B+MoiI8Dk7FbyANWjEibB8eZYT9VURb0wSjyPxhddVHtGly+LF1kSaaRH9zrjeSdf9L+/R5ftk6XIJkhK7XDFEyftvMV+glCLLCyDim4aqlXVAbc/YwitXhVJ4ZOpvjKEzGqKqlsXBwXIjkeWnFj5UKlyXX+Xyy45SYqplM5UcF0RpqF0I6MJKom/wLKoSZSO5ycmKggxpMlpaooriXq5LFm1FcDJoHW1uc+XmbW6/8SZvvv9dti5cwauMqirZ3z+kqUtc2+DbBvAYLaJL9Em8cQ4fDErLN2ZtJg6hQq0QEz49xyiV1tPE1aJscrrodO8lkUFF8LGldQ1Em/AJGteUtG2NJPw2xNSIFUUXFT1VNaEsK7SGxXxG62qMIRXKcDoZs3Vxg9uvvkqn02cxnRIpsNkGoSfcbWtzhhtbaKvY39vD2AxlDFVZgTb0B0OKIqduKmyW8ELBrwLjVEqHDsGLAG0MeaHp5pHp3j0GpsGXMx5+fpciz/ned97mQT6n3btP3wYYGMqyZu/U8cXHX7MIffTGBbJWUZdj5rMJUbd439I2gboOTCrHTAufO9eWje0h59fX2FjbxGhD7Vw6Iy3GRjIjXEofIqfTGV7V5NmAtbVNRqM+733rFc5vb/LHf/ILfvrJDB9qmqomzzJ013L1+svsXrrK9vmLeDTj2ZyohTvW1ZbaRe7f/4LT2YK1zW12di9QvPkO7fiYO3fukWUGtbPG5OSQ3/jut/mjf/N/cXy4T7fb5fGz55zb3WUxm4ErsVZx4dJ5ds+fR2nL6aLi5q0bPH54j6f379HrDLly/Sqvv/k6WdZhsmgYbW/wZ//u32AWE/7Hf/4H7Ny4RaUHjEtP3l9n1sDdTz8gt3B6ekxVL+h3+wyGOd7BwcExxuYcHx4xWFunqiNrO5e4ev0iJ0djvvj0M/zBE2wxBtNnejAHZejlEBdTFr4PPdlsyfsNh+NHKOXQOuP+/Qecv3iJ8cmYiRlzeDyjPzrP7/z+O/zk519zfrfkryf7OFcz3FxjmF/jf/rHf8h//89+nyd37/Lnf/THPH/4mBhL3n77HfYf3kNPJ6x3DO1szuWrFzmZzfGhYtA/T1QwqyvGpyU/+9kv6WWRfrfDST3mzmdfQKylSdXLVWXZUImIAKsSHy6iVueWUqzQM0otNVo5aPXfYtCKIfHMEbU8qbVRnPVfajXISw8URDg+PuHnP/05b3zrTW7fepkvPr9P09QY3ZU7SluKosP+3gn/+n//t0xPSm6/+jqffPaI9dEm11+6wv0HT9g/PKFqFvi8YXStgz0XKfWMejGjqiqyToeOyomlY3E8x48rrLboTBHd0s0jQzKtdQp7TOdw2xD9HBVSAE/rUSFCBXm3g+3kIjKEQG/QJyJ9GUrR6xbUbYX2wqpV0RKDJipL7QKT8Sn3HjzgwqWLXLl6lUf37hObhtYpMOJCJCK4uCA1dG7tai29N+pDiLi2ZnFaEr2mGPbwOtKWLg0BRXjv9rqYtmVRevr9Pj44dOO5sn2O999+jY1uj8VeRdYZMhzscO/uZ9x/+pST2SlECQsyNmfYH9HOxlwf9fnWaI2bRQdVO06eHxCVpuM9loD1aXgbxQlqkLM0+EAUWmNykhp0lkOmmLc1j1vPrNPlmYucAplWNE5wNURNWdcEJIV9d2ONzb7iwGjGkylffnWfLOtw4fw51tY2+eWXd/jgg4/Ze/SUN2+/zLtvv8rzg2OapuXZ3iFl5VKdEFb1wovcSyKycaeWeAJPppUIps5B26KQTUZT5Cte83I8qxOLX+omEQlD6i10uudJopxN26dLjNPSWSiB0hZMuovSyrZzAdVIyrxOiDgZcov4maRK0pNN8BGWXGAl8qh8q2eDY1JfKs5YQLMSxLQ+C0WVM8OnjSjhUpuELFyKLsthjzUZy6m7bOEk7mrCDyigqipq17BoHNOyYdY4FnVL4z3Oi3inlE0Ov4gKfrVRtxRml9kOMZ1l8kUkcVglNuySma1SpksINK2smbdNQ9s2tG1L3TQYrcnygizLsFlG3inIbIZRFm10cgqLQ95mRsK/ok71rQRIuUhCFKoV11iwDYk/m0Tb1gnr/UzAl5Xxtm2EyZtqZ60UmTXUbYsPHuckcD1qaL1sG9ato5NF2XpLtbEKglxRSd9Qy+0HzjjlcRmMlgR3FWWjVjAEhrJcJFdwSHkKZ5iDJa7MOSfv+WUdn9y5y/dFm1Assin9Yh8nzmvvpdZCK6ySoaJSWkRDE7F5LpsAKWBNNsrle/LOo9BkxhIz4ciq9DwvQ998+lpdCOjEZM40BOdpULTK0MZAN0ZMK/g5TcB4edZ963BGnh2j03Ono+hlCeFRVRVVWROC5IsoLNvnrzAYjIiZOK6ruqFuK9BQGMPpdCzhulnGaHeTfH2bVhoscKkQB7JMwo2FaW0pekMyldAjQVF7wdD4AK0T5KDziSUdAlEb+oNN9DmH1Z7x0TOa+YzgHE3TUjctMbaYLKPIO+RGwie7vSFFnqN0qtubNm28i8HOxmVYcCHcXZ3R74/IrKWtOxBlqzqGF000cp+pcMbU/tsff6dFWlvkbF6/irVWkAa6IDY1ykfmJ3PasoYQyWKkrJsEujZkhbz5rSkSdySnGJzjxpu/D8V5qoUmBIPJOhgioXFAiz+6i7/3IVmYUhTSnOdFgYy8IjoDnCANllVbVTc0TY2PCmU1JMaeNlAtTsHmaN2h1x+wVnSZzaY459JKf8C7BkIN0RGCx/maED31okW5msYnWLOSyVb0LZnK6Xf7XLzyEr/7u7/H7/zWb9LtWLRV/PLTT3j+9DGdXLGYHHB6+JScltGoT12VHO4/p5xNuXbzJi9tjlg3mmGu+eDTT3lyOJbiKgqHrjccrAQFFaFxLXWZQqS0FHKydprLOor3CRYtQuUSHh8dbGxvsb25zSdf/ILlyu/S0YUWJ2n0YrWXtReNb1ustauVFhVZrbJIIFISPrW4CFWIFLrLjWs3ee32GxRFB2Msj58e8MOf3kGdf4fhpZsEm3Hw/JDb57e5famPaiao0MhhDlibY1Kgijx0oiYUnQ5FJs15lsuFE4JPKZEWt1x7U1DXC2bzGdYM6OWSqG2tlc0tbQgYtMkobBdUWE3WYgh0igKlrbgBhHCP0iLurq11WMv6ZJ0ef/XJQya1ZTjocG69oBNrCA7n5hAccRbRtuDdl3eIbctwNGB7Y0iu23S5SAAEkPhHZ4KQTGg1WdHB5qmQ0XA8qbn3qKS/PoIs5+btc/QnjucHgVmtOS5rxnOH1xk6C9y+1uHldcXp0yPe+1aP/vs7/OV/fsbPfzHhnW+8xP6zMWEB/TCnH5/TLhY8Px7jq336nUJEk/qYOL1LCAOOupGvrWfvMHC4qGlURrsoibGHNl10MMRmjrYRnWWMtvps9ftkx45+d0F78oSTeZd704qps8wrS92ANsIkw2r6/QGdIifvdRkUmrU8EFzDyWRCr9/ldDzm7v0vGeWOYc/wyqXzvLMuP2NjDW1dMT8dQyi5/tIVgnuH9fUBWWFplqtKjUxThbWTAgSWrCAVmU7GhODIbUF08kyoVM+uVjGTwBZiRLb5U1EQYUNZbnVGXM26DGMkC46Tg32efvAB67s7qGEPna/RqEjsdNj61jv0z+/SPnvG8cPHjI8WHBw84PDrEZ3NXc5de4mN/gi8plUlg2KbWeukMENL+IUWt/vk5IiDe19wcvcLhqf71JN9NkYXeO/3/wndi7vURUHtIq509DtdfHQiDCooq4p5ORc8RNOiQmRytEc7OyQ3rTRti5LJk+fkARbzBU+eNPi2Zb6Y8atySuPmTEMrLh+lObe5zSDvcu/gGe18nloHaUZ3r1wg9jIaIs6FlGabYfJMgO9KtjMEOZoCExC3bAwhTa9fwE6EiItnicYmFXgvct6WuJcX172WTO3lx4ucqxe5cS9OXF9cpwVW7o1ls/VrDKxlIIcPqyZk+XmWHPQskzOqqoWtnWU5w+GAxaKUTYrUrelM/5p7YBmu2MSIHvRQ8x6hqtDSnf7a733x86l01iwbhmXgglEKn5zJkSR8GoU1OTZ44iJSN00qoKRB6lhL12i8CzR1hQOCzhlt73D7jbd5/wd/nxu3btHp9glRM5nXlOWYaj7Gtw0xCivP6qWDIwW6CWtE7jKE4StrgjKINQm7A0qagAzBGMQgTnElruBBd8Qi72B1QyAxHuWFTyy8yPpGh7r2NEc1s+kxu7s7kGsWizndTpfhcMR4fMJ8LlP56OHhwwfEqIV3HCM6eE4nx/TXdzi3c4lFExmXDSbvMhyuS7cdHKE8JYYKFzyj9TVyK/yybvCUi5LS1WAVNs8wWXqHBggElJfBq0bWWeXuNehgKeeBPBuyvTVARahGOfPZjDzPufXOt3jyixZz9JztviFuGLK9mi/3aqaTBTZfYNoxTVni2opGSZBdeVry9OkBe1VN79JFhr0ePW3YWFun1+8xW8zTW9OIS8tEdAqWDSEFN3mHw1EuTmVtsG25//iAy5d3eenWLh99/hUxFAzWNtjeOce8KRltn6O3dUG2ODwMtzZwrkEFCcLavmjZP3jO0fPHdDSsn9ui2N7l3fe/y3Q6Z2/vEdF3+eSTjznc38PVJR///Gdsbm1z69U3uHT5Gud3dvj5B3/F559+TG84RGnDzvlrkHX41nvfZbi2zt0vvqSuSk5nJ9z9+iuGo12uv/I6WWEougO0gsdPDvni0ZjX3v177Fy8xNvfHlJVgZ8MLDYsiCoymU7Y3NxF24zH9x5RljWvv/UGX31xh04nUtU5r33zHdY2RwyGLXtP51TNmF6umU6POX76gFuv3uLi+U0e3D/meHpItz+kaiNNM8e1C4q8wGYZnbygm1v0aMjTBw4XNOcvXeab77zN0bjhy0++Zmttjcu766jeBle/+T5/+Af/Led7Bde+cRv2Jvyn+gMOjx7yy7/5G2gd9zpDdja2aNyUN95+Baf3WN/Zwgw32Ts4gukR45NDRt2Myy+/xP605ODzrwlugbE6NanLlW5ZdzcmiTkqJbC/MPiMcmiJMYQzoSapbmmwnvxeZhkek1yDWhxeJNF3xauNZ+uvEnwjztXj42M++ulHvPvu27zxxit88sk9GdJqcexltkDnPRaLBX/6pz/irbe+wfb2Dvv7Y+qvGlyTuJsDT3YOiquRKi9xoaZ1Fa6pKWwO85bmtCROGqyT+6JtmhVDN+CFM2qtrBoHL264KKG8L8z7QEWGwyEmz2i8w7uWxjdoqwlBvveNjQ02Njd5vvdsVfsoFVBkYI2EI1Hz/Pken3/+Bbvbu4yHA+aTCc4JTs5oLaG93idXmhg8ksWNrJPRW+vSNsKhNLlBtRGvnBgoCkO9qEXAaVuyPKNHj53NLcaTY3QJL62dZ0t1cEcNjz8/4m5zypPxM746uEftmsR2HvL9H/w273/77zEabnL88C7Tn/0I00ypmopuNMSQhKaEqRMEWli52SQoSoNq04RSRBKtpX9cxMikVRyEnElWcNiUzNuWnSzDdCz9/hBCRVgs0MYwHPbYWFunmwf6XUfrI3XjoA0M+z3W+l3ObaxTZDkboz77e/u03lM1gfF4xmJRrYK2lu/VFz9WQ1Yimdaybq4c3jsiIpQTUs8XQYco4T1R2jrnk4OcFKgUFMsc+uWzGBHEgYRIZSIYuheE2dQmurbBkKVnV6Wa4azW0UkcXtZCIooJ49V5UepMkC0q4SPJz39ZZ6CU1NnIxlBIwolskOjU8qvlbS8DcpIIl8RRlPxZMQCYlUNTRY0PLm1dJoxeDDQeZr7GtY75fE5ZV8zKikXjqJwnoCSUlIgxdmXswkvInlrWoSGJdD7x/tVSpF7WMNJfKq0xMXFIW3GoihDaygaRb3FtK8/88lkzGpvLENfaDJtZrLGyFaRlWB9IfXk4w3SFhKgAknCZBl6J9RljWAXargTOJHL66BMqTM7sgEuvkUYZI7i2dGZhDFFrvFLUwVN5RxECBYIy8IkxG2KUcCyVNoRSDhAr56tLnNw0kE788pQyt7onhI28fCrODBdEVhgFn8wgIH21NWaVt7EMlVvmX8S4HACYhFoUnIfUXD71F4L3sEa4xwBR8qkSVlMCy7WOabNLQdQoI6FqPkaUzlBGDAfKLAV0T56Yz6EVpTPqZCpIZhartTi3fUCFAN7jkmsVUpaL0agowXE+RKq6pqoWNE1DVdV0igEnJ2O6axN6a5sURV/QRoUM3V1dU1eVcH+zDqOdc3TXN9B5gdYWa5Kz2IljNgTHoqyRCJRMzA+KZIDQ5FoL36JhAAAgAElEQVQT8PjGyQYtwpv3wUlOTOvIjKXX6TPLLIFAXS0oq5K6blHa0DEakqCa5Tm9fo9OUYhxKrSovl4FXRtrk+gumFWiaFlKi3c7pHPC5ok9u+zRtMb+/wi08HdcpFXGYPp9MAqnoiSaZ4ost+Rmg46Dtm7lYFiURO9pygqjxZXYBoexHbTdZee132L9yjucNuKOVKlhVQGK2NLUBywefEiY3ifPNN2NHbEmO0frPI0LaBuwhRIekYdYS/I4SpLL27Ykt9DJM7QKOJujO32cd2RGE0LN7lrGeHrCdD4Tbl90hHYBscW5BudbYvQEL9+X8K5EnfExkuUDtta3+d773+X3/uE/5PXXXyMEz2R2yldf/IpHD75kc9glVAue3PmSZjHD5AbdLeh1+6hyztZwwNBoTg73qaczbu9us9N/l68eP+cX9x7yZDIhywrauiaYswO3rCpxTaW0cqMkPMsmt7AEwMih4yNYpWidl4MMEd19iKskVeedXOycsZCcd+SR1eRneXkvXQpaa6zNZSoaIt55PDLR6gTLxfUd3r71FtcvXZc0eWP4d3/5ISd+jd7ODXprG3x95x4bJvKdl7cp4pzQ1hADdRuoG7+6WGJYOuTk82baorKz1XKlGk5OxhRZIdwUq2XqpyJtU2FtTsSuAOgxyrpA09YEnWOznvz9xmCt4DOsliCCbqeP0rJWpbRdVsV0igxswRsXeih3kf/nkz0ePz7ki4HlnRs7qLZCO4fSYqevFiW2G3n/5Q06nR4dkxIcYzpckwARlQg2PvF7lVLkmSHLNCbTtEYznjZ89MWE06njxq0+ZSMX58u7fXomsD/T5DNNHirKNjJrI4vJgjfeGtHdLYhzz3dubqJR/PAnT3h2UnFj2/CrL37Ggwd3KJID2dWHdPMOeXcTZz2xHlOrA3J3QLuf83E5IQ5fxsdNggoE05ViRGmshtwWDNY7OJVz67UhIxOpH8PB1z/l4PkdZvl1FmoDPejTH3UwbcPlC9tsbPWp2pZBTzjX87nj5HBCYxRV4xmXkfFijoka193mo6d72M6Etply48oFFosxa+uKRTOnXJxiTQm6ZrQxQlko25KmrlIRIxdaloswZmxBNQ+Ui5KhImE2NApD7Zp0ICZbA6zEN5bOnChCuwLyqHgpH/JyZ8i2MXSUQfvAjo6c3r/D3b/6D7z0g++z/tKr9IZrGDTRWbKdi+huj+s3bqBDRjVbcOfZCQcPvpQE5tJwcHhIiDU9NQJV0DEZdV0yPp6wf7TP8d5TysM9usd7dPYe8MrRCdnoIm/+D/8LF37795gER2Ugak1sPG1Vg5Kwv0VZcv7yQM7LNNk1ynB6csKoq5js3Wf/+ROme0/IijFbW2tsjI85XVRoq+ms9QkGqnmFdzK9D8DxdMqJH1O1VXIYyEp6Z2MEgx6VitTBE43GKJ0GIpo2CFsIZP1InBcyAXer82E5VJJARGvVypGkWCbpSgG6TCBeipTL11EC4M66oxfX5f52EMFZwu3Zr//2qsyLDMQzttrSLcDKdbFkpr3497TOgQ9YJK131BsQG0flg6xipWbOpoAI5cUhIAxTy/rGJmvDEU+++hpVt0ShMKAlOyQ1D8kNs5Q41NJxk4Ta9G+ikgZrVi0ospyQSdGYJQ7YZHZK1TRkNmM4WKPfGZB1c8xWj/PXX+b2N9/mtTffYbS1Q6MiVTljdnJCaJ3cu75F+RaTkmE1PgnHIb3mSsIXlvePUkQt7w8Z4km6q7ynpGBfBhBpJWgAozN02zLfP+HLDz5i5/yQizcuipsi8cEym2OMwmZgtYaNNeanpzRVxdraGtZkOOeYTqd477HKoqykFBujCEGfOZS13KbHR4cMz19j+/JLXHrlZXa2unRyw8F+y+HTQx5++XOm4z2mkwmj4RBlNE3dkHXE5VBXDXXbgLLYaIgkd5TRWJ1jvMcqCTNs2laaDSVhLc+e7zGbzzl//jyd4YBgFG1wDDeucaPX5/EHf001f8zOyHLORbK1HebrA56VU4qgaKqKyreMywWzecn46ISjgyNCltFXcH40QLWefp7h0urj0mkHin6/y2A45HQ+p2kcznkUDm0zytmJOJhb+LP/+BGHZcPl61dYu3SOwXaPfqfL84MnPL37Je3JhPPXu2RFXzZ0CsPJwTOCq1cYqAsXL9NOD+kqx1Y/o6TL8Pp1vvcbv8Ff/od/RzmfY43l2ZPHwvvTiqOjyPragGG/y/jkmK3NXS5duiYdV3QEX3Hx8g22dq5yMvdU9Bj2emQGDp4+4PHDj7hwcQeC5c233sBHzd7khH6vx+effk37yUOu3LzFuQvnuXLjFj0r2Ieyajg8OCIPA1Q74/qNa1RlxcnxMVr10VnNwd6YalozO5oR64yq8mjdcPDsKc30GJoZu+dv8vLta3z++QPu35+ymNfUbUuRFcxmNVp7rl+7SGwX7GyusbHW4/GzKc5ZxlPH4fMJj+7d4aVrF+nlBb96eMgw75NHK8xOBa+9epNPPv4CrTcYds9xtPecg8mc773/Nv/+j/8tH/6v/xvXru1y480d3n/7ZU6zNSYPHtHtZOw/f0Jv0OXd7/wWXz2bc/z5r6R5W+5Ov7i5JHZZlgney+28pQAg/3khCCwJMUrJFlmbXIS4FxFfSYjVirQJnVal4+qcI4JKjjP5Q5HpeMKHf/Mhb7/zNm++dZNPfvF1argtWZ4TvEJRMJtX/PVPfoo1lhBz2eILitpUbLycw7mShR0L76/V6FjQsQa/8JSzGW7eoKqAdhC9o43iWDOZIet2JJiobvAhiIMvBKyW4Fe5wES0iSFQ+RbTSmBmVmQYDT4KBqhT5Pjgefr0iSSbJ8de9ArVOgxgOxmtCxyfTPj88y9Rr2lGoyHlbIq1EroVlSI6+dlbY7CZbFX45VAvz9BWM/ASnFyNa6KJ5LEjolut0IVFt7AoS1xyxXa0oR+73Lx4m227SzYf0HUdZofP+fzJpxyGPUrTUBRrfOP2O/zm7/wuv/U7v09vtINSHfL3HPcvXOHwr/+EB0/ucQlP1xhsdAwi6GAJUYESPE5QNgluKfy6TeojAUwgmEAdPbPGUds+8xhxBDrdnF63S7ff5XgyZbqYE5HQ0dFawXB7B+0Da2VL62tCgLKqKXIt3MXYUs4mFFYzGY/Z2z9iUQlCp14K7/EF5+yvVxPyBMRI67yEBnUMxjga78i8pZMcnGKwkS2UNIdAKeGs+jbZ1nWqW5LjYLlF6cOyDAh471jUJR6VBm4iFLogOKOVKKqXjFEZsJCCpZ1rpcZqBY+noqyCL3m1rl2GQKZV+zREWQ6Q5etY1nAKqwXXl2XZanvEqOzXBoPC9BRR2GiNzvLVtpFyiQcbxdRTt/JzPzmdMZmXlLUI+yFGgvOEyArRBDo5NyNRBZQRnIoxwvldDiFDWOKw4grFsKz5Mi05NiJcL52Zio4t5LnU8nfqHOoGbEJFiHBqwVgKXUitGBTKS4BbVAhiIOmY0stKqO6yhl2xX19wi4Yo6LllDWrM8ms7w0U0bUtZlTR1A0rh2pa2bVZ1sTEiWjovpog2Rmw6D3xM8xtliFHTRAnpM1rjtcIaLWdwOvONSZxkJYHFCiVitZfXy3tPDOLaJkp5GL0IsT4GfPqEsonx66YEuTNSvs7y/giCfmFp8EhCbVCAFsZrTIN+n9CR1orwHtLnETdsEIMEgtUJMQmzipVzVBnhqqooX3iICrRB2xyddTCmBtUSkecpMxarxHjQaEFodQhEo9BWNlFkoJSJ0YtlxpA820ZrMe7Uirpumc9mTKcTut2a09MxT589oVdWbG1u0usU8hwakwYFiroS/IsxBQaVcjA01mqck3wIZ8BVLeW8lN5Ca6IypAw5MS4FQdqU5RRXzvFVSV2WRAKdbkG3W5CZgLOgQ0s5H1POpjRtK6F9yTxSZBkuOkEZGkVMpgwdtRgVlcErjzEWm4v4TxrO2UzEbxctbYv0CXFpkpG+K+90MHY5VPmvf/zdFmmRAyPEQIg+MWihdp4s5vigiCmxObN9qmqBMjnLBtkAeTZk/fx7dG/9JqdxRNmmcix6nPO0TYvxNebZV/jHn2Hjgm4+AtfImmrTQkpLLNsabeTPBq/IbYciN2AtZVMS3Cm9AnodTW48LotM6mPKes5pU+FcZK1Q1CkUqJXOghhaopdkxkjEaLXsaFeXWIwCYr544Qr/9B/+Af/o9/8BmzvbjCdTjo72ePL0MQ8f3uP8do+ednz8s5/RzKYMux0JG9NWnHbeMeh06NqMIxdYLErsyYTNfp/feut1zm+s8dO79zksG6rocd5LgnZd4wjkJiMECccpsoLCmrQCE2TtF8FBRC8HiDYyNdw/eMbzZ09lBVil1DyWoT1pQh5lmrVseFeYg+XhG2QNZukgjH65QmRwQS6UCxcucPHqFbprI7Z31/nZ55/x488ekZ9/j/WNLU7HU8xizPe/9TJXdzr4akrKmKQNUSaDRNpG3LoizixFD4Xzwi7S6f3VK3JicOiUOuldRYie3Gp0XhAT6GBRV+hYgWtRJkdlPSIam/eEDxMjuc2InSjUHGsBcRAsGUJLqLurGoie6+dGvD7z/OJXB3x8Z49ev8vLa5rp+JRuPydL3ahqTxn2NcSaGKxc7gpxBnKWZLyc/mVZtnIEK2UYzyMP75/w5HDGk/25fD1Pc85vDthey1izgc6uplMgl0GbMa1awjzj+dMZ/+nDQ/7x3z/H/uMjfvrJmG+8d4Uv9jw///wRj+7sY90xrjlBdbugLJ2ioOitUzdKVnqiZ9gb4P0pavEY3zQEV6HXbtLYHVSwxAjFAF66usZGoekPLfeeVjx8MkP7htOHz2mPGwJDstE5dka7FKM+53Y6VNMZ64OCTtfgQ839u09QyjA9mbOY1zIw0ZrRqItqG/aPJpiupnUFX96bsjUYYTunGDfGB8egY+j0CrybcTqb4YMn1zk+tFgrhcPSRC7FrCLPOmTDNaqqZjI5RZmMoDSLsqJtaoJyiWspH2fIA3n5lk1mFmHHFrzSHbCpAh0lZ6jzLVlbs5sXPP38U+7rwCsqZ3TtJbJeR4qarCD21qiCF6d3p8vrl67w5PAUmgW1sYyPD4ih5XD/GKJiPptyfHBAOR6jXMmmrxnsPcM8vc/g+Ig8ei7+4Dc4/863OY6WeeulSdOKGDRtFCZPVZWyRj2rUCrw8NFdjo+PeO31tyDvYHoDtq8NyYpdzm9fw+Ydxp/+nH63w3RRo/OM1rVyXgc5P9vGgVJMmlOIcXWeoEB3cvL1IbUSHtwyCdZkBpUritwIwyrdOZGwatSJcbWOtQw7y/OMzNpVEa91CqmJaUVL/39cwgqW7vWly2DFGoYzp+YLDi94QaT/W79+8f2xFIVXmIH4QkBDOHNjL10My+AzldxdoQ0cHB4So4QHKicFokKlIIHkgnHyz6zNQRnywZDOYIjzE2IUR4K4yESkjYmdK8JoKmjT17wSpnX6Hoi0wbOoS3RUZErT6XTQuqVqGmaLORFN5Q397Su88e53eeOtd7ly8zam06GpW05Ojmh9SwwtzlVEJyx6k9wmMdULqxXNGFO4hAWlRYhV4oIy2qK1Fef9UtBBCm+dhBtjrbDXq5andz7jVx/+iM9//Jc8/NXHXLixyz/5n/8Ftt+XzRiCFMZWoRKewxhNv98lRjBWXv/p6ZSjg30G/QHdThdIIRoBcRqkSU2vP6I7WKezvsugP0RHhStrvv70GdVixnzW4qqKg70nzCdHhFAz11IEe9eQW2FWUiSzYIwyuFNKkpu1rLg1ZUXtzrYttNGS4BsDxgUO909YW9tgY2ud0/lcUtC9ord5kUvv/4Djz35E1RywuZ0zLHb5cP8Ub/sE7WhUZLoo2ds7ZDI9ZTabo7Tm9quvcvmlG/jQEnIIUdzLS1e4SY36YjGlqkSgleJfNqyUbnDOEKImz3tMZid89vk99ictppOxtnkRrQs2jOJWp8N8NmbQzRis5bQhQmioWdD6BdQBV1fkVIx6hp2tEd3CsJi1mLzgtddf586Xn3D3zpecTkp8V9A33X6XXjfn/t2vmZyM8U4xHK7z/d/+A6aTYy5dOsd8seBo7ylffnWH3SvXefe732dtYw2jNY+//pI//7//iL/493/CrZsvsXdwRLA5i+kpfkuzeX6HwdoGDx49IreGfn+TjcEat974Jvfv3WF8fMQwc1y/usWlS5v87D//lKppKcs5vWrMwd599O4WxwfP6fYt3a1tnj55yKIuWV8fMpuc8Fd//hdcvnyJc7uXOerNaBqDtkPGx3usj/pcv36BulqwOD3BEIVv6AyNt+yd1BydlAzW1ulv5PiqYX3Q4elXd/iTf93h/ddusNHv8OjuE2LloarY2d5m40ZBc/8h27sbzKuK6aLB2BH7ezMWCzh37jrjhwd85ze+z1//xZ/ww7/8j/zL698iek3d1BTFmWMWQAvPJGFm1JlLVokjZ7WVAMTUQK3CXpbrot4lzqWIP8Gn8Jkk+GiTAoTSIFypJddxGVIU0vGf7vUIs9MZH3/0Md96+5t8441rfPbZfdrWMJ1O0MoKGzyJS9LoSwCxt2AuBMJuS52XOAKhbIi1JrYaX9ZoL8zTUDt0UIQUdhuTGUIlEVnYtBIYo1U6g53UoTqJMJ2uZHNUVUXd1ORFIQHLqQ8AxP3knTB2V0FLaXfcR3zZYLUh5pqmbjk6OuGLL77g9ssvyc9OQ57lBIQN7pqWNnjatpW7xnuatiUzA4y1dPtDQuOoy4poDdZ0KRtx4hK8pLgbha5bmrpifDzm1pX3uL7+Cn/w3/0h979+yEc/+oi6icz9Ka1u6fTX+MFv/iP+2T/7V1y+fIUQBXpkjMJ0h7zyG/8NhJqjn1oe3P2SSx4u5TkDAj54WiUhhMFaorICOHA1OgZ8UDgFrQ402tNkLQsC09Dg8kFycsrdvJjP0UQODw6pGghB0clglGfkWpHlHeywh481PtScTstUA0S6RYeT42Pu3n9C8DG5bX0qHs9KC7X677NaQt6aUo0sGs/cBZQtiE0JQe6H6Dwm09iI7BhHEcJcK3WQNrKBIQIhEL30VUEEseg9JgpD0ykJg5aw7hROlXj40Rqily1VlRyvaulcDeKy806MVTaLq/rLanF6GqMSYSSQKQ0+kOXCs1VILofWajWQiEiQoE0ZEDqJVyoN5JU2uOVZ4PzqHLDGiCvYWly7FPuk155Xc5omcLooOZnPOJ1XGCsoBJsCmrVaCm0hPYeswriWNae1Jp0jL6za2xeH/3qFMTBaQHo+BoKTn7kPAZtZnBd0lU2cZYOEZnsfCM6h8xyQu7/T7crrqTTRJkdI2ggguXlXDlqlVvXnsh5dIbISEmr5LhOsgX/BUJDE3jyHNJhpmoYw8+nznGkDaE3VNOTOUWSGbDWIExepnN0KYy1ZlgmqwS63ZJdmhaWjO6bVdYcL4uZ1zuNaT9s4nAu4NqR6N224aRFOjRa8ZeTXN+TOchfOzBNnWxjJFK0NbdOIyBvF2UwQvJrWiqCWiA296l9U+r4iIh7r5efSGufCKpxOK0FwECPBp4g4K/9cO49q5SyKjcNYT1Sa2nk6Coq8I1qNMuRZTqsNuTEU1tCmsDgbIYSSpq6pyjGLyQn1Yk7bOHS05LZDnlVSNxsRMZ1vWZRz2qZKr5XC1S2HR0ecHOyjjeXqrQHGFHiSML0MiIuK4MFXDa6pxem6dBajRLPRiugbmralbmrqxYz54R77zx9xOj1CqcDG+jqbwyEqNowPnjI/ORSObpbh0msgqK0am1napqFpGzItPH8UeGSj3Nqc4KENQe5XmRAkHU+c+zbLaZtmdbQ6HxIvWmF0tuJZ/9c+/k6LtBFhjGgtK5Ck4KjoJZHNkIGWiapWBpN3GazvUOQ5bWgIjUabDdavv0+7eZN5BYEmOaIiPmrwDr04pv78Q3rNMcOeYatnafyE4AK5BluIxT8gE+eqqal9QCmPqxX1omVazbGqwYQFo94m83pBXdfM25qyKfG+xWjD1WuvsLffMnmwT+McnSIjRAHCay2sDWHgKGlCYiDTll53yM3bb/Av//m/4HvvvUP0nv295zx8+oQ7X/+CyfE+r796m5yGX37wEwZW0dvZotPpUCfOTFmWrK0NyYuM2eIUbSIXLu5SlzXVbMLmoMs7r1zj4sULfHL/MQ+OJ9w7eM5kMaNxHmUNhe1gzLKAMxir0ZrkFHMpvCu5kLysLMgZ4YVhk6zpyzervL5m5S6IIcjPIjOodjkBWtr/Q1oxiavGX+4JWX9SJuPGa9/gyu2bFGsjsuGQP/2rn9B0z7Gxe4210ZC7dx7yxoURb1xew8Q5ddtirU7iSJq2tTXl/JRub4hKMHy58DVVvaCuK/rdzqrIJgrEWs5s4dXkWUEMGpSmDVCXc5rZIYPcMFrfwmayWm+shABI6I+smFgloq6yVg4nh3wdkH6POJNNaPnm1XW8b/jlnRM++OQJnW9cYHO4QaSF2FLkGdqKiBlI4RBaitXl1DGmwlcrRaeTo42kMkYUjw/m/PTLZzwaO7B9msrRVgcsFof4S+d593dfYqsHVRUY2pgSdg2mKFC0zLB8dH9MbiK/9f42x1+d8n/++TP25jmqt8PcVQzchDxEfDujt3WJoHYwOiPMj6j2n1GOj7m0uUWbVVTVIQM/wx2fUFWHZKPb7Fy8zXBrm5aKC9sWW1f86rMnHIwti0aBDmizxvq5b3LrcsH2+Q1aFONKcbA3ppzOOTmc4dqWo/FMXArK0ck6DHoDBms9MJqr53psDAu+fjShGBW0kzFPv/yMv/n6hEF/g6FzjIqWbtcyN4q6ajk+PuJ0fMyFC7tkiZeFsmRR4VxG6zynpwuKfESWF+yev8po+xLd3gClDZUrCfgkBqUxIWfC3HLqnzQaRspwo+ixrSM9rbAqrbcoRShLdFCMGsPzDz4kNJqXvlexfu0SnfUhWScnKzqy3o+idi33954xGKzTLBbMxlOeP3vC3uNnBB8JzQJTL+h5x3pdok6P6B7t0T06ZFTOsNriX7rNld/7Q6qNTUrvwWiCa5hP5Oc9GA5FIPOOajHj+ZMHzKZjFpN9up2ck4MnZJ0he48eopThyvnLdPpr3B4UPH5wj8V0Jk2QUjI9bWvhdSUQv1o12meu+GLQY/3KRUKR0USZnmsimdVoG1FGVsZk9UmGFq1rJXU1hRx0jaXf6zCvayZ+jrWZNKgvJK+K6KrkzIu/nvq7QlZozbIxUmkoJNPz5ahx2Sjxwp99QZhNHdaK7c3ZNHn5++V/xZGhjYao0KnxDd6vmhlZz5VPmBUFzsm6+ZLdJd+7nHneuWS+SetbUdwO42YijUBR4LTGN5Ws12H+C2FZK3GznLWE0jQqveR3eaKx+OBZtBW5ESRGbjOMzclUwdrOGm++8x3eevd73HztLYbrW8QIp3VNM58R2waNgyADKBUamqYkhvj/UvdmT3Ye6ZnfL5dvO2vtVVhJgiQALr2rF7XUWkbqlkb7SBo7JDscYf89vvGdI+bKDvvGE15kWZ4ZSe1pa213N7vZXEASxEaAqCrUevZvy8UXmecUKMn3cjEYJEEAhXPOl5lvvu/z/B6yNF8l+hIvF0ppTGtA6Tg1DxNzFW1mIchPrtQjEK17yofLnIP58TF3336Hu2//hP3H95k8fI/CzOjYiunTpxw/ecr1N99g3jiIqcLByRCsalU5xzrLcG09FLDOkqYJRbcIuIHIsUcIkqQgywrSPCXPC4pOH5kWGCF4+vAui/IO/d4abdXw5NFDBoOcGy9fZ/P1lzk57nF0+CmL+RzTWrpFjpQOY2IQngthn8aGC2BgnhlcZE8LLePrjwoLNN5aet0eEsHxsyPyPI0BbAmJSjAo1OY2/Zduc/rBDD874WT+CXM5RAyHTMqKo+NzDg+PmU5ntMagtOLWG6/z2muf4/johMYZ0qJAShUSeY0l1WlQPRjLfD6lrmu8EOSxoW3boE6yviTLZuxsrbO7e4krV15AFGtM5i06zVCpZjtP6fcyDj+t6GSWtZ5iUbZMzs6hHbO32We+mGOrKe1izGI+o+x3QUnmi7AXbAyH3H7tNt7UfPDhAxZz2NgYcPPWTZI0RUlIEoXUCd2NbVRnne3uGhaLSmBtrU+3r7l3/20yJThZ36O28MqL17j68i3+9i//JNr4ExpTs7GxztMnD9i+/CK3br7IwiZ0c0k7n/LjH/wI3d3k7PiUvfWCTrfLxuYO0/GYqmyQKmFWTujWOf3uZS5dG5LKmsnkjHy9z7NjRVoU5ElCawzzyZT3j05oX2swTbByDgZD6nLOZDJjOpnRLqa8dOMqWzvbHOwfoJRlY7fH1qUug40c4wZs7G2hvQ9rTGnu/PRdPvrhfTYHOfPFKUlSgp3w4Z132bm0iXINf/kX/wHjDIOtHRqRcfT4Af/tf/3fIFTGMHf8xi9/ge/82q9xeHjM//Q//PfcffyYRMbBftxtls1ThLjgr9rwc5YK/uWFfenoknGfXuFnPAgZFDU+/rsS4d89QZkn4uV4pSETofmAJ1zmI3tRLgeIkeM4GU9560c/4itf+Qpf/vLr/PTtuzTNHJWkq8NgyTnEe6p2Trar6N7IaYoZjWlxRuBLR3U+BaPokoVkeSx142gqE4M+Q00iE4Uj1IFJlgWhY3Q1aB0VoXhkItF5GoPNJEWqoAysxbpt4LmTyzRB0aiVCgFxSoWz1AZVmWsNpqzRXuN1aCo9PTygakqG3Q651mRZivEeY8LQ0ywajGmxVROaY41AFjmdbheZJMhEkXQSEAm5yphVDQaLrQXeWJCBqe1agyKlOq45PD/m3/9v36VuPEenI05mZ1SuZvPSFf7gj/4LfvXXf5disEY1X2Cqkm4u0CKhtXMGW2u88ou/SrHeZXJnndnDh5yNpqTCkWYpqhEXjawYNhTcKi1WCRrvaYSnUdBMc98AACAASURBVJY6scy9ZCwUMwm186R5lyqKKc5Oxwji8FiGYMlOkpN5ELTYJIR/locTZvOSPE+ZJQ06Keh2hjw9mhCUjMuSY1kk/OMG7WfO6ihjabxj0RqQXaLXBW8Cn1wIInJr2TgMQUfeeqw38bF18fFweGtIIDLnPULp0JiMdZCQYJrgSlQxqMg5MCzvXMEd8XxdFJqCYQ3bOqhlrbGYqLDN0jQ0Up3HE1j7ro39hZDJFIbv0pPoJNR7CKTQcW2GobIzjrotQYiAtpISqRNME2zkpm4QQlLWE2bzOYvFgvmipizLEMSFwjgb3JgqAeRqf3KIiFMM1vy4U4SGHmG4JCNmITRr9YXCd8nyhzCQIHCzq6bBOIfSIafDucgjbZbio4BTsN7h42tCCpIiByFJk5QkS5FakaaBPS0jw3vF7o3qQ8uFUyA0BkNDHu9pbQgnC+Kn8LmF4LzYdI1NyiVj1thgTbdLVm0cli/r3hCuG5TRpjWIIo/354gpVBKdpgihyIuMPO+gdRLeB7Hkz0ZcTRycOWOxJgoCHQgvwlBegncN1oamrY9iMZXooNZtW4T0eBNRkPEZXqqElyzFJW9XRumxQOCVRyUp3hpc26z29xCi50MOAhdNXucJ9Vf8rCURLxLXlk40xizXdJAgeCJ+g+BQRChknuGbFGdbnFZopwOuQIb+TvIcMzdRCqXCjyVS4aQKAgZCfTqfTphPT5mMzjg/PWE2myNdENtZDL3NPp1unzzP0YnERpZukNbDfDpmNjunaRYgC3TWhzRHy4Qsk2Q6OMa0BCmC0yP0W3R8vpZiMxkU6FJFx7CPQ5Qa6xYYO8LUJfPJIU+NRQpL2yxwpg68awl5ktHrD0jzHNfGZ8F7TNNQeYnIM2Ts3QTRCVgs0gUHuY/PU2vsBec+3h2ECEp9F90mrbE40aLcZ0U2z3/9s2/SWuGAi9Q9Gw8YJ0Kn2rvAxmjbYPPwTtPOBOfzBbgOnUuX0NuvUFrAtlG5E1iCSngSN6I+eptryQl7t3cZrHXY6PQQCUGlEXXcy4CWs9GU0/GY8bxmPC05ONwP7AvXUntDsbnGeNxSVRXGN0gpqOdz6rZBa829J5+ES5FtV5BxCDzX507LwMAVggxNP+vw8z/7Tf71f/LHXL/xCtPFgpPjU05PTvn43ntMp/u8cfsmuZb8/ff+FsoJe5evoITn+PSU89GIXrfDcNhjc2ud4fYGu3u7DNYGNKahrRqqeUndtkzLhqESvLa7x3pnnVQp3nv0gDO7CKmsTUORBeaYUkEKLqyhak3ATPgw6UqSBGvCaw5FbLDDgF+xZ533GGcQLaRJQpKmGFeH9Ealca4MG48UITBAeHxs1vo4UnLOIrxAObh86Qov3nyNojcgLzLefucO736wT2/na6xtXWI+HtGn4bUre3TElOn4FOsFeRZSzSUgvMGYGtPWSHpBdRaqa4RUpDFMpTVtnJhqjGljE7yi2+uR5V1UDHxauhqU1HSylDxTeNNg3RyfhMZyaCSJEMEjHIkSJC4wgK31+BA3AIhoxw6KLSsc64njzRcGjMZTnpxMeeuu4uu3drnc76EowRvwGnxIFfc+bPLKh6LROIdxIYAgiSen9bBoWj56dMxHT+ccLjw66yC9wdIgVQtGcOPFddb6mn7hyaQgz2BeSlShyKYu8GFFwcgYvv/RmIUTnCxSPnzmsDonybtIU9KOHqJpaYylIzQy38AIhcKTd47Iehs4YSnPD8h1Rn/7EuQD5vWC05O/I+02XLv5S3w60rz//hmZanjyeIrq9VnbHgKWXEu2Ukcng0Q4Hnw64vDcMRmV2LoODMm2or+xzvZWRmonXN27gsoydKE4P5szOTsjU2so33L2bE63SEjWN9k/nPPOwxG/+rlrTKf3aKZP8O6E1swp8hzbKajqEqdUYNpIiZQ2TmNDU987UHmO0yo0RYREWIdzIc1eeEmoGv4J5WSsrXMhuJIXXEkUhbRopcEsSxCJtuDKktwINqVk/JO3uD8558bPf4P1V2+Qrm+gix5eKawJDOatnV2mswXCjNkcDElv30DUJU8/vke3nlOMRqhnB/THJ3QWc4ZtQ648VkqmaYeb3/wV5LUbnNQWoVREI5wGRbFzTCdjVCz+kmSIEJ5+v0d69QqibTF1xWz8DOEVV67dIO0UOFty/85d3v3RW8ynY0R3gFACmWiahSXNE5Q1QSkUhtarxmV/OGDvxguc09AId6FW9B6VapJU4WVIq18qNZbv9YpXBWSJ5tL6BiezCbO6xDqDtcHaB8uQw+fKpNgMlCtV6/ICJFZpxLAsxJaq24tARCH+QTvTLzmKQQGyatQ/d3b+w9/PRztUqhOsaekWXeqqwlgTrLPGgYsqMweJSiiKnMWiDPYq4t8O0ixYMGeTafxxcDZYU53wqG4Hbfo0RwvkqnC/eA0h9MDgxBL/sHw/4rkfKtF4IfNBEdtO6WZ9Noo1Xr55ky9//VvceO0NLr/wMkJnVE3NaDKibQI/VxJ8aQ4bh30ghCJNC3zkdkmpV43ygJULF6T9/QO293bpdPvPccCi5UxInFoWsgmJSqkWU/Yf3ee9H77F4w/eZf/Bx3zx9Zf5vX/16/zbf3OfdDrDJ5KqbHh87z7Xbr+KxGG9iHy66OYwlvm8pJrXKLUIZ19bM5tOOT45pd/vk2Q5SZqQFR06nT5FpwiDSxSttSxOj5mMx0H5m+S0qibPCxI9YzEdM5/36Gzv0e8P8FymKiu8cwwGHZxpOD55Bk4gvUULaJqWtjUYEwaRbduSJAlZlgeXTwzFVEqAV8hEk+YZk/GE8WhE0c+DVTKuM+dBre8yvPklDj66w3gxwSVdJrM5T5+dcvjsjLquw/MgBW+88Tpf/cY3MVawf/AMIRSdNKdb5JzWC1obXAbluKSua4SUNLalsWGQUKRFsC86z87uOrdvvsTt196kcRqLIMu6rPcH9IZdnKt5ev8BB/tP+eTj95hPnvLL3/591roDzg+e8MEH77O3t01ZNfR6Q+a1oaoNpycnlLMZWZqG15xnWOvoFjn9bsb5eM5kvODo6Jj1zQ2yvM/W9h7HZ2POJ2dU9xuU8GwOB1x/6SYbO5tsrCteuLbBWz/8kPbxE5LOALeYcunKi2xdeYVGSqhLXnzhKl//uZ/lz/7se3zy4QdgPddeuY0RHba29yjLmh/+4O/YWR9gSuh0u2SJx7cndLphHSdFwmQx4eToFClgNpqjpEf1Cnq9AffuPmGRZnS7KV4rdnd3EVqws7bBnTsPmU1GKJlyNpqyNR+QC8X5eMbO5Ut88YtfoNM/pp3P+PidT5iNp9y4+RIHx8fYumXvpRskMsW7B5wd3KcSQ07m+7hmzu56TieT7B8doAYF3/ntb/P1qeX9dz/kcH+f88fvMh2P2dxa58r2i7z13e9y7eVr/Nbv/Cb/65/8O0bjI2QWVGer4dhz++jSxXUxCPMXe208a+VqV1pNvlhhbuKmJZbCimVid2zQsgrpgaVq1rsQ4LN0FAgk0jncssnrPPNZxY/f+imf//zneP31F3j/g8dUbYtWGUkg7OEIDQo9lIhLlrme4ZpwZnqrAurAJsiyCU6IRIQGZx0uyEtOZCJj0IwPSnljAgveRWeVTJKg1ExUGMwoMCJYOp1zgUHbhoHjckgpBLRtDJhUOgRECUB4VLLkTjpE24QWoBZ4DSSSg7MzZmXJWl6wyGvSIg/7rlKgZbBbL/98TtDOF1RS0pQ13nmKTsGsrKgWNUUvY2FKfBIQX4bQHOsVBdfzXTZEh80iY62jmeeWu/6Us3bEm1/9Gv/y93+Hb/zsz6GlYnTwhOl4ghaCdLiFMyGkctKU9PtrXHvjZxhlGn35Os3dD3j26BHZrKKvErQIIqMEQSsEi9ohhMNoQWMFFVBLT6085y2MZMa5F5TWsrCGxniaqmQ+X8S+qkPFYOuj0ZSydQzynEZmeNmAhKquOT+dkIgMpUKjygPWRBWf+EyP9jPP/vNfoc6IDhcBlfNM6grtPcJ6EmlwzqBiF9V6F4Z4UWkXml8CIUN9EgQ8MoSwWotoW7TQOOGxuFDn6mDhblobQmgJgh+pAr7KB2UJ0hPvlGFIbWKTUsbmEm0cfBKUp9JarAgOz6DSDYpyJSUq4t+sDzWcEEExF5jRLdaGgFRjWpypMd7ikHip8EIHBJGC+aJkUdaMxlPGszltZPYu3VGh5nBRdCSQzykvfawVW9OG1/QchkpGdJeIm00USn4GabXCLqxqzMhzdaE+tMaGYCpjl7KAKN5xsUaOoVxKI6UgTVOUVBHHFHJV1HKPE8tbhVgN2mUMuvaEJu0y0DugDW0cWF0Eyi1V4qEm8CinVnuqjwrt0IBtwYahkjFmVT8LRGDzu4CdaVwbkGUyDNYRMjRlVUqWdcjSTmhyL5EWBFEYfsmutxhncNbHP4eMzriwlS9zY0QUEqwEE5HesfzMgttKPedGEBcOORFEeBGmGn4/lSBRIVzN+/hsenAOFZ24S/GC9xfvnvXLQEtx8YzFQWOik3hkRWSmDzeTUPcS1iphwNAKQZpoEDbsD1IgrcArSS08etkbEaAkaO9oiYNJgptdE+6s1kHVNswXZ5jFAmcFSd4huZahVAdFSiYUWZphrMVYcI3FtE3ME5DkeZci7wWxUOJIc0mmPd5L0iy8R/MThZMhkD0E6YU63tqgInZhFZMAtQnPjncBVVd0ChKlKBczZuMpuDYgqiPXtt/rs7m1w/rm5moPMDYo4eu2DfBOJxDWoXTgO6dJFp+p4LAx1mCtpTU1bcRpLs9AT7yHZDnJ0iny/1clbXg5YYoonCARKaK2mDqkurWNp5ktAkjYB/aYGRkSkbJoLcn6VbZe+VlsvoWtLHLZ5Y5Ta0XFmjtgUJxw/YuX6Hc8XitymYL2NG21urj2uwOkVGSZwtsaXxt8mnAsLbWtQBjyTKFTz2x+TtsaWmuwztI0TTgznOXw8DBMqIWMqZDLNFiPUPEVe4dwglQpNgfb/OI3v8Uf/9F/xtrmBnU5Zzw65eGT+7z/3ntk2vMzX/4y0sOdn75NPZuy1c0Zjc8x1tDr99Fpytb6kH63A4lke2eP9c0NvDOkSjHYWIf1NZx1tNYxmS04PpkyzGt213q8srPDnSdPuHvwFBNqtKgWc9EuFjbsoEJqomQ/Np25CMEJ/1Qskx9B0OsOqJoQZFXXLc7EtEuhcEisCRuv0AEJ4I2Ll0GBd2G78sKTpzlv3nqd3a1N0iLj2ekp//Z/+T8x+hKbezfI8h6HB494cbfD1pqE9hxh5xRJ2AyINjXhwu8l+msrqwRElZQAmSasDYeBjYSP0O5gebaupGlDYn1QYIUGtVSSvD8g72ua2ShsZtbQmClpUVC34Rl33tK0C7TWZFIjvaPyFc5rpCwIk4NlM8OTCoGQsJ0qvvrqNlk+ZzQzaKUo8iRMop8DlIftOxQNwZYGiFikhG2YxkpORxU//vAx956V1OkWLskQ1AhTIVSKZEin6JF0uxyceA7bmkGmGXQVN68nFCeCIhMII1ksGk68Z247/O1HNV5leN1BCEeRN3zj5avce+tDytNTMg3N7IQ036I2Cp0NkLuhmWGmIzrbLyGbOU26genu0OYGWT5mcvAxD+5d42CxRVMZpLDozjrXXxjy8rU+tnGcni44ODjnwZM5Wo+YLwxOZMgkI1vvs7fXoUdNoTVXdjSjs4TxtOb0YMa8MUzOJtRlib5/Giat3pMkkCoPcsCHj8dc3e5we3uN84P7CHNIXhhUpuit9VhMJkxmMy5fvoxUMWET4kTZ4lyDlppE58xmC7xfThpZHbarXfG5Bq0nbGoaweUk45WsYFukDIRCR2WeFxLlHcortBRoK1HeM6wapnc+4u7ZKVe/9TXWb9+i2Noh7w+xVkKas7m+weZwyIMH93h0/ITt7ct86Y2X2VQ1j/7jd+kfPmPt7JRt06JaE55tJZiplI2vfIMrv/ArHKVFUDDOp8xGI1IVAid0Iun2ugihg9pgNkUIxWC4TrdTkFjP0Sf3qOop25dfYm17k8VixPvf/yv+9H/873jw+BGNEnQJDVAdbS9hL5LY4NJmOaSUWkGiORqfUyWCpFcAYpU8GyxqwabmjIvN07gDLAugeIFfNA2Pnu1TRys18ce9DUVDsOWpWDz7VYHk5WdDt5xzwX4lLvZKJZZs1tBdjnOpgChZSbUCSyvRmtpVn7WKiWUJLuLeFl0HEtJUMxwMONjfpz1rSJLIO3RBmWNjiCGx+LE2NudEmNaLiHkwdcPMhEu6kiIC+0VkgUmE9hT9HuVohKvqeOZdNLxtDIFhNaiUsdAMj7rD0vrA/JLG08sG3Hzjy3zr57/N57/wZbb2LqGLDg7FdDLmcP9DpPIM1gY4F4YaFo9cMqLwBEUQMexCXSANolJIRAxPhmDQ79Pt9FA6RQodOZYeTRKaDlrgTMPibMT777zDez/4Wz795C5bl7b5zq//It/9ixI1TLl+83W6/U3a0RFaKJxo+eTje7y2f0h/dzcoaqzFeYvUgSVXVRXT+RQnglVVeDg/PaVtG7RW9Hpdet1emOBbT9PUGGOYlzXzecl8OgHn6PcHdHowPz+hzVNSZSnbivPxGZ3hEJGlbHYuAVCVJVIExn5eLnBtjfANWIMWYb9aXgB0mgRVsZKr7pb3EfeQhAWTZhlpmjKZTun0ChKtMXWNFQKkoBaamciZ9fYYnXsOTmfsn54zmc5ovUT4kPT90ss3eO1zXyApck6Pjkk7eWDeSViUC5TUtD4obqqqYj6fI1UIpNAxQVig6RQ9vvTGF7l561WUcBhnmFc1QvfwVUVbOfpDyc5eh1xeoR4d8Szr0tSGurW0vsEpTZEPeP/dD5nXJS+9eotOVoRwI9/y7PApV65cQxjH6eERaZIxHk3YGPZZVJaT0QLx6DF7VYUUKWuDAccnpxwfPGVzexsJbA57KJVzejbl+PCYenFMv5ciRcL55BQ7yyj2rvEL//Jf8fTxJxw9+oCiN2A+M+xdusbJsxPOnn7C1tYap2eaJFnn5hufZzo9R1pL08xpnODp/gGff3MP15boRFIUOefn53z6dJ/dy3uUTU1dLig2B6z1+qRJwnQ6p+hkXLv+Im++8TrP9j8lSxV1OWO6qOkNNlA67rc645NPjjh8es7VS5dIioK//u7fMK5ybnzhVb7xC1/l7PSMt374NkkxDGtANhh3yv6zfT66c5dUa166/k16gxw7GSGlJNOKe/fvcjwa4fOCP/4v/yvu3fkxHd3CbMbf/ORH/P0Pf8BJteDx4RFOieAKctHuvLricqGK5Tm8gY8usKjWCtZ9f3EGP/dreO4cJiqkEIQCeXVmxCaMkviIDlsGNfml48MT2YEBmeDjHj6bzXjrrR/z6s2b3Lx9jQ/uPqSuDTIZILzC+BbfaehcK2h7DZVziNaBCRdmSWicZmlG09igLvdQ182KYWmfO9eU1rRVCBFbJr0jBGkBqUoQWgVmpnEh8MV72jYEYHnh0TrBa4k14ZKqtMYLT5KlDIfrYY02dWg+iODGsKErjbcEx4KXKK8pq5ambsmrhAFD8iwnlWEo5oTByZge3xoW8zlOBSFDkmUk3Q4+S6jORtjWIlODEDVN22CcQBWa26/c4OdufJ68tPTTnC99/Qu4bJt7/+aYP/rNX+YrP/9VNne3aKuW6eQUUy5w0wmT2ZTcteTrhrw/wJsKa/t0ti6RdzvMPrmDcZbKGxhPMJMZ2aKhYx1SCbDBKu+cpUFSSsdcQK1hISWfLCpOXMG0jfFaxuLagFcKeqVYxRuLSCTjyYTxZEqv18FawWwyo15U4Dz1oqGcN+SFJstDiLK1IY9l+fV8LfJP1ZfLWgLCcK2yMDeCwiukdzQm4A2kd2jAOBsEDwCuWrH8rTcIJDgZlKpS4o1BWoeQLoZCG5wKLg1JSIk3NjT4rLNolriC0Ghunud8Qkh7x8eAu4CuCzee0KB0tGghkdKhnQrrN7JdcaGRpnSK0knMCQCLR0hHWzcsygYTFaNIiY0DdusNdj5hUi6YNzXz+SLwS5FhOCkuVJDLUK0QMOjiMCdkA/jYKFz+PIj37GUz3cNFyFtYt4F16j9bn662p8CIZ1l7ek9VxQp5ue+IcG/XOgSyhZyCgGvIshyd6KgKlYE5H+b8NKYJymcRasxl6zUA3+N1xYcwLItf2e8Ds1dEVxLoWPsuA2hF5BRba2mFCE6a2FRfuaGEiKiogDySKgQQGhtcQMa52LCHRCekWZcsyYKtXAiUUCgVBxU+4Jy8DXgSYxuaxoSQVBe+jzPL5my4I6wCodzzobsB46JVgoi8UedsaPxFJ9rz+RIiDumWPSAIKmZUqLOXo8Q4onhOKX6hug49wdCDcdaEe4IPNvrnUWZLPI/wxFt+fEZ85CjHwDblQog11sccgYhLQyEcJHgyAZkPGR42Pp+hOStwNqIllEPIEpVV+EZx5dotfvu3fhuZbTCa1ljnwufnw69NU02lFK1xNNbQSSHvpOHO0zpM67Fh6yORgIW2MSghEDrcsdI0YCyaOrgkZHQlSi8RFkzdUC9KvPHINDTQ0ySEgdXlIiAr0XgjqMuWalFTZiX5+oAsTQAosjwEWy8WLKqgCvdZGtS4QmJYus88eIM1DcbUwSUdByNSXjjzlE5IdBpQLs+VEv/w6591k9YLQe0VZm7JW4d2EtfUtE1Df6OL8Ya2tWgRGnwCh0oqnF/QuC7Dy6+TXLrFlAzjZhcPrQ/d8Q4l226fy/05vcSRpAqUJBEB2IzwCC3p94fcuvU6/cEQJ3MO94/5y3/3f1E9fEwqgy1YCBFl5i11XVOVzcXFRoSmgfeBqyEIylIp5CptO0zhw6Im9mY2t7f43d/6fX7nN36bLEs5HZ8wnU15+PFHvP/Tt9ne2eIr3/gSSap5562fcnRwQFNXNKnAWcHZeMJwY5Nre7skeJT04ZKTBqZGWVYsplN6wz6dfpfpbIppWzpFl24h0aMSFlO+cO0qr169yp0nT/jo4ICD0zPa1uN1OGTkcweGFDLaIMPkydrlBuOC8jaqcZYStzBtCp0UD+CXB6MMgSmtBSdQPjJZhL9gPMbauXKGjfU1Xrj2AsI5OlnGj977iLfvPiG/9gsMdq4xmszQCayvdVjMR3S7kERWiIh/pYmKYQmQpDlOKKzzLKoZbdOwNtjEWEuWZVghaBpDkiTxs0/Y3tldbX5B+RvsvFpp0lRD0zCZl6wNMnSW4YynXkwDR1lY2qqkqqakaUq3s74KmDI+ND/cSt0RGgw4g7CQKcONjQ6JSGhVweX1BNuWQV0nJD6miePixo4ICmapSLMMHQ/BBsH9gxFvfXDEs6nDZ1t43QEZlGxNXaHzgry4Bn3JnYeeBw/PuLxZ8PIlTbfjGGQwkIYmV8xyz/1qivMtstMN03Uc20VQtowWNY+etfh8A5ueofwcU06wo32MGkDWI812qc+fMn/2KZsdgSEeHJ11sJakO8bVFeeH7+F6n0MWO1y6ssHmekKK4nB/zOh8TNkITictTvTRUjPcyxgUkuEgY2aDKmRrq8uzgxP+7vsnVLVlURlaLyn6YUCj0ozOoMugV4TLTyJY7+Y8ffKEg08/5QcfHLHR2+XSpTeZHM3xYgKuRilBt5NRTie0xiCiNR4BOkkjc8lSV45OsUbVKhaLWYS/Ez+xi4vlan9cXjARbCUdbhZdrqNZ84rMhMmpWYYgxZujscFqk3qBco5cKY6ffMr9/+OMvaf7XP3Kl/F72+jeGo4+JtGkOmVv7xIy0Wyur9EvBuzurvPqoMODP/kT9PiEtDGBqyk1DkHnhVe4+Zu/x2xrh7kIRcSD++9T9Pq8+NJNGmNZVAuM9WgVlHhpkpDoPKThOpiMZ4xnJTuXL/HCzZd49Og+b//f3+Xv//zPePTkY6amQYiMroqGsBjGioei06Ouznn+7NODgnRriNWCXIeC0HgXmE4yFAvBjhT+W/yDk3PJwkYES01NKB5YFaQSqYkWmc8Gfi2VtcYYyrIiTdOVCkLH4k8IQRWq6JXaS4jgGlk2Z5eFtfdBSWSf+x4XuIPn1GBxdGudRXpJXVU8K8uojPGhSdjUofEaLz1SCHzrVzY6YpMu0/G/iUEIy8ReG4JBhFwys0JCrNaafDikMWeYxiLkBfLBu3AGOu+jallGtUU4I21rUNrTX8u59tJLfOuXfoNvf+c/pcj6LBYzDs73GX9yTlktmJycMDk55/at11H9Dt4GtYn3QS0QLjEBRbMqcEXY83y8+ISGbXBLJJli9+rV+CyHPVgISaI1iVCUsymHD+/x4Q9/wKP7D/AKfuZrX+HF21eZTUd84Zs/T//qNd76/l9Ty4K1zT1On9zFq6AGOD894+nDT7i5vRUs00gSlYCQ5L0ON252OP/JOww3Nijygraq6PR66CJne2eX9bV1lNZUZYVtW+qyxrQti7LGu/AszeaL0MRPctqqZT4TFHmO6qY0raExhn5/SJZkeG9pbGjKeJWRFj0aABta/UqqsHss1d/LZ06IcFYTuILhyVgqmyRZllJWC6aTaQw4czRNC0pRzg2Pnxzz6cERTw5PODg6p7UO6+OZmWhu3niVl2/dwjjBk/0D6qam6ATMgXN2uUIu1pFOyIuCpmoQLoSkOKXJij5f/dlf4Etf/Arj0XEI0UEglaZtW/ziDJHkNLOECZbh2oAr11/i/OQVdAof3v0YlXUYdjts7V5jMp2jqxknJyfsrA2pywWNStje2sRaw+H+Y7yAJE+59MJVRs+eQqJYPKg5OS2R4hwl4OjZQyajQ9776bv88r/4Dtevv8jW5hanp/ucj84Z9hTnx89wTrC1s0dTTXn08RlCaF54/Qv0OkPMfMp4XnHno0/Z2LxEWRo8gmfHh7SyT1okOCXJig6iqTk6fMLHbcuX3rjOtReuMx0fkWpJJ8uYpxnPnh3R6XW5p8xXowAAIABJREFU/fk3+PH3/440SRgOu2yu9akWJd5Ydja3GJ+fI1xAXLRNQ6+b8eabL3PnTmAep70hadalrj0Pn56hhGE8PqPRW1y+epnL6z2u9nO6OP7mR3fpDtZpW48xnm5vwHg0Dkzd4YDOep/XvvIzPP30Uz78+CHdwZDFwycUvQ12rr3E3/3Vd/nNX/4a+/fu8c7d+5yWDZXwiCSETDnDRVOC8ExbG9T9y0AWv0xbjmqYpT7sQkSxbEKI6IZYqmDF6gIe9r7V6RybrYAMKBmlQ3r30hUlnMPEswIhgtJHXDQPhBDUdc0HH9zhhZdf5KWXL/Pg3j51M0OnPRpV0d3VsFYjiqAdaluPNhJtPKJxURklWbqo2rbFx3pHSrVCP0gpGQ4GlGXJfDKlKUucdUHF6sFbQ11ZmqbFS0/uOiHAaxlcQwzdEWLFPBQyWKhtWyOakHPgRFDuyUSRKklrTbCMO480hM9CeoxwtEk4rybPKrY2N1jr9FYX3RjZgYrbkhIBqeKtxYsQJqbyFN+0OOVA2sBFzTJSLK6d0F+DF1/ZJbcJD+5+zHCjw7/+w/+c7SsbtH7B9PgYjGE6nvDs8JD1fg9Mxfj0AC8hzRIgIxHBak5nwPZrX2NjfYfHac4aLYOmYnT3HuP7nwRxSxSVOAk+yynLkloLmkxz0tSc1IJGZJycTslzHRibbWyy2NAUD2xVh0/D8+sxCGlwruLk9ATjDUmeYKqG0XSCriuMt+RFRttGRaP/xw3aC4SW+EwtgRTL+QSVtbRCkaLxvg2vyBP4rjIgDkzE4iy9PVIKpPQx6Cq+V4lazmix1uClQHgblLQiDB+tsbhEUVctJkh2SFgOOAIiKKgz47J7bt0Qz+zlmjQ28DatDDg507ZoFdaudbExqWOV7C3WOByOtq6pW0PTWqbzhkVjsR7qtsU4qJuW2aKiaQ1SS0hC8zfRCUlEm6zUjhBDzYJ4J4iNQn2yzAJYBrkuh0ZByeFXKlQXsSwXeIDPDpmWbNfnFbbPD8bb1rBU7UoVGPtJkoYBtQxp9cH9GjNKCMOCpchKqZABBKxwLTY2BuUygAuPlmrFe3XP7WnP1w/LZnVAwIVnbCm0aNt29T0bBG3jkSpBqoBrSNOU1joyqfAx+6Y1jtb50Ng3QSCntCbJMmQS0JhCK4TWUbUalaWRVSxdGwffLdY4jAFrL9wRywZ7+HPHIUBUmavI8g9383C/lULghWN5oixza7wP7w+SOMQL+zNG4BIij9lFF25Yr8aGQYZUyxt8GG4557Bti3CW1lzga54fCgQHHXgf0CJ4j1r2XqRC6AQjNQpBGjENftmPEQR1vDW0TYvTBpWCF2CAUGqH9egcCOvRHlKRYIQnyXJ63SFFt8v21StczwY0VvBsPGc6GVPPZrTzCdbUuKYBU4OvmY2OQGTorEPpBUYL0OATiWg9TVkHYYmKYX9yyW3OMIC0Ch0RWwGf3CBFE3IpGkmWhcFEtzckSTK8C6Fk1sK8ajGn59TGsmiaMGD1fjUwmU6nTGfT0DyPavBlToUUoJVAEYKBvQj9PunCnq20Js2C6l6nCqH86n72//X1z7pJK7xElxI/aWgXoajwrsU3DQt7RqYzRNNinSHxhlYGpghS0t+4ytXXvorVBdZ6dKppK4PxAci85sbs2IfsqGO60sZOfUAoVMbhUOiiy/bOLjdefpX1zU3qpiFNe6SdNW6+eUplFIenh8zqGc47mrqlbZaby/LDiwVgnNBHXdTqwu0iICiArMOUNRGatf4av/97f8Af/t4foITk5OyY4/Nj7t79iEcf3eHW9Wt885vfYFZP+avv/QUn+8f0sgypBuxsDimKgk8Pfsy9+/fp9z5PZ9Dh2pU9rG/odFIQjqLXQQLzeYkTgU9a1g1NZSiKnMGw4MEn95HO8tIrt9kcvsbuxhZ3Hj3h0fEhZ+UkJMprHYtgt2pGLCHWnvAa8ywjzTLGozp+uBe2DCEIqkHBSjHopcBJcCIc7t5Ge7gKiiZrLRIVlWgJaxs76KQTINc65SfvfMxCb9Db2KP1GWdn+1zdXaPT7VBWZ9i8QGoZpkHeIYVDa40yYEzgpDkRQusW8zl33nuXq5df4PqLL4WC3PmQqutBK0XdNOT5sjAITQKI06vlAYgm7QzRnTWUTtGmZTabkHcUWZIhcsIky4tggRAihAUagxA2AuXToD7TKVL4MBRYzMgzybpuAo+rHkWFm45dCBuVZBrhQ7GSaI2KAWEyzZhWjnfuH/DugyPGdQefdgMvSUQFsc7xVYUzFQwLpngen1cUwnM8mSMTyc5OyqKyJKmlj6OXwkZfc1IG/lS/UOxsCN683gMveDDO+Ol7T0grSd7ZwDSCTiFozYJCOFKhQfVQwqB7Kc5XoBz17JSid8ygO8QOuizGc06OPyZRQ/Jrm5BokkRx9PiUw4Nz6qoGEtJ+j+F6j53tLlt9iVaCqrXMjuccPplw+sTSGEM5Aq0TsiJjZ9gj63ZZX+/iRShytjf7zKYVpyentFaR5z10Z4tnk2d87+1DvvONF+nvfBEmD/H1Y5wbIYVmuDZEyDARrZuGpqnJs6Bw8NZRLqqVJakqZ/h/tHGvytHPfOXAtSTjmigYOshV4ORIRGDmxQsN8cKID2ona1uEt2ymKZ3KMvr7H7PYP2T3c7dZu/0qrK9RVhPyfIjIcvZ29xBC45Wg9Zq1Nz/PFzodHvzv/zOnP/oR69aTKaik4MpXvo6+fo2TtsLgmE8mZEWHosgZj09prafb66Ok4OzkCCUlw143TmYFi7NTJqfH9Da3eeH2ayFI5/vf4//58z/l6acPmNqaRkh0LH6kismkMtj60ixbNRRDMzyhs7EO3SzwgJzHtIF9RUx6jX0nrAuWuGWHN9ixQmCAjJNvFxtUKy61CJY8ECFoaamW8s+fAz4OqxTdbpeyLIFlOqpc/XN1QcLHRHAuFLRxP12qcG1Mt1+m47ZtuyrSL/bXzwZMXFzOCLYntywkiX+e4O8KAS062FJj0S+lZG1tLVzm5/NgzbMmMknDZSFNEpq2ofWQdjpQ1VTVOYkPKtYQ0COjfSykMTuC3dF6x9pgm1uv3GJ7p8v6pYxLL1+nt77Ojz/8Gw73DxifP6NeTDBNzdnpGdSSX/q5b3NpbwdriZax55ASYhmCuCxg1ep8kpEdubRFKgle6uAYUJJEKFKlwTimR0e8+8F7/OSH36edzjjd3+eNL97kW9/5DvunM1689AX+6j/+OQdnU0YLz8/94m/Q6a+xvrXDoQ8KUmMtjXGczyYYZ1AyRWeB8zYZzxiNJ0wWNcO1dfrDNTbWNzk5OqLo9rm0vkaWZSzKCmfD3i+lIEkUSaIpOh3KRU1T1wghWCxKlJ7ROo/SGUXeodfroXtdut0+icrwzlGWC+qqAgSbm5tsbu5wdnzI9PyIaj4JKq4oml0OWJdXhf7aOlpJzo5PMW0dLhvCRRunxBnH+dkoqnMkTd1QNQ3nZ+d8+ukBH95/yPl0jrVhwKO0RLiWnZ0tbrx6A50lVFWFk5BlOQKNsxYldOAW2zC0FDJ0bKRKQNbhXE4Kdvau8+LNN7n88huMK0PZOrKij7HE9HBJlkryQjM6PqaadhkO+2zsbbJ59RWaesFHd++QFV16t15jY+8aSZazud7h8OAx2jW8fuVfMD4/Zn1jk9PTUx4/fcjt117nyvUbbGxv8NZf/yWXrvRoGsdH9/YZjxYMeglPHj/kk8f7TM6POTt+yvbWBlm6y7CTM50aEp3jvabT7/PoyRM2BiHQ9tmTB7z/wUfcuHmb4XDIZKJwJmVAhk67VNUMJxQbmzs8fXbK9u4eRZ4hFxPe/8Ffk5odZmcD6rKh2+vT63Q5PTrBCcn4fMpkNCXLUrxQbO3soqxhOBwwnlYIoXm6f4TAsL21zTDvoqRkbdjj1q1XOdr/lOOjM8azjLJqESKjdQ5nFvS21rn04lcpZ462bClnFVk2ZH1tG50XVLXnlZtfpGlLJtMZmIZHDz/lxeQmqrPNK69dYVy1vHjzZaTSvPP2e3zvP/wlDz58wHebOaOTU87KliquYSkCk1wtQ8KiMCBu13EvWO63cfDwnFJ2SStkyX/loqnlY2MxsM8BKVcX5OXPCd8nqsSSsAdhIiM9ps6vwsl8ECZ4ezEYfB5n8+j+Qy69cJ2XX7nOJw+eUtUj1LrCdh2lNegquKHKRYOpLNSgbLj8WREUnBAumtZ5hA/7eSKiKh4Yjcc0ixJT1YFXK2VEgPkQyPlcQ8UbF26P3gfU0LJxCqFmXfl/gw17US8inzbyxJOExjraMqCCiL/OGocUBqs96MDWrMuK09EY4QXdNA1njQNig93G+5WSkroKgypHaE5LnZAWXeh5pCuxBpKmZbuTk7ma6dkxsMaT9095LA3f+LVfpBqdUps5Ujm8dUzOz7n34BHDQcHOWoeqXtA0DfPpDCdzulmG0hlGpahOn+Hll3n9VzY5339EdfyUXncdMdygOTzAPjumquco78g6Baq1CGGQiWI8n1L0evgpOOtpGhvqjNbTmjoEYzkTcEJSQBut9FicbbFtw2Q8R+icPM+YNQ2NqZnMZ5zP5isVd3DpXDQ0/ynEwfPP4GrB+IADaNqWfoBqEniPBit0bPwRw4aIWTEyKvlCTaEjmx5jw6DWGbz1uNYiYvNZCo+0wU7c+Do06URQ0i3XWOtdUJ27iKYSkixNL5qWCrwNbsHWBTZy1RoSrbE+8MCrpqKnCoTUIadGSoyAum4xxkbMT0vZtpS1oawtk3lN1Rqqpg3hWsskeCFJpUJ7H4a5SpJnIaxbiqVtPggRlg4lKRTOusi89pF9KlfqzM/w+5e4wFUNE5SezzfTw5BdYG0b9o0Y2rps9i73GR9xLMY0oC6G8WLJ5vdh32ytQUdVqNZ69WdJkwQhAypGJbEhiVzVkUGtKld7qVIRJ7VkgcOK8eusW70PwnusYhVgHVS9OqKxotgrseH/GxfrzjDUVXF/r5qWRVWjsyZ8PsscI+HDIEDJMCwTwa3jnQ35DAg0Hm0tWoc16XwIhHOeiE7zUVQW1qeMjt5l8fzc8cLKPRFUVat15mOjVQlWIXPGOJJEIlVKaQODX7rgrPUuBGV5H94XHVXQQsglDGw5BQjfz4XnwHuPUEsldzjDljlBzrnAgZYB5YnQIBVeBHGMEiK4FVxgNmPbwMuNbODA0Q1BiMrbgEVSywZyFKeJIDrQSY+yavnTP/33bF66wtalq2zvXiMd7jAcDMiGa9TTc86fPSLxDqk1m2vrNHXD+dkpKi3JZl3SXJN0koA7bQxVNQMXBiMh9M/T+AbvZAx1DgxrQRRr2KBqDarbbNVvSpKCLO2sBhcgadoQGGcdLBYh20Dgo8DQMZmMGE9O8N4CjjRNovMrQStFpxOcYyH0OTgGtdBBiGkd3jR4mSKMRQKtcSu81z/19c+7Sdta8vOWBB2k194hvaBQGaolcIGcx9QVwlV01tbIiwLd32LrzW9TbF1j1FqUC2FjxJCUTFbsNPfZKd9mezhHiYzjoxMOD8Zs7+zR29hj69J1Ll+7xtbmFkoKyvmMyXjM5jpgYOfSHp/XHU7OT3l2dgSiDhuvCh9Wkmi8XG4uPqpl4yYZyz9jDGmaBvuECKl0WiZsdNf53d/4Hf7wd/8A3xqOzo45PD7i/Q/e59Hjx3zx86/zja98EeUtj977mMXRMWIxozNM2b18iaaa09YNL7/4Eq21HB4+Y23tBlmRUs7nZJnEYFlUNUpret1esM3iybOC6fmU3CrmoxHdLEV4w6cP7rKxvcNruzsM8y67W2v89P4dDs9O8UArRIRpRwuDj6wbAnNwUZYsqipcsJY8rsgyFD5wj5ZMHe89IhGIIsE1ZdxICbN66+P7Gey7zhu0L7iyd41Od0De7XJ4dMxPP3hEvnmbzvouxydzkCkbmxtAg1YZSuVIGST9q4msNyRa4KzCW0HrwBjL+vo6t27epNcdUHQ6zBcLglw+wcMqXCcosfTKXh2YowZrDZCik5zhxh5JmuE9aKnJCoOXGq8CO0pmHUBi4/TMyyxY6XwINkJoUIGl5wkXjVylWN/QH+Zhsmk8qKAMxsUU4qioU0qTpAlIjUFgUXx6XvHD9w64f1DRyAFCpytOo0fgRBKsOKVD1lD1DN6mGCytFMyE4MlZze024/xMMugoMmXo5JBnkmEu6OWON18t6GhBu5ggVcpaniClo6wd0nm8T1lYh7IVojplMp+QbFlSsUAVPbJiGzMf087O8dMDElmRJ5AMelgq6mqfdh9ORzc4PhhSj+cImdNd36STK3Y2E3Y2EpwUmKrik8M5z04WVPMGJRMMLVm34Pqtda5s5AxySe//Ze7NeizLzjO9Zw17OHOcmCPnobKKVcWaOEoU2S1RgiRYjW4L6DYsGHAD9u/ybfvGEAwbaKrbAiixSYnFoUbWmFk5Z0RkjGc+e1iDL9baJ5KEZN/qAIWqisjIOMPaa3/r/d7vedspj56dcXZ8CKrF0dGI509OGI+nVEU4HHhXgWpBtsnD831++vmI7339Fu1M4OdT8DVKOXSeB3aWqTHGUJQleRbGC5M0Ics0xXJO5ac4Fxg9jRgSOrYNj8hzIZNAXydc1gkbXtESEnzjPJAocVFEEp2EEhAuuEDDyImgn2R0leLk4TM+v/+QzfsP2HrjFVqXdnD9TXRvHdKM2nl6/XWsTBgbx+DGHW7+1X/k3vo69378EzrnY9T6kHdef4Op9yHcxjnaeU7/2ksI4Tg62ufo6BBrPd1OF60CJF+4AaasKRdzzOgcLyUvvfMOo/GUn//Nf+GXf/PXPHt8j4mtMEoCwbWBCK546zytvMV0OQfm4Xwdi5p2v4vO0uAcjaJsE7OgZdhLfByLb67p5iGlZHd7j7IsOD87R8dQK+svRpNEdPY3btQXHy8W0iqGp5RlGUTQRIfnYu3qHykFwvnIQScexIgNr8DIapwJTREcDgwh2FLAKmm8CQxDCNqtwN6ezeZBbP4d0aGRaYUMI2Faa6qqCumm1mJtEG1ns9nquaokugMQIeFYeipXhu8rSZJoehvroZm6rFcQ/lCweOrKoVJFe9Bi89I6m7ub/OkP/x2Xd29y/+n7HE6+4NP77+PsJxTTJbPpCGvnVMsFmWyzObjC7/+rP+bN17+DqVUo4ryInG+PiAefRoBXOolrQgVmswSkYDGdslgs2dreIdM5qc4R3lJMxjx88JAP3/sV548ekCuBrEv+6n/8Kx4dnfLpl79hsH2FJycPuPfZXU73H2KLCb/46S94884NvvP9y3TXBpQqod1tcePqJYbXd3npjddI0gzhJOPRmMOjQx4/fooQmk5nQK+/zuh0gjOCxbKi118jTTOm0znFosRZS56nDAbdgOhQCls7ZpMFzhjqMnBmF4sZSdZi59Ilsrak08uwMXm7nSjqsqAsliRakbfa9Hp9tM45Pz3H+sC09a6OQoCJYldwWuStlF5/QLvVYT5dMhktca6OB3UVHQ6SxWJJUQTm6mQ25vDkhHt373Pv7kPOpwtkmqGbcA4BmVZsb22QtXOK2oQ1rZv7qlt1E1KVoFIZDtTGgPBIHVyjre6QyzdeZ/PKHXRnncNxTSdxtFQSwmrmJU4r8k6LJGuRpC0yX7C9s451gqzXwqd9ikXN9t4lWmlOr9+n3+tQbPRoS0NHG8rZOZc2Nzk+6/Hk2bNwQJKa8axgaCS6vcHOlVtc297G1BnP9k+ZLwrmM8NsUmMr8LVl/+ljnKs5Ozvgnbe+weuvvETeavHkyUNkvcRWliePnrE26KOUwZsJ7737Y3b3rvKN7/wRTqfMp2Pa7QGHT+9zdj7m2p2cwnrWepugDL/4xS/4+U9+zM7GNv30B8zG32Lr0pDBcI1f/uJXtPsDJpMFdz+/jxCCojQ82z8iwWNkhm4NaHe71MDe3h7O1pxPxljvmU1n/Ob9D+h0Bgxe22YyW6C1xdVgkdRW8Zt3/5Fp0UGmXZ4+OiUfrLO516e1sclH739MkrfZu36d9375M/b2tnF1yenZhFt6wJPDCYPekPHcoPdPKYslUhWk7Q5o+Mm7/8jdew+YCxdE1dhMcMHfGUONolGiceG9oE39FirmhV5o0GblynwQ9t/oeI0j0TJOyQkRhIhGvG3u0LYJyjJuNXrqnEdE7naoh+NEnXiB273al8O0wuHjp/TaHV5/4zaf3f2SqlOxNAa9kCiTYm2FW5aIWmJcCB52NuBzjAnuWa00VilsHZ5TXdfImLZemxpbm/A+RfdQVVVkWoH0QcoQDXvWYepw3vE+hFAKFVLerbXgmvDNRsgIdb1OQjMVKcFVqERR1y6Mf7umSRr57kKFabdWTmEMZ7MJrtOhlyRBoJCR++sF8+ks5FwYg1IJVV3jrSdNWtDJaak2hRwzPT3j2u42f/q9H9AuFE/u7+M7A3TawyVw+Pw+mzsDklRgLBgD8+mCTqfL2fSM+199yFbe5a3X3wrrKGmz//AL1ja26a3vUdcL9icl64NNBi9vYLevMnn6AJl2ya9dp3r6iOWnnzE/3KeenCNsaADaWlA7DVpTLBcs50tkSyO8wdUeostPqjBeLoUgUxqMZTqaUgzWUHQwS0lNRaoTUpVQFiagcOZzlotlCEIihOOturL/P4+Vo5PgehUS0kRSLl0IPqstLa3xPoj3ImJFgnzSOHMbVFScGCUEYzVYEW8dzlm0TKnrEuFkCBYrCpZe4GKdYSLCK5LuVs8vSYIgFvstWB/DngVInWBdEE9rG0ata2tDOCoKLTWlhUVVsigKirKiLE0QaDxYDF5IitJTGceiKKO5itVGIUVw46YSEhUMIEq46JoMtamIZiPvXESvvMDHjg7Uf8oJK33osQgVuiDWOZI45q11MOI45/Hqgl9rnV817K0LGTGhwXKx12VZjpKKXq9PnrdQOkGlOjRa4oh+00RKGqNB3COlCIaixswgECtXrQBqU69yfGzZBDd6dBLqr7quowFIUNZmxfCuaxNq6+jitcZS1WEqOSBaJEon1GUZTSYquDxFaOgslhWJXKDTnOl0Sqc1xnuF8B2k9yRKBhyHkKu6XUgJUWR3PjiMjalQqkYIg6k8tY/88hjGFv4t8LJ5P8M/WqnQKPbxWon7uXf+4vwlJAiHVhIhPDoJtXhAfGTUZRmmvKKLFURoZHmHtTWJjEyhKB4GdEN47k6GNSUjugshAmItfm5CgEZRVWEKDqWRaYYsSgTLkONANPE4h3IGWVUIG6bKnQFTGpy0uCS8Tu0d7TShbrdI2jmqyOkM13EW2u017rz8KlmrBxKWp8c8PZ+h24/J84xEJThTUS2WKKlxLuXGrVe5dPNl5tUFlsHUhnJUUE3n2KJkvhgDFmSCc5FJHUPxytoyX8xYjMcsRudMJzNmszkIydbWDt1OL+TrWMd8PscYCz5MUiqV0G1rdKLjflGxXCyoqxJlQ8ZFP8/A5MwXU7yr0YHxhqtqfJLgjEamSTD9pRkQU7Wkio0yhVAZZe0RJk6jy+yf3X//RYu0OBBljVAN2FpQLSu0lGFU01QsqwKFY6PX4bXr1+iuDTjt3cbsvsXCpfHi9tTOYfAoYUjtjPbyAWu6oN9OWMbgoCzLydt9NrevcPul1xhubCEEzGYjijIklzocSkr6gz6qu8XLb3yL93/zPqYqUbpBG4SboPGx6xEvUsFqaJkmJbyuqrBJONAqI8tbfO8Pvs9f/vd/CR4Onh9yeHTER598xPHhU955543AoJXw2Ycf8vjul7SkpDtcQwrH8clzrKm4/dJtpJI8P56wWDrGoyUHh8ecnR9zNluyub1Jt9dHSk25WHJ88Jy14YBEaWpjONh/zLKu6bZ6gKAqK/YfPoT0mOGVG7x18xYb7YxPHj7i7vNDxosZOk2w+DD6QdgQEq0hCgihC6ih6WBJjY3We+J70wC2pZDIFiH0oA6dWONCWIJwoHzDLYQs77A23EBlCVIpfvaz95h4SXswpNPqsH90ynBjjXYCwli8siAdUujAU/E+hJyhSIXEK4lxocs1my9IJFy+eh3rJcvaUrvg7pUychSFI9EJQiV4FNaF0RUvwwiA9AYlUryA5aIg0VnYtJ3H2hi4QhiFbRhhDqhdEOPChS5AqCDO+TDW4G0I/ZI6uG4lwcGQJsG1FA4RknruqesKpRTtvEMqwSmP0Dl3H53wD58cczQWGNFG6CSCzWmsdngMMs1RW7v4aomJ4xNLL1iamkw4TkaSj76Y0tM5r98QvPpKyuOjY06en/Lq9V1uX+7SzhTjueHZqOLuszFj0WFW51Bn2KXCnO6TZYbhxhDna2pnEItTtBJ4mTFfOvKkQ9axlLMRrl5gigVCKVrrl0it4vzkC2x7iVj7Gp1On73LG2yva9TkmKOv7vL0MZwmOyyXiqKSJKmkv91ne9hhs6tptRN0rigWFafzik/uPeX0ZEZRWrxfgIcpVSgQVUJQaSM+3wi86PLgec3OFry2dw1Zj2Ah8CZgWHzTzFCQpCnWOpbLikS0SGROKx+gpaU09WrUPNSxsRjEN8AHhICOklxttdkSCV0h0DHYaXXY89FRi0D5kJIbpgZCSICTgLAIV6MEDJOUpIbTX/+Gk0cP2X7tDjsv3SHd3cG3c7xIEHWByLp42WKZgW13uPVv/z11f8jBu+/iFyWf7z+iLheYLEOkGbo3IOl1kcozGLTotS9zcvSc44MnHB0849nBI77+9ju0szb79+6xN9zkzlvfJtOKT37za977+//Kw8OnnNmK5aq4DUWscTXdtA1ekbfbFGUB1kQnkKTV79DZHbJUwfmqvMKJEIzQGwyYz6NruTmoI2P6JrEr65iOJxhTr9wBgsDIVlqF0KfY7Uf89qG9aTpVVZPaKgLryoZiyNqQANp8D4JDgtjpXrlcf8v1Egq3JnTh4mf9ijWoRDipCClI8xRrLGVRxgmEkID7tl0UAAAgAElEQVTrfWiThU6zXbnA8B6dpWRZxjKiEWwcs6uqKjDW4/tg6hq8CGEJhBAp70GpBO8czluM8PhWRrFYkCCR1qFlyvbWdV5/+5tcv3OVQp2Rrltmswlrm11mszHPnn3Jo+MvmczGdLI+rrLUVYGQhjxt8fWXv8233vpDtjZuYmy6YmxfiBsxuTxOMkgpECoemFxgFIuYiNDt9hn01uh0uvjaMHp2xN0Pf8lHv/wZR48f8Nq33ub7P/xDbr/8Nf7xb/+Gjz/+iJtvf4fFr99FeegOOrSlR5UFoizIgP/nP/1vHH75KU8e3+fOD77Pt7//fbYuX+b5yUOcWzAazdh/8IwH9+5x6doOV69f5vBwzHKxoN0Zcn58xngyYrg+IElT6sqyXBbMJnNaeUqnk9FpZRhn0KlmPp8wn81YTufMJzNanRb9tTVEkjIYDpCJpqhLhPOU8ylzH8JT1/p9Wp12KCJtHYSZLGW4sctiOqIoxjgf2JMi2F9iezWwwZZ+CUJS1iawdePYnUBSWMt0UWCePUdgOT0/4d5X93ny5DmzeRkSmImfkQAlPTJJUVnGsqqpnYxijMPVbjUJEFa7ot/NKJYLjJDgDUpJ9i7fZrj3Et3tl0nam9S1p6xqvKkg95TWkIhQQ6SJJE0VSeLRSYvloqRUhqICYxWjsxOuXt5hc2PI+rCHVoauTskd9MSAh+fHPH36hFavw6wsSZKMUrQ5mVa0RgVJ1uXWG7/HRidlUcNbJ6f8+oNPODqZ8MEHn3Lz2lV6eZfx0Sn9fo+v7n3J2cEJ3/ne97h8/RrWGlpZys7mBqNEUdqK/uY665du8+jxM/CG6eSU5+dzBt0uxXzO+ekRre6Aq9e2sFmfJ4cTXr+zza+yFJcI9vefcnj4jNHonI3ddXqDNnVZMjmfUHnL04PHvPPdt/j2977FdDrhybNjLBnd9R0qU1EVc54dHDMcbpA4RavbZ2NzjfHC8Xu//wMGa33+/sd/R1WMsXHcb2N9m+Pnx3T7z/nm915lMp7STwek7RSdQCtNMIM1agHlbMz3v/stnIMnB6e01raojOTR02dIK3lw93OkWHDl+sssK8PSesbzkkVtUFmO7nYoRmN0ND+I2KyTniDeOl4YlY6H0obpLcRvibfex0koPNYF0aARcS9GqwVEkwGxadcIF0KCSnRwYhHXrheR4x0mXlxsCHrByqgQFRJW7l3ncEZw78u77N6ckm6ASUB7oHRUpsa5GlWF+5vgYtx1dU+IjtnGTCGQ2NqC9tg63NskAq9UcAn5iNuqDVJoZOQ4Ou8RSmGKChKJbmV4KQJWPGimUfwQ0f0XX0swdOGFZ1EuKV2oXxEEHqP0q33FetA+TLKhw6RA7R3TYokGcqFQJrjgnA/3O2ss7VYLpMAWJYmQ+CQIF1JqRJWjJzmvXnuVN269wwf/5T3KrxJGHcnmlTsM79wkWU8o3JTUC7xM0Knk6GjE4/0ztq4OEF7w9LP73FrfY/PVIbVyzE8PKBdjhLf0NrZRaYtaOSbjCcP+Gpuvvs18bYvy+VNIclppyvJui+Xjh9TjObU0yCTDFCmPD8acLy1aSMrS4CoTQhzj4pWIyM8MQTRawPj8lOetnEz1SFtdlrOzgGHDUpkC4w1aBfexc6FBEdbu/+fpe/WQSJwIa9u5gPcj1RjrGOPJjGPduYC7IoqjSDwSvEUgUHhwIXBO+MigFRZBjTAGbcFqYt1jIdFYJEezBRPrcJWNiyegkISATAenoJYBI1U4h04SpAw4A2REKEmJsQH5JqWktjZMhriEeWk4nxbUVbjv1aaiLAPGoSqDQ1drQZLIlYCqYnPGx4vWx/BPay1Jp4UOUnQIUgWMMKEmjOFjqHhPC12jsDepeJ1GPm1TbwW0Q5ieEjaYbJoGygW3Nu5PzT7iwzRXXdnI/g9BWUki0VoFnJgPeSpJlqMSTZrm5O0cL4Npo/ndNhrbVk0vH0Ro10z5ORvfg1CTWxtG6lU8wxpngzAdp2xlXUfUo1i5ggM+xq4EYIenjqGErjYhW4WY4+E9WiiyVgsE1FUZ3uNa4FxO7QLyoDCWZVlQLOfkWUYdG0ZJmoQwsRfEajwIpUJ9mGWBZd/QW4XHpR5TC6yzeA91xSovxEU+rVQB3dCI7R4Csx8Bto66RhCZnTMkMoaBR156owslaYb1AlFVwUjjA3rTexs/g8gh9sRAsvASRCBYorxAehVxPrG5GPMihA/TBl4I0jRwUZ2IsmwSGuommk9cvBcpa8BahINaKZbCYU2NqCusVBjvSURAN6hE0+n18R7SxRKPodVu0ep2Wd/YQuvQkDRGYrzD2ZLT00PmszH4Ci0MstVhsHmFrNNHdxVZKpFKMJsbTF3jqpKz8Yiimgcncm1QKkUpjxUW56AqCqr5mOX0iNH5IWcnzyjKOd45qnKJSUOIe8B6djDGU1U183LJdLFA64Re0qPbapPJDirNmU4nlNNzFospQgSXrZQ68HVNbFIIsF5gbMAMpYkkVXl0z4f328aziW8ayHFCPNP/vBT7L1ukhchFA+UlVVnjnGVRlbjaoYVhs6+5em2bG7uX2BquM1ebLIZvcd5Zo3AC48ObZ2zYRNp+wtA8YjM7Y9BR1DYwCdc2NhAiodUbsnf5Cv21AUqCsXUYe8xbpFmGTBQ6VbR6DlMm7F25jk7bFOYcYyOSwToELhQ7DYNWiAjJB5SCJAnCsAzcLJEoup0er995jf/hP/x78m6bJ0+ecu/Le9y7f5+T8wP+4Ltv88bbb4ARPPryHg++/ISd9R55tsF8Nqff67GYzfjqq6/46t4DzsZTvFcUZYUzS87PBuzsbHJ0eMZ0suDy5UtcvnIV3VGMxmM+++wLWmmL0dmI2ji2dvbIspQApw5g7em84Omjz0nyDjcuX2F9uMG1s3PuPn7AV4/uMzcVIknxSkO80CFsakIpNra2SJTm6Pnzi5uQ98HdSWR7yVDkyURDWTE7H6FNEBYkKqT+qSDUoyRbGxsMBz3A8PzknF98dJ+ku027nTEbH5LLkpu7l2nL0MEM3NkarUPnriwLOu2ccrHAo5AqQ8sEK1OcSJgsF3iVYF0UkpFUVU0r15FnqNE6Q6tgaQ9mn3DDVUoifRhLTpUODlYXRzyQSJlGu310CnliZy8U8c5YhFex4FZhdMMTu2qWuq7i4Tb8bhmh7IFZaVBSY+oaKRVZnkUmFpTW8d7nD/nZhwdMXBeSHqE7GHrgQewIIRQQxD2VpKB1gMX7IAglOqHTVwx2c977ZJ/dYYfN4Rb15wZrHD94e5PdrZxOWzBbeB5NK/bHjpHrsRQZSAf9HWx7QHutT26P0S2NEha5nIdUVpVQ1nOmk3NUr00iU0TaRlDhygXz6SkDX5J3LtHxI9J5SPNtJ9fZKEqSB094+uHfsjjdx7e2KDZ/H73xNdY319jd7dHtO+bjGofg/HjC4cE55/MSW0vqRShyAqVE4cPiDNcwxM6kI5GOrCXJkz5aWp4+PWJN97ncvYmvPcrNkc4ivSURHpLggpBSUNcV5+Mx48V91i59h6STsJjPf8vBgAi3/sApCpiqXMCVvM3NpMOG07Rk4Nx5IRD+wnHWFEKSuAcFwjwNT887E9aktQil6AhBlrcYnU45+fEvGH14l/VX79C+eYn21gaiWuKzLklnDV+meJGQtAZc/sG/pv/SS8xPT3lqC8b7DykrS95qk/UH5N02UgnSTJAlgpSSXqtm2aoZdgQHX33E7Pyc0fNnTLYvkbYyvvrNp/zdf/4/eXj3Y07rKUvvsfHQF4D6ksViQafTIWmnLOoyQO2rGu8lutVisL1JpSRIVjzBBltgY2JsaKaLyNE2F86qyAxdLherwrhxVK32K7gQb2PDSSnJhVjIaoStYc9aWwRxtHYofZE+Hn48fDJa6wtnxAtFe/P1JnSh4Xc1h5CmYdOEHdgY8GWMWTkqLlwajQNWopWOBWBwYTTC8ouIBCEEWZatvi+bVDMZDmbOeoT0YRQpHiJqayFLEFk48N++eYcf/uAv+OEf/Ruu3L7Os+dP+dl7/zcP939OIiWYKcXMY4sFxXiMN0uq2tFtb9DNN3np1ivcuHKbW1dfJ1FrmFrhrIxBPOHQAjIW3k1AWOCWeQHGFCyXBVpAlrVJdEbbSYrxOV9+/N/45P1f8sk//BpZzfjjf/OXfOZK/uIv/pz3P33EZ/cfsHPzBh9/+AHf2d1hu7/OT/+vH9Hr9fjgpz/h9NGnfPDjHzHaH5O0JKKX82f/8//E7s3rkPaoTY1fTinPFnz86/f51Y9/hk4Tbr9ync2tLSajikldIXQOMoiYeZqxXJTMF3Osrdne2WBne5NeP2c6nlHVhqKseL5/wNnxiCRL2bm8S6cbUC06b9PpDVhfXw9rU2usA+cL8qwVHQRhbRlbkyYp6+tDWnmb6WTEwcETZtOz4Bp3IZXdGoGxkrq2WGtQaY92Pzg/gqEurPv1NU0+WOBrw2I6xUlPbyi4oi9hraQumwTnEmcLcIYsy5F1j8XEgxZYaXDUq2tNRqzJfLZgZ6tPf5lRnk4RQrN79TpXXn4Lsg1sso7VOUobqGqUktR1iXIWLSFJoKMMncSRpAKH5mw0xVuBF3lI/fWGRIL2Fr+cIxNHXc0xqcKmLdb2bvHuP/6U6fIBW3s7JGkL3e4zqyw+69De2GU+OmI9S9m9eo3vOsvJ2Tmf3XvE89NzXnrpBhtba5yeHdHptHjnG9/m17/8Fb989x94+PA+rc4aW1vXGWz08LbmwYPHrG/ucTx2bF65RbUcMxufYGczPv7sA9Z6LdLE0Eo0k6Njrr++hyAlyVps7mxx6coOjz+7y8HRc46Pzrh28zqmtuStDtuXLvPs5DmPHj3m5PiMtc0+ly9fZjkveXZwjjFxvyxKvHVkWcVsNsLLHJX0mEyXfPHlI/JE8d4v36ez1qPd7TIcDJnNl4ymY5Z2Tt7xFPMxy6nHlwMuXdqieGWHh/cLqnkBZk5ZFOikzdnxIZ9//AE3Xvsmg+E2zw8OqPOU3/vuvyIRkkePvuKVN9/m6aOvcM7T7q1x9Rvf4uj+fUZPH4JxIWMCBzpZjYmq6Mpe3V5fUKx+d79zLrCtTV3He0DonDZus4Ax4wWXWagxnXfB7BP3beK9QKumsfdCqK5tGrIXTbcmtExEAVMgMWXN07uPkT1NttUnG6RYYaiKKjwnHz4jrWKDL9aJSoSjno1TXwgf0QpR3BGCJNGoTjuOJXtM7aKjzYYxTe8RXoEUASukgxDrnQMbplB4If28cTIG9194DiZyMSsb0gV+twnpowjshUBEHJl3hizvhPuMd8zKEqcSujrFCRFq+Twl0VE8iqgxpRROgkgktrBYKUlUBuOUd//6S7766QEbfsBCGwbdNu3Na+S7HarlBEWJsBXT2ZL9kyUnJ4bz42f0RxNaj/Y58z9nN0to3bxGK8sZjU64P5+xuXuZ3nAbUS+ZzmZYv0an3Udt7pD1h+hL12D3Gt2dW5y8+488/eLXSDWi29HsP54wmQuc1HR7HdpaMjo+W7E1pQ6OaxdREmVR4RxMJzO8PyBLZmGUWkmUCsJRUS6xQpK3M7LCsFxWMeAuCqkvrPXmc/hdZEdT5wY3dHOmbiYZwxHBuoCGCLTSwLpEKHBmFRUQHgoX12cQcePUkPdYEwRNJxRehxC9RWGZW4fFhOZqfC6hjoM8+JtQSKra4MsapFq5dq2zoIJYO19WJEkSUBtVxWiyoCwryspeYKWi+UGKcE6SkpBA70xw8boglArZOOKJtWBEgThPmidhkkeEkWvrLF6G2q+5h4n4e15050spg8u8qdnlBSrCR2NXgwzwNE77cH0ZY1bhrMaYFdpKqTDRorUk1Spgh6RAyRSVZCRZFoTtF5Al1rkV+7ZR8hsEgRNhgrmsK6q6wtmIrRBydYZPtUbE83+DlbI2MOP5HV5qs7gaFm9Tk6dpiq1rjKxQ0lGWVXCTiuC6T5XGuwRBDAkLCuYKgeG9j+d8E4PiAwbAGEPiHF69YIrw4RyhRMCjSGRoWkmDSDSlD9NBUoe6MnwuflVTy0YpxUeXOBDDafHgZPhMlbwwVQQnr0R4GWpoIeOkUKjP0jTDeBeRd5bahvuH8T4sqng21DqKy6IJnwoNPt1MuMUGHb7Jp4kioRIx4FNhKwFKUWuFtzWJYzXJ4K2jdjVaeBIh0UKzVBIrwApP3mmTEnQUpVNaeU633WcynlKWc7I8YbFckM4m9Ho9tE5I04ADcdZSlynj8wLvKoSGVndA1t7AkqIzQasNOhHBEOVSqHNGJyeUxgTBWliUMwGNKImhZBXOLqjrCXV5TrE84fz8KVUxYTySzPprdNpdsjRH64wsbeG9YDabcnZ2RpamzKcTZp0R3V4vTphUEdvhmM2mlMUSCOd3h0dLueIcO2OpygrhJVmaQxLRnt6uPh8fGzTBWR4MJP/c41+2SOuhrC2VsfjaYOs6OqEsG2spr925ze3ru6wPu0ghGFWCZXaZZesGpZU4ExMxkeAkwno6dsSwuE9fjbDGUNUCJTRSJ+isw7VbL7GxvYVSMowcO4PWEmsVAkW5XCKznNnoHJkOGPYHDPpDivI5TbJeojU03A9/wZWSUmFl6JooIZF5StJpkbUzpJIMB+v88Q//iJ3NDSbzCcfnxzx4fB+H4c/+9IdcvzpE2Jrjg6ccPvmM3c2UllYIPKWylPWCmy/f5tqdl/jyy3vsXLrGfDHn9PiYVqvF+fmEyWhCp9Nivphw+OyQ6WjGzTsvkeVtlvOS6fmULB7Sev02G8M1nLWU5QLrDNeuX2J4fM7Hv/mSpw9qdm/c5s7OLrtra9zc3eHDzz7lYDyiEoHz60UsaAkjE9PZlCoW+VqsjDGBdfKCeOAIRatu5+iqBbMCZ9yqU2WlQ+YJrVTRbme0Ug04Dk7P2Z8YxN4eebfHaHzCsNdjkBoUYcyA6AhLpY/pezXCa548eUivO2Aw3ERKyXw2QUhJr78GPmz4HhEZtAVJClpppM7QDefEe7JE47xbBeGEUQQPUpPmbTxhBEGrjE6SBYesl0HYicK2MYHzmGZpdKwZPAFQ3tyEm27mhcMuFkfx0WwMSmuyLA/iSlnihGA0W/DJl4+YmHV80iFsHqFD510AyYtmM3EOb4K7ARlHpYiIB5WyLAWH5w6bdpnZlM8eGbpJzesvrfP6nQRqz5NnjpOyZl44HBqpQwEi8hyncjot2Mu3KJ/fpSqPEAnYskAUBbK3jlMpvY0tVJKG56U72HqG6ljarsQXE7L+BuvDLsV0hp39BlEd8fSrCs7vkS++oFNPWI4GiInj1o2rbN65wawwzMeex4/nLGfHmMUUXwnQKWCD2ITEu5DMLpShlSt6nZy1YZd2p0Wvpejmkn4uaCmJsI7x+ABfTlj4Fll+HeuWUDtqf4L2JalS+DQPLsu6RAnJlat75O02k+WEsjSNYee3HA/ihRvxbtria2mPHSMZCIV2F0FJIhbbWqmVW7P5a8L9PboB4jgNxDGrML9DAuzlbWrnOTubcPjTn+O/GLBx+wZbd+6g19epOme4TEOSMVI9hEqYmII6T9jcvczNjR2ET1BCM69LZrMZZ6fH3H/wiLOjR5jFGVni0VqRyYRUelRq6Wz1SXLBB7/+O+pxzXJ0wNgsWAqPIaxJGQt1AZSLJYf7B2zv7oSGkvd4IRGJorM+xKUZFTUNWNM7gylrhFSURYHUkiTJYlfakyaaJE0py/LCYfXCw8WRTiUvQmdcFGSbQvPFA054n/1KHG24Y1LKILBGgbYRYpsCtq5r0jRdIRSEELTbbYqiDBw4ayPzLRy6BIJEJygpIpIh4A8aNEFzGGhE3oZdRXNmi+4vGddM81oAkiSkeTeFbh0FC7zCeQPxdYEISAlnkF4hbAD0D7otdtfXuHJ5m3/73/0HXrn1LWYTw6eff87B4WPm0xGzySnddhelPM+P9jk5OaDXS0lrwd7WdV698x0Gnetcv/IKqcoClsYpQEW0g437lopFsqDhScroIBBS0O50A5tVSJS1HD++x+fvf8hnH71PohyXt7bpYUkzxbe//wc8mY04n8+YzpfMyoq3X7nFjSvX6ekEv5zyN3/9vyNtgXSe3tYmh4cnfOt7f8idd16nf/kWwikWZUVVS6xTtNtbmLNjKCpYLNC6E12sgm6nx+bmkN76Ov7QUzkLqkNZLplMxqwNe2xsrmFsxWhcUBZBoA8Hi4AjWNtcY2t7ixBWkaLSFmmekaYZaZqitKIolxhTIcgwpoDSh0AQ70JjNgsN0bX1ddqdDuPRKaenzxlPzult9NjcukSn3afV7pJmbXSare4PKjYVrA1s56qqQ1ZAFGSq2mJsGCeuS0ddFRSLGcV8xnw6pVoUEMNb58WC2eKcRTWldpaqttEJLQDHyblEyDWklgzXttncu8PStFkWhnbfI0RNK4NEC3y55PT0KVf3tqiXY0TlOC9G2OE6vfVNdNZj2MsYlyVeOF6+tcN2zzPsdyiXE7QQJFKTdtYYL5csa0+lukxtRm9rg6u3b1MsFrz2xjf5+bvv8vjJE/LeANVpo1spHTugNjXXr13i0bNDxtOQEnz99k3mxQxvBaaGza09xqNT6rJkWZxxcjYi77bJdMJkXHA2WnD15dd5/PSM3cEGzx98jFuccnW3w/HJCb1ei04Oz5885HS05NW3XqGaJlza2OalWzc4uP+Ao6Mjzk4nzM5nOK9od/u0Oh06RZenD/c5O5lwfHoG1lMulpjynF5/wP7BEZ2sixBwenpKXUO3M6CoaibTEffufhoDjiqcddTGA5rjw3067TZvvvl1drbWqUdHHBw84+Wv3aGfWfafPaTbzjg8eYaiotMONflar829T97j1bff5OqVHe4/fsAf/bs/YW9nl3sffEWWdPmP/8v/yvRon8cP7iPzLmtXXmIwvMRXJJw9e4KppkjlQVpQ4d6ghIrTKb/tKGwmIF7cv5tQDymCahP2W1YNdb/6WY+POK9m1Hclukq5YsxbH6cu/AtjqFHsFDHZfsVT5wWxTAQxxDuPnRgqM8PNFbQlsp2HKTMReJxh76/DRBthqsY0E21NLaHE6vWqRJG3c1SaRtaix1nIWznGlJyfjsPrj5WDjqQBZzxSRdatCOO/zloMLhoNmjdVrqbkalOHFrEMaeKNA9A5h1cicvuDW9TH72ferhBctXfMbRWS20VwJdZ1wPJUdY1xcTrEBLSREy6EGsngJHz2cJ/ycEnfZBjpMEXJ2dGYayIhyduhNsfQTjV3H3/B/onm2u4rPPv5j+meHfBKovD7T/n0R/+Zy7//XV76znfod3NO50tO9h/hTIGvpqi0RTFXYKHb6VGioLVGeqXF3uU7ZJduMv5xi8df/lds4lkKqBqTCp61tQ45lpPjURjxtyK6tQMb1ppgZLRWUBQ1StTxfQTvBFmSI4SiNobaXIhSugkAbYTx36ldVutDNC7u6C0iuCNL6zFx+qFZ0y6aCGzkEfso1jf5HZ6AZZJChukd51bBe3EoCiHACgtehSnERLFEUJrYTGmmKKJbuzSWelEGY4oQsfYDLwxBMAvXjNRyJVgaF/iyZVnRXMQ2jiv7KMAiQrMxSXR4TSZMYhDxUaIJYmr8j82UE6BkcLGqBjWlBNbGxgMNgkqsBMwXa8qmBkyS5KIpL8SK69vUhtY5BGJVc1of3ruGud0wZFf1ZjQkNKP9KknIkhY6TUnyHCFVmAiLLkof69umqW+cXTVhnPcx96HBScXrOv5MMA40omUcr08TtFOoKNI2G62I3Np/qkmQaI1Xmlqp0Lj3QZSvbR0PMOFrUmoSVMgR8CKu0LgHmTqIyy7wi521WBPqEindSiQW4mLdOyReuLAPJgKqkJXgCbiDxvEbMj3sau9uzBdNg0pEVJmIZ7BmWkLGPdd5QqYOF2suGCZcFLxTnK3QVlHZgJKo6zr8jDdhKiReu40QH/BrfmUIEUIELSqat1TMgUAEp7JujGAiTiMojdcJrmmsxNdTmRpsReocOZKF1jFwLqM3GNLe2KaztU0xn1OUS0bjMZ3unPlshJCOPM8R0lOWRQiejE0erSRFsYCmCYgk7/RYWkM1n5O5hFRrrAvvZZaGQPYwS6piPa+i4B32Bu8tMqYcKqFCw8BZqmJBtZzjPSxnC9I8JdEpWmckOkOphEVR4h3gJbaG2aRmORtjrA1iv4SyKqjKAmfD+cfG5qZxllTGpo2VOFvhnaI2FdKoWBcrrG2MBhF7Efe/JjD6n3r8ixZpnXeUpg7OJmeRxrDRzXnnra/z+qs36HVy8iTHC8+4rJjaLkXna5R6HeMJ3S4C88QJQ0vOuaRn7NYz2mm4nK0NNu3KCoZrG1y6fh2tMxbLOVrF9Nc4vmBrQ7VckoqUo/0Dhpsw6PbY2BhyeOhIYmCPNw6cRaswOh4O5uHQLJQgyRLSdoZq57hMUSaQKcHvfffbvPa1l5nPp4wnMx48ekDe1vzBN7/N9tYawsw53X/Kwy8+xi1P6Q77rA8H1HVNp6uYFRWbexvknS4Pnjzk/PgYJSTtLGVne5OTk9OwUVlHnrcZnU/44NcfcfD8BKUkR/vHrK0NuPbyDVqdVgilERaVQDtpkaUpWatF2sq5/+ARD58eU3lJnrWZLObcunaZa5vbfPnkMT/9+COmVYVTYcNRSuGMo7CRMStEvKETig4TbkI6TcPm56JYoSStToeidlSuQGhPpjSqleDTILpIJVeixOODE2ZO0u8NUUmbojrhSm8L5RY41SKwPSW1sdR1zWI+Y9DvMxqdM52MubR3iURrqrKileZIMjxxVCWOTXkgb3cREdfgnQhObWcDEDwWNUGkD2O1zkscEqUCqwYXRoJFxC04f0Eost5jnAmOWIAoWs8mU7rt7qqLKnxwZSjV3MQCgL7hjgb8oydLE8piuRpjmUwmJDrl8t4WT6ah8bFKfW/vwWwAACAASURBVMAH/pXQochWAekgEHhvwuelRBil1hqZCOoajs4kqWwhK8XdgwkdWfG1O5tgHdgwCC29oJ+nrGeO+bJCJJJapaiOZ3s9QS08R9MFxegJ25s9lKupootZdTfxKqN0YY34xONciW5vhjTy6SFOOjyKRAs23Rn17JR5oXl2cJ8kX7DekajFKfPT9zn69BYu2eRo7jkZgzURRaJySGQQ7hEQX2PeVgw3+mwN2+z1U7YHmkE7dNZ87bGupqrKEEKgJINBi7oIXX6bJMHBvdAsxiUU53Tbq6EoWq0WSnVpdQZI3aLXk6suLKI5SEXBNmIPMqm4nna5Rsq6FORhxwxuwuYGjmO4vsloPAouIOIRK6qcIvzB+Nn6sM95h/KempCSqrOcG+u7TOfTkMJ+eML5lw9Zu3KZ3s1rZHvrJL0OMptReYF2DucFR88PKKuarLVG2urhhWB9Z4fLN2/yqnmLZw8+5Vc//RHPHn5BkqQkOoGqYjmb8OTpM2ZljVCK1EvmiwXn3mJjgRuK4VhYucCoVlJQzBfBJSvASkFna4hc67BUDidDwdEUms46pAetJO12B5XreF2GFGxjzIqd7V4okF880ISutFsdeFbOAC7YYM2jcZ43h+SLA5NeiYgvfv/FELGyLFeFVyOuxr+ETrtFVVYr1yvOYayLQVDR9RH//uC8r1c/3zzHJhSi+f9+v8/5+fnqeQMrYbkpTHu9HtPpFCUVraSFsZayLPHeYIlj58MrvH77G1y6tEPFmGl5SLcnSLpghcGYBSeHz/j4vf/Gs9MPUb0Fz6dT7j34CuPaCJkilMLXNVrn3Lr5JmutG7g6oTKhK70KtMIHl4ZMEKjVa26WeyhYFVmiwdTMTs/4/NPP+M17P+d4/ynVsuBP/vzPyQdrXL9+h15/i5/8zV9TCcGg3ac6PmcrT/j5P/wU8/ALHty9ixmP+fRXPyPVlq1bV3npG9/kaz/4E7ZvvEK7vUVl4ej5Cfc//wwkvPnON8nSDJv32Z+EpgU+oJxM7ciyPsP1jCzvkOWhAN65fov13jqfvv8rajdnOFyjKkuKZRHdHZokOvNa3S7d4QbDjSHgSNMUoRKETsiyJDSDVAgtWcxn6ERQ1wXChrWntMTZ0BzK8wyiK69eWLprQ5JOm+5ij529q2xsbCNlAiJHKhWDekDIUBw751cHk2bNWuuiaOCQKgl8QB+YmRJCsreXQZgmuLtdbfC+xNkKa2zYM53H1KGwtzaE5iyKgmXtqLykdp6ycqg0wXtLikdimMwn9Fo5whoknjyycBMlWE6nyEVJp9dns7PBvCrp5m1279zCecfB8xqbSCoEpvYsTMbpdE6xXNIZ7pK1NEnaQni4cukq33hjyedffEJxMuD6zasUsxEb3S7DrU1eV5LpvOCX733Mhx99hlRw+doNXnnlaxwdHrKYLakqy8bmFkdnIz7/7ENaeWCM37xxk3kFmczIVYe6nDMY9DjZ/5xuv4vOFUKkLOYLrHmOLGf86u8fsXfpFqpasr29x/rmDicnzzl49pyz8ylOJOTdPtZ7Lu3t8NGvPubBgyfsXdvl6OiI6fiUvd0+b33rLf7hJ++ymBqccJSlQYiEXn+NGzcu8/DBF4zOTrHCsbOzQbu/xnRRU5eW8fk5WMd0NOPo6JzCCpIspV4u6WY5b77xOu1Wn/frEjO6zPjoACcEb7z5Ou9/8BE/+j/+E3tXXsUkHRLdoSgq1rotfv63n2OWZ1AbWmlOf2MLnfXJO1u8+t0Ojz7/hIP7H2HnI4QJCfEei9MRS2ODkrMKA+NivwijmReMcdHMnkjBi822xi0qaEZif1v8uvhvGjUlfK3hCjZNdimDhwBBkiTUxrzQWI13bylCUeEEblZTLkt8Ksi2JPlaG+PrgByRAiWCGGeq+kKIDjZBdHxOrmG6p0ngiwvPbDrFFBWtrM2g36bdaTE6GQXHlgzP25WBL+6FR7qMWnp8K0UoERLULfigJARBzgWRx+JW/EnvoyjtRXTDgTMm3hOJn40KuAgZjAFhZDigJybFnFaakacZtq6ZzeeUiwIvJYMYsuikoLYGW4UpOic9hZtx4/U7vPW1V6nmJY++mOI1K26xlpIs61HYlPc+OOHJV0vyp5/wJjO+vpbTq2smTjBOEo6/uIdMMrZfuU3bOO49+BJbLZA+OEL7GwKrJKejWRgl98GdppRCXtrl5T/8M86rZ1Tjr5AqpSxn1ASWa13MuXn1EtSWg5Nxc56PYUAER3JVUZZVCEr1NTY2b8si7BftvEMxnaKkJE00lTLEkSJMXf1WQ+LFtfrbjYrwiyNsjtI6bHR/KR/qyKbZYF1A0hjrwIcJpRX93gusadjLTT0U6qbKWWoX2gm1r6kTiZMpVjVnRFZ2XO/jJWA9wtkozqwuLZqLZlU31zaKl8EF7+J5hsYGIZqLvgl2DZzz8PXIHxXi4lrEIWSY7KxXTfwmzPpFY0VojACrwLNm0so7j3H2ooHcCL3iIuw11G8KZ+pVUz9cwqGusc6uGvzee5IsXdVnzZ+11q6CX70Io9hKBS6mNQ5hDFJDWVUkSZjmFHEtaK0v3gPh45RWNJj5hDzPkEKt9rFVQ8pdiNbN9b967c1e5wOHuKmlrY/O/vixmLJamdu8E+AVSiaITONMuOcHHq7HNFk20c1tbeDaGhtEVVPXKFnjBWhbk1iLlIYk+W35yyMwhElEqRXGGYRWSKuQyuO8jfjM6EKN4cBChcaDFC989j4YpkQU4qRqrqvQaQgCfHM+uAgYk0oinAvcUikjMiFegi7oAgi3WsNBHJaRnhGmi1X8LGSTRxEF2hBiTrhu8RC55DrRuPiaqQPLVnsBNuAdrKmxVYmqClKVktYVSxS2rBiPx8yA8XJB4qHXbZPkGd1+wekxFMs5SiuyLMG7i4acR1LUBcVyRkCigPWSTm9Ap9umDsl0FAsbTCARV+FdNBzJMLXXNFkDRofoJAt5HlomaJUCHm9rpCRMlAiN84F7Ds0koUaqhCxPQ3itIGh+3gbEU1nhnKU2IZjXmjLu0hJroN1uxcmXJrRSkeQZSifoNKDYmpDb5joiXusBecQ/+/gXLdICEJkmwhm2Nwbcvtzjm2/dZG1jA+sEqBS8p3Qtxu0bTJIrmP+XuTf7seS68/w+Z4uIu+eeWXsVayFZ3ElRW0u9qN3yTHvGngb8YsOwH/xkwID/FAMGDNiAAT/YTz22Z+yZ6Z6Zdmts9VBqSRQpUuLOKtaalXvmzbtGxFn8cE7cTKp7/NwXKICszMq8N+LEOb/f9/ddBNGPSsnIKPM1uR9xKTvmm9f66P0lToZThJ2RZ9F4OAi4fP06rU6PyWTOeDxhqd+NxZiAQitC8OhOi6q2DJaWqMopea9geX0JoRSlrdB5lpIt42YYm28WAFzRKciXutDJsT6m9WVCcvf6c/zwO79LrjQHewc8fPiYQkne/s7bdLo50lZMjkd89clvCNUpl9YvgJMYY9BZoN0ZcMnkVKMhO48fkWEj2BYUWkiO9vdZW1vBek+/3yN4x97uPvu7B0i9T5HnkTmztELeajFYXULJcOZ/JKIvrXYBGWCp12d49BUuSLqtDsPJGOktl7cu8vbtF+kOlvj5R5/wZO9ZTIbNOANXlIqpicLhiD5LSojUVKqzAJ1m+mc0ZrmHGrQxSqNclDyXIsrJghDMq4rxeMrO3h6V8AStsFWNDNG7SPkZ3jdeXTopvv0C3M2ynIsXL8ZEx+TzmmctylpjLSAVeStbeIoYGSe3kY0Wi8wYfkbymwWfALVgIxyndMCoeEhFNmwEjEVi0EKzOURpm7NA+n6tcoo8UJVlNATnTEIdN76Ucuhj0mJkuTUAUgRZZrMZ3W4vsubsnCvrXd77/DFzZ5C0IjArUyhVHPVBYiUEnxh3Ohqv+zS0KF3yzc0zyAPjuqQOgdOq5L2PJywXS1y9FLhwUdFqCQY9icBRBkvIcmSm6HQ8T5/N2J84RqZNu+ggkOh2jyzPI3u21WNGC5UmtdYGpFJUsoOsPZQ1R/s7KCFY7vdi6ntV0V69xo03v8vOl79ClQco6fB+zqRWnGzPmYccETSCMjG9TDxlM0GrrdjcaHFtq83FgSGXHi0C2pXk1MjyjPUR6ppyMkEbHQ34Q4YTgcqV2KBxcpWipZGVo5pPqOwEKWoCFiUVSmfUHkzegiAoyyqtA3EGyou47nM0l02PLd0iI1AYRaht9Pkh+rM14P7+8WHyTZKoVGZGcNHh/dnEG9H4EKWvCYFwDgMUrYx2bw0l4HQ642hnj/3Hz3j6yccU1y6zeuM5epurqEEH0+uhswJHiasOmFAzKSfUVcXRgaC/vEanv8TF6zf53dYf8+HPOsxHp4ymE/Z2nvLx/QdsHxxhG2kzMaTAS5lYDE2lHovlIEEXOZ1eF1vFYBRJbLRagy5lBk5G7z6fvCIWhaw+Yyk0zHWfZF3NcxdlKGIBxMLXwdrI7l/0BYvXecngeYA33pY0tW8kbild93whDixYq2fFHfR6/WTRUqKVotPpJNbAWQF09vu/3nCdDy5rroHW+uyzJJnY8fHxAixuwOPZbLYALpp9J16LxlIhQHC02pILly7w0u2X+ZM/+k/Z6N/k3V/9lL94508p5S7tmce97+i/fYEstJiMTnn44FOG00dc6C4xryY4O+bVl38HJWvub7+H14ccH+2zu3fAyo1bceDlI2sWb0AohErFmpALkHbBUCNeZ+kcn/zql3z+i5/x4IP3OXz8ENnV/Jf/9X/Dr+895vKdu4xnFc92dnm6v8vNuy/S7bYopOInf/6X1NWIh7/6JU/qEplrRpMdLrxwm1fe/M947o23WN7YQpgOk5nl/hcPefDwCe//5Z9xfO9j1i9fYK1taPWW+OiX7/Luj/4Vuw8+xQsRPeqEIc97WBcDHY1UrG9e4uq1Wxw/26YuZ2xtbuCDZX93nyJrI5xE2AqRxxpm7cIWGxcugffMpqMEjIDUAqUiyFFWkS3grE1p2JbgJaBppNFVVaX1FplJ1tcEa0FIBktr5EWfykWbFy9rVPJUC9bFpjxLZ5yz1HUVk2tDQGcZWqpUUEfQRPgovY73S0JQGOJaVEKTmQIlO1gbg1mV0YszLdMqDieEQJs8Mm2aoDEZPQ9tbQleIEJNXW7Gpq62iODQCoQKGOOZjqcMT8eU8zmbymCnU5wG3e1Q1haZr0BuGM+GzOZTEAadFdjxhI3NLQoNwTmMBGUCr9+9SX38mP3PP6RVDvF1ibx8mSvXb3B/PuFbb73GyfGQz778ig9//RFvv/0aYDncf0KrHQNwD09OyfKM8XjC6WiElIqDo1MePdrng/d+hVA5G1vrBHvCvCwZmHVeeelljva3efLFp4j5CbmsWOmvcu8371AjuXb7DjefHvKv/8X/waPtbWTRotUfoLKcWTnn5Tt3kNLy6PF9vvX9b5BnFVsbbYKvEb5m0Muxs4CXGuNqWoXh5PiE/VabKxeuU05Kdke7tFottJZoEaiqGSenJ+meBMa24u7br3H/swdUZfR3n5Wa4XBMVrRod5c4PTqkv7bOa6+8QgiWn/z1e+RS09l4jt3HJ9wflux+8SlH20/o6AlPv7qPd47+2iomL7DkZOsXudbuka12efrph8wOd9B1iZIiemM6n0CYWEs56yJ+pVMS8zmw5LctEM6zDqWIViva6Oh3fo6t2vzb6D0nFmBW4wcuAotQsvjDw9nvTt8bpceSkITjQZyBZ8IJxAzq3SlZCKiBhoYJ60NssJ2NMmelFsM8KaKdWCvPCMGBFMzLMjK2JhWudIwnI+azaQyJsbH9FOl8ss7iEkggfaAez4BA1soRKQ/BpfMuhqWkkCgis85Zu+iJGratEDEUq/F59NYR6kDQEM3Bzq5/EDB1FfWsSXiPfqlOgPWWWsSQoKAlNlgsDlRskvOOQfWn5CsW0XLckJd59DBghWJmJS2pETLnl+8/4oOfP2Franh+ss3r+SGrcs40WFr9ZV76e/+QSavNJ59+ymc/+jH95T4by8sUPqbNF502WS4xueDwYJfjw12MF1y4cBXZ7lDXJabIWVnb4GT6BEG05lFIVJDUkxK5DOsrq+wensaQVOKwNXprCuq6XJzTMZG+pK4nBAu5ydE6kisEgnbbMJvNsC75yJ8bui6ua/ibaiCfav8FgBai92JGBPtFiMxFbRRKgg+WTGURRA0eH5qBuqBJW48DPAEohI4y8Mo2Mu6ArC2ZlhSJjNLUs4TQzETis+UjuCZE8z0N4HxGagjpf7wPCWgGaAbvzbUjDeRtBE1CoK6amuLMikPImLMiZTzfhG2e9VgrahX5xqEZYCQE6etDm8bv9LerRr4+tEkvqdSiB3DJFkXrCJKGEBbM++Z+NXWgUpFNq5yNwJaPIdZ1sNisQOk8grbSopF4LxFSkWfZwm4hsmn1woPVhUhuCCHuIVqpBVjZWCWEcFY7NuG83nusr2hMVBcet6kGDkTwMASwdb2w8KrLEuEcNvhIZnKJoR1qwBJCjfcWgiKIgHcx5HoB1FqLrWqMtsig0z12BKIyTCq5WFPBBxQCJwK+9rikWJVSoVUaVDhBneoPa+2il9dao5Jdmk+K6sX9E/G9nbdDkyLdMyEWod4kZnpApCDgcAbcSkle5NjK4Xwd10Sy6FBKkedFvNahwVliD7QgYCXQNlr1gZARnMSoCBi2cio3RagALmCEIBNN3yPQ3kGoUPWMfB6HaMhAPYk2JNVsymhWcnQQqEVSbVRzJpMJUs2j/YrIEUJhjEJKQ1lWeFdH1rT0YKHf72OyNkoa2q1Ap4h+tCGRbOalxdlAnufpcZEJpBZRXeB9vD7SIqQlhBm1HeGZ4sIUY9rxudBxwKCUQascrWMOgjFpQOgdtq6orSXI+CzXtoo1qJAoncWgd5khdQwaS5ModFZg8g7adJAqj/uflHGogIjPkGyC3UJUsbQ6f3MvSK+/2yBt8IS6ZLlteP2ll3j7zTdw9Zhuv4sVEpdAJEubCW3Kzk1meoDzzVQjQChRYUKPCb9zu8fF4ilP9qZx+iI1AcmkKtm6fI2NzYt4RwIhuwtmiScCXkJLggvoluTqjcs8vPeU0+GY5bVVENFzRDUblg9IEZDeYySQ55BrOst9vBagNdpLpPcsdXr84Xd/n43VDerJjOHwCK09L9+9TavIsVWNrWbY8RHXr6wyPJboVsHG6gaZgcdPHzIcTel1WxwfH3F8NOL5F17mtZdeYn/vkOl0zmh8ilCCTLYo64p+r8e1G9dZ39xgdDpiOpkyrytscICn32kDEbwoywqlDFJkeOImdOXCJjevX0CYDk+e7KIzRTUd8+zZU9ZDzd2tTa5ubPGrLz/lF7/5gJPJENVqoTE0uZbRGzJuNlk6cKqyPJvswkIC1mq3UtFpI0AY4qSYxKqpqpLaeQ4OjjF0GRQdfDljpaXpyAnVbEZLGJTJKDQR2Ap1TLWUCpUX+CDOHioRmIxHODUgxCMsgsZBRMkcPgGsWWTNhsgESs8pPrizQkHG6TNlRScXZMbgbPQ4q60lINODrePmnaavhJA8u2IhpLXCpcTQMx9NCSGC30rFBrasSrIUNiaVQstowH10dMTp8JRupw/ScWOlx5V7h3z5bEwQJsLlC8YFxCY9VWdJ8ySQsalP00JXzpFaofG0EHg7Y1JHcP+rgykfP1VcvNKm01ZI61BGcDTNcMDJeMbBcEblB0xrxSRIsv5lqJ4xHO7RyWB6vA1CsX5rNbKYHdh6TCgrrJJMZg4t23RbXeS4RgTHbK6ZOENbwpw2t7/zjxCbd7n/V/877XqPbPkyYvU55vkghtrZGmGj/F0VhpWVgqtbhotrLS4sZbRtzd69zyhdSXdjCwt4WeBqGRv+5Oc06PVo5IiVCAhhUDbgXGTs1xJM9xY96fHze/h6GxUC1pVYVyYT/ppZOYvgnGsasgTqpd5MScF6ljNQhkIsWh1kQzkQEGQMC/AumtWn0ijZIDTba/LNSomgpORfAC1UkkFlCKkZHh5STqa0paaztMysqtibnLL/wa85/OIrxHKP7pVLbN6+SWdllXzQBTopZXeKsoHKVeyNdwAVByXCUxQtTg/2ePDgKz794gv2j2NaeMNuaGQ3sY9LgKhovFvjel1dX8EFz3Q6J9P5omD0IkRmDwEXRCqexKLRbJhN3nuwHp0pVlaWKMs5k9mcEGB5aYngPaeno2ZE/rUjyicWfJTyxfdmTHYG/J5r8s8DtsAC8Py695tYsEuEOPMCi4MrOD4+XgC3ZVmy/XT7nJ9RvC6NF23zGRcssVQLNnYpAEVRUKeiOB1zyZoFXKhRGEJIU34hwEuqWU1lxzEUwnoUjq0Lq9x9/XUuXxnQyiUdtcrKoM/O4wd88en77O7ch84RWncoJ4fgK1zIkFh0FgjzgPCWdq4xKmdr8zKZ6SJVxidf/IzJ5IjHj77k9rU3CHSQMkMQbQ3SZCsxeuLAIdqyQAiNJE3y1Wef8qf//X+H235M5i2FtGjZYX1zlfbRlP2DfTYuXOHJg8dcvXKFVljhn/3P/yOfvPseo+0nIGvydpeNO7d44c23uPud32Plxm1Ue8AsaI6t54tf/pzPfvEzDna2ufXaa2Ryzny4y9Fkh7/8X+fUVvL00X3Gp7vRh0tA0JrVjS10llOenKAzDVKhVcHnv/6Ig70H0VfVq4XNxNHxEfhAd6lLnhta/SU6S+tk7Raz8ZjaAyJglI6KHg+BOnllRhlzlhfJOzIOPMpqhg+O+Sx6goYQVR/WJksFadCFSEOB6EUndaQyRza+pyotdWUJ3jOdTvHBpcJXRI+52qZGK1mPBAfE4ZNMLAPvAtbWBKVxomF6S6QIOFc2rgnMyjL6mllLHjyZyVAyYOsZdVXRbrdptwzOBWxlyVpt8nY7yi5DBLDKakZdz+ks9VBZD+8tx6NTjkYzSmdYW9ugcpbJvIZZxXh0QsCTZQFnZ2Ta0mu1aGcKrQK2dCjvaGnHxqDFl795wnw6ZWV5mdPTU1aX++zt7LO5eYHvff93ODg8YnI64uG9x1BHW6lL1wTrm5c4Ojhk68JFauuZzireePNNHj96wvpkytHBMSYbsNQ3HDwrWRpcYOvyC9x88XWu3L7LydGYBx+9y9r6MkHOaXXbnB6McbXllVee50d/kfPkyTMOj07xSDrdDrs7R2xtbHL18iUe37tPPZtw9fIWmYbT4wmPvnrGlWs3qOYPKCtQRY8rV2/y2aePuXfvHg+1JuBZ29pEMqeelwwGHXzIePTVl5ycjrh24zZXnrvDaDRj/9kew4MDvOnz/ocPsfMhx9ufkbsDsnaby5c2uX5ti4OnV/n44y85OdxhdWOVycP3Odo/pToZcvvOJe7f+4SPP/uMuXfk7RznPXWo43maGdZvvAhZm0cf/Ax3so+zM4SzION514A3yHhGCOcXgFBTEAW+PmxbeNOep/g1bUto/MrD1wCLZG4QAVp3BmYIcWaNINK/b86KOBALCdBYbOiL9xUtrQKidswOpqjaUKx3UUZS1SWVdQjiYN1ZTyjjnmNzjbDxmQkI6nmFq+vIavcRMHHOY+d1GswL6rJCBiJDTEqU1ATr6C+3cQaG5STuM0pisVGRrDQipYw7BDNr0SEgjUIloEMqSaYyqrqGkBiMUkW2nI21cklNnukEloQUiAMWmNgaGQTCQyUCp6dDVJ6xvLGOFVGS6oSgdjWZrXnrpde5qrZ4+skRTx895vUXvovJHIESX1VIk/H4wTE/+mc/Znlvm2+ZKa8yZ7WaUay0sZ0Oy5evUCvB/vEu33zrTe5/9SW/eufHrF+5yObmFuV4RmUDItNkRU4uNEfbOxjp6LYzxCxnPjyhGh0jfA3CcDKpEUKRJWsGheB0PGJ1Y43usx2OhjNECuKTEpSJQKGEGAyGp67n+Lpk6mrmVY2UmnYrp/aOEAStlsHagA8iWWolyXSyQAoukTHOrfWoyjpjktbWUnrPwGhCLRsaAdZ7FETAzJEs/kAIj0dQ+zjoiyy/1J8n8IoQUlBSJH3ooGkR6CiJBurFIDwF4jbvSDTsxbN6J37t7KkM6QuBr9dZTZnpkxprMf9fPIdhUY81GQPG6PTfqVxvfp8QGBVVli4xxBPCu7huLg1NlTpjmTakg8bnNBDByEUomIxeqTaBmXFwdB5ET/YHaUCdZTnWRpCyuR7NEEjIGJTtBUkpZhKLL2CrGpXJdC6KmD9yblAUA5IcSmm0VtSJZVnVZ7WkhBjuHcuvCM6KGB6mpEqZPYlZmgBEIQW2GQxIFYlTWYZPZZwLHlfFbYHg0t6YbDSAEGLt4YIj2IqqNlG1k6wbqqpR8EQSAd4ljMbhUqhd3F5TfxtAeEfwMUSuqit80MlqRMdeRNqFwiL24jVCejJRNHFj5/bnhoCVRgsy1UtSIrxckC98iMQsj0/nRkAnz22chxxCWaHyGh/UIkRMJHKbVobMmMjoBUzjFZ6s2AgpdDDdUykkKos/X0iBaLUh1IjK4jT4OpHIRAQWVbr/XlT4Og6wnTo7u5SrkcFSOsesrjkZHlPPJvFpFVDNJ7RbXYwpaLU7GBPthhqln3eOljGRdGJrvPSIkBFCDO3TJoZtjqoKay1ZlqOSl28QEhEcvq4SQ9bjrUXYGulqdJgjg0UkVaQ2mrwoaLV7hKDQUqOEWjzrgXi2n1+rkUGuaBU5vW4RCQd5j7zdiV7MyapiMp9G2wjrk6e1RgQd9wkZotLZE9+vSwzw4FHC8O96/Z0GaUOA9eU+3/v2a3zrm6+mSXCf+XhMXZYUrTZKK4a14VBcZqLXcAR0c7D4gMORhTGvPZfzwmV4/JuvqG2dmmoFUnNp/QKvvP4WRd6mqjzz6YxOp8DW9eIgIURGqVESUxhMsOjgOXy2w/LSGlneJpQRAHEBdFEgWgbrHHm7TdZpgdFYHdlXbSSZyXB1xUu37vD8c7c4chlsAQAAIABJREFUOjxgPp6AhEtXL1IYjQw1Coutx/RyT8i6rC4NGE+mKAOtVkGvM2A0njAczvDe0Cp6bD/ZZnVtFZNp1jor9Jd6HJ0cUc4tWil2dnaYz+dcunQJbURKrZM8fPwI62ra7Q4rqzGpLxA4OTmJRstGcDw8xUnBneef59PP7jObjlktltFApgVGOEw15fJglf6rr3FpfYNffvQb7j19Qo2NzFGZDtbGX4foe1ilJvRr7K/GgDsxbFUam0qi3HVWeSZlhRhPOR0OmVuJzBTzYcntrVVWC89sPKRotejlK/TyAhNq6jLKnY0xCKVRWTvKPUQsKsdlFTdsZbCAClFW3RQJLI79uNaklItmNRbjZ+vYC8GsigmjXaEJIVppxEGARxkJWJwLBG/REM25g6euLVqZyH7QhgAYkyz6Q4BgF4EBOgQqF9mQJhXgjU9Qt9tlPisTQTagg+e5y6s82H0aPcTi6RclxjTja5+mnyJNTEWUsS1KD09wNfVkRggGFxyz0tIyOfe+OmTvyTN2dlb5vTcu8I27OcUo8Gy/pmyDCQXzyvD0aEJpNcvtNleuXGT51u+z/fgTHn3xMbOJwJYTeqv7lO4YNxpS+hHOKFpZi8wYbNFn7KA7uEg5PCYXA1SRsXt8CrMV5FGPI+5gL/0h+7u/wbQ3yVWP2jbemVO6fcPmxVUuXepwfU3RzxShqjCuJAtx4FIHT+Uc86qkCFCYglZukKoJdiIWAjKulWaSLpTGB0cZWtTZKh15C6k0/tTiyz3w8/j16Yzj/T1M11CW5aLQbLzgSGtNEOgYRUsrtI8JwL4Je0tAIYJUDEeAM8GSaB2l0dEXLIBKTV66nQvGgogAvw+O8WjM9HSCqyxB+NgUCFjv9Oj5Did1xePHT9l++oTPPvmYpa0tNm5c4+KVG7SX15BFm8o75t5hfcXpeMThwREPHtxn/9lTDvf2GY7GVM7hRfMZ43BjwfJcvK14LZoCWyvF+soKtbPMT6Yp6CQ11USPpsaTV6WGvHk1BBHvXJS+ek+310VIEkgbOB2NwIfkY/V1BhXEIRIiSsCaYq+qykWj89vgbPN3Dfh6Psxr0Yake3fGlGfBtPXeY8xZyGL08W4YHyz2HDgLN1swv5LcKJxr8MvZPLKaQpTSGqO+5lWrtMQYRVXNqOcVeEWWa1ZXWgxWO9y8cp1bz13HtAOqYzk5ecK9L7Z54fq3mU1H1PWMlgkYV2Mrh5gLtq5ukcsMV0NRtGm3B6hJZHVUNXjXJoSc5f4VvvuNP2Z1sMXPfvEXHOzu450ly3S0lwliwb5oPnOzihvmebMBSwHtTCHLKcaWdLTEY6mmE44Pj+j3B3zy85+w9Qd/hJmN+bd//k85ePAl1WyCNIqNrXVuvvQaL37ne9z6xjcpVjeYiZyyKinrWKgrKTnY2eGv//LPaaua5+9e5e//x3/Cv7QzHr//E/Y+fhclNM8/d4OrP/wun311n/d+8ldcWF5Da5PCCGITZuuK4fAZ8+mETMWB5ngyRohAlmnK+ZxOt0t30CNv91jauMxzt17kaH+P6WhC0WohVbTiUTIjEKVywTtMlpO3O+R5kZjzkYEffcli4JBMnmqQ2MhpoKGVTMUmizV0nhkePeAiqJvl2cKrrVmLIQR8kuu5pD5xiTGutY5ggYsNgavLyOapIwOrquZILTC6RZYVEchJd1xKgfNxgKuUIHjJbDolz/OFbD3LM+q6wtr4cyfjcfRVlxqjNbqfQwhMh0OOj48ZzU8Q5hHtbocszyjnJdXc4YKlyDQ946EeI51EqhaD5RWmY4cdTbCjYwZKMMgM9WREe3ODyXTMk6N9ukULKQV3X77LgwcPeOedn3J6OqHV6kSvYGfxztJpFwg8q0t9sHNGR0eUc8G1228wmr2HDI7p6Ji5r3j99bd5/PSIn/w/7zIYbKLkgMm8YlBbdp8+w1PgZE5RGFrFEjeuXOSLL+5z795jNjY36A6WefzwAULm3Lxzl/f/9J/yf//LH9EufsjW2hI7j3fJ+wXrFy5SzaY8ePCETtHnwuoSn/nPOR0ecevF1+guLzM/fYKfzpBG45RkcnzKaDznpdfe5NH2M07nFYWE4dEOr775Bu2lFtdubXL35iv8L//TI0ZTuLm5ws3nLtMqBM6VIBReSjYurEK5R+HH1GHOuz//BT/+q/+Xo+ExaEM9K6OMUYSF9UCRt9m4eoeW1Bw++Jy9R1/iy2Fs2mQD/cR6Uil9lmjerG0hFiDt3+bd6ZxD6sbHOwIA8ZyRCymzUrGxbryaCWFhJZUOi/isCbFgrUkZ4S+lDcFbECGxGuPeLFMQTPqnBCcoj0pc5Wht9MBIlDT4Op5/tqrT7DOCrqH21GWFQqBqx1Leot3KIyMwKLpFm9zktFoFxgi8rXFzz/hwiAye5dU1nu7ucfzlLqKtyU3AZxU+i2BVyCSyI1FFFkkxSoKKieA+OKRPIFbjG648ypi434iUkl1avIzgjyAgcwNENpxPgyLrBJk28Rk2BcHD9HTMYHWFkEmUVlgqxtMJNzobiJMltr+oefbRPVwm+dxuI9c3kFIhZeBkMudf/ZN/zez99/iBmvGdbkV/PmPqoLO8xul8StbRDB99xQc/+Sknz93i1R/8PrO7L/Hlex9Qnv6Ia3/0A2ynT1mXTEZzNreucOfmbbRwCCPZP9rlg3f+iqVOgaknnI7HDGc1LtVrSkmMUszmM6SAa5cvMJp8RWU91glmZUVAoXstBDXz0TEzWzMcTXDVPIYmiYCSim5u8AkE6BWGqnYInVNZwXQ65+R4SFnWqaY6k8qfHx7HMzXWXtbFvA2lQNQkwE5iSICtaELjUn/kG8Z0JL80wGpowLEE7kpiMJL3Hg0YIegYiQGsgMVmv5hJp8ExZ4PoxTcsfkdYnFNf/zzxFcOav/45m0dbivO1RbyWPvk6h9B8nub8icw4mwBBkYaLQkTVT1OLkxiq6U2f7SPpv513ZCZbeMoqGfvDhTD+3N7TXL8GvI11TgQ/mwwCgHa7G/epEPMItNbkWR4tGAULgL62NUorXOmYzecRnE5etY0Vl9EZ1qnk7+sWnq8iRIm5StZZjbWeUhJlVBw+iDNrh6iUjX6pQp6tueazxLM6hrYHE/Mh6qqOdhlEQDMyIVP4oHeJrQ/Oh2TbIGM/HUICxpMXuHdAZNW6OuW6LAD7WL+X8xmzcsq8qvG1oK6bgGGZQLvISo1B3h5nA045tDaLNdnYbZEAwBiWd1ZLKS0W91BwFmIcfLTNCGm96CxPQY0mDjy8jR8hnStx34o+zlFFmHo+Fa06fTovRIie6ZFw5ZPdQgRRRfKZbZmcLAi0ip651lkQLj236exxDlE5wOJNTVAKqTRKWqTzBGtx8zn1fEpe5Hjnmc8c+IA2VeprDCF48qKVlFsenfdxwrB3cIDUBlt3qbodQvC0hUaoQFU2wYeJBa8kKA0uECqB99Fb2to6+sK6CoElmc0CMVvIB0u720LJjEzHnWs2mVHWJSHEPCkpBcaEaLOVCzqdHivLy3S6PfpL67T7axTdDkVeUJgWHs+8mjGfVxwfHHI6PCTYWRqYSOo6ZoQE58kylYYxSZkYzmyVfvv1dxqkbeUZf/IPfsidW1dxvmY2ryirGucCeZGjhGRUenbrjOPsMjPVIfgZGQKHxLqSqhxzZSD43Vf6lNvvMzw6ABxZniOlRuqCi5ev0x+s4Fz0rWu3c+qqjJtLmrY3B4+zDsoSGSRFblhdXWIqBSbvM56PyaRA5BlFt48uMupgUVkW/RQRlKFGK0GhDXkQ9AfLfO+tt9Eh8PTxYySwvLqMMnFzVKHElhMKZRksdTgZniKEZKnXZ3R6Qj2b0Ot30SZjZ2eP0WhGu2gBsLu7y3Q6p9frc/HSJQaDAQ+Pn+B9oNfr4b3n6OiIK5e3WBp0OT4eUdaW7e19lPqEb337dfIiHhhFUVBXlvF4yvB0zv7RlEePnjE5HbHS69JtGbq9DsvLSxS5xpdj/Bj63RWe37zIcqvHhbUv+flHH3FalcjcEIRApeTKuq6pq4rZbLagskOa4iVA42uSM84mpJWzzOdzhB2iCHR7HWb1HO8smytLXGjPqUxJllvaWUWeFVir0Fke763SeGL6t1xMPwVG1lTBEdPnGgZDmgCGCNwLH6eFIZCKkXP+ZmnavwBrUYxnFVDRNpF1DaB1Do0cLNgIuhInvFIIMq2i5AFJFDyJszAoAVrL6GqTvMicq5nNpiyvrCGI0lapFO12KxUTAi011luubgzotXY5mtcgM0TwhOT3iNaLhiA+AsmQvJlmiwaULnHzOaP5jNbqCq3lAUvtDmWeMxsP+WRbY8QhF5ZWuHmj4NoQcpnRngkmDpwpGFhLZS3dTGBEh1bnMqEvEe1XkONddnceoesx1XAPGwT9ixugYDY6wttdpFAMLq5QOsGRWmImQVx8Ddu+wb0DjQtrmIu/h+y9QBUCXg6QvqI/yLh8YYUXLvRYb2eY5G1vagceXO0obU3e7WPkAGEKlCOyHUT0P6qtWNxLIaI8PyaKxilmVdUYqfDK4IWglJJCZig3x9sZVCdIZRkNh5wcD+nJNnVZLorRMwZAbNpkCBgfJYB4T0O2rWNKIlky0Bci2ojINJUmpNRPIZjNZrHBC+cZE+c4QVIgTWSzHB8McWVMj3bBJflZIEhBISWbWUFhDEe+Zns05vD4M57du8fn/SWWty6wcvkS2XIfpzWVtzzYfsz9Bw/YefaMuqypa38GCJ0D2prrCY18P/7dgt1NTBU92D/g1s2bnO4NGU/n8b35Zsp7Njl2zqZzOiyKxRj6JRYN9N7efpJK+cWUF8GCPdEwXxuQyaeghyLLo5+nj8FGAXHuvbJ4hn5bCgssCmApfwtEPmc50Pysxj+2KcKbgD/O7Tvy3Fo8/16VknibUschJgmf21Mbj0KfQuQMGuq4/4S5YLmzxjfe+jYbF5forniqMGTQXoZguffoNwQzZzw+wM4kvU6f0jta/R5rq5t0TI+T8oRCDrh17WUUGUpnLK+us7K6wWg+QKuSLBvw/O030KqNrQXtfI03X/4DtlYv82j7Pq4GVRhQiX3g5d84G0LzpDRbVwJZti5f5NoLz3Nv7yktERvBurYc7h+ycvEmf/bTH3P/p+8wmU6oxkPaWc6VV17izjff5oVvvc3q1duodh/rNQcHUx7d+xSRS64+dxtlcgKBOy+8xK8vXeH4q1+zd+8L3vj+3+Pf+0/+C/7PyQknn3/IUgG3X3mFN//+P2Lyzju898tfcuHSJY5PjqlR0RtSZanxmaNFSWE0+8MJRbuNlkDIkEsDWq02/aU1su4KvZUtytoxPBkmD7gUBJKGC15ILD4W7iZ6+gZRk+fFmSdx2uudDxidkWUFPsQ9Lkr/4v6hVFpf8qxpbNaqUiqy19PwIB2ThNB8bzxHPZ6qmpEZjVYSpbKFv6dCos9Q4MhKr0ucnTKbVRSFjc+rj357UaoeGX4LlYmKUs35fE6n00YaQ1nXeBwieGw5YzgcsbK+hdF5GlQ0PtKKVrvDXEhGpeV0eki/v0Soay5duEDwFVpMyYImG2uO93c42plSmLtUlWV/7ynZ6TF+PGK1nXN8MsaORrjZhNHBHrdee50r168zB65cvcylBxc4Pj7i4DgmuRfdPkIbtC4YTufcuHwRJEwnM/aOTgjdTS7euMV45zFHh8eETICRCAkHh9t8ce8jBm3FzRduY8sZTjqGh2P6y22yXHNxc4u33nydP/uzv+Cj33zM6voGRafHaFrywa8/ZWV9k6q2PHm8zWhU0u841jY3Kcsx09MhF69dxdaO7QfbnBw9Q8g589mIyWTO8qUltp88QpUGZQz9lR7PHu9w+9XXuHrreUyrRTneo9XOabcyJlOHOJrSarXZ2Fzm8o0bPL1/zNKgy81rl9l+8pj1tXVM3uLtb3yLk9mUVwdLZHXN//WP/zfe+eWvqHwM6nHOMT44Zvn5BrWMa8IjCUrTv3CNVruHznOe3fsQPxkiQxpUuuTxF86xB5PlU2QunvnQNgOzZm+NAGna5gOLdd/gLwt7GCmQQSbgJvkxKo0IYG2yb1nMvhs2Vjz9pdYRiPBNfkOiCaSGvwmqkV7gTmsmjDD9HJMpvBJUITrComLNlpeKtsnZWtukn7fJrWdrsEQmINSWYAP9Vpd2FhV1IswJytNrtegWJbdXBrzwne/x6YOH/Juf/YSn8zF7ruTx7ICTaUVetAleMVjq4yUc1zPKeRUTywFHBMiVEORZCu2UAqkjW80lUFY0G413lGVFSOFEVVlSlxXeeoysCJ0OpYp/5+rAtJ4wOj2lu74MRkV7F5Hz73/vH/Ifbfwx904esDvfZrDU4/b1VznNClqtHlIbPvrwQx7+5Ke8Xp/w7aUZl9UU0RMwWOHYe6YEqOY83n7K0niMfLbDye4zrl65wcnHDyiPhihrGc8DWaXJjCFTgX67hbUltZtjJ0NEOWX14jr7jx8zHB5Tec+4dGRSkOd5XGvW8ezpDp1el9XlDjv7Y0JI7O/GvslWjGcjXDnDhci8NlrhhYp7q14sP7xSTEYTpvWU7mCJtfVlhBDs7h4g/Vn916xPIRYmHekrIgFhcYCLcNQ+Argmpgwv2GGxDokAYxrR0XhlNp6aTX0l1dmwT4pA8A4tJB0jUanZi0Po84SFs/rqbwNgm9rpt22m/rbX2dfOP7sRCFLJFzSGibvFMxfrxFhteO+ZzuZomSNVtLvQWqV/rxaqqvP1bDjn2d4Abg1I3vxpzr9m72ksnM77zn79c8ae0+R6QRQoilYMBRVxP0QKRAN0JbKUTPtZ7VwCohOzuIr3WakIwDbvQSlFURSJARyBJykFQolFFotI21givyPVuTAzWGxgIYREhHAEHQHNhF7GtbKwdwkLi47ISpA4F0G7xiIm+Kg+FUHE3JS0vnzwNBGPITHGa19He7Rza8Rai61rqnmFqx12bvE2xIGQCwQZYn2sUvgvDQs2vi8tTXy/woPwCciPz09AndXrIb5nIQXeq0TLtjgXLQAIPlofpGGHVBKpInvUE6/Xog9PZ10zTGzq+AXwLcTX7CVCiOzmpouqnYvKEuvRQqOwKKlx3lIDprFu8B4jPC0XKAJURI/xKojoNa4MBoGYeZQEo6OVgod4f61NQV0GSYj4j87IlME5yNpLdAdruKzA+0BZO+y4JBCVkFp4xuNZOpejjZlvgsQSszs0FpM+4FxSCBIDl0djx6ws0c4QhCc7OSEv2rSWV+kULUTwMPMgI3M+yzOEDAk8j+GTvf6ATmeJwfI6nf4y/cEyRVaQmyLeBhG/d7yxxWx0wuhkj/39A4ajEcFBXVlwUNdRMSKkp8hVVM/9O15/p0HaleUlXrhzk3lpkbIDYZ48OzyVnTCpNc/qdQ6LS8xULyHTgVpC5WqEn1KIId9/9RJd94xfffZr9naesbKyxNLyMlIX9JY22LpwjfE4GgJro/F1ibc1WasTH+hmSqSid5s0hnarRbvbhvEcUxh0u42WfTqDHK8VTmpEpjEqo7KWYC3rK6uYXsH+7i4EyKTiO6+/wYvXbzCbzOh1irg4Mp3YK45yOsZOh0gDuruEkhptMkyWIwgxAEQpVlYHtFoFjx894WD/gLWNdXKRY63nyZMntNptWp0W4/GYtbU1iiJne3tM0WoxHJ7w5huvU1Y1Dx4+YTar8d7x7Nkut249Fx/ylkIry2Q0ZTazfP75V+zvHdErCm5cv0SeqwhazSd4aTEZnJ7sI6YTuoN11luGu5cvMR2f8snDh5yWFitAKBFlZgmIzbLsHOMsroOmGGlkMme0sQjEODtmNtnH5CvkUtJv9ZBBxmlJocmVINMSoyt0mOMrjRAqTkZ9NG6W6pyHJHGKpbXCzebMaoc2GYUxMek3+Dip8QGjTTok4sYgZJzuulTgnJcih+AJQlPXjmAigNT8Pini1NRIxbQs2d/fo93tovIWoSlxhIqMkiQRhWRzwBnb0lqLkoF+v0twcTrufJyqaWMQMmBtRZFlBFezPmhzcaPD8f0RAbUIkkDqhD7Hn9vIxqM8SYBUEeCOp28MJRhPCHNLb9BiXFmClJh2n6W1LltXM/ZOoHcEjx+OKZ1heXnA+sCyua4QeYuHuzVfPhpzOrcc7s9x2QrtlZwrL9xiPno1DjdyzbMvnzC6/0vE4TFeelobA/rdDqfjMacTjeyso9ZuEFrrWNXHhejL5VSL0LmI1hXdjuTaZsHLd9ZY6yiU9Yjaol3U0FUu+tEAFHlBZ7CCTwVUkbUQCUyvK8u8LCnnc9ZWV5BKp3saFkmbSmlc8OQqSx5EkjIost5NXDVGVqd4GwOdVjc2cNouAJOYtCwWzWAEOARjX1OLdrJAiDc5EsCjXFGIxDQPaW2k58b5mLbpffSeJL3XRgpPY6GhFTo32KrClSXBRTev0ExkQ0i+y5GFlynJqpR0231qAeOq5vBkyPHBATsff4QtCk6V48RajuoK08mRWuPmFp+YNL/NfDjvlRabYo9PYQsNUGut48nTbablnPloHpteQWKjRP8w76LMutk24uQ5FbkNeBoCRigm01kEuVIirpJqYV3S7A9Nc954FjbvTasoJUNEr6nI6m1YiT6xHFgU2E3hfp7x2sif/rbmI4TAdDo9B6onlmOSu8nk29sMtZrC/ry9QWT9qkVxbL2nriq0UlH65h1lXZFrzaDVpZ13WOmt0FrL+KM/+iE/+OEf8ulXH/DRl/+W+Xifa+sXqKspmQjsHRxwfLxPsJK/fvdHfPrpPW5cehGfzekstzjcrbmwdZ31jWsEF/2pVtZWuXHtNpPJI1qDGVcuv86VS7cRPp63QgRys8TNm29x8fLzMUxMRMucspyQ6ezs+ixQ2aaljAMK8HhnyU2bt77/A+69+/M4HAkGvOfZo4fcXttC1FPKsmT1yiVuvfYDXn7rm1y9cxfTX2XuRWQxzSyffPgr3vkX/5zjLz9nef0i3/sP/kNufPObFINl1rYu8fwrb/HX9z7m5NFTDnf3uP3GN/kH//l/xT//H/5bJk+/4r2fvUv7wm2Mz1lav0hvaZWTkyHtwTJaF1gXQSeJpcgl49EpyuT0l9eYT0YYITGFoj9YZm3rBp3VTcrasrvzlPH4OCav+4D1YEyL/vIylY0hrAsMKIGxJA4TQiyumTFgTI7WJjWJDqsslXVIZZAqnnmes3XbrEetojwuhnJO0TqLbNbUbDZ7o1Ea2W6npiHakETW7RlhipDGU0LEHsY7ijyPbF4cBIe3FpNYimdNjY81gwjMyzkm19G6RWp0dJ1DOEu71QLvqeYlPtliEAJeOVrtCJZ7EaVuKx1NGWYs9QztosvJwSmhrljptxk+GDF99pQnLrB3dMq9B5+xKgOXewXPXbjA47DL+PCYcj7l4soak+EpwTmyVouV9TXuvPA8n3z8EbN5hZCC+w+2uXI141vf/wOkMjz98jPa7Q5Odbn24hpPd0949NGvubBk6HS7jEYj3vnRj1m7+jx3v/ktJpMZs8MdZH1CtztAZDnT0SmnJ8cc7h+x2mvz2isv8W/+4kfc/+ITvv0730ZlGRWK3aMh33n7Lba2Nnj69AnaZAznU3A1070DlIDrL9+lpbpkStFbKnj1lefZeTZm/3jI0tzy3GvfBVvz5P4XjCenYHq88a3nsLVleHJCuzAU3YKeH1DZwIOvnrG0soL3kls3r+BOH3J5a5kP332fd37yM65ceZGtK9d4+/t/wHA44d7nn/PhX/8Vv/jle9g6pq5HmbRkNh4hRYjWZCHK8mPzFHDGYFbXuNJ+k6JXsP2b95ieHCJT6jqIlJSeghw5A6rOM2sXHrPiLKCFkMJf03bdnAs+MWVD8hNFxjM5ziqaDIP0+0OUWoZIk02D8YakINJ7jBYjwYczu5FUAojU+BIkYuSophN8z6C7OUZnCOUR3rPW6nOzs8Fqp0cmM4T1hKrCPxtyPJ0wr8soaS8rvIs1rpEC62qWjeY6gRtb61AIzLNn3LITVjNFma8wVqs8K0vGQjMKNfVpxfFwilIVeBtrWRGnxkE6vJCEVkAVOUYrakEEb5tnWqbDnGgRUaXBpLPRNxIbqKppzL2QyT7NRe/to8Mj8m6b3mCJ0XzId29/g2/feZPqyYyT+oRX/+QtyuExS3kHQZe2zPjq3jY//cf/hDuTHb43CKyxj6gcnbUN9KVV2jev8Pzzt6kzRfbBh3w8GtFfX2Hz0kV2n+7jQuDSzTu0N65xWGYMqxx7PKec3aMcn9Ib9BHCMz09Ic8LeoMVdh5FmXtpI4PLlxXdTsBkOZrYb5TzKavLXaazitNRlSxhAifDKe1WQSczFC2RPFjT0FsbpIg1U/DJr18ZrJOMxjNG5S55XqBUhs5ioKPwLOzWzuT1cW3FwVuslZwLSA2ZFJR1IDqExGfI+8YcIZzjeIh0lkTyQkgqoGaNN4okiKCeTn/6RpI1tRHn2bBnZ875M+j/7/XbtlLn//68QqtR5whx9nMbuwObPGiV1hAaJmT8d842AWUSrZP601qEkAvbkuYaEeJatXUcJJrkg31elXJmt3AWXLso4tKrCbjVjV1FiCzUppaMX8uiBFsQ2alCxaZaxBpAKYVOhASlFcIIBImQI+L1QIDRBq0MSkalpZQSLSRCi0X97oNDJHYtDeifvH6ba9FI5M9/Lh9s9KG1KScihMjiDAJr6wjMhrN75Ul1glD4UCdrq2SjSCBYi/Rx7VsfvfEzpfDOUZUVyiU1qpSNLfmi5gCxyJXBBVxV40O0EcDH0EIloo2LEBIlVLo2kRmMSDJ+GS3jonItkrBE8Is6XSag11qXgHfwzlCHWK+SYNgGR9CJud2Ef4n0PoVsQoXtgtUsidlBwduvfbYFy9o5JHIBkAcByhjcvMIbjfOxlpNa471EpbPUK4mRASE8+JJQepyUTKsK6wWVrZiWUyYMPHs1AAAgAElEQVSzSQSak12CTNZ5KLPo92ieiwAeT9Fdpd1bwcosfl6jcQHq0jKfR4/b8XiKCxaRWNg+kQAicciBcGnvUngnI7NWaPKijVCG09EE5xW29hzsHZFlU6ppRb/TIcuKaAmiUr+GotvtoKTG5FlUxqqcTHcxUpKpQJHFMGIRHC4IRPBoJLnJKfoD+q2cvOgSnjxiMj1B1R5PQ8KLfr++9gT1N8k7zevvNEgrhKSSBd2tddpFi+PdB0znJ9TOUs2hki1Osi3G+TW80mRegsippaeaT1DljBc3Df8fc+/1ZFmWnff9tjnm+vSuKstXV/ue7p4eg8EAGAI0oEBCooIC3/WoCEUo9K/oQRHSE0VJFKAAgwZmiCEGYzAzwEybaVfdXdXl07ubed0x2+hh73szuwEGQ2+4EW0yqzLz5D1n773Wtz5ze7Hkvb/4Ph998EsWevNIoKpq2o0eqxtXaLbnqMuSJA2m08PxkGI8otlpx+sI15MkCVmi8MKhVfjn7OyA46NTklSRqCZOC5wEoQV26rDtw1S4rArMmcEbx8SXXLm8yquvvByo7c7S7jQicOCwpePxg0/J3ZDLy/OkUmKNo9VsU1mHUJpGuwNCkudJaGgbnm63xeHhEXnaYHlliTQ5pN8/49HjxzRbTYRw6ETSajd46eUXGA6H1FXJzs4uV65eYW1jmXuffY4UkmfPtkgSxeXNS3jnODw8xDpLORni6hHz3SbeOHq9Nu1WgrEV49GYcjIkz7s08pyD4318NUHnLTbaXb7z2stcW1nj4d4hHz9+TH8yQGQaLc+lYdNDLxzEs4chhvyY0FDGm6K1xNqCk/4e3Y0eOlNUpmS+kWPrFK1l8HWJ6YZhylYTPJwFQiY4ohfZjI0GpakjuGb45NEeNSmv3bpFQ1azKddkNEY228EewAeAI0g44s7BuT9kmHGGllgQZFrBDDsa6XuLjCw4U4XU8xu3b6OEo/aCuq7iYRsL3Ck+KoheuOeG7EpKrKlwQs8meQKBswZrKsaTCd63wwaqDZeWWnx6b5ealEiPurAKIyPNRgm0CADtFA8JB4lG64RayFBk1hZfV2gs1y53WGqlmFqydWIZV5bTUnJ03GdZNVldUEwqOB1bTk9GnJyVHE0qrBUsdDOev77M4mKbvdEcnz06xpxlVL3bcKdJXu2y2GszKGsOT3YwNkMtrqBaVzBqAetUCHbCAwZ8yeq85s7VBVbnW7RTRUdY8lpQFBOE99Q2FBJSC9JomC+8IU+jlxceryXeSqRTpEmKVOH3F9GTCgRaCYwNxWua5YAPQXxGgkix1BRuAdV9CWcnTA4eknqNjJNYrUNRNR0AnE9NofCOx9WI9W4v2K9Y0ASZh5PhcA6BPBEADEZhs6axKCYXbq+PFhcigrSSJNPoPMcKx6QYIZ3FCxVAGeGxTNlCYWptvQtpzvF5kRJSPHNKkKE5M46D4Yg+NX3vqfMk7LUTExhIzl9IPw2XdZ5ke24xMAU7p593EUwl1dDMMEVJ4jzS+1loCZGNE2vw6AdtZ022mnpECRETWiXTICPnXEjLtqHp0fpCsJcnhBIRgOpJMZ4l+PrYsM8aEB8DaOJFzGThfsp8lRf2vC+yPi4yL5xzMy+s0AhoVCxYp6DrLD3Vn7+HSZKQ5Rl4GA6HQb7mpywlj6sN3gpy3WCuN8fa6hpry8s8d2WT9lyDtdVLiIliaXmZu5/8kg8//zlPdj/h8OQxZmLodjoc7x+zu7+PqSY4J5BscbC9zbPH79NstKjEKYuLLa5dvU4j71IXoejRKuHWtRc4OXhExRYbK9dIaGFt2OeccFTO4iuP90EhEuTwjnIyJmmHQtl5j4oBPheZKEIEX1VBsI+58cKLrF67Sv/+x3jvqKzjvV/8lAf7B9x68xu89OYbXH/xBRYvXcPqjKPTM+yoRCYNfO2RWgbW+JOHyKNnjAZ7/PAPDjnt7/HSt36DpbVL3HrtDX72H/89p/sH7N7/kJsvvsK1197k6//s9/jB7/8fbO884S+/+4esXHueK1evg07o9ro0Gw2cs9R1hUhCgvdkUuKE4MrNm3R6Sxzv7lBVBUma0J5foDO/AEoxOjqgHPWDhY4MtVMqNXmzRZY3qceTqAoKhXrwJosySROlcSIE/igVpIB1fQ5EGePROkPpLIBAyGDBc4GFMn16hQ9ndbDl8FR1MQOA4cJ6FgkyOWe3EIcYTAM4fZCYeuFDqCWaNAaeSBFkzFnemDXK0++tIlMr0ZpGnse98/y8AkWSNWnJJHjCR0WEViHR2cegjMnkDKdHtHKJG0saWpBKi5KOVt5GKsGTBw9IzvpsJIrh0R5lf8zxs10GtiRZ6fDC9ctcWVti/6ygfya5cusGebvN9uEB3eUVVtc3KArD8ckpn33yKTdvXWU8HHF2ekazs8CbX/0af7R3yKcfv8/jvQn//f/0P/Cqk/zfT5+wf/AYeXDMXK/HpSsbHFVjVjaXOTwc4J1lrrnBw3tPWV3p8OavvsXx3h7v/fQHDE5OabVbrCwvcLK3R1GWqLSFbsxRyQY+b3Hp6lV++sMfcf+Tz3jjrVfon/Q5Gxdc6cyx/fARZb/P7Tt3aDQ7nB4doho9XN7ieDDg0o1LZIniuH/G0YGlkmdUpUMkCdnCIisbl9i4tM7R7gmd9go7ByfUVc3+To2vBJdWVxlPBjy4/zm9lXXufv6A1twy3gqW51Z5ePwuf/1Xf01R12FYHBl7xkFdV3hnsDaqSWRQUFTGRvA2Ie0uceXFr9HpLPDJO3/F6HAb5apYE/oZ40hAtMOQs7P3y4DJTOXAl18Xgdzzz01rQSGjmsnYmUf6NNgTFS0UpIxBQRcAL+9nTDobzO3i+RY/N1NqhJRwNzaYOkioF9OE5bTBmp4jK2E8POG4qhlOJnjhGI2HWO9Yv7xB5eDUjalcGXMAHMo7to1gD8/uwyPmnjxgYA2n3lErDTIhTTJ02kQnTeaTFNvIWOh1aJR9zqg4qYcMbYGRLujCrKcaVdhOE9VpInTYo4JsOpyjUdkb/qUUQiY02zkDe4qzdQwMirWDlKAd3muq2nJ60Kc4Kbm2cIXf+Mq3aaeSh3vvMm4+43f+xW/zkz/8Cd/7d3/K3MZN9K0m77/9M7IHn/FG17CSm2BBk6Y0FueYe+l5rv+jbzMwNR/+/F027rzMw3c+YWTCHjrc2qM1v8zlN7/NSfsym9cus7d/wC/e/RHrc57l+QZJo0FdlBzs9Xnjm79Bp9vlw/d+SJal5I0UWVVY42ZD+RCUaJhUBWmacnVzmc8f7gTQwnuGE8PW3hkLvQaLnSQMLX1g2VoC4Fk7h0QjvCNR0Ggo5BDq2jM2JUqZWGv4We7BOeh5zvgTkbDhfACqkmiNU1lCrStA+RjC5SFUVBd1YLHfcS7UXfLCzxAhIEk6G84oZ8FASrhmTOQMXmALfpkZ+7cBtf8l4Hb6dVPgMyxFEetQcWGti1koZYCs7czGYPoK9lMq9Gg+9v7xGkRsnaZKJxfB0TRLQ00alVHTevAL1x5BunNrhHMQV2s9q+vl1J8zfo1W4c+QEjONjxeh18WHYYfWmjTNEATrsCRJAkNUqMASjlaPoQ+ReOPCQyXAOsNUMRauKwD6pTXIeOnGBcBwWrtOAUrEuc1JeO8Cs9A7z6QK/UlVVTMyhCd4ec5skyDYSXiPMQrjg1JMqHBdztaYqqSqCkajYchrmeIJQpJnHnw4E1QcRk9Zt1oGK8qqMjPAeGoJFYZyMWzLB8WpkiqE/UVbAzm1IFAKT+gnpBKzHh18DC0GItwc2mqFVml4VpTCmBJvJTgTPVEDsDsFyIPdY7BJs8YGhq0QgbAT5UtCSKwL6kdrAksaF0MYncOZYK2AkDipqBPNCEMn1eh6GvsWnl8rNZMkYZRmuBiUJpxkUjkmw4LSGcblkLos8NZi6zg0iIHwOmuQ5k2cjOYmziLkuYVPkjaQKkFJTZaqYFNjDFKHZ3lkPJWpw7OAiHalMigh4z0ztacSRbQKCtYG0/0CptlHGVmiaDTbdDpdGnkDbLCirOuawWBCWRZxoAhZ1mBxcYFGU9FodJF5RiVLxskQlWaUiQs1pwTlAht9MJngixHeFAwHw6DO1RoSTWFMgFmiets5FwJU/zOvv9MgrU5zVq69SH844t7jzzndvkfiJyR5k6X1W4zUKo8Gq9R6LjChlMA6ifUOYyoWE8OvPr/KeO8D7n7wDpPhKfNXr9JoNBBSs7C4RK83h/U+JMh7gTMleSMjTQLbqK7DAmlkCkmNsDVFVbC19zn3PnnI2fGI/e09xsMTXC7xMRBH4OLXijCp8I6z0RneRC8qpXnphedZWFhgNBrNJvnOVJii5MmDh9z95dsstDRivMGtWzfI0hyXSbR1jIuCPM1QHUkxGTMajTk+OuLRk6dYJ3FecXRyyv7hEd57BqenbF7e4OaNq0wmY7a3nrK5eZUrm5cRQrC/t8/W9jZLK4vcunWdw8Mjjo6OOT4+mVHk0zSh3z+mf3JEpnXw/dzdp64rnAvs1Pn5eapqgjUuMKCdYzI8ITcV7TxjYaHHtY11buwcsdTp8v7jRzze38FYj0xTpgbu0ykmnE9RhQheVeeKF0FtLbaq2Dk6Yml5RKORYEdDqtNDWomK9W0oFYx1SGkQlIDDqyROeuImHGXQDkdVDsk6cxTW82D3hKFJkMkBX7k2j3JFDDGxGFORyAy8C7Iczll3AN5P2RYEsEZ6skQGppQMHjVhUj4kTbIgK1Geazeu0mw2MT6IvmpTE5arm/n8TQsVa11sjuMB72Nqq+Z8qi4E3gS/pERJ8MHMXTjDzY0Fft54xHEZATCCJD5sbFPQNv4zo1y6afkWQgG8hJgwaYohq70m19a7LLYlroSH257JeMLNDc3X31xg8aBNUWi8EtzfHXDv2YDdYcW4MCw0m6xf2WCl0ySThtPDEQ+2zzg9rlC+Zn69R+fW86wvvUxWej76dAeYR3oFukvlG1gnwNVIF6Qii3OayysNXthostELgL1KFDiBqQ21s0wr1DRRZIkEJwiikDCd1DI+bzYUDcV4TJYEdkJvroWPaeZeSLQQZGmCMB7jA1Na6FC0YG04kFvLiKyHsSVqBGWp6B8f01nq0ltYjEODcEembGoB2ERx0lA8FTUtrWkaEYIFAO2m9wRELJqcD6ml+CAR9tHgVU7B+/jcCB2kkUkrR0rN8OyUqihjYK6LRXW48zayi8zUCsSF713iGNeGIRa0pLQwdJ5THAMfrB50noEPAOkUu7wouZ9+bgpaTtkcxCIksNUl3hiSLGPz+jUanRbj/igWSkFg56OX7HlBL0jTnImdhAPcWLwOTOMk0eH9iI3ejDUFkSEVGh8RZbXOBesHrVOECPe10erR7bTZ3dlCT5OTp8W1gymr1tovNvpa6wjanoO6F1uL0HxPJ8QyPGM+FDHeT1Oz3cxeQyCC31QsfoSQ2NphvMFbhxYSZYMfVyNJ6LQ6dBptfvsf/i4v3nmFn/34x5we7HP//Xep9BlfeeOrvPbir3Bw8JS//MWPuPvsPU7KJ6QNg9pRdE/m2Ns5xEkZQiAQuGqMqycM6n0GE4USmuW5ZZQI8kyt2rPU55WlTTY3nmfv2LC6dBUpUmzct2tjEEkE8KRAxKYhSRTdTieEf3o/k+BLcQ7oJ4kOAVTO4YSkFg493+HON7/Gn28/QGYp1y5f54WvvsmNr3yNxfVNTJ5Tefjs2QE7jx6x9fhzXn7ra1y6+TyVCID8pc2rXLvzPI+375PYivHWfX78//4r9p4+5pv/8HeYX1th7foNdt75CZ9/8DZ3vv6rLGw+x0vf+k2wnj//v/53dj9/wGQ05trrb5DkCcsrq6G+rg3eGpyKT4BU5M2UqqpotVr4xUVMXYU9RWlG4zNG433KyQgtQOgkPmcalWRYLxiNJ8H2QEQWH6FG8s5TVSVKabJpQNGUnQF4YXHWz3yMs0YehlFSgQ/siOkw4wtArRBIpclyiTU1xtYxgT2swSmLRmkd75+bDQZnwwof2BAiyimTJCPpLYb5oJeMhgP2dne5euU6WQwVdf6L6+oLjfy0qAgXGM4u6UmSUEyMxwMm1tJoNAMAjaSrYXGlQ1UOqCZnLK5tML8wx7g0NFtdklLQsAZTF1xamefJYMKlqy/x9P7nOAMrq+sIlVIUA/qTIes3r3PpudvsHx/z4NPPEDv7LC4ssbS0zNe+/g22t3Z58PAZr772Ir12h//0p3/KoD+g220xP9dmv9/nB3/2EwTh3q+urvHw8/vIRLKZJsw3FvDkeFNy49bztHPJoD/h5PCAydklnj56zNnpKWdHExqZ5s7zz/HOux9wvHfI+tUuOsl54eU3WNm8wZVbd/jB9/+Cjz76mMubG2AtTmt6K8scP33C4dEBKk959Ogxn93fZv3Gq7zw1a9x9942pi5Ym+/SW1pk6dIqy4tzPP30CUuri7zw1ZdwOuP99z7nw7/+Be1U0u21SLMmv/jRQz754Oc0koIrVxdZuXqdhblFnm3/kP7JKXvPthmejXh07yP6p0d4JWdsJYdBEPw+nauoY8VCbWfPugdqbwK7See0rt7hdtri2Qdvc/TkE3BFZGnLUGdKEVQjnAcRfRkYugik4JnJTKcYzRRsOwdepl6FoXme2ugE8DUAAgJQQs+YYVM/o+kgMYDHcWwrQCYa6QUynvOeoJ6yeNoqYUGlLOQd5rOcnkypRzW7wwOOfcHYGyrhafQ6mFYDg2Uih5SmxLU8NFUM93FI41AoBkKy6zypVFiZMrY1AKquYTwiGw1ZyOZo6AbFUYXblTTaKQtzbTabXfqiYLvoc1aNsd5Slwana8hrnJBTkl9cy4GI4IXAExjEdVlSeYFKEua685wcHIYzU0LtqlDLJIpiMubMwObiHP/s1/8brmeL+ElBc9myP7zLv/xf7qMOl6CUjE6O+fyv32PvZz/hpbRgTYyxtcWlit7GCpOGYmgMHZ9y96c/4/Of/TWv/YPfQS+ssrmwzHBY0D845fVv/xbNr3yDnbEgV01kmnL9xm0GBw/ZOxpzeLZFrsBUNc+/+hr3PrvL9tYW7UQyN9dg+6TAOUFZ1SFF3kqKsuTsdEAjT7l2fZONtZpHj/cxtcXUgrIeczYYMVlqsbG0QKrUOes6bOSUdU3ha4SxNDoNOmXN0fEksCilxolodeTPvV1ntlLTZzsYfYIX0bZCB7uJ2JeFv2enZUesWc/Br+mXi1mqVFBVaKUQMgCyE2ODF6x1WAt5ktBILH5qVTWFBb+0Dv//vL64hsWFz0tC0Oj53wtg6pfPuDgM/xIALGPgm3UutE2emZ3A9D3A+5n/OgTSgI9EHmOC8tF5F9mqcb/QKgR+ztRQAmEvWG95P7MrmPYLUgQQXEYwPJzb5wMnEet1negY3h2AO2+DXZcTFwBjMfXSDvYAgZ1qZ2dqsIohgLTRR1vEWtY4R6JDTZ5leQRdQ/0sdPAwFgQ7FxWvQ0XptyoDBuNsUHsVRbCAE7P9OOx/Ok3wJr698TpDNsoENU7IYyCVd4aiGEMkLCVpGCJrZ2Zg53QIoLUm0QnWOmwasBznApkq/FwZA+rDcMH6YEMniYO9SNzy3oVzSsSwvNjzqPjzZjU/RPZoQpZqvKswtQgWN94EkH5az4gAqE9xkdoEz1VJUAYGO8bwLIPA+Dj0E+cqYeEvhFeKcE4ZQRyUJFTeomwYKGgCkFp7wVBIhiiMBycSZJKSCUOqE07PBoxHfcrxiLJ0pFmH3vwqSdagkefkeYZKM9KsFZSGUbHubRGZvJrRaIxIMqRIQx/nIEs1iRZMEHgrzs+G+DxrqfBO4EjQCpySsTYIVgiBBOnBQ5YmWCNpNRvMz88xv7hItxsIhb6Gsq446h9zeLDP6ckJxyfHVLVhd2eLvJnQbffotZbJGk3SbgPd6DDXW6Hb6OATiSIQl4qqpH+0RzU+o67q4F3sbGB4yzRmH0m8DXW0j1aSf9vr7zRIq9KMooRPf/kLzg4eMN9M2byywZVbt6F3mz//qGQsuihnwwRJWrwtqesSX/Z56+UWm40hH77/MfNzPTYW5mnkLZwQdDpdut156rpGywSMw7qashiz8+wpeZaysrqONYEunyvFuOjz8MF9PvzwQz5/9JTFlUtI1eTgaIvR5JRGY4GgOY5G2oFQDiIkm1pvQkAWgtX5eV6+eTvIDlRIX7fGYsqSvaeP2Ht0n5Vem7oq2Nk9RKuUyaig2e2xtDyPszWnJ0c0Gil5lnJyfMLdTx+QN5pYb/ns88+ZTMZUVUmaaq5sbrK2ugp4et0m7VaDvd0jskSxsr7KeDLh+KSP0glra2ssL69yfHzM3bt3UUozmRSsrC4jhGJ4VlBODJub6/SPT5mMR3Q6Ga1Wk/FkRG0czWaLshohpaLZ6rC0tIQSCmVLlucXmWuuk+JpNFLW5ue49/QZ/bLA67B5h0wjN62MA0s1NoXTg1UATgi8SjgYjHn89ClL85s09k9Jz47RK6sII6IvrMPUDukmpFks+HwAPYH4cQA8hfQ0mg2czvh8Z5fDkcMmCR8/2aWRel68PIesSxYWFnExpc9UJVMGnjGWLGswDSC76JkoIggrpcBLhalqjKkZjAZ0Wx3QOYNRQaPZxCBRiQbn0NIjqJEonKlnRVgIgSIA0c7FsLAo6Y4HiLEh9A4hg3RNKUxdo6TFVjWLrS6XL69x/HACFzeMWV8ro2QjFlfTLjp2LsI7jFL4ZpcEy8a84rmrTbqZ5mBvxOPdM5xq0cozDoaSx08dq62Us0lN6eFsYDg4HWGThDs357m13iGxgsHY8P7nu+yNHRUtskbOpSXNc9dbKCk5OR4zqkBlLYyUeJLZZowNTU93QXH7apPXN3PmpAfjKAcj2u0Wwlj6Z6dUVUGr1aHRbOKcZTIeMhhbsiwHIalNYKxICVVZgvPU1YT9naesra6g8zalCmzwadNlvEHplDxrURpBacGYirKuGJ+NSGRNnrdwtKjFZdpLCcXZLo+391nXKXPLl4LUpDYXuAig0pR0roto5+zamqaHZiJQzpA6Qe5VPJx89NL+4qQ/SCmnXkXnnkUohUwTVCrxUlIWE+qyxlsfmOjEpFUfinkPGB8YqyICqbVzlMJRCY8XCdYJzvDs+ZoTfLhH0pNlCQpBUdsYUnQ+dDh/TcFaMSuapwDP+eeDTYp0HiY1iQ8p5ZPJBExNbSw+O5f2OwdFWRLNKEJTDAglZ+vp3O9WzAComRUKITBjalMQgO6wx2sl6PQW6PV6bD15gkahpidAtEGxzkUp4VQarvF43Mxf9oK0bfZeBNAWBELpwDJR/tx/CxcbIuIARcUZShj+eGEwxlOMA9A93+hwZXmVm5cu0T88oZFI5loa7y0vXF3naPcxH7/7E9xkyPL6HINyn/HJFapqhJCOuXaTajhmMB6w2GoxLAZsrtxhUih2zh4gk4zluRVWuisMT4aMTUFpCqSD/mHJD/7iR3izwKsv/SrYNEjVnGCut0J/sMRk7GA+HKOhugQvDRcTxc+3pzSC8OdSoWnR65wN0/A4qMBapAUtHG98+zdZu3SV7nyHjSs30Hmboqo58556MsYawY+/9z3e/vM/IRMlc3NNVq/dABHulc4ynvvKV3jwl3+GdSXPP/cCT46O+OX3v8vp/h6vf/s7XL18mYP3c46fbPH0/mf0lq+QNlu8+uu/yeD0hJ/+m9+n0W2yee0KJAqUpDJ18A8XgS1sQgIS3jpGZ312tx6RaDWTAo8GA8qiBCBRUXqJRwiNTDKIDBEbQxMCWzWwcqSfyu+mczc/W1/OmzDA857aVMFLLMlJtEaKAIoRz7LzNcMX17A4983LVD5r+C5ahSgZQDbnzlUCFjvjvc5ksITzUsgE4npLk4Q8y2PachzKTP3IZpdwoRkP09rIqo1rVwXJqrN1SEaOstHa1ugkIZEViSvwriZvtPDectY/BifQ9YR7d3/JZHDG/uE+xfEBAyO4urjON7/+Fg/uf8ra1ZvcfP45TicD0idPyFstyBscnQ2Zi0O4p08ehuCuToev/8rX+Y/f+z4/f/sDygo2L22y//nHNFsZZV2wPN/h6cdvs3H1Ckf7j+ld2eSb3/4NPnj/lxwcHHD1hU3KwQRlHVsPnpIJz6XFeY4ef8Z/+Ff/EuvG3Lpzm9svvMQ7P/8pz730Ak92D3i29YTl1UVWFlvc//RTsixlef0yKs/4+N5nvPTG63RaOc6aICtXCePS0z8bs398zOrmZYa2ZrC/T1M4th7s00ubYDWHO31euX2LX3n5eXSuMQIGk5JrSwkfjbcZ7/cZPKzoTyqO+wMEnufu3GT10ibjyZB79x7x6d17ZHmTV19+jb2tz3n3nZ8xLCegZVASSAmRwafTBLzFmhpnPThLRQyNjOyt2tVYpSjris7iGrdf/QbeOk627+FsGQebF+AbF/zXLz5Tf8PnMgKt+Agoxj+fqSRcAFLCfhXDaqJix1obZbRutkZnoI4K+7q3xGHU+XkW/HYjywmH8WEVKe9JBCw3W2w2u2w2utjKcjoc88QMOa1KSiUYa8tYWIzwnBV9ZJ6gcg1+DMn0GiQOj3MClSZYQhp7gcTK2OCHUwlfWHqNNq/deYvnb75MtzfPZDJh9+kWTz79lLOtfRqpYHWxzXJ7g4N8zNPBAaPUo1pNah38HqkcmNAXoaPtkFYgFbUzYS8jUEWLokDlWWDFSR+VRBJbVxhjoVZ88yu/wQsbL2Oe7aE89Obnefj5Lvax52argxItVjbW2frwI+aH21zvjmnYU8zQ0+h2mVvc4Jfbz2gtr7J5UvL47U9pHoyZd4q2zrh96Qq//Ohjbrz4Jpe+9mt8LBSN+R6TskS6mjzTHFtP5WCu0QQ7oDff5PTskPff/imTwQkLywmtXCIlOKsoiorT0RglJFU1Dh6GFAzOzlheXmBv/4SzUeg5cAJrPXWgkesAACAASURBVHsnBU6e0syCD24jz5A+qKTKCgYTy/B4gnED0piDYZzDVhXGuNkQ4iKTczoYuAhQAtQuWFUIrRCuDnWg9XgRFRrexD1XxqAffz6ImD7j0zMjNhpaBT9V40B7j7WgpGClkbNbjCgRuOhx672Yfc/zLf58v//PMW3/5st/6ePz/nIKeEbLWM7zAnzsjb64FzhvqU1Ns5mjlQjp81wYsExZoTMg3GPtlK05VWvp870lnluhRg73GEIoV3QoioOcAP7ZmCUSAkAVSZIGGwMlUUpH+6jgqxtA5KBCcPH7Wu9A6WhLZGeqrOlZLITERAB5OlBSSiGkg6g2s85Gq6HzYRRIpAws3SmjVqupcpaZRSBxj5YR2M7zLOy9zjEZj5mC49aYGAoZunehBFromTetd57S1GhrSOqasq5wpsKaEqSmLguMMeQ+D/emLAIgGK9JOE9VljgXgtZSH5WNFwYVQkmEmOIRUeUQe4JQ4xhAR5sJSaJSlJZMmdTT+t64YKUxZeFaCWCREXAMbN90RlIR/ov1LvioQtZ4G62pKhuG/X4a0BqCSC+y0CGsVYSYqc+QEpGk6Dr0eSZwCdHWY0zos7Q1ZLLGxEPSKI+Y2h+IaJ3nPMNRxUu3r/OtX/t1+qcTqsIGawkhME5jvEFbi52MgaMg+XeGyegMp1OMa9JGIr1EptFWz7iYNRL2jtA3yoiyacCgVDDqKI2lNiFLQfgApicqpahK6tpSVwmHB8dUdc2kmNBu9+jkXVSS0VtYDJhTbZiMR3gbbLXGI4cpTnCFIWs2cacKkTc5zo+Za8zhtEJqibM1dVVQV0UgXDg7Y4rLOABQQszqgKq0s5yQv+31dxqkreuaex+9jRjtcntzkavXrrN5/Qqt3hLf/2jC3SNFkbdRUpAKhXSWwnp8NeTGvONX7sxz+uAnuGLAxuoaWE9ha1SSkLXaeKHxXiI9VFVIWFdC05tbIE9T0kQjbE1d1hwf9XnnvXf4t//+j3m6tUNRG/LGfbyXDIYjrAQtQoCQk8FIGRTOG7wNsj2cI9OO9YU5/unf+w6XVpbxNoYAOMdkMuF4b59njx5RDE9pNrMQ9gQcH/cZjyYgd3jx5VvM91pkqeL46JhGs8Xe3sHM13V7ewcfJ3bz8/O0mg28k/RPzpib7wZ53KU1siylLA3HR32sNSwszCME7OxsM5lMUEpHZmxNkmhOjvtkukkjy7Edy/HRLlpJ+qcnXLqyxOraAmdnCbu7B5RlHSZfSFqtFggYjwfMp118UZB4yfOXl2k1FZcXemwsLPLJ06c82d+hslNvLTE7M52z4IIx97TdmkrSrPQ4L3m0u02iEhouxfb3USsr8eDLKcswtfMIjHHo6A3mvMeLqWhDxiZWolSDBwdDPtvqY/I5ajQnkwlv39siVxnPX15A2gnSCYyzgRFEKEyUjk2sILLc4sv7uGEEBq0kLNRiPEF4R20rdJrT7i0jdfCo9YQJXKZlZCSFIl04MQOEEVNzeQ8xjMHHw6MowgGkkwwhdcDnXEhRtXXNeFLQkAnXL6/w0dNHWJHC1LKBaQEST90I2AYq8zlTD2nxTjDfzbi+2uLWRk5VO969e8jO8ZjCeFq5YL6XY4Xn7sMh+52UeixodzVzvYzLS22SZoM89bSE46MHuzw5nHA4yZDNjEvzDW6t56wvaMrC82h3wN2HZ5Quw1iPExpsaLoFE7Km5MZmm1ev56x1BE1TgjE44clTj63GGOPxdU0iLLYcQ6Koi4LBWR9EgtApzjnOhkOEUjTzLL6XAilSEq2py5KsPRdAca2RSZiSSeBsXLO732f3aMTZxDIcFRR1QW1GqKpAERI7tS6Zk3ClucDNpWt05xZod1eQOsOaembCL3VCa3EO32swsRUHwmOFRXuFdAlLJky1k7g+ovAJ413IIYFw+PggAw1Cm2DhgHckMQ24nBSYssI5i41A5rRR84SkZUewhpj6EhscpQiG+lIE0G/kFIdKs+NqCu+DmXyWkGQpdREA6ziCnxXAwffb/y2gbXwKhcBbj8VEX0zLg3v3SRsNmo1WsB4h+rPGZsPG7y0FVMWEWTprDA3zUkcjemYFzBTbvshY9/48NCZIWeWsMBHOsf30EbtbIfRoCrbOCnJHXO/+3DM2/owIj5EkaQgSsOdAuJ/JbgXe2CDzju+5NyHxW/joRedAECxNhLH0soQ0hVZnmZtXv8qlKzfBTHCTAZeW5nnv6OeYwTFPto6RKuHf/cG/5tnuU7ypWFtZQGcVt68+z/raFZ49fcj27h7Hh8+YaygGlUJaaLU7vPLK17l0OODtDyynwz1WOqt8663v0EzWKCpH7SuqYkx/f4+Dwz4P7j9mvneVy5dvgQ3Mk7mFFXrDdcZji7U+2mm4WViH9TYEoNYX/c/8+fsb38mZb534UlPmQqFVSYHudLn91W9gnWPvdMDOZx+wtr5Gq9PFO0uWpNy8fpmPfIXpH/Lko3d55WvfIusuYrxAJSk37rxAb32T0/sfoue6fOvXfo2f/sVf8ui9txk8e8btl16g2+swOuzz9OO73PzK10iSRUSrx6/8V/+c0bjAVifMr6xwfHrMeDJBqum5IWZ2FEoFWZgzFcf7O0wDjLwIVgZ5o4VOUoQPzI2ppFQqFaWXIaCyKIrAhNE6+qXFQlepC+9TDEe1dQyDcTGkSJIlKUqHMyQ0nWo2XPnbmKvOTWXa8WSV59JGKUMqclmVZJn6gs1RkAsmswYjgM7yvKH3oSFttTq0rrVCUxm/Tgs1C9XwcQ1++XURwA2AbdgHhYy/owoBTV4JyvGEajABDGVdMvA1SdqgOB7QtpYegu7KOv3tLTKlGJ8N2Hn6lJVr16ioGeE4tTWn1nP75VdJkoQnT54yGBVxyBIYGpPJEItHJxmvv/EqP/zBz3j7nfcwxYT15Tnm22ucHhywup7S7TVpZRZTTbh3/yFra1dQXjMaTVhZXmJ4cMiw30eLiu5Cg8mgz+HuPZ48fky32wB7hUaq2Vhf4+RIceO5O7zyxutsXrtMp9Pm+z/4BR9+AOP+Af2zIXv7h/RP+vR6V6jKCffv3kMJKK2l9oaX33yFxZU1Prv7hKcfv8fEJ/QWr/Pjv3iXGsfgeMDtpddYmVvk4GjI7tEJa2sLPH9lg59353m2v8vJ0R5HozErlzZZWlrGScHgbAgCBqXjm//wt/n0Fz/nX/9v/ytn1YDdox1IEgQu2j7FkCkh0Xk+hUUIPuGK1Ifn0DsX93yPtyE8xkhBc3mVm29+g525ObbvfYgt+kjrSLxCKImT52fARbsD/zf2n+kzFkHUaLsxBb2m+/4UtIEAWkUqB3Vdh37gwpoMg3YVJf1u9vkp+0ox/V1CE5gLRUcoLs31uNTtkntNMZywX4wYaM8whzMRpLGVqzGJQCQq+FWGSJwwBJVxmCPD/iGtiyoSh4lDwen7acPYA60UN26/wMtvfZ2FuXU6cwukeZM7X9eUwyHPPvmEv/7ed9l+/IBOM2fj8jLduSZPJkcUUjH0JXiHIbCOBCqG+oZDUqng/bi8ssJoNOLk8AQXQw6DR6iNg63wvqbkvH7rLb7zxm+h6oSqsggtyNMmOmmBASrJ1Veu8Vu/94/47v+5RX3s6LoB+BGFSBCmYm/3mHR+lXHpSbs9nvv2txl88Cm69jQOj7j3x39KPr/K8//s7/MEydsffcjS0hpZM0dimEzGtJo5l9cuoyTs7Q544dWv8OCzz/irn/yQOQ2J8jRUSFWva09Z1QwGQ5p5RquZkXYbIYDJ1izOtel1WgxGob8KmKHAOs/p2FIaUFQ085rFdgIywaEpKygLx2RiEKJGKhHltn4GHuLP9/KLz/P0eZsCUrUJijIlQyhdZYIyKUs1FgJBhTAYlxfO5KlKA4iWVMEqwstAZFIiDAGc8wgLQjlWpGRNCLa9p4yn/HR4PQWVv7wGv7BOvvRnF//ORcupi1938Xf/m+fIFJj74nDSWkdZVGRZShIZp9aGAbOOoVtaqy+cg3hmYKjWMqw5IWc/Q0oB1oMN4HQIgE0RSs96SyECU1apJHgFS0GW5RH4BJCRCXvuNXwOHsdA3fhyLtj8Tf9seg6L6XA32mxN98DzIDCB0pLahmB3wfl9MWU1q3un30tHoDcAzcTBk8MbgyHs29MBrHXB+iXLsvMcjdoGi0ApQ6iTDHuYdcFCrTI1uQ97ojV1xDMUUifgPEnapK5q8FPrtuDvrRONRFIUFVOPXyF8DE8L70sANDVpmn6xduGccS3EeeCcVJJUy+DXH4PDRHx+lLAIpQO5ykEtQYigLnKJAu+QLnZqUwsDovIxYhgeqKtg72BrD0LhCeQeYw3eB3a6MSbcFxGUFkytGIQAKUMGQR1Vnh6UN2g8MgLD2tU0nAInsU5Teh88wr1EkZKlXSaiitdnefX1F/nW33sNYy1FYSknFVvbJ5z0Lf2xYzy21O4Y4c5opYqN9TVko8XEhGwpY+uomPR4p5lUExxhzxHTcz9anQVkx6HwKOGDIr2cUJYDqnqIx2JtqB+V0kyqClzNeDKi3z+hkbfJ8zZJmiC0pK4KirIALyLRxlHbEiFrxjJkXrVaHZLEYcsxAxNISsbWgWQQM0rkbK2HBlwqidRyNmhSSpI30v/sHgV/x0HacnxGzgnXX7zKpcvLrG9sUnrFR1sFf/bBCYP8Jk5IUikQBBDPVSVZdcp33toknezx7MEnUXIaDLETl9BdWGLt8g267YWQ7OuCL1SYdmjanTmcLfHlEC0cR/1j/vi7f8b3vv8X7B4co5MEnSSURRkOExypUKFpJo3SnPPCTiiBcJ5mmnL7yjq/85t/n5evPwc2JJx653C2phiccrT9DGkrFhe6tNpNlhZX2HryjP7pGa1WgyRJePrkEWxu0Gr20LLkk7v3ORsMWFpewSNoNHKazRZCCDqdDt6HwJmzsyF5I6OqLU3v2dzcYGfnKDJfm/R6PbTW9Pv9YAkhBGmacHY2QKmEZ0+fUUwMWZ5zdW2RwWCA3TliMCx55+2PmEwq7jx3i6pyPH3yDBBkWQMpFFVZMSkKWqYRdCDWoIXl6nKb9cU2S90GS70OD3eX+ejBQ3aHp1TaopKUYA0SQNbahuTmMNEKm6ATwUJiYg0PDx/TzdY42f8MtdDlbLnF0vocIgZdTU22ffTlCVMrAcKF6yIkTZde88G9B5xWGpdkeC/QzTZn5Zh3Pn1Gu5Fzc61N5iuq2jByNY7QHLuA88yKGmAmT9MqemdFXx4pJHmWhk0zonFpnuN9CCeDcHAJHKmWeG8oy5KyKOn1ughCYZDoNAwCRGhQiFOzsixIkjRYKcjgpTS1nXV4FubnqGvL1ZUu6/MJz46Dz1vAzuLmF8MpwgQ8bIw+OnYHeZBnsZvz/GaDpqw5OHTc2zpj63CME5JWS5NlkiQ1tHoNtrZqnh6VtLOcS03PC3cybl5dot933HtyzHuflRyMUirvuHGpR55JXrrdIROCJ7sjPnt6xu6ppfQapI5NTig8s8yysax57bl5ri0mpJWBSQiNMtEWQgpBohVVPUEIS7fbw9Qu3MeiQqiMNMspqjqwHwW0Wy2UEFhT44Gs0eDm7TvhkNRZCAMzlpOJY/u0Yn//jIOjU47HJU6kqEYLlS0im4JElzS8R9QgdQqupDYnbI92+MUnuxgvaWRtpDyXQMhE05hrI5oJtTB4GQrWQ+H52Buc17wkNFlke4apHTMvrBlTFD+baDpnkTo0oqqR0lmYRyvN7vY2tqiorQssWikw1oayMR6M7XYT6xzD0wGB4+2oRSwNHOAtYyRHtmYcLUy0gGazgZYq+AiZAF464aKHaDh8hYgM14DMMJWdCSmidUxk4wHCCaQXsyK4KgqYFVdi9n29h1azwenpKaGJC+tEp0kozKSME8/z5OyLEre/2YzHgiwKUCWKRIX3NDQnU2sD+zea+zQNh3JIHj1/GWNIkgTP1FPXxz1KxCABj3eBWRnuhcE6Q6YUmTU0bEFHW9YWmtxYnuPy0jL54m16179Oe+Ump6cjfvjn/4FMVNRNwfaTexSjU7TOyPM2j37+NlkKveU2qm0RzYS3fuXbjM7gD3//Dzg8eIasxyxudFhbmmecFPQ6S6wuX2Z9oUc9dnz68EcUkwFl5bm2cQPv8pmdRnbb4bzj8OSY0cRgrEWiSTNI0yWuq5fwXs7sJMLb7ZiyoL/s/za7EzP2T7RDiHtX2AfjMxaHfDgQWnLcP+b7//HPuPfue3hb8U//xe9x89U3MCish2u3b3P15i3u/2yLZ59+wtb9u9z6ylsBHHYVrfku1159jV88+oSHW9vc/Ae/w+/9j/8z3/+3/4aPfvA93vnh92jqBCk02w/ucfj0CVdeWcXrJo2lLr/+X/93PPrkbY6Hp5SmJs8boQ6JNGHvwpg3yDwdVVkG8D2yk1AJeZaBq3HGI9Op9+q0gSUGxagZUzs836G4T2TwyRYiNJd1bdGpioGFHmOreB8g1Q2SLEeqJG4m51YpF0Hai/djeg+8FDHQK4QBTZs6787XyMVG+ssfT9dFoC6F/1gTQPsw9DyXkksZBhhefjGUBE8MOYts4ymYHH8HrTQiyy+AbxqVaBIlcZMzoA6SunJCY2GVzVs3OX70DD0uSFqaxvI6Tktuv/YVdKPByEkWpEQnIQF5/+gAleXM9Ro8ePSE/YMjbt++jZaCp53HQcGUpHhKrl69yQsvDXnnnZ+Hr1Oe8fiM0+NjFua6vPKN1xFpg0tra+zsHnL37gcUkzF5t8fp0RHDQYGmROcwOBvybHuHSmf01jZQvuSkf8R7b/8Vc50Wu9tbFJOCtfU1lJY0Ghmbl9dpLqzxeHSGUClHJ6c8fPyEW3eeoyomHB706fVatHodjo8PuXRlmdPjHcxol9dfvMXPP3oA7ozh8JDK1Bztn/Djv1S02k2GBaxf2WBYHPHgs8ek8zfZeL6Hu/8hp9sPqZxj88oGi8s9FubmuP/5E/L5Vb7zj/8JCQnv/OVP6RfHjE2Fn3obhsUS2F9CkfV6pI0MU0CFDfvobNAYnx0XrJ4kgtpWjJOUbGWFG70eOs/Zuf8BxclBZHv76ZxhRrrzs+LugsYlfiziWTELVXVTy4IvAUcugLHT59YBymvcLPhkCmzFPSzKp52bsnAJYZ4S8Jb5vMGtpRUuN1osGkHiLDvjMQ/LM/rWUTQCCDuqK2rpokQ6SJlVZADVYlpT+1liedRwILPzgFxb1dE+IrLcBeAkt67c5q3Xv8Xi3Dp51kWqBsgGabNLd+UKV26/zJ3X3+Rnf/5dfvQn/4Hjj+5z/cYmby6sUXUUD6sdts2YoQSvVchWiBkU1sTzUClO+6eB2aVCvR3q9mAJJb3HC0uqJFc3bvK7v/67XGptYA5PES7kToBkfmWeva1dTvN98ut3KNw+i11PoQ3aGAqZkF+6Qn025sRYvvnP/1t++sEn3Hu0xUvf+nXGq9f55R/8P2QHhxTe8dxv/Tajbo8P7n3Cj//TH7Pc6fD3f/efkDS7NFsteg24vLHCxx+/y+JyjyTL+OM/+iOePn7A4q05lHC0UkGaSCZFOLtM7ZBNSa/TDcFtVR0k9CgaeU5UooMIQy/vg2+qVpLKeUbVhMFoQppoUJpJVVNHhVmQ07vgU+kusFz54uBhCq7OnvE4XHAQgoFVICbVUakX9ncfwZPQVztjQLgoz4/fx0VrovATmambAmMpshaDIrWdeDoafAUB8p2yvNUXrvfi8OQLA/L/wuvi1138ePb7X/jvxf//8t+ZrUvvqKoKIWIt6acWJVNw9Bz8ndaG8atnb7SLwGTADxRlVUI866wIBPs0TUPwm05IYk3pIsNUSh8Dfl0EQM9/nrVBwCtmQbYepTRJknwB9FbRo1ZLGYOyHUolsc4Ir+kZHnxcE/IsJY1qTmfDna2rKvrRht+1qqoQEvZlAH36fjpHEf1riQBhYODWBDvEaIkRn7VASLN4byOvS85sxrwPKtK6qgKrERGCtIVEK0HtXWQoS6SV1HUArG0cSgVbAoPW0aYgqm2kSlBah3Xko0IpssaD4m7qMxsGL1q5IAzQIZVmSjRAprFHUcFuM9NhXTobH6YQ9mjqKuABzkabs3hGxDXitUNEek6wWVPUdQhc885GsoeY+QO7qeJ0OpCLQy6pE4ghbcLEwYDzIUAVhRYaJaY+8CE81gqBlSr6hYOQjizLef+DZ5TqExaX51lbybl2pc3GRg9rBSfDgodPBrz/zhGmTEmzJVoLa3iV0tIJea7QEooqWG2ZymJthZBB2aiVmFlxeO+xLpzr1lSYuozPjAksYkL9aEyoqWtbMxkWNPIWWaoxdU1FQV0XcS8i/LwqZI7oRGEqC85gPZwOS9xI460jKSu8TOKQREcgPw50a6KWMjTjUitEqkP+CsGrt9VskmXp+dL/W15/p0FarQUvPLfJ0uo8aa4RqWY4yvnZvX1O9SoybyJFkM0Za8BWJNUxL27kvLiWs/PxZ1RVEaRApgxvSneZ1dWrdHuLpCrDG0sxHoWixQkaKsGYkqoYkriKo+Nj/v2ffJc/+pM/Y1zUJGka5YZh6qd1YIhVzsdGMJhCez8FHMDXlkxqXrx5k3/ym9/h2volXKTsK6nxxmCLgvr0iNQVdOY7FOWYuqqoy5q5uXmMNdSmQipB//QM56HbLth6tsOjx4+RSrK/f0iaZ+R5RrvdRClFo5EHcC1L/j/m3uNJtuy+8/scc13asq/M86b9A7obpgHCEARBcYYUOaJGI0VoJYX0R2hCf4G2XClCoYVCiwlShiMyOCIHAw5BAoRnG7R7/bwtX5VZaa8752hxzs163QS1mc1kRMXryM7MqnvzmN/5/r6G5eVlHI79g2Om8zn9foc4TbDzklbaYjgcsr6+ztraGuClRHVtODw8ZjqZcfXqNeIkweHDWHr9DlJFFPOaR48e8u+++zc8vP+E6zeusnV+gyRO0MoP4MHwxMt7pULpBCMM+7t7REpQVQUtkXBxqUcWpSx3+3z86D4Pdh97Nm4U03hOORk6X3hm3MIw3RmchGltqOwxaawY7X7IYDnBrr5CrDXO1tS29osvFiksxjq8k5dnCUgVAXA4yrl7MGbmepRVMCWXGhElnJY1v7j1lCy9xsvbGW48RMsaG4poKTSNq6TfFA2mNsSRIosjtJaLw66pK+oqp7Y1sUixdY2tvRzFy1eeM8n2H0hVlsznM3q9LtYYiqIgilJvWC6Ul3EKgXWGbreDUtoHmjkXTNVrzxZCogVYCT1RcX2rzd7RMUYocBoWRKhQWQWfyzOftBqlLVtbS3zuxT4tKbh9+4CHOyfkKkPHCas9zfVLfeJEcvfeHk92U4Rsk0QxtTMsV5Ki0ExPc8rcIlTE0WhOu91mux9z/eISR8djdneOGE1K7jwdcVplONkKfoYSrEWJinPrgleuLPHKdkpfCXRpfDqncpSVwVSQJDFKGLQUZGnkN/3A+jIGZJAIeYmX9cmraUIcx4F5PMc5Q7uVkagYKTWzXPDscMCDnSP2hjljm2J1izjboL3WAqE886AylNNTytkBhTBIJ9EIYmYINyI3cx4XBZE5pWXHJHFEMRMorUmX2uilDk4LTJ37oeC839CB8h3ZVCuQsFwpMusDxBQNCyLsyFIs2Eco6Rm2WiISTdTKmJ6OqYoKU9X41GyDcGdeR1VVIbWmlbUYTybUzodgGWGxQXJsnaRAcWJrxs4Dijqw7rT23q/+cBD8bDnr0nvZlz8wNEUbQiDVWTErhAAlSdvZwk+ru7LEdDojRnrwRggircmfA3Wn81m4D/6UEEWR75DLEKpnvB+Z/Eyx3zzODgIyFIue0WicoNfuYJxlNBmfgYbus+/zn7mxscHx8bG/l8914us6hPPhx6QQDSht/XSzjn7a4tqlC+w9uk8+HdFuaTaXetxYW+PGcsZmS7PRT1lfijidwaC9zpNpzqOP3mX3yUN2nrxPJ9HMh7tMpwNuvnaTb3zrt4mijL/6yz/n5HiXV954mSlTNrbPk7aWePLoEVhLJ0pwTqJsh5XeKof5ARc2rtHtrqDMMm+9+W3SVsTP3/1rnjw+4Mr5GmkmJHELIWMq42U9S0vbdPvhYBYANCGg1V45Y384D1QS5qELB8SA04UXhO8nMG980epftyj+XRNMEHzTwvefpQnleMz+rQ9pZZJnn3zIlZdfQ2q/X2b9Ptdef4M7f/8TxsdHPP74l1x/7TW0zjCmQGjJtZuf49YPv8/J4TFPHj3i2ptf5Xf/m/+eje0tvv/Hf8xsMiJJYLDzjEe3b3Hl82/hgCLPyfp9ZJQyOt1nqd8HW4MR6HDYMlXlk1+cZZ6XjEZDbF2gdUSSthYSyboqUOGALlXs2fw6Wvjj1bWhLku/fAvP1kvTzMv1IEgbfVPAF4NeaVJXNdZ5X8AoUigd+YNP+FFKenmx+4eMpAXDJqQ8e/aC/FRtF0X+YPmrAN5PMY0Wz3tIzBhHbe3iMCQJh48A2IlmvXhOsuuXvQDUfabR4r1yJZH0991ZixSegVzkBYO9HS5sr/H0wT16OoFJyaUrNzjNMswsYVJO6WxvsrK5gRWeYbOWtqkFVOWEe/fvsbezA0YxOB7y8OFDlFQsrSyT53OuXH+BO3duM55MEcCjBw9ZXVmi02qzt39MkiYYUwAFkapZXkoZ5yUbG8s8efyY/d0ZkdJMRifUxZQkVSRCECeK1fV1rrz4KnGriy1r7nz0HrPRPgf7R1hj2DscYIXm/t0HvPLyVS/RDeus1DEIxWhyys7ePoOjAVJAIS3TvCDLEuxEMj4t2b6wyoXLmjuf3OPk8BCn2qwsR9z+6BHzSc7uYB01mDCeDHnw5Akq6nD+0hYvvX6Nx7c/5vGjW7z5pTe5cv0Sg8N95mPBcV5wcnBE99wNbn9wlx/93Y8ZFzmns5kHk0QDxDSgqQUVMS8rxoNTorhHpDWNl7vDnuWgfQAAIABJREFUh1FJpRCV90hWwU6qtgYrJa2szea1l7HOsvfgE8rTfd+ENo37fgB8rVtsTXwKoDkDL5rHYn1//jUBfDU2NPjCZ+lI47TC1GYB7DYrVhPaKRZTogmjcWytr/H5rYu82F5ipYb84Ijd0Sm7dsaONJwqR1nXuMp4JZUQOAVGgdMSowVOh+CTRoq7YL57hqb3WhQoFEk3xjkoTElVFNRFTT/t8+arb7G9eZU46qKjzPtjC4W1Ci1SrJD0Ni/xtX/yn7K8tsq//7M/4ZNbd7iwssyFGxd488JFXlpL+f7d95mGOe3tHFxQE3jQe2amC4DhbNJ7+avTXl7dkR1+7ebXefnCK7h5STkb41zp6x9l+K3f+yazLx9zOhrSWc/527//17TVgFYb7EgQr13hjd/553z4wx+wd3zMpKq5/uab/OgnPyGaTTj45YecfvQ+XSTq6lX0Ky/w9tP7FPWcTBjWsgjlKsBQlBUrK0vMyxnHwz3ObbzED3/wQ378s5/TVobaVYgoJokVWRoxnlY0F1iW3l8zFjFaxRhTcnTkbe7iSHtLJ+wClJLBkscJReUE82lOrL1hZ1mZAM4JzpQKYQw7X08+DxZ8CkBzzQ33z5W1wTjIpAhrqveppWkVCheQQM8cM/ZsJgYR06dwCRf2ER1e68EjD70r6UiUxGHCe2zzP+FTf+Kvtjj47PMNWPnZ63weNHwe6P1Vj+fff/a6M4DTiQbgC+QC2WQHhJ/gQyuAJuS0OYc0QWDgmbNCBZZjaJ4090qFgCqEWNSSNPcHzyzFNtfCAoS1wT4hXP1zNoIN4O2ftxasFSAjb02EWJwDnCCoNX3AlxJiYUnQXE9dG98EjVQgLAS7AuNtzpoh1agOhBBBoHnmk+p/amyoza0JzF7pgsWCDRfpmzZeCWS8f6vzAVrOBj9Q59DCP2+qgiqQ9yzCh4fh8yJq6+tUaSVWyOBbTwDhVABqA4Ct9cLCwQXrArf4TpW3O5DewqFhv8pA0GquWy6UQo5IS4SMsIFdvWDm4s9Ogf7nSQv4hhQ4VFO7KI2KDHXl/Y2NswtMQTQzyJ2dCb3qs5lsPvzPKk+U8IxPj4+YWIFWVEpR6QgbrAaUgNIYClN7Bn2j3oqgqByPnx7x7HDKwweaJ0/arK1m9HttlpfbrC21EM5Q1pYkU1ilaZowWgqkdERRsMSqfK3rbA1WIDTEscZYryZ24X3WBks+69NkVKSJowRnBUVekudTHwBe1RBbtI5otTOWl1aRWlFVJbPZjEk5obI1NTUIg7GVP1/g68/alYzzKaqukXFEaiNaaddjQM43PZRUwfrD76lKeAatsD6MLEkSIh2FcfLp+vj5x3/UIG2r1WLzwhZaWsq6YjK3fPRkyr0jQdxdR8QZypVga6raUM4m9N2A73z+RezwE05PntLppIynM8p5jnSSzXPnWVvbRCAxtcWZGq0VxhqGg2PodJCuRIuKyeiUf/3//Bl/+hffZT4vSZMWTuAntVBh0TIIaqCiLksy4TcTYw0RAukMiY748utv8pvf/AZbK6uIGowI5tvWMR+dcvD0McOdhyx3EtY21jkZDnl09yEHu0eAYGWlR9bOQMTkec3O7kOcuU8ri1hfX2F4OmEwGCLnOb1+j/l8hnWGyXRMrDWbG+cQwjGdzSkKw2Awxl2CdrtNiqQoClZWViiKgvF4zHg8ptft8mxnh9u377G8tAzO0ukkxLEfYEu9HrNJju0Ylpdf4f79p3x86y460vyL//I/wznD0yc7WGtpZW36vR5REhHrhEk5YzKdo61lMhkQt1ewdYwsCs4vt9lcfo2Xtlb46OFTngwG5CKwImqBioPk3jqkEzghUcoG+b2mMAV2uktdVzy+A5fPdVlfX8NYR1WVKO1QxoOegkZiGqQmIcDt1uN99uaSKo79gmqhxqFQlFryZFzxd+/doxdfZLMnySpFbSzz0lDXFhUnno0QwKfa+k1GhS42At/hq306rZexKB8+VedordFRgjH4cdrIt52l1+/R6XQoyhKtNb3eki/ppMIGQ3OfA+MlcoSOtgjsjLry8hOLpKxqojghEpZXr6zy4d0jjkdTnG77FE8krjYelFV+k3C2Jm1FJEnC1laHl672cEXFR5/sc//JiMpJ1tZaXNrqcmU9Ixbw0ZMBB2P/GWtLkKqS+XzO4V6LO9ZRzGpW11ooXZOYKYmTXD+/iTIFtjb84t27TMsaG/VwOkIllb+/StJbEbxyfokvXU1YiQWihCr3c9IZ45NnTYnAH7jm+QzVbpHqGOm8V7RwAiW9V4yM/HUWriRNY3QcUeYztIro9npUzjGZVzzZP2F//5gng4JBpZDtNeLlbVKdICVU84LRYIItS5SpUaImLY7JiiO08izKyOS0ql2i+hShIqJIMTMFSg94+YXrPHioyMsCE0tK4UFn6cAIR22cb1AJwZ6oEFTkSnLNxFwQnr3flGKNN7YNRZFPTPcSHxVrVBxxfHzM+GSIKUtfRIYDqXN+btV17RksznG4f0BVV1Sm9kBtCA0AqIVkYOFEWnIDOInQESKGuJ2SVwWl8cmwSZo+J79yVJXvzPtusS+Qvel9AD3Dgbe70qeztuI3TWPpnVtj9myPMq+owwEnjmNy5y0VpJRUZbH4Pb4g9J3o5X6foihptVp0Ox3uP7i/KGKbgqthxDZd8Do02cA35GbzHKRfR2yQgcoAQjYAkzM+COvps6dUdeU38cbwX5zJaTE10taoALJjKhIpWE0iXt7o8o1XL9B6oU8mC1Y7msjNyXRFIiqKySkmP+HooWHXLXPQPeTAGhAKYU5RYsrB/pCPdoaUec6j1iNk/GMuXbtG1Epw44Te0gZJVbLz6IQ7n/zfxDLipRvXeXAbfue3f5/LN15kSs47H/6UTtKlmNZQndJtdfn6V/6A9XMvcP/eR7z7i1+wc+8WK/1l3vzqd+hvnMfVOthmeBa+cwaf3y3AicAgDn5jzoSzqm8MWXPGOGnAOBck8b4ik2cHslCgNoy0uq4QzqJVRI0giVI+//oXuf/Tn3J69JjbH73Pi299na3L14PcXXP9c59nZXuLo4f3ePzxBwyPjjh3/ipF5Q9TF2+8xOaLr/Lw73/OzvsfcvKVXS7feJm3/vl/TWfzEn/7p/8Hxw/vsNTNOK3mnE4nPlXY1FSmYJbnLK2s0OukzCcjdKSJ0oQ8L3FBSmqlD8kytQ+uaKcJSilq5yiratG8cMKSthRaJr5QV9FiT/MWOb7hVNU1rXaHWHlGh9ICpS3GVAg8a3U8HmNNSZxEOKeIE/+ZLtSRItT0/ptg4U9ngtRYBUseH94WfUouuWhgiOfY5RDUR8/hLuKMbSJ0U6Z6/zMlBMYonDP+4Cs4e60INkP2OaYTfv4JIQiZggFKeI4d9dzI0kIjZYSIUg73D6lTTR/NWrvP4wf36C71iXt9bCqYzmEuLOOyJInaSKc4HQ4wdcV4NOHOrXvcv3uX6XjO0vISrTQFKXi285TZbIbSktX1NU4GA2ztWFtto5Ti8vYW9+894C/+/Lt88YuvkKUtptOC3WeHPN47YGV1i1hrqrKisAVd3abf1Tw7PMKomKy1Sj61bJ7vIaKUt999n8lgzOWL2/SX19jfG/DWr/8n6LTN8PgAYSznVvrEGsqy8EwwqbAGxqen7O3scv3F6xhbMZ7NMaak3W1zNBjQbrdR0h+0rl/e4mg8pJW1GR08gqjDC69u8ejWLTC7tLrLbF68SHtpicOjEePTCVr6hPHjgwF3bz8gixSrvR5mVvMX3/tXPDsecfeTtzHVhFpYIhGBs1gR1vLwTbZXVuktr1BN5sypkUmMk6HpJr0fv5ISFUUIpPdhVwpXe1/sAofMepx/4XNk7RaPb71DcbKPsrVnv7jnB8rZYXcxxhasw6a5+Dy25RavWTQxXCPpFEEKG5jdkV7MJ8+6dQuv/QaIsSEI5tL6Km9cu8GqkdSDU3ZPRxyNR+xLy1NbclzOscrXm9YYhI5A+5RwpSVOe5/JRu3g5JndCGFOSgHO089wUlAriYy0Z1UlMaJwvPHSF3n5+k2ydIlIp0Q6RUcpKs5I0tR7HFaGfFpQWsn1m59nbX2VP/nf/zfu/fI9jk5POT/cRK6lrIuYJNNMZbAvEL4h5xlcwUfVWkSkFpJkgyOJNaBIdJsXtl/jS698A1FE5PMZZT4mwteCWSIZl8eM3TNo53Q2l5lVgtdf/xy39t+hrCSvfutbDFc22Gn1SFstfvqTn/PWH/wB5yLN3/3hH7KRF2xHinGny6Vv/gZPheLDO+9z7uIlrt94iagsqSpDcL0ky1o8ePQuOhJ88P67/F//559zPJ4Q9wW1q8nLHB1lQQ7va1sPOFlmsxk2qkjjFKEVxhl6vTYryx32D4eB9aiRUmCswOQVThqM83LosrReqScbA6wzQHExxtyn1SnNwzNWwxq5ACLBGEdVG8+O5Kyf7rALqyYpZcjEML7hH1RKNI29AF446cOHmxrSCW+pL6X/m+JI0os1am4JpEfftFgAzs/Nw880Tc4A1OZ5udh/GgJMFEWLz/CqjbPr/VWf+9nHGchLuEaxYF0KIWioCKapVRpIKbBVn4NuQ/izIEtbgAcGjW2sr3y978K5p9lnq7JcALdSNR7AJoBoAq09+zOKYjwQC0qJQDRorC7Ovv/meXDk+Qyrk7CchXHi3OJaGiZpaYIkP5TyDdHCGktc6cUa3DRTlQ7ZCS748OLrfC0FUntFjxSNfUCEM5ay8tcZaf/fUgBKYI302TSLJoEPYLWV8T6mYS2tyhwlRai1/ZlQSo1FYCsbSFreasA0QaRaAApBQ6bA31elSGLfaG4edRmIJ6JhpQuk1Ajl9xtvexEFklloLPq7hggkA0/0swtA3Fsy4j9H+FhI3wwPYLnydZCpaz9WjGcZG+trI2ucV4+EcDG1IJCIs9qNsE9JiQ1MbackzjiQfn0tqVHKkUvHXIARGiUkKjRbhMJn5QiwRiCEZnPrHFG/RV5BheJwYBnOSuJI0E5yppMxs3GOrQRRIBNaU6MQVLX0DVbhWeNFUTCfT6nrMgSE69Bs8CGJ0vla2dIEuluc9fc/jlt+f48d5bjEGYhVhBaSNEno9Zbor6zRW94giWNMXTCdnXJ4tMfR0T7z0QgpBNP5DIvwjGEBc1OiJMTOIWpDZIMXdRi/Sgmc8vM/jmJ0HAcLBK/WFsKDuHVtPtVs+uzjP2qQVgRJto4TrE04nkW8+2jITK55702cb6JYC3VFmU959cYG5zsVDz68HzxhfLei212i119hY+sikY6o8ilKxb5ThDfLbmUZcRQhQ4LoD7//U/79935IUVREiaelV+Gg7g3R8awLJLHSOOE9MXFeEqmQLCcZb37+83z7279Or9v1JsTg2R44TFlw6723OT3Yw5mSC9uvUuQlh3t7CBy9bhs/Ww1Z1sHUglsf36OoDOury6yuLLN98QI//fk7FLXlwrlzOGryfE5RVkihWFnuUhY5sU6IopSimDGdzTg9nTGezFha7qG0P1BNp1P29vZJ4phWmjCfnzIanXLl4gUwE472T6nKnNW1NbLuCnErY3Wpx3h0ys3XOpR5ycnRkHxesbzcZWPznPeRESIYWFsm4xGnp6dMx1Omkwk4Q1yNODzN2R2O6HTbpFHMWqvNN27e5OOnT/jg6SMOZhPfUbS+WGvYMc7hWSyhnpBaU9WWujhhd+8Wt261yeIv02ovETVdKlt6OY7QYeOTOKfQQjGcW+4d5BiZ4qRnp/qp5qX9QoJTiv1JwU/fvc/XPn+enhJoa5DU5POcVhRjpfc79vJ6XwjM5iVkMbGWSGFpdzvUZYnWJdbWtFop1irK+ZzICUQU+03T1h5oaTqyUlDVPuCkeXhWsWdn2NrL3XGQz+bEsaEyvqiKQpr8PK8pXMFq1sLZis1+xquXl/i7d3cxSgERoMEqL81rJHi2Zn2pxdZWFyUNp0cz9o7H3Hk0wBLTW8q4vNnn6vmMYlzz8aMjHhyX5C5ite14aTvhXDcjz1MOjyz3dqZsLiWsrmjWV7q89Zrmr39ywO7ukMOjHfaGFa6zjDYWYxUiTnFKok3B9pLmCy/3eWE9oi+9b6Vz3oe1NHVoojhi5T1FtVbEvR7WVpRVibViEVWjZChywqIfRRIds+h2WikZlYInh3Oe7E05GM4obELUW6eVtlBxRpFb8tEUW1UoY9EYtJvRY0CvOiau94jqPdJqgjATsHNkPUMJSywiIiuJC0HiHK+//AKvvXiVhztPefvOh5Rl7sM0pApeRE0nFCpl2bOGYlpyPAe6y2zGEe26JsKhnTflt/iiGClAC3QrptXpIBDMZ1MfVCZASy/nkAZQglp4YNgoqK1B1d7Xzjrffa2FxAjB3DlOXcmxVBQ+sQ8ZLI2jToxuScxJiSmrhb+Vs97PTC7mGoumReN/1QRuSSkgi0hW28jE3wct/MF2abnHfDBmZPEp3cYglT84u8pQV4ZYaySggwxbas10NsMay8ULl+i0Ozx++ITlfo/BcPApRnzDIldCeAkhDmV9wVtWFQ7n2VtCUlkD+Pnviz6DqS1IhcGhIgW1D6UAiLTA1CUYgzYzesBW1mKjn7K91OPqapuLax1WM02L+yRpiTMls0mOK+fMqgnTMqcuFdNKcjJP2FteY2RLTusj9o4fo8jZ2j5HK23Rzpap8hxbWN57+yc8fHgLKn8g/N6/+QvGozFrG6usbvYZlCVf/Sf/Ob/5rd8n7rQoypp2tMRbr/0an9z5gO/+0b9iNpqxsrXN1779T1GlZXJ4woMn94lmOdnc0o29bM4KcMIF6wG38B09g9LO2BwNq3rxaEC54Jv3D9gw4WMWzFscpg6MIVP75N+gLKqp2Dy/zdUXX+Ld3YcMnjzl2e1bnL94yRd71rK6vsG1z73O4ePHHD3b5dn9e5zbvkoSpT6gIcm48MLL3H3nbQ6fPWHn7m0uXXsJkNz82tfpr/S5f+sDrrzyObZeuEmcplRFjlIaW1m00kSRojY1Ft/VT5PE22Ao/MFACFScECUppnREKkaqiLIoyPO5927DgILEd+qQKiLNOn4drGuschgHSmumxYTaVYCXizslwZZgLKXNmc5yhuMBdTGj1+vQavVIkogmpMVZFzzcBdb5Q5SWnnEh8EEoWnp2ugz+aqZ2AdMKPrVS4ZwA6ZtI0gaQVvrGUiN/Ff48BcKHyeD8EUzocJCzJnhXNqixf5/kOaajHynAGeBkRAPPejaukxKMlw3qADo4oVBJglCC490dtrYvUJmaLIs4PHjCdO8JhbGoLON4NPJBX5d7RJFGipSiHHD7zn2GpyOSNGZwcshkPGA4HtNqt71XaprR6bSRq4rl1RMOdvdJ05Qo0qyuLrO/d8CHt++ztNrnxRcuU9WWk3FOknV46ZUX2Nvd4/H9xyiniNOUk8EJqnY8efyA4709WlnCbLrL0tI2G+tdUnmOWx9+QJqlWFIGx4dknRIda1CGVieilUqMkeRFTpYluCKhKmccHh+wPd8iTiKkUCRxwkuv3ODkZMB0MmV5pU9eGTbPX0IcDnn2eA/KiqKckI+GJJEla3Vo9VbRrRhnSsrplCSOefG1NyjMlMODfYrK1yZlMWC4f8LRwTNarQSpKuZlCMbx/iUeaPVUMaySrF64zMrqBco6eDorEfzDPTtKOYWSihqHNRXaeYaVtV4mb4INgIhiuttX2ahrDm5b3PiQdpowGXsWrwn73iJtO4yk0GfiU0MvrG5CnNl4NMxaz3wMzy8YTpKGnXvGelM45/3fbfg9UsJat8MXLl1mlYjjwyOGx0dEqWS2FPFoMmW/KqgcaOmLBJ1EyEh7YFZy1tSSnkULeG9zj6IFlrmfeHUADHwjhNCYdSipuXr+Il945Qu0sj4qaiF1jNAxKm6RZF3iJMPZmrKYU5UzhLQYCb21DX7r9/4ZfzQ8YefxI8r7u3T2E7YurbPSafFIjNBpxlx60gsWjK08alF54oGTtb+3TlJXDoVlNVviW5//NtfOv4o9yanL0jPJFEgrULGmv7rM7Y9/xPb5dco659Uvvkg6yShMRGt5leXXbvLLx4e88p3f5tKFLf76Bz/gwaP7XL5+lcNEsVIanJEsvfQKnc99iUd3nzGellzrLvHWt34LWzm6/R4HxwfBf3vGZHDMeDDiu3/1A3YOT1BxBMqRaokpa1ppRDeLOVA5pvbkjLmtGE0KVFeiVRW8SL1NQCuLAmAa1rfaUpeBQaYatqhb7I3SNduoC5YwZwDtwl6jgXHd8+ofuwARBBAphcKSm2A7Es7p1lgksVeWGk8o8LBto3z0v0M1jYaG0Roa2QTZva1qjPMGdzGOWAriRKCEC+5FChHYlp9myZ6BsQ1oCSzIKYuZGlSu3uc0DnZAn/ae/cdA2X/M9qCZ19Y6jPPqXosn5QjXnM2CbVcAytxz60Vde7azkpK8LEHKAPI6dOR9fgOSGYA1FfxnLVKcgbkIh4o8Y89bhIGQdvE9CuEWNmp+XQEwQYlEuA/+Phrj63JjchqVjJRnkJGS/vf4mkNg8Wdw61zw3PTbsnOC2lpksJryzaBwPg0s1wVAj/NjKtwYKSWmDMzWAFDb5tDvAoLp/BnNCofBIIUKAcd4Bq0psMTU1oc4SaW81WRVIyLxnL+vW9jJeEW09g095UNGPfDuw6FVAFRNXSGlt0uLYh0sLYS34VMKIfRCBSsQ4fwewn6dB2ptUJiZxoKATzcY/LQM63Goc0Qgz7hAaNBxTFXOca4mgGLY2te8gdLgx4PyjUAJCK3C3AzkEunOlGzWefsFF15tBXVVImSMU3gvcw+2YLVE5TXCNA2zGikjOlmKVAIlFVmmSdPIW21UlkFeMj0+oZoMAZ8bVJbgrPfSjYxeeBEL7SirkspUWOsoXY0qKqI48dwxKTw24ixKgBB+T6+KkmKeB4DaV5WRijG29r67SqKlQqoUIxKSNGN1eZlWHKG1YDAaMDw+YX93l6fPHuOOD5gXE2yzCUpJaStMXlMriVYRCQatM+JEI7FI6W0Q/HfvPcB1FOOUB8OFkFR1TWV/9XoD/4EgrRBiCfhfgZv44fXfAZ8AfwxcAR4C/5VzbiD8ivmHwO8CM+C/dc69/f/3+b775JjPcgZlwp/85DF3y21MuoYWsU98M0EuXozYSE5568YN9h6+x/DkyPuLWIeOIqSMWN+6QBQnFHkZFiwL+AmWJglpotDK4UrNL35yhz/707/kdDhDBb9Pt5DU+S5QU09J5ZlqhhpMhcCQCsXW0jLf+bWv86UvfIE4ibyMXfhUQI3E1CXT0YBydsrweJ921ubo4Jg333gDU1ru3r3F1auXiZIYY2qOTw4ZDKesntvg8ZMd9o6HTOcFRkb0essMBxNm8xndbkpV+c71dDyk207JWm1WVteo6pKyKEjjLlVRoiNBOS+Io5jR6SnHx8dESnFuddVfU1Vz8cI6Vy5tc7C3T1kMOT4es7l5gXw2Yv9gxLS/hlQwmUzodjs8evSYn//s7/nyW28ipfDgSBKTtFpIKZiOJ0ynU4SEOImoSjg8PGZSGtJYYUt/AI2RnNtcofXCS/R7S9zaecqzwYCirnEYzwIKg901B9TAqPEFaMWkOOGXH/6cVqvDSy++gY6SIBvwi2xlalIRYYUFlVA5zf3dATuDOU53vaF2YDN40DNMJiWZq5Rbwxn1B0/4+ksX6UeaTidGpz1KGxbUhTTTj5zCWMgrVCtamHJncUwaaSaTMdPRKd1un5lzlMEiQUeh66s0deUD5uI4Io5TjHEoLRYLsf8tTTHtF8gkSTzwVdeoJKLT6VBVFYWZkVclxWxCFEdoWXDz+jq3d07ZOzWAl88LIXw4kZXYfIpQiqPDIb3lFmVdsf/kkOnU4qRmbSPhjZe26KaK0bDm49v7PDs8xcUdNtcSXrvcZTWVFLOK07lh72SMciXnVhNs7biyJWnHKdcu9vnJh1Oq1hrjkwOcypBRTGQKlK7ZPJfw0laPF86lJFii0hewZWWYzSdEkSKJYw8AViVS+q5vEvmi7OD4GIlgdXUDlGJeWCZ5iU6S4JkIWgUWtZCczmruHU65tzvkZDiHrIdcvUDWzqgnMybHJ5j6BKWhhaWlS3pxgSr2kOU+/fqYdj1BuwkqmqJdjlATpKgwtbcRsFWFLS1z53BpiyiPaLdavHT5EnEk+ODBfSZViRVQhGLPCfx64hz5dMrOdM6gsoxNyRc6a3yu1YM6Z9GWDU0DK3xxEqUtOt0ex4eHzOd5KJx9gdkUB/5+WFzt2aEmyGK8KFMuGESlgxMnOBJwqhwza6gCeKMx6CQKBbOXB5nK/+v9moX3k3PepB88c7eRdVnrmTy1EvRWeqyur5BXhllREEURsyInixPy+hRX1ZTO+gZQLwbnSxEd5K6RViEkSIHyKgLnHJ/c+QRbWx/WqBVCKw8mEkQ4i0RaP5u9l6AhEpL1lWWqomA0naDSBF3ju+NCYK339HKuRiNxwVtOuYgsbtPN+nSziI6bsexOeHm7y7XNVS72lumniszlqHxCUQwoh8eYesy4sswLQVGUuLqmMhWuMtg6ZmhbnKgljsqICXP2T4bs7t9mdS1hfesFrr3wJTLd55dvv83h8TM6UcZkOOHF669xfDzi3v2PWV/r8Dvf/iaVKfnZO++SZi22rl3n4GjEe2//gDu//BnrSy1aWcSjD95jfW2LYtjjx9/7Lk+ePcSpmre+8iU2l9fJsiVWNjeY1Q1UZmm8nxzhcNQwzRpRZANmOLc4YPi1LUiKQ9PPS8yUB2c582sUoYi31rdglBS4xjImFLH95SVufuUtbv39j5gPBtz95TtcfvVznLtwEWGtD71589f44Ec/Ih8ece+997h49WUmecX92x9TlwWbW1u0V5Y4HR/zyYfv8sKbXyVdWqW2Nedfvsn2Cy/T6q1iREQxmQTZngDnw/vGbAbHAAAgAElEQVSEkhhnMU7R6y4HACeEcwCR0lRliTUVkxFYJzBV5cGlqsCYFB1FvntvDM6YhSyvSYMGz+qJowwhxkynU1ppjzjy+0dVeSVBY7ehtaIuYT6f0e0uhSTmBXlwsbcYa6nLChF75p1W3t9aRxryGac7z0iSiDiKEUF2KaMYnWSg4kDR8+tDWZfMi7kPXIkSRBQ8vqzwrg9S4KzwoXnC2woJKZDENHJOG/z3wCEXhwwXmiuheQ5IGRrl+GacdBYr/WGoQoCwWC1QrYzljS2evPMzsm6HtcuX2LpynsPBgA/ee8+n3TvoLi0Tl94u6uKFS8yd4ng4wjnJuY1NTmONlt7CYm1lhek853Qw4MJF37TfffaMWCna7TbzPAcbsbm5TlWVvPf+x7zzwScsr55jdX2Z49Mxr736BufPX+XGjT1uf3iXWZmzef0qJ6Mx7Szl2gs3ONnfZT454d7tfWpzmxdvfoH5rGKSGybzU7pty/bGOlHaZzoZc7J/SDeq2N5a4uMHY2xd0m61GA1PmJU1o8mMyWTMUtRlOhpTzhTtzh7Ly0s8fnYPYw2no5zdg9t0l9c4d+E6F/YmPH22w97Th1y4fIny6Q7SwujwgFZSMB2NiCPFZF6RZB2sG9DpLmHKgid7O3ztt77D137/d/nbf/PnPLj7MfN87scMLmRI6DCEDDptcXXrIu0oY1wVpEKS5wVSKlb7fQrllUMiSXC2giJHC9/wbCSsnqEGTkhkkrHxwk3SbpudT95ncrBH4UC62od5WQ+wnHkfByYcZ5YsnkQQWg7uM4y/wI573gMyUG4XlVzzd9VV7b1IlQDt5bpby0vcvHCFFZ1xsnPI/YMD8kxRScNgPOJkmmOVQukYhAUtEUphFTgtEGrx67DCBaZ8Y9EmwiLaYAbej1EK4Zmc+IaLEoLVzgpvvPJFLmxcIYvayCj1AIVOSZI2WdYGJ6jqgnw65OnjO6yvLKGlpMjnrG5u8tZvfJN/+/+eMj6dol2N2i/ouojVvuagLJjpCplFRFFEXRsfOIoIbGLtvS9djbCSWHb54rUvcfP8TVaSPmMNKk4pRePn65m4aafL8soWs8mUj355C1FkVOUGzi4jllq4/jq985Ks02ZvMOR4OmF+60P+6de+yfLli8zef5/03DUufvv3eX8Gj4cz0H10vEx7ZZNZUeCymCTPSasZCMvh0SF/8/2/4c69J2TtFOkq1rstsjhCSsO5tuLFjYjjQ8dB5fdD4yyTcU6qQ3Ct87w+JZTPSVADqmCntoAon1MpEMABH+Yjqet6IcNfnBfEWWPzV1o8NexNa2lnGYmCxNZ+AAmf71CVzttiCO9RbKQI7G+zAIBdYEcuvGKFCNL2wLJVAmcEwilsbT3oF/nxFkWSCM/ic80h5zOsWWOeD/VjwRKVwdJm0eQPF610UBfWZ8zR52uOxfV/uuP3Dx7Pv9ZZhxYBmK1rL+kIcuYmGLQJg/VsWr8W6MCobT7PN0MtVVlhlUUEMoM1vup2wntKS0LgrBDEKlnMW1PVvm8pm9NgM/7tc+C8W1iMGdN4BtvFPfMB2vo5trJc1OMQ1gN31kwS4TsVoVbzN0EEYFg2uBbiuXNIkz/ReHgLIbB1YIMuar+z0DEI4abOBxgbYxZgt7fJUDjrm+zWVVhXYaz2IF8V4ZI01FgWrECFMfl8jemtDGKk0kRxhBINEOgVD42tjXVQ1RYpa0/kkco3e2XjQyqDNc/zEiRvsSDcGYO5ub6z7+NszDX7g1yA9g27+KweBoVSjkpqEBrjmlNXYD3X1UKFtvBxR3q8pMn5EAJhDQaopfT3URhQAumkt98qCpRK0KamdLW/LqVJlKafZszynFxFOBnT7qwSt/s4ldBPWiSxRilJhW8yGAfT2YjZ9BQVRSTKUVV5CLVOPHBZVWgdAkKLCllbD9CH77u5Phea904KRKSJ0gwZafIyZ5bPcKZAOA+EKx2FIlB7xWwUURrLdF4wnY1JY42WS0jdYm31Mv3OJstLW/SW1nj67CG7u08YT08pbIH3RsbPqaqiyGeYuqKqCjqdDu12hzhJ/L0MZCZnLaaqUNYirWZWViBUUGX+6sd/KJP2D4G/dM79CyFEDLSA/xH4K+fc/ySE+JfAvwT+B+B3gBfCz1eA/zn8+48+BN53oiwN93anPJh0qXubSB2jBNTlnKoqqcocnY/4tddX6HLIJ89uM69yvxBIPxh7S2usrm+R56X3o9IxSkXYgP5XdYVSDqcEBwcn/Lvv/S27+/uhYAmG1FIgbLPINAnMTfegwlmFshWRVmyd2+T3fvM7vPHKq54JUvuDkFCexSWqmsnRIY/vf8LW6jKrmZcUWGN49PAeq6srtNst9g52SdOMbrdHlna4dXAfIRTra32OjgccHp/QerLL1tY2nW4HgaXX6xLHK+w+O6CTJcxnM6aTOVtb3m+3yGeYytDpdUiiDFMZKmp2nj1lMp6wubFBbUruP9zhydNTts6fY//4kMHpgOFkxqyw5LWj38+IB1NGp2OkcgxOD1lf22D7/Je5/cktZrMRrVaLLEtZP7fG+rl1Ot0WGxsbtNsd0jTlcP+Ao/mYPPdS1PF4jLWGrfVzpFqgbc1WfwmtNUvdLs9Ohnzy8AGj6dh3XIX3X6U5kAp8N0viu8XOMCmGvPP+z+n1Vlhf3/KefGHfLfMcVzvSdstT2GvBg/0Tpk6Djnw3zHr2HPg9L7i5UAJjEfHR7ohOdsJXXrlAJ1PIwkBRn3Vmw4ISHHoojWWe17RjkNZQVAXWGrI0Ic9zpIRer8e09JIl57wJu8SbnqdZy2+W+I3TSzM8EIFzZ5265m+WMpi1l7RaPv24tpY0SZCyppxNULqPq+ecX+nz1uuX+d6PHzGrZehAeKaScxakl8nP85rbt/eQSlLkAq1iLl/qc/FCB60cj56d8mR3wvHpBCE1l1ZjXn91iSzW3Hs45unRnLwsUCbn4nqfOFYMBxW3i5r33n/K6dQQRcuMCnBKUZzuE0nBUq/FyxfO8earK7SY0aJgOpkxq2pEp0NVlAhn0Mp7MjvhvYYQNUqGTUpAmnZwrqauK9KkjStyoiiwqhGgBFoJUu14tLvP93/5jL1ZRtZbZ+3SJiZRjMcF490BJs+JbEXbTlg2I85lOX01p6dmRGKfstonUTMSVSKllwbNphVVaSjyMaPJkNk8ZzafeYN+5/wBVClSHbG6tER3qcf2yhpPjw6ZY4m1pqg9syhC4EZz7GAOxjIDHtQF9eiQ3Fa82OmwbgWRq/2WrgQqiRBZQqfXZTAcMhicLoojgWjcRDyAFCQ0TWlfGIPxi2soysAIwcxZDq3lONLMFTikD+uQfmxGsZeomNqFUAH8JwZrBQIDrqm/Bd5DUynlA9ycJVteYvPCNl988/PcffSIxwcHVMZSTiZsLa9QOeMBaJy3k6nNwi7B4OeFsAJlfXCLC+CvDhIWZyEv5uRHc0zD/PNXsihOrbVh3wi+qngGnlN+s7Vl6XHAqvKHKqFoRxmtdodeq0srienEMRe2LnLztS+yvnaB5SyiM3lM8cmfc447xGKIqwbMjgsG8znVvKCc15h6irEFtYGyDKiZCUxJA3UNQzSDpT4TlXCaj8nrIctLmiix9Ff7nDt/gc2VyxRFze5fP8bZmi9/9ZuIqsXduz9FSYGWlroY0u+v8NaXv8HFK68yszXjfESrq1hb65CqlCI3rG1c5Gvf/E0u3XiTDz76CCQ823/Iz955m2Je0G73+I0yZ/PCdZKsj2uYk/j56JxPQW7u9VmR2hyanmfciIUsTIqwIAf/KZo6J8hjmxqiARedn9YIZynLOSJJ2b5xg/VLl9n54B2OHz1gNjxBXr0Wvu+U7csvcvnKizx594T9Dz/i357+Lzw63GPv4IALl6/z27//X/DqV79BEmuuvHoT5wwUuW9wSoEjppjX1KbEmjKQfTwbo9vuINzMgzBC+LR56zDGM2N8oKS/F1pFRHGKsY6yyMkLb92RZm105CV0ZVWhIkviXEgz1ov1HyeIk4xW1mE6m9BuTdA6xhjfkLLGS4urMvdNFS1otdKQOE042Hspl9ZROKxJUC58dz7dPdIaqoL3v/9XPPjZj2mlEdJYbF54hlEc0+506Ha6RHHsmflSUklBbgy9pSU2Ll0l6/WppbekknGMQdDr9H1zJdJYLQKjAZoQTu9xLDCBkGJNEzjHotFkrA/DgEDCsQJchbMlDXtbBuC4EpJ07RxrV64wnE0YPHvM2pXr2Cjhyo0bHJ8O2dndoxSaUkSUVrG6vs2znSPm05xeltEWFeXJAZPpDCEVWatNnhfMpmOKfMpkNGQ2GrG1teU9J61jeHLCyuoS5zbW2D7Z4MGDp/ziF+/zla++AWKP5e4unTTh/q2PGJ0eEvXaDAZDzp+/yLWrlxDEyDjDYajyIeOTIx7e+5g46fHFL3+Vt3/xE/Z2n7C2soSoK473D9h6bYtL16+QHBzx4P6AtW6PdpZiKsssr5nOK4rKsLm5zScnH3M696n33U6fKM4oawciozCOhBRhHKasWeqvsLS2SXt5mfTkhOHRPuNZiakFh4dHbG9tsn+wjzWGleUlNjc32X38CFPCjZduIqzh/fc/YTQaE+sIof3ehAtuTDiUjji3vk5kDfODPUaDQTjAWaq6Rq+tIrIUl7QQbgkRaQTe/85Z/5oG3EmyFGMt86JESEFn+wpX2l0Gd26xc/djzHQIhIAVzgCaBcLizurQT9V/IcHz+XXs7C2fDrp73hO98SoXShDFkjSWLCcxX7p+nRWbcfB4j/3hkIEwHM3nzOe1D9VTPgxMaDxTXEpcFNhS2ktJHY5AfvN7nJCBeSfOOv0uKNQCWGDCtUgniIXixsXrXLv0ElHcRUWJZw4lLaIkI0lbKKm9b21VoEVNvx3hqjlEmfdNrS3bFy+yenmDvUdPOJoWmIMjVirDul7FGMtEzhkVOTpJkE7iah8e7AAd7MrqusCWls+99jq/+41/xkqyyuRk5MFkHSFwGFthRUppNW+/e5fx/oxMVDy8v0NWbvLKl36do82blPaYqNdha32NH/3xHzG4d5+nswHdjqB+83Xa59Y5iTMuffPXqS++yP7hKWm7TbdexrqEp3tDsm6H0fGIajSlnbWwZsSdO3fZ2d8jayek7QxThJR1FaPljI4ccfNymyc7I46nuY+7cY6itNS186Gh0u8NEkGapLSzmKKcAeJT9b5zJrA2HTh5Nk4581n1ryMAc2eA5/Mk0gZ4bII5wQZACvKqxsaxn4tKUFmHrWu08GoGlPcz/rTdAMHTORyKQp2nPS0PjLeIcM6has/WdkrT0jHLkWBa+rPX4u3hjz0DuJp74JmDSgXFa7CyU5HCmtqHxQZ5eKDxLliunwVofxWr9rOMWtH46DiHRIazhvdQjWLPwnyeqWtD+GsUBYKQ+zSL0X8x/rsxoeFsjEELz8BFeJsArZWXVTsRgET/ESoKdmHPvVdKEcKoPTuyYfbKYMGnlVe4iBDCKxC4yH1qjXN4ANm4s2tpxlITCOpdaIJdgLWhhgGEWASGIf06pwK42cjzmwawNYaq9sxXrb3ayA8hidIaY2qiOELU3re5rmuKQGARSJSUlHVNZXy4rnEhj0Y0Ng9AY7dlTahHPdtZCogjH44l8IqnJpC2CRz3QGm9YCVb54PB/JjTfp4EDKIhIiwsnEJB6vNoqkXj/nnLqGa9FQTrjDB+m/BGJxb96MU5RAgNIZTZ2z3579iJoMBokGVPvfbzzYnmeO/HjfThlbmGzEIMYXwBVYWuK3RZoJUmjxSlAvv/kfYmv5Jl+X3f5wz33piHN7+X81RZY1d3s5vFZlNNtQmSEmmasOGFIQiwVlrZ8N/ghQEv7a02hr3ywjAsWqAAUeymTLLn6uqaK6sqpzdPEfFivNMZvDg3IrMo0hbEABL5Ml9kZLy4557z+31/30EppNYkcY0oahAnlpt3H7Jz8y6LzKJV+CyttShhkEojTU5uFhQmoxFFNOoxcSwwTiGUqK59uGfKLCdfpEE9sRyGLhXF1d7lqzUnPMQ6ppnUiaQkiSKM15SlwXtBktTIbCC8WZZ9SDiL87RgIucIIorS02oqlIyo1Ztsbe0QxyFcjVMHKRRljlJipepxZUlhbFBqV+BxzQripFExr4MSxCIpy6DkLZxd9dF/1+M/GqQVQnSB7wH/LCxeXwCFEOKPgX9YPe1/Bf6CANL+MfC/+bC7/UQI0RNC7HrvT/6//h8VJYzmgg+OFtj6HkorYmlQSEoXAm5cNuNWP+HtO2tcPP4rJpOrMOGTUXVfSza294hqbUAEKe9yulRJp0JyoMIYzYcfP+KXH/6ChVuE4gaLswItRMWetSzldYgABBpn0IAwOffv3ucP/9Hvcu/mLZypqOx4wtEKrsiYDwbsP37E40efEivJjb09Wu0mpiz4/ItPeSAesLW9xfnFBaenJ3z00ScIGXHr1nV2tjbp9bq89/6HfPlkn/Pzi0oilrG+vsZ8vmBz83YlJy2ZL1JOz88DG8UWzGYzhBfoWKGV4PJywGKRkucpm5sbCAmnJyc8eXbEx5884fnROb/xzutESRR8S4Tg9OKS3La5msxIkjpFlhLkqIb+Wof7D+4Q64haLWG+WHBxccHTp0+QStLr9rh58xa9bo/xaMzZxT5Xwym1WkKn1aTbbXNjb4dGq858nnF+sk+BYLfZZrvV4Xq3w5OjIz559ox5aUJBuiw+loeqrzYjwqF2Nbnk3V/+Nd/4+re4fv02QjjiqBYCxTB4XyCImKUZx6MJVq8hVFTJ2l6SwSyLDRsOIIQgj1r86nCMlZp33rxLJErwJavs0qogX7KkvNRkxoAztJNqTVS+kVEcGLUbWzv4SJEWwesYCVJpalFcARu+Kpk8WIutEjS1UiH9XQS/tZeTr50PxU1ZlhRVcmGzUWM+C2xOrTRllvLm7TUuzhf87JNzrAh+QV5UZv1RVAFzgjIrUVKwttHjxvUeG03FbDTl46MBk9RR2gZCKF65t8abd9bAOj56NOLJ5YKFU8Te8XCnzzde6ZK4kvFVzqPnM/aHGu9go6khLVCuJJ5d0K3DO/de596upllOuRqOEJ0upbXMFlfMZ6coD83WGliNjFQ40EWYNnsffGpA0u608d5S5AXGFNRriqauMRgvWBRQqpjR4JyNpuRiOETWmmzvXkcBi9GI0f4CS4QSklhm1NSYLXnOtjmkn56jijG1yBIpQ7cWvIank5TpfM7FaMjlcIAtU5zNsNaEBNeyXAHuSSRQQOYcs/Nz9GhEu9MhUhGpzYNVQGVGb/OCfDqtrns4dEofPOkm0wvOzYJfa/W53migjCVOEqJWHVmLmM9mjIfjMBF3wfcNWPnMlssJnw/+yt6FvczIytPIe4zwXDnLmbdcekeexEFSbIK/UkiJDSy7rAzgtLfV9PNFq/qCxRP+uLrflp5ccaPB+sYWIPns88+ZpRmRVHjrKUqDkkHmhBLoOKJRr+NrEdksD/67UpDEEZsbG2RZFiR6rGr0wCBQoJWmEdeYLubBeN+7Su70ogmCUCQnSYwpCk4vLiq86EUQWKQk33z9Lb7x1jfY2bpGv7dJXcdMhufMJ0O67S4bO7dY37xBLEvEyRl5NsJkB0xmc+bzgiy1lAUUuaewy7CBYKzvKk8TsZT/W0/mBGnSZhK1WTjPeHJOlk2IRIkQber1FsY7Ts5P+eLxlxSzjN2tHg0BxyfHFMMr+lGdBjGHzx7zzveuc/3aQ/ZPn3E8PCMrZnS6NX73v/hjtjbuki48w8sjijKHesL2jRu8995P+PiXv0LHlkYrYVGr85f/NuP+177FO9/5PaSsr5giAXANw6dw/WWQsXv71UbIUbFhXvJOgxCCWK1PKlaIrwZplRNzaCqVWgWcCEIQHUrS3VjntW98g5NHHzM5P+fgs0+58fB1jBMcnz7j4OOPyaYznJNMTk4ZnJ0S91q8evMmD9/8OlsbW7zy2lvIOCJOYnRSIyvLypJGI1RMafLAyPaBaYQP7KNarcZ8PMK7MnjRIWg2GsxmM7xzKBnhvA3eYEC9XiNPM5TW1JWi3moRJcH70XjB+voWStfBQ1GEofPLjIw4iqnXG8zSMZeDE5RUgU3rgr9yaXKcK/DOYE3JYmFpNlpEWlaMxWBzsEqdRuBkoDVIFZiNZZrx2V/9BR/9qz+hMx9Tb7VgvkBMZigHDkssIY4TlFRcuZKxtdhGg7jd5crDxeY63a0NSmeYTqbU2k0K65BOkChNo9mk0W1DFKGimLhRx3iPTBLqrVZgDyqNTGrBLkhHCBWCdxKtq9C0cNMbLzBC4bxCWIOqQFo8GKHIdEx9b4eGhsFsFgBi4bl55wHd6YTL4YSisIyGI/J5wfnaCfPBgPVGwtUkp8gX1IVlXGSgIkaDEfN0zu27N9naWOPdn/8SU+RID1ubm6RlyWI2I81CQOON67sMLoYcHB5g/zrjwSsPSGQdl024PDlCa/jWr38HL5Iw8J1NGC8KOnsPaW9sko4u6fcPqSnHyemAwdkZF6eHFIsrJqMdkoZhMjyjWbtFvdEkiWZo70knM0YXQ5x1FIVnvCj58NPHrK9vYZ1mls5ZZBl5Ybh155XgSZjs0JjBzt4uP/nhn7F/fIiJu1zrbdFY26R9MeDq/ILR5SkiqnPj9i0uzs8wxYJsOqERAWKN+TwoBv6n//5/4OjslJPHz4I2tmqulQhyUyGh1dtgfWuP/vpGUKTkM5qRRKtlEE0t2HmkFmU8k+kMumtYHSNkSKc2FWtHKQXCo6UEZyhKg481UXuNrYdv4YRk8OQRxWRIUTES1dLv9eW9iooxWB1jy6Hn8vHyGfE3PTVXvuS8OAtVpEF46lHERr3OG7t77EVNzp6fcXw15Eo5Jr6kMEEFI5dScBf6FiFVdbZFxLUIiwt+9SK81+BlyfI0DIBE1QR7sWTPBtsDJ0OQaWRgo97nwe5d+s0eQmnSoqAZ14mihKTeROkE7yxlkWLyOdIZ+q0GeZoifYlUQd01no2YywX5hiRqJAwuUhaXl1y3lq3NOrWdPk/8jNE8w2od7JOWPp3WgHD4rOBa5za/963f41rnGiwEi3yMtSUNBULYcDYQ89mjU374w49Zn1/QImOeFnyRfsnP3HvsXrvFwdMLri7PWHv9G0RZyY12nVffvsN7f/6nfPZv/pSLo3O2773F5ve+z88vL1lMC/rtDuv9Tqi5vWAxz6hXLNBapDk/PuXi/JwkjsL+XJYsFgXHwnJjq87mTp1IZbQ6CffurPPF2SnTvPK8F4JFXpAWJY1mM0jSfbAN6HVaTGZpwF6UxlXBTFKGEC7vQ/0kZMV2xK9A2JcBzlXZ9fJCfbGgq4UsyPISKSOkD6rA3DmM8xjjmROsF/TSQ3w5cRd+BQiKaui6BApVxc5cMuK0JuQfeI/HhgGigUatxlaiOSvKMJz7Su34N9/s8kYLv+q1uPLHFURxRJqlYS1UNYa1lpcxx5cBtZc/o5fvyX8fuA1/ts4FX0wHArdStSxl9EvGqav8eY0NodShXRWV0iPsHbaySNBKUVZ7gnVhAKMQCBsY8j4YDocavWI4LME8V4FY4ZqIyvM49MtLf9tlDguw2iuowttkhYoFJXGwinDC4RArIsXqs6l+hqUvLz54DQvBiinoCVZmTkISxQFstKYCosPPHnqY0L87B1mRh3qoUk4orYhFXO1pClOFq/nSBrKdiFdDa+OCLVtpSqw15HmGj0Kf41BVOG0AVKnqwiCDD19LJV5igrvASnUWQQFCBnuzKK5qIVfZNAgwIZwy2NO41R6/3N+dcxVAa16EpvGCnLBawrIiFsDKIixYPvjV+reVZ7lzAdgO4acVFivD/qEqvMpZGyw4hK8sqpZz7qAY1VGM8J6pK0mkJ6nIYUKEzwRn0NYgixKj6qRCIWSEjxxJvUmjdCAi+v01BB6hPCqOiOOEVSg0UGRzrCkonUNGNZJ6ixc2JBUhqPoorbGkWUbhDF5BpCN0FFUDAxf8Z33IGzKFwRcWbxyxUnTaLYrcMV9A6QtsHmzpMCVlCaUtqcnQq8UywpaW+XyOcyETIo4ivLdEUUS312Pv+g2EUhwcHpBnAXdTSBQaZ8LPa41lMV+wSDOkvCKOkiqLKFznsijBC4QKeTiFyf/WnWz5+Pswae8AF8D/IoR4G3gX+O+A7ZeA11Ngu/r6GnDw0r8/rP7uKyCtEOKfA/8cYHd3m1J1ef9wytNZH9HqhlQ/LH454bUl3ajgO69dx1ztc7L/FJO7YD6sC6xzbO9usra+iZd6dShIUU3RpKjAjTCRn15ZfvLTdxmMTiCWISFQhgbRu/DBUh10q9ASQOuIVjPh62+9xn/+n/4Ruxtr2NwEmR+VfAABpeX89Ijz/cecHR6iUGipqdWC9DCptZjOCvafn3Lj5i7tdpso0mS55eDghCIP7CzrSm7fuckszZnPA8CapQv29yeAZGd7l2t7Ozx59gU6khjrOT07oshTiryk0+5Qz+rMZlMGgxHOe9bXekRaM74aUZYFDx/cQaqEX/zyffI0GPVTOFp1TZHlHO1nFHlGrVbj/PyUOK7RaXsuzgfsbG/SbNRZLALbWQJJHDNbLPj88y95/1cfcvv2XaaTKePJBGMNUmo211rcf3CXZqPG2loPa+HsfMDZxYDJdEy91eGVvV32NjbodXp8enTAyeSK0ppV0rtnWRwEzxUhwImC8+EBP/nphP+k/o/Y2b5FURToKEbqKKwnHzGZLBjNC6wOxVbYKZaiNY+yBV4mwRdJKHywa2FkBD99fI7SMd+8s41aeuQ4CEblEmcNxrog0UIF31IJkRDkRR7SeoVgPp8SjRvU2n20jtBV8VVajxBqxThbgg5SCaIoTPmUECRxjJLRCkxaHqJKSUpTBMN/HSQXSaSx9Sbj6YxGq0dalNTljO99c4/h6Iovj348d5kAACAASURBVKa4qIkXQZqLF2E6KDxIj4oEr9xu02k4Li4GHBxOGFwVeKnY3qlRryXESjAYpzz67JyLORgVE8WW+7fWubNVYzHL+PizL8jjDnmyTme9y8nTL3gyHbGzvccf/9YN6kWX0ek5t7uaThwOnn6/S1QFEvQ6LcppGVjBLqUu69h0xDxPyfOcdrOLUJpas4vzBnxJkc+xZYlQllotwcoIo2M+eHzO08ucSZpzfb3Ote4G62uK5+dnTAdHRMaSqC61Zp2GnNBKn7MuhqzpIXU9o6kdcTP4b84mc45Ozzk/e8p4NmNRHRIhsC6A30qH9RpFUZBHOV9NRTUlIU1SWAdpSqvdYjouw1RdaWIhSbMMX3la+apIE0ABXOJZLGZcZBmvd/rcrne4rhKaMqKcphTTGWWeo6REi1D8GRM84IxdTpgruZEI/BtkYLHJajibSsW5dxyYkistSGJVvUa1OypB1EgQWlGkOUUe5IpSSlCOZqNJo17n6upqVQQH+Q8v/MSkIOq00UmdtCi5Gs7QUqFVhA68ABIkLi1CIEMUpFs4hzOWONHU44gkitDOESsZppjLCbZ3lccg9DodvvNrv87P3v0FJxfnK2aRMWZlvbCcdJvS4hHYKgxwxYIAhHN06g3euPsASkE2usQ4TzGfkk9GzHLDYlaQzlO6rTpqNCfNY45O5pg8pSgcpvDYQhAIH0FKuGT8ehv2JgipzhbNXLbJ6tuUSZc8z1HeEmnN4GzAIjN88NGH3LlrMKng/GIfHStIL1CDT/naxm32Xn8Tj6RgRqdTY32tx8ePf86PPnyXRb6g0+/x/X/wh2xdv0vpWjx9/pi//LM/4+zgEd1Ok1g1+PzRJ6AyOp2IWsuytdfj5t1tFtkpg8EJ6+v3QkEmKwaMktjcVh7FKpBj/csGLrCkD6ykklXwWNUlVL9XndaS8YEnGBEqUDo0NoE8htZBIRBHEa9945v86t/9kOHBPo8/fJ8b91/ll+9/wMc/+wlueEYioLGzzbV7D7j72te58+prtHodFtMFl6MJB6cf0uo0iGPNvTe+FkIsnAcTrDusL/CuYGnEJoRDSk0Ux5Q2DMe8AINivbfJdL4gnY5YLFIWWcp8NiNLp3S7bUQSMzOGRrvNtRs3kSphnqbY3NDurtHurDOdz5jNZ1/Z++VLnzVYZrMpSmrW+tvVAC8MWMEgRCj400UaWHxUrJhqzS8TjEMhW9VhMnwv0Zqrx48Rp8d0EkHLaFy2IHJV0+It0jgaMniCmbgFsSOVklhqup0Wo9MzZlcjnDXELpxVdjzGzjO0V+ROkolA//AoSmnIpaFQFis8GoWVkjKOKLXCxhGyFhPXa7S6PaJmi6TRxEcRnWu3uPvGt9FxgyIPaIT1tmo4NVZGFELQW+vRTWooIdm8uYf3Eednl1xdDrhz5w5KRwwvB3z63k9QZYr2JcOLYxBQ4lnMFyBDboHzjoPnzzk6OmA+mVNkOZ9/+inX7tyj1e+zfW2XdJ4xHg2oJwm3b+zx0aPHPN4/ISsdDx+8inOWW7cfUOo29179JkI4Lg8f8/nnn9HZ2KaLZ3urz/68wOkuWXaGNynPvzihEUmcguHVJenpKel0gplNGB2ecXU6Imk2aXb7ZMYwyzLaeUm93ef0YsyjLw5Z77cRWnF8cUq92WA8yyis4PWvf4v06Qk/+vMf8OTLx9hWj2//zh9AVMOJGrVGH1NK5ouCe6+/wvr6NqeXI9769ne5PHzG6PKYxeySYn7F5OqI9z/+hMwY6nG0akyFDRxYJSXt9hpvffO7tDeu4yommfUerWMkhIBUyWrQOD4/Z3J8jF8b07/7AKFjhA/1g6sGnMYEf+d6UkdVYSvOe6i12Hr1aySdNiefvc/i4gRZsVxXgVsvATgrQq34CmwUvv4bAM9X5OWVhHcJdIWhHOAsLSG5u7bFetzk4uCUJ5fnnDvDVHkmJgVkCDSWlYwcj3CSRCe4WCGSALRAaN5DpRxsfCD4uLsKjH3hmykCECQAS/BnFIIEyXrUpScbNFCgQn5CEidEcUy90cA7T7ZIMWX4pUyBcpAoiXEFsszI8jEfP/2Y0+ySQkOjE1EXDdKLgqvJjM1Gwo5tUW82+WB8zITQs2kdUzqHywusTWnqJn/03T/im7feJMnDWR1JC0VaDf4CGHI5mPPn//Zdzo8NWzLB5jOEdixmA370i3/NKzt36SZdPvzp+/zGrdfo37mFOVMkTrMz9wx/+nNMt8/eH/0TFtu3iOM588ETFuM5169voWJJu1VnOknRUjCYjYml5Gc/+hHH+4c4YRFRUDQqCXOjuMrAqZhJkTJ4sk8U91nrNVmcTSpPfIHxnqwsUaUhiWIKE9igmxvrXA7GLApTgY3+pRrKVaBHZbtRrcslOLf8/t+2Fl8GIcVqHYc1U9rQN5QuhLSGnANJ6R3WerwiBOz4wFRbSqqVCoDiMrhLVsFXS1Bv5YWsFM6bFbkls466dzSjUDO4l4YaLz9efs8hfKuGVpJ6UgVXaY11nrwQ5EWJK8OacBXI5SuQ8MU9/NXhyd/1eBnINa6q16uAIKSiLEuWaqAlgUhqVYU5yxegnbNEcSDBBGamQmpVDYIEZVGEDBIZXterypaMALTmJvw8xhisMcRxjFYKranyHQJ7Mvik+r8B2DussQHArWwxoBqI+yU5KYB1QlT1v1j6GS9tIAkMWltZhElJtFSoaY3UGmMN1ruQixGeTgiSfWGrgQie89J7dBy9xFz11fMdSmh8GXItlFbEPq5qiwiErtaOxbiC0sbEXmFMiTElEoWXHiU8Hr3KclFaEUWaONZoKVAqXAdf2UNYa7DGB/Vd+DiwUUSc1MK1UkGd7Z3FS4kpc4L5d3ju0k/W2lCXWrsMCKvWD+4FAWt531TfCQOF6qmClbWErSwTrHUURVn1fhWxzBqEsyEsTKsw3LEOZz1Chp9JVCQaqh7IaYXzmoiE0qQU+BU5EW8RzhAJj1CSUklslBDFdSIjqCUCWoJuq0uiFdOrC3KnyHROvdak0WgEH2PhcaasshgUvfVd4noH4x1aCBIdh7mQK4lkxMwapkVGLjwKQSxDTR/2sNCbWuvIioK8zCkXc6azKYXJAUiSWgDphcb4jDgusXlOnqdMJlfESYNmo002H5MkCVI6vDOhf2u1iKMIohAE3+5skJcCY8IeNpteob1AeoUi9M1SSYzzlY1e+mKQUQ1Pqg1l5fEclM9fZaa//Pj7gLQa+Cbw33rvfyqE+J8J1garh/feiyVP/D/w4b3/F8C/AHjtjdf9o6OMD58toLaHUHGY+HpHUYWsJGbE/S3BtXbB848/Ii1SCmOoKYV1AiFidvZuEsU1SvvCvB8sQoJ0oXHQUYwXEWdn53z00ScYwoLwWiB9YH4Y63HCrfzuEOACbkVSV7zzra/zR7//B3TqDRazBVppsB6/ZDR6wXQ04PzwKTad411Jt9ekUatxfHJKs9mg3+/SaoYAs8vLS+JaRJIk3Lx2jUatydHpGcfn5zQ6DYrZnG6vg3WOWi2mv9ZlOpnz5ZdPeL6/z/2732V9Y4sf/eQXKF2j3ohQIkw+s7xgOLkiy4MsptWsYx1cXA5wzrC+3kNryeZ6h2t7WxjrmGY5WRkCtKLIooTm2rVb9LtNimzG+cVl2JijhMvhEBVtEtcT2rIX5AhFQRIl7Gxfoywsg8sRi2xGLU6wpaXRrFGrR2gN7U4DR7BkiJMder0Ww+GYp88Dy2zv1l3efvCAazu7HI2H/OyDDxmlC3Ssq4m5WDEDALz05Cbl8HzKj3/213zvN2us9bbxJkwviZrgNcNpxqK0uMi/mO6JAMYbSyhUdZg/Ke/xrsSjkEqQFZJ3vzyiEce8eqOPdAXe28ozV1TAnMU5g0Xi0RhniTUhVM57yiIYkdvKyF4RpGqmNMBStiK/yrYQwY/Je4eQanWYhCeETVgiYSkbRhApjZBgvSdO6iRl8AWMogiTpTQait/+1l3y7AueX8wgCfYA8NKh48GUhuf7QyLpOD+7JDcaESesd2u8shvRaCT86osLHj8bk85zRFJnrRPhzZwYx2CU8t7zA872zxAdi2or1usR6/0+7WbMvb0e//g3aqzV1vjlz2uU1tFuNpjMUqbjK3qddSIV4TwknTUm1mHyBdlVzsnhPnGi6fTWGB4coKKIzev30UmbxWLB9OqCdqPB4mrCMM04mgi+nNZ5NNaIzibdbo18fs7nH/yYvJC4OGbdXtEWFmnOqKcliRigFgc0RcbWVptWs05RlJxfnHB6dsLp+TF5vsD5PMhwhWDpycmqCAzFmqoYBeBxZWB+LMPaVMUOrClFv95kMJvi8QH4nwZ5PRUI5b0Psp/KKiPFc4hnOhlyMJvyhrdclx36OIQL/09pHLFQGGMojMH5aspOwB1z78irlsH7pQe3wyiYCs+5Nwy9R2i9kpQLWeWiSo/QgkgIbOFwRQDZHBBVfHNbFZaqSnr1/kUYkaxpdLtOZ6ODjR1WeJSIVp9fOc0wi5S8LCvv6NCsWmOwpafd7vDqq29yfnrI0eEB1ns2d7YZjIbVNr5kEUisM6RZzocff8xwdLUKgIh1KBaNMwgEWspQZFWsPFUBcyuPLxzGwtnZKThDq94jlp7FfEocK7rdTpCYmzkHzz/lWCm6skSJJtNRTFSk4TUrb9uVvPwltgQyNE66sjnJjWYW95g1NsmcZzK/pNvV9Bs1ai0wJmc8veD9D6eMBzMiHwZCHeG5sXaNW+tbpHXJz37yKYWfs/3qbSKlaNcTfFnSbUSMLg7467/8c27tfYMkSdh/+pRPf/ETOixweYdBYZhfndLuadqtmEavxvW7u9TX63TiHiJaNowVQSekNBFHSdhTKmA11I0vPOIqIk/FyFnisQKEWwUkVvUrS3dbQSjgRTXBRlSBCUJhhUC60FRt7N3m9sO3GB4fcbb/lOPnX1KPBTry3P7G2zx45XVuv/YmW7fvIKzk5PiETx99yWw+pV5v0e/3KJ2hdI6yLEBUYY7e4op5GLrgA/M57L5VHWLxlGEAhiDNCtK0pNXsMRuPGQxGFFmKsw4tY6aTObVGg6jRwIng6yWIQDp0UsOKKEiprKskdy9Yeta5yiJCEKmYTMxZLIZI4Wm1uug4weQhXNJXwFStXqPf71R7lFo1aEt5GIRhnRAC5RVOgJIlbjqiaUuaZUQyW1CaAHq6oqT0FuklC+mwznDtjdfp1+tc2ZJmr8U8W+CEIk4adGLJsw/fQ3nB7d4WpViQjsf0Wh0iK0mnC7SAhfToXpurxQRXlnhfYkpDKRQpnlKWWGEp8AwQIZ03ihgvFrCxS/zPYm5987cwIrBuAjM9yCq1VBTGU2YFuSkQaUq/NNRqDebzlLe/9jY3rm0zuBwwOj7k6nzEbHhKlMRMZ1N0ElFrNFbNk/ElV1czOq0mHouoprzDyyHj+ZTrt26yubVF0mmSSMFwcEkcK3qtBudXU07OL/nhD/4d/IPfor++hikcP/7BD7h19watZkQcN5mMLknOzjmq9xAWmu0ucUNwdnzC2fE+12/d5vZrbyDiGsf7z7GjAc8Pjmh1OiEMKlZ47UjiGrYoK0lw8Mh3UpPmJUkUBc+4JCFOIvJZyscfvM/wcsLF5QnX3nyLma+zc+se00nK5k6fxDt++eNfYLOMbDxlQkKrWWMyu2Jza43zg8f8mz/5Vxw9f8JkckVe+ZWnJljYKB88iZ3zFMIxzxc8efwp5vETrAmsI+dC2E2WpoFJ6j3WWbwzmDzDCsnWG2+HcOBqsBlHEaIZZLOLeUYcV019mYfGVAU6k05q9G7cRUjB8UeQXV0gq6AT78M5IZfAZwU6VeLUwJwR1UZFGNp7QhiMX0quRUjlDkBUaOClCNLPBM/DnT3u9TYYnA84GlxxYQvGvqRwgWQlCPZEXoCkCvXRCmKFiENYzyp9ndDoe3wYiEkRAnsqUFboAHQsyZBa6qBGFw5hYKe9y1v332Zn6wZR1MDrGjLSRElCo9ki0lEVRJpTLGaU8zFahvAuZOiLrDE8H+7z+OoAkyhECaU3yI5AopiNPYPJlLVBi9txn4nt8sQNmSYlzgaJtgUiG/Nr99/knftvouY5OVdBwegy6krj8xxnQeqYX/zqEZ9+csiWV+x5x6RYEG126W9uUm+0EbWY3Xtv4RuOoydf8PA3vsPZo0949H/9n8hpThRr1h6+Tnn9Nj/78oj65h6bO9c5evaEIi9Z20pw1rG9scZoeEEtETx//BEf/updxrMF9XYNHSmkKYOnv5cUNuZ8HjO48FyMcuJWik6olI9hOGuNp7RQWkNpcqQTSGXROiJOguIOXmbEhiXlqmBTKdVLPYRbMRarnvsrYO3LYKeq0uMDkCAQ3lMTkmv9LvXFFbEK++nChuHGkskt8RghV+CnEAIlwFfSaSErU2RXndcVICV8qBfRIYg2wAceJw1xPSEam1X9KUQIq5IVicZV7zfSgmaiaTeTMPxcpk76YDjnfZAnCwS2sgx7AbR+FY9Y+rO+8Pj96ufzNz8zgcQYSxIrlAjdklsSKKAKkwrWQEs1B6sztQI4VeVn7V8wJZfDp2XfgHPBE1SH1xGVSlc4T6RUCO9UIbxTEhjMotobINTIrqrBFQJTEYiWg24PK1ZmyG9xq+sIIYS0FicvbNB88Kdf9iFShHPNV360KjSbwVNevvDhtr6yOrM+UKZFsLJayvWjCjtZ9h1L2zNb5cnYpZIKTxRFlXVCqMWNCy9rigITa0pnw3/jbSByoCrGc+jJIi2JVFBHyGpIJhzBG7kqWJchVEuGsbMOUxoMBqU9cbwklgR7EL/06oWqXpMY63C+CGRl70N/FFZm8GxFBLAQWbFsv7LSqsB6GcLRRBgqexMCFYN9kwr9kwzD6qA0DmtDyYqJ60JQphTBk18RBoRGgpSeehyTWIcS4XwS4VBBOId0oR5QkYY4wmmFFhFNranVk5DnEIE1Kc4pvPPkwmFMRhxHCOHJ8gV4gY5rxI0azpVVkG5MrZZQWoNWgjiJmM5dRQjQ1OKYSMcYJNoH/2NR3VzLwYO1GdliSJFPKMsFDkPuHE6EPsPFJpyNtqTMMqZXQ2pRQtxqE0mDLEJ+wCRLMcWCbreLjmJ0FNFotlhjSVwySC+wRYG3ttofQy9vjaEWhfAza23F6g5YjJbBfzrN0+DjLauBzt/x+PuAtIfAoff+p9Wf/w8CSHu2tDEQQuwC59X3j4AbL/3769Xf/Z0P5xU//vicEVtQayGFRaNwSFJTYNKMXZXz9VubXB5+wvjqktIE+ZJxDiljNrev0evvUhoIk+VqYrf07TRLb5gYh+bps+ecnp9VpRbh8PBhyiG1pLS28ixbymAVUaL5B7/16/xnf/D79Bud0DxECtAvhY1Bvpjx6KMPMIsxO2s9BkJQj0MKnLWG09MzBqMhWZYjZEyjHrPICtqNJtmi4PDwmKTZoCwdi0XJ7u4O8vKCw+cH1JM11vprRFGTzemCTx59yWKRc+/eHbKF4+TiECc8ezvrtBtNlLREsUFLxdbeLloJsixjMhmTJDG1pM5wMORg/5i1/hrz6QxfGhZ5ShIr2u0Gm1vbXL9xm6vhgK9//W2ePT/g5HRAt9+j19+k2+2FQCTraDYatFstFvMFT54ccnU1I8syklrMxkaHV1+9z/pGl1o9ot/vEyUxhQlS9ChWKO1YW2swn3X57MkRVxdNWp02LQyv7e6wtbbBp88O+HL/KaPpGBnrYEQvQtCR8xWbSMOXz75AEfH93/pdup11rM2IdB2HZzybUToDoiDYmWvAVpOtULg6DzgTilulEOiwpmqScZ7x48+eg/Q8vL6OEgXYErxdNbaukh/ZSgKro6iiw2ucX9Dp1YmSBqxka+F+UFJSFmF6HemoMlYPh4HWYSJorKlM4MFaQ5rOSZKEWq2GRCGFCu+5ApmWaGuj2WCeZSgJHoUvSm6stfjD77/Ov/6rz3h+kWJpIJWv0mWjyrzbcno5q4zyG0jpuHu7z93rbeYXA04mM64mKYXRJLUmN280ePV+l8GgxaMnAzKbk6UK39nDqxhKx9hn1OuOa9tN7mxHNLUikZaH9zawQvPsYExZlGxsboKHcppji5SoFqGF5eriiGZNUY4PUVoyHJ+g4hrPTs44Ojnjla99m067zcJbpqML0sWCZ/tHPL10lBtvsHfrdWwiWZyfMj14Fzf4kk6zx1qU0HbHFMOnzKZDrC658eA6/ZtrHD0/4/mTQ5RSHB6fcDUdBjaLDMMcr6LKTkAiZDVRW4K01q2YBiqOKx+eEu8cjUYrvIYKIQd5ltKII+ZRzKIsmIwm2KxYUnRebJ7V9Ht5vufOcaFggWE6OmdtfMH9VoftJKauJc0yFBypM2HK7EJB5q0NPtxu6U0XdjOHp5CeCYazMmdYGjIh6CRJSJQPI/bwfKVQ9YRpnpLmBd4urToccb1Ord1gPJ1AXVcAkwqhCSb4jia1mEa/g6xpChWM56ULe7PSGpPlSCGZzReBCVUBq4EhFQIiLk7PGA6H6DiAJlkeJG9VaYskgKtahCCx50eHYdOWAfg21qKqeaNWiihOmGcpxgabBVcN7gIRukqglYLjwQnPDj/nrbtv4e3SE1ghZRzCxIxBS8hNyVx4Ov2buI3XGT77gK6YE/vAuhZUjIaqUF4C4MthlBWeuaqRtdYo6g3GF6ccHz7DmBYPt4Nn4CKdktQFKnK025bB+Zjh6Yh+XCMzlvlixniU8+qrD+hs9Wjf7GPKnN2NPa6tvcbjp5+yu/uA3a07nJ4c0Os7rm91uXPjOtnlGZKIbDGm362zd2ubG7e36Wy2qfc7LIqcTrdNv7dehRiEoncp/4qiaMUokUpU4RayAjfd6l4JP7+s5JvgrXvht0VQNYgqEEFKFeyewo4GZUGezRBxQtToAoH9E7fb3P+1b/HxJ+/T6rRxTvPr3/4u33nnO/TW1+hv7/D04BivNB9++CEnh0dsbG3yrd/8Lbr9Ptbb4CWuNcZ4jA3BDVqr0AR6gVIarUVgp/sgNSuyBStvPsDZkvHVkN29HQaXp8GbOlYoFVEUOYt0ga43uHPnHkqFMFSLpilj4loTKTXD4QhTZlVwWJDmha8NpSnwBAY+eNJ8Bt6RFXNqjRbeO7JyjgiaSxqNNvVGE6kjpIpC6ALB/27JrJICnJAIr8K9M1twdXRIUpR4ExgTSkUIISlMgfUWqTWlFLR3NmnfvYFUMdZZsmxBXhpuvPE1Oq0uxcUpJ/oT6ijuvP4mw+mMOIqQXhLljsHT52SjS+68+QaN6zv84r1fkhjL9b1d5vMUISJGVwOO9x8RV/d2UNpakNAsHWeHp5y8/yH33nonwGmiSrSvWFACweH+AdlVDREpynbBl+MpWzvX2NvdotNqMB6ccXZwQDFPqdfqnGc50jpEVGM8nWFsaGpVHIMXNJuee/duo6Tj8OCEdDanliRkec7w7JxOo8buzi6+yNjd3sEWhvFowXA6x1jLJ4++4OT0lFdeecD9+/fo9FvEynN0tM+rDx+QzQ3v/fSv+PzRZ7z51td57dXXsHmbyeLH7N5cI64r9q7dodHf4ubN1/jB//0vuZoYWv11cmuJBhkbG1tsbOzy9PEzBJ52o85kNAIcpS1o1GP6a5vcvn2D06MTxlcjZvOUIitotRXv/PY7PPp8wOnTQ5zWvPvjY2JTcDW4ZD4ZcXrwiHw+YvfaDUpX8PMfvctf/NmfMhpdhGGyFCt2qncugAqVgsdZh3OC0ggWp5eg4mpt+qBGUgpZU8S6RqtWJ4o0XkpkHLG+e42ot0kmg7dpFEVEWhPriERHWGMq2bEjjhN0HKGrwaMxFl9rsvdqh/7mDgeffsDl0y+QRVYRNxxBdcULf8vlefyCFFUBNhVrqpLtSxE8+8RyaOjDEizKkkgK3rx1j7du3mVydMbR+QVnRcZcOkrvVzJVbyq2nqSSqArQCuNtxT5TKz/fMPSq3p/wVV1rAqirwGu/POxXg33hPHWv2O5t8ptvf5d7Ow+oNzoIFaN0DRU1SBpdknoTYyymLHAmZzYZ4tIRrX5rSbfDlAUXV5d8cfacrCFpdjYoFwUuTSmKjLgrcFIyGaUMTi/YtnArgSstmWNC2KHTCK95+5Vf4/d+/R8zP79C6Ixuu4t1luOjQ3q9NbSSeFNysH/FD//iV+QLy27d80pLcKoEd773NmUUg4y4vvE206LB/Tfu8vi9/4fbO5sMjvYZfP4Ja64g63R55Z3vcqHrpKVkcHZBu9Wm1WkiY8UiS5lezVjvecbDE+bD5/zlD/+Uk5MjhNI0mi1K4fG6Rm4hjjco2eGTp5ekWYOcBn7suLiarvqFACY6JtM5UkEswUmBweB8gbHLZPgl8PqytHoJHi5tal4Aikug1tqVmfvfyhgN7L4XYJaxjtQYnIXUBtsFKgKHEKAFxDIoT92q95IgXHUbhLBM7xyJjhA+WHt5ISgruFUqsNZXYJoEy8p/NSB4BGWrECgJtVpClNRoNGskcYRyBdgC44IlgLHhfReFDWzfyocdXgqmXd6iq1ojfE4vf+8/5LFky8nKHmwZaBnk+i8k75IX99cyUM0tE+2r62WtRejKh98bnKCyNwiMPSFDPSlkAEaFJ6hlPNWw1WKMRytP4VwlxzYoITB+yaZ8AXLHy6AwEYYEARkNUv+ldcYy9lXI4N2qhAghXHFEvd5C6xgInp3GlOChyHNKE4BJi6DwRbVfy8qTtcp6cEtlWzXYXWVFhMHxUlnnbPj5nZc4W6wG+aU1mNITJzWsdaRZST2KKlB3qRMIwL/1Hm9MCFCOgmJV6witE3QUV9cr2L445yjyFC1f+AuHQD5ZKZHCtbc29D7KebSu1lFlcVVREHDeVuxPwFmkdJgyXKvl9Q+hWZp6vUaSLDN0Qu1FBelWE45q8FAp00RFjqmGc8iQOxAUZOF6Lv1+V+z6cCShbKv0rgAAIABJREFUCOpPrTTe2BDy6iVRGWpWJx06ThA6nLehHQokN6010lasW+cwWUGeXVE4UCohrtWROqJQCusM0/EQ8DSaTay1nJ2fkMR1Gs1OIO/EmqQWE8dhqhhHEUkU02o2kVrhtQLjsHmJy/NKsR5ITmUV3qW0wqOZLVLyItTkRVGEYShBnSCF4Go8DPeMs+DqwUZQQ2E96WJKOp/SaHWIaw2SekK31SISoQdNopg8W1Qe2IaizMmLnKIsQh9vTLAdrTkKZzHGooSiKEukCtdcKf0Sa/rff/xHg7Te+1MhxIEQ4qH3/hHwO8An1a//Gvgfq9//ZfVP/gT4b4QQ/zshMGz8/+dHO889R4smvtkL0wBjiKXEeIc3BlPk3L/dp2lH/OqDn9FIwuZnyxKnFL3NHe7cfw2vahhTEiuqADBVeXvYAJjYYIZelJ7jkxNKU642SryvPGTCFHhZVIFDSU+zGfHw1Yf87vd/h16zj8kLkqS2MmVfTtRNnjG9uqSuBM31NXrdDpubc7bX1rg4P2Fne41efwOH5/HT53z+6ZcUWcad+3epx22iqI6QUZDxRDGfffqY4eWIWl1z7/ZNnHNcnp9zcjYCoanVO3z2xXPKwpIkNZJak+F0zmC4oNPsU6vV2FzfIElipICyLIjjmJs3bnJxecn+wTGDy0tmkzk7ez3GkxlaSlrNBjdu7rC7s0Wv36dWqzh1TnPn7l1q9Q5lUTC5mnJjd5ek0+P4+JjBxSXOORqNJts7m4zHU0pTsN5aY2d3k43NNVqtBjpStFotpFJY58mKEklJFGnyLKNWr9HtdCizBaejAVfTKc1uh05vk28/eMhGu8P7X3zG8eACpzwqilZTTFsV0SjH04PHdH7Z4Tff+R5RUsObAiuK4A/iS7AZihCwsPSZ8dVGKawhEtWUzieEnHtCQEMUM8xTfvroOSrS3NloI12OqxJpWW7wIjBxQ5JkCI0LcvxlUvnqTsMDuppAFzYEnKCCXcGStVHY4JsiBJVPF+hYU6eOXoW9yCoBU0IVA+VWzYUg1sFgW4gAMGBSttsRv/fdV/irXx3z6OmAkhh0gmdpdh1ezxOKe0HBWqdBBDzdP+V8LHDxGu12k1vX67xyo45NLYPzCVeLHBMloAyiBOkEEZatXsKtzRZ3dhpsdyXD85JUG3Z2Ej57dMrwckpvY4ckqTMeDyizFG8yxumYLJ3iXElhClRkmU/OqTf73Hr4Bnu3HjCdp9jZkLPhJZ893me4KDgZTknihM0bD0ijFoOLQ0aDEWrynA13TK3fR4gFG5yykVwx4JTrN9dotvqs9drM0wnTqwvOzw/J8pTcmtDgV6xQUU1DpRKVj90LaaQ1BktguJlVwyap1ZNgOWCKMLGsChRTGvK8CM1oKfCFWU15w2rhKwUmL30tUXidMNSSK2c4mw3Zsw22hWZPxPS1RDgPzlKKAKJaEaRJ1gdQEO8xBK/cqYBL7zk1ljlhTeo4xtsSKUDrMK2P+3XW7uxwMR7hJylxFGF8SdSI2bt/k/WddR7v7wcgunSYoqAwZeWzbHGJxmkdCjYVCt8yD0VevVGjSHM6rVYAP5UmisGJIEV1hSPNc+bTKTqSaB32kYBre5QMjEPrQtMQDvbgVRgOT0mW51gcutpH4ljSbreZZQvKKvAqSPVC8Wqrot5JGM5n/OL9X3Ktu0lNN1fsJaokUqoCta5jEBIXb9F+5TeYLTJGB++xpkOttWRI28pvOnzckmCj4jE+IquvYbrbOFUjHc9IB3NmKmJyUfJs/5D9/X0aDUGvJ9nc6lGXikRpnIXpLKN5vU4kujx7POTkizO+tv0NyvkY1Wlz78ZdbOF45bXXuf/qG8xyw9nFCY1azH/5T/4p08GYo8Pn/PQnP6CXOK7fvMXenT0KDLVaDwG06pt4r16SrvnV19YuB2FhqKmk/uoaprKt8RWAFjx/YNnqVN7worJlUSIwjIssI13MWMzmRM5SljO62zskjRbWC5STWCXZffiQ3/+v/in3bt6ivr7F1XTGbDLms5+9x7W9azx+/pzf/P5v88rrr7Gxs8v23h6tbo95tiAvijAYI0zTfXWNvQ/XKczRQjCmrCRvZZGSLiZVyMayTnCU5Zwo0tQadXQcEemIWhJRmDrru7s0u33avQ2EiKjXm6TGoVSdKK4xn03wvkTi8CYEYigp8LbE2TIErAlLXiyYTq+Ik4jSLiiylOliFBKohSRSCeDp9XooFWGcJFEaKdUqYXgpz7JLxogIDIL5aEJ2OaLtLAq1OktM5aWmRGD4Se8ps5Tj519wNssQjTqtdhtlHXk64Xw2pjg5pkzntFot4oYmEU0a7TVazQ7p5ZBoNMKUKe29a6TNOv8vdW/WI2mW5nn9zvJutrq7+RYeHmtGRu6VVVnV1TVd3VU1QzcgQEKIoe+4QFwiPgo33PEBkBASAgEaoRHQTXXta1blnhkZGZt7+Grmbtu7nYWLc8wjqroYCY1GApMyMzLT3M3e7Zzn+T//5ca771KdTxjc2EfVLYtFQ5HnNA8/RnlDkuirZlh4Qeodqixpzk9RJjCgg1WShBgiErzUBNV8QZYnLNuGw4NDTncO2b/9CpeTUx4+/orN7W28zDl8+oxFK2irkiRLkVJw7doOp6dnPPjqK4pOHy0Um8MOaZby1YNHmNaidEKe9SjnNRenE+7eukvdbTGtYDgcMRrNefL8KAZPCE4vp1y+/zsePnnMm2+8xvp6n6dPHnNj/zqDXo+1ziUX40d8/LsFJ4fPuH37Lteu7yFdDk7ywa9/Tnd0jXe+8R3uv/MdHj14n6OzCU3bMBj0OD5Z0jYOnRds7mxz6+YNxufn9Id9sgQ2N4dsj7q0TQUIet0OGxtdZrNLOr11Th4+5OTLMY1V3HzjbeaXUz7/9HekMjB0J+dnVPML6tmYqrX84mc/YnxxjhdulVUV+CqRaaW8oBGBAeW8ZLi3z61vfQdR9CNIqMOA2dvo9ecospxUaax1OAlCJ+isoLEeb220lwrrqpSSNElopUZIRSpBJSkqSdFKonwIZ7QE37neYER3fYsnvTWOP/mA5vIcpVc+r+KKkide+nvcnGNT7SPDf/XfuQJlwvtXcmsYDYa8srGDnzccH59xYWqmqaB00AZqWPT7DLVDkLIE5YVbCZ9EzCRwK4bvy8y++L2lD0CaEAgRamXhBVomCCfIHex0B7yxf4+99R3ypBPYct6hdUKW90iyHnVrQzhxU+Lakl6RotJBuLbeY9qWxXLGw+MnHJYTqo6iFQKZFOhOgm8z2rpmLlpUA0/mC9wZbI4GbArJuUsosxZvYdhd4z/867/lO/e+zae/+iUn80PyeF2zBPr9DlIpxqcVP/vFpzw/NayplKE/ZY2SbLvP4VefcmoN01nNK3ua63f+gsvTJecPHvPh7JKDn/+QjTYENQ7ffINy4xoL1WFjtENzfslsPsXh6Pd7NKal6HY4OX6K8jM+/uCnfPnoUypn2Nwa0ekkTMsamfaRao907R6XYoj3p3j1DMOC+fyExsRrFG8lbx1V2VAXCSbPEAJMY2haS2MCiBK82OOTE/fWVdipj/YXL4djuatQrxcM0ZUs/0U2wKqwjOFBCJZNy1fHZ/QEDNOCgZShP4n1q1KBTZsIiZUhH0EQWy+pIkga5dWmRSPwUSbsI2VSxL7COv8CzFSCNJFggpzce09RJGxu9Ol3coQKykR83P9s6N2C3aCgbT113dI2kaAViQ0raf8f2I6snt8/Aq3/FIv2xWvFOA2qlTaer+DuIGMdA20T/K+FVlefobQKNVD8PStp/6qWXz2vK1COFWjrFFYE5rzzFilVCJmOGSQ+9nfGmLB2GU/bmBiQHK6Xjp79Sqsrhitw5bkt8VfBojhIZMj66PQ6dLOMYbdLNy8oipy82yXRGVoHVqv30DSGul5i2pplVXM2nrJoK2bTCeVyjmnr0O/bCLzjg00ZjqptruZbwdpAY5wJbFprA8D8kuLq6vx7Q2NAW03rffjLWIx1iEyFWkYrVJKGQV2i0Ym+soXQSUKW5GidsMofsqbHysfYmTbYoBFZyKtnkPCseprAuhVEAD0okYL5bQzWE0G9AC7uCxKlXthHrML6jDEIIWPtFcPEpAzDdBfyYawnklokVspgyyll8NAneFQHMlAYrCdRtUEMuQr+vx5viWC3C2pfHwcI8fd6rYN1hYzgvDV4YWmFRwPOhHA7gHq5YLYsEVKRFR1kkobn3hrmyznOGpIsJc8LvIPFcklrPMuqIs0Set2CLEuZzxdY58nSFJ2m5HmOynOwjnJRIXSKbBqMN2FdwCO0JMkysjzY+Si9ZFlVuETjlWK+XGCcR0TAfFnO6fX6GJcE8qWEVCV4C1W5oK4b8qJLt98NeJrWbK6v413L5VxibIsQKdpm6LZGloHAk1hwcXja0zpYuzgo65qqrmibQKR4MSj7x69/HSYtwH8J/LdCiBR4CPxnBPTnvxdC/OfAY+Bv43v/BfDvAQ+AZXzvv/I1qxxVNkIJUN4ghUZ7wLckbsGo73njRp/5kw/IZfCqMDh6vQKJ5NqNu/SHI1ovSLMU5d1VeWJci3eWuq7AGPI8p24ch0fHodkjTrV8AFUEQVqc6OD/5z0MBl12r23xNz/4Pq/dfhXfOkqzuPJT9M4G+Wy5xLULjp88pFnO2N/cD1Nma8nylL3r22xsjuj3h3S7Xd5583U+vvOAH/3oJzx+/JSj52cUaQe0Iksz8iwnUWHqf313P1xkY1lb36CqPQfPT9jZ3aauA4jQH/Z5fj5mOOyzvTFiWS7pFsF/dXsnp22bsHm1gfXivGJyOWW+MAwGG8G7VUs21tZpbcXe7jYbGwMGa32q1iIThU5SkiRjuNZlNp0xn8/4u7/7ITdu7DMYDFgslzx5/Jj19RHLqkJpx/37txltjej3ewGo6GRkecHR8Ul4ELKcwNUEbz2d7oCygm6/Yno5oyhSdnfvorXAioRpteD+7oi97b/kZx9+yIMnX1JVNVLruEmCkwE4qm3JR19+gNaab3/7u7h6iRcpdV2RKo8ngMPhXgg+LVIJcJY15fjee2/wyedf8OXJGSLJaVHRrN1hsZyVgl98+gx7b5+boxx8i/SWNEvxradparxrydYGUb3yAmRYSaZfYBTBdzb4z1jG5xP6wzV6gwH+pQ0diKy+IJ+TUpJ3OnHCKgO4I17IdoIfEoDDW0+qE1KdsChLWixZUuCalhvrOf/03W262vLRYc2ibvEEz1ThZQCelAEZvDM//OSQRLfMzuZ41Uen8Nqra9xYV7jK8uCrCx48PcekPYRJg3m7VkjfsL/R5S/evMbuUJIbSyJSjDWclx4kLJcWvCJLNN4Y2rqlvzZE+C5luaDb75OKTS7OHjG3NYKGyfg5J+fn7N5+m2QgOTo+5afv/54vT2uGN15j9NYWeZpxOZ5z9PycxjV0mzMG9jE3uxPK2rCYn5AOE5Is5ZvffI+t/X2eHh7w0Qfvc/DsKWU5x/gAzq6kW8gVH/+KuoKNDAQpxRWLR0sVbC6ECAyDSJ9WUgYmvg+DJGMtWoTJv7EttmnDxvtS3bgK9Vkt+iuZtxACFFjtqcMcAOclXyyWPPCwJuC1Tp89B7n3ON+SRFmV8R4TJ+5SQolhLuDEOw5My1gKGh+CiWIViQayPEN0M/LrA3p3N5k9saQHl1S+QvdSuptrzKmZnR3RpmEzTTKNtsETykd2iANEGkL8NBpTt7SL4PWjO2tgPYnUTC8uWS4WqCQNcjEX2MHOW1COVOYURQEisFCEiJ+ZpDgb/MCauGmCj3KxaBOyMl/wnrIsqcuKxkQfbB+SsT0+pucGZpSSOjwPnz/hrZsHvHrzZgCtksi8tZ6awMxPBEEG5ATF+h7b736Xp7NjprNDht6RSH8VIHV1XQnFOSrF0qMZ3KDtbnJ2NObo4BTVKpbnLZ/+9iFnp6cMOn3euPkWZ6eH9O0Gz09OkJcJWuWcnM74qv+QYX6X9evXWFeOaTkjyZbI1vLFZ+/zwUdfIWTCtf1X2dy7RW/d49qaQmVsXr/Pzitv4POcw2cfkPULZFqQqZR+d5eNYZ+it4mzOkggX7QdwD9uivzLxxgLr1DcvgBBhVZIr5De4a0J0izhcU3NolyymM3AOzp5zubagDxJGJ87ukUXvMc6jyLIEUc7uzRlxZdfPsI8fEZjDcO1Adv7+7g04ford8k6PYqiS2+0jReCaVXTtmGvNzaED6VpRkR+4n30wkdXSkmWFTjvmY7PsGaJEg6lU4yJjR2eg4PHSOFD2B4O5wX9wTprWzt4wjC5rhZMJgtkkpAXFrGssKYOcjYlaBuDMXUcAurYhwf57LKcgbCkaQePoWoqTBtkpDhPnvfp5T2KLENJHVmKsblYNf0EwMrFpc7hUd5xeXaKnc3IhAzf1Ti8CMnMSqehgW6DGqQ5O+Xg4AkXTYuLTZJxQfkCnoFUZKbF2YpPfvpDlo1nuL5N1u2jLEzPT2kWcw4ePURtDVk2Jb1EMx2foHsDlu0CKy3Gtjhh8V6Dd2gRpLbehYTmZjHHmRqRBndrRHTrFBKdJPR7PSZPvmDQz+l0MgrpWF6cUV6uc3hxwVLA2Fr+4bfv0yuGyOEO46Nn7Gz02droMthcZzAccn1/n/HZmNn4AtlaZvMJ1bIMTFEp2FhfI89SZheXnJ5O2NzdZTqfs7E7YlEv2D7a5ODohNqFoXDdthyfnDFaX+P4+REX40uqskIUjixT3Bzs4IXn8vxzHtsJr92/y+v3v8EXn37M4ePnLM5bJuMb7N+/wxePPuLo6JzNjR6dYcp4fMK0XLB16zavf+PbWFKMl2RFl92dDbSwVLXni4fPwCvapmKvv8Ff/eAd+v2C6VmDbhrWbrzC+aXn5PSM1LbMp+dkvYJCZ9jlgsdffs7vP/yI4/NThIzKILFaC+TV3mV9YNMKJD7NKHb26e3uUxmB0gVCJQjv0QpyESXdEXBXQoAIUtc6GvUkUiLSGIAnZfQJBHQYfvh6gUCgVUKeqKCmcA7RGmxtcWlCtrbLvW98l04+4PNf/4RycUYiLN6JyJiL69gKWHmJVnsV9ijCf1+x6wIIYa/YvMp61lD4yYxjM+WkWjKVsCD4L5sop/We6Ecrg0VSHLJ6RCCk2MB8C8BfOFZLeN6VEGGftS5IaQlfWkmBFgmiBlm23Nndp2eB8xniekW2HmTBSaLJs5y820FKSVkusNUcW8/B1qRKgldR+mmoTc2zyXO+GD/hUgcpsnUmgHdJghQZzhhc11J1DSfHJe5kzk67xuvZiLa85Eszx6iMv/rWX/P1179L4ju8843vcHr4kMMnj9ncGDLc2CAruuiiw6OPD/jlp6cYNSS3YzbFklw6Nneu8eDxA07qOY1RnMoT7uw2nHz6kDf3b/HV//4/szE9Qeuc2XDAxtt/xoOzinl5jlga8qLPfDGjU+TY1iKkYGd7A1ee8NWjT/jNL3/MIoIDTsF8ucDJAaQ3KJI/Y8YWszIl9yN6QqDVIUpdRN/LUP8EW4wwVG5qQ2Msxr0gSCBVWGNXPFX5EoNWiD/4dx8ZliIyBIUI4CfeB4/YCPivhgRX92usI1cSdWthKSWtSkhTgatLiOw0gURGtYiHq9Ai6cG1YU+M84AQpBlZ8zb+bKoUWoT6yAuBwWG8IZGKzX7GZQu6k1N0UrrdLp1E4K3BtOHcOOfJRLQMiCxkLwTLZUlZNhB4u1eM2ZdrkJcDw/6A7BDP5R9bHrxct6xAXx/rGuttIAHIoMJc2SZ4CVLLK/LGP6rpIjgKMadCBKamFCGgczUk1UohogWFWDGpfbB7EXH9ETJaNMZORCpB1klRPlqriWD75EUI99KrkDMZ1k5rDSuvYH91vP5qoKSUIs1zsiInK1LyjqJT9EiTDnnWCQxKGeoYSfic2XzJsmlp6pKL8RmnpydMF0vmiyVNtQyWRc5ivKVq60AMCVLoYKcok6BCEyv7hnBjSx8A5NY1NLXD2pQkTVk2NVKCsorFYkknz4JqUQh0klAUBXmek+dZrHGCRYgQwetX6ZDv4pMVQS9UPDagyjhrqZsaY8wL9nVraW1N07asguaD+ilgEVpHBW6sdRKdRF9/QdEpSJM0PnORREUkFYpo4uiDpF7E7xEUy8EWxdowyIxmdUFJ4qOnuw9rhiZkC4T2PwwzAnUrDP2MgDaqKbWQWEAmCVInYb0hDNqVaWl9YOA21mDblkRpjLWUywrT1KR5hhAprbG0jaGqSmxdYq0h6QYcQ+oEvEKnGY4QfDtzlvlMMJvOrgabxgTv7VxIamfCDqc0SkOn00XKhvpSYUyNlOE+HQyH9PsDprNLJhcXLKsSnWrqeb26eaiqKuB0vYJur0vRGaCTHHwI0a1qQ1O3XE4mMSRXhABOZUFa2qa+UjwHolCKcoH0FkhZEq8EaQzc1nmKWiqqMuQ+rO7vP/X61wJpvffvA9/6E//r3/oT7/XAf/H/6vcjkCqNN09g0BgEjXFoO+etvZx08YSz8QF5KhHeBnZi1qEYbDDa3cd50DLsZc5CPV+QqOAheHEx5nIyIc9T+v0NnJPUbQtx8ibjmHs1nUEJMqUoOjmJlnS7OV97521evXubtizxJsjJrbAvAWySTlFwfnHM/OKcfjfn7OyYalHR6XaZlXPWR30Gm1EGGhfR/f0d/ubf/j4//umvOHx2ynhxQesd+SLn1v41Xnv9HuenR5wcHzMYrvHkySPuvvIKo40hz54+YXd7HXzN8dE5+7dvcMM0nJ5N6RYJnTxjfX3IwcEh55Mx3U7OaH2dwXCNs/Elk8mM0/MJxhhu3bhFWc9Jcs1gvUeRrbO9PWJ9fYgXikW1oGlrhAiLy82be0ynMw4PTzk6PuX3H37Ezs52MO5PNK1pmU4vGY1GIWl6tqSpG+6/9ir9fo+6ben3e6gQ8xl9HhXTxQJvLU1dIbwjzzS3b+7RH/Rp25ZOp8v5xQWPD47JRMH3v/4er9/Y54PPP+XBwROsFEid4JwI3irKsGhnfPD5+6RFwRtvvgs+SOawDdpWMfRFINAYL2kNaCfoC8P9NcfwdgfRTHk6K2ldEv17QrNrZZejacNvPz+gePcuu4M+yiyAyIAzYVqT6FDAxFo98FujnCc4bbyQJBAb/W6/R6fbjQzWAGatFmIR77kwsQtMJudBehkndWH6x0r64Ewo2qSgWi5J0hQI7EPvUzKdUs8nZK7hu+/uc/225zefHPD4+QIvcjxBmh5udg0olsuwmfh0E0SCq1oefv6M2VqHujIcnkwwIg/+vq4FKcml4Wv3R7xzZ4NRoikEdAaKykOGwnnH2aSlNZKimyMwDPoJ4zODF4GJ3OkPkQLMcooUHQbDXWohcbJmMq1h6vjqdMnHjy44brbp3tujf+M2jfEcHB4xOZhQaEFHCzb7cHs743p3AyUFmbqGo6IpF5xeXvLZwVO+evQlJ4dPQzaR1niCPEZ6j/ctghf+oVdT7RWDwLvgdV3kWAxKq5BU7yGwt1dBPSATHTyErCWRYdrrXbBD8OYPpVgvgpX+iBkAASDxwQJAeEUtPFYFZs2sbZhcjtlEMpSaXqLZFIpe9K6yIi6keJZeMpGew9Zx4hxLD14KOkVGqhVV29Bf32Br7zrniymDzRGtFFTLinpWYqylGA5J1jqYVAVZmAlsfq/TYHLvQWkZJUXh+zdtCwiWszn15ZSi0wHjcI3BO898OkNrfXUOtAxTZKQgyUPBlmgdfBdRJGkSCpo2TOadkejof9ViaOs6sLhWSeGrwhximnIYiDi7CpeMbBGtgpdtG1ivF2XFbz/5kGtbI7Y2N6mrCmssbdtgm8Ai8KSI2DgvrKO7cZ2dr3+fs1/9S+ry9CqpVVwVywTWphJYldCqddrBHo0uaG3J2t6Q5VHLzRv3+N4P/oYf//DvKYqcf/63/ymfffEZDx98xLf33sR/U/H84BG//+J9xvPPubursa7LwfEhyJo3vrbHcHfAoJNQTyd8/sEHeJ/y/X/3P6C/vosTKY3zNK7CJwnvfeevuHt2k2UzBiUwTpJnm3Q6G0hd4F1sAsSLIdSKSbtqTlaF91ViuiAU+kLFA18xYRzgsG2Nby22KSmXC+q2oSi67O1dhyhxGq6vs6wWLFoY6R7GBZa79R4V6QOT6ZSL+ZSd7W2+8cbrFL0BSV5g4vkWQlEZF5vVwPg2dY1WgfVXVku01ldM56sUayEDa8F4lFQU3S7WNiGsQjpSLRFeUNtQ7J2dHgUmupK0tcErCU4FH2Yhr3zUmmqJNoYmNltBRREGDNYbynpJO29IEhlDVFLKssG0NUkaWui6rimrJR5PlmRolSK8JdUS2hYtBDr6B668fZ2P1nOsGjwfjgXJ4vQM0zSgJE5IWhOCyBIlSfKMtmkomzLsY4MB+dSRVA3tco6UkkKmgcmPxSJIsy7ttGI5exYak+dnQEKiCjKdob3l/KOPmJtLWgxpkuJ1wtbdO8hej6as0NLjrKexhoTALpQ+DDi00FSLJa5pIX1prYz3pVaBPVxkCa4paWVLruBiPkNjGQ26DNKcs8mUbr/P6+/9GVme87Nf/oTbd2/y2q3raFPz/k9/zO7mOpyd0DQVH/z+E0xbcmNrg+WgpjcccOvmPjjL82NFqgK4UJYVg36HG7f2WczmzOcLTqcXV99RSEGvW4C35GlCWVUMNja4cXcrrNxmDq5hfDnHtpbz8wVad9je3mJeGdaHfS5mY5pZSb2syG+sc31vmzt3bvLdH3yf9f1X8GmHz774kN7GFpu7eySZQntHkiiqSRmAEKv5/MEhbeN547W7OJfSKXqYiwuef/CI3/zkR+TKcDkd861/9j3eeOsd/pv/6r/mo48+43x8CsLihUKJ4NsvZAypic+/UKCLHpvXb5Nu7FDsXGOxqKgbi1AtQkYptLeoJCaYR/kqRJsLH/ZVby1GCHxtInChqOuZAnl2AAAgAElEQVQaECQ64db+FuVlxeH5JcZ6WsnVuitsWO9rExzaM52z9863MGnK4w9/Sn1+CC4wn7yPtgOs4LMXIFrw0/R/cK+tWGwSgtLCQh/Jtk8xy5Kj+ZRTGiampXIGGZOu8UTv0rBTCilDA7m6mVdsPBcGXUKt9lSHtJ5B1mNtsMZgbR3rPctqgbE1pmkRVpLJnNHmGqO8y+XTp7ikS7+bk2hFkhYU+Rp51iNLi2D10iyx9QJMHc+Fw0uPa1tMW3GxOOfTo894tjxhnjR4JKkQWBnWLYfCaY1ey2AgqRScLUs+PD/mrY1d7qmccVOxdv9VvvfNvybzHbyT6LTHYPsW89KRFpr1tR5CZTRW8+NfPeTwQpJLzTqGTTxFVtDLhqwnfaoi53xWcz55xOHR+2xe22R08xqTUY/cjrmUKaNvfJtq4zpnFw6RNRRYennOTGuSLKGsDWuDHocHT1BiyYe//xmz6RRvBL1OQWsMkoxWXsdmb1H7G7ROY7yl9gNQu6S+pbZjrF1do9V4clWvB3WhTsL+pSTBVioOtQObcFX3hTtvVTsGlmAA15wPANRqi3XeBzDGmyuCyB+Cle7qn/ELhc+ynixPaaTAeEFtgxdo2PcU3pkABkWWaKJ1dPfyuAggr8I8V+Af3lEkmlndBiasFLjW00vgZregbGEpFXXTMqkvmBODkpQONodC4LQgUwLnBcZ6yqqmLNtwvOJFzfyHIOs/Bm5ffv0p4PaP3sHK4MQLF+yWlLzCEa6ecVTE1wUvq4e0VjhCrogjqO5W4WI6KnOJPWGoOILlk9bBbs/5GIArI7EhyK/QSiOEDsFtwgfA2MXPl5JEhAFKY19gHzYuKs45rAt1UtM2mDb4wAblmedZolnr9Rj0+xR5RlFkbKxv0++v0e8N6A16dPo5nXxAqroUecFwEO9L09LuV8zLivPpgsOj50zOnjMdj1ku5tSuIc0LlBKU5ZK6buJAi2Dj5BVOOLI0o/YeayxaKtJAR0VISVO3VFqReOjrLt75oBaVAhUZz8aG44xIOD560gsZ945Yxzn/spVNcN2wLnjxto0JONGKfOA93hpsW9M2dfRgDr9TxudVyiQMvYUnS0O4lxcC6zzGh+HZKuh+xXpvomrLeht6SRMA2rIsA1BrDDiLaZrI9n2htl2lQ13RIKLiT4q4R0mPcC707hJMzNZYMa4D0B7vPO9Q3qJ9yDAw3odjrRvaaCXibQgZS6SgSFOcVDQ62MYtmxLjV0z/YG+mVRLUwFqT2oQ00dR1ffVMCRHUptZaXNtg2yYM4B1Y09JUNW1d4WyNaUqaqoz2D5Is0XSLgsY0yCSwia0xmNZi25amrJnP57iNNTKt6XYKOp0hIg75y2XDbL5ktphRLpe0TR1VlGEYlCZZVDl6hAxMbGsNqrV44wLOEhUeEoGTnsxrIKEs23+jTNp/oy9BVO6o4O2qopn20sJ6kXGtW3N58DFtPQ+FhwuG3SLJuL5/hzzvRpaiCz4ZdcMXH3/EsFewsT7k+NlTrLF0dndw3pBmRWSDhU3RszIYDwutlxJVaGQ3wwnPxs6It954k3pR4StLovIXX3w1eXQOgadbZOzvXmO0MWA5m/Ls4impSrh2bY+t6xvoJKWtDcZ7XNtQ1kuSVHPjxnXStMB7yXxZMZvNePDlAzqdhM2NdWzrmEymKJ3yxRcPuXnrFpubaywXl9y7e4fxeMrjR4+5c+8ubfsUKRxF0WFzc0Rdtzx+9oTpbEZdGTZG63SLgvF4wfOTS5x3PHj8HEHLrdt7DPtdiiILMobYtGVZzmhjg6qs8FiKTkav32O0sU2WZDw9fIpKFFjB+vomUkC+XLCxsYFOEibjS1w35fTkBGsNw7UhndGIuqlpTSic8yxjPp9xPr5kMQuTtl6RkaWCyfg5RdFHyoLr10YI4Xh0cIFvau5tX2N7c4trD7/kN59+wGW1wNq4QCqBU47LesbPf/dzhNbcvPf14O3aOsgswtXRUlSjhcZYR+Iy7mytUZ895e7WOpujXf6Hn37KbBwl6KgoJQmL7dG05FefPOYv3r7FtV6ObWuUVORZgTDl1YLnr+wHXiycK+aYjaCtiTYcg+EaUqdY93JRsVrIwjS6bZuwMXiFkMGTzYuVbnq10YefquqaNE1om5KLi/MofUkYTy5Js5z+Wo9OpwtK8PbNDjd37vGbT4/4/MmEs8sKY1MECVFvtdqmQmcVGSGTiyWT8RykwsmckELRINKEzfWE9+7s8c5el0y0galuoCwlLklAOZZVTbmoUPHZ0lqQJpa1fg8vBZezkuFgjUQpnE7ZvHaXerDGtBiSOs0s3efXj0s+fDrF9/dYf3sXb+HR8znTWRmsFqRnJ6+4t5Ny7/o+W/mInBLnZgw6fY5PDvjNrz7j4w9/x7JdhqRKuQr9CrJB7x0IFyPrwjVxAUvC+yBHCRuEo1yWWGMoOmGK68oX18aLsDVqFaauznkswWO5tm0wjbf2aqNdvf4YoF1ZawgBDhHN6qMfHj6wKKzDK8VMeubOk9iWvKpZE4qh0oF1RBhsGWuoBUyallNjKH1oNpWUpGmQwQz6I67ffo2k02MuBZ31AbNqGZ4rLRjd2MF3Elo8WIuxgUGlhGAVqLJi+ugV6xsQSpGkmu5wgG0bikGPZbnAmOAz1FQtRZGjlWJRLqI0luBRG1kIXoZzkKU5m5sjTo5PQtop0DQNztkrtoCS6sWz+FLDEgDZOGGO6nvvoW3bF8+if4khJSyfPP6Ce4/2WFvrY41hNpuRJSn9bhEGLSIyK7TEWUOFonfzHZLljIsP/p7UTkmE4gq1YOW76jAyoU7XEd0NqtqgO4JRt0s3NxQdTdtULBclTw+e8D/9L/8jSM9nH33AWmfIN//8n3D/rW8yPp/z+y8/5+DoY77+ze/wZ3/z7/DB73/Bl08m3Ep7fPrJYzpJj//4P/pPuP7K6yT9fvACszL6wEapY5KxtXcPiGEjiDCoceGc2DgUwgfWlo9MtkSG4w83sbs6d96/WAs9BD/iKLMydUW5mDGdznCmpVtkbG3vkBc53lkOnh7y1cNHLKuav/zB9/Ao8s4AneY4L2NqbWArtK3h3v1XefO1+0itkWmKsYLSuCs2u8CEy+pF9KnzJDo4A2uVkKU53ofmLBChVithSMN1Huq2IakV3oR1TmsVhxFB2tlWBucsWZGhRELb2uCrJwRVWYYGS6fkWRqCBq3Dmjo62Kh4jm1k8Tpm8wnLcoaWkrwoqJqKxpSoRIZ0XWcRBBuj0cYI11rK+ZxOrkgzHZ4BHwr9lfedNyHxeLXCSQ9KeETTcvroK7Q1IBROhdK+tQYhEjItqZzBKMXOzX2shG7WxWUdpuNzEg/Cepa2QWQZa3u32BjtUJVL5HKBmS0ZDEZUywotC7zXeLckXVywbita76AOXvGnv/0dTVHQWEdmfXhOY5iGB0xUm7jWUi2XV3srhIR0H6+vVAopJM8OHzMsBNf3triczylLx8npIZeXl9y68xqvjDYob++jRMtkuuCtb36L3f19rl3bpjp5jhWSR08eI01LVmQs5ktu3Njn9vUdnh08ZbjWY3st52IyYXs0wCmPMw3D4RApBaOdLq/UlvPzCxZlybJproYMZV1iTU2iJb3BGp3eJk21ZHoxpkg913a36PbWGG4MOTg8ZDo5Q6UdxifPefz4KULmZNIzPjvmG39+P7CVEs1wY4vaKBKd4FXBaGOT6axkfhlAFOcMk8mcIs/Y2r2BaVuEzPn4o3O2ru3T1im//N/+Dx58+BGNW5D2e+xubfP86XNOji75+S9/yWx8HDZHuZpSh3ttFa7hIkvUOYerG5LhGtn1G7QolHFxgGZp2xq3kv43IvhZSknWKdBpRms8zraYug6SQxkY+CLukW3bIiODb3aiuD7a4PnTQ5a1RWZpsA0hsO5DY61RKsV6RZJn3H7z6+R5ysPf/ZT58QHO1OjYBjgR9s64uAXWqljJmcNybm34DkpKsBaPQnvBKMnYTFOqsuKsXHAhDGXMMvARoHHO4URo3L0XrOxkV5Y9QsQQXATOBgBZakGG4ObOPt968z1euXk32KcsK8rlDClhcn7O+emYra0dtq5tcXp4gJ1c0raOxbKiM3TkvYK0MyDrDFFJTtvWNNUCUy1IhAsBR9E71dqWZXnJg+df8Nn4MVPRYITHGRvAxghJWtsidfAgbpRDbBeUiw7PDhZsLy7YX9viW1t3ee+v/zl3t+8hW4+TLcZI0myNvduv4ds5UjmMUTz47IAvH5zSyA5dWvoYuhIGG1uotMPW7nVEbmmPj3HO8OY3N3l0eMgv3n/CKM9o0oxi/1U2vvN9HniNHhRUpmVxfhrtw8BaQX9tSF2VOFNx8ORzPvv8E7TOyIQnyXJalyDyPWTxOkbfoW1zPAatHMoJKgPT8Yx2NsG3kTl5FfQT9sO2tRGsEiiZULdNSKXXCaY1V/tSqAWJ7GyJEjpOGgmKhagcStM0srls9HuNgUQRiAoMSn81pBZX9Uf4GGdDsJaWwZ7O+XC/ixhshIw/LwMQO64cJ4uGyoHBs95N2U4T+spjsdQ++EQKJYIVoSdYu+FJnaUnG5K25rKsaAnPzSoQWaoQ1COlYC58BOsEZR1CsULPGmuJl4Yi/ypLg9V7/tif9k/9TGD7gXeBICBVXDNcALaVChYknhfg68ufoyOLflX3JEkS3iMiIOsd1lg8PhyrcWFwH3MchAz1svUBEF95ECuhIiAYZPCBWexj/Rhq+ta0tKYN68ofEIOIwGYbBz2BbBJUfsEf/GI2YzpfRBZlQqd4Rrfbo9/rsrYxYLjeZ9DdYK2/zaC/Qa/XI+8O6XZ7FN0BRWMYrFu2Nne4GO8zG48Zj085m5xyfnGOtTWNUFdKQyllGE4RhlMy2jQ5gnoiSVLqtkUQQrm1DBiOi0BuVdVxAJuikzC0c62lkQ0ySUiUxxmHVwGkDMoaB9HKagWoBQZkIMtY6yJ4ba/Cwpy1cb0NgHcIOTOxNxDBTkdHO0YvSVxKkia0dRvuJaVArer86FMsJN7VtMYEcLhuaZqWqiqj/6+J9hQNzplogaOuhj0r73Mbr6eLGUterJSL4T6XgHLBy9bHPlPKEFaoVKjtjYfWOYw0WCGuVFVE1nSiZABVjaGuyuBlKyWdIkczIGsaBsMBCGgbA7pFaRsssaRASRXJGZIkkTEMN/gOTxczgltDuB5N09BUFcv5nMXlBWU5pSnn4aiFpArEcALXSNHtFODh9PQcqSVN07KYT7m4vORsckFZe7Y2NWsbA5Is2B6pVGO9IctSFguBalsa06KcQmqBT4JKx1qLVhmClDz3VFUNpMHGSYZeQlsbbSiDyq01/z8FaT2hcU6EQHqJE47WearZJdt7El8+ZzE7DUEYMjTPUip2rl1nd/d68AaRYVG0jeVyPMFbQ5YlNG2NThR5ltLvd5EKtNeM1kdAaJiUCjJx70GkCflaF9WBRiVIYbn9ym12NjeZj5ckgxTrTWT7iBfgifDU5YzZZEKv6HB0eMbx0QGjQY88k6wNO3TzHI8PjZNxONvS6RY8ePCQpl1y89YOe3v7DAZDPvnkAe//9reMxxPOT85omyCvXd9YB5EwX9Ts3bhJVS0ZT854/f4dfvv7D/nxj85I8h53rm3T7/b57JPPSNKM9bV10jRhtDFiMj6nVIq6bbhcLOl0ezx6ekyWqgCqSsVgMKTb60evOofWktH6GrZvr5IrIRA5u90MrSWLxYJet8+g2+fk7ITtnV3WNoY451nb6GKs4eDgGaenpxR5wfbubmA4KcH6+hBrHFpp8rzD+GyGaQyv3LlDr1eQpsFHp1wuSJIB1/e2aeqW3/z2E3R3DdUd8vate7x291UenTzlg48+5vhsHAzYlcdJy7Se8KsPfgZ5l0H3HsNBn0tSnA/eSvgWJTw5YTr7ys0dOtmETz75kFuvfYN+ppHSBUm2sSFsKQGhBK3UPB4vSD5+zPe+dpthniO9RSlHlnfj5h+AfOvc1aJkY6po3DKvmn5jDDLJQjHk40RRxCECQc5graGplsGnLStQSRobutXQYVWIhECbPO/gnKHX76GUYHZ5QVPO0UlG28BimZIXneA30xh6tPyzb1zn3dev8bsvTvj04QXjixLjEhAqyhZVADcio9cJCSpOl9E4b0kTxyu31nnv/pBrXU1uLUqmQfrmXEhv1J7JxZKqWrLW7yO84vzsHG9Lbt7cZ3wGMilQaRLMxbWkrmccPz9ie3sH7XM++P2XfFVPmCVb9G7cYzjqcny04OTZBfgSLTyDpOaNm5p39yS3R4L9ayNcW3N+/BTpM376o/+T99//GePxCVqrwPwwDhlBVIlHRvmhe6n58iuJCS+Y+daHxGljPTrR0UtYUeQ5dVWBEFjUFQAcAgJCcyeExDhLG710/tRQ/x8xAaSITLvgESWi1kyumBEigmVhzEctLEsHE+HxtkK0L2GDBBadC/V8+IOHRCvSPCXRBUVnjSzfZNHUVNawsCUXlxdUsyXbt/e5dec2j48OmS8WKOtDQAGrYIhgH2AJjCOtQ3OhpaLFYZzFJ5L+/g7SwfTwFOsdZd3grGNRLYIxgYrpwDohyzUq18Hjum1DIr2B+Xx+5Y3mI67qRDgerRX9TpdyuQzFjVY0dRMalRheIFzwUfaEMIbAbFlxp8JxCR+A8FnT8v6nH3Hvzl1G/XXyoqCT56RZYL+1TSi+0yxFigQnJFp0Gb7+bRanR5iD9/EELzGFIE0TtHZ4abFkuN4mIsnpJYbKd7DSIGmZn53x21/8AyeHj1FK8Juf/F80xtLrFFTO8vMf/R2vvfEuf/4Xf4X59ncpyznD4YA5lrNlxeMHjzF6yOtv/BOeD44Y7d5kbWufed3grEF6CNVHaHasWxW2ofB8wb7xcYAjXlp//BWYHRqnF9YdK3nlqg6ACATiaZZLJqdHTM9P6BQdNja36Q8HVGVJa+DDX/yKjhIcPDkkzXI6aYKyjrZakuc5TkbvOIL+18UGS+tgqdF6ENHfy7mYDu/jUkaoMYwxgUG9+p4OkjQPbFb/gjmzkpsGHgIILHVd0tQVWgcJXJplgKJpDN6BUgnd7gAhoGoCE0lpSVNVYfAmDVIrOkWHclmyXMxJ04QsL0IStLEkOiFbW2d8ccKivGSxvEQngixP0EmCc8G/vMg7dDvBA76pWpxp8d5RdIroI5ZhnEcR/H99VF+sgjuCGVCovdpFycWzx/QTSSp1cH7xwTMv7/fJlKK0ht1X7rJ5Y49PPvwAZcJ9UPS6+LalnS+QacLdr32T9dfe5sbXvkbTttSTc7768HPeee/bTC4vyfMO9WRBzzV8+L/+d8jFJZmQOBmsiTSeehF8qx2CJO+QqQRhXWTEhBwCraCugy+ekDIGgq4GXQpHgs66lN7hlzO27YDlYkbrNDJTnJ2dMZtX5J0hJCmXj7/gdF7yzl/8gDwpOHx2yPHnH9DJMiYTh/SCVCtMpti/ucfasMvFRUYnVaRSMjmfcDkvaZxg7+6rDLb2OJ/NyXXOzu51vv2tQB74/WefhxA6B+PLGU3dkqcFF7OS0e0ep6fnLKZL9jYHJHmPs8kRR0fHXEwuaBdzEJJBb0A3L6haB6Ll+eEp0/Ml9eKEVCV08w6//uQzNjc3+PM/ew/TzrBtGYYriUSk0N3oI6xC6w55pjk8OODJF19yefovuTw95PzkcQip7QzQsuDJVw/4+W/f53wyxhMUNxAVRD6wmkSc9F6FaYiwOJtywcnBM7Z2b2OcI5GRbXZFhghNnbUmyCJNAB86/T5aJ4H1ZA14hyIEtpq2RUpBnqVxoXE8ePyM+WQafBjNEq1Ap2kAdAVXwTBSh/XD1A1aSDZv3EclGU8//jXnDz/HN0uEt9GbPnprrtabuDc4a7liwUfFTUB6IPOSzU4Ph2Ncl0y9YWHbsFd7j5IhZ2AVRBq8A2P2QvQztATAQK4UVURGVWu4uXuTv/knf83NreukUjOflgzyHqPREITkjTvv4JyjrEqOTw9oa8u9+2+jkw697gZZ1iHv9Ul6fVReMJ9eUi7GmGaJxMZE+WAtZ43FtpbDyQm/e/o5Z66iTgRa6QBYiwgImOCpq5IgTTHCI3JFsT1EzVqOn8/oyw7XRpt87frr5LIA24ahiwmDMOs9WdonyzJOnp3zk198iWBIlrf0mjF94RgMe5Cl+PU1vv6X3+aHv/spWxrS4ZCxuWB+fkh1ljAwGW22wyt/+e8z3rjH+dkZLs/QVnMxPidNc7r5AEUgDiybJYqaX//iR1xezkjTDkobDJpaXkd0vkGb38T4EYkXtIlEoUjrS6rJQ+rJpwh/jlCatNNFYGjKJbYN4I53jrZpAtgiLE5AUXRQQjG7nIf6LAKs4Z5yeB8H8lJE1mD4s041SZ7QtA0yDvaECD2BUi88Pl9YEK38lAPT1hHCdWyUVggZhw3WolSsKX0sGIVgWrb8Zuz4qnU0PgQqDZqaN3vw9kAHqxAUbSQNqCTYkEjlkcIivaGQEuEsVRsGHS9ovYEZB3Fg7hzlVeXwwsbgBYPkBVHlZWLDH4OwL0LWXni1/j8xale/zzmPNz76xgYpudY61LKE0WbTtLTS4K2j3+uRZRlaa9IImL183hEyeJ7iQ0CgX/kNr/xu/RVrFh/Cw/I8D2q9CPh6HE3TXAHZeIctzdV6eWWBt2I3ixchcyFLY+W3u2IER7DbgVI61EPRM7U2LdVkzPn4FH2oKIqcJEkp8i7ra1vkWYest0Zv0GWt32fQHZKnGVkWgqHyRNMf9BhtbnI+OWM8Oefw+UEYWDdVYPyu+l//wsoDF8geQTAQe2Ib2aVJhrGWqqlIKxWGgKEkDSGHyiKUQScKTcB+rHN4bMjEi7khbsW2lmEfhgjGxusVGM0OrMPZSEgQL2pIaxrw0WrENKR5ByEVxpaBfepcDLQL/X8rQOsQkJzEXiiolkDq4Jna1G28L8NnOtdiTSSM+PC8rowarHNY08ZjcVdQVfBndVFt4UlNS9oGO73WWLy3uFYgMxdY4s7hHDQWGm+xUoR6OnoYa5XQmBYhJK1paeYzkrwIz4wnEjEU/eGQvNMlNR4hdQh8I9zrxlmscSE3SSmuaGVC0FqHcCHYVQgLLoTH2cZSLRZX9ZwUK45+wEUCCzfgEEVRsLaxxtnZGUIpqrLm8bNDnEzodXosqpLhdEiv10MnIfBMxvq/yHK0VMFjO9bDjQt1pY9kiThfoSgCedNEBYPHgfIIkWKtJc0zevzhWvLy6//TIC1xYVUuTiJMA96xqaZsuRl+eYy1YXqDFHinSfI+u/t3QWW0dYNQATGxzqB0wq27ryC8YT6/pNPtxwdL0NQ1WUdx5849lOrQ2gpEYF2iBbKToPoZFmiNYaPX4ebeDVKVMlrPEfKlBMzYdEpikl9dk2jwtuXps2PG5xd08oRXtntsbgxwTtHaII9OEklVeZ4ePmc8mVDVJTdu7HHr5i5Hz49o6hnvffMt7r96D2ct5+cTPvzoY54+fU5dG548PSQvOmxurfH2W/cYn1/Q6/aZLi6opgum3Rn37uxT5B2m0xlZkUOcTt2+fY/pdMbp9Bndbsbd2zc5ePKUKnqQjieX7FzbDlJeZ1kuliBEMN3WwWfRtA1SesqyYblcslgsqauaRCWMq4amrrj36l22tkbMZkGevLu7zfHREceHx5jGMbn4MtL3S+7ff5Usy6jKmmcHz3EuTCZPTk8Zrt2h3x/Q2oYEFQLbEsH1/U0efpVwfPycrKkpL6cMNjd5Z/8Vbo12+Rf/8EOenB5FFkZgPZ5Nj/n5r/6eN94tGKRDFlZivSa4sRicaZACNvo5mjk7m0OUTvj40SNOJ1Ok/L+Ze68ey640Te9Zbu99/AmfGWmYNElPVpEs3z1d01MzgCCMDCCMIEA3gi4E/RVd6Q/oQpe6ENCQgBlI6kF1T5tyZJFVRZdJMpk+IyLDHrvdMrpY60QkqarRbR8CRDIjefKcvdde6/ve7zXDOAywNcqWBOkJugteYYPg/smcD7/a5zsvbjLMAr6aYXo5QWbRISkxrp0LCG2emdhdeM6ugoOUVKnoj3INT4tWKvqirABBJVE6mqA/e7j484IlyroRASOLVHg5Oh2Jd9C2NVleoIseQRqOTk6YLZbsXr1GJiWUC7aLnD97bYMXr27wxaMzPrtzyPSsJDSAzhAmjzLD5G+EF2ABUVN0JK+/uM57r4xZMx5tG4RcTd4iA0RpTVU1zCantNWCUUehs0CvmzHs51SliCzhIPHW82TvLloEBqMBs2XJyd6MOwcVHz+s6V1fZ/e565St4t7XpyynM4yvyFXJlX7DezcG/PDmJuumZHl8j9xlHBwe8PFHv+SL2x/z5OFdQmjJTfRDiqzJ6FlotMZoGb2UQgzbcGkbMFqDiZ6y3rkIMoYkk7EOnbwghVh5bxJBSR3N/KXUsZHxHpkmxT7JRMSf3tcvWJ9CnIf9xC31AkCCC5N6FxI7J30YF9K6WY0JBKkQjO+htY6AR/p5lufknX7y8unSOMF0NieoQGMt1WRJc7agHGvu7T+hbppoa5Cay4TcpSJ5tYdeMBecc9Fr08cDHBeLs3pZI4OkLSuU0mRKs1zM6PS7hGTlYLSmUxTxGROCZblESVgsFud/Vbwq8SW1pJvlvHD9Oe7ff8B8uUAm774oR10xa1dNUJImpRFIJKBIovo2+kx74Xl4dMzHX37JT3/wQ7rdDsG22Baa1lJXMY1UGxEZkUJgig7rm29iqoZjP0cvH6P8Ei0leRaB9toLnMwJxZAGyeH+E/aO7tFbL3CVpy5rZrPHCCz9fMB4pMi7eZTSdnr0xmucHO+TFTmvvv42VVXxi7//WzIj+M7b79HvbiG04Z/97L8gCMh6Q8rG40Mcvpx3YWldCbm6LpyHgYFI4RzhQn583im5FDgS/5xI4EL64Xkz5G30DtY+LbQAACAASURBVD07O40WEcGzu7PD+uY2jZc8PTjk09/9jk7RpamWzPHsXLrE7tUrMQnb1UzPThjtXKEJgmic4VGJ1YAgBWPEJkkisILIzluJMVOatLM2sYoE4M/35mcbG0FITKi0VojsdQm0bYm1ZXzmhUxNsaHo5NRNE9d9iF1InucJvIlnRKz/HdZaZtMpSsB8MsFkWQwmk5rMxPWTFzl50aUNFktNpjKMSX5iUtDt9pEiDpeda6MfnG3BBYTK8Wg8kbkrpY7+dEF+I+wtCJksXmA5nVAdH9OLXwyfgPui16M/HrGYzTBrI0YvXOPOgwfMTif0TcZiPkdpRbfXYblYULaOo9kZuWg5KSfozDD3NYwHtOtr0OtSGY0cDNn/8hYz1zKW0QIm9usxoGLFei96Hfq9HnUCMYQIBB/ZjYO8S1032LKKgRdKEkL0dxQoUBrd6TPY2CEsBLN5i8x6vPL8y3Q3dll/TrO2tk1Z1jx68pC6XvLclee4vL5BEJKTyZTJwSG2rKOU/vJVltMz7nx9h6apEapPr9/He3j0YJ/J2RKvIiNqnBfkIkBTcbQ3p5f3WFsb8sabr3A0P2Vv/5i2dRwennL33iN++hd/wXJRc+O119m89hy3Pv6EvBDMqsDB4ZJ+GVObq2VFr9+j0ArjAp1ORqElCxfYe3yAlIqsu8l40MWXc25/8pCrl/u8/NJ1tPI0VY3JBDuXL9NYz9nxlI8/+iWimnN2eICtSxYnJ5STKeO1dXauXmM6P+XR4z0++ugjlosFxggCq5CWyOyz1ibfxkBrLSok37wkrRUChA6MR32sj+nO/hkmnFbqHGCoy5LZbB5ZOEqTZTlCSIosS021S9QaeX6mCRH37kwrlkpAN6MrTWTCJtuLLKFfTRs9n0MItCF6m0sRGG5f5WaWozEcfvUJoV1i1Mp8QLDyhgz+wk9x5RlqdLwOq1DYTd1lIx9wNJ/wpJ6xEJ6VdW5kSIn4XdIZJIRABoFCxborNenCE3XxaS81XrHWG/OjN3/Mi7s36ZiC5XLO9s5l+t0+eZZh8oKi040J6WVJbzBmd/d5lNRUjaM3iAGGnf6YTn9M8IK2ntFWU5R04G1kqIXo8R4ZdxM+efw1+82MBodPOQlRZRDOawGVGZRZha4KUJ4wBrkz5OT4KXvzCd2nUw4//ZIrw238YIj0Mu1rASUUxnSxYcDHd+7zaGI4q6PfdM/Bmlb0B32Ozg55/t336F/e5drsJnIv57/8H/5H7t66xb//X/9P3rz8E8R4jZ33rsNrP+TW42NmvkchczLZMOoO6OkMIRy9/pCDg30urRV8/vtP+PR3HyCFwUpNYwM+bCAHb9N236BWQxqboY1EyArlptTTBzRntyCcgATT20L2thF2RhaOqcOM4BL7zWvKqom+llKQi4K8yM9BWqP1+RF6PiQ9H9xfnFltG+tY27SxblmdVeHiT1p3URcmMu35+3qgdI7SReuN4APWi/i8EIPs4jL0BOcpLRxZz0ysVDOBs9Zzd9FweaC5rDXaQUjgipERnDRCkEuBISrLOlohsYQVE+KP1L3fBFW/RVx4tth75rX6/54Fap8NpVr93rO//0feJZ7fgCIxTn3yliXWRN576qaOw6GiwAUXn2MVg5pWNaVYkXS8Q2mBUibdRpEUXPHzSsn5oMYT65fG2bSv+Bgsa20CEtvzQFKBPAflYSVm+Pb3jLuWlP6ChZnCbn0IUa6+2jtVHvdqtwL4JdZbZuUSv5gDpzw+2IuBvEqRGUWv02XYW2c0GLO2vh79WLVBK0MIkGUd1ta2QSjy0yMmsxOqusS2TWKWChqvEFmO8HFA5ev4+bRSsd+VK8DWIVJYlk9ZQVJrglB4KrpKEhqHkg7nPFpcWH0Aab2t1ln0WlZZhj3PkYnWjF5anGixIbofu8RQFURrneBjj2itxS2XaJMhVVSm+GDRTkc7LCnQSqG1uGBGQ8wPYBUq5pI6LV5zZ21SiIjEMofgbDyf0tqWSZWuZPK1DeE8gM0HF2tyZ1FtC62NAzAEwQQsInrVWo/SoIOM4bFBJvBRnZPGMh0l/66Jimgl435FAG9bmrqltZ7GeaTUdPKcTi9aEggFwQVsGjjGdRrPMCklbQJEhZIpGHeJtSWtXZzX1trk0UaQOMARXuFDzAQJ3iGBTGoyZWiCBS2YLSvuPbzHaDRAGsd8OWVjbZNet4N3nrZ1qbdTmE5GrxOJcnVds6wrqsahRUi0u7RHhNWvPSt17apO0VpiMolPIcN/7PVPG6QlJYsqQwgCIxybhWOr37AVHiOrkxRkERIpx9Af76CKIfOqRaagnZV8y4xHLKYTvvjiq5g2f/1aTO9FUNVLdHbKKzdf4crui3x9/xgpYhqg6nYQnZw6pHTGtuXS5lVevHYjNXny3DNkVWTG4BiF9DKG77QWGRzT+RlSK1rvWZQ1R0czlOqgM4ExMC/nVKXj7HRC01hefflVet0OX3/1NV99+SVbO9u88cZrrK2PWS6XXLt+mVdff4nHe/t8+cU9fv+7z+h0cvCB27e+wjlPv9+nv2xoPBxPzrj76BGL6SRdU5BC89mntxmPt3BCM19aBr0u167sEKzl1pd3mC5LGjvm7HRC27aM10ZMzs5orWM8GjIaj+KmgKAqa05OJswXy7iYtWHY77G9uU1eZDFFMTX1TVURvOXmSzdoqpL9/UMGo3WauuTp4SkfTj+kyAu0zqiblvH6GjuXtjFGcnR8wNbWJiHAZDKnLB1b22sYo3j15Zu45ita5xCZxy1OaGnpFyP+8sd/wQeff8wXd2/TtDaFLUhOTvb4wwd/w/iFnzAoNGUoIjMpsV21t1wZZ4y6ivt379MZX2L/tGRaeZwKyGBBNISwAOcRKosyZiWxwfDVwRTvGr7/6nWUVSwXDYM8Q2uJd5HRsbL0eLZYkEqmUAdPnmVERVyUIMQss5YQWkJbxTRUHb1dtI6HIeHCGNwnEDesgIc0uRWpcJKZZriWp9A7j1AKZXIubW8hT06Zzs4Y9QZ0VU6oa4x3XOlm7L65yes3xnxx94TPb+9xWnna4GI3kRqsgMcrWFvP+MEb29zc7pEHh7QBHwSTZYV1DcNONzIqgeAtmZboTFEvl7S1ZDQYs77RxVnBYKhYzlvKySknTx5gmyWL1nMwnfP1ydeUxTUuvfF9+utb7B/NOTpe0pSndGnYMkvefrHPOy9c5c0bGwyyhmpSsqwmvP8PH/CLX/4jDx58jTECQhuZlESSSpYptDLolT2Kj4miyTE0bsUhoGX0uZMiYK2jbhp821IUBRXRX6hpGozJnimkIjMvSid8kppIhIjBVD74OGt8hhXw/9k5V6CsvFhPq/vNM4VYDNZKwQIyNqwheKS4+CxBpgY5sWajTCY+6yENePJOD5V10UUPnXVoQ0NVzRlcHZANC9QjkI2jbVqWpyfk2kQpphQXgJeI3pys7EhcLFa1UtH/1Ufz/FXqtAkG36ZOIDHEt7a3uH93htAaqQ1ZpiLrD0Ar1tbGZDN9Dhp6ovftxniNxXLJoioRMoLBX3z9VTR0V+LCpF7Gz7cKHYufJWB0hneJqUWIDKrz5iAyemfW8+tPPubSpW2+8+LL+CayJ4UPSJFM+9OkWQpJpzsgW7vCjXfHFLMHhP33CWf3iZLsmtZ66ragLgbYbMxsXnPns9tMTh6gcsHLr7zGopkjdcFf/Mu/oKmXnEyfsP/4EcdPTlnrjvjxC6/gTk756P1fc7y/z7DfZ3G0T7a5xtvvvMuf/exfUzmPzDUEaG2Udl2Akt9sVp4NG7lolOK6XQ2HUkZ6WptixYUhEH2aY9Chx1YVrimplnPmsylGRy/1TA/R2vDw4UM+vfUl127cpN/t0VQ1wnne/cG7ZIWJ566NoQ7Lcsna5cuY3pDKr4JLouxPKHUBBBEZZ8Em39wUvrAK5IPIJIU4nU+zhbQvqHOgBwHfbOJEsvMA6xqsq8EFMBGwaX2L1ppOp6Bu2hRgF4FdlcQ5SkusvRjYBRtZEba1HB8fc3J2ytraCJNncXi1ABssg1GPvPCJNZihpMGYLO7LOn6fyewkqUA8w96ItbUtur0xShcEaRBSnQOzFxYq4uLsCIHJ/j5hOqGXUqu9iAm5Wa9L2baUVUm2OeTRwRMe3L3LoG6pa0db1oQiR5mcTn+IbFv27t0lKMHdD37JcnZGaFp2r9zkuDvgeL5k68Y1MqkRviQ3Cl+BEDrtAxLvW7xI4NfKrxTHypZDaBAosmAQdYWtKkxiXagYTxcLeREouhlrww3yTodeYdjevcra5V1Oq5atDcFz12/w9GCPjbUuLrRsXX2R8fYWB8en9I1h2O2xt/+Aej6l6newTU25WPDwwSMWkwnGGObLkpPTGVeu32C0ucGnv/s9Dx88JO8c0oqA15pHRwdIadja2ubf/Ff/hs9uf8X773/I0eFTfvX+RwhpGO9cZePvf8sbb7zFK6/9iGZxxqCjWD8JHO0/YjTIGK1tEFzL3S/vcOvzz+kPCm59/jlKG54+PeDevbuMtq4wWLvO+qDD3qOHfPb7P/D2qy8x6HdYyjlKZwyGO1y/fplceH7T7/DJr37DqzeeYzY95m41ofUFWXdA5SSLpeXR46cEYej0hlh8XO/FKkE7AkLRJ7ni9Pgo2jxFBDWyd7Ui63SjmkBnMfsh7R15niOFoG4atNF0Oh16gwFtaxOwYMmMRqTG1vuogmmtpalqdFJwCClpvMT5CLoq4vnS1FViaMXnPctzjJJE5ZCOoSkRLaG7eZWXv18wXlvj3scf0C5OSVl1aEFiN0VgRSZ2n4Ak+1dYHxmDu50+2noOywUz76LNQWLjoZLPbmITihV4q6LnqFhlDwQu9lgRgwOVUPzwOz/irVffoVOM0FKzsT2kPxohvaRtGtrKInQgLzqsdYf0ByMWZUmQksWyxNqAzgo6gxFIxWIxB+FiwGVrETisb6PFhK1Z1ku+Pr7P58cPOBMtrQKPJbi4NzofJdo62YsIEVm2UgHeMRNL/E7Blt3l4Hd7bExOufPLX7J14wXy4RApNE64xGiNKfAffvKIj76q+fLIcOxyVK7QtWJ71GXup6hul72nh+z973/F5Zeuce/+Pn/3D79g+fSYZuk5XQRuvP4y6z/5c+6IHq5nEdWCosjJAlRTR7lc0Buv0bQNvq6w1YK//5v/m9PjCWtblzmzgkaMyUffww3fpDWbtFYgtMTJgq5tqR9/Tn30S4R7gpI5+egmerALMkOYOUWxRtZ5Sjndj/7r53Y7Nlo4hWjNJNNAQ6hVrZfA2XQMORfXFwks8X7FyNSRvRe+eXYFor9+tAtMw/sE0MWWO7BMatUow3Y4JbFAriTSBkIig8iI6uE9MRRTxtrLB8kcOG5hIzMEH4ftNsS+y6YgMy/Tl7AOrWUiDXyT7frtOuRZosKf8pF91u7g2560z/4/z5Ic/rQnrUjX2dN6Rybzc3a7TSzf1fsYraNNhTER2BOR/OX9hSLJiGhnYrROYKw8/z76W59tlSDvuWBAR2V1HEh2O53zQdOqF3j2HI9ep/b8+7sEKq5AZoFIny2CwisLh1VIcgzEEngZ67iI64Vz/20pVmHYydPWCaqy5fTkAMkDtNR0uz36/TGdbo9+f0Sn0yMzWSrvJb1+n6KTsSznzKYTqrqKAyofWZkyQFktkVLibBuVdFJiXSRiee/PIXTvPda2LOYLGhvIiwJkTuYCwVukKCk6kcWtdf4NkH91fUmgaZZnkGWxZ7cukXga6qqmaaq4RwcRg6XDBeNaS5m8fz3BtSD0ORu2DS4OKK0iWB0twVR8lm3rcT5a3rXJkzZ4mwgPLuVrRBYqRKKIa2zEA4TAqBjMHH8W/cKlSAqxqok2Dk2DbZKyysZzVomMrCNpvUwc4rhfJGOic3KJfCZ4VSlNLhUehcmLSFjxNnZeUtE2DZPTE6QQVEWXxntMnpFnESdazhu8qxGktSuS7UOwtK6lbTzLxZTF2QFVuaBeHmDrE0SoESLS+wUSoRRaKUyWnWMnTVXFNZMvCX5J6x1KBeqmYjqNYaejYSDv9BiPBpgio2ksddNivSU4S2YMSqbrajLUEsqmpvUB6zzO20g8Sz08JAwmRHB3dS6vfvbHXv+kQdoQouF3FiBTkLkz3r7SZ1RZmqdLKmujsb+3CAFZb0TRG1PWltl8ybDI6HYzBDHd0QbBsqpZ29zi0qVtuv0e3gUmkwlaeXy7ZOfSmH/205/y+H/7nKadkBWKfNDByYC0PnreBMeVrU3G3T6yTZtX2izqpsJaS6/Xi2iOj0WSMQUnT/do6oqtrU1Gaxvs7c+YnN2l2+vS7ResjUc8fPAA72E5ndPJcq5fuUoAPvjgfXr9PmtrY5qmpiqXFEWGUpJON+OlF6+DD9Tlkul0zu7uFZbLBQeHh+RFhlIC21SM+j10pnnx5ktMJ1MQ0O+PWMxKHjx6wMmsxAHff/ctlGiZzs5o2gZH4ObLL9MrNE1TUVcNuenQVHOWixJjcrK8wBiFmzfMZ0va1lIUBYPBgI2NTTpFwWI5p6yXdDrP0et0aauWpq6ZLwTPP/88ly7tIrXhzld3mU5meG85PjlhPI6+vcPhkOeeu0anmxGS5DvPOqypLmdnE/b29hiPhozH6wx6vSjnHww4nczZu/c1w43L5MM1vv/am6z3uvz284+ZlQuUNCgNZblPePx7+rtgii2mIcMSQTZDoJoecXoU6EvJ3sExT89KWpGhFGgdCGQ4ZwghWmVEUlEEQudOcOdgQZ4/5eXdNZwryWY1vmfQATrnxVVkHpC8WcJq+qISy2w1lZOC4KLcorV1mqBJpNLRV1GoWPwn/8dV3AurSXZif4cQmR4XacrRwFyrFdjoyYxmc2ONZVninWVeepTO8SKyjU25YFdJRjc3uX59nTv7Jbe+2OdsusB7HRt9Fdje6vDd1y7x8maGaSuUzmgd1GVNEO7c73OFfBijkd0C3TVU5ZzloqZtKiZnhp2dLZQKaNNQFIKT6QkP955yUhtO50teef11svVd9hctJ08eMzs+Q7WBQXPE61c6/PCFTV67PuLyzhqDgeFk/yG3fvcLPvjFz/n63hcsywUmEzjX4GyLMYrMZElmJOKGXZXxmgWPSIxCgcA20Qxc+uhplxcxjdZoRSihdR7bRNlRTAXlnEkEFx5Vkf3JeRPWWBtZRwRC0lPIP1E4RsAodpb+mUPi2dcqjMsYk+xKBLgYwGjSBLpJ30WsukliIbpKiVZKMRytIXXGsrVkskX6ObZt6I92OGvneBsISqJS0rz3MYkbYq0XAs94/MaEd6FWNvVxCikTT9WnoZwKMqZWG0MQkizPebq/H787MgKs0pMVmqauCQpOT09iXyvic7EqPC9tbzOfL/ni7leozBAI0W8qTceDkNEfzvtU7KWGJV1H78OFFEqsALwkDxRxCh8Q7J8d89s//J6Xr91gfbgB8zk++MiqSQWzEoJMKZq65Ww6R2cK19+gci3jLER2iwiEIClDl6UYUtGhrGoWpwtkLTFSs7Oxzdb6JrZVvPtnf879J3eQRw7fcVgylic1rcz4l//pf8aHH3zAndu3OTs6otcd8Npb71KMx1QyhhiEVMBrFSXikegZzhNNv+ntlvhiIrIWfVrDz04VBAF8+nPeI4JDK0loGxbzOYvZHGtrunnGcNBnY3gFG+Ds9JQPb93itdffYlE13P7iC954+z2KvOCNt95gOOjS4pnNZmRZTq/bY228gdSGVkRVgyD6qK68j8+fneSHLBKDVxCblfAMjAxRAmdtGyf76MTUSfeP2EBKKZOv6cX7CyRKRpaLt8kqIj3rWV5QllVUdwBVVSGESAycBHav1mCIzRs+DrcGA4PUiicHj9l7ep/eqIfSJu4/yoNwCBFZiybroKU5Z/nO56fMl2fUbRWZDl4xGg7p9/sIFPjIiJXfanpXe4lIRbMIMH36FFUuKYSKDYiIrA3rPaWtaIC2aenqgmFngFucRSmci8D/fFmT5R3y/oD27JTZ3Xt0pWBNeLQUyEf3ufP0hBAylp+ukxUdmJ/SaSMrMkiBTN5znhCDGoJgfnJCM9MUxsS1qWNIB8Q0We9amnJJL+0/IQ0JICpQim6HTnfERr7J+vYaxWhI0IYQGp48vEvuah49uM/Tk2OcELzZOE4PD8mLLhu5Jr+6gz26x2k9xdZLLu1sc3B0yNlsQd16tnd2OJlXTBpLNl8wbR1PJzNmZYO1UXHw9vffwwaFd9Dp9ekP1njj1Zyvbn/JyeEh08WCjz75mLdlxs//6q949NkXvPHWd9MQSrM2XEP6int3b7N7dRchNLVtsL7EWcnu5cvMZgvefP01Opnm3t4Bi7NDQjXj2s4GJ/tP+PCXv+bHP/wetDWz5Zyzk5a9e0/pGQWhQ9kE7t76mP3H93He0ekNmU0mPPj8K54eHkWWeNah0DHwpVPkdPICqfU5ACSVpK5LpmcTrKvPgQeEQJqc/miTqnY0dooIgRCi5UFdV0mdEvepXhr0riTMy8UCrTVK6fOhCiL60+luJzKS2jaNWAP4LAZZeoc2aWgdPMbk0XPOGIIXBBwiJNZQiGdDi8AM19l64TWWyyVPvvyEpjwjU5qIXcTvgw9pABp/TYjni2wd427GWp5RLWsao6jLCFiFNjbbimh5QCIQnINHwUW7GR8Dl2JJIlFOIL3HeMkbL7/G977zQ0bDNZQoIivP5GjTIbhAruPg2XnHYjFjNBxim5Y8K/AEFn6BFlDNp6jjPfL+GqFp8G2JCDG4RgQfP4trca7lYLLHH558zkSUWJX2Wh9ZYIgV6Jj2XGsx6ZyxdYura2xVU3R6/PQv/4xfP/p3HJ1N2Hx4hyd/+JDvvPIyFStfd4WQObe+POTnv7jH3dMhT9shtr+O8gu62qFES7Z7me/+7Gf0Ll1j8dd/zWL/hI1iyP/yP/3PiNKz7nPmoWRiJPdOZsxGhl5Xo3UMP2xcgyi6eCDrdDk83OPqdp/bH/8HPvv0U7JuB13kuLlHdi7jOzewaoMgM4zySBkgnNEc/oH2+EOEewymYHzlXUz3VZZOIlVDaFvq+hRhPKpYRIDLRmalTHtxlK/HekasvJ3PT9lAdPURmDzeV3le/6zOtaSsCxf13cpbXUqRQI7EsRTg7IXipPHghYyBsTayBxsf6AZxniTvbWTNGi3pqMjsblnZrwUUkkzGWk4KICkIn2UgBGSUYvsUePbMuf1s7fGsZcE3iQl//HVug8A3Qdo/BtA+y579jwG1ETyzWKfp5EX0fg9RBq9kVMhlKoWKyThYVCrWnHI1EFYyhSql+5iszi5q+IvPsdoGQgixlkp+nsEnxZ1OhJcQvWV1Ikc8GxDXNDXWWs5LuGeYw3jxjesSEoN29d/nQamEOCRRGustJHZorKh8zBZK98aHlLRLDJ+rbY2bxwAslWUondHrDuh1e0gdr4VWMlpaJpZmDDVzBBdwvsVLGfuYuo6AqfMYEYdWdV3TG+SgBF4JQgKag/f41tLSUlIhCkO0vkrBkyaqWs+tKtJ6sdYmu7kLct658jHLELUiSBnVRDY+OyoAuPN7Fm3snqk3xQVhZXVtXbp+RspIOEt1t7cOGzytjYCndxbXtslqI9pohCBwNvZtcQgmEErR+BafQuNW9j1CgG9bNBDqBlM3UFcRpHXRgscHCLogU0OMUQjXInT6eyIKjncusuilwqf+TUiBNhk678RV6xQ2QGE65EWfxkPTlpRVzbys6XS69Podep1+fJYFIALeu8gaT/cnBEfdOpqyoZzPWM6OmR0/oJwe4poKr2K3SEiEEATCC4yOAwWNwAgBm+uoqeT47CQNDaG2lqOTU2oHpshZH4/YGHXp90c4RBzu1jXeu3TdBVp7er1+VBJYj3aCson3iODjekws9uADzoG1Ecuzrv2Te9Q/aZDWhwBKk2mFYY5ZPqB5UrGwh4TlNHo72jglD0Kyvb7NYLQBAUbDPoVSacri8V7Q1NGT5dr1GxRF9Jg6PNjng9/+mu++9RpGddCm5l//5/+Ku3dv8evf/Jy8q3BCYoOlI3Q8IHxg0MmRPlKyfUoJVEom2rhFSmjaGgmYLKeeSZAZbTJ5Pjo+Yzav2b0k8MIzX86ZTUsW8wa85c03XqPf7wKO2WxOURQMR0PG4zHj8RpZHqcrHs6DLmzbsLOzRVvXfHHrE8YbY27cuMrpZB4fsjZS/e99dQfx3DWef/5FJpMzptMJvX7Be9ff5Lef3OLg6SlGKy7tbHLn3gOG4z77+3v86je/olcUPH/jOlIpbGtpG0tVR09F5z3aaKbTBcfHZ7SuJcviVMRoTVWVTKdT+v0et2/f4tKlS1y7dpXTs1OePH5K8AFjDIPhiKJT0O11MEaDCGxub3L71lfnwOXWzjrb25tMJ1OcWLCxucWlSxtY1yCQlMuGXpFRlzXHBwfsHxzz+MFjhmcTtl+4SVZ0efv6dS5tb/Dh7U/56qt7tKIB3bA8+RLlBf3dN3HFJazPEE4y7HS5cWULLVs63S5HZyUHp2e47jYCiwwCITJkvkEQiiDyKLXwLvrnSMXcCT558JSgJC9s9tBNg/WWjUERQQ9n8QFsmkJ575ORfzTuFiEGC8XySp6HITkXAwJM1kFkOdavpqgXxYT3MYU+Su3U+UTcwzMTd5GKt3T4CAjeRamz1Oi8S1mXLOqa+WxJEJpukdHrFIQQqJsZfSl55XKH3fUXeLB3xq07B1SV47kXLvPOq2tcNgJTNwhl8NazmM8pTEbeyWlsFcETH718tJZknQ7H+48oFxOuXL2KNjGAbTE7YTo5ZDpd0Blf5iyss289bNxgfCWju17w+MFdTs4aMu8p2obdK7u889I1fvj6Ls9fGdG2Ex4/vM3+geX9v/23fPr+P3J6fIxVLa1vUlq6x2QZuTFIwPk2BpH4kAoHQbfTZZUUKqRC1DHRVosoSZRCJjDsEwAAIABJREFUkBkT75OIB26RZWSZZtDvIoRisVzifWQYGaMwSqfDyaOljhYj4aKpkysGQ7gAg85lm9+a/F4UVBcFqJSSPMuoqjoWkEJFPyUJwqQU0iCIYgURk5dDlHARwvmB1un1WdvcJEiDygo8gqqsUELS6w05qhe0lYsecFJBcAidQBUpk1ffRYOgdQw7ybLov7VcLuPnTuvUp6IoNAGTFXjRsnvlKp3c8NFvfo0Acm2wCXDJtInG7iqFMfhA3dSRbSQi4Hz37n2GoyHbW1scn52RG01d1SnkLQLZIpA8iGK4kGstRmmUUnjr8DamhSdabHyGWElfIhuyDY5bd77k488+40ff+zF5p6CpS7wlMjc9BBGLorIsaesDsmGfbH2HiRBxgpvYxFJqlmQs9QDZW+Pdl69zdvCI3/36HygGHWbLGUjLcuH47e9+Q6uWNKJi6ua88eN3uHntLbq9NZbO88Z33+Gt775LXbasr20w2tpi0jQI5+lkBVIIWmGZL5cQAr1u/6KxSwDD6r6QivZn26w8z1k14SvfRSljYViXS8rlDFuXECxZlrM1HtMf7OJ8YDZb8IdPbnN0+JTnrl1l9/Iuy0XJ22+/w7DXo8gNTVuhc83S1nSHa6ztXEUolZKJBW2ISc+EaBsShEiBYM940K2emZBC3IREE2AF3nlH3VTM5mfRXkD34nMQzqlFiTUho5R3pQaIFSyBSKdzNhbq2uRIqZFKxqEuUFcVWWaom4aV1E7KCC46ZyHEsAFvk8xZRdBnMB7x4jDn4ZO7VO2SqprTtjUmqVY8gV6vR5F3cNaiNJwcH1CWM4L0aB1ldFoUFEUMkzG9UQSdfIs2RSqMv9W0rhhNznLw8AGqjZ9bZFliCXp6/QFmbYNZXbJsK1wweJVTKkW318U3La++8Sb7+/tMT07Z3NqkoyTV0Un0vnctMgSkdXRcTU8o5EkVJZ51RWihlhIv0721idkhYjhcFgSiDfG51CoNKBVSG1RwhMWctoqBnqsh0Co21pOhizE3XnmDzX7GZDlhEWCgDcI79h98gT96yOL0lEeP9wl5h57yDAZj6rrlxrXLrA06XN0YcWncZTxeIwjJxuYm957sY1tPuX/IcrmMwXJVQ1vXlFVFWVu6/QF5XtDtb7B16QUOD49SAFNJa1v6vR5CRFL2/uExW0/u8/33bpL5R/zm559z89Xv8tZ7P+SjX/+K6eljiq5hUdfUZc33fvJnHB/tsTibMBpscr++x3/467+lnC+Y2ZpXX73M8niPtrWEZs7P/6//g0dffMzV3cs8ebzPaLSOEB32H06YT09BndFyRrdXsD4YYVSHX//+c754/IRGxuA6IzXKOzIT2WGOCOYZZTA6Q2eG4aDPw7t3gcTcCjFUSOcd+uOt6M+fPBZDiOfq+VBMCqRQ2OSzeM5sJzXW1kXGuxSswM14nkUWr1Ey5S0k4Cqa0J0DqN47lI6p01IUab8OsFJmBEfro62L7gy5+to76Lzg8e3fUU1O0BI0MQBSyjioCsQmWSUGXU9rLvcHCO+YtxXTtqYmqZoQiDYy3r2U58FMUS0F2gW6Kp31WiaQ4eJcffGFl/nZX/wrtsfb6GSl1DU53W4X4SUmM0gZB8aH+4d4WzM53KesGq5evxHlrMRA51DPmOzPCeIReaeLdRXCWtqyRIgoKba2pWoqbj/+gq8nj6lyYn1EBF6CTE28NtFbMsQAHhqQPtA2Da6uGMuCm9k6/cYzXB8wO3rMbHrIVx/9lpt/+TPyS9epvUfmPZ48rfi73+zxeLLGg6nBjq5jrKS/uM9wWjHsZzz37nscZjlm9zov/+w/4cEv/o5XegN+NfsbAgUqNzhVsmimtE+eMNzcjIo6IZk3Hocm63UZ9/sUvYwrWcvi6Av+5uf/juliwfblHVoEbSuReQcpeyB7KJFjTMCIGYuD31Of/AL8XYIMFGuvI7feo6q7tMKCypDCIslxLMl7FQZBuZwALrFUE0C1KsZCZMxeDPuj2iECPhc5F8/gn6lKicCbDx6tY2+HuGDTQqBtI3gqlUzAUMAlgDA3GlULytrT9uL7G6mxBKR2CCyjvuJFm9NMauYhDplzLbjRyxirgAjR81GLyH40SFTyqZdBxZo3iBhA6585e9LrG5YG/z+vP8WI/TZj9ttM3P84kzZ2ZRG2MCidmJHpGsnENBSJESsTy1gkJe7qHVbEC+dcymhIgZc+DY0DqeZfWWsR904Vh6Mq2SZ438b6M8mtV2qm1nl8cOfBX1EZl7yKnwW+034qZNyvVsOAFWgplTxfR0JIpBIp/kImW7Y4HL4A/tO/VsNsDK01cRDsA8JH24fWNbS+pSwXHJ9Ef2pjDHmWo5WJxB1IastkKSHjfiJaQZ7n+DphIs4hW4szPsZn6BjGFWT0edUyWjV562jqMn5U0UU3Bq0DLpPRqjKdRauXVrFWsM4mxdgzwwIhyIsOQsVMkaYqI9NXNISmjj1Uuk5AsoxzgGZVhsb1AR6PDS2+sc8wqUm527HftG1DsG20T0oszbgHrELJItNeG01mskSKSP7CiURivUcEi/ENlCWqrpDVEnwMrpUCvK2Y1CXabyF7I4wwZPkQKxQi69DahuA8NvnaxuBKhRcCrTOUyeM6MDlBdxivb3H9+ZuUdUtTz3Gtpayi2nS5WNJWNto/Cr96MmJVJjUaicgMrYuBgZnKqT20ZYlvGkQQCBEVAiJ4gov1fIDkeAtakghoGaPBiNJa/HLBoiojON0K7OwUpSVrgwFF1mEwWqff6WOyIvo52xg8u1wuqNolTbNEKEW5qGgaUIUgT2rbc29gKZKKIKBNFykt0+nZn9yr/kmDtEJKgtI0tmFy9pD61j+SrZVc39AUoqYKgtpqctNhbXuTq9evk3VS42Qb6taTZVkKn4lJiKPxmKLoxAIxIeDb25cYjtZpraOpjrmys8V//9/9tzTlhC8e36FxcUNrXZxAKRSZ0GndxFJeBA8echMByeCiN4uVAZEphNHknR6Xr17j0ZOHnMxmKKHJM4mW64Dg5HhGr9/hlZsv0u1opAzUdUNRFNx4/jmCt7SuoWwrTGcICKzzSOD09IzTyQRlDL1+j7Mzw2gwoi5rnr/+HK4N7B8csnvpEk1Ts3+wx+7VazgEdV3jXcto0OVf/PkP+M0HH/P113fZWR/y6isvsL01ZtDrcXl7i+OTM37/8Wf8+U9+yMHBPlVVk2UZAsXB4VPatsWYLFkEQJbl5FnG2ckpSgjW18fsXNrBP/BMziZsbGyCiBtmt+hwenLK8eERRydnLKuGGzeukeWabreLyQ2z5ZzffPBbtjbXeP2N11BSsH1pBy0jWNXWLZPpnKODw2iZcHTCbLlgOltSdLtMp1PU/a956aWXUFZyqVPwl+/8kMvrO/z+8084Pp1idMns7B5BKfItRye7QiMKEJpRv8/s4B46aE5PT2jbOUZsgKixTuNFnJ7lWUZuMhZlE6WiSIRvCcKzcJLbD55SyG3Wrm5Q+4qTeYk1lkJLpIrTOx88TdvStp4seZ5FPm9KAJU6Jtf7Bi89wRQEnUW7DaWRickbRPTjkYIITKwm7ElaQyAVXPZCVoPAe0dZt2R5gRCJ7SYhzzRBKpRJkqQQOJ0tcEiq1qHznKBb1gvNxs0dur2Csm548fo6HRHwtkXKaBviAjFltjBx8usFKoFUzgq81kgRgGjBYVuPDy0new842fuayekRn909ZPDyT8h33+ZSd0kpCk5mM37/4BR3PGeweMp6V3D5xhX++T9/he+8vsPGUGPrlr/+f97n/V/9e5bTQx5+9THC1SB99PEhMgCljKBTXVdxH1Fxw8+NQRuNNoput0tVlYQqhqEMOjkEaFubfOPixDhKcX2U1EhFnhm6RYemjew65x3GKLq6iInHImBxaClpvMdKgbexmJIJZLxIKvvmhP8CrA3ngVzxJdNUPRb2JjOYTBNEhBQjXhrvf3zvC2+dyMBTia3gQMBg2EcVirJs8LWk0xsycXO66zmmaHHHE8qzU5RXCJ8SZ9Wq0FTnkr0VQ8/hwUFT1mSZYXtjk8lkEotyKWOia/rHmAzrY+O7mCxQWR6Bc6NwSqBSuItEpWIoHtIO0EKhZCwmJuWc2kfGcDfL6JgcHQRlWyfLExeHcnbFXgJpog+3WxVqItmQhBVWFz2vhYgFnfMeKQzTuuX9Tz7iuWvXuLZzGQG4xsZAAKniMyXjd6jbirNZw7C7hutdYTLZZygWWKlpnWMBtPmQjdGIF196keF//d8w7A/Yf3oH5xseP7zP4eNT7n12h+uv7dLb6FI3SyrmnJRT7j/e4/GXtzG25bXX3+K9P/9LsuEGy7rm9ucf8fDh12xvbtPpdDk5Pebrhw+xbcuPfvBj3nzz+4Qg05AyspJVkCQTREgBYjEoJzYahmiZ0DQV1Xwanxnv6eYF61tbmCJnsVxyNpmyt7/P7c9v0dYWozMGox7dXsHu7mXKsmZ2ekSnyDg7fUrRG7J+6Qo6j/L8NnAxoEpFryAkywxS4yBWvzhvfKInroMQm44gPE1bUy5rZmdnTJdnTBeHrK9t8vxzb6ZnyqX92iYvNZ/kp5GB7VJtH0uEZH0kBDrL0ZnBuQjIex/Zhc7VsfEIHh8ENjikUHFYkPYHqXTEwp2L4ZYERqMdxv11Do6ecDw5YNnMYkABIIJg0B9RVzH1d3J2QllN0x4jCMFh2xqd5fS73XSdRGoAV4F+nO8x5w1xxC3wZcNkfx9sSxs8LtjUqCoqAsNr1xltDGNthqS7s0V7csKVF15mvmxYX9/APLjPndufMbj6PC/u7FAt54SyYv70iH6RY8uWUFvmR6cUKHKRkw/WWYgFTdsgjKJtPaVsaVqBraMyw/uA0J42+SdL55A6WqoIqciDQiyaWEMIldh4ROBOgJAalWVM6orWezqdDl7Aw/v3ePLgEdnODrnOuXL9OTCG+fExuW0Z9nsMMon2gUHepbI1VV0iheLq5UscnU7YP5myLGu01vSLPPrEGs3u1jbT2YJep0tvOGI6mdIbbNLtb3B6eoR1gaUTbGxfo9e9y3QxxYfAkycH7N9/zPXru5w8uccn0wWhbXjy6Gs2xh3GvRGH+4dgDNdeeo2sP+bBndvItub06Ckfv/8Bd76+R29jTF1ZRmPN5OEey/mS1lXc/vIzHj/eY3d3g+Ga5uHDRzw5uo/wgdEwZ3t9i0uXt9FB8ctffcjXT57QosjynBBgUS4IIZDnGS0BWcfr3u9kdIucQhmW5ZKmqdNuHa1tRBD0ti6jByMa4dE6I7jYkCqlIrs1MWRI59eqoY1s7/iKliGWcl5SNzWdbicOLgI4BFbE51aKADI1V4howaNlIkQ45osFVbmMdmkhIBNbzbmoguoWHXRRYAYbbN98B9UZ8PCz31IePkLSpprC44VCBInEgnNkQnN1bYPL43XqkwnztqUN8RpIecFkEzag0sBdEOhqzabJ2en22OoPGHR6FCqjyHOMVlS+YZllvPi9H7GzuYvBoESU8coE8lZ1zfHTM0ajEZ3+AOcdhdE8eXCPyXRJpzPg0rVrrK3ntE1FUy3p5DnLcsn05AnO1hil4/OGJ/iG1lbc37/PFwf3qDJFyGQcCnkiO5KVC2by6UuMQWcjS8q3LR3g7a0rvFJss5YZfvDO6/z9gwMO53OKo6fsffopr126gdWGycLxN7+8wxdPDbenOUuzhSoC64N1Nk5bBhPBCy9cYT494fYXn7O5+zz90RiTd5nt7/H6lWvcOTuhrhZYPeHBo9/jJk955/pzNCqjM+hR1xVdM6TfMRg8dTllc73H3//bf+Czzz5la3ud4bDH8VTjQ45SY6TK8CLgcXg3Y7m4RXn2IaF5AKHBrL1IfumnLJsdQmgI1EhUZLDmAzyXcFKQkQGBpjnDtY6sk8WAI+vS8Ml/w491tUmv7NNWjOUI5LlYgwkZRQVJpmxdlHL7RPKISzWceyeDSHmxgqr1lLbFmMjKq4LgdNkwNAX9TKO8J3iHQOO94JWRYKPoclxDEIp+Jhga6IqYRO+ERKQ1HVxkznnpsU5gjMJrgeVZ1c43wdlvWx5825929eellCnz44+//pRVwp9i2J7/Hh7bQl3V9DrmvA8WSV0TgbZ4bvpg0dIQgqN1Aa30ub2Ekhf1ekgDxyQij7YrYRXeFXs9raOcGyLpRj4zrHKtTTZpkU0Zcbxwbo8BkZ0an0QZrV8AbXT6+8M52Le6HkpeBFDH4e0FIUHiECqgicOwRBA9t1dYKdECKqqyREApsNFxI4Vfx7XpnMe1gcwYyrKMDEitybP8vO5UyKia8QksTVYMTWvTnhL7hhgyJsBH1rYuVFKnAjLaHLRNg1AKWWm0TFYTJvbQSoYUMpvAeu9p2zbdX5XC9i4YkVJEVnGrDTLZdgjl4kR1JUGD1GNF5Z9M6sXgXfLHT4qe1De2icEr8LRt+pnz2BDfVngfme4B3Dk7MzKrI/tGYvIMI2IdXLcOJy3Ke2zd0MwXmOUC27Q0rSMPHulABI8SAYPHL2tCuyCoErMmyI2m1ZKsGBKkZFnX4Hy0GSIOU1Qi/USpf1Qn5nkHpTU9lXAwrWltSJ67nslkEYHn9B2CDNG+USgcyUJABYpCo0ZrIC1nk3twKpEiMa+VjN87Bcw5Z5PdAlTOE5QkBIWUhkJrXJYjCFR1Q1M2yBCYzaeczheMFiWj2iGNx3QkWbePNBl5a/9f5t7sSa7rvvP8nOVuudaOqgIKCwlA3GmaomTLHltexzHujp6HmZiJmIf5+zpmIrqj7Xa37bHkTZJtUSJFgiuIvQpVqKrMrFzvdpZ5ODcToEz1s/OBKLASmTfz3nvO7/f9fReSsmQyuUBPL9AqRskpo5HBmzqQmxwrUiUeameCKjFO6Mg1NjcvceeDB9+4Fv2bBmkloJxkMnrKpz/8f5l9/gPuxnNe2lvjnddukHa7RK0e3W6f/csHdDtdghLDUZQFOkpeWGQFcRyvJATOOYxz9Pp9Xuu/SZJoTJnjvOXs5AkH+9v88R//Ee1/7nI8GDAczyinBp0aUu0Co9EHX5PlrP5Fw/EXpbBCabb291m0Osxmc6I4opUk4ASj8ZCvvnpIHCdBllvPcO4aGxtbnA9OSJKIqjKkSUR/bZPCGOLGV0M0oQdSSsqy4vx8QL+3zu7uHmmaMR5P2NnZQgjBzZsv4Zyh1dL0ehkowb2HT5jMFmAdW5s9+r0eW9ubpGnGJ3c+49NPPqG31qfTbhMrTV0aNjY3OT97RqfXY5EvODm9h9YJp4MLJpMJ1hq63S5KKaIoJkkSrDVMJ2P29/bY3NlGaMXB1avM5jNm8zmLoiCKIjqdLmmc8vDRI7JWi9FkwvngjCIPIW6vvHqbs7MhOM+zkzPWNzaJlCRNMzrtFovFgqPDYwaDMfPZnPHogtHFjEt7ezgipIiQAobDAQ++/IIbt26TdtvYquCd6wfc3NvhX37xKV88PmaaX+DOv6TnK3q7gkpvoVyb2fiCvKyoxxc8enoSCnxpghRBhWRNSsPBVsrlS9v89JOH1EqvKPtCRzgk06rizsNnZFmb/c0ui6LGWsNGW4aET2wzdQwpnkIJalNQmQVplKLQ+LqkdsHrOI0zVJQGENY10vFmAOVpPIMa4Lfx7g5FWmODIEUALLyx+MbYvSwrLsYTNreCx63zywAPQSQ9OlEoHTGvYWRz5rWj9pLEKxIkyli8y3lpu4MTDmmbkCcao3zrmnTQEKSlhACpqIzBC6gqg/UpvUyxvrGNrUriNCHRGtdb48vPa44Hhil9FiPY3Y3o7e5y/PiCWaWIfUxbCK7vZHz/O69z+/WXePnVHdqp4PTwjM8+vMNP//6/89ln71MXU7QomzA21xiLNx6ky4KR58zZYGQeJF3eOuaTaZCUNDWvkMutRWJdTVFWYfLWsBmWU9FI65XxeBTFSFujGiamX66BMvh8FUApmtAjKVFpQqWCHGn5+Mapf+P7+ssFZvhrI3VxYconlCCOI+oqALAhdhtUpBCGlcctPrxGksTs7GwHCYqKkCqhduBMRba7xXk1Yza8wOYFcXctFE1KkSQarSOKvPp6Md0Ug5IAriw9tOo6pFojwnertF6FlgkhqE3F6ekzjDWk/T4ukTjtcdTBk1IHwDSwr/xqvX6RVVxVVXgvYynyMbqxgEikDH6JIshpl4EJcuXX1RzzkjmJZ5laHprqcH9JQrFnpeDRyTE///gjtvprKCGoiwJshWyC8KSAJE6x3jEva+JWTLb3NrPjT+nKKRLNrPbMSKlVxKKYcPT0Ieub6/xv/+f/xYMHH/Mvn/+AdtWhXsxpWc9Gp81oesZiesHjLx/w9NMhO+t73L5xi3I+o91dRycphSk5Hxxz/PAr7n74U76oCpyxIX11rUur1+XR/S+5ffstVJSFYrkBCq1zTdiiWoGewbbDYIsZ8/mCRb4A4emkLfo7O0RaMxlPOD49Z//KFX7yj/+EspZiMUdoxfrmOi/fvo2iZmNtjdH5gKI2RFmHTn+LtNVGNMBs3fgmu+Y+XjZS32T1IV747+oRqC3UzjAcXjAaD6itoZW1Wdvosbm7ySLf4ujoGGtrpNCr11iyYZw1LBYLoiim1emTJknw+3IeW5eYplnWjUecEIKiKILMt/GfC8w9izM+JPyKCCV08MhXjjhNw/ppA5CrpEY4hRaKtd4OaavLeD6msgWLxQXtVosoaYEoOTs74mJ+QRIrkAJL421mLN1OQqe7Tpb2ECJCyIg4ypBNuMjXWPks14+gaKryGmEEpTdIZ0jRWOUpXIkTNaPTU4pFjpYRFBUbvXWGF2OcijmfTDh46Sb3792nv3WJS1dvMJ6MkQJ2b75CFiWBvejgqzufsNfeYjEpuXx9j2dPN6jOD9m//hIojfWeab4gz3NmFyPOnh7i64Ko1UJFEfl8hkOiRYSUYb01VYHw9jlDxzb+14TmeVoUmPwCT/DqnownPHryhLe+820yoXh87yFSJvS7fYyr2ej3aGUpl7a32FzfZDq+4OnpCQ+PHoeGTEicEqBCHRnFMZ1OFyEkW1tbrK31qa3HyYQobTO6GJN2pvTXNjl59oyzk2PKqqbfabG7s8304RTvPYOLC/7zn/8Vf/AH32Oz3+X89IiL4WXW1jOK2Yz7J8/obl5i78o+H/zsffpr67z+1jvc/ewjRGr57u+8yRvvvsp//asf8oO//Ru2tzcpTQVKkiYxvd4mWbbByWjCwjzk0f37CFuzsd6ns57S31jjs8/v8eTwlIdHpxidrrzxpQpNomuAIWPCwBNvqG0YOl2MJzx69GQlDYbQuDutaG9u4rTGEfbNVsPwN00qdvBMXsq0ZeOxHhhVqmGcSkRTk1pGFyPwPgTONuCEThJIEoS11Iscb2oipRv2YYAUjbGBaSODp6QQYVjoRfCVVCoEs0RRHDz5soze+jrbe5f57J//ntGTL1H1AqEFSge1n3Eea6ATRdzauUJUlFzkFYV1VKYBk2wTPmI9ynn6SrHbWePq5hYvb22xE2d0RdivYqkQjhCWoyQL3UXcuEHn4GVsnKFjhVISHWcYD3lZ400I9p0vIhZFiZKCi4shdVUyHg14eviYK9evU9eGSCtqGVjprVYnMHlJKPI5Vb2gLAouBqe4yPHVky8Z1WNESwZwoAEFTaDWETx6G+WWd0RhCcY7S1YbbvW2ea23x57q0I1j1q5d5f6NA47uHFItJtz78Ofc+O7v4brb/OP7X/DjT+bcH68xba0jWh2SFBazKa3xBVE9R44HHA8ece2VV7l48phLGzvMvrxL9eQerx3s8ervvccHdz5Ga8mjL39OKTfZvHaL9Zfe5nxRkrXSZogfcTo452B/ky/v/Iy/+9sfIoB2uoYwPWypUaqDFi0wFqdLEAuq8WeUp/+EXXwJtiBav0Xv+h9Q8a0QICpEQ962hJYywqt1rFc4maK8w9cV3s+oiorIxw1YHwbsSyatWNZLzZ+68ZcK9Z5dqbaWtdCyf/Wrjpbgi+kd3of9SggaD8xQ05TWcjrNOdjsBMBRV8xrwbCwpC3QVuC9DoFGWBI8l2LFdqIQyx7HWZRYgn7Bh71stuJUaSLRbMwiyOSLGpbw6otgKr/0//wv1bwv/v55qCmr530T8Pvi7345VOybHkuQcJk1IUVgHsdx8rW635gAQqrQwDffu1+931JKvwz1MsYQraT30QqgZXlsQjR2BY0c35sgxbYBIApUyIam6QVahcJ+ef4b4RfBmjFaHau1Fi9Zffbln2LJ5m1k3DTvvww1DmHVIQtl6WO/fM0X6+7l75bX4NLvdemPGwgjIfhpec6VDODzyhd3WWsTnlsWJXVdgfdESYbFUpmSWTELfq9Vi1aaopUmSxsSkHegPUiPtTVlVa5CWou6Crk4kQ5hW87im7CuZZCaMS4wfBt1oGr2H88SNPYNuacZkPCCJ/CSYd0Av1XZ2Px4+wKrViKkauzpQm1YFqYhgLmVjYQxy3yRZQ0TuiRnA7gbepxgzxfpCKGef36zyPGzKe1iQauoENZg8GRE4dg0xFmKTzPKqNVYdQicFIHQ1mqh0oTUeYSD2XzOfDFvvP2b+8mFsE8pNEmaUVeOsgyM7zgO12ernRLFCiljBm4Ygnobe0apMryXWLegqk1jlwM6jojjCC1DTkaY1QZ1qI4i8MtBTYRzdjXMtTZcv1LmtG2vsTKwKNlY4UlNnpcMhxdsdraZjuZEUZu4LSmtIIljiGKkj4hjg8wsWkBeFAgMdV1SVGUgU8owaFGqCeFV4R5x1lDl5TeuJ/BvHKR1zlPMc8YnD5jc+wC/GDIzli++mqCc5b3vvkuWZaxvbLGzs4ezYYqglCJLM4TSLyy2biUzWIKoUkqSNMW6EC7ibc1iPuP02Rlu23LjxgHbW5sIEfHF3fs8Ox9iKYhUwe7OHkVZ4Y3BVIY4jv7V1M43fhhSKZxaW9rTAAAgAElEQVRUtNY3uHTtGrt2j+1enyzJmM4n/Oz9n3Hy9Ji9y1vs7e0wnU756t5D1tZaZO0WRTkkihUIR6/bXU3sw3YapCHn5wOECGmY54MhrVYLpcPFYRczPI4bL11hMZswGk+I44ThxYLKOA4u77PWyRpPFcHezjq8dosHDw+5uBgTxwYhK/JygI4jBqMR//CPP+aVV17h8sF17t57yGQ6RUvBpZ1LGFOTRCGcZD5fUBQLsiRlc2szePU4SxTFtDtdZrMZaZwQxxGD8wFHh0+D7Hhnm8FoQJZmJFFIjYy04sr+PveLkgsP+Tyns7XN06fHK3BYywjpJWmSMXAXpFnw5zN18L7VkabV7nL27Bmj93/GW++9x3qvRRRrUuf43TffZm/rMj+58xHD8ZCZNcRRSmtLE+t2YItayyQ3nJkUqxNKU2OEDtMvl9OWlrcP1mllMZ+kmnEZAB7ha/BhwRJxxMzW/OzuY4y+yY2dHYy5oMYgncOWOUoTJAIiMDisY9XQucph6pKyXqBVAMOdCv5iSJBOEKS9S8+gAMKK4D6Ls5a8yNFaB59lKYmiBOPBNWzBKIrY2toMEyC3TDEP+7xqQGecoS7qIEfRAmE8rjbBsyvSRDpBUSOdbcLiRGCC62XSecXsYkpdVaz1ekiC30zWbmGQLMqQPrmWttFxCy8l47xiHu0w67/CqBiyvp1RRz0ePXqK1wkWSVIsWGfEd35tj++99R5vvXmZre0U6T1ffXHEf/+vf8ZPf/zXjAZPceWEVC893sJkdxkApRtfLqkbNs7ySyBIhKw3+Po54LMsfJVWGOsoqooiL6h0hZICHUVNWIMijiLSODAjwqQb0jQhTWLiWGHqOvjZCMUgXzCqK0olsCIk6OpMIWKNq4MhfTg8v8KdnAsbtAg8nec+mS8UmLIpwLxn5WUVPkojdZMKh0XL4Kfn7PPCUAC9fp/u+hpFXaOFpJXJlYel6mVM6zl+apA16CQCFSRUIbzFr4qQVUHj/cpYPRQ0gVkQRVEApeRzTLosC4o8R0vF2fkp08kFMlKIRFMrh9CB3VH7GqwIkUIvFNovFupChHW63QrDnspZ6iooMZSURFKRV6F4iuOlfGUZniW+VoQGBqRdFZ2hYA2RRlaEgmZuaj768gveePU1bl+9gTM1+XxMp9PD2uBpFje+WIv5nNwJunu3mHS2WIxPiLxj4dqUcoNFDR/+8P9jNBhw/eUb/Mkf/S+k/Q6RkrRjQXuvy97aFiapyEdDXrr8Eq/f/h1S2SJrdel0OrS7LSpnORw+xnuJ8rDR6fPylZtsb25w9PSQ2XzCwbdukHb7XNp9mSxpU7kQlie8R4rGgsM5vK0oypLFIsd7qE2Nkoper0+/v4NSknZrjfv37vLo0UM63R6HT4/p9Te4evUq08E5b732CptbW3itmJYFtpbMFhVJu0+v3YUkxSOpmgLMeYEXAeBfFvvPQzKWzdoLzFl8wyB5EbAPAFJeLnh8+IiD61dZ31xnOBrwxePP2Vhb59rlG6SDGRcXQ7Y2d5+/toeqqgFHVeZMxmPKoqTXW6PV7oSi2GvKqg5F+ZLEsWzSVGBmy2b440wdahYfQhZkJIj08/CE5oOF68tZ8kWOVBFSJHQ7PXr9yxRmxvHxfZI0oqpryrpiPBtR2wrpNE6E9NvSGMrakMYZ+byiyjxplgS1hlCNPPGXWETer3wxpVJcufES9//5R2EwIhxSKaxQuKLi6PPPqOYF52dn5NM5SRS833JrKJ2j1etz49o1ho/vc9zSPH3wCaY2ZFmGcoJUxfTXtqi8Z+/qZWITUQpJHlku6gXp+jrRxjqV90QqYifdw1jP9GLM9vWb1MWMs/Nzbt++yacf/JRiNkNFMdIaojimLAtEM4RznmA5EqZtIATPjp9yfvKQq1evEMUxL7/8MsViytnJMUVVc/fRAzKdsDUbsd6JSaOI6WTCZDJha3ObRZ4TJSlVDQ8PD5kWJdOywiPJWi36vT46jjk5HZBmLebFgs7aOkhJlnVoecXp2QDrNReTKU8Pn9JrtRDW0ut06GYZk8UCj2e8yPnxTz/i3V97k2vXb3HztV+nqOeMT59RcUqpLKaacnE2JLI1x0XJw4dP+Nbrr/L73/9NRoMJB7du8NEv7vDV3a9IWxJvPFcPLuNsYPo/fnzGcGA4uLLDertFu9ViNJ3z5f0nfPLJV4wXNS5q41VgA7pmKCh0jMI3Q0GJEkGOXRqLXZSB0VmVDSDasF+8gyxCJRFFmYPSgRwhI+IoRhBSrWtjqOsa1Qw66irIL5drdpYGqw9vg/3K9qVLDSMsNIdJHNHKMoSOKRYLKmuDvUESgQdjXZDctjWtLMV6SNOUOEkbEEYxno6fe0mKYEdV16Gh7+wc8Opv/iEP2h1O73+KyyfIOoR8uaZ57bcyWl4xmxWMy4qpM9SElOvYQcvCRpzxyqU9vrWxxZVOn57SxKZG14bI2DBcCIgXBlgIgTzYp3f1ANNqBbWXMaRJRpSkK3uQSMD+/hWk1jx58piqXJDFEZUxxLHm+o1rDWBSY03FxeiCnd19Wq2UJEmYz8YIochabU6ePuGTT++wcGMm8QzbkaDDHuyW8u5ABGNp16RlWNtkcIcBNNfXL/HeldvsZxu0rQuAXhRx7eXrPPjsEbP5jOP7j/j8w3scRjX/fF9wxlVmUQxpB5UkIBzFaII8PWdfS87u3ePSG7fZuXbAcHjGjrEkp0d06jmnFwsivcvtt24yHI2498UhbjHl8NNPae++wixpkZucvfWUbjclS3cYnd7nL/7Lf+T42VNEnFA6TVUJapeh1BaCDpgZSeWoymPM9OdoeR9rF0S9l+jd/CNKdYN6JhAyA6HwTuFshbQCnAUyPBEVMXFckbRyitkh1pXYOsiZhQhetbZRVvlGKLIcprmln2vTn2qtV7Xosm/13hNFGu+W9kXNQE7KcB8SajKcD1Z/wnM6rzjvQ6/VZVYNMFYyWhi6nZp+nIIVoALzTQgZ/BqFC4CY9yuFlPAChaCynnkZ8mYyLUicAOmRKuKiEEwLu9xuVwPyFx+/DNq++PhVFgcveou+ONz9VSzaX/0IjPdV8DE07FW/+q69pxnOqq8NkVegsngODvsXXmVJzJIrS4MmwNU/BztffD2lJM4FxYgnWMc554ijpBmqvAA2uzDcUk0A2PJ4AbzzVGbJygwAqkQ0ap/A2g31ulz1R3ZVb4V1PIri1edQ6vnAfKlSFCLUTgFgk3ifrMh1L5IqXOOP6m0Y8MmmiBKA9Z5Wu01lakQe8jYkgAnBWVZbjLAUDRljNpvhnSCOEqTSYRghQChwTmOtpCorqsqR6yKEz0eBtawCroo1hjzPGyIZz8Otmn5C66V3b7DKeZHgIqXEuobU0XwfdV031wYNSBt69YZPE2qTxq4tKMWCt6+1Fc4EsNbbMPRY3iDeL3M0aOrG8H5FUWK9RXtLaix+NiOrK0Q9pyxzaJi6WqeBXKYjojRBJCkqydBRFJi73uGkwkADTgsSHeGkoDIVzix9fINnbqhxQyCvacB45xxVHSxDjfUoB1LEJHEPnwBIlBZEcUS+qKntIpx3v+wZCUrUOqjNlorQ2geryUhHSBlsBKVo7D9qg5QOlYaBJVqjohghFDpaUJYl1lnyYsGzZ0dETpDIGCsFPknZbK+TZD3K2iJdiY5nuDpCmAShYpSOGoKcQjgf7JY81HUYfGBDmO9iMcfU1a9cUf5Ng7QeT22nPLv3AW5xhlKEm8nCfOGJdIu1/iaX9g9QcRaSskUwl8axMlZfpiQLB14uF/HgZxIk5RXWOCIRoXTG/YdP+OrBQ/6n3/0DLl/eI4kzbt2+gccTxTFSQV2MOH7yRdhwGvmv1vprLLZwA4VmJgA6nrTXpy4XDPKcjhMkacrWzhZPHj3g9NkzsiRmOJywtr4O7OK8J2tltDtZmKSJ4Gn3/DsCGg+sJE3Jy5L5dM5kPA3pgxIuX77McDSgrkvWN9YRKub9n32MVAmX93aYjgcsxp7J8Bl7+ztc2t1lOp2CkiRZSqfbo6prRqMRvV6P119/iyePH/Hxnf/E/sFVdJRyafcydblASUWnl9HKQhjD2eCcsiro93phuqDCIlFHdfDX7fXDooRnPp1T25rBaICOArMkjjKG0yEbm+sURUFdz8haCZub6zw7eYapLf31HtYJLkYTLi7GZFnK9Owc40BFwbzcuVDEl8aQFwVp1qKuKv7pRz9ifWudW7dv0u+tI6Tk1s4227/zu3z68D53Pr3L4vgRsWuRRS2k36bb6fFsWpBbEaZ7WjQG3AZla7bbEd3EcP/xffIix64Wy+BbKZVG6AjjDcN5yS/uPiLSV3lpI8X4GX4xxZUznDdEaUaSrVFWNc6VIZClKnAWvBSUDiZFQTcRWC+oTLDeSCNBJ1Zo4QPg1oSKLUElpRRJkgRgzgegfwko+UYWCqyCNpYb9vJhnQtMyKrEuOCPqZsiUCaa2tWUpg4JtTLIQcLUqCKOErQWVHmBJ6RjWmeZzudIIciyDG0dSsUYYJrnYC2ddpvKCI6nNR/cO+f+uaK9cYv1nW2mgwHeVEgR0VUFO23L926/zB/9xh7XDlLamWQ2rfnxjz/kr//iz/nko5+Q5wOEqNE6TIadDUmZy2LAe4+OdVgrmo1FiiBb9/hV8+WhCfgBJ0LwhatrnA3PUUoFS5BG7hHAAIWSCiUafy/vmjRrTbfVItKSBY58vsAgGRsTpO3eBy8r4TFaQBZBXoZQrcanK0iGWBUEwYP4eaDCiuEvQiBB+DkMAIwNaZ2rQsoLlAjrmjM0lgiiKWgEQiuKssKYGmkd6zs7VA5OWhHZWofJ6QRfWOIkIU4inAq2A9ZbQi/5nC21YiwEIjFSPJfoSdmY8NOAQ05Q5wUYg04jZtMxVVWgZIRvwNkkiumudZkv5oEU3IBhyyZ6WRwsi1IpJWmaMp5MWPq2mbpJiSX8zJJF+EtMi+VrrQrK1WsvP1dzXhp6shWCw+E5//TRh2ysrxNFmqIuiW0dwjArw3wxp93t47xnUZbErZT00m0uhg9p+ZKZbWGiNipqEamI4dETZuePEYsTXnnjOmt+SDsuWbvex9uc2XTKO1c3qBCcn9ylsCHALuv0qL3nyy/vUswXbPQ2eOeNd3n3ne/S+s3fR0jN4GLAcPCMbL2NVAlbG1cIkR8OKTxOhLWtqAry2YwqX6CiiChOaHU6ZFkLGacIqfji0485Pjzk5s03+eD99xHC8fprb9DpdclSzauvfYvR2Qbe1lxMRsRJQhLFiHaLOOtROUUtdWAxC6ApyHxzbbimOxWNtcvz87TclxtfLwThIvylhsxBmiS02hm9Xtj7/p//9B/57PFHrHd7/B//4f9mb+caZ8fHbG7ssvTmXTWNLrBRvPPUVc5wUPDJx0eoOOGNt94BgtxrCbZ+jWViTMPmDOnHAFJrjAhBlEonOBcCQKyzhARbhfeC51WBBq/ROqUdR+zt3mAwOMHWCyaTAUU5w2MoqxDsZSEwU4wHA19+/hVbv/USKk6xhEAMpRS1qb/eqK6udQdacvvdd3j8d3+NPTtEC4Pzls76NnJjndJ4Mp3RkglRFApTogRtLK4qMUXFvcE5QsDjX3yIt46WjsmFRDmPkhGDtEPhJWs7O8SqhULx8M4p08ERrU7G6PAJRVVDp41utRgvSoSOuLK/T7vVYZI/oTCW0gYQywtBnHWIbQiFeu6/FxpFraPAmlGaXr+PrzfodDukWYaKNLdu3ebw4UOydotvf++7nD1+TCcK1kzeh0HLw0dPKGuHqS2VA6G7tFvbjGanRFGExlHkOdPpnCK2GCfJraK1vkvaW+PJ0TEVYzY3dzj6/AtGkxl1MwSfjs4pFjnOWg729rn3+FEI73Gew6fnFMUHoHu8XkicTRFxn9e/e5u03+HOP/+Y4/sPWMwLdrZ2qec5b3/3e2jdYzA44sa1G+STGWutFms7mxw9fkgnbXPj2g0ePX6GLbc5G5yy3s0wteHewyPufPGAaVFjkZBkK4YYQnyNIOEcKBUjlG8UmEH27gjPU8uQFsJAz1tHnMS0WilVXeJNHQagXuAbb9Ov1SfSYYxvfO3BWIsrzGrtFzJc05GOsdYEdpR1TMdjJhdjsjQEnNjG03E6m4YGV8rw/CbQ0zpHni8wxtJf22RjY4OLwRCPW60zcRQ3A3BNVceodp9rr38bFaWcfP4hLh/jfXifRCu2el2ks8yqgqEtKYRHWYeynstxyht7e7y+f4UrWYd+bYlqi8+rcKw+yNMDI69hsUmN67XpXr+BX+tRiSAzTrKMJOuiohhkkCzHKtQKVV1x5fJlpHAkWmJNxWh4wXg8YfdAkrXbmDpmbd2TZVmAYaQmy7qolmQ8HtBp9Xjjtbf48Ud/S+nKQFRRYQ0OEthmr/QNi00sQ54E1oKoNW9cf51/9+7vcpCuM3zymHp8hrAFykn2Dy7T3ejzbDhDnQ35u7/6ewZX/5T7xSYnpYQ0C/uSsZhYELfbdEVMG43wsL6/y+Vr19iYFZz8w49IZkOwBb31ffKowyd3PiZNFb/9R7/HYuQ4Hk14+uguyfVXkS1BFGucmZPIkr/9mz/js88/4uqNqyjdYrGwLMqaynuI2ngd4aoT3GxImT/C+sd4tyDuXWP9+h9SpLfIp5oEi9AKnEaoGBBYJwCH9B6EwgiBVDvEWYmtC3w5aBLd/UoOL8ULYXvqudXH0gLENV6nbsmy80vGXRNIKYK0GOcbe6nnNQ4+9NVKheE9HuYWHk4K3txaI0tjyrklrx1HwxyxmbKepigrKKvgCy9UyN7AisBw9w5hATwVMCsti9KhIoWUwRRD6piahIfjGRMTWPbWP2e5fpMtwYt1mviluu2bngN8rR588fE/AmhffL4n1K1hzQvWYDqKVoqZpQXLkuyy+nc+qLPC2hcUSWJVrzx/jxBYXDUli1+pDfRSPdCAf0ugL1jBeIxpFGsEYDEwL5+Dn1IIhDcI8Vyuv/xuLM+Zx8vj0DKEUiOe2zhY75DB5OD59+lDLxGOU3yNyLb8MyyVspHn+9XnWNZoq3PUXH+rHq2xG3BLi7GGhNHptNFasVgsArBpHbay1KqiFWeoJkfCeouxgTxjnUH5aEXAEV4gIh+YmSrUW8YIqiq8h9aSNE2CXL/dJkszjAk1mTWBseqr8FrL+3N5jEtSivNL398Qcuabz25MYIcGJmgYXIS42hCe5axvAF5HXdU4VxPyLAJ4bU2wGcDThCwvhy9BSSwQDRGppi5yXJmjK0NUFvjFhMV8ArVBOoFEobVFNgz2cPyKyAs6XlFZT2k8eWWpfPDJF1JidchfkQQTDduoY71v2KtILi4umC0MIIliRae/QZRGxHGoEVgOjEQI2NOxRClPvqgwpvGlds+9dQP12SC8C5iPcJRF8K1XKgoDAe9I0oR2ux2O01isdeSmROqAiXS7HZIspigKxqMLSueYzy54amqEcGznEwpjabV77F+5xlqUUBQleeYZK8GiqCmNxPjAftYahFTB+tCEHhIZPqP1ISBb/g+g2H/bIK23uPKUxdGnSLdANpOgSCc4YiBmfW2HrNWnqGpMbYmiABzN53M21zeb1/FBQuxDurBYLSqNrICAtGuVsL2zzubOA46OH5CmCVGSIWRE1MgLolghUERqE6VaFLMz2mm8Ar+MMc0G6BFCB5ZROIrGKzQKbAIdMVsUDM7GbG6u89LNa9RFydnpEKFijPGcng5x3nL1YI8kSQMjzgVJl3OWJEnBB7lXu9vDHj3D1GGyE+uItfUes9mUw8MnZFnK3t4+0+mE2eyUS9vb3Lhxg7WNPmWec/eLLxkOBjx+/Jgka7F7+QqLsqCdZAzPztnbv0yZlzy4/5D5zjaXr1xleDHj/Z99xPUbN+h2uly/fp3ZxZBYhyCGosiZTCdkWUoURVR1hS9DcMOjB4/Y3NwkimP29i6RJgmXdncCYH10RFXVDEdjBvWIVtYBHyTP1hrSRJPt7DCf5xweHfHw8IjDpyfEUYgd7/f6lHVNVVdIIakqHbz3mjY2y2LWOh363S6HT485fHjIYrrg1ddfJYpSpE5Yk5LvfetbXN24xJ2PvsCPHtFrp+hpl/VLV4mF4MnhKWf4cINZjxWQSLixt8l4MuLO/YfkajMsys3CERwwBcaGkAkEDCclH965x/o7V9neENjpBG8mVFVJUWiUCgxG50rK6ZRCxei0i4x7GNnCxYKZVVReUNXgrSdrAKJuolBhTQDncV42vbVHN4zAgC4ExCNseL6Z8obmaTmND3tmEywmJFZIKieopUb4EMIjGh8/JQUQUVQVWRKATWMtSqsQpmVCk6PjiDRL6Ha7jYwmyEQCONxII6WmcJ5qMuPTu4+5ezJnkexwcPMVvC24fzTClhWZm7HVjXhtR/G9N/f5rTd32NuUlM5z/94JP/q7n/CX/+2/MDp+ADZH+8D4NXUNxoEN8iBE+J6CVYGnNnVI2ZZyBcYKQjqna/5SGbMa0lRV1didBAN/T9iYwv7/fD2ItMb7JmxMiJUvVBrHYGtirYjjiIvpnIWCSojwvTfAko81cb9DMS2gDOdtNb9ufpAh9Wu1Dj4vjJaFpcf7ZZPrETLIOZcgrW8m5FI0FgNNcyWcwMkQ7lXNQnJ2ohOEVxRlTpHVVKrAmJy8mKM6iiSLmVchGE8qiXBNMSmbMLBm+uy9Q7hg754XOfP5PKytMjQS3gjKOoCBaRQjnMfZGtGwAZbfQb/TZXtrh7PzU4ypm1C3rzMXngMHYap5fHzcrN0B5Au+bO65fJavMzVEw3L/2mt5RxxFOBe8Eq0Jxy1Vw+ZtAIkc+OCTT7h+aZ/Xb1zn2fEzZtM53f46rVaPvCjRcYGOJGVdMq1brO3/GqMn9ymGnzGxCaVWXNo/4N3f+C1+2Eo4OfqIvdaYzuITdlsVnS0NlHhgJAv29tocHT9gOD9CRWtUcYfx5IxngwXPHh/TlSnbO7s4M+NiNiLpbeKEZm13n7WdPbwCj0YSUZgFpiwo5gvqqsBWFVoJslaL9c0tkrTFYDikslBOZsxmp7x06ybOVJwdH5LqFvtbO1y+epl2OyNKJIv5lMngjCjSJFkCQmAqw2w8ZDGfs//SbSqV4l3wGpMNAxu/lMqFQJUgz3/e4HyzTPF5k/Li76SQRFrT63Y5Pzun1W1xfnHGuB5STS44Hhxx68abnJ6csCgKsqzV+OeJZin1xCoh7cQ4b8PaQU2mIurFBNck0AfvU0Fd16tGJ7x/UBNYY6jrCh3F+CYIQes0DAyMwTiD9AFg0UmMlNFqoOR9YFtIrdAqwxko8xmzyQgpLHXDYBABlyXPcyKn6GRttjev0eutrUIOhPj6AOLF4QZLOxg8my9d4+Xf/i6P//yUrYZR1N7c4NU//VNOCoMsLa9Iwf07H/D4wX3e+Z3vo3TK7OyMD3/yE64eXMYCcdLmYjCgoyJEVWKKAlEZqCH2Gr1w5PmI/b3LlEagvGIyGsNoiBaC/KlhZiydrU1mec7Rxz8nTVKc0nxha0xZo0UEMkbqiKTlCBnIIZRUCA/CrVg9QimUDk1dFEckrZRFkfP06SEo2Njd5s133ubi6JjJs2fUsxlFWQdbo0VO/ugQ7xKSdp+Nzav01y6j0vvMq4KyLpnpKZPplMl4hvECPZiwn23QbW0St3O+uHuX/VnOfDFHxzU6igNwNjijMoY0y9ja2CTPC56cnVA1acLDwYB/+OEPsCbi3W+/hyJHpy1eu/E2b36ny0u33uTh/bvcf/yAVMEnv/iMs509It3m9OgUakuqNJlKuX3rFaR1jIdD1rsxndvXycsD3v/gQ+58eT8wZ2WCTts4IQgjA9vUxSCafW/JXI+0Ripwrm48q8VzAEjrVTMbmmlPFCVkrTZJdy0A8aaRgq/AlwBILMPfaJh6chke3LAwy9pg8cTWoaOYujYU85yQFB3A0kU+QTRDFASrgJ+lR+JzKXnjce0gTlLm8xhrakxdIpdWCJEiS9OgaLNhbRJJm72XXkF6ePr5h9j5EOkdmZRsZW0wNZPFjIWvscazKSJe39vlNy5f40a3T+YtYr5A1FXwb3Q+SEE9yEZtZb2j8FCvrbH2a29hdrYofGAo9TtdsnYP2TTtWoZA4dJCHGvqqqbMp1hTkiYR0+mUl2/fDpYzcfAWDuzhGJAUZQX44EGNIIo0adLizTffw6SeH/zirxDFFJE1AK0UTdq4XWIiDUYbgEFfSQ7WDvh37/17Xt9/hbaM6el1ntz7ADMZYJwl67S4fPWAj88fMDcldnjOYbvk1Cl82sJrDSrBN8Vv1t2iFffxE8t6J2F09ysuqpLzR4fEDx5xScCs3WH/N/6Q0cFNeDjmwf2fsdbu8sa7b3Ewhp9+9gWdzV22dm9glUErw0/+5s/467/8zyxMzf/6/X9PXHt+/I8fMp/USJ0iOxorFpSLh1SL+yDGeOFQyVXW9/4En7zBfBJ8sp3yeFEjpcF7F0LhpACR4RxIapyMqP02CkfammFsDm7ekHd8SFZfgmnNnvYieQhCENhKyt7kIIgGVLTeNeHXyzU/XPdSBE95ax122dNKARZKLzhelFzKF1xaW0OIKdNpwbBwLJ5dcKUXc6mTEGtNbRzI4KnphVr1xc57amuZGFgUoeaXSiKExUuBj2OOpxV35yWzxiLkX+/nXwdMfxmQ/aaffxXr9mvA6wv18q9i6H7934FtvsM4jtEN41OGIAZeEN6s8AdN4wErQk0Z/RKRgOa8OhdAJ+eWVjxhgIpsQF6lVscgBCvSg16qDzx4axuLKktdGxrYbmU/B6CjqLG3CEqHF4kdWuvV+7iGSSmVQrrmMzrXsEkbGzupVuqz5fe3tGZ4ccAW6agBbJe9SqPsa86RaobhWZZhjAlgdbigqeuaqqqoTb1iLGdphnOWoipxGCpXU7iKyEWkxJim35NxHPVXTaQAACAASURBVJQzNsjq67IIvXIVZOgyiptrMSxWqrHtWaoz0jRF65isla7uq7IMGBQ+9FTOBaZwbUzoCVeAfQBpEcHiTCyHBE0WiPVhcCOQTbiba74PiZCNErEBYoMKzCHVknTU7DlNlkhV1SgtgzrSVpi6gCpHVQXRokCXC0w+Q9aWyISerNYWY0oSD7IZ4uFprP1M6NO8DWpc4/GuDju/CIok24TVsbyHCPdFt7XO+toOpfGUZUlRlKhkAVI0NpmSOBa0XUxVOYxxzYDChXtLqGD/RcCEyrIkX+TUVbmyGPFS4EVEXYfzXNc1dV2xKBbkZbnqPa1zlGWFVlFQ2CvQSJJEs9ZdI1YJlhLvPY+fPmI4nTIaThhPxlyML9i7fEC/v0aSddnYzuj0d4izlOn0BDM1jcVkqCEjEd5vec5F5IheUN9/0+PfNEgr8AzvfUh+fh9shW5YWN4JnBJ4LciyPs5qyrwI5v4uALllUQT5uVj6wDTTLRcuZmuD1OJ5kIjEupC6fuvWTbZ3NkizDoEBGBY5aFhpQKxTOp01zo/uk0U9pIgCE06IsNB5j5MBlFoybYQgTB8JZt9ZuwXek09HbG9s0W63GY1GpFlKq93B48iLmsdPjtne3qTdblM3tEylI/CCxWzGYlHw7OSc6aRJmSsKLl+/RJIpnjw5Zji4QEnBydEJRVEFkM1a6nyOKxOySPHrv/YG80XO2fmQBw8POT09w2N57/tvMb2YkaUt3nj1Jvcf73J+eobwlpdv3uDZaMz5aEpydMx8PubypS2QEXlZscjnJElMK2thrGMwGiOFoN1uYz08Pjyi1WpRm5pWGpNmKUhNGkfksxmzyYRXvvUqm1ubCOkZjS8YDC+YzxYMhqf0umsYLylKw2xR0G5l3L/3CCUV3V4XC2xvbRJHCZFKQFZIgpQ0SWNeee0mv/7ua3z88Rf84s7nfPCzXxBlLbJWh5dvXkMYy06vz/d/4x2Gh6fkozP847t0N9cw0tBxFRcqJQ9XBtIZWrHiYHeL8+EF81qEcCFTsJlJttb63DseUjqPVxYpTANEljyb5Pz8i4qt13fpKbDCIHHUeY4t5kglsPWcs7NDehv7rPfWyL2hUj2IUoyI8TQyCQSFccxqT5ZGCOlRPjSeyzvLmsDukVqBCJJWCOSXIDFcStqXI19W4JV1LjCMjKRCN8Chx9RVk2gaJPaxVihJEwISFk6Fx5QzqqJAxTFCxjgkmJKymJNmbXzg5yEaSU1ZFjx89ICz02OenlxgZUp3t0s1WTCcT7DTKUk1ZqtV8JsvX+OPv3PA2y+nbHclRV7yLz/5lL/487/h7ucfMhk/RfkcR05VLairqmm0moJsyfh1oRCtyxp88CLFg8jLMEWNM6JIIbzBCYm3lrIowYsmvXjJOggTzCgKMqKlzUqYmktKU5MXOcKH1GSJZzybY2rDWqcNOmKCpW7ODwRJDs4hnEC1W0T9DtXZxcqu4UVwKhQJQRoVWBYySPGtbUDHJllVeJa9bRgqNAVnM7FHeJR8HirmAZ1mRJ02xtkABEUpp+MxuS9Yu9yjdDl5nVObCqkzposCVGherTU4HLFOSHREWQUXslgrbJNX5lwYaSyDC/ACJxxagJkW+NIgYo2p6gCEiuCZpKOIAsdofMFkPibJUpZAEp5/pXh40W9MKUXIUpIrYD3WEXGSkOfzVXCAb4opKUIjJV8AcJVQaK0DC9e8IBlsUnYDsB98DkeLnA8/+4yr29sIB6PzIZevXKfb3+J8MKTIC7JWC1MHDyrb2iDducXw7ITCdUCtsb6xwcbOBt/+7e+yOOvSsg/oZWOqekyqWzgnMHVNpiFRhn7L0m87oixnWFvqjQMy+hSDnP2NffYPDtja3SdOWnhCQ+28QXoJFuoyZzqfUdQFiY6I05Rud5ssjkB4JpMxOooZjKd8/PHHxMKTJQmzWc7+5R22L+3w3e9+h73NHRyCyhouBqeoOAoNQLtFVZbMC4OKE5JOn7XeGu7kKUIE9rlpzoFxYSCiVonty6J1GZIhAzAiAvi/tNhYss3kqsB94Rz6cK1trm1xdPKU3d1L/M+//yd0P2yxtbHJ26+/RxJntNo9xpMJrXYbZ5v3pQH5JAgdE0lBkrV55Y23VunUWnic9Fhn8DYKSdZL2wxoPOxCIExe5CSNvJC4tRqUeReu5cBockRKI6SGZu2x1mCqGl/V1HaGkI7pbEpR5wgVUo1Vk07r6hqtNe0oQ2vJpZ1tpPCIpjlvrviwPnrfgJeiuZJVuC8lGCW4/u3vcPbhL6iOD9lsxUhXkbRaCG2ptMXXNXWcUCcJ2c4W3c1LWBS+22f3tTcorGfjygF7i4J+kmCKBRJJMZ5QLHK2NneoRxd88g//Qm97k+TqBgfpexitcPmcp3c/p1WVzE6Peft3/4AHj57w9PAhSvggXcPhkxQtE6KNTaoiDwFJ6+tBjhba1eCb6W0I65Rh3R6NLljfXCPrdalNzWAwYDweEZ1EXN67RHu9R57PidKMXqfH4HzA8bMTkDVClLRFUB60+2u8+vbbDEYj7j+4T6ZjTNTCzxcYU9PurXMyGDKYzRmdn1LO5ox4isNTYynmExaTCVmaIU3w3Da14eWXXqa0lqPTY2jOzsV0wk/+8a8Znx+ztbHO3tUz6tLQ7XXwtqacLrh/73P2djao6opHhyd8+93f5ODaq7jacXZyxrOjp6xvbZClMd1+Fyk1ReH46Yfv87NP7jIvLV4lyCTDKdWAl3K1ji6T2JES19wlAS0IP7vmZ2MDsGuMae5PgXeBhVWVJbPpmKzVC/enbDy+XRjUaKUDwNuwkkzDaPJ1RaQiVDO4UcI3qpVwLwopQ4OOQzdMaufDwK6yTcBfI4PUy8Z4uZ7jMc6iVESSRJRljsAHbzyt0DIiVjGRirG2QMrAkFc6IYu36L32Lqlq8fjzD7AXJ6QCelFMNZ0zrwpi49hMWnzv5W/xxs4e/bomWUyJXLCUCqy4sFlGuqGDiOZuFQITZyRXryKvXKaUkspDJAQkMV7oRhYaLEu8XMqQHWcnh/gqZ3d/j6os2b20z/WbryB0Sm1pAAbVDAMgihVVWYU1UHranR5J2qY2NTdvvMasnDP49AcMFhPqWOKswOEAGzy9vUM3AyNfwY2tm/yH3/7f2WtfZnRygWt36a/tcu3lN3j6xYeU0xHomO3dS9Tii2CpNB8wHI/xazcgVgjiEEikQxigF6ClJiYKDfx8jhyPKM5Oyc+HJGsbdF95k+jGmxzNLJ2dWwx+/CP+4fGPefzlCS/deI1OneDPT4mu7dLfyHh8933+6i//G4u5QcQtPrrzFetJRJy0kaki7eyB1rjqApEOqMsB1A6Z7NDeeg8TfYv5WCGd4f+n7s2e5Mru+87PWe6WNzNrL1QVgAbQ6H0jRWqlbdkOeWTrxR5rnibmHxzHPMxMKDxepBnLlCmJFCWKbDaJ7kZjL6D2qlzvdpZ5OOdmoVvUhB811dGB7kJW1a2b557z+31/30WJkEJuXPD5FFhwFi0DoON9ASb4uFoxpPEduB3Q52CasF+LsPaVUqikt1+L1iLOrvrgcA5GQpeMQVarvZ3YBwS5vDU2ArThL5Tqg6dAOIlzBqkE89bw4GxOcTBifWOE8I7loqFtLEfnS7q6Y5gppAAlLLpn6gpJbRytDUDM0gXliFICqQX4BJTiykkezBZcOY/tz/kVI/XvZ8f+KlbsN4Hcb9od/CoQ9+vEhr/7fViV3aFmbOoGO0xWQeOhhL5W2/RA7bV1UcANVtdFULl5D6hQt8sIiioVEu1VzEB5fVgafn4/sA5DL+vDNRkbQkutczFELO7PiGgdEMkEWpMoFfZSiFYIAUfJszyQKiIILXUEGfFYLNa0sSoQq31I0g+iAygfhl3By1UpHa8j+HNbG1i9XdxbPD6EdglBohMQrALtehykquoI3EmcEHTOYttAvvE+9MPOh0FI1zRUIhBKVJZhnMQ4h45DAefDM2NNGxjf3tD6ZsVG7TMWEJK6qZnNZ2itSJKMLIakSxnqt8FggBCCNAnf2xhD27TUdU1VN1gTQHJr/cpqUqkQNiZiz40H58I6C+S80Mc7G5Sf3ptQjxGDw0RYB9b2fs+BdR67DlzwvaNtl7j5jLxrEXWF6Bw+DsN9FywXNQLtdAhH9h1JpiI5KQ1WVgQ7v0amuMwjnMPFfscR9zKiAlVFCw0PUmfkZUmW52ghKNdKpBR01gWy5QSKQpOngjSRDIdh/15WnnbpsV4hkgxECeaK1FRIY5jbMGjQfaC2SkmyPNq2xFwT7wPZyMuQLwN0pkUJsF6wrJd0XReJSZo0U7RtVJlJT9tWTGYXdLZjMjvl7OSQvf3brG9ss7mzT1mukaYZtu2wkVTorAsAd7S8cMYgs2vWdt/l/n0f/6BBWi0cYnGEb8+R0gbKtwh40tp4SJ4VFIMhECniUqB1CALw9oqj42N2d3aJvLcVHR4RgQkf/FSUE6uNrfOO0WidLA9+d564KfTgRKDtgJLs7d/m8ugJVT0nyQLAIqXCi5418PUNX0qFt44syUOwE1COE4ZlwXJywWI2YffGHt52lGWBQ7C2sc5iOePl0RlN9Yz5smJjY4PtzU2s6VgsZugkR6mUug4bwPbmNltbW2jteKXPsE6wt7NL29YImbCxsY5zluPjI5quDimGiWY4Krl184D9gwOePXvBs2dP+eUvPmM4XOfTz37J22/fpxyN2N8/IMs00/mc99+6z4/++rPgQSs9iZRsbm6SpimdDYqzxWJJVdVkWUaeaoo8Y29vj7qquLq64sXhIffu3GJ2MiMbBC/Fi7MLhHW09ZLz08AW2VhbI0lSXrljLq8ky6pmf++Ao+MzirxgZ2eH5bJjPBoxXy64ms0QKqGqDAjN+sY21rQs50suzs95+OVD3nv3LT759ifkww1+9ukDqqqlnsxpJjNOL59QW8HdW3coTYeqK2YPH3A5TMjf/IA0S9GdRxGTGI1nnBUM0pSXR6/osHjXIJsZt3c2+Y2P7nF1ecGrZR1YPLggH3cN1nU8fDZBzF/xT97bYT1NUYlG2Yaz0yPKskALz7hcY1gOyfIRdadxVuNtF8A4lSBFOPi8TGid4WLeUKSaUZYgabGuRYZYcMDhnQAVgdgoZegDCELzEhiywQPHxecNIPjINVaumKBt25LSy8mDxQeEQ8r6KGvCcXl1QaIVxbCMz12HdWEKmsWDxZqGJM3xMuXwcM5/+4sfkoqOnfUNFvMTpqcF0itq06IWR9zf9Pzhv/iYb394wL0DxcZAcHFywf/5f/xn/v0f/1fOjp7i3BzbLXBmSdsGzxnhehJtlHslSbQxIBYRMizi+Py6PjFTBoPxIDeOe0IEAAVhGNMfjGkagtfClDcUR70fmHMuhIzohGExojMt9XIJQrBoDC8uJyyQeNEHv0XGqVSY1oJWlHvbuGWDnVeR8ixCY9wXlj0LTlwPmXit8IT+vAgeY6EIC8U+keUkpMDp6CNjLV5a8jxhe3MbZ4NqQKdDWmuoOsPmeINF1dBOFiRCB7N0Y0lk8ARK88HK3D8ElgUpadVUgEB6eT15Xa240ERLJxCNQXow3tHaKN+SkmSQY4QjLTJQILTA2MhydtdhUv0Uv2dFvS6himV0tLBRYeK+rPBEz6V4z3rP3yCn6ZnHMUSpuQ4o6wv/VbrtawyNxlt+/vgh924e8L1Pvs3pyQmt80znU4T0NG1LXhSkWU7VtFQ6ZXznIx4/+JypKVDlGsPxiPPzEx4//ZyhP2KYTfCuBm85OT1jWG4gheLiYkaaabSCctQhVYOSCWQ3+OAf/w+8//ZvUxvHYK1gfXOX8XArnnue+dUly+UcKaIkqByyk2+AsByfnXF1dc6rp4ekaYLHsrO7z9buPpmWpDjGZc7m2piuWpBKRTpaZ1ktGQxKBnlO2xmWTUNrDMVwyHBrhywLZyAIlvNZxFJV2LMAIhuEHliLzDope5EVcX8Bohd3z9LoqSH9uU7PPokeX0JAOSgp8pzFfM7v/s4/59d/7Tex1lAvDc+fPaGu54xHm3Ey3lNABEIFTz9L8ByTPiY3K7BtS7WckReSpjMoH57l0CxJlEqwPjCShYRltaRpJa1xJNmIoozMVX8tXeysJ80G4B3WxMIv+pA1dUXVTnCuo24WSCnQaY6M6geXwGCgcNaQ64TRaJM0K6ibmlQNVgWic/a6qPSsGgPlY2MsBT7L2HrnPT78g3/Nl//uf8XZGdPTV3z6/T9h4/67LCZLUqlZyzNmJ6948MMfkI+3OHt1wuTqhK5bkG9sIHSHEw2TaolzBp0VDG5vkzjPvDEYm3BUT6kffsG3/83vMXzjJkakdFWFuPsG1dExlw8fcOPDj3G7N7n9m7/FaFxycviStdGQoxfP6EzF2t42Tz7/Cl+M2Xvzbnj2vbqWIcTnPLy/GVoVLBcNx0enOOt448497r55l9lsSprmLCYzDk9PSZRm69YBH92/y8HF1coy5+pyyuMnh+zdv8ft+2/yyy++5LOnzyk21kiHMG47tBZMFwuarkEnkrfeuMn8ouDoxXMQgqIcIp1jczTC2Dyey0GdVC+X5DpBSx2DDoPc8WJ6yV/8+AeURcnNGzdYXJ5w++AW8+WC1jS8efceaaK4ffsuxycX/PCvfsQ7b71FpjJu3rrHdD7jyy+fMR4UbK9v8vzohF8+esrPvnjEojGkeRnAqPhMhoGHisOOaM8j+zr6GtyU8TkTPgRqGC/wXQw+UuGZ7myHl57xeBOV5MxmC7xISPoQJEK6tRA+1CGEr++9/aSQtLZBSEUqA0N+oAsIPE5kIklUHrxro/VPazqsUljbxXR7iUwCeywlDUFoMvh2eyFRSUaiUrquJUvTGHpDYK4JhZvPiUmYmC4QBRKpEGnO/rsfUq6v8eynf46YndAKx3y5RHp4d2OP373/Ph9u3UBWFX65RHahhpBIrAgE4URppEwwAeXBCsESyO/dY/jOeyyzEi+gLIsVe1aqcH0hGMojnUAliq6pEDGMJc8HeBSvjs8Ynp5Trq0jdB4m+SY8Jl3XUsicpK97nMHYoBbrbIcSig/uvc/CL/jjL/+SY1vjdQDrEB5roTPBX9G1lp1in//59/8Xfv2t72FnHTar0CIkhp9cLJDZED+/QgjP9u42Kk24qmaI7gprpsAiqNa0B5UH21sR9uWubZAJ6ALSxLOlU84EPPU1bObc/8e/wzESORhz953v8sX+j/jqL79PdfKY5z+5YHfnPuNpxu2bG9gk40/+6H/nq4cPUXqA9xmvnp8zzzJ2D+7y0Ztv8ei45smrLxCcoJITvKgQcp3B5reQ6SdMF0OsFUgZQmZEJBXZyIrz4vXgqwB2iZiX4MwS4SqwAWAIuRMysNMjCacfDr/uLypEAHD6wCgfg55WNZLwYMOgcBVAxvWZ0wOZpq+JVfDr91JwXnf87PCK926ssT0eBKZm62ms4HjRMW06tBKkKjicy+hhGuxnBFJqGgUKjRCOVEmshaPW8HTS8KzqMFKumL4rTVpPKPkGWPvfw3p9Hcz95tf+fV//TeB29TVAzycQ8d7gBZ0PwYbC9aC4Wr0+EARC/WitQerooU84y1c/B7t6fbjvikQnJFqH84kAjEp1fT3OOUx/NkeAz/lQa+c6QfjAfl+RyPr3WQpk/3tISSKuVT7BLqMPabR4KdFC0DQNTVNjvcUBiZQrAkOiEtIkwzkT9lSC/WTYd0JNIaXCd21YByqAgX2oolYKby11XUfAMEwY0mj/KJJrP1npNcoaWhdUDwFsCwNpLXW0IqiZL0O9JSQo5SjSHBF/btjHHJ3rkCrYutnXmNtd1+ERaKWQSlHXnjRtMV1LXQWANfjWBiC9SzPW1tbY3FyPRB3DYjGjWtbMF0tm0wVt2+GUxLmo9u57FBmCjGWgzIbWzvlV8HbfIa2e8XgGXPd8LlotXPd1Xd1BU5Eua9JqycAY0qaDxQLRNtB1aByZlyReoJIE6cP51QP7gyLH5AWzNGWRJkEhgQ0DVxcG/D44EiBlulqjvVF2qFEMnQt1udIKlRSkaYpMwhqbTrrIQBcoHUiUTRvD0Tx4HwbUw/E6ViuOH1U09Tza9SlcDFtTMlgoeu9DQK9zFFkRBreAo8C6UEdLEUJ8PYK26eh8S1HmuKUL56VWeG9pmjnSdlyeC7A1s6sTDg8fkxclWic4U7FczLA21MumbalNF3twj1maEIjmPUL+XTvJ1z/+QYO0whquDr8CG7xMLQKvBGkhefete9y/d5/hcIRXGh+nEUoqqmXNxcUl6xvrOH/90K0mOXEKI2RgpEgZFgWEzco6gVI5xvYyrLjxAdchGgolc8rRJi+eHTPAUeph2PDoPZb6psb3Iz8UKuZRhA1RphKBIpeSzsPF9Ip6ehVYiKlispyyfWOXvds3sXXD48dPmE4muBiE1XUtSZbStGEynRcpW1trXF5cUNULQDAYDCjLAWtrI/JygLWWxXzO1s42i+WCs8srmrqmLHMO9vc42L/Fe++8xf7eDp9/+ZAvv3zI+uY2Xz5+Stt2bK2vcffOPnmW8Pa9uxwdXaATxb27d6kWM07PLkjTnLppqJsaJUDLkJ472tpYSdunkwlJklCUBctlzWw6RSwauq7jxeFLynLEfDHHL8KdvKVus7e3izUdR0dHTCYTZiyZTafs7W2jlWJ7OwC51jvOr6acnV1SL2vG4yEbw2Ew2Sf4+7ZNy7Nnh8gs56vHT5gvF6RpgfBwdTmlqyqMMUyOTkkWUEYW6MnPf8JGVlBmI2hsCH/Q4X0flilXyzknl+cICnANWwPB3ppiefkSzBItMzwiJrKCkC3ag1WaZ5M5nz4+4dffvMHu+pDRBsyXc7zp8G1IlXS24/zsHIpNppenmKZhONoiKcc4oteNzABN5Tx1FZqGtVyxmJ6HSV+SxmlbgpYhWEzEoJTX5VJ9qEM/wcTHRFDp8Y3F+cC0632qriX04L0NTJdUopQAL1Gi90/OiPRIrOmCPGRZMyjHIewsTalQPHpxwS++OiPZvc/BVk579pR6eYpMR5jJc0rt+O47Jf/s19/he9/ZZW9b4VvDg18c8sf/4T/yZ3/637iaXoG5xJoFrmsxdWiCvY8NoguTXed99NrVWBvTpeMUOU0TBBIlM3rZo7EGIT15lgWgTodgrs50tE0bwpHKEq0C0ykw98JatsaEMBXnyHXK2miN7c01jk9e0XpBMR7z4KsnvGoaxPoYbwMYHEuLuBkFAHO8tYG5nDJb1AjXg8Z/f6H6+ueupeARjPWs3sPX/bm8C02wRGBwJKOc2/fusDZeYzJbIHzw+Ou8pyhLtJTIRUd3NqVQCSJJ6ETYo/vU6fB7eNouyCXDzYnFSWyihe/3yiDf0UlKKhSdceRZjlU+FrYCnaSgJS4RZImOciD/NT8w7/1KXv66nK0vOoFVCmv4nImy15AM/ro0vgccvLc4r3AueL1JJQhv13Wh3zc3cB1YFgaG0DrHT7/8knfffo+33v+E5XxKtZzjfWBi11VFMShJlGTZWfL1fdzWPRYnc8blgMGwZLm8pOvmOHGBZIppgydokhTM5g0IUElKVXWsbyhMNyHxkKsBVf2K6uoR77/1z2lUCakANDiFdRac4er0mJ3dbcabG9StQTrJ5ckZjTP84C/+nHE5BGtpmyXb25ssri65dfMmH77zNqau0EmCx2OWFUqEQLTKWeZVRaITskHJwc5u9PaWHL46BrFgZ2c3qF7ic4iIbDzvwZvov0cA+1csFIJM1F/f/xCcEJghwftLrPa1uNyDn3Z870WU5JblkLPTM0znqKomeG4JQZKm3LlzD61yrHndrw3CdMDH2sNH2Zfl8uKYRBouLg7Z3FyPIR0epZIQ+mAtzlhc23J2esrR4RHzxQKpJQvV4clIByOKMsW5LuwnIsiLQ+MQ6o7+PrjoTzlfzHB+EUJSm2CbtFZu4a0AJdnc2GZyeckgz7mxd4fBYIT1MiotHH3K+Er0+DqDSQSGkAOMVMjBiNvf+6ecffGQsz/7zwyqOS/+4gecPXzIvHFYr6jnC/zVOY//4s8ZbezipSSbX/Hpf/lj1t54g+liTjVdoGxHIsEjGK1tkKYDRhtb3L//NmvZgA1d0pxfMXc106qhyEvSUY4bpOSjkpdHz8lH64higMsSNu7dA+sxZ+d4IWC94DK1pKMNmkSROgc+2GSElPGYbSQ0g+EaXiiePnlKVuSMRmPK4oDt3W3G4yGL6ZyTo2Muzs45OjulsR3/6vf/JffevU+SZiwXSwajNZzOINFcTqZ89uALWmPYyAp8pnj+4gXW1hhjKdKEQjjcco6vF4wHBUU+CJ5z0uGVRjmF1gIT7XWQnu3tTU4mF0znc3rFgxABKJgsplSP55ydHLG7scV4bcza1gbjzcDG7x4fkiU5SZrw008/Y29rnU8+fI/j03N+8ulDfvqzh1TLmstlzcKCS0qUzEBrtE4wtovMPxXxbRHZcnHIF1lbUgTgW2oZGzmPyiR7N27QzGuWF6/i+RaGYDor2b//HnqwRmsD4cL379FrsmIpJSL+d1mWeB/DOkwADoL1jIHMkyZZVK4ovJBYYQPYqSRCqxX7EIjfIyanSxkYit6T6AyPIk1ypE6oqwpP8IkMbByCbUs+WBE9fGygnRcYPEmSMt57g7cVLL76KQaBaRoy4/j4xk3eGm8gr67wTY00bRhM4cI+afumPCZae09rLZX3mM11Bndu8sqFRrZYG2OahlwpMiXBd8HGyQbgOjByLcv5lCxNSZIBOhuQqYzt3b0ASksVQJEYGKSEwhIssuRrDM0wZ3fYrgXnyGTCt299yOnkkv96+CmNCuea9IQAFS3wDYzUmN/77r/kw1vfglqiRILQoWZSXrC2cUAyHvKiWtBMTzmbLJDpgG5R48yMsjunMRfc/tabHJ62nC0ynHABTLcW5fDwcwAAIABJREFUDYxHJUpespxMmV98hpkvUMOCl67jj37wlyR3PmT93rcYbe3yvT/4Q54/+Bx7MaM1HafPD7GV5Gi74Pip4/TRC4RVkCRheKkyrMk5mTi2tzStOaHzT7ByCosaaTcpNj5ADd5l2axhnUQqj5QeYUXw0ydmEzgL4jrsJwyIAWexZop2Z+Be0jZnSN3hVYKUwRbEGBOfHRHBzwDh9XWLjF6MOumBWh8Zew5LkOb614KoevUcXNtSCRGYrsIJTGeDvFoIjhuLO5nw3u6I9dGQdFnRGI8zgg5P46GysabEowgkCZ1IUhXqZ2M7lIJOppwby+eTlqPG0hCAP6LkWsp+uPoNsPRXAK59jff6PXi9jvtaTfeNmvm/x+6gZzDGUiQ+A8F6pK2bVUhokiQoGf703q0GPlmWQrzPAXCLVjvxc0qG/qy/bh2VeT3xgAjAKh+81Fc1bbSs6PuYJEmCnZwM60JKvVKRBQJHONOdC89dkMvb1X7ehy55d90fVFUVXxeGao7AoNVKg5IoYVfsxMBCDT1g78mKCHuI832dFo4O0d+vEEaEjuFzJtY9vZpIS4lTCh9Z4c51JGka1W7B7q/tArlGRTs1Y1qMqXFO07YOhUApjdZpJKhEdrAx197qgLXRwxlw0q7sDZx12M6s1lZPAAkfkouLC7TWJEnCYDAg0eH+F0UOwDyqJ92qzxMIguJVypAb4HvffAIB0HoT11tYe6GXIw4teyZzqOE9DmE9GIOta2RdIZuGpGmQVQ11jVss8F2Lcx1aK6TKwTqctCQ6BaUjjhYyeISUwRZDh+At48IawHuEs8iYwhbY2KHINha89Nc+vL1a0nu8qckKSZKlJFqRp+H+GRtC01vjaJoO2zm8M1i7ANNQNQvmV4ecnjylredoGowTSB2Y5FJIqqr62nNunQERLMT63h9nGeQ5aRJ6/aWuaLRGq2BRMZvPwcWgMzxGGmaLCTpRCOnIhaF2dbDayHIG2SDaJbaBWetiHyNEsCeSCdZ04GQkV/zqj3/YIC1g5suIeAvwQSJ8++YuH3z4Dm++9TZep3TWEZLbUpRK8D5QyNu2ixsQ0QMiMGiD9EPHMAOCPFmwStFTWscpnYoH5PUG36fXeTxt51FJgdKay8sLtFQMBgVIjZA9oMLqa4OPTi85uWZZOcDrhNHWDllecOlBekvdVTz/8is+ffA579y/y91bB9y7d4/T01OWiwUISZ4PQFgm0zO8b7l1c59ikHB6PGGxbNja2WE4HEVT5BTXtTRtS9e1CCEoyyFpWoB3vPnmXYo05eL8gr29PYblgDTJGRSPmC2WmLbl5PSSahk8DiUGazw3djcwzrBcTkmShKuTU+bVKU1rKQc542FOkWY4BE1nmMzm4YARkjQvUFKERPXOMJ/WVFUFMmFzd4d7b97h/PKCpjG8fHXCeDRifW2Nd966z1/91U+4dfs249GAl8+fcfjCsbO7i7WGwxcvEEjauqGqW7yYg3Nsrg/Y3tshS9NVU31+fsbkIoCXTjiUlkyXFcKGLq1ddmiTIaRG4VBXV5z+zY8p9j+gVJsYpbFS4k3L+iBjenWFtz74j9iG/d2SNPH8/IvPmVQGnxYhsduGYgpalNCQJCy7hAcvr9gcjLmxf5c0FRRJgRKKdrFk0b3CeXj05CH5aDMEMHQeihzhMrxM6WyYXqI0TiqEc7Q2JEtqrajrKsg4CXJgenkEAqmSMGB4raiB4BeUqGhlIEPBKIUHZ1YT3jRNMcaEAiMmnKIEIozh4lDEMRgOkSIwHANgXJCnGUURwkYq66kWji9evOLR4TnNvOGTj75Ntzjh2ed/ReI9ZTthlHi+++Ztfu937vDu+zsMRpKracVf//lP+L///f/F00ef0TZXeFvTVlOarg3hYI3BWKJvJXRdgxDXBUwA8JtVoZRlGVoKtA7+UtZZlsuGtuvQicRIF3z0vMMRGAypTqIcyWPiPgRiNSDqmm4Flq+P13nj1k0S7ZlcJWSJ5nJZc3ZxRb61jonMo9UeZh0qyjtdZzg9PcNKgcg1ogpMHcuvLiy971nTrIBJuSrY5AoM68HbvsH2sep0AtK1AflaiS7LYN0hBIv5nKY1dNKxtj8iSTR22dBcLcjI6GddXgR5az+gSLSKxWRo9IQODYQXsZj2Ye8OfrKwPhxhrmpMZ8kSBcLQdh3OOvK8QKaKJNdxzQVpa/hdoffTAuI6DZ54vf1BXzBbGyS3qyCG1+6f4trPDSJMLghgbpSEtW0EnePkOzDNifc9MCRFnDxHbjIvTk754d/+lI3hBmWW0hkbgv2A5XKJTjSJgtYaGjFg8957PJl8hswSEi1pFjMmk3OSbE6na1QW9rambrFOsayW7O5u423LbDKhHDq0TEClCFkzufoJnVpjbf/XMIxDg+gJHsV1Raol49GQH/3lD5lO52xvbDOfzNm9eYdRNmZztM7ujQ3yVJKlCU1nOT58Tp4EEEBpTdsFHzFvPVmWUq6tUZYDvIOLyyue/OIFl1dXaJlxdnrO7v4O+3u7eDx1UyMThZQO6U0cf16DAvT+af0560Q05/f0wVw+Sgv7fU/0AC1iVQcQ5f02gkvDchxCneqW9Y0t8qJceRM7J/Au+hyLUFQHf2IXGd8hNEIEgzAWswtsO2E+OSURLePBAGE9xnQ0VY2znquLSz7/xQN+/OMfc3pxydvvvMuHH3+MsY6jkxPSwZhbg1H8+R7jDB6DbzrSbBD8xggDQ+89zhoWiylpFtZ3YlOUytjbfgPvJBezC7xJ2FzfZ5DllOUmiASBJsgtw+8QhlZxmBcVRl6AFR7XNeGeeInxkK6v8/H/9If81fEhzS9/zlrr0OeXuKbhatmipWZTpRhr2NtZx2mFqa/wXQXLOVxdsmY83eSC3Bs0EnF6hhUJi9Emv3j4nMFSokzFo//0/8Cm4mx2wfbBTdRaCUiqF4d8+vhLWhz5xib5xjp6MOTuW++wVmS8fHmEKjM237jLvY+/QzJeWwVCrhp+fPDkjTkCVdNwevKK88sz0jRjOXufF08LsI6ri3OeP3uGUppyUGC7lrPTY5TWSJWGxOI0Iy9HTOcVOitRXrBRlpi6YlY3CGlZnl+yNRyhmxo3n3K5XJBqzdZoDB4aV4d1LzWJytACNCKGjQjyQvDG/k2+ePxVkKOLXlobwPvWw9l8weWiQr6IXAKVkOdDxuMNyqJAZ4qucwzShD/7wY+4mi14eXRM6z1WK5zOEWkSdi7VBTm2lChSVlC+6AHY6EMbn61eXSaUiEwXTxdZ3NY0zC5eRg9nicfipWK4eYPB9j4uLUisj7VJtBbDR0l3HLz4axZZYAHGoY21NG1HZ02wKDCh5uo9h52zzBZzpLXR9iCcOb03qHU29g0K5T2p1DgtQGiENEgLsm6xTQ14Uhn2n246QRtLmg7i+R+u2+GQ3iGcw3vBcOMGw1tvYl5+halbBij28pKiaVBthWnDANZLYGVfZAlWTGHdGjydALs2YuOjtzmVjvPllLt37qCznGq+ZHI5Cfv2wQHKsxJaOu9YTuc405IXA0Zr62SDEaLrGI07xmsbqCRjWTVIHzzgvTXhXLcWVNzrPEG23ywwdWiivWnJfMJ37nzMw/NDnnZn2FzgZXivtJAkPuV3Pvpd/ul3fo/EZiH1G4fQMpJkJIPRDoNsh8Wi4/s//SN+8cUJPh0h5g2lMHw4bjgt5xyUC+6vl/zHv75k4UY4Cd52DIRgXWfo1tPWltYGi4b1nQP+djLh8fd/yLd/f4cPfmuN82mDXhvyrX/yjzj8mx/x2598Qn1R8caNd6i7mmc/f4qcdyir8V6RZxqtPF5mnE1bHv3kz5mbZ7jkCqFAuJJR8S5p/g5VU+Jtn9vQIjFo5VHeEWctIU7Ve3Ssra33CGfwrkV0V2h3RlOd0rVVAKJksHPow5fCmURkaIaBQ7+vaa3xMtT3PbFi5Y/p6SmUARhErIYLENiNzjuECq/XIiqDvIhqKMtp47AnC+6MC94oSkZJizfgOktrPURw3/vg3bqqi4RkkKXgPUvTcrLseLqwnNSe1suebcU1incNsK480l/vt18bjP9/Aa+v/3//2l8FyL4O9v4qawQf9zp8n63Qz1AiISuAAWRpsrKF69VbTdNGll6vgJNRAi/RUqxYx/11dF2HxdBDw8JDHnva3qoigPUE1YIM2Qn9oMl5i/BqVQv3RLLQqXkkYIzFCTAxmb57DehMI4u3//2D52wIBzXOIvvBd6qRXsSwqwCsiwi0y1iAyXjNQkZbiH4oEAHrzjp0D05rjbc2BM9FS7pgIe9jzxDUkH1/4W0AdXsgsbeB6NqGTiWYJEV7jUFidbqq9Z2NALKUK1uO8Gj4KI33Icsknnitd0EhEAFaH23dfNy7mrajie/d9OoqnJ0+WtER8i6E9Kv7oeP3CR+B5PT6ugzhf9mqT2u7FulsYP1GFZWIi9K7QNjAGFzdQNuA6xC2xTdLmsU0fr4FE/YPpwRL25KlwRPe9XvR9dOw8llXiUD6YBkhCGeKpM++CcQK64k4GrGmUtE2sV8T4Hzw7BVNQpJCPvAUeWATG+upa4ESGbNJx3y2ZDmf0c0vaWcXLCbPWE6PkLShtzMeV3dhzCsCk1as1lmwYuwHi1JKbGexUU0p4pY0KgbkSU6ddKRpQZrmVPWCxXJBZw2N89i2RS4WeBTOC8qiRCc5aJDkKNEFK6EsiXZPYc22zoIDF60t0vT/pyCtdZ7GOtLhMDbdgs2tMe+8dZdimPL45SE6GbG1uUWS5UECbCx5VrC1ucXa+ngFtPS+i65H+0U/EYTgqxb8R4wzwT6gD0OKy06I60OA6N9YFCXOQ1YUONtwdX6OsBtkgwIh0uBrxteLRi/BCbcqNGVcEH3AQTYYsX93gHeW84szlq2mOjnmiweP+Pnf/i3vf/Ah773zLrPplIvzMJ3Z2FijqjvOz6Z4B8NyyCyvaFpBUZShwW3BmY6uqYOcW4RDUScpeSqo64rFfMbMWj77+S958vQZB/v7WAsff/g+dVPz/NkrrIcXh6cslx3vv3cPrQ31tGJ7c4uToxParqNzEmTKycUR+WxOtSxQe1skWvHq6BSdXJKmKd6HkKVBlrK9vQ5CcTE75+JqyrgcMB6OGJUlzhnm8xbhFC8Pj6nrJYOi4O6d25TDAQcH21TLmxwdH4GExbLl3t03g69Y6zlTU4TyKBF8zIo8RSfBlFwIyflpi8YxGq0hVIIxHetr6yuJej1tcKaNZtUwEAo5OaWyv2R772NcWrK0EnzLxjBnMp/TuLARKW/Y31zD+47nZ3NMMkbiSGyHEm2YPoXOInrgSBpV8rPDKcX6Bb/50X2G6YC2rdFeU6w35MWQg7sjjEwoiyGz+QyVDjDOg29JvEcYgZc5Jk4atVaYrqaX2nSmDeC8DJ5g1nTIfgIbASXB1wseiJ6JPgQUlKmkNh3Cpby+xXgfpEwhIMnjbHhe1OvsRa6LHmMNwrdYYzBKcdUq/uaXzzirYTQY4E++ZH7YcfLqCamr2Nne5c2Dm/zGR3f4tXdv8sbtbYZDwfOHL/jBn/6A73//PzE9eYXzFd7P8LamaiqaNjA7UpUikwQngrG5lDIae/e+sWHC15vyywgYEp9ja10wgO/ZmxCn0AEQzLIsBKxHgLAvlgJoYlem+ePxmLXxmP39fYoiZzI5QYgQ3PXl54/IVcLtzQ2mXUMlNTNrAotQgBQuMqAlXkl8mZHtbtIeX2DrWDx8gyVwfZ1fP/BDSJtb7VFwXfQqKXshAUJLkvGAjf1diqwgSUqsSBHSImUbmLYppIWmrmuaqsEYy2CQIlMdAB0Z7ouWAVRrunYFjEiVohKF8bYnJaxANyElFstiMqW7qCEJE/lmOqeaLgGFSqIPXZzYN80S522Uk3uUgv39Pbqu4+WrlwhUkMMotXpP+oP8m0B1XzynsRDuX98X6z1o27/X/VHh8SsrhL6o78EvIMq0JAvb8dMHv+DNgwO+9e77JEnBaDRmNCz56quH1FXFYDhE4Knbls2bb7D28hyUAGdJlEBJTdMIzCDBuBCA13UN1kKmPW01I88daZ6SaolzHeBIhMFwynL6OYPN20g5wnqHUqGIXNbzcE9USjWr0FbgOxOUGannt777cQgm8F2QynqH1pGN7DrqpkMYj8wGjNe3GBQFXbWksy1Pnj7h2ZNnHL08Ym1tnenVhPHaJuPxmBs7G3TVlIvLCfWiYmdzA5ol9WyBSDLSYhjYqqsGpm+84kbkiAOVJWU5IHipqr4HpX+jpFDx+ej9mSE+ZCAEB/u3kVoHb0MnA7PEe4STYe3KcA2BOR3ACu89telQguiN77l5cMD0wjMdjEmdwi4WkDRcXc748sHnHL865sFnD3h+/IqqbUBI9LOUdz94nywf0NUNL49eMV7bCAOtWDy7OGzJC/HavirI8wydhJCRRTXH2grrO2zjmc9njIfrpDpFoijzIUWWR7V6CIlx4QAI6cRR4iijTROR6dFVFedHR2xuraNHI5yXGCzJzT0++Dd/yE+XNcsXT9hxMkholaXyEqdShIeXj55i8SS5xjhHN5lTSkmqPEsktgtFdpKlOKlZXk3RFw3rchspPYWrqI+v2NAec/wSWa/TOs+GV1RVi5lfsDg75sI5rBBMPvsZvnEsbMeW+IAP/sW/It+7jVVpYPQrHe00evdoAUIiZPAOLgcFbVtQNw2L+QzbNiRKk6Y5n3znO+g05fDZc9bXxlxenXN6fsHe/htMFhUqzVnbuoGZLJktW/YObvHVwy/orEWlCUWTYK1nUFfhDLeGQiU4JJtFidKKea2YLBa0FpIsBSExCBIV7AaqpmVnc4uryYRXp8chAb3fX2V4Noz3GB/tBqwIqd7GMGsMk2aBxWC9QNguyNJVgkvS6N8awjxFBIJkX0/YYNsjYl0JYgUour5kFr1vKgTQWIB3iLQgLfd4/ugLqrPnYUYsJSQJG2/cYevu+xiVI2SCsCEsK1y8Cn6LhCGCtZDqwE4Piol2BUyshvIuDBtCjeKxtkMaw1AJbNegvEHLwKSxMjSV1ntENgznofHkBkYqY+BCWN+aGCOMp/YOqUvwFmO76B8o8FOL0EsS1QfjCGyU1DhvqVxI5JZ1Qjf1lCZDqoy8UzTzBmEN3npUjJ1ESKzpcMaGvUuGcFTrHW48YvD2PdrtDbzUHGzskOUZqdIUgwK6YOHQzJcIpUiKQRioJ0HdJHyKkFB3FrGokCLYlRWjzWiTBc1iFoI6ZWAzB7BFrQAnITzeNCwm5+SJisQQw5oe8P7ObY6fnjDVAis9WI9Ywge3P+IPfvvfspnv4bqAbjkRkgmQEusMaZKTFCNcMuHhC8+sHdOISaiDbMvInfD2WyU/+fIJv/G7HzJ9O+FPf3FGl+4gceTWoJoppjvDmBo5KBm+cUD57U/45c8/5f21m5SjEU+efoHKhhSDhO9+7zfx00Nu3d/isnzFcNdQn03IJhXStuhIcMiUCtep4eLiJQs1QY6WYX2zjirvY+xtRF0EtY8yeNGhZLApE95jTR3gMRHOk/4cEb6XD3d404CdY5pTjJmFQ05IkCaEDkXwsgfjgBUrsC+orDHoJFnVMava1F/3uKswsciAUxF0/BqwSTgPdKIxxsV+ymO856wxLM/nXOYpawmMUskg0SSZooiAno2Wg14FUNMZR43gtGp4OTOcV5a5DyxCZLwPhNBVXguA7evVb36srvV6Gvu1uvd1ELe/B69//H1A7Tdff11j9y8KAKcxHdYmK5xBqSDRT7QOe4B/zQIr/tnXnj2pQxBsE4TvlV2RHBD3JR3r1x5sd71KOBISAouS1b/ytVrWGIMx9vr3cC7UMkrF9zb+vvF60jRd3UvFda3c/6yATzuU0KgI57k4RBNIpNQREA7MRRdtohKlEUqiiD8XGV32ohLCQesjIButNqSMAby+D4u9JtlBAI1d9DkmDiNCLROGZI2zdPMZddeyPh6F565aMsCSJGmsAcFbEYf7gSBDrC+DX3//TIWfYYwjSZIwNPPh3+C5G+tEEf/04V4E1YWKw0C/uo+Kb2RkyOuQsX5oHvx5w5DSOQdKYttAnnNmpXmiV/spBF3TYOsKVzf4tqabTZHTKWmzxBsDxpB6GCQZMlwFrQer+kBBG9oNYxG2RRlN4gzKNmjhMFIHr3PC3hMIEdcD/f7NGRQDyvEohAhGlUsgAAm8t3RVi10aikawsZaxNlYMMsgzyLUMwdoupZ5a5pNTmukh89MnKF+RJmCFxkaihRTQxZA5Y0zYq/MMLz1JHn1xddgL57MJy8UiXmaoTZSEItcoLXEY8kIzKHMWy6DGTXQgSyVaUw5KhsWYshgBkk4bUtdB5eicI9Uht6rtGqT0gWWukmjpcL0PffPjHzRI2zQVbtAyHpfkyjMqCz587z5337hFlpe0TcegTEnSlDQPIG2QBmhuHByQ6EC1DimVDtM2tM2SIh+gkzw0GT5Ihqy1q+m/BJQQMTyC0NhJBX3RHgtfJwX5YIDWCUWWc3zxkslswsGtm2zlm3hvwqTQy+sz0rsYIOOQIhRpq7+TcjVtkDphffcmrZEkOuWNm7s8eviAn/30F5RFye3bN9FJxunJGY8ePeP46JhUZ9SLhouLGZPpnLYzXF1e4rxjd2cb8HTGBF+6JMXYMK0qyxGDPI/yhIThaI1fPnjI0ckZt27dZlEvGJUDdne2SAYF1gheHZ1x+PKM0ajg6OSMq3lF19QMywLbNbS2ZTQsSbVkPp9zfGxZf/stBkVBXbdcXs5YLuchEdE7ppN5YHH60CQnSQjwOXz+gqppaNoO7yVlOUBpSWc77r91n8vJFSenR9zYvclwPObi6oLFcsFkMuf2rQPyQnJ2NUG4sAFubW2QJhovDDoJh8/G+hDPLVRScnF+ST2b44cpb7zzDsNyyN/84KcYwkEggUQppAc3v2R08ggBTLIRDSEpt7MOKzVSCwqZoqTmalqx6BROQSodb+9tsj3K+fTLh0w7AToGWAiBlSlTcn74eEYyXvIbb45JkyA7HpbrIDTFMGXeQSsL6m5CngTXRaXTMKXC422DcSF8J0k03tjIdg0JvULqrxUIOIfH0DbLcGAkaWy4WG1c3gVvaBm9iNbylMpKltZjvUB6v/LsCamg0R/R+8BYJ3gy9YOOAI00CFNTLzsO5xWfHy65bFL27x4wEHNePZxSvbxknYpyoHhzf4NvfXSHb39wi2HW8eSrz7Htgj/9kz/mr3/8Q6r2CiUszhm6tsHbLhadkOU5qU6ouwAKS6AoBivGHUKgpCAtiujhYyOobWi9iWbvbWDKKRUKCedIkjD9NM6EA8e7IAOO3zdJEuqmwxpDXdVsba4xHAw4ONhnc2uDh198wXJxQTEY8tXDZ7Sd4TuffMjt/V1eTS54MruiqsH4UIxIpcnintc4g1MSnaUkSjJ/cQxtSPV8nR0ArAB4RPBUCs+bW7Fow8AgMioSiSEA1kgYbo3JNtbwSqGkjt7fGqFTRpubSKBihioEy7airZsgvRmk5HmBIjBm+4RQoWRMmfWBvSTEap31HkyhxvN44ZFaQ+OoZ3Occ9TGYJoOPGRFSjrMSfIshOHhKAaDWMSEotZ5x+n5OabrgrRJabyHrusi20CtJFSrsK/XitoA4If10Fso9FKZfj3go79WXzzGAvjvMjoC68vKICuUSjJtlvz84ed8+6NvcbC/w+Hhc66urpBaUzc1SZoglaJqagZ5wcEbN5ksFgga1kYlOzv7TF68pGl0GNYkBF9w6ynzUDbnqQZanJMI5XBdhVSQyZRq+Ypq/opBdhOPwniPcp56WTFKM7xzfPuTj0mlojMdjWlDUa66MEX3kmrR0eFBKQaDIWW+jtIapTMuJjMe/OIzbh4c8PTJY4qy4IsHD0i15u6dN0ik5tc+/JCkKGitoW0q/st/+CPaxvBr3/0tLs8vsdbQVnOG6+vkg9E1kyTeVc/XAXIhJINBcQ0c+dVBHAFbufrqIMEMn4kdB73yxVmuveaR4ZlR4Hxgf/joxeZ9KJCdtShPCKwyHcZUJKJGeEmhS65OTzl+fsTTo1c8fvKY589fMF8sMdbiEiAPgPHJ5QmPnj3irbffRWpB1zWcnZ+zvbUbisvIdsqzJALFMjRVQsYBLTRtTefmeNHgvMGajsOXj7nIhow2dhlkOgy31zPSLCOEpQp0EpRLPgLhQQFEDGKIcry2Q8qgPgrDuCDpWixmdDvbvP8//ls+/9/+HZPTV+TKE5TWHu8EComrLcZZskGOcA2zszOMdBgk6fqIG7ffYe/OffJRidfQLGumL865/OUF8+mCwrZkwpJaj3eQGshyjSpLXNNQoBinEpElXFxd4s5eIWVGsbXD2x99wvb+TSYIOmuxpiItEoQIAyCcj82tRGc5dWeZzOYU5Yi8GCMIgZtbN25w+43b5IOC4+MjirygyDMWyyVfPHrMy8sZTih0VpKeXmEtnLw8JssSJrMr6rphMByTOcnG1k2GdAjTYE1H1bRYITBVTTYqETb4+A20QgmBVQp8FpQIzpBIAUnC7tYOV9Mpy3oZG6T+KQlkBVbVrCdPU3Sa4pTACIkjDew4pQN/QcrITAr/4KOPOJFVF5tQ63vtWQC248L5GmAE/vpZ9RYvNWkxYmP7PldPXtEHuyblkNsffMDuux/gsiAN996vnlbn+yRygxNxwIiIe3hgqaKSoKyIoTtSQuqhcJ7UWhIBqZOk1pG0DUWWkqk0NF4yib7AKZ2Huc4QLqUsctZJ2c5GlCLUR1olAbTOtlCwCqmzLgBg1kPnLc4aAmMIur7fUJ4unjXyRonItvC35igp2B+PyUXw53euQ0S5ZGc6XNPibbAsEN7hJLTe0aUFF8uWiy+eINKCzQPPfDFHocjygps3b5OkedzXNE4Fxp4SAu0HqBj60sWhjNYJm9u7QYpsDFpLGoKengfeAAAgAElEQVQ6QApBVdXkeR4UKyI0xaZrMW1NtZiTDkus6bBdgyDhYLRNaTWXTRX2qhYOxrf5g3/0r7m5fhtp+lCia/sZ6UFpSZJKlk3N33z2jDO7y2m9QLkcpVOWbcPpqy8oTp+RDd7iyeMrNvWQvc2EF3WUdf+/zL3Xk2XZdd752+aY69NWZpmuNmiHbnigIRAgQyQoUaRGoxkxRjExD/PnzaNmhlIwxBhNiEOGRFIiAYIwjTbV3dVlsqrS37zmuG3mYe1zMxsg33kjujs67c1zzt57rW99xjdkuqMMLeuuYR0GvPa992hefo03ZnuY0Yyq1RwfHbGuG/b3DvDrK8Z7W/zxf/gj6ssLivGEre0dvv/ee7Q28Oi//jVrr7AY2qbhfHFEo9eYsRdiUTNmsv0VOvcyvhmgYpbqq4iynjw3mJgL89AHnPJEpdHKyfr0GoMmhgbnK1Ssyaho60vxrkwnkuiPzabGiyomc580uEsK0B6Ydd4LWAiplhEgN6h+oCM9q0kep85LbayS7L73vIwqhW+nXlYj/pJd51iFyOfrlkJFBlYxMJrcamZDvfGNzKylXkvIdNt0rFEsfGDlwce0Z6QgTqNMqh3VZuDS11R/n23B5nUD4OvP+Ztf94WvVWoDKN0EZH/1d/wqoPtr78FH8FKDZJkV1mmyjPCpfhfQNWBtkvRH+ZyxhogwrUMUVZCcv2CtEG6MzTZ7sahYktougOo6sdzynuiTvUrCFSKi5BKbR00fAHZt3SUAJD1wpDVG2/T+SNZu0i90bSf9ghJAMfi03yWLgA15IaF0IUiQUpeIMUorgpMQR+U1MUqOg0lsxz6cN4km5NwIfgNoxbQH9UxxH1IoWgpNbepaAiXT9wv43cv/I3XXsF6vWSwXjIYTdiYTttoho+FwEwRmlMKFgFeeiIDlqq8j0/kWY0jDwIgIWoQx2TmHMQ6bAFkhvRi0NUIKymzqC7reqlX8c9W1H20PpusN4S8QvMcrd31RVPJx1wYX3Rd6b6Kchc16KVZjXYv1LXF1hVouYLWkq9fkaZ+NiCe2Ss+01gLQAuioiM6D6/C1ImAxocV6i9GKDnBEgpb+UJ6o6/WUtjhMlmHyHE+HVWqjNleIqgXDZj9rW1guPYORIs+hGChGXtFWGVm3RVFt8eTyiLZdAyH5AA+JWnJeGtfioie32YYNbqzBdw5nHd6IFeRgMGA8HmL0tTWCbC8yGCq0IkZD54WIEbzb1MBFXnKwf8DBnTtsb+0yHov6tesaFos5lxcXnJ+e4eoK72WIFSOibojCcs9Uxj/0+kcN0nbdGpvVRGWYjQu+/e4bvPP2m+zvHzIZ7lCWE/JyRFaUUkwlyVcE2cTStEUbobcfv3iG1oFBWeK6FpSmC34TBmONlWZT6RQ+KxtQ7zfT78sKARhcjIwmW2SmRJmKtl7z8NFjLs/OuP/SPabb2+zfPhQ5UAILlAIfpSn34YuSiRjjxmzcJWDn8N4dLouMq1XFdGuf7MUZH334Kc4FDu/cI8sLTk/PaeqG24e3OD8/l2nBoGRVz8W64OBA6NzRJ6sG8bTJcsV6VVGUGUVeUtUNu7tbtJ3n+YszkU0qxeVixfHpGbcPb3Owv8PXvvI6TVNxfHzKcjXiqqo5uVxSWMvB4T73d7Y5PZ3TOEfb1Nw73GN/bwtjxL8xzwxxMCCETtLcXce6qgm0dG0nIIq1XC4uiRFmsxmT6ZTnL15wtWiZbY3Js4LpbMJgVNDWa05OXhCA9XrJwf4+T5+84Oj5Mw5v36Zt1pRFic0Nw9GAsrA4L1JrazNeun+P8WzJ1bomH+yyc2tMiJ4HDz6gqxz1PJK7UlivRozrc5UxCJHm4jmhA7X/EsvBkGZxRV1JGqTxgd3tbWwx5OTyGTYrCEQmNvLW7V0Od6Z89vAhi7ZCdiaLzUf4GKjJWVeaP/3Jp8yKL/Hm3SmZDzjjcTFitWaQZ7QxYHUKrctyoi7wkZSwCTYGCgO51dg0HxuUI3y4ljr5yKYoi75lvbigKErxxdLiB2RsvplGS6q6bOCFkeanC+LL6XuAMjHTdGrJjDL08/cEY8haSsDC2sNHTy/49LglDHZ55Y2XcM2aR0+PUR7c6gWHezk/+O43eeet17n/yh32d0Y8+ewjfvyX/x8/+vFf8PjRAzrfom1AIx5B1Wq9GbyMh2PKoqSqKvHsTN6gPoUPQaQscmwm3jublEetiFrA585L8WwTgFutHVYZBmWJtZrgHcE5AnIN8jzHGElRFy/bjrKwzCYTbt+6zasvvcbl1QsuLk/Zmk6ZX9U8P78iKLiq1hyfn7Fqa9oghv+45InkPavVSu5zLkFFTfQUo4Ly1jbN2ZzYBHQUmCEkhpNK/LCYfoYxmslshus6rq4WG6CRGImdyKCigcnuDtPDPdoQUoKmxRpDiJoszyQoqWtRhSYONL7yLOdzlNU0ymHaDpVJYqzINROgphU6ij2H1eKDaZIMpb8nImONwhyrGprlkkzntE1D0wqjNSty8mGOHRQyE1NygGptQPU+X4q6aSXEKUljN5BpGlZoJE28yEWOLcXntVTwJmPDp8m9TLzFbkcYvA1tU8lzb0wKoDMbJsRGXqilMALxvq0C/OyjD/nxL37Ob/2T32QwHGEzzWQ65LMHH7G4PGNndx+tNF3nuHVrj3xRSsOnLYeHL7N48SnPzy/ZHXvGI0NZTlgsl3QxXDuyBilMlN+IXdE4Mr1EuwqCS4WEwrtItVrhV2uatkUDdRTJYZbnmCyjaRs65ciKgsnuDkVeUK0qlsuKxw+fcrVY8PLL9wkh8PHPf45bLlisVnjX8s1vfJ1b+/sooK0bmrqmuVqjbMZ6seDZ0RGvfel18kHJYLxNllkujp+Q5TYB/GkQ0Z/NCmnqIDVz1z5uPcOkDx7b7Hlx8+3CAktSrZ7FIoNejzEJ3EqNTERkVTE4fNcKEzSxKKwxyT9QUl6r9Zzz48959PAz3v/5T3n8+eecnp5Sta3Uo5kmmBTOp8T6Axep25oPP/6QyXTGcDQhywouzk4YDoaMJzO0tdjEcPQhYJSScENlqOuGtmtkr1URY3MMOY1vGQ3G7O3cIiunrBYrXJ5j7H5q2Ei2L1aK9EAK87hucntlQdt1ZIMCk+epiRFQL8syitu3KPd3KPC8/x/+iLNPP6CIBq8U3nVYFdHWsLe3hy7EquaqXZLtbfHu7/w293/jG5jdMWayy+Xqii6uGBQZ00bx8ilcfviEj/+fP6H59IQtA0Vb0Zw6GObk07jxbNNKUxQDxhOPVxG9fYvv/M//K3ff+y7HdSVeulaGqZmxeJVu8o2BvLHCpLVFzmxrhneBLLfMtqdMticUo5wil1Ty8d42q1WFsznlZJsXp2ecnszJhyN2bx1QVTXL+YJ2taBQmrdee5edvUOKaOnmV7QXz/H1nG69wpo0mOlaFvMrlIJpMZBwOgJdBLQEMwavqNYLjMnZ2d5h/2rO46PHMrBVN4rXqDbkMqUkxFFnJSEFqSikxgkqEk0KZenBV9iE+YkkN5P9UfeWIRqCNLM9y31DZFMCGfXYh4qKJiiMHbBeL6mXF9L0ZwX3vvwV7r37dVZYXJcCUpK/ojYGEzPAo2xE9+scpNbesHo1Fhh6GBnF0AcmruPuoGCnzFCnx5RNx6wYsLuzLe/Je1xd49cNdVvhqel0AVszprPbDPIxg2jIQ7IziXIeOu/ld0c2TbxPII2kkWvA0IfmKDKMMoQAHtkvVDGEgz1CjGRWJMvC0kIkoj3IFsT7Ee+Inai86rai9o6VdrjWM+laWfvujMaeCHNrOOVypVF5wWxvl51b+6y6hizLCVrWYpZZoobCZslyQmNijq8quq7Fq4APnsLaDYtIhlvXIErb1ATnmYwnoMTf0SiFj5BFy9gOGYaO0ASm2Yw//Kd/yFfvfwPjIzF2mzWrAKLYHFkg1xccPfqcTz75OU/WY1ZhyrYZE42lyHOm0zHBZJzXBb/8yRnf/uaE1++MWD+vUUGhJiNiVTC0A1Z2wPR738ffvsOTtUOPdhnt7LA8vcC1DTZ46tWCTAW+9PabLD7+lBdPV1xeLlifrnmyf8DWbMqbtw/4xdMTuq7m6nLOZbskTApULAhVwbh8myzcwbUlOor8WWvxnCyGJaVRaKep2zVGeQkhJqBDKzw0ZQiuJoaaTHW47gXryw8J1QkKAaxUYtNGJTWpStksKka66GATTnkN2Pa+slmShvdS8J7MQBrsKBTuhpQ8JBJNRAAyt7EZEGAnGjkDCi01r3MeH6FyyZYteri63PwOlYbVsd+b0isi9gmbPIIQ0pasv3De95/rQdL+9QXA9MbXbT6HqP36cDSxcbu2dtDq10HffwigvVZIybUJIaIDkgifwEEBHYVhq5RGJdWaMXpjNdb/UfK39iBRwqitWE0YLbL9zGaCfYawqSl9soLwdUPEi9Lca0J0m73Dahmj6UQyMEbOauiBPrUBYeW9XIfOaaVo6lrAOyPMUu8DSsvvValOV+lnhbRfx+SXq7VBaUWeXSsvlb6+fkoJKC3esHZz7XtGqdgtSD+jEmajUOSFJsvz5DsbJaQpRCgK+iwCElkoprPPKIUylqA0Xdcyv7qkbWuqZsS4HjMqhoyHQ0aDIRFRhEadbCi4vt/9oED+e22Jo6MQBH0MKJsGlelZtNpgrbCGQSwIe4uHEAPOy8dNzxZX5vrZ8GHjH9x11+Au6VoEJ32tx6N8ANfRNRWx7cAFtAdbNdh1ja1bbBswWLSTHtcrTYewSDUKE7w8c4jfsXYKExV1GjTp6NExqdNJxBuhY8vaTmFlPZtCayWZQZ3kLxhtZCihNEpbbJGjxeab8UCR5aQwMmibSHCy141nJaNsl4yO5eqKs/kntEuHcsk+wcjg3RhDluUQxO6rV3DLc5/TupZqcUXdDMhzQxe8qOaiB5/qFW2wWjMaFtSdZ7GqWdctMchZ1bUtJxcnBDrapqb1nnI8ZTSaMChHjIYTyqLk/OyU5y+e4doWnVkZdgeH1TkKxz/0+kcN0qroGWSO7eGIr771Jd5541V2Zgecna5Y5i0v3R+io8eHSGhb2ralKAqZWgA9hB8jVFVFWZaMhgXi49RIYnryfREGVS/V2hw5CJgkEkcJElBi4C4jJwajMcVwSmxXbE9nrLdXXJzP+emLc27dPWS2s005KGVDg41c4aaHTv+bviDdiNK4Z9Yy3d5hvVhQjKa81DnWV3OOTxaY/JLMBMpBxnR8i1deuQ8ElusVpR1w794dquWSq6vLxD51BNeS5ZatsmAyHmOzK9quFRl3iCzXS/Zv7TMYlJxfXlBVNXVT88HHD3h2MucPfvhbvPbyXdarBT/7xQOUtoyHE7pC0kmPjl5QrUUCaAjEBNRubW/x6msvc3J8zNV8wWAE4psnRd+yanEhUg6GbG1FirKkdY6t6Yzbtw+xWjEaDriYz8lzzWq95uzshK3ZjJ2tGZ+cf0ZeDrh9cJuLswWvf+k1njx7RNc17O6OKbKMl+7tMyhLtA5k+QBjDIurJVs7uwzGQ7wKKO0oygFaGXKTc7a8YGA12iWavzIY7VEhkEWPblpCd4SyhgG3WT5/TucVA+XoaDHRsVqvk3w1khHYKhS7o4yL0xNWdYXWURqfKJI+rTzK5CgMF5dz/uzHn2CyL/PlgwlN14KPMjHyGtVFsmIIxkpgRXCyqSubnjFHYT0ZHoVODI/kRdr7UW0WnPxrPE6eh3LCoqLZhENI3yqNK0GkdlZFBhboItEYat9AulaovkAMROeT76tKDBtAGS7XLR8+uuTToxXleJ/D115mOT/n+eMTsrwgz+GwhN/93pf5zd/8NtPZjHKU8/zZE/77X/0Ff/7nf8Lx8WNi7FBW4X0rhuetS76/Ch8V66qiWlcbDybvk89rFHlMWQ7F4qLraNt2U5z0X9vL+ezGFiE1ZUaKC++TtUoMIpuNYEyGtZauXVPkOWVmGeQFs+kWb775NoNBwdMXC+6/epfL84pPHz+jnI5ovefp/IKT6oq6aSRtuizoIULvnEw8jcZEK1YeysqAamvCoCzw85rm7EISVBOzE9gU6D1YWq0bghePnJ5B2gUHAcrRgNHujHx3SqcNnY8ypMiG4LQENiLBJV1UDKczWiIdgWq1QpUGHQIxOsRqo2du9L2nxrkO5zqmsyk2s5xfXCQFUUR0T6mY78A1HXleYrWlq1thu0WwRUY2GhCzjIDD3rArSBv6BigVPz/5/UWWJ9N7kW0uF2u8D1TRb+59f71uFuk3C3iVpult20rhdOM56UPC8jwXP9bYD+bo600pIrVIw1ah469//ne8dO9lDre3uTx7wXJ+QugktMp1LWVR0LYyET7Yv02MhqgCB3dfAfcbfPLThrPVUzrXsD3L2NuZgl5jjMhujCrwsSTEFomHSA2/24ZQSIgJQdLWNWzt7qK9w2rDerncyHO0Fq/Z3ckMrS2LdcWqann/Fx9SXa14+PARW7MtbGY5HQ54992v8vWvfZVBUfDqyy/hgkOpyPLyDKU1bVp31liKPGN7d4ff+u3fZTSZkY8mZOUQn6SzxXCUCsNUgPd72AasvQZmb35CAEi18XuTwNAvbIBy9m/ouGLJo7XCqBTs4jqC7xJT2mOI4BxZqlkWiwXLtqJrlpwdH/Pi6Qs+/eQBTx5/wtnlGRdXcxkMGY0uDCgIWq611NxJLKgV4Dg5ecHRsyNeefUtYcLGJTZTzGZD6iZsvK5CYqiDND9tW+FCS55ZfKsosoKoNAd798hMxnpdsVyfM51MmU4m0jz1wFqqicRDu0/4/uIrpod4o8YgMZ4SmxOgsZbJ177KO+WQH//R/8ny8wf4pkb5FFSiIm1ToTEsg2P45Vf5yv/4Q269+zZnqmPZXrFvJqxzhSen0xFbKkYvD9m5+w5v3Mr5+D/+vxz96Mccdi2lNzhX41ZnMl/MNFVds1hXNEZT3HuJN3/vX3Lw3R9wgaZRgWw42ngQu9B7p8t974c5eV4yGk2xYc6dwwPyPGNQ5JgMtBa2dDAGazSVClzWK7zTLKqGs9MrqmVNjJq2rrmaX1It1oxtwTfe/SZf/cZvouyQi5NT3PiKuQ5UF5G2bnBtzWiQkRUDmq6DxEDqm+zadRIu6J00hNqwbmqqLrK7vc3FxRnzapWea4HSNu1ilMGuGY7xZDJ4jYk9ZeXxE0aXEd/W5EEHSeaK2viVK9UDv3FjEyIBGWqzNnvpcUhrUPwvFYPxLtXFU4KfY4qScu8Wk9v3WQZL5TzRd9IwbuyHRPKvtDA9vY90rZPaxndJYGnxTUMWHRMU9zHcdbDtHftdy0RDe36KacVvbssaGYTGwPz4BbZtmBmFzwfo6W1ubd9lMNmXngE5A2PXpjVgCd6kxO2IdwJ2NTjW1ZoQYble4VwnQbmDgUh/vdrIkevUeKs0SApElBUWUoSNdYsy0vybzDIaTWk7DcpCXpIDhsCQgM8Chl5N5NAhg8agqzneKJaPL2i3nuGMoZiMsZMSO8xRZY7Xiq29XWxucQhDN2pFWzUSRqklWV5rg7XgXIeExIpKRoCCQGYzVHQbJlggcnZxymo+B92gOsUPfuv7fO+t7zGKg8QB6N11JfRHoTA6MtAdcfEjXt094Tvfzfjrsx0ulwtafyTnQOu4WrccHVc8GVpee+suW5OOtw5K7twt+S9/dU5tC9ZOs9aWve98m73/4d/wf//or/GDGesuUqmcLC8pckvtWoiOzChu7e7wxpffwB2t2For1s0Vjz57xr/4377FaDDk7I/+M6ddw4oF6Ja4dgQ/IB9/CaNfp1kNiTG7vpGANZAPIta1RFejoyPELnliBjKNqDddoPPSR5j2gnb5Eb56jCYx6RK42A+TsmS7EGPEu1SrGp2C6+Kmdu1BPR+8DAi0IvprcC6mmhGtsFbqo/5w6QkYQmySnqKv67wX0lPwAvrr0IdXJcKUNRKOyQ0rASXsWwWJjbmZ6NzITIDYB3j3LEZuDAy/cCaxeZ+b/+/ZsX3vEfmCvdemREhsxmTkDagvgMB/nwXCF8/EZCmgIsZe3wvnBD8I6Rpba9Lf1XuletoUPFWWZVLDJGwCYRnGcK1+6GK3uac9iSCqBOimtRaihB9rlYmXcAgbaydjemsFu1GFZVm26XG01mldXwOuIH7JMYTksyv3zmaZ3Lvg8d5tro94kQuga9QXw9pUlJWubrJFb7Bv5T1eB/5671N2REjniPQSaCXBrVqTZaL20pmccc52VOuVnIvq2krCGIML7WZAr5T09uu6xkVP4xzd0NGmmntUDtCZqHxj8BsrhuvB/vVz+QUFXbKscCls1hrxgtZazkbdB1WmIaaOAec8dbsmOLc5T4XNrr44DHASamaM2Zwh3juCkyFPVBHfNLhWFBeqbfGhw61XDOZXlKuarOnIo4JoMUrjSH1NUHK/onjNZojvPV6COlUAEzosGcY7dAhYpfBKGLwRcWFTiuQJewNJ04bxeCKqyjSk0TojaoPKtPTSPmWJFJrcKrJSYSw4r1guYLnyLFc1cV0RtKYYDbFFntSrAddJuJhOVn1u7TcWEj1Aa63Ge5ee74712lM3UK1bhsMRxiABfJCsG2SDMOnsM6bv7SLzxZLles7FacbZ8THTrRPK4Tbb0x0GZYHzrWROtB1GRRSe6K77yiyxfv+h1z9qkFYrz6vbBT/45le5d+sWezsHFKM9Hj7+iHv3ttjZ20ebARFF27Rk1mLFIO566h8kETCzlmwyQSELYb64ZDLdpszH8GstiKyakJpA8bgK9Pu5bOIBryLWFGxt3ebkas5kPGO6teTTR08x2vLxg085Xsz5znvf4aXbdxN9XTa7um7w3jMajTYGxsCvHQDOe3SWMZxtESPcMpr56Rld3XL0/Iy2Ome9mDMoBpxfXPL6G6/z8OFDlmthIE+mY7SOXF5eElCMRiXLVY0yl+RFSTkYShq9S6Cx0lzM58wXC7IsY3d3i9PzcwKKDx98ymw44Ld+8z1evnfIal0zXzjKsqQsLcNBSZFlzOcXnJ+f41ygaxqezRfM52s++OVnbG2NZDJuLKuqZb2qGA6GXC0W1G3NS/du88or9zg/OyZGzWxrxmg8ZFAUFHXFcDIm+JrBaEjrNcoMKIsBL790jyfPn3N5seT8bM7B4S2+9KVXOTu/4J0vv85omJMZg/hnewwa5wLn55c8+PQRg2HJK6/cFysDo2lbT7twqE6ThZRE2PnUvMtUzalAUI48Bprzp+gYmN05xBvLhZ8ztGN2RorT8xPmdUWHxoTI7tYEZTQfPHzE2itamxE95JlsjsZaGqWIwWFyw5Orhj/90QcMvnWP27sjaBusNiwu1kQzgN6fJnREF8mKAT5G8frTMDSgggR6CZCoknF9kiMER2/wDQLUIU8+rXMYJeF7oWfiobBWgkN6D8fSaFovm7IPga5aUBRDdFbIBu09XdfgQqDIJIm5DYrLRcOP3v+M45M5W9tTZtOMx4+es5wvGGqFXh7x2nDN//LD72BiTVxfUKmWD372kP/6X/6UH//NX1EvX2B0miY7T91U2CgebmVZ0HXiI+ucSyEjSa7TdWR5Rp4XjEYjjDHCgmzbNCTxtCk5u59WW2s3ha7NMoIT2VjnUwJ6hBikeDXZDTBXgTU5RVZweGuX9777HV566S6Pnj7G68iiafmrH/+MdRfYurtP4x3zxYp40UihNxmAvy6qvPeb5Mro3caaJSgFuUVnGlMUEmaxWsNa0uD7YjwSJawOxWqxEPmTEU8g7wN2kDG9vU+5PaHxHZV3FCHDx0CZF2KOTi9pTcEC3jEaz6hsTTVfUq/WmMGQwqR9OQhv00S9mUK7GHBBggHapsEFueY3JbIb1sO6ZX25FAlTCvAiMTqn+9t0NoLuQdsclwLF5OtScu6N3T7GSFkWECPNeo3OMna3d9BacbG4/CLzIt4AAm8W//GmDYI0IyE12zcL+vV6vbG98N5vmvHokwwtpiFe8Pz8wUd86Wd/y/3f+SHdeoXragkIynO6tiHLC5SCrnNkNuCDyM5sXnBw73XaquXFZz+i4xFtaFFOgl7Go4zMHGDsbaIZAWtc/RDvTml9hh7fJ5sc0PiGiAZtiCjK4QAdAyfPn2GsZX9/l+AjFxcX+CvP08c/5fT5MUVecnW1QBnNq6++xq39Pb7yla/QdS1bOzPadsHe7pToHK5dEZUoXsQjXQIfZrNbFIOSxWrN1dWK89MFq6Xj9MNPeO+f/IYUYS6iTM/GiPx649QPPxOgdUOtAkjonrW0rRRpRifgJxXVPcOBmBJ7oxRVrWuIoSP4Ftc1mxCkLgRi19HUFWdnp5w+O+KDD37K0bNHvHjxguUq2fUYaXpjbhIQqlA9W0bLcx5T5xAjxNS8VnXFk6Mj9g5eSZYfHY+PnjGbbaNUalzSvhsRb2KSLNqFlrIYgB4zGBYsVksu5uc065oiH3D79kt471mvrsizl8mtSLiDD7SxJdOS3hs2AQ83witCoChyVLL0QWnatmaxrhkVI2HaW009nLD1jW/zG7cO+Ml//Pc8+5u/QV1ekA8GhNaxrhxOR25/79u8/ge/QziccGHgYr5ktVhSDqZEZfFJatbhaYuKYlDi37rLW9t/yGd5zuK//QQdAqXK0BHqZk30FT4G1hFGr7zBN//t/87Be99jYQ3r1QqnFLkyrKsFKgaKwYiAsMuqao3VIsk1JqMsBtQXHoLn/t2XyTKDzTXruqVpO168OOHJ4yeMt3aIaBoH80XNcllxePuQoshw6wq9arg/u8Ubb3yFw1feIuZbZMWI0RasVGQ4vUW9XGKLCh004MitwSotthIxSiCZUuTakBvIg+fsqiazGRZF7GqyLOfu7UP80RGrpk4Jxv0+lqBabcEOhMnie+JmYvmrFOwTEWmpkRoh9B/rV9umiZFnlsS0u8ke6vfdmJrz4CSeZvfwJba27r8KBFsAACAASURBVPDo0/eZ3r3DvTfewowGuGJE03phkCL2Bir0ygipwa2ShrtzgUiHcw3aKMqgmPrIjMidGLjtWna6Kw5bxcQHmLf4piLvOqzSqDYwXzyQdPAYMa4j05HMa1pytDIUUTMyOR6F6xrwIXlKXu8V1sqgxdiINjlFsIymJcPhiIv5BcfHpwB0rgVauk4G59vb28k/MoFBRix4fBoYBO+JLhBQLFcrApGBHTEc5axWF3jXUK1WaGUY5AUmitLKKAFZjTJibRU1rDtQkbCsaI8XdDFQW0M2LoTxZTTeKM4GBfl0zPjWHuXejGJ7RGfAtwGrjDDStCF2ToYzSOK2a1uMEs5w1/aWDA2elvlyyYOjT1i3NZm2vP2lr/F7v/GvmNo9lNfC+vQKFYXRrSNY1TFQK6j/jmr+x7T2kKPTu7TZHcjO0DEjRE/bOC5PLlgeVBR7OSNTM8qm/Mkf/4Ts5bdxZCwiPGnX3HvtHq/8y3/NAzthXu6yu3OIcoHFasWkSGe1b/BBs3t7j6ENbO3v8/3f+xecf3TM+ekj4q3A1fwEf3XOQZkzmm5z+vyUyjuU3aYcf42o32DZTJOUNf1NOgGLBEK1YlB40Mt0f4WBjgaTwBCiJ/oG5U8J61/SLh6gYyNgrlFkucXkcm75ZEHQE4G06sEdyVUIvUVBjBt2ojVZOkWROvMms5T0PZsBTGKFKiRbJdX+8syqjceo+KQnllym0MEIy1yB0ZFgEQLHBjSRAZA2CtAbULRXmtIPILn25kSrjRy+9++8ecbfPPNvOK/QDxXl/7/Ya4cggWjXDEkBM0P4IkO3/9rNew+BX32FEKV3T2zgtmlS7SHM2RAiXefT+/CbfURrRZZnFOUApQw25SX0oV2i7IqExDjv75MxBpOJZYI1Vkg/CnJTIGHG6VonJnKIfgOONk3zawSEmJ4frZMHeVIsKSv7SH+ltdYCsCuF8oo8z75AQOuHvv216n9PlkJ6++Fyfx1jjBuwuH9Ob742z2YMySs/iepD7/Oq6XxI16HPGoqbZ6QHTaNOWtMEOisU6/WSqgr4tsYSsSpQ1wqlIwM9En/ZhNX8ai/QX6+IWFhojfhMh4gHYc4GT/CezOZYW2JtvlFaKq3xUYBhgmPZNhvA1zk5Z4y5tqfQPgWGpV4phoBPId7BS1BYRgQfqJdrsnoJrsYvLlDrNa6q0J2n9XKvnLLEpOwLMUpfphRBWVRIQ4voiaFDKYcKGusDuQ/kzmPaFpNbvAoYLSSP3o5DR/DIdRZQWomSPYApFHluUcaK77SC2kWWztPGwLqzjEZQDKPUlx6aLlItHe2yItY1TePoGrdhc0ef+sBUyRutca2sF/GldZRlsWGQx5g+nghuTdNgjSKzCpMJGNtbGTonPzUvNNrIs+0juNahibjulPN5RVYeM8wHFIUQO1zXEVXERYcLsl86H7E2p8Oi1T8Mxf6jBmkLq/nhd7/Jy3fvYbOCwXSfwXCLH/zmP2UwKLG2kIRYpVEdrJZL9GSCtXmSgcjDEbykjta1XHyb2XS43JA1qJ5p0LNHSBIxaZg61yU/GLtJAPReAriG030Gk1OWV88ljdRCFwJNF/jRn/03Hjx8xh/87u/w1uuvMhiVuDQV6v1Wgr4hKdD6eoOTN4XS0rwTIWjDYDqlHASeP3vKyeklmkDnGh58+jl5UTKd7VCOPOVgQFuvsGZKltU4r8jynK6LXJzN6VrHYDBIGyscn5xw5+4hjz5/ynJZcffebcajIdPJiKrp+G9/8xN+8vP3mW2NuXOwy/7uNjEuiEBZKO7c3uPp46dMJyMODvc5Pb/i+fNTBqNIWZacnJ7y6PHnTKdjbt85YLFccfzilL29Pa6urrh9+4C2rlkvVtw5vMPB4S2msynBO6qmIqjIcrmksIqt7T0GW4ecv7jixYvP8H7N1myLGDMyWxJjR0QarGq95PVX36JaVlzOF1IAezkoB4MR+armk48f8uLxCXfv3WV7b4vReEietSJR8h6CTFEiMU2VZd8yOiOPkXFXszp5SvVkxujlV8ijMFxmkyEtDa5zIgFQUJQZq6bheH6FN+LrNrKBu7s5R0+f05kMRtvEqLB5hveKp5cr/vzvPua333uX3WFGfXXK8uwMyhn5cCweKUS099ApMlugtSbXFqsgeidNmuoBjL59At+1GJsBwgjc2BX0DUgqHkA2tJCm6kpLguhqtWK8NaML0AWNNVbCwEKHppQ5sBZgVyQdiqaD44sl7z844uSi4+DOPXb2xnz+8AlXdUmuO3btilcOWn737Tf5zrv3OTp6zNX8Bacfn/On//lP+Pn7P6aJHYUB51uCczRVhw8OW+REZbC2wLkGhUggZZIp4F+WZZRFKTJ6hG3fFwzESNd2tI34qoqBu9kcqn2AVOjZIz6Kd590oSgQvx0FXddgVKQclIyGI771nW+BCvzNT/6a+XLOuqr52x/9kmrdgjEyZdOGbDJFTyLjyQRn4WolAU5lUZJnGW3TEINYD0jOkXiSSWIu6NwyPNxFtROoHD6x8GPdEbveM08YtcoqdCHhXjYfsHV7n3J3CzJNvVjSNQ2668RDmyjm+tFAkACRpu5ofUtR5rSmxS9bYhsx4xwXpJDSxE2BCBCDl7WUCvvFcknnnbCzbS9RSuNuA5my+NqBU7gowDsRVKZwJtCqDjoJsGhauW+j4VACBLtWgAjVe4YKY2CxWCJs/hQGVyhc24KCsizpEjtWBlhp7WxYFVJ0ZFlGU/cs2SS9vcG8gGvlxIadTWoEFMneIQVQaYNvW37x4U/57rtvs70z4/xUhgaz6YTWfxGUdL5FJ88yosJmA+699g63bu1w8vS/s5o/YrlaEhpPwIIasZ4HardgMpI1bsyMVu9z6/AbhGxM1ayxpkDFSPQJeAmOqlpzeOcO2hqOnj/jL//iL9nf2uX42XMybdi9u8Wr919iMBoymk152d8T1kiW0bVr6srhOkkEN9Zi84yyHGCzAmszmrZjsVjy/i8+5OjZM6zJmJ8tObxzh8qtmJ89Z1QOhAmvLb/eGsGGDkOvipEGVifZVX++Xge8JR9mJeEt4t3mBVgKHu/axJDz+LYhxBaC+IXGEKjrlvOzCx4/esTDh5/wyWcfcTW/oGtqgpIwHx8hFprYsw6NDBf6FFlRlPR7LV/Yo6OW5+Ls7ISLixOm29vECGfHx5zt7rN3cCi2HOk7XLjB2FEGlGY43Cb3BbPtMfOrD7i8OqbIBtzeuUtVrTk7fcGr97+Ugl8EsG6dS+Y4Kezpui25AdTKW/XO0+lAnsvgznUtMR/KnVAKspw6gL13h6//mz9k/849fvonf8LRs6eMo6bFoWYjbn//64TDbZos0HlHno/Zvn2H8WSXPBvgWinEq65iUc2p65qyyIm3pnzpD/4Zf3t0yvLz5xQqw0WR2jZesRxMuP2tb/K13/9XbH3lW6xMQec7TGYpky82IVBVFXk5Svu3osgL+VvSwH48HvFiXfH44efs7+2SZ5bzi3MGkwn5aEztFPloxvGLM5zOaMlwQc6RplpT6iFZ1XJ7MGNveouCEpwMQpq2QWcZqhgSizGqGFOOWrK8ILoqBdAFscrSRgJGtME4S8QxHE1wdNQn9RfCC7emM9rOMV/OWa5W1I0MdHpSgAASpBmtsFyjIvnHC6gi+0wnxIXAZjh2A5kF3UvU1ebnx5tI7ubhgRBlv1ejGYP9N6ga6LIh9956g8HhHaIGH5QM9SISzpma9n4P7VxDEwJ5Wcr6Co7cdZQ4dpXhfojc6TruuJbteoVuVpQukkWAgPY+5QyIl6COAY0B7wlKQHDnI3XrMM7TBp+YzIbOiZTUJxlvjIGr+Tnr9QKtFdPJBJsX2DxnNBqQF5b9cpdbB4c4H2ibVtaTNWilKGxOiNCmMFIJE7kZ8OOTDNYluXRyItWR27fEKqara4KPKSFe1E8o2XPQUv8ppD7QSthDTdtyVV8xX19g9YhhNiA3YhfULCvc2ZrLp2eYnTE7b9xjducWlyRQfpPOfX2WB98RXEPwLd6Lj27wnZAAXMfjh59xdPKCugvc27/Dt9/6Hnvju+goNhAgPvoQMcpggqPQS6gf8eLpf2K0teI//e2KP/3plGAOmYwecGdrl/Vx8i/1QkiY7hh2BpE2KgYHL/P+mcXZnOOoeTya8s++/x4P9Q6fXjj2XvkG27N9JrMpx8+foNq1WLC1c8rScmtvyrNffkDOiDe+/g6Psk9Y/uSY3YOST3/6c44ePWdrNORwf5vK3+Oj58eY2Tt0+eusuwnRaBxgEygpdgFWLHKqQO06JkahoxPbDm2J0WFTFkDwFcYf46uPqVcfEdwCpQwBudc6t/joNvdZvKTFg9eiaTrxLLbmmjDQp8b3AOevqjt75Q8xJmaevKyV4CdjBAC8MaOX+6d6ddz1P9rI4CIk5YrSChOTpVaQv0EA2sRApAceNckOl81YSfXnO5vN5+bQ8O9jul7XYH0MpORqaNV7rd8Eantq5c2PX/+8X2Xp3rxmX/y8MEh9iPgYZdUpNgN9kpdl8H1mgdgGZJkly7IEKEpf0bVt6j2SJ7dKIWvJEiHGuLFrVPTEBpVUThqN2fyeGKP4WYeATyBtSNL660Fb8kNNwKuxVvoYLT73vby/V4olhESyJ248J/3X3Byi31SguZ4p+iv3bUNqgQ0xpr/ecq2T2m+j8AkboLXrGmK6rs41kL6+Zwcbk20IN8qG63sQvFjTOI8PgUW7RHmRsdfDhqmSM6HMBxiTk9C5694kTTACJCaz2vzdmycrSuBddI7lakHbeYyxFGWRiD+ZDMmIG1KJQvyMhU1+PaiQOiAREL0E1FmTfG+R3qbrWkKM1KsV3WqB7Sr0esWgdqjWoXwkOgG6vRL7Pq3E810ISpHOQOM0PhO1VlTQBmG6B5tJv+sDJgR08IkslFjCKehOgQzd0t2S7ILAai02hKZrcd5RlCVFsiLQXijjTSPDwK4Ds1JED20b6ZqI6hzaOQlGbipiKzWS5F9ISRJjSHYQekMM6zpRbfZ9QIwkEkIkIGpY7xpaFSlLRa5kTfg00GhbRwiiWs3zUpR/NsM7R+cirq1RnScPDcFl1I3FaCtQijF4FYlKYRUbVYwHsYj4B17/qEHa0aBgazZk2XoO9vbYPbzL5eUV08EAbTKW64aqrhmNx5DksSpJspXqF6tMF7QxlGWJayuIgZ2dHbQ2eO9SUd43d6QFiJhBa1kMXdNQVx1FXmBHKQ0QiGhsPmT71j0WV0fYyxP293Z59uwEsgwXM375wSMujv8d3/zG23z/B9/l8PCAPDOoPCOFD9LDZv00smcdBCIqin8qRFpnGY4nTEcjirJgWBZYDS+eP+Ps+Dm/+OABk/EI7wO37xyA91xcnLOze4tnz85xi4rxaEirHG3nuVqccHJySlEUzOdznj49ousE4O2c48WL57x09w7vvPU6F+eXPDl6wYNPH5IZmU6MhxnK5jx69DnPnj3n8OAO66rm088/52rZEoKnLApslvPOu6/z5PEzzs5PeXp0xMGtWxwc7rGzs8X9+wdEH1ktViyuVrzx2mtkNiM4x3gyZl2vCM5J8FVTcbWs2X/1kPd/+YJl7WnbSnx2ixK/qvDB0dUdTVNjlOcXP/sFb7z+FoNyyOXlJePxmNlsi7xoGI5mTEa7PPjgAZ989Dnh488Yjkqmgy2iA+9ks/cxbIAtrcWsXwWI2pLhmPia9WcfMS4ypoN9rmKGChabJpnGtUzHJb5d8fmTlfh7hkihIncmOf/k7UP+an3GJ88vUfmISEa0hqigDoYPnl0Sf/Qxv/feG4ytYqBqLucrQjwQqUcM4Dtc6MiUR5sSowqC8zgtBZBKRX+fYFlXLSF6QhvwsZUCIMrUTvYVkxibsedLoBF5p8r6yTZUnaPyGnRGFi2mLFiuV4wHE1AKoySb2GYGVMEnnz7hg4fPqFrN3ddeYTgoefhsztpPseEZd+2K33/zkG+/8xqHt8CblslkwI9+/CP+y5//OcfPPsXoikxHgld417C8mKMw2Mzio8L5gHOVHBT9lC2oxFiRELFIn3Iq0p6iLFAIMz/GKFNpJWBcUZTo5N3VF2ddJ36Ucp3Em9UohbWGzAobyUXIMstsOuI7732Hd776Zf74j/89R8+PMJnl4SfPOD++Itdibq7aQDkZsHItnVIs6gqMSpYEEVVERsMBRimq9QprDLVP8rcQCU4kMkqJvMyXGWFYYiKMpyVh3dAsVuJjGKSZtkVGMR5gcvl7wyCj8S0ZGbk2uFSgaa0YDUYy7e48AY/RGS4GVGkZTgfMVxdU8xXaZuSFSLdCYqjHBIRJIWIEYOR6OFWmSbzWyWMrFeVaaar5im5VkxUjmq6lqSphYJYFXgWKcgBaie9wU4OGvMzoXItWSljGkPyxRPrkgoDOpCl4Va9lX1eRyURsP87PzjbAR+9hlg4KvPdMxmMG5ZCTkxOyLBPf3fTqmS19YyTHi9oUxFrb/gBIzLaIzXOenR3zX//6L/mffv9fclDco20r6sWCR0+OOLhzj8l0JpP0riWiyLISk84+7IBY7LP70g+Y7X+Nbj1nfXnEcv2YyxcNzs1lkmwNgSkHu19mZ+tN1OBVWpcJUxSXRPciYXJdB96jkQJ7azbl1ZdeIlcZX3/nXcpCUsFdcHTO0TQrtDG4TkDPSMTqgul0i7IcoIxhuV5z9PyULMsTWA7vv/9LTFTcOTgAFF9982vko5I6VtSrK9r1iq3tHbQVVtsXXr/CjOmljcKeEBle35wR0zA2umtJtjapaXUSfkEkdA3ed7R1Tega2nbJennB1fySZ0fPefDwMx4+fCTKkdDiYivJ7bYPY0nWBQqxE0lDuRjF81P3hXyq96XQ/mLToo2mrpY8f/opZfkGWVZSLS45fvaE2fYOJstkH/Me33UoJexglDRWk9E2MU4o8wzn5PcNhyO0znh29ITV6pLRaLhpopTW5Hkh1js3JYq/MngQ7+Wa4WiEUtJYZlnO1mSGcOn65l0TVKANHqYz9r/7Hb49G3H6wYd8/Jd/xbq+5Bv/9DvkL+/iClGs6Jixf3CPUs2wsSR2gUxFtM0Y5J5xvsPl8oS6OUeVBdkb97j/z37AJ//H/8Ww6Yg6oynHDHZf5u3f+SGv/PYPiXu7XEVESRANQRcQRfZo84IsKqK24tWtIC8KjNHi5+8d5aCUAV2Wc3k5Z11VPH70mN3D22KZkOxmXsyX5JMt6qZicbUkM4putaCuK/aKKZPhEOVhdXGFzY8ZTmcoWzIcjRmOJ/jZjGGuWD3V6NUV1hd4xAqkbVuUVjgvIHQ0YktRVzXDwTANSAXUs0qGiTuzLWbjkvV6xcn5JZfLFZ0YxoraQ1J/BAzRBmMtpJ/bP5xGp2DJPkQksaD652Wz1BA2LsokSWgC86PsqZvHPSrsYBs/OGCxfMb4/ivk4zFV2+GI5EbAAWUltFeWbCD4TlRoLqIzzdpVGGUY+o6Za7kXA6+4wCs+stU1lG1N3rQo7wRMUOLVr40it4WkeqEEFIomSZVFFdMb/gXncU1NvV6hbUEIDhX6UNGAUh7JqmxZrdZYFVDGUg5GZEazqOWcyvMhxmQM8ky+z0pN1Pv/aWs2f6/Rwq6KCnTyaAwuCCMoDc+DR8KarCYzFmvzNBhywore4AcBvEdpI4x+pbCZpu0qfvrgbzl6/ogtNeONO6+zN5gKqycqXHA0BK4uG87/7kOM0Yxu79EpAfNJjGrnOpqmQkdP09R0TcX88ozghFWriSzOL/nglx9wcXnFcO8W//qf/1u+9c5vkKtCxkDakylFUHLdtQrkqsP6Ux59+mc8fvwzVuGr/Lu/uMXT+BaDrZK333yV+d/9pSi9lGJUDPnqm6/y0F2xMz3kz3/6nCM3YlEMyRSsRlN23vt92q++yacVrCMUw13OV4o1ATvaY/9wiDm4xeLsc3ZmJdXxYz7/8GNeGt2mWi7Yf+U+ty/f5OknP2W+umR3e59X3nidRVUz3XqTYbbL590ez1oRuEVtEkAjzD3V+xBHh68jtBFdZGid4+OaGDt5nrSAL6E7RbvPqBfv01Tncm6pSJZbsmGONkna7T2o3vdTE6ME/mgrwKhPtl9iK6Bu9JjXIGQvL9/00URUYrdxAyRzXZJZx+S/nsDbPM82snUSWBWjEeAq9dMGLWztIO83pmXm/3/m3utJsutK9/ttc0z6st3VFg1HggA4dCCHpDTDq9E1ivumv1NvitDVvRrFxHhxZugNfKNdtS2bmZV53DZ6WPtkFcDhOxMBNLobyM48Z5+91/rWZ3qvzZiA434Yob7sNXvZo8dExFIpvFBdnvmJ2dhbsfTgqAq9n67aqAH6Gm0zhFd9HaY21l8h/HFLhas/v7RWuBwfO+/JjCXLMyHqQNoXg1gOGIswZkURo7WhaVpU22FMJqB+J0QIAWsFAMx7v1XVKyL0xo5RLkXAu4ALwhx03iWAWmy9dCZ+uDbT+ERCUaRB2xWiWM/yJA1ldQpA6+vaPpQyJEDOu354e2k31ucCqHSNQspCCJEUOJjqnCtAbthYaIh3aH9vxYNXBtAmDR5CCu4yMdCkAZhWitZ1hBTeKMOuDp8CEfGBEDphu3oBaUVtEOi852xxwenigslkxHa7YmuyzXQ0E5/R4Th9lkuf495qol9UITFU+xpUhhuaPLOE6Om6Cuc1naukz9ZmM2iPSUYva1VAd7F/sOJ52zOTbUR1UmMJGK0gCIu7aTvWVUVsKprlObFaM6o6TBvRThNrsUzIrPga6ahRPiBQsgFkyOBwKCUhiF4poskYzHYIwyFVDHSITUJQAQjCxA0CnGsj/vVKgYkCyJdliTGWNvV2rmto6jUhRvJ8QHSO9XqFyQcMxluEwRAzKYg+0jaBto5E16FcjYodKtQof4HqKsHwUu0bVJReP+1RYh1iGI1yvPeJmS7ne68Qy5PiIXhPtb7Y7IW9zZKPDmOEBKVijlI5qESKwDMsCkbDMS7IkDc3miIrMDan6zpq127Wu2tbVArfVlHUen/s9ScN0oLm2auX7O7n7F+7RTmcsG3EV60NERISLQ2WIisLfIxEH3C+FQDFe4ZliSKyXi05P3rB9YPrmKJMUq5G3qBPhdUaZUQ+roQ2CMHRNRWff/4p3jnef/9bTHf3Uq0kLLFyssONN77LsnIMj5eE+AptIiYr6OrI09M5h3/7T9x//oS//OF3+e6ffYvRYIbYDkWUlz8vKiQARBtI3on9IbFarYlEJtMtolXsHuxTjAa4akWWZ1T1muVqLYyw4Dk7OeX9975GMRzx+0/uY/WAp8+fMxgUjIdD7ty5KZLBGHj5/CU7Ozvs7OziOsfz5y/o2obz83MGuWVv7xpv373F1mSI1pr5fIF3DhUjxXhMkRU8e/aCYT7mjTfvMZ3OsHnJi5fPmE4nnJycMCxL7ty+RQxQNy3zRcXe3g5KGd56/R5npydcLJfs7m0zmg7QRg7/ar1iNBniQmQ4HFGvLjhZOUIwfO3r7/Hg418Rg8ZmOU8Pn/Pxp59w8+YNvv/975DnBdE7lssLXr46QaE4Ozvno08+52tff4fxdMyL50eslhU3XrvBzRvXWa8a7n/0BatXawpVSjBE5+iaDhdFshx9pFPQ+harcpwBSyBr5sy/+IzJW2NqnXFx/IJVHcBohqbgzWsz7h3s8ptPH1Mjm3ZmLbf395gVWjwjrSH4Om0IDhdBBYW3GfdfzfnbX37Kf/7eW+zsO9T8hCasUR04wPmKLMsxpOLQB7rOYLN+CCAyeYWHqPG+I7MG5zxt15JRbHxaxVpVib9MdKyrFa4LsrEYS/SyuQ0HOWdtxAeFohM7i7xANSLVR2thaNlI5TVfHJ7z2wdzOj3h9tdvE5Xh/pOXdE2k6BbcG1f81Tev8+17M/bHLYXPePDgPj//+b/yz//095yePSWzIouxLtDWjTBeA1grxYzrhAE3KMoEvCBAnIqbiX4vO3ddg4+BLM/lYOpauraRBskaVJQiQxsjU0trabqOrusIzosU1YrnmPhNWTByQHgvcv796R7f//Z3+Z9++EMePPyYpjrntds3+OLRMx49eYVWkvwZgqdaLSlnw9RwxWTTkMIOCLRdQ12vheGJpnMBfCQoAcOiSkwlhCUV1OXUPhsWUFrMtGQ4nBCBtmlE6W00PvrE2o9E5xPrR44zk2ksJdNim0xZmtjItNKD9xEzy1llDt911PMFOrcQPcYoMitralO8px2+By83fkshoFT6EU2IPrFAclavXqCbiLWKxiVvJFsw271GMZ5iC4syAZ1pIjl113K+WCQM9tJDUaV9W6R8MgGnfy4SvhqJnJweoVPgnUpyqd4v62phfn6+oCiKLwWp9L/373mmbZhoiVUOl8VpBFqAqPnwiy/42sef8/rtO1xUa5qqYjIeEboWokdbCVMQ+SxEm0NqWrroaTuDMVPseMzW6IBr5ju45oLQybDL5orG1+TTfchnNF684myW1ClIWEdAAvGi6whdx8o5gne8/cYdTFQ437KuK/kuiXWBFn+p0XBAnufoLOf8bMViXXP4/CWnp6d0nef41UvKQYlSmt29a7z37ruMZxMGRUaohCHQqo4iHzDY3hMvWpXhEKZsTEEncomveKcqkZTKDVWSwK6lgTFKCcgSW5xrCM5jlUZbTVCRel1tCu7gGi4uzpmfHXP88gWHT5/w7PkjXrx6xcnpBau2SfudJWiIZCgtxWLsWR5pAByNQiUfdmm2ZC0KoyN8eZ3ouBkSa2Ugek5OXnH7zi3KvKDzLa9Ojrh+fsbO/jVhxESwqaCMMdnWxIBWGW3nefXyOZPRmNX6jBgirnMMipzMTBmPR5jEXvdBmkeb5+nJl/CEfv1+aW0LvITR/fcUf0PnHCoqrLIbVlEI4rOpZyMmb73O6Po+9ciyrE+59sF7rHONVR1Kl+xP7jLKdtCxwDgS+AAAIABJREFUIAZPUzv5blgJurAZu9OC43nHqlngCpi8dR1154DTR2fsHdzj7W9/h1s/+IDyzTdZZzl1UpMIczqpqIKlt3kKMYq1RYgbz72Yxvc+anzUBBRew6rriPmQa3ff4sH9RzT+Fbs3bzAaTyhG2wSVUV2ccXFyjI01hJxhOaXMEVVL10BWUS/OaBdzypmhrVeMhwNaFDvTawycZ33yHFWtoV1gtSNYQ+U66qYWj1igNYrGO86Wc6p0DgbvWbc1zknAY2w7tqdDtrcmPHj0jFfnC4JSFEVJMDLUJIYEDKqNr6LvFV6JNqdTgFV6xNgwqrXe/DxtsALCbPAMlViSnhg1Kpsy3r6J1562njMeadbO4d0a5x2tyaSOSZ6zIQRyEyQLQGXYzBCMMKgmruGaa3g9tLzTePZbx7htyfGSi9A0myBPk2VS3/RWNlYLWNpKQy8ybpVCwALBiB2SMgpNQHthh/og45QYPSC+ntPJlGFRCCjStpCXdE3Furqg7Vp0eq88K0CpK6w5YcX1QzttMnl20zOnjMZkGVpbfBcSMMyGqRRaYeNopWlcR4iBoigSMz4FqoWA1ZEsUwSQPTdXGK04nx9ztHjO3njMzmCEpsRqDVHAaB0z3MWK5eELdq/v0MawYeD50OLaNa5ep/suQGQ5KFivOrq2RYWOJw8+59GLpxSTMT/57n/ga3ffI1clKngCLTYTxZpWEZTB6o5CX3B2+Cs++ejvmfvb/N3vtnk6f5duMCarGpxWzIa7LL3Bai893uKYG+9+nV98Pudht80iG6NVgfdz3vr+u7z/F9d45c/Y2hoRzldoDaPpFo0LqOg5v1jy8pMPsf6U7eEdPvn5L+nOV+iZYbE6w+qcO3ducmd7xtHRUz764td89vnvsKMSo0tuZJrFesVKrVmpjI4MdJLNI37dUUufp6OCqPBE8sR+JQSsAuMqjHtJqD+iWd3HtadEAlFJ+GpWWGyepPZRbfIielafVhK4Y5TcYzlLpIYM9N7l+g9A0EvfywRU9uqsvn40QizSWs6YqOOXBtd9QJU2KV8lWRnJgD6xP3v2dX+WBAGXiSox2xUmS57o8Q/9YGMUcotO54qAyCaBgskTNZ27UgenvxL5SiWgs//em/eWQ1s+96Z2S/L2K4zOq//Pl/5/1b9vkiak4VdPFDPJKqZpGoq8IMtKsjyDKPdhUxcm7120xmojyrMEJgZ1Cab3ar6eeSoBXY4uinKzvy9GJ3s2K97iRZaTFxna6itneX8/pBbZDJK9T4xUlQJUO3ozyY0thb+8n+mOyvAm+BTGblBp31FKgOFAJOttKrgEyvt9t/c810YnC7P+fsh75Jmca3LN5TlwnSfGjGg1bSuDCRsynAviCxtVqvF18kcVWxlpd+TaBYXkmqTclpPzOcv1BYtpzWxaMR2v2dvxlMOSzBQoJeGqAbG82gwE0t/9AEHWprxvlmVYbRmOJlgrKuYYRa3tvBOygLpUo1grVg79UCVGhQQySv3Ytm0CZ3VSjFeCAXUVbe1wPhA7COsG37RE54muoQ/t1lqTKankxPpA9nEdYKTFDspE8Ii6qBhN0Ls3UJnURp0HGxVZWkM6CD80YIjpu0jhbSU/R1u0mLuhoqi/1uuapu5YnLzgxbMnaFuwtb3HdLbD1v4BxWBCQPrj0LX4eo0LLYqW6Be4rhGfaSW9aEhhZrIP9Z7aUpf2DO/eGzrG3hpBSVhunm3oH1qrjRrA5gXoQJYLuC4WX2KxkRkrAzBrKbX0goM8I8sGYunmO6guaLqW1jW40KG1RxHIspzKd/yx1582SKsMF4uWW7cmqJgxn68YDAb0rNOiKLBGkHEV0yTO97R2R2aNGKknmorzHmUt6ERvDn2jAVZpqnpNnufkmSEG8T9r25pqtWa1OOfp40dcLBfcuXOb2fZO8p/0dKmJmewc8Mab77M8OWa1mON8x870jOP5HIAYDR9+8oST4zMOD4/4yf/8l+zt76J1otH4y4NCp4mj826zQeV5LmEjuUVr2ZgGkxEMS4rhEK9geX6Ca2uKLOfs+Izf/u4zgoH5ek1wF6ybNZPpiM41VJX4JA4HQ6bTKavVir3dXfIsQxGZDkq2JyOc61gu54TomE5Kbt64gXOO+dmCQTFg3dQE7xmPSp4+fwpGkecFzjtu3LxOlslB/+LlS1SE0aikqtaslhXe1XRdS1evscbgiUy2t3l5fI7znm++/xbEBu8qQpRUc+86dOj43S/+kZ3ZNQqrefbshNHtm7z22j2Ojk559OiQvCj44IPvsF5d0JzNefrypfjIlTmruuJf/u0XvPONrzEoC6oKlhdz6nrCZDLh1s2bnDw6RvsUmOEktbEw4qXTOJ+YJwqvhOavjCIHusUp3YPfM711l+nelBWG0kS0i4x1JNcwXy5ofcRmlunWiMF0zMcPDjm7qMjyAhdEpqS0JrcFUcQCdKrk08NTZoOH/OD9O2xr2bTbVqGUZbHyDAdj8nJMI5ZuhNgRgkxsVfJxUxvwwpJlhrK0lF6aspCKI61lKuWSrODs7JTRaCITPZDpeoz4CG3bCeNFUAd0NmK2nYB2FFFZGhQfPnzBJ58fw3iHm3cOqKqG46cvCC6QrQ454BH/9Xt3eeumYqTnmFDw8MEr/sdf/w9+9Zufs67nG5alajtc06TCVjEdDgFhq3nAFAVELj1AuSwGNv5cRDqfWJIp5M47aeB671fv+6mfsG1d56nbhtY5yjxP0r+YPKfFmqS9aCitYTwacv3gGu9/4xv88Mc/4NEXH/O7X/2S/Z3rnJy+wC1fMh0YzpYdMXapofbYiPi0ujaZ/+skZYp0yVtXp/u4Af7gClNJaDSC04iXsskLsrIktmsg0oROfHWz5K9LIHiPyXKRc/ZyozRNDDGgNGRZiVYWlbiMbdvQ+ZrJ7ow6NqzPltTzFdl0i9YFdI6w1FJx3jf5/aufyqvLX0gg1mU4TLduqS/WDLNC/pvkI2UySzSGddegqoYi14zMgNlwTHV8hMktzofUVARU1NKAJuWFVprCZpJcHSQQwVidAO6QrBn0RlLWf96rxXrvDWWSf9hVn7I/ZIKk4pZespUap3499ixtrXi1mPPZ4we8ce+ehLCUJWVR0naOar0mH402NiQuOHS0aGUISknwoJVhXe/LqvKcYrQjcqyoQQVKFXDK4L1NSGcqzrlkV5CKd6Li5OgEm+fCcgs+Adfy3+ZFwWA4whYlbZAU4wcPHlIWBTdu3eYXv/glq4slGtkvru9f4+DgOtPZlOlshrGZNAvIBD6fzhiOJugsI6i+wVSSaK90KmaVAC7pI14uqt5jFujZfMg+bvJM8A8XCL5ltTwj+pY8NzgfCd7hmpZXL1/x8IsvePT4C169fMnJyQnrpqKhwWuF0gWmSIwRFTcNptxvadh6X6zLm3/pYxfSmv8qS7U/65umSQNaAbwXyzmPnzzina+PKYoB62bFi5fPme5sk5kcH2R/0EqzrtZkWSZp7RGsyVgt1yitGJVj1qsLclMwGI4piy2KYohw3tIARWmMsXQ+sX2vAG7C6hBlks8svZlJ/537G3F1SBGVAqMTi9ESJxNWBOybd3jz2jc4Y82Lx4fMptu8fffbmJDTda0ME1VEFUYGZiZ52GmFNgXT8R6r01PqrKXYn3Lzr37CuCl4+xvfZnrzLu2wYJmK9H5PVAoZiPfFeRqCy34fNkyVq4wpASsyjs9X1KFlfP0Ok8k1xtmIzx8e8fDBpxwvlty9fYvJZMLR86csnj2nrFbMhiX7wykjk2NCBNeBacC3xHaFW8+pVaRqGuzBgaQBz8bYuI1vKyrnaNcSSBV8ZL1a0bpWPL2J+Cyj6zxWZyjV4l2SyjpP50TJ5KPm8Mlztne2uHnrgFXbctF0mCxZhhHlmUprtweulUoJ3fRnzGVjH5JVjTZG9o1090O4BC8UCTwACWfUFjPeYXz9Tez2a9RVS7s6Qk0neAIa8dFXSkAzOgGglBLg2Wojo0oVyZRhEgKvdR2vu4rbXc3N2jMKYLtOhg5a4zPDdLIluQzOo8zlvQ1p1VtrhGGd7EL6f49arHB0srDp9xOSeDp4h/cd0Ttp2jIBBGICj7x3aQALSkkSdvCtXBftk8dd/1xpnG9RziaLs0DTNMJUNpYsKzDJi90YTV3XMpixNoEUMoRQRkNTEBFQwqTr16R9NRBp1xc447m2tc2bN+7ym89+y/0Hn2C9Ynt0jWFeoGMgeFguKoIKqPMK24j3bts2+NgIQhyTpUHaNwRE87RNgw2eMF+QnSzYIuPet3/If/rJf2V7sENoUxCeUugI9DJ43VKaCtaf8flnf0OjBvzrZ7f57bMDGlWi2le0QXP/+Bk7izVDm6OUYzjZZrJ/i08WGR9eQD26Ruwa/PyYg33P+2/MODk5IQs121pTVWuMzpkNtsgUMrBoOrQN6HrNb//u7/nsZ7/m7TtvMB5M0DrStAsOHz4g1g1Fqbl18w4n1QlLvyS0JzSLNTfdDZQb8KhtaQqPtSOMGcsAAEemFBaktsGhnKZ1iuhkTWkfoD4h1Pdx1WfU1RHeS3K9tYbpbIzNoU3r0Hk5azMroXYb8BA2dgaayz2vX2v9c/zvMVblX9MzEi79RJXWKc8iXL63TOgERCQmXkZ6f3s5hA/h8r0FKEveuTYF0Br9pSF4H3Z11Ze0B2jl+0moWQ8ywtVw2Ms9SKe8hk0mw2WR/Ae13FfB2L62vvoZvhQ29gev3j6xxxau2Br0QWDhSg8Skr2SEhLIVYxW2su076ShsVKaLDObGsJ13UYlJAFffnMdilyk9FmSegvxK0nQAbqYmMcyoDNJxt8GT3T+0lZBfbnOtVaA1/765HkuMvMUUKeTDV4IsjZ1skchXjKcC5uTZ2J/570XQotzsl97WUNXLSUu75n8mU3b0sQvh/qq3vpSy57obbb5/RAkr6S3IlBRgHiTrENIvUAIPn0HYeo672malrP5grb1rFZrmq5mMCqYjqaMigllNhQrRG1SjxO/tJY26ykEUUIiZ6v3nsFgSJ4PyDKxvPFBVFyuawUX6cRaSyViizyDCu/1BtQ3pkAZCZbTSvoXFxp8tyYrR1R6LdYzXSR0geCdEK+MAJACkcXN2Z/8jmSwroKEQHtZE2q14uzRA+rnZ7jJEK7vUc622SvGtDFwtlqzqmsBSW0BxuLRxKjRmZFA53QNYl9nRMmJyHXAV+ecPbsvOMTFPrG6hSaQD6ZkmQR7B9dRt2LX41cLzhYneNrkPZ2GxOnrSGsg96FLwxLpay8tNYy1hM1eFzZezP1988kqqOvEs1YbnYLFNHmQ+kIG/lBXa4o8UpghRZYzKAZkWUHr5MzPs5Z1rVnVEYVBqYwQNDFe7r1fff1Jg7RGG+7evsf+3jWGoxGd18QgzbsxMiEyeUZTp1CEqJK/h6FpamFvqWTGTmR7e4ut2VhuVJ9eCSLHDZ7F4pzdvV20UvgoG55SEaMV0+mUP//+D1iu5uzsbic6vhLDYCMMi2As0+3rvPut77GslpwevWA8HkL0RGMwShHIeHVW8//+/b/w8PFL/sNPfsS7777NqCjQSuMSUCuNOpsDoqddZ3kuYQcxChPLe3wEMxhycOc1huMRq/kpRgVC1/Dk/IzaeQ5u3mZrOgWjcG3Dcn4msk4fGAwGlGXJZDIRn86y4O7d2ywXSxaLNaPpiFg3BK3JzZCLpVDL9/Z22d6a0TQVw/GYl8dn/NM//yuvjo/42te+ztnJEW1dYfUAozSjwVBsG5Rib3eLp8+epYS9gsPDIybjMcPpmPsPDvnwd59Stx2L5Y/54Q/eZTQcsFpXVMlQe1TmlFGzOnvC19++S5kHHj9+yMGNW+zubbGuGx49esFy+c9s72yhlebk9JjrezPu3r3NbLrH55895NEXT5htj7h54wZFvstqveTXv/ktRRjgzz02SmpgL4+W0yNuDhxtROoXtaRw6gBj42jOn9N0FXFUMt69w8gaos1o6wvODz9m5k+pKOlCwZ3dPWbjbf7100PWscRkBVloINSEaMHkoAQMdb7FefjZp09Baz54+zrDPKLiGpPnmHKHrpUNtbAZ2mhcU9MpNhO83ozfhyDyFTStC0mqJIdTTCzQpmmoqoqiyNjb36fIB7Sto3Oe0WCcwp8iVXNBzCSpVJ6FLEk4pDiZVx33nxzz4f0jxnsHXHvtJsdHZ5w8P0f5jrGq+NbNmr96e4+39lp0eEk37/j4/il/988/5We/+pmkdhpP9J6uddSNNPFZlmFNL1WW6aPmSnJ7jKkq+fJEvn+2lFKS4K4kvMkYuzmwlNKMRmWSQMtzWFUVUSkpirWWVFaEsaCUhASo6CjKAbdu3uTeW/f44Y9+wIPH9/mbv/5vZMqSDSc8fvQps9xzc7fkfNniUZTJC0xFxaAc0DYJuEvyVRU1zl+m6Wql/6CYCTFgrAIVyTLxuPXeM5tMmE5nPH9xKCBH2iNsiNgontc2K8nznNXF8rLQEISL4AIq14wGo9RQmSTPWjKYDNm6scfp6oTVyYqIMNt9lpp9QGkBekO6J1Lgmw1QontZlU7p1n376gPV2YLoPcW4JPqIa8VbKxsNocxwRiw4QDEuS6w2TIYjFusVPvbyPXBdhzKGmzducnZ2hmsavv7mmzx48pj5YkFAvKhsCqzxAWL0m6CDHri/CkD1e0MPuF1lG/4BW6MvKlMx0CuK+6Lbe4/JRA60dI7ffvE5f/bee+xPZkQjjdrAWDyR4DqRITufhntJeqwF0M/yQibyQbyZmijnGUGn9Njkv6xVShhOgFxiRYbQN2+iHji4c3fjyX744CHj6ZjhZCLPgVKsV2thmJ6cMl+uxCaoqhkUBTcPbvLGG3c4fPyIe6/dYzKayFluBMDpQiAbDCjHIwbFAIXFK0XA4GIfziDMWK2NhKwg6xIjAGGPJctzC6Q1pPqiLYI1mhhcCghsCO0aFSp8t6RuPC9fHPPw4SPu37/Pw8dPOTk/pUuMBq0VyhiitiijEG9AkYJJ9yGfR20KLrX5Z88w0WmQ068lrjShl2CNANI9+KshWTJEXh294ubt2+wNStbrJUfHz9g72ePg4A4ie+2ZKZfMmP41GU04PV8xGU6YuzPO58dkmWVvbz+xZqVYVFqUATHKdUycwcufb4YJvUepsJtIoFDksqn3yc9XaWEbVPM59fqC4XiAnU557b33ibYlNC/Z9h25HjIe7nB0dsaiekVULjGmxIomMxlt1TEZbmFNgTGWUTHjojvFzEa88ZM/Z2quofMpp1ha7zaBGn3jHNOAxHt/WQNyybAicinlp19HCpuVrOrAol3iHjylaQ+ZTrY4uPMaxXTM6ekR63XF+dND3GLOpOsYW8tIWbYyYTbaGNCuI7cO3VSQFZRWM50MWaiI6moO7z/kxeFDDvb3KQrLBYHF6gIbPev1KrHWpT51QOc8q6ph7Rzn1YUonFJjKkyXSDmcEMwpDw9fcOtgn63ZBHfREG2Rlm5qZnXfoKQ1qE0CdxKcGZN8VUG/eQl+0AeqKFBm0xglcj0xdoSoGM4OuPX1D6jya1RqQjf/nOFQYXO55ib5DCoi+CBqIu8FCI2eVgcCDhUdowj30HzTO+7UNVtNzWDDrBPZatc4GbKfn2OUwjkP3m+er0gkRkNRFHiSVyIRVCA5VMu+mNjpJGmpMVIzNPV6s/4VKnnGClvMpORumxm0yYWVIxduw/wKQfxCTUpIJ3oZDIYEqvma6ALaZjKw0DnBicKmqdYC2gyH5NqSZ1YA2tQCh6TI0zKRlO8cxSs/NA5FYCcb84O3v0u4aOhCQx4NqnO4EIm+pWk6uiYSMbj5BbFq0JNS1l5bQ2iJ3gnjL5B6ChkUBNehqgb37CW3yfnLr/8ZH/yn/52D62+gnaHtaqIPZLlYblijUViUrqF5zPnLf6Bpz3m5uMuT5j123voG86qkmrc0yxO6boleLimVeAsvusjhEn5fwzKfgo/o8yP2Biv+8zu3uTtYovyadetYPXnJeDyia2rOXj4Rpmth2d8Z8tr33uXDv33I73/6UwqvuXnjNfb2b+LaNavzY8a54cXpGX/zq1+wvbPPd7/zZ8TTx/zZt78J7ZDjRw2/+WyOPl/yWedYxy06CyoWFHkhIAsKjcPEFt9pPAYbHcp3dM0x1J/QVZ8QwwqUIcQOYzN29/bZ2tmiqpd01UVi5uXCRN2MN1NNoS8Dm3Rfj9DbPanNgJ9+jes+ALWvR+T8MNakQYWiS36OOlllqb4+jJE+lNDHiNUmWQYh9gY+pPXf26bEjcWV61zaZ0QWjbq0v/r3AeS4UWD1LM6+3up/DAnA23y3VCdvzlj40nt+lRV79dev9gpXf+2rtgdffvW1M5sCoM+7KAcDBoPBFbBXPqNL2QfamE1mDWn0pU3vB+vxLrCYz5MtnTCr8zxnOBhirPxcp36ot57ozznnnOxqok5PQJbUDCEKk7P37rdXgkKzTKAiay09cWOztqzYMORFsakN+oBc59wGYI7pegtQfRl6JecrX7nfWj4gfb0hAGRvudH3Ov3llSWYzq0gvawcT/rS01f3902Y4EreVIZjTmy6rFHJa1vWq7j7yPC2aita37JuK6bTMU3V0o1adqaBYTGUbA2dbCoTcaB/xnrVUb/2+qFGVTW0XaAoA9aKWkLuocXoHGsL1uulgMcbYpEndB7fyfMeg9ScUVvyLBPg1lq0ztE6UOQDtFpB8Kjo0SqFXgIxOvCGoCUA6zJYTqxOnAKnIqtOCD2FCjTzY+r2hAsFp/ctL/OcxfYOqhyh8xLyjMFoKFZRQaxMui6SK5VIY3Fzrgpob8hzjY4dMQ2uVfBoN0TToLWD0OCagKUkMwpvIXjNuqqoLpYyVEjZJlLDJuBTQfRhwzonRkwIuK4Re7AopIyrJInOi7Ku3w+yZMHnXJeqIp8GKwGtILcW7xq0lhogyy3KGurWkVmPsVInqygYwaDI8V0HSpOZjN4O5I+9/qRBWqVgNBoyGA5BaQkJaJ2ABWlqEiOU5UAkSD5grcH7jmfPDtmaTRgMhsQAg+FAbpKxAoY2tTy8RnzEurbeGDiH3ndLKZEoTWXqs7d/jc6Jp1Of7BqiSI01Sh5SPNlwyM17b3J6Nmc0HIgnGXJDlbEEAuvO88kXjzk6P+XHL7/DD7/3PW7sX0/mPSkhkCueMP00KQRcCrPJsxyNovOOoDW2KNja3Wc0GnMxPwV7xtbOFq+OTrlYzBnnObO9LWJhmI1Lzs7mvHh1xN3X7rE1m/L02VOKIscYzWxni63dXR598ZDFsmJmcyKawXBK1zZcLOfMtiaUg4Ibt64znozZvbbP4uKCf/vZrzk9OWZ3Z0vkElFC3cpyyJtvvs6jRw8Zj0bcvX2Lum74t1/8mtn2PhfLC0bDEeVgSLVuGYwmzOcVn336hLuv3WQwKMmyiJhoe8ZFsjJYrHjj3i1GA82jw2d0bcNsNmVLaVbVmo8+/owQoMhyomsoy4L1umFvd5fgHednZ+zu7JJlGbv7e8xmO/zs738JTb+JSIKlVsLG831jnWRGva+YJ+IQQCTD08xPOfnk91z7/i7blHRljjaB7uQZ12lYti0rO2F/MiK2gfN1hHxMUDDRHffu3ubpi1NO1g0qyxIzpSGEhlXQ/OKjxwwMvP/WAeu6YWAtnZf0St/UDGdbCGAhQKzYMMkEa5MSqTUhSnMR4+UBI7Khy4NeJ49alPjK2N4DWhsBf2yBjwmg0NKweRTGllQu45PHh9x/+Irp3gE3Xjvg+YuXnL06R7vAwM9573rgP7+7zUF+hAoVRkUePXzA3/7Tv/DJoy+wuXBAOies69AGbPJuEy5MSvVERM9XGV16wxq4LMJ6j9EQenC699HSFHlO0zZUdSWs6aZOhYk0Y3lRpMJTfCul4JUrG5wcNIXNGZYDXn/tHh988D3m8zN+/etfsq46jAocPf2ISdkxKCLbWxZrFF1qvL0LNHXDeLILwLpe4xIDoPfqQslzb7kMMuzlQNZY0FLMdE48KpWKtPWaOtOpuUqHfmqnYyvNZSSKBOiK1MxoMV4XYH4i3rsuCPNDyQG/e+0aw2LI6fkr1osLTCmsf5UAwB4gQV+yBSGBISTOYRCw0Sbbh9xmDEYDqsWKUMkEfzCZUK8quX8K7KhEDXK0FTUFBNZNLczmTAZ2/QQ7qkumxfHxsaTaes/Hn35C68UzyqcmPEJKTI1kNifLMuqm+bK070qh/iUm8Fd+7yqQ2685dYVRYbQRL1tjWK1Wm6qzbjoOj1/x248/5L/86C9RMU9hVnLu+K4ly/MUwAbGeIyJ5FbS6YPWKBVFjRFimi2JN7X3juA6um6Fj4GtnT2sLYgx+bUpKeQDl0WzMOXBdB0heHavX+fRo8c8efSYQVHy4Ycf0bUd1/b2ef/996nblslwJAxj7ygHObfu3ERZxbptKMuReOMWBWQZMcvwStNGkWH1IUZR9atUX7Il+pukeq/feIly9nOFGNBKAgN9cPhWrFiatqauK9brCy7mZzx/9ohnh494/vwZjx4fcn5+jgsBrzQxM2CtXLckA+tBYGGIpvute3Dkj7/EtuCykezPc2AT1qjSve/ZSz34rJTG5jl123B0fMze/jW00ZzPT3nx/Cmz6S7FYLxZO2U5SI3LJbN3MByzw3Vat4ZJxrKa07RL8XLPClAie89NBtomCXa/jaoNMbmXgKoegAteBjEKSZ4OVwrwdGb018tYi81yinJIUIGm9jx++pj7n/+CyXTAe995A4yhjStO1o/AOMq8JMsGHJ+ckWnLeDBhfX6GoWB/7w5FMWJ5NifmilZ7VsqRJ0Z49EGucR+Klfw8e4D2avDLppG/0nv3DX+MHptnBK2JynJ8Mme1WvPi6WMOy5K8zJlNxtTzczg9ZhwVZVQMUIyVIvOevCjAB2LXYl2LMhaLY3l6TF4OuL6zw8MvPudFk55tAAAgAElEQVT/+/v/i8XimIMbd3jv639GVS1o/JqqbanbCo8MbGNU1N7ThsC6ajhZLbnoasphiWtbsSsyltxkWJMznm5zfDbn6YtjptMJ48k2tck3QzNjRA7775E6VG8HlnwA+2YxLYg01LlMYxdWUs9ehhAVupyydfAmsdijCSUxdDTzI67vTsjLQtKlQ0QrYX8L6COyRXrrIB+wMbKN4y0i70XDnaZmu2nIXT/sSAnoQWrozGZ0bSvc19h7OIq9mNIqedCtk8VJSCqNHtsIm+8V03USUCXQ1GvW6wsGg8GXPMdlmC8Da2MQluAmeLV/ziUbwDlPzBJMkUAkbVLIoYoMy4zenxEi1ijqqk1AiEksWp8Yd3YzVJBaBhSBGHQaJIkMHiKGiI0yzMuLKe/few+PZ2u8RXTit9sQUDpSDizaR+arNfPjY4KeUjUVrl6hgiP2EnOl6Zx4l+M81oM6W5KfLNjGMpns887OHRpV4iwMcrMJZe1l8kYHTDzn0YO/ZTn/mFbv88vPM775v/yv3H79dT56UvPTf3lBOFYM1q8YtjmsHdFk+GKLL44UL8YWV2qUr5gOOv7LX97kbXvBlg10viM3kaYNrC8uWMwXHN7/hHEZuffGHd7Yf4+Hv/45P/t//houGorJDqYYMN09wLc1uou4nZqLas3cKU7nc9a/+w2zgUffd3zrnW/xzR+/zvU3HAefLbG/fsXn82Na16CyMXa4RZNBY3IKHDp0BAxKeWw4x7RrquoRq8VHKE6wxpIXAr7d2Ntma2sHry2repWAFJUS0xPpoq/pw6VNgE4Du94aUBktA8/NWZSscejZiP2e3Q+W+wFWqmUSqBXVZW0DEJVIvnXPTEsPkYAQMiQNQSTIIQhCGKMASj0g3LNprwKhG3/cBJF8FdC43K8va4CrQccqna9yiimunExf3uP6moIvD9i/CuBuzgt9CcBdfY8NGB5EuZMVhkAgN5JXYFKwVj/ElOt/BZhO7yWAqJKBUXSpBwm4CHmeYZKq0yYCgU2kDRBgyvtwGWaMALRt16ZnzeBdb20m105p8QqWc0BYmtoKuawPTO7PzbbrLkkWCagXn88vg+WbPVFp2mQH4IjJl1fuUx9ArfWlJ3K/fvvhb4xpfaPwXsDJdMfluqe9O0YlWEmArvOA4CVXwfxL4pu8g2zpamMxGUOUulJpjImbnth1nrpqWKmai1VDPW1ppw1dI3jDeDgWEpRKdVvfbWu5Lz1YfNkPJP9oRFnWpaHd1TXkuo4QxZ4hRGF1ai1+u75rUzevBADWEi6plRBhlMkIsSHPM/LhgJhZfNdAAKuznkAta0pD7NnyiF+w9x0XOjI3jqExjFLmhPcdtusogmfs4bR1vHz6iDOT42zOaHvG/o0Dtq7dxg5nKCUM4z5EWKw05OHsfaVBwkKd759dTdN2GyJZP0D3ocNaTWYiwVrJ4QhC3PIqSE+YBkg9oA8yUC2KAmMtKsjwl7aFdC96kkyMSRF7xYc6hJisQRJbPfVIMW2oMiQpsFaxtXvA3rW7aFNSrWtc5+kcxJDhYkfbrsV/PRPbQu99whz/eOfwJw3SEqHIS/Z2r2FtiQs2FTmXB5FMi/XmQmd5xnq1wlrLcFDSuY6yGJJnGSE4PJdmwHkuMvLeA3Y8nhKDomsdWluszhIzD7pA8uuycpOAQCDLBTwT1oL4TJydHKPQTLZmDJ5ZSmPovCdamxodRYiGVePoThb833/9d3z68ef8b//xP/KNd99JUzMHvQQixuQrKUVq0yXvkswmGbQ0QT5tTuicrf1b2GzIZHZK7T9lMT/nN795Sl7k7Oxusb09Y2dvn0dPn/PxJ5/w/rvvcP3adV6+fM6bb7xBXuREpbl564DlfM4wswzHQ0ZbM5aLBW+89T73XrsLiGcKSjOeDPnRj37AaDTl7/72H5hOhuzu7LBYLFguL3j16lg8PHPL48ePuX37DtPxjGFh0XS88eYdhtMRx0cnjMcZO3sDrNHUTeDw8JTd3W26rhJZZ/REpZJ/mjDwtmYzlhc13hfMjGG1Omfv2g1u37nBq1dnjEcTru9v8fDJE6p1za1bd7hz7zYXqxmHT59SFgXf/+B7HJ0f47qO6WCCJSfZ/W0812JK9fUxEpUROn/oiAS0yfEh4HRAK0/18jkvfvZTyjtvMbh5h0kxoztqiFVDt6optiLBrTg8nrN2DlWUmNBxc2fEe/cOaC4uOFucoW1BJEP5BuVrgso5b1r+8ee/Io/v88bNXUJKobN4Vusz8kFGVs4EpI0SkrSZ3V4pLi4nlz1DMIECVtJGu65LwKZHGwfByTPgPFk5YtV4osmgDytIHMiA4aLW/O6zpzx4csrs2m1u3L3Gy+dHnD5bYoiM9Tk/uL7mx29n3MjPsWFFs5zz6eED/u4f/41PHz0n5habgfGeUK/xdYNWEqbhXctqvWI6nWJtnj5/Ouj6wi6ZdffftS8CNobg3pNnOdYYykFJZixN29CnafbsseClqLl+/TpN24qk2GaoGMiMJvoO5R2TYcnu9j7f/uY3+eEP/5zzizM++vC3HD1/hevg/qPHjIuO4VBRZIrdbcP+9pCnRxVt12JsRjVfcm1vn8lwwrkPLH2LVwpvJFG5lylFIiiNd46iKGi7LrE0o9gw+BSMBSyXZ1T1guFwQNO0OB83hYpJxZ13Hb33UX+9RHbZonROWU5EVtnI1N8Fh6NjvD1FdQFWFeuLc8y4JBoocsugzPDOU5Yl49GEo6NXsmdpkdT04LlGikH5zLLfrVdr6vUaV7eUgyEmtzTzVgrILCObjOjSos5NhtaeLga6upJ7rjWWdK168DWtfZtZvAanPCZPxW2IxNAzejVWqU1ardYK5+IG1O+LrQ1D9ivH11dZIJeStEufqn599qwC+bNkwzHlAILjw08/5VtvfoP9nQnr9QVKaYJCLHlSwRsItK0BZRkMhoyGBd45ASySFDZ6R+OqVDApQnRcnJ5xPj/Hdx2znX2sLRKYKOFtEZXYuYnfFiF2HYXJMCYj1zmL43OynV3evvcWt27eYjqdMJqNaVyH6zp8jFw0NeVgzGS2I2CVzgAjnnZKzo8YNGAISXaniJsuS2lkr7/CRlCiiUsqms0jLkBEFFlXF1qqtmW5OKeqljRNzfHxK16+es7n9+/z4PAJ8/N5shbwYMS2xuQy/BEvSmmi4qbpTAw8ZFAnzWYvK9aX4NWVdRDjJZPkKounD94w/c/pG2Fhe2ZaWBwKaZhCiJycnrK8WDEcDvGd4+TkiMX8nBvjLZQVtoC/MiQwiakXlSXPpqAC6/aCYbNkvTphUOyiVIHW2QYAVz3Ipi4bIPpGPfnldm2TbIAURluauma9WpOXA2yWJzZQ3/RDNBo7GqILGeBYHVm3coaHtqVZg85ynO9o2hV5ITc+1zmz0R71qqMsLIOy5GJe4YN4PPogz1DnW4KyWB2FBeRlsKCUSp6pQcD20CclX60142ZfUBumR+/NF4h4TCZrzntPV9WMhwNKnVMtF5weHRKHQ0ZotmxG5oUVlhlDrhWxafBKQlACHh9aTDBkviFUCy5OnqNdha8WZLrFuxVVs2S5XjC/mBOMZ7E+J7eF+PI3Lat1g0fTOgGp8uGQiSoI3mFNxs5wIgC3zfAqsBV3MU+fyRBrsWa8vwXaCgCbkplFfs4m9Ktfk2laDfRzhb5mkN/sgZhITMnK8mMfBhTNFrODdyj332LRGZxVdIsXmG7OYHyNvLS46PCd2E70z2+MkiYfo6GwGSWw1ba87gPvh4bX1it225YyOJQLtArAMJltI7LYtQzllxe0dU2WGHv6yrokqQ20Iqlv+gG8tMDGmA2gIMEznqqqqOvVxi9yA0goTdvWslY2+z4oEvh91d9SR4qBhOJ0oZUBhs2xVtSB66qS9VOIpzQxCrCfizWTMiL7DT4yHIi/nooJgErfMaRNq1cdCINY1rtAdZGoIwfXbtDVDhUtMRMbB7mRjagWjEO1a549+IK4njGYjTk7PaJrK7a3pkRCAlsC3XqNbxqyztG9Oma6bpnoAnVac/HxE3Z//BpnqgEMNstIqwZrIoNsydmTf2Xx8iPm3S7//R8Mr+Zf44Pr19ktGm6UDQfTAUdnJaOsIEsAhTYD6myHpRqC19DWZKrlR9/c5s9fKynnntDVhGiIzQUZgdF4m0LDiWkY6YZvvbXD8f1f88v//t8oFhW5GVAWA4ajKSobkGdDRjvQ+kicH6PLIXZc8uRsyXyd8fkXn/EPf/N77t7c5+bOAW415I1Ws6Ut50RW1nDuLS0KvMKFiujXxGiwsca6x6juOd36EfgTZtvb7MyuyeDYrfiL732Tuq75p1//nrqu8L7bEAT6urf31qY/cxICKPtfv0ZjCrjta5fL4XXfIIQYxIsxyYV7FqPNrJyBgY2PciKoSa2VZZcsR5UUOukvrbUQXRSbsDGVzifvOxQiSY4xpCCtS+VRSHv2VUbrV0FTpQwxekiDGJQw3jeFn5LP3DPq+uFLzxyMPcirLmu3r7Jm/z2mbf/jV1VUTdNycRExZsSgKDcDS9e2eOcSA/qKEutKPRlDEDsTdCpjxa7AZjl5nknv4y+vc/Be2Ot94FQCgPtBVdervxTJCxuy3GJTWGJIdgcmXfcYkwVM+i49qUVrnfrBQB/ShlKpfrpUBfXryTknKfZBelOVwNwizy+JCum6eB9S/oTeXJfeb7YH9Ym9i5Xmal3ds3NDBMn2VgwGA7quQZETQqRrnex7WifFA5trLZ9ZQ5BQtRihdU7AVZ18TlNgmXOB2jWcek/bVJzPz9lZ7bC/vct4MGJQisQ9pD7mci1tSg0iMpwwVmwIQYvKMNUfG3ZziIRgxBYnynitqltaF2lbOSN1qj+JLZqAUmGTA+ADGJvRWIMeDMB5Qt2kkOEe7E4FdhAWcgxBHnACa+14qVpujHMGKtWhyhLyQO6giI4Sx7iqeelWPFkucY9h9+UBB3fO2bt9j8FsB7BkRUY5HFI5sTeR+iGF1PpA6xzGWMajCU1bE4IiBEtwElxsdEBngQ6F01HMkVSkCxVdrKUvSypgheAXxlp8kJpPp3sg3w+xD037mtZ6w/7uug6dnrl+/SslfrVdDFiTIY+DBKIrbdBRMRqNef/9H/D2Oz+kHG8TDSyXS54/e8ni7JSL8yPmZ4esL05AeXyAro2YCMZeDnm/+vrTBmmBQTFhNNpBqUwutlLolD5b1eKFOhoMsAqUjYTQERUMR2Om020J19lQzsG1HVmW0bYepTxaC405BI/NMrycShvfzYAixA6iRwdJmeuDb2KIBB3IbIEynsJ45mdLXhw+xJrA7YNbvHjyAoKSrGMVZdoYIxgwucbFQN3CZ188Zf5//J988MFj/uIvfsTu1lSAyOTtp6JOm5k8KINykGRoPk2ARKod0DS+Q9ucrd1rTGdbFIOSw4efszOdcHK64vxsSQyBrBhybf86n37+kOW6486Na2RZwaPHD/ja196mLAuuH1xnUA5AOW7d3Ge2v4dWdxgNRxupLem7ocQ37I3X3+T+F894+vyIa3s7dHXHxaKmHA04PjmnLHN8gM8+u89susWt27eo1he4ruLstMZqzTvvvMm6vmA5PxXm7PEJTx4/YX9/i+3dbcajIUTo6noD2q/XNatVlTyYFDuzbUKEl0cnaAXT8Yjlck2mx4y2Z4yHQ05OzlEahoMRWZ7z4MFTzl/MsaEUD1z6ROO0kamIixEXhQWolbC6Q+xTXOWhNkrCksrouHj2CO0Cs9GAYn8LvbXHs5P7dI1iLy+IXcfDwyc4hihgbzrkG28coL1ieb7AKGF0d1HjdYEyUcCjztHOT/n5T/8R/d3v8OZbb7E9yqi6lqzIUNoSvVzPmDxVPIrs/2fuzb7syM4rv98ZYrhTjphRqEJNZBWL4kyppWZ3a/VqL/vB9n/oP8H2WnZ325LVvbppiZREskgWi2SNQAGJBJBz3jkizuSH78TNBJtaftV9KQAF5I0b98Q537f3/vYuawqbi52o0EY8gLwX1Ygk1JtN4uRoMhFPrK4Vhs21kriZZIyp9xQypiSFPM6rDLNFy++/OODxyxV7r73O/p19Dp6dMztdQGEoafjuvuPP34Db9SU1U2bTM54dPuInv/oVj4+OsLWMWsVOWEXXRZQSNVYCXIgMBkOKMieAQt7cY1ajiM+izpxj31D1LK0xmrquXznwu+Bw3kn6aQ5VA7G2QMFyuaQoCka9giYErIXYBsbDEbf3d3j/W9/mT//Fv2C2uODxo0+5PLkgBcXlxSWhbVmHSOdKUkyMBopbOxUvTyXgZFAUdF3CuMiwMAzGE0atZ+ocq9QSCSST0Enl70waytFwSFrOcMGjohHfWq7UfkbLWKH8fYPNwXQq+7JWhWHRyHidiSbfU/FljR6MLhgOBtL8aUUMCa0to/EYM7a0bUe86GiXDWYyyYmdEgCjlcMYy2K53DT7KYs5VEqbAq4sCtqUCF0k0OG9WG60TcPWzk2iBteuidFhbU0goVLApIDSOZgDZHwnekktVaBUwmXVjrFWVHEpEjs5sCU00mCNASO9isqFY/QuF1WGqi42vmkCsF6l0v4xpUX/6pUAm8YjZVubnkCI+bYkGbdJMaJCwgMvLy/57eef8KMffE/UvUkK3xQTi4UArM4l9m7fJ1U1MSWqohBiJwVRxesg0yZEnGsl3Xw0obirGUwmUkj7iLYpj1InyH5NKo+0G61BZZ/SQj73rTu3+OEPv0+VQbmgIGrLOipMNWQwKbBVidJG9osY8RkMijHJ2WgM/eCa0kksGuiBWPnzHhTtA0tIYrovRn++/9dyYqdIs17RtWsW81Oml2ccHBzw9Okznr98ycvjI2bLOV0IuBDE8L+yKCxoebeoyEB61txkT+O+i9M9sZVJuyyEyw2zuiKKNo3xlZr0Sr0pigFpYOUn6wz2C7Qiz4W1vR+0wmBYtyuev3jOW2++S0ya2XLO5XzGXWOErHVuQzAlpCGuB0NMUePzvja2+5ycvES1gVKVdE0jAGpOlO7Vez31EJPYLvQgcoqJxeyC9WLB/s1bYKV5F+sLaXgkTVnII5J4pikF2hYZXA9obdm7vcs3x9+X9WcKSJGtepvC3icoj6aitrvcvzER5WBoGO4pUrBUesgiTlFG0bRrCg0UchKkHpyNm9WUJ0eykh3ZQ/tmlqxeSSpI/7Jp5qV5srYkdIHlckk1HmBsjVGWgS0YjLYYkBgoRYWhLjXROUgeFwyFghQs9XCLLjlUCqjQkvya2CxppopuMQMC9+/cox4OqIYjZtNTZvMpoZ3TNA5KSzmwYKDcGvDWG2/x9PApz49eUBY1hVKifDIF1aBGWUvbdSw7TzU02HJI27a4IFMCOq/DYAqSMWRKAnSeDstNzeZ7l4ePXjm5CUZBAOyYogiX0cTYyv83W4zufo363vvMYolTgZtbA86fvaRLS5p2AWacvfbEi98lIYZVSOKNGsFqyyRF3g6O933LG92aSddRBAlb8kpAgYRm3UCKLW07p1kvST5SGEm2D5lwKMuCFAPdciVqnMzEi0ddEAFHUGhb4X1EXF0VXduwXC2oqppqkEmNdKWcC1FCcZJKm5HboGK2Wsn+mCFmVVSvOhS1rdQtAiB4J1YNoj4KeLemLGqUloBMYkRjMEZhdJHFCldzzEmFjSJIbUCN7BOcQYEU8pqPPgPOoNDy6XWBzZMYKoFvW5787nfoyx1uv3mfi9Mj1l3DZFxT1TXOyXRG4xr8ek48PKQ6u2CMRqXAoHUcf/wRt7/9LerJGE8k5P1Oa6jMkrT6HU8f/x2qGPKrj0o+OdgjbD/g8nzNuk18+OGXLM9HdOs1s/kcZnMmJKzRRDuipcCYiFaObz2s+csPhjTPD1GqYntrxPLiELeacfTynDfeLii0Ybi9zTffv0dYzPjFX/8Neu7YqbZoujWD8Yh6OCBGhTE15WCb8V7Ejr5CaTmrT9eKiyZShwnFasXhoynVwtI1iR/+8N/gQ8GzyxVnuuTRoiMtp5TRs2qXuOgxyqLcCd49hnDEqPbsje+xvbWPtZbZ8hITFG6tuJg2XC5XNMkjQFV/NqTNXt2rRVNGKgVMI9ckagNUptzHKqU2Ktvek75fKxqVQY2UHctVVltegb4xWwf2qsC+3gGI1/MH+vdGah1j89QOcWO3lDfeKxU+V+nrvQ2T4M7Xa64ryx0B7NQVyZSuPrPe7Och73G5Nu4vMXHlt5BeBWB5Zf979TO++kpZPCE4l0Es5oyS1HhM/ndRnn9ry3zMyDWFKGdUm0n7oijze0mBqPIe0eMacjaHDRmvtUZn4ZnOilnk1mXFdVYO9pNd6koJLfVdJq+S3OsYQgYLpQ7XSuf8Bun7feJKgWutgKQblfQVc26sGNlYa5lMJlLz/YHNk/dezhxl8z2Jm5C0fk1sCsMN2SRhqTEEsYvQGq+E2NNaYTrFupHJAYDospANUEpnixW9UVonBJhtu45CyVqPMVEY3cOZYKX3d77jciqTuU0IdN6zPd5mUFbsbO9SaEthS4QnyPhPIlt/BLwLoAJGC6jYE/Zk7FQeK401BWUxJmTMwZaBOoYNoBhjILgg86Q6bnxsy7rGmpp2cUHqWvwkYFRBCmf4CJ1fYwqNKitAkUKiS721VU+AJ9bB08aED9DFJLkC2qKMpVaGXR/ZMYFBdHTO8eJsyvFixtHFGfdOXnD7/utM9m+xf+sORkkwprURZQoSsg4GeQ1UW3tM7ryBmc8IAVI5widIoQVV0HkvQhmliGGNa85YrS7xsSMQ8RkvE5JVej2U2tghpiTq3S6rvstSSNE+uFeeuWIz7bhZZ7mvlFDcDlTEmhz4myLaJJqu4elXjynsTR68/T4P3n2Td77xPm9ezJien3Hy7IAXj7d5+vh3nF40+GzJhAOS/yN7ibz+WYO0Sit2b94CZXCuZTlbMBwNUdpkxRcU1mBNThfOoGZVWG7s78kGlL11YlYC9ONXVVXJ4s7pizEKii9ebNnHTiW0gcVsTkqBne39/vnJm36QZjsEgmv48tkjfvb3P+X586949+03uLVzm3Xb4XJ3EkPMnro51VwnQsjBSzFyeHLG+X/5MY+ePObf/sVf8O1v/4mkxIeQu5u0GWHTiAfg0fER9+7dZ1APZeSpLCUpNatgqtGI+288ZDAcsJjPGB1dcHl2zKiytMslVVnx8M3XuZzO+e2nnzGoLMbAsul448F9xuNd9m7eIMU1e/vbjMb94+RJSWMsKF0IU+Va5suWJ08OmV5ecnR0xPLt19je3eH0YomLcpiMJ7u8+eYb/OpXv+SLR5/xtffe5f3336ddr/n0y0ecX8zY39/jzu1bdOuG5WrJarXCNS1fffUFu/t73Ll7h/3dXZLvkyU9bddSlCXT5yes247d7QkKzWw6xyc4vzjn5cuXVEXFN957l/0b+5yfz/Ah0jmPKQsuzi9ZnM6oKYT1jVFG5DKwEslFTT6MjNUbUIGsitMm+0SmiI6OoTIsz58z/6pm/9ZtGO6yHu5hdWR7XOBWlyzmU9JohFJGwqjsgC8OXjDvoBqMMUUJIdIGhalHqOgpUoV1NefzU37++89RW7f49vtvQZhJA4pmvZgzGI7yeH4nCrwuUtohRtuNbYewl5YYZawmxiTpiVpnpjtSFuJfhxZvGVMIKDMsNKHzErhUVTQRLhcrfvX7Lzl6OWfn7uts7084+OIJ81XEhBV3hw3fu2v40zuOu8NLtoaBF08P+PjjT/jwNx9xvm6JykCC6DpSbqStLTb+Ws57yrLa+Dv1h5brvZ30VThB4IpxtdbSNGv5rnS1YVS1MSxXK+bzOSG4V8dTshWAWKJY+lkHlWQjjz5QFgXb2zt87Wvv8b3vf4fF4pxnB4+IbcP5yRmHh8fcuXOP7dEOj756wosTz2g4pKgjk5GkV69cotUdKM3Z+Rnl4AY6OG4NR1TNmtNlw2gwZB09a59QVkAtgLPpGQa1GWkU1OdKFdD7Dbku3x9BjShNwc2dPd5/713+8cOfsW4dnkTXtfSe3CkpBmXFqK7RDkprcoqqYzQpqUYFzdmK9bTDe4tJCqs1bdfSuYbSygRC27oNyNkDJhrF1s4OruuYzeeiMrAFyRq01/h5h9aWne0dFrM5oetIKVLUQjZoI9KOFAXUBLV5Tsn/VUCpFcF7XAisplNh8wtL2ABqGSTThpCkEE4kCZ+8BiTXdb0piL0LhJD6WvTV9+z/MP/+lZI+qwJS9t9Fy7mSYpQQKq2QbKvEKgZ+88VnvPPGa7zz4AGr1YplIyDkermg61rqwQiFAy9J8kkNhTQhkFxmahUUsQISKXq0gnq0RTkc5XC8zDRnQK4HqRRC5qBkn/ApsWw7nj47xMVAVZWoqqaoB9R1iSkrtKmIGXAOAEmIxpjBMgEP5JrCRjGj6V1AVS/SuNZ4qgTRu9xABXzISbWEHM4BMTqWiwuePz/k5YuXPHn6iGcHz3h5dEzTObEbUgjZW1iqwuZGLYMXqoc2+99cfYda92x3PsMzstonx0PfuF0pgPrCMP/AjYVA32BeV2LrDOL2kgulrgB/gxCxZKj04uKc5m7LsBbQ7eTshLvTS0aTMa7rBGxRWgjt7OM7qAvWed8rbcX+7i1Ss5akaVOIwnCT+M2mCZTr17RNKwT4QPa/wmrssEIlmTAwRQnZG1FrhXPSSHRdJ81mf59NHtLLe2rUFj3awhKZLs9o1wGSYVDeAh1xPhLbgmGxTUzgfSUEkhHlctNJs2FUjWWI1lLWxjwmr3MT3A/Nam0w2aqqP7k3ad69L2NuCK+r5AflAKssbtWwvzOmDB1d02Cco7QWHYMU7UbIpi7IWiUldKEZDCuKUkb/YvLYYoCyJdF72stz1s0CFxzDyZi97ZsElVjNZ5ACnYusWkdAQ7PCKQiq4PmL51xeXKBIDKuasqqxZYHVhnXT5HpRo5UAACAASURBVLBLEQe07RrnJD4qEVHGknS/xjUy4pl/nzIoEpNw07z66lVZXFMIaW0E7ERGIoMuKW48YPve+wz37tAyIoTAuw/v4U+e8vjL33L74R7jUQ0arDZo47P/ekKbAmUV3stY4Khbct85PvCOt9drtl2DzkqxqDQuRQaTCQ/f/zbzyzUvHn/OznibtutwSCin1A7y2Vz0uHVDcI7ehdcUJlvaKEICbCHWIVpG+RUyOhmCxw5H9BM214EGURCajD70KkKVARGF72TCIKm+apT155xDESXcTCMJ7FpUra7tsLbIpJGSEDYladty77NyMib6rzRGuTZtDD6nedu8HyCwjoBYqQduIQWf9zl5RlNMG69Rawy6dZwePmG2OBL7odGI2Lb4bD2XXMA3Dc3ZOZcffczDaBnu7kH0lLFl9fQR5x//hr1/+SPmSRNVRCePZU1qP+f05d8x7xo+f3KT//ohLNu73JzUTI8P+fp7b/Df/+ibfP7JEb+4+JzZ+VNityCmDrTGF5WMwzZnlP6YD3YecNsaZiGwdnPa5hLXLNnaGqJNycO3HmJI7GxHbo0S//Dv/3eWL8+4Ue4Q/YrQrQU0MyVGGVIAjaEsBowGW2hTc3x5yWVrqEcTVFWTyi0mO0Pu3b3B0eEBz06/FPuqANqOKRvPYAmjepeb9YAuJZxbQTxmVCWGg9uYUkuaeFHi2oZ2tWa9XPOTDz9m3q5og0LbAm1C75YjoIopoA9n7Wm+XNtujrRMKG7AB66mymQ0++q8Suk68NtvZTHbVynxVeTqnLhuBdV7qvZqSq0lS4Ekgbj9zxYyMGGNKGuNFfJWIeRaCL21YaKfgPtDu4Me0OuFWP3n1NluK+Sx580evwFb811K16YK+5uZrpOpV3uevN+rdd2rrwzmIApnUFgjftMxCNlnkuASISScCxurFGOuvOpF7foH6loiIfoMAsuZHrKdGfS1q7DKJvvK99dXprQZ+S+zoMU5yTToXy4EyLVUr1juWrFH2CiYr6mP+89fFIXYrmUlrurtwPKXk/raOatdQw7XLcqSmPu6PnDs6vtgs3YEhL8KyoJsm6F7TEW+p5ASOoenbdZhUVDlvU7FRIwe70Wxe/XcmOxyE698b7kSWZjC4oLDKPFnTl2HtZroQ7bWU0ynl7impdlaMxgMcV5smoaDAVX2jC7rmpDFGDEa2k4CsFABlZRMb5sik6Ni96WKmnKwS12N8tSLxhSWIufNFEWxmQxKQQRlzjUE16BiIPkOv1oSVnMWxye4s1PWx4d0FxcsZ6fE1ILS2JiDolEoYzJXIpN0USkRvLgW1TncQOG11OpBJYy2lEVJlWvqNkXmiynzbkEzmzO/mDK8dQ8z2McMd9HVmMFwTDko0EWNMoZCa3RRsNM9YDjewTVrVqslpqykh0nirR9SJLg1wbdYv2B18pzQrIka2OxDEe8jKTmqVEkY98biQkgalwP3nHMZSNd4n0QImveImBJGI5ZyIWIzOdp7GAvRIDVliAm3anny+BNOT075zW9/xr0H7/Lam+9w4/ZNdne22d6esNreYnt7m9XqnLZZkaIi5t7on3r9swZptS3Yv31XFKJRvCIKk60NtKIqC1GXpKutUVSMgIr46DOoxCYp0lYWtLSCWvX+JoqyrDdjrb0Kpeck67ImRmGJ0YgvVxIFl8LjmhWnL1/wyccfcvjkU9puxWqxy8G84zef/B4ndI80lBoZs80jjCFmFlhpbGFZp8jvPvmS5dmM0+NzfvhnP2BnZyIWCEGad1loUJY121t7FLbcsGv9CLcg/xEXRa2ye/cBw/0GMzqXMYfQYXXifHqBSoHd7ZrtUUHTtIQYODk7x3cNe/s32d3d5fatbTlETO9besW2rlZr5os1T58e8sXnj1g3a6pK82c//C6z+YKjk6c4r6mGNaURJuLo+CW3bt9kMKxZrJYcHj7nnYcPubm/z8vjU14cvWA0eoN79+9y8Pw5ENnZ2ebo2PP5FwccPDvhxo0bLOcz3nr4gNdeuyNeSCkyW8zZ279JWdecHJ1QDweMt7a5PL8koTA28vzFI07PDlDaZpP7Oa/df412rlg9XVAq8fzxPmzSUfsTQkZyBGRImd26eqgNIXhc8DngSewHytCwfvaYi5u32f3m90ijGxjjGA8H3N7fYjKZsEhaxhe04qvnJzx5eYG3I1FIuI69QYVvVkRlssn4iBA6fIqcMeIfPz9ie/8Od3ZGpBBYr2acn77k9t37lMbg2yXaSAAKqUSrIo8wSyNhtAErh2NIAcn1kWPIKE1VSAO+csKQhhixpWFvPKTuPGtl6UzFYtby68+OODxruHv/NYrtbQ6eHtOsNaV27HLM97am/OhWzTs3W25sV7w8OuDDX/2cv//ZRyxdQFVDUaV0HaHrhCU0hsJaXPYYKsvsFdqIv7Rz3Ub12nt8Xvec7UdwXO+npKXAAHWVRprHeowpcvGjsprWk7ItSgwe7xyFFU8hhRS5k/GYd77+Du9/65ucXZ6yXFxycXHCfLriy68O6VzEucjujZs8SIqvHn/O8xPHcFyzv2+ZjDTLy0DXdhirWC4uSH6MBnzbsTcaU2jF6XrO2vnsqa0YjCqariW0Qh4YrsBPOfyviioZd9RX+1yS4vr07Iyf/P0ZPjhQBmMNO9s7nJ4ckZIiBkVtaipdC/CthCxaNw3D4ZCEZ7WacXl5gTYl49EIUxpCDqsSAFRLQEt+LkbjEfPFgpTE40r8yhTWlOzu7tHGRHu6xE9bhoMRq9mSxcWM0MnUw3h7i8GwRBVgywoXPF3npYE1fXErBaAEfxmKQrGYzWjWa8oe8M8+lQlIGWjw3uO9l5EZZSisofMO7wPO9Qe0yyNnVwRAyiqCPrSjr6Cvj+6l/PsriEj2atX7VmUwT2mFjhFC5MXFOb/8/W956+FDbFHgFo6maxiUlkJFitIwvTxjMJYmWxcVhbYZIlBZhWmJtsACMXQZDIzoZDMBmPcBrp2n17ztyKPj48k2w0GNLmtUbiZkTM0QVSJgxA4lScEn+4sUMz0bDeSG8Arg2IwexpgVelyBpCkRnZOAPwMxepx3RNfg3Jrlcsn52QUHB0/4/NGnHD5/wfnFlKaTUFFjK3Qp3txJ51FNJTWAVlfqItVv8/01p96Psh8jvNa09VXCKwDt1XcNV2D9H18L+d9fC+hQm1E+Uen2ftOKhNjHCVi9blZcXJ6x9doW3gcupue8PHrGO6OvXWtC5eWdZ7lcYnVOgQ+OrmtJMTAcbTEe15RFRZHVeD2ZkzIR2auTyqom5cmStmnwrqNrFrTBs71XUdVDCqWIXvbXqqo2djmSSl1sxvgEFDBoW9G2nmVYMag1ofGMxztsjW9BlICijhaTVcQpyZhgP74dYqBzDapIkDSaEqNKUtIbUoXUA2HQu42Kv7zKwWRX+2O/1pp1s6kH+7VpjJURQu9YX57hlYQwDYbDDE7KGaUhg8PyXMtEhiiU264B5OzsXEdaLYis8CnRxo7GtRTVkLZtcMERvUdr+cz1aIS1BhcDUSc675ktVySVGE7G2KLAWPGaI8h5HqNY2JjoUL4lhQ6tNfVwJM2YKUQlzpXnfP+flERRm3qfjySWHX3TLQrbfk8TAlsSywPB1FQ33mL3zR+gxjdoYiD6SGVLdoziy09/jukumGw/hGwnkKKXlOwEqfOipgW0Sgx85F7b8D6Rh8Gx3a2pnFhMJQUBg06wvJzy8S9/jkoW7Vu6DDyLgEOJUEDJbh9cBiSyKrCv4UhJJqOMReUwlxRzfZQb4j6IJIaYa+Gcbh+y4v2aR20PPJB93r3vrbHkHNZKE+nDlHp/30xnJZlsKAu5Do3CGksuwTZggkImNUgi+uhXs1KSUdC5tWRYaEVKHlCoGEURpRU627UEQj4PpbYn7wFRxUzuaCZFgXNrkre0JLr1UsQwSgux27Ysnx3gDg8p925jYiQpjVGRyXrO0S9+zp3v/oBiOMLrDpMiNi1YzT7j+eFjPj2o+euf3eI03KeLHX51yDv3v8WYFd94/yF//vV9vve65n/9X/6W2VeXlIWiKgrS+oTu8BcYOpg95imv0d74nylNRV1Cs55TFBXT+YLJZIeL6Rmv37vJ7ckd/v4//m88/eRzbo/3GI/3CaMxs65hMBhRVwNIWmq+vO5VSoTgmS0avN2hjQJc2rLkeYyEF8/xizmDbsF6OeXe/btUg0CdFkziijB7yu6tt6gGA5rmDJVWREqC4EXMlnM8c9btmuV6RQBeLM7RpSHmgBqd/ZT757W357iqKvqz8+rc0bqnILPcKGWFd8rgBOaVswx6sjm9skfGHL6n6X3UeyMiXjl7NoRFfs+Q11zIodw6+wj1IVjX1bH0nzEDJzEHFV73270OpL6yh+uMGZj+HmS6JF3z3UVd+a5zDaDtz+LrZ/cfef03JPx1EDf/uvd9NerKdkdcODMRlrTcc5V9YjNAeh2cjXnKqx9FDyj6jId+IhCkHt8IMkyx+bXqf14f5pl/TkqJ1WpFb43QX3v//v3nKY30WdZayIGbKvsKCxjc15mg6T2Sr+0dWdmvUChjcaGjbVqcEZD4+v3qAfMeTOu/r6v1m4He4PHZP3YT6Os9MZOM/Xcj68pSFCUmaZIKaO/p2o7o/ebvigjnSk9eFIXUDVHL1Fcnf64z0RWThOOR+y2D9IjL9TKrbyODqmLdDtka74hveYwUhcmhXoakLFoXRJWy0rMQciKJotkoxXCyy3jnHtZWoEw+W2y2SjDUVbUBbLVIzXGhw3drUmixJJQPtKs58/tnrGbnrM/OWB+9ZP78K9rnj2nbOQSX7y8bYZpMa4LzHQunaXRB2XQwDrikpX9RlmRKyQ6wFZPxiGJ6QSRgC4PzDdPZGStbc3Z2yuDgS4q6Zmf3PpN90LXCVHW2KYDReJfRcIfgO7bdWghf5+i6gPMqh9sFUoi0bcN6vUCRp2Ss1GcYEVD2diY9sdPvRU3jr9XsQqyiZXwyeM9qvd5gBlVdbfxijcn1a1R0rcN1ItBJeRrQR48LK9ZnB5iLc2bnF3z1+SfUoyGj8QRrLN16RrO6YDaf45ynLAfZk/yPbjHAP3OQ1piCop4QKSiyP2ZK0sBGJ2OKBo1PgaJ/OBFzZe87bGEorIAwJE8KkmyXwtUBpLWmquzGA8dlb5wEYstBoixKiIZmvaRpZgyGY1KCtlnj2hmL+SWL6YxRZXn/6w/x3nF8csmvf/trDo6PSaXNcnrxQezN0YuyoCit/NqKb0pIkag0x5cz/tOPf8pXz57xF3/+Az54/z0KI6NRuRZDa8Pu7m4+BNPGuPuqqZZDW8JfDLYecu/1MVvjEedHz8G37BWWg6dPqIqC8WTE5P5tlNEsFnO6ZkVVFSgVqaqKyWRC0zo656mqAUkrptM5v/n4dxy9PGY2nTMcjtgaDRnfHvGtb/0Jn3/xiK8OnrNae0rX8to773Dz5i7GaqzV1HXFct1wcnLCqK5ZN2tu3bpJjIH1suHZs+cCvE5nqKSoqjGTLUmePnx+RteuGQzPsKWlLEvOL6aYQnxki6rGlhVRK6bTKbPZlLqy/Lt/92fcu7vFxfkJxlp2diYU1tCuNf/P//kLSlNhUnEtzEWq4f5g3RjZqxzwokVVFXuv2sxIkYv7pGWzYz3n4KOf4suS3Z0HFFVNjInpsqWLCqUitQ68+/o9Xr44Zt4FKEq6ZsVerfmzD77G08NnfPToGcoakrXE4Q6xqFnZLZZLzf/70WP+9fe+zsBYiqpkNKpBCWilFMynU1bqkspYqkE+XLPFh8rkR/ACHxml0CpidaRzK07Ppuzf3Gc0qMV6QRkSwjCNBhVKV5ycd/zi4684PGp47c33mIwHfPnkBU0nIz/36hU/umv5YMdzfzznzu4e89kJf/VX/4l/+MVHNBFsNRRWq3W4rsMgzLw2RsC8rMQE6LoOkI22B/9khMG+AtD2DVVKSfzcgDInKvvM5l5nmvvNPWRmVin5jhXid2iKAqvVBjyeDEd865vf4Lvf+Sbr1ZwPf/1zRuMhx6cX/PLXn3F0dMHu9piz6SWqNOzd2adxK14cHjIcGl5/bYfxeEW6XJKSeB/ZFKBZoMuCZRfogmN3dwdbVzTHL3C+RRWGyo5YL1ck74XE0aCJhGyGn8KVJ5hgP9dCEYCQwEeHigljRUlmtaZtmlzLS+r29ngbQ4HPoyGdkwOzGg5pu4b58pTZ8oTBqESRcG2LshqM7M0hxCuWXSmaphWje63AuxwaA2jFsl0RPPh1Q2oDo50J3aqhXS4JwTEcjxjtjIgmoYyiqEoKVRHCUpTeRl01Hko+U+iLbqMZbk0wlRRFhbkCabTKtjIkbFmIqlcZbuzsc3J5TozdRlai0Hms22+K6b7g3LCx1ywOrhf7vd8nqfcD7gvVDIqprDTMXrqNCnz06BEffPWEdx+8hjWGQVVxfPCY06OXDIZjbt5/gCkq1s0CXWSLgTyy009wKGUwlmw3EDJyJR7GSV1T1/ThHT2AksMHNeIbWgwGRCUjkyhFbziQkhbgE0DpDMrqK0QzexCj+oag956TNSvEpZOx541CRtQXwXUS3ElkOp9xcXHJ0YtDDp59xYsXLzg+OmWxXNJ4R9KWhEL33meq94TMY/D5e3gVmFJ9WcAf/CI3HP39uWp6r6uUNkBr3xxdbyLVVfOq8/ipunYdEjaUgWDEf07leiaGIKpPnb1UNcQYOD495s6NuxRlyXI14/DwK+7evMNotE23mYIQK4kYAj5bwLiN3zYQg0wZaS0hI/QkwtXn6xuuhJC0MYh1RoqBwXBMNZyI2iDfkxBlQqj/txJipnLQosoNp9z3shhJsGq3olQ1aM2imbO1dY+6GJEC1Cbvv3nkUJ6JQFKOs/kRLnRoK2rDstpGK8vGrzuTFKl/aJMnxEb+DiZjj9ee16x2stnv/2qvFPuUplkQujXreUswhvFwhELhg6eyliI3V2RPR5KhKCWcdt00hEKCrJRKdOsF6+WcNoKqB6iqRpcVPnY419K0a5QSgmk8lpC9pm02BJlXAaWTELb5OV22S9p1S1kIiBi8BG91qxXnx0fE4KkGA4bjXXwS0LH39o9KrBKUyuSM7vcsIaLS5hnJLbm6ekJCXuc+JqIeMnzj+5R3vkFTTlCdE890AwOt+e2P/y9e/PI/M9rfwutEs1xLI+/lfCiKMpNciuQ9VQrs+8A7KvF2Suy4gHVBAmKyn6wKEUKiiOAWM7S1WK3o2pSfd0VCeoDeW9kaQ1XVdM1aPHlT2qhbnQ/4oiRlrzjTg/2ZkIpB3leeI/ErTD7kfVttiB0BEZSMN+fcgv5ciiGhrKizQladV6UEgXrXydG78csriVECZqLRuWbTrJu12JnUNaSI67oNsaNzQ6+VpLOLgq4f9xaln9FZrJLBaUXv+al6B7N8fsSsrJLwstW6Yb5cMtrd5eLinP2qJCmLdy1xesHq0SOGbYPKIaRoscaqCMyPXnD55Rdsffs7tBiUMjRNYjh5wMq9w49/NuPg8nt0dgvXfMXLgyc8/vQR/9P/+K+wYUmlLftD2Ck9rXJUhaGwHXb+9wy7f8SULTtl5Idf+4BmeUk92EELM0dZjrlz8w6XswsmA00V1/z8b/4jH//t37FTb/HgnfcY1FvMT8+pp5c9C0evZGzdmqOXz5nPpxSFBLOiI9GvcUUk6IqjNjKNjpqS7zx4k9HqnK39mt3dXZ6fHjExC9btkrP5ir1qnz/57psQRnzx1UseHx7ThMi0XdClDlUI6aMsJK0IyDOvtXhDp7yOyWsN2Fi19HY55FoiH9WoPmApkT1I4+YMiuk66fjqmfaKj3cP5iG2V5uj8xpAdn1fFbLgGqCqBRRTCsldIdvO0KsoyeBiFjelK+/S64Fd/y1Am8G5rKbsCabelqXPcOkBX631BuiOmYiVG3vluf1PAbWv1NHXQMb+KtI1YJjUK1CzRVKS86wn5lEqe2ReAdH9/ZYJQskq0HkyrshhYRtAWykIPaF6DezO6tE+7FpI2rAh3zdfZ68aNQaTpw2ht0AQmwKttEysGENEbPGyWHjT+6YkobTXa6q+BuqJJzKh1bbNRq2qtN7snX0tnVLYiCD63qy/J6U1GysEGWkX1axS4nkbslgixBwiidTR2ooIw2i9yQiQG3gF4PecgkKjdCSkgCkkg0WeobQB2lWu62RdSdhYSNB0vdWPpWgdRTUCVVBWY3Z39nJ46h5FvUNSBmOKfD0pT+5qlNHYssYWQ4wtN8/w9X4ihEjbLSUbwKjNmaGiJ7g10bfYCERPKg2xLjBb24y0RhvFtJkTj1d0aw9eBI4pBjnnUBgj59Tcw4V4NjFWAU0ptmjKkgyooqUAqrKkrktSCJRGUeqEih0DoPaJeDEjDjsaM0abimKiKVMi2QKSTH0oK4CrLgxKSUCytY516yVcTVs6IBYljZKwdhNBZRs/YzSV7etmNtMEvbK+rEqqusgTMQGjLTYLwGIMFEVJ0zRSOea6yhiLMrJGyTgJIKIwJW8Sc+2udUEisFi8pGlO0DOpA4UIFwssrYUwwEQKU1Jldfsfe/2zBmll7KZA6zKPoIL3HTE/ZEZJqnvbNui6yEqRQCRiC02hHMl3hJAoigodA64LxJDAaExRoa2Vhgh9zRMFpCLLXrSA0olmfcn0+BlxvE3bwXR+iXMLAWs7h3OeNsJHv/uCX370GSezhRyyWpj6clgRoicmKCtDWVicE9VcCg6VcrJ5AVPnWa0bpp9+wpOXT/jzg+/xL37wQ+7cvQtJ5NzEBFo8iYzSjEajzSaWcsHVp+3G6PMCU2zduEE5HHD64hk6BFIy3Lp5j72dLQYDWWD7e2NWqzkxWkBGvE5OzqgGFUoZFBHnPCdnJ1ycTwku8PrrdwnOsVqsefON13GuAWBvdw+rl1ycT3n65ACIDEcVw6Go6na2trEojk6OObm8oCoHvPnGQ5RSLGczLhdzbt26zcXZObqoqQcVy1XL2rXcuLGLLSq+/PIpt+/e4nK2YL3uWDanXE4v2R5NWK3XOO+xRnPv7hbf//5b7O0avvx8yqeffcYH3/wRu5Ndfv6Tz/ErT1WO8G23Gc/pAVqVk35lbYo6JqRIDFHUtbABICCJV6lRLJqWAJiUUNMLDv/hx7z5p/+Gcus2XddysOzokkElz8h4RqUi+E4UM96hkufGzg12RzWPfSAmvdmgtbVoPcIxIJgJX5yt6D5+xl+8d4f7gxHj8TZK18RkGQ0mqBhYzM45Pjrk7v23cmGiN81qjKKS1EoO6xg8AUe3uuRv/urf881vfYdv/+DPIEqho5ECvCprzpeOD3/7GYcnHfcfvsVou+TLzw5YLwOlmXF/sOIvX/N8++YFD7YCu6MBXx18xv/xH/4Dv/rtp0RTCWjaRbzvCK6DGLGV+MZ0rntFxdK/+pGbpmk2rLP3nq7rsFaaE+ccTbPOhak0Z6PhgJgSnfMbsHczVpP/XsysbVFYqrLMNgh90SKt33hrix9++7v86fc+YDY74smjL9kpSuaLhp99+BmHLy5QKTJfthg7g0KzZxIP33yL6BXPXhyxPYrs7+/zxfO1kFABlkvHdNpw+4ahUDN8q2mXitfuvU5ZVDx6cciq63DnK+6MdvCV53Q5xfVBErLqgJRZdkBdUw3m4t1oK2tdScOfokfFxGgwxALtek1ha7ZGI8RvRRqWGB2mUoy3B5y7U5rmkmY1pRzvSiopcg0qKgmDKjSubUlJCjyUwgVPgea9N99DhchHX3zKyresg6MMimZ+SWENo2qEXzYSqKgT1bgimCj+tU1k1bWiJAlyoMI1tbDKagKM7L3l4Mr7U11LJ74G6KL1xmOt847jkxO66F9VWfRFsvcURryTQUB/wz9d3KtcIAoJBD4FyMq/mCLWiBl907UYZdAauqg4btb89Ne/5s6NG4zHW6xiohrv4F6cEKcLxoMLUgw060UWySiqgdgDpZRHzLNyxWiNwZIiOXwgH3myRIRsyoqLGBNJiXcXCZLWwqSnmH2wMsisZd+Qp+IqKOIqnRmSyYCOFosipSwperxv8cGJ3xMBn5/1mALBO+aLOZfTc45Pjnj2/DnPDl/y/Pkxy9WKzrfEKD5Zxmp0XQk7jaLHh1G5KELU5X3T13vSKa6pWXODm2LaTKfIyJ/Yfmy2npSJu2tY7is/41rD+4qyFgHhZcxOwDBbCliNUkSV96CYwREt19wDuyhptubzKZcXF9x/4w0a33J2dsTzZ8947/1dUazHlBtAAXVc1+Fcl9egkFUpOnzoJJhUK8hNGrlZvk7m9J9b/ndkNBxiygFlPZQAzRDw7iqco1dQrcQgNPtqBobDMXU9AGPQqmBst2nsDikkyqpkvVoxX19QTcZoI/VHStJwi5dhQVIN0+UFl/NDTBFZLFcM7IS6GqOT7oU5m3AblMISOTt9wvHpE+699g5lfUMauHi1Vl8hW659pxqNbxp0u6KMDhUqGbGPMoaXpJOEFFFFgbGGMnvvai0gblQJ5QLeCxjsuoBPiUaBUR7txdalbZcbQrGsSoqyxEcn4HFdCuicEsF3+OBYty3OCci4WM1JMTEejYUs0ZbVasnldMbFfI6yBcOdPVQ9IaYC8ZUlky0SSGh0r7gKG3UesGlqE1fP1MbgD/HvU+WI0b3vUbz+5yzNCB2WDJOMc1qj0dFx8fQTQjNjvHcXpTq6xYqYvPjJGUOhFHVRo4uasdGMm453YuRrRG52DXbdgOtAG6y2QKBpVmhjqMqaobV0wWXwSD4fKRJcroE3CZLgYrsBt+RsDEQfSBR4xEbhOgkjlkodpIgxVwFGV+CQjNL2AJbSUlOIH3m2SFKSkm2wmzquDwM12S5EKQGaYvIYk8McezBEhfzrmJ/Tq5rf+y7vp35DVhdFQVlUm+u0NoN6CMjts/JL1r3JdU8PruQzIVuHlFVFZ6XO9a7FNSu6Hn5y3gAAIABJREFU1ZJmNqesh2jXcvz7T4gHz9lCUWoR0oi1lEWlDtanHH30j+y++xZ2MCbZARQ3scOb7L3+gDT+Nc15RQyGxBYuPuRvf/yYnZ0B//pffkBs4Kc//ZDTwwN0XDLYHrFKDWp5wk4oWTeevTde57XX7tB0C5JPTLa2adsVs8WCyWjAjZt7vHVvl9/93X/lF3/1fzPwkd2bb7C1dQOlKkrbUFcDTG1xKlAoUCbRxY6oIhhNEzpcWtI5j1UFSe+K8koVrFWBs4ZfHJxSJI96ccHOZMqiKbB2CzXUzNsLTg5POTx/QmUMc9dxOVvQBohGkXTEhAIdyX7DGpPE3kqsRfq1JgSYQixDYh9Op/oxdVm/EjblBZTsn2vVZ2mIeq4nE/tJj/7Z+ENAUmuFShL8ZK3ZAGnX1aTXbQSuWyHAhq/deM5fTWxoXPCkINuL6rm1dKXU7InRK7C2v75sWpKk3hVQMOXnqQeH+3P+ao/X+ZySa5Dzoq/artdvGyXntc/1//+6NqmDPNM2P+OohC30ZupLG5Vtp16tF3orN2N0FgE5UEom2HK/Y4xBFWrz3aeUaJsu2zl2Ajjlmt9aizJm0xv9IcCsr723QtZG/9qMjAtrTXD9tHIPGobN++evLoPw+TMlAXM3woY8udjXzlxbP8Zk1WjeT/uzWf6B3wDLvRCgLAVILstys5/FEOk6j44ej2z9yhiMTUJg5ske0hWp3r9C8Fk0BynEPKUotVjI66pXr4Ykz0pEY/JEiykL6tGQalBiCos2JUU5pConlMMxw9EtytG+CArU1VoxqA3g7aPDhTYHswmOI8FYMqnjOk/XtaIMxmMKSwxaLJRWM9aLS8Jqhfae6BZiwdiB9WvCYk6hJJg2Ocnv6IMxCRGDkQBapeg6x6le0g1qGtdRF7VMuCtNMiWlqdExQFmgywK6JmtzhEzf3R3z9ttv4k2NNwZViIJU3IK1rBFVXBHGnSMkWX0+BdBBxCVRyGSItKsly9lMgr6MQsVESgGXQn9oZYJKSIWYhVzGCMja16hamWxbIXaG++Mxznup2ULEB78htawVjMJsj/MzGlmtltIzJrBG40NLURQUSpNiR+wSKWqcS4TkQUdsWVJWAr9WZUVdV//kDvLPHKTVoEqcT4Ckm4aocM4zGFjQUUISSovOgJlKHuVb5rMZpY6cXV5wcPicmzdv8fabb6FipLAlSdtNcynHhHxBKWkx4k6JGDu8X0oQyXLJy4PP0CHRLlacnV+y7hqK2tC0a87Op3z+5WMePT3g6HyKD4lodPbzkp9t8sicsIo+M+qZZcrMlAibcsNUKFRRcHw556//y9/yxVfP+B/+u7/k7bfflMReL4eq3jChKvtP+VxY5sMkN6GyryaiSpSjMbfvP2ReT1CpYDWfcnJ2SVVbtrZG1HXB7dv3WK1alsslp2dnNM2Cd955i6q2GC1+Ncl7vvnBB3jXMZudc35xztff/zoheJ6/POPy8ojX7kxQN7dZLnZ48uw5X3z5BQ/eeEBZ3+Tk5JT97V3GoxF7+7t8/YP3MEpzfnrOcDTC6ITHs1gsuH/vDhezJY3zKCWS9cY5zucLzk/OqOsht27c4ej0M2arOW88uIePHqvh1r1bLBYztncLtF1TVDXvfeN1xluGulJ0XeTx4xdiXhp7j0NhnFUuADbqIsSnUxIALT448XZLsvGHICN/MoKWwQ6h4Cg0+MUFz3/9M3a+/m0mt26iqjFGG4qUGJXgF6fMp0ckNDFE9uqKO/s7PHv+kicvzsX/KyAJ1tGLL4qSkbLODHh8MqdUntH795jYLbSRlF9bDdita3a2d5ldTsniLfqmIAVPs15T53AoRWQ+u2AyrNje2eH23bssm1Ueq9NYrYCAMpHpquNvf/EFX5203H34kO2tAZ99ecC6Ddh2yhvbc/7Vm4rv31nz3msV+4OC3//29/znn/yEj377GUHLCF+IEe8cvu3o2oaqrinLima9xufRRLhi7Hs1mrWGTglbGsOVsrEsS9q2w3snQL02lGXJ1taElCLtei0+pZ2jLAvKshRVbkqomPDeUVjNoJIQrX7MJypIMTIejnj/3Xf45gfvMV/OeHxwwHQ5Y1Rt8fGvPuPl8/MMkMGq6Uh6gSkMVVVxa+8GX3vvbT761ZJHzy65cfc+g7qgaR0hQakNi2XLGw/2mMQF80XLaqFoVzd5994b7Gzf4vHRMbPVjPu372JLzfSTX4ORwlk8UxNoRVlXpBAIUfbMHnEpipK6qlmuVgiZ03tlKsbjEavlHOcc48GWFD/XxtN99OhaQ2EIF5Fu1hALjcmqOvEulp+lrWYyGdN1HfPZnLIsGQwGdN5BDDx+/Ji6KNmejFHtinXbElaO9XTBZHsXigz4KgFpymqcbQ1s9vbyFNayt7fHet3Qtg3ksKteRahU3ARu9bYEqJ4Rvwaoquxn6YP4MmpExRiCPBd53XnnEd5LE5V4bWok0T3mz983ExqF8x19iKUAx1bsIMj2CDFRmoKisNy+c4fj4xMW8wW6sKAtoe344sljfvvZp3z/G++jbSGm/Fs7PP3kM14cvKCazti6fZvReFf8nDSU5RCl5LzTqQ/3yAPKCWGx6WEGUSCTYg6mTNeK9z4RPY/PpatiJyEjWj2i0XtageynGyBBhqJz4Q3RrenajvV6zvMXTwmx5faNfQEhl3OOTo45fHnEF18+4sWLl8wXC0k0T2I3o7SMJBfaoDNJS27upDGQe9/bJwiRdq2R3FQbKjPi2Zs3phyOwWasL6UswsvorlJ5tJ3eX09C6KKKEk6Ul0D/JiZ7G5ucmoxSYp2kVbaSyNeblT4yKHg17odO2V/VkrR8R2enZzx88x32d29ycXHJs5eH3Lpzj9t37oriPQNuIMqC87NTBnXFOAf7JSJNu8YHjymuA8pZ1aH6SZIMeEVRNmhtxP5AFzIOlhLBeVbLhdhSWQkAU0oxrKoNWRIqGZIV1abcv0G1w8AvWIVLPC1VXXK5OEUpzd54H2uHvWEzMUVcXDJdHnE5e4EpHEVlSWlEpbepyy0IovAxGXSUBOmIToF2Pmd2csyNvbtU9Z7Uf0qa996vUecmPQSxPSmsqM0WszN8u5AQkRQhePELdS2DwmCSNHNBe1RRyrlLYLZcUA1qitIK6el9HrMvKMsaUw5QZS1gSow431FVAyaTCa1raLoGHwXk9TGwaloWqyWz1ZJ12+B92HiNzpdzAR2SYlwPSDqwdi27D77Gs0VAcUaotulsjUn9lBWkvA9t6p2+Mo7k9bdJWwEkkJPgSTm4iJSIasDOw+9g7n6Xmd6lSxpLi1eGwohipVmd01w8o6wLtvb3odCUSWwZit4mxTnatKJQYjX2mlZ8LUTud45h06KdE5ItKz5jitnKpiSmSLdc0aWALkrqukYraGaXEnykjEwVqEjSHhfjRvARkyQum+EYXQ1ZdZ6iMChDtr5Rm1FbIdJ0tjyTxjKkfkRXJjmUzmO02QYhBZ/fw2erpVJUbi6QVKIsK1JygAAxcl5ITWRSv29l4CnvKVUlnvpt1xCDp6xKYjA4H2i6BjohXqtyIBNCxuY+R9ZaCF6uOSbAZtCuN+LJz38S2i3FIPctJUbjbSaTLTrX4eYr/GCNUZr2/Iz1k6dse1EkKWtIKgnQSERrqGNk/ewx3dkJ5rUxXTLoYoyLxf/H3Jv9WpJl532/PUTEiXPOPXfKOStrzqpidXexms2p1SLcssYHCRJkw4T9IL8ZgmEYsAwI8J8gGIYBGRYgQQAhG5ApSrRoypNMiZKoFskW2ayuoWvIec688z1jTHvww9px7q1q8p0XaFRVdt4z7IjYe61vfQNvvHudv/5fvsE/+OWP+b3vH+K9RestZlPH7320x0tvvE0zn/Pg0T716pDdomP30jadnfD4R58RNFx6+Q0uv/YOR6cr9vafcfXaDSZbE15+6Tr3793h6HiPn3/tPZ589gn/8lf/MXaxZHNnh9xEfLdkNZvSzGeo4BgUAyxGAEwM2uZsXrhIPn/OyaqiDR1OOUJniSYDlaMYYU1G1IqFVgSn6XzO3rEXRhw1KsDJqmbV1jw/mUsIl01hR9aijAw3tZLaiRSo2e/N68FC9IRwziZI6TSY6v1Zz1iwvbpBpwFzjKyTz1Ua5PVjmL4+0kqdsdVTjdIrKyQwyqHXAO5ZvbDulWJMQKCcjb3nZz/YjBF8FEWPMQZrTVI99dJzeY5UTJ6SxHQtONuvzzFjvwTI9v88N7CXsNvEVEx7fK9cksdKfel9zyZSf/jPefD63J+S0O4UvBbRCSBXSU5ujE0KTFkE14lPtU7gqdgwnbFWoT+j5AzUvR1SUvx1XSIIOGHNCvNUresOyddQa7/b84znHpvogdI+0EvWTHJ+PEHyE5yX+6u/f5JS0aozZm9PdDnDOWI6k+K5tT6znYiceXm3bUtd1+k6WsqyFFVIqqGN1rggKgr5bGFtWWGVqC1Nptf7lzGG1bIizJ0EeSrQVs5pZeT8I/VEPn55yK40qCCKAm0yrO59azUm1bbi2S5DXKMtg7ygLErKQUk5GLAx2mA0HDMoBmijaNqG2WLKMCpgTuc0QRuC6gPy5DwNriUGcEH844PzSRna0bU1vqkFRA5itZdnFlNY8nyMzaCLgWyQYcwmzmqoK/xihVtUNLOG+XyGnx9Rrg7JXIOKYl8SVFxfw04FXAJRvXfQLAhVQVNVWC/MUqsjPkBnwCmV/Ko9SoUUeG4YFDnjyTbDizu4YoQ3QwZ2G1sU5IOCrMjE7iAxkZVKQW/KpEFrh48tnYu0TYuvV9DOaE6f0a6OxV5CpXYr2RGJt6xkTg0GpVhM9EMCL0qvPvBZq+TJHQ0+ROqmZp0/odTaNkqeaQn70towHJe4lLNUpcD6oKTP9K6jLDbI7QCjM1CGZbWibSuCkjrAuUinAxSRTGV/5B7zxxqkjShWbQ2c+dC61tO6jqEqkFS+FmMcrmtZrCqia1idznn08AkfffQpP/rsU5pmxbtvvcFf+09/kUtXLtMGL8UpKTlQ6FfSSHcOSBe4XXF6+JzZ9ATXtZxOj1gtVmhlaeqWpnM8e7DP57dv8/TZM6aLSoIdMo3JLTZKK2wSsCPJ9+JF1Tf7eS4BZuLll6aFSmMNGKOYbG6znAnweuvBEw5/+Z/w09/8Ot/+uW9zefeKpMgGBOlXsmrC+IGeQQLpMAR0OkiD99iiYOfSVba2tzk+3Gfv+TNOqznH8zmhaRmOh9y4cY2b77yD7zoeP37MdFYxGm8Akg48Hk+IQaGUZ3Nzwu7uDjtbuzx/scfzZ/tsTUquX7nI5qikHAz5+PO7fO/f/5C79+/TuY56vuTZk2dMNjfZ2t5iOBzgnePqlSs8ffqI8XiDyXjMztY2J6dTLl64wNb2Fp99cY+jozmLeYP3cDpbcnA8ZWMywWY5r954hVdeusb9Ow8YDgcM84xGO9o2ktkxy8WMLA9cv/ESAzvkg997yJMHR+RqjA4KFVQiicQ18ykmEAst/79GzNblgIuE6NKkWtYmxkjrOvrEZJVkb7kOrA5eUHnF8OJlNl96C6siNio2ckVoT1HdlI1sk8rDhc0NJuMRX9x7ysGyQZUlfQpnU61AgS1HGO3wShJCbz09RnvPn3j3ZS7afqIlcgCsYmNLC1jgpASIwUMQtrFOfsZt2xJ9h/eGmFv+1J/5c7IGPtC2NeVoA20tR3XkN39wmx89POXKmz/BeDzk3r3HNEvFAMfbl2v+w9c1P3Fpxc0bQ67slHz4/d/mH/3qr3Hn6QFoaeLbrqFrHaHzaAXj0Yjxxpj5YoE2mkFm15PaflIaY0TFQANrNlNAPEqHfUpjYgcYbSjLksFgQNd1HB8f07athI8NBqAVTdMApMACyG3GxniItQrXtnJoxkDUsDWZ8K1vvs83vvETnJ7uMZ0dJabSLv/yN3+Pu/eeEc4VeD5EmrpjtWyYnsx5kT3j+ktXuPn2m3zy0SfsHxwzLIykVzphMS5mM6rFBlevZSg35WAeePTgFioafuHP/VX+/JXr/P1/8Pf44ScfE6gwI53cBU1i4gSUylhVK1SEzCS7lVSQtG23Bl+0UuuZufMdDx89wLkOjXh2KxSdcwQnRXXTtEx2t+U7Vpr6pBGZqZFka5NlFEUuLCYii8Uihatt0jQtp9OpvJk2zJqKNnq2d7folKR5dy6gQsbulauEtmW5WhCCZzieUI4mFFtD2qyDJkLUlEWRGDuKzc1N5vN5+jYqNQsZylq6tkkFuQwbemavMSaFNMIgL2ibJjXdQQAvoXSsG4wsk+A9gj/z3g3C4shTE991bg0C2yyT5yf2LAVNpg0GCJ2jazo8La33PJzNiTFilagwtPeo4JnNTvid3/13vHLlAhe2L7BYLdjY2eat995jdTIjKwdQFuRFKZ81DYh6xUgMiUETIzE1QtJSJCkPqRFAGJExxnXRLgV1amBU8nXXds2YXAcxpaEEEZzrpfWRrmtp2iqtU9pfug7wtF1Ls5pycnLCnc8/58HDhzx98Zy9o0OqTuxjessTkw+waSDDumkTsAajRHaWzjnpgUKPlydbB7UenBBjYkz3jWjPrtFYhUiv0hkqCv0e4NWp0Tu7H6Qx4QzcVmdMmL5xNlqRZRLYpEEYyurLnqj9ILAv/mMAjQGT2D5RLESCDxyf7jOdnfD2O1/He5guTnjw8B47Fy5irQxL+nogLwo2t7fEU9sHZAKhqFYVTVUzLBPDureH6UNo+mGGkvt0Pp8xLAsCwtQkCuskxshgMFgPebqugxgZb2ygnDBqcpMRUUTVDwsUWT5iI+xQn86oqxl5WVKOMw6nD1gs9hkU2xiVoaLCRUfVzKm6U9nviPgqozATNocXMbGk92Aksf9iL6P1nu3tiwxHBYONHWJIIYuqZ8OkdPsESsYY6dqWzBqCb9k/eMaimjGwwpT13oF30ERszKQWMgLcGptjMxkiu+DJZJIqXnImAyX2B0YJiEFWgJKQqNhCWZbYPON0NcPjCCEyn885PDhgvlhQu47OdzRdI8C/sSibo4xFY/BOnkOHRW1cIV58m9JdJHcrTo+fCHs6NGLJlEpFncDX3ue1J5xKDXRmHhFVXDeUYFDBowKojSuE3bdZMaHxCSAIJEugSFCa5dE+fnnA8OoOg+3LeGOxeViDP8556rpG48hsTt45Xuoc17qWjUWFahthLCevSt8l39o+IDiIf+rm9g5BKYpBiXOOer7mA6dz7sz3FS9WIgJMaQYbm8TBEDVfgslQyTKt98ouyyF5lqWmTKWBlP6Sykobk3Cavk7xAsh6CbnKsgHWiF9z59rk9xioqiV1vcLaDJPyN0LwtG2F0VnyiyZ5Kqem3VUsFguKfMD29gW0zhiNrQQrJquY5XwBo6GE16gzMEK6z94WyKYhFok8IqQO38lw1EZhK6kUyuRaCVw72dsjhsiFyxc4uPUF7vAArSIhy8kHIzzyHXIAlZF7RXV0zNHtW2xeuU5DjtcBhUVHeO+tXf7rv/4n+F83PuRf/8vbLJcalW1zVF/gwSm8NNliOj0hNAsuXtig6SyDCy/x3b/0LZZt4P2f/jleeeMtFqsWmz/h0pVLTDZGRN9R5HDjyibzF/f5J3//7zC9f5u3rl5nPNzAEFic7rP39BjrPDHUIhXuAunD0zoPxtI4z6Kq1sNAgLaa07YNrhszGG6CsuiocQSCIeWKLKjrI4gVwXWpJpcn7PwA2KZBno8RdEihxQp1jvV53utVCEdhHWjTq6X66yjS+rPr2n/mM8/5HmxMHvtayA99IJdaS23OAOIoRWR6HVGwKuS9eqC2twjKMkPXOdF29SCvEjsWo6VWEhBW+ille1ZfD6acAa/nB+pfZe5Krfdln9rem7IP1+tBvfM+uOngXgOJ6N6fOq0ZP+5T+9XP0r/fOmQL8K2TEGkrCtQYncjujUZbg48RqwXwbtuWPLFmZSMRkNBm8lwaLZ7RedobpA+S//XfwVhLmdixvR2A1qKiW3///rP1llbpPoixD1EPa/Zuv8Zr1nHyNPYp+8OkgDiVLBJsDzKnGqJLr0c8U6iYpFDrB9va6HXdEEJY92D939WIgqHtnOAdiXzRW9qpFNzYdR10Lp1NiuGwZHNzk+3NHbZX2+t+r65rWmQwjXKELtAHkZ3PHFCK9P79syJr5UNI4aes2eHDQcEgL9namFAUBcVgwGRjA2szsqKgKHKCjzTNgrpeoo6OyPPnMoA2OaYYMCiG6LwUcokS3CFi0jDBIT7EAaPBFgbnAs7LQM/5gPIalARODsoSpbZQEXy7oqvmhPmY+uiINl9QZ4ZpdSTDea3Ww4MugdNWHmRBPlUKM/aOejWjbSuiyTDKovF4rVkpaIJHmYjNwHiwBnT0DJXC5AOWzoGqKcoRKldkOWRZFGsCpXGk80iJQjf0RAuklGudZ75Y0M0Paed7HO0/oG4WCdQV60GVQsLoYiIkQds2ZDGs70thSKfzPt3beZZjCrMe0TgvoWIuBSq3XcegKOh8WLP9m65lUBYpJ6MlOsEPsyxjZ/cKb73xdcp8QgwSoH0yPWY2PWa1mLNcTHGuAuNlb3d/9CTojzVIiwIXA9aKz4QmkGcKoiGzGoLDhSVaNdRVx5NnB9z67DYf/eBjHj1+QecLXrrxMt+6+QrXdsdUi5oQvPhI2H7aEoTVQUQpCQKLvsHVC06PDzh88Zy6qogq0BJwFhbzGXfvPOTW7Xvs7Z9QtY28lpbAHa+FoaKNFG5xXeoKcNEfGLIJ9kwZ2fTEI0cOxbbz7O0fpqmagLeHJzP+7W//Pi+eHfPd7/xJ3nn7DQZlifPnDlzd+yrqL22w6UNI+IEGh8g7dJYx2r3AxVy80gZK8dkHH/Lk6QuOTw7JMstLL73E9s5Fjk/nFMMh21sTWhfI8gIVIgd7z8gyy4Xr17h3/w4HByeYaCkHY3Z3LzLZGNA0NT/1U+9hixE/+OEnHO3tc+XiZS5cvsh4PMJqy2pVcfveI57tHXL54gW0ySFC3UgzMpueUtUVy8UCgqSCdrVDKcOydTy9c4/QeW6+8hrtquXo6BTULtsuoqNic7LL5mSH2XzBarpkPjviyuVrPLz9DF0VZLqkiS1tsi/QWiX2pBzga48hpXCJoWe0kWustAQ8WGi9o207kRi5kP6+hDkNbAbeMz/Z5+EPv8/rwxGTcgMqz2YpiZeZCrx2YZMHz/bYGmyhreW0bqEc4RSUKvLa1cucHhv2j0+xKhJjgwsi6W6V4c7Biq1nC759c4ciVmLXoPy6CW9bB2vmVqBpG0nNTvdrlhnG45EEdQUYDARMnS1WlONNsrxgVjl++5OnfPJ4xqVXXmVro+T2rQdUtSPvWl4fz/jum5r3Lyx5+bLilRsb3Ll1h//9//7n3HmyT50aA+c8sXHEJJ8RO4IhTfJPHA6Ha1C2B9NijDRNQ/R+DbKplEwsAxBhay4WC5qmkQNXi63JfD5jtVqitcHHIIAMrIsYBZRFyaCQpGwdI0VeoFphTg0HA977+td5843XuXX7M+r5lNFoSBM0v/3vP+L2vadyzyiZIPfPXtcFZvOVHLRWgteuX73BG2++xb179xOgJMBPSN3zyfGU/OURF7Y1bag5XZ7y9Nl9Pr11l7/4U3+Sv/af/xf83b/3t3n45FOsER/hLBMGcQ9Q9u/vvCMzeWoeoffdNQm4BdafQWnxvrLKMCpHKKJ4znnWXqZlkeO6Bt846nnN9uYOOzs7HM1OU2MgHsd9eEAHFIWwfHUIKCs+20RoYuDg+ETALZ3TtguGow20Nuy9OKBaLgghUIxL9MDKdD+GdTEagKqqGBQDinxApas09VcpqEj804zO1ozItktBOgMJjlwsFvJa/kzGe9YISBHUMyxkz5f0XpG2OOrQ4mMg0zkGxcnRMYNhST6Q0CWlNFatyz7cYsVyvsA17ZrpvGauahnmaSXAqVWQxcD9xYx/9b3f4k9/97ssFitym3Fhc5vReAOvoEXmjjoqLMIS00n2jpLhZETA5R58U5wBq8qcsWRj7C0PPBEPUc6i3rdwbZESRYpF9IldFwm+S4C4MLba4BLY42nqhsP9A6bTU/YPXrC/v8fB/hFHR1Pmi9VZwI/RGFvImaZl31VGn+FwaS+Wxkyn5lQKXHVuSNmvJ7BmBvX7ROIAJVDlbO1NYiSuCdbpbDWkWjJ4aaBRaR7aD1kRFpLNsFnOYDhEa8X8dEps+4CGxCzh3NlM2irUOUuFdXPFGZvJCaM7qkDnGx49fsC7777P1SvXmN76lEdPHrKzc5HrN14hRgH8VqsldV1LyBVB9gatIGiCQ7wsEW+19bpy3vvMoY3sqZuTCXW1pAVsPM8A7sMZ1Do8SQZAntliSoiB8XiTLC9TSd0z9TJyxoSVZX6yYrAN5WiMMtDGitWqBhVRadCWWUtGZLZYkkXLYDBhVFxgYCbge3l6TENVGUIqpel8S+sjo81dohnQ+XR/ryX750EAuQdGoxFKQds1HO3viRReW6IXQw0dIllQuFXNwku47ajICSCDEXLKkQxFWtdRDnM2tiZkRcHzZ89x3tPVS9rVkoAitxl5ltO1LVUnRIBFNWdv74DZ6Yy2rjAaPF681aMnsxkxsXGMzciyAptpgo5MO9hvLFe3Xmf72nc4Pd7Dffo9uuOHEBvEn1Ij4VgBrT1OpgvJriYBLzpJaRVrRp0ApQ5Ch0Njty7hyh0al4sUW3lsdCIVjwqMSexKS3npMqEYoLogZIv0zGqjKYaaQmusd1x0K666lnG1wjYr2aW0xisBCk1SjESSYsloymHJoCxZ1RXNakXbNOgoYGqWi+JuzaCTB4vohSWjVGR1eoLLVrQxoxgVKCPBLL13pU7Dtx508N7jWgmR1NqSZ4P1PahUBOUJyWcbwOgMawZobdGmDzWR+897GfRba5NfaAKK8MIsSqCvNTk+BJpmybKaYzNAQArEAAAgAElEQVRDWQ7XIIO1di1vx0bUQNR8OoEqa8m4kX6jaSsZ7ibyy/meIYQg6dlRWLXChuyIsaMoLE21YHoQ2DSR6uFjRl5CbMaTC0x2ruBCxLkV2kdsCufRTcP0wX0ufOvnsONc7FIiRCdM88sTzV/7z95ne6vk//z1P+B06ui8Yff6ZeL0OdXBbbYKeOetN6mGl3jzO3+RS1de53SxIs9HHM8Um1sT3njzJm3nsZmlbpdcv7LF7gh+41d/mXuf/Hte2b7AZHOTl169ic1Lti/usDupOXz6kOPDBfPZIafTQy5u7Agj0miCCyzmC5q2IUZRcXknTNcYlnR1i1IObQZolYG2CbCqaKoTQqjkgI5n8vm+9uwT7F3XrfsO0weAnvv7PVvxS/Z26syv9Ww/+/LZ0it5zoOL68+gFCGcrxd7L96+I1j/cWKIJt/tNRPhzKPzDCTV6+DI/szrd2eU+OlqJc9w2zZrH+zzNgsh8qUciv479//dP8u93+vZ+cWPfdfzv3fG+j3nnZvWtAeH0Aq8+rG1PW+R1b/mVy0QVOoRfRCQqzdwFZBWaiQBluR5MSGIl5BWuBgwfWBjz3ZOPrF9hoZSoJPdhTFZkowLQ1+A8Z54EJMf/Nl37YNx+6BkxZmVQb/GktcjViu9ZRWRpAjuF4h1P6lA5OGhoyxLWaf1aKz3Tk7gbJR+E0A5WdseRDsf4C79iZA8+qGcj4Ess2fAsTqrXSOKppGBcd02tF1Hlg0YFAXb27uEFDi1Ws2ZWcNysaANQTIQEvnqvB9wP0BfX+dUF0qZlKyrjKgzx8OhKDKChIIu6wprO3x0+OEGBCWsyqiIoaFtVlibgynIuw1i01KMAmZQonOLyWwa9ESCN/jQIYo4CN4QalKNTqqzIstlRV11aG3JbCG4mTJQbIiCsKqIzQrTaMrJJoSGzje4akFQss97JTEiGZDHiEFIEg7BMLp6SWMhp8DbjFYbWhc5bR1VW6FVpMg0+FZqcwvFZEI0luACvm1w+YpWOznDswHGSi0leFkQk76oiKHDu5q2k16iaSuadklbL6ibFREJAO/rVrHW0Fiby/0SuqSiPBvaWGuxKoWFr/cOAWpR0Plz2U6prlAI1uC9qJa6rktnrTwXWZZJkLHzXLp8nTff/BqvvPITjMYXGZQj8qJgPptxfLTHdP+I5w8e8mz/Li6uaJoOq1v+qJ8/3iAtCmsHAtIqOcBDUzGwntCe0DUNy+WCp48f88GHn/GDDz5ndrzg6oXr/Mw3/xQ/+fPf5tVXRXrdLg5o5ofUjfh4rjc1BJRoqyXBNcyOTzk8eM58dsByPsc5CD7Sxo5HR3vce/CQB/cecjKd473IJ6JSGJVJAaRBazm8olIpAMWgrWw+fcPbAyT9xKr31JEpkExtiOIGI9MBCYGJZkgVA5/cuc+LoxPef+9tvvMnfoarV66QYfEu0nsv9n5hX/IT6lc2itRFk0IDjGVjZ1cKj7bj6+//FDE0fPajH/Kjjz9henLKmzdvEok8fPiExWIHFWFYlpRlwY3r11PRHpjNp3Rdxeuvv8bW9hbFYIyPiryUQ+Pdd97BO8UffPABJ6envHF5B2vAEhmVA8o85/nzfabTmr39GZcv7RJ8TYwdpsh5vv+c49M5VV1xeWsz+YZ45sslxlqu7O7y/PkTLl65wM13b/L48R4ffXqXjbHhnffeZrhVcOvWPk+fvODdd9+gqRX7j5dc234Z7y0H/hDddvQTbWOk0IghkuU5XdemdHBZ0y4FNqFIKZMChIrEQ1NqhQuBzjUErYnOoXQk8zUnDz/jTg4X3v0uRpWMTEZdRZY1lG3DmzubXCst04MXHE5P0fkmhJZhbHj7yoSTARydTMXD1YNXGT4Ku2npNT+8+4wN0/DeKzuMckvXVms7APEVFUagNYaQWZErQALkWpaLBXkxQGnLclUTfCDLc8rxJvPO8jsf3eLDLw6YXLrO7u4mX9x+RDM9ZZTB2xfm/IW3LG/tVFzdVly6OOR3vvdv+d9+9Z9x5+5Tgja0MdA1NXQRiyFESYUcliVtMoAfDofrwtSmJqMoCuZz8d8bDkdr39le1hOVMLlWq9W6iCOSpDRSZE0mE7QxNG139mwo+d1ROaAcFKnoE6+24GXqdWFzm/e+8TW+8e47LFcLnjx6ymS8AVXkX3/v+9x++AzB+M7JRNOqAjSNY75sGJQ5L/aOKYoNrt94mflqxfz+/cRoks+jjGFVdSgsk7H4i2WmYVpP+fxHv0/zKyV/6T/+q/y3f/O/42//nf+R23c/JssgOGEYmh6sghRkI16UfXiKsHXMmu0vxZ8AQCaTQLR20TEcjNBRvI6Cl2JMp8Ow7TqWqwWr5Yqd3YuMtsYcTk9o0zOjQkzMLCm06lCv5XaFtXS+IyKprV3rsMZCDDSrigvDbbqmpk4s2szmZOWAznqRjwbxh+vlWtF7ltWKZVWvGaybm5t0bcuqauiCMBEuXbyEMoZHjx+irDCoq6pK94o0/Vr1aovUKOu0Pr5nl8iaZUqzOR6yu7PN073nTJNHUVXXNE1Dvaooh8MUPCBJrjGKPLyrKkLXpevE2kIFFNEHYnASfKPEG6wOHm8Uv/vBBwSt+IWf/zYmKqrViuFwjAsCALqYGAlKk5uM3Fgp6E2eBgcQlFmzaftGK8RA2zYURZGk9sKEEXKhAVIycBD2m6dN8l9NTNLvPnEmBvGT9c6xWq04Xaw4Pjlm73CPx8+f8/jxU2bTFVW9AuXTVDtDaQkOsJlYKLRO2M1Ra2xmv9RMRGQ9fWDNZFPEMwaQMnIOSvcoBS1grbRhIYqEXAY4Zt38nJ2bOoGpYmNxxqLxQMBqsZLxiUWQ5QX5aIQpC/KyxBYFxWCIipG6a2nSvROTbE7EGl9u7mIaAKz7ugSoqATW999cKY3H8fz5M/ae7/Pu199n/+iAk8Nj7ty9hc4yynIIROq6Yj5fMBqPiRjQAbE1lGCfajGlbeaUtiAGs2b+rpukELDBYAvx3WrbBu265HtrGQ6H9OnUsWeNGrNuZscbE9q2WfvRGavPraVhkG9y/eIbTAZjGlNRL2p89IxHYxbtHE+b6ieDySwKy+boIpkZsTG8xDDbxYQ8+avGdaEjjXVvtQFklqhzAuLLF11YM5HOmvW0WyuVGFSBrq6ZnhxJE+Y8k2HJ5qgk1xprFK6BtmnItaEC2tJR6gFZkcvz2DboDF56/RrXbtxg//CY4/mc1emUuloQlUmMbofW0DWe6WrJwckxR6dHVI0U8VmmiTrSNg5jFQa7Pu969pzNDa2vmc8r3PAyM2+4NLnGk5PArBoyfOXn8cHijj7DhBZrkr2BFluH6IXNYnTysU6gjNYGtDBWpakX1nCIBjXcodh6CW9GKB8h1Cgj8skuRFEnNSvyzQ02b36D66+/SlGWzOrTM7/BdN9EDV3wbDctL3cdV/BkoSFGJyQHLN6162cade7ZT5vVarkUWxTniMmCSgHKi/dr78UYnFu7sohaDwgtvnbobIPMWorMritnozUu3TPyXIoNgA8OHzzWGrI8k6YxWQMQI23XiARyMMBmBUbLMLy3BlGKNAATYCTL8jOWOsLy6tl8znl0Jp83y3JGekRms5To3gNxIdUbGmsNVicll+qtPBwxeIyWs7zrOqzJ0CaulQA9KG2LHE8HrZYw11DRxBXiC9igQ4NpI4u7d8gOT9hhwEAXvHT9TV7/2vscLRacPrwLdYXOLCpAETzHd+/y0osDeGWMJSNaI8HNEXTXsTuK/OJf+RrXr074pV/6XY6OG/7vX7tD9/DfEfcfcHFL41XGN37+TzN66W0qn6GGOYGM1rX4DmanC8BQFBVbW0OubU74nf/vn/Iv/p9/ylbmGW2MuHz9dV558xuUowmDwYjV9opqOWdR7aEzj48NzjUopSmKDJdqDBfEu96HnlUZEuuzo6lOQBu0slhTiMVJaERaqwAMXglpo7fO6ns/EqszxmSN4wWU6ocRIAOHNeNyfVap9Z7l45kKIq4HjT/OBO1/FxLYufbzYb2f9MPYM4l8D06pVCMoCTDUUrP0Yb1SV/a2C70PfKpHY5DzLQ18vPeiGkFY+iJfTr8Te5VKL09O6xBZkzbW30MJ8zHEmMKcf7wH7n9UOmx79tzZ8CL1dud75nNn9FfB2PP/3QPnPVgtLxzPDfcTkz+Gtb+ugP+SqxGIZ7WKkjrAOY/rUvhiUUhQYFGIhFv3Q0kBd8+GqgGlPF3nhciSGNQ+AbxN06z33SzL1j60fa/UWyQoBVpLD9SvtTGyr3yVSRx8WFuCdV23DmgTG7AzBnYIQWzO0nrpxCLu1/p82C4xWUYoxP/WBxwB26a6LtX4kkNxFs7Wk21m8wXOz9ZkB4309C75MttMbJnathYfZJLK2cjnlc/j15c/KlA29RvOrwkiNnn5S12scF3HcrkUj2rfUdc1KmoGgxHj4ficT29ERZ+sgyp0HJFbscNTmXiDKy81uvNiv0cM+OgEdwgBk2UMBkOxtJORqgCzUbAdFyWdpI0aX+Q0A0uoDH48IoQJy+qEqrLE0GKVGOq0KlAEyIPYHiilcFpRxY7V8TN8NUSbDD8o8HlBnhd0XWBVr4Q9aw2ZySiKAdvXbvDm2++yPdmVXjsbkOlc+knvcW2L0uKZLm2pLHZujfjkWiPKNq3IrSHYgg7oGfMqPZ5ZnsmwOREdtFHr4cf5IYvso+nZToquGEXpWZQDTB8WaoyElbdtIrKxZm9ba2VI2rb4KErKgJAodncvsb1zGZWNyMcTsnLI7qVLXH9jAN7h2pq9p0+5e/cWTx7d5vjgCbiaP+rnjzVIqxDGdfAdrW/pqiW+rcgzxf7eEQ/vP+X3f/8DPv/RZ6zqyPUbN/nuX/7L/NT73+TKteuMtnfR1qDxMDKsBpEsk4spUkVPWy85OTqmaVYsFic8fvCEk6MDxmNDlg2YV4FHD55w595t7jx7St0JU6oPWrBFYmgFkjQyrhmtEdl8e3mFDwFr5JDr0+jhbGOXfyb2RwiYRKnvZbU+HYgoi8Pz4mjKv/n+7/H0xTN+4dvf4ae+8ZPkNqfunCR1xx8/nCIRlWT8OiKSChITBiDL8VHR+o7VconNx3SN4tGTPXRR8NL162RVwfMnz9EKtrc2WRjFS9dvsKpqVnVFRHHl+hUuX7vE1vYuShtm8xmxdajQ4J2lKEp2doTRuv9ij5dffpmPPv6El27c4N1332X34IgffPAJd+/e5/rVq7z5xg2sBYJjezLh6uXrHOyfkg9yVlXNhWaL8cYGw3LApZ1tPvjhhwxWQ3Z3t0A5PJGsHLFcVjx7+oR79x+RqQ2uXX2DD753i7zeZLe8iikzxsWEZ3svOF0crUMdALTVRJ9M088zgRSENHExsWchyMJqJbIdnTZyl5IApUCO5K7h8PMPUSFn45V3qashwQ6JWA4ODrm+u8VoVHD/0T5eiXeLxrE9sITlEftPHxOTA6JTIiNVUT4PWrF08DufPaawhm/dfAlfi7erUSHJTgTUF1+bXLxc+tRVJf6uo9GIPC9YLk8pBgWjjU3qaPmDzx7z0b0jLl68SDYyPPriM+pZx4Za8tam4s+8m/H1CysuTQLFMPDp55/xa7/+//LFvcdEnRMRNrxyCLsbKWTKwQCU+B0Z24eYpILWeZGHBrm/h8Mhw7IU8/A05dRG06XgsPWkOD2Pru2wWUZZDhgOS5pWWNPnGYxlOcTmwrDVCpSxMpAJgY3RiHduvsnL169wfLJPtVpy6cIluqD5V//u97mzBmi/yj/o/0yexbruOD5ZAoYXe/vkRcGbb73GcjmnfvhC2CdJpjtbRg6PG752cwcVjlGhI8taFhyw/+ADfuPX4a/84n/E3/xv/iZ/67//Wzx8+AXBtJwJdTi7V9NQSNFPotXaC0wYDwm8TT6M3jvyLGNUjnFdoOnE79q3jnxQMhpuMu+mVPMpwXXMFkuaJ0+E8ROh9S2ZMiIxT823TU2GQoOPROdR1tD5QHABHSPNbElOxmgwoqprXNdCjEw2NxmMRtRW5KPi93rGcIhKCkPvO4w2DLKccjBgd2eHJ0+e4jsB12azU1Z1LVPYcwyJtVQQJYn1oW86ZB/XCVwWMF/sIzJj6JxjNp/LwE4npnCWMdraojqdUp3O1sy+zEiqetdU4IXNZJIfEzGuAXQlNy42MapiVAStaWKkXTb83h/8kI1hybfe+0la1+KWc4yxFFmBNorlakUXPSMrTJxsMCRT5xJKjSLEvhiVoaAkgRsCIvfRvWQ8SX37oSbJq8x1LculWDPolDreuZa2bTiZTtnfP+Dg4ICnz1+wt3/CdD6jbhsaL6wR09slJOsAm+XE2NsOSSBKfz2UT6E5fbHVn1lBmHoCLukvh5REsTxQsAZGUX1MgDyjPRMEopy5qamU8B9J2e2ZKC7IUDZYYVC0xmLtkKLQDDdyisEYXYgXMMrggVWayKtRSVjVAmI5kcz117pvOuUe5kuA8pdqIq0Ez+6faWNoXcX9B3f4xk/+NNevvUxTCdvg0eN7XL92A2s14/GYrS1JEkYZssEA51rm7Up8VdsVrl2iR9trMNXajF5S7ZzHKYX3BquhaWqM0WSDAb0FxJm0W4BOSdgWED3PSrKsXDOw199aCQPeKM14Y5fxxoTKzZnVh7TdCuMVqiPVTKB8RHeBwo6YlCMGdpOy2EQzSA2hNP89yB2V2Mx0bUNTLxkUhYCRQa3B277RXLNn9BlzqpdqdnXNYjqVIYuF11+7zvbGAKs1p6dTmiViueMVPgYa1xEUTLa2aJuW+amoJoy1tG3LvQcP2Ts4JqATSzztzUTm9QwXYFnXnJ4esVot6P0pfRBpnAviQa+ChH4YG1HG0jUrliqybANkoihQaEKQQFdHgR9eJX/lZ6hiJMyfQJhhFHgVsShiCjFEJUsDldhPRGKAEBUqQOsNwQyJ5S4b194l27pJHYegOpQKeKWTTYXD47BeMdq8gnnlJo33tLMZIfiESYT11qd9oOxaLruOGxo2Q8B68c/ufMAEJyoALYnaMYgFk6jQAvVyldZUoxIwYMsBmc0EtE2ZA/2a6yT1TFdfhtgJlFDGiM1a1wpgnQhlksAtUxQfOupmBUCmy8Qkl9eKCDsxRUwTI2umGJF1va+UIioZkBojbCuFFs/qxGnmnAJDa/HVU1hyOyQCXeuIVgbYvadewvukl9IiX/XrXkOleg+KfAAxl+uLl8+VgFyVALNca2JV061mLKpDqqZmVGZcHJZkLlDff8xG01DEAZuTLUKIPHv2lGJri3JjCxdjCm+MZCjMYsbpg3ts3LhGCIH9k2M+f3iHV1+9yfbkEqrrKKLjOz99iVX9Lf7hr33G448/xe59wg01Z5gZajbYuPAGWVZKsCcaFRvwFatZzWJ6SjkscY1m6/I23//N/4tf/qW/x/HBAReuX2PnwhWuXXsdo0YoVaJUjlYt2aBgNB5KeE1o6eqpDA+BxWrGyeyILobkRW9RUXIoQlRJPNVB6PAeyBqwCqPSWRuiAGzIUFDH5NQeIpm1a8blOsA26/9MbEdQ/VGh1oCB7FM9UJlKzSjWJGevlRiCqmcAfAVsTIM/nQYGyqR6NZ6BZlKH9EqWFDAZZLjS2wOIDQrr4VffI/Vydp0AUK3F7kArk5RLZzVYWzfrIbj5Cpjc17I96NsDi/LVpa7oLXr4yu/2/67SsKLf/0mDCa0UUZ8BNz0I9If9fJWd+4fZMMg0K2KUkgFiTNYxPuAVWGPTHih7bvBe/IeNQUcksKpXEKagrzzPRZ5tpJYJQWohH88sC7quW/c+/XncYw7Cts3ODSXVmsWa5/mXWMJ9XdR/BhneiBpqrTpUZ96z57/7uhbQKRAthDS4FUVAnudrgD2zdt0x9WBwzzBXEaJWqEJ6Qt/bT4QzAowwhp3kE2m73ldDjBgr50JfG7arOtm8nd33fa8u1o2JFawEdA7nBrhy5ogNSVQKlzzJu+Alo8hYTDBkRS7KVdcRbKpTlYC3dVOTZ6KoUF4G/iZ0GJNjTJ93ozBoxMFA7Lt6oDAEGS42dU0AiqJEZRn5cEyeD7C2wOocEEscHz1111CtMmoVaLzD1VECR9uM1ahkWZc0lVs/Rx4t6koFTluKzNCFQBsVbYgsq4rONnTtEoyVAMN+JqGlt7PZgMFog82Llyg2R+gcSm0hy8kLYXvH3mqB9L3F+4MYvRzx0aCzApt3FLkmFiWZ26ExL0TRKcYIyetdQPe2dQJmr63J1Po+U6rH45L1oxHCSpaJL7NKdgjnMbP+eejJOtpYggpEHGiwuey/WcwIzjM7PeXwYB/PEG0LNrVmVa0oR4m0MSp4dXPCzrWrXLl/g9uffsjxwfM/Ypf5Yw7SoiD4munRIU21wCjN/v4Bt2/f5eMPP+PpkwOMyXjnrW/yzW/+NG9//X0uX71KUWQErWhihKbBqhbaOZn1Aq0FMdp/9vghd774jOnplJ2dbfJMY4lsjEdUzSm37zzi+x99wf7hCdF3tIiaTsJnpPjXSmGshAuIH57GkCR/IaATyEQIIv/0SAEVZEIUkudFPzXs0xrFjy4k+XY4Z/YuN542lhAdjQvcuv+Mw71/zotHB/zsz/0MF69eQgVPdOpMbpDCHWLyEiRGSAUDSjxeSKy3LC8oBjlFOSDPNljNFyyXpzx7cUCRD9iajME7FvMpL148Y7I5oTw94fmLffFZM4ZhUZJnBV3nWdZLbJ4S9DycnEw5Pj4GYHNrwmg05kef3Wa6qpnfusvVy0teuvESP/ftb/Hs8Qvu3L7D48eWt996g1GZY6ymKEp2J5vcu3+Px48fMBxNiF1LORnTNhUxRubTJaMiI9eRMLBEFdCZRtuSjfEOud2kbgvufLjHlr7CII4psgHbly6yOdzlzrNbHJ8e4mOX2BrC2NVaghmkgVcQfeppEtshTYb7Ze4BFq00Rsp/BFqS1NhRCBzf/ggfHRsXt7CbhlxDHQJzX7HSgZOqwsUCFRSD3PLaK5eYnTznyeOHxPE1Sec2Fq1zYtsJywVNh+GgUfzWh3cZDga8cnGI0TXKtRAlhd5oJUFL6ZAXFmVGURTsXriYgm40G5NNsly87z78/B6//6MnjHZvcPXShHuPHrI8OsFUK956bcKf/UbBT17ruDbJGQ4DDx/c5df+8a/z+Z2HRJMTVIZyEFtHaCWpUynxTYwhspgvZA27M+uCviiok1eoFBXi6+a9l+FLKlyd6/DerSX3IQQ650SGmyZzMbIuaBRgM0nSliBCCM7TNI5WdVil2d3e5OvvvM3Xf+It2mrB3v4J8+WCtjX87g8+5s7Dp/g1m09+vgrTQsTYjMFgwHyxTIdBAAI3b77Ke+99jWrR8eD5YQL4O5Yu8vjZjHfevM5oWBDaltFY09jA0h1zcP8j/o9f7vjL/8kv8jf+q7/B//Q//w/cevixpGH2ASacgRAhRmJiO8g9GnEuyUUSaOScw0VPV1W8evU1sqygasTLVStNGyOD8RiNQTtYzU7lvVC4LkionOqDU85LzvoEay1M2+gpBjlBATqxRr2imzUM8zHlYMze4QFd69EYsrzA5Bk284TE3LDWojgXAmF63yxHCxwcHqS0ewkBCt6zqpY477GJRRAS00AafZ9APUk31zo9032wRgK3UQoXHG3XsgqRZb1a+43FGMBqhltjRuUA1bi10sC3La5tCW5IXTdSS/Ts3B6oi3F9D4XEEBCARHxTtYXZouJf/Jvvsf9ij595/30uXr6SwmDEImAwHCBBOS7Jhhoya8QuwPvUwIc1q0qYCTIc6FxH8GJfEHwrcIOWpkwRiKGjqSu6uqKuaurWcXI6Y//wiMdPnvDsxR7T+YzFsqH1MjSMCGMbI6nsWkvKrhTmssYSgGSwWcGbb77OnXv3WC5Xa9N/79LwMgVrGY0wmvp7rd9zg3jBx9AzI5O1QJRWQEKz+ssoycpi25CYaKn+19rINbUWMoXNBuTjIeW4xA4M0eagCwIeZTwOK+doAgdjUIk5pcgnY9r5ElZNOidAJqUKyXBLrKPeGy/2zB61Zgn1/rskLkBQkRBbHj66zbOnD7h47TLPnhUcHx7TOieBNNExGg7ovKFtarJ8QFEW67pjOCzRKlBVc0aTFm1LgpN1SJ3/unAdFBlNUzEaDrF5jkmyaiAxZc6GDBK+lkaaMUHlveVG3yCl7+tSiJ0mZ2AvYMdjum6F9x2F3cRRIQp7g1GWIhuRmRxa8HUrCSxa82VPOXXW4Gq5DgLgZ2c7szpjh/W/09tkONcRvCe3Ftc1rBZLWXkVmC9OsXbI1uYG42GODYGm6mhjYJzOoQhcuXaN0+MTDvePcBHu3HlId+s+s2WNtgU2z9aAe9N2rOqK6emJSOyUpqqXuK6hzAqsNjIkSCy0tnWoFMgTfBqqEqgbizcj8sEWR8dTGGScHDyncyI5bEKGGt+gvDkkHHxO+/xDnBMrmZgXqDzHty1N6NDKY/C4ZMflPASVkecjRhcuYyZXWZkd3ORlarNLG82auN43UIaI14GoCqJXBDTLZol2iMcgQWroKNfHxsi2i1zVigtaU7QO0/WDmPglkCb2zK9+cMOZlLhraxQwGo/ZuHiRtm5YLeY0VSX1dBq09U14oIfBDE6BQyxLvPdypmU5KgFe/f7ZdS1tW7NYzMiKgkE5OPPvTCy5GGFQDlGxT3AWmwg5dzuapmVjPAal6DoPMQ2SlIWoE4AT+ulNGob4s2GWChTFAJUYt8k9m57t1tdAMT1wMcm5jZVrZbQmz0raWizWZDNKoKCSq2hCpNCG+uiI6fwxxVCBcxQ+4KYrqtMpo/mSIYG8tIx2JigTaeYnsv9F6WtcCnQhQukjB/dusfMLP8dpu+I3v/8b3Hp6hzdO7vH+Oz/L1Z2Xia0jC4o//wuvgFH8o7/7v6BXX3BhpNG2YLj7Kk5tMLIlY93RTKcsZ4cUyoIwotYAACAASURBVDH1DqM8mxsjXrm6yaPPf8A//KW/w+3PfsTWZJONyS4Xdq8ROsVyumI4moBriaEmzxSDPGc2nXO49xQfFVk+oHMt958+4ePbH9FET1x7vZ7b95TcgybtAfIsBFQU2XjUks7ue0/XBKLp5KXe700CVun1tRDeRwIUv7LHnbFM1fq6qRTCE9OAQGmNicnXPCmPRCovtbBONZvUib1EuH/WeoA2AmFtySce6b1lktzb/dCl90Dtf3RifvTy9BhBGTnTImcWB6BSrSHgW/RhvTb9AFaUgD0grdavHzl7T7+2rNPnFBX9Wqi1jdB6L5Gd5WxtYT2k+zEW7ldA2f56nQGbaQgYRb03HA6lRnUurZcR+b8sp4RPx3D2eZWQemyyR4Qz0NN7T0dLCJJ14rzUqTEN08Qf3uNdWCvWssyQ4hbkfcLZPdS/9ldZ1j1pTNZM9iDnxF+796BP3xylxDKsv59Jd3GvEs5zuY9NYpyaLEuf5ey9+iCx/nd79aNK9ZpSSoaxUfYTpXWqTXxaG4tNGQIq1RrOOQnVTniLWMko8iITCzFjcLmFGKlW1boe7F+zH271djo+3e8RYQz3fscueHQKYTRBbC9NlktNmpBLrXrGNykY8Ox5my9Oqesli7rFTueUozHjyQSbF0JQSEOOLM+wukD5gvFwTEDhURLWrCwRS4wGtCUvRmRZjo+OoXd0ozHNxoTxaJNjcprYsWxPWRWWU22YG0udRQiQe00HrHRksrHB66++whjNaiH1/mJV4yyAR4dA1Yh1kvRiabChNANbYGJg7+gxXRbZzCcM9IA862QYqS3K2HXeg0lqAqUNTgPRYvMC3VVYqynLIYYUWhtTfUfP3nYoIwqbECW8K6bBaO+d3AcihnBmOWaMKDhsr5RLTVivhhZVpahidc/aJxJdJMtyMpNhlUkgfMPx8QERS10HmqpmPp1KwKt3lCOx3ijzEZPNLd54+20G5Yi9F/vwK3+fP+znjzVIG7xjNT3lZO859+7d4/bd59z64i7T6ZQrl6/z89/5Lu9986d57fU32d7dxeYWEyLOtXTRE8MSHR1atQzzlkhHM5uyqiuePn3C3U+/wBrNxZ1djNGsFgvqVct0teDR4VM++tE9Hu/tyzQ9l6Te6CLRy6ZmjUlTeJH86SiNPVqas5DYXH0K4TrZO8rvBqTJ0lqvvUwwel1Ank1N5cFRvYxUp6lfYYgYGiLPjg/5jd/6LT59dI8/92f/DO+9/Y40gFGtN+b+wE4mCkl+3E+lWEvJpfhV5PmQ4nJJuTGgOFaMyoLlsmZjo0QbmM0XdN6zeeEix7MpT188Jwa4sj2hiIHC5OztHfD4+Qve/dpblMOCalnzfO8Jz19IKFgInoPDfbquY2M4IbOG5WLF/TsP0Srwzs3XePP1l/nd3/0+hydHbExeJisyqrqmqha88toN2uCpm47ZbC7hGk3H9vY22ljaNpBZizaKaxcv8OrNl3ntmz/J4f4Byzl88fEj2rlhnKboigHEAduTCd+Y7HL30Wc8fnGXrqnIrCEzWtL96DdZmQYRxHuv59kqJVIRCdNJsiCj0X2tTUCbTA4PFcj8iqPbHzEab3DzZ/8DZmWGb2FcbtLOGlzlpUDpVhjVsZxGuvkc7zt82xKzhjxtFrVqUDQoX6HMALKCo5Dxz3/4iL/ws+9w8/IWYXmEikGCwlTAWiUy9hBp65rgPTGTULsuevGCRrNqHLfvPeJ7f3AXM77EpasXuPvgIUfHFSOree2K4y99PeO9VxTXdwpsnHP37i1+5Vf+GZ9+/hBvCynufEAHqJcrKUYzafad+/+Ze7Nny7L8vuuzhj2c6c45VWZVZdbc1dVdPYAltbotW4EsCxuDsQhH4CB4IcARPPE38AQPPBCGYIhQQIClwEELoUAeJLdkWm13a+ih1JXVNWZm5XjzzvdMe1oDD7+1z7lZkoBHnYqszLx5h3P2WXut3+/7+w7ugu+aXcluYoxiQp8m913XpbRi8QfKsiyRVSKuk0laD87EKKFFMYLNRKbQOY/3tZjNq4BWyf9NQQyOEJX4ErvAsBjw/NXLvPLyi9y4cZlqcc7ZqbCsF3XgW9/+Yw6PTi4YG0jR+ec9vHdUlbzu6WwpFilGc+/eA15/6WW+8NYr7J+c0zkAYb0+PfdMK82ljRzXOoq8Yu9Fw7QNfHxvn6d3K/6vb2r+5i//Pf7+3//P+C/+q/+c/f276EEkIMW5jooUoSMSTR/k2ql1Om4fQBijTKHzmFNmG8RoiCjyxOoMyjPYHWNHBe1Zx3Q2JxYF2maMhyVd07CxMebKtavc+eQTgnMIEqtSYqdM1pXXuMqJ4byO5FmGm3Y0Z1OuvHCZLnTMT0/BR4rhGDMswaa0aKPplBP/NrUGWYStIcx3pSKta6naGmsEKJL1JPu2cx3K9gV6L5uVUt27IEBw8krSKXmY2LMFpNkKMZCbjL3JNmfzKefNkhhl0BGjTIr1IHknhojODQUjRsMh1WJJU9d0VS1KAx/EdyuxIIxSyV4hpfoahVGWqDXe5JzXgT/40W0ePXzIl97+PG+8/gaX9i6jUJR5SYyJ3drVON+Bb9E6x4eI8w0BacqD64QNlIp774NIwVSk7VqR60ZP09bU9YKz81OODg852j/m6f4J57M5R6dzqqbFhUiWWwnIsjAcDMW6JOqVbFclZm4IKjEt5PVWSYantebT+5+KPUk6A/s2qW++UOB831gEjLU98QffyV4h7AgBsiRoNIG2K2kgKGvAaEIbBPQiKWVQeBUpJ2NGG2OyUQbFAG8tOhNLkBAvsEiCSF7Fj1dk4zomZl4PBueGbt7KfqMs2ieAWloRVgBLCjaLCZQLJE/W1N0m29CUPJwznZ3xo3f+kH/rxb/D1educHB4hHIdR4f7RN8xmYzZ3r1Mnhu8a5mfLanqCmNgPBySG0ddLQSALcbSayVAKrOZeFNnGUWesVycY7MMYwtI17iuq0QAUwJmKWQgrDQxMfpVkrHSX/fUgKHiqiZBZUQVseSYLBKtoSQnxq0EVqW9KQRC7YhtS9e2KBXIh2NUNkarnJ7xJciG1GdFMaRJ6xClkhnNn96pjTYiZasXtPWSfGsbhQwQjJWm5+nhiQT/eM0kL1E6IytzutkCiFgr9cDRySnT0xPqZkE964jGMNreYbS9k8JFFXXbcjqfcnZ+Tt22iSkjQ5CmqYhAa1xi23l88OKrGpKkF4+LYM0AZYc0MaPY3EKVEzidEQOcLWui3hXWjyoENC9uUNzYRI/3YP4EZSx2coliMCa2Ne3inG7+hG7+WFjWWqNUwWDjGpMrL2O3XmTpC/AZrSpwcQ1MoDVRaUK0BGXIoib6BcvZlOg90GCUxtgSZbXUST0o5QKj0HI510yC+NrGmEK6UgMWo9zDRIheZKeRdMQkuNV3HVob6qah3X9C27YELwoikldy37Slww/wBB1psQSryHMLAawWb3bveg+7nl2WZOFWpKkRi0pJzcG1dJ3kVdjMYrIinSUgTDQBAcajEQB1VUmgkDZobVHoHu9I7LPELFMmnStijyFMvCF5ZsW3m/58koR3bTRKGZzraJuGzNpVbwH9PqiQVG6fZnUKFYVI0FPSlTaoak57/x4mMxRaUWQlvvMU3pMrAbeLyQbFYIRVBlctWLS11HIklVdiQ1tlmB/uszg84I+ffsTv/sk/Zev6Bvnu83zru9/kzZs/xa2rr2GjZbMY8LVXDf8ivoc1T7i+N2Lywk0+97Wv47Mhh9MGWOLmx5h6TtUs2bq6TfAtL724w+nj9/hHv/Jf8+4HP8bnmt3hkJ2NK0zGu0ml2JJZvdrD6qai7TqMiTx5eJe7jx6wvXeJ2fyMP3jvR7y//zFOC5dUxbBWOa4qQCWsuzzte8FLrxhlvwy+Z7WS3nONyexqWChWAeYZ0K8/E3pbHhJDrA/mVCqt/wQ8okghpTGJdEKP3ROiT4B+TOunZ6bqVL3GZwDg/rkrlRQSVkA7q3tAMiJy0lSr9AO7/r5Ke4JYEQjjWZ52xAVZwzq9Rh8c2iZlTFrLKTYtkTnUMyxdAbJZAbaftSPor01cXQvZp56xTiBA4E+9j3Ju9VQnVt/7s+AsrIHb9Z/lnm26QOcCRsugX3JLslX4lPeSQq9X9an4UdssTz05a3C26wgx4l2XXm7CCtJ+ptOeaHT/XKJc9/5Xev9ij0WA9HoXbCH63/twujy3icSg0v4TV6A9qUYYjcbJokWvaq6AZD6EBKwLGSL5KRtDH1YGrAAylwgSKwazAu/T8EG2Ifn3FMwoAWYpW2eliJKjQakoLMf0GrVSqDxbEahc59IQoBRbEltQ13W6N6OoxWAlcIshCLEtrSltVcrTSKM9LQQUo5KFjRZykw8a5QGdhvfeIaT/QFCSG+Kjx3eexh1iq3MW85LZ2ZDhZEJWlFibpXPBEIzBYMTPVmuiUuT5gLyQekzUygFnFEF52beVAmPQNmM4GNFsbDGvzwmzgjAcMB8UnIWKNtktFZFE8orUVtFtbHLpxk2uKIMGXnCB8/mUdn7M9OgJx4cniWwlAazKB0LncIsznt75gNNqzu7Lr7O78yK7k6tsbW8yGG6RDyZgWxQFviuIdoC1BVlusToSlENpC0l56wl4E9FGBg9iK6rxgNUZIKpQa3MhaqXg55AGWIk6J8SAIEP42EmdahPW0KUw0n5t636PVhpjEpElSP0ViPimIwZNbiSfyYWWqjrl/ERDqGmaOVXXMp3P2dieMBkP2RhvCxGyyLn8wjWKzSF/3uMvNEjbti3f/f0/4E9+8GPu3LlL5zVvvPYmv/QLX+Slz73JztWrjCdbaCvM2c53Qr92FTG2qNiQZQYVOuanU44OHnLy9AHz+TkhKra2R2g0xwdPaV1HMSwwJscrmFctxynEBtJxoxTKysRHR5EkxBgxSnyfYpruhOhXk8EQPa5LSdm9olWLtEwZnSaGIoXACBNEWfFk7Nw6GTzqmA6otLGmhdcDS7YoqIl8dPces1//Dc5++mt89Stvs7UjZtkuygGqvGysq8KMtV9RPwmMUXxMQpRpY1YMGW8rBsOatlsQgiczGXXd0oXAhx9+zNbGBrPZkmIwZNF53Pk54clDqtbz+PFjLl+5xPbOJvW84uDgiCdP9nn++ZzNzS2c12RmwPR8SpFn7O1eoq5bQux4+nSf52/c4Ma1K9SLOVrD2dkJTdPSdS2nZ2fsbGywvb3L/YcPcQHOp1OKoqTIxWu1KHJsnrGzs0VuLT7kkI24fm2PH/zzd7FRNgatM5TKCVGB04wG27x+622Mzbn/8EOcW0hTHCWRk5CKMbX2bpQJH4ml7FfMC+JFOaWwfiSMJVH7Q0S1FU9+8kM2ty+jdm+ilGY4HNChaLUhGE0eKi5vb1HVMw4OT1DlhjBf3ZwXRiVbE8OP71dSiPhWQBo7wKmCp63n9959yKB8jefHE0J7hvOB3JjECBcJjG+FgVqUBa0zLOdn4Dw+GO4eLfiXtx+Qj3a4eetF7nx6n/OTE4rMcGvX8rfefp6/9Hzk0l7g6f1P2H/0kG9951/y3if36GyGU9DWbWJXrqflfaBXz4g1xq49qVKxWFcSBNUHgg2HQ7TW+E5sEVDiQ9t1cvD1Cai+b+IiZFlO773adS2d68jynGExEDA9pdy2jSP4wPZkxPUrl3jrjde5eeMa9+58xKf3H3DtxgscnMz43h+9w9HRyWd2rj8foIV1wSWTPcV81pFnHZmdc/fRA65du8yNG1vcuXMogxQC8wr29xdc38lRIwGmL1+yXB0Ygm/45NMpJw9/wu/+1v/Jz//1X+I/+o//U/77/+6/4fD4U3TRT50lmKbzARcdMQaKrFwV+he9oGS0oBiUAzYmm1gjII2ejHDek+vAZGcTpzzzxZTZ9JxyMiIvcjYmEw6WFe2iJlQt2q1DynrmQs8O8DHgY0j9pNxDku4asLnl9PiI0NSiPCgzYqHoEP+/2IUE8PnVvbWSKCtFpnuTfy0JsP003oi/cExsBW0MrvdpTo1Tvw68l6ZVG/FrFn+itE+n4jiqQFDgVEz7rFxnn86AVViHNYTO0UWP1YpptRAAaZTLwC0IM6zwkeZ8vvIhU/QMQPGZIiisthIepANt0Nw7POPht77LO7c/5vVXb3H9+ee4evk6Ozt7mCzHYAldTdPOpdjxgRA6lEly7q4RIF2JQf6yXlDVHSdnM54+PeLg6IS6aVjMlyyXFVXV0NQtvgspgTpJK61CYcBkuMTkaoPCRb26n0O6RhLEtmZSxBhp23b1d/E1Myu/NDmm4moi3jckKrGgY9pP0aCzFMyVwrz6hsX2MujE5vF9CJlRUEozYrOCbDBgsDHBliU2y6TR1gGnNC56aB1KBTQyWFpJ5OjZNyRGtkrtpTyHfDTBVS1dXWNC8mJO6yxEYZkF+rN9zV6KgImGTEkwgtJmpcZQ2uB85IMPPuSnDg557tp1jo+ORQEzn3N+fs4PfvDHfO6tL/Dcc89jteb8eEpdVzx39TIDG8mteOs2dUU5lMJ43dgq0AZlMjonUvHGdWS2IC+HCePqAboLVjkrAbla1Ry6Hz737JD0N51SjA2etp3T1Cf47pwYJVxE25wskxATsSBpaJoFoa2JoSbS0nRj8uIyeXEJa4dESnn+Qo9BZxm5Nqucm5j2uH5tVFWFtZbReETw4i8arBWv2WJIWY4AOd/nCwlLXCxadsYTYhTf35DCRJuuRdeG+w8fUi/meK3IRiWYLA2DAp0PLOuOg6MDptNpqgMDzrtkMeHog2fnyyVaawZliTIG5XowQQL+yEvs+BILp1k2S4xSLBZTglI4rdFBJwsOaSqDUrRR4dWEfOfzqM2XMMUAU07wQBY7Nk1EuTmqneLbSqBPm2OHu+hyi5OZY951wuCJyRDBe2lYowQNRiJOZ+QsMaEmNifQztG5RkUt9dFq4B3BQx4CW13HZoho3wq7NjH/+ia8lzr3+8faroDkW6sIWdrDOwn2UjGKckiudBoM9WSIZEkCuB48SzYU1iZ2Ulyf3TFC13lJgU5nh/i7g9KJIdtWSeIr9kvyMy4GN61Zfj1D0BqbmupeYqkSmKYIScKplOyhverOarMC4iRk+IJ3aULqgpIaqCzLJFKX8DSffN2zrEhncvIljelsdi7VILJuBsYyCIpBFzFErGvJtCak98UOJ+xefx6bjeiceBy6pNqyeYkO4KKcaYVS2GbOD7732/zWgx9yYA6JseWHH/0Bh/enfHr/kL/xtX+Hl6/cojs75o9+6/8gHrzL1bFlUI649YWfZrx3g2UoMEpTLSq6pmKSG9qqwTULvvTlN+kWZ/zar/yPfP+P/hBTGFznycqCna1rTEY7jEdbDMYbgKgyeiDLe2nip/MzvvvjH2M3RtSh4e7+Y9roEkCoRLIb1jVNIswJgBB7VmtS6/Rwn1IrxrVOthti+xMo8gLn3TM2TH+WlL4H0tYsyPW+uh4k95+3/j5r39Rnwcj1c5XmZu3nGlbDgv57XPgb0Nd28qtfsyvVZ7IkITFufYgXXnsalaVedO09C51L9eiFn6miSvYO7eoeWT8N9cxzWytPpf7skdyQlC6qh6P7+/HCefDs9Ymr17+2fPgMKH/hz2vGsTyv/gw11pDla+9SF2MiEihs8hzmwmCm61wKKFrX5kVRYGKUwadSENPna70afmqlybJMsg/S+6e0qA3atiEEt3rfLq6jz7KD14GG6xDQXjbOypJKgsy6LuBcjdZiXWS1ES9aJbVz7PsL0lqM/fsh//epZlJIVg4x1VFJCh+JK9C+t3LppxAxenqLhN6yrVdVKCCkNa+1xiZLh0iyBvSe6ANljMRoiMEKqzkoXOdS5ZJAfBVXw4r+HJCDYu3fXRQ5o8GIshjIoN8YVFKNBaCNkvlQtQ1GW7TSWCPgttQ3Og1COlxX0zWWPMvwXZRwUG0IwRJsTEMOGXZ0ztF66Xu1MmiVoWuPMkt02hda5/CuJbQtVadog8ZhaY2lzQyVVnitJQtDa3wUde552/L+hx9xcDRld+8SV65eYbIxZm9vB+2vc3Z4hY/MhxwdPKXrGslnwOOAZbeknbU0y3MOj/YZj68wHOyysX2FrZ0r7Fy6RjneoBhuYrMxOh9STrbY3N7Eqoy8MJhBwWAwYsaUaXuO80uU82ggtxkol6rsPmhZ1qk1knEjilqxJfXeo43GB8FcehVub3Wg0l4WgnhBd12b1JRyn4odiFrtW03TEDpH9IambfChQ6soHsRqKkB3BEwu3yd43GJBNZszHo8ZTyYYq8n0s3vxxcdfaJD2+PCY//1Xf4PJ1hW+8NW/yltvf5E33niTzZ1dyKwwVkJHdDXLekk1PWJUeMZlZGAjOlZMT8+5+8knfPj++6gIVy5PKMqCuu7Yf3LI/TsPmB4e8+Uvf5GrV6/SeU91cMjh/gnLuoVMNhvvRU/WSyyMtauwnf7GUkpAHmMsLqWGSwKmJstztDUy6U5f03kPQa38bcW/BXx0qNXEMzGIVNoMYqTfxdcSANlGKu8JCh4eHfPNf/ZPeffjD/jG17/Ba6++xqgY4NqGqP0zgMxFEOyiEb0cWlpABzSmGGFsgXaGpl6wPd7kyrXn+f47P6JaLCjsPuVgwLRqGE0maKU4Pj9HKcOlvV3qquHOx/eYnp9jbcbNl1/mhRvPszHZ5ODggGpZs7M94dq1K2id8e7t95nOz7h+9Rr7+08gBq5dvkyI4kk6nU7Z2dnh4YPHnB58ysGTJ9i8oByO2RiP8Kn40Qo2JmO2dra4cvkSvlUszj1ZucX9j+5zdO+YkdoBFQlGDqaoZONXQbM1usbnX91gY7LFex/8gKaeCcjTsxTQoCyka6eibHJcmCSvNg+gcyLNTNu+gL5KJp9DwM+PeP+7v8eVL/4s46svoL2j9ZrCV2z6OaWNPL99jeOjKbNgaQc74D2TLPD6lQGz86fobkGwI2KSe4XYETFgc+6f1HzrDz/kb/70TXYGQ1w7x/pU7Cg54IeDASY32DzH5gXWRNoWHh3VfPu9J1Rmkzdffp2Dg0OeHp8xoOXaMPC3vvocf/mNjJ1iSVud8N3vfI/vfe8HPDmb4vISryV0A5kXyGGoYrIfMKvkxL6AiFFM7Z1zadPTZFaCNUajEVmWMZ+LDUqeF9jMMpvNZIiipdj03iFm4mufoz7YIIZAURQUg4LS5iLF0wrXtBBgZ7LBSy8+xxuvvMR4VHL/wSfcu3cXZYe89+GnfP9P3mc2X67Ehf9/Hp8tgkD8ms7OZ5jM4A9P8cZw7fkrPHx0St04lA4Er3n0ZMabr15mUI4YjsZs72yhi4ZXXxKv3vsH+zy++32+/TsZv/h3/y72PxnxD/7Bf8nJ+T1UCTZJN6/sXeHk7ISqXgpglm77GNfpwSL9Vkx2N5mMt9CUjDdLhmVJ5x2jdgmZ5nh6xOHxE5q2xijxj328vySicNWSDz/8iKzI0JnFRPEg6/cZpaQ5CfiVBK5eNLR1Rz4eU3UV07NjVJKm6MkAV2iC8aKa1j34A2VZJpsLd/Fio7WmbRoJCrhw/fuitEt+xIq+GZGNV/KmhJ0ZCLjg6eo+gXPdDIhvsUZbw7Re0iXzeGstuTE0TUv0MpFvGwEcVJrKR5LfeBDZZNARlYl1w6iUsBHfCQAQ2o56Ol/JewX8jZio0CZD2yFdcHzwYJ87D/fJM8uVS5d4/sYNtnY2uPXyi+QFLJYL5vOK5dKxWC6pq0bkS/Mly4UkVk+nM5q6xflI61NRreEiI2UlT8uTJzDQ65xlfUtAXUgMV4VM2EPo2S9mDUCmpiHGZHewAjEiEh4tCc/9OSi1r5y5K+nxyoqBFRtq9Z/qJZ7SUDsNujAUwwFlWZINBwS1tpXIjDAUnFEEa6mcT81Ar0aR989qTTnIaVArVt7qXA30NCZ69bN3DmyGGY7onMM1DW1UEiaxcYnNzW32Lu0xmowZjsfkRYlPa/rs7Ij7H3/A+eEhi/kM5aOED0W57lpp5vMpP/rRD/iFX/o3uXnzFo/vP6Braubzcw4/PeT0/JgvvPU2z79wE20C29tjdra3CN2S3CpcULimYz6dMt7cppeHaqNR2op/sUvDjgsMLJWGHWgZuCmTwt0SSB8VqxCRiHwOqYnX0eOdx7lApmHZnjOfPWI6vU/whyhawBHJ0LYkywoImq6bUVUnWFMzKBw2C4R2jOuuEbpXKAfXsflliDatG/EWNjqiQsA58Zoz6tkAlPVA1YuPoPdUrmIwnDAYTfDRkxmNtQV5VuCD4unJGVmeiXIqKpEJBkfsGnQQ1qY3GrQSLzYj7M7zxZL9wyNOT0/F0033fmkSLqQzObdccNg0hKxdJ2nvKVPBE1DFJuXWZSgnVKfnhGgl3MoFOm+w5SZRDwjeyfUMhVieaIuLFhdLYID1iswJg0UlibzJxwyGN5jkmi545m0DxYhFE5lWRxfa7KSOiB2ahlzVaAQY1UoIBnlWQiWKDKKwgasmQifNj+/Ea7YMHbt4LsWIrZYYJyxym86Ifl+PStQh6KQWC4G8LLFZTr2shDmUCfMner+ysdEJObHPgFVJXQayn6lI1GoVCtWroUhWNiGmM8E5vBfGWUD0xD44FospTVuR5xnKKfKiWO2Zwlrr4bp1PWCtXZE2BNiRaxuS6gDW/p4xpvpTiXXCcnmO1pYyH1DkxQUQJOIjErqY2Gfr+3Zdk3jvaFuX9ucE+JDAtBgkTMyllHlkL7ZWrCpkbqgwtmDnynPoYkTdOHQQj8giy1OAW7celKaN2i9OePePf5cP1SNObhjcMtCcV8QlfPULL3Lr1nVKBz/47nf49j/+JteLyMQadm69we7LX6EKI+ZLjzGOshjCYEBZRGw2ZmtSkHdL/uGv/c/8zu/9Ni62xFwGThvDLfa2rpFnY7QpQRlcUj945zjYf0xphKzQeMfT6RHEJcX2iJnytEJQOdzlMwAAIABJREFUTIoGASWVYiVjXg2LSapLm3wy07B4BaIKArkKidJK0Xbtyte+HwBeBGt7Bu6zwGHoS5MERco+65xfAW3Pfp/1EGBdLukL31PT+0X33rPyWtY2QpKdEi/cQ89ax6z207QU+7O/74dCKjxXPrWsZfch9HYJKZQzgaoh3XNK9/fR+tHXJheB1BVjVit6xlXfq/cA7bOPNZmm/1yeuc79Pfhng7V/6mNRekKVbCWAxO5LxAIXGAyG5Fm2YjyGEJNn6gU2LNK/BO/p0s8oipwsMysCiuASvRWEp/N9ry9glDyfNesahFz22UHRZx9rsB+c63N0FFkuNZzNDL1vdnDJvkppgiLV1s9+T++91OlprfZkM+ccRVmmIFhZEzoRiHxIuQghEnxNb+uQVtrqeV+0hqAnw6TX179ng7LEJRA4OI9Jfu8u+MSkluuoraikjJLBl9TzDT1o399zWgk+1HlH3bSU5ZCoRLWprFhXosRDPCTCh9hcyhBTWt6evy5KcKUMRimWsymEKCxZbdDGkucFPnb4OqKUER9rwMcOpXPxtlWa0MwFjE62lovFgvn0FNqG2eyE07MDZuczlouGpougLS4GlDF4ZdA6w2oLPqC6lunBE5rZlGY5Y2NzzGSyzaWdy+zsXOPmrUg5GHF8ckDbLiE4muWSToslnIqK6viA6vQMZYYoO6QoJow2NilHE8rJDsPBBmWxycb2FTb2rlBuXWawscHmVs6VnQE39q6hug2Onzzle09u0zQzWctRryZjCoRtnljg1hjyFQlJgF2NQpkMWxhclklPGoQcFoJYGmhtJI8oZVH0AXF9mF6MEWNlS+mUYjlvZNDA2v7G+46mXcBM+tPN4RBf5UwXgePDfbI8ZzKZMBqPUvDdn/34Cw3SKmX4uV/4JV5988s89+LLbO5uY0tL5wNdvSS6Ghsb8DUPPvmIdn7Km2/eQnWO5WzB6fFT9p8+5eTkjLzImUy2qLuWj+/d4/b7H/Hg8VNiHXj7lde4+eLr2LKgmp7Qto75tEJrmySTEm7RW9qoBJwGn36PUiwXRU5AGn9tLUoFfBcpywEbe9vkoyFNVdNWNdVsjvPJg8OsN7HVIYqUjL1UKcS1H4/uvWwS2ECafhorh3UXArPg+eMPPuDT/QN+6itf5q994xvsbm3gPDgQI2/WDXP4UweeTn61SOgPCmVyCruBNxkH0ynLLnD9xgu8cOM6i+kZxmje+/ATTk5OGQ0KNjcn1NUSg+bp06crZkJdV0zGY3b3dgkhcP/hfW5cv86lS1fofMv+/lMWyyk3rl/n859/k8Viwe13f0w5GXB0dMBkskHnOo6PT7h06RLbr9zi4cMHLKuWre1NUIpFtZQNr2t47to1sjJnNBoRvWI5qyiyIZ9+cA/TpOLYaGmK+kMxAeK+hdyMuPnc5/Au8vHddzldnBCCk0bKGKKXotN52YwIKjXnKnmUptJfSZEuNhfSuAqIoCk0+E4a/ersKfvv/itumIDf2sSUYwq3ZCu2ZCpnuzA8bRu8LfDFBsZ3bI0jW5MJH33yAXULURfrQiw4dFwSYwWq4OHpgm//ySN++q1rXBmMibER5pC2RAIuepqqYWBybJYzHG9xftbx3Q/vc84Gr77yOQ5PTrn34BERzd448LVXCt7am3N1NGA2PePJwyfcufuER4dTuixDnDxUH+IuTHDEDL9f96u1eKFwusgWGJSlSMISy241bAiearkErRL7SOwQng3QkAO6/zqAPMtk4pxSrRVSKAQX2N3a4flrl/n8q6+yu7PBk4N9Do5P2bp8jceH53z/x+9zPl9KERX/38wN/qx9bV3E9gWT85Hz8zkYzenpgslGSTkoaRrxClRWczx17B8rXnphh0s3b7Bz9UWa5oCtnWNu3vQEVfH47Ij9Bz/hO7/9e3zj5/4Kf++X/0P+p//lv6X2J0QtAOloOEZrw+OnD2nbBqI0FaspOfS6UTYnm+RZQXSWfDAiLwp8vWQ4sWAiTaiZzk8pxwOUlr3PZjo1HRptNYPBiBvPX+fp0wPOzs6F9RxTcebdqrGJPkrTHRR5MWBZN1IURVBZRjEQH0yvRD5ulEzo+2HZqgHUa6/dPkChc47hYCDetAmwFeBfpWFfCokjNTxe7lmVfLqJ4kctsq+QBgHCgu9ZIsGIZ1Vwnk7B0GboGIlKPKtwbsUa64OAZAKfBnFRZH0d4K1CGYsuxLvLKEU+KnFVTXSizmibhuA81gvYFABlcwJQucinjw558PgAZSLldwbYzNK5jqZt6Wp5PT4IMzAEVvu9VkZ804wUp72Etpe8aXPBQ733S6efSykIYqovgEgE363OEDnbepC571HTPpVAPaV7v7k+ZVWvgPoeuFixXSTZb1XwiwQ6SsCjSmclAibbQU45HqDLgmg1OhfWWtCpSQ4iquxSs6rQwi5esW/SMDaCUcIOausmNd1RgFy/Zo/2DD8fhaETnLBkdSbsio3tTT7/9ld5662vcOPGy2xu7JJlJSYvsbZEG0vVNLjgaJopt9/5Dp9++C4/uf1DHn36EMIa8FBG7Cs+vvMebx98mZ2tHUbDkmluOTicYnTg5PAJP37HcXpyxObWJjdv3qIsc2Ke2AdpYLxOjBbgQAbFToLmgoQOWZulwrJHelh5Cipkrw9pX4laWJZN0zI7n1KUJaONCRHoXEddL2mrhkEBy8VjXPeYMj9CqSkx1Lg4Z9nUHO6fMT9vyOwQm3l2djO2xpbMtijVEuOYEBpcp8WSwozxMScEjc3yHvVaMXak6U/vl9IMh0MBU3qZ7Qo8iORlxqUrl+g96GyWYTKbQHuN1wqlM/DCH21jQHuPTf6hPnqGoxF5llM7z8HRMWfTc2HIKmEhJTRZZJPGorTF20AMCLGgbTmbzbFZCo6xFmxOHGzR2lGy24CyGNI1HU0X8KYgK7fxuiB2AWiIKkP8S3M8udSZMUCzwOgBxpQUVgLiXGg4OTtiMJiQ2QzXdBQm0FRL8DXC4CxE2t3fij6i8GSxwYYOo8BmhtLmLM8dWkeMCgloDUlSGIkqkBvF2AcuZQWDZoltHaoV/3/vA8roVX2gorC4SGCQ0uJR33QtbVeTpXCdkPzEfRSrA9/XugmwWA10EhjQPyKkxrsmy0SOqLUm9PLnBBqvwE4tnoE+eNoEingfqKuarG3Jsow8N4TkpRe8ABsXZdI9wqZW4K2o8ULyR1dKo3SQ9xpQ2tB2LXU1J7M5uckIIaNXgQCJCSyAlXcdLtVAWWaw1qbQUE8IbQK0pMYKxuPRROcT4CENa1zhXSp5XkcMhlExYTLaSICyWGmpXuHCejBpjMUg578NHRu5Zndri5luaecN1gz50utf4Rd/9hcZM+TDd37E//3rv0oxfcCVnRFb167z9b/xt7EvvMHd/Rl1FVA6UI4zBoMN8rLjtZeuoOozfuc3v8k/+ye/wTK2mEFOwDHwmt3RFoMezFasvFJdArFn56e4rGU82aQNjk5HhsOcbDyk8RGlLFEnr1TVC+YDOvZg0LPMxL426fcXYfpJ7xeJK+ZgHwLmvXhbrhikz4Cp/Z/Xw0xZmxLQSlyvyd53FdSqFnbOPVvrffahku1TOqD7r18Tetb1uoQsJqn6CoTXK5A4rRKEhSh9UQhe5pep/+mXfT+ZiDExE2PPsO/b3ZCuV183PMsuluGhXg1xeuXW2nt2/RJXPr5Bnle8cF3X7Ufsn336+f/fVf5nQVtIQ+bgCSEx+XqLRG0pioI8z9K1kZ9njICnvY1FP7Tpv5dRwuA2Rq+VQySFWHAJXPKrXmiVe5MGNVqLolClAeVnAU4uXNuLHsD92b+ySUj9Vz/0CUEswnpzCB/WoVvifdx77Cq537QWT/uVF7MMk2KMqD5fQmmxKroA9mulVh6+IQS6tqH3WbZWAqBMIv2IPZDY3fX3o/MebS15VqIKeS9810mdqeOqjjRZlu5HT5Ps8kBINRff4/46+BAIZR+k5mXQrnNhaSIMapusLLIywybQVSsj531MvrVxrW4O3lEt5tTVErSmHIzkIhhN8LIOuiAKOBegKEtUZsnygkFWEGKqy10kUxq/XAgwO6tpFo5u4XFVQDnRMuX0gbkSV6YBncmZo3C03YLT40NcU4vtnrFsTba5dOUqo8mEnZNt6mpG29acHJ3SVAsZmEbk3KKDsMC7KSqcEd0BbVUyPx+RF5sUdsLxwxExH+IGG5hywsao5NruBjeuXOLFa1fYKgs0DW1XEWKy/eiHGFH+7LxL6tGQBi0yKLYJ6/LO07WaXiUg+4TBGgt0ZFmGsNoDF5ns0ifLAEu8cYtk0XGOn87lnE6+y9ZqlApE3xDaBXkWKHIDqsBHy2Kx4GC+jzaGPC/48x5/oUHa3UtX+Ou//O9RjDZRqsR5x3K5BN+hm4pcNWjmxG7GXrFAZ5puus/x9Ij56Smz+YK67QgRZvOK997/lHt3PuHk+IRl56hdYGewwWufe5ubb7yNyhXVh7eZLxtm82oVKOM7Bz6KxNAaovcCRCDpjM53gFCchTUiJtohOsrhgOFkAoOchXLEMicrCpwysKzwbSdAg1bi0aYV4utzcSLpMdpeSBmUTVgn9q2T5BlMVGIMrxQYQ9SGo+mU3/v2t/n4g/f4N37uG3zxC1+iyAuU8kliGVdF78VDSKfkWtKiJ8m0fMxQuWGyN2I42WZzeoKKnhs3bjAcDqhaz4cffkg3HjHa2ELrjAef3qNuarTVvPTSLd7+0hc4eHrA7ds/Zm/vEju7e+KpVpScn5zROIe1GYPBgNa17F7a5c0vviUhUXVF1zmccywWFfP5jO2dMW9+8fP85L0PGI8GKISl2bQy9To9PWE0HnL37h2u3rhENT9jenzG2eMZu/oKVhWU5RhjczQ5SiMBHcgGGnxAYbn1/GuMR2Pe/eCHHB4/QgWPc7WkvIZebhQwVgmxVifriwSoq1Qw+JiAJR/xwckh4VrZTG1G6T318QPufL/DGMuLb/3rFFnGsuvYGE6wIbI4PwMyYTRpxeWrezw9nXJYG1Q2wCoB+WOSiygchI6gIhVD3nlcsXSP+dtfv4mNjhAcUa9Zc8GnAUAILFvP77/zCQ9ngVfe+DxV0/Hx/X00getj+Ktvjvn6LdjLpzy6v8+TB4/5ox98nx+9f5s2y4hFhkER6hadpC4BsFlGNIbowkqGIAdETEDrWsZSluWqiOjZkmVZrgq7+WKRwgAEwDXJ8Lv//HVxocizHKW1mH4nA3vvOvHGirC3t8frN1/i5RdusDkuODk5YVFV5JNN3vvgLj/80XvUdUeig5Baqmfun1UT95nC7mJDtpZEycfqqsacw+bGkNh6JsOc5dzgVYbKM6bOcOex4+aru5jJkMHWDnYRCf6My5eWEDWeirPFKZ++911MrPiFn/9rVPM5/+g3/gcW3TkRzccf301MVGmcgo8om4FhVYiJR49la3tHpro2x+iSGCxEi85g2c2p6xnn01OyIheABwUhkmlLNKyY0IePnzJdzIT5pWRSXhQFyvSeWCJPapYNykMxGjKfzXGdk2lzIdPhLErQRPBRgNQEzPfFpkw4RdqiYmQwGEhasHPsbG3jncMpJ+spQt11mNzi2i6x56TglfA/JzLZvtHSa2C9T70WcC7g2havBRDo/cCM0Wkvkn02iQgRrpZ4Gg1GA2KMNClwUZGGYmYtVfVB7BR8maOLHB0iGck3yreouiMuxXqgbaSZ0TaihB5KFzz1tMK1HmUCg0FJXpY083lipGq0FiAxKpXwRlmbfUFqtFjtqCQnSpdBQLyLzVLo77XUsCSZl+7bsRjX102mi+szpwdhlTA1oW8WL0jvLjBbUKzsJfqwuKgURmfko0JUAGWJyTNMmRMLjbZ2DTxqhbUZrXO0bScDAhRdAomz0IOt8n19CihTUdFGYSfQrRkvPSgrjKRUNyT2lE7hP1qHdF6+wL//d/4DXn3ti2SmJJITPDgfwGfCutAB5RWhixR2k5df/graRU6PD3j6eB/fOXQ0K5az1p6nhw+4ffsd/vLX/wqTyYjjwgKOMrdE72mWcx49uMf52YSbL75Alhc0bQAyTJYTCRRZLmyWvjmMAa1BE5gtZlLfjMYYU6721D7YThGIXYWKQfIAtFj7xBgxbY2qz1G06CIStcUDg8IyKizN8gCjpygzw1jxN3M+YpRDlR1ORabTU1pXsXdll71LhlwvMaqB2AlLhQLFU2LcRenraLLkkRd7e1q5v3sriQtrsr//eh+zXsmh09D2xVsvYm2Wlm4QVRJICnT04EF1nsEg0sUAXZdssRST8ZDRcMiybtl/esjh6SlNU6/Dbazp21RASd0Q1sxR13a0TSvWLDHi2pZ8OIZsiCJSL2a4qKTp05ambeiixg63MBt71NiElHUo1xBDh1g3iG1GoQWg9K4Wq6iipFpWOBSTnT1a37GoKlRUdG1L6/rhRGJK90eZzvARuhAxoWVAQxYDdA2z+SHTs7sM4xnGS1OdlSL1dEqjI5QoLmvDnsrIuiXaB+gcXunkK0faD0zy6JagR+8lBX4xm4lPofeE0IjNQPqiPMvEExUJXnMkoCiBNDGK95xJABppLQjIJJ8gw5seONNoY1FOJUaUxRqd2IsaoyX0Zzye0LlapJNaPPMiUQb6/UaaNraVusQn/8/Yh4QFQgLKXOdRylIWgxWYWxTZCnTpz/A+tAcl60saVgFGcD2ILMMXawxFWUqYVWQ1jAghceRiFPm0E1g/V6KgUFbhFaAs5XiTIi8FoMsMNoL2gdjJ/dPXOlqJdFqFjizCWBm2ijG3tkYcPHpKrgt+9u1vcHnzMg9vf8g//+avcv7hu7y+PWLz0nW++m//u+y98RoLLNvbAxbzQ5q6pcsGKNfhEdbud/7Ft/iH/+uvcDZ9SpZHnOpQKjLMCzbKEqOEcRhVICLNvPh+tmxvbYA7R8XIsq0hg529Taa+w3mfyAXJP9aoZ84AnVQdcs6wCohy3pGCE5LSIOHDiRXey/yV0phMrf4egifLsmeAgpU8Pa1bhdRyXGBr95Za/eOiUjLGuAoOWwGlMa5VYQr6EEat1kdu/3krNc/qPgkrubBWPXMtDVOUDHPFAnD9fXoQVT5nDQK73nM+9bqroLCYPLgTyL1GU3uLgsT8/gww3hMh+ucuDGPpIbTpB8Trf+9v9/QRISh9BhDuHxdBy/51XHwtMUa888lKZ7h6HzJrUx+uJEC3bclyUfNpbchslghaCVxPP8KuUuoNMWqcS16bQYYs/ScaYyjyQX/LiaWc6tnzayulXn12kf29CttMQOdFULb/mhjkbFRKE6IM0vM8Jxvl5Mk2z3m3Gtj4tB5FKQXlaIRSJKaj2NP0tndCrnKJ3d9JIHFa6z0j1gRRvGil6Hqf2TQE0Wkd9iCzj4G8yMUyTffKmTSYVn1OREGe5Whj6ZqWRjWoaPHBgavpzZ7FagqI63ux7zP7YHHnZLAXlGJiDNpkoAyZzsArrMrTANGmAZqwy4uiSPirxftIZiWzpm1aulZ8hJu2JcbAYLwtg9NimFTaAqtqXWCzAmsMZZ6hNaA1Rlm2drbZ2tnh6aN9so0rjM4OmQ6HHJ8YlqbCVTWqlSyXKOWSgOVBiy2aAqMi7XzJSdXhXItRsJjNKUfCBh8ORuRG0dQFeq/k/PSErjmgcx1Ej9WCKxWFJVdQ6IAOHYaWwIw2NgR/TlhG/DLHR8MSODcZn+YT3h1uMbCGw/kT8SUOapUD1flAl2xiFEoUUz6peZLNhUtDBaKcfT741bpr6nrFwO2i9D5C2+j3BtkotErkMiW1LSjJayjy9b2UBigq2RMtFmc8fHiH7Ustg+EmO5tbbFy6TOcDVVVT1TV/3uMvNEhrswxdbtB4hWvnKN+i4hLja/LQomPN+fGn1MtTcI5mseDxowrnWnzbMl12HByd8cmdh3z64DHT+YwQIMsztLUMVGRjc4M3vvg2V154lUW35Mr1CpO/y6JrZEKRCvu+AdNBpyl1J2+CEY8477rV3M2mRUKeYycDfJnL9N2ATgFH+IKiyPHzJe1SvAl7X9MYSXKORDuMkah82hwuTAVVFJPmkJ7fagOOeBdlIwmRyis+uv+Q49/8x9x/9Iif+Us/xfUrVwFheMUANjWW2gitSl0YPRrSZNikI1kZjFZkQ6GFz0+POZ1VZMMNrj53kw8+ust0NoeHTzDa0gZN0zie27nMsCwgSkHtfeTOvYc479nd2SXGAMHz3NU9njx6yid3PqEoDEWm2dvepMwzqsrSeDHqPz+bkSnNk/2n1E3H9vYOT5484erV59j2jvmyoqsb5rNzzk6PGBQFhVG8+713OH80J+820FlJVqSU6kw8bFWQQ9LmJRhF13qybMBktMvm5BpFNuGdd7/Lwyef4HA4pXBBpuoqGuKF/1Rf/ScPYaN7Aofwylof6GKQsBLvCFHAUq08y/OnfPrjP+Lq1etsDSfMa8cozyF0EMQ3xwfP1uY2165e46Pb71D5ApMPkneugKwoJNwMm/yMlnRK8eDQ8cmjU75yc4INnuBaUCK5y40mNAuqEPn9H9/l9oMZV1/9Ms5k3HnwiBgCe9mCX/jcZb72muWFzYo7tz/ghz+6zfms5kfv3mbhFWaYAUEOGe9W/qFGq9Rc9b6NMTVQkbqq0oRbwjiszRgOC5EIp014nCTDXdvhgrAlRRIiMhWdrEmqppJ7MhiMtkzGo3QYrqVnXdsRnMMazfWrl/jc669x69aLFFZzdnxEXVVYMt776BO+//3bIrdKAFWfgP5nTdk/K1P7LBtCJdZDX2mHGKmqmuODUybPZwxHhewxdsTLb/8ML1x/gbt/8tt4M2SyOaLrZozHG4Rwldm8Y2vLcTMa7u0vOJme8fDjd3lnY8LP/fzPcXj8iN/53V+npcHrANqibU5hNK51ZFnO1tY259Mp1uQoJcEexhSgc4hm5XulraYrA1VY0tQzurahKIYQvYDwKgVeBEVbNygkFCWkptOrJOvxHSnoGR0j1IH6XLyaytGIs/0jYhfQ1lBMSmyp6bQEQhE8UQdiTEUT6yKy3zONtWxtbnJ2dr6yPVhWSwkMS1583juRo1qLc+sivWej6MTk0NomFldYSaK71ExErbBGs7uxTV03zKoK7z2np6erRqsHM3q4spfVZDojEunokl1kXBUCIu+S1ybFQv//VGxrhTYFxhaYkSK0HbbtWMwX+K7FdAJ2Gm0wmUHrFoVM8ocjGYAZvYJPiTHgevZJTM1beq+UUhiVyTMJJF9XVkwX0nOPPfMHtUpJ1Uqtm9J+3a/uh7hSq/TBGaS/C4sjhdolX8WYwhmUToCrycjKIgUIiu2ENgZdFug8k883Uri3Koj0N0gooTVW9pzOg/NylsfEwiXQhDXzGZX8ZtM+tbrf02+9fYqsPycfTwDnKiALCJ3Des9bn3uTWy+8Qq5LVBRGbzSGzEoyL8qmaX1Ep/dsfO1FSms4Pjrm8PCUOx+9j/bSwGulxB+383z0k9t89UtfYTjeYDCcpIbMU2QFPkBX1zAeMx5uYI2lDopoSHLMDEwuZzyKzstAdDAoUlCWkxAknYFWLOdTFJrxsITQUJ8f0c7Paeo5TbVAJz6GMjAaTZgMRtSLM+bNAVjLYHOPPCvxviL6A7Q+xZYVSrc0ruasPiXLW6z1FMPI9uUtCJFLl3IGuReWn7LSdAk/jxhqfHdKDHO0Ga/Y1FFuP/F2i+mtixLu1oM04m8nQVWCTujUEDt2Ll1jtLFHtTgieodzAnh1LjI0mizTuLD2KA1Gk6fANVsWzKuKw8MjqqqSdR8FuJBZk5iGCNMj4qOi9YGmbWW/jUGS5IMwHYM1dEahiYS2JsSGoAyogXiIKkXQQ7auvgobW7RdQx4tXSxAWblOqcYLgFMK7AB0JNcKpQI+yP4wHkyYzU5YLqeMRkNQBtfVqT5MBU3ofcwBleF0jg8Qg7Doneuop1PccoHPW4yBXBlUrFEBiIYYFFmMXMkHjFRA+Y7oIx0e49MNpftOyRIDEoJlLV3b0cvINaB6dVgCXFVih3vnpNaKgMlQ0SeAecWXg+DJFHidmLPRE70MAXy6ZrKWBHzqgwKFwaWo6oY8K9Je58nLjCE9U0b29D6ksW1bnJOhoYSkyjqV4OlADG51DgmgIszqLOE22hisLXBeGNi6D+BJFlEmM+AjuZZzOc8yQrD43jg1ptBUQBtZk8GHJCUXdYlRmk6LNVuf9q56eb9WEDyDImdnbw9bDIjBY5wjiwqUwZuQTj05j5SS8GJPxMRI6RWmbjlZLMAo9gbbFLXm6N4Dvv1PfpP7P/lDXtkesLE55uV/7We48ZWfoTM5Jnp2N3N8PaRaKqKrGQ0U20P4V9/6Lf63X/sVjmaHxMIQ0utHObIsY2MwEVDDChNWA8EjIExwTIYlnaupW0fTLMhzRYwtR0fHyWYprEgBEWFb9edSXNn+kJjG4i8aUj9GROxL0vqSXk8UO8EHURrBCkhDidonlRECCql+oNqDinrdb/Rgfw8WJpS1V4RK2RkSv6BXiazrUQkzXg9V01Q1Pad0pqd7SCmdWK89YHmhFuvhjf7notZqHJXsQ/rnEkElr0gBC30CAOPKCmE1LOeCp2wacujkyyzeySENS3uQO7Fl41qBcxH4JbIOtNJJVkRvz8Dqdf8pcsWFx0UbhP65Xvw9BtkrowrkWUFmLHmeo5D1R+z7fgH/fYwYZVags2INCHrvxNvSNSJJtxl1I+BdZmUPsUWeQGBW17uXb/dr1KXAsM65C56xF9/j5JebgOE1wCn3fq/iLWyeBi8KY8AYGWRneZGAebEXattWhl9aDBBEdQoejwsR43ufZ7EoUsjzJu3dsjf5xK6Vj4mtQI7OZJgRvdgD9fN8hexf9GvNS50nLi5iUZBnBdZmKC2/2rpmPp9RozBOEaODPKNJnuB+ZXOgVx64vf/0bD6ja1u2tzRTkvvIAAAgAElEQVQaSxxGscyJEWulBzU6JwbJNpABnCKzOcYYsqxkMt7CaAsqkhkNHqqmFk/ZGMkHA0aT/4e693q27Mrv+z4r7HDijR3QQKMbwCAMMJnkjDgaikGkSBedVCybT37z/+MHP7lKZatcRcomXabKIiVRMi3OcIaaPBzEGaRGAx1vvveEnVbww2/tfW5D5Dt1q2YA3HjO3muv9ft9f98wwuaarMgpim1MVkrNrkwC9SOtk9wEokPTEaKh9WCnMybKkGWOkfIoD42viGHNigYf0rMCWGWkckrseWwYLNd0BJyna1a0zRqT5fK9MeBah3JgkPNTnmEZLESlhCClMjJToI3FFjlORTIb0Vp6MxMk+Mt7T+MNXXfMqspk4KU6tJEhc3CybgeliWJgacdmE0QXo0qPdurpjCYgfXdM+02/0zVtK8QNzaVhEKA0Rmu0DygTaauatnG0dYsPSgD2zsnf0pE2SM9llePs+BHrxQKlch5O5ly99jS7+9cYjUfk5X+mTNoYI21V4VyDa5ZMC9CqxVfn1PWCs8OHnB7c5+z0gM57tDJUbcv5csX56Tkf3L3H8ckFdeNICja0tYTUUFlj2d7aYW/vKuuqowoBrzRddLjghom9eAgiht9DoRExJrFrvENH8TRVucFMcrLJhLIoUJkipA3SJq+roDy61JhcUxQzzCSjWa1x6wrjI9ZkaGVwqVE3SidZl0xZVBp1CvU6HS5pIqdU76uVDjONsIDQPDo949//1bf58O4n/Po3vsFrn30Vm1mijuI7ghIvV7OZ3F32/dkcPHKQRwVZXrB79SmauuJkUWPtiGdvfYbHD+6yuDgHFM/efIb9nZcpc4sLHV3XUY5LstzQXjSs10tu377JW2+8hdaelz7zEpPxmIvlisPDYzlYYmR3Z4edvTlN3XByek61agitYzbdQinN7s42pyfnnJwcc/3GU4yqmkcPHjGdTWnqiovzJffvPeLkcEW+HrFvr5LnUyaTOXk2xtgRxuSomFHkY9l0tEZhZTrYKaKxXNm5xZe/YEEbPnrwHsEJENUzI0KU5sBoQ9CSQBlQBC1MKUlmDjL9VFLo+OixeUbwElgV04Tp/OAjfvbD/8BzX/w6W3mBsTqlfEfy6Iih4YW9GWOtOVus8Rh0RCTaINK6xCpVSqQBOgZMVOzM50xHiugbiF42MO2JnSN0FStvee/whB99eMx8/wUm5ZS33/mAdbXianbKf/0L+/yTz84Z2WPmeeD08IC7d+7x8OCCpgO0+HDF4IguJHBMpvnr5VqYsIjktZeCKelI5IBIkh+ZestmanpWgnNU6zXr9RptZFKcW2k2og+0nUvyn5QKaw1ZppnPJsIycY51V+M6R5EV5KOSG9ev8spLL3D7uadxXcfh0WPauqXpAn/5re9x595D+X0x+bXRBwz8p3tXH060YQBuANkeFEM9ySDY3dlmXVWcnp4Rg+Pq9X2KIqfxEWLGL/7y7/D+u2/x4YM1X8u3cO6ClobR6CrGLsmLtaSi6AhxwXkV+fnb36Pznt/9nX/KYnHBd773/4FxkA6knb0rLJYL6rphOp9Ttx1t2+FDZDaZUOYjmX57O7BkldVEq3FNpFquZfKfZ/SS1AEshUEd4IN4HfXrEiWeUkZLErYO0Kw6TLDcePoZVGaJXYsKgfFswmw2wsUOObLS2vaeqOMwuR8CxKIUt1Vdc+fu3Sf2LpC1U7tusHlxXYdOTBVhj0tj0zcUIUSmo5EE2zlHTPe2b2CMGSh6RKPpoicPSoqEKHt4X4RrvSn0vXOcnZ09UfyLF5ywCOXTJgHGCpT4ewlLIQzrrEmybG0VOisZlxmh69A+4Kqa9WJBcOJzqZQEIizOF+RKpLnoHow2YMSbT4BFJVKn4bUlhnDsJWwb6c8wbMAOkuE+6EekfamoZmNJYa2l8400ID1AFgLaWAFDjEFndpDrKmvQhUysjc3IJyVkuQCvsW/4ko2GVjREXPRkIWKjHpKvoxcf1Lquh/fW2xJoreXcv8Sl6ZuRnhEsN+vJaxK8NCExSqNsdWLyp6bXBfHb1C7w4u3n+ZWv/Qrjckp0kc43hNiK72sAbTKUtsLmjklp4cG5QJFNePmVX+DW7ed5880f8eZPvs/jR49o6maQBh4dPuKDD97lc1/8RabbuxTlhIOH99nZ2iKzBc55ynKUWPLSBJrEihHJl0EreZ4uzk7IsowiN3gnoYw2JTNrI2tYhcCqPufk3rvUp/dx9Tmri1OU8ywvloTQMd/dZf/a05yeL2mcIysyolJ0UbO7v8fu1RnTHU2mV3jVcXa+4EdvvM6dB3fZ2x/x0ktXmG1l5KOCzEA5MujogcRsReSx1iDJ1aHDJs9Dg8ir64tTunaNGY/IiykxKtwgLexBip6RL+GAeEArgleMp3Om2zusV8eEGGk7R5a29ulkyu72jGq15GKxFCufLCMvCrIsY7FuWC2XLFeVMOqCNA8uSEhH03WMRyX7e3ucn52xqKQp6wgJl9TUrqN1DmMTGzF6fFsTophj5uUElUDfNmbkW9eY7t+kMmOmXmxtLnxBUDlRS9KzQBwKbyy51thY4+oTFk4k8OV4Tl3XNJ1iNNmmKA1n52f41RJ0hjIZxJ5RMhxrZMFRBIcK0JmM2WxEexqwJjLKM7IYyfOSYCA0FVoJw3ymFddVIO9a8A6jLJoAOgz7XrSWiCGqiHNBBnzpmVS6t9fYsKYkz04a4uA7VJan80+hlBUgNHgZSCkJ0DMmo8hGzCYzacZbR1Qq2UyroeYmCCM2BkWRFWiktsAYskwG3r23p0my3p6xUxQFZTm65Du68WfcMABlvxHQTMnZG6UZJYrtiCoUmc9RKopcFmlSy7IU1nD6XQIo6MS46q1kLMaK/552QRjwiiEorGfnqgQO9lkcSilRR6UBw3QyJWpofCQzhqB88nOU50fsbmI6ywSY1MaQBcMktMw7h187vvjZX+b3v/S7LN474N/+uz/ire/8JU+Xhp3ZmOmNZ3n1G/8YPdmSPRZAebanGbE5R2vHU1dm/PBbf86//MN/zuODe/ixJlhFpo005F5INEVWkOdlUlPZwWZAhcAok5CXzgVq19J2jtxk1HXH6ekSoqbnkIZkF7RhAaalGDbns7D85Dztmds9S3IY5PfHjUo+yIDYKsm9jglk6tWTCUG9BFxu9rAeDL1MEIjD+Sz9iR2s0NI7iemcSworOReD1DVDBNPmIwQPKogSkIixwgYUReHmfz4FBOs04EfJwKRzHcYkJaDvgVc9AIomscljCEMonYS6bobAwfs0LPjUNYybunrz/jcA7bBP9TWh6gEeBpao1OZ9ra6G332ZTftpFm3/ucvfBxB9lP7HJ4sRbSBEuqbDGGG3oxRGSe1gjJahRoTo5J709WK6hOSFWJpkmQyoR+MxCqibSmrUIAFV6XIki4Dky60Unfes60oAJ7VhU19+7eaJHkYNPZpOMvJ+1cUojNjOdayWLeu4SlYMMgTRfZ9ElH1Ga7rWD/fyiWunZAjfg7shBKJjAOplHWzuq0rge5/P02c1eCd7ndEbqwaA4Bwq2X0obYg+4kOD6TpAhgI2s0ynU2KM1JWXgZYyaBXwLqKjGQas/b7RK74Uwph3naPMUgC18uIVHMTPXulArjL6lRxDQMUMFTOMLojRkucTbKYoipwyExV56x1N1+GcgNH1uqJaB/I8UpQzbLJAcEHhHXTe07QV6/US7yBGh3MtXQ2urnHrI6jW+KZDh4gKAUMceuZMyZPfe2nLve/PPhLLNlAY8UUO1uCj9FOda4VV7FtRDAUvIV8hEK0eaoYAw75pEzgfkl1H13VEXFK4poG479suM6zRqJIthrZDWKAMFyymKOntTkKQIa3S8v02z1FtQz+jHQYaWlMUVs5WBT1rOsSItbnsod5TNy1N1xGD9HUxSPBk8JG2aagqjzGgJ5pCSU3dOEfwhuXZCaenJ4y3HmDGU7T9z9STlhjQ7oIRHZgV1Ct8VXFx9IjDh3c5PTlOabKBzjUcHZ/zwb0HfPLwkKpuadqUYpi86eTmCfCqTU5oHdPpDqPxHB81y3XNRbXm5OKUznVpKq2HKXmMETzSYCSZsDEQjMGMC0ZbM1SRocsMtMaFSED8tExmUQjgFA1C1TaWmEeycU4sC5wxxGWdiAkbbxQfN36dg6wjgQSbz4XhMOqBoX7SGEjyWatZ+cB79+7z6E/+JV+9c4cvffHz3H72Fk1VkdkcF6FtK4o8kyKzLwLiJpFeaZE195NQlKaYzaBu6GpHXpSUkwl5IfLV3Z051irx9ipzHh8esrOzzZe+8iVCiLz3/ru89tqLVLef5Zt/+U0eHRwxnU4YjSZk1nJ+vpDpBIbjs1MeHRzx4MFjCJHd7V1G06tMpzNWqzXL5VLYCcFz67nnuX/vHpPJmNu3bnN6dM7F6QV2adkxW8zzOVk+o8xmFPkMnZXC0MCgshybj4BIrm3ypxPvGDLN1b1n+cqXNdHA3fsfsmxrfEzeQyriYyS2HY2TlEMPtN4lbzSRGrmQ2DpK4TpZTzLokQA6rQJ5WPP43Z8SWsf1V79KkV+jaT1G5WjfMc88Vyfg2wofFBhL66XpMGkgEVADdheiR3WeLCx5/vlrXJ9rtK/Er6XMiN4RY0fbae4dnPOTD84YX3mW69eu8+F7b1OfnzPWDb/+hTm/84vXKJafMCby8O4D7nz0Ce/fvSOMHKvxtSfWwjB2bUcMEqDUg2lt2yb2iBkKA+89wQvoVBQFXSfAQAiG2WwGChbLJV3X0tS1PM9KAKCmblJIkRz0fQMh0qKc2WSCcy2ZMXRtQ9OsyYxhazriudvP8tprr7C1NeXi4pTzkxPAcHhywXd/8Dp3Pnm0meD3Ra9sUk8M2uT2qdSzpmIipfcqkm/ZUHBIYSiFrKIsSyJw3jacLypseUE5LqnO1hze/4TFquLlL/8K3//Jv+CVV4/5+pfnmNhizZhbtz9HVR2ieUCuPCFc8OHDNevWcu/dt9iZX+W/+t3/nrPzBT9563tkI2GznJycYzJh1H909yP6gJ3oHPu7V5iOZkMQEz2LwQiYo5zi/HSRgEphn1dVDURmsznOdTI918JsdoJSDuCnzTKMtnSuJSpomprc5GzNtzg6PqSpVpCSaaOSYlUbRUg+hgYrfnHJ3iJdUZQxGGvxbZtYCHInZA9WtK5LEhlheBgUVVUN9zGGZJmQBl4hBFbrFQo1yOTETgMgUNiCIs84OT0laPH5S6X65jX1Mq1La73/uMzsCL2kvmcqpPMjgjS8qFRY68EyAiJ10+CQYCubaZTNQUMxLym2J8yKERfnC87PzjFo2qZD4dFWJ/9QAS+lwUEY6WoD0KI2/ovGiB9r753XByjIeZPOofQMCggoDBcfAtZmsr+FxFTVwnyNCSCxWUY5KtHWYosCnWWyHlODEGwKtVFQRY9SfbvcM4sCSTuK1poMnUDS3qpgc837Z3VosHvQtQcT0uf6UDudvp++Ke6bv3Q/iyyXIZ3fNMjESOhaguuYT6d89sWX+M1/+GvcuvE8CgGYScw1bcVvTkLILNbmMtQwEhrlAhT5hBdf/DzKBF767Bd54TPP8eH7P+e9d97mznsf4F0HvuPNt/6GZ577DKPxhJvPPMf5yRkhSlCd9jCfbzGZzmhdRJscYzK0shibE4OjXre0XYdrKoiOpupBCWnOYxBGRV6U5AQeffABJ/c+pD25z8HRx+xszdFe0awWzLanXNkeU5895NFHH3Hl6nXmoy2qquLi5IiWPSo7Yza/ijKBg0cH/OW3vssbP7/LhWvJR56TxTlf+wcvkFmNsYhtCmLlIBbSBTGUGDXn4qhmffAR7XzK9g3N+ErO4Ucf8ZN//WdUh4+59uqr/NI//e8IOtVxmuTxKes2FTVINFccmHEmK5jOtngUZa0KRhcYj0dMZ1NpXqwAKkVRUIzFymTd1qxWDW3dUHUO77pkNZUSvnvbKu85vTgnJC9B2ccMLgZW65rWC2OvMAa8p21aUAZrM7Isx1qLT85y5c4NZs98jtrOcKFEhVqAS2sJukCZfLA2EXax2CHYqDEJGJpMRkRlOF8s5bksJ3RdzXolww0hLQjLTwePUh4VnZy/ISkDVAYosrahPnoAek3wSuospbBWE7wdWGu5gqlWZF1LFgU0DIICoLTFKM14voUtJ5wcPcbHbhiA9WypkIB3GfzI82lSroNJzEcS6OgisocojwfxpLaadYTcFmTFBG0LYtsD/v3+IXVKSCwxqbstKDkXmq6RZlxbAfVU2qOisHRCCJhM2FN5UQ77jIC6G0n7UBdFAXntpYYzFRcSCIoMPYfkeiXBNbEHWINIh7tOPOkZ9vXkR6kGPcUGiEp/IpIaY8RrmpiGVWkzHRUjRuWI6Bxed1hdyJAt3RijM2IfNuV9YrYJ68sqzcR3jC5aXrj2Ar/3W/8Dv3jtc/w/f/XP+Pl//BbXlOPWfIdsMuOFX/o62ZWn6TxY42maNSoqtkrFZH8MvuIH3/wz/uCf/y8cnTzAzDJCLr2P9z3AJ8OVR4cH7E7ui02JikymYwItikBWlOTFDFuvCL6laxtG4xEXVSUDTN1bzMjVEcAg0tsFDAVHAoc2gF6y7+mvrFagpT4Vv2A/AJHqkqVBamGf6PP+tvqhBwiVVkMYbL8Y5Evywno/+d4LvlcfDb82kmq0/mcY1uPwriNpoGUGdnC8BDoPAcBR6oMnzlfVM97UwH4jgXLaCPNbzmX5Ws+IR+vhexQbq4L+PfTgdBq/bOqo3mOcJ8HbeAnMFcXOpetNbzWTSt/QX0516X5eelZifOJ3D9cV8a8n+QVHpM4KKFpXJ/akyN+Ftd+vj0hI9VHwEjAVvKfIMkblKKXCi4JEHmMhHGSZWDl4LwFrmxotPlnzZJZROZJ9wtgE3jIE1klYYa+MUEP/3wO2xN4PX+NjoOtasXlJ19G1ojLrAbFeIRBS7+eSrHyw7VAyxOkvn9S/SWGVvt5jHQBt1w2fH+6DEiWBUWL7Qww4L2pL2NgZxRhZVlUCuXO8a+Rv0Xvx9wCxDFc6FQh6Y/si2QJxWBjpcsjrRiWrCouPgdVyzQhLObY0XU3AYQtNUJYyKxiVkzRwFUyqc57u4oK6rsmLnPGopDI12mg6H3BevP3bRkDMuvYodUaWjcgyS4iaEHM6b6hqx7qqaOtabBJCQAeH8R7fVLjmFE1NF5Y03QqjFDatf601wXWJaSrPUBcjTdMQQyQvSpq24vz8lNlsxmw2JxiNzbMUeNzRtY6Ts2O6rklrSPrGmBQFUQFWhqoo6e2iSlaHrqGqayFyOFHTFLkd9ixlIPpAtGqon2QfEsaybIxC4JGhI4Sgnhg82IQLdM4J3qfV0MuEpIyWLSap5wfSCRRFgc1z8s4Ro4RCOxdZL9d0bQtB03Y12ihyK/cx4lEmx1iDVRYXPefn57izJVH/3R7hf89BWoduj+jqFYvjQ5Znx5wfPcK3S84Xp7QR6s5zfHTI4cMDjk7OOF3V1B4UhpBAECmmxYcl0zk2GzEux8QuMCrEi7Qcj1H1BYu65vj8fMPMCf20DkARvEiOdJ7YeZMJ2WyMGufkRU4XAq1rk4IhiOQzepkcEGR1pT4yIK8rKNCjgondxRcrFicXeNeiVSQzlt4GIVWWG5AnbgqDAQDoD3kFMaVK9oe7yLwUTYBQ1Xz7Bz/k5x98wK/+w29w+8YzPHXlKlpLgvC6aylHJWVZPlEcDJIYRQq9YbBm0FZTTguu3rjGuj4jN3Pq9ZLj4xPyZCVgWsd0vkXdtqzXK65evcqzzzzDerVgb2ef2XTGYrHi5jM3effd9wnBoI1IXx8/PuTx4SGL5ZKbTz/DZ195ibpa8c577xFCZGs2Zzab4X1guVhw+Pgxz916FmJgUo5py4hXii29zU6+T2kn2GyCsSIBVFhiavYZqPCeqCIm16gsgRNRDr8yK7h+5QaPDx9xulzQetnUGi90917G34O0LngaJz4oUZFA3YiyijY4YZkqhsIqErEqYmPL0d2f0ylDubtNkd0gGEOeK0aZYjLN+OjuRzStR9scZcC3whrR2iZ/QPEQQ0lIx1NbhleenjNVDlyDzgq0imhrcGpEXRs+vPcRrdPcvLbHw/sfcHbxmMIavvJ0yTdul9jlJ7T1EScPT/nxj37MX3z7uywclJmmbVthhSlFdF7YJQmouZwiaq1N3xtEtpu8Y4o8ZzweU1VVStSE5WqJ8+LvpBVMJxNJGBaiIn0ggXCDZEIssmZDWeTkRfIRc+IhOi1y9vZ2+MxzL/Diiy8wm405Ozvh9PgEazI+vveIb/71jzk+W9IzT5Xqp7ibIuzTRbPWYs4/TPfVhkFpVR/iIa8z9mc9kcOjo9SsiTx3sVwzysVGYHFxyPe/9x1+8evf4Dvf/lf81XfvcePqZ3juZklGjbUz9vZfwbmSGB9w/WpLFxwPHi1ZV0e8//aP+YWv/xa/81v/DQ8ePODx2cdkk5Q2631i+fQpxQpd5OzvXcNEQ1u3IinSlsa3RB1ou5p2vWZxIkxQ57ohlM1ay2QyFpZzzyzA45s2ycfloBa2SkvAbQrszKKUYXFyRuhaKcbzAgrLdHtKGwNd6JmXSvZHs2FKKKOGYJQiz8WTyl8Kt/LCIvQpIVjLCI3dnS1Wq5Wk15rNME8msnEA5vJ8E3Qn01/Fs089jfcdVSXghVSnl9eDSKYvF5QDQ0pvkmf7wt8Hl/y+VPKG7uV9PXdBPjKtGeWJiZzWmk92BT56sQEAdJ4z29nFT0rG169Q5AWL8wsA2rpmnOc0qzVd1Qj4hiIq84SKomtbKayAqDToQIjiZRujNFm9pEgA6U0DZa3BZAKw5inMr2f6GGUpxyNUZvAJyDc6nSlK4SFZtQhQEbSAZioqgpGwg3hpaNmzaDZBeOIlHILIa9MGMazL/gy9/JHUh5v7lJrYJ6pxEAZEf7/770mPvPxrRAVPFiO3b97id3/7d/nCS19ka7KD94rOCdBVFLlc83R/Y0S8LpXGa5GBS2BIuvYY2s6h1ITtnafZ2T3nC18suDg95+TgBPA8eviAu3fu8PzzL7O1u8fulSscHzxKIR2ByXSamLsGYxTaSBCYMRnLxQXr9YrZbMZoPE6MdwGf8nKEMlakkj5SjEaY0JGVI0bTHdqLM0blnBvXbvDo/n0UkdnWnMVyweOHD9nf3eLq/pz1ak2zWpIrj40ddDXRtUSryXRBtWzResxkssXF+pDDgwYV5mgDJyeP6eqK+WyGosWgUWqbUXYT023zN3/6r1h/cMKEn7D7wmd58Ze+xqMP3qf68feYpfRp86tHFNv7KSiOAaBQSqSaGlFAWWvkfEmN+Wg8pnMd1gRRSqVB+LpeU1UeomM8HTMei/9gVbcyQOkkbXvVNgmEDzLEV6kv1Jqq62i6VqxjTYYylrqqWNcVrvMEpTBWPO7yrEBbGeEYYzD5iDbmVC6n3L5Osf8yld0lC4ZMK7zWRCzYgigsAdn/ohAN0MJgHxdbFGqGi+KNmI/GxHVFcC0hGurO43ROsBa0MFL7ta9djYq1gE90RKMJzjPLNe7gHs3Bx0yeMvhoWLUt2jeYWiSROsvISdiXitgINghoGnKLLkageuaMvPasKPEouqaR92ENxWiMMhn1eoX3nTAGwyYpXiFZDS6KbUvbBTSRUssZ3SlFaxStMuQ2E3a9ElJFSD6usm14QuyEKdRJcE3Uimi0+GTHgM1sak6BENM+lmp4vfHt7BlKMe1l/RnxJAgkTazWVlh5KcwEZBDtkbCaXt0AamDl9UOzIt94hYtXtOw5G6/Szd/sVSUD4JWeDaM3gJrXYEzG9tY207wgC+IfTFI+kAaJ3qdUbdVbTojkGA3RBazKeOHaS3zjV36Pm/kN/u///f/k3/yLP2AreJ7Z28XkOdtP32R89TpHxweY8YLZbEqzWhFDZGc+RfkF3/7LP+dP/ugPeXx8nzg2tCYQHKnfUphkizKdzNja2qFzDQ8f38cYxXhccHBwhDUZo1HG4VnF+dGCs+qUs9UFZitjcb4W5VvKBDEmY+Oj3lsL6KQc8sNZ0TORBZhM1zeKpZwKAfGejlLHhM35Yq2VoXBPRGBTa17+5+W64jIY2n99ACd96OeXUi/zpIRfAL9Ul/TvB1myA0Fn6AX1cOT19k8heCJh+J4Q4mA14JOU3XsvMv8e+EvhfcJsTLYO/ZxsmHNuzuEnw63S3x2MbtUlVmgkpqBB8Xj2Q4ig/A75nif62lSbKrUB10nrX96D31zTS3XAp+/JE8Bjeo+NdxSp5lVJxaut7GOkYZ+P8t76YVKW5wlMKlHpORWPdEVdN9hsQI4vDWfk2vtLA57LwWBGb4LXNhkgQuBCqQEvyFPtrLXGObE8inETxCtgVnp/iX3sfcBanYDV5Int05DJ+wRIi3rDJJBsc+3lNdlUZ2xA2XRdL61TrTVlen/9GpU62gzviSi2EN5JLd11Xdp35etZUnHGEHFK471LNoSJyRsDIF6vXnt8q5JiM4VJOd8f3GLB0IfPafXEdRcPcs14XGByUS3k1pIbTVkUlHmJ1YXsTeneSB5LQ9dWNOslvcIpuSTKsMchr9EFLhanhHCezkaLosQHS+dAkZN5i28rlM8xMUOrBStXE+howgLPEmU8eW6JFBgtz662QDR0zlEUOT1BUHx+Hc5FWtdSdRWni1MhMmhR9agEYLdNlexh+rpYNKjBRdro8EChFZkSaz/pHw2Q07atMMODXF/jN9YtKsiAfV2tAQFmM5unfTgb1qVSqUZXKWclywa1i/NeBpn0Z+xlz28vhLy+mE/rUTTqoZ+jUBQ5XStWieOJMKF9Z+kaj2qFQFS1Fdt6JkPpPAddEoJilI8psglG2U0B+rd8/L0Gadum4t3Xv8fy9IR6uaCrKy7W5/jgWC5bHhyf8eDokNXinOB8kpdbbJIzS03wY9QAACAASURBVCp13/ooimLE9tY1ytEEg8Krhvl8G5uJYfditeR8taJqusSsCBibSXK2S8nemcaMDOOdKXY6gtwSM0MXHN2Gi00ITiQbkHxrExJPmmqmYgwtDXaMis4E9PaIUWboVhXULbmxhE68SodE7UsHRN/gd123AURCGCbkvZTTKENucrwWX5cuBrq2ZfnwMY//9E/56he+zH/xa7/O/v4uW9tzmrZJ1gqbMKYegNlM5VIaadPig6MoS1CGrd1dPj//CuvFkkf37uKams57LpYr1qsl42nJa59/lbsffcjdO3d46qlnGJUFkY4vf+WL/PSnbzIaj9jd2ebg8BHzrRllOWF7e5f57hZGG67tXxV5+HrJ4ckpJycndE3LaDQe2F0/e+strl29yq2bzzDKRyyVI/OOSbmHsTO8zSgnI3ReQjTCoknkgiKzNFVF5zs8AZ0blqcr2rZhcX5CtTrF+TXnixPm5RS37Ti5OGHdiA9u4wNZ8hlzzgv1Pzic73BBzMwFqI8y+YxJlt/fY8QMO2KIeIJbcHr/He69OWL+9d8kLw2665hahYmB08VSmGVaUyqDyg1Ns0T5mqhLvM5FFukcs0Lxuc/s8+x+RhlXrJo1kyxHRQ/K0KqCn9y5x0eHZzzzwkucPv6Ew6NTsszy/Hbk11+dsKMOaBZrTo4P+eF//C7f++FPqTpNNh7jAPqAjDTJDF5SD3sm4lDA+I1xd//veZ4zKkf4JCH23hGjGcIJ8jzHasX27hYxRJartfjBYblYLEArjJKCQMKBDJPJCKUVdd3iW09hC5579gYvvXibZ2/exPmWg0cPqdZiGP/Gm+/z/R+/yaJuUcaQGZsKt/DE1PwyUHtZGiSeZXo4oC4zEUIIwlJMn+uf24EhD2gVaZuO4GpC8FT1Ca//6Js8+9yzfOkXfo23/+bf8MPXFzhvee6GInSnYHa4dvOX8Pod3OHb3LxWE33NJ48vWB7f5923Xuflz32F3/hH/4Q//Xd/ROUuMKUheAGPxRpFGtD51i5b0y18J6w5Y4QNEKJCW+hcxfrsGFdXFIOfTu+p7Xn8+LHcJytDlrruMGl9h7ROlQ/SpGUZBNDkXLvyDL6OLE/OIURMVmDKEY0B6x1e9WyMhIMaSzkqWC6Xm8I4RFEj9EEpaeDhOinYbj37LPfu3aNuGqzNKGzOjRs3ODo64vj4OLFDwmbqmoZf8tqlUO0LeLTh4PiIrq5SaqxM8qOSeywskE0hevl+y3oRSeAg0bEW7ZMEqmdypqJTmuNLTBylWK3WoKSoV1FhAomNoQmt7DGdd9w/OMTFQJblNCGgSgnPs1bhlcLaKXY+kbNSWxRmA0hGBt85QkgqEp/YtE82bwA6N2SFPHtZliVWewRrE2tIGrEQZdonoLD8IZsYFCn3XJrd1HwFlcJOogDW4vPbT2HD5vtgaFI2Usi+CPoUIHupOPp08zWcpcPXUjURInya0ZRuSz/R79lJdI7nrj3F7/+X/y0vP/8q1kxpmzB0yslNK11DKcSJYHQuTO90LQRcluIwdJGYghb3t57hjv8A54TpGRDGSNu0/OyNt3jqytPkZcmNZ59lcX6WAuqgLAucD2RZKYwRBBQP6QC0ec50Ph+kZ855YVNOpqmJK6WhV2Lps3/zBfb3rrK88QIfv/cGH3zyM9xqxfbWDJWYi6dnp1y7ts96teD+vQdYk3Pl+jVGeYFvAhfHC0Z7E+bTKV/6/GscnH+fs7YhM5HtyTb7s5u8994H/OzdD3ju+W3Gk4yyyDAhsLsz5sr0KU4+qjl5/YArVWS/qOneeZuPPrmPrhpu+0ARYf3wIW/8yR9z/Ru/yvylz7Mi4pSSiAgNupcz9w1iYoMpIuNSvHmddlDkFEWOVpq6aciNIs8zyqJEG816XVG1DV1izi6rJeuuFQ82m6NNILZN8kNMlkRa47WmcZGj01PWdY3WilEhVg+mLClsibGZyIF9xOQZZGMWbUa2ewueepWquEEbFMXyDNMusdkIU4ocX6mMGMX3WKuOLNYSkqEKRpMtomvRQTw0m9Zj7Yg2gleGqoMupCFM/6goaVx8jGgiOjqKuKaMFYX2zMqSB4/eI2fNeLSDVhZdmOT1mlh2IVB6x3bQjLOAVZCVJd4Im+qZV17h/OSY86NDlusVpmnSQBmCUnTOY6LHFiV7V3ZFcrrq6FmIAhKJxFIZOW/2P/Mq4/0bHN59n+rR++QWiIGmqwi5NNC+aSDa1LCJjFbsawIhOlzsqLuKzgWCDikYU4OROt8mxcVl0NVkmWQfbDxtCCESo3tiH900+2YAU0SKnUCI4HC+FdluArtCAqT7s2o4x9AJfPJcXFywvb2FyTJ6wJUEsvjEqPPei5VD/zrTQFknmwirtNhTlGP2trbBKVSIGBMIdU1eCMM7egGpnAtkRiSp/T0nKqwKFOU2v/97/yOrK7f4k//1j/nXf/jP2A1Lnru2TzEuMFtz8v1rnC3OMPfeJRiFfu45trd28M7jqzN+9Nff4o//4H/j40f3CaM0BHQq+Y5HSU4PCotlXs549sYtnr1+mxAi29vb7O7sk9mSqmqoXMNk+yqPHz/k3vEJK98xm+2wPDqh81G8+q2c0TGxgvuzMiQAbjKd0LWthDtqnQADRN3mhBk5nJsDe2tjDdDXxpHEAr80MH0CgI2b39P/jKwZfamXSI+qUinXRMAOlYYHSm3WWB8Y2gfsId8y/J0+WEfWZi8D9ptaOIEhkRT6e+k19j8rry/5G8eI7cN7U1/UA9LSKySdTA/mpTM4hAiJHT3YDvQDr57xhoT/9NL7/qMf4HaXQj+97++B2OZwCTyEDUj9t9UNl//70/dDPimDPxA1o4kMQK1RYgego/iPSlkpYKo1osrKiozJeEzTNrRNKyHHTYdK5Jb+vV62X7jMFlRKruHwHi7VRDqFgym1kbYL6cI9sZ76f7at+JQ3XfeEj29IQWKT6VRCwLQo8vphzyaQWA0/M6jf+hru8gA8rVFr7PD3Jb8kvTdjhzo9xigq0QRO++gGUoxJwK21ieGZWMW9FYLSkbLIUUSch7bzEgxvcsxkTIiBXbWH7xwXF+dUyzXWrCTMK2EivR0fw57bUdc1WmVMpyNRc2Y5k8mEIs8p8wKlNUaPMLFAkyyDvBmulQqKrgsip3eiQDVGgNwsy4hKhh+ZMRg8rnUJLNcoHM6lgy/K+yyDR8UuBVHW4NdATVAVkRqjHFGLBYTBoJSwhWPQWCtguaj2SCFgMhzpa3uVwuFINlG9DYy1BmNEkayjqBxRMeW6RHSMKGvJgsNcGm5kmQTHo0xSmvZWOxKAGRN71mSWNtVYEZ2IkrLOnXd0XYtKdZXJctlf0nPS+4SL97VYPZRlOayRtnGE6DG9n7U2FEU5eBG7ZFeZtlbGo5JxkeFbx3rdoipFpxsBuIkYm1GWUyQeVTEqSmbjkt3tOWWR8Xd9/L0Gaav1mtdf/yl0LUYJpf7obMHR6TlnZ0tWdUvdtcSQHtosQ2srshHdoaIeipcst8xmW0xmOwSvaNuaEBzWGtqqwWlLdJHJbIfRZE4vd1BGo6xFWU1pMybzCabIIdM4IxJc0kS0/9BqMx0LIZAZC9FvpiwR0jhANqhkLB2IRK3JZyU6M/h1TagEACV4PMmXU5tBniFSvMSIC2EjAUjNXz8d98EPC6t/EJTJCBEuqpq/+uEPOV2s+O3f/A1uPXON8bgkBi1BVwopiBuRncQgflN9oeW9F/mBycgyQ0BjshGznZy2a7l750PWyzXHR4esF4tko2C5ffsmB48fcHFxxmya47qO8aTg1u1nOD4+YGd3TqQjz3JG5ZjZZML+/g6RwHg05uLslPOLBV3nUAYOjh9hTSETFSLaag5Pjjg9O2F3fo1pcY3cztAqR2FROpPJk87QGJk0RwH1zy5O8d6zrpfU1ZJVteLR4WMhicSO9fqcEFpcEB/CkSnYnW6xNZkxrxsOzk45r1YCTKYEwQzSVFxROUcXJQU6DJ6Q/ZQ94vBJjujR2mIzTdsuuPf2D9nZ2WXr9udYNRmlUbSLFeuqE7sGRUozNBTZmBBaVGjpVKSLDtMFXn7uGb72+RfJ2nN0iCJ7sYbYNVR1xTsPVrzx0T12rz+FV4pHRydok3FlrPlHL4156SrMlSc0jrsf3+fHf/NzztcdpizFpsN3WGUISjbuLLNDUEC/AfdTWe894/E4gf/yjEOk7RqR7hKTV6/8nnI0SgBNZDqeslpX4m+EIyChF3meU2Q5o1EpxYdRtF3LerkCH9mazfjMc7f4hS++xvWr+5xfLDg9O6HxHW2AH/3oDd54+33qphPmRAgSWhQ3cpy/jUXbMyRsChOMeiMhBEn5RilhDySAtn9mN0V1L81SKHQqljzQ4JvHvPXTv+KrX/8N3vnpFu+8u2JnZx8dG25ei/hwD5VPuHrz8xwfHoF+xPXrhsoFjo9ajh/f4fHuDl/72lf54O47vP7zHxCCA1ITqBWRQNs17G5tU+YZofU0XYduGjyWYB3ROkwXWZ8v6TpPXmy8oaTgkolw55z4ZKe9SiSSpDCExCSPEdUGurMaG3L29q7y8Ucf0KyXclGNBJwpZajrBmW0yHqSB5SOkWq9xnddks1fKpB70Ayw2uLSmnt08AjnOkwEqzV1W/Pue+9Kc6tlojo0yoBOh/Zsa4YxJgWCQR8Y0jqPMlnyeRMwL0UjDE1YP9SSvbkP7UgeaNGnI0Gxt7dP0zScnR6jdBwAjM0qkg+ZDkujFZQWe5XQyZTYSyOje5YLIkmLPtDFjkg3TP61Eqa/2ESoJNcMaEgBJip5Lhl5ncEMfmnBixzZJjl+egjEl8HImnBK4xDJFNHTemHCCltiA1Js/Lzj0HT0bI0+qCukMzT9sDTfQ2PS//30DKl0Hl5qXGJ6fcOzyyYw5G/7uNxoxXRmD+yNJDveNBafBn/lazpGntrbY386IzSOznToPLHy0/9vwuCSvUQvtUtAuUrNtWsdIUohDRKCMB7Nmc92ODn6WKRqSVLmgQeH93nw8C5P33qB8WSL3b2rPLx3h2mekWdiM2JsgfcOtEIFYRBkecZ4MkG8LyWYRCsvrBIfiJi0Z8QELkGIGdl4l73nd5heuUHx1lU+efv7dCw5Pjphb2+Hm7duMdmac3J4wHw2ZjKbo4zi9OKcrStzFmcLyCIxV1x7aotf/gev8LMPPiCS8erLT6NCx8XxOZoMnRk6X2O7SFCRplvg2hMWjxfsuIKdEBi7wCi3TGsFIUcZSTtWjePjH/yQ+fWn2X/lNeo01HBZ8sxO1hgxXFprSDVljTQNREvbOqxp0MnD0tgMbTU20xJ4lfy9XfA0bScAT1YMzYZ3jsxHtLFEAwFN0znapuV8UVHVAkSORiXT2Zx8MkHZXv5qUMoQlcdlE+z4CpOda7D3MnV5g5qJ7LU0xM5h63MsGflojDcjnC5AGZSrcBePyOe7jLa2aZoKFUU2q4N45roYUcYSsLSuZwiqxJgFHXTyatUYBRkeGzoyt8bEmub0gouH7zGZZxRZma6r/KwLTmwdAtimYVbklDFiIsnTTlg99z66Q+haYucw6bmLgJ7MuP7ybU4PDzm883NsvebRvU/ouhYznM0aMciQZlJrRZZNmO1fZ7J/lUcff0jMc4LR1OuK5ekKNS/xwXO+OidrOybjKVZnOOeTx2ig9R3ruqLpWrCGJnSYakWIQtBAS7ih9wHFZmikVAJPtACgfdq8T2GWl/ce+RnQSgLlYhBAoD8vvOuwWWKHZZmAbOksjilwMWrxGA9p3yXV9IpUdxqDj14GQmm4ZKzUw+kBSF69wgaPUQgnmbWMRxN0TIxZFdDOyXvzSoLj+gGZl+a+Dyj21mJ86kOi5vHbd/jzd/4t/++//zP2VcWt/Rm713fYuX2L6bWbxHyb07NjdrLI9Vs3ibHF2khsar777W/yf/3x/8G9wwd0OTLIDUgGSALNexaXCZpSjySxnIwyzymyETYvGI0URT5jS0V25luMJiNOv3dOef6AcrqNcx8n5mMa4Nh+IL85LzQCcGbGQhaxWhLih94MwOq0r/PE2dOHD0n94QdgXiux8CD1f0ACK+ITw0F5LVIXydzSp3MoqZQuXYeYzp9BKZL+O0Q/1BayxlKQ6KXBMvQg2vDnRCSa2Or9QFtYmYl5mAKAezKGVuJrGVN9AVFIQSnAx8cOUAO5YXMOJ0OaGPstZPO1XtmSjmWTQOfwqTqA+GmLqc2z2QN/aiBOyLj40/6zT571/+lw94mPGKVWDEFk7fqyfDoRCZJyRmk9AIz9enGuY7leiYy6f65jWm8qqWWRfwZiApzlPMqLXIYiSmT4vT2LTmBZhNRjyOsMyVPTB/Ft9T4miyHxsc6yTIg0ZbG5Zr39WYzk6fuCc+TWEFKmQuz3FiV/r78vPXDf15/94+Q6AVq7tqGvAUPaS0xMuAzyDDnnxUot7ZchKVJNuofGGIzSAuypOPw+TfJWJV1z51JegcNohbW5qDi1wmQ5s9k2uS0o8py6rlgtlrR1Q7QSBu+9yPwbH8SqSmlsblBWs7iQoEs1M2RGhu2ua/GIftc7CShfVxWd69IA08tzlYbGYo1T4H1NNKLAsDqXM011BJ38naNgErGTGrGNYu+mEEDVhZYQ17RxhWNNDBU+COCsEOX2sK4RxUkMHqPTcx2NqG8SsUInQFZeZxqKAqqvl0O6b4mZKnVCqlNjpG1biq4g5PL89gMlay3jsRHlhb5MshA7O51wsKax6Z5vVAMSRJwP/YLuPZKV1NxFkTObWbGDaFphfKe1qVIfF1Id3jZuGIK0bZcCQiUnqus6eWaVMKatkWtsjWZUFJgImbb4pmVUjtnb2iMvZ0zKDBFBRqwJGNP+ndvH32uQ1gdPFxzr9Yp7n3zM2cU5y3VD23m0yej9+0yeEXHi45kMnSMShGRMTlmOGY3mZOU2jRPTaoMloqnrluVizXw0Y3f7GueuxWQFUUWK2ZRyMk7p3YbMWnQmP2fzjBBagkcWgdqw4voURkhGw2nzg96GoD+84uCXo1OyNEoCTtQoI8sLQlbhQ4S6EdaENQl0TTKPEFFBD5OozjlhKwU5GAR8Sb61iJ8kXJZkSCHZhsjr777Ho4NDvvK5l/j1X/llru5dBe/wUejmuZVUYBAJmNEy2bdZRlbkaTKWGjklstf57lVe29rl4NEjdFZgrzlOj4+4e+cu1hh2drZR0eG6yNnZktPTM65cuUZVSwr9K699VkzQ6xbvHIvFOXkuk9fWOe4/eMjZ6ZLtnRm3b13h8cMDXF3z9NPXuXXraeq64vDxAfVZiwqKWbHNKJ9QmBFZMcaYjBjc4F+6XC25WC+oupY2ONbrC0JT07YNjXcQBXB1QQytlTLkecbVp25QlEWazI04XZ7xF9/+C7TV7F3ZS0xB2fSqtqXxjvPVmtq1LJuGs2pFGwNBRfEv8mGYdvsY0iEfcdU5b373P/B8yNi+9hyj3ODbCqKnzHO6piOqiAqyITntxY8udNBV7I0LvvL8Hlu6okW8eIwxZFrTKM3dR4f8+K2PKUdb7Oxf4c6DE1xQbGU1L+9ZXrqSMzUBV3ne+ps3+NZ3vs3JaomdlHhjCN5hlRSQBlJYTyTPDXXTDazZ3o/We0/TNMPENySWiusSYwXZ3LNMMxqN5OcVNE3Dw4ePqOtaGkfkzCjznPlsNkhWvPdU65qqrilMxs0bT/PSi8/xpS98lr3tOUeHB1xcnBGAg+Ml3/nrH/PxJwdDs8Plw//TxaLaFJFa6Y3frErgD71HJ0PxZK3FWJk8o5U808YOoI9S0rCpoXhPU1+jKXHce/dtbj77Mrc+83k+uvsmX+ye5t2PD1gsz3npeUP36A67+y/y2S/8Ng8+/gHri/e5/ZSmaRwXVcWH773Nl7/2j/iNX/0dzi/OuX98h3Wok1+WSCaDj+yMdylNQU3A5qUU07EjKxVN7sAHFqdnEgxgDJ1rEDmkGXqHVIUPXj59AjEasjyjrlsC0FYVzdmKZ66+RGZyDh9/QnAtaE0xmZCVBTYzdNoNh37PpvDeERFgXgIp3KZ3iRsvb/HQdZRZznqxoO1asqwY0pK7rpX9Xcvhewn2kwmxgovzc5QR6R4k5kKIaXLbg26pOeolZmlgJ3eyb556ppRIGrXRVNUaa3POzs7pEtuOtKojly0SepAwsS9jFKaG1ajoJKneaLzvhiZ/kPeZmJglJg0hQzqL0r1Smt66TtaoQyEKA5+SaCVEIILqmbZhKI4GRnj0KCfPBioMXrHyKLmBQUH0gw/YMOJUbIDbVFD1QR4923AAKdSGZdP/sAQIGC6Dpv11cJfYMKq/f5dB2/73pN87XOfhd6T7mW5NHzJHv977v6nkssSk2xSPqpj2BNnflLI90p7kyn0TLEWu0Jx6OZ++1IjHYW3LX9Rs715BfSgAgTZWhhVasayXvPn26+zsXcfojCvXrnN+cYwKLWVRYrSsk7brKLWV8HPFMOzwya5GKwlBatoVdVNRjmZpX+sDbSIqEz97j0PPd3n5q7/G9aee5u5b30E1Bxw8eMDx2RlgKEzG3pVt8jLn5PSEW888w2Q+550P32I0CUTfMZ8YfvmXnudzr13H2IDOWhbLR1y5rti6ch1sTW5LxqUlzzIK3bJa3qO0U7an20xokv+aYpyP8FrOAqsMY1q2lGO0WpOvTzg/eIBROWZ7Hzua06YhkgwRkryNBGwZw3LVyCBQaWHdFFDmGXkhTbExiuW6plrX1G2DJ9A5j840WRoiWSsNuTEFPiiqpuJkseRiXYtNjzVMpiNmsxlFOcKMJmByVvWKZr1iNJqByVB2zPTGazB6mjbbYpHvUcURLiYQN9vHbs2IfoFSkTyscFoyEwYgJkSRYBYlylWEzkmdGONggxM9rKqGtmogOAmbjbKPEBSEgKEljw25r7CxI4aO6NdMJyWZicz39smLET4EutZJY1MWKGXJtCELLbqXS0cGr1eloDo7RQdh5mGkZtXWUo4mXL35LHXbYbN88HTOrBWQJu3FKqZ9WEeC1jRK8eY7b1C712kWF8yyiK/XnJ6cUi3WzGdPYeyImBdcXCzwIbI120YbjQtSE7uuxfuOZbMiH81pTKRenJJFRWYLQONdahDSXgLSfKaHPA2/SIqKDUix2Zt6EMHgE3MLIpnNRCIbVdrTLVpbGeim5jkm5V4MaqgplIbJZCwDNCfqOxUDwQuooY1O6oWNjD1tZvQdtFzLQF6OmUymGw9u7wd7COkPDF1i4PVe5W2UszLXGmctF03Fh/fu8ub//D/x/uKcq1sZN65ss7075/+n7r2e7Mqy887fNsdcm5lAwgMFFMpX+6ZrihRHjNHMw4QmpJh5nD9vIhTzOCYoaWQpSuymusl27OougwJQ8Eh//THbzMPa59yLalHPnOzuaCAzce895+y911rf+tb3ffD7v09x4y2mV++yWjtWDz5j07YUgxLnHKvTE378o7/kn//z/51nRy9oM43KxY28Axq6yCvScmLQM8iHiH4wFHkm5lcq4HwLQeODYz5fEJVmNBhQliXOB5qqlXHlzApQr9+UFiCF0eA9m/V6C2gGRCczNcL7pmOI4pGQgC9Ux2DcTmlIDksfwzMrv9flQUp18apr5qXuL7tAv5xfPum19rFL6Z7UA8nA1+j+s3X1Yddw7F7Xe58k7rbAbVRdBJd1Iky6tJ69SAbIEknMtdS0N9okxjC9LIlPJsPbXOnN6xEzWv1bU3lEemA49I02iaO7Wr7Oe1SQf+fT2t31ClA7ecEbIPYbjZPfnmrtfofd+Jz2jScm3de8Z9+BxFib6T7/tiYTs6GUy4YoGqjUIqmi07VrOif6mPRsk9m3CqgsyWcokscI1G3H0o80TZvORchshnNCaDNJN1ol5qdSUOQ5WSbrSkAxWX+q12KN/bX05owxELwYAZpMTNB78pF3fS3V1Xsq1XhKJfNbVN/8FR+TxJxGGgA+BHJjBaDugcSO9b2t1bQxBNdlVvTkIJCJrE5TvHtu3QRkjEH0+NNErs4s3rfSFItyfcYq8iKT147Q+tDLEQnfwNG0azYbkXRr25r1akO1qZgPCtroMSHDkhOdIgaLIhN5v7ZOwDJkJkfrEqURg816JeChbxNYr5L2QfIKSAAoEWHmRoMPNVFFvFc0rcf7BqU8jV4TWKJCnfAyTwyi99vtsxACdV3RkaqsNWR5TohSBxVFLuCmF+8MyavlDHLO00mPKFRPVrNW8kvnRUpSRU3dNsTVqj8He0Zxly8p2zO2xbAznTdRcCllt4bF25oH8kFnLCvXkmcZ2khTZDAoyW1GU8h+kLpLo7VNDGEh0GyqNXVdJ+mg2DfT8jzrmwQxJvmqRBDRuSa4wKapWbs1o1BQDgaMhwOuXLvGdFJSZCExryMmdpJDv/319x6k/fzBA06Oj5nP52ibbTdl9GRlznA4IirFulqhopgX6CBdOW1LynKf0eQS2hY0LSgnm995j46a5WYDWpgxmR2hyBnvH0BhyKZD7FDG54kII6ipUUbMAIKKokNF7IvFXfFxEkjDzqEOHQOnYxOloJmCfleAKqWIRmHHQ7QxNBcLVN2ZTiSdIiMI/rZjuVts9pVj/7m0kSJXK6Gdd6zRbqRSKzi5OOMvf/RXnB694k/++B/y/jvvyLiAVkQTCanrpLVOowjSndq6bMp1BqUganRWMBgMuXrDok3O6vyU+WLJ/iXLF59/zpXDq0zHI7SyRGA2m6HNiIhFm0BeFoyGJfPZBatly8Foj2rT8ODBI8pCki3fOup1xav1htViQ11XDEdzPrp1ncmdW1weX+LhL15wkO0zzkYYk6OLAlvkhBhZbRbUVQ0R5ss5x2fHNKFFZZbMKnFRDsLiGwyGFHnB4ZXL7O3tsVouWVcbysEA33qq5Qq3aWiqJfeuXBdAKjM7bqWeodYCwB9cBqXZNA0vZ2e8WOAj/gAAIABJREFUmF9wulqwbpvUAerLwwQIgvKe9fyYRz/9C977nmJ45RJVvSJ4h1aeTDWJ6ZERtRbJBKugjeTK8dHt61wfe+qL57gQUOTkqoAmEmLGg2fnrGrH/Xs3eHW2YLVqGRvPx1fgD+5n7OkT5q+WbFYr/vqnv+DF6xNaY9BpfRmlpcu9s7ZBDsim6Ubz5NDu9pV3nvV6vRWST8FYOs5SKIfE3u7B3balqeskIyGBeFCUDMqSTJtUhETqjTzXyWDMjevX+N3vf5ePPniPwkZOTo6YzS5wPvDw0TP+/Ic/5/hsjtiDbEdrYDvuszvO1O1zSVKjuKIb3SfN3X6UvdWNBYUESMu+M9YSterNEJRSZEYTWtffO20kuW/qCuNWfPXgAd/4wQ/44uFDjs4t3/rWH/PV4/9CXgTev29Yzp8wGH7IcHqDev2C6XjDdKrYuDFVveKrh494592PeO/ex7w4ekpoA1meo0yUYs0Y9sopOlisgWJYkpkSj4MSvBEtovVyjs2tTACk2sDFIGdv6vz2yZgPBKTj2o0JKTSj4Yj5usGYjNu332Z5scRX0lU0RU4+KfHGpdEk2QsxmX34IDpjmc24evUq57OZMPq1jF76JE4fUgGhNUzKkrvvvUNQ8OLkhOcvX/auoP1I1u6Z2ctX0O/JN85ZtX2+kR3ALq3xbqxRPveOu7D8ElppnBf2kdFi1hPCgM1m1bt+668VDbvfQ0tBGpzDIKNNRhlatqxUAGs0GotWW/apxvQSOgkdpWOqdECu9zJW5VxnJKHpavcOdOikBXrWVCpUBYxI8SDdi84IAuReqtglcUmLzRgBMBT9ORETExvVaeRtP+cbRXJfpEFX2HVFEmxN28Sd9k2WjhRsno7FC2y137t43DHDYvdz3bN5Ulsg/U91/0XGtZK2o5JidRdU7tjEHcs8kZOEbZSAMp100GyW4/1WaoiocR7Gk0vkxZQQDdpqdJ7Jv9OG89k5z1884+b12xRlyeXDq5y9foHWSfPWu1TQbjXtdD8BkIANLUD9fLHA+YpiUKKTHqnky1LAQWr06EjUGdNb97lvA8cPf0lUA0aHa+68dYvxwJLZltOTF1w6GDEqIm55THXylDofM74yYGAL1HLDRAlevd5cUK3PKYYtxju8jwyKAcNBwcBkZDGjqleMD29y7cOPaX/zJYO2QodI4z3GypRJZnJCsyaPa1guWT/6nBePfoWrA8Nr97n3/T+Ua6PHpGRtK9Wfc433rKuK4bCkLAqmkzGZER1yvGPTBGbzGavNWkxfteRIIQZhpRstskfes6la5vM1q6qidh5tM7LCMhgOKAdDilJM9NBWpm58wJgMk2VUPmKn1yivfsxZO2YZcyoGeHQP7jcUtHqIyvbIY42NNQZHGxtCGKCzERy+hRsNUdoyKQeEwmCNZbFYChsUzXgypmrO5GF0PgtpDDNqA8qjo8NERxZbomsIMXL16lVsc0HQCo9mta5kQkB1khJWZHS0wZicWG9S08mAixweHlI3NYvTM0J0IleghbHjW4erz/nkh/+RerWi1HJ2aCPnIEphsLJGNQIiegc2Mj6YUoyGXL37AQ2Ws+cP+c1P/jObxQXKiZalMYasGJBfKtE2Y11vBDBRARdaVpslF4sZs3rFleKAYIXVbZXum07B+cRW7c7sXemj3Xx9+3MBjTKU0qKR3oF7CTSTUWErkmwJ3In9QdS5c6e1m95Hwo0wuLLkJO2cx5gghpSJxddJ/AS8SLwlJqGKAatV38jMrWEynkj+7V3K36UuaxrRNjd5gQ4i56WtNHs68ka0llnb8tMnj/j89StClvPupT3GB0P23rrOvd/5LsPDW2zMhPzKLUwTOFhvWMyO0UpTL8740X/5L/yLf/Ov+Or1c0KuidaIqWkCOb13/bh0CgYy+lsUUqynhp41VgxxYjp/gyczUqhnZcF0f4/TthVtRJu9oRu7bQbKHQ+kKQu1fc7ayNSiMAi3gJBSCFgMvR9FZ1Dtnegl7oJPHfuSFJ+jittY2MXdxEqVNdWBqLHPNyVESwwPqQHSXUIfH5VM3qi481pdzN5GLrp8QfJd3U8MddcXfOhWeJ/vhBix2vRmPx2TUkBhyem6PdKDcynX6Ef7E3Dbvc+2YZm6vbp7/iHFNN3ncyAgUvfvTCcx0O3XsJWj2jJ0Yw+C/9dA2f8Wi7aL+STwU0gDIj/S6eNmViShVFp7LsZeJsqkGNuB7RG2WrtKkdlcZN0QA7oQXWoeBdpkThlCTL4eW7BbSFc51mbs7e2lvFXWQ9uEJBUJ3kVCaJMUCmgtdZ5NBAy3U6fEKBPFAST/do5Y1xhj+4Z39wz1Ti4mAKCMnhsn7MiEpSJj7pKT2TSB4tqWtqr7PLvT8CW9rkiOiZ5zREDpzqy6A+SVkunKzgA3hCDTRF3+5wPRCVu13shUCwGCa2mrDYoko5HLvpY+upYmeTIP9b6lrte4JJHjXaB1DYPBiMa3KG/Ay9RNjJmwzY2Qi6wVMpK3FtRaDDaDQ3sgBly9Edm10BkBOtGQTc9WiKcy8aRMACWSClkRwK1kv1FjtE91lSZGi7aKum2xVuNbEfQuSplctAk/8qFBKxnP72oU77ba0k3Tytn2X4tNkExXu4YSoMXMOURFludkVppgm6oiT8B6VddpT6QaJ2EMLsTdYym9y5aEKL48Iuuj0ufFgTFePEucJzOGoDXWdPKEyXg8RAG9zYjJZIJia/ppjVy/aDfLHusmK8W0jl7S7eLinFW9xi5nnJ6+ZLo3Rk8s0+FYJtSbBnb07r/+9fcapN1sNjx++lQSnbygGJSEVjoxJsvY29+jKEuWyyWurrGZADpaZxT5Pnl5QJZNsFkpYJlNQal11FWF956z2TGrasYle5OgDJPRhLt37vKz4YCgFS4GXOpAmg6U0WICpUySFdg5qHe1J7XRktMqJZqcqThLofONjpKCpNHRsXgCKopZRCgV+eUJoW7Qq5q4UUQf5POExCxLxCalNE0jzNdOiHm3I7g98Hc6saRgo6Xgqrzn57/5jEfPXvKD3/ldvvOdb3PvrdtkmabxToCKkNT0zLYAUV2haVIXQqxaWFc1UUdu33uL6vIloo5EV3F8dMJqucKgOMsXTPemVI3ns8+/xLmWq9cu80q95u5bNymsQY9KhuM9Tv2Mp0+ece3GTW7cuoFzNfPzczaVY1MrFlXN6edfgc74+MMPaJaWkTmk1BOy5GRdtTVns3PqtqZqN31nrW4bVu0agMKANSXj4YiDg8ugRV92tVyyWs05d47Tk2N8lE1b5CVtqHlx/JxIYH//Mov1nPOLM2HIgjCqEjiX5TnGWMo8492rV7l/7RpPzk54fPKK082KKrhkRmawSpJJtEJ7R3v+jAc//ffko4IbH/wOFiMOukqxXjc4Y4nKYqIEjzYE9sdDPnr7DgPjqRYLbJaTGY0NcHFyyqcvlzx6ecbVt+7jdcbroydoF3jrUPNH71/m/SuB5mTO6asX/PI3n/DFwy9ofEarhCFmYytrO8iB6IMXrSBkbRotwt3e+3T42m1SJCerMNPSmuwKmagCrXMsV+ukWysFlEmH/LAsGA4GTMcTNIq6rmg3CQiMgcloxLv37/Pt73yDq1cvUa1nPH7xgk21Am35xS8e8LNffcZy08i+xKU9SM/2hS0gtAuWySYQJCEQ+uuUPSX7PKSAAsJk1KnQJAnOC9DhUrcY8jwjaLl/Sqs0xhRYNy1GKZ49+ZQbb7/F23fu8sO//Gs++Mb3uPv+n/Lkqx9RlDW3rwdePP+E/cvv8v43/ymfffJvubwfOJtvCHrC8etnXD64wve++T1eHT/hbx/8HHzAZOJmOSrHXN4/hKiT1IrDmK7bGLhoF8yOT1nMlgzHE5RSvRlE07QolDBUvJfJd2tpQp2YIyHpMLdkNkdHTagVN67dZzza49GnnxKbNOpWFoRCoUuNVzEFQElaldYMi5y9vT3Oz885OjrqmZJKKYbDIW3bSnKazlkfA4vlkth4puMJM51jkl5sZi2k5DjPRAw+REnSOlmZ7n13i4OYCpB+nDD9TkQK9r4Jl5gAPjE4dEoGnQ9pREme92KxoDcsS8nKrg54F1u6pHM4GjAclMwXC7QW/XKVOtY6bmOTsFVCcjl/cy0DnVF3/3nbWp4BdHq0CqtlekWW/S6jRPaKT+z/GCOkpky3b3bB1OC2LsHKbF1TtTWw48D75te2yOnOht34CYJB9HtSdTqPSSMyvYZgtt117bind2weekhD8owODE/XSLorNstom6YH4uX73Z/VFqQPkc26pqobpj1gvPNCqfjtANLoWqq6piwnSRakc1PW9MYzwSVdR4UPkTwbMJleBpMTtUZlFhuFWeuj5/nLp+xP97FZxqXLV6g2K9GeTUVSUeT9XQ5BzD6yLJMPqLZFk81zrErmESlRzbVK5lcy7bFYnbKuZuxPrxJ1hiunxP3rvPv+RzRNjfKO3DRkccbtcYZxS5r1MSpe8M5Vgw5L9MmCuAiQK/K8oMUTY4PREWsj+cCioyXPBgyyIXkyYwxGU9Wgb11HvThHnRyhdcvaLRgNR5TFHioKA6sMnvXRKeHhl9y9eZ2qiVSZAJV9U2ZnvXV1QOsdAZgtVxir2ZuUdHqORgsw1LYNLgR8D36pXovTO8d6uaGqG+arinWTQAkD2bAkHwwZjgZkRSnJfl7gFWhlsUoztRnBOdoILgyYXv2QhZ6yVIZaj/EUxOj6xgQqIyiL9oFG5TKS2iwwNOjxEGcGoPbA5vi2ZRM33LpxyGQ64auvXnB2dkH0gYP9AU29ICZDMRAT1agk/hnfkiE5qUuyTZcuXeOD927xk3/5f5APBoz396h8JRJaMeI9UsjrSDSBPCqy2qNHUjA33rFcr/viWWnROVSpEeqdI7YtfrWk0EpkyVK81ElOAKVxrsXrFhUiKnhCXVFdnFBXQ17nI6b33mV847qc5W1D0OBMIOjIcrMApRiXe8zPZ2TGoDTUTcXJxSkX6wU6y5iOx0zLEc5pfOP68xt80u+WJqEw1FTS2vdbY6/YnSBgMzFOrZsGo5Uwo+j8IJCDKKZCRCdpNXzKt0NqYqaOTzoDYwfM5DlbI6cuR0m/bhTaGwGyE5HFtW0CGRK7Vgm4lOfCMO1GryEklp080xA8tsvrVJJEaTxRaTY68Osnj/nl6xesmg1XL+0xGhW0meLmO/e4+4M/oJpOWKsRl67dxeuCVjtuvf0er54ZVuuKrx4/5l/8yz/j0evnxFITTDdN2IFsXTNya6rU6ekOcmFcq6ghGvKsxOqcxlciURUthR2RZRUey6UrV/j8wa/7xptMA6keZJIcVh5HTLFG6dS8taavl5TRSYpsq9XZMzi7GJaApq5JoExf2PUxSSlF61xfT77J3uz+3MUZ1f+/SaZKvdZrWnc6AW5vaCHHjmixA1b2Bl0SJ7RKMSQBZVaBS9NFWu/mvfSLzKZadzsdo9M9cCl/Y+c9Qv8ZJd534bKbzIk719Fl2F1Y7UDwN8lLu3lF1+zefe0Y6GtblW6k2vm3XweGv/71dWZ11yRWO89FyL2i59k50XvvUSHSRi9N8BDIbQ7WYDJpStVOmg7GmK1ebZZBAsSrppGzLmkZC0itiN4xHAxkajdN5QkzVqFUZLPZpLOqwwcUTS2yczFoYmz7vM657r7Hfi37IH5A0heQxnV0wqbFGNpu0jEB5XmeYzvArdMoVlaanKmB15FyXOP6xlJZlgmQVjTDps8BO/1cSHIjSsA+iTGO0LhUw8VepsXkeY9XdHq3zonRk0ZhM9ub2SmlKAcDNqsN60WTnlfAt47QphouyP10PrGyQxQmqXK4VshFTV2jdcYqHyQ2dIbFpjUhOb+QwwNKFXgVaXxAG9DeUOQlEQFxo67ABoKTaXPxpRDjczkXAkpbclsAMikRTQ7RY4pAdDUkS3MdVZK50ZRZLnr3MdBWsp6EHZ2mEnuZtM7kTM6FLDe97nK3E7szN6T6yKQ8iYiQCbr7aww2z1Da9P4m46JgNBpJjbRDzgJ6Q2HnfZIGk6ZkIKZ1TJIgSE1P51BG9VrXMe235XJJ65wY2luRc1OJ5q4yidF9Cy7VcnlW9rhEd35kWWfaSd9A8j4yGY4ZDoeMJmNmszPm6yVfPvyCGB3K3WOgbrO3N+lJfH/X199rkFYmgq24pMZAW9cQhFpMDGxWS5bLBXVdo9EEF8FERsM9BuU1TDbCmIKQnFhl/MlhLPjgCG3LxeyMZ0+/5Made+gyozCa/b0DBuWQzXqDtVlfesntj70Yv8elEaMUHLrCPXaMoI6NtcO8S1994Qo9IEQCTkPSzTJdsR8j5IagC0xekA9L3KbCbWroRm/jluEl98fgWtcngaSCUZkOAaMvJE3aSG3b4rXCR1DKcLRY8u/+84/45IsH/NEPfo8f/M53mYxGvYusjIqQOnzbgnhbOEvn/uT0lIuLC95++z6jyYi33/8QV605P73gxZPHlIOCs4szZosZ0709Xr464uXL12w2ouNxdHTK9WuXgMBoMOBMzZnsTRhNBly7ecj+wZBnXz3lwW8eMypK0JZI4PRozq/mn7JvrzC0+yhUck1sWW/EkXBVrzGZoSwGGJ0xGo05uHKZ8XDMwXSP+fycdr1hs1xykTRonPeYPKPxgf0rVxkOxgTXYBSsqxWvzjJGgzH746mMONSO8/WcNnXZu266NlZMsqxhrxwwHY64vbfP/njAxXrDq/NzXs5OWTQ1XicWGsi60g2ri6c8+Os/Z7p3yF62z1lTY3JwWY62Bd4bCEF0y5qGuzcuc3OiadcnLBcXTPcuSdJu4Gix4a9/85imOGR4/S6PvnrGZrPkEnP+wbvv8d61gqGp+fTRYx589ik//83fsmkdPuYoawTk8ZGmqfvga5SMxbmmBSMA7S4ztQNqiqJIQv4N3ahXF4C7BNa1jroWdo7xiqJQ4q6r4NJ0wng0wWQZy+WSxXKFbx1lUXDtyiEfvPcO3/zoffb2p8zOL1jO5qyWNY+fv+KLR8/48uFzXCQV1OzMXrMjNL/dv93h3CV4xgp7R84sASFtKp4iYDCE4EWXzOikTyYqeVnXdeuSxBh7cAsEJNYmGffFiAtrWBzz2U9/zPd/7w/56ssv+Dd/9v/wT/7nf8Lte/8dDx7/JaezU96+U2KKI3KbMTq4QT6bi2mBzti0FU+fPeL9D7/FNz/8NkcnL3l68oSIJdcZl6YH2GxADNKhx8jzNVZ0uP2m5vTFS1SUbjKxG4sVkwut4PDwMqenpynxaVIiZ9HKULuaGCN13bCZvcbPIu9967tUVcXx8VNc26C0Jh8OibkmZBFx6dRkWSHrxEtxsQu0dYX8oCy5tL/PZlNx0jR0A3PKZLTO8ckXXxC9J5A674nx243+GW3wOohcR/q+sQJkNa5FoZM5FCl5DcJ4IOmIadFh3WVodizNrusf0/djamh0LtEh+L4p0MWTrqD/egHgvWez2lBkGQrLlRt3ePXyOc1miYn2jcKlY0mEpGGuOhbMTgHY/blnf3SFCTqJ56dCnA4clbRY6vDE8ghIck4q3joAtgNld+IfyO92IKq4f79Z2MUOWN0FlHdB8tgxS+WVxQ07NVO7uLdTUHXTIz50jcuk1fi1AqzDenst5XSlPaib5Fh2i8DQJQLdHVcyneKD7AExhEjlX1e4dSAJwn54efya47MLPvr42/I93U28dFyAmApbibutq3Des7d/GW1yGu9RzjHISwFUVeTk9IjZxRl7B5fAaC4dXk4skwTa+wg6nbdB1puwpyI2F+DFWMt4NKFtKxQ53oO1AaU9VTVjvjpnsT7lb3/9Y65cPeR7l/4YxZTXy1OezV5T3DjA5ENu7x+QhyXL1+f45Yx2+YzN8hW5ahjSgo8MDKi6IjQOtCE3goC0g5JlcGJqNhzIuG3URGVo/YaoKp49/ILnP3nNlSPHZDFnlHvyzFHqQHF5n7rxqNBwc3SZ88WM2WeP+Na3/xn21l1erANVpJcz6Z6jVACyVzbrTf+8Z/MFR4XhYLpHnkBtYxU6BEwm0ligiM7Rupa6aajqhvUm6ewZRVlanAvkhWWyN8XkYpRos1y0phE2ijYmNbUiLTWbuiHfv8bw9jc4nmma6PHQF/8hGlCWDqQJSloITomO3YgW3bxkbRsoDymUIriGaCIqGr569JyXr15BDEzHI+rNimq1wnbpY4zEpDynvce6BSascaGF2GAi3H37berVKS8f/oZLd6+gc4tqxNQ3ooiqkwZLjaCqoXQBG4PItQTPYj6nIVBGaTjoACao/nkYRCdYmPE7BlouoG0yJ4vy/CSHlzOoWa/ZLJaszs759K9/xGwxI8zPKPC0KqPRmqVrePb6Gc61HEz32Z8cYIyMVbZtC1rMP7TNKbzGOhiUIxrdiLGW0sLqS8aAcq5L8ysEkUCr6455aETHMBXBHeoXorDVrBGgXw4OTce5F7BV8qXWNWi9NdtRShE0xE6jPGmCurbtAbJITPm87Q0PVRSJH9HMT+xjcWuUVoxS5IMBmS1SIZx0cqNPZ5askTYk3wqraYB5teH1csnzxYzXqwWMCm7feYsP7t7k5Og1T2YLhrfuwPSAOloOLt+iHF/CRzH/yvIhd+69i28W/OSnP+PLo1e4TBGs5Foqxj6G9sZEfdyIPTN0Ppszv5ixNzlkPByS55bBoGCz3GCNJjh5HsFHXBCCwNHRcWqaqW0+keKL1tv/xb5Br9Lz6RrHOjU4RCdVZA++NqWTmjnyPBUks7fdpqGY3Gxzj98iDUAfm7dfaidO7sTS9BmJ9DXd119jy0DdBYK7prTcD78T/7pJkZhk1BSqUwQS35YU/qS93QF/aQS+J0OkY7fLRYww9Toflu7SumcszdguZ+KNPKG7N7tTUb0+Ktt8KnYko7jLpu2D8xtfX88nvv5eb9xjuTG0TZtkALvaX+QCldbShELWiEHYf20jn8dmpscThoOh7LMgo+dtAv9cyq07aYpOh7MsCpl41QPyPMO7TuM70Jm9OZfyEsTgV86HgA+t5LUmx5ouh025j/fCQo0+yaxoskzqU6NEusAUFq3KJHe3XTudiV63Hjupj24imAS0yb4xguukteZbh28dxopUiU3yip3WbvSCC0UgOAF3rTboge7PWwFuA947kVhApRF8izUWq7v7naRp0hlilKbcKxhYS70u8D6wXCyoQyWappF0PovsXYgiGxe0sLB1DGw2Lsl0SpMEbyiTRn1RjkT3VykyUwjOpYXoYbJOhsyhdTLP1QqbdIitFn8B+X3xPFE6ineH0cQgBnmhbWhdTYw1bayovaOqKyzSvDNJkFFpK3E+00J8QKYTIPYTaFuDv4j4++gkj+DFG0EhEhEguVHad90gjkYn0Fbub2YysqKQ+iMmHeEkjdixaHeZ9B1xRYBtafBopcgy2+f0Vhu8CQhLWNqY3eRgQFjREYR46Fq8F9Z337BSKpk8yqFUNw0xBAbDQa+pLASlQs73IFrWwXeyBxIfysEAF/cIzJhvFjx5/gRrFAS4HW8ymZTY+P9TkFZJKyxpUESapkpjAyp1eF3q2kkRqYxF5QVmsIfOx4Ky4wnRCbiaRja1DvimxtUVp3XDl18+5MOPv8/oksUQmY72OLx6mycvPpeAn4n4v3QLu4JT7xzw9IBMd/B3o6+SNGxHKLqA2QWTXtdNJ2wojfLGkMThA8ndM4LWeAMmH5AVmbANlmti6zEJOI4JMAk7QUfGTOXdo+8COulg6UrQiNGJJcNWX7CKgcfPn3P8Z0c8/uoR//AP/5B37t8jM4ZYd137mBKjtJzi9j5IsBgwncj9aLy4CGblkDtv36duKlxTs3/pgPVqRZZn3LlzixAV8+Wan/z0F+ztj/j+d77Bd7/9IRfn58QY+O53vsNoMsLkiufPT7FZwbvvvsfx6wv0fMZgOCVTGWUo0LWwI9u8oW0b2la6KI1vUDpQ2JyD6R7T8QEHlw+p2obzs1NePHvKbHZOu9mAUtg8pxgU7I0OyHIBg30ify5mC3yzpq43vHXzHrkpMDHw7t13uX33LR48f8SDJw/BanzbsKg2rJsGrQ0DbZkMBkxGK8aDklFRcHMw4bAYc3Wyz+dHzzhdzVNCLqYwUYuL8sXrR3zyo/+X29//HyjMhHUdyEyZrDI8QQnDqbSK+4cTbH3M/OwpddUSJmMCBa3XPHx+xFkduXH/Ho9fnnK+rNjfG/LNSzn3DnOa5Rmvz14wW8158Pgp5/NKDLK0ItOiRdsxzoKXZKwDF6XzJmuuruse4Oz+7L3HBy9O4iHg05hdt1+0lcM6KzLKpCPj2paiKCiyjCLLIQRm5+fMFkucD+yPp9x76zbf/sb7XL2yT/Atx0fHNJuWPB8zm5/xs18+4OXxqYykKkmIZHynh5K251Da5zpJiwDJUE8nECN1+ZxEobCThGoticDB5ct471gsFsKu6nWwusRYGkAib6BT0MmoKxnF69BcX69ZnBxzcXrOO+9+wINPP+HfloZ/9Kf/mNv3/5Avv/gh8/kRt6894fq1NSbP8fYWw2lGvfCoWDGfXVBXLW+99T5v3/6S04tjmmaNHQ7Ym1zCB4O1BcNcodKZoiaKZTgjuorl+Wk/jhe8p21qxJClgAgvXr5Eay1M17PzfpzNGBmfFVxI0a49Vw/vcP/tj/iPf/4vaJuVJJpGut3lsGA0LtlsGgjQ1E2fiDrnOb+Y0QFXcg8Dm/WGF5uXfREqzyGkwkfRKlCZTVqpaaQu/bmum6RvK53UTseqrisi22cmNY4kcjFEskKKqw5M70Z5RNIjMixK9oYjlNUcn51Rt00/Iq61gDt9EcW28Om6vrsxpFuP1lqigvV6Q0TciqPqDCTjtskBXVXZRSBJQOJWM3d32qIzeBB8J01KJE11uddpvL2LOSi8knvsfeDy5UMgMpvN+iS++wi6a16ErrAjjf+8xL4VAAAgAElEQVR1LIiUUO3cC9S2idkVXLus4u58kYZqN8mxlVDo8wnopR6kMdr9bNcYJKb4Lj/pCsfds0AplcYk5f52rOiQAD25fTFpzIsjctu6LYCruk+TXrlbL0qxt3+JwXhPXjOB5dI/in0sT7lfKq5EQmT/4BLlYIT34jbsrRfTkOBp25qTsyNG0zEEGbVcb9ZCg9ACAmU2wxqFA0xmCcFzfnHKZO+A6d4+wQmrAmWwmbA1vV9zMT/msy9/ydNXXzBfH3OxPKbN3sP/ynLj0lscXTzn02e/IjvwXMqnTOMCNT/i9OFPyTfHDOOc9WrOKrHdpntD8kwYH1JsiSWkJWJVy3g6oChHor/uZAQ5KkGi2tmcp5+8xJ7D1eltiiLDVXN8CCzXCw4KhR0MmeaWxasjqvmcxUXNb370cz7+X94jlNJM66ajVKftlo5oV9csZzMGZUFRZJS5xbuWo9NThkXBILcUed6PtvsQksa3p/HJ9LDMubY/JTMZJtPs7U3FqMWLk3NWjMiHY1rv2VQN802FE+FsnA+QCkznPbWH001g02QEOlMUB6oEVRB7kBbQARMrMhpUW+FOvqK5OCG7/R30WyNaH8jalnJcQojMZguRP5iUDPOMi4sFXma4gSBFMDIOaUJD4VdYv5T8Wmn2RwW3r1ziR//n/02zmVGO7xAQADkaMcvzUfTYIxGDEtMg14rjs6BuXL9xFacUs9NTok8NovT7KNIZLkC2nAku7dZAdA7SSLsKAgbrvKBxDVXbkhtFqRzarYnrCxyOyntaW9KiaEJgsVqx2aywaA4PDhkMSlYrkWQYlkNiGxjkQ8ZZCU4Kweg9wSQAzBqUF0O1ummo661WqerXmRSXRZ7TukBVVz0bbl3JVNegyBPYazpcDbFn6ca1k2Fp0rPupHm0gnVTE5DRzJC+l1krXgexYwQpulmC7nvGaJzr5F+EHeQj5EVBluWpEPeokK470E97+XTWNt5zvlxyvFnxejnjpNrgtWL/8j6H0yG5Dlwcv+TZySk/fnnOyx//Nf/TW+9w+71vMb50i00rAKFVitV8xqC0bNYbPvviCyoVEqM1pAnESPRiGNw3IfuqTM5OozSL2ZxfffIrHjx4yMH+Ad/73e9x5+07nJ+f8c79d7m4OGGzbjk7PyYox7qtqKu6r6F02gMxxUKVJItQhq+X2n0ciV8zsUwxqI8p3X8UqRm6Y5i1E5u759pd35u1JX2Totv3OsX57nNv84FuDap+gkulGC4s8M5p3m/znPSqkrIqojLb9+x+kGreroGplTDe2ZH78rumaEluQPdNDHkX51waK7ZplFiaxURZZ8SY9CN1D3rJ9YU+h+iut2sSd7l2B7p067e/9hBTTvbm15ZB/NsN391m8fYevvl3ld4vdsB2WpGdRnEv+RCD6L/nhUwdWpl6UiEmDEPypk4mLqZ7sM1JPZkWCYSOUR99oE0yezF9ZgFb5fN0CLqPnraVOqwzmoNInmmsyQE5DwaDQcqV5VpcEKPLsHu9Cai11ibCit02wCHJD7geYPNpUqtjrvpWPmvbtmKeRUiv795Yq/I+O5M+qW4KqYnW7w21Bf3k3wZcJ32T9kW35rOU1/m+/pT700l0jYZDcqWpatHxDa0n2oD2mjb4tD6lySOfS+KU7p+vhFCNpshLrMmwmWEwyMV4PS/StJKAtCpphHf5sU45idQfEWMULvnk6Ix0hmu0kWejUBgLMXpaV9PSEEIjE8SuFSKi1j2bFaX7eAoR59M6CiEBxBKtQ1Tydy8xva3bBPCqfl0qJfmUSXFaq8RYTbiU4FSRPCvIbNY3GbJE5tIIluCSKXQH2vbECS3rLLeZYAnd8+2lImUiTGqo9CzT0We07c2/QgiJ3LHVgW+dI8sytBUjQZQiQ5oHbZImCGkvCqlKCc5SijRSG0NPwAFFlheUwxFt6zhbXBCfKSBjMB5i80vk/w0o9u81SCsHmSRcHXDZBZWun6mSBqb3DZktseUelSpp2oaJMZCMCMRZLuDaADpgdU0bFqxbz5ePn3F+dMTe9IBLk33u3/8mv/sHrzn716/wUYaIopghQtJYMjGA0bTeIfoyPr2PbDAVVWKXkQrLrlMZk9h07PXngnfd1BJap+BIpKk2qMyiiOIASJQDFNCFId8fkxU5m4sVrq5F+ym9Xma3gslCj98Grq4oR0VccnFEkXTxYhdr5b4qAY0WdcNf/s0vePDwKX/yR7/P733/WxxMp6TmVf+66Q37wKSUZn86YX86loM1KqJRuBCZHl7mHfNN8sxSFjnPnjyhdi37h5e5vKkwaJbrDSfnc371ySPuXL9JG1uapmY6njKbLXj5+jXHZ0cc7B2yWtc0rmY8HNFUgcIa8myIdobW17S+FaC48UQFk8mU8XjC3t4+Gs16VfHlF18wWy1AeYieMivYv3aViKJxjuFgxKqqadsNMSi0zbhy5ZDF8UtKYxiMxkz3L9O0HldvUFEz0CXv3rhHriKrZkWIgXVVMa8qFnVDU7ecrOYcr2YMi5z90YQr0xHTcsydvcsMreXp2REv5hfM2opWewHOMEDLxbPf4LTh4OM/JhtelmeqJCENweExHByMuXV1H8U509GIg2mJLksqH3n+/BWfPT3m4Ob75FnO+eMvGWSaG6PIx3evcvPaAcvTc37585/w61/9mpPzU4bFUBJ+m0a4SCzSLvGPUe5/noMRIDZ4R2YsIUayXFiNVV3jQtKmTZ3OLuEiQtvWvUu7sQajFIOyJJ9MybTBtQ2rTSUM56YFpbh6+ZBvfvQB3/zwfcbDjPPZKZvGYXVJ6+Anv/wFP/zx37BYSwHUd9Bd52zbL+M3vjpGhFIIS05HkZ/Qqu/SdkF960Yph3lWZDRtk8wDpMnUMWyURDGMEmK8teJePihLqs1G9lGUsRBUJLiaanPCrz/5Kb//J/+YV3t7/Ornv6CplvzhH/8xd9/9E55/9Ut+8+Upz17UjPYnfPz9f8S9797iR3/xE54/fsimXvP67JTbd9/hxo33uPbsEc+Ov4Co2d+/TowQcIzLEWpds3AbNiFywZKqXrCeL0EXxChd2OFw0CdFm6qiaVtykzOdTjk/O4eoaHxDFpPhCZGwjtiq4Af/458SVODp44cUWUYbGuxogCmM/F5dUxiLyi1VtZEEJaTxV9RWY7VPkLtRY5GJ6AoaMWCTrniMYrKojDhsd4mvVhofRBxeWS1nZDLUIL7J5iSteQkL8v5ZnstEQuqkKsAozX455N5oH281F0cnOKXTKKQsuOBTIdIVSjsgHsSenb4dAez03BStd1gDs5PXuGotWnu7ml9szc/EtKortwQsETBR4ULAtJHcGGyhpZkZFLWPOBwWkwogaZqKWd4uu1dhrGVvb19AQKXfKHoSp2AHbFRo0xHXUxETt2OXb44VboH4Xc24jj0tv0+vNxYTw3r3LnabWqcm6i4DKYQti0fWC32xpfrnnYDlJH/RJfmKVIj2n1liqUKYe3UbaBuZANplNyecSZoOCgFAhlOyNK4s76nRSGHbNjUhGQ1K/NZk+ZDWOYzNKEcjuU9EfPRi0gNEPEcnz7l0cMBkdCCfLXrwHpMbrIHovSTjSWdXG81wMEDpSFut8XXLcr2knIzJ8pLnTx/w7NknzDcnvDx+SLQVeZnz4QffZL7a8K/+3f/F3bfu8Pade7R2xoNnP+aGmbBeRuzRazh7ga3nXN4fc76uqXykyCIDbYjJ5Ev2rxjVFVozjoHa1bx+cca9b9wnzzV164iuIW8hW3je2S+JQ8+eithoWETNvNnw4tUTzrXn5o17DPwI30QGqsC3Leef/IbqD15i7tylMIZWOdqwRWd1KmI3mxWz01Myo0AFGtditeLx81d431JoLTlRDGI86pzIuxiL0aTnBptmRZFbBkVOkWUMBwVtVUEtBa9xGwaDnL1xwSQrWAXFvPKsF+e4CFYHNCXTvesJwG2IUVL5qDXeN2CLtOME0tTBEimxqkFfvKA+fkgx2WcwHdGEgHKOYZlhioLleo02Gba01CFS6oyL9QanpIlC0L08CjFiED38mMx6lFZcnQ44+vxnPPnlj8mnQ1b1ithIY0lifehNXrppsc3igqaqcP6QQhc0uuHV6RnFwRWY7FMqmRirFnNC8OQ2p64qIEoOTSfDJRvKIyP8PjgZ71UCALgg+YpRmjYGZusFrXeApolQI4ylyXDAx+9/yGZTM8hLclviXCrStJjc2DKjKAtya3FtxXq1xvtInudiaJfnCdcWwCR6J1IhuSXLS/I8l7MmNRCN1uiImA3qmBQNtqY9MQH2crBt6wulxO0aLeaOSqeR27aRJhtSeCpl0JnBK6jqSpjA6XVDcJKfpNfUWgmDNmkWqqDJspKDw2sMRgMa7zBAboVF7iNUHirvmbmG1WzJyWrD6/kFjQ7kueXq3h6XC0MePX55LjnfcEhoI0d1zVc//yVhcoX/7c5H6LrC1Q0qRhYX53z6t3/DlYMJv/jl3/DoyQO0VUJ6SDJTOgFwwQWyLBFb0nnulQD4+5Mx3/3Gt7lz5R5EafROL09pYsWXTz7j8NqEn/3yr3j4xVPOVkdkN+B8NRMQyBoZ5wYEDReCijYGneRoSDE3wBuxevvQYg/I9jI53VkfIIQ2yXrIb4Qoo+REaZQqLYB1+K341emtvinHJNRNYXh1hIge8EX1IOHuhI7Uqt1kj+ilR62I0ffgpu7yhv4YkM/j0/0mNRHpmaKyx6PQ6JKHgeQcMUrTxVrbjx+LdFKS00vAiW8dBNkPUQlM3rrflt+Ty9vKXMitSSCsSQz04EWlbOe638w32Pk+fV3yd/3e11+nuyekHEDHgCYmrf6cECXGVVWFMYbRaITRCZzSRsDGmCbFnP+t97JGUxY5RTFIYLqAtCI7YAihpWkbtLIQWjZrYaB2gFRmLMaalBdK7W6zDCWHfH8NJk3RFZkY83asSJynyIX5WGctm3rTSwl0bPGqbijyjNAm8F2lsfoQ+qne7l6KTFBNZw5FFLawSDRs7+kbjY4Uf2IU9q3VmsY1FIMB0Qnjug1pWk1tp5m992iSga6CqhbJgo7wB4hfi+oMzdJEZQjoAL5p2VQNvmmwComfCowRPABEB5doJK4oORuLYsAgH2BNhsYyGIxQiBZqZhRKewgbvBLSj2hbBzwuaQODVgbf+m2DB4U2kTy3YGXCShkj53gIZFbhg5jS6yxiUbStGHFlweOMTPTqJL1RFgMUwmBumgZrDcvlBQFp9ouhcEtEE4IiBHomq9GG2CbGesLDYgQXk3mnMTLRozUuOqLTKGuJbYPNM7T3vbxLBJbrtZwh6Zxz3kuuq3WS45LnBOm+bzXbklav7PUYI5ntZNQ8WZbjnNSBWZ71zZoIiSDmU7wVvfUYtTCqrcFmAsZGL5q2SmvW63WSy5C91UmWqoRZ+BhxdYsHTJZD6zg7n+Oqz8C1NDfvMB1Nfuvc6b7+XoO0Etu8HCIJ+OiE8E1MuipFAjW9AmUwKiMzA4LTqSgKfWcXDGjLbH7OanFO9DXRa16+eMLzZ494+90PUEFzZf8K3/voe/z6Fz/m4fMvyHOV2ETSEUCLNqtCWFg2FdsCUuwUpTudto6RY4wUtvqNi5TOS0xdQnHoS5qycRvcpbSNYqZLxFiNmQwpAjBD2MVeJBhCl1spGQvvwOqvB5etRlGXmFm6YjQqTdfbNKmjeXQ648/+1X/gq0dP+e//9I+4cf0qZT6QEeHk7BiJUux56VrJa+segCYxArJ8wPUbI7KBUNnfKgecnp6wWW8Y7u+T+cB0PGV/us9qveTLJ8+Y7I04PDzk8t4ei/mc2eyCeuOZhxWbZUW1rrl6+SalVfjKUdctIQid3hqD9prhdMxwNJISJkZev3pFU7ueCTwaDjg42KNtavIsx7WOTV1jjWU0GHL12jWssZwen3A2n3P08im4ltbXhBiYL+ZoJY6Qioi2OSpT7JdTSE6KEzvg6mSAizBrA/PVitPzc86XS+Z1zflqxa39yKWpZjoaci+7SV4MeXT8nLNmRTCyH0qbURaK5YsHKFVw7aM/oCr3qIKRThyBLCiujUv28oiOULUtw3xIORyyruDBs2PmasLdG+9w9PI1JkampuUbt0a8dai5dfMSz6tXHL94ydHrY7TOxMwkdHIdEoCttdR1JU0MY8nzjF2zjCy32BBTZ3/LRtts6uSCTDo0Y9JcEpDOBzlYy6JkOhmzN51iExN3va5ZbpZYMoblmGtXr/De+/e5/+5bjEcj1qs5rQugLBeLFX/xn37El4+eUDfSOVOaLauv756+mXTt7hXTuR9H+mtWit4RuRtN2n2dSOyBu26kMM/ypIMsmkDbPZJY6VGCZF03otkZkNApxxwxVFTrU548/oIPP/oWP/7hv+f06Bk/+ov/wLe+8w+4/953uDg54ez4NXW2x9OjFjPOGBxcJz+bszx9xaaumezvc3jzLqO9a6jTF2g1YDzaS6NRkf3JPsXQsly3VK6liZ7NqhLdzHwA0VMU5RuFgnfS9d9UFV9++aWMthjDsByKoUEr+yK2jsuXr3Pz1j1++Of/GbdaMR6WnLUrzDgnGkXrI7YNtG4JyeCL7kyCHUB9y4YUtkbYYUFuf8cHSaZUQsYkMZNC0+jERg2BOiX/bZLlyBPLKTjfP9+QWN8C0nma0GxZDXQdMvmMr0+Oef3pl6gyo7aQTccpDqi+8OnGzfvmWkpAzNdiyhvXhLA9g4+MxwXT6ZSmbnpDh57hgDQAO4ka0U+WJFDFSIwKG+FqNuTWcMxgoBgfDDhe1nz+4ggfPYLmSdIUk2RDx+jo1zuK58+fE4l9wbhlHv/25w87MfIN5i+88ffd/dh9TxqDabLlaz97Q4v97/jajYe7e//rrBg53t4sZncZOMJ0YOd95T504GtI2o4xMS22TRwZ+VYocVh3Mh6sTZYmiIR14NP5ZE1GUCEZ4qnEHjapIRsoi4LofUrKA7FtxdDKKOqm4uz0SBizFhpX04aKTI/QVtgJTd2gbYGOCotlWIwweYZvHU1dU9cbxvt7aBUYjQfMl+c8P/2Uxi0oiowr129z/fptytkM73/G89cPwVRcXDxnFAa07Zyz56dcC5owW7FcrNgvL+GqwHK9Rg00y9M1Q1WijKz7qCB40CoyUopqU9G8fk1z6RKD6xMxCtw05KsadRG4mWku8pr52UvKpqBpaqqqYeM9zdFzRqakbgtshCzTDPSA5XzN6ZOn5NdvijltimqyFhCQwUcuTo959fIZy8WSqBVtMoPx3lMWGa2GzelCNDytoXUO33pCD8anBrtSWJPGo+PrHrJRUdZMJ5+TWQvKoIqRAL5NhdKKvCgxB1cZHd7jpbM4ogQFOgBPmktitJeYSGRoSpxSDA7fZjjex472aQZXaaJmmOfkoxJVFP2Uio4RH1pm8wX1ei2720L0DhW9SGyJW4M0wDJp2A4zw7hU/Oqv/jWb+RMOr9+i9S3GWpwXIFCkQRJ4FQK0DcvzU5y10qwxImugR2Nuf/f3qGZnvP7qEW61ZDAYi2lZWyWyg7AFO+dnMbvLMVmB11YYweMSV1dcVOcCLBspvJarJev1RjSEo+TWKmryrCTLS+qmYjgYMCpHaNKkRGJby5EoWokxBpqmpaoq8h58TUxHpUQrMgHISmuszQQU0eLTHrScIxFAbxtFWx2/zvFcmIJbiI9U1CqMEmCkbhuG5RAUuOCE7RkR02GlMCanrWVPD8sh3ai1TDR1eqXpLAuS38Uo2vRZUaLHU9rJALfeyBiv9yw3Gy5Wa5auZeYbFk1N0zgKrZmUBZNhiTFwYGDS1th6jdcKleX4aHC+oUaxDJ6/+Kv/xLJt+Gf/9H/lrdtvo7XBGMf9d+7w+vFjfviX/4lVaNFaWNg6AcrBdxtWWHh9U0+BiQrtPNNyxOXxPtcPrjCa7DEcjDg4PKD1Fe/dex/fwAfvf8yVyzd5dvKIr1afMz+ai/GcTRqxidlpUs3WSXdp3TVuOz3XLq+jb/r18SXFrT6OIQ3fN/5N1wDtUoSuHlQSP7pG7ptM0TfjmsRhMfx5EzTejVdx5/vibt7F6g5o8aEbd5bPoo2MQoMArrprdO9cb3etWuuUY38NlE5fxhjJq7TuDaXKokgu86kBnmRA3rjGBHpu4/wWHO1kBuNOY32rH7ybl4RU2/oe0N/NIztiBnTvo9/43F0u8PU85Y2/R2FXehd6UpciJvAyjZqnBrxR0LRbuQ5rjOhrdyBjukZjhUXqUs4gy0SDl+kNH8S/IniPj8IcbRNwhhI5rhAcWmms7Tw+DKrI+3pNzoCYcr5AaD1NWpO+cfx/zL3pr2XXeeb3W8OeznSnGjkWSVGkhhZlUbbc6YbhuBF0kAABGsiH/HlpJAE6SJAggIdOJ91u2e6WrcGyJkqUSKrIGljTHc+0915TPrxr73OqJOWzL6Ch7q0695y9117rfZ/3GXzvKMpSFM0+jDXS8NlF6RxzgNyw9slBu7LfDfskeXW4EMQOJ9d+A+YzrK1BhTlcr10PpkmI3y1IbSThT57e97kMFxzFeU9dFtgyhwAqIQ/0riMFn4cwQjgIIY7EDZXE/qTvejbbLaFrCb1494YQ0KXNYC+oUvo3lbEfxRAMLftRXRhqK2vWGiXndIoQ8wAzyHuNKtIHR/KRwpRs215U1jlYTpOZqdqSYqQoi3y+2OyFLkAtEWxdEgtDjAUh1mz0WtSrQVQnfdeh0EyaGVVZY4yhDOIX3XVbfHDyPOf6QqwBBwuCMFoJDWpuwQFMrv1F0VJkP+KqEsapDLL9eP/TMLQxhqIoWK/XQuoacLSU8M6NAV4mk2zELmgH5Kvh+VTDvjiEGkLqPVoZeufl/RhDSnrcM8py18+aPDBLMQpTe2Bkx5wVAkyahpSSsHJT3OWOGEPd1HSuJ6RS2PEo1lcrYggsL6744IMPOH38lKP5gt/19Y8apFV5Vcvhl/2FlMIWJRotC0NBsZjTmIaIoahnstkXCqMGPzWTEXcBDdt2ScLJ1NIUdKnlg49+wnvvf5ODowZrKu7ceo1/8Uf/Lcu/+Ddcds9IRjxSfMrAVIqoELOHhVD6YwzZpsDmMn8v4TJpVMqJk8jBFjOSOkxrhm3EGC0TpMDoVyObSZICWSspwrVMJqvDGboq6VYbuqsVJg5IPqQkm+SQ2DweZfkw2Qcynm+Kd6mXMojUoMVjxbme7/74Jzx6fJ+vf+Vt3nvvPV599VXKosC5RFJGvFfYk6QmMduG4QA11GUpf06AtkwXR1TNjNVyyfLilLhZUWuNXSWullt++sHPeevtL9Cu11ycnuK8k43YRaIJTOqabtny7NEpk3qOAVIqUcpgdEVdNFR1iTaG7WbLZpMDw4DpdM7BwTHzxZxEoO8cp6tsxXB0xO1bC5z3rNdXPHpwn3a1wnc9bRAQuCoKjBEJWFUOPmvSqCU0hbIsyimxX7PeXBLxGCMT6aOy4Li6xsuLIx5eXvLrp5/zbL1i0wdutGtuHSyYVhNeW5xgCHz89HPO+jVJB2praEqD9Z7tg1+wshUHX/p9vFV0SoPy1ApuTjTTtEFlMLHtOnTnuNgWfHrmuHHjFcJ6yeXlJQd1wRdvGr54q+KtV2a0/ZL/9J2/5d5nD7BGrqdGobO/cfJeZLV54yrzhGkIpyENEp092ZaSlMYyyxGGAizESIqRuhTgoanrPGXWTCdT5tMZ7XbN5XrN1WpN13cUheXk8Do3j6/z0qu3ePMLrzI7nBBcoG0dPiju3v+cH/z9j7n72QPSELqhFErtALLfvQ+NEBDeO2EPa7FHGJqZoWPal1hBLryztQFKEZAACW0MBDUOd4DnwN3gg3gd5SZPFXLIBx8lAbYPYJbc/fjn3H75dd588x2ePPgVS/WUH3z3r7lcLnnva79PPTnh4ZMnfPTJfc6uWmZ1w/HJCX23IfQdq4sLbly7xuH8iNpOWDRzGlPQ9Q5bNiQ0bd8SVcLriO88Z4+egk+oSgqJ7balLAuWyyVVVY0suGldo42E7aUgLKqQ5KA3SUHUvP/Nf8aTpxfc//WvqGzk6vICSkOqDV5HGlvzhS98gc8//5SL1SazZ/fWS07wHRodaTRl3agM5KdROo8Um3GXZJwyAC4YhyblYjapRF3XkAtEkWXt1vJzoCFyMO8zPLPKiQGdDArCrMKUdiykVBrYNjsJk0x+d+yG8dcMzVH+/EOTIZJCSQGXQlbhh0Jzfz/Xmph9SCVgUOfAMvHTnQTNS6rhCwfXuTUrmDQ9k+tH/M3lZ6y3W1JT44kU2mQwKQd+mawiyYWxUkqsPxRjA7F/n4brkz/peB9fbIz2QdsXG9B9pu0A2u93hoNUcr9peE7qya4BffH7+8ykfabSUDz+tkZ4fI24N5RNko6tAN93RO8EjEq79y5ozNB8QbfdcH52xu3X7lAUNUrbfGbKAhBQWlgIWgmLQTBfYQgtFguSd7igUdFmxoJYNIUET06fMZkumM8mrNctfd/RJIc24qvpvaeyGpJneXVB13UcnJwI68Yk5vMJlbWoBMdHx/ze7/0+6YMl9x99wrPTJ3z86X3Wm/8g4QrJ8+qbd1jM5/jqkOlqQ3zykOJyQz1b8PnlisJUbLaep4+forTFFDPaC8+j7gptFc2kxJaGgMPYghI4Lgq+fuNV3NmG7cUlKgYalZihKFOBmwAnNZ8/OSX0FaUpmFQaFRQ+OM6f3KOMloNmhpoeEKqagCdpnRmGJqfDwyBvEpZb4Omje1jluHntCGUtRSF2B8aQ05sT63XLcuvxLopUNQ1wWgZXlCYZYS6apCmrinLaoIzF2oK6LqlLGRa5rsf1AYzFKEWKntVyxeVly9G1a3TNy2xW4r+flGGX2q7yr/PYFDBK0esIqsGpGb6qUM1LiKIjYmNHNavRKmGNJrnI8uIZi6NjDk5O+OyTT0jBobSBkFDRo5JHZVOfpLU3qLwAACAASURBVBRKW4oAKbScnMwJ68c8/uSHmNqRCgtK0q6d6yURWmtsVhMUShHWV4R2jZ4fEpzHaQ86ErZrnt79mOQD3aYVz/PS0vWtKM3izvstkVmVWjE9OODk9iusXMQHWJ89YX2xhEQOeFQ4H1hvNvQ+4EkSEqyUBJgUDaWpOHv2EG0U9kQ8IcWaRpOcHxVzg1+e1orFwYLS1kyaJgMfOdHdFjQ5kGUIDAvZHmaQWWsr9UQQE1n6vt8BeIYxvEslqfuH/WkAnpLS9GHDk2cPqcoJi8Uh1uZgoVyHCgtPBux1PRnBrRgCtrC44OX8CDIwtKYgeRkCBg+Xm46Pnz2jOw9s2zWxc8S+x4UAuS40WjFpKq5XlgOdOFKK0nX0LmCUeA6XsvsRA6xdZN12ckZq2HQrvvt3/5HTR/f47//V/8A33v995pOSMk740+99l4dPHqMaiy4KUgrCOE5DUHI+Q7KUPOVhOlG8gZuipi4qFAYdSwgFKpSoGDle3EShOTxoqMoFvd7y4P5dlus1SYuU2MDIAn3xPIkxjiDjMLzbHeBSBygY8wsGUHc4DwZ/TtixcMdz3ujnvrd/Bv425cluqLizSPpdTNH9n0MmNjGAvynvYWJrJELofA5m5jCwZ52Rwb189g1DTnje8304k6UfzEzGJPYKxJ2NQ/B+7I0jogJSeo+8pHY2EXLdUv5d5IFVBqnTbl2MYM14LdIuIDjt7uVwX/frgP2v/Z/9rq+RgZuxTvHgHD67AIwD4Di4D5DBVaUgGZ3DbIvs/yzvzfmetm1HEHr4fmHEFxWVazJjMdhR9q30EFDVixTdyJCXlIkx2d97vx/zLo5AdOhF1SMWwD2678bgV+8d2ohHpzAzbQbv+1GuLmQHAW/LspQhW845CCHusj1izOFUaVwPg4Xkfm1n9p63AddQeQ/XWlPaCqWFWapzPk8dI00OqCpsgTaG4CN92dJ14jk/Mry1BHYNw1Xf98LU9x7vWiE7IKxg2aqlqrVG45VYMAyxVtvNina7pSor2qJk22+oyorCFMQokv4Q0zjQk6FuwMeOwlYoWlzrdn7P2Y2pKBuq6VxU4oXOOQ+CPZXGEsOQG6JJSYvK1kb0XFjX7XZL8J7eOcQ+R4kPrJVw7qqqZK9S0LdyfazOVhyoMThuyE+JIWZLEjWet/nWkZLYccwmU5SxNHpHYhzA8WrwUrZimdH1vay9FCFpSq0xCFlKMk88MTg2W7+zTsvnruCHVgZ12X5xGAYppWi77WhfUJVVDh7bz94QBZwo9jWhc/IsxTjuUTD0ZUlYtEbWX0IAd2MMTdMQfcAmhfJZUa00m3XHvc0DHtknv3MP+UcN0gqYI5MhUJiywEqCDZPpIVZpnApMj4+oyim9i8TOklxOZzQiw0lBQhGUClycPsBvr1Ah+8NoRUfg55/+ip/87Hv84fsN9eyYWVPw7ttf5psP/5Bv/93/S+e3eC1BOUm667E4V9n8eDig2Jv+DczaYbKgze5AURlJ1XqQ4w69ZkSg0dyAJpm+5O1e8Nk8HQcBT1JjaewcrRTd1ZroBtq1TAOGBwU1bKh+PDAHGcSLkpehgJMmOx8EOqBUwhO59/Qpl397yf2nT/iD97/B1770LgTFtgtMposXEiOHzyXAVfBBQD6VwXRkEyhLzdGhZTabcPH0MXGzpplXLA4nnD9bsry44vWX3+Xh/c949PljnJMU2e1yS2Fq5pNDYq8w0WCVojAlTTFjUkyJPtCFHuccPibKsmI6m2VZgSYkz3J1he97VFIcLw5RRrPerLk4fSZhMUZkYSiZTOHE/mLbb+j6TopgW8jUiUBT1TSFRRMplWJWTum2W/oY8SFLmIJCq0RjLG/dvM7RYsonjx/z8NkpD85anG959eQmi3rGS4fHIpN5fA9HFEYOCqs9NStWDz6gmE+Yv/4uigkuJioLi0bh2iUptiTv8aEnRMOvPn3KWVfw9vVb3Pv0LjY6jirNGydzDpvEYlbzDz/+B779l39J33mxWVDkUDDxGY0GumzOK8VCQulEDJGiEDN8ZcxYhGnAuV5kC0ajdUWvejabTlhGhfj5TCcTqrLkYL6gsBalDE9PT1ldXdD3jmRKqukxL9+4wZ3XXuf4aMFrd24zP2i4uLpks2w5PVvywc9/xmrrOLtYMgz0hckmMqGdHH5XiO3/eVdc7ia3RSXea965LKvaFc9DwjQwAlqy4e8KaecloV0p9VzxNRbl+VlP5ANAD4EroIywtDfrNUGd8/GHP+Vr732Lx/d+zXa9ogueD3/yQ5ZnV3ztG9/ijdfvcLHccPH0GSujUb6jKgzd5opf/PTvuXbjBo21zOsZN4+vix1Alm+cX61QrqOrI0kF8I7N+RVWWTRDcjHEkLIfraZpatp2g3ceHRO99zKkWXsBSCO4jWNxdJvX3nqXv/mrv6brL1luzgixp6gXRK0xNhGS48HDh6zbLUqLJ9YAvA57puxXuwm+0Xo86LssJwsxZtmghBVMp1Pc+bmYxqu0A74zqKpUZkjsTfBVjCPbZZ/xopV5DqDN6Kw8Izkcopw2hLrKRv9SDJMCIULXdrk4zk3L2H8Mk2G1B+LuDQ1SInhPQAqR7XbLKPlJA6incq00BDuID5SOSQJ4vKJAcxgNL9uCaygObSJsL/n1h4+5++lTtGqoohGfJZNE+jisz6FxHJlfstkPxckAYMQovk37z9NQeA9rfgQ491it4zXd+9oBoblpfgHkTXvXSFjNPNd07TNpfiPYbLyvz3vL7Xsev/h+xzOTNLKfpeKMpOjZdj3OdahcrkvzijSceb1pbWimc1IOEBL2UwYZ0GMBK/tB9pzXKQeRyb2t62qUi8UQwBbDBQNlaH3Ps/NnGH0DFSE5R+hainGoJuwRpWF52Y7rOETPs2dPURoW8yO67opNd07ZGN7+4pc4unHMD3/yXR48/gU+BaIXQGQxPeb9r/wBD9uC9pc/oX+2pi4Kus5xenXJ8ck1WlpMHZlPG4q6wRmFT4q6qFHTCaoyGOVJKtIlj/FOnuErh0keYyrqEkoDwck1PTio6a7P4TRRUzGpS1ZR0QXQEXTq6dpLtDZ4XdG8/DLX73yBS6WIRpHC8AylkbnUdy2uX/HN33uHm9evU1U1TVOSkiOFDpLsf/cePOH/+Ld/w7PlBmMLGcDrREIKfVs31E3DdDIhhUg9maDrBqwhBC+BkzFhSrATqH3EpYjrtpRNQyoalpvI0etfprUHeDpIAnpiCpSK6CgMZKOgUAEZhRtC8gRTQbFAmYDyLdBTKJjXNSrB8uKc6DxXV1eYQgJJ1qt1HvqLogwVJYwk9dk7WeNjxIZEqSzXTg44+/CnbJenTG7MUcaOIGZRFBRFmVUyiqjAeE/oW3QMuJBD9spapNjtmkc//xFKF1TTA+bHJ2zXl2y7LQQvjPHsmakUDOqoq/WKzb3PUGXFZtPiVpcUWpQoMkGTIVPrHJ4oSjtjMAmSsWhdAJqqrPChxwdh/MQkjeFqtWS1XDGbLtBKGLanZ6ecHJ8wbeYCzOZGE8STUM4VaeJDCJmoEdm2IpdsYk4gT4GyKNFej3tT3tIZCpidRzi5kRSSSFUVlHVWwxnYtBuKbJkWk5yDIXt+C/AiQAIp+8UbhYoJn+t/rRRWFwQN3m9o25bT0ye02hGNxUYlg5CyQduCksQsOhZ45snR+EiVH6dCawpdoKPGx4BLCqwlVDWrcCrBXzFI26Midz/7mH/zv/1PtN2af/oH3+LR/U/5+5/8A73egZYQR/siMvtvBD9z3ZUUYDQ6QFlU2KJiCHwmgkLCkqyy+ADOSe3jXGC7dWzbvaC1lMb9e9z79xq6sNdHDSDBwJyVsy7b8ewBTzaH0RWlsPhHtmfaMQiHwfBvq1P3z7X97+k8CFb5OPptIK8se/Pc6wzWPzsLOwEsRsCR3EoOHzt/TzhFu8++B0//xnvcyct3DPH9L+k5/fO9byIPZQfHzN3vG+oIpRjr8QFkizFibSEKrvG6MfbrQ/0/fL0Iuu5e84W6Yq/uePH7z38YSDHRbh3xIKGtDBRI+wNhsTmLYWdbkZIo8EbgcahJYhqfX539XiWkDUav/hRHNYbJlmxK5TDzlCj2AsVBwCQfYrZE2fUaKcYcMgo+g3/a6PHmSz8i76usSsqyYDKZ5HwAWeuyt5jxHnV9Txzwh7wOR0VyfjbKbIsjoHqApMfQ3cHeYT98OuYhzDAs0Gmw31OUxqIKAaJDEGKBUbm2SpC8YCRN02CtAHkqszt1XiODasnoCgXYwlBZxXalcH3Pcrsl5vWllPit20ICzlSQ4Y3zHW23pXc9ay3KKK1MHs7I9TS2wOdn3jtPiB5dKDQtGgk5TiFhw2C3AkVTEQn5WiVMYdm2LcF7vApYLRYMJp/Dct/yoB/wQYaNkUTvHTEhCmIfx6ZDhgZaWN35AbJasgB0Dtuy1pCI6LJksJpxvs9K2JwXoeW8Wq9WKFtQTydUtfjgD8Ov/eevKEtMDglrX+jlSl2Oa7jve7btVvbpPDwymWFNZrikFDPrWu3OZS1nUd/1EijnPVVVMZlMdn7Jzz3KCd2JtY0dvaBTVsWIlYbSdpxStZ3U0cYW6CR1+mwypYgFbdvhVE/fOrrtbx+ewT92kFZl6ZIS6d90NqWoLaksqSaHlBR0oQMjsk1jDWmT0BHKsiLqiIqa6AP4nqvVY9zmDHyXDyxh/IRS83R9xXd/8De88/pr3KoLqmbOzZMb/Is/+q9ofcvffP/bqNjjlUdhGajz2gwLYDe9LAozMpuGxTAsDB/DCLImcoGESA/k3+8O9OF0TWlgLCSiFgZxQZ4ykUHPGCiqkupwSr2Y0l2t8astKU/khr+n1V6jqmXaopXC5GYacmK9yXYRw5R+WIxRfIRcSiQsXZu4+NlHfHz3Mz7+2pf5/a9/ncvLS978wrscHt6gd1luRWYDa4QFoFKWfiiwmRGVT+KowFYTrt+6w/LsCVcXn2NMSWVKVmfn/PDvfySyRFtjomNSW9ZdD77AO4VOmkJXTGxDU83R0dBuNnIttTz4146Ocd7nkOCI9w5bapGHOEfoe9r1pRTwIYinWEzCjiXgYuR8s+azsyc8Xp/ikjByxXdOin9U4mgy5Vo159BaTpqa2hqm8ylpE3CuR2OyhClidMIQuTWbMq1eQafEg4sL7l2c0afIF26+zMwaXjm8xsVmzeP1OSpJmIgxEW0duFOefPgdrsWO2cv/hFUqqCYFZZk4vzwnuCtUUlTFgqL1/Oqzz5lfe5XLNOF823NUR16dB25Pe24dX+fRwwd8+9/9BZvzZxRKgKSiEN+hhACSnU8jyyOGSCAyrSYkI5vSKNExNjdIGlxPiFBVVWZaRo4PK8qyoCorkVKQmDQN1hjWqxUXV0tW2w2VtUwXB1y//TqvvfFF3n/vPW6cHHB1/oh2e8mjhw9YtY5HD0/5zn/6DmVpmR8ds8lrYAAfSMNEfZ9J8Lu2IpEvGGswRrxsuq7Lw5jnAZz9MKbh3/ok5vh2eM4SVJOGdrMF8jOZG7Ld4ZALCZ0ny0ahSo3Rli77x7l2zaN7dzk6vsWdt97g4w9/RKMLlu5z7vYt63bFF7/0T3jzzXe5ef0Wfe84fXKf1faCzm9IbWSzqgjeM53MuXHzJWFiodCmICR5794knGvxmzXb80uMMjItzKm6fS9G/Tdu3ciNJRweHnK1XNJdLZlMpsQU6FuH3zr6TeT9//KPWXWBx58/YLM9J8QeU9c0B4fopsLWsh9cXF1iSrn2TdOgtJKU9T3wcdjTyrKk6zq22y1N04z/efbsGXlR4Zzj/PwcpURqFvJgIeXiT+s8Nfd+9EA21tK77bhOBumctZbpdMpquWQYaOWRfm7ocgiDzmmmiMdlCuKJZo3BjY2TNC27MyM3B0NHpHcN0fDenZfQBkmGtfSuk+J2eM1hhA1iT0DC+kSTDMaBbuHabMZLR8ccqESRPJdPn3G+esK9VUtt57xUz3HbLavOkeY1fQl9yvyA/AApsirg8JD5YsHHdz8BJChQ3ov+jedrAAGG4n0ouoefDc/F88yb/FnS0IP/FruE3ByP9yq/Dvk1hjC4AdjfZ8TsM2xf/Pnwvl4EZoftZLhpErwgTNrgHO2mG4P1lNovxnJTHSM+KWxVM68m8j2G8B5LTCLXS0oYNinsfJAlhV1kViYPRTUC3u5aMCRAUiWenj/GtRvefuNVDIFuvUGrBkxFUVUyGjaWo+NrdF2PNpb5bI41muXlJXd//RHf/9Ffc9U+YHFSc3iyYDJbsFhcIyXx9yrritrOqM2M7ema+OSCdLaku9qgTg5Zt1tOrh3x2mu3sbXh9us3aKZzrr/yRYr5MXo+p6xr4aQkYSWn4IluQ99dsV5d0l+cw+YK3y9puxZHpN/04BV1U3H8yiFr7QhbTSoPeOnlN3HbxJMPf0XhBcxtFczfeYPZN76BunlTfOh0GoGYYaggw7iezeYCQ0epeg4nU8oaXITgEkbDZFpRlLf5+pfe4D//6BcUkwZjK1ASYJuUopnOmc4XVFUp/rO2BCXDvtD1+L7D1AVhqAVTzI2nx/mI15bpySH1wQlPtz3Jh1wJ6qwySGAlnEssAxI6Beroaf0VyiSSmmKRvaFqauZlKenaKEiONipmhyfYasL51ZKtG7rZkFkCMqhXboPVkFIlgGeIEipVTrj/q1+CUtTHRygTM+tbpKraaGkAgWQkudq3LYpEGxyrbo1pDkkU6EJT5256cXjArVff4oMf/1Aolwx+1uwmmigUBrynd1fjvl5pIAegKGNkOBY8m74TqwMGOYXGFhVVWZNyfZI6AS6EtdOT4q6mVojqJQtz5FnMA5IxSTqnug/snUEd0wUnTN6uRynF8ukTnOspi5Lbt29TNxXehefqixhlXxl8Rk1mxqUUcu/RcLi4Lc17VbBcrVi3V0ybGcaURCLr7YZtK36v7brl2skx1g5BNzFbN2VAUUM0FpUCRkOtIy/VJcqKj7chYoj42BOCWDccpMBx8pQpy3y1BRPRWVmBUuiyol4cM7txk89Cx+rRfaIaxlFi0pFU4v6je/zP/+Zf8+DXv2R9ecGTy2eESlHk+5WUHpl2Sg0y6HErZmjQSWCVoTKFeKsnRVKepBxlrVl3Hh8gRclxiNGx7TZcrZZsW0n9jhnYUQhgGPfOqBcBUp+Ze6OKRw0J7YmdzCYDZClm25+dp+0w5Ny/7y/+rueIAWoY6OrdGZj/zmgXkJ4Have/RpA2wuB1nFKuZZEeaQB9h/CmIZx6+IzWGEIGJMng5wCoSQjYvoeyEr/jvd+vc+0c0uD1znjOkTJaG+XPxmgC4le+u807q7GB1SvPfwY7IdcYcv2HgapYGQ5nfUSl3bXZH8YPrzv8nv264HcNkoVwka992u3Tw74Qo7DprbUodL7GOwAyqSF41I2WgiNrL9cTgw+/0ZrSWgZ/6ZSZtTqziYU8BgS5bzGIlZwLgW3XEbxYMg32C8N7MMZQVhU2lRRlkYM9h1C5HUahsjIixoh3ntFOYVg3KfsSx11NNaoAUhKcJtfMblynkAs4Ucnl62q13a0nBICOuRcJ3ufeRGV7MlBhUDtJnRS8fLbohe2uQ5Rln4HCQUZfFFbun5LPKB7dshZNYaknYivTKMTmKKsIFQofBPy12qANlKWhbiIhJFzfybphIBCI/3Tv2lwrizpOa0V0nq53NM1UnmW0BGGlhCnV+HyY7C2rtGE6m+E6B8PgL2QcRg8kwWI8C40tcL0jBQG1lcr5CUSqspT3kRLJp7weFNvtOj/fSTxtczCaqOdkvYXgM+M90TsZBptYEGOgjwKkq1ZCMq0RKxml88A3extn1yaUUlRlKftXZmUP7O6iKKnrBlvY7DUt+6i1diRQeu8zfyWO69paizaaKTO6rsuWZGlc8wPzPsQwBkKH4GXIbBRt32XV3vAsCo5lixKflYPyzCegk2yD3mHQmMJS+AKsxqPoupbf9fWPGqTVCqaTCfOD6yhbEHXKiXcW54MYLGvx5pBnQ5OMPCQpWyS0vkW5Le3VY7abU4Lf5iIph7ZYQ6qgV5GfffIr/u673+FP6jmpXjM9usWta0f80bf+KcurUz786CdsQo+UdEb+2zAKQcbpQS8m3SHGbEBNZn7JRiagnEyWet9jjIa8GIagF5IUoBKaRj7cRXoyHBBGW0l9TAodc0NfCN27PlnAbEp7foXbyGc2hSVFzyC/UwzSVKG4i+H4wHbdJfWNk+AcQJCQdFh5j4ouKZ6tOv76+z/i6bNTvvHeVzg8mFGWBUklQpT3h/L4kJBQcwlxCC6RSjnUB7YB+eOiDYtrN6maCqNLUrhL167Ydls255fE4JlNplhbYQuN9RVt6GjbltnsgEV1TGELCZfItP2o5HA8PX1GjInFYiHvIwR820oK5uBzZITpYVUiasUmOtoYeXR5yr2LxxLipRK+SEQ0MYL3HU4FutShQuLqas1Te06tLabtef3oGtcOFhTVBK2tBLxksDj4NPoQV6bknVdfx9iCT55+zuOrC6ZNzZ2jY2pVcuvoBk+3F6gUsYXC9RGXoEs93fIxF7/6IaWpaG6+RaVrSmMxusS1ifnhIUpVPPz8Pheblpt3rvPrx4+JuuKw2HDnKHByqDk4avgPf/GX/OLHP6fRJRDRxqJSojQanxugQiuiMTmoQ6xFFOLXNjAeZUlnFl5mcmy3YhRfFgXFZEJVVtRNBSnQ9x3eB9p2y7bdslqtaNsOrQxvvPYF3nrna9x86VW+9NV3qazllx/8mF//6ufMpzXHJ8f86Ac/4vs//AdSgm9+8xt8+tk9+nGSvl9Q7SbU+wXDPsChcrGkjKKsC4w1wuQdQLiB+aAGMFeP6cxDET0UXOJj6pnN5hwdH/Hg3v2xME9JQB/y64Q8oUvZA02Tw0+8gyD+YDF1rJdP+fiDf+Cb3/pDrr90h8tnjylNor14yrlS/KTb8vTpE9798u/x2qt3iO6A4FcsZnNOjq/x7NlT+m7LfDZjNlnQdg5blBRNQ0LhUUSVcD5ydnmO71tevvO2ePl12zEhUynFxcVFZmJELs8vpICpaw4Pjzg9P6eyhqtVx82bX+Tr3/xj/vzP/oyriwe4zQVKKYqDA8xiQllamrogREfnOtn+EI8mbZSAKfm6oGS6a4xhNpvhnXghOeeoqxqTFJOypksSqhKRhsJY8e7GeZRV2AwkhhhxTtitTVOjtRJGrhagTGtIyY+/f71eIRK2gfmoxgEAufmIwUNOTe0H2apSKCUSsZj2hmkxMobEMACIenw9GeLJ+tTGIumNKXtTZs9zKw2KVplxlM8V1Qds71kog9l6jPOUfkltpjjfcffpPWLquCw0m3rKvJhx+fScy9Ul1Y0TytJSqESvPJE9Z8Qk13XVbuijDBkGFu2ukdmxnIZnJZGy5VkcC6N9MPY5VhLZ70vtGr0RzN1n3w7XKO9DI6MYRvkx7Dzq5J/syYfzXjCEFoygXdoxd4Z/o/M92nnHy3/HfIbF1kEvAxXUjsErjcXO809UBlIUkqf/ch0E0BmA5hRk3RmtCcETQgfByesZI8B/CujYo6MlGmHli6+tBe+5XJ9jKynY2+2KoqwoJzNUUWG0ktCHomJSNaMEb9v1tF3gwb37fPThT4nVOWcrhX0m+9PLr7zDG3e+yMf3f8l7732Lf/bNP+GD7/2Q7/7f/5aXNlf4qyXTwwknr93k6PgGpYVuc8HTs0smhwvMZIpdVIQy4U1k67aSmptkLWtt0EVDtTjg6PorNNoQNmuWpw959vAuq7OHFMbgQqLvPaowcLsmlsccv/k+737zT+jPOi7+x/8F8/gxJnaYV17hvX/137G+eYurpEghSFDZ7uHKjDtPih7fdkxqA3HLtlVsexlO6oT4//UeUxS8/0/e4Ozqgs/OWoIpQEc0FlOU2FKAWx80HvH5X58+xvctk7qiXW+J24pqOiMME0QfiCGigid6TXX7Nba6ol2egYukYkbK/pgqedCaIoJYtMlTaghMTCSwpvcbVGkpipKq0OLPpwTe17oEHLqsCWjZWpSC1RnagCororW5TjNov6JgRVJWGP0EHn3yEaeffoQpLBSN2DUg+5IE/shrKul8xebj/IqFB4wVm588FA0JAZR9YLlc8vrRCQdvvMOTn3+PiYoypE5O5PkJ0Gr0AAYBzwkRk4z8fmMJStF5z9VmzaZvBQRXQiJwMVDZmvl0RmULmqpmub7MwIii33Yoo5hPpnjnsWWR7Yw0N65fw1oJ07G2wJqC3sv5ZWBMo08knPNcba7ovM8KD2kkZ/OZhLeeXzBtpjkgZcdKlOGt7EmFEj9gk4dgxli0MpRGpLRD8rsyJWVVoDR0saPdCLunripMIaCYGQC5pPMAdlCqGLROBKT51DFSu546dIAwmgbfRRJYram1wiIgn09JalRtUCahq5KinlE0C4qDQ9JkRru64NIn0mADkD9PIhFU4uzqnP/z3/052iicjhgtkm6VwZuBACMZJJCyjHuYbealgFGGSdlQ2wqjSko9paws0+mE88uL/HdlGOGDI0S363OiWD4kbVDo5860kVzDAM4p+TtBSAz7cl8BaqWLUoi03Bg7Am1KCp3srZwQT/LnWab/f6xa4eyn3C6KNQB6GIRmxIOdccF4vqls0aMG0EuuRYwBZSQ0bgDaEgNwImf34AgfcyCfnKuD+kSJDZDWzzH5ZAAp13HwLs2NLoMyJ+bzW+oEURsmzWgThWJUoQ7gtfdiJbJfH3hB3+X6D7VFivl36efagd2Ttj8ofv57LzKRX/x6UYUj3uCy8fUuYI2CfA/3SVyohBa68Ji3IB6sGatICpU00YtSUQYpUi/pvYFivsVoIz6rbbsVKboWQC4ECUeKiBVin+vlqqkFjEsy9MdIeJUyRkLPkih/onfydpKwJ5VWOcMi4HtHVVZoJUQUUZ4qcGnvpXK+kAAAIABJREFUeVQjcL+/lmXNh9yLpd1aUNIzpphGhWKfxDt7sDAQwNXnoDGF0wLquuDFDVbtqaX6PmMxioGFPM7Y9T45QPoa2Q93FhDD+eUVBKOwTU1lFGrr6WJEa0uGdlGlRqOzitpQak3vPIOaw2oZjokvq9gVgVxPAd6N2CCVzZgLJD7CJdZOBKRPWli+xlBkIojVlropxYYpOpzTQFZ2KHJ9bil0wdaWbFYr+r7He1GK9CaTClPMLN1EURmck/AutKJ3AlASEzF0Gaw0KBWENKIlQDEkYWEnrVGuB6AualFr5p48xIjKa0EhIZcDAEtea653O4vFDNqjFM6tx0A6pRTJaLH0IYPXSmNMQd00WGtwvSMkL4MPk5+tosxB67uBV1mWez2MDDh86POzr4jRUlVNtm8SMk4MicIUlJUhBk9KERciXecIg3pCJ6L3hCS2ekWp0Kr8nfvJP26Q1hiOT65RNnNcEglOyDYACgEKJbRLEZ3cWNBSmBEgOFaXjwjdEr+5JJFBmgzUJKWoqhJrLX10nK6v+Hf/8d9zMFnwxjtfhtJycHTEW6/c4b/543/J9emE//yj77AO4oUr/iEJZZKkJavMBlIqh4AA7FioMuXLDJ0YEe6lkslWPnBlB0jjRC3v2XmCKwe+YvD2zGdu3pVDELP8oSHUlWF6bcH2NNFvNiSEzTeYbIeQJU56SMIcmtc8lcobvXde5Au50U8hZHnF0CBLKMHaK35x93OenS7p24L33nuPa9ePUTrhItJIqDBOWkFxdXnBdNpQ1zUBZEqidPbRFdvOarLg9msV9WTC6bNHbDcdk+ynuZgvMKZmud2QOtBeUaWSw8kBVtvfYGd1bUtVVlRNIQ++c1xdXpBSoq5KUooUw1QoBJQ2BBS9SqyIfHD/Ex6uztjaQE9EJ0NTVFg0lS0xCTbdlivvWLq1TGJ0YpsCpoBuc87TfsVL0wVFCNjhkMjDYu+FcaOMZlFUvH3rZbwPPD5/xnqzYTOdsrAltbE0psyDAkMyBb3zdH2PSuC35ywf/IKjciby8QgHJ9doioKqKdluOz69dw9TNyi2tJefM4lbrlvPBMPh0RGnZ+f87d9+h5TtHaIXYFI2LwMuyLTQGOpKse0lOMkqKcYk0TyzHBBPKRcdQwhG3zsOFnPm0wlaF2htROoYxUIgxES/6YkBYiiYNDVVURBc4lvvf4uX7rzBJ59+jFKB3geOj6+xXV3xp//XX/CLT36NT4nX77yG0YZHjx6PxR8Mk2814Dnj+hj/N1cUUiBmxuR8gtKJvu8RFrEMkpS2DJ5SWosnKDD6pwrjYGDMCxDjvOPpk6dS4LgsJcks2iEdVeuBUS8ArdIK72P2Axbpi/jLO/r2kocPPufLX/0637v4K3y4YrtZoyvLNrZsuxXnF2f8+ubLXD9eMJ9WHB0tWK8u+fz+p6TkKArNarPGFBWqqNDG0reOqCJOiT3H5mIFSbNcrei7nmldgnNst9vxQJPP5/HtBmMtZVlzdXUl0pdtR0ia9//pv2Czdnz20S9w7RWahCktzawiqZ6UYDo94NbtG/zs5z8DIs4HTs9OJZE6D43kHqYR5GuzZ9IAhru2xxpDYS1tn+/LMMUPIYfYJQprqauKtm0BUWVoY2g7YU4J+yJLalO2WRhBth24L18JM/rh5bWWdtLpwd6C3PCY7KU3rIEw2HCMv2togva8dWWhyp8yq0QNxSigQiQqGfIZrSiVhm2PXrZMfWJhC8qgUcmSXODpo8/pLi/wqcccTtnogkJVLO89YbNZc+PVm0wmNZNmxuerK66Mwikp3o3NvrjBs1qtRLpWWKq6od1uxxT3QcUxfJaxaM4yIRLP7dXPSRCHsYna/XlfprjPhM3f+I3XSZAblJ2n2fBv95mzwzXWaidfTXEv7HPv95EbCjUA5yqzl2WCQnA+Nw8veNdlhsEOgM8DSjnoxyJ0eG/GFKRRXh7woUeRsCmw6VoKY6mLGqutgLZm3OmknkCucQye6WLBSy+/gtKWlHpc35Gix+p8mA9rOA9Neyf+ddNJw1e/8jWSXvPBR9/j2dUjTs9P6WNHWR/zxXe+SOfW3Jgf0ZQVT+9/Ru07pqXi+J0v8ubbb3F0OGdSlRB6fvnhz6hjYnJyjW3Xcv/er8X3eLGgaqbS3CVDKg1BWbyD9abD9y23rh1yNJ/SHF7npari4+UVpbUsjmc8fPiYtm8pF8eomyfod+9wefs6quxIh3P0ckNyluLmbdy1I5Za0fq8f6e98yHB4M2vVCLGHpJjvTqnbVeUlTA7dJKKdBASWlvwza99ibO//QmPl2swhsIUGGsx2mZFTk/wuV7bbEm+o/NOAMqUsGWFsgXeOfHITREfepKZMDm6wdZlTzSlJHSOJFCsMlnKmYjBE1WgR5PKBVZFCp1w/pwUphjbCOifjCRIx0DrhpCVROeCXBedKCYlmkDK0laVh9jeB+qUQ0NM4tVbR9z9wV/h1ueUB5ayKimqEucCZWF3YTsxopJGGyQwrHe4DJJ2bkOgF+mp93LNlGZ5ecrHH/4Db331G+juksu7H1Epj+8DPoqHYdxDXMZhiJb90SPMMQ94RMkVQhwLAIG4xD+2KCToYzadcrkUpUkzqZgtFnT9lq3bEkKkqiqMMWy3G4xRLBbluG+HKAyi3vUUVmOwbLat1AcJnJMmzpQlk2bC4YHYOhlrCH1EJfGvlH1FrKGMESBqs91Akma8sLK2tJEmfEvi2cUZh8cnzGYL2s2SzXpDVUFV1pRViTWWSdlIuKvRAwaUQ4fkPAw+kTJTUaWIThETA9r1FNpRqITRg4dpDutRQSwjUAQ0pmywVUPZFJSlpaommKIhqoKQEikEut7jQgZlMkghxBAZmGij8Uq8gHXSmLKQoSZpBL2HPSvFJMPQYbgwoKMJogKnoI+eqi4oCwlLcl1EBYMxwx4eCMHBkBuhlYCUQQDcqKMADnHYK3brTYaQw14v9V/IIOUAQibkPQaklisLK2A3QNLjShxVHPnfKwZwUjMeh3tnykjwyWeXzIvzADg/C2kY9KYE2sqgEAEgEsPwcHdOj2BwtmEZny1y6Olwvip5W0MQkZyvu0AtrfV4ng0ko5CZpNZagnNopel7vxueqh1kqrWh9/2uBMjMteR3Z+TYayi119Pmmz+AmOwds2r4JAMQyPiZnzvjX/jarylerFN+198jZUZ9Bs9T/tzGmAzUyvv10TMwKQW88mB2yp4BkExqN6wRlZ3slUlF+rYbz4amkUFrQvCUsiyAkhhlvw8+UJUVoPLPdnVNyvWpc25kjbu+xwFGCzHCx6HuzPiE1sJIHP+94BKDN7IovvLnyzXJWLtpRQh+vBcDO1HWjEUXO2uJF0k1zjmilwDXqqmlDjYaHTTBS83X9/24FgemZsghlgMbdagPB3/oLq+vGILY/2RGpc57lKzhzLTM1zyGiC6sKOjINg6yIgS3MlZYnyHm4DuxuhBgU/qDtm2JEaqqzCxYAeuNEQVdDCmrN8SeYaIGD+4o/XWQfdl7R1J5oKEUVVmNg44BoLbZlqxvW7zzGVCWoYt4HmfLBxRVZSG1GZtSdK2jqkpccrKfWb0b8sRASgFixGpRFRiVsyussGaVNVmhEFFBckD2LV6838r+mZ9iHeW9hCAgrs42in3v5B4NwV4ldK6XYVkUzKLPYZLa5OuUXy+EICrb/MwPz+SgehmGKfIM2sxu93RdJ7klyFp10ZOcEDGTUZSFPFfGB2y2ZgjB4V0PKlLqgh5PiD2J39xnhq9/1CBtQhGUoXMuh1cJO8+HSF014omhBMhcrZZcXi1pbE1pSzZtR1UaVFjRb56hVZYAak0cJIcKWVQp0tgCP214dPqUP/1//pT/uki8dzTlvFtR1Qe8/eqbXD8+oJgs+Kvv/R1P+zOiBeGZMTJcVZZSDCwZrXJgVkrZ7D975uXJkTbZL3Y4ANOuiR+avhBlwrZD+XeN3A4ESnk4KM19RIpRYzX10RTTGDbLtXgwpWE6KOEjMfoxKVJeP2aT6TiydlJmd8U0PHCySYS8MZmypPOO6MGdbfizf/9tfvzLD/jjf/4HfOVLX6EsJnQuIJ4kQ8ES6PqOqhYA2AfxK0Xn5FQiKYrnmTY1BzdewU7mPHv2iO3qgpPjA0wsOH2ypLYNSUsa/UGzQAUt09MoafLeC7v56PAIYwyXl5e0bSsNcKHywwsxQtAxT3IiOoI3hovQ85NPP+bBxRO2NtL5iE6K127e5MbhCSqKrGHWNJxfXvDw8jF1e0nbdbgojbwpCjqreNJ1rM6fcrOecK2oKYzKvksZyMg2FEpFDquGL9y8jetblu2GrfPMC8XEWKa25NRdSYOiZfOeKsVyvaXvN/QX92kfNJiy5Gp1nfXikNn8AHyPT4bHy4764Jizh5+gN0+5dQBv3pxz6/Y1rt+8zf/+v/5rPvv019SQvVcDrndUdQkEYXGrlD3BFFYptu1WfOaKMgdkiD2A63s2bYsycu/rqqKYz1jM5zS1JEr70BOCp+97ei8TWastqii5fetVXn7tZX75i5/y5NEjvv/97/K+NVRGWK3ttuVnP/+Qv//BD1gurwgpMT864M6dN7g4v2Cz2Y7F/O8qvJ4rvoaJnYoibSkN6ETnOjFKHzxEZYA3gktibp7EfGf4jQOTL8t8lBYPuyHxVhuT/z/jgWAKS9d2pGyZorRmu23RSIGjrRV2ARB8z7a94P79u7z+xru8/aWv87MffZvW9awe32N6eEiMIiftt1dcnc6YzRqqekL0gYuzZ2w2l1y/fYuyLkTCq7U8eyRUaeiVhB9tTpdoW9Jut9jcFIZc1Kg8pCJAH2RKWRhN23UoZUg9bE7XvPrq13nnK9/gP/zFn9Oe38e1S2IMzI7mzI+nbGJLiI6z82dcLk+xhWY2m3N2eTUelmlsDhQh+0cNkrZRAjjsU0YzXczpLvwIxJVlidaa1XotjUwMmQGcMoNBGom268Q7GZtZvJrg8p6vBpD/eWaFUvn3jgNBRubGUGQOnwPiTsKW/25RFAS/AxCHzzQCwTqDhwztHNLsZ7+7kOmmRmnKqCjbQNX1qI2jdpFpUjQ2UBYFojbpeHT+hE1wHN66gW4amqKkOz9le3XBye2bzCZzDpuG86sVfbehnlTUQDSahM7ynsEHN+FDZLla5TNwsIh4HlSNMTKZTJjP55yentIHP4b67D+nLzZFw9cAnO83aS8+0+M1VLu01v33MLJn9+7ffnNm8hoyaq8hHV57LHTtKOtKKWVHFz0WwsI0EEsCTd4fhpSQLJMeB6DjwGgfEt41LNrk4tWJD6rvtwJWGBmGpCT+YVXTIJM1AT6MMsToCL7njTtv8dJLr2GKBuMVznlc22LLCZ99+hmFNVRNw2xxyGw2F+ma9/i+Zz6b88//2b/k3a9+nfuPPuX+g1/x4d2fcfbsko8/+resV+ekds3Hn/yS/uIJb18/YtK2fPkP/guagxPu3/0Itb5P7Ld0AXzS/N33f8x6teSLb70qA/UCrt+6jUqWyaTh6KUTDm6+ijJztmvH6uyUR3d/yeerC47mB8ymNTrC6dkF124vuH7nLe5/9oCL6Lj32cdMm9v80ZvvY51n07WU2uDLhvL2y2zKgjYmQm7STBrgfxCbgrxfVDUxJj69+ymlihRlyWIxp67q55pKaw2lUbzz5h1Or6748NMHmEKYe5s+4vXOhiTGIE1pCqgU6V3YsdRSJPa9BGORhMnrPcwm2MUxV51HxUShRYFjdIlPGowAmkrpkWEZdU2sDjDB028eUiC/pCmnWGPpO0e7PScpQ1SGsqpJMbJqnSSCp35UUY3MAJUgaaKydKYkUHDtqGFWJVb3P0AZz+LadZq6JipNXQsZQltD27aUZQVKowm4dotS4r278Z7Oe/roKGwDysrgPkQqPE8++im+a/nC21+lPT2lXz3NcJGcuSnbsOSHaPdMKYVGhp8pg0MjiBBlGB+FxiC1NZkZqCyL+YFIeEPAlpZkaraXT4mkkZlfliXrzYpJ8EwagzLggmPbbXHBkSiwSkCyIcTYFgVGZUuFFIXZXFYkoKpFtuxcT9u3tP2GyWSSBzbCdjU5HEcbYWMNIZJKKy6WV1SzGU1VYbSh7TrKQupqU0gTWtU1hR2UFhJqHKI0vLYe7C/SOLAGMGhKbSkRMFYIc9l7PYNdtrBiGTGZUzcLbFVlW1NR/6EKCX5WQrxZblZ0MeJTAqQJT3nQJfW5qBZFyhJHFqBRe8qLlBj0T4Nv4QDUZb00aMXdB/eZuh9y/vSMw4M5b779FuHhlhASxcGUtetx2rP2KzoCNFOOX32D9ukTVhcXKAKqUKAjKe1YkPuMVthXwwzawwxchp3PY9lMKGyRwTqd5e9ZapyBo0QGSFNmqZm92lUPZ9wOpGavFh3AtvHnAxCbgMxU3gG/CmtMBnd252iMYsWgjR0Zs+PQOIPSUvIO5+JQkwiTMiZhDA//bnfm7p+z8h+lxRN9CLNOA7iK9KjDOT+syRcHswKwDGSINNYSL3rQv1izPXeZXhiMP/dzdnXL/uf5bV/P/WwPFRaiiFgeWGtpmkaCj4bahB07eqxr2GEB8nr5fSTZsQZGqg8e53v6vhdfzaahrCqqotwLJc4s1jAM2shdBGKjpAZAe/i8u7yH3b0SxehAvsmHpTCYjeQejHYQZB1HBj+HWlf8WPW4Vod9zVqT780wtMmEvL1QvRcZ5PJ+dv6hA8i2f9+H3mS7Fcsyo+UeDHYeslfsAtIGRq4xg/+/lgB6L/2p63ti0FkCn8ZhvrGG5HZgbyLR9S1p99gLucYlhkG8MYYUIj5lm0ktUn2SBEWHvMfFrMpu2y0KhUlG9lGgbVsmZSFEmGTy78o1d/5cZSmhsxJYLfcuZLsHW5WQoCoTXdcRfE9KUvMpo/4/5t6r27Lsuu/7rbDDiTdXdaiqzo1EUAwQRZGyCYpDQ9SQNfwgP9jfzV/A1qDlQVmSbYgSLVEkCCYDROwudKqufOumE3ZawQ9zrX1ONUA/42JgVOp7z9n77LXWnP/5D6ANMaQ8DZvMNj1MJnbM5NBJCTfev1QDB7MDxidlKedOPRHPWGOJSN+ca15Rj6TP3FrarqdLfZjcBz+GlGXrEOc9Pvh0JosKVZSz8t8MbUPO9pB9MYwg9T6An3Ew5xxlWeLStTgfyFYPUUFd1cTC4IY+DSaCqDFlqpds5lJPET1VXVBXFdmGxDuHGzy1iwydE7b/j3/uVvKLDdKCQhsJ0SAECRzqB7q2Q5XQ+UhRWAgB120x0dFuLulBUG1XgO8py+xfkX5mWpBVXaKMom8bkeNoQ0fko6cP+fd//C1Oz045OTqjrwdOX7mH18f89m/+HtX8Ft/602/x7OYBFF5kOlFLEzYenAE3+HGxOeewyMRs19wLwBp1fOmAAFnQYpkgzZ21dgxsIZWl4+tlqZKSDTdEj1E6/T5STGvqxZRORWgCrpOpk44vb3jGSDNGmjAljfG4eEJITDQFJE8o8eRNnluFIURFH+Gia7j65KecXz/lybOnfOPv/TrL+QJlqkSDlybFCn1HFku+ugRQSxOrU/EtB/D88ISyrrm5ekZ3s+LmfM3mRcOXXv0yLS2hcfjWUZgSFxz90FPWFYvlgqIoGfqezXot3iKlfXkyR0xp5REfZePQxrAxgR8/esCj7RVtpeiiCPtOFkfcO3mVCYZVs5WQjV6A7bqoWRIoVEnnB/q2w0SFDRZVGlZ9A0PDxJYcKDGWJjcCWlg5wqyLHEymnC4PuX685nq15mhygFKR5WTCs4sLNtsttbWyuZJkP97RNtdU15+inlecf37I6fKX0HOLVZEXm55rV3E4PWLz+CFzNpzMayZTKGcVH37wE/7q29+m0gobIgPCPC+qQopno6mrkqbZCpiNHHRlIVJIkS8MlKWhLEoGKwX2EALTyYT5bEZZSHqjeL11bLdbmrbDuSjBXDGwXC55/fW3eO/LX+O9L73HfFLx53/yX6grg4qOzz77lE/v3+e7P/geH3/yMW3fjf7Gi8WSyWTKj3/wo52v58/bZb4AvuRnQSfvWVuINclmu8VYPRqZCwgnRYyxhuBJTbUUFyHJ3YhZlp8sIIij/EVFJUz6vaKxLMtdAIXW1PMp8+MDHj94RGhleIAW37LCGKr5hHXTcnPzhB/84K/4rd/5PabLM9qmY/3iEdtuS7vdoILG9y0MW5ptQVFNUSg2m0vafpvWg5wtRoxwQUViERliR7u9pr24xCTPKrT48gh7wo/XEBGJsjGGqqrRytN1PW7dYcKE3/jG7/DxBx/w4P7/S7t6gu8bTKHRM4vTA4U1hLBjXE0mU3Jaa5YFhjTxFIA7JLmQ+OB657m+vpb9UCtc8Fzf3FAmL9KcFjqZTASkBfphwDu3Y1fCWISeHp+xbbbcrG/S67OTMObGgR3TVQqAFMYR80/bedaJ9EwnmczLz+J+EwA7BsruuRxr4iTN3gMXg89wBRCph4i92lBcd0yxFChKbSgTeNEFx9A5Xrx4zoaB4nSJnxTMy4rNk2dcnT9nerrg4HDBRFsePnhCU0aKueXN+YLKVjzpWi77jhAcygpwEFLRFJzDaA3ajNY5X7zWXDjn4nj/fn5xjabvern45uViff979+0M8p/z98mU3o2fxT5gK6xYAe10AlbGhyJ9ptlLNzdL+YwcWdZ7/sJeSTKtsO0jI+tEJVuE1PjsGGH5xXYgc4z5PLAYPaQCMBB8hzYqgUsi3XI+4nqPMTsmUWY0GA3vvvsek9kBhoIyWoauYxgcMzRHR8d03Ua8N6MABG3TcHOzoixFAmmKKbfP3uLW2T2+9NYvU5aH/D9/9u9YX98Q6VC2wxQtx0cVBwdzjk5v8+xqw6ff/QC/uWJpOy6ePqRpB7pty6PHz1jMFtwfHrK9fsHdd16nOCt5+OBTZrXCuOf0q3M6V3JzsSY0DXG7onYtrr3g5qKUwUiMPL+44OT1E05ef4urh58RVeThJx+zWd9wOjukOjnm6vEFRVVSHx7hoxY9XpTPhVRjjeyzNGy3Rc10dghR2MXNpqMuKmbTOdpKUGFd1SmApKa0il/72pt87b07VGVF1we+f/8zvv/xU7xWDC4SUGy7LU4h/rVGU9qS3nnxB0zelRK0OuCjZnr4Kk7NxNLBt9hCzk9bLvBBgj21LggpfdlaDbYkRC0gcNsxLTS4LbUesEajtGW9bdG2GNeo1xUuDNBvoF8DXvaXSnzIQxgwIeKxbDDoouLw6IhPf/jHrF88oJxVLE5P8RkUCI6oxFLG2pLpdEog4ro1fbMRX9oIPdA6z2YYmNaHEqgWJJHZhkgVem4+/5Sn1ZTTW7d43F7j2i0aabhl3WbgTM6PqPTo927R2EqzbduRAS9AkgD1AWF0iXWIJfqBuqzo+m4MLulcR9u0WG0oy4oYAv3Qs91uWSyXoEnJ0xk4GQQI7rvELE4WBqkJaNsON/T0XYc1YkMxrxcURp7r4D3PL54z3U44Pj6hMiWzyWQMbHFuIEaNjrvE6bOTU6y2RC/AbF3VVEWFMYktF8W7MQY1egc656nqSvayKHW9RuGjIirD4EHbkmoyo8TKXmSLBAwLOFyVBXVdCau3KClthVYGl5pTnRQDMmBWdK7j2fqaTfCE5LGZB5EgPQVKrDFUBJvWp44KYgbsZBih0mefa4EkqZR9OngKU3G0PKTrB+5//AGvvX7E0Z0Z5zcPmdRTJrfu8qMf/YiLixWfPfwYvSwZJgcc3HuPePoKLx59zvnnD8APyb4tJCXijuWYlRGy5ya1CLJXxyB7vfg4GmyS02pEzSjh0pLoLvkdCu9CAhd+9vyU1wxkm6UMbmnSkHA8WQTIlRZx76xJoC1KJbnujuW6L/sVYPHl2jkriL4I6Jok+wxJ2aTS/ch2EPm/G0+5sWfWAnbFMILHL73Pvfp9lL0nfDq/5/06YKzho1xzVqjtzmi1G7TqDH6+/B73Ab6/a1D8//e1GxIznk95eG+SzUHTNKI8ssVYF4wM8bE33VNRZcZwjInwJHtXTLVKURQpZDkBUN7TJQVOHijHKKFU2WIp16eCXckAbh+c9T5fd0yMzqSUizn4TeqaOHhh5hcCROvMElaiGsj3RGykdrYWYx0VMis/H8cCCkeikIS8T4x0dteXnrOyFFJQrpX7rhuJIwBFUaILPT5X2Q6EGNOQS4MBU8uz1HXdyLLNfUdRFEmVV9BpQ3AJ3wkS/udcn2oFg/L5M0mvqeIuZ4TI4MR6TWshMFlj0/DQj8QAre04qHAuBdWPfaf02BGNtdUIgKNBMhGEHBh6jzEKYwq0MclG0EEUFrDWkq8UQ2Rwg6hwFFLLwzgIyOsvEClFkoFXGwEwkzVBFG8kBGPbhfLlZSVqDzOC30opisTyntpaPKb38BiTLOkKL/dXWMIAVnowne2DQM+SHVEvgeSZTCPBY8UYhJcJPTJAS/cqSoaVc8N4fnovlot5/QnRT0iG+XnMZ41SarSVqWyFMRaH1NoxepwbUigsQrZM3sam1OgCqlmZ7Bl+/tcvNEirtaGqZri+ReVNc+jp1ysG1WN1QRsVfdfgXY8tZBpQWIRW7HuiE0uCmPw+jFL0XtLGbWGZLmf0akg09Yid1LTXWz74+BP+l3/9B/z3//yf88bdCq08J4enzJbHvPrqXV45ucW/+dYf8Pnzj8RnS4exsc/G5CTmbAjZn2aX5G4Su04pmbhrKw1WnihkHNRkfxof9w4NwHmMsoTBoYwZj7VsoK/QiRIvHoiOyGS5gCmE3tGvNwzrZmT5+BjHzd8m5kEk+wPuS0Pz9EyNTWVMizw3wdlzMXaRT55csvqPf8LH9z/jH/3mN3j7vS9TTxbjhGUyrcZFsZOr5funxtcUxuBAUJqynHF2+jrb4orLpz8lrAO2NRxWh1xsXmCtyM/7ruHo+BhlDV3fs17djNebJ75BDBGWl4CbAAAgAElEQVTldRKzKURoB4eLAV1FPjh/xIcXDwmlpkdhfMlrh2fcO3oFs/EMwaE86KhRHipbcjg5YF4vaGYdj1885cX2grIqmNcLYesYyyZGnvgO0wfmUQqcvImQpo9FYZgYwxtnr7DdNvR+4HKzojaa28fHPLh5xnq7xZclJJaGMuKD40PAtRu4+pwnP/oLXjk5QdvXmc1KNljC5BBlS7wbOJ0Zzpa1GIU3HX/yR99ic/GCqTX4XhrGwQdi31NXJVDvvKRSA1RYTV3PBZjwjrZtKMtSpsX9QFVYmn6gtJbKaAie1eUN265js91KUaUtk+mcw4NDFtMFd167x1e//qucvX6Xy6srCJq333oXAvzld/6C733vu3zwwQ/YdhIkhYYYAmVZcufuXa6uriQ0ip+dvO9PY18GhoS1YEtLWYmvsniGagnVihnIyXLtmFJRSRJhkQ3KMlHjFFcCIXZ+pG4Ykvn9rrEMPrBarSQZFMQLVgdCrZkeLdg+u5LhipF14b2nns1ZlAu26zXPnn3IZw/e5tf//m/xrX/3vzGZTlhtL3nRbOiaLcuDY9qDQ2xhUaYiKs3gWgpbSNiiE+aDiQiby3iiDagw0Kxf4F3HZLKgqkrWmw1DE8br3O3bemcj07QMvSMMga7Z8P5XfoN33v8l/vf/9V+zunlG06xkyFQahiJw1aw4mB9QVRX90KFQbLctTSNSt+12KwzQKNNmawzDXiHdti2yPbrxPVlrU0ihpayqNP0WINcYgy0K+q4bATsJqkS8AlEcLBZM6xofAq/fuUOMkY8/+gijTSqcZIhWVRWbzSYxFSSAIT93+dciBY3drFbJloYkW/oiy4TRT3Y0sVdZpqN2xfoI+O1JAz0UQ6C+bpneDMx0Kd5XUZj6RVUQYmS7WXF5ecOqb9HTimW0nEZD8/QpN8/P8SGwtDOWoeBHH3zIUBoOXj+jtgVnLVz113gVca5DFSnARpYghX45mRwFPn1O+ZwIIdC2LV0n3tR1VY/3YFyJX2hMv3g/d+ya/bpB/+waz+s+7pjMOUBsf2/4Iktm/Dnp77w87i8NJWTHCAnDlWaciITaaI2LkXbo0vvIfK983mSRtdy53GznYW7+ksbfQEzeZekZjX1L8ApbzyltgdUFLraADImMNUJ89ID3zGc1b7/9Dt4rtk3DdH6ARROiNHzT6YLgO04PjyirKRoJLvFDYHl8yHRWj6/vfKAql/yDv/dNnjx8wHZziapKymrBl956n/mmw51fcrFuePbj7/Pwo5/i1lecnR7w2WcPmE1kUNc0itPjI56cr3n+rMNMW/r4mOg8NijiTcuw/Vyk4l0v3pJFSVHIYHzTbLm86VDVAVU947rzLA6PUdfXHBiLYsrm+pKz27d47Zd/hb++/4jDwznze6/TBZ88kYfxc5bPU4DtNKdGF5bTV1/h5tEZUyvPeFWVKK0oq5rZcslsOqVvO7Ep8APTylBZ0ESW05K7txf86KNPaJtAiFLvqaixkxpdFeKJ7SNRuT2pYRSgr+/AzJgf3WXrKnSu03SJridEazHR4Zob8FPU9ARV1ATfiH+h8hirKBcHFN4RC+jb57RDh60XaFVSFTVKGwYU112gaxtoL8GviYUV8ECBVQk0IoqiwzluTS3z4Rk//NGfEYYNy7tvEKsaCSsXhquEhcnge9uIqsYAvu9l0K+hCZ7Gw+X2isODUzBG6ngFtp7itxvoWx5/8kPe/NLXOXv1NT798QWlsqOHZ8j2MyA2ad5RmETmCJ4YFH0a0jjvpPlMoA6C24yNJyiMLtDW44Y2sd4GJlbCSqaTCSFGJvVEzislsnzvnfxZi1x/OpmM5IPM0lFR03Ytzsmzd3V1hXee46MTJsUUHQWYKIuK+XzGdrOV2tVKvsIISCMAR9P2DM6hjeL04AitizT8UhSmEKAsNb8qZrYhrNdrXlxccHh0zGyygDi8NDBSUZ5hTWA6KSnOjil9gy4qyqJGK5Inpk40lCC2JVpjVVKJRcnniEp8+ILSaFXQDB2Pri9Zx0hUZrTusNomDDaCUYgdTNopYxwDcL4IzBHiOPgXZUyS0kbHQVnx9fe+ylunb1GYSDU33H7jVWaTiu1qS6w0P/30PufPXnBxc8Hh7HU2RUWjKoqDCUd2gpktuHj8AN9swQ0JPJXXz4xU0lAtA1gAzkngTT2dslweSK2aAdG4e+9yp1OYkRJprtuz5EibkzxX4xBvd+7lWlPqyZjAlfEEA7KfubCn83mY/fXz2smMstQo5Rkz2WJon1mp1A5EDEnyKvkmoJQZQfMMqozvMf3E4IOQhtK5rROzkATG5s9bJ1skmxSd6WB8CUjdZ3fmW5afZZ/CfMbPil3Qs1Jq9KXOPfoOZN1bCypf766+2K8hvvh3+Z7J36c8GuTsdyksXOuUBRMEXDLaYFJFoFJPmu95fq/WGmwh5DBrbcITZFCfc0BM8kIl7gBqYxIhJAG0bddikxWPTmB2SOrTDH5rrUflWb7PRVGMTPc8LO+6NoV3JfuAVCPVVUVh7Pi5iO1SFBYnqXSLQLI4zJ+rSNXTZ+PTIDypIFTK/cg1Tlb0ZWaqUgrXD+P788MutDBh+2Rbubwf5+vLfUC2THPOEX3A92LJYZXG24KqqrBG06oNiohFFLhKG+Sc07ggRIWY6jyi1HjW6jEob1dD6uTJm/vRdP6YnVXI+KxGn/KEYsK6xGPVVgXa6jQ8FFuA4N2ID8UYmc6m4/DEOTk3AgFTCpipywLXBaJWWFPgvVheyt5hGKJDkXAmLatLSHcSBC/rJlsNKXS0yQJQ0w2DsHK7Tgg0UdQVQwLgnXNyX9MQww9uVARBfh7l52fP6l1g3p7q2xiKhXiXa2OIhVhTebuzOxv3Gy0/fxi6l2r+nd81TKcFfT/gXA8qMvSOorBiPZGIWW3X0zeD1NJEisQs1wnA77fDmD1SlhW2EDUsSgJE/66vX2iQFhRd58BFogts+wYfO4ieOAw4YDKZEI0lBCksgoqU9ZTe9eKlGfc8ABEKdCT56JUKtBwK3stDP1nO6ZsO7wMfPviMP/y//j2//81/whtvvCvWASEwKWu++u474P4p/+lP/wM/ffoZjRdPDqXl8MsLzQcvkkOl08GiMiaTLATEb06p5GU50nb2H0R5v3K4Qe5Io5KFFIJHIfIa9I4ZENMII6TFmjpAylktPlQxEpse1ww4LxOcDDLJtFenRiH5dyhFiDLBsYUdpTAxCqARk1RQq+SBoytCMFxvHN/94GMePb/gV3/lCX//V3+Fs+MTKluiDxb4IeCGAVOWoFLAEmHcSFRUwnCIcgi7GLHaMJkthVHoIsEFukaK2MlySdtuOZgdUVQlm82GIfuEksCtVJDnrszHAD5gVSEBIjHijWbVbXnw/Amtl0mMMoZJYTieLnn/7vs8/PhTNtsVs0nN7Vdfo42BpxfnDNuWYlIxryv0xbmAmEVBjMIokXsXuOwbCtejUcxtKXVakPmi73qxy4gicSitRpUFAUdR1fRK5JGd80wnhvmkxK/WRK3FMyhCNwzYq3NUCHz2t9+mnH4TbU7ZDl6MwIOwPRelYmkj08Jy8fwpTz69z6zQxEGmvGVU+C7gAdcPtG0rXkM6BTRoQ5GmTNYoJuWEMnnt9l0/GoH7weGINNHR9wN939N1g7yHyYzl/IDpYkFZzXnrzS/x/ntfQVnDRx/d59mTR7TXN9x7610+efCQv/nud3n46AEh9slQXElhp+DgaMnJyRHf/97305r/2Qn4/qQa9oo+rTCFwlQGFz1hcMKu0RIaFaLH6uJng47UrpjKxe7ZrTOapmG1WskBlyX5MYUYRfm54m1nWd2spXBOzUU9qZkfHuKtwSynFNsWv25T8SJ7Stv3zA8O6LuWZnPD97/7F5zd/u9498u/xPf/5k+ZVnOadstmfU2zXXF985yyrinrOcoY2s2GN+69TWktmwGwEJWEGgYbiAaa7YbnDx9JERcDbddLQa4UMUjhrK1BGU30UVjFOrLp1hANbjMwnd/it7/5+/zkJz/m+uIB2+tzdIhEHdHzmpiZxcmzWCfPtEgQU3ijxOImfW51XWOspbtZyVQ0RC4vrtLzqNJhruj6QYpD5xiCT6Fusp8ZrSCIj/iusE7MxSSXfPzksUz5VaTvWmxRYG2WBsp3ZLlVVlEI+GuEsZAk7jnB2UdJvpUwArGzkUczf+67RkGksDFZs4DREozjYgrpMMm7XB5oZqbEX6+ot4GDFmamSp6ZYqZvKoNC9soX1zdcNhuiglOruTOboBJrUinFG3df5Wy24MEnn7JptxydvcJhWaJWWx5dPqE7OiTWBfdOxVP0cScBjcJoIxVXu0In9/0Kxol5HgLuN1kxRmwqoPcn67mA3jUsUsR6t0sCFheB8BJzdwS40z0ivf54pu0xe1QGu+Nuj9j/t33AfLwYMqi322OyhZFSBh9DYm8HYpACd8eJlkIyObuhcgK9LlCqSInH0nBrFXGux7kBawtiGBi6nq4fWE6nTEpLqQ1bFwhKpFcmiDukUhEVHIeLM06Ob43MQ1tU5NBQ5x3bzZbnT5/RtQ2L5SGzxQGL+YL+uCNqYaj0/ZZqMk/haI6DxSG//JVfZ9XecPDqAXVdsTQnlPGcbb/h7XffYTJ9RFhd0RjPyektzi823L1zl/v3fyJ11WzGi1WDmR5y0yjaxxe889YdLm/OUf05X/3Ka8yXJc2wJgwBP0A3KOYnrzCvjjkJFcFMUPUCX814cXODnc6IfYstNM51NN4zf/dd7vzu7zA/WBJfuU3jAj4goUC7g0ECqciMogjacnB0Qtd7ai02WT4ENJqhH9huNvRp2JABP2uMKGOsZlpWnB4fUJnIVdMQTY1WKUU4PW/90OO7Qey4VBYSmZ1NTr0gTo/pooLCoqLFmTnYJSFFU6vKE70amScqRnz0+BgwpkQPmtDcMJkcE6LY4RTLI6bHrzEpZU+DgPWBOHh0MUMXEkJWGIehw4WIVxpHQAVhcL32yiHqyfdYPf0EW5ccv3aHMK1QsnWnIN+I8z1WybAsAl3TJd/FgANuvGcoYb29ph0aFtUh4AguUJY1hVJ0zQYz9Dz++EMoC07vvE5oe64uzhPoonB4ClMStef43i2urzbcPLnCaosbAkF6TgHhlTDRo5KJ2aSqMSr5QarkFekGjNVScw+BaVWPAJi1llk9YTqZJraVZQgSBpttUPIg6erqis12QzWdcLg8ZD6fp/MM2q2E5U2mE6KKDH4AxHf26OCUo6WEkqSxnNSyKp8dnsEPrNZrjo+OsEndZ43GpX2q63qGfqCYCEOJIPur+CmKssRoIXgQJQROLjGik/xYx0ipobIFWhlsdOmdGGJwAtjqHa4nXs5utCAIYRBbDWNBRy63DRd9m+orAda00hib1HbRyz5aGMnm8EKqUIidh04SaJeAyZDATh8CNt0rkN6nNiUH9ZzTg1PmixmmVJwdnWG0wm2uiFvLr33tG3Tvdtx/cJ8L1ly4QGkKYllBVJyUJdPFktXVC5pn52xX1zD0EmqF+N5aa3c9p5L+zBrLdHHArdfvYIpSLL18j+8HQgrPsQmMM9Hicm6H23FfUbvB7U6NuQNNfZDeU5nsB0sKokzVbQJtfeoN1X5fR2ZkqjEhPb+GWATx0pmah8TCDA7jezDJPiP6DDylwUfYndnjWR9TqDYxPSwCPAvTMoO+MUnSE2iZHxKJshox5NTYjWdyTM/rDtRSZMsg+fkjbDWe2Rm8G69PDn1ymJscDbnm2x+g/l19xV49CUj4nCNQSAB6Auczc1als4PoE4M6+YuTPEWz1FsLsUNFNfraZuaiJ5IDwPeB3cwyDaFJ0vQ9L+cE4isFtjSEICSLPAQC9TMhsDqpKUevZJdyG/zLzF/nHFtPUs0WY50GAnVkFicZYI+MQw4QEFanPqcf+oSdSPW0X7NrpTBFMXrLZsKLSdepgljZhODRUdiiVZlU2hp8l4NbVV5qcv+TfJ30mmJRJHZeMQqIactSVKbWErdrhkGAuOBTPZ/IPKI6lofMJnUZgM4MUSW1CJGRdZ+/TLK0iSExjgkQhZznfKBU6dpUidGy/9jKolWNc5IZkj1bdRS7B2MtVSlety556pKIJWo6HRmwzg10TUtIHu6uG9A64MeARSE9asCHATc4yrIgoUHC4k3Abd4jfQwwCKOYbPepd/V9XdfkfKV+cCPwOgwDRWHRyLcUZYGOEZwbWdYZX8nBhNnTVykBx0PYAfF934/7QlXVac/Ja2XX28ugoiCEify7CxSFSZZ6AWMtkyhDeuc8OZNCGS21OGl/GmEGPZI3tRYrpr/r6xcapI0x0g+B0A00qxtcHBj6NSaIFNdaGKzCWijKWiRdSlLnyqKm67eSTCc/TW6INaAMi5MlZlrQKo/WBoVliAFVF9jlFL9pcdFx/+P7/OFqTb9u+Yf/ze9i5zNMOeVwUfNrv/RV3rz3Kn/8nW/zX//6O1w1lwQrsqGgJBjBaiWLBpHJ+uwxqTQhOLJ3IumRzr4rGcRTqVgnebmM8hSl9mkf8rODFwl1Am4hHWrsD0QjLvboSjE5mBLrAgh0m1a8NKIXSZLeTV72Dx2X7BAisjF7BaUt0yajZAOMCSBWSV4BtAQ+Pb/k2X/5M3784Yf89q/9Gu+99Q71rGI6P6DvHSb5TAnisnvTPhUcuVmVSYXBB0XjI30BV90Nto/MFlNMqSliQWEsfd8RvBtTK5XS2NLiB0cMfpScFUoYkwaNLQzFbM6V23BzdUkbByaL2diIVwaC65lNKowJHMyn3H3tNZbHxzy5WVFPJrR9x2bbUOqSw/kcxRllaelaCdKZKsvEFnQ3a0y1A7x1OvRian5cN9AFR9tvAUdZGCa1oZxoVusbFA6jFbNJyenhkmlpOb+5oWk9k+mUsjD0mxXdtef8o+9SFIr3fuMf47zI2rq+R1vDorJMlEOHlp988EPa9Q2TwtKEAT9EirIQU/o+CEu2aYhIcIZNspIYBQjbbhuqopTp6jCwbRPLNUJhpGGtqoJWd7iiIizFw3YxP2ReL1gcnnDrzj1eeeUObddy+fQJl+fnRO9p2jV//F//hB9/+CF910FqJESSE8cp7517dxiGnsePHu+KOF6edud1tvP6zOCe+GqSmmWtNb1zFLWEbIQ04Q9BDva+78c1ndnz2hjeffddYoysN5tkNp9ZC2EsBKQAE2+gru2EfeGlGQk6YuoKXRV0IaKrgmI+pbveoiMUpkiMoEDTbJnP51ycX3Nz8Yjv/vV3+K3f+G95/vgZ5+f36VyL7xxuGNj4azabFagX0hyoglvfuCWWG0Mu3A1D36FMxEWH8p7YB5aHRwI4aUVVT4jB0yVvZwEWokyJdaTrByKKsijwPvK7/+xfcvvsDf7jv/mfsXFD6NdEP6AnBeV8gq5K6kmF0jCkkLoQA2Vp5ZBPhWGeKq9WK7SR+64SEKq1WFNElSSVWhQFxMgQAoNvU+ghwnJMrHqlzAiyZvAw2yLsJq/w5PHneC8NbR/7l0H6vecKFbm+vhpZCHmjdt6xWq3GAjlzKNM3paZYmgGUSoVpanSUFEJ5gizVseyTBqj7iHrxgnnjWeiKSRS2ZQ6RUqWEFm2ahscvznmRfJruHR/x9ukR/WrNi5sV67bn7muvcOfsjE/uf8TF9TWmrjlQJfG65emTZ9jFFJTmzmzO0XzBh4084yGAiX70We6Hnpx+qbQafcCiIk3XdxNt33U7j3NbjBYB++zb/Ul3zOfE3jmVz7o80X+JlbtXV4xg7R4AvGPNppW59zr7r73/5yxtzR/HrmFM3NjCErSmd0OSOu6elZCgFjmCZN8fhm7veQigrOwJUfYjqQ8KYpRgxt47Ntst89R4loUlBvHnsqSiMMY09IRbp68yKecYXTCdVeSkYIXC9T3WaO7evcv582c8/Pwz3n7nfSaLCRBpNg3PHz9iNl8ymcwF3E0A71tvfYXlyQmxgLquqbqWH/70/+bdN97l4OiQZrWirms6W7DZttx96x4HiyVYyzv33sF5T1SB5XKOC5HN5RUPrCa2DTdlxxAHzl6Zc/bKnKODKa1TnBzeoj59C6enrDdigxWVZXZwG7U45uGLF1xfrrnG0fkObzXq+JC3f/e3idqytqJ4UGkALCDSzkJEIwPSPFivqiloK6zWhNCZoJNcPPk6Jj81H/weuydQVhWF1pwu5zy8fMHgElNfCSAQhsDq+hLvPOWkpkgWO8OQfeng9OhVTLmAYCgGx3bb4edHOF2BMoJzlGBCQNMSgyOGjhBLAhI203VbdNtT9mBnSw5eextPxNpKQjv7gc2woVsNxMFT1EtUtOhhg+tXeLdF6YKgSoJ32CDsnemk5JOf/BDfrzm48wp2WtNrRWE1iQo2DjFRapRkR5QwppXGEbnuHf3EsG0btpsV0/lc6ooYwGqK+YRoFThH8OJbOz875fmDR7gQMFqGeT4quhApzgp+5V/8Et2g+Pa/+jOaxy2lLXHajYEqUck+IF7emrKcoJISCaMxMdmARYjRiaers8TUxCtjUEozqYUZrqLIiYWdJ/7sbd9R2IJts6XtWjyR2WTGpJ4kpDjtc5nFFQPeeYokUy2UFV/sPAhSAkANrhfPwyhJ2K/cuk1dVSLPHJyw8nQaKFQ7KXtVFng8fd8znc6YL5ap9oyURSmKmij9SlQKr2Q4qGNE+UCBIqqIVuKlGUb1SbJdi+Cd3/n2pyYd71EBiBpnAp9fXnM5+BGEFUDIjKzmIiWMC9i7A7NEGryr+VQC8rTK9mkF2WtTBlIFi3pJaSpZ1N6gQoFlSrvpiW6Oipp7t99hs11xubri+qaj6zY0Thr9wTkUhunRLerlEe7oNjcXzxm2N/Sd1BXR9WzXN2MdEGNmj1uWBwdgDX3wDFEC2oyxjM3Nvhdrxs9UZpLEBEKH8d+zOmuU/SaAWp67BG4mhd7YZ4YwWiztn43SOybpsJL6aDc0JYFOYfy+zDdS6c+j5RPJ19P7HQil7Fgv57NTwpSU+PsrtQNqE0illAYtfpAhIkHbPgcQp/syEpp2ClKd+uKdx3/2N2XMJ1DJGjCvuR2TMYFI6fOI6XX0+KfUko51AT/zlevHl+uO9L8ohAAXHMRAaUuKwlKYgsLKuaG0kpo0ijxc2HYaWwpzM7OQ+74j201kP82Y0D2dWavIfdT5c0igVwbufZBQq6KQ+jREAZ6KoiQHYOUv5zxCPkgKLqL0MSkcLvo4qkD3h+PyXEgYmhDE5b3k0Lj8vooiBZNHz359p61GaYPBjOCvUmDHz5cxJGs/k2IEopVcVw7TjCqHwWapfERpg/cCAvduQLMDv40RCy+lVQpWdAyDxw2eiNgTtMOA63sBC5XG+07q7mQv4l/qEXY2eeOf03MV0LKXBhl2yH3aKTLzorMm74npU07KbRWjYDJGahpiIgsoRV3WuODFBzaSrA4iSkcKK5jL0PfiCR1yqK9gVkVpqeuaGLwEx/UVfd8xOOl7B+PG3CUGna7JSuinihiNPJPJvkBCMC1VVaKLAheFsexj2A2uUz0rvb3YVuZBj3NmtLKI/S5gN3sKF0UxPgs6BW0qeMmnuEg5L/J9ya85KWQHJ2HTk8lkfG58SOdcCICFUqdBRVbViuq1KmyqIWMCkpONZmrsFElFoAQcV+lZ3ykLfvbrFxqk1UqxWW1pVyti3wnjKphkcB0YVEehDZPlDKUN601L3yZWlA8MbkheDykgy8u/qdJQzKa4EpxOBvhK0QPaKOrlglgU0Pa4vuPJi2f8H//nH3L+4hnf+K1/xGxxiNUlN5eXzJaH/A//7F/y9htf5g//w7/lp4/vE8tINB6CMGNjAi8NUkwI8L/bUFQqakzyV4xpmpQXoTE2TeHE00kpYejKdEGl6W0h4HCWxuSfmw+MuH/IyDQDq0AXTFhgykIAWB9wfpBwsLj7/pgOeWuMTEKGPY+fccKWEhtHA2eZhkclHlJeKdZ95P6DJ1yc/xFf//IDfvnrX+ad996m63qir1nMD0EVhKiSlFc2ednoZW9TQIgKXVS8+d6X+c8f/BGfXjzktFjSB8f2/DGTqmY6meKdTyzfBBhoQzGp0CrSdr2wn0OWv5Z4FE3bslzO2F40PHz2iEigLstUpCt0HNAEnj/5nKPpBNBcXl/w+OKc2ckt5vMlzy6e0bktzc2GIQxM6prpbCIpgjGwsAVfu/cmN0+eEYcBFQJ9GMbpKTBOtV0YaPotqEChDNO6QqlAPzTUhQGr0bEH1zItI2cHNdem52a7pbJzjpdTGWoM15z/9C/RVcXhV7/Joq65GhxWRSoCJgzc3Ax8/sl9guvQlTTxLkrCsjx3gwRR9L1IQFyknOzY1hnE6Nq1rDVjxoJSNkmFNbIWpmUNyhCrAl1WzKYHfOndr3H7tbt0wfP8+TOuLp5wdf6Em8srht7z4cef8PziEh8zGJNhrVQMxUg9m3J6dsZnnz2g6/uXJt2j/BleLga0lkC0BKiI11jyRVWBsiqZL2ajRDtLOYwxNNsmPWNSAGWJ+ma95vz8PIVPydqWfmw3aBG/6YLjkxMeP3osB6uY2RCNwlWGhiBAY/DoSQmVJfTidUMUlUG7bSgXlvlyymaz4fzhfS7Ov8RXvv6r/Nm3X1AODZ1fC4MoNYU2yd7K5ZTl0RFDBsgQn0Y/DOilpYkd65trNtfXVLYU5qY2TGrx0lkRcX1PdMlg38gAyiuNUXDz7Io37/w6//ib/5w//IM/4OrxZ9w8/5gYOnRlqJdTiromGsXgPUVi85MlfVr+H4JIiL7IZrRFgY8wmcn09er6WoBLLV6Rfd+nIYgf97SdqkqjEhtpJ3/ZFUg5sCCHiimlsVaNcti/61mKUcLJ9p+9fU+07ElLjKmx2PnHmeTzLQ1EOrxHqWeyRYmZZWo4Wi4Znl5iHlywHCKLckIRI9IyQWkKhsHRtWv6tjN6pQ8AACAASURBVOd8dcNluwWluXd8zOvLBd3lDZvNmrYfeOXWKa8fH3H59BlXqzXGlnzljTeprOEnn35OdXxAuaipjKXYNjz44AUvjGdSVKjCSAMakw9rur7cvOdiZJQxjqC4eAfn+zUMQ2Lf7faUfRuDvJbzr5mtu8/UePnfXh7OxJ/z/eNrpTPtJWD2C/tHbpCz1In8UyPZ+AClwBuFI9A7lwYHIhzOO1f+70SyLM2vKVJ4gffUtU2AjMKjiDo19TGgTcnB0RFFNcWoAqJKQ6TEZArCqNVEVJAgwOPjU4qiInqD0eJPZxJwni+jKCbM5ocou0EbxXqzYn19SVEYFosFi/kSo5TYJDlPtJrZ/JCqrvnB3/4thb6hVpGqPqSYHfLZZ0+wPvLaG28yDA5tDZdX53jf8877X+JkOeP+Bx9yMJ9hgM12y8nBksPZhItNw/VacfXhCv3TC6aTwOHpnNtv3+G947dQxZROlYSFFdBpOxCGnnp2iLFzHn3+A7p6ikESqVvtkZo8eRYmwCc/X/nZ2WdqgzC6iqJEm4KhaykLg0KPBXnbrzk4OpLBaF2PfoDCng40mw1ts+VwMUPHZ3Rdi7UmNS/CCqunU4Z+EOAGiN6nZjZSL8+49dod2sFRxw637fDrDntg8UoTtHi4WwKljUR6qZ+MRUWNCY7QbSkszE+OGILCB4OdnTCra7q2Z315TVGI9NDSU9YFk/mM65tBFFQOrC7QppBzKnkiHy4WTPzA5YNPsaVmeXZC0/cMSZJubTXWs3kv8z5gjEWh0V6ho8YFTxNhEws2/cBms+XsEMJ2oGs3gKeoKnRZoIoS5cH5wNX1isYNuKAoyXWjpfcD2iiG0DCgMLXIYLWS1+rcICPeBIqG5CNtbIlzgbYdMLbIxyXbZkvTrDBacbQ8YTKbyToOcazflTIp3Tx5bYZI13dsupbjw0MmswnGKBaLBZOqpu86Saom0my3YgFiLVrBEIWtpJMqar8v8MHTDS2bZkXftsnqROPQhGTjkr35Q2Jf2T0vfZca2xwgZhJLyfcBraIEFA4utQ2KkAJoBKRNLHGUKAM0qBgkjyBKQ5732DzMCEGAuyLtexFFMzg+v7lmrcFnoEErQiR5/MUxj8PnlTjegxQSl/Zo6Xty0y1DcFPqEWTU0bCoxUddK4tWFpRFqYqmaYlBmN3BO1zb0W1bLm5WXLQNa6HPSO+lNc4rlC6pTs64fXIiljNuYOh7Lh58xPr6Bi3Wi2nvgGJaoa2h946gIOiIT/1MUHJvffAjuzWDSz74vREg4zmX1Tn7Pdp+r5cDkUamYjrTiFmGnIBb5HussQQScKYF3Nl57f9snaPTUCOqHZgraiOk/osCTGYlwI6Zm22FMnCZLMJQCQDMdZYaAbmsHophLzw1YbqZzJJ36lxT798rqfH2maW781yel9xrC+8xK6heqgfSOkhCLrmzajfA3T8zfl5dkUEz52VoVyWrrrIo2fcbFiUZCSOQHttYOatVUr+E5A0bwg6gFXWYcEzLUo1DamOkZ8/AVB7yhCj5JzlcLz9Hct50wnoNjAFIwzCgjZZf9Q5ojTHFNsbMfo3jGtyvpyXMa1e361R7wA5Ql+cgM6jlV2uLtF/s7nUeUnmfWMUxjp9Ftl0cnxMFUUUKDJ5E/nBh92ym17eFZTaf0Q39yObONb7zjkIXCYsRxbBWhsH3tGEQO8lhQCdrAR8GfALpZGAiPeXI+9Ga4OTijZY6SoZPAgYr4piXoORxSPctKzIEzBRSiVgQuH7Y3SclDNF91ZlRGoymVJI3orWmH3qGQewZYqpjTL73Shjk0XvR6GgJqy6UwjlPYSvBS/yAK8RSJ3+eMdX8iowNhUQyUBKOOakx1lAUFUVdCUYQpEYOfgfSoxRGKWazGZWrxkCv3fMkwXtaa7bbrQS6pZD4/Dzp5BnetC3rmw3CmK0oy3I8/xjS+vEkfCKrzBsZBqBGSzad0Hel5XnWMeewyFrJNiWipLJJTbgbHOSNqh98ImVIuFmZhvs/7+sXGqR1zjNsW5SLaZISGJw8lOW8RpeaxcmSalrROo/rIuXhlNJYuu0GNyR/KiNTAZm+B6yyuOjBFLKQojRJKsiC1qWFWDMMgc534iPRbfkP3/4THj9/ym984zd49813uHz6kODh1utv8Q9+7Tc5OnuFf/NH/5a/+P638T5ijEPZJAlIU804LiX5ypuW0nFsDEOaamot02gxB5eH3xT58IW8glXcTb1GaUgCVmWakjY15wnpvagsg9KgpppyUhO3W9y6IQySNhcQ317Z1NNiN0asExTjwgsxT26kUFIq8cMyIOwDUUtzqoJmUIHnq4Zvf+/7fPL0c/7h5dc5nM0wyvLGG+9zevZ68v6UJsVnrxqdp5FIgaIii4MDGt9z//FTytffYXJYc/Hkgv5Fz2y+YD6dQxA2n+udyKBcy8Xqmq3v8UaBl8RGVC4uYPv5T7js16z8BoWiCBGUeJopAt4Lk/bgYM7D589xVuR/0SiWywO6T3u2fkvXD/RDR9s2TNopfZKzzp0kr989e4XV6obL1RWDipgYBNzwSY6jIpthy6pbg4FpPaewiuc3L7hcXbCclxxXNYVWVDbJepTGLCcEHxmahuUrRxRW4UKg79Y8+/F3KOoZJ8fv04cC7xts7NhuWzYvrrl69hAzOIZOJZlC8mrK8o/8BCoB+Zpm+1JhktmiUSt858YJrxyYis45jC0lnENXTCeHHN06486dO0zrOZ8++Jjz50+YTmqePn3M48cPefL4OdfXKwY/CLtJKfJ8OxcYIADn3Xv3KMqSJ0+eALvDfddyM77X3dQ3iqwiRnQh0oaYJvlaiwVC27bJK0e9dJ2ihpICgQR0Bud59PDReGBJZZ0EIAmwEj8aRVEWmEKSr6OXpl6VlvpojppPGJTIVm1pMHXF5PYRzbNLlItoJ8x9HRWr1YrD4yO6ruNgZlgsHfOje3zla/+Iv/rLb6GqDlXkT0/htQWjOLp1i+lySTcMDINGhYKmX7H1G2wxZeVXrDYruvUGO9cS1mgNNzfX5ECW6XRK03W4MNAPHtAo7ek3LVN7wD/9/f+RD374IT/+7l/Rrp+hYk9RWsy0YnZyhJ5UHBwf8eLiPDGagxQwIdINW6qyEqZblKm7tVampSqOzUfXdQBJ4hRQBEnf3NuLIBUOee/UGZyVf8uN7H5wRL5j2bsI1N7UXhJph2FIJf4OTNxvnPLf5eIzT3/H1iA1BdroUd61X/BnUNloI9Pn5LlXKQ0Xa/SjC856sUyRZlasSQpr0TFS24JVs+XZ9RWXfYtWmndOzrizXHB9/UKCBp3j5PiQs8WC88dPeXFzDYXlK2+9hVWah48f4YOjdz1LM6Uael5cbejnNfNJxTu3XkFPK7776HNunKx/jOwTUjAGhnTdRVGMjVtef6jkrZuK/cx4GRkD8td7IGz6+blxNHuN5F4D8PO+9oc1O7/1OH6PT4PH3PCHBIy+3Gi+3FDknxHJvrYGr4QxOzZRUkXLdaRyLjOb8gACxMojRgnizMwLeX8x7RsatE57qMb7AVMIc0TpxP4JgWBkQK287N9HRydobRmcsGAtIuvTGrquwxrx8Jovl5R1yXbbjIX1bDZjOp9hjIAmg3c0zZr5cklUirqa8pX3vsTm5oYnn/+E5fExh7fe5emnT7l9NOfLv/RV3vryl/n0o0+4+es/5+LikoPjgqfnL7j16usspgseffIJauaZVEnaNplwcnxH9qZmxdCs+PjjGz56+GP+9gePuf3mmxzfeYPbr99BR02z7pkXG2K0LOdL1jdbzi/W3Kw2uCApvZFU84V8gsgAR8DRvaFfZARZZQ1bqnrO82ePWd8Ebt86ZTKtCTFS6pqyqJjUU2bzCUVZcHN1RfSK6ByX1zd0zZZJoamMInqHVxFbWHxwyaIK2VuVSl54UjdND5Yc33uPcjHn+uIZs+I2w3zJplqQHAARlnXEuoYaj/MV3s6lhvQBPawplOZgfoCKa/p2oExSveDkGk1ZoYqCuF1BHDAKhuaaOLR4QJeTZHflCDi0CkRVcDSf0zz5nP7qnMlySTGf0af1EHwgGmENyp64s+mxSrO5XhMSucCoSBfhyeBYxsDVdoWLA1pHbAiErsODgKjeg5fz2RcFr7z2Ouco+o3Yt5TW4HFcP1nzn//Vn9M2Pf4aKl2BjqgoDN9A8qcl4okUSmNsQVHV2KJIXs3CoplOZ1xeX0AMHC01hd0DWJJNj05ZEM45tn3DeruWEOMEKszmcw4WS7Q2DP3AZrMhEgS0nU4x1iS/Z5fWugTs5kCmfVCyHRoG11NWJbNqSlXUbJt2ZBnlnIf8Pd77xMZjDFLJks/MMnLBQVDi0+wheumLbAIYPIrZwbGE8DQbTNqrZdCT90bJ0kBrTLK+icFhoqXShiFEehW5cj0Pm4atUrvQsL2Bl1JK5KIxgwZyD4wx4/m5//v8PTnjYif5BjxMbEVlBGxRMUoImRdWnApC4/Te8fz5E86vntMpj7MSvGZURBsBnqxRaCsKCQXoUuEHz+rqmsvzc/GaT2BzIKKLkuXRGdV0QZf2G6ONZBCGQF1XNNsNoz2eAmWN3HtZwD8z7JX7bMdzKLVixHyWpDNOnp8w+ocC416jjRmZtz7K6xqjRyAclYG+TI3ZnZ2pIc2rXPozJFU9g56Z+SbEosRuzAQjslJlx3j1fncGq73rhDh6OyulCC55y0YBQDLY7MMuYHVXr+3ecwawR9JSzD61uZdQY3Gxf7/l/ezOhC8yZV/6+exdw8+A53K8WCNKGO8CbeiIQez7FvM5WRmorZCxBIwdaDuH8wLXDM4lu6NdQn1ZlgmclmuXS9z9XqkURJ72hBzgt6tdXsYkurZLyp80LPAO+lSjREMY7RhMutaISZZwud7d+ftn5bDCmMTaDVnBthuE5xC+l4bxETmfUl2t4j6bPJJtX1REgi/NF4ByLXYROu0f2mi8GsZg5sySJLrxNbXW436Yhw/7NZ41Vta3ilQaoh8oIgzNFjeEsefLTGfJ1EmgPvJnEGxntGBQKue+Jp9dC8kTOsv4sx1DCDK8E7KJEmWPkuH+SCIIAT8MAsb3QubRSdlTFYWoJaIMEEOQGtC7jINkgNMSg9gQee9TdyMBm1obQnQobTFWgGsySzVhBDrVFzlkt3fi44rW4340OIdK9wegKIpx7xZSjhnViFVVjZ7JOQjPJrDWLhbjZ3pzcyP9Rbpvk9kUrTTXN9d0bTcSJHUikI3EhkQSwij6oSN2LdbIMGW73Y6fm2SR2ORjrMY+YfCizLbWyMCwqsbzK1tvFGnoMKTP3AWXhsYv7yf7X7/QIG0I4nmhlGxMk1mNnVaUk5JiXqErw6Cg6xp8gD46Tk5PePPeHaIbePrTz3ny8BGbzVokNtko3WhiCtsS7yApIlUU+UnUmlAboKaIgdD1rIae1jn+5oPv8fD8c/7Z7/4eX3v/qxye3GZotyg74b077/M//YtjTpan/Nl3/hOr7jmEQCxhCOLjUdhq3ED3G8gvFhby+2RxkC1LUImBkBF5mWpYI5tmIO68ghTo5AdVFAUnJydcXV2NQBQ+bbwqeaVoRbGYCvPMbuhXa5GgOZek3GnTS/dMpYY6y9izDQMxTUaDF7ZNBJRIFbTSaKtQpiAEy8Z5Pv78GTfrP+X9N+5y9/YZwQ9st1dMFgdMZkuMFu+vVGfIARbFXw/Ep+yNe3f5zk8+oTlt0JVlcrSgv7qijz22thA1RVFRz6Y0TYfzjnpS07WBptuKj4qXEIkc9qJKw8FkQe0NOhqULegY6AbxSAkxEHVg9f8x9x5PtmXZed9vm2OuS/98eYfuLqIJgCREUQq0QDYhBgAFGRwwxAgNNNBUf4zGCg00UQSlgSgSogFCAkG0FESgQbRBO5Z7VfVs+sxrjtlOg7XPufdVExEa9u2uqFf5MvPec87ea6/1rW99X7Nik1qeXZ5xeXvL8i/+PX3oWXUrTu7fpZ7W+GXHbDZFoagnE7qmYVJNsalARcV0sqDN5iCpd6RR60c60yHJaJ6xlvlsSuc6zm+v6JLneLbPYjYdmZo+eEKbMHgW05Km6WnaFruYMp0vqHygcyte/Pjfsv/GkrcffsjSdJA6mq7j9OkzXLsS7bMkUiADQDaA/QLMSVCXLjUjmDICXHm02WSA0mg5FMqixBqDNiXaVNTTBQ/vv0Y5mXBzdc2L5jnrboPVkcvzWz766BO+ePIEHyODtrM2+aBO5I7xUGzDbG+Pt999hxcvnnJ7czsmaemV4vvVbrd8LeJdZovrLGug5ADXKUvM5HEKm03+2rbNnT05LKPilYMe2GHNZmBAQUoygqKy+3DXtTx//lzSRC1C42pvyuzkCLOY0Lk+m7XIHp8eHxBbR3d5i7Eak5LosIVE7wP1tOb07JTf/4N/zlvv/Tq/9Vv/NZcXL/jxT67YPz5AW4M2BlNU+Jh45xtfE520zhMCrPsNy80N8UAzUYnYNqxOz1EpCYNMyXhjyHHMR4/VRgTuk0SJGCNp1eOWlr/2n/1tqmLCP/mf/0fOn/2M1N+gDChTcnj3LmpRsg6Oxf4e67bBB2EiGVNQFJrF3j53797jk08+JoTA3t4ezjmRMvGJ4FsYGBUp5fvIFkjLMYpcnAza2975XEjIZ9aZcR92iqKBAT506dE7zscj6CssvYRoY8cQRqCOoWO/CwDujrao7ZoEKZ69S5mJ8xXWd4JkxMhJ+8gsasrVBnu9YdErFtZIAakkkUIpKaJT4rZb8+Tiguu+R2nNg/19DicV1xcXLLsNqjIc3Tng7nzB5dkpL29XJGP54M03WJQFnzx+zMvrJWE64cFiD9M5Tq+usSeHzPcWvL83p/SOz56c47pedN6RYlYrhesckbDtsO80Tshjq0kqy5ERkxgYU/KM7FDCD02Z3CjcTW++ypofCvmvgqq7BdUuID+wTHY13UaphaERqrfAx1eZNChFoQ2EjNtkINU7R/AdyQYMw7pMZCFCkQeKw4oha1oXFCZPyMSetl3n8WUlus8R1suGvl2R7IqkPaoUqaKUPCoVGRQWQNgaw3w6FbZMUljF2Fw1uqAqLG3T0CjDZDoBVdF3PTHApJ5RlDVJWYIS2QwZ47NUZSlN1Ziwdcl+fYfN+oKrq+eU8xPmR4/4i7/4Y5SBt997hzZF+tDz5IvP2D86YlqV7C0OOH95zsGDB7z/jQ84vzxnMq15+MZr3Hv4iKuLS148/oJnH3/CxdlLXLMmrToe/+BjfvhnP6OcTDg+ucd0fsjDN284OHnEGw9e441H73Jnckjrs/Fldh9OWoMKEhN0LqiGwjHnOa909KKM3b72+lvMDfz0h3+Od894883XmS3mKCPNo+uba26WV9RlSfKBZrWBGFmuVlgDpS6pCk1KnhSzwaEWpnnwYqgyGJYVRc3+vQfMjo6J5QyPwpYlQVuaYo6vpvhQSXKE5MmTIvFX3zzk/KblyfUGZafMipIYekxUKDulqmeUC0vTSsPYOZkmK6dTNj7QrBv6dkOqLYaAzWwhpaUhKbmAjI6qYkLoOj77/nfw7pK791/HVDVWSdMx+J4URWZrCyBEVFCo9Zr1i2co10OMhABtgi/ajrul5Xx1y/XmhiMzyeZdMsYbQ5DJo+ApTY1bbzjvRK7LDI3OvE/nep94kZh4I1qoZLQxx9445gcZVJPgQ1EW+DiMbvei/10UHB4dZ4BLxunFrVpIIFLUI+OwweN8T9O1lFVFXU2obc20rCnLiq5zJAOTuga1BaR651BsZBQSaViZnGNJDq3GOqFvO/q2o5hZbFFhywlzU1JWUtb1vRsL3ZRE1zzGSFFYjNGYUqZEXNuRkhjhNU1LoWrZAXobq0W/Fkw944Ovf0gAPv3hd0ntKiNqRkgYyPkXVaI0GehIkkN1XYcPEW80fjbly+trzryj1QoTk0z2KQHXkhL9wEFfcCgvRjmjNGzLDJzmez+Y/bCbiyrNrJ5yOJ1TWJP3eMIqKyPYIjaJTOuJ8XGnEq3WBK/FkBqRjBmavymKvnhKidXFOZdPv2B5+gwVHYU1BKEDo8ua+dEx5cEhwRY410tjVymCCmiVmMxntK7Dt93IJCZmICqfcUbtglnmlTNrACTTAL6q7cROHOX1coyDERAhbfPUYTJs8CDZAmxq5+zcPY+37MXtuZtHgodzMkvv7R7QoxZqDq+DnuVIesh/DmEAtoZonNg1Qosx5sbFkOftAJL5l++yOcfreOW8HvK4nDMOQPJOk31Y+38pQ3bnzwOo91UQd/v+MDT5U1J4FwihI4bIbDrDOU9ZZOarltFwySnkukU7OmRwVcyhtwxUiRMha9YO8haD/EOMkaZpUErh8ufu85ShSBkMgLbcR5PZlUNsKsqasiwpizLLhW2NYYMfDKMSkZABrVfvM+ywoPMaDNn7xWa5mJhNDoeXfDaPeN2kkUU5kMPET0AMnYfGS4gh3yeR4gs+iORp9MQMwqfcREmZkYrRGOQ6AgkM6AwSKsjeD4Zt+0AmoopkIAWiNviigFBJ7AviI5Ti9r6qgagQY2bNg7Yqf06ZL4gMOVXWGE7bGDauNQIphXFLieSCvJdReZI5yBopbCH61GVJcJ7ei2xAVRRjvTydzaWG84OOrjTEYorEzOaNIWbPDZGzsLbIDHrJq7M4ipxN3uNct40/OY7FmEQWMSpkvlrjlEMNzcEsaTDEJGstKsd3l5mxwzSIgnHNO+de2atKa2bTqUw8ZC+adtNQVxXTasJiOqfr2hHQJSUBxGdzlDZ0XUfXbydlU8YEZ/MZXdvSNA1973LzO1AUWYIkyplHkL0aU6B3PYWq8VHua9O0wpZWjFIYWmvUwHv7S16/0CAtCmxtqG1BoRey4EwiGPA6MZ/U3Ll7h08++oi+aUWz8vaW85cvqEsRKy7KgglT9vb3ODw85MnTp0wP92l1IGlwbTYEyKLXWgtI51KAiaHSM/qrROxlNKopDc9WV/zTP/gXvDw/5z/99W/x4LWSsixxMXIyP+Yf/t1/wOvHJ/yf/+af8eX5l5IQiE4/vfNYK0Fn6BbImAdjgQoZzFHiuizjw5JImuFQzQtsG7TS+NDld22p/ynJWERRFjgvI3goMc1JScCvlItiUxfMykOU1YS2J6w24AOFlcAhH1NnENiwNSmTxErlAw8YhaoHwy+lZHRc8AZhHaRkeXG+Zrn8mNPTc371w/dJqSc91xzceY3XX39ftDLJ75N2D8CESoH33n2bJz/6GF0Ymr4lqoSyGhc8VzfXzLLzdec8Pgmzs7KW/XrKpMhWzVqPwEYfHBpE34+A6zxN9Fy5hhWB4Bu6vqd1DfSRlzennK3O8SlQzqDAQlthjXSVog9URcHtaklIUBYFs8k0X7+si9KUxNjjY8J5R5VH3hrX451nWk04OjmkKEpOby/wKmLKksHxUpjbBmMLyhqU8yQcRTbVu7y+YeoiJ0fHLPZnXK023Hz5Exa25M50Djh637O8ucF1jjQr6X0Q44Ykpg+oIZEZZABEc5iBBZ6ZBbtrU2c2xfDfoLDKUpU1CdFj6vuGVbMURq6G1vU8f/GMx4+fstnkgJoNEYbnDkNyNQC10mi4e/8ek8mEJ58/2XbJ0/AzsJs8vQKuoLJbJgzukX3XS9KnpRgbzfJiEtAlhDGYhywWrrUeR8CEsa4IwRN8FOZGGti/g4aqEjbOoO2UoKhLzGJCKg1N1p4qi5K+7eR4i5r5wT7udkXos2mXVvQE1ss106rEliWXFxc4/0Pee+uX+e3f/Yc8efIxzfKco3t7JJNwKuAVqMLmRE1ji4I+BTZ+Q1lI8WBah7tay1rKxjJ+SB5UGg+3qON4/6IPtLeBt9/8df6Tv/63+f1//U85f/Ez+uYCQ9a9DiJNcesaXHB89tmnGTwWjfAY8whNMjSbNo9a6Z2CM40JvYLRaGooWIZnLAklkA/WqqrY39/n4vyCrmtBJRnRjGEc+xkMOoYRlaEBMhQRQyFUVTUJsvtpfj8t41zispzEwESRCybzCkCpMjg8dIilO450BRi6H/KZYvD4GCmi5o4qqZseztdMo8aiMwsXTJCGilaJelJy27S8uLri2vUErbi7t8ejkxNuz09JMeBRzG3FvJpyfX3D6XJFg+aDR/eZGMPzZ8+4bRsm0xmP3nqD4D2fP3lOebxPYTR7yqAub/nk+iWXlRir3FnMeH57k1k8MpqakjAHxzMLRpbAEDNeOf71lmkrgIEaQW2GPcTPN112AdehkBgLrp3XLggLWwB9iBvD16fTqZyhbfeKbnGKKQtKbJuuSknTU8xII4U1OGPouh7vHKqWYjfmAr+s6zGkqXydCejajhh7FnuHuQjRFGYwKkgiIWQMi/0D1kZxeXNO7zome3uoshT2booYxPgiIU0za8ud9SfPpXdiGtptNnzy6cc8eO0NpvMpSkkS3HaOaV3LeRVBmqMlk8NDyUuil4JCJQKWGDz7B/d59vQZlxdXTPcOuVw6vvvdH9LHyN7egsXdY7h4yaP332U+nWJMTapn3HvjNd7+xvu8TmIyr8DImrlzb8qd9+7y7q+9y9XLF9y8OGV1ec3LF6dcXV2z2bScf/Gc1j3hyePHvPH2L9G/2/Do7gN+5e/8fcLizgjyR7W1RFIpkbKe5iBAoWQhSVzO6zbEKAYaneOd995nUhm+9+d/xmeff8kH77/LYn8hayAp2vWa1dU1Gk1wDrwwdX1KJGM4Wkx5cr4Co7L8Q9biC5HsEYOpaxYHR9iqhqKkCy1TH5hMDrlKE1pV4GNNohRWaILYtUR/QxEsU9Nhwwav9tDFPqYsSSHhoiL5GrQhqG48S1sX2JtZVN8L2GYttjDErgHXYLXkl8SA9knAUAPWGK5fPOby8x9S1onp4QExTySpYSwzRSxCeicGdEpYlQira4rNJfu1hlji+ojrIzcucGs1123D+dUVzugLWwAAIABJREFUx/f3KSZqBCx8dDAW5wkdA7Hzmc0nDaq2F7PPKssARBdIGHFoRliDfhQmeRVs0sawbtc0/S2lrUje4wf/iJzL+AxEFaZAa4s1YqQVo4yoGyVasJPJhLKuqW2VNUIV3g9+E9nZPW2ZQ0nKcLQSllBhLFZn0A+yGbDkW1VR4p3D94HNpoFksdbQuW4scL3zTOqpsL/yJA/I86uKEm0NpbWiu6gUVV0TO7mPQ/MyqkDUEqB65/j4o4/ZO9inKidMp1Ouri5JLhKVJ+XRXbQmaEMyom0fQ4AYhABRlGxU4IvbKzZJJNyMVmC3nhtaiSEO+TyNMRKU6A1Lui730VjRHJRzP5vr7DDPyA18o8GWcn+sMRS2pCwqiMLuVEZJfaWsaIWXBes20PmIJhB1DgxZH1eawInV9TnPPv8Id3OBCi2ltYxyHnXJ0f2HTA4OiaYQiDefyy6K7EFScHl7k8esBdwh54/oAVQcctUBiNw2E8k5xBCyhr+XrTJ0kRn9Lsh1GMjPhwz8yxnGGO/IoCKJMSqOOa2SJiI6kULWus1132j65l/VWBz216hLS5Y3yM9qaISHIG86zKMotmCaaBEPE4YDK3hrGrp7LxJb8FZnqQ4BmRm+MYPIec1l1miKMUeFbV2wm5fsNnt3c4zda9y95gF4zosnA0lC3kh5iqYuSuq6kgbCcO0xkDx5cm9XjkiN928Ayb0fwDODyezbAagdvE5AgKKYQcKU89GyLLFFSWHteK/sOI2V19FAuMnENpns3YLRWpsMmOYJ3Li9LzFrqobg5TnmmnCb/2UQGdHgHp6nMXa4ZQL2Dd+fGWshyveSAcaiELMsk6c9U0psmkb0aI0i+cx01JpikDlA9phb+xH4i+S1trOnzLD21EAg0FnH1qNiRMdELuMw1mCDFezDGskFszk0KHShMErjQsD5QTIyjXLMfjCsUnaUS5JnYsd9Nzx7RTYgKxUqPwONED0whqIWKZvgPamMhJ18d9jjgzZ0URT4YToxX+NQnwTARInRIUaqqhylKYY9EnwUWS2jaVuRLSAl4mCoGGPGWQTrsDaD3kn0vgcTvRACKqgsAyD3eys/F+m7Pq+PXJMbS9+7UX5M5b1eFFJzDYTC1WqVv3/QnxVAd8jZxaAeIUOZIrODsw66ETPRaVWzmM3p+p5BDx0YWbul9+hhqyshUqSkckMOdGmyRCG56R8pjBEZkhH5+/nXLzRIa4xmb28yimprpQlEXIp0fYfveuqyghDoliti77m9uuX6y+eScOgCVKKYFpSLCmYafTBhcnJAWC/pXA954clL0fc+J0+KqDW+0Oi9GWm5JmaTid7BabfhX/3Rd3jy4py//9u/w9tvfQ1TRKZ2yt5sn7/7rW9z8uAh//vv/3N+8ulfEOnRNhcIMYyLTzZeynRos+0Ajj0c+bcx2dgihJxQJDJiMAY/ESjOnVU7JGXyPsvlUpZBTjRFKzbryWjyQShAq1eJ6mifdrWm0BCbnq7vqOuKFLUUFlqhChnJGQ2XjLhPppRAyzjleG9VNn9IAmJligBRWUwhxkifvFhyvvoBH779iDfvn3C9XGFtzcNH76ByQTlUMTGH0a5vObh7yLd+9+/wxU8+5eLmUrry0dH3TpyX24ar5SXaGOpqRmGsJBdE0diUjAuMHBZE0VEpVcG03qO1PbpvWfc9odugdGLTNjy/OoUYeXH5ElUZjAGf5HdWVYmtKxnHajvOrq+wk5L5dEGZQZG6LAlNKwBfVChlRKMleKyW7kzbd1Rlzf3jQ2xheHn5nHW/ZLaYE0Kg2TSE3lOVFbaMKCPd7rIU8fe+74mpIKkKHyMXtysWiwqjFQsbaC8+pVL3sKqkDxuWNxcoDC5m/SGlIbo8gp2ys6gkK/WgvZfiONqUMsBFzimG8ZS6qrC2QBtJgn2MkByb1Q0uiAFY321QCfquY3Nzg9YJrRP5kWQzujQCGmkAsfJeqKqaN996javzF1ycnpGzvC1Q+xUA55VueP63MnL6tW0ngdgYIhoVIsnIAdd3AhDa3UMNhJhFRFnZB2UpIvybtRcAkOzKqjVGGXrvyJsBlRQ6JqIGMy0p5hMccrCq3EVPSlGXFavlCmM1k6N9NqfXuN5TFQUqQHQ9Xivmh1Ns6HDtiu/80e/zD998j3/83/73/C//0/9Au+ooZyXBJpJVzOb7aF1iDJiioqwjXp/gK3AWupsV7XrFYm8uexhhglhjRa+pKOk7GalRJNymp7vqOTx+j299++/z/X//p/zs+98hdhdE30HSxOAxs5omm5NNi3JkL2vAWMUw+nW7vOL65oKqkr262QjTqCwrFAJ0DCMwRVFQFJbVZpU74VpChhJnboCmaUR/L5tbREQ/VbHVcBrZHjnBlIJvCzaazH4rSivOqdnwQOKyjLxO6inGGNq2FffO3DizxjC40FotRY3K2umyGnIxljUvtYKCxOzwhNT0HDnFmw786gZlC3yQhom1Bd71JBDmTQicnZ9y1rTctg6tLe8+eMDUKM4uz1itNxit2J/Pmc8WvDi94WqzpleK9x/eZ1IYPn76Jdebjulsxodvv4Nr1vzsyRNum469fspDXbN6esrLfk3cm7CYTHjr3gm2KLhZL1kGiYnGKDR2TOhJwz0fAE6D2clTJHdXY3EyMGvJIPnIhGXbbNnVKd5lbewC4LtFFTk+gXTLtTJEFTIQuy2y2rYdC75xs2/7hOOXyGvHBUgqICpycub7YY+nRMLTB2GvynVJIi+AgsRShc4Mi8wiQ1EUE1zw+NhnvCBhiyn1zLCfsr70bEa1f0BwLS5I3A5GANTSFFTVBJUGDbGKRKIsK/qu4+rqnHt3jjg42CPmfT1fSDLcNS2RiMkjwW2Xdb+0ZbPeUJYlRVEwnS5orq9pvWdWzXn6+Auur8/5pb/xX/Dg5IjHP/0eH3/0mL5fcb1aE4xlkyKTynDy3hvUs4K+UCQ61mktrr3Z+EErUHueO4sTHr77EL/xXD5/ydmTl3z60VPOzm6YupZms+LzH/2QJz/9KbOTe5jJnDvv/jLHD95ienCPVEyFHRWlwQS5SYY0kJ3rR9b0UNT64IlBzpjWee48uM+H6Zt878++zw9+8GNef+shhwcHwhDyjuhFS14N4H3SdF5+z8FiQlVo1tm5OiUwSdF0ko/O9o6Y3zkBY3ApomOHj4Gry+ecHM6ZVJqNsihv0SoSxR2Q1Ld0qyV//tMGXVagC1RwKJpRd87lqTNlS5pmTaUiPim8Klht1lyfvyQ4AEvvDUTRGE+hwQOpW0EUoK2ylrlqWX30p/QXTzl4dIArCzH5SInUZ1ACOJoUPNivOCgKDqZTrE2kfkL75hRFoCpqmpXn+bMLXjx5xs3FNec+8uz0ggd3H7BfV4SmI3ovIFlM4oqd9V9TDAL4pCSTYVHlibOQ47tDEdAGClNShoDzER/TCMoIcGQwVnF68ZJnp2e8/vANpuWMzvfZjAphilWJQw6wupL1ExLKihQEudh0Xc9ms5I6Y76HNWbUP04qMq1mFLYkqcimWQvTTScBj6Ii4FGlkvfwTqQtlIC6SkFVTSiLySjHEaNDGZONljzaJHzrZRJHG6pyIhMaJhutBAEvUeRiXQyKmq6VpkuU3F4rhe4lftVK0Z49xZ19TlHW3Hn9bY7vPuTy7CXd+hLX9/i+RyWZtjGmIOKymU4k2ZJkC14013y0vGWVaxalwZYFvXOZ3SyxXiuRXhhklV6J/YpRszXFhPO96PkriZ/yWAX+8Hie3Z7zFx/9iIdHS37pna9TL2q8bwmxYVJPCE5kd+qJpbSa682aoC0qiRxJUoZSGywJ369ZXV1w+sXP8KsbdASMETk0DQcnx8yOjqkOTgjkiUStKI0AEClKBWO0wfuO0gjLO4ahAadIfsvAhAFc3b5SPkdTBvV3C/0BF1TajtJOMY81C1gpzesYvej9jsCUQuktoJphUqk5UyKmDCwpGJzNBw1XvbO+BXzLrPfEq2eu2soh2GxUNOhIZtwZvZMjCYEGmSiNA2q8K42RrzkDL+z8TYSxQb+VLMjgawYcJafItTieXUMyMe2UKZqvTs98VSNfru3nP9P4XBIjuUNruX8qJabTKXVVMgD0Q06RkjQGtTUYVexIcwlAFIZJ22E/JEWIYLUAXz4Eid1RwF5b2BwrU94jIodVVBWkgbGfdVAFWhCsIAOiMWbpnDwGz86lDw3dGP1YbxktYKYYykZ8bkxrlQ27lKIoS9ASqwvsqGVsBunBJPFBJyEhDSCv3CtphiRSNg+ToKC0pirtGM+1URJb+x6SEGqccxRlSV3WMvERI8FJI32XfW2MIWTG6PDshQGc69EUia6XloLOTSMnNUxKkbb3MqVSVbIeQ5JcUAnzWPomScbs2fEHSNnkHqkTB58TRa4XYpaYjAoyOE1KI9PaWJvfL4z7QsetPMZANhj0cFMGSwtb7EgaStyNKRFKkdcw41RhzPFE9pA1BqPBkZhOpjjX5zjnSSnkZoM0CkKIFAUjm7kwWR822hFHGF4+BMoMuistWsAhhNG3p8/GgwN7Whi/LssjlHkPmxH03e5J2atD/En5Wgd9a52JjIOcwmhOlhJlUeTPknWB8/2rss7tCIRrlQ3PImUpGKbJGJnWmRSps/wof/nrFxqkVUphCiuaTiFml+x82qTEer3ms48+JrY9ND0myGEVnRdxZisk8v62lbH2ZzA5OODq8kK0l3Y6iCp3qAdKtVYKq4yM4EykA+k3DYOCfVTgVOCnH/8U83uRb/9Gwy99/UOirlDqhKKc8eF7H2LthD/4wz3+5Ad/TCBgC3IQDISkUAyOdkJlV3Hb2Yz5YIhkQDev3cHxzyotf5e1XIYxr7HATNsuxsAGUQpClETIKD1uQul2CYgqx1xiMhcGcuo950+eyqbzQ5Ik4+4hRkySA9/3vbB9lBIgdBgZUMJ2G57pCExnAMrnjkUMic3VmtXmEy5vbvng7Uc8/vQ/MJ8uOLn7EBcUOoTcFc1izdGjK8u9dx5xfPcun/3oZ1w+fUERC0IKbNYNSUV8kHFEY8XMxyhxEFdGOmsC9GR6vs+dyjyROq0nBBKVLem7lrVviSny+Py5aN3qSGUsTSPFSbO5paoq9uoa17a4tkUBi9kcExWHxZR70wUVilUMbJoNRWGZz+fc3F5RFSXKJLqmozCK45Mjyrri9OaSl7eXJBU5XhzgnGMdV7TBU5kpgUCZ2aohSAeoKku0tdkoI7JqNlxenjOrSsryljv3Eje3jj1zR7pAPpJUEgfiEEWaANGsEldQNY6Vy97Jmo25Ez2wZYdOnTEak03ZJFOyI/BlMvMhdCu6bs3l2RnHh0ecHBxyMJ9yfnvLi9Nzzs+vaVzeL4PGWl4D8pLPcnx8wuH+Ad/9kz8VQfSdoPwfC9DDa2QmxDDqzAgRYNtNLYphZCyLumfHWqM1ycex264RtsxQ9g0Jlfw/x5ec5IqTpgCFRVliIjid0IvpqEusjXTXvRdTCdfLKHmMiepgQew97fkS37vRyKzvHevVmqIU9u3l9Qv+1b/83/jH/81/x2/85t/jX/+L/xWlodgrmM4P2av30ShMoURrThXMp1Oa2tH5JbdXZwS3QZtpZlsIECksU0PsM6tJJUyEftUzs4d8+zd/m6uL53znj34Pv74mOYdFROIDienBHMo8LJMZDSlJYjEkwTGlsVO5KxWgtbBhJHFzWzdPLfq4LjjatpWnoLfgnCnLzJbMnVeApCnLisV0xmq5ovO9sKHZOrMOacMuCOi8p7+9Hb8+sjLzN3ddxzCyJaNO2RQjM2QAXHaVTTl5strkPH2oStK4hmLTct8pXgtw0LcoHehUoNcanxQxiKFhmwJrH2jbwKoPtC7iVeJ4MWeiFKvzK1btBm80R7MFk3rC6eUlF+sVyRjePjlkr4Snp2ecLRsO9/d577WHFK7j6ZOndE3L8f4+b99/wM3lNZdXV5Qne8z293l4dMh003LaXpG6RKEVpVbEaAhGYv6gU2WVHosyGbNiy7TIhmlD8VYURUZkt+dZIp9pWmdAd9jT24R6e+Zsx0HHZk1m16SYcKFnkKVQSuLZKyOPCbwLGKNQMQO9uQmUhmIyJ70pSQHtAR8DPgX6bHowxJuyLLL0UWZKZfb3yB4z0vT0SXTLwtD8TLJHUh7r69sWFBRlhSlKdFFCYZhUE0LTyFoKDhcDsaxRKhJ9R/AyKp6iImkp+IwxHB4fU1dTvBM353oyGZNcO+h8hYTvHU2zQStpCi7blZhjTmfE6Hl5dsri4IAnn3/Ocrnigw9/mTfe+xr14pg/+YN/xheff8Frb7/Oi89f8uL8GR/8la/x1nvvgTZ0DnzIDrwqYg25+StNah0DsWlZXSxRPTA55sHXH/Dg65Z2dcvlk0+5vbig36zor8/5iz/6l5g//XdMjx9w5/1v8PC9D7n/+nvU0zkYQ4oSS8j7PMaAdx6b9f8FDpCYvrq9xRtPWUSmkwlvvvmIl89OefzZE9Jbint3DvEe2rYRZoYxAnrERFVP2Tu8w8lsweNbz8ePnwoDPkjxVtU185NjZif3UGWRjV0EZCm0YnX+krIvmb7zgCIljI4iz5QEGDSzObZ+nTYEinoi0l1dg3ItUVmSLumSw3hFpRQqiv6aMcK27rqGqDWhLICaoDXaBkJwxGgJrqfQFltNsFZThzVm9Yxw/jnWKqZHJ2ImNbDxEmNMnBnF20eWvbBkagLFpCDWCVdPWK2usbrl6GTK63feov/aPc4/esrykye8WC45vz5nfnw/AyiBLMSb96kfx1Jjlo5QpqTUCpKwdpNPNM2G3gdsIY0KF3rRnc7g14ALDs95MVuwN+8JIdB2DetmyWy2h9LQ9U0u/gusrTJBQqTZ2r6ldQK22sqinWa5uWW1WvLa/dc4nO9ncKoU4zQFXS8jm8IA8xAdN8slt9dXHB+dcOf4XtZTDhSpHD8nWfrJZo120VTWpOhQqqCqClzvubo6J4TEvbsPqYuKlKLETXGloCgG53SfG0TsFMt5YiBEknco32EJWBzJJ54/+Uz0e61M/Qmb1YCx1NM9Znv7xKsLVr4lJgEYvE68WC258I5OK2wp8gsqbO//LigiTTSzzdny160ZXMDV2NCTpp+QLVJCwPw84XTdLvneJz/k088fc3l1yje+9jVO7h7T9i0Hh2/zyfMvOD094/nNc7xSJKUpqprClrS+F5fy5Lm5Ouf68gx3fYlfXwlTKoH3CZJnstjj4MHrVIsD+T1Z/9cFL2wzSZSzFFjOL4YG43CewJgjyLMJ+dzK0kmjFMVgZpR/b5BaTmSF1FjjjjhhSpKzI8xIpRU+GxZL4y68MokkslOWgTUnkgNy8KWwk1+zzX9G/c60u4a2AJGcg1sgZgBspUm5/R1Dbarz32sl8iQDi22QXxtBHZUzp7TLAB2YrDuN3piZwLvQyPAeO42AFFMGhGTa8qu1w1fJHv+x2mJg0o7AapBzu65rYUfGhNYFKaoM9oSxITz8Pm0tPohussogwFBnKaXH2tp7ySNdljFUSiZktdGicQtiIlkI3kDM8jVZrgACSXlpjowMQ3kGLjMjlVL0vQPEUMs7nxs8Ga/Q22YKiFE0uYEgAF2grouRuayT4BjWWApbUJTDpI/cM+fczj7YmpCpFMe1JCCaz6SGMSkbY6oQERZjLOvajqbv5O/MMCGc0NNpxiwEsJRaQ41g3nBdw7RV07f0neRfwUcxnsr/C1k6aSDB9d4JW3Uwd2c7rTeyy4ccNeem3keqvE5AQHBjs76zkfsZc4N3YEyrJJMkwTvcMox7YCQ6ao3O8WgAJ60V1m6MicJGtNdjTNkFTLXWYw475NHjWkwKbRVWlQIQG4WyZuisZPa1JimZrLW5OY4SqUBbign17t7ZlQN9pRERRPJBzMN0JuwMdZ3IYIYQKctq/MyD1u1gBjeA1KORsVL4fO9DlO8bAOlpLfI/Qy0YRua6Hf89SDRsP6sacyCS6A8XhejbYqysu3ytKrGNmf+R1y80SJtSYtNupONTGFJmVpVWU0/ntK6nbzZsrm4JvVDPfRLtC2OMuOPmjE4bQ7U/Ew04DWVRSZExjCjn9ytzIeK9dECCQgJeXciI1m2L1Yo+eJIR8PbHjz/h9Oqcb53/Tf7qN3+NRXDsHzxkUVS8d+8Rx7/zj1jM5vzbf/9HBN+QkhMWKZJECjjs86ErD1hc5sz4uQYR78GkSCHjKkmxZQxmMCjm5NMoxoU4mUxommYEeHUOZNN6Rp+Ty8IUgDDLdBIGlE+eorLM7x7TXd2yud5A3HY6h1GklDupWglTVjZCHA8plQP1EISG8R0Zk4jCnissURk2MfDR0ytOr1c8OHmOtolv2r/O/v49umxyIDpgmhCzY6NSlPs13/hbv0J7u+LLn33K1bNL0otz2tsN9J3IAriEni4wZSHBMoiLblGWlKYgObA6DPGDtuuYFTPqskQHYcLMJ1MisGkbMIpqWuF9TwyO4CKu95T1hJvlkvXtks53FEVJjeXh4pBvPHwT2wdWy1uWfUtd1+ztLXB9y2ZjZUQjGhbTffb3FsQi8uXlE55enbNOjr5pmbkFi+mEuixo+p6maZlWNYXN7IWY9XqSAGB9DHSrFanfUCrNfDKnadd0/RrVBmI7o7IVlS7pVC9mHj6AEo3Dwd3T9z11HtEdDkHnekJIEoSsuI8bLaNlZVHgekfjW9EYLQ2ohDUaFT2h7wiuYX17C31DER3Gd1RVxeL+Cfu15c58wvOLa85vG3ofZSgsryfJWURj9e7d+7x8ds6LZ6fsJmC7idRubNl9KaMoqwJbFhkQYUxQrBVxdAU0bc8gcTAYFgwjUEpJl9bsgC4je2+nOwtZ4ygXs957yqpEFxY7sRQHc3wMWK2zWZawKeuqxrks7F6JJt7i3jG+6fDrTpwkrYGIPKdyRllrmuaGx59+n3/+e/+E/+p3/hEvnz/nez/8Q2bTfY73H1LbGckH0fwrLCkqdFWDSfiuY31zC7ag7bosbyLUBNHYFhftkJODbtlhvOGv/frfor2+4d/8X/8Kt3xBcBs5yJF1We3N2Ds5pA0OZRSTsqAPbozVcl+k0VAUJVprNpv1WJR535LSajwYB8C17zpW6xVkJ9SisOwt9rm5uc0C7mF8VttiQtbSoLelg+joKTM0rHhFlxtkqsPmYnDs+O+AgbBlcA5/1sOkTcjrYFiDWov+k9bUVcVqtcLHQEgQtcKSmCXFvAncaRNHCaaFYnJ0yO31DcuVMHVbJ82uylra3nOxWbFxjqjh7mKPg+mMi/Mz+q5lNpmxN9/HWMPF1RXX7YZUFLx5co+5Tjx5ecrpsmMymfDwzhGpXfP5+TnP12sm0xlv37vP9fklL8/PKfcWTMopr00PaU+veLK6YFla7swWvPnGfc6alp+dLYmE7BbMaIQW0laiQpusw5ZlM7aAvM4d8sArcgNDUZSkoB0YAMPYJbxa0EmxtLNnwzYxGgqC4RkrtQWIhzN0nHyJA9tVSd9pBzwYEuzdAof888714/sN52L+lEBCGYNNJUbLFEP0Xpq2xmCNxo1rLP9ESujCSkPBGwpTUZmaRMJOKqzWuHWLCgK4Bu/wrsO7jr5LzKf7kLXMtdFMZzO0KUnIs8hV89gUlzNOxt1C3zEtSwb9wpTg6vyCpt6wv7fPwfEJd46POTy+xw++/108ipum5cX1hmcXHe9+8z/nV//m36C7uUU//ZhiesD5FZS1piprFFVmtfRALwweJdplzWqDbxyh2+f48AFvvvsGZn5MUZQo13P+5c84ffIZN8+/4PTZ59xendH7G5ZPzjj97If88A9n3Hn9Pd7+2i/z2ntf4+DeI3S5oJrsQ2YdqTx6LLlMROQIGq4un1PpnkllUSoxnc24d+8e55cXfPnkqZiIFAYfZCy67Xpm0xmLk7vcfeNdjh+9ibIlG2948uT/wIdAUJH5bI+jhw8w8zlqOpMJpCB7ReXi6+ziBfG6Ye+dX8H4JTYanJ6I1r+RgqgLVlhXZkJQhqgTsb/GaM/08ARd1UzLUuSV3D6r1S2YgsV8wfW6IXlLcomEAIYqKVIfUalDhQ6Nh5AwrsWdfkLz5Ec0F59x9NoDFnfu0adBdmDsqaCUoukc682G9dmXbM6u0UVBiJ47JweUpcJWJXYaUGnNrCg5+bUPUB9+wCd//Od8enHJnfkhCyMNwaG4lDgsbJ6QNepDiPjYYaxFEUhJ03iY3nube/t7rK/PaK4vSM6NMWiQ+ooxoUyB0RMWswPJRZslq2Y1xpGUR3mNtdiiEM1U5Lzvup51u8ZHRwoeFx1Gaw4PD3FNz2w6ZTqdoTIjPyq5Q2VZ4oIn9r34ZxDZ399jkacI+9RnKa7sTxABZGx20HM0xmJtIdcQZBTV5GbX7e0V8/mBMOJioGk3TKZTmWzKjV3nHMvlCp1Ebz/lc2vwxuhjQx82oKVRVVDkkX9P6NasN4FJXY0jpGVdo4sKnwxoS2HFk8BUFbd9x88uLlimiM6mqYGYpRy2o+tbsEea1CYbRw28I5X/STGOk0kqKPlcRpoYi9mEdt1jbUmw4PA4Gp6dfcqj+3sUpuPi6opnz7/gs6dP+fGnH9MVkQdff49iWhOLQozYPPh2zfmTxyzPXtK3G3SIGMhGNEZGnScL7rzxDrM7D9n0nhhcNjqK6ExOEBZrIqaAqEikXL8JGSCgiE6mrLQx45kznGdD7iCN7a2sQMoHSsrApixZYWsx5ijDuPPQiBS5iVyGCrCUm+Hj/U8AepRPkDN8kHxQW5Ahg2vEreSdMPzU2ICVMzuzx/K5aLKU2AC47WpwjvqqCZTagjYM+EcGd4f1MLJcM3gzmonFlBnnjJ9tiFDDOhoYwYOMErlR/1V27O79/iqo9NW6Qq5j++cYxDtCWHvCvAy+p3Vd9uqQazTZ/C/l6x5JC1/JXYf1MLI/c22JsVLzAAAgAElEQVSCkmaHyeQJopemkBaZQ5XXRwhByJhAiGmMo8M9ksvZBV4z4KdktL+qKmmQxfgKUWK48JQShRGzqGQyqJWlCWLWpCU/x+HnReuz2ALFw9rN+IF3HiPz8TJrnBKTqhaZShdGRiUIsOlJGDR1PZE6b1FR9C0uf4/I1slzsrnWGK5n1z9C6omCQZamnFR0bSl1da4XQ9fLmpI+iNQP+Rn5YVRf6VHWYRek1XrIUTPmQ8J7maLZNvHC+PdKZaNdpXKDRT5DUQgxS8DmSHCida+U1EPKWlze3947mlY0ZK0RspoZiFn5OciUxnZP7t6PUV4ThfLbXNsWBUVZoJHrTqhshpkbUTFPvORGy0D4+7k6S4ux5XZd5QkZdr8vZaBUUZZ2zEcFCM0xCsFBhvfx3tM0jVy3ta/6Vvhto7AoCiKMpBGXWc1DzNtlXXddl6c8RRpjMp1RZXA8pUSXNaBTDIQozGdtTJbv2YltX3n9woO0WpEDlwCZ0iHSlNbQ9IGbiyuScwySLSkh4/t5TFor0XCbVBPK2YKuSBRlyXw+p2k3uaCT5G7o3qWYhqnqMcnEGMq9Oa3SxL7HeEHZHYlr17A823D7f/8+T54/51t/69tU2rI4POFgUTCdnvBffuvvkrTm//mTP8zFt8dqkHJrOODMKxp9mswuI1/Y0JHUavxcQxITvBe9p7H4E0bDKyY1gDElCek4aGV4+PA1UPDTn/2EyNDNlRJl6GR23mHKgvpoj5A0sfPZHVVGdEYAluHIYyxOX+lWIl8aAvOQbInx0nbRR6Vog2Zz3XG9fs6qadm0ka9/8HV823D33n1m830BarW4TWqESeGMoTqa8cGvf5N+2fHyi+d89qP/wM3LM/qmw/hI00GI5dg16fqOsqyYL/aYzw8oq1KCuw9471BtS1VVHB8c8aZOLNcr1q6l9RHfB2yh6dqW0Pd4F1kvNzRtJ4V+cKBgr5rwwfFD3jl5wExbnp0947bZYKsCrQ2b9YYoc4aQoCpKTKFpVcOnL7/gy/OXNMETtMG7wNPTc954cI/X7pyg8Kw34vSbEH1NVUp3LAQZmQ99hyZRWY2h5PziinJSYIsKjaJd3lDuHTCpSzYbGbMkAxfCQBaNIDt0ufUAgkgSZMwwai7gt9FiYkQKpDwCKEmDHPChd2yWS1IMHB8sKPcXfH51w2q1IoTIwf4+lfI8Ot7jteN9jg/mPD275MXFkutVRx+3emMK0TY9Ojrm808fZ8mS7Zr7qgnCV5m12mhhtlUlaIh+0IdNqKzFLJ3jMAJrwQcG18ps1o4yArKJfl0YQZ64ow095Lyd68eGRmEt3aYlLqbcf+cNzje3zKdTXHblFJwkN5p0hd9sJLEwUM5q9h7c4eKzp9JVjQMDIOL6jno6k5HO0PDRj/+UP14c8Rt/+7e4WL7g2Ysv2JsuRPBdGZSRjn4MgWQgRU9sWtztmv29Q8q64vrqSu5PlBEWayWZ1CHRNx1FKvjwG38VHx1//G9+j9vzp8SwkaTOiDZg1IrqaCGauN6hlcXnA2s2neFH1qEUzl3b7yQKEv+n04qu68Yk3zmXDQujVO4MrBHyuDqj5tVwIA8dVa01XbvhZdOQMvCmAZX1aZUWKYGt/pmMvw3Jxm5iPjDIB6BuGJURZ+Lsqp0S02z2t9qsxoIYYFLVrDKg7PN7zZLmYSx53U448kumvhd5lHrO/oGh78+hj1iVcMlzfHiC6RWfXt2AVdzb32cymdNsGjFNnE44PjzEBs3zywtWriUqeHTnLrWyPDs75abvqMqK1+4coXzP6dU1z27WFHtz3nv0EHd9w4sXpzQxUMYZR2XF6skp55trllPNfDbnw4f30DryfLWk3azoY6CoSpQx4hCbzy4FWD2ADEGkbHbYz8AI0I6jROlVfa3dPT4wk0YTD16VQmAAWvPP7YIB8t9ybm2/zs/plCm9/V0jWJzf31grwL4SHVmrjRQSk+l4PqO2umIS8kUTuihLVITb9S1VPcGWIgOhxvfdMlxsYVGmxHsx8LK6YFrNMMqQlMbOZrgAfr3CpETwIZsXKEIS80uDSBwZo1BlxWDyKTrcsmad70nBc31zxdn5Oe+88zbBS4ybzeaI+UWWNkqA1pzcf0g9nVFOD3jf9bx4+QWbtmFS17z74Yf8lV/9Ffbv3MMddhy+9TXqsiKFSIyOpHtZB8GToiPGnlJZjK2wRYm6A6WRc8ZWC5KuWfXCymvbwFma8/BXv8Vbvxq5fPmE8y8+5ubsGRcvn3Lz4hnr5Q03P/kuf/LjP+f7RyccvfkW93/p1/ibv/kP0HqSGVuyHrZoQMD1LWUJm9tbVtctnfMYU1KZkr39PWxpWS4bDg73eP2td5nO99FFyWyxRzXfJ9maTetRqeONB/c4mi94fn1LfXjA9PgOajJj7TxxuRQjsRxbCqVxmwa3XhKSY317QWkTk+AwxSFey8imc47CFmgNbbOmKGcUxRSUpyonlPUUbWtC3xKs4u69B/ikePriGXvRCRAZnOhyqkgMjuQbdJT8GqUJHopKUzU3XHz8Z4Srz9HGUR7M6YIbNR3LzIgCAdE2SfHJyw31RrG+XBKbntIk1tfXTKclVW05PjqkrkspuIqa/TsPef2vf5Plf/iMF31LMdnDaJ9HbbNUCnkCDClCVRRdX+c6GROe7XH04HUefPBN6umEZx/9AHxPiDq3RoaYzbjPy6LCqIKqnNB0KzH9zSZ81lr2FntU1YSYPF23Jimo6pIQPZtuTRdaJlWNSgpDwd2D++w92sNqK/qERZLJpAwGDQZJ2hisLSSPtxrXeW5vljSt5+jgkGk9QaU4glWD9qQZGioMQILFO09wicIUTOoJd46OpMnhPMF5Qu+hlKg1xM6iKIhuW2gPkmKivB3AJKIS9nVKwmaLeTy4NhqyLFD0Pa7TpM2KrutxXSMu8FbTKs1nt7d8vGnprcaWGUzXIiegcszZzc8GIGoXwBA5gyhj6Fk7WjPoSoqkTFmVfPDeO3z68ReUtqQuS/ANxB6rPCeHM04We6Qucdms8LGjVS19ZegQiarm8oybvsO5jtX1Be35GSoGrIKUSSJFNWNxeEw5n1ItFswOTnCZ7DJ4dmhBvkWGKEIIg6b/mDmMevVR5fHgGEkhERAzocHXQ2XZrKEp+MrZlsUx43Ag5TMu3818L1NeQ3nfaJUnFQTA+zlmX9reezJBSBtDiJmBuQMakYGilBsRIXg5m4ax4q+c38PnH+qJcXolRopKmHDtppF1OjRo2QK2aseUNZeuklvsAM4DqEbKxKGhNlWvmoRtGwTqlXwi7uQS49PauT//f1+Si8jzVwy/N5BUoBw1ecOOadLOPoAx1919z4ENKp962+AYamySSMMMDR5h12qZTs5gE3rLRJfzX3IRkVvwaGNl8jQ3hLQ2FIUAykZrykJYjF3X0TshWrjeZQa5wvleakijs27q1jzO5Nqq61qU0lsjKIbplTTeq91n4VIcJweV93TOMWAQKbFlgycBn33yhGaDNSK55cK2AT9IdAQf6HMdMYKgeX0MjYtx/SI5YF1PmNiSpmlo+xaXa5A+BJTKz1ObrYlb3pcxmbEW2ZWwGPaoyaxSl4ke1tqRLTo+46HZFxPWKJG0KUphatoSY0VbNWYAfNgHCk1VmAw4VzJxmMj5Xl5vWYpkMCkcWKjDPVBaYVU2PEs7msN5T5RlmWVTFCrv/RASITgKXYz3L6afz8V3Gby7DNMwGsuJsbJIGhkGbHD47CNZIwm+syuVY4a8pKokx8pA9PBzKaVRH7t3YsZKgrqsUFrhejfW9cPzHFi0A8t7uVqx2WwEn5pIo8oH+RwhG9SHzgspxVhKa1F/OZH2FxukBdBp0JeRbiRJdPpWyyWrzZrgHDolqsJmbU85yFI+HENKWWTYgtHiutb3XF5eYK3J3RzpzJdlOQa1mESryigt/x0jMWrqgzmuafHLhuRCVj9IGBRXt2u++70f4DaBv/Mbnve//iuUiz3qouLR/bv87rf/Hgb4znf/kE1/AwUoUSiRQ1UnVDLjYRdUeCVQKERmYXCYH2j6oDC2HEWls2LLDpAmzo4jborKTGPFsyfPRetmLEpygaoUJoNgCQgazKRkducQ6xN+07G6vpFiOoq+CkqJgY7W+CTaPlpvR9Qhjd0epWQ8QqPHMcOtjFQ+DGKiTwWPX65Z/b//jsdffsL7bzxg76BiOivQeiIjD1lDSCXAB0KKeJ3QhwWv7b3Jw3cecnt2wfPPv+Ts8TnX5xdcXl/KBilLond0oWXdrtm0LZPJHKUMEXAhkLoOlGJa1Lx38oj1bMOL1TVqfcmz0xcoHamrkklRsulbLAqbFFVRUMynTOspr+3f5dH8kLhpeXJ9xcZ1mMJQZ80fYZQNz9WgbeRifcGL5Rmfnj3HZb0hpeQZt53j/PSCR4eHLKaGWTGn854+eK5vG7qmpSiyy28n4+9RK9o+Mq3leVRlkdd3YLO5pqhgsVdyceFkBeVRMWA0tCly4B4CqdEyuhBjJIVAyswspRS+l89qlejaKZ24uXyJC5G6rPB9R+gdyyygb4xm1TYsmw5TFYRkKJLneG+f1473Odnf487BDc/+P+re7FeSJDvz+9nm7rHfLe+tzMrMWru6mpzmAjY55GA0IwkENAABvQnQ/ziAIAkjEBTEAQfs4TZssrvJXmqvrKpc7xqrr2amh2PuEVndeqcCSFRmVt4ID1/MzvnOt1yv+OrlDWWasBmjePToDYgtr15+A3Gf7nv46j0tDwvE/l7cg0IHBY4SZoOEe/WT+CSJQhgEMQWjKGMGRk7rvQRhxCj2BFo8J7s0MJGAvSS5SgMiHRXZYsJtvYW0FrV1wzSxqm7v7ri7q8UqIQEo3geq0BAzgxlndJuK2Pb2KZqu6dixoxhPaMqabrviR3/1/2Aw/If/6X/hT//Tf+TLTz7m7PiYk+P7BJ3J8bcdXlVEv0PttqiyIj86wrocMKAUzhlpvLyGWlHdbhkVY37ju7+D7jJ+8qO/5fbVE/HGixqDQbeBzgfcYow7ntA5kb9ETVq7BFDVar/p9UUf9BYHjhAjRVEMG7uC5NcEylqyzEm6dttKonQrDA2lFXqwaUhFSYxDGEu/2bbep3tfCxiNpsgyNrvtcA1V+vl0wwzNVr9OvzbtNv3CpjBGGALBR2LwOCtJqyEIy/fVq1eJISBrSBE19xrNe3rCu2ePsOaW3YuvoO5oVyWj2YTcjam2G3QA7QPWjXn/g9/kF9evyHTHpCi4Xq7xXcdsPGU6Epbi5fKOm6oCo3ljccLMZDy/esVtvcMZy/3ZFNu13Kx2vFjtGE3mfPjWW2Ttjhc3V7Qqcu/klPcfPWa7XfFqdUczKZjnBd85PsXfrvjl7S3Pqpb5eAq5Y1VVRKNQJq35yZ/dpCl3lzzXzTBR7699728WRCoHQyhAhNfWpG8XeYcMl75pC6H3emVoKDVq8PnjACh4bQ3plxQlxVeMArgcbK6QmvMQGfaCalf2kF//4wxeVP29k/6gjGVxciZT9lTghcT60MZggpV1THmxp+n6XHUFVoKkQlS0xuJmM7qyJHYiAVveLTHOMZrmBC1yQ200VjtRBiXPfKv3xe/y7pa7m2u6pubs5IjJZETrPVdX19zcXjMajVgcHTGZjsnzgqAsOoJXFpMZTt+4jysczW7H1fNnXDy8z2RxhNIZTAyZsSidyf4dagLyzCkE3BZTypD2EPnuVVlRdzVTN6FtPFVTsVzfEpvIxaPvMJpNaAPM5o+ZP/5tuvUNm9tnXH3zC14++YirJ0/YLlfU25e8+OlzNss1f/Tv/gPejlNDLIzQYejSBdq6wSjDZDQmOIcua0JUIv0fjZgvFozyMVlW8ODBe7z7vd9AuZyy6Wg6T1lVVLdXKFqKUcajx4/Y6ZeM75+j8xG7EOiC2FE5bYgakQ0C9W6Hr2vcaEKRO3yzIdutMeOGyp3gg9SCQee4PKfQObkbSzU4tvimYrdacnKcY4g01Zanz5+TjcZkuWZ19RVWBXQwBDfHmLHsUb5Bxx1BKaKy2HFBPrLEyxXd6in4DcV0hrVO7F2MTut4jbXmQB7Zcd0GzosF733/Q8rnz6hWN9hMVDp3d1vKXctsNqIoDF5ZytjQqoi+d8yyhElUHOUZ1gfwnj58LxDT8EIGlDogHuFWE13O+N4FDXD16hWV71B5jrdtUoYL81KsKSOogNIdxioKXTCLx7RtpNrsCJ3HuIysmFAUY7xv2JQrjHNMpucyDCKwrXdMJxMmbkbmxkxGMzIrTWEMgaA85XZLXe8oipHUG1qR5zltWxHR7KqKXV0O/6/1Db5zOLtf55RVw5rT1/q9z2EMEhZsbcZivsBZAW6JmiLLsdqKzFlZhN+hyfOCjo6u6g7WPwH9DA6DEUmo3GmJEQj4NNCvK2lMiajooavFgsLXRK0I1nLrGz6+uealgi4zcrwqzVVjJKAGD0tphPXB+p1qNOIQNNMPwfeYVJ8mrqh2LT/7p8+odw1HD09RPqDagNORwmgsAdrAvfk9QiIVBNUStebzzz/hy6tXwrYKHW1XQexwaSjvARU6rHW88ehtZvfuw6ggKOj68UEMELokK5f60VoripKuX/dlV7DW4NtkN5HYjwLMSuh0D9B5HwZV5a+owVRi8KU2biDcBFFcaj3AY8N+pdIxDP0Ze4B1oNzoKMOPvttMtXXP4hNbvj3Ac+gzq9N6EJLiYn+fJoJDjIPV0SGBwvQS7EM7tX53DXEIYiL2wZ+Sl+HxOG2SEgRU6lEkV0Cl+b3qT1AK8NqDvD2hYj/8jYNFxaGVw2Ft0P/+EFDqv8vrytH+nk3sw6AIXcBYhTW54BEICNZ1XsKgevZ4ApR6P9GhD1Fq+DzVM211sigZhtdyv1hraapKrEs0wnANkagTwcZaiBpl86QwlvMUiInU1VtGCaAZvBfDFC/HkjtH6DpClDC0XrUblZJcgggBjY5eSGUHJdOeOZrsHpJVWX8Nh5ZsOJfyHNSpB4yJwNGk/WYymcha2+MmMdJ0Kg0chC0t97BOQ7+IMmJh1t+bhxYe0j/o/aBAKdF1x4iNKUzNSHA3RqOMTqRCUWMbTQrJi4ONZT/Q+DZI2z/7gPicqm/9u/TMGhTWZWSuQDtLZjMBQI30aEYLa9dlOvWj6RPSefGdWA5OJ5O09srnNE0D6f7ovVelF2uo61qOO7G1pU8zMlBIa17btqKCMuLLaozFGrnYPiRLAAVdymGSa9NCCIMlxlCGK1Ga9MfVpvvDWukHVWeGZ8/o/nolyx0UwXdJLSJ+zP0z019TY8wA0vpWgGaV1rDeTqVf05SSDAYfPH1Qekggr7EGFaEoClF/5hlZVsj6qxiCyJzLMTGT0NI0hG/C6+v4t1//okHahS14f3TCp9WNyO+Vx1hHFwPr7YZqs0ElBmzbBIIS1J7UsIk5gsYUI9zxjJgbTJBUNe99SqwnNfmymfgQhs3P9aANSICQShKSPBdAclsSqxobZdHrgmLdNfzkk1+y2u74E+X5V9//Pi4/pjATTqdz/uc//hPA8+d/+3/T+RJtZDkIKGw/HQ4iF9eIzC2oJNdUagAlgGR3IJOR4GVyINKrFLIVhAZvjB2mLjF5uwkPPHC3vUnNz8GJDx6T/DN809HUNS7PxN8m17TGo7ICqzratdg/BO/TxE6mP9r27lI921LeWg2ghtqDXzFIc6zT7CwkSU0qHLoQebnccb38nMvrFcqN+f53FaenD1C4IWSmN+OXTSWgfMQrjc4VR48vOHvnAe224u7VFV988gmf/Owjbm/XWGVwWUbwlTRSwZPnBfePzyFG6rYmhpZpPiUrNKP5jPPTY9739/lqMadrG6yOxK7FzzxG5aioUTFQjAoiMn1c3b2k2dWy+uSOqAJVLYwPbQ3WOAKWplvz4vqSV+slq6bCK1lwJiPH0XTKrtzRdYFNWfNPn33GJFdMRiMyl3F+fkExhlCWZJlIFa5vblmt1xiXQRD2x2iaU4wkWE9rg6Fhc3fDaDJnPBvRlh2Fc9StJ3gBl4zEM0uREMRb1SiF9y2+CxjjJM06enzyWuqilgA5Omh32NBA1Ow2a8ZFzmw+oalLoofTs2O6KKmcTbXFeMem82zu1iitODo54Ttv3+f0bM7Z0Zinz695ebtiOpvywduP+ejTz1hvtwdgybdfe1/KGOSZRSmMMiiriSbdN6HfhGA+HWGtSLG6NtkgcCBZQaG1+Mv6ThJKDQrt04AkeqKSVF/S5wlrPHlfEpjMR3L/W0WXzO2XqxVKKdbbLdYYZpMJ6/VaJM8xopNUqI0iO3PnJ4R4Q1iWiAYvEJoAjSRnLk6O2a22dM0t//j3f4FW8G///R/zX/7iz/jrv/wbfuf3/5A3H7+H0tC0G3ZqTaVq6rJmMp7z6ME7/PiX/0wTRQ7jtEMH2N2siXXkjaOHPH74Nqu7FV8++Yy7V0+hbbHW4MY5vunompboFJP7R6hCNsHohV3gg7Cfuw6KZLLfdZ2sh7EvMh3aGNqqYr1eowHnMro0LSUVxd6n66LED3KQkqSQCJ+CZlQUaxyUASW+oQEpcjs8Jkhboo2m817Y8cmHWKdAhN4rDfYAXNTi76dCBC2Z8tKEppCTuLeCCbxe9AcVCcjgZm4UJ23kfhU4cTCOhgcf/B5fuZzLr36G2+xwruDi5JzN3Yatb4gRLi9vePC7Z/zg9/49P/3Hv+Tm9oY2GrJRxmQ6o93uuFnecdvWaGt5c37E2BqevHzKXVVzNJtxfzpnFAOXyxW31Y7RZMJ33rxH0Wx4cXnNTetZHC04P5/z/PnXrLc1O6s4Pp7x+PgIf7Pk2e2SSzyjUcYPPnhMReC/fPwpZVSYKEE1RCXWJz4SfYcsdSoBCPK8ip9vbyWwZ8H3wXC9tUj/d/2zLudVJFKHTB0p0swgi0qTm+ECRiWN4KGdvwxlhk1MGkffy0W1eCAefLQKwmo2KAiBrmnxbZfsEdJAcQBBUtOZDkFpkaxJE22SJNan0MY0PFCiOAlEuqaia9vkbV3IoCz5symnsYs59XJFbDuuLy8JbcDYApSRJO4YqOpWClM6qmqHy3PGxYSyqqh3a+bTAuvmjMYTVqu17Pc+wRGd5/blM1brOx49egebzdhWJaOpJ89HbKuSum2Zzxe0Zckvf/5jyu2G+2++hZ1NmM2OJYRUKYIyxCDyXJOGIAMbWsl+oxCPs6osaaqS9XpFVIr54pT5/ROitpTe04VAjAo7OsYVM07OHnD63vd5d33N6tnnXH/9GVdPfsnTb54QRwXWOHZdS1PXxNihErPPeOiakrurl2yW14zzSJY7miawmEzJnCMrCoLK0HZCno25vSv55OOvuHj8JsV4xLwYybVBsdsuaduGi4cP+ejVDY0Hm4gAJjFdlFFk2uDyAmrP7uoaRcbRe7+JN5Fuu2ViJlS+plFLgg4Y7zB0BKXYeUvMG8YZjPMJuDFNiEzGOW3tiV1LvV1xd3fL8WzGbXlLvV2SFSOc2tBWa+r1EqUbgknsLy3dpq7XrL/5JbHZApHFxT3cZEzjPbQdSipX2rbGB2HmaqXZxchKeyZvTHj36JSrp1tQBW2rWWYSaOabwHq3oWs73PIKaxdovSCMx9gGcpWxEJNmiAdS77SGGtPfHzLECLGhXN3RtoHl6pK4vWOMwoQGHX1PZ0AnFqE1GcplmEyjdp4Mx9iNoOhQKpnhoqUB0+LVX2Qj0DLsm87m1L5F45iOF+IdGBs6H/Ed1E1NRO7dm9srptMp4/GEvCgQdqgMx5vYMBlNmU3mxM5zt7yhbhqKfEToBHgJXUtIAy+xAkhsryTZbpqG+XzOaCQARpanECmieM/rSNvWxBgpipFYLUhRBGoPXHfeU/uaLjbike0DJiaP6OSHKGE3CjGWVShtyUdjCbett0QjPc7z7YYvyg21ETePTCs8YlegtSVED1Gkt6JoTEBsQh9V2K/jgglEoveEqCSzIMgwRyMMuk1spHbQEjgatiXzQmPrHaHasPWKEEfcvnhK++JrsrZmND/m8umXbO+egRcQwGghLHQ+oK3DGYtzBTbPmb9xQTFb0GmXkr+7tJYL4zhGP/RfTSehbEqTBlACzHS+7zsFBEOBshqieDgeSrgPKo0ByNg/BxFinxuRAlSU9HoSjNizDRO4n65bbxfVHYDjvcxX9ioNSsBxDoBHAdMFfBJlYiBEP4SyKmWGPdM4OwxITSJMhRClV0yDhUMlEqikaksBR6nG60POIn3eSWJFpjCe3lqsjwSUHxOmtdR6PRwmr57J3gOoAqIKOKz5Vc/ZX/fas3l/lRzSA+ExCjGpaSoiDqXAOc0oz7FO2J1GCxM44tFexj79AHrw6tU6DXD7HiMSDmX5ah/YrZQE/Bpr0Mrgxhmh6+hCPMA8unRuD9VIIMiHAHzyv+S6xeglsyPKcH3blYnRq2i6RhR9iT2K7i1TAlXdDdkeil7xlALB0jH211/1KN1wDuWiiQ1k7wEqqh/vPZ2XPqfzXnpplSwsVeqzEhtUjgW6uiVGsHmByzM5XqOo2oq6qtOAUsg+AbHTyYyo4spSQhB7Zd227TMxFHhP14hK2cdOhiMqgeVBSXC2j8IyTZhHX0+a3m+awGv+r3pvl9ffQ8IOtcJi1TK891rRqYiKIZGCWpquIXNOlOJDH2XRaZ0PibltnR1U18EI4KhVz66WtcLZlAsR92ziGGNiWSP9lkpr98Ezo/uMJ+sPLOD2gwtjDGNr6LpWrCvpme9IgCIBpeX+6IIA/G2XsqO0TwOMSO27wd5EhlvuAIOS9+uZt9aZZPMSB+C3bRpIwyzVs2VTsmbP8DZWLEG1UhR5nliyst5bJwz4cTFiMp7QM8EBYeCmnk8bi08Ylfc+DaH+f+pJO7EF78cztmUlEsnghXWpFHkVaDotTFsNpW9YqUqKt+AJyVdDZY7iaEZwihA7YhrL1EgAACAASURBVJoKtW1ipmiNtU7Q/5g2QaVk4w8BayzEgNIm/X0ApchHBUWeUy7XhHKHGK6D71p2ET755lP+9z/7j2BbfvPD3ycfjRjnObnL+Hd/+G/56sUTfvbFz2TqkQWUDvhOFkulzTDFCTHi7F4uoqwZHibvA51v0s2498DLXEYIKjGO9l4lPnnT6WGKo3FOAAGlDdbYFLik8Z2nrkphNqm9jKI3TVbGMDme02UF7bok1uJjanRKH1SgVDiYWoE0y3u5S78Im2Gz6f0dxYtIBvQRjSXGjk5pvnx5x92f/xWffvGMP/qDP+CN+w+YTmdok4k/ZLp+pImwx0vz54P4sOSGi3cecfrglMnRmOXzG+5e3XJ3s6QuS8ptw/VuSzHKWUzHKG9puoZK7dis1ygN42LMKMsJynOsc4rZHI1nt12hVMRpR91FWcRbL4sHkaauiCgKlyWgRqaM3ov/nMnkWrxYXXK5fknUmvnRhCmK2WRK6Dzb7Zb5OAMlMvOq3rAqGxofyF1HHV5SjMeStD3KRfpYTVBGUTeedV2hrGZU5CyO5rLRqchkOqeqStq24cHFPTbrHcvbDV2MEETu7WM3LOpRSRp1gYQmhBDIXWRaOObTKYtxzmaz49XtmqA01llGozEmOsraE0KJtRqXO7SShQpryFDUux27XUkVdzRFgTOGSGS9KTk6OeH04h5H4xEXxzO+/OYFo/kJNkaeff2s79YYfKUOXwnM7208rJPpqNIMhvdN3QgzJ4I1KXXUiTG9kD0ifTpq3yT0/rQhRuIQDpQ+X/dMgzQ82e95aCBzGdPFlFpFSh0Y5RldI9KUoigIqiNzGXmWs9uVeHovKlmHFPK+xXyK7QKbssUk79fG1xCgKSt823J+fsLt9RIVdvy3v/0z7r/5Nu+9/w4ff/oxf/9XP2R9s+TNd98mjAJd1hEC3C43LG+3xPANqo1kStGVDV5D2bZkdsQbF2+Sm4yvv/qSly+/Ybe9I3YC0JpMJss+eoJS5IspMXc0wWOVpAEnBFOeWWRwEareGN4M64cPLTRNX3UTgLqu5NY5kNOFENL0Vcvkl15SwzA9N8aKX5wPSXbS++B2iT3ds19lDe7VCz1oCN8GaA/YPD79amWgpq2wzSPdwK44ZJX0DU7feCqlyK3j2BScli0LD8qIAuSNt98jWM1Xn/4cQ8f67prpmw956913+OePfoEJHaG85cVnP+Pt7/wGP/6RRXnNfFZgM4eKgZvNmnXXYKzhZDohV5rr2xW3bUWW55wdzaFtubxbc9NUFKMRD45OiOWWp6sVL9Y78smMRydnXF9d8/JuSRXh5OSYNyczbr96wdY3bEcFF/fO+fDxBXm34dnlNcYHctVhg6fTGa1Ug2IRQkAriwTvxaEY7Fk/r/t3SaMWojBJh2eCHojdy9T2Tez+PPf3Qv93UjTuQdxeodJfVME24n7+c8DIUerAmigxQpSW2mQIPPFhWBO0loFrz3SSpkSAV63t/nP7PTQchKjEgI6BqDxaHXjvEjCZxWR6f2wqNReTMcF76ps7Lm+uaNuaPBuLMjbVQ03TDCm6WiuCj8mP2zGdzujamvFkijKO1c0S37a88cY51lg+/egjfvGzn1CWawpbcH7f8M1XXzCeHvH4rfcY5wXKT1jeLblZLjl74z4n987oQkceodptCTEFVTphZsQERhstC2bXtZAa7bau2axWIrlzjtniiNFkSpZPiOw9DcW2QBjNNRYfLUqPsIsZx7M3OHnnt3h0+4x7X3zE5bYjaAOdJ8ROeietMGgZpu5uubt+itEtoyJPfuszmqYRdn3dsC0bmlYzXxxzcf6Q5e0Lblc3vPPOeyxOjvBBMR5NcEYT10tOjo8YFY7Kt2jfB2sGtFHkWY5LNedmvaJar5nMT5jOC776xT+gKpge30efvSvWFqHGdLWACr6lIlKvt+wIzLc7RqcXuGKCDx25s+jcENsdUQe26y3WaUKeyf3cdahQY12NMjHZLoi1VEFLuP6c5uYrrOrIJxPmiwUtNV21xWATq7dF2VYGinpEoSLTQvPmkcHFNVV1x3RqKbIcsFycj6ibAEGjKNg1LV8/u2I6y1kcnbAhoi2MiBzNxujgaTYCeIYokveQAG6U7NsBoK2wzRrrDHG3xJdryHLaukqPnjxXAqilOh+R/frQUNUNtW8Tg3aMsQ5nJOQkAB4JoC3Lis1qQ1ZknB+fi3rEWTrfst6s5NlPa5g1AhQtjo7IXE6W5eTZiAgUWUHXtdzc3SR7BNDGMZvMsdphlQM8qJDIGR5wHIJDSivxuNcmMZFyGUoamwZCWvoDwvDsO5cxmU5oykaYVLFn0kmDGxK7ySiFMEIk1M46UR/WdS19iE4Anja4LEcFT9xqjLJsm8Bnry65ahvMKJdhMmKzEFGDKq/3UNXDWi0A+DAk6+uwqGi91PyjkaMpm+TDumdk+hBETmoFECnynFzDxCjeffcxsQp0reFo8oinH/090xhRRkFTY2LAG0lb11GAVGUzTh88YjRbELUMcVrraOqKoNqe5CbquBDwvpXzhVBxYvDEFAg7DAVJ9yEJlE7Lt9Uam2V436YBhBkky8OM7wBg7Fl2UanBB9cYl3rAXrLfg6b9eWTY99J2KP9WCauZfj94rd45uC6xl5ZzkEHyq+zRw/25B1EIaViZZP1KbjA5DqXxXZsAQyX2hfJtiep1Rq8ATwcAX7JvSLOGJDXX+NAJUKb3oHJM32tgKKrDrAJe+z7ftjw4vBc5OJ7Dl/wdr50TpQT0KVzGKC/QCQTqJfHK9PeCGqTqLsuGc9ivWT3j9/Bcv1ae0H+l1O/rZJGSZWKYEXrLmMO6JqZa26e6W9ND2ocM3v48NW1f0+wZ01pbnDWJqShYgBxnso3rvAC537IVECsENfRpSon6MKS6yiZlkVICnvcsSGOM2AJ0e2VFaNMQScv9bLQRIDaT9cwnr9X+edBakzlHnmU0rk5AqAzf6e0KktqgKMTCr7e0WycJPIBvW0Lw6OgTKCrDiBih8x02AZQ+ehSK3lLae5/WPYZzLOuyRSccRLAYPaicfdeC0ljvZF1RluilV5cbU/5t06b7NwrxpW682Ps5h4rSI/V5DD2Y3VvH9cFth/2K1lq8OOQG34O7+Neegf7+7FpRJ2gjAV+90nZYD9KzlrlMvMszv1cspnuHKHYOLtnOtY14fbtE3Olr5j53RM6hFZWM93SdXIOeWb7b7pInu0ksWwnCa7t2WGe01pAsPYKX6xUQb93MWiHYpfs2gvgzH+5Z9FCUIqH1UjN4sXSTTAyp0439/4Zi/0WDtEU24uHoHN8EivGUqc0p8hydObqu3YeIBEUVPd80V/zkyc94ub6VKYhTmJGjOJ6y60q8b+lVEsbuZdm9L2Ecmnyfbpy4Z6CmG9VoYe70N6abTfBG0222mBjJjKYlUoWaz599zf/xf/0n6hJ++7f+CJvPUEFzsTjhf/zX/566Kvni+WcC0BlB5D1gYkQ5WbA630mKn0oSTXXgm6sVRVHI9IA4NLAi1TPJF5Y9OJEW0qEo6DedHjQaZB7sA4sSa0wjjEhpoOQ9vFbY+QjtLHrXUG62koCNLKI+7r0CAWlO1OvTsX6RBsT6IAGtne/SQn3gSaWgiZqbTcPf/fgXfPP8Fd/94B3+1fc+5DvvvcdsMqNpZLovhUQPZqfvHgMharZtTdeUZFPLww/u8/D9B+zWO3a3W1Z3W376ySdst1uW2zuyMJKJjoUuNLRVS7XepOmiTHWMs6AiVb1LhZHGqAxHMqoe+BoBmxeJsWFAGzoVuFlf0/oa1VpM4ZidzmDi2e42aKOYTKbogHjNqIK6EeBpMplSjI7YNRWb1ZYYIlVZ07QeqwPR1xwdLXj08D6PlOGb5y8hhaBMpyNJzY4tKMtkOkMbS12VZBomRUY3zbHOUbcpgT56JiNHjIpd28gmqxSjzHJ8OueNoxmn8xGTwpIZzctLUF68e02RUVjN2I7FnuL5JWVdYydj8eVNjLfZdIbynl3bJP9OhctzYUsFePnyBdtyw4P7b/DB228xKnJuVju+/uxjYidhIP3m+Dook0BV9gPaxXyOySzL9VKSxNPk3lhL2zY4kwsgHQIaNVgMQFrsQwJyQgJlFXvQpC/KIHm3WikSdRwYKj5GityxCx1dZrGTgkePHvLq+Qvu1lt25Y5xXuC95+7ujqOjBdvdTiwAFBhjOT05oRgVPH32jOJ4TrfdUV2t0DGluqah1vrujsw5jk5O2W63LMYav7nk53//DbPTBaNC8+nPfszHn/6C4nhMfk/jspybJzeEEnZ+g0HT1g1UDWaa8+D8TZzLuL28Ynl1zXa1hNCQ5ZbpG/eomzoxkBuIgXw64ej+BRvr8Z3HRy9hd0VGVe0IeJluIk1MLyPRGuq6oWvbVGxprJPBWp+42ad2HhrAH/px94MmlaQ7x0dHnJ0e8dlnXwz+VL2XUdt2GNf7e8t75XmOsxIqBwLOm9fkB/3KKkXB6fERF2fnPH/+nG1VEYOnD5nar3m9y6n8aG/ur4kUUVOsW85KzZEPWNvSrO745unXPHz4HpPJBX71FF+XvLy85L3v/RanVytePP0CF3c8/fjH5GcX/OEf/jE/+W9/iddryrJku9mxaxqK8ZjHF/dZ317z/PaaMkScyzhbLOiahpvVimVVU0xG3D87xXQdr9ZLXu1KZrMp33n0kN16yd1qhTeai7MzHp+dcfviklfrNfpszuJswf/wgx8Qt0v+69/9I1fB887ZY05Oj3l5c8nnqx1YS5v2L9OzeXwnXuMH3sHBJ11MKphkqr33RD8s9qX4l0Z5D4gfMmJS48J+b+8bmf5SKiCmorgfNPZ70P6qxaGoPnwppQe2UUjgjA9+WBO0UsTeXkUrSOEwKio0e+YRStwMjXGIR1xKGzYBFbzIyLIcFzra6NGhZZznSabFAJZkowJlDF1Vc7O6YbNbkU/m9J6ERhsW0yk6BUSOCgkQ09qA7+g6LwFYc/HBPTo+QRPJspzby0u+/vJLvvfBB8ymI2IMvHr+DZqO46MZJjX7McDx6SlHxwsgoHTEWMt0voCoabtIWZbidaeUeDb2aqc0xIkxSLFvLbPFEYvFEW06r1k+JqBJxITXnkuxtkhFdlQ0MdLiMPkJ+o0j3j5/hzfqhgYDGglGa+vE5orE0LC+eUFXLhkXFp2CWDLr0CZnfbdiWW5AKbJsjI4l5foVbdRsm4DyFWcX9ymmx9h8jLIibb9/dsZ33nnML56/xBOw2qZ7LFBVFS2aqANtuUXR0pR3XD/5JX7TEbTjst0xMTnqxKD0HG0zGcq2O5R1FOMpo3zGZrfh6vklWeZYTApyA7lqaW6eg4p0ytJ0gS5EMNCFjlhuUdWK0STHa0cXG2EP7q6onvyEkV9RzHPe/eBd3vrgLZq4pm0zxtkIV2iyUYaxnq4tyWzOxGiyWFHELRPtqbcZsQqMs0ICQ5xYbTRNIKA5ZkzTGr5+docrFuQjw7N6R8RxrzhiXufERsDH0DToqBCHrSA2BgpUgHaz4fnmF2Ac3guz/U5bql2S/abhWlRR+s60LmgFysKyvGNZrxhlI3SwyQdPrNVaFQcZd/SRo5nkJMQINjPUXcOnX3xKVe+YH83kcwhk1mGtZTE9QjuH0ma/lyjx+5yMJhAioRMg1SqH0xlWZWjTS8/7tHORYHbek2d5yiHwuFyYT1Vd0TQtWRRZs061UQwCmPSqgsIWNKpJg+gwhDL17ExCsjaLIvvU+YjZfI6KkbvbW+nNrNRIPmjWqw1ehaRu1Lxabfh0c8fKQUxgrnUueRcyAHJtsq3ra8KYhuakb00CqUS2bZmdnXJ8csTVV19Rb8o9aIaAgC5zuMJiMNg2kMfIvWlOnmn+5m/+Bqss3/3uhxxPxtjqitYLOO9snjxPA13r0XnB/N59Th69jcrGVG1DiJ6y80ALypMZR1HkdEGCIo0VynD0Yv+mlBLAuN83YhRZe4wCcqT9rGdGdq2AQVGpYV0Tn0k/7F2Hdj79yFhqz14L0oOjwriWQCE/WET19bHRyTIK3e+Mw16n0r0Zo5Bqhp9Je20/8Dg8pv73h6/Dfs8aN+zTogTtPTMPIMZEhDDGDPv+4XD1cN+OMEiXXSZp7oehrsQ9yBmJv/54YTiffQD2YTjQrwNiv/29DuuR/fEmDCFGWe+MIbOOpmlRQY5rPBoRlEkB3FJnuCSz5+BYxEbgdb/Uw88GBusDkF6+Vwj39RGpHk5xOBCgi374exUCbduglE3s2TD45WZZJt756Tkcns0YEpBohn+nE0DVe68KizoisvhmAP1Vwsh7ElB/X5o0YCCIHSC6B9Xlsw5Dn/qKrgseema6UUNAZD/Yz5wlWitgcQJNYwjUdYO2RlQSCGO1852oRw5YzFlmUMh+UhQyYHcuo2lqwYI6Q1OVdJB6x71lgqy5okbsgd0eV+rvz0PWvGA/EaVEnepDQwyi/HZZLgxYgtiR2EiWGTqEXFiMpB4Tz1hPaJu0a+yxov68NE1a99O+0B9Trzjvj6m/pyXk7sAP+qAu7+9955ywTZNFx7f7saFmH54x0pDCyhA09MSGfvgi6jGlLC4Bq/06YbRFGyW2Md6n4UayL7CW0WgffOd9YL1epu8uz7S1lvFkJBlFdT3473ZRSJ+Zc6Jk04a2ayl3W7a7LUVRkB0MKruuS/ZLe/yrt4TQWsheIUaME4BYISzoX8cp61//okHabFSwmM94q6s4Pj3j1IzJlcO5LDHXPJ6IwhCi4rfzx7w1P+V/+4f/zIvqFm8No9kIN87RZSN+KSnhVGuDjwcbEHvw0mnxw4npxjTJSDjGmDw65KdCTBPR0RhtMtrtTph4MdKEgFGaT7/6hj/98z9jPJvy4Ye/haLgeDblvQeP+Te/8wNW65csm1tUEIp6CJE+odPHvcShTz607nX2VQ9Ug7BUe0C26zrxneonr8NGzLAAwgFzKMbELk5FqtbEaIfGt7coIJn0K6PpEvNV5RptcnIbaVZbQi3JpPsMXrDJJ6gvLuBgeppeIfl8iL1tINLT/VMBp/qF0hAiPH91y+1yw2p5RwwtH7z7HcbFDKs0PoLvN9Q0qlGRZBovRuVtWwl7y1rcwnAyP+bs8SnTx3M2yy16HVm+XLNarvBlh4kaE6WAafrvbiB6kZZtqi1lW6Ezy7xIQ4VRRtBWNt4ok2wfOtquoQsdt+WKy80LgouYvMB2jsVkxMliTjFy7HalsBaMFB2zacGoc1xe3rGLEINsmGfHJ5TbkqYRsNxlkhpa1w0uc2T5iMw6Hj98wGa7YToZoY0UxGW549luRwj7JFilNCdHC+q6o266JO0IzCdi37Bcb6lqmf4uxoaLowmnU0duOmhr1jtP8C3TwqGqhpubK/Rixm5ZkxcFx0dT4s0du+2KzEq6a9u0GK149PBNbpZ3bNZbnDWU5S6xGw1V17DarvFPA0enFxydnKHMHY0PPHxwwd2m5Or2Fi+Gc8MGMUzN496Ta7lcojODzWUyXJW1FGYqYjNJp1RaoeJ+Ex3YjzEloQ5gnSz+xsn97IMYg+PDQRGhiD7KAElrlDMEZyHPiLkjRMWTJ18TDwICmmafJrleb6QxS89kkWUczeY8e/6Mtm6wRcH04oTMGjaXq32yaJosX1/fcHJmsc5Q7UpUZsgU3Dx9Qj4aY8wE22maF9dsntUCnvkOh6atamzmmE2OMVNNUJHl5Q1311dUuw2hFeDl6OSI04t7LKstvqvEV6ztJFTtdE7MDcUoo25qTIDj42NGo5yvn21RCqwTX6e+8BQJjCcSmc/mlGVJlmXiH64UIyvsoCp5WLmUits0zWvMyqFISoyPm9sb2rpMjcfeA89aOxQxpD9nWQqzMXo/POJbhXgqJGRdg843LJc3NG0NpETWsF/r+glx740FwjgwVth8bHdw58nNhHHmsCEQyxWf/+wfMFHxm7/z+/zkv95SVw26bHn54orv/fYPWG/WNKsrwm7D5ddf8t//yf/K8xff8OXnP2KdPHVdZjmdzWjXW5arNZso9jbn0zmq87zcbijbDlPkvHl6RgGsyi2bJlCMJ7x9cY7fLHl+9YoyBs7Ozjk/OuL502fcru/YWcv5qOC3336L3eUr/uGn/8xtYzg7P+Xt8wt2VcnznTCVurYFa8Ck4WAn9iD9ALUHzoEDuaN67bz3fz5MhtVapWH/niXS/0zP/OnDR77Nut83ZHsQfmgcD8CCnu3R/8zhz/fT9cN9i9TgStOlh/dViY0k7j8StmHSlD9GME4PicwqgApOGOgoDBEbHEVUlGVDYZMPVgTVW6p4CZN0ec5ut2G3XXJ0cg+nxun8SNJu17U0bSMSwATmVE1FWW7JnCHPMnwMNHXJ3c0NoyLn808+4dWrl7z/zkNi8Pz1X/8dFw8e8u6HHzAd9+8vDfJ4MqEY5Tz54ks+/uhnKB05vneOszlFMR7YHKM8R6EZT6c4l1FuK2zmmM8XScnj0ZmiDR0+RpSyhMR+1Cam4MTXr4lSvVO/lDIhynDNE4nRQeZEhNWTG/o6LwYULdv1NW2zw6iAD/JO3jcoa5lOF+L5piIoS24dmQMdA11sWd0+pSxX3H/0HS4ezqlCA0TeODvlg7ff4Z+/+oaoczyd2AdFL1ZVKtC1DdXmDqLH11vuvv6CIpsxOb9HO4rU109oN2vU/AH5/D5FIcc96jSh3jFdzFm88R71dotuduy2GzZ1TUZHXN2SWRgdXRCT5N8rCN2GrFtRvXqCGmfovJDGySrKZ7+ku/4SU69xE8vZ3PLGuOH8ZMJkPCYbaUym0KqgqnYslxum4xaNot6siPUGGzy6gKAcr15c4T2Mx46zsyNU5ml8hzHw9qM5TbtkvXxO225R2lCOZmxnDsqGxfEpY+vY3d3RNjWdbwnAeD7F+1aCErsWHyu0qtFBJPG7UFM2tciK+1o+LcrGGWwm6qJtuebrl1/ijhwxenzT0sUJKE0Rx9JIB6n/2tCSZ8KKLauKXb3jen3D05fPGI9H5E3B6ekJzjrapjnwNmTwT/fB07aipsu0w8dA2zS0XUtuHCMnYZMagxjlxMG3eghH6r0mtTCPFGAqqVk7L+v8ED6mkp1KWluqqmS73RI7SUMfvPmT/DQqRRuTrzsKFyKbzUayCGKgKndELbJXbfJk0aZpCWx8x0d3L3kRG2oHysieF5O012qTntm0jaY+oJcUwx70C6k3Qinm5/e5/93voo3i6vkVMVbynPeDKlRic2u61lMoyBSMAELg4Ttvk6NRoWa1vQEDu+gJ4xmTyZEQRqI07MVkxvzsHJ0X7LoO30k4UB/AlOcCXNVNPQCY/V7hfbIL0BaVfFCDjzLwiTEN/2Uw19ceUTY9NOKpGhEwpO9aRb15GJwl31XFtFspZHjRs7nYs10PWYz7HiwmRs/wz9Of1WuWQj2pSQaHh1Jd8dIdBquJxHDY4w17sFJDL6h6Kl36zzCQVZI+P7B/6Xv03qYhDMPMpmklg0P1wws7+NsT9/Z5Sh0AtcN5g8MPOARW+3vu1/3+269vg9Pffh8gDT/knm87T2y9PK8IJG6MsDZDGlrHGOm5rEOdk1igh5/bn+PBDuGAYXt4/ns2rEcyRIwyNEnKbbUmy7Nkk+cTS9AQogCveZ4LWcE5tO4Z2qQaQ1S9cs+nz46y5igsIXiMYV9rh47YhYOaWQvTMGEdfTh6//4xRqIPdFHIGF0QUkx/LyolNghAsqtKAHUXJFsnna8+FGqvYuvPTz9wg9ilaxciTdvgUtiU/PIohDjS+93mRUGW5/hOWLR1U7NZb2jqmtC14FMvonSyX5PB8ygb0TSNrOlarJxCAkYPsxREDZT8kbXFOOkntXOYXMJUQwSsToAuKKOwzgBGfMFRhCBAp/f7c9cHTyolqisJoGcPwKfj6mvrngUuRJqePR0TIUhRVzU++BRKJghQf+7qtO+BAJPCVpXPcemeHgYLqQeWvUkGOaTePYawD8tL2JcMC6Tuk59LnrVaztvh9QfQek7X+RQcZofPHuUFzlq8lyGCqMl6xQ8oY6nrGq2gbVsBw4tisMCLUQLHqraBrsPYOHxHYzVRW7q2oatLjBUWr4r+wMrmV1//okHaEAJHOEwVmXWKhXHoTosELSAMDSvMFB2hKRW/WTzgFycPub3e0s1zojOstxu07Ztn2ez6qQC87jkji4tKoUAAMflc7MFR7yNZnlFVtWyEVsCWrLD45Zpuu0Vp8ZXZtiWfPvuMP/3P/yfGRt5/93cxyvLo/CHGaF5ePueH//gXmMxImm4MIo0NcVih5PD2LLHe56IvRrwPWJMxBIkp+X79AzIkUaeX0rLB6eRx1zep8l9F1/nXUiOBAz8+YbwqwCU5gFKKqAPFYkwxcrTbimq1pd01KCXSXeg33zAYUffnfAgJ6BclL2zG3kRfvn4y59aajkg04lXbNh0/+qdP+frpS77/4fv80e//gLcfvo3ConV6+JLZvhhwC1N3V1byXWPE+E42CBXwbct4pAWMioaLt86IMbK8vOXJL5+wXW4ICAtQQrcUhBTuooXd6KxMkKbjCc5Zqk4GA8YatmXDTbVk22xZbW5pY0s+zUBHnAGt4XZ9w6rSGOdwNsMZh4qKtmvplPhozuYzVss1NtNoa+ialvGkkF/tiLrtaNuGu+WGGCNZUTCZTDk9PaIYOaKKjMcjApHl3R11F2g6OZ+xrFEExkWkaxqMUuSZYZLnHE/HBCXm77e+pe1qQhOhc0SvWe8E3LMmx5qM3AWiMuzalsubWxazOYvjY5q6wt47pfWB7W5D2zbMFwtubu/YllvyPGcyznHGML84Y1vuBAStLRgYFSN29ZZsPOb0/B4xG1EsTtmUNU+ff8PT51eUVXsw/WMo2vv7OCKBDZNZQbPzdG2HcQZSQdr7j0YvC63WKjE7pfmpKkkkDV7e3KS0RptAeXSvbAAAIABJREFUpz4Qoa5qWi0eSBopNoKJ2HFBHI9w0xl16CDIWhMUQyiDgEEMz+dsPifPc5Z3S8pdyVdPnlDuSlmXokePHEwLzGon90xVUeQFoCjrirvbVxwdHbE4u8d4MuXzTz6mbUuUCRSZZmRzlMnpOkMba8zYYaylrBvK3ZbLu1vauub+W49Y3V6xW96htWKyGHHvzQvy2YS71R1VuRUOTCcAf340wywKat9wb37Odisb+mqzoq4tx0eL5Ncn57FJQ6meoXx6csp0POXp06c0TZOSN/cew/3a0aa06b4wPWTWQtg3gcBqvRZrGaW+9e/28qfMZWy325TWKfdPPCygeumOl8GVfKZlvdmyudugrSFqUSCQGmn5nD6RtC/uBWC21lLt1pQvb9CNps47qpBzFEc0qkZtIq9efsbv/uv/juubV3z0ox8SdxV3z55xfP8x9x++w9c/XzKKHTef/5zn33zCH/ybP+DTn/8VNgRsnjEZj9FNx+1qQxk8o6LgbDFHNZ6r9Zpl1zIpRrxzfk7c7Xi2WRMVvHG84Gw6JbYV39xecVt2nJ6c8O7ZOS9fveLy5gavNbPxiLfGR3z100/47PqSYrHge+99j/v3Tnn1/AlPry/ZdJ7z6YytUmyalngw1FMolNkHArwGhB4ydsL+nPeA6SFw/ivMFlQK4pBrd5iU+9orMgxDBqAfULG3NBj+GT1LaTi+4fcMx9rboYicWif5ph7ACaXBWjmmui7xnUd3SU7txa/dB2GOoIUJFZoOq4SlFZTG2wxMgc5kfY4hYH3ybwtSs/i2pWlbmlpURSiRL0cCdV2x2Wxomxa0xWWFBMaoyGp9x+nxMbvtmrpuUUozn00Yjwreff9dPnj/PbbLa374wx9ycfEmH3z3e9g8Z7laM5078iIjGxVUTUPdNHz22Zd88stP2W1vGS+O0h6X45xhvV6JP3yMuKzg5N455xcXVGXN9z78kGfPvuHJky9o25qiKHj0+B1Goxmn9+5zdHIyMFF6BpXcB+L0GiOID0kY2DUxKDwCcuXScQzPqPixybBxs76mbbfkWSAmgCsGT+garM6ZLY7wsaNtPbtyxWp1xeLkhPnsiPWqZLu944vPfolyORdvPaSuNmTacX58htWGJnqxFOqE/WXQg/Kp3m6IIbGNlGe3u6F5XjI+PmU8OaXabGhXLyizM9r5G9j5HKs0oS5Z7p5z9u7v8eD8ERbHl3WJGZ3RlBu6bAImUrad7JO+lT0uRpTLyI8WzMaGXVXB+hLXLQmXP+ViUfH2b9zng3cveOetc9r1NZuvXxEWGdl8H5ChNUxocE1N7TuM7nBTUWWFEOhMwBSG3V1Ls645OvPYXOE6Re4URd5x76Tl9vMVm2bF2dk5erpgs8iIVWTcFahijMaysMI+uLm+JB9PJMSsVSgaLArfNWg0i9NT7GLBi1eXfH35bL/uRHkOTErGFtsETT4tCHmgZsO2WjL1C5zN8NHT1HVSdggIUbcNdVvThpbn1y9YVxtmR3NGxZgiH1Nuatw042h2DCFSNRUheAEXQhDPSK3E711Zat8ymky4N5+wvlkmD9xklxB1sh1gGDxLCIs0sFmSR/uuw2SObrulqkuxfUDCWLQ2KJfJcNCId2qWZVRtnSwgoLd9UVrY/4uzc4pmAl2Nr9a0TS1e4vJwpeeuQytL4SwtAR81r3ZbPt6sWWqNT6ypiEcFARJlExev/wjDcxB8ktmmddoHqd99iEzuPeD48XvU+ZTQlJRlQ2g7rDMDqKjSYM8ai69rQpDhitOA0tx76x2uPvmMq08/Zbe8xc5GBFNQXDxE24zxqMArAY6ctRjrUn0WUVZ2AaO1+H4qPXjL+igkIhVFOYWxCTAORCV1QJ4XTKcTCJ7b6+t0TqKEDvmQ1iJe28cGuzlkXetr270/qVhrkX51fep5ojuGQPJtZiiE9nsm6b1J1iGkn+n3PAE8TR/YGfeMvBj1AID2x9qHRh/aFPUgWT889Qm0JPV/JCWEMUaGjBwSkdK5SAcWEthLP3ilByllv9RGQjCHkLmD7/waApjesFe67GXY++LgsJ74Nl5w+Pp1dcfrrxSA1Pph/7fGEHxMRACDD2EITh0A61Tn9ESmw+PoGYrfBoj73w9BqfRMTQlks0aTZ4WwCMdjcucwVmNtjviiQoyauq4SyLonmwTfQnpvZ6zkO2hF2/bMR0PnxZosqMRYbffHLCPTOFhdNF2bBjDpOJNfp0n1cz/M3p/TOAy/+x6vD3pSRpMl31oJqPJUVVITZO4A4BOrS+fEu7RrO6pN8vdXolJWSlPHmtctPfQwWDgEwaXmsygdsVmBsRmxbYmhldor+ZEbmwFx6GGI4utKGj4c3oMATks9ZAsnAH1SUStjsC5DO1FaWZuRmUx8f9HEtmdPGzIr95gwmSWXQ/YOIY719m7KuoMhitxrvZo0y/MUhK3RRp4PY83gjxyjePXLsF3qXG3FqkApsNGhMpeA+E6uoXYEogzcvaeu6uH65L3VQAJ7fRAyXNs0aX/rFbMpnMzqQUEZAaOteOWmdSjGlHNCHAZE1hiMSaHFbUub6nWjFCbLhzUhelFIW2NRWcSaxWt9oPj3mmTp4HFdK6B09AdAdDbgWWW5E8Yy4t9s3B5r+/brXzRI22535LuKRilM5RlNx5DAjIikpnWd+I2oGHFKM48Z92en2KogTJx43jU109GEtqlFOhekKZamXdgPpHCr0CWWm1HClVEq7Xdp6h5FiuNb5Gf6pk9F/l/q3uxZsuw67/vt4Qw53/nWraqeAQIEQGIkSJEUKZpQ0CFF6MFhPfnF4f9OYYUjbMlBBy3KMiVRokiAIBtAN9BDdVXXeOccz7QHP6x9Mm81IfuVzojuqrp1b1bmyX32Xutb30Cm0dMB1kS6upbXpyKr0PLhZ48Y/cc/482HX6GYzEBnHB+e8P1v/zbPXzzj6eUjkb3onu/RU8/ZggiodAjrnV8tACnE6K41gxSbdjdB7SWfIXk7xdSohiBeNduNZrfwlDjGy8Gn0oEb0yGemLVKxmOgRQI2yhSUBq+nBL1Gt2472VUxtbRRPG9QwiyUszAFBGmdUnB9ugb9ZpUm43dk7CH9beMiLy8W3C7+mvP5Ld//5q9zdnjK2VvvCRUdRfTJRB+NaxrqapXsIGQiHFyUSXe6fi50dLHDFHKIHo2O0IXmxeMLXjx/znq9Js8smclpXINK7N5oNYNhjsk8TajYrANdJ9evioHz1ZJbt8L5Bk+Ht5ArAXB8E8B01E1LtaiFzYNmPBwxm80w1pBZQ1kUBB9ZbzQRjTKW+e0lbSd0e5MZZtM9mlqjY2C9XlPmGVluqNuaLLeEGFnXFbPZjP39fZF3FSVt51guFlxf3bBeV1I4hsBsOqVRiovrWwlvahy+6yRczjVcL1aUeQ5eQmi8qzjY36cclNgIKrMS5FBVVHVLW9WgYH82ZVjm3M7nrFcrJpMxN/PbdIABPrDerNHWgJK1MRgMODo5oRgWYBVNLWz3vb2MwShjOHybyWTCs5cXnF9cC7jfh3KQ5FQyjoc+Sd44WQrJGiMaOZz6wISoekP/JEEJIp91zoEX+YkMcNJUTMOoLDk+Oubx50/oWk9RZCIw1o4yM1BmFLMJo/EYKkmPzo2RhNL+PiduQxUAVqsVdV0TnEOHyHQwIvrAuqlkMm9ADQry6YD6ZinbXZBDyxpFW1VURc4b7834yle/zvHpKU8+fcT582fcXF3RlE4kkzhcaECJ5KftfNqPOkJwXL96iWtqytGQ8eE+5f4YXVqu5jesFgtMEwitJ/hAMRsyOJxx+vA+q9WKp59/zng8Elahgs476nWTGowkSTKaqqplsKIV88WSalNt30ufylonb0GRhMtEvN8D7xbJOk2Qt1um2u2b9E2MSkWLFoDG+0Dlqr432UrtZSrdA3C634IFwEUmuGRSnPq4nfalJitg7Y6hGWOEIIWS0hrfdajaUbYB3znq3BJUTvQdaENwLTevPufZZ5/yte/8Fi+fPqJ++giWCz7/5Gfcu/+Qz21GpgxFW/PXf/a/8zv/9J/x7pe/zmef/QKbGyyRxWrBwnfYQcG9/QNC63i1XLJyHcOy4Gw6wa82XK3mVG3LyXjEwWSMdo6Xt7ecrxv2p/u8dXzM5vaKm5srgtLsTfc4Odjj5uUrLhcL1KTkwdkpp/tjPvvkQz6/vGYeHKdnp9w7PeHR9TXrtpNjXQdJGtbZ7tzRPVBAOkd2jPgexNpdx54l33/xzkebmlApcMN2CCqqjB3YkZ4s+ZnvGuT0AhKAe9ebbgcY3/lj8lCEvMhptDQ1wXXoGFOoRSC4mq5riTHQxIjrOjbrNV0nzY0PkdY7XPI+cymcoms8TdUQnZzfwUCWDWlcJPqG3Bpq74gY2W8iErDa1OgiR+mI7xpcXTGYDAHDcrXAZpaiKNHaopXFao1TWoZRWmO0pWvXtG1DU2/Q6oDp3j6xqfjg/cc8fOs9vvmd38TmA1bVhlTJCwAWpCkJwXN6esrZ6T/m8vwlo/FYBqbps+waCbOr646qriiLgtPjezx79oK66ri6vKVre99MzccffUwxnPC9g2PZe5PE7S4rI0a/ZUxu10s/sFOKGFx/NKBIATXKYLVCeY+v14xGA4aTITpsJLVYJd++AKPZHgfHpzTNmrpeUirPxatz1sslRTlmPBpys1iymp/z85/8kPNXT4ko3nn7S8wmY8Z5wa3zxN67HCO+2RqaqsE10hD7EMkLw2Q6JDOKGG7ZXNwQ9ZT9+++xCRWr889wiwFqkGONw1evuIkdi5vnZIM9ohmLp12WwfRAzrzocdUKv5xji5IQPa5eoKNn4yKlbfnSqecgi5x+40s8PM2ZjjsK64jdLSpbU7VzTDPlYHQP5zsZWFoNURrdwtWE4MgyOYdNjAwHE4ajfXyrEhuxQykvSjnvIXjunU6YjEe0XnFx3dJGz3m75mRaUIecx6+uYLHi7OCA/cmE81cvuLi4pMxLhuMZk8MZno6LZ5/TLpa0bU27yWT9kBjnSmgHnkA00sB13jOaDTmJRzy++Bwt6X2sqzVnM5FbVkFCpKwVZUhdbWi6mmWz5uL6ktFkzHQyosxKpuMJi8WS28Wcpq0ZDgZ0TiSm49E4eUB6yuGIIhuA1ygMja9ZLhZEoHMdxgRiNFRVRdPUjEcTBnqIyWzfMaRzesfUNYmV1nWt1IdaGluleoszOe+U0RRZoNXtNoE8RJ/6AwEON+sVJjZkSV0kVgh9ZZ3OQJVUXItrXGaoM82jmyueNBVVYQkoDAZtdnuueC3KIErHnqUWsIkJ6X3AA1EbdFYwOThkcHwPMxjRNh5XNUTf0jMp5UzWaCXDT6PF89urQBVhenQExnB1/goTPddPnqC1gjwn2oKY5UST0fX+2HlG6vjRSjEsclzo8K7bSlhj9ImxKcDzZDzj3vEpjx4/omk3EJQMapOfJcHhOqn1jDX45NPay4b7oyykv+/aTnouSAquBNBy149YzrxeidL3T/0gW6mdHHl7gt0FLmE3LFVSH0vteYetqeSzjqkfiymUR/qpSEz9XlQhhbgKyCvej373D8k/xjaoK7BVjipF6u8i6H4A27Mre1Wr3Vr6aWN3taG1dN6TFzkxGkLnEgCuEoB7h8EbhSEe+wH6bny3rSteZ92+PgzelgZ3fv/LQoBeLyM0wXl0WYj1ibGoIoFhCXPoQ4nlB8VzmwQM6uSzrrXZ+jaj7nhhpgF0D4ybzGISGKxSjWuM3e4DxlqKXHzWBSD0d0DZ5HuvEBVgDIQu1bXp+jVtu2VmhxDwLrAdpkdoO7lH1JYVGTA23w6SjBFvZw3kttg9j/cCbHq5DkWei5WgNti0t/XDWNdJ3pBgJLKwAhGtLMpahqMRw1GyQQuepq4JMVIqARqV0iir0F7hW4d3EsputEbZfuilyDKxKWg7sTr0iXyltUangHBUJM/lDPNK0TQOrzXKWgxyf7euYTgc0NQSJN55R08M6okJ/edfFDlghISTWUJMgcPpGghDV/YmlYLIFDKgi0Sc75m44m2hVG+EIut9N8zWKCXsfOJOCcCde6AoigRKpvs9pjoqJCuNzMoQs/eFTWvHYLaM8a2yNUp4nTGiUsxsz87e2QSg2Ibe9YzbJgV0uaSwdK6T/tbmOOeoa8k3yPMiBdX1zGmVGLJdOm/TYKRJbGaj8HW1vW/u3ueZlTMkVDXOdTLo0nJ9MiuECkXAN03qWTVFUYgSQOutBaNSQvzam8zonAzHe4vE/9rj7zVIa3xk7C2bLANrKcYjvK4I3tMlY/CC5IlD8qPoArN8wqgYU1PjggM062otE8EQUqOWfEaipk/zUSEm2VrffO+kIf2EMnhHZnNcQtZV2kA1wvBURUmR5cTFCtd1W3+MZdXxNx98yI//5of81m/9I7QeMR2PePftd/mN7/42539yQeVuyfM0OUgFkBRYOh1ymoATf8w7QK1O0qCYJACSwBmEkr3drMWbQw79uE2Xlve5O7h7aviOKZa8jxIoIpJ4I41Keg0a2VwO9mZ872tf5v2f/Zznl0u0tajGsVmuiJ3DJPllf6j0kiZUet4kXZZ/MIEd2wKkP0j7SZvQx0MIaCsSsCZ6/vrnH/Pk6XO+/MY7fOvbG77+1a8wG8/wMUkziLSbFV21STLTnaG5FOpqC8T116RuHVprhkcj3p5MKGZDXj59QldvcLWwSUejCetVLcbiA0ue6xTE5SmyktFwwM3iBmck8Vg8WqCLmq7zsqFbxFg7SoFOBJsVuBC5XSxRQJHLZjLbGzMcDbi6uqXMC776K19hNZ+zXq9oXctyMSfLc/b2Z+wdzBiMBvgYccHTdg6tFW3Xcn19TWFlCnU4G+G9Y1JqMq3Y1DIRu766ZrVaS1CLUXSbmrpucN4zyDP2Jge0bcvV7YLTgxlDY1L4lchkBnkJaA6mU24WS16dnxMjCbRcYo1IaWNo2axWWGPIbC7FBQio3nQ0Ttio0+A5PD2lKAe0ztN6sY6IKmJNYH82pigUk2nGaGK5uFiyXDTEKEWDyPB2EmPXeQn1UhHvApnWZCl4IwYxbPd+N532QXyio0+MLJ0GCLr38koHUapjirLAWI9BiccNhmg15XjAaDzmYLpH07WU4zFllvP85UuMlvt5K1VLIEMA6rbFRJhOJrz37rs8f/6Cx88/x2pDmRW42JHtTwkhUl3NiV239dImQrWpyfKMoiw5e/AWp/cesrq55Mmjx3z26WMu5pfgwzbIgpAkI/3eqESSOzs9YDAZo4YlQUVZf9dzYueplrXcb1oxmIzYPzlks1njguPo+IjgnUi2+7DAO4VJORjw5oP7fPzxR1RNQ4ziE6v6bjAmFob3lGWBIhXeCUyNW8nbF8DQvjBJe3rjRAlhjFzf/uA22jAcjNhs1tu9qi/OjbWyT/jec7QHgU3as9R2P/GJLWISyL4dtqX9+27RFIInOkV0sgNprYneJW/OSMik0dEukjcdLz99xPTwId/5/T/kP/2v/xK1XlA9f0o7m/K173ybT3/+Ae1qzuL8KT/50Y/4jd//Iy4WS9bzl2yqFZVzlMMhs/EQV9VcLRasvHgvnU330M5zcTunDo48z9jf26PtGl7cLrjZNEwHY9453sMtb7mcz9l0nvFkwunhHsvFnNvVEq8V+2VB1rT87Y9+zFW9Qs1mvHf2BvcPZrx6ec76di77nDJkRuO0lRCukHy2okoDkHSt++KVBJzfbWq2RVW63vCa1cCOWaW2oRny399tur742A5rVc9GSowv3/u675perUhFW0zhAOC9yGPxnvX8Ou0pDhe6bdhB6JFCDT4xPLugJAjGytnXVA23NzfcXFywmt/SVjUuRKwqaNvATdigg8Okhk4hTb6OAvqPjw6ZTqc431FtloxGE6zNGY9neB8oykJCxbQoN9qmobCWarVGR8XFy2c0TcWq2pCXOcZYPnj/x2w2a37/B7+LHU4IHglYKktsliyOVGQ4GlKWJQeHR2zWG/ZPThkNZA8vBgNpHFKQX+dEYXFze8WrixsOju8x3T/mV78+pGlWDAYlm3VNXa9xJNaLXDq6qLYeaH3IX19UROR6CrMqQvTEKDViVLLWrMpo2jnz6xfcXjzi5bNfMB55vvwrD2jXN3RNh3ORqvLs75/wrd/4A/LBPre318xvXvHq+WPsqOPZ489ZrJ9wfHqKdx3VZo62gfPnS1AD9meHjA6OON3f4/LzJ/jQyWeN2DVlGsym4nAyZO+NIw6PD3jzzQfsT0us6rBGMV/U/Pmf/4SX559y8N5vMz455ubqgs3tNRkVg2GB8zWb+pJseoYdP8TbsYR5GkNAJNLD4QCTZ5gsp2orVKHJ9ITc3XASXvK1Bw0Hg4B2FW0156ZpsJkkTOcm5+jNh5TlABcyCShpA7FN9lUKiAVtG2nntdwHUe4JfLJ26JxIQ6Mwx4nSQGZZTlEUGNdidWCzvCW3A4JynD64z6jMWNYrrm4uWC9vE6zj2WyW+GpDG2VP72ohPNTLFZkyuKZJe7qci9El4CYLrN0160VLGysW60uuLl6hteHNN9/Er2A0HDEcDlgubwEJu6vbitY1NK5h01bipRxhkBXMxmMmsxlZnrNeL3GuxeHJ8pzlYoE1ljwrwHlMa9E6w6pi29c0dYPVGZgEPaQBYVHmImmNAqBgkuw4OnqPv+C97EfecXlxQZ6JwqtzHbHdeR9OZuNtYKYE7rHdS7fXKUJdrdDtgkIJ+GYS2NvX7f0eGGIguIZgC17VNb9Yz7k1imhNqpXEN1TUezvlizaazrt0lsvZR9QyuM5yir0DDs8esLd3hM8tSmcYDF1nyXKL7/qeIWCSx3NRFMKW6usAY8gmUxbzFVcXl7xpLMOkenKZodMWrZM1nJeEdmOzbdBi8IGAeAC3nRNFTBoE9ixYg6FrOhbzBWVR0HbVVh5tkgdtRFNXldRCiRyj2GWl9GBFb7W1A776QM2wA+nugIiSOxFQUSdgVNiNr4OHrwOPdx/xzteEpf26v6pKdWj/OStliEq+YpTIqmOU9aH7QVjsVUdhu677daW1bAMCokhv4lPYjzJ9Hxq3oE9Mr6tXm/WFn5KUIIKD4XAoqjQvIPgW0Eqt55YhrtTWe1nTq3Lu/F/1Fkl/F0j5ZaqdL17T3bW9o4gLAmT3DDufBlJaa6I2WNuDsySiTvp51VtEyGsPUfr7Xj3WMxr719EryvIsZzweb9dMCH7L6utT67uupevY/gywS5+/c72F4R62LMu7/qn9v7mzFhOy2LgoEnlBoXXPZrS7YRJscyZ6uzJBWgPOiQInhCD+vP09qAT0t1qUjUUpxCqtjfRqaQCitCUzJJuQnbfsoCxTqLBKNgIRYzNGec5oPMF1jq5t04IRAFYpCQ5TpcIHR103gkfE7WoSZmu6R0EspBYrycxomlqs37SsUxcS0EnfV8m17AFF4REEuij3TFZkBKPJslLYnpmV3gCNj1EAYCIuOIw2sk8lKX1IFgE9Y9a5ZLkSmi0TWc6UAq3MrsJOuJJ8fhLGGXpVlyJ5x8pnlTjW2/tUJQZ0b98i/fZOtdh1HWVRvhaIOBgMiCHQbdnR/esQW8G8kHC3fggRErtWa51sOHZrcuu/TExngCEEqJuGtm0kA6q3A0RUedZmqPScMezWfwiRIs9pGrGyqWu5jwS4LrfWDH0omE+qN2vScCQRD+XXSFABvGcyHEoGivn/aXCYQTNAEt9cdNRdjdWQFyU6JAq9D9tJbm5yQtTsZxNmruCy2UBhktdTxGChk03IB2GdmQRMykNo0yF5TUqjz9aoWylQ2gijLk2j4nYzl2cIUVh3djzEdy1hucGESOs81+sVf/pn/46T42Pee+tXId9nkA14791f5eGbH3L9yV+h+9S/dOiLpEMM/lHmtYNJ/h+T6bCYOW8lAzHSNlVK5CQBNH0BvDuGpJiTorn3POmbGpHkqmQc3sspfLq509QqRELoUNZQNRU///RTLm9uJOQqK8iGA8yoZHV5A00nr9fJYvXRY1KadX+49ECGJKNKcSH+JjItjVH8r2wK9pFGTCcZKEStuV53/OVPf8H5Qjzkvv+tb1PkBa0LqOhoWwny0Upm+lJQsDv87xx0/U3qvbzmbJzx8L0zDo+HXLx4zsWLS1SmGA8liGA2OwDfCFtJO4L1BOtYdSuijfK6O9mMBvsjPn/+kljYlDYPm/WGyWTEdDqjquutMb94Ekc650Ablqs1o9GI05MjPnn0hGH5DkfHR4zHQxbrJeu6Yf/gAEKgdS1d8GhjyVP4UQx+GxQQ8BAiy8UtZZGRG8XBbAJhwWg85nBvzMXVFZvNnKODQ6bDIavVitVqRbtZ0mRGPIC7lrprmYyGWGuoqzrdTxC9Z388pshzzm9uqVxgVXXM52t88MzGI2YTsYfYNM22MHVBmMExBhaVSODb0BEQCVvdNDRdjQtp8pyYQaNBRlnuMZoUnJ5UPPrsgtvrpbAzUckTR+6CrnUiv9AabdmyN733OC/esovVQmSf6K1Rfr9mVAJp+wmjsQbfeqqm4emzZ4QoQG8HqBAJGob7M/ZPT9jbP+Cjj35BsGLevoqQZ5Yiz1hvZLCklcgttuERMl1gtVny8acfCxshKkqb8d7b73D+8iXnF5eoyRBdN4TbjfjhRNkrysGQ46NTMc5HEoSP79/j8PSYs3ff4NWrZ2QKfvr+z9DKMB5NUEqzWK0pBwOygUVlGlMYvIqgAs3NkpsX5/hKppIEjR1kDPdGDGYTCQdbr+m6BrSVpFNl0nCpZ/eD0pGmqri8umK6v0/16hXaSDJrfy8qpXCdYzAcsDfd4+b6hoAwkXRiNN8F3u7aEvQHt7VWDuI7QYb991trmYynNHUr4QlaIQGG6azRO3lP3yRppXYKh2TrkhnDdDrFGsv19e0WkO2L4DzPBaiIwpLzTlQi08mYvHKo+hbQ8NtIAAAgAElEQVRcZNU0FCpidSS3OQOd0S0rPv/4U77x/e/z1d+Z8/6/+dcM6jWvPvmU9777HYrJmOvlBXlUPPn5h7zz7d/ja7/+ff70j/8FeMdgMObgcJ96s+ZmvqALjulowDDPcasV66ZFZYqDfMykKHFdx5PrOYu2YzIc8ubJMartuLq94aZyjEYT7h8dsLi95naxpiVyfLzPw719zp+fc9025Id7vHV2wv3phOefv+DJ7Zw2Bt7c2wOtOW8qsTCKcu4aI0MSE9U2VNPqXaHdS8NgJ/UT+f7rYSp3gz/6z7lfR3en5v3j7vf9sp/ZNjKp6e5fy90Bo1I9+0zkTq4LrJYbzl88B8RbXhlF0AGTZeTDEcVwTD4YobMB6AJUweHREcuNo2pqOteijWF+e8P5syf84md/w/mTT7m8uODm1Q117aiMg9ChjbAlVNpzhGGqePjwLSaTferOUdVLbm/P2d+/h9WFWCBEmN9ckZUDqqamXs558tEnDMqM6f6M508/o3Udb77zJcoi58O//Ws+/OlPeOPtt3l1ec7Zm2PKcoxJNVvoxIfs1ctn2MwyGAxlAFLVlGXJxrWU5YCoIp0TYCUqDRam+3scHB/gAhglCfDFYAAckmWGXuYttZhO93ySgSMWI3dtqkLPLuxBjV3/jNGaLNOo0HLx4hFPHv0t7fozlL/G+BWT8RRnMm7aSNeKz7sLllW95m/f/zEHhw8YjUYMBmNmBw+5d/YuJ/ffoqqWYveQDXApAMgHTeczvPaUI8tvff8blHsZa9dicotSAR0Ux7MZb5wcMFCBpmvpvGc2nXB98ZJqPccER5lZ/vAH3+SDDy75iw9/ysGv/z73vvJ16vktfvGMUi3JipbhdI3Xr1is1tRxTN0EWpujMkmPd5sFNkAxnpHPZjgzRQ1KShfJXv2Q+vqaK1XRbpYEDHuzCd44opGBQNc0WNMI20kJMUGCiiR5u26EvdRUa9qmIQZp2l3bEVwgOgG6rOmtJHoWnmI4GDAqDXUNtWspyhGtDnxW3fDtr7xNljtuf/EY3UZsnhO7Fo9Hq8hmfoMKggIZa3BdjQkB75vtwF96UWH1eOV4fvuEed2hDITOMRuOWdcVq8WSkZ2SFxnrak1UAWUi5xfPWayX0urpSJbnnJ6eUthcwoGahuuba66vr6jrmoPDfdabDc2mEssEa8mLAeO9MdV6TTO/ZjycptoUymKQanYZIMYgDKCQ6nhjRC7pt2DUnTDkKMO9PM8ZjydYIzZi8q0Ga3ufPrlfvOgH0pBLb5lqcoV8Ai8DWgV0TEqGRPhI0JGQNpQiGkVjDZ8t5jzPLG3MIbG1otJ3vE1JzGaR4UYk5JdErAghQJYzOD7l5EtfZjI7xESNxqMQhqxqrTD9QtwGHYnFWXotLqIDlCEyURalNEcHx+jRhM3PPhCLK8Q30hNkEC+QA1FLsGEvqQ4xWVbF3aA1piFgDKLEQSvqtqG+vEj240n2mwa3nkSoQW9Bis457J3+Z9efieetVpoudEnQEV/z2pSzSarSkGzrei7M6/WNZrfx7b5+99cv/n63ju6ch+xGXygZ4Gsl95kEZ5Kw0zS87G0Y4A5LW8asXzxbhYWnUtiu33qzSg0XE0Qct9kw/Svp1a4KJf60LqK9WNrd/VajtdwraVWj2Nn5vXatfvl12l3vLwKxu6+//r07fCGiiIG0TqQ+CCm/og/BvQti9z+ttJLej93nKACRDLEA8ca0dlvT9EBWX6v09SUEgg4Ewjazow/evfs+e7CrS0FXWZZJYFQChPvQrr4eu2tNBb2FStwGJ9v02vI8iM2Q93jfyXpAepzWy/BMwFfIjIEsS4FkJKJYIBqL8x1ay35ljd2SPIzSRBUklBGLUm7HckXA/KwoJHwq9DVE2ieCDFGKMiPkJdvsIyehxiqkAZMxmGEpiqtE/IvpHtXapHBwS4wl1mRsmoqiKOm6Ft858hQIrVW29WmN0WOysK1ZrE2ZKFbjE5u4D6EajycMhiO0FouVtu0QK8lUPxuDZBRZopKci0jEh3SOJB/W6Bza6GQh56ha6b11P/hOZ4lPP98lvMWkercoihSoLcGIfchf/8jzfLse+zXVA/n9vrftzfr7CUXWW35qlTAiKdmil+exxuARwpUpy3S97DY40KXQ8d6msL8nrbWMsxFtJxk/MYgPr1IaYzVlWW6HYK7r5Hor+SyNMZRlSbWpaNJ51Xsoi8oy7sIKAd+JJVJ/xmXWbu0T+nt/XUnQZZE8b3/Z4+81SBuBTonXIp0jVjUhKDofyIYlRVkSFSznC5GMe8DDWBcc6gHPuzmVAW0lJTPPCw4PHtJ1jqvVJd7XRO0hJNNfBJSMqt/s5cDI8zxts9JMayWLziXWR0weZ5LgLVI4WxhsApObxYqQ6PefPPuc//yXf8Hx7IT9vREGw2y0x9e/8W1+9uJDaj+nMJrQeaG0IybiSolPkzKJCaJev1C9BHRLlVcK0JiEub7GCENuBJ0K4rYToKCfOvTnSw/g/rKJYQ9KKQXOR4iBRVOxWqxlKmCEnt4liv5wb0pY17T1BpX8lrRRxM4LAyBNkiFN2lTEB0lzF8JdBG22/kV9QRRCwGrxQemLHlDUvuPx86f86z/5Y66vXvGbv/Gb7O8foVyg2qzoJ5O96+fdguaubOQuqBJjwHcV1uTMDmeMZkOGezOefPKY0Db42LCp5xS5WE2Uo5zOeco8p20863VNVIoyL2m9Y7VZMh5nTMcjvI9s1hKU9eDsVBIqbwNZnlNXLZv1ZttIBC9shPm8YrNuyIqcl+evODo8EDnzsGSQWUbTEYOypK5rNnVF2zk6L5PLclCglRTHTSsyQ+88m6phUBaEEBkNC1aLGw4ODnjjwSmXF1doAnvTMSo6hoWl7ToWyzXYHKMU8+UabTSjIscYhfciLSiKgsl4QrbecLta0UWPU048vBCvrUwrBsMCUlCDS1PioMDkiskoR2nL2dk9pntTlBLwuu1awCSZevqsgkgnhllkcDpmPJpxdbngs0dPuZkv5FBRhtAJE0bklbIIogLXdeTW0LQtvQVJZjM67+nTL/sUdWN3AGJE2MoqWSm0dbcFgzxizZJPhqjxADMoISryLCNaI2vYB4pByWAwYL1eSfESgvijFjmrzQalDJm1uKblan4jAWUWqqbm6vpSZJtWkZcjjvYOePazj+hq8eZDKfYOjphO94kxSZuipw1gbI4uBxy/8YBqeYWeFmTFCDUc4aLHZhGsobMqsXYafNPS3qxYXc7Ft8darLYE26AGlsHRDGcVF1eXybNXLAbyLCP6SEwMCmPUVhXQdY6Lq8stG87ebRLSlhdioChE0dC4DqJ43+aqoO38dorb38/9oyzL16avIUmj+2JVvl8+fwEY1JbBEpNvobAZ7sridiyHkPyieqSuqqrtZ9iHkPXTWJm6RqFmIiwcY8RKodUBn2k20ROdBAENNfjo8QRyBc35K14+u+R3/uk/59nTz7n5yX/Brhe8fPyY+w/f4ur2gtjW1Jtb3v/zf8uvff93uX//bTbLa1SMLOdzrtZLYggczfYZDktW6xWbpmIwKHn45kNs53Gbmsv5LbeN43A25mxvim9bnt8uOa8cBwcHfPnhfa5fPmd+PacJinv3jnhwcMTF05dURpGNhzzc22MaAx//7AMuG8/aZrx1dsq33nmPD5894VW9hk4m6E7vzjFJJhZQpwdGt3tyUmf0n0Qvseu9ze4+7jZPd4Hbv9OA3mkat41LCkHp5cTCnkhnavqZ134lrRutUEbRbDp+8dHHLBZyPsz295juz9g7PGG6d8hgekgx2icoS+cjSllQBmWHZEVHiBqrS3SeYYsh48mU07MHLObXPHvyCR/97AN+8dFHvHz6CV0MGC3FpgTOaHzXktuML33paxTllNatcaFls14xGlYMyoLRcMh8Oefpk8fM9vbZOzhkNp3x8OFDHj/6CJtJ4X40OeLk5Jgf/pf/zO3lJX/wgx9QjmfYooQITSsqi861FJnl048/4t/8yf8BMXB0dMR0OuX8/Jz9w0OOHjwQ3/aqZrWu+c53f5PhYMj77/+YyXTMbLZHOZDCuK4ajk7P2Ns7YH51KT5gNiO3Bh8dm3XFdLqPUtnfAdrvNgmofs0oUFoCU4yCZs6Tz37Ks09/hPI3FOqG6OdUmxXPbi6oNrXI5dsGpSwxGtabOc+evmQw+JDZ3kQkm/mEo5Mj7r1xwGB8L7Guc7QeYOwAj8b5DmUMrYfvfvOrfO3r7+JQ5GVJ9J7OOTQRE50EMHYdbevIiiHjyYznz56wXl5jctnnv/d7bzJ9a0GF4+D+hCI7ZGDOODs0EBq0DkRdcLuO3K4DmyYQKKm8xfmMrtK8enHJq4uP+daXv8dHzy5Z38L15Yfw6iNO381psobgHSazzOs6eW1mwmD0GdprHCZZ7CSGpFY4p9hsHL6NqJCjlCFoGagr41DRgQopB0L2VdnnBGTo1p5VLWo1FR3tZk05GXF+e8ntW6eM3trHb66pXiyxVY3VitxmoNTOk9MI+4pguLq9Zrm6lTqeZPmFyF7RULcVq/WGvdk+J4fHdI3jpXvFerFgtDfCdx06RJq64XY+FyZNbsmLknVd4TuHRZMXUldc396KCoiUPq80ZVEwGYykdtECBm7ahuVmTW4M1qUsAqUg7lh8d1UBTVMTfCC3BUYJAGKU2YIjW9ZjDAyHY44OwZpMfNhJ4J/SGCskAa31jvmc9jqRHXc4XxFxqXfQqFQ76MS20kl5GFECeBlNaw2Plgt+9PI5T2NHq5KMVsugJCRrKVRvXyQKP8tOStsFhzIF03v3GL35JuVkn64LVNEJoSVCUIpmvca17c5/NO3LW1/LENFRMcOwj2U2meGCBE/vv/0ml6+e0q6uMJkVOXlweGV2+3CMpCWdwOOeLboj05gUOqrUrmboHwbx7cR3xNgH2aaBY5IGC/wYpCZJdcX2nEqkHfEv9XdwP/Et7VVccRu0pl4726RG0a99/Ytn3N1z8ote8H8HtEyDru3ntwWuhcB09/33KiISM7AP2em6PmhKiDc7lij0HqA2NbAB8VUPCQSXt7h7f8YoSAo4tKJ1wmjrvd+DkvfjkqojSTjZAtZpMPTamf+F/u+XXasv1g1fvLbpydmGk97pxZMuXwhJIWCzDBWFCWpSjkwIIdkUCCs6z4vU66d/T+vkL613UvQ7A2qf+j3n3JYd2HUteVESo8jy+9Cm/mdtIqr1770PKhPLxT57Q4C4nhXZ//kukaJ/eNfRta2EJKmekPVLrlMUNZv3nk4pIRIZLX1/v65IZDIlPaIHYgBnRAGQZ1naL/t+LKQhAluwMEbQflcrJgCFGJ1Yl9yxnexzC3x0RAK+lUF2TBYwxogUP+q7/syB4EDwREVhMlShUEnB0HVdAgZ7j+A07Ceke0d6F51UzmJbkIJPFYQghDTXObIsY5AXDIpSnrttt1hKf1174N57tw3L6m0GijwHJUrFpm0kCyQKGUJCxYQN2ipR/+Z6Fyhps4wszxPYKuu2qWvp62KkLAeiiuo66YPS63FO7GGKsiBLA0JrRQHRNU06g1Syw1NbcN+7XR/Qq6jvhgXLvqG3a7rrPE1Tb4PBYhRMyRqbWL0G74B0XhLBtQK4GqUxebEdQOz2URiOBgxGUl+3bSuEI5tJ3xtjUmSKPWLbtYIHKMEDek5QFzpRkivx0+6kEf6lj7/fIK0GbzzVYoMZgFfJqqAN4pVDFOBSTieZPCrINQyVRiM+lgGh6N87OOF/+Of/I3lZ8j//q3/Bj3/6l3jvyDPxzVIqSd7T4WtSYp1sLD1tWzbHEOW8ttZuLQ0MKcmZKHpHFxgMRuQmp9kIYr6Jjh//9Kd851e/yf7eEZPhPl2Y8eW33+W9t97l55+8L0FFVmQzvVxSGlRhx/TUe9KG16WQHdeHEMDWOL33skSl4C3VT3zSpiV/CfQG8XenrbsUvS9OWRUxPZ94c1hj8VpKi9CDHwgY7GNADwtsmaOanPZmiW/abYMdfUw3pnj1yCEmfoExJnBa92EDpOIgWTMoOZC3hwgk30+Fi4pnl7f8q//zT3n/w5/zB7/3u3zpjffwEUyWScqqSu9e7Q6BL77fnUeMsJJC9NKEW8PZm2+wv7/H7auXXF9cc329ILqMxrXbiVFWihepNoqiyKi6JoGuMBqVTMdDKdS6inv3jtmbDnjx6gXjUcZgMMANCsrc4JwXef/WTy3ggqEoS4Jz3Nzc4KNnNB0z25tRbTY0VUWeANPQepyPGBU5Ob6HNYqXL19Q5CXOBZqmwYVAZktZ+96LvUFdMx4N2RsPWW1q1ss5mYpkmeHe6RGPn71gWXtciLQeqqplvdqQW0tRFlibUQ5KtLWs1ysyYJQZBtmIurDUjedof8zx3oTBoCC3iq7tWDWyrlWMBOcYmIyjo2NOTk6YTSfymusGbSzCu2fLalBG4bpI7CJZrjkYD9gbjxgNS37445+wXtcEp6k3rch6wi7UDgM+Ta4j0rRkeQJoUwidMQaNeLb1TEq0FIEmHXA+iIRCR9BFjrWQD4fYvTHOaprOMR5AXhQEI0MT33Z0bcfl5SWgMFoRvGI0El/iqnoqwJVzTMYj+Tdyy3K+QKHYVGvyvAAVGQ5LimLA4N4ezdWc2IiM8P4bbzMeTGhaKdZc19F5hzOwcg3ROj5+9AgfIl/9lV/h/PqK2+tzlHKgMikig8bXDfMXF7h5hfJgCgm6w3vKWcnowRGMckkXDbvCI6aCW0W99VBTWibpJs9o64rSFhIKpUWuGJywkcWfzaKi5vzyEpTcYzp6yqzkO7/+G3z26DHPr55v77+7RXfbtq8NnOQ1qa08pi+MOt8yGBZ0rpZrrO7I5bTeSk7luXZhGb3fbH9YN02T1AyG3merb4JkGMU28CCEgEKz3mxwyzmFFsnTOnr2OotVgSzv8G2Lihs63/HBj/8MrOPXvvsP+PePP8KtzplfvMDkGW/cf4vPHn1MqTquP/4RV/cf8Ad/+E/4v//kj6G55fn1JYHIdDJlNp6yWq1YrGsCirOjYzJtWC3n3C6WXFcb9qcT3js5o96seHp9zbxuOTs55p3TY6rba56/vKSKkf39KSNrefz4KZ1RBJMzzXOGMXD+6ROu244qL3jn9JT3jo949eRTXlxeoKPhaFjS6UCdRpR11yZvWI1VessU8N4nhvXOo1yKsDu+W3qntvj/ar5e2/e/AN5+8Ux47bn6Yd+O0LOtE1KeIEEpFusVf/Lv/pQvvfsO3/3u93jv4Zs8fPs9RpNDWh/poiFg2FQdznui6ohRw6ai9S2+7dAo2rUEUBRkjIbH2HxAllnu33/At/7Bb/Hnf/Wf+Hf/17/FReGByRgSWt8xmkx5951fwagh1kTIMoxSVOsNg8EEbTIGg5IHDx8ym+2zXq3RxvDVb/wa1ipub685On2Ds/v3ePb5Zzz97GN+5x/+N7z13pdpg2W5qri6uGW6P00AjqLICgwGV/XMxhWXL17y9NkTprMZ7yyWKBW5XSzIhhM2v/I15pdXfPLzD4hKFFAnJ0e8ePo5Tz7/nH/23/1zfu3Xv8f/9r/8S0LXMB6NMAbWdUVQln/4+z/gwYM3JSD2DljTN2ch+lTXCPNWK4XVHavrpzx79GPWiydMyxrchvX1BecvnjGfrzDWMpvt8+DhfQaDLLHpbRpuJz/druF2fktmG2Z7Ndpcslq2qSkxZPkQY0oiSkKjYiRGzaAsMCbDFANCnWPzIdoEXNOQ5QV5mWPHI2JQoDIm0yH3Tg8IbkWRBazNCLbge98dEjrLi4sVq6bC2shkKOEwhZX6Sp8UGDtA6wKdDRNjW/a9i6s5//Ev/oq2+5xvPhzKeX0wQ5/8Kvt7HeNRpGtWNHVLu1li0cLYVgGbWwhgFag+LTrVntZasiJDBY92mmhBB6nvjDUQM6L3It30Mfltgr8zjPcxojOFjRbXio/f7fUVL85f8qV332I9VhQnFlNYNucVdq3JQpYGa31AYI4d7THa01xVGzmTVNyCJV0nZ+/R9Ixhuc9kMGM2nrLczKmqAVXTMMwLCB6jMowy7E9nZEVOIDIYjcmLkrqumN/c4myGLXLK8RDTCUgrsteG4XCIVWIb1HrPqlozGk+Y7u3Tbioa3xIIFMYSMRDvBIv0DE7YNts9+OM6R0j1sroDPGmVPP+UFgVC2q76oZLskyHZfJGs+IUtJUNNh+vE4klsnGS4uD0bNXItkdyKoBRz7/jw9ppH9YallcZMJQ8oHcReyjmHzcSGTQrxsD07PQE1yNg/PaM4uU9rC1arChsi0SLDzSDkl7aupAcLEWOlFgtBrCGsMkIKiVAoTWkt07Mz5leXeGX5y7/6IVefPGcRciqVE5QlxkZC14ylt73Tafja7/dG90n2cbv398Ch6tlbJFDJZAJcGtJg2m/Z4j0bTykJOVI9JSgmkDldmi1rN13zgCI1FlusSQZQOyXgDhST5/ulwOGdh1K797j92p33tV2CIWBSzab0ztMZSGxjWSOSY+JkoKbNFnw3RuOcSkCtSgzoZFuUBtUi0e7zVgLaiCIlzzK0TSGeIabera/H+oBtyJOnpZynij4Isw/XA5XUmrvD+4ug6xeB17uPL9YT//Xfpz+zWyaxJ4T0wGhipcqaEfujtGkJgKsyyrLAJLZgz0K/a0fQD/97sla/R7gQ8HWdhjAqkUocoGiahjZ5ymZZnshbFhUDRS6ZNs47emVaTPdUIKThhyj8TPKf7wdEu+sX0iAn4JK1QggSvil9gCN4vwXjt5hpDMkGJKJ0Jj3CnbWrtLxfwW30toe31uKdjDvkmmag+s9bC5PVS3ioDJfMro5MfUhwLVVdy37qnQS5x0BZDgCVFDk9kUvWtbUSwGithRjwQXxmvffbsENjhWFb5gU+KVrVHQKKNq/7w4oNnKccKJQSqwcFBL+z+Oq6ToZeSqFC6te7QHBiSRCJW4sBoxVeyX0mW+1ujVhtyIYjYsLSQvDJF1/O+LLIk7o5MUXT1qHTfiHhcwVlWW5Z2UUhIOxgMGBvb29rrbFer6lbyRcxttjurd7LINV3YgHWg8TujuVAjJHQRWhCGiDYFL67sxrsQdXhcMhoNGSzXm0tHUJAenjClmluEys8pP6wZ4dvFXvpV7lOycZBi4WFANG9hUQr3rtkiawV0tm2G9yFpJDYgc5ylvy/+dL+vQZpAcSz0JNnloOzU4Yq4/biWj6UTsJz0lBtu2EntQlBWbxJaGqA88tz/sNf/DnHJ6dcXp6jELNhmS5qovfiu0jvU9L7ospD98V424oHSPJQ1Vo8QXQ6NJQWME+KeESChaKta+qu5uL2gg9/8RPefvsthqZgMppwPJ7yjTe+ypNPP6aOG7k5osE7lw55Sx/c5WMU42ydGENmF+7lgtyYvaTjtemnkll377wTE0gJO8BBDiT4O4dW2ji509zKACrJTvq7ViHNYR/Ik9hGIbH7UJbycIpft9TrDa7pyDKz9RbcfuxRJA8xxCRhlufqJ4gyyY5bULxPI1XpNfSTGQ+su46fffKI69tbvvmVb/DNr32F6bCQxmDLTPDppvVJjnKn0EqHTojio6YVZOmz9d6RlTknDyRdWn36mMXNnKqqUREGg5K6qliua1SW4XxDVW9kQ+gCe9Mca0AZzXQ85N69Y5pW0rfHwyFVJR5uRWHZ35/hg+PqZsVytWG5WWOLjEkYUBaZTMq8sDzWqzVZkeED0HVoDUWWEVxNCEF8TVVE4ZkMRnTO49uWNgbWG/EbVAryvJSQsdU6sV01LoXdGGvYrJYYBVbLptQ0Hj2dsH9wwGq15ma+5vT4GKUM603Fy4tLQlQc7B+CUlTVmkxFzk4OOJqUNE1NmRmMipg8YzgIuLalaiLD0Zijg31GZYHRikVT4aLHaGnG+jVqrUw2I0GA/uDp/ZCCl1AM2TAieJFcovrk9366KsVdUYjkpGlTmmmUyWaeZSJRUj5twmwHBduhjvfbiX0kkuclxXiAGZa0JrLZbGjrVtZrZmnqGgVMp1PqapUY7rK5baqKOpnMb+UjqeoTzzppRObzBSF4bFFQWMtitSSbjjBKs3h2gS0KTk7P0NpiTKQYjglRM1/dUPmKDRXRe5bLNePxlAf3H6CNpt4scU0t+3HrcJ0nV5bZcMJi0+GCFOJNXYOKHJ+dkY0LmuiZzKYMB0Muzy9IFnSy18QdyBUAlHhjgTCOBsMBN9e3DMoBVdVgCOLVmeRRg3JIURZiC5GKkmfPn1M1Ndr0nuN+O4jqZUX9MEf3/kB3Je/b671JRVoKlIwik+uDNLYNbuxL8GSHk4qrruuwWfLYTuEnPYP3rvxnO+UNPa8jUlcVvmmprBU7Bq9onKPTCte1VOslZB2xHODaBR/98D/wze/9Ll/91vf50b//Y0xbUV1dMDw+ZTTdZz6/JHMtn/3sR/zRf/8/8aUv/SqfvP+fUcowGeRMipLVes3F/JY6evb399Da8vzJC1abDQ2ew8MDTkdDNqsVr27mXNcN9+8d89bJIeuba168vGIZYXYw42R/xtXFNTWKkOWUSnFkcl4+esomOtrxkLN7p7w1HPDy0494tVlTYXnr9AHvvfGQX7x4wkVTs+laAUy1SXJUAb81qThM7PS+gRBPv9259UU20N1H38Ts0qbZNrfqzrklR9vuefrGe9sA0zfliZmmFeJv+jqo61Xk8N4xf/iPf8Bv/tbvMJweoLOSxoOPmpVb8zfv/yWPb8+pYsALFQmlDV3b0nmRcHddjWoc337r1/nWG9/EdwGiIURhBbxx9iZ7+wdc3FynwrBvQD17kxl7+/ugLNoUZMomOxxR7SglCbTFcCfdU1rTRM8b732Fr5QlJjNcX17wi59/zFe+8g1cUDx9/oqoc/b29smt4fbqHKUUJyf3ADg4OOK//Sf/DK3gdn5OXuT8/MMPKPOCYebZ/EAAACAASURBVDnm+uaayXCP85u5jKCVIXh486236VrPfHHD2el9utZzdnofi6Ze12wWV6iuYTydQNsSQ0euFdoALmxZMr1SJqT6UCyipEGyKnJz8YSf/+2fkasbCrOhnt+yWlxTr24IIXD/wRnDUcFgMEiAXIfNFEVhyApDnqRwzhUcn01RBDrXcru4YLlYkiV/3qAWRJcCRp144aoYqGqFj+AwBHLywQl2YLk8f8Hx/jF7Rw/Q5RSUofMrVOzo1ktyG1Da4V1L5yPGTgjespd5puUIk5UMigFa5YSklrImoHwjbFMUTb2gqhsGg4y3Difc+6Pv03Qdyg7Q0aF4Gx2+S3C34BYSHNd0PPvsUz74yfvJjl3IDTYzGB22ktDoRZqd55YMjyPK+/cK7zo0MV1PT6gjm3W9lUIrFbE6EIIjKwzeB2yW2LbRE0JLjB23NzfE+AZ7p0e8mH9AM6ioyxXmxrMX98h0htEKrSMhaCZ7x0wfnPHi+bO0t6jtOUCMuC4wzIc8ODiGTnz9dIBcZwQdKbQkaOuoGBbF1j95tVmxqRsGoxE2z7BFJjWvkv3fID77eZ4zGk0o8lz6lNZiXMfLl69wzvONr3+DxfWcNp21EQEKjNHJy1C8+WxeoLSSkLUYIIgkU1uzHWK5tiOGQGaybbiT9x6dgnJ0lPrfe4/xHqKWIVffS9EzPDVRGXT0xOAQH2dhParUBzgvgXuqBxiU5srVfLKYc+Mj3oqPo1VAUInNmxpXH8VLVGAbWudQ1jA5OmL/7AHl7JhYjIk6o2sdygtI0nbCRlcJ4CCKvUGIsTcFRysoM/EZNNqQmYjNBKi6ePmC/dOHHO8d86r6mNpaOpuhdIa2GapryLUmGiWeqzFZyakd2Bx7FYza2SpFIvRMvQTS9bYJKLFs80RUIrL0IUCRBPxG6FqRgfP/MPemvXZl553fbw17OPMdeC/nKtagKo1lyZLbsRwPbXe3A6TRHRhGXuYDBPlQSV4k3UAQBAmQIHDHbsuxZFmyJpekkkqqYhXJInl5hzOfPawhL56197ksqYG81C0QLJJ3OGfvtdd6nv/zH0IQ9VvHIoxi/+ZdSB63Kp1/HeCq+h5JAAaFUqZrkLu27eVz7trZF2MnKFNdx5V6PvrBdOcxKb+k55UUcy0WHAnMS15W6RzTiWEWUgiQDLtVuNYnQiLmBPZBnOolybPNlVyXZC0lDMkUAJQs/XRSSrSuFSBfgS0yfO26Si0NOmJ3zCfATvcD3a5muD7Q/3QNcR28+f/70XW43suQPjdawrdROOdFB6oAbfcWTmafGyOB2rYfQGutU1BSx0ZOPuDph1ljU8CbosjyVPuG3vKkC9JS6Z5pbbmeWk8Ui5VurcTQveeQgkyl9mk6BVmqn73be6Fq3a1H8agNIYqtSXo/nZdulgkjWCuu/TwhxBHVSwzRmHpTbUwKp1LkeUaIgd22StlBokQwRhR0oNjtRMbuY0jkLyOkD5UCxCDlDSWCRRRrvBCUKKeVKHvBy1AreDJbJJsmUWKTMoSIUcDetFaVUxilUtBUAiadS72Poqnq1KcaUHvih3O+P6vknigym2OtxbnEUk0Pr8jo077iZE346PF63/OEdF/T9ptqI4+KOj2fnS2cAM7dOsiyTNjaIeBa3xMiCBGlDMEJQcmWZQpYFmsTm7KQysEArTXlcMBqtRRANIGhSmnKMpeMgralSjYBAtTKEErszaCqKqq6StcuQq7QEcnwuL4PNtU+YyoB1W3bUFVV8tBWqbeL6ASogyj3umdVhkNy7azRVE36/LTGI1AURQLnVdov9zaZAh13/Z9YtxmrQRlC+rzY/7Rf//GbDdKGgJxTMr1YXF1ihjOMMvjWCXKd2cSkCyhjMSGxYb3HZuJbFCMoq9m4FX/znW+kBbTDaDnsxfOmFcBSK3SXIh3pNzWZAskNU0oJSJqmPSEd3ipNYlRIaakqTYaUwuaGxitCG1jHHd/56fd4+wtf4F4ouXXnkFuHp3zprd/ihz9/l/cf/xQbxXpAG4PNVO+JanWG1qTUuG5amw78KIb/CjkEOuuFPv0zdq9HppMSltTZH+wP4E8zjXovRvpZl7Bf07/rNM2SIsDLJqIkNbtnGXUbbnDYPCezBXlZ0mx37DZrOZhb+TnG2KQmFuAbv7eRiKT3GeO1ab8cMkIl16mITIAZKkkRNE/OFpyffYtf/PKXfPVLX+Bzb71BnmUEJ6nQ/XtnL5X+tM+OUpqI+ANDTOCUJh8OmB3MeHs85PL5CxaXS7abLYM8Z7Xasmtbdm2gaWrKYYnKPEVQZLn4c5a5GI7vtjtcdJgsS6FYgdYFYZ+awHRcMhgUXC1K2qcNVduyXAUalzMYZnLQBMB7mjpi8hwfI7mxzCYTtuWW88tLXpydk1vNdCLTJq0Nq+UGkxka79HBMbQZMc+oqh1Ki0SvO3i3TUNoa3zrZFrmHAfHR8znC+bzS6yo+ri8vEKhuH3nBpeLJetGEtztdkdhDccHU0qjGBUBo1uCb8isEv/gAKcHEyaDglVd00RNMchxvoG6Yj5f4qJGqVTYRdkQjVG0qUmXoMoA0RK95/zsnLpqZUNVMlnvBjHByfOtbfLXirDdSpp3CLK8rTboTGoRl4Y6HbuvB04h+cOlv1Op0C8surDp0IaqrgAxEVcVxDaQ25xMGVapqe4Cquq6pQuAMMZgtWFXCTufdND5KHtEkWUoa1it1hAj48kEXwyptjvybMRgMqNyDmMytM6lAS5KfLuk1Q16G6lXO4JX/NVf/SV5UXB8dEQVDZ88+pgsMzTbmk3tyG1GMSxxbkPAMzgYM75xgJmUtF6SpKvthqraijdblAbGWGHSpHL4GtAtgRNNXSNyS89iuUKhyBMbS6HwLnDz5k3u3L7Jz372U+bzJW3wfPT0oYDtpgusETDYGAvWpJoi9GCq2CLofu/rQxUhFUEuTetl4BJDYLPZ9Ad32lC744osMz0DRzz9umAp2V/1tX212zuNNRLk4vcyI2UtjZU9b6g1lVM01rJrHYEaoxS5U0yyIX5+yScP3+fzv/cHvLi64OmPv02Yz9k4z5uvPuDhQ8VysWD19Ak/+vY3eeNzn+ejRx+QV1vyUrOrKxbrDY2KHI2nHJYly/MLNruKrXcczia8duOE7WrBx1eXLBrHvdu3ePXokPXVBc/OLlk5z/HpMXdOjjl/diZyaG04HQ559eQmHzz8kEor9HjIK8c3uTEY8vzJQ15UFT4r+eytu7z+6gPmyyu2iyXbtqH2LbrMxDYlXkunTX7SMUaii5CsLVR/RqXhZQf+s7c36JgeXfrs9SarY1v2h921r31JxsgerCXG/nwjrV85U/c2DNZkqOGAP/2TP+S3v/IOmbFsFhuKAehSofOSCzfnP3zy9/xUXbLLpGlRRpRAulRU7Y7WN4Bn5OEou8sXc41uCmw5I1M5eQOa54k90u1hwiAzwI3ZlOlkCqkAD9YQnexTPkZC3PtZbuoVZVFSDAqqzQZURj6eEX3Fz3/+Pp/74td48OZnePr4MdErVss5bV1hjObxw19y9+5dovf4GBiMp7x1fJPN+orl7gWqyPmd3//nTAYjRpMZTx494mq+4PUYOT45pa4q/vhP/ozXX39D1CKuSeyWmoODY1rn+KM/+uf87Kf/hNaRo5u3uHz+nOePn/QgkTFG5O3dPVVyHmkUMYVeZFqxePERv/zJX+OrD9BZw3q5oVpd4l3LYJhz684N2XdMV8f41JR4oCF4SxMcoZamO4ZA21Qs5xdstkvG4zFZluN8TetqQpDv47wTRqY2aFPIfugqdGhRbkWoB1htWCyucCHH5LsEwLUczMYUpYRfhbbCuSVts6bIJPRtNpwwO5riomG5XLBartitVgyGU6LS7HZrpqMxR0c3KfMJUdes51e4egQhIzOyLzV1TdvsKAqLMTUqVKjgmB5OOD18h3FpWK2WYsgVHY2vhWGnrNShCnR0uN2GUG0xowwXMto2olzAtY5dsKw3jlEWCabCtR6NobCWsijITE5ZRhonQKT3nrqt8W5FcLBeLKmbmunhEYsbR1w9eR/GETVx5NuaacgATetbwHN+9pRnl5dsN1sJWfEJxEcgR2tycjWgIEMbS+sDsYnoYLDOkAeDSQSBYZnRRgmIVUrUbxtXE3ODORxhlLDLfIw4Ddk4Z3x0wnAwwtUtddsQdUEWLLfu38VHz3y7xmYZw8TSjjFS7yp8kJoli5bcWnSW9Sq+1jUMsoFYKVgjoF8TCU6l5pHUpFpCkMRvaSIjSkLB034lYJpWBo2DxECWx8eTBdl/dAfkoTAgYXdKoYKU7V5H1gR+cH7Oh3XNTmuCyjk4PqTMMi6fnQn4bcWnNfoovtnagzaMj2ZMbp5weOseg+kJLqawMWWoVWc/FchDpLDCWlrHKKol1ZFZpB8ry4zCCkCovBK9lXJcPjvj5qsP0PmQm6/c4d2RpfY7MBESu88k+WoH+AKoZHMQAZ2u63XwTl6beomJRVpbwRiIEk9lQiKE4IRNG5F+McjP6FSERPEvFzVSSH7ae3uJ1BSlcyikgVQHeEool8wz9+eclEVxf8+TcrIDDDpQLXafG8XqwSQCUxc6LdZ/AuygVJ/HIsCd1FW+s25Q3b8ZIulrjcUYYWqapBwV26nYD8B90wqgr2Utt22LSkGvnUpUACVNXhQ0bSVqNmNoQxQ5darBfV2n969wLqSE+3RN1N6z8ld74F8PxH4atL2uvnkZ2I39/ZVJicYoK4MsumGiomlr2WesgLAmy4CIST20cy3eQ+sanA9Ys2fUdiC1SvfOJy/8buFqpfG+TZh3UhlpiFFhQieNj6CkBg5eXX9jfR8sLNSYEu6Tr7TRvV9uluwG5PONKE6sZjQcAvSq3+7a9LVVEOsFAYTZ+0oncMt1ZDVF8kBN7HZjyDKL0QJYqgjjQZk8+BNYmQZw2miGgwEMB/iQcnUQQkVITHYFyec3T8xNLxYCaZhgjBViWHRJGZeeXaNSqF0Abci0gMfa6D5EMoTAcDDohze5tdSuZbndiI1+Agh9EHVMnstwzUfJZgmtWCOURUlQAW1zVJCBRpvYq9rE/n53KskYtQCfTYXRBptl5Fr3zzHJusb7VjAbBGiGmsxYuSda4epr9y4IIWFQDtju5PXH9EzrdDYoZN3sku+qeKdblFaMRmPKUoDcthFLQJ2KtGE5SBlCba/66NaJNYZBWbKtdrIXdM9Yh711YWVRBkcqmt4SxNqMvBxQ1RXb3UauU0+yMBgjnsQ+rRfv5R7TJoa0ythtNmLdkYZOSinqJk9AtKLIc9q2pm0bUQoZnRjS9Hhi27rU62oJtKcLTvz1H7/RIG1EzHdjdGgVqOstV7VnYAYS2hXFH1LbBKqGrtSKtE2Nth4dRQ6jfQTnaf0cFBgtU+4glrRAMs73+wmGUlHCNOSfQe297jo/Q50kQdEHtDViWt2bpKv+gNRaizmwj+zqHR/Nz3j3Jz+kVAOMGUI2ZDQa8/abb/P+xz+WTUjysOSAQ1gF3imsybDW4FwLKrFNtciYdPcag0gNOqBSWGtKrhkpgCBtXCFJPj49FewOGpOaYoWS5NX0/pVOmwoBg6Y0OdvdEidUUzqGU3c9Y7wWbqbBlDlFJuFDrm5wvkZ7SVXVXap18vsNnj4EAHTycUwbUj9plINQWHqG4FMBEeXaRKWpvOcXT57z5MUV8+2W3/7SZ5mWA5lCxnQA+UDU4VoRc00enQzbg+82Bgls2NQ1jffYLOf4zm0msyO2yxXetax3lTAqlEj4rLZk2lIoTWZFgmFTobFcLDi5eUS10+yqDTHolIZpaJuaaAOZ0pzMCgp9k03luJyvqH1L22oGo6GUFE7uCY1MvXZtS2ktNw6nKFrOnl1CXuByS20rxqMx08mQ1XZH0ziancPmHkKgrnaQ5ZgoG2GeZTg8MVpwgclowGggPjCv3r/Ds6fPqNZrtDaMRyNCgNW6Zls5XNT4YHh+teJ4MuD+7Rv4eo0xMD2YEpRhWZ2n51GeLWM0hwcznLFgLbvWM7+44tnzCwajGdo2/dS5Y4LXdd0PMVQyc29c4Gq+SjVbB6TsWdpdUW3QRB9wQQpkYueBFVIBcW3bDHvj8+tFmkbYIlFB1EpsDsYD2kwRlYS/ScEb0V1RbeWQX21W/XoTNot+6f1574kqYBJ46L2T1FGg9W0q0hw6Pc7OeVzbMrl5g9HwgOHhlNgEbF6Q5TnNbkfUkB9OGMUpV08e0ay2tLs6TZEjL37xEF8LuyMf5MIEC+BimroWGeVkwPTmEWZU0BAoypKbN29yeXnBbrtN13Ev6enUCjGEpGCgL8RjDLRJvkViw/pWwFw5QyPLxRXrzYL1Zo22iS2iFCaZvYeOFaFIe1zsB2kgLJMsy/fG76mYksIT2tanoiWgomK32/b3umd6CJUMHwKZsRzNprw4v5B9Md3Dbv+X5bI/X7o9tm1bKXJjRFtLMShZEVluGzJrKIqMeRbJ0ZioyIJMfhXCbMqAq0+eUL39Bf743/wF/9PHH8HmnLBdQ+t58MrrvP+Td2kJ/PLn73Lvs1/gzd/6Go+ffkxcbZm3FXUM3BhPOB2Ncdua7WbDlsBoOmI2HHJxecV6u2bZeG6eHHPvxgGrqzkXV2vWPnB685iT2QHzi0suV2u8UkwHOUdlweOHj1hWDQwHvPPGm0yt5tHDD7hwG6pyxL2bp3z23m3Wl89579FDlm3LyeQAbSzPdiu8QpKXjbAeQpKQdc2IwexZ8LAHxq9d55ea1HSmfbrJ6gDaSMeweZlF85KUsTsfr/2MvolJg0+uNfAGRaENvqrYhBX58ABUSuTV0OawzBou9Q49LjkqDglOs2i2tKbFUUlQU4hEr2iUDBMjhhgzVITMTjBZIXVAlGbf0A0xFZPxAUUxlFejLZlOs0YlA6i2bWlbz9nTJ8wmY4ie9WaBiYFBXuDqLf/w3e+QDSe885XfxQW4/6AkRM/B4TFt2/Dw4UOMzQHNarlhdlCitMFJKhSXF3Pmy8f82b/+t4zGU+qq5v4bb/B6lqO0MKxGowknp7dl6I4iywrqtmJcDAnaYDLNG2+/zc1bN/HRUQzHXDx/xr1XXuPwxq2++ZOhVro3aagLhhAzMhuoVi/46L2/I+MJg+GO7dWCdlehVMtkWjIej8jLPLHyzR5IiZZOLueckwbSewGlvadpNrS+YTKZkGW5DKcbT8D3oB3aMBhNKLIS1+xomyXtdon3UOIZDe4zu3Ob8XRGXk7R+ZDt9oLNqmKQZQyGBzTNlrZaUVeOsjBoPNvNClMMqbYrYIcNLX53hg8VB4e3iNFyef4RwyKi1Q1iaChzxXpdET2UxZhBOcA1rYj2cit1GVu0alEZ5NrjGsd0OCRXoGPAWk1V74gxkJeFnGXRo9qKy+db6qqiNAE7sLI+2sjZ+TNePF3w7Jnjc2+NOLqbo0yBb2us1jQ7z2pRcTgeUowHVDtP3SiWlSdi2DaG1bamdZGsMBwc32Ezf4E3W5QesnvusfOKojHYMqccDhmaku2uoTCalXBlCDEKJKkURTkg01lvUaOUAIihbRnmOaOyTMVox7RpaV1NllnyPEOXGZsiYosh7XJD9J7B7SNUYSTg6nCIGY2hcVSLBWVWMB2NyPOMqqnZLDZslxXDPJdhS4w439Dsdkmaq/E6QJKQQ6pXEVlzbDvQJpOmN0jocCRirKZ14mWorAIl9bjUWteoCX3zLr91HqJOaWE0qkb24263jHQWkASjaTPNx9WGd+cLXqiIno64/crr3HrwKpnW7Nz3WL54Rpb6NecjQSkGswNmx6dMb5yQTw/wOmOzc8QoSp0Yuh6tJcutZC3EiNWGeifXWoiu0vAH78hMTpFnRCfXwaMZT29w6/XXefLkBTY2vPu3f007vyIbZzilaOqm7406ckvH+u02/47F+JIFQHfp2BNeSAMAlfZklFgfRFui0MSmTr2pqN1C1MSo0GkPw0YJWo4C0Ajo5Htm2XXWV5oSClCEuka6CakG7iS13ed1YL3q/11FAS9D927S21NRGKxGi61Yx0dQyYZvD06Ga/tvTP2r7OtdhkP/GtJZKwGhnaVc8jf13bm0V7tcD3GWQXwiQ2nxTUWDLfIe7DGpVpeaUoKEup+tP3UvOxnypwHW7r3s7+zL4Ox/ygqh+7yXlKz0JSreR9omYHIt9W8MeMTaYjgcpqCi617U/YMp2HyINF6suzpfzt6rF1LYdsIq0rOqldkzzK3YsfWeqKpTHnVAuaMLDQyJYNAxu40x5EUhIZHGJFwhrZgOi9Bd/5+GQOl5sda+5Bvd+ZN2ysNO7SagnHjUdusrhJAmCN2FlDtS142cTekvYvdfdw9R+ChSd51sFoRhHpOlhsEmu4MQxYPbJN9SpSwmvc5ugKWUAi0spOC97K9BAG6lBYcShaeAcjbLxNZF2cQGNkm1bbDGMBoMJTwzdHWtEOgMCqwAmwVQNxLCGhL5p0lAeVBgddY9qmil+gCtoiwAGSCbnU0Wfvv1Sex8ha2AwL6rk/drWogrsrC6PkVFyPI8DWHA5hnBx97SoE2WBd0eYbQQi1TbJB9xelypWzPO7bORlNbJykzOpOukCmPEXtNqk2rstDfGgEb3w8uITBM1EiisgaIccDCdstmuZVDb214oXOr/nBcyiE59Xfc85XlOWZS0TshJy+Uy2RakftukZ1GrpLhthfjgu2GP1KQ+pCyeYPBBVOEhXLMz+tTHbzRIS4ToRV5DcFijMDHJfmInR5cbqbUVmW+Sv7R1ReW3kA3QNidGj44KreQwlMkGySuwM75OIEIQyYy1XZMmL8dou7cQSKCM6+j6yibpJWhjU/ES9ocOUuwU4yHBKpr1hg9+8TO+9tkvY4wjKwsO1AFvv/YZvjk64Gp7gc1kEfvkuSoy29hXAwJ4pEmi3vsQ6ZRUF1TaDKPIAzoD9+57hRhRaZPeSwxebk67X1kCpjoT5N7QXqcjvXG89dYbOF/zs1/+ojfGvt4Mdww1laauLjiUhvJgjEGzeHFJvdygvBOD/OjSpANJr/WSsJgcYXsGVdeMdT2ZBEh1JVMCp2UcgzIZQSk20fPX//A9PvrkCb/7zhd4/f598rwkugaCx6lAjPol8K177d3rV+I3IQUOgdB6WiWATDYsOSwKdrs15XxIvJqzXm/wGLJBSbWryG2GyjRKOaLyrKs1R+WMo8MDRqOSDx8+ptk1WKMpcpmqbnY7kZlEhdYDopdD3W83tK1nvaloa0eR55Rl8h5SgXrXMMgNN29Mmdy9hY2KZ88v2GzEDmA0HHNwMMU5J2zeABFJ8XQBhlkuQwg6yZeiLAq0B6OhyIs0sQzcvXubpq6pdhW+iCw3GxrvcVG+1gdNGyJXyyUDGxmXORHD5dWay6sF1a4hy3LyQuS1tW9RXpMPxyibE9uKxWqFsobGNcRW5Cw2kwCMqq5o2oayLPpiFm24uLpivtrKs6uleOn7kY6dEILI6JxGZ5psUCTfWSmOtO4KBmlOukl2B9D01iDyMBIUZIOCozs3cYVi52UqqwlYFCYqTqdHXK2XNFEmkccnx7w4O+tDCwVAjDjXJRdLGqyKSaaSCheVim/51dmBKLbbDcrL+7tz8xYmQsCgbJJkBglzUJkmWMV8syTUDtV4sXFJz7DyMjxRjt6XqmkbitGQG6c3yScDXK5otRz2rWs5vzinrRuGwxGbzVYUDp28yMgEF7qS/XrwgJjZe+coizKFFkSMNaxWK5TSLJdLuR/JUqKT8Zgk9/KpCFF0+1i394S+AK2qSvbmlF7btr4v1n3Yp0+/9MzTsaZlWBNUsj1I328wKNHu5cTc7j1yjZXQ7df9lDn9rLwsGUynLM+u8G3gioYQG7RtsbrEeinorFbY0qIyTbud86NvfZPf/s//hLe/8nXe/7v/iyy0vHhxxp0HrzM9PmB7OWcca378jb/hs1//Y16984Bf/PKHoOB4OuHGcEJT1VxuVmyj5/BwxslwTKwazldLNq7h5tEJ9w8P2F6e8+Tiip2DO7ducjwcUi9WnF8tWLWOG4czTqZjns8v2TiHHZZMZmOy7Y4PHj9mFRviqODejVNujUd88P5PON9s2Hp4cHTEZ159lUcvLiXYTBlcjFiUsInSs3Xdj62zLzCdD/s1T8BPN13Xm6+eAZ/WHLzM8OjvW1eSpM/t7+u1M7O/r2kPAOR87CRm3hOcQ2dB0qeVeDfGqMnIKIImj4FRNuErr38FGwv+/uff46o9R3uF91KwGmNpQqRRlkyLSkCh0KrA2oHUH1omvD4BDMFFDsZiY+FVksAirE+T5TgXiNHjXEuRZUynU0xesF4uibst29UV7/3oH6mD4ou/91W8taigGM4mVNs10TeUgyG3792UQbEL5OUAUxQUhWbnWqLNuf/K6yx+8I+8+/2/58v/7HfRtkQbzbapMCYns7kEioIEAKZnVmmRh4cUBKIzw/ToEOcDSmfcffU17tx/FZQVL7vu5O8b8CCSOGUwWUZsr/jw598mtB+TmSXPnzyi2VTEUHNy84TRaISPchYUukiD0mvriD3bolN1yV4mAFpmpZlrXIvGE3wtjawy5MVAAhmVYbNZ0G6viGGJVaL6skZxcnqTo9P7NK5B21zCTt05pV2SKYslx+Q5w3KKUiXBV+x2G3TuuHEqLOary3OMDty+NeByrbF5xsHsDueXZ8wOTxkMJ8znVzI8C4oyKxkWJcbmogbIpK40HlSr0CrHWkOWQmyOj07kZ0bIrPjLaiU+h2gHoWYz32BihUZx+eICY1cMRhPwFa7acmNWMBuVDIqWTGuIFUUp1yA3nu265eMPr3j1M8ecnuRsth7Wmvmiom0FMNpVW2yhyMcjxie3uHj+MYPCsqkX+LblxqZEeXBBWKh1dUVQDTF6bGo+HYFMG2aDMYXJhbVLslcIss/b3EqSuhL1mouBR08fu9iUgQAAIABJREFUUXvH7dv3xIJgmFENI8HA5mpHZjTDg5JPzp7y4uKC2+097t97BaMVdeGIuQa7ZTaZUe088/WGZTsnjxmHh8fkNuNys2VZLzmczIgmoJSj8AGDSh6KnrptyMh68oRCSA4+CsuqblsyIzVkVxoL+Np5d+vep7nf85J0XSdwNqLxKCyqr4nE4iAB1lrhjeJCRd5dLHgSIs1wwP2332Ry+wGtLfAKDu+/wmp1RVtVAmEqTXl4wL23P4cdTlHZgFgMiT7iXA3Riew1WQMpZWnqGtfWkiegDNvlKu3JST7feR6rjNyWhNDKOg2Rg8EYV3t0XnL7YMq71RaFA1MkdZQAey6KFNxom4LSkkpC6YRzJupK12elIkbsM2T/F3KISnVoqtGUxuaaNmph7mqHtgp8g4sehRaVk4K2baRWSfcTpVFWEZ0TACv1rKpnPXfgegcM7JWMIaT8BL0/s4zRiN/l3hO/UzHv7X8gdDUWsff77YC4rqbpGW10/dL1M1es9vb91MuJ7x2w7dNA3iYWoY6BvMjxIVnTBdLaE7YhKoWpRQFk0CkQ21hyLaGQ1W6XkPN0E0LXO8uDELkuJd+f7/tr2MNaqbz+Vd/Z/xSr9uU/d/VeoKoqxpNyPwTQwsIbj2Y9m9e5lMGQaohu+GKMgcT+BHoyQgwkxYd6GbyNHdFH1kbrJZS5A6C6+km+Zg+cdt9H2KtG7BK0TiCZMH6N1pIBE2MaWsX+uobYqeOuXY9ra7MbcHb1VleXX8cdgBSclWxUXNvjD0opfBD1RgfQdizkLv/BGANRUW2rBB6nak7H/jzvbq/YBCRsRPxKhDUbxPvV2kyYoEpB8Ggd9/YUVvf+sqoDxRH7jkDEJmWmTf7hDgknjkphjSZaTfCaLNs/M94L6Ni9voEtiKYLupTBiQL53ulthCBnVnDieY2RfT0zltlkKkBvYt92e1a3/xc6KRxjfwL0a7f7XWtN41oJXHAtVa3IiwKbZZjC4lMwWYiBalsLYSaqFADuEwM14DtrjrgfKPTrIoU2+/T6rJHA5Q5H65jP14c7HWPe+T0+FVL/rJRKAWlCinKt+AwPyrIHd4XFL3t6kQv5MPgu30nYxUZ1GUMDtDZMpzOAnimMlnXcBXFW1W6/5yrofIytlTWhjCY0jrZ11/aYX/34zQZpicTQoqL4boXWyyLt0HzdfU4QeFQpgnPimxQ8elejmxylc1y6yAI9iR1AkecE5GCAtHEH6M3gldDpO/BFm70EKaaGXScflqhAawFnA6Twg+ussc7rA1kcjeNsOef55Qve/uIAcoPOp7x26z6ff+OzfOuH30o2AnK6CCovh6A28lBqlcAYVO9FExMYEWLyaVWdP54ATDK1Mj24KdYPvzoVvn7IxChTu/SHvvEN6f87CcLF1SVapUNFmQSe7L17VCpu0/GWNnCPznNQmsnJAeWwoF5KUmtMnjHdIZwXefLR8Uly4PtpsDAB0hnbH4bC+hXGnkrm0klGEQKLuuYH7z/ko8dP+d133uGfvfMOt44P2awvCU0nNdf95nA9ufKl5j6mzTrKJK5xDtCUec5oNuXeg1fYVg2XVytGZcmN4yPmVx9jorBzcmsZDUccn9zk9PQmB0eHWKtR+ZgPPvxIzLObHdrIYMF5qHbiU+iCbAoKRb1rJJQgj+x2O8rdTsDaYYHNDJtqy2a94fjGmM++/RqRyMXVkm2tuLicc3wkSdp6sWY2HnLj6Ih6V9E0O46ODsmMQkUJ66pdSwiR3GYpAGHv5eScgOzj8ZjxZAZn56zWW6KCg/GAEBTrKpAZkWRMDw7IyzHPnz5BRcW4KJgdzVA2lw1fBexojB0MaV3gcrHiydMzbt65JwFxzkvIlFK9qXeWZX0xiFa0reejR09pWkHyjUoFZ3wZZAES21uKuXpXozPTy1YksM6nZ2jfEHVFa8fAMFpLyrrNMMOcNot4HTFp0hecsKqmkzFf/uIX+eF7P+HFco4ncHV5ibEdS7YzwN8XtpIoqpJ3lLB1m7pGAXme0wUCdqBgJ4Uqs5KT6SHWR4LOk81DxGtoDbTB49uW9WpFMGBTkWK1sGmVSUx6LY1CURiK0YBiPAJrqJVPfk2KYVnivWdXVxBhW1coJb5RWZZJ0my3v1zbc/q9Vlt5BgIcHRzTNg3bZpv2MRmoyXuVQY8Pwlb0wSevLBLzQ/fFSAfkqdTIXme3DgYDiqLg+bMzolK9JKzb/67L4JKTBScnJ1R1xWK9Sg0LVE3TS5Y+zaIgFSEm/X495Ko7V0Lap8ujA9q6ZbdYUSWp19BAoS1aGQa+RVUKo3OiSaFki3N++r1vc+f+Pc7uvcbZwx9Tz88JDz3T2QGL5YLt4pz5aseLk1u8/ebneHH+hFGz5WA0YbfbMd+s2RIYTyfMyiFus2W12bB2LUezQ+4eHdKu1zx/MacOkbu3bnE0mbBbrzhbzKlC4NbJMafTGVcXFzxfb4iZ4d74kIMy58mHH7H1jrY03D2+yd3xhGePPuGT1RWuKHjjxm3u3Tjik08e8/xiQakMcVOjc0NAETrfp9TsKKVfKvB8CgmJUZLOPz147NbXrx28ha5BMFwPg4sJ+L8extEPatOt7WWtn2rgusR0T6RuHbu6oTCOie4orDHJ4nKUySAa2s2O3fM5s9EheYjcKCfMDu6w3jXMN+eoege+xSSppLBGRHljTS4hFgluiUqlRN/AaDiiC+BURsCdSGQwGFKUw9SQeMrBhMHoEJWJ1O3Z2VPe/fu/hRj46h/8C6xWNPWOTGk8np/86B/57rf+XyazCZvtji9+5avcv/cK3//ed/nSb38NMxjx3s/fYzoY8t57P+Xb3/yP6G9HRqOM1978Ah5FVozIi0ECPhuIiiwrMVqnwEDxawzBoRIDUKXQD+fkPtpMAiRDAi+iEjmm+JIlxhIRaxSXzx5x9eynzEYr5ufnrOYrZpMho9GI4VBSiTObp2Rr0FqY+OIrXcvfKWHrNU2VaooE5KZ73zpHSEGSKAGOB+WEwWDEerPG+TbVtzVaRwKaqAumR3cpRkfULuCailIHDkaayWBK3YB4Cq4haqJ3KB3JTUE+LGCoUUFjlOJ4esR2u8Zay3QwQHv5fqend8mzAav1lrpumE5mWJuTGYtV4LcLTPRkRjywrXe0LqMJAesjdVyTFQXlZEQ5GoCPLOdXuMZTlgOyPENrT1sH6qoltwXbaAhRkXUSchTj6VQ8udP5LEKmSMTio0YXnpM7JS/OGi4uLimKAWCYDi2b1YK6ilh9wnZTMRiLkmQ4m7FeDmm3K+wNTR0aNjgGuwi7DfVuS+126dRRiQkkAJhFM1CWwhTEzrOSyNHsKHmfynDSe/G59M5T1RWD8YTRcEJRDGh0ZJSksWQFw9mYwWjEYrni6fPnBGPYVokp3O44PjykyHMenz9jPBnj8oA6zLhcrLi83DAZTFjtFlRtRRZKglY475mRk0eR3zrXEnYRa6cJfEqDZC/sUWMtpdaoqDFNm0CTdO5eq9nkONr7DEoj3+1pGpGqy5nonVh10GV4xIC3mnZY8N78ih/MFyyURw8nZAdHNFpRbWVAns8OOLxzj/OPH6KaFp1lTE9uUUyOiVkheyEacDjl8d6hEpkGFN5LeKI1GpsZMmWJRZmyMbq6vLt/Bm0sPrZAwHhFhubqcs6LywvsZkFTbfHRY4u8lzNrA5kSRhc6SfyTu0AXyvYrfqSR1Ivuz5SuV5J+TQBM0ehplM0wiC9ndGJvY02TJMpyvhhtiDqRUJxPg+iQzp7ubCP1rZ0ZnerPpE5Z2H3e9ZqkAw6v110d+1B1rNvrveT1cWUHoAV/jXwDoF8aXMaYgLtrIERXx3464Azo7QT7ASywrXZ0qe04h80ysRMz6e/Se9VWLAQUoIyhDV6YbMkaIiL3R0VFFxT9EjRy7Xp0r7+7sR3QDOpXruH+vb589u/fm+AOHWAp/xT7e6OtRWvDcDikKIo+0CgmoJMYsamOreta0usTW7BjGKprr6XvtXvsgUSa6gC/PRDahSRlyT6lY2B2PqBdnRPSz+mIBJBCEJ2TellLMGG3X4QEqsuXd6xaue8dWacjaABUdY1SirqpxYO1B/hJirdrryvVVdfD0/ra/hpA3fdK19ZtZ/PS/aegt1oQhq0M+fe1odw71zGLUazXK/G07wHEIl2n7nqJEjN4YdZ2azp4j25TmLFWeOTfYjfbjRDd/j2IpVrsbT06fKMj2GU2WQEo1bPfuz29C2MTeydRCSsjDN6X1i0vk0a6ddP3Psk+NCL112A8oG5qmqoWC4AQhU0cQWXJYsVkDNQAYw2d73O3zozRtK0Te7cYe1b1YDCQkPS2paoqnHM0TU0Igdxm11QAqY+LgeAk6Mt7LxYVeU4IntYhX+sDVbXDZhbnSoqyhOgS4Sk9Y9csU9L8pq/tlLGpx9jb13S+z1priqLo+0rnXOrLNQZDXuRkJku14Z4QEoJY2tnCAhZFndbg/v19+uM3HKQVOVFC5sDLw93GFqMNeSYHsPOx3/1iouRrFRggAxOTZex8g/Fxb1ivA8HHfjIih25q4BCpstDEpRiJiG+EzUw/+eua7tQppc0fkUdFkqx2fwiFKNIctKEeDnhRV3z3n37E7//ev6Qcanbrmlg7Htx5wPfe/b6EQFkjE9QoQKQPMm3SRtEZf8Uofj8qBpRN/preE/vJzssfMUYCAe8dJst76Ud3OHYb4acPHqVI4GhXwEUwwkYMBp5fnfevs/vowV+VCvA0TVBpwmuzHJUZWueJBvLJAGsNu/mKaimm2kFLwRWMks0xFYXde+lA1G6c1DFr5fNkshXTvSFGbLp03li80lw18I3vvcujx2f86dd/h1fun1JmGW3dpp8nD62Le4ZVX0h0aydd5xAjXsn1xzVkaCazMb/15Xe4dXqbs+fP+OjhY+rdhsGgwLkWOyy4cXKLG6d3KAYjVus1Vb0k6ow3P/MWRwdTPvzgZyyuXmBUROcF9S7QNjVexX7SI49JSJMZz3a3RSkoVMZkOkEbxXqzoSgiw+GIz7z1BqsfvktVeZbrLTaT61iWJaMi58ZsjB+VzKaDPpnT2IzhcIjKMlarTSrundRmiPQkIkWF1hqbZdy8eUzwns1ux9HhjPFozKOnTwlIvkvjWz55/oym3vHK7Tvo0BLx+NCANpiswGtLSwAdWayWTGeHaJ0TAGvVfhKfik2bnvMu9XGxXPHixVUqlg09G4prYA0C8or3n/ieEUUeqKPsFVqBq50k24bYy1K6or37XkVZ4psddphjhxlVaCCmVGUf+iHH1XrJf/yHb9LGQEgKAe/axHBRBC9BUpLIKl9XFgW77ZY8Ge17L1PToiyZzWYs5guaVkLGYipeYwRjMwk2MZaocpnEBvAK1srT4Fm/uGT9/BydSxpq9IE2MdOyPJOCWwdGswmTwzHRKpw8IBwcH7KrGuqqklT3gWY0mfDk6Se0wZNpKZyaxA7pJiqRgNFZv1/I0Eg8CW8/uIlvHcvlkttHM5588gm3b99lt6t4/bXXePjhByyXc8q8EAZ0N0VWYssBUmhIIq5CAmf2hYNSiqZpqOua9Xrd7SLsGSd7xnQPfEu5z2I+Jy8KsceIEoawrXcURcloMGa1WvUT3/15FrpN+KWCviuIXStNiBqWFAcjaSB9oFWaq6AxbSBoxyEGFVqsc5jaCYjsd1ycfcTx7RO+8J99nYsXT8ibOXE1p9WWB6envP/RgkbvePj+j/jtP/4veeu1z/HBez+kWm052y5pY2A2PWAyGLBbLtlsNjQxcnJ6yp3JAfV6weXVFavWc/f2CTdHQ5aLJc9XS66alls3Trg5HjNfXHGxXoHS3JjOmBYFLx4/w5uMVsH9k1NeOTni6Sef8PF8QVOWvHr3HqeDgmdPH/PhfMFGaU4PTzi5ccyj+TlPqlqYp32TIQV0CPsiSBFRKRjn+tnVnW/Xz+PrH1KIXbsf1wBcrv259xrsmrBPWVlonYZFqQXo2TlKs9pse3mTSHcVKoqU1RotwyEXGNuCt27dx6iSkSop7Yx3bn2O0fiAb/3yO/xy8x5NNHglEveoAygHSs7uTBt8I7WDJDBHopPwoYjUDiGSgp7y1ETJgNfaDGUCbbTEFnTUzF+84OFP3uWdz3+OwzJnYA2ruqJtW86fP+U73/grvv+db/LFd97hp+/9jNVmi/vq7/K//2//B/dfeUDIlvz7//G/549+//d490ffZ71e8vqbr/K//Pt/x5tvfp5N65gd3+C/+vP/msFgxDf++v9hs97yb/7tn2NNzk9+/GO0LfjM25/hww9/waAsCC7w/NkzirzgtQev44Pn2dkzMlNw4/SY3W6HtTnT2YzoI5fzK6aTEUbnQODskw/J1Za2WuPrlvGoZDIekOU5OtPYTAAg29VT6Wz1raOpmyTzjZJEHDzGkKSKPllOkcIpkk0VkXIwJS+GLJYLfNhgUxCtMoYQczwDDk9eYXp4j6hyjFas11c8+eVzzi8XzNcVOi9YrVf4xpHlhQwPW89u3SSFgzT/uECzbdhsalovA+c7927zx//yT7n7yn3Gs0OePX9KXg4YTSb41tE2W+bzS977p5/w6OPnuDZwcS7+8uPDIUenN3j1lVO+9LkHTA6mXF4umS8W5Dr59PkgwZHaEPHUO4e1U46PR6zXa46ODxkOhmx2FU3tyYssgVgKZcTqx8SIixVtmwaE1nJyW9E0OxbzHU0FBzcyjg9L5pcwLIfkpoQg67cshkzGU54tzhiUijgKrGuHxVK0WtQwymK9SCWDltC2QPJ+RJGbjAA0TWLna810MCG0HotFB1DaUBjFg7v3MXnBKBugsRgfKRpRbo1HpxQHU0w25tX7r3F8clMsCZDm1JqS9aZmvapwbUNVO27fvSU9TYy0rdho7aqK6WCAVcJiisExsAarrKiYBiXWiC1HB5Rsthu89wwGA/HF05pqW1HXNaGNDIoBJpNgtGCSB2o64TpApgcx0iBJJUXSyz1Fp1JLLFrf8IOzM57FgM8Uw8kIVQxoU3hr3TQoqxkdnbC+uqS6mmOynNH0QILBPFg8KjTJg7MVgMR7QmxQyuBdI000Un9FH3uZdIxafpFyQoxIuMUKTsCG8eEhr3/+sxxeXfD0p+9RuZZaiVVDJxkXbRw9e7P7sMaiUyBoG/ee5qazRKHzutwDdfQ1gxBMgtKAJsszok2y67bBO+l1tQkCyIYIiVXrYiv5JNbgGmEPdt76ck69POy+drL1QNT10KCOOdoBagJOieRe6X1fKbWYQkcj/afzfe/bBeh0oF8HYqZ2r89T6PJKVOoBvXd97dWd5V3904O1iXGntKYwZg/8pv4r1xa07gNiuxoqEojJctAkVqUNhrYJ2MzgKr9nEX7qWsU0nOh6up7hGfbX9aVb+qmPXzf87e5Bd3f6OkWBElPjnqnuWs/arfsshM7LUtmX+/HO7uH6z3XO4RsJKu5yQ7Isk+fWZsnfFsq8ECDYtX2N1Hm/mo6RDCLHT711TwpJ6yj4gMP1+AZRGIzBC6YS6eweu35I0zatkOvS6w3RS37K9XuudApWFB/xDuBXKvTPVHcNO+uE6yS47veQ8ntCwjKMERC6A9mEyOGFoRuCsI+1Jk9SddfKYEh+vk/rKq3d4KXmt4bdrmLbNGwbYQSbzGAzs+8vUzhcF9ymtdR4Rptk4yh4jgue3OyZojIs4RrZLPbvpXsOjDG4RoDYLqSLJNmPIfQM/hC8BH0jisgucE+FPSalO3Cfzne3s6nQ+OD2A/9EKinzAh2F0ZrlWc82dt6jTew/32iNNQqS4sInpjRGJYKaANBZsvYQsFgzm80IIWC3G9qm7dnbxppUX6dReBQfeHTKrEB8zuWeRXz0tG2LccmS49rzF0JMOIm8L2NMUnBJz93lv3jvcM73AwytFc41onAI+9Biawx5lvd7GomkmWclSqve/kFpCEHUc3mWMxpklLmnaX697zX8xoO0EqrTtDXDMJKgpQBRRWxhUVrMeknJ4sG1hNiya3fsQsvGt8SqRk0HspAwaDIiHmN1CiXzKJMmk7rzZpFwCKstJnmX+LSA8FGmnwo6Jo9CwCiZatE3aaRJvEwmZSLkYyDDMCpGYEd8dPaCD558wmcnN6m3Cxbzc05ObjGbnfBi8VRs1rWMYVs8Ay1yPpVYQmKpgCywmF5bAgqJYoys6OaI7KeIxMQ2TEWFMenBlOsOoNS1iVz6fkpLWDlIqJeOgRBFggIprMQItU3RTfWkVIgk2j/In5TCZJnIdkIUar+OqEHBbDxmsNmwObtCeVDBE3xL5ycTfEp91OwLD0Uao3ZyA1kTNoFURPm5Ln2hVonVpiON87z/+BMu/s//my997nW+9uUvcHIwJbZOvOYU2CgBdaR3YJK1RuikO2mCV1qLCy2udbg2EtOBcOvOTY6Ojlmvay4uN6gQuHX7Dm+9+QCbGbyruTrb0roam1s0nqODAQ9evcV4qPjgA2EA1LuGotQEcraVo2mFBTEelpQDy2Kxpm4axqMhWVkymkwTcCFBYuVgwmK5RZmM0+Mjnjx5gXOGzbalKDTjUQG+xbuGQZmjcLRWU1UNdSUsokxrCqtxeKyRzck7R13VWGPJhmLu3uxqKANlmYl3UIgcjAvs7WOenl1Q1xWbDdw5PSEMRgwnU0ZWM18u8TFSt548H2K1NEer9ZaqckyPT+RQQSwwjBb2UIghJUeLhFMbTdCKx0/PWW3r5NeTihOfCmcfQUlBlhlpHF0QWY3NCknXVfIceefRaAbFkO12S3AOZRTRC0O9B5GMohgUHN2+xemr9/jFxw/7QEGRQIBRwoIOQG4N4+GY84tzdDqM6raRZyTPKIyliY3IlJJ5v9E6JUxGirLk+PiYy4sLMeePkRiTZ1KzQauM4Y0ZthwTs1wOWiyBgFEVPrbsmorLD5/g5ltpmqMkNgcig8mIoxs3mC8W2FHBYDYGqySJWWkybXnz1TdwzvP+B7/AFob1esNgPAJS4FpSIvhUVJjEAB0ORhhjqKpdKmA6M3/P5fycq4sLxuMRWQX4lvVqTp4VPPnoIVaJj2DdNr2/b+xkYUkCU2SW0WDMfLOUQsY7VIQyy2mcx/tIXbX94a2NShPe9KSrrrFIISwIqNB6h9sJI1qh0CTA3Ad2u+raACmmvVF1be8eMGS/f8RkS2PzTBqa6YyyatmeX2G0YeUDBk/uYZxBozw7J1K+gS3RXhO2keePHvH6l7/GF//gX/Gjv/xfGbkd88Ulp3fvM5wcopuKul3zk+//A29+/kucnT3h8dMPUApOZ4fkmaXarFlvtjilOJodcjqc0O7mXMyXLOuW26fHHI4GbLcrHl9esvGRV26fcmsm4YHPFgtapbl7esp0MOD8+TPWXp6LV2/f5vbBAU8eP+TRfIkeT/niG2/y5q07/PgH3+Xh+Rl+MOKVo2MeHB2y3q1RdUXuPU1qzlBAluHaVmwfdJcSq3o2AUYCD6Tgvj5s3DcGXUP1aVbU9YYrwkvM6JDuazek69qHl32NZSBplbDBQxBrAW015ahMjB8FSJq3VZpMGwFtFTSNx8eKKjjqxZbNdMtM3aBZ1OJHp5o+AEssgMQ7GyIqvTbjPVpDbBtoarKikOlkWndKZSIZjRL8E5UmL0e0TaBqd0yGIz782S/4/jf+lqOt5/DigvWHP8EYy9VuzfzykuXVnLNPPuLg9ISv/9l/wfPzBW0MLFdLtts1Hsd2sWV5fklupPksJ0fcfeUt1j/7Obfvvc7o8Ab/87/7HxiPSv7wD/8F3/vmN7BZgfrzvyB4ePjLn3FwdAPeeo33fvAD6rrm6ZNHvPWZ16kaz/mzT1jMFynAsGV+dc7hZMblcs2//vO/wGjNX/3lf+AP//APuHXzLr6t2K4v0NqxWuxQyjAaTVE2Y7necDoq0VrjfCvs5CyHmBg7TopvHxzeNyk41uNS04NStKELXZJzJaDI8xEazWL+HO8bCZ9MQW2NjwwGp7z6+teYHH+G4eSY+eUF7333u3z/777BkyfnrGpDXUyoRlM2bUvwkbIsxWe0dtTrHbvzFfV6h1EBqzS+kbNBWVGIqR98zOOzFf/tf/ffUI5LgqspMwkE3baRn/7gXb79jb/hZz9/xEfPWpoID9464nd+5y2++vXf4u03HjAdFuyWC1588kIAT5986jpQy0WiEo/vcjBjPJ6x2y4Zn9wmNEuuXpzhK5eCX0Qy71wA7Qh4Ye2E2ANFIQhIVWSaaCKt2zG/chxMA9NxjrEZNtM02wVFMSCgMGVJPiyJ7Y5y9P9R9yZNkmXXnd/vDm9w9/CYMyLnqqwqFFBEFUCMJEhwXHS3tUxkm8nUklb6QPoCMq200kZbqdtaaLV1N0eAIAiAQKHmMYeIyJh8fNMdtDj3PY8sgHsqYGWJzIjw8Hjv3XvP+Z//kLGq1iycQ/uSMpRyvitJUtdA1KCSvVPUJrGyFIvVnLatmZYTMmUhH6NtThccGjkbM52jERlwpjUEhdOSuaBVho4WMyrYv3WAWWQsFguyZF1lTM54MqYsMmyWsZgvCdGAsmSmRHmH0oHx1j5TPSGPRkgoCpwCpyIZwtCs24q2rTFTAVO7uhE7oP19tnemRBUlRFUFWt+hOk2hMpTK8EYCpjQbAE9pCI4BcNMhEpwjdA25iqn3kn4iGnBaca00Pz054dNqTbQZQQWm2/uMyy0q16EzxWQ8lp4rzzCPvsTj5n0OHz6g2D/AE4mhxWuRsQcjrCRjtKilQiCGLlk+RVyo0W3AqpzoJFBY6SBhvlrz5lu/xc6oJA8RFQO5VUzzjJ3tKZ/+8pd0bUcW4fU3vsbfffQ+jUokngjRdYReKSmopCTCe9mffZD7oHV/VkAfytbDFH2mwibEUqMTW70nkXijsKUm2gxd1UDqp3wDSB6HNhqDluY+9JJwNsSX2A+PRWWkkoJAzjcEtFRbq4tQAAAgAElEQVSRmMBStIDYKgzwEzH61NMxDPdvnndKG1wfNqeTiksZ+b4e6EtMZ5V+vx4wjFolBqb019YmL0o8ARBrSUPUuj+esNoSUjBQHxTas2dVCNg823i2KgGaetWctYX0lCrgXUCrSHIzlAXv1SAVHw7v9Gm+oCjtfYXhRbXcFz9u/tuvfz68UH+QegTvHZiSqDRBBXzXoZVNX7Lx293c502t0jaN1BBaFKXDkFkpRmVJbwPZs8qLTBjHNuU1mMRAludED36wPZNQKVEMDGB6/8yhhkClzGqCk0FWnxHg0v5ktGI0KpNM3VKW5YukhNhL+j1t2wAyKBK2pR2sGqSm2oTr3VRs9vXeAG6mayOvG3CuS8xOi1JQFOWgHtz87HZQ12klz2lZbqyunPPUdU3XtnIdk+xeG81oVNJ1jrpp8c6JR6zNGRUFVhvGoxFt23I9nw/fT4Q8z8TbOfWCzguw3LQ1WssgRmslAXlovBOQumnrRPqQYPXciMWnl0WK6zqqtiEiqqJRHMk9TXYNvTossxk6CihujME5ed3GddhM2Lc9s7rv/4S9G2jbltFolMiCsldpdMKfxKIKIjrhObEHgZUSi4R+30mKy95qIUbFYrEiyzJiwlaszohWNjcfA6HrhL2qNToF1BujMZYEgMu5UeSWPPc0TZ3UN7IGOueG96KMxtgEkicMLURRwNpMrrlzYgvSdB1dsgfJiwKSittHua5iXiuBY8KuTThEEP/Z4EOy4kzrUUmoWd2tBMNSGp39/9WTFjBeoaOWjReF9k4e4GAJw6ROwnO862iD4yo0PPeNpDx2DtN6goaodZKk9/YD/WGWdCxsQMqeReV8EElFkIVi+l7oBnuuD7sBkrQiDj6RAg77zXQtTap9lBt3sVrzD7/8KbfvPCS3VpgAmebW4SEns8fD1FLDAEaFGLGCfCYpyWYSlTpUWVw3xqs6/X+tNnIU+X0NMboXvDXlYNL9OhomECFGLPHG18h76z1h+glXzzxSJIP22GOnUhzEJDELUeQbspnaZNYtiaBoxXRvB9956vkC1YlfqBh0S9ECqdFJ0/xB/nrDDP+FgJgEoPf0/h5ACURJxdWKy6rlr376Sx6fnfG9r7/JG6++Sp4XhLaRMIwUnDZIYHu/4PRM5XkByMRdoWnrDk9gvlhQ5IHp1jbf+M43OLh1TFO3jEaWre1d8izj2ekZzy8u2dmfJnmFQxnLcl2hbc69+y8xKic8ffqMpvXkpaF2AXybmiLxoZ3NHJPpiOPjI4xUj4Ta4wnUQUL1ytF48JbJrKVu5SD0TtPWHnzg/OKK28cH9EEExlp81VDX9Q15r2i/e3ALFWnaNV0bmYy38CEym1WsqwZrDev1ksvzyJ27t4lKcXYxo2k7tM24fXSXIresr68IJpMpWlYy2d5FZyU+ehbL54wnW3K9Y5CfST9xTYyKmCxBxIOEuu54+ux06DgEJBUpmdz/MNxDSYHueXCysQ9TfCVMW4NhvV7jOpcK8GQf4r1I47TBRY8eFVTK8+TijGj6gYqAwbs7u6zWKwk00ErsLg4OOL84H9jy/WjDKE1Zjnj00ss8ffqM+fyaoiiGybfvOtqu4+nJSdovIr0kzhgNOid6w+50l61yIunBaf/yrUMRUBZ87Vgs1+T7O0Sr0cgQw1jD1vYUFwO7d27Rhg4XhQ2kEiDqvee9D95nNB6LxYFR3Llzl88+e5xsIiyKMBQK0uCIFLzzTq6zlmasP8SCg/OrJCVWkXVdEZWwwRVraShROOR+j/KcUVGyWK8BRZfSfE2uWK5XdM7J3jIMc3q/LVkjxhq6rhE/uLSX+ZDCKftCNX1zD96RCrs8zwfT/BC8+GknmV36snSu9J5PIQ2Oovgktm1SgCiq1VqmxkZT7ExZXs3wSQK27loWOiPaEYSACw2N85gmMNKajMD85DOevjfhztEhn+zfYnn2KaGtmM+uuHt8h88+/5zFesn66QfcfemIV157wMX1KYWRhNP1cs6ybmkU3Nrb5Xi6Q2w7LuYrFk3L4d4ut6bb1Ks1J9czahd45e5dDnYmrJYLnpw/p4rw4M4x+8WI8/NzrqqaBjje2WGaZXzy/sesVEvMLK8/vMe9vQlv//wnfHR2ThiNuXOwx92dEddnJ3w2WzHLDJPxiMwp6hhw/XBRDjdZByE1kUoYB3JE6o2EM63hfv/+TWDtFxusfl+/yZDhBqul/3uvQLlpmxBCIOo0w49IEF56LS/V7dAUy1qzApjGFpsBXmPR7OwdsbOzx+z6OduTEfqy994SkVv/ew3AsopEvQEJfNNKOA1pKK1FKhmIwtrW/YKAtq6ZTqfYUcFH73/IL37xNt/+1ndZ/uivGZ2ecv33f8Mvfv4z1jsHvPxbX+crX/s67777K55dnPPBp5/yyeefc8sFXr3/CNd1/PCv/5p60eCrlszkBKfI7QgdM156+Cpf++1vsXd4h6eff8Z//Hf/no/efpt//PFP+N4f/4k0oCHSNBXWaHCeZl2zs7NDd3DI6cmJWBNMx5ydPubhw4dE13Dy2Wd867/5N1z+9Cf87X/5AV/92m9zcfFcAkmVp6kWNKsZWVvjWkdmIC9zfA8K9GC7SqFLscMHT9e1eN/hQ4fzjaQhOz/kFFhriUEamTzrw1YtRTEW5s16SfCNvA+s1FjGUI53ePDgDXYOXqalIDRrHr/zK372F39Ju5ixOypR0TInx8cJo1FBoxROW4IyqAx2dizT/Ybnjx+zujqh9Q5TyBmnjDDhXOv5+bsf84t3f8Hr/op6veLg8A47W9s8/eBTfvB//4DHz07ovCIfW974rYf8+X/3h7z55uvc2h1Tr5acPnnKcraEaJKVjB9suZTSQw0QA8nnGLQpyPIpy/WSLBtTmEjbNjjf0bWO1boiyxU2F++8PgSXSApM0mJtoWEyHROcgAlZruh8Lb7BBJxvZThajBlPdlleVIzLHFNW1OuKUlsygKClPtOK6JLkWClpjo2icx1aZazXK5arJaXJMRaK3AqTNMiw1qeaMreWLLGUpJF16FzCTYxWlKOCUk347NljZrMZeZahlWJ+fcXFxTllWbC7u4+1OV96/XViDCyuF4Q2smVHTPMpU5VhvSSyO+9QTvzinRHFiAKRl0afCBBSG0UlIIoLHoVhPJqgQk2m86F3EjZQv+OpDUMuHVw3gaKQ/AaNEoaU1+BspDWaj+YzfnZ9xaVVNAaiNZjSsKqWuCg1uwspGCd49HjMwcsvMT3cw+uIc7WQNW4AF9E78lzsvIwCk8ugNIRAF9Izonr2E4j6x5NZy9HuIVtG08wXuKjIkeDJxeUFzz57SvSRw8NbjLd2UOMtqnZOZi2uaROgpzcemVonIFgYWCqFFd+U4RojXoO90rK3uFMoCKJc6BmrAjpKw650CjstCsBLT6F9AukF2DDGonJF1zapx0hhOQGxhktdoARfbyx5blo2CVnohsIk9W79177wDKib56D6wnkpQK8EIKb+L2UGDHWrSr1ZZpKyNAUx92dVqoMiAujFxBpUMfVlUcCkkAgJqKRENUZA236fjr2NoKHrQqpJk00EAiQHJ+9PazNI2bV68Zzvf/+bdcAXGbH/FEB782v6j2Fgu1lGL7ye9yH5qSdApxOWnckkB6TvTfv7BBu7vZv+6OWopMgLsefJc2EXa71hvHpPSNhEjCIP7706+7qmD48T5vqmv40h0iGZC31NY43BZhZlk7d9ZsiMoUjYSi8HV4C1KSgs9eF9vkav/ut/p6bZ2J/1OETXn8VA8OKnG1FDTkRMRI7+vfZM2ZuDeFItlhlF17a0CfwTj1/prfLkc91bxA1K5fRa2miKshiUuz4pIfCyJvMsT/6j9cZGDSU2AM6Tm4zp1taL1hTJglJZzbgYg4Kmbsi7YrBkyrIsKXkyiGK/ua7WtOJ3JApOpQSbSHhP27TkXYELMrzPjKEYjZJVW6Rr2zRQBdd22MGCIAGErcZ5J4rEdB3NDbvHGASvqapKLBwSc9eavt4WD36lFFalIPvkc97f15h+PonQ4r3D2izZWQQZ3IQO79uE50R8iIN94eCdrHqAPq1NYzCmZ1YLtlfkZXoe/fD+Ex88AcsWpYR1raKsFx8iNjeo5Lec5QV5KYzofgiitfTG/TPStK2sYeWHzJUIydIjPS/qJulH6qambvCB5Euc/cZ9Bf6Zg7QxBlpXoaP4V5oetNBK2CFB46P8kgqZlrZNzdV6wTK0OMB2AdN6KA1tunlA8gnTWJXh6ATEDZv0uI1vjnrB3LpH/6VJl6JpkCIgB0QIUQDFyHBIDtOoEJMNgRxQjQ28+8mv+OPqDzjcvs3tw2Pc9XNevveA9z78GSoG4rCQBBjo6ddap4MDmQzqXuIpVy9NSvs5gkrNpVg3DBMOZJLRLwBjhPEroQAmyfiFlShgaAKc++a2f63UUHm/SVlUWqV7IyBK8BvZgjB5dGquw8AEds4JuNl1tK6Gcc7W+Bb11YxuVZFZQ2jd0CgTbzCe+gNHmeGw7q89bA7Jm9PBmIBbkPfqtKINig+eXfH07C956+MT/uR3vs3udonyER/NkMDoh8Zf07UNJycn3L9/fwg/MTbH5grvWsbTKZktaEKLzjW//Z1vspyveO/dX/LO++/w1Te/igdWbctUZRBadnd2KMdbNG1H0zq2tvdR2nB6doGPqwQIikQ1zwratmHRNZTlmLv37lAWOa5ztG0rE+wyp209TdMRWSXPP8Xh4R5tJ4OJk2cnxGjwzmOtoW466maNF9z2xnUTNpm8th42I3nmrRTKeU6mNLOzFc4FdnenRCdgbQyerfGY+XLNxWXF46fPxIKjbbHGsL23h6LBFiXK5ESlqZuWqg2YPKd3Xe3vaW9DQjoYIoBRuBD5/MkZs8WKSL9G+u+TotLYNFxIrIj+QNZGDymRRlkBdo0ZDO+1Fv8/rUTGIumbEl6EUthxiU++fgO4l+Q71poXGAir5ZLVYjkUTUOxgVhnVHXF+fPn4KXwPD46ZraYU7WNsF4V8nrDc54OM2PJbUG9ChzvHVPoguiE4aetIXQGozOU1YRGijS9W4AxWGUobMZ0OqEoCi6uLulwKCt+w/0kUWtF4x2Xixl2vUQpTVVVzGaLtG/pZMmRCsuypG1burCxVrnpKRVCQJnk5ekc2mTMluu0liFxfkBtPHJLY3np9j1ef/QqP/rxj2lioA0tq3otfrj04W7dUOjNF3OyFIbggzR2qiw3k/4QIIhdikio1LDf93KrvvDqi7B+vzE3QLzhTxjui9zZyPZ0m5cePODDjz5itVpBmmL3PnB6VDA+3GV9ckGIYuOxxHNarbEqw2YQlJLwItOiraFdV3z+zk9p1y/z5te/zU/+dkm1uKBeLbi1e8ArL73Ce598BN2SJ2//hNe/9Sd8+Y2M9371Y7qmYlHXeBSH+/vcnu4Q6pqT2YxlU/Pa/Xvc2dlmNrvmdDFn0XY8unubvXHB7GrG5+eXrHzglft3ORiPOT855WKxoIlw9+iQ4909Pnn8mHm9Yjwac/dwh1HV8PaP/4FP59d0ec4rx0c8mJTMT5/zZLFmqS3H29s8PD7ig9NznrRrfFDEToLkopI03V76Cels6wdJyNlA2JzpL9yXeLOJkvvSf13P9v4iE/dmA9a/znD/6ROEEzvDWowxNFU1MBvk/cb+ScZqQ65lsKdNRtU0mKjYHk+wSmEKxf7xHp+1iX0RNux+pRiKRq2ksM7zTPZopaHriM7RJkaIUTYBM7KLapWYG1phy4JRlvGrd97ml794m+997/fZr+b89X/5Adu+wz/5HDrPy3/8L3hw7wFtOWayd5eH0yNef+1N7h7/kLe+/i3+4A//lOnuLaq65ZV7R7z08Et8+atvMp4e8rOf/gPztefg8A4mK/G+ZW+6Ragdro7sbG8zGpUyeEUznu7zwXsf0lQtn33yKX/wR3/Eer3GbI355OMP0Tqjaz1aWWJoODi+zf3XvsTW/h7/5//xv/PLX7xN4wXM0gRW8+c0yysUNUVuKAuDNYGiyNgyOaofTKc07KpppHkNMWXYSvMb05BQKzuwf+q6St60BpSElnRNQ7WuCb7G2IDVWarDFOOtPbZ3bzNfLDl5/jNG27fAtfz8R3+BWy4YZxmdMcS6IjQdq1XD5Og+5IU0nYgnedCKYrrF7UcvMd+fsF7MaZcLXF2D9xRaYTPNcl3z83/8OQ/u5xgCMS54/vxT/ur//U88+/yEUGoO7+zwr777Db7//W9ysLvFernk5OqC1XJBcB6tbZIdahRG2FNI8nvP4DK2BxkieV5wcHif2LXUPkL0FJMRIQTq2mEyAWmNSeonLyCE9zI4JgSUFTaUtsJicdFTFB7fLImxRukCHxohMpic8XibanGFi46YO5qioWoKRmhogyhQhv1BVn2eGdCRzrfkxrC3syNDAKQJtbmo93RMDKS6BhTTcoLOMhrlabyw/UojOQsRhc0s+9N9XnIvc352nsIPFTvbE7SJzGdznjz5nFu3bhOAp89OuDi9AKe58oZXD++zNy4QjpPsLT56TCZhPlbpYeAigUtit6SNQVtD07WsVhUERWYz8kxABu89WWJO9R7sYtFxI1wz7WNqsOzZ9DooI0IAEzmtK3588ZxPIqwTAERhaZSjWl0RgiHTopozRic1omFyuE+witDVRA86QBsaAbAUqOCoV5UEmPbDAIQRGH3P7ovE4MEz5HW0bccPf/R3vP7wAQfTbUw0ZESy7R0mx0fobAZd4MnlOc/qlk/Wa9ZlxsRadIjEppXzVxl5H+ksUEoRQIB886KVW2hD6ntEvt6n0Ys83QxDXCCBMYhqKtWLJu/7Bss6zMVDsutQxKSW80PdozCAMHe1kcGBNSoBLDcsAFKtMqhMbpx50JN0emD1hr2d0i++1x5gRISSPeEn9uduYvSYxBMKiXFMelYH0CuB1ioBxDbLMEpsX4JSKcg6JDuZRJdI11hrCcCS8D5h8Fub+jH6IUWQwCUrJA0B3SSxve/PUZsz/GY/03/czFC56UH/TwG0XwRkYWN91Ne2/Wv09YL34k8ZYiB6YXJaYwd7AVTvfa2GZ74H1AawPEZA41wg11bYeun3t4looKIiZBuMIqQhYt20cp2GPiPZfPT+r+rG9/TDiB7ElplDCrdTFEUpAXRR1mP/bAffDddWgLdNEC/wgry/B25v4i294k4lwoxPALvJ5Dp1N8DETXCsGdZq/+/GaFzwuKoawtKsUQOwO2RDaIPrBys3QPeNIq7/OSQf3AabZWht0rXowV9ZYFVVCSCcMkoSX20zIImRpq4Ta9SQFXZQCQzX2YndjlaK6WSKLxx1Ip/0OTiiCNaMypI8z+iC9IsasX5zUcK5svFYrm/X0Zha9ok07MjznB2tadt26G9d54Z7I7Y5hroWyxwX/MbHmhRCqST4rHUdTdPQOYexZrDli1GyU7rOiQLOWkCsALrOpCF3ZF1VtE0rayGB6E3TpGwWGeB0QchYxsj6z6zsYf2AIMYo5CE2di7WCmDsEpELJcNW0l7T55f0vb3NMhQa472Awv1wIVm3ZCnEbxjexM2z2K/P/j5CbyEh9z3PBXSu6gYfIl3X/sa9Bf6Zg7QhBmpfgfLkWqFDQGNE1pwmrT5KaJgiYoCYJkchxCF1kCgHhZBI48bo3IhcQyVr5N7npX+gtFaIYX1IzVoUAFCJPkqYtSYtcJHGbIy8Nx53KtGjoZ/Q9RIK8dS4ml9wfXXG7b0jtrcmHFvFw9svcTDZZdbMxJRZ68TQEnCpf12VQMZw8/xIxdVwKKQEu97PQ8VkX0AU64QBaE4G6z1BKIQkIU8eOlKBIP3uxhNWDvgbHjkJPPM9oJ4OS5mUbgBena6pTg86oQeZZCPEgMos2liKvSnZKCe0jma2wCQDZgFRkkeL9ym0TADjLzbkNw/km0WHTq1y78ejtaEDrtvAD99+n2enp/zeN7/KN37ry1id07SNeKh4jwSZSIjR7u4uxBs/WycpktZkeY4xGb5tCDEwmU6Z7u1DFrm+OuN6OePi+pKiKIg+kGWayXhMbjO8a1kvV7StANg7u4csVy2z+RIfpDmyNme9rqmqiuPjOxBgvVwBmrptUJmiNIYuBJarlrwLWBvwoWUy2uLenQO2tsas51c8P1/QOs+qsixXDVppmrahrlvG5ejGcywbodYZIl0MjEeFbLpRvDnlYNUC/hnNzs4B+I5qVeN8xESYFCXz2TWzizNym3FwdEw+nWKynKwoMNbS+cByVdF6IMnO+zWAMuR5wWq1HIoZYYIHGhd4cnJOCElmlZ4NKaIUmZUGzAc/FEcxJPAnJmuNYclJydBLckT2Ls9/m2RdWZmTlQX5pCQrc1yUg3JYHUqKjudnJ9gsJ88lSds5h3d+Y0uSitjekL+ua06Xq+Fzl9dXrKvqhaKHHlTynhDlwPO+o2o942KP/d09YTUET1WtycoCJyZ9KO+hc3KeGCli8A6UpmkrVmuxn4hKMy5KlNGs50uKPOf41iGfPXmCsXLY51nGYrHk6uryRZ+lEMkyk/xhZS/r12Ge5zKNVjIcUoh0lihhJTKMcmglBcd0usVitaSqa7a2JriqpbCWaj6nWa+JZU6MQZgxqdGPgvqIJFDLge5cNxTvfdPe79uj0RhrM5bLJW3b79t2APTyPE9KAPcFdv6LrIkXm6PNRi0Facfjx59TV7Xs2VqlJGXQSUq6tb+LW9W4xZoArGPgKnpGQQnTLCqM8uiuxSKsKh0bXDVn++49vvqN3+NHf/EfcJ3n/PkpDx484u7REc9OPsNdX7O8WPKNb3+fD9/7OfX6Cq0Nuzvb7JVjmvmC2XLO0nXcv3XInZ0d1tdXnF5dctU0PDy6xcH2hOvrOZ+dXbLsHA/v3+V4e4frs+c8m89ZhcDtW4ccTLY4OznhbL0gZoZXDm8xVYqnHz/mygVao3l0+4hXDra5+OwJp9dLmrLgaHebR7tTFufPWS/nKKvIsNhosEWBJ1K3TfJq3wwhVRQWRlAI8ylumE9fZL7I319s1sqyZHd3l7Ozs2H42X9+OP/YsBpimrz2Esmb/uUxhGRVIs9KEiP280EMmlxJ0RpVho+aIisorOVyfsHf/uSHPJjeJhZxUJv036vS86uQ0MPCWGyUnz8uSoK2VD6mtNmADhtGv/Me3bbYIkcrQ24MTz//mLd/+iO++c3vsDUpeefv/xLdtbx+cIfTp5/y1nQXXbdcfvgh9t5LvPaVN1HacnR4iz//N/+WL7/1Fnu3Dnkjavb2D5iUU1zUdDGye3SHN77+DUIIlGXJbH7Jf/h//h3/+JMf89/++b/lra99h//tf/1fyEcjpDAxfPs73+fxpx/QrJdkec7WdJtXX5twdvqU3/v+n/Laa1/i9PQ5n3/+OcVowlvf/R3seMInP/sZ+4e3OT66y0efPUalpGXfNXRNRfRrJtMMY4UdNt4aC0tJJ9Aq1VVd24psNg3lQlCoaLBWoY0AQrDxAjTGEJRlPNqhqZYEXwMObVJjpSIxOowpKPMR3jUE79iZTlF2zrvvfsj1xTNGNnmA+kAILWObYa6vyNYTjnZf4nnViSWDyQQM0go9HrO79YBp2+LWa7r5kuXVNc1yTghtqs0844khNFBX11yeXPDxp+8zmmZ897tv8r0/+C77u1sQWlYXV9SLhiapT7TSONcBDpvlWGPxQc7JmM62YV2kZrT1DpRhd/+Qs2ohdgyZPK+TLfErbNu1AG3Imo1ELIGmbYZhQl9z+ORRaq1mmnUQV2LdExw+IQjWlhTlhNAt8DoSbKSyHUtXs1WWwvBRyfc9gUbGKgKeVbXClHZg9bZ1OzD6jNJYk5Npi7JiWyR5BZ7WBqI15BhyneE9dDHQNDWV85ydnNDUDUYbMpOxtb3LfWOYza6w1vLKK69hsoJHo1d4+OBlLs6vuHx6QaMc6+DIgvQrVVdL6GpuU5BYoO3EgzoQJXjFe7IiJ7MZXddRVzVd3bK3s4fRiqquub6ecXR8JJJkpcVuLPkyCoiQwCW9Cb8ZmIqZFdswbahU4J2raz5uW5pchhwqBrLRiE5pXNeh8MTUEAuzSGrumgAe6aGighhwfaYHoBFJckT21h7oM9qmYYEwrdq2QnFD9QA0rqXBE3RSKhiLyyZc6oLs4Bau86yN5uz8ObPC0GSWUudCaNCeoJMd2lD+CWDVByZ3vZw6gYc9CKW1JmgJbhtscW74d+rU8Ks0TFSoxOYShzyTa0ze4JuIyiB68aMNXhi8/bMofryJCabkghmzkcv359QXa44v9kE36xPRUL5Yv5Dea9/XDcQbJfVy35fq1BtqrXFR+iLn3QB6aWNISGJab0ZUbPRkHxmCb8gG8rWDXDrGwYdU1q5kR2gtNaX8uwzVtdK03sm7NgarFS7vcEqRkIHfWAPcBFVvnt9frN2+2E/e/PwXP/fFn5MeA8Q/WdS7xmYYq3HBiZeJunkPEiM1AUdZYs73AGPXdUJ66OQcEvDKDkBR4AYLemjuNySVrm2x1lCUyZM9DUP695BpLYzN4GmaRvq+pNIxSuEayQqwmR3q6gH6TT+yr7u898nKLLzwLLqBYSkf/e9UFAUxiN9tTCCz8W6Qlfeklv41bg4lBsZtOpeBYT02jQdVDz/fWvuCx+3NgNkQNsHYPVDes3jrpiGEfoiThuQD8zQ92z3ekX6WPK/ys1zXUeRyjkYUrZN9L0QvrHEU3ifmd98TqnTWxjQQCT3YHolIH26tgRBp2gal9Ka30j1JcaMaBzmj+r3DGAkE09kmZ6VtW8bjMVtbW5RlSd3UG0xHCYKWWQkBnagxXd2wqtZybY3YJmR5zvZ0Std2rNfrTUBeAsHzQqyIMm3wXvrqGHlhX+2v/Wpd4VwnGQxZJlhh225sWtL+KMPGkIaTWdqrAz7WaKBpO4KK6ChWPANeGAIEL3W9F4Z+f4ZEQlJYJju07msAACAASURBVC/bQg9+zP3v0xM6rbVJ4afQmsS0FVVQWeaYzLJcVujsRh//hY9/1iBtVNB6h9KGLCtBGZwTLyhR9Kapb+jEQMkaWt+xbhu5MFbTBc+6qwlFnnw4xOsjhEjnOkRuspnmEHt5SzLLjiTvG5Ue6sSU1TcavX5DDkLBt9aibe8jFOh8NxxecshJ0SCAZWS5WvLRh+/xW69+hSwrKFzOrcM77B7e4ezxItkE+HR4CtDggyxEeZZ8ErjIIRkhGTXLwWqUTv6d4pskb3mY6xCTH9emSU0buhafDZQsf5Ht9FYQDIfpxv9G0ubFENvTV1oi85b/9fA0iOTDJ4N3dD+1lE3MJAN/HyWQhzwT8GhcMM407XyNazpMlE41+JgKB5G39kj8zUOyf/0vhsqEJNlHJ9YACnwgqEirFB9dXPP8P/4FT5+e8Ttff5PDgz2ZamtNUEL5N9ZycHCYEnUl/CcmFp4UpHIgqgBZUVKMx9hyxIPxa+wvjlhcXRKC4fLsnL3tgqKQKXXXNDhX0TY1bROYr1Z0bWBrusOycqA7MqvpupoQHDu7U5q2Zn2+5PbtY7rGUTcOEwzGBmLsePrsnPFkzHic8+ord2mrlvnlGXQTHty7xfn5Bbv728wXC8yp5u7d2+SZHIa93xcqkhcZ5Uj8j7wT7+jgA77piCGyWC5kzfpA3bScnp6C22NrNMI1MhE0aG4fHJCPjllcXaDR7B8dpQAXAegVEdc2XF5eUXeerOgP0+QPqaFtUlpkAun7Z/z0+QWXVzMUOgUZ9M+AHFJKK/HMUjc8YYaaMA5rqh9eBC/rrWcgKGQv0kYzmW4RM40d5+hxjjcQ8ZS5pK23XYvWBlygyHKiUozKEU0jaZZK9cVNvzIVZV5QFiU+BBrVDQf/uqrkkE/sPaM129vbaKW4vLhMJ3AqOH3gYH+PrckEnHgb+WbNWG1J8J/uMMFRzVfEaDnY2yc3ivnsOoFOAs5apTg6OmK5XHF9eUlAYbVntViRZ1kKD/B4pZhMRlRVNfhCjcZj9nf2ODs5Zb1aDZYzxoo3U1/8xSi+PhBYr9dkmYCt/eRToyltxnQswVyZNuxOtlATeHL2jHc/eE9sXhqPSqESpbEYZbE2o+5q6n5qGXuvcWGo5nk+TJFD3yBoMbKfL5bUTZWaRdk7uq5LzOibRfyGqTGcY3HDyuybgL4AXy0XzJzIuXRiMIRUaNs0gMu2RuzdPmLuTgjrlo7IHE8eQUdDFxp81wEjxozJsxG+61hfnfPs2SmvvfE1nl+e8fyDt5nPrnliH3Nw65j585xq3fH47Z8wuX2b3/3Tf8k//PV/Ymsk77FarVi3NUvnuHN8i9t7U+azSy6WCy6blpeOjrm9s8319ZxPn1+wcIGXbx9zbzrh4vSUJ1dXNNrw0u3b7OQFV9cXXFQrUJpX79xllGs+f3aGzwqWnef123d5de8W54+f8tnVDDeZcnt7i7tbYxZn5zxZrXHGsI1lOhpz1XYs2pZotIBfxkgzG4WZ+vqjR8yuZzw5PUmN8IvNUj+Y7G/VzYIxptCB+Xzebwm/1pS98Do39g5S490DS1oL063pWlrnkvwqotP9jWkAmhvxh/VETFmg0UneqTm6c5+J2ma+WhGION8N56o0/iJRVQpKbSmSXVFTrXFNQwyeq6tL2qZGmZw+ILEfUDVNQ6lL5ssr/ut//gEHe2Pq5QWfXl9hTeTW7pS6aXjjG99Em4JffvApV+dLjo9uc/frb9IqS9c1fPP3f5eqaXj67DExiu3H0q0JGKzJwYBRltxIE0GIPHr0Gm++8RaPHr1OF+Ff/Nl/z63jW8QgTez2wQ5f2/867XpJVa05un2HvYMDvuy+QlkUgGbn4JhXvvwVtBE2yN//8O9YXC/513/2P9JUFfOqQ5mcgKFtWpbzFaGdM9m+Tdt1GAVKZ+IjbEzyYJMbKrLbICnsQcLBUCEFbGwaCJEaG9AFSm0z3X5IU31C51epnsnT86PRVjOeTFGmoPUt41GOUh31asbV6TN07DB6ROfEi206LTDGYmLganXCuNpivHuX88rRRNBWwlZCiISoCNZgdyeMDm6zdddxfX7G7PRz/OKKcmSwpsNbIDjOz88IRcWf/Q9/yne//W1AsVosaOo2nfketEUhoSgaC6pnFqnU3PWSZpUGoS4BEaLO8q5juVowXy64dbDHeFKyXi+JAcrxiJ2dCcvljKZuMZmV2jZ6TJ5895Kvv+s6rNGJ5diiszWuu0SPRhitcSnwM6LIizGqiMTY4tcBl0Uen57wyuQuRVmk9x8TyUFsdowVdUYPMAcXBkZMcB6ba6w2GDTGbkJTugDeKKLVKJcGbAgbbj67pqLj2ePH0nwq8b7fmk558uQzqmpFP2vVStbJ/v4Bu3tTMq24enrO7HrGyBQYK2fEwXQXVxia1lMm5mTXdXRty7qqmEwmjMqRNJMxkluDHQk4HYP4Se7t7pLZjF7Z0SvrYgJw6IGd9J/WmqglhCcvClzdUKN453rOPy7nLDOLM8ngN8DRvfvs3HsJH7V41wdhMYXo8E2DD4Gq66T+DyRwLe3TIYrvJj4BJQysP+9jYqs7jIYQGpp6LdkA0afhjhBExoVY1bWupVMjHCOWvgQD+TjHVS2tPqdTCnRGJEMRyLTHRYdPyj5/Q+q6AVo3oGf/8YI1zg0yCyEOfWRf4XlxqZX+LAp0KGBXTj6eUAUHQSS9SstAlwQWdG1DprWsEx8S4Od/DYD9NbsD1ROHNjVLP1DZsGjVAKz2MnCtJURWQK5OAO8QiMggPESfAFGFB0ye/CHJNkqUdEBqLUCz1UqyPpLtYEBA/z54SQggimR7K/ZAehMipNK+u6m9QvK+FQWozUQqHqKs4clY4a7X+NiDdptr8ALZIV2Pm/dyYMd94dr9UzXBzev5RZC8Z915n74v1epNstnwsVfKCph/M7gOGABNk0hXOjEg+z5Wa0Pd1snOjcT0NIPUfzQaiadmAvi7Ts43oyF6J7aQWg3WiMYotO7BayG3iKVNslNIoGxVCcqgtcYmUplc4g3T+IskhpuA7XgylvesRG1nrSXEgHMtzgVslicCiliE9c+CcyLRH98AZp33A2CnUMkHOe0fIdB2gob6xKqMSVGc53Zg9W7em8baBLRqAcxtZunajs75NLSEEDRZJtY3/T3qnKPzG2tIYAgrkzojsFytREGiZR8oiwKjUmCfEjwlqg0g2nvoWiXWGC5EmibZ/amIS8A9QGbsb3yOY4Q8PfNd1yW7LsljKbL8BYZoryqXMFbpvTObYUNSW6Q/VUz7XGYxeZGerS4NohCijBd70NFoNGSr9Ix4lFhI5mVJUcpwsVf0GiNMWwmWm7CzvU1VVcM96nt/Y7PBfiFGYeV2LuJDR5tCDwU4D8QuUHdikZRpS1XXg0rNhz6QXVMW4qcsQLoMKHyyPxBSSLqu8YZ1xLDnJpuMlCMl7OGY9ms5b0ejMT0L9zd9/LMGaWXq5imzgtIUBN8RgpMHMAjLVStNhqKLkc6tcXHJrL2kDR0hSAHi204kZlZD3/APslMpSLQSbxxh36bJRAwbpmpaZ0aLZYJDvib4Du8jmc0JwclUTAswWhYlVb1C+YhGJN4xbnxbQxRQsQ0d7338Dlfn32Hn4D5aZ9zav8WDe4/41SfvoHMBxUJ0hCApogEBqKJiCPVqXSdeWwp6oHWQM6QQoUDEJjm47JObA0ZMtRVqmKSJ9Exboer3QMkwaewXX/qkUom5BJupXbhhQn/j8B8a5hATPpoA3YA0Pon2r6ImOEcXHAHZ/NV4TGYs7npFWDfE4GRxZ5aiKJktV/ie5czmUJUJuwDjWvXegf3nBWT2vi9QEQl4iERtWAXFX/7je3z25Bm/+803+dIrD9kal1hydIzizwSAAx/T7yCLOoZ+YiiNgLUWYy1RaXQ2Zro3wtqCGBSurtDKS1KghrpdsVwscC5Qr5c8OzllezphXG5RZCtinOOiZ92sCBo6H9Has7uzzagsWK4rWuexwJiId4HLdYVTGm3AtV7S2mcz6moLm1ke3j8iGM3B7jaPPztBGcP+wZTReELbNMPkrshzrDV0KUAnw7BsKmymybItUJH1umK1ahhNJhzdmtKsVsy9/H5NSkgMPjA1E45uHxODwo6ErasQ5quKkeWyYl13mCyX+9Y/fzEV9KEdJvmytgUYPzk5o66lqFSaoaBQSYYiD8CmKEOxkWoaRZZndCkdU9ZKGAYP/VQ0piC+osiIZYYfZ6hRho6KTIl8p3PCWNcIs3xcbjHZnvL88pzxuMR1jlrVtK1MB2PYSOeu5tf90hsO+qFhSQdUiBHXtkxGI2GvK7A2IzrxIzzY2UcRCBqm21Myk+FVxKnAWtV419LMFoyKCdPxLqNCWBBt2zIejVmsF8QUoFjVlUhCMnm+W+9lHpNYyl3nsEV6xqMYrldVzYW/lEI8iDVG27bYaBmVJfu7B1xfXeNCCiEInizLuXN8m+v5THxoo7BMfYTPHz+h6TryPOPi6kp+1xDweSaMOS/Jpz3YEmKkSUxCCU9M951NEy5AuRKZD7BarlmpSpi/zknRGjaFd2/10VuuhBjEBnkoxGVvM1ox3ZqSZRkXFxcDyCuTApE5kZ7JiBRnHk8ISEIsHjUqKXa2qaoLYohUPjDXhonR5Gkw1OFoVIsyGdpYQuOZnZ7xTnibl15/i1i3fP7hz1mtl+y6Q15+7XV+9at3CNU5z975Kb//P/3PRA3v/u1/xjcr6mbNwgcOdvc5mExZzq6ZzSpmVc3xrX2Od3ZZrBZ8/vySeed5+f4d7k63WF3NeXZ5RUXk1ZceMs0KLs7POJ8tqWLgwe0jdvOCs7MLZl2gbmtu7+9wXI74+P0PuWhbwtYWx4cHHFnN9ekJZ3XL0liKvODVg0O2RyUfLmf4umbtpOEwVos0WYuciDQYMZlFWsgXwfP+/Jeh3WZ4E4IUc13bpsAHvvA9N/7OixJSOd9A9a+bdg5rDW3XEpPEMILEJKUAEx3AKllPDR1X7oL12rBYzRiNxxzuHqDXHrTHq0iDwynI5V0Pz49WFmXSnhzkHIq+Q8XAxfkpTTVjMhkTkyelNprSlmRlQVMv+a8/+L+4eP6E1770fSY7h+wfHDM6OuD56RPu7u6wf/uQ5oPH5PMF+bLjyV/+FftVTfHoJYrJNnXt+eC9twkEjo7u4F0nXncYtsbTtG4kACL4wP7hLY7v3CFGYcQVCr7/R3+CUobo5cz0rqZrV0Tv+d73fw+TZXRdLaEMqhCGchSGPTGiteX1L3+FyXRKOZqwXi/5/h/+oQz6o2G5WqIM7O7s4YMhs4YyDSbyLKdnb0iYigzmYhCvNGF5SiBb20kau7UFISjx00ascbTJadpA41YYf8OXLIA2lqycko0m+NDRhZrFumVU7rG9c8j29i6n4QltI7WlD4HRqKTIMsrjjPG65Wp2Qmwc9w6Oue7gfHaNzwowli4EvBLGmzAOMya3jym2tmgvP+bg3oEMP01H5x3T7ZJ/9a//iNdf/wqXZ8/paofWRiTmKXBU9ecPUnBGn2qk3tNN26Epj/1iiGLn0bUN1WpBkeccHh1z69Yt2qpCh7WAoyFQlBPW6xUmC+jMiEQRTWlKvJNQMacEKPLBo61CK4+KNavVM0bliKLcJwaHdy2EjqzIcC6pmEoLTnPWVFSXTzkEPHKWiLRaaomtcoutyS1yVRCCow2tnGdai+VXUEBS8AUwmSEaTYfHaQs6oLAEFJ5A6FpyO0YZK36zIaKzDO2h6RwX52ecPXvCwcE+GsVkMuX05Iz5fM5ksoVWlmVb8fz0OThHVoxQJuNeXPHlBw+xWjOxBaXO6HyLD57xeMyoHA+AWoxuqCX6PTDLc0ZjK6nvKoUy+ZhAAY13UreGmM41HzHKELMM5zqadoW3mvPO8avzS56hqDM7sMZGOzvcvvsyFLtEZRgHYXgJkC9EiM43+MT8iqEfkoWByScD03rYW01SQwTvMNrQtUKyKYJi0QNWSfovm2rE6Cj2JC5Q7m/z2td+m9feeAuiwkVH+7HFnz2h9annMJZsklN2GbFZ4ZQnpIGbC16sOJTsB0pDnhX9qpDwL6HKDz6QIYQBxBC/4NSspYIuxkBgAyahJfTHmK0UllPTrVcCFBUl0Se2pBJfxeA9WnmCC0T/4iBRa43RBpfkviG9D2Ic/LOlbkns2Jskpb6G0QqTWhub2Kq9Zz8EGbwB1spVkIFjAuNSDzj44Eax25NuEbG0SjYENs/RIeDSWdqDMgBBy/f2yrYkQxmG9yqdudpYXCJv9B/WGvHsNwa0T8DjcPmHM/0F5jDcONN/fSD7RUbtFz9eALx5kSjUf9wE5ZVSuLYd8hK09xRAWRRS5/fs7OCp67UMhlLmBEBRFMnujUGVqoocRQJ0o4BxfX5OjHFgFxNBF+WN/j4NnbpuAGZjAyEuh+vVJUsN2TfjACbLABPath2YosYYsRbIc6wx5IkB21sZaDaBfFme4YLHmmxQMpoIeVkSbpAhQoypx+5D9LTYltkNCSLrbapCQIXNWuhzPEYTWW91U9O1XZK4k4BR8agfl+m9xpBUiRImJc+mId/eJYTAuqqS/3rKRADGo5Hc1xCo6mYYsKAgKFEOZlkue0MeiC7QBkdwLlkyKIzJBSRPwJ7zMjTqiTlOidWhEEcUVV3RBZdYv4l9jR68WnurLRArii7LxLYuvV7bdbRNw0oeYgAyaynLAmM0bVtTN70K1aT3qAeLhroTHCA0jewB1gzhY9572q4T5VZ65uWeaAnjilGGwUFsKwiRPMsJJkjvnPaSmAb7mc0wE7Ff6G1kemueoihRCYCPEUwK4O4B3yIvRHkWInq9SsCr9PzaaKwCYyI+wGpV4b2jHJVCQguBPMsQW25FaNqEGwjonimbnjup+/v1L8+XSV7Qnrpu0NoOQwlr81/bR/qPf9YgbYgRVRhUtGTKoEInTC1txWAc5GJomT5BS+2XXKwuCCoMIKFRiKFmmoakIbGI3FOjgo6pyOwp4WIyrI0WMDWxaL134o+VXqhHy5UWyaLQpicoZVivV4TEtAg+Dsw9uNnsRUKmOLk65fHjTxhN9sjGe4yLgpfvvcT2eItVWAIh0bcZGGCxX/VKSWOZgAeZ4Ce6fo/sKzkUddzI+vv3YaxJRdINjycCvnPScMZNgR5jX1AMLzv4vPQgqE5/9vJdld4jw1WVwql/vzZNvm96H3kvgU39YNwYadp8EEsDOyootCEUDfVySWYNx7eOsFnGqmmgT9SDGwfwjcP3xj3oD9HeoyXGFCamlASWBDkIuuh4fD3n3//F3/DeZ5/wu9/+Jq/evY8NIssLMbF+bwB6/WYkB5NLoLqSULsYUyq0pphsc3w/I88zrs5PWXcBlExG101Hs+poG89oXJIVGYv1mjYEqY50RBnx6XLOs701YWe6xXx2xfVshs0kuKRrW5qqxQWF94rVsuHx4+d4Fam6yEE5QWvY28/Ji4yujswmC5arFTY37O1MGY0mVOuV/D6J2WIyi1Ga1sukbDQaMxpPmM9mzJcVrQtMraHMLLqUwcn29ha7epvrq0vq5Yp1FSgnOeOtKbEwAnArkbo3PjBf17iowCcGU7qLOh1AIJ5CSgmjJ7eW2fWS52dX6eEHlDx9DMOZvqHcrImbvpYEMXTXQ7BBKrJTMdPfU6UjdlTgdMTkBjIzDEjEakT8a6zV7O/scufwDu+/9z6z6zlt3UhTSR/6kFjw6YE1maWIpUwMu25osvr/tNLieakU69WKdbXCR09pCyIRYzMKW3D76GgAeQeVgBJ55zq21K7l6uKC7a0tonNcLGY0vhYQKshz2HnH548fszURyUvrOqq2pgtuYJRuT7eByHw536wpnXyEug5S82WtTWbwQAg0VSVG9tZQNU2azEZm1zORrHh5D1ErfPSyvxtweIJTrJuGXjaoI4TQ4Zou7VC91Ku/6wKiaSSQpreCyfM8Aa+Qm4ygwCfvpb5p6CVVPaivE3PbJTZsnpi/Ie1f/aM22FmkgUY/zX6RDaJSExrSHi/vNgQBiG05IlpLbKUoWXrHeQSrDDYqlO9wQaO8ZmRKMcfvlizOH3N4a5t7X/oSnz/+iKatefzkMS89eo29e/e5/Oh9Zk8/Zn3+jLe+8S3e/uHf4CPUPnBr74Adk7Oaz1hVFfOq5vhwj0e3j1hez3n8/IJ553h45zb3trdYz2Y8u76mjvD6w4ccTcY8OzvjZDGjiYH7B4fsZjknJ8+4ah1rBS/fv8et8YQP3/+Ydezw0wn3dnZ4NJ3SVSvO1g0LY5lkBa8e3aJwjrOTU2Ztg84tqvPJyzIQYkcksupafvmrX0qSevKxUi+cBTfBVf/CPe1PN6X0MCz5TR8Dkz4BtYqkslGbnxW1Eqmr0nRdCjUEUdH0z+bmNCYA82bB37z7N6ilpysMd/UDCXVoa7pGAIow+B/LcDVEYbgYk2OzHIcUirprcYlVcXF5wWJ+zf7+cfLtlrWprSLD89Of/IiP3v8lv/N73+f1r34TU0zQNoe2YXL/AeXBFJVbYgzsjyYs5i2f/uTnrK6uOfz973L4xldwzuCqNcd377I12SIkm4CskER77+T9u84NTSNus6cBN8AMefZ92+I7l6TpUf7uO87OnrN/ENia7tLfpBjFqubg+CgBv5JYvL+/hzZgTGBrMmZ3d4tbOyNQvW1BQ8RjbSkKq/QevGvwLuBdS8TTefF3V2Ez1InRyUAlgfzKaMajLa6vZ3RtjcZhTUYfKpuPCra2d5lMt2nammruGY222d4+Ynt6yMNHr/HOz99lsaqYlCVbkzE2E4liZg27tsBUkdOrz2nbax6+9AaZyjnrAmvncMi+YmPyesTThoDSjgePjnn0/zH3Zr2WHded5y+GPZzxjjlzFCVSpGSJsmSXq2x3N4wG+qG/ZL8W0B+g0F1oVANVHlqyJEuyJFMkxWSSmXnn4Qx7iqEfVsQ+N1Pyuw5AZDLz5r3n7B07Yq3/+g/vvYcbQAdNUVTcfzhlVk+5ubphtWowymCTT7sKoKMeB5lpmSawR0BZFS2uGySgLJWbgjdIwxucQ0VPWRbYg31ciGzWG6wtmM336FthSu0fHIsKqNuCi6km9NLIaBClifiyhiBWPFpD21xwegaHB46qXuJdjx86fOgBg7UzbLGBaSTONJ89v2FTWKa2JOIw6awptKE0xfg8933ParMiAGU1Q+vsd6jTMJ8de195YhoCC/riAc/2+UtYnRAXBlNqSl1gykA0BuMG3tpbEpb7fPv9D3n41lvMFns8PnyAC8LAGlxkPj9keXiPodkSk7+7rQydGpiYCoUEyJSqSAEk8p7SAzHW7jsf4bBTJEqKnewVSNhSjNILeO/xqY7XwBDFAiBow6CgU/DLyxM+8w3r2hKUAIVeRfRsii+EnSTDzYDSWVFiUbrADzmwNQ+95WcXZZnO4g4fhNySmWlaaxkuDy6BzoqytCK/TmXbSMYwsp/2fc9y74C//tu/48MPf8B0suDy5BQfHffvPWJveUg4P0UbYcgFXVHYCmULfBjwXpLPfd+ClsG9G4aMQYpUVxfjcF/qLjsOewNZ9SX1Men5LBIrOYMJAH4I9Dgm0wmTEOlbAUO0dxADrm8IfQcmEYgSENYndl1mr9kEgIQQsErWrUtkEvF1lMDgGGWtqsTiE6Mwxhol26lBtqfz6ZyT8yZEIUSgktVWOkNFgRnHAC8UQnTKvZa2qRaVejT3iSEFD/kgtjxam9EqQvkdMOlyf0gcvSRHKw2dQUlPNLue2985y6X1/Pd9Zl8h9rwGuL7+da+zlPPrdeD37iuEQNs0xL1aiGFKmHqmsGgtwGb2V2W0Rchs6fQx1G6wIaHbNg2Ks6TdoAszPmP55UMK5Us9TkzPjDGWrhPfVgHSsvVh5C5L29pCGPha7Ri/6TOOfr7pZ2XQODMMs5rMpHuUCVoR6Q+6tsHaAqMT2Sxf3+znmNZZBv5UbsciEpCWsYkIKqT6zIgthPMeNcizV6mKqKCwZSJZ6NFXPoaAd4GisCkAPCmsLBSF9GnCXhfLqel0QrPtUj21yxTRWov1lLEj2/bus15oK8Kb5MnsEsHNOSdjrIRX2GS7UxQFw9BB16fBv02M15THYjWmF8/XEMQL3hgjIdOokTEbYyQU8syKRZ+okbRz9H1H3/c7v9mqkkG+MQmI9yMT2TlHWZZUVaIKKCEXZRavGtJ60buBSw4d10aPlhyFtQlgl7XYJeBTwWi945yTYVkKQLvrz5y/d2b+erdTixfGYE3N4D1eK0pjKQsrXsJp79624h3cdx3aGKpJNX7vxWyZvIUNQcswwWpDNZ0IMN22OysgdcdGMwcqKlFYyZkaxHtWQVSRtmtQWsB1a6o/2CPy608bpAW6wWMVDENLkeRW3ns0MaXrRgEfrVDcV+2W9dAJTBY8QUuiaJU8R4IPCQzJTUBIslg1SpRy67Rr5NT49UqnAigdisZa1qsVfd9QFBbnAsfH9wHF7eoGpeIdphWQQFsBCeU/Fz0X2xsa17KYzVgH2TmP9+8zq2es19foQqEphEnseoqyBhhBUZU2AjcMO4P7EJIP0F2PlZ0/zGhuHoQVoNM0ITecWqtxA8iTXh92h16e1upMd08baN6gs6T5ro2ES+CySgbKmiT1uRO6k1lp+R4IuiL+Nzqxk7QxUFrK0kJtGbqOq2bN+sUtrnWY5JWWJ2tVVY2g6e4l9zZ/DcnXb/wv4Xkiv5LNfVCKGxf48W+f8tXpJX/zg+/y8YffZjmfM/RDaup31ydPEwEkRFPR97347dh6LN60UphywuHjNwhFwc3lBZpAZRXbVcOq3QgLRwXadst629N0HUVZcbi35MYY1usNs+mE/b0lkUDbDbJxIu9hOpnihlus80QfcQourlagNVVZ0fUDB/tzLi/PcYNhOd1nMZ2wuexxmgVJrgAAIABJREFULnJ2cc1sUjOdVNRlifc93jkJLXKevm2xyoCP9O2GzXaDCzIlN0pxuFxS3dsXo/JagjVsafD7LdV8hrYVypZELb6SWgNW0TYDN+vtKyzFDAAaLYmUChLbUWS8PgSefvmSzXaQ4kUFmeQnKc8oRSKOYIwcirvAP1kXSRIN0iCmwiFkOYQCZRRmXmMPZgwxMplOiN7RNk0KnkgSuRDRAU5evKTrewiJpa4iRVEyDI5hcOOaiTEmP9T+lWJRKfFKy9PGwlrwkS4q+uApq4q9xT6X15fEEJkupyyWS2F96SJNlAuc79j6Na1paPsNq9tLTHWARYDu2WwqQHI/oAtpAKrK8P3vf5/nz5+zbtacX14wDMJiLhNz1hgjgUV511QCeE2nU2IINK1IsbRSTKdT7t875uTlCU3XjkMlhdzrpm3ZPzwgxMh6c0uMsNmuZdCT96QoTBAfAtqnCawOtG2Xpsm5mA4C5qVn1AWXJv0iT1qv12MAmEnFpx+8FHfpvluzCx3MRTJpXFaVZQJZRcYz7olK5Gh9LiJzgXpn78lMgTGELzU/YwOgFWpaU97bozu7xPbSQN8ER5mkfz4GVPRUfoCtw6oWM7S41vDs08A3v/8feO+jH/Gbn/0DoWt4/uIl7338A7Zdy9nJC/7rf/4/+OZf/s98/Jd/xa9/9Y/cm05YWMt2teKq3dA6z8N7x7x9dIBvWp5fXHDd97zzxiPeOFyyubzkxfkVKx/48N23eDxfcnF5xsnlBV1UvPXkAfeqJdeXl2yHgc3gODw8YFlovv7qGX3UTGZL7t8/Yt8oTr/4nJe95wbDwWLJu4f7qGbF0/NLbrDMJxPeOj7ki6sVp0NP631qLITBXNgiBXQ4chJttrPJc+6758EY8HEHeCWtsVeOjPR6vckbfz8OAuVX550M8JwweWJilSlIA4VItGnYqqDTA9rAfH/K1rW0OIqiwunAw+M3+ez0K3SQA0UpUQjgMkAsrJWoBLRWzkshZYSRf3Z5wZvvSvq1NUUKcez45//xj/z07/87H3z4bb7z8V+i6wU+anzQqHLG3rvfwhYDtBvUtKIoFG8uZ7gXlzz77Wd8enXJ1Yuv+ebf/A3f/fDbqGqCNwUxCntFGZFUykBDGB3ZR/BV4Fya16KskveeyGKVLTC2kPPSiwR5sVjsmCT5PkYZrGRfxZhqn6ZtmUxLQPP4yTd59ptDor6kNBGlQwITFD5qnJdgFz90dM1GWISlZXA+efiL9VWuFrzfKXCMNRizR1nNOTn5PVVRYE2Q+xcGbGVZHiwpKknk3js8oOkii/kxoLi4PGd5tMe9x/c5+f1TrFVYAyZ5vhtlqS3YuaIyBacXV1x/+isW+2+gqgU30XM9ePqoccqgQlKL+IbKbvj+n32bJ/ceULgrtHIEr9AE1psbmsZhrdhs5LpQqUjfdyIPL8tciuHcQNOsKcuSup7ho0N7klQZGTQRUAYKG4mFgGmDSyo1BW3TUVYVg3f0znFwcICx4k0esTKMC8lnsgAVPdrI9TYxSZujx2hP25yytgVFIZZowXWgowTolNKYRddSLwybGHjZe/bKgklhqF2LIQMOVgDJoefk/IzLmwv2D48wRSF1jC2SSsVgjBI2lBaJepfCZIOXWkMTiDcrLj95RqsDaz9QRIWpLJPFDF1X9H3LIwzx+SmnV7csDg4xZZkGPRKWPNcFxaymN5p6OpWhSqkpg8Ikmy+RzGfpas9kMklByGIPYK1NgYG7Pc+HIEFNTphJKgpbNKb+IweHGatxDpq+RfmBidX0UfH5zQW/bK75ulIMhUYHhyairMUu56ydZ3AB1/fC3EqsWK2lFvXeMQw9OcxJzlZDN0SxJxh6Qhgk+KcXVY8PXoK9xvJdJK5BCmmxPEgFhFaWoY9EB9//ix/yzhvvE1pNO/TcnF9zc33F8nDB4eKI4/17vCTgvLA5vSrQdoqNHcHIPhvQAoRYg7Weoe+IKMackqjHWltFNYYFibIpJtBUbDOKomDwbgTXhLloKEoxi5zO9yjKio1WFEWF7zvi0IkHaBoquN4L2zHKNY9B7KPqRNZIVJF05sl+ZbUWe4KRWCNgz8ioDcl+Lq2PInmhZlKLYge0+TtqshA8QekEOEooLYhdXRRUItlRxFdqJ6U0If09SmMSbVchob/mzt6ukt886b1K4KusBWHICts0q0lVsgMsk4w7aDV+jgw+/nvM2VeHuH8cyL37dX+gsPkjgO3rtYJLQFdIDNQ6WTKWZSmgY8hB5zsCGenPAxFTaOnj0vcoC/GVz3gDZMaiGs/BbOfV9x15cJOBV2PiqJIsy3Jk3ebwrWxzeBeYHfuk7BuqFDHZdwgILJ9tSGe+Uoyg1nid0s+IPlCZIjHQhWkb0hkknsdS43ulRntE8YHV+egnhKRujJngcAcw1smDX2u2aXgcSfu1kjXoXBgZwc4PaO1SnlBMfWFa187jt34cXsq6kmGmTZ7BPoTEzjVU1S4YLd/vcZifcBqtZb+3hVzTHOaY92yFhMupSieA4lWMqi5LSit7iXNhDEbTaR3UdQ1RLDkHP4BCVCLGir1gVco5me5H13VilaFlTRWmpK7kfO2Hnq5tk12OBrzMUpRBlwKqtm0n97Gu0UG/Aqh2Q48PArb2Q09RFCNulZmn2ec7E3oy0Anc8WCW7IhMsrHp82diTb7/AVKOUCA4PwK+SilKW6BR2IkVADVG8FLLVZMKq81Izok2YoxlOp2KTYOxo52KT4GntigoUqi0DxHnxF959zxCWRTE2rBu1qBg227/3T3mTxqkjTHg3YDRkcF1WG0JSqdNIIF3Cgia0Ae62HHRbNgGj1aGup7IZM6oMQ3eRwm00qlRUzo1+cnzyGS/CWNSk5wepLShzWYzilLCZCIIKGrtuIFprXj58qV4WniXvEwy823nlTn+GsSyYAier89PGILDDfLg7s/3ON475mz9XD5rDMTshZZYp7upi2zghS12UwglbEfSxDUo8e+MQRpC71zaILQsWC0TjRBicoW48z7zRIud75LcoziC1sC4yee/y6/88JkE2EJmMb6afpkBYgFPVZJ2OBRSFGgMWgngqZWmjxDqgqACt01D07aUXv5tQt2SdUXyHVI7UCQj8lIf6Fc+V27Mc/KmrJWU0BgV2lZc3Gz4b3//Y7549py/+au/4tHRMfVkRteLHFwKJNl4vPe4waVpr3jVVCr9nMjIwtXKsHfvPvPFguvTEy5PXzCdTIiHkb7tWa8Gtl2L6wc0sJgtqIqKxw+fMPS93IYggSLiBxuJvqO2Bc55FBLu5YaOth3wk5rZdIJOAj2roS4t282Wq7NbVmvxOlqtNlRliR82Mqk/MCxmc5rtmqYThjshUhSF2Cy0G4bBsbe3T9P27O9PmM8n7O/NCCrQdB03N7fEEFncu08fIs5rKl1RpYRtjHgi31yvaDYNqq7HA0QpRVFJcRmzT3LyZrPGcrPe8vWLcyIimVUhoguRoGXwJeZpV2JA5YltHi7cBUtz2mxITIiYAF1tNLoyqMpg5xPazYbNekOW0Qc8NhWV3TBwenUhrHUDSifDex8oip3xPTCytCAxNcqSbdPgnaOwFm0KtIFJPWFZT3nj/gN++/mnvLy9ZDFdsF6v5DoFOcSq1GDnJFA5rFtut9cUxwVD04gcZGF45523+e2nn7DdNjuWffL7UkFxc3PD1dUVthIz9hCElYFStG2LTXIgKQxTSrOK+GEg+MjDe/cFfE6Mj/XtirIsaPpu3CN8FDTAOcd6tU5BSVYOQg3T6UxsFkIuoGSjNsqwnC/Ytlu61ol/Igk80H4XxlYUo0wm+9L64FPy567wjcQx4MxamwBbuS8ueJQLWJMCiXz2rBTbg1xEkRiANrNmEBBRpfecB1EhRCAB/2o3GIRkbVNo7MEc17X4ixUFChehMZrbGCmUZvDQBUfESOiIcxACm8sLzp+f8N773+PZF0/ZXHzBZnPL6ck5b7/9Pqvra1ZXL3nxm5/wo//1f+fs4i1OP/8Nw+aGTdeycp4nRwc83FswbBqu1huuB8fbbzzizYMFze01L69u2LjIt956g8eLis3VKV+cntFHw/uP7rO/mHF+fs3J+gZH4PHBEftVzdmz56xiQE3nHM8X7CnN899/wUopur0DDmdTvnW8T9xu+fzklJdRMVsu+Na9I1CRL4dOGEBKoZWcxfkaZgaWNMtJPhnFCxAF0admIhWA5g4rRJiAu1TseOesGs+3NPgh3vWlVYyFQ/pOMSKS1Ch+ZEGlYM0gTUH2y8cHVNB8cP8Dvrl8l7//9T9R+0ihIrPpAdprimCJOGJ0EM24p8Uo1hsxgS3aCNkRFFEZum7g+vqGEDwFAWsVpVb8229+zW9+/Qs++u53+eD7P6SeHTCQC2botaXaO6QrOqpCU9w/YnlyyupkhQ0au92i/SlPt/+DYbvh/b/9X1jeu88maAavCKTmOjU7fS8gUlmW48A4X0/vc6q2k4AH11GkptHYcgTAYojsL5doW43PZ0hNj3rte2qtsWUJ2hKCpqgW3Hv0AS+e/j17sx6lPFVdYIwiENBRrAu6th0DN6wSz3UZ4GRbKDvWMUoFhsHTO3h07y3adkNkk/rqkojBFobF3hJVVAwuQOcI0VAVE25vr2VPco6ymPLt734D5bdsrm9xakjNJ1L3Rk3vBpxyLJaG9WrN9vx3uEKC7qyecOYD22jQ0VBgOFwafvi9D/i7v/qYo0rTr1aAxyXrhmpSELxidTPQ9h4bTBpmJHJBkMYsh/KEKMM2paGMFVqR9j5Zg/L/Djd0XF+fEkPPwfLN0QexmtScPH+GGzrmC0md7vs+NfzCZMogioDwgRDdKGGXfTMPs5SAkrGh2V5DsOIBbJT4iESH0gHomVYCWrc+MHQtM2s4MIap0piyRikrLC4Dk7qmakpyiJxNHrTeiW1VURTCUEoDGG93wFV+78MwsDy+x8f/6T/xxaefsbm+pppZTj79hImZsTepQTk4uaKc1vSnNwzOsW0krG3wQcKEovjtTqZTSQEvC5EBlwcsj98k1skTPkns+74d6xXx4k9gTbgDeqFT35PZk4mUMAZbpYGV0rjo0xdFvFa82Kz5l+sLTrUnGLH8goi1UC7nPHn3GxTLI7rG4YsO5xu6PiaPeuiHJrHjYrIDCLJmoqPvGiSwWUAQk+q0ELxc52R3lf4Bq1UrrMQMCKbhWFlOQFnqquKNR+8QujD2MfeOHlDaiuenX/Pu2+/zVbPl988/h67B6UivLJXNAFJiIkaV3hdoVVDXZjf0i+nMueN7Xlid+gpH27fEEMfzRRuDykF5IWC0eOYrJSFj2+1WlEXGEmNWZCU7iDJQ2gJlOoa+J3onjG6td/dWx+R9acmSwrISq7A81BoVWam/0QnszUFo2RIsosQeRSlUCKOVgboTrhQHYcBqhaicVD4KFUQz3hMV1VhDa5PhB6nd5V4XIxgMjLJhla6bQsA2lRau0qm9VSkAMH2WGCPR+2TfIf2WLQvQyRM393/ceZ/pvHj993cB27tfO9YAvPp9Xv+z14HfLLk3WiTYSidyk76TFI/0mVEJM9B72ZOzZ6oGGUCxI1zlvuhuSNfduiUHNVVVldaaGqXuIO+htOIlbHOAIBGiRZtEcki4gSfVK3eB2hDGnlorzeCGxHhP/qsZqHZuJDBk0o3zeXAtgXshnQNZnQKKorDjGpBzXSxrQhoq9cNAl1im2YOXGOVZuQv+pbB0IesJ6FZWJWHwuCbvR7kfE6C1LDMYuXvdrQWVtsLoJqvrcqCZvHd9x7969EOOcp2y/60tijFoD5IVcczWjPLsg2BM8U5NSvq8CoS8Y20KBtMjKAqMdoDRxEQUiOioiYPHx4GgEwEogZtyXZMXa+6ZU69nEvib13f+zGXys40xUhZiRZDBYpABhDGGOikUM6A6hnGrHVvbuUEIPXeY02VZjl+Te/QmBWj7EMgBus572e/T2YxWVGVFYS1tCISmQcfUxyPevTH1aJlY2Pc9Xd+P10NrPWao9F0rz4wWP1uAhBljtBlxHUW8QxTSjPlM0WCMZX++z958n+AVP+bH/LHXnzxIG9WAmVZ0VoIDClXKwxKlKDRaJuvOd9yy4Vl3yWXsicaQHeEG79BeJlcZmAXGAzs/9Bk0zBPQvNfenb41jRTu/dAzODd6YEiRI6ydbbORG5VxQqSwTsfJa1O2iEFYME9PXnK5WTOZHGEDzOuaJw/e4NPn/0YfNggY4VLBLtNCa4wsQnY94euSA5PknvKghREIyYtnZ+wu10gmUfLe76bVaZXZWjsKfp6ijYdb3B2q2XuEdP2892P6dgaV5f2+ehCmfT4BcDnFOrEHo3hKqsRk8cnmoaxKVGGZlDV+09OttlKf5/eUgNl6WlOWJavbtTzU7A7P8UC+85nV3UMzTaUNEk4TleJmcPzs02d8+fKKP/vWe/z1jz5mf2+O6ts0OTPj4SAMr7wJCaiVD7aYGXlKQdAU1ZyjhwVlUbK+veLh4T2iD1ycvMThWSwOOD+7ZLtesb+/R12JbHt9u+Lly69YrVfEWNC2PfWkpKpLttsG5wNaB8qiYrXaAhZjxWOo63rW6w0xFsyWhyjT0McNznq6XoqwECNt27PdbNlfztjbW9KcXrDebOXZKQRsa/qAD4Z+vWL/cEkIA6vNhvlSPFObzZqbq2uWy2NiNAwhYJKnXjSympWGtu25WW3QRYmLEZPXotaj7CTj/jpba0TN11+fcbtqZO3pmKT1WopgxBcoHw4h5O8pYJg1sjblfqtX1mr+OTGFWxR1iVlWFPOatm/zeEECbeKdKS3QD54hBpQyaK0otOxjgwus15tXAH3YMd2NMSyXS9quS82iFVBICdO023ZYn6bI1tJ2HVViKEHk8OiQsiqJbSC3Xt5nf7hAqeD65RkGjQuRT3//OQAPHj6gaVpurm8hWY74wfPs2TOMEW/Hvu85PDjk4OCAlycvJRFbKdpeZILWlvjkbVvZCms0q9tbtk0j76SuGLqOi5vr1CDsvMzEPzYyDH0CbT0P793j+vIKoxSlkQRfuZ8S/rU/XdJtGrqhkcANlScxyVnuTqGUh095Kh9iHH2UCNmuRaPCq2mvdxmTB4sly8UeT18+x4XsXidrJwYZYOViOTdQUphmb9I4FmAxhSBmRmG2YRjPwqhQhWV6/4DWefxtCzFyO7T4KJLLiQ8URoFYDVJqmR4XzvPFr36K+rOSv/zrv+Mn/+9/YehuOHv2KXsf/Blvf/M7/PYX/0T3/At+/ff/D28/fperTy2r1rH2jieHB7xxsE8Yer6+veV8veGbbz7h0cGCq/MzXl7dsO0CH33jbY6nJTeXFzy7uKYPiu+++xbLwvD8/JIvzy/pQ+CdB8csipLr8zM2ztMozcOjiimKzz/5gq6yhL0Fh/MpT/bmXJ2+4GrVcu009+4f8fBwSb++5Xdn56yiYjqZMLWW22EgpqJw8C4xG5OyJLE5xCIpjmfiXfA1xnwC3a1D4iv/3fkLWcN/8OcJ7IhJYhkCjsjaD2xch4+eKsMJ6ZC22jAtKkoU3inul/d4Z/YWP/e/pB8Cfe94sn/I9nxLHAKh6HGhJ1KSD2uVwGBrDS56Cixx8MmjUVjh52dn+L4llAWlrfnid7/llz/9Z37wl/+Rb330PYpqSVTi5ayCQ6kCB6yqGS/KgnI2wZqC9ulXDGcbKCy1Nuy5Aa62fP5//RdefvI7vv23/xNvfPwjzOKQXhscjOGMi8XijponvnK9lVJYUxCVh+jZbtbYGJnv7QESeui6nsE1aKWZLvZB2zFxPM07xj00n+uTeiKDeddyc/U1k0lJXR9SFD3Or9luOlQcKAookqx4SOyHECNtkuAZIz5vGcCUd+9I7SRFMeHg6A0++c0/I4YShoA04sf372PqKW3vRPXkGrF9ihFCj+u29N1Ax5rFsuYH/+HPub5aMQyeSVkynVX0vaea7LOYH7DerBkGT1nMUNpycS2e33bvkDCdc3ErjchsNuHe0YwHR0sOJwXD+gLigC1k8B+CrJ29/TlVFWgbUZ8YW6GLGq0Nzeqattmm/UueqaOjQ1ASwNttW5bLBVVp8W6Q5igKNaIua+p6RowyKAkoptM5hwdLri5O8L5mtliwWjnKQu6Tc4M05VoAc+8CwSkIYlSDsiKfj5p+cGgTUHqg7c5QsWJSLrB6QlRRvq6w2LKmmhs6vSIqjYl5KGcISlRS2oqHrzaaewfHTOqKEKEyJWb0kE42Q6lOJsoa6d1A1NBFx8LWWKdwDh5+9B7FW494cnzEtK7xviFOJmwvt/zF3/w13dDgXE+MgbKqODk5o9k2tF3D1eUZfujpG8fcTLh5/jXRdUzKkh7DzeyQNxcPYSre894P9H1L16c+JloS1CrPRJAhrTD6E1AVMwDIKD03WuO1NJU+eGGwaoiF4tQ1/OTqJb91Dc2kwIjvHEEZWhdYLg8w9YJt00ugZexRCSyJwY3WPwq5hlmR5IcB74a0h4mHpdKyn/mkXKwqCdoySuOI1FVJMXjalydsY/o8Wth61lRoXWJVyayYUSgjvqdBmO17+4es2i3z6R6Tckbb97hmSzADyhQUqsjTPYgBg8EWBWVZCcAiJTxuyIzvXV0x1nHe4/ww1g3D4FIvkoZ1gTshPQFrhEEanJMhntZ45YVdbTUUBaEscX0HKlnDJEAGH8R+iwTwKJVIMSo57ihhS7sBSKBnBi1z/5NqF1MWIhNPXoqiNBA/WmAcYufaNveCIhu/CzTm3A891tFG5x4x24gJgKS1xuMx6m5o0R1Cz+6UEPA79WMhhNE31AVHgeSYlKXFO08MEZvCCG1hcWoYv+Pdz/D6mX93OPsKseqPvF4Hdu/++vrXZSVXXvvTeip9cUQGk74hhkBhBLjP/q65Vsygbu5rZU9WDH0/khtC8uuNCJhbFMUIcGWgLCfQD4NL566E0OVMjBgSIC4gASF42juqPtixsIV88KrvLchAPAziKxq8SOUzE1iFmMBUO7LpC2sojKEoCmzqZYIPI/s0Rnm2jRJmqNGipiyMZfAD/dCzbbY7TCMTd1JNWKsa0vv1XhSguU/TGqzV7ILnNNu2oWk6YmQEiXM9aYx4orZdl/xqHYvFXLzx070eBrFBk/09jrZpRlth19+xpWnaRogrCa8RsDP5WYcoVkIZX2EH+sr9SPqwNLS0piTgGfphJBiRfr5KgVfD4EarCcmGkeFnCMMI6GewMQOv+XPFGF9RQhmriGFXd+V1JnveIGFraa3I+7PyzCvNMPRjzpROgKy2hrqyFLak61tCWiu5H57NZokR3ifg3aO1wiZGbtd1I9M2RoHfej8kv+9kUZQC55RWdMlir64riqKk63ucG0b8J3ghZJEHRcjzG+KuR79LILOJSZs/r8lB48nLORBxrhccTmuyV/cfe/1Jg7SBSDTi89j5js4FJgRKU5JNoV0U2XE0jnVoeN7esFZB5K9+GJFWW1qRWwRPTnTOXqsikUnmLDEmGrQ8sMZaur6X9MoIXS+Jc5PpFO89VVXtEPIgh01Mh6ekeSLTkDzxy218noAINwGl4Pb2hmZ7w3x6iAmBIgaOD+5hTEUMWwFoYyQqKQjlBtt0WOcHLORxePrRyQ8oyiarlCQC+rh72CJAnkDymjE4CdyNpEPxDrsIKf9Qd4o90jWNAoQZlSQK6dDK3p8ZtFBKJfP7DG9IIRHIzVuWAIsHWW5sNXIv0xcLe8ZqZocLurqTgIN1I766EfGSshJusdmsk/F6BtGTd40iSZUz4Ld75fcXY8Al/z+PAlsSA1ysW/7pX37N9fU1f/Hn3+Odt59I8qqTgkvYPBbnA7awVJNJKvCRzwHjdRm3AVOyd/yAyWKPptnSNx3Hjx7TdFuODo95771v8Iuf/QyrFW+88Yjr6wvms5KmveHZ8xcEavzgqPfmzGczrtoeqy0xgFORqhbvWPD0vePyZsN6KxIHbRSzyZR6MsXFluAcVWGT1EXuzPnlFcdHR0ync25vtrjg6QY5iG9u1/SdQ0XF4AY23ZZpVfDw4REhak7Prri8umUy3Qfn06GniAYcAZssD7ZtR+OjSDf1zq4j+/gE77GlEUacd+iipO8dL16ej6wdhRTSWkequsQWBU3X3pmEhnGTzDWYyjMVGNeKgDrS1EZAVxY7q7CLOcpIQWi0Zjabs7e3x+XFpfjNpmfDGsuQNnUN4rOo5J5Pqil7e/t0Xcdms6bzQxoUBZS2dF07hmmJP7NIZFQa0pzeXhGNHA5ucBgk6MOUYsEiAKSVia8yROVQKjIpSzbXt9yeXTKp69F8n0AC7Bn3sZim8U65URJXVRVdJ0VMVVaEwdMnj93FYsEwOIzRdF1ioSnNetuKgXtdc3u7FjZyUi5k25OQdqNvPHmT5WLJz//1V+ztzXnvnbf5+e0NfddiK0n/zYXBdDLh8eNHvPj6a6KTPXx3iGq8T3uN0SPDUlQEaeBnDIv5Qg7+wVHY9LnTQCimRjHvcxFhLLZdKyCwsncKetmPfdjtJz4NnELc2baIf9vdRuGu/PuOBD8Pm2KAqsQeLOm2A3oYcDHQRlgHzRQBr62GKnu0pfde28D16Zc8+vg/8tHHf8Gv/vm/028vePblZ7zz/ke88fhtLs6ec/XFZxwvjvjwgx/wk1/9mAPTsLSWzfUV113H6brhjYcPeby3pL264fnlDZfblu+8+zYPphXXV+d8eXbN7RD54K0H3J9azs8vObm6JKB5741H7JWG07MLbvqeQWkOl3P2leHsq+c0QLAl86rgXmVZnb3ky9Nz4myP4/v3eXIwZ311xldXt9xExWJS89aD+3Qh8KuzU7Z9xBuDMjvWRZbQvTJwy41S8glO/T1aiWd4Hszm+0L6N5kpl4cJ+f6M9+3uuZEOGacVKz/QuD4F44n9SWZUKKUpbSlhg0FROphgsAoear1WAAAgAElEQVSUKVHKcHt7w9B1RIKE2KQU+xhJjKOYCnFh2EQCwTnxQnQBpQ3X15cMvqH2JZcnz/nlz37C+9/6gPe/8wMoZ3ishELFXPDL2Txoy7YouDQD+w+fYL/9Hc5+f0YXxQqgjD1T17LoNtz85uf80+nXfPnZp3zrr/6Wex98l6Kap4BBn5hQKgWe5iY4MZvzZZUjG6ugb1uCnxFtkRpQT7PZUtaVqE/G+YfYJO28Ynf3Ru5ToFldcH7yGX57yeHeAWURsfaIrluzWV3hXEOzuaHrNrjYoEwcQVkZassgBSUkAOfTeZCKntlszu9//xtWt1fM6mSZwjAmBqtg2NvbJwRHs9lirWG7WeGHTlhmTna+ISisrTl69AhMRWksIbSU3mPMHIoKGz24Qbz1SsPD+T0G1+MVzBYFTxYlIQYJIfS3xLYgloYYRZpYVzXX7Yqhj2hTMp1aYhioqhpjCmw1o6iWlMUMd7gYm86+7XB9T9dtRbLeO/xkwmRSYnSka3qsKSmKKZpAO615efoV1mjqeopVmsEPzJd7ONfgfE8MHm3Ewkyu6c6TO0aF1paqMnhjhJ3pMyASpW6IEWMCkUGGgoOEBxa2xA2eejLHmhq9cdwoaEPgqCgonWfrxC91iIwNkyRPa0pdpsFtKc9yBKuLcaAqz18K/FHQhwGHMI2N96k2NaybDXZ/n84YTp6fce/PvsOkWqAfPKBfXXN4fITSmtvbWz76wQ9RMXLy/Gu2zYrZdILrAkXU/OL//q/c/vbXTBRUlOghMKzXzO4dU1QVcetZNY6+6zhY7lOakuQ8kbYwhY5I0JDLoQ0qhQqrNJROYTP0I6PNE1GVZtUF/u36kk+6Ddel3I+YmJPeB0JZMz18gCqm6BjofEfbrtBB0uMLI/YEqpoSXBhJFnJGK0iBOs75NOCW59qNNaIZmUpWK0IQC7bMrhXf6sTo0wLuutjj+x4zlcF6iJGBiMaymO2Jyqnr0aYQVaUfUNHjlMdYAVx8qkkkgLRN53ZHJCaGtQUS0FrIoFpk0ioRAEQy64MbG/fM0FaKO8QQk5jiGqNUCnbT6cxQyZM/Eq3DxIqSSOx6ohpkIGiSrDpJ3NPcl0BWUElNjBKWJlqJxVTIXrVhZPpprYlZUaqEYCJnZZKsZ3JNthxITG0fcz+lGIIbCQXaCHHH5/cVZW9Fy/4ZpFGTPIYovXIOzAoJcVRj455qqHxgIJ/bplCfoijEesMYVPTJKk9hy4IQN+k9vaq4eB2AvQu2vv5nd///j/3+9dfrAJdOXpu2KGEc9sjAKwSfFG8J0EuEKFF6hXEoJMDPHTYxiZSgVAqvFNsxrfXIcFRapbUZx+A4Y1NCPZGIEHJyiHIMUXqtVEtm8NwlObkPAZ+CkUNixOd7bbQo6opCUA4KS7bzQkG805/5RFJSUQKnykK8TsuiIEZFn/qHrJoBkiogqRsNTKqaui6ZTae0XSvK1bTt5Xud2aVFPUMcoyRPYxgGlBaLgxAjtRXf0slkipsNKZtC+ngBhwVIXiyWQtjrHU2zHVnDWktwvLWF7EFuoGmavFKQsDNLVVWADFN6N6C2W1lzRsvzEo1I85NCY+gFfAwxKYRSGJpANLmWEqWC7JdCrHMJiO/7PilPpV/bAadpT0igqsuYhUzgZC+L0Lb+Dugt56TzHu0lqFpruaYu2RRkhm9RFCPeM+51CQsrtJwhRu+C7qN3OBcTszjfQ4iIyqaN8j2rqqYoRFGZ/bGV0hLcNp2N/VVWSOZn0BaGoq4pvYSZOTMIMBu82PYYRaElRyCvO58CGEFsydwg9jsx7GxCInIdyiLIs+zDqN7MeFnUEaxGRY1VCq+1eCP/O68/aZBWAcaWlEUl/rIx0IUW4aXIDXNegCAfPV/envFidYvPi5osu0oS03Q4hbRASBtK8BL8pVVi4iXgrjSSUO6DJ7vVoSJmUgM7j49A8hRFMToU5smk0kQViEnGmoO/jN6FkoQYMErRrG/ZXJ3w5v23pPgxhgdH95iXMzabS5maGp1uukwbxKZATuLckJpklE2MyRA+FUNaGGcxpsmrdHeJOi/eeUopqroepcB3pwTkwzcyJlGW2hKRJNsMeu98/3LyvIAbOu7eI2QASqdDXz5DDuCRg2RXROYDWaHx+e/FaAQXXAJVNb33OKNQiwmTuqK5WeG3Ha7tMdOaoe+TN2GaJMbMbMt8A/WKZEnBCNblDZAkNxjHuxq8taxcz798/gVPX77kB9/7kD//3nfYn89RXhpEKZoUs/kCpcUfJ/j8TeKdn5iGCTHio6Ksp5iiYqtWtKtr6nrGMAycn59xcHzEpCh59uxrXrz4ijfeeouD48fM5ud89dWJsJ61om03DK6lsArnFUMfGZynu+6YTyoKo3Eu0PcBbRRVUUBoE0tcDh6joN1uMFbTtrA+WXN+ecvecsGmHYRhoDXWaKztOD29ZrnY4/a2odCwmC8pbEnTe7aDYrLYR1UlpioSmCGAoEqHe9d2nJ3fcNv2GF1gIrJWSf54IeJVBral8dBW8/yrE84urqQAVdknT57Mvh9SA3ZXypQn3D4FGdxlRCS0NgFzppDgHF0Ypkd76HlFrCpZx31PUIHNZs12s00FiYxl5pMJ1bTmxclLIMn50wOjlOLJkzcIQ6TbthwsFpxeX6GBvuvBeAbXATvTfxVhPp+Phf/ae5QfjULS8yuHf2ELjNWURgz5jRKGT2EsU11xcfKC7nYrYHCb2NZK0j592jvrumY6rdlsNvR9z2a7Hs3fh0Fk1EZbXJB9YzFbUFQlXbei61q0loPz6PCIL796RlEU7O3t8Xy7lVDHdHjnwQwE6qLkaLHH/f1DPrEF3bbjl7/4Vym+jMZERT2ZMDjHMAy0bcsXT3+fAroElNbJp6ysKow2XF1dicdkkrAc7B+wWq3ovQcf2G42yWMyYI3IWxSSctp10pRl0Mdow6rZsu17ijIdsion7yLDtwTmzedzALHJiYkVEQVoz5kIkBkpO+laZryEGGVwEJCwwbqknE/x1zfM6glh8Ky9eAJGHzCDpgyOopA9LvhANLA5f8Hv/vUnPHr7G+wfHnP+4pbNzSUvn37K22+/zWp9i+saXn79jO//7f/GZtjy2W9/Shd6tt2WVe9559EjHiwWXF5ecHFzy3Uz8I03H/Nkf8bVxRlPTy7ZePjmm084mpWs17c8Pb1iiJrvvfcui9Lw5VdfcrppcAEe39tjZi1XZ2cMxuDrmsVkysNqxuXXp9x2DXoy4+DgkEfLBZfPn3HerrkNBQfTGd969BAdPJ9fXWFDRPg4wrJzLoDWBJVkRmTZl0rArPj0eWJKlk7MgTxADGEcqipIQ6LMAJJmM4d2yv1SuQKQnxUVuiygtAzRC7tdjl0ZeqJQeQKfLJyUkuA5YSwqWu/ZDh0PlwdMXIXDM0SxuojjqZXeF6B0IV7Y2oORs9mkv9t2DYGBr599zm9/+TvefOttvvvxj1B2gvTfEtAgx25q6lUkRDCTGWFi2fQd/q33aN78nIuXN6McOPrIDAl43ZxfcPaP/8Dlp59z/NGf8+4Pf8T+W29iphO0NpIk7AdRwKQ9Vgrx1PBHCbGJznHy/BnaGA6PS6zWDDFSlTWTyQxtC1QKQANR1mQFQvYli6lGUwTWNxe0t1fY0CebKEMIlrKqKKt9YnBcx2e8PLnEK0c9m+E6R1kFysJhtcGLOTom4QVVOaGoFFdXlzz9/Rfcbj/lwf0jWRMaFAZjNOvbNRNKimpKXU1gZvBOGjyTWIXKyt7sup6h90z259x7+BZ1UfEvP/tHhn6DVufECN73KBwqNet1PSMSabsNZVXxznvfpu08TXtLXc9pmi31w0cQG7Y316yuOyKGajpnNl9gdKBXDUPnaAePrRomc0W/6RiGDdpainLCdLFgu7rm4vKW+WzG3vGBWGf5gb6R/TwSaIeG9eqKvlsxnUyZzxcCICEsMTXfR1mNGzpc34mHqPNSnxkrPr+pBNRWiZ+6gxgK+taPoIC1hrISBk1E0/cdhe0xepBhr9FChrQaUykGrbjsPYpIpQoqPEOUMyUP2KR5Fxa6sJQ0u9Fces6jHof8MQacH+iHjmjEJ3rwjqZtOP38Cz765rs8/fVvsdMJ94+PuL66Zv+NY7xRzI8OuW0bZos5z05fyDXpHV9dX/KtDz+g73rW51fM6pKz7ZoyFigjsvtKG6IbxItXwW274pOnnzIppjy89wjloRva5DNcyHqMOdzJo2ORhhDJh9n7FMAYx2FJ7wb66NlEx28uL/j59RVnhaEvDCidfN4dLkQmR0v2ju7hfcSoiAqe9c0tQ78l+kGyIdDYYoLJ56uWQCQdNBhN27cj4zSDcCK5lfyOoMRDN4aIGPuIHylKcgyUyH5SYJCn84GtH3DaMPgAMQiTy4MJntu24WZ1hbWaPgEbWov8XEBbz7ZrBbBOoDXB44LUZFQSKqQRdlxIDCqTgHxpvIJ45iYyTQweFxQgQJJLA/CiKBL4kIA5n4dEIQWQiWetWAVI/dBHAT5VpTDOv2K/Y2y2vJOeTLJNxCNUmxwanYOn2b1fJcC3sclzMTD2gPKF0pfl6cRI1hvrI+nZtFGjFYaPaX2R/5nYKciRm1UJAiq61HsOGRTWu5wVn+yKYrwTxKaEhYdSYHQKm3UUppCKWCmGGKCwImr1vNID/IGN0Z1f775ekbi/9u/uvu4Ctq+zamX4LvL8wQeUDxRKQSJRFYWcc2VZEYIMEIzJtkuKwcnIQK6JQRuxOTTGUJQ2SfOlvtkpaiXk2GqLD06A3qQuzWxkElQrb5pkPZRAWSfEjLIoBIRMn08pxXQmYFg/9DIYTgQ6lZrnGOQ8sLYcw3eN1aiqGK+R914s/IzsqX3f47wbWb3aCmgZYxiVaf3Q0XaiOAu3QsApy2K0k8iLUsBgErg8MPQddmoIKhN+ZK36IMrDIWNKvQwYZtOJAOQuhQGnaxPjkCwiSqy2WLPLR6mSp77Nnq1qKjY6ZEBaoY1cG42oQiaVDGP7vqcPco+N0Rg01kqwlDMFrvQMUXpAnQdXZpdLEX1IxBm5t0VRoKdTsYl0nqZp6LsuMepF1VtVJdaK3ZL3g1g/BfHoVhpIVnPSG3ncyr/CbC3LMtUe3Y7FmnrvwpZUcWf/Y5Nfdcz1NlGwrCiBg+LdLWCvj4lYSMQDKigKLRZfwzDsam/AWCHcqJgZ4PIMaCvYhbkb/IzUmmVRCAnJe2JZJnZwCuNLFgylLTBKmNCCtwnpR1thnrvB0w0DBA8xBdsZm1S/8sxn9Yj0uUAI1KX8rGHwGPXH9xH4EwdpUYqyKuj9gNOJhWQUfZIsRwLBeAo0jXY8HW65Cm2ic+sRtZebmI6B+OqELJLsAFR8dSqoFL13GBVHaZ5SBo8wBX0QMFQa7OSfklLM82aSPUR2UggSE2Q3nRPfEQ9a07ies8tLPkT8M4bBs1/vsV8tOLsJRKtSkyCLsLTFGISWzbPzpChPWzIjJm/yIU1xYqL3iyQtfcYQmUwmzGYzLi4u0nveHVgZOAiQUmFlOpDNuBX5QN4BmiE9iKOslIRN6Wwpcefr9S7p/I8dmiOAma6h1uIFqc2O3TR6eWqFrgtmaslgt3S3a4auQxlhH4++RHkam+5Tbu4ygCtrJB3mkXFS+KqcRzwGVSmeT1et4x9++mtenJzz3W+/x/vvvklVWdQQqaoZi+UBPrx+bXOjn/2b7oD8yAaz2N9nWtdcXl6w7T1GKxYHR1TWoC/PCU7x219/ynL/iG9+8AFH9x7wu9/9jr7fcH6xoe89B4f7RBcZuo6yKBmGntYNdC7i1z2H+3vc2z9iUtesN2uarpcpfFHio8JHSaAtq4L5bI+u6zi7uGa9bdmzBQeLJZv1hsE5JtMpe3tLprXG4plMaryyeCJ7B9LEmqJKk18jcnelhKWp4Xq15Xbd0neOspLUX4JMkmUNJJuNGBOIr/AYvj49p/c+Fdt5QpgmwfCKdw3snu+7z+iueNuxnLVSwrCcVkwPl5j5hJhSMiVB/dXCTMLoUkHmHMZ5qrJiUk+JQNtuRxb1V199Rdd0BO+wRjGrJ3z4/gf8/sunnF1fyr2KbmxaFLDdivw0D1Tye67rmr5vCQSCirw8fcEnn/yGe8tDFst95vtHoKEqKoxSvPj6lM2mZbG3Jwe3UolNbdBx59XsnCgHfJL1l2WZ5EJwc33DbDolBGGWLPb2uF2tcM4zny9TUTXwxdOnKK1omoa267CpoM6sDh+ErTg1NSpGri7PeXL/mKPDJaeXVwxeLARcZkWm+5X3l7brpCGNChWEGRBSAei1H4uKuq5pmobr6+tx38x7QC5YUVkOxyhdyV+TmSMolQpfP34PkZFm0E4nSZal69uxcNoVxvzBfnL3zMiggGLnh6zSflDvL9lsGvkZBvrg2OgIrqfCUAWNRSb/MUJwjhh7Tp5+Rj2Z8vZ7H3B2cYLqG65fvmC5mPHwzTf57JPPWN9c8at//f94ePSYi/kRN80VQ9C89fCYe/tLmtUtZ7c3nG073nn8mLf397g4O+Pp+QUbr/jw3Te5Pyu4uV3z9OyKNkS+/fYT9ieK5y9fcH67oQ+at+4fc1DXXF1dsSHQKU3pA/erOdsXl6xdh5pPOTo84l494fzpU15srumnU/b3Dnjv/jFmCDw9OeOi3TCpSvb3Zly0LdsQRZMapNBUqTGMmUUCBKUp0NRlxbptCEaGh5qdz9vd1x+wbeQP/+DPx30AOaessSgnDVlI9kTyj0O6v5pSK2wIeLTIVqNBR4uLHV73RBPo6XDK03qRVYufukoNm+yBEsYiz4XVMvSSn2XYXyzpVit++uN/ZH95j+/96C+xkymDk0Fi9taPacyagRqZJxWU8z380HO12FL9+Q9R646bX/yaWQxo5RhWAyrCxHn8zZp22/L8+oazz/6Vhx99xNsf/4jjt79Bv21ZNy0PHj9Jj3AU5pOShlpFTfAyjD84OmY2mRCcS1ZLBlWWu8EIO+wg1z+v3zejDHEY6JsVhBYVewHDkXCz4FV6Tgv2D9/kjRjovOX97/xHzi/O+eTf/hvBnTMtM5sIlDYYC6YoUAYGB9umo6yKBJJIMrk0jmnPSACNvMeBrmnROkjQjxYpf1CIb5wCaytm00MUgdl8ye11Q20Ng2vRDCgVQAUBVtgSg7AVrTF0W8d6O1BOa/YO99hfPmA+28Pi2FydgFbsHzxgMn8IGDa3L3B9JPSSPF3aAqs9Xbfi5vwcpQ2zxR59WYiabDLD2pKuc/RtKzYHPmBsSVVNaNstk8mUspA9qCpqWrdh6FsmkxprpMZqwpou9DIcrgqUDgz9jo0n8liRy0owkMZrJdkK6JHFAmIdURhhYqHkWQ7RJfddOTuCUjg0Z8GhlQzO95VB2RIPFLk+T/WX0dmWxgljUgm4EYNKtl56ZMwX9QRDBcZQ1hWzquby6Vf8+D//n7T9QFCayWJJ6xzNR88oFzPKSUUzdBzdO2b75VPWfU/bO0yE82fPKcua7e0tj+99gzcePGb99QU6kVa8H+g3a/ptQ18VXG9WeB84fnwPbSx927HdNpS2YDIR6wPnxRs61+ZEsT9CybkXkE5XG4NJPUwAXt7c8vPLU57qgW1Kd1dpWOUDYCqO7j+iqGtWTYOKgeL/p+7Nei3Jrju/354i4gx3zptjDVlZJIsUyRZEUWKr1ZYMw7Dd/WK/9Zu/lT+DDQP9YAiGYRtGq7stuN2tgSKpZrE4VFVmVg4373ymGPbgh7V3nJNJUn60fAmiqvLevOeciB17r/Vf/6GqOD4+JfkNq9UtTeUYfJQgoRRJIWTma2JAicS/kma6sLxMBm5CCAx9CzF7RGpREhVju7I/F8ZtpSH2PdXeMfrgkKG2qNZjc+8Wkicaxe1qycXlBd4NSCQ12RZg+9ljGMBI+GQuEinp7v2wQQePUmJBV9fi0RuzBB9ETedDIHiR10rfuA1jSknqqRKgUzxEpY+DkLwMzMhKxspBNOLRXyTbwyCBrCHkKWAg5n1KIbYHiYC2FoNGKxlkFvu1kJ8jle0P5DMqgpfQZgX5e4zkllKL5jY49ysSfqSVyPnJtk9KITWZgiHIczzW2YXMk8rAUWopYeBJzS49osFmj3OV1SIpk57QQtYq3psozYCwflMeyAZrwBrIWS2/CYj9+75+U+9Xarrd3/Vr1ki8gwPA2Lur/GdaCcvcGEPlnJBQcmitWIdZrDNYW8k5EuQzqgzwaCRIrPiG776XGCPeR/zQje+rME1loCAKYGOMqPWyQldCk7cqnV0LtsLmLKFNdVWNXq/B+/Ge7ebnFIZm6IKwNJXCWiOsQluUcUL9j0McX2/3uR5VvPlsKLJ2v/Z478Y/L5iErK9sl5Dfy+3yFjLYbBBmZNjBDoYc8htJWbG7tTorKs6yB/ggz6WrHDZtJf1t24LqRNmUr5kxBpvBvhgHhrwv1MlkVrtm0kyw45Aw0uf3XFWVDKdSynJ5L96whRiSEhZhvdfG5meyKIaF2FbNpxzO91i1G9q2HfGSErrlKkdVyWtIwPkgpAVjaeoJiRzEutmM170AwUox+s9WlQSARmAgoGK+74gveYpRrAbU1n4j71IMGQxOKVsmRS+McGvooyeoSIj96FMOQqIxTvospSSjqtjooOSe+eBxrigehOQXc1hkjEK6caZYi4SR/JASWJMtBm1RVEvovcl4knOOMIgVqQxCI3XlRFVhLW3bCeEq76FaS5/ujKFv+793H/oHDdIqBW5SiceNF7q5ci6bqecGyihaFfnZ4g2fba5ZaJE5DVmy56xMmIMXFqqiJLbngyU/lLsyyEymkYmQB+NkShBiyB5AWsCXtN28Rp9Bk+UcbAO0diduhYWlYPQrRGkGrVnGxOcvXvGD4JnMGjbdgMVwZ37Ir14qoi2bhEzDRzr/zsRZoxi6fpTQKv3Oa+b3KTt8NpvWJhuzy8GyWCzeer+jIbmSKWvKck2lsz1ALhyK1UKIMT8sCZ1UZhKD7BbCIDJsNz1hMOqt7cHOIWhyamnKYLPW5fW309dxE44hH04KbfLmXBucm2PnDTeXV9AH8BGd8iGmtiBIec1y4L578Bpj2U4cybIUnSXroBBwEWVYe88vnr3mxdkZZ+fn/N53vs2Du/eZH96lnszwoTCNw1vrw4xsjjJZZgShlFLouuHg5A5+6OnaDRhHNZ9zfHqP5ANv3lzy/PUb7t495Du/8zVOj+Z89ulPubi8Zb3q6YdFtslI1Nawv1djjABw0TasNy2/+NUzHj64C9niw1UOhaLvB5QR6UwiMfS9SB5IWFcLYKSiTKWA09Nj7hwdsDc1rJfX2Mqy6T1DhNn+QQY2s+y/kvuvMjjufeTs4oZ1J74602mVwVM5AMjPsVYKXYwdjeX8asGLs4tx7b4Fsud1UqQvMRVrieyro40wrvJzWzx1uk4YE5Lk7FFNhZo2UvAZLUeLMnkIlNBK9ifxwzNApBt64kpSxLuuZz6f0dSHXF5eMJ1OmU5mvFwsODo8lOGL99xe33LvzinXy4WkRfpsZYIwzcoaHafTmTV2eHjIar3kZrmkDz0vXr/g808/pVKG6cE+Jw8ecrh/SGUM63bDZ5/9gnoyQxnLZGKpXMV0MmG1XjGbz7m4uCDGSNvKRN8ah7ZFri9punfvnLA32+PNxRl91/L61WuSFrbvMAyjGb+EoxZx1bbQhbyX5HvkSVTOcLVe8O/+9q+4XtwwxETTTFBa061X433p+556Iix5rXIwRRJGaZ4U0a43aGvGgq8kh4ry4G0/oBJ6plSxUtgWpuOEdgwFEEuDlNLWj2kHXAAZItxcXwuQa7Zea4XFvT3v1M4/t98bgfmyB1jL0LZUkwp3dMD12SV2CNRW41ViMJbbFKkGKWQwhvl0RggDyUecTdzcvOHBB9/kO3/wx/ztX/w5Ztjw6uVXvPfxJzx89AEvXnzJ9Re/YG5qnnzrW/zkp3/DUW0xMXB1ccHNZsPFque9+3e5f7THcnnLi6tb1oPia4/f42Q24ebmki/Orlh2gW8+vs/pXs2riwteXS8Y0Lx/94R57Ti/vGSTAq2GCsNp3fDq+VM2oWN+94j7d045shVvnn/Jy2HDup7w4b1H3J9NWFy84fn5JW/6AT2d8LvvfcDJnSN++NUzfn51g1f5mUw78sa8NrSVwMu92YyTw0M+f/4sSzW3TdZbcsdS5CMMfQqpaLyPqtzIsnOjkPUc+kEa4Jill1k2VQZHBmisEwZp1FhlqbWjMZaz4Zy//fKv+LL+OV5HWtPRpIkwf1V+DVlpaGOpqloYG6Gwh2VY7WrLbDrlRz/8EU1d8/jJh2AtPjNfhAWegG2Dt3MwMsQBrxJdTHTTGfbJx3zYHLNIFW/+7t/T4Dn4YA/fTTh/dk6FJnQDZmXQr+BsuWa4Pmf5jcdUeycc3vsA228kSCsjmKKgyc+AMUz3D9k7PMYZw2p5C4gPd1U5jHW0g7BGptPZ6IW49XHe3j+F+JwO3QrDgEYYdSlFlJtglCP4jhQ9zjUcnNzjZuW49/4fcO+Jow0dX/zs/6ChxWrF4mbF3nzKZDZDGU3fD2w2gYRhUteonE9g3YTZvGIYujyYTvi+5fo60LYtKXmUsdKEGJc/uzRfEc0wtBgttZarJAkuEairQD94UlJjMrTWoCuNcpqUHF9+9QuSUXx4/BEnd+4wnewxDAFlptjJIQcHM+YH9wjMiSGhzS3KrSD1aCXqpjRs6Fe3tLevcZVj5W+pp3NcNSN6xaZX7O/NWXYLhm7F/v4exmgmkwn1pML3NUPXUgK3Bh/ofcCEQGUde/vHWOtEbq4TrjJYp/E5kDKliB8GVpueFMEoqYqMVihrIQ/prVYYMlZtcvWkGINYxLM4CYM316CdSryOnhYIxpKqWoZZSc7pohaz1knCNcW/fnsOkwFcowzGOlKlIDlCMtTO8sHjJ9w5OdPfDpEAACAASURBVOD84g0z3eCHjv76mioEXv37v8Q1FbZy9MFzUddYDS9//jldSFwNA11SzOd7NE3N8sc/4c1nP6cJPcEmXDKk2HN7+Yb67AVHTx7TTGqOTg6Z7c2zKm0bsKK1yVLXXEMlP37eEEV5o7QSNQy5vs9nm0+R882Gl33Pam62hIy894WkcLN99u/cA1NhXUTFgFaJ+V5FHJoctCbXbsjhcEOQ9PSmbrh/9y5n52/waZtMnpLYC4htWcKZ3HtFDzGglaPrJK9k+8yDTTB3FvzAw4ePmO5N8NazdzTBr3s6q8Aa5vMT4vMr1jGwGnraVS8AmS41uID/iQQ+2wdlawWTpcApglLibaxzHzUM/QiAqFwnFRsBlRgT7gtA4ep6BD1GWXIGSkPY9qRFbaRQJCW1pXOiEgq2Iw0D2sHQt+MwXXo3sTRQ2UjXWAdBGJX5EMtWEkJUKiCzLHGRuwtjOit6dggJoLJnoxXAXUu4twQZSM23rW1yyJEVENfnmg8FKokNWCKN65QMyOnR81GuRVl3ykj/pbPloIFsPSEMXAGmIWFAG1w9RWtLSm9bzJXr/tvAkt/0528N7d8BaH/b3393mOuHnuCdAKMZIA8hkIzdyqRzHybKEIW1FbVzeUilxu/HwNj/F/sBuYFCFNg9G61zuKpGZ8/vmCKEiLMVNoe3SVCS9PGFsFDyZwpDN8Uo4XVJAqU0OXTQKBSC2SRtxj1I5N+CQcRcQ/c5S0RYuPJnu8FmwzC8Q6TZ1ua7pK5EYvCK1XI51vQaRd0IsaQEUMUkYVIRJbkFSgZXVZbkJwT0K8SSgkmMYWdk64782oWdueu5Oq6BCEoPbwHN3nuh/AtljhjB9x7fb8TrVAlga7RY05TPNwzDOODXGRcJKYGGFISQU66NzSrrlIRBLWceMAjG0jRTnKvpewEOhz7ghyj7kRIliK6ltxUbPzPaOKhK0biarhdlodFmBIqdq3BOZVuI6VvAvLUWU20t9Yr6USnJi0jGZuumilobvB9oh54U1Dg8ImN5PttSBu9JRPqhRXUSGq4yBlR6PGMMLg8V27ZDaQmlHG01VVa8GbNVQRjRxes8MHtXWV5yYcT2JU/orQCqWstzUXKHdEpM65o6B09TcEPvafseo4rxw2/++gcN0vYp8kW3EC+gPJ2hN3nDzmmFKXDdr/jLV1/ymkhwRiaEWhanJLVq8bsxKvvG5hdQQAZfUYoqgx2kNB622oi3Sz90QEkyBFPk92o7zSuLKIYwyiXT+LvKhp5QtiQnR0qwTdKGLiZevnnN7fUF8/0jrAWtE/PZFN/L1LcAg8VMPCdYjR9nN+WxbAJvsbTSr4OvSYmZvM6QVcyAQymSigmyyYuOtMM+zRts8ZoVz5gsByWHuqXCZhYmpirgao7WS2n7XoY8XSlMhgJQvEWN1+XzShFfgJZyuBuTfXpjoE8eZQTYmN8/gXZgc3WLb/ssR84M4/j2Q/Ib2bIjkGrHQ0ErQ4yDXNZsjqcUJKtpo2fo4C/++qc8/eqc//Sf/lO+//33icqhdC728roQmv24KLevn9/bVsiesHnibivHarkk3Cw4OLlDVVnspEFXFcPQcnN1zeP3HnGyN+Gvfvhj9tvEatMzaRpi6klp4M7JHQ7351ycn3Ny5x4xJZ4/f8nnX/ySg4MDkQN0cv9DjEynU5TROGvk8FQqy9kNXe+5vNrgXJWBEA/Bc311g3MG6ypiEua1FLAU3F4YmSrl4YLl9cUVN+ueqNS46SfEV7gkVibv84BFGAJKaZ4+fclmI+CdMFnf9sERU/vtfRa2+xbMBYUPnhhiBoNlUhh8oOs73GxCtTeDusarmA/V7DuWGIsRZ2wG7+QpLCF63kszdHNzM8o+1us1vh949OgBQ+9xrmITA68v3nDn9BRjjRwuKqcC54njLrvdWpnmee95/fq1TA+tyMUSniH0+BC5eXXLq7OvJJyHhE8wnc95+Pg9Vu0G3/eoCGY2J/hA3/fjM/nR4ydcXl6xadekVDx3JEH329/+Dpv1htevX3F8fMyb8zegNIvFTd7nNCqJb+zBwQHnl5dZHiX3wGqDRg7/ddvSpo7BK1pUPmgtVWOkoe17XFXnAjcwn81Y5rAABUzqCZFI13YSSqCM3NMoxUYxnJdn2fxaYaUo3kgCJVeu4uOPP+bZVy9Y7hSAkkhtfm2f2GXGT+oG3/cYZ9G2oeu78We3exrjn73971s7jjKoqeqa/b09zoeBQYHfn+JXa1iscEAXxEJGBY9KAaUTqttQGYuyCoywMTarG64u3/B7f/SnXFxc8vSnf4Nd95w9f8GHT77OennLZr3g+sVTPvzud/noo4/54uf/kW7oCDHS+cg3P37CgTPc3Fxycbtg1Q584/1H3J3PuL2+5NnFDeuo+fjxXe7vTbi6uuGL11dsguLJBw+ZuoqX5+dch55UVRzP99jXlvXylnXscPMJR/tzZinx+ssvOB8WdPN9Ht17wJPjQ159/iueX1+xUJJ6/snjx5xUjqc//zmXl5fUtfhJeqVQlctNRdrK8aLCKs3i5oab60tU5TBK/BkLm2m3qcrlAjLUKcPPne9t795YcgnLLMlQdBiwScI+Y2brjmtAKbSTvUlpy97hPpP5hIOjQ/o3L1jGG57fvpbmXUWO9IwUAtjc1GZwAhTOOAxaXETypM/ExNQ6nj17wd379/j6154AmtubSw4OxdZJfk8eWObiv6ADCRh8z+XlOSloonX42R72w0M+/i//OX89LPj8R3/OvFtQ95E4BBpnscGju4CJG/wQ6H/2U7568Sm9duj5XfY/+Jh7jz/i8L0PaA4PwRhi37NuOw5P7qIrR0SY872PbFoJRWzmByRl0TqS62W2AXzp157pSCKEnhQ6ou9Zdy1KW+azQ+48eMJs74ib6zdcvXlB110T0SSjWLQbnJ5y+vAf8fnPf0jkFVppri6v0Arq6VTOr6hpuyANdNXI/VaJyfSQw8Mjrq4vcg0xCIjnxcZoOp2jk8eYLJNThuh7Ou9zFkFNt7okqcTpyQEHM0PoW9p+SUgSMjKb70kgjpeQIltZZrMTGbLtT2nqQ/x6xXLTY9QE5xrqeoJxU8IAy8UZlTFMK8e0PqXtVsLOXK3wfUtoW2ZVxJgWg4cuYLVheXHN9eWak+NDJhOP9guGVU9yho0XADUOA2S/07ZrZbCsoNt4mMwEENCW+fyAvl+LhyUaWzdjwGhSWR6qFFpgIGFfKQkd0dmqzOgsAVdDzpnQGciIaCUPg9Uwpi8k2CCC85lSUAmTS/aIsk/kxlxbAUGsqJ2cFYZMzHJZfAcmwqwiKMWwiQQs06MTDu+fwmTO5eUFe7XjZH8fpxW+b3MfExkGj7MWpw2+77hub+kXa9zQUy1aun5g0Q+YpOgTJG3FLxfNpm95c/YCc7xH01i0Vdwub2hmFgaRbda1ADJJqewvWQLZxE+y7dfC4rOZ8Zgl4cYY1JDofMc6BQZjUBhs2g4RA5FgDXfee4/m6JSBimZiUN4Lu1ppSAY1eFCDgOXaUDWaOuV8DaVYb2SQmvowNvfee8LgR/phCgVwlh23gEiFUaUQ0o1KicaKzcDR/gGT2mJMZHZacXu1YX44ZX2zoBsG3txesuw71rrHK8RqTCuxFVA6D1cN0/mMdrNh8EP2+jTZ+iazkpOE1xSAdauayZ6/MeW/YzDajkqAGCPtZkPX9yMIsFsjaK1F9gu5F9r2CNZYAUWDoVeJZGTwSPCozKpPMRC9MMOMEcak78O4vaMNKXvkpxjGmkinbfDtmO9gtnZOpR4N2Vs9kkhZXSlBRwrIdhZsk+593g+SLrVxVoEaWXTZmlbYkBS1aWa12zIIhWHw4z4QxqyZrCYpVhNJmIURTcQQjR1VJuV82DJc3+4Bd4HVd3/mXbB1t/b7+77G74/DT/ldEvAm6yAhQaKVk/2o2B4Yw+g1LOChWMIonW0JFKMdXAIhi6UMuGcrjV0mrM5ZE66oSo0obslg3zCEnOnw9jVQeUhdSAnDIJ6rXW7oSt7DluSQP7ISgkd5XsoAKA7SV9eVG4fXVVWNDM3CKi/XtzwTkgekRsZsSDLcrKzLGTyRQoard+r8EAKhFxu3kcE5EjAEw3EZ6/ApknLgbBnMic3b1n4jpUTXCzGuKOQqJ6xXsqtksQAYwValaCaOylYoDD5E2r4T8oDSRA3OGOqqkmcrxtHfND8OlGCvpqpHILprOyTgNJ9LKMGb8pLrhz7vAwI0aiWfpQDNbdu+tV6tsZjseytsbLm3RY04DsIBq+yY+WGUxlQ1A0I4iDEi3oTyRpyzNK6iqWq6ts1q7KycUBZnxU/eVbWESYZsc6I1WlsJcwTEQ1uYvSVc0rlKFJ8hMAw+h8QFIeYl0JkgFEMgJLnuKoGrmnzdGD/TMHis24aAjXtjZpAP/ZAHXDZfd5O1GJGJbhi6Pu9bomIpAy8y2z8Owha27xCF3roHf++O8v/x1yp4/s35V3QE+uzn5nNiuVJaUj9DoOtbNpUiqhqt5ALFKI29dQ41bTBNTdQCaKqUmyilRsRWEHiVjbWlULFaQI4w9HmynjJTbjtFSSmhjM0ybEbplSqTE7YbcwFVYGuWj1bitZnk4WzXt7SbG4gt2kRm+xOOTo/l9+XJgalM3gicANjFhmAsKPMCyBR/MuBAkk2e3NCZzPIL5b3lzb8cduV3xbz4C9tQa5lAhSggVfmeys2mAM+Zacp2QeetlHwZxwcfJUVzmXw4m+0I8oMy+usWf9Ay3y6TrQzolkJuBFBhBM4hJ3zWFbNJw/L8is3NKl+WbdFT/v67XyOgnbaMuZQnIhFIWoEWED6EKAentoSoCd7w5asr/uWf/a+8eHXFn/zJn/LowQO8UnifRo/ktPNeyvKM0Y//LYVAeZ9yUM1mM4Zu4GaxJMXA/UcPaeqGn332Sy6uF+zPp0xmNSen++ibFXUVqCqDdfu0XSs+da4S8/TNgvlsyve/+zE/+o+edScbbt93XF1do4wEfvgwUDuH9wOTpmFSVwxe4a1Mtz786Andes3y+prL8wusTdy9dxdbNWz6jvW6lQm4zgMOpcbGqQwVbm/XErBU5D35AG2qWqxICutAm9GGYrlY8eLlmeAL431n/O8xwR0J8WJHLlHAsAIoGgV9DsRSSqTtyhmmh3Oqw31alcRPOASsyVO+HHRhreHh3Qe8fP2Kbui3z2OUSWM58BUyTPK9hHE1TUNTKy7Oz7lt19TO8fzVC2G6kbKnUS5USsGQi+KUDdxDjGKNsTdn4zv65TIzHyL785mEuC0WWBQpp0w2k4rVWnxZow90Q8um26C1Zt21DH5gPpszmUxI6QKllYC/SZoOZxzPnj7l7OxMDvtiaxUDhf1eGK790HN9e8s2VVhSRetJjU6KRw8ecvbmjPPFNUnLQW+dxhnDpmvpe49Shr35hMViwXw2o25qbhYLMe23lv2DfZbrVQ58jOPDtCsBKwm0u01RaQrLtBySDONi5OXLl7S5ABrXUn4OVR6ejMx7JRz/pqr48IP3+PLLL4gx0vfbvy9rLe38c9ssSDGp88BtO1AD2Gw2dG2Lzcmqg9FUh3sk7+lbAZ5jikzrht4HNioxTfLalXKAJvlI36958/xLnn31gu/98Z9yfXFGe/aCxcUFr/fmfPC1j/n53/0Ev7jlzRdf8PCTb/Lq6VO6AIPf8OS9hzRKsby55Xy14vJ2wzcfPeTB/oSb63NeXSxZ9pEnH7/PceNoN0uevrlm4+Gj9+9yOHU8e3HBxXJFqBz3jo6ZJiV7Rrck1Y4HrsEuB57dnHGbevTBMXfmB7xXN7z4+We8XqwYrONgb8Z7d+4x6wOfPfuUZ6sl05M7fPPJEz776gVfLZd0Gixi1K8QBo4Aehm00MJeSPkcV3mYmMvccd/YPSd2z4tyT/NiG88oeW5zU5RKWFmxYcq/OwFKmEVRKdap59OnPyNdJV7dXJDqCdFGMIGUvAxaQzm5pTErPaOwBmxm7QpjWMXE0d4eJ8cnPP7oCd/9ve/T9y0k6NoV/WbFbD4hZJsEzS4gXR4foSg6V6OsYXG7oVUR4zT7H3zIH/43/4IfTS1P/+3/TntzwYyabpDAIUtE+Q1pWBM6i11B01QMV0sunj3j5V/93zT3HnDw4D2mhwfceXSfer6Pmk0wkzmqcgQP09mMqplQ1ROsdSSgMoqqyqFFb/kqKgknyx9D7OkkiGLTtvi24+j0Hg8+/F0m+/eIyrF/Zx/b7HP2xd8S2yWKyHpzy8QdYN0hxu2j1AVNU3H//j0K4132YQGvYn6mQ5LAxKoWeR2Z9SaMOgm4PLn7EGOn3F6+YbNcSliR7+k3A3sHR5imIobE9dWbvLdpJvUcNdljEg9QOmCydVMiUVXC2rZaGCUHszlpUPTdmhiWQMJ7ha3m1JOK5Cecnz/j4tVzGisenkmLjyhB3idpQAePxqNjZOhbum7JdVwxtBts6Lg9u4B9jaJns7ajDN97sb6wRgDNwQ8slys2bUs9aXjv8ccEpL6r6gnWGbq+FR9KrTBW/OQclslkIvLfPpKCDM9UDkBLIeIZcKZGaUVVWeqmEjljUqKoSN02GCmJx6dGmt2UkjSWld15lnaVKg6jHVo76noKSQK2tKvAKIxKTEKk0onkrLAIewF2vUqsNi0X6zWtNSx9oHY1J/uHVEgv44wjDIHZdIbVFt97pusFh+0awoCJCR2ieAOHxKCgQlEpRdQRnMbuz0lRZbWIous2pNm2WZfPpMbBUkoiQ/bDIFZdGkL0+GHAGfGtL/WF1ZoUPX22ZUPpzFaWHS7EiJ7OOH74HqaeMQwiuXbO5JBSaZwVkZvrM9l7MhAc8lCFlFguFqCLV2YcQ1CHzDbaDshyL6MkULjKUtSYhJ2rrRHpawKlDO1agIfpXs39j0758vlPefjBKW/OLug6T0w9EU9VWYwTr2md08dRiiEgAVS5bqizUqGENpncbQibU97j2yzLmNeRgLPWucyUzzYnuR99d+he7pHsKXHc2+TcCiSViURKyZoLRhiTIeCqmj5lAlIGT1UOnEqIrBpyAJXVKJ1ZXgYwdiTqFHaeNlqGEjGikvzdoiASX/0w7oMoRRwKy69YO4iPpFzFwn4EhdgnjKCh0mONW4BUlcHi8Tgqn0GrbNEgvaBWipiBuDI/tdZkwE7A3h7AFfufLfj4a6qZna93a7Pf9L1S+7017P8Nv+utvxszqSgzTYMfMMbl2liNtan0DXYETwtDPoRuZA0Xf9qYWei2chDys79DHinXRpe7kJ+jZMhcrzRiJ4qEH3qZ0+4MPsWuEIahHz9LCGEc8koIlxYyEEk8PY28gLFbnGX38myxkoD3wmCsq0pCn4YhB1brt67pluggZ4xVNrNEG2EHZyxmXKcZjFZKzmWdez+dFUTF2oyM32hjmNkZZFsKyTkCs8OK1VozmU7p+z7/zBZ0L5iSsZaqFms4n4HamKCqxEefqEDJeSSSeXHQN1l5E5OQuLzyEHNfUPaYJGqRmlqerSTKvdB76autgZyZJURCsebrkmAjJucrCMlHwMjRt1UJWO6DDBALsFl+ly6hYkF84a2x+bmO2wDokfkuz+0QAj4FuqFgGWJjYPJzDUIYVEo+szMGQyIgIKtgUAKzSt+m8V4yU/qhB2S4Ya3UDDH3+G27wXvBMyon4K9BaucheJY3C4YMso6woFJUk0Z8elNWiYuEG6e1sGvzeeS7jrbvqZxlNpkIlrVayu0FwrqsQYt1NjOlzbguN233W/eJf9Ag7UDkjJ5BJbogxUQbu5GFYrweNzrrDDY/IDGpMVHQ+4Ad5XxF7p8XeAYJyoQwUWQoAtaEVBogNT7wmBxQUaT3ZJlukp1LaZneRvkGJaCrME2VMdvmRymKHCMoGGLgtu/ZxIBxFqMiScOdO/eo7YxNXIIK40IVv63irbvtqAqDEKOzyX0cG5eMTgtcWtKlAWMcQ9/T9Z6S7lqAJZUB0ITIM2KUCbZJOhd3xQeo2DGofJ0VKKicSBeGYUClmAvANIYMjQFeZfMbN1NGX13ZEDOgXg7xfK3FWDoH6iBgdnkATAY2gRw8F9jfn3M8m7K8umbx+hLfh7EwKCzNbXDU9nDeguHxrT83yOamyz1ICmKejKRE0tBmScO//b/+Ay+eveJP/ugHfOe7v0M9a4Syn8CHLahewP2002gCo/xBZXkkaCZT2WBvbyPrHh59/AknDz/g05/8kG7oOTk+ZTrZY3m7YTJ1bDa3+FTR1BMq66DfcDhtRIrmW5xu+P7vfoOnLy84v1jitCYc7tN2Hp2EMWoV+ASr1YaqEpBs3fY0taNfr6lU4JOvfcCLr15we7ugW68Z2g3LVUtIiUndCNifiwBtdWZAGIZ1T/CRyhlU0IQo7NG6chhn6LpulFCMTCml+PKrV9wslgJ+lmeRVB4zYSHk/4XskQMaa3d+LkRcZWmamjYPIlRKKKMxB1PU/gQaC0NPlUROlvzWPw8S00mDRyZ0IQWRUgCVq5nP55yfv5EU2jxX0MYSYuLZ86/46PFHEgqhwUfxZAwxYMlAZ5LBSJmojpYrOg9ilACvBwcH9OfnUhjVE0zVsFiuODzYJwyBru2p6oqTk2OYNgyZheacyDx98sI8SCVUEV68+JKr6wsp1pN4AmtjCXg+f/pLFFomvwpOT085v7wkpsismVK7muvljaSkdm1+NArzXROVsN2fvXxBYyseHJxwuV7gU0CpSOx6KdSTeDOt12uskjTs4WrIrBdD7RxD19JuurxnxTyY08ymU8hFbsrPpg9hLOxDbogYt0/54FEpbpebDMZZvC97jspNf2Z66SR4TJQFF0Pkiy++zEMbLYFs2fS+sLOKYqGAsFv5ltBJ1E6BDIzsyyLvrK2BvSneB7pXF6gYCTqyTHnPHsI4nNxTnrmdYGKFTZHQ3fLFj/+Sf/Sf/Bd86/f/lL/83/4lxq+4PHvNweERn3z9d/j0059w9uIpatLwe7//R/zdj3/IXmzxfc/Zasmq7YhW8c2P3+f9vT2uLi/51Ztr1gN8++PHHE9rrm6u+PLVG249fPvJexxVisvba9ZDSzOfsX+wj0mK88srlpsl3iju7x8zq6Y8ffmajYlM7p1wZz5nrhTnXz5lET2bumZ/b87XHz5gc3nBi5tbXncdx8enfOujD1n2m1zeAT6RnJznEkwgqazoJCFjaAgpBzns2BOxtUsp4MZvZ9UUNiuj1RGZxaC1InaBru1oh5apH1AxgkskFXDBUUVHSp5OR362+JynyzNhJpmIG7KkTkHUnkCgR+yeCqupnJG2siIxHTy972gqxenxIQdHd/jBP/kT6sk+XevZm84wytL1A00UWwwt6IuoYPOHSSSUSUDAD4H9gzncLHBIuvNaDzSP7vLH/+K/5d5Hn/A3/9P/yO3z5xzFhCVhQhQPdgMET1pqTNvhlKiTBn3D+tUZ13/9Q5Zx4N57j3nw0Sfsv/ces/t3Ofnw60TXYGvFbDpBWWEJJ0XmVQqbaAhiRWG1eO8Lg08Cw1ICbSua6T4MR5jDB3z4yfeYHD9kvR4IwVNXDc38Lvv3PuT10xu87xm6gSYlQhzQOlJXM6rKcXTX4YftuiEMhNCilGGIHqsUlWuorGa5vBZQMAMsPgxU9YTp3vv4aKmmDSFekcI115fn/PhvP+P73/8jHh9/yOChQqNSIESPrWoJQbSGlALBd/hBJH9d3zKdTAXM9GGsGpRVVI0mJYtfbej6NVobFrctqMhs5ojdgB8GQvJYBUYrrJb9GQM6wBAgqpoutihaJlMjPuR+IPmeMAyktCGRGLpWVC91I4BKSDijqEi8fPoaZQx71R6H9+6J5D0qCQmeTNB9i0otQ2iJBPFVNpaoBpQ1JF8R0kBUAl50XZeZrx6VHMZOsM7RdQOSsZMTqJPm0Uef8O0fnPL8X/8bIAcK5323aWph3iYhekDCuZq6mmFdQ91M0NmaoaTeg8jdm2rGXu3QOgdZGakhfT9wcX3N2c01Gmj7Hu0kzKiyluVqzbSZ4qwlmoHJxNEng5kfCTAdPDoqnNLMT+X8j0nY+NoookEaTuNYrG8Y/ICODocWX1dTM5tN83A4AJoYEv0gapIYA0klkUdTBkcJpURpI+CL1GXiwxtBWVHEKalHU9Kc3PuAozvv4ZPBqoEUeoaYz14lQFrdzDg8usfN7SXed8SkUHEgBunpfEoklQGf4EneMLSdAANamKvWWWKS81GZSOwH1pu1DKNUVsalSOMkWTyGyGp9Q0w92hguz1+itWcYFrw5e46bHLAYNtzS4up9ZhMB+l1ViV9uSvRJPAuVh8Y24idNFCk30vcJuBGps31BAV5LEKg20n/FIIOiEFUGxQXMqKqKSd2M5z0pZfZttvVLYXzNGIeRjTX6YyuNdrWwJpVHx4RLUZ7Nso+nHL6DQgsBFxMTyjiSksR2k9IWlDNWfDqz36Uak+QFqKhUlYd6Cmc1QQlYba0l2sx+TJBlhjJQURlgTwlMATYhZuWXMSaDH4y+p2LZJNtZosjOAVtsy4CoiqBULAlRQpJRORYvg5BaybUOVUcaio3e9hz/bYDtu+f+u6Dt7t/7f/sq6pngI926o5/2BC15M3WRSOc6UFRs8jvNuOeQa5McmhUFTLXOAWZkDRoULgPuIxs6Dxb7oSN5CEPAuYo+A3PJS7cpoKgZhztl8FB6dJMUVdWMWITK5K0R59B6zATRFKUiIyFC9s08xhZzXQkLzO/VD3IelV54ty8fb3ruh4IPDGSGqBWGp7NO9pGYxNooN4HRhxEvKWpoUhJ/9By4Pg7fQwa/tUOrLTFLAPJsZ6ckVHs+m8m+2g8jVlTAXE1EG01dOQYvrNWYFUsx5FA0bTHOEZzfXkMlFhAKMNZI6GIGk0NmCpdrq7J112xvLqDhMIzAMkSMs6PfNQlWqxXD0BOT3DelE8rILLnYmvjgJaA4JgAAIABJREFUib30J/0QR4IfKHwKpBIsHRMmGGpXj89oIbONNpj53mtt8L1HG8XQS26MdcJ+t1qoMUprhqFj8N1oOxHZWl76JIOeFFMOds5WDMqOrzl0PTGvZaWRYbazEsRmDGnwJKOxzjKbzpnWNZtNR/Biv1PIFVXViNKlHnLPLaC/zXthGaZ5H7hZLkSFExJGVyidMEbWdUjF3krA7cl0KvHGUe7P3zfP+QcN0kZgoyI9gWAh+IiqLAwioRkGSeHzwaOczjhFhiu1hiTpxrausK7Gk31LtZamXmtSkaumXHXkL6XK4ZebHyXm0uOexXZiVphyFMm8Uhm00W/9TIzi26NSaeaKCbUSMDHJNG3oWvFeUmAxzKs5jZmy6DbgdLZ5SO+87zROB+UrSYr5zoQPpEklIVO57OmpEEBhWk9GIDcRiWmblDzaCYRdr1bZrIqnrxR8ioTJ4QNbY+9RWsKvH2ilENmdlBX/xgJoCPi+nTQX4FjYtqns2RQ27/hzxTNMqzy1h9V6Lb7GtcM4S+z7t+79rtxo96sUXy6z2Mp73/3euw18mYanlAgqcTO0/PjzX/D66oxfPf+SP/7HP+De/XsyqU55upoP3rjz+m//7sLeymssigfs3v4BfddxcXnF3nzGN775LV58+SvaIXF0+oCgLKcHDTdXb1isN0wmcw7mM+aNY7NZs1qviTFwfXPLpG44PTpgUjesFksqZ7hZtjRNQ9euIWZPHx9YbDpWbc9q07HpO372i19w/2ifh/dPsA6aSYWpHNc3N+Bq6roZZTsxg6DRKJSSAvx6sRrTXS0KoxN1Ld7Uu2zHcU1pCAFevjwjRmFMp3zNihxte3/V+NqlQCzruQRjTaYNm816O1HTmmpvRnN0AJWjGyR5fTKtGfpOpFuJ8T7f3Cy4vLoBJf5RKQwc7R+y3uQAj6bI3rfALkA9aXj27KkY0ettoZZIwgrL73l3XeRJhhTWpDG06urySgZUVpLL1dEBoa7BOrQdMBXUR4fs3Tmh61r84KlqaUyOj48ZOs9itcT7AWM0m82KtpPnZssElkM1Jo+rK3RShDBwfXOZvbX8mDp6/8F91l+saHvxRCrPTVVVWGfZtBu8j1il2Tua8vD4lPWzlkXfkrIfmspg1O7911qhk0jutJUzodu0OdwioZSwphOarm234FvZQ9T2+RIQJe/faqsQKMz58owXL9sts13kO845uqEfQb0hCCNNJLRh3J7fBWWbpqHrurekYdvb+/aQqKzVspcmZB9o9uf4xYq42pCIrGIgednva5u49Wu0maBiT1SiKDBJ0d5e8emP/4rv/N4PuPzW9/jFj/8dsV1z9uIlHz/5OnfuP+D1m5fcPn/GnaN73H/0hM8++wmGgSFqvHY8eXifu3szzs9e8+L6lmXn+cZHjzmaVSyvz3n++oLrPvHJk0ec1Jrb6yte3ywx1YTHD+/RrTrevLngdrXENo77x4ccuYo3r89Z6MT8aI+7k4aZ71ld3HIx9PijPfYPD/nk/Uc8Pjrlzz/7JWdhw+nxCZ88eszqasEXr79iATTW5nWqCDqviyB1QnZG3g49ooSXCFD5DvMsvS2R/E0NWRkspvwfKTeoCfAxSGGch4k520XYHgqiVQQg6kSrB/q0RmGpTU2tnNh7IBJRkSp36EbeZ9EIKMSOx2o513TyvP/+A1RMNI3j/t07bHrPpJoybfZEBhp1DkLNu00qxIfE2PkCk+mUO6dHgKauatp+IERhkLRKkyYznvyTP2Gyf8gP/+c/4/rHf8108KQhSniG0bhK01iFK8/REKi1/HtYrWmIpOevub4IXP7NL9BHe5z8zlM6FYGOw7vHzE5OmZzeYbI/x7kaV9VErUkYPIrK1CSlCFoTBckFIk3TUL3/Nbh/F2Ubqv17BCxDlHtik8LYmoOj91lev+Z28ZQhdCgjzHOS2KX0PsqzHZUECpFG321tCihvqJsJSht86ATMzYMtUiSZihAsfafZ33/Awf4psObo9H2wp1ytBj7Zu8fh5ICE+LWnGHFVSfGu6LoNfbce9yHvPbPZJCc3B5wzVE1DySBQGPz+hqvL1+IlOLRMpxOa0w+pbCWZC6En+g7v18TYiyQwBCrtqOsJ09k+m/WGMPRMJg3eR9aLW1SK9N2axe0VJE/lDFYbMAYfEl0PVWNwzZLP/uMzTOdZ3y6ZHR8RtUZZx2TvQMLTFoHQbcTOY2fwIeex1KJ9n+j7jnpeZy/AfE4qMCaiVa6zY4tiQCXFJjjuHL3Pf/Vf/3P+w08+5+L8GSg/gmnOVWO9ppAwPhDWobY5MXxHUSXepFufwkoZ1nGg8z19cmz6SGUc8705x0fHWGv4/IsveP3yFfvNhNA03CxuSUphveH8+pJpM6WuJ8xme3R9x1dPnzKt5yitmDQ1d46OR/AjklisV5je07iGmBTWOSon7Kmqqqhcg1VWgIyhE3m4hsG3LDYLATYVLFdLnHM0kzorCYVtDAiLe8cjtnxFpD8wTcP+ySHrzYK2FyBRGwFagheFYCHAGBRNPcVbK2ClB2MEEPDeY1LCKo12lZzHxpMym1fnMBxtpAZ2lSFFYV4RvTAqy46ukLwAq3jw4Qeouqb3gfVyjdYOkqbfdOgJvLq9oiViVPYwRhO6VgKFMv3FlABKcohoBtViDJKAnof9lROGf0mCT0mYxglZu34QtZl1dgSfjBEAZld2vEsEETC4AHLZNkHJXh1DHCXiKQ/pk1K4ukIpYV3rmMZ6I4XtPS3kmtLLkQE8ObsMSiWcE1C2SIBjKCw+jXIVZLuOqm7kzMhKFCFc6Hy9RN1l1LY3K3uW1FriM6yNeFuqEt5Teii9tR6Smh6Rkcv4YLRfKNchN7gjKzs3nbKekEF8DDFfw1/v196tu8rXbz7vt33M7vff7QN/25fJII9CCQPWZnVpvidKpXFdxCjWJYUctluDvPVc7tSWIffWuwQjECA7hEDwMXvSpvFe1HU9AnqSVyO2hbLvyPkWox8zJMogQhmDQ217LiScTGoS+T3e50G4VoiLeH5mo3iNii/tFnPIF/Pti5ayfVHuA0qYtwQRMtqGAAx9L0/GWLP9ei1njJHMokzaI7LTJ4TRRqcMw0udXgDIcT3zdvC5HZ9f6c+dKeprxt5dZfzFGCPD5bweSo+BEoa5hFQJAG+thQwUjuxmpUma8bpZLcQmH8XOZsQKkvjVzqYz+qEaSSsxRqxxBBUw1mCKXV+MY79ldtjM5ZzshyErmPS4XooVxWazEXZryOtASWZC3TSADO6Hvmfwcl6H7P0eMzlJLOkCxuq3mNSyviJh8KSOrH7XWZ0mgW1SI4iaqfi9CuwlylsQBc/gB9qulVA+o9FYJCYqE+VCzADwVuFR1nNhtYv1Qy22KlGGUKJeSfjoqSc1zWyC6+qRcW5MJfujUsDWzuc3ff2DBmlRmQmuDERJZoveC5u1bIoZaByZl8U7B0VUGl1XTPf38NncRmd2XUb0GJmcMKZbFuCngLRAZmptwbJdsDCN+t40PvTyZuII6tV1zXK5zGmfW49VbbZm/qRE0HC9WnK7vOXq+hZLYq+aMGtmvFpfkKzCD3GUFMckACQZ9E1p+75iDNvpWX7f2Q12bMRk+iRS7RC3vi+jhcEIhhSJrzR0KGGaaZAAk/K5SdJ5JpGyG7OV7ZaNQi5VGiVNxVBfPJtUvtwaYp7S5Z9H7bBK07bYkGFtkTXn60Daev6pzFLNU1yMoouefuhGFmu5bn3e4MuEZJxks2X67m7MwLh5ls81btTFu8loGQSnhHKWIUVeLG44/4v/k09/9Sv+6A+/z+9/73sc7u8Ts09YUnmitfvw5ua/HDYjCw9hj2utqSdTKeYShKio54ecL5bcffSYD558g9ODCcubM7748pf4YcO0UjgVqaqautF0feT6eslm2dH1PZP5lOPDOYeHR1zebHh9/oaT4yOcq/jq5WvxPdQWpSLGRCa1Y+jXrJYL1uslRycHzPYTIWmi1lTOYnLDY7WkOYcoE0u0oesTt21P1AaV8jGu2FnTcdwgx8ui4NXrCy4uF2R0hVQajDJ51iING0s4lQEZrbPFB1JY5uZnyGwBrRRuNmFycoCeNeL7lSUzCjn0pLgpoI50ENrk4BEE6BCjcTmshs5naUjC54KEJJKN6eERb968IaQhy/PlzytlSEhozlsA0c4/tdYyEVWKxWIhchej2JvN6K1lXa2Yz/cYaouJieOTU/ZmU47mj/j0Fz9HJ0nfRCnmkzkpJr73O9/jhz/6G/zQk/LuERN5yuiyKX1ulkIQA/sSuOIcKE0/dDx79pS268Yp624QgLBJsuegFgb0m+srOp+TjX1gUtfyu3fZ7ClxcLDPul0TvMiqwtDLfpVgOpuTUiDG3CgYmbTGEk+MyqoHkdeWs6Hs+2OhlL/KPlCm+kop5vMZy+WClCRgrsiQtNbbPWHch7afuXw/pcR6vebdr93X1e/sxeVLKYWOkRAjk/0Z0+GI2+cddoC+D/ioSY1lYhQzwGsnfoZdy15txTcZz+1XX/JsfsQ3v/ePub484+b1z7l48xXKOR58/HVu+5729oZfffYpj77xu9y5+wE3l8+xeuD0oMFEzfXtkq9ubrlYtHzzo4+4u1dze3nG568uuA2KTz7+gLtTzeXFJV+cLbjpEl97fMg0BZbLBYvVEtNY7p/epVaKi/M3bJLCzhtcSNSt53a5YNUPMJ+wN51yt5mw+Ool/+rvPuV86Dm5d5+vnd5lc37JT796yo3V3Ds85u6DB7y6vuKr5YpNGrDK4NBjoyeLOo7rRracLTi7O/x8d8C4C9qWNVK8igtjYyx2s1VMaYVLyCUJQhzAB2a+pt10aBWxSaTRx3rGxFTcbNZsemE2Hcc5ug0wERm6z2nAIIOOqa7oQ+TB3WPunRzzy198zsP3LUnJ+6knM0w9EwZSynVWKSpQ2U4ln6Nak4wFpcWGJgZCGPJVUqQQGJQ07ylFDr77Pf6zD5/wk//lz/jZv/5XdJcXHNmKaVNxdGfG3ryhX3XcXN2QwprkPXEIOAK1tRwnzTxoGBLD2Q2bzY+46Ra03RWvKgWThvruMXce3if5yN7BPsEq5ndPUU2N3yTQFowloUYLLBKooWe1ukUdnPLJH35ATBptKiKBkHRmeM1o9k4J6oU0glpnC6qOIQRiL+nkkqQtnzn4QWqgbGWRtMFWNSGHDI1SaJXwMTOHQiBpg3INPvQMIaCbO9x5GHj2/DUDMybuCKU0FiQNvdSqgE8GNzmgDPmmThQ1rh7EAy0PqEMIJO9JKTCtPX0/sLg9ww8tm43lzoPHNJM9us0aQ8T7ltXqEqMGCQKxNSo6mskUqy2mXmEzIBoS7B8LYzn4nvVqQUo+B+KKLdEweBYvXqGS4eThKV//3RW/+slPCEmhTI11DlvNaOaH9MFj+46huxGlBgqtEfZpylYcyTH0BqXsCO6kJEn2Q9fy2U9fc/9Ry72791HRguoxxuJDxW1v+IM//c/5Z//sM/6H//6/o/dLNAlrTK5nVUb4xEtUMimEdrhuRTVkjZOmFDX6ySUU9IGYeoKGNiqcskysZl5N4ZX0Afv7+6xWK7phIAKdH5jMp+zN97i9ueXq8oJDrZkxxyhD8OArxXy+z3K1YD8lpjkUpht6Lq7O0cZw9+Qu84M95kczJk3N4mopzMxkcn1b9qpI121Yrq9Z9WucrTBKM20mAs5UFZUVm40UIKU+9xh63O+koZcBSNSOg7sPObr/iLX3WFPlPmzAGYNVxR/SSz+kLca4zFgTdlZdNbjsK0iIOG1EFq01rpkx9hTiJyYlvDG4ypJCog+Gy/zn0rBDZZ14c1vHe+99gLU1e/sNVkfq2YzrzZrq6IB6f4+EeApiJPdA+mxhREUiQ5Swzdlkynw+5/Lqir7rM+iisp2HZKWg1EiMKQCZLr1YjLnHKddSjz3G1nNTbABKL2SsZvAp13eyLmMMOeivvM9AZNtvyFxKQw6gVQqiEjWprXKehsrWBCUXI2c7xAJaZQBUVL5mZJElEtZVMnRSKlsVWGJ+FsRzEXSU+k8sE0KWJkndrzO7k7GmTyijiJmJqU1RQGQWLAqVsidnOY4VqHJms82KQacdEhTZd1WS2NFa/Dmz6izGt8HYXfBut87a/drtQ37b90v99i4b99d/dguIzqYNVtu8l5eguXc8c6PoRgqBoNSZxhjcdDr+3tKbFv/QXeBw+/xaJvVkW5uicuBoqcHVCJIqpWjqbCmScQLyOlb595ZQLvK1HwklOegq+hwQRyZ2qYhSJaBMXj/s2KOVerq875CHHs65PKjTYxhYqdXL5yug4rhfhSGD9GYcEiilGLpB+hRTLHrC+HrFojGlJIxPK+fBbobFLllD3pfJtkvyf5/tGkaAd7NdO+KZnFnJ2oxAbiF47PZIgx/y0H0nIyFttdPFlqvgSiUsq9xnax3kwYqAq2JTV7nST4stgzUWKlmPICzuEMJoYzBez4zbJC33OniVr+82XDnGOPoKhxRhUrAzQ1PXhDhQNxOC93R9i+xrKdsVyd+rpw19145YT0q8Fc4mrHtP33cjXlReexgk20XqrEFAYq0JVsKPyzULuV4XZxstZ26MWV0LMfRSN+qtfWm59wUvGq1pxnsmai6lEzqpkThWOUfbCTmrQANa67zH/v8UpE1JEgMlJVTAj6Q1KWQfDa1x9v+h7r2eJEuyM7+fiytCpK4s1VWtxWCUYUDYArMLsTQjjfvAfaLtA//ENT4sDRQASIIgSCOAJTSwg57pnpZVXVVZqUNd5YIPx/1GZM+Az2CMtfV0VWbEjXvdj5/zne98XyFsyixBmcGzCLq0TA/3sXWFc50k0AhQKMVUWrjI4U6IZI3afMvyVojp0MjXpXeSFu+lu5cfYMJL7wT0pmnGAzsDRKKbGcFEPEJdb4mcL25Zt6LbZKymqkuqqkzXkvRSUsdCsX24OQmTw3VnTDP/vdZ4v9WIzMHAhyD6lGGn45CYX7vFZ2aeqcRK1TEmHT/p7gTnx/EX+dEEDiMAbQYYd0HPGLfBYxe4kWLHjSzB5K+WEuJ0EAUZI4jjtamxuyqAcBzBbOTOCetIIe/beVzvxG1VCxtjtzOa72m+zm/LHORAsfvneX3kJAQYu18iDRpF+0+LAcSnL17w8vf/kK9evOK3fvybvP/22xRaoQaHH9KaS51KyVVFkF9rjXPZKEWhTDFev0pFB0oxDxEXoO8Hrq6u8N0B7779Jsf37vHs+acsr1/inThDKqOwtmAy2eP68oqzixv2hsCmGVDagilxruPivOH9Dz7kyRtP+MeffkJVT4k+MClKZnXFwzcecDhLulsqUs8mDILvU1QC3MUYx/VZFJLYK2Np+oZl3+OSbIWKcogphRzM3o1rJYMgQwi8eHkhB04y4xIWzBZIkecCMYGs6O36N1aPe3MYBqISxlIIgWJaUx7u4UuDNjCxltW6RcVINyRtvLHpkmMG6Ji0tYJo7p5fXkGMnF9cAOB8TDWHwhbSJVwsl2w2Gxm09NKF0yqNphlN1w/yHXb2/Lc7+FudZ9kvykduL67powD/N90aVxt0BG0Uy+sFtxdXKKBpNhhrWa82LPslPnqeP/9GwKrUXVZpXOTJG28QfODly1dgNAcHh0QfuLw4l2eZAIJcnPhBGgrOuzvAVtZxiilohuB4df5KpEuMxpYFta6YVBWbpsE5Nxq6Bedp2pa+H9if7bO/t8fN7Y0Ue0qzf3DA7eKatmkIUXH/4JDNZpPGPLcpTmbQbgFkMyZaOSmTrbudXhg1utPfj+ze3NXdAfG2SdfdTv7u2tzVDNtNzHP8yQn37s/J3wsrwhEw8wnl4T7d2RU2KFo8znWUsWCuStog+nmoIN11q3HRY9yGlz/7CWVd8/53vsfPNtdc377m+vqSo6dv8fb3f8jP/v5vcK7l5uxrfvT9H/LTn0U262v6rqUdPH3suNl0vP/2U+7tT1guLnl+dsnSad5/7y3uzzTrxZLnF2uum8DbTx7z6EDMdNZtR9CaJ/fvMbMlFxeXrKInlhV7UTP1lvPzazqlGCrLYVVyqi3+4pJXywU3KnD86CHvPXyD9dlrfv7iOQsdONg75oOTezTrDbFrUb7HkHKFrCOd1p1S2dwvMR5zAagzC0yP9/4Xiq9UGOfi0Wo7Nk+U0mgVx8bU4KQQ8X4gRoeKlmbTMQyw7wy/e/+HhOMC7QLaB/amBzw9fZPC1PRe4RpPXU0wwXAv7Il8gHcMbUvfNXTNGkJgYgzFbMbj4wNev3zFxeUNtp4mvU+DKUu8MkmOIeuiR9ROfFFx25TWWrPZtCxvbrBG4zxEXQjQFqFvNkRbUFU1wWjKBw/51f/mv+X43Q/5yR/+Aa+/+IJJ11P7QBk9vY6EwmB6hU3NKoOhUhKbZJSswLqeuulQbUfTtfh1j1qtCYtb2rOXqOBZVoYu9iwP5nQ6srpqcA5WTYcn5ZB5j4dA4zzv/e5/xQ9+/J/TemG/Wi2SNBI7A9V8H1vOUFFjlabd3FCXkuf5IMVGVE7Yp24QJo6Spl5wjmA0xpZ458dYq7UVZm+EvlkRfcPB4THOI2CKVihdc+/BY+4/egdrJskMQxGjx+fGfAiJxSma7XmSSwoUMGUlbMAEXGpdomxBCF1igZTY0soEjrLEaOldpOsjk3pKPZ9jqymEHh0jKgpLuSgmdF3HZuMwKtL3LdYUlNWE5XKD1jCdHmGtpRscTdujdUDR0Gy+Yr3sMNry8O33MUkCCzPFVhPRxAyaqAp0MUHrQqAVY4TZ5LfrUBuTXJWzgatsY+cG+i7SdSlttAZtDW5oQXmIjs36gqha/s2//bf8yR//Hs+ff4xBNOYKbdD5M0meCKkJnhCdVAAX2CSnFWMuVB1BOVCexnVoVXFYVqIPODju37vHsm149OgRzXpN0zaEGLh3794I0lVVOWqNl7agUJq33nqLZ89eEsySp288RivRcVUEXBhwvkdHRYyOotD0TUuz3pDRLJnuUfgwEOLA0DvWm1Vizpai+zgEClNQl1MpWEmjSamI1DEXvsNYE4QQiRhUNWN+8phNr+h9xJqQagxhe8ukfESpgBvkHg7O03YtMUpjSXLtBI4ZmbmNStP1LrdSxQBLbWsflGYIoDHYohafvuRPYFDUtkxamJUAsCEwdB236wVP330XZQq+fnmBrWsqW2CVSC5FSR4lXgRp8JpkViv5zNaANgMfymiZfgp3J13y5B9EVPZDSRIF8j6S++xO5kHK9VMd4ZMHS/4srQ3GxFQPbOs12JHyI7fXFEVRMzhpqGUT7OgcWov5tUpygSHlJ1op8ddIGowq10o6TYeS6ywQgoJOcgNRWPAkAkl6DlFp0HKiZP3hEFNumHL8SESHxFxLZJksmRdyhzSKqWJ0HlTKxdIZrLOfDHHUVRWfcImLvR9ENzjE0a0983V2CVe7r1xjfBu03c23v/073wbX8vt8+2e3YHyg6zpmexOIMeWl7hfyTgV3TJpA9rW2dsyFrRFwKQOHmZGdCS35u5TZdNoYyrKUHDxsiQnRJ7DSp0o61fy+H0bcIE+pyf1MRK2+lynQ9GzyWpTtJHmW824LLCpwriFGMDaikmaxNRJ/sxGypGdx1GbOrM/cPM5A8i54ugtGh5AYsiFQVMXoCZLrpL7vhQ2JjK/nEfb8nLquQ+GF0OW3QJxN9z4/82EYaLoW8RbQ4/NIAXNkHbthoBuGtI/NCGzmddUnnV+jRXZKa40pDH3o72jFaq3FaLIo05kujFsxDksxYGft2RTDdg3Y8vochoG6rlPzRjE4YXbGhG9kADzvnRCjSHWRc96t71B+vwzWai3ApxD/pBGUmeNaGaLy1FVJDNlQK+fiMr0ym1RCbHIyqRRJGvdG9nZZlqM3VWbxF0WB1pI/uuAw2ooBXBSTSzd46qKW8zFJo4Qgkj9KC/N7CAkz8Lk5lGT5Ql7TapTU6Ps+xTf5XkYbyqrAGmnO5f2YpT/yutRI8ysEn4gEv/z1zxukBbokWRCVIrgkKF8V7M2OuL26FpFpK+P1MY1iBIDoqLSmmBQM0UmSlxZZpuPHmIs1NTIx8+aOQajzNjm++p3gnA/Z3eJbUFlQ5AMYYbbsoO3SmU9Ji45EvAC8xpAJvkEpbpYrtCqZTCrWTU8932M63yd4MBi0tpJ4+bgDRu10StgJjuk7kQJ2DgbG7IyCIACmyeCxuju6/+0DKqasWIDLFBBC+v8mj5yQ2/djF4KwTSy275n/G/JoKMTRpC0DcXlBaFIyQj4ME7NZbrgUQiMIzJ3PAhmTCFqhWk+4kYJWfnwbvL4NvGqlRsZjfvZ3gtcOa26365mTuTsHtVGJVSuHGUazGTx//td/zWeff85/8bu/w49+8APmkxnaqHGthHEEI7GgdU4c1JhAiYSFaHMNSWtq//CESVWzWtxQl4Zn33zN69ff8NGHH/Dk6Ye8AG6vLxi6hk3bsbzt6FvFxfWCQRXcrBw3yxbvPfcfP+Rgb87V1TU/+cd/5PDwHoeHxyxWSyKR/f05s7pgGDqcC7x+vcSUU2aHNdFqysJgiuRImlaJRqWuvqYfPMvVBhdFB9QonQo0L88tJrdlLcEvdwBvbta8fn2d7k1ILHgB6jPbeOyGjYfFFr2XQ0/2kYwiGDCRoiyZHO0T92o676g1HO3v8cE77/Hzzz9n3WyEcaAMru8pUhKslKIuSrqux6vUPWY7Gq9SB1ohoz7TyUTcKb0fv1dMhRBK0bc9j548YLXecHF1yXQ6FdZm+g6np6d0XcdyudyyN1OzyaDYn81Zu551u2JiNBNr6dqO25tLDIbCVhyenNB1DevVmiEOsvYCvHj1EqMUD04fse43LNcrQgy8evVqHPcrCoMbeqrSUpYpWYxi8JKTFqIAXfPJPInsp0M1JSnRO5HBCJFpPaGeTnh9/lo0bkOkT02ukfGQwBcT27XpAAAgAElEQVSPdI2HXoCSo8MjlNGsm4ZXr89SQ0li42KxEJ0lfzd2j8BbStCGYRjBVAljufvP+N86Fe3X19fshBcB+GJyldV3wdpvv3YB2TxRsMvESEExxTJJDGUESF5FUXB8csTLFy9oNmuUNlSHe/SLhn6xRmlN1/dc68i0rlHei6YjYP2AMjYZZEVCd8vZz/8TT975iCfv/5Dbv/2P2GA4f/WSd77/PY4fP+Ds6y9ZnH3BxeGcB6f3+Yfnn9O5HlUWXC9ueP/Np5zMSjaLK765uOZqUHzvg7c4mpcsbhd8/fqGq8bxwVuPeON4znpxxTfnl1y3kYenp9wrJ7y+umHpHb3SnM722FOG66srXGFgWrM/LTjWBawbVq6nr0pO9/d4sn/C8tVrPn/1jJWOvHn6gDcPT+hXt7y+vWKtNDNjOahrNv1A0BoXJF8YG5dpT7qwM3KntuuDVP6Oa0CLYVNeADEdZHdYOWnRyLkkkk1FYTEGLi5eUs8OiUExPdzjo+PHPDk9pTzYo1+v+exnH3MyecjJ5A18H6mnM6gMUVm80dCK83moRJs94mmLAl0o6mlFafdZLm758vlLOqep7AyNZTapxHAkQjRpEidRiGV8NI4u37vr//r6hqrQzA4PmNqK5aZhcB3etQmI1uIuTqR1HXpW8fRf/itO3vmQf/y//5Sf/V//C8+XFyjTYQaHCk5G2YKFXhqFASuSDontbmKksIaWNBmDNBr0MLDXG0wYsEOk9h7XDJIgrFs2TUfVD4ndpre5RQgMEU72DlGmJA5ioKbyvs15jCqpipkYaPmGq8sX4lgfFL73oMT52nmPIuL8gDFiXJJHnVEmkeeTgY+y6CgmO83qkpfPPyaEjmm9j44dBI9SNdpO2Z/P8E7x6uxrZrMZ08mUwfk0VVBjjaEfOpm8SWyQ4IXxIwYn0nA1RiZXNAajRPag7VrKsiBEw/HxQ4lZfUtdlTgfaFYbfN9SasWwWaG8Q9uCFRofYxoLH2Tc0IlZ0+31NZPphMIY+qZj8NB2PcPQQXBs2pbYtSyvN0wPDpgfPcYNPbrYo6gm2KTL7mPEFBNCEEmPIo3YGh3Hkclsjje4YdynMWq8h3pS8+H3Z+zv3yfGmsAmTRp5jGqI/RnXl5/zxtsf8Tu/9bv8d//+E3R0lMZQKE2hLSoIIBhD8qtQ8r1tYaUbE2UEXStLUHKGb5qGdVhhjkrmkwmVKtFRUyhLYS1VVVH1yYxzUdMMnZiu1hO88ywXtxhtmE/nxAFUUDIens7X6D2Hhwe4vqNvhc0OBqMLNs2Kxe2CEKEdxEXcKkuciflbs2lYr0UWoygK0IrJdEZ04qyuokKJsBRlkhnw0W+JJkDbtjtnj+Sjreu59+ANZkfHNN4RnEyF+OApS5sYtFGAfFtgTK7OZG9L/NT44MZmLsEJK7QXaTWpNQJ9kIaD0oqiqCjLiqig0AX9ckH0A8p7vBZ5ilwz9sHjleSYXdfhhwHfdXSupV+3uNrz8vKKmACTuAu0aQEStDUjwLFIpqe5Me9jTGY628be0PfyHsZQlsUW7GT7e+TGmNKjHJyMs5eoQjP0Lc4NMrGgtrWcvEt2v7ibL2SAVsBgJcx7Iyx+EfGW2GaUGRuKArh6lDZSP0inCeI2d3HE9GcIG1ZLfWO1IipporgEkI4N6mRk4H1EWOnymTERSXLDQ6U/VIAKEJWMdks5ncaaY9jux9QsJY3L69RUVQhIH7Ua2cOgRnm+TPYwRSGeClrYuqMMxE6elnOyXaJOBjt3GbS7TfXdnO6XsWx3f2ZMJIl0bUffC+tcpO62deSQDLNygyTXn5qc06rxz3Nmkn9mMpnsAJXbyc/dnLbrulRDyXoahmHUANZaEwc/ssHz2lJKpn+NkmrJR6mFXQKIs1m5SXWyTVJTWiuqoh7H1ieTir7z+OCludQPrNfN2GzMoOvI5oWtXnGSBHQ7YPYIaicMQyHN1KEXcp5JGrsC/uk7v1PYZJpHlMZwqtmNEVkn5wKD64WxmdZuURQQI7YoxNTLOdouSVkplYhfKtWDwkBWWtH1PcYWaT0LxpGZoy74UVYnxxIxG5RrLssS55w8pwSWEmNqmMhztcbSDWK+OQzDCA6aBMpnsodNrPaQpFuIIjkDKjV1RG7AGkNRlBit6Ts5W3bXtE6SImIwtpV0gzTpq7Icg0LFrSyB1kp082O6FhJLekfXOKYcUCENF8y2uUXCoYrCUtgJfT/Qd/J9Je+RbL6wVqSainIE/ENIJtxKUZQiw+W9p2k6YpDp72wgjpU4Nbhhu8a9Y1pPx/UjmvgBF6SxkTXwrdWyn8c4K1OPWmf8Kq3ZGPj/LZM2d8xUBvK0wiihbk/nc24WC7npSjYLPhAGjYsBPamo701QBQxDKx1EgiSqIaBVLroDKrFOtdJoss4piXWXhfO3rNs7YEHcgnSi35KEshO9xseINVUCJFQCj2QcRWdjmATuqrRRlutlEkouKes5fdTU9UTGO4CkXCfvl8YVJTiJLoqsCZ0WuwRYnUaSIWuKKGIanVFaOllK5RGWLZhK6jLIwkXAXi1sF2Jy3EyfJdT2OD63ECOWpBmTOisjrT8mDZdk7kECHGM6OKWrwhiMtJZDTDBJlYrM1AXmrt5Mlr7wXpILq4Vq7n1AGXBdz7Ba03cdJpkR+CQoPgzJmM2a9LzSekhAvQs+SVTI5nPBo7yjLMrxkMqdJdl/IlAefBBwOEUxGQtKSaiWZPLl9SX/4X/6n/n008/5rR//Jh+99z4GLQZSY5cm3e8QpAgccVqVOn2pPsyJkFKUszlTpcCYZCwycLtYEYPn4OAhTTvQrFtc03N7dcXt2jGgmMzmOAd959FFQegd06pk9vgh1zcLTPRMDHQEXHA0XYMPPf1mxWpR8uDBCfP5jICjtFOKok7peWYASHcfJSyuddtx2/WyLiKgPNHk/n12HU3JTIhgJCg+f3bOpmkTy0anjpqXZkZOmqJilDhKsWRkPGS2kjwKQnAMGmYHe4SJRRmNclJsXF/f4nwUHTSiNB40lKUVwDkG9vb2eHByyldffUXIJlXIHgRhCOSXxRIG6cYpLXGG4CmtRQVwg5hEvHz1Ssb/rKzl4BwhGqKS/ZJ1TUWUPpKZwVEp2jDI+9mKk71D1l1LXVbcZoDRRNp2I0YWfiC4SFkW8nlp1M0FR11WLJcLqslEGGmt3POiKFmuVqwUHB+f0GwalpsVkTx2aOlb0VzNiYNJC1cAXem8F0VBDIF26OiWQ9JwG1IHmREUC0HGaaOWkUdbiHP6crOk6/sUnyUeWm3Hvdi7bmx0KKQ5F5RKXX7Pyf4++wcHfPnll3hi2lPJgbuQEU1iLjRyInpXEkGl99t93T0vtmA9bHWpdvVodxPpXf3e3HAYiyfnuLq6loQjCqOcquDw6X0uPnsGg6O0ChcjV74lxoHSTCkocF4kIBS54IHbyzNQBR/92o+pDk/5s//tf8B2KxbNFU+/+xG3N5c0Z6/4+cc/4ekH3+Pdd7/DZ1/9nNVmyVsP7nNUl5jgKeoJTls+fPcx96YFtze3fPb6huvlwHfeeZs3DysWN2d88c01iwF+5e3HnO4f8uLskkXb08fIyeERh7bm4vUZDYFY1lRKsRcrhtZzoxxDbTmsJ9yfzmnOzvny/BVtZXh0+pD3799nc3XJ88tzboPnYP+Ap/cfQVHw09evuPUusQHU2MTxURgCu/JFI3CeTXNyAEnPJ8ey3ekQH9MUSgb6Y4QoxqCNa4lampm1iczqkulsRtu3XF9eYm3B1NfY1nHKhENn8a+ucUNkHa9EXsYUoCwqGjFS9TG5oA8M7QqrIkeHc86+/IavP/+G1iNGB3gsBmNqIpm5IM0wAWcBlQ1RjRhjpC/bdz3dpuHJu0+SGY1L4K2nHzx1VaPLmqAtMSX+ylqcMkzfespvPP53vPej7/PsL/93lp/+LXzzjOkQ0apAmwI1NYQAQyzoTUUbDF3XMi0jldJoVWA8BOUpAxg0ZVRYDCqKa7hLEgmqBxW0NLSREcTBezweFRW2KDk9fYALAp6GEAheZCQ0UuRHZ9CmYjI/wPctN5cvmBcLrOoELo5eRj+9F7akz6BCJHqHV1keK5kGpVgBUnBYPOvrZ3zTLzg+eQx+oGtWuGBoBsvBwSP29k549c3XzKYzjo7vEZXBFDUx9KgwcHH2AmVEPiF6z6ZpmMzndN5TlhWPHz7CdR0oqMopXbsgxhUhtOwdHOAHjXee1eYG5wbKcs5kfkzE0jQDq25NaBYM7Zp6skdUEgNtYZhMZjRdT9euOT45oainFFVN0w74YcCFSNOuadoNB/sH3H/4Jqvba9CWtu1wPhKCpU45oPOBtm2xVUExnUG5x/r6nMO5TePJaQpOG5ngUlLkxagorCFGqQ2MrgUIXXfUdQGqJyKai0YZdOzplt9w7+FH/NZv/w6//3v/ntXmispILhWIZFhAG8kNZV8bjCmSQVXa+0b+XGnRfa+9o00Ak+8dTg2EwmKN5dX5GYN3zGYzur7H9QPLweF9pK4qTk5O2d/b4/b6luXNCh9dGtWGqjAEBa/PzpjWFcoHGR+OkeP5IZWy7M/3OTjcx6tI2w0srhdcXd8wtL0QAtIIbFFIE6UsxPylXbdEH6n3pqmYT/rH6aCLPuUgSsbUvQITAm0ImMmEkzceU9QTht7jlMdYhQoyGuyck6Lce3zOVSMYZZiUU2J09EMkqoKirOQzg2foOyCM5msqWmF8knRti5KiKhlioL/ecP7lM2I/CFkmMfHq6RS0xjUdt+eXlO99wJO373P58hUXZ0uCKbn/6CnrduDq5haPaDjG4AXc8Zn5pNMEUGAY+m2Np6UAlzJoC8r5kAzYNJKXqCxtlCdtkN+LAsgFDFU5YT7bE4kcrMh8qIjf9MSYpqmUlkZPjCgVMUptiRsjsJibwXEk5owmW1olmS4lEhj5f1oYraQaJ5Il5tIUWEwAiSQ3REROwBSlABIxJumLSFBg4tbhXikxcgppzxhldt5HiAR5L2VDozGXSnmPGP7KmlRGpxo1MfFQI0En8YbkmpJosejOioRRUEJYMNqgSotKzSw8Ceja3rdd4HUX6PynmLO7r29P2XwbtM11qnxZKX1FIky4xaJtnFiIymC0JSLNwCID8qneyzW6c240kjWJ4Vkkh/vM0t8dzc//rUDMunKFEuJYB4UkuSGpS8o/EziqvaWuylxoglLUCRTO02KZLRiCkOeMEQkTkyYhhj7tL23l+yLfd/COmK45NyYyMJpBXwE8LTqR6TKzHzJrXc4Lo8CUpchPpTUtrB9GMFVHieFWZ0MzaRYoAJ/G721BaTXTuk5a7sMIRgcfUAVM68nIMvY+YFTO9UXntkqsW2ssg3WJtZn8iDLj1BjqsholJfLzMka8TQpbpPpWAPYso0UCFLVW1PMp+/t7tF3PeiMYBypS2ILZbA7INYco8jJFaUawMCZgmfT8hkGazWHox/tnrDCeh/T5aRkTQpQcUOd6JtBsNoKLWTH2kr2V5DKNsIVHeoNKALbJ7OhtMyvXQZkoKatFYqsbJIc32lBXBkol94hMdJHMwdrtOkifOOb3JhFgMstVa4P3jmwMWdUTlJokaYUeYhwNIrUxVAmgDiGyaZtxf1tbCN5nDC54kaDz0kCqEvlTvn+OCb/89c8bpEXYVz6J8woTVswXXp69kgMjIebS+dSYomBSV5j5BDVLcGZMeqSENP4lWpJKbcEanUWsg4C18kC35j05APmwDcKZXZN1hiJxdAeUw4wRRDQZwMzduKjEcVaLHpLRlqDkIO/6Npnu1BRKwEVrrNDorQCpKk9qpq7NyE2MGSNICzTpWmZwIhf5LgVB0dYkSRaUCPhrUmK7q2+bv1c+HOQ6tJIDcFxledPG8SoAASGsFuBT7dw7dsAXH/I1kTolqaOdRvukq69GsHjsemYmc14z6T0yBzcQRXc0KhnB6RybZYOO0pMWIF7GsUTHJL1ilFGfGEcdzqjVqGNrjYDVSt/Vn8zXlkX9t53YkDo8qfmg8qh1HIHXZdfw//zd3/Ly5St+9zd/zH/2az9itj+XDZ3cGr1P2k+JDa1VHrsTRk100rQYgdoYsdWEw6qiW68Y+oaiLqjne1SlxiuF6wZurxdEZWSsVGu09ZS2xNYFisBsYjg6mFPXE07vHbC4XVEWNQfzimdn5yw2K5oIuMDp4TF7B0eUdYmLgbIqKcuSEJyssfEWS6YSlWGxbhlclCIsBoJKh4bSmMRkcMMAUY3JxKbp+ObFmXTscnJJBvwj2soInHNOQIfkhr77yslrZhJ4FbF7M9R8wmAUMbEZOufouo7167MxEdVpfK2w0jRwTlwcL64uCMg4UGHtVsx+zEFT0lFYZvMp63bN4eEhVVHSrjes+w5T6LG4GjvmKSEZ94BWI4M2H/TBOSlqNAx4YtPy3bfeY1qVfPP6FavbBVgZR/SDo2k3d5JjhbrTgVVacbu4GRNQpVTS75W9uFgsx4Rwudww9D1J8JMYYPDJODCEsXBLGCVkhoxSrJbLcUxGKWG/5DEb5+TAVGoLiBVlwf7+nPV6jXOe3g04N6TRRFlbWYZgnH7IrP6cHiRAzhjNerOhaZqUbOU4vwVMrdkahynYFl67yXvcJu+/wIwlNwW2BYBIK3zrhE6/o3Zj4E5sy8wGGZfr0ZDWX2JcVJbpgyM2Z1cEL5+7CQPGRKpug7UT9mczbFni+w4fFNF7oupZLF5wdvYF3/u13+XTT37KsnvJ4ekJ1fF93vjgV/j59S2qa1icfcV73/8X6KLi+VefUuNZXl1zenrIze2ap48ecjQvubq84Nn5LVcbxwfvvMnjw4rF8pLPXy7YBM2H7zzmwf6Mq+sLXt9cs+kGnj485WQ25eZ6wSZ6OgOVdxxMJixvl/QmEmclR3bCkS65/eY1580SNy05nM95MNtncX3N88szrrxnNt3jrcNjYrvh5fmKvmtQRSmFiAoju9j7iM6FrNoyoXOhM7I1ElAfxrMnFyWJ2WG2MgoEkayZzWfcXpynsVjFcnHLbLaPGjbcvL5kcD3RR3woub0UyZX5fEo/9PgQ6J2Agtpo4tDS9zL+vt6saZtGxpw3Ky4vLri6OqNfLjh/fUnbebQtEbanSC1EJXqSGrAJoCUoUg8pnetp7afC3xjDyfEhD+/fI/iel6+v6PuOGJCRO2PGxrAPok2ZdcaGODBYzcF3PuLgyUNuPvkBn//+/8jVJx9D14EuiMYKs5UpdvoIOzmmXV7S2DWBgda1RDegikCMGm0LmVIIYTTJsGhscARlcPg7mu4KyQN1NKhqwt7hMb1zolUfU3MzZQw+So5pyoJ6ukffLOnbBdEK408ovZlhlMAQ5wGXxteCjM9bS/AtwTuqSY024i4tHusejWdoF1yea3zviK6j9z1DEPmDo6N99vdL2uaG66uG+d4JhdVcX75mcfmSfnNLURV4InVZsb69JrLP3vF95rMJh/szgp/SdT1Vobi9OiOEBdPpVD6rN7S2ZzafM3Rrbm8vuby8EsKD61Eh6W6WBT72GK2ZTCf4ANpMiNpzu7xk7/CIajJFGUvvW3RZo33ANyuadoPWmuPTh2AMzXpJiDDdP2C1XInMktYMvaNpWyois9keewcnhOaaQncy0p/O2ZimTTKrUyQqfDpL66Tvp3BhYDCNPNsRJJF93SzPWN58w/37xzx+9IhPPrumsDJC6WPKP0jjtFq0mDXCGJRYvM1RM6BVlSV7CpTxIlMUhSWY5X2qsuLFszNWTUPXtETn6Iee1/E1R0dHNHst1zc3zKZT0JEhDPRDoBsc+weHFKVh1TWsVksOpzOC87g4MJtOxbwlSqPZWk0YDTIV682Go4PDxN5J+usg3gAYukbubQZ2fGokxBCTOaHEjbbvZAw20dlVWXLvzXfYO30oOucyvpjuo+zHzJTSCQCXuGooS01RFAzDQFFOtiP9WphZwzDQD30C8KQxmqXqtDUYKw1k5R02VsSHj3jZLMefK5SmtGL2o0Lg848/5gff/RWiO6TZdBg9IQbQpuSrr7+g6TpMZQha2PZW63FqCyV1nBi9ksZsk2EpJrHPGPOKkEA2maJLkhhswYHcqJGpKTH0MVonwx07ntddJ0zaTE5wLo+sh5T/xTEfyDlDhirz2sx5R4z588KYP0htm8AtLSQhkYgzY60VlYCDGpHkyt8154WDE/ahRlNoLYQKL+xLHZLggtKIpKXAqvkeZJ3tDNIqJQSLMOZIgez5mOVqyLW61olNuQOIZuA3M9dI06q54ZqYvdFLTeBzjjVinduGa87hvv3abZ7v/nv3tcvEzdf6i++1ve7CFqnRI7Et31tjtNT8GtF+DmlqI+WbI6tWb+U1dkknWU80X2N+9lkuYPdacyzNJr9KCWGiKIvRUOnu95Xp4PFrJRAtP+WyEM3hvuuwhSXoHFOE/UquAdLzJErNLfug2I71R6RpLlQCfHRjTauTmeZuji3pgE8MzkSWS58xhGHM34T4RdLZzr+7g/UQxhogDANEJ7mDETBQ8I08kR1o247BuDR9mKUXQ3r/RNCKibWq1PjMd9dV/h5Ga2xh8D4/38TAdDIpk8F5ay0m5AkhqZGMyQC/YWomaKNx0wnDIBIIMeV2xlhMMNR1LfckrQ8xibbs781AQT/0DP1A33V4H6jrKkkBgSvFZFPWWTKfC8nky2TMY0bTdkIeSgQra6XB5vGyh4Gubem6bjRRNDrJx7AltWVvGa0VZWLFjnGCmABfqUfLqhplHVSeAEBiIFEIN0Vlx2lnweNiIliScBqD0nGc+q2KMuWZeQeQJiXkPhTp+RWl1PoxSk2ptbCka13TaMPgTAKi8/fJpMpfjDf59c8apJXiYTs2GGNiTWrR0lHaUE0qetcTrKaeTqmqmmJaM2gYQkcMUZg9g5dEXEvhUaYOyy7TJe500ozWyQlzW2R78Xu4C1bIX44LKh+KWu0i+bssqjGyYW2BUpIMBJX1ekIKpI7SQu9lMVtdoJGxXlNYnPPokFml20Azgpekr5UUivMIyV2ZhnyASNU5/qzWyXXVpANsC9Tmjqw2iuBl3EFb2SDCyk3sMOIIciqTGLPpXuUulmR2KgHnO0CKuhs4c3cuVVJb1lI62KU7vT1AojRqMFoxhJAcSRE9oxa66xX0yR1RZqiwVgvTMm7p+XLw+zuHrs3jITHIyN3g0ncP44bLJ38+RPP6UTqPNOnxEJDvIYdQVAqsjI58fX7Of/8Hf8h/+vRj/vW//i0+eu8jqrJm8APaSKtP9A3jCDrK2IUX8EiW2JhwyDOw1AcH2H5C3zWcLzfMpzUnp0/Zm865vV2weXYGSlMWtQihDwN1BbO64P7JnIPjOVopJhPDpDYsblZMJ5b3335MUJbr2xXr9YYHj045OD5MuqpgbTEmD/l+ZrmKEB1tF1mtBhnLNDD4nOzoUSMoBJnaMlqBMqAKnn3znOVqI0V6GlOQA1TAefLYSGI1xN1YmIJ4Tlg9EVMZZocH6IMpsbB4ItmQoe27VGzob+O8qbkj66bve0l8MjiYurtlWUIQR8yYGiTODbw4e0EMkdViidk7QClD17YQI7PpjAcPHvD8+fPx4Gn7Vq538KPRQh7HE0a/NBPy0gje8/zZM8qq4Gp5Kw73Xoy1utiO43bSAU06ViTX3rICJeZd0uyJzOdzVquVJBoRrFJMp1M2mw1t2yZARPa/S4VSlijJDFYZBJCRXJQSV+XMKnWew6NDlsslwKj9JPc5y7VIbLq9XSZdriAMvrTmx2iQANmtllAuFLYHYwZbezfIeE9Vovzdfb/7zy7wuvvProbZ7t/v/v+7oG1yfo1bt9Dx51OszN95e613GbdKax4+eEDX9VzcXsv901CdHOD7gfZygULRemH4VFZR4djzPUfVHtZouqZHKU1ZamZ7lq+/+HtUvc8Pf+Nf8Ud//B94/fKMYtNyeHTCOx/9kK/+7j/S3Jzz/LNPeOuD77K5vuL26hv25lPa3jGdTJiXhsXyhi9eX3OzCXz3/bd5dFizubng8+cX9Krg+x8+5qA0LG9uef7qikXneP/JAx7v7/Ps5RnPrm7ZWM3xbJ/7e3Oa5YqmD4T5hHlRUzeBl988Z+UHwt6Et956m9Oy5vzsjGerS/rScjQ/4K17D2EY+PjF16wIHMz2eXJ0j+eLBbd+SMzzNCqaQNfMYN6NVZnRoaLAbLkx5L2nrmsODg64ublh8OIqm8FcaywTY1goGBrP+nZD0/f0XYuNEFWgnNZM6j1MMUfbCl3I+HfUBfOjU9q2o2s28nyDl9F3H5msWxbXV6y44Or8BZ9+/HecX77m5vacddOBNmMB3vStxKI0ep/XVtZXRG2bWzkebItOjbGKYei4d7JP5zyLTZcmG8ANEu9CYkaKU7NLuYQTp2NdEOcnHPzot/i1tz7gxd/+JZ/98f/B6y++oF+vUDYwmx1gTt/k/rvfYd1eE/w1qm9YfvwPuGXEuq0MjmtbtI2YaOn6AVuVmCiTVyo/HyPNex0tuIHBa6qjE+anD2jyGR9UOtO9GLgRGPoV2hhme0c8++prQmiIYUhTRiqBXfL7wUdCGDAqQkzrCclPCQYfRBO+KKsUQz3CTBSN20f3H9D3kYuLF7jlUtZD6SlMIPiWvr+haTzzWUm36nj11WeosEbjUOWcqiyJfk1hPNNS8eT+MWBp10tsUctnOofRnrKomFT7NMuW+dF9ZvvHtJtBCmK35vLVGa4PzGYVVakwxmF0pG8HQjRoSmZ79zg6esjQD8z3prR9S1lJbuIAq5U0j6zmwYNTbm8XnF29RquIrguqquTp22/zzfPnknMZy2Q2QVmLH3pc7xmGQFnPCH0neVcp5qRdO4yg3hakyA3TFDKVsLNiLvJU1v/0lKVm6K9ZXn3OrD7m/Tcf8fWXP02F0rZ5KO8tjQeTGmm6SIWVSQ4eoXEAACAASURBVI2NGPFuwCHsGlMX1Mg5EjwiM6GFbXPv3n2+evmCL58/59233uGtB4+J0XN1c81nX3yBD7BYLZJ5rOOd+bsMzvHF18/48L0PMMbw2Zc/p+t6vvf+d6iLEmsLdGE5PDpCl5qgI5v1mraRM/3k6IDjoyPW6xVt04hBTgioKNMv2Ih3E6JXOB/YbDomk1pYnNrjXc/gHV0/sGmbJA+j6AKoyZzpySN6VTDIlpB6wwdCAhRt0vZVCqzdGvwIszSKvFH6s0CS7Igem8b5BWyxOSxJrWPSPdUG7wJmMqU+PoRnFpzIsphSiUxGCFg0V69f8Q9/+efc26/w/cCTd57y8uVrvnl+xl/85Z8TdESXBSSWrkImaFw3UCT9YVtPxmbVLiEjM/B0YnkGleo3drwCUh2WzxittbCvnBa9XKUSO69n6Hv6oaNtNwlwDCPAnYkt23o+5xZJL3L8nLDN+5V4cLg8LaYVxhQYI2SZstS4pJMuLFUzNuZi0JgkV6WVojCWbEqMUiJpoaKAYRGRq0na0ejUUB9rtpi0lBPYrpKchyLJiqg7OZuwcC35T5XZmjYDdyQndgG2gCJGP+aSUg/nuKDIZp07kKycV5mQJAX7+Nply/4yUPb/6/XLmLbjk0v5YjasUkoxmU6Jwck/0STygpzfZVnCt3LNvBZ3gWCXNDKzAbbfyWPrut7eW5O9O8S8bJxe5W7tmnWQ81qThnUcQaaMN2Tw16TnKrIJ0r3Jzy1ft3NuJLN572lUs82LR8JCpDAFSiuZVh3z/+1nZ4AtEzuEzOLpum4E8o3O5o6a0MUt8U5pnJfryobx+X5kc6ot6A0xODH2TNiQNtKkyQxmIalILt/3jqrUyPRmQchM5JTrgxrZ+JkNHlMd13at6JInUNU7YaoXqX72O/dOrlNWs/cihbR265GhLHu0xFg9klViFLMsq6QBGZxPJKOS0mxNvY0x1FVN17W0xtJ3XdofspeyuVhRFIQQ6XuHNgJ8571ZVZVMUJsswyl/XxSWia3keXpZM1ppirLAWJM8aLZElywnEGOk6yW/ynIeufnUdu24dlwYRqJgDDKzvhtbBjegOu7c+0CWipGfK8tylCbtBwGqd/56lMTcnXK01ojJWpVrPFLsls+d1BMKb0YwXwLkDgb5T7z+WYO0kMS/taDeedREArd0y7uhJxrF3skhxaQWjR8ibXCiMaeF0Zg73sEnGr5LgCICjsUEpm5famTJZBYUkMxGvg24ZkOwPI4bEcdLEmWa9D6SIGWgJ4ukE7OOoXzmMDi6rmdSKtpNQ11W7M3nCfDRSU9D3Ooz+JE+QK4mL4B0eVprMZxi243NhZQcqCQX0SQ2HlUaD9mCHPk+xMi46TITLLIFTregb7qf6i5IkROALSMsjRBHPY5n5++QgQt53yTfEAUsysEuIolBPgC0Njg3cHp6igqBi5ursWDzUdEu1/TrDqLoKFmltklCiIAe718k6dMm8WhJXLaHnsvSDUkUPLOsFNuEIwMs4yETQxIU3/5ZTPfNJJ2YqKBXitvY8zeffsz57SU//tV/wa9+5/sc3DukrLJpQdJ0jYwHqrWyDu/cs/RIfEzXWVRU1jIMHVe3G2LvqS3cf/iEL7/6huX6HK3ErbnQiqODPepawPBh8BSJ2Tj0Q+q0ellbxjN5sEcwh0yms0S21lhb4KOYR7VtIwdHOliromDTOi5ulzSDg6QHpJVi8AFrCowx9H2b7pFNAt6KddPx9bNXabtuAYY4woFpHSWna1mHqcNm9LhfIhCVdNjNtMbuTXCp4kuSgiTO9TY6qB12ecwdvZ2ObGKECAAKVVnx4MF9bq6uaNpGNOOUSJ9Ya3C9sHQv+gsxwNCin+icS4CoHjVou1aSEKM0ZVkw7HTHJQFRKGM42TtgtVyyGNactUtoI0UpGkrRe4Ze2FEu3TthdWZmiICgLjWgfNrTMcL19Q1aG05P79M2LW3fUVWVGHYBs+mUg+Mjnn39NSF4SmM5PDzk8voK0lhTlvoorDC+Q2aHI6yN9Xo9gsdN02wTmR1245BE9r2XeJ73qHM+TV3kAzKSN4HsOU2Wgcmjh+OYToy4xFrefWVg2FrLarUa9+5u4Zn/bAsE3zWZ2E3Yd/f+nfi4/YExEfhl6y3/TvCe65sbOX/SGwqDX1Htzehv19CFMbZsvGdtPFfthvpGMa8MIQYKM0Ebi3MwdA1fffGP/Og3/jVvPHqLZz/9nL3DGTeU3L//lEfvfocXP/8Jl998gTaGp288BrdhcGui89SVYd2ueX614moTeP/NJzw9nrG8uuTnz68JFPzg3TeYWNgsrjm7WHLbOd5+8xEP5wW3F+e8vFmwDIHHh6fc35/TrBe0waEmpejENj0XizXeKMLhnMm05mExY/P6ivPLS4Z5wcm9Ux6ZGX6x5subS1YeZvtz3n7wkKKoubi+YOEDCpPMd+QczgBtSLFkdKlNxbk2MmKPSk7g6dkNw7CVxMghKT2nYRjQKC4ubvjkk08pKsu903tMp3Om8zn17JDJ/IigakwxxdgSlCEoC7rGFAVlkOTbeY+xcvYUlWIyPeDhw8d0vePwwStCWfHs/BWtk2kElDCKet9L0RS2TssqGTDIhaazXm2bjtv1DyhDVZepkBHGQ1kX+L5nvdpwc3vL3sEhk3omupJBgExjrJjyKLBKhjrN4X3e/u1/w+l7P+Srv/1r/uaP/oDL58+IrFn1DZvYo08OmR49Ynp0xJdDSrz7hTSpEPM1rSw+OJq+oTASoELSOiyKAq9EZmJIybxDUx/dozo8ZqN00im3yRwpjXl7R79eE7ynG3p++tO/hyimLikrkKZPlAftUzNfKTFGdD5ShEhV1qLd6kWrruu6pIkuzbnCWmKE5WJBOTmiqObYTnT5go90bcvx/gEmttwsLlndvsaoEmt6lJYx6KK0mEIkcyZ1jVGadrVmUs/p3Qo9DbiuJZqC6fyE2XyKdxq3fo1SJdPZIX5YMPRLXNdQGo+PHZqQGCcBa8Hh8K3cg/PXz1G6YjqdU1YFzg/YIM1lmZSQAkdbiMqjdWRwPcYaCg2Dbzi/ekVZS0xyMXB0cEDRFqyXizT1YtC2IvoSVMRYKy7dUXJEYwu8cyi05K+pEaeU7MuyqkApvIuYoiC6SIwKrQKl7mlXzzFFy9MHexzXJZZctMnkVoQRpNUq5WUxjpqKSinRQSfQ9dJAObp3itIaE8UkLmvPmSTpZbSw46y2FEVF8ANHRyccXF9TVjWmbbldrRjalmryir4dWGyWeB1pfM9Nc8Pp8X0msxlVIi8YbYgKqrri4OiAelJj1QLfe4ahpyxEx3zIYIIusLZEazFkroqSIYrmXp/ygaoUJlznepqhJSi5hz56ggJvNIf37mMnM5rEssLHrcwLihAUQ5IGU6pI8lCk8zmBVCaZFCkS+CAEgxDEuMZqPcbZnC8bZaSGChEdNVhDnxieru+pqmKsjbwfUNGgFXz9+Wd8+ugBJ/ePGbo1y+tz/vRP/lfOzl6iZlOCFUkVAXdE9mRSVwmgD+Pk4lbbUzKKkZ2Xc8DkC0HMTNKUecSIyqQgJflkllNar1es4irlKKJPqI1C1LdzPXU3jzDGyPspJR5vIaQUOOXBbHMEgKIq7+hDFkUhZkaQdKxzbpQaVzEig482xSNhrKGzzECqWbQmOj8CpvkLZ6YrKnNFYloXcj2Dc/Qq1WxJZg8FKo2iZ3pUBk3HI2qn7s7kmO0BRsphUx2mY9LIdakaEDJMNm/zOe9i/LBtQrbzeduUTP3Cn+0+k92/2837/imwNiYQadu4cGkPJrYsyZxWC/N8RBt2mLK711UkNvxuzZnXM+M92+rWZuxByEcCjgl5SEb5pQDwo5+GNlmuDZSWGnQXqIohMITI4Fbjdeb8OIPCIPl6BhpznpEbMFExTq/aQlISlRi+IFI0zvlkGm/H71iWIr9QlCWTyWS8LmmI7tRl4/2Sei7v5XyPFIyyDPnaYlR0XbOdmFUqnfmy3mIU0ynvXVJu1CIVEIWJWVQFGcge+oGYXGYzaGmTt0oYJP/sErM5N8+1EjKLNZbBuSQ/kxsW0ugl7cl+yIxhAUfzRJTWmqjCiA30XoBHpbXUgM5R2hLxV9IELxrFPiq0KTGl1CMu6eHGMOysaUVRbM9FMSLcymxkSQlU0qT1GbZGTLPVRGJKMv1WWlGYApTE17qux/fKzYeqLDEJK4gxpngWxkkQYwVwjt6nBoIfY7fzDh2lIZenbDLYO+oxE0Glpp8SMN57P+IIVVmNAHL+3aoW4DqkgFKWMsEmTf20JyO4fpDJkCjkRIXi2/Xm7uufNUgbYsSriCdtuARu+jQGUkxr9KSimJSY2uKtFNneBVDCWCAm5l0SQo8qoK0SM6YYyOxZUGlUbWsmo5DfDSEfrOJMuTtyqlQC5FQu+GWzOCfgTA5AKp2zRhuCOAOgkrtbTABhaQxWyUboup7isGQ2K2j7jv29OTrpxRljU2c6jKPaGSAaDwSVF4aAsman+y9n7RZkCMHjXRAdUK3kUEvMwswWSlXa2K2QHxW3wigyQSITEXLnUg5IFYXJlw93+d1E75cL2HasdoCKXwA3w/ZAykDw7kG4Zawm4ywn2mg+bToZ6wwMnaPESNfXKFRQaC0b1xgZN8pANogUQmHle8nnJd2bpDOr88hEStrYua+/+NrZjHdA2lTVp3unlSbawJDE/j97ecbF5R/xySef8Tu//S/58KP3mNQVldL0UcwYxKTBj2BvvqfSpc1utGoEELTSVNWUsqhYb1ZcLxrmJ0/50W+W/NVf/RlD07JaNqA08/09plMZMWg6x2A8q+WKq/Mr0dKy0KzW4rRoNNbWRBVpXQ9RZBmM0jjfjWL4u9o1tzcrFqsGxgaMrDdr7chyS8sWawrEhivy8uU5N7frdPAIw0xY9luZiQDbbn86rLf8+HTbVcDaknJvQnkwJ1RGZE1Gpnoy0PGe+Vw05YZhEK3hpMuczaLys48+JnF22RvRe85fvaLtOuqqEgF2LWCziZbT+6cYo3n+6gVIK2aMMxmkJUh8GxMsvU2od/e+Vmo0AIlKHC11YVIilDV7RRg+s+Ri3Hb3lVIJQNZ3krDSWhlNHRxGB64ur+i6FqU16/V6TPxD8GzW61EnNwKr5QqbEkjvgxj1hK0bbQgBjySrwlSKFCZJSHgv2oDa7MTrHWAzfR9jLA8fPuTi4oJuR+A+JybsFvKkaQrv0zhQSElo3Mannb28y9jYLZSMMWNyfyf5ZTsuf+e+xrsNvn5wY+weJWLSMww7P5v/fUffLMXJvuskiU8x3yRGWDGfMDnax12tZJzaR5Z0aA3RD8Sh56gxTIqKutBEF3GtQUfD5uo1P//47/neD3+dv/jTFZeffcpeVbIKlu9//0e0qxXXL75iefY1J/tT3n3nA7569hlDd8OyW/FyueZy5fjBhx/w8GDC5flLvnhxSePhVz98wNR4Xl+veXVxw8YbvvvBW5zsTWmWt7Qp5n730X3qoqJdrml6T6c0E605qkrOX1/RFwV7h8dMS8VBjHz5k59y3WwIexPeOLzP05NHvPr8M765vWVRWI4PDnhycoztBp6dnbHcrAmmIFdpOWEihMSel2d27949nHNcXFygd9grYwc+JeCLxWIsgsa+aWKfyc9q/uxv/orL9RU//N6v8OStNzm+fx9tJ0Rd03tDN2ywDgobkittR3t7Sz90VEVFPZmjoyUi0ks6KOpyxmefveB2E/kv/+t/x7JZEWzJn/zh76FjkIYIAed7Sa6HHnRAFYZIboRmbe58SmfQOi9vGd0zVgwz3OAE6PFBTJS0ZjqpKdIeGlFqvT3ndIxoAi4GmujprEG/+YQPHj3iya//Op/8xV/z2V/9hIvlhvjVJ8yPZhxUTynffY/6nXfZm0+IzS1DsyD6FVfnL9jzkaA8Q4hQeGLjcSmnUoIuoENMmsKRPgTu3X8A9RSXQGRhkIHrRYYgEjC2oCwU//B3/yc//fs/5tG9rGUt+pSoSPQiLRS9JwZNwMq4Lr3EBa2FtWhLyae8xw0e34tJxXx/n64bqGqPnRj2jh/R9i41CBTXV+fMqglqcPjVhsurBWLEZKgqaTz6psP3orU79D1953AO9vcOqaqaMLR0fYepC+6dPsbYmuvNBUp5BtcJQ2hYsmkv8bFhNq8oysjR0cH/S92bPVmWXed9vz2c4Q6ZlVlTV/UIgJjRAJukKIoDyBBtSeFQhEN+8KMf7P/JT/4X9OBwSA8KyTZNSeHQYBIm0QQaQHeju7qmzMrxTmfYgx/W2ufeaoB6pi+i0FU53OGcvfda61vf9y3q2mKdnJeGGdvc0fgaNgOYyPLOEuszm/UtlkBFJKWeNA6cHJ9gXc2zp0+ISZhF3oHFEiKsrq5wlQdrWdYNs9mMq8tX7LoNs3auXoIzxrGectWM2pRhxcM0BWB/3mYrjTnJk43m4g7nGkQyLlO2KxcI4zXrzYr3Hs/46uNT3DaQY8BW4isq3pBgjNO8XZnx5Rwm88Wzp2QLp/dPiIi/Y7IOvDSBhaSRWa03nF28pPWe9x49Zthuubh4ha9rLq4uGUPkWD3xqqZltV5zs16xXW+53dxyu1sxxpFd7MgSEjFqLxDVN/D2+ppoRnKMrG9XXF1e0tRztR/wOFdAao8zFd7UYCOGQLF4izbRDVtCtMSU2I07NuMW4zNNO8c6xxAC9dEx9x49JqVAt9mSYsJbTzZWi0/J5YPO85BCe65SVgUkEoQ4TACsku5kz1iPzeJ9KgBnKb4t4zgwMR4VMCJlcpRCfAyWbMRyZYyGVj3pHz1+zGI+Y3HUsFw2hM2W7vYWa6GPA9shUJPxWc4vmyAAnQ7nssZNQGPxMAT24OyUbwdyLt6Je6uHoggtBf0wiKejMUaa8sYoeIiw7IxRwonOHzmoi3LOxCAkJAoQl/Me0HRuAmBLzlIazCmlifWY4bX8QpoQ+9qhsAhLbLBaVzhVRoonpZ1yMoPFOA18qhqMqgQtyXHJgwpJA/b1jzV2qmVKLiUNGyi2BYV9eHjdCwiuF0hr9j3RJmljrPhDFnsjpt+Vk72wa39d5Xb4OMzrDh+vE7deB3N/HbArb3ef8xWVYUwGGzOVL2zMPbPQlbpG89NyDcdxJGy3zBeLSTZeLMu8zlOYaoQkM2KKNH86X3XflppZcuUkw0nT3i7B4Oj63dQQOSQPFOARhNVbvHEPc+MCqO5rwKg3oSiWdFYO+58xBfhHhq1Zv78m9uCaeO/J+tlKXlPY5YV5LGvVT681hpHsCtYT900K/X5VN9Rq91GAQqPsdbHDkSZGdE7rfyu0Fq1bm0rA87Zp2e12MkPgYD0XoNxYA5Hps/R9T1ULWDmEII1KtQGErAxjsGmvxGuaRqxqooC9skbQ/Sbv11qxdgsxMGvaqX5p6pqmacTuKItVXChzdjLi369gKezXoADWQa0WtK4ZZGZLUO9dm9Sqy0gdWa5vGPY2fkTJP5ezxTSgzGRhEntnSUnORzLkmIhJB8OmRFPVJLcfcjcxcqta14nUnVnJFyFGaZgq03dUEHYcR1GDWqu2BKKEizqwbRhHsqrdvd4P2X8Dm+2KEII2ChYCVqegQD70Q0eIo+SXCmqLD248qFF/9fF3GqQ1RryArFP/TaMJY+Vx3tAczWFWk610BmIcFCyUiXrZKlKdC4gmgc87yzCOk0dsCRUSHJURZ6WjHg5PbT3R96w1lZMIuVPecP7ygXzIvyteJiIbKXBn0oWovy4AY4wY46gqy7rrcL4SOZd2TKemnyY5BSAtYGp5f/IjmmDqK+6HJqX98LK0Z4NMoIAau6MJgFHACd1gpbtqcHjv9LBBvbsk8Iq8vATNclDLa+0bMWYfHPW1vWTI0wFWpt07Xg+Eh4BNkUEZE9lstziz90+yxrLrOsZhoNUNIdODa0Iap06w4vVSbJf7mcSoP5Zra7SbbNXI3slGK8yrw07vtArKc0/fl3tVQMOyvnLOUmCWLzkZnLGNIx9+9jHnN6/4/Ze/zR/+/b/P6ck9mkZk7mMYJsBA+eHaKTxgOB8kO1kLU+Mr6sUdQnasxoH25B4f/N7v89nPP2L3i09omhqMxVW1JkaRIUaqpuH0/l1I4GtP3dSk7AhYYcDkA09eldFUdc04DnrfJZiNMbHpImOSBCoq2zwbYZjWdTUxvnNSubfNxJR5efZKWJPG7Nc6Bx6eCniXQC2sG5G1JpW4JBJ1W+EXM9xyQdJBISUxNJR1Lfu1bmoJ0vvtvQd3Du61JLZMNgQ5ZpleaqGqHDFqJ9xYYobdbsc49tOzuHJuIQlYGaxAUt9r/TnpzIovdEriW7Ss57SV5/zVmQz68F5keTlhk1wHawyuqicZR1mbaCFSOU8zb9hsBAQvckZ5byUJCxSJaNPULOZzri+v2G423Kxumc1mVJUXMIOk54WcHzkdApdi1l5uWuVlIvZmt9WzWK6ur8RrtoDL07U2+0bZdifTpfM0+Vj2nfdeGkpZABZjYLlYKMtomFgmuTSjvgSugngndbsdbdNqIuD1bLTT65T7FXMZ2GgnEK94lRaAt2lqUtbCq6zRkpBmnd4q2kJ85dSvbn/mlebZqBKoZJh+P+VMzFAfL0m7kdBLUReBbQp4m6jGjKfBuQqGHdkkGtNiYqYxcH3+nPe+933+m//uv+ef/y//M6G/5frZpzyfV3zz29/mP188J41bzp9+RvWVhjcfv81HP3lJqA318ojvvHGHB/Oa66tzPnt5zWpMfP833uK48lxdX/DZ+RbfHPHegyPuLT3bqwuenF/THi/57W9/DZstnz9/zvV6x+0IODhpK9Jmi7WG6uQI5yzzMbO9vWUzdJjTY+6enPC4OWL79AUvLs7IJ6d8+2vfwK3XpHXHs9srzseBYAx3Zg2Vb1h1AwPqXWbMBFYaa7m+ulZ/QMjaCEpxz0adJhCXdUiJ7SVQy1kQc+boZMEP/+Ef84P3f5N33ngXTE1IYF1DwtA0rUh6TSaOnUzjTZHaO6xJjN0GY2tw4kHsLDz54imvzi/41ne/TzCJfr2jrufCYNDiF12DMQd8HjUw79UE4sGcmTQgZg+2OC1qh3Fkt+0xKbDd9gxDoB8jMYOtGrwxGAsxi6+91c+eka8D3G42+LrGOLESMsYyVp763a/w/Tff5d3f+2Nuf/4FqxfP+OKTn3L76S9Yp5Hu+hULb2gf3Gc5f0yuB/onM9quZ5Ejs7DFmsTq6TUhbRmGACFBjoQxELPKB53n+P4jkqvIY5zOtKKayXjGINfm+uwLPvzrf0/uXuA5JqWKEa95ViRPbJmosdEwhmKlohZQGS1yxPYgIQNYVquekHuePvuCN3v41ulj3n3vG5wc3ZMzLATOX7zks7PPCf0tZuwh9hK7snooBwHYuj6y2Qy8ON/w+N1H/Pbf/wFtM5dBtNYxhEjuNzhbcXxyH0ckpw6bt+w2V6xuL+nWN2LhYKBua4Z+ZBjM5EGakgFT04+Zqq5Jqef87AnjODB0O9Y5EsPIOIiH8ur2ivm8JcbAfDHTOD4SxoGqKlJemc7svefq8pIYR5FRGlGCmGbOuKmoJ/VUUckAWKwreXSG7MReAohhmEAfrFOgyMo9SxFnDGMaGIeek9OWr739gPOPnuF1toHkvlkk6xpjYgzkCI1riTnT9wPXt2vaecO8XdL6lpQSu91AXDhaX1EZr7VGz/HRHRaLOV0/sllvuL2+YdNtSMZy/94DTu+dcLu+Zb5cYqzj7TffZBx6ut2Os7Pn7MaObtcLoImsJ5stBksymbae4ZLkEr5qaGdzmXatEt3at8yaVpioyWIU7Pa2Iqde/KhJdMMguTwCwoVic6R5aTKOk4cPqGYzxpiZ1TXjoMNAfa1Yi+bBVr0OY2IYBlEkGB1QjMq8FQixQDZiJVNyY7lvAtBGVfgUGbVz4qnLGEj9DpsTEUsZlJXJjHFk3sxpmoq6doyh4+r8nCfG8ctPPmMM0kBLgngTQo+zDQZD18mw6VTAJH/QIDUOb8Tq7BCYE6s6HSirOXj5tzCCy0fTgUe25OuF4RbEJsNVkzy5wIdliroxykrTXPzQNq2cZdMUdfbA4WSF5fbNfw6+X/5epr+X3OcQHJUSwh5IfTPWqKzdGZwziifre0Pk3rbekwCmZvRU/GUKq9EgCs66EmCqeOdK3SKxSpix8rvOWYlNCg5ONZaqYYQ4ZcDIeWMR5nllPb2x+opS1GYF/QtY+OXHlwHYw6+9xu6dcsiSi/2qgirr59dSWsAc3adZ7d2cfs4yyySlyDgGagU9jTanvPMU9a7R/0ljWAhhJT8+ZJEaI0OYZNF+yY7AucmjNqekDR47AVzCnpb1PYyRtq1U7SyqvsPPOYGmB6qcYieAruyYosx6SOUOaPtFiTdGrRXJ8rUUI40OGdx7tEIKOhwtHpC7piVmJj9Rc0CScmrjIGQaASKLmmJiXeYw7WWLAWOpnFe7EDlDJXfY17nl57wTW0qMWDaQhe2cMxDHvZ2mlfPPGUPyEg932x1BhwbmDE1TkZHfN7pHq6pi6DvaVhTk1u4VtSEEARR5fe1hwThL3dSYcT9kK8XIGAdMhEiY6h85c8TeIaWMcTKIPWdIITP0g9QaIeG8Oai55ZwLSUD9nDIuCbEQa2gqYehnk2VYtVp45ZyoKk8MRRmArtU9SSZTsDwdcln2IQnv7ZSH5xzJUa6Hsx7jBZMSxeUe84khUlc1rnVq12fEusA7saMB3GwGBra7nYL0YmdU9uBsNiPlSAgC5BqzVzjL3ClLxpP7SMjity1QmZ4Dr6GErz/+ToO0WTeNd066jvJV/KxhdmeGazwDyoI0SXxInddz1pCtUKuttdM0PbKAqk43B1oIZ7P327DGaBeksEmtToj8kiGCFtOlEH+N/WkQoCDtPQ9zzlS+0aAiRUq5iRkphoImPOM4ENNIpAI8POrZGwAAIABJREFUzjUSIG3EmbRnpRozJdcxCbXcu4qQtTtVulvOSeBU5mehX2dTWHgH0w0VEDVJmMfkrL6xen1lPKIcas5roNBgXgKuKa8r3dsUEmMYcclN96g8SjIQ476DmjSRscimD/oGzGuL+fWAmFJJ5hNjCIyyXGQj5iKPzuCsDhwxMo1VPUenXmpW8NUWnzPpfO37rHIIF7kEBkwp1BUMF2uN/YRK0EKYRPHpkve6tyeI5AlAN84pQJPxOqQpkHl+e8W//Df/ms9++Uv+5A9/yHe+811qX8lnTsIwL+puZy3O1fvkKAlYViwlSpgx1lO1M/KYRaq5OOHxu18nBcNudSPeoCbSzmrCKINTnPU0c/HhMRlc3TKmIjWXz+Oso2lbClPToF3ULGBEVdWs1hu6ZMnGY4ywPXPMU2JqdB/tB8DItbm8vODs/GIC9w4BNmk2mD3whSR0BfDKlCWQwBma5Qx3tMDMZ0Qjdh/koKFZpeyIt+LF5aU0gqydgsbhJNI9y1uCW9TOndMkN+fIbrvRe+LAStBYbW5xOmX0sDN9mEB75wgKnNjSXdfuctKDfz6b88aD+4Sh5zyOJCvJQlNVk4G8FAdWGGd6ffVolQQuR+bVnHkzo991DOMgF4zM4fYrRYNxhiEMjNe9+AIbQ1t7qspL0q8G+wJUilS8VuanMKs14fReJMFGgJ4klTY5GUJK1BjdxzocrBQgmlAQE9e318xmM8JWfAunhoieuMJGEMDq8uqCUpTL3s3lR6ckBTJ13UiwVnDcWEsYBZBom4ahH4RVYmSFlpMixTSdr/uuvvwRWXSYmLjWGIwX5UFQANDq+YwmpCnvmRBlTSzmc7GZyFkZtMrAiTJ13lSO9nhJ3HTYQUCpMUa2KeHJzKqaORI7t2NHyjCzLZV3dOtLfvR//2v+5J/8t/zBP/6n/Md/9b/Sd5f84qf/L9//B3/MB3/wQ370b/9PmmHH82e/5P6b73L64G0ub57zxlFFlQeuL65Y7QaM93zrvXs8XM64vLzk4xdr1mPiB1854d6i5vrigk+fXnIbDO9/5Q4zm3j5/CVXN7esx8RsNmcxqxmHgeA91fEClxJN6NmuO1b9SHv3lPt3T1nkzM3zF1xubhjrhgcP3+S3vvUD/tOf/e+8Wl2xNgHbVLzTznnzzQfcbAd+sX3FKgaSF9b/Ibtot9vh1Le6RO5SYJXp0WhSZvSESVlWHBqbU4IcI9/75tf5ne9/wNHRfVKuwNTCdDVy36xrsK4ixZHN6kY6+m2L8bL++q7HNZJEGmv54skTvvjiC772G1/HtRWXt9fSACq2JbomcjaEoPFNJprqmjzo4Kt6pJwFGKYBaZlIN4xcXt5yxcDF5Zrrm45q1lK3MwXdElFtCQpDpAza8taTUuDm9obj42Nms5nE0INE3DjD0Vv3WTx+yJvb7/Dg469y/eRzzp494dVnn7L1iXt3l8zrO7zzna9iH1aYy0vMesO9Bw3L44onP3pG+vyKcLmhX22wRIbtjm4I4CxxtuTOo7cIKiXdH2lZVRgOEyPDsOXixSeszn/OyZ2KunLkKE3FnIKygiX32u22Uqzpokhx//mHviOmICzeUUBCDDhf4VzNG288wnvL9dUlbzyK1O1dxtCwmC8gnJKGhuvLZ3S7F7g4kvqOGB05Joa+4+pmx250XG8Tz6863v32fZrFKcZ6zTfA+ZqYDJvVirZuqF0mjVu8OWLsNqxuN6yvV8zrhjEODMNIHjYMMbA4Ptb8tqzxpEMaL7FmHwOkeBK2DAaGoWMYOmKMHB152vlCQcwNzlnqmQCfWImR1kfu3juBlFnfbog4qrphYy9JoSMSJH7liNWBOq5y4iGcIQUP2ZFyZBg7chp1sKowLDMCKDmDDuSx1DMPwfL1r77D8OScyknhWCTSEDAWnDMMQ8+u76lqkdvnnMBa7t19wLyeE5wMu2orT6wNM1fRuIrW11Suwg6S8y7nC47mS9J9YXtmY8nWElLH44cPycbQ9x2kxLKZ85W332WzXdOnTJ1rLl68YnfyJovFqTQCnLTerPU0riVXFkNNTpbLi0vCONJULXU9F2ZR1nifBFDzVoDkhDQy27rGOsswBk6OTrDG0puB682GMSbaxZJqseR2dUvKIsNNJWxm8VWM6vfunCdrI2EiB+RIjCoTTRKjnS9yUu1wZDmjpOmsFgIHIJhk2ImMJQ0DeewnQoAw31q8r/HRMnOOmsS9owUniwUpZY7aJXGUeR/BCOBbWfElnbUz3n7rLX720U+lWWAEyIlFMpszMVjGYThQhKniSIcC5rxncotiUPOUUNitpalbCARSgxZVkagwS6VZWH3yb6skgyk31OtU9h8JZWclITUpGlDUQeUaHv4pYGD5+6GK6NByyTs/DXxLOtinMIRDDHjjhdk9xUGmnLFYUBRJcWnOT3WzNVOcmBrkxorqVZ+pvA/5vJqval6d0n44dsn/AfU5zkLwMBGHkHlS8V+dBirl4sy3D4cHtWX5969TQx0CsYc/8196DrlGem2y1DzOm6nmtFaIGnXtcdZJQ0CZybaQrrT5WohpVpmgEwu0qH2SOZjroQ0JlYFPeIU+7EEtU6nNk3ipHzQpNNEpBKg9ueB1MPjL12nfMAiMY5i8X0vKEWKQPWIE1JqGmh/gJxOLORWrhbi/zlJgqcJNvay1ipMhxKWpkQhxxBgd+DztNJikjyhWnyEWq5YCgIdA1msq/qJSt3tT7efBWFFjVr6SGi+nCWew00wOxS2k4JEYZaVx1taZVImi2RohmRULkbaqpz1aOxl4KQrt0jSS5mdh15ZhanI9LbXz1PP9PoshEDFYbyEhMdaq8tqK5UqxdyiqI+fMZHklaj61aKgqsUDJgoGMcWAcZTilgEhJBzEOE/FojPK+k4AwrDcbrPFUlSXmSNftPZabppG1rLV+ea0YgyIrUutnY6isI9tMjuOkKs05Y7NRFep+nw/DQFVJE3E+m1FY6zEUdaf88Lyd0TatxIOcp8Hesl4z4+Cp65YYopIvxWcXMlVVM5vP2HUdMWVRd5uydv9/yqSFTMgZG7Oa3gsbyc9rZvfuiHfhqwutOTJtO1P/SmVMZe06Uja9m6wTpoPGWFKOMsEww3TI61/lQJRkVwbFlUNt7zeYDa8Vzvu3L4eGdK2l4slFUqidov3Pm8k8PeVIP+xk8JmpwFTU9ezAP07YcNIRkCSgzJMpHinyWfJUMB0eoF+WXhwG5f3DaGdIDe9LdwQ04SpSBOS+WCRhiGoToNexdNPKhPqofnGHn1sOFpX6TOCUHmAhaTBLOIN64ch7EGsKR+nKH/oGlmevnLBOcgyTDD5P3Zf9tYmT16x4kI0hiBfJQRengPwg623qYuc8+ReXFy+X89DbrwAo+89s9g0Fir+w+DBPg2xixtRywMmhIIDzX370U569fME/+J2/xwe//bu8+fgRPorXXcglMTp8nVzi1QTw75dpxniHNy3WtIzDwPHdivn8iIsXT3n62cdcXl7TNp5uu+X45ESKLiyYCucl0GSgarwctpqwy7USZmPSRotT6foYM2cXV2y7nkwlPQUNVEEbCodye+m8JUiWzz59StePyPREBReM/L5TiVlUiUu5F5NcxyEBCaiWc6qjBaatiQomlutU9kpVVTjr6HI3gXF7v6JflTh9aXvtAYusvqm5IowB32QqZ7X7a7+URMsRdShrms/nbDab15pBxWfY6XCg2jlshq4b9sltDFhbYbNIpI1awWSKJEwShzSB+eKfGEYBEWd+xnboJzCxSLSMFVlSYePO60YaKgqMxyiNF2cNx0fHXK9Wco9znia4yt9LkyWQkkhljLfYIu9JkZThzskJZ+fn05pwzk0Dy/YFTqDrutfui8gLBxkoZISJ65yTTrSyBg6TVWudsEKmeypJyjhNnBbfWmMtd46PsCZzfbuSghs5IpyRLjWZCVCWs30vjTz0ERYZpUoAjTBfyjL8snKg/K73nnunp7yKkaEfMDljs4DNFgHXcA6zqKlPlnArU8VTjoxkdg5WJrEgUxuDTYl+HPBNhcXTWIjXz/jJ//PnfOfv/Slvff27fPbjf49LA5//8mN+6/f/lDfe+YxXX3yM85Z+e8tXv/YtmqctNzefY22ishV37yz42tdPMOOOs7MzPn5xzbpPfP/r73CnNly/uuT8asPoHd/6yps8PJpzdfaC6+2G1QgnJyeczGuuVls2lSVZaHNkMUZW1xuuh5Hl/Qcsjo9pY+Lm7CU33YZ4Z8Hy/kPeuveYvNry4vKclZOi/EE958HRMevzS55fXzJiqXAY3zBvW3br9XQWucppUriP8TkbHTq479wf3i9T8gQjU+GFuS9+lT6CTYZuGMT3zzosntq3WNtAhn63Ytetmc0XNFXDEKQ54XxF1dRUvubzJ5/z4vkZ3/z298g6dMJhcGTm87nEmjhglO2UQsIksS1Q1G2/rg7+lLP28EwDYatcXFxxfNTIWdQl6qbBOI+QvBPZivqoyGnLM2qvhvv370+FeQZlIcu1LTWgcx5/NOPxD77D29/7JrcXF/zyL/+Cs5/8Fdfnz1jvrqnvWDo6TtuWYGF9Gjj96h3yqy21ndOe7vCbkcoY8tUtYSPMlPr4Lsdvv8VAIOYy/VqbaqX4i8Kq22xvRG5IhORIQa2hUsBbmcLMKF6Y3lUCHsqVwprMenMDJmKtYZg8sy1V7dn1lwxD4J333sS4huWdU8Zk2K0HfvnxC07uPOB4ecq9e3By/JCby0+5evkpt7fPGbqe1A/EMRD6TD9mbtc9s5MTvvnBH/Dg8SN2ty8wRvzjYhKGX7SG7WaFpWPc3lCZB9icuXp1wcunz3n84AGL4zlh6Lk+v2IIkfniDskYymy5rCAQWQrfAh5NayQVSy43Nd4AbNVSV14Y4Gj8GTowRpjV1so5Pg7kEKmqOW09Z1vPGbsrBR8MdT2n8jUpB2IKYn2WIQ6QAiQGchvJOWBtLfmxKWdu0jiXRL5eOUzrOLl/yoOHdzFRJnhjUNWUFK3ZQlXVSGqrHrVpoOv6afCTsZa6aXDeMJgIQeJ9yCP90PPq6oKj5bGsrVFYVO18TiaxWl1wfXtB2yyZLRbEsWO7XnH84DHvvf2uSGz7nscPLhQIrvGV04Z1xrGftm6tKC4a3zJvFtSmZV4vKExEc7DTs5Gp2JVvSGVCOEZUPM7i6sTYtKRRyB/GWE7vPgDf0A+RZPLUUAQZyOJiNTE267amqRst5j0xFXsjSDnono/EoXgG7gc+TV6jUnSp/N9O9UwGZYyKd2cBBENIGN/g/Iw72bKkwWG4d7zAxcQ3P/iAuqq5d3pPYN5SH+hZt1rfcnbuEY6EsL50gSu4sj8vYpLXczo4OZus4L6ce9LOk1ozsy/ID8FJO4EMUcFSGeRVvl6mh/86gLD8vfx+YZMdHx8TQ+Rms8bmrNyEPWhX8gj5HK/XKId2CGX/lt8JIUz50iEbdiIVqKVMzqURKEstq9JAarpDRmfmUO4vZMMD0FCL8MPPWX7Xak2PEVZoiiWfLDGk1MFZgWTJV2NOBCN5ETnv7+/UqjuMga+TgH4tI/bX/Pu/9HOvP0qOoICX22twCqAXQ2TMgTAGJJ3bD67zlVFfdjsNRC+lf4gRFIgt8wjKGmuaBmsMbdNM674MRXXOqUWKTrI3xS7DM6ky9Z6j4JjzCuTrxRvHQeZe5L1nbVkjIQy6XvMEEh9aeJVmjwlipei9J4bIMPSSP2nTwDqn4JeCp1r3WWvZDQPkfs/+tjrvJudpjgVGZv8UJm7JwQsmUK6F0SGYIYzCoFXLNUymD9IgjElsJ6P6jtdVrevKYlOecI2UhUwj9zCoj3okAg6peR2eYRzI7ImDxSLlEN8oa2scR1UoKKiqtWnBm6RZVtitgjlNrOZSZ1hL3baqkNzXJTmDtxJTJoa9NpeMk8GQs1YUJF03KMHmwH7FGGbVTO5PZqppUpIGZ8qS6xXbQOeFCySfxeGVmeucMLTL2TLqzBBrrYLviXEM0kBXZa1vakxtSYjt6BgTIUqz3GSwXrxuD8/fMQQBXfW5QwFqYySOYrsy4UB6/RJo08qqGt7grVWix76WA8CBsxVVBT6r5/rBOf63Pf5Og7TOOk6WS/X5kcWRAePE+Hw2b/HGUkZ6y6YvdHZLRo3sjW4YZRhNzRIDZTq6UZq/0S5OOYSSzZM3pY6JotCk5VG8gL7UOdJvSzdQZVgHG2xvam3AWJwR5pUwXCJ9vxPPDS8gQVW3WFsR80DIhhzSxPATJq3K/Y1Tdp0cpsWH6HC4TTk0SyfrMCCXg9NaOfxSLtdPAFtyng7KGILIcFPGUeQjJTFBD+W9JOjQl/FQclPYYcVCwdg9Smadl02l4IMs+v1QsXIbXuvgKbuw+MaKbUPxERKJk7OWUaXzRm0rDHvg3BffomS0pj1kavLavbYWMml6LwWw/fIGLAPXnNsPP+IgSBmj7FsNkCYjnisliJSkJxsCibOba/7Nv/0zfvbFE/7kD/+Y733jWzR1A+qdwwFQJbVonhKXQxDKmNKprzQgt9DMCU1L1w8sVzcMm1vS2E8MKKzHuooQZfibscIKNXptDRYOfHIpV04DoHGOro+EZBXcsjq8TRnhyig9vM5GA/HF1Zqz82sk4GiyOQGxbp9MWCP7QtdrViDXVw6swc8b2rtH2EVDAMY0QpbGUOnylfvkrJsaMYcshMPHISheaoxy76XTCVXV8Pu/+0d8+OGH3KwvKfYch89R7tch0yGoZ85hw6Xsw6BFUVNVzGYNT55+wS4G3nr0iLcePuLHH35IkZ9V1nG0PJJEIGWZFB8Dx4tjuq4jhiBTd3XNDYPYaKSURJlwkLSKx5whh0DTNHztna8whoFn52d0w4j3yrSJkdVqTZE3lUBdkiGRZukUV2XROwWq0yCM49p7YQZpV7sE1t1uR2GCWGunSaAliJefTSmprCmD259BwATYFmlPXdeEMOpziXl8KSrKo/izXVxeTM2VnLOsb+Q8cM5jYHruMYyvvafDYivlOCUtjx6+QUqRFy/PfmWNHa6/GCMvXrycmCnF5kSK8WKlknFNRXO6pBsTcSOJTMwZ5y0344gbIr6dcVq3OAPkURj19QwTB158/BFjrnj09nucf/ELtldPuXn5BT/9q//EO9/4KjevnpK7Lf3qghcvK95461023S3r9StqU3G8WJC6LddX1/zixQ3rIfHdrz3i8ekRt1fXnF1tSe2cd9864s1Fy+bqkp8/v+LVNvL48RscL+e8urogNzV5DDTZMcfSr2/YpUhz9whXOcxqy/nmlvV2i797BztrmQ3w2Ycf8pP8I65ih6/mvDG/wzwmbs5fcdEPJAsPT4+pmxlXqw3OWjYxEnPC1vUUS/fn+es+bhOLo5wLuRy46hGMnfZTUKmUFLRgvHjlSbHJfkCGdSyPj/G+ZhwT5y9fsTw+YjmfUfuaTz79lF/+8gnf/e771LM5q91WztcQcQbm7RznhZFrkMZfv+uJwUBtEHEwgrqVM07ZAMIYkbNSchlJKJNxtLM577zzmJcvL2jrHl9XxGwUYHX42uKN+9K+MeQUhTECr50h+7iqBW4Sv7xkM9EZjK9YvPmYH9z/x3S/9QEvPv0ZL55/ymp3ybC7YdYOtAtPvXCEqmdnNnTe0lWQ5zXWVzLJ/mZDiIH20ZtUJ6fq9y7NpGyQqeQ5SwM3ZkiRzWqNQQqzmKUZHaL6splEzkYAiJQZU6Ca9p/kcKvba9qFwVWqNLKoN13Ng4f3SDGT0oh1MiQOHGHscKbmR3/51xwfnfLeO2/RVAvq9iHVrKM3W85WL4ljIowR52uRL/rA8o33eP93/wknM88nP/4zMjfkHFTK2DHsRuazmpMjT19VbNe3zI5XvP3WfV48+YRPP/mE73/wHZras9muMNZR11Ik62TdvQ+3RF0OizqRCe6Huez3h6zrtp3R9Z2QCkLAVy1tMwfr2WzWjEPApECKIjncBBluEnWAaNMeU/kaax1dt5LXq+QeIIQltv1ITqWwkwFeZW2nkKfcMutgkxQitjY8evMNUp8muTa5nKNSO3jXMG8r8SDMwtxr2lZBWpVTWsF+UkzqE6ggdd9RuRqTJR/uO2mAGu+42lzy45//BWfXL2lmxzw8fUhrK0zIzOsZJOj7gdM7d6idJww9fbfjJmaMg6PjJc45jo+OWR4fEcbAbr1jyIHl/Ija1Thb7Qca5j2oUWoUZ6w2CB0WYfIl1JsyS9GZcqZdLJkdtexchbeWrGykpGdd1jyeLA2d0A+Muqclxmm+rAWs9a8PY92D+1abSbq+YhS5shVFzZ4pCE4VWKXeMClKfmegqr3UX5Wl60aqqqdtZ/zsFx/x6uZCajYjOUnI0swYxpFXF2d4WzzhVe5r9mqfcl6lLAxtadhZVWdJo1+OOGk+qRxPaz2meDHVUbGwH+V3desQY+Tu3btst1vx9j/MhfUsPZw/oVeRMGrDKxe1QAI9r4pyU/ZtsWhSe4KDuqXs8QksNyKJ7rqOynvm8zmd5lpln4cDoHgiOaTyfpn+Kz8vRJ+Sx2CK8m1PnEHPZmHlKRiizfkwjsKIVyWS5IOHakf5mlWgzYIquiy2qrHeE6Q82FtR/JrHr8u/vvz4MlGj/N7hfXmdvLUHhHM2dLsdfd8yXzSax4mVzUiALAzHMlNEGhR5kpSnJEzz6T4gNb/3MjCwDN1dHh2pl7kwEYu9V6nDp8+gX08xavOhvGfdw4UMFaSpMo4jdmS6b4XRPAzjfj3ZMqzcTb6fOUPuXwezMWbysCVn6qaZBqbN0mx6n+ngDHD6Way10+8WosbkZ1usQjA0s1ZxefleqXnIwugcU6IuQx+tWPD5uhJ1wTDIMEQFf53K4b3e+10vM1d2XUfMSRQMzgspyEiDIKmFTCar0tWL6gXx9h/GkTDKGq9qtdpLh3Xh6w2Lsv/Ff5ipEVbO8zK4OqX90MuiqIXCzM+4rIp06yhzYJwC11IjjoQQaZpaVEVJZ8UoNmcNYlsBr51PYKh1yJZTRbxzgndlwBkBsXOWtVMIrlJ/y+80td13H1DQWuubyldk53HWU+dI0jrZ1w5fWTDSLBbLK2lWe2MnZm5VVdOeTFnsAmWNy+EQoryvUa0jplQfVQXrY5qAYgpTW3E0+ZI0FILYNForILeoMoLG47/98XcapM3IhM6Yo3heYqGpsN5yc33F6lqN43FCO895OgCslcSpACtQhsaIIB8kAEihIlT7EigK20kOMU3qlDlZ8nBg+n6KwuqcJn0eHJi/rqtWCrwJNJ3AoIidkt4sHoxG5MltO6epl+yGrbAqNbhmkwVIpPjxaAF00JH8MuPvy92OEihLkiR/d9N7zQcRrBRcBibgau9Ta8i2AJ1iL1GSmkOAqbxe6fIJyJ0xOUGRYpm9pLT2NX/we3+PH//Vj3h5faMDiF6XahSPS7neiXsn93jvva/wk7/5G6IRiULUrppBJNKlQJZERtlQJSlQqUUiqTdoSTD21xC9v8U6AuQaCBC1N8gvwK9myFOQ0SdQZsd+mqQBiGmatplzlverCTTWk2JkMML++ejTT3ny/Izvf/t7/MM/+iO+9t67xHE/dbCA06WhIK+jsp+8fy/OWh0MJ0f4/OiEZDKb7Rp/7yGb61fkuJNBONaRjWFQgNBnNyViE/ikCQWlCNepx8YYdn3Paj2wG5K0UoywPMkleLnp+pb/WmcJMfPZZ8/Z7QYN7OLrWtZ+Jk9JcT442IUha0kmUVU19aLBHS8wi4agfjs5gXcWq6PFCtg7TXBUX9p8sKcO18LhY38d7HTvDSIBvF3d6n7P9P04CY5ff57XGxApJVarFU3T7M3v9Y+zFmukg315M9CnSHaOvhtocLz14A2eXZxRtS19N1BXFcM46GAPuU4319dy7b2nrmoyhkYHnI3jIPYb5Tbq/RVvHvlc3jhyCFxdXLHd7vB1jfcVfT8oG91MQDoYju/cYRwGUk4M6qlazjBrxFrCWCv2DyHx8N5DXGX4/MlnU2A9vAfl+jVNM62XkshN553K6nIsHnSBWifiln+nlNlutwoGH1pYSAMg6iTpiYGfxQrFqIew1SMia7OibWVYQLG94GA9T8BqAYwN5Bi5vryU+6rPb7RILo/XwOcs672wxEslXiZMJ2URuLbBnh6xWW2wIeG9YzcExpwZY6IyiaNZKwAbiZh6bKrw2eNCYvPsCaezO/zOH/5j/uOf/Su6m6c8/+RD5suGb333N/n5X/+IatiyO/ucWe35+m98k7/4qxXWG2IYubq94tNn5wxU/PZ33uXBouby1RlPzm7ZJMc33n3AvUXF+vKCXzw959Um8PZbj3jrwT2evDjjZoy4yrBwjqX1rNZrtiFi5y11lsFhN+cv6Gxifu8+zaylzonh8pLnV5fk0yOWyyX3FndYRsPLs1fsZpZYVdyfzbk7W3K925G6HZtePKcPrWowhR2rexM9CA5BBg4GuKRMMlIYVFVFkp4VndrwVClRleWgFjcxBYijJKrO01THGGPpu8T86Jg7J6dgLP/u//i/eHZ2zg//0X9N087puwGTEo5E129JccS7GpNFYh2DSFH73cDQReZzS2EFS7xTAMeWGLVXsqDRP8RA320ZQ8MwBpqm4uRkye22JyQwrlFc61AVc2il8KsS0els1PPOWqMqjERhX2QjA3zGpsa+/TZvPX6Dt8bfJa7PuXn+Cetnn3F9/Zztiy25Smxu1+xuDP020/gZXUxsQqC3ltTMae8/oFkspzgHKCirCqAcyWnDbnfFanWLjdC2M47uPeD6ak0MK4xzhDGSksizQ8ExMjJULIlCQibMZ3ztsDZjtIDquo52Vst6sjLYcQgjzsHzLz4nDpn33n3IT3/6Cz75+EPGfsfYbzmaVczamjsPHrNeb1hfXJKC4+qyY72JfOuH7/PeN36Ly+dfEHMlrEjEBSD5AAAgAElEQVRf4a2nmVWEIIBaPas5fXhP8t5xxXa75uT0DhvniQR87Xn0+BHdMAjj0WSsq14rDkueYijTwKVRW3Jg2DPsxnGk321IoWe7umW5mCN6G89ivqTre/pdR1s7AWz7iHPCHgOH80e4xtK2whgaxx6fI7lfEYOsV+sF9POh5Px6fw1YZ3DJEJ2u5yk/iBibCXnk+PQO5pXkDzlFTdXEKshZ8cnNrmwYWK9WOKPeftpAz2RyTPhocBg8wqhpm5aHTrzsu6HHu4oUM+Mw0FQVy+WSs9UL+rjBVvDg7gNCF9juNnjnefr8CRfXLV3fMZ/Nubi8YFbPWBwvMests1nD8ckx7aIhRi+D4pLEHpItjiuSJ5Enr/Oy9YwRxvDrNi9KWsgiBc3WsLx7D9NEIlZnJWh8zJmsAIHE733tY63aOQRhrVltgm62O9IoKiVjtbFvRX5cwNwpx3YJU1QnsG/2IHlxP44iX08J46C2Fq9ZHNKP5+r2mpOT+1w+PePl58+4vLkioixzIqMW3mXSesmTxzSq3Liw0ootAFOtV0BWyenkeu7ZqaKU2ts1iEonl8N3OguN2r3tLZpiDDx79oyq8tPPSD7PRPTo+w5gao7EmNhsNtPZLmeMNL4LGKuItp7xFueNeo4aUQRY89pnytpUiaOAFwLIeOp6D5jt/W4LuWJv2bUPob/KHp4AQs2bDs8NkGbBa7VReU5jJfcK47TWZHaC7O2oe1/exwT3T00Bq+vXIHl/VhDvsK778t9fq21+DTB7+Dn3Ye+/BL/I94cxaO5ZM4RR2eHS+Cy2g9abfT1giu3M6zG1qipmsxmz+Rxr9g2Fwo7uul4Gzhkz2fPBPo+ewE+jzSRlRk4+rge5qzSg5araLBYGxlpizBNEUmb2VJXFWE/WIWjOydT7w1hxuL7Le6qqSq7FQVNQsJb0Kz87nTX63/l8LvV7ztL8oxCxzF79AMznc1mLIdAaI7aY+r2Sl/umUWA6MA7SKDBW9oBzXpis1rA8Wsr3Y2JMopyx2eAqp0O1BHnqx5FeVU9gMNbR1s10Noegtla6bq3u/0JEGYZBwOWD4YDSHEFDnqXvhdlaMJbCbLbWUXlDzIHtbjc11dqm2QP0WZnB5Tx3+3oDYxhDJIY4NeGtYj5C8NufRfs1vt8X4s8qzGHZ98VvO0/KTOcdvqzPnCAb5rP5fmibNcyqesKoAIyqGYrVYiz7QvGWqhLbgdQ05JBkbgL7HN96T2WEub7bbcWZQZtzVeOpSy0cRAVTsMZDG5FegdwyU6ptG2EGW0MKYjfR96OqhM1k5VkdgL2/7vF3G6TNGRwY6xlclo7GrMbWqr0iy/AAIwmRBMwSHAub0kA2eK+DtbQzWIbfGCNd3wLCSoHFlICSFQBEAlqIew8U6XpKhwuyTruUfxZ2bdIipwT14nciRbVOtivAYZTJ3PJcwh7oRpHXtW3Dg3sPcastkUCfRpHXKIPTHHQPS5dI5PlMQEwBGg/BjbKBysYq8sOszAkUNCkBw1n53BkzMT4n30UO5D7avSkeSmXTRp1kVzaOBGtl21o7DQnKaJdTf/ajn37E9fW1MgfNHszUq28OPpO1ju12yyc//1gOMm8FyPCOZHSaepF3k1XCJAE9531xeci2I5nJjmIfqPd1+nSNk8ivkiZSkg/pNct7gP61jvhBHC/fP5RIYwpzK+u9Uc6yrxjFRIbLm1v+7X/4D7x4+ZJ/9Mc/5IPvv09d11OgzTlP9zblvbxD63NlHOvra8ISU8bXLQ8evcXd5ZIP//ovSNHgjcVVnvNXF8SQOL17jzKgyyBygkS5nyKPTApuFUbrq5trdj30Y9gnVilijHjwWi+AWAxRn0fsStbrDS/OLiZAXaMpRdpRAA9trUzMNFl7AVt7ZscL3KzGLFoGHXBnrMWD+P8aZYYdBBpnHe2iZbNZv1as/rozy5rCENknc9LRz8Q48OGHPyIjhvj2QM63P1f2e7UkJIV1MY4yXGWScxlZZ0nXbiKDF1n1ze0tf/Ozn3H3zh0a5/nDH/6Qn338CR/97CdY7yTxA/WlzTqszWJrjzee69sbShMiRzkDp6Q97pPwuql4+913WF3fcHlzjVEmS2G5ls9orPh3FhZ+XdfMl3NWmxW3N7dSZIQyjBCIMlCscp7tek0XOhnWpXuiJFrlMcnu9Locfk3OCfnfcrmkruvpehYgoUh6QBjPh8WH3O6DKbYlCShxRN9SufNJfbHjZvOaBUvZ7q8VAOy9wkyGruv3yYO1CgpJsShb5cA3Tp9vYuVn8dw1Rrx/ra4dXzla6+HBKZvnr6icYxgD0Rh2DrbeMHiDz9CHgDEZywbvZ9SuwQwDL598wg9+75/w/u/+Cf/5z/83vE88/+wLPvjN3+Ph1zqePvkJd+cNu/MvOF7UvP/t7/D5Zz9ns9sSc0W7uMN3336Dk5nn5vqCJy+v2BnP1772HieVo3t1yS+ev+LlNvDNr7/NmycLLl5dcnW7YhMSbx4dsXSe65sbNkNPblsaV3NCRXd1zW3qWdy7RzVvqEIirG5JjcctFzjXcK9aMg+w2W7YmkxvHMdNzYOqpbu45mbs6HPGVY6ZrRhz1vu7bxiWRFbCRlkHyuBnX2wao/ZmVtU6WmCOYSSkIM0/u/cxzQUgjL0ABdZKMyw7fG24O1+yWq35d3/+5zx/8px/+s/+GTNlM+UkIIbRM06SxwpjnHhqGUO2mbHvGfvxtYS+rMESV0qT8zDJLi3n4mkvrJKOFCObzYaQDM3MgQ7noMQt/b99A0IL58ImMPs9UfaQVZ941MpIgF9hvVLOKd/g77zF/aOHPHjvfdYXT1kPzxmGM4awZrW6YNhGYtuQ8ijXSD3m69mcqmoY9IwlR2JUD8i0z+tWqy2//OU5FQN3753w6PG3aOZrnn32EXG8oVjshJgYY6aqHMcnd3l1fi75pa84OblLP64p7HyZieUYhh7xWUfjbMCQiUPH7c0rnn72hMeP3+E733yP7WbLq/MzUujIQ8fN1Su6fsNm0zFud3Sx5mef3xByxfzOY6xrub7dEGIU0FMbBhBxRnzrxjjiai1qrGfX9xwd3eHh/UeYSpioRyd3qIeBqPYzc7ViOVwXpZh11hKCDOAwXpqz0lC2k41U6DtIntB3bNIoxaExjKEnhowlYHG4yrNcnkAWj8YYlpi6oW0t3hvCEJSh2jN2hcHqGIdAyAnrDa4CYxOYSE4jIYhcVYgcaWpKeOdxjWE2b+mNWC+UfBTjNSd2OONkCIsVzz0wtM2M+UI9xbVgCzFQNw2Nb7BlCF9K1E5ovrWvxG+/lqGR1hhsteT73/hNTo+Pubq5ZF7PmbVzbGPZrrZkn7Desu7WGGN0IveMZjajblrGEJiZlqYVb+u+6wnq9ZrN/myZKoQDYNZo3l7ILDmBcaXysRiTJoAvk/FNg2sTlQ6TNQo6FNaQc+LnnVPxfDSTkk+upTB2T09PWXYdm103MbO9d4QkTK6+7xhGOccEVJGctORFFFs4Es6IT791dsrZ5lXDcbNg4Srsrqd28PjRA85fPOdkfoe4HljfylBSXzk8hkpJIcYgDRiVrTkjE9tLvVFyhEM2moAPefJnLGepyHIdTs/bYn+UNd8UKyfJ29q2EbZsihSP1pIDxBhJhZll7ZREHCokm6bW2kgHl+V93JHX3IN5pckfk9xf5514zNoCUqO5hzTSEhlftZgGncdg6IdOop3WFZX3U72JPt+e2ZqndcdU75X8XM/dkp8d5LwxyZkvijgz+YyWQbqFwW016Aa1yyhHnjCTIWb1z0WshypfTZ+xSKhLPRS1Qfi3PQ5BxcMa7rXc8+D7XyYS/GrdIMrKco7sQbWapq719fYqzZQSrpJhXRhRdBV2a7FlI2Vs5XRvO7IRv2SLDK2Mowwhw/DabIipBi+fR3N2k/OU66Sks2JcpWtUYn6tDF1jCvAq71ssz4LiIaU+MsLIrOupGTA1KkaZEWMR9mPZCwXQtcYKdqObNWdheO8BSs2ZJ5sS+b7k6tKwlqaJ3COvg7kLluHrWhXNmmMnwAjDs64b5k2rjG5R0BATQ9cLgFoJYEvK1GRyzAxdj8kqbbdOCTUyZylHwYsSYo1WOcENvIPKeaTVkA/AbfnTtu107Q6tJESmL3F6NpsRxjANRi7Vj9f34GyNt6IejyFQOYcvqjFdu70yg8dBBqRWdaUxQnK3IYzklOm6Tp9TbDuKFZzuGLq+n4aCOmdUWVFIcfuhgcYYQuipqoqmymqJI5+/+CNL7RjBV/u6SWtu9TEkp6S2CaruNYKrFaUIVRIm/cFZLv7CliEPEps173fGSSy0Rqwzs5CkCg4ITPNhmmYmfsthP6PEWVWjY8nJYF1FpZadMwX/hfE8/K1nzt9pkNY5S7tooalIlcNUnmASQwr4yXs1YWJmzHtfk2JQbmLGGJEh5SxBziv1PeY8yebLkGPdj1rUyOYm7gGtUtAD002cWG3a2ZRkIejhbLEFyVNgLBH1vdg9/TxHCTQKjKYsU3AtlhQkqWw8vLE85jfeep8hR/7Tj/+K6IT1ZEyi0gFd0/swRhIpgCJrsUZZAmWa+qE/kBygIYyaROTpEBQrguKnCjGWzk3ppEiXzJDFM3QPsypAYSbgU3qE5fXkMLeWgyl3RlPETDIRo0Ojnrx8Jt1jDaQS1HTDK5os70XfY4pshg3RZrkHmpDIzF6DSQpCk4RZrQAfpYBFki2ZkPmrVgcYGW7ktUlQ2JIpSzHqa49T39NRqfXCOlEQM6Up8JS1fMiQmzqFxrwW6E0xmzaFei+Sc9uItcPPP/uYF//8BT/+2U/5r/7oh7zz+A0BqKN0uyQA7ovylEXKmHMmRyYvHeOsDh+yNL7h/OxMBjTZhto6vvf+t3n+8gUf/+wJ3lXC3nAOGQZTPksJppCNTvk0Fl83zOawGlaMJsnrkibJhK88yUQxHEeaIAkBn84vrlmtt1OimstyQ9e0JsHZyrqcuo16rd2ygeUcjmZEK+tMpsGWz677kMJ0FADGWceD+/eJYaDvx2nfHN6rEiwtFoyfkpKUEiNhYpwvjpfsum5ijKD3fvIVOwAB95N090mgtZblYsHtZi2NE6OSQ4MGKEsicef0hMenb/HVt7/CTz/5G375+RPOz86oKpmuLs2DDGoRkXNhk26xyRBJjEmSuQd372GA65sr3dsOGaqWqZz4zY2AraQgtQqoGK0MYxa/1CJz23Qbqqom2+IFmfC+omkbxhAYwqjJOWSbWA9r6Y46K8bvmmRlidTliFWgXxmtuvistZM0ZUpgVBJVZITlfk4+Vq81NnS5ZSaAK2vxUNb0BJbqDzrjXruH8/mcYRzou37fDNTzbrk44mi54Nmz52DFVseVPaTXpnJ7yxx5X/IJQ9j7yTktJIs/2JTUOik0Ez3tvRnDriGsBy12DbscuCTydLdhlgy18Sysp8qR47mnrRviGNjdvOLjj/6S93/nd/niyTc4+/QXOLPl8y9+yR/8yZ/yr//FJcP1c2Y2cv7kU07ffI+j+TFXw8g3vvkV3hwGxs0lF+fnPHl5wcUI3/jqGzycWzbXl/z8izMu+szvfPA+dxees5cveH59zarvefToIaeLGTfnl9xsNozOca9qWNY1Q9extob6wT1q39IMgetXl1zvdlQPTqmrivttQxMiXzx7zjivyYuapTHcMZ6bmzW3ObI1kYeLGV959ICX244nNxuGIIBq9mIlVCKb1BxmAmVLk0VxEaV8RUxZB95gvCOOO8zQY9JIMhFrEjEbAaisI6cghYF1OFdh3YymblhdX/Kv/uW/4NMnn/E//I//Ew8fvclm0+OzYUwiVYspUTczbm4vMTbgvERVYSEl4rCj62+J5oHGa+SsV3/8UkmXtX9oNwNgfMV2u+P2eo0xMuG4rhrymBj7AV9VZJNlKEgl0nA7ee8z/bfrOpqmFr/XAtRmjfw503drkq+p24UonLIMp4zGYQs7CDCuwsxOaN9cMMtfIYcd9x7+IdfPXvH8s6dcPn/B9vKMoTuTQs1bFotTKWyzKnnQKcIIaDLEjj72PH15xk8/uSD0I4uTN/jg9+9y9+FDQoJXz3/OdnMll6xu8csZzWLO8v5bnF/d0O3WJGoWi3sMNz2ZSFs3hJgZx0xKlpRGjM2YvAdrxjFwdLqk++iKm1cON0QqV3M699zcjKw2N8RhjUkR5wxdClzcDJJHecfiaInLGTt0ui4NNidwmUQkhERTyVlgXEvd3KGqTrDuAtwAJmGzA68TkSuRyRtETTJrZ7ru2TeIsoDpvrICVOp5aCkNxOL5mZnPF5gMt6trGexlEzl3pGi4uV6x2/U8fvyIdiGeft4YlndmxFDhECWLrSogEYLX4aoBa6RRmGIgDYlg86SsSwFktphYHvhKZJQmF9slw52TBS8/vyRnYf2HYaCZ1XjXYvGYnBmHHcY7qtqTgZOTYxbzOa112Jx0poXHW6+MKWEVmVQ8/Bz/H3Nv9itZlp33/fZwhoi4Q85DTV09ssRuqUmxqW5xEkVJMATYDx4APfnBgP8B/0s2DMiA/WQasADaBGXLZLdFNptNimx2VWVNmZWZd743hjPswQ9r7XPiVjdpA35hAFU5R8Q5Z++91vrW930rM7JcLghxpKparJNGeFM94N5X7hBjT4yZnB19t6M9FACl9TXnVxeklDg6OGS5WEoNM/TUU0Fp6Xcj2+sNQ9/jc41B1RWuAOolXuYplkmMMIQkhA8UqJMhNBFrVV1kDSFJ7h3jKIoo9ff1bpZehxyneqHETm8dzldTPHytOUhT1QJ2hJFdL37/hQFpkLxd5kdYySu1hpqA5izxS2agFYsJx3K5IJE5PDxg6HuePLjHG08f8Wl4wZe+8TZnYY2zI5WJknPYiqHvcbUnWzPZ0RgEtBbmcZSzSNe+t45sZqn9hEtpFPDeU1U1BwcH3Nxca5DQPN4UdaLWVwqIgAx9JmeyNZMXo7MGXNF/yt+PIches7JXd7tOatipKV1yB7W2gFtnORidoJ6pFHCTfEKYts75WyCttcIKL82IGKPkuSA1hBX/zZIz5ZjI6kFZ7AhLLSm5tdRy5TuVXCdqs3qqq1EQTkHXlMr7aC1psw5uQsgjiKycJEBfzsJElVBXhmUrmUEHaAqf9jaQ/fNYsvt54n6c3GfX7v+9v/HnRmNthlIjOWMIcaBd1GLtZzNYeXLWWBmMlOZ80tV+AuzKZ4cQ6Edh60+fmZjOQqeKrKJSAej6gHOWoR/FAss5ZUsb6qpWC4FZdbuvApX1JjNmKi9qPuvM5Nuas6VtalIUsFAY2aIWJnm67W7yi0XBuswMbBevV6Ks9zKgq4Cr8xwZuR6rYHPxiJ68bvXsM1GxnRTFIgIh6E253F6tLTlGqenFf9ZaO1lJmACVk/M1ZZlXkeM4gdyS9RjqpiLEyG6njHfn8FWFd06Zo3mqbWNM2rw3+EZUvuLZLEzMTr1Y66oScF3ZncMwKOlwztsq77F1RVV5Uqqn9TfVN87hmlrrkpEwjmDMNEhNzq+KYqcn9nhJ7UUMvnLcb4+xztENPUPXT4PZ66qS97dScxtvWa/FVs+6Rmokk3DWk5JhHEZClBkqch2BfhC1qXcSAy+vbwghsFws5BntdrfsOUWZLcO/bu0TL3EqIkxfIb8lXFKygg5WDCFgosY6U2OdYxxGMHaytvN7tbhXVjOK6ZRBvjE56lQzqi3fEIZJeeD0rE5ZbHWcV+ufDMum/Znzprz+ToO0WIM5qsnW4msBw2w05DTLJhQaBJiBLf05BTibpG3SqRD/DjdRlcnCoBPwDu0coch+mLtWVqe6ImBDASAk7u51oIwkL3OA0r5SLsi9AJNliJSZNbIM40ikYtftSHkUAIWMsxVjHzh5fcbq7qH4M+VR2WlzgJil0HsUdRRgKPeFcv+KbAf9vdtBKk/XoB6SClA4M0sg0l7QRUGZGINICvTK54BXvstt6YqxBpPi1MUp1o+mFJA50zQtOUexUzAGnXmkIKafnvvUlbMOctSEVAJTVdfkeiB3YQ6U6NArBU/LgV9AuhDD9D1SilSVJyZJHGpnJZlNAhC6ukIfJovVAiwMXUcemU3SFUAva+U2q/l2IPxZv6m96zN7vm/lPstq5Ga35f/6wfd5+dln/Pr3vsuvfuc7HCwPGPtBP98S9XvLMK9ZdjIlHcj0ZOMstC3hGrytGHcb7MKzWC34j/6Tf8n/8N//ay7OrhjHgYODQwGqYH4+2klKMdO0C9rVAavDQ8zNhhcnl9KImDxx8yTN2PUdBplq6b0jIV5Gn376+cQAwJnpqtlLknRbYlKmUv+zkYRbtVSHwqLFGOpK/FKDdk7LKi3S8v0kbBhGXrx4wb7H7j5Ls3igpphu3Udgkqksmpbddku32zEzbQuwsy+vAmPKn+ep27+/N0eV5ss+EgC0gL45ZxbtghATQxg4vTjl6uaa088+lHs8yVHk7Hj88NH0vidnZwxDjzHQeC8eddYShxHrLE3Tsu16mmaJM4ax39D1HR988AFgqJqauqkm/7D5/jhkCrWbrrFtG5UEyUTTuml59OQJIQY+/fQT6c56kd+N41g2wN5AuNKVLXdztobwVSVnUJ7tRWKMkydWSW7Kde9LdMS6Zk5qChs4Z2WS7VmEFG+wKetFPJiCXn/p0gobZm+I4PSsJcZsNlthpOV06zkXlsP+v5msFvYm8ZY/c87hjb/FCi5+xjlKB3l1/w7r7ozcBbL1YDw3feJzO3CQM3eTo60WVKslB3eOaKzn+uwcaxLnLz7gxb1jfuO3foff/fwV2/U5rz75mJ/8+Y/53q//M77/+/8LQ39NMmtOnn/M8f0HOPuQ9fWaaCKb7Y6TzcBlb/jaV97m6dGK9fVrPnh+zqtt4u997Uu8de+A81cvODu55PVVx8GdYx4eHrG5vOL0Zs2A5c5qxXFb0207dibhDxZ441kGw+5afGnbu8fknGmyocmO16/P2LhM1TgOq4anR0dcnl1wE0d23nDgK94+POLYOE7HgRh6higFq0uOZPKt2DDF/KxxRJu+tpTgOk19ylIMDENPjALcxTDifC3xFKi8JycDlAkKwho5OXnFX/3Fj+mGgf/sP/9XvPHGl9hstwL0abMAY0RR5L0wcBDW34QdGMsQRrbbja7f0nhIgJ3Or6mjjDBKi11PGKXR6J3n+uaGRdtS1xWL1mM8hCwNY5LI1J2tJH9TJhp7clW3WmIMU9FY8idUNXN9c02MkadvviMFVYzCELOGyi7ZHxUUdXilwWP8gubOfZ7ee4vH3/j7jNuO3dUlJ59/wuXpS9abHXffepvkHEPX0e12LBopulJMjDGQwkgII69fnzCMwpa5uLyhHwK28SwPH3A3Rg7HHlcvaOoDYhoZwo40jmTbEKLFmBaMAzOKDYp1LKuGwWcqHzm7OMUYqBtPxnHv3hN8c8ijJ1+icX/C5fkp2+s13tZ0Q0ff7Qj9Trw+Q2Yc4PI88eosYnzFYlmxXApQOfY7LBGDFKA5SfMo20yzrKT5bVvIFTEmDo8OOevPCUny4hzSVAhbk6AWlUtGVSJfiEWFCeO9V1/KPMVkjIBM4r0urL2qcuQkz3S73dE2K6yDkEast2zWMjDPKRtM2GICqBQLGPlsWb/ZRHxV46qGfnMznY1SJNdSQE954TwlO8SAyZZFXdM4h00ycNi6PSaW1hd11ZKt1B5YYYxWjReGFAbnavl3JiPDymTjZSe+g8QRYsRbMNlNQ+p8ycezxRgPJuGrhkoLwqLKWSxauq7jYHVAUzeknOiHXobyWhkaWGVhuDpbYXGypseOFC11vdAbps1TbgNISUGcL7KlhSHlsd7LcGIFC0NKVDmJwsPauZbCqE+sUf9gK8wqPZtEDp/38oCZ6NLULckIKOKMwdbLiQWX1EPYe18ONEWJCvnDTACP9xVXV1ccu4YD33J87x53njzibLvh7OaMH/7x94njhmahTSUiVA6vzWtn9Hwx0qiWAmiuozTgI7PYbufmpdm+P/DL+4p9D1ajrC5hSJZYgrBaNY8rnovyvmkCCkpDC2Opffl8M+WCUnfNuXBh3xW1RHlGxggz8ItAY3mVPMqYRCgK0Smn1R/NHpiZZ8/hModk/zV5+yoYZfQZZ23eGSm4b/mWzzUd054uv18sdcowJpOk9o3oHkdkxxZDnuzMpAlRVx7f1GJxYQxlwHemVFE/+9oHYv82huzPA3p/lj2r61evLSfZA4Ls6VyGJBYF3nlV6YhFlVz3XNsXksEXSR4zmGoxet5lXQtJSVrOuynHFGVZhCzqMtQb2eo9muqbAqIruOn0/I8hMsRB5zCY6b1TTDhvJ7ahUzJZWeNxGBR813Vn5lp5IrFpIyQhZyYllw9RsZwyIMypfdpI8VtOuu5KTei8o6lrIZGkTNcXtZ/bY8Iz7R1rBfQfhmEi6RWVq3f+FvAZYyaMYW44hCB2Cuj3wND1qthAhpqXgZMSby0hzYPCjDYPQpy9eDFmeua+qqY9KE3TmSxUzs2qsHtB6wUFg6OoxysF4gsgWz5nGCRm1nWNs2JDMw6DnFFOMCnvPc57fF2R24Ww67MoMoLaF7RNw2Kx4GCxpOs6QhSCZVXVOOtpGmn8drsdu243geXl2StqNZ1hSRWcpZYrf6/ve7HwC4EY83TuVVU11UmF8YsRVYMoPI2qzsytOtEY8F4Uq6LunvGWFIRwZbysc7GrlMZGVNW9zMoyuHaBczNZxmDZ9R3Ol3Wp+09t+n7e6+82SOsd5mAFCNA6DNLl9l4emEj5mLyOpmQfoV1L9wn1H0vq3ecoEnrJK6Sz4tS2QLDGJCE/ZzF+1q9jQIPlbSN8SfrSbEJM0gc9gz2mGDVh9w5SDXhGAp5FJqvGlNntRoTV3eB8j3My7OP9zz6humxIThh0E/BamoWFZq7AagGY5deZ/eE3JXHIWZMEY3O/DDkAACAASURBVKb/ymFYLAgKcFcYQ9NhlrOaQbtp88ifFwZtYRuWwCbARPl8o/Io8sy6K8BVOVmTsgPRz595aEw/ltcElIMWcyonJglIW1WEPk5J15RcaHAPY7kWICW8kUIyRTU7d1J0ZCsdfOscNnusd9RtK5MjnKNZLsS713tCiHTrzeS7JR872w/cCviZ6Vr3k4G8d223rtPKs3KVF49lYzBOurTPT074n//Xf8P7z57x27/+W3zl7Xem64lj1M92t4zJy0ukHqVr23B87z7j2HO62/Dq9JT33/+Qr3zjq9w9ark8OWfZLMTr01hMNuIRZgxV01I3DW3bslgd4usW6x03L0+JKWvQHqa165x0jXNIGJlEJtI54Pmnrzg5v5I16WSfZjOvXVnLaSocC1s5kamPVtR3V7hlS1a5RhxFTmF0HQhBc391sbfPy1TVGUQrUr594LzI1ApYW1icwzDQD70wJVMxvne67ufmjjxb/Z8WudKZNbcS5d1uR+nGW73XpYKQBG9k6EeerZ/xyWcfiexD7Sy8DkosBvH9MMo6ntaUmwpVPSLphl67kpaqavgH3/w2zhq+/0f/B01bYawE7EEB0FlKUgonKc6qygvTzquvY0wcHyzZ7TpiypyeynCwSs/pnCIxS2JRwLFyD0oiC9zylTVZ2epBZCn73qLFuzWlxGKxuAXeznvAfOHXt08ap75r09mGxJ2cs0jNNKktRUUBhaVg8zNoq+dU13f0OuChSMOTnqnA9GP5eXnP8ut9b66y5vfXplVgwjU6aX21pLkb2L08J+cgMugEg3OsDpcstiNEw7bbcXVzxf2DY+I40rY1MXZ8/P5fcf+td/kn//F/yr/5H/87wvaGv/yzP+Xhm+/y93/tn/PHv/+73MkGF0fCbsOD+094dXbJ2cUpKQw8evKUx284Dl1kc3XCXz+/4GQbeO/rX+Irjx5w/vwFJzeXJNfw9NERq4MlN1fnvLq4Ypcybz58yJ224Xp7yS5FzGqBxbIIlpurKzbjjsX9O+Acfkj4kPjw9DPCosKuGpZVzTIkTp9/zsYkYttwUNXc8RXcrPnw7IzLFLmzWNBmGUaEjVNBWbYipWhgltyVs7ps5JgymSBDohCP/WHcCWPWFB9Wu7f3ZS87J0Mfnj37jNevX7PebPitf/o7fPmrv8B62zOOaWqQZkRyFjUHqSsBBcqA7ZQlVg3jwBh6vDNEtXiiyL+Rjr75AkgLcianJCyHumlom1r2ojUqGwSvwJyxhppMimt89mqfIz7tskaFZeKcxUWJPQWQxsieOaq8PNeho3KO4EUqJqiIqlH0cyWyF8AAKeiMwzYVtl5wcHTM8s03eTd09MOAq1t6CXjUVc0wdDS2DOgQ4HwYBs7PhLmYgbOrDZtuy6L2mKpidecRdbNkdfQAcsXNzSkhrXnx8TOy8fQjWFtPQ2sMmRwTxlvu37vH6uCQ7i8HLi/PickwZkvKnmxqqsUR73zj6/zoj/+QcH0CwUKUKdACbGY2Xebz045PX48E61kua5qjhnbVYAwK0CL3CmHbR2NZrGraVU1mR8yJseupa8/R0REX5xfIUFWdes5cIFknIJ2x5RzK059lBdkF0K/kHDToECUBa5yvsc4wDB1dtyPGEYiQI1cX55h7hnv37/Lo8SOWyxVn58NcIGs+KZ64iRgGUhi1CBX2ZwmX41hqA5E6Olup0kZAHKs++rHMj8gKDuWENwaHupv42cfcaEFtrReVmjY2i38rGYgjcdgyjlH2NQlf17QHh+SQGOModk+aBztjppzXN7UMVkGGimzXa/kezpMokkrD0fKA1tdSGBs5M1y7kCnb3oms1giznWgJgzThY5I8oKkXAgxTfNkVaMsld9qrVfQzJ0DKSKN9Ow6sGRhqsVLJKU2DnSbZssavmMTbz1g5a7yvaJqGlKS5LGsABRWiPr8R4yoFZkrtUQBGS1XdXhNonZKiWA94Z6kqaVIt25raVTTO4m1N4xbY3nDx/IQmW8aUwIqKset7oq3YbnZiA2VKUa3nklXpdZ4JFpJAivTbV2LlYGXzTQC4DLgKWjfpftL3aJtW2L8TMJQVKMyUAugW4QTkeeq8EGuEwSq17JwPlf0pQEc1gedFebP/rErOVHKR8trPqwDGEGTwjYKJdV1RGh76ptO9KQBceT4osCK55jjbRyG5tDV2spHbW4a3XvvfrVyDMZmg+Z2wK9VrOcu5M+VM4r0mwpay1g0T+DJFa7Of9f/NYOt+TvhFBi3MDfQvkmt+3mt6X7WUOV6tGGLA6XuHIOurrq1It7mdUwITSFkIP7UCblVdyzloHRgFnvT7CQvZkGOSnF6v3BoBnXIMQqwJgWwNMtfttqWDd17wlYIhwDRUMeZEHsuwY7FrmWMGk7KrrNk4FA9wIXh5XwnIHgOLhQwMs85NTMYSGwwFGCt2B7mIg6c9lKL4wlu1UYwxYp3sbZszxrpprStkJkCign/OOywFYHbT9YcgCsNK7SJK7TUO4/RsUkoMY1BGp1hRGCxdt5PzftQhV10nnrRaP+bMJH8XMo4wXCdFXFAP4528j3duaioVML0oBUv9mFKkrhu1RZHcLsZEzpvpmZRr2b9GGUJmJ9BzAoQx4lMd46Q+KGsrW6i9enHrs1u0LXUl5J0Yg5KjAs4ErIO2rnBOFAH7z7gwjhcLGT7WT8MKK9kbarOxWq2IShBYrzfT9ZTvba1ltVqx3WwYxgHvrDbPpHZzzrHebiZwWs71mqpSZrFz9MMg98MIaG1Hq7nBTOLcb1A55zDOqIe04FEysD6I9UaKhCx2ZN1V9zeeE3+3QVoMY0qkmHHGEsdZhrE/aR1QoFFAmhDixBS1OlW9yMOFCCuHhsTprHToRJ45L9L5kCeoTAs9SLIUC0aD6Awu2r1gV6YaF/BtLv4FdZ/RefHlsVO3xWZJO8cgk+UwjqZegIKZl11HU4N16EFTQLy8Zx5fvHHN1I0vBdQks90PMDmRk0p2UyaXf7d3+JcrmCTaJaiZMiFSJLizmfP+5+wBjHtxy1D8YsqvZ7B57gypNCYVjy0pSzFGA69IoiaQDEmwyGgAQTxUFOQRmfIsaSjjwYwvG82R0Gl8WClQKGewyOhwwr4wlfjQTNfkLKifoF009NsdblHjtzXO92IAr8ENyv0oAbJ8p+I1aWcAZg+YmotTCl4wde7YA3OzMQwZxm7H93/4Qz57/jm//d1f41d/5ZdZrZbiG5YSmDyxRvY76vJspCuWc8BVDYd37jGEAXfdcnK+5vv/7gd4LH0fwDYq8xfmxfLoiOXhIYvVisOj48kcO4yR58+fc3p6irOGYQzT+hA7i6zMF9mmSejNmGR4dXKBcV5YJnmczP4nyGTP8qQMoRltwjQV7Z0VbtWCF7mi0UBlnXRQYxQ/q/J+xhrxndG1nKd9LgGqqirquma73U73rjxHNGClnCbZSAl6Xn9eKYt+GEYKo2L+7pakQxBy2X+6pSZAXZ/RlBDuZZgiTTMkK+YeZWha0y4m0/MwRgoD6uzqQoufIGC/Su4XdctyseDk/FQ8gnPEasLw8cfPGHZb2raW5oBzHN+5w/X1NbvdhuK180V2PhQLB/G/JSUubi7le4bEbhypqppFu2AYB/E5zHD34JBd6MVLy+ap2z53sucbcHh4wC++9x5/+qc/mpOnKHKpYkjfNA3L5ZLtdjsV5PvBNcaZGeG8Z7Vc0u+2DOMwN4H2GmNl36ScJh/o/e+1/3x/HtOk7Ocv/t2fx26BuUFQ9s7+3w8hTIChMcK6LuD8ECLJGRb3DzFjz/r8WgEdS7/ruDFwpz3CJUc39pycnbG73lBjWVU1tXNcry/48Kf/gd/8nX/JL/7D7/L+n/4hNg38+E++zz/6rd/h4Tvv0b16hguB3c01IVoePHhCzJGryzOaHPEmcnV+wcevLzjvEl/7yhu8ebzk+vyUl6dnnG873nr3LRZ+ycvTcz4/P+emTzx5cI8HByt22w0Dht5AHRKtcXS7LVdjR3V8wBAiywRVyJzdXJMOF5hFw6M79/jGG2/y7//oB+RFDYdLFr7m0FTUIXO167gic3C44u03n/Lq/IJPwxU7AiZpsWwQ78b8s89KGEZ58pudvdEy1jhSilpoyWBI8sxWyTnhnUxT3+02/PSn7zMGid3vfPmrfPUbf4/trqcbegVUHUPYEUJkDEGbTIn1zY34ehsjioYyVDUF+n4n7MgshbPPlKSIcpTu5waFCe6dBx917dYcHR1ydbMhxESVRuw4sL6+YrNZ0w0bYc+pJNVSfANLfCqNKCsDH5z42Vovg2caPDXQXQaag0N81eK8p6oXDAliLlCyxWSLIZHUh1MKfZ3Uq8k2OZONJ3pDxkKIFJZKNwz4psEktVUwib7bcX19M52rN5uOq/U1flUp6J64vlmzHWC5OMDYxKJtWW/WxGQIQSZy13XFanVM390IABoDNzfX7LqRqmlIWMYx0AX4/NUrnro7nF9c8PY33mOg55Of/oTr0yvGPjKqD1o3Zl5fj1xEz+HTh8Q80CwNdZvwdcSYnqoODOOOFHZYL/Zbqzt3ODxeYl0gBhj6gYPVEcZ66iZx/+F9ri+uGIPYH9kSd41RAB3xfNTGe0jF2kdjkUq/jZU1niIY41iuWqraY62ANMXWaL3Zsmg8R4cHky+g8wKEHh4dIlJPAaUw+mcRUhzIeSRlKfbk7JM8KidVkOUgeZRDGiEGlSeqDBfEGzZDVHAnRwFXjXqLGmcmr/bCdiEjNUFOJCIxBDabK7Y356yvzhl2W2HFYTm+/4h3v/4ei+MjbOWwVU3lDONuw/nJKy7PTjDOsjw4oF4ucHXD8uAYX1VTw85XczMvpzT5R2aT1SLN4p2ZhqlI7TNQBqNNTfwMOSbSpLpAr01bPBPQXkT4qCQ5TTlltobkLKZSpiayHkq8CkE8ZKu6lkZ7AT70jCsDnYv6YB/EKjVdAXJyFrVMDGpdpCQRWQql8Whmr1KhVELOLNoKZ2DR1FTG4GLm+uSSH/zev6MfxON22Eau+8AVkW1OkOwErMaUxGrGyp0Qfk+e6qAJqJsAVI81Xu9DEqKC5vFRQU3h58yKwhAEpKiXjUxOH4fpz4r0vuA+hchTgIuog5NKDlVCv4ARfgJjy69LHRRUfpuzMsgxE+BhCzuu5LB7JJFyrwtwUf7Mqo1JWVAGprqxNDBB6rOY80SOMhixrNF/mtRqzBhpKM0MXsN+/bmf/+yzVjW4TmQAI1ys6Tv6iQGaJ3afiTLp3dgyaIyfeX0RjP3i75Xv8/NytfL9vwjg/ux7yHoPagdgzIHuW8kVfBlKVdRalCaK1vEmi93B3mfe2leFFMXebBVm0K7kkGV4d1HD+qqevp4Mcw4zQ1Pzz6pq6DtR3DkvNY+v/ARyloZEeRgFC5nyYmXfZ10vBqs199xwSElBZG3KOAVqY0rT0CZj3aQMzHtD8Xxhnvs8KV+temIriKD7RVjElOZFytgo33W+L1IvrFarWZW2tx+LkiAbaKqKsYCoSXK8qm7w1mGdo65qVssVIQVCPwigrY0MY7UhoxhFyoIX1LWfakoD01yOrYKw0ci/sxon26Yh6HcIMRLGKFYysQOEwJgRcl0Y5YwdhoHdbjfZZ5R1KkOUwzzYsdImWoxUzhNSJKpliAx/L6pnedZRv0d5v2LbkbPU0GKDEfFeZs40dY3zfiYMGSOfVVVy5lTzAFOxmjNqleeoq4bgvNhilJpTv/e+TcQ4DpT5CkXVYK0Vm5yc2O12dF0ntk2aN5QcuJyZMSWCKs0KaRNdp8M40qs9RNvUAjRTsAWm3NQq41+Gqc/784uvv+MgbcKQcEgS5YyCHnXF0PVTl0CSytnUvTAUZZGIT5J1KKVe5CclRUH/H9UXrMC0BbIFlctOD95Ohf8kGywduanAEbAmTciJsFXl76LDxLRMMEUuKdCxdRaTHcMg3csxg/UNbb2i9gcYKgyOMpAkagJXwD231/2XQqiwCjUlM+oZtldkGgPOzRTyqqr0fihzVsFq4FYQmEJkLgf8bbBDflTZwcQUzJNtgiQA83dIE6PHTECsdKhl+FiRfpVuaI6JPWLwlDwVb8asfi9y3x2YRH2wYkiQRilUc0hYZ1isVhhnScYQtcguUk+Fw8T4X8/4AqhY6yTpscXKQIL/EAPRyNpwladtW8auFxZeiJQpqDElKu+mQ7+wjBNzsVyAcWEsz7JUY6wksvoMCiAva0IZ5s5gnOWDTz/l4uR3+eTDD/ner32Pr379q1hdPyUg7ktmHArIA2Qrw+sWS+4/esJydcxuu2O9DXznH/4qLB5wdn5JXS9ICVYHRyxXS9rFQmWIwrRMMXBz8YpXL1+y3W2J6iXljNtLDHWYgq6VrAfp6etLTk4v5fs51eEkpnU/JygF8BVGc3v3EHvQYJe1sIHcnNAXEK0khzLlOE37xxpLLpYK2TAPwJO9st1ubyVw++BGaYikJId+o/5B/SBrYFE3eF8JwDKOe4nYHigMM4icVCKmncGyRkpSczsV1PfAiHzPWsaQefjwKbWrGMPA+eU5u247BcOcA9Ya6kqkpWGILKqGyngIKOAskuacBq5vzjleLXn0+A2ev3xFiIHT01PtPnuVAjGBJ3LWFIBSzkQJ0Gk6iwjic3Z0sMJ4x/bVa5mMff8BQ9fRa6FRmMrOOZpGBnwVYLS8rq4utQGkg0/0/NuXUg2DyGPKELHyZ8XWpjBUnJ5pSUH7/QKiMGPHcdRpqLMaoa4rxjFMwOn+GpnOLFVYGKU92r0hcAXQLsyhwqIAJna2xLJyDuu/M0zJ5RSqcmYce4mV1mFqw+rBEbEfCLsgbLtgeHnT4VPF2/WKNlvGMbJNHbZdMoQesqVl5PX7P+bDp+/wnV/7Z7z86GPGi8/YfPYBf/aHNX/vm7/MX61v6K4+xdWRkG+ompYnD55gYyYOF1xfX/L+51ecdJFvfv1tnhxVbK9O+OjzS667wLtfesy9VcXV5TWvLi+52iUe37vLo+NjurDlYthyPUbauqZKht1uS58S7nAhxQ0WFxLbsYfDlub4ADcGmiHw8rMX5EVNXC5YuoZjU0E/cB0DN96yWFQ8OVjA9QVpvaGOmUEQGhW/GkiluVpirZ1YVlkSCpzGKYvVs7ia2Dze+jmu2NluwFnD+uqcD9//a+p6gXWO3hje/fJX6YfEEAMZpSug8rlsuXvvLv04st3e0DQNTdVM/mLWWh14lIllerTZYw7l8r98q1FQzsTpXNO/3nU72laKRxtHLj99n5vPnhH7nmZ1SHN4zL07x9iqlmLDGEIScE0aCKUQi8K2ZCRhJceNMtzDkMibzPVFhfELqsUhy6N7+MURzrak7OX8s8WqppzTmkfkTGbeLwXwsOrDXc6Ptm0FdEuSDxgyfddxfXUzeWJ3/cjZ2SWP3nhECAMpyuCVYQiE3ZrFUs67bjfQdzJ121iRg1rTAhsMWUkDEkvrpiEZ6MaRPiR23YYQO9pWgODV0SN+9TffEs/alMhG7Df6YeTqZiCYlkV7xMXFOU/euMvV5QkHzZb11Ue4esfywGNNS9U6Voe1DCbqtoQxY/ESPqOAcb7yPH7ykNVyxW69ox/ilEvP55k2LsdADsJeE3bXdJLpmRhxSQC+pvE0jaw75yDGUWxkfMWyXeFM5M7xXZLGvpiygONEDLN/4pzPZnIOxDiAshCdEYsQsUCDvpcGWOWnjoMAelm9ePdYiSlnss3SlMxKFtBmwpxYlsbL3FxIKfDis+ecvviY3fYS8ojJQeXbjnp1zJ07x1jvGGNksWzxOXFzccLp8094/dkzsqpq1ouWXDlsu+TOgycc33/M9XrLOI48fPhQ2Fh9T+W8FKlW5l6QlPGoDH7vHAerJevNRvI/1K7EeqINkjuWW5KYYow1VodklTyiJLcl5yl5pANniVnVHKpySSnJIMSY1L9SBqLVbauxUUDaECNOh72U/SgxaaCQOspz9tZhjJf31Vwwx72GF/K9Gl9PA4CsNeQg6kJvMmkcGMbMUdXypXfewrQVj3/hazx58y1e/uv/iXh2wjWZVDUsvGfMmeQETLRYzX+hWBsVNlY5T2+fkXuMcmXFSt2UJvB3ivtGAKld17Ebu0l1ZK1KfKc9ZbThJGy64+MjOUuvb9hXKZZcRoZqCdGhxKCJFbb/bKfCkMn2o7xK7bYPhMI8xBgF2ItKdR9/nJmWTEPI5PsYrK2mnKfeGwDkrEyqT5rbZgV099+v1IZyfuv3MnNzvgytBvlcJ2iBnEe5yPFlsFW33RHDiElR5mto8DMqTUYBzf8vr58Hvu7ndl/M837OOwDFZ3mePSHvZScSSBm4Jw0rAddDTng/+6PuW2p1XaexrOAcmle4GeAuitb9WF/ARywy/C+LNZN809mbPues+W4UAKvYGFROZfNi85E0lchKWttvAMyEFoOpPJVXxUPOJF1Xtvh46/MWWzS91ylTW/U9lglxU/5Uho7msiaCKqA03/Bq4ZYoQKsAoMbp4DhmBdtU27nZyrIwS0WBqnsiQ45RgTdDpUSicRSw2uhZh4LO3nlyQH1nkQZYCJIPKXGorWphzuu9LPlKedbOWp27Ujxw5XpleJylalsq74hJnu20z/QsN0qmStWs1i11zfSe1tK2Ldvdll3X4ZAhkQ43PUtnYOxHQkiEOIgtwhgwVtYD6r8qw/7sdJYYZYZ7V+xrEjGM4v/b9zRNMw+WT5HUz0rT8hyMMUJGygXfknjUtq2uwRmHikGULFPMI1LsYUqdZ8nU3mEXLd4ZxfyEUW2dZdE0LIv6MkVh8ocgn4dAEjIEbGS9WTMMA5WraBcLaj8rPQF2gwz8LTnJvnLhi6+/2yBtRrrjBTq1UiKNfaAYKtuC1+wt4gIOxpgkUdaiyZdOHGUDlumEBpsE7JKOTIYknh9d102Bq9ZFk3QoQAFybsnOTQl0hc0HTEO1RF6VFQS0mclvZYICcybEjqvtBePY07ZLhhw5XLQcHqx0wIZKDFIWmf2yYegH6WSa+XDJRpifwsZkCl7ShZCNIv/JlGIwejAygX1lOFbpkolsq4BaBQzP2jjbmzqOJNWSSIhfi8iaREKU98AweSAWUpzkk8aJFEmmf+ok1Sxgt4AZwhYtgERJ+kqwLOBj+T2jyVx2lubuISbD2A/icWYyrm6EuZk1AORU3KgIWcDE5IwWhHuWFST16xL5Q8xooNEiJyd2/Y6x27DwDYmErz2LVmQcwzAQh0GeTC7AtMpn0yyjLS+nAJV0jtXLRwuLSahmDMkkkpVEzOSMr2u2aeTf/vDf85cffchv/eNf55d/6Zd4+OghuUoqR80kU+SveUJ45FnXxBhoF3dol/e4E0dqH3jzK9+gMws+fPYpthIfvrZtJ1ZqaaI4I8/z5cvPePnycwGXbbESSepbJ+BzNDIoDCTIjIx89PIl611PymJTUBoQ1tlp7RlNsrLJUFvsouLJ199lMAKo1nXFdrcRcMHqED/12qswUgCSsUn2JUakjSITVHnXFxIxSRjnJo6mxBBliF+RkOQk/m2lC3p9fU3xlxJmQRaGcGFKUCxcsiQaKZIxk92I9jBuA7RGDeuzIUWDMwljHE8ev8Hp2SmvT16yXCzZ7rbaSXRTAeK9Z7vd0vcDdVXjvOXs6lyKoUVNiEH2visNw8zV+oab3YYYAzFDZf001KYw2CyZuqqnAYIpz8yIpDKlVKa+W0PdNlxcXzCof5Jxwkq7uL6iy5HsZD1BZrVacnR8zOXZ5XQt1jpubjb89c0HRBKukiZP5cxUOJRmVEmK9wHe/QKlFCKjeh0VVhAK4Jbm267rp32HEd9zi9EhMMi5apwWzaU9p2egsywPRYYzgVM5S4PPWKqqpnim+apis93MgJP1+mMpug1t1bJaHnC1vpD7rZ8h1ybnGCaTjcUdHnL0xHP5/DUVI4nMkEZO+w0uBd5ol9hgcckooAbZOhrvcGnkg//7/2T5m/+C7/76P+GPfu93aZpI7eDqZsN7v/xd/v0fnJCHDbXt2F2ekGPkwcOHvHi547OzDSf9yNtvP+HJcQvrG5rFIW418vj+knce3WV3fc5PPnnNy83IO08f8+a9Y9brLS9vrjnb7rh355j7hyv6qw0dmb4ytM6xyAkfM0O2vP2tb3N6c8H27JxDDCfPX7KuoL57yJ3lkvtVzfWrM25IDMuKR6tjHrQV3dWG19sta2tYLBue3rvH2XrL6WZNsOKTZooXlS3nnCSLmaL4sTLB12jT18MYYQwic6qNgkFWWCjeeT79+Bkvnn/G08ePCUPk42cv+Me//S8w1svgBZQ5ZkRG7JwMQjBkbDLY7GiaFRivwKyA9yEEal8x9r0yNsQ/M+YsIwBjUBsCYXLEpE0iWS7kLDJxdOBg3/UY19BvNnz6l3/OOw/v8OQffJNUV9yEke2wo+svCDETcsUQenxO1PUKWy2pK09N5vNPnpMjvPHuu+phqSxOLXjGELXAgKurE9puTXt4D1sdE4PB7PmW5hzlPuiei8mCRhJynmTXIeUpJ3KVF7ZxTgI6xcj25pqb6y2FrdSHyIuXJ3zvN7/L9c012801TWPoup5+7Fm5uwzdKMDQMJJzxLkaXzeYm8Co7GkTAsfLmn7ouTh/zW63YcyQs6VuoNu+5tmHz9h1PZeX57zzzpe4f+8xfQhcXt+Qc4/zmWpREbst6/UNy0VFDhvu3Gm4dzeTw2c01TUPHi8w2RHSgDFBmM05YdH1YiudzpwQFaWlbjzN4q7MbRgHDAnvKrUMknW022xJIcpaGno5wxPTtOOuk2JssVpSV6oYM1YsmIwMFknZUptGsSKRu1fW4L0MVAtx0IxfwdsI1qa9pkJSCb6sWWslfg59B0S8ArTG6nBg6yWXzDLQ0TpP0Ca9dR6ZvIxmIknZ2TPzJSuxojJgjeR664sTLs6eY0zEV1A7eY+qaXn3a1/j7uPHBtADXgAAIABJREFUuLbBN45hd83ZyWs++smPGdYX1CQa6wgZXLZ4v8B4I4VhDlTeMA6ZPo7kOHBx+pJ+u4UuYm2iXi04fPCIatmC8yyWB7SLBVVV0S5bdusdIcnQXWclP5dYUwpkg8llfCxgZ8DPmJJDFaAWsArO1kvqusZYJ4Oa47xP67aRPKJqcLZ8jjDQnBVVRtCGpSg75HCRAUheGada/BuR8hMscRSySvboYMXCvjRgHDkNurYFkKvaBu9qTA/OG1xT8eX3vsbxg/vYg4ZXJ6+56a8JJmNtRa5rbF2z0EIyFfuaILLWpD6UrnJaVM9+voVgkrUecs4yau2pmbMWn2KlEpS95a3UQCEMk/xfjygFXmbijrGG5XKJs+Iz3zQtX1ReOSdT2osaSrwaZ4/Jfbu6kqcUsK78d8suaqrfzBQPDLMtVywD1NRqJCUxL5CzezIy3btPynZTAkBOAasqgpKLFc/dcj3l5wVA2c9z9y3f5DiQAWgwKyqTDocagzRhQk7K5hfSFosKvKzxbJmHi+29fh6wWF77LNlbTfcJsP/5YO9co8JEs8jFjz3LkD2L1o8N4xgI5El+n7MSHVDLxyhqQrEtkJkRMepQOQQriEpOAxTQUqsttT1w3tF3PWMYqesGv1hAStSNDB903k45ztxsMNO9MfqjtdLcoDQxUiIaWSlZc9GcyvwRGYblvZfGX2Gm5kRWrED2wcwQDmGcayYnBCWpHwRwLRLynJiUswZRHpTFM4ZhalTklAkmTs+tAN0S9+dmjAz6jooxyed2yuT1ahNnUOVDiFgEM6hUVVJ7tQCUbwsp4MkkK7W5846AIWf1601Q+Voq4AJS2lnRnHMmO8eyqkhFkaV7whUrvzhq40e8r71vFVTWdRgzddPMAHYBNbP8HaM5pnWW4zt3WIxiOTix7wGswduKg6piGEeGofi8yv2NSchrvvbEHGWtqtWQJJsZWzENZx9CRwxBQF6HEAqto+s7GWiYIaZEGSDorKWZGM3SZM1JlTGlGZFkDaQUGRgwhYhgjRIx5TwTgN8Qdj2aPQg2aCQviVEZw8qsddHRtE7zaQW5bcZ7S1UvMFZmiRgr1jZSrxtVcopfex8Es3NO1s3f9Po7D9KW/woIUiTzRTYz/958YJbDq3TbjSLcwNRpTBO6JY+kPNDysZWrePTwEaenJwzDqEV38d3yQBmqJQbmGQUUySp5lsUgksMiUy9yIjMFHVEiF/DPkOJIjIlu3BGDsl4zrK+uGPtOkiInwBBZQFNrarzS+A1mYnWmvaSiAAgFqHW2AAdZZWOoXHLuuBUgO4P6lwi4W7rK0onVG0YBrMpzKP6zJRnwCtTsGcKjB05CTkIRzFPYikaHHwipQZhDE9h6Cyybl0wxk94PoNNhaw3GZoxzjMOAbcVDzRo5VHPKBARgL75A+x6ypLhnSyD3Neaog6zydIh4v3eYGiMDZ7ylR6Z9V1UFtWPVrqhDYLveMOx2k9l36ZBVVUWfZplVTkmGQeyxAZN224pfTHlZBWbEq8FMpugxOl5dXPJvfv/3+av3P+B3fuef8ovv/YJMqkyjdqYMkNQrWR6wFMIe47R4sjJY5OTkkkWzYLU6IOJIWQprZ8W3KKUymT7z+tVrPnz2EbuunzquJRGUYAKdAl5OWWoGw2az5vXr86nxgYKjU/KUpaNWmhKurahWC2LjuLi+JKmEuPj6CAMlqC+VnVg1KKOzML0FkJX7eHB0QF1VnLx6PSXVU0IGmojOjOcQAhUVKQoD9d69+9IhbFvuHN/h9cuXcvAn8UUywGp1QDdJLfbPwKze0jOQiO6Qss6MEY/Fo4MDcsqcnZ0TCThTcXlxxdD35By5DuPEmi4gXiyngiaBnU4aLhIRX1WMu6AebXLmHrQLLq+vOVouIWeuNxu1xkjThG+MKgO8MKzmLv4sZyr30RhD27bUbSvrO8l5uh063v/4QypXa9LpOD485O2nT3n/2U85ffUaY7wuCWXzK5BksoA3YRyxwLJZIVNAw2Q5UM6KLzKiJVbo8ANl4RZGa2E2yH+FfVSuQx9bFkYdZHKOEygU9JwnKyPeMElDi304e+83DOM01dRXFWm9JufMMMzsd0korPiexsR2u5kB/JxUuSGvBFMHdyTjFjXN0YLhQhhylsxm6DlJkftHh1RkbIj0oce5hgW1sFTTSNqe88EPf8Cv/Pa/4Fu/+du8+Olf8Kvf+Uf8ux/8iLvf/BZf/sXv8Fc//Lc0jcHmyPb6DFs3vP2V97joBg7vXvHw3iE3lzecnF5imyUP797h6f1DdjeX/PTzC062kSePHvLWvUO67Y4XFxe83uw4Olhxd7li7HrWYWSoxEvtwDps17Pue8zhEZebG/qra1w/sgkBs1rQtI57B8e8cXDM608+5qzbUN2/x4M7x9zBc/XiFVsL66bG1Z637t3lnTef8qMPP+Uq3JBqAeIxChjoMKEShyamqBagwtaQ5zCOkV6lv2DI0xAZw2fPX/DR8+d86ctfpfE1f/ZHP+C7//g3WK4W7EZhFxYWbEZyGe88/bDFaNFm9DwMQfMbw1REhRDEnkXVGiX7IWdyiIxRwI+qaSeJbol91qrMMARsIwyfzW6H8477T95kea/lVXfOn//xT7jY3HDvwQMuzk65d/cO9x+9Qe1byJa33vwyKVWEvqffXfP5s0/5pe/8BnfuPsXiyFWNSQFnhYWVshQUOUXGsIMcwCZi3JJGqOwCY2tMjlgjg2N8Vr/JpGCzkSIrxECjDTNp+mbNuxI5j8TQkYaR68tz+t1OvecBa3j18pRu01F7z1obUYul5IJHxyteff4Zw3BFYkdOUPuKEAa63ZoQRJ45BgO2ZrvbcX61Zoxo8Zr59JOPeGGfc3N9zbbfENPIhx9v+fzVC6qqZuhGhnFDVRnu3XsowEgYiGMk9Je0C0/sb6jZYvOasb8ip56YIgcHR1jbaI4SCGFQb+EF/dATtUi2WkxLc1I8I8duR7IeW+kwKIfkB1nWtUhFA+MYGYct1nQ07SGLpfgKVt5jbUM/7CiWZPtMnZzlMzLCBjVNA32aVAsxSbPcOYPJUQFaiSPj0JOtoWkWUkB2HZZMNk6bEKBaKvGwJ01gU85RwPQSO5DwKqQAczupLJCb8XjruLi65OLkJZBxVrCemDLWNrzzlfd48ta79MYyxoG823Hx+nPOXr4g7G6wakcQyNAuWN29z/2nb3Bw9z7dENluN2yurgnGsrmKnLx6wfX5CWG9oRktzmaCheqz59x/+oQnX34XXxmSR5oBZVq52h/knGSIT8mBzUxoKMBFnm6A/lyScIo6IKdMHEbwhmwclaupKy9zA7RB6CsvnrPosFxl6o7DgDGWPkhd0zQ1fd+LYs/L8698Lf6plbLZUpR6Rq/VWQFvDAIyWeazVgrzqI3tzLJpqX3FwlTUOCpb8R9+9Bcc3b3D1W7Nhx9/IISdqpbYi2XQ4dDGipzaWUusxLPQWseo4BCWqan/s8Ace2t6BgmctYQ4Km6hhCNd/87JPSvEoInbqakopuQgVm2xmBRXMc9WE2VIa7H42wdZ55/PeeJEJshlXoCnqOj22ZazRF7qvKI2yllqXC0t9HsZUkgylLAAtHvbxxjD0A2UnNO50vCeB0gajW2m5GIYtazJEwmqDLMuOSRKRMlGyDNZo5bkRZIzpxgxcVYqGueJ3hOmeyH7vVzL/n2a9scXXn8bCFvu/d/2b/fzTJD6OsZIXanUOya63RaygKTA7C+svskpJ5IOeUxEsY0xs2p1UPJBaRtYle87Vwm5zc5s3MlbFTRn0YG5RuT2jQ42KkrOYrtRhu+i63cIw63z3YAw4cUIV+sAvdHGEIeeCTkcByFGyWKdbKEmkDZCYQYXpa3bU/vIDIqge8lMcnirEgJjSr4tFpr7OEfxqiXLsKymaRXsSxRF5Dz8W55VRljuaG1uK4/NQiIaUqByKpEfB0zMRANxF2VYpJmbIFabuGVv5AxhK9Zz5ffQM3u/3jNGmkkxjRI7jSh9y3DrQkgpgPQ+sF5qX2sdMWj8z/MaKTVCll4mTpsltXESu8p76ec0dUVWNcq8DmcCUNu0jKPMZgAUR5jVXM56losVw9BTVwr+Z0tlHfXBISnJObfd7SSXJUxzPpbLJQAhzH7Nk/Kh7EM970Lop0acc466kjM+k4hRWLwhyoB452QvxiAMZ+cc/W4rTcgCNiPX6b3DpsygFj3CppbmMEksTqP6kwtInakqp+depqr/Zij2/xdIa4z5b4D/Gjlufwz8V8BT4F8D94E/Bv7LnPNgjGmA/xb4FeAM+Fc554/+3z4jB5mw61B7E3O7czUFxC8Ad3KgzWzK2dMnKlBTAJikIK4lMQMHKScuzi+EZm+EklyCqdEvEpMMHEi5/J5+H0pnT4NAkRNREqICQkoimXJJkFWmZBLD0ImsKydyMpyfnTL0O8hycFmv3X9r6PsOh8XqRMUycVU2NAo2qam70cFXOd/azMZIF8oYK2zdnxOkCvt17hZ+IRiz/2zKszCIrCPNHbRbnysgpphISzexzEuwfj+BtgpMMyVJ8uMM6hbK+JRI2NuekCkmopWCTwKbXDOGCQQrTFVykR7L2opIcmgxWvjpNRmdSKrrcJpqGQImG/oxUB8d0h4eikzCCGCFdYTK41cNhwcLwqZjc35J6ESWIJPeR0zO2AKWW5GST4MT9NDeB5KnwxmVs+nTCCg7tvLEmDjdrLl6/6e8ODvlu7/8bX7j177Ho8f3sFlYE4U5IxYK8hmW8rDVaiHCyckNd+8csmiXXK87BR2tdA29NEeMNZxfnPMnf/ojLi7XWPUVstZKBECShMJal7VWpCM1rz4/Z7vubyWY0wCHrNZpDpID11a0x0vcwQJXWUKOmCSeSTfX19hqNj+fGKvZaIKmZWrx5MPo3IHMru/Y7dkbzAtemy5p9n0yxlDVDSbBbi0+ddubHVm9VHfdbgrQMnxH9tP19bWwbdXvyzAnXH5v+uZ+kmcQsoZBfIL6rueNJ0/ZbG5Y70ZSiqw3V9M+yTlzdHSEtZabm7WcdUl8VPcZDKUJUNe1mr1H2sWCmKWjvOs6rLN0w8BqsYK8U3bIKB1ib1kulozjyDCMDH0vnlDe3bp9JdAVEGm8uZHfryrCMIjdQ1WJCiEKCNXtOk5OTqU4sU4GKOrzLIyMqJK7yWYA6IfC5NLGQ0n2/pbXLWsRbQB5L/YlwzCwXt/IILYp6S7V45QflJ7C1Mt6990vc3lxyeXVJTZbNtsthWWbJ+BI2deadKy1kVCGzhUzf2Py5HFtkIIwpYDx5vY15FneVxI/YyFX0Nw9JPQDw6WwDLI1rEPk+eUlD6uWo5xpsyP0iWhrTFXR2oQDdq8/4+Tzj/j2d7/H+cvP+YP/7fe4vr7kz8cd3/rO97i4OOHq5fus3IC3lutXHzGGka++8y7XZ59xeXXBp6/OObnp+Pq7x7x5/4D+5pKffvKaZ+cdTx494UtP7nF5fsInpzecdDvuHh/xxt17EBM3feR06Ghdy6PDY5qUeb3ZMDYVq9YTbq6odh0Xl5eYwwNWBwsOgPu24fn7H3JyfYV/cp92seA4ec5fvWaXAmHVYJ3ljaNDHlrHR//hLzm72eFyJodM8laBQSt8mLSXhyDPbGqOIh6pIUVStsIK0LjYVC0kxyfPPuXk/Iz3fvFbNG3LH/zvf8AvfuvbPHj0lO0QJ8VEzlHXiQBD3jmC9bpn2SvsmfZ8Kdwihs16o8CsJPNVlnibUmIMkc16x4PHD/FVzTiMsj/UTiqnzG7X0brM0A/cbHuMX/Dgq9/i2Uc/4OL0BZeXLxmuLe985Zd5aO/z07/4Eec/ecnX3vsmf/LnP+bxf/GUcR344Q9/xGJVsX19waMHT/mzH/4ZZhz55nd/g+cvnvPsp3/N/aNDhn7gH/6jX+fq8pqPP/mAhw/u8vlnH/Po8RtcXq958OAJj9/+Ch8/e5+mtlQHR3z2wYe89aUvszi6J9eZs8itNf6WYVNZT/w47gjdNeNuTR57zk9O6PtOmGFe2JWnL885fXnC4zfv4kyk9mq1Yh3rzTmnZ5+DiyQGyIa2qbm+vqDve6pmgaFiGHrW2xu6cSQbR704IOaMCY7dbuArX36Xb3/7O/zlT/6M84vXevYPVJXlzTcecHT0DrvdWiy8xsB2lxiGEWcTJhsuTj7h+uI+w7BlHDuOjg4wOKq6pa5XbDZrhn4nhZjzYDxh7PR8U5a9NtHFFiKSYmAYdrihYrFY0rYNOTsK3cA5S7e9Io8RayOLRUW9aIQdFCJRfWJTTKQgTXrnnD4HWYMyRdnjrMfqAN9xGERZYFSZlAI5jcTQk3Mgp4Gh78i+YrFQhlmM1M7hXYMxMosixlHz6FGYkzkS46hMl4hHYoo0yNXHMCWxQZjAIomxkkpHTl5+ym57jfcCpnlriVQ8euurPPnyL2Dqljxuubk8ZXv+mv76AhtHWpPocyb7moP7D7j3xjvcffyUbddzfnHF7uqcT589w7YLHjx9yvOfPuPk9eeE3NMay8q12AxV9vhuR3jxktfjwMP3vk5zZ8U2DnTdVtR8RIyVHNbP3T8pvGOa5zWUPzBmashr1EIsOixpCBTebQLGkPCaTzokZ7+5ueHs7AwsasvkFRiUvNTpFPHiHx3DSAoSm2JIWCu+rF5l++X8ylkK59kSagYacspUevZ667A207oKE5Mw5qoFVXawjoTc07iKu+09NmHErnuGONDHxJik/sBYYfhX4pHcd53WH3PNYpUMMw0s2suXUp6HsskwGq8AqGGgKPBmya9VBnch97C33kDUoQI4MjFO5d7MFgYFnN0no5ScZd++rDTl55fs7/LdiyS6/Bpme6WitoqxKIhklUTyxHQt6jTvbrNOS90l9VKRUyuonYX97JwXwE5nqQhTTgKe7K2ZFJNKPad1t3UKsk6NFG2i67qT4ZjIIDoF7chgYsSoJdEYZ9LQfuPii2zZfZbsFzGI/Z/v/7t90L68vgjQ5gxjGImxJjmdj2FFpVWGDpX3qKqKMCaskG9nAkEQMMi7ikUz+4paq7J4zQlEfVNpc0RUj0axgpJbFiAwhCgN0RDodI3tD2KSmSDzOjH/D2lv9mtpdp73/dbwDXvvM9epubqqZ7aalDiYpEVSimXJsAxFhm8SRwgQOEAAX+ZvyEVuAgTITYAEAhQkiC+ExDBsJ4ZjR5IdSSAlkuYoNptsdnfNVafq1Bn38A1ryMW71vft092yDGkDjaquc/b0fWu9632f93mfJ0mD9K6Xz6X42PXK10MIKglPSJd9ff0KfrPOIM7rOco6TZc/REVVlMxmwvKX6TeRufTe4Z3HhX4NJ9LUE5nQzNq2fd9jEovfB5GQscm411ibSHayJvvErPcxooMfNFqH6UDvwSu6VppSdSmyQoW1yJRd5OT8XDCoODZJROqEJA8hhMDmvJV9Yi1GG2lcKYkL3rmkWyvs5CqZZKlGURR2IMU4nybg0j0QMB5UDARlBmnIfO+tsQNhKhOPCCE1/5K8SiKvZLZtbvjZNIFcFYWcK6nwEQPwAptqyfzcGMXYXqVJQYOmLmph3KrEgo3CzpYcwQxxqSwLetsPa8MYjTHlOD2Q1mpMATUD3aYoMRGa1SrhOIbpJDXKopepjVQj9qmBLSZkcuL1vaf1HVqNJmFZmiSTLYXsmfAKTdJCTg0Wren6LuF+ka7vxYTvo7jC2uMvDdIqpW4C/zXwdoxxpZT6P4DfAn4D+B9ijL+rlPqfgf8K+J/Sn8cxxteVUr8F/HfAf/bvf5eUNETRYVovqC92uz4BUExdEEgA7EcAxpwEyHMzey6PE0tQa5p8oc2QzGQzAueSu2z0a2dfHmVl+Ez5IDf5oBSx0CRYPh7KGe8Xwm9k2cxp2jO0voqKhu3dHS5d3sf8zBAHTaJEbY/i4mrU2hhMCiTDG8DQKRQNIACTroEU7jnQ5C6nMODCOI4DF8DwHLhygpKD1QhWSHcqhD4tSvlnkViQsR4RbR61hnSAy5cv8/zwkBD6JN4Nopkp7JihO8wYIHLynw+MdWbpuqi6RTq+WQPJJnkH8clQBB/RUSVAWUB8lMam6xMTMydRVMluq+NVHMc6IDMJTVrJct8VhqigJyYKvcJuTCi9w6tzfNPIdYqJSRQyI/ziQQeMYOfantBaJ92dwBCl8ufTaZ3XJT5Gnp284Pf/6N/y+OAhf/NXfpnXX32VorD41uH6jr73TKcT9ADyqBR4E7PEVGxvb3M2X3B6vhp+los+aw1nZ2d857vf4enBUxlpWwMMlRod6kU8P4OPshfnyxUHTw6BJAavsrMv6fpKcwOjUYWh2KgxmzWqLrCFGBSEKMypYexrbd1Kspu0pZ0Uu73WidUYh/domxUaYTePyXJq2mSN3HQPcgfPu56N6SSNo/WsXDcUHDYJvRdlCVqxWCwGHZ980IimT6Sqa8qy5Pj4eFgH600U0JRlSdM2rFYNT54+TUlPGm1NiWuKAmtmZwzrZf01M1ibGacCeMooXcxhS0FVlnR9z3yxICKg7ssvv8Td+x9ilKHQhmpiWS1XBCXJtlLjKB9r6zlfu/H/R/3dkFn8GpHxcB1Pnx+gC9lHfo2lOwDZgs6w7h7cu/5CUWNVjtcXdZnW/8xrNGvADtpd6fMKm90P92L9+fLfyILPult90zKta05eRFQlY+cywSBOn9ZYSGL2uXDKCW1+5BGbwhYoL+z1XOyFGEhzZhfiH/l7KQYpF6UixayivrRN33bQe9Ex7HtO2wYdQBvDTimA8LJfoW1k01rKoND9invf/RbKB65evcT86YdMQsPZ4V3uf7jN577wZb7+B89omudUhaH0ju7wIaW9zY2X3uCs+ylNf8Drd65w5/oO8/kpHz445PFxw/XLl3j95mWOj4+5f3jCk2XL7uYmt/b2USFy0jQ8Wyywdc2V7T02teX5yRHHoWdSTqmLEk4XLM/n6GlFvbtFqQxl47j/9ANO3Yr68h67e3tMejj48AG9iaxmFZXV3NmaUi7PuffsMYfBE8qSrckEo0uO+14adx+53xL/xqI1B15rC5Q19MHJ2aE0VVnTzFd88MF9oip445XXmNUz/vgP/w1vvfoKb772Bss+4oIUamYYS5Y9mO9rYS19JzEzj6fq1NAb95XEqma5WjsT1BhHtaGqRVNOaSOuwiTWd8oRjBWjjc3NbQob6YKnDZE4maK39tk3lnAcOA+KK3feorYVhwfHNG3Dy7ff5Jtf/ybf+f1/S3Saq9dv4pVnUkwotObwwV0++N73uL63x2RiaE9esLe3w9e/8S1evXWDg2dHhK7HRsMHP/wxb958mcfHx7x79y7XdnZ48sFPef1Tb2L7lne//22uXbmC3t7NSA+KkHT5knFbSKaQURyZl+fn9KtzND2Hz54RvJfzQ8n4e7NY8uL5M26/conJpMJoKCuNj5GT01OatsOYCigIsSUiwFXXdFS2YjLbZFJNWS4XGK25eu0Gupgx3dhkNtmmWTkmk02C91ze2WFSBrQR44mi0OxsT9nb20apTZaLFavlnPOFIrCBUh4VYHt7gnPi1ry/f4XpdMaq6XA+iBRAcBACRV3mbJa6nuJ8g9IxNSZJ51sQ8y8TiKmp0Dsnhd1Q/ASatqHtelAWZWbgHdFL01TFpJ0aHXrI+YyAMH5oQ8qfCUxv2w5UBp2kkW7QWGvommRiks6mPCWXY/9kOsFEMYRRSeIgr3GjLbYo0dqkJkmRxvIVvnOEzoMXAD8ENQAXCZkd8qfF4oyjwyfE2IIqCWhaB7uXr3DjzqsUkwnOdRw/f8TRsweU0VGoQFSejshkZ5fLt26zf+sOppzw4uSEB/c+oDl5QRVarArceuUNXpycYkvLdHODpTc0rufJ8pSd6TYb5QTXR0qgPZvTnJ6wsfEWxXRDXKjnC6KSSShtDcpLwA+IiVpM8mSCo0QyUSXmc0ZnTWfJjXwUTW6tDVZHrClSDpXNwWTMejqdSpNwbZotA2URJRNVMTKpKry1hATyhSiyalopQhqZjyqNReuIcnGQeCkLGQEXZqAG54Xlm2JcVVYJBAro0qCjZVZtsVFvo+sSVMFPHn5I2zmCkfVYFxYdg7RuQoCQwA0kb1JaJVPclLIIanYBwBsWiMra4rkWIgEbhdQW2YvCj6afQnZbB1AZ8pTMCpM6Q4yPtNUpPxvN8+SzjGfO+iRpzufW66Dxvf3wfnENpfwoqJib9hn4JV2bIoNTqQ4pynI0V0r3JO+lXJMJMO+HvNv7ME7+DWVxJuGMxnEhCmElpnuQY1hevDFE0U1ORJH889xwydIrOoFXkZFNqda9ZriYxw3r+ALmwMeu0yf92/pz1l/nI88QoK2qBlZ4jApjIkVZyPpLObqwneW76JjvoTRMRHbCU1aiRy+j2QLMeeeTLrQGdJK3Yy2OqhFsVXka2eNdQJEmNtMazJc9175D3Z/WzjApG0eAX9bkSHLQxlAnHdgM/inkDMj1lcSZUUqhrmucC8LYj36Q9oghsJjPadL61FpYjCo1fEis2XzeC+nFYlKN9dH7lf8c9ptRA5haFMVQT+SHyaCySiI5M8UsNZhVjAQF03oi5sshsDGd0fVjLZExg7KqBvKRUhq9NLSuxyGx20VPYUvKoqBrhYgFmujCYORpEp4BCud6lssVvfPDPS6KQgDj6EULPgqw3CTzycJa6noymlb6kCS7EqkIwbTKJI9ysUkk16NZrdJ5L58jTzhmbMA5h01SgDHGgcQ4VtwZg8veIKCieNFk0lDAU1bFIC+acYSoZfojM51Nkl8okibsMOGpZEpxvYlijGFqJ/ROckTnhQ2d62el1OCBkjREhn3jvacwIpkpsg1eSBCVALgQBlDdeU+zbLBlkXKzdtAU/qTHX1XuwAITpVQPTIEnwK8C/3n6+f8G/DcISPv30t8B/jHwPyqlVPykKJcViAIBAAAgAElEQVQeMUbR8UkdiKzlqmJmgoYhOKy/Sg6K68X0OqgIDILBAswFgksHewrkMSDgWsgatgnkDTl4Z6BMmKc+OAEEUuEv4Gai/ecOSVyDYzPSwRrYCIM2SNc34HtJKM2EevMSV156FfWnaaR3AJhIY8g6HVypawbkcfHxTEljVoyH6gAsJxAuB4nBWGANvMiAaR530OmwjIxajiMzToESDSKljLB0yWNBpEMgsVujJFyFLSiMZXNzk+OTE/rkEKxJox0hg01Zs2bNMS+ENVHqj3c8B0Z1oq3HNaFpBgALgs4IRg4qOsePYdwmBNB6BJS0ke9prXRbRF9rHH/Paw5jxsIXiGQtQIU3BrM9Y3Naszo5pzufD6YQJq1/iAR3sUObNUrXgdv87zHHvgzCKwVRWN5RpwMlaNoY+O47P+Heo2d86Quf4z/6pS+zv72D6/uk0xfEzTyvpUG2Q1hGxoB3PUZnNuOYLB4cPOX73/8+9+7dS+DlODqldXakNQJSDvtAoZSwdR49esrZyVzez8haIq373PHSpcGUhmJjit6ooa6JhR5AaaNHUf64NmI/gKkxokJke7rJ5sYW9549FckcJVq6MQRsOkDy4f3RpG0sPFMiRsBaxSsv32FaT/jZh+/TL3oCikkSEl8tl6J3ugbCT6dTFgvRHc1aqUPnem09X1jnClwMsr5CFNBUBVTS9DVJskgSmHghgZb3HUHa/LBJGmKVnKZVruJSTmytxRSWLhlfZCmRelIlXbyG5WrJ/qV90WxN61FpQ3SOkIAr0eDN90M6saBQIWDVyGo32oAOiVGr0EWBiw6CRqWDb+zEG0ojo0eTupbPGIOAk7mpFNYaQzoXPZKwTqdT2q5N2lghgb+jmQ5A0zTpesWhCMp/rks6DMm+1gPL48XxEX3nUTqZgikBXQtjmCX2cUQNmugMMW9sOub737tOCkNryRs+lTfjOk+nQY4EksNJTDUx4guF3qyY7GyyPDyFxLJtVeRF3xK9ptARV0yYRUfZNUQ9ofXS3eqOnvPTP/1jrr/yCteuXuVpNye2Zzx/73vc3L/JZz73y3z/m/+SEBxaFdCtOH1yHzuZ8vbbn0bFwKyCftny/uMTHh6vuHljl9vXNgnNCfcPDni27Njb2ubO5csE53h6csxJ22LKgmu7exgfOTw74fHJCdPNTbYnM+Ky43y5xNcVelYRvcO3PadnS5ahZ3b1Cls7u9h5z+HTZ/QqYHe2qYuCG7Mt4smch+dHnFeWzpTc3rvM1UvbPJyvcKdzThNYMMSSdGzEkBgnqUgnJl2xVByKS27F0ycH/OhH7zLd3uNLX/klKlvyJ3/8R1y9fJnX3niDxWpFlwyPRNder53lEtvwJM1WTbPqcL6XvRIzy0ZuuMgkaBaLheimKZO0wESZy9hCjH2MFYfznC7nYj7kuCwjcrONmtYFnp+1YAqu3XiT2B3xaHmXSb2Ltpu0wdH4gJ1sU29d5qUbr/DkvQ/Y2bvMG7/yc/zgnXcwRQG+oVDw0pVr/PG//Gd84ctfZqfa4NZLLzMtv843/p//CzvZ4mt/5z+m6TpKXXBp7zJv6pJ/8bv/K3+4mlPvXuHS9i5PH92lxrNZlwyaFMTca5X4EnNhLkCUMSWbmzusYsPJ8RFPnjyTpw4gu6dtHc+eHzGdbdE5YV5qLbp6dbnJ5f1rTIqaaVlzXh4QtabtPd6DIbBZT6QYOjln1QU++9c+y9bWFXzfgnf4qqHpGvrYcXVvmyu7E2yRGjYqTSH1gaKwXNm+hJ9tsNhYiq6schA1k3rKcn6K73taZVieFuiiSCPiwlLr+4aiNKAcrl+KrluhUl7jJV8j4vseooxm2kqYqb3ric6ha493Lo2DQmUMyiYn+SDavpaIVx4Q6YqirKkqS0xGkl3X0/seHx2BQO97dC/yDCbJ4ygFIbikiaiHaRWDJkRDUZSiXxpkJLWuakLf4bwTLXkFSlmsAa09CkMI0qQvrTi/F6rAtw2h8ZhQD3t5bL6kMy/l2AfPnjKfH6O0l8kYZbDllL0bLzHZ3KJtFzx5+CEH999jWkRUWdBFhY+Wzesvce2lW9SzGatmxcmThzx9/BDXrqgIlEYz3dzEETg6P+cXvvJVVjgoFIcvnvGTH/2QK2+8zadef5vF8RnKOVZHx9SzCa5v2ZxeIvaO1fk5SoMpNLEXB3vJ6T0xjABDzvnDcFaNeU2uBWKMeCKLGOlCYn96T6c8OmqUkua3VgJ+x3T+ZqAl1xDZsC2fSSDAp0lrTwGzjSnBS/GslDDdfGIruRhQaNpezGWymScRMd1xnqKy1BsziqqkXywwE4PWBdpUQIl3hhAsXSsyU7bQlMbQp/NOacWkmvCZt9/m7v17HJ2cpqb0mLMTs8zdRxvlkhNpa1JunAG1PJ0pZALx6bBJf9lfAFlzfpmQJExh0UZTVZVogCsxI40IQPtJOWj+PB+T5ErgVx5rV4rhc4UQh3H7kUU3gq/5e+TnikFUMY4UMzJ9faqX8/UZPl8Gx1LjUCTHBJwPMWZ51hHcHg5TJZNCKuXfqa5v2xZjDRZh3g+TsDBMFko+CdYIy16lpoS4wRfEqkC1EZXkXnLjO++N9fX60dx7XMcXAfaPwhnrz/n4z2AEpuSai7SG5A9VkhWScX0GEgtRobSlrqeUidSRwXOfZH2UVtg1ScNcP+baOabXyyPjspei5ARDDSM5v/Pp9YMT7fEYRWZCRXDZjEpTlRUEicPSsCbhJxJHMx6T143RemCihqQT37ueorDENMEcYyD6JM/VdShlqKsqkagiy8XyAvnAh0BwPapI+zEx14P3yQclyVaik6SeYA/SeIypeSB5gZiDhUEiraqqAaQLMZGKUFhtpNGH1N1VWbExmdIaS9+0eCI5KhTWsjmZEaMYSveppui7jsl0Kk3yxOrd3NoV+bu2wXtPVZRpX0dCVSdzd9nXJmFOmXBS11OUgrpeMV8sBxPBPEk+m0xBj3IHLBdSF3ohsFmlsVZDIXjSarkc8TSERS91SCLdhICPsJifM5lMUCjKLKGRMbZUc8YQ8UbTuVZwnZhjj0gPKCVMaJEbyA0lIR2M2FT25BkJTS4xuDMOFEJIU5b5+QaiPL+0hZAnjJHva1MzJOW3IQRcn+ZHghi8xwTM5unpHAOHeJkadPXWNm3b0rYNozwLGFJzQOs0pY0QhaJaiwIff/ylQdoY4yOl1H8P3AdWwL9G5A1OYnZNgofAzfT3m8CD9FynlDpFJBEO//x3EbYT64E+0TG1gj5pluSOpUAjUVz/GEcP05lH27scGXH5MMkBFyjKEqVE2yIESRyzK7JOB1vWic2asD6KgLxWApAQ89hzSnyMlqJXyWGo00i/xNo8IiMLRUXHoIHiAn3naJqecrPEVjP29q5ibUHvGiamxLmIC3ItNOlQTEzJi0ByLtIT/RqVxtmT5EG6QFol4C2z0dLTLgBTQEyFpgCcKrEOR+gxH2oCrocBLIyMAG0+13L/ROjjPcE77j+4hw/jIRu1GrRDI34Awwfgh5hGP/yF1x3AvBTM8nuDQltD8KTALdc8oUjkzFzGjeIAYuXRLJPurwBWZkx2g0hVaGNQ+dqsFfA5EWZNyFwnACYHXFsYyq0purT0q5b2fEno3TDGPYKyiUmNdNkyW0+aAqLDpNNBOaK1ckO11mM32mQA2HB0Ouf3/78/5MGju3z585/lrdffpKpKyrIQun8E17vhMFda03vPi5NT5qsF2kChpfj3wfH+Tz/ghz/6M168OEqjSYauadjc2EBr0TvNDFCSdEYIwiaPWnF4fMqHdx/jXKAoC/nOJonGey9mIEqhCjDTCrs1QdUlIV1iiKmhw9o9VBeSBQkBAd877ty6w2/8xm/y2//od3h2+Iy6nvDSrZs8evhQdIXSumY9aRuSYGRENI11oeTwuffgAVop0dJJTIKu68QNNLP7E8Xdh8ByuUohaSycsubYekc+xdEhvrm+l4KCOKyvQEhJsc9hDqstre8IJJ3bAc5L61GPZhI5KRyKVm0otMWEHt970cBbi58RuH//Pm3Xy9oInhcnR/LCRljy2Xm9LAr2L+1zfHwspmQh71GdtpbEbmuMjITYMo2vhuGzjtdJtA/zCi/Lko3pBNV7qrJCTTVH56e0TsT+FdCn9RiTAYrRCpK8Q13V9K4fYl+Wg5AvOjZFJKaPBmRDoy2MnzE/lMpNA03vPIGQ9C7Tz4JoIi0Wy+HwX61WKfbK60qyGVKszuyS8XzMIBqKIRqPyXIyBUyxNgfJoGT8VBtFubOB6xzt2Tk2in6u15Hj6FArMYC6ZjzT0NBpmBYbTGyNI9L7jvb4kMs3bxJD4NndnxBdy49/8C1+/otf5aU7n+bhB99HFRZbBFRsOX78IUa9xLVL+5ycHPP4YM7hyYrbt67yxs1t2vkLfvLgiMOlY293m5cuXyE0jqdHxzxfnjPd2uTa3g6qdyzajkV0bO3tslnVbJc1k+mM07bB2zQB0axYzlcEbZjsbTOdTGHe8OzhExauZXpjH1MU7NczzLzj8HTOSWkItuDKbIsb5ZTm6Izjk2NWIaIKYU/IZAwjAq4lP0gYQsIKBSzpfcS5wPvvvc9P33vAW2//PJ/78ldR1YRvfv0bbGxt8fZnP8+i8/K80AsrwZQp9muijvRdT0jTPOdnZ1TlhMIaYjRoo9nc3mJzc1NyCVLfMSjOTpeib1gmmaYQ5UxN+pXEODRNchGfelnJHCrSdh3TyS7LZgVn5xy9OGR5esz+1pTYVdSbU4IG37V08wXTK7vEesZrb73N+z/4AW9/+StsXb3G6nvfQxeW6DpUVHz1V36V73/n2/zRv/rXvPnFr1Js7HD1pdd4/7vf5HNf+Tl29i5x7/4DojZgS/b2r7C7tUNzds6nf/4L/Oj73yG6Fo2MwQrDXvZD7x2FLnKGmFtueNezXCyZlgplFOeLM54dvgAl4JUxCpSY9jx5cojSNu3liLEVXddxenRK3ywpleL65atsWdGQ1MFRVSUojTKa87MzFo1nZ+82e/uvEXtNu3pGszqH2KKUF1f5UFAWlbDkc37gWlZNS8OKsnSIH4ihSKOEMULsAz44losFxKSNr1M8iEAUs9dQOKJZ0YcV3WqFLaSB1Pc9fefkzIgCtqoUpHIRTYxYoxMjM63HlF/bVHwH71mt5jL6qRQhKGxRoZWhWa3onGOyuUEXOrmOqUh3vQyFK5QU63bUhYtBRhV1qFA+Ersm6RGqoYhSiMljs+opigllJe7SOie2CMARXcRFh/eO46MTLqkJhqTFB3KG51NRRdL4HE275OnBQ7rQURSKGDqKcsLVW3e4dPUGQcHje/e4/7N3qGKD2poStWZje4/t/VtsXdrBu5aDRw94/vQJq7MTxIx1iq2nzDa2mOzuctyuqGZT6v197EZNVRecRcenvvglZtNtDvqe7dvXcW3D7dfu0J+dc3Z2Rr25zXK5ELkzJWZJPgqALyCMHuoLabQPcC0QpSGvImAhjdSD7IMe0W8FCCTJFS9nVvRxmGYJ0Q/NqQwGGlsM51NMZ6owRC1W26H5FIMaJtBCOueNTkwmI2tkMIKBQSZKacnnldaYokArg8aQpT6MLZjUE4rpBs9PXuD6gC0LbDZV8x7S1BFK8fzwUCSIgkw95rpmOFdjzv0vNsxDCPjOD7VeZhQP0mh6Tee27xJYFsbvH0e255CPGcOV/Sucn51zen5K70QqIrNA87RRzgsvGn9lqSaV2M7V2uclESQk58ogK1wEfteB2DzllRm16wBurhmz3vCFEfAguym/lkhgyd6PhKR/yVDPpGIqgdZhBMjTz3QCq0MCakbzbol1ufYcgF6E6KKQs3ow3JzO6M+74X6uP9Zr3o+ynNeB77/o8VGwd/y3dXmsBMK2fWLdST3hXYDYY4IYQNmBkRoTmK0Glrcxwk5Vrh9AbO89NhQ41cuEAlJTD/lfAuiddxL7QqD1ycRayZRfVZZJh1ZRFDMiMekjJ/AMNRBhrC1ACWtx3cR9ANNsYucH0YRVMdL4rGG7dq3CGHfy9erS548xNQnKJPsXZW157wVPQV47KtHHdc5RT6q0NmRNaaNHnWmyZEdI69MMtVaWWBnkYWKSQEygeF53sg+cmEBZS9e19N4lMFsPuZUOac8g5prTSS3fKUS6oiDGJCWAEukfY5gUJV1bSt2tlBB3EpNXJ9DP1rVIozmfRunTRFWMzKYb7Ozt0ayENBO8Tx9L4WOAKHHBJOPokGShrDFJJ9xiC4MxiuViNfi3WKMpixKZeNWpOdBjbcJDfMAUxegPlG6tc7I2lcnsYwYg1HlpWokPh0+1WIl3DmMLutaJBE0KBPk+COtaAFyRIAhiuAx0atxf0uhl0L+OIYjhYarjome4Z0qN62/0JgnDiZkbE4rchNRy5qTabDqZUBZWTNCUHkkbQfaHcKCTUaNmkEP4pMdfRe5gF2HHvgKcAP8n8Hf+sq+39rr/EPiHALqy6eZK50LBwN6U8U/5mTgXy03RgFeJUTowRcbNrteK2BiTu7EREKIsSlmomTqukxR5OtTGEelxVFongf4MEWe2IFkGKoxjqia9pzBD4wBcZUA0d2CJmq7pOT0+4dIlT/ROXMAnMzY2dzk4eyjdIGWIVgJT5oWwHufWMbp01InIuvx/ZiFEpYYgmYv6dNoNQSk/smmJUiJWboyMMRurk6D/CIYOLqBrZ9w6E1apZBCVwSWSdlwa2cz3zCQDKgXUVclqJewyKYADRsuXFNfXTK0fQRxtjIBmIQwg3e7WNleuXOHdd9+FmO+RGrQFw5CMqUFEXbp7aTSb8fOF9HuBmFhoiaGc8/z0l8zcTs8cDjKVihAZJQhgNeXOJqausWVFc3aO0Ya2Ee1heboi60GRNZ5Ugsrj+NmGrnT+zCpr56SukE3yGQkIct7z45++x/0HD/jcp3+eL33uc7x657Y40QaPNaWIZpcGpQznixVn56f0fYcxAuw9fXLA04MDHjx4wPlikYwS5H1tYnyXZcm0nkjC1rsB5NdGUVQVi87x4/fucXK2FEZBSki8czgv2r8hyp92Y0K5NUPPKsTDJ61n1HhN0hX4KBOWFFM8MF+seO+992lXS4rEnjx49oze++Hzi6fayBof2Sh+7X0UCgPasEpdeu8DdVWBksDcJyMIYWmsMbmz5lfM4ysC6ubE92MJI0oKDZUTmzDsHZO6zTEZwVlj0th+izaa2cYM14i+k9ZJKzMl+pnFu7+/P2rCmZK3Xn+T/e1tvvGtb3KyOk8ppkmbTeGDguSqnhNjOTjzLQgp3sL87BTnuiRgnxPfJFifmgl+KADWGykI+1mlEU6jkui/XE/X97SNYrMWU7Ombei6Vkbh0ndcT5iNSrpBlcE7z9npqbjMxossyd75pC90UV5kPRH/pMRdfi/mOk9i/VCNpDibXqcPkmyWOkvNSPyR11krEC7c/7xeBFC5WFiM8UBpI+OCOfklGSsFSfh0VTK9tEvXtvhVS5EkKnqtOPeB0rVsRMXURxZ6SUVBXQuLTkVPvzhlOd/grV/4As3K8fzxBxSL57z3o2/xqV/4IsenhyyPH1GUYvKl2wUHd3/G5uVb3Hz5DQ4XDT9/aZO97RnN/IwHBwsenQU2tra5feUSq7bl0fMXHDcN040ZL+/vo5zjdLHi2fk5080pe9MptTIEFA8OD9GTmtI7dCejX84aZrvbVFWFP51zfHRK6x315T1sXTMNGnc656jvWVpDKDSXZ5tcrSecnp7wfLnkOPT0heQmccglSJMKmcUsrAWX9odWiqg0QSne++ADVvOOL37pl/nSV76GMjXf/c73KKzl05/9PJ2XhrIxliJpWrmoBu1MDczPTyiKmslsg8l0C+c6qtrglSM0nrZrRUpFSdMWo1HesFo1tE1DYTSKYtTSD0Ho9iqI8ZJKE0UxNR+jp207dFXgvaNtV/Idu54P3v0xD+69z6WtTWb1BtOdXRyRxXIByqJtRY9m99oNrr72KtfffJO5C8znKypd0qwci2UPG1t88Vd/ncOTF+LGXVbceu0t3v3+97ly4yUOnjzl6OlTgnOcvHiBnU3YvX6Do6fPmW7MuP/v/pTbt25ibSmM4BRPhIkjDdTgewFlAJWMpMrS4twc5ztOz085OZ+jrUrNkcy3hfsPH/P88BmFkdd13rBctPz4h3/G4/t32SgtzVJYSr/yNz5PPVVEWqZlyfEL0dC2tuTq5dvU5QbRKAyXKepKRlttQde51ATP+zexmn2Hdy3EQAg9dlJSJv1W7/oB9KmrCXvTK/jQEmOfjGU1hEjXLAjBQXCE4CiKgrPVOSxCmmSyFGnKKHrRu41Bo5XFGFkjvu/pQo9WkufYQoCfDAx61+Ncj1aW5bwRyQRtQSusLVnNV5zNz7l8+zobe9soSKOVnZx9SqXCRnJFa0pZizqgjCFqSww69UJsymFlT+iUV1oDk2kNRHoCznUYE4laGFUmvWdUirIKWJ9GWFWgDw6rLcJWUwmsBKsM7fyUs9MXonMfQYfIpa1d7tx5jXoy4fGj+3z43ruE1ZxqotDVhJ2rL3Ht5m1MPeXpwQMO7r3P6vBQmnvasnP5Btv7V9jY2aOsKgHhDh4QmoYHH97lKDh6t+LJ4wcY4PLeVa5eu0XXdwLehkiJFMi9b1g2cwFKE2PIJz+PnBQolZr5ib0TEnPKKCWmO2qNpZkaGkRw3tFpT+/Bhx76iI558i8MBa1NwPoweTeMo47AUJ6a8VEA0gwInp0vscYMTClI+pTGoHwQLWHMoB+rjYwseycAhthLKKZlTZhoajthVs3YqCfUZclktiH5c5S2VYiKzvUiKeY8GE3bNnx47+549seccymyoVoG8EU/OeUsKearVB9pI4BLzhFFK1MAioGpN5Qcfqi7si/HcH6HwMGTJ0lbNSbT4JRhrskHfFKD2Jhcb42s3wyc5bH59QnIYZQ936mUa+T3yZ8pf4d1sDI3s0cG9ZhnBO+FPZcYiSHV7mISJhMiAnQojBIQsQ/jpANrNR1KamcTjbBjE6km50M+hMGITO6RSlNMSQpLK3RhqSdTzvU5UeWp1E8GYvM1/ei1yb8DfCTf+vMffz6oGyFAs2owdipAYQy0fY8JkZkpBh1QkRcw2MIQgpC45NpLPpeZyFkiQ66Jo++E6FMYUlzLxtOeytZyL0gkmTU5Rq0FINZmnLar62qY1Mx7NfgRJ2naPH2XdIoHIlNaE0owkz7hA7FP8hNray3XaTKVGtN0j6QoTdsO05ry3mI06aNPgKJZI34E2q4hM9slntjUAODCPc57Z1jrSiqzQotGddM2ssaTd0+ux3SqaUMISbZOXdifSinRudVCtlnFCGrNgD0Kk72wBapLNVuIkq+na4VOMdj36VrL3jbp8/s1GbZsKO5Sjdl7R1kUbG1sDvvPuR7lBdDMe3YymZAZ1eJ/4QldQOmCaV0PsUmMxjw6hAHULm1BURhKP8ogOJeMsnSBsSbJ/nUoEEmOxLTNTFiQ2NI0zTC1WJYlxtQDxmKMom07nMtSLoItiMGgI8RA33f0TibKtNbYYmwqrVYruq7DmCI10BR90umNQeqwNrGOs6ljH+PIzh+ahWGYzkJFYu9A2QvM9ryGhgZacALQRiFXqKhkWjTEIV590uOvInfwt4APY4zP08L+J8DXgB2llE1s2lvAo/T7j4CXgIdKKQtsIwZiFx4xxt8Gfhug2KxjSOCDkrpfCuwEOmqd2FZKCyMkj7JHSSCFGK5SUJDiSafmVUgaSCLMFOiCaHBKoHJrSUYGGZKDWxJQz5tbFvgIqqx9j0H3L12f8U+lILuEQjLqyiM1Gh81nQucnLzA6oBVMlrX+8D2zlUevnhE2zumlRUXdPJIbh5D18nQjMT6HQGC9OEkqc10d5WA2wQ05sWqhnUzsnKHLkT603svTFcl3YSQgkD+rutdWdauxQB8ZoBz6DqPv5eD6jiSEZhMtmlWDS64oYiMcRyTj3nMTd4ofW85kHLyqYCzszPRAhnGVBU6JfEjE/niIbzOYFQ6gUKCDA0dXhCGQUxFRn5eTkzU8HoClEayBo90Q51Lo17eYSpLUW9y+dZV3Krhyb1HqD51ItfAf7V2byO5gTEmZfn7rX+HdR1Sa4o8bTQA+SeLlj/85re5d/8Bn37jda7u7XH5ymVeee01SMm91iJV4duepl3x4ugZT58+4sHDB8znPT4dVAKSyyfc3dmiLEvKQsDCxXwp+psm68talq3nnXc/5OnTI9BZlgCiTjybkOQuKkOxMaHc3kBVJWgZ0RDjBjXem/T9Q4goczH5UgmgtGXBhw/vcv/RfbzxyfjEsVgs1ljksg+MNdjCSlKlNbPJlLPFOdpquZa9AI3jtdfYpGWbAVHFuH/yIx8kQyd07TE6SV4coSfd7wwkSJfToKKwnk1hBGDV0rmsbMFCPh7NYjU46cbEgMoJR17nIppepANV8+jhAw6fPCFEn0wiJMENQQT9c1dcKemaGiMmW5mJOuyHKGZsZVVJk63Mrs+BrHOV12dm9V7cq6l5lMaOyYViQkBXXTsYb6yahmgUFkVphZm1WC2xZSmu3MZglKHte9k7Pjc+xoNTpaQ2ZkbZ8O/j/Vn/9/WYkZNmrdUFDTDWwNYcC3UaAcvF3XoMWf8sebdqnRtAea2tJZlwIWZ9LA1QYCl445XX6dqWx48eU0wLtvb3mR88R7lAqaTYbzWcho5tSnZMgffQ9UuqSjhoFojecfj4Ibs3X+PX/v4/4J/+o/8F9+Ie5wcPePz4Kr/wi7/Kn/zBP2fVn4lmcfS4pmVx8oLZ3iXefP01VqfP6Zo5z84aPjjpmGxvcfPyPr7tODg84rRt2Nrb4eruDqrtOTk748T3TDZn7GxssThb8GKxZLqzzWnfYLxnt6pZLVboqqKYVgJOzxvmR0csvGPj6j7lxoTKgZ/PedEs0ZO5cdMAACAASURBVJd36MuC62XNLoYXh4ccRc+51fRlKTIo2qRze4yd+cyJaxFZJYOE2lg2JhUHB4/55a/9Lb70pa/QNY6vf+PfsLG9yee/8NeIuiI6j9EO33cyHlUIu8J1DfOjF/RdQ9s1dEXJfHHG2dkZW1sbFDowb85QwaVcQg1NHGEmBZpmQd+1lLNZajanqZB05vWuT7mBFAs5RhqjqasCYxSrZjXEBtd5mmXL/HzJ9uYen/3ar2EnU5QumW3v84u//hsEChwavbHDV3/j77Kxf5VlF/jUZz5PbWERLNc/9Tb9ZINqe5Ov/b2/j4uRFsXmtet86df/LhvXbvLDH/yA08NDdrd2eefHP+bOp97kpbc+w6Wbc8rdS9x4+VXOjo7ZuXKdNkkWKRQ+gWrB+SQDQ9p7kgwao/Au0vcdzw6e0bY9elQ5ShLCmuPjBXc//IC33riJjwqiZj5fUtgKHTTNvOPosEGXFdPZJpNJ5Hw1p+jcUHh0fcnBkye8/gY4D1HXVJMZZT2RfVt24gqcRqEjAsoYDb6Xe5OLbHF/zgCJI3hPXZfUdUHXrXB9iyabs/Sslkcs5we4KHIqZbnNzm6ZyAyK6XRG1zucS07jIcp3Uxal5VzxfcdyeYrVcvXE8Esulnc9TdskkxPLzt5YTAY0ptAYBU8eP0AZMeds2obeCcMwrmnoS2qepG6MwegCr3qUsUSv01iiRakoOaf3hODo+5Zm2VBPt8jO0tFGlO7ROrJcnKPVgllZowrLZlmjjtuMv4FK48AxJO28gC4UJmrOT05YnBxTFAEdFBvVLjdvvEZVbXLw6CHv/dl36Vdn1DaCmjDbucze1dvMV4Fnd3/M47s/JazO2drYYPfSDTZv3mb70mWqqqZdNRwfHXFycsji5JD2bMH+pT00gRfPDnjl1qsoDc5Fnj87ZFKWTKc1ru+ZErh88yo6ONp2QaHHqQ2UlzM1gWGQps58BhuEdALCwg4hk1vGPSIkkECuaJQa29HWjiYyomlYrmn26wRm8LHzqCxLYb4lYC/nyK13AwszP6d3LjUhcqMW+VTe07cd4szt2NjYoCwrFvMlkyhyFrO6xpoClKVZLmmbFcH3+ODp0HT4BDSIhqDPAGwC/mICC7XSZFJWZmnGJN1FYsJqGakcz2ZkVH8dmMzn/5DLDAnDWBtkg+JUqor2bHC0SRqhqiqKwuL6nqZpLlyrPDG4nlvGeNFwdj0vyYCOH6ZSzdq9G/OODLCu38MhjVh7zSxnsP4zYyxFep9hImntfLJGjXqNTtZi9pMhy82RcQBp6BMYGs4fnWTKXi35c/kQZOVH0Zsm5c5FUdCtfc4/D0Rdr93XwedPas7n67r+u/++184PkR5IHhoJ4BJPCiF4hBCo61rGspUYxDrvhhxxwCTWWH8DgK8LaluSnep9IpUZlNRdepRnykliTDEiy0k65y6Mka9/16yh671PtVm4eE9SrotSg9yc1gzkg7z/rS2GBkLOp8UQSif/iHGqMKJEQiWIBJAqEylKrWuzyvXvewErhXWusdqitRnyA9RIhIlr9dXwHJtkR5Tosq/L0IUQhG1qZdrGhgLnHOfn50PdBOCy3GMIA0i9/t0ByqKkqvo0JSq1jIzopz2txZBbKSDI1MgqxZOMUWW8qiyKpM0q8g9N0wzSDZlUOHzPJK+QY4FaW/OEQHRJuxVhrBZ1Te+EsRtSo27ZrLBpHcUQKAuRrhRSTMB3AWUjdVFSJDPxHGuC93RNi05Gdvn7ZPwnJhxLG4MqNURNXV3Ek7J8RkSkI7IJuV2TZhEJkQlt24pEWIyJ5CNat8GJVIhMNQd8s0rxyYg2dNLilzjVi2xYmoYkKrQucL2wzLNxNQgZMmMY3ot+em705j0yxruPP/4qIO194BeVUlNE7uDXgG8D/wb4T4DfBf4B8M/S7//z9P/fSD//g/gXRC6lFCa7XXkSuDlueskj0iGC6NvgxxHurAnKsBgZN4iSDnDMNUr6w6Ux8byA18WuY4x03aghNBwCKbHIAWwI0n50Gx9iFdL5h3Qoe0HV5aFBSYffhcDh8Qu8a1Ddgmldsr21xa3rt/nx+z8khJQQpO/p0yiaViYVIZBQ2hSIGDffBeA0JuKvGpJia4SWLZ81ko2+8j1h7bpn2YOAH8y48uMCqDkEvrXRXEbAcL0bm7sjoNYSHAEk5vN5OgBGyQQUqLiWXMJ47+UDEH0egUnXyzmWbuxgEzPYmWQf1kCXC0BHfoM0CqWVgFshZpB9lCSQX5NmgNE66fql+5KKEJUPCtaSqhAIaal7FXBNpFCKemuD/mSBj34AhTMDb2Dwjm994boP32Ftb4WYXI1hALcG3dw0hv3w+QuePXvB9Ut7vPLybV6cnrC/u4fOSXXXcnp+ynI1Z7Wa0zQN3osIeogqGUAIQFWVBXs724QQWa5WLFcrMYzApGtR0PWRH/7oPT68+xjRlxG5kawNFtNn06XFbtSUWzNUXRIzqOBDYnj4NY0pub55rwzXIYHsIk+gMaU0cUI6jI3SH1vvIIlJaQs6WgpjmdYTzs7PiM4TgpIR9DUQPbKWHMubYgtLXdUcH58MQNvFjnzSY4pr9wsJIln/VqXr4WOS4IgC4M+2tri8u8/9e/dTw8WsJXJweW+fo9PTZOghyWtee9evX+f58+eEpMf6/PlzdnZ2BEB1jtOmY1JWdMEPzKdctMW4Pm4nMU9MWlLiPFyNMXnLSV6eYJAxlfzdx0IiC8FnE4U8biQ6QkoYywi7RaVDcuUllsTEHjBaRnSqsqJpWvquwwUvCT9O9Lpjug9xPelPCZmTfZ7PhwxIS2FxMeblv4+xazT/yEnI2LBRKWGUWJhB7ezyO8YhLjyUuhibxth68b3XQf38WmUpTqjEyPnZCW3TgIagIrO9bVSInD99hkr3MypodWSlDU20BGUESHM9EzvBaCusvQAPfvYBtz71eT7117/Cv/tXj5iEnic/+zH7V27yqS/8Mt/7+v/Ltm1keiAG/PkhB++1FFu77Oxd5sP7c7oQuXX9EvWkpFkteXJ4xvP5gq3tLa5sbaOd59nJMcerhtnOJrsbW7SLhuenp2xv7xC0plKGrUnN8vwcXxgoS6zSlC4wPzmjV4qNK5eoqpKij7hVw9nJKXFaMykMO9OKrR7ODk851Z6TChZGrpEe7p3cmNy8HJoLCDuCKL+7aQu2Z1O2y00+86m3eeutz/Deex/w7a9/h8mlS3zpb/wSzmhUgKKoUd5xenrIWScFwWLVcPj8kNXZKcH1RKMIxtC5QIhwOp2yMZuhgscrTVVoGdWX3SRrA0/fL+n7lrIohJ0ryLIUAeR1GAfnZg3E4IkKyqqEBF71fU9pC+qy5tXX3qAsa27ceoly6xI+k46KmnK3JIaUzBclamOHWFQUxnDrtTeJWnQMX9ndQylFFyOb115CaVj5gJ5ucPvnP4ePntc/+3lsDJioCdZg6oqu6dhyjr6u+Lm//kvEtqXrHXYywymFCkAyDSPKuT/kZ4gkjPMd3guD4+CJxD6TcyAjcAtaGqdPHjzhzVcuQdB0bcH52SmFLairGW0/JwaNcxoXFChDVWwSA/R9NtNJr4docjsMRTlDKTFSUsYSlcZYRVEpIj7JPAVQMopY2AIXJM+VGBBQwVEojbGaqDVFtY02PUblKbAl1muKrsV1LyR/sBOqzRmTepMQNNoUhK4lOkeR4qUxJTqKTnFRWAqj2QodfbciRgG2sgRSbTTTqBCXZY9zLTG6VDwXmNJSGk3beU5On3F0eEjUAjqts4piir3e9+m8LlNB7Ie9Jg33kArPHh2F+RsCFEUpMlYqg7k6NXsVpyfHlHqfjb2r1JMJ2oPrFuigEXvYrIsu+zqm/UsMnJ4cAj1ERfCK2eY+O/tXOD494mc/+RHt4gylerSdcenaa2xdeYmDkxc8uPs+7vSEInqu3rjJ5Vu32blyg04hudODe5wfPmN5dsKybShmM4wROY/L167y3rs/pW9WvPrqHVauh6g5eXrA5nTCtY0NHvz4HYwucF2gKmp073HBDTnw6Afhh8nAuKaDpw2JneVBLLJGFjqphsgTWUqA9pwHKa0HGSeUACeZcWVtITFQSR6Y82MQRlQIwhBbZ3PCqIcK6WeMNVXwAipFraROAYITU86qlAbci9MTrpQ7qMKgCmnAKy2u2m3X4ELAK020FpPy75Aa6MbYtDdH4zOFMI1z/pmlIAQoSoZCVjQRB43+dJ7LeSzkgQygMPz7CHTl98omOj7XvTEOmo1ybYRpqpEayRg75Akj+SCuAWCBseGrWNeWze+vlBq0QS+CtpK3rYO8Y+6xVmgwkj6Ge7YGUMrn8AOQtP6fc050OXMO7CVeyZpikEIBAVtDJyBvSM/PxJ51gDbn2OsEGR/CwKbVqMScX6tp13K9fF3+Qx6f1EBf//+8lv+i14upQA9+zdjWaIrCYpIcRd/LGHiMoO1YI1trqGsZrc5ksbyfYowUxsoZHsK4jmO8kFfGGAlKpilCFKb9OvEgA+zroOL6dzLapngw/nuu3fN1sEWRzEcNZVkMuISAdaMR2frUoEmM2VwbxBgH2SXW8nXZpxIbspF3boxk4C+Tz+TzrbFggWlikWbZj0wME5KRTtIamsoYMcfrRQ5NFaMkSGGt6KRrxebmJsvlcgC3UVDaMq3nRKqJwownMoC9prASr5Si7336mWhoq7gm76FGHeIcU4aJv74fCCXOO5E08yE17FMDNOTvGoixH/ZTXhBlWcq5rBVt06U4ZQdCTX7/zOwOIdD5SJHP7tglPf1E+lFClsnxTOqwEpW/Q98T+m4A4SHhG0MNL5/LpPqIKHWkShiIgNpJBqSqBtA8nylZwqEsSzZmMxbp3jjvk06soayFSDWbzeh7J8zppI1sBy1vNZCgYhB5H7IhpO8h5lrbEX2gaXusLphO0/rqRcvYBY/WEZRDqXUM8OOPv4om7Z8qpf4x8B3AAd9FGLD/AvhdpdR/m/7td9JTfgf435VSPwOOgN/6D3iPBN6saSmlBT2c9wBKpcTakIN5jAGdDlylFJ68eGTELcQ4sqWUGNN47wediayLkjfqbDajaRoZR1s7fEbnwn4owEM6EDLTM+sS9X2XHE3HpCRDdGIOlUSRifTR8/j5AatmwYapKWrDzuYGd26+jDWl6LeK+hrKpnGQmMaKEgCizAj4KEjjTyGNLogzsTBs0vVOI/BxAA30AAx4L5tUEjmGDki+/sP9Wgep167TRXbt6GyaA2N+vjw3Ucqj0ODFGEW6dc2qRylJBGMCaq229L4fnpOFt9cThazRorQMOWYd0HUQf+zcyIbPjICPjsePf09Ad1QDqCPfae27pOufLoLck4v5DWq4dwJW5u5LeorQ+4FiNqEqK+anZ4S2x3c9hc6j5sg47PAZLjL58j1Qn/BdtE6mEqQRFkbd4mBEi/bhyTmPvvsDvvXOj/j0m29y55owN5bLOYt2iXOiR6O1ZTqZYYqKqKTbV5aia1tWJU3Tslw1dH0vII0xqQgoaVv43g/f5e79x8QYqaoSpaVhkdkLprSoQmMmhQC0lSVqKVS1Sw2aBLx7n4P02vcNY2BHgTUW7x0+RmypKYzGtx/RwRrCzFqC48KwRo6Pjtjb2IIYOT4/J2gzjMTLEwU8dymZ9kkHet7PqaqSGNXAdh3XWgb+8npOe1ulBHXctQlQkM9llCL0jm7VMptM2bt8iYePHtF5l1w+TeoAanqC6AtihgPNpIOsWXRDjLLW0rYtzvdoq5huTVmengqDPo6NlhDEedV7n0ZKTOqqy0iaSTG7dzKWYowZnYBDwCbw2wdhxeb9V6RxFJ/iS58YNUZpru7tYa3m/tOnmKIQXbu0N2OKTUoZYpBRuDa5qiqtcL0HpdnZ2eX87IwY+mHM2MeASSwhbXQe4hAtZiX6bDmhyImSUqMxRly7LuJImhIptQ66jndxiNTqInM4gzDycqmptlYgrb+PgNsfL6TGtT+apuUkNETP4fEh165cpVeexXKJMgVma0o8rQiLFTYIcLIKnqPomFnLzMsERnAN2lVURnaMVdC8eMw3fu+f8rf/i/+SovB86//+J9SrU9755h/ytd/8T/n0F7/KT775e0xkWVBEj2oX9CeBsLnF1Ws32N3dxvVLThZz7s9XLPuWra0NLm1tovqeZ0dHvFitmGxscHn3EqFtaboVRV1xupyzzwb7Vc3RySmd0cx2dtEhYLuedrHAG9jYv4LSUHWBbn7Gs/kZflqyd2mbzaJiJxoOD59xQmS+UTFXUZhWUXSziZ7o1cUbCETJNkRGg8hMK/bqAucKXjw94Pxkzjf/5Bv8/u/9MZ/5zOf5zb/9W9hyQgieIkb88ox3vvcNjp49YHN7i9Y5fITNnUtsbV3m8v4+pqjonKfrA+eLhoPnz3n65ClHz57gYsfVG1epK9GII0jxG3B03YKuE/YVfjwT8jhyjnv5bFdKJcMmleKQgHerVcfW1oSyKLhx5xWuvfQaWil6AipIKyaQ9L9CAEQv7f6DR9y5bZhubNLGIGenElkTEjPBxyjNdhTaWpQydC6iqxptFEpXoJRMP1mL0oYmKJQpMdMK3Xt6xOxMR2HZdU1LaYoBFNIDc8vhfEffNczPzzh4+gwQnTry5Ebq8YUeHt59jPvya0RlaLvIanmO9z22LDh1nj6CjprFYsW02mJv5xZniwO810xnW0xn+2zvXOHo5ITd3asyUdIsU/NHpkmCbGgUdtD198FLc1IBeJp2KcBUVSWmkcbkeBw9GjETjMGj8BhToKixdoNmdYhSjj64FNtKimqWZIRKTJUbwJrCVhA0vXdiGqUUkZLlsmcynTKZVjKe3LaUhejohdQkda7BuxbnOvouUpR76KJmsunoPbSnj1FW9PeIcg5FFS4wxMQNuUc5lfI9+X7iTQBKy9hgDJrClug6SRWoUvTnUiNSJEeEFUXURGVRaoLyjm7eg5PRdo0ARHn8N8tN9KHh4MVjvOox0TKb7nHt5ZeZ+4Yf/Nm3OT14QGk1k81Nbr72aa7dfpUPn9zj/bvvsFkW3Lh+letXrrGxs8t51/Jn7/+MZ08eoL1no5xQaMXm9jY3du6weeU67737M975xp+y9/IdtqcbhMmM+cFzlt4x3dqktAqrxLC4I2CnE3zU6FjQLVpwyeQrNbidc8Loz6OwacokEwRIubRWSfbAjw1cqZUM2hTYbOaCGsELJesjEghGpeapJio9sNBDymdyozCfzVrpgW2W89R1Zq3EnzH3yvlIIGkZZ6JKTEw8H6gSazAAqrAEJSZhi7bFR08TAo1RxGSSVWhDtJaYtDVHgXEGwohCGsLjmS1SW6Rr1HbtcKZmgFYnVllupo5N6DhM1eTzecwt/3/m3qxXtivLzvtWs5uIOHHay9uQTDLJZGZlFquXS4ZkW5Zf/SDABgzZv0Y/wo/+D340BOhFdsEqWVA6i1XZMJPJJnnZ3P500exmNX6Yc+0d5zLLgGEIqABIXt5zTpzYe68115xjjjHmnAMIcUOaSq5pBQD3TrwTNT0sA14P84EC3pT66bD2KsDdYY4gTEpPo96WXddNMRLuWiiUZ3BHyWdmhVB5/3SQa0hD+m4uMhGcciKkSNC62jmvrDhVchYARmHxpLnh69c5XV/llXjymnqz5EZa78nsC1mXptTr+tQP3+8wvyrX+Tphqdyjw4b460Dmd4FcDl5S78WU2O53LNsFy9VCm0NZ2ZyHSi1DDiU/Val+FMCyEADuDI4rsx6mZm0W66UD1mhKiZDCNKivDNk9BFkPr7fUyoeWGwLAmjtrMoSAM25aMzJkO4q6Up9R0wj7PtqoWcO8J6QLIzE+jkGaQtmSTZzAOWeFmBZTmhuaB3VvsY8o5CmxgvgusF7W0yF4K+xXAYDTNFzPYxGWqy8kvJTxlSeFANaxbBdU1hNT1OFg2ghIsGgWggPkPAHrMckARpk5ISQe3wgrNyMxmzQPTHTeslgsaJpmyucLrlT2uahuYCzKqlwUwHlq1Ej+5xmGYRokV56r92LzUFnDbrcjKmFg7PZUlVNv6tlWI+XMru8IIU5WL6Wmdd7LmtI92A0D+74nJVkLRcE5DgMS96JuVWFSo89mWotIHV1XFaaqJnVxaUKVfSAEOa2fM6RRGkJtVZGcPJ+C/xiYLRIaR1NrU+AgTpfrqStZs0GZsSknYsjq4yyWBvv9HmsrnPXTPkHPKYlpkTHsMYT/NCCtfuh/Bfyr1/76M+Af/57v7YD/4f/L+xeWY+la5lxYihrwKeCU/I1JCsLpYiYKwGutdBRTjFR1RUrKfDWyCVNOhFSkVuV9xUYhIwHp8upKAoB2F6dgnIqn7XwYWvXImAQtRhbpGMQLDNRqwJhp2mDWQwPjiIz0ceT55RWXV1csFieYNGBN5I3zc9aLFdfjS4YgcuZyUDljiVk6NsLWLR1L9e6RbFWCsrJlijVEIgvoAgpky7TxoIyEqfupd78ceIcsuqhTI6eDCe0QuZLMlL+dn9/0ngeAggwVkAOoriqOjo64urpEvDXL4ZKwmiTFg4Rh/h3zVFVbuvXaeTuARCRQaVNuvl+aZChdvXRp7hz6xsy2AijaoElFee9MAXbKIeB0wMUMuAm4FSm+oRTwGj34knbxgWTAWM/idM2w2ZOsJXUDKchE5BiTMoDjFIDvdKK4mxCWdSgAbWbWcwEpi1eXkQ7MmGSNbveBv/n4E569eMH7b7/F2XpF3bbSUVLWjrOVMHCcI+cFKUeRNOz3XF/f0nU9XgeqOGOIGW4ub/ntp1/z5VffkikJu6yx4iNsncXVjubkiGq9IHvx+hHmRpzWds5avJlZVmI0bpTrLvcmhEBRLAx9T/Ku/Fr9HGaSnzgjBXsMkT5200HunOd7b76FzZnrjz+ebU6m+158i5kaAEVWsjo6xjnPs2fPsGgxk7Mm9uWZKXPcumngGwhTL4vuC5IanGfLGALb3ZZ9t2e73U2JeMqJy+srbIIxi00JyjLKiB/Q7778cmKKlvt0c32tctRMNoYXl68IaAc8IxO/dbhAXddkTRqY7rXGEGcnz6wYIqujFe9//33GrufXv/m1TusWW5di0xtCmBLjMUVO18d4a7m6uQELi+WSm6srOdS9eDSWwjMDdd2yWq149vSZeJUb8fD2dY2JI95VnJyecnNzLVZ1Ns9ND21EdYUZY4pEyk6J0Z0GQJ4bTodFTt8P0kSwXhuI08nF1KxKERBWRJFG5zyrBayea8bcLT4OX+X7596l/I/sbfUb05+fEn5ricDT58/FDxcYYpB9dr4mZrD9CDESgavQc1TVHOcMIVONI4t6wAK1l6EtPvVcf/spH/31v+VHP/kzfvsf/wP7bz8hbF/w0X/4P/jT//y/4PHnv2b/7DNap4wW6ehw+/Qr2tMLvA6kIVqGPnCyWrI8OaHrB55f33K93XF2ccGDe+esnOfV7Q3ZZlI3crxYcNy23FxeMeZIvVzL/hgC/c2W0WXasxPx4RwjZj+w23ewajh7eMFZ27IaE9vrG65TYnPkubWDTHIvagzdp2BFBpUFeIjq721zxluPz5nWObw1PL3dcLvv+PTzL7i32fGDH32P//Z//Bccna3JY8KEwNXVUy6ff8PVy695+OiCN7//Hs+vbqjaEx4++oCYI9Z4YsjYmKlJNKeZ5cWbDPtbHn/+az7+1c/48svPaRo/NXBA2Gshjuz2O9klWc7DrE3FZAQovMtMMqrQ0Cgpm4RxSLx6dSUMHYRZLZFO/EFlmCXsNluaRiRn3jse3L9PXUksSQZc1kZ3FiVUzInUDTjv8b7WeD7K8I4Uud5uaJoVbaPnipGCvORcCQOu0lzkwE4qJ66uXrE+XlPXjSb0KnGOkb7fc/nqkpcvL3WPlaZHaaZkMJbLl1tiyNStIUUZAOK8xTeeZB2bPrLyYqFydvoG7bLmZvcCXy1Yrc7IODa3t/RffknXRY6WKza318QwkOMotgbIoIy2XoARpopxAtjU3lM3Fbtuh8Ey7DzFOocs7AxbZeq6wRlHDAPj2LM6WlBXNZVZsdmAcbBciL3S0L0ihR7jhN2UR82ArRU/V1tBCoSohaLxnKzV325M4lGaI2HMhP2WZMSKKoYgw7/wZG9xdskwOqr2lLq9oh2W4jVrrIIoMkm8H3ptFloFXI3k7KaA/8I8ySmASrRTFqavN4acxV6BHMkmHpxlUFcLTN3gXMPx+j677ppuO+JTwlK+t5oKuzLUaAgDm/2GLvb4quHk/A0WZ6d8/OknPP76M9Yukd2Kt3/wh5y99S6//PQTfv7bv2G1bPjwD/6It77/feIQ+cUXn/PJb35J6na8cX7MW2+/w6P7b7FYrQk50e337EPk/N4Fn/3qVzz+u7/FNS3Z1XgywRvq1ZJVW7FsGp7XNcdnx+Tdju5mRxxh3I06o8NACjhjwBmGPui0a2GomSxrCgVBC9M1p6hAWFGvWN2PWtwjYK7zdgK9TAgCLmj+VM4gyT/THWlnaT4C04yQrOfiDAypmkuHe+Ti25pFNZhI4rmvbOqcsrD5kmHhPBWWxnlWiyXeO5qmwu0NYwr0OTEag/GeynpqnMi7BenRPNZNOXvOFusFoDbW6ICbSGGSxyCqopK/ZDQPUFBE3mdm9t1trM5MQuec2tPNuUHtKrGnyFlUP3lWQFpjZWCaMQqui0VKua/TtHJ/ANjlwqwXFmpVVZLPDgNxuyelme16CPaVOAizlL7kEYf/HLIgZ5KMAKAzi29WiPmqom4aNpsNVm3BJjA5lXpIc6xcQGZVo5pZCSJAiQJzWpOiYCO63stgNGMMvq4ZnAx0LItRL+879RGI8uh1UPjw9Xqd9d287Ls5W/krOV8M3le0ywXWlnUehTBjLSnMWIY9wCUKAWyub/PEPp0s0nKeQOqoVo4pxOlavPMCAsdEUim6AF3SrKoqWSfGSkw/zC9L5lVYjwAAIABJREFUjQ3Fg9lO4J7B0Og5FMaRkDI5pGn9xhjU03YGRstMjgk8zhzc16xMd8nBC26SctBZOxnjUMasAq4InmG1zhQQ12iNOA+ds24m1kxM8CT33BXzaCPDMckK+IXAdt9Ng/SyAqxVVZewiJBJ3IST1HUleygmUgwzU1yfqdxnAYZVBkRh8ieKj7XOihjnxkipZVMSiznnLM5YPI7KVHKfYtJ7LvmrQcBGX4nncVPXjEFyraZtJ4KTcZaj9RHjKCxusaZ0gmvoZ27qhn7oJY5EyeMcTpvLgnVF3arWWIwqKXKYG285RsZhnOKnxJEyDF32weTprThRsS2xVmZKQWa/3031TfHKl30yCrak6zpqfHH6/ILaYqQ029HknPHKFEaxukq9nK2B2gvQ2/ha5vVkJTRYsXvoahna55QVLx7PQjxIOTL0DTGO0+/+fa//XyDtf/JXVuAVSbxQYC4pK2qeUsiBxYFMKJ0mP2KIJJITlkAJMTZnBsT/R9a9JYbCgJWOfTLSpQnK9CJL199QmK9xDlLZMA+typI85IyxiWHs6QfxyHDWIaWEyo1y5vTklJQN19dXAsgpk+p6c8V2t2G5XNJjaBrPvfMzHlzc5/bpK7KJuMox9CMYi60spEw/9FI0mnKPpEgxxkxT73MWnx7jZllPAS1NOfAJKh+QQ31iW2rxQwEXynXLN8p7WQlqNtuDA2/uIE7/5bsHXGG9CqAjfmxNLX41XT/eAdyslWEVFLsDgoJscoALMFpkF465X6pAaxTAeu4OzxAueq0TsFnWi56ulgKCpAn8sSqdL2B1AXPhELw2E+ibEhQf3eLFZJQdm0rRitD1MRAI0Drq5pi8H+mvtrDvyEECPjoY7lD2MpnBK/g4d0edJl96COXZwHoaZGd0vVgFUshcbbdc7nZ88rtvePPshH/6l39CWzV8++wZOEdb1xgzkGKgqhwxBnZdT7/vuHpxyYM3H7JaLNmPIy+vrvnd11c8efqc3Xav5vbyWWMGq+uuqivqRcPifA2LmlTLAUIUucGc8dyxBftOgvR68pVBWfYJjGVU7CplafhkwDpPSoPuW3neY5qB5Dj2/PKz30qHuKnwMUls0P1tsyEJDoGakQgrNESurq6ESewMEfGpceauRMroVNKUwsT0FOkn1N4xxsAQxik5zWMmplu6oad7/gQUoK100IypHDaIbKiL3Tw8yJiJbVnAQ+ccq6Mjhq6Xoi6DMQ6XMzkm3nn4Jm+sj/nm+TOe3V6z2e8wKQuHJ0aZ3p7L8C9D0ATNe8duu+Hzzz7DITF9CJEhStFlYWLRZ8T83nvPSbti7Hswhj4GfvPFF+qAowwTEmU5G7QDrJIWkYpJ8yUHKXj6YeDTTz/BpIxQfZUxk9BhHYgsx0DXDxLzrCUOoxYP8jMw7zcpZJjiUylUYgFuTVE2KDPMFFBeBhsOQzfFp3ndMjGPX28Wza+5MSH9otneJSt4+zrjQ79DvAC12RFSxmCxywo7NqTLQBiTDJWxjpsQ2JiKRWMYaeljxNJT02CzpXIV7bjnd//+r1jEzIcffshHr74mjx3XX3/MJx8teO8nf8HHt1eM+ysWC4utPHHImJgYbm8wyzWnD97j+uuvOFsHlsA+Duy3G277Hr9seeNkTRVHbm9vub65xS5bzk9OaIDN7paxNpwtj8E4Ugxsrq8I1tKenOIrzyJENje33Oz3uOMV52fHnDYt+XrLV09fwqolnC3pXMTXDox6SQNGpddZgYIyWECG6Ehi1RjJK0LK3G72RGuIlWVxvOLBm4/407/8J5yfnZHGjqHrePH0W7a3zzg+WvGX/9V/g2tbbm83nN+/oF2dErKl6waqypGSFO0pZ1Iy+KrBWji9/5A/8P+IL37zS7abj6dYJgMFDf0QuL65Flmtgil68uOdk2TYICw4I7FvaoAmHdDhK5IR6buxHp8ShkQyFhJEMjkZLVgczlVYW2Eqx/q0kkFSWDx5YqdxIN9NVn+nSheFJRKwaeDJZ5+y2+945/0fcXR6QVU3JDJhjFgnzTkZ4giFvdXt9gz9Hl87rCtAlMRyYWZFUhy5fPWKy8tbiX3WiMpDz0uJe5bL645Xlx333qgZ9oPct6qirj3W1uxGw8pa2qrBmMTLV1dgG9q6xpsFjx8/weYb6uWGtmkZh44YR16+eMrTb77A2UDb6sx360kJVosF5+enbLcbun3H+cUpR+slm+2Op0+eU9mK9XrForX4KuPqRNPoZG4sKWbGvqJpz2laJ9JrbZSF4YqYR4Yhk6iJAUjl/lnCGFSFAJUXtmpdH9HUYlvU7Tthg5ikZ/YIRHIydLuBpmkhZXy9IhtLNhU57xjjDmOK93skDBHvK8Yx0A+RukosmgpfVaRs1f8copXhUdY4kjWYLGq07LLG9ESyRpq/AUwuGX7GmIbl0Sl5eYpzax68+SN+89VHfPu7x7ybVxjvRFJalFwxkirJC7p+5GbfSS62aLn43js8vXzJJ7/9FSkHxrrmnfc+4PTBW3z08S/57PNPuXj4gD/88EOO1xf86pMv+eS3vyKGPQ8uznj74Y85OlqRUubZ7Q23X31Nv+8Yux0hjrz3wx/x7gc/4NvPPiXd3gpLp/LUFvLlK3JbkY+PWLz7Fqul5+ab3xG7xHYfoV6wPD6nqhb0+0FY1lWFc5YxjlROhpoK2FDILyKhzylhnDDQ0ebwGALd2IFHiuiUcL7CG30O2hAlW+IYZwKM5hESekrTQ+qlEnMKGD5qM32S3dpZ+l+GZmm7UfJ9mxhCgtBhklR1vm5wvsIlOPIVCxw2GoyphNCAeEN2BKLJ4C2tr/BUJG/JIZBMkOaLd5CcFtzCWI2pyIMzJVcXMFGbnwqmkgXMKcBlAaBKHHVOiv0JYNSaYs5J9YxRm7Cs6s9iPSP5IzhtGmfQye5hAjXauuX8/ILN7ZYhDMQcqbwMyxnHEePFq3u3200g1jS0VvMKa5yCwqV2swc5x2zvc9iQfp0pm7OoTgwKoGawTn1Vx4gNAe88q3sLYaxlzbmt+vnG4qEquXOZBZKyx6iXrdG89XUGawERo0FsFOycpyUS0WWR/pRGpT0oSvVVnl9pmh++DhnGrzNNfx8we5cgo0mq/sIYMptND7Xj5HghQFUWO7qErKe2XYiSxMh+mu+xNE5LLVqeyUx2MlTeE0KmqloFm9P0bJ16bQr2UZimM6nNGvVkxkg+MDUX7JSPSo1pcRniMIoHqxESWlvVqmiYmZ4hJF1vmaHMjzAGc2BvUEgP46ixyMj9KIzdQ7awECoSRLnPYQwT4F7wgMKkFZa9mdY5MNkcGMxEoHM6eN4aSx8GBr2fTr9ebBVyBJsdYxBsIu62U+0k36uNcpPZ91u1prQTmF7IemAYhvFOvEja4Cr3I8Xi5Vq8gjXeJrXvzAljCnFQ6miPlbVtLdHaCUwvlibFBsNXnkUtSkbvlHRopEK21lHXXmKMl72H1kcOubfLpqVyjlrnrwjb2BKTDE2sKoeUrQabBVQ1dTP79NYO4xzDOOInYpuQIJxzLJZLmmGg7zrGENjt9xSLFhS3i9qoKgpNUNVjHHXfZ0wKgkns9oIr1LU0QMyci5b7XdaXPCM7EaNet5hIORLDPFBx2udJzu1K/ZZTzIScJuW9cxXeVTgX+Pte/6BB2gzEaaMp6zRJB6Ak2IXGPzHvmDejdJdEJpY0+SgRWIKSgJZRu8AWK5Kg0slAzOJtNoDTxEPtCoIyLacunxRosmGUHWCNsCSZgcipY5wzISRcpcbI1jCOA8ZXWAy+9sS849XLb7A5QnI4aharNY/efJPffvsrUgjEwVB5p0E0y5AMpMjIVrpjpRBy2oHJSZKLCOojKz49kwwwpTsTzCdgQAHe0k0qkzQzCkCYA8BVO5/GcOdwy3nuktnCVD047EC/rr97PPB4Cmp6PTNsErPjQkmAnCaFIMmPSsjJCkjOzGCU83jn8C1/NnOQKPcBmDxNy98VaYh3HpPm5LOq/O/17zncwKWILPfIavtt/l0C5hcpjAy6i5QpF37ZUOdMaj2h64j9QBoVrMVgsiFNoI1TduKhdCkpyMT0zJ0xKgH4PQPnrALRtSPETDckgvPce+sdfv7RL/m3f/UzqCxN7VmtGh49fINVW1N5z74b8NZw9MY5qWr4+vkNj79+wpPnr9h3OlTKGazXpFBZ3CEFfFNTnayoVwuCt8QUWVQt4ziQUyIg4OXsjaagHTMTUZKIu2tl7vSb6ZmXlyvM8zjvj4JyyzqaE8JkmJhbaRyUDSGsZgN46+hL51/jwyGjV/b/7Bc6SQM1ObwjZ4u6XqL4+rzz6G0q2/Dy6iUvr15oQhwltvh5UmocA9YZ6raeDi+jy31OsudCAU2oQgjcXF8ThxFbVVP8k/tnGPqBWA/YmCHI9FxnHL5pZOJoSjB9/CJjUalbjNze3lL8kNOB76wxsxl+JmvnM/LN02/xVrzmiOK5JJ1jSTS9tVNTJMQw2RIcvpfJMxskK2tntVhRLRpuNxsB3xALHaZ7JMWqNJDQM6Yk2zMbpiTgh8/s70/eS9IuMck7p5KjMP3e+efNnVgys8MK2ycf/IwCUdMbzHu4FC6HCX5Jpgsbw5UEtrLYVUvY9sRuFMlSSuzSyBU1Z76FdkE39FibcC5QWal7Kl8Tw8BXv/gp5/cf8fYHf8Tnv/w7zNDx9Wd/xw8XCz748Z/zq7/7P1kvGpZNTd+9IkVgDLjBs6pq3nrwiH4YeX57Q46ZZbugXR/jqxqXM7vLLVe3N1TrFWf3LojdyPbqioffe5vbYU+/76mxXL58yegMi/MTYQZ4T9rvuN5t8adrjs/OWLmKeLXl8sUL+saSjiqihZSMJP+2MCrRZ26xORMGYX4aZ6U3GTNLX9FmKxLClOhJkig6SzeOfPCjH3N2ek7YDXT9nu2upxu23H/wkPXxmmg8XR+p/IKmWRAG8RYLYRDgwFhpSKcs3t9JWAgpJdZHRzx8+JCf+0pCFmZK2CErk1biv1HLAQowQCmSSxyQRoSuQPbbDftN5Pz0COs8Adjut1RVw77b03V7jtanOCuex+PQM/Y96+NTtWlhWpuHcbg0hYyZhxEVCNkYIAW6/ZbVsuVkvZIkPgZiFFZC13dYC3UtzCKSERVIKioRowMkvEy7VplhSiNjHBjTyKtXL+j7DnS4pJMqTiaAW4PD0fUD3z655PT0lGEQdUdMmf1+kEFgGFCQ7/bmhqvrLYslLJZHbG5GvD3i7PQ+5w8eYIh4bxgGaBYr3nn/PT76m7+GuKOqxZqBnNm2LetVpKkNz14+Zde/5HR9RFVVXF59g0mWfbfgaNVQ13B2scSvFjR1ABz77UBTnRDCFc8fv2K1iNS+oR82wrgp8TUGnLcYq+yRmLG9rKv9zRVxgFBV9EPDvlrhq4aconjH5hInAyF1kAQU6Pe3WGtpFnteXn3LEBKL1uEY1RrBEEImxHFSy1SVo20avGvFssJqfNKitDBgiq+gMQaHWHKlLNLSEosNwqJL2YGpWayOGJuGZnmP47Pv8+zZv+Px777hB9//CbmwJ0HBwxLPM6EfpNmVHCdn96mXR3z00U+53d1QecPpg3c4fviIn/7ip3zx2Re89+4H/PFf/CkxJ376s/+bm8019x/dZ1FXhP2eL3/3DSH0VFXFannE0eqI84t7tFWDszWL0xOWywVNteDJZ5+xv7wSKnBK+MbTHh/zxvvvcPbWQ15dv+T+0RGZgRfPX5CbgWwdy7VlCCMBqBXYyUb2hclFBacWZYXRqkeaUZJFRs7dLnR0fWIfIt4a2UNBPWmNFNdlqLLV31Ea/tZIg8taq7mrHEohRSKSl/XF+zzJdO6pfaTfa5U4I/7vkhPnBH03aA1gWLYVtbW03tNWFZWTpuMQRobNLZu+o0uRTpm03RAwEWortYw3CFssJbyyhEVunOg6LcBVMRSjsGgLyBLVwqnk/2XwWAHOFIcQALVd0HV7xnHAaRPsMBai9aGsvdkSSsDSAkxNby6My5Ro6oqq9iKzVWbc1mxxzlP7Ruc7wDAIo0yaWWKVUgCtpGxyUT9aFu1C9+Y8d0XAs9lbd6qD9IILo7ackU5rUw2nOu9kzn+3/Xaufyj+j8JuI4rf9SF7tCiRxJIFqTP1pszzAiQfG7XJj9O6XS17QAFBb0kOiDOgVz5beZU8uFzv73vdBWDvEo/Kz/x9P/ud90gJnNQDMUV8dpONRPEMlnPRHvxcuTdBQUyBdpz3NHU9/Vzx8E0pFTRec4E8rYGsKsrKeQpeMqp0HJgGtpXrFLuvOH2u4qEcgnyWva8mkpDkLma6wynEyc7QGKlOCzO1MESdM9R1K3txuv7ZcmE6A5yb/lzX9bS+xjAy9MOk4pMmMbRNOwGiXdcpKKpxx1ppXihI2PhWvGiHkdAPdIoDLJYtrnJYb3BILExjElVmUv9nZvJbmUc0ajNrGCSuiNLITzG4KECtFU/cCS8wZcCX2C8ICUuea4pCqnPOsdvtyDGpLSbT/YHiz+r1jJNrjlnsuXKSoW1jKmS4hKiSZb0VO7fE3HwqpLqUdQizfiaUYFnqE2ME5M9ZBIul5hU7HAE0ay9KjQk0NzOe56ylbRqcMXR9z/nZmRB63Kx6KHZ9xb6heAKXM64w8Qt7V6wZPF7XaHk2hTEexlHqSlUdeO+kkdwHfXYoUOw0PpsDbHJe673tIWeapsHkoIQhifXOu+kaf9/rHzRIC5q4639jKnTvQocWGZRBUP1szZ3AaDSAF1DEIJtEvFoNJkbpvpCnDrpiPLMNgSkdlTlhy+QpiZk+pzUTa7SAuUY7f4cFMsZqN0gmo49j4OXLlzOQaxBZc0rsYuTJq5fshw7TLOQQtBUXF/elixqF4lDMvnMSj8nj9THPn78Qhp5BhiLoYSkyQ7lfRlGanBL5Nar/5Mny2uKx5oBth3TfgrJSCotzAiEPi9lymGuxOA2CgDs+RuV3Shdn9s2RQ3/uOEuSNFPhy8+VgmwuAmfwwhpDye6Kn1td12y3W1KICmYoU1gTl3JP5vXIFHSLj5y8f75zME+HOuLxdXgvp807STv0PWDqFJZ7IF3NOBXZ4hOcRdprEmZRQQVV60hdzf7qhjSKf5x1XruIMplxSsgP5EjyGZn8fdBnWj7PYTEta1oLH+OINvGjn/wRuzHy819/yj6C9ZYhRDY3Wy53HY6MtxVFthZDZBgiY4wY71iv19TLhnGMkyG888o3HTLWVqzOjrGrhuQtyaq3aN+TD9aLPegsl31U5OElkOac7hzq5blNHbs7QOksHRcWmiwio02G4k1TijrNcZTNLUCgycKiffPBQ/oUePLsqew3vadVJebuydzdd0FlLNOanp6TUcmE1QMwc/nqkvOTc01AlF2sQEdZhwUoLn47xb/IOcdqsSKqf860TzShqrQjaozlaL1mp1Pds64pyDx5+YKXL15QNQ1jko6+DCJJOOfJBC20tXFg5ECTNa2fOc8MmhJXBETJTIMgtHCw1jDGIIPTNLaU+HHY5CjPuHjkig+tvfPMnXNUXibElmFiYRxx1k/P06jMO4SeexcXXN/cTJ8LDhUAwlgvX5sbQfPePlxrU7yb4qt8nmEYKMyI16WDh3FofXzMdrMhpTlRLgGrDHw5PAsLk5kytNLMoGwZRlBsbqZC0YJta5YXp7za7sUzNCY6B98MO7wVY/x7yXKvrdQ+Qppk2WTaxjNurrhdnvFf/ov/ibA44fOf/RV16vjmk49458/+kjfefY8nn/+Gde0lLkeRJ5mh5/LJF4zGsG5rbnctNDVtmxmieCp2fc9lvyd6x1sPHrDv9ry6fMV+GDCvXnG0WlK5ipevXjGmxPrsTPbQGOl2t7y4usadHnFy75w2W4arG569eIlZ17h7x3Qp0+86xhBZXRyTUxDJmbIj9KkDatGDE/mV7rVu37Efey3soU+Buml59ObbPHj0JhbL5vKKzXbHYr3m0YN7GOvY7HqqZY3zNTaJt6TU5KWBXKRX0oxB5VgpBirnud30rI+OuXfvvpyzqCxSJ6LvtpvJ4ibnIOd2FglXAe6ndZyNDv+Vfem8Zeh6rm9uaOqG2+trvv3mawyZrx5/ibWGP/lH/4R2UbHbben6DcfrU2Hgao4lCT5TUagtBSnS0uwnGJXRKUxg2Ow6qsURF+cXJCtD0/rtltXRmqap2W5vCXFg2YpNQExRAXQZzuWcZ7fbTo30HEfy2JGGnn7Y8/z6JWbpMMmSRrWQwhBKfmENIcGuB0xDYoexhmGMbDYdr17e0A+B1WrB+viYze01Xz1+TO3hgw9+TPY1b9y/z2Kxom0XBBOpvGN9fMzp+SmvXj0WyXu3x4x7YU7WDbf7ji8eP+ZovWbTDaTYMfQji8WSbkikODLkyM1+R1MZunFH5d9g1TbkBM+fv+KtRnwOz86OMHmgWLf4tgXniBkaW0GOhG6Psw5fOTrExqQ2kRAGCWQ2kvKWEHvxsqwarBUv2BgDw2hIASoHgxmwJtG2MISelEf6LtKofJYyEM0ZYhrJ2VHXLdbWIpKJURjVxqrHcaIfBowyEUUAoewrk8CUIXFm8hIsoEyIWZp41nN09hYhr/n6myuGPlJVFTnIz9jKUZhqhTHZDR27/Z7Vesn5g7f4+tlTfvvVZ6Tc8/bF93j/gz/i8beP+fzLz/nxj3/MT378pzx/8YLfPf6Ci9MzTs7X3Fxfc/n8FUvf8OD8IQ8fPeTevQu8r6f8BSw5OfWLDpw9eIfV2T32V68Yt3tSDDTHK47un7M6OyYaOLnfcnJ2zPW3z4n+OSkGwjhMA21DCrjopTB3ZqpfclDArACJWXIwYw1Zh4xiMoFMnzNYR1N7jMqwU4oydd1mjE6rlgarMN5CEGmt9zVV1ShAlwlpJOYoz845HJaocch7YeOFUaXpiloEjbNJ/SlTFi/FlCSXd86xahtsjHi8jIBTwCKOI7fbDdtuJ978MQIVYezIwZKyJXuHqytpzlcC7kp8FcWMUfAk3mFUFiDZTMBUVPDLlXNbsskptjrn2O86MIjEPGe1YzkEMcssFmG3zcOnD/IJTVBCCPSjTFr3vqVtFux2e/Zdx5dfPaapaox19P3Aft/dIY6UXLIAqrJTrJ5nAe90kM5yyRhGttvtlIeU+u7gI02vMrUdmHKiubF/N48pbMnyGbzzZGT4kTHFyk4k6yGn6f1A/g6tyyeQq4BBev9jjMq417rGMg3nssoIzHqmZ2ZwrHy211WehzXq6833Q6D28GcOc/jy/4eN9PI+xWtzHIQp7pyjblsqX8l6Qp53TqXGnX+uqKwy5gDcVHB+ArHuMlQPP/MhyHnoMSp5RQEMzQSQH35u57ShZ4VAM6nFlGkblC2N4eCzqeep88pkFDxlsgPL8yDBqhJJe9OIWujwvoutCFOtdlgDlusJ2sC2em1Rr0fy/wpfeakTyu9OwpQscyGKx25TN+QQ6fd7hohYT6nS2FqxZrTGUXlPU9UTuSwq0aeqPE1zpOCgMJ37vprk+QUITSnKYDVtTBQyonN2qmGMNUokktxzt9vJUNFKzuHKVSyWLYnM1e2NsE9HUcvVdU3UmIExhFhsPBNhHGjadmJGWzM/96SqixgiRjlfla9pGkOvoHSm9PyFFBhCAMtURxbAttybYmtZzugEeKMD6KLs71rXTg5ineCdx5lRMDTFgCSWJrXHSNR1g7WOFGRwaUBPk4zmB1B5j3cFEyjzP6CtG+qqgixEnxDCVH8656iqirqO9L14+QLTcOvydWmCScOx7JVabTBSTvjaTh7m+77DV38/FPsPGqQ1gEep9AahfSMLyhWFvTHaSZtBpunnzczIBCYmJkjAHjtZqLYSQMsad2fTy40T6Wrp6GK+2yUrD6f8f3lNQOVroGVZkDAbOOeUps8fono4ZcfXT59xs9tydnQhD9ovOD95g2W9oou39MOAqyssjn7scRm2+93EOp48haJ4sVjEQ7MU4sKiks84D/qZpbt3Qe+ZhTWBWSkp+Av6oSdQvfgxkfPEbivWCOWwdqVLdBBcS9ejeD9iDU2zoKpq9vs9Ic5eLOLtWQ5rAR2k4zR/fo3/6hNcgMoCiMxJB5lJ8jIB8cwbUALV4fulggFPSYE8d9SsXZeMbnbnNCk4AEcLkDwBobZ0zdR7KL0mJbLakIiJQMI5A5XF6FTIpXfcPL/EhIDLYQJH9dFMhxB2HgpXwG3DYVf8IKmwRuiiWQwjiImcHO987z0++OGHfPLrj3j24hJfW4w3WCcNlYCwjIYQSEkkWU79G5PJeAv7YY+14hltrGV1tAKSBLJljV+22KZW/1S5abVKMbKyCI2xMgzvoNNfEl6Y9505aCCUNVfWM6Aeo7qns3T2MIVFpixT7RbnrAxUY5imSulzjCGJ15XADcKour2ZBvmVe5v1eTjvaduW29tbTbb9d5LBnGXoYRpFYiv+ZYZtt+Fme4nxlXj0BumAZ/UBJsPRcsV+tyMD2+128rIahkGerZLmvHccekJNibUGROecFm9xupcBCFasB4JBijak0QTizxT6fmKSyF6ZD2qMArhJGDcysTtPSYIxMtG5XbTkFGR4mXUcLZdYY7gsfrQa6w+fpzGGruv0UK2nw/YwdllNFpu24XJzLdYnZX+nxMXpOcvVgq++esxut6M8uBIPJPEwB7EdBZteGyQxf3n6WWst52dn3N7eToXK7Nd2WDjkqdlX/LHnuJUIoayn8jsF/Djcy0m72t9hdWSZYh9yKaKYQaycic7ijhras2PGV7cyUCZnbsPAtyMkD4YaHyJ5t6M2MmAmIQqO1XLN7W7Dt8+f8U//u3/J10+/IT37nLC/4ctP/44f/PhP2F7esnv1lLZCbTISjgjhln7Xcf/eezx6+EN+8dvfcLm9xoSROI4M40BuHI1f0Hc9r56/YjMODCZxZgxpCDx//pw+JRaLFh8jK19xc3PFZhh6JulKAAAgAElEQVSozk85Pj9jkQ3d1TVPXrwgrRf48yN2Y+D28pb9zR7bepqTJVRT3079wSSrM9bgsvjQ1s7R7fZc0okFk8rrbYK6aRmutiT1nhi7HfvNjqZuWbWNAAMhCHhhHeCIaSRG8QvFOGnOKnBRWAYSu+UfUuTm+pq28hytT3DOM449YZQiIqXEdrelKCrKINCcIzmXJpVhVF9U8Z2WoaEYw2K1ol227PqRXReo65YHDx+w29zyvbff4uZ6w+XlFWd2wRgElMZYhlGYkzHLYDFMnM4f+d2JcezJKbNs24mNVVUyPMM6y8n5BTkEovGEKMM2nPcKKksuUbxKY47qoZblOjR/K5N327oi20jsBmwY6Lcbnl2/wJ2t8Maze3VFVgWaNE8TOY3gE/0Y6UNQoFsbp8nR98KYO7845d4b93mRBjCOoU9Yaup2yc3mltX6iN1+x+p4TYgi23PO0tYN737vHb76ZoerLcvVkso3mOQI/Z7r7RZfi1+qc5Zu7FgeLaYBFjFHsm3Y95nb25HTtSflzOn5G3jfCkjpK3IQ46aYDM4vcM2KmA2WzH5zJQ2yNOhALjkXXLPGuEiKQSwlDAISZGlWWVPJma1eqMFILFtVFfv9VpuAmco5xpzZqtQwE9lstlRNS1O3GBzjYPj6yZdcXJyxWi210Z0PmtrlHBWJa/FOpIBieVa2WGum601ApGJx/JDl8QN2XeTJsxdEY8F5coiTjHUatKNg2G23o8+JR+f3aI/WfPSzn7Ib9lycX/CjP/gjnj9/zmeffsaf/vFf8P67P+Drx4+53l5zcXpCHAZSMLz94Htc/OQeZ0dr2kqeozSGNV9Ra7UwjrixNB8dplmxeGvNGouzEEwmOsN+hKaqWJ+sqI6XLELNo9Ex7HrGAUyyrBZLYgoqXZ/BvZgzBGk6e+eVtZfo+k79JAErcSgbQ7KWIUXGPmEFjSUbsSTox05UTIXhr+dNVMIBBGKQNTMMHWMYcAomRCPy/5wLewqlwSTxzFZWX9KGksnSBCQlvIOh2wEydHTdHtHg8CnhMeKRbg19vyMMPdZkaQQk/TwWnG+ojcM0NZX1DKOwRotlS0bP6lLj6L+tNsV12WkuB9kYbeTL94nnpAyW9r7WuFZYg8X6IWn+pTYvTsRHBUSpvJ8IFiV3FE9WBXPVEqEfOuJNxLtq2iMhReI4iKVLnm3qDFpnRkMZVmwAVzkdpiv5436/Z9/t4IDgUXKnshcPCQaHdQPM9UY+UFAd1lwFjCu1H+kQ8CzvIbG77BO0LiqECaMg5KigWmnalwGxUtuZibghgwlR/3L1R9Yz+ZC8cfjf1/98+Hev1/y/73sOv1fu2SEeUL5PPEPxIpOvvDCji4dmzhAGqVGyMeo5P4Oei8WSzDz82iCgKeFQUTjnvgWMLWQAQD1b74LQ5dk63ATwFvZmUfpZZadWVUXbNEq+KMQF9SzOwsAWgor41M8UNr33+rzmXDjPRCVV3oqNgBB5ysBu+acMQZ0Ve4UgVteVAIdOvXdTnlTURVnslbUaQ8Rbp3WUYjJjIBgZbFzXNd7ILJuU47z59Rq896xWK2XAp0kZN/uSWtqmIgQZfFXXDSiuJYzOAjCr/ZgC3eX9q6qa6hZnHfv9jrhYCMlJY5V3nqppaJqGo/WacRgn9v84jgx9P1mgYdUjN+tgblusO1F7UbG5TFnk+mLXmIgpk2I/YSnGGIZxZNRnvCz2HBjKMPeu6xiGnkZjXQhmstfAGJ2BNONHKWeS4KB0/TB/zcjKsaruCwoCxyBwbFE86m+nsjJ7o5DjxGrCi/WTYjBWY76oQ6RZVCVHqus7+Ag546yQUJpKGwEhENQv2lmLaxvJW5qaEEfGYVRLLFWqeUulZCDxzf9O2Jhe/6BBWpBkQopvGRYgXUpDNm4G3qxREKB078qhYSa/C3mJXCBkSf7f/v4DLi+v2PR7jBXp1dQisMhhkOXPEvReA9TM3Ekq4GIBbEVOICBS6YqCJICHPj4STA7ZabMs0frE5vaSq1fPOX/jbSyOZbPiwcVD1ssTNldXYupfVVRe/EJSznTdgPVeafJpajOFrJtS2SqUTjBo4X/3kCoB6lDm8t1D2k4xqkgZUBZsYbdNB5niXocdxMMD7i5odpdBOB1UJVXSr8n91udS/t7M0oBylSUxKdeYSFjj7gBzFCAO6dJmLVhnQMZ8B6Av/51AJ4qP33x7rbW0vp06TeXzF5bAwTl1J5ExWnpPHdDp54oSMpKTsr+dAeuojpasjSV3HXkcGfY9liIL0vtQsspJKq2AsIJBhwCmrGO5dzGXTl/CGMeHf/RnZFvzyWePiSZTLSqyKtowCe8kic+KbVZVRVKZRwGNY4iMRCk8vcVVTgbsWbFzYFkzGmXKFoBK95YxklSSDMXWYgLsTJzWgzyvubA7XHOH4Hr5s7WWxlpSTJL4lQYMiK+ernVQfNaKFYfRfWS8HAjOCYM55KQYd56S78NuYlvX0zosMpHymhLW4huLvo+V4QcpBmG7Wcdu32GyJcdRPNey+DqHMbBoF2z33cSgLdfbdR2JTEqRyiu7YGoiye/v+544jsqCfw3oS9K4SLLQRRZlM3VdUyRV5RAsydYwzOwUYPp5o95uYWL0zUm8tZZuP0wqBY8hir54biodxJPil1UAaZAGSIpxil0xRiKGMSWePHsifuVGvNpKY7Drd2x3Nxhr2HfzsDiDFFU5MyWiczwzM+ugxH5dgta4iXUD8PLVK3ISyU1ZA0VCbfXnMnlijZc1cH19rZ9D4p3EWWHgzgzZeSKxAK934/shw+POMzVFQiwxZySxvDhlyJbu8goTDS4btmPkmsjxUoZweKvyNevw3k2f26cdv/zrf8N//YMf8M/++3/Jv/5f/meW6Yb+xXNefPOMDz/8c/7j//W/M4QrSb5NZAw7GtfSGM/Ny5ec12esfMPlGPFkvIHjk2PuNwuuthteXV9ztdmQnOP+w/s0vuLp8xdsx4HT83NcytTWsr+9pcsBf3rM+uSMRfKEmxuevXhBPllgz47Z9yPXTy/puw5qx+p0TeUc+zToHc+SJlinDbOAN5YH5/fod3u2+yto60lmZqM2k3DsbjtSSMQwsrkV0LtZLBUoyWz2N1SLlcTfrIA/UmxXvsZWEq9lOruZ/GNFpiqMk4cPH3J7dSmDbLQoCSaIT2LO7HZlmKAOEDUCjhuKekCZdClByWWMpLHOSdCLKVHXC2FSrI44u/eAnDLjIHsK4wkp0raVAHfF79AYyvAb5eTIQI+clek/J+2HBf049AIOhiBNWSOxvqqryYdsHEd2+w2Nr2TQT9XIuVJylihFe+MrYpTvxUTGoWN3c81uu8W2FdFVsPHiUZny1OQsssCQiu1F8SuUBrg0pgJOn8PFg/v82NZ88eljPv/iS+69eY+T+xfYqkwXr0hJkv1uvyOlge+/+R7nJ2u2/TXDsKPrOmKIONvidfJ501Q49VIU6xZRATkn7Nd2AYvFknEE31Ssjlusqwk54kzGOGFrVakm9gJaGOsJMTDsIyHXEqOz+FKOWSwQhOllSVnit/dOAOqcGIa9gE1GChBnjNgjxIT1tbCxsoArwzDSjz3WO2LIPHt6xfXNhocP3qSqGgH5TxcsFg1j6PFVjc3CrJaGV1aW9dz4TxqUJ5Ak6/2wAsqThDHpzJLz8/fxzSnPnz/js999xiNxx9Cc4oDRWKygSOzDSPKW03sXXN5c8+TF13hr+eH3f4Q3FX/7yc947wfv87133ufrx0/YbTYcHy2498Y9lvWKk/UZi+WRAIwK/MUkHrookGCdwYSAJ5K9AWvxwWGC+E4XXqa3lsoaTJOpjSf1ge1tR0yWpj2mrQ1DF4ljJIZRGDzWEoKwUEuuXwgupSFYztlirRVTUuVSoI89A4FYoSCurAUQD+gwBLyzDGPA+0omn3tLSoEwRGWKZsbQY0xm7PbMgzCZcrSsthYmF9sJiUxJFXAF1DEmY1PG5AB5xOGpaWhcQ50T3hgqJ5PkY4rUbUXfdwQirvbgYDTin22J9LsbbEoYHNYWRY9F7OwSMZoJOJBmgLI6SWqDIQCbUWuO4u8+qVoM9GMHxuKNABSRKDNOzGwvc3ge55yVqZWJqn4SlqLEIxksVWq4si+UGaZ+nyGOE+A5Nb0VMDN3GK0CEhrXkAvQpaobsjzj+Xvn/HTyykyJGEstfqByVDZeSfYmqy0zS8AP84+SHxX5e0YAVhnIaZTtKOdIAaOtyq0LOHfYIJ/r3JLv5SkntU5BOSuHrDGl9p7v/2GOdGhJ9vpzev3P/2+vw/d9vd42GRnwWAm7tO86USvUtVgYKEglj1c/l3qe2uKjjuTpOWWGfhBl22vkqsNa51AVmPSzJK2zCuO1yL0PcQ5rZZATuk+tFRDTWScWF1qXTrYByNroh1Fwg5RllgZMOTrZzPm61qniAy0gIkkAxWjCnXrcaI0YY/GDy3SdzAHyzt9pTpR/JkKatdhxFKJP8eXWr8tnEQVw34vSzhZswRhsngklh2u8qBVhvh6nFhbDMFK5hPeORbMQ1q2qbWMuTRj1lrWWpl2QQa3Q5PfnmBjjQLVoWdQNVA1DGGRvaAwY+o4UojB4q4rsPUHtECV1FfsY7yWWGCNDn5OSZArL1ftCVsxE6bCT8qjs4RqvwDUZbN9ho1hjVN7jKqeDudzE9g4hErrdhGdMakHrwFqGYSTFMN9/3cuT7aVab5TnLjZWctaTMyGMkHSwGLMytMQPeUYZId7Le8hgbInlJoktkNXrdwjBrJzTpEjtPdhi+enIleRXpcFAVusOZ/Fe2PCTFQsOmz3OeCF7VH//0EH4Bw7SSjDKGOOQaWgCXEVlthYz3xLQC6PSmpmFJEWnfL1MZjYGjuqGP//Rj/nFxx+zfSoLRg4iRf1L8a3FQgHSckraMS4erkWufxfMBDDOTsVy8RctEytL1V6KYjRAFz+nDIwxcrnf8vibL3n/gz/EuyVt03CxvsebF2/y9cvPISd2+60u0KRFUFbP/4C3xUpACvnCADKZqSOJAlJmOmyKNHnush1KJaB0kgvjr3jkzN6I1jmiFjMZkQNIF0IW9ahATDIGM7HnZrnB4YEUUmLcidTOWJ1mGaJ4AKskU8BZM60TZw+BJLkWYwwhHxy00mo5AGCNdNDzAVtWP1NhQZZHd8hwLYF+BpUFmMSIzyYwHVQzQK30+skj1kydn2l1WP157S4XzyZZe1HAYAScyir/jmSqdYtb1eRhJF5eM+46KsPUdZdZRXa6mFwQJObrkiTeKYOvGJgrx8HCu2+9zbtvvcXPf/Fzfvf5F7hafF1iDhNInozVThq4EOn7QRgdgEEkwKVBkWLEJs84BFJb41YLTO3JRu0EyFhn7/jdxBjlOlRip5tf9gAlISn3ega/D+NLeYbSYZWO5fpozftvvseTJ9/yrHsCvpjZWlyZ9MiclOUcsbmsAXn+tfpBA/RmVNlxyas0TbByXbvdbm5OaNGS5AHM7IcYdeigrJEUEn0SSaNVSXPOUjalkGjqmvXpmpubG7q+53h9PCVdxaenWEA8evgA5xzffPMtRg/GfMC8LNecdU9ZjAxAU/A+IQV7NsKoHeOIi1b2p5fBcaW4zgqqFv9j8QsXk/mcpSMq1+7mxDFndrut3DW959Zazk5P2XUdCTPJEJMe2oWZWgZlhBAwOeOqCuus2sNkVk1DW1Xc3myEa2WQYtA4ZRsL68LZipSCDnUr8cSpR+gUGWQP5TIwrMTLAhx7Hj14xOXVDdebS8gDVoGQQ0DK6XvENCefTEPK5oImpcRqtcJYw83NjX6vJpDcbbQJ0C/xxmhskfcqRQsH3yuAHNlobIVYGfzZArPbwC5MYN5N7LgeK+75Y26HRAx7TrzFUU2+aK2D2xdf87P/7X/lD/6zf8b3f/ghX//i31GbkRe/+w2n5w/443/8z/mbf/+vcT5DSoR+nDy+cr/l6ePfEsfMO/fOeHa7Ff/VkBnGW8b9nt1uy/HZKctlS+0tz54/Z0jSdFhWFeerFVeXl2xzwCwXLBctywTOJL7ZXGLOFvijJZc3G66fXQu4sao5feOUetGwubxh13W0pyua45U823HEGctJU/PGaoWxmSc311SrRpq+CdmXkiSw3W/pc2Dod4z7G7rNDd0wkq2nXqzxdYupaurFSuvKSLYGkytsFpAmZXE5Kq26bCIm9aQwSFLYLGlT5NZcU1cNzohsznmHsRlXGbaba8LQY0yjjcJp4Up8cQZna8qEZm2TT9Y+6FnpvNFmkGHQoU1lMnqRDjqnrBpXGoxaOFsonvVe3lKBbDmTqoWZ4hNlwMjY03dbvHPEkFgvjySxIOPcQuSddatFRckhHCmMUwPDIMn3GAacqxiGHfvtLU+ffMt2u8ccHeEEHyPmURgVucSdRErCKCIETDI44wljJgQ4Ozmh666ojWd7swETqNuKH334B1xdXdGsFjx49Lb4WxLYbV9haajqFbvNDXUdMCHz1efP+Nnf/pxvnzxn13USt73FGKcNNgH0nBEfPIwM1rJOmlBvPTrmhx88ZLWs+Iu/+Eecv3FBFyR+khB5tzWkHOj7PamL9CHR7QfqesXx+UOW/gRMK+BTknNx3G0Z9l8Rh6dYxBPduECxZpnOVuOofKurJoPxWCdxjRileWAtMcHjb6+pFo94c50Zhy3b21vuPbjPw4cX2Dwy7jpRz9lW5IFFihul6SBe0HK2FkIHGbGsMZqLZRgyjNGzWNxndfF9bH3CT//63/Dpb37OWz94k4glGYOLGZP0jEXUKzlHuu6WplmzOLvg15//msvdDe+++S5n52d8/Nvf8L133uODH3zAq6dPqa1hff8RF2+ccXZ6ysn6jBgTfTeQ0oAMlNeBZjoUy9hMTIMO9pV4n3LQXN1BUfPpDAxnCugxynkUIiSRQsdBx+IYGVock8U6AWza+giLznQojVJJkyQnU7VMNDDEXopTkwg5YhhIMZNKQz9bDF6GiKYIxlE7EExC2Zkm6dpQwDKL11+MYh3jsuRrISddz5J7lFw35aiFsJzpqUyCTwL+hFQ8/QU4IEdSSKQ6Y+sKrKWtW5rjBVfffim5qPOkNJLCSIoDW419DrXxStyxzzKK80mtMTNAQ2lk6ZpLOYGTWbYTExuJcwJQJ378oz8mDQOLxvLpl1+KZDobxn4vKrnDesQYHYCksvMDsAvE5qN4yZczniRD+0ouUfLfIpcq4FFpsHsdyFzyinEciGGc8hZhj8UpBo7qH1pVnpRFGrzbbmXIr3PaOC+LVdY2xmKrSq/lcABnAZgP1E05TKlUkaUXpYQMUFO5csl1KNYIVhtyFeRD4g2QtC42YLShDsISt64Bthqp5nz7kMhRXq83tH8fyHr4vb8PeD/8/zsYABDHSBgHYAHI8KthGHCVfN5F62jaFmcrxQNnebyxWdZdkvcUdYGd7m2p3wtR4nWAdrIc0PtZSCTWiMVaIV8551ks2qnxX/tKgXerqtgk1nVoc6CQYLQ+z6BnStT6NhHGkYlUZc3UVCp2LRPRwQgY7Jxj3/UMwzABiOV+GvKU908ko/I8DmoHzIFqV1WJMUnOXYYbkgtBBJlPcee5z7YdxQdVnqW8536/n+77IZhcnn1HN0n1i51PTqL6eZ1sWH7GOzexS53RuqjbTeus2JblbBRoTfQxMai1QWlaSCPJY3OmquR6XBb2vFXl0v9D3Zv9ypJl532/PUVE5pnuXHN1F5stzpJoyaJs0TAgWYZsA7YBC7Bh2XrVP+NXPfnFw5Nsw7ZIA9RE2IJlUqRINgdR7e6urqmruu5w5jw5RMQe/LDWjohzqwj4kUrg1r11hsyIHXuv4Vvf+pZXeMBYo/IABZq507Lv5fuhbSeMyVrLsT+aMCF5/oLdmekZWNpG9aIVRJUc04rUjXPSXbTbMY4jIQRZV2twVuVZvJDr9ocDXdtJLKoFHeMg2EDKae7wKNqNYCSaFf1kJp1xyYV7eXZF9JVrJ7QxRtddQWcnnS/7fpgkHKoki/cyVM/OgTIx5QkPMVYkppwBUyS2SCVPQ83+pNefapC2LqAkw1ppNSry7jzZGFIULvRsAAUsSRXAs5LMeOcha2W2GO7utvzGb/1z9sOAtV6DDp1yaqQKpbGLBFG6UcprBvr1Ktrrfy8rBaY6gcUhtHro5kxpfv9sLPvhwPPnz0ljBCtt1F13zIOzN8jR4XJhOAzYpsMi2mJgSOOIdUgVphTR8ZrtTF1guU65AarDqA5g6YSW97y8/pk5Nle0UBDRmRnQyrlMA61KAYdXBk2ttOZ7RnNJLxdQUoynrwGiAyv+H6NJQlpUUCvjNikAJPFCwWoAT6nTECUUmQZD1X/DpJlWBwQ4FyhjmlpoJgNqZvBkeu5GnNGkTVUq05dpneu0y/qaf24uAiy/DgvmZy0aUIHdea9Za6WNx1mO3EOGzY60O5AOvRofh6L0UxFh+VmAtpFUsGcGdoZxpOD51gfvk+MdH//ge1hXK7F5WntxztVBI6051uGbwPZOHRhSpbTGkkzBH6/w647SNZhWRetLncYqoKV4eYMLkoSViprrf8tyVe7t6a+yBr/u7Bpj2O13fPzJx+wPe4x3wrIxCPNgUfCaqt8LO4EC8FlByQQaeM3PtbbCLc/iJHFQmIpLk61Y7jG9v5LypPUaY9KEVBnFTpz10ydPubu7Awx32y0+BB49esTNzQ3jOE4FmJwyXdOyXq2k3S8nSspY/fwqxF7bRWqV0OpNBGc5OpYW3uD9BFLmXBn3AuK++fApm7s7DnFgyFGqlQr+d13L0dERd3cbQtOw3R+mQFCelwajRt7z5vZGwe2iIH0FQi1HR0eTk18+V6fBhPBfhOHSNg1ktZPjIOwXI0WurAwZ+X1pP1uC+t57VqtW1mah8VXt3b1zjSRx11fXbLdbbanJeOPxql9Vr18RU2pLzziO4tydn+xsfd+YErGP1IEiy89csiZet+VyjVX/c+HPch3GWfe0/KywIhuOHpyx6S+wRYKXbAqX44GVETpabhxhOGCJrNuggvqOk5Xn/Pt/TN8n/vxf/mVK2vP8u79F6e/49MPv8md/6Zf55rd/jh//4DucrRoYkenqMq6X0kdsNPjuhGdPHpIvb9nfbunzKH7AW9584wlmHHl5eU571FD2A63ztNawu7vDWE972uDbQJcM/fUVL7d3hAdH7Mlcvbpiv9lTUuHkwQlnbzwidIHLF+dsrze4xtMYR2tF373znmcPHrN2huGw4+X5BdZ60eJKAryE6ldyFrZqLsRxoB96bBM4WZ1gncc1ntC1mNBKC5emsfIwrcociAWowFPRgkfq9wzjSNYizqEfNJk6UoaAvpeRIub19RW77YbVkaeYOZGc4hUneolii2arWgtszlmM18/OkhDvtneSdBcwvqFpWkLTzEMhFrGH+HbJAuoelWvQvWhqEVnO3STHEuS6UkqM8UDGYRTDTUmG4axWK6yxXF2/YhwST5+8IQXTnAnB4m0rcYS1jFkA88Nhx6c/+oyEAA0uNETf0Oe9FKaqDdZznVMRWYqUpIiQE/v9Du8buhBYd0FarNOOTOb49DGPnz1ijIn97sD1zQ2rlVxH8BBouLx6yZtvPOZffe+H/Mqv/hOubndkLC5I14m0XSfVjlffpQd0WtdSKKlweX1D0xiePT6hPxjOHrzD5affpe0MziUgYo36rSgar/t9ZIyGkg27neHowQPa7jGuPaE9PiMEy/b6ii8//gOung+k/QXkPaELSDhlVLLGYkOL9WtSPmApeG8wRVINSa52GAoXlxvOz3e89413OF57Vu0jHjw84/j0AeOwZ7+9pkkrQBKnmCJ+ik1lAFLXVf1L1QSNAhCEIH4wDQOFiM2GXAJnTz5gdfIGu/3IP/xHv8Zue4O37+sOVBJHqYX3eXDO4XDg9OwB/Tjyyec/woWGn/jGt7h4dUHrG779zW+zu77j8ckZx+szjo5POD45YkyJmBVwMkJsUIMFCEPRlEJSX5ljJI9VW9LP3WPTcCTEHpYCCfb7gYwAHUVJJTlpy6jNOG8Yhh3X5y+IMfP2s2/S+kYkmZb+oMZ6WdjqeKseUsDBqOy5QpHBKiXhcFP7MjDNo4jDMIGNANbJXIaUIqnIQNNKWKjnV/yygDaVFADSjhyahnXXsRluRVfRWm13NoxDD1kGsvTDntyuZR6DsTRty/HxCcEHDnmgHw70Y0/MkVgGiksiS6UobEkZvAwMrTreNeKqoGvtzplifI3NJN4pOoA5MYEUZh4iFoIXNu9+z+6uZ4w9QxyxSF4i3TMCiBT95Cm2J09MvIKcs1wSJlfiR6ZE1Wmd7OkyZxBGee34Cl61e3KeCmpTnIIACU8eP2HVrvj8y89JJQnYrPHTMI40IfDO229zcXHB85cvKYCjxkBa2suFaCQ3E6KSXIsUwqvPmf3Pkmkr9lYAEKdSOdSc0BpSqWxAKVQ45wlOtMhNqRr9QpgRVrCSTQwK7HhC0zIY7UKquW+tNf0JwMnrYGz92a/Ll/+k31smEnNxC5wXDeEMjClKV1muA6+M7jVHoa6Lp+bUwj4USQHrEo1v9Gcl/q05hgBfTOu7BHCNEZkQYww07UREk/fNlDJM8eIShMxZWd8GDJlcRt2rdtK4rgOwknb8VkCrVGBUsYN+HKeYOxeZXeFV1sg00h2DMSJ1xHIQrvjvdbdSm6myCaVM8l2u5lF63fIe2lVgixqjOWYpCoRbJ+ues+jV5oy2+yfa1jNGzZ+Z2ZRLgLiUMjE+nYJ+4yjybTELYcQ7jw/z79d8vg49rmzlo/UaF4SBv93t1AbVVnvpRrLW4rwXm5vmM+6syALWroll3Le8bq8do6YUkUYoBevDFMRNMp2LM1tf9dnV3L5ot2UhzR27WWyegKCyL+MQyU4KKk3Tqizn/J6uCdMezTnRtpI3yVwRyTnr3shFQGn0ZGsAACAASURBVNkqw9C1rcQmes8xSkendD+oRAoGiqUJwijulbm87MbUXliisqXFJ8rLOUfbtnK+jBCHYs6TtrFRKQRTMiWOFANjGkV3XPPKr3v96QZpgZgzTfDqtMsksp7GUQ5/nuUMZiMpht8ow0kwraqVpC0VprAZBpIRp5STDHFwRpfEGpmW552w03KhDrp6HdRJSYcV6PeWrNOJyl1ZqParyXP9N+oAUWC5KBPn6vICUsaWRDIR33jOzh7hTMCVUYL4nHGhkUp6For7k6dPODs94fmL56R9om2a6RA6U9mB9x3RzKZSdvIC3Hrd6VQALCWpLN3TZV2sF6XQhEBMUYGWuWU45wrE6XQ+NURJg8IqH2E0wZxafgoKNMobOecwWcJKFqDc8u6MMQraV8BLK7rGqAOZl6QGX0arvlnY7jrBNlWsUFiMr1W8pNpdAcSaUJWFM5gTbvm+4euc/LQvFn8v93ndX6+D5zXwSQVspyLYqzX2dkM6HER3xcytPctEuf7+VHU00lRoCsQcyRjef/cb/Jlvf8B3//gP+fLLH0miZgXIkUqnl8FO0x4DYx0PnxxzenLMixcXXL660n0CTXC40zXtg2OKdxS/AI0tGCftWxJgWWKR4RA2CNhutfjxug7osr1rBvvzV9Z5uv8qYZAzprOsmyNud7dTQmFtZRbOgdnXBWWyR19j7SKs0Vbbc2NMyi6XPda2rbQOlTI5E+MdwziKRp0xCwdVeP0o1muxRhiqMSc+/OGH9Fptrj++3W6nn5XAzXF9fS3arU3gMA6cnpxw2O+J49xeYoxRzSapYlpnVQdIEtC7zUbBUos187OoQHNoAk/OzjApc7g9CNCbVBLGGPYqxVCXU6ry7t79iZi+sDlSFEkC49wEatdnfnd3NwnZL0HV2nJdP8caw93mjjRm3nrnPcbz84mtEotMnbW67pV5XNdtBmaV4bFY09rmVMpcPKnFg/1hKwmdoFFa4JDxwpM/KGKbWpWMeO/d99hsNlxeX98rphhjGPpe1lfB8VJq8alew+xrpsNIBZElQJ6kNGanOX3GtKcpRGNoTo9p+oHDzRarrWVXjJRyx8n6hKPg2MURT2K330IpdN0xXbcixRuuf/w9+KV/k3/rP/nP+XuffEjoL8mbl/zx7/4GP/MX/xKXFy+5Pv+cgOiGZmMwGXzOtAnuLi5oHzqenpxyMRYOu8x6taI5PWPoB24vL1kfn/Dk2RNe/Pg5XWjYbXe6Bzu6tsOVwv72ltu7DeHxKftSePnymr4fCNayOl3z5I0n9Cly/vwV2+sN3gfWD085Pj7iaNXx4HjNcdPQZsvt7o6XtzfcpUyyAZMsxiZOu4a3Hz7kxcUlN30viWIqmDGSY+Ls4ROCP+J2t8e3LcYHvPWaIFTwqZbhzORHjDHK+h+gyLR1msCQYYwJ6wMZqywG2V8yjAni2HN7e8fhsGN9fIo0c+lwPt0fOSWZ1q6H0boKUEjRw3thO8Qx0R0dA9B2HXebDd55Oi9Dodq2XVgojckWPmppN4UhOu/JCuDaSadHfEjJcpZXR45xSBPDMKcyBfUpjezu7hjHhHnyjDSO9P2GFBPr7ghLYRx6hsOeNOzZ3F7y2Rdf4NpOipvW4duOg7lV3XkpTBkrSf5+v5UYgcRuvwNTePzkERcvN1AKq66haRyhNPTjgRQPHJ2ccb3ZMYwj7epYB7kVTchlkObV1Z5/9E9+i1ebAdeu5fM06ZUc1k6dUuIANN6p/1syySYutyMvzrecHR3zgw8/5Rvf/nM8e/YB19c/IrLF0GMI5AR3Q89+b0nZAZ7DbmS//5zz5xc4d8RutLSnz/jGt36GdXfCw6d/htjf8fJuSxzuOGpaTKr6b8LTtzQQjnC5JY9bUHacsUUHwATR903QhjUxGT7+9AuO2xHvDfthoAnC2jHWY5Dhjo33lKSsqyIslVmvVIB/kdyIWCN6pClJ51a2lmJPOH38AW044dd/7Vf5znd+E4sk7nNEaqeirFbqSHHkMAw8fvqUV5eXbPd7fvL9b7EKK66uL/lzP/MLtLbh6OwJp6dnWNeIxIfxdEcrxgLJFZxvsVaZYUXYsq6WYkqGGIlpN4FcRm14zhlbWyMR0C9H7bCiMJoo7NGURU5K41xLIQQDxrFaNez3g56lQmVs1IJ/MWXKp2qhPaXIWCKH2LNPI6NJEBwlSSHTejsV73NKDDFNcco8MCqRhzL7aBYamNrZKPGYE7CGzKjxhtQgCnEUaZikmovCXlXQqkiRInhHcA5bZDhccFIgss6RS+LHX37B1e0V+3igWPGJ3ru5bbxo62qR51OLy3NSH+/lNzFGcFX/NJN1ZkP1q8siaREHTM6JTz75EJMTMfYUBzjJL53GsMXUAdZzPEHJVPbsRAKpVa/KptBPMobpZ1nkQIbKwNZ4tyghQLU5a/xcKATnsVg2N7eEB8ISHHvt9kLJSkXivi+++ELXRUOHfB+4BASgA9565x1urm/Y7YSkkagt+K/nlfPvVmmuGkcWveaY4tSaX9dDQOiZRTsxZoMnjgLk1jyvGFkla6pvRdfyPjj7up9a5mlf972vu4+v5s33X/P3BVgbdT6H9Z7Oexlu5UVPPkWZM5LGRGgl7yqpYiAG5yRPjjERTRTvbs1Xnsny+irjtO67iXyihZthiFPRZegj/SAAvQzVE7xjGEbGccB68dEpjzq8SZjxTs9zsYambSfA2Xs/PYNc7ssBFlB2tJsY5PXzwkkjhIqvyYGXf8QGCdM/L/JaY+X8Wyt2Z4wjNalfxihC0DIao8/s45QSh75fdADnSQ6i/u44jguAbh5m1rYtGAjGMUZPMlKHjuM822jVdYQQ6Pue3X4/Dcr23hNTwhrwIXBycsJevx9LIuUDBhmktVqtpeMslano1euzNkDTNNPnVaxl6g7WZ1LByZgi/f4wncMK+jtlU9drrWuXVGbF6aynOb6cZ3LkItqwDq/rFSGaKQ+vuYrsUzm3WfVkSxFJvRAaLV5qhzhA0UHZTStDyCo4qoQJayztusPZw/1CQ7WVxuCFYsyh79ntdzJsLQuRpmtbTCdzFvq+n7TEqzyDU8azBfIog2tr4VTcjcG4FdYYPEmL/f+aDg4DAR+HfsAq84KMQmsFsgjES9uPBh2F2ZFQ6d+i2VXBv4JMkI/VGMo7UIxUIp1zSj33k7GQvVfb25eg5Uxxf92ImylgyVr5zPe+J+8lLejWSts+WCZTZSR9ur29Yb/bcXJ0TCYSfObs4THGSSXH+coYLuQ81mI7mMJ+t2e73U3XK+3uloU1lKqUc1oFrlpwc/JU72k5/bG2xC+rKEtnVHVASlFHq07E6zTNooelGrgpGF1Ud+r6zQ5GmLgVfLDG6dNHgVq7cNyavRnurUdGAhujrMxSzJyeemmxkG1W8JVZoey2GMdJXLw+u3qvy6CsJptTa3wFXqydnN3yZapxqc+jXreZA7OlptAS3H89YJh+B4NXMCh7Gf6zbgNpu2V/u6MMcTJINZhbBhqCM02qbxQrLJuuafjpn/lprLf88KNP6NNAq1rOtUoIhZyi6OZR1HhBPwykHOlW7bRKTRPojlqasxPMqhHNKAOlyNqnnCadHtlDwk5u2zqEQUB/D9NAhlLmVoXlWsmzmp2o0SrupFmzeB6Zqn+nCfpibUzdcIt/18+qN2aw2JIn21HbeWS/8xUbUKdE1s8vmpzI0BwZ3jM7lDrMLtM0jegWVjBtwTzOKesEVTet9263uxfU1LUZxpE0VL2eNNmHZeEhA3Ecp0JPSiJ8P+lS5xrAz+BKBTlLLnzx6iWHvicbYWGerY447A8MOYoTTCL6nsvc6t+2rQ6dAWccbdMQewkGhaWnutQLxnp1ljP4I/fRtA0Yy7jdYKyyUXKhGEPXdTRtQz8c8Jp8GZj0uErOHHTQYG0Zk6EJZmIhLJ8fmGlvlMX+rVVv2XCWUpQJXfTM1b1k1K5gWbUd27vt9PyXyaL87P1iARlOT87wIXCjg9VUIHX6HWM0WdY1qNdZSr63ZvXavfNkIDcOf3aCGRNlN+KNJebILiee93tJQK3DlIAfBn0uTgpTpdAOO77zj3+Fn/6lv8Yv/42/yW/+g/8JV3q25z/mx59/zi/85X+Pf/brv4oZLxlij7UNpQhDBgOHfeHqy3OefvMD3vrmN9h/+Zx9f2DsD7y6vuD2sOedo1OOwpqT9THXt7fcDT1jyjy1npMIl5dXbMYD9sExm6Hn8uKO2GeaJvDw6RnHD0+5vb7l6vyKlCK+C5w+e0A4W9OerGmDZ9j3tOsTLs8veLW5ZZMSRZlXNhjOguftkzV5t+f64pK0XlHt+jj2mJRZNysijgdnD3E+zIwy9ZtF7Z2mDAoGaIJeErlEXJGA3RkzTWT3oSU0HT60WB1+IaxpqVMcDj277Zanz3SaMjPjYwpWUxJ96slGRUnCrKPkKhtl5mm5CCO8aRqcd19JWiuj/+Tk5J49rj8xxx1ZwWWjAE2c/KuxFkodppEAsVMpZ7y2ZOaSGQ496/UR3oUpsN9t9wzDnjT0rNqG4bCFPOLI7Da33O32pFUHWcCx0AZwKsNT2V96bmv7NiUT40gInvV6zad3L9gfeu62WylwORnsudnccHO7IxuH8yc8ePSYtm1lmA7CLv2pn/oFvvvH3+f84grXSpu2HFldK5VPKsznmGKYm58rbisF5YurHbePD3z2o0/53v/7Xf7iX/rzxPGWzeYc53rpcjKOIRli8WAbCo5SY9DUU+IeM47sL17x2fCK9foh3lo2N5f4pqVpxO+DsJ3njp5MTAVrV2AMKW9xThhZTWtwhy1jGnnjzbfY7M8pDJydHdPannE4CLtw1VFU4817jS1MZND9b10gWEcdUFmnnhs8zgVyrnZNWiuzsYyIHfry0x/yq//zf8dmc8FJ9XdIwc2oPEiN2+IYMcosWx2t+PD7n7Bujnj3zfe5u97ywbs/waMHT8VOd42w4tsWEwKpDbijFQ5DSYNeVwYd0ldMnTRdGPsBdJBOROQMnNVBKNlMHUP16Ag709A2Dhssxsm08VhG0N+3VlnMxnN2+gRnd1BEBs6KmPUUL8lZrAU6zWucgVSIJdMjep6lFlZVry/nTIlzPFCcm4o6VMJJXnTsqW1LC8Akp0QyZSayvRbbxhgZU1x0xEEiEodMGkcoAsyuu04A2uLpmhXWBvqhZ7/biRZ+igw5EsmkEkkjOjhKTpBowctwnRSTlBzy3N2WS8ZbYcE1NswAdWYuLJWa38xarTirawS1P1NmSBSqlEDUgjMmLzoPjHZ+3me73ZNZW8Sdpsx+fAKqFuQOs4h9564ilcbQLiXvPBYZmj2OkZfnryhWADungGpKyr5MibthMwHlJSeqJBPUie4KtlqrequBwfWMuTJdF2Du4t6WBe+aH+UFdmOLnJs8p0uS/0/vJ2fFWissu/pZFRDWOGwqhJoK1N4HMZfkjuV1fR0g+/rr6/Ky1+Pu1wk3EhPKWbGqs2kXhfMYBXQDiIdI8KLx6ayj7Vp9rzQBswIy+q/EjHX/1K9X4kgFKXNKMiyTQtJBwTI8T87gbrfDOUPwQTu8HKv1Gh+CdC2bTPCemJBh2SrLZqzF12tRH1/zkcpCryBi0ZzZaOw4D4aWPTthDLnKlM2PNte4Sf22dZVsV/PoyOEQdUBrzdFU7qXcL8osgeta9IBCCE5tm2cYh3tg+HLux721nq5BzoJ1jmJlIJwJVUrNTLn0er0Wybaum3AXkbqxjDHhgycEAcNTSgzjqLmvJcVMCA3F636JUYBU3XcpJZVpuD8cPemzl30R6bqW4D3WJ/phmAp54xgpCtKC2M8yFeeUZFcKxcySmUu93pKla7rXLkLHTB6r1yH+389dn7l2+s14lHeigVzJbrkUzZeLFDxKxphmYm3nVDtV7svM1ZwxjsJcXq/XVAKM5O0y+Kuy133rWHUdow52W2ILFui6jm7d0g8H9jsZnGot4AqhsWqPLUOf6Yfdn2hH/lSDtAaZFi7OXJ28HoRKka7JpgsCWtTW66o5iIJsJUepmBlhfaYcdbiQGPaxZFyxlAoKlbkN3DknbQeL/NrUBEodV530Ka8qJr0wxihz1ppJczalud2m6rFVI0jRRJ3M0B+4u7nl0bNn4DzeWo6OG5ouSNtwMcQhEVpPFfMvufDyxUvRNVIQQ1hTfBWQKhXcuQ9oLYGH14FnYLrnWfvovuNaanOIDqVWo+pBMgZr59+fmWBFHf/s2KoWmzgzg3GeKZs1koiZhaGeBjtp8DRpNSqIX1QLzC6NsE73Baa2iLpG+o97Tvd+G7FUeMSwVCZguV/oXqzlpE+r+mfzRHZ0ffI9oLZ+5jJ4kc+5L4VQ/y2MQIetiT+Qg8WcHtE1DXfnV4zbA00T8Mzgcb2fiSG8uG/nAzlmfvCD7/Li+ee8vLqmOWpxXiRCZGqm7MAmBL0HqV7HnMhj5ssXL6TNqPWE4CgOzNma3DpmuQTm65EFm5x7EzzWORmUNwzsh4FshKEzF03uG/qJzS4rLuuT5mCgPiCJ0eT+9ypsbhAmnxXagbC5WDK0Z4bY9FwVlLUqhF7PoOxH+eNcoGh3QKO6YEtGszEy+CIVAaWPuhUHBStLQVuPZKhXDeiKts0UtB3fecYUZ0BFv75k8hs0iDJ1HxqZNr5oDal/gvMU43j04CEnp6d89vmPpgIEaJGkiO0xzulMkpo4ZO4OewZlQLTe88333uf58+dc7+4WSY1OIZ7ApVkSJKUkbGM9H0advLj3+Wx9HVugson7/iDsKvUrvvHs9j0ff/IRxsh5crrPpmBDAYCU50p3dfDOqR7u4rPEFlWwc265qllqZXioKPG9Fr/q6KUKP2KBjz76SPSbrLlnA4yZOzTKIomo7xHHmemQXzNC1Y7XpKaC4cv3Wf6tR5JsDeHkiC5l+sMFsT+wahtKgUsyNiUCgSYZmjHS2AMlJ4bUUxBtuv3lcz78/d/kr/4Xf4fNYeD3/+H/wlHZ8eUP/iWP3vqAX/rrf5P/+1f/Bx6ZCDkxjrA+XWMypIMUer749GNOnjylyZFDHri6fkUx0LQd+8Oe569est3d0uee0ARcgbZtuL285rYfMGenvJxYPYW2a3n89CHdccv1xSVX5zeUnGlWLU/ffsqTNx+Dgo+b2zsBFNIFm92W2yERi8HmwqoxnBl404K/vuLTq1uc7wiuw9rE3sLV5pZsDHFM+DbgmpaSrNon0XebfU6hlsrkb9XnI9J4QxkzfX/Q4qOwUnAerMdYpwNI7DRx11rL2I9cX93wjW8qkFL9aN0XFSTV81Rb/JzzMoTD1AGoMmS1aOK7Wh/p2923kPN5uV+ALRNqw2TvU0qEYCZwspREvx/IpdCtVhhkgKQzhtu7G7Z3d5w9fIR1nQTp1oFxtN0aaz1DTBjrWR+dEbzn1csfsW49J0driIbDMHDY7RizoRhZK4rFuQZjvTAhpOYysQMnO+HtFNPcbbbc3m6VkTIQU48pA9jMMO745NMLvv1TP08IDSmJhNLQ9xgMfRx46+33uLq+IZUBZ1q1yZUZMhd3JqCGCuIzgxRFtGljSZxf7Lh8emC1avjuH/0e773/jKfPHrHbfqqFM4MpHm8Do/EY64Xpretug8OURDARlwcOmz397Y904GfChSI+LKuv1ThbuZHih4wD47UTp0zdDG2zpqTC46dvcPzoKde3OzbXkeBbXHC0ocGURE46zRkgy/T2/nAga4zlfSPDXowQN8aURYfZey18ZZwRdiJErB3Z3b3gf/+V/5U/+P3fmuxwSfJZpUAuVTNfh4wU0U9dtStyytze3vDmkzdY+zWuLbz/3jfoVscii2ENvg34VUdqG8w6YFYduR8pJXDXR2IeyTnhXYt1jqYReRTfCWjPqiWcrnAZbEwyAPYw4PK8D0yNZa0yIFNk3a0wGPa7qHGXAH6lRCBjnfik3X5HG84UXBfZDlPKdBalOCISBabIGsSc6VMk+xpHWELXMvYD4zBMuY21AuIMY8SFQI3pJTNNOu/AaXpTpngPOzOgBHyZO6B001NIGBt0X+n1FpGHoGQFCgRsdM4JeGQcL1+94tWLl6wfnmJcIBlhYA8xUpwmBMrILQWN17NgO3pRNY8zRhhlJi86UxITA0sk8uYW4GWsnjWnw0S1mdr5Zwy2GJrQij5hjlPM5BUwmmJyZeJJQV+JSmUGBYq1UzzwJxE87sUOS6BQ93ydOzHEgYwQUwwyrFtaxKVoQjFkVaKZNChzpuhckqLFlLnwl3nx4oXGYhL71jbumh8ur3kCd5WpXH+mvqy1eCPSBjHVAo3GK2XO+QQUi1MuUpSYRUrUEteUezEXDZdrvlzP5ZrVa13+XV//f0Dc+pri25i4vd7QPH0oV6YxcZWo8F4LUjmpxryhV6krHwIi+VLjN5UlUp+7HH5dAbR7XWbIcCSjxCJZS+nKW69WolmLwdpaDK1dZJVwJfbEWYdzHqNDNZvgVO1XmeI5TbmLDOoyjGlAWJtWc/g6JDtDVpIdRrqQKqBrzfQzNW8ZB5F8kUFyEJpAHOfBz/Vnc86MY08pmWRm0oNzon9aSSg19/BWsA4p1iLSkzDhNMYZHQZoJ3yqrqtzjjRGnBLxKghcEIKJNYotGUfwM2FsCVBWmYScRRtG9oKfCFRVusB7j69dulPtwejA54J3ju70dM4by9zxWBmgtWsSW7ERfTtraYJ0R4ncw+w76+eDIRsZOpmNzCORbhg3nelutaK3ju1+Vzc/WeUEagcIRmUKEHvrfcVGxAbnEil51k52VvCA2u2YsmgeF4p2ayLDu/MsP3nYa3EvhEkbN5Tq75PMu4jjIg+WuNv7yuCuHQ1zLhWHQYaoqXxdHEYZ5Bo6/JFTrXXJxayfiQi+sbRuliB5/fWnGqQF1GGVyXmXaVJbBQREXVAAFHMvkC2lYOzMEsmCtgDaxl0EKBv6AeMluHdeZQfyXAl1VujKXgehVLinMjutrS3BYthmZqWAPsv8uIIlRavdAuRJRTOXRC5grKPq5GZTiAxc3bzi3fwTlCRMmVV3ynF3wourW7wNOGsoakTqRNJs6rRPnSheMinOLFeQ5ZichGqeCb1fHOlXWuElklJwu6jhnkGxZeVoMqYajEmlRdqcc1k4uOkaygQyGSsBojNacdN1q9UaXU2MMV/Roq0VelAgmVlkvoJqtmrdFXlmZQHhVWyp6O+DGKnaJjQ7bLmGOpQNjDyHBTC7ZN1OgVGpuZDRdkcF9oqFnCfArEYMy9+9X2nW3XjvmsoU+BYtVMg0Shm0gAHXNZy98ZR+u5MEtR+xSdjeIrCvbG7LVIFO03mCTz/7mFJEl8aFeXp2ZVWVnMlGK/R6PalkctRzaRJN4/HeYtct5qijBE+KwpZIJU9gar1X60QTtGtaYdUBxRd27MklMUZ5Xk5Zz9VxV8C36j6nPGsvLZ+HtVY1xhaJgWx1XVs7/buyfOUo1IBSfj5r+5gK7sjz1Nbhuuedq4GeXNwyYKqVQLKwUa2zmGxIQ8ThGIq0mFtk/ceoraTVTlozAbQ+BOJ+q2sgWorO1sqynfSBJGQQKytBhBK3dM8X3WfOO7quwzrLod9rsuk4Wq3JObPv++kaimoeCrghQ/6KkYF+zsq03u999APRFTxaC2ChwbNsPdkBg75nKUt5BKuFtzpIAm0HrgHz/aETtQOipMijsxOuriRwOz0648Gjh3z0yccKvMt+eOvNNwHD5198Ua2MsGd8DbDmc5Yzwp5yTto0MXi/SKZRwJfCMA7Tvm5DwGn1expOiezDJ0+fcnNzw2G/n7SkrLLJql+bbYDh+Ph4Gj5XX9vtdkrq1IhMz4JFOyWFiRlsjJnkI6qtWSYlpaAM50J3tIYHA/vLawyW4mBnCq/SwNoFVsXRHhJ2HDlaJdbG0K2OMNbzwBjuXnzO97/zL/i3/8P/lM9/8H12H/4e9rDjh3/wO/zV/+xv8eXP/wU+/f1/yqPGQYpsd3sMQcGghE0j21cvoF3xxpPHlGC5vrulW60oGG77Dbf9njyOPHt0zLrpuLq6ZdPv8WenvLi5ZbPZ44zh6GzNs3feoOTEiy9fsrvdY53j5PFDnr79lEdPH2BJorvqAierNcMQue17dinhfUMwlsbCKhfOhh5303M7HuiOj2jPHtCFFefDwKbIuTIh4LpW9IgR7VrppElkazC2TC3YVaNVtoglx0yKA13XchgSP/zB93jz7bc5eviE7SFqh0khp0HanTWcj8q8HMae280tsXYEKRhhTJ72Rk0m6p70PkhLcxrpVmuMnfXg7jZb2m6FD2FKzGuSUNR/tU07JVjURFqBhqIn1FqL12nnU+EXuLm+4jAMvPvuexoUSwzjQkPTdaq7L8wSRyE0DTnHhW+0NKHFW8OzZ28y9ncYHYo5Dj3XV1eUAq5pBd82MpXY+5a4H8lGcKba4eR8YHX8iH60tG3g+ASGx4WzB6+46G9Zry0xjaRxjw2Ztl3xwU/8JO+88y79kPAaEwjOJMH/7eaGzXZDItO4GiGqH89zklLjipp4Lepg+p5ysftD5Ec/vuTkuKV89gV/+Lvf4Zf/nb+EQwactG0HHLE/RPrtnvXRqXYh6UC0YES6wHnIA8EmrM0Cbhix37HYiaUFdd6DtDZbIp6RhOiQlpQwRkDhEFr6fmB/2AswkLasOzg6OgYLq+MVYz+QS4KSVMsUbQUvHMaD5ANOnm+KhpzUFocZBESiaondraM1G777u/8nv/b3/z77fqcevWAFncUh07qNgoLOB4ILpFJ4dHLKh6++YBx73n3zbRrreff9dzg6PsaEBoLHBA/Bk5tAbj1Xwx276xdcfvklL55/wdWL80lzlgJN23L64AHtasXxg4ccH5/w5MlTnjx9SuM8edeLnWgjZkgyHFCZTGXREQhFYzuDdYEUe209FW3UOiW8CQ2peD1+mjvlrAPA1NMZyHAGjQAAIABJREFUHXJLLRrJ/wubGQTyzewPB8hgnLKL7CxXkkpWDVAme2AVBKlxvilWwRswxkn7rpdCc0qVuWcmH4qRtmmcxPIybFOGlonP9YzjQFZWWWgCq6MVj58+4Sc/+Bafnf+YLz57KbGFanyvu5Y+jbOd02JMKXMBqcZ2cN8PSmu2me5xJmpI0Ub0Nt3ELKt2VAQuamzksKbw7rOn/Oy3f4rf/L3vcL0b56KL0Q6mXP393PWC2sHgAylGhnGcP2MCiaFkyUeXoJO1lmTmmPP1wna1K9bMcUDtnLQ4aUsuAnBLzoAw+BUYkbZ5JgAZJP521lGSaJfK9dS1ySqZJwCksD/nYolXyYpxQbiw2nFa52XI45qc5By35DINg7YGshEsoVKisAbjHWVIc9K2eJWv+doy11rGYq8Dt18H7i5B3a+su+pBm2KoaUgcIoVM8B1QsNbjg8OrPmgFqSzKEsxLDKIODdfh1Qud1Crh5ZybNGpLYZp7MPTS2WeNDAhtdbBYExr6YZDBsEqGG0fRwjXUbsZ5jkspGeOEcFK06JJSIaURmzRHLeI7hnHO4+dXmkC8UorObqikOAU+FzINKAhdcibuRuICnDZGhgpTajd0keGQcdStExHt5nTvOiLCrqz7VcBWP+nUmihAvymiuy06svNwNqOHdRgHfPHK/HX0SSXbqmwLTF3VVnWb4zhMMVmVewEo4zys3GjeJnnnHBdYZ6eOnPrM6xquuk7OpdoFsoDmwXmSScQ04kPAOTvJXOVS8D7oLAqV1lOt13od0vovHQml5EnOp3as5phovMesVkpOEda2M/V3Jc5qVGYBJU21nWgRG+0uHMfI4XCYzxfC+Eafquggy34ozASoCqrWIeEiwTkXNqytxQbLOI5s+4EqA+OsDtir+FkRoNgF1atVlm+VjhjGATMo1qeD/LwXW1hGxdyydGVVmZave/2pBmmNEaMhQZcCLZoUg07pNFn6IJZAieoKGitBmjWWmIVlS7GzrpOCJsE36Hi4aXqsfP7MNgrK7KpVwTq5ugoCr1YNKY1qRNRJMYNrpRR81dnSDW68mYToazXSKoCEgq2xFPblwM3hhiFlxjySiqVtTjgKx0rrjhz6SNsE1TBTIFU16UyprLkyvX/OWVo/jFEGXJqvC6h6L/efxwIoLBqALfTjXnc8Mz29grZ1UNrshOtHVGaN0TYs5ywiNF21msBkoNjJsFsFSVAQsh7A5bVWkFBwr7ldvFCB0grgKVibVd/HvOagc5mMba3+1iplBQNrqAszoFlZwbYKcWMmyZWiG7tYKFnX392XNFjun2Ub8sxE+mrrTZk+76sTRkuBYi1+FVg1Hr9q6W83jMoCcqqVR6lgt4B0lU1QSsFVppddtBHVs2Ln9aw6y/O1ziBkJLM6PaU9OyZ7L4DB4p5EyFt0q5xWE4MPkuyXopqkiJg4UjCRSrDc79F6jbWWzd0GTG2/mzV2li0Upmjrt5cAWy5UBmfVfZqzmdpMhKEyV+rTtK8qI0FB9jK3W2k8OAX09VwsmQS6QIstJ0FNcI63nr3BxeUl+91WquhIGwZG9dH0ORUKMSdhL47a2qIJxmrVcXZ6xu3tLf0oA0esFRC47j/uAdNIEGtq6xz0Y89+c5gmq9Y90nUtWNjt9+KMa9t8UeaZAqty7zJ87xAHdNS1AFHG4FSHtUzBpMGoPmfl9Uvl1knlHE00TW2xXgxh0/0eguf09JThsOdb3/omH30U6do1m9ue8/NLcpHigiQjge3+wG67naaLenXCFTCtr6lwg5SrrLYQovtCjr6wZUIItEaHgCGTSuu61up0PafX19eTzEVZ2IHX2S81+a3V7yX7pP7MxJp2lpjidG1o8XCaMLt4VTs3ndfKaDIVdEuEEOgenXI47DnsR1wSNvcmDlwUw0MsR9bjKbhkaZIMHWxbse12jHz3d3+DR3/mp/lr/+Xf5u//3Vfki0/pv/iY/+cf/yo/+XO/wMXzH7P98kMaa6bWNOmEyJwcr7FhxfndltxH3nv8Jk0SBtC+ZDa3O+4OPe+//RYnXcfl5RWXux1m3aquZI/xjiPVnx3HkfOX5+zvDoS24emzJzx+4wnFZm5ubyklcnbU4dqO7d2BmBKHOFKQwNZTOEqJkyHhYmKXLW51wqOTY0zn2Wxv8EROj1akUars1lh8kDbzWhCTIq26IAO1XVueWhD/UGC1WhPjyKvzC+42OwR4a9keRLOzPxwmO5RzwiTV2coSL2xub0hpBKuDR5hgwQlEXe43sf92KvhVYLBg8E2YipFTwaoCF4K1Tkn0xHSSytIUt6U8T2mv8HQpkhydnD3gbDHgJ+meXq2POVqfgHHaApqIcZhZHTmTc8Q7p9qUDmMbutUJadgTk+jonV9cUkD18I2A7s4S1ivGuy2qAABJri9myDSkEjAuEZpOWZEyjOf0YUe37uj7gcN4xXp9woNHj8AkxrFnVY6psgIpC1v0xYsviWlQIMcqa17BRlsga9uuqcBkQpLVyduoHRUbaL3lxeWWZ5cH2iee7/+r7/HwrOPtd9a4ILIG1jt2uxs++uhHvP/+B+CgWTVzwdk5CiIV5p2wJCVkkYTTWWHkynpLfOecgDZp7DW+RLvKqt02MlDOGfb7O8Yhcn11wenpKd4VjLMKPnrRHk9JWL3W4YtnpHB7c83J8TEgwz9KFtAmxczAOMW8FIsxkviZkoj7C/7BP/gDrl6ca5eagxJxRoogJer+L1o6MNKx5Qocr9ecX73iaL3i4ckZnW05e/SYiJVupJMjovdshgPnz3/MJx9/j+vdOSb1xOtr+qsL3GHEFyO6rcg67F59ylVJ9BmycaxOHvDG+9/g3W98wDfe+xZHq1Ps2jLs9pTeUmymaMtqSoncixxLUoClbddEZylxhDIS0yBgmmvp2hVJC4MiUzAPxUwqueOsp7hZ47KoRq81RrtPRCJnVEdRh2JlZVRVVZ0Uo+YWyrifYh6JGKVtt3bmyfBSo4BGSsM91meNnVKK5CTDAyvrzXmPcZa27XSQqpPvW8s4DOyKZbQ9/WEvIG7OWBfwJrPrB5EdUJ8oiiLiw1OeB4EaXQvx71H9OnpGJR+pts9Zq4VMq/GfFkCpHTQ1+ZCFMsZwe33F5599zDDsFYRQm5kLidqBpZ2CCqRbK0DFWEa1GTPwbk2diyLMeCGESzdqHCMhCEHlHnFEr7929UxxQ5HnNpSMocpuabGX18gh6NwX7sdJ0l0mxd0KtNb8sg6eKyVrmFyBlfka6vvVzj7RQK5SYpo3Lq9Dw/0JRLXMRBIjWpF1JkuxDhsC2UXKKLZj9mNfBWmX6/V1X3s9lvq693gdnF18B2cEb4g5450Ba2lUPkSAxYzR3MVYN8W6/aHHOY/zIteC5irOGZo2TJ8nLNJxArvr87FWhqu7aYj6rFOaYuGQe43nJWaMMWGaVs+z0eHITGdWmKBCILHJQCMFXLLs5UzdQ3KWJuBeWbZehwtaJ2f5oF1hwihNpFwk5ymJlAXETVk6qpvQ4Ftp47cxaRwhQGP9HOflzLRNEJ3XGElRmJT1+uvn+dDgfGBQuTOAfb+TDmUFu9frY7Uf0g7vnBed2Bg5DD2rrqMOtI8pAlG/n6Y8sjJSjT6PnBPjIMCxAL8iCyfd3dVuiW0SAmG+h9t453Vg1ywbWeN5O+EGAtrGsWo5i4yJxEuZkiopRQhfcRyE1BEzxVoojmzmXM8ZiS28b4ixxzijX2Pac6UUurZbAKZ16LvEV7Yg8qa6N8T3uImIY43Roc2riY0vfzKlGNq2AezEtJU1mZnoGGFti2a9Dtk0RrTWi5m6cl0rw8v2h9rBWmRgeSmquywyPLVLzRhDzFsandmSS2HsRyXvzBhJ1agFQyqJpnGMaZY7fP31pxqkreBsQYEfBSCNmSsmxs5tuzIkwKhOUJ6GolgMq66bpvJZLA5hDRqRDKojGJhYRgj2WyeaVmMY46h6hlJZyKWmFLM4dH0ZI4ZIvr7QDjJzG4yAH3ZG561RZnBlwxqGXLjabDDO0rUrhjzQmEDnGloTyMpMG4aB1fGRODdbK4jKOqlakUYq3c4ITV9uWdpXpCKna6/07qXuUa2WlDy3RVX22fLe6mtysouAa25rMdPhsLjJMNcJp1LBEcdTlFlZwZ/6OZIIwhKovNcSYywZYZBV9u0EeEz3KQHVsjVnCUZ/NZCZA4MlYILuVSYwct7HNTmWKqPKHNS1LGXSkjL1emogp///dQy6Gci9H1DUa17qQU3rlQvJogGTtCO4dcdRF4jrlUxL3+5pFISngqxLMMfMchfGSsWsTj9s2naq1pciYuymoNrOuR4IUkycvPWEd779E1xcXkquXqTYUmUplkBvjHGaJjkBRUYGmf1JIPZut5M2tKXkyGL9lvslOH+/Sql/10E0U0U1JZytdkhB1Fyma62Oakry4N5zKwWaTgeEvfZc7g1vku/InsiZZDIvz89Vb0ja61vf8t5b7/Cjzz8nlwgaAGAqmCg2B7VPKSYGM7Lf79Vx1za9QvBBAvgF2DcVAnIBh068Lhr0L4A9A33fM8Z4b7IwzMUMp8MakraTVBCoAsAHFZyvTrttW5wxDENPpkgClhJkeUZNExgGkRjwrsG3gf7Qk1IkNI6Tk2POX15MgP04Rq6urvDW8kd/9F2GoefRo5ZD30t1W/fNerVijJGbmxsZ1rbQLFoWfCrDJ2tCVPdRTT4rULsMzgXwddrqNxewlsyGSepAW0irU5+GTpbF4AM9i2jgWffOMsBc/iml4K0weilgirLNa+CyuPalPcnTvS8Y6NaLrnBYsX7ykO3zc/J+wCMMqtvcc9cd0xpJLNyY6EzEmULynhg6QuPpdxt+6//43/j3/6u/w1//23+HX/tv/xsehsTVj37A+ZNn/Lv/8d/iV/7Hv0t/c4Evhmikk8E70Z1MKWPSwO7lc/rLhtOuJa9O2HtLsz7hMMgzfHFxzcVmQ+8sd1e3ouHmHWdvPOD49JiL8ys21xtKLhw9OOLJsyccn57Qx5E4JjJwfHREaFuubm/Z7A6ApVhhZJEi7Zh4kKBLiY2BdNTxoOsoKXN4dU00kffefMrD1QqbIyYnnJH9i/GkcaBrWnA6jdkasEEArhIn4GwYIyaOOgAm8tZbb/L45Iz9oafExCpYNptb0rDj9GjNerUC5DpNETa8MZab6xvSkHBtwpg5wFW09t4+WPrx2k1UkYRSqtRMJqWZrTENeKAWo7KaVzv52wmISNod4IRBVGz1sfL/3jcsZPkmHyPXUfXIRg77LYd+i3ctZ2dnSGJbAQ4BPzFGCiUmMaYDu8OBl1e3FN9IW6kLGOcwznF0esrdqwtJvpyV9uQiDDC0FVy6n+TeDr0AOOvVijZY+sPAGA+sjgJ3e2EDN80DvPfsD1u8d3Tdmu1uz9AfePb0CWdnp1xs93iCMmrkuQvSUidEB243G2XbCAAiyyHPz5nM6BJ9LHzyxQUPjg3lqufjT3/IW+/+NFjDdren6wqrozOOHx3IoaUNlt3mluOTIyyJkgqH7Q5TEnZKqpSBtfbTs0hJZElqu2FGEqM+HQjKjml0qMrm9hbnkCG2OZFiZL1ucQ62u1spimm3VBxH2bMIUUMaKSxHR6cyRBLRXdW6qSRj2SLNIuJznA2SL5SB0hdurrbkbLQ4oWSKnCkpk6UaPa2l7LFM03W4NnB7c8ubb7yNN4G33n6X7vSUwYJZt/QOPv7sQ/7w93+P5x99yIkbeOuNY954fMaDN884lB6zH0ijTPMOzgkQ4S3JyJDXnAx3d5dc/t5z/vnv/Ba//eApH/z8L/KTP/8LPHnwGHxL8QUTLDaO+FGASOu8Mpw8cUjYGHCNpySPMcJCdDbopOmRNriJiWtYyIZJQIIxEofHMRFzIWLJTYNrPSsHtmSCUWC7CKCeStY2TpGdcyuJDUUmxVGMyFVU+1CJHpQig6WMALUy9Lih2Mr8VAkn0ffQmEZsT8aKtq2zdN2KnGDoB0qrLe0YUil43zBEAXZiKSSEGWxHlSHS/MHXwYMlq5Suzg+wUuiaZYmqHQJrxbYYU9urRwE5rNMlLWonZ4mp6lu991jn2fU7vv/ZZ4zW4rzoEmf14TV/k1bw2fcLa62ZYhMfgrAV1TTXGKAoK9Ug4E8yAkRIXF71OL/a4j2z44PIS1AmUSnXBAVHFnHiIta5Fz+WiveLnRD2X5rWZJmjWI1pan647PDBiD+Ziu8af6HPb9ItX+Rl9VpqLl3q4iAxspPK0T0iQu2o+kruNAFBXy998HWg7uvg7Ne9Xr9Way2hCTITAxmA5BshQzi1TVHlXoyRmRTGGJrjY8mZJ5JZFqKEbbTIoaxO52l8YIjzbIk6/GgcxqkzooJK1ZdXEzGqXmdKif3+MD87O3dnLdvh5cwU+sNhAoMxyoLVjr+qYV+ve5nDgsbGqmfbaiHU6hBx6cqVnw2lxrZMbeqnxyeAxN8xRmmj14IPCHjfhoY2NFO+N47j9Kfmlc5JF+GUg+bCOA4MwzhpVVsrZyOEBu89x8fH05yUGJOSU5Sp62C17lT/NbG92wnWZQwhCMPZ2Y7UZYbDcK94Yoz4KdHhl+JkLJmURvaHPdYI0HgYB9HlVwZwJQQ2OkAeRDe1gvFV1irnjA+BtmkIQSW0kMFeMUkXiEW69CpoXEqhbVvVmwUsHPo9pmRWncSgk02Swz6d80raMbIAUmhzsh9DaLFKQKjXUJRwWQHyui7OVXLkbD9EomCWLa1nrn6GMQtbmRI5zfm+MYamkc7T/X7PatVhjOzH0HQ4Y7nb3kn3R86kmBWgV61cjdWgDigTn++8xfiGXKABUh5w5l9juYNi6tQ/MZ7OWLwGoxapYmrMTLB+Bhn1tJYs84sNEIyVCaUlYvCUPKootwIl1QnpIqeoVco8T8czqj2VakFUY+ipRedeC4lMX4R6uDyljNP368upo5CAQASQrTGQtcJoLLt9PzmP4Byt97QuYIu9B2iNUe7JqEOqrEot3BJzwus9YVTQvYKLOU/XMQNVNem6H2TIGutgNmZwpjKFQ2gmB11/f2LZLIBWYRpKgJe0oiJaZkyMU9Q5ClC/cIx6GItWeatGTgUbcs4T4GfVCExaImXWEZ5gsdcc7VLPdNpV90A0vmZNFKSr5DMVtI5jXNx/mX52wrqslVYJvaCacy1B8ToUagYZZ6mJ+S7uv5YBhrCUiiQlemasNWTrCcdHuKYhrDr62w0lChuz7rnqtDPz86xtm3W9xQGa+WvWqgFL8zRVa7HBsD47ZXPYEXOagu+yZJ1aS9ZpiqAMxFwIRloeku66uldn47wAyhZrUHdo/Xpt8ZlbHebfnVmYwtAEcWbBee7u7pQZAqTMyekJ/TDcA171DXWNdc0XDIh7xYqizzipFhtz8aHqu2YS22E7DbArSEJwcXExTa3NFNUoLNhiwMvPpmGUgpZqOG02m7mqqvdv/Hzml8UWYSWYaa/Ue6yyBFKRFhdSK9QVbDZmqUGpm1wlaUqZGfgVCJ73lFuAOmL1a7XUajC83x8kWI0J34gzr/IGcYxsbm/lzCuokRUIiqMAUmPMPH/xStisbj4fh8NhTnr0vu4lEYu1CSFMAc3re2hpR5YgaUpZBhoFT3/oWQ7susccglmepZR7e3kqNCz+XV8hhCn4WhYu7hUnaoXhtfdb7vt725jqI6rdEYAtF4i20J4eUw4D++FimqQ6WPi8v2ZoOp65wLpIVRsXSaMjeQmIGwvbF5/zO//oH/NX/sZ/wE/+hV/ih//in9Ec9nzyR7/Lm9/+Wf7Kf/Rf8+t/77+nHa7wWRKuru049CPD0NNZkWLJY49tDI+evMHeGLqh59X1FS8vLnl5u2GbI/teEv627Xj05AHhqOHi5SXbqzuCczx4+pCHbz/EhiBtsKhQgLEcDoOwsXKiKLs+WIcnE8aRB7kQUqI3idw6TtYt5TByvr+jDQ1PHz6kzZkvX53z/k98UxieyhBsTODm6oJMpulWuCZQjOii9vs92+0dh/1WW7Aid3d35CyDGTOOm/MrSoawbuljz6E/UMbE/uYWj7C4xPY6jLOklLm5vSalAZdbMHmyn7Ifyr29Uf/tp0JCBe4FKimlJmPyPvW9lkNFawK87IJJynSt2ncT0wy5xhyTJuYyvAs7n6ka1xQkphGNtYiz0HYN+/2Otm3mRD9L3JfiwDgcoPSksWe733G921J0cJvLkMdMxtKt1ljrsAriVXaLsU7AFGsWIK1MpbfOYY3n4vwVzgv7+3azYYiO05NjVqsWawvPv/yMMY08e/oWR0enQMc777zFL/7iz/J//fbvkOKBnBwU0cIjS2vmeOi1YCXs1DTtUqPa8FY6DAw433J50/PpF+f8/M+9y4MnZ2QD223POGbG2JPNGd/++X+DMWbKuGeIkZQz/faWVdtwffWKrmulrV2Tolo8kn2Q2Nzccne34Z133l5YjbllegIINMFNqpMeY+by8oZSMm2zJo6Z/W5HcK34gJwIQckRRYeZ4Dk5PkUG5EpXkrHL9lpA9f5qSFAK5OQp0UCa49Wk8aE3Vhnf6uvUY0+kAFPY93tizDw8e8zJ2UNOnzzGtS2JxIaR3//t3+CPf+e34faKN1vHuw+Oee/xGU+ePmJ7fiP7Kkpbdxbnjo0jwYq0RlY/v248p85z1Y+cn7/ko3/663z+L/+Qb/3iX+Cnf+HPcnxyAmOHHUfMYcC1EddaVsdHOCzjYSQOo8a5FmO9tkLLfRijw4Ut2OLuFWVkudQHZdXnK4XsHDSnEISZ58usWUkpuBDIpoj0UhH92/+Pujf7tSTLzvt+e4iIM9wpMysza+jqgWyKlESKNE2KpklooiUDlmDAtgzB8IP/AMP/i/8AP9iwnwxbMG2LpCHAEmWQarCagyg2h2Z3VXVVZeV0M+94zolhD35Ya++Im1UNv7YPulDVmfeeEydi773W+ta3vk/u7yhrstQYjaN4RUTV2QTJlYUxJ2AiWWTR6tljMlOCpm1VWz4TQ5IzeRhpmobWt9jkCFNkCmImS0yMaWLImdEYbNPQh4HkhJzeNI1o02qOElKUM0YJIWUEfz7bZrJEmZyShmwBbXJlr8bKGrb6ne2dPEFis6XxIncTwqjr2dE2DYf9QfeZZ5aMK4x1wChIm+ZJRd96NustQ9+z39/WvSh5nIw0yMRDwliPwVVmYqmLrJ1JFmaxj+V7KHgWgk44LnOVcr6jEghKQqkiMZI7lN8rGuV3AV3ZG4VllpGOXUY8aAoJ4A5zuKLAS1BRAJu6zrzDIdIT0ZTiSmuHUkukOVZBAX3mqdM3Y2GpXeda4Ysg9fL1JkHkzb+fm/syGWccFegPU9TnJprjBmod1ve91CZtU6XelmCy6GuKkZixs83kGKZ6HUGNj2Q/T/U6y79LHb5s1sq/572wfIbr9brmygL+FVC+5BXShPa+mdmjWrsY+0buCqplPXtkzJKMHtcK41OmCZfPNlcAusSrtm2rtmtK7s49mp+lPNe2bbHWMgxD/dxyTeQC4AnTcjkFF1PGhFK3Fk1geV/hzkkx5WhoG4tp5fMbowQnsrKaXa2tuqarpl+VNGcM3lgBlm3J31tWCpqWNYUynUtN0/d9Ne4q4LNf1HDLukael1FvgwbMCJNOMsd8Z40IiCogfoyirT2OB2lw63dvGmEtD8NAyKnmEvN3Ug3fOOjeo+7v8bDDmlkqZklWKc/XGESWS6+9UV10Y+S66hR1lthV5OCKEa1vtKFRdJmN7JlVJxKLpankrOiJY2C73gA62atHUZmodNaRTaJpjBDWjFVij+zzRoHumCCG/5/KHQB1zNxQdD9UuHkBeNRCU4Eg0SqUbkMMUXU5l4Lqql9RDvvCcFQgjCz6NaXAdW4eZHe42rkB3ZgqqaA9ggpWNJV9WzbtfFCX34Wiowkpm/kATqK/la0j45mSBLsUJwmHyiIUp9K5+zcHASlI26YhBdE+sdbgran6nLOWS1SgVoyfyAorLQCK5Wte5MrGqtA4ulGKNATzteSl3MAMfMYY8NbiLIzlsKPkiGokpGxkY2fDMfQe5ZzFI8FkFSSXZ5mypAdeQbb6e3oYi+xCLvXElwbO5Z+VrvCX/XcZdy9s04yMF5eNHkIgLgDPO4y1CsxkvG7uAmSVn6/JXaaCYKUgKV+BxbO6Axovv1OemXhlTVprRZPJgN10tJ3DtJb+4pY0yd5pSqBJJWUTEE4lQufvmiSIFSMFr0DoNCngkROp8axOj5iIxMNB9M6M1zWs12tLwigUznK/Qpg4jAdJZFIZG5nvxZvgWHmVhKYAzUBlHxojo1NlVG++h4XFMHfstpstfT/I2lLGt/eNjLCEcGe9FJBdAK2yF6yYM+nPpKznhia7ToODBHthu7fOcXJ6Ksy3KOeatYZsYNcfSEa+X1KGq8uGTdtVh+jJZsYUpJg31BERo8Cls44pTFJc3WkwzeuyJH5lLTrryJrsxBjZbDYzIGNkjTi7PBP094yFrFIIJSlNco9XXSfsqXEiTbF2icsel3/mESmwdF1LikmKK/3wGDPTNNSOpgR9lRjw4i6/3+81eZNt07aSYBSQtgT9mhS+8V3qnlag+sv+fqn/BMr+i9QCx2LxxpOtNJ7qmlgUcssCZnkf9f9AOSO0SbPuVgzjSJiCGurcZYAs2Q5LI4nl+y9/dvmd6jVlHXq2ThgdJtOeHROGgelmh288kcTOG54MO4xfsTWezjlWU8LFiWnssasTOu8Ywp7Pv/N7fNDBz/7ir3Lz+pYXf/IH2N013/qtX+dv/6P/kr/xK7/G7/3z/4UjRM/zp3/mZ/j+p094+uRT2qZlIjLmkTAmLp5/jmm3HIY9w+GWm5tr+mHEes9J10HjOD07JYTIs0+eYjI8enife/dPsauG3JRYK9MpwzCwWa8xzhF09Ms5hwNWydANE5uQacNEdIbUtKycJ17vmFLU7GGDAAAgAElEQVTieLOmXa/pdwde315z7+iYjWvJw0DY7Ui3Eyk5zj/7iOvLlzTdFjwcbq958skPuL295fzymsvra7abDV99/2vcv3+fRCRMA/2uJxx6zl+/4qYfCMaAdbSuYeonXl+8EH1bZ7URBikmbvc3jFNPu9rqOipnpTZD1KV8uQ7q+kypAqRGG30gphNTGPG+redIbcgyM+WNNs+N/n5p9oVpFF1bZVgW/eQQhFGRCtOX8pmS6x0OB/a3Oy6vziFOvP2VrZyhUc1NUiTFiZxGUuwJU08Oe2IYeX11yU0/0r51iulWWtBYEjJK7b0na/PROEsKIvWRMeQkY+uODDnQWFitGpyDFA+QA64RFlDnVwxTj28hxgNt60nDxJOnn/JTP/k3GHd7pmHgV/79v8njr32VD779ba6vbzkcRil8xkSK4huQchLNbiNgWYhqioElJUMKCWszMUmD7nqCr3/zG9x7cMbFxS0xDVgDw3DBTb9jtbWsNmdsTx+Rc4PJPWnas+4sX/vaN9gf9kwh0vrujfUgU0Dr9YqmccJy0leMEaegQs6mMpm8b1Q7UcCl7XZLSpm+D+xuD1xdXdM1a1brFusgq2RZjlm+W8w6eTUKY0dXbpHX8U6drlWrPdtMIDJlS5gsYmBusGSRBtNpE9EcbFWfWbQ/jVUGUgy8vrykaTsevPWY+4/fwW43sG3ZXZzzwbe+xXf/8Fu85QLvHrW81XlOvWUdEs2UsSEyhklMbDIYp+OOpmEqTWllDzfeQgyckNisOvqUubp4znf/79/k5fe/y1//5V/lGz/xU7huRWh6CJOYgjUNRsOgc44wDKoqayjjz9YkrJkNgr13pDg3aHMuZJSs+YCAtdka8K2sf4TVmhcN+pizGMt0Xd1vhozzLWUkPqdM24oWYM6Gxs/xroJemjvHFGVSkYS3wqzyjWgBhmliChPOG7yHOAYa47DJ4pLHm5YcDWlKfPrhx7Snx+S1Yz9d0zQwpYk+OqKC1966qh9rMlX+gJzxrugYlobUwoDJGgqSrBilnKNGQJyizSjnHbVRPAMoaAPWgGlwjcEmab7PP1OYrhbrGkrRkREAAOPIZmbATtPE5XBJjtIMwKQK0MiZYGk0r2oaYaIHHcVtiplXnEG6moPrWT6D1VnrjsXk6JwqznVQmcS0DjT3WwLDTokDYn4sjXkxGPSaoxRzN80ZEbaz0dqteo9kidWlvjEqPVPBMyu4QTZSE5emc0am/Io+gj5CyhTccop0We+/2bhf5mxl4vbLwNt6ar4B6C7/bBxGmYjdriT+pUyYdAx87UhWfB289XXKKedcwcRljlfir7GGMSiZIxU2uKVpWtq2XZzZCibGBVBvrDSRsqzNtujXphkILf+UtZBSqiQYU8/T+X7kbCqGkU0iZanfvHfkSF0fitiSjUV6LplpGOVZmdnAt+u6Wjsv/4kxaszxd6bLpC6YyR+FMWu0nls+E2tMlX7IWeoTASyp0pHez4SfFAIhJQwWJ5o6tTYta06mRAIR6LqO1re4lWVUCbqyoYKC69bKpMB2u5VmdCpntOT/RWrKOQEPY643XnIs1R0uJmS3t7ccbbeV/JUVC2qbRqRBw0KvtcgxGMOq62iLQXeaz0KveVLbtmw2EGNmCAO7PaLBnjKr1boaoBljOIxD/X2p0YRNaYGmnfdQVGkLo3if10kNIhWAL2trvV4Dgz57eQZLIlzB2cq+WxJjcs6kOu1ephCK7I+Yc9b63hZJ0BnfWTbuvBP8ylnNNbpOYvIk+VjXKZCeNe4AbfvDodgfaZBWOotGxmecdJUSklhlMlMMtE1DTGKKY11WzToJjDFrgmFm5ivZqB5NgUONBMw6Fi0PJefZHbtpPYYyRowEo9JxNlAYnbX7pwDPOJUNJT87jmPVZRQZBQQAKUFZ435hUWXELTQYQ3LimOey0OOLDEPRlSygSDFDQK+mJFvWGDFRKIB2OVCzjrIow8bo/TUKABb2ZnnlGkT1AM1Zrl8/Iyp4VqQnvI66zx03uR9Zb+Q0jeB91YOruwgZbRVN19JFNhWsl5/QRDJTQegY565RTMqIoNwSIx1eq89Sky/LXPwZ7d4UkK08iSI0XopDzCJg60FXANdUdGcWXb0C+qSU5jWs600Gt/R9FfjWZSYJT2UnLoxXKEs1V8MrwTeN6lrd7agCVROndPYLs85muYaYIsYZ2uMtbbtif3nDsO8JUQtzhLEpJhAlORdGjfe+rmNj1CQuI07MiOZnMOBONriTDabRJEOlSTCFhT0niEYfyxIwHMYBDNr9TmpYQV1T5fdk6cu5EXMZFy9dfgm6vnRFK2gun+WsyjwYNUOJiX480O8OrNcbphhrUrS/3QnIaQxN2zCNMnKfKE6ruTqil+6afFdJGOd1V5hk+gyNZbvZsN/vRbpBQVannf9Df6CMlhprCIXB7hseP3rMyxcv+Oo773H+8iWfX5zjV8Jsj0lGARtbDBjms6sEHecdYdIxxbR0UhV2ddusSSnRdR05Z/b7gyQi2vRiAc5IQiQd3BLsxdhI1pLWQ8RFMmBVj9E6i1UxeIMEwHKvnPOcnZ1x/vpcCx6jNZNojBs7g5Elca6sUiMdUhQkPz46IqbEer1mt9vVdTQ/l7uJdj0fmBt55WfL3y/ZF+XssxjRkkzSD04l2WK55ueiQFh5dzWqlwwPoJ4bBokvpFQTuzcLinq25QVzV5/Xm4m27JeZTUNdJ1qgJenQBDK286zfOuN2HEUbLRsmIGQ4H0fOmsTGG9IYsPsBkx2tD3jfctJ2jHnk4z//A9yq4df+i/+K/+m/fUl+9THx6af84b/6DX72l/8Wn/7gr/PkO3/Aybrlkx98zPn5BW3b8dZbb3Fxfc3h9QGfM+HqmmR7jk6POH73PaKxxJevwHo2x1vypuHi+obry1vWmxU//s2vsd6uuLy5VkZTVgAuEmISnVEtzmMWzUasxaVEExLrIeNDIjmHbRs60xD2I1OcaI9WtNZx9eocY+D03gOmKfH06TOef/IJ559+ThwS+33PMNxyen/D8VuP2B5vacwOFy45WWXufeMRN/092m7Do0ePlVE7sos9ly+ecri55OnzZ0Tf8OzlLVf7g2SJxnFx6EkGAVasNsps5rbf0Y89R1kMHksBUZg2ZXKpmNaklOgPPU3T0jmvxkxzAWI11hfmjiuJLEVLUMBjPakXa1JiYt/3NUZN06RuyALcVhBZAl0FCLJsALpVR9u2bLcr0PwrURpn+p1yYBp3xGmgdYZhTMRp4vmzZ0wxsWlbrBZbZVLKNR6/WTNMgzQx69mMFjxe3eUlR2l8JtjI0VHL6anldveKtl3RrT3DmDnsb7m+OQca7t9/i+3RlsvrS85OTzjs93gvzcCf++mf4a1792QklcDt7pr97S1TygwxsN/dsru+ZjwMONey3+2FIb7utDmV8SbTNh2nZ2e8/94DfuzH3mOKexnPjIHGGZrVns4nDldPMSlxdnTM48fvMw7XjPsrnJkYjaXLFqeGKNc3N2Dg+OhIwJ1G7gO25EHUZ7TebDg7Peb29oLb2z1t20iDxiIolYHVuiNMkcNBiqu3336HYQyEOLJae7IB7xz7/Y6pP9CqIVjORsfSTTXNkfrJs9oec9jvRHc4CKiN80wxMU6p5t0mG9WmhVxd0XWEHjXBsTKm/fr1K06PTzm794Dt6Sn+aM3r/S2/8zu/zQ/+9N/wzsrweNWyyZEmJWxKpCky9j2rtsF6YRdKjiYTI65pxAsDU/X2TCMAhY2WJgjj01vDmctcfP4h3/qNcy5+4Zf5uV/6ZdrtlmnqiXHgcNjDIBq95IxvPDkGrVcMlgZnoW1E3iilIJq0ep7LY5PYEaLkFILRSqPDSJJN48WlU6Hx+rxRSRGZzBLGrEMbkCmDEl2yb+faSVn5ZO4QJgAF8IosgoAaU2GbYkWarRMztDZGOuc4XW94sDrh9Oge4xT55NNP+Ormx7Au88n3/y17k4hxxK/uY30HU896s1a5NykusxEWdkoR3yxjoVxX20ju0LYNN7sbTcXnZmeZuBTgXZnKJkPRStYaLzOzPZ11FPjVWdFebNtOgF6rPgjlOmourFHfGGIcKghsgNYXjfACWMneLOPyxog/azGKRGsGshjnVRkCYxbakKXWo+b2Od8FHJ21xCAyVEVf2DlP0npcrl8Zb43oiM9yUZGcCggyJywpJVRhDJDJzVLrpbQAk43RHJEKvIHUuSHlKm/wBVa/Add68J6cAznUD7sD4pTXlxFglrmbGNhNd+7LHfLGl+SSy98v4LR3Vr0lkpA4CtlIcSPvDA5bQTVrLDjmCTUkjy+m4Vmv3Vnda+nudxIATO6hMGQLUCsfKLVcJjk1cW5sfXZhEoOuqDlkAa3m764asOlOkV1B9hhGXVsL35+S5yIsxDnPLrmqaGOnEJV5DaHKaWjuomu24C5SvyubX7/b/F1RcG9Xn/Ey564T1doModS4utdLRmKN0YbcPDkcc6prztiZiWqtIR6m+txL7lUwj4wA00vihPeNNLKz3IMYE9OkJoBZpB/EpK9M/dmKWZXm0cnxiZ778z6h5nEiAZJi1Ea8NjX0fPdFenHRqy3s5HEahfnvHK3tBE/IInNjvdP7lWm7jtV6zTiNwurVCzRmNgjLSoRMUcDNepZmIYmkPJMBM4IziE617rMk5J0CBJe16J2aj6kerexVqQOdmY3zQggUSZ5yljrdSyHGGq+bptH1II0U5x1J9ZlDnIgJ2m5FjBCTwRhHCHn+HinR+qYsoi99/UiDtIA4ujoZh4spScFRGHsIQOgw4CTYkcR0Rg5Yp6BV2UdGKZoJ5xtxfytRSxAxvEbRnGScMaMi+MhYXdYNYDCV+SYXKoeZgdoRNsYoCKXdI/3/RacplU61FuvC/tWxkCTdopgy2WS8MaRp0A7pSsZVjBf2RJQiyFhDcZgrmzbnVBe9UdQxg1xXLgmvJFLOvGlMNXcS6zWnomEXNSkw9QDMOWMRENRZC7GMkcho3gyyyAFYxuNrZ3RJM9fPtdZic0kU0AJ6AaKULmeeg015HDL2JmNbDnU5rD9rdDx8LkvFVGXhWJoF9M+qSdU2wvgkZQHiLaodJQus5pjWqmPw3SCfcgZnMMliXFYAU8E5BVjncR/mJsAClM3MsgfLAA9gS8IP9T3r++hXFOaPFAwyNjR3ici5OiKmztLcO6Y9WnN7dU3c9aL1g2hKhSjFMDqGUxIzufeq11yots7iNi3roy3+eAvOVkAXDNkxJ2dWv790C2q3TxJgcbn3ztHp+iFnBdzKQV9vlQYqlbpImhSUmYSciVOUMQZ7NxEDPTNSJgcFG3XPSyAUpse6afiZv/rX+O73vs/V7lZ/T0wsxrEnIc7Jpblgja2LxDtHVKF3q9rQBcTPWcY2urbjcDgwTZOcK8WcJ0sQ2h5tGVUPtvQOYk589vln2Gx49+Fjcog8u72i6VqsjvSV86mYJxSN2qOTYwHBMZgQ69ozGdq25SvvvUPOiU8+fSJAYooCuBpDEWe3tVtZRgWD6Hgb2fgxl46200RHgv4UQ022Uxajxvfffpcnnz9hmEQqRpImeYYxRXb7nTBhDHK+emXtI+sk6t4UfV5l6+lo00o1yldNy6rtuLy6xLctrjAh4uzOWl61IDUqR6N/V+LDUju67kk9nwSwQlh9WdnyZv6ZEkecsgbKZxtjqkNt+YwvSFJo3JiKXtQCxC2JYlneX2BL63oy1pKXwp8wN4yyFoDW1ty+MIRajIzgbVZsH5xx8+w1Rhm2AcMFkSfTnm7Vsh4iebAYM4G5IefIdnOE8y1xGHn+4Xd4+I1v8u/8g3/It379f+BovOXy0z/nj5zll/72r/Gbz15w/eop6fkzaQgaz7PnLzj0vRTXWBrrGdNAf5PwBr7++DHvPHjI9W3Pp+fPeXVzTTKGhw/u8ej9tzHrhhc31zWnyDlqwoqyjhYFKtIQIwRcSNjdgWkM0LasjzbYnMi9GCZtVmtabeKsjeibvr7d89FnL+h8w+9/8AHD4ZrLyx2Q+eaPf52f+/m/z8njRzTbNTY7vv4TfxXrwfqGaFbgVpBlHPL29pbDbs+D00c8/fh7hJy4HSOX33/G9X7Ath7jE67z2JhEW8zquL6x3Nzu2B/2pb6Yi416fpb1o6BClgZPV4oMLfyF0WJ04iXV9R6VwVIKJWPnom7+UMlPSnHXtqKxKOOeVnTKc8I1nTC6dBzdLhpyFPaDM1i3JcSJ/W5HjlGYOQroyn5S1m4ELOz7A0+efI51Xou6JI7Nuikyjma9Zbi5xFk1VYoTjXdMsQdbwO1Et1qzXq8Z9z05RKxtJFb5jvv37hFSy0cffcqzZ084Pr1HiIGb3TX3Ts94+fxzrElsNi0xBq5ePWfTOR6cnjJOPSsbSEctkzHgPMTA61cv6YcDJ8enqOw+Jydr3n78gHsna063HV235fXlLfvdLdNhT4oT3lpikGfRmURMe85OPDm/4PmTS4wTOQZjEtvNmpQDxhrWTUc2liNrWbUNXedIoZfnFxJjTCjkR0xBxuIbS0ojOQemYUfjNoQwAAIier/CmMjQC9h1fLLBmszYT+Ath36knTLdSUvrHCEnjENZrwFjHAKnWqyJZILqCTcyJZeEvZqtxr5pJMSg9apMo7hs6FxT2k+1FyX5usVbxzSOXF1d8d77X+Xt99+nOzphioHf/Z3f5sPv/D7vrj2PVg2bHPEJUgqQAyZNxHEkR2htS7BedO9Cxno1UNSYUXJh6yEnAziyFaayR4glD1tLiAc++df/iv3VJb/wd/8DtmenhDEy7K5xeFzTYmIgh4lowGSLyZZsxVjGqlu2dY6UDEbZkbKnpag22WC9x0SRlIiap4LkHRLDtTbISeJghpQjOUQtp+RcKHFL1sHMDl0CjvNYea7yGM75mnMN0wBW8h/jDCElspGmp3ctje1ZNYbTVcfDt97i3Udf5ez0jNN33+Lxew949fo53/mzkckMrFee0WaarsGvOyIJouT5QesSkzM2C/FFGFBBtD5LDHUW1zS07apq+xbyhkkKUJkFYULBO/T7j+NUa6uS1xrtAhmKpuU8es0CJC7gGUbrl5xEt1EB4Lt5rAKN9Yw3MqaM4ez0Hte7m4UHia59myVn1efiSsO41hJtjQspzc3oSkJoGql99CVkDh31NnPeAWDc3TwpYSrpo3pY3Ml1YNI3qkQWZX5bK9easkyQzT4RFmLEKNuv0c8PMWjzxpK7hmRngLPkY8saq1zDMneq921xD9+UjHrzd5c/+8W/FxarNUljn95oI0QxkfoowJuYKbXKMDfM9XoIsqcl77NgMo1vqyZnyrNBV5gmmlbHvJ2SoCyQi8whEqcN5ByZxgMYQ1BiWJFQkMc0A+dAnTbLOdK0DcVoN2WpiwrxqdRk1gTK1Gy5P171rpmW+0nWekB9h8YygSuTs9NUpFSUZZql2eu8J4yjAI965mQlrUiCnqt+abn+MikQkjSeMzK5Mg2BMIk5YozimUIWSZaYVYIkJCGhqaH0ar3CWV/rroAAmEtPEmvULK0apcoeFkBRyG9LVmzJzUtju9VG+ThOrNoVWEgmcuiDrjM1kDdF7sdUiQCT5gnjpLmudTJlm3SNyiRE8RcQLMTXcyKRcyAjk7OFQLXZtrV+qHlbyiIXtvJ6tCWsc2JIp3hK23hMY4hNqJKjxQzNOVsB3qx5qzNKWjISL0NKDENfpTSLjERhV7etMMnLc055llfs1h1gmPQZYyxDmT5WDKqYqRdN30lZ6m0rMjQhBmHKHg56zhdmtCGmgNE61+R29nr4ktePNEgrSZOIuMvhJOK7hUlZOhlZQTdjsgJYpZMnovgpZUnacsIaCQIxZijAaT1ojdbgVoOQ6rQoPu+8CHMLv1WTsfKqhjpyPTLKrEh/LsFEkxJradqWXt3Xk6aN4gwqHdZUJAj0uxodKfdtS04G6xIZFVG2MlJXALqoB0od1omiMWILKALivFvBAiPsLjsL1tdnkGf2VrnnRXe2di9RUEFZMVWGwMwmNm8GtjfHI2BmEAN1ZEaYfXLw5JRqxweY/151574QPI0YyxGzmkIgv68AdUlyMKWLpcdFlg6zgHvooatgO1nMlktAR+5f7QBmOWxIsfZG5jWWIahWVZL3iSlJAmqLmYqCjmkGZZaJgC0Ysa5XoAY/k+eRsfo97uynAqSa2sW8Y0yk6zPESMBgGoN3DWt7ytg2pN2AGRMp6qicJphSmGX8ogNZBN1t4zGtZ3V2QrddEzAV6KksbGdrklGeb2ZOAGWMAQ59j8HI6GuKmkBLQH6zc126saWjjzECLGgygQJULPZ/XTvkWsQVdklZn/00ELKAXv048Md/+p3qjFnGq/qxJxa3TDuPExoF/gHVOzN39kZxGZ2miZwiF9eXqhuszF55QtKU0IS36Ni2RswHv/buV3j57BlDDHz85FNevX6tun66/nIWppCd9Xkycm4e+n7uPJatqNIKY4x89uQpMUzs+p6m6+ZzjhlkngHKu0Lthc0qCXCWs3qhaVX3iX7sOIy8On+FtR7nIsUABaMTATGL4VhpTGmHfLPeioZn32tAbCjSFXnxjLwXOYSu7STAhkDS79A0TTU6KN+rGCskSkMFTYDBq2B+PXcWe74+Iz0Ly1hPY2f92MJi9V4SuCINYbUwaQsTe5HnfxnTt+ybylT6wms+N8s4Gkm6yOU6lnto+TmlQNDNJuC4xsVIxnjD6t4pOWQOry7kZ51hTIbzqcfeXPAgexrnaGPEjr3Ec2/ZWMeJc7x4/pw//eMP+M/+6/+GcTzwwT/9H7k37Tn/7r/h6PiEX/iVv8Nv/9b/TvbifDxMkigbK9MAyVhS48hDwITAeHmJDROPv/pjnJzBi8tzHnVHfO0b77ObJl5NPcPUs+o61qu16EaNI6EUN9q8CHrGiZZ7ZDVEjoaJLmRi62mOVpiciDsBPdebFY6MGSZWxuI3K66ub9kfRjrf8N7bj3Gu5fz1LSEHco6st0d03QaCoaHDNS22dRzGAy9fXtAPiRh05DQLAyIG+f77fuTm9sD1GDjERLIW6yzb02NCDPSHAZzRZpQYYI39QL87yP4tI85zCPzCsvHOcXJyjEGTeG0GZzOzRJbrpax9Y4wAZ4sGQKawWKSI8d7TdV3dZ8YYUNC3ADvF2frO+lw2RMoUAsKu64NMIGw2Gyr6nEXzMmEYhpGLi0tevjinXXVY7wgWch1509yiazW+ZoyJWIuaVknDxXshAqw3K5y3NK1lmAYia4zrMHZNji3HJ/do2ud0XcfJ0ZZplL3/8uVLPvvsM77xjW/QrVthX0yaubmRNI7YlGmcoXUW4y1Nt+a4e5uQEtv1CcfbI64uXpLSFdv2wLYxnHQNbRPY5Z7zV8+ZJslL7KojG09IhsurG5yFk6OWrmsYwo6Ub1i1a73LA9ZbbNvQ+A7rLJvUslq1pDDRKxgbHTQ49nvRCvcW0caLe66uBvrDjhAmYgo0jasj9RYxPDo4g7Ee9BzcblsBY4MYsnhjOTo6ldHf4QaLNO4zRrF+aS6nKeK3MmZqFIBIUwDrtEmqenIm1HPMqJlHiXlz7hBF89NY9n3POIy8895XOLp/H7qWP/z9f813//B3eadLvNMZjnLEJdFkTUkK1iKDZI1jGIsGOTPAZNCpHp1EU5ZPnaTTA9e7Mi4Ox75ji+fye9/njzD8u3/v77I+O2IyR3jj6C932F4mU2IQYobTfZ3zLC+Q5w8o/5K8fAySJjvN5w0Eo2Cxk1iZjUj3ZGMEBFZ3bzHREUAmxiLzpozcOGGtkxH2PLOSAGKZhjIW6yWP6XtxRs9ap0g9kCt7rGlWDNPEGCNn3RrrPFe3t6ztBe+883XcquPB0WPe/7GvYX3D/XvvcXv5jEhgiOJOHxGGpcXMMXBhdJi0cVfiS4mRxVTIqTa1cwLUCBDg6nO2FXAEQ9HjlaZmUL8Ta2WqqZhildo1K5hVpoOcL/fO1DgPpk5mSn4VKvkhxVTXs2OeVnPG0rqGv/Lj3+QvP/yQYTgQY1CAXBqvSQk9s8a96DjLn1s16JF9ZrUOilEBfiOgbtP4CjLZLOPHy4mgcoYbI0a41nmV99OFaiwpWbwBk6UmccZUX4IpRIxt8FYYaU5xgRK+BBSShV9ks5zzpBgVcJcYaWJmc3TE7cU18TBScqQ3gdplbPuy3Kr83Be8KX7Ia5kf3v0MAeqkbnZ0q5XoJ/umxlmrQGzS2Fsa99YIaOqcNExCjHVvLsFwk0Xmo8oaRPH1KVrhd7q1iKeP1KMW45zkHQhRotQ21qp+snF3av7SVBgHNcPV+GqsGGQt77VM/TZ37q/U/82dOqk01GpNpS+poROrzta9V+tJbWwUs8q26+T8Vym/UrMun3H5HnMdbbDe0BlgU8bcU93vIDGr+BxhBcAMKrsQpky7Ftakb4RZap34DJQmNzrpm43RhrHF20YmN5PEK6P4UdV0jRHfNMQUGIOwuK3zRDLeytkbQqzyDyUW5pxo2k5zLKlldv2BcRwrqCpmdDCZiHXCNhcg3Uk8DhPDNLLqhAFLiNIIzTOpyDqvcTFUwklSzeoCnKJCD85aKPWPdEywvqOQI0OMIquYoenWSvBbTC0avXcZPCLFlJL4BcQoBKWuaUUKs+SaaA1WpzaLL5WleJ0Mg+jket1nBTsBkXPsh54U5T4WfV7JUWGcRoZR5PViymTnsL6R751gyhKvf9jrRxqkJYPIskiSaq0nMo8qV2AmZ1Ky4tqsHSlh4C0SkqKNlGftxyLwC0jxX1B5dZ90Znaek4SksPOU9RhmQLO6qVMSsRmYLewVY+aOZZjE7KYAW2QxUhhTxITIqmkIOWCTqUGo7TqabsXhes80jfTDAYzFFF1JIwZHVsHeQuvHythKBTdZgFpam5WixyqotQwe8z2aj+450UsCUqaMoe18iWIAACAASURBVIxG5FqULQ/c0s14c5yg/DO7pwprWppbWXRW6sF/tzO57OTeXTupJsO1RivHe148o/JddBymvHdCx4TKe5fvXs/jXIGf8kwrIB+jAhjyibOBSlbwXjpZ0qmyYGVNxihAEVlZn4trlevVi0hFQ3kuhu2yCE53JSrm5ChBsnply0ShJOrzf5funrEWv2pZdS1pPXG4uiUNeh8qa6L8rryvRRoP3dEWv1nhNx125Zly1o6YYqUa3Fkwo2em63zd4jpq7hQaEnTKOpuBsPoe5WdDVG3c+dnfYZXnuYtZXnckEsz8yJPeH6dJdMyZwzTUNVPGF+QZazG22D8lwb4jyi5IcU3wuq7DeUc/jhLnzTxyU75reY9R3ZJxshZiiLy+uOAwDPRp4sPPPhEHYa8SCzEKa3L53Mv6ZTYGK8y0mEszSkBVE+Dhg4fkVy8YhgnTeEIM1VCofFcpOGRoAYQVLAZeUc8AHe/R277c97ULnxK7Xlxnc8xYpzIpCEt7CpPqEOoYkZ4R9mgrTpsxAk5Gf72vGsTlXpYgO4WJ3e5WR8A0oRxH/d6zfIdzjsCELfdMNQtBuudlxKs8m/J75TOX320JzpefnYvneb2kmMsGroyS/Mb7Lv9d3vvL2BxFSmR5Pfq39Rm82Zx7872tKdMXKECmCWlJZL1jc3IsWtO3OwyGhKE3mWuZxuM4JVYh0DWOEAZ2+xvAsm7XbBrH7Q8+5Du//bv80q/+h3z/2x+w+7MPWPmBz//4D3n7J/8aP/+Lv8Affet32KxaAdyMxWU5Z49PTtis1rx4+UK+WU70N9dcvjrn5OE7/NSPf4NI5ub2kkO/JzYdtm1ouxUJ6MeRaRK3dNAzIksyue7WHK9OuHz2lGbfk8eBvG25/9YDpv2B/fU1bePZHm1FJ3mYaJzFGM/rqx2HFDk5O+btdx+xbVo+/fBTnHW88+57PHn6KWEMfPTdv+Ti5pqzRw9ZbY/BtGREe/D49IzT0xOVYlGWgYGb3Q2vz1/w9Pkrnl3e0I+T6KkaWG1WnL96RUgBq1qAkocawjhx2O8r06qWZQpQyGO+yyIvGvampg75C2uvNscWRY6sq7vob2HuvTk+WoCKpI7ipSiJUZsji3PeKnOCUlrm2Xxwu90wTVrcJZGemUKQ6ZUYGceBy8tLdvsD68ePwTnRtnd2bmQ6z+poy42T0fGoOorrtRR4MarRkMmIgZhI3dhGmHZx9JjouLw8cLkbiSmxWa84PtpgksG5luvbA7z3jtz7ZGhsSzYDTduwXnfkHJlCS+OhWckIocPS+ZZ+HGWkfj+KHmnIDLcHegO3CbpuoPWBo43l/KJnSlY0WpOc2YfdHkdks7KYI9X0NxNTvMU5j286chb2cLZBz/TIfpImgXOeo+0J4xg49CONM6xWawVLItPYC2PEGbbbjTLdEGmBlIl5Ykwju92tFIzeyz+NY4oTzlp1L7dEwDQem1pSGklxlHFpzXFTzOQkzb2mm5SRaSlM2xAUmLHz9EGmyPG4evbq0SYh1Yjh6G0/kAzce/gQu1rx9MVT/uCD32Wbeh62HdsUaSjxzpTNgLWO9XbLNEy6HwKN9Ui+MicWxkoz3JXmdiEwZNRYtRSeGUfm2Du2fsXl50/44//nX/Lz/9Hf5+HX34dh4GXfz+ZyynbPGOIkxpkxRNFQNCqJY2AWOjFVhqI2t9Ocw4ZpkgKeSUkjIiXhvauFfdO1pCC+BMUJvmtbJZ84ynSjooELsEUAixQiMcln5Zy1zhMyRG1e6n0iG3KMNJsyLmpYdWtW7YppmLi+vuXB1Y4YLPfO3uPz/YEp35BcK8WynfO7lKI0sfLcNJ3jpLmTZ5a4uSzyhdWdlGE1s4hzlnOw65YGzKYCIOVWlKZQzgKkhgVAC2KSuozJ1sqeSFFys6h0epMLIGW1hjJEAOvqBE8k850//zMxTUsip5bMDM6V6agwxUUuUYAvrQ+MMNliDDhlgRUt2aaM2Zc8CDFTc35uPgg3ZmHeE0R70lImQgsIIhqb3sjnN/r3zhVDsqR1frnKkt8U0LkYgMskhjFOtEKNTlM6+a3WNfQaSUr8+rLXMndbxr4f9t9v5oBvvteb72OweCdsauPUeFzrU8r6kT+UCQbGqivrvBciVtMwTTLZsMwvy7lijBEGX8m1lbgQkxLQNIaXRv6UZK+BIU9l0lRquUwB+GbCVCFAGGOUvKCxW+uUYRxpm0al3xbyE4je7puNXmt9rdPm/TaDzktdXKPPtSAdmVyn3lKSGOOsaBQX/Cfr0l9OtC0JZKW2rvWNle9mm6YS2ERzPaqEiayvrhHzsX7smYaRolla39d52m5N0yRtfEeK/ELZS847mkZYn+MgusJlLZVr9N7TGMMYtJkzBcgqd+Ecje1oW6n/iwEZMco0tq67N5snUM7FjHVy1gmgK82gaYoyUaHs4n6acAQFKC27m1uMs3jnGRjByOQIWYhpMvWnQK0W674VRulcR0ruVwiKRgHdnLLkA/rZVkl3jXUMygyfpkkAXiNxreQSYZT1aEHxPKMYmDRJyxpw5QzXPGCz3mBBz7xYmbgxxtokcUpk8br2y7k+DI71elVrxGLUJjmmoXFNnZ7+stePNkiLABtF0zGEICNPyNQ6tnQVQRavjkSboiejQUI7N0nNm0qgrAAhhb0Iha0hi8SLppr8QQ2OOauzvI4ZlIVe3LoFDjTKhpVgnBV7Ckk6AYCwW/R3xBQhyN9jSL5REFcC1Nq3ukgCwxA47EcOe+n8mZyxWBrfyCJHmMJZ2bMG2bBALbLfLMhrMZUXDBhra7JSElsoJREKYDqRACigFJJQFqH3ZXAq967Rw60aqpnF2IFeY00SYXHfmceKzBKQyPBlnwUKJMhjCSli05xoLcGhJYs3pVRZa2WzyZ/N5awxqhSV6iOnIJxl/L50RMvLWoPxvjIIMwKcmJyJUVgHGgrrZ3/h4MxlxDLPSf7i7+YEY9lllAAgz0YPRnMXnFkymyUxTiq5IZo6+Aa77vDW0KYNqR/JISqzPNdGRKfdUbynO9qKvAepatyk8nwL2M6c1FSgT//c6nNJsehVibGdOHnr75iladjs1EkFI2ewN2rANTp+YgpoukiUKrhgy7NQzFgRTYOC4HLB6AcJCFY674aqRV2S7GVCVkG49EUW2rJAI5f+oiQaTeMl6CmYKjqZorudJbvnYnctUhaq1e28rWul9KDnICx3uozxzHtgBsljLnpfmaPNCf/5f/pP+Mvvfod/9pu/gfWNjB7a+Tu9/fbb3Nzc0Pd9PWelGymsq67rlGUT631drvO6nrXAnsaIxRCmAawjM6/VO/qpmlyfn5/jnMgZlDXxJmhZRrK990whMFX28Hx2oM+5fE4xfCuAftHFAph2u/pzb+rHLpP6qku1ALLKemuapq7F8m+MgMF3CunF7y/v1zI2LT/z7hnJnT/LWcY8C8D1ZiGx/DOJZ8r44i5YWzXjcobGsz49Yj8O5CHKPveOwVnOx5Fj07LNjpWTONeYIHqK2dC4jnx9xb/9Z/8H9u9ZfvXX/mP+z08/Yzr/hLZ/ymfpwM//6j/g+dMXPPn4e0gzX85c2zQk73j+4qXce4Ow5BpDnA4M+0t8SnjXcL0fWRvwqzVjTqT9nj5nhmmqEji5aJAbg4kJZxJtntgcJqara44fnLJ9cEocB/qra7arjvXJFu8sh+s9XbcGA5e319xOgeP7pzw4O2Y8HPjkwx/QNSvuP3zMZ5+8IEZ4/vkzPvqL7/LLv/w3ee/dx9x//Dbd5h7DIIZ2eE/IlkN/YL/bEceRlCKH/S03uwN2tSXZA+RJ15lO3jRO5IdUV8saS8ySqF9eXs3PXk+EEsMKA2Zp8ll+ZAm5vll4lnVYRh3LWpT3KU1QicsgZiEV2AI1gxQDjhgCTeP1krICIIvG7hvXMTeTlYGi7H1p2gTGcaCxkEkM44Hnz5+J8kHXChvcOqyuHadxvF1vcF1H2k0qKaOfXYrmXM7YJE0bmzk5PaVZbzHjSLs64mh7At5ye3NTwcSjzZHoHedICh1tKw7OKSa8DXSNpWsCkwusG/lclyImRY7WHUNIssdSIDFhmfBthzUt1mwZDpDSgO/grUdnuK7jcBBpnDxKDmrSyHa7oXWeqb+h76WQDNbgm5bNkZhBYTw59aQoDMK2afA6wXB79ZoQBAQPU2LlDbZt6ft9BUei1IykFAXMUydj6xzWiSN93xddc5EwMNZJzEeaZsM0Mo0H1Tk1IoGTMm2jo/ZToN/vaaxns90Ky1mNR5Ox0gCPOr6LAtIYXRvS1MuusB41FzaZjKUPie7oiLMHDxlT5A8++F12Tz/ir5yu2eRMYxJiNifr0HuPbxq2x8c8evsdbq6uuTm/pL/ZzUAwIuvjKCy4uS6x1pK1CV00OAVUckiWmOksvNO1nJ9/zvf+6Ns8ePcRbedoVg29gWycAhGGwoR01uEarzmTgoVYci4GrA7TOKYYMAX4yKph74WE0rQNDqNGuLrvQiCpMVqKEz1Fs7mjabywTZtOGaJSV8WUmIYDOYs8lG9aQgzK2ovkpq0yQrkimSWOybh3N2Uaa9l0DY7Eve0xZ0cnuGxhygz7kauLa25vDjTNEdl0TAxE19biPip7zulnFGDVGKcg6kJzHqNSbk7Bbzm6JD6CVVOneh6VMW47A6Yybgy+bXB2jqNJjaBTyozjnDvO8dcuzECTAuAF7Jml64wmrEX/MysgnHLGqK5jwtBPk9a95XvrRAymglfGlEm+RCJX4kwMkZRGXatOQFTvFaibc+gylZVVTmMZL0o9Vye3ksYOLJv1mtvb2zo4UYB88ZKy2Ow4Wq1onKcfe4ZpYFTA0JsyHp5wTkBGpyZuVoFq70rMyzgv90j0y+f8aZmPLuPLMn9f5nHLn1k25N+s35avL3yGRD4OfU+7anFYosoN9DHixlHjmqNp2roeao2pMVGAI1PPmpKTlrHu8jvW2AoOVSmEBCGM1aCpgIEyYt/OrNyUZSpXx9BLfVRG8cu9WK9Xgmtovl30c8vUrTRc5msoptMly5A8em4WFCB4SXqb60ejINpUgWKvk6IFgCs4RkqpsiOLpqrgH3LUlIli7xyTSj0uiRWV1ax5f6NEILk1+sz1zzOxtrtFGsCJtFgBWgtYnObryMznSo6C4zTek/Msa1FlNfWc6BQ0TMZAtiKdZgwUDyGQs9Y19Icdxfuk/Jy3Dodh1XakrDE9TNQ8WGtB7xu89fQqa+gbnbITgIa28WwQ8L/ENH14lUFtg9OcbBSA18rUUqhSjuiEal6cy7NMRd1DzHWzeCWIN4czIotTzuGUk5wDzETLlDLxoJMd3lWZOZFEEFJU1FzYKXZRpOuclcYSWRi+m9VazkiddCvrNefEqmv1mapcRhgxac5pDbka8n3Z60cbpDXKhgUR29W0PCdhWhgrGi5SoAdUSYOUyyIvBUZSIGdmHc6aQBCz6HIW0KL8XfnE0i1J+rALAASoVqscNEb1JsqoN6jBUiwBVIXY1Tk5RqG3y0td7kxJQuSwchha41i3LcRMtknHvT2HQxCmCQZnjOiJSu2gANQMKqHJgYyWuHqL7xTmerjEGMX1Eup9KH9XNlABcU2Wz0bB87y4b28W/uUAWna+KvipYs71ld6QLtB7tAQpiuxCBWNqIlA+S8fo9ZBx+txnzsRyrd0NmpVRHJMCRprAm4VGlFVzE/QYWoBcKeciuU8Zm3LOaXdB4W6Za9AuuKnXYYzoYqV89yoLIPFlhfEyQZj/XIDTqAWljP1Ih7Voof0wEFhqFHnPosljsTSrFlLEdaIf6IrBm5r7iWNwIltL8l6LbkOOQfaz82rUpsZZi6R2GYjz4ppKcLVW2QoLQOrN7w/ckdsojo7F0AZlS6UkAJLJCqqWZ1jeL6aZRxYLCChd1MIoTCQF0Oa0Al17VpPcet2Lay6BfZymO+B46TznPAu/F6BEktREZNZ+rKBg0uLWZJIxDGq2k8mMMchoU+kQ69jkAn2W8SfnCGleC/Id4GizxRjDfr/n0I/80//t17l8/Vw6tvr8rCZ9KSUuLi7msRozmwnmnImxFOoTRSf2zXUr303P5RBpXMNX3n+XTz/9mJAkmDrXLpifs+j/3QRZtfSyFE+ieSb7trA3SuOv7N0Z+Dd31lT5bkXPtjSA6jNnZirUs2Pxfm8m8+X5dV3Hfr9/4x7I2VRY2+U8KIzHJcC6bG6UtfLmiF7dT/lLigJNvJb//8vOAt0VurdED7D8XrIiwVJaatEZ/MmWdjiwO7+GlEkhM4aJNsMuB/rcsOsnSIYjPA2BkEdcY/AG+oun/Nm3/gW/+Gv/mL/1D/8J//x//u+w43PC+Wu+/e0/4dFXf5KXr19x2L2WUVHvYdNx/2vvMabE5fk5TdtxdHKK7SzRws3FC/oxsD16i6+++zVe7V7zKgRcjPRJ2Pai2QzZJKYUSRZa67Fj4Pb1M85Ojnl83HGVN5zdv8fh5sD+5pLj4y33Ts/ob2+53t2yWW1oneHV9RW3u1s2p2cct2t2L654df6Ce8cnuNWaP/3Lj/EOvvmTX+fq9Wtydvh2wyd/8THf//MPOYyR/ZDoD7fYBtZHJ7SNJww9MUzs9wcuzg+8OH/Fi1cX7KdAQMZLU0xM41hZ/zUPoOzXzPXtTgrwnOoTzjlhszafjeRMBSwQgK7Tc2NeR18WQ5ZNlCJVVM5DDCItYayYspq5wJUxXdHzSinhyUxBUL4396WMB5q6Cedm8t3YKXsmMgw9zdozTgP73S3PXz4H7yRWkbHazIgaGzLQdB3eN/R6dkgRK4ZkMcloX7dayb3WGH9ydob1jna15uT0lHfffo9PP/uErmloXMN2c4yxDa/OX5PjQI4HpmHAuoyzidYYbBwYd3t8AuuFXZhjj02RaX9gc3SCPWqI4wT5GudFAifFRL93JKua4UFY1PfPjuge3efy9RXDYaBrO8bTFe1qzf2TU6wduLocGEewxpFjJoZI7jLrdUcYIsPUMx5u8fYIFLwap4EkKQBpDFy/3tN2regbpkzCMdzsGDMcbbcMw8SwPwCZZrWiW1mWesMG8VowZNG1TlFixu5a1r0BmxMmSb6bra7dlBkPA2MjbPhUxjqdk5Qr1xMM0FxTc+zKvFoWx9r4zIhZ2/r4mM3RES9fveLj7/4ZD1rDmbOsTMIQJQ/IMpbcqHFTypmb2xtenp9zOBwk5sRcAavyqjJhueQ+mrs4S4oK/CnjMWRlT8bIsUm8s1kRry44/+hD3vvJn8CsGlzrMa2pwJ8xUpim4gmh8aXkCJInL/Ql9ToimdFkUmNpO0erRX0yUfM6p98zsQrqD6Cj8GX/O+crUOicTLR0nYygptW6sgBjSjCJ98gccmZCggDVSa/ZIKzICW8QkDYn1m3DZrXGOc/m6JjJBO4/eMjQK0MNS7SerAwyATJFhqBxDTin9ZsQGrquI8XIOI0iX6W5ni33s4Lg4L2tRkcFtJJSQdihKUZhx2mhTspVjk7AMKtF/sLkySkTLC/iMYCxrFdrvvLeV/joow9JOdE2TdX1n/9REMmIfFqKMmUgT1maBIVktFySBcAu6zFlVMpAr8G6yiZc5iASa+IdQEXyp0V9g9Zmi/ePMdI4L2BKEiPaO9NIVkulLAz8lDONt3z90VsMMfDRZ08IU1Bmo9TPunwqECVr0GFSJudI1LZ3ImPaBrfqSP2AGe8y2t6sqd78u2Ud8ubf/X+93szTMlJz9f3AahxxpZ4h36nHrW9wvqn7tOZ95T10ArI81PIZJUctoGQBMtuuxTciVUCmml7XOsOobEo2NEWaRFmSJT+epknOa5VrK+shBMEwyKkC8k6B2Vk2SXNHZSWWxkCuCbDEv3EYcM4Ky9jMbPWZbJWJcSLnmYDlvccbW2u8JVtWwHyVzVNWeWEYF3wDqHIFzrlKECqM4WVDmoSec07hAcNw6IUEkoo+rhVTMZdpvNdp7CV7v6zZktdkRKJJpEYMUCd8NW7ZRbxy1oHzCJ9CTNes4hQ5g/cGt+kwWXCIlOQ6MqLl7L2t2rHJJ6JXwpZtMBhCnDAWWtdgVysBsIvBoYKOzhrWbUtqGqZxqs02r5J83nls05JyYuw6aRznCNYqW9ZXU7Ck2EXJP40xtE2LN1YM6rUWGrW2r00zY2lbL2BziNIcj6ES5yQPlbxwmibykKsHRds0ckYaaVjGqTQxC8t2NpErhLwqQchcX3rv5burpGYqjSgnBu4xBJ04kDrqh71+pEHanKH4iFbWqib5lXWpCU1OluJkV4sOHdvQdxBQLxthsGZ0ZNUiPqQLINU2GENF9eUQUap6CVwaUFIGZ7TbqDq3OVtJdImEMAeblBKWcrBL4mUNHB0f4Z3j9nqnQTHP4GCSouXhw7fIxhCTwWbPNCUOYSA67S9nsW1IRrm/Ro24oug4RhXkxs4AdbZGRPMXI9VJ721KSUTVy0ChAoQeeycwiMaNPCyRPUhzUsVdSYPSeRrHsQINICHVlG5zkkRPTJeMgiy23vOcC+CgRgMWSeitMFpMSiqfo9eYkzAKSuy2AhrJQylJStJ1M9d8OQl4X4ATjCXpGI43tr5PYd0K+F8YbIWpLYXpatUKyBOKeYKhaJ0WWYoSjo02npYgpQpgytpPc+KwBIUKKFb/LsM4RayOZBfjlgqmFA1fHf1JOqrlFNBBk3cQA+KcZbwhKtiP6vZi1JnWOXCOoPc5Y8T5Wl9Gu4dZNUyjkRErB2LggWjVZiPAeNZ7Yo0CVpQCQ79fMTtToI6yRvU+CjAvYKy1TsbkvKHomjl9rsJYtBVorfcPXd/1HQs7W69Fr7kw7wrIXyRQjDqvLhnZhWHeqp7QECbtaOt760h6ZgaOZR3Iv1OMjHEWyS/62+uu4+HZfV68OmfIUbQzyXoeSfC5d/+Mp58/1fNOWRG6N2MMuBRrEJJjTp7Bqml4+8Fb/MUnH3E9vOb6ySth3DhISXTZyGKymDCMw0jIEXJi267ZbNa8urqQ/RozYz+QoY6T6P9qklG7qEGSiGwSr16dy+9ncWQvDZSiHZnVBddqopFiYgz63Ovoiana5ncZrqJbbQrQq+wtTKpFTrkuX5pbWZl05i6DtTAMwNQpj+WaKq+c52S2jIFWkHgJLvHDgdeSICzPgbKvi6HADFrLPvDe1rNiuV9KI6uA9zYXRs1Cq1bjqACy6HmU6iLNZpaHwBpW9+/Rh8h4cSNO50aMEp6EHeu2wZuWcAhgRrJ27H1c0zZr2nbNeP6cP/4Xv8W/94/+E673/5h/+b/+99x3htvnT3FHZ/zsL/wdfu93/i+IO7yTmPHq/DV9HjHrhofvvE2IgdevX4vWcko0bUMfn3O0fpuHDx7R7QZe3V6xiwdCyticaXOmMTLSZQAzDrjdnmNjOV2tOdoesVpvuL664ObygtPTE443W3ZXV8Rx5PTomNZ6nr845/nrSx6995Czky2XF+fc3Nzw6NEj9sPIhx8/YXN0xFffucfLZ6+4vLzkp3/q63zw7d/nxcvXbLYbVuu1mF0EcS1uV2swhlcXV+wPPdfXO3Z94DCOwgi24LyCGtbgW49tLDdXtwJCNlaZcTIee3V9QSRgCZicMMnVwRCrh17Jiw6HPSGMnJ7ew1pPjZy1SNcGQ56T5Ky6+lZkxuS6SLicCJNoPq9aR0hGJdgTYewhW6wRlq1AK4sNYTKYTM5q6JBnVkRpsscso3QVhNPyZjr0RL+in0bOL855/vQ5NGsmCykGXLumcZ5hCmSnBYmxtNsN++vXKmHjSHnPNAn7exwnuq6lW6/JNrE9bllv11ib6PwasuGTJx/x6acf0jUd907u8+Ct93j9+pzd4QZv4ez0AaAMC5vo2ob+sMeQaRoD2SmrUYvtmAn7AUvE+Rax9e5JecQnyOOB4J3c0wEaB3k60GwtPsOYAsfHx3i7oT/0XL9+CUykNEo8psXZU8JoeHL+lKPtDevOAJEwjiR/oO0aca12kZgCKYpO4hhG0qgFrFMzPw/Ot3SrNfvdhHEdTetYrTsgM+XAerth6AP9GFk7L+ZFCuZYMv3ugmk/CsjkLDk6TDakUMyBpPjzriGOkTRlcnYY2+AyOJMgB6JmtDlLs9I6q3FBEpeUDTGbanpiUyQOB45PTzGN5Xt//if/L3NvtmNJlp3pfXswszP5EFNGRE7VlVlUVRcpUkSD3a1uQRcEJKChKwECdKs30ivoDQhdCJAgSILEbpENQSSLZJGVxarKOSIjPXz2M5jZHnSx1t5m7pls6LIOUcwIj+PnmNneew3/+te/4OKMZ8eOBTpMF9WMNaWLCnkeQ6LfHujv9qRBhmw6L7G60zg8xqD5hhMgYxxr3JugDr7JiPSCpDYRT6ZtG1rXsvSe63/4BZujY5aLE8ZlIA17EbsrrCsnbGKJ08VP5SiSbTEOesAEDbPWaQu8oQf2CfoM2VqVBLAY22Ctw3vLGAPeLmoHY2mLL8Njm6Yhp0Q/7AgxMvYHfNPivGPoe+qwoJTkkqOyHG3R2HTazTgVs4UVDNlkhgRRojEgi64zgW6xhrzE0pBMZPSGjMM1rcSxcWTpW1JW9rPGmsa3kitqrtO2pdgUqj8Uv+9rrFxIIRNRxCkuacBlsnd4L345jIFYYr0s+ozo57RtU9unC4BaNGInwFqs9O12K1JWSlaR4doS91pr6rMjJ8kLNb8pQ7mSUSJLRrSAjZyhw2EvrcK6R4t8WtMUsoHem3Y2tG0rQEvKskcQX2o1Nk7Z1kJ3zonGet3PWeMSacu2SAdozMJ+bypQE7DGazdsIuTM9b7nm6sb1qs1bbMg4nCtJ6juf9v6CbyjxHcRYyEFDWQ0R3BNg1u2DNfU4WHfR3qpbuhBLDZ/z8M47z/0+m7RHCAxBkPCyqjrbGicpWsayMJCNzmRUwRbBolp4b78OUTGIdG0nrbrZF2910KBqyxnievknDd3HQAAIABJREFUdxrfqBxSmjENVT80I5qeKdduUmFxpgrmZjPNokExmqF0PKZMdrYWCCJSfDMKFlslQYVxgBhF2sWL3evaruZ/XuPa7X6n6ecUXxfwrHRdl7UYx5FB45JSPCkg62q5lHygAGdkgoJ6QM2PBh1M1raNaH2nREqFbRzrNVh9znrIKpNU4RG6ri0rD2QFs0sRQckyvqmfJzZR/ZWCgiInJEmT1cBKgMZBNc3luXkFCTNgokr4xUnD2PlOckCT0TSRnAYF8ScmtGxRkdQTRq+trHprHU2jZyFFMK7OiXLGyblrDElZ876ZCg1Ty7+Ct8YQsuZCOcvMHpBBYUmJbYrXOWNkqCYC2BYcw8/IUOU+Y4601uKjFmqMoeqie4cxLX5sZC0E6JAY2BraRYvPLfvdXrpXFdNK2l9vFHsqeuSS10lFuAx2g0zqIyEVrKH0s6KAsxa8ZvMWHr5+q0Fag5FpoTpQpTzAmIv+yJQIW22/quwKTTSLtqbNMp13Dk6lWObRShWmAIIwgZL1z0ytJCUYcM5iLYxjj24BSpVcWJ6WuY03CoAWw5CN3MvusKNx0nqrcYhcVVL93bbhnWfP9XcjfRi4ujlj6O/wKwUEEdDIyekVA6EMzRjjxMxDg6yqYWoE+GTSNRWpAotNBfQu4PR9J1SejYBpBQpH7/v+pptAkfuAbdbPzmrJijh0YeTed5ZSZS9TRUs7I2WdnSOlMo3PlG2gzEcV+Fa9UlvBe2GfyDAxFLyTvXdPEgBbE1YKuGNyBb3yzLEXcLF8Q6nYiZEsR7RU0H11av/Yq4DKxjARr5kqneUslD/nnDWBct9hKxYwqgLxur5mBhSiIGRZGyy1fUomgEJGh6mIl1eAX5ILl6FMtJwb+7J1Sgt3LptK109RqQo+FWC2SBiU9SxnUcDiXJ/FfK+VvTztGwVlZ+/Ls4tKubS76JlnAgzr+wsIwQzghdlZmr/3+6RF5I76vq/t8xl57t57qegBbdfWac/32JgzusOcaRBS4jD09ONAVPaGyeKcLZYmO16cPOXq7FImVKodI2fKcK0QJIGzWhjKRjRpr66v2G+3DDHgvN5n6TrUszyGsU4stc5i9ax0bUvTNJqkZcYxYrWtv2jTFpZvuVenQvtYi28ajo+Pub66qpMzH7I9Mdqm54wwv8RoYJBWo7ZtOehANNGNlOTr3stoSxxO9Y/dDHwqE2mzBslT+2ORQ6gVX2C56FT/8AFL4kHAX85uZfSOY/3sAkIXGY55Qazce90bD4FbM2mBwiRnYozh8ePHNE3D69ev74O7ZT/odaKBXrl/oBaBmO3rZHSohG74WrwDTOtZPnnE2I9wGHEaEO5T4nV/h2fN42xoxgAxkGJDh8HiWOJJMfH6lz/nZ3/+lP/0j/9L/ubvfsnbv/q3nB5lLr/8Dc9OTvnd3/+X/Pxn/5b9eCDvbrm7umTRdpycnLDv99xc33A4HPDes1mvRVd0HOj3O3KMHA4jJgQ2vuF4ueTr16/ZD3ua0xOyd7gx4/cjizGzWbSYDLc3d9xtb7m9uuDJ41OOjjdsb26wObNZbQgh8PbiDVfXtzx79pgXz55xc32NCYH3Xzznaj/ymy+/5fk7j3nx5JhXr8642w/89CcfYQx88utXbHcHXLslgLDbC/MDOeshKZvMGKIOD8naxVOKmd57jk8fsd1tGcYrus5DEvA1pYQzhqvLK/phwDcrrQNmSEHOR03oM5gkbctuzu6fink5S/JW/anuS1uNNOov1VcidqfoTcaggyZMJo0jGUuzXExtlAUEwVRbW/y+xHiozSqxWg2DAQ3aFejZ7faEceTu+pbb2x3Nk2eiR8vEoBDbhHZAGVzjaryG0eTQqC9PiTFIm3fnYbNqsdYp47gFvT7nG8YQuLq+Ynfo6ZYnrI/eoWkdz568ZKkt/zGNmJwYh5HdfkvrHc4LcFZiCGedMkgkoXI2M/Q3jOMOZxyWlpQjMQ9sb885pD3W9lyev8UaaJuOm6sdTduyvbthHHrVi4sSv+YMZk/MPbvdnnF3YN/aKht1F3vcbiQRMCaovptTKYegtrgAUQ5rWnKM9LtbVsuG5mRDiKMAduOoBf1I23a8PT+naQwmjRr/tcoEt+QoINZh2OOMr91AMUJIYF2rw4EEfEhJgIOkOsy52LeMAgymJl4CNigwlyVGsb50q0B3csRNv+PXn37CurMsvPoY3wqolDPGC/AUxkDuhMl+d3sLWYDKMfYCghpp2aWRiL3a3cmUgsYfEnsa1Up21f5blS/LIdFf33F2cc51n/nJH/1rmkXHYT8SDz026hk191lkxgA2kfNIJtRYu4CChKzDq8S/ppxIWSXhchKQJSZQWL8MohHG2RRbVVAxTfGV9x5rVMaFiYRRYrWkAC3GUIb8CkBXcgewDiGyZJE8aNuGq9sbTtYXdMsl3WrJanPE1eVb7ra3HEYZGJbWLcFbvPEslgvV7WRq59Wn7yw6ACcr239JIV1EpWbnPA0tlvhbP0uLw5PvBbAaawlbN8ZMQqTCXFJgwhgdHq2s26rNyqyQWlhlA+fnb+tukeFfUQHUKS82utht21SCTCnSlvU2pXqd5XwNQxl+NYtfNTYv3YgGW2OcGGNtWU/obBa9zhBGUg4am9QrErbmLEYRltlMWs9Ip0LZH2XOAbM855urSzaHXiUOTc2Nqt/S19wPAQLO6D733pFVDiEbxEGWHGkWw83jt6n4fT/Gm78e/n752fz1ML6vz7t0djiHt55F29ZcqpyVEALJptrSXzrkauxYuuL0+UWdaO+9Z6HsxTLsNoQgcZLzNZ68JysUkpLYI5FRwF7v66DhwsitmIw1UghyDouc8+1+y6Lr6Bqxl856OWsqBZkxLFYrPNK5UBm2mkeKzIMMAS5AZVIcSFrMYRj6eyBd0dS12t1ZuqBjiqSoM4nU1pRW+KSDomKSXCHGRNt0IuFgbdXmtm4qnMYQGFRztuQ75RnGGDn0qhFupJDSdi3OiaZzwaFSTlUDei6lYBxkI9ID+7u9Fo4NvvE6f0jWBZsZgg78ypOkgDBHp1xRtHMDXdvinROZtbLWSnaJcd6J6gQktgaPxvdG2dEww2ECzkluJ7jYrNNVN+I4jjPMZs4e1nxCpWe6rhN/oZl2nOlx+9Ktm1OdSxUTtE0rmI2dDXxTH2qNoTHCpE9Zhp6brDrWVmKrrutAi6aSh1rGYcAYy3KxuNfxUVjVIM+h8V4KeKb4TNV/dhkZpCd2JWiHRrGZUoQSu7ffl0Lpd1+/1SAtUJmac4AHJgAMPZSl2peLc9SfFe0sAGNzwe+0SlSmB0+asaV6NPklregaKoBVktQyFbA4O3Eexch9t8XUGCP06SRGqvysH0f6fhApBPUStsTKyfLk9AnHx4/ECGfIYeT8/A192LN0DUYFubOKx89dQXEm0+EvXMqSxEwJj7SEIMFgFMMpnd7aKoIaBO47oQIoFFChOIq6aLP3l0M5BxUx2n5lhG1oZgd8+n0q2Ddnr+mmIJOJIVemNQWsKYCdVuwMWQz/LMmsgB6JoR9pXINzaNA1Ta83WareKUaEiJHRYqLuncI4+y4omItxqKDhxGguazAPAso9lr1emG7z4ODhf8t5mWvtPnyOcwMpQfO0TgWArN+RtL2qYrWFvSz7zWhwHso1pCL8X9bmASCv91bo/kWPWQqisgdTyviqkzXdUwGXS/Jl58+KeZv79PymPXb/DM5B7QKU1j1a/jxZGErlrwTn+lNKq325z/IZ+gHKQZ+A3/mznu/flEQf6WEQCFSnNt9Hc+A9A7vDjv12SzKABqBZ7yFnGIeRX/z9J4xGHIhzXpxxUBaDn6QvSrImRRvRG9uPIziLs6gTKu2Yqg0lqe0E/Om/7Q8HDn0vybTJ5CGwOTricDhUe71cLRn7gV6nkk6t0RLQXFxciDaRfuZ8v4udR+2zYbXZYDDc3N7inFTdK0CbZHqnsTI1tLSQNVYZOKph6a2XCbDDIDavPGd9/kdHR+z3MgH1Yavb6ekpP/jgQ37xi19IEjsHPuFeQGKMYb1e0/e9VrTvMzdKG898H5fPsMoweig2/48lDwXkvbq6+t6kY342ynfcHzD3YG8bU09BmgWAFbBWO20XHavHp/RnV9jDIHvOGc7zSO7vSM0SEyzWO1yMmHEkxR0mZlq3ZmESv/qL/wtWS/7Nf/Pf8SeXb7l59QnNcMNnn/wlLz7+Kc/e/QGvv/2MbmHZNB6XPWEM7G73xBg5PT0V9vA4EoaR46MjUgh8+/YtbbfgaLFi3O+4ubjmcHWNP+6wOdJkRzOCGxOLLB0aYz9wOOwZhwNPHz/i5HjD1fUljXVsVhv6w8C3b76l61re//A9jo6PePvtGRZ4dHxCPw7cXF7y3jtPePLklK+/+pqYDD/+0fvsbrd8+uUbmmXH7/3OD/m7X37O5fZAVOvvAONEjsE5X9egdEI49bnOWgKaECw68jhISz+F/Z2r7dze3tEfejZro3I0JeZxaud9tSVe9UMNpTggbIKs4INohqsNKd2tWRkgMYifNBN7rPj+/jAggxYNOPGdjQIK+13PctUoQCSFY5GCmm9a3Z918E0xfnrlKlEVc2S1XhMOt4TDgf3tjmEMLBYNNBaXYBx6QpBuEmsQRo8xouOpk42xWdkiGYEkEmN/IIVI18LR0gtAmw1Hmw132x0yl6CjDz3tcsGYwNklT55/TDKZQ/aMe0/TPmY47OUul5ZlM9aBi8KOV/DQTowZ5xqcgf5wQ049BiNDy2KCPLLeXJDjHWN/SRhvOdxd0zhPDLBYrtkcr0U/PGpR1zgat8D6FTHDySMp3nkyu/0O5xtCThyGyGrV0TQJS8JkBz5j00jjPb5ZkNT+Dn3isO+Jqce3ntPThqPNKZdXV3I/xqq2nePxo0fE8cDu7kKY5A6G3R1tt+JwMzD0I3c3t/TbPb5tWG3WLNqGfjgQorTcxqJrrOBiiJlspK3QZGZ+vexRHRLITI4sJozXeMtaFkdrLq7ecn3xmg9aWCgQFUNSTyv7m5mtBrRl3da4NWnOgDE4Kxp6tW1Gi40mTvGY5JETIJb1wpOR4Zor5zBD5OlyydX5OVdff8nTH3zEofNkr/F1UpJBprbOk6UbKc4KvzJcWIu0VmQ/CtgWYyRbSY7Hw55kxe8fDgL2j0GGSDVNo4ChgExDEFDAokCIMZhxVLkA8UHzzg8VBiQroGJRNm7bVD8mzzcTU6Axlv7mjuOXSxaDY+h3OGdk6vj+wBAGbu9uuLm9pckGqyxlcmQMwv5OytAq2vsll6v5SS7daiUO071ip1hOy1/f8cX12c78tzEW7w1ZgU5yroODcy4Dq+Wz2q7FWWEcF9CygEAZVF4A/UwlTjyIJcoeKrM+ii0pHXyCTZoK4nRdd4/8MS+i3wcVJ8Ch5nYlT773XlvJKdaKL/V6PSlJPuV0ZkxhT2NMjS0yU45aWJfCysv0YZT8zEoBs8RqJdcwCItc9o12UeaEcU6BZrDeV+mHuW95CMzOfzZf24fP5OHP//++csnvQAYe21Z0y7nvM8s5kPc2JFOAbE/XdmQSMRaN2ftxJJlJb1W7dMr/jDGVlQ3CvrQlh8qTTELOiX7oK2BVgLoCxnklHllnaZtG/PmhofEei8VbK3N5jFjOxlnRaPYeZ6DJU46aU1KyWpD9Y1zVvC15inT0pKrrPSc/WLVTXufg5CTDCJPTAo92sRk94+1CmJnDOCqID9KJr12lTUNbGaFih3LKhJXOlCmYQ2GslrZ3LWRYJZ9472SGkJ/LNiQOh0O1PdLyn7Be7M1qtSaMgRADFkOjnw0tjW8YxpF+GIi6njkm/KJh0S3rWY8x0h8OpDASgzCyu65jqTM8cpYuxt1up2dzxLdlwJupjN4xSiG5PO+ua1Sqr8w/oO6h8lzAqMatbhTd1yFOA8hLXKMOU3CdOA2OD+pjyHO8xNTzl7PabL3WWn9KSTt55Ry5aiPFDhXCWNO0tehT1gTtnhbw1lcNXykeTGfFWLFlhT2NnjlZI8uo0goCFHv9d8E25szih6/fapA2F0C0Bl6ytIUeXdrbmDmmqhmYc9WLnICNXIGncpjuGdw8MeoMaDunygHEVDdaDbT0ZY2rQR7Eamyl3W8CFJwKt889QXV8WSvEevDLdEqbHO++/IDVckOMBhOg3+349vwNySaydyST8To58zD2lTnq8iSybJVGnglgS9ujV6H+AihL5dxZh/WGMUetwJuqYeWgAhbV8Os9zsGkMohtclzqAIumK+U7TWVoTM/B1HZiWZ/7Q8PmbEj5aEmYZC2kjV4+ypasU0EPacvOWdmzxcjrf51x2EZaMrImmPMgpWrCKhKes4KSundKMF7AWamcK8Nwtl+mdS/P8Lt7/x4Yq5bGwNRSwv2goAJk5e8zIK8GWbP33Qs+dF/LuZBzV9bClqqusaotY6VtXyt2dS/nEm9OgFZdU6iFEyhTRAtjtqTW07Rh2RtK19Tcu/xu+cyHxY/5c7VWzmvZK8bYGcD6IHCaB9Ll2SiIl7PctzGT5ur97/rumtXrskadz/ScS/Fi/hlzRmw5T8Mw3FvTh8D8wyAcpOJqzcRii3JgCDExIi1jEQFMHm+OMRjOry6IyRDmrF1bihrK4KSwTKD0xczZpGjg/97L99jutlxeX4ljahqyVoY1z6H1DU8fPebVq1e0GmiFMTCq457f76JpOTk55ezsTNpYZnsJijMXW+6QtpjWNSy6BWM/MKZJS9ZpxbgfDlJAiJKAPtpsON1s2N3eSpucJms5JxbLBdr0Pe3dnLm+vr63DqWqmnPm7u6On//854zjgGuae6yHh3s1xsh2u53AzVJc0X+fFwjmPqq2qc33rz6XOXg/f5W/94dekhJjpy+YXVP93JRZr9d0Xcf5+bkGJ1MLaylrZG1JcrYw2mItmGYNRFbHG9wY2b+5kGQrZoI3XOZEE0ZhxEVlK5tAYw1DNjx6dCyM7H7Lz//8/+Q/e/o+f/xf/7f8j//Df4/ZnXF39y3ffOl4+u77XO2vudue441oYx/GkW7R0SqTe7/fY3KmbTv2h4Gbi6uqT3x3u8X6hpPFksX7a3aN2GM3JJwyIE+ONjhr2W1v2e/uePfd57Tes7u7o3GezXLNcOh5880ZMWU+eP4OKSU+//QLukXLkyePuL65IqaRH7x8Skjw+adfYpuOf/KDp5y9veD16wueP3/Mex+/pB8ixiSck04bjMj/eGdpvLCKMIXxKYCq00C48R7jPXnZkhcd6bDHtR5mbMKSut/cXHN7ecHTR09JYcQ4fY8OUaFB2kw1BrK2tF7nKRm3GiTnGUibc7WNYk/LcBH1YWTiGAgh4ZqEzYl+HCT+sRbvF1hjWC7XTHreKFO42H7xWaUYONn1rOdBmCHkICBxDMJcMNDvbvnm9WvGnFk4Q4yj6PFhZQK5cQJ+OIk9mrbRBFf2TNssyVmGeNjCYgoj3sF6vRDWawJjHMdHa3b7ng8//IjDfku33JBxdN2aYQgsuo6UUKaGfH+OUT7bt2RrCWHE0lHkdlwj7diRAFmYd9lKMp+Afoy07YJFd4JtFuRwIF61NKZjl2/JRlgd1q1YdCf4ZmC/78EY2m7JYnXKcnXCEAbCeIAErfcs1I51i46YIovlUmQrTIYEQ4yMQ896c0zXbcg50/cHwpBIoRdQMA0M/Y5xLAMl0U430RNMKTIcDlgyXesZhp7dfs+yXbDanJL6Aw7P3fWWbt3RdFJQPxz2GJ1TITI1Tk1j0NjB47yAQEXz3IqLnPaOYPoifqYAQkwZ6x2LruPs1SvYXrNuHSlk9hj6uGfhfJVlMo1om7qmpWk7Ft2C0I7s8laKHCV2syITJQM0LY3OvJCkriWkQBrTLFbOGDLeedaLJV3bioTHMHJ8uuHle895FBKvPv2U5+99IIxI5zA2SAdXEghaOr8KyJl0DbT7JRph25sywFLiMec8beuIvgELrbPYplV/EGjall5lC6x1cs/KGnLeYVXaaBwHSXJV+7U89+J3SgJrjKvgSyEneCeMsJBHsV9JckJjDZeXl7w9O+ODD/8jnjx+JNc6Dhy048BZw+NHJ+xaeBvvGGwipoy3jqOTNdfXN6J97DytruUcqCq5QKoMM4k/rPVVg1U96b3YdG4PUwr33lfXdJ4X1N+ddDb7XoqbhQ06zUvJFCmC4veh6PBPLGx18ALePGjNFpkJjfw1r7F+YkQWMKzECP8YUDv/c5k3UeIUbx3GeiEnaVuwzdQ4wRphD8ueE5/ilMxinVHtUn02KuEHtnbWlmJaLPtIu/skzhYJvXm+CtQp7AWYyZja6g/3CRQPi93fB85+3+v74rDvK55/589Z4rTl2GKMFA6LbFmZKF8AvJJPTNeaiGmswGBQrc+cVRYrJpnLgdiqAgzV/ZNhjMM9vMIYQ9OJPBtW9UILWQIqwOu8VxmAWP+t3PO6W9D4Fu8aYdaOA8QkupxJJA7TGCXnUJDeOAFzQwwYm8nZigxBns7VPDa21rJcLmckJLGr6DXe60JjNg8DwTOKjm7V09XumhLvwP24Rt4j8YExhibLoLXC9kfzYOM9y+WSMqejPNtyTVHlYMp5a5qmxvSSu8jcH2Mtq8Wa2CTVwB31XrRdPlvWy1Z0tFPmsNthjUiRxDjpDzvnGBcLHewcNU5vZntK8JG2bdlut+SUcI0nIdITbdNIbplSZeXLM0+VbaorP+s4kNivzuVhOq8hyvBrqyBoY1W31ohO8Kj/K4WAfhzZ7vc0ViU80sw/Gu1s0C5ipxINTsl2SeNfay2d2pigA0TliqcCoEEKOsLOV1KakY6W0oVdfUOeZsiIQU2TzJ7VQYtZOrXELqfKCifLULL1ev2P2pLfapDWIO2wovU5GaPi2KwKKsdSXTWIluVMnwwjQWDmPrB3r/UHKnhaxLhR8MowO/A5Vwo1zIEVaZPPZB0Udp/JODcQrWuUpSKBSNlk1lhsFnDEGQlPUkw0bsHLF+/hvbR9HVLg7PqMr998jl9YjM1SVdCD7K0K92eZbFuDiuJETdHLTaQ0Y8/mUiFWG5EiNpenaNQhqjM1U2vy5CCQgE+dZgEymX13cYzSZSYTcYXwkuoiqBoBqAaxTFotoN33BwuF6QuqdanGP2dpwU9Von+SDhAOEAoEoxo7RhNJU4HdOmxOAcWUynzd0lpihJpfg62MsH3i7PcKw3DuYCY27/2KLffWS342Add29vOHwOy8VaKArw+DLLIEQTWnNfX/KbCeqmMy6piMroVVAf6sshEFCDaptHSV8NOAvc8cdM6pLvJkzKwGDjFnGmPruc0lmzcl4dZkX9H8UkQp7KyyDR4Cz2WPlkc0PwsSOOdaZZ8/75gi09TbiQ09DwoeAt3fF8zeKxjNAts5KDbfyw+lKeY/n695BaI1oLe6rgW68FiMU6ayd0SEGZMBnx3vHD/i3Rcv+T/+/b8jqvMrYKLB0LYtw34n1W4rdq11DdlkDv1BkywL6uBSylxeXdZKKmT6Q4/Pov8TFXyJGb5+9bXYa00ixlEqo94VfVw5N/vDnuGtOOhaDp3teWtt3RuDAqyHvsc1nrZbMO729wowMUZhwBXhaeCw33OdIhcX58IuNo6MFI28M/VcoAFUYbjU5AepgL733nu8fv1ahwdItRUmQPX79kkBXGye3Q+TlICb+aeHRYmpsEJ9Bln/PO9UmL/fWqsJzOTfjCZ+tfsDuWUBD6Z2uPl3FnBz+o6pm0JA2EhSwMIbg20bmqM1h9stcZdos2MMmYNJXOVAR6TNDueAMdJ5i00jbrejXR6zefqCkC3/7//+P/Gf/Bf/FX/wr/+Yv/rT/4WYdgyXb+hOTvjJT3+fv/zLf8/t9RvaxuOaloUGore3t3RdJ75z6BmHCDgWjaVV/5KN5fTJE2LT8Pr6gnjY42LC43j+4gWLRcs337zm5vqGp88e4azh9vqaZbegWxyzvbvl7Zu3ZDIfffQBwzDw+us3nBwf8/zlM871bLx45yl9SHz+xSuWqxXvv/+SV29e8+bshg8/fJcffPCUt5dXfPnVGT/54bu8vTvwyeevSdrdYhstdBbAcg5gOtGfP4QBt1rw+N3njM4SDOJLs8pQGFPbaG9ub/js17/k3RfvkhcO1wpn11oZLpoDOJexRlhLBVRThym2Ok2OJGfu2a1in3KW5K12MBhhz0l3ZWTY77m9vsQ5x+b4ePIZ1lOnlsvpEKAEKATAWjDIuRYQsmpi5xSQFv6AyRFLoj/suL4649U3X+OaBgPEMTKmQOoSzrc4icA5jCPGazCOFju9w7slOTXEZIRt6xzRgLHgG8d2uwXjaboGYyNN4wjR0PiOz379Bdaf8uL5h2zv9gyjMJi6VrTX7NIT+sw4SvFnvV7RNwMhCNtMpjxLMfhuu8f4ViZ9E6XQM464FDAp0B+kkGrtkqPTdzlsRRbgMIwYt8Y1azALkjH4riEbaJcbXHuEbdZYHHGQBGo0HtPIemXr6TpPNp5kHTENkpzSkL0j+w3JrBXgXuI81R/FcMDdXXB99Ybd/o62NRgSMQViHNjd9uRxZLVoaduW/c0txjh2Q6DJhsNhZLePGLOgcQsavyCGzH4fWHQt4DHWEcIoLeVZYhasw7tG8okC/5VEv9hmlfkoUltR5wb4rqXpGi4+/ZwmRnJI3GCxiwVpHFhlw8IL2ygmaIyjW605efQE1zi2t3uJ8wrDvKT9WZk0dgKTcjnglNhQzlbjHWkMuGxYdp0w5mIQMsaiYblZ0uF48/Yr7s7OcSePaZoWxlE04lPG5mm6eYjKhoujDMuxRgYPF/uusVeJ2cXvBe32y4RYJp5bgu7V8vf1+oic4eZO1k4A2pFxlNh5AgslgdbICNBBrxjadkHfH5Q5bhQAtjrcRZxUAgKJuzzys998woKGj8NANpn1+pTGL7CmwaTA3eGas/GWfiF7wZpE4yz7f2CwAAAgAElEQVSnRxvCsGcICVwj7fyzafKlyNt1C2W1z4gQxpCzJxPv+eoSd1sjhfo8YyFavb9iu4Gqw5hz5uTkBO89b9++lfizgIzF4ClQKy21aIxKLWa1bVMBkRijglyWUjQtoJRoIQvLexyGmnfYUAqy94G68hzKn8W+S1fWBGx5IE5AnW7gVIYQ5nL993X252y0eaxTurIs87xJY8BcwNcSTwugUti5MmCqYRgGYgG2S36RRM4r61m3zaTBWdfw3hrfj8cf/vn74rv5785fD9/7fUCv2Ioy8CgWyLmyCbuuq2tRus7KmpR2dmk5N9INoySyEnOXQV8pTQBh2QutstprV1RdA1O7ELwtze7SZl46G4dxZAijxJYZckiMacA0mWyddqEIYSIinXNYYRLGNDKMidY3tIsFJLExOSXGONZcDqhgp2yv6dy1TUujcmmS1kpMEHMZXBy/k2MBk9yhgrU1F1PAcCLoQSl+lN8vOR7AOAjDVRjELeMwMg4jftYFUK614E9J2ciNSi15ZXai51QGVIsma9M0gm94AYelw1TnszhPxuF9CxnsYkrIy8yhcg3eN6zXZehb0rNn9dyCMZLfLRYLASszUqyzXrAWY3BebHEIUdmxihSZSQ8WhDk7DHu1UbbO3/D2vi2ZwN6sDG7Lwnua3NJr12LJp9q2oWmckC72B4ZhrHIfpSO72itr6gykoLmfd44UVT9c5SCSSj04a2jaVuxWFidTZlehsTNZCrxOC1pF6s/5iWDVlAKIk/lTGcFJSq4UQ8R4GbaGzRx2++/YgfL6rQZpQZNPNcoCqChQigQPFmVYauIh2isNWdvdctmkSJVDKoXyexOgMgX7iYxjMpwShN9v4yyvesiziAiXC84FGI7l2lE9DAVTTYGypOVJ2pFUn5EsgbWxxBx5+fQ5H//gI8Io+k+7fsvnrz7lm8uvsJ1o1Bo3A66MqXTt0sSF6nkZZclJxcHXxD5Wg1Peb1itVsSUhBqvn1cCqhJwzF/eWZxrNVEqhqik7sXx6b0bCcyLg7HKKkBbFrQ2oswCScyKPIAMRDOUiag5l9FmCnJAFWj2qt0m1a6sgw1mlW699phlojVGQFzvinwGNagqMg+GGRspy3XmmdE3CmQUXa35z+eOWX0fzhWgtTiB+un1O0lMEgIzZ1H36INgQR5llvbuWVAQ1XmS7stFFL3AsscFu5H7LFeWydKOWoCdKO8TptR0HSBapoVFXRxZYbRSPiuJgy4aeMZZaYet6yPnw2i10ZS6iSYRibK/StV8Ar8kaJhJAmiiD4aiG1ScY2l1zCnJ8DNmrWla4QPVxXWu7tnpSVNB7Hlw87Aa/5BJPV/Dh+CyMYZF29E0DdfX18rMmoLaMhyKrDi2JpzlqaXMzM6Uooeww9qu5e72hp9fnEuB0Jra6lQAnH1/II4j3nmcdXRtSxiFteJcUwcFyrXL/tnu7gSlIJOCFgucJWmr0JOnT/HOcfb2bdXlXq5WxHFkHAcF+sUWNL6lH0b2g3QFmCQsitViWYPMpBpsTdvVRNI4x9XtjTj+2VT6wj4XBuIkMxJjpB9HsI4xim2Rcyb7u+yFnDM2RgL3g/by73d3d3WflYEdZc/AXAaFST9tvjZ50r8r75sH8PN9UqfW53JPEuzIYAcJeEpVdr/byeeU9yNaYtK6GdSGSeRddnQBtvu+v/fdADHH6v9KDaXYzPpetX8ZCEmm8trW0z45kYLKbsQnaRTfhpGzuJNiYGrJ2RJyoHWJeH2OH0fef/mCR8fH/M1f/Iw//Z//hN/9oz9k9fx9Pvv1z1m04C/PudzeYoDlcs3poxMuzi+4u7llvVkTc8a7hqEfGEYpEjkDOaoSoxUm+fk3b3j+4Qfk3R5LYn204fmzZ7TG8tmvf8PV1RUfvP8+q/WSN69fcbTZsFquOb+8wDjLhx//EHJie33Dm2++5cmTJzx98pg3b74lpMjjx48ZxpFv35zzzpMnvPPiOZ9+/jnn53f8wY8/4vTxEV+9/oazs3N+9MP3sW3Ll6/O6LxjICvlz2qcMQ2qmfuikBLZWzaPT1mdnBCzkeBdk2VjHTg1vc5AyvT9yHK1AdsSUybmgAmxsnGIjmxlKERhOOUMKZQkiRrAzjqnawJ1j8FipvjDWIs3lhgz3WJJDCP94UAcY/UtmDjtdSPaowIK27IDp0RN7VD5n0jRREiROO4Jw55xvyP0ey4vzrm6uqU5OgbAo75/CETjMSZgsq1xonQaANniref4+DFdtyHlKwFoxxFSYdEYbXwWX3rY7vXZZH7xi0+IybC7veH26oLD3Z7z87fENPJtI0XMxjd426ievOfuSsgHjfPsY8b6lrFtIAeMiYiqgSHFERmKqehVHOj7gbZpaLslWENsG1zbsTnZsF4/o21XYD2rpiXrwCjvW/pewOwJEMmi4YbWyzLECK6x6j9kI3jfsFkc4Zo1gdLaqgXAFBnzCM5gmxVNsyAMAVKiaWT/tE1HWliu9z3HzYocDTFYwmgYD6PGPolXr97w9vUlf/Qvfp/lcsP1zTX7IWCs4267Z7layt7AUKSwTBaWnyo2oiRwwFSGTRm+a9RmF7Zl1y7w3nNzdcHKOaJzfPQv/zkf/OQ/5v/5sz+Duy2HoSf3A3kMpAwbDNF7NsfH2PMrFss1u/GWNEZyYzAxQhTJHasF6mQcRrvXkhG2kTEyDWHUgSSNyUj/rSH0iWQNwxjJEUIKEEbOv/yKd45Pyc6QnKnxiUkgmkgQxsB2dyN33omsRLKBEAdSDDp7QBLSMQlhAU3k0TPXtUuGYWAYBy3cOkKKnL19Kwxa59jvD3IekwDKMQyS6KZMykHDMjPF2kbagLMXsPSw31dnY5jiLoshhYFsDKOFi3zg//7Vz/ibLz/h8fEJT48fs+42ONdy6Pf8+vIt4/vvMjx7RE4Ob8Tub3e3oLFDCmNNCgqYKT7dAVL0LSCW+NMJsJjngv1+rx2ZU7dPu1pwOIwVCCkxvgyuyxqPRq6vL/FOGLpGP38CJLPmsdqJZvTZUUgfYnlk0I7EB95pbmWt5lRKXDFWBi15h1NCgrUioSQ6o06/X55HKTxPuV8h7QjAU3VeUz1N5JwYBombnZFhWGXYE0X7Gs2VS+yEU6diKtsWtTnkKTa3xhGiqPo6Y3RfZ2Gr20kbtWkb0jhQYkHxX7I2TnXccRPbu+ZZsxhv/t+HoOpDgsb8798HwM5//jC+K3tPfKVlHMYq5bVYLLQbVgAewQckL3LWIZyJ+dAvIUGJDS85OZVRaYr0AxMAbp0MjptkDQo5qLAh5bkMQ18JOlKdLJ+RpuFNOkAqp8T+INIIO8UXKhaiuaSWzCAJc/wwDGSk260O9NX8ZrFYiP0KYy2ezp9nasqwOQE2RapBTk7MiTCWjuxJmq2SrbIQ42IS7fdMrmdCdP4dnQKXOU3D12TQn9iyxjcwUsG8MYyMMdR7KK+yjwtAWYFn7RCQdfKCdeRAGMcKgGZNGrq20X3sCXHkcNdXCZmJgFa6eUUOUoZHyvU5K3OQnDNgO1KIhCiDncvAR2sdjeYQJW+RokmZCyWsW7Hf2l2k9jylTLaRrlt8Z++LJILBOCdxIpmUHRiEaKj2sW0aAYPHkTFnXNtKh7kzeNdgFpauidVGpiQD5iQecaQcGdT/FUlOq3hg69pqw/tDj0GYvcUnG8AU5q/KRAyDEFecNfgk6xVSkGHVw45RGdKl+8pojNq2ncSDYy920zUVU3N2Guj+fa/fapA2o+1LaryjAkI5Zx2UYUWjNQkAVSotxghjNKWoNGphB3ontG1rBZgp7QIo0GatEd2zmtRMmpVJgwmniP49Y2xEV6Pq0CIVoxBH/Zkye03Z3BmI9fCUADFowlOC4c4a3nv6Di+fPiWlkZhGdvsbPv/qV2yHG8xG25ytI5nCDkjKwsoU5HhuBJ0TVnHKE6o/gT9JpzfqNEdtWaoAoCJlDx1T/ZktdfZSgZsMUf2dbPUwRZwzWDO111SpB1mSynJMOeFMuc65Pqc6EmfrczWqTSe6WjPoQRZGnYSCsOXejVQ0chZwJ5UASH+3BBwStNRROWLU1clUgFaTGeedyiVMb58cn6VOwFUHCG72XsME1JbnMe39+5pnrhr6eZAwSQdMwGVxitNdla+bABoM1dDXoCRP4BI5q8zBtG8yxfAxsdr1+ZRqWdWUstT3W2PJNmklNdbJmGnGMpaCQmEd5LqezPZjeU5lPxanm+s9K+CmnynX4fBeAMrTkxP2+32tolbHlh4EUjnXpcmgukpmeo6zvT7/ewH6yrOYO+i6b8reUHsTQsB7x9FmA8aw3W6FUZKZNNyiaodao4CoOJgYJ8YaKVMIMsYYxhT56uJMksJG7aV+p7CdZa28BuVFk6ofepKRKvpmLTqG0zCpXOVQyv06JyLtTvWbhr4nzhgj1gqDo2k8xrZTq3zWNkYjQFJjHTlEfNPw3ssXfP7FFxU8MMbx9Mljzs7OpvOYpor1XEOpBJsVjDamPmMpDOne0qDrYXj90ObPiw9XV1f15zGlyvyo+4FS6Jj2RDm79YxpUaOcyzCWwTkTK/7evtLPGcbx3lkt9wV6jsv1q3xIjqEGv5hpX1a7kKkJ8XwvF05VKbQYI8M4sz47+eEEGFZAWf1As16Qxg2H/SUuZ7y14By3YcAMgM/EMHLcetpsaV2iDXvOLs44v7wAE9lfvuLv/jryo5/+GN9F9odrTk6fsL29xTjRmfvm9bfkmNhs1mCkah5D4vr6lsZZHj9+xO3tLegZiynhgDj0vPr8M46PNzx7/i62bTAm8ZtPfsnZ6294993nHB+t+PyzL+jahscnp5yfn9OPPS/feY+m7fj6s8+5u7ji6ZMnLJcLvvjiS7Dw4uVLdocd37z5lhfPnvHO02d8/tU33Fzv+b1/+hEvTo/41a8/5Wq/53c+fp9s4Gd/9xvuDgM//uFzvjnf8uZqi0Hb34od0/VJMRJNJFk4evKI5ZNThlSzWiLgUqoT61OKmGTJyXDy+DnHp0+wfklMMrQzjKEOs+j7oRZeC7hqsPdiJ6dDNUpAWuyjvEE1q02WcMAUPyAnwlkH1nJy+qRKUaGyBsaUWEneW2KrlAqT3WiuLx0vKDgrXUEFoB0Ydtfsby/ZXl9w+fYVv/mHX9P3gc2TVs9epu26e+BJTFFsn7HEXLTNpC19uVxOLbki4k8fgnQfOc9isSYCy+UR+8OIBe62lxib+dHHH9E28M1Xn3N59oa7mwuMMzgvDLi2W7BYrlmvN4Bhv7sjxkEYfniMa3DO0rWW5cIBI76RInTVcscSA+SYuLkb2XnR0+26zOZ4xWLZ0XjHMGzBHHC+w7qGMEIcD/T9Qf3MkuVqI0l1GIk5aCdRi3WZFAdyClgrQIx3MPQHTEjYxQrnvEiTOYONDusyIQCLNevNKc63ZA6EmFiuj1ksVmzvztgPI/t+oGk7YjDcXvfYbFkftYz7WzAB08pEcYBhDDV22R32+K4R+YqSjGLACHuyFIXzbJMWW1c6d8rgMJIAz23bYbIl3t2yNIbkWvbdhsWPfkxzfsXz5ZLTRxvOP/uSL3/5D/zon/0hm87zzVdfc7xcMTSeO5NFGzoEohMwEuPoU8LlTGusxHh6GYapOy8n6dTKzhCI9Ic9XStT22OI3F7fcP7mjGbRYcPI9uKtgHyNI1qmDzTSHUUW+ZHDcJAYQqZwYVIiGGk/RfVXRzKHMDIEyz4csF7lPYzhsDd1+FvUoizGaryWiCFpMTUhkLPG7EkZotptdi8/wJCajsZZUhwYBwV51ScVV2ONgTiIRjKW5CPXeeRy7PnizTXd2de0OsgmpIA7PuG4eUEYewWWXNV4rXGYNQp6lOFe8u9BW8BTjIRRhkwZEDAAKVjIZ4htjXHS1y+dSY9OT3n1+jXDUADtwqQzxDD58P6w55DF1pV4dcLw1Ifnafh1CQlCEOAxhBEMMvRZIAgS0pkjZCCQgXcep7IfZYhvTpHlcsn27q5+bimKt22LbzxRwXYDwjg2BTjWYrTa09pFlw0p5AoYpZh09lxUmz0BWpp8SJyhOVXJRyVHR9mOKh2YSjEsVZkTcmGnS/xRSDoFcLsXj2dh+Q6HgxTrjeTGBTgsrzm5Zv6aF7D/Qz/7PuB2/nlTDKbrrvvcWQHplotFbeW31inAqNJTWbAEic2mPSvDCbWgqs805kxrylArKaKU3EOuyVaA9t59GPk3cokCISk+EFOSXFfzQ6uDgEmhMlFTlmK9SFl4cogUbfU5kOhKN12QQVi+DEeMAi6X8wbQNF7Au1m3WqMSYzFFDHnKA7Mw8f1sHcvwameKvjzVrpW9m5LIEphWBoCCSLaVYeFy7kpRwyNqZVYZ9BLLNG1XGdDzuL+s+zx/TzmTreAZMQScB4yhcS055crStKbBOggxSe1eu31TTuwPB0zBwjRe87rO3vs6MC6EgZxUWsBbFouEIzOMA2MMaktilbYQprWA+PJdCozmQqaTQk7TtCJ3M8owunKe5rKPBfienwNrjMpToTmcSPuElGi7lmw9pnG0batYjwywk5kBTbW3xQYZI0PPHJZ21Uw5txYcx6jasNr90fqGOI4yc0htSGMdvpWBr6W4MY4jOSWazgsJL4pMZoqRMbS6J8ZKKm18g3cNKWe2h712GiaIgk12XYPHY2c6vg9fv9UgbQEaCtQocZjS9nPGZQOxVBjz7DCIY3NGggFXPFHMNRkNIag0gCaTZgZEUSoBUnGfJ8HfB7qIkaH+Xk6l0lP0lkrmIhfmyvRTdCqoAfVAoOASMXLkPL/38Y84XR+x63v2+1venn3Fp59+AjYLA8GiSLw4X+ecGkArsgQoUKSgWCKpk5UHUdpkKnNS72c+yKi8vq+KWNaptuXID+797hzQKCy2pla8pord9wEg9btmQGl5T3UuGWXopDrxtWic3FszTQJTjDUwyFFbwRX0M2rApQpS1tlRWCo1YMozw859cK6yTxAj3njDZrOpjLvpXgt04xBZB4toGt9n5lbHx5yJe78F42HVFzMZwIcgzveBhfNr/76ApOqpagLjtapb2K7z901nYgYCIQ4saxZvtD0hZ8i5gHOFqV6YUt8XFOUH/73/qgFVCerUkUx60NKSUMFcMweRJwB03o5V97iZJCVmiFutztnveW5zu/HwGh+u2/x+Qorc7Xayh0rbmbWqFzn7XSOAwtHRmhBinZiMVtGLAxR2rYiXZ+sEGHDiwK1Hg3up6PlGWvur9MB+LwFvjLh2ajup1w74xjMM0sVQWHgF9AbYbrcz8HTGPJn9rLxi0KQ7JzbrDcu25XZ7x83NjQREGqyllKpmarUvRq8oSauqUf1VreFPAYcy5A3zqczynqbxtWI6b3t8WCD5TrGKmV2Y2a/5/ebZvpoHafPzWPf3LFEwTIBvAees2qyimVuY++MwiJ+Zsbkb7ymSP8qr0uzvvn14mFDUf0OKM5npXgtb6N4eN6aeXAMVvMN7lo+OSbue4fIGb6TteCRzE3tZK9+wXm1YHZ/QAMebEy5vrrDGsVm2XFxfcPmrc8b4IYtHGzb+FJNH3v3wBZcXT/j5X/01McNms6nsmH5/4Or6Bmc96/VaJurO9rbzDptFEzPFTDsmVsZztztwfX3O9eUl7718wePTU77+9FMsmSePn/Lt2TcYY/jwBx8QYubXv/w1u+sbPv7gPcYY+PLLr1gul7zzzjvc3Nxw9vaCZ0+esN5s+Ptf/opxCPzhT3+Hrsv8/S9/hcHyT3/nY652N3zy2SuS9fyzP/iYhWu4fHPDyaphO47EEGSIlT5/ogxIom04eucxpy+ecXDCejaSneObFsZDBaCKnh/WcbQ5UdDE4nyLbx125aTDR4P/ECKlOCp6apK8pBjIKdAfJGErurN1w+pemffcSPcComcaI963Op3aqL8syZ2Cu6UoXvcoynIpTCuRNhCWXhBbNx4Y4wFDZtjt2N2eM+yv2d6d8+qrz/jkk0/JzmI7SQJ84zk6OuJw6OXeUpbuJGeIOcoEagNN4+g6h3MTC2kYB7zGJiknukUnhbIQub29IyVoFy3GOtXj9Hhvubu9ZLe/BPYsF8cY12B9hzFOJ2fvISX22xtSHGnbBa7J2l4aGIZIGAEz0jaBxkX8aoExViUU5JyPw4H9fhBGiFkxDIE7ttzcHggh4RtL03SEmGkbGTAyDgcyjtEusTzB+wUxHUg5EVLgsE/4dsF46CX2dI6MZRgC2/1emEFRIKJFu8A3HoNntV7J8LZ+5PL8W7b9Ae8zNlk23RE324Gb7cDJo6f0wzVnl+dcX+05e3POB+99SNMtOD87sFq3nJy8x/HpEX3fE8YDR5sNR5s1d3dbiSO0j8xqDGeNDN0bFCSyFmw2qiuovqGCS6nGJNlAs1zS40j7kcaCt4az33zOF3/7t8T9lm2G1ZNT/snv/S7bnBmfP+c8BZoPLPnxY667Fv/DD+luD7z+/Ete/vQn7LZ7FtZx6HeY9YLd5S3h+hI7yvkyWA4xSrdRSjSaxwQy28MAbi8DYbwlO8shDoTtSBsDu+sr0tCzWB4x7m9l4Gekdg1hEs5bTo5POQx7xjTiM3jrCUT2vbRejjYzpsiQIv04EEwiBVAoi93urjgmARNaAcdTJZqo/02qOzgfxMlUFDZ5aqvOwJgGbrY3Iu/lJZ8qhIca3hpEK/jxCbvbt7TOEkzCZpHlGHLkkAYaLxqFy+MOlp6UAzYaARs1Ti8Aa87SEZhmsVjTNJXlJiBjqJIMMo295ARaIJn590blVEIY+eqrr+j7XsFFsRXS8alAnU6Tl7hB2LYyVA4dkgWT7vfE9J5iBMlBXeP136Z4JaeE8wKwPH70mIvLS/phZAj676DD3lJlRJd4KSVhNPbDnpiaeyCg1Zx23oZuZXtNcbNFC8KF8KGkFMVlpbu0SFdJni7PXot5Ct5kI+ez6BbnMBv6TSaOaQKtswB8uRAHdHmKz5/IBRIDOyvDS3FSRCEXktc0D+JhjDfPp+avfyxHnr/mn/ePAb9jP2DMirZtSSmy3+/rfvTOk2JWaYdA1tkzKSctMNh6UEosXq+zdCrO8tj6neMgLFmj0n4qX0ieZD8kXxKotuR3YQzCnNX7scqSdAqyeuvx2hpvjQFbBjTen1VioF5rIUyFMWBbV/eYSKWJnIAxQhoppASnSFFjPZOcoGIBxtbOyJwz0cR6dkrsXfZSU7RZyYRhrDJ95Vk5Y8EK0co5Oat939O2D2QEE+rvfdWgnWMSZVYGqBxcKXIASdvlRYPYsFh0miMnxiEwhqFqsha91jKYMYeoMg+6/5No41pjVMIAwTOiWPIQAsMw0OgzaF0nw7qCSADE0untdQ2rFKAwn0v+LB2qckYLSUrOXag5TmEIlyMfw1jZp5Zpho+zTqTuQOUOnGiSB9XRNgmKb3/QrVWeZ7HrJQ82FLwLFgqeT3mUxXeyX4YYxA5hyEGGHDor3Redl8GYGem+tr6hcV7ttgy3K7Y3pECOmaZppQBojc4gEFlPsaFKlPyOlZhev9UgLXAP/KhgYLHnSrcW1qi8/yHYIYxKVxeqniF1TuV3ok7jzkaBOv2/Oag1B2+MMfXgWU16k9KfKdccC6iYNWuVajlmMt7qU2pAU1qJHY4Xp+/w0x/9Hq1fcrc/MI49r19/xevXrzFJhoqRM0bbxSpojAqu66EzBaC00tpVDJC0xCsrVTOplMB7q9M3J4CiPs+Zg2L2/ChtFspoYEZZT3WdihMymAe7ct4eLh8K2cnzsOrY62Gb7YeSON77fTP/3hnge+/jzVQR1uWRZTLqmCagpA6Tmx32AkTMQTwo0hcyvdJaS9ZK9PHxMYfDoeo83n+OkhTUFs36fO4DP/Pfm0tOlJ/NQceyd4sB/T4glroDH4JMcsAeAjYUUHCmFTsHwx9+9kMQSwzqFPwJQMR3gKo5AH//+U6M7YfP5bv3cH9vlTstgxbm13Zzc1OfXyn03APW8owZoH+3k8HRZ6FMrwfn4yEIOxUrvvu+h+vctm3V+5rfV0ql2q/V2saTYqTv++kzciRlOxW5jATLCUdWMrhDnI53lrtxhBBxTcPTp0+5ub4mJRGHX+jkz8PQqz5bV5MXKeY4TJIgqWhXpSADIopkpZWFuPcM5blOLICyVk3bMqrUQQiB7uiIq5trLs4v6l4pQ/kengWjiY3S9mQfp1LNrZGpgJhOmCfGGGmNmQGlTVMq3LHu2dogO/MH83uZrx1Qg7OaKOh+KYUKmMT15bInO1OC0RJoTFE1977nob8rz+c7ZyFLZ4LJYoezJlgPk5Diz+ZfVIN6U0y7+pPyjPMsWZz54gk4V5DXe9ZPHmFTpr+7o0Ovx0DqGk5evEvOhj5nbEpAwLrI3faWu9uR4bAHZ/nq81/z8nd+zOr0Hf7i3/0p7737jNWy49HTJ3zw4fsMfWR3t2PYb7m5vqZrRLdzGIZ76yStcKpNrgHyeHfH15/9ErdssC7z0Q9e4kzHt2dvwRmONkdc3lwRU+L9995n6Hu++uIV25st7714ToyRy4sLnr3zlKOjIy4ur7i8vuXlyxe0jePi/IzHj1a8++I5aQx88ssvcG3H+x+8x8XNLZ98+jXNesUf/O6H5GHkV//wBR++e0xzdMyf//WvGFImE2Xwgl579pajd55w/PwpgyZYLktbXOMaYRJm1bEFSV5VlqNbrqoWs8mWVIJT3aOFpdT6TnXLpgEQqSTcVux50RXLUQa4CdMmEtRH5yRBdsqaAGbEdljHMAyM48ibb9+w6DoWiyUAi25Br/9mnGWxWNIfBozzrJZLZNiDIYbEOAZWyxWZjHMyNTpjOfKweP6COG7ph0gwDrvqSE3xKQjrQxPMVPdDwvqGbD0CGGS6zuOdURZWFHCFWHWCnbfEPNKPPY4FZdL8arnh/fd/wHK5xmTDdnvDGHtc61mdnLI5ekQ/BC0OiWzX/oSo78gAACAASURBVPaOw/5O7hEdMtI23N3d0h8O+KbBOoO1Pc4MLBeOtm0YU6TxHYvFiiEm+n7EOct6teD8fEfTZCKJu9stR0cbvPMcDj2rxRIsxNhr8gfeLzg5PsW1DcY6DB5yizkk5LYzi5Un5pG3Z6/Z9Vs5/hnGmDgPSQqGNrFYLHSfNRgihzGwaTdcXd/iFyNjSLhmxWLZcrO/5PztGZcXd8Q+sV607O/uSCFwfHTMcrkAEiENxCiSOdYaVusNi8VS5MFSxlkFoDIMIRJUxqY4Jqt+lHRf3soYo/Fyxi9bDiYxjJG1aWhI3Hz5G372J1+TlwsO3Yrzv13x/MVLttst/sOPsMslh3TLYMGcnvD+xz+h/+aCv3t9wb/4V/85RycnfPqzv2A4/5bf+Vf/nP6m58/+1/+NH3/0Q958/Yr97R3XV9f86Cc/4frmmstP/oG2l8Fn2YF79hiwxN2WR6sl9tEJdkyYqzty33O4uWa1PlLgUxJqq8Xv/4+6N/u1JMvO+357iIhzzp1yHipr6ondzWZbbJKtpkTSJCWIAmjCerBhGYaeDBmCAcvQv+IHy4D9ZsM2YMMWLNoyQUGkJLZIDSTVA5vVXd01Z+V4M/NOZ4rYgx/W2jvi3Mz2c+sUsirr3nNOROxh7bW+9a1vpSxJiG42Izlt2lfOCGMgRnzbYHPGZLH1QxiIjkl1YakQKRV56ovnWLvHjwm+8RwZu1gbSqM0oPp02he7slzr74rd1jM8IxWW7uoh8fmC9cUFrclEY8Cje9gwpMzi8CpX77xOxI3lrtZhTMLrXMeUZD/n0Tez1qr+s2MY+nokpiBrRdirxU/WJqFxbFKUUwEdCohRmm9GlW3JCtIYttuS0B7P5BCkkqCdNcLq08ZbGkJJ/Lbjv1vSEHbO7vK7MET2DufcvXuHF6enEqtSfBf5fQgDm81K7O5shnOebb9Rd8kwDKHOl7MiJweJ1ndq+wVMtcXlKP5wtmDGGMRZKyXgpkhQlTWSxUmt60b+CVXPXPQdZR0ARsD2shZzzJDFhx/CACZX1nKRvNrxy3OuhKZuNmPlTI2VX+VDvTLuvfR6VbL+x33mVSCvrJtU5c2KVmaMG3IWPdrZbKYVi26MVawR0EjX4ZRMME3CjxfRBs4T8Gx630AFsy2Wtu20sVUrYC1jP4/S2EmAVKsSHkaY9eoOSsMxjaOgNuee3I6QQPLYm8MoGSYMscZuxmofojDuUackpqHvJ0QaKgA6GXBKIWzRfi3rcZTRUDukmEIB7I0xGjMU3WS5awFqC3gte68kk40B74UA0rZtJS6UcZ3GgYWEk9QOFbC6VFuXJAxGEug+FkyLmuxJOTPrOmwnJLshBjICZLvyxwk5wg+SmBdtayHXCFFvrH4M/SDSGt5X2130owUglnUzBZ6ncW7BCwqBUuQbfJXKCClgXYMrxCkr/qo1lqA4S4gDMYhcSUwZF5w0x7UGshmxv5zxVnX9J2s/kcCKfF1KIyO4bdxknqSiO+eoGsDyfdZIBWIKiWgKia5IE5R4JzGkIFKgucjPyZWd9VVqKMZM23Q0bWkWKmB/ioGcd3sNXX79xIO0Q+oJfaDrOowV30pANT3Q1MiYooFSAocCdDlX8DY9DESaoPFekh1RSgidCtyj2bcpsFMaq7xqMeacZRHHJCVx1mB2SvgVKCiL3FKZfJLto2rHGmUSeutobcNXf+bnef2Ntxmi6Lo8PX7Od77/Z7w4P8EfzcnZ0npheaIgVskAOiMNxMhQtnmOCetE0waoYHFh05YFm3WsXpWZ2CmdhwoCGpWXyFYAYqcaP1LOT/2OImi/Gyw7im6s/E63gDEKXIwg3Q67TA1doaJLpmmk0Ts3glvlukYZoTFEAR2saBORRiBlCr4Y1HHNSJn/BGAvP8fugm1TULscOI8ePdoBHses2vgsBcCu1zbmpe8r7y3r8zJbr35u10/bAWKm/5U5t0ymQxz6gkHqaaPQeh2TAsLLXnzVdUbWbP15RpMYTJ41XxqPXbB3F3Advb+iYzXNpO3sTQp4im7pRIovPz9GGLKoQc5op8bMS/cDsmdLaUp5AjMB00y5P/PyPBaH6OVXYaCNyYucTWX9le+pmT8rnTgP9w94/uwZOaXarbMAibJXVJdKy9osBjt1VjPilE/A5RgCz4+P2arYes65gr+lBOb8/HxnbgxiI0tH1HFmqXNgys41U8Be7EEI/c78xxRVJ9Cy2fQ8f3FKTOB8I/uvHmiZUWNa7VGcXK9I3uwwVKnnhACwY2dO55x0U86ldHEahE2vOXYBnQaadZXqXJUOvEHLcvTK9ft2zxMdF42Wy/slZo7VAS6fn15rCsxevpdpssF7y2ZTmBLatIzdIKR+Pu/qZhUPM0/WSrnS9JrGSnl42asl2MJo2eW8o7lxxDYN9OdrKbsOkfPthu99/CF7xnIQDTd8w9HJc5ITAJFhEDvfQGst/XnPZ3/xZzk/jfyz3/1tmrxiMbMs9vaZ71/h5MUJm5MTrh7ssbe/IGPYbLY745azsI6dUUa5tUQS64szrh/eoJk3XJxd8OzkBbPFHtev3+D87Jyu7bhyeMjq/JzHj56w3fS88dodyJlHT55y/cY1Dg4PePz4Kav1hrffeoM+Djx88pA3X7vLG3fv8Pz4GR98dJ/ZfMHNm9d48vQZHz54yo3rV/jyl97i+Pg5n95/zJ3b19g72ONHnzzh6t6cdR9ZbreEol3ZNHRX9umuHJKclGDFJECJcw2UpMdqMwJSRppp+qZhvljIqjQKbGTAaNibI9J4KzGESOkjV+V6jFFtcCsMeu9FP9pC2wmDPeVcg62cMzmVcj8FaYpTq+v8jbc+KwCwSi056ymJ0pgTTdPWcrTCpM0UwFRtVBRpqBQHhs2aOFzQDxts39EtbmKsx3UW4zscsj/G5Jw2g7AWkyMxBIKWhKehx3tL1wm9L6ekrDgJpEW2QKSXxi7JHZA5XZ6xt3fAfLbPi2cn0lAxJfYW17CuIyVIcWCzPmW7PScF0cfDSsC5Wp8SU2a5fiGMIGsJmzVDjFiTaVvDerumaYRF1jZgzIxtD+cXW46uHLFcZ45frJgvHPO9BcvtGbiN2LHYE9JWA0UIoVf7c85mOMXYlpQM5IbF/Bpde4h3Lc4Y1ttzMInGSkIgk+i8l8QXA2HIWDIxbglDIGftYG3EvicMz09O8N4xhDUX51tiD9tVYHl2wa3r18hhxWZ1Tts0bGKgTzCISDGGxHJ5jnMtb751RxlAW0Ic5FmiBKIh5FppYU2u55ZgtAnTjLayaEFma9jbO2S9WZEzONcwkLjxuc8y2z/kkx/+ELM9Y7k648OTF3Rtx/f+yT/m4Ogm+/ueD58/pnUdKQQW14/Yv7LPn//pH/O5r/w07/zgHW7duI7Z38O1h3DzNp//jb/G7ZMTvv2Hf8TZ93/Ak9bz5V/9Fd5rWrpN4MmTJ3zpG7/AtTdeZ887/vybf8jh25/h2udfZ1iuefrkOawHVqcv2Lt1h2wsQ7T4pIq8VcdaSRROfp77CNmpXJcSIhDQ1LctbWukFBcwSeVzzKiJnrPEVTlJZ+0YI6bsfUafdxiGyoqrTqbandEnVG9Tz5saX5AxSPWgaPga/GzB1bv3uHj4gFiYvSRyiGAds8Or3Hnr89iDa6wztCZXeacCrBo9J7PaznI2hBhZrtZV/sigxBXd+0HPeJDGRwWQLhV/mTzJWZaYooCV6qs0ntJY0ejZn4tDirC6N+uVlOFqbORUxiGmUMc1xoS1hcwyjmsqpCYyJ6fnvPP9H7DZ9kTQcne9JkYBoFHPU2yidLGfzmEZsxgDJNjk0nAoSyWj2r5SfVPnVWOnQtoRoLn4w2P8WmMElPhQ4yZZAUZjXGtLZWjWOVApE7WPqVTLTMrLRx9QPxOi2HkyqA6vMH3NTmDzKh9v+vNXxWmv+txlKYFdAJe6UgpoKU0ngxKRjCZKk565rjJtM8UntXUdWlMa9g2TG8jqk4YKOlorfTq895Rq3KS+UbkhYy3WieSAMQYHIkdgLZ3GCLE07EoiA0hpTmedeq62NugqSfGpFIAzpsooeO/I+jvHhLSjQO1m24++JaOEQBiCErfGZnbOKBPXgImh+hC16VgSiaQyL2MTKy3PN4WN7tj2oqmdARNlbQ/DiDvlLMlaqyDwMEjycRpHVP9C52cqf2IYdZ/H9VriAMG1yKOCqVQLitTDthe9065pJemg5fWNSmQJHpXpWo9zM1IUkoq1Ddb6WsHonOiCB+slQaBVQiKZouQauXg14aLNGutYyb4ToNYbo1VEk8aAWRjP1jla55k1rST4NIFV/HHvLYOzrNdrCkgac8ZoTyI7GbuozNtiY0ojy5jiDokgxkjTyufattMNF+j7DTEn+mHAGses7RiGHt8onqf4hTyL+gmuqbiSkDLBNSKXk7LIeaWg9+LkDBuGAWcs0Ri8k9Sp+3cZpDXG4RpDH4KWb6LgnQQAonk1Gl0YMxTWTw58a+vBKpOax4NCvlKNn1HQrTSfkYA2TbJr3rt6eGSyagrVOJba3dIY1Q2RkgpMZAjSBKCAO86KNlCIAWdEY7c1Dbeu3uJrX/sFjLcslxecnZ9w//6nvPP+OwQXaDoL3kozpyLIzYQFYAqTVQHFckgmCXwKkOC043ki0TYNIUlwFNVpuMxSnQK1BSyy1tL3g4IySilH/2eioyeGKk3mKdYMi+jRjI5azrmeWgKIZZW4Lc+RtXOpvqeCxWNZpMyreHoVWFEjacs92THTb6wmaPO4KHYAGjMFGRX6noB5BYiUOKCMvqljXZhbpgSvBawq5acaJJZs8fR76/ebMfNfjT5ZhbNLWUoRbZ8wFXS9FXCTYiwr2KYAoTpVtXOqLQ3bTGWhSq2C7DnhCTD5nnI1qjM1Hb8i2g1lLF8GYy8nQmSP5nFOytLS6+7aC1OdyKl+ZgFVLycYyLvAmdU1OuJMeecy5SCYShuY4nzqoitrroDpl8G4Eeii/j/qHE4B81clhKagrUgziEZX07WvGO/CitObdBI6HO0dCOPv/Ext0Mh6z0CvnV+B6kDI5BUW8CjjUm2NKZ8eS56clQ7x4/36uk/LS7LKxR7LjpGlVxpqZNbbXicgMy4DO2E+lzEdy71iiszns6o/Cip9oZpEqTrvhlnXMJ/NMcbw9Pjp5NnGRMMUSJ2WyEpSyOzMUcnM98qCngZvtWnYZLzKGp2u8ZqBTZHZfK5aSC9XMZSx3QFKdaym6wgywzDpqMx030z2v3xgbJZ5ia0/TUhMn2BH3oHyvKNTKohbJnmD35+zGA5Zb3r6bQRj6UMgGsPWGPpocRhMP3DrxhWsMRw/foLrWq7fus3Z6Yr12Zr3fvgRX//l3+Dxw8d8+J0/JC4veHG+4bi7YLY35+qta3QY+u1QA8TZbMam3wKGxgsrJIVYgzt5Roc1jjt37vDx5iPuvX6V+WKf4+PHLC8uuHn9hjR9Oj6GmLh39zbr9ZbVcsntu7dZzGd8+uAhISbuvX6PmBIPHz5kf3/OYj7ngw/u8+jhE27fvsbh1SMePnrKg+NT3njtFp9/+y4nT455+OCYO3dv03rLO+98jN+f8dWvfJYfvv+Q5cM1zhrmB3PaK1eZXz2CeSeNRIIGu1Y1IknYpsE4U8+YnAWE9d6wWMzKgaVBtZzZ5EzWyg5DnqxZCc77oWcxmxH6ntPzC7r5nP39A9HHzYZotVLJIF1tozBdnfN42lrJFPuBMAQpibfgGtGGTUig05fO8b7BmyzqVrq+4hDr2W6KnlxM5CRnVM5GewlIp+s+ZaL6ce1sjrHiYHsnRWcGqaTyzuMNDDmPrEBd313XYJ2lDz0hSlmf4FCqG2o8KRga3xGSYT7bx3nH6emFMIJS6Wa8BZKWbVpWF6dsNxeEfkXYXrDe9GQkwG28ViiYREwDbdvgvJTE2jxg8ORkMC7TNo6udfT9mtUShpDZrLdYd65dwaW099adNzF2D2sD/XbFZp14/OwZbduxv38IrsU6WC2XnJxdIBQky3y2Rzc7pFs4tusVmxBIQc7DtvW0Tcd22NRx79qFBN9pw3bTK/swEFOg7Townq5rGMKW1bZnvTzn5rXrLBaH7O1tOG0vaFvPNqzBJRrfMZiMcZbN0GNzBJMpjZW89wJuK9Qh3ecVrDJW9NmNzlnMtQpubPKUX7KM3jd420qTYjLJtRx87ov82n/6t/jf/v5/y5PvfIuf/+u/zrxZ8J1//k0O9makfsvVg2uksGZ9dsq//N3fJWzXLLaJkxcv+LOPPmQ2DMy6Bc+//Q4Xm4A9O+PD73wX33VsX1xwY7bP5+7egyGxznBw4yo29LTXb/BsuSYsZsxu3cAsFjw8PeXmwRX8Yp/t0xPOXrzgrtHEpm/JfZTyeKO6qUlYmjFGYoiSrNAnxHuyc8TQkyxk73Eu4y1456TcWsFG66QJZYz6HZ5a5VL878s+eGH+GesqaImhsjvHM6awdovfW+I8owxSYU8dHlzhoOtYnjxTDecBlzPzgyOu3LwLB1fYor6xgZyjnlFaieisBM1Q7UONPRLEypAb+1iUIy3qmVGe1UpgOsYeWjJezlOjZddGdYL7fqtgkjZlU7+g+FnWGgUZxtJzCgmJkfmtEt9lNQtAXBLymkBPGS7WW3m2ch31MZu2Ye5mpCzNdAs7L+de7rVei2rDjBVN4qja/t43CrSMeyhrbGI0lqiMRfVtynxS/p1zfRbRlBUgPDOSpVLKY/8Sa4XxLZZYS7wL89FCJSvl6mxnhA0t1xrBWOstQRnclhEAnPo/5fXjgdaRWDP12S/7bGU8p0SQglVYUykNNYZwzrFY7OnecbXBm/SNUb/SWlKcEEsmn6/zp9rO3jc1dm6aRkHahsa39f47LQmPMVTm92a9kvWsYK6xY4yD+uChgFY6vtk6cigJDkn8FDmjGGKNSSNSgVeqcYs/5o0X6QQdx5giIQ6QM30/VEZv45vqhxZcojSEi1nK92OMdOr/SyJY147624PGPmUMKsbhrMibxLGiOsSB4jfL84u2fDmDyr3KPh7nwGlCqHxPrcozo+arMdSkVs5J5Oh0Vq1xCsqbqqUfwkA/DARt+Nz4BtcIazUqMFni/rGS1KnMiTB+m2YkwSQFHCma7kkY0s5rc8Gcarxb1mnjfY3PXBl7I+urjGeMpbldHuNvJcrNnPQICMOAKYxs74UAYBSq1Cr1mHqKhrL3UtWJF6BZ1nwBUYXwaAxsNtuaRExWxsJ5YRjnLBUOod9W4DYbVIc71uca4oAJQYidzglB00jj5xSS7JWNsHe9dXrvYlfyIPJY/TCoVq3De0fjHIGxcuTy6ycfpEUGMQxbnHVV24HSAKAEGClOqOdFG7UEJRKgpywlUMaijqNKDyQ5NMfNxg5IB2OprCFjvZXud9ZJ9lgD4pRTpdFLB1NqcJ6ilJhttn2VQbDGiOjwICzclCMuWuau42tf/Pd4+/W3WC3XnD5/zpNHD3n3vR9x/OwY11qsR0ATPWytHkwxoWB2KXmv/WxV32c8YMoBXzrMCYhmpAu3go1jM7aRCTg1/DFG+mFL6VJVmZcV6CvB71SrdGSAjuVPo2NtFASVBl6ZlAtwq3phqi1bdEYFS3uZ0bbLdlRgIRd2s7xq4xGd3SLajpVnMUbYVaAOWGXNFgBCs83e1+ct0ak0WDHVycnkejCqvRxLgfVQEn3a3QO9Pldhj2qZU2ZsLiHOhyVZNFs6suKmAPL49wLUGGJZ8JnaUAgFlLMxpCyHadN4wkSuQ4dzd8wrADcCpCPAI2tch7oG/RUgnYD/O85LOdhHFEkd0XpGjPOZd1nwRZlBHP1dkLPszTKXEkioA2jGOR7vozCrp3OUayk/ChqO1x2fQa4nbBV5vqjP6nRvyKDI26WM7Mc5d8aIDMDDhw9VT6c8d9knWQIgVBS/PFtIuGw4OjhkuVypebRVhqDso9IpszDUC/D/mbc/y6efPmCjmnUFHJ3eZ8kg1q681b6ayXeNzE/Rkyrzqk6qtZXtkhX8MMYQY1CnOmkQQt1/ZWkcHOxx7do1Pv7kE5arJU1pXFZ0iJ10aL16/ToPHz4ikwkhEYfIarXSecj1XqfO1RSwLfdcfP9xDBLOeV5/7XU++OjD0UlHx5pxvipgVoKEKViue89qqTVmEvBO1sF03e/sD1PizHH9lTmDrPphatfseB+F5VKAvKwOs97hzrUVCp7MX72bCjrX9U8uejcyBwf72D5y/uyUrM2VMIZkIHqLWcy5cvMGhMjz5yfEnJi1HV2zx/7RjD57nn76Ic38gL/2W/8R/+fpcy4e/ojWBtYh8PnPv01j4cN33sPGTDZJuscXfVPvRNdOByrnYlMyjXeslktWF0vuvHaX89MLPvrwR2y3W167+xpxCJy8OOFgb59u0XJ6fsH5xYrbN26wP1/w4NNPGcLA1Zs3OVstuTg758rBAW+/fY/jZ8/56P5jXrt9nVu3r/PR/cd8+vyMz33+Hm/ducaHH97n+Nk5r79xm22MvPveA5r9Bfc+c4cnx8c8OzlltrfAzGfMb17BLOZE57EpY3PSoFRO/EzEGyu6bTVQVQkpEgvvmXdSEpiNlXLJ4svUiZbPjcC87D+TE0GDgpSjOuhiY4Tv5MkKHqQUBPAJKuGBAjRJ2XheAIrtekvXdfimk7WANvFEwOO64rJuvLIBJ3Y2FVDCSgl+1oDQ2Y6cV/RpQ3IZ33UkY7DeCwBpRFPPAMYJyzdlg2+9NA5SsGE208YVOQjYo+ylmAKuaWjaPXI2SJMejzUN3gkQ++z5MSFs2Kw3ZALdvCPEwHa7pO+XtM5xfrri+3/+Qx4/O6XPUlY8bxu6RhsWWWla0c1aaVyZElHBq3nXcLg/wxiRw5jN9rhz6zZdN8OkSNcY7t27xXzfcvf2LfYXtzg7f8SzJ5/gTEvXXGVPtV1jTgzDwHzWMm8z0WQygbZpWSw8s1lm6LfksCUZkbDIg3RTNkSGmAk5MZ9f49bNNzk5ecizZ8dIwNwzpA2nT8+YdQtu37qNs4lgDQd7+8xaaS6z2vas+wHXCSNczhMB1USUIhERHXLrHNY3ypgZgIhz4j8alVUZIdhEzEppyFmax1Q/KknpIuoLh0jXNhx0nuwdOYIj8/63v81X/vpv8vW/8R/wDx58yq2v/xIH+4cc+zk/8/M/y7v/9jt84S9/gz/9vd9n6Da8+dY9lmcnxJMl6cUF/elz9tuO9fEz8vMzsoWrQ8+7/+h3CMaR1wFy4ON/8294sd2yffacLZmULe//i3/FW1/5Kc6ebtg8e0q/77l5803S6pzGZBoMsQ+yX6zYukQgpkEOZG3iM4QBGy1t8thsyQlsNrR+rr7EhiEOXMQ1IUdp/Bkzg5XEhjWGMIQasBe/RvxhN1a8pBEYKDqMVhnbOcdR59SKL5rVRyxVeNNzrOz5UhFgnCOnlqZrubJ/wIFWyGHAtS3GNPRqFzAIC8uMUi3GSOVf2zpSLD7U7jmn7rw8B6b2DPG2gGkyzlnXk5nepwJuJhsaL7IFQ2lIphJ7hU2Ixh5yzTT68BklqBR/W65Rm/ikVEkDGYk1K8MZMKpX6awhpFEWyqjN9E6S5znlyiR2Wg0gsdquH6yuMUmTX5CYdXNm8xkhiB9lNEbL5Grzx2FRENrI+ZKzgioKXlcZPidrspT+V018WR36MxmU8v1WY8dCwCmfK35bnsZAJqsfXvBcjc9iwQFy7UnDxJcpz3DZHys/f1USfbqepj97CcTNWRnKnhhKQrHD+6ZWZwg5jFpB17SNMFwxtQ9OIY0YfV/TNJW9KVXEo5+eM8QhEEMkuECRUdAbgixEiFE2TzTvt2FLCKHq3so2Ub9PWbUJR2n0udlslB3cqMa8rUmb8sfPO/EpUpJ4NmViHpirvi1GkrcHi5lUvinbN+fSqA85/72jaVXvnknz6Sz6sSEJW7cQupyz2sipq8SKfrutRAsUaG26RveVNPyLWeQJClPTWFSCSADLxkhTZHIh8ei8aHwj1Uci1RCGgYG+xqKz+VzHPU5iJRjSQB8GZrMO23gKuSPlyBAHzpfnWONlzp0kgMgja7nY25ySyiBYQuiR3jsCDJf3Nk2jlY0igeKdIyozuzT4TilhtNlX00rzrBxlDRTWMEYlrjC6vgreY+racskp2N4JOKpScN4amsVMdHKjxBDOSqNVb6WRpWtacg4MFBLRBLvSP4u5yIQ4Jzrl052bySxmc2azed37OSZtGtZUIlPQJEbWSpyCBTXeQSNVUykGtqU3DBnjLVH7YfmmYYgJq1X0QwhqyycN6S+9fuJB2hIudJ0KZiPAylSCQBiQTtmYI5sypiAoHFZFsI1kNFNSWYICaJgdh2AsFTc1AC9Bb06ZGATEGFR/FlMOGe32izSaMCLFUyP5GIRllY3BJFP1PGTLyyJorefujdt84+vfwJqW09Mly/OeR0+e8J0ffIc+9vj9TgBhazQzXEJlAQSFKWWLd4OUIptqCIuxHQHSkrmVjVlLFNPLB8m0fHZ0MBTk0SxFEXCfZhWnAG/57OXfQwFDRmAnpYiV1hxCCTejlqyAacrGm3SlLAeJ6GPm6viQqcyY8aXPaHahBmutNnAoqk+5OgLjNWRepwyBGCPJQOHnGgVDqo6jjqc1u981PbxF67gkBsasbNHz0aaoZHWgks3CPNMDrBSdFy1d0ZmkNnbJKWk5hhrKS45GBTLslAE9BXH0/Zc/l4ouUQGexvVSxqvOsyng9Mtg8ggojd8vAJbsv+L8l6B9mjioa02dQxm3XEGHjDhBFRBTJ7qUjKHjZOr1xzWKXq+sGVtYxuW9k/VcnPNp2UxBtPf3D1ivL6Qhj4aO5ToyRkUHdVfTasyAyu/29vfYm895/PjRzniV+65MgOIAGkPI8ODRE/lO5wWEv8SWvHJ0BXJmeXGxs0dX6+Wo3Z3LOLyCOVDGsDS60O/ebrf1WE11aAAAIABJREFU/oqm0dSmXJbuCCFUAK0st7Kmy726S4fbarViuVqJNpzq41jNehr9DkvGkWm9ZQgD2+2aWeOV8S8zUrLxU1B5ygKujKDJGi0A5zAMPHj4sDYXwry813eSBSXAVd3wkvXOSMItDLtldK+qbLg8/8Wxm14z59G+6gaqW7gGibp3iyxMtY+T9k87Uiu2rDOz81zee4a0G4DnLAFXBoyzzK9fYUiR88fHuAgN4I1j/3Cf/SvXOFmtCC/OcEg2fnux5cmnT2kWCxbXrnD1xj6P3n+XL3zxy/zmf/Z3+Af/498nHr/Ptc6xfPJU2JI4ttslewcLBeTD2EnVGO0yKzaw7Vo2/ZYUEsuTC97ffsDe0T7trOPq9Ss0xrPdbDl+8gzvGnzbcnGx4fDwiBs3btJvtzx4IADt4eEB282Gp89PuXn9Kkf7C97/4GNOzpa8efc6144O+dEH97lYrvjqF9/k2uE+Dz++Tz9sePtzd3j6/JRHT8+5ev06i+tz3vv4Yy6WA/feeA1//TqPl2fQOoasTIwY8dbifQlhNeA2mewsIYmAiMNKYi8aZn5G187kPNASZ92sFRIp0hiZIiFlEYkQrz6YYbFY0M4a+n7LMGwxOAEwjPhd/WZNSr00UMiJNAyUkt586ezv+x6MlCmCNLwrNmBMAE7Onck+KO8Z+g1ONaVTTNWfK0CEaRrZm0X26tK+TClKB+o8BqbFduzv7dE1DeebFTkFmsYzxETM4Ezkyp4npJ7T0zOOjm6xv7/PZrtV/9FyevacYXtO13Ts7x2RgKG/IIeBT+6f8If/4lu8+9EjkjNkI8k6mzPOKJPMlCkyOJuVVSL6mFaLq8p+brzl3mtX+bmv/RQ/9fm3SHHg+tWruFYAdkvD8+NnfHL/AR998Iznz9a0XYv3SZPJBu8ch/v7mMZz9fo+XQfLs0cM8RNiSLTtDGsSTWOYzTzWRbw3eLtH2ma62RG37nwWYyxnF6dstluW5xugZ9tL87Jr4QqL+R4zOp2DjOjJOry19JstfWMxccA4J43zcgJEE9gakfRw1pGTgexJsadUIuQciQHWq42SOaTnAqWRTGLUrES076xHQTbw1tI0QGPYDpFD17G9WPHN3/l/+K2/859z5y/9JU7aPdYDHH75K6xv3oJ7d2g/9xn49D6/9mu/hmsaYi+NRPx6zZ/8o/+bGRBenHPy7XeYxYHteklvPbMrV1idP2QwPWdPN7CY0y4M9AMHpiMcP+CdP3rEbLHg+rwjXMzh4oDNyTmr0+fkkEhB2E7bfqvec2KzWWOxNM5XN8ZZbdqXkPhFf59IhJzYpsBgRp+5+ExDCOPe1TUpGpBOQT3114yh6JGWc6H4WknJBFXjOknyJ6a0c7ZOz17nvQDPSKmpc47eCvjpnJHEBVCE+JNq6qJMJQkHco3Jil0ojZmmvuRIHlDfzhpNGAkoVZp9TZORmGKSxkRlSfhYawhxYAi9nkG2jsnUvo3yRuP57o3fOfPLq4Apo18CRvUW5Y+A4SlGAf0qiCnjUCqlYoxsthsF8nPVxdyVplO/Io2+l/ce4z3eOYbNlqj3e/3GNTarNcvlUgYl5SpLUNYMGjemHDDZUho0Wy/l9JGM8S0pl67tI5hXYpdctaUNMTNhIo5+Yy2pn4xdUvvhrKvn3U5sVjT3y70W8Hwy9q8CZKev6Zly+X27vvrEN9Tfhyhsd7F1kaHv2SYqcWLqa6WYSG70U3dkqvRVWItS9m/G3hGUZEgCaxlSIOexb4pgBCXJouxlxTb6jQCkwzCw2Wzo2q5WzQr7V/SWfSvM37lfVKAyZ9HkzDlLgs2YUXKhmwO5gshT0Lk8Q+NETqfxUk2YCr5QQx6dm6JDmsE3rUobaDVdJSTI5BtgPptXZm7rvNg5MzadK+MPBtfNql9EzmxDL43OrMWrJElhkQYFLKP28Sjr2DkvTcGAlAZt/rxmu+2xVu69abqqr5tSUgmLqE1vpWqoaTyLxnOwt08/iLZ9jEFjKAEHZ34uIGtMbDY9q+Wy2iuXDY3OQ9d1dU5LTBxSxhhPdImu0UR1SoQglZzOIBq41moDMxmzFBOb7ZZBq80NTiqn3ChHOcbVKjlnB43XRlCmxC9lbZXXEBJNSewYCEliF9vI2MYYx8bbirTFlGmc7PsQSxWdJvcbj9M5M5laxVAqTpmJPYgpVPBe1mcSGS3vCf1AY0csEl3jzgsI3jWtxPw5V//l32GQVjXPFGgJKexoXlQoIoqRDaEAJuWAK+DWoAeAbJaqmTQ5yGQsky4EuxM8FBaJGAGjBiHj9DDWaFqMurE4rwBXzoR+LN8wNtMokFS0elLKwmjL0uyjpeHrX/s6n33rs/R9xPuOs+WKd9//IR8//BC8lGVIZlUWljSEmYBeFMemdDI3Cv4NjCW8Y4amZGxHsIbKBNwF6UaAqPzMObcjli8HKPU9UwDo8n+nLN3dl5SppTR2YCwOTyYro1QcwKj6oFwCmmrZT65WW+9PV00BRuoD716/gPc2G2XSUkXmX86UUrOx2dpq9VVBSVgaYqEkaJwc2uWAwJSEg5XnMyObqa49Z2tRWin3qoe1Op8VVJqsX0AzwhqYOFeBXjKjaHE1lrvOsThkEhi9ygG4DJgVuYbLADSaRSu/Kz8uTm0xwqYEpIyfLWyBepfle3Ou4NOOQ1T2M2ODQJn/EcjNCqaPYKxV4lgBBe3kc44S2Yz3aQBlrReGt5b/UOVUxrEszyH6sWmct5w0SZMV6C32SO9DD6vLY354cCjdht2YYX8V6D++5J57LZOiNBso34ms8c1mXXVap/N6//59cV6046hz7Y5ObrERfnJI1ysbU4MPOdyDDo10qJ1uwGHoaxJuCpBWRnqdn8I8LjpOmb6XbHPK4uxnUL02C3rdOASePnok3xulPGa5XNK2LU3TqNbhhJFQzpuJnbps28aOwQJErjbrXbt2yW4Co/SBfEn9nbWWvb091topvSQoCqvjVUmzqdMuTrWbXNpQ5VnGW5msJXbX2853lb02JvjKviuJCQmB1XmfjEeeaA46MzYRA7FfvUn4vRluPiNtew5vXOdwb5/NcskP7n/IXoDZkDmaS8l0jJHV8gLTrwimZ7G3YPnsjD/5g3/GL/+13+Ibv/jr/PHvHcNwzvrsghgyX/0LP8tHH33Ian0OqvleEkSZLEwhY5nNOrnP5Anrrej19hmbHUdXjthsNpwen3Jxes6VoyParuPs7JzF4kAYdE+f8uLFM/b35uztLzg7v+B8teX6tescHuzz4OFjrDN84a3Xaazjo/sPGVLkK1/+LN5aHn70Ib6Bu6/d5uT8Akzk7c/cZrbY4+n5CdbAm2/eYb53wIP1CZaATw19Ngwy6DgDRBn3ETjQNWItxCjswaQNadoZvlFgLGcEqVEN4FwqT5D/N4asVSjWNTqO0uAt6p+UI2fnp1w5vCrJYyNO7tBvsVbtgp65ol1oJutLEjd931OLPesZdTkQnjCiUq0DASPne2HmluZD4pwn+n6D857Z/j4bayvDpmyCWt3TWJIRe1y0pY0iUQd7ewJIDAO+8TjXEjaRkBPOZFonft75xTmz+RHbfstyfUFGmj71QwQTtbLLggNLYrXs+f1/+q/49OEJqWvBuvHMyWlMFWf1fTJEEsnk0bcwhgFNMOIY+sR7Hx2z2fS8+cZdMpHNZkuT4WJ5n5PjDe+/+z7f/Bff5dHTFX0UG+NU3igmqRJpnCMaQ9uV/g5j6aqwYoRJ4r1lPjPcvL7Hz/3cV3jjzbuEvOXF2QnL1Zbl8pyYtqqjmNnbN3jbsd329JtepRb2q6zL1WvXCJs1lkDoByyZtvF0s7mU3aqrUkqUQ0z0IQIOaxs5Z4Ze14GtWvLVZTdGpaHKuSsl4dKQT/x8YsDkxNw3zLqWvMy0WK67jod/9j1++L3v8Yt/47dI832O3/sIN5uzHAKmbehzZHHrJsNiwT/+h7/DycefcOPKAa/dvsGL7YYvff1r7KXE8bs/ZHux5UWK/OLf/E8wVw75v/6b/443v/zT/PKv/zpHt++yPX3Ot//JP+bBv/23EOHel7/Krc98BpsDca9hfXiE2WZMpHYfJ0t39Aaj3dUH4jbg9vYxxglIgq6fnMEilXlOgtmsNl1AVEPjHdZ49YdH2bOoe1ASA8L4TlnOWgvSWT2GunZjHJtIFf8hhCCA0KWtfjnRWCrRrAbZ3jswHSGq1q1KOFCqAfP0KyXWSbHIo+jZ5EbmYJFumJ7tFtEYNIhPIH49o8uivqpVn78esOVo178vNyv1SROl6Y1oG5p6bxKPTZvoFsm5cRymvgYow0+lr0pTGm9Lt3fRncxWxrLslRQjbdfSdV3tOeCsE+nAVMrFHU1jFFAvlY9NEdWTsUfLvRXIyBpTLlcrckwaM1HlYkrcl9SmOWROt/0WbIOt7Mai969J5UlMaUzxlmWVpix2v218jaVk8q3Ik1XG8ySOzMWnki/u2o6tslGFTKPfr8A8E7/tVWBt+fn0tYsfvAzUvsqnnILIRYc9BQHvsoK0i8Wi+n0/juAwXRvT95RrRjMSTACdi9HfBmrpv9zb6Ee2bStNnnwjmELx/VOugFdp+G6MpXUe13aiR67xVozTsvtdX9pqgsUZZcrrd5ZGxd6LzucQdSea8rkxSZM1KE8p02fRbpa4RcvwNWaMSRmVSYxF3/c7DcectYScasKixDTeepVBUQmYpqlyataMFbkpSMzjjKFrO3LT0nhP3w9CGLOZOARJMvqOlHpmswXetVWSUWyD7LrZbC6N8YagUghZYk20aZw1zJ3Itw3DIGCvH2XqjHE0jce5hq4T1nLBwrz3krw0htlsxuHhIdvtlvVmg1Hte6eVwVZxClQS1CIEyLZptB8RNNZBI5Iw1ca4htQm0Cqk4qeGIYARXVuTFfpWvKQwlZ3z9T6tLfvN0vcriamR5HJpcBeMNL4uYHyxVSEEmsbp2eY1Hh3IGXxs6tlijaVxYltLBWdSvDGGBE4TVYonFrJESkF9N4eWrmO0cZsxBqdJppySMKFzFo33H/P6CQdpM8RMMrkertlMhMeLQXBWsx1p3KwKbJVNKUZ/ZIFN0fjL4KNBD5XJd0wNWj3QorKCSrCBaFYajDg6mqGKSRi0MUSyGw+aIQRd3gKWtDR86TNf5Fe+8ZdpredidcHz8xN+dP9H/Mn3/pR13NDu7+MaW4HDMWC26iRQg+XpkTE1tmMZbzGYhe00Zeq9fAgBO+B2eRm9oFXHsLy76B1dBnaBlwDaKRNvnBMLWZlOBYRURMEgAWCcgHfT+SuysvJeAyoQoEcuYLQUewRoy2FQHXTKs8i9FIf+MgDmvTC8pwyAaWY9Jel27ZXNlxWZLSBTJmvpka5NZaNK0yO9Xy0jVzUDTHk+NGLbAQ7H+Zs+E4yOsdMDvgRbJRGxc2+MYNR4SO+up+kaGeeZGkRPXzt7bMfpod7zuD9HsDfn4iQha13fWxwsqxrS4Hay/0bBXwHax9mc6slKKVbJJst3l3uY6jGXPVHGIedxzU7BwvqcOj/TvZJlGtn2kiUtwJmMsfw+ZWn6V8rzardha1WeoDC3HY8fP4ZUhC+KTtfuOGcF7WNMkrVTAXPjhHUQw1CDjzIuoe/BjVIHk1kWO1x0u2xptjjalGJPjBubBJbX1AEc7VFZqxOnDcPR1SucnZ5Vf9saIyVMTbPDyC3rNcZcxxLEbKSUaXzR305jMK6OiMmZxnlh7WXJqnZdB8NA6MemHJed78vs5unzFOZBSRjWz+h+Kgsl51x1qS+fPU3T8Nprr/Hw4UMulM1cSg4vs56n4PjlhMjl+35VcDHd02WOLn9men/1c+rwpOn7kKm0Ru1nuvQZ3RcGQ+M827ylWcy5dvcWDeLgPXz0mNXJGS4ZNsYxxxC2awESmpbWg4mR7Xlm/fyEw9aRnj/kX/+//5DcNdz5zJf49L3vwvIcy5qL8wu+8NNf5bt/9l365Qk+GawTDXZrwSTDbNZgnGXYbgWMaASUizmxXW45fXZGbgzROhYHBzTOc/z0KYuDfa7fvMHzp08Ztr10nV/M6DcbFosF+4dHWOd59OgxTdty7+5dTNjwow8+IaTEv/+X/gLzWcuffed7XLmyz+JgxoNnz0nAvbu3OF+teP78IaaZce/OHTCZ09MnHDQtb926xWYI/Oh8TQSMFcZNzhGTRbogpUQ00oTBWYsJEaMVAQlo9/aFXaK+kUUagdgiy1FBfQO4Wk5YqmWSJjOc94ClaWYcHV4j5UyIEmAOfU/jG7r5DOtbCQWzreViZQ2XtVe6GsviKbeQNfG7a2tFK70iuWXZi/RQECaJIZO0kZgB1pstSRP21oyJIxCgAfXTyncWxhEpkxMcHhwo00rlM2zGO0l+ZmPI1nFwcIV7rzkwLZvtkuX6hPX6lPV6JVJb7RGuWeBme6TUM4Qt73/8iA8fnZAbD95pyX05D8c0mqEEoiXRIOWETqVtslaIpCRBVIoNHz885/vvfszNW9dZLU/JZotxngcPX/BHf/TnfHx/S246TFMArJoOJwF9EqBt6LVfQSxAlDQDK2NnEJv6/gcn/OCDF/zKr36Vv/iNBfHpe6xXS3zX0NkGiyEEhzSeaskxs1yuGIaBa9eu0fdb2qbj2pVr3Dg4YHnxnO12hYmDAOR9L2CQlRGJKTHEyLzMPSgxoxH3EX2mIpGWhSloswDQYsuK5EH5o2dtDMQw0Lo5N67f4vnTYwwCcA7LJe9863v8xi/9GsznPPz+D9nbF713vCeSOT9/gU9b3rx7jSff+td88J0/4n7fY9s5X/nlv0hPoreSsBgODrn+sz/Le8dP4Es/xV/5r/8u267lw/c/4tZbb/PLf/tv89v//f8A1vKrf+/vkTtH7FfMY+Bgr+X4W99j86fvklJi3nVSLTUEvGmJRs66lAbSEPGtx1mvusql2gVN8Njqc5SyZO8s2XlQ6SurZbIpJdIgfkFUe+AdFYwr50fIALGyZ8c9PCZDAQHUzEgKGauzxlgng9qezPJiIBtJ7Ba9XLEbCkqgkiu5+L9qr4p/dYnJ37btzrWhsOhGCa3Sz6T4uMX8iBtrNME9nsMFzIwxMwwBa1VmheJDWfV3x/uYEgQgstlsKouvjEf5e4yRw8MjttsN5+dL0W80TnzKUs5f/daJTdchD2HUzSx9A6zaWWtcBSPKdVXOsTaExBiVLjBC+IiG9Up9NNeIHS3+sE56Uhb71cMjPvuZu3xy/xOeHJ9TKhiZVIJ658hOGIM1PqwJBEsK0twyM54lpfeHsQYNcTQuVJIVKnNSmPjdjLZt2RgBjSUG3C2Jnr5eGssf857yukycKPti1w8eXylGhhClsiQF2TfG7ZTjFwb2Zdb5zvdMvn9srjVUH5jJvRjvdr6r+LI5S1WOKfJpJJXv8PUML2s/51wbHpcx6jfbWrVbCAcoQDp9lSZnU39gmkApbPqYMmHYiM0m135D3jukpVDRw9czPmf6EAi5sPftFN7AO18xnKHvWas02m48m3d8/T4Noxa3s3jnCQrahpQlvoMad2SN0WfzWdV0zQaGnBj6LdswFJhD8SdXbWxQ3Vh1O2ryZNpgTMY9aPVfVJDcMZvNQZsOphJkImM0n81IbcuggLGAhyPQ3jQNbdsKhqHjIOS9NM6Pb7HzGbHvRRdf46qiOYw1UuWuDVm9a3RuUl3DW600CiEQolSbOO9lzaQMOSkImmvCqMyF95a2bTTRsyZE2TN93zPrZlhnNUEZSCnS9zJv28GoPdXmj9bRbzb0IbDpt3jn6dqWxlnsulRhpWqbYyXsjZha28j+qpXoqnlemowNw1BlcVLSdTuEyrD9ca+fbJA2I6Lg2VS2aTLiaJXNbhRoihp8jMyrjHVGnUe3a1AnBxRQGXDVGBSrPgHcShZJkRStVFHAKEszDZExkPsoWaVYQJeYGIYem01t3FUOctHMsdy8foO/+qu/ztXDK/SrDdvNinff/z7/8lt/yKNnDzDe0rQNzawja3bVMh7AZLn3ops0LVcvZeiwG4gXw1ey4pR3ZWqpwRRcmQIvO8F7ngB3VsqZGrfLOr0M1u4cdNaMjaQoJefKvFSWsLUGX0pkogCH1grotFuWI0YlF4OdCy9AmQKUuQPjpPRNWBdhBNeAmMUhqZlCk1+6b9BmAwoAlc6orzrE5XiTpALKKigoVM5lXCQjPc2SQgFGyreMDmD5fqPZx9KBcOoUFJmEnMuYFCc573xdSqk2mKvzVBw2Js+uAZlecXw/Y2Z6p8nfDnj0aoD3ZYayAJgC0BZ28vRD8i8BtEcG+FRqwABZGzuNPMLJKwmbNpvJ2lQdpOKk37x5k+VyqeVwysDA1PVUQMZc/l0vkncbt5UTzhjAMETpIFkyeSkljM0jKF+HQUoQ5XYTxKSMEwmCIipPMdmTxhiISbq6xzKnujaT3JsBjAat2ALUjXYwaWZ515GEtm1o2xmnp6dY6ydrdnQQMxmi2iJrLznOk9JlXfuyj0ew0TopT7JQBey7tsN6y3wxr1nLMYFWVl9haWR8Y3QN5sk+1EymEwc8G+i6OU3Tsl4uJYlmgjhtzagVd9mRfhUoOib9tDkRElxcriSo01ocojKwOWvDCHnmjz76qOrolsfbWd8/ximf7ufL++6yLZ4Gw5e/c2qj6/1On2Xc9pOfKao2CabLtYqTmpF59c6TfAPZMD/qCMsNH/zoA3IfaIzY6bU1ZGPJ215IngvPlbbB54iJFh8afNsQ1ud88vSYw3tv8fVf+g3mXce3/9nv0JF5+NHH7F25zVd+5uf47p9+Exd1zSsM5Zyl62YkI1pljffkmLScHzabnovTC27cu8Pe0TVePHzMowePIWeuXb3KxcUZ6/WKq1eOGIaB5WpN4x2He3tst4HlasViseDqlUNOX7zg0dNnzBrP59+4zvPnz3j6+JgbNw65eu2I9z66T7KJN9+8zfm65/xsyaybcXjrGstVz8nJOU3nubJ/gFltGVYrZq4lZEPhoscYsUkqCIwyFdpGGoKkXsoYjTPEIdEuFtJABAFe8BFrC8gx2jZxQksgMNBqQ4hUg21pdpmzoWnmhDhIItFamrbDW4txnmxEpzYbq4EE9RyZMoFeWtOTdT0medA1lnf2uLxVdNQFgIkMw5aYt3hnWa3WIv1g28r00e1Vg01JalrtgQBx0wsg4C3z+RyDBBQSvJYqioD1LcEII2Y2j1gnjKPN5pwUe5xL+HaPvYNbtPM9utZhCZyeZJ6+WLFG9Ow6fVirG6YwgcenE99SPV5N9FOrb9R1lb8naWb2g3cf8MUvfh5vIeaA7zKr3nD/6ZrghEXqMLReWR4FBMEK2yeNa8EYJ/62MXir46zEGmGhWY5PNvzzP/pzbt6+xdv3BvrQM58vICf67WqcUz05QwikmDg7O6ffriEkbMyYMGCINO2CYXtBzBLsOIRpNoSBlDIp5lqllHIUP9I6Zp0nJ+jTVkpxkaSuUZ8r7ySgBfB1edT0zxnC0OMxXL95m+Mf/IB1TKyGJfs//QV++a/+Bg8//pT51SNyzvimZQC6+R5t07F5/JTvf/ObfPFrX+dzn/8pPvnTP+bPf//3ef70GO86wrDBZrX7xpCahvPNwK0vf4lu/4Df/T/+dz75vT9g7+5N/uO/+1/xud/465wePyfP9/nmP/pt+k8+5fWrR3zu7bu0Z2cs2oatNczmMwDCZkNurDa4kuEOQ6BpO1k9RqRQpDGlbCwrx7fI1RhITljV234LyVByBiWJPZt10qAmJprSsCeXSiWjYNouoFDOsQqaMIIrYynyxH9V/7ecmdL0Z2x/abIlhUx2VoEeVO7KamI51QRQ1OqUrP7j1HZcrhQrYHNJqpZXrOX7RkvmqXHpblXXaMLm8wV7e/tVa/Glc9YYjVd2+zIUbcmcS/m5+Fwi9yByBhcXy/rcmFGzf7Sv8j0+J7Z9r6z+wFoBNGHEOxmTArqVsQXxH+NoiI3a9FIO7awbATwj4GlMiRADTQEEJwk1pz1bTExcnJ5iUmLRztimQUhVhYlS5mLiR1f/Xm4MZ8vw51Fvc+KjWWXjFl+fTI1zhOXoIUgTKOq8V3P7ctxQxuVSHPiq30/vZfr6cf9f1kHW5GrO8t+mlfsses4556pRGkKoTSFlrrUBOtO4cvx+23jFHKhxtTFSaZaINE1bH160VQMmyDmXYmK7TbuEEPX32rat9wQi2WAwDCnQT6ptZU5GOQ8orFZNFpT7vRxn69xu+360BZkqZ8Y2I41Ojfp2pXmYV//Csu17SpLOWP1c3hBUK7eMWbmnKchWsBDnpNpovVnLfZRYBmHDi3SZANWFnFHnKsVa8Wgu+TpO5yxF3TfazM1aJ2A9sFqv1VdhxLmsreQkAcihyEkZPV+N2ow0iN8SCpCrCbOiV1zWVQHmG9/iTDOeh8oWjSlVndYUwRiJmUriqzQsszqfAh6X+BBN/pmqUTyNRTIjA9w58XFitHjfsNls1F6idsbgvcW5OfNFyxAGhiHU2FCA5qayoFMSea8Yc5XOaxthz87bjn7oxabGBCnhO5F2KOzq0PckEtuwroBtTfhrfBZSlkSTsZhcKk89IU6qNJIlkarEx3TfXH79ZIO0SLBmndWAQMGFBEXjZsz66+GtDjY5ifOji9kqYJTy1BHXTTQFpfIIuBQmXtaNKiAWNHr4J6vXLUY457GsI0n23htIJAEHTaYxwlTJ1ghIMkScaZm3Hb/0C1/nZ7/805iYWW3W3L//MX/wL/+Ab7/7bcIMmsN9WLTCgvENjR50EpLFGp/norU1nm369xJoXz5YpKSlBmVYcmlchDSAqIAHuZaES6lBJqsGb2m8Aajz83LzowI+TgP+pAZOEw+yAalQUt1MMY9AT7KGHASoLr83OpcxjvT2MpuiQ+JH469j5YwRxsmgrFVlbFuQbFjSRIERmr+pQG0Zz4w1JZtJoxcTAAAgAElEQVSe1VjnusbKkxcdLos0INvJ4E/GLem/s67X0n1UlW8quJRz1mSBxaLN6pB1bsxknCpwTmUNqxmsu6Y4wBktW9Z/UhKgfbFYcH5xLvecRm3jXT9D90mRCiklZRVoHd2+4vRmBUsKQFieezTYI1AwAgeTVWtMbX6Vs+HK4SHbfs35+VKfDz0I0xRWrfNT2MlGdatzFkF86e5ugF3wX5pxUXVZy1ga/VZb1jFIZtaWgKQ8q647Cxg5tKzeG0Yy1ZKMyhUEyeK1aNkVVXtJnj/jnadtWvrQE4vN03sICbBWkwsGrCfbXO9vUO1hdClJIFBGN6lXmyfgiCRNXnvtLqvVSprlTGQgoCQEMtdvXOdieUGvTpG1FpMSUdf70cEBISUulhej/dRXCIHnJy+qvW/aFt+1rFZL1pt1ZZVKACb6QPPZHGsty9VKAg7EDpa1aQwF6lZmhTCrMrky4bMdGdQGQ6OBx9iReVx8xYaVpIy1npyDMNiykdLYSdBQHM4a8ORxXxSnLahNsCZhkqlrTZjvVtd51Gx6gzWprj5jpCEXURKMyeyCqDs7Nb+cbNoBuSa/L/9fnIgaTIo3hskqIaP7sEQ1yYiuHApGF/csx0TCEkzEG4fzlhAjQ2OZXz1ic/yigk6lCd2y0fLZ7RLbZY6ahm3s+fTJj7h57RbeLzBxjdmuccz5xq/8hzz86AGrp+9D6vngvR/wlZ/5Grdvv87jh/cxWRmh1uIaz+HRIc9evKjjlXXdW5PxxpE2ifPjFwwxcHZyypUrBzjnePHsKefnSxbzOcvVkhcvTlgs9mm6ltX5km3fs3dwQDvvOH72nKfHL7hysM9n37rN2clzjp8teeuNe/gG3vn+BzRdyxc+9yYXF+c8ffKMg4MrXDs65MXZOSfnF/h2TtvNuDi/YDUMZOfZ9y0xR85zIhiH9P2VOXK2sMgyudHERxJD5ZJhf75HqTKSCdS1p59H91DKlhAH+l5Zk0bAGVsabsXMqDtZ7I8Af/hOGHg6/wXMMEa1FyfyN9N1mHMWfVH9XbFTk1Vc7ztPbCJGLL2hlBKqppggwgx9X08+ybXn8R6sANvejvplxogfkJV5vbe/R0qlUaEEOs61EB2tb7lx4x6Glr4/ZrHnSSFjoqH1jjCIjubR4RVcMyemhDeJxq8IZJqZSLYMKutljR0bphlT7XE5ZmzSQLXm3KUiq1hjYxLZBXKE1XZDzCJ3EaPFJY9v9gjZkJ3BuSjzacXu56JFlwPiagh7styKsOXVJhqLU18blVIyNnHy/IJvfesH3L1xJP5EHhiGLUM/qJZkqtl0ExPL1QXx6lVMli7ijTOEfk3rPCaqvnJO0iCPCPTk2BfEHu8a9uaHLMMFyQRAOqFjBpwX3y1hiKacR8XZ1LWqs16qzHIK5GiJQ4KQObpxl+g9F3HL7DOf4zf/i/+SMw+//z//L/zVv/U36fse6z1Dv8Y1LYuu495izge/90/5+F9/my/86i9x7+e/xtU33+S3/6f/legaWK3oc5J4ZtbSzOcEIjdfv8d2ueLpt7/LlRcnvHj+guMHj7nx2us8eP8+CcMbP/VZ7p8c4+Oa/bCGswsWCU6BZjZn6Ldszs+J1zpIkdAPbFZrZkczvHX0SbRAHY4h98I4j+LPY6GU5occ2SRDb8GZjEsQbdkDCrbp3i9+KM4y9AOuaPkZo2BJhElT1JL0ziUOM1TN0+I3WGsrO88X/8q5HRJNiQPI0Koe5Ei6kTJbKfN1bPNGmL8FoJ+cccVfKa8CylhraZ02eVVWV1b/rxBBstqSKguk8WNKSRPHjSTO+4EQA7VaQG1R1fOsOrpjPOG9xFPFJ5bO7HEnkVx8cqsJitIUylqUxatJuiwrvYxt0QkuvlsIg4AUdtKBXadazvaMyx5vmkpwMGS9nsFgSUSMKb1QZG+JRIE8c1Lpoacnpzx+/lyqV6zKjSC+9vhS24eC/FV+zmhSSsFwDZJKaXf5bKzHmaxNp5hBJV0Zo8x3jQ1SFtm6NNpaOZPKfyeA6v/P63Lc+6rXq5PoCqqljEkG10iJ+rT6t6z7AnJV0oJqfUYFaku84FRv1GgiwPmxeW99HiRCCUEAwfp+15CDjHtMmdaVaoUCiCdlJw6EMNQkRanIEamhfvd59bsbZbHabHHW69OjRK8ocZjRRI/xFTCzbqzeEwanxAIpy5mc0kQ/tuAGwHwuerdFQ9QawxC2tDRIkll8/qREJGNNJRyVqhurDe0OD45EQiaqNnUBIVOia9vKyi+aqBV7sVJmX3peGKjJ3mGQCoE+DBhnIBpsQvv8jPIwUiKi1WzKmDcKdNdKUvUZCg4j950n+0P9XLUB9NoA0hhhtPayDgtr1Kpv5PR8jJtQ5SJSiVMRcoq14gcEtWEjWcnqXKqUqVYdxJQwCTy2MvdL4iAjjH5rLI0XsFRyBIUAJHPvrPhgqc1shp6sBEliorENrWvruJT1KEtNwHrXdsTYaZ+SHu8tviQssjDLzZ5hCD2+b0hRjNWsa8XrVtnBYQis1ptq962zNK3HZbHJq/Wa9SC6xCabscrzx7x+4kFakoKCKWP0gQX5lAVfMpxWeO4Ug/7/UfeeT5ck2XnfLzOr6rrXtp8e0ztmZxeLhSdFAypoQBIQCRqRlPnAkP4q/QGKUFCK0BfIhxBiAEESNDC7XCzWYM3smJ6e9q+9pkxm6sM5J6tuzxCM0KfV3Zidnrfve29VVuYxz3nOc5xuQANNQaoFFLDXKnHy2ktCYQzUsrWf6BuzbBCnyX2Mon1W13Wh6u8xUvV7o1Zyq7oiZwUCM4Rcs6oP+HNf+wV+7a/8VRZNQ7vd8ezFM77z7T/hgx9/j667ojqaEeYLknWBqH6HCNjnMpTKqQGxKq4l3Fb1NtB6eq+QtSJrwVMqa+c1gJouwMgMlcAsWDBkQuBu1L8x1u5UzsD+rrQ3K3hY+UruaxgkqcrCDwrmtECC7JjxhTNizEOrFom0hHdemLBuAtIpY7q81PDGYSAPQ2E1yvVGvQbKAZJgyNbNQbZ9kSAbwDIyczLs3XOMArAm1SPOtpZ5BEvRqj9a6S+MAmegsCSP8rAdydaeVwIKBX/KMSqsTgukKM7PQDKvbSMOA5Fg6CPr9VYNtRiZaEwbZJ1TngCZZZ1K0yClcvlKIi4JtcOc5rRlfEzALQj0lLGy03XN0uaSkrRtxSGVQJUshRY/2RfksVJqhf1Q18XRAniXSxD74sULrLBg1zzVeDL2lUip+GI75OutLcSNTl+lDKoshRZwtEMvFWtdGxti552jmc8l+fOiuTe9934YoKm5ceuU3a7l5cszsgLJySWIAyE4+tSLPmhy2hZbNqfYw2Taq5OhA3ZE8piEuODZdR0f/ORDoragFImTnPfuebO5Ls8VtHBiDO+q5svvvsd6u+UnH/2EqBVGsxPijCtwo3bP+vqalE1qhQIuZX2+MnV8yfp6jQVCU6ARWxOYMPYDfTeQZp9vu8q6/t77yRTifSDTCi/232ZbHX5Pz2t6HWXi7uSzpmdiLBLKq3aBO8cntNsdL7fXhFq1pybc8JFdMsLl9t+vfv50/7x6P1PfN/3vVxMMG6xRvpDRjrhJ8GUgtOgSjgXQmBNVJUl7jIO8v644vnXKsNkybFsBZjL0aYDg6RLMFjIwc7vrOJwtyGng6vKck9OG1+7eZN1v+eM/+rf8wl/8q/zGP/5v+N//2X8H26d0Vy/54Aff492vvE9dz/nwJ98nOGFzDEPiyZMnwixz9jzVBrtc/F+3bVmslizu3MEBm/U119cbTk9PcM5xdbXGV4GmaWQqcNuyWC6og+fs+QvOz6948NZ97tw65Pz5Sy7O13z5q1+i7wf+9AefcPvWKe+88xovnz/jk08+4+bdW9y5dcz19RVX11cslgc0dU2rTIHZfIYLFZfdjhBhUTd0QLZWWFC2oBi5ppnRcYXD2lszB8slxtT21s7qAKbDHqVd1LsgHUAIeJoz5DCew1EGCXGNBsjqvkBB1rLnFCgoe2qSgIKyUwy1sT3KeEYmG3dvT9v7pjZl6Aeyj/q8B00qlI1ngJ2dFz2/TL81Z+Iw0HiTSBg0xpKhainF4ssW8yXZQTcM1P1At7tUu5WoKmgaabGVASM12VdkN+Pk9BYHJydkV7Hb7bTtL5HjQKUAltN4wRhE5GksNl6vTI5W0DEHMpGjoyNu37nHsyeP6PtEdonHj5/T91FaiWUR5Z5iJPUDEheK5trgRpAiqUafS2PhyTlKIZ+srNrBcb1uwQkbq+t2OsBINPWur69YzueAZ+h6yJ5217FYzPChJuUeHMScqYKDQeZSmHSByf5kKOyji/ML6ropHV/TSdWlKM0INEMubfpi5lUbXu916AfSIIPWTm7eoj48pss7bt2+zWff/T7/7pu/z9VnT5nPKnZpRxUybAZcSgzdwMuzK6rZAecXl/xvv/W/8tav/BJ/9zf/LifvvcP1EDlcHrD1MqW8vnMDX3t2l9esDg9wKVHvOg6S+PpqiMx94NH3vs93/vnv8DO/9HXe/y/+CfVuQ3P+kscfP+V6uyV5T71a0fUDqe8JGeIQScPArGmkCDGJ9zySfA+530sVc4Y+JXZDD/VM18yTh1ikT4Y8FJAIoO9anHfMliuJx4iatE8BJvv3FLDRYpICP9YenXNWYGVk0pm/k8HB0kWWnEh8eO9LDF5yjywPV/aBTCDPWWYzjOxei/v3GbwwJvEWBwYnhcWYk3TduH02bIppvFacDviRGCjt2hI3JUawtBS4rNCpTyIp+uj170z+6lWbV9ZFAXHxY7kUrC0GBWiaZjI/QoctKoBrUbx1Yfqgn+EsR7aCmJvkSqPWqV1T8KE8aKN9ZAdpyAIM1YEYJR8LVPi6kpxYdbAjY4F7L/+2a9yLn+y7KbI4FF9RXI+CkGPuZLFtUh1R6hqCRynDZX2msfB0racx2/Te/7++9vKjBNvtlvm8xvS1+77Hu8h8Pi+/Y+CfrZGwIwNNI+DnYIMzDajM++xt+ydpZ4TNAJL8ItL1+4O2DXS0goBoeaqPTGMMLEx13f8+MGtE+z7q4Ea7ZgMyF4sFs3omDPUojNpo8zZ0bYICt1VVFaC+5OSMQLz5Bbvn7BA2t+4BnMPlCE5mZzS1kHzs7FWVEtywWEIHrRuJJQvI6rwMfDJGaNd3gPy5qqWtv6plwKz4RYkVMkmkpSZ7p6oqAdRNozv2Jc+xIfBlv6VETMMe8O2co64bZioH1A99ia+sIGFFIInDpHMspVSYs8LEdprjBoYhFpC/5Lq15qaV2MTUD3RtJ5+BECvquqbySecVRZVrmA6WdtRVrezUUcrAQGxb10IeGHcflmtUQfa5FMzV5oRKbYDJIQiT1WycSKkMNE0zwRjklVIioAWMUDGbOXxwWK0sx8SQB6oqEELNailzGdKQQAcbLhqRIhmaWOQdZN9YbC2zfeaLJbtdS991EqekWFjGX/T6qQdpbfiEAWNFKzQnaZdzTthDUn4DBykNpRGmBGiaSFCChSztPQZ25SQtG68YMTNYKYpMgQVwOQswY5u8XK/9vp8kwtnkGcS5o4y5KgeWYcnX3/4Z/t7f+M+4eXhK3+54+NknfOf73+Gb3/smF1cXYuico/LiME1TxXtrPUeTBAHjcNYOJNpHZjTttWd0S+g6HvapTpslcbkEL+pw7fdyBmOyqoaPS1IpsW336qTS6csCG7IkVnY1VplH78mGn+GUIYQnFg9sAvVjEOU0EvfOC3DttQplbNJJoOO9x1XS6jCC3rI2NulxmiwmrRgrPqXGdNTjnK7lxK3vBxsTozuCISPAIlVRBcxSKhNqna+KBo9DARU3Aj823dS0e6dguOzNUJ76NFGWgN3CKRTn8lL3yFZRG8+crEguAN1YyTcQ1JXvL2uga2X7x02SamNVGENS1tmCJZ2wyzQ2GxNUcVaBs7NzvAenzGLbMwaGv1o5NgdwdCiDgbbb7ejYct5bu6jtMT6M61U+oezrqc35PKCQy71KG+n9u68RU+LDTz/FeL4pJXylUKomFilFYVp4eR5TgK3rOh599ogqNMQI2buidxTwOKkfwBdcD4iG9szalKbJRtmmr/zMyfAJqRAqswq3t144aQXaCwTtGeZEjD0//MEP2e52AsI5TVf0O6oqsJwvWS1XbLZbur5ju91iLYr2XrHLMrX+6vKSi7NzXePE/l2Or8yILzb1jG7ouLi4KNdpz9I6N5Kui62Fm6xJSiNjvxgCfZnTLfZzug+mwT1je1exF2ZHsrTPHp+c8Lx7hg+BmzdPWV9vGPpSltnbr1/EzHDOlfa+NPnZ9BmX65nYDBgT1VeBWnvuoyKydZ7o9VuBgsn+0EAyaJfFEAcZEpcFMHXBc3D7BtfPXhK3Mjxu1/U4PE0zIznHbohUWYoy0WXa3Y7zsxccDj314pgqJH70/T/hrbfe5LU33uHRD54RcuTy4iWfPvqU9979CpfX51ycPaGq5tqZIOscr9cy4dW017KAlF4T7xRFW2+73bLZ7Lh7+y7ZRTbbLbdu3SCmzMX5FburK27euMFiPufy4pK+bfnyOw9o5jXPnzxh6DrefudNdtsdH3/0mLt3T3nw4B6PP3vCBz98wtvv3OP112/z4vlzut2GB/fuso6Z88srnPMcrFZ0KbHebmhC4PDwgG0KvGx7NnEQQA2ofD12CwTR0Ur2386zWq7K/g3KfjBwz9rlit6798xm++FiJpN10EzKWXy+HHGcJvb2zvGY7Ce2kuzbANP94tfoOUYwUGIRgxLGJPrVfZ8z2s0gIElMyuDOWfXJtQij/wSNkxyTien6HmsFr6ogmnI5aUwKOUfRLY0DZGEvmfTQweEh125N9jWkBbOhwleBlAaCR7TIvGe+OubOvdepZz/Cz5bUR4Fdu2W72ZC2WylwWSFUu7m8nrPPv/Rn1kWQPeTI/dfvc3x8k08ffkJMEKjo+qRs2AorhOY0lBgbpx0cGm+VThR7RnoNFh8Who5z2sHiaNuB7bbH5xYLnFNKUhyLjr4XXdv11ZqXL864uLzk1q0bEKHyicUssFguSbGjbuaQArvNJVhRN7sCynVty3a3EUDNB/Jg15N1cNWEHKD7cjrkBR0mZISAjBQAY9fTdz3Hx6cc3b5Hkzre/9KX+dHv/TuGjz7kdLVkGWYQEwezObvra84+/jHdm7dY3T7lV/7mr1EvD9hetyQHzTbhLzc8/eGHvP83/zpv/JVf5ZNvfYe3/5M/R6rmPHn4Ge/9/Ndot1tiN2jy6KiaGpci1dUl3/+//k8efutb3P/ln+XtX/hZ3n7/Z9h887tcdQP1wREHN26yaTtSO5DbntSLnu/ycElTz4iDFJWzrkFVNTQZ6HuR60lJGPlVIOsQqopkB0dibfWZBqhK7CsJaV3XdL3oLLow6tean9qLfdU3GKnABmNZ7LVerzUJH8He4qeco2v7UkxISQr3U4k2e//4+1nzN7GDWYfYhFCVOMXYaCnJ0JuxCOULEPZqsTPGONqsrCSXoJ2TKZdBP0E1vdHw1hh1hRmLAA1my6YzFOxn0z9PJb6yMuGjsieF6CEEBWcJy8T+WmxbgFY/DnwqMZHaFcsd7PeEPOD3YoVRpcABfhLDK4BYubL3XKVsXueomwYHtNutnOuUSU6npjuVb0mUHFCNv+QjwRjEkhdPwWMpaqnZQvImnHbnxqifJZJpvqqh8uQ+7vmbPTxgQsIq+/cLnst/7PXq3nz155Yn1HUt+Z8TkH/brsueMaboeG3yjOQ+J+D25FzVelZfleGy52/XkywHnpw7Y1xaPt80MjjY9kEIHpPWNCakdwHHWLSwl8WHTlp9tHsFKudJ3uIXX86TFQBdYTjbtcqgxClFwRV7DkTJpyjn1MmzVuKf7K80yi+kSNQz56zgozJ1KY6ykNM9ZkDzfDaX55Zy8Y9RByIGJ+3tAgfl6RaWV7K9bM9TC7JRO00zVD6oVCJEDOR0BX/KWWLwppkRwghCTucImaxBqCpmswYZFL0re2oK3DvnRukDw4TkBgh1owUqAR/TTrq2shbBim62njUbzGVnyDpdc4ZQ1VTesdleaweCK+dUZvmM/qXvxdY3VYVT0o3Dq2TAjpR1+Jgz24J2N0DX93Rdx3q9Jmj3QKW2OGfFWWy9vGB1JtuAPldhlGfwEiPnKAl2CF5AV13D5XxRQPeUEsEpmUH1oJuqolGS5zzMPjcLZPr6qQZpc85EDSKcs0oQkryavlAvFQPnfFlcNMg0cHoPnMnmmPNotBJlI0yDiLrodShrKwrl3zmUuTeUalCaGEJANi5CMY9JaddZtLOC81RULKj48usP+Ee/8Zu88/oDuvWWy6sLfvzBj/nWd7/FDx/9iPPNhvlyxXK5IHlZCwl4ZCASqMFzrgTIlsTYdMBXNUDl8iyYH5mvr65VAR1LoqZn1GAQA9NyLtq45JEtZsbs1aAL9quvegRG4NDJoCfnQgngojw60bpCJBIEGLZkwhy4APVWIbUgRSzEF9w/UBiP3oZICWgUqhriWFkXJ4EYEcSQ5hhxToKsaRCpn1wCfmvHyHl/nUugh4IeFkQ4kUWQlguvuZHqWNqzUlFt52RKKtmR+0EAVq8tZAZmqn8qejg4IQALGiuOzwCqNAJu1taYFYD3IQgr1mBFP2WP2jrtt4YXEBrVgtI9R3nur1TKswUPI2A77hvbn+WYUVpevEls6OC1XKBkU7jd2weSb3jOzs4m7G6nQbhKSDiTz3DlPNmZmgbQpXo7uVbnpmCEOLCk95aAjx99Ks4oDRweHHJyfMKjp4/pU2TIElibPal94N7de3Rdx5NnzzQ5VgZIFK0j5x0uD7jY47InZ08OgeAb0coOY/AHcs2zZsbR6oBEZr3Z0A19eWbToM3+bMFLYaXrc5gmT0OMsocnZyGrvbDug81mzenNm1yur9jttgWEF2fl6Lqefrhg1sywQQ9jRGPMdBHtTygmYUUC29+MiRh6vpzLOJ+Z1Q0QyXGQYTv2nJydVy16TTalBYlWkCi7SPfq9FmLj8hjUjHdB2ROT07ZbDaljXPvdwEfKoYUaXPkw8cPiYPYl+12qxNLVY7FWM6TIMwGKloCbAUrA4unYHNMnw/WX00aXvUhxZ6on1XESNu3nT1tCULNljhPhZytvu1K4IMXZqf3jio4msMVRylz/fg5dJFlM8N5YQad9xuOQ83BbEWbwKcBKkd3fUm723DztuP45l269oxv/esfcfP0Brs33ufhRz/Et1c8+/QhxMTNG3dotztyjhBhs14T6obT05tcXZyXVkwr/MlxSQxdR1NXLBdzTk+OaNsdZ2cvODk55ejwkE8/fcTZyzNuHB8yX8w4vzxj1jS89aX3WG/WfPCjDzg+OOCNN17nxYvnPH16wfvvvMnx8YIf/umHPHlyxbvvvclbD27y8cefMMTM7dt3GOLAi5fPmc/muPmCqz7R7nZ4IgfzJRXgho7oBVCMlScjjM8UnWrCBuqmYWh3oJNmj46P8d4JT0slY8D+0ees8j8pa/FIz5gwe4bCMBP9Vh3uaj4HVzTNZa/FPdso23NMDrPuJ2vrHW2oAA8jZGv/nhQAGQsiDmPaiQ8MPtB2LTkKOyhNijxO92ROFkON7e7GVncaXxwerzg6XpHyoG3tPW23JVvTrcnSOHQKcsdq6ei7NF4XFifJQDOXHYvlijfuv84br73GB4+ewWKBX6xkaMfygBAzud3Q7zYMWvwi23doh5Ab7XTOY8tvjANVBV9+7x1N+GU9cvKcHN8QqZyUcZWd24yrA7NGtdKzyl05Z1B7eQKiXSsvrzbU8uMUJU4KVLgYGIaMDzIdXjTkUmEh5SxAy807tzg6PCCnxMsXz5nPAof37+K9p+sjfR+pXMQh7KZ+EC12G2QWY6TvWrpKWtu98/qs1fcqY6UUhMuzSKIhV2d8trOQlVVT44aEa3vCoePuO+/x4Y//lONbN7l7eoOzH/8YFyrm9Yqhz1SzOXmIbD7+hKuDBbMnZ3z3d36PcHzCwfEJVRP44Y9+xNW//za7jx7y5O0H/MV/8Pf487/xd+ibGT/89nd58u3v8Jf+wp8nXW9wQyI6TwoVVVUT2x3DbsON+3eYhcSz732HXb/h/j/4e8TVjGsSt05OmR8e8eLZx9D2MgfDeZrZjBxHmYqkz41B2LQh1LiYSLGTZ+sdXYSOXNqn8SKrY/lXXdclD/Jeh+45ec6nN2/QdQNOZZ0E+BQ9wClxw+IyiZ+rvenqZmvKHpvEWyHIwEKnoKkAE0OJzQoTM6htywZYmJ+zAUwTuYBKmGjmT00KwHIhsy2aqOxdp/hPkRwL2o3ggrX656InakeoUq1HK5JJ7mHySd4+WHLOPH5HYf47Vzp2xvwKIBe9SIlpRuBiPMKj5v40djdZrf0YfBqfiAak2Onxn2mRu9jiDC7rMCfAWp1FIUvjcu0qjG2vuZHYMu8yTRVI2e2tszGQ0dgcZ/dJ6f6b+oMCXqNxv8kdJnRAr5yDUDW4poG6Im8FTPd4TBHBXtP4aHrv039/EQD7ZwG4ewUL+z0E9HKMklfe+6LfOd0DtlescGBg/xAHUlawM49EnrZt967TwNe6roX1jRRsrVBhwJidB4tpm6bZ+5npzGcyOSbVinXk7LVzymyr+I0hDZKDOpFDGNwgoK6z4Xsj3hDj2LnnNI/1ph3qtINVv1vOfypdbi6Jr0Hz7JwzhFEeJcaOqm5wzjMM3SSXMc3WyTONbmQJa8xQWOgFX3JFts45Jx2EWpERHEj2ebTnrv9noKidndKd6aS7IxsG5qSg6r0CjSoBYMWksWCVyjBzy1VtDzMk6qrGBacAdd4jho1EPbGbgu1nBZOdSoQKe3XmZM+MOErAu6DFslqKMFVDTPKZch7jZN+KXZmlGtHjHj/LNw3kUPSWu64XYgcQB5nrUtcVicyQrHtAiVUpEfTvvGb7FIQAACAASURBVBfAOynA2qcoPkk7KuqqktxcfYcMeXXlTIF0lVTe0/cdQx5E272qpcCguFBMNgtqzBO9c8TkVVZPCHdxGLWzP48b7b9+qkFaQPSJECxIDIcEn8MgIFlKUmHY0z/NSYdTjFql5kCGIVI1oUyzAwsUKH82xmBMY7IvwbtSmFMuBmB6iKfsgiFGZZVMKjtoe0LnqMOcB/fu8w9+/dd5/+0HbK6vSXHg8uKSTz99xLe/810urjfU8zkHN47JdSZV2noMozCzE8ccCqigSUYSFlCK06Rb3lHalPVHFvRPK4UlwddsqlQ4srW3OXCjbkyy5M5Z6/3n22X9ZL0tSLNrEeM5fn/wjpxHnV0Liqwl23sBz2RQUCr3QJLDmnwWzU1Q3UTV+/RjcDJ14mTTjqLco1RA5JoMrM5O9XpVhxcF8F9tES6gd6GXjc74VYc+DW7MM+eMal6NTQvOjRPqyZns7Hr1WXltg1bn7mySSFlDBfaS7SMFkXMu4G1UpjeMepsS20nC5pLsLavolV4TRo0gYxhqTLcXODFZn7IvdPCbvUb23gTkyxmbqps0YRgDyTxxqBIUmM6sMw+Y3H4iWy7HYyNYpBKtQIE5xHEDFiDeEvoCXukNhuCJMWv73/AKaKd7LYtGVtbkN6eB1+/dZTlbsN1sZBCL82X4lFOZgtVqxW63ZbPZSkeWajX47MjeMyRhsh3XFafHBzjv+PDxc7JfEOY1LjqpZqJFC0awZLPZcHBwQF1VtH032tHJdVsAIg5e2B5BI9jynmTyDmFP57tUnZEhjr6q8CmTiPRDXwBaC0KHfhBnFmF7dSHgX11jbSX2MtauxlrjWVaZhCnb2fZBihFP5u0Hb7Dbbfjw40+LiL09S5NIydH2sS+g+KtnWaMrch7P2LjVRyZKAowVQs5cXV3I89MAZUyShDJiTBqyAEs2MbXrO+q6ou+NASBAFGihUX1CcnqmMxwcHeok2kT22tqoieY0edgHy9j7+as/c+VuR//o/D5r2PaNV3DeORn6MJTCn/A260qGdBkYP1Qet5iR0o7KiW5T27VsguNoueSq7djFzMHMUwOLxZyQM5fnL6kXT4hhjus7XJjxS3/t78O/+10+++4fMGyuuDh/TDN7m/e/8vN88MF3yMOADxVf/vL7vHzxnOvLS7xqSQfvWK0Oubi6xHmY1ZVO6s6sr6+4ur5ktVpy5/YtPnv0mIvzC26dHnN0fEA3tAxDz527t7m4vODRZ4+5cXqDN167y7Mnj3jy9CVvvvkmB0crfvTBJ1xerPmZrz7gxo0VP/nwI9pdz7vvfIlNt+bTp09YLJYcn5zy0bMXXOw6am0PHHYtu/aa4xs3Wc4XbF+8lOEULuBSwvlAjaeaz9lqchScPLflcln27bSQl7INAtRkMUhL4bRlrfjQIg3gsGGYNrQMFKRXJtAUgPgiGwMCcqQk04xDMGYHBTgvNiV/8d4d96tMchZfFQgu0KWeXgtI4uNz0ZIzgHW6w7Mujn1f3Qj4N5Ygxm4qWT+JrYa+Z7Fo2G5ecnJ8TNtUbNYCIIY8sFgo6ytlNtuWBTUHizk/95UvsRt2PD27ItZBks+ZZ9EsIC/YrWfMuhWu7Yi7LbkbGCasL2MD5yzDwayF8Ctf/RLvvP0mZ89fEFxguWqo6iUPHtzk7Xce8Cff/4EOKJHTbD0hxZ4acA7qNrTdWRNofcdoP5SF1YSGr3/1Z1nOVmxzYr5oqCrP9fUlu+1W128kNxwdHXHr9i2eP3nGfLHg9o1jbpzepG/FJ8Uk8ic5DgJaRfNlEzsEoEWdFA24sWFGypqJWhrOqZA+yHLNknu6wsYtQ3iHntz3fOnB23znG9/gX/4fv81JTBx6z4VzNIMj9JnGybp86Vf+AvObx7z81ne5+PgR64trcvbM6oa5y9wcOnLf8kf//f/A4Vfe4+TWDa7Or/nBH36L06cv6H/wIx6dr5lfb1jkTIvj/JNPmN085d677/Lr/+0/pT5YMOSOsFhSp0DVJY5OTji+dw9c4PrsEp/G8+arSggPyUZu5dFv6eC/bAgdopPY9j19owVRJ0BimT2RrdMnjW3IQqNniANNIxqsuR9IpW16BARLq3aWiRq2d0cAV/xjVU26qpzEtUakMEahnfsy2CdPBpIZc9qNviwEYc4Og9ikujbZlmFvZsJU5sC6zey7/CQ+HYtXmdPjY2ZVxcuzs9IuTBqBTBsUY7GF/d60eFDXNSkb+5bSPWf3NO10NCAZKJJQAnRIzJE1/7FhzMUv6zWHMGEFu6jfIwObFdmcxPQi8ZLzaCtTilRBhu/ELMOl4hALuSEivtQlyzPHjp6UIwyqyZkSQdk+IynAE3Msa/MqeaPYabmzEr9PyR2uxKlSoKfYN3AK8mNxVPBl4N2EFrzHoJ36mlfzPnsm09er/z39jL2/yyN7F3IZAo2Xz6/rhrqqGYcNZ3Ie9goJWYG5nHPpIHFUBO/LUD8rrEzvq+97FouFMAwJhR1q59qu1VrGU4x0bSeg7oQYF5XkYddnhRC5PVfsNU7ub4hDYZ7KUxnKXpyuTQiBvuvLGY5DL50oGv+XfEzlVYTFrTYgw7bdSYv50NM0DU0TkLkODlyi71otduZy38NgRWivcpAC9tV1wxAFB0p5ZAl7PZMGWnvGjjpb6+BNHnASQ3tP3u3GRFmvSWJQGejn3Xh+cYpngH5eLmue8zi7qRBEdGUNo0rK2kVt7dAPsg6eYhcKszPvdwWORQEb/AguZ5qq0rzYlzhKWLYUuTwDk+VjQ4lbQP6+qeajFIzFNKEiR5VPyRnfGPtV8B/yWKSYz+c4RylcZdABZyNuNJvN9uwf6stCCAKmK3ARqgoDT8z2O6f5ow/kfsC5QM6qf+yDYDdIjjMWtLPmaZ5mPiOTdSjxuM/aVvRz/0Ovn2qQ1jmoPALWRUG5hSkrATHOlYl4JbbII6xVAv886i6GEMiDtKYpBUgcWRLUPyZpJwvOj63dVpk1Zp5uaDLC8NQg1vugep2i+TXkRB1mem1JGbuemQ+899pb/Ne/+Z/z53/u53j5/AXtruXxw4f8/re+wf/zL/8Fj58+I80d8+MFeeZwwVM7p0DUeBiz0eKzVk9TJkaZkJmyGLygjl+CqWGPWu3dPmgp1TA3HnT2D3hxYAhw57VtQAAoqRc55M+lUo88u6nG0PiMJwxnUJbm9DlaUCQXIv42MUQ17N6V5mbJHwSYFY3Rkd6P/oyU9wYkpZTU2FuLayoBncuJpIlKzDrkxPSL1CEaBvg5EENBnZLm6H51WtHXd2EXHoy9ga2vGhY3GkiTsnAuF0DDmJ/TIU/jYUhaPUt2keWv5SIULLYT5GSB5V406NO97RDjG3OWJEgDlqpqcHkcYDANjkGDMlsjbbd1TpIBY2BALgLkxoSfsnE/B2iXPTEJdNxYQc1JmHlel0F+PxUtP3MiOckES7w6lizIuFfGctFQnTBGjZ7v8tSuiC5udvLZexo+k3uwgNJh3QGOTGCz27HdtZyfn0trjrMkwBUHfHl9rWdV9hHeC4soZ9BhZ87Dg3t3+Gs/+3V263N+6/Lf8jh2tL0McUpawTUGlHOOXd8RnGfz8rkGZhaITs4mkrSuFguuLq+UtY6wyL3Kjuj7g4rT5xz3bKcFxGTRd8w4Xjx/yZAjdVXtndOM2Nqsa+xDYLVc0sxmnJ291N8fOwCiBlfae420wlpQwRi4SP8W2cHHDx/Stq2I+juvxY4JmJzc2AZj1+/Q+xq1vS0ptfMsBQBjhIwFAUtyxhYy2XMpJ2z6aWG1uvGsekuq7Buyp6pr+r5VGz8mHbuulWFnWc4T+lw22y19340afMaCLkCTifOPYPW4f8fEFmdDQGSDZLUPLmUdRgLZ6XrkTEwDPmeaZk5d16x3Gwk0PZOE04ChRLdrteUo4hY19JFu29HUNfODBU1dcdm2rPvEUT0n94maGS53eJeZzRyfPf6I26+9w2uv3+XlesthnPG3/+E/5f/erTn/9EcM2y1nz59QL1a8/vZ7fPzjH1DXNZ98+DHb7ZqDwxV9J/qZ5EyUg2IpIH3bMcSOxWrF4fERPkeeP3lCu7nmzft38CGw3mxYLJa8/vpr7LZrrq6uef3ePQ4OjvjgJx8Qu453H3yJw+MDvv+Dj4jDwM//wpcJAX7yk48Ax7vvfontZs2PPviQG3fvcHLzhE8eP+bs4prlyU1CU7NeXxOA1XJFcInd9QW3FzN8gstOQLpMJHod4iZ8OWERNTXL1VICa9X1lMQwg5vsWST5MF39GGUKtlcb5BRgSIz7RAqhQwF/hr7HR6/yKBY9UOziaNPVPhkDnRHEw0lidnW9ZrVaUVW1nk3K71sRRVo1My5HBZwlMW27Lf3QF2kGdQKim+mE4e+tpU+vyKMavtGxWqy0ECGJUoyS6KbYk2NP8AJ0xjjQzCrm84r5vME5GW6YMrjo6bvIwVENvuLs4oLddsPh0ZKbRyt+9Zd/lkfPnnO+3bHTuJShY9cnqtu3uXF0wvb8nM3lhlk94+Xzl5ydX9C2W3IcIIk2YAiO1WzGG/eP+du/9udIccvzZ0/JbkfV3OL4+BaJDb/21/8y7XrDw8efse1b6mBSUTqoiCRdGURhr6BsZf2/wmqzeEHBlto7vvaVd/nFn/8apJbl8oD5vCHGjvX1hkePHnFyesLhwQG19zR1Td+1+JhpfGB+eMjJ4QrvdKBargguwdDQ9mHPh0FiSC3L6pimmY3MaBJd32Pt3pWv5BwkGLLI5DjJdAmqITgAgQTJ42Ii+0gVK3yfcUPitZt3+MqD9/jsG9/gxskBxynTnp3zJ//Lb5GuL4hP3ma+XXN8smJ56wYn8wUH2bPeteQBaj8wa1T7MsLw/CUXT36PZ0NHbDuOkucgwZ/8T/8zDInDfqB2sMiRP/xn/yOLu3fJLvBHv/07NKuGw8MZt44OyVXF/OqSZtZwfP8uu7bj+uwZq8rLEC+Nc0IV6DY7QFiruFz8rM2isAecXCY6R6ibIvMEqGSb2PuQDVCNtK11EYJP0mrfzGb0Q0u/25KzDEEypn1MUZJh5/BZtC4lTqPEhXhXCrQ5C9PMAJ1ElqJl00guNin8sxfzTYqwk3sYYho7JZLGEtb1F0YGldkD5xyhrkocGlRewexeTokqCECdcyJ7RC5JbZKb+FsBBcdBQHuxc5ZnUmYBYHRO8ZcGLkAuYFqBBLTlMMVRWsJsbMjjPIJXC87OcksC2TqlJvHfyNw0WQcBSkXexYMP+FCRU6TverbbNe1uK7YheGazuWqqOtVnFH/gvVfJKv2u5Evh2tatDB59JaaeFsqti1bwusDYMSb5osVS2VPKirLGQinqY8bXtQ4p19jXaV7q/aQYZJ9JeZZfBCr+Wa//2HvtHmPMxByptb27dKsoSSWlgZhkqNww9NR1BV5ALIuNhxSlYKc52axpmM/mhKVMekFj46SgJETwjp3qlQYF7Iqso3fKAkxsd30B7QSsTvS7lgxFNnDddZIjxLiHM/ggDGgfZO6NE+RRu8Aiu92ugM9VGNvwTa4wNCJPaO3tlBgV3a+6Z73E1vP5nOPTk6L5mlIqZ8TkiWx4l0eGpVWVVO2GYaCzwYXNvNgvwQhUv7Xv5feR91dVRfa+dF/mnNm1rcRC+iwEcA8T2T8ZOhWHnqpWHWg/UIVmxHxioh+6wtQHYa5WKp1kko5yj1FicWVzGngsIHsa41qnhBsliDnnxkGNVcXQS2Hbhs955/e0heXZCdYSfMAl676Vz4pIDDmo5I5TnV0XFMsyf5ANlZABq04xGB8geAFqRRpN1rnyVdl/0uWgxaUqkLQ4KVIyEWPQo34H3Dj02DslwQjnzHsZ9BqjdmUqxhK8x1WVFAEUIwgTu+i9x6dIXdVlH4i0VU2oKuqZ6tjGSHKxEM2k2+n/r3IHoBVWMIQuK4hqlRNLHp33uEniR6n+aXtMNqArjq2tkwqhfIMg4saokmDEYdWg4CAxJhkFvFQHXbAtlwkOstM51crq8DlQdZ4Hd+7zj37jN/nlr/8CcYhk73jy9An/+g/+Df/6m3/IR589FJkHPGFeQxXkgQo1QK/XBsiM7fTGYPBOq6glaREgQjbFtMI4gj6SZMl9pTzemwUOU6kC+X0NZNF7LsMz5MlNfdAYBPgSlHwRa6v82bnCaJ0CcTYMalAAz6mUhIHUpW1HnbppFNm11FVFzMPkc21gyNjKnrpOQDL9ReeUWQQFlHU4AYoyCvhOgbgR3HK4UnmnQLYejy+MZ6nMjHuqBGYKhjsoLF4JbFUkXv+XMwXQyQqKWkVwfAQG1E6CjDwKaeNDYT4ZW9WX+GdsOylgc7lH0dyxz7bnbM6gTJO1NdbAQo6yx3s54STVrtSEK8Ukky0Z2bkl4JoEZl5bS219YxzkrHoKu7qwgTTuK8zhPCb1VrE2YNRnVOfKWkRG5wX6XkbwMmW08iYJegGyJvt6DKSlsORApm37wOX1hpwTThMWslQ6SzBn5zMqZRSn8iyOiDhcrxXMT58+4TtVzduv35V2pE0rwxpIClpnDpYruq6jahrWm83ogE0rdJjaUbERdS1BtYDoUpyxdSm7yom2WNu1wvDNueyzAqBrYJTQVuSggvm9Dm4coj7TUQNrGAa22y0xSZV8Ppuza3elfdL5DNGSO8d81jBEdZJ52gKTijG42kjSKMyiQfe/tkMlSYxs31iigoImVhgDsG48SwJlv+0DtHtgvQg3yffo575qD6fJ1XQPSOLhpPLqhF0YXd7Tpzw4PGSzvqZVRgMIeOucKwmoU13SSp/nMAxk7TqwgHwsjEx0d9kflgcCxgu4p+zpDDlFUkzMGgHXU4Kr9Zo+DyWYdlCA9JwyaYj0u1Ztd6aaNTQnDVedMEMXtUzF3u060aD3jpgDVdpx0ASOljNyjnRty9XFM6pQ0SyOOXv8kMNFzZd//i/wbx4/IaQtfb/l088+5I233+Hk9j0e/uTHnJ+fUVeO3Xag76OyORPr9QuqqqKZSXu7c5n5YsHpySnX2y2fffaQWRW4d+cOm92Op0+fMpvPODxYsd2s2W633L19i6pq+OCDDxjiwFe//DbEnp988CHBV7z/1bfIqeXDTx7hXM2bb97jxdk5P/nwEcenx9y+dYuHnz1is95y++YtUt3w7OUZzsGNmzfZbrecP33KyekNDhYz1tcbrmInfaXZE2NPpqZZzGm7XgqNdc18sYAsNj+UfSp7soA2uLE4njK73YaUEqvVAWQ9Y6BtcgogeDkrTvXc7HdOTk5117C338cYzEJ0iWfYe58E85KQDtrqDKVgYr6vXLfEZKgflnOcdIAlpaAmjk4KK95rgQxwZiqslTJnjo8OqZqKttPWXB06Ngw9wxCpZ0tm8yXNvGHXrul7x65NxByIybFcHrFcHrLetKQ8sGgW3L97l/OzF7iYee3mHV4Ljns3T9gNkW3XgR+I3Yazq3Oq2YLjwxO2lwuGIfPavbe4c+s+T58/49FnH3H27Cmb6w2ZxMnJMXdvnXLrZMHRqmborqhCwrmWxWLB6ekxl1eX3L0z47/6x3+LP/7uj/n2934kjKIciUmZcbGjbwe6ToBoj8TF/ZCKSu0ekynDajXnV37xa3z9K++w257RzBoq52SolIPlcsWNGze4Wl8AA/Nqzuuv36dvW67OXhJ3O5YHC1Lf4vIM7zXpHwbRcWtrdn2LMesySaUfoJnNIEu75cBOQXOx52VgKqgWrRQlTNHQZzfKeOnAPJEQgrjtyJsWDh3vf/3rvPzhnxKHyBzP7Qwf//Zvs6kc33zyCD9vmL3/gDS8zWEFlzlT+YrkUomrvSaJTUzcSI4+eoYUyHh2OeK3LSnG0klw6ByLl9dw3eObOetnv0dcBlb3b7F89y0OD4/wg2N7fIP66JiLyw3by3Nu376j50Tsfl17iDWx02Kdnjjzk/ZPzomISJxUAXodomgyY35yplyJVbKuWyaqnYldK1r/SYafOW9+30DQXIaqmA+ToW+91MMHuR5h0vpJ/CZxW6ilTXucJ6B6mnmUXJqCYmM7cSZmZc2mzBDl5wYECpusYixa55I/6g5SvcExfyHDEHsur3sFf0zf1QmANmGfSvyXyXEsiCaENOD03uqmHlvJtf3Y/HOKcv3mT3XcXblW7/cJAk5BbIunLWcqazHprhQ/MP5ZPlOLX3nMP0ZpOYl3u17soOnhzmaNxoqiN9ooI1Ok2Cg5SsA6btyY67PftTnORJE8XWIYChCE/a4kfrIe6ssyqUgHOAVk7Hu8MXdjHuPb4CBKMd/lMSfSDT8itG5c7+m/p+s+1Xotz36aHE+e2fhTifO6rme33VLNVnImhkjbtpA9y+Wi+MOke73rO3DCmG2aOTgnbe9ZiBlJn3O32xGqBm+DlpJIAyQ9rw4ZTto0DRZFFsZtHBQ49TrwaMyz7BlVVU1W8L6qZI6P91DXVVmTmOTsOkZta+8987rW1nNZD9uzxtgPWqAIlSvzV6YPxNivXdeTk7AWm6re0/C1V4yRtuuKDjTl3IcypKzve2Iain2w51DV4zA0XwrYsei7Fhko/bdzolPadV0BSk272yQsnMnlpUTbbSWu6AeqEJjNF5IXary+Xm/o2lakXLwU1JpKcriUVWIy2l5z5TuLtMWiLtc7DFGKLE6KTrZWfd+z2+328pMQhGUt570rdiT1UuCy+zFQf9rxamvlnKOuZjLAsDJSSKbv+kIsJEseXwVjHzva1BJ8UIA44FxiNltgPksY/KqDnjOxF6kd5012QzoUYpKORF/siZ5ztSsuGZZUS4Emq16vHfkQaGbNXq7mvScgdr4UNcJQYlHnHFWQdTHJUkGDetIwsJiNwwBfff1Ug7QA+KpQzaVaFgo7ImHG2Vhv1j6KJt1j1cSpQdKsefx479VQiYRBaRtJBuFMHUWWRD0rlT1be6w4LAHkJKiq9DpTGggp4wdP7Zf83Jfe5x//nb/Pz73/NTaXV5ydP+fi6pI/+uNv8nvf/AM+/OwTciMVr4PbR/hFw2BUaDcFAJkYdU26VfcUvUWnQKNnwlZ1bs9RG8iN3Q+Ug2XA6PSA2ucY49J7FVg2I61GAixoT+X7pwESTEAou4tJkGbao0kPpLQV6n0p+DF1fnKwR3AuhEolH3JZqMQ+8GFf/UXO1DsnwUPKRas1xiTVYgV4pwZoKuVgr33nPK5p2Vl6H1bdmwLhORsgMq5RSqmwQPecI1nBMwlCJDkFJt8zXacpSylnIKbSKhkYAVkMANZkW7aTL2vvbc0ZQaXpEILPr0NGlZohCePV4QpAJntIuDopys/l/GYFPsfnN2UwWOuFnP9c9sL0Pr0WWrKz3xlZgrZO1hrTq7bSlPF9cHBA27Zl+IPdD8mp3l0i9lGvYdSStSDbOdOSVtF5o6NiGjx+ornkis0Zdw+kmLj/2n12Xcv5xXkBFINWpVNyvNz1/P6HH/Htzz6lI1BXouk6n88Z2pahl1a0YRgYhljkHFJKbLc7/aaMTccWtphjGODl2ZkmaCKvYkE+OVPX4xABGQxhZ2Zkikzb7WT1Ek01p6oqrtfX8nfaHu0DHB4eqt3o2e1aut1WK7vyHVn/l2ygSQZHoKorQuVLUNL3XWHfWPJmrdnWvm7b3c7TlEkiR0m/wFjYORffoZn3uNf8mDK9au/sz3ZtY3KSx/UsVySvMZlCgVrT6LW/T9oWmOiHHptGO026TIpiBF81ifQy3COX29i3ZVntiIBg2Q40yTkt5GiXCbL2WjriaLlgXjdsNhuudjuwyrT6U2vTchlSP7Db7ei7Tqb8zmc0swaXnDCxLq7pr9cMfU9wQBVYDx051JAzsQ/4bWJV1cxCRXt5zrZecVDNePSDb3Hx8gm//Jf+U97/pV/l23/wuxwOidnQ8fLJY+6+9ha77Y4njz6kqRqGtteETe1FJft1Pp9r0VZarJ49fcrV+prD1Yqbp6dcXV1xeXHB0cEhpzdP6fuWXdtyfHhIzomHDx9SBc/777/H9vqKTx9+ys3bt3j9zTd5/vQxTx4/4eTkkFu3b/L8+QueP7/k9PiU45MDfvzDD+n6njdev0uL4+GzZyzmc1ZHR1ytt6zXa27fukVdVVw+f4ZPiXsnJzxdb+gBlzwhgG8CbewhwfGsoZnNsfjG/JMVCL1zxddF1f1MKRKqQIUUPJzTqbXKprB2P/EHlHilaRqGvmfoOmH6NE2JlfZ3ujK+wqgLWlBTHM4FlsuVnmVtrdMYx+y92FcbDaY2KkeGoSfFgWGQ1jJfCouQc2QYMqHKyKAtlGHs8QlyigSfWa0aPNIJYC3xFdKF0/WR+SzgfM1uu2MYpIi9nM3IcUZKW7bbVv1jIA8dqe9ZNDOW9+5zfX3NweqIUDccbpd4PLvdGoKwRM+vj5nND7i+vmI2bzg4PGJWe0K75mTmmL12izdvHxG8YzaT4TEuR1xsyX3L8fEhh/OGz55ecrisOTmY0d48pI8dtdvxV/7y1/jFX/gqfRxoDg5Yre4wXxxTV4H1+ooXZy/46IMfsL56qV1RsL7equ2vwQkAfnLjBq+/+Qb3bt1gc31OFWA+r8gx0bY9q9WCWdOwXK1ILjP0Hdu+ZTGbc/v4iH6z5uzFSzyRi7MrsvqWIQ2kdhBd4yTSWy5LXOLw2kIoLKT58rRMCJ81NX2/VZKGVwxHrLPPjsqFAuYb6NgPPbMwsrhC8HTbLdvPPmO+POLW7bvc/5mv8Phb/57FcskyJ3w/cNRl/Pd/TLWoaBrH8rXb3FkuWKdB9mnO+DAW/gV0TJASVXagKjDB16TcE3OmcsKoSh7m2nHS5MwqRZbJc5wix3UgtzvWqePwzTcZfMXZixd01xtWbywYJcLknARfkVQj0QrOJb9RzxWBPiaGJF1rol2opcuqEp3LwriPxT8lHZ4lgGcWjccsv1/bsBgylXYuxZRG0oUTX5QmcbB3ju0gdoMsGCe1kwAAIABJREFUwMwUzEpDZN1da8w/djN5F5QkMPrUKbMqmeSD5jOVAiSusjhTB2IlG46ZS64pJJ64lxuNjH9KDGf+thS8J7lWdmDMmMoraQNvqKAAEdFkgnSQWUoltpY260QhTVS1xuxyHgWo6vaAhClBZmzlHoGpGzducHFxscc4nuYe5htK/JtHgHmMkxzzZg71jOCcgO26r0KwYj30sdckwxUJAos3pnmhtExneU82xrfY6SnALDGjdIm4lCfP3ZUiG3btaSRt5ZTJ3oa5efysIXmPV/ufYy7yZnY2zLdMX1OA9tUC+6sg7avv/w+9TNoRBWx7fZ5VVUteHEaWa3mWStyagoA20M/i2Ha3I6ZdkfmyFnD5TKex8ShplFIqeYwBnc6JzJRzruRERlyR3EVlJHA0dcDa820vDSnrsDhH33eaxwQq72mqWrvY5Lx0bUefhdgRghHmHDkmGtV5tvsXVi0EF6RLTjvLuq7b086uQgUOmqpmZ8P6FKzOMZKVFbqczSW/QAZsmdyHyRVVtaxxhsKsNPkIci5n0nnPfDZjpvOLJP8adBi04FhByUi+DtR1oN3t6Fwr+7VP1HVQgpfEo/WsgXJmBHtpqqbkXXYuis3SfbdYLApwPJvNhKQxRGIWzdXlcin3pL83DEOxJfZ7DrVz+l1d39NhwyMp7GXbPzJHYxy45pwnt5E618qYFr/Q9p0SvwJNUxFTKH7Fft97L/df11ytr8tnBi0cpqggtQKsPogEpnRXS1fTZrulCQGnEkiV82U2kmEYUsRRWRzNg8v41Mn5tv2U9d739pkOpPfeFz9H9jrMzNPUM+qq+UIbYa+fapBWgAmZri0asFrhKzo+E8F0B96H0hI83ZgwOk6nbKgSVKRxgiSMm8xMjukQGc1eHKQ5O9WhVAMVQsVAhuwYUiY5T46JWQqchBVf/+qv8F/+w3/Cu2+9RXt5xXZ9zeb6im/84R/yL37vX/Lx409pY4+rHasbJ6xODsiNgMtXV5d7ephT5yjFJYdN5vVW9TM9mInjs3/21jmPwYSBhkbxHivIY/uMHZSprmhWoGCIUYX6TUNU6OVmor/IOe2DkyOYK39n7B4JEKbtulbBslZba0/GOVwaB0FZIlha6gtQAdNJruUaECeexrFBgLFmx8qJXe/0wNrPpo7THJjJ05rzKb+b8t5zkX2rbNrJz7O1FryyjjEKc8ChbQZIEcEbDoh9L3rPvjwb50Z9K2DUt9F1MOaCbKOMsQRTTqo44nUowOf31atBisRqoTiOwpZSNoJo+BjYqheML+f01fUdgW2nFUCdTI7sB5+tTYyi5WwB4/Q8kISZV8ArN7bG2XPebDZln0zvD0fRjTK2x40bp1xdXQr7cwJSzmdSPby4vCh7chruTe/PaeFoHLAGvgq8vDyj63oVKLd2lF5spXMMwFmMvFh3VKGWINeL86sqT7cb6HdRB1qMgHYpJ6ot6PvhlWc6BtAxJ5pmQep7etX0tNdms1FgpsIqycUx56w6y7kUtTwwqyrWztilogOd0sDV1UUJCL1H9HyjATCS4prtFZ3lwOrggMvLC1KSYSJ+AuxPhxQ5RFtKbMioH2xnA+9L0crOhQ0F0tUQ0XlNAOpamJbjWo3P1857aeljTHrsPVVVCfg58Vll3fS/Y04lgC7t5QhgjrYIXlxdyQnwAjYX3bxyb6kkO7vdThIgMYpkRLPdAmyzt6UN3IJwZ61nYo8SWYHiTBMqls2Mg+WC8/NLtm0Lwam2Mlh3ABmGrqPvZe29g8OTI6pKWAWDtIQQVg3DrmJz1hEyVArMDjlz2be02eHmC2ZkqpRYBYdziavrl+TKsVpU3L11wrYb+Lm/9FfpGfiT3/8dDvuO2PZ0bebNB6+z21zSba9EPik70MEGTlsJr6+vCHVF5UN5zq/du8eN40POXrzk8vKa+/dfJ3vH9foKcmK1mBHjwNnZBU0deOvBW1xeX/D40WPu3r3Frbu3+ezxp5w9f87dO7dYruY8fvyEdjfwzoO3qKqKP/3BRzgHb7/3JkOOPH78GcerFc3hAY9fvKAbIjdv3SFUDS9fPqf28ObtO6yd4yIlkmg2kUj4uirSLTO1Ra7snX27NvXH6LlMKeJ8LmCs2SzvPUMatQ8t0DXbVVUVV5dXXF1cEprA6uCQWbMAXwnryUPOVjRj7zpGXcRx8KicC+3EcHLtYxyXESA9Yx1Q291WBlE1lcowyH51Gg/0gxaPfINzoSTw3llxIlF5x+HBQmKs2CtbXP4xULcOlWgxDi0x9jhmXF5uabtITANtuyb4BYv5MT57rq+uOB+e4ZwE+QdHp1RVTVMfkIeB1Szgase23/LG7VvcvHWHzWbDxZlotj56+JCr9RNC7VhVgSFUzGY1h6sDttstm/U1Q7slOJH38mSIHS71XDx/Qr++xFUVTV3hQs/BwYKrtWMgcefWIcvVKVXd8OxZhw9zArfpNjWOLPY/mT/NzGaNsh8zVUj0u5e4nDhcncjAuq6j2+24PD+n7XYEHKvFEX7puXvzlOOjQ3brS9rdjjT07IbE9WZD3cwYQmRIPbHbkfsWT2Q+a+hjZLO+RsiNjn7oaNsdt24e03cCpGc/4BA2Vwg11nkGUkyIZLIXnfjkYEiZKpvf036lDKSBZw8/5fTklOXqPg++9jWefvhjztdX3KxrARDxLH1glj39k5d8/I1v069b+k1b2t5FS1GKE9Yq2WWR70mVK7q4dagKsKSZEGgnigtQuQbfQVx3tGdX+MUct1owu3mD692OqyeP8Vp867uOdrdjPp8V0Edcm4K3yeSFTKtWGLPROfpscw/Ub2dk76fMQCwzHgSohaoOk+FcA0Pf0/c9lbLo7PxG1Z50TG2P/Nsmipt9Mb1AEJ8jupnI7AmXCkhT17UUKZPpYVLadr1Pey2lNr9Azv20ZXsEPdTCaRzuGbvIhOVFysWneu+ZL+aslkuev3i+Zz9tMEzMeYx1s/jXUE0liIpVBfTaJwSYPbuI2EyRrfDMmrnkTn1XCuaTyFL2mwFZw1Bsf9d1ZZ37vqdRUK+ApH6/+9E0O+USxmJ+yYmyzBJwgtGTs8kX2FqKkZdCwYRoku0aXwUts9pyHTyZ9H6S6ZxP11gKhvaMxvWidGFK/CNyWNLqbOxqKe772nySMGrrptbOCWHqTYHakZe/n8P+Wa9Xc8Xpz6fOL+dM09TM53PV145ljSqVRAOJzwyUN23XArAyrk0zmwnxyHl8VdP1IpUwDFIgF6AxE6qKppkxm83KMy/5FmM+5F0gaLt5mMnAJ+uqzDa7RgdsW5HIyHWhqqjMruUsEl1OyQpxoO+U/WigJTJ3yAUtrpk0HVIw3bRtYZk75wiVSBaJzRjnE5Wc0TlcPdPnlamdDaoSext7GSacXKLLrSgGhJGAYDl7O7RFJsK6cKwQZEQdi+GtO9tYqDCybe38xGEQaRcd3NbMZtRVTewHeU+ENookWN00VJqPWZegd0FoEln2fwiOSMSFUU95JCHKvlkshN0bvdiaoGx3y7fruqZpGubzeQGfsxa4fNDn5oPGMKMWuHOTIXNIvGm22CHguKWdjcaT9UGN34rdC94kdrKSmMZBkM658l12lkIVisxRNwwMSbprvKPIyCUtCIpubpAhsoPiVaGSc+1EZ3e7FYaxSX0FZRcnZVeb3S92lK6QFUqB0Xu6zuo74meMcd1Uzdgl8QX2YPr6qQZpM9b+rWCQtwczbri9BxVCaXE1LRXnIE70ZIIX9DxqpV3+QjRHBbzR784ZQ9VSFvaZsEsCOBUx9gIMZw1QvAtEO7Ap4YZMcDVHzYq/9ot/kV//W3+X1+7dJ/cDT58+pt2t+ePvfYd//q9+lw8fPaQdBqqm4uD2IfXxjC71pLYXKQcUQMsji9Y2/KBJtP3Mrt+muEpr0ucZXaXlyElQEnWdXfB7gIF95pTp9+r628+DsiJNdwl9htMt+CooOwXcpxUf++7p+w30ySlRa9WoMGbz2DLyuc/XHeVVgNopqD99r32fszVWMGLKWp0WBqbBzDSx/aLrlkAulNYuez5e27+mQaIVELwfmUY5Z13bKZNaIqHKS/U0plQmeRqoZr/rnBm86Xfsg6ivAuiiWzN5Xvb+lFQv1SQlYrnHqbGZgnz270E1j0sSpDG6JQDG9igAvAFsaAKhLXpB2b2SxyhwlCnvtbjfHKrcmzLD03iGbLBfzq4EEXJf+2tklUnbg+WZJ7E1WZn8wTvOX5wx5KG891SZdtfrDaHtSIw2TeoPo9ZWaWdLY2tkuQ8D1nTdDlcHHBwc8OjRIwHCciKY/pqKkwevDipGYtI9omwUcUryTJrQlKRQdKEnOlz6SI1J75xnsVwQh4YXL17iglQuj09OyjVOp7GW/a/fKrckAW/tPcsQ2NQVOTh2ux3eS2ugBTl7gLomdnZ2yLqGZN5958u89eBN/tW/+l2sNS/GXMBWK0bdOBXGCFDawJh8R/COEGpa0+WyYgsTn6HPxmxA27a267Fp61K88GWiJ/nz50GuwfT4ctnznwPuJ3tZAomIhzJgrgLRVrJEyc40IytY2uImw3a8w3TlUkrSnhojziW8l1bPKWgs28MYM/IDFZOQpMIHjmYNszpwfnHGuuuJTgJbn4V9RBa7st1u6XY7qmbG4Y1T7CYlFbDzq5PCj5bM2iOGi7XmbMJex3u2Q+Ss7wmhpvIVVYrMKui2F3TDjrv33+Z4ueST73+P+ekNfvVv/B2ur17y0bf/kMYPtOtzzl/Omc+WbK+vwfYK2vbkZPhmjD2ruWof9oOwGVcLrjcbHj97wc3TU5z3PH/5/zL3Zk+WJNl538/dY7lLLpWVtfRSXdU9g1kxM8BggAFgIEgAxk2kjGbSgx5kJjM+6u+SniSZjDKjiaJEGSRCpAgBINbBzKB7erq79urKPfMuEeGLHs5xj7jVQzzPNSurrMrMeyM83M/yne985wzfb7h39w7DMHBxfsFyueT+vbucn51wenbG/fvHHB4c8vTZU9brNW+/fR+bDC9ffI6x8P77wu59+vQFe8sFH3zwkPPLMy5urvngvfe46To+ffaKZtbwwfuPOLm64fHjJzSzhnvvvs3NdsPT16fEumU+rwVANZ6o+s8+BdqmoZ4MmtqpFiGTgr8wdXbipzGZLV/pmdZiSba/7HYiHO4f4IeOs4szjIHlYp8QzU6A+ubZGmskxZgrYCJFHGsrjKlKUTP7t5DlaPR++n6LmYBcKX8N1FYneOfrV9mmmMAkq62DA3XluHXrkBQ9KXq2mxuurs4wFrarFXEYcCYShy0xeoZhYPCBpoZmVtMNln6wWFNJa1sasETCsOby/AJrKvYWC2xdEYYOZ7SdMBjwCdNEhvUGhkAVLTM3Y9bOMVjmraOqas6vLri+PGdYrzDGif6qraitpe8GQj9gVYLr+uqKzc0NyVU0+/vMtGA19IGuW/Pkp39KN1igwtqIqyOOnqpJpOBxtmM5b2nqpvhWP1iub67oh0htZzRuTgqR7XZL4xxt01A5w97ekvmspesHbt8+4Ohgxrbv8QHOzzZcnV8STOCtt+/R1A21q6mpWfVbun7D5uaKtq3Z27+FNTXW1FSVAIUxDXT9iuglSey6QRJW9RXFdhkKcSDHDwkBpbJ0RyrbztLYmuHqnGcf/hVfunfA4Z37fOvX/w4//v1/Q6cdeE4cDLPlPsvlHrEPdNutxDOm9FYImNnUol0XogyhSdKxNURh+2AVsMqxTwaZUlL2KyRrqOqKgcj89iHLgyM2rmb7+pT1syfMZzWpkWEtUQepuUoin6zHX7t8cnY7RyLC3k1IfmA0xow5NkxRNfwiuYBTzrwxJWcyVthaOVm2RjRmd+AscY1fSOxzTFw6vpDk3OUYzuwWgYHS1ee9SJJMc4q+HzUx83NNKWtLh8Kacs7qYE6TV0ZanHX4ZX7PmIYC0Fpr8YPn7PyssMaaptG2/1aGyaQMHuc8gqJ96+zIMs6mOCXpIqoUsJ/G6wnK4GtrDMvlgnk759nzZ2w220neYshdTTlnyV8DBYyz1rJarWiruujgG0wZ2FPIS4ly3mezOU0j3TKF4RtVCiZZEqbY5uxn+r7T4YtmMlTZ7jzHvKbZD2RN2hR170rwrM9Xfm61XgNQ12MLeondU94/uZNn7ECMIZKUrSvXlEMbYVfPFjNmixldJ1ramW3O7g7W/bSbC05zq/z96fd2jkCO8yf/J/q4Og8Ey6xtcJXVeQZyzgavJLYYpcBd5UK8yFnlAek+SvG9ntU0VY2rIl4Zg3m/gnQTp2r3bJWcl9zNaSF4NptYfq6c+zL/OWt/QhySDugb18gg8adlnO8QJLynG6RwkCUMU8px73gunBu7L7te43QFR3PskEHl/KfktcZwM6zo+76cPQH6KmmkSQl0IGeKsTCth76fvKd81nbo6VeD6Gvr50wHF+avs7TAF/P8MSf3IWC3W+qmKSz9XPTGyXDFwQcSEd/JjIkiYWYMlYO+l2FuWa5BsILRnk7zyTIMPelwX0spSkZ9Xn4YCuvTZJtjNExOEHU2kLOVzi3YxYhICT94Yb5WUsSe4k8pRYahp21nOOvYmy/o3UCKFqyQz6yuYdM0O90EI6lG8ysnsoNuMhQvD1w0dhycl4C6aYgq86YODqfMdLGRe6xWKxIiS2P0czOInZnZ0z1dq2Z0vj/JH1VeC2hmbVn37XYje8qLnEUezvezXj/fIG1KeK2cpSQBgzVjBSs7iwwgDVoVzCBeU+VWAGkFjdgyaCxXH6JgBQqaKPuoMDaCluoUcLLSlkIcWVEhiGi1U0aVRVrkCDCn5p3jB/zmd77HP/vdf8Dx7WPOzk65PDnj5YunfPT4p/z+//sHfPT0E4YUqGcte0f7VPstnY2YKBTr5L18Xmaw5gRcN59zdQGJZENoKl0CKgqrJXcYpgyMGdG7xGb5Ag1Yg7QUZmAkJ0g5mJsCllgjtHG5KnXkjAOa0nht02p6PqhqsncM1g7gN3FgU6c3TikfQeuURkDDwI6DKYBeCfzSzmdmcDMP4xKQZwzspmDRTpvPxGCM76nDU9Qo5CE/WacFA9XUkGqwIYzxfI95XRQ4sBOQOJ98GAWwjVhPMwHlR3B5ZCLLku4GQvlV7hNJYBPoXkia6ECOZCxG9SHHdZ5W7HKwNQKk0nRTAKjJWZVnHcuzkaFcSQNMQxa8jDrswahhxYxgaWaHOGvLkD8jG0OlSSiyBzAGyvImCprm90uSGIUozM6E3K+P4jSs2gO57KBBkpPJw8oyzjZlu+30PDhEVja3PAoLcgeEZLI4UIaYZdmQbHessfTbLRf9IMEceWKnMLYrREMbI7rBzlW8df8+z549k+eSRnZopaLu+XzKPuCNl0xdB3EyJ6ensn/sWMSYzVo2qxXCWJU2Z6km9vqs9dmXREOGAVmzEK+fLLV13L93l6vrG65vbnQvFcsi7yMHWX4/yN5tmpab1Q2PP3tcui7yfjaFjReZtTPadkZKl6pFNygj1sigmIhUnv0gQbw66JLEF5M0npmcLEztAciQnRy1ZtuZgSyjTifvodwymu8r27PxOaQMcev5t+zPFrz7zrv85OOfKJtVWrszP2m3EBN17aTwYozRLhWLwRXbWOyUDmMoA+6y/I+CBXltQZK42lnapsYaOL+4YBMCg5xoXLIyBGzoJdANAWssh0e3SHUtwekbNthZAd8DUdiXd25xs/V0qw3F0yRpSVynyOvthspYauNwKVLZRPQDl6ennDx5QrcJ3Kxu+Ju65vu/9Q/YXJ1z/uxjZibw6tkT5stDbt25x/XZS/xmo3s3Jz8WEx2b1YamEjat73t8P3D//j3u3b/Pq1evePn5KxJwdHzMZrPm8uKSg8ND3nnnHV5//orLy3Peeuses6bh5csXDDHw3oN3Gbqep89eMp/PePjwPc4vrnjy5BXHx7e5c++IZ6+ecfr6jC995QOapubVJ59yOJ/x6MuPuLxZc/76NbcO9jm8fcTryyteXZxjXMW7d+8SrePk4pIhRpzsEmKIVFUjmotq+1IunEyG7FiTAUzIgH1QiRopaltprTeW2tlJwG9KYC0sC6hmwgqqZ03R/vPDgI8DTdOSpTIA4iTGe9MMJVTbPI0F4bp2DIOCurrPrTEMmlAvFgtS8PTbdQGQMzIUU4KQ29O0IB+1ET3mGDDR1g37ywXGBDbrK66vTtmubmhmEuzL/ImItZL8GmuUdbEBU7G3XOKsY97MaVzNZn2BsZaDtmJ+dEDwkZMnn9DOF6zWl5pAOeqqpnI1g42sr04YfNBOqQ5rBoyV9j3fDYRhSxi2bOOWpmqpq5bKNeJDTcXWb6ibGqLEq23d0KfAom1YzA7ouwGTVrg4YPya1PUqA2GIg4DfrmkkvgwDeIOxCaeDjerKEpuWs6srjKuoTCKFAR8987099vb3pCOssswXC9pZz3wWCfGGvvdgKhYHt9jbn5MQfzr0W7brKxazmqiTwKvKkaJnvV7hXKsDfzfE6GkbA2lDCBXJJLzvJKZ3tTI+1cYYjZu0m8PEhDGxJFSJtBO/2sqxbCo+/dFfsf/wXe5+9dt86VvfZX11yfM//WMOraEyEjMPIVDXDft7+4Su59pleQNTutyMtZhZzbAdhMUbR93IwUsBLoXs8yGaAM5JsSEECBE7D+ztz6n2FtT37uGrOdvLDRcvn7M9P+PBw/eo5zNiGosxRmOmummwYVCNeI3DyF0VattT0iFYYuMjKjMVtTgXcjFE/oQQ8UMQ4EXBzxgjtasF/ImhSI5ZJcsYZ0eigvo148bBQgWAqBu8F13Wtq5FL7HryAw4Hwby0OPl3p7oTXab8vzeBMeE7SYt4FVVEbxXppfV79flZ521DFbmHVROB5+FgLNoAS8oeCX3tbe3XwD1zHKsKmVQ1W4SO0zBvBxHqG1SV+us2zGCaeeLMXe5urzkmqsSi3gfaNsGYw2b9QYBrn3JUzJAknOP/LkhpQLwhBBEX1JtKjlnjAIgBh/Y+HXpJpDrkfXJsV7UHIqSI+Vux9wxKTGkIZEMKpWFaoDaQvaRPZpzyKxFPcY4dVUzBF9ilKB5UC7QC8lFNaezlJUWvEu+K1Wa8p7CMu0mkmWWhMZPX/BMf/ur+NRp0fNn/ExOR4wRGYCryxsOjg6YzWdUlQ5a0wK9VfZoZp6nBO1ctUsrh3OVtnwnZX2nHftX1ZVqtLeI5JWy3DXnzX/7YSgYCRZ5Vgkp8tQ13nvdK5XGrhI3yXvbcu95TTOgK2CfxN7WOs27KXFw8KGAlNlGFdKE1+5J53RILiITooUZV9VFjxQo0l4k+TqagG1UugGjoK8cNVdJR3AMUSMm8ZemqsqgVGdlgK/YJtHEjjHi1eYlkAFu2n2LxviD7yfxltxTO5vR1LV04w2ejc4JyffqbDXaZCTljskTVSYi41Dz2UwKKl0sEgpBnw1A0zRSMLNjx+Bmsyn3bUAHqCpYr/cxGp9U7GW2nVkOT7TsY3lvEBuqLA76vmc6qyXFhKmM2tskuUgQNrGztkhxxMkFOGNImZAWfLE5mXFtdM0X87n4Ii8ER6tdilLoESNiTaJuW+yghbZJXpOZ0Pv7++KTSdLBohI49XxG0zYqWTGIr0BlAPVaJOaQs+qHoci0iFyISgVlzMB8sWt7+vq5BmkNhsapJpBEBcBYaTPGYJPecIqkIRCMOMbaONVdmlDZEefih76AKPI5VtpikeAgIRsi+IBX7SFJqiUpNJrQYkQD0yYHUZhKJjmih5mp+dJbj/gv/uE/45e/9R2WyyWb9Zqffvwhn374EWdnp/zhD/6Cnz5/TJ88VVuxONqjOlgQK0NUUfi8DjloymBbqdoJRqrObwStrckaGAo+ATGJrmv+vR2atYJYDm1DNqZo/oYYMwqq80VHMC5GaUstEzj12oRxrPIRSVvGyMOediudOTEHUybHuqxBqt/JVYvS2pGBXBIpqdHXdRoxmcnGV+R4BCvFaZV7kNsr1yeB34QdoE9C3uqL1dApsJzvJ1f0jDrWEuQozJCiBgyaEFqbB2R9ERQWQ6xt+fp5FlNYncIiGZnPYxtZ2lnfzC6Q/9eBdoVRPIJbOZktyYo1hKgtLIlJsMV4kCav3Wcr9yDTMzN7IaiAdmZr6Z4K4pAtCWLQSpgaUKfaNTufm9lbqnWr9yyMWG3VY7yWwKilm+2GsVUBpjM4kVlcWROuTKHUQC+TAOLk9/LLqQOTdbWsVutd0ExtTS68TCuqhZmSmf15PYHDo1vcXN/ogADogsfqGhmtNiWTNBFSrqo+0957nr98RTRGmPK6Qyrn+PrXv86PfvQjaTPRYksGDXOgEKNKUGQ7mqvPbgw6z05PpHJvcpu8B4Tp5ozZSXpzQLoJA0/OXkvi7z2VsWw3HV3X6WeknbMlwCHkliq02BDCwKtXz3ih65C7LowK4ue93PcdL1+9IgRpjXbGMm9bul6kYnofMCEW25FBJwm0xoml0/vINrf821BAaDM5y2FSKCiTtHeYqhlQTlL4IOFwBdR1JhFU2qbCcHxwxKP7D3j2+CnrsBGASplyWR8rxFBsdzYJOXBNRuxyHhQXNdBPRnyqs1XRCN5h+OQdaQw+eJZNw7xp2XRb1t2GwUeR+pms3Wq7peuERdMu5sJK0gA7n59s63YtkCZWtaU9PuTae+Kmo9Y2pJTkvrYpcNJtcMFiTEtrwMXA6uI1z6PhwcNv0N455uTlaypj+NXf+F1+/1+95ObmkkWbePfRHaq9fZr5gic/+RG1AWMNDrCNox8Soe/p/IBpWmzt6DZbiJFN13Fyfs5suc9isWR9c8X15RWHB3vcunPMy9NTVusb3nv4AJMMz589p53Nefudt1lv1rx88Yq95YL7b7/N55+f8fr1Ke89fJeDW3u8evmKy/NLvv7V95ktW378k0/ZXyx478E9rs5e8/npJXdv7bM8POLF61N7na/aAAAgAElEQVROVxuqdsb+YobpOzbbrfj0lGiskTavGGjbhQT/SBuuHR8pGIqemOzrXCS0mCSyTv3QU/S/QVu5JAkjjZ014m8tUVnbrppLQGogdx+bFMSOGKd2N+wkBwImaMKn8ZkhcfLyOR/+8K/52je/wb2332ObC5zaAhuCJ8WAdTXtbMFmsy4TmI3JA6MsRu8jhkFOrJFzGBHtOxsSta2obGB1c8nlxWu22yv80DOf1cyaFouTdnpryuReax0heNabLXuLJYvlkio5Xj97zsXJCVVbc+vwFqenJ2w2a0yCw1sHNE3N6dkZm+2W+aylchWL/SWLvQOMqfEkLs4uwUkyGi1gArMm0TZzjHHUzjGrlwSfiMYzn80Y+htCgrppsTXYFGBIDDcXXKyvkKHdYqfn7YzGWfp+K+tvI1VTY61Iec2aWtoRgwxViUEKZtuup21q5ss9ZvWcs5MzXp284t0H73J8+w4+dDCAMY6bmxuMdbzzzh2ur6+5uLhk6Dr25jVt3XJ5fkHb1PjBc3J1znJvj2Z2QIiJukoYV2FtTfAC0MU4ULmEocNipAjut9S2JoZpHEtW9hFywhSY1b2RiITosclhjZAJ9vYO8OsP+eRP/4SDW/eZvfuQr3z/Nzg/PeXq4w85aiy1CQzDlm67ZT9ElvMl14s5m/VGuymEUeoyYArELD+QpBtGaNxi24LGq1jdj1rgDyEyxMDWGfbvv0PcP2Z9cUXcbnn19AnX6yts1WDI7E9b4omIDNuUgakSB4kRFmBYBqiIrnHWeIzeS2yRItMOQzReDikWkLY2FQ5HiL200lLzzt17vP/oIXePj9luOz757DGfPP0MHwNVW2f0DWuMAj/oFHnN2bSYL91otgAE4mczG85S1Q2r1c0OMJTBkxyDxShxgLWWum6I0WunUc5phBiQY8Co8wKEVZ/9fR5gDalMGVTWngLhzio7L4l2JnWNMZbNdl26hDJIlMHCGAfVzc2t+XlXJgV8hL2WWZbJyEV2Q49VZrXV+P7u3Tss9hZ89slnOznzlHgCrsxiMQ68DmDN8whKATt75ZA7MJVMo+sSQ1RphLH7DiP2tdLfDyHgnCkaj8W/kEj6dSSoTZb9apW9nLzX4p5ehwJzGYCyxlFXasvVQ5RuRz3bEqvnYoTs/xjkrIuercySGfKsER/Zxh5rsvzGCEBNi/TT18/6/yl7cZon5P/b+TnNTYxJhAiDT2gvLN4PhAQpepq6ZlZV5MzOamKUhqBgmy0drMkkOUsGPJ7kk7bwa97hcpeaPNMQvehwd0IAGQbp2Rb9VNkvRvWl8aIT7r1n22+lxdxOZOasBXKuMA6lzXu/qpvCxK1r6cqRgulEji3H20heIu+fQUj59zAMgr/YcRAZiVHGQaUZBPTVKFZj+dwNaYx0FSYSs0ps0lT72VV1iWcTYwEGhJEu9igyDKGApK0OmCqPWcHnQfMNA1ST96mrSEhB7JOSjmKKqo0+Dg7M+eqgxaUYI34Q25GZmdl+ZOwkyxWI5IIAuxmkBVkrowSkhERhheWrBZ4Yo7CyseL/LaQojO6g3QvZBjZtfmrCpI6x07ObaKqq4BV1XWsHU5IuqLQ74FChNoLOUckkuHJedIvEGCcDJGX+X8ZZMl6ROz6c4kMyLwmNa+JIyMkxbEy4BF7xBqv7pakq2qYmeNUjDirpmeRcGVfharHtXd+p/rArGuPOSYGk7O037ML09fMN0hqYAnUjg1G+n8GZXGVxRlhhmRGbwaoMagFqYIxOrpX3kr/18MWkLL6oItVOh5LlFgkxArnynVtDrDFYbyHVtNWcb37py/yTv/cP+M1f+T6WxOnVBU+fP+Hpi8d8+uIz/ujP/pSXF+d4IvPlgmbZ0hws8JUkJVaNUD6M6P1nVlS+n7zxXGEsjq0cWoOX6hS2JJ1JE3WD6nWo47Mk6qpiPp9zc3ND9Dlg0+8bowFkdi7SSiPPRJL5bHhQkAjEqRijeqFvgJkxRmJ+znZkbCVtja0qJxUtg677CJ5MWX/GjM846bWOazT+7FTCoRzEArqMQV12xlPHKr+z61Sz4Z/qpbzJRiyMiAK2jhpOTgOv/P/ZeeXKaDZyGbR4k2FU2uIn1zgNUPP/vamZNN6/7JGsLZeB9JQoRjTLAMjn5eBqbDcp1dk31mVc93zPyloIuSdGWad6nzmARHdj2TMKJI9trXIvTs+w3I84dQGA5V6yVm5xapW25OiaCUZvS4BcgGyyDg4FzM0BmtOEyajNiQpwOFdx//59zs/P2W63KhjOrr6XyfuS8u/4RvCX1yVLlJBBZmB1s9JWDKeOS4sjYWQAjey3VOxH3huDz8GDLUBbjPD06dOd6xzB4lTWL5/3KQN9ur/y7xnd7wGQlnlo6pZZ03C9uinQWzljBrCuOCyfIifnZ5P3HPfreBZ1L9vJ8EN9OedYzBccH97m2YsXLBcLIkkAATVMMYoeV+UqHr31LrWxfPryOfVyzvXNNS4lvvzwEZfXV5ycn0nwkIR9nNdmGly/+ZqC0PnfIAUwV1U0VcOsaRkGzxB6Bt8XtvS4nqkESzmQ1G4/aa1KlpOzE64uL+mGTgtTptjBnBSVtVF7nKY2tKyvANBGAxFhnUhQGKKwKGJMZTi1mmtC8Mxqx+FyyXq1pusGkuo9VcogCCGzzCuqupZkVdckarCbg+Vx/XLxQxNi/f9qf84y3uL6xWtSCNST7hWMYZMCp/2KZCP3FkuWJJxJXN9ccHl1wTt37rF0sDo7Yfn2bX7jd/8JH//oB6zPT9lsOkwyvPXeB/RDx+dPP2FujQRIGmwfHi65vLzSwN2wXm95+vw5rq05Oj5iNl/w8sVrXr8+ZX9vDm3LDz/8hEVT87UPHhLiwPNnz2malrv373FyfsbF6Rl7yyW3Dm9xcnLC1fWKh4/eZf9gj2fPntFve77zza8QY+Iv/+JvODw84CtffsSnjx/z+cUl9+/fo1rM+PDxU649LJczmuUeVxdXbK5WtPMZi1nNduhJVDT1ARt7Qdsoc0VZqeLLRxs0ZTZnW1vV0oYnLbgSnHrvtVVL9qxBbF7M7GgjvrxyDlM5UlVhDWzWV/jtWjT3fE8PGOto5wsqU+O9xmZRlENzom1TJIWBYbvmh3/+x/zL//G/51d/6+/yX//z/xZjaiKGELeQhDnllWmfpx5vu07OT3RQqW/LQJj6j2jAJmVgGGGB7NeO2gXOXr/k+vKSlBJ974lBgK4QPXXjsA5S8IVVl4ey3Ky2HOy1pE3PD/78z+m2A3XT8Ojhe9y7f48Pf/IRVVOx6noWB7c5uu1Ybm9Yr6+5vr5kszmlWx9ys+rZO7jF0fGRMBmTxyMxQ+1mcl6SwYREp+BlYuBku2azuSSaDbauCV2QhMd3dMOgNsThqlYlV8DZRFOLRpt0sAWcMcxnjtoJKWHwHoKwJ7GO5WJOM1uwd3jMZt1Rt5aj40Ochccff4jvN9w62mexPNQhHIbrzZaqaSQx3nakkPAm4ENkbiuqpqHbOjZbz9HRMT7B0K9pXUvbzKiI+MHh2oW0I5pewBpbEcKW/f3b9FtfOtCyr9T8buwyQ2IZorCDLUouUAN0cOcu88Ue50+f8pf/4d/y7d/7xxw+fMD3//E/5U//18jVk49p69xJ46lqhw8O6yQJH7oesnbkROdTOlK0GJLnWkaJ23OhKhkFO7A41xBtTR8c9t59Zo8e0psGh+Py9QlPnnzC3mxGvb/EmwhBBm7lBFF5i5DjM72GiHQWmuQEpEYKwT5AqIT4IbG5sEaN3bXP1lkaA0aqwyQi++2M73/ne/zi17/Jwd4+9+/dp6pausHzgx/9Jf/bv/nXfH5+ApWBWmMG1YjOrbMxIAw0wCZHTGKrop5t5yqqKsvhBbqtaAaOrLYo4FzKcYTmQAmGblNk4YRllUpwnXODEncYpIirgJOPwqLLcan4XI2T9D0H7yedYtOOuYB1EKLbKWiFODD4nI9krXrZD16Zn9ZK51Nmw5IosuJ+kAE/dd1wfn7O8xcvCEHkbSAz2rLEEeS421qZeB60yyUpWSAEzZGcUaAl4nC4lGdBTCSRElJkSBp9a1wfgxbpNd4NoZczsjO8MReuJyCv7ixrVZ9Ui0Gqa4ZJUFdOwbuES0JQGAdfC2EiliFvIxlHWNcSpwxJ2rWFwOBAtVTzfg8xFBvwt4GzY5xvdnznm4SbaU755vtNfz4lAcVDSoQkXQBBbdLgPZUCZ5n551yltkfirqZpJVdIUqRJKTEEr3vPYPzuPs9syJ282dvx3Oji1XWNq2qRLVFpIT94fW4CimUJAWutdBfbUTppR9YC8c15UFW+j3wdcik5PjHIEDkDKdIN0qHnrGW2XO7kJgYBzpLX4dt4xS0yCCkdxClmQorTYZR5z2UJworeyBkWGTijsbSwVGMIVDq8TLqBHJWtMBiG4KV4obmcU/A0uUjtfMEagCIN45wVYpDiOsZmzGnSpasD1jJWkIeRTfOx3D6fUmKxWDAMwyQfELJa09RYuwfA4IeSMwAYa6hdXeLALAMwxulGQWMjHequYruVwpT4GcXOSFJISomtDt62xhKi7KNhGHTwaC66ZYKPDu8yRnSiEZkxGd6mmJ7ev1VWc77fXJjJklaiIW4LRiY5scgKlTMbRmmd6f6srOwJp0VOkzteGJ+fdVY05PN5NhT8sbKOajbHWiuSeOJAmdUN3njFkwx2opf+5uvnGqQVwCW3Z2bQLBs+CthhrcHZWhaytOsHokkyFMAnDUQg+mwcx3YKaWvW6mLKJkHAhsw6kt8pR1vArRRVvClR2QaXahbtIb/167/F97/7XT545xG1s7x6/pyfPv6Yxy+e8v/94M/4ix/+gLPLCzm4VcV8f0m1aBmUBWeNaG4WICR7HLmKci0SiAiCPwaa6DpRWgdiDBgmazYBEKTqK/dijC2Vlrx5HcJAsNpWYRIFWMzgaAYVQTVLklbrDdpm4XbYr18ADDFFk8pVVTH80noYy4aX1klpI5R7zC0kpuyJGKNW/O0kOBqZWrkSNZVVGK9HK6zlfcf7UvxiB6SZOuIpUJvX30BhEmWgOz+7/L4ZdJo68KlDH69RubEpsziNgimuaMvkT9g1puzc//R9x2vNw1t2A4qUvhg05NYoCfLekKVgN0DJ9yqfL9/LrTkZ0BPnOzlfZlc2YrpmGay2lp3PHsFEhbGNtjKBssKztpMp+qN5/VIahysZbbPNwJFsSmX2FnA1FV0q0eUVhnNV1dR1o4OQ2HmGO899537Y/d7O75iy3lb3da6ICst9dMjGjOtugMpV0vr1xnpmUCao5qw888DFxcUXzmQOzGTPawKhTLUv7q2kzzYPCxrbaQR492yyZm/lyDIW2dJW1sp0zaiar3aUsZCAYlqYsSPrkwyrU+4zO9nNZo0l0W034Ky2aVGchrVgLJyenkqrcAocNC1uCf1qTWOdDCxwFl+S+i+em5/1ejMQzy9nHG3TMm/m3L51m77ruV5fcbNB2Ap5unOx8WigIcYkFd8nCcy637AKa9CJt3nvyiOwO+BnBvoxuxrbb+49yHYrSAtSyq1dFcMU9E2Rpq7YWy5YbdbcbDcMuhdtgjCZLN22LXXTSJDyBT81smeLrWHyYMtqiE+xs5r2cA9/vSZ5lZXxQZj+RqWN+g2ztmHRzAQ0oOb04nPi04q9w9tgGz4/O+fhV77OnQeP+D//5f8sQNew5tlnn/LW/fforzdcn7ykrg0gLXqzdo+wXBC8BI9ZZ2xeWWzTcnp+xtX1FUe3Dpm1jovzMypnePf+XdY3K168/pyDvSV37hxzenbG2fk5t4+OaJuGi8srtn3Puw/eJhnDhz/5KU1d8fDRe2w3PR9/8pj7bx3z/qO3ePLJcz5/dc7xg2Nms5aPHj/Hp8SdW7cITc3rE5EiaVoB3MJ2Q1tbXNtwVUXq2nCwP9Phfq7Yv7Lgk/Of2Ruik4Sy0Ibyc4Y8jEP8eE4gUpIYJiIt05VDWe2yd85PXtGtrpjNxgTj9eevsdbx9V/8VUwzE6akQQLZhIIYshsq6/ja17/G89/4dRYHe0SbMDEQ/MDQdxPfooM1lUXio5chE6rrl1spZQNKQJ40uA8qgxC8Z+/2nKa23FysSD6QUmAxn9HUDRsv7cSLxQImDEySoYuie3d1ccXJs1csrOPuW2/z+OkrNh4+P7vhq9/6Lt86OGa+t8fF5QX7+/tcnJ1w+849mrri8uoaZ6BtZ6y3HXsHBzSzVnyZq8ragOgnD31PjD2+7/BDACJXV6esbk5Z3Krw3vPi2edsVucY02OrJFqHVYOJFQQ7Yc4YwMlQI2vx0hhFwmOIRC/TmGUIoxYu1yuuByn83tlfcHQwY3V6wfrkc1xt6GaOdrHH7Tt3GMKW588/hwFcMsxqy7brOHl9wqydse06Nus1w9BjjGNv/0D0IUMiJCesf3I8aAkK7sc0MAwyHyInbJm8kAkMVmOZGMSnG5eno0srtydQVco6ipHZwSFvvfseP/3ox3z2Nz8g7S/57tE/Yv/WHb73D/8z/vIPfp+rz37KHRwpSMtxM5+JZIB2TGlwQA5njAJw2c6llEaGpiZ8EmNrOEIkmIhvLIe/8D7zh4/YREPsOy7PLvj4ow/ZbDd88NVvsH/7thZKE7PZDJcHfKZUNF0lv2DUTLfITAYHHQNd7BhiIEWnnUkKZHpBBkfgVpPX4DE4kokMfuCXvvF1/s73f4OZq/G9p44WGyz7zR6/9u1fYe4a/od/8T9x0V0TnQw6jCEvjjyvpqrxQUkm2vVlbebyGYyJxL7HS7CiBBwZlmc0picFAcfLcFQ577I15LzvABFGC6MFnRtJC9YJhO+TDLKKGms568og0+z7By/sOmsESLAm688LIB4ZsNGOpB+bwSMBWo+Pb3F6ciopmrJmQ5YXMJNWfics1lzsNibhfc+277DGalGuEi8ahR0odlcGqHofBDxVEo61luiDdF8qwz5l8CQYBoCJ37BW5zLEcehbfk4EYcqCSsBN4ijNGole/mXIHUYZcImFuCPgXCZSCfsxep0pMI0rki0gndEzI3G7VEAU4inAvZCPZKCksTqTJedeaeoVd2PAaa4z7Qwdfej4c9O//7b3mnwTrYFI3qIdmdYKIFSZUbYiv68A7K4QYTLolYf15hzVpwSDyMYIYSXPeLCFsTmSVlBpI+musVYGY7WN2BNjzI4OZwECU1K9VJlkn/Vis/0p6xtCAS9zbtj33U7uMubBej19kPcGxUB6GRJmZZBwzstkz2hHZdRW9Cg5D7CDSQjhTjqFMIYQPSGhA9cgWUMKudMik4uyz81Ao9GCRI7HK7Uj+nxD0rWULh4fgra8VyJbNGGQ1lWF95BBG2dswUFSTCQzrk/ea1PQN++pvEeyZMcY6yfV31Zm5zAO4srvJ635I16S90++70wbq52jmjUFEyvXpF05GftYVKO+dejUZmqhSf6WeC1rBZOfn+b51jkqldcouIMxo6SFMTtnMZWtZsrP6gYs5LAYx+7s/HPTToOge1TuQbo1fAwM0YtETvBUTroXKqMyMsiZs9YyBCkkTIeEOSvxlWjRy9kWrfif/fq5BmllTcdsLYMWKYmTs9aW9mjnnGjFaXXfJuj9gDFCoTeMDzA7qKrKh0kTipSZPXKI8tcxSbtAXVVYZSiHKIEX3lCZilntePTOI377t36PX/3u97DJU9nAyxef8dGP/5qPP/uEP/nhX/KnP/kxq9BDY2mrmuX+EjdrMLXDGakkytCKkOtHJEOhr4cgCVLZuFohyIlWEXiPmc01anvKdQsYK1jIKFBb2oOBq8vLXfFrlUDAGCo3tlBIcGmKFyvgptFgykQwrhhtw8hwnTq4DIrbNJl0p1haCqGI+Zeq8eRQjqBWNlpZBmUXBBv3DzuGJyYJwHMLVQbYZI3f0KudHOApODk1DuW6yr4VL58NWjak43uMRnYKOk6Nr50AvHn4UV7nqIHHm9fzt73eBI/y71hb63WMILhUnSJJNW+nDGWrxmb67zc/fwxC7M5n5fNoTK6WsvMeU9Bw+v5ZksGYXeD5C8B5DvKTFFqS0WQogwkKBuUzkI15sRVISxBJixsSpWesYnwVm+J5/PgxRS5h8gwLiG53iynZSTkrAvBvnou8f7J9y3tvCvQazM5a5c+bFid2met5P6UJs0jAmLqu2W63el3iVKTaqk7F9wV4HfeanTw/AXPb2YyYYNtty7MeGeKUe8vAeoyeSsFan4Lq84x7OT9fSTIzGC+Pg0SZzpzPUNd3IgFTWQmKQiwgkrBq8j6OXPUbTDLUlePq/IL9/SW9M/zNpz/VFlNldap+5RQQnhZmpkDnF2xBfuZJJ9BbuL65EefuJJCTAZSqgKUFBQnKlJGSxiTepKCsD0NpjcAUCQ4Mqsk8vuQatHVxUnDLdnIK2OrGKcFoSEBIRcvNxMhyPmMxn3F5s6IfBnxSBmKMbLZbQvA455jNZiSQNqQ31iafH2BnT0//zWSPJpOwbc38aI8Ow+b0UqYVpyQBdOXYEtkET7tZczCb09QVKUSG4ZKL00jwHXcffonDO/dYbwPtfI/9Ow+4OXmC9Tf4bUeVDA8evM8T37HXWpLfslmvuD6/xLmq6K8ak4hDTxwaOi3OHN4+pN9suLq8YtbU3Ltzm/W6Y3Vzzbvvvce8aTg9PeH89II7d27TtjNOXp8AcHTrFtvtlpPTM45u3+bu3dusrlc8e/yM+/dv8+6Du3z00adcnfV86ctfpnNbPvr0Od46Hr51B2MSHz7/nGVTc3h4wNn1inXXcXC4z+Fyj41POHtJTeLo8DZW2f6llfXNZ8PoXw15ryfm80WxLfnZ5NhJ4gVDCOJTCUFjmkSVwMSeq7MzjO+ZNxUxDqQQmNU1927tsbpesbl8Rb08pNk7xBoZDpaitPZKQl5RzSreef8r/NP/6r9BMISKvu+IvicpA4UY1f0qqzuNnSqSiGfGdlJF3Oyl0WJ0xfHRLbqXr9k7WFDXDS455lVDGjzzecu8rvBbw0zZ8aGPhD7KcLb5HGl382xWW9ImcPTgXW7drdgyo21m3Dm+g6fh4Qdf5t7b73B5dc319TldB/1mTTM/5ODO3TK9/aBtqJsGrKGdzbBOkpaEETY4sF5dYFykrWs2N5fU1jNrWz65OVdQZsHe4X2qZsF6e8PgN1T1nLpdMp/vQzB0fU/bzIpG5OB7rq+v2ds/oLIGYiD5LbG7IYUeXEXtZCJzMpFIJHgZ4rXubjj59CWfP3kJxvDV7x5iHUS8FKourtlcr2hNTevmrFYbNputDEazlv2DQ3xtOTu/4uXLE2bzBcd3Dri4PGO9XTPcXNB3G+pmzma7ZW95QBgEWAw+cHV9KkxfNaJWK3ZJAQoxNkZASmVDxSRgXLJaHEoJzIxHX/kGq37N+U8/5M/+6P9hW8Ov/tbf5979t/m1f/qf86M/+Ldsnz/GNw0DievVNb7vBVwiQhL5JFKk38oE6agtu6hvj0wK1CpvYIxcR58CZq/h0fd+kbe+/U3ibMHq4hqXAp9++hM++exj2sWSt999n6aaE/qcDGq+H4uLQHpVM+tIlyeiYJZlm3oGEwgBjBVoO6Edc6DScHkopsLfKeDDgDWOg/mMr335yxzO5myu17RVhfGetp4Lw2wIfPur3+Tlr/9d/tX//a/pQwIX8VFyHCm6QggDKRlsGu1RCAGjxJKU0MQ9FdAox4e52zHPEAj9ULo05ot5AQLV5ckwtDInwpQYydky9rRoYZvkhR2NxFzeaMFapV2MMdSVIQQYho7KQTJO2oKjDF406lpNJsswEgyIluvLC/ywncSqkPJ8hjjGmZnlGnTtvN8CVvMpS79NzOdzkgKxMQXFqMdBi8YCUSTxZACYEkT0rCTVb84g0RgMW0S3GGQAmxT3pbAiwFfJozI7bgJqhqjyXkkKZEVjtMSAmqcnq5qgQQaAp6SSWijTXM6PD5k5i54plYIrMhZy/YEo3QgWYjBFa7kQOfQaflYuOSWHZN+Z//5Z5Izp12/mNT8zb5vEZiIhVstQpKqmriSWE5BpKrFnZJ7CJNYuXZB6LuqqmQBW2jkSguppOmazuXYj5w7TRCryQxlHEUZ2Sn0ZxlSGCqfMhJT1Dn7AM5SBS5nNn/L9pkTf9zoQWUkRgw5L1zNrNM/N+zEXRHyIJC2AdX0vtmiiZ58JIyFmjeuRvZ2HcAM6hE3W3CQpouTCrqybyiCindoa62bgbRgS2822vIfN4PUOTiAG2DDujc1mI/Iuqdk5H17Z7FFlIlOKst/z3k0RPwFDc+d3DKHE29M9mvNmwbxGuYSow+RgMpA9jd3FOb/JAOaUhFbp9QiJSQRD26ZR2xlLzpoUkMZAU7lCmNqmNbUykPN+sfpMMgs4xoitJuQ+56gXi5LTioSNdInkeT2VMrLFxQZ8jIUxm30AOHJ4OAW687XkWSoxRjbbjY7Dkc+3zlLpUOXc2RVSFPKA0aKHVSB3GMp6VqqLmzGnGFLZdz4E4nZc2zdfP9cgrZowsuPKFZvRKCUNYMTQmyRTU2ezOd12i/XSHmGNwTlJhPMAImN228uZgDsjii8BnDUGq0i3TU5FxhMpQGNbjhZ7/Mq3vsOvfefX+OpXvsn+3pLt+oKb88/55JOf8OMf/zX/7o//kI9evcBri0XV1CyWLW5REZ1ER6KzI4cwOhlAJgYiayLJQc9TBDOIDBSmoGw6owxkCTKsFeMCkcrYEpSIw0DBrBFkcLrpLbuAT+Y+FkeU9YFQh6LWQZy/tr0k1aTNiVwOFvN6ZwDOCK2/QCkxizkDU+bXBBCeGpRsEPMrtyW8CaTC1ElqkG4tb7bCpZQKuIfRwCgpY8hkcGp8n7Edf1yfZJJMw9VKOiaVycGQQdkRrJvKIGQHnadYQpY2MAp4G9GHnZyBUmUbzXT5jB2gdwcInJyx9CZrUYLNZFIBF6cVu1cJTcgAACAASURBVJ8VXHxBbHxnUfVnyGwWTRom15Y/304qh/K5MAwe0SQa90NKozbQVKbCRzkvWTNVtJtNudtSBY2TokBME6mA/FzteK35XnWdMWoj4nidGbyjfAZ6P+r0ok6T1D0aYyQMI7t4d/3H55WHZenF75yD6XMdnxElEbV2ZFUmyBscGRoliRUI26bve2KRkJA/eW9mVl0GV8vnqWNK2molgdE4dTTv13w6pwG6MHOkYkmSlv48SVpYF26nLUbYxJkRLReZwcDcChNTYuMH5IxpQM/Y7pbXp65rbFVzfHTMfjvjk08+4fz6Ck8kWmndSWlMRUZrxxfOyptB+vSZzGYzGSxAZNPJJOTatVhj6YdBk6YvAqYwsl8LQ5bJWUljRT2lhDUOY0IBd0txzFr1LZH5QgC2lV8xfe3agl1Gd9aJcso0WLQiX7G6uqHrvTI8lAHRy/CVpm1xGrzHNLUIaedclOLN9Gema2iMtl4Kuys5A7OG2W1Ht9ngNz2tE534PPAs2cQqDry+ucHt79E6i7OJNNxwdR65+/Z7HO/f4vnpGbU55nu/9jv8wf/xv3D66hlH+3O22xW2Nhy9c59Xz54wMxZoaPVSYww0sxpSoNt6YtfTLBc0TcPZ1RXX2w17bcvB3j5X1xtevTrj7bfvEI3h08fPuHd8i/cfPqQfOq6vrpnNZrRty3bbcX51xTv3jrl375jPX7/m+mrFg3fvc7C/x8d/84SuH/jq1x+w7gM//uFLTNvylYf3qYh8+vg5dxdz7t075vXZOWG95ujwkIPlPtcXa9bBc+fWktob9ua3wCqLtbRE7iaTRQpo4lutcaI3r7qyYzE425ZUbJcxopHoKoexFTFE1tcX9OsrmsrhjDAhjZHhX8v9fW7flfbYYXNFcpZ2cUt8gU04YyBalPSHB/YO7zIET98nSKIrWNg3WuyxVlizdVPTNDVslVVlJ75YfTuoNlsyWGe4ubkRSYdmhrEV3banX2/p+zWr8wtmzRyMw+GwyVHZBothCJEwRGaLOda17O13LI4W3H/vAz766We8++4j9uczAomLyxu6/ilXlx1Hx3c5WB5z1Z5zseo4Pbvk7fceMV/Mubi4oHI1y8M7ONfSNC390BORqdPtYk6MgWG9wdrEcnlAayocPfuxZ37yAipPcguoLXuz29xbznn1+iWLxZL95RFVLZPoq75nMV9C0k4qmzjoeuqmwVkgeIZuTRq2dKtL+m7NfD4XOROpkGFTwprI+eUpTzcv8BvYdBvCtqN1gWYBVdXi+0PO+gCxwriWpg409awka4vlktP1NZs+Ym62PLj9NmBw9YbKeIZVgCRDWcSXhZLgh9DjhxvadimswKSxnJH9XuxMFOmfDPRUlcgsRIUmrRHWnqlnPPzGN1nhefnjH/If/v2/Y9Mlfvvv/0Pu3b/Lt3/v7/Hsb37I+tVTfFNzfXPDsO0KocE6WwALUiJ6LwUt06jdAyzS/YeyjkLAVTWprrj19n2+/hu/wq0vf4m+MqzOLzDOsry14OnnT7haX/GND77Gwf5tTLCYaOg3Pdtuy3K5hzVViQWiF3+di57ZHhsrA4D6oEIjJcbR2C9EmrYtw/FQQDQTCEwyGB84ujVnllQ//dZtrDX4wWMXct69B6Lhl3/xl/mTP/+PfHryWPRQkdiyqirNK7ysBRCi5j4xT70fAb+RLZY1GxM5fM6FWWMMhFh0eDO7CQPESCSU9zCl/UbYhEltf7KROMQy8XsEWNT+xSzrJTYyaLejSUEYcaGXuDTlYZ4JmzuLVNErpUS3Heg2a2EsOwEXstxaiaussMFDEHahj5342KiQmg5o64dATBJneu+LnnDlavpe5CFsZWWQqg/KcLQF/FDUUO2qshVjryCwA8b7FQkdBX2zpMFkZkb2LxJDjZ1YmUSR89Gck+R2+cw0zIWC/D7yfLz6JQhDIOR8KEFMOW9w1IjcSEDiIQFp5WddroYoG84KHU6e08TXvQmCTe+pPJv/xOtN8PYLxfHyg7IUQVvs60rAJ98PhD7StJXE75M9PJUYyC3nWbt6WnCo61p1SeV6Mpjk/UCMnj56AV+dVV+q5ypqmSZB1/c6GCmOAKeCTiJjIPskA3uDdmb0Otx9XEPplg7eYy3UbuyGK8QS7TTN57tSPVMDhHzdKUGUAZ5OdVVj9v3Gir/Xrp9EIvQIgKdAYI5hRHJAWuiHKMMOs9RBHobXNI2CvOzICAzDgKtrUpJuxiwrYiyqa5vou46YEvPZQnNLCH1X9n4MSjTppMDhtBBmnVPdWwWr/UikmhLJOu1gG/dnpK6UXR0jXTfiLpm5WnSdMzNb7WvbSrfOlNmaH5pJEIeITx5rK4Y+qK3N+bQUJVOciFUFMCaUNczYW1UL6Emi7NGYosRgRofKNUoGSolkLD55jK1KrJftsHRyK3HK6y4zsgess2VNjKlLjlTiXMZCWCZbzZpW5OhiwiZEo1aH3dfOUTkBX0MIuAwwG2jdDEj4EFmv1yrd48AaatdANPS+YwgDyYjm/3/q9XMN0gIygVVlDKStEQ2w3PgwQhThcQtx8DogQPQgRL8InIhJEpLHVRAUfUtBgoKYJKS3SfRzonFYKw/FIklCZjqRPCZYWjPj7Tv3+Se/8zv88re+w+2DYw4WR1xenfL69Qs++ckn/Ls/+mP+7K9+wNnlqSRBJuDalvZgiZs3BBOkTmWyjIKlyRbaKlMyg6fGyEAW8Rsl2BTTmdsOtbnDqnZhQfGBMlhpCpKiEhE5sZkAOezqU4oxkP/POr5AGbxgTAZoVcMwagXI5MqZgJ5R/z/pcKTM7DPKJstVkwJ+JEF2RerqDRbuG2BtruZZu5tcTtlsMDJ6M4CVMoqYwGnVK4MV00TOwOSgo98bAdtybchl52oe2u6d7KjxkgOulMJEF1kWPymIm0yuC+bzYMr7FkZhhr8UTLbWEsjrYyfJt1zDlHkphioWDUBjohrvkf5fGNOM+0v2QCh7zqp0CDnenXRu53vIwzrUZIM2kxmdHixgqKxXVE1i3eIaII/tXuXa0pjI1KpLA6L/GWIowBwpkexU73cCROXCge57AegNGFsGjSU0mFatrcxQsCQxsgoC22QIk2ruTjEiJS04jDbM+wFSUqa4TEyXATkSkOSHn5nB02F/Ze/+jEDRGRkIlLTQVKlNkWRKigcVhvl8hjWW1XrFzeUlBgEngyY6fd8xDH2pzDdNW4I6YyjaYjZJdTCmxPXmhjys0Ona+Sitw03bMAxBWS5pDICNEZusDzvEUew+P6u+78p9S0toLOD8zc1NOVcZnJ4yGqS4kW2EDFubt8J0C9uOy74nOQWfMVQ2AuOwMjHHWct397lO92KxSeR7Smy2WzR/AxLrbkPtBnJx0TlL01b0fRCbkEbGbwYTxgLHaGOMvqexmckYBNZNFG2tlICsvZ4S276XRNOofSp6pMoz0OdK9g3GkjmGEdhvLPNZzflqTT8E2V9aNe67jtlsxqxtpZrsvUy6N0Zty8jYSfGL+/ZnsU9GO6U2Jwmzr547Du4fcfXylLCVtrpUKYCXYBU9j1fnbJPn7YNbHNiKMHR02w0vnnzM3vKIzabj6vyc977xS/zef/nP+Tf/4r+D7oRv/NIv8/izz+iHxPtf+w7b83NOPv2Y2klXB072ZU2NxVJZARy3PmKaluO332Np4PTFC84urnnrrXvsLRZ8+ulTHNA0M/puw8nrU+7cv8P+/h5Pnj5lGDyPHj7g1t6C50+ec3m95tEHD6lqx0+fPKN2jq/+wvtcXV3xo5+8pGnm/PI338cPK548ecnxrSMObi95fXLC6nrL/Tu3mS2XvH59Tkhw53AfV9cM1Zq9/bkm/uJ/UgyUxho5ZZO9HUXDQsFcRWP0nArzY9a2ECm+wVgLthIgpRIf1F1d4jdb5nWjnT8qweLk+5LUJ4IN1MHK0DwSxhlMdAiumpRdol0BWIypwQQqF4mD+jwMyVayc4PEG7VrGHxgCAHnLdYhA7SwAkIhnTjHR8ecX54LWOEH/DAwm80YouXV2WsWVcvV2Q1nl5f4QTCsbhv40i98XbyXgsJVVWFN4OZmzXa7Yu3XHN95wO3DuwxDx9Z37B0eYm2N36y5vj7lcnUDZiB0PU27YFY5un7LW+8+wDUzfBDGUIyGzWagH3oG1f91VUVV1eztH+AqGSpWzSJDH+hSwtUtztQwQN0uSLRUzR7NbEuylnb/CGtaTB2pF1GKn1rArpxlqUmIS4F+fYNvFxzsL7i6PGN1dcl81sjgGETPzlUVrq44v4n0veHo9m0eLBuOb+8xnzfcur2g63vu3n3E6+M9zk/WrC46bFURPTogKbHtA8G03Dq6w+HRWywP7nJ2doqpFtjYyUDFsAECPvZYC1Xj8IMEIElCdmmdVPuTYxNrjHTRac4gw02zjmEk+kTtBIgPCCtof3mH73z711mR+I8f/pD/8If/F+ebK377t3+XX/iFr/LOL32X4foD0uaa+PKSnpcMQ8JGCARmlcHWkjjbmcN3XllNOX6WAWFeZTWiScxvHfLwW9/ivV/8BqGxnJ2eMPQdq2HD3vEtrl6dsfJrzKJiebCvMiECRvkoWqPeD1QWra9oXKfrICzMQASCDlS96XoF+swEOJM5EQd7ezKJPGx0YKDGMAFSsnTDhrC+Ia6uWF1dML//gKpagB/wIeKsxBK+jxwuF/zdX/sVXv3vn7IaAqYSKSaiFztjjRJW1I8kjY3VP8egDF9yVwvkIpHER8LC10HkYEVWbrW+kT1grZBYkjDqJe/KPtYIcJkZZUDSVutxCO8EsFNfJx16Oasw1C7x/ntvkWLko48viLZVXy2/k4rPnRBNpqBHjPgwyPuTGWc1JNU3jhKv2KhDxYwOoA2hyIL4oACZdoSlkLQzU/QhQy/3lpSdKstvxvXUYFQGSCohRMGlpOtRpsIraFjkMBD/H5NIbUWVigCje1X3vwJXSXPClBIhgY/5d9GcQ0PjlEhG/VBUWw5F1hCUmQ6kECCNA61zJ5ZzVXkvo92TGd2P2hpPMhPCzhiPvRmvvAm67hInxljxTZm4nT2E+uEEYYhsu14KJiEQCVKIS5H5bMaIa9sxh9ecC2NwTU1NRd8NpBDpfCd72Trqqirt+UOUwzH4QT53Ej9blRgzElgK8BYDIY6YgPdSnHe2EulIDE3bSAE/g61x1BqVpRfW4t7+PrNZi7WGftuTyWd5zYbB73Q5Gytt7+2sJet7gxRQMs4+ncdQijNIgamuK2I0ymgMundFRs8qGGyNpVVJjZxPxJTwOqQLI7Iqs1JIogzDy6x+6zK2AYv5HonIbDbDe0FZcgHc6mfUlfjbvu9pmka7F73EUCZRWZln4cOArZsCrkbtbMjPK//p+l4kTzqRkKkb6UiunBRaffDaJT4Wteq6lsKOMaCAet/3RWrPIB0mebifEEKCsI+HnqauC2PV6eyUmHxZ40wAKoPcuq0+Uz1SBpUhMuUct3VbZB0HlTrwUaRh8jDmGIPgfVGAUat5HooHGSshbMG1VIIyA9UpJdVSNxq7KdZlEilVBDMWfmMQqZCUJFcGqKoaU4pzXqRXjeS/brEQIk4I1I12zgZD5RayT9+wA2++fq5BWgOYSgAbYwyukqEV+QHHJIFPQpybTYk4eAnUraFtZ0RntEKkm8MIQ6uyFj+Eop8mbEFtp1CDkEIcHXNAQBIfqKPlqDng4Vsf8I9/7+/zm7/6PRIBmwynJ5/z9PkTfvzhX/Hv/+gP+cGHH3HTddgKTIg0e0va2/vYRa0tL5RkW3L4BHYKAsrLWtGLta7S4QKajJMZaexWBLTKRoz4wZdKQ8EqJ8CmGGKz41gyizC/Xzau4+9Mrm2iJ5nZj/nbQrGvyvqLdEyu/Iw/k3Vlc3WpgKtocF2c1y4D92dpsGRgJ69bSfiV8We02lIqMNpOmVmUuVIMRtv9pq0to2GfrkOpBqeRaZonNmZjLGsYyjUaMzrz6T3EmMgTsAXQzsk0eE2QrQZ2cbIWwgpG2j9TZuFN18B84TPl61FSQViT49pOg1B9MFhjZOovlPahwBt0fTWIOagak/9UPjMPshf5kgxuiTA60RR2eJ4AL5cwMiLz8/beF5ZlZn2GlNlckgw459huNjsV2lIVd2aUAcmgYZDfLxozKY3MbgVMy9oZC5Uw33NFcKLusHOGRsDKslzusV6viDGwXC5Zrdbk6l5m6uqKlWe1uxf/Ey8DvfQtytBDC4MWt5pGArMYA56ogzDS/0/dm/3Yllxnfr8Y9nCGnO88VN0qksUiS6RIqklJbKllCEIDMgyhDevNDwb85H/F7340YMAwbNiGYcNutNXqVtstSKIkiiIlTsWa6445Z5484x4iwg8rYu+dWUX7lT6CwFuZJ8/ZO3bEGr71rW/hg6JtBTAUAKUfkJG+W/Qo6y5hidYngrCpairSKcmmeEHjJHhxLX7j0dF+X2NDhNj+EWA8GbNcLj9TUU8LIq0xEgBlWYb3UsWW/ai7NfADG+C9F43y+LwDsKzWhNaxWM5FIieKt2uTwO8IDt4AYft2stDtwTzPO6kIVA+mCxMg2dR0lug00KXIEJhOp9Jes9pIW43u3ytr1BeXhnsqydyk9weIIvcDFm7oTl4XSBJtmbAMok0dbCDxqfHMRZbUyGYYo5mtlqxbB8qI7mXUKC3LkiLPpUjqr5/REPqkOvje9g8Tl2GBKz37xGqQ203FDKmm51tjJo1jcXQOtcO06fkrKteyCQ63nlFqw9Z4WxiwmWU9P+PdH/8to+kO5a1buGrN7Udf4o/+0/+C//G//i/53ve+R1kI6PrFr32DU62Y/eJHqCJnbCy+kUESWW4p8oLNckXY1FDkTMdjTKZ5+uEzqsWCew/2GY8LXrx4xdZ0xO39XWazSy4vLhiNSozSHB0eAfD6669hjOHlq1esq5r7Dx+wWtccfnLMZJrz5MkDTo9nfPTRS/ZvH/Dw8V3WV+ecHJ9y52Cfnf0dnr58xWq54P79B2wcHL54iclztre38XiuLs7JM8v2ZIxFEbTYe6U8watY4I6+xgfA0TYVxagky0tU1A/03kU7K762dXF4mIJgYltplOKwOuBdg6vXjIwkcgGwiUmriW2TwjpZbpYEV1MvzpmWOUqXNEGhDbHIFe0GGo/k015FNr624FoJyn0qrglrzBFwKuAiUBNUQHsPsXVP2gk9FxcXtL4d2GLPqBAAcmtri3pV4dDMFy3nFw3bW5nYotGY2rW4RhjHWZ6zWFxxdn7G7vYeWpWsNmtyKwDNer3m1fMZeV6yNZmSFWORiMFR5JkMRDKG0/NTivKIvCxZbyqWqzO8P6MsSmyWsdqsyfKMLOQURUFhxda2IZAbS16M0aMRo7EWtpEO7O3uEFTOerUhz3KyIkMhwC4Wisii2lQbnPPkWYwhlEdZjTcBa0p0MWK8vc94usNoVLBcXLGazwT094p2XXN6ccF8MafUCm0KytyyVQRoV6yXS7Z29tjZHaG8Yr3Y0PgW7xXKBNCyPyZbWzRVICun7OzfxascX1+xvqxQaoxWwmzXoUZbj/Ea34r8ikEKiBLn09nJzr8mO54AjiBAlmslznNtK8UqHf8owKic8O1vfJvpzi5/99Of8pO/+zuOX73in/6z3+edd77G3bu32H3yGsXOLZpszNH771Gdn1NXNcpuKG0JQdOEQIgtvk1o2TSVsKSUhaJkenDAoy98gUdf/CI+yzk+Pyf4GuMd56dHPP7qG1BafvbuuwTV8sW3vsTj154QtKJ1PnYTWcaTjDwr8e1AV7zzKyIL4ONel/b2gDIaEwyZNqLJOPCn6816wLCS4X6RWoBDSDFVvWG1XrJeLWnqDcrk0ungQGlHnhWo0PDsoxe8+fABX7j7kJ+/+JTGRIAqnlvlI3nBJ79+vZMq2QNP/zyH3UxDoobkkaZjwQbvY74VHzx9h2UHsMUYXA38UvJJqctRxWA7+Wvn2hirEkHBwKtXRzEWsvg2oLQ42BTf++Cx8RpTZ+gw0eqBYMlXG9+gvJRQVYjTzI0Ru6YHMzJkQ0dmeZQHED5Al+u52CpdxVx5mPsl0Ct1UuqQdDzl5hJRQhvdA3c3mK5EIDWdvh5QTEXhmAgn7WaVOmjoQBhN36WR4gQV47zE6m5cP/w5hNCzsRGQXwah9h1cBAF1rLZxEGMQGQXf66ynnPDa/Qxen1dgHu7P4bP7ZX9/87N7cFdkA5p41pL+ce0rrJYOsrRHvfJCJguiv26znNwYiAVY5/pccD6/6ghUqcgveXro9nh6xjrGXCaCVwrptk06swpkgB6SBxskjvZKkWWWTH3eUCQl+z/hAc5TNy7mtnIeyqIgEKjblrZpCQSaOrWQK9q6kW6tVAywNubDkmOkQKbLL7UCLXuPSKTJ8p6NKfswQfrSwm+t+OAQ5HzWqo55qe4ARZtZXOuwJkNpRWuk8AG9rn2ZlxJzeCfn37XUcchfknQwWpNlmQxTdY62bVmv1/F81WilyLOMLBPZAOdcZ4NtzNWMlpb8LMs7gk0ICDCs5N7yLMcYxXicsJY07LWNtlLippTXTCYT2laGdjV1LQBs1LlVEa8xbUMdtWWHbFhjLZkqOnyo8Q1t66g2a2zMt2xkMvsoZZjsj3OOUVGS2awH9we5TNMKOSTZ9baVoXjrtQzAM0bywzTHJDGFE4DfmaaYo2QJrzGGuknX4jp7IzYogse+94XpM5SOBSEFVSQ2EWSf5VlGEL0v2V1acqTU3P95EpTp9SsN0go4En2nGoABSsBV0V/pkzoVEc8Qd956vQIsPrK4THp/kMm8zjmUMRid2vVU5xiV1pj45YldResJ3rI33uP3v/27/OY3/glPHj8mR7Ou1lxcXXJ0csxf/c1f85ff/x5PTw8JbSCElqANdmuM3R7hMmGK9bys3iinttybIEwCeJIOqTgB3d2zTttnAMZJi1LSHLEdOCD/ncTBY+V3UDnr1nsQ4AzBmpsOiJAmYfZO2xgR0U//3TvrWEmMAUSqPDB4hgmQuwZ8+hBbzyKyd+OlBtfbga9aX/tZh9rFT5D2hlQpCxF70x2IloZxyBrJ92otw9rSWnRL/jlrMwQZ0v157yNDIsSWFDoj4gdBTAIDr8kMdJ/rUNbGuCZW1mM0E+1ct4aJeXuzwiv/o7uvw6sBIJOYgNcDjHStSYe2Y76G63IKg6fSf36Qa/Gp7B6vpYPzQ+ius20igO5i60nSNfa+0x8FaBvXGd8QQld5TCCbjzo31WZDFtnkMgBPmMvGRlA/gpZaC7iagsThPjLGCBs6AsbpNkKI7XIxCbSRwSqPsAfxhiB/qnoDEdCE9XrTnZUEVg+DtyFT/BpYO/gbkFYm50TYXCGBqQmgHNA4Dva3qZ3jYjkHJaxO3ZUxxUFleU5Tba7prSaNyRAGQCgigeLRTEYjDvYPeP7yOSmfkjWMEz4H9iXLLE3TfsbGpWB/tVr9kiC3BygT83yzqbtzmV5JFB4kMdBpwAZ9u5b3Dlxsq1EKbSNzIh2OqAM11OC9GYh3Ba4YzKSAIQX6qaKc9gncLLr0z3exWAhDmX6Y4fD70n9301c7f9GftA6gTT5MXZeA0UoJwzb0jPgkodIlLfR2LITIVER0hsssZ7GZs2lrvDM0myWtayiLkizP4zUE9vf2WK5WbDabzm/IOsqFDgs/wwQ62cw0tGj4TEMQIC9oJGhHwI1ib5t6U7E5uyKTbK7/bKBWMPMN503NTpazv39AcIHF4oymWbJ96wDbrvnpj3/Ed/7Z7/Lbf/Av+Pt/87/RXB3RNBWrixl3H77J/KunPH/3JxjlKa0VhmF8lrkWDUtftRRZS1VtCE3Fndv76ABPP3nK3u4erz26z/HhIfPZjN3dbXZ2djg7P6euK568+TpN03B6coJSioePHrJYbvj005fcvX+Lhw9ucXp8zPMXpzx+4xF3797m8NULri6uuHPnFju7E169esVysebe/busnePk6IyyLNk+2GW+rlmu5XncPrjF9mQLA9Qx8BVZFFnoEAF+oxTzqxmnJ4fs3brNzq07GB3wTgqJxhhyowcVKWG5EFumQWxbHuDi+JDq5Aizlna/tvVoZSDaZ5sZtqZTVps1H3/6IdYq3vvgXd759m/yxW//Hnq8K8yX5DNUbE9UiuBTC2UEfVFRWxMQSVxcK7IyJsZQaGHCGJUSChkmobTupnl7FQjOoQKUZU6RWabTLY4XFTobYYsRRR4oi5zVsqXIy+hLhPW2mAeKcszOdmBr6xaZHWNNSVM3Ai4by/nJM/b3bxMmE8rxmHW7QGHQxYiqqdk0LVkhz/ZqsWQ8ntK4hratyDLD9s4O8+VSzopW7O7sUdqC1jWsVktyG8hMzWZ9TqDFWg/BEVzD4fEhp+cXWGvIy5xNVWNMKRqsWoNSXF5esruzS6F2cM5TNw1aQ25lGnzTbMhiUWm1Flal2Hx5Novlkp3dXR69+Sbrq0uq0HJ8dsHOvQITFFtbE7RyjMcZq/kKk3m8avEoqjZQmJyApyhyRkXJ7XsP8V5R5iOycUa7WaLzfdDnaLWRrpY4tNYke+ccdSuDxIbFNxfDrE46J4SOgZq6uTqbHSeAE+JgrwAlBV978hXu79/n79/7Oe+/esa/+9N/xScffci3v/tb/Po/+RbZnVs8+c53uPvaG9SXM86fP2Nxfsq8WeOalrpxtCiUzVE6o9zeYTSesnPnLnsPHjLdO8AHeHb4ksuLSw4O9qDZcHz0isnulKv5jLW7YrGaU9iMJ49eZzLZYnG6ZGSEaRl8kPbm6JglZlN97KVi503USCX6Ya+k+0JiHPl5R5iI5AsB+GKLu/doa9nOx6wvL1ktlqzXFW3ruLo853Y5El1nm4mGnzEE1zIa5eRW81tf/yaHp6ecuzVtTHgJ6lrsMPQJ3QRwJI8oiqLTPh/66KEvHeY0WmvaAbtPchhP2zaxkJuliwAAIABJREFU+Hu9C+8m+DssmKfiYNJ+7IrxEO8BZvNljOfle0zs8vRRW1HFGL+LSaJd9Qw7BqPNUzJ4KMWlWitGec66qgUIT9eFxDheNrLY6BRHBLAmxsnGUmQZTdXr7XfF7RSPRD/cyTzd8OVdHDqQzxCWoe/At6RXCyoWEEwknPgePIEuTpP7j/8XY5Xg3aALRGLckK4hklvSgNrUuZPyIWLMkdrlU8wNSRZO/IJXctk3ST+f9xrGhp8HxN4kVlwvknx+Ltvvt3ghXkD9zFjR/Y65YSoc9Hlmr3vZtiJdYaKsy3BAV4r3pa086YK2FEXZ7fOU63ZDsnyUjtQC0uZZ0eUpOrImU0zXdXm2Dm/6M9jjCNIV47zDtY6mrmK+1Odziv7ztEKAV5PiFUkq6xgrFlkeP1NYnkNMKKiehRtJsAJmxtyrwwj0gByWii2Ryaq1Risj4DT93yQ5ikC/ZspKfOJdYn6LTZFOAMkNVACbcIF4rW3T4LwXySAEcymLkuA9zmtCkO6KyI8RYDFqsOrIWPatQ4WAVQpblDibSaHRhwjwC0israyVPLdkD9IZpANpE0idwPA6DqUzcfBqkocYlTltUXTznrp8JObOWgtRqm1bqqoiqU0pHZnLEZRNa5rY3lqpbo2TrJ0PgVyJ1ETbtv26x2dWFmXUTHadvfIBMpXAdsF7klRF10lhLaiAb+hsnoDlEa/JMrI8dtb6HgcZEhFFokkwmqqu8V7Y4i4WFJRKXc9yvdL52Uskft7rVxqkBfAJPPWRfWgtQSt8yk6NwrUwGm9R1ZKwpymQCodrfWdkvY/MP6XAxoeqNIl8n6ooGhXb7iMg4hXWQR4s9+6+zh/809/nn3/3d/BtxXp1yWYNy/WKn7/3Pn/5t3/F93741yyaitYYjHLkmWF0sIPdnUg1RYtmYwJ2uKEfmAzcTeMvP/RSBVKyOsZmYog/A0j2IG5ySj1D9HqQEVICTWRmRtAygchDBzMEDm6CLENQJQ14uvb7QTX6eiClB++XCYlBUL0BHJsclhj4NMGy++0A8IDeuQ7XUIajgTjmBNTKOkrL5fUhSJ22VQcY98Dx4KavYcadgxkEOddBOnn1bMS47l3lWdahcy5pD8aEQ3RajGwDEhCpuswjINW9NkjLRRaHLXVMAYlqoph3glVUZ+RSsOojyKli21Ey5GmoxTDA0Tf2QXxcdBONE6opd94tlxjMtPfkHkQEXdqMtFIEp7r9EYJChd6JS6VL9kVdNVLFi0OieqRQ1rRpG5S11MkeQJysHLBK2i/SIBFrDbV3ktQRh3tZK8NlBuCX0gptMrxrZapo6MHVoQ7n9TPT6yCuVqtuL/aSIqbbm+lvh0DlUCOa+PQSU1FrQ55nrFctVmlCBLQnNufRwR2q+YIH9+/yycuXXDnwVlHmhUguxADLNXVk4UoyISw7Rd9O1bf1hLjnElBvtCI3GXXbSKDr00CUJLMSgzlEmyo553TO0j5vmvba2RjKicjzHP7bX3NwN5kLSYYjJQ8JANfpf2OhJn23iZ8pwyU+PwkZ/iwlY3XUghq+JwVPSWt8eI037WgXbKSCxODV7bcY5Pa2oj97JoLBMt38OqDc7RP5sP76u6RTEVzqIOnXXCHAXZEXWGtZbNasGgmw/KbCty27B3uMyoK6rqVNKys65sWwymyM7loH09n9PCAeuFbYGq6l9wiYSGyxI2AzzeTeAd57mvO5JL5amFIZkmQcVyua4HnDHrCf55QKmtkF1WbF+csX5FnOSmV8788bvvs7f0A9X/K3/+d/yyi0/Ogv/j37r32J1568hVs1vPzkY25NLFnc06ld0ChpFWwWc8rJmMcP9lmu1pwezblza48Hj+5ycnjI7OKK1x4/FE1GJ/HJvbv3mZ1fcnx6yv7+Dju7u5yenXF6esW9uwfs7mxxfHjGfL7kjS88phyVfPThR6yWK1578giF5hfvHdIGz+PX77OoNpyeXLI1GQsQPF9ytaoYTcbkmcU7x3QyRqkQW1sVWnkMiIZn26C1xWQ521tbTMYjdJGjjAE0JjMUVp6RkyyH4JwMqtqsadqG7a09MAaNp7k45y/+p/+ezfvvs43BFpbRZIqrGrzywhbxgdF4xHq9pm5bglVUF0d878NfsHdwj9e++Vusq6grpxLaD816xYe/+DEPH79OOd0F3xKCIrik9yiDe3zd0ixX5AEKpVDWooxGB98lJL0tiicmEAsGoovaeh9tm6X1NZNJSaYhuAarPcpDs5HimLWayXiH6fYeSs/JiyllMcU7sHZE8I75bM5mU3F1dcnjN77IZHuHyc6u6LY60bNtvaxPXubs7h9QNy3rzYqmVViryTLD/u42OpN4aDwe0dTCQtzUK2azc5r6gqOXz8jyhukk59nzv2R3/yGj8S7Qcnj0krrZMJlsUzWB9WrJzs4uxhjOzy8ZlSO++PrrbG1tU5Yj5ssFp0eHnJ2fYDLL7s4u0+mEUTliMhqTaYlJVasoi4LJ/fvk2vPe+z9lvpyxcJpXp3Mejku0DTShIS8VO/tTWqcoyzFnR7PoUzTBBYoiw5ic2D7EejGn2N9ma+cOxi3BX1LXFyiVUdcye0HYXQbvLdVG2uxBwPcEYBFBLwmnxfEmm2qNifYyJek9KKKVxmBpqobbW/v84e/8B3zr6oKfffAeh88/5U/+12d89P5PefuttxiTM57scusrb7P/ztso51B1g682VE0rNsSDCp68LGlCYFNVXByf8skPf8LyYsZkZ8ydWwdcPH/O+ekxb37hdZiWfPrqGWqnwNUN9/fusj/eI2wcq/mCkBfkJhMWsVd438aifQAXOo1Qsa9SqJYhKI5FteRqs6ZSLVXtCEmfcuDjRnlGQNM0fdefAjI0i8WG+ekRy5kMY1yrGavxlO2D+2ib07iWVoHOc+4+fMj68pi3vvBFvvniOf/3P3wfp7V0tvg4SCdOGk86xVVVxSAp0jZCiDqOnwXCbvrs9HuJY4ja90rmR/BZMG3op0SXPw6OGTB6BbCGphl09hG6AoAioI10EPjI9gxRIzGKZsUIqf9OH8Q2D4kJKUcyaLGvCpl94RxN20SJLwEJUBHw1aovlHcsV2EDto0QZJq64uJcdEHruu7Any4ujZ1DEiem3Pk6USflVgn46kgEcS0kfk0xYJ8ruRAk/vABn0DcGFtKECbF8xBBWKVFmslEebwEkslxTrn0oM09xAFyOmoYK93pHstzh9Q5ZK2lGeR0v4zhNoxbhnvkJiA7fP//238PX8McFoSlilbkZU5mrYDOHSCaNKGd5PyxMBp3cAQeBRg0JhX5FcaKPE7XrRaZ96Z1nbSZMRmp9UDsXpzho6Qw0NY1besoCtG31cYIsB31GEPM5TZthYlDo2wiISiNikBrCIo0k0FHoNQ5xyoWwZM9dkRZj3jfobsuz9qthXDFoCMCYdWm/ZrOrwCJbSdj18WXwXXFiPgHEle2K7LM9h3BAxso5CAhZ2gd5ZlInyfv1VqxqSpCcGijom69XJ+Ls1NUvJa2qnB53l1rXTciIaTTcK9e3k/S+dCd1STz6UJguV51rFqtknZ3lHHxHu90ZPlGYDHIAK40GyjlmgkkTYBwwl26NYqbIwTIspzMhs5uJLuQcg6ttZAGtrdZryrpDFd0co15nl/Lb5pGJDqCDwJ8x5e1QgC01jIej7tcw3thM0/GQpipm3XMrUTeTpse6HXOsdlsojSFMH7ToDNZUxtBVEsIdbx+UuWmO591XdM0jdxLBHVTl2fbtixXK4bM88zqTlvZGCPAfIwxf9nrVx6kJSmpEwSg9DLlO3TaFsKEu3f7FufnZ1wtFp1WRoiggExrjS2ykXWYNqBKx0WJ09KECKGoaPBEY6vUljfuPuSP/sM/4pvvfJODrW3OLw5ZLNcsFgt+/Iv3+ZN/8+95/9n7rFVNyI1MTSwMZlyS7U+gsPi6xaVprkSn3OFg1xlbQ+3NHlDtK3wqASRxIybaeDo06cEnMIXQM16HQNd1pxIgaqAMWXrXwA9SZXL4+3g3EQf00QCnz0jXEVD9pNTQg8rpEsUJyLAqASl7VocPvtMrGYJl6bOTIRhWM4eA8HCaYd+m9NngLbU5KpWWzXcDqGJ6GB2FaD6FGHRIxV9HAHB4b58Fd4b6qcNrlveruB9j5W0ANPX3Fdk+IWopD9qdO1DUp7OTQDK4BkR3ARbXn1/cClpJQhTpJfIszEDP9sZJvQYudc+nbx6R69YR6Na4xGg1kb2MOOuOwWyEgYCB4IcOVa65c5hxGJuP699GPSoJ5lQXYIrjaXtWegoSTQyItMZYQ92I1p9SaRqptKm0QbRuU+VTY9BW4x1RnkCY+EnH7yYwF0J6Tj3ArJI43rXzJPq0w70zrOYnI59sWCrahOBYrZZRP0ijQqxiWsPh5Rm+bqheeU4uz3ExDnVOGKVaa/Z29ztGp7ZD5qbqNn4C8vrAIuA1rJqKT58/G+wfAXmHhRJh7Ipkgh44uhTM9WeuH0yWzqsEjX0hSn4WW3NuJGRJisF50TDX6T1axRbugc1SEtSV4zHVZkMaDiDa0T1DqNNk+kwQLkFaXVfX9lSyIZ2NiQm+Hti+dP8psUnnd/j8b35fCkim0ynL5VIGLhjR6KrrugPbhzZwCKjLYWcATBn29/aZzWZs6qqTTxFQQjMqCjRQb9Y0dSsBbhtbeKYjlFYdQK2j351dXtK66/Yqnd20lxLLfXh96TPS+1Kg069DL1mUWJUehy4yxrf2WG0awrruCjxKGTyeVVVhPRwyx714yd2tCbVvUSajWVxy8vwperqNsRmzqyt+74//mHV7xg/+9f9O3m64OHmGCQ0PX/sy88WG5dUryix2fGiNigVQYxQtjqZZUYzHjKfbTIoJRWY5fP6KxWLJ6689JDeGy9klewcHvPnkdebLBYeHx2zvTBiPR5ydntI0nievP4TgOXr1Cufh0ePXqOoV7/38A5TOePz667Su4uknIqXw1bff5NXRCc+enXDrwT22d7c5OjnmarYhH00wSjO7nJFbYWwba8ltzyhUwaFwlLkAETYvCAhQZTPd6XGF4HFtTVbmZErTVBvOTw7ZGpdcnZ8xGk8g1FTOkxk4/8W7nP3shxQvXtE4CKWFMscGhcdjmpambamMwWqDtZpaKfaaDbNqzWizwtYVZVC0IbLNlLQEr67OuTp9xRuvv4ZRgcIoNm1LXVeUoxLlHYRGtBe9x6QkLuXhSoaqdufWGIhqHV18YrS023thCjvnyW2G3d3jeHPEYrVBmwyMZl3XhNagTCAEjVYFbXOFzXxsQ7RkNhO7FZPIxeySvCypmhq8Z7W4olpt2N3ZpyxyGt0DVKNRyXQ65mJ2SW6NtGIS9exGGcZknJyf4qlxyrFuNlzNzpmvF7AMVFWQPVBuYe2E6XiL2dUlLtT40LC9tUVQDmUVo/GIA61Zrzd89PRDtNJsT3e4fXBAkVmCb1gul9TVkpMTw3g8YW/vgLZ2tJuKcjrC4xnnOc1yTuM3mNLQKs3VouGxKYUlaDTKGCq3Zvdgh9zm1Kua3BTs7Oxxebkky8cEVbJpAqPcMppMWC/mrGaXnJ8cM5/PUKxZztfc2rfo0oLTOCw632KkPa5dRaav6lya2Ka+cyDxS5N/SMBs6rXv4tsgMgIBzXK+Im8LHmzd5uFv3uVkdsaHzz+mvrzgZ3/7PaqLKw62D7hz5x47e7fY2tqjKEqKokRlInu2WW2YX15wcX7C+ckx1WqNxrB/64BHX3jC1fKK7//9D/B1zTu/9g7kE37xi5/RlA23tx7x+PYD7u7co1QlBs3Bzj7Ot/jWY23e+VBClH5wqavEx4MgwJ6PlBUXfCcNkmL+m9Ji0q7rr/kZ7xvmZ6fMDl/hN3MuTg9pVkt2J2NWV5eU4z3G22OsiVO/gwaf0WwcJsB3vv4NfvbxhzxfnaGtIc8Kyu2Sq+VChprGeEJiH8v21hbO+Sg1FP15kqUYxF7JNyd/bIymcb2MlvcyUT0xxMTXhP5z4j0OZd9cLHBZMwQd+1ZxFRmPeNFqNVkWNVOjvJuCNtwAM+I6SoEpAks38jDvPUVZcGtrn7PzM1xw1G3Lutr015807elJFYEQByhJSJ86BwgpHnG0bZ8bOue6VmxhXPZAV4jXfFP6KXWapWckoWCIZNAYl8acpgsqE3NYG0luAzELT12XYrclfOyH//j4LH2k5SmlyGKelrodhbkrxcUU90DqPB12GaYOStXncN2evp7HfR5wez1/7OO24c+Gr5sx6808e/habVbkZYa2IzkuIYi0hYJ0R4EQmX0CtKlYEJBYlz5fQsgcagCUKyXAXhpe17ZpXWUInY6MyYRVJB3QNu6PNuZhMryV7lm2cXYFhB7EikBvEigRIk/EYKJMgdYq5s+h60RLw9BT/tZp2ie93GSnB50xCgGOtTKkgdaJzJDyKRXfm1jIKsoJCsNbrreqKxarPg5NsXHCWwSXCVFyUgILjxTwlQpyT8rK/TYBTYNWUtSHlGPKmZV7dJHEYiJRSHK7PB9FQNZ1hR6gO38+grRpPfIsw21a6VrEYK2A8xqLjXu9rmuaWs5KjaNpajyKPALFTSPkJ+edEPcSNhJtbZYXgHRaEnxve9M+Vv1eT3YxxKJBHgtuAo5LZ0CIzNu0N12UFhueG9d6mSMVWaq9NJqV5+A9NsvIC0twjqoSP2VNJucwBIqi6ED3tDcNGhc8eXoesdBlbRa/oxUJoKhRYCOwm2UZBKgb6ejK85wsk86OoixpW3mmMljOCuCvetkFpUMsZX3+61cepFVBWCrC7JShHSoa7LqqsHmOUnB89IqqrlFBUPC2dbhGKOYh9ju44IXNEwETo23UY5ENJo5AySTPAEobtDNMsynffvvr/Ed/8Ps8efiAwsLV2SGXJ8e8ODnh+z/5R/7mB9/no6fPCBmo3NC6lnJSYrfGqNxQaQfOQ91E/Rhx7l0rD5E1me77BqiXHKUksgLMoFQ3mMXa/rME6Ezv79lePjKQFDr5Qrx3keUk7YdJR3LY/pc8lgQnppsb4jt0zxA9OCiN0V0K0g+Lis7PuTa2QiKRgvMDR9mDpwIqJMMfHR+9w2zbNrZe6Mi+vA4KpHVLeqW9E+2B14id3AB6+7Zy0b4csnI1aWCUip8VBLmKn6WTj4gBiwBDKsS2Ca266l33CtBN2B0+75Act+lAy2vBVqd9Gm8iXbegnGgFxmYoNM5HpkBIoKAmqRMMdTJlb8XLUICX70qVOxW9/XWQvDfA8ZOAJKXh4/oqgsrxwWLsNtNyTwLWPEObAu1lcqaAqZ7lak69Wcpgg9rh2gbnNihqfFihVSs6YkpaZryrMSZDGxvb28XhSaAsLe9W2wgYq5Ru0bgWqw2uFaBWKQWNp65bCAGbiUSCdx5tpYRjrGV7e5uzszMIgaaKgUx8Ll4h043pn+fN89y3s/fFDFkrARcTC0K2hyO0gb3pHrvjMaeXp6zaRlhCUQLEqL4ts2MwakkGvGuYr+JU36ZhVi2xmQxKkLZc6VXIjGEynbDerKmqtVS54/Xc2d9jvF3y6afP6PRkSWdICglpAFYH1gUPXWtHiNInEFyLUZbRaExdb0itUfLrnvmfnNx6vSIVEHxI7Y1DUDMy4WIrqoCzkkD3ydRAWzkxNYbPI8QChNKgfHfGU9W6e4Z6MAQjHV9BesiyfJCs0p2L7hVZLCmRSYGU932hqAOd+ZwOCq4nAF13SPz5erNJaU3cS/3k3Y7VHUFy0XBLepuO+dUM37YCZitZo0zBOC9RSrOqN9TOCxjrA3lmmW5Pqds6+iyxPx35WfWB4/Xik47giEK6NHvbnwqHcq0+/ttjbN9emtY9xD3V+SAco70poa5ZHZ6hNm1kX0j7si0MjXdc1Sv2yjFow8Y7cmtZ1DMWlw0HRYZar3j/H35Asf07/M4f/jEf/vw9Lj75Cf78ENtsyFXGO9/8TX72g79gvjxme5xhvMJmOQ5PUIbQbFAERnnJZGuberng9PSE9cbx+uN7GKW5WmzY2T1gUo44OTvh/PySne1ttnemzGYLrDG88cUnXM6uOD4+I89yHjx6xPHZGS9fHLG9PeW1x/dZLVc8e/aKvYNtvvilRxwdnfLppyds7+6yszXh1dErllXLzvYWl1XDfF4xUorCwF//1b/jslpy/8mbjMuRMMi9l0nDGkyW07arOJTKs65XHD1/yfpqwWI24/z0lCdPXse3FefHRyxOTqHa4DYbHBLEVpsK2gY1mzO+uGTfe2zrYAl+LdrpWilG1jIS5F7snzNkWjNSirFS/OP/8j/w93/2Z/i8pDGabHsbNZqis5zga6rNnKfv/ghtRuzu7FNMS0bakqmA8w3G1VDNaZolq3YjNuFGp09ivqhYDExtx845isIyHRf4WPxqnUObQJ5ljKcTlqs1bZwSvlhsCG3NZDqmbWuOT57H/T+iqteMyon4OWC6s8vWzhb1ek1RlJyfHLK6mrFcXmGU4er0EK8UKsvY2dkTVozNGE0mWCN+PdTCfqybGu8ceVGgadisL4GKq5nsLxcK2qahcDnvfO2rbG/d4sXzM/a0ReuANZbtnV0IilsH+1SVaBre2drBty3O1cznM9bVktmVFQmhMkd7ieu8SxpxLVfzGdW6YuIaILA2GnxF3ThG4xyP5+XhBft3Zuze2qLMLSFk/OynP+Fg7w46zosSxvc2rs2oWsfs6pKtnZLVuiY3nmZ5yfnRB1SLQ2aXl4zGgflihvNCsBBmjaJ1iaHl+mRIRdDHe7o5CSikRdJ3zOoUDyp0Fyul1yayxlsf2FzOWc5m7Oxuc297l713vs7WnT3Oz864eHnE5vyS2acvOH//aYzXpBDilWisZ1EmJCszdqdbbN19QDEeM18u+cGPfsjh4QsePX7E1772dQqj+Pj9n1M3lxTFhC0z5vUnXyZUGion5BCt0eTUocXkGmMsbb3pgaZYkFeoqCgrnWYGaHRAW2kBLfMxlYE21F0SqqNMl+vaeGOhUWuMsrTVjGYhutIf/PQDHm+9xuQbE8zYcetOA75BxW4wnKfdrMmMIssK7o3v89vf+g3+5V/8W9ZB5BPu3LlLc+RZrkWz30ZWr6tb7t29y3K94uWrlcTXqFQlHhT9xCkFD95FoKn1BJfaww0JEFSRDUfUnBSHFbtMQqQ7BNGY9dEXuwBNK/JZ0vUjgECIf6eNwcY4VIp5NsbwAwIOaS5ELK4qnfpySd1izvnIOPRsmpq8WVM1mw4I6mJxF/2+D7HDMsVqQ5klRRaH3wzBxOSDU86WQLZUqhiClsnHp65A5xyubWmjXe+Pmun+3edVsq4xehDdX6PQIclphO5+UmygCFGCTYC97reyTBGE7Yu90jHXs2y7wrVSoE0P0jk/mEdgCZkR4kftCOr/mxWbPvuXgbM3iUPDz7gZ3w1/nz6raaSDsW5qGVTkAg09+y9JRvgul4v5qQ8oQydnNsyzhVQSOhBKp++PxB75XgEIbWZRadIsCYSNObJ3NFUbCxbSgal034UafMBqkblIUgvOOerGRYa3xNU6fqY2whzWWrphJNaTHNsYi1YFJhNd+wRU6ogNiI68rF83t0JpGaTnnAC2xgiDVJleTqQjcnnxqRHQttaSqQytIXjRkdcmgrAh5l0xXhb5K/DRb9kYqWqtu6Ks1oqqlg4A51p5NloLq1kb8nxMnhcdy1PILBavwbkmsp1bMmuxcbC0i6zj+GCu7T8ffx9UIARH4xRBK6wJNDHv8EDTVvKsnBMdZqWpIzhrjaH1jqqq2Kw38XqtYFlKURLZu66lqeoOu+kG1sfnOyxuqGgbrLUiYRYk32udp2n74WtKaxluF6QzJoTQzZdK7wO67wqxK0qAi9ANaMuLPD4z+f66rq9JrWTRHnsCNspDhOBjIUNkDoL3ONfL2iSZhrIsBMAG9FJHLE46RK3NyIsShUhBSTeQPOtALKznBZk2seP581+/4iCtJH+hq6LFpfSB0WhE20qlxhjLOlZSlZEqkQ9tnwAG2XioIIF2oKsuC9sq0EYGZ2opV15hnGKkM77z9q/zL/75H7I7zvng5++yd2uf9XLJJ0+f8uff/z4//MXPuFpeoQtJHB1QjgrGu1NcbnDx8BuVplrGarDqmWSQqjy9Uxjq4aSWBElMfdd2FDzCREjp+TABB6lwqb4qSUjCxXJoXPBSQfAe0BgTW5vxsfU2gQeplUTaTdvWoTPZjK0PqOCi5kZibUWGZxDDpaKh7e432nytBZRIlS8PIjgeAbtrzk2laYkq6rT0bKyhhhL0VRv5s2H7b7i25qm9sa8Gp/cIqCD6v8LATftoyGrsAStQA11HSQIiEBeBkWtaTaG/Du9TcCTPIMQ2CaPNtfsXp+L7arVJmsS9tqzoTvaf3zQOH5ouEO30uFSqHF5n3fngI/OQDkCSNTeDNQuD6/fxmMrvnJPkV/vI3g0Bo3fY2vkS5fQ23kyYTh7RemnFKPIx3q+o65qrxRIfFLefHFCaQFAapzLatsJtrmg3p8wvf87y6jn1ZolvW4xqwOYxME1NY4qkvTaQgAGCSNqnKqwHHUI8nz4GtNLqv7u7x6OHD/jg/Q9k4IyTxKVtW5ZRAzCB+saoeO9Ruya21KTI9POYgkMmpYpnITFrE5Ce2tiUl4LS7u4uF4sLmnqNybOo8eOuPb+098ejEh9aNpsapUSX2+a2GxagIyssKE/wDofn8PiQtpFx5R5JLiZFiTW6K/rI4EXXsa2V9FPFsy8/k+FjirqJIGm0XalVCaQ1pqo2JMizXx8VnXSD64Ts+8SiY1HEqq4EGmkityRWEtwkNoDsz1RsALoKam+LZBKqSjZ3UDi6xmzwIQaWKk4KDZ1tk1tTn3kW6fnLyU57UXfgcTq4PZiZkrf+vN1kaYQQWC6Xsl5RqL9jEpBYBIPzqFOBJ1ZfVOp8kEByVa3lvV78QmEt4zwaLk/lAAAgAElEQVTDYFisVtStY7FeQYBRUVCOSmymcS7h4qpDruV79LVr/8y/u/dJMUNAbSTZ7O43FqI6zxaTsfh1CZwO8bm03lPsbOE3DcvjCzRgu0KHsC83ytHYwO7dW8xXC+q2wVpD2665ml9g8y305Rnf+9M/5e79e/z27/0B3w8LZp+8j6lqro5eMZpOefTml3nx8wWh3hCMl4Qpl0DPZqIVvryacTWbYbKCcueAyR5S/a9rHjx8wNXiildHR4Dj3p07WKNYrOeURc6d23c4Pjnl9PSMO3fvMB5POT095fjomFu3D9jb3+Xs/JLL8zPu3z/g4PYBz54ecXp6wdtfeYLzLe998hw7Knn88AGvji+oNhvG21N2ihGLqyv+9Z/8K/7q777H/Uf3GI130LrAKo13NUoFRtaiWk/b1Hz1rdeYas3f/F9/iW4c1gWUCzQ/mqCammZToesW3XpMCGgcZZ4xdi2qdYyDZqQtBoMmDvlQimA1RB+mdO9fdZGDljhnqgIXL56yeP89Nq5mqaDOMuZeUaHR45Jg4EdaU5oJ25NdimmBKcfY7S1cpmmpMUZxeHnKsl0TTA+MBKU6nf4kq9MVC3zA1y2l1YwKi8GT5bl0k7j2Ons+TlM/OTljU634yttfJssyVhfnjCcj8C3VZoXRGZktxeYB+WjCZDrl9MULrs5OOTs/ZTk7j90cLcYKo7nIC4piRADK0Yjp1hZZZlAabJ5Rty3np6cURUE+zdmszpnNz1jMZ4zHI+rGE0LLaDTi3t0HTMa32dm6y8XsiGwRODs5w7maoiyZjEf4xtGsDePtXWw5pmqWzK/OMCagDTRuzbraUOS5mBQj3T/j7QnT/V3msyW+qfFtTW4tWhvycsRqtaAoMxbLipPTFU5l6MsNrnV8+vExF2eOrXLMtJzQevBOk+clZ7OXXJxdoHVGOd5iU1WYUHE1P8RXJ4ynhjhRF+8ddVXjW0eRW9qqjrFVZFdFYC3Fx0HQHVLx25PkilJRNfp/HboEs3WNgLRNy6ic4KzFtxWLqwuWi3PuPHrAbj6i3L/L4+27qE1Ns97Q1qIT6RO4YMUX5FkOxrLxcHYx49mrl3z67IecHB8zKUd842u/zhuvP2Z1Neflx8/x6yX3H93iwZe+SLlzm0KPqEMrCaNKNlnhWo/OhA0fkCKkaPZLLuKD65NMrSUhdDGvUjHRtIgsSARNszwTcgievBAtyLoRoK5Qlnl7LnJuAS4urvjpP/yM2fmct77+Ze7cu0c2GhHsGIVGB8fs8phpHphsT5nNV7zx4BGPD+7w4eyYdbXho08/6QgjCVw2WuQsTo6PqJpG7ik5hujntE4+sycRaC25SyB0+ZYxGq2TD6YDM5USqAUtA29UELAr5Vk+CCnDWItNA2pMizFZ1HgUfybFfYOlL6SHmG9GByXsLBKjV0W2GV1s5NJArOjPqrri6ORQNB/pY9Eu34vXKWAOnQxCusebHTxDkksnE9DFL7oHTgY/H+ZXKbZNwEy6LyEDdB+EiqSXLvxAOp2wRuLeoCQmD677fUhnUz4kRQN0rFfnu/sPCbSKeZmK0nmSJ3WXJZGHIs4OEBDPRAYtmZEpbKTc8TqQffP1eSDssIPs8/7ml72GMeQwlw2IzJgmskJjPm2NxEdKGbLcxvw9Pv8O+xBwMQTVEyKSlB6Btt0QiKD7YKBt+u5q0/Zs1QhCOVJXmIBdcbVEazoxpSOQb5SAffIj2UdlGQtf9N8DwnDMMhliiRW7bLvqv6y/sVKEc8rFVn35DOsFhE268H3eHLB5FpndIWqsyrlQ0ElFSmwp7fxt/HtjDEUpQy1RabiVx6EwUXpPW9MVQ5KefSeZ1uWIct7KQny/jzGHc5GhGjt0qqrqhodpLfrIMqR7JIPsdS+9k3ZVYiwnwFajxC9rFdm+cgabpun8nFbCuB/lGeOEQzgnevnDtTO6G0iW53lkDHvaWohCNgLfIcpB1LUUi+V91yXPklRC6kboJDi1QrlWcDsX51I4R1tVzNuWpmnY2d7uhpIppUTuJu6HJIcxGhVRLkHOeFVV/bkc2KcA1Ot13Buqs3cCxrtoxw1EsibIzzUqSnQABBpX0YAA96rvju7tdbSzKmrzRnJiV/BCQesll9f/vwVpA21wnVC/kh4NQghsNpt4aIJodkRgJADr+ACEFi7Uf5B2HqNNdBx9FUYMgY3VuCDTR1vNSG/x7be/wm//2tcIyyWtDuxt73C1mPODn/+Yv/qbv+ajp09Z1bJhMpuhjCIfZditEp9rmXDsiANbZLCPV33lUa4T0HE6sUrDwUIsdGlSK7v3knBLtdF3G8AHRBw8Gs2UMKdTLM5dDqZ8h4C7IQRpnwBiZIcP0Xmp1A4iLQghhMg6brtN5mMrdJKFkPfEaq2PAAYD1h0xkIrAJFrqqIHE9gqdIw8q/WfvLNP7esBa1ixCD1hrqaqq01DpW2f7dYjnlQT49GBND8Cq2PYRSKBt//c60vE7BxpiQB9ZstKyE7r1kmv2kfXZTz3trqd7SInZm5x9f32d445RjzJRzkPicJQfALld1aq/BuV6o6C0Fqao7qtCgcREJiY5vdNM15I+u/8Z/RCjoGh8bOEKEEKLUxZpM5pw5/5vcPDgt3l50rCpLUfrAkJLsz4nY4E2OUEH2jDCk7P0WxitcdYQijG2sJRTxXin4smjtynaI9x6w9nZKUfHH1CvX+KbFYE2BuYxuEJaTnwIVL7tDKUUYgL3bt0hzzM+fvEcFSdmJsDRaM3x8XF0NEaA2DCwPfR7MwmIpzVKrVafF6ANgbaeFekQwDxJUQSZoO2brqByOjvjdHZK4xtMkck58woVAUtxxPK/xhgOdvZYLK9YLTegHIk6nYDkBNoT94TzDtf4bl+pAL5t8a2j2axpjqpYABOWt/deClvRhg7vU7SGrsuD6O5fxBZ5CUYS0DEEIocFDAErpZUlAXWxo6gH6dAReFdRPsN0+z991vCzEyt8aCfSPh8yZ9MzlOA1RC0n3wX4OiaFMlG311u9nuAMz05/DfI7ufZ+7ZLG8nWQE/rBjUm7Nq1Z0qEafreOLODOdgz24mdYIHENvQJtNbm2jLIc1zrm9YL1ppJEP0CWZzKAhngGQuj3q+q/f6jH/LnfObivPLdMJxMWy2WcYCx22CUtMWLhSJvoj1ISGu8VsT9tlE2Z3jmAAMvTC2EFxIKN956lq3m5nLF/ckRTR0kTH8jzkuX8kqLYApMRbM5ZveEbv/ltJv/xf8a//Z//G+qTI9gsePnRu9x/8y1ef/tbvPrp3xJURW4DuBjcWYunxbc1ioztW3d46wtf4m/+7nscv3rBW09eZ7Wac3J6RADu7O2CV1zOrihKy/bWDqcXFxweHTEejcnLgtl8xmq94PHDexSjMZ88fcFyseLNJ4/Y35vy/PkLqk3NV956QhscH35yxGrVcnd/wuxixmox5/bWFpNJyXzZ8OzVOdo4mqtzDt89YbH2rBsplmodKAKMtWZsLDbA/Gc/ZqQUeavJg6JUhpHNyeYbjIkyUSYjz0wnB7M9nbJZrnBNTe7E3jraaAySqF46xz4WQIxMXrdAlmGNMLqpPAWALtkEx7r1LBpPFTyLzZJ5s6bynnUwbJxi7dZUWlEVGUs8s7ZmfGuXMCqpTEDbvGe1Rw8sgXwESFqJa3SQwkqmNXmW4du6C/Y1StjTeGmr89KR0FQ1wRuurja0raPeVCKD4WcoXeBdIDc5NssxJsfVjqfPn/LRT37Ce++9zwfPnrNeLJCBTAGbGZRRWG3IrJVCvw/sbG+TFxZloRyPCcHTVDVFkbF1MGa6PWZnf5vd/V05/+sNkDEaFRR5xuzijCyfgFdYhF2NW6KoaZuNFOLrhtXCglfMlyvqzRqjFcvFOU2zZDIWFm4bJ9kbq8lKzdbuLfJ8m08+ehcdahaLmovzV4TQsFmvuFpA8JpPPznk+GSGcw1N66jWhrlqKKyhbhWjLGc+X9G2jrbasL+7hdUOTYO1Ad+0bO9OmV9qQhUIaMpiTKYFdPE+gMlwJCCjlxhLfoQoqdW7p2hL/dCeeRmNDp3dbaKWrNVGClflNiE4NtWc1fKS81cvefrhh6ig2JnsMhptd9re2WgkevHBSNzvWi7nK04uj3j/o4/45OnHNN6xtbXFO1/5Kl948gajTHP8ycecvXqJQjPdmbK9e5eD/YeofAItuLaWXenlPImefwQAU8IoGEM6eN29diW+gEjJBdH8blxDCzgVB93GFt8kKWRthnOeQlvyoqBoYUWgdTXGBLxvqDdrDl8cM59fYrTi67/1XfYfTAUE9YHJtKRZXYIfM8lz7uzs8Btvv8Ph986Ye0+rIDMGR4hgZixkasV6s8ENCisJqOuguAQMDvyQAd544wtcXFwwn88HoFhi0aW4X/JKwRCtfGdcqUlZsonSdXmex5ZYF3O3fpDTzRi+15alAw36aeOha6EWeaXrrEyJA/p2bWlDj7IBKV6QuxbWfUcCud5lOLyGm/HFTbBxGJv9svcMX/2gUN/Fy0KekfxuGN+EEDpij/xMTupNMYFhDpg0WIdrk7oViVtbJf3ca7Bu2hKJFZ/2QwQJY16s45wJrSwBYdUHurd95nUzlv+84nRas+G93Pzvz4uRIGIeqehgTGypl2dblAU2gvsp7g/B9bEpYttU1pOt0r20rZPCBKEj1qRzk5iA6Zyngbh9vuLJsoyiKK7dp/xvktbrByoplQZ0+cg+LCOwLvtEhhTG2Nt7YQvoXpYy+dxUcKlrGeKolZZZI0p1HbvB93vctZLzEQIuMndDZICmwmx6L/FvBRPS2Ngx3NZtJI5YEhnKxBx/OINkOIwtbih5j1JCqEvdtkHOcIuKhQFL0J7MZFKYgG5eR57ntK3MF/GxE28ISnbDa03sXI15aKYFNE6xVpL6zPM8rnHAKy+DywSGEbtpBBhPzyTJDRRFgTWGzNtO9q1NchkRr7I2IzOWPMsF7B0M9bLWUpQFDJ73er2RveM9PigckGkZXijdsNJpXiEDg9P1FGlNrO3OTJKr0nGIWVeoIBYZ6ppEBFBaAHNjLW3TdBI6wXvyzGKUzJ9RrUgwdN2TEfkVMNsLEcs7vHd9kd/YjiiYZdmNnC8NJ9eSLzqHI6B8wLsGtfn88w+/8iAtmGhYUSG24MYD5ugWvquxxWpFMhpS8U3sNASEUAPgLi66pWsSxXuF8YZcj/jut77Dd7/+a9i6ZW9vl+nelFevXvCDH/8j//LP/4xXx4cCVAYobIbDY8claqvEFxqnolGMbSfEymXaYMPKpQtJQyj+/wDMcd09xKwG1YlBi9MZAJA6abUIgJM0bDrGJ6EHX5PT9b4TYya4aO1UXM/kWFMLAz3AZ3TXlmKiY2jS4CYkMEoc38SbciHqPDoHSndTGnUEMeum6YD0BC6kl/y7r3qnRC+9Y73edGCrrLVJn9J9RtLloVuzZNQFDJKfi3NURtr4RApC9mEKOjoJhHhdqRpjtMYai/MugnWBVMlNzOChTm7SVIa+TSn9zrmWvqV8kDR4YXuIHiLRAfTAeVfNxOHj4Cd8oGkbTGaiU/FAi7F5VwRIxiQZ06Sx2/++j+3leuJ9+zg0xQUIIgvQmJLJ3hPu3Pk6e3d/gw+f15xceUxWoHRBcBatdmjrNaHSBOUI2oOGqppH6FjjuRTAPoPMBrb1KVv1C+7t7bN35x3G995hvDlkdvaUV0fvsqjOILRgNFo70ZhWRtJp76XIENf8YjFnVOR414in0ooQGeSr1ao3qiG1aOkOkOwrhLIe1wJYL3pkwwCsA9XcsL09DJ6vVLrjTid4FyvQcYqk9rQR7G/rhgqN7WQ3Qmf3EkB9eHgEyjMajRiNplzOL7uHpyM6EhLDNT7cAN06WQxKyXmvvGM8GnOwv8/R8TEGTZ5nVHWFD1AURSfFkva3p5clMVpassbjEZPRhIvLK5TW7Oztc3p6GjWBkq0b6kTL2mdZLgMdBsFip28Uz3/nsGOA2TRNd96HCdLNIPpaIO0H51+pwbkVG+CQ56W1aJwn0FCaRIc26rP/zrKMLMtYLBbXAvs+wO3/Zhj0D+3U7u4u5+fn1667+/fABiW/ln7PjX04/J0KUibTAUZFxjiTIGi+WrJpRSvUoBiNRp0etWtluEwChOWZB9SAjaRVfx4+G8j3a1M7x9nsklRQ6g3N9QJbR90mBuKqvzfftjJAVMmwvPLWjrREXS3xtYuseimmncxm/KL9lG1vmRYl67oSUX9Tc3H2krau2Nm7Rzke8/zjp7z269/id/+T/5z/47/7ryjOT5i6imcffMCbb/8ae194h/NPf0qhFJaodW1yvDKgHK2H2WzJbafJywl7t++wWtfM5xcoo7h1+xar1YannxyyszNl9/YtXh2fcHh0wuPH99jZ2ebw8BBjDPfu3qVtWz795BnOKb781psYrXj//U8pJxlf+eobVOuKjz98znhrh2++ts/Tl8e8Ojnn0aM7TCYFl1cLrs4XjHPD1taYtt3QrgJTo9nfKZg3npNFxQbP2jsuG4f38HS5IVeBQhkKZRgZgwkKoyBTYBWUWpMrhY3ntlhcQpDCeKkNNtAlPzomNsGLvjBKih6+bfCbFSyg8gGvApk11I1EDzYzbELLsm1Yu0CLYukbFrSsdGATPK0HqwKtArzHo2hdQ4VH5zrql0tUIgW468m0D9JJ5YNHBwmmtZFk4urqisViIfGSNiRZFptZvGvxTgZN0sDZ0TnnOpCXmia0bP0/1L3XryVZdub32yYizjnX38ybprJs+64mRXYPqeaQM+JInAE4IwiQBAmQHvVPCdCzoHe9CMJgKEF0I86QTbLZjl0+q9Jn3rz2mIjYRg9r7Yg4t6veW9Govpk3jwmz9zLf+ta39h17Owsq7+naNTEEDvZr1uslzx895k//7C/46NMvaI3BescwfKLtVIJLdf9ABrO8PJXzRQvwzuA0Wa2qTN00fO2bb/HN77zH8e19juZz4mKH2npS6NgsL3n+9Amvz894+uwRT58+I5mEqyw7O3N8VQMWZz7UriawPonMQgjk1HN4uM98thCJBVdjMiwvrpj5XRpbsTOb0bYB5y114wh9JmTL9dWVFrRrUjAYW5NTS93M2d3Z1Rgoc3BwgMcQQ8bbRmMry/L6innjcAaOT+7h7IrLV08UXKsEMIsG6y29LTFv3rIlwto3uhJKwS8N65KJnSq6h1PgbTabSRLZtmSdRG2sx1SeerFH5TLpyeecPn7K1cMnEGUwi68rqrrGVJJMxhTpemklvbhe0QLvvvsW9994g1vHt7HGcH12wYuXz9ksz5g1NYd37rJ/5zbH9++zs3vCpu/oujVdd4WJlhwdRu1nVdUDqFXmUaglRh2FxHdRmXUaj6QM69Czti0BSaKNtZiQh0nlmahSQhJvt10ve6u2IgGaJS9weq/7646f/fVPsHbOP/1XxzS7jpgju/v7rFNLTplZU3Hvzh2+132Hv/v5L/jo8gXZSngW0YKOKYy28akWSbwiJbTlH2Mems3KwJ2LiwvVsS3+qTAIlXGt3VbOmQkL12mcl3njwQNW657TVy8VZJQ2asyoCXkzxpj68xI/1nXNer0e4p6xuLwNjI6+c4xLyn8Wo0PEzHBHpsXn8szL+p3P5zJYp+uG136Zb77ps6eHKXlnGkHYUtAo4KvoRmacG+Opcm8sktfGFEQ2AtmTzleTOEzPR4E2eVZCRBqKuMZAGge46ckNSYpC9UP36lDWL9eovxFwVmTScIUsIfmAyeOz/CogNud8Y9gtX/rarwK3v+p9gAxVCwlnPXXtsSjIWsgDup76rsO6osks52+sEVZoKmvAgzF4Y7QNXwr/hcGIGYsHxebNZ3NlBk4YlnacbRJCVFBq3AelC7PsHVf0W5NIJJRoTghCcei2C0G73dw4pCvcjCFJxNzjJkOsZHi6FDK992O3sjLWYwza0ivrwahuiTDrxxb7YZB1lnysxLYYIWiUYd6JccB7iHFgxhsl+OiiKFYWMyFnhahD3ox0DDrrRHKgPB8mRRjdZ1ZJfdOiTwhhQDfKGhBmsQL2psiBDTd7tI2ap/VdR7QibbPFoNVnP/2+YlOmw+eHAYNBbF+J52ZNQ7B2kB9E4z+rLGarg7pjHIdzF8zGOav6sgnvhchTzkcKWX7ArqDkbWMXZrELhdXvJveu2DpfeWrNyXplIvdB8tmui1SVxxkPuo6jruOcJdaKJms+nsELjhVUIkK6JMsAx0Lmk2s1MOQ5CtXRxZH4+GXHrz1Iy8DOU3CBMjE7b7EgY5JBGAXoGqbB67U3TUOZTmhVO3QAAwCbNcDNlhkNP3j/B/x3f/zHrC/PuXN0i9lixuePH/L//uhv+JO//AseP38h+kaDlq1ltreARU1qnLT7lCmyRqYeppQH7ZetJHwK9hVY07nBiIygXqZUqsqCE6xzhEFhBGqM3XYig2NHWnBMFnq+sEIixbqXz0FbnOT9Ihfh3FiVT0hVKU2+Q65HAl50w2LESeas7E+MOnGG1h4ZJmaorRteP/1M+QtDdSrr38vGEWbMCChOpQ9KG6P8eSjSDR8qm1p+Ud4T4hQELozbUaB76nxtzpJ8GqOGXET2jRrpouFbRMGhTGpMw/or9P8yXKk8u62AabDI+iOm4bqHD9JCgHNj4FQADecFiK6qihylCmSQdgnhFxRwd3u9lOqkWtohGCOLEzA5kbInxBn7eyfcOrxDam4xO3yPZuc9Hr3MnJ635OQJ60DRjCGByZ4cWwpEiE0Y08v60fYYcsK2kdhZLrol7WbJq+enmP0NOydf42TnTY7uv83u3fc5u37CF48/ZHn2EmsuqN0aV4oZ6mBBhsGsNms2m/Ugih9jxKYMTpx6YWQO6yIzBOHl+Q8M5Mlatc6BHVvEpsfNYE2Cu8LkZgjOTc4smjmV95xdnJFtpjaWr7/7NZ4/e8Eqioi5JCZlLY6sBIO0v9gs4L/XgRWZEnDKuZTp2VhhqqQYyTFx6/iYylhOL84JRu5XyjoRGXFaOSN6Pwa6ths1iNSxly6FMqWzWSw4OtjnxfNXhJRo+27cb0Hud9M0W8OiSjW+fG45irMtbZBTezplu0+fVdl3JdgogvFDgaMUt4YNNj4z5xw5RqrZDGOMsD61QjQNqG62ABpjcN5xfHxM13VcXV1tg4+MQOv0/G+yMFJKnJ2dbQ2T1B2pe2Tg5P/KOius5q3v1NdEhDG9M1+w0zSEvmO5XrPpemJK1FWFqsFJwmVHe1JA0mJ/yrVDSaLHc58WLMrvixEvCVHZXzfvTbF7wz0xmjyVZEweHq4SBl32hsXtA5YhsmqvsBgZGKW+4dX6mtYIG70yGZtW7C4MySWuL3ra5SVN5aj3jvn5P/yE93/3t/gv/tv/iT/9X/8X2vaKZn3Jp//4U77+ne9w9OAbnD35hP1KgR9naaqGuJGul52dHZ4//oK5s6ywRCx7B8fM545udcXpq3Nun+xzdHTAq1cv2LQtJye3qauax4+esLe7w/HxETFGHj56irWOb773Nn3X8ujhE/aP9vn6t97l9OULPvvkCUfHx9y5f5fPnzzn7MVrvvHOG+wfLHj28gXr1YZ7Rzv4quHF63POLzua2rDY3SFh6dZrEo5gPdFIgh2MxXopuLoMLiW82pyUE5WVwNynhE0Zh7xHec8yhddIoOmknUQ7o9T+6eNOuaxhGZQTy6NG9DJdWa820yoIm5VlFI2hs7Axoi3uEvQh42JH7Ty95FjMbKUuUmK9IajHqNahHDFrQTVK+7Fz8j5rLJ220AH0oZfgO4kMTN/1WAx1XXF1uSTlSD1zXC8v2VnsM2vmNE1Du2lZLq9oZo7Xr1/yDz/9Kb94/Iy1h9pXJGsIWTp6RJoBrKsGm1vs6hCnWWGfpSxEhj5krrvAxY8/5YtnZ/zxv/59bt3aw6RMe73h+vKa169O+dnPPuAXH33Eq4sly3UkJ6NdTOqMMDibdf8brCtyAeCcTFmu64rFvKb2DbNmwcHBPu++9ybfe//bLOY1OTaEbs3uQjSEk/HEDDMdoGaso24aYsjUlSSA7XKF7QPr2S4kR8yGqplhcqAPnQArWUHCBCnXGCoMHTElLZJYiXFCR2VBhVRk2ZVOqTQSCkpQVeLKlEthVoG5GwDbkEBbGYAqOsXCjq68Z/9oh93bJ9y+84zLL56wuroQlnVOYDMx9thqQTNfsN/coqkb8BV2vsA1MzCW66sly6tr+nXP3v4xd+7eZWdvj52jY+y8olrs0Iag+xPm8x1Wl2thGqnHV0hiO37UaxzM6cQrFOnJkKDNiU5be4v8zpC0p5Jsyj1IuXQUOYySUHI0BGCTWqrYMzML4lXmH//259y6e4/f+ue/T8Lj612a+Qbosc4xa+ac3LnPN976Gk9/fsGqDDQzWWRSMuC2Z1HEKFq8okW8DdrlnMRvMQ4Bffny5ZDID8D01E8NPk/lwYbcSv57/OQJxojEjbOWvu9Eoin0W3nb1OdNYxpr7TBAtZx76QYtQMM01ygAhcR22/6xdB2W2BSKhm7CO6859CjhNGXufilAq+vEKMiXVeZpOjx1mqcAA3khK+CymM/ZrDdsQit2ROUohhLBVv49iYm1FVrOR3KzqVSFxBxqA0s+O4kDZJ1GkQOYrPcRnCq/k6J2UGZugfw7JR5g3Pj5Zf+U+30DNJw+45ux3PQ5Tf88jQ9vvm4bG8jgyuwPyXvFDwjA5u3YxRpTxGFwVoBm51RWKI/xbAhBNV+FMUgBvbCs1muSsjnL2q28yHgYksgt6Poh20GCoxQ+xC4mZaRP7lcE24/3u/hgqS04xQTk9TEFchCN9fG7zFaMnYlkLHG1HvZmkcZa6+MteVDJHdLkXmcy3Ua6n63iLOVZOy/t+wbIQfKLvmslZUWqRc4gDjBm6rqSoZebzZAjegWKKfdd8YoiL9FuWoxVILPkOnFfYB0AACAASURBVJN1lDVnKtdbe48rw6LzJD/XvZm00zAVwo/6r5zlmYkKnB1sytABO9k3Vn1ZuUdFP7jYyDII23tP23WD1GQBOJ0bO4izniNZOh+scYNMR8ET5Dka+fdhKLv46DJU2BiHIQ3SD1Ppu4FZjRTvnJMB31vFqwlYXmQiYkrD/fZa2HJDnqnzSzCjtALiP7wtrF/RqnXW4RrRvS9rN7m8BaQP6wvIOn9bcnIrMaUB5410hk5xrhvHrzVIm8t/WQBI6z1kneqo2oC191oRjeTS1m2kopNCkJ8pEbVCYxDQomh3Dus0W0yEua357a9/j//xv/xveOf+fc5nInD/xZPH/NXf/4j/4//6E569fo2rRDzZGUc189Q7M1jU5NphyFJRUOavVZ3RwaEyiZXUQDhT2lYYqpHFUWJGOYCqDFJBObFWANEyUCdRWoIU0rVOWB4KJnntFU6MgYyBAagagF79m3US3AjIarTdTqsSKLPMQIpBW7DLlG8rLQxZK1MWTDb62nGjJK2Ml/y8UPrL9YwgqgLumXHY2hBYFYcuV22sVBOn8gUD2G3NsFEzCuxPgqmpzyzDxcpRjL8YiTJhVrU4U1KQKynA53VKpryzaCoXPcoCYkiFZpxSKQCHVKaKVk5piQJh+ZRK3VjdiVjrh3uQ9RopuZYCcxhLTFkqeaVFbAhotWW+BG9YXYdyjUnBHmkNtJgsgzRSdsRcs7N/n68/eJ+dxV3W15bTpeHsecOqf8lqAzm7AWQnpwEDywSM2WC1VUD47JEctcZtMjYnal2jzOfM5++RCXTZcn1xxnLleVo1HByccHjyNb5x+4csX33M2bN/4Pr8Ezb9BVUVVBNMAgznRevaOYFwkpF1lTEqmJ+Zz6W6VxgMVg3/YIB1z0yDzwEwy9tg/hbCPvlpxyxxYKUU52utoao8R4cHxJzpNhtySAN7OSLPMmk12Vlp46iqisXOnOvlNd2mJYbl4BSHRFRtS4o6ZFAMD9ZIy/F7b78NKfHi9Uuss6zWG5arlVynSqA47wX4D1JFnrbRlQr0vJlzdHjIxdlrXp6+YrleK8sGDcTUNpK5e+8ui/mCh58/lPscy+CvONg80aKVAH1INIpN14TLIkWKtmtVf3Z8NuW5bFWqS7JgS0HiVwNuKbApayVlbJYA8PjkkBevXpJCacnX/abPNqVEt+l49erVoB21BR4Xe2a379/N7y8JXQkmy1na4dztUAgbWnTULpJHtogEkgbRJjcEEovZnP2dXdq25XK1og1BNQcRUf1cziUOzP+csia4o+7vCLR+dVJy8zBSi9Hz12Bn8rotGyUPUQtEmdl8RoqJdb8agq2YhTDh64qd40PWm5awbjG4YehLb+DKRJrUsYvD5R63WTKbz6lqx+b6JWevjji89y5N3vD5P37Am/e/w3d+8C/4+Ed/yoINeXnOs08/4Z1vfZvV9QVXl0/YnVnmiwbvKtb9hr2dXQ4Od3n0+Cm4zN2796mt4/rilOXVOZurM/b35ty+fYvLy0suzs65feeEvb09Xp2esru7w8nJHTabFY+fPmN3d5fj4yPOzl9zdXbBg/t3uHX/Fk+fveTZk+e89fabNLOGh59+xovzJV9/7y0O9uZ8/PAz1inz9ltvce/2MT//5UecvrxivttwcFRztQq8uuxoYyZloxJRDtGvlOcXgKhtpTlnjDNgPO2QTBa7J8mMLTGDFv1ilEJPSVpkEAlDIU4KisrOcYmctJVO46Ok9leCNk3srTJFoibzRor1GQOiBkOXIWrAX1mPdEpMzPCwTwbIUwaMWA9tT87ga89isSDHfepqRrvqBoAo9JnlsmNvZwbZUNcNITmOT3Y5O30twFyEbtMpS6hlubrGGDi7eMnF8jVPXr+Awzkmz+g3AUIgBvFB3krM1fdhmNyedO9ZAzlFshZ0bblu67BZEpJnz8/46MMnHB9+B5MNe3tHxJR59vwV//Djjzm9XtNZi6kriUFzJBmZVJ2UsR5zJhuHt5bQ91rAzhgSKa6BpUwbz2As/N3Pf8GqPed3vv9Dbp3c4frjU5brjntHJ+wd3JJixHoJKVPPZ9y6fcKzp0/ZWcyxBpZnZ1ycvqa9WnF4eEIzm2MdpNhxeHyL5brH2UiOgeX1FZtNq7YtgA3ELIMwxTdKISEX2E3DcnUIMhTHlriHyfpiYKllpCgxZcqlpDMRnA6mUQ9ljcUax/zgCLo1e8mzO7tNSv2ga4eCX7ae4SpJrlNI9EkGceUYiTGzM9tjt9mT3WSlO8e6imSFLRVSoDKWpvZYP8Pbhhwu2cQVOWi3ifpQsmiI5VQ8FIPmafn/AQCyhi71bFIg6GyJ0pM2HXoJ290plffY7LC+kvufEpvYsaFnz2bIhio1pCX83V/+LQf37vHN771Pm6QMY12iCzJYeWd/jz/8w3/Jo7Mzfvb5h8Q6iYZ1hqxxeulAKz7G2iLRVuJemVcSSju3xrx1XU2K66OPHIAz0C4qN/hOkC61+UIGxaxWS3IWoEU8WBSASb5JNXmVPZqlVX1aOE0KYBhjeOftt3n69Blt22KsGwgaWdeoNYY333yTx48fS6eht0PhxLmJ3x98bB5i0D73lBi2AC8hbIZ8tMQcA1gbx9wol3wmZ7xx26/7CqDRIK3Pzlc4F/A+boElo4zaaH9j0eFFusSGHKswZadgklXdcGc1jrsBiip5ZDjHEo+MJzjJPQX8NyW295a6qejrSJo3hK7TfKWYC7N1z7bzxhGYmd6f8ufp8ZWx0A3AdnhtEnZ/HwIg8o9tK+e2mM+pVBtUcOk0dIEIO1nsk0FA9rbtpLtEQXJnhEWZydR1TR+6yaBoAa2E1KbdLjFKG7vm+yXf6bSlvOTxRbaDLPs09iodoYSsVgeIGSuMXl959W8GW7lRlnLTksKozVskPkLXKwgr197UNRm14ylpjquGQJn8ZljrTmW7pFtVgLmCgZRQ1lBXwjp2Gpv2QVrbg/pnaywVldg9ZaeX3GKzWcswYURGrPKeQhYr9/fqeingoQ7oEhC0kGmySvYk6QpUbMQYI9IBKPklS1603mxE5sI5ZtWMLoi0VNt2go1lvR0qCTCbzbS41JNiolct3bJeveaRABeXl3K/UqbvO9quw1c1dV1TVRXOWjabdjjXYYh9RjA7YzFrva9KuhRGrtXYMComEjC92PYieZA1voMxZBMguui+yuD7EASLqiqwNosdNYXsJ8/VGjcU48cCgAxNxWvnss0qiSBrMKg+e06JpHGo5OYogF3Js8oiIVGwFpHoc0MuZIxK5jiV0/A1KUWVppjYpy85fq1BWpJoHhbqM0q592oYYozEvpPgRx/cwGzQm5z1YfdtJ0xII0yAwvSyFAatw+eau3u3+Df/8o959+23WbVX9Cnw7MlTfvSTn/Enf/XveXZ6RswyJEMwozl+4cgzS3aZnMKkMlCcS9TCUTHc222nRcQ559JaLyeZB31SBlA6BKk25xJgGMiaUBsjA4GIUfRFsgSX1lhw4EyFISq4aDT50VYhGO7VECBQWMza0pSlraBMIS26N6CtSKawU8DotPWSV5UqT0rF5+YSSwyVtKQtGVnZcc4IwF6qyHK9YlBjEuadmbBiS4tSGSxUQs9SRc663wX4toNRFma2BncYnC0bTypJJYgwBdhKicpXLOYznHNcXy9H0DXL/fXk4ZlCFgkCGADWwk4rG1ohcbmWnNXpbrMuTQFp9HqFzawGLMcJoKWGZAowq8GTNuRI0nQBI8ziAVDUNWeysNUwJRixgqhkHZhATU4Ns9173L3/Prv7D7i87Pjg4wvasEtnd+mTI6UCDkaMyYMTlyWeMCQ8MkhDpEMCRnBULBmfwVtpqTXWka0jJkPM0o5fhTUhea5D5GrdcX614ej4gL3Db7G/e5fu4iGPnv+My4uPyPESYwLkShZCYYFbi0X0r7P1pIwEpdlRwlWT5E6XNn4xT2lYtzgnbI2MXkunrV52wmougERpqSttdUZWhJFvyCmTLLSpx2WHryp264YXqzVfPH0s05gzWOM1WI1468QJGBFMD6nX9mthwGc1FypqBRhir4FMpVpH6tgM8JNf/Iy263RVCujnrFQOrZeBGruLHeq6xmY4PzujFBgskHQv7u0c8u7bX+PVYsYHn37MOsrAwZx7CT4VtMkx8fTpEwmYnRR5SkA9FK00e07kSaFG7AVIYaLvW3IIZCNtKSNzIw/74CazZSwKAdYOicowvThI27fzRjWwRNv7cH+fo9u3ePLiiazrLMXBnPKQ5KuJJnT9wEKf2n5JELR7ogRJjOdaftPUFUH/vVR4h0q4/hzWVpYWaNRHjAz9YiPSYGfnTcXtvX1Snzi/umITAjkJyFFXteawej0UeyQWbNQfKz9GiHoMTsZEpYDtW2A+IwunvOcmwFuYNEzvXc4CZOn5ZSTBRH8Ga3C7DTtv3GL1/DXxaoMxyic3hj5FTrsluVpAduROpiXPfIOxhvOzFzz84Ce88+3vsV6u+elHn/Cd3/4htYUP/urf0aSW67OXnD3d5513v8XH/3jJurvm7du3WS1X5JTZXK+4vPglKWbm+/ssFnNePX/G5vIcm3sOD45Z7O+w2izZdC0nd+/QNA1Xl2d4bzg5ucN61fLJw8ccHe/zxt07PH/1kvOzC95962125zM+/OAzLlcbvv2t92gqywcffs7lVct3v/U1MpkPP/qCNgTefe8++7Oap4+f8fDRa+a7c05uH3J+fc2riw2XnYCatTPMbcJYz0YHcBhjB1ZeyuOzYLKnBqOey7oTGz6sCe1yycN75d8GgNSNzAhrLNmWYFzjmiHhMiWLGtawaiUBhYUrjG+TIRlJWCsjhVsJXQTgHQdNjvtqXHcJIqQ+UDWVFKtTpvKSmIS4FjsdRf6jahqs98Qu0bVrDvb26HcXLFeJvf1dutATQoezjqaSwvDmekldObrU0ews8PWM3PekIAMur1+f07et7N0UMc4M8kUlEe6D3jNnMEkHCSIgN9bSdfDZL5/wn3z7WzR1zd7+Mav2mi+ePeH0+ppoPcYbXIk3keG5DiELFYDHmMysqQnW0AfREASRSxmGRpBJ0bBaJf7yL37M3XsP+L0f/jOur6+pLs7Y2T1iZ2fBYrHDy5cv2Swv5bsbAUq7zYaDgwNW1pJTR9cl+n5JU8PriwuM1UnN0eMaqOcOQkW/zFx1LQbpaDLOyJ7WeConYUWHEESO1YJRG22yxmxZI7ASv5b4qKzXyTqR31tsSfi8DsXJCbKAqZv1mrZt6VvZS6ZIg+mtstaQdEJ5igL2pxRIOcpgq6FAmbAeUjIyW8AkTOoxxjObVezuzMFmuq4XgKpIrGHo+haToa4a9bNFRmzseCjDxKYwWybT50CyWfOOIu1kGF8ozztnlLQBOTvwIjM3rypWoSOlTjSLC9gdLa5vWL1s+at/++fcPj7m1u19nl+cUzVyrtXM4WcNd+7e5z/9/j/lo4efEeJahtNljSdLEjzxEyV+L35PvjMCaWvo1Vj8tGML6pCrqS7/kLO4LZDOgABbKq1TtAZT0kTGSJ4GhmQsphASpnG8EW3VmDMz71iuVqrfOAJJIDkfeZy1IVr/yJ4r55wEjEu5aFPKEwxBGKK2ABTWMUpTqM0124zjAUBlPHK5Z/r3MtRJWq3N9uvNOE/l6upaCTtu258XZrBXxrP+fmp7i4zVcJ4wEGtK5+woSyFsvKj5QxkG5qxI75W9OmWoFmkL1A3VvpICT07Md2bkdWRjJNfkRtF+ekzjyClAu73GDDeP6Tr4qmMbyBXfF1IibFphyRsBtQYMQUEvdPjaQEQwpqj74YylqWpZszERTSLkSG/i0FVSzs8Mcw2k8FD2j9W8uQC4VeU1PpTCU5mFkDqR3Mk5YypHbbzYCCVZzKx0KY5zefSeZIN3lZIrIovdHUilYJgHUN7V9UAcwhhM5amc39prg80hDIC+MDc1V8pyLtKKLtiSDGJOmCyyhaKD2iimY+jalq7v6KOwyr0X7VFnHbP5DFTiI0XJofvYY6x28BmLrxoWi7mA5UnA004ltyrvlf1smWXZuykm+tgPQKYxIrUzXSchRPpepBFDDAKc6kCvum4wJLq+Z71e41TrttJuBwFZnQwd0yFdIxYgLNr9ppEdoIPLSJLfGZ1rYqzH6z633hNjTwyKe7RrjLHsLBZK3hNftdFhdKGXdSVyauJ/Yy+2a9119BNdW1ckXYwhpEDXBlLS4rVxWJPpez8UspPK36BF+kZlKLMwDYY1UvxIkdOTgnykVTmYjHY+k8mFZW0YcMZCAnLO4V0tXRUpSb6hRSWZuVAJcz8bAfm9Fr5w2hX25cevN0hrlPVo8+hwcgkanWhDJJkUHlRA2pV2+VwAIVkYA1XeOmGeDXo2GWccjam4s3OL//pf/Rt++/3fILQdV2fnvL4650c/+wX/95//BU9ePcF5A1FaG+vFnGp3BhUCiqqhi6UFOaUvMX6jQxyo2WRMFqDV2hEUTYPhGzeNcXbQry1OvFTEinGVhDgP7M0haUJAo2lePTCxjFyTQcHAIdQrifmkwppVsNrbYcGaSWtFWbyRPLL0jAK+5dEyOrfCai4tytlYde7bjjCXxI6MVz2dcam4Qatw5MSMR2FkuTxpYUljwlMYpGVwl9Gq/NSRChNa/q3tO2ECWhm6NAqbj0DClz17QwG7SjBY3lN0WwyYAsKP9ySlsXrsrBNAYqhKmeFcrXUTBm/Jo0uAaMbvSNMq83YLf9k/RjWDrdg0QhYH4vwu8+YOh0df486bv8lqVfHFk0tWq0yfD2iZEfOMFGW/GgX1jRF9Mu8cOXaksCbnlrh5Tegj2YvRt9ljHGAyfc5Ek2nLOjb6rK3FATYm7KyhdpKcry/P2Fyf86pZ8MZRw53Dt2luvcmTl9/l7OF/pF19qHpEHdZknFcQNafJwAIj7YtqtMshrQqFXa4MbyDbPFRwbXkOxlEGNkr8pqmAsrtHNop8/qjFWpKPTNe2pF4CjN3FDnVTs9m0g9MoQYZV5uT0mLaGbO0fXZ8pig71/Xv3eP7i+ZBIOSdtUKvNklyYW5T1mQdgsARum82GrBXJGESCwSKASEiJF6cvePX6FGt6rPOEIMx2Ed8fCwXeTdopY4YU8U7Y2jLwMA57KmmVVp6C2ipr8M7w4Pgu7fU1L5fXWtzLg9xFTBGck+GNMQ02IjMJmLO0PGVlWJS9XDk/gLTWSOJ0dX3F2c9PIZdBA5pAIiwNstpcK0yFcu+3bMpW8lEA5WFZDDYphEBk1LvLkwSnBKZlXW3bPAa7awfARf5e1TW39vfo2o4Xp6dcbzZUjQy38RN79quJ3LjGviwRKddRJvWu1+utwLmc2/CZBQQern/83mFflPdrh4BVdmE2YGvxBV2UZCM7q6ALzPZ2qbLh9fopfR9xWbCMbKBLmUuzAVtj6zlNSlSba2pfEfsrTp98RGyXvPXOt9n3C9ZnF/zeH/wR7dVLPv67v+DAGF48+gRj4K2v/QYPP/4xF2cbYttiA8TcYmKPd5Z+ec7jT6/IMVBXnpkOY9hZ7NA0NbPZgrbrePHqFUcHu9w6POLs7JzHn7/g6HifuycnvHzxgqurK7723rt46/j0s89p+8g3v/Ee3abl848eM2t2ePu7D2hD4IMPP8NWFd/+5jt4E/ni84+47gzvPLhNdpmnp1c8en1JpzIEjbHc2Z9z73iPLsMHXzynxWJ1jyW2AfYhfpk8fmOVjQeDL01oTGE0tskj2GoHQCUOn1VSc2NG31b2aPHBxcVb3dvYiY5dgQ/yuFYKoGScsjz0M8t1TK6AmDLWZGGpxsj+3q62csPO7h7r1YoQl1gHxvZ4Hzk+2sVXUmyKSWKDw+NbPD99AS7w1nv3WSx2JWH2noOdXU5fn4o+G8JIz9bh555kPbeOb1MfXdJevCa1S3LbimRWF+RepUzue7yVVnMSGOu0aCvMoYShcjXrZUsImdnc46ua09cbuj4rQJe1JU+KuoEpYLf9XPvQyTR0W2JKo2tDumuy+nii4fnLJT/+8c/5/X/6B9w+uYPJ0K5bUojs7e3w5htv8fmnH3K9vuTFk6esLq/IfRTN3JiUeWgJsef66pzYd8TU8vqloan32N+5jbU9i7lnM69ZOUfUAtoAzCR5xrF0Deh07yLZYpMZ1soYNWYFpgwyEFekyqZrvoQizo12vRQcZd1Bu9kMMmYxJZIOpRPgNdCuO2LoAFlXlVtIazEW7y3ZlMHGcntLp1WJpYRNKJ021huR0Fhf0betAHvO0+YsupMK3GER8YKyZ4ufyaXzQzRnM0iXjoKPRpPJCW4mz15/YSZgJVEG7aFTtAvw2Ya1MMDdAYtsaGLFxedn/Pt/+2f8V//Dv+bw6IC69nR9oI+RxlbEfsP73/gO3373W/z4kx9jqlLIyaQQyXbsGjRTIH3ik2IMEt9PGJdTnzX8HIC4st71/WEqL5QHHVdgIEXkoTPHkLNVsF7uk9EprNMOrGF4qzFsVmtW18vhPJwpGoojkHB8fMTbb7/N8+fP5R4P5zpOHwfoexm8Ka26YuOkYxIZfDuAs8X/jgO8xm6VSfak+Yq1ZigalJwtFbbNuDMUOLXKqmQoc6Q05kUDE1fJQ9P2YGclt5Wc1Q65zTRXHuMcMz4DBWOGblAFnYwzkMbut5JDU9ZxlrkboeuYzRoo3ZHe4mc13YX6jKl/m5zHaA++PAbazl1vRui/etwsTpf3Ygx9CNTUOgQqs5g1WNMoq1I7UZyevxNAtA099GoTjWilGi0E5KyDytHO3T6pSy5MYYP3gqUkMlgrwLquXQzUdUUMQcFFKRA0k1zEIHZEXb3E0LUbBvGWdVHWYAyyV20Gq1OxjQGUmemcxHwW5LkWkBYF2HKRXJjEKEiBy1svAwaR3DemKLOBEJAMY6SN3YxEp1S6FI3Bq37prGlk4JcVjGIYlp0SsVebrBIjRd920LlPmZADznvmszmdzs2oKhnoJaQzORenfsy5REWlXRFRbYqsC++9dLb5TKoVFE0ja9Yi3efGwKyZMZ/NBokKWf8i11A0W5PKzaUkWuNT5nJVeZx17No92rZl04dhX7pKnmmIEUeFoYYdsXMDyOq8FoINtqpY7DoZ3NV3MrjOGaq6whoBbMtwsM1mI7mKAs9k7SJK0h0SZPiADp8D4xLeCLEpZSn8rtYrrPUE5wX7cNqVpeuub9tBF3w+n1PV9WAvpnKFZU8XrV7JR2WtdZ2QRcFJ4cKkoWsxRPkpxQ0nRbYokizBGEIMxF/J4Mfj1xukRYL7WAAHgwKuTp2IHYKgLvTMK5nc7jRgJI9MCaNVCasDfSxZDQGYBLVx/M73fos/+MEPySGy3mw4Pz/jw0ef8e//9m948vIZ1htsZTExMVvMMFVFnsl0PhAmQsxi2L1zyg6RDVXaB4rjASaAx5jcFzDNDsy68cg5iwEenJYliaT/6OQV2S8T/SREUtA3ZVzlxXkhm2gQFdBWIGlZk8EBuYT8ZgxOs5E2q5wyuRfQ11rHMF5xCHoYgFBb2oj1c0zKW9d088+jDu8kkU/jYKIhUC4GPql+adFx1QE2ZmB6jQCvc8pczWLUpkCwVd0qinyCntdg+I0hqK5M+bdiqKZO1WnV7aZzlhYnZb86YazkabXebCeOJRgqVTS9gQOILD81qErjlE5gaCUo6ykPe6EwJoE8nfx643xLtpxlNImxFb4+xDV3Obn7Lod7b9LHHT5+1HK57MA0WDujW7f0EfB6P6wmdTZSZDn6bg2hJccNJBm8kTGQLBhPYoHBSRU7dcTcQW4hR5lIaRPJZLJxEIVZYrse38x12nCmbzOX51c0/YJ+ccDxyW9xvHePRw//kovTT3DxubRMpoC1Mw3YpGU6Z0BbQYpBds5tBfLCXlAnrPSYYrStdTLoZbKuf3W9CaB+cw+klNnbW5CBq6srkoK2+wf7nF9cSCEoC0gYQxTRcTMONynfOwVpi/1xRasvC6i8aGpu377F6/PXhHUYklVhLopjjloxthr8y8RoWSdt28pgKSPTxzOJHCPz2YI29kAmBkmU8DoVVQNKsrC3ZF+rXSj3QjBXylBB0WNiGDBRihx6dwdmrbVwvL/P7PCIl7/8BWQBK05OTri8vGS12QzSIaXtNOVEVdXaamjGRMWM9thZJ+sq9ZSiFTnS91Gq5NZDyhQNdNnKVhhmSS6mnPP0c621g/Y4peCGIUeZ7GzU9mQdxz1ts5tKb5SAbbAZeWyVKklFSgVkM7gMO03N0cERXdvy7OVLVn2Hq6V1y1svwPtk/XwVa2SanNy0g6UdarPZbOkMTwHam59zM+EZkiIGXG6r5bIITAzZVEYZFsNupZrPWBztszq9gF6KRFH35Cp0GG8h9qRNIlk4Wuywu5iTcuL64ikvnjYc3n6L9DrzhQl87wd/wPLsNecPf0GTDU8ffUbVfJN3v/59Pvvwp8zMhsYjLMkciVF8sM0luM+cnV9QVY71Zsnu7i4Xl5dcXF5y6/Ytbh0dcnW95OmTZ9w5uc3du7d5+vw569WStx68CSnxyWef473nvffeJMSWR198wa39A95++21eX5zz6ccPOdjb4/6DeyyXlzx99YJq3vDO3RNWqyW//PwVn593rPGaXMHdgzlv396nawOXZxfc3Wu4WEcuNoGsgW3fB0ne5OEM8RWTWMVasEUTTxOpzFiklZhNwR006cOOTzgXOyBt9wXQyFm2k/Nu6NpJUYtaJaayysxOCeeFBdhHDYEter5mAJqgQDt5aIPPWfl0UVg13hm6tgc8db2gbnYxZinMzirRVDMW812qqsGYin0zwziPqyreee9NcGuaRYPzFd5VhNDJDAVXM99ZcHR8m49eX4lUR5LC9suLK7oYqfZ28TuVJLV9Ji7XhNVaikU6fdzpHINssoIyqmeLtOEfHh+zt39I314Su57z00tycix2drluwG0d0wAAIABJREFUl5S7ss2hK4fEbdJZFIcEsdw5U0DyoQil8ZH3PHv+nMdffEzjdtndqTg9PceamsuLjQxXDR0pJOrGkrSAcnVxQQg9O4tdvK8Ioefk1hGVybw6e0G7vmLW7GC8JUXIESpXUVeOVd+T6ZCpwkmltDLWG0LwWF9hjdXhJpBDkYQaY8wYAtFHBWtLQScTY9jSRi8DEwVDsWDswPLJKZH7IhOFyiZAlCmvsr5SYrm54vziJXt7+9w+WoBDBn5lyOrnY1IdUDsZSmTkWWw2a1Yrh68dm7al3fTSGpv9CLopaGK0Q4eSF5W4L43xR5EYCymyij2hsM8KKs24dSSGSHpe0+4HAXVt3Qz7vZl5klnT5Uy0UmSwKVMz49HHT/ng5x/wzjfuc728ZjbfUV1SkdXZ29nlB7/xfX7+0U/pu0CuGfKXFLXgw7Rjo3SJQAGzYxxZt18GlpXCcHE7xV9+GSAXQjfEynJPE1n9WeWcdMxlq7MaKInQlk8rbcRN09D3I0uuFJhk8FJ5MyyXSz755BNgWiTL5Gn1QH+X0vb1jflSuvG6bb3cYm9Ld9709xITMcR8ZvLZ8hnaop2L7Rn/vZzvFMzcAjApMdZYpJbih4b/ep7ej2u6kBhyzsNeKnGj/LuyK3FCeirfPzmnrLlSUzUycNFIAT50HWEtck/ZGAbi8Zesmek9mK6rm/HSV4GvXwbu3vyOlNIwP8ZjmO3sUttaATzJeaPGVrnPJAPWKQ6gzGIQIDbFhEki8VLATZH/qGUdhqKDWv4TQNfmLC3sWQhtuCmpYGQjepUzsnrTu76TDhAj+EBpL4+9FtP1fWWoeop6rjHRJ2GaOm3/N8bocEbJx2JWG61r0yCa8OX7SwGldKSmmCYxojzrkt+VnTZ0CBcQW2UiMZLrxVByIYlF3BCHih1IJMlfDSJbk0bJRrkuAfFMiCNOoj/rusYasfcpZoJKSxYgcVhDGWXuR2Locb4a9GTRXKWsB7QzuQw+ddptmZKcb4wysC0l0a72TtaSdxXJaDHIKIs5lm5aIawY4zTPEBscup4Yk+i8liKo80OhxmFk7pNz1L7CWU+HpXaVSrmZIbcqa3IxF/ZtHwqLmCF/aKoZ3im6lYL4vtjJYDLvdQCbyExY7whRAPrKO4zXTogsgG+R6ij5UkqJuq4Hf1/ISCGELRuUknRoxBgJMahUkWFnZyEFfBOwJhGCMIILBmWNSHzEXgenGSmOf9Xxaw/SStfrmMwLHpIUhC0vkkS+DMoB2UjJIC0XGkCJ7kUUJDsJsGCAxji+8eBd/vN//ofs7O1yubrmfHXNZ8+f8P/8hz/ng4cfSImTjDeWetbgFrUMryAOAvrJKDszC0hWnG4BZASoLa0EExBHQRv01Ri5zsJynbI0i9cvrafSJp0GhxWLTtPgtFAEXz4zhABZWYC2ANbbg14GQLVUIIdBEoDJGCcAskkazEzaR/QLFQDUoDAVw6eBgZXvDBMK/01nNgCmjI5tYNpOnL21dgCRh0FZJXlgBB8LkDYumrG6PerfTgMWafUfhrqhz5SxzZohIBxbjQsoKkBtYQjJ/bK6nvMkwCqPtLRYlXakKchWhMwxRgEpTVqNOIik4M60tag4ppuMgYhem/5OWNNKLRvc1eQ9JhKjY7H7gJMH/4RVOCa4Qz59EdisO643ichM1lQIEKw+f5lgaaVXBXLChF7aOXGAh7wLZgdrOnI9Ize7NLfuUx++RUCGm7m4ge6CuD4l9NfE9RV0Z1jWxByHgC11rQCWXlLWelbRB8/L8560SlT7Ncf773Hvmwew9wFXj/6afvU5FUuSRZgLCgzmlLHeTtjV41pLKZNjmQqut0pxNt20uvXKGtwGlcp93XpOE1tgrR2qd37ShvHo8WNijDRNI2temSFlYnNd19TOs+mF6RHSWAkdChy6njHy2ev1ip/85Cc6KddoQSxCAmfckMQuZg2L+YKzi/Ph3Iujshq8lUAYI61wFtWjplTSZX0NE5idVBCHINWM/26M2NLilJMB39TjxExtcTYoQ0bvXQiJh0+ekvteWQLatl9L234JTouGqi2tO0HlYob9p89qklz1fU9M3bC/i72zWYJMKRpM8QrdQ84Mz/imhtlwTGxHCUKmwf9g+78iMYgxUtc1OUsgPG0dnHyFJF8xUzvHncNjYt/x9PlzViFgfcW8EnZnef+W/pxVPerJ+W+xPRgLVuV3y+WSwnzx3us9lwAlxCCDlqzb2mMlGZuus+E72ba1cnIUbHZyrUNmos8ls3vrkBQj3fm1sKt1vfcpsI4tkUhnPAlP7Wu879jbOSCsN7x6+QXZWO40b/Pq6TWHt+/zL/74v+d//9/+Z/rVmoXJPPnsI779m9/nN/7J7/GPf/fnuNjhraWpK/oIPZnKCavv6uqK5WrN8a0jmsUOL07PiH3PnVu3aapGtExT5I37d7l1eMyL58+5vLji3r0TUgg8efacpml48NYD+k3L89Nn3Ll7wr2Tezx7+ZLPHz3h7skJt28dc3F1xunpaw5v3WL/8JDziys+fPSCz896Nk7YcI3JPLi1x8nhgtVyyeuzFfsHM3YPFrRPLzlvO5yvtTjktpkEZvTNAj5kYbVr0WC6VmIq+mCGmIuMkQSqRWpleKhoOBGV1aE/nW4wHW8ibYgmD7GMjIhLkqkmXbca5JfNWTqQyKPtSGkafwmo0fcbUgos5jW+8lxfXmOMpZnNcL5SCQNYXXWkzgM1zsNiB7yv8VXmYL6HcaK7upgf0HcBcqSPkXqxQ7Ozxze/9V3+9pNH9FEGz5EzOfaiuwYybMtaTGXw+zPq3QNS35K6DbltCX1HBRqzlGROp1HnwJ2TY3YWO5xvzug3K1IXef3qnNhL4pUHMQvUVo/xZLknMSeMdiWUmM3qnwvrU8LtrGy/ROojjz79mP29A2ZNQ85rjS6ELXrv3h0ePnqEMYbDwwP61YbNZkPbttR7C3zVcHV1wbw5Ydd5bNrjqg3Md+fCeusyJhqcEQ1hX0nnRI5JiuDWYZzDNw3NYg/nT4fnjrbJjrJncsSc6GNLlTw+V6QsbcTOCUOwaZoBUCr6diYhHTnWDZ00OQp7NoYwxpMSCmOMYd7MmM3vUM88kHCVo0wfRwGzwm4dW+mVQavLN8VM3cxYrq+JIeFcRYytSDNpO7rzFahmahn2KjGxA4K2p09sZ850KdDmgK0cOix8q5wx7M0hwZhO1oZsDX42IyNxSttvmM0rvDE4EzE5COsoGczG8h//9G+Y7/6QncMdFjsLEjXL5Rpf18zmu3z329/j3sFdHl4/gVqKslG7lpy3g8Zj6SjKlDU4+tPin6b+Ycu36nrP5f4PdmGM00fgVv1vmvjhnFU70jKrK1LKdDGpNEHaivGM5omzupGiQPkHa7RTRLtdshR+r66uuL6+Vg34TN+3w/fe7GyY/nnqo0ffvA0Ybn2GmRTdxhdpq/dITCnEmPLKcj8K2Dc9t5ug+NY91++0k/O0CjZJ7LVN0rlZKJa3jPNNctYuvSI3lUfSCoxwWYntpC09yOwUDBlha9pZQ18Kf2GKM4zXML3X23mr/ZXz/Krj5meU7rhp3JP1f33bEcMMg8gLhCDa4G3Xiu/V9n25I4EyZl0KR6WIqTY9JGzlh8JFUvDUKRAmM1UqeYbIUCavuXeMAo6mmAZ7gtr+GMqwZcnLnLH4yo0Fiwx9148MTOeGHKAMgp/Gyc5ZaAvZagTvR8BSY8EC1JobHTeaA3hv6fp+GIKG4h3Crld5uZzxlUjWyXOxQ/5WcpqCOY02JulnyntCDORWu2v7keWes3Qd51z2pdrvG2u69o6UAiihrlyTURmH4Y0mD3lc7rrJGld5CwSk9t6TQ6bvZXZJkcxM2kkUU6SbdIuWKxZGr9H1IPc+9IHQB/VHUfyiLTKdiRTEBsfQC2vfGLwZC0qu8pASfdviqxo3WX+V90N8lnMmRbnukBN1PcNXeehYKLgOWaVXDECFtRVV8FpMMEpIEoxkd2dH8LIg8VEpfJaYtVEySVLQGka7b62lUhZ1Sonr6+thfTnVEraFSGoyoU/0QYoFOYOrHNZV1E0tZNJOZP5CTCQ7Si0Y+9VQ7K83SGuE0WnV2Y7wWml9HC9SqOvSZluo9AnRqLJqBLxWfU0WHVabLd4YTnYO+aN/9p/xxoMHrGPPKnS8OH/Nj372U3724S8ItFg8RdPWzTzRZpIx0haXleuUzRDoihPRpCT/anI7TcatYXyNRcXu42AQym4vwEDKUhUp09YrM0oNyKIdg5Ai95BSoqobUui3jFhGroPyPt3vkqyPbCprS1t1EVxW42MdQze3WKHBYWbdozEl3AQ8F6BlOyHfclgM0dJ43XrcbOdF73sxTBLcRGkvU5Fs+Q5+5VmUnwVQK68ZjLNeUgnKhY1oh2sv1VsJEsbnOX52+Z4S5gpgOdwflNXKOJiotO0kYyS2xmw9r2Ksy8A1ccTqeBSUk7aAKSNZ10MSPWeJKSeBgAb/w3Wrw84pE5LDVUcs9r9Hz7sse8/10tO1XhJJkzFRNOTQc8qSrWGsaBoRgwqJW3AH2MVt/O4d7GwfUy2EQ+VqmDXY3UP6akcqgIIsYUmY3FGnjnT2iPWjnxCvH0JYEnLGpp5KNW+Dakutr1s2/Q6zyuLSklV8iQmJ5tYRzYN/BrP7XH/479hc/QxPh85FkAF4mEFTR1Rpy0RVVLx9fH6jxtd4bAX+N34v+30bbBuTMWGDbjYb2YN+DLyMldbVRJbJymZbyymEMIJo1kAs6+LGeQ1ar+Br0acim3HAlq4N1BmToA+R1Wq1BZgNzgVJzEOOOO80gFQnaAzzxQyDY71ZScBvpXXo/r37PH36dAgSDFlRUpU00KSgDDUIMQzBUQnUsq5dZ61oAYXAxXojw3bqSvUGE4+ePJH2ITcGKGU/A7qX0HsnzyNPCmlZQXdrLbu7O6zXm6FtSIK8cYsPSc8A1EvLJGrvZejlGMiHsK0rNrLmbyRRuVy9GdYWE7u5adsxuRyzav2cJFrUWQLWqq44X16yXq1pcwDvmNUNlXHDgIhyj0tQKW1w2sFgS1K7/UWDFEMeB4SUIQ0C9OpaVTF+qfBPWVij7MfUbpXrH8/HDHtwSMNMufysQe44nNA6C9awc+cIcmZzdo1DGHXeyTDSnsgqZSocs7ZjVifM1VI+O6/ZXL/i8rxhNjvi/PQ1R4d7fOcHf8BHf/MfCO05zrV8/NHP+c3f+X3e/cZv8sWH/6AsloitDJWt6HMm9z337t7Desfp61OePntB3wfeeuMNGut5/OQp+4cLHrz5Bmenl3z+8CFVVfHNb7zL5dUV5+dX7O3ucHz7Ni9fvOTy7IoH79zn+NZtHn3+jKfPnvLgrfsc7x9w+vwZy/aat958C980vL54xS8/f8XHZ5E1horMyZ7nwe0DFrXj4mLF2cWK4/0d6pnji+evWW4Mtw8PuV6v6DMDo68kYt45ZUkXfyfxxjRZR20EyJAYYY8b+pKgI8yTsWBbJEAM1jt85bXtWPZHr23r8pHqaydrrxSXS0LivMdXRR5pBGiL/yw2TSb1FvvmCcZiUmJvbwfvDTkHrId65omxJcaO0HfEmHG2Yn9/n+vVFTH0+Lri4HiXLnTsHx4wW+yx6Tq6XgaVOOuwviZkeP97v8F3P3vEf/j5T7GVI7qxHTojEkMlNcR5ojUkV2Nqh/M16XpJ364QSxmpjCTtm9DTzGe88+AeTeXYnc8I7QZiIrQdm82G3owspWwK8KibKWdkWjp6v/WeiWCwssKFHdMH2dMmg1UQduYbiIbKiX5rXVXEGOjaxOX5BYvFLlVds1oveef+m2yul1ycX3B1ccnF+RUXl1fcOtoDYL1Zkom0q2s2G5jPZngjRZjCYPWuwbsZxnigovKOzm1wPpJNjZCpzFCT9sUOy0MfbGzMwopJlTKfrIyM7Lpu0MVzSg4Y4q6UlHlXJopvA4CmrDnEvzhrybbiaPeETILkyEkZiRr4F+IEZmpzx04BGQoMMYJzFc571m5N6BLErB1uhaEke7MMSsp54iC4YYOTwDxYIRc4JwM5jbarli49a8tg1aERRPaTRVjL1uKcYbla47PnwC9ksrV2jhksdapZv1zy8Jef8sM/+j02bUdVN/i6Yb3e0Meew8Mj3v/2+zz868fqWyIR8b1d3w15kmg8aiw74CtjXFyOoQgoBmqIocV+lAJuAdjkd0Koc4M/vllwN3pfRIlFC1lR1pMUhUsb+DgU+fziAgzSmjsAEONQ0bIXCzu2MLmMMaJV/CU6hpnxXMrwX5PH3NBM4n8pnm4XScsen/racpR7GEsMM7HvBczIJf7T9Vu+86Y00k3wthylGH0TCJ2+ZyyUl/2VhveFFLElfTQyc0VY4xr3auxnMToUk7JqwVjp7vKSew35OiPh4mZx+qvO82aBcnp9X3btN9fUzdf3ORANbLoOvLIpQz8UN0MOMgQxa0w+6bbKKQ8DwCnPQocuFdCt2LOSA5dnHUIguywdelmKtClnUDkviWkTfeqHzyvXk1IatITFLtihQyuRcZpDlzVd2JRdL4xIYwX49M4Lk1XtM0YkyayrFIOwA8BYcvJiB1JKhJSkA9k5tc1yf0XTfdSrHQJ5a0FZn2Xujpy24Ep934v/cJ5kpOBvncVbwW3Wm82Qk3vnMDrTwzo7YgS6j4oNcs7JnBFbCUHFIoW+pJ2oQAw9IYhsTq3SAFn993RAWMnnFt6JlF8Urdp23emaAmvcIPNXOtOLzAFGMLSqEkzND8WD0QaVQYgldvBVRbbQ90Ht3gSryVmH3smXh5xZaY479XMmj5JVBUSfEmoM0o2ZsxkGtIvsj9hm7xx11Qz5p3QligyItRacIUQZlOY0p4ghkK2lrip63W/DzKZcwHAzsLPn87kQYVSewumaEhJCpPIG3wvYXvkKkcQQID+ESFXNxB7HSMgJrzb8/7eatAK9OWAEtmTTSFKfTBqE0aVdOhOMTGtzQ7VB9ViKDoVxeAwmWboucuAWfP+97/D9776P94aLdcvZ5RW//OU/8rd//3dcrZbC3kgZu/D4nZqkeiPZyBAliw62gDEJH1qZR+AqpYQtyCVWHb8ZDEqRJLCmCFpry9T0hpDxRvRSehXsx2ryYzSQUFDSGkM0wixwTvS9TAykouejLNOYA954goEamfhNTHJnUxlso/IQqE4wRhm2hTk8Bj0wJmzkRLL6lPS8JXhky4lt/URBETWmU0Ygug4GkXxTnHYk51GvaQAXpp87obNPAQUxohLUDsy8XEAuZZsMAFgJcEoQPCaL0t6Wh/YNUEb3ZB0Wyoa04+o1TcCOkjRIu7ecyNbAFYUeMsDACNNW5iwSCqi+qjMjO6k4BmskgCnGWFAOSYwFJytgdcJSUbkDDu/9LmH2XZ5ezWi7TIyWFHUae06QPNYkcu7lw00U9mxy0u6SOnKy+P0H7H39dwk7J2TXYGxFTzNouiYcyVhiZBgcIEGVBTzeLqiO5jSLu9CeYdpLTOoIV88Ir36J7U8lGDYScMQQ2OSE6zO277kIHbuVZ/fet9h98z4LM+fVBxVx+WNcE8kugQ14FfJOCJOp7JM+CjN4BCQyiUhOpfo4rrcxaTHaCp8HkJIka0T40RIEZlMGVelwRO+H9V6cnS8i5ROb4VxZF1kGoKQoiZD1FKaLLeCkBlSiTDLqlcnekOp742tSCHQpivSDE0Zan8QWDQ5TnVm5loIhpJylEOG0WKDBl7PS+llYbC9fvlRADm1NFldk/ch6MaZYd7Er5X4WXyBBhqH0pA0tfdbKM1ObmZ28L2E0qWcAB7cSB4FEFJAfizkFODTGsNl0o67TYMfHjgQpHqoB0e93VvUac5F8mBxZ5HnKyVrd/+aG0y76cc4qQ9lMkgZ0QqoR9kLSVrDCfpB1l2lmjVxD24oNy8K+2nEOP0hIqDe1o08aEqc0MvUkGdR9MKkFWFPWp1yPXI4Eo0puEp+BmIjS9jZNwIyCIDCCbyItkidJdYkCxp8FxLaDPc3DejHW4hcz9u8cE9uetGrFVhptFY9irq5Si20TxwfHvPvWA64vrzg7O2OzueD81LB/mJiZyMOPPuDBg68zrxr+/s/+T6oUyZueX/7Dj3nvnbeYH9yhW5/SZGkVjN4RQ0fthenTbzoshp15zfzWMSlmnr56yeWm497eHV6/OuXJo5fMZnNOTm5xdXXJ6evXvPP2O5AzF2dn9JsN77z7JvP5/P+j7s1+7EiyNL+fLe5+l9gYDAa3JHOrrMyqXqq7utCt0UAaaFoYYABBgABJ0Dzr39K7oEdBgIABBEhAq7X0LF2t7qnuyszKTCaXJCMY+93c3RY9HDNzv0HW6LV0AYJkLPe6m5ud5Tvf+Q7Pvv6Wy8sbPvrgA+7sz3nx6gVt73j86Cm6qji5fMs3r8/4/qplozUTEzieT3h6vIO1mtcnF7Sbng/uHaC15dmbC7yCD+7vY4zhu8U1Gw9BVRgl3TO2qSFKIc65xK40Is+hVO70SIcgATwqnQNGw61UlNLLeDhGToy0Tgwb70UrjCggUJ68ntt7s0SRokwDzjJLutaYSVXsZDo4ZYeQ4heVitAS1xicE6buZDpBo6mrhk6OLNZWNLVnxUZAY23YmTbE/ho/qZntTtnZm7FeW3Ymu2yWK5aLFVU9pesd8/mc+e4+1k6ZTFr+y3/+z/E4fv3sWzbrDik4emS4pYBlMe1XlIDXwTshITRzurZF9S3EwJ07Uz44uMeLV2/46Mef8rOf/yG1cSxTorl/MOcnP/2UavoDz1+9YdX2xArK0CxtqI0k1H0IBIzEh9HjQ8RaKE30XiYd69SFkSBGKmXY391l/+AOWhkqrWW4mjZ452kV6Oh5cLjPD683nL89YWc652Bvh4PdKWdn59zcCHtw07X4tkWpKIPF1h2+u0ZZsWu2UVQNSUtYo4wM/1SmwtgZwa0J3ZpuvSbpeYktRQak5YGtsj0CRItL9jHbaJQk2SHmAaJJDzE9kz7IkM7coltPa9YbYTlLgi6+nSgdF16JB45RYW2DVyEBqECQQnAeLCMak8JAF+Ap3WcQeYjJzow2dPRtW/RRXe+pzQTS0KQc55FsaYgpwo5x8JXB44IXLebgwAVCTGc2G3uSpJPRaQBLBr6S/c17pK5AC6CqtMZUDcpUaQK5Lpr0IUToI8++/J4/+/N/Qj2fsFm0UkCzAd8tMFg+++xH/OXf/hXXfkEgdcqYBGoXsG4AuTKAOQZVb/8bPRAysp4wDPlG+l+6r6Hddvz9cV6Sfduq3aSCa1qTFLZnAMmn7jqrheEo3cSpO0kNjP+Q5FZ8CMmWynwIiUU0mSiyDepFvBcd0kBIHTA5Vsm8zJxDiMxY9sESi8k6bpFmSkH6/WBj/rvrOgFatJF29JBsvIq3rjMm3/9uMbqQdsqH51xgeKnRs4qknCadUaXyfQ6/p5UWGQAlLdcuZjbouCCuiMEjFkxjJxVuNGDo9isE6QQZP/9xTDbee5kdehvMHb/GAG3JIUbF/qrKhA2Fij7JCOjS1aIT89doAQWJaTxgEOkyYZsqeRYqdUbENDhP5cKL6Psq2NLiDF4KNH1iUhaQyhrqKrNshUnZ9R1K69IlayrLZNpAVEXawFqbOmN8OVMxxAJ2TdOQKSkEJcaty3zzvE6ST+ffCd6jjaayZmDI5twmYS/OOSmO5nOvRFc3d0yOn1fO92MUPAlEDilE6NIAvwyAE6Gpa4wVGa1J3QizsjzTRA5UlIFeznua6aTkTFkGUZ6eQlWinxqcS/lIJAQLIkFMXdVbuclkMqXP8gwIe9oklmjsHbaqmDg3Ys5Gqqqi7x1VJYPEJM4KdL7fsmnjgp7SJknr5eJfZkB7KjvAiXk9netxfY+1lqqyZWCbDGvzBZAVEqXFWEvnHXlYtOudDNlK5DNrrAwYSzrFfd8RCci4kci6a9NcKvHpLutjp+deSDH5fsNg2/zojEbvhSjJkO+OiZXei6axNgL0ZyKoUhmMr6SoGUTmURtLU1uJL4MM7cvzkYixSPi87/U7DdICmGSlc2Kemywysh3TpOoMHuRJfVI4SsOZ0mCDEMFEpNJGxAS4f+eQX/zhz5nPd2k3TqYpf/Mdf/GX/wfnl28lQAnQNDV2OiFoVUAlYV+q4nyLYUXOp9ZGKgs6tznpomUFGWBMmiDJ2AjtmwTfqKS1aNJUOLlPl6rhjdIoo+V7CQSVu5UqqlRHxFi4rgejS3BdPl8J82HLEaX1IYGRaJLumRh3o7fbMgprcOSsMk3e5wChbPThc263/5aKK4mhGIekfezkB7aWhMuwfXjyz2RNmcz6G1Pqx8CLvLdmvAT5GZpRG+a4lSXvv/zKBkeuQxYxhkGjNBviwlhNiaoUy5OTTfsoV2/H957Xa9yalEF8oOiNxdL+/R42GglUTcCdIgfsDoVGx7SGsnnx+pDjD/5jZod/xLcvepZLJQlwBKJLb9dj/IYYXVrb1BoVpa1NBU/AoCbHzJ/+gnD3C9bY1CoT8SikKpsSxBjB5XObz4jccgd0pkY3d9GTO5hUxazDivruJ6xe/4qwfktcn6LUGotDB0WbpRZcy9WbyKozHD74KbsP/ww7PeT0b3rc4kvqWU8wGqLGaJkKLgPBHOiR8H4J/iSB8aRqcKQAFDAM98rbKgPwW6yFfIZKUjHs+bETHqQ+hmeZ16UkGjkQywFrAoDHCYUaXYucNZGnCGm/HdyZE/sNry+Wg1MqbEd59uNJybfZ2ioDMvl/SgsoqFTBSDLTTiklTOkRA33cCvWOjYiU8yMDEBS5ghVCHjzhCwBDsqtKa0Lvkp0cguj8GtuIcQV+bJfyMxsPDjHGJO3wJLswNiDpI7JvSo+k7IWcCNnEPhkKRiYFMQPjutjrdO2FITFKICKicfejTz7l5YsXnF2eJckItWWr2ralTSCtDCuQFiHZWJS7oe/8AAAgAElEQVTnfPveIZZ2qfJKdi6M/B6jJHYs3SGJV9aKp/zO7evLDNgxq3iw/QLabwWNo/2c1zWSALoMmqfvR21Q0yk7D45Zvj7DLzfobJeBzjkcwrBYKo8zih6HUz02aLrlJafXKw7uHIOtmdUTHn/0GaubBf/wV39B1QW6qytefNdzdHyH67DBd0sJvL2jSj66X69wAe4cHLJeb7i5XLDxnpvNio+ePKRbdbx+fcLjx4+Zz6acnZ/iQuDho0doa3jzw2vquubTH33Kpl3z7bff4brAF59/SgyR7549p2osP/7sYzad47uTM56dnPH8YsXaw9zAk8M9jg7mdMsV351d0FSGD47vYozm1ZsLLPDkwSGRyPdvzrFKsVNpFk7S2NpUBCeJvjG2JPrBB7KkT94rWg86h9FkBVVKgK+U6K9lG3Q72QUB2cvAnbz3R88+Mkp0Y8SkxN0D1XSKbRp8jn98PjMRHYcrjaQCtBEdvugDdS1DPjZ9jyPS9o627xOjUBOCFuksY2jqCZt6gq08k6ZmOpmwXq+5vj7l6uqG2WyP6XRO75Mf8JH5zpTeWh7chf/2v/5vePbyBafnN6y7JeeXZ7y9OGO5WkqbvbH0fc9ysWJvf5/FcsHiZoFft/R2l76d4juPVhatK37yxY/5+Z/+jPkEutUC/Iq6bji8s8cX1Yzd2T4Hszl/99XXLLoW2zQopZnWNbuzBms0qqp5+foU7zZEhC3qAZTB4KVolAb4EQWAj8FTTwzH946Z1LusV1dcvr3AWsuTp0+pdwyrRWC1WjGdzPn8s0/45jffcv72hGlTE2PPbNoQg2dnNk0JufjW6WwmiZHfoLXBWml5N1YVW+QD4Emdc4qudUTfFX87DvRy95XO/kRJ5B2L7c7xlyo2KXe8lCQcATK8DuAcXdtST5siGyb2JdyyZWXzliRcqfyeKb/QachIjMXPCbQqg1iU1hhr0cpwfb5gc7NKepwRo8FWWgC7bKtDso8Rhtgjn9UU1mUb5Ry9dzgvsgj5tGWGognCvDaZKZau3yeppMnOLmhD2zpW65a9aRCFK4T8IeSFDdEplPJcX254+fwVn/zkc3wV2KyWhK5DG2iaCY+OHvLB/gO+PP8WZ6IMJ0seAQY/l32XAARua72zvbltM/L3c245xDb5vVP78XvsUrFvW0xRVfaLvGsiQCRmKyoRRqxJQ2PySwpTd+7coU3DbPL7Z0k3HQW8z9c1jhVjCMWv5pyGtHettYToyv1HRJIlJgAYNXS13M6z3nePt/dx0Zwfh0A6y96F0XWSrn34+hisJQPaaRUTAjvKrVLvTJbnywcj5wnlumJGbMmgr/gPuZccC0rsZ0sOn1ZWAMLKEjc93NoXt9fmfV8fx/jvAunvB2Rux3SSu4PSSfosZtLKNqCbB8VZZcv+23qvbJsTOzwXedZdu7V/yjBipItP8JQIWtH7XICLRA3G1jR1TV0L+JZzdQG7vEiepaLntBE5vKZp0jmAPooU2XA2KftDyFIp77EDQJafH2SN2UQmy0C4d2hVD3s8kWeic4QgOthy6HWRa4ikTiskh45G43s3kGRipPe5gyLJYxpbhrejoO1a+q5jMp1irEmDrbJ0wzaoIAUz6SzOhLA6yThIrpWJZL4chNLJkPNKK50IOT4e/wkhiP6qkvtYO09ta7SyVNZQVU0aLib7XimT7BtMJ1OMNmz6tsTtfd8X8onEeTnfG858HqrqEnBprcQpzgk4HIky8B7xrNYY0ZGvlbCSc8dCuvdJXUtRwDnp1OoTYSNheqg0U6f4OPn9EKWI1TuXNGmH4miIAdeHsq/ytWZ7maUOBMzvy6wDkZ9K96oFp7FJygOECBa8F8wk2a2266isTR1T0vUga5SukZRHGcm9pah1C3wavX7nQVofQwI2Q2n5GSfz5CrgKNgom1ylg6cgpKqvgVw/pMbwxac/5vPPv8CHwLptOTk74a9++a/49tV3BOOFcq40ZtKA1biYhs7k1p/RZ5bBAWnBsz5s8pOFul4Csvx7IxBlHEigSMM1QgFpjLZYZbh7Z592uWax3sjuTQGmT8Y4RtG9iDp9S+sElGih8wPByQAmbYQF2gdZmexItTZStcsJTxiq1lt/UAUYGSdPAYUyMqgnt2EUHbOR44UhwSo3nv9VQAK2fm4rqVdsgbPAFjjg06TAMkQhO4b0cNTW38PHjz93/Hnj15iVWz7Pi9TCELHk8DdV+MitYrGATpAThKHlaMAdBqccBOEoQXWIER2kypcNxxhkiWE7QBi/X8ifExUqyPUqJZpnQVXM7nzK7PhPeP6DZbGQYoUkvwGCIjiZ3OFxqZVZ/q98hKgIsUI3B9QH96kf/B7x8EPaaPBKiTJC1tZNpQMZ6BlBOVRQBcDOTI6QkpWoFC5ofLrHnjnm8A+w+z9CL57jX/8Sd/GK0F2AWhO1xkSFdz3d6pzOQwiKvYefMLv/CY9/+o/5/m/e0PVvUFYheoYDG70EATGgoyJPCycgAz5U3itDEOX9sLfHIN94/beCLT20243B/5JAhMzeHAJwrVMgfutciP17187c/lvWVBjVSpQ4WC6WRLcmlv0oIv25sJBtQ05cx8FDvs5sE4L3xVln0LhUvtM5ynbt9t68PWjK+6FNWkVKFTQnaO+zESKDkKqdPlChxsc72VNT7Fu+rpw43G7fv/1c8jOPQFKRKLb+djKTz6tKCVEowdhQsR/fx9bv5q8hbdhNk6aexlGyoBSud7x8+ZLlciE6vOOzHgKbjTB8rLU452RialUllCHZFx9KEj+2a+W+b62xUqrIwYz3+1ZyoqS9anwm3leAGq9rRHzWWF9XoRIhLGdycdh/o2dX13UpGJYDkBNFo6l2J8zDHa5fn+I3PVU6z6YSFsY6Ol6cnbA4v2C3qZhUlkltZKDDasVN8Nw5fsTN+SnaNvz45/+Yq+WK069+yaHW9KsFiyvN/fuPOTt5RQwbaYdOrDSDxDOrxYpgGuqDQ2L0dJeKk5O3hLblow8/ZD6f8PLlC6bThuMHD2id5+zsjAjcO77HxeUlp6dv8H3go48+hOh5/fo1k6bm0ZOHLNYrvnl1xj+8vuJ01bOJMJ81/OzpA+7tTnjx+oSztzfs79bcOdzDdz1npzfM64b9o4a273jzeom1ig8fHHKz6ugurnDKEhHWjdbZHohfyEXNlPNStGYTYFX2xyhx11oXXezx+RrHBJlhztbXsx3djjtAErSQWlfr+Qxd19LCnVq1vQ/ZWifgXw6uSYMvVAQdA1ZrppMZla0BJdIlUfaT6x1Gaya1Yj41AhSqSAg9xMBicUO7WeF9y/7+Afv7d+k7L8mTX+JcoJpMqZspb9+eMJ/WfHp8zNP7jwnRsVwvuLg+5+bmimY2YTKZ4HrHZrXm6PAunes4OX3D2dkpy5sFHz/9jMo2KNey19QcHuxgTGQiODJNpagtLJcdMUQePTqE2LHYLHh1cs6qbYnOE1uNI2KnDbvzKboTNktMGbbrPOgKpwKVSVGdSix7H2kqzccfPebDD5/S1HOeffM1fbukqisefyCkg8mkYnHT4VrNnTv7PDi+x83VDa4Txuzu3gHznSmTqqZrhQFrtGa5vKHrPZPZFD0xKIMUnHVmcSsUFpSh6x159kJwEWOETS0AaGbBkiJ4seTWprbYPAcg2fdkYum6jrqqy37JNjwXQGPSTw6py8R3TuaYpeYqBYOWqdq2gVv/ztIycbC3AoJlQoUGbaiahsvLS87enrC+umF3b5e6mVLXjbQmhyhs55jaj70w6FLWktiGmogw81BKSCUqs3uydqNcU1673jlkzoJCGS3Xk06TQxFthTIVPrT0QQCVEFxyNKnrJTiBMLuAqiLf/P1XfPzjz5jN5+gQ6JeXwkze0Tw4fsAnjz/mN2cvJEYyahTriH5F7u647TfHNmUMlEdu+9cCxwEZ9Mg2atse3QbiYMwMTeusLKo84wQCmxxHCVAwLlTlPGaz2dB1MjhJ5NBiyX0hMjBfVbmWMPJ3GcjKcaICJpMJSkcuLy9RysjALGtS0VkVkC2/cnylzVCk/20FtK3/p+6FmOMlCY5HBefh58cFt3FONga7t4HQbO+H7sOBzJLZ8AOQG+JI2z6RtIixDN4OiV2eu7a0saJRGxKnPce7iWb97nN+F1gZf22MU7zvZ2//zO0ctuyxENmsNtjGoCZWiojFLg2a/wMYPvhaUj4fY5Ig0rp8Lw+wG1+DTmSUKsXplRFd70TgLH5WMZqZ0fZMJg1NZncGnwoMkq+GVCxZezfK/1M3zCgmUEixK7jR7IlWWIjb+yySAwyXcnspUGRw2OSrTWAsRS7JoIodzAQWUXKQ9TFBBm85J2BeBnC9D7gobf4gNrwfMU61VvR9h/P6nf2RZ9KE4GT2Sbq6PHjaeRnErqwU5aIZhjsXZdwIrutlaKoXVjNqyPfG+ETwnjxwWtimIj2VAceYtPqdcyVPQyk2mw11Lc+wDNRifG7H+384u3n+QD6LmfRSpCaL44syGDNJjWmtMU1dcua8f4XwpJJEnQyky1+X99ZoDdZUaC2SfW3rkpayGex4jGDls2WmyEhqTivRyU33o7T4sa7r0FHYzk1dY62ckU27EaZ417H2nknd0Occysig8OgjvXdsuhbUlNA7qjTDwTkBgZ1zqdtRcpFpMykg9m97/c6DtFFpPAGB/BKTJi12LEZYKk656gOBXGXM8gghHQ5Har9xnieHj/mzX/wZze4eF5eXXCyvefb6e/76y7/mvDtHG080kWq+g5tK+45KBiaDGxkYy1Xz4WAODhUllTvZ3IoYszHWBfQYBwt5I4bkfCQIFGfng2cWIn/8yY/4d1/9mvPrS0wzSToxcuhVTt5T66lWiuizZETSFCJNsiek3yVdUzpQPuCRgDoDEKKBIlWuELaFzmFw4tI2MUyXNTpXw6B8EAMoPQY/MrAUo4Tb44rgbQBj/O8COoWQGGISaGdAIv9u1tC7DQxlB5SeRgIMZcFSzCOLl4XFY2J1j9qq8t+5gm7MKABQCWhTcn9d6MkMBK1AhWHtcgKLYntfpMqfjwGjxkzeXA0KpViRL3n8+94H8lCQdLhKwC8rkIZLqDn15CGT3R/x3bMli6ssjh4I/YboooCYMSaJB03sWqCXWN3MMLN96qPPqI4/w+4fs441PVqmqnuXEFlpS0eHwqBVIYrAdw7ISM9Bi4RITL1jGrmGSKRH47TGmF2qw89p7jyluX7B5sUv6c9+RYw3eAVeKULoCOszuLTS/n73HvvTQ46f/CGvvv5LdFxSNxFdWVBKNKpiQCkvhjiEIejM+E/WJ86DamKaMDvaX6OoqXxt3FJkVZWKKIMGWTmPo3+LbagSE3XQ5B6/b36mSqmyB8fnp7wfSjoGVRrCoAwXVyusTELBWiua05vM9ZB729nZKUOhYhTmYWYYlcJN2XPydZToDeVAdHw/t4PS24B2WadQUOLRulK6KQQMyixKsWld18lno8uvZtsizjJsfZZSSd9caZqmKdM7t/SB32OH0hcoad4tGxWSjczgIlrjk51mlPCVoD7fI6AKi0Ta2Yy2AlYnkDzvrhBE2F4Y32ytbV532ZtmCCRHIIOGrSLclo2VXy77f5y45rX/9yXGIcQtqYffBsiNk96xbS9rMX5/xZbucp7GKrihTiDu6CyFIOuiI83+lB0OufnhnM2ml2REi5Zm6D1XmxUdmrWrOJrvUHcdWmlsVbFqr6lvmjT8ZQYffMw//S/+Bf/r/whXX/8tDY7LkzMqU/Pgg494e/KS2LeofoOODhUjjbG0AfbuHbL74D7PXz6H3nHTnvH4yQc0k5pXP7zCVIb9g0PWyw2n52co4NHDh1xdXnH69i3z+ZTdozk3N1eslyv2dne4e/eQ06sbfvX9a747WXDuA3Za8+nDe3z+4SPuWnj1/HuWywVHR3MO9ue8Ob/m6rrl/sGcg905J5dXnF6umE2mHB/t0nlPaDcc7cy46gI3a0eVB8qonBzLMzHa0nZ9YcFkX1ae5W9Jdt8Bq0Zmc+C6qoHxliHWGNPw1YEZCBEXNXpnRnNnP3EBZTJxYyoWqzUgg2ZD/pj0+QYtxWnv0UgyaUyFCpLkNcZiUUTfY7RIkFRGY21EWY9vO24Wl+zupsESVNT1DJINms8mbNZrzi9eE7Ti7t37tO0N33z9Gz79+FOaZhdC5NHhIXtNzeTphwQ8682a1XJFnM6pK8tNu+bxnX2e3jtgtVrTVFN25jPWq2v25lP2ZlNc11ObiqUX/bMYHNdXNyw2jvnBDvce7/Inez/h99aOkzenrBdrtLIy/dr1+H7BF588ZG9vn2paEYOjW7ZsWk/re9o+oLB4L2C0MRUff/KUP/nj36exhrM3r1hdXTHf3eHo6Ig3b045OJizM7UcHd2l6x296zCVDPHYrFdUlbCqQ0zJprWEXkMUdlYzkZZHH3t0ULjQo7SAtVVTU9cTgrN07RqtI9qAy/tpBAzJfk2xXo4rtLTyGyPSVD54KmOTZmNmgI6sc3pfYSTK9/q2o12tRZIgJdoiEZZs1Ts+Y3hlL0Eu4GegMF0rSnIZ1wVC5ai95+jeXaLr+eryhPVGbJ82hqYadfmFKOTDhG+pKG32kIrQfvjsECVO1dqidSit1TGdhcw4Vgxs+RwzCwlECakln2+y3mRE65A6k2IOnfEhEtrIy++ec3l+xsHde2gFN+eXrLs1vVLc2b/Pz/7oj/nf/p//G+06go5URpcznWOJrCmb/cHY790GGGOMo6JSTOD5IGsAg2xC6RQYFVXzn3e7btK2yD5fJ7a+KsZs6z0KacVL3Htzc11yW+d6jLWS+yoK6WKcO419JmwXyrXSA2imfCkmKJ2Zidu5lc/5F4NNzgDabZ89rPkt4pSi5H9jEGkcV4TUGpw7xQoAakbdhgzDovJ5iAmIDXlANuNYZQDF5L8j4EPJICqVSFsxSBu7T4Cu9wFiluSyWFuJtI3Kue3wVuPccbwO4/W5TebJaznef7fjm9uxU7o7IjJwy7W9DPSNohFb2H5al7wXoKpqAXL10B0qedTgQ0EGNmW5BCFSDIMUy/UqMOk3CtEpAX95WFQIAXwk1FkSTUg/EQjes9q04n1TDJgJEFkObYitJb5s25bpdEqIXuQY+lDi1rxmLgGPGWyMMeJ8z3qzgUgB10IIxNTZpxXQj+KIILqm2U5pJR00ZW6OD7SrFYoEaKe9XdcTuk1L13XCHDWGoEQz1iet/nHcOxQOYsEapPsyQrLxRht00FLAD5E+SpFPhSG+ds6hnVxr5/p39pFOEnN562kvgKV3wshXCVMSIDNjPmKsRG7O4lYrfBw6uyMxyRsMIHAmod22OSIfM9iM0iGXtGWVTjMgFOTWkIwJKSRnNjlHTD41S8Vle1FVaahZ6rQOXnS1m9rQd9JFIvajvDmgqKsqddZQ3i8X/qNPOQ0kX29KsUJ8hGZ3vgNK0bYtvevJ8h4GizWKylTye2mQXy4AGmOp6hr6Hh1TYQIg9qAVDmF5B949+/n1Ow/SSvQQSmsxcYA7IjK1ThIDLULpqeqogjz4DOInWZCyiabK8sUHH/PRoye4qLhuHW+vFvz9b77i5fkbeuux2mOahjCvaTVYLa1GSifdkJyU3wLTBuebk9iAVFRTUEcsDyvHXmOnnwMEeS85xCAgqQ+Ou82MR7t7/F9X5wlgSYCmSmGg2nbaggnI2hBHFZWoQBkyaJzF8rOkoopRqMcMTju/X3ZM+X5vV3S0UiI5QWZBpkEeo+u6zajNhtglSjol0Bkc2Fb1nG0jMQ4EdDL+k8mEtutwfZ+ATVWM6NA2pJI0gTCNMzs3QgHdyrNK99v3fWH46VStHt8/WW929Jti4+WzTHq24tTEuAjuOGikZGmMUlGNlJYVUwxyahVIz0TOiHpn/SRYj8V4jO9J7lNJsBxqps1Djh7+KT8sDljcJMeRwN3QJ+cRAzH0KHp0FKaNqi1675jmwU+pDz+A+QM2sWETwOWnFUHllqUQ8H2P8sLsUYmxgbaZmFEY4DEGlE/XrtKhySBBlPYN5yEEgzN7NPuf0UwOYe+Q7uSXxJvXGJMCaALd+kykQmxPPNhl/+mfcr244eb1v8ZbSfon0yadYU/vuqH1MI5hcIrzzgG97NWhsq/UKHBWg1MdP1sfokzFTPvRJ7umSqIwnLc8zbiqTJmoO9iN7YDy9vmBgb0a014x0RC1sOhtM8FEASeC82irmDVTaZFP7fBt25b38d5zdHTEZrPh8vJyVD1Nn6lE5P+3FVpu/52vefxztwFDSbRFqzzf63B/ctakdUbawLIuWwoDS+CQPoxYAoYhyQoh0HVdSSLGn7Gzs8NqtdqyW7evPU+cRQ1tPAKsZg5EflZjWYNhzRQDsFr0WZVis2mJcZMKZGkd0zXO5zv4vpcWnJw8pRV5Hyt2tE1KNX2cdGz/cHomo4La2BMPQGoc7OIt1ixxO0F5XyIz9qEw+IjhMobPKszd0b3k9ctJBySbivgkHSR59QrsfM5kv2Pdncu0cHlgmNrSxz4lmp66c5jYMZs2GKOIyrG8OkP3kbae8ebrL5k0f8Iv/tE/418+/w3u8pL9yZTTV2/QdcXe4UMWV+cobaFbE/t1imk066srNusNjTVM7h5x984d/GbJ69M3aAPHDx+yuF7z5vUbDg922dvfY71Ycn11xb2jIyazhpvLK26urzk+usvhwT6nZxf83cu3fHm6ZBUizdTy44/v88WTh5i24+TlaxY3K548eIQxkRevz7hatDx+eMjOvObV60uubjbcu3PAwW7DzWLFxWLD3sEOGMP1m0u0ikWfPb+8Ty1+UeF6n2xi1kiGAThPzzIB/jkZRCHxVRiAnzz8hsxIuxWHjPdFvpaADDzU04ado7uEWlrPsgbeZLJLbx2t65Iu92hP5RbiEFCJGawzy0opUfvRCtNU2MqyvF7Rt57KTtHaUE8qtJ7Iz8UuMfknKFWz2Uhr387OHNevCb7FBMfy4oJZZXB+yVff/gOzyQ6bjeMf/dl/RGUaDDWViTTzhoP5PoHIerNmPt/FuRZbG5p6ynpxxWZ5zrSCuor0/ZLgAhsnDEZtIloFAh2tW8CyFb1d06FNx/HxDH28g7ai6erSIJG6sjy4dwQmUJlIFRXW1Dg15WapmNRzVuu3LJfnHN454vj4Ic45zk5fsr4+Y2INvvcEH+m7jq5tuHE9s3lNAG4WC9quY7la4wLcP3qAMqBSMrlZynC2tl0zaSqqOg0H0dKynaaVFZDBey+MJwUhejbtGpXizDyw1oUgMg0xxd9pSFPu2LhdgMt20VbDsNscr3kfi2ZojNL2GZDP0alYmtlCY5sWEsg79nG5UBgHgyb+yAvzVFuDxJaR6D3tpmVnZ8587w537j1Ifjt1sgQgaalKCCHF19Bn7rAqoCyKAtr59EcZRWUN0UFQWYdWYh1rbbp26cyTuE1jEzHEq5CKNIjWZxi0/I3W6WyrZBKk8LK+WbC4vGD3zgF9vwHvWd4siJOK3Z09njx9zN3ZPsurG3oTcUpAe8zIT9zyKwXAuAVqjiV68tdRMTFghw6esS+6bWtug2wSK2b/NjxLef66DNsSDcwg7b/juEWJRMftWCij2WMJpPcVMvO/M4ttvN9EzkOGJgU/DHa8nceFGGTo7Jafl9cYjB7Hr+PzsVWUGz2DcSeS/Ixn7P7LM8gt6SqBiRFCcLc0+pPvKbKfObaTPT3E56R8TmLbHKcrhWjul2KLKsCVMRajLKpp6JuabtUVkGyrYPxbYpL3xbi3n8/49b732/p6ujOtFFZrnJfugL7vySQmnYDK/MyDDzKvpzx3ca46xWlC0gLfS8FYa51YsYqQ58ik+LHveqJJg8c8ECSebV2fGNYS62/aNmExaYFTHhJG0mHeeag0XduV/CbHutaKBqsxkjd3rhc8IkZIgNjWMNJ0PqPrqSoZUqijoe97+s5hK4k/u74vLEVrLVVdic1KwKH3QrzxPkgbexjHrFoGVCasxntP5zw36+siLeK9h6aR7r4Up7RtO8i5IUMdYwxU1TBnhCiFN5/Y8kE5VCVSUF4b1n1LDJHQ9WKjQyisTUAG2BuNcx7Xy8+44KmaJjGL875WeN8lv+Rw3jOZTDBRpfVOkkC9sGZVVKW2YYxBRcpAQJBu8DwoVsgrpmBZuVM5RmGMaiVyPCR7oI2h7zbEGKkToSLjF1qrJJMghJwssYCndFnJNQjGFWLEWE3bbui6Hq1tRllKzp1NayYHxQQ25/U0SULEp8JEAJlnE0cgc7ZryW9M6jpdeyg5k+Sjsp5NXWPSntKVKntQ1hCMrZI/t/goco2Qhkv/ltfvPEibk9pIFEH6TNdXAxCaGYoRSTatEpp6o/L4xigAS4iiH+bh3myHP/jRZ9TW0vkebQ2vTk/4uy9/hWMNdQBTU+/M0FYMiUYl9qAYvZjazrO8wG2HKS0ziCEqjjBN0ysYgVQLxu2ePrWZEAYHnieHxhjZP9jn5uaGm+WaOK2HgqHKjjwBhsh0RNLkwOhTC3ca42i0pndJ/MEm3SMtrRRZu8MjzegxRLoYsQlQ1An4yBWShF6OHpwqjtEHl0ACjVGDHuVYO0knndsQMmNaFQxgCFwDWYWKXBFUA/ARcoAl/Jdi1GtbEaMkSC4OwXSay0FkYOcQsyZuCmBD1rhURZMxM3WBxDZUpaU783IGMHRwKvL+o2SQVGEffd42jJKXMhmC9N16pA0jj93IAIzUamTTZznvyHor4zfOrGt5bwFHweDiDDt7wPzwD7lcHXN9PQMaohYqP15BABMj+J4QW2JYC6u2ucvk6e9RP/yUsPuQNta0HoJJAHZMjIwY0K6F9ZKwaQEN1RTT1MRqmDaZ1zwwOLXyd9Ym0pJ9KGuxqYVApibK55rqCPvkP6TaOSY+/zeEy+cQ1xB7lGlRmxP6qxXL5mPuP3bV/k4AACAASURBVP49jj9es7h4zro7wcYebRums0YmwZuazl2ngC+kAElAQJ2fp07GfSRzIvZJNKMH5jxJ3ykFjdqCyoyMVPCICbi1gx5RPiMQS7GhaRo2m82t8yS7QgaPaOpanGw+D7nAkIsTwz4SUCrrgEnAK8NEJJkSUFRAYZjMarp2w8XlBW3XElVMQaRimAKf5BRSv6d0jqlSAAGxS8Mrd0hsg4pKxdL+LkGnBDkh2Zry22YAZnNDMzGSFDjSc0lJRIgywTV9o6qqoq80br3JVf9xAjRmTtz+GyVdCs578TvkJCQVxFQ+8+XHE1iQLduQtORJ4iElLxmId87RNBNqq1h18vUn9484PTvnei1yJEoN2uk5CYyhWDpIyWoGCkICzcwoodgCVbPNyPeqRCJDgIQ0gCvkgTvytUF2AAHEwmDBh8vYTlDy570vqXnv76ltFnIG/EBsotE2rWoaRJe2tm0q9u7fJbQ9/eUNJq2Zd050u7RmFT1v+zVeRe47RaU006YhdgHXr7i+fkXX9ZyfXfDTP/0F/8l//l/xF//Tf8/q+oJZbTn74QeUqpjvP2Zx/RbfO6lBKYUl0G3WsOlo7uzhouLm8prV9SX7Bzsc7O9xeX7Fmx9OubN/wP7+AReXlzjfc3zvCGs0J29es1y3PP3gEZN6xncv3/DrF2e8XPa0aJqp4fc/e8TnT+/jrq+5PL8A5/n48UOWyw3fPjsFbfj0ySFeRb7+/hTXeh4/uMPBzpSL8ys26zV370xxEU5OLtmvGioduO43kIayhCggnDFG4pckKQAOVGJqjPZ3nhCfYxqdBz1EXwYRKihxSIyipVf8QhyYb2kMjPjukObXTyYcPHpIvbcnyYvSHN47pqoqzs4vEqNMobUtZ2EcK1ptqSLsT6fszHYBK4za2rDZtKxvFnTrls7DptdU04ZIj0rSQ1XVMK2mQIWt5yhTc319wWazwBiHcz21toR+xeuTV6zX1+xMak5PT/CTDQeHDzBNzURZ1osFzm/YtGuWywWz2RQXPFZrKmOY1DvM6gpnFLGqaKYVdVWzWi5xfUsMK0J0YDzLzRKnerzy9H5D7Q0oxyYsMEaGo9WVZVJrJk0t4HYImOqaykKlFToaqkpz/+iA2ewRSjV8/c2a4wd73D96yvn5CW9+eM7V2QkmyiBOY+DtyVtWmzWz6YRYadr+hqapmM32qA92kDAlYhvLer0huEB0Pd1mTfQ9MSq0rpIfcgSfYyklBWMdUEaV1kOlNSpaeheptElauhKLZLjfBy/gjMrdVBrp8EnFgkgBHpRKCZ+L0pKbfHueu5Db7knJr446TSkXBt+YNRgTyBqI6MSGi3kfFtumSus4CPvHRI2Jcm+7u3OmBzOcUngfOTg4JnQ9y6slWkbAJ/8jwK68JF4PqasqxJCGiCW2Y5A43aeQVSedRp1AWm2tsJD0kMyqSNI/1wS8MNVdwHXSTtuHnk27IjT7AqIScNFBSKSJ1Pnhlp7TH675+CdTlpc3THd32deBnf27rFYt8/mMT5484fXFa3wI9K7HVpbokAKoGvKqLPckcc4grVT8S94LW74orYFWJb72aSBRid2URO2EAEpT12OwIfvynAOOJYNyMq+TK7KE0I/8nbCvZECZTiCk6NkWX+t9yUFyzqiUYSx/MJ75ke+pzAfxGXzLYGVM8We2yjGxJlWxuSoORSxrk/xQysPkukexl9ZUVUXbtgU8jHGYL5GmiBVwLzvqXBjPeVOW7pNQ34MKMtBsdE8SqmSN+jjS483xU8qlM8ErjM5VTLl8DhVU7rySIDFoiYNDAlvy+m3Ho++PYW6TIm4Dte/7nfe9tsBdraTYgqbvOgwWFYdW/L7vhU2OSgN7K5wLoCV2tWmAtErAqdaCMfgY8CQ2uY4Ya3BIPpMQVvq+Z0NiYiqRysrAXsZBYCj09H1fSCPa6IQzWLSVTkhtjGisEoVhHiKDVnPEq4iuZHBzNBqlLFYbJgn3yfG5VpmxLlq3JjH8c6Epd231zhHiQCzJZ0fpyGy2U/SIM2jsY+rciwk4rKwM/DWi3dp3wpbtXU+76eQMGmHu7s53CN4RIcmVBNFHTXIMmWyjjSnWOOdimTSjtQxX26kr6eaI4HovufxonhFaY6xhZqSI3HYtXS/EgrIGxmJsRV1XGC3D3DZti7YW33ZgNJUV6Z7MuhdZtDWul6GkKLB1JQB2JoUZIYsQIl3XU9U1xkisb7LEDorFclHIEpOmoWkaNMKyX63WKb4LSWJNBtEppahslbApl497IqxI3pv1+WEtw0q9dHpMmmnJj0LIAxSHeS5aKeq6lqFu6YyJz47SaZPyPJ0KOz6nFzFCTAXMkIsOpM7emOxlZt9alHJb+WHu8JNh4ck3KYMKHm1kmNrU3hooPXr9ToO0MaYJtykAF2ZUMgsp0FFKNpdWAhrmf+eENgNtRqnsh7ABPn38hMcPH9B5x8Y7urbny6+f8eL1K5kuhoa6JlorkyGjtDMlU8yYpYSPW2ynceVQfNoAwKIy4zS1qsZctY0lKDDWSnt3FDZbSK1cJsC0sty/d5fvXnyPMhXWVAQV08aTtnryoU+Acm61HbfujFvtSW3oLk0pLveVq5cpYMvfy/dXHMjoh4ozKjT/WKrD+f7GgJKsSxZ/HmFxjMHu0furdKDSVUoFJDnqxOxRWpVJuSEZLlIwnKuvIcQCrovTTlOmIxilBjp8ApekEMAW2JnbqUoQc6udWy5xG2zO7UaDjtkg26H1u7pEw1upkuRu6Wpl9injQAFizJMzGUA3NRAIScZMQRJqFg2tg7sf43nIxXWFD00Cchx0HaqPqOgIfgk4kS0IwPyY2ZOfMfnwD9hUc1qv8AFp30/3JnvZEZ0jthvoerStqKYzom3wKoFoMbcqJVAJVTZFhFT5HabWJ/osQRt0XROMJsjtAIYQ91C7XzD/7JD+5Nesf/hbwvIHdPC0bo3yDqdPqHcf0Rz8iJ17P+Xq+Vu8EpZKXWuwE6p6QmBD264kwExJfjYrKsY0ImLEIoX0bPNTTIlXBpRS4cIHX37GGKko1qZmtV5LPK/N1iTUzCJ3znF5eVn2y5gVoXVuMRuShvG+GZgnw1lLaWJKYNLZy8FQAXMT2z54+t4wnU3TYBao6ma4zzgkSTlAsFUFpKptDmJLQpAClMTOjaMzLpejh59HzpVcvhpQzvTZCoreMkj3Q9QD07nYnWK7Bp0sPwKMx4H3mMV8c3OzZZtus2lVhKZuMDqBfaNnktevAK5yM+XzywFOz9QWtnxEW8ODB8ecnLyha0U3S4o9Cq0MV5dXLJcLnDzUck1ay/+zZE6+6xBTJTeDobdtzi2gNv9cTL+Xfycf15DznLSfjLYYLYF1DuKF8aC21mtc4Bx/9u3X+GvvS3pysFuGKY72kMoPJu0RENNlasv+w2OuXKC/WWFjSjZTQSACrfJc+5Z6HYk+Uu3UmMawiT2hXWBtjbrxfP3Lf8N/8Of/jD//z/4F//J/+O/o3JpJ33D26jW1nXJ49yEvbq6Yao1BEplaix6r32zQTYNGc7B/h/07e2zaNeuu5/Hjx+zv7HJ6/oYQPUdHd+n7ntPTt2jb8KPPHkMwfP/6hF99/5ZLF4iV4Wg25bMPH/PjD45YXp5wc3VBZSvuHx1zfnbJmx9OuHe0z+NH9zk/X/Hlty+YzCuefnSEdvD29IKI4+7dPW6WHScXF+ztz3j84Igvn51ytYooG8HIWTRpwrRzuR1OgACVgmydB5NoXbpPMss8xtzlMTzbkAoxg/3Pw0JHLbMpjpKBUWmA6nTK7vFdzN4cb8SxKKS9s6pr0RdLQF2xQxHyfANjDdqJTZ9OKqazOTEXfp3j6vqa9boDRPc0KqinlrZb0W5afOwxpqbvPXVV0TRTbN2glGO1OGO9usZimVhFt77Gqo7oWvbnM44+/YS+g6ANFyevAI3vWtpuhet7Qrvm/PoMWxvqqqZF4fs1yrdcnb1lvbzm8GCXdt2KvwXqpkEpYdi3yyWnr85Y95Hdgx0mlRQY63qS9HUnNHXFvAGjPC52YBQqdhhfgbcoo1A43r59xqRe4PqG85NTDg8PeNM+4+3pCaubK5QPWGOZ1DVoy6///iua2ZynH0aiDlSVoalnxKDweKbzhug961XLarlCeYfGE1xLDI66rkX6IPYDEUEbAuDSVHFrrQB4/Ybed9SmYj6/I3HL+PjrKHIGPhUE014UYCYWUxG8l4FzWp6/VhpPL0CUzUXXkf2PYHWVUpaAx5fi7XiArY/SJpzBpbqukVBtm7ChUtCpTIpzg0i2yCAyxXxnl6Aj7fWKuqq4Wa5YrzbMDnaL9xQWb2JCohLwVwypfBYqp0cpiZTfISjR6VcCFBEG/6sSe8gogxAdctimsKbCVJI7RcCNWJjygYE+dhhvMLpCq4bgK149f0tEM9nZgb6jmjXoyZxV2xGJfPH55/zrf/c3eO2IxmOUSYmxXK82FkXOM0qwW2x+Bu+0yi3QOUYaAFYZrJOBSUso60gC/gNaRlrfKthmJqvFGL3VhSO2Lc3ESHZw6NpL65JtaHofpTPQn+dc6JLvyv7I7ODtoac5nxj7VLGbKQdCgBKTCBQ+AZFZji8DtD4OOVhuY9ekuYuj7+W9CkP3j2jiR5yPpXiXgRKtNb1UayGkXE2ROp4GKcChID90CuaCnipgrMRmrhRABpA2P/oIQ66XrjNLlkhhISYwUSfASHI920zo1aoA+e+LV34bcDvEXvqd+DD/bPFz4/Ou3o2NEhoxxPNJarCqB03ZnFdqpWWoZyJMxBhxsUem25vEqBcpF8ntZL9bJZqkLnoaWyd2rUbrmq7blBPkeiesfqUw1ibmq3QS2LpGW0s9acp5kbgwkcNsRVULG9QoKdzJfk3DnYITFn/qFBRmYlPuPUYp4JHA5pKnwHZMHSPSeZMKjUEGOPVdDyqxI1MRRFfSku6dFDt611OpEWHMJ+A/tdXbpiES6XpDZRtENzrinKdrWyaTBtGRVsPZyh3KSTZNmwEPqasKnXIeRvszP1PRGmYLZxjjJnnP1FVF23UiDOp96eRTyT4brWmsYjrZERDZbsrAXIWAzCZJQ9Z1jUb2Q4gBbeX3J5NJ2eOTyURIb32SjhzZnKapBYzXiq4XX6mApqqG/d2kMxACXdsWNnNdiZY6yIA2VJqb0vVkiQTvc3e65M8oRJoprAqxhZybB89qtcqHjqrrSk4UU45EetZGV+W5V5VInlhriMg8j9yBnQtlMcah9Ok97Qj8Je19nWIHW1V06bOzAoB09jig4t9DpP3dBmmzc5AKybCwITEZSwuLGlitJlV6RItn3DYeSvJeacunTz7i+uKGamdBtbvLxeU1X37zFatuI1Og0Ziqlk2cWI95aBNaDTod6TAQh2pqYakJ57w4yDxxLsZAsnMjMGdIRPIkzyzdIHOMAibAvb05u7OKv/nb56hJlRynQlcC6mYQK4tCkzds8g+ZDi4xSw6Y5Pp1OjQRVQxLTOufgdoCjDAEdvnr4oC3nY+0NiU2QLrHrYq2+v/WpRwAneGyi4PM16MH45wBChRpyJQv7K2QDkks78EwlGQUzOnk8AszOV3v2HkOgKyAJM55hD2tkNapHqmwDMH52CHnoAqy5ooqf0Kq2BRg7VagsH1O5BrGYNLWeqa7GjPh5HspoCFI+2qE65uAUw0u7qJULchp8MR+k7RbegjCRiXUmN2nzL74BebuJ9yYHfoQBbwlsZ4j4Dq8cwKo+oiqKvRkAsbQqyEQKZFVDmpyAp/ThxiLH1Mxsz8Te6/bEJxDNbWcWy0D4/CAnbKcPKZ+cpdmekj73V+iF98RCKxcQN9coE/f8ODhE44e/gGbk1/Rty8JumeziUymmmayQ1XPaNu1PHvn09CptOfTOiqlCDKCdwtgewdQKoG6Irfty3OX9970myG4YwjgSjVWD1pS2c5IgiA6zJnNAFKtDSEUgfecMI41cUsAwLCvjTGl0guZHU5hyVWV4dHDh7x49pJoa6y29H1XHGcpTqTPyC0wKuZC0XYrIgw2NO/rnIjkN5JkWva0RhXbOtwICZBM1fnxe5YC2fvO4aB9m9dnf3+fxWJRNK9ua8+Nr3scsGsU9w4PWXctF5cX9Ons6RhHviGWRDLb0Jyk5bMQozjzrKOtFHRdi/eOiCdGRetSi1qIbJzHBWEDZPxZkQuGagC7Rnb4dqKxlRyMgkJhd2+39QkAb8qAg7zPgxjXrfY0lXWC8yMaPff3gbTj1zih2QLDbyVI45bK/BrYtWokOzGgNZ5INW/YfXTE4vUZYbEu3i3GgK4s0/mcvu249A7aFmNXTKuKSinYRNZmwb07O7C85sWvv+bz3/99fvGP/1N++b//z+iuo0bz5rtvePLZT9k9fMTy7TNm2qOjx2pDQOQBDg73qPWE1eqG71+8ZLY34+jBA2gdL1+9RJvIo4cPWK1XvH17ymy+w9Hdu1xtOr5+/ozvTxe8bQN2YthpGn7+kx/x4dEd3M0Vi9MzptOG+c4uF+eXvDm54P6j+9w9PuD09Tmvnp/z4YN7PHpyj+XinJOzM+4f72Primffn3F53XLv7g47+zu8/uEtVXR89vAuz04u6UIsemcyGEH86dDiHIu9Gj+TEuSOnm+WnBgfZ8HBUlEsMRJ9KhipIB0aAAFFNZszuX/I5GAfpxTRezSRNnie/fCyvGkueg15UVYMleTW9wEXPHt3DrhzeFcSDWsBjbE1j59+ws58n3/1V/+Wc73CmEAInei/GfEHMlzJ03tHbWZMpzP63vHi2TNqk+I1nboOQmSz3NBJLx+eFS+/XaE1WKPxrqOyFfNJjfU9brPEd8J4rOi56pZo7+gW17y5uSYm0HP/4ICmboihw7WRiZrRXb/CNFPmkzlHB3e4Xi7YbFosBquA2KF0jVaBSS0MkL736Ji0+TRE1dF1Le1myWYJ7XLNlz88Y39vh+Ajy+WGuqpRlUZZxWxnj96D9bDe9OxNZyiraaY79F1H8B1EB16mlOsAXdtRWdisVtR1w87OjrAPI8SoUxJV4zZpEGvutIs9PkZC7PF+gjYN3nk650aDBzVRBfoQ0Ua60QKePAAtEFJHWSgAmdYU2RwfnMgKKPl63s9WW5SWQqSPkboepqaXVtWUsxhjiErdaufMdjjF1dlmaSl4++AxSmM0tH3HcrWU1mYDxiq875k0NXXVJLasgKu3gTvZ8inJLZ00qVAZAlVdUzeRppIQcEhHE/GFSG6Llk468fkC2jiaSc1sd4/Lqyu8EzZ2XTeyPip3XPSE4IhaJyk5y+uXr7m+vmEyncjAv17joqGxltVqxf3jB8xnc1b+UsAOBntvkkZtlhwYfIT4ptQoQiHGKGmvjpGSN0jLuy6WR6kEa3thzgpjf+iUcy6U/SRmKvt3+Vrpfhr7u+CLXct5RpZa04mxN94LoRAukpYn2+Dodi7Clq0tsdEo/JTW/lA2mbXvSizIfpfJ7BJG5QFiYtuFzSaDdga/DFpbrBWAJAQSgB6KzuOY3OMB0SYWIMl7CfDk57IEnzDCY7kVlWRyBNCV9RYtwyyVF1PxLnFHh7ydIU4oa6cG2Yas+Q8RFyKmqamamn7dvhNXjOOm8bqNX7d/53YOcBvgvv1MyzNJca/3nrqZyNClSAGNMg4R5PDSxY66ntCYNHMhbc8oAhtyrWGIDeezmegedwrlUv7pPdHa1GKvUv5QFYa6T3mJ9yGdF9Exz11nSgljNANg3ov2JiNJhJyLE7PfT9qtysiejwrfy8/njsr8/mkKnDzfIhsIbbdJOYpIwQnDX3xYtBadJNCMVrTtBu980q8VaQCjdMkdVRT7K3m9SnmLAKd1VUmeazUx9viIsHXjMKunAIYJllDIcF96l9j5ikkzkbwj7VmdchSfigV96KVYM8obYoz43uGDK7mKUorKSNdlTHTyEIPMYkr3YatKYjOtqPQUooDLsn4yr0fY+ppJMynD6CTGl+ch8k2aysr1dakrQ+yPEtsUIlpFpk1DU9c0aRhZ3qcmdQLnfLMyyWe2LaAK89TaCmV00UEO3tE7ITcELwB3Zji37aYMYowMhBxjDFM7I0uCEKUjP2vzSuHIYGKk76QA4ZzIN1aVJzZ1ma2Q44DgQpEMkYKDJigptvZ9V4LWGCKmqqiqSljBkdJxHYJ0Rbg+ybma/x8zaYHUXj4w7MZsQ/kjTrWylioBEeO2VQF1Em6gNMd37/Pk0VMau8N0skPnLc/fvOLlm9/gfY+pauxE09hG3sOFRFWWN4ohQvQoQ6GyB+I7BykEn7QoMogiI9Cy1ookaCENBQCUSgLOkc1mjdKa2hg8qbU3eKyOLDdLFq6lrSeFmaSSxkgInuACurSjbLMudaoWZg0mbZJ2lRaHKhRIcd5KGUkgRho1xJgElZMeZKSsPylAkkqHVG1FTEEW34c8eGFbZH1ckc1rOAZv5fqTk42xPMeSwBUwWp63Dz5pFCfGrFwZLgVa48+NqeVDp4ogCcANCYzPb08CqnOCPwZ7sraRDFOLZGdjEvtirPmU7ysWY54DtHcnvY+dvLTVSyXV3/o5Urn4fUBG+TkYZ6TD+YogbWIKZebY5pA+zIlhQuw8uA7VrVGhQylHwBODgQD24AN2f/+fEA4/YBlquqgl0UpLFmMg9p7Yd0BEWQ21JLo+Ds9MprckxFjLgA5iLC32kEQhEg06etLfqXpeWais7LOuI7Q9apKCiwhEDbaS67v7BVU1xb34P4lnXwlMExzu+oxwcMDewX12Dn/M2asLdFiJJlNcUFWWSVNR21oqllG06KTqJ+taa9Gb6YMfDQ5TJUEqQN+IdZ8LBYOtkt1aGT2STd1O3rJcSGnB6TvGOqAysXfbfgLvyIyMr2H880OL3vBSSgJYAcIMdd2wWq358ssvUYE0FTSkXK2IVJQEQvag2IWtZHXE7n2fRunWvY8SJ1JhI+S9olKxJtshRnYllIa7d953DLhm3af89dVqVYYOju3SeE3edx9KKd6cnMhn5mR8NFgt/65Oe11rBSElFKNnAOD7nsePHrFYLrm+vubk9FTOQ5qo7aMvwPf14lpsrDaDJE+SjpBpqpQ9mD/j9prfTmLK30qRJ6LntFcpNeiXj8C1zAbbAoATIBXj8Lt53d5bWLqVsOT1yIFV6RQZ+dwx6BxvrWMGRsLoGcUgjPigI9XBnF0U1y9PiL1oMtdIkrFer2m7ng6DjxLo7VU193f2OT68x7r3ovvprvj13/wlNzdv+Onv/Rz6jn/7V/8L0XXMoubNy+fc//gpfmeX1cWC6bQSQosPaO9Znl2yURCVppnMODg45PL8jNNXJ9zZ2+XpB4+5vjrn9Zs37OwfcPfoHtfXl/z1dz/w1ds1fYygNLvW8sc/+ZijnYrXL77BrTfszHeZTWecnJ7Rucgf/sHnRAK/+eY53drxRz/7hJ2dhjdvzlheLXn84B7NbMp3z94SneJnP/mYm82S33x/St1onj46oFsp3hqJK1z8f5l7sydLjiy97+fusdw1l9oX7EA3erpnIdXkUKJJNJEvMukv1T8g44MeJBr1Qq3GZRaigcZSQFUBlXveLSLc/ejhuHtEJjDSa1+bmkZl3bw3wsP9LN/5zneyhIEycDQY1/bXGFPCE7SwFdTYqTVQI5933/g/2faRFKNjZuQkv5E6pyCmGZSWowcPmB0dw7pNhQv0eyRoW1z6aGdNamHTumFunWRyZkIY8HHg9MEDZvMlh87rIFKnmnrOOFarh6yXD6mrM2WfWEGkw8qMtp0RQkXEsd93VE1kuVjx+Ml7LOcLfH/g+vKK1fKIppkhETabjZ5ro0zRmKZhD3Eges9hv2O/r3AGTNKi60MgHHq8HyD6NLxEQDzdxrK7uiL4yMNn77E+esnm+hU3mw2VD/z0uqO7vdaWzhjAebb7W4Ic2M9mzFrDvLFUpiLEFlsJpvE4Z6nqiqPmOMmL7Whcw8n6MW3bsjtsidJzfHycYieol3P+6vd/xc3VDTc3t3zw0YfUs4re96xWK65uevquxwRh1lasVnPeXF0gdcViecxyMWOxaNkfbohDKjLZ1PZrLLO21RZMifhhzzCkkCJCDGr9vehekihEq3t210c2vedo5nF01NT4OBCip66bYtd9jCqjZsZZAApkJYZatk+JVUrUZK+u2zGxDhl4ykO4DBiHTa2S00FOGkuPRyHHat4HXGNwtaOZN8zWczDC9pBiLAyLxTpb6BJbkIepoHIeWYddAUsFvNJX6B9rcU2LtZpAZvLL4HXQjnVWh+4kRroPnoAkhp6hXsxo1gtS5EkfIpWraasaEmgbRSVw4qC6n04qNmc7zn94w0e/+RWbELm+vmG9OmY1mxGGwProiMdPn3H++obKjl0hIAQJBcg0JuVd99r/S4GyqkjpjD4Tck6TmVIpHE3ybiQ/m1fIoHsix28mMU1zLiIJpMrDmvT6ciFc31qLK3FK3hcxOdR8XyblYTm+L3MqohT9zmlMktu37/jedFnq7rTTDGsLr2XqR7O8jO4bve6xAynZSYRh8AyD3PH7+fucqxLIGss135eIQlSXMnr9/LqqgIAfYgLtEuAeQ9GFzEzcnM8UFjSGplFGoolWW/0ln5kxX8ztzt77Isuk8dC4VhHNb11Vccg+YxJPTO/z/t//oSLzLxWhpzHN/d+9Xzg3aG6gLfsr1cUePNvtlqZpVGvVVYgRhhi0+9ZYmlZ1ME0uXqR9V+YFCDrs0KCFTqO6tzFoESG3m9fVCBIW8Cv5e0l5m7Pqbw0gMcm4kAcGKokpGBCvjNlodKCjAu5JXzUkKQOrbeOS7F0ekpUHlw1+KGzyHAc2TaMdu6TCE9B3wx09ez94PUtAdGr3VAJEyQTje115rqqpq3al7w6F8OCMxeDSqmaWq35eP2ghUQHlvI+zdIXiLzGx9fuu19h6spcySNn32h2SMYvs6KTNwgAAIABJREFUi3KOkoklwzCU35nuId3/WuCIUeiCDquyVUWd1tdZi4motEXXpWc53n/lHPP5nL7v6bpOZYmDZngZwLVYKlcpC51JXpUwqaauFdy1GauQYiOMsUit3aRNk+8r4/hqZ51FJRqCwbncEWLv5MDO6jV6H5JvTQC5gbqu1N7WNX7w2BBKHuqco8pSm/MUG4iUuR7GJKB3NitndvCewXsFc5H0jPW6q7YtzH4fvJ5dUcBZROVk8vmThOnFmLGnX379SYO0+ZUNnIplW6WIp6AmRm2pskbbauu6nkwaz7qIinoTYEbNew+e8/D0MavlA8Q1XO8P/P2337LZbKlq1WadzRYYU6mmK5L+L5bgBmOVKZIqD7niPU0qvfdKCxfh9va2tANiJtPhJUEKSXMx32dVJd1RkfHf0U0Ugv7xvac2qvUSgmDT75BkHzJbNK9h1u+FSQuCtRgjSPquUpVDPyM1b+vv5QrtPfBo6oQyaKhaUy5pfiXDbjXIMfeceq7OTZ91/u+74M3EmWYAKrd/RUrworiMRrhi1NnY1D5jGcFRNQSJjZfjS7Jxyd+o/z9LaUyPUmZJYiKq05XBivzz1PRwD5wd713IAPcUWJ0CQkWAPAW0urb3hunEWL4nyl0HX94Dd34vgxb5cntfUR89oZk/5/LS4oegA7n8ASSgdW+fKqEV1YNPOPrNP8OffkgnNUEMCqRbsBbiAEOPeK8yGbUr7aRqj0wJ8CVfhBlBd0n3BZSWV0N2PqmwEYIGwTmI1BsDEWQfsE2Nq2fqVGwaBmdmyNFn1J8eEdpT/Nl/Rvwt/faC7fYx7nRFc/w+vP33BNkhAwR/wM82xGqZihej4LqQM6nIrJ6xnM14d3mRijbuzp7VV2opSzebA2ES6Kh2LaaAY0zQMriWQa0yfVNGhiyT9+a9k/fS/SB5ytIue0RktDtJNyz//jAoWNm2c7S7JRBIesdOB+rEmPQguVMLmOz3u+D0nVY/RkDt/nVlGxkUgyqdE8qCGAHCPIhlyhoh2c/M2hVEW0gN5WfT17QwdFf8f+zcmBZTpme22D9RrUNS8lalczYFccv3kZlIk5bUlFkrKOS4uLhImll2UmNSto6rHA5lVui/j2yXXCjKSVe2ZqW4NLEF46eaZLru2xApiY8udwa0cjArjMM0LTq3x5YkUNLvl2LhPTufQVZy8D9JYqZA6/1iXpVatKaJ5n2w1xjDkFq/pwmftq7qsBhb1TTHS+b+Af3lLXHXKeugsMzAS2RLJPbaPvW0bjh59oT6esv15RXPnr3g8vKSd6/+wDeV46Pf/BW9gb/9P/8Nzve00tNtzjh9cMJF2OP7Pa2zuFpw0RCGnna9YH50zHw3Y39zy+bqhufPn/PsySPO3n7Pu59+5OnTJyxPH3Bxfct/+OMbvrna453BBnh6MufzD5/Qxo7vv3qFCZ6nj58wb1vOzi+onOWzzz6h73u++OJbrHX8/ve/JUrP69dvaFzNZ5+9x+X1hr/7m29pZzP++h//iqvba85fXfP+s8esTxt+fH3O7VXH5x895/vrG364uMGazBqjnJl8pmAcQJFbjQ3399i4l/Ka510raU9kiERBD5WgalYzZqfHtOsTXLOAKv1bGD/BpjM1TYY0DpOSTBQWRpW09KqKZy9fIMbh/YBBqIzg+46vv3vND9+94/L8glnTsmiPMVKDJP1OW1NVC5aLY5p2iW0WGNfy+OmH+AdPef3Dtxy5Fe9/8DHdoce5iuPuwHwx04EiYWBze8PhcGB9vMLEyG63JUrkx++/Z3u1gRg5Oj1hiNpCaZ3qqAk6dVjEcHV+y267wVUrjk6PuNxs2XU7/M0VxsJbMcxnM5p5y2K5YHNzjakNt5sebODkaEbswdiW2XKBdVDXcLSe0VgHoi2iy9UKiZb9/hqMUNcB53r6LjCfrzjsdtQ2UjeCayrmJ4+I4rn86XvmbUPwkf2uJ/ae4AU/ePphoGkrlqsV3XaLSIertHjbHwZs71jM5wUkLYUd0RgpeC3Me9/rMU5dCkpKMEQMg8D5zS0rEahmONtQG0us8gBXRq3D7HeTWF1hD6UOueIrrMVWypDPBfgxcJywHpONZlLUysxdtY3aJRdDTGCfTQwsNb/L9YzZqtUBQEUDusLZBommgAyYmGLiiJHMDjUFKI6eBLbkaFdtnY9KYBh8RzzsadpWT2XSJYaYWL36M2fQIV5Rc5L58RFUjugj3usgTuZ3OyI9URmXYqmBqvNcvPqBT3/9KZUzLBZzjLP0ElislmBqXjx+yhfffQE1pOnETFzSxC9nWz/OkCg+gZyJjOdeCz9Rs2pj7zBMrTUpP0g+KElUCSNDN8ujFXA3fUvOv/PzyHnH/dghv+dnMYJQGLnqf9Pn5rxI7rI27/tuSTGRsRqbSyxB07g/k8XV74nF3k5zWufyNTuSOS3rnPMSzbNyK7KSa3KBYnpVjXV89Pw9zi5uuLw5p48BY6qSI+b7ynnSdG0mdwZiikRWzrN0TyeJEasSd6PsQNokzoDX52wTWy8z8WrrqJoGcXdz6CkTuKzrvdcvxXj3Qdf8Wfc/Y1rs/9nnxrHTrev7JE+XYnxjwFWFLGQTcUNioG5qjQ3LZwoOm2RUlL3p+6EMiULG85lnQAx+UJtWpIwmZLS073OBNoPBea2iqP3KczPqOkkEEhn2XVorBfAigeBHAlOWd7BGiyhDCIS+0468DDKntfUx0NQNUYQ49IWJqjlaSHlA7nywVAnM1cFkKh2mwyMldW1nO6ts65jIDwbD4EMiQbh07wMkApXKR8TUcaGFXYmeqq7JnUBCLgxYHZSVfqeqXMmHjTFlvsaQ9G3znsnEEcpnKYDvnHa1jSx0WxiaJsfpMRL6ocQ7OX4GWMyXHA6Hst8yvrE/jF2dMRm77BuzlI92Gox5X47JjbU6hwGDxJFNG+KgIGY+B2aMzbImrFjVfjfGICGOMhuJPCgpdodYbE9lM7aR5fFIxD5lQlfWTnIik4o9Ju0FvY6qrilSRDEoOTLlxS4VLJu8zsn2Sio62pRnd31PnWRD8lpnG6TAMgmn1NkldfUPQ7F/8iCtpCmFwfskKOx49ugpYRj46fynhPUoOBCjgpXehyKMrRWLqFUdYF21/Or9j1muT5ivTrnpI2/Pz/m7L/5AFGUciQFHW3RRBKXSW+fSkACtiDibD/nYanIHBLNOJ4SXqnsC+dJGj0HIjFTr1OtJiFQ2t8yPzTy5JW7fDTxcP+LR4pTr20vm66UCKInlpvfKaCzdaMzUwViyXkuUADEPl1EDJcnpZQHsfC/G2lHD0RiMjNqqOSjJB7Q4mhBwUMA3yUFMHEGpbEingctUz8kAVaU0fFGfnALbVKGr3BgsGKPMYP3K0u6scYUOb4hhZJHlIMoak1obxgBOMQUFEtPSqBG/F2BlkGIS5+g6ZlzZ/ByALk48VaYlg0XZWCBF6H5kKVP2nWSHk/4lV+dtpWzSqIKwZU+apD+U/bRIDtgT80ME51YcnXzKngf4zqZBXx78gISOKD0m6rAHd/KU9W//OfHhR/TitGXQpLqiBRGDeGXh2qrWYROQ2qWEAmIjiTWbhiVk4JKUPKQKX8bdUp6ijyRom4DR0lpxHHnNTfTIIERbIc4Qu5hALEvlDHH+ksWn/5KwesT+u39HN1xxtdly9PR9FidPsPWc6HOLtiH4nuC1LaZ8TX62MQU8orqHRgwxJ4wZFErDFkxxCHmXjlM0LWnqcGIESgJ6p2dBJs5a0HNpc7N5CihNCoqnwOK4B3VPxahtLjkQHsHJtM/QdY4Is1mLxAw8GgUs7Hhv2g6jFxDRIskojZ8LEGCt7nHJxQandjVKZmuMYOaYLiY2qC27Pe3pBLAl/bwctGDHpGJMyNJzlDEpwyTwyNwtitwvPOVXTjTyM52e5+l7sj2U3IKV116mrZB3h1zlcyGTYNoYHe5g0Mm5CMnHaZDcNI3afQHrVCusqtTWF9J/Bv8lpnsfrzXb7hEKG0FszcNtOVPa/TC1YTE9p2Qbc9FhXImyP5OBK2ebybrmz7JFTybZAyiMoTtrnOyccZb5bJ4m+Q4T35Gf291EKQPLmQk8LSamxtVSyGsfrDEIe+8JnVc7bDSZIQrewN4K7/od8fUremN4tljj97f89PY7lcju9nz/9d8TjOUv//pfYAn8zf/+b7CbK/bdBcvjEx4/ecLN1TuGfk9TNUQJRK+Fre6ww1rH4yfPePnyJfvthjdvXrO7veXley9ZLmZ8+/ZH/vb1Bd/cdHhrmBvDR0+P+Pzj5+APnL3+HiuW918+gyDstxuePHnI0fqY3e7AF1/8kfl8wW9/9xm3m1u+/+E17WzGoyePefv2jG9fveXRw1M++PAJV+fvePPjBb/+5H3Wqzl/8+UrDh387i9/ha0c3/10TlKCxAdDTKAQEQYZJUSGBHRlvbSqqsZ9kfaLmkV93tOhdyYxdhUsg2gsbj5jfnrM8tExdjGnj9CLDoHSJEn9TGHQTvaUSjilTzcq8ZRZZKCDTVbHaz7+5JM0pCfg/YAYYbGYsdtusTgwHcY5mnatfjWmRK4fsFUEU1E3C+3k8ELTrnnw+Bm2WTBrF8xnSw6HDmNg6DtuN7csV8cYEZrZHkE4OjrG+57usGe3veaH7y+4uDpjfbTmxcd/wdHREVVtEL/j/OyNGoAAvh/oNtdsbs7Zb68Y/J7zd+fMZ3Oq+ZK2abTV08PucOD2ck8/CMNmwGNZHB1xux24ubyhdj3x7YblfAmx42plOFq3SDBcXGyYLWus02fro2foA841VK5lvTphuVzRNDXL5YLmdE2sWoK3XFxvGLo9DqHvItubPYf9gEhgtlhwdLImhp5+2PHmxx957/3ntG1L13X0fc92u8WigyydSxJn1CxmR/hB2IUeQ08IGodH1F3n7jVxhq0/cHXriVULXlivTxlCQx1qajsDEbwELHmQo6ZNPgQIEevysF7GIloGO5L/U1mL1Iaa8wULEsdWytwhEBML11pXpk3refAQI4cusr/a0n1/w4dLh/dwe71hd72lsg3G1qmdefyjDjsWkC8LhKSDgQRTtDljAl/6vmeooO8OYITB99oWbTXJtClPMfnjE0ggorHgbL7EuArxPWKEfb9le9ixrhqsJbVRU86pFYN4+P7rV/zu9hZnoKmd7qch0M6WhCi8/+Q5S7HcRo84UwAI9fEpIU++AlFmWJZ4M+nBTz1WTqCz73bp/rLdalylwDTQ+6HE0m6icV+KjGnFq8oloAjy/JGUVJQYN7c3F0JJ9k0yxvn5IvMAM5tYz6Z8JkxMaMkl9D6yRnveh0DI5AEDovYud6CUGCSBWdmPFmKEdUXmLxfytRV8BADFCHGin2sgDXakgE+iFGo+++ATfvNpy7/+X/9nuhiwZpznIHmdJHWaJaCMyb3lSCMP5s3XGSbt6UziOiVcpVwTNHdMV65xdxLFMwaxFtvUeJvBd/OzmCK/fqkofD9+vCvj9fPPgJ+TaPJ7bXp/k1rH97uttsenZzf9PWsMbTtLn4EOf5rkGmW/ibIgDYbgByQNmXaVyxF2kltMwGCIZQCZiLLIS/t3JswF7WLNQBzGlH2i3bsGj+6PGCPWpQ41CSlGlARypUHL1iRC3rhermqZzec5rCyxs7U2aaWrHrZ1ut7OOSV2FFA8r+m4Zhnkz/hJ7j7OkkgZ7MwDfGMMuqclW5G62HYSjoAxhJC78Opi443VPda0OrCrTkOdnVU2qfeeiNAmbda+79OZpnRn5nNgnC0t/xK1O8H7gRBdimXUxlRVW4axRqOdYYf+UHIM55yyWC3UbaMg46EjStBhY0PPbDajrhvNAUXIhJsQKcXLnBPkTCPGSBgG7fgZ+kLOqKpKO8ldhXGiJDOn5MIQ4oRIoZbjkDRtERJJx2p+nWxWxnQQKd0BLg17tM4wHLTz1bmq6PBmP2Gt03kyWQ4ICH1fgFfIna6qmRsSLqYdY07BZxGMqwgRmrrRs+pqoqgfL7ibKCiuxeKogxijUN+zFfdff/IgbRSPEa1qSlTx4cY4xAizuqILQwn81Ukk9FuU8q8sO03oGxwnyxUvXzzHVjUiCkb+8PoVP775luxjZ80MkwHaFMBbYxMHTinuOtBLEipvte3WaKIRi9FwDKn1X4y2wEwrqQBGTJnilysASoa9l/wnQO360PP2/JJPP/iI5vYIljWvXr8tG0nSTs4gbQYijTE6jdZqEJCny4fsFOJYCYvJQyq4rNfgXFUMdJhqYFba+p6Nn/483glQM/NgWv0aAZeR4ZsBSZN+5pzDT3UNTUnZiiHIhtGkvyj9XsFVrdwYrNNBDmCIFg1EJy2/peoyqRaJlu8wcQR1MhtsZCFC4d+mCk5IbMiMKsr02u8Bd3mqQq7OFy3PODrpEEY2YwFoc3KZr2eiyZOdd0zAiH5MkgkowK0ZAzuxBGvArmiWL/npstLW69jD0CnYSYQYMcHgTt9j/Wf/nPjwA/Zi8XKX0WiMEPsOYsQ1cw3cM1CUAmVdg7Q/xcBkP6UYUe8tqnC7+JRMWNXOiZNnEiUZ+Hxexg/QH3ltObBGZRaiAW9Mmn6wYPHsL1n0HZvv/h3d7S37Xc96/oDZ7JT9zRuowFY1IVq6biDIWJDR6qopGqvbbs+2O+iZslaLEjnaTPtFA8z07PMpMI7HDx7Sdx1XNzeEdP4zeFoqeEaDIWyazppb0wSqzJxXuEGnsFbj5NISbAMioTiqHKxMEwwdnhJKsB0Gn5Id1UY0JuYLV+AV/fzaOdUjtZr0jRPeZfzuybkTGZ9jnpA9rm0Go8cEJh/4MRDW9qx8xoqNYUy8TDnrI1ib2bR6HM2d95mJbcifAdxha04D6TsJnoyV5pATN/K2VKt1X9dW19ikczC2Q46J+QgqVdayWj3g9vZWg4XU3iloUuGTjbMpotHgPh+E1AMyuc/JgSnrjAET07Mp7I0ctjP+LJ+3tBXGQHrs0tDvHtnTxfab8f4wIxtIT4ot6fNdNpGUNRQRhuB1qOgEQFZJpMSYl7vXacpZnCZHeQglxfeJgfZ4TfSR3dklplddLwVZdM9EYLBw5fe8ev0Nw+KI42YGmw6HJTSOsG84f/U1TV3xyW/+Ebvtnr/7v/8N65mlMbdsKsdiPWcfdUL5AFTWMBw6ujBw+vIl64ePefPmNbeXlzhrePHeCwzCl9/+wBc/3vCqi3RAJcKnj4/4iw+eEYcD5xdnLOuKR48eYQxsdhuePH1C3cx4++Ydr1//yPHJER9/9AEX7864ur7m6eMnYB3f//AT33//I89fPOG9l495+/oN282W3/76Y3w0/O3ffM0hBv78dx8TQ+T/+o9/wDr4Z3/1a/7wzQ/8eL3VhDb7f1BfKijjz5gyEV1DfZsgmhwP5MeU/p7OqBghWrWVEmF1ekpzckS1XGFqp63sQTVg8/CnHMQXCCP9Twbtxx8mqH6ik937nmePH/H08WP80KsOLiQdTHj08BhMxX6nXUdiFYQOIkQswQ/YShiicHl9Q9XULOZr+jAwzIT16hGC4dB5XNUgEnEVrNaOpm2pMSwWK6LRVtF+gLoxNEPHYrmkWcy4uN3w6s07fnvymLqdIc5RNxtt+65EAWLnCLHD+x1NPcfRsF6e4qpG/YJTJqyYlmg8i/WSqnFUi5rPf/vnxCBcX79je9XxxX/6e7Y3O3w/EHzL0yePqeqK4DYcugNDHNBmMaFuNYEbonB72ODcgb6ztLPnVAbOfzrn5METhlBxdXXLzAnb6z03N1tOTlbUtWO5XmCrmijC+mSBrR9QNw1BhKpV3+DjQGV1KMvQDxz6Dd5c8fTRCVVdU1WCH4S20sQ1AmKVAWoTMIDTouoQPZe359zuthwvjlnPj1gfnTJfLHVIj6CJpXEMQ8CHSF2lYUeu0kKmaBIbUuJpncUnBpEVQ2WrNPdBZQSMvWuTRj/mEstRbaICLhCNdiRZE5AucPbDO+pmgXhD5RqcqTL5H4QUC9sSK1osIXsDM4Ickjr5rJDUp5L/MVA11QieoWfLOk1uw6B22FUWE5WNFBAq43ColIMXTW472bPxWxwt87rGGEdV12OclP5cXlzTdR0PH6w5P9vRGIOzNSEaFss1z548ZdXM2YRbqJPTCpnwoOc95xBAIZgUCZ6cM5ixcAoKgk19/zg7I+VDOR6IgjjuvO+OT09AO+W3U16WAMcYRf2egJWgoaBJrebZRwZtGa9qixa/c9GXRBZJMX5CHCWOYKIkj11khNDn7Kwt8YwOrR3B6AKGyhjXFIk5Y4qMQibqZFArx3bZR5vyObH8bILpjDkSlv/8xZfMmpaAIdpEVMjg+iRVkTTfIhNeBBIHJcUyo2HX/AcSWUBloHIOZI1AkjAypHzI5LzbpAJxLtwZcLasyzQuzGsy/e/pv98v3v9DRf1x3c2dv9//3ZEoMuAPXdJNVWmuPCg9g9/GJgmsFM/7VKzMf48TYD+33Gu+qAzb4D2ZbazEjIMO0rSOwYexmBQirnLMZjOq5BNxDpFaQXKb1t9Y2saWc2YnBZDpyybw0mbyW1QbXdUq/+jcdAAb+FRgyKDplFyVwWstPqQCkM3t5SlOJxYgz6WuxZhjwExIIHetxqIp67JNjoqDZC3d/L26Dmk/mCp9Vzr7eY/CSLZJxZCYwE+XJPNijAy9FDBbu8JjihOq1G2TOzJGG5RtVj8MDH2nvskoTuNczl30bBdGskHzCKOyIToHaZQV64ceV1fp95O9zXsyFY8ionryqftAC2W2xIJ5b2eNXle5ZINMwgWkxO4lr9e3pqKqXrf6r9R9YdNgNav4xqE7EMPY7eKqFM/pgS4s4RgFV1XUSXon7zkvfvRzInivsblzCbBNfjGI6hQnL6N7LckebXfbIqUCjPIsmTyUChbGJgkEVJrT/39MDvuTBmmNMbR1nQTwc6Xcc3F9qTcWA9ZpUJIXw/dD0vUyuKSPBBYbBCeW0+URp8sjpfFL5Oaw5Yuvv+Bmd0U7d1TtHFc1RGNT0K9tbxYV64+poqfaozmR0J3lE8rurCuBu6BtHsYZAlFb6UiOGgXeAqOzjZk5aKuy8RXjUeZZHw3/z7df8Wyx4tFyzR9/+glJ0/tiZtyZMdmI8e60eSY+YtoCBEyMoPwMuDApAJi2qeaPylWH/PvOqcxBkQzIwY1kdqBNdP/x36fVxwxe+GQEs5Zuse0TIEMKIAZglMmJKNBodIiOsnVyEGp+/p331iAbcknPYhwsRgFU8/vGaGJc4/tO9pfacCUFiWMgTdIKy5+oznmqP6MWSybPU9dJ7y/qPcsIzkhGXQTIQ7wScGvSzzXOMlTzR+zliK5X/RbpN1jfI3hNZGKFO32uGrQnL9lKjZf8LUJ0BusD8bDXe2paIE31xWBTIpowGkjAb74IEWUPF1adccqSlYAQEB8RArHbYzP4a7SaOPLhKNV6/QzBxAGz7ajXC4LLz7VCsAyxYseSxcvfs9xv2J1/y+3tnuNZw8n6JYfrb8DfIibivcFVakuy5lEOciQ5BhXHV8ZBFAVHa5eKOqUIcbeqnv9+fX2l+85IjkARkSLePgwDkocvpP2l3xnKudPNY6Bqef+9F1xcnJc2I8wY2EJimRsF9HKQm/WWJO0esZqYOAMnpyecX5yPp97kvaYt6q2teHB0SlOpzuqbs7PS4qbBV97T6RqUWp2SjZ+3iOXrmdqFfFbL+ZSg2lX3zt+dqcrToDift0lVPb8/txBNv3NskcsgoCv/fZ9VewcMnLym319AXJjYj2yLxgQqxLuyKFMbkm3e9Dpzx0f5vPKUJ9dBSrzlrn5u/v7y9/zL8stJRQaMRYL6qvzh+XsKQ1hKIjxN/Mb7/flnl/177z0l+J0kO92hK88nR+ej9nNKEO+tYwb+7z+jKftFRJDK0jxYMwwDh/MrbEpgILOcwNQVXeg5G3awh6p2nDYVjQAm4P0W2++5/PoVoYv85V//N/Tdljdf/AekC9z8dEaMx6yOTjgcDsxWK0SE29trhv7A5uoKbxsijsdPXzBzkfOzN3z7w2v+8PqGdwehM5aTRcNnz1b8+vkp/eaa6/ML5osF66M1u92Ouml4+eH7eB/4+ttXXF7c8uzpE148e8rZuzOubm94+fIlguGrb77l5nbHZ5+9z9HRgq//+EdqV/HbP/ucq9tb/ubL75gvj/iLT15wdnnBf/rqLcfHKz746AX9IPhDl/yyMuSsS/4hZpsSSxtwZlwEJojJ6GbT2TSj3nsA0zbEumZ1dMTqwSk0NQNGAdrs52OyXYnlPfqbcQ9qjGLLOXPJJ0bQxCt6qtjxm4/e52ix0Db8oPY7BugOB2azCkyDqxx1bTBW5VFELNbMaZolp6cP6H3k7Ow1Dx48Quo5VT3jsNtijcGHWKQ9SP4LA1dnl8jgWa7W9GIJQYhDoK6UpPDZpx9xtGz48ssv+eqLf89iHnn/gw90yIrVJLmyjrZtaRdrusOO25tBwWCgbmYMvcFHQzcMRC88ePyQkwdHtPM5r9++JRjHxdWe9aqlaSuqI8fRyYo3t+90AEkz43rnGUKP2AZvLdGo1mDTzsAH4tDTNpqk160O5vBRWK+OWSxXWCpWixPiAcJhg/eRk9NTFoua5XLFyfERXbdXNooY5ssVPrWxagyUh3YlQEkkDRbRIuMgQow9VWWQoINdC+AiQmVSrGgcwdb0psIboamEPnZc355xeX3G8ckpi9mcqm5Zrk5wtk0DkQb64YCxc6ydJbkPtd/DEIh9TBIuUTXzjUla/KSkVO7Yp+wHFNFSfVQNb5XIoUwqg60Ns/URZm6ZNSuMqzDzikZqum2HiQrC5XZYjJITjLUQNN60oudUySdSNCDxql3oK0c9mzOrtXiEUD4rA1cqCR1g6AkY7eixCWAUletxbYPfb+nDwMH3HMKBig3GLqlMhaHCpNg0pMT35uKaH9++5eR0QfQD+91iaPlLAAAgAElEQVSBo0dP6KlwpuHZsxc8e/w+P775W+34KlrkGWQbfUvu8CsA7Wj0C4hbJ/m8qf+f+nft1CHZoRFomMYZd94v06J3AkBQxljwMflPIYPkeb5GCa1SruTSVokoaJ+fQb6/aa5W5PPIQz5J7bp6P1NJrOxKjblbfI4xEMJd2b58UdPYZeqfpz4UmQAx6ZW7lSTFHplpLdbwzU+vkRDxTotfVkqwcCc+0M6vMUbMXT5xEsvp84U8sA1RMNiUZyfk3EdZwYLIRCIl581G2cJGIvP5Artc0u2vy/3enyuQ1+L+636+d/9905hreq/T/HNcX/337tBzOByYL+YYk4dzjfdQZMCSr8pzfHwII9knSbBJ2mdj3KcSM9YosaKqaqzR4VvK/1EgM+ejoPmHs5a6UfZg5aoEit+NLUPwhalYcv+s+zxZgyKREJJPTMQngzIscwt+ud6gHRQqZ1KVQWUZ/0BUgisiabYIEy1iXS+XGKCgOtVZh7TgAjEmogn4IdwBQxVzScQOieSZB+mgKsElAbwiTOJujSVzvpWlEvI8G2NMiiWyzIqhqRuEoOxcHBgd9JXzPgWRVes1hEhTVcVuqx4zEDX+Wi0WtFXNoTsk1q9iDzYD+sbR1rXOGggh6e+iQ8EmhDEDDPmcixCtgSx3kvaXKkdV5TmHpKVvMWUvTYtaEsZCByIF/NS8Pa9xBBn3QZPkCeZGu+u0+DxKINWuLp2luraqq17IlFbtkeqS6z2rMzRKHjIUxmzKZgEtxMYwwODT7AUFgYfEnhWRAiQ76xJYnboHDey7g55PHwpj/Zdef9IgrU591AA/L3gIgYMcqFydUHpt9q1Ti7xOyoulemqTl6uNY2ZqPnj5PqenDxFbs/Oeq+2G715/g6ejsTPEOEJiEakBiEQfqN2YrGfnpcCh0cEfziQDOHEcOeNNCa+qJiSQLBv6hMmEQtt3JYiMkifEpwqmaCi/j4GvLn6kvniH2FqDFDNJsklOIju8dKCcMUUIvYC3JMOSKs1TfR+SobIZXImTZF4XYjKsZdp2oo4wg8+mCCvnVpu7jLf8yoYaSNecQhIzgg9p8cr7AXwcgyWM0eAkhLElJjv79KdEXJIAqhQs5YNcrif/h9xtoZK0D3MAkL/7fiX1ZxXRSfARo+qjjImplCr6CBKZ0ZCQBoYlsCtmJ29Hg5GXZmTMpsR1+qc8V5ucmKUxa5rZUy6uAyFaRHqIQ7oHj/UdZvEei1//c4bT9zjQ4AVly1pSJc1om0AIuMWciCWmtqMcWFpXJeF0T/QJpBUVARcfMZIH3ilTg5CA/FmbjGpEZi1xCMTQY4YOVzlkdgSSz9vdp2eNgaHD7yLt6Ql9Sk4VtBR6EWy1pn3+j+H6ln5zS9dWzNfPqZpjhm5D9IHeCE07JwMHQsS5BpU8GM9OZpVmx3cfvLtfECGd812ngKatKlTs3dwBJI0x2moCSKrmTgM9tTQRQiCYhtdv3yhjR3S/5u+tqooXL97j/OyMzfYG0M/KrNWis1wMCfjgubq+JuuUuaTtl5MBRNuhzi4vtD0xDMo+zAnp9L7vJS7pUdw5H9P2uzF4NiVo0n+LZX3yGcnXNtVP+qVgefq6Xxya/mw66AVIbUENh8PhZ/+WbSpp5aaAq7N3B2dMr6OwhfOJ/YX9YowpulFXV1c/C2qn7yOtEZP7yafB5XvNp0OEn69IstPYEljntSw2O051FZP9megsJkWdHKv+LDm5AxKX+8zA3N0rmq6Xy35oNHTIhNl+3+bm35+C7veBkTvgbPpcLa5Y1o9OCLsDw80OnDB4T+0cPuj0Z4t2B9z6wNlupxNxncOFSLc/0DUb5u2S63dvaNcz/ut/+d/zb/cd59/+PbMmcvPunMrWNItZSWRVLw38bsfsoeP06XPefv8db85+4pvXP/Dd+Q1nvTBgOZo5/umvX/BsbjlcXnNxveHl86fMmpbL6xtCCDx//pi+G/ju1Q8cuoFPP/2IxWzO5cU5tzfXPH/xkhCFL/7wFYP3fP7rj5g1ju+/fcVyvuSD9z/g4vyCL79+xYcvn/Ds+SO+efUD37255MMPnvPwZM33P13zx+/fsDpZcLo+5ouvflCdal1k7UAyysiOUTgcujTMQYOzHGyrX4s4m+Rrkgp7iIKrG5r1MW69YL5eESqHRyVbBMbEoGwm3fXjwFgzAUTz3khJmJiUSAUMERM6Pn7xmL/6s89p6xkHVDeuspZhGPA+UNeOEJPeZaVDE7UV2RGlQaSi7wZmiyXH6wXd/oZ3+47l6oTdfsNuc4NEBQJmbYMxerZjCHz7xz+wubrhn/6X/xVHDx4zmy253t5wIGJtIIY9j54csVz+GVdXN8xXDc55un3Pu7Nzjo+WrI5WHHYdu/1BgQfXoLJdlq7v2W4DVd1oQuEHXA1Hpyvevj3jq69eM1udcnE5EMOW1dxyvGp58uwBs/mC3SYBn9ZxcvKY230HIdB1O4bQq5565XBiWa7WiHg6CQQToT3BtAtMVYEIy/maXb+lbue4B47DYc/l9S2Dh/lsDaZiuz1gGVgsWwzgh54Yk99yljh4ZQwJtM2M4+UKQiR6j4kBi9AloAJIXWnZNxkFaanoxGKtslx6E2lnLVYim/6G/W5Dn4ZmGetYzJesT9ZYV9H4A4v5mradY40OUqnbFmucDkgJnmhiSqAng1XjKG3gJknl1F5Nbbs12rqrzSoN1lSJrWrZ7feIl9EGZ1AxAXu5xdnk+CXGXBZQwEQ0pvEEbui5wjOIxYmya8WO8mbWutIa3lQzlu4IH31ie+qwS+8DroKqqelRdq5KeKl0Re8qgnhMqKhdDVUaAENDt+n5+j9/yclpw/7mkuiFfljhrWAry/Hxivff/4D/9Orv8D4mXURXGPlGcrHfaF4zyduscyWPyaYgzwDJsVadWojLILfyxEh2OqROFv0X733xf/n38+fnWKWqqtJdozmZAdHijtq67JdHNpx2HaU2RZmC45HgfQKabbmuwhozpjBSRbTQX9d1iSFiAp5y7DEOrItJy1tSl5bQNq3miEmXMUuNTP3tHYDtHvkmSwIW0CL5ATEQnNHzZBLwmthqud055M+SMW4szB9G0BSmYC13/p51o8d4OcdLuldyuBFRhpuzhiDapTZvG3zlSv6i3zl+9y8B1dNY4h8Cc+/Hm/ke7gPAU1ug65FJLlkmIyRWXmaOJiZ7ep4xqr4mqbiDsakoCnUifIhTNqzuN41xFBATqqqmqlzR7DSZuRhjwQaAMhS3P3RYjBbxCuiUbE1UPx2S/JFNmMCU+JDjzJj2gXZI5/zHlkF56VPJRYEQRIty/aDPZsLKraqKEFXmQkMMQ1bbE0RBQ6+avDZjH6DnK8WDIuOzyLeV85B8veOMklEGQrsUNR8f4w4l+QyDrsPU7uf4d2r7NURSiYicz+uArswANel3IpjUTYQt5KtCZCg61FKIXpmRrefFFZA/ppKbQc+irevy39O9DpSBZdO4SusyGlPZui6xrYhgnEoC5pkqqpOtyYL3nmjvxucx6pkUoWAdViw2DYaMURKrmgkIO5R1zeuZbarmUiqHqrOs7mFZGY2J2v0QyazedF4MWBGNwxLLWZ+aMpxDCMznc0T0frzvi+9lQpYdiPghlD2ZGwp/6fUnDdKKREwUqmyMjcGqxabzfWLe6QHOTChlOyR3HTTwb+uKFktLxQfvf8Ridcwhtux2A+8urzi7uiDg8RKpk06isUptj8mB5hZhEbgrtj7RGirGN70vmbGQqPnExCw0WhnPiSx6tYl+n6q41qbDJrkwmPMYjK1gNqeTNEExgcrOuTK50pjRiJH+LcrYnpJ1WFOfDHA3IYYEYCYQyekkGG2LmFQvc0u0pOeVP2c6uOwOgHonSRqd1xRYIQEylqTHk4FgKDqN0wTfxvwZRi1ElDuHr0gBSF6TOGJQyTAZc7faXNpr8zqlV9YXztc97oOfT3ifOthfrNDL1NmnADNrfJkMoppEWUhaLEnSIlfgskPOOqMZFNWBKJm1ZBIoyxjw5GcTHdGdMD/6kHgzp7IVQ3+FZE1iMUh9wupXvyc+/oSDqQjGYELEErCokLfvPBIizXKGbRu815YEC1ibh+DFBETrdRjSc4peK1JhIA5CjF6NVvCIs5imhWqGcTXHD46pZ4arn67oz7fEfYfUi+SYU6XcSGlPEQQ7nxEl0lhDsEpOx8ayX4NY9usXmNMP6A9vOZgVg1tj2jVyEDIEejj0OJcmSqZkJ4qQhzWNVdIUoBYZjSRzwkSMfhLMlZaTxGJVQDKzRkcwMA+4CSKFMaxBjhaKTDxgJBKIHKL92bCMXJR4/+UHWCpuNzdJ30zfV9eVJj2pPTE7PU1uTXGsahtyS2QKEqzBS+TQ6aBFl4ZLGJK2agk+x7ObNduK1jWjs58Gv3fsxSQwT4emXOd92zI9g2Wi7WQ98neURGfy/fmVAzDVpOyJ0acuiPHs5oAgs1Km3zEdnnQfBM52Ixf97tzn5HfuyhNw59rvPF/u26S7r3EfyM9+/rP33gOOp0xeGAfRpSsqwLC1jqJ9aEZbdtevZHcp409klEwA7jyv/Dv312G6V/I1TpPl+2v2S+sx/e/sY1zO79ua1ZMH3PjA0PXaHZP2dB6UEaMlGksXA7f7HU3d0tYNEDgMG7q4pLWON3/8ktb+hr/663/Bv725oN+8ZRGF24szTqtHNKsFPniadoYzhiFGbt++Zntxxvb2Fmsq3lwf+KkXxFmerlr+/MOnvFhWDLcbDpsDjx6c4qqKq9tbqqbmeH7MYbfn7PyCOAR+9/mviUE4Pztjv9/w4MEDrDG8efOW2lk+/eQjhMj3r15xcnzKwwcPefv6R97++COffvSUk4cnfPnHV/x4dsuvP/+UZlHx1R9e8eqnGz746Bnvffic1z9eMTOBLhiiOA1qrWihKAI2JyAT4JyRcQXqwoMEqCtcO2O5XlG3M5qjNaFKiWgMqb02plYymfhpU+KtfK7iPbuSdd2Imd0VcTKwaCzvv3jGP/r8Vzw4PiFE2O03CKrDPWtbnjx+wusf3tJ5T9972nYORqU3nG0QHMY4Li+vCWfnOAtV3YBxSQcxEmVAQmBz0yHLhdrefg/AMHTUtWU4bLm9gr27SQMtKhDYbDbs9tc0VctyeYQPPQbL5vaaP375BZ998jEvnj7h9vKKi7N3VKZDJLLd7jl0A4deB5Q9evyAy8tL+g7aGbx69RVffvUDYai4vrggRs/D0yWHwTAzqtE4BOiDwTWNtvdtrwlen4eViI+e3XZDU7UcrY9pZwtUixBi72mWD8HNEGzS7ItYNF5tGsO+j+y2PYf9DSIVDx8s9dzpo6KuKpwExKfYehgIQ6czFKLQzmfM50uiV6moYmVjntKdGJTqeFKsqXswRWYEYCceYypqa1WTtHEsaCFGfAzshlu2Zxu1d9FQ1y1tM2M+WzBrlyznR8xnCyQEqgps1RCiZxhUC7KqlBkZQuBwOLDdblkulywWS2DscrsL3FKkBog1eGHY9Vin28/3Udv+s401uY3YKcM4RiRajX9Swi5mjEMG6bncXvLj7pKrdaSj1kK7FUJuqU6AVwyZoKFDwbR9OA3YE2VG1m1NPc/6mBpPB3r6CJ1vaEwN3lPVqmcttWAqhwyBd99+T/hHH7O5vWG9PqZtZlhTE/wBYwIfffghi/9jwSZudVhemW1Q3InmLpMiZtkHRcNwjD36viu2YbfvC1sT0UTdlYGqqgOPNVixd3zjNKa31hX2Z103mvCXXCnrXia9WKMxuXOOOoHNSLKZQmEnlvwTdHCONSX2ycUo1VyUEhc1TTORJqAAtSPAOXbpkMBTH7VLpmmqIqGVQdghyc/9EsiYn7Ewsjvzc5g+gzwgNxNklDuugG0G5zJrTr9LYdIYI4llVHKmqU0f4wFdDO14tRn7Hd9rUidZzoPyeqP3jmjMut3tOewPk9jmfvfPXRB2+volEPeXXvdjr2m+OM2LSQXOHHdLHlyXwKB8PdZV5VmBp24a5rM5ufU84wMShOAjTdOAGNUmd1Al1uH0DmNQrdO6bcrP66oiJMZg3/fkokTWvK0TsGcSfjL4VLhJQ5NUFWYE+Mt+MomYZLTTRIZxaNbIpE2g4oQglucC+dTNqOB1AhqdparyPJKqdN3EEAl+SMPNBw69amdbxgFXxij5LssnHfqDFtXsOMC7rmvdN0NZHvo07EvxIldyp5Gx7hkGr7mVKNip16nyDrmgOHaHWWwCM0OAKJ521tJUFX7QnCSEAc3TGsAm4PZufjPNWTJmZq12YVsSGSNaRHzCnMZnJNYWcJqJNFQ5dymGtwWPQ/2RG9+Xn7P3XtckxqL9m31zfk9V1WS5Cl2nJFEBqOwoqctGcZPCnK1HDWBrzMhgTSB325rSGZXnHxXJkGSbo9XrxmSbOV6/qxzWKJO573uNIYz6xabW7qr83qpSP5Bzlxz76r5UdjYpR/6HXn/SIG1CknRhUoCASKFoV3Wl0wDNaNCrqkJcMsK2KkBobS0nyyXPX7zEtUtCBwff89PZJdc3N2B14IEYEJO1fNJAgNRuZAhk/TtrE+ouWXNkdPghZiaI3gKpOgcmseBG8FfvJxYNt3F4xRhMGpMq2MbqxDsRjDicCNFGokW1OmJQ7ZY8GMiPDNNSyXSWPLjjzgEz4+TKAuiYPCXXlyABlL3s0hTQkMTCM0A4AiGxfEZ2UzocarxHNWC2HJ4peIUxhYl4J5k3Y4U4O6xpy8sIcprk8EX1cZKTIyXZU42qu4y0BCTlLTjxoZJARQUD7h4qXWZTWkyyIZoGQnkNxt2dWOIZZJgEY+nyy3XkACjrNkUvWEvSvFQKvctBTQ6AynNNWi4SVTPKagulEUOgxixfcqgeMUirFcTDQQMdaxC7ZP7RP8G+9xv2WbAbDYSsU3ZHGAbi7kA7q6kWLUMKJuqkg5Mr8Rn4xqjjtINHuj2h2ybUJiDRl+DLGgj9gPRbsDOo5lz7nvpozuLBEU1t2Z1fJ8aBGR9cAr1MVP2a4CzGG8Kg0za7ECAaBT3FgbF4C+7RC4Y3t3S+oZMKceokrGU09JLqADECgap2ynYvQwlS4G5yFdCVlt3cAp43jDomOwn+UoEnjoGfSfeTz4SgwXdJP0Xtwayp+Sd/8WdsNzf8xy++xU8qsbkyLhKZz2Z89823/PjjjwpQJG3gzEiVmM+ATYlGSMmGJJaC3DmnkVDaUbLmsEhQVo216fsjBdhLzDcjEUl2jSC0dUNdNxy6bmID8zpkbaax6p6TnHLWJ+cknxx9qxTbWTZWtmX/PwGyMYa2be8AsFlv+z4APA1s73zm5Hz/Q0DttNCj369r27ZtCYDvA8p37eI94Hny/mxP7OTv+ZUBsvvvz8HXnWeQ/RUkG6uMgGwH8xTZAjqbfF/mzjLntp6pbE4OoMY33dUJJtnW+8nYfUC8BPMyflphyxhTquM5OTRMAH+480wPiV3RHM1Z85jN+RXhZkM/DNq6lIbk7KqI0GON4PoIYc9RfcS6nRGGPVc35zyZL1k1S7776kve+/Qz/vpf/Xf8+//tXzOc/4CzwuX5Ox61zxPoAe1sgTvs8Yct3W7DrGqo2oqj4yWv+56Pnj3kv/jgMYvYIV3PbL5itV4RQs/tzYZ2saCqK7qhZ7fd8ejBKavFkt12y+XlFYvlktXyIbe7La/f/shqveKTj1+y2Wy4ur7kyaNHzOcLfvjhe66vN/zqs/dYLVr+w99/zVUX+Ys//xSM8B+/+Ibvzzd8+vEzPn7/KV9//QM/nl3yu19/xFffv+N8c9AuGomYFB8glPOdC0BSwG8F4qKtqBczZsdHNKslzXJBtDCIMmctmXUmWMkJlIFkE+6f67SlKF1DaWcQNSETG6mN8OL0lE/fe8ZvPvyID148Z714RO8D+/0WSXqrMXhqV2kiMhxwzlA3CtqHYHBVk7qhHIfDjlnbsFxoq3zVrDC2pm4WVNWOwIAfAkFgOHS4uuHps+ccnTyg3205Olpzu93RdTucNbT1kSbR3rDdDpy8eMLmesNs0eJMxWI258//7HOOlisuzs4IfmDWWja3t5w+eMjF+Yab2xuePH3Ihx+8RIC+3/D5rz7kydMVne95+uQZfjDcbjtEPCfrFf3mwPJ4wc12y3Z3wFSBjz59wbPHJ3SHA92QB8l4dtsdb9++wxodDNXMatpZi6tn7A+eqp7x5PELXH3EzdUFbePYE+gOO5brGd7r8LlhP2DsLbNFRVU5/KC2ZtZmFk2FBGX7aRIX8DHy8PiYdrHisBcsEHqhci12yMwnGSWjbNZK1PdmPxUFBmvYEakjRCtUThmas7pRHU1r0UFHuvdCiHSHLZvdNdgKoqWtWtraUTcV7WzFrF1R2Zq2mdG0DbN6VkCG2awlJyu53T1ZPY3ngyBGWb5WwPdeOwSjSiOY6MAbiJGqMOc0kTbRIiYwZFDKgqSYcQg9fei4vr3m3cU7Xl/+xG2zZ7uwbIaQQDTtGMCoVmFFlexsILXLYZ3Bi/pBZXlaKutwtbYT98Gz6fesfYcZPNbNqWptw1UXH1Ni3+FMYHt5yaKes/rwM1Su0WJdg2trvPQ8efyMRyePuL3cQmtQJothZL5o3KCjEO52UhQfb2Sccp86e9R/RQLaagtS/ETuFMz+cupz8/TvkZWqn5UBmn7oCrMvD0KNaBN5RJJsl53Yp7s5hck/lxHAj+R0X8GRmMAOSRrqPgSGYSgdMfn3Uxqd3KpJLcxgxNJYo+3N1qbBbondeoeZmn2lJYOsMTEl67qmso5hGHSNElA1lR5KTruQRXSP5oGrkr12ioWlnJFyD2ldxjxyfB4hBLjzLNP6TOMtsmSCvUvGQUHGIKq3irW42iGVSy34OTZW73O/CPxLgOsvvaZxxvR35d6+gkwSqErsGPNaZhafqLyidoGqzmZVV2XwoHMVsR+oXIWrapq6VbCx69MgpIDfB6o6jLJ+Zrx2m+LJGAPdfl+Yz7FpirRVegsSI10YSoG9dNkyDkMm7U2RUWZM96/uuWgMzloFu6zF2KRfijIk+yRBaWKEoU/aolUaEGZTR7AgdcqTY6AbOiIuyTAmmQZX4YzB1bG8L6Q/PgRsIrZZ55IdBee0qBSNzimIomBwQIdgzWbtyCQ3IIMUrGC/3+ODZ7FYsFwuAZVHOuw7+t5z6How0DS1MvmrOhUHHL0fEiMzaQIHASMJQ8rMeB2kHaPQD6NsiXXa9ZCByxgCh0OnQ1CjaLeIUe30tqlHcDmOOUbmkWfmqSAM0adYLpb42lpL3VTYdP713yJ1AqirSn8/d47UdU3fDwTv8SFoF9pkuJdzHXlwdsZ7ClaSF9lkSUtSzKH29dB1+kzms+Sf1W45pzrpVe3wQXWPXWLDhkS8MLVLG1o/NMt4xBhU+kbA2ZrKGQxuxJWMvjdfq85LMZhqKpEYUYaz/l4feqIYqmq0Jfdff+IgrSbjoYCYAMooq63l6GjN9dV1Auoco2M0SMjTyC1D0Faok/mKhycniK20pUEclzdb9rtbXCXQCr6OKpwfhMqhoBaCRfAhjgxRAwStduaAT2uICrqUaqgIJrWZYZRJa5Ogecj5IzoMI4MIggJcUbJWhzpOn6YDSjooNr05C7yHoO1YYlTc2KAxS54KWOjfRhl5FnXkOaQZq6vKfiwDDqo0Ndcqe9BCqXSq44jajh4zOzGBGAKS2AzGGKiS046SJrun+01VrykoaUDF2xkBWTHj5s6VO8iaTRqQ5vVNMVoaKsUYpGXQZlrtnQISjCBzcZ7p+jPYVkS/yeBLwFpSm4dTDbmommLWZvZhYiBMtJViccrabmOtKYDjCDOMiHEUME6rQBE14PrvUoC1/OYCPgSvRioFIg4VXccYnGnw1TOak88536wI3hB3FxA6aCuoFiyefc78kz9nY1p8yHZL95ZNlTW/O+CcsFw12Fr1n732FGIt2Ch4YwjWYH1EQkD6PXF7i1xfYBZzquURVE1CQH1iDjXYbge+wx8OGFMRO+h+6giXjpPHx1SPH3B9sZ/G5WpgbdYpVlRVDBwOPfVimVi06dw5qxX8GHHzE/zsAXHYQfAqvZCcobbT6bppq5jaF4f+26gpk5nq6tzzcC+XpqyKCLkNJQejMSh7T/ddriinoV5JQ6kEyYwTLPPtWTSBPF6tsSiTNsEPZP0jay0SNOHabi7pDhsNCJpa9Y9SC2QUlMVchn7plwQfMJUWTqzRKbBh0MmjUUi60UlDOg9lyUFtYnFn2RYRteV104CBw35H5RzvP33K2cU5F7fXJXHQBCqdcrnb4l8S0YndyiBnbk9TwFsLBTrILPOlSFpzZgTBJ7bGpeAspETHWDtqPctEriKv0C8E5JIAdEnvtffeKynql8nmLQkAUDuXptWna/wFoDX//T5LOKRARnRRytCTPLjN3PvdO5+Zct7S1WDGQlrRNU7ArWVkSmdQXMg6gOqb9BqkSJmU35cMmI4BSgFVGYtu+YrNvXvPScD47DM4kYC/tB/SapdrznZXbbICe9OEe/A+3RPEymJXLUt3jO8PxEFlSYL3+n0uMpiKq67DuogxEeodx6sltVQM/Z7L87c8evgMI4bX337JX/z+9/yz//Z/4H/5n/5Hhv0VcytcvjtjffJIbaaLGKddRFa0W6WtKn734QuW6xkfPn1Ke9hw2G5YLBb8v9S92Y8lSZbe97PFl3tv7LlnZVVXV2/s6Z4hR8KIA4GQAEGAAEIP+mMFQSQoARRECSQkjTjDmVZ3V3UtWZVrZMZ2N3c3s6OHY+buEZlNvbYukMiIzLv4NTc7y3e+85228tzs1mx3Ww6XB6xWS87fv2ez2XB2/x7tasG7ywv2u46Dk2Pquubt27e8e/+ep08fcHBwyJs371iv1/zo80+pveWHF6/o+p6f/vRTHIZ/+IevwTr+8pdfMMSev/kPX3MzCH/5i085OTBKv58AACAASURBVDrld7//njeXa37xi59i2yW//fbNCLAbyYM/dMONQzmHGBQkcQZbedqDFbaqaI+OqRctMQ+z6GLIPjLr2Jq8TwxQfFGJlcQQGDBGB5rqZ6YMAkse+BEVbBVYNJZnTx/wxbNnPDo55WjZ8PT+JywXLUO/J8Y9ziS63ZbWC/vr97w7f5vb3BQkdJVDxBOSttHVxmDEIUFwC0uzXOJ8g7Ge2juWZ2fcu3dMCoF+u2d9c8nF+9dY71g0LR5H39Ysli3dEOglUvucwNQ1y4MD2mXDgwcPOH/9hrOTI5p6QVW1NAeW3XaLtQsqv2TD5Qhyxxjx1nB0uMSakIHcDcYG9t2WxcLxydMjJMB2v6BdLFSv1AhD6nDve1I6Yb1dc+++5+Sew7tjYkInhAuIPOT07BhDm4v3iaePn3Hv8aeEZHlzfk67Oubg6BFvz8/p9jt2uzUMAUmezbpjvw0Yv2C7F/b7yKJWXbq+H2ibCu8NdbMgDnusGZDeIFGvsW5rDA5vE2LBeIs1NcbsIdtSMcqd9VnTNsYOsX60H8FogC8xEZ0ObToUjcf3EiBZnKnwRkEpZ2taZ1mdHCm45ZU9mnJiN/Q929iz2b7PMk9aNLUpdx6gpIGqqmiqBVXVUPmG2ldUxqt8hMsDw7wlpJ7QdyRrsFVmoWEwSXDGq53zUyEyxIEubOm7nhiFm82GMPQIA9vhmqv1FTfrHZfbG25MoPcV1lQ4Q56irV10AmNB0nvV+G3bVtmXQRQnRRhSJKWQARk3ajVudzu6RU+TGmVuNRYvHmcczluVahp6fNOwuQlcXK45fXSq+VsKIBHjFvi24fRex2dPn/HN+++zz05YNzE/mfmROchY4jRT8gNud0YmUcB0YpeWjqZZm3VxkyVnyHnCXE5AE38FfLtuT4iBMqBYBLVNJs8uEQOJMUaf/PLM9yaV6LCV5j/W6J4nJpXIMoIVQww5ppQJZBk7lfLaTDq46qeV1aoxqzFARWYdOrqu+6AArfGpJeT8sLSyG1BpMKZuFkBZd8Zikoz5bGnXLr9j8r0RoAx1FXTOV5oKvcYYshjteD0j+F5+Ll92BDwZAdYCbUtZ1ywjOL2HFkNihIqsee3tGKtoXD+txRxYLdcyj0XnYOvdf7tbdP7474UQoPdyjOMoLHsFlr3zmmvqVeCcDuYr7NMu9pghUPlq3MPeK6sUY+i6LvvUDLZVfmQtW6vgYUyRbhi0mJCCNuFaS12rjF3lGypDzpNzTmrVjvo8eNx7TyGnFWCrxO/9MKgUjVWgVkllXqVjityjCCKRMMxAQmMmILBuqLxTu2OLnEe4FSeSt1ZVObytqXxFGAYEjUmYneUMjOB9Rds2GKMdGkMIxCxzklKicl6lJWb3uBC1hqBDmGOMyqoXcN5S2xrnPAuZGO56H/RzrVcgs3VLhl4Zv8pqViJTXdXKvPXk7uYse5gUAE4xqdyaU336Mki6aVQXf77nMFqsaRYLnLUMIRCGoDq8WfoMyINT1Q8pMOzoux6JkegMlamwzlJbJZjEIY0DysrgrgKop5LEWsN2vdV801hWq4WCqUmHZacY6fpu7JQqxa6JmYrGlSHkuVBqI2JVESVgrZ/WLeNENsuXFjkWzW1S9sP1lM/kzlK1EfnfjEEkqD3NRSgjFpWfD2NuI5JmHVylUzBLVZJUYsWo3/zjEO3/D0DaYkRG8AVlyYYQuLi4HNkzwKgjVCjxbeUJMVJhqY3jdHXCarHKFSRtY3n15pVqmjYe3yh9PPZD1sGQsbUZshOKEePd7Pp0Y5XqtCb/isozM6jFEDnvxuFVkCiwrG4K/S5afQncMvIiM6HvDFia0ranoKJzPrNPNen0eepcVVVTZSMDlVEURDR5UNNd/cYkylDWqev6WTaJSkAkbXM3ZUAYem9sdmIpxVz5z4BUBmRFhMp5ZAR0J2c0AhdlrWZg7/zfJRbWw5SAi2gQU4BXkx3FyO7LgVa5ibqOM6CCPCVdQCSve17rD4YzlevIYYlWDBsKo0PEEMLEIi6PEMJUzZox6sbLmgEq5fvONWBKEGQTYCxOcpAGlIEJkmQKBI2bmMKZTYuxBLEUHcneLFk9/k9Ix/+Y7moF4QKz6zVQ8QtWP/kzDn76T7jeN7mlLbdVGYO3CvQPocd7y8nhgsbbDPYJSNTpqBkcM8lgUiB1W1hvUMTXUd97QGw8Ui0w9VIDVhKGRBSButV2waDtOWnXQRcIu56LF2959NlDzEPL5fs1kxbvtIYlpjbG0G+2OO/xvmYYIlIY2KLtQ8muYPGAbfqWyoDPMg0aF0qW0VANbElafLEFKId87swtEfDCsACIUSigY0pxLHJYq/HQBGIKxqbMvhdtETYZbDQTW0OF7y1BhPWw51/+6/+FJMI+WZrGjO9fzoT1nqubG4wxVE2Vp0sq898bS8igrvNaWS16XkrsmZKVk9MTnLNcXl8Dmmwcnh5xcfGeuq7xzrHbbaZdm+1olSu1JZCVlEYWyb7f8933z6cuhDloOgt0i2b3/HE3yC3vb3KApcGgTDYjP78EgsWGFMdf9KY/hF1HF8Rkm+SDayxMqNvs1LvvczfZmz9Dz8xmsylP0CBq9t0+prc7/30O2pZrucu2nUBibv3/+Dqj11KC+rJO5RrHwXki4Owkrj9mVFOebIwdZVsk2+PxM2drYowyi0bbVzKskrTN7vOH/iNhrQdTBkTO9hBoZ8BsLaw1o3zB/H2dd6h0mlHmrDH4Rcvpk4fc8I5+s8c5izeqe5+iEIzlYhiIDobrDbX1fP7wIZUx7DZXrH3N6vCEYb/mxXff8PlPvuCv/+v/jn/3r/57SFfQdVxfXrI6OWJICecbYuwwRrApQrfl0dECwzFX796wjZHT40PqquJms2EfArZqwHrOLy65ul5z794ZB8sD3rx6Td/3PHnyhDAEfnj+nP2+5/NPn9G2Fe/eX7BZ73j27BnDMPDNNy9p64p/9NPP6Lqe33z5A4dHx/z6i0+4vLri7/+f76i855/9+ROSJH73h99zQ83Tn/yIy/Web377FVXl+OxHT3nx8rVKqBgZCwR1W5GSwVU17dJBVVEfHtAcHiLeIcaRVQ9JooMcbI5V5qwwA2MCNhZRxeTYKftEa9DBk2BCpCLR+sTxQc2j02M+eXyPZ08e8+TRU7x4jg+PcNWS/X7H0JdEp+f64pw3NxdsN1ca1zij0gVJJ9lLjCSJdN2equkJoePq4j2YY6yvePLJPYxxGGfpuj2LRYttNM5b9A03IlQ2cXP5it16T4g9myv12xLB2pbaqw7y0cEBKUW22y1PPnlK7Sr26zVXb78n9Te8fHNNt3P0Q+DotObguCLFPa9evSaEyNm9B+y3N1y8v+Tk6IDKJeKw52K7ZxiEMAjdIFR1xdFRzeGBzUyeG05PLYtVxfrmJSlcUlc11hpC6hQ8skvuP3zGqv2U7eaGbrhmGAIvfnjFj3/+ZzxZHrMdBNmt2W6u6Tc3DEPgcHVIHw27LrDdddjKYHths/Yszhrqtsb7liFGjKuwtsJ6AclDaaxQOZ1NofMcpuRIbVSe7p3tk7bTxpEBGFPEu+IrNG5Jogxh64QdgjiLNYKkQG0dVqzGRS4wYPF1ja9rXFXTLFqs83jnlFHqK7UzWm0ghsh+u6XvB/q+p+t6dsPA9eacsO+yDdM/jfdKAqirQlzNAwy1CCyirfRVZq42bZ0TRu1+6YaBrt8T9gN9P7Dt9pACdWPZp44hCSIVoXYEhN4ZqBxV43De48h2LmmRuvjG3g4ZeHEKDhgtjaWQCEOgrvV6NFGR3N47ddEZHE21xJoKgyNhkOjxsmDo11yeX9AeVhonCkgcSMbhbE2zXPDJs2f433iC6LBomfmbHEGPuY11dtSTv+03SjEx+xM7+Zbbhd845gF344+7UkowlwAoReHJx0z+p+QcEzGjJPIhz23wlcsggM6s2G121HWNwokZQ4JsI6duRx3qmf2oIcttGc3H7BRv6HbUeRBJ4q24pJv5Vil5OJJJMroXSjF0JLPIR3IbGH1/ydE1br4NEo3PncVtRbKmTJufYhQZ29nLPSgxRUrT+R93w8zvT7ENUxde3jIFjHLWYr3aa22HZ4qjyvea3ct5XDn/uXz23f0x//ljr5vWUHL7vwLpw6BMmbpWIMmaIr+ma9D3me2NwXtBpMTLmneGqMVlnX2RWaXezQhDGeY1liiBQlZyTokZ1umAwSiBYYgqjRET3lUsfK0xkVEG56i5TVSd5qQF59KJ67Muvckt8k0I43lIKREGlU5JISImsyBRAplv/Hjfb2EJCCFEREJmzDqccWAycSjHCcbpEKso4Vae7WeDwcY4WyD1A4NA0zR4LMY4kjOIcSPYF6Nk/wHeZ4mDHPsYb8HX+lwMNuk5MgK1c/h8j5yUmD3rpkfFWpZV6bTQrr4CghgKy1cHaVd5yFdqmqwxHDVHz34opUTdeNpaAeWh73UAVkoYMdRVQ13XpKRAtaBFPihs+Pz9rDJmbc5H97sdKemgbGcURF1Udba/k13puk5BbV+xaBdqPZJweHBIjJHtdoe15hb7V0RYLhfjLIwQgpIQrcHX1YjNpOhIg2pZOywhdw5XWY7OOpv1wxPrzXrMzY0xeOe0kx5hvd6MZLqq8gqY2yKHoHnkfr8nhIG6qqmrRp/rlQxUgGKNVYUkBiMquZGyv5EsVekzY/quzZw//uRB2iknNqORHOndMOqlSko6ic6psL8ehqyNJEJrK05XJ6qfGSIhJNbbNW/fvcJUeoB8VXNyfMxus1ZnjrnlmDWBVNF2DU5tbrlQ4G8IA876MUlVNajS1qeGXjJyJNnDKnNzGn6jX/V28j037Nbk4V+jMS16PmaifY9VwdsVXtBgVFwGe4aYgxKZBpTlQxFzayHJZFaiIYVcPTNW2z1nYEER3U6ibckJHdxVWK9FyL8AyMWpF5BgPiyorIHe85nzEk3wS/VsbLdgAhUKa7WAPyPwOa77FLyX9bVuknooRlYrtpNzn0sq6HIbZbY4T11XbLcb1eMaW4A1GCqvuztdddzfM2Bk/N5ke5ym+27KYShkNGtudXapQbDj39pCqsnkEEq7QBbRF2UjpeqY6v6v2Lc/Id1sSN0b6Afa4xXy4Bn1/R9zs3N0QbKWnm4Xbw3OCBIDaRhYHDT4xqkzFZCg4KIAfVAA3AKy2SKX7zChx1Yt7uAQKk/stxDzFEzrAI9KH2RmlBjVTa0SzjiMDYT1htj1nL94y9mPH1Hvarpt0EnihXWfPcq4vimSOm0rDUXES2KuugoxeUxzTOgb6qZBqfSZPZr3YTFIKaa8byZmZQEkETXmc4bFBJZOZ7xsxJEpKIHPHj2g2215dXEFOXjCQBcD3ni807YgIxNoOoqWJ0AMta+Yq5TbwgIV1TXUXET3SAhhPD/GGG27y99R21H624mHgRAGttse0OAx9B3b6yvtQBiGEWhVINrmc2DGYX6JKYnBMLKMQ4q6FuO5H3e+vj59PKD98CEj0ULG5CSvcTlfd85cKY4VnaTyGG2NaFGvtNuMLJUSJJup+GKApq5xztHnoGT+WeVvY0oL/vT7HHwtNnEM8O9857sa2Mzv4+xz7gLeUyD+4VrMXzM9948/z2WZHIkKoCNljebvlW7ZsrKudpZkjQnUWOrMgHS59iSjDvPt6yjfrbxHHJPaMok2Zh9drq0kxGY8t/OkWj+/ylN/x70P1EcrjjC8e/Ga2PXUubBnc1tTL8L71CNUNDc3tN7y6PQe1gn7/TXLtuZ4eUh3c8m33z7nR1/8mu6fdfzD//YvMPTIENld3nB4ckQ/DCB5fSUS+8j2MhD7PfQdvvaIRDabPc5YFq0CWO/fv6duGx4/fYx3jsurK0wyPH30hDhEXr98DQl+/KMfYa3w+vVrjHF89tknbPd7nn//gpPDQz7/8X3eX1/y/LtLHjx6yKfPznjz6j2/+/0LDo8O+bNffcbV1TlffvuS+vCQB0envHz9hrdvLzg6XvCLLz5nnxznb95p0gR4X1G1Ne3BEtPWuMZTrRzGeahqorUMSRP9sbiAGad+l6nPo6SF6DAvERkLSiklYjKZyWZUi1MCDXC6anh0csxnzx7z+PSI48WCw8OGbr+nEcPJ0X2MdazXO8LQKQOYRLe+pN9c0u/WdN0OXzfq3bJ8Tb8b2G9u8F4ZtweHp3jnWLQL4pDYbTp2m47js1P6QeVc4hB4/eYF79/8wMpB2K5ZX/S8e/WO7W6Hs6D61wnvaxpf8fZVC1nT1lqoK09TOTaiLe4mbfAusFoYNpfXXF5ck2JDCgvOHj5BBOq64fJijTNwcnyfurZqq7xht+kZ+siuj+z3EbnpiXFgs40Y6WkaT107ltKw3XZ0+w1Dt9N4TyKYisPDFcvlqSZjxtB3Qghrzh6d0vUBcTXrqw1x37O7ucJjefz0GbVveP7DD7y/vMbXC+7dO6VtPb7ShHR1cIyvKk344kAMuxHRSZkQ0VQNxmStvTzcKkli6IZx7kC2NmN8MMaBFHbhzLJIHuAL7CUQVWkdjxapA6UwXrTyMsCmLWQ4VP81GYPNLB5rNFlzVc2isbSTdSWEyO56zfb6hqZdKLgQJRu3SBQh5iDM+YrFosZ69Vndbku33bLd79mljspYmkWDpMRg4zhlvHKGg0XD0GfGZXAMaHtrMpBH5xHzeUMGvK9zS6ymiz6TX1RL32T2MMQUiClSe09tFBxxlWqnlhZ8g7bNurHgMtl+a7RF2orBJcP1uyt+/Z/+GuNrNtuOJL1KVdQKvj55/JRls6BLg4KWVmN2jdNKG/aUF4xFyTtA2C2fOosRpvkTMtqdEiv8sVi+vG9p958PBpqDvnPSx+jfkZxDyUTosUp8qH0NAkNmypG7YowoAURMlvKYgXvWWqwo+zL3FOTPztJv+XkxJixp7BT8oEsIjT3GGoOUyeVunqB/sKa37HT2p4vFgq7rARjCMMUp+XOMyYORZIoPxhb/Wa50F+wssfkY/zAV5WGKNyZJpOnciQhxCDn/yzIM1uErg29znp/zmJKDFjLM/PFxkPX/+/Efi78AkuhnpyR03UCIQttoh3GZcVN5BbSGFNl3OwyWGHVAU123iEzDrYyxo6zD1KE8Y/vCCM4azNiJqyQYLcq0VaNEFxGEiCFrvJrpvpd9XWXJE1NYxnl/D0NQBmwGTStfZcAwQ49eRlDNWss+7vHOUvmKJDJqf8JEXghhIg6EEGibdgTvDROJyFpD13dZl1Zb7QXRopRzt+ZMWGuxSTsBtvvdOPhq3AMlF7Cl8BfphwFjFFB2TnVmy57TGCXPBaLokWou4CplfY4pS74XZIIOQh5MmIcHouzZMITcWJtZpvk+GYzGUzHSD1kCo8rvZcD5CidaCFd92IG+U1KNy5hN0X+NOT4vXYZFV9pYR9u0hKGnctoVXnAojN7/YdBB5FVVaUzjnMpZGIPYjNm4nKvlvLSpav0cp6z+oR9GLduYtJPbOksZemaaGh88KRP2dA1lJO/N9Z3btpnkOMp3sbp+KSW6rmO73Skm5jRGtRmTMgawhtB7nY8gQu0cYqwWY41h6Hu1m1njmlIwIxMjk3adpjiMNvWPPf6kQdp5IpyiGgJBtEqRAThr/FgNL6+BEuTrPGhLwkriwdkZta/oehVA3+42bPc3CDr8ofI13b7HGEcURnHokryHMOnsKFBnceTq/BBVyyfrXTmTq0/ZeBRB9yiTIy06kd75EjZ+kFzf/d2OQWmpQLkJiRcZmWbGkqepCjHlapEFJ1avQbQFUWDSccnrXfQfTYq03jFIJIjBuwpDGkHyAkhgp5ZxND7C1zUSJn1RhDFISzJjbxlzq5I1D5DMLGAq2i4pg4/Wapu1YaomCTK2XGkHURoBpxxjfFC1KBR2JRmbUZdnnrSPADICRgdiJZE8XMkTQsejRw/p+j1vXr+dwIoStpcATaZgbxy8Y8iVyDKIZ8ZGk6lKrUB/lsrI657SnaDFihoZSVmjyNHUNft9l1uGlKEKQqTl4PgZy5Mf8f4iEq+voF9j6prFk5/QnX7G9aZiWPfYA4txMQOgCtjW3rLbdTgiznsFxY1W+4MIfUyIOJ0QjCFst6SLK+z2GnEBc9hgFh5ra0zoSSFhSoXdugnTsRZJUQMEMbiqAhwmBGQbGTY9Fy+vcIsFpGHcayUEY7Z+rmnAWZw3mKhgp8oKgPUVXQq4RYP3R8hQoS7QgKSsuyUEFOgxzoOV/N2jtp0ZxkTNWvOB7vFdgA4Y2/PUdQjHBy29GXh/5Yk4RIICNaHHuIRrLKHvR0a+hh65M8lXkKAy2s5VkDKTQbMxaRFGBk5xthZlFZZhaN5ZDg8Puby8yOsnqqFmHfv9frz+EDWI0UBDA5EhDOrMrc9BsRntit4PvW4RlWkownSjdO8smR6vuZzhGZA5TwL+2KNoBE9BV7x1/uePlNItDdhbtnd2zkaAcZawlYJV+b0eJzxP7/Wxa513WkyJDVMQPfMDc7C3BMDzNZgHHfPP+RDYZLRL1tz2Mx8yPT6ekM6eNAYf84nSZvb/BjMex3Kdk00sXQvZLRY0NV9HKXag+dOtazGmlIJkYnsXn2TKSWRmWxnB/7sJ1Xz9P7YOCRgQ3MGCw8f3WL99T+xUB8yQNeuM2oAbiVTDgH9/hcHw4OiYrr/m+++vOF6dcPb4Uy67ntq1/OLXf4XB8zf/5l/Sxh2tDOxvdjSrhbbeGYPVFJoUEmcHRzR1xXa/Zr/b0ThP3TR0MbLb7ZEEhwdHpCRcXl9TVxWPnjxhfXPDDz98T13VPH7ykK7fcXl5ydHhISdn9zh/f8U3373g/oMTnjy6z7fP3/Ducs2nnzzh9GDJl7/5jvOrDY8/vcfnnz7i/Pycr394xb2H96mOjvnd1z9wc7nl8cMTPnn8gOvLC86vt/zki0+5igFjVWvMeEf0luAMyTsGVMvbWw9iczowjGC57u2k/mu2h8reKn7O5D3onKUuPqPfc9hanj56wJN7Jzw4POLh8RmfffoZB1WLTcJ6d0O3PafvhSEKV+/PaeuaFAZMSGyuL3j+1W9Jw5q6Ngypoo8h+yPdU/1uy359yfFJy6KuePToMWmwtO2C7XaNdxXv371RPVFf46xjfX2BG/bcP1zw1R9+y7/9t/83P7y8Zt8rCFl5S1N7nGXshqrbGusNVWU4OmhYNhWLxmFbQ2U9p0en+Noz9JF79w44XFUcHi8Ra2jqhV7Pbs9vf/cHPnv2jJOTQ1wVEW9Z73ui8bSHLbUI1c2WrtNBJJiG09N7PHxwTEwd/dCTkiUMkavLa3bdnhQdlT+mbR+xODjj6uZ7jHhicsQUVCN5v+Htu1ecHp/RLBZYLLt9z8HqmCHCEITPv/iCk+N73D87o/LC+3ffk+JGAdPkMb7O8X5Qv2yU6QYOXy8RdPCNdw5rDYOE7Otg6BXId1kvaMwaMtirCaHLoZf6JevcKG/WkZRFBfSinUXeWmqr8mRVJnqYuh6TukIASIgOZLEqKVQkuYqmX1PVVM4RmpqDk1O9FpOLfDFStQuMJNqmpj1ccXhyzOp4yerggLat6bod25trtjcbdpsOE/X1xsL19TXbyxvSzY7d+kZ18NLA0EMSn4fwBW2RR/1wDELILZ1xP2AqbVE11kBXdPGVfKAatLpehQ3qjMMZz+roUIGHIWSme4YLc0tuIIygg/c1lfOYlHAC78/fY6zHVg3tynFx8Z4YtxwcKyv57OSUx6f3uXh1gSxc7m7KVt/kFuLigwW6LN/k7TTM864fl+xzRAqIwsgynIOXd/3rx0DDuV+ZSzTNY5r532OOoc/CoGCvNY7V4YpF2/Li9SsFcTOQY8bPI8eBk+62SCJkbcoCjogIRP1ucSbzU+YgfAxMjinLByWZ+cjSsVleVwCr22Dq/LuVvKjynr7vqZyfhq3m/LXoRBdylP495ad3C7Rl2W9/XjnUcmftZ4y4fO3ltbfeV5SZHlMimUzmhY/MvpheP2rGpjTmdvPcdR6X3e2k/Fh8Nf6b3uBs4wwpkMFMIUTtTun7PXWdlPUnulbO5UKBdSOgpXnJbJAtylJ13ox7SGNCO8NccrcuqjvtnDJELVDZbCsBJOfRCLEAm6LgvES9vyGGvI4Z7MOThkGJbqikQNf3iOjvJf8tLGrtgA4a50iWTJzdP40XpjMVYqDbd2pzMpGv4DbWl/hZO06GQmTr+pwrqP/ohwGbCVZiLWEI7LodiFDXFS77HyMqRaLgrJL3nHVg+hFPcN6Ps0vI+0GLXfp5RR9ORPNK8vp1fTfuaQU66zxs02SgFsIwkGnGSJZGMcbgvMcYtLM5CWkI7Ha7cYZEyRm894jVMz2Enq6fsIaxIzO3KqSQMummDEDUPM7NcpKY0jjUS7sBZPy8ymtu1Pf9OOulgOjW6YyXKudPIQQ8k70oALrJoHbxnwbwxlIvlvS9ymiFFDGWPChyynOstSwWC0pxf7J5CgaLCIvFgqbWgeNFtknlLO247xBGFnHRVHZe5TlWK82D+36PMY4UdRCjns0KkTgC1xq3Tt35dx9/0iAtMAKaIwNGpimZZYgT3HaakMESYzGkHDQYjo+PKBW3EBQt3/dbEgFrlJWx3+01MfTV6HDGDeY9hIkePyXh+olCmVZuc8ACfWbRlatKkpCgFSzsLHlneh9jjVZG5mDOPKHMVQJrLMmU6caWZGT0H2U4WHnNHPR0+WBZ0XYuTNbMnD0kCfeOTvjk9IivvvuanfUKhxawNa9jqapIzCB1BtJNEpKZQBIBjIi2qzFjSWXgthiyUWMEPvj+SdRhl+TNFxCFKVgpjnOmEKr/L3mdcyBWAgDQSm1J8mJCv0e+qPlBnoMCxRmkNGCt4+3bd5SKl4xaYzIyOErwOK/sjsGdFKD5dmADuSW7CFM7FbQeGWCZQSImjWtfpng6QR32EPC5UiNY1YMFDEvOTj/naHWfFbudwgAAIABJREFU+PwK1hfKcD26z65+SJcOEaOVLJGeGBJV1WAsaAdAJA17VqsVBoh9wqSUWalepQ1S0spa6BmuLmDYYRtD01QYH7MWXI1pD9W/uAoxdmJT5lOl/I6CW1tsW0EYoNtj9kK46miWR7i6JvU5Ybjz0HtPboHIgVyI2Frb7NIAxkZcJdihJu4DJstWRIPq1eRrigI2V8YKq71wAkXAO6uKM3cC+aIxdosVkFsiBM+A4/ffvsClQPLaflE5w1/9+Z9zXLX8T//7/6q60yOFWrJNgWTJSSYYJmC4RKJJUsbw74JxMu7LMVcVZcuu19ca/FvVYbLZeVqBEKbWx6IAOlblc7FKxGRtrAJ2TmfJgibB2YaWGr6zqp9cgEstTmiAWtfVJPVwixUxBb4TID3Zs2Jf7gb0Hwb9ZV2mM1qeX5I2ZsnaXR1YmFoft9vtLYB1/rgdoJf3uA3IiuQCXPExtkB1HwK/8CH7ZX6P50lCeVhjbjGG5/7l9s+3pXDmwHX5uxy3j13XrTOQr8XlKvowtrdpxlNVtTInUsTnoKfkReX1d9dUNeLVfsb4Iav4Y/f57nt8LKEuyVyUyadao4zv9viANAz0767UHybVAyRZYgrsUuImGlrxXG32tN5x7/iQbezYbtcc7m9YHDhuXjzndV3z6//sv2HdBX737/4HXApI1+G8Y3mwYrfbkKKewdoYnKhkkLE1ddvivWM3BKJx3H/8jGHXk2JPCD33zs6wzvHDy5e8Oz/n4GDJo0ePFLTZbnjw4CGr5ZJ35+948eqcBw/POD454svvXrK56fj5Tz+n9omv/vANNzcdf/bLH3N63PLixXPeXl3x2bMHNO2K3719Q3Ow4NOjI9pFw+XFJb6qePDwHrvKUfuKHi0chSREIBpRYAit0ai+WWS8TWay2cVn332YnNinPHNAD7k2TpMG7h23/JNffM5nj894eP8xi+qQ44MTmmaJDELsI23tODoU3r9/R1XVvHr9nLN7Z3jjSF3k2+++5tWrFzx5ckw/dEwauOoDnAOGge3mktXqCGMsXbej2wWqCprG0vfXxIuOqqpYHZ4RQ893X/+We0dLIvBv/v2XfHm+5yYautBTB4i7HkunQ5vQ4ifW4Aw4DLUTaqu2NxqoxbGsPYcnC9q25sHJKb/65c9oD0/A1XjX0NQN6/WaxeqYrk/U7SHnF6/4u998S7fV6d1npwccHy1xJGqvTKKwSxysEpc3W/pug0igrluaZoGvKo7aGrGw2xm2+xu4vqBpjljfbBAide2JoWe/uWK7vuInP/057WqJXy65uDxniLBdr1kulnzx9MdglSDgzEDTOq6uO4beYn1FHHLCGdV3WAd11bA3Dl+tqKolMWpXSylWJ6PJ5FCGh4nkYoDaX2stWmfVydaaMEmJ2EAMNhmSnWJH9bIW4z3UDqk9rBrIenb5ZSOwaRI5MVY5HFd5JR3kdtYQE2SmuHHq0/ehIyZN5EKng1qJgZB6dmFP3EFPYpGUxRQlkqxKs/RDVEa5gFhLtJ6IZYhCNwwMKdKnxCA1wViScUQx+nnGItaQbO7GEpAYVHYjF0T6UFjeXsEHyXMStJwE4jBVXod8XlXPNmCa7CuDEIyQvFXWsFgMWVNX4N35Gy6u3/Hws88Je8MwdCrpIInVYsW94xN+9PQZf3j7NQNmFI8bY2yEpq4Y+mFsC5/77ZKwlyKPoK2503DoopHKB37vbt459ydzoK7EEzqbojizAi6mW35bRPB50JhejxCjYK1nGHqsMZksFDLImrtFMpBgxjgfMEKZSA8KjO73+1sdKSMYncH1EgfOv1uM2t1UmF6T71R7W4rK+oKS43xopzWHEdXcnOVUc/ByAlALKSXnZ+nDuOKPMc8UvInMysS37tvHfv+gYGutzpbBYDLIpSGKuSVlNj6/xMHpdgx3973vvmbCDz5k4I6/53zaGkthssak+caQIpJ0YFiQRAmW6naR26hlJHGJnXSWTc73C2EpZVDVOX8r7nbOkaKehzIvRYyh6/rcqVI6nQoIph0sxhq6QdnSbnB5fwh9P+R1yh12+dwNw4ABqrrRAlEcbs28EaOsUElCGAZs7v6NQ5zlAFnuETsRF5LQhV6HZ0ke4ix6oE0q51uZoppXTFIsoMXflAexlM7JypUynWHoBvC5M9G5PCtJi1lBNC+UBGEICkRnLei6qoqJU1wCyXOQ0ogvpEELZH3Wsi17xeVZQWrL0jiMq/ELQhx0EGtKhHyeYmbkg4L7fd+N4GDZs8WmNI1KHcSo2Fg5UdaZDBoz2gtrSjFrhmPFiEPGeE7PcCDE4dZ5m8uSlnNfivIGkyUJlbzinaPve/quY880oPHWmcGAs+z3vQ7CTtqtMWJe3D5fc5Lh/MyVQe/KNM8DGzMrWLJcm5Dxsiz1mUKkrRvN4yx5rovaZe89zi61SOELcG8xYnPBI8t9lFkaf+TxJw3SGmMwSWnIpZqmxqK0MghhCGNQZa2bJZRAygwMC9Wy4vjwiDpPbB8QeunZ76+xKVFZg5WkuhS5yoQ1mgCaogOoeioVeWBKjBRko1SmysTyohMDTBUhq6wY3NSihVG6eF05hqAaaMYqE1Yyuj9tSDMNuyF3kBoFmWx2jvpv2QjHaXKi2iZROVIj+v6x6DKSWQUyVgQMhiDC65sNe9EmL5E0Mcr0asbKb0hxDF5Hx4MO1VI5CqEwEosjsPmN1DHOW2snFlSJAKxR3RC9rWms2gDEmQbRWFGjBEd62PWacq1ZJuBd75tetzFZB8Zwm3FrJiDZWqfVr3JPsoMo7ELvvFZfU9bEFBlbyw0TuDQHNBLaxlQSU5OZhaTCvB4xS0ogNQVjt8+LSCSFAppZ+j5MxtUok9ZYD6ZhGxouvnnJ7t0aGTb6mqomNWeIzfqwbqBqGoZNx2pZgVfW937XI7bCtzUpls/PALG3+GgJBExKDNc3SLfFmZ6jswMk7rm5fIddQX1YI/UKi+q3hTylOeTvrYviSBLy3rKYFDN4mxAistvQrxf4dkE3ZD3C/NpxS8l0NqXrKKbPicFU0Ivgh4G2v8bLoELyIejEZKc3v8DoNgOSRhImGazPRQE7Ob4CO84DIzFZb3Om0axgouThebCPgnc1MQfwxMjV1QX1yQniLV2vAVXlsnPHYVNUPTibiwc5iCMDi5JBZJPF0pWBL2P2JKIa1WT2bULtQ9frdE3rPFhLDFH307QTwThGvde8t9VJMRYftBgDkgbVKc7gCsaig0rV5lpfgcmFBNHhG1VVsdsNpAQx6hk1Ru1KualFd80UHWugVON13TMQHCfmRTk4U+JUzljOyqQAc8q6yGndmMDckpDJbD5hapGcs0E+FoCP4PJMwy0Vu2TIgFWxsOX6NVD84H1SGluw9rvdmGiFOA86S3KY/ZkApSUoTYyYyY7MNcOLwP4E2M42wfgdSqGrFOVuJyDljy3GQhPNXFjMrjAH4NP5sNmuxKiJ1/yjR8Al63DlYcejhER5zt2kafqOueslV+e7rssFSJdfS94HaoDzfBeMtSyOjjBR2F5c5sF9+azjSCaxT8K70MFGWWFH7RFHR6fsrq+5vn5LIlH7wJvvvqRaHfOf/1f/nNhd8dXf/CsOrdDtIlVdc3LylHfnrxHZ6ncPQmM894/OiAhhSBjfcHx8xLDf0293OISj4xOqpuLt2zdcXb7n7PiQ09MTdts1KUYePniItZYv//AH9n3PwycPaZqGFy9eEiP85ItnDP2e589fIQK/+OWPaLzlq98/R4zh5z/9GSFF/u43z7kW4fTJffZ9z/m796wWLQ8fPeTV9Zp1GFiLJRkFYpIpQ1WLT03gtOBYuljKXiw+HMzYpVCCed16ohqh5BkA+awTEydtzV//6hf8/PNnnB4csmxOMKYh9sLNbo33OuTTWsfpyQPCkHj/7i2LtuK7b77h0dm9vD8DB6eHxCR0/UDbLpGtAmUWS1U59ruO9eU7DhYdvVhe/WCwrDg+fkB9fExIOlHZe0sa9qRhS4xbkq35P/79P/DV22vi4RntiaFOA7IPDNsdYbdFwqCtczkO9VZh2yiwi4wDYq2B9T5wcb6maiq+/eGay+uev/6nf8Hq+JDNcAMiHKxOuLja8PvuOV9+95bff/Ocdxc3eJdljCrH4aphtWiQPLBDjKFpUHvstdW/qhxtW6suXOO59/Aeq4MD7t1bELfXfP7JXxDjG7bb79UW9QNXF5cQEpfnL1nGMx4+fMj26i3b3Y7dfs/pvRPa1YLN+gZDIKaefhjY7yKLNuHDXsETiUQDpTVxiAOJBVX9GGtPwHksQkw9oMVJgJCT5KKbaSQPVMSQjODJQzrFqW9KIHmYic3Dy0SEZB0UWTVvkcojTUWqPNQekk77VqA22yebZX/IOq+1x6U8GDEPliEVdlUgJSFlJmhpC7WFKIHOfQjDwOBUQz6FyNArTBpTQKJKQ4lIBm8SN6lnY4QuGYZgiOI0zsjxUco+HAeVVWabSNJYARkBGVPaR73PgHKYOvFsUr1FhG7o6LodYlIGeoUkFnDoPwXEa6tusglrK5WvE4u3FdurLX//f/0tZw8e0FQLaue1yHBwiifRtjWfPv2M+u8WxDywJeUKvDWG48MjTo+OOT9/S5CQga7bgybngGT5d1syG5OyT04fgHPFN5XcrshPjSDnCCSUQTkgaTYzI/vfMVfM9m6MQQwKCojQDx0h9Nxs1yP5xliNw4vWt2TWJ2aSM5D8PoKw2e3y99MzoOFZtrkjMGGznFqOFWIpVAg+++XCQM0el6LZaezoLLMkHplcbQk6JY0gcRw2lfHGqYiR19+RpblmHUq3wo2SkuWAwZoi3ZDz35TBuMw8HQGW0nk5kzQpz4cpZy85bBD1LdZ7BWoH/X5S8i65A6bOwNryuAvazgsEcwLA/O+PFstLrJqLIGHoqauW2jlwnqapdd8aSxJD5dS3mcLus+onkiKgSvZJRcZR/19BzTQucCEPgbZzK1u+dIxJxmR0iFoB+mJI9L0O0JaU81xfcn1LXWWWLpojlmJFU1W6GWxZoyprMBccwdC2LYiy78lkuNszNwocV7ohsi3NRX9jM35g8h6OGZMxlqZtRyA0SRy74oyxWfJORjkJ5xxL75V5u7cjziOiRbS6yUOnkrKfh2HAeZXpsbZoo7qxhb9BQVwF/CaJxJSKTYq0iyWIsN93I35QwL3KV1jncM6ycEuGIbDd7YhBC+DO+1H2C2upWx0gVq75QyKRympUVaV7waBs/pyrIOBcRdu29INqqUvI+XCS3EGo7xVFtOCXZTCrLN8nouSMkp+UDkYj2jUkfY/zlrZu8n6Bynn2fa/rmc+woNq/1lpCMvRDT8FHhpABfJcBUANDP+Ru0TQ+r6p8ltmZy2bpm4ec13nrRjnSoRsIYYu1lno2YCylpB0aIsSoxD3BEEVzWZXaUDtpjKhWcc6BC374xx5/0iCtOhRFw1MKuRqZN5boAmTIBCHfdMxsE2trkQ53sLRtS5msJimy267Z7zY5gHJ5U2rlgAz8WVsqimnUrAAZk4KiS6kgo7Y1OZcTZJmSb61mFDZmZtuNlVbh6OiYvu9Yr9cjcCk5AXbGjYfHZUdRJA9Km4pzLjMEJef4H07k1GnUBVAuIGquWNnMSkrg0URqvdmwNoZkKtXXtdpGaHJQRzaKkhK18yMQMgKYohUikjI9EUbt2qL1YvIhROatNPq9ygS+8c8s+b7VwjJWz4pd0e8WgrbBjUl6AU1nAEqRGFDGhMJ+dlq00VFNnyt5YINgMu3dmlLJK+w93QPlwAsZwJLSUlIADH125S2lipfGFr4CfxdHVfaCzT9LdmppfO9UwKQcpJkCAqEAi04pVAeVvMc1R3R9ZkeHARGPbU5wzYrKt3TbAYZIaxwxBjZXW84enjIMgdBp5U2BK/LQuMwgn7Umpf0W2V3C8BZr97htxe7qnLZaYN0xQ2YS1o3F1+CiQXZagZO8eAq05lY7q/o+evYcEU3KY7ejPl7QrYMCuTLGUbfuobGOAgKlnPQftZYdkW7T0e/2LGplm6SYqGytLf3kpCxX6cWQ9WHJAKGepWSMamHbDPbn4Mj5aS8VAF40YlVn6uzIKi1Ps1iExO+/+Y6v7XOS1eTFlmJD1qnC6T0wAofNASeHR7x691qZinkJitaqMTa3P1mixBHjL4PyGEFkwM7a74zKRMxZlUUzbJI6mAJnFUfQosGqrvnRs2d89e0fGArbgjzgoZzhUkzJcjGYMhRoAgt17aezM7cbY2gsBdYsZ27GALmlS1gC5+nnYgtsblfK/zPuN0mqAVbeby45ELMt97mt0MhtiYvymvnfH3uM9yEnV4oP5uDVfYTBK1OLf+kwKetQpmqXz5zkUTSpKefL5M6Bid1xO4GA3IlhPmSAzG1nAYzHa8vXoTbXzPZSAdKZ/GcGhtV2Tu1R+cZr0mFKYD8NIpDsqyi+NLPd5kHovDtjTMRnTOwQwqgbPQ3inO6ZZNspSc8pxuCaiqPHD0iSWL+9pMLgjSXmroYgia0BF4RqLZiXL3l8esKq9mz31wiwagM1ia9/8zc0jeev/vq/ZH/1mhdf/h2HLdxcvKdqDjl7+Cnnr7+DuNbBHCLsux67WuEqlT3p94HL8wtWjePs5Iiu2/Pdix+AxGdPn2CN4eLigvsPHvDo4QHn5+94+fIttnF8+qPHrDcD3333ktVBw6ePHrJe7/n++UuWy4af/+zHLJuG7799TpDEFz/5nM2+57dffU8X4cnjUy73G9bbjscnp1A5vn33hmvjSVXFgXUsVzVdDFzuerC1Jv+5PiJJRh1xq2jGtP6WHEeZEQSZg+5FLmZk8Yvev3sHh3z24DGPTx/Rtiu6XSTGfrQdQVS6xhjt4Hj8+DFffnXJcrHk008X9JsNb8/fst3d4H0e8LVolWkSYLPZEeOAMZ6rzZbzizWfPDuF/oZ+f0XlDJbEfjdgnWPRrjg8OGToO8QEVu2C6+2W333/nKGqiJXH1RXeLPAHnkUImBAY9lv6/Z7tdkMKAzEMmJjUV1iT/ZkhKhmUIQpur+zXv/3tt5w9OOMf/fzH7LstB4dH/PJX/5j/8V/8z1SD42a34dX5hmjApMwKTsLlbkMKN+N6J4EU8nk1eq69VZ/tXC78uxcsVzWfPH3EX/7Fr3j84Cf4yrLb9Vz3W5YHx1hge33Fl7/5W5KrOD0+Ztks2G6uib2CaFeX12zWV1gbOTleUtVVTraVoZNChwqPKusoRmEIhmpxSru8D7bFOE+KPVFy6z6GJHFWJsoDTU1OPMeCgAKipUOmDAuNSVlqtXO6z4zGEc47qkaHmlV1PTJjnHcZpNX31fd0uAygVXWtKFaOdYcCBCZG+6x6sJkN6fLgIOtomhZXVZogZoA25qLmEJSVa73DBLWNIQW6lNjGxEZgI4ZeHAGPFN16RbJyIq9/nJ3YdCqhp90NyhSCqq5VA5bSxZJZecQMSEJIA76q8FVNpM9xsnbliJFRT3cc2JkSUQYsDm88KXj6zZ7d+prVgerxh7AnsWe7i2yvNzx7+gmresE+3WC8DlSq6pqh7zAY1uv1CKrJ+GWL1E6cCj8z3zwWTbOHYea35gysMSeY/5soOULSpIFaEnhNMZURWVWelMLox4qEgUHycKf8edkfJWSMSbR7UePEKMqmHM8q5DbkgmaWfC/dai0eAWHDqMM7gQqZkGBNUbGYwOFMOBnXSqa8qnyPMkC3dGe6WWFWkhZNrFfWZmHUjez0mNtGmDPb5l2eGWiGMc7DFKYuY7xkJed21o45dw5TxrxrTpQpuZsCdUxrkwkKZeBgITLM16A8SpwRZ7n3PI65y7q+C5Ddfd78OeV+lXNpncqJeO9nuWQBqJQp6b2CnTEKgayNmc+BMUCcxXJ5P8+vqaoqHQye2eZl7oDzGt+Pa52/d9M2SC6+usaNsgYmx9TWmFFD3holz7ksK6CgnZ6HMtC37IWU41wyoFueN+6IQnpC99w4NM6YTAgxSMyaqpKJazneTJmMwphTZKCXnC+IRsppCBijGEsUzU3KYK98AIjFVJgpvtR9qeBm6V4TYwilsJJZ+ynmuUTGMgwKYhZyQBoCxtoRAEV08KQxhv1eO3TEe1zuAnZGu06S6KyIUX86aWxdt+0t29R1HU3TYNBBYovlcoyLRabZTmVf187jjKWtWhxlLlPBavLSW0PlPN55hn4YJQMKScRZqHyDryodqu68SkhmjKeqVRbKeY8Th9iEWKNSBkCSOEpvVFVNTElnROTvNBYZMvtV10/PSpExNEZtt5CQmH2fKcznfD+CZZ9B68qrfN8QAlGgGwLOqY4yOZeZBsirVJTESBh6rPX5fKoEa0pZe1xUF/g/Ikn7pw7S6qOk3SG3ymsLSEksmVU+lFWp1Y1cGULwrqKtdQptlKg6X5IIuy1hv8c1Tp2GnmdiUKBOckAWS5IpSQXvixPMzivlfs8y1VvIzNS5ER6TX90cOukdSrXn4uJiBO+AbMjseOA1OJgMnMkVxzJYqNj4+VRsTX4np6CXVADPiUUEs0RWLbWCTLllx7uZzml26hMqwqi7W67bFKBmbOXNxk+zdsrgo/L8mIHPUr0a13a8r7crlDAxFFMsQcUE0BYn7r1V2nsM46TCfItmDtCMFfZ5wKTF5DKZVY1OAXkEQwh9bsOo8FYB6JTvUWHwleucNDRNBsqyYzHFsU8gkc3fSdm3uepXgCHJZ+EW+KDsTAVoDSkDuiJC27a0h0dcX19jckaswKVjsTylqo9wtCTW2JiQeoU7eETA4RtP3yckWjZXHa5uwQYcosPAJNFUyhqxOUgr91ATp4CxENYbZHuFM1tqttw8/4G2sqyWnzBYZa6nBMMo6QDGahU7pYikEi0ZyAmpYDB1i19G0maT12fg/j1Pd5mIkgsiTIH0uLczgb0Y5ATUBpqF5e26xixPIQ0gqgGZogZ6qqs0gWc5JiLEiM8M4gKmM+4l/Tfv/fj5I4OeAuwGxAGFzY06IJvPic0TQaPRpB+rw0skn9kognHCsl3gMCyrBS45jo+Pub65ucX4NGqw1A6YNILYZb8Wx1xi7jkLcgJm3fi9Ygw6BMRYIneG+GWjZIzq9R0tWirjNFDKBQRXzoiZdI2KrRCYzoSd2hN19+bEaiYXw/i50/PmYOJ4tnM3xhysZEzU8jBEPbgF76FpWoasnVXO9K2qK7mq73Orpinch9sB+WgbP2Ivy+MDpqp+oZJ/jGB2+bnspcIEKPeptClO33H+c0nWPvx8gLpSqZ8CzGJUD5sEo2THjAF8q/XTFBt3B0zLiU1JhpS5ooyB+XXcXatpvcr9vC0jIla19SxknfCEM2bcv2PCPVvXcu/MLGgeP0cmna35o3RDlHZR6y14z+rRffohEC43Y+G2fM5gE2sRTOhwnaW6Mcjhiso5hmHPbtDE3IXI1//h/+SzL37KP/0v/lv+9abj+vXXLMzA+7ff8/izn/H5T/+Mb776e0LSVsMUAiZBrAy7XceyWfDo8RMWlWV/c8Hb168wEnn8+CEhDrx9+5bVwSGVr3n9+g1v377F+5qHjx6x21/z/v0lh4cnPHh4wma34eWrc87OTvnsk8cM3Z5vfviBw6MDzh6c8P7qiq+/f8P9Rw/51aN7fPP99+yvdzx58ghvBl5utly2DYMz3Ks8nz48Y3FQ8dvnz3EYBlEdX0NUSSTQZEJDjukeGzXQORwYmRx5wzBL03Xds311SVi5mpXxrPwC4xq2aTP6TJd1R1NmkGuhwrFaHXH+7hUPHpwS0sAQB07vn/D25VXuCFJgK5t7hMR6s6ULwtffX/DrP/8ZhkvCsKfxgRg2pD4QsCwOW7bbNfvdDanf0lQN+92G7W6PYFXvXxQ8DNbi6hpbN/hFi5NIEyJDtyeu18h2B31PGDS51MKt+sVk0GKSEa5i4h/+8ANPnzzj5OQYXzUsFkm1U23FX/z6Z1zu/oZ3l1cYbxFndUinURktm+0f1pC8+q2EEp+jgS7pFOViUS6uOq7Xz7m4WFPXDV989jMOD495+eKCy8sLDpZLUhqIuwFf1awve7w13Fxf4l3F7uYarOgE+9ayq7UIenx6yKKpVQ6FxNDvEaN+LSaPq49ZLu+xOroHmY2JKT5O2wo7hsxmKgVvlazAmKxZW/pkdP9hpgKbRtuAUV06a52CjBm09ZXH15W6PKuaesVHznOAkjeqP7Vj4g4ahw9Dr/vZKPkjxphjKgEitbP6OdbkOrOuvLWWIbfFlm6MZA0ihj3CNkX2IgwYonEEYwjGIkSN3XJ8pWCKAvGluyKFhM1sJWttbv8uUjCT5JHq9Bus0XZgxUAFtzqgOTpif7FmyIlvSgnjoLKVFh5z6mGxDKEHa/G+xQSLt56mqdjeXLJa1OxWLUKkqlsWqwVP2iUPz+5z/uI9fqE63v1GW627/X4EL+dFuZR0yJZEje/mkgejtqikDITOpJWcy8zNzKyd+T8zu48uxwEhhAzcTzFRYaLudkPBIm8BcSLgrB+7NFOUPAx70o8ci8s5H5jiI/JMlKmz05hcyDG3Qb/5QzuNpnkco7+WzDIvVlamvHceM445pe5sJSqUOKUEk6LgPDl/TXm+SPHDBRCyGdgo8YKU1zNdV97243kyZlo7BWdm8HrOjxHN4cg+pAB5831hMulAYswDiewIGAsyMjfTneuZ/z3/+WNF+Y89/+7v8/s0j1kAum5gt93TLlusd3Shz/IXNmtm6t4bogJJes2SOy4sGG2Tt84rwaTkElmztQyPc85hvSMFXeAyUGuMjfKalhx9ZInmP0XuQ3WhQSQSkiibHIhWwZY4i+8lKvEsxDQO3hMCIar9qqtKuwDtBAwPwzDKqHhfMRDzoFirQ5B1g+s6Zm1yAFKWMLQGE4tDn+RGQgZQtVims1J85QlDIIzXpmsQU8CgfuD/Ze7NfmXJsvO+3x4iIvPht+c0AAAgAElEQVTM59yx6tbIFkmRFGdbBAQbhh5sQbAN+P8UDPjFgK0HT+SDZA5qkTLH7qrurqo7nXPPmFNE7EEPa+0dkaeKfu5sNO6tvJmRETt2rOFb3/pWVHkI9wOxZIyxYkcxJmKY4lJrBVwNQ6jvZcV4IiIl6JwOWcvTfiILmD3EWPevyD9JjlokQWVwvTwbIYwUbeJxHOtal/yt3+3kfDRvtVqYKESI3WZDv9rgnGOx6BDlOyUuag6XAcYMjcEjMmGmEB+z2KhcfIRxUhjMYpPHGMjWEU1i6Hta39B6j7ce2zlCP5CzIYckRKMsRS1npEvTZAV7Y2YcBhaLBV4Jns47ggkMIWjnytw2yPPQNm0FaWXInMVgyRFMtjjbSlfpGMml29SKhEFJfUEkVaWm5CDLQLUxiZifkIcswzAAYdK5/YHXLzVIK5hKAcecADZW2lAKKiessPLp8gDrguuC2JxpEDZoyhBiIqbArt+Kk8ZRha8riCGeQNDzwsS0Cgrq7xk1gnqOctIaZBWNikdJeg3QUGOMJJ7jONSKsvybtnymx4CcJVIGZ+U6XGaIskbWTkOqim8weo4hRZKCw4VGDrKPQhzx9VqlHcaWJDtnDdhnTKyMMAoyoiGpgYi0hOYK2tUBZ8VQ6BNc1qSClEwOSdqHpemoVtlngMjeempAVdhc+okKxMQcSEQZImYKIDMdozh8Y6y2hZXfAJGFkEQerRgbvSeNVoBMMV57bDC5/0UDx+i+ECKrVIpKQBS1giYfKQm+VNtt2U7lTul612MWzSk7gSGpnCvCOCs0/inwlOu3tsX7Bf2qJ6WAweJOL2iPT9kOa9ZpgOYI03Syzt7RLUWXJoaEs+CdUWZ6xhnUCWTCOJCJpCGStwNmTDQnFzTtOc3BBUfHZ0S3ZEwHeNuCc4zbyO5uR46ihWObBoOToKKAoNZCES9H9GWzQXTadltlL0Ac5d7leiOnfZGTOAuMtGm51rMdhCkz4smuY9cHwrgj55EUelyDtBSiTBW9HyZlvLdqf2QPOflpvZ+Tc64BTCzJYK5tQ95LxXEYwxTwZtX20W6BYmfMDNBPURy2S5BDILuG1XbN9e6O7BLPXzzn5uaGzWaLPr2iG2cNy8WCzXYnYJmZtwBO9qdW2OcsSqZqaU5RAkHrtEWwrLKR4rGTdvabzYp//5f/AetaUklwNbAuAGkFdss5qB0u8jYlMShrWof5PQp2S1pdkkdJcKeAfAIsHwfTM1BRs4uydWoCMQMj58WXUsXHzI45O355pdl6VhCKfQCxAos577038/17f5ZfeAyIloCrALKiT1a0tsUuT/Z8Opo1lqdPnhHGgZvrG7Wv2oaUJ13zPLngvcTjcVIxrfFUjKrXVDOsIv+wvwfnCWk574l1K28axGePMco1emkzMszY/GkCdh/r8+4D+FO73xwwlkBZ2UW6VskYGSR2uOTi1UtW7gO7mwea0klgJHbZ5QQu48KA3zpCzLw4PaExmWBG0vqWZY5sc+QnmzX/9Pf/Of/1f/s/8X/+b/8z6w8/4yCvuHn7Ff7TX+PZp7/K1eufM4xrGuPY3d9jDg754rPPWRwdcXt5xduffc39zSXOZl4+v2C7XnN9f0+3WHB0eMy79+/ZbLacn19wfHzCh/trHlZrnj9/zsnJCVeX19zf3fLy2QVPL55wf3fL2zfvePr0hMVywbv3N9w+bPj4k4/57POXXH33FvqR3/z8I276nv/07SXdi5dgLRfW8eXxIV1Y8+an7zlsDzn8+CN+ennNTovEJks3TfXhsfhkUzZ2fX5sNvvPl5kz9tVeYDhsPR1AH8hjpFk2eN8w9H2Vtiga2wnIxjLGxMHhMYf9jtVqQ9N1LA+PWCw8m9sr4rADm+teapqORZc5Oe7ZbNf84rs7Xr+/5eWTI8KYuA+3rNcbrPWcnT4j7jbcfhi5v7vE5kDbLMBA27XkbVA2OBIzhgHrLGMBE6zBtB1N03JwfEoaenIY2d7fMdzekYcAEazNkAxRqr9g4Ga15eFhx5OzC9YPG66urjg9O+bNuw+4xuGtDrPIDpttlYJSQmWNsedD+0qb63LRcHS0kKnX2w1NI+D3m7c3/Pgv/4pXLz/j4uIJ2/Ut47Dl/OOPOOg6Lt+/wznL0fEB3373C26vr/jss88J44YhDFgaiJlhN9C2hq4T5vWwK8CsJJwxGsbQcHh0wenZC2CpGvFRouQwSAKXLUkTfwGZheqZKPFQlqJc3XemxtfFFtTWWqst4dYIWu2cTH8ucl1qy0R1Q0BTb1wdImwywu5RbWMDVT/SNS3WRWzTkMZY5xEM44ixhrZrcI3DeKdgrsSnzonkxkRiSRo3IbqzZJJRsCEnnIFkVGu/gNNGfK03EZsSRBSoF+mC0WiBLZZ4VJ49qySPGIPocmfDuh8IMdIthV28ODnlzrwGI0UU67RQQmYIAzEJkabRQS33u3t2YYFp4PrDLSkGdtt7lotDFu0CkmNxdEzXCNDx5asv+erbr+j7geSozDHnZjmOPrdSbE2VgTiXoyqfM0aB+8qKkq68Pf+roKQxZtYmX6QNyiBVKtgoMzFS+TZSKJy6OqwtwyEn/cmUprxvT++1xEpFL7geVdl6zNir8qZ0g5VOP41vCuFDnpksnUpm5stn558QfdPyvJTOknLutbBqDTbpc1RAPD2Ngi31ZViY5sKuDIBCu7JyoWWV4xsdlKblkpKv5f1u0RgTpcBSYsB6vTlTT8RMheUqdxCFeIKRrsaUEtE6QkK7PLT9Xq+trPe8oFxy1Ap4mUfM6zyPt74P5v7wK9d8FYRBudsNjCFgERbk0A8Yazk9ORYwKZd4PuKsZ7FocTpU2BlX2//Ly1lL27bUmQvGEsJY/62sk7D5Z0UAM9/L+ySBeYzsjK1AYHKuksfmz521Vos7ua51jJFhGGoH2ZgCzk4zDUIMFEJHwtCrbIBRchsBnFeJxCIjaWTeTynOYGaFBrRdv891HkIYAyI9ZjHjQAijyEtYpzrahXwHm76n1U66MYwYjD5z+/jFbhxFjiMLOE7OtaNAtqmBJN0LzpqqnxvDBKamNEX/IgEhe8U62ZtlPbMyPwsmJPqzU4dvCKNCZTJs03tPGKUDwikTl5yJIVbWuzFGc9xMDKKJG2PE6jMm+14A4TiKJm4DgCckWRecVQ1eAfmdd+QILR6bwQeVngxZEvpkqj80YxatdYSwQwpV0iHnjFHnZpMMsAz9QA4CYqcyS0W5UqI/DUYH7hm1NQLMynBQk00Ftq01tK7Bm6buT6LBZYu1USWh5D5mHd4XDGCsyL2oVnhhRVvbSbfE/8/rlxqkBRjjIEGhqJ3TzILsossZU8S7Yhzke6IjaDFECJlDfyC06YRM6TNwu1oTUsZrwpmjDgAxhhgiTvWlnLbp1JxSk7nS1lsco/hMg80KhjAZrLlBqsm7Ef6D0wd5/hLHzp4Ri9oOIwZWmJPZTv9enKotBpCpPTaWB1MBj1y8OxrPG2ELWgVhJZ5QQ1sGsljpqa5VTl2QkjYVUKyAkCYXsX44WB6wXq/JM8da2bsV6IASiIQQSDFU4zVnn82/m3OeBMEF0aSCyAosF9bw9yq/eT/hF7ujgZGpB1BQWf9EGH/eOkoXTgHhiiB2zjPNIcq+mRhm5fynarUEviHNAilmAWM18ALcToyAucFUEW4ztQ8PQ8/VdkuhKlSQhUQYR1YP92zXLYw9uIbu+JiFT4wPH1i8eMVGk2eLo/WOxlGrQMsDGSImXS9S7a/6UFFAzzgM5KEHY3AHT2F5gG8MvWukFTE6svXSkrjtSesHvC8tUxnbLqsGpEhLJLyRamy0IgVAHCEn0ZcbIcfpPtZqZ3mZAuyoRky/g9wQmgUxOWlhDGvCdkXfrzAMZMbZs5TAqSPN0j7kq5xGvUUVPJsc6gQ+CcaswboGf5XBUwIMdR45Zw6WS4ZhEBan4FlasUTbMoXhNwwj2uMoyWU0fPhwXfVSy3NmsuVwecCvfPElHy4vGWPg8sPV9wPFXNpCY907GFuLEcbsM9ALSFJsBNryWGRkshfN1pJ4COxFWamiIjM932Zi9k92YbKhj9d1j4Fazg2jRIjvg7nfL57tB8sFy6zPf7mx8+002xdZ7V8BPn8w7jamts3V4pe+Pz8meWJt1H3Dfqv+HHScs3LniWdxhoX5YIrNz8KcqUlfvQ9yzZvVWgaVKBsG9bPz5OPxBOOcVaagsgD2bicl2aj3ol7bHBBVUD7PgObZGgh4UtqryjMDJDg9OiXlzN39nTKP9m9AsZnfS5SYntVSKHj8GaDqqhu9fzkLyykRaJcLTl4+IY4jcb1T6SGxg8ZYApkVids4shgs280Oe2Cg66TNfNzSNA3jJvP13/xHfv2f/R7/4r/51/zJv/1fGO+/Jfo1b775CU8/+pyj40M+vHug9ZY2ZswYWSS4efeeq8tLaBzL42NODzvWmwf6fsfR8SnL5ZLr62vW2w1Pnz2nbVquPnxgtdvw9NkTnG94+/aS7WbLi6dPODs94c2bt9ze3vPy4xecHB/y7Xev6fvAl198RrPs+PonX5G3W169fM7Vw5q///oNg+84dY7jtuFJ1+B2a96+uWJx2PLpiyf87P6eLkcGHBEnRbWcFMAqxXCmZwRl9TEVXitAr8+luHxT99jCW0wOpByIMWgQPB9EI2y2rLGCsDvAWMfTp8+IYWActiQc2/U9Fk+IVmQP0kDjGxadZxwirfccdoa7m4G/+4f3vHr5O1i/pmAF47Bjvb6jCwnfdhwdLEhxYLvbEJzj9PgIe3sr52T1WpIyOXO5LpW1KViNbbGLBctuifGezbsr0jgIDSGXeDQSYmKz7Xn/7j2tl1b0+/Wad7d3vLleYf72K9Z9T7JOCuva5ZO1pVieVx0SUlyI+i3RgctgZSaCBEOiwxrNwHdvrrm+uee4jey2Pb5JPKzuscYJ61PbaM/Pzlk0npOTUz7cfKDvNywXB+TsSMlgbQdGOth842l8Swgbhn4gR0/XHXN8/BxrD4ip2HOJv0OSNTDZMEaIubBogxQFNDHzzuNw2rmmcjdZ6oTeFWbYNHjHFvtijQL9E2CH0bhN184YBEj1TpNtjUnS1HFmrbDHnLfEIPqfQxAANJPouhbnJe9p2ga8HE8GFUumUYbBxKSa8sZo3CebprSR5izsMAERiw8wNcbNQDK6A4whG+lUqKwiV6JVK+eQpm4zmaItEgbWO8gQjcEtlxj1F4OCpMaDsK9kQI4rWpEpsRm33A9rlosl6/WO1f0DD7c3rO0DzfIA17TyPdfgaPj0o09Zmo4Qe5KVNm00Jiv3pcgeFcYsQHa+5gXAHgNQcJKo+9/irK/fLcSSzFTcLiBwzbdSIV/InizDZKqvi8LOKz4npSzTyNVHTnJwZt8X5Vm3iQJaU38+6kNFA7foBJusw5CLs5OfFHJNUg1XvYmPC65T7EB9v8Z6et21U0x3Rka7GlKuElvlvazFd4kRps6s8qq5tBEGbwHWkrIsjTIAy33L6ouVPFhjjKI9CvP4ohSvZd+XPVFjw8wkGZeT2BPjME51PVOuv43mluX4j1+PyQTztXtcIJ6v9eP35Pmcis3G6vAk4ypTfOoMm5EYrNP7n7Q7TvZwASaNaFjU7pQ4jNimUXORNH/WPFr9b8qREBUQVBs4z0+FOb5PnnDW0igwaIzohg6D2IBlt6h7Ls/sk2+8dG+kxJgDLgs5KI2xgjAxCmDbqC5oie1CjGQTGcaRcRhVC1V0R62C0WWfYQVEK7NKxn6ga1tp7R+D2H8dHGcM0vWYE4wDMWa22y05ZQ4ODvCF5e4cIQT6fqg2uQxXL3vW6RA0awwmSYFreHjAIPfWOY+1jq5dkFOm320qSGqU4SpD16iyOjFG0eVWFq93TqUkJqkOYyENge1uVyVa5Hy8ytMISxhkOJw890avXQyH5G7yv5gScbedcIiUtX4p98sZ0TwvREKRf0hgIkZlKYyJWOcEcE9C8EsxsRtGuqbRZ01m62QrMikYS9YhayYbYpB/y1Z8UJ2zlNRKa+EpxdIJKevvVb4Aq7KbMaikhxGg10jnRIhRQGKV/EhEQpBralXuwBpQoXwBYhFb54zo1ws5dCQqduSNw7cNu37A5CSDQ/+R1y81SFucgDUOwwQSVNaEREBqNecglYBR1ohQP2Om8y1g2fUDmCUZWK0fyEGcpbyy6gmVhBNyliBKgDgUZZ85zpLblsRcjRramgyzlnc5S6ZWp9I6sF+Z0wPKZD7nqlMpx7eptP2JRo1s/lgp29JyX2qRQq0XdqwyQ9VRTYFCrEZrXzy86JmoUdcgsAjO2wLiZX2Q51m53qchSuCxSRoYavW3GPMSjJRg02RhRIUQ6Nqmfq4Klhu5PtBzxQhIV25FFtCrDpoz0jZgtJ2rDCwpp5qLJAQT4CCBlwK7dgKMZD/qdSoYW6ayG2OqIyrHcG6SnCjHdE40VVN1+AIaphRE+0n1qDLSrjbDM2ogXMEgO1W1y/UZJgaMUY3YGIKG1UavK9N4R+caofAHYaa4puHu8i1513PwyrONAoI4Cx5hVwQjrUmHx61IEsQkH0oG52Eka8uBwYwDKewk4PUtfXNE7zqck8JKwJDwYvjGLfR35AFybsBLW6HoJcsVCyCtdy5GchwxaQAi1jWs1pCS7MVs6iNCnv3FWGgbcXLZLPCNMh+C3CebAzZtgSAi+ymIFi2TYynDamSisTgno1qVJTBPGjzLJExbdYOFRSr3rbQQ9cOOUKeoTq1HKSWWiwUpRqnClR1TQbCMcSLHUpP7DK4RdlQ/9GqQ0Iqt7LNh1/PNz35Ov9uW2tee7alJDPPNp3ttMlQ1wUD3X2FHRNVX9r7BZoPORFF9SQnIYk7CQFKrOGmdKYNCtUol65iC6sLknOs9pxRLNjaL9yeQRz6fZslBKUZRj7EHCpYHPc8D8FzBw7JGcvklkZD3lPCxl7BVIBuZVrpYLFiv1wWhLJlFXeOyP9Kj75fPTAMVkEq33qc5s7feIwrL11YWPjVRkdecVWKAXb+T8/COFBPeSphQArv5WpWjmNl5lkQgx1ifwWLrpGig7Dyo1yL2Wi2z2nija1aTl5K0VWBc9v7SN/yP/92/4v37S/7t//V/VH85nc/UHvc4ISr3sq7GLFGtbxllc6tvMeU51+NEC83hkqMXT7j79h1hCLTWg5UAkJSJJrO1md5k1kOPcWBbQ+NaxjSwWt1ycJTZ3b3jp3/9H/mN3/5D/qt/+T/wJ//7v2G1vqZJa67f/pyL5885f3LBw80NjfNsd1u++8lPSW3Hp69esd48cHtdphp7zs4uSMay3W7IZJ4+eYozlrdv3xEzfPrJ52yHDb/4xWuW3ZJf+eITXI68ffOWfgh89vknNF3HL759A8byT370BTFHfv7VT8kWPn/1nNv7nh//5C1h2fDq4oQXBx3nhx13l++52m44Or9geeC4ev0NIVo+PnvJL+53rEOmTHXKBklwYsTqMDlDYWxnvS/T/ZjfG7IWLlLCELE54NRGDzHg4qA+NmoSrsVrnWZdJHqc9Vjf4J2j7we6xSHEwHJ5yHazIYdMCGJD2+4Qu97ReM/Zacft7chf/3/f8Wtffsrnnx7Tj1sa7zk+PmD1sMUaj7NG2vGTdHK1jeN3fvVH/OS7P+N6vcItj8iqB5pncZvICeoQDEHPMDiw0J2dQ8qsLt+TQ6zXY8pexdAPa9abG1zTsNlu6UPmbhe4+Yev8a0wQxOi92adkcnK1YahsUSxSUk7hsUuX93ciA30hlGHe5ItD/c9D/drTp8t8BbSOHB5+Y6uPUDDd25v7jg4XHJxcYH3DZvdhuWi4e72mhBGlssF3h/SeEOwkaPDA46PD7m+fksKntPTZywPzmi7A4YxMo5DfX4tCZwjOwfRIBwF6exodcCwDG+xtF2HGydXV1oRm0aBuSIFsFdIUBuHaIg2yWOttKMmI3Mkik+ggExJSp7eO4yb/KrucKpm5EygznlH27a4RobuxRgw3mNzxjaOdtEKoUF1QMWQWQXzcrVrxjgBnhVES0nnRWTZUo6MzVYILNaSrDxz0UhHnVV7KowrAS6EXaQdEmrn6p/anRPTNHwlp8R27OnjQEiRhSuxuEjG9WnHuOsJRAZ60hB5/+6SD+9uWD3c8PBwz8P6ni/+6a/z+dEh3fIJQ0q8fPkJx90pm/yBSMQkkbkoAEkhMuS5P6ntqTMyRYkxrQwZQu+h5EjqUotfLc/C3I/MfEzxvzKktehkTt0YFUQsrNuUaNpGdYungWZlPzpbwBId8lm6RTPCAs8T87SAMpJroODNRKKRUxPJBlmPWZzM5BPluZfW4fngtOKLczayl+cEGs0/RV9XhstltUUxCEjjrTxTEZHSE18tuVxOhX0r5BvJ2aht/AUcLTJ/85bksQZfks8VELV0c5b7N+8IKq+yfrIYCpIimqW42ec0DjR6D+bx4Jw4MD/uHCT+IaB2vq6P/z7FIgU30PwiCfgIWpRA4zOsaF6jLEO9pBgiYwokG8A7nJEhlAImJaLq8kPWQVQeDXgrASzlJIMkc9aBWkrCQApd1kkMX6RaMtCPQ41l26Yhx0zTisyJ1+FmoscqTNwYA2McSCHTNh2dan3XvFnZ0nEWi4YQaVuHdYbGNCR08NWBdH2Spw6YMEp3qfXCxm0ODrDeEULEHko4EkLEdgvKrIaYpXXeekfbtZASwxhp207lHKSjuWkbshWJjKOTE1KKjGOQnaj3MSaZW9I4AYydDgLu+57NZkuIGWOF8d8uFhweHtG0IqMQYmAc5f+F7ZqjyDC1XUdOvnZ6p5wZd73YBO8Fs8rUax9jZLteq2TBQuxdlvsZU5TBYwWzQcBgYw1NYyuBJMbEpt+InbUWb+SeWiMJX7LiG1frFV4LAMYUXWIqrjPteek2iTnSdC2bYVc7KkH9VCPyetZIYXK726ptkmKiV634MQX8jLgY+jjlKCqVNMag3eWJo+5AijBKaHTeVE3mrAziMI7VNodxwFg3zepQGTiyIYaCFzqRQjWGvpfB8jZrl32Gse9FRjFOw01/6PVLDdKSwbtWhM0pbB65mpRF0DiGgGvaGsEbY2RIFRLz2OxwjVR2u4NDpf0bUhhhu8aaIIGc1Y2dgjyQml5m1FlZqgHKJdnXhBptVclGgDCplluZUD83ylEqtDFKG8Lh8pgUR3b9QKF9z1lhhtLqkdWAJox1WNwMCNDfj9IWXRyXs8KagxKUFCQm6cKoo9cKlrTiWgVtJHAselUpa2s1pQVfgacC9pagcpYAT2wp2cBDkFYza8EwH5pGTdYTgseIExXn0HXSbr/VqeU5KyaozkqSrandsaTbUSstGpnItVH+vbBaVWewJt9UYAQUWC0DBzT4wBqlzk+VMfGnxRkXSuDkGMr9L3pY5bPlPocooKUwgov8w/TUzjUwq+5MLuzgkszOgBtjSHFEIgzZxbaASlmE+Nu2IySPb84IaS2Oxnjicok9brndJZI3NG5B50UPNUawvmiZmTroQC9fE8RMygaSxYwB4ijXUtqry4OJrm3OkpguFsRtR04Dy6MGd3LAFq/NrAmn+6sWAlKAvoc4ksn4boGkZrr+mmhNq2gq+BPGRO4Dy8MF1ol2TAzCLEg5YPpriDvSbmrLyiljmxLYJUyKeGNovEParpQJWOjFIPp02hoacpoCxQooyp4oMiOU+5epRYbrmxv9TTmuDG6ZWPpkWRs1NaIdPQy1yk0JwBWgyGT6cUc/7qq9/MHKfnmmdCfmlFkul+QsLVYYU0G8LAa5Bu+lNS+lKHtRh7wkjKqGiH2UWE/06+bsSNA9VPKQnFW2Y9r3lS00u7clI81ZNbJMrgy0eo16A7I+ByWpmQfF5XmuO6fY2vlvmsL6LBrTWYpyZkp65oxXY2SgXNeKr8q1AIe2bVM/t5dM1RWZ3pvfK2OmD82HX5RrtTN7hPqTx9eyl1hk0ZPOBpyuddfI8J7drKWt/EZZu2ILk56n0T+Lhp987xFQWi9J9aeR5D4LQiRV7FxR73p+sq9lf4m0TuTf/T9/zP3DQ71hVoGYlALgqjzNPEGar5UzdhZMlz+lwo5BB6hM4GwtFiCFtcFY7OGSg2fn7C7vYEwVxLHOSuDbeh6yIQxbzkzAesPZkRemXwoMYaDxnoerb/j7v/V8/qPf5Lf/y3/Jn/7x/0re9qS0IhvD2cU5i6NjNg9rGt8yDiOHJ6c453jz5h2r1TUvnp5zdnbG+u6OfrfBtQ3Hp6eYBLvdjuXBAccnJ5yfP+XN3/8Dp6fnfPzslH635c2HD1hj+fSzVwxD4NtvvsNa+JUvPqPf9VxdXXFxfMTpxSlvbh74q59eMraGj16c8vnT5yyt4f2330CK/Monn7Eaey7fXdIcHHJ+fMrNrseGHm8tQzaSuDWWJ08u2Kwe2K43AmxZ3d8pkbOdQJRqs+TeZSPa3LLnM94ZTk+OAMNqs8Uvd3VAyTD0DL0E291igW87TfgQ4C2XGM7TNi0HC8e4veXm7kaSALeoOoD9EBnDSIwjTWNZr7b8+3/3Y55c/D7OwW47kqKczxh2jKteWHney6TpnPjs4xf8iz/8Tf7vv/hrrre3WN/JpOws15yC2nzrSDlMz3iIYDPetSxPnzA8bBlvP6BRKqRMiJmTwwVNkzBhhUktR97w/PyIN1f3PKxlMjNOktkcM7bxLNqWvh+k+Fd8iK63mIpc9facLwN6TAXBTTKkkInDjnF7z+3Vd5jGct42pDiy6Fr67Yb7h1u8veDoqGMcNywXjhyzDKslYwj0mzW5acCPfLh6y4drT7/LPH/2McuDY3J2hDFKcVvbCU1OkERbvWlksvZ2N0rs4BKZRrRCI3jrabsFJmy1ACl+2VUdVqP6lE7Y1hhlcHmVTUB1NGUdjeicCAibleVnMjaHajMK+zGQZmxJHXCUMrutFMmK1JcwWjUbx0gAACAASURBVAGXSdq55xvHwekBi8WS2+t7+b514kfzBCBni4B4SL4bUhT5DGMlhsqW7Iy0qqrNU34hNmWSlXtf4v09dmcu/hlqtdcajHbLJTImSa+PM+LzhzQyEmTCPJbGOWI2DHFkN+wY+x3ruCbkgYPlIZv1muvLG37rn/06zsJf/vhPOfYNLgaG7ZqbVc/F02dcnD/n9eWVAnMKWKu/KGDAnNEIiWxLXjSbJG+o4J6htF9PQ30n/yGfqbF5Fv3DtmmEjZezFAlKXkOuhI2SGhXg6+n5GWPfs+n72uZdi52ga1dyquL7k3aymf38zs72XelaNIZscyUFmSQxmskCvuQsHSLWiFRKBWSz5NvzXKTmvRXwQLU/NdbSdmerrdPGWHa7DdZmXOuwyVYf7nGUAWs1pjDCWHPMuyWZzkFztJSTzDIxZTaNxZmWnKMQHEr+XtfRKKOuyONQ72G5rhpHYnUOSwZnMI0X5miUeMPWYsj8u/vrM39//t7jovs/9vnyqvutBohSmB7DiHMqlZKL1rrAOaPuI9eID/PWk4Ddbstm2GGcZdEt9n/XWpUEFMZfmQ9T4mOvnXDdwVL8pQ5HLySrxGzGijHCPLcWs1hofir5jyNXeRCnAH7XtfWZSHr/xLbodZuil2zoDpaSM6dYAclxHFQKDymQQR0q5XRvhaLTakzV8G0aXTtvsZ2dzehwDL2Qf4yV++4aI3vByZybthVCRgxJBxwrCIjBO6vxRsuyk9xgDAGMyqiQWTQC0DonLYfLruPo4FgKaTEyjiPWCNN3sTyQ9chF0zsTg9yjYRCZyq5t8b7IFcmekg7MtKdlfbBc8PTJOTHDZr1hHAdiTISxx+BofINNiaOuUw3esbJrYwz1GXHO07YLFu2CoMC5zQjgqH6z61pM7mi8ZzeMKmUSGXYDxnmaxgsQGmP1IwXwTTnhG4kHiiTKOAY267UUhtQWCgYnzGNnPJbMdrdlvduwaBvZP87JgLMo5KBsjOS3MWO8MI7HYaSxDcM4sN5tMM7ReC0uIvrryXk8kGJmHEaGKM+SMYamdFMjM4VijCwPDsgWhjgSSbWrp+Bt6L22xjEMPf/Y65cbpDWAtsUaMzFDxzgKUOgMeMhGE/w8BY8AxjiERenwbYfvFiwPjlitB2KKEAasS7hO2mJDEAHq0lBhrdUqTJzbSNxM1D9WxyuB11haEpyvg3FKgOCEiltp6DkEYcCSoTobMzPcyuAxVgdqlHS7gI8FhBAIpLSJ56RBWJwGccU6hVDZVkkYkAanLTYOy+QU0TZqmcooSSbGCuNTE4U9NhQTyCSDweQ8S8CTFRgu3q20YTvXEOOowVDxRcLCEyM0zACJAv6k/WBx5sBnnGQKkJVzCbhSvaa9LaaveeuS7J/pXhRN3VoZRVtjrFbbFRQoRyyD7IoRKueZUyhnhingn5UhYTVQKCcmyEzVaarBxh7QUICicp5ikE/Pzni4WzEOAe+noAssMRmGABmLXRyS8Ziuo2cJR0+wR0dSTTTaJiIIKY1vdKKlyAU4p03rORGy6GmFLDIkKUvRgZiAiDFSlXZGiZFZ5ApyCiRroFviLj7i6NDw/GnDwxbGh4xJlnE3klt93lPGmoSJgbTZCBDsPa5rhS3pSgCla1kBoQI4WpK1GGcwOdHkTL/riaGlcYllXJG3bxnGB8bdSiaZGqn+pSygY2X3ennP2Wnnyp6QhGUOxJcBfYW5XezKEIQ5LUwVBeaS0JeljawAfYXJOYGqJWHWpkaW3YKTkxPeX75XUNjWZ8LUXUcF9uZsjXngbbVCWJ8R3VtlHzvXUG2PNLhMwWcNsB5XSXXf6kaszKw0JT4/xDqYA4nzf6v7X8wfbSti7yEGvHW0Tau6UEhrjHYEzB94KezsMyCKvZjbiKRJT9lHdXiaslnK2sntKLZoP+Auf0Z14FWCQr8zgZZT0P6Y0Tlfk3IvHgf0xQeU4HQKxPcO9b3vljW2zokOYUrEHDDGiKaVBlJz4Hl+jvP7UoZJlOudzkPZMjnX+7l3n40EopFpjwbVicqzZ7kk3gUgGXLk55fv9oqc5Xrk3nxfc7myWsrxFJqYkXkxBg2iC0j/6Psp443asSxs+uXZCR7H5uoWUsLWqpLhYbdjh6EdA2NuWTqPx3G4WGKcpw87msHSdS3rmzdcvj/l09/4LTb9LX/7Z39MHga2d3fEEHj28hUxG7b395Aiw8MtP71+z2YYePrsBZnI5fUtKYwsuyWucQzDQE6Jpltw0LSs1itW66/55KMXHB0uef/2W64uLzk6PuT87IyHu3vev7/mybMnnB0f8XB7zWqz5vjkCN8seP3mlr/67pKdc3zx8gVfnJ+S+g1ff/OG46OOTz75hE0/cHv9gYvTc2zT8vrqlnsy5xfnnDQtb+9WjCYTItxe35DCSEYZtBrmOOvqczVnX5RBnKVgU0pyi2XHixdPOVh2PNzfc3R0SrdsaBtPiIntdoVvWmWflH04xRRkR9sssN4QhsgYnIhLWbHNMWV2/Q5I2qViOTqSz7x+d8uf/vlP+KN//qt4A8N2TSCQk7Bgm8bStgvaxTEtB4SHB373y485PV7yF//wC755+4EQIY2JMVthAjlHYsAYYTYKINGQTGYAmmBp/BFDusMSxOXmzNJZnp0f4EiMu5FoRrxreH665Ivn5/z8zTXrccQZx8HRkhAGGRLVOMJWnlZvkOss4WMFDbPErzh842o7cooC9jnn8MZw9+EdDzfvMZ1nu9lw8eQFv/97/wWb9Zq/+5u/5P3b14Q4st1s2GweOFgsODs75c3b7xiGnsOjJW3bYBvHetuz3qx4/vQly+VpJS5kLQBntKvHKDMrCCAzhszN3YbdGKTA70pXg9zvu/t7zl0jID1IEqdFTmOViWkNGBnc5ZumDtFJWkBQM17jT6vzGDK5atQX/ViydF1Za5RXUTRvpXhYANrC2jEKflpnyd5jvcd1Hd1ioSzamW0yEpPJcZJMEUeSUqwRcFQLwilnGmu0y0VbMm0m2CRDwCg6lAVENpNcgDF4pgnhtc0ZEAaqwRmZEdAeHpOdZxwGfHl+jdHuI4kgnLH4xrJNgeyXRNNinWWzfuDdm9f8zu/8GrvthpOTMxrfYTQuzjlxdLTkybMnjN+OmFaOWQo61Rdo7FGLHGQZLPfIx84B0tL9lpOAEjlPAC4zX1jWftF1tG2r7d2hHiPESMbq7zHFIBm8MXx88Yybu1tWSkSZ+yn9JckVcslpVFIqaw4687H/mKxP6R6YgyClm8haaR8WIse092UAkXZ8mv3rfuxLSzwhHVBz/yvnNsWW8lyU71c/DLWIAflRnDGLhzROkBxM6QpGGbhaMAeN38wM5MQosCPgtHX7A8BK3DeXAywEith6QsULJY4n7e+F+XEeF+fLNZb9ML8389j3h+Lf2YFrXDIOA8YcVrCzDH86OmxoXKPszkQcRoaUsa3BeE/TtGQrMjDzcyrnaYxRTdepEBpjFJ1/jYGdl2c7G9m7kwSIEYBewTNjChtdrycJQ7OwfkXCUpayaDN77zWpcdRB5dpVGEr8P2jbuZHuwJwzre20GyZO+XTNVyyN8xAFaBZbJbrD5TncbLYq0WKxzktR1DuG3YD3YptsEl3WEKKyXS3ONoB2SYD6HpXwSBMmYjDCGjYGV9aWTAoBm6V4DBlnpfkqWUOz6BjHQL/d1VzNWenIbBsHviGGQONkPR1O1k73VdHeX3QLLEWSUbCecRixxnFyeCTM3hTZbtcM/ShDg4GmbcX/AG0j8qI5iZRD6VB21tI1LSkGJWelioM5I4xiawzH7TGddhmnMBKDDLUT/FTiXe89Q46QEuMwEnLCZfCtx7et4EE5cnh0JMPiwiB+0zp809A2rYaIGb/bKJku4NoG5xsaI4PZxKtltmNPNJG2abHG4rGcHh8xxiDKTUbWKcRRxBG92lwjnf0WC1lYzCEGRmF54fKUn6y3G7AyLGy922GsFVJFjiKTEMtcmkzOs3zw0euXG6RlMopiNKzqz7byfg6AJSvAqXmWMkkttgjfx0SKAzEOBOOwrmPRHWKXS6KzNBjCOIj4PbmyLgoLqRiRPZ07U1iLCuqlhEfaO2KWIQXzCqE4vUSykzPrw0iuD/YEFhSnZRUUkDZTaRGx1ouOyRgkEPG6ozI6OVCdCNLOk2JhjU1OgVLxEkhfnI2y3SSiLIuZNLiRADJp0l7ObwrKCiSqrzwx2Co7QQEm66wCjlJJL0GFJOAAk5C8tY+DplyTqblTy3HGUkSguL0AIEvyn8nCeJjwl2rU5o5zPu2w/NZjPcgpEImV9Sigup6vBhNFsBuELStSZqaekwS/tk4YN5i65mVFy2Rx2YP7vz+t/AyQNjLRuAyBk/OQ+5B101ocaQSbPMYusd0xzp8w5IYcG7KRymm2CAihvx1jImEZhlS1lCPCaG+81/PXvWSVVRq2xGEnAKXNmGTkWdEWiSFkmfK9bEke7teJEC15syatt9Jt5M9IthEMNg2wvoPtChNG7HKB6zrWu77q+lVQPJf9PW3S2iqdEt3SYxrHze1Il3tOzI5duGc33hPChuaoIaCVeQXT5RGypAgDkeXCVWDSlP/JA1KnlxoNXCyWOmSQAkDN9FQrwClONYTwvcCtdpaVfVaDOdESEga+fqYkadOGn1qMZsyO+YC5CqaWNdP/D/1Yg9cKOpMxRgc2wEwKQgPdel15qjvU+zOBLnMWaA1QNajOGlQX9rupRzIVICuvwhbp+6kymdW2ZDMxUjIl3p8BsLPjFBZZhbdVE7kMmCx2qA6VLI9ifW73Qeq6+mZqvX/MYH18DnNAvbz7GFgvhbIC8ma9b3N2MCVZzfvf3wem//FkQcAQ9vzTPAGcg7JlTSaA9Pu6egV8mA/aKGsQk1a6UZul2yCTVWuqHHsC7rO1JIcAEDELa5ySeNi983sMTGeVyqEALsUXP1orSTSUHTsHDHNh4Wo7lm/ozk5IKbN5fw39SEqhyrSMwOgstyFyPia86wlkDpdLbLaM40BjPc5tuf3wNe7A8+qLX+f27VvefvN3mDEybDYMux3L5ZJ+fU+KI+Omp7OWZ4dLYogYL4Vpt1hAjmx3PU3jsU6GIDysVhgDx0cHkCNff/UV64dbzs/PeHJxrgMHN3zx+Se0bcu7d28Zhw3Pnj2FtuPvfvGW93cPdIuOX3v1nE+fXHB//YGff3fF2fkZL56fcXt9w7ofeHHxhOwsby6vycby0fNntEeHrDYbaBtuQmKbdKiPmQaBWWxlLxdwfr4vo0p9ZHL1iyh4nmLk8KDFBf0eovUJhtOTE9HuTIGM18Km1YKrIcQRY7xMk06Z45PnnJ6tubu7Yhg2xAQHB0d0Xcvt1Wsa5zhYZj7cbtnuMj/+i+9YOM8f/cGXGEZIUYL4nBh2I2P/wGb9QNsuWC5ajG/47PSc3/jv/xU3q5Hr6w+EZNmOidVmRwbabsluu2G73RDGyDgENv2OzXbD9mHFeOyIDy2xN6QU6LqGT1+e8+zskMzIYCw5RcL2Ggx88rRl0T7h9fUdmyHx6uULVqsH7tYPbLc7xjEoy85oZ0wBHjNxzBgrPiMFkfwpsYzVGPL48ABvweXIj758xeHJCZfXD3RtW5mirz79ks1mQ7dY8rOffcvt9RVPL07omkTXQkwGYxPYgZA81nc8e3bBkyfPhJkeg8Z9BfTJpBylcGoEMOj7kdW657aPxEZYQtFMbHyJmyNB9ZGNkYIsmmRmgwC12iVRNePNbJhY6SzLChRZz9SZpetmyvR4g8HKXizxgKaOkIUR5fyePbVOOriMd0RrsI3o3BVbZmteIonymLIEbkbsXkyJcYy1C6A4P4nFRV7DIFO1e58IjbBrvXHgjErq7BforF6/9b7OZMhZGKVGW6CtkakgrmkwbUve7hTkiCr9ZEhRhucZY1m2LQftKclYohlYjdf0acX1+3d8uL7i6sMVz5++5PZuS3OypTlacHSwYNE4Xn36Ef4/CJhQuwQpl1o6ACfgK4MkyarJaUyRYAMBXmb5RdZOGfWlk++Y1qJKHaT0PdB0/p06T0ITfrD85OuvxG9rV5FBigNzkFKnUVAISNaWwTuqS6lodzlnaxQzUpmEAhAWXcbix+oecgLUFmBT/k0GRUkRTNbFmGktalfrrIA+xy0n/86ezxSZPI2WNffb962av4RQ4zTrtPir/15jlKyzYQxVzm3+O4rbUOQPnPrx0rm2F5sYlKikYLISZ7K1ypjLCpQaymDivbx69t/zP+czA8p7j2Os+Wcfx0tlD0xrrcUGo7NbkujOrtdrDheHNe/MWXyqdw1lULW1antme3F+TqLJHCn55Pw8Sg4DU/G6nE+RmMwFLwAFTEtOKnZW9DsNxkbFAEr8mLG2F/s7YwdPxxcb0w+9gL8zbGU+lMu5KWeKUeQGBis6utlPBAch3EzX3fc9eVB7bZzahKydCQaTpBsypIjHEHIm00uBS5+PqeV9rDmZtVZniBRMxyo2Jf5pRMFpEt41tXAge0I6osdZLlNyrwKOl70zhhGIel8MWTVppVAnMdIYpHPG7DJd06lEhWrb+obSEC1aszvFEabcFWtFE1ZlRUIIxBBofYPJmcY43YsD2QjbNDlH07V1MN2YEq4VaZKUMo1q8Bpj5HyNwXuJ40wUrIBR4rfGOnyzFOnE3il7VuYAEUROA2s4fHLIk9MLdtsNo85iao2jMTLgGmtZua287xotUFla62XGwMFSmOLjyHq7FQasKwl1xiRoT05JTggiYwjiA5Eu/taLVEg2Mmcoai4/lkJ2zuzGofogh5+bze+9fslBWoOxXoCGnLDW14DEOo/BMqaslf1pep+JWXHGiEF1T7JMkouqebp5WNH3QwVcyBaLEw2dJIupcRrGOBXQz9XhGmvKeAVSTjTWctQs2KYgn6s+XT+PgFxSEXfVADkng7myMmJR4KQ4MjT4zTmr8HoJKgowVwTS5e+lxYQsbUZY+X6tSuFJ2ZD1+CZLIBxzAYUlsPPW1yR3n0Fq6oCs6qCggs3FTdbuJ+vEkTpIeuwi7FwroyUgMKUNBdnkufw1zxwdMzRYz1nBdHHa+hm5sRRNYxHun6rEwPfYsVN10dV9VoOqtA8GzR1qaeXIeXrPWludRc5Z2+4SMSa8F2aQs17aF+IEPKNGv+iTGUOF2ArAlNIk1l9+ozwv5Rzv7u7xbUsYhMWaTQlQNRDD4GxDShZ8A4sjoMXg8E0rjowJuG+8xztLv+sJ/chmM7BcdvjGQbb1XhmMtlNl0S3ykIeRtNniTkS7Ryp0FouwyDsHAdEozSFx+7DFNq06hJEUB3w8wHiPMxl2a9LtFWbYknPAosLpozBpct1TpoKNxellGVuMwRKdYzOKllDb9HRxRf/wmtX9FXl8AHpsY8BZGeoQZQ8Vtl2VBcvK9MMKqB2RIC6nPUZmLgCUne5XVRhWJ071Bbk+s2VP1ePMQaLyAJJZb3est9uqNcbs+UopY31TvzdpjImNmQOGU5V7HzDE7LMkawWdXB18SZlttXtTEFskQnL579lzOAejmQXyBWwXRvf0uZRyNQPZIBOwjZkYn+Wem3r2WDuxj0syEGfn8fhVzrkEozUBqgzaKQAVmzxb00f3am4vSmBstdIcFXTc27PaFpPj3H3nvbUTn5Cr3vFeAsmUPJXjkvfP54fOsdq4PP2W/qPa5O9/f3J2uk4laDUGpyx+YRvsJ6t1jR+tTcyZFDKN9QK6BK2/Ovn9GFRiQ5Moa0qLLpL4monZraf9A+c8vVcKKpqWqS8uyVWuRUTNYGtRwRgJuIpeozGii5UttOfHpBTpL2+hH6tulvQVwConvluv2OWOc9XV9s4yZEcTPXEXaBzcv/kZ48ETfvRbf8Dps6f89K9/jElbdve3mLalbRwpSVufz5kxjqTsOHtyQUyBu9sbwtALW6Fx7DZrUogcHnQcHR0y9lvevXnN/d0Drz56yvLggLubW5wxfPn554wh8Pr1dwzjyIuPXpKM46tfvOH97Yp22fKbX37K86Mj3r7+hteXK56+fMHysOXd1SXGGo4PT8jDSLBwfnLCabvkfozcfPMdF8cnHF+cM97c0W8HKSxpXDOrUdbXPkOmPHQSv4nvTqRxZOgdNze3PJyf0S2PIQfCOAiQmLNMt89J29LUH6vfa5qGdQi0WaZSm3bB0ckFn7UtD/dP+eof/pbV6hprR05Ojjk+u2B7d69thJbGj9zdjPy/f/5zUsz8we9/QeMt47AmhB0pRVKKuGYAdhg8vl0QbgdyNizbI14dRlzT4NpTsA0Gy+HREdvtVlvtG4xxbHc9q9UDm+2KkCJ317f0d2vGOBDGHh+3pGHNw3qkH3c0VkBXZxLHB5bz06e8ePaEr3/xjvH2lrje4MPAAZajwwUP656QJK7JRiY1W2uUkRRJiJ6mMA2lkNx4jyVyvFxwd3NDm+44XMDxyYKL0yXr3cDl+zcMY+D89Iy27dhsVjSNxdmEs5HN5o4x9mQ8bYLtbodzHdYtpUU1KkBrIJWuMbVDBmHV9cNAHGQQyG7c8YDBHB2Sdr10wSB6l1LUkxbG7DNYi2tED19iRWG1orbJ6SBM1T/DO9FCTjESVWZgtFFjHPVnpsSSMtTXOm3fRWI8sWQKKKqdmPvGWoBLCdc2wvpy4uMPDw/Z6LDC0IfqS1LRds4aUmQZ5GKV1CKTsqdhUiVmHyz0xhA0rjbokLQZGFWAgpD3/Vl5JsWe648aAZd919FrN1JMwtSVNbcY2+JsB6aRdlvjGdIOY25JaeTu/pb1sGOXIh998SOeJ8f9biMSXGFgiIlXH7/gqFuwZlc1+qdUYgbO6p8FDCmkAqP7oIJw+m9l6HDxCVK0nbona36gvznEiIv77NEa26Hsf7KymS3JGrY6nT3PgHdm52+KWcTUvEQAtyl9n/xydWwzUC1NQJYphYUp7jHGSIea5sn1vRLv6B4ex7ECRCWXmIOUOec6M2ZOUKq5HtQOy7qnZ2DcvBMmpqTD5wxF/ESRPrFhytKMWYg35ZgWSzLC9K/SczU2kxtsNQZ/zKQ1GLLLVXKvsNpDzhjnyVkHV9WOi/09NS/qltdeXFMHF+0Pey2//0PA7d5m0LSwzOoIQy8M7ygdHdZYxiigrdHBXkVuypT4O8swL2AvbimxstxqW1nEUniZYv5xHCQnidT4aBpMnCegUrJVicuRuTc5Z8IYpNygU+6d1wFnel+SshOH3VCPJR2X8qy1KhdWYrzHMiaP19AY6VpwOuMiKTM4Idq4OaZpVgPUDlLRYJXnvB8CJklnonGOMWfGKEMpQ5R83ToDisNQ1jiXAYxI7Ky/XzVgZYdgoHZXk3VOj3M1h/JeikdlEFmrLNdyzWV/Fbb9FA+ptISRuNM3npDEb4Ze5BcK2C9idErCSrH6u/J8Zr3+qdsoEUcBJ+l08CMiqRFD1MFllhBGhhjB7Ghcg82CeTksJkdcNoStask3sj/DEEA7VUw29Jstm7SuZCen8qTjOIBrGIZBWMYxYxodCpbBJ+kIDSFgvOyjhAxQ9Sp11+LJRCF6xMyi6UQDPFlawDkDjaUfR4k7Ed+KdYSUcVgi844QsQveORnwZqTDt/MdY0yMQTSFyxDJEIWYIvIaP/z6JQdpQdolCoAoFRBDCc6kUlPb/LNQ8DHiXCOGxnmM9SQNrOJui6Fht1tz5FqenJzRm6iAmGp36MT2FNUROUHtDVNFJM4AgJwTL58/45NnL/mL//RXAu5q0DrpiKoBsl4Cp6zgcNRpkgo0NTpxbjI20k4MlpRHSKkGTjkmRR2SBpOFRRsVwJHEsiSVRTssG6uAYtbqo5yrMCIkeExZq5TWKNCtDmcGbE6SBXK8rulkemsdfKAPvS6VVZBGBmztO7TMJEMwTQif5BawE+akX6j5XAlnyi0pybP40ymALKLjhQEatNXcmBmgAbVVOOUy2T5Pv7HH/DXVkJbPzQMU5xxRrPgssRRjUATX0Rad+QCyrKCnq20m+wFV1aUtVdf9haQI2ovO5wxYkd1KJDHkiD/wMHZk35Jtq5Cpti3oQcUoerx3eGfoFZBLMRNSJoURJzsSk2XoSOMs4zCI1nPjMSTS+gHf7whkrOsqW1oKIRGXHWFIarBGGutwiyX++Uvi5gHfOowJhPWadH0J63sIAzSednnIOEi7QQkUcs5kFfwvbU5YCcAkPpbK1ma02AA5RMbdNf39a3ZhJUPMUs+YHUmriQLuBXWqU3ISRhGDd94hAxpkzZeLBd46trvCIn5UmaawH40ydkrgSpEW2y9OwF5gIkGkkSqfRAL6nGvyUDZ3nkBCkdaYCiAppwr0dW1bn+15jDhndDhbxBV0+1Lq5vI57xvCOAibZfawlr/OdZnFlsreLvpQJaEpQaOw1PXYTcOoCc1eYKnRZQZhHEEtysyBOnk2y4Cqcj8lmC/yKvPXdKs0uLcTo738oyQsBTSc7A+zZ7acb2nPmhe4gt6nPM8qC0JVXAyGwtyYB/fW2gmQ199UKHF6b7Z3JCiIyhSdkpS5DSuByBxIFq3WtKcvWxMqbWfMiC9J1aaJjYraClU6N0QiKNb9abCVzRRiAJMYQ+KwPeR3f/O3CTHx3du3XF6+Ywi92E0x2JTCHloUmu9beTaoe18A5NIKN1sTJHGsNqIm9Lkm7pUVbAw57TOkRIten8UkwWvCgLcsn5zhQmZ7dSMFGk2SsJbRWG5jwqaRRXY02w3eeZrjliFu8HTYjSe5B7ZjxD77hF/93T9iGHt+/jd/znZ1R9N0+MWSxdEZ/RgYhh3BiITSZvXAarNiu9vw/OkzvLdc31xx++EDX37xOWdnp7x7947Lt+8ZInzy6iUHy47VwwpnHU+fXLBar3h/dUXXtrz66CW32y0/fX/J3arn4viIX/30Y1oHP/vZz3nYjHz0yUsw8P79e07Oj+i6JZfvbsjDjmcvBNJSYAAAIABJREFUn3J8fMib2wfuhp4nF2c8PTvhq9tbVqsHDA0uiT5cUPaNyOZoAlP0m+dJWH02qXvBtx3r7cB3373l5fEhB8c9Q0gsD45xjRSw6+R0Z0kpEoKlaZwkFMPAGAbub295+vQJ3nmWi0PapiP0Ae8XHCyPuL27YwyR5cE5q5s1427LwVIGeKz6kfuHzJ/82c+5fljxh7/3JWdHLdZIEdF5g3EG14imq7EJYwf6h9f0OG237OgWxwJeZcPtXRHhygxOwLYhBBrgxFlG03N4FglNwNAwDJntw4rV/Y7gR/I4EHvDOEZM2xBM5PAg86OLM7589ZTNekffb7i9v8WahovnT7i6uePuYeD6rudu0xOiMHucNwz9wBBE4zRlGb4xjpF20fD5R8/45OU5m9Utrgs8rFbc3b1hjAbrjzg9X5OiYfNwCUDTek6P4KA9IcfI6uEe6zLYlr63+Nbg3IA1DeTEOAwyPNchhUdBMNFciZSEGWXGHoNhPWxZpYQ9PCRf34qvLYUZtcspSbLkVKqpTEKfa7sXcLzMMjAlkVRfl1OWqd5JY3krclG+kVzFJCvnbCVezjlJvKBDtmSydJHPKsCVxMrS6ioDfRovenlDv2O32bHb7cSmmeIfbJVac5W9K7ZNEnaj06tttd0hyvCxERitIVsZNCZa3IVdOLX3jyFILpElAogpVoNafK41TqStksHrbAkKUcIaxkE6F+0Iy0VLoiGSGOOGwKiFuYY+BC5evuTjH/0TgvX49pDj5ZI0joz9jtdv33B6csjFyQl31/cCqKl8GgpCzP3w40KjU5b0fkw/te5LDjcdY4qNcmV35iwDl3xl/826UgqwMR1BfGuiEn9MNjqAeZqTIWzZMiB1snuPJYcmXzyB08bYCnrNoEgtVItvzLP1KF1wzKT95N4hU9U1DyvxRVJW78SqlTis5L0FrJUQVGKkaf2nwV1WmfBFfzmRIUrOJNqzUduUy7FUO1VFvjQFr+C1SSKxoHRq3bfiS3ISGzHfx61vpjbtklBOiyP3tOsIvsGYXnNMW6/n8Z6aF51LHjjfD+W/H+/BPbB09qr7xswAXWuxRsAo67RlvO1ou/9M3Zv82pFkaX4/G9z9Dm8kGWRMGREZ1Z1Z1Y2GUJK6N4IgCNBC+mMFaKWFVoLQCwkQhO5So6aszIyIDJLB4fGNd3B3MztanGPu/hhRWmffQCL5yPvudTc3O8N3vvOdDhccbdtOnZkxRtPIYWL74TwxBGKY80u74SlGButiLYViesbOzdIKFZitvlQ73fQzVKJAPzPnwtAnxSb0MpRNGe33B53YKKLDA52DMR9niRUPIp7goeu6CT+QCrIKs/2x+BIU2My5TMNunfcEwLnWThMKhJqOeCU+adeAddUYKtJ2q0l6KRXdj03KJrGBscDFovY5P3fo+ZZqCy2m8U79AG7OAL2R7VRCyxlIWrsHK6EMy1XC5BtA16lIMYCQCX/JNrG5ICp7U1o9V4iR8gLDODKkUQdaU7sW9Wz54On7wTRf5+4lbwMfPeofhn4woLvYcLLAmJP5M8cwKiDcuMBmtaKNDZFWz/BYSGlUCdHRyJgu2JmErKLX5JyVRR0jue/VNudCG5NJi0ZIhWPfay6JzcxxytI/9gPBCIdN1+GbQM5Cdoq/OedxBSQVovM0BIIENt2KQz8QnSP7QkmJMQujCCmN2hGBDml0JZGHUQfgBt17jWnZr3wkDz1RPDG0kz1et5ExZdr/Hyj2zx6kDSaurxplWrlxgORkVG03VTA0UNLDUQczIApBRg+NAy8qqHxyfslnX/+a52/+npc3L60SobR6sZa72bl6Szqr4xQ1kkARfRD3Dzu+z6+U2l6U6ZulDrwRMtaSZ5B7tgqKIrQORHUvxLsqbYJQ2UcKvGpKu6igeF0Thxpuck0u3RSsVhs/MQlNK8U5pWZX4MFby3JtafeWeGr1fw48ps93j6v9ZHh2/gm7w4Gru/eIFwI1WEMDIEuY9deKiiwbYDRV/Bwa0E4goZsqgtPgF+9xYXb49k41fjXBnuCNmUVZK8UaVOu2qVVtZVNj+iBV56wwK1yI/fsM+rppXWcQaBmc5VzF7R1aSdTgoeAetRZ5V1sX5ntWsp5NMa3PMVSjrq96v646HadDmiqlHxEVvJYKCFqIVZRd+8WvXnD9Q8A1G4JrGQ2I9M6RyaYtoz6+oM9xvWrYr5VV28RIYSRgbKQAXefIJbI79GgEsVIg5u4t6U3EPX1OWG8p7oTctPgxk0Qr4sOYlCXSduQhUWTEtw3N6RkxPZA+vGF8/Qp297iUKKFl/eQF/vI5ZUzUAV6GLNs+mPcHRIQAToEnpx6JYRxphwE37ul3N8h4QB6uCI1A1KmiYqxmfV7qxGpIXIfe5ZQrFozzwm6vwEsF9lyZgb3p/BTsuozVLjbAjAwSpvOg52xuD4IKOjkkG5va+VkficoKBPGOxocJ+Kgo1cQmqRrbbm7NmjWWF8AIbjpD+qv6Ocq0set0RSeRu18IZKn6yjUknAsb9T3LMx8qIO00OBp3DxODYpJImxj4Mp2haVKwaIJQz280Pa2+T0x+xFXML8+/X7TrQuTjANwGoki1T3UPVDzUeNFFzIbN7XtgQZOz+1rajsU66BFcAOwWxGknyGx350BffYfuzUVgt1j3mhQKMuuL2d/WdVwWg6SUaW9MTBDHlHjVe9Fn4afOEfGWgIlntlQOXyNcqiaftg5OnRzY3pHMMPbgIk8un3CxPmPbbblYnfD9quX1u1fs+iPJAl1HsVZsUfb+9CAExE9s6ikHseupu+8Ro6W25S1ypKnFtf5sz2fJ1AhmM2dmjcq/eAEJnnh5gh8O9Nf3BJNBM9yCY4C999xmTXCG21tCEOJ6g5diDCthA1y//hOr1Ya/+ut/x+31G66+/wd8Z4yjU0/YdKxPVmQGnlxc8OMPPzAMOqhqGAbevbvl/vaO022Lj54fXr3ip1fvaJuGz794QXCOfkysVmtW6xX3Dw/89Ponzi7PuLh8yoe7e/7w7h3Xh5GvPvuMb56ekw53XH24I4TAF18+Z3fYsT8cubAhZn/87jX7h8Rf/cXnnG3WvHr3nqMI33z2OaHxvPzwnlcPe0r0fHl5RjoMXI0DztgNRUSJ0aYHO8noGLA0e3gmgAUXOJbCm+t7bu7u8W1L9Ae6uNaJyF07tVx65kFIh8OeECI5a9Hq9uaO7faEk60WzQOO9WrN02fPyBcndOuVDg2JA6XA9YcjEjxDEaITtuvIarXhH3//npubHb/59glff3nBi+fnnJ6eaFeAjHb2PYVMznV/eSQP9PcfFJh04FBmhkP9g3eOnEbGSQe+ZxyO3F/f2+RsyHJEwpF1m0njwO1+YH+Aw7G1pDpzf/ue9eYEkUDTNbx4fkpK0PrEp09WnJ+0vHh6QfEekUBJBSFZzNbSp4HiEr4E+qHn/LLj86dbGtdz++ENASG2wmp1Sko6+HbV9IRVx4ebN9ze3tM0LcNw4GR7wjAUnGROthFiJpeBMq7wTQO5oSRH9iO19VuKdn0oW8ypxn06kuUIaeAwZN7c3bMvK5rVVllwRQd/qlxBoVt1xKFMcW4RHfbXxAZvxdjotdNOpYQiDp3cXHA0JimVc+b2+g4foXGRaANNYqPtxsFi37Zt56E2Zk98ZVGaVqIYiAwayul+9fjG03SONmoB6X6307kNvjEiinYCuoAWjazLIDsx6apqBT1kBc9ygLOzc67ubhhlIEXV6avAA2Zra1FUzIzWAY8qlVY/V+w/iz+LFo5X2zWgoOEhHRDJ+FD3MjgZ9Fxnwa8y23VD3F3w7j6TcqDpVqxPTkmDQ3JGgkNcQ+sauhDZnp3y+Ysv+OHqtRZhrSAvZMSFR3Ydew6++nDVxplILsKCCZoKwXKDbI4ko4xK76M+HKwrpvp15+Z4XAQvsvCvNRqwaFyW+qvqJ70lKNpNlC22chMwVqYCpRaZ6nOpPsqCRgU5Sh3KM7Mq9ZE6BSVEi5Fjyqo3au1GtvP09ioA6vwExjoqEMnU1eSc+s9sYHyNM2GOowQFs63kPO2T+vLU7qVFZ6bNQ1Eii0AdVmv2GwfDqPcZgrFpJ6evsXlwjtBEBVVMBm7SqCzWfYN2wjR4smk1xxhZrbbsw73lQHMm9fFryQRWl/T43pex5MdA+7w1FzHwR+AvaNGl5Mz+eCQEh4seEnRtp+sfnOkH6+BI5xyrdq3YQ9CiwpgTOAV4LRzTzy86IFzXTgcdmqGfBsHVHDwnxSNyzoQmEkKreTUqKYHXnC40gZWBwTHo/gpBGamrtiOP1m3qMJKL5jRj7axT56f2zwgJwzBQgPVmgx2lGnqZr9Q9WqSQxqQx5gIsr4xMoRBMgLTkQjBplxgig2moOhEdPGVxbsqJrmkN9BTEhnxF03JVjGAupIxpxBqbVT7Gnn0x8pS3M1NZ28p8tUGzpgntQpwHJ9t5r5mH8yb9gBUCF/c+g/K6vkV0uNcswaDYzxrHmAZtsnVuIuR5rxqqIjWnEFKNwYqeKR2UWWzekuJm0Xv7WYs5IWi3ayiOrgQ2paWVzvYqjLHBRceIIFnZuS5HGlHQFBcoPjCSENH5N8G3uu7Z0ThoXJhIUgFPLqPmdqWwaTvA03ghJQeGyZU06rBPPD4Xonf4bLhVyTStyqqGVu1JLpkSMnt3xLtCY0RHFQEMDEAOegZKVr8xJtX/9d7R4BWANyxMgJKKdh913S9YFH39WYO0NaHR5NDAQDtwjx2FGmoplZnlbcCPbuxUMikPVkVz5DTQth0PuwN/+tNLOBFcDNqyNHlzIZQRYjSHvhhQ4R2EqIBHAUdh3x/ZHQ+MUlSjI3gis9Gd2KUOSzCZDIowM7S8D+DlkVFfMillCpIWRkcvVz9+Ydg/dg4Ti64mnyLGFrUKig3o8JOu7fz6WAfWe6dJhau1IOHm/k61XajJvlaRastQfUbThHYRax2v4MOcBNfFUsaVTWIEO8SzKP/0XgMeKmOWxT1PDEILSLQCVgzQwAIuA2mdgiHKdNDPVmkNIRmL8udAyay/VF8TK6+CRos2dlBDXq8/l4JqpqumsCag9p+fW7dl8ftSDIiiqJ6rc5O4esICmYmt5qzCGKxVONP39/z06kf68SnSniIEnCTwQVv8kydIJnhjpeeMC3CxjvRrBXGdZFoD1MaxaOXKg/M63EIS0K2Q2CCHa8Z339OQ4LNfMbAhZ6ERR3ZGgm0CLga8b0i7TBgH4klD3N1x+P3fk/Y7ZBxxuaf4gD89w22fcMw2bChEZbVZAKs0AA2acR4fGyuN1MReK7lRhDb0dIcrDg/vafsHjuOBeNJQrF1bnanpuNpUztr+pHo1WlmrUh7ezkw99x/vw8luiQYLeoYUfHS1cMOCIeBmkPhRcWSRUKgIuTe7MmdklRFUUl6cX6/Jg4EewXuOx6N9ZtUVtmDeKEoiorIPlmlUsGN5Druuw3vP4bCfvqeeh6UGlJ6Bqi877+t6Lx+3hC2LQiJWbLL7r7HuY43Vub1+/jzVoayven8V2MumkxS8VtInNiYfMxw0Ilzgn49tLtWGzXuwWAEM5lZL+4UZnK1/5edi0/S9NQiFqdMAsE6IGVyUrIGSr/YFy5Vg8l+/xN74+LnU9ryltIpbPL9lZ0a9PEQePc9lUml3ZoAX07oW6yCgaCFk1W643J7x9bMXDA8HZJ9oG8e/+OxXPNme8PLtT7y/uWbXH8EYac58fU1M50LbL/uw6SnWP0/+xvaUtTrqOs3A+OMCXJ7Ob5F5sOT0vpJJAj4GTj95hiuO4XZnckX6PcU5Hgq4NEAM5JS4ur1m4x1x4yke7g939P3A6faEN//0/1J+9Wv+zV//t/xNn3h4/QdcGiljzye/+Zc8/+or/vY//Ecerm+Qklm3Lf0w8OrVS3b7gfPNlufPnvL+3RVv3t+wXW357LMnjOPA3cOOb7/5hv6w5/72mqubG549f8rZ6Tmvrq/549srinj+7V9+y5O24frqirvdjidPLxgFrq6vwXueXV5wf8y8/OE1m1XLt7/9knUX+O6HH8lNwxdff0Uvwj++fsNN7mm6jr/+5muenJzxD9/9QO7FioJB2w2LJeZi+vh+LlLj3OP2WdHYInvYPr0gk1QeR4RxSJquO2f7m4lNuTKW3263Y9WtiSHyq1/9ihC8snbE2UCJwBdffMXd3TX7Y09wkS4GHq5vePXjHf2YaDeOTQMDhfNLlc96d33k7m9e8sPLN3z54pKvvvyMzz/7hNOzFkKhFGiaSA4FybOt0qLQoO1xAt63NtFacEE7VKT0lAxIxOVI2zaISzg3QMqsuhX4I8PoCEFsWrPGrcN+z3oduL8/kEbtvImtB+9poiflwaYytzTtSoepORjGI8EFTrZnpHuV17l8csLqwrE9g4vTRL/fI2lPoYPYEGOgbQO5JB5277i9OXJ39zCBnillgig4GJqkSblTfcH9/V7bXKMO8wgOYqegtaCJa86ZPIyk1JPGXpMjEjeHkTfXmdFFivOAtVCLkJzQ50zJgvOBbIzWaGe0tvwCU0EK89G1nVXBjkC76ugPI/uHPU3RoW9SRKerN62CRF4ZbKM/aKE2eNuPxj6zfe2rPnwtIgRP6FpaL2y3LeNYiB3E0BCCavr1w2gdam42Z8jEhoshTnlStcUKVga8Fz55/oLb4UDKxwkUBCtIe9UrrbCXgrcVSKsm1LF0YrWAmHNmEMGtWgWKMhz7nv2wowmBQ39gKDvOueSseUJsOpIrhNCx2Ta43S3jKDw8HDh/+hzXNpRc86VCHjMP1+9xLvPZ80/xf+snYkLwGvdJnjU2l34MioEzUUHYlAzsqP5WCOJ1Mrd1TujKuSkeqnnAI5mAugZFSUXjEiwx4HIqkC/eP/+5mK/M1MKm982jHExjyFSfiOZVFKILJGP/nm42lGHU4bR4xM9+yjun+bCzeFQKZLF9aJ0y3hZLxIBn0x3lccegc1rY0muYrkihC8v5arfllDehuaxDLF51Exvw41xzWexWsz/Hts7WsrUO1JRHiwVm8FwqIcoerGA5VdGuwnqPOB347Yoo+cn+usA0bMsoGz/LzZc/L2P0j59x/fkXc/uP4rDpZ7veuuf6fuB46Ll8ssX52oWmrNZAnCQPC5mcMgMDsWnmtc/CkAZyUkZsrBKPGGLoFbSPxtr0JnERY2S9XhNjVC1y88k1xldA0tbQa0elC4HoA7LQaa4dw6u2Q9rCOCZ8EwhNyzgqMBnDXExQP2hZsXO0xiSVxRop+BvIeZ6f4IpjvV6pfbf9JrUrChDRTrRiRJYRBYpT0S7MbFIIZUyoQo7iSrnotYgTgsnyiYGzlflar68OWRenerbBB8vT59hZZyg5JFjRx3u8zIPASimIgduS9AR6U96oJK7YGFO5yoGKx8VKYtRnWnIxYBUaNM6PocF5zzAcpg5f7xXPULkL69q0Tgmx/YFhAkGr5yA6/DUnlRKIqI+tfifgWbuWVjwtgda34AXXRorXc9gn7QJbtSvGY2LtA75AEzsSmbEkjqlnLIlBBL/2OKe21RFJodC0LSknAo4x1bku6qdVb7hhSIXiMkmEfd/Teo0lGhcY+p7iPJHImBI+RIIPZMmMaST6wKZds5ZCExWP7MeRQQpX3kDqYINuRXCh0ZhtzISi+ZnH431DLdqRIPznOjhM3bBVrxw21MPAUQfERfAgVUtGwQOthuqhDiEwptqGrw6jbVtwTnUlLIuVKj1QK5Q4csr4qFU1BXzATrhS6X1lJalhjU00REcrJ7nqe7g5uaj6HhVdcB+JkE837x4b9BmQ/CgYoCYtTAxN72YmEfbZpeRHSc4SxFQNTWOKmVZMHZJTA5Ala3RO9p0Br4XdcUdlwUkxMNjPwYlYUjQBhxWactbSTJ3+Od/P8hmWow6cqK3RdcCXxVOP906ZdQMfO8Gqa1dwTtvRqmZMXeeUi7FbbW2sTdaHiFsk/7/klJeMxFqhl2LVxV8ASBRI8WQbVDC3HcjEihMM0DZNMwXmjFFoR6EG9RWC1H3q57Z36voGPDAOd9y9/wG3+ktc01JGQYYjbVjjAzAUYtC2Oucy2iQndFFogufhfiCuTvA+KQAaPH1/JB8TGMOgiBC6NbI9RY7XMDwwvv0e54X28zU5BpIPBO8oSQOpkhKUTNu12iaYd6SXP5BevYRVxImyzd32hHDxlLFZkcGYs8ygUWWMovvJtxGsci6285BC7hNtG4nphv3VHynjDa6/hTLgmw1JtP3FWXFE9dhU+7Rp5raTqtOmIP7MzJyA+FzPlgYcCvBbYSConZv0z3AmB+GoDN6p2LOoBtfTXyfoVu2iah+dBRIiqgW1tBkzYFxb3B9Ld2BAp2715RCG+aD5CWSd9/8wjNO9L3WTtHrLo7MzfY6xdupZqudoabuWRZHg/RRw1W6HjwFH/fMM0tbPrNH9BGxLLew9Dprr0D3n9L3L4VmPE4aFzZEZANc/z6Aniw6GWnDB/I4zcLEOFJzMvMzXWgFXZ3ak/v60nvYcaiKSZQagxRgzHjc9vxqo1ny0fs6kDec9dTBO1QauduYxuCnmM+cEuB6WSSZg2qtgikFmf51pjzgQx5OzSz795FM+vXjKk9MLHh72vP3pHU0TefL0km+e/4on20teXb3hw/0t724+sO8P2nbrloAqk51fPptf2nsfJ1P6b4+TrI+Lk/ZuqpP+2ffUPeaANuLblhOBu5wZd1oIqQXlo4yq6VkaZbz3hXf3e5r1CSddy3AcGPo78ipS7nre/HHkxa9/y7/77/9H/v3/9r9w+/aPbASOb9/yKifKWNgfDqy86q5lDxfnp5ydwna14ebmlrvdPZ88fcrJ5oT3794xDgNPn1wyHHs+XF2z39/z9Oklp2dnvH7/gR/fXnGyWfPrX33OSYD9hyvWbcPq9DlDStzfvKPBc375gtvdkR9fveN02/Dtl5+Sx8yrV69pYuSLLz7jfuj57uaWow+cb8/55vlTNuL4/m//hiSey3jCuzFbQmSdBKIgraudMnVvV/ten2mNR7JYO6fHlcw4Dnz4cMV6vWIbA81awS1qEX9MU3Gt73vidqMAoKikjwsKLjnn8bHDx47t6QUlJ9ro+fyrX6k0xLt3xEZjvZubkf3+liYWtpuG4IVDn/mn797w/Q9XnJxsODtb8fTJipPTNadnG5ouslmvWMWG2LR4CjFYck4iRu2U0eFLPQVl5PgmIFknY8e2dhz19Icj/T7R+ZHgA9vthsP+wN1xYOwzSEMMDh9U7quUzM31gZzg9LSlaYAElIRwJOcecYV125DzwPXbW3Z7YXvS8nDzAS8NqQ/kfQdW4I2xwfnI4TASY8F5jbEPuz0yalIcXaBpW8hJZSCsiyuPR427Y2Ntq6pXqLGPlqdSTspoTiPjeNTfSb0WSUrhen/kfmjo26BxQ9BYow778yHo1PP9gAuepjPWVMqkkLWVMkRqN533gRAa9a2ijLLRJ1auY7PZqNZetvZxMxGSktrnEKmtG5IL+Fq49IhXrdbqjx7ZKu+Q4OE6sH245/TZBZ98+gnhbKXTyEOglMHiSx1KE4KSEZJTgLLaeu2SqhCaKJgl8OOr19ztH5C1xiJjTjbRutrxGgfN5AtAmVQWk9bClrLeAqnGwiKqtxocZD27xY306YHRFfrxgNsJl08vOD3f8O5ux83NUW1o8KQhcX11wxdffaWTwYtX+YQCJTuOuweO/R0XZ2vWXcMgNpSlUofNVtQhrcU6ZSiZKr1UWXo5VxCv0DTxUbG6aVqOR2UBu8qMcW6yT2WK2fX5RevCUikdTR5rJB68AomPCs/me2aAVl81tnz8qu+tPsdARQMkN23Lv/qLf8Hbd6/5w49/QkJAGXH1emXy60vftdSGpe4P5thmeU2PAOOsjl1cvRfbcAagVX+pZtpIQK7eQcWR/DzbYOG/NZ6socsiHhYtkFS9UGU9a84XvbW7m7/ACsRZ5nyoVrCXQ+aQ2kFlw51Qtqprgp7DXLvYtHj4cT6n1/5z0PVj8LW+71E8BY9+f/p5+flOSUg5W7dn0Tw4JdUrbYoQg7I6g3XWpTGpLGFsKF60OZAqn1NJGJ62bei6TvU5ixYwKtmkXlOMka7rwDq2h3EEUTvsrQhVfTJAyhkZ0hSzT/J/RfU5a96ezEbqPoLBBrnrAGxl79Z8foqfRHU8xfQUq34tMneZphh12Jf585r35H4k56Q+wUV8owPfvQC5UIAmtpQxmQSHzhPJaDFDnJ7J6AI5jRPLPljBbZnzTbJcONKosjLOzmkd/Oy9J7SQykAl0gWbXVTlV4aqq49qmdbZOVN8Cgx9omrI5pyJTaMdG+Kos0ac14KU2gA9l1UiT7GyNPnWUhRcbsyWacdooosNq6ZReYYYTPKg0DY2LBKHGOAuopIywQdCcXhR0FZ1eIN1eQjRN0hKhOLpmhUrpyCtCxFfnHaHeAdpUHyuiNprs8Wqk6+50ZgSJeu/jykr29jA/VEK4oUhjYQ6FBUH5ahDvvC0oSFLwRW9nySFnEdWbUdnRddctNu47wfwgdWqpSAKUvtANGmW2pFeSmEYRmOJi8anQGNFkH/u9WcN0oImn4XZwRWr7hVD7wsaxFe1nGAshHpQq65qziPH4471KbRNix8GnA96GEPUMQIxMgw9ODEhZDEQwJJur0yA4CMpj5bo+smITi1LGtloyw0G8D62u3pAvTejVfA20XXWfTXtxSnxrKzhMIEglc0kLD7fV4ACu/6a+JsxZk6aJ4aTOb1pKJt3s26bfa4GM56qIaRONUxsK2VuJeqUW6lC9DXhdZj2n59AR4+xlqgOS4NMZ5pDgibviGO3O0xALjx2gLkUO/AzwDsxaxaaSVUHdjl9VbCWA1c1Gi2AMgdYslYeJXgLQj4Ct6lGeG5DmgIgajuNClfrs/15pbRW713dv1LblTXQc9Y+XSuKbgEZtK14AAAgAElEQVSY1aC4ArgTyGUASbH/hcqiCIEg0JYH4vFPrPxLijxnzA53HHFyyioIgwWXEzCDBoJdEzjfrLi6uqcfCr4TnGQgkrKySV30SGhxLkFc4c4+gaGH25+gf2B4+T25z4TLF5RVR/GBXLCihzr6gjB+2JFu38P1B3z0ZOchNPiTE7pPPqd0ZwxTy90vNSFJjf7ABxZNIlQgxkWPpFvc/Uv6uz8h6Zbh4TU+JLy1Oeh5KdP56NqOcexJKU3VxrofQvDWAl2lCubzWzWQNfgwOQY7T0gdqhfMmZYpEayBez27y8KDBgNLzStPcIHiNJiogV2NuT9+VTtU/23+vhn8nIo98vMAdPmx8z3ObcQ1uIoh0IQ4id9XAE8niC/udXEdExxmZ2oZLC7N6cdgbgVRP94L9XeXoKHBndM1zxegtqZ+Z7Qp1h8H1L/EnFgWs0Rq6WQJArIAmNzk26bCVbVhzHv658981gBUfal5VeTRd8kEgLuFo6h+5WPAUtlWDvysWTsNwJP5faCBTS1RLoFllQLSnTEPGZkLA8vPCA4LzD2fnH/Cv/ziW1oXKUV49vQFu93Aw2HP7f2BVeg4W58RP4l8cv6MZ2dPeP32R24e7uhztoDb1nSxXv9cEvRL9z9Vt5nMyoKBa4Uy/9gPLtdORCVmtFyj/m+k4FaRzfNL7t9eUY7DtM+cg8EJ11nwYU1bPGEQws0D4dzROMGFzH7csw4rxv09b3/4J779N/8F//X/8D/x7//X/5nx5pr92/eMt7c0p+e0TccwHMBBF1tiGzmOI2/evMFL4tmLJ8R2xbs37zkejnz26Sc0IXJ/e89qteb88gwE/vD9n3h7e+DTZxd8+/mnHI97Xr56z+X5OZdPn/Du5prr2we6rmHdnfDmzQ0/3dzzxedPeXZxwmF3z/39Pednp2xOT3n34Yo3/cgDwvNnz/ji8inj7T2vbq45Oen49ouveP8w8vD2HQ85U4oNQSVbIjYXZbwPjxjl9Tk7wAvc3e/YXWx4WhzrtuFhNyg7dTqX+t79bjfty7Zt6boVpSSz+2HaBME0E7MUzp80bM7OOBzu6Pd7Ll9EvuUB190h2SHJEWLHzYd7HELbjgQlyJCd55iEh+sdr9490PzB07Y2MDl6njxp2LaerlvTNZ7VytO1a/pxx+ZkZRq2WkCLTodfFYEQGpBESkf6MRNc4f5uz3Hfs+1gkAbCitW2JTQdu7s94yEx9jpUNMRI23acNitKLnRtJgRHjGpfVl3EuZG2c5ydbGibyJg8uQRcyDReJRWO48jt3TXbdUPXRZwfwCW82zD0mlw93B9JfeZke2HgkljnQrJ4rDGwp8d7WK06vFMWbQxKgihALjpkpaRMySNS9P7zcGBMhZt9z3fv9lyPa3qX8W3EOVEfawDNkDLSBAieJkQis45kyVpod8Erc9l8c/V7SC1sCpIL667B54IkZV1X+10Wfq6In/xdBZqEDKKdLZg/0XZXHQgkaBdEcoWSR9q2Ybi4QAKEGKcOGu/A+2g2SR51/lWcULGxWbYIA80ednuOZURCNJ3tebJ6lrmjpxYY66lTQKFAZSRWe7sEp6gST1BwBiodGFydfRDJpWfXX3N4e8do8mPDOEKE3GfevnzFw7dfUWgIYU3bdaQsNKsVzz/7gt//098iJbDpIh92IyVYj3Gx+RCuSgypREzOCbGummEYaKxduWq8p1wortHW45xpmpbT0y3Hw45smvsVwJxtUEGyRU8WM4q1kCvZhAUwaw/DpMy8/ZXUNba1izH+zIfW/59yHMnk2uFUC8RE+sMeZ228OfiJwLMkxyz9Xo3L6t8pIG/P6CPgsL6n5on1nifgtuYP3qIaYfqfnvcqOWZ7SFgMSX0MbFb27xS7WIFmijGr7XfO8hyLPbyn1AJJjbBsQJOSu6wjqPr7ae3nn2MTCW1D6FpyDBNwOQHFi++e9v5iT/xzQOzyvb+0rss9IJYb1rOnDP9GB+9JZhjGOZ4KM6TjXdAhWUaYqgzqYHIrpRQjH+jejEFJS752TuHAwKVKZMg5q963m4dIjTkZiGVsbKdSB8WBC4HGG8BX9ZVF6FNPT6+IRCn4JsLxOMX5eUzkkhnLkZzSzDxHC3sTIWmJdbh5PpF9keE2fiKn1ZzZiRaAJDvGNJJLZhhHolNByWJnO1iHVuoHlYkIKnojtgcruUjjzYoLWGeHdbXF2NB27WQvVCpC5twqZ2JstGBp7NdaPKr7f4pN7bvwFmF6R/COnJzK/Ygw5FnuLA028MpyMETo2pYhDaRUTOtcu0JFDHS3juZKrCkCw9Br3OEUEA8SkALjmGibZpIjdcqemWY2lVKIRIgtEtBOWSIePXcp56kgKKgEQcETfMMxZ9IwqD66FxKFIWfTLdchmWPu8cGRs8eFQtN2Ci6bFjIihKBSQEWsEzRorBFDREb9/jwOJK8EMIAkOjAvemWNE5yyaYcD+9Tjo7furFpccuS9xpFjcbQhIr6liZ6mbZHoGFIith390CNSaJuo+rxRB9X9c68/e5AWCzBwznR0DGpRoUKi99PGnYAES64c5vxKoaTMcDxahVKB16ZtqVM78TptFGtdVrUc0elu02CQWq2sbC2ACmIwGTTvbXqqJa+uAkUWICkmI1NSqSw6dY45Z71+3ATqLduJP3YINaCsSLwGuQYomvOrjKpSZNI/qS/n6hRaoA4Tm8DZ2eC5KSB5zMQF1f/NU7XTDni9vso8MuAWmDVSDaiolSMsYffTneirgtdTa+zi76bgxSKA4GYAJucli8uMbpinQi6Dq5Jlvt5p/4jqlNTAx/ZiLoViOqAiYoceDbTNiMkEiKieT2UV1MRyajvyBuSK6rxFnAXx3gJrva9qNL1jCp5rdUaCTiKuDso51V9yubaM+Ol7C9oK0cqBePgTJ+vX9LkjscEVRxl6NrFw8Gj1MJtGc9AkyZeGz590vH/zgeNwQNo1oFXRXIwRmgRCQ4gdZRRYXxCfBpzvSFc/IPlAfv9H5MOPSNsi3Qk+dhMImHNCxhHZ72HsdRmbFpqWePqU5uITcneC1vvKBFjroojFcvNUSkKsYen0TPTpOKKH1fED5eZ7Yn+F3L/jcHhHs1KJitA0+GLDCrzq7Qz9UbWomwbnMHaP15YTUQaylEI03TjqM3VV92wB3qJrhrFJYwhkS4Oqw9dz+Lidbm4hn4M6LeAsbEItHsxvnADXZQDsLGF9DJBqoDsVESzZnIC6uoqLYHV5fcvWchEh5WwOMyxsSrXpeq9J0vz9zj06p9N3L2xMBaDVvH48pKEmSo+Ti5+BzNVWmi06OzuljQ0fbq4fBcsfA7H1u36JLVFtjmp7LxIXw1U10Z+TAWrSX8+qiNlZe141oWNO1Gawek72sXdUQFUMkZqGbQQ3A8DVX1oCUF/1zEzpQ73PooL6P3/WP09O5vc4W4fHUjB1PbxTLUacUBL0/cDhoafZtMr46hOfPv+M1ekp97sd717+ie1qRdcEtnFFPL1k6wM/fXjP27sb7vsD2RmgsAAVluv7+ELm6/kZ2OfmZ1z96/yWClPIlKwsk9vgtVVt7u5wSAxwsuKkXHJ4c0XJo2odJijO0VM4eKF32ir//uGW4Eaebrdsmg0lZw5uoAtr3P093/2nv+HL3/4V/9W//e/4u//wf3K8eUPsB0Jz5Ozpc3K75vrhRq8tq98/O9uyajx4x9AfaRrH08tnNE3g6t07Li8uODs9Zb/f8+PVe/a58K9+8w2XXce43/Hh+ort6Zpm1fLqp7ccx8TZyZqhZH738pr9IfP1V88437bcvH9HyonLp08JseGn1z/xfhy49y0vLp7wzckJ99c/8eHDPedPn/Lk8pwPb15zN45cbjeM+56hxl0ArmqBTw/p58/Mnk0Jjptx4D47NudP6ELD7qHn/uEBomfjHI0N6tntdvTDwGq1IrSNnV09nyHE6XOzJcjBEgwfHbFtaLsN47BntfkNhcLL77+nCxlfEsPKM44OqoyAQN9n+l6H2oJDvON4KAwjOArvr/cEJzh5YL12XFxo+1zKQttFLp+e0jQesTa/nIRjPyCM5HGkbRTIXTVrCh1u3bG32MkL+MbTBkfXbWFIBAqHfuT2IdEPgdV6Q9c6QjMSvcO5Vgv/Am3X0q2UxVPyyNnFmsRATpAOwthnckmk4hn6nu0qAJlhPBCaIw6NIfqDMntXm5bDcWcTw1VTsQmAH0kI0WmbfmxbvNcWyXqkUkoMxVhvUiglkVLPcRjY74+kVHj54cjrh8wuBi2u+9qMLTZ4BG6PB75795ovtxd0TdChO8xsKKSSBwLKALQ2ant2wUdi0OEgw+7A+1evCAjbzVYBnhhpu1b9mQGH2pZdcNkR22i+Ic92WECyDimp7bklZ5ouqta1iOYrRXTAatV6RK+3+khcjRm9Dq3JRSdhWxyS0CnWxXmSMabGAllsaJgHse67Gl7Vwv/ypU1ds4yT+paZkekEglN5B8GK8SWRrNB1tjmno+P+cI2I43z7jO3mgkOvra3e7fnw9h3H3QOn5080liqJNDzgGsfnX3/LcMz83e/+npP1iuHDkeIUBGhsSEvxs2+eBkUpTAgI49hP8YCSerR7DK8zOsY8cHi907ifgiuA6VnKwrnUgU0iWQsvrpJfaoHPSBYys9n8IncrBSUP1binFJYxyOMip9g6Z5Vq8MqUHZOCRP/pd39PklE5ezkbuDj77Go367PSz61syHpU7LunnCVRpaBUHsrW0vaFq91+YneUZ5B3GXdIKVPH4Bz7zIXhae8wt4xXwk0FUvXyrDtKZh8w+2Nt757+3nlj3U2leRZHTgF1VyUgdG8Mw6AAV9vW+VsLv/PLIGu9xmX8uASwl6/HxAKme5+fMROuYT9ojGGMVRFYrVZT4TiEhgpW+9AQQ5yA9CrdQs093GPyQX/sGfuB2OrgpeA90QeS6L+rnEDmcDhMe8g5NzEU6x4YTDbMIBGOvg6xE9q2tTOYKSUTvTI3yzhw2O8JThnruWS1q17jlei0my3lzDAqgzYElcNZdSvrjFkAt9nkAG2v5TE9itOatlEiUxHtRi3COujwqSKQymhDwoLNN1Jb7yzHdE592diPtI3OH3IIbaO54JgyJSWc8+wPPbt7R9N24HVdQwiMYyLavhiGo2Iffh5cGIJ1Mtjzr8Pv7FgSoqdrdKi39ggoNnE8Hqc94p23z9Gfow/0uwMpD4gVLZoYKVL9T+020J+D1yGlMVhRxbrEj6W3HLfhcFTfHoyRLaBkHMtBfcgccyGs1jTRc8hHitfhbwSVYUmiA+HG/mCzphrKOOKkWFegpzj0u2pHhAhZRrWzviXnxLi3wYe1AClKivKxUfuqQrl6fkrBhWh70fBCsw1pGAmrBoL6+SJCDooLZhSMPspAFsE7lcvZHw4EF2hdIIgjSKCNtVvbClZeGeveq35uzoKUTPb/vC358wZpnYJqJVenKjaZdQYQtPXEWvNtA0cfKCWRM+AzeSxkPISOEFu8RPqjMkAm0EPEQD3VNRE0MBPRJExbihRAnbT+DPRwBuqK2MAytJLkUXq8syBptFaL6jSWjF+wipIzNpd3U4IPy0SyTMlideIej6+Drli02tYkffrsBYgg9fAvWGzO+JJFJ2KKPAaFKlO11Owz12tRuYIKFDvvjOat/+ZE28PF1mwCHbwzXd/HzNRaxQ8GmOcqVo0OIqhgR3U09dqkJCQ0BixkXQOcatt5KKW2MS8rrgZSSG0hqeCyabp6D+ghK/U5xEap9aXuRx2cVXBavC9Kup9bY+fJqBX41hbqkYvLp+zuH0hZwatUErhgOqr622PVPwQcJsoNOvzD2Ah1H1BlLjQqgVKBq4pw6b14SeT+hpiukOECX0CaQOp7+oO2HaYsJDKrpmEdPdLvEDnyyZMVz56u+el+xEtnU44H1l3gmIQhWyAeI0Kr4NzJEyR0ON/AzU+44QY3HGHcI/s94tXQGU/AdG4c+AaaLf7kknByTjg7R8KKbMNWcK7mTRbIGEhoCcsUjAlU1MS7ytQOxLIj7l4y3P4RP+4YjjdQBkLbKaDvCi6iqXnwxEarvNFH1l07F2wKpofroO5HqQCqAnMxajFEgCzFpgo706hWlrZzDi9iciiqSTazZ/Umdd9ZAcbOQb110ezBdHRmOLpOTkXmljSHOvVgMgk1CZuYHhOIaOfVGJk1AI+xNdu0DKotIakILkwDHlWyQ4s5MXoL8hW8naYx2+/VFErszC0TofqoKxNIA8hWdZNKmRKCunY1/q0Jit6etqo4rzpT9R76vp9AxY8B2ClpqVWc5fUsQKO5VVGTVfVVWr3VyamZecQ4mijWxLooyFiwgl/tIEGsOyHYNVRrMFfXJ/DWrlE90xxMFz0YICZh4OvTepwgKAtmTh68gf21WFkTS/10Tx2k5uqzMl+4XLs5YQFHqBiqFqqK8PT0nLP1RotCdr/D0NO1az775HP+9W+f8f9kx353Sy4j3gnrdk30Udka3Yrb48Dtwx33/QM4m5I7BXjK7MkpP7L9jwL7KZma/V5lRzwGnpf/m/+unhsnuvqzXq+xz3ygPTtFRHh48544CqmeCwq3/Z7QrkEc58FzMyZiSrSdDjQYxx7voIsr+oc7fvr+j3z6xdf85X/53/D3//H/4nD7ljwm7m9viZstEjwhqF4geFabE479gWHX063XnGw35FJYx5azi0u6Vcfb9+949e4W8Y5ff/MF2yby5vVPnJ6e8OLFpxyHnvdXV4QQOT874eHQ88NPH5AQ+fbXL1iRuHn7jpOLM07PtjzsDvzhT+/ZjwOhafjts2ecrTf89Icf2KeeL7/+itg0vP3pDSk6vvnmK7b7wt3hJwYpOLRNtzIfa/6/TGqnZNYehTg4EPnu6panr37iV0+eEmLk9u6W8UMmlIjbRsLasdmsqfUu7wPHY0/bholVP2mROkcZKtPM450yYzZdIIWO0m34zW9XnJ6e8/b731PcLU8lMvSFw74gztP3hSGrb9bkU0gi3O+FlJThMg5aMO4ax0nbMgqMOYII/b6wO95zfrmmaSow5hkGR0oO8S2nz57zyZMLLk6e8PLlH9kNd6S4otHqLqUo+0PywHbtaTyMCLurxN19wnmVlGqjDj8TrwXOECLrDjYrgaLsq7OHA91an0N/0KQry8gwQpQAaSB4GPqRLKYzi7LAmrbhcHhQ8DEGfFC/pYySBPmAj47gG8aUGYeRy4sVvhQkqZxLzkIpRygqsdP3ew6HB/oBjoPn1YPjTlYg5lMRnA+4YaQYq/mmjPxud0MPfCPQNd2kH6vtrVo4L8WSa1QOQTwUL5QAEgJjhvF45PrmHYeHB2LXUdBC7tn2gsuTC9rNmm3T0bqG0Vv3Xhbt5jGf6ixOKTlTKOQ8sH+4ZZSRs+YplK0mfw6KOHYPe8Zs/iWrXxLrekPmTrIaIxYpNLEjBM0JctJitLOcoVQ5AHUjGkKKghjCQnrHmV1TqvEc+09Fu2KdWGpXYzMzQktRaYdVp3FHCIL3hXwUnERiWBH9hnXT4scDPsDhvufm/QckZdrVGU3bEpqGw/GBYy78xb/+DVf3dzz78RPid79nDAUfHdmNCnoUFJBxAW85hTKNZxviTRahDl/NOWveUnOcbB1TVQ/SWx6Y9f6mYi7OwJ9CiGaQ0GFAWpA2723xae0+wpktK6P6EBGdI8CEvVMWGuweSKMCBXWKeXE6qFMH5xgzzPK8UvPHBdiZrfuv2lMf9H5qXFS9mxj7WPeGatyWXLXWai5q8dcU+y6A1KmtWtmJum8sv6ta7jZwJddY0ut3lFw7TGscr9eTZI4zcFXfXsGXLEocqdWGYnlRJb14MOmTZKQIvS5dLtMT1bcSrWCu+9/48YsO0CWY+jGJ6lFBnLmL6+d5/WNftnxVeQaN4QqSCykNFInaVt0oy3+6Hq8dH8X21Wq9sjOXtdPROVIyhnmMVFabOO1hPRx7nNN8fvQ6INF7T38cqBrZVa4p54yzeNd7ryxa9DwoGKvsRSWPQRbFZaL3rGxYUtu2OO9YVYZv1qGh3um8Fuf9RL6q8n1j1qKEdiIr2GzJuy5abAiWR/vgaWOjdB6n3UVDHlXr3f4zpzhhLsehNz16JrtWC22VGR5O1ebllMDBOAzUIedN29KYzviYM2lI5EqAM+JX1+hgSr0/1Uy1bIB+GMDwpBA7agFsHEeGcdChaDlRZxt4LzqTxQfiSvfqmBJtDCrlkDNjyWQptE0DBI7HIykXA3kNVxAtTDmHAtvULl+v8kVG9FBpWq8s0ykoM2Z1Gm1IpT6rh6MWPLpjp3q0oaFptODYGMGpOIypOujn1UJR1hzDi+6t4qygZLlTFh3OLqKgcanVRfNPFciX0WQuSlHZqJIpThQk90pqU5kLzeGLK6Qy4txiD3iQrISNXAoUGyppHQBd206+MxWhz4OyyakMZbVdftCCSRMb8pggC137n/HgsCiOZNG35KJTmKv1B0v8C421uztqq6UjmRPpx4ExJVLSQDAXYX/Y6YPB0Q9Huk2jDkoKIpmck6LsONrQLlhTwdo5Ffir+qshRqvLLltXtVIhpeqTMgU61DZ8Ayo9znKBWiX8efX0Y9DAYXR8ZkehrbMVkPmoklfBZQNaJs1BA7cdj3UplxVARUP0wBYDoGt1LC8E7uuTS2k0YHv+vQDWyl+vy0DeBXC9bA3WawCcAp51iugs06DvmfVmBN9oNdwhM1higWHwLVSgfLGepcwVzimoLUwstgpcO8dU+SpZGZMaMOmzdWj7mfdeDfbiPpZAxZhHZY/4wOFw5DgM9lneKlqPmb4K7CzPxeMgoLYMipSpfd6Jss67pmHoe11IJxgFAPGOYbynkTtOzjwPfcc4CpJHjodrvnmx5s1rKGFDGwqrRnQaY8msO+HLzzZcP3xg3MPm9ILYtRzGpCPwnDpxiraj5arD0m1wT7/Ab05wD+/Ju1vKMODSgJhWET5o1cs1uNhCu1Jw9uQC161JOLIBotWZaIHBWwA2245citE87IwUbPCeN1D/AMNbHq7+EXd4A8f3pMM7nCvk4HSoSKsDbKLzU9TmgzfdNTftF4vjF+DBskLurfCx2Pe+CrToNvZOBwdNLNYJB9QAv/4emMyIVbcr+8A5p07bVcDPtj5MLP2p0GJnZgL0JpC0Bozu0X6d1hj9vjqsKudE23bqmD/SvK2L4pxp99h+7bpuodW02MMLkLeChjnN2rY/2/Myt+ZVxnGtHaldCxQptG2r02BLpkpQqO2rVeop7sd7b+8tE7ugJp+1O6GuzxIkWgbc83qh9tcZSGv2XYs7j4Px5e9o4jTbp1y0bS9E7VaYWrxNM7eC1ctEYAbLbV8u/UZ9NGYDKfPfVXbrdH9m9ifQnllnuNpYMRB5WWRb2tOlHZ+vUfXenSiD7Osvv+XLF19BDnTthq5pubu/U5kWCXz/+9/z/e//SNetiAF2D3fGfPK0seV0tSWPhWfna4anPd+9/pGb3a0Gz76CYsrq83VYj62R6jfP+12v0dWVs0LhvKE/lhtZ+rHpntFnM51FlFUdfSB0kc2TS1JK7N5cEZx+hxMtdO5TJjZetTBF8IcjuMBFtyaUQu4hhZbQeva7W969f88Xv/6W7OBv/+//g7K/JfV7Bkm064aUE8d+JMYGEW0Hi13HkAbu7u/YbrYIXrseJFBK4PmLF6zWLf1+z/3hirPNCduTLbf3t1zfP+BCILQNt/f3vLm6ZbXe8OzFM4b9Ax/ub3lyccGz81PeXt/xhx+v6Efh8y+e8OVnn3LcH3n5ww+sTjd89tVnHFPh+uoDzbrj+WcvuH3Y8e6nDzxp1gRx3PajMpmaeWjWxyDtfIb0uXnnKC5ytTvyD3/8jrMYeXL2hIuzM0JsGMdEvr9hxZqTi0tK8QxpAMkkayEtpTD0I1234vzyUgtq4vBZW/KHoXA49Ky3a2Uv5YbtquXr7QlPL57y/R/+jvubN+zud0Dm7q5wPMDxwVoUW7ULOXmGXjQRlqzThsWZXfcMQwI/KksmiyXehe22NfJAtUsKaDy5fMLXX/wFXbPi5vYDV68+6Np5T/Sqq59K4u7ultXFiqaB2EaaJlNKoomekh19n0kJdocDKunmaKLnbBspcsQHR3h3UBCjcXTrCgzAtol8+rzDMdLEFSUFxuFA23Vs1xvuHu4pY6JtWzbrNVZX11bc4HA2PdN5QfyK6xuhjY6Lc31OXgq4hpJHUu5JSYerDf2Rfhy5P8J3V5kfH4Q+NDjxBLEOhhDI+QhB1zgBN3kk72+5PR74MBz4bHvOp+GCldcBK63Tbqfo/MQGDcY4VLvigKDF3SbyMB5I4wEfHBzh6vaOV/ENTdtw1nRctKfE1Zqzy3ParANxUy4gCqCJKKEjlcT+4ZYPV+8YGHh2uOWrTcPhcMLv/vF3fPbNN4ylQFCtXBzkVKjdfA7t4ipU/VHPyckpUiAf+sn5ZWOd+aaBUMeYOhwaMAlSDfgkV6Rgw8ycLR/571rUFNHrk6Yhbk8Z7nckB/uU2LpIEyIlCcklkMCm27BqVkTRdt7iGqRk9h903kFJibPTE5WncJ7Xr6+5v73Gff4FF+cnnHcrtqHjjoFkBTN1c3OH0eQXq1+y/y+lEEOjQFgpj2LwykyrcnQ4FrnS/JmPYiARBcENoKzs5hqneQMXq++sAHYl05RSSIw6hLppJvASmAYYpZynG0g5T7INUJl39ToVUEtJ8PLRdVLlN7yB0o6yeM7LTk3nqrzWvD6ZPP2boMDy0p9qTJDtjPspjhWLYbWj0NmuU8Co3h/OTbHYNCQV/yiPnL2zW+g66zOP3iuYW3T4UpVYqGBYze/qIMAag6nj1sJMndlQpXaUcOQ+WkOmNVjm6MuOsuV6LP3Wx39eArfLuG75OWPf47ZrBUbFMxwHxKmUQTBZRimZwVrr21WnwGkwqawKokslgQSVEdUDZEgAACAASURBVBAdYlmvQSUSNLfqmnbGLwxDc92i4G34QmvX4EClG02+r3a7CoYf2Np4ryBr17bTfU7yFhZX1XhWCVCVAZzUxlq+CxiQ7wxRs8Ka97RBpS2TZKQk9Qem5+1Au6jdPLxxYzIy4zg+ygfqdzS+mbotBuf0DLl2ygHaELTL23uCFKQ1m1qfp3eqcSTgYyAiuBhJ40gMjtV2rYQCjOTi/fRcUsoc+oFh0MFvYoQ0ZUY3uFVHiGG6dldPlfM0bcN2swER7vd7+nFUTCcp6Bi7FThH2zTaEWoEyZwyJWt+72RpDzNdt9KzN2osHFa1c89kSlpl9/ckRsnsxxGKp/GBphjpxDkSaRryWBLKqg6ap7YhalGr5lPOcCDPpBXTto0+q6LA7ZgGhqSSkSlnJayhLFkR1RhuQ1Sg1fwNTgew55JxBMgJREkjbWwUKC4mE2IY2jgkyytlGvwtaFdsKlk7AaKnH4apYJEOyuKuEiNy3P3MltTXnzVIOxlMs5kh+EetNs5pZV5YtOnrv6hB1YiX2GolQvJI1d6IMdK0Db6JFMYJca96kZp4Mul/1WRX8HYgaoKm3wcyC1gbIFqkkLWwWGMca/+YDfAEGLLQ9KGypnzV9bf1eGy83QSiOgXgCtS2avkoUVZAx6aiCrMMgVMgubbvT5/tZqOIXRv1UUzgDnW1F63Weq/afsDEKvTOa8u/GSrVkTWQgUUFsohVOxaOoui76nWIVM1XFoGXCWk708k1VLxWWXXy6AzyauKcf7Y+rrJ5zdFr4DlX3A2yJUQ/scHm1wyKz3t4/nOIcaEBpM5tv9stQPgyOaPl71YGQh3Qtrzmek4Aa293U+vJBMBX8MUpQKJs2ggl0e/e4Z905NULOCij4Um749/+uuN/f3VNT2cNntXUC00QXlxGfjoP/O67a+LqhNjWYQCCc5UJq3owrmvoTTfVrU6ha/Enp8Shp/Q9bjyQ05FSEs4FXLOlaTaEboVrW0qIjGgoWUQULK37UCOBaf0rspSLOgl8mM7bxFyswXE5UPbvGG5/JByuKXcvkf4KfCE0jRZxrHK4bOuqwfk42HANqVIAbrIH3j1mcM5AlwF2NQ6EWZdpCdwttI/n/eAmcE3bL6sW7uMhW8tzMu1MN7Mbli10dYhfCHWNqq0yeRZfCx56fyEok0jbdcYpmHocVP48+FRweDkMojwKaOv7KqMlW4W3guBLDbb6PROAWtfIVfC1FoWsilqDbsxmVYc6HWqZNKu8tSJVza56XVKD+ikBmOUm6rXNkgt58ZzqojqdXLtYI/3sWTKhfpfBfNZhYOtmg4umrTwx6+ff+9h+P5LEsH3G/FjgI3vzCDhefGZNLuskWb23WuzSD5zYMMtE+NHzYvKdUvLEpvFOONuesm5PQGxv2TqumpbVesXQD+z3B07klK6LdN2K9WbLqltTxoHhfU/pM12AZ08+oQ2RN9fvubm/4XZ/TyoK1AavXTFUnytCIPxs/ZdA7C/9vNzXy/uc779usrr2TgdgTPpbge3zJ6ScGP8/6t70x5Isue783cXd3xJLRmTkUplV1azqZjcpUqSWwQw0MxAgYP7vgQQI1IiiuKgpUb3WkpVLRGRsb/PlLvPB7Lp7ZLOB+ch5QHV2ZL54z/36XcyOnXPs9kGONl3b3RC5E4MvbNWQegWgVj3n9QIw7NqeZeWpUmZzd8X7Dyueff41X++3/OK//kdiGiC0EIQl1UcRaVXeUVWOPgyEtmfVrFit13TdANmSrGN19IT16RE3N9fc399ztFpxdHLM5fUVd/f3LI6OwFfc3G/ouo6Xz85Yn55yef2Rbn/g9YvnNMsFb69vefPuniF4/uRnn3NyVPHh3Ttubh54/eVnHD895fr+nm0XWK3W1MsFH9594KE94I3j+XpN0/UcDnuCN3qWuEdn9nzezn+2WLCeiOW2DdzutqzqmsVqzdn5OdtNy/X1B879Ge7JU4kHVVpZCh/GWLE7QFkzRhig6P4pe0SNMU7jDk82Fc1iwfr1MSdnZ9xc/YaPl+/5eHXLzdUd93ctTQNhgEGbWtBnamMJGdKQsEYct3JMdIeBVEe8h2QtFu3EjahVPIDaJJWj7/LdFV+9/AluVeN8Q9cGQn+AqqZ2srZSYc9Yi61Ennd26nm437E9DFhlz/YhE40lO1gsBazZdD2+tjSVrKH9PhMPkB9gCCJL/eOvz8An7h/2NJWn6yOHPtGmSJc7Dn3ABEsdYZESPtpCfhG1ihOFXJMqjhen7Hct1elCir8mqjwxE4eWIbQiTe1bYhTf4ZvdwJtDxcE1YilmCwtKPBqjNQoUiJQ2msyDiRxSy/3tJe8eHni9fuD50QlPj445J1LlFcYtsVGK5smIusYmKUiH2NM9bOm6juwsdVWTieScWKxWGscG+gTbDhYuYVtL6iTWMMbQHlpSPzD0Pf0wkEym3W/phwN97ok3A1+4r2mHlneXt9QnpyzXa5ypAfHaFbJEnuLZslaKkksniwBZZjzfZT+UTvHWGVKWPYsk7ESjMXrxq8w5Y9wUm842xdFSII3KD7BVRb1asjOWIUYOITKEgKscYRhwzqt1hHjqCktaGkX73JBbx8Ivcdpt3ljP7rAh9C0//clXXL37QA57Xjx5Qs0sP0lpivesncUddgTpSk4iAMjUIHTezKWwaef3OzZP834ELrBOi6baiMc6ZerPmr0a7Q6i+3yxtPr0LJliOPF+LaBQAXBNlvVSgMk5kPronILx+Y3onGYy1pTzb4pFxtjQFralwxpDiCL/lq1W1TPj9ciaFE9NJqB+9io2TMU/t/Q0AZH9yphqHBHNyJwdYy21Fso5Y50nq5KzsL5HMo2CPvLZiez92GQao93XycQhUsKzlNNI4pjiszSOfWnGO7LI0+PY+h87k+ZEgk/ji0/f9+mz/31grnGyWkOxmkhy85X3kidnZVTHiNhxiG+osZbKV/K8rQL3eSIfWW/UCvGxB2rOOp5Zvrua+dWWHjwSDwvISCr2c0z2F0ghKEWx4SgENExpkDxZxtV19WjsxDogCGCof5dmnquSywihI5Opaj/mH9Z6eYR9hBiUISnNslJhckdU0m/GpoEy/jKPix1EeQalB092EvM678BKbl7VFV3bje8NMUKUJqgYtPCjz1nHxRr1dXZG/KO9x6CNzRFP5CEMylyVYmndVFhfAXuGoaf2MjbeOeqmxhq1ybOWbKxepxciYNIiijUsm0ZB3kSfpBjuvCfonK2qClMZKXBUGZsz1hQiopynMUbqupIZIXwHwdFUbUMl+VBwkZgFYAaoMsLAziWFNyRrMJUfFcxO51hBf6z45kAqeZz8e8xZLRAY9xVrM94tCZ30drLaKNaWOM8aZcNmbDbCRnaaew4Dznqdp5JLkqQBn7UO6yxN02jBUvZg2SPkmpyvhE2cMsbJedcFaQiXrORB2Rhhc6eIq2SN/r7XP2mQ1hjDkAXVdl7p/FopkYrmDExTMDUm8YgokIjJRoEaCKHDkahsxWrRYICqrulMRxggJUvO4jsl4Bw460cvqYkpVZhRKmHJArVkhPmUUhYfL72K8qfFYis7bsSkLJtaAQmyLlo9CFxJgkcAusi3Eb9QIBnt8qg2CAW4EgDGykKdA4cjOCBHt3gfPva8/RQIGStbehAa72bJvnYI1EZb5pMNXvuigZHCkXV6SFuRRTyqMqL+QzMQqQBb5TUCIp8ebkmqSMX7sphol3u2yu50XiQ28yrxyDwwZryOselCLkC6Aruz7xT7A+3SmCxYxkpOOQTHezOGoe/V28mJFQdSScEIOPSYYTgd7EGbR3grAW055K2CDjkpEJ2zNC7JSAXH6nd7ZVnEqAG3AQzORnL3kRz2GJ+FRREjD7fSifriwnLT7cickKKlto7toePNh5b1asHzZ0/57l3Lw37DiT+icpZFzqSY6XKUqlXQqrPTQyJnkmkIvsIsjvBOrEBcGmR2G4/1C2KSBBFg6FpS6BV0hdICVta9dqw0hhzDFIwq414k3XYEZXBgXYawp44PDHc/4PoN/nBHu/0I9Niqloq0c2Jt4J0m7MIaT6SxYQcxjxIXUVo4NbqXQ04CizDOK7IyozPjcwhBDv5SmJB5rkzJXJh6wpap1UspxMm/tRz8ExBrNOCeB4fjiD0KAEvAk2EG0Oq+peujyO9LYecxCPcYICyAnjVuArZFXKZzuew1j3/302t1zrNYLPHec39/j9gFTN/7CFDUtVzYrgX8noOUxZ82Fp/mcq2fgJxlHc6TnGmd5TGoL+Ae8CiZm/+couyv0thPqv91XUsin9XmwmRNaKd7S2kGhs7GpbzGJGKGBT56pjPGzaev4p9e1sVYxJmxeZglHXPf73ENZalOi6fXJPsr+2j5s4xp2RONyWo1ksUzLMm62e/2xJPAerXEhsDDZoNxNf/yX/8vtF3L3//934PN7LYbUlzg64r1+oQnT86pKsd+6Hnqap3EjqauuXhyxunRmncfP/BxsyHkNPnP65Q0utGOz3eci9P5UObCpyDtPza+j5M1LUaqusGhDVCNnnvOs37xjL2F4XZHbgUcSy6zjwMcIi5Cm2HQPcUew2ntqWKPacEuGnJI3Lz/jmwtf/DTP6PvBn7587+kDj0MguSdnZ6S+oFGgcfQB06PTskGdoceaz2fv37NEAIfLt/z9he/xlnD559/ztB3fPfDWw77Pc9fPCdbxw/vrwgp8OrFBaerFW/ffsAAP/7yS0zO/OaHD7y/3fH0yRP++OVTlo3lw9u3EDM//cmXZGf44c33uKbm9OiUth+4vtrQp8jF+Tl+uWJzf8exr3j95IjLPhJm67z4I87X96O1oR2+g3Xch8DPv/uB9dGS58az3X7EuQVx6Lm/uWGxOqZZHEnyGwH1cJN9IlP5WtiJmuBj5CxtmpWAthmJA2MCGgG/7MDy2PGyWXDx4kdstzsebq7Y3H/k4+1HtruW7UPP7qGj3UUedtrAiox3htBHYTvmgcZKYxCU3WsrI9YJcWCIDjX9EdKB8Xy8uuHv//t/41/+qz+jaWoMlhAixgRClkTIGcPqeEk0gS4aMJ710rNqOm43gZ3GG6WBSFVJQpaNlyZlldMkLGMqGLqB3RZSthiT+Pay5cNdot1FnN1hfcY1Ht911IdOfNlNJu5b6trhnCSgwnZ0eAdLn/jy9dcYc0Z/+IawThrjC2soKYM2BGlCZXPCmIrLh44f7iMHe0Q2DTYPePUXTllkqVnte7KV87tYUQ1kNiay6R/4vr1nfed5Wi34bHXCk8UpL07OeHp0zHK5YH28JvuIS/Lsu3bPD7/9LbvDTthbes7HJGy+yjtSEHZs7yxNA9kbuiGTuw7vHG3XC5vaJHztiTngamHZO7wqUjLr4yN+9vwlP/npH/P+6lKlvxJHMTsbC1GEDCZPDX2ssTjjiT4i3dDL+2Tfsk5tHSzKGp1yiHkRuF4Ia3O/30/7IkpqKbGX7oW1q6ibZlS7tH1LyIGcvZx1rsaYRDZJPf/UCxcL0RKGTMoi/cVKk7/DLlM5R4XhsL3n8s33VNawaBrysMcax9RDIz0qJJYY0WpBHaZ4YG5vY62QS3IuGd4UH5UCskXGyTon46tgue5IeG/1XbN9ClXtmcIylf3FfHL+lkK6EFnEakXOYARk+wTUmwN9ScHbQiZxrhSctGfBuIfK7xwdrfHec/PxRhoU6j4r/o8KeI57bFGGKUHGGRWszX36x+4KAtrFWVwiYYSSe2YEHDONT3kmY+w83+OzKjiNkQJjEhDVWAOJEWzHGIIyCjPaaE/HxFirRQgzi38jecbExEBdVwze0xurzaYmgHo+3p+ukX8sRii5dBnb+T3+YwDto9xdB84Yi68r+hSprBcFQ8rCACRBmBqJmSw5GNlgFpaqqpTgJHPIIUSIkleW5tplzRSlboqRLrSkqpIcvYC5tmASAmaFfhjBO8PEvM8UkHKyssBYbV5VQPo85uNl/JKOV66EJdmrDQBaCBCv3Zra16QcRWlhrTZnaqmqiqBkkpizqKoygs84p4CfSOqLurngIlPRfYqRjTHaFKwfcyNZW0JaIU/kL1H0iYw/xTTG9NZK88ucRHWKyfR9IGZR31pjMM6KV2xMgNOilRJOco/1HucslWuU6ZvoQ6Qd9gLKKphY1lQMg8QBwKHvhDynRcuyl2AcYRBwt+8D3f4eY2G1XOKVGT2OfcqEOACGOCTtSyR2bt5ZwqCqupjF0kCVmslJ/Bt07SYr88I7P7F0lXhpM6RBmbXqty3XYRUHFHDcZbF2wNkx3ypknaquyDGqql6Ud8YafCPrJgcBrUNKoxJ3US8lRXAWa6WxpKgYJY6ovMd5R9PUZLXQTCmx7zuJA700PpMmfFpUSo5EYoilCS40i5oYI23XM50Xv/v6Jw3SZpX/VM5puUy9HLWilqKAskaN3kugkU3Emoz3lXhW6MIJQ0cOA3kQf4tFXVM5T5B+fmMAmLN0MKx8pezKeRXMaJ43SVunymwaK6pFXuStVX/MTHZlUy8+jOp9MwK0qJfRVG0rB9v84C2vqRqpDWrQjoJGDs1cFp+8ewRFrC1V9Yn5U1ha478rqPMoKTVgsv5uATNz1vQzKWM4Krgk3ibeazfElMAkDF6qy2o7QPkPxg16vjGWauo43mN1ZTq4CsOQPL2n3EuOeaKQZVivV+Sc2Wy341jOAWg3k2AIsC6HqU2ZqIFuwY1HVjIKXpcIQ4On8lnlP5HfF6m8SEgsAvyWg3t+IM9Bj5QSiTDi1eMBTwHFGEG9Ai4bvRZXDlVnFNzLOG+weSD1l6Trn7N6/jnb5gV5H7m/vOX//vcP/Nt/+zMu2sR//25L8CeYnAg9fPs+cLQK1IuKi4snfPvhgdaJAbmvFzRAMpYhiSF4DsKcIyObcrYTYDKiTDWVr8nGMaQkCZVWsgUgBKPsaAFnLSJfd4zNA2A2fvrZ5Tt0XToDVWrJ+w+49g3dwzfY/pbh/geIB7I11Ksj/KIhTp1/8N7RqwH/7zzfJLC+eDVbNUyfrmUqLCizRZOpwkAYdP5RpKvK6Cr3MwWDU7AgdrxzBruZva8EivNGHhP7vwQazjlhziAeT3maXBK0MAfqZLY1TSNNGPt+9p3TtY77FEU6hq4lM+6Vn7IJCjOtVMrLZxTrgXnQWr6rXNs8OBaJCqMFxPzzxz1ax3HsFuucJgzyc2myMK3FKeEtRbKsZ848oP6UPWqMBhK6Psv3C8vdzAJNI/vwbLwxiWSkCCkBR6aAfrLWJdl+3IRt2urnScKcDQzKhtUxIKtdUIxM5huIJ5gmceUeozaQsdk8uk/MZJFT2MefPhdjJBnOJcrLYI3n6cULjlcnHDVrQggc9jsWrma9OqEPkeurW1KKLBdLYddFecaH7YBzS9ousD0MLNanHJ+ckXLm4/V7ST6SdEZ/ffaUp+sTrh7uudzeCvA0dl5nDLLnRQYpbk7zssy7eQImy+R3/eWmsdH3zHwY0WQgJYlJvPdUT54Q2ygVfyNgSTZwiInbYSBVNSaK1Mz5PckYnhCxWfzUbOXw3ZaPb78hx8gf/OGfEmPi1z//f/C9BITeR+rKSzdaPYNCSljvqKoGYxxX11dsdht2uw3doePi4gxjLLv9gRAjZ08vSDjev/8IGf7gi1dU1vL9mw8YZ3j52UuGEHn79orr2x2vXp7x4y9fcNhs+PDxjqZuePLsnD5Hrj/esFgsuHh+QZcSt7cfqeuGJ6dnVFXNuw/vWR2veP36Odxs+HjY0hkonbnn++LjMZf5mIxBRLiZ3ldc9wO/fH/F+dNThodrmnrFcum4uflItpbnL79gsT4idEG+o0rsdltSgsViRYyZGAdNSi3GeDLFL1f2fOcsIYqKpB8GrHH45oxq+YT6OHDx8g/IoaMPO/b7PdvNjv7QkYbMdh/Ztwf6fk8YOva7wP7Qifdc7Kitp089oR9EFmki23aQOAdPDMMEjoTIt9//lkVj+ezVZ7x89pr319fEMBCVMRLVxiup5zwpMewiQ9sLqKGe1c5C4ww1Amos1hVt32FIpD4Qk2GIlsp61mvAisXY1d0Gp81GKg+5hyplVgspkCeNhXIWqWeyBkIkZSmgZhLHy1OOTj7jftOTssV7g/fCho/9QEotYeg5dAfEj87x2+uWf7iMtPaI6NWKIFus1XmREninnoAGY0v8pooCa+VadB+7z4ntsOX6/kB9c8nyg+fJcs3F6ojPTs94enTKk8UR9JHN5p7r2yva3IutiXdAUCbYID63mmcMKdL2LcZWwnRKkRwC1giZIBlRFKQgZ7TzntBnDJ6cnQZRiXfv3qkfoVOw7zHZIgQBB3JKuCy+fikGsnTooMJox+yBZCK5MmQre52zHvR9JceanyniAfx4rxcwTVQgBqS4ICU5AVQqhw6BxHhYyHaSfKZE5S115SjtBlKS2K+PHTHD0+cvwTpiHIjKsOsPLSZE2t0DD/vA8ZNT7OWtyHHHhP5xfO2cG+Od8nelkJtSxrmpgacxpVlPVmZswlpXCHLqdSs5U7ELSnqmO2uwzo/nR9aEvnhuJmYFUr2eEleOzzEOOFUV5azWACmrivRxAXHOys0j+zOPecMIBlPitaSxh1El6YCxcs5atfeSUHI6+0J8bG1VYsliBwGP9+as3z9G5hrjfhrv5ZzhEeEgj418StxVLJ/k/vTz9HNzZrT6d95LLoqBqAopq89cz8BcbPSMkX4GGqNkzc2tcdIPxEiTSKPArkXJJ7N582ls8P+lsPspADuPmT59jZ+f5ft8Ufvqs7QYmqrWXhdWCSICrhqkUWDf9wzDoD7rZorXkDnSD71aFWiMUlijszwGIPcD3hfVmFzv2PCtFLV1bgrrN44scMFGEqGPI7ZR1Gsi0d/inB+bakt+a4ghKPA7j7WV9BYz2UScszRemLiLIynaxxTZD4Gh60U1kTM5COWzFHvFFmEqFhg77wdkSWli15f/RNWT6LqA955h6Mf4rgDxlfcYa4RJ2Xak2Tg0qxW1VT9gfVkjfWoG9cHujIGcMHZiL494ghEGZ7E/K83BMIa2laKZddL0LCMx+jAMVJUX+6KcRNmcxK7HJKTHkOa37aEVz9jKEdyArcy4J8YQJRaPEe89fddhrKFZNaIWLBhVyan6QVXfZiy0umy0F4ieFilpw1RG0BljdL9ExjKBGoOCMsMzyqJN0Gvzx8ZXso6VVNOHgVKpOvTa5Cw4srJ1hUGelDQja6wwvHOUQr3XuT3m/0l6JrnKE4PgND5HnNPrybIfWieqEqcWLRVJWLO2FAcNy0XD76746fVPGqQF8aSIUUyvnXVUpvgxlo13qtw6rYjnFElGDpPiKdNrtbLvOnbbjtVqxcXZU1aLFZvdtVYFlMGZoK7q2UE+S9ZnB4tV6ZnS+xTQ07fnLObJOSvUVA7LOP6GULgNpZun9QLOxEOQazeVVlok0JHKbZHmqvl9lIAhFUDByrjJ5lukLDOZbAGKSvIdhhFMgQLoMUpZp0N3ZsUQhdmXdDwKbjLKGLL4dmYFNY2RCrHXqlE5VMr7c34sFabci4GMBBqyX8omm1IYwfCyQY3sUCMdDUlRZFvWYEwJfwzb7Z5iog5ZK2xp9F4xXiWFqUgqJPDJSSp+OU4gYDn0MyrJyXm8rhLUlSDdGHl/UIBorN4qxGsw6lusoLRWngoj0iqbyqtHC8aMcpKYI0kTxbLZ+LLJ6AaEzgORZhbWSoJ4B7d/xdHJ51BV7JsTUv2Mm8OW7AzeBUiGts/Y2mFrTxsD4QBVSPjlEVXdsr+/I6ee5uiYan0uoKxWkYZ+IOPIzslmmcQTNuWE2JVK9TqGJIlTSlhb/NDQIFl/zmii7DBWZRY56j1q0qD+Q+X+BSQSULWyA3nzluHdzzHDD7D7lnD7a8zhEmsHsq9oTk7Ji5psxNfJWNmMHVkaG2mAXRgN2RbQL5OD7DlDSPTDXo3fp+CkVGyLF1TOyuZw0kUzacLojB0D+QK2x5zIOVFVzbg25+Dr5C81Mb8LVj2B+NM+kDMKKJRAWAFFDfaLfYzsJbqG0lTksQo+jl5pxcw9TYyV+cva6TqLFHLy85zAxPLzMHQKBj8O3Od/2llAacpOney4/6RxHTMGlBIY6DotbBg7gaQTuDnt/cZaUtDv1OCUct2lDqBgr6H8vlbSlZWXk3gZGRQEKdJB5zQokOYk0UQ5xK1VF5sJdC8/jyb/5RnDOE5zv7bxPnWPMsUXOWkQhPxduR9T3qc4cgm4SgAzB9i9JmVzexqRh+n96ppI6sEcdQxMTDw5Oef52SucrTg7O2e9XPJwd49JjiWO1XLJux/ekeKAdZCGANlQNQ2nZ2esVqd8vLkBAxcXFzRVTRh6aldxe1NxFyPXb97gvOP07Jzm4gXZwqbd0YYesKKwyRly0uYrpeFeUv+7eXEBci4zrCRUU/GinIBWz+ax0JlVmpV1bEljUSUD1WpF9cKyjZmw38vZqGv4kAKVqai8p8qwC5G038IyccKKPERqb2iMIfd7bt6/wRnLH/6zP8cZ+PV/+0+44UAMPaZeYtTX0NYVXXvARsNiuSbGxPawx3rP2dkZy5cLFs2Ct+9/YOg7Tk6fsD+03H24YbVe8PzZOc4kLj98oFk2nD97yv7Q8/btFX0b+KMff87T0wWbj5c8bPecHD9hvVpJg0yTOD89xTcNNlsqa/nixXNSjFzd3rHNhtMnx5w9f8rH6yt2d1uOqiNisvTan8DaWUH7U9B8jDdQf1PPYA2/vr7H/I/f8C++eInt9izrhtPTNXFo2d5dEfsWuzgi2URFxXJ5JM/MiJ94iAmbMoYg3n1GziBbFQkzVE7XlhFwNScJxhfNESl0ZGOo6gUnJy85+vqYEgGkLHt91++IQ0/drIhIUhXCgEmGQKQ97KFvaXcPXF1+xFcNMVu6YaBvW7pDy9C2dIcN3dCx3ew4P3vGdhfpIL8ALAAAIABJREFU+g21t/QxYm1F5QwmWELsaPcH9pvAdi8+bJXJBDJHjeH8qGa36+i6SDItdS2JYV3LGMQscsOKxBASVWXJtWXRLCAHwtATgiF0mWiRmCBJ13XnpUhonIyzdyIdtQa+/PIPWR+f8OHmB5anT3jyZAk5MvRRwdkdXdsTyaTs+fV3H/nPv3nAvfwZpm4IqZf1ahxZfQtdXVM3C3YxEU3GRjeRKlIGm8aO2EUdE11im+WaLocD3x/2LLZXnFy94Vm14qfnLzn3C6qq4tnnr/BHC25ubgToDrJ/ujQw5EzVNORSgE2GoW01voFki2JL9xVtwiTdoBtEPejYbVr6MLDMSwETa6+2ahqJlg/UZDqGpAxxQ1010AtoO4QIoWeILW3u6RewP2rYLfRgJ1FXnlWzYLvbkTWIeFQUSXk8U6bzec6OnH7HO8PyaCXy2UHAthCF6e9Nw8KswNU44yBHieVwAh4gDXW37V66l+/vCSo1PX/6DJczznqeXVyQ7je8+uwlv7m5osdgFdj3thnPxpIMGVVX1LXYRUys0jmglmn8gpgita/Azggkmkthik9hxI77jxkBmRk8CVbUmcXqwOq5M4SgwLaCxkoMEuZjueYJPM5kfFWNoKIc1QnJKtU7t/Q3SeIzWogs2idKSCNZrimnzP5wEABlpiwp5JJHz13/LOpS5+x4/lsMzoktTIxhln+WeHmWv44qFQU5lcAiIHdSyz6xZhmL/6W/gUQYkvcZBbA0XpG81GhTIyvM/TxZMqFnd+HnGtLY58aaYlehzy3DEOK4l8TYj89sHJ8ZwWau8PgUbJ0XrctrXkj/9DWNGbMYT3LdMARpcKlWdFnjDW8slfMjK1Rk7wargGuIUZU90rTJV5Wcb0EKRyWPCiEyDMJKLQTTGJW8VtW0bdA5Jj6nAlpL7pmyFCOqqpLc3DA+t6oS9uFyWY83lWKkqmpiCviqkXmQ3KiOyxo3NnahJDkDoRQkLIuFxCtNI7aWVeU1twyklBlOIofDXmJgeRA6h0T1KXiB4DS2MEZBi/VCMDP2sY2XryoMhrZtRQ2qappY4v4s7GSJeyMnR8ccDgdZSzFS9KzOWoy3+LrGGEPXWWIIDHFQr1mZ36WfyZh7aAzfdR0pJdbr1WhP01SV7v2RrhdVZ/HmTUPCVY4h6RrqJ0VmjmqbovYmumOx3+3YsxPVglpaVK4CY+n7gZKKPGweqOta7BTyFIeFQRr4xSREIOPFG17yKfmWaLR3SWHcwpjPOucgBUw2DDmSQsR6UZ2V3kC2MiQh9tJHUYdZI+rqnIzagwRS0ny2zThfyV6HFss0B48xjLYnhQ3d1LVQEWPQhpjQDwXELz2fpOFdDoLo9GGQpn6KpWU7NbqzSOGhqM8r9/uh2H/iIC0K8AjkYJPFeRmAAoIZIx1hpXGNboxGINNkwKZEcrANPV2QSkKzsrQGqnrBanVM2pSKomyIss4sQwzqa1hAh2mjLXLPIl3OGkxkI3VJizIhi9m8ERAKMyW3ch+GoA83qm+OUcl/ArKxGPU4yhoY2Vx8bY1e7wzIpLwPLOWwUBPu8r8F+EEWSanMjoAeApxGBYUl8JpJhY0hZTGC1yII82YrKRWpZ0QtFeU+9EkWUGcOduljE8A3C1DgvdfOiWZ29bPKkzJboAS3heWsEhxbvFxVJoR4vZRN2hipJjo9vNycpVPuZUS15NeSKYdnGQfd7DEQJ5/dEgimlNQEP+FnbITpsJ4kYaOoZ0TXSgAgy7SqK2LM48aRUgk0tKvioEzP8jHlO4wa7c8AZAkmIJmWvv0F1c1fcHLxgq46IgWLGeCb71tevD7G5kQXYOcyFQrsZAi9ocexOj9nd3tNuLmG3GIXayq/kgYFOROGjmQcBukqWW6xWHzoDxJsmUzlZQxDiCKLVrm/vgFTfGXUF8gkMYPHZLJxZCzGOkwWkDWbrMFCB7sfyJd/R779B0L/Fh5+Q777LaQD2UacrcgLR/JAEosJjBwwRhMS8eyIknSRtXCQMNngrdUOkXrImwIOBkoxZ1xDSSqRdVPr8xsUGDBjkWAESXWdxhxJfffIGgMF88EQY5DEt1AKKEUsO861ebAo15+mNaZrHfUOFeBKmydYKXIBKnMyEgyaPJtzSc38H8v7ZC3kR3tOjMOja9N3iRxoBvI9TnTmn5fGPwvjcc5Ame6xrIUZ45cJkC2vicUwXScwJkYUZlDZE3TtS6GQMTkuY/mPgcpl7PzIUpWxSwW0L8vBCQg0DOqpZDPGZHX7yKD+SfLM8iypKkBsmhL2kviTZ760+uyQqnUplGUkoMMwFo3G5CpPe5oxBus9q/WaraoSnPMUUHMEqa1ICrN2n87ZcLRc8+zpBSZnhsOW089/xNdf/YSf/93fSNHGWOk6bBHfOGV2x5Ro+8CXL77k5Wc/onn7hvfv3rDZBvKyIg+B2ljOjk+pDSxcxWbzwJAjPsOPzp9x36+4vLvm4dAxKEsLBaxLIIyZCg+m/H0BHT6ZK/Js7ThPyxwbE3lNH53OQ3kKWcFw+QzXeFYXZ2wuA2Gzk6YbRqRgD92BgMcu1zKOIZP2e3A1NvSk/T02rahdTeg3XL79lpgjX/3xn7Pb3PP2139FpUUwZ8A0DcvFiqP1MdeXl/QMHJ+dgW84Plpy9e4H7m7uOD455eWLV3z8eM319S27fcerV+ccrZfkGDh/ei4AlPPcPTzw9v0dhoqf/eQ161XF/cMdKcGrl59BhuvrazLw7OUzokm8+f4N1aLhp3/8z0hdy69++SvC0HP+6iUsa96/eUtIiS+eP8M/fclf//obbrpIrmvGxqWlSKrr0BhTAq9x/WHAVp67uwf+4199z8dvvufPv/6SV8+fsaxrdoeW3d0V+80DxxevaY4qQhdxTYPzdoz9vK+1s7OcRxaNI1KEHJV5lSXAH3piv4O8gyqT2lpl+S1ttyeESOVXVG5B3wX27UDXR+5ub7HWcHHxFO891nnqRcNiucJ6T+WOqI+PWSyOWK5PqZuKum6ofMUwdGy3W4ZuIBwOxNiz37d8ePuRpW84O1nhajsWbkgJ4hHOR+43G1zsCTGQjWWzO2AXFa8uFpwuPN+/3fBxe2C5UMVaSLjaUlVQGZFH7g9IDCSlGJyRc6ILkkRVtaNqRP5nbcJXjsWiwlYC8pIhq7ff04tXnD97yWazwZjM2ZMzmkVFiANx6Njvt9rgzfOw6/jlN+/5n9/ccu+PeLFaE42DYClF22zFT8FlT71as0W36ax+nsrw8SqhxIq6KaPMn5gJAM6TSHTO8DEl7vsN8cHws9PnvDo5YnV2xrM/+IquHxgOHfd3t+zvbjGHlt1uw91uh7VOmwJ6fC1F9ZQDcTz+DIkoMbvxI1BljVzHh/dvOXr6BIvD+Zrl2YkwwwYhpqDhXwqR1EdMdtgsSjBiwgFDHNinjuAiN3ZgayPbxvFDk3mwCZMMlZecQGKSPBJfpj2wWDzF8fwZz8QEBku2jGehNbA8XmG8JfcoCSESU8BZz6I6xtmabh+wBGovOUXGYrKFaLi7eyAha+zd2zc8u3jG6dkFqQ8cnz0hDHuCgaOrWxikWOBIuCwDY62nFJtTztSlKaTmdUXuXSSzQ5R4DAtW52gI4u/oZSeQs9k5nDH4egJPSgF5KkonIfAYVYapBUABf0ovDOeFQW0rN8sxUim5U4rYTpuJzeXhcvZ6wOJsJmUpRlrjNLyWM794snZ9p4w8PW9SlpaeBgGRFEC0FFabgDhNI99bGJclzpUY0Y3XLOOtOWrOCt7HsUeE9XbGQlZ1Ehr7GpS0ZMb5zyxmk2sz4xkKxR7Qjs2BcVOskrS5UlExxpzGIogid8KkjzPAVGMf5xzBGGxVE3I7fqb55Jp+HzO2PLdP+0RMz9P8znvnPxu1xZJ7lHnhvDREDknGWYp8or6oZ83jspJhah/wSuaKIZBjwoJa9pjRv7o9tIK5pMQwDNR1rdL6ScXSNDWYhkKy8t7jFQQ2xtA0DWSZZykqa5k8PmvrLE1da6MnAVtLLiiEBFVclHPcluKP1QI2otSwXu0ti7JaciLpZ2HxTgozdUxyTbruhzBI/qE+ygJ5yPPPEbyCc5SibwHKgWKBlRT7qY+ORgJDH4PaNwjoFoOAksmBx3ByfEyIkf7QjvdceWnQJdJ6Q9MsSDERYqtEE/t4fyokOqSwE0KYGLpO7IhWinOkJIpHdD+LMbBoGsWYjIYvUzPilCIhijrBWT8qP63iNMMwKHDtVMUH3jdIQ17IfZa5pM/DIHme9RKn2SRerTElDGncO2r1EbbZ0Ce1ZdCzxtSyf9S+otfm4hnoY6Ddis+rd47K+bG4lICkRE6w+MYztC1xUCasWoOQotgulOcaAjZDO7Rko9YKalV26A5EhBzjjcUm8ZEtPsbeebIpBB3ZUmJKpPZAVdXCuE1JCCDW0IZhJJXGIWDo+X2vf/IgrbEW5wxRsYBSCTKGMSGKWuko1TwBLR2ls3u2iZAj97t7rMkslgvuDx3JOXzVkNNUhczjJhEFpPBiZt0P0pTAacUqxCidXhVgxEx06KzJrjfCjMJMG/Y4kXQDerQxQyneqSm3JuRG0jtrnEgztFJVqgBjBR2F+uQDps/Vw6SAE/K+2WGAbPpTZbBcc579nU5wHssNJym0GcElmLO2UMmIHRlbj8ELRLaj7/dWmv1YI1INCfomj0OPyFRKVVikNAaMK5jDyGoFkVr4bEYzecFZjEi/kiyYjJWKvRNmY0gAwuosflVGJcpjFRWpqqQoDaqmLrJxYsQaJ1UXIyxXRcFHgKg8j/GpaFAGj//MOsGGQXwLBdyaSaIAdF4BI8OofEYB9DCF/ViAbGE9DiFyePs/WDZ/xvrpa+5STdje8u1vatziiGbheNgP9KFmaTOVrcQ+JCc6xVmXizVD1TDsNywYsDbRP+yIIWCaBoPFYdWUXIGsEthHAWUSCW/Bm8QQwmztFPm904RZ7EpyTsShk8qdt6WJroxosVOwwqiqTCDc/0D77i9xt/8DN3wgbb8jffyfEDZkE6l9TbVeYxrxEcpafauMI0ZhQBpNOrKCbHZmEzLNVwUijRWpuoKM84CsPJuk7MqyxqYgrgDLephmWf9FDjIxJc0YuGkFRhsiZF68eAHGcHV5SSm2lBxrshuQcSzS9rJ/Zq3WlveWjsY5Td/zqKYwA62mv51ArQI0l41qWv8CghV/t0nCXyQlc0n/NGZzD9XfaXTwCTg67bGTT++Yas72xvKagFr598nLbnzHNJ4URvM0D8Z8e8aQ+JSBVADBAmiO/0UJSuMg0uuSDMvE0gSzfG4Zj/xJl21rx2so11iALMHJpQgHfCIr0nEtzHsej/2nVgalcVyRPZX7LE0cJmsgOZOWzQIzZD67eM3z85f0bebo6JTNzS2/7P6BZbNguVxhsWzvHyhuEW3b0zS1+FfWK1LKvPn+Dbvdns9ffYUxlq5vudttyf2BhTesVyesViecdnuurt9z2G+wQL044dnrE97d3/Lry3cMaeqEHhNEkzQIZmTwJAUd5oWC+flVAspP59E4t2aMT5MZ7X704Ymn6NGSo/SUu34g9uKtbZxhiIldHKhiRzSeEAais9T7HTZDUzmGEFjXa6qqIbZbPr7/lqau+emf/Su2m2tu3vyCZROwTqwUaFZUlcdbzzBE2n3PYrHk4faB3W5L2x4IaQDzhGHoxIrg7IT1umK/240JdN3UXF/dcH2349n5KednpzgT2GweWC5XNE1D3/Z8vL6maZacnJ4wDIE3796RsXz22RkP11e8/f4N/RD54uvP2Q0DV28/YFzFs+dnLJaeb777BeeLCr+oebtpoaqI2eJMUQtojJKTSFvx0llY95yua9nd3jE87PjF/ZbcDZyfn3O6XrIwjTKuHLE7YJdrbGGwJEe2hmw81lQMQyaHRBhahn5Dij1h6LEmYRkgB7r2wP32wP3tPW2/IeSO3aHl9n5H2w10XUvfR4ZB2HZ9HwlBnksYAt6KCqbIF31V4Vyl53amqT2+EhupmAKLxZKmWeAcKhsXb7eUBsIwEIbE0fqE5uREZf6ZoT1we32FCYGTkzVHy6f86E+fsVyuePfhLSZn1qfHNDbSb/dcnL+kTQOb/Z3KjWUv7boDKUesr7l7CNxt9jTLmso2+v0966Uok5ZHNd7L98conuNJgUNjLQlZS8+fveCPfvJHhGDYHwaenJ7SVDXDIOzSoR/YHgL7NvDh+oHffP+RN5c72gD+qXTcTtlSVbUwsqzYCdhKuqDjvdhhGDv5h5pSPnHjWVJYNOLpV4qUcu4nqWQRKsPb0FJtbjk5OeO0aqBZcHHxCmsdz4aB2B5YW8tm98DH95eSBO4OHG4f2LQ7rFUQL0ZyKoyboD/3GESdl40DF9jcf+Dy24aqNwyHlu32QUCvPtFrb4kchOXWD5EhJLHW6FqGtqc97LgPB+4rQ3u25tZAhyU5w85m5WHKnhUIo3x5ekk8OxWO7WgvJJ3gZ/7sRgvUBnFocBbf1AyHjj4E+jCQvIDhKRoq17Col5ioSb2yqnPK5CHxcLehXhxhTcWLi8zqeEGthZaqbqgWK/Yfrnj+9ILjZkGMnTREMlJIC5qrGAVjyz0UIFWAxtLbQ87OGAMxZGFSZUjZkIPGE3YC3mLxcU5qiZCnBrPWuJGZhTGTGstJXGuMMAzFbgC8r6dz14p/sJvFCdN5XAg0UwNVuRdRLHpTY21ppFTO7qLsNLiqHmNYMJjCvk3qPYuCLVZiBlOUAilTuVqKMaWZmcY0Tu23bJ4X6Y1ev7DVZJjUSgNhQ5bu9ERV/1DAfbFfKfc3/9MYYYSWaK1M00JaspqnGIsQl8gjY1nO/ImJW9RtnzJdYeoJYp1T7/LH+dU/du5/CsbO/216fo/tSX7fq+SbIOrgygopzTrL4AbiMIAxbLZb+r5jvV6L3YHG6yklalvjnOQjBk+yYq3UaZEEEt6KsmG5XI73UOI6Y8wI1Hr15CwgdlGygczpSdlaHowZcQXrirepxImFSGU1LhKQSy0SNG8uvp4xCrCuJW6KbWTMabQtM0YaP+X4OMeerAws3kCvzeAEpFW2d1IrHiUExGFQ5mixP5ysPXKGGPII+Keodnep9A8xBKbGcQlRLeacaap6bAxNngr6yVq8q/HO4hGLwhAmXKFy1ex5WJZLbYAX07jPll4l5ZlJnhQnAkLOY1ztFUge56tRQDwlZRQrXqPPy8wwGW/lDBVCAaQcWCs2ZqxRtqk257KzPDCLHVSKqgp1pVmk5CZBx8goASXlhLOIp7my303KBCP5jAFt6GU0PxWbM7AyR73Mydp4XC05rE+Oth1U4ezGXNp68XWvTUPIU5P7Mn9isUXyQhBommrcH8aG8E4XXcygxJuYAmlIDDHI+eotD7sNi8VCYp/0u3vO/PX/A5BWkGn5YUqUZXPQ5Fkp8FETLqsets5Kwx+Txc/ksN/StwdMs6KyFY1fcrw8xWYZhiJxteqDagyEMHD65ITVesnNzQ0pmdHTZazo5QJ4TZt88WH01o4eXM7Z8VAr4ENh7lgNsEaOa8pkM1kWuNGbVReUHiqRGeBSMsYZODF6284AA2CUdxawc+5dOco1KIeKfk6eAYojSFECmsKcAoqURL/SFQZbSqMcaJKElKCoXMdcSp5nz0M3C6MbkoJTxIzD49wCsqepl6zqBevVkuVqwWKx4KhZUTmHryrIib7vGMJA3w88bDfcPNxw6A90YeDQt/RDABPxLoOJODM1KjMGqaFrkOS02pYUSMOIjK8EeyVAKptxmTe/cygX8Gg2NmX+O+NHAAf9LGGlFan1BJyXMR1lIorMGSNAyWSbWwJWAymxXLS8OHlD6v+azv8Jh9WCm01H/M1HvvqD52xDy82ux62OhM2bZC4mkzlcv8UPcPL8NTcPN+y2e7wLdB8+4FfH+NUxAU8O0nwAJqDMGKMV76jJNgx9T8giVSJPcwsyVSMSmhR6QnuQKqArDSIMmTjOv4yFqsKaDr97S3j3X8hXfwvpFg43xOvvsftrDJFsLTF7mtWR2DJokxGrm+hMJTeusSGGEcAsB+54ELoJmJ0Cv8dB3Xy9leps8YmSl0i9SnFEmODqnaXTJ8znUUaT1EQycHX7UYIJPcxyzmNDvZElYUsA9bipxiNwbgRWJw+smItf+NTR9dGc/gRYnWR6M5ahmbq7fhrwlmdewNvHYOljNuv4f8ZIXZmjs0C6AMIS3Mk+Zj9ZN5+Cu+P9j3vVtJYABZeZ1tcn4zcPwOf3V8C94oOW8vT8JaOVQCmnRFVpQ6yYhZnE9OyiFgMK63Mq0hQPZCPzRvdRsQyZNdHLmVFdoDBkTGItYsgilZ3ZUHjvx/lZEsLSoGNqplBASSHrSYAtz6Je1PT7lstvrzlLz/j89Y/43/6P/5PN9oa/+It/jzGwaF6zXK3Z3N1z6FqcdyyWC5KBISbWztO3O7YPD+w3O0x6xhdffc2KFSfnpzhnuL9+z4fvviEPW7xLrFZHBAOh3+GyNE764vlndDnxzdX7cY+eP+emEiuV+ZxMeWJXF+bB3CN1LhH9tLDw6P9rAFuKqzHLs3WrhtXFOd3NPantcUPGComMTdeRXSZpAlCHgGv3nPglOQ2kds8yR9a2Ie4G3vz6l7z66if89M//V/56/8D25i1r5yBa9mxHWZmvDe1hy2bzwPHxkrOzJwz9moftPW/fveXp0zNefnbO9cdL3rx5x/HxmrOzJ3z7/Ru2mx2r5YqvfvSFeJf1e2IeODs9o+8G3v3wnv2h4+nTM87Pz7m8uuLh4Z6zsxNOTk/Z7Vq+fXfJau356usX3O02/PD+hsXJMU+fn9G1ey4/vmF5dsIf/+xrPnSG93/zC4Ygc1tENjKOxlqV2IllDCkK7JYS9x8uiQ8balsRUua376/5i7/5OV+8es6Li2csFw3OZHbbaw77W46aNdbWRDKRREyGLiTCkMgx0+43hPDAMBzoh46u72j7A/t2x3a3Y9f1tH2iGwIxJ0LUBqoK5hs8IWhDMKJ4xeqZblOizo7YDcJsi1uNdUqRICvzVPaBfpD1Zl0BzzLOyd95b1gta+q6Zoiy1y4WFYtK5INr77jdCjBULc558vKI/fsekyOxS+TQYVLGLRqerc94zhOsj/hKuyAnR86Wo5On7A5wu2m5eP6MZ8+f8f03v+KHb3+FRwqG2UZpcSZBB2RJXhQxwWA4OT7h89evSTGxedhyfLwGAiZHYOBhd+Dy+pZvfrjlhw8P3O0GdoMwtZLN1DgcnuRR1o8WuZyHnKmbhuV6LXLLsoZ1r8tqhWOdFNar4kVtZf9y3pGTNCApMWxOho2J/Ka7Z3V7yfrJOQHHYT/w7NXn9NZjVyd0CRbNE7588gXHx0fCzOt7Dpt7unZLSgO19wz9wM3NR1IaMCYRB/GprWtPzJb95iOxvaPvNnz//a9I32dsXXPbD1y1e6IFgyPkTNe3kisYSz8EUpKi967b8mAD1avPWK+P2BgvLN4ozVy8c+r6Z8b5Ks21pvi2zLMCrBlryTGoVdqsAA04L7FCyOKBvVit6W82RBLdMFCfNlSuxlhHzgZnPd41AhJYCVgNwnDb3m7xrsY0npTvOLQD9UoaArl6wer0nOevE+s+s1ou2PSdjIEVqx1SsUSRwqaxYyuw8Rw2ymIIRYliPTlIkZAkRZqUlWWtAHJK2hAmq59sSnhfUU7VEIOy0pStGrPaajiJvyIKFugZbf3UZKv4JOoctabSc0ZIRRghApXeHeX5GLL6CJfnaGdnWPl9vZ4sYJm1TvbNLHtTxqhSdN5fQ2KCUliaq+GM9RT2OeN75zGUmZU5LUXhOfYssFbY9LMz1Ci4XNRcjwvyiWI5UQr9RflYJOpFbVTITZKvKxA8Iw2hw1fycmkGqUoX76BydAoCYX4XVP2ULPAp6DIHlsv7fx8w8zset2NeN1mNxZjpuoGm8lgjRa+qqiQ2aBoWy4UCl6o2NsLgjynRVA5fV8KMTlmepcZ0i8VCQNgZc7bE68V3GAqj3D265pgiURm4VeXVilEMGaSYKiutxIxd34slglWrgCDg4Gj1l6RIknotalgzPSOVmRsF2/shSBHGKDNcrynlqDmEzrPASDBKWnA0TIQnAZIlxi3klyFMLMcQAnXdCKjsPNImJuvaks9s2z3mIMzebASwtFrYA4n3QgwUawWj68I7RzRatFTtfkoGjDz3rutp206AUTvPQ6bn5BRvIgspLZkoOFlpbpyzqhEi2WkhyTDuKdao8oSS85Y1pL15lCVtHNKMywpLn6gkOCvKdsWBcVnA+DL3rbU0i0aamRXi0yzOxixGfMNkIUs5J1iPH+M8RiwwK9g7DIM0L1RWftk/Y0zEmPF1TW3tuL6bdaZrO0iZYZB5YJ2jso5VXUthF/H91uAMdMxr9bytKvE/7nux5bPqRd8Pg2I/CvpnsfdxSez9srWcnB7rmSdkl99neQL/xEFaSegn4LHQoI0p1cM8mpWPmyC6OGMm54EhiNQyZLh/2Iwbd+M8Lg8crZ8QApDF+ymGoGALymTK7LY7IOumMDEpCyhakv3KeYWGDOJxksYDy6mHq4GxejF5QUJhBRegNiWRnpUu4KRZ4qcbTmEOlw19zsT7FDQoC/pT1tOjMVOwaEo4FZjRyWQ0YJNfUl2VjkF5WQ1Scs4sFrVuvsW/xowg5Wgyb6bnNj11+VzvDEICLd8J3noylpwcLnlWbsHp8TkvXrzms88+5/PPvuDiyTnnZ6c0iwrnPRUSeIpZswARUf1XhiFweXvJm7dvOLR7rm9v+HB9xfv3P3B7d8V+tyWZiKmydDx1WeXBk3jdJEcKAVdVwoLTMUlxJtOxMnqF9VbkAPPDfg6Uo7KOAqQIxpe1SiTsUMjjBi8+QCqZmh3yc8aDPEOngYYGailxXFf8m3/1z/mTP/2Kv/i7G/b3l4T6gj69kzTyAAAgAElEQVT03H94y9068bMfP+dv//4ggfGiHr2giYm023L27BSzalg1n7N72LO/+0geDlT+BLwF4wRkUgDKGvBOwXdniNkwhEQMGUJS6Z4EiMX031U1AEPfEYeuTE4dO3QeWiQ9kLGvCPj2iuHtfyVf/j1VvMekDf3Nd7C/kXVX1kpdERqPz3pdus+I55sedBqoFTA0p4jRoMJZNbEnU3kvIJyu36wB5OgtNAN0SnA3l+wXUDelieVR1u/oLWztGPA8Alc17xCGrgbJOZGi/Nv8u1OagKcyF+dsjel9EjwsFkvatiUb+V1nZgWF+V6jf5b5X9gZpchTvmPOos15AhrKmEyvxwHt6AM2AtCMe1RSn+n5/iifX64169iW4OHTQtZjRi5I0m/MFLhO1zsDXeeB+2j/kmVO5sy8SUABZEvDy3Ht/874ayJiLIX9Po6xsrTn7C9m31ruQ+yc5XekcYTXItJk1wJGC3fyeyar7QXu0WeX65pfxyMmcCHKU6SwegYZw831DX4LtJm//u6/cPnqLaGLnDw9YrVYk7F8vL3nYbujampqW7PZbBhiz/nTC148/5zKr9jvtlR1zfOXxyQs//Df/xvOWY5Oznj56kf80T//16yPTvnmH/6Gvr2lbjxLFmzTAFEbVwyRw/4gZ7CZVC6F3V8SlTwbE2sez8HSaObxfPjdJG0qiEzJgNHzoTDWjTVkZ1mcnmAwHK5uCW0vUl9jOAwDMUSCrxkQ9UblwLY966Unm0DoZC4dLRdw2PLu29/y5R/+mH/xv/9f/N1//g/sbz/g04AxO7ra0qxX4unZD5gY6YaBk9NnnKxW/OVf/SfqxmOt4cPlJVdXNzx5suTJ6RPaQ8ft7QbrLC9evaA7RK6vPnC0rrl4esZ22/Lu/RUxJZ5enHN8fMIPb9+x2x/4/PVnLBYNb99+4PZ2w9PnZzx/fs7V9TWX13ecPT3j/OVzbjf37NoHfvLjz3ny8ikhDZhDIPYDgxd1lQABjB57ksAmSkHLmszhfsPwsKFWADfkyDYk/vZX3/IPv/2O0/Wa05NjKmdZ1I7KWSrrIEsHZpEaW7o+ceiEOdt1B1LqySbRDz3dIAwJ4wxDiAQDWI/xtez3zmJSUFKBNB4zvjDwK/UTNWQj1jwH2aRlj6WAScVTMo1nunEG5yTJTjbjK0catOmGhZgN/T4SN1tGMY2VRoTOGNaNI8dESPCrH655enHM7cOGvg8sFlaLJjVHqxWny480VUVTw2ptWS2XWFPjfc3x05f8+IuvySzYHfa8f/eWh82G1foIbwKVM5yeHrM/7ATAqhuWyyNpamIyVd3Q1AtIhvv7ezbbe+p6wXKxYN8fuHnYcHn1PW/efuTq44GPD5F9sBjvyM4i5q8ZsXoV0EkS5wKoSMwRYpCCY9Idz+cx2RXgbTpnx8ZOKY0elSkXskLWGMaTvWcfB3758AH/neeri1fYZFiuTqhOz/k3/+7f8Ztf/YZvfv4/OW6W3O8GbAN11WCOzzBVjU096+Ml3jlWF08Zho4UA7vdgaqqOD7+f5l7s19LsuvM77eHiDjn3Dmzcq6qzBrIIiWKFMUBUrfktiBBbjcatgEDfvKLn/3mP8mAXwz7rQEbBoxuQ625RYkUx2IVqzKzcr55xzNFxB78sNaOiJss9TMPQFTy3nvOidix9xq+9a1vLYghsDzbZXVsydstXQgsN0vOz1uebrc87JZElXOVttei3SnyS0WCqXeBZYocNZaqdsI2DNKRVCkIM5L8SyHVUXtHSGPsIbY+UIq4I0AlrMrBf5GlA8iAs5m93T1W5iWlq8M6z3wxpwqWnHpCAGtrvK1GG2osKVnOj894/fwVe9cPwVvqWUPbdrRtT1U1zHZg1raszi9LiZ6kLO0hxit54tBtYgY/WfkKr4OHhk4H4Hy94uz5M2azHYK1+NlMSi06xZ6cmc3mgxzcdEiSc5YqV0M3RYiRWVWPLG317yX2KfGEIWmMN/pa7yX+lYKuYnf6PqvzPooevfcVmBGEwmr7rcY8aPeid17ZtvLMrDPSgKoA9MAcNDJYzFgrepJFpkpznaLhPHSJmgx5zHFGcsgY82YdYlw6ppy1AnZLADHkxtXkc0ffmov6VMEwJV6XWyMlyYxSDArIWmUcKsvWlJiJ4XwXwFnqYTooSc9BAUF7qzIqeoFv+vtp7Db975e9pvHllFA1jcMlhnbDWXNW9lwOhrpZMJvNcZaB3RpjZLGzoJkJyzwrQJRiVp1kq0QXN4CjTa0dsZNurPLcp/FLzpntdis/twbTj7m8/K3YyG3b0277wXZ6rwCys4Q06hB3IWiYLFqd5TtF1sAM56Gw9HMuzMrS3ZqH81zytAw0TSOsdP38GFWIJyaqyg+4i+AgEn9tt1vRgFdgNaWM1/k2rrJSdNH72XYdKUgXmVNspKorIQQaKcoEjetlwJ+BGOlTpKprKudUXlFy8VJksRZES9VRBoGmZIYzEoIWwpBhVlVVUcgmoWAsWljxCjSnYY0UuE3lPFuc1Q5nsq6tPJuqqqj81P7mwdaIvZAhmDlD6BPGKOCNSqlkVAonKUtWC5sZUt8PhTCraJJ3Cl6a0pmmvgGR4ygSBdhJgQWku9k5DI7aVyrBWeZSqf6ycUDUsyDJibGGeVPRzGpSL0PsYowka0GHE1tnaXQo2KxuICeylWIRaeyiLHhaVXmckzWrqx6s5N9F4iAmh1XiAEBjip/JMJ9flVl54/UbDdIahIE1MFSRdo3RfI9s2qQt9Vgk+UEOdASytaz7wKvTMzpkAFTTNDjf0ezugxURa2ckaCyDbzJ6+JM43srXpBQJQSb6FTCCLBohA6NOgY/MyFAtiGdMqJaPAMxRDwZmZAkPwUMWQ5JDkI3uKqXT66FKBYwdA6qyMnIox8TRWDtol0wdQ05JB2GY4aBXldDqt203CLlTnNnk4bwJZIztYcrOQx0EUqWgBCWMQFXR2hFwyQiAkKKI4ifRGRaGjMOaioaKxXyPG9fu8LUHX+Nr97/Knbt32Ts8oGlmWv2IhLal64NMI88Cmlln6dqW09evmc3mzBY7XDs65Mbhdb567wMw0HYtMUROz8/54tlTfvXwE375+S/44tlDNv2lUNcLuwwN/JyhauoBSDG5AHlecJk8ttVoSCiOvwS2ZZjMFIjKZcskvEcrQxbnje6FCRALAzBehqeUNbXWyVA8o0EFI+hrcDSu4ZsffYU//f73SSHwvfsNy09f8PMVdO0CTODlM8vubIf37u3x48ctrXdiPBFtoGb3OpevH+K3K1i8i50d4A8tsbJsyZjNBltJ29FiUeOcDOGyRpOnAF3IJC+Bg180BAXCTQxUztO1Hf1mRVKQVA6nGyM0ueFJMO5o6Jltj+lf/Jj26T/g4zn0K+LpQ7j8HJPX2s5qIEfquSPPDClLYJdSlhYWklRbtZXF2BIkqgMdM2BKxTkXAGF4DqJitru3S4qR9Xp9BeyCMaArYI60nZcihj53W1jDBaMe98EVBmjSNjsNFMqGKkMcBEQTp/VmkGlMYRhwhcmaUmKz3dB3/aAz1CuDZmpTyt/HVNrmZM+X1o7pM8t5BILlvYnSvhdCGNciyZ635XDoawCfB0DTDBV2+f0EpE15tGH67KSdaLruXBk6JoOwymCIJMG/Gf1O0Xpyk6Cm3N7wfLSSnxWMs8N3S4KXkWnEBoQob0qmML7KAAi5dA26jB0YEJpVyXcX8Np5KRpoG1/WokMB6kMIGGcwqkeLMYPvGXadGQH96XMu6zXdr2CG6rg8KwWvjRENp7M1+/UBH73/AefH55xfPufv/+P/y2yxy1u33uYP//hP8QvLj376A6KJHB4cMJtXXF5c0rc9b995j+Uq4us9Yo60XeTOzdvsX77k809+wtPjl5y+eMbDwxtSvJnvs+3WpPacmYNm/zpdEMZytFGq7+q3UVs0LSSOe1R86ZDMDWdt0P6YPPNxP5XgGsQ3kgpzQf2fsTI4J0vinclQO+ZvHeKdY/nyhNR2MmRpVhFi5DL39BnSdkPqAyHUcq8zmPmaTQyE9YqZdVQ58urZnHc+/Crf/cM/42///P+hvXhF167ZnPbMDq5x9NYNZjPxXY8ePWOzyXSbSyo/Z3+34fLikrYLXL+2z2Le8PzFa1arNfv7u9y6/RbrtuWLxy/Zm1ccHBxwdr7k1asTqqrmnbt3WK1XPHr4GF9VfPjBA/q+5/PPH9O3PR+8f5dcOz751VO22463373N/sEOj599QcyR3/7tj7j/3h3W3YZnr8548cUJlbVEV9qhJXYXP6odDbr0FkO/XrM5O6MKGYMl5ERIvbBSsPQJNpdLnp1fCjMGpOXX6SBHPV8hZimYG/lOq5rpCUPKBkwlBXpryBVSuAQZsJoSHovJFcZUpJi1GCIAf+x7kccyapvJ0hquhQ7ZRaJTWiSyChswaExgvSOhzHptxbQKoGS1vXXlFIgUW9mHxEVbbIph27Ycf9ENzFE22uJrAiZvZKEjWJOpXaayDu8MVZ2pmx8yn+8K647E0f4eu7tzRFY6cbC3h112LJcb6qYRvegd0ZibzRtmiz3I8PLlK0IIzGZ7LC+XPHtxwufPn/H4+WtWbUfXZmI0BONwtcYxyZCjFvRqTxtbLXBnSdqy2DFyIoYeiwDVPo+HVmLpNJjcss6UAg5X2X0yiEriWUvGGMcqJz4+f07MmY9uP+Dk5IR9P+ezh09xsz1ltPZiQ2IgeitFl9AR44aTk2eQAl3Xk4HZbIdm5y0Obt7i5bNH2Lwh5cys2WG53nDZrXmyOefZes1xSlzWlt5JIiv69+qHkbg6xF5nXECfHV2KbGKHdTOck7ORIzqHwozt+bp/CpigeewVfy8ArB1AAowZ7JnRmR0xJ8iJ+VzA6D4FNtstbd+xWi+JMdPUu4Al9K0M1bTq64yjrhvCtuPi9By/U+NnFc1swXbT8qtPP+H6wT4Xywu8h269wsZ4pRXeKiiFMcM1WUbQsKok0R6yLw1TnLPszmY8//wZ7WzD9bt3aepawE/nBiDM638LewoFR4yRgTJSp03Urh5slKyvU1BX2ImS+Cecy2/4VoaisxTmJQYpWreFESqfWaIkBQHIo92YPM/KVZpn6d7G4N3o77IWgb12jqLkjgKQvEkCstr67MxIDtGQfBKnjh2rCbEhhQSEMTQ668WAdgPK3gohSCckY4yKjloZfG4uZ3k81yX+FizBUWaYFIkcWWOn+1OfiX5vyWVTCFIIrLzY2jgyA6cxN5M1Hp/vuMfefL1ZzJ2SzaafP2T0OQ/t7DEkuq6j6zt2dxZUdYV1jpgCddMIWz+IJIJ1HudkkFpKiS70GB0Y7p2j8g3G2ZFhqcBfySed94OkibGq460kpxgjlfe4UtRW4Cn2om1qraPtO9q+AwTQLexZ60fimnGWEDrBIWKg23QCpDo/nLEhJyETgthJmzQGdcJ8LTqs89mMXFVSmBNuDRYtNGRhs/adaKw6jGqjNnikGJs1PvfOkLvIZrWV+SG1yEZECybJzIg+dPQ54Iwf4uiore5d6IZZJZu2ZduLFqnzo3RESAEibNo1XQgYLE1TUTczwUSMdGKHPg7317c9u7s77OzsUAh61ok2cdwIQNy14gvreqb5/gAD0LWdxCzGaHHKDTJn3nbjfBQr+ZD3Am6LZIYhZ5G2KXKc5fOLnXJm7Py0KqMxEBKM7Duj+Mkm9FKQcjpUMwupcb3dYhRwNtkQFVOrnCeZEVcroH3UA++911ymFIIgpdIZKxiZDJq2g2RbTiqbob4tRmHSJmDVbckp4psak4ywoqMOlNdOcOccXShMf7BYQgoFHhQmrXVUXuIwiUtKXjik+V/6+o0GaQEF9STYMG5EMUuSDAxViZSzDBqyhmwcHqtTsOWBLVcXnJ0esxMb7G5FPZ9xcHgdb+dYIiYnbB74SoOBLKxV7z1tuxWD7cZVDSkRstCfs1ZznJWBX4DKMMiGSpqJW+e06q9NMQUMBRmy5YGUSKlXNoUhpDBU9wvgotimVv4ZA/MsVG2rAG0fBo82HKYyEd1EYSlnUABKqOjWTKaYGgspqY5XaUMvjmcEGI1+LsaIOLkx2hYhrC1haInVTCEI+9AmcjIYHM5KhUWqDxmfLfO8wDBnNtvn6+8+4Nvf/j3ef+8r3Lx2g7mTCkkbesJmy7ZtqVzg4uyUs7Nzbt+6AdmTnSfGlvOzE5aXl7B/yKL2tCtIeGEfpIT3DbV3NNWCm9dv89sffZOXJy95+OwzfvHJT/jFp7/gycsv6OOWqlbAJkRc48XxRx18lEewf+rIkxoSa41Uhiixj2VkV4k0RjbarhF6yEYr6XlgrZkiafAG8zEpU9VYTxGFLzidM3kIpm2suHvjQ/7sT/4bdq/NOX/+hOs7lo9uNFzWhpfmDuedZ5Ph06cbHnxwwMGO53QdSTOLU6NJCpz/4AeYnYrmG39MPnpArOa4w7tyrTERNq0UG9ZbmkUFlcFUotXVhaytq15kAlyEvseFSGy3bLYt+ArqOSXngjy0yIkORBoSTg84eszqGdsX/0j34kfY8BLyiv7yCflCkh6syBIYIFmHW9RghXlvsgBVhoxT54wOHygV3qLraV0J2kSwvgCATBmrOciZHwLDq8yAIopfnmNSbcykjGA50+phKcWRqxj1VdBXEq00nEuLG/RxGQBGOfMTPWP9PJldKFDE9OdRAdCh2GKKBAMD+AuQDEQzJgiy94XFIEP03LBfC6t+yngtzk/kCaS1MucSl5sJUJ00uGAokhlnwVhCHFm2pTyBVpXzuJGGAkoBlUMfhja7vu9VC7o8G/T9qj+urD2iDDiUKrieC6APExkbI0BxHLKXrAUCCSFHBtJwaYN9RfebJA/yHlkvTTqywRgvQayuc4hij66sQbH/RgaTSUCk3SjaHVGuFX5dh3a4ojcKA0OyriCRrECCpKyIHJn5iotXr/nk/Md4XzPb2eHWzTt0bcfTh7/i3/2f/zvzvQXXbx8ym8/Y5CXzxYLDg7f46td/l5wdH//sH5nPG+7df8DNW3fJyeKaHY5uvs3m8pSctsTNKZebFpwhuTld2tB3lziXyMZTec/uzoK93T3OTzZjUgpYrf4L2K/7Gg2nzDjIZOr7xiTMDOdyPJOl30JWZJqUFVa9AI7CwMh9j61rmsM9Us6sjwWoLSRsUfhJBGtZhh6TZPiOJ1MvDJhIHyGnGoPh+Okjosk8+OCrfPSt7/KTf/hLuotjcgx0mxYHnJ1fstjdZ+/gkG7Tc7m6YH//kBxaZqZhcbDPtRvXePLkBa9ONty5c41rh3Muzy+4vFyxv7vD4f6Ck7MzLi7W7O3tcnR0xPlyycnJCW9dO+Ctt66zWbc8fPQUQ+bDD9+m63t+/vOnkDNf+ehtnA988fgp1czxtQ/f5uj2IcvtinZ5SWy3dDGoiU+QHSF2UgCI2pJqJbG3zpK6wPr0jLheYZO2O5uJJMjkeZbspYxXzWUzaCxorBXfoiyywkVLANrREiTvl8+2RtsltVCkSRa5gANqtxSwzSHgvEd5s+SYh26CrAZBQknZS0IqUfue0pB5SdE9Qixtgnq+rSuI1JDQWCuFzKhAhjVeGJdqm2MSWxaDTDP2lSNbsTerrtfBmZbcZdLFhsxGkjULtTulrh0Hu57f+eg9nQbeMV/sc3B4yGJnh/nOAmcMbd+TcGxXF2y3G/aPjnjy/Cl/+/c/5fnJkk7bDJ2x+v1q/zFi362ASH0WUK7xNT0Se2Utco6DLA3OV+AdcdMPw1qMYZAwGE670cFQg22b+EpljQkeKbFxCpGL3POLs+dcti13To/5IG1JsWXRXOdwdw9nLOenp4TQQo5kAolACBteHT9hs74g5Mz1azewzT67N95j7913+fjTX3L7qMFUkc32gtOu55OLUx5ulpzlns47kULR/WGVTliAL2EJ6b3lJHFA6jDanmuMwXiIyj60CtIUYDHGTB/LQKZMoYIYPUNpsIeGFLMWRnVEohJDYgpC2KgMyRlIsOk6LrcrdvMMly1Ns4+zDc7U5ORksJuReKyqPNlmqtkc72uccVhbU9mO2Lb02w1PPv+EqpZBYzZ2xBBJTUWRDBhYd4zA+xUvq0Fy+V2RslocHnLnq1/BWktVN2rXCxtT9lAJsCWLGWOqFCMYS9Ti8xj/jxJZgHbnKfu7AOxmbDXHaHuwKQMupd1a8NNCepl2tchZtbbkgwKSl+Fc1hrqSlh7IU9Yk1ammxd/JXmIXGNVefVtDpMiBpnLYrUtXIbmpvG+NNwsQ6XlWkRjUuI1N7lntYmMsxjKFyfy0Cpezn/O0qEgD1SKwhGxqdMBsZX3YuPUhqQktgGEOTi0eyNAtNMiajJlwrzIPFmkUGq9I7XFgcCXxURf9v8H9vAEsC05wHBfE8B72lU5/Y4hDsuSJyYS2RayhZy5SnWB276TfWks89mcuqokxrVyPe22pU8B5yp85YccpIB+5ZqT5g3CPpez442S59pWBiqRabdbrLXUzpGMpa7rYT8J8FUYo079uBnAKWcse4sFtnKEvpdCSNY43QBGPrfEnHNq2VdGryiL7bF1JbruxmKcpa4q7YjWLtyUCVosCzEMerQCRst+XDRz+bxUpMBU91X3prWOWeUGn1E+L4vm4TAYsKpq7L4Tv55hr+/ZbjYCcueM9466qqGZQ84sdnYJMbLdtoQ+EHvpmDXWsZhVmIVqt8bIcnkJOdG2Mmy+rissAgbHytJ2HTllNpsV27ZlPpthrWVnsRgIFLHrWW03ZKCpa4w1wniu7dDKf7m8ZLldk1JmMZtTV56mlmFnMXWklOi7bsAvQDoSrJPu4hRlOJe1Fpstta+omlq6aI3FZwhdzzb25BB1cJwMF3Z1jc0J27dDHiZSGhVV3agdTArMOmI2Ap5mkUB0pVvYjpJ1BaSOyYx2VW1mDMKA9k7Oe++rARMLfSBfZtlPGiJkBMCOyiKens9yjqzOFQkxAZG0lb3gzDjnxSmB8Z97/caDtCmNrAONmylMzKJfakzRM6pIKZCxWFuRckcKEnR6a9iuV3SX58yba/gd8FiOFnvsNDXkFSmqaLHRoNaMw25KwlbajM3Q8qOMOecIQ8tq1tYghuAgKmPVDUCEthJZq4wN1OBAGqbYSftojJFKJ3lmo6xdM2mhjNLaM5CMEQBA8weZFprNkAyWIKCqKsgi0h2KBIO14+dmQ+gTEpNKq7yxY4I6gH262crPSmU0qvi3tOyoNqFS3YWB6iTkSwquOUuIrYY6Hp8bdt0+9w7e5utf+Qbf/t3v8NH791nsztm2HZt1z1m/BRMI3ZJ+u8YCbepZL8/YrM94/nxJiXtCv+Hs5CU5JjarA1bLYxa7h+Aa6nqG9TXJiIOpqoqdZofZfIfm5tvs7+xx/857/Kt/+W/45Wcf84Mf/S2PHn/CZnNBMh296bHV2Krh8ZooyPMYGIYKgr8J0OWcVUetOGEJhuuqptLKeKf6K16doIBHCotpgnEl8Ixa+c4ScIkMR8QbT46eg52b/NG//DO+/q0/YHnxnItXx7h0xj6nvFNlTH2XvrnHsoVVguNV5NatOfFVy+myI9YN0TqcaTCH92juXqe6dpMesF4mTWaXwSdMTOASfYr0ywChw6YIUeS4s3EYVxGM/B3W6zY2mGauARNy1kESCDlIFPaGsVARmMct8eIp60f/iXzyMTYvMf2KdP45+ewhLi7BRJnWrDiX31tgdmuSL8m2MGustVSVgDbWCzfD6PlFk+3yTMcA7WpQNUp7wHarrCT93Zs6VkOblAKgYuvGz7zaIiX7q9j36WcIOK5t1EzgyPIdJQDTIowACAUAFNvjvSWl8ftK4Fb2p50MNjNX7l/+7W2R1jDaNZC0mGRpdMroZrMZnNqXac7mLACMQRg8MLI8i87ZwHYdzkGREyjMBnmHU9s36l7LbQ9MyVS0dZMOppN7KcxeYdKGwYZmDf7JJXk1dH03BLtX2EYT8fwh8WcET8u1lu8vCdqoNz7uKhnMMYKHYK58XxnYWFj8ZU0K20nWeVpsKF0qV0H+K3brjeSj/LfY+cGfOZ3grE22aEJljGG2t4+xc7aXW9Znp9iTzMnxKfPZjLqqWK3P2Dxa0fyq4dbtt7l27Tb1Yo+797/CrZsPePL4MUd7M16+eMLy7IR33/uIG/fuspgfce+b77JeH/PJpx8z847NF5+xvlzR50xIGUPFerMChE2zuXjNxXqlz21kyVrrcFaGcZWg88vA6FFvr+wR+8balX+PidrVzxj/pjznkigDZG+ZXzsAMpcvXuFCxuZM7hPZGzokKe9CpEuiD71tW9G89DJcKlUNses5ff4Mkwz33n+PB23LT//xb8jbc1if8OxxJLmGi+WWo6PrdP2FBOiuIcWadmVoql18fZ3965bZ7oy6ijx/8Zpum7j51iGLmeHy/IL5fJc7t/fw1vHs2UuyTbz77j2auuHF89ecnZ0xX1TcuHWdlycrnj05Zb6ouffOHqlf8+rZGbt7Cx58cIe9w4a+vyQFS+o7Xq+XvO4zyTcktZu1rzUdQoygE602+kh3fkm8XOOiFvd1qqRzZfBGKZiKnRX2UHkm4xmSvcuo81aAgyzFJbQA/2VDYMq5Kra42DdQ4KzEjm/Yu5JQhBAUYCrssXGfFYaKALgK/JbNo3GkTLkuLDUFsG3RZYuj1JpKzsxmDV3fQ8q4ylD5mm6rn+lGu+WbSgFsAYxNJeyXmKNol1rYnc/4+nv3eXDvDnXtyH1W5lBFzpmu65nNHdiIQ3x9tJmf/OozfvjjT3nx+gxcJcONKEy/PJ7XJPYth6QAfAEHgxQIUxQwRuMdaw0WZeA4uUaZqiOdTMYoiJOzdB9o6/gV/zwkovL8K4zoDXovxbaUaIEv+nNevjjn4flLbh/e4cHN93jn5l1uvnWLW3dukbQV13pDt90SY8e1o1u0qWP35g1+53OobsAAACAASURBVNvf5+K05dWrJb/66c/Zme+RaPn48SN+8elPWPYtx6nn0iT6ypKcssA1JyqTYSRsSKOmvDqRlCMh9JgkswVCDNgkfsSIg8Eg4H5EbHu0Ym8E4BKVe6/Mra4Txl5hJJUcCKttujGKVqR11M0CW9X0247WRJFxmUeRDklrKvVfNnucb8SWuky9sCz7JaenZ9y+f1fBEEs9n/HR177K8fOnHB7sksicX6xoZgvSspUidcrKkHeT2Hpso7bW0vcdmAb/ht8uHTxNs6P+nyFWsCZi7Dh8LMSkg6HNAPwUg2IZ28ibpiHGSKfF362CW7L0I/lo6Fwxsu5912GMzEkZyTMlJzWDAciDzyrSUSWnUPuh9qDrOokfzVgwt+ThGQ42iJJe5GHWhcSQ0mqcMcNAbfnOMLQ7l9ip+MEYe+3+MQNrzWgOL99Z7Og4U6PEq0MMYiSmeLODaxikJo9ImMdpKKMP/thZAc7IVrteLdrCVMJgRrqB2s7aQ12Jti2j35++pnH8m37+zSJ3eb0J3JZ7mb6vdG5e+awkbek7uzv0oacMf8sps9luRHrPSPFJWKPd4CetsapDXAZyyZ6bKZA3jccxEIPG5WUtjHR+5RiZzeek0JNTpq7rof3bKYs2xYT1lcqCjD4o60EyyPXUXkDikCLOeNnKSiiKyha3COtTOgrN0EksRA5D5cUfu0KGSaXjVIY6dSGSC4EMIVoIsSNiPaTcC4PfqcwcohGfcsJX8n1WaJSkkIfiD1mYkzgh19isAym1AOj0/DV1Q10Z2rYjZ0lgKyd7tGlqqroihEDbdKO8g9riqhZ5A6v57+5iQR96lS8TNr5XEBvN/0S+IbBpt4O8R11V1HVN7Stsht24x7ZrRdsVOQsp5/FvnMXPRD6CqQydEUAXRF5CGMUSr8Sch3We7yzAZjbbLakL9CkTOin8Ou/Yaea42jG3XnxC3xETrLZb6FqcsyxmM+pZg6s8cZXYdC1bHSrunNjJuhB0FEdZL5cQE66SboGqqtTmie3ctp34ynKOjcF6j3WedYiEroe4xphxlhQZujgO00w503atgNu1x+tzGDopjKXtepz34gM1ZizFrxTLXBEhFf1zr994kNYV3R8U8DQjwFUMSuXteKicHJaoiaIEXwCZLvSELIfe5ESN5fp8xlHTcNpdKDAr4GRWWQHn7QCcpSRjBqxVcBELOmE4a/I+bQ+dBu3DvwtjKQs7rLRRyy8l+EzKpDTq/MRpaJKt1TJrRiZe0TSsfWEASXKsKfLQglDEvQsL2DmZvEvbXpkwX0AoAUgm0+sn7Z6oQx6QDDTEywpuaIXAYkghkkiaFI2O0jmnwxGk5Tb1CaIlZ8fMzXn35l2+/61/wXe+8R3u3b3NrPGkkFldXrBcr0jRsVpFNusz1utXrJcnHJ+85uTijPPlGZerS3UOSVvkIzb3ur4Vi8Uhe3uHzLyjMhU3r9/m+vVbzBcLFnt7+MU+VAsq33Btf5/d3T2sa3j79jt895vf4/NHn/KDH/w1P/nlD3l2+YIUA3VtsVEKBVElDJwzOhl1TOAkaBlbf6TFSTTiiu4MOTNrGm4cXePi/JLu8nJohzYZqRLH4mjKx06Yjll2qckC4lsjIu42zTg8vM1/+Yf/mj/+L/41rmqo6xZfHbKNr5mbC476n7Luejbu2yR7n1VqOH6+xSTL0VFNiIGLVSRVmbT7FtX3/wRnLBvmZG0/V9RMBo3hMNqGIJIQM3IM5KisRQVapfDrwHhtqWJIzmTVYsHcJMBShlNlDDPT4lbP6J7/jHj6CDYPMfYcs1nB6SPy5WNsWpFtHNuecsLNGxY3Dgg7tUhsDIG8Bmq5JEClvUEte5EimERsV9rzCzu6SAgUwGuwZb/+vmIvCnDwa/Zj8jdSDAFjRubH9PPSJMgtwX6BkIqOtisaPgggXk7ylfcNnznaFkn2lT2eJ0x6BQjKDFYzJCpiH5wxYLMmCL9uI8v/rBmB0ALGWzJDp78pgS+/BnSnJAyKqW2Sm1RHadzAcmfy/QUkLcrbI+NBgp+qcsQorVaFrcHkWU8BuWng/WWB+nCvhWUy2Q8FLJ6+D6PPZxIA/HOsDfmeIjtQgBxh1Ba9vALYF/sz1bWd+tfpviyv6XWWQmMJpoffxTKADDAO6xuq+Q7XbxywV89ZHr9m+fIV58sVJ8tX7M0XeFMxayze9KxPX7G5WFHvHpJMw1//+V/gTWA+r/jud77P2cWKjz/9KT/9xQ95550PuH//q7x7/13u3695+NnPcLZip65Zd0u6sBX2djVjuV7z8MlTOhNYd50mPKMsBzkPA0jHls3yzKzagC9f9xFgM8M6y1oy7OUSw5TXVH95KNglAb9c45kdHdBuW7rTS0ynIBiZdegI1lMbR4Xjchvoux68463DferKcbm+5HBvl0XjefXscyKRW3ffhW8ZPv7hX1OFJVVM+KbibL2h3W259+Advvntb/OX//GvePHwC+bNHttg2XVzAmfEEHn56hhszbv3b0K/5fmzF7zz9l1msxmr9YaXx8fs7M65984d2q7n0aNnXJ4uuX5jh92jXR5/8ZrjV0tu3jjk7s0D1tszTl5f8NaNa9x/cIvZLJLClmq2h7GBZdvyqxcXXLh9cj3DZGGpalOqgEVWbU3KbM8uWb46wYckPgTASWfPcG5LRbvEMuV55JH5XwxHaZ8tciixDIyUTfFrSXZK0vKr20kGs5R4qZxvTViLjS6dMbIP8qAZTWLQWHVOimnSkmqI4aqOmdEk3VoE9NA9WYDNKcBorUyzripti9VuMWuFyZRSoo89rhYANelZLq3RRVHOaryRJHBlsah57+1bvH/rNrf29/HRkTro+o4bN2/ivWO73dD3HTk3Ejf7RLtd8fDRM/72n37FsgtY1VjMGZEyKy3X2kVgND5y5UyaYnMBHRyXgxSjYoqyP3yF0yEs2Yw+sMSsslYgmpZFz7bosSsZIY97JGedVi/B+ZCrbAiEpmKTlhy/+ITHxy84+vyAw91DjvaOuL53xLWDQ+p5Q4WlsR7nF8ybXWLn+fTTp5ycnPHi0aecvX7C+cUxLy9f8WJ5zGVY0ztonQErg2aKVJY1VuJMvTbBZOWepLtC5TRiGvRTu9DrPlU9VZVzKu8ZdHhNmeUQpfUZJtq1aRiyJIB6KjWRoYW2wF5+voNvZrTL1SA/JDB7TwobetdjCNSVw7oFpIqqcexdX3D69ILtuqXyNdvtVrqecmK1XvH06Rfs7jbcvvs2f/+Df6KZzWF9IUCJla6IEMwQN5QYO6ockDzbRMqjXyt+MCYB8AdN0/KyiATIpMtGAG8tSsdRRxRlN6aYCF0g5iJtIFrVA6PZoP9f4gyrzG1DJugAIyHUjDFEzokQ5Ww6lWrJWQoIWTf0lTkYoO3qmj9StGoNRQtz6OwyAtoKMFzyPws4KlvRp161OGXvBL12uT7Jna2zml9elXUbY9mpTxSAtuT803h6CsoawzAcKGVpTc8pCwipJKGis4rGiWXNpGslqaS/rmHJoYZAYPQJxV4Ek7FNRVxN7OAbMVj57/Tfw539Z+LAUVLry7GD6e9ylm6xvf19dhY7nJ6fEFJS1iwSBzg3yGrlLLNMOl242WKh2IKcgRQjvX5u0Y8drjeLfnnxR5Lj52GujjEymNH48d5K7NR1vUgVyOADnL060wE9Y5FEp6CkSHLZYY+AmHyjBbF+2w75EcapBEgaQLShQ5FMHyK5y0NhUjCTkppK59lQaDSSr3c5qM+ZxHyDLZXutBgDKKgJEsOJ/CU470gZQtuJ7UuSh8+aRol2ErMUqbltJ7hLF1rqUGOMyD0wyU1CiMSuVezHaLeQ/K4U9sd5RKoR7B3ESFPNsXaUbIshEZ3IuNlsqBoBP7O26ucBp8pkA/VsNoC0JotsQLvZ4CsBlcvahiBF0RBEz5UkXTuVMrSrek7sZG1Dkq51eY6CA7nKMZ/vsFyvCX0Q3MgI29g4C87ivWOvksJgytLxWHyz86Kt7YyhyRnXtRrHIMU5XU9f1VhncU2tmrFlomshu4GvanJTkXqRRDOqTS0LbmmaWn6eEpVBbXNP2/c0Tem0MII31Z6279RGBWkxBWrTiK/JmRh6xi/49ddvPEhbDCtoi5bmqSMAokK/GtzmHIl9BldpGCkPoE+Rdey57Dt2ciCFLbWdsztrONg94PTFS/AFd8lA0mB8wj4zRf9Mu98MygKUt9iMVG8ylMmRZWCLIg2KvaVBpLyAcZlyTyO2oDDS0BqMkWEQMYahZUM+wchG0oCZUp0TOFeDW1Tgf0ywozJo27bFWst8PhfKtwK2MAJKKSmwlQvopDNgraw7xZkoey6TCX2gsrYUKeVq7Ai0W4AI2SRM8phQc9DscP3oLf7ge7/P73/r29y+cRcsdP2K1yfndKsecmSz2XJ6fsnzlyd88eoJT198zsnFMWerJZvQ0+dAojjeHmNkgIEzmWySDut7gTceHzpcgp3ZHjcPj7hz7Rp3797l+rVbLGZ73Lr9Dm6xC/UMUs9OPefw5j1uHlznt97/iM+efML/93d/zg9//g9cLE8IVltQzOjoxLkW6KqAswUEYQhKvB3ZVBhD33ecX5yx3XZDBXfKOCyBVNKAzCDJKMgUQUWnFAzwuDzj+sE9/us/+2/53vf+iMrP6dYdUFM1h2x7R9+2VGHJ3nbFYVrTLTqye5tNv8fxS+i2DQdHM4wJLFfSrhiqRgKFEDTothLwe9kzw1Y3EkhkhI0u6dYk8J3+7ZWgqWTSFpdkaqShxxCxcYUPK8zyOctnPyZffEqVWnw6J16+JJy+Im+e4syG7CCJEIjsPw9+IRODMQlUOsU5BWlyJqegpORJu2wuZ6nYpKtBWQkWpuw4aSE0eE0OC3v9TS2qYSnyWIiCXw/uilMu9qL8/QBYDkkSOgRh3IOpAIOFBSybZ0hQphX28tnGMLnOYp1kEE3Zr+VipiwJOwEhSyJchuqVALi8ShKUJnu8nB+JOcvNjmHcNHiVtZddZQrDTZ+R8hGGlsPBK//nPOTkO5pmRtf1gyZcVlvuh+LY1fW/yq68GrCXtSn65PpD/a2ZJERmABKLJE4ZejIATpPPHv2U00RcgHGj1dxip2XfWpW1YAjQS7W3PPtpS96ULchwpSMjsRzRod0yASaxM9/l3t33qVzFzM842N3lYOeQdOMOVeN4+uQRlyfnXJ5cYp1U72PYYMnE1vDxP/01n3/8M+bVjNlih9/73h9y/70P+MqHH/H481/w+NMfsT475fXzl8wWMyrridHRbqQdc17XpAS7B7v45oKfP3xMazLZSgtWVmB2Cj5P95XVZySaaVOgewrMlUEPIxCYJ/t2ylpmUgSpKj/sm8IGApEVySFS1xU71w5x1rJ+cYLNcp4iiS5JMNtbxyaLTp1brphXnto0xBQ4PX/NcQx46+kedsQ+cPfdB6Tu2zz6+Mf03Yq4WmIz9Js1F6uGg1s3+JN/+2/4P/7X/w2TMtcOr3N6+prt8gKX4J279wm55/TsmPXlkkWzw+HhAS+PX3B2tma+s+DuvTusLpY8+uIZq03PzZvXmC8qHj9+xeVlz93bb3F46Hn16jl9H7l39za37+5T15EQ1lTNghrPZnvOJ49f88nzNeneEaVwPbgMbXXNWVowu82G7ck5ue0luXOi95qHswm5SKgAZX5AcTomqzxA+VGJu2Ic2CaugHVB9leBwso066xnwnyJWRmBRDPZPSJnUK5rKM4lZDAlBuvF3oYQJ3buqm8orEBhwhVwQgsNavesbFYF8sAU5lFKMjnaO6y3eOMl8QqiTeu8wdqaGDRx0Vb4AirJBOrMO3dv8OGDezR9pm9bGl/jfMVit2Y+n7NaLem6jrquiH2g7TvOukt+9KOf8ZNfPmG5idhaitpFPspgiFq4mJrq8hzEvosNMhhh/GTwRtgq/VaGvPXWsTBG1DIiGD8OvcpZCRJMhghNvmwAPosvQzTwck44lVUTfwZkL8/OZjqXOA0rTjdrzPI5zfOKxnjmvsZnaKxnXjXUvqJPiZR7IpF1HzhbnbEJG4I35MrQE6Cyos2nraImieKGMZlkRDasXLkUAaeFhyJUwKCrH5PIMGVNNHEVaAdPDJE+RpV6Kv41k5MCtrkfH4ayR8uQGD08IvmhBeecZCBstZjDiTyrAqgINGcgB2JuMU5zBSzdtuPVkxWmr4itxkrWQuzZLC8hRXZ39+i6pUprtDjvoZynKISbpAAzCGD4ZiE65SySXOVUGhn0RQIzGa5V/KLsy8nkcjMOSp36zCyoj+wxEm3sgNHmT33sGEKpH4hB1qcUDHKkDK82GheHKB11KKCUwshgddYrAFw+exzyOZIA0gC6l/RjAKOzDN8KXT90UTrrybknWx38lCO5SKcMM0bkRrpeOjXHafRig0IY57UYBbdLN8/4GWNsMmi7l9xWwV7pdhafOCm1jjGwSk3IZ4wxcgHAyheVYcoTbBAN8CBmgkmYyuFqL3JVchKuxAxTosD0Gsq/x4/9dQLE9Odf9nqzECjfGelCL1q5VmQJchmelBJdSngMMoxqJJqF0IP60YExi/izTd+z3W6vxJ7OOXzldS9Hye9jFPa05i7Oj0zC4uO890OOkw0St6qdiEEY/sVOZUQ3W4pnXpnYpZNQCG2FzBZiwOt8ihSEdJZjJiRlaau+bunaIxv6LpKS6Ng666m9J2UpNsU49mhIkUYGikt+mkRjPos/NVZ0dPvQC1irmEdfpAmCMnV1P+UssgIpQ6XAbyZjrBSoYpACTY6JzXYNSIdzVdVDOmC8od22rNYrrJLbqkq7T4ZOAHmmy+WK2Xw+7JHCak4pEVQuoBR8a+swCoJ6U4YTS94XY6SrZMBc6cSQrCOpXUx0q42CsCM+hTEyyFTzh64VkFP2qO4hI7Ym5cSm7Wm85Cu+clRNTciCjYDI2/UxYb1ib85KU0/sJc/R4q1RmTmjMd7CL+QeOvVR5cyaxGJnTkhRJKj07IYQRGrTyv1a41QLO7PtumEQXdXMaJoaH4PIeWCIfcu2bUX6ZZLHp5RwXkDaEANlaLycKS/37CRPG4iaX/L6jQdpZUqjHRZfHAwS5Gn1RUAAR6lQpJxxWikSQWBDDyz7jqcvv+De3Xchb2maPXau3+TarXf4/Nln5Bw04ARjxhbEYTqhtWw3G1IMoqFqJAF23tH3gQHf1f86YzT5kx9ZQTnGBKE4aKvtYuJFhg1f2BCyDipIb83AQC0G3ZXgNEvbo8kqA6EQdUaC1nJASiBagBhrRTS7AChTsEd+ICEUOiF5uChT9HGTsnPFMUtrM1hlVzmtcFgAkwREjAIaO2SoRm13uXvrHb7/rW/z+9/7Lu+/94Bus+bVi+cEAq4yrM5fc/L6FcevX/Pi+BW/+uIhT46fc7FtCSYRrVRmqAwZJy3zCq4lEiEqoOUQZxYTLmvC4SwnYc3L40t++eITFr/wXN+/zr3rd/jtj77JnXv3ObxxGz/bFR3ZDCZG9mcNv/f1b/Lhe+/xi0++zw9++Pf8409/zPOLF3RxTVV7nNGxuzmTCphhynNNBNWtLPIQZRuFHAltz2a9xlmP9RU5Xq2symNQbZZxIsHwfpOFPVECmjs37/Nv/6v/nu9++w/AVfSx1+p3gqpmve25PD3DdoHZ+pydzTnuxSOq69/BHX6bLh5ycdLQdrssDmYcXWu4WCfaTU/qelJlpVhhHMFlTMiaLOqepkxYzWOQk0WPz5ApOpkYZWOUQkuWQLuiZ5EDaXtKF06I4RJ//oJu9QXd6gtMWlHlHtKWfPIF8fVn5LgEo9VJVNw7GVzlSJXFNZUkyG2kNlb2p3NUlYiZO23lG4K7EujlCYZcjv2bgX8BfwoomPPALCjPbvq+8u+iK3rl58ocHv9uZFJMv//NgNEaaSlKWWzb2Gom1fdcNqQmBzmbK85Gt9TwfWVIxfA7W/b0yBaeFnkKg8JqwNC2rf48X7E5b65HKToZGFqhhr8pgfsExEWLEQZDNkVPtNhABrbVlCFpyvrm8VDm8mD1/aVT4eLiHO9rqsrTdVsNwgToGIHPArqX5zJhTA/3qFOcJ2BdAWKnC/4mM1rWY2QDZdW7ywrGF2ZYKZI5Jy1pg5+w2s47AN152LyFOTPdl2/amCnoXD6zDJrIA7ioQHC2OpzEcf/OuxztvgXtlrlvqPHYaoY/mFPNGm7cvE2/2fD4s0c8f/YFsduw3bbsLhxzH8h9S7/pOF9ZXp90PH3yK5rmkMWiZmdRkTIcP3nBi2ufcXh4g8NrB+zUM8J2ztlmRRc7FrMdYoR5M6eez9m2G6qqhixDk2rdm6Q0sAkALdbAvXt3OT+7ZLm8HAqdBeAfWGs5a4v5lNld1k72x5syN7L2V1nXGXTQRyQ6aPZ2qJsaEzPb1+fKasmYbGjpgEQ0liYn+uWKPmb66Lm2t0vf9Wy2HYf7C2yOXBy/wFaWWw8e4BdzfvQ3/x7WF+w0M/qLC1Kzw//97/4v/ujP/pT/6X/5n/mrf/8f+E9//rdc3z8ixERdGUyOvH5xwnKz5OBwh4P9HX71+ecsl2veffAuR0cHPHn0lFcvXzOf7/LgwU0ZIPboBc7XfOXDtyAGXj59jTFw//5dbtzaA7slRGFi1FXDdnXGy+fn/OiXr0n7+1SzhhAkYXPG4lwlA71yFi22Tcvq9SlxtaFSBp0UAJ2sV7GV5bjrni92ZARr1BRMwPZBTzJnSo9FRhhFzl1lm0uhogBjWe1A6bBisFmDrVCGT3l31uR0OK/ld3lqV40O7WByjcqUM8K+KQNhi401itRkynCjcf8K8BFJvXSLOFcNhbTSOSBdSROL6kTrXva2JO7L9Yrnz56zW8/YX+zSOUOVK2bRUi2X5BSHqdSPnjzk4dNjHj095vnLc0K2ZC8FxBiSJL1GCrmlE8sqOy9qwanYneKTEpmYMhEG9lTtSiEb+q7F+IpEqy7ZDsw/rWdi3PCIhgda4jMU7K6qamA2pRggy2Bh6xwpSgxsXCI7KdhHm+n7yLbfCoOvzxgdjpoYh0IJMJEhR4KzRKcJvbdUVobf5igX2hvJB6z6K5nHMQ5fGW4gle4qhtyjrmoWzQyTski7KBtJhrRIK2pfWlxTHv2jEVadt05jzonfzFJQcAqY5SG2yFibCL2cs2Yxl1wuJ1bthjYmepvxFmq3x6zeo3K7GKRl2GdLDBW1MWyW0qaacya3W05fvWBvMeeD99/n4aPPIBvWyyWha8kxEntJngepoyjX7OxkONTEH8ah7dcM56Ww297seLCqxzsUswuwxfiSAmDUAbSyjyVWsuK/B3NQQNt0xZYAqmurIFCexKIomKoApOSskuP0vXSJmGoCQrjRHhS7JGQbIBfIrMgWGGVDdiPIrXlCjEHu4UpBSnJh6yTbyGk8r3lYG52RkhlY1EJ60jNMmYUgUi7lXDIB/rN2IcjeGtdY7LmXWC1Gsj4HWf8wyNeM2r95yN9LTFT8+lCc1Xy9xH8pi6SFbunBZ0xj/ilAO42fvgyAffM5fxlw++bfTZ/7+dkZvjHMFs1gsGJKVL4aZBRNUpDcixZ/RgkSrhSmhIlYcgs7dAcWwMtgvLTYZ23bN97h0HxBfaQFQt8PsXwqXY4AxtEPEh2lI0GhP/1ueQ46iyKPz3+IOVXXVuyqFkmVKd2mgDFWiwcJE8A1NSDxqEkyNDEE0Udt6gZLlH3rnMiyZCHoeAPGW2xU9jfQOEeIDIUtrKGZzwgh0oVA1ydi6pQUIkWvxXwheZSDTOByvYSNAo1WtGPRvME7Wd8UlFXf97RmIy7WeZrZjJ3ZTAiJUdiq3bZFdG39hORjqJvmDQk5kTwqOJCz0jmzbQObnPGVkCKsku6K8QoxktdrzRcFB3PGCjExBlIrgO9gC63VuQCWMsSclOW5WajqWslPXuUQeqqqpgstfWgJm0RTN5PiYlL50EwPrLdbuSdnpRhQCztWSFSG1XKJ9raTc6ZqajmnjHsu50zX9/TnwrDNyHXFJPhV2wVikqHYBtGm9c7LymmA1vWdFvtQfFELYCjpykq+7TTHN8Ywq2ticAM2Kd14gcqAM5FZY6/MuHrz9RsP0or+kdK81TibnMh66K0xmDQ6mMLcIsviZSMVGpMDnTF88fQR33j/t9jZuUEyiZ2dOUc37hArD6ZXrEKCkqaesbOzC4huT1VVxJy4uLgQp4OwOCrnwYhBKIdl1BCTXS8OyGBxwyY2VgZaiNPViYCTg0LiStAgAbxUc5xTB5GyBqAygT6WpFHtiYQGZmjvLYm+sI+dBv6yAStfEUMcmK+l7Ql16oBUcnWNBHfMorli5IIrPNaowLwRynwua2VEHyclYRV6UzNzO+zV1/nON7/Lv/ju97h/7w6Vy6wuTlmtLkkEEj1n5xd8+tnH/PyXP+PTx1+waTu62LHNG1LlNWEoLcuZjCMZCbhJGrgycfJZgoNs8hBsZG136k3NZddzfnHGi+WaT549596N23ztKx/x4L0PuPbWO/h6TxxJ6Nn3+xzt7PNb733E3cNbfOd3fp+/+8kP+Msf/DVn2zMyPd5KcpeNJJRGHW/EYi1D0icAh6y/U3AtIFovSYcAXXXmGmQVDUhNRFNhN5e/MpaZnfGdb/0u3/jaRzKNMAtDOsbAdrulzz2rfsvJ6TFkw2od2J4fszr/lNXLx+y9d0p19A1WaZe+O+J0vcf8zg3qHU/Y9sTQYpoF2fqB1l82soYuUpXLEVt09IwbAkVD0uhHhqY5BW4xFoenomXen1FdPuPy1c+I3WtCWBNWp9hwgbEbnMm4bUv3+nP6y6cQz7E2YowHdUQ26Wo5i9+b43fncko0AZVzKGClBNQO68bKLhhIE0A2lXS8HLsS7I1tc8aKXco5D0z1KwF/adMpz7UkCZnx7DCK+QsgWUbdoN+XgaInPUlACjCphS45x7KueTjeBXoww1ko8YDmWAAAIABJREFUg7jGzy8A4ZhYuFJgmiQOEruNWsjZCnsJZe4XRhKUqc9cuQdrhWVdEgCrtnVsi1OVMWMnaz5+5jTMlfcVwFfvT4tVhjKEowAp4yfljDrOTOolWBMJkzC0o9ti3zMqBWNlr0vWM4B0BXiZ3OXwTRnt4CVJHSyP+wbeAPE1oM0o4Kpna7p2A+NCg6mB6TH5XQGtkw7CcyXoLYMkJ2t4RSfYKBCABCQyeE4GMIjp8dJGWVoebcXuwXWu7d9gkWvafstme4lJgflij73dG/ShZbN6jSPzla98yN27t1ldnvH5xx+zvrxkbcA4T+i3BKSVL4YV7eqC0+OEr5wGUqpRh6VpFjz44Cs8+PB9DqtdLrZrll3HyfNLutTSxY5sRacsJTPYTLE741qKnTXkHFmv1oSunxTRdD2tnpuUcdlz/doNlptLYi7rNtWcG0HbsudG7GPCyC8JnZ0w2ivH7u3rQGZ7fIbPRtkm0OfE1kI0CY9j1QVenp3hHezNZtx55y2885y/fImxcPbiCd573n3wAaSeH//D35Bii92suTx+xSIb/uI//AX/3f/4P/D7f/yv+Me/+jsqk7h+7RoXl694/OQp203g+luHVHN49fo1KWZu3r7F7mLB4y+e8/LlMW8d7XF0dJ3XJxc8f3nK3v6cO7du0G63vHz5ivm85sH9W+zvNeS4lEDYWmZzhw+wPF7z8ednrLewe2tOMJZgM14mhGGNU5BQWIWbswu60zOcGZP6kW1uhnOxmM9JKbNZr4ezYwaAQvTvig0ciiPlTMMY/+RM1wYWi7kE93bsaig6ggIDSnIcU2D4AG2fNkY0kq1+XpHLMOpjDA50iKRVaZ88ACyGaRtC1s1UbC+mtK1LTGFsARpLZwVQxqCZYlt1f6Y4gM0wgqBlDUuBS9iRVu/d8PLlOacvz6hrz3w2o8jh7M1r3rp2xGLW0LYtXeh59PQFF6uWmA1J50BIYjkWQUtsmxWQTClC1GKYDvcpclm+8trZNmG0WJG3GUCHqmZ+dER/sZE1KbGy3rxTtDbFURLJmhIjy9kU1pdK56gtjhmCjdTW4ZzKlKkUA17YP67OtOShxdJWkjdkoEPaQLMmlhIPoD5O9wZJpMNyErZ3sVWUcEsSfjDEXhhEo46uQN2lo6Xvt9KOLzQJMB5ri7yckCsKsCbtpWmID8RPlc65UdJpKBqYAmIxnAeyo3JgScx2alzlCG3Put2yja2I6pLxfoe6PiBnGfhlrSVlp2QDw6btZa27nspY6npOyBFrEiFlsqnI1tOlADmSQ9aOOpU4SBmTDNkKgcZ7P4mRITLOHinRxDCJO2s+kzX+U3BxWoSVMzIcSfn/CAhljLRLy4ESQDtn2dcGYdVZw1isNWN0X/xHYUnbYkaMgGeCHYk/gHGIWIy92BcDOQSikb8bhv7mqHZStDND7OU+rM5RMZmkshJF13KUe9ICUhJ71BfbZSXGct4LhmcRTVQrg1atttnLevQYND8zo70R7U+DzD4sMWKxAXlY7xEERc5t1iJrLgUP/V0qkQ0KaEs8E4fcWglgJBmkmjORjEf0u2POGCyEgDSnmiEWKjH8dNjWPwe4DvlAie+HZzvGb28SN8aYn/HnWLpNR9f1NHNhXrbrHm9kqLl1VmS9QsSo9qqrquEacyF9KQiHK+xi2QzSOaIs+zcIJaVbSHyadBu2XYtxbmiBz6Z0ko6FzgKQi4SHxN7WWGwlfsyWLkstwgxaoKDSFJaqriRuB2WhJlwq7NJaQUk/zPCRWDsP9h1jVPqrxMWSg8qJUt+fIc6EeZpiYl7VSqBLUsjMEWe9WlQIMdEnJYKFnsp5Zk2j+W2mj3OaZibPXnMggGwCjfXUpiYaOUMxCDu974PaYaDrafYaZr4ipsyma4khsN22bLtWi7GQszBRUxYMxxjoQ0fXR7xzzOaN6reqJnYrg9ZdVskIpdFXXnRcY+gIqp0tp0/wtrquMCbLjJYsRZBV21E0iIvcQuUrjGrubjc9Ocu8Idl/gcXOjuZQlq4LbDadDH+zMnRO7EVi6BROOtjUO+wmY02Fq6TrNaQMUYpKMUbmcSGdVEa0c72x9H2g68Ow/jEmZmmOsZbKeDZtSyYTNsLq984NJCGMUa3iSJ8j7WrDarWcaJAbMInYF3au2Peu13sZcm29zm1HdKLfnHL3awWc6es3HqS1WQSb27al8R5j3f9P3Xt8S3IdaZ6/K9w9Ip5+qZGQCUkCIECWmGF1VU31ovucXswfOf0P9Kp3vag5Z2pKkCwKgCQ0UounVUS4uGIWdq+7RyBZa06cA2TmexEe7lfYNfvss88SAwaUSoyxEPoyah99FjFJJR2SuQhdpPWO45NTNIqynNCgqIqSa9duoospgboX9gUx6W1Ti1EymjgXYElcrsE5DD37Rg7JwVBnAywGKfgoDnfIBPKsJRLwfgQQ5GYXQXSLQpAO8xLUJcdcgQTo2VHIDF3RJMqT3uslhQyuyitn1lV6DudaFKmLahS2qw4xiYyHlIkeso6kzKkyitJYooq4TjpNk1gkOiqiyfAcYhHRVKrAOLi2dZ0P3/+Uv//5/8G79+5hUUTvaOqay8tTFvMzzq8ueX7ygs++/JxvHn7LVbOg9jFlOD1eazADW86Tyg3EpxFj3JdGJ8dTZgSlxKnITBOUrDWvFGoyYRECbWw5v6o5mJ/zxdMH7P1mjx/d+4Afv/Mht195lc29PRo/x7ee2WTCjTff5tXX3+aDH3/KX//VP/DPv/wnPvvsnzg7P8DrgCsiXomDkovuY9rAk6pkb2eHo8PD5PDJgWW0MEKEtZbnVJ4xEqTRRRy6Z6r0O0UKdLSsU1zk/lff8eC173jvwx0aD13n6ZqGq4szrs4vODg85Xhe0zVzTk8uOT27YNE2uPiMs6unzG79lN2bP6Gd3Ka1r7M8nkA1pSim2L0pDi/lIzo7UoXMjfYy/kH2QAzJOdT0pYU5oy6G2zOJC8ruEtUuoJ3TXp2yOHtCnD8htAdAh/KB4Bssc4pwRX1xxuLkmNicAEuUEqafUj6hTyKarwrN7NoOxfYUbzweJ2C5CqkJgtxL1zlhJZW54UxqnABrhjVFJCpnpVez62PWJGRQZjXAXnHO+miHxHYlBUy+7zia10B2yDN424OgI0BOtl9cRTDjapZR/j2wsda1ScflaWm7yHVHZSNDFYCCPmiTqM3nsiHoS5TzWKw23ll1UHuIXw0gZh6n4UZySJUA15id/aE5AjE5Gj3wonoWXZ/1j+J4Wi0Orrx06sUiJZP9vY4CfEUG2TKL+YfjM2ZX5AM7xth3i++d/SBPHEZrzOhRk4wgWebYA+/DuGWsOjs0/bMyAmrJgI9A8iExxPoGSHpo4pa/0zknGX81NLLwydlVcdCAI8KsnLG3fY3dnX2u715joif4BopqCjXMzy8haN555yMAvvjjCc4FvGux5ZS9vYrJhzMuLk958uQRx0fHBO8pTYH3gabxKFVjbIGPApBEBZ3zNF1LvWw4OHxOiI5X33gF7SKHB884PDuhDS1dbIk6EIyseWsskaGMfMxEzyyd07MzrJagM8Th/M6ntouBu7fu8NEHH/Ivv/wX5vWCsTzT6voe1v0PWJjj9yTgRVgJwg7ZvX2Lk87TnFxg4wBmtc7TBWkq2QVPu7jEmkjY2mJrZ4cQPLV3xGaBaVt48ggd4I1779J1Hd999huIHd3lKWiFV47/8X/9dyyBwjdcnh2hy4r9vVtMywn18hLvW+aXDYWZceP2TYieb758iLaK11+9y6QqeH54hCk3ePPe61gdOTs54/TknBu3trhzd4/tjQrvlqA6dCFdpq2y1M0Fj54f8O2TBXEyoZhu0imVkq7kGm+00hRa015ecXF0TOw6TFkMY5r2/A+D4iw3MAry0/t6/28EzsV+bsS+mMSYzAxINbJBMDT9kaoE0zf66qU0fOybqGQ72/uKaqgYy56L7zy2yPeQNTRVH1CPWX4hlXyunD/Z1g0rjew/5kA6nxUD6CZnzsCgH9bocL+IRJZ42jgvlIpm2XGxaMg+44GCB89OpMrLZMYrqERbjelcEZxe9Xaut5OZxRRZOWMGvzL1ishkhGQIrbW4rh2kz4xhurvL1fNDfFNjlSUDcP2kpz/FpklZo/MtfWUEqmfWkexqUNIgyxUFpTWjJlK6P8Z1ChiVT9VoybaodGYbbRGWs5dqrZ51qYZnyozwJEkwAOeqv5esCZuZnkp02fpHNNqksl3Rhs+awiqBX87ndTHY+szwFT3bBPooBqCx/7v4pJmVlVnb0Ue0j9gYKYwlJ6CbrmNZ1zChlwsQMk6qtgoDOB58x/xyTkRRTCYUasruNc83X/w7Rgdu3rzBzvYOe7vbLOeXaEJKjMsaClnnVBm6toXUmXtAVU0/Z6tAWa5kDCkOk3uJSnzCsT8B4tPm8zfPfUz0fJsbTscMYsnvbbIXWoMflOwG3yH9X6ksfZKYn6NzYizTkxPyVVURibRJokn3+ywKAJL3U/J7cqfyDKQSU5VNJlMoRawmxPzeoARYClEq/bLfVYxAxaRTYlJJtUr3KBWdOa4MSaZFAPIMSkspOsmdFcZuX7nVH5tiG0KO40av7DePmfC9D6sGJrKY3vGaS3tJD+eBQRigpKar0b0cUF23j/1drvn+L5OPyr8f+6eDtOOIxBHBFBLne+foEsHMh0DbtZgQqQpFWVZ0btE3pxt8eXlm56TpX1EWwgC0VmytE7+iC16AN530RdNZYY2w3H0IxM4L+cYoqfhUikrr3o4bayDOaLu2P48zcSU3uzJaJ38uxSw+kpvP5bhFK01ZioxlXg/Z59Xa9JIOSikpRVcCqsXgMcb2iaYcv3VJbif4VlwKrYidsKW1lgoMU1hJiKREYSYCqBCwyXeLhcWrlHgIZTbtknRLWNPWdCbrjIjrOiDgfYtBE5zCq4ixQszyIVLXTWr8LAkDqQqRObd2g6ZpKGxqJp/2q9YWrSO7O5uoaGi7Btilrls61yYgu8AagzYGHzapl0sBYaOc20YbyqKiLCyKwLJe4oPsE+88MQrga2wpsp5pE05nU5yTZmXWGGnWZS1FWRIDdM7RtS2d62jblqqqRg3mNNVkSucc8/kiabeKRFcmwpSm7Cv9vHfSGyQ4cA5rNUYXlKVUxNJF5ourdOZCURqqyRRjCopCmgY2jQDGnetAKZqu6c98lLDC27YRe2sMRWIsj+VrmrZJ57Y8g7VSXZNJRq1zRN+xrJv0nKmXi7ZMNzZpmoaL+UJiwJF86frrzxqklZsXLc1qYvusd7ZTISIakkm8P+svZqMc0uHQd2CPlqigmk6oyoKLq5rQBfZ3rrM53eF0foouTW+oO+fonNCyY9LpkI66wrjAGMkqkrXOsoMnelXaJ4aV1oneDhk3y0HtClMNekPjvbD5VC8SLc+iEtCZD7EQQt+4pQcLUjMyEaVPASe5u3m+0uDklUkoPDhPYSzTagJAUzdSfpgZIpGVMhKUANZlMUFpzTIsKCfS+beuawnoUxMplViJpS7ZMhu8/eqb/Oe//Qc+/uhn7O7s4tuGtq3puprGtVzMz/n++6/53Vd/5OGLpxxdnVK7GgqDs/kpFJ0iyTtk458bpCUHIEpZsDE9D0CmKKf606Uyqy2vr6giWE1q4ogLgWVsODs75ODfj/jqmz/w3jsf8N77P+a123eYVlOUbbFRU812sZNNfvLBJ7x+61V+/uFP+PXv/o1/+e0vOFqeEG0kmIjHJ6kKWU9iGFp5DkJy6Ib1kbO1Wc8WUtY6OdRZ4iJGOXA0SQ/YRVTQbG5sc33/Ot4HvvvmS27cfgXvYbGcc3Z2zJPvvuX44JijszmXZ0cs57WUHBCo1BXdxRfM58+Jp9+zeed9JnzKVJcslxO8NqjZLrbcwpqSEFu6ZklpHKYocUbJPXsPaHTsUMGhtRj+4BpUqCk16OgpukvK5QHq6hHu6gXN8hTnapyfo/wStLD3iqgJbo6/eopbPMMtz1G+RenMSpESqyC0dJluFSk2KqZ7m3gjmlvCyElrI9mQbIOy/ljv1JF847UgOL9WnLW8UtUQcOffjYPr7NTl7pAxfUkMITm3eZ4lQRRC7AGeFZbTCNAcO4VjYGgcUIzvOYPJZPuQfzb6fG+rYs54FnjvkibS8DtyGV6U+07EiN7J+8H3vgREGd+vOHyZ6TaUfGVGYv5cBlvG9/Kye1+/h3w9pRIbKUm7jMdQGoGwEsS9bO7XvyuvlXWgLv9s/HMJjDOwP7pmTE1qRs/Ug9hpTebOr/nx8/Vdmqsx6NHfZ38/qcQphFEZphp9n3QizTY2IrqphghO2Cfb2ztsbW6zu7nHdrXDzFaisa0Kqt0Nls2VlKWf1SyuLvj881+xubWLMZq2g2XdEpRnVk7Y2L3Gzq2bbN+4yYunzzk/PuHs9ITz8zOaekFhLWUs8TExrjPorAO2DFzMD/l///n/Zuf32wQTWMQWvVFKAykCxaRAW4tPw2BS8JzXmlIaa+2wrmPEeWEDZRadVgqLoYseFwOXi0t+9atfMF9cEQhobVeArfUxHe/79YBtWKMDlOhiwJSazZv74APuYpHmPWmJaVhqaGOkjZGqc4TzC6y20iG3rIiJbTSfn/PsiYfJhDfeep/5xZwX97+m0C1heYU7h6A1B2en3Li2R7NYcHGxIG5uMJts0nU1IXpeuXWXgGI+X3Dw4pDSWl578zWWzZL7j58RArzz6k3m80sOnr9geVVz95Ub3HvnNoGapl2iYofWUkpvdIkJiuPLOV8/nXOBxVzfp6squrzuoiQm0WCtIjhHfXEJraPQqw1E1ve5c575fJ7meUh8kJtUJpu7bvfWbWAu/S9Km0CI1b0o5ZdSMj6U5Id+SrNPNQZoMwjc712VGp8lEGVIkA2A8DihsLpueOnzjwElMZtqsAFA1zqKYqTJ+5LnX7dxcmalHgOjxrEhZtBKgYl4lQEzkWkxWuPDkICKgcRWEZZ7rnJQOssMpWv1AUAQIkCEGANl6uQ8fu5IpKwqKbdVoLRmur3NZH+Xq+cvIIrEVP9sURKIPg7sNT+qWFlJtiqGZKaWf8SuJUSDVgarjQCi47M/R47p3lyq9CABEj4RM9ZtQQZWVApa1+0IDGDh4HuMKvAQ3z36iE9VHzpJOvVnhk7sQw0xqpXAcby+YkxNPBMIkldkRI3IKRmojclZEruqA0wnE6yxON314GSIMY2lkwa8puwlmaJKCHMIuK6lazuUNTilseWE5WLJjWvbTKYTYuzAdyjXYlREIcSWJLY2nK9aoaLIlazvkbEkTf4v+2q5EkjirmxTUtmv0qBj76f36wWxF0VRrPgjPwDplAA7Awt/qCTKJI31fZhLmmMKXvoEcNoDbdsKCzAlVIVVn+XvVv0AhditmFjRPaAVlUSLSpGlNCIRa4vU20PhkvzeIOEzJPU1oMsU/yKMZpcyq9k3Hq/vYV3rVJYc+vUcQ0yNiYZnzO/VZCJC7H2mfm+tsVeHRE5OiKVklUoEjOTzZ4A5R48qN2J1q6DsoDVpWLeT4zO+/+61/TRef2PfYEXWYtiNRAQotUp6f3gnVRqydh05+WWMMPnUqHoPwBZS3VHpMoFikiAokk5pWU2xWhiKPvmFPYEt+/K2wBDRBf3+VYmhq2Xxij1If05LYXL6IFIDuXmdRmGUkRgB1VeSyp4yPRBptEnED8FAtDIj+TepjA1JBqdt29RMTCp9SYzfnDTxwdPUS5q6Rit59hgkKeA6kTYpyjIRqERSZmBpC1OyjSERBDXoXBEjFa/LpsbFgDIWtEhmzqqKwlpUWaCCxxtNVIbOKq6ahehfq4hVlspOUQWI7J9U2qgolVIYgy4rGcc1mR9jxW+NQTGzE0n4xUhZie3JPZWstVQJfBz3IIpRntZYgzFgi4IYhQjpnKdta9l/KEpbYE1iwCPj13WS1MwsdmstxlomMdA0Bu8LnKtSs8HEcrWiqTxJdiDLBmQfu0x6ttl+uq7DO5eq4GKSHiiwRjFNTc7qJI9grcg9imypQZuKoiwFUA1BGMM5BjPDGaESm7tLzSJ9DMIONqUkTpDmm7mvUyCmpne2B2R9iAkvk3Ex1qBDpPYNi/qKorAUlXym+9MY7Z83SItS+JicJKMpjCEER4wyMF3wzGZTEcf3o0Y+aaO7/oiMoKR4um4aTk6P2LtRc3G2wFa7XNvZ49b+K5xc3k++mFwrcY5EQgCIWjaDSlR+KY6IqCDZhdyFVhzg0B/cA1tCsAsBjsX4hbSAsn5TiD6VlWgxcmroEg3iq3SdH0p38nsR45Rp+SI4P2Th4uiACMnxzeXdRhcUxhKt3FNdN7L4C52y7KSO18lhCbKRvRej13ROGjQE0IXc17TaoiorLuZzYhCx7kk14bUbr/Cffvo3/Pynf8nt6zdwPlBfXuBcR+uWvDh5xnePvuU3n/+Wh48fc9421NETjCJaKZ/LAuY9qkpyONL95fIsYcTpntUIUYDL1OU9g9QhlYH1nWwjSY5AgG8PCRNNjk/0XJ094fmvT/jDF3/grVdf55OPPuaVW6+JeH7dQFFgyordjQ2uffiXfPDex/z0L/6B3//xt/zmj//O48OHLP0Crz0mOd4xRM5OT0RSQudOlHntjMG1dNLESAxj5o8EqJIQDtB5jCooygm3b9zlP/3F3/Jf//N/oZzM+PUv/42DJ/e5d+8DLubnPHz0Nfe/+QNHz55ydnxK62qCCVAYYqchOjQOwjH1wb8RLu9THX7L5q2v2du5gZvMmHevUpevw2SPaKeYUBPqObOdHVDTxJZbEF1NvDqD5QUqtKjWo7o5xl0S6nNCs6D2c7r6FBvP0VzR0aXSpIihkgxj54htTbi6T1ycQGo2JKx6Kffpgyp0z7avtjfZuXtDmnE4h1KWLEgnAvykNTXoUscMkqWAW5Gdu7DiTGWgMyiV69jlWikwVyNHaR3kzdcwWssBrzI7KDsDKjFk1sHTAZjNr8wAGeOROVAca4uughD0gGcvFp/lWkZO4jjDP870j7+b7NSTm9olhlgGDEfB5LpOp8udRmNmg64GpGN72Cev+u9P3VrTgRvy+IzmYhzUBr/6XICUeHmpXshXDUF0i8as4nWAZPX583z8ELQdf1++3thJyutNrbxPyi+75ITmMrAQh3uQ+Yv9elyfk7h2ffk5/Z8S0OSmZGtskJh1BkMPxBgM01KztbvF1uYO08kWMRiUh3ZZU+hI6yIb2zt89PEnOOX57o9fsbmxxcnpc87Pjjg7PWRSlWxt7FDYirpZErVm0TVsTraw5QZ3Xr3HX/zl37F74xoHh8/45b/9E4+//5rF+Tlt51g0DS54rC2YVCVeS+PItm64vDrG08FEUTWbYDXBebb39rB2s59b39OX5JyYzSYURdE30YBU9ZJlHpSApngBlrTWXFxeYDPLkzEAl4GWVeAv/359b43XiE7zEYJUUURjKDZm7Ny5yTkHNOdXVPkci4omBSO1D/jFks5aCnPOtRjY2dgSJzcGPI52eUl4eB+jDR98/CnONTz//guKzuPOTym04ua1m3jl+dGbr/PV7z5jcXECxvLaa/dY1nOWVxecnJxweHzO3u4mt2/tc3JxxrNnh2itePX2LZbn5xwfv8DayNtv32H/2ibTmaJpFc6B7zphPSB/Pz6/5PP75zw803S7U4rr+9RWGqOQ92uUgNA1DfXFnKvjE3Ri54QwlDP2e1FLQy0JNAdAth9zGNmyVGIeBsmX9cB7SJAk4CRkfyLpSoYk5YIwdgBsKg8UEMas3N/KK2G1/ZmC6sGsGCVENyaXNg8gXr6vcfL/5cA/I8CHpHMv31QUUsqYk0R57a4DSuOzK99j/oz3sQeueymjpIeOBhVNKttWAsoKAp3AQpWSG/lci73fnJkowSftwhwcEiknJeVUyAUSeErlmE+M16IQpljUisl0yv7duyzOTwltK01TYtbAH6bAeylZDASyzGv208S3V+ma+Vyitwsq5EoDaUgyHNOjZ8L1IFLGPvJZ9qcSf1mWRaRZsqZx8stjPuOzDRnb+BHjVRnKsgKEABKVRilD8J3oHBrbM2xzo6k+4ee6fiwE38x+gu7vfXyeS7WG+CzWGnQAU1UUVUm9WPb7MBJpvcd0SyZ2Qxp/RSXyQloajkk5cIfvOgo7SZqSBfvX7nBxecSzw6+4efM297/7Fh2kqkAZJXI4KfEWV3wFeWWJkRC6fi/1Pt/IV8oxXA++4XuAVPUueUzgmOnHJduVgQn2Q/C7309aE2NOZI/GM9XbrCZh8lrJFVSDD5htluhqDiBjn9BGiQzVKNkzvpfeF0oJDOfcik8GwohXqVdJbk60DoQKwUFkRFwcMVkR1mVuMCRVzQnUT2s2+49aG5FWSc+lUqOnMRCcN61RqWdC+nfeBwIuqn58QhzO3fWEKKRmbCYlfLQ0pfQKiYeQhLZi0Kwfr6UxOJtfYzZsHpv/6PUfvU/A5BSvKsWkrFIykB74KsuSGAPL5RJbVlSTCTkZIqXYAt5K8yOol4s0V5G2XqLLEltWPaCX78J7L/JWSuFpU4O+lCyIvicVZfmvGOU86FIDJ20E7O2868FQkdFK1wxB2LJKC8Erg6MxEkLyE7SWfgsx/13OrBgTIzENuw8hSaX1yyPpocPVfMHi8gJLpDKaIu0S7yPKyb2YKBXchRFZpS41wGs7QZYEK0jzbWwv64gP1G0ja81KozldSi+LDVVQJRDVK42Z7VJsX2OyNeP09ISr4wNwHZ2DZb3EtQ2mKEQeRSuC64j4pH2qEu9JDpcYoXVO+iNpi02VAn2MqhQi5RPoIvgkb5AgL1mvUUBw13V9rxxNAudV0nlPWvRix0bgPalyJTUB9DEIybEs5KwO0tBwNitpWzckQRPpobCWrdmG+OP93vQYKzYxpERBUQpLV4oj5WwmGoyOVGVJVZY981UrJUxbStiIAAAgAElEQVTwtE4JimlZMq0mYj9ilAapwaeKcZGFiF4SNyEIpibjp0c2IyQwPPaNpIcKQ2k+vrExk/0QY6oAbOi6DoNiUk0oKpHuyHrwf+r15w3SgmQ4EJAxIAeTThqRCtGU01oTzVDqEHOX25SBgATcoVk2Cw4Pn/P+j8AahbGandkmt67d5OuH4qyh4uBEohIbKOm6Zo9RKVQyAhE5W7QCq0XrQqeVr9IzyKJezTZmuCeMytQlDhGHsVA6sQqQ7GBaVBB63RbxwAQwzYdeLrPJh4QxZqUhjGhalT3gp5WiKgsJJoKUooumjUJhaMOgxacZyt9MIWVdbd1KhrMo6TrF/uYer167xd7WNucXF1xezCmKik8++gl/9enPeO32a2gii+YKFQLLZs7h0SFPXzzm829+zxfff8PJxVlqKKAICaBQwePxApLHCD6mQzId9HEAcow2iWuKAAvp4A7RjQ6+CDFgIjKffcBBCgCkxEsl8D9/xivAFpx1juX8hCdfnPPN08fce+U1fvbTv+La3g329/bATZlOr1HYClNYfvLjj3nnrXf4m7/+G37z+S/5zee/5tHzJ5zPTwlKAi9tDDZ1KhQWeXbCZO0PwcyIPRkTazwFXBqNDgUTM2Fna4dPP/2En378F+yU20yLgrptmE41f/zsC9plTeM9D77/kkePvuH88DmtawiaxPgQsIqQnNwQIHb4+oDFwRWxfoS5/jrF7A5BfU9XXGey/QZMtmXdNQ31eUcMnm55heuWRO9QzRVqeUUMTZI+aDB+jnELTOjQKoiIu+pQqiUG0eXFL/HdkuiWhNZB00B3gVYemxIrXge0LjHKEL0jFeOI6Hxl2djfQU8KOjoSro2O0vAia0IrJc1LrLWUZUnjWmkQQi7XGhyv7CSvOqg6MZVGjn4C+tbL39dfw2E5ZsOsOuA/BAdHazp9f/+zkS0Yo7bxZX9Pzn1U2ckaAxSDk57vySWx+1XmycCWzYG7isN3jJ35saPsnBOHUP2QBSafEaDFxwzwDr/LQVH/PMlGy4ikdFt/f6tjJ3ZhAHNIAADB9+CuNLNQcuA63wcaOZAbj8vYSZefmZfM19CZFQaW/MuAkDw2JDBD5XnMTiGZoTwER/n7x0A4o2u/jNUxZtYMc5zTnOn/IVIay97WDvs7+8JcRMCBZlH3rME2QLQzpnbCcrnk+bND/urv/p67t9/mN7/4N/au3+Dhw284P3tBu1jAZBtbTrh18wabW1NevHjG8cExRiuKsuLF0QHLLvD2++/zzvvv8/TR93z3xRe8ePaMF8eHnJwcc3V+zmIxp3OeaCNGB1SwaBVRHmK9JFpLs2xoqyl6a6MPCtfH3DnHYrFY2Ws50RcUiYkljqhysrZMDjgY7yvS/P5w/vNrrDe3bhuCD30zBG107x8U04qNG/u0TYtvHDZIN3uRvhEW4zJGplpx6VpYXII17ExmKB9TGWFHMz/nxeMHYODdjz9msbjk9OlTKhs4PXsB2nD95i0ePXyEi47ZbELdtFydnlKWFfWywSjN66/eZjItOTo84vRiztbGhP1r+/i24+DokJ3dKXfu3kRFh1ILIhIAl2WBo4TQQQAXHF89vuCzh0surWZ7f5NgIGRQDIhatAQ10DYdy/ML6JwkhFIp6ngvjOA+Ge80ngTRVRsSGybZ9JCCTdUvj963HNsNlQG3OIBjmVUbkvcQSSW6ab9n+5OAoR+AnTqV/hJ7DUigBwbz4dPfh0rl6yprUA4a0mP7sX7WjJM0Ym8FyKS3qdKzYP2zq4kbEqsmA5r57PJMJiXGFizmy0GSRSthIoUBhIkM1Q8RUtOfVRuWBkaC0Szble9DK6IHZQzKSlAax4m3xAKKMWnYekWLY7KxwWRzk8XxsWgMZlA/7cHYg2bZxxKQvbAFk2pG0za0qQFmb0OVgEC9jnpik4bUJDfPZ/Byvvjet6Qvkf/BK9vjmHzRBEJpHYSpnMCanv2N6vsd/ODMianqxupeO1IFud54fUvJZk5CrCaVbZZDS9+ZAYDcwGa8PsZNbVRa01FrYmEot2ZwekbXOtquw3lPoQI+dOQGpxGkya+SPa+1dErHB3SMuNBS2oLp5j7ffv81W1sV129cZ3Njk7ZpCTOD0rYHXQPSGT53LLepd4YiNxIVjdQxKzKPSU92UXlcZbVkcL4fnxRrjYHtPB5d160kdwXkGdie/X5E9WWzefyyjMcP9+8qECh9C4b7URnMg6S6Kf8LKSkRlHi043vNgCvQg17jRPLYR8ggbB6vdXBRWGdpHafnDDFXfebrgjjd4/Vt+vWfQfzxM2d/qU+qRQWE1HuFHozurb6Y6tGeGDNYs21VCBszJDs4VGoZZZNPKWOXFBV7UHJMPFj3GcZjsT536/7/+ufWffS8bvKJ09YNYWMiQJkepM8gCnEtaf2aQpiLzjmUpwfdtdIUdpAyqLuGxnVylnpPNKaXMOhZsAgbO+OhPqRqB6P7vgl5noOPtKksPIRAWVXYKLIuMY1ljND5QOcdSmvqpiFrIFtrsGUCy2XaZLxVS5ebp0chVlTVdCWpgpKEnXcdrnN0XZvmIeLaBte0RA100CIgYVlVApoZARttYeXfaIIWsoQLMn5GkWQDvDSTjwGCRweoYm5SGFDaYk1AeQ/BMakqZtWMjZ3r7L32Hnfe+5jZzjaPv/uWR3/8Faq94Pxqydn5Oa6pWDSexfySpmnpfMAFOXe1LRKbPaK0Zdm2LJZXGGOoyilFYQmhTTIPsidcK+Ptmg5r7dCwMgSCd3iX2MJqwEq0KdBapcSngJoRJfro3sk4lyVlWchZEgSclUqlTPBL/aK0wrnQ+ypN0/Q2pygLAd9D0pZGyfWbQFlWZMKa9ApJ4LDSeN9BlHXXNk2fkBhsFCkBKfakKATbiiHgO5cwjZDWdEAlDVmtAi7mRoVgrOp9Le8dhba44FAxiv6uEozQkYh1XvTwQZ7PVIouJaCNsRglwHGIAR1X49fx688apFUkUf7k3IoGRuooq6RrmsgDhARapY6dicmik6FWUbJHLZHz2vHw4CnKBPb3tpg3MC00t6/dJKoJbZhT2tALoqM13jvRKkobvw8AkPvxI+fEuWS5RiVJuVxKmFgDi0mnSdUJBI7BC3WewYFVqrdLxDiUu0Rk08mC8YQAIbQrB5hS6fAAAdqULDK8Txub1AVSFmxlDEErgi97XUaixkWXDkG5l8JorDJM7QRbCe29msyYbe5QVDMKCiYYWHquz67xyXs/5dOPf8Lrr96l1IambfC+IbRL2rbm4dMn/PK3v+V3X33BweUxTnkwIv4fUAJC5m6+iGMhqLdDi5I/URvRqiGPV+glFlRUAjrKpxPDkgTqItmYSK91lJ2mLKyeyyt6qDZqXICoI62SMoTFxRGPz4/46vkj3r3zOn/9k095/e6baBcI0w2KyQYbdoqaKDbvvsFrt17hb//q77n/+BFf3f+K3/zu1xwcPWfRLEQr0QSMSeAWueulMBKJuTuzjIeLnkKX2FBQmQlWF9y9eZef/eRn/OhHP+LV118ldI7nDx7z5MEDlu2Sxw++48nzR3z25ZdUquT44pCjgyfEtobKghLNvVyO4nxynlLpky3Axyv8smMaK25t7tAdHnJx9Xva0zsENSXqAlKX9+AbFE5ycjFBP74muiVFqNF4TOxQoU37VuFCxLklMbbEdgEhErua0F2iaFEhl7BEUJqgTNq3Kjn5sn81EiRHa5jub1NtzVKDvWRncuwrK4EMkppeuyf07+1LDZOhVXEItPoAE0XE93svl/zl8sYcTAXiyJLEPkiTg1HWsvOewhRpXa8CBD5LvfT2YQAus/OvyGs6oMw4KE7PkwBmcdrSvlAqAYvZoRyeOTOmhFEk7I4xo1R+n3ZadiqTAw6DYz4OCgaQRI8atuSxkHvPJU+53G6s5Si6TRkQS2yr3o1NOV4FfSluevXdY5PtVYqVigOZ00BVlX1wJXOanOx0FshyUWS2e75vyA736piPHfNxMDdO3uV3SCOXVDqZ2IA5cNEj2RuJGUM/5uvOvYyfnDnjQCqExNLOn+sDz7weJQgqTIHVmtn2BluzTWaTDVRQ+FakLnzoBv1ABSpqFhGuFnO2txUvDg74X//rH9nZ3OD+owe8cmOHH3/wEQfPtnn48KGwIYqSs7pFT2ZMJzOa+WWaAw++5eLoiF+fH3P91g1u3rjBp5/u8vzWIw5PDzm/PKepGxZXNYdHR7w4fMbi4oyAk4nyirB06AJUJ3vQJ7RIj8ZNZHAiTVMPgTQD05BR+XlkAE7zPssNwwZZjzwPw/mRY3LFKDmgxmtnWB85aE1HWQI7wCsodzbZbPZYvDjB1+KjkADkrN+y8AHrAm1saN0Jahd2pjNi0xI7j9cN88tTnj9VvHbvHT753/+Bz/75/+H89AE+NBwfP6ZdLvnwJx9TVCXHzx+zOa3oFqfUlzCdbDApS87nlzw+OcJoePetN8AWPHzyjPnlJbeu73Dt+h6f/vQnPHrwLSfHTzg/PUJRCgOyKomdVDAcnS3445M5c2uY3trG7mxRCzwlY6kz6KrETnhHt6yls7i1qbGPNNHUeRxjPgtGmyud9wOoJP6QNgKq5U28CrjHPqAYAv383tgzmbL/IEBWTPeSAR/5/hCkAYbsFTXYt3Rz/V4cJYIyQziz17J7kve3BNICUK+XbI8BgWH/J3AwPYv3boUx6hKpYMXtVcMYxjjYEO88JjFmrDFoa/DRoW2yhZmdHDOInq/RD6D48SqPO8N5IgOWfH1ShZnudSyDFr3rqCQg77qOopCAL5+DXfCoVJLadoHSGHZuXGd5ekroJL6ICbTIlFqTdTlRYls91K7BuZGtTmOp+zUhZ52PvtdUFHshCR1CluRSRDWSqslnXmLdZtC1P68zE1TlnZCkCaImd5TOxiVk25LXbiYoJKOjIpTVFFROSEiS1VpLaFrapu33To5xMnArkkNyLuokB6N1bt6SWb2JsZq2nIpIKw5CkpsBPd2AdJ7VdcuybpjOthMOExLALSxGYxQ4KApD1yxxdUPTNky3KorJlOnmFj5qDg+P+PWvfoHWiunGNidhQU405nHOQXZuBmaMaAnmhy2wqZQ29Mnfnp2v1SAZFyO5pHw1oSCsbmnAHHswcny+DzFc+r3WqQJSBqrfpwms1sZCBolj1n5fTbL2Zwf5pEknT0xCDzGA1hg0Ucv60v0n6EHW7PtKQgE5aEYSDllDUpipCTdLCSdIZfRRGoUZa8nN8/oKsnyerYGZOU8ZexsXh6NTxd6fzPFZjLFvXJgrreRphqqi3q7k3gijecjJCNX7b0EWafJdhkaBKb7MSTUt8gKJ/z/6njhaA6tn+Ni/XZHCGNnlcTL9Bwmq9Bonc2OMdC5wdbVkulFRTipsUcpdhZR0s5YYREKDppFqAi0M2rqpRbaJlqYNFEXBpLLMrKXwkugKaT58aIkRkUvKhCXJKqWkmICeKEVVTQQMS3JsPnhJnnUOtKJuamITsUWBNXZIWFgNQfXVa2L7ZVTbrkv2KK0xY7FWbHnXSSM3Hzzz5RVGSxMxRSrVV5GymlBUYDtphNW1LbOiwNlGNEuNprSG7c0ZZWnTVtH4zicwVqfYLaT1K4xLq6VXRdu1dF1HdB6jItEHVFAsFzXOR5xSWAO+XrBo54T6kmZjg2q2zbS02OA5eXZAfX7J1uY2odO03hO7kmBgf6vA7Uypm4bLuubZ0QmXF5dEhMBQlBNA03UdKsL86oqrOEcpARarqkIrWQ8axdV8QZ10Usuy7NmxssbEPtZ1Q9MJG7jrRKqlKIr+fcZaotIsagHUWS6ZJBkbYw0ilxNwnSf4Fuddv/Ymk0mS9Iv9XmjaFjefI/q0kz6+zbardVLBl3WMS2sg+l4iyLsmPWPBvG4xRlEUFUoJ87vr5T7ErmV97OyjOSexu3OdrKkkI6KNYHRd06IL28NBShu6ThIF2uR9LQRH5xLrOUYKK+tVwgODiSKnQXRoJR4eIdC5lj/1+rMGacUYqEGLL5W0EwctR506v2VBdpXfpzLLLVcoK7oYmcfIo+MDrhZnzKa3abrA1MIrt28xme4xjy0hNiI4r0jGISbND5/ATiDSywagpfRIpYxtzvD1YGpyyjJTAxLbVg/sB20T2wr6jEEOzEg/y3q1kuVIwFQ6kHLn3sy2UFq0Zr33fQBKFDDGmNTRNTkqgUjTtFTGYI2hKkrquqZA04RUet95rDJYUzAtSq7vXGN/c5fZ1LBZTolBc3G1JC4jKnpsYbl16w4f/Ohj7t27x+a0IriOzjW0oaap55weHfHN99/zr7/7LY8OT7h0Ha2dpsMzYqxhWlhicJhJhVIR7Vt5bsQwu65h2S3pvEtBclojSoBbxRhoTRnA6JPWW2Lc6JzxHQUPOb7rnQsBSCMMAXPSYiMGfAG1j7QXJ5xfzPnu0X3eff1NPv3xp7z25ltsbO5j9AYhGbCoDLt7t/jxznXe++AT/ss//J88ffaIL7/7iu8eP+Dg7Clnpy9oFnOC8gTfoaPCe3rAJXiPLS0bk012Z9d47cYbvHfvA958/R5vv/UWt27dIoRIWy84OXuB61oePH/Cgwff8uU3X3BwesTZ5SW04FwrnWAttK5FI7IWAGkUxfB4l9Zdh1GKsoDXr29y67rm0YPHcLakuXiOKWZEpfrmIMaIgQ+AyxINyoFvMKFGhQCpXUZm5YSuwXdzvFsQQtuz2K1WohmX90sKrpTWqLSPrC1wLsh6LyymUBQ7M8qdGdHI2pEefAl4yUCkUig/7o4rgvE54z8wnhJApoYyh6gz8JLK3OKIhZD2sexvlYDBDLYnoC5KUFAVJbrQvd5NVKN1yCgozwwlMtgnQWJ2cAQQVX3AFHLJzIgdk5t8aKVzTSlEjZTXDazYGGNfoZAZIAPjIAf2ualaghoUvd3J+0YzBBUvYxSoVM6aAZQxiyeielAr66vmxFx6Uz/GQ2mKGpQOYgaYh47tGbMR5sYa04GY7GrO7MYexMylZmSbwQDeCAsppDIsT7biY32xPlG3Vga37pjn9/TASk4IjMZQQKCBPbgeAJHWm1ai35nv2GVmXwYZkf2V9fvKokAhjQQ2ZzOm5QRrCkAROnGafHB0rkllsDIuRitJaBbg8CzaBS7U7M4UT+//gZnt+PbLzznb3ePunbu8dW9Kg6KOhv/23/4rB08O+cf/+T/Y35niI8yXC+rLmps39tnc2Obs6IAXjx5x9/ar7OzspXO34Pxizub2hO2bd3jVvUO7vOTk8Dn3v/uWer4kuoBvOjAKFxwmeIk1WGO0pH2uVA4TRkCq6pe8vC+uBlsqqr5EdLxPyTBjz5b7IZC+zo7KweYQtA+pB7nHyNb+LiYqLp4dgI/977Jede09y0VDpRXNpMLqc0yh2ZhUEAJN19IGR3sSUKbkxx//BZ/8/O/413+8oD5foJM/NF8umF8taOsWCsvGtKRuHcoI0FNY6Xi/tbnNvF7w9MUZi2XDrRt7vHLnBtMNy+PHD7mcX4A2yaFW0lE8AN4x7wJ/eHzBURNwWyWzves0tqJLYy96oQpjCmFLho52uUhdqC0hs77MaC7JIOEwF2NgPAMPMleeHAvG5BulqVpZE6u2N4Etcdh7+dpKKQHrGMqsc8NEVQyyDDH5LLk6qu/SHoe1mddH9i2N0Qm6Tv6eGux+/v7851ChkEEA3QO0xmTQYJV9mxkr2U6ObVT+PpU+a63Fa9/vFKUUjZPAWtuRrEPMLOb03twEN9m1/mzIew0BTDIbZgBtBdzTCHNQGcN0e4cQhXEYohPgwQ7lt1ElFZIQBZywkeneHlvXr3P1/EB0u8OgyZotovjaksTPWqYx+dFjwCfb1K7rsKmhTy9Fw3AuZ/9duEjDWunBmTRG+SzLlT2i+SjPHoIErybpNUrwmhJ4o/NhWLy9uRIQLGkaOu9F7in9tuuc+MZpvjIo3q9dlPgLSqOM7MfSFn1S1SQ5Cp1ioLyFsr+RY6pgNXZzJk2ZQmTpHXV0KGukmkmDVqFnk0oBi4C2rl1wdXHI1vV9umbO4cUpy8UVKnjefvNNzk4OeevePb4/OObxwUOsTr7WaM2qRLhJx2K/vmXYhyRwXrchhBQzZF9lSCLrfhaT36FVKuEXkNzqVY3SDKZL0ih5H9nGj84g2YdSlq5UPsPl+3wCOHK1ZkhAZQYdNYAe5BpiHJjhGi3ybmvaqS+TKiDFlSr5QZkZnUkGve+nsjau7EWtVJKe06nJbfJBkw/dk49itpdDL5FMYsqx7rDnEwBLjql9H+OH5IePA7exzySAbhq/9PPWdXjvKYvUYIrQVzFkvCF4Gf98NrjgZBwhkWdWbe0w3vEHf8+/H0td5J+97O/jdbD+ytgBIAxYq0GL3VJRo00GnRVlVYpUSCrLzg21yqLCB0nCeZfKsdsOFNKDxwhgRZYHJMVM2c8xCqusAO46YkthBQq/JiamcaQoC4j0TMNMipBESMSU4k8KYFgRYxRN0xAILiW6VE520sulGWMw1lJOZN610lLhRpQyfRSltdJfIl+/KAUPmaTKuxAoC4tNwF9lFDrJRiogFoGqLHuSSfbbvXe9vJHWCtcleR4fIDV2bhonQJ4LOCWEwUJB6Fqaq0uWi0suLi94fvCCzd1fY6otru3vMpmWXDQidRCdozCKsoRqtoEx27QhcvvaPmeXc04vLrlYNNRO8KNqMmFiNBtbW7iuxXUtub+JMUK6Mcays7vDdhzWhEu6+SHN2aSaUBYVnXe0bcfGZNSUTwnL2GgNGqq9a7iuxXsnTN/QUpQl08lUxtxII7amaXDOs1zUdG2LLgQgLipJaBXA8mpO3dRMmpZJJZKGyhrRgU6gb9c6urbDKmlMV1WVAMcROu+oG2E0CyxnKazFGvG7jDY47zk+PVuJN402FEVJG1pc6/Ah0nTSuEx6GYmWr+/aFCcL2Srv2aIsqIKw610nVeXKiFxH4wwGsVPGGAHzI1hT0rmQztxIiP9/BWnzwiA51LlrKKOMopGuk+MApgdByICt6p0lFw3HZ+ecnBwyvb2HNQXO1Vzb3+X2jVt8+/QAPSkk+6zF0NlCJnGxWDB23tItjn42CrbzfeQgOf87AR8mdd+1VvXC7nKloaQBRiUZCRAuy1Io4inTC0NZkU26FjHKojJGskpdkjqQg8OIw5M2rbgSgdZ3BKfYmEzZ3tygVALSNVFKH0qt2apm7Gzvs79znWs719moKgrjmS8aLpY1i8ZTVSW7O/t88uOP+PCd99na3sEHh2uWeNfQNh1HZyc8O3jBd/fv8/jFcy6Wc3Z2N9gtJ3gVaNoWfGBSKcrCoPBYDVVpmChZBW1QNF60RLrQ8PzwkGXd0XSO2jsB8axB6dTkILEvMLan30M6lMV69UETSkCWzJrJbJI8v9KILss/SGfGDBg23nPhaxYXcw4/P+H7hw959617vPPuB7z79o/Y2NghmilOGULjevC4NJYP3/uQj370MVdtzfHFGaenxxy+eMHV4pKry3OaxYKudTjXifbKZML29iY3buyxu73PzWt3uH7tBpPpDKMtTV1zcXHG8uqMs+PnfPPV7/n9F3/g8YvHLJsFdb3EJakKHxxaizi78iTdt+QMktZSUUAsIKoEQMa+uV4MLTrOKbmkrU+gSxn3ILCdTs5QTJiVjL/H6JDKFUSPUEPq7BnxrpP3EIi+FZDXpNLBxGroy42sJBDKagJKymd0iHJIG0W5PWPj2i6hNISkSZwPHj12hIbtmuZ9cGhXSmnSHo8xEs3YQaMvL1NIY42ghgA4W4uVfZ1+bq1NTBthe48dvfFrfK0fNh9LgC/yWRdH+nAZtBsFjHkdK6UGHWQ9GLgxA0SbfFykrq695UvJsJE8R9+IIQ/rGPhUauWZxs8DDMyItaBFo0GPAorRdbP9fdm1IXU1zgyKMXspDkHOGOQc5j/Sdq0EChEhWyiS/MsA2Ob7F8AnlZuFoYzyZa8xGzh/7/j+sz0fB1DDvekeYe5Zm/2SekkZnfxCbFjS1mL8vShEgltjtWVztsnGxgY6iv5XYa1ogLZdmnuxiSGVNknJjpzDvvVUukJF2JhVxNjx8P6XHD78ls2NGbdv3mJy5y4Hzw84Ofkjb//oIz755C9pvOa7rw94+uBbXOhYNpqyqihLg68Mzi8piy1CMJwdz3n46AHT6YSyKimLGZNKOsZbVVLOKrZv3iJ2HQ/VfSnF7FIFSWmFZZcIQMO4Zvbw4GPkMzv/fnWd6pW1+zKgfbw3c2A7LmvuQfd+TeY1OMzlGESWzL/coksM22J7g6nfpz45x7Sih5nfo7Sm0+IoW+cprpagFHf2dplNCvxiSVsvJPCIikf3v+b6K3e4+eobHHcLFhfHEDu+/vJzXN2yUVqWdUNRlMxmGwRlcF3H/u41Gqdp246j40O0Mrz7+h12dqZMZxqoOTu5QGuYTivRzPPCHoupJPLRYct3Zw3zylLu7dGUJTGxZaN3GC0JrO2dPS4uLnCLFnc5x0aQnr0p+A9iZ2Tsh3noA8w125nP+Lznx5UBsnfSvK0F3GOb1jMZ/8QrO+n9ZxJ7w9ohcb+ytpK9HrPeJdFvGScN+jJQBJyWqjM5h7J9yQBtvoeBrRVX7Hu+ZgYS1iVY1m2K0QL4hCBNNZRSvX66MUNokZMN6yXTMQOiMScgxLiKXZZNEONYKzqVHqbfCagbiGiKWQVWki/yDJJg7W2n1n25MkiyyhnYe/UVfNsyPz1DgTSISeW74hvQA0Y9KL42n+M1te4j9OsJfmgr0pyuv384I9PPs/8ZBMHN4AAJWM+afitNR/vvHioMoxM9wo3dDYrJBB8HuYI+qRSROEvJ3JKq7UIGXdXonCJKn44sf6CkIiUGvzLXudEMyS8JIWCKAmUM0QdaFWiVFx/Uiv9hC0XnZO0HFWl9S1SRZrlkMb/g9us3efH0Eeenx9fBqwQAACAASURBVNy9fZs3X72ONZqPP/6UX/3yM46OT9P3jbalEr9Fk8/MvJ5GPtJozeY4zIVBP1H8zeRz5TMh78iQZegkaWryWatyYi32fgqpUjNElxoO5XNmYLmTAMKuruUeEiiZqyS7zG6OEKIemM4oiAJijs8w5wapt9UEIv2aXPHFUkVGBuHXmZx5jeX/sp0ZSEqsvEfGJn2ewZ70iQ496P0PUzYAs8M9yb9dDOCEOJV9oPFZuZ7cziBpBstNYUSiKAorOqZmzToTvnROinREBFzMki2R1b0+9t3W/75uE8Zjvf7z9defAm6lslJA2MmklPvq7dtgu40Wya7gBzmurktJu5QgyNV4PkjzpNZ1FFaYk857TEhYQWLkayXScEZbsf+pMlcbRdTC2LcqNbI20hskS4RlANyTtEITRpFjE5VYiVYbXLLDZa4WzOcLKTnU+25AVESTxqqS5IAxAr5qLfGs8pGJNShl0bYUXCRGXIToIfpAmfaqSXZtsawJ3kuzQ61QQfrc5BUp84ukRoyh68SHDj6gJxXWC93FaEV0HUEpRCW6o2kWHDx/xOnpsVQ21He4desm1rUUMeBTgspHaLoW1Un15ta0ZFoY9rZmLF1k6QO1C9K/ySccTCnqtqFu2sS9idLoEM10MoEVIoGnbbt+Dipbip1P6yymRm+d63o/tiiksaMkcge/d1nXfVLYWJtwKDl/urbFe0/XOXwMvSayTez87e0t2rZNCVCRWTTWYgtLYatUsSOVe6U1Q4IxrQOtbJ+k8b6j6wS0L6z4+5PJBIjSEC9Gkdlx4vcaGyiqCmsLacDmvEg/hECIYLXIphltJA6MuWmYp+s8ITTiy6EpSpsk+eRZO7/WvwWNT+6Rc57O+ZSwe/nrzxqkjQyaLwaFNUVyHBJokGZoyG7Kv4c/h8YPvWOO5mxxxbPnD7l97RVKvYMOjo2q5LXbr/HNg9/jbXJS05WcDzhfD9dKwb1WonMU46qgPOm+dQqS8sk0BO3DopZAYjiEhHU7GOc8sfkga5qmD/y6ZLCstT3rbuXATOPQN52AvjwrM0gU4khYa4nO03UtOkyYVVNa11E3LQbL3s4u17b2uXntNm++8S4azfnxEfPLMy4vF8SoeeX6bT788GM+eP8Dbl6/Sew66rah7Wqa5or51QVHB8d8/+ABj58/pw4ebS17u9sUhWU6naCULOzoA4UJlKXB4NEECh2pTCQArfOEqJCy7Alv721xtWy4WrQcXl3x6MUhrvXUymHKUphdyAGf98PQGXLkaKvE2Ov1bkPvcIgjmgLvKNncGJFSHoQ9FqJ0U3cegqo4vLjk8o+f8fXjb/n33/2S9958j9ff/ojta68QQupIqTy+dRQmMt3YZmtzm+nGNm/cfQv144BXXsr9gpTL+eBTORy9Y+S8dF9Ha84vz6kXNUdHx1xcnHJ8/IKvv/gd33z9BVfzCzrlqVspG7MhBQw6aRAFlZx3nwI6uaaxNpVLlcSoILhkwBX3nx3z/OiSi/kC5xompbCfI1AYGVOiaLeENjfiERaVSHyIA6dDlMMyRjAKZZLemTGgKgGkGDKaKJVK/eSgL6oKbXUqA4SgJeNVVBXV3hZMLE3biBD5SI6ENfuYd3GfKEkBlSC4ef+q3kKoEHsnJpeJCftAmhVmAJ+YWVdhsC8q6VgGSSRku+BaKR83aaxkoQ0SAuuAgazfsT0cQIYeKGJgn44/lxNZ/XUYnOgV0DONlxslosajNnz/2LlMThQp+GTk1OZ3jOymJLbSWTtyUPPPJTjPvxt0/vJ6ELu86kTnOuehmcEPx2e8EMYMiCFhBqLLPDDWYgRtZbz6EroeVNGjdTK8xt+5Hhi+DAxZd9J74D6DiXGVbdkHgaPPjddJ+gJ858klOgrpZLs528AaS6ktW9UGs9kGruvonMc1oisdSQkcLSW+CgGuJbki7DtbWm7uXkdHQ9fVyba0XNQL5u2cs6tL3nj9bX7287/l2dNnfPvgCXuvvsP/9vO/51//+Rc8efyIgKPpFDoGuramLCa0KetPDFSTkhAil4s53fk52khn90lVMt0omc4mzK9Ouf/dA7wPFEUJJlWSTCeiyaiUyI+YvIb6iXjJ2K2DTP1o/4dA1so11HDtcZCa98c62DteO31wG+kDBO/F6afQTG7sYYzl6vkRKng00kkdDbqwBB2oQ+RovhTnNkZe2d9na3OL+ZXopXVX5xw8+I62WXLj1ivsbW/x5Wf/zvzsEBUCVTlBBWibwMI2bCgtyjhRcX61ZGfnFtV0k8nhYzYqxd52iTI1IYpggUaaEkmn3YouSiM2XMP3Bwt+8XDJYVRUt/Yoru+zSBJGWht8lIZn2nVcLRfUbYONiBZtCDiGeTJWpyRC6MdWGs5GrDW9feqBNsbA06rPledvbDPWk0pD0u3lKO0P5jUKGC+gmuqDZRK4mktpw0oCLvmOcrdk9rz4LFBVJTdv3uDJk6dkjX6d5G1y5VDWeRyAaNCjc3B8pmStuvU1nD8v6zCQu6HLLzILdS2Z+RLQYgyGh5jvJWtaJr/dJXAlvy+xl0j+VggBXVqm1/fZvLaLnc1QzZLgPV4L2FpY2+8XnbUclPzdEdjY2eLW2/d49v331Cdniembxt6oFOCmEs++ok/8gXw29FIUozWRfzb4j4G+M33yCURmQK+NT7YzGawV8C0kEGQA0gawPQMdWTIj35sA9qY/dyGirGFzfx9tC1rnadu2v1+ttFRGJN1WopQlay3d48X3yD5QBAREQMWkBWqSgUos4ZDioqSGGqJUbwQfKIxlczpj0V3iu5Z5fYXbaGk7L36sCRAcV/U5HoeKJVZN8E2kqz1VWbG7NeOPv/0FV0fP+OCD97n/8CFRK+6+8QZFVeGuzulcRGsBkA25cVIAraT/SILec6I+IoH4eC+AzEtgVUs/xoFR79PYZ2mm3Hk+hIA1to+/8grp9wEI6JjBvOwuh1wVEQne4Vzbf/cgf6Tom4wF3wNvqp+fOAJNV23W2C6NAdf870Euxabnj30zvrENzL6H7Nu1yqe8rtUQxys19H2IIfbjnt+fEw7rfmcmH8hs0PvjWcIkj+96wis3hM4+W75v6RQf0r0k+0xOeg1+X+4DopUWRmRRoEtLbPwP/dO1sX3Zz9Z9zpXnXLvOnwZvpapTCSKKayO6SLYoYQkS3wvRqrAWVYjd8kmLNhN6swSCzK9LiSBF23mqspT2ltn3VhmQTz5garTXA/UY2TsqJdCCh6B7+yMgfW4UFylyIi/59WIPhbBmjR2qFSE1gopELWXqITX30jo3Ts/jpwGNNTIWGgXei5Z1jFg9lbPGe3QqcUcZXJReM46ICoEiVX22XScxNw3TwjIxGgO9pIyxBoVJawUp5Q8BNiF4SaS30aOiaL6G/4+1d4u1JL3u+37fpar29Vy7T09Pd0/PhRyRHJKiKYoyo4slQHEcS4bhAJHzZgcB/JT3OEAAA0kQ+DVAgABGENh+UeK3KLEiRbZh2JItyJJIkeIMZ4Zz6Znp2+k+fW77VlXfJQ/r+6pqn26KgeINDrvP7n1qV32X9a31X//1X84Rw5Q2hg7gk/t2nD19QL04wUdSdbhFGzm/rFHE4NAJQNcxUhkYlwYfDY0X6Hez8aAs60bK/C2KaAwhOJwT+312sQBgPM4avhpjRU/Wtw2NFykELx3IsalxX2ltp2UcmibFjuJnCFGwX1Md+J5iZqs1eiRAa1GmOpIQCK3HhchoNGJnNqd1rWgYJ8KI9wGrCibjUar6SQ1DQ0gAa7+fBIRO1c0EvM+6zHQyLUopdvZEJjWv6Qwciz53SnCoKJV3xK5yxREpjKFINkdBB/THKHgg2c5p1VV752qKEALL5VKqjwpFWY2Yz2fEoAjR/Yi9/v8BpFVK/a/ArwLHMcYvp/cOgP8deBX4GPi1GOOpEgvzPwJ/FVgBfzvG+Mfpd/4W8N+ky/73McZ/9OO/exCcZKMXer2YmFDx5BfQAwKQA+5s87LxczHQeM/jx/eJX6wprGI+GVHTcOPwCKsqvGvRNh+ACaFP1wpZsCzKJhYbn/U8+kynTmUikpEb6Cd295PvqY++Mkg4ZE/0TM7eYEuQI8Bs7oJntE4GLDl7IaCtCG5rFCTAMSQGllZaHHdjsVozKis2cS3CzSjqei0ZN2+4/dJdXrn9Otf2j/jc62+wuFhx/7N7XF5cUG8clR1x585tvvaVr3L3zisURUlo1wI0RcemXvDkySM+/fQejx8/ZrVYU1jNdDplPpuk4LulKiLTkQTmwbUYE7AqooNHR090DdFJk4GgJYucG721RtFg8bbg9b193ji8xsdPn/Du42OCj9jCgs5MKdLBn7Oc4tCgVMoaK4wukDL0mAISCbKVFvZsZrCIjyqHgcLgo2iZ7B8c8hNvfpk33/gc0TQ8O3vM+dMTHm7OWD94j93NGT5KWWMwkUk54cKt2KkPseUEW46ojBWNuWQ8FAZUyvBqMR516/Eu0npPiJ5ms+TZk0ccP/qEe5/e4/6jh9x/9ICzs2di5I2idS110xAFSU5sCHGYpLQ7djsohoi2CbyOSU4iOTZaW4LSPDlfpOAmyEEXZT3apOcqJaaJopm7QybZBKWMBAcIk4IYKcoylbqJcfMxomwCPxUo3+tDkZxEnYLtEMUwhuhxBIrdKTtH+5h5hVMBXUpihThoOMcVpzkDeQNL0juT/X8xsbCFyyPz1LGxYxSAZOCs5rHoQFuQDHiM0qRvEMiGxAKKIWJtYnFknax0V0OgKC3qwb/3zrZNgWoOVjsdqG78BlfIt657DcE8NlcZnZlJ9CIn8yr4GLORvuJ8Z9A2fyZrK+aDb9vZTfPeBQp5drYByg78HNxLSOVx+eerwEQf2LD1jFvPlfQCi6rkxtER9+/f70Dzoc3ux2Q7AOk6nl95/yrcne+r78D+PDM2O745KMvfFQbj1r+LOMF5Tce0Ln2g0Jb5ZMbuzi7jaoyKCte0tLVjHVZSOi4aKwn4kqSJ9w6Fp0QzmcySnmfWR4SysKhgwBcEPCgvTAcNUUUePX7E7s4Bt155lXVQfPzhB7z88i1m04pvfutbKLPgw3d/yNNPPsbiqSYjlNUcPz3DKCn5vFwuadoGYwqKUmEKSxta3n/7benw3q65uDyT0qyIaKtbTTEeUY4qgtGia93N+dXASHVrQ+s+IB3O0dZYv2jND15XgZzhdYbfmRMJ/QfUABhJ185zDUQtzO7R/g6hdayfnUtDhEhiR6tUghxZK2ERjjYNo4slkxtTrr90kyePHmCMZr28YHNvQ/m5N7n1yhs0LvL+H/8+7eUzdBHYrDdoYynLivW6oZyWlKVF1Q7nN+zvHjEujqjXZ2jdopSHKMnM3P04emjWwvBYrzdcLBvefdjwqFaYwymjg0OavFejAFUqJbecc7jlAoWUTALiXyVDptN4ZumYPF557MXJf0EgrNRzCf3t5Mb2HF8FNq5eL5cedwFs9j+ddD7u9XCFKZhtrM6l9rE/22LM4Ccp1SXnciCD0P3vZ2ZLtnnZTpPBnATyi30flAMP7EwGRKFngV0t3R02wEyYS/d/V8+EbmV3wMc2Uy6/hmQEpRS6kEZ44UpzvwxIBiLluGJ+uCsySm2LjpI8IgZ0fs60EXbmM7yXQMko0Lag9RE9qti/9TKnBJrzS3CpikFBDAJc5DXUy1zIWOZGvv3Z2M9ZN2YZvMpzqHrbMRx7OY9Vd04Fn3Tkc1IhCU9Z0zMAh69u7AZay4HcwER8zWI2YbwzJ/rY+TEh61yn3h426fFFIjpAiNKM2OgMPOYYKKnqv8huJumIGCE4ATrymgVFoTXznR3qiyUhOC7Wl6xjw8gEmlBzuTrFR8+quaB2G2bjfQpd4NqG48efsbi4xUcffsionPDk8VPeesty7aVrjGcV6omc0f4yEEJKTmedbpI5jf0ZKnGR2KYw0Cc3iU0dI91e2mKdw1biNqb40AePNREVhDDgfdtp2ZL2LkR0tt9RKhzFpw9JkiBCksvyMXa9SpzrteUJAjAbk77HRZRuO4Bje3/1zO/h/hs+U6+7OqwiyEngJLuQfMxtv+Sqjza4tlIoY4WI4nv5DwVdD5BuPAdn5pYNyb5e+lGqFrIvK37lsIrt6rNZY+SsGPihne+UP5+IN1aLPnAvt6W7ptnGWqgKQlnQqrqzC8PX0He8+ufwddVvGD73jwJ349azyWeFneiSLmlysXWKRpOdIMZe3i/jDrGXL7BWmusV1nbnA0rki7RW2CSbaFMzrW6+lSQ3XALWdYjSR8XkKjMZNx8DISV5ZKh1WlnpWbxL/q7EfFopmlRdGYLH6ZbWGIkXu3NYnhPnO79WJWk313qM0kzGI4kDg+9Co3qzyYMn368NbRC2qnTAidgo68JHISOYGGmDsB7VqJRS9sy0jmI/TDfukiQW2S8t8i1RJztjpcpAaTzg073HEFjXDQTPpqkBxXq9gUSeMMZSFIZRJTrr2hbUmzWShJZqHGMFKN2pSryDpXaUZkbtJe6uXcv5cslyvWFTuyRB0KRKHpGEyGdzGwKh3ojfTh+b5rXkokhKiGZ2iglKi9GCN/ngoRVN+yz1KfIU8l3GGJqmlkaKXtiqq9WK0biSPd1t+yBJxE3Dcr2kKASHMyadk5ktbgSolxx0lg0VwpkczwEGetq5D5NUpOSwVBOCSzY/x80GA7SNYD1G5QpjSQBYK7rK3rsUqxmUAde0aTwV1pbpMxLLmWSLtFYYpZiMJtIj6f8nk/YfAv8T8I8H7/1d4J/HGP++Uurvpp//K+A/Bj6f/vsZ4H8GfiaBun8P+IZsFf5IKfUbMcbTP+uLlVJYa0T7UKwHiqT5F+hKBTOyMLSDYrR7rS2S8fPK0wbP/YcPqNdLqhKhekfF7nyX2XSHk8tzbITSCn06xm22a5cpjfLd2dEBOqMnGkrPB3XGqC3GawYdMgDA8KxLLIIMuiqlsNr02UYtamfB9/oYwNZhLJqpdGUrfYn4IBgMiCFRGh/hcrHEtS0Kwysv3+X1O29y/eBlvvKVr3N5ccann7zLs2dP8a7m5tFtfvIv/CSv3r0lnb6Dw7WSxalXK56cnvDg0QM+u/8pp8+eoa1mvjOnKCs8Hpo1qt4wNZG5hr3SMB6XaD0W/RjXoupIfb5gc7FAOS+G2VhMaYl4qonBW9j4DawCQTt2CsO1l68zLSwfPzrBA04rvDKp0Vo+iPv1kn2Gjh2ROhcKa0PGTAxjKhMKcvgFHNaWqFAwH+/wMz/1LX7pF3+Jaj7l2+99n++++0eMSnjjK19CRc39+/f507c/YLGpaYm0pkWj2S12GDGWjFxZcevaSxzu7+MQfcj96Y4chkYCrOBFkL/ZNLhmRbtZsnj2hOP7n/Dk8accPzth5RV1G1FlxAeNQsqWvVNYnUsIPEEFRBNcnE1jpKOnrfoEBUTK0mSbJwYuaRYnk4dBmgUYY9K/iZOsrCxsOxoTiXgUPipi9BRGxt6opOmSmicEl5g6Kmn5pTkwVspjguv19bz3HVCUxcTHOxMm1w8w05I6NOI8pDLv3KBAtu0VWYFhcJ68wwxY6tjvZ3HuAZPZKokDpaAYOlrJocmgQUjfobRJ99Ffr3fI+pLUbQdODq90YTJIKXt5GJTHTr9JPqmADEwPS7C3XzloyMyIbJCuApZDp3E4dkMg6ipotQWmXgGXJagLg/Iz1TWNzE7l0M73DvD2vfXgrTyNgu7zXRlb+sC2PlgOjnNAPgRrxDFwXubWOcdiuRT7O3j2q/Mk9zh8n44VlfnKLwKEt8dMRkpr03VazuBNPjC6cchJwQTi9Z/Jdk3GmRQ82bLgaH7I3myHyoo2lGsDvo0d60wRKa3oR/l0LwlqQ6GYlCNh8OgeLPbBAZKAUZUGFVitTzFRsvGVsUxLg1steXR8zGQyoSxLvvftP2TTOGZ7u3z1a19kNjni5NpLfHbvXXYPjvgPfu7n+a3f/KecPD1G29SJuG0wQZSVp7MJp6cnfPjDH7DZrABhk+R9ERRU4xGzvTlRQ+ta0Vbs1k7/lzx+zwPp/X54cRCW9+zzQG1exx2or/r91i9gUuJ1EKwNI9TBnJoidd1N51kDjK/tg1JcHp8ICJDnPwSC1ujCsAmR89YRz85ZNjWv33kZVZYs1yusKSl8y/17HxODYTY74O7n3+LeO98h+A0oqb7xHtH/wnFwsMurb7zMx598yqPP3qawitHIoEx6hlgQIkQdkn64gKX4yOXlmu/dP+PBMhBHhsnhIaEcEREJA2IgkBLLkU560GhF3bT4mJzpDlSAqCMG0ydmlOzt4H033yqzOdNZkKVPtvbdYP9qnRM9PypBNQgelSa42PmGMURp1qNIHbCNsE1Cz3RrmzYBuMiaDaKzqxIsG5NOvwSqgMnyMrIy2rbho48+TuBpTOu+P9cUw+ZjstB6wLRnjgnBwPR7eZAoysH18EzKe0F81Pz8zzPG+tc2iHE1udVLeCXWqsoMxAFYqYIwF3UkFgZTVTTeEdo2jYf4In2JulQGLZdLykrWVuucVE57GY9yZ8714g7HH96jOV/KvvS+Y1UKY1RGzmSWbLILwfdA5bCssQe6rrJlc0K439dZviZEKacVLU868DuzcZWSZK/oZfaxjfg0Md1HP57eO4F2Peiq4PCll6hmM1rvcTE1w8J091GkngkZ9HDOdb04cvK0bzCV/OLY7xkfRe+zLMuuwVrugeETs84ag9KByd4u9viE1aZl0TScbC6Zzed43bBuZf+EGCirAq09MbZsNhf863/920wOAt/8xs8zthO+9+3v8Ju/9c84uDHn1ddqPvjwY1xsOoBVxjd2vvzAlZA9mjTkr/pLxtoBg/h5ux+76etZ+BmQ90EIHtnvySznDFLKtcLWGhFtQvlc7lUgDZxkLHzWHI7d16bvEfum0v0532J0sXV+ZFZ3f5b0Nm7oM8Tc+Eicjk4uIqY4Mid2FKpbv92aTsB+hE4KomtwnGxoXqC5C/xVGZofBWYqpTpdUlngdHsRpNN8BLJ+Sr5MZttdTcCFwXXzvaRvFJA8s+VRxCi+qC41dWPBGpTRRP88yWN4/1eTsj/aJtK9/2Jf8iorN/m4SuIcrRTa0BPBcjSWzh/XOmmOl8Yh2/rMMvatIxpNUCo17FMd+KYUqKRtmuc3rynvPUVZCgAZo5S/e+mhQSKYuOBTCXnvayskadzJXKRzlhjxbd1VuGbcJ/OojCmwhU3Jn0BuQJfPK9GdFuZnNZ5ATglpYULbQnyAEIJUiHlPUJrGR0JiShutiEp0Sluf2ONBwEgpf/fU1iT5JU1VVXJWJ2kMY02Se5F4IwbdaQKLv6FSryOwpU1VGVYaliWcRmysMIed84Tg2DQOFwPWBLRqUQSpMNUGF8SGtQE0Gqthf16yo0g9VyKeyLKZ8ex8xXLdcLlxrNZr1us1IEC8KUrROtcSJ9Z1Q+saEVBJ2JNNIHpQER8SkURHaTKG6H0XRZkqK6BxLavNGqN10kPWlGXBciXvGSU+x3K9hoVK0gQZNE7sVzyu9aw3qy7JLU3B8hkv0gUBj9ayRkSmSKqmOjJWFGDVGI0xCMksShIz295ccbCuN1hjGJdjfCt9PJSV+bpslzhCD/qmZEjApXUfCE5Y1oIR0QHMANpIA7fgIqvFGmF+X43E+9ePBWljjP9KKfXqlbf/OvCL6e//CPiXCEj714F/HMXC/L5Sak8pdTN99ndijM9kf6vfAf4K8Os/5ruFpah6kEio9KBM30SGrIXY+9ldYNY1wEEcfKMUUVWcnNesFkv2DwK7h4e4Rc3udML+/iEny8dYlYAcq/FKhIgJgagSM9D7PtNKll7IWomJgTko8bBJd2XISOsAWOhYbSGVj2mtBABS6ShUiqIsZUEFn7JcGrTuuowrayhTp3M6UFmcAtE4k7PN6N5JNsYQfWS5WWKslAUG7zHKsDc/YnfvCGUt+wf7nJ9e8MFHP0QZw+HhIbdv3uDrX/0q+4eHBBRtXdO2NfV6xeXFGcfHT7h3/yHHJyfU9ZrJuGJ/fxejCpZr6R5ogHkVuXlQMS2h3WxYnS1Zb9bsTmdMTcH4tCYet7C2KF3hMZS7B5jphI8f/JB27VEHFUVZUY0DygeWZ6fMCsPnSsPO0T7Hm5rjdcOFawhawDpFBC06oLkBQNAkp8ZTpO6TQAce+VSeJrsfpGGtwYQxhzs3+JVf+VW+9fO/wAcPPuLX/9k/4Qcn9yjLwE+/+VXCdIpBcffgC9yOnqeXpyzWS57WlzxbXXLaNpSbJeebp0xaz6i+ycljw0YpJuMpu6s5q42njQGlIyWBmYId7ZmENWZxwb53HN6KfPVz1wmzL3D/3PDJ/ZrztWK2d8jRzj4qaM5Ozzl7dsrZ8WMePP6Yxw8/JipHNSoYl6LNslmt5AAOAe8FeAk6M8IliGrbmrIs045VjGyZdOmk5JaYuskioIRVCh+htGUHVColnZNFvyhp1yrwoQ8eO3BK96XrmAw6iQ5SBLx3ok04Lpgd7aJnhZSbqC7cJXOnSYCqOKfpR6UhJVhisi3CwPaJCdM3QlGmdzJsAmBdEp7vYNTsCGbHsv+iLhDO2fz8WXFWxaE1xvZB7WDfZrhsYC1RqVzWuUAiP2+BQMkEiDVMfvqwfDJGyZIHFFnTbPgSJzt2pWtXtRvzM3RBqBo0M4Sku5bg7HTriZAujtsWCEAPpKcxJg7Axyt/bjMvQIrXtp3cjiE++GzvqIduXHOQmz8rLEpFvjsinJ+ePQfsbLMgFIQeaCc5kaJnzdacD+8rhz8dEJKc16gixIG0Q9TdOoL+Gl2Tzfg8Y4YMcgTZW9cPDjjav85YFeADq9AAUZpRKI2x4jxIwFpiigLvWmxqMFnYUQoEJEjMTn+IEVuMGJUTFFBNxrx0s8FHMGbM6bMz6stznj57RhU81XhOYUsO9w/QVnHv/n1+6zf+p91ugAAAIABJREFUb0oiX/niF/jmz/4ynz78lD/4/d/nydMTmsYRG4dv2wRICfNtvVzxyQcfEYNnPKnQRNq2wUWfAnDL7v4uxaRgk9Z3x0jbAtwYzCPdPOcyZ5sqVDJbcgjcPq9trPJq6Ma/nxS2trAkf3NSbLi3Uwkmvf6xiqBDRBuD1eCjJ1qFV5rycM4kOFbHpxSIz4PJgVBAR1i4lhrF2cmaUVXx8sEupQ+0m5oYDe70mOMYqA+vc3jjFlrBJ+//Kb5eo6Kjblq0KQk+cFE1fP5rL1NNC9793vcpbEWZZXiilGkXZQl4KZkL0LQ1l5cL3n5wzntPVlyWhuLaLn42o07+SvSRrNmeE3SSYxO5nzY48e58yPKJXRmbNEwcAIII4yzvL52AFK1UYvjSOfK5PNdonUpEA6rUA5kr9Zz9iBlgib0+bdM02NKiCkO1t4MdSUJDG9vbmLQ2XV2zPr3ArTe4KEGe9w6bdEZJ8x5c+jM9q0lgik8VW7Fbe/29yc+pG/mgZLuTUBgsycxSJUoydMgezcmKoU3NQDb0jcayJqXWuiMkyDXyomdr7DrgJFV9+BA6Jm+g92ONMuIXEIlGYccVs8NDgq3wUYGWktUYxb7m+EF8bEPdehq3krNFgW5dBxQ5FOVkh8O7r3J2/z7r03MMKpWipyoCIz47UYJ6a3Xnk/iky5hB6M4eKJPNfw9mZaDEKAHhMhjSAUgp4Zx8hJh9ByXPpeLA6gzPjsTIFm6KZAWshugDUWtm+/vMDo7wWHwCMKLSAsrlvZKMVf6TLCel87P2hJSgApg0jyGX3cN0NEYpRWULKQsWxwylDUZnfy3SGEWjBDgKMRBCS6Ah0hKC+IKVKanGBSZW+LqldksmFEzKkQBTWvG5L7zFn/zJd3j/T97l3e98j7N1zaZdELWMmzKJTZtkNLpzMJ3Nw7G3xpIbP+aGmkZpAS8HG+UqIJcblVrdg0g6gZxke0bvAg59EDmrxb+W9zOok78rJRJjSDYMIYdE8akFkEjXUxprq+5Y6Xwj6NZZB7LnL1B9sqojPkHaG0mOJNsYpVJzt97nys/hQ+jW6pY/ln4WsovvNa/Z9r1C3muRrX2SXaj8UD6ELiGU/ehA9m98d+7me+ikQLbmK/kqJHsS8iYVDzgmHzRLKgbvwaRKwNIKFqwymSLdZwqwh35g9oGvvoY2b/jecEyHCYFtsJc074qqHFHaRGiKHo1JuEKAUGCsnIPBiSBQdF6qakJDejRckju0Vio3syxOiCFVq6RnKQw5pS1VpUniK6aScG0EuNaJ2VhoZuVEwFwKST74YfVGPm/Eb7LGEgoBRIuiEH3VdObkfhDaCkhYFAKw2SSDICXkBQBVWXQJ3dz43ZJkY7SmUAW+sASkIstHaXDtNNJ/KEqU12YSTggybni81mxi7Br4tes1VgvK4pyAcQrRQq3KShKtSuxP5hqG1uPJ/W7kWlYrATGR5pNKl2hl8QkoXtUb6k1Noxq01lRV0Z0Hxmh01EQnFTdOBakQU7JXjDEYBddmUw6nM9arljpoLjcbnl0uWGxEu9YDVhuKwjAelYxGVddQPKSYrbIigRF0IHiFcy0Rj3fSpyakxVmWJbawTGZTRusxTV3LXHkByLXSFLbEWE1BasTpQgJuTYrUI8pITK6CENVi3YgEhfc09UqSh5kB3LYYG6g3oiM8KktZ+0SRKFCKuq5lEqJIDWVgIXpEo7owKGWo64YYI5uiTuxnhSkKcr+ZQCS2URqFGkNhitQ4PEmphEC9XnfksaqsOptjjCQpVMKZ6GSQXvz682rS3ogxPkx/fwTcSH+/BXw6+Nxn6b0f9f5zL6XU3wH+DoCprAAuZqgFlzLQoTfEfSlyAnC6LNgwM5XAUq1Q2rCoGx4+fcrLdyOFiUwqxdHOnNeObnLv3rtgAoEkYBxtOpiMoOBK0YZmcG4kynfK/ivA+xRUGL1laEMYlOEZ0+mOhcSOlS60Bg1J5L43zs45NNvOgdWG4B2ZvWiNxQfR+bC5y2oUZqQcFr3mklGIDqaSsTNoCqXRwHyyw9HBDfbGu+xN93h4/wH3Np/QOs/nPvcab37+NW5c22dSWupmw6Z1LBYrzs/POT17xqef3uPs/FQalljDfHrAZDLCh4bLxQLnxXCNJoaXru0yHysuzp/x/nvvU9kRo5HFtJ75heJgVXBj5y6LHQPjEWVV0SqDrQpujKbcu/cBz57WcOc663iG8g1+rVlsNsSiYHesKG3BzMIPn15yEQva1DhNp262knFLgYRYd8mAkcCo2Acz2fkXuQtNaSbceekN/sZf+8/4yje+xh//4E/4rX/zG3xy/gGMAsV4xruffp/v1X9E23pG4xExdZktbYErFWrPMLMTDnTFS+aAiVHMdYkLkaq0GFPQBHBe0dYtpdtwa0fzuX3LblSEM8/mJGLsiNmNOU/qwB98dMK9izEHt97ia6/+JDcOj5jakhg0rY80jaNeXPLk2X3e/u4f8+9+95+zaZ4x2zNoq/FhQ7NqMarEaJsAIMnsRyWGpRwZETd3on+mAW1SWVsS7lFKdyCqVkacGyUOgzh1EogWRpo0xJDZvEXHcA4+JUyCsGt12u9R9xnktnEUVYGuSsZHu5jpmDo40RlSYHLkoYSZ2DmSHSM/26Ak65C6RhrgaG8PVVgePn0C9NImV7WlttifsOVsJesEpGz3AAzussqd8y9h2LBkcmAjiXHbeRsmXSTI7iUNhvZCHPQM9GUwo7uwPJsCUlZ0GMDnAHsIbF59XQVQe3aW7vHpAdisM3ikMoguGqkyHeq560s5KB3TdejYdqWoKSAY2lyVQNKhLR6O3ZAZNxzXIRsrpkYHL3KY8xhvsagS+CNBr0KpDDfk4DAxkbp1J/MqjWu2H1sat+Q3+9+PZDCgD7I7dnZXNi+jKsGPsBj3Jju8tH+T2XhKgSKGJBfT1pRGJWZ7YsUnWRkTFcV4glFJJzSAzuVFCU9WUVNoTWUKrDJMJnPGswPu3H6Z3WsvcXjjgFW94L0fvMsH773L2cUJO1jm813WdU2pptx++S7xRs0HP3iHP/yjP+Cll4949bVXuDCRotQsl5tUViXznDWzTp4c8/DBpzikMkET+0RojEx3JpjZmE1I5a/Erb0xXLdX38+N5zJ7o9ujavv3hszA566XKje2pI8GZ4qMYU58bDdxMakZRS7tDyqdS227ZTfa4NCFYXRtHyKsT84gSuOD4ANoTVGV8m+bDS54zpsGc3bJrCyxRUXbNlzfP6BtG54+fYLSmlfuvk41GvHx+++wWVyAa9E+EKuC84sVH/3wMz7/5l0e79zDhQbnG3Q00vlZFxidKwc0fl3TtIH75xvee7rh0lbYgz1GBwesSY1UVd8cyXsJMK1OJehp3nxmLfhkw9McSUCUgqA0xOIjqi1AgsQmugrOZxBKfpbAKw7+fZiYyskQ2XsJDEnrzhYFs8N97HxKubuD0iaxpBObLiL7yhpKoNrfp12taTYbmuUSv1wLy6l1UIi+uS0szvkuYSbP3d9rjKL7GwndunhRdcNWYivGjtkEKXD2WU/VJHu7Xeo/TAJJhULfKHE4Tt57aTKS5jPvn+EYbms99+xQuZ5OJfaxA6QgEnVksrtDNd/FoYlddUjIO79jDQ+Bo7wGujOEvB8VbXRUkynX77zC2fgJl09PoG4wIdvOXn4oKgGKojiIae0lUDXb5MSWzfa8Y77m/Q7iYyRWrhy78uxbsgodTD1g/UOXWOjOLJ29BiBJI2llKKYTzHjCwc1bYEtcTIlYxYBByPNzwFVAL3bPNjya8/lzFdDP8UwIEUvvo/hUYaVHJdEqlBMWae1a6rCi8SWzasxOtdeV7htb0cRzRkXFX/j613n9zS/xyYNP2JtfZ2Tn/NQ3/iL/8H/5Yx4/+YTXv/TFXmszn9dXdPivJli7fTGYo27fKE1EypSHduJqwk0pJVrtShhzWZQvMwVjgKh630Mnm6+SnVNZhzbPb0S0IpHSYpvWU44BfefjSaf63OwupIXZxacD31R1C7S76W4dkePSDMAOwMvOZ6LXah3aFu990nE2OWjq/cSuqlSezRrTEZi2bUEueddb/vDQ7xzOX2Yi53UXujNTd/H+1bWdXzmZnH2mDPLCcGkLwJN1TlEKZQoh9qRxFyAxDFjE28BqbyOf74WQnynf3xBIvmqvX/R5rRSjymAs1Ok8U9okeRJhT7ogDZiatk2AkUYrS1VVXa+ajkCipLpKa02RAM+Qz9jsEys5gzSqY9bn8yyfbfI/uc8MPPb+7vAZdXeu5uo/ic10t9eE5exTsyaFtiJrZxPbkrS3FCRJzHQkxkDiBVFYS6GNgNPRY5WisAYXUhPy1hOSdqhW2ffVUqmrFApDaFtUDFilIHjQWarAd+OnjSIaK2eJa2kbD1G0YsuixFrRQU5cbbLTrLQQ50pbiB1IcZwk2gzOeYw1rOs67Q/xYRonScbSFp28k1JOGJyk8nqtO1kLpWqMLrAGJuOKg90pNw52aVrHarWm3rRsvOPSNXgFNpSoOE7a9kqkB3zeb+Lf2OgQuR9F8I62abGmFEattRRlQWkK3GhMTInvEEPnK2SgsihmnV/jnVjONgaMFuwjJwSm07ngWFv7JXb4VowCnMYozdjbLNmRbI6PgaigbTdoVaCUVBnFoDCZzaoVPtiu+iHvX9/JI+YILq3DEHGxlZ4JWtO6Vs7BCKa0QqqMXirWlcK1EVzomk/HEDHx3z9I271ijFHl6PPfwyvG+A+AfwBQ7YxjkVgrEserDuLoDo7YGwhDcpT08ECmO1zEpigcioum5oPPPuHLX12j9Yj5eMzhfJc7hzeY2oJFe4GqItYUyeEQJoYdsAOMTkzLfEBngxUTEy6xaZWKXXaqE3DPRi+DK+mgNUYMlAoSFIcYOyDXaEOOH3Q+XIHCWAmYUzZXKw1BtFhi0vY02iTnLTN1E9idD+uYAkgihZnw6itvMh1N2JkeEDaO+vKMw4ND3vrqN7hz9zZFAb5dcXZ2Tqw3rFZrPn10zP0nT3lyesJqsyYGz2w65XBvn7ZtWS1XtL5Gq4LZbMa167u0zQl7uyX4NY7A3uE1Xr3zKgZP/eiY8ukplh3mrx7hjEYVJcE7KmWIraM9WzFeeg4mE8rrt3nfr2jqNXF/xOnDC5RSjIuC0LTcnktjnLefnnMaEKckjTFJxF5YNomRmDRylJYDRIUolHpjpJwxKAoz4ujodX7tb/5tvvaVb/L+J+/zp+/8KavlOf7yFC43XF6estybsDG16JGsLU5JnsEG8CrijWJSTNk1c4zVYDyFlpKrqDVt3WBRyVfQHE4qWMCmCeybwNRrxrtjMBM+Omv5w/ceslY3+MKXf4mfeOWbzNQUFZw4iqQMfxmws4r90Yxv7t7i1s03+N1/83/y6OQHFApUNaZUU2bVHoUpWS4XuLZGq4AygAZjYbO6wDtFWYyTUxMwVqfKI3Eeq2pMvalR6XASLdcAKqSSjkDjRc9Fad0dxiTAVpqkaNHIROOjT86owsZIG7xkequC8bU99Lxig8OrBEYOA2uSYxyyTZH3jZFDOjo55J0XMCc72aOypCiKFwasnaB66DPF+TUMtnpIVLLw9PzM7vdyIuc5x033YVp2gLPd2Q7Ek25XBi6G359Qw5j3fUpR5MArByUhyEGYHyMHtXKNvqt1fl0t7brqjHZO9QBs7rLkKrM/E3i1xRjurw+ZwdGzevOhuf05Oge0A4XZvpf8/UPAtgd0t5+jc7qTPnSuXEiKNFfmePB73blwhXGs6LWx0xxsSUYQB8m5ASuD7SYYPVhI/3Tp34bMqBAiuVAtJKfucPeAShW0tcdTYqoDxjev4VcLmsvHTFmhokuAlQQDZSFOpPcB5yNtK91NJSmhB6U/hs1yg9aGppZmjqfnNdOLJY0yfO5Ld3nti2/y7vd/kne++x0efvZDjp884fbNW+xNp7z3/rscXdvny299iQ8/eJd7H3/Eo0ef8cYbr/O5N17nBz94h8VyTWkLxtOKyop+eDO1KOsJzqGV3dIALsqC8f6M1kAbY68rrnqtvqHu5tUAL5DA71w9k/0PtrWah/PcrRv5oWMihfRzzsoPg7p+DW8nIQ4PDwmt4/j0BHLDNmsFIGKb1e6VQpcFOzeuoRWsnpyiEms0O5FEaYQQteKzk1OOQ+Tm/h6vXj9CBc+mbaWE1LU8PX5I8IGbt27xsg/88O3vsVkvKLQTmxsKHh+fsX90yM6N61yeneA2NcokACEqYhNoY2DZrlkul3xwvOQHx2ueYdC7O1SHBzhrcoy3BQxlvcFubFKQkjXSspZ4V36ebGanAxlj6lQcO38rDt8f7Nurcyd7K9vB7SB7CFx0He5jkmUYVYx2d5keHRKswWkr5YF5HrI+oDb9qVBaTLnLNMyZuH1U09KuVqwvLqhXS4jCDI9BwjylpQQ6DO5DdYmHAWMzr+uwDSIME1D9WksAgOn/bdjMZ3uc0nrzrpujnPBS6RmNsb3Pm3zwnEjcAvNiz3gLg7Wa5zam6oPcI6BILFqKEheFcCCD2J+PGQglrZMOHNNa9Fc76ysvF4TFp6sROy+/jKpKVsdPiKuNIGZaUyiDqzdoKxqvOslpQC49Fwue125MZ24GErozNtvvwVrvzivV2/bcHK4H14YMxf4Zc8n+YIZEriBGJpMZe7duU+7sssnrhcH5qXISo08gbWkHx7wHchK1H7gXn9P9PoqKJHUgYxHyvtEaPSpRpcFv5Nq1q3F4PA5rLFWxA64kJgAiFgrd1jx+dM7lasXO3jWMnRCx3Lh1i/Fkig+exXJB3QrjzHf3ErsYMt+nTus3B1IxQlR+a23m8eljpXyl/pUTNHkHEtNaRZ6TThJCd2C8TsBv7gWRbUcyfh0Ymle0NLjSXXwSgnRz7xMdprsffQWQHu7v5+47xuf+vAoUBkJi7ZseHCHifU+Qyud+ti/Dl1YCzHSNwgZr5yp4Kmz89Hs6N4WSfem9MH0zwSKf28Ozt5cbMVvr8UV6vGTfP83v1bXcjVEIQmhSBowiGCmNV4rOH83gYl4bL/Ij8t+H/ueL/uzG7QV+6uDOOsY3Kgjr0YtutFZG9PdDWthKMRqNxAZp6WeT2ajee7qEVkpaks8wlVmBsftOkr4oMRGXVPIpUyJOkhI6SQpKzCwJyWTjQpAYqrN1qqv+Epk60dmtikqahxGJqUpLhYhWNpH2Qn+eI8A8MVVOpLHTul9Dgb7sXex2ZsyTen5oWhShjXgjchZ45Hm1xpYV0bWdr0uMSdKlEeKeVhA9LkaImlhYGu9Fbx5YrGuqVHCqYqTSUKJFGx2Rdqg3LTaxlSU5ElFaWMaT8ZjJZIyPwrR1bdNXGqYqjhBTA3ifbI9JMg9GpNJc29KEFq0tdb2ARqpax0XJfG+Kioo2RM5WK55cLjjf1PI8IaY9F9JciZyUCqqLBa0pCFqaqPWa6pG2bkTHOMXgGihsCSqDnvI8MSjKspI1YxPeJ1ufIgHWnQxjJXPba1rLBpSG6nLuBS+yQTm2l+M7JXKMXNi1yBfEAEF3kiGyFqFNpEYVo8gyKPlTqq/k+13jOl8lIDiAG+jPlmWRqpBTAgFF07RoYymKQsy9f57sNHz9eUHax0qpmzHGh0rkDI7T+/eBO4PP3U7v3aeXR8jv/8sf/zUSEXfuZ4SohNpuVA+SZOhC6cxyypllcSg6LZ6YAAalWAfHR/fvcbE85fp4j3XbUpQFR9eOmI4nnJ+fogOJCVCQI7PWpa72MWd5pJxPKP8poMhMJlTHWu0cSDVojgOd8yU6o/ROMj1LWFuZpu5AillvJjn7MZW8SPsiybaQAjmVtDwDSXc2Gfp0P7kpRwwK5wOTccXh/JCjo1sUSlGaktmo4Obnb3Pzxk2u3bwFGppmxWZ9SbNasjg95eHDh3z84BGnqxWbVHJ+sLvH/u4ObVuzXtcpE9QwmxbMpmP2dg84P10g4u4VB3sH7M8PpYufc2AMz9o1NmqO3JrZfJ9nl+c0qyWFLWmblidPH+LMmut37/C09WzaRrrwVQU3bhwQvWFWlGy0pfaKw0nJtZElto7zesMmKGLjMQiLNjNcosrdfJMTopOepwGFhlBQmRk3Dm7zN37lb/K1t75GaGoef3KPT9/5Ps/O7jMZl3jjWNFSt0uCElaolVQfnggSw+JUy9qusWPDcnWJWwujMAP2sXXggzQbMxKUVCFSuciEhiIGSl1QxD0qbnL9+tf5hZ/6ZW7tvUHhRoS2xgfwQRrINDHivARgHk3QFUevvMk3zV/hd3+v4cnjzxgVU2w5otkEGhcJVKIFoyOtWxNdS7txrJc1SlUUxUhKN11LqTSlluYuk0nFzmyX480TGeOQ9dRkW5alJEI263XaH04OyGQMQxSdZ0jlMlmKJHFTtVWMJ1PsbEwxm6AmFXVsk+OcDup4xbVWqpNH6VwfRccgIjPwUARjeLa8gOV5x0C56vRm9mx+r2Og0AOv0AdD+Qu7A23gPF5lv+ZXTOVgWVcqB2xDhzV2Dr7qmBa90z24Vta87QIR1TnOGfiInY1INikzmngehM3POQwM+qHug9LnA4IcXW9f92qA0RutLhrvnkPYurG7TxA7ncdy6IR3we+VMb4aXF51pIcBQQaSe0bklaAknwHd+89rLw4G57nfN13jBZmX6MNz49IBWfSs7m6S4zYjJwMBMQRsVOyOJ4yKEucDrTH4WFHtvM5idpd6pmn1+2wu32NcP8aGDbNyzqgcs9qsadsmNekJbGpPaF0CVmSPGi36tEVRUhjLplljywtQT+D4Qz797CO+9yd3ufva57l9+w6/8Jd+me99Z5eP3v0ujx98xumjBzTO8f2HnzAdV5SVYT6bozTUjefhZ/eTTZmgbMHOzoyd+YzNesX777/Dpl6hC9sBo1ororKMZxPspGRNRHmNjoowCNiHa/jqmu2mKuMxOWiX305z1c/Z9npP4x9CCtyT5FKMnV5Yvx7pGIPDtQpwuVgQfZDSxARcqXhFdzo5hpkd5wvD5HAf7zzN+SKBJf19FNZiCin1W7eOs6bmsm2YVhWrzRp8TBqugePHD1BKcfe117DW8v73vo1fL2ibBqLCucjHnz7g9p1r1OuGzUJAEqUV0ctZs3ENy7bl45MVbx+vOPEWtTvH7s0IlZHuusHLvAxY4PnZVGIn5FLBNsV+HRtQqU77bTgHQxYTw/0at21SP+/5v34dqDTTV9eEXGZ7T6qyYLK/S7m3gy8lyE24Owbds95j7LS4u72a9NhVWUJRMN2ZMb5+iFucs7lc0lyu8E1L27TyzYlNLn/GvkpL50Y//TP4zK4csB37UuNttm0IoUs85v/ys+cxzRUSw7U+OE3xwVOWA0ZW3Ab/8rx0zN0rtjSE3BhNqq7ErkYoSqaH19CTCQ3CZopJnz4tg87mXWXpCqjsyazn/AtptUgwn/yNnevX2ZnPqc8v2DRrRtWYuHE8/eQzSi3M1eGzqLxOc8WDFwBFayuBYALghudxt/7yPEls3jMjMyvD5BL8wZmVnJecCAQk6ZDBYmspR3P277xCMZ+z8UEqhJTKaYEOJHwRUJfHrmMopn3Rf5ZuTw3PwX4/SSK+K93PoEwCs3RpsVWJi5dkTVVrLVU1Qmktsk2xkNhGB6pyztwontx/yvGjh7z51teJFMKIshtuvHSde59Z6qahruuUgImDFTnwUVBdZc322brtj+VxIIO0KlU1hNjt1aGfZ1KfAXyQmC7Hr+nXdbbtCPkgElNRaAbZJYln0poQEC4BXD7Zmq7JTH9GdO8otuZy+HrRHIXEOHzRPunAT/r9nQEwleOhoZ2M9IDf8AwcrJm8Bob30q872YGZYSnXid2+6u+NrTnKNqg/B3v71q3h7M/H3v4F7zuJh+7+Y+zlLpKGv1FRVnLrpfotsS5d1udV+X58t49f5D9srb8rc3P1DLrqKz83f4hk1WKxZjSu2NnfwYeAax1FYm2qKKX1Gi19A9K4GiXxtScRArShsIbWuV6js/XduZa1N5US/yGvNtGWlrFqmoaylL3ahkgMdHIFXvU2RimFLUsIUp6eK+KMMTSuxWfpwTakmE+qkUtbgNbUTYsLHp1kkEh2KcdENmElvhWALS8Wg8JHn+ShdFduj1KEAK0PxEQWcc7R1Km/hzUooyBECmM63yn6QOs3aC29EZxzSVpCwHyZO0VaEbioWCw3nY2bGMUoKqyKTHQJikR6cBibQe7UXFsLGGqNpTACusZCZAW99zKXqUmMrAvfx5zd8pNn0ZFUARJonaNpHZeXF1itmY4nFLZgYhSH4wprNBvXoqI05ay9k3LU6PGtA2xHgAkx4FUAo/EuJxgVrROWcllIjL+upTFamfoOkJI90uw7Yy0m6bqGJC/UkxtC0gcW4uP2PrfWijyP1p3MTtas1vS23FiDb0OS5JLEBohcQ13XaG0ojaHMeEAr+sOmEolGQkhFworKlsnGiVSO9HXqK4pyEqOXbIxUlUca6ib8sDRXcIHt158XpP0N4G8Bfz/9+X8M3v8vlVL/G9I47DwBub8N/A9Kqf30ub8M/Nc/7ktijLjUGRjEePnsHOh8eAibbhjIx+y8YDqnXDKcyfCqQBM9Ty9PeHryiKNrt0QgX8GNl29z5/Yb3H/2GO/rJDpdkpvOhJi6xCWHKx8a4nyYDsQwuUwjZj2ibGCT2HJ2plEooxNLoNf6Ifb7q+/kmvK1SQhbKUWSeOqDiyRUrLVoTUViYummTHYQOQVFL97tvXSCtihG2nK0s0vpFK+88gqvvHKTo2tzYmhxjadtL/HBs6k3nBw/ZnF+wUf37/Pk5JSINIMyynKwu8t8PmW1XLC4vMCFCLrAtxFbGpp2zbvvvoeOa+JG8dqdI3bGlvV6SRtrgg4U1/ZZ/kTLw0+e4e6/Q3EyZn1xRoWiLCq8NlAF4rzgQXvC6f1A4RxnRcsnAAAgAElEQVQxeKzz7LWewgcqJcBCrTXz0lLs73DSOD56dsoPH57gXcQYaW4iSyhlqFJw4p1P5TAyhsaOMcUuO9cO+dX/6D/lF3/+P2TdLvn2O9/mN//lP+XJ6We0vgEzZj1xLCcLovKU7RitC9hEmnZDa2JqjBFF67V2XK7FUMTgiSk4McgBQQSNRXlZCy3gVGQdIlFZKjXmQO/zlbs/y7e+9svMqgPCRtOGSIiaQIEPOjksXjI4IVDEiCosxsy488oX+IUQ+KPf/xd8+tFHNG6TEOvkoNkSYyJ+vWC5uKCuV0QqdDHny1/+Wb75rZ/n9PyEf/uvfofjBx9hbUUIcH52gVVFt/4golWUgy3Zr92dfQhSrrCpN7RNIw1Wkm5RcNLIzYe2Z0yWlur6jGJ/RiiMsAuSgHfCutBR5At6y7ldopptTe4+a4yhVRL86xQ8oCX7ljtdDgGEmPeb7MBtwDRdr0vGJDaE8yKAnp3zbN/yNcSO9cx7adAh7A+NgpACLC1gUw74hkFUBlyfs430DhPI9MZAZ3+Imlx2nUGf3vmUK3UHD8NAZhCEDQMXIwLuOVrK4GMekxwAiQkbzFF2sumZ0J0d7Jz9nnmYp/gqGLAVULLtKD8Hfg7v6wVg2fDPH/W7Md1IOoZQii5ZtwUC52fIZ0Meo6hgEAB210V1WVuFZKCHjspwDWljaH1KKOZ1GmBeTDicHWAoabym0XuMD99isfN1Pgy3OPcGPX+NqbnLwfkfsNt8jPGBxfHjrqJDAmhoa9EmzeWaVmvQUPuGNnom5URKpdo1RjVQBxbLC06OP+L4/nf59MZr3HnlDaJz3Ll5m88+eZ/z86doYxiVmmenT5OW+ZiXbr7M8fEpjx49pTCBcTmims5oW0XdwGrjuVw3FKM5gTYNpTQxU0YzmU9FU9IFtJAxRX+KFzCMBqB6DjwFOJf/tuUs5ADOjnG/vwYJh2RrjLbd3ukg3gFQIwsj/ZESzhkMu1hcdiyB7BRKh9s+eO0BEAEg2hjQo4LJzev4GNmcL9ABCm2wZH1bAYuLqsQXhrP1EqPHzKqKZr0WENE7QtxwfnLMw9GIl2+9QmkM77/9XdbnzzAoNhcXGB354HxBvVlQWY0iUBpLVEEaiTYtnz5Z8KeP1hwHQ5xWzG9cR88qGp19k36vim6s60GSPGZBtMuKoqCwJbFuRVZKvBppdGR6e9QDtBLAZyC3O+6v7ksGCRpF9/msqT0EofJ35CCpHJWU1/eZHRwQdQKSVQoUEoiplUrnu4BqpquAkusbbZJeolR9aV1gdvfZ2d2HxhM2NZvVmtX5BZvLSwi5K7zq9WDzNXW2H9KMa9uWQVEW3R64mqjKjRGvgrg9uCqlfEMG+jA5medqyOTLycys0RnJWpah+3nLvoY+WReR8tTxbIaZzQmphFEpSKueXNau6M9ksYd9Z3AYNlzqDiU5n7XEFDEolLEU8x3sZMJMBwwWvfacPXmKd5sUPAmLOpehEoRtlJmnmgyaRhg0Hc0BW+4V0cU4nRGSN3OSMVeS9KCjVMqEpMcsa0mIIiFIQD7Z3WP/9l3MdIeWIFVFCrqMQQazEsP7Kjg7PNtC7EyT6KOTWby9bnw+w7vf0xIoXwWuhmM+mUzYxKdoLRrOvm2ZTUYUKIJvwPSsSB8D+MikmDIdzdHG4oLGRbBlxed/4gvcf/Qxo91dPnz2niQ6kn919fvlHtl6qW4uelsgMV/ome/5GrqfLaWyTy3jGGIAnbROo+znDG7lCqfO/8wNVyKJ4UVqRhy7OASJ+kBnP0De2ZqntF87pyP2/pCAjinhkf893b3VSTNZZxZ96Pbc1qk48J2yT6xTdaYMV7IZ9AzP7NvEvJ8ZAs+DRZ/e65umDeRjYgK2s21KhKuhzzN8De1yHoA890OflRhTv5sUNw/8yS7BnuQnfEy2XxuCj+iiTLKHXppf5+dTonuaWZCwLW/4Inmw4dk/lHD4s5+Pjrxyfr5KZeIGWyiUskLiyn6x0gQXaEKDsRZixGthi9d1g49SDVUURapCFn8nM0ZDYjtqY6SqM4Qk4ahRTmbce5GFdOcNpjBYU2C0lP3HQXLKOYcxhovlJVYbyqIUENwYnHdprXhChOVG4nithdVamEJAuCg+U0gyjlorae6llZTFo7qYSafKy5htl0KwgXTeGSd+YibYdXtLRRqXKonWXhoGk/wmY6TxlBXGaGilwVaWmEsnDxFFmXRjjdaoqFjXLa5pGY1G6EklWvfe0TjPbDTCxIghJJ3XgDG2IyMpKwBlbuIVjU70ADnLbNFXnBfadvspBGjqBqVTM84oa8QYiy1KbOnZbDZE71mvl6wAZQpGRUGhNGo86hirCuFOnS8XPDo/4fziguW6FhKhrtBWd8QD1zp80yJVJXKmlGVJkZoxrpsNi8Wil87QiTCocjIQgpa9mNec1qJJL8zlvoKtS9KkeDU38lIMKg9jbnImc1co6bNBkGhBjlepIOpAb5Jf7yNtjNCKTm1hJKFhjbC6TaqWUF6hdUoCp4ofbXMyLFcj5SoKm54tEp1CFT8aiv2xIK1S6tcRFuw1pdRnwN9DwNl/opT6L4B7wK+lj/8m8FeBHwIr4D9PhuWZUuq/A/5d+tx/G1MTsT/7u8XWJdYzOpIa4ojqVEasg/cEncAYn3Ss6GNe1Z0kEdCo6NAqsGhWfPrwHl9840soX2JQzKdT7t5+ne++8zZr/4RgPBHfiRn3OXdZtZ1Rzh0h88LwAWMGwbrugQ+UZH6ks6xOdGc5LGKQTRcgOXWq16sCcrlROpYZEtH2Z3usLhYcvXTEYrPkcrlE+YBKY+VDQAclZZIRlI/oGPAtxGCYjOe8tH+dtz7/RX76p36Og719jHW07YLzs2eMRxPWiw1103L85IR7n37GYrFgVTfMdveo64Z1fcrhwSHVaMRmveHi4pK2aRhPJtii4Ly5RLGLVpHgNrgQeXzS0LrHvH7nGvP9OWfnz/CtIpaG8e1rFAd7rC5XxKbBzkrRk61GFMEwWjvWbaA9O2O8ccy1IagSY8DYKSUtbrHAW01bFQQNN3ZHPPWBvUnFxGjefXBM8ALUEj3KDRySECV5lH52QbQhoy156ws/yc/93C/QEPm/fvd3+Lfv/B6P7QP0zUjTBurRhtY4WmPRBhxO3GwPrU6HliA4EIwYtrhIAWFaZcmhDl6QNO83BC8dJIvKErVN5Y8BlGW88zLf+MrPcWNynfU6dM4jWf80GT4dPYakVUzAeOlQSTXj6KXX2dt5m4+aH6J0wJhRev6W4Gs2DVxcrPAOyvKA3YOb3Lr7Bn/5r/0n/NQ3fobf+X9+mxgN1XiGNQqjo3QNBhon2etROUri75HLxQKNaAuOJ3N2d8asNxtW6wW20IzHo2TrI61rOTs/ZXF5gSo0O0eHxP0RoRJ5Cgke0p4IYitI7KWusUbeSzkYzZ9XWWcp2ZhULiOHG+RyMxUzqyqVmmTHnYw5qg4cHTrSuSRCIQ75ENDLDmLyF/smW93Bv80+UiqQYQbVBSLiZPsQiYl1JlBJxKBSOJWqEnLJUgr8BBTMjAQkSE3OvSI1z+oCnQxE9Ywaeb7seG8HetlyCSidgrkUEPRBTxcCyv1ohcoEufxuhFzq1t9DDgDz98jfuwM/jU0/jgzez4zsXJady3z7f8vOwI8CafvyuuQ05ICHXlJmyPQbrhPRojKDe8sZ6EHQns+OKCBEV9aldQf+D+8ppOfJzXdiJDntEoDO5lNGpaWhwHFAOPqLPN79ac7YYWdWcHHasgj7uOotOKhoVvssnnyH0WLNtKxk9WjHuJqhoqd1IVUdyPkmDSt8GkNPjElqJ+0ZTUtJjV85Th86mosTZrMZOztTduYzCBs2mxUoxXhk2Gxqnp6cE4KjHI+pqkJski3Y2zlEF4bLxQUPjh+iioJyOiO0Na5NDQKMxs4nxJ0RXgsQ5nXas1FvrYX8kji2L2M2KSHcNVVJwa7J1FrVj323f7XeYp13zkja0yr26yG/euxC7sklZzE7niEB9znrHunXeX/vPSgnAomgxxXzl65z5jzuckURpYojpnPFKLBaGF0bF1m0Dq0t08mUtqnZtI6yANOsePrgE1Rw3H3j88Si4ru/9y/wbYs2cPKk4eb1W0wmY9abc0IqXWxw1E3Dh8cLvn+84hRNnE0orx3AtKJNtsHowf5KwYg1fUUQQdZ9mYKwwljGZcWqbcEodNTgRYNPkvI5eUU3T3nzDWN5uvnKGocp4FaDRE/eubH7QWyWhtC2cnaUFaP9A4rdXaKRBq5aq6SyLfcjTGkBfLRS/L/UvcePZdmW3vfb5pxzXZiMSF8m81W9qnr1LPnaAd1sgU0JkiADShwIIKCBZhrofyI00UQSBQ2aLQlqkWI3mmzHp/bPu/JpIiPixjXHbKPB2nufc6PqiQNBQOsWEpkVce+552yz9lrf+ta3vJOGlLmnQCy+BqnpVWbAiv3FBPRixmI1Rx/N0eslcd+x3+/xbY8eQqr6EZskJKBQgsXgI8pYpNxQ2Ljk8umcPJiuS5XkoHQGS6dbIIO6o4TBtFT8ixJ3U7DMDUOaK5KfnECTUikCAQEJjFKEIaArS320grpJ531M5dQZIEoN4SbsurwGDpr6BZMhIzJjilhOn9LAt49B7kdrPJpqbpifn7J9/hnO+bRyRVtdJxs4BJc0EyVYVypLKo2kjrKcVPY/Mlgzjr24LgKUBJdZy0qafU38m5A6p/cuEI1mcXzMyd1zVuf3YL5giImxk841adikxzmMEZ8k3KaA/AjQJoaxGgGskN6PIgk25TgnyVildSEgSEBFTUx2NMQgieWA+IFa/O71fsvVbicNyVQA5VHGYVTDZrfhcvscb7Y8eO2eNIxDxsEHT+8G7OqIX/vN32K37/nT7/1ckvrao0yyxXlNJgCn+GLjiKMn8xTw5ZfSzG1SZl3W+FhRE+NYUl1sBAnsi6OsQWGfRiXVthMQdpqwVzpV5GgjhJsYxjUQo6zRCFEpvAKD9IJQoRi9SbWPLja17O+0EH2UzxTAsJxTySdJJb55P/kg8bDSBu9uSaGUfZ9Y/rmbfQKOxO+LZa+VsyyNi8iL30qWp2c5bNh46MeXMzwemHluA7UxxtIoUva1MGpVKqeOPm1MFNkl9UHiPmNlr9vK0msSeD8C0UojWtV6JEqFcLin8v1O7zu/CnP44DnVwXsPgNvkB3f9QD84TNVA8sFc8AQniTuFxkfpGxKCR2mLsdLPwxjD4Hq2e2HCWivarVoJeUYbSxh6go94N4ACG6006cqsca1E3s7OEkCtcUWwO+0CraWJVnJuB+/xsQOgImm+a5V0OkFVluglZnQh0A17rLXUVUMMkSpVaBij0ZZU1q/xQap481kaSPIu1mK0waY+I55Iwl6lckeLfm9MBDhjNcaKZJJzaZ5DEH9EKVA+rRHLIrGUg3dobaTcXWuRRfQBkyQiqiZLZ0ZJMBqLcpoheDZtz8xEZuIEydpxIbG5PUPvEkieG2ulUvwQaaxFKQNVjjsgxlG3FS/JVGE3R0kuqJDK8Wv0UuNSpW4MIZ1JKSnqArYyaKVpGpH7Ozue8+DOivVuz8W25cXVhlc3LT6KHKglUlUKb5Oua4g4P4hmsRukSlprjk5PcF2fWLmaPjUUq2ez5H9BUIEY3bgOuk407tPpbbQR2YHB0bdt2edKKeazGfV8jut7YT47J43tFFS1Rauq2LQYFb3bY00lTegMSP8c2d8Z54shiMaz86OdNpr5bEYM+3QeyHeElHgOMZE2kw82qxuGvqcbemazBpTCxFGu5vbr3wrSxhj/8S/41b/7Be+NwH/zC67zT4B/8m/7voPPkACI9G/R85KgKT99Zjtki10yZfKlk2ukA8kLK8YZxTZ4fvrhR9xsrtH2lHk1xwfNa+ePuX/6kA+vX6G0FAXkACw3BzBmwqZT8cCI6qJjGcqhpmIywukw9M4Ro0q0/exAIp3rYs5WZSdiCoik3GpE4JUo3RmrasajR4/50eZHvLq+Zt+1cmhkUE5FrIKAaAqqWFHphkWz4OzsDo8ev87X3n2Xp/fv8vqDRxytTtnubhg2G4Zhx263Ybfdsdnu+eSz5zx/ccGu61Fa0czm3KxvaNsdD+7fp2kattst+71smvliwWK5QBHZ7Xe0XUdlK7TVBAcDDT9/foNpZjx5dMxidkTPHg94q/FzQzxVRN9gnMJdtwzXHWbd03SBs/mCR6dn6Ps1M1WjfY+Lezbdltg7rrcD3oPvIBJojzTzynJC4LUvvcaT1ZI//8EHPN9c46zGmBqFTWd1YjoT8EGhncWYBe++/U3+8//kH7FYzvnn3/l9fvf/+l+5aa6wb4ALkX47EKJomdWmZjGb0+237EIrTqOKqKCS1pHMa1/YHaASvTQmLValFCoavv7lb3M0P+GP//xf0SthHMs+0MzVijdPnvBg9QiCIfpBOgGLnyjrTEmXW2Lm6ZICHGkQZGeKV5/t+cmPf0qMGqUsAfDBYbXiaHEHzIxHb77HyckJd07u8s1v/wpPvvxlTF3x27/zz/id/+l/IAw3LBcrYnRoInUl2S+tHZW1zGdz6rrG+8BstiS6gc51zOZLat0Q0XR9Bymxsd3djOV9VnP+8D5qXuHmFqcVIUjZtYm2GEmfSrC982UuRcd2LIPPjYXIdiKO+1EpW4I8pVKwHKG2tgAz2phSBpuvkR3sg1LIyf4d3zwFXcV5KSBy3uTJEh6wfibfE2IsGjxT25cD3sKgyMFquieVM5fJWc7Aas7Glu+F4uSKky+BodYmNTKa2KaYgazslArQkTuoR2k7Xex1ud/ENBPNxGT54209vkiOPQ5sPIeObB7YEggxsm1z2e50HgSg1WUuD7T4JufG4fUP5RDy/CoYS8PyoWxMKusKJRDXqaFjukB63BHgKA5mYo1MS4unQMdtLdXxmnIm5MBHKwHAVssl8/kRihnEFZvmK8S7v8FH4T5PT3v+q19Z8sOf3/DPvvOMT1vDs+pddnfOOTb3MZ/9JYvNz1kOV5gq4sJeyiQT0CDJDYWLoeie+eDoHdhKQLOAsKtslLWw313QdzdsNzPW6wVHqxWL2RzvBtp+TwgOazSzpubq6hVmI1rmPkizR987qlo6ia9v1my3WxazFWa+ZL2+xPsBoy2rO6fousb1ncxh1mrOg3VrHSk1BsKyR01iGvmyBmJIzRH1eBVtTGmSkpkZebGL3lqqwkkJARirZMY1ebjGpuyvKSMnA1+3QeYMMoru6cj0rpZzTh7eY80Lhps9Ou0Hj0oNNAJVZfhsd8PWVazNjsenp6zqGu893TAQfaRtO9p+YNv2vPbkCV/59i/zs7/5Kwbfo43hZnPDrBFdvGHf07eeve/52cWa777a8cpU+MWcxd07VKdH+Fy6O7HBeWfqJEpW9loyf1qlfVxVqKqSPYIEip5QgJK8j8q4ZuxET4CZWzZVxt2MdnhiQ1Dje8ReBYbBAZF6seD44QOq1QpvtFRuZPhqapdU7p6dKqmsKqzpEsAVGz0CcMTcSE3jokdHhZ4vOJovmWFo+479ZkfY7qBr6fZ7gpeKErGfucENiNSSlA2iOAAQpoSAkX2mypk0BWDHBpmx7JdRM/yw+c/BuYfYxdJsKJWofr7kb8IkdRCMoTpasbhzitcmSdyo/PWAVNrJPhRgKutkCqKZGNkKqqxrmJPgYbr+BDzzwZdr+yhsGx0jy7v3cH1Le3mFIRZVeWl4mtlolDNQzu+8P9NCzo+aF1b2Owp46iE1M9HGQmLvxOSDOO+EBQlCHDCWOJtz/uAR9x4+olosCMbQRwEIibJOpwDjBMn6nH9xmGDNz5P08lVKaqYdUno6JCanUQrn0/qKlARhKMCNSgCjwtQ1urK4zuGd4+XNS67313ijWTYVWhmMEgZWjAP7fkNQD1gcP8Azp3M9tdFcrTf84Mc/46vvv83KRerZAt9fCRicgbrErCZEAdL0xOdTY8ymkp8Yw63Ge34EUPN8FQZelqVI4MGBXY4kgLxsuXK+5+9QSGltTrbnpHXRJy9mMkOCpPNX9oeLKSmrKOdjXk/WmqIBWuY+vbLPkP2jQiYIY2MfdWs9lERDGK+Tr6FUavyY9kQmJ5X3xBE0JowsWwHyFNG78pxlP8TD75G4fjwXD9io+d4YtxbJN8oAbVmzk7VNAcp1UpeYVlAlwCi4xPpLPTMipBK0MiYj0D2yM6fn9W1Zs9vSL6O9pFxv+hpt8qRRotaJCS/uyDD0EtPFfG6JvxOCZ991WBtYNkuqusJHTxNnKD2U/aC1pm5mefsSbJViSFlDSilsLUBtvh+ZV5mL0ry43HOWDhxL8GPMJJDkBxmDqVKFJVLaLs3CKElM0s+M0mhrk+SYgI9GqSRLOZM5TuB7JtPFIA3MtZKxquLYntirCD5SW5V8wxH8k8/LmqmsPO8wDAdxSWa7a2uTnfQpNhLiVUB6m1S2JjfO9ErhiDT1DJXAcx8DHi0MYmIqYNWooEFJ+b+PkZ5A27VAxFQVTTOjsmNlXvZII2GU2ySvR0ps6r1HDQ60whqLEHVE7oEYBcS3Gq0iMfQiNeE0VWVZ1RXHizs8ftDw/PKGV+s9e98zeE+MUq1kKhnrwXl65/BBZDGamVTdmaaSFmo+yHmgDyvJnZfzN1eQ+QLSVsVu5gZ3fdeV5mS5MVlV11hjmC0WxBAZnMMPjuCGVFkr8aokaA1UURIZzrNve6l806qQtUAqD6pK1v6+bXF+oG8H9rstUWmaqsZaI0zrZGcG54rvP6tqbgapunIBlBdN/77f8Ite/68bh/1//RKAihHQSMBkyTCGmACVCaibDVsBKTLYkKjgSvIQfYw8v3jJ5dUrHr9+F0JDP3TcOz3h0fk9fvoyYmoBh2srDqBJgE0OoPN1YzgMtEScOpdpjeDI1OjeBhf6Qg+n/Dw3cIgBeV7y4aUKy1grxTC0fO/73yVEhevSARsiJEZH8BETDJWuOT66w73zR7z79B2evv4mbzx6xOnxikVTYfwA3vPi0w+J2uN9R9ftWV/fsN+3XKx33Gz3nD94hH/xEqVhfX3NMPQ8eHCf1WpF3/dEImdnp9R1w3a7oaoN11eXqZGELmVBtq5wLtI7w7NXLft9x92jinunC0zsca7FR0ffd9Igbd/x/Hs/4aGf8fbDp+i54uzuKV0FvVJs1jv260v27QXr7TV9MCiqJELtiVqz6XsGN1D5wLnVLO+ccv9rC77z45/xg+fPaaskBeFhoJfgKKRSJVNxducR//6/9w95+52vcdVe8v3P/gp/vGF2DGhFt40wq4lxYD6fEaKl7x0D0jzFRCBISYpJy8HHmIBZhUqs7QLRpTVuTY2OFdYp5rM5+7AnxoABar3gwdFjvvXWN9Gqpu9dcVZyCUgIEZsObZ/3h1aYaNEqSCdGq/ijn/6Iy5fPscqggiZGjyZQVw2PHrzBm1/5Om999eucnpxxujqjWi0wdcXv/96/4H/+p/8jfvOSk2UtWmKmQhUnU0nZihGtIdd7EedObFdraojSbMRaj7UVbXfDxcUNQ9+ilKZ3TpqEELBLy6CCNPzQow6MNICLhYF4AGApcQ4OWG4pkZEHPDIGjCH4VGqhqJQAvmVPIvtvSMHqbaZQVVXj9+b9fAtIndqB/LNpIDx13EYA+RD0vc1eyo0dMugZtARyIzCZvyuP1SFYfMC2YKLHGuJYtu9jKSfKuGvwYXJdYYiWrq3xFptjUl4UYvpQmrfkU5CB8ORnldft8crBwhRcKDY/CjOV1N31tv29DR5Mry9Bg//ce3IDnoOxiUj5Vvr8tPFOnsP81VJBkRjNYyRRgI2RHakK6Ba/IJjOc38AOqsxGMxjYpWmriqO5kdSEu0CQ2y4mb2Ljw94VPX8wyeGo598l1+vDF/+9XN++28u+cNPBrrVI17eucdy8WV4/oe4T/81zXBNDF3qVK2lK7VJjf6UEfkcL51n50oxeI81NjELXNEa67uOfbuh7TRtvyCGM44WRzR1Q8DT921x5lGRod8Tw4yu29N1LT7AnRCwFrT2bHdrqtUZy+WSjb6hHwYWR0tWJyfsfFfGqqqkiVMeoWkZpFLqIDjPGmfSWCMx9YrswxiQjoDuYVA53fOZaZjnRdYuyac51Njyt2zKdF1/UTny9P6VUaMOJOIDeRWpTlacKMWl+wS/61PiOGX90exDYN/u2PeGXSqNfHR6wnFiI4QEXLntDe1HA8Mw8PRLT3j7fcVPf/A3KAJGRfphED9J16y7PT+/vOFn1zteaQ3HRyzO7lAfL/FGnp3JM4oh4UDGYfqc0wDVNDXV8RLT7rDJlnmjRHN48vl84Qyk6Fv24/Y+Gk30yKCQoRzLiTNjXUXF8vSEo/v3MasFTsoQ6PuBppmN5XaT55iuN2ulRHOaDMp2kQISRHJDDmW0dBhPLA3RX1MYO+N4tUQNA26zpdpt2V6v8V2P8gEdXM4nFJ+4gN8JoLid/BqB/wS2hASm5HU4AR4yKH67BFGGSx2MQd4LGaidrum8RzJwRbKbyhhUXbF6eA81m6FcQKeE0PT8ixGikoRzOcfS0OokIzGec1nvL0t/qKJRGaNU6KUBkjVjBDSqm4pj9RrRe/qbtZyfagSOYhTt/FEjt6ChYw4mAgW4HXtUSAJ9HGPnhlKF1l1dAeBcj7DlAqausYsVs9M7LE7PWB2fQdUwKOkxEVUssUeeu5B8sSxjFElMN5WlLfyt9ZHjFwFghelYcMqyfgtoERNbNzsGaXyBsRQ8MVntYoZqLKGVPd8z0IaBZQ3BtuzdJTHWMETm1RGLxTG1PcOaFdgK1Yk+Yq0NcfD81V/8NY9feyIxoSY14Rx9A501GApOHstaHoHWce1P7fDUjuffTfU6iz936xpl2tUIdobkE+WYNlct3bYV0+uo6VkVBfjNbHuVwCIfQplXeWBSfwe+8FWS/ZOz6ZLAmFMAACAASURBVOA7p/H05DP5+X1ipk1th8pnZLpfpQW0nPqvUhwwslBz0ztpcD3KooRcfUpukJjX2+cB2um95/9yE6vpfWWQKuaYi3FeVJJiywmn3Osgg7jZp9ZGtErjIPZTmywpmJ4lglJSAXE7kXrbr8/fP57X2Sc8nJ8v+nwem77vOT05QqmIcwGTWPxZW3w2X6C0plG5AiudobrCGMtcLwTYJBKCx1QVVa7gCWMzvYN1EJPsoq1KfJE1kYMPVImYQwipGiMB6UYaoGc4cUzCRkhjFxB7bVSq0Eqxh1FGQMTsE0Ut2vpmrIRIl0Ep0W8NRIKSOLPw2EcdFpQS2bwiwRNDYfwK0U2VRH0+Ew6SBKQK7uAJCkrVapiSg8Qp1wacj0kLOFWAKAWpcVlMsYDsa5ElVCrSoCR2jxFtNbPFgr7rIJ1THlcSp1l/OPsq4Ka7QxpZCbOCvu8LOYXok10P5bMmMY+NTWsO0c4lBLR3YBwNA2eNIuiam75n2wWiURgdUEbhtKGNnmq+pG9EIERF0XVFaaxVRKsOYpYYI3X20bNvESNdemZrbdHMr+ua45MTgo/0XZfWoE4+ZJSmuVHMoDWG6AZprJeTpVGqBqKaERMTKMQBFZPtyDYnBuq6pq5r0a2fzfDOiawcSMM2JckCkxICU7kin6qII6CtsJhRUi22mM35Ra+/1SBtdtIUSgLBFIBKZ19TNoTWGucFPJk2KMhZMKA4EOTupEGue3l9yYcf/ZxHj97BGMW8qbhzsuKtJ2/yJz8+IqqWFC8LdV3ljFkOreVONZDrVItjmgNvRg2sMXuW3pueVRojUAzr1ICLoU6sqZx9Uqqwc41SiZETMKpCRYVFU2mNURXVfMbZ6oyH9x7y/pff5UtPnnJ6eoeToxXLpiY6x+7miu76krbraLdbSIDi9XrN9fU188WS2XzFrltz78FjlNI0sw19v2e33/Lo4UNms4Y+ifZ75zk+PuHJk7f44IOfs16/ous65s2ceTNnsViw226ZVZVoT0VPpOLF1Z4XLzfsXoNH92bYek6/d3iMUP1ry+r+HXYfX9K2a+6f3+XjD3/KNjhW9+5TL45p+4bd7Ij2bM5NMARVlVI0ZWsG73B9Rx0VftcyuIHVyYJvv/c+82rBj6+u2aLQVuNIB7jT+AHsbMm3fulX+bXf/HuESvFXP/oeP778IcNZT1f3qMEQFoaKJRWaoD3t4PB1QNc1TaykUsIjmi0ueVA+YEpmUsBbFUllTqCCJqjA9z76HnSRVrVi2IJiUS+5N3udX//ab/LWa2+x3++JLmkPSw2OHBBKVN2IHpMOHoOVwxpompqXzz7kT/7174HrU3m8CJlrY3hw7zHvf+vv8tVv/yrz0zNsVRN62QPf+dM/5r//7/5bhs1L7q5qTHZQYnIUQqDWTdGYlX4FEpwMQQpC67rCVpWUdwwdIQz0fcvgO8IwSLmLlhKwfrtnUJHq/Bi7sji8OAxxdMBVjInRRNH5KyXL2SYwYa8mezPNBFeVLQGI1hpMAqbKzj/sVm2tPXC0b4M2X+T0Th2uKZA6/dkXOe/5s9NnmjqtkQz2mGLDJlgAMQYC+gAQKfYmBR7ZwZ0GDPIdE6B4EpyanEjLTxGnzrkZ36/HwEQc+MOmZFnfO8bUuTvZO3FnJo24JuM6BbhuAw4mJYam40QkZW8PNXTlXnUqE1Yl2ZbZQkFPGiFk9kkK+o0SRkh2WkeGSv5i8S+nHZjlWTKwNIKsn5eMGMc/syqnTn5ehyI7kNYs4vws50tq5gQX2CnNZvaYm+oBpt3zD96xvLH/iDv9C/YvLzipTvkv3nnKa8vI7z/f8lF/wqb6Cv7xHZbLc+KzPyNe/oCKNUZXZa5EA1q+1ztHDJGWjohiMZvTVBU6aZV57wjRE6LomSmnuNlcQYhUtcVYg7U1kCsBHD4O3Gyu0FrRu454GQjesTid40OH8z2XVy+5vrqQMdVgl3Oc4qDJzrRB0XTdlPM2BxOTxEVVVQnwiJBYYgXY+QWBYn6VtZptyPR3jOstv9dPEgO3r/t5lsovCuaSw6+Q8Y6SrDFHC05ee8j6sxcMmz0Cl6ey+6bGzmr6zhEry8YNbAaPUZ6maojOSTMxoKkMbr/j4tkLlk3D3bsP2K5fQXDsuo62d/TK8sH6mo/3O7ra0BytmD+6iz0+pgsiI5XBG01mFSOl42X/HgJ3+Y9zMkbV8Qpzc4Pb7sikXGvNOG7JCU+m6BfO02Egnf+MAb/icN5iAg2a1ZLVvfuY5ZIuBbOkQDhrnJPcPZXWX1FHjRmny0D1ZE4TgB4KcOTwvUtMSykLNZVG4xm8MLoVETOrMHpJNa84Oj6i3+6Ig0fv9wy7nUgzRF/OlxhF8iik/gWKw/Ep44JPmpcTWz9Jek11Zw/Hdqxmuz3uGdjNNq3o6U7AQZ38Wk9kcX5OtToWBopSY6CeziKtNSO/EzkzEtirkCRdlg3IscR0H8skadGHiyNBQuZMQIaIsAFnd04xwMsPPqC/uUEl3dJIZjzLfeUSyTzh4/gegtb5FWIqo05s/wBs93vibid9LLTGVBV13bBcHrG6c4fFnVOCbYi6IiphqcakXz9uAvFLrK5Ssxnpi6EnyQmjcvMzii3J9tIga6U0PM7je3DGCWM4MIIXZdbzPk/j7HOcVBlMXZdrds5zsV5zVJ3y/tN3+fjjl1y9fE41zFnO76FsA4NlGBzzpmJmFJevLrh++YxvfePrNM2Mz569wHdOWOhBE7X4gYqYwKOKuqpErzzd4TRJM7UJU99uqtmcWVzF17rlnx2cC2kQcuwWEzhRokeVG1VNgc5pIy+SiZiwXBOYZ7QlJLphDONZku+raOqa5FuQwR+x+yqV7U/Pj+krP8ftcn0Bp8f7HKVPDv2uEITNd0CKgOIjqgSSxcQCDiFgtR19skgC9zJQO34m76H8PXnNyXVGhnC2McJEH5MWJRbPcXkMwDjH3mcDHZOmqVSE2bqhN6awLhOyB2RQKzU4nqwt+Z0pPvX/E/id/q/cxxe9L/vgINXBISSgOHqaqhYWLXnOhR1sjUVpKeG21kplgNFJY3q8biQDjzFppwvDW+ZQ7sfaqhB/nOtFF9WaMo4xwtCnngkRYbf6VP7duTKHxtrCsJemhxEVSNJqHk9IchkCKFotZxUpqaQRRqIbpMqgrI1ynkM3DAlHkjhQay3xRxrfQMSLyK8kvrTCh0E03EMWRZE5HpvKyRozSRqCCME5sZVGC2Mz5OSnfHwYBPDz3uNTkioqLUnUbPdNii2jVK/6JFV0Zz5nYQy1UjL2SlMZK03egoeQK7MVZFZ9zJUtcdQ/DbnSSggTknz1OD+U9+fVp7UieInbrK1k/wXB0IYwEHyP2+0SuVAzMwZda0yMDD4yqy06RnRjcHXFEBRXQ8d619I7RzRGKqqNpts5IYyl2FrFiE2xvlLQxSRPkdaoGwaUEuA1Bk9V1ZJ81KqQJ2Ja31qZdHZLw/QQwNgFWSs0RIfC0tiE24UAekY2JgpJMsRkA1wQuTRtK6pmxlyLLQ/DgHNObIS1xa4orZOfnZdROotSEzRrjciH/ILX32qQNiINUskHW/J0U95WBiEBs3LAaTE6IYzU7inIgQBCWpvS9W3TdfzwZz/hG1+7olktRXejaXj8xlOOVg+42H1IU6sEAisxckAuY5KDJGKNTcFEKptRkEsmpsFcRv9zlk/OCGk8EJL2WFVV5E6fcoJlpkWGKGLRsQIldPioiFhC1Jwfn/Lg7l1ee3Cft958ysO7D7h7ds7x8THnq2NQmn27x7uW6+0F66s1sW8Zhj37IXCzvmG7ucYrxTAETDXD1kd89NkLKtsQY6Tt9mxu1lSN4cmbr2Otpe87hsGz3W5x3nNzs+Pi5RXLxQnX19cYU7Gcrzg7ucPQD3RtB0qx3bUYbVjOl2g0n13d4D54xbBd8Ku/9FVuzDM2XIrxN5b5k0fE+Zy//vGH/PTVR6jaoM9OuJwNHJ/NuLQLdk7TW4uzNfvB0+72KK2o5w3WQ3VUoU2F7gbU4FDOwW7Hm8rQP3vGh5s1PY4QNT6A9hULfcSjB+/yH/9H/xl3793h1c0Lvv/zP2enrhlMh6Hi9aMvsTAz+uhp+57Bd3SVxw09IfQSyBkYIrjKobwnRNGG89GLA5XkNWIu4Ve5/DLSxoA3FkyDVRara2p9yjuP/w6//O6vY/sZw7Zlt91T1Y00G0kOnWSuxOhbrRN4J8wCObACf/RHf8DLZx9hjaxJpWWv3bvzOq89fZcHb77F8uhOCtgczbxhc3XB7/72P6V99RHnRw2EgUCgbuqyV0TnxUgpgM6lGVr0nbYbmrqWskcF6/Ul290N+24LSpxq5yNaS/YsRnC9J17tUNoyW51KZj6VAsbcpCOBZ/IrCUKlSdwYxIfE7CgBZshlaMIsFvZctkcZWBw7cvsoB0FuBFjK2vXYcEXGYCxXvg3g3gZaSDYFKPZFTd5bfqYE2AvEYo/ydXLzHOkgnGxnAv9ycJ4bTdxmJuTvnYLE09KsqbMuTFw57HTK3mqlU7McDq81AQBilILfwvFRCqNzwCxrQ6cmQgcsx1v3NQ2o8r/z/I4BhyrOuIB+I4Az1Vob7zWPly7Zda00QU2cvaIHq1KwkuYwKnGcioMv4zxrmtFZSoDEbWAjRshND/Irj/sUdJ6yKm4DuPnBVHIGI4qmbqiMNC/xccHOPub6+Nt09R2+der4jUeB5sNPeO/rb7Pp7vPz7/+Yix/9AX//tff52tN3+N9+sOFPPmm5tsf0Z79BnD9mOH7A4tmfUe1fUClhZ9UorNFEZXHeMQyDsCicE934SlyVru1TQyhAJedPQR969sMeTwUatLHUszldt03MuhrvBVCczRY4H9hu1uzcjnYIKFMxtH0CJwKL5YL50RzHAOqwaUtOoh+Of2ZVHe5TlYIHT54vk4LkVBLN5xny02tO5y0DcHl/5xjvFyV1bq/1AzbuxG5Mv0spU+wrMYr2IZLQC0ZRnaw4VorrT5/jrnfiSJOYd1pRV4YvPX2C33UQ4NnlNWfHxyybCh88VoEOntDt6W5upHLEaKLR3Ox2XLZ79lHxbLfm0/2efaPRRyuOH95DH81pVSToKJ2y0WVuxM5IYk/plHAjA7biB2llR7BUaaLV2MWMdr/DoNAxonQsdk7elnzFDCDkvXNrDPNYf5F+IClwEpBODOlsOWd5fo5dLuhCSCWa8myRFCx5AUFzwJgTUGXyD9aLaJsSPD415KLYCjex/9JQrKZG5Q7yHoJ3eJvWed2gbGA5X6AliuXm8pL2+hoTpWFJCB5iKNIowsQJhSGb7c+oHX4Au33hefBF4MPt/XDIHpsCGfJvY0TrMjfJ8y4wO15xcn6OUxYt7VWSPc/3OO7lnIybglUxUkDzjP0opYoNmO4z0cgbwSBVwI68EgwBhT25y/kTy/qTj9i/ukAHAT7z9+TzTqVYILMn87UzOFHSEVF6R2hrmS/moEWX2gWPtoblySn1fMFsdUwzX9LMFhhb4QX/QAVLwBOUlABrlUCGGETnFVDaYKJC2UQiqSphYuXEUwIeRCItn5eiv30gbSRhpqxZpVKpfipsz8dr8r1IDOxD4Fh+PnhP1dQJEAi0vaMdtrT9mo8++jn7dqB1UNdzlAFCwHUdVxcXVPU9um6P1ZqXF694483XOTs94+LVjUgjKZEBUNKKW2Yxrb3BOWB6/sayL6dr+HbC93O+2q19IIQhl8b/MAEYYyxswqztG9O/M+gmMlL+YL0JMOQLQJF9EqVtah6kZN3c2ovjmk5zUvRuITNbtTap50a2fYfVGbdZ8rcB6NII8JZ/mMG5XOae7fhoYzNrbwSWI7EwIrMdNsYIaBiz7RkZqJk5mP+WvRmLLcnj65J+sknVPtPqtjyPxRcYVycqlWDHDGgDLvnNpkrkFlulfaAPGOvjHIzjkddK+c6pf3FgM1NiOhz6uvlVkrDJX4RI1/W0bUtdSQ+AKumOB6Cu5mRmYaUTkz5Kw3DxCdM4exiCyBp1bS+VnlpK7cucpnvph51gLFqqTkkxR+7j4JP9yDKRWuvU5DA9i0l/91HOnwTSW1OhY47ZZK27KOzQ3ClLKSUM6JCbCqbZiYmwMjlXpZdGIr0lnVOjDbHSGOSeXUjM16gIUeI9nUC9XLGNKu58qqxJ9jGOYLnK82ty7JcBuRSXkm1KADuRAMoHEkJy0VFBkMR6lrhp9wOrpmJmDMsqUFlVCIA64UQZN/AJN8jXzmubsjcgRJFgq3QlmuOJDBZjTpKO789Nq60d7SPBYlQEKw1xhTkPFZG5idREbIzM5zVNXeMGT+sDfQCvNN11xLmOdrcVvdjUV0opMFFRGYUKgSwn4gN4FD4lI1RuE5P2hLEWHUXORif2tDJJcskLgStqwQtViISwRSlDCEIW0cqgSX8rBSokWyyVmD6MVQ8CxAvL3CeSicxrkhQSWFfuU1nwY7wXQ5AEu9KgIegoRsVP2c6Hr7/dIG0kZXHSwsj7T6lEaU/GmBFwyNqMggONrC/yoaUNSiUhdhXp8Xx68SnbzQWr1RkBWC6W3D9/xNtP3uHFX3xI7wKmscnR8qOTXe5LhLllkwuTQqWMpUoPkjdkLvFCqVGaKoECOjc4SmLTAjZpNKOocPAOlEZryVIEHyFaVvNjHt1/wNtfeot3nn6Jh/fucff0iKPFknnTSCMDhQCx25bt5oq+29B3Pbtty26z4XJ9RUBz+eoS17XcuX8fXa84vf+AVzc7nD7l+HgJocP1e9CGpp6znDdEpEnIdntD3w/MF0vads/HH3/I6ekdtNIcrU5pqprV8phP159QVw21rfnk+gXn5+cMQ4tSnsVixs1myw83e2z9U56+saSuK/q2xcWItxbuHNF8+U2UC6gq0jaavXZ8ePmMfoh0Q6QLA7t+y81mh3eeR48e4lsJSGfasKxnNKtTmqiovWM5dKzO73Ly4HXsT3/Idz/7GbsQqUzDwhyxbO7xS7/ym7z97vtsb254dfEpD++eEl45fLTcN4/4R7/2j3l6+piA53q/ZbPbUNcNrh8Y+j3b0LLverbDIIzeoWM/7Bh8Szfs2fctgx8IiU3atp2Ud5BYViqw8x1tXDOolqhmnNs3+eX3fpOz5WtEI6UPYNnc3LCvd9R1I6CSBvyAsamZT9bMMxGU5uXHH/K97/wxjZH9JJo8gdXqiCfvvM973/oV7r/2JvPFHBcG0czRmn/5v/8vfPj9v+RsabEmUiktoKvRdP2Ad4H5fA5KWE5u8HLwBdGVFO0Xgw+em5s1V5cvcaFL5c6R5XKBMhqXMk/GGPquQ6PZr9fEjUUtKkIKhEKEilTlFUemrDjJpDLt3BAjSMZOqVI2HyOorGsXM2MoFKZCKW9KQdeBe5Ud70kwlv/OTmnR+ZvomH3euU6OQmYN6QQgi8eYfpYSNsnWTLvq5mDUmLHhYWYvFI3BmMGEcXymbMLsN04dfnmWW5INKjkgijHQiYe6X8VgEkvgmxuMZO1MOUB1sZuCqaVxK3ZUxiuPqQDDcg6UIDoHGemZM8PJq0PQK12ErOGZnyXPqxzKFEezrhqUGhvUjXM+BjO5QWM+d1Q6q3IA4GI8CGwSAizOYCQ5qym5MAU38mOXMyeNwfSMS88eCEU/uaoss9kcY2YQLUOc09dvsl885XRp+A/em3H04vs8fvwAN5+xiT3333nK8nTOT7//lzy8d8N/+d77vH4a+IOfvuLnw4qL2XscPVhRLx/iPvtT/PXHLP0Or3pxSoxkmRtToaPH+4DzATX0hDA6OZWVAK7b78SBqSKD6UDlhjyG1epISsTcAEHYLVXd8O677/KjH/6YdreFKBl5W1XEwRGdp57PmJ8cMQQvTlDyFcqekwiHnBSZVr5kpzkoQIOLvlTvxBQIyLoYyypjShTndGoBAifrbRpoZQat0mKFS4AXUlCeEMFsM2ICBm+v33jre8bNwph80bowKgCi0VTHSxb+jJu2IzpxHGMuASNycXlJv++I3lO5SFh7qjunLKoaFT3KWppaAPR9u8MNLfu+47rr+Xjf0im4CZ7WKPTqiNVrj1HHCzoiLgMKpcpJl+R3vt9xb+ZEmjhLApQnb16DxrA8O2XYbgn7PgEyUhIY/AiEZNtDAs9kLMTN/3yQPP47g+oxgx2JmTZfHbM6v4NZzemRMkelFNGPnxabZrLTKo+gEliVbIsPMZXmj/s3g/i5eaUEvIas7VjAMunCQ/GClZYGTUqjQhBbqiBojV3MOWlqFqcnJXGyu7rC7XfQDUQ3JBuuEsNnJCBohNwAUtaf76GcZbm0stipw+QZk/E4HF2Z65j8YZ3PR+/SPIm/bWczVvcfUM3mRC8lyJFpgnMMnkggSk6ilLlNeyP4FHQmXwRUIXXEdDaVKktIyQNhPRHHvehCwEfP8s4J92cVF0azeXUlzXi1SushJSYTS0tFVdYT6dzGi7yB1/KnOTnh/sPHNFWFSnq0QYFqaprZXLRnU7zRp4SgrYSNJChBjnOEuFESHyjpTxHlm2XzxMJI19pKybzWib2V7cvEXk7mNScaY4ylM3wBIlTebWl9kBKZ8WBn4YKTxsYy0JBYXr3rGULLs5fPcX1kZk9o6iXL5oiub/HOEYYe1/d8+vFHnJ8e8/qTLzFbrnCqZkhsf62NaM8K4oW2NnX9zuexOUiKTWO0/IyZtTpF7/LeVZP/z58fz+JY9mlee/lcUVCICsXuRFkvOu9vUrO8GFLwPwItMdkwRfZzSHIHh/sq+xm5dDvfcakNSGNOSsQQRn3s6X5FJWBP69LYqdjSTDgymsoYYlATsHKsRhGG5ZgAld4Y03GX5FxI9XtKKakU0Dr5DHktZvupqCtL6z0KRZO0032yR9lnE03qDHqKj2X0iPDk8zUDbnkPhRikARVGQLd0LhsD+10r3d61dIIPiX1ZbJ0GqyuxNcmGWmuKfvm4VvLWymzZ7LOPv8tn/e3EYTZpmdnY7jpePn/F8dGc5XyJaQTYr2yF73sZX60K2SOQ+1nIXAomESGdzSFC9BGffYdyJoRka2WObWrSGYJUO6gILvlRSmt0jERCAWJVKsV3Q8BWlZSA57WiIPiOIQRhKiqJIbwC17fiERpbGtESpPFplRpUZQKONqkpZJAGqYKxymoLSqFtQDmJ7zRggsgKGGUoguKpq5hWopDrBlcwJrFeCh2SnVM+VcsoaR7mFFgr+2syj64kQE2qrJbfhbQ/VADl5APeC4PXKkOMinbv6TtHpRU3VYtWUFvDrK5ojCG4nspIgl2hSqN7H6T6JhDk/GEkPsIopZb/iE0fE4ygcH7AedCDaOQvF0vZn8qirUmElZj2n6fyPmEWCqKn64Rtq23N8axmOZ+xajzbfcfNtmXfDbTDnvXmBoJH+wEbPFXyl7KUmjTAUwwRQvQoq8fqSiM4mUrjKX/EJ5f7E/CWbCtVaq7sHTGKv1FXM4gxVRmnmnsfU+WchrGVBNoa5rYBFdC1TTYqEFJ1qHc92jagrTBpNdJgV2vaAFEbWuckZtEw2MMKhOnrbzVIOx6m6QCKmXY8srL0RKe1AADFKc4lDCmwCohT611i2EnA8MmLZ3z/R3/NgwePkzBwxXIx55233ua7P/ljenWDNJtIrFhSIJAODKVMThYjrLzkqAWVDJXcd9ZE1JnJF4Vqnx3KEKTrqRVqlqD4Opc/WYgeFQ0hKoyqWFYNp/fOeO/tr/LeW+/wztM3eHh+htEibh2Up+927NaX4AZUDOz3O7bbPW23Yb19xa7tuL7c8+z5BfPVktM7p1zeXDNvavZtx3J+zm6wNKvX+Mo3v8FnF59y9eJn3PQvOTo65WgxZ7+9wYce5wa0USwWC+qmputbiJH1WpwLAQsMVzc37NqOxWrF0PccrY64e37OZnPN1dWlZPfCQBvhuz/+iMv1gidvHDFrjIBuXjr9cfeEEDXWSnfC9XXLZ6+uuN45OhcxtmIYHN0wUFU1mzbSbi4J3nF+55TgI/VZTW1rZk1NDA1+ccz5+SNe/9JbPPzJ9/hXf/FnbNc7KlPz+NETfuM3/z52tWD/6oIPfvhDXlx+QNXB/eUdfv3JL/G6ucf80tMYg7q2nJhzFvWKLuwZosg66HlFnGvOTs84Wi3Y7G94dvEMUxsWqwVt36HrGR7NzXoLWhg2UXkuty+5Hl7yez/4F3zv+XfRZsFX7n+F9++/h3EWH6T74NHxCc1sJkyMJNqdwS9h9VEyoSolNP7i3/wh159+SGMlKJHu5Q3nZ494+72v8+7XvoFC4do9Hs/x6R3+zR9/h9//P/85jQrMakPQoGMKfLQ4acZq6qbGaEPTNPT9RuQYjCW4SDObcXR0xGfPPuXy1QXdsMP5TvZuiOx2O9nd+WAOUQ5VYzAK+vUWa1aoWicGSNKeS2fkBFIksz6z3EkpK1MJpEksrpgYxyQHUmxN1gxVyeGMuWJi/IZ82k3BtfSvGGO55Kg/dmics1PrYzrkmARHKd5TgoYWZ2kSB09s56EuqmS3UzOPlIGVrGp2DkcWWdasMkodaG1PGVDlb5XK5ZIT6LPeIZ9npYzjMBkPNTJxVfmTQdh8/3ls87OO8yDatnpkMKuJfMHk2jFSGHX5vsr9qRFsExZwBsryoiu3LkCIyo5NPBhfOGQGk8FtrRn6/gDoztUfxWHIIIUsgjSHk/lMZ1oG2o2asIoT0BBjlpuQ2zZKM6vnNHYBwUJoUIvXGFZvo3XFv/O64Y3+gpW1rB6dsXUeP4B3kfmdu3z17yy5/vhTXvz1/8FvPXyLb377Kb/zoedPnw2seUB7es5q9hqL53+Cvv4BbrigCSLVYozHKEuMomu+bz2DF7ujBSHBaI0xwr4NJbjyDD4KqIuhrhtWqyOIgf1ui6kiPnguXl3Qu56AZ3OzISANCnWIYC0n9+6iFzZJIkVh9TIBM0kAV2J86AT4B5XWVyRwJgAAIABJREFUJhFNDsYDOo4NcfJ8l6ZOeV6cQ5nsyKsyh4oEwqa9J3NFYZqMJcRTQFE+GMO4ZpjMeQ58b4O/AjgLYDMN7LKdKPvRapb37mCIXH/yIsVnnuAiXYQPnr0gBGEg3F2s0N7xfLPhfLni/tkJJmocivV6zYurl9y0W256R2sMl8HR4qEy1MfHLB8/gqMFffKDxvu1qBSUZzZC1iLVWjMMQyon1JDKHrMNlLJIKS2s5nNO797j+qNPian5RUzA7m0N0pywK+NdAuRDWyW6ieN7g0+2ScNsOefo7jn2aIWT2kwBPpNdzoF//n6iNG4lZkAn9yoQwCUiY2+MztBLAXMzczp3hw8hJI30zDw2wqaxFfmkS27oBAiJuJgICotFsROr5RL6jrhv6TYb9tsNQ9ulRlMZWEnl0kru+zBRmRokJvDtIAkxBb7yM46GrKxnGYcE+oVAZcemXyp4hsGzPDuiOTsHUyGsJPG5pRQ3L3vxC4w1JQECFCBRKWF8pZQmlbVFmiiokSWWTsMJ4JiakWlSF/gE1huFNRUDUC+X3PvyOxxdrbn87DP67YY4DCiVtOqUKqBhti0CWOTJUgJE3znh+OFDFkd3JAZAEkVyH4YeDVFKaXOgozD0vStnhdFGSuAzmILIviTDJmvbaKSBsJPIKpIq81KkNUk6pgCkgDvT5oVlL6exlTOYSTyWzvCyPlJ/kSjrwlqLso7Z0ZzNhSE4eWPbD7RDhw4VJjZJRgeiEyJLHyKmknL7+WxG13UsV0fY2ZJ+GGiHntoYGlUR6tzALpSzWMdpBY0pv5smqbMNKInU6bLVE/84Thr9qTEZdygbkLiWCbSaJl5jSjopI81vKb5RKDIZGjUmcjOgCcleyNqvjB4TDWlOixxJHH2pfD+Z9EQCaUIEHcdnyHtK9oS8N0aJu8S3EZsU0/qNCRixSXLDJWmBKZtdKiMm9iwlM2JUBWyJMe8VXdi4kcy6lb2pjSTgHK4kTod+SOtTE1Ru9iuHhTBtBawyCZwhPb9So2yLYlKB5gI+kpIIOo1R8imbimgtqrbgpIljJnEoqwtIHJNUgjxXkDjVZd9h4iPccuDzWThlYN9+T8Y58jpzg+dmvaPd7VktW+qqFuAYTd3MqWcNdVVhbcXgBkl0xWyVZdzEbYml8ka+RDO4zL4UfdQ8dlprhnbAG0Vukma1JBOHIJWh1iQbm3ylLp+BClxKYCqSzBEyH3lfRC1Nzo0VEEyqmQZ0VUsiKe8ELftGaYN3ER96MotWQMlAXv4KcArQScotpnNdRbIcG3GsflYIDhNjkISq0ZIU04h8Q0xN+1wo32e0kdJ9bbApjpDYQqU4PBZJJ5EqSHIsKttJwZO8z1IMIeVSNHsCl65PQLVn0VRUCqIbOF0tWM1ES1ibSnADqwjJp7JoCNkWRFxwRHSKaSwQiMFPSJ2HdgAtNqUfOqJSGEximCqWi5k06iKdEUF87rbd0w89Sin6rkWjqKuKxaqBowUDmutdy6ubLR8+U1yv13S7LevNDTbI/UirHgVojKnSjlKgUqNFrel76XWRJTiKz6c1dd0kkoXsO5MSRopIJZkB6rqCJuK6Fm012AqbmvzGIA1OfSJ3aaUIg2KIHVioXIVC4/qOIUh1nTUQ9UBubueBuTGEwdHYir0PGKvZXuwIGjbx/6dMWkiGanpwJMfXpLLFnE0k0fizgQmJG5/y1XINPQmsYyRg8Kph6wZ+8OFP+OVuy2J1TNNUrFaGN197g/PjMz55dYVd1FLCkiLpMdOQysLkh9IpLgS8Cygj5ShKWwi5QdKhZmIu5SjNYaIYhErb4twifhLBW2o9Z2YqHp/f55e+9g2++bVv8NabT7EK2psrdlcXEL2Mh4Z+v2f96oLN1SUEz6v1BZfrK64213x2+YJXmw19a9BUfP3rX8Oj0JVl8BGfslRtv+f+/XO+8XcfMvzFjufXFWqxYqkM3u3ohp6+33N2fofFcsV6fVNAjME56igHX9fu8cGzbyuqRiQd2rblnXfeRWt4+fI5Nzc3RZ9DGdg7zwefbfns8hVffvuMJ/ceoSuFtpK1cc6z7j0fPX/JxfWOi/WWto9YW9No0LamscIk7X3Aa8n8+ahKSZhNzczQhhgHhsFx9/SM//S3/kNOViv+5E+/w3Zn+Po3v8WTp09xBH704Y/4+OIDFueWs+GYyqz4jbd+iTPfcPHBB6gQ6b3m7O4D9p+tuXj1nIij7Vreevs9+iGwfnbN5Ucv2G3XOAV2vqB2iuP5EfvLFkKgf7EBrViu5pyenrB+9oxF07C/bjFUnJu7fOPR11npJX7v0UEC8pDo+U0jBqptO27WawyBeATL5QoXHYpIbTWvLl7wF9/5Iwa3w9ooh23QmGbJwze+xKM3n9IOHetXl6zmM+4/vM9+s+Zf/u7voELH+d1TdvtrNMLEcIMj9hGUdArVWjqCDn0vJSzBJ1F+nZoZ9Tx79jHb/ZrIIAchoiEnfkgC2hAWmjaWZj6jqis6FdA+4gfJqutU8pIz6DnYNkVXUJq2kQ9FhK1k1IS1mfYlMU405UabFENAqmfHcrbimE8cqhSTjLiLPmTDZVkWOARbCtMiXyf/Lo7/LmBpAhUzCHC7PD6/1xhbMuAl+Fej7mxugpEdilK9MH2eW86iTk5vBqOCzw5wBn/HYOUQrP2C5yhBQQSyjmv+XQY4Msh7OMAZnC1NPRIbKIMzSsXyXCOb+dABnjJiwvSeoAR3vgRKh+zVkRHz+e62UxDo86zKeOCU5wDZZNAg3196xpi+Q4UEpChdGGRaabyL4ANWgTWKWTWnVnMilnV9H3XvVwnV23z1/oq/99gyv3rOG+8/pVWB3W7PsG/xw0DUmma14u67b3D84iUf/fx73N1e8l9/6zd4/zPP7/zVcz68MXT1U9r7inB0l/rV9wmbj1kMN9A7UA6Py2EKAQFMbN3gXAAGbF2hrUFjMEnHaWQiR7wbqEzDanUMKNp2i3MDz589o+s6lILFfInFEZycCc1yjplZvIoTvTNK+aXzPjlPubGdeAq5uUUBnKJC+WQvlAKfE1BKnN2QpUbSmk3+R1QZ3I3FVwgIqyM4SRCX0jmkrC2H7ZmRVgBDnYAxdbiOvugVk6NPnCQuyi8pe7kAvQpm56c4H9m/vMA6GSQXBZCqK4uPsHUDVV2zcY6w3XB6ssIYeLVd88nFBS/3a268Y+MCnXP0OmIXDbOTY1Z3zwmLhj5KBVAO6JOD8IW25fb+HLd6SrkUMEETosL5yOxohTs7YXspSd7IISNuCsKEUt4YD/bYFJQQkz9pIqOAqKhmM1Z3zzDLBUOM0oBOKUjSQTGBshloiBOAZLrv8/dle6RQk3L8BBqRg/yYyvJkHPyQysyNxVoZB1tZKb1NAeDQ9/R9X9iLMYw6ykTRGNV1hWoq1HLB4vSEerejvdnQbbcMux2uF903bTRVPizTq7AJEwB525ZPz5/Pac1ObGtmYuZS6pjGX8cogE0zY3n3LhiDS7/PCcpc7qm0LvNqrBUmcIxF9356jiktlTi5IWB5lil4FjOrNvvo4pMbY2WfqtSFmlSNo8AuZywXR9RHJ2xfvmB39YrYtbihxwUv/r1zZQ1obdCNZbVYsZivOD67y/zkFF9VdD6Pw1hiaYpNIbEdcxIxraXk7wn+MFbgyHJM45HmyQ1DiV8yKy0SDhI5hQGZ5LCCSnY0jonQ2XzO0Pdk4FpY+KnsO04kgTJT7dY4V9oIEwuP+uQZei+ajm4IaAWr1Yzj1Rm0FaHrGNjhlVRl9L2nrhtOzs7YrNf4bB2SDzObzTDDHhOF3Ue6Fz0dswRSTff+wRoIIRFrUpJiYjuVGt+T369vndllnWebhviYec35ktGV+Q5oid2SN6WMTfackdELxORjBTUy8lFC5MjNW1VCVcfE37jfJNZRyV9M3e0h6derkdmnyqFRbHX2jUmJM5VA2uyI+eCLH5qfGyaAMaMEgjTYUuUryBVN+T/vUWgqU+FjkAY9MWKUBWJiRQshSc7ZpMsbSdUYAuwZk2xGTDiA0QX8Kj5+tj0JmFTGSjVCAoqLnFg+Q7UArwdxQRpDWRcjYJ6rWKRE2o5r57bfG8ckQSFrTJqefVEycbpevRcgsR9uUAjTmAi2uuH+gwdC2gk+MQgTs1KB8x7fDyXJknW8SzPlZAdLcz0xEpIADVLtYPJ9G2nsJSQE6U2AEjlIlOipyjgFhjQm3qVKChQkBrNKyewUGiVSjICMXSJS+ASg5xL1nMAIqR+ExFCBze6GpmnIeqsgvo93rlRJGi1Smc4J4JuTu3VVC/iiBMDPZ0kIAZt8LK8QeYmES2mFVLMoiRkygcWYifxOIpdkiQiU9MCJCpzzhKjTKEX60ONSDKvTcynAKNiu11RKPJV+u+OVFptgqxmmrpiv5syWM2prmZtU7q8gBE8MDh+0yKYEOROyHM00hhn9JwGLg8us5MzAhsrqEk8bLbItCqjqGmUNbhgSkVEnzd8Oow1zbdENNKqisfdYnyzZXK949sknDG2LGwb6QdZmHweUHmTcvCS+ZZi0kAv6noPgUCWrpnZpbrQA6AoGN1Bbw2o+o85av95hjOJo3iSJFA1KKpOtVaiqkp8j5M5gNMwqnNFU0bKYw/VmS992guXM5tRWocNA7D314Kki2HbA6pohRvqoCK1j0+75Dl/8+tsN0qrMaBgzlcVpV5NygYxmxJjYgXq8QDKIPqT5y55NzNlhjcLys89e8PzFBW/O7mFRrOYLHp0/4q3H7/PyxXMBnIwYAJtLG+KopVZK0dK91VVFiPmgFDAwnaaicZH1Wf5v5t6sSbLsutL7znAHn2LMjByqslBVQKEwAwQIgt1ks0GaZJofJJnJ1M/6Wf2g/yDT8CDS2KQRItUNAihMNaFQQ1ZmZEbG7B7udziDHvY593okQD3DzYCqyvQI93vvOfvsvfZaa6dkzxoZSCMbRYJRTBm2pQBfMrVz3v7il/n2177Gt77yFR4cHlIpBb7j7OQpy6szfN8SosfHSOcD55cXnJ+f8/zZCWfn5zxfn9H2TSoaFU4poikolKeLHte16CxhU9C7wKZxHD8+48P3PuaPv/kF2m7Fb1pP7JasVhvWzZLgxZC5KCq0XhNSx5ToUxLu6F1L13XMZnPKcsL19TXT2Yz79+9xfPyUEHzyHxXpgUKjBfPm/KLnnV8e83i+ZjFfUFYVXduwXC5ZblYoM6Eo5+zs1thNA1FRZsk6kd2dGTFGnDZUZYU1MnxBjzDaAATF2HGzuuZmvebth4+o/6Tk6WnLn/2bf8tsZ8bTF0/5jx/+I8fuU3acolOeLx29yas7jyg3Jet6yvHxU85XN2zaNqVcgbZZE7ue65MT7tx7yPn5Jb/8xc/xfc9sb5/pzh6XLy45Othjs25Yb1rQlslsht9AfTjh1fsP+aeP/4mLqyXTapev7X6d13ffJPbDTpCuvSKtb5I0omRST2jWKy7Oz+m6NklSFIqaX/70n3ny2Udo5YjZ09AYpvM93nj7W7zyhTeZzBbcOdhHK5EK/uhHf8eH7/+UMvSsN+D6BtcG+q5NvoDie7vZbFgur4lBDOdjiMwXi5TwaJxTPDs+oevXKCVATp6OrLXFe5fT1qFwESZGidaaQhucj4M0WZO9lNIeRYZp5IQ1EsFostH4kCTlRknGQ3OypRmS61ueUnosjl4KW0O8yqwKmWjqb7EucrI/DowKAzA5XKsSuZFOQI9Kye4t+RNhWMXbid4t8DC9chKZi2ujM1MtFaWR4aC+/ZPj79sGVnISqbeS8Jy35+55Lvzy73g5luf7dPt3jx6MqHQ3ohoAmuFeK3Wr+Bvujda3vm++XhjBm/zz209O5Fzjnw/PcvufW0Xs72M53AKW1JigZxaJMXktxVuFH4zf8/cVjSrt5Zw0j4U2A5gXlfhIaxWYTafMbI02c270Lsu7/4bNwQ9YEPjP3y7YWz/mwd2KVX/FetkSQsSHls5tIGqsmdGjKOoJ3/jaWzx9+pwXP/k/+S+//G2+/mdH/O/vPOE/ninOzSus53vsTt7AXb9LOP9n6vU5hWvlu2uDippms9nav5q29VIokSSIWoHOoE+SgScQe7HYIYRI3zbQ+WRFIp5ai91dbroGU1pc0Cx2J0QdReI6AF0aF31i0aT7ubVvMyCaPQNV1KigqIoqvT+k4RuGPvlQmdSFF+80OS81Apr71HzJgH5mrOXfnff66HM1Wn+w/cxVblqolLYktlCyb8iD78YLYYg547UNv3IAw4aXNSzuHlIVBdfHzzAhUhYKoWdECluI9ZK0b+lcx+fHTyiU4sYFPl5dsomeXkEoLB2gSsvk8A6Twz2oCoLOTCPZl9qYNAFeDzMFtq/393mdSt6Up4XnWyn3xMeA04pyd8Fms6ZbrTBbAxx/5xVHpsz28x/3cwY+4lB4xKgopxN2H9xDTWp6JYm63NxUzOIZ2KzDvga9FS9ugUAJQNP5UlLsyuCs1grv4haDLsIAFuSGlU+y/dTMVJqIxRYydK/vpXAxKsXF3FBTgItEpXFKgbXY3X3mi11mriWsG/rlis31kmYj4JhSSoCUDL6x3ZzaipnDbc2A3qgEGa99bKL1fT/cG58aJ77rCdqy8+AV6r19vNZpTyUwKgqzXafUPwOHRJLoURQSSlt5JlqgAZHC5n0k54D3IzipFDgXbj2r8czfYq5HadgUxlJOauq6xvvAZLrH4vA+bb+mb25g3dKtbuj7Nt8m6qpiMplQLOZMpjOJNboAU0AM2NilaxK1kUVYaUIiHpmSalw4Uhhn8GRbbq40Hp97pgBUVYUKiWGmVDqn9VZeQQIk0n5Mzz5qAbGy375RimiFDrzdGN72MpX/VsSoxeZEJZVVuo/eaOKkQs9r2usbiIqrmzUb56h3pAmPr4hrcDRgLcHDerlBESmLgslsTjZQMUqAFmssqkOUV9kfcCgdxwZJCOMQrfyAcpxKd3eI0y/bD0muZUYADzXEKmNIJATBeIzeAvpiwn20HhoJMfg0IEn8PYchYzGCirfzq5S++C0fw5fzhwy25vXq0/5TOk2Ul2875LuiKiN995c82Rlzwe2cMDIy5mVo9RZrcAD6RsAx/9NaS3BiaaSNop7UuM7TNg2olLuHdG5rPYBzyth0v2VNZdCtsAVEkWV3fQdoAQ5NHmhqsEok5liNd54+AXP5mZnk2S/3UMBylcC3qARsVEpycLRGWYMnYhKmENIa8mkwoaytOICMOY5Ya5LFCAP7dDwbxnPo5UFrL88vGJ85t94n9ZTk3T79jokShqtJ+7RQGkdMCgGTFJOpoaNUUgNlv1epv+W7KTA21UkCOnpcircpNvlEfEqNN5lynzxPlYBpMUYZSBFjWsOSH+iU00Ujw6xUOjtddGSLAI3YeLgEsEKUQU4hWWgVNkWCDPLDfDrdehayzoMORJUG1AUl14ahKMxW7SB2Dlkc5RKgGpHjxGCoCiuxLEj9qVJjoA9iNeGcp7Aiee8T8KeUovc9xiiUKfDIe3yUteNioGlbjC0orKUwFm2k+RpCJCY7TO8cKkSiEfubjVfYqOk3HadnpzR9RzUpeP3N19jfnVOEnrq0VJOK0lpUmqdg0vf3UUmzKzIA3TGd99vrzPuAiw6bFrcPnvVmTW4rE5EB4ekc8CmGFEUxEMe64IguELynUJFZoSkWFftVAfsHfPXRI2L0XC6vuTq7wt10nFxd8Gx5TutFoRKC/G8QO9xSL+Rg5YXUlfaFJ1l/KLDB4J3DGYUncLB7gDWaSV3Rdy2bVmZZZDyib3uMsRADRVRibaAMk2qG6iH2jlIrbD1hMdtjcXjIzryiWy1pT8+oPMxtgdEB4yObriUo8ERmWz7ZL7/+oEHaDFTc6kxmPy8vkgkV4xBgsvcf6d8Fg0leIFpMo0fWSpDkRBmc0lzfNHzyySc8vPsFgikpior9xYIvv/5VfvbznxD7JUF1FKmoUimYKxgS68ycAIhIxyCmgkCkUtnnMx2AMJhjy3eV8EIyQI4edLSUdsrrr7zO97/3A7737W9xOJ9TGejbJadnp5jgaW+W4Do2mxWnF+d89vwZn5yccHp+zmqzoXUykc5ZhTJi0A0GFz1RBQoTiaHHdQ3B9wSlQAvT1QWZWvfOj3/O8nrJfLrgB3/6ff7pR3/DqlnjXU/feZ49e850OqOoSpzrxE8weXT0fSfTBBFWikI6WTuLHS4uLmnahsViLkVW30vBq6EsanrnqKoJzgUen60or1sJfOSHWTAp5tTVnNnM0HUtFxdXRCJWK2azGXVV4n1gOplglWJWl6PfZZQBH3mQloADPTEIM3V3ccDhg3u88vAVmm7DR5/+nJP2M054zvGLGyo75c7OIevzNfVswrrvOTm9QFtDu1lSFQX37j3g409uOLh7n84BaC7Ozzk9OcHaisvlmnpyweHdI5RXnJ88RwG2rNjbWTCbz9iZzVmbS37x+c/pcBxwyHde/SZ3p4foHjye4DJLiMFcLe+hxWLBwcFeYtrK5OiisLiu471338X1Gwob8NJTp7IFd44e8Orrb1FPFpRFAVZB9FxeXPHTH/8Yt7mmsNB3Sc7RO3xwCTiTwlx84FIS3yg2TUPXN2T/K/GP6ZETHojJPiRJFW1KXOXgEDCkrisA2qaj1w50ia2qQfLlk1eVStIauSeJpRCQA1WJ55eGQQ6htliNMUaUkWJEMhhhulktxvgGTUxDYm4l/ZDdfvOxlfZ/imu5SNB6kGPmgjaDpdusgyxtz4WEUltTh8ky3rFQzeCo1BnJb4xInlKpk9+ssWmgTUhyt/wFExjE1me+/MrMqC7J+HOM3h7KdgtgVOPPhZcP0637LT8n8TPbChAzgBwHQHv4vVtnxABQK5XkUCkhC2G455nJPMrwUrkSM9CikjffbXaNAmI6RwLx915Dvubtz8vFU37GYzdfCg1jLaHrZfCcl+eUQZ3t9ZHB6mGw2rAW5HeF3GlPDBajKybFAoOlZ4qbfhF1+F2aYofv3nO8Pb+hPr+h3jni5GZJrQp0YSi0xZhJGjIB7qbh0w/eZ9daXv/ymxweBR5/+g77kzv8L3/0Fb70zPN/fLDm6abgwrxOe7hHX1fUpx8wufiEsr9CRy/qEi+sOZ88J5um4d7OK2w2zQC6CTNCQeghhiRh8xAV8909Xjx/Ru+dMGEJQ6FR1TWz3R26SkNtafoWFBTKCNgVvKyTMD5buX96XBdKCl9lDKHvKZ1hVhQiITaapm0hwmI6A5WGz6g0DNSINLzvOojQR/k85wM+7buYAoMbYLiI9Um2rsZ4Sc4Ncn5DCospxmRQOFsv3SrcGOPGNuipdAKLb+VS2fLGUOzMmYe7rJ6dQ/AJRE32Jcbio8IFYcouN0tQipvWc9L16NJSFSUx9Cir2bl7h/rgAKoKl+wHjBpBtq1NP+yvl1lFL8eazMiXvZgCeorBHkVHRNcV5e6uMEGdGxgn23szx0ifhiWNAwDHgjcEl5AQ+WlPoJjPmBwcECYTnBotXgKI/5uKW/EkX95WE/+l68vxAFLsZQsoJjfRUmEZwsAINUqBFhuQzCA1pkAbOwxA6buOzDq2OnkD5hi5BYhnVm3+JG0LYedZy3y+R9zr2Gk2XJ2dsbm5wvc9oXOyL2/Jp1WSGQbyIBs1XFtIMdgnBhxbChS5N1kanYcEEUFZTTFbUO8dEG2RhinlhoOcwTENRszXk5+xD17Ot2THILkQGCvn+Ah22SEXl9sygmx5mrk80y17HfIZNq7TvveiPjIFhbEEG1DTCeVihzIorJc1JedaImIYg1Pir2uVDPhJ4ggKbccYkdjVxlrJWaIa/txYub7ghWlrtBY2kWKwcsj3VcWsLoGyKCltgfPSbHLeDTmC8x7nnahughsYZRKTUuUUR+nucM8TIGkyG+3Wa/wdIECQ807kuFp8IIuqprHiy9j2jst2w9K13FyfMXEHzJU0EGPf4fAsz17QrO8TgpwpvQ/indi2nD47wXdib6NSPqBjBpoSMJZirk/EkO39PzRFUt4nfr8vZUIpDo0N8TG+DE0lnWK3hpxJaT0y1Ab2eBwbDSrJzvO9HXIdldmFOX+LSWa/DdQJQxCd1CgktmpqVeZ9sq0YksFK+cmqWyjsyznO7RiWgOp8v0je2Sm/GdSi6Z4PRYkSyyCigEMx/SKdwFiXbAP0EEHk760xxGwKmVDj4NOgHy33zXud5PYGE8XPOxSZjKCGOKdsYuor8eyMMatblaDKIVDaNCQTTS+ww9DAJcVUkNrG5PpdKxmQGvzA1M9EC6V0aq7eZqO//Mr3Nq9Viau3lQm/D5wdnpn/3aGXkUjvepQR107XO7SxZBsJlVmTKsoAplSH6AwauxwP0nq2WqT4wae8YoTxYwKrt+sAg4CyYXim6f9TzMqDpaMPVFUpRBQl/scKJT02rUmYooDhwVOV5UisiQzDnIY6C6TJkxi1WaElNhujimpUxI11DSS2ZVGQB8DngZQZbypT/RQUENTgEa/i6C7jekdRFlhrb8XF3EzKXqZ2YFgHqr5j4nratsFqJSCdibS+oWvbwZ5QKQH9JQ4JycEnV+e+c6yWa4hTlpdrNss1br1EEbB1wd7ODvu7+0yqCaU2FDrQxigKbB/I/s8osWTN+eRIyhGrthzX8jDekK6/67rhXoUQsSazsQUYr2wNJhP5oHMO1W0oCg0YjC4oCs3B/pTN/j6xU9xdrdg5e85qec31csn5coN1hjIqmriR2LdVcxNTPqxGNQEpR1NI/Hc+UBjN/v4Bd4/uIbwLwZ/6IBYfRbQElRuhGmMsfQCtC2xdUU2mzHZm1DFQVob93UOMmXATenSpibMVy+WK2jtKIsZqCiJ0kc45NKIq+Zdef9Ag7XZSmV9a5aEAaVCOeBwwDH/JCW4uetIG3uLWpsMyF0aSNKyaho8//Yg/+sZ3mB7sQQmbTvG3KJATAAAgAElEQVTolUc8uPuAz84u0cYRlUWRA1BEpQmqpI5qllEGRNJttE7SpRQIVEweiGPC4LMfSkiHedQQFFZNuXdwxPe/8Uf85b/6Ux7eO8JqRexa+psl19cXXJydsFk3LJuGjx9/wqfHT3h2dsrZaslGQVlXYBU+UemJEhRlQcvEahvB+B4THM51bFxL1IoFYoAco3jVnZ5sOFsF7r/yKl/66j3WXUvbNpigklTASyGrxSB+d3cPYqTrGjabG3zw1JOaGAMnJ8+pqhqF4vnz5zTNegyG3tP5hhBLImJKjYZZvUPVNxSlpSgLetdJ4NMFD199nW9//dv8+J9/RN8umdQTdFFitIBPbfIs6poGqzXdeoneWwBTiMJWzGdNWRY41wmoj2E2n/Ha21+nripeXL3gnQ9+zDqesmxO6EPLnJaf/uif2FQXfOXL3+Ds9JTLy2u++Y1vkAehPX72jPP1ms3ZCw4PDmnaG85eHNOtl1S7lqosmJRwtDfj6vqCrltTVyU7u3voAhZ7c6JyvP/b9zi+fkJVaO7XB7x2cJ8yatq+4/z8gmkxxTlPNa1l/6TDwhgtAV0LU1vARkl+PvrwQz764H1sYVA6oIzB6pLJfJcvvv019vbvSNfKOUwqun/5s3f49MP3qS0UVqGStNhYDaZkLECT+b5CvGFcwBeW9WYNRKqqwlhN222kLRbF/89k/9B0OApLJmILkywcAjc3N3LQqoB2UbzTUqcVJZ45OQGOUVhu0rxRgxdoZtMOAGUqPrQeD+8cS3J4hyzNiUNQGVkPKZnfSna3gbvRj2pM7EcwMYG1ScaVl2SWn2myRCvFMZUByhEaCCEzlCJEAbZHYECSABG7ZoZEYgds4Qs57uZ7npmpOb7m58q2HCb/M0nYso3D6CsbhkI3gyS3QdxRnRDzNPr03hgyIOLJgxIyUyMMYOwod2LLO/A2+Hsb1BqA7wygpYeZm4Hjz5kRUDI6DZrJCd+YPA8FmlJDIZvBmIG9osb3AnjnR+aKMbfM7m8DOinpjlu+6CSJIrJnhu+hDXU5x8SaGDS9maP2v0pf3eGO3/CDwynq7Cn7d2YErZkvDjBR0dCjNoHaVJLQK0+0a774hdd4/smnXKxumN+/z5uLHT791Qcs33nCX735Xb7y54/46/dO+YfPl5wzZVN+hztHDzjYfQ118g7r04+hb7CFsPwikcIa5ot5qt0i3jn6vhPgTKWhEYDWkqIUZcl//z//j/yv//7f88lH7xN1JGiNUxqnoKxqZvM5je4To14sgwR7yVPHxzUx7MstoM6HiC7EEqTbNMzsgqk37E93sEXB56tnNG3L5nJFWZVcXV8PTYM8rEJrRV1UTIqKYBVeC9Ojnkxw3rHpGtogtgylLjBBCtoQPUOPNo4MpYzcRG3IDLoQc9N5ZOoP6zmDBokVNEzklpUtvoF2bOqExL5Gg1nMmGLYnJyhEoMzELlpOu7cv08RFJeXl1w5ub+b3qPKgrIs6fqOaGD37iHTu4f0phAAXQJbYplsAc8qFQBJCq6HPUkq/BiT7JeA26E5E0ElkmQvlC2qnR361TXt6mbYz6myS+BH2FJmjZYqeU+ZwuKdS3mk3P7Zzoz68A5qOqM3mt57YdIoKeh6J3meLYqUi6ZqkqyOkLNsYEkPxTNDbMsFJJB8x+U8y0UMIKCaRgZIBdDGonWBUgbvY/I7HONoQn5SHpAKFbPFMPYh2YEk8C8I2KeUpg2ANUwO9tmd1JjLiu5mjds09DfrtG/sIJ0lATIS9/LVJ3ZejIM3YWY8DYUU6jZIloo8U1ZMDvax0yl59WYmmpItTUx+ojlmZ7ZnjopZvixAZYqUya8y+0JnWbQ8GvkcY3L8la9kjLq1/vJ7dFLjxJSzRIWwvpRiUpRgEohg07NkZBMGkdPhfZ+G6iQv+LQWc6zyIQ06Q4YjifJFDXvDWIvrnbCqtE7gS9w6Y5MSJwrDLeeDsvgUwfXpc0a1hw9+KNSHBms664yxQ3yJ5KF1kpeYbL2Tc6AhNuVzLOASaGyVJfZOvPddxGqLMZYYHX30nFxdcnB2zoP6Pnjo/BrnG9qmRe9VXJw8YXX5EFvXzBb7uHVDSF60j155hXd+XRE3cobkHEaeZWakJqCYpGrcVh8lGbOKohASgErYuN6H0TYvxZMhrqV8KZ8tQ7NaSzNnm8mbY3eWhhdlAoOyTYUecwVRWrjxOwRh8GdZ+pBLhOTdmogKkTT3IcX/oRGy9ffElDPmTQtD7jbE2wQ0Ds3wXGMnwGzMOdO7t3Lf/PPye/0Qj4YxPzHSNKJ8BGHBaxJjPTVzhr0XtywlVKQsKwhyD1UUj2NiIAaVlBQ++cr7odkRibdUcQaFtgafWMBO++RFqSmMRaV9YDPrHokZ2gooZowGn+/vOKh3sMVSAmjFfJ/lkgBSrB4JGd6HLZXM+FxvN/y3otBWXZH3XN6DOQaEGNi0LVc3Kw7v3gEUwUPoRzKINZaowwAmp+ACicCSbQOsNmlorkjtSes9pnw8arCmTM8HygTMZaVbjGBtQW5K5/2YY61CY7QV3MRY8VCPCmVSXh9znaZA50bmcNgMrPb8rIhpcFtmdW/fO2QPiYWNGuoUnZ+ZEuarKN9Sky4B/SEGUaylushv4UsEwXIye1MhgK2KEErJD7PlRW5OkvalT8+3dx0eJ80z7zEhsO6WuHVHXZWEEHB9n7x2rTQQiEmiL1D4pCxYpzPg00+f4Pqe2CdQWEE1ec7OfMbOdMYrd++yO5ugK8tifyFAacJhokr1jh+C1wC4DoQRNVqjaCk7t+ph+fsQFUYrnPOsltdoYymLkqoQUF5rTVVbxEdEiEZNs8JqxWRm6WvDnf0jDl49QjUtq82GJ6fXrF+s8asbnq+ec9nepDPHJV96BZnFLw93OJMCsHE9hbZYWzCfzTE2ETldSI1uT2kUwYt1aDWrmU5mLOb7tMFibMnh/SOOHjxgWs2YTGdMJhV3D+9wdXXDr3/zHpfLJSYq+qKgTs0hH6HRHmMUtTOUtmBnUgCX/L7XHzRICwwywjEgjVRs55PHU+4UJt5zbnpJYPQSJFVeMDl5lgFcCnn/RkV+e/qUZ8tT3r73GtpEdic1Rwf7vPnGm3zy9EOqqh6Mx7UZ0XlhL0lintkBMnjHjJO8c/EfRnAi+9vGINIp6YAqbCxY2Blfeusr/OWf/QXf/tKbTHTPenVG23W07Zr1csn5xTmfPT/mt5895/HxCc+vz7nxbQJlDcoIAJyne0qSmoJzAGPiUPRF5bm+OqfYf8jaw6QqRVLABhUUxhSoScnO4T5BG37y09/iNoa6mGHKVpiDISXJyZvq+vpaDJmjdBfLoiQSuV5dg9IU1nKzXvHi/ELo/XpkPXedp/c9qBarC6wuMArK6ZSqKrFFwepmiTUF9XRKjI6f/uyfOTu7BCWd2ug8WaYZo8eHDt93GF0wn5YEOmJ0KIxEUZW83lSBsToFSM3+/n3uP3wTrxXHZ59z4s/YzBzORBa+4GBdcvrrd1k/2uHhn/0lzz9/wp07Bxwc7IuPpfecn39CYS3tuuH+20dcnp/z+LPHoIW5O59NUUpxfXXO1c0qBcqe2bzE4ygqy6q95t3HvyYCD+f3+Vdf+h5xHVm1K6p6xqSaU5Ql2jtJCpNOQxFRBrRhSLylyDcEF/jgV79gfXUhHmGFwdqCykzZWRzx6PW3mS12U3IuQfnZ02P+/m//b1y3oqpKqkLANBdEhlIwFl1aa6y1aXCPxk5KlF6K+TgBXajhwOq6foAOyYBmymisoO1oLfu+S4OAVEwDQ5zCRIuzIQFscjBopYdkQtisqcBX4qUUY8DH0dtOGAsjcCiMI0lGYyr25XBU4pEXc6Eir1zcK73FZIuZtaRSETzaFWQQSt6bwU6VmvZxOPAGQ3QY9jPpew3JdcxDvxIWQDZST1PbFSJZJL0hJXHRjN8/oxlDYpjuC4rB6y/lMSJj0WNSnQFG4hZgmX6nUlJQ5wFOQ9x8CYAcvHjVdnMu3ir2yPc7AZ+56ZWbd1GNjAK5TD0AVUViOGRGgwy/UfjkrQepOErsEhUjMaaBa+o2CzjLPofvT7puLwNtQvrzzGQ0SieJTrj1/q7t0FpTlqW83zlhaZLBhMSuRVCpbX5gnkyu0INnZV1apgUoOvpYo2f36fffZNOs+fMjxaP2CXd3p0x3FtwED9bitMXEAjOxaXAl4G548dljzPKK4Dsuz8/oioJN09HjONoraT79MUfzz/l3X36b13dr/q8Pb/hgU3JVvMLVzh2+8OARxW//gRef/lL8rongPb3rWBwcok2OuxHXryGK/UZdFbL3XY/WcHl1ya9+9h5WVVTlhD50KOexhcQXawvxsVYCAlpkaAMAXmSJPu+z9E+TimfvPQZJnIMXeWzwnr7rKCYF+zsHzBZznjx5jtUWW5aU1jDZtdw7PKLro6hGtGK9vKFtNlzeXOOILDc3Yi20ccxnE5St8N1aVAqTPUKALjVHI4FN19BHnxB9BOBSVgrfOEJbuQlwq3Ad9tvIIh/3ax7OJUUaCeQkqR60slAWsCjQMbA+OSO2HSGpD86uLuS8pmWjI94FglWUlSEoj7OwOLrL9N4DXBrepOIYL9KEmLGYAbHoSPEsyu4mX/h27BAwIbPQx6ZMzKzkGASE0qAKy+ToDqBx1yvyROsMwoY07CM31AkCoub36KgIyVbFK6hmM2YHB6jdHZoQB0akUhqdrHuMIjVAM9s/Baf0j4jEIxez9JuhgI+5uk/gSgY/BH0WYE3mE2Qmj8RS8YYL+OBQ0Y1DOpWQA3JsIQ1w9NGzzRglgrFF8n4d/4dWhDj68i2bVrxvdw8oZ3tUKJZnp6xOntP3ncTAxMbLzOE4Xvq4zraeZUx/JmdlTDlwKqu0nDPlbM7s8JBQWgETtxuCMbN/Bxxacp20TgziiSfrOzXmyLFawFplZTJ1+D37Z3s41q3ziQy+iadtWVbDpHiNJvqIKQqs0ag0sCgqOWN89Hifm3sJZI7CgvbRo20G1z3GjOenVsJyEzDQIN0OQ2ZaW1OgokErS1mV2EK+s7WG9XqTBiZJTPcIKJHVLD56Wtcn9r7Ge2kEZMm2MIjlU5WKovZAMYhOGG0BBPMV5r2P4zDELOGXfCez3FQCsyxeCRtaWQEp62mJC55mvcFfrykrCLHBuUgVJlRFiQuBy5MLLk5fUO3NKadTgnPEvqOYLbh37wHz+Q5+9Qynb1tVZC9+wW4yYSXnmQKm9wpKbXjt3hGn51dp32f8VQ2WEwEG1m0ICdBSI0NyyA1STpXX7mDXpRQkf2QZeiNryDmf2OZpHeBRIdL7fhheJ/mxGZRbAEpbdMz7RGIUEfFuJA5/PgBdSvIGHSWXi4JOjVYLW8z4oFJDR0m8lt8toINY1niMtrdyuvyKKMm1E5grg/qS2ikNXcys5My2N8YMKqIM9mijE8Al3zMqAX5ssjWQZFlRF7UQP5oNLkRUGkAh558HbdFInm9MIUQGJYzI0hbJak9eWhtsVKjBci09mElNO5sRmxUqxoFNSxiZhjlv1wOzWY1/F0IC5GMuT/A+DPhBHM6KeCv2vPzabgbIjsxJcc6pU56a4rQBoi3ofPIrjyMRTmqGoQLbym3lV2Yvd2Jml+fvIOtXaYPW5dBkLdJsmbxvrLXofG+jDNbKdV72fY0xYtIaN9YOAwmtzkSJfH+21HFDM0QPeVPGiG7NmQhpSJ+S2JZrA/mOqU5OdZaPYQtQVXkhy9qPWoh0csOF8JM+P6hAREBtlDTvCbJvTMrDSMveaCv4kM54kXyIraZEhAXsQ6DrW3RXo63kt13X4aNjdX0FvZfKNCk1lRUszJqKLsL5apOA5fHcVEpxs+q5WF9RqCVPn15yf7HPfDFl5/CK+U7BYj6jthZbarxSqKClKZrug0Yl/Cwz1NNzUFlRGtMeCLlIIyKEKh/EktCHjnXTMJ1MpGGBEXIWCq/FFiGqiFcdlh6ro2yvQlGWM/b3dugf9Nxcrrl7sc/xxTl96Fmur7lZ39D2AtbKJ0tsGHZhamQYK8D+um1oz3qa9YZ2s8EahVGe3cUOk3qGNYZqWnCwf5f7dx9RTGaYqmb/6B57R/eoJzOKYoJWUFWadrOhdp6FsThlsKYQImPn6KOmNBWmKoh0+KalXa1+Z2/n1x80SDsWGbl4lvCR/zuDPyItGGUE20Frm74egkgPRVoqkgqdunK9NTy5uuSDjz7kS4++ArHEUrMztXz5zbf4ux/9HU17QZW6OtJRHZllQ1Klx+7xOEERyObzaCkKUpKZF02MWqaZOnj14C5/9f1/zZ9+/485PDgEt2F9fcF6s6FtGk5OnvP548d89Pgx7x8/4aLz9AGigZDMqa3RoCTQhK2AJnT0uNU5VaAMK+f56MUJttihNiWxly5x6xoKVVCaCXfvPuRb3/86YVLyH/7x16jpDnMDtFdE36FCT9ACJPSto+ta+t6Iz8dkCjFw02wwxjKdzAghstk0NG1L1/eUhU2JnMFoQ990UFUUsymT2ZSd+ZQYejbNGtd0eC/Tn4N3LK8vaNcburaR4GysUNULTbtpKIxhdzZlUi7k/iuZYt52PQRFUShMUaRiKbGQMERdsbP/kHq6Txs8H774nOdmxVXhsH5CeHFDf75BnbeEg4b33v01Z2dnfONb3yRoxe5ih1/94leEzjGpJphJRVnVHD97zs2m4WBvD1NUmHLC7s4OwXlggyorbGmJ1rJ3sE/Ugc9Pn/Dh2W+xdsI33/hjvvKFb1P3e6hQo7RlPp9LEamN+OekiKrU6AeTJRdyQMk0xU9/86G8p5pSVgUmaFS0oAtpTBRWps8SCVHxm998wPHnn1IZKLUcdmVZYmOgVep3DkelcpdbURQl1mrariHLsZp2nbNK2bNKSzKKSJpijFRFgS1Kur4nOkdhLdPpFOc9TdPIIRVi6owXUgQmPG3Yg3pLjjZsyyhJbESGDQZga5jBABCoxDiF3KMbrjNPw87d4pgnoOZ4FH/XJ/ZlFmn+99HXLTNfE2CaWLaZIZN9ZLfB5MwSkSnXmdmQpUcWGQ6SZaPymUZrItkLdwuMHmLwFiD4UvI9MFfVOIl4uD9apcEEY/GbZVsvx/ThGhgcOvINRvr04+8mMY6G4pxkWZGtM4aE0wxPKgPcSmWvLzVcf34eZVmORQEw2h8wsF7SUhieU3zp+d26R2k9Z9/xkEz382vbEsHHICyKYG7t0W3wJCotLPWXPtNnalR6X1EUsle0wXlNV+5x8OrXmRze5Ythzds8xl6ccf/tH3CtZEJsumNi54AUd7aoMAZee/gap7/4Gc8+/IjXv/dtJgSevHjGi6dP+cLdu7x274jL8+ecvPMp33vwNm/9yZf4289X/PjxkmU/5QP1GsXD/wpn3iIev0PVfg6xxeC5ODsXy40ohv5BR5QWFUqnoaxrOudkLXcNP/nxf8IqzXQ6Y7X2aAIWQ/SgoqZQBTpolBlBmvHRqDEg5HUHkPZ+TNYKxCQ11Zq6nnK9WvPJp4+xhaEwGhMLbpY3nG82FIVFtY66WtAsb5jOatpNS13VLKYTHn3xDd7/6DdU5YS2aVjdLLm6uWZWV1yfn3Fc3lDXU6rZlMODO1hrOF9ecrW5whiZpJ0ZJ0MsQYHRv9Mk3vZIznEBJA4YUyS5oHhrheE+RPF/Qzy7iZFoFOXBLsZolscvCJ14aa67ltg3RBTVZJLYHE6k5cYwPzpice8eqqrxwQ17l9Q0UQD+doy75fEYRxbZdlwYnpfOlgdbZ0vaO9LICMO9MNMZ87uKy66hb1psLAZWe7ZwQIlkUsc0cT5E4Vx1Iv32KMrFnNnREWZngdNgdfp+yd9OJ0VSzCBfyINMilH6r7IENuBcj1JqGJSlsoJDjWDP+BJGjhSwyScvfaYUXGoY0qOUGjzYMykgexVvD54hAff5TN5upOaYki273MAmzgzcUow1jWXXlhRYzp89xXUtRfIYHqwFtvfYv3C+SQyUmJw9EbUSuaazmp2DPUJd4jVon+HYpMhI4FOmJsYYx+tOIFTfJ7BESQdS3gPgyFbCRVWijaHv+1vnc75n431jAODlegLee5rNGmPE6oPBQmX8TsOAuhDkjJVpg2QJ+ihlHv1Fhdmmbz0jpRR1Vcna1mYEnEMkJhaq1XZgExZWhjAWuqDrO0IiPpiY/AXTGuhdJyBSnp6eMCyVQOCqEl9BDcTgcal+CCFbN40g0ss+7yFKYz03H9VwZxiam0opXOxR3lHeOaB5+pgi5TCu65H5WFpYpACmpq6mbHRH1/RMpwuKeoo1llBm4F8A+1dffcRPjj8kepkSH9R4Nltr0xCfBNLmfaAUKnkWT8qC1x+9SnSep+eXA5s2782c3728brJ/4zYg+7IaVM78iE0gTghhsAcwCQjfbognA0+MGXOGbZ/XvC/G3EUUnrd9dLeaDDlHNWJBY2yJT9LrnGhlQFZ+JrPNt3I5n5mX+fuY4ZnmPGwAF7X4u5PbJToP6xQ1iLE2WaIJY7iwlqIQxqVLtjUwDqLz3ovazojtSwwB74S4oXLenpjecgP1kFvqrEhBfk9RGKm9yY0JhVGIJYcLaaiVprDl0ESTxkVFOZ3QXm7Ae7S1A6g9fi7icaoUOE/fuyGvZwBh5czYtk95Oafc3msDeeKluPry6+XY60Ogd46IFkUGQMIFfCJ3OBcGIDJEqb+ssUkZNwLpoNPwxTIRC0hN8lLu85DbMuAPWSYu53w6K7QeAUQlT0nqLAbgVsgaaRC2MowEl8xM3rpnclMhelzfDzXvaCsyKiayynoYoKyVKA2iSfE4JmA6JhzFpJ9J6gI9Nn0gtY5T7aV1HnxqBu/cW89LFv+t55kuQmJQLj6DNI2ssdh6gU17WmlN2/fU5YKb1TldswYXiN7jnacyhZBGkzrGp2smf9+091RUoA0XbcdN+4LiUlE+h8oadmZTjnYX7OzUzKY18+kCW08ISmzyXLIaiXkwZ6rlQxgHA+aGZlpUKU8VG50cs6y1SUWkBosTBfRBFClGmwQUO5wXQpGoNQNlqTFFxZ15yeuvHbLcrLlcLzlfNjx7dsnJyQnOrWm6jj6pBZR3wvCOilIbTIio3nN9fkXAs9k0omremVNYy+H+HrvTXaaTXeykpppMqGc72GrKZDajsCWhczjbgypRKrJcrvj4k09YrTfYyqLLgnI2o19fS+M9ZFWPNLWbzkme8i+8/qBBWlAvBaX0p1sBLAcJrW/LQ29JBuL4czqK71FOctL6ISrDTdfz/vsf8MPvnGLrjo0rMKHg9Yf3eevNt/nlb/8fylpTFBof3TBlMm51mmLsGcExM3TDVLJpGDwolUiTZKMrlCqZlzt8+c03+K//7N/w7S++iVId7fUL+nbFennN5fUNn3x+zD+/+0t+++wJTYg0IdJZQ9RQaI0OoBIzSenU5XTj4St7VQ4tHximEXoUp5sVs9PPefP+a0QMbdtiS0TaoQyu9Vwen/HNP3mL//avvs7f/m3L1bnBmILYXKPjBk9H1/Z0TZvMvwu8ilRVSQiRwlgm0xld29E0HZtNk+5TBhUVZVlTlRXewWTvIXfuvsL9e3v0mws+/+xjLi+WmNSNNDZQFjW2gGAVui6pJzvU0ykhdpSFYXl5xXwyYXdnwu58wvVyxcXVFX3nCUENbLXgnQSVqFJXTRP1hL2De9ii5Pn6BR+cf86KDe56Q//pivo5TMs9vvCtb1GqCZcnz7AqsJjPMUrY2s9OXlBNJ7gQePXhQy4uLjk+fkZhRSpaT2d0zrF3cMDzp8cioUCzd/QQU03Z37tDr1veffw+Z/0ls2LCrp2zX+3j4hzvZbKnAEEixcgFAKTCNU11NIm15H2Pcx1Pn3zG6fNjptMJ5aSiriaoNuBc4N7RfTSBygRCcGhjaJqGD9/7JYYWq9zA7svDPzRbh4HsYMqqlKooJRqFLajqEmsNFxcX3KzX4kmjxqEFbE2XNIllUJUVRVkOn0WUOi34gOo8Bo0LicmRipHBQ0frwWOJVHhmVl3wIfnRIs9eSZceREorspnEFkrea+i0t8M4yCfGOPjHRjdOkAe2DmC2AOIwFJDZX3D7NcrEQhp+IX9vU6zLkujfGQaUri2DJKkGTsmhvM9sxcWcUw4FqZGk/GX/WK1Swyf/WJLFmTTRNXfmJc7ooaO+LTXMANJgF2A0ZFnQIMOL6DACCjENkYuJEaKjDByQ9ZLPCDnoh1i7ldjKhUpxOQxcGmwY3K1CK19nRKwHBuD999zfbMORrSHydY2/byyqRPI1nls2+Vl5L95aeY2GJH21SQI8TEZPIMvtryFgjbCgekpbMJvOqO0E6wsaNcff+9ec1V/lyAd++Ipm9/gZb7x6xCb04q1ptBT96YiQCa6O2DmuPvuY1QfvsRs69quS1fEzsIrdiWHyhXs8/fxzTk6PefXOA7725Ud8+NG71Oef8e+++j2++/Ahf/PuKT973nBTHDG//wqzw69xdfEe/vTXLFa/YaF6dHQoF9C2IqjcqQ90XfJFjyp5dhn6ds10d4/5fM56fY0hyftcILjIpJyggyHbZYztlATypcIyP1MJXYlFjyRu1iRfPKVRVuO94+LyjL5pIAaqoqZvO6ZVKfHbWi4vzum9p7yyFLbg2dOnKK3oNi031yvK/YJZNeWqv6aiZE5NVBPQBTpAu2m4uLgghsBqs0ZZKKclWgdicAP4l0pwaaQk5okwAcbBPUNxlEBSkaJLAYLJTVo9rp3cJk7vV1bjVMQuZuyhuXpxSr+8oY0eW1m88+LLH4URpEvL5GCf6b0jgrH0cWSwg8gelU57+KXGndqOwwlYHNd3ZNwtAhLlPZLzwTwETmuF60VKba0laEM5nVLv77I8v6BbO8o0cMan84EkHSapO2XPRmGwa818d4f50RF2McMbkV3q1AQMKj+H9MMSUeT7ITJdNTTBI0jqmggAACAASURBVNpAqQuKwg4F7FCc5fhg7BbQpQdpvCSXETAD4yazX8uyEoa9lsFAznvJYbamSI9nSo7F8fb93wKT8rMh6iRLZQCdFOkzjMaWUxbFKzg858fHIgnN8YnkVzucA+pWXLwFvCvJvTwCsHoifQjUe/uUOzt4FKHzGNSt6zHJ5kwl0DkifrMxMgBigw3JAGKNBbophh2PUYlhP6jy1ABegAw0DCGiYppar0zaf2LTIY0thanNyDoMPjHoDH3vCM7jox/PBiXWPdn/z2fZKyRGYjncQ538sIuiQCFWKgNQlYF8o3G9o+2SX2FdUaZrr8uarusGz/0YRPnjhv0kwEceEmYLiy2krikG2XCEmO2W5DySvoYfGgGjjcC2XF4aElrp0eIkW5mQ1pkSxUQ932W62KO5vkzNGsO66+lcTxEqtBKmXmZfL6+v6HvPrCjo2oauFTBNW81sMWN/b5+JqWitIpiQgEklQ6bSx2dWMSmWKRRKC1EE1/Pjn/4chZb5HSl3CUHOR6WElei9+I+W1g4A1cvgi1ayd4b8KsW8nFnl5oh3MpMhx6Jc80r+YFH2trVAHiyNSjnwEG9lffsBTCY1QRgYdT5E8asOEBFvbwXjuRhGpWeObcOAzISNbQOBA2FhqzbPoKrWhqKuMMDNei3ycGOIXgYJCzFCekDBi8S86zphr1XVMChqiE8SVqVJqA2ltejEcHWuT/MoUj6VlEvaGIwSKxaUNHAtpIaN3F8iFGWFQmJC320otKFOTYbOOYI2hNAntqUAjDbtgRA8JoIpTHpGOQ9h+M4xJuVOttTYArRvA/D5/nILDPz/A2R/P4lCnr1L99DaEjf46KpBCSIkF4YaI2kPUBmYNsIGtLqUZ6ZU2j8m+YymRo+4tKecWf49z1hQUYBD0lmvcs5BasZ4lwmoci9Nyku1kHWUlkZbjAw+rrJPMvNbWON57WWsJa/Ll7GhvHmGdRtHWxGl9MiU1yYxn0MCZxnATqmpR4BttJmRRqfzjqKQ9aO2WOqkGG7SZ/fOpdxCrs8UYmMzWpwoSjtHaalxCztBzwtMYembFaurC7pGBuKpKI3zoNLvGwrOnK2M60QUe5Eehe4VqpcG4ovrjsfPz6krw/7OjIP5DtPFhMms5M7hPrbUWFtjdJm4DxqlgmQuqWHuXZ9CjwDf28A0SupYYcA7Gbma9q3zDm1F4ZD3skKRB7OVRYFJaZFSnlgEgu/YqRXz+YLFYofDxX3efPCQq+tzLtcbzm5WrNsG3zYE1xOip7QFXd/Tti139g/Z31ugUNw5PEzRs+dgd8Gr915jOr2DMyVtmq20bjs6F2hbT4yGoqigTM0Q79DWoguL0opqPqPfv4NfrzBtR7Na03tH7HsKrXGFIRrg6ne2NvAHDtKOBb/a+rNw6+/HgDYW/7eTYJI/iEpJluwCAZNS8oAieihNzYvzMx4ff8wXHn2RrlWYcof9RcnX3voi7330nwjOCeNny2dGG5sSs7wBR9nXCNLIZnGuS8NTJKmw2uKiYree88M//hP+4vs/4OHungzw0h3n52dcXZxy8uKEjx4f885vPuJ4fclay+caa+UYUCLzzqovNci5R7Ajd1YHAC2C0hYf3QA0n91csNfssj8/lGCOEXmI1rTtiieffcykCHz7u2/w3/3wO/zNj37O6WkCfTeRrm1ZXa+GAUzN2oGR7zCdTpkVc3wING3HerOh7+XwKMsaiPRdDzFiTcXOwRE/+OF/xptvfYl//Pu/41e/fJdufU0OMhoFQWHR1LZkvivyM11UTCYzilJjNDy4c5f1zYr5pMQYw2Q6xRYVGsV0UhJdP/g2kUA5SXI01WyH+f4h0cDJ9XOO22PasGb12Sn2M3jjztf58x/8kKDg7//6ryk/e8rBvQeEGCnKis+fPBV/temcpm042Nvlk48/5ma1pCws3jtCDEzqKb53ci9sQTSWyXTOfDanLitWzZLffP5bXPTMqhmH80MKVdGh8KHHe0fEJCP+/Mwl+5Fp8jGt/9ygkPX48UcfEmJgPt/FViVaW1SMzPZnfP3b3+HV1x5RGjHY1go+P37KJ799n8KEYbKpkUp5SBQyg6RIyQ1BrAZQYjtRlsJg8S6wXm/YNBvYSqCz11ZOSMuiYDqdorWh3TRprUrh32wa+rYjRoP2IC7LIjd/WY4uHVp5yBqd5FZRfHSSpyHIPcoDBvOgnizrjzFKZzlGGeyXJLgDvJpiVowBFRJYN6Ca8vfBj4VOTtzyYI84/Hy6xgS26mRRIp5xqYgcQNcRrDVDwpEZOxB9wCGH8fhVUtEabye+A1s4AaE6JSXOOcqiRGVwNRdbIUrBGZM1Q6aL5sFmW7E4N4gy6ykD7RFJipPPRB6qLr+TNEQid0JVspvR48CfPFAu56hxYAuP61EK5AQeJ8sJpUbWy8sesxnsFX9JNRTG2yDRkIJvF2QvARFs3c8RKJH7UpYlVhs04NIgo1QqJlBXklOjTQK6Mivu9mA5EDP6uigodUlBAUwJ86/Q3P1z1vGIb+0E9sMZd3cqDo72WLuWTkHEoqJDx4DvO5FP1yXdakl/ccrbr73K088/4+t/9hf0Cv7px/8v8zu7vPWNr2Cc4/2f/5z12SXTnR0e3LvPzeU1lz//EW88/CL/01cf8dq9ff7m44bjruSqfAv74A12995i9fjv0Nfvc3euqXxHs9mIdxcy7CgET+hlcI1yOk1yD6zW4jNrrEV7L4BZWopVVWGNpU/lbwxKpI65VklwbO78q2SUKphb3mse5SPzskL5llJpvvzVL/Ls6TGPHx/jgkrOOJ5ZWdOubiijsMVWy2ucsTTrhvnOnLOTFzRNh28DxbRmtboi+J716QVGa/x6zcNXHtLgU+zvWS+X2LJgMp3KoJwBPI/CLNFSFGyz3fN6zAlwzj3E5geEdSly2W3WRo4ruZjUSTYaYkAZi92ds9CwDBHXNPRePDCbrgOjqRYzpgd7lLMFThucF1/dwes/F2BhbPi87LeXh6YOgG0CYXLuRirItnO7Wy81/iwJuA0u0EdFMd9lYSyb8wvcupHCWMXB/xOSlU2UItUr8Eaxc+eQ3cMD9KSmRywOCFK2hhjT8B49PINtsCIOIN0oBxVfO7s1/Oo2YJPBjMx2UckzPiBNQgEc7AjEJzAwgpzj6TspkEGg6dzcZtzlWPRyI3AbsM1nSrYYQ41FpcJTaCOTpInoylLu7KDPxBYD4mgpRsL1tq9zAC3GP1dDdExHmYJiUrNzeBdb1mJDlGP4FggxMJDTTw+eh0Ti1vXmZoGA4KS9v8XidL2wvuVSE7B4W50yPMv0sCJxiMN58Kzre3xhkcnqcXimwvgTf1el1TBMaLj3WgaRZA/FDBLnqdhKKerE0DNG2HzWCOgRtKXHMZ1OCTHQpu8zsOrD9r0exzDla6uKGqstmyjr21phcOqYfX7ZGlKVh09tMYy38qFtJn9+Za/VthWwbbA+MTo1V1SKuRl0NOh6TndxAT6gAjTOs+k6ZuUOE7XA+BqZNGDYXK+4PDulixvmizlVOSdqSwwCls8nM2pdUMSeoMVnPGYDYUg5nEdZYQuanE8oeSa6rFAUoCyEMFhjCag77qFbjEcS0JNA6szMzKz6QRVBlFwn7eHtJtsI4qR3xjG+ZzZaZvNlIFBkuzLgMkY/KieDNOJynNJapNdGK1QU4NoojUvWTwZh8BqdrJPiaKUgMUAlJr80O7uuGxpL20zq7XWQ1QDWFlij0F0rVjlpPznvky1RhJDOtiiem1prdKoltMqN6uFDyEOJexcoK6n9Npu1POdsyRCCSKa91LgesfYrbEFWvUqeLaw+mwgHRKhNwRfuP2R3WtE2G56cXnDVtAmMz/mjEsIAkGiEA6N6BGCDWFikZFepcWZBPuSUEvZmjj9wW0mS19r2Of/yGtyOe9vviSGzLB0Bk5R/UhcQ41BvxSizAUDUtkEptFFgLEZJs8IYYcxu5++y7KUJJQM0GXLnSMBKd4DUVks/p2SAuTa4vhdiQGL0agAtNZRPOYNJ523wspqNMaIKjFsN4ShWIWbrrBlz/5FwYkwx5ko6zQQI2S82kZhcvxXX5D6HGFFpr6ikqhHbSDXkU4E42L0IyCzMZa01yiuCzj8vQL7PNWHIFiyyZlzyb9bCoJPrI1veZUWQwdo5dlKgvGIZz2nWDT4PAFAMDZYMkG5toFv/HcZsDYA+wsYHrtaei9bx/FJmBpWVYX9nwuGdAw7373Cws8+krBPZzxB0YuGjBrA64onBgjZyr1TIQIR4OmdVI/LHRmeLQI/WJt1PxJImyu2wZZUGl0HnunTOOjmzAiwmNbuTXe4dLbjpHC8ur7m6XrFZ3XB2+oKN36CR53twcIdHrz5ibzZN9ZwQGcqyorAVGMVkVuPNBNUaLi7OOD09JfrI7u4BmILZ/j5TI/mhKyx37x7i2obVcklUGqqaWNWEvgeTGhERut5BaQj9bbXF9usPGqTNr+3kfCz6R5aSLIg4JG8CmwAqS5TlQMuJXowyMV5yXTn0NAarC1ah5We/+QWvvf6Iu0d36H2NW254640HPLz7CscXv5XPtgptQBfiG6IyIBvjIG+VAWNJppcClbElEY0BilhgvOGtB4/4b/7ih3z/q1+lKg3Od1w119w0Lacnp3z26Ue88+F7fPj8lIt+A5VIQ0H8+gbgOWXHHj8ATAIy5ER7NKzPnVe8bE4dDDpqVm3Lb46f8KUHFfcPFmhbMZvvUtmS4Bsul894990V7XrFd7//Vf6H/+JP+d/+w084e1HSBdhcXXKzWlNqCURFmo4dgyR9XdfStj3NpiFEmM5nxI0eZO0mJbJluWDv6FXuP3qNd379a/7hH/+BOmzElyQIoFHWNQf7e+zOF2gEzCtKkeYbDZUytN2a5WpDWf5/zL3ZsyXXdeb320NmnvGOdWsGAYIYSQAkSImiKLGl6O4IO8Idbkcrwg+O8H/hv8lvdthWR4fDg9zWbElNChIJAmAVgKpCFarqzveeKTP34Ie1d2beAqhwOPTAwyCq6g7nZO7cew3f+ta3CoJSnF+uCdFRb1rmkym+9RRGkYc1dY4uaiIlewd3GU+3OF+tuPfoY46aJ2yKNfNru7yx8zp/9JM/4tsvv85nn97nH7a2OTs654033sEUI+yo4uj0TIJz79nf2oboOT56zvLygv3dHXSMuLbh4NpLrFdLXF1jxxWz+RyjFbs7W2jtuffwIz59co/RVsmNrZe4tfsahJJIS9OsAC0C60kPWM5HZguoBFz1EF1ZldSbDZ/86mOqyZhpNUIcnTCFdm+/xEtvfofJ9r4Av0qCqPuf/JLLsyN0lCqZTgGwTpORlJbAqHXtlcBtNBpx8+ZNvnz6FKM1RVlxeblguVyiU8XcOZd0AeWMurZFGyNsEm1wzjOZSKutbyWxCE5a/6uixLcObVOoKdEtQ0H4mKasK6XwaSJ71vkjRGl/1dL+q3RGT3OrVOiGjmlNxyZwuUUc1QmpkwDWzBSSt8ln7mqwBQOQBZKGm+6GMmT2gk4tUeLTxVmZbFvoh1QFlyrQGmnLTY9cK41KZycDoDn6EO1fASySH+yDQJX/k9ZMD5NX061ziMLm1kp3gUa+t7ztWpeCWXLy3DM7us9M1+QHEgyFtRhrqOusG5ueVceYzWtIB9YolYFrTx605IOTIo6GGDXgAGnBGbJWOrYKfQLF4O990jQMjtNeS3+XP2WIhVaK1rV43yfSEgg6qtGI6XTKyckJbRBGkrEmdXmkQT4xdoL8Xw3eRa5DG8OkGlOqEh9KFtVdLg9+zNLe5XoV+RffLNh6+CV3X36JjZ3gvELHFiK0dS2VfKuZzecENNXMcBYVK2P55m//HpNrN3n65AGvfvPbTCpLc7hkV0147eAu9WbFJx9/wMW65pVXXmV/b4/n9/8ePfuCf/3WD3nzxi5/cm/Df3q+4bgZ4dS3mH/rJpPNR7SLj4nnn7O+fAShpUDRRhHX99Z3AJxWkegddePFvtsC1QqjSVsthQLAFhYXBYw0aZ1VrgSkVw8QRTKPllzACLBbTrgxnVPUDS9t7/LGSzepD5/xTCvqVtr/d+YV77/7Fn/zd3+PC5H51gwXPU3dMN/aYrPZcHJ6jDKay9USfWZp6jWKSLTpPG8azm1FKA2TnS18E7HeYIKm3TS4IC3nUUlcYVJ3QPRB2JJGded3uCdiCrm11thCJU3Cq4mKjwlMSoBcjJIwoSKNi2A1jYro7RmT1nFxdIwPwlZFw3hrwmh/jzCZsAzCSIxGoXXuLFJkKZJsQV6UwOn+nZjibeuugLsZXBiyX64A0rnlMH1Gp8/oI15Z0BZGY6YHkbDc0K5rfF1jjOqmK4t/UEStKCYjtrbnjK5dJ5SFlLViFL+iTAInevZvv5/6tl/ZW7ZjaMn/dWpfFuAg5WWd/ersX7JXRGHloVXSQ5dCqw8BlRLf7nODrF8vxXM1YfcdMNwPrhwWr4Z2LReO8MnGpcIUQFRRmq59BK1pJaPEFgV+3WBUbg1Ndnxgl7sNkO47D38cfnZIjKXdg2uUW1u0CHCuYgbpxR8458BESfh0z27sc4EBgKESq/mK7I6s9LDjYXidw+FP+TUsNirVd8X1xU2Ja6VdNiYfk1rXk1NSUZH697v36luc+zglgyVD4CUPeqrdhmALuX4fMEbJwFWgsCIrlmULssRGXvxcBO7avSNoZSlMRe1DGp4lIFw/DE6usSpKRvMxp+dniB4Csg55AGkqSGTyeH6mbdPivPjccZKWyH5NQFMBZqKxMvCsqohGY9AEAuerFRvnCNZTVgZrxLfZqNjUK9bLFaO54ex4zd27U7yOWAOXZ2eMy5Lt0YTT5YJgs4RUv/dlULNHecVivSCziI3RWGUTGBBRukjxgWhRi435aldn3ltaWQLSdoxRSaJIST7RbatckMkxZn8um7ZJPs105zekvd8XpBLwGuOVc43KxarUlRT7oku2pYUtsMZQN3UP5irpHEzkQGHgadBYyXEBFa52awCdhn4uPlzpuhp0E9WtY9PUaCS/M4XY3lFVUmgr/iztWToQUtPUdTrjAugIbpWLSeITvWuJUdGQNLa1yBRECZBlHdONOS/daFpbyZfTflephGGSbKLRFhU8s61tbu0fsFMpzi5hsW44Xa5TJ4WcqRgi0QlzXuX8O/mhzrYP4uxuz8QkvRV7coBJw7dDKiLKvUj+fsVGqaukgavt/D1O0vmjiLD5Wy8gahCN8jzLISD2t3WOED1t21AWJUVhsbYEY9CIDGEGLYP3KcYQYFdl25n0d3Ocqj2EqGWAY5qdIEPfDaptoShE2sR7tDWdbytNKdI3vhV7pA1Ga5HGcF6GvGb5yJzDJbwn2/thvNO2LUVZdLZfJDayDFEmP5gkiaMQNrB0OQupRnxa27SAaH6bRERpW4mjlRmwo2MkOpGDymdD6yT7oRQq8+hj7798DHI/yS2JjrOC6NG2ROmkLY/vZH2MEq1aM1GMygJtoF3XlGXBbDRm2TaZqN77F379q+f3pxhMQR0C7aaWa9u0HF7UbB17drZq5qNDdqYVN/a2mW1NsKUUvJJuWqpFCfnBJz8mcljSHeIJ3UwTUTGSZ0yUzuaYOlgigm2oKAXIEEXWIWqxVcoUsi+co6LB+w1GF0RgNCrYmR7grh+wvFhxceM6q1jTrGtW6w0HB9fZns6pjMirtJsaYwVQ39QNzw6fs1w36EJyo6dPHhHxWFVweXGOGU2o5nNCCIzGJVVpGe1tc/LsGefOY2yJKkaoosJWG4yqqNcrdBQJouAixT/xTH7jQdps6IZBvbyyTo4eAA4JFEFJEpOqHgEJOPuzrFLCmwKMIC1UQXtaIp8/fMDzp495882b6MLgTmumo5LvvPkWX/75Z1CkqqwyItyslIA5wcnhSy3zYeDMk7eU9oEgG7MyBd99/X3+y3/9n/HKjT1Cu2HdeNbrJadnRzw+uuRn//gh9z7/iOPVERttsVVBIGDScCGTXHYOTpUCq9IEz2ykM+CQAgIfs9h7JNe3IhJUqGLE0gWeX15ybe82FcL2LZQiuBrnI6sQefDoS6IyvP7dN3jnB+/xt3/zGVUxQ2toNitcvWJSVYxnpbR9ucDl6hLXOprW0bYOY0oKW2JM0+n5WFuileH6zTvoUcG//1/+PV8+egD1EjUKBDQqBmaTMdcPDpjN5hQp2alGI6qRaLlaUzAqKi4u4HK55NnxEdVpwc7ODlpbtAmig2sNjkBhVCfk7lNb46gYsbN/AIUMfrh/eI+NXbIpanZuXOfdm9/j1jfuogrLZDrnzTff5XjviFt3b3J5ecpka8KqXlONJtSrJS/fvc1yueD46Ei2gxFhbqOhrErOTs/SvrbM59toFSkLxWp1yb0v71FPG6pyzK35DfZHO7ReEeqa0LbYYpR2gWifqQQ6mdSaKQNxVKoyatCGZ8eHHB8fsTWaUI0nRA8xBGrrOLh1k+lsBirSuhZrNOv1il9+/EtI06u7QVdKp0Avtc/YArQwVW1igjjvOT07lUQXCRpbv8GFBms1TVOjuveQIKWqKsbVmNFYWNbitNL+TgwPWyT2QNKmtZMZygg7fDaZ0rQtrm0hAXHiM6SQ4nPkC10CnllPPmQtIdA6ryySuKQTo5IIvug7DUESkj5R6CxVbhelC9zogjPobZwkdHQBmNjABIxmcfhkU3ptyf5nuspviGRGqbw8Wdr1yueS2LMp8FVJ9D4zcbIRNkm4PwMNEBMeKUBCILMgZJ9lHd6+ZSjdmxLAt2f49GwnEp4bkyZobqE1Ep1gonQ8gAzdyEwfuUbSHunwUXJhCh9ROmIpJLB28u8IoCJR+e6ZZAA5LVS6z/xsr7Y1ZUA4t33mPRBjRMXQgeQxQnSyv1SMIpmh+wF4q9WqK1AordPwNHl+WcvSWumaCOk6ldbSAq6lwDauSqZ2iqZgrWb42U3a6SvQOH74esGNcEQbVqjRHS6XG2xZdSC/1pqmXXN5scCWI4pqjhpZprdv8+kvPuQ702sswjHt5ZoxmsMnT3nzO2/x4MuncHrKm6++yhduwerpI47OD3n85Cm3Du5w59ZNvvz051yb7vHfvvseP7ic8D//9Es+OlKcbm3jp99lXdxgK0yx6w1x8QQSeNgSsEH8aFQKZQ2FrRI4IAmZMo1YOyV7TPrdIrRemP397panp/tYYcha1CkeUAp0gC1tuDWeMR9r7l7fZWdW8IP33uB777/H+eU5h4dPKYzm7Vdv8eD+PZ6fr9Basb21z3S+y61bd3l+fMjjx19Qr864vDwTsENPaJ2j9Y6maVAhUtdrNosGaWbW1GcLZrtzTCuHoYlO9m5mNCYmk4pgsR3ok02QIumkCiyLdKdeBe7EjKVziLAGMoMrhEDUEi+JHJNFz+aUraPQELTGjkrseCyDxrTBJp1+YTakGC1pGmpFd/aHrLuuEJIKOj4E0cqLfVt6b08zkDFg70SVEu60LgaKQmxCxgCVEp15W2xRzXYJTcPZ8VE3XEc1Ig0QlMIWJeP5FuVsSiwr2tyCmix4vl6fnwG9vQ7Rd0wf0l7M4LHr2Pd5/TOJIJIHSUriKPGhSFDIztVkLesog/IGzxrEt4uJCp0tijlBDOJ7X5TC6QBNqUAJqJAluJBkVqnEph3YM48AyDF4mcasclFPrrebppxA1f46Ff0jk/1my1JiAicM3CxPM57OGM/nOGPT+wzi+oz1DvZ6nv3QA7ACTrngOqZanh6uMyiCFBLk+aju+lMp50rrsUnFgyHIkot5JsvEoJI8gKyFS7qTJktOpD1irUngRXoOsU+dQ4iYzMyi+zJA110BovuojZXOEi0Aj7CB5P2dc92AonwPuXARFZS27N9cgQqeyWhEVVo29ZrG1yLrgUpyT+nZxkjdbvC+Tfq28gapDizRUB9KEdPgPaLIfCijQWtUkkTQCdwCGYDnnfhDU46IqpT9rALLzYa1a2mcoy082qTBf0EzqfYYF3u8/sa3OT4/wRZzDI7NxRmjQkgJI2MoIlJQUH0xrt9Pafi0kZizbjYCOBYRorBJC6PS7hYgOhcDhwXl4b4M9L7ZIy3ZKvl9ARqvAvB5M/vO3qSCQpIwUyrLQA0encpFB3ob5AIhsRh1ulZHvPI7IDGaxvSxIJk/l/aLkpbv7m5ix8FO15K7lgbx7iDWzXm1Tu38nUwBYItCOjWCxJmzcsbBfJvDkxMuo8ggGKXTMEW5AudDd97ynhLdbyB1hhKlgBuIuODxxCSlIJ18ApwHaZdOcSyIFq5SEtUFFFFrpD1OoYIm+EDtGpamYu00m7Yl4tPAYM2oqGgKhatlL8coxQcZTqtwjZMbV31LfQfIJbBfbEHspNiUVonVnW2RPIe85kNQdmj34Ou6uOje34dI6wKhIHW8IWAmYhez3m5pC0ajEQBFUTKZTNjUrUQnOkmDIAWM4BxoI8MRtU4gW+gLGGTbELu9nfodks80OO8ylDMoQAQZGo4UIXI0E5UiEIiaLmYwxpCHucnA5cyIV7TBY3XikuoiDc8E1wZ0MCKjg+igK1SybdmHSSFHimEiVRaDANoAWSYRwW5pmpY8ABUiykpBTz5TsKisLa/TQDVFAucTi985+UwBNaUIptPe10aASR3TvtEKEyIutHgV0VVFOakoG0/bntK6FlWWEm0MGfFf2R39K175bo4p8r/6f7gQOV8tuVyvqLRiZi0nW3OwsLU95ea1a5Qjix1VmFLkQgqtiSF1yKViZRpvToyOsrCgrMSvXhbVdPl1Yvor+bp3LaFxKJvkgLTgfUVRCmM+VEm2IoqWetsSArg2Mp5UlKMSW4kUwWazZjKZUtqSeiM5kPctEztGoURvXykZUl96JtMtJtMRRBlI731kvTjn+Rdf0CyXzOcT5jsTNs2ay8U5zrWM9UQkWZQQO83IEIKlbWogUBYq0Ta//vUbDdJKwj7UD79miQAAIABJREFU+OuDpb5lNiTpAtlkuSXCB2mjUKoXbhdDKe+RNRljqv4HAi5q8HB4esm9zz7jW6+/i7IFu9tbQMUPv/d9PvjZ33G6fIadSTVEKPYRWyTZgQRUSbIDVpUQJDAkelSsKALc3NnlJz/6ff7lj/6QeTVitbokhIZQL3n+/Ckfff4Ff/XRfe4/eYxjDQapsJgIIWk50rNsOqFoWaguCMkG0mQtvtBXPpMgUWLFkVpETKLw20TTD5SVkQqG03hXE9mwXF7w+WdPeHq54e477/K9H32Hzz55grYTbseKs+efonSLKURvrWk3eKdZLDf4IEPVjPW055dE5aXKTwqhjObo6BmHJx+xaVtM9IxLUAR01Ozu7rK3tcWorGRRtKKaVIxHY0xhCUROTo+5OD7h6OSIo/MTmsZTacukKmh9w2g04rVXXsWWU9k/CSBBk9rDNduzXbZ2r+FV5PDyOU8Wj/EFWFMw1mO+9cqrHOztY7zldLEimIJbL7/CZGcbFCzOL1A+EE2EyjLe2+bRwwcsV+dMRpYQHbqcMptt4ZqWy/NzZpO5mGdrKaoKtOZodcL90wcsyjWVmXFz/xYjW3G+XHJ6ckhZTUQ+ICc1MSd5fStB8IFNXTOejpOuVOSLzx5ggmI+2RHGaiGOozSBGzevUxaW6D3r1YqdnW2+fPyYxw8eUKieoaZR1Ekc3RiDTYG4Tf9WKle4RXOrKir5LKXYrDcoREuvCyJTdTJG0a6dTiZyPoPoVPmNaEDJIDI50zYNdQhNjfZjyknFpBhjbYFvBKAVwKw//7mFJqR2uxCy3IEEBCTAuGe6DNpyY2aupupotj8ZaFRdk0kPiMY+yBXg13T3fOXP9PxyMPZiW5NKQXBMgf2QHdUH7zlo7oP5DJpA7ijwnR2QfZMYvypb3nT9IXasYp3XKw5scZf4yO/lGvEwoc0yBb0+IN21fYXRlJ+Aj5Cmg0YXcv7f3w/05zWBEjk5zUyE4BJDS3qw5TMH2uUoOvmX/jriFZ8xZCgM1zhfa57sCnQgfwgxFZKTduAA8Mm4RvAJyPEuDQsk6SKnxGaoi5gHwnmPygM6JBwG7yltybgqkh+s8PYao2vvsZjs89p0w+9/w9A8+Jwbt26wahuc91RmnLoFIkZHAbioCMHJwKrCMr95lypatu/c5YMPPuDZz/+e3fGI/W+9xGhri8X5BTdf/hbnlyvq40Pe/sYd7j1/zi/uf8bhasUKzY2dPZrFU774k1/y3nd/xLf+4HX+7EHNn3++4YHfZVnts765zf72N2gf/DUXJ59QuVPG0aMLjdeJXdB4qFLAqoWt3RSltCy3DmsLCmMpi5Lat4O9PywC9ANuuoIGSbIkne/oHGOluLM9xy1WtJs1QW0RVc322LAzGvHOq99hcXnGrT3Dqzf2ODk8prmMKDtjPB7hKbh555vM5rt8du/nxBjZNA2uaVHaM1aKcrfg/OKCTdOgleb4+SHlqMLVa04Pa+ykggQ6Rh/xJoKSWCezpjIIlAs6uQDSMUrJrbdij4SdI3alrutOGkUNzmJuzRU5F1n7ajphMhtLghMCylphMMSY5KKyDTOdbU1f7O1XTkJVbwu6b6W1L8qiHwA1+N0XQY2eRa8oiyrZQi9Fm6wtGSQRDIkBKpOXFbODa+lspW4FpXFa9PWi1oSikMQwSmtjBhl6+yvJV4y5UBO7pC7bnnwPPcOpjz+z6F62J5lFm61uTPYtv5dSisLaK0W7obFUiq+8X7emQ3sVUxKWf0bJvo+h/9n+XKRkOg6eGX1ruhfDR9PWwnZTsZf0GTynfFfyfHv5HHl/JQOLvJNusMJS7mwTynEHtEJiukXImuM5ic7gYXe20+f6DPindvu87obeT8rgKCvRi9bd8xmuW/bZne74AMyOpEGZCbw3znSAeAYWvM8DyxA5A2US6JbiCZ18TIwQFV71/qZMBbQsmSGauAGSpnphBewyRvZf3YrNVoLQJV+dYpB8hrTufZVS3fRy0bxNg2ZVyKirTOZOZznEQL2WDoLCWlCJhZg2YczPXJFsrKIobDd0zFjTAbQZFtQKYccpYQsGH5jNt7kYjQluRVBQty2Hp8dc25/T2IZCBYwWHUyM4vDxCe0mUlVzympKjC1ffvY5qm25ebDPzmQChy2qLGTwbZKtErOZCiP9g0+dfi1KaazVouOdnpV3AXKMkOyeGsx96ArvKQ+1RSGt053fj8J+0xlcpQNZc1zTF7AH/ilmHdVeKiH/nABAAzsSQjdcFCTWNPT+Lp1GKRCSAbF8/YhcSf7ZBGRKjECXTw4/L9vlofand9Kp5aPvfqaP+wIyFFrusXUt63pD61pc8EknWaffyYOcUvwJV/RSh/YxRlDe0yRfWhYFrRMtawAXA4pIoZUUtqMMUh5VJVMrRKs2RNbB433sgOTL5YKHXz6mMuKrz5cLebbGEJTFD7pZZN16jdms0+y9T9KI/Vo41/u4TkIr7YHCSsdgjDHFOqoD66/6lH5/DOP+F4HbbNOGgLlPHX0h2aqukKfEVpZFSZbqaFuX8pu8DwJt23TXEILHFLbbfwF5xkqlXM75FGNlWcp+H2Vd2iwHk+qT0kmWsZxkQ1BSODTaoKLk1NEklrjPg+tk/4UYCUkSyLsoTOEoUgYET2wDdfREJ+z4xvs+nzNpqF3siy1JDyvptOc9mGIrpHgmw5q1xB/aQqOxtsQog1GI/AXIfQaRd1RIzG+NxgdPZS15Pocy8qfWGudFaoUQk5xG7kaRYadKK1rvICp0UTKZ77DWlymfTYv3T8Kz/19fuegj/sMTcT5Su4ZFvcETsc81j748YjYZM5lPGU0q5tOK7dmI+WRGWVRUZSoe44lROk6UNl1RWxHxOlJojdVpHoDpuyAiEhNv3EZ8QXoVidmfSZO2UBBFL1m6JgMxQJGKPFrDfGcrsaojsTTs7G0TY6AoLYUVfXaloHGB6Bt0dMwmYzbrlewREzGqJfolp0ct6zPLerXFKrQ0bWQ0GjOdjgmbS+lOa1uUb6h9JGKIWuPbVqQjf83rNxqkzeHri4ZnyATL3xfwQxxPyr+74CHGSPQebeR2FeCdiHdn3xdipAngg+bSNfz8k1/xw99+xs7ubVztMdqyPd/irTff4y/+5j/S1huMEoMkVUMn7K4Yu9ZhrSIxtBANMRTEUFDFEd/55jf5N3/4L/jOG2+Bd2yWhzjXsNksefb8KT/7xUf87JNPeXi5ZBU9uoDSWDGW6WBqlZkcUlmJCSjqgJ3O4YvFyTO8c9CYwW/RCh0c4rR41lqsVmjladoVmorWQ9M0RN3QNg2XiwWcH3O68rz+/nvcfeMO4/mUqqrY3bvG4fPP2axPcG4DKHa2dlislnjXCIMl5qpK7ED21XpJ03hWyyUqRkxlKBMAroNiXBpKk4E5oPWMqhEKxdnZGc+eP+Pw6FCGudQbogp4k4x7NWKiC4pk6FeLC6Zjw2hUEolSVY8apQtCHDHZPqCcjNjYyL0vf8VlPIHCY6JiPp5x5/Zd5tvbbBYNs+0tbty9w+7+Hlu7e0wmI+7/6j7VuKQqS7yyeKU4Pj6j3myYVpKMtEFRTqecnp3RtDXKzqUNP66Zz3dRRnG4OuPJxSFOK7bG29zYvw0YrNY07YbReNYlvDmB0SoyHo1onQyyM9ZQqZJcRHBtw8MHn1MaA3jWm7UMMIqK0WSLa/sHFMlZjscjlIJPPvoQ1dQYogzXSUnbkKFGlCKC0tLObY3BFlmfVNqdRqMJzjmWlwtc2xJ1RFthhUnriIApXsl1lWXZBTNFYWk2NRtXS3LsnYCNIXZtK0bpThRcAoKYQGW6irHVJv1dDEBZVmRNJKWgMIU4yy54HrS4IUBBJxg/SI7l+33FPNuxXInOSWUO0F8MeofBVrZ1wzayfKZfBDLgqlh+ljjJZeoQkw53RglRNI1IPoi9ED5B8F3YDtAlJbLWOVikZ8MNkn5pZ5KWv3ztHTMkr08c/C4k7cWcQCT2FJLs5L8LGE13T92QEqU6vUqGSZeWqcU+hiQ9E/u2Oa2SYH1iGIXwwvr2r6sMNGGOD8HzPEE4gxBDhoMmtxymcsYA2M4Bd+yzHwEvUsAqci6yrzOQngPtfL5zTqx0SVmMycPOPDPc7Fuspm8yKeFfvTZBP/wl22PN1rV9Fk3NtBpJAQhp4zx88iWXp0dcv3WTysoQMhNLqGbMXn2Nzahi5+5t2uOnvPvm28zuXOfnf/3XVPMdvvX93+GL+7/i8vlzFmcLTFnwzvvfYbGo+ezJfZ6fHfH262/y7e271M9/hTl+wr959R2+f/sW/8M9x4eHK478nNPR99l95Rbj/X9g8eznhPNHWM4RBUyFDtJel4FGHTXTakyd6FwmKsbViMqWXPhFSsp7bT49BPS7QC6xGkNfwCiLgvl0gqsbzo9PuLH3Cgd7u2xNS4yCerkiNi0jraHdcHr8hLffvMu1Wzf587/8O7747JTWz5jOtnnrzVf57hsvcbnY4sGjRxwdLWmbBq0LCIqooW1l0ENRyHCard1dTk6OZQiUFQmiPP1Y6h2q21fGxK5jJhd/FCYNjokJTEBihFSkLcuyB7BiZttHOp3DGCXRVtI9EqLYLQG2DF6Fjq2iou+Y7C8mhl835Xy4l4kp2SZrisrPWmM7vzJk2UdUYnGl4ZIxx3cKawoUHhddSuyF/aJJw3NCwPlI0AZsGmKpNUqJOJiAVRqUJmhFbEN/LjOjVH+1SNPdy+DvQ/tkukJlKl4l3enOb2S8EWGelVWVwAuRYcgdJUqrK/FuZ1flH0mOqP9e/swr608GgGO3701iQQ0Lffnar96rQkcBUlsXks+INJsNoWkoEyCY43CVdaKT5qhSCkLo9q9rmq64qoiE2GJKQzGb4Y3Fu9R5kXydRkB08QAqJdQd/tj7EqWkOGwNKkIbWvEPXgTArtyPNkDfBj5Y3L7jIe0Bae3ttYNjiEkGQtbIOdfJQkgRyNH6hgxGeKdZ16HTa39xb8jk86IDd0KIVGWBDv2QmTY9c41I5xCTvw+O9XpDCJ7pdCpDVbR0AGXWo/gsL/cUhJGWCwzrTYPzSXMVOQuZwZeBFJ9bm62wvHI8FKP45izRJICiaCaXeRhmjm/IzMAMhmgZuqY1lTGooDETxfa2SIspIsrCsl6ybles2jWFbpmXJT4qXGh59uSJyMJoR2trbKE5OLjGpx99zPXbN9nb3cU8THZHS3ypU5syUWI4aVeWjgx5Bi5pncrz9F5mf2hrsMYmH507lEIHxEIq9qFovUh9FcaIL88xjaxwB9BmIIwE+OQCiezlq/lt/1JdfNn9SyGDzSJiz3MMmc9kTN11QVHHuiMmxRcKHBIb5tjiqjTK8DquxkW91EgmPmQwMDPAh8WC/H7GWlb1muXikjyQFgMqDFjCui+K5WeV49thAUZ8UbqWQnckgaZpyMNrdafjnuL4GCmVYrsaYU2kjoG4XrN0XrrvQsAFx+r4UHxSiAST97gCo0QOJ9lSRW6/D4NnmwqjtveF3ufBSpmSRHeNGbDvO+iS/M0Laz58Dr/OF135nqIbvpb3RUi5jvfiP3wUCUgBOgOmKlLMH4nKSMdHlD3cxVODHUnaS9IEF9PzyPMcet/YX2O/Z64WE1XqNJPVscku6kxUcL4bjGe0dDNkgLZtatp6BSEQhbWGDpE2yEDwNnhC04CHlha8x7sWrE7Dn2PXBSJdflrOjeoH+MYsnUMQDMlYyqIArSjLQgYlaotWBcE30vFVWpQuUMqiMKLPbKvECYqgE0EDYY8Oz1Umj8QA2ighH1orbflpsFieKxJCZFSNccl/FVo6Z338+vzm//8rFUeTHWuRQghKoUNgc3aBPb/EPJeCybg07G6X3NjfZ2u2TVEU7G1vSSEs25iQYx5hH/sQwCRpHhRWyTO2ti+I5v2c87426VhDyjFjAsGtPFtrLWVZ4BpHs26JROqmxXoZeucBY2W+hEn2Xgo2ERUEa7g8O6UcjSnLEW3boJXCu5rN2tPUgUYVeDx2e4vxaIZvNsQYKcYjRvM5zeqMolUszk6Y6AJNpI19t8zXvX6jQdouwacPAjJLavjKYEQ3wTRGou4ZIuKo8rAwuna0fAgUKlXUI0FpfNQ8fnbEL/7+p/zoh1tMijnRVuxXFb/z4x9z/4vPefT0YywOazzYRIfXBTFPL4yBAoPRluANKowZj3b58Xff5b/4Fz/mxtaM1WKBUi1Ns2C5POdXn3/OX/zjR3z4+SNa7/BGWpmkoC7U6+hFz0OGZgn4wuDAkBIfcSYpyIz91HmdgBxiX1Unb/Q0aCx6xXK9ovUt0+mU4D2tr9nUDt80hNiCEg0jZUrahw2/3DS8/v3v8uobN9ieWB7fG7FrRjz54hP8+ogQG5q2ZjQqadpNAvJUCiIlMVsul1K1DiIUXRYGW1rwgbIYcfP6DaJbc355yXy2xXg+xWrDcrXkw48e8PzZMxaLhTCDrQh6i26dJOgmHfrgA6WxWKXRUUlXjw4ykc9YIiVKzdi5dgNlDGtX8+T0MbVdEalRAeqm5h8/+wVPq2OKqFFVYOvVbexsRGs9y2LD/PUdtl7ZTvITMBlXfPu3v83tV6+JMdYFTfRs7+9wcfic3esy1Xcy3aaqxmxPp6A9j44esW5X7MxnvHX9da7Pb3aSFbu71yjKcd9uSGp1LCI3box5/KRJAbfodWkimsDp+RnPnj0B7Vksj1PgPycEy/6tl5nPtrBac3F5ztb2nKbZcP9Xv6IgsKhXKOOlVUXJwJmIBALee6qiFHDceUajkVSSfWC9WaNNy9bOPs6vWK7WEpyFBKxWFU3TopWmqCqapsZ7z2q1oigKJmMpADxdiq6tMYbGu1RoEL0traQI4WOQllQjOkDBZ2ZOP61aHHBmzhgy6y4nMMMqXdaqkzBPgugXC0f5T50crgBAOajpAVsG9uxFtsEwKB6+74uBegZ69QA8GCarV4Lvwdcyx7cDkWO+ZgnSpYVHfkrn4V/k9mgyMpJYDT2rOA/ei5KNkVHEISA9ZBq8GGDqpNmbLraTpRh+P9/7VfZtTubzr6oEMomeFEhQ0yU9ccDACFn7qweN89oMn4X4iv4Z5J/XGYwlgafSW46U6fLzyEytIdNh+Fx6lsnwfjOj3Lk8vC0H5qIrmKdK63IKeiz3pbdYFHfZHLzPhd7id3c2vNJeshMCB3dv443GFiVRGXy0XKwb6uUlh0+esjMtGBUF67NTUAW6rYlK4SYV8/EW1fUbbL/xFvalb/D06RNOnhzxvZ/8mDCa8vDJIa+/99uUr1zn4fIEVRTQBAosTVScnp4wm1Ts791msnE8/vAv2N+6zX/3gx/yi9MJ//3fPOLj1YyL4nXqay8x3v4t3NH/w+rZnzJePgUCTHTnu2IIlEXJaFYxagua1qGNZVSUVLYSJrOmAxxkzTN3KLGl6VmEeRhKSHt+4xUPnh0zNwVtUJycXFC3a2bbc3b292mW5xSTgovFguPFOf/Nv/u3/OQPfsTv/eg9ZtvX+A//61/xZ3/6F3zr+tsc7G7z7FBh3RHvv/Ydjo5OOb/YsGg8dX1JqS11XVMW4qNG0zHjZipFirTltVIYKxp1SmnR/4xRfDV94iqmJfTgT5fsSQup804kYWzPfNEDs5JZCpnlp9BYrdOUXdnj0sEgCX8GTvOZyO+RGUJXBmK9cJ5RvU5bvvaY2/JSTJI7FeQ96YpMUpDIhSNH1KITbmIakJTOWAjColERvAvCwM1nOoKymrKoJH5L9+tiIMn0yjWpQSJBbz+TKSEXaF4ssg1tSvYHMgX7qiZsTKxeY5QwKqylsAkoRUEejkIa5jNYv7yceS0635PsfE7Ic2iQh8FnkIYofjez72SSskpSQqmYaYsE6CshNJTSGRPbDdo70chVpEnz/TTu/BiHer3DPRBjJLQNRIetKrauHTDe2sKbCpskK2JaZI3qiqJ5qBaRfvCn7n1xp61bFFRl2e2xoQ3NAyOl9Vx3hbbh/s3AevZb2ZdpleL7ZFO6x5HByBgkLs7vR5Y2kNxDpb3tBz5QgIg2gTgCpjjX5seMsJCDDJq0lkIVxBBpNysyO1oZzbrZsGlqSdCTpETXEjwAslDSeu69SI+Jy3apSyZ2ZzfbAgGg+9gieN/pz3bnMBU7VfbDXQzV5225U6VPpMUaa22w1YhgGvZuXGd5eIJvJX9pg2fhaqaxYZzkUFCR1tcsDo9ZLS8Y745ZLU/Y2tqiHI+5fueWyF1tTzFlQUR1OsFlUQo7LxVFfQjI1HifnknWRVUQZT4BCmwpnSreSeG/Lzr38U3+ujUygKrb90NQM4Z+XyUDH1JeFlOXUh4eSrJleVbA8BxprbucDpWrPUlqKh0+Y2zqpkvSN5EE0MvnevyVokxMsgpaZeY8yZf2gOIw1sznangGuvv0IcXMJJDQEZUW0CrdY9CKYBRa+telFdwYxqMRFxcX5IF5XRyZrsKl2Kcsir7TQcm59kRa14gGNGLflNK4VEyIIVJaYTlnTqSxGp1w98Z7Wu9oU/4QlcIjwHfOAVyyT9paKXwlXyb7vQdcM/AeyP6gj8Vlqa4SGKJSRO8H++nXv16Mn4fr/6IvkqKDIwQZ0CVS3lfzjzw0TYBayVfz85O9IPHTECAf7oWQ2/CTfYREjjD9+R/e6/D6unsKeUBh2h8+AKFjUMcMfieww7Ut3ktBJYZA26xxzQYdwSspGBRK44hobVEEefcYMTpgC41TOg2Wa6ArfpuuwJUl5ojSyWatRaeuCNGPFzKI8x5XmwTuCc5QWCN6saMx1WiKMmMhiPhILAKZIai1EP1cU8ucwkEOqFDdLBQfAlYZAkGG6yYb47zrGL8xRKwu8KphUo0YF5amDp0f+Wd7pRgqv2P21T7KYK9IpPWejYssN3C5WnJ8sqaqjtDacHNnj/3dXabjEdOtEXYseIhVBmMKieOCo2lrIpFG93FkURSdj1VKcJ4QwAcnjOkkbQipiJhzO5VAeKMoJkVHHtNKU9fCZs15nnQEKEQjt8Ja2GzWLC4vmCsoqql05yhofUNTr8WfmIp6vURZw3q5JgbPaFwwmowpt+esjwvq0zOoG5QRENmHgP4nHs1vNEibjTNDY6R1areSwDrGXAEisaLkMEcQjR5ycKVTJbtnIYUkYA1I257O3UIaFxQ/++AfePnO69x+5S2mRUGzWHOwvc3vfv93OP7fvqT1Z6DFAIrTNSgSlVsFgjNYP2ai5rz2jdf4ye/9Lj967y3KsOL89BQXFIENpydP+ej+p/zZ3/+chycnbFQEG1FatFIFkpVhDWVRktICMRLZoab7VHTRU/c1Bn9CDwgMNS9DWhdJghWXi0vRDNGW4DUxOpp2Qds0Anip9FzqJaFe45tLfr68YH38Lm+9/02qb9/i03uGg6h4/sjjXc16vQKvGJcTIlEAPKWoNy1lWVAWlsvFJW0IKBVEuiDCZDTh2vYOd25dpyosRydnuBC4WF7Q1GsePH7Ms6NDCQwsWFOCFgkKgqJNw52ktaphZ1Zx+9oBu9u7GNsPX8oVW6UUthwxns6JwOXinCeHT6hVDVExLsfUsebPPvpzVCvTeUttWDc1S9cyMSWFMaIVozQmasa2YqwrZsUEWxVEVaRgDg4vFFtjmE4kiNC2Juopz04WbLTi4y9+QQyRa2afd66/xURPqF1LiJ7RaE6MAd85XLBGo1Tg+GhFnloOaT8kPbbjo2csz0+ZlgKQN7GlaVcoNcIUKrFnFePRmFFV8emTRzx/9hTfbgjRSwtf9IntmJx3Yka03olushHwo3ESIJmywBjLzu4uR8fHSa9PnPlsNkNrw3q1EVZNYanrTbdnY4wsFpecnp7gW0fUmjbW4khTwFgUhQy/CYHgpF21UFomarZSiewGbGUmecjAWcDavhU+MyOzjMjQv2Wm5Ivv1YNwye4EKRrlM4eKg6q5GLivY2LlAKZjjOazrTKDSJEr1MNAa9gqLKZyOChjMKm7S1a/ytrNTionk7mFP4M+X6nwdi1ygeBcGlKRBglBamGKV5LpqyC02HmXwZ4u2b0K0L4YeObrla8nWYSUXGltErip0Lq4EjjnZzFswXvRPg7tYg+mXNUrpHuvBAql4E/LBKWMU1wJSvMAmOFn5XsatlUPn/fwemNarJw4KaUYFQVFtOioadhjufMuq/nbbJcjfnI3Ej/7Ka997zs0Rvzd+fkF1XhGiCN++vN7bM0qfOuYBpPAgBqrHavFmqdPnvLw4RPe/+GP+ca3Xke//BaPVxecHB5R7e+xc/cV7n3wAQUl22++S70951q7ZnVyyMNf/Iz92ZSX3n2Hl19/jedffsGnDz7lxq2bvPn2Nzk/WdF89Je8v3+L1//z1/jfnzj+w4fnPLkcsSpfIRxoSlo4/Cusv6BVms1mk4ZHFGKjtUaXZZbIRsVcqOnPdd63w7PTnxGVwMLEcVLS3vfs4pRniw0jrzlrHMWnDzEq8srLt3j7m7dZnh4xH4+p28DFquXepw95/uwJR8+PeOe93+L0+Bjf1pQmsD0rWSwKbt7Y44c/+G3u3f+co6Mz9q5d5z/+X/838/k2q7rm4ZOnLJo1Z8cXtAG82sKnpM9HYeHpYCEPNMx7dAAaaqMxWvTwvvacQc/6U6qPr+j3KBEcSfs6tfMpo1JiTZcMhBfsyIt71gxAil+XmH2dpIvck7yyFEk+Ay/aIDFRgaappb3a5KElcr8hJzcutQsO3jwkPdigSMMnIQ8H6s5ZZ8d7TbfBcg8SnyEgTvdZQ2DQ+16ioSMHKPkFa/LgHWnFVMZeSYZVFAmZF9dPWNIpns1JTJc1JfBOCUCV4xpD2k+Ac62AGJDa4cVGxA4QomOrQNLVUwptIpvFisXRMQSHKmxaq9itSmaWqqzIrr7KBo7eo4qSye4Bs2u38aZKwzUz2N6vfZakGhY1Veztfn7PIXiUE+7+36RW4sH6chMAAAAgAElEQVQg4vzQ0msI+JJAeaVFXz8EKeSYjuUoRZOi6NlPMYYElA2YYel9jdZX9q/WdANzXyzSdRImuWCiZX+EoIjRDJ6TMDOttbRti0tTyX0aQOXaFl8LUCsau5IU1ssFRud1E73DEGWQZvQD8odLuU3Muu2RPJR2CGY750QOIO2lkPZY27YJ9NVYW3S/3+0BxLY5v8FoCGVBC/iUq126hjO3YRdPEx1taDFW4+KG88UZj774gm9fe4vLs1MmZcV6tWY+n7GuV4zHI/EFPqK1xMibzUbAwPQ8lJb77SUs0rMyZWLl0+mMaq1p6IsZPrguthoCUXmWQQy91nNn4+LVmA8kTnSh7YDXfG6HYPCLNrTfb/J1g4CFeXYA2XZ1uaCcTUVqvVagPMLQS3syZg3NVFTK19Gn4GJzJf4wV/Yr9IXlXMjonnGM3bwCIUhpvJOhmALDCdPfe9FDn06nNE1DWzfktm5RrMpzHRSz+ZzJeMzJyUkXo4pNEzKG956qLMnDszUC2BACCsuoqDDasnYtmyDfcyEI8ILk3KITTVccy/vW2ILWCe5gTUFI4HJMjDiVikqdhwgJazC9NFpX1AxRugdVlkLoNV2zDf26tR7uiRfjya8UxOQqZH2zvnHai7lATewHccneSh272opebxTAWgaP98xSIJF1+v1BYkPKtYt9GsodyPYM+MAAh0hxvE92J1ePoxTTtJE9JecqEl3DZr1ks1kRo8O5hkjEpmsNStbcBzBlhRlJ567SoEsj+FHqvGyd4BlaK2yQNclyZYL1hy4uUIjsgIqe0gp73WiF1VaKEa7BO5LerkY3DZvVima8AmMxuqQqK9qmxJoCrYzI2+gi2c2YBpoOCIbJrmRZP1IcGxMpKhK6IWiZ0T0qK2ajipG1nNdN3or/bK+rb6W+8h0XyV4QVGTloPYOtVnio+f56YKdpydMRxWTacV8d8Zsa8RsVLKztSWD2WLqstLiR7pcLcRkw/oikdbQE6fEbrVtwhdS7FPYMnUqRopSQFph8xqmMwHmN5sNwQe8jyLroS2j6QRrFIvlCUo3NO0CT4tvW1zr0UZLYd1HvDZEWpbHh6zqDWVZofwWVBY1rmiNYtM6tClZNuIzowuETfNr1/o3G6Ql12+zcVeo5AjISKt8F42iMCmgUSQkXn5GK5lwjJKpodlRSKugByXAr3RORtoIywiPj0/5+JMP2d2/gd0pmY8t5mCH3/r++3x07xM++dU/gFqiikYCG2UTKqHQ0WB1xa1rt/ju29/jD3/8u3zj+h6+WbBcXeDbDXXrODx+zl9/8Lf87ONfcVo3tCqAFsdllOiVCOtH7iUgmjq2sCifguqcZ0k0mBHoBOUOwBKVJyGrbt3yIU+/LO1oUYaXBe8wRqeJhqJ7snE1OvQTLAtjKKwiujVu8YiHH3qa5Zp3f/gW77xzlw+V5uLiHGIgqBOMrSl9g/dpsnhboxW88frrPD865PT0DN+KCLcPMiBsb77Fwf4uo6pEY9i/do3WtxwePufhF0+4WNdgSsAxHlUSNKVgzntPZRQH21vsjMeMtOH2zQP29vYwxtA6h0t5rwoBosbFyNbOnGo8gRA4uTzkpH5GsDW7k232x3uUVBBE90hpmEzGrC82nJ0cUWztCzgcPaumZrPZcHNvn7NNS7N0rJoGrcbcuX6bi9PPORgtePe6ZlGf49sG31QEb2hC4HxdsrpYslsaXtt+iz27hXYQggYsWgsDQMVIVopFKZSyOJ+KE6mClNkDaMUXTx6xXF5SjScUVYXZrAltg1cwKi2TybirMrk28OE//IJ6cYZyawoLRWFxbcOmWVGOpmktWwlSjKLQIqlR1xtUao8trGI8mTOezjk6OcJaYTiVZUW9rtHaUBYl3vlusms1HlNYS51kFpqmRnUDY/K5kH1dGENVVtQ5sItJWxFpdWi9gLs5afPdUIM02TZmMEd1rWBK5Qnb9I46BaGRFDSbdK6SPRLWSgJBMgAypKyRQceeZfRiMP+1oGS2AQNKlU4FKvm7/srv5n9nRkgGs7qid7ItMebxQvJDzgvgKm8er1zjkHWqUnJASHYlteYOwd2o8u/37Wv5ukwKTIzS3bPKg8n6pD52wV3+vczwlaiNhMhEiB5tjEi1iOcWtmDMKUFi5aYCntxbBp4zEyLSt4lmbor8fk6KO9+j6ECFrCeZhyGhJMEvrEnBeCMJ3oAVnI5rJ7vTJcBcffYhMUFEujCii4JxNWWkCsbaEsKEs+IVmp238Yx4a+YwTz5na2TQs5LlquFsuebifM08ztB2CtUel5s11/dus25OCQg7fVxYXGh49uRT2sUlf/en/ycf/uMvuH3nFYrxmDvffJPRK6/w5PiU+x9/wjtvfRu9e8BGG8bVmMlmw8HLr/L04efc/4u/5NXv/oAbB3dZLmvOLpfUVeDON25TOcuD+w+onz7hj779fd69do0//uWGv/vinFWomEzfZOrOub7jWZ5+SX36XCa4FhqUsIx99PjoUBiMEh0pldZRWvVzlhr7YaFKCaiVIocr5xTRY2c85vJshT8+x2rLZrXms0fP+OWHH2PDgm/cvsV4tM26NfyPf/wn+OAptOH/+LOf8/jpMSOr+NXH92jW13j89Av2Dw44PT/h4PoOu7vbHB2fc3l5zo39HabjGbPZN9mEwOVmw8OzM1ZWdbFPHrCXWSS58CEF7EhR2C6ZlrAox0Y981OC9x50RPVt4/lnYxQd15wEkN6fAQtGJZvQA7K5YBxTAt9xua68vq4gJEXzHhSLKbCPDPRGE1AHfZtxTlyglzhx3lNYafVuXJOGH2V2WJJUitLqLQCQAGo+DZwZsleIPZiaM8t85odAaAaqh7ZW1jEnunKf3oc0LyAzqAaAC4Op6enZBFwHRGbzljyQtF8r8X2ovnVXcPvcvi+gosrrrELnz2LaGwpAq27oZQxpUjjpAwfPCYSZpBPTz28Ci/NzaJ3EP1F1zDWUMAS1Mgm86t8ny9aYVMgLiI6cnc6oEeZU3bTdgJBcgFWRVPyStST0g4nyM8mAeG59za+Q7GWWA7kCdihZw/xePXAr/9MDYFnaMFOhMeSCoxSijUnPRUvc1T3h5Asy4KazzqBJoE4QBuxQOkFAdfE9RZIMkH2S9HGzJqJSVGXR7dtOGiNds7T0C9vMJoBRYlWFUgY9qlC5k6h7PgIsZTmTNk1t98Enzduk6a9EdipLTEmXlgYzAOFD7h6RAW06KrxPcFEctHEr0Aa8b3Eu7c3Souu852HdbGjaDQ1r6mKDcoam2dC6DQ8/v8f7v/0uhanYLFasN2sKo7g4O8ZqQAWij7RG5MGI0EaHDRqfzot0pZh0veKf22aNMQlUhjSfQ3fPB4Xkoj6Qh87GAQDrYy+ZkGNFsj1Lw4Sy8Y0qw6d0RaYQUidIaiPufj+zbfOQ1hAw2sjQLO+lUI7MtMg/q7TqBsJ1MZPKRiCfBcmhZaJ9SKBHH/PmrDGTMpxz3T4VEpQSbf0Uy+UYT3LhXPBS3bPPsVm2UXkFvHccHj6X90xSXN7JwOBIFMlCLXqxTVMnZrKw77x3HSyQJT+yr8rXnaWDgtY0SLtzfoY5qhUdTOnCyB2fMsCRzmcqrQhKoaqSaDKobfq412SZsEwOSxKL1mC06VrWfUhSKronZsg+zNqu2S9Fhl1Xw7zhxXi/N2+ZyY2cgSz/ELPvdMkXyn4yOR+hC/shBqR9XxM7Uo5sBpXJE4kYIcxXJa3vyR8JwCp/xtjrzca0lqiYopScxKR5OE7a0U1EulujdEfG6FleXkBbA54QapSKhDSHoEXIWDlWCnhCW4vfsaK9nVOVGGW/+QQyy+A6g0iIi5/vl0HOoXO+B9tTvBU6rEXiKx9lrxqEfCLrucEFKe5slJLBvdpgtcWWFaPJnHIyITSps8AUaXaPhxAoq1LyUC3+tXUywrBNhLnWOaJzsj+18JFNVSUb15kaOkPyz4nY/pr3kl2b1pukUx0AFfGxpV6coy8j8Sgyfj5ivlVSFYZr29vs7+4wH08oqzHjicVaT0GF1SUoGd7Xp9QifyZ5pgCzzreJYa27AjURRklSKiLM6DZ4lMp2Wvd+MOVkRWnQOtDULVoLa9e1GzbtWop7AUpKlELIlDrimg1x4xPhM9DWNYWFEk300AaotCGYiBlXIpOhDBw/+9p1/A0HaaVC0bUiJsdmugAy6/Lk05QCe1I1jzwYQ4L4EMQZ53YncZBqEJCKw3BK0aI5bx1/+dP/xI07d3h9PqYqp5TFCFMc8F//23/H//THlg8++Rl1vMTaNCQsygHbGs/4nXfe51/+/h9w8+Z1DJ52eUrbrFmuLji7POP+o8/52w8+4OMvHtEYIxNbte4CR2IOMlOFOkSULnDBYaMSUCmmSkF2lClw1VGC4L6yHZPjid00QXn/gDapwhrzxHuIwbNZLqnrNaWt8AGIitVqzcgW/XRgrVEGovIEt2Z1+ZgH96RN/Xs/epOf/PhlplXLBz8NrHRB4S5RYQOhZrVcdFXGx08eU9ct4/GU8XSKDxIEbE9mVLZkd3evYwGEBGTfuXMHZUs+vnePcSkaL87VqbJnKFTBbGbY35pyZ3+PndGIoigoykrYEWK5sUragI214A2Nq5hvbVOUGhdaPj+6x5F7hi0j12f7zNUWlSo5Ojxid2cPFTWVqRjZguvX9hjZEp/a9lVUjO2I2c6E5dkZzjqOFs+5uXOH69e3WC3O+fY3jvmv3h9jm2N8u6FtLT5EGhzr9S6Tj2t++nHFG9deYWsy75xuCDnVISUVuS6RBuYhGyCGIOwPJY7T+8C9+/dZrZcY7yiaEcp5olLM9ma89fZbVKWladYoraibNV98fh8dGzZxRXA1r95+i5PnJxwdPefG9QOMMTx69IgYPaNqhtGwWq2AzAAJWFVSFWPOLy65uDjFqlSFKioCAjZgDaWCne0dTk9PU0uaZ73eUFjLfL5F2zS0TXuFEa6toark+daqxXkn+zwVbqQdMwowayRQMglwy7IHEpyarmofFZCdXIiIhGHfYtYBq/pq8ifBlLoSSMnXs3P8KiM0J+8xJdz56/k1bBvMwVhOFPv37n92WOnuwACJjBIQqhJwG/u2tPT1TgNWRTSp5Y8UoA+Alp5ZKvvPJuqBMI56oDvfb78+XLn//J45UM0BkQTzVwPPmAAkAcLpbV6UJENpldgS6X0H6y4gSWrdy7Fmelbe5+QoPws/YIMh9lX34E0Pnuafpwtc+5tMa+RTYTBV3KWFSs6oaB+GpOssln74XPNnSLIDKsiU7KqoGNnR/8vcm/bYlWXpec8eznCHiGAwIjglk8yxMquqs6qrulXutmW4W5IhGTDgL7ZhGP4L/jf+DzKgD/YHuwFLrbYbKpfUre6ah6zsHCpJJskgGfOdzjl78Ie19znnRmYJsA1bdRIJkjfi3nvOHtZe613vehdVFIdlbW9xdfQH6PkbvLev+UcPNxweL/j619/FGUMs5vzVLz/iso0438HkktVqze2dgof37+EupITv8vyUT54/4bX7r7F/Y5dbN3f50d/+mNXqEtdu+P0/+k+obh6xu1uyOj3l8GvvY+/cZ1NMicBmdcajn/yKo7alW7ZMSsOTH/0EO5nxtW99k+X+Ib/+/O+4ml0S6n3eePc+x09ecPxv/5K7r73Bf/+dr/OTt/f5s58cc3q2R6y/zbL27O69g5v8FJbPidHQJZ3JAXFKczFwmBMoryXQMNLIZ2BqB9nbOcDJg+0jzWJD2HhWV2uKHWlSs24da6XYvFhzsDvh9eltHh2fsqFm2bYU1RxVTYjaUu5pmssTfv7hR3zx/AnPjo+5/9pr/NW//ht8cLgucHK+xkfD6aKlaa/wKko3bqOp6pJNHLGBE1aag5uUB5YANYL3gxZk1vfLwJA0CZE9b8ywdlVvW74c2OmMDKbPEiWU7CMNQFYGMAZWawI0+Sq7l+doWNc+2dvxPfTBhMpa1Pn75Lmzw+2dT051siVdxLvUyNU3/fP3zwujhl5QFDo1RxpKtLNNz9IufQCc1lNvU9LezSXfY9udn1dKXYcxzbZgDHxk5kfTpKZMRZGkKGTdyufmhkf0Z10crYUeMx6Nd8/W7+c63Ue64T6gz/ZpBCyZpN0o4zAkqrTS2JTw3SxWbC4viF3Xyw7hs90ebHQGSPPE5oRWDBIImbJidnhIsTOXEsmYq00G4F6l8rZeKzCvozgAtGNGoU2d1bfWmZefZ1Ztntfx2ZLXycCkFTBSALLYxwhEMKlTs8g7uV4eILPGQKWeD9sVIKk/YbpnaZKkkxRXfrLM8DSp0Ux/zkBfsj9em4UdWNdKKUJmRXqPNTaVhsr5MqnqvrIHlZOzwjqTZsc+AbX5VyRuKHSJD25UqQOFlZLeWKRSX9dJH4IRMBm8+AsZkEOlRnBANLn5s6xnm9mnE0W9v8vl4hIbwXcdF1dnbGY36fSSjVuhTUXTtagY+OLRZ/i24fat21xdnLNXWF4eP+Pk2XN2qpqjnT0uL87pyPGQgCkuAeMm+XchSV25MCQBXNf15dqbZtOvDwHTpOP6oFPsUcoOgKBWfdAvc5PAssQsH4CNwYbm3ZL3pk/2NWZWZoqVxAb53k6F5Cv4NA8Q0amZL6SqhrSEt2xbsrMkgEHkZRRDM9iRT4uAxlLmHfqmk719HPmsMZ3DGbwmjuQPGOQKY5BGmEqJbTdKS1OoJAGT10xm9roga7osK1mP6fxIQ4KkIfyQGFHynqG3AXgvc7xsNklP0mfvFq2l+XJUUhWQpRMzhUkxjJcCaXyYfpYbwWb9z3x2C0PTbCUVhfnpep/TpOSG61zfEyInWsR+5ITHYFuvJzzHf47904HBnZi0DMnVkJMFqD6Ro1PSOp/jIaaquBiSZKQ8r9YQU4d7oNex721dag4HubpBwN9eV94ODaKzJrxPIG/nut7WyP7wNF3HarOm3azomhU6BKpK2MuD9m0mUCSJEFQCiAPOtbRdHHrwREmWjWXfFGLyUaOzXMt7cozpg0cbRXCyKjJekkHpft+oVJ2sEMKcD6iUMA5K07YNBkXjPLaopDnY4gJrS2xRMpnO0bpAKbBWEaMb9eIQ0lUIQrBrm43oo2rBszLZpJrNMEVikzP4I///XfHav+Lo5YhL/RAUiqv1mqv1Cq3g2bMzbu7tsbczpyprqgoODyoO9vapbU1ZWIqqpDAKR8CFkSOUpLlcmoNh+Uec69iQ/ABj8CFVn/b3l1nfOcYH37WsFiFJg2nqasJqtcB7h0qxmnMd0QfquiIEYcQWVogTwSi8Bkuk22yIRqN35xTaMpnUFNMJ5bQmdB388EdfOYq/4yAtZJZTbzDDAEooNejV9A59TBkNnQoPtGxSn0SuQsyGS5gWWvf8w3Q0yQS54NkozYvVhp9/+HPu3jlg5+AuxirqAPdu7vIP/+QfUO7u8dOPf0mzWlKrivlkwtfefZvvfvBNvv3uQ3YnE0K3om2WdL5js17z9MUxv/zsY/72o19yfHVBW1uUliYAqIG3lUHjwT+MdJ2w/9q26wWjJWskB4vKTxKT3pwayq2ylY/JcGYNyOyTZkAlxshsNufo1m3JgGnVNx0IIdB0DVVVCwPFh8RO7uicxypPbODp5x8CHX/yJ9/iT//4XULY8Nd/47G6JsYrlFoR10t8oq53Xcet27dZtw1Ki9PWbhqapuXo4IiQy8asZdOuOH7xnIuzS6rZjNdfv8/q6pKLi3MmhWFnZ860rri5u8fOvEa5llpFamuI1hIQ3RRJ41thQyTdSm0LDAX7N/fRRtH5hs9PP2elxIDENhJUoJrXzGc7FKaiNAXz+ZwXZ8dkHURtC9pmTdd5qqpk3Ww4u7qgpcW5FTf3ZyjVcXbyjJ23Gyb+BOPOiDEQTRL/N5G2WGDcBtccoRVMpjOUkkxR551o7IV+AglOOp334BWZhZiDddg0G14eP0dFR8TgXEehRK329t173H3tHjF2gEdZy/npGcfPnuLbRkriVOTl82PqouLh/fu8PL9gtV4lJwtc2+CQ9ZIF3+XgMmhlePz4E9arC4xKDW2SffXIviNGrpaLfj8vrhYSyKbypWwHckDdB26pQZi2GnzWchTHuW3FeGaBdp9YIiTnIQOUMQaiB223m6+oFMj0mFAcZBHwIZUBJeMeUtY7DsFUBt4kWLwOYgxO1uBwDQytsd3TI+e4LwUbgSBj523rygE/ErRLV9rEREtOVI9dqsQWiDlATU5ntiFbBnr4/F5GIPahRzo7B6bX1i2pITD90v3HgNW5gDY52aSguQdhs8OYGBd+KC8cymByKVWy+RHGQG1+v+lZQNmZCUPgGyOZkIka65xmkHrUQG70bHneM2CjksOmyUH7CEhCmMY6gytqDPKk9QagDNbW1MUEGxUKy0btcFndopncYjd4vrevMI8+4uBoQqciy8srWrPL7PA+Hz66ZLHRzI1hZzKn3q3ZuMCtozt0/gpbF5jKMNvd456yfPbrnzOpI8vVU26EPf72336fh+99i3e//i57R0c8+A/+GLfxNKYAH9hcrrh1+x7vHO7z2ae/4s6bb7O6uORv/9c/Y3lyRnnvkDcf3KNZB06XZ/jDPXbv3WPn5hEXpxec/vD7vP/amzz8e2/ws6cTfvYbz8XGsWzn1MUdjFkxMQVtu2RiO9CWmDXKnMPYEmMLnI8p+JZxC2nuJFAYGHH5cI2QSi493bohbjw39/e5f+cWuztznh+/5OT0ghig8QUny45Xyw3nyw2FrSBY6ukhe0evcaNd8urxR1y2Zzz//DldF7npas4uTrn32h0urxY8Oznmzp27NC5wsVxxtVrRhsC6bXBlQXV0S8KftB+kuy0JmCI5oHrweUK2Gf0qToFH9gcixKyLp/p9lAPIHsBDGgiOgybvcwn5ABj2gY1So4BKLh+H5Mi2fjRfsk0ZANOj3xcbu53YycFln2xWCbxIjc0yozCEIE0oyGOUSgbzWojC1Mk2YyxhIkkoqVYaVzl8OSjOgOLAps22a9uejYLnFATmkvj8e5lFmZte5ksbBDyNOQweQN38bDA6QxgYVn0ZdxykYHIjt3w/g50dEhcqrZPcuA2GslaLQatI221YXZ7hlpfCrFUCior0TQJU0prI8y3nbAK1U7ltVKCmM8zuTbwtRMIskyhCb2pl3lOiUI/GePwc+ZJy6wgjrfn+HvI6GK3HLVYtQ9l3itTEN+iBbY3WMUkGbGvI51hknJDM4KP452Z0r2przgYG8AjgGN1v1qglvV4UxZaUSNaCzcCXipG6qrBKJ3a5TeCkprSl6PUndldfvqFUYpgFuvWStmv6ppW9gn/MYFLsAV5tNEVVEptGYiafgVx5bmu1sGfj4A/JV6azLQ5McQGwNdGWTA72WZ+cwnJJiIF1u2HVLvCThhA3UjFRlQRfsDg/58Xxc954632MLWg2a0LraJYbjl+9ZL/epT6/6pvbGBRBiSTYmHn8Veslx5YZMHPO4VJpettGtFVUVSWNbCLE4HJNDblsXHzUcfXTUMU5luTI13aV0vC3DBr0OpDXfA2l5F7K1Dn9+tXHiVmeKcfJyV6E6Ef+xiDHsi3/MdzfVuItxl4CJOSYHIhBmniFLD1gNJ0f2TmlUrJwpOF9bQ7y+KNA+wxaRwj0DRV98AlQNyJxl64xqN6XjFtZc1IJqvpYWJHkK2BoWhuGZJdO9yum26dzM/d2iUmWRQmA17PIc9OnDPOSSEmxP8f72DuBR4rtvjvjM0qGZpskAF+uoMvvG/9bGyMJGxAfk5gYq77/3aZrKEzRrzdZ1xHXut7P73XBo4BZWukebHbeUST2efBKkjYhrxuRmhmSHEMCIZf3h16IfHg9Euliy+JqIf14fIcOImXWdW0622RcMqGH0XO76MEPZ3zTtigtzQRVFJZ016Xm2vnM1KMeEDAwun2H0qIdnavq8hkcM7aS5jzL06iQEiMhSyrJ78QAXQjQeamya1siirIosWVJaDvqyRSUwhudEqkRaQyrUDEQXEv0Hb5tcF2LtQJ+S98Ci7UFVVXRk7r7JXMthvv3cGXrNZzLcjb6CJsQeHl+wdVyjbUG7zr2nlfcu3XO7nTCrJ6ztztnNp2gqxKMJeqUbA5C6MzNVH3yJ7ND4cNQmdDbmJ4MMKrQzHcZYxrbtH+8YzKdEldL2f8hQFT46Fg3HVZNKEoNQhinmuxwePsum9WSrvOoumJ65xaTqmIynaIKQ1SKzWr9W8fqdxqkjUS8gqwX4nNpcwhDGQ9yyJg4OPhiaUUMOiRx9gyMKBX7AwiSoDmKMfvQh4hVGq80K+f40S9+xcH+Lr//gabeicRoqYC37h1x795/wT+4/FPOz045mE64fbTH4f4c5Td417LenFOqSLu+5OzijE8ef8HPfv0hH33xmIvocFanUpLQ68yJQ69RfefQxPiNkomUxZUZQCKur5XoGamUOcqNfXpB8xSoGGPFSQu5u6N0k9WovN4IUXSB5vNdUJLtDypQVaVoFkXdl9ZJaa8s+M4H0B2F2hDbM15+/gk/+EvHH37vff7hH3+T1/b3+Ot/82tOLqFpVixXV4TgwBs6H+gC7OzuUtcVJy9fEJxjOpthq5JopHx+vbzihz/9MV3XUtqKxaahnM64sXOTg5tH3D08gM6xujphVit2pzV1vUv0gaZpEpPYgkpMpeRROO+JeAwabSzz+RyPZUHki9NndLGlsgWL9VKYaHScX12wWF7x5p232Gw2fPLZ37F/6wZVPaUsJ6zWa5q2YbNesDgLTOqCG7Ndzk5OsMZwdnVOEzuqymLUCh09BI2PwnYzpqTzLU+OV6xDzcnFJZAdfhGUEmcyAWwx8OL4mJcvXvD+N77BdDqlZ9WQi0o0JycvuTw9RoeGtm2oqh2ghmi4dXSb2XyK7zzBRYrS8vjRY148fYpfr9AmUFUVulAUM8ODB3c5/eklXdcwncNAAYsAACAASURBVExlnfkuGUr53qKwKC0agJvNipfHTzFGURdTlC1wnTBR3Kbtu1e2XUfXdr1jPK1rrC1wnfy7D3ajQifnQxmDshrnhyYcuUGHD9JEg1Ruo5IWLiFIeYxJr+egknyoDYF2DtDGMINRqUQ0XZnplNkNPQAQ/ACgbAXzw3vHwX4udxo7Y9cBDpl6KYnKP88O1xgcHgBBUClTb2I69GMGXFQK9OU5HUPJUk6AjbOO+f5VQsAisW+gANulwJBN11BurY0eP/rovtPfsclxTzL0IScbUiVF/PJ49KV3eugkn8cSYnKSMtsrOcoYcoOHwbFNc5vsYz/nUYIkUkZcJ0Zd+qhh0ajEVk62O0uMxKRr2CfMlADQKt1HBClBzk0Lcl0WEAk0aS/VkwmlqjDBgtllVb3L6ug/pCt2uG3OuXn2kllcUO0+YOEkdWcM3Lq5h/r8imo65613XqNuz3nxmw+5N7vH9GAP7Wp2d+9x595dQud59vQ5r05e4bo101rx/ItfsHPzTcLqAc8fH3NxOeP23X3MZEJsA6Zx1PM5Lz75O3726HPuv/068/1b/PjHv+D93/8O73z3O/zkJz/k4x/8kHe++QGzowNOzhc4pIHT4euvcxgiH3/8MfrpZ/zx/l2mkys+sxU/ehF4ot6j2H+TuQFz/pTb/hfs4FJTjIAtSqqyJDMdUQrvXdrbGaxEynlTsCN9y9NCjPTB8627t/nDb32by1fHLC4ucMsl0XXEYFktW37969+gNNy8scfezg3292+z8QWr1hOcZbZ3m26tWXtPoOXDTx9BdITJGucjjSqY7R9w7+4RZWlQtqBDcfX8Bc26Y4rGkLvcJ5cmh5VRQJMYY2K+jPd8KmmO9HtJArsRa3i01wbAKDWgSKBBNjveD3tfSmYCOo6aMEFqzJW0KxM4fL1xmNJ6mIJRwkf8at83vNE6sz4G+xVCkCoXuSFycg6rkwYjEKVzfF9GnfZizPtNiV6vBOp2u2FOeti+cVYApbYb4+hU4ZSlYbyX0tVswsZghoyhpSiMJBev2eQcnef9LZ2efTqz5FyzCRzPzz3Y6dgHFpm1lkOeXOLeV1fEQWM/pLU0BqW3wNrefA3grYD3Mk9BCQjRdR3t8hIVuvQZY6AyM6J8//cMevZJxRiJWhONwu7t4uuaoETqwKQzok9khYhRINIUAvQVhfgAfTn9aK0Ma8ZurfM+YE9NGMdJha8EW3M8IMrzpFrrtH7E73Uug1UZkFf9/9fB38EHGMCz64xYRp+SX+9fS0GsV2DjkGQIPkjD14DMrxJA2CrDdDKh6zo6L4Cs1SIFVRYW5700DMs6uz41B9VQ1SV6lEQ2Vio/jBqqZHJMEnxk49p+HApb9Lr+vS+VgCiJZ4X5FQOUxhKN6EGGtIak7ZVhMpujC6kmyxqTS9cQikDXLSh0gbWKLmo2V1d8+PMPef3N9ynqifiNPlBVE27dvsMPP/qEShVcBUe0OrE8x/IY2/NfFAU5+aqTFItLY6itMC2zz+ND6EGfnjmfyUE9+BAGn2YEQI7n+Kt0ucdro++ZIRBeqoRM/lcae5WBRbZ1u7cA1phkpRJomOg6NKOu6AMwOgJhw7YvOwbZpAk1vZxaWtxyzhrx9Uxh0daKXxNJ4Nh4/afPJn/2dn+HkPYfIIxEpXvpBqOThCGDbR3s8LCrVEo0qNQng5Dau6qhudDw69cSiT0wLWeXtZbGy7dqI02fTCbnaInTRZokJ69iYqqniq++gk98Uq20JDiS35dtlKzF60nCbVv9Vdf1RFb+MwSRiDLZ/42Ktm3T9yTpjrQ+us73YOX4+1VR9vMl/Zp98hFkPrtm+L7+vYqtRIT3ni6B6jmmUEr14x9T/JuTx027xndrTIyp70UC9dJzBJclgHyP7Uj/GUdM2rjOCd7RBY8mEtzAmJRzIfVkiIH1skVFUsNhacCXm5qG2NE0MmZZUqMsLN5HVHAC5KZzxCS74JKt1UqSPT4EVFo3vnMEn2PZmGRXNLp4JfiLNmhjkx8g57ItpDdB9kOc61AgYLr3RG0xUVFqy6SoUtzy7x+YHV/juWZ8b+m8aH2g85teUmPZdpxerZgUBdN6l4O9OXvzGfPdOQcHh0zKElsE0ZhNDSdRoIwS2cdUxhKThET2T4Fhn47srcgjJamPHrwXAphVFUVhWCwWgp85WXe+00TVYLAELetl11pC27FeLKl1yeHhHYIGok8JocRkr2e/dax+p0FaBYRUvmGKEpWzVYjmJT6IXkl2MkA2rPjT4lwYK6g5JAd8cECNzpqVCKirEsNB5VKTgCPwooE//+sfU1ZzvvG+RusarWqObh6h1ZT7N3apv/YOWgcuL0958fhTag3VtCK4jkWz4cmzp/zis4/5yaef8upqgTOaYEuUjlKDAX1JQH/Ap8SSBGqSGRDdCzHUIQQBqn3EiJAtEKFLwYZS4D3eeYISNo6PTgIqLRT6PhOfyr+jgth2xNQx23WBmMq8y6KgLEvadSOGxo5LS8Vh3rQbNm3LtAq0zZrffCrC6N/59pt89xsPObqxwz/9n/6M05OlOJdeuvIZFJtNw2Kx4Mb+LmVRcPtgn3IyoZrURAKb9Ypf/eLnHD9/xnQ6xUwtha1oVxterhr2d+do73j6+BHrqzPeeP0ORVmDLlBK45FuoHUtWV3nuxTJJqaGksxgVdfYqsJZzcV6zYvlS7x2VMUMbeRgat2SqB2tb3C+Y914yrqgdStCo9BFyXw+ZRoqNqsFXbtGKXj56hStDIcHhyxOFmitKbRNHU5bcsdtWxiwlsXCcbko2Jm8hu0U+CAgpAvoVI7edwHXmuViwfnpKdGnLrUpvBcnD4yOvDh+wvrylNqI2LpvYeMabLkHAQpjWa5XkjWKkVfPvmCzuaTQwuJu2pbOXXJ2eU4bmpSJlCxV1m0b/JyYmugFTKnYbC7ZbBbMpzuUZQK9g2dSV/gQ6JpOpCjaDpQ0N7HG8saDhyzXa549f0bX5SYL4qxZbQiFxhNpupYuOqIP0rW6D4azxungIEtgIvpTgklmYx575zAz7TNQl0vxifQNC3MR3XCJxbnuqMO2/7fN6qF3vLOTPA7gxkH1mHUzfB/9cwFbTcfElshhuNU5NJd1kBmv2Znz/WflzGJuGjAGI1Q69DJ4oDM9YHS/fQOUBAqTQRtUDxqMmQ557XifxyDfYyozTs58dtCuBz75z22NwS08WG6DrDPmkwbfAG6MHeFxQJWfswd1gpwv2x+eHQ/5HK0VLo+xVkQ3bjTHIEUDSR5iAJFNaiCUddOt1synFTfmU+JaEdWEjTnC3fiA9fQ9Huxa/sk7it1HP0RNWi43N7h99210VOh6yoPCY/7V33C5OCa+dcCtGzssCou10CwvePX0cx4/esR7773L0a1D7ty7y/rqIcEd0nYNP/7pj1k9+ztCVBzcfglFyfO7d7l//zX2Du+gTcHO0V0mX2959uMfMTu4w+cff8LVyQkP/rN/zNoF9ospLxrH88dPaF8+46JZctm1vPbm29TTmvnuDR689w5Pf/UzXn38b5i5wPfuv8PtG/v87UnNry4rXvmCWWHZbT6kcjlpFnFesWpWac5kHRkrzDPR6gIV4iAHkPdQv4Yk6KuritsHNzHAF0+esFmtcF7RrFu6tkHrSFlZ5vMdFFJuV1YlN/dvsWgdZ6dnKD3FFfu03RrUgru3bvP0+Qs+ffyF6IdhePzFc1aXZxRVyaZz3Dy6xRuTGb/88EO6dYsqC5SRNaSMQqlhbeRELUpAjzHoGZMedi4jlD2UGarDNQ7MQcrtnXOjPTle0yM5Ca378Q2pOU4vx5K7HiP3oRPzRKXPyHZuaB6UAZrEeE5NJvOV70XBUPkTcmKDEdDke+0/W0ogmVmqpO7JWgvIJ0HwAM6Pg1CjDb5PwKhr9gTGKboQYtLYowcjFdluRrYYnRKJJuBPAuRsJzK49uUknZRRC8uq6ANO0KlqICRt5WRrg0ufN4DofYARIzqVrMSIJOXVYI/HYz0EK4kPaAw+OgwWmhZ3dQVti466b3hoU/LTjZpXjsECaRQk+8tay2Q+Ybq3SxcDMeheziuD/HIGD2doD9gkoKM/n80wbhk0Hs/beEyH8mG19fp4rWll+uY/MYHEeT/16+Ta53ofhMWUGydd21f5s68D4mPQdnx/ed5yQsHaIjVZ1b1mpdGiaVsWVTrfIkVRiA0IEJMEiunLQTVGGYITUEMlfyekhmB+lDjtwXXoWW65SZkf+VLXtfH78VRxYBmmjapNBtAE9A7BD+CnklglQdxUs5pyd8bi/JLohERytlpyujinthXYFl1U7M536bzi4vSSiGUyqSi04Wn3CT/76c/5oz/5j7l79x5Pf/0hphS9Sp32YPBZR3Y7IcRo/OVRxHb6GCjLEqVlzQu7bmD80QP7iZnKSPqBwc6Nk2Xja7ChAyBKb59gKJkXu66U6mX/xA4PLNT8veMkV++75H0iC1Bsmh7r7zNyUgcQOa9Lay11XROCkF6UUkkub7ChWWu0LiuUUmyalrZrex96fOZC8lV9TtBf893GAGECg402aCPVhBm27O0WOakRtt+rdF8BYrSRxlbpjPDeY7IvrLUAgQkAB6nwy7YlaPl30KCMkSpTayABrGMJg6KQuDMEhzLQbIStnPsexHR+xPRMMtaDf5llcFR/5m/7uddtbL7GcUfefzFElqsV67WwE3WUcXDOCWM2seubpiHEDGSJrbOlSU2roL1mR8mJvLTu8l6y1iat5wHkyr8jjGGJ2/rEWfB99WKOGwB851gvr1CpSV8Ikah0wkaCkO98TA2xg4y1UnLepDELqTlh27U9iB+czEUf4yXwLufcvPfk1LFqu4TDDFUpISVoiIngFWPvh4q0R45lxFcSH8WlXRUxGrS28jwkORQdWHcegiKsFyxWVxhb9CCt0ZaoYFJPJDlgdD8mUn1h8F7hfCDisEYzm8+oi4JlWkv/b67ftt7+v7h6xCIl1RyKZRNYNh12veDF+UJigPmM27dW3JjvMp9X7MynlHVB0JG6KqVnk/d9Xxkhz5Bk5pJUYu5z1a+bLLkiyXCXdGvFnzZErUEZkc3sHNEkqRSftcY9zkmDsqtXz7g4O6WLkdpqbF0QEp7nY/IDvayF33b9ToO0RCgwoBUqQKFMcuXBJSfSqqQTMtZ/Qpx9q0WcOWuWSAc8YdYYZZNeju8zKIlklgBHOUisggbDxckF//Nf/AUqtrx5/yFVfUAxv4GKDW55xcXpGl1ZTs5fEZoVjXMszj2vzk548sVjPvz8M54vrrjU0FolrD+FlBqnbx06hcu/tTIYpXoIVPQLTB9kRi/Og2RjfBJAj0Tve+A6G1DJjonGUq/hQu5C6GlDwKqhVM3faNFIpnuNGHZrC24d3ebFs+dcXV0RjaKyBUWzSXR8hTZy0GzalrqcElXBy2eGH8fIZHKD6c6M9WbFanlF9BBQ6LLAmoJ1sxHQzRQcHNxkVpe4KAeZ855f/93HvHr1iulkgjWGpm3xykg5kXc8On9FjIHZZML9t97l8OAQW85RWg6htnV0nWM2s9I9UOuk4SQsCaM0RE1ZT6C0YCLnFydcuUt85dmtpkz0BE1gvVqzWCwpzRSlA6dnp7S+wYQSHztCaClsQbPpmE6nnDdLVusrzhZX7M/2qIuSV+sVvu2IFEQCUTkat+HqMrK3P6O0isVVwF3NcBuLmRUYLDmnLs51FsWWAOb+vXu8/to9ZvNZjx3lAFnFiIqBF8+fEV2DUh1RBVzj0WHOfF5xeHiIVnD84hk3b97A+5anjz4j+g1Rd0QV6VpHs15hrGGzeYbWFlOYBAIMMgsgpQKitVfgXEvTrTg6PGBSTXn67Bld5yjqmta1+BjQhZWsuA+JqSQlHE3bsFqvaNt25KhoMcBB+sOqke6RNWb0/Ikhk2Su8g96cCABZcYksDUZcCW/hE16lulNycmV5wteWEYwYlOpHG4wKqWAnv0+ctDHme6Ytzj587eDwfG/x05aHL2/L9tPAMD481EQMhCcmcRK7ouYxmEE5GidIIkEqvQBM8JQzOw4wSBHYKbc4FbwE9m+F5ecsKETMikQlPsO0dE0bmB0qDSWWwDtaB6j2MxILqEbzUk/4YnBkIDl6GNyynx/bgDJvuq8hHsAKX/fGOwfQ8BD8JXnRJhB/a+ENLdxFJCk92Q2kezlUQAXU2IORYGljhA2K2ycsoqGs8lD3P7b7NqC//wNzdfNU9771tf41aPP+OiTR8wO7rG3f4OrdYuLlvt3Dzn7+JjLk1c8Pt1QlwYTOpaXl+zNJzxxjn/2T/9H/tN/8o/54Pe+wZtvv8cP/s//g9VqyTd+77tU0wl1ucOjR7+hmM75zcUJy7MLfu8P5pSmJpYFZucm04dvcRXh5z/+Id9+/z2WwfH9/+Wf41+84Ft/+Accvf81Pn3+mM9/8ZRbD1+nntWs2ob28pKqrjl66yEHD25zfnrC8eOPeWt+h7e+8/f5H/5qyfGFZaICOjpicKlhiCc6x3K56BtB5ESAIgEBxKRXp4d568982VPtpuFGPYOm4fjpU+rZDFvVVFWNrQvOz87ZNCtQnvVGmAxd0xKj4VaMUBhWl88oInTNhq4RpttmvcHagtJWAtQFcK3n06cnuK7FFJbLdcN8NsNqAy7QhQ0mWnSdmBrIWVhYCyaDLDElW3L5vTxNLpLvOgnCVNqofWf7tDdJ1QH5GkrwM9NkAAxk/28Hzv0yTfZGmslsB8kge3dI4MnYS4AyCtzhWoPFtMOUSmyTZKegl56JhP67B0BP95USeQ2I1ufQbAckiR/7+x+Wg036otlpz/fV2+gElmV9yDTkYvGTvchMjLz1x2e0aG2bAQTwvmeP5XHuk1OJwSOflROGQ0UYPZA5/p6QghJZ8z4Mpcz5XFQ69nY7MtitYW7pX/PeC+txtWBzdk5Yrim1jLFKTN6uc8NnjFgp/edlrXAFRVWxd3CImU2I0RCCNM4RNltax6n88TpImy2uymdsBtf6tSLjH/Pcy4P0xru/pzTp/Wf3HyBNRDNju6+6UwPAPl7742fMazOv2a2fZYsTQp8o1ckvzc/SJY3fzOAeAFshSOQra+HmNS+/I5JhWsldtk4AhJAYfcE7ulZ0C0MUu+FDIIShWZXrPC4k25mGLD1lj9vpFIOkLx+C9jwm/V5N95qrZwgD69L7XhrBWNlHMdLbqagidmeON4rQRiKatY9crlfs1yumdkphDeWkhFBycXLJ6asT7t27Q1nXvPXwAc/feIvDm4d88I0P+PDR51z4pfQngN53DjGvX9UDZyHmhlEgVUqI9qwqxC7kgYiJWdVXxQizOASH97lFKcO8q2yjRq+nvZdldyTIH0hDvbZqpJ/rreRAtjejOeg5snEMtufVrbe0nfMez98hIGjsfxZj7JuaxTRHco4ke95XS+ihqSMQghM95NLKs+US8PTMarRv8jjY0ia/z/caoPmM7u1baoBGer4MaEayhMBXf3a+MpsuSzsolRjB2YAz+Os52ZJlDnI1WfYjcuxgbYFPjcUYybTkz5hOJ9iiZrFY9jgGUc4TKYmXCr9c+UV//2z9O19jAPu6jd1aV6N4QRjDwtZtu4bCTnBeKvWKsiBXJQafG4mnc9BKZUZuKCg+8yDdoZJNTK3AUlPDIW7KsmS9DnK6jxxTjJMJeeyFNCfsVe+lajI6h47S3I0USyitk2TdqMFmlIROPhsFfPWiExzjABqDjElaT0qrVM0pRk/6kgyJ1l5q00uiMVcexCj65K3biIyF9wLcK0mCOh8oCpPc+aTnnH2gKOSLoeI0oFQg6mSbiKig6NpuWAtaJ7C8oaxmVFUtc5XiuhzXGK0IKDBaksh5T48swf+T6/8OQHt9Df671udwPiqGX0vnWvZVZUQA6TkQlCaGjlW74vj8FdOyZm9+g53ZlKPbB+zszdnbFT1lpRS2sGglkhyE/FmkhIRDbH9Odg1VMvneQhQNeZVkhGIEbQps0vKuqgrvOmnOR55nxWZzzsZ72ghdVWO6AlWWAuoqIe10jRcN3d9y/U6DtD5GNlHYjRHQHlCp9CYJs3uEeeGidNPLjcAG7aNU0KgFiGs2K6aFhRAS9T1lVnSSl8iOmxb9TJ9+1haRD0/P+Gf/25/zva+9w3e/8V2MqQENwYEPNIsW7da0vuHpy1d8+vQJn33xiOdnJyxchwNiKc6W6zZizbWS6pCYSlv7IEio9dbYfqGG4HGuEWc2RNFe2mywUUvX65xNTc5Vbh5W1pUwGKISYfZUoO18QJMMqREnWg4acaKa9YrYRZbOUVQ1lS2pq5r9vX2uVgvOl5dyCFd1Ar+ly57Sms61eOcptGK5dBy/gH/5/Y+4dAVPn7eEboPvNgQi8+mUtpUs1IMHDzjY20XHQLOSBmR7BzNOlwuOTy+odvcotKZtGqKObNoljWupbc3R0R2KoqIuS3Z2dgh9UYxICDSdo202ZA6N0gZbCIhvlaEuSqKaMNvbJ5oCHzzPzp4S6FAodssbxE3HrJ6wcLA7NUzKCbPacHKyoiwtzaahBM43a6bTHa4Wa1bNGq1bDvdnvFi3zMsJrul4cfaC1jsMDuNX+Ogx2lAXCqsnEGvOFwV1nPLwta/z9v13qHRFE0Qnx3ctXSeC1flgn+7MpXwlH4Ihw/FytZuGLz7/DQSHisKoCL4DpTm8dZc33n4LdGQ2KahnBVfrBY8+fwSdI9pUmhEchQ1YI81ExInxdK3szVzigxocxa5riEDrOiaTCetmzaZZMZtO6Zy8z5aG1WqNBkxRJCmOQNt1PP7iC5GqsMKcj7mEFYXzHhMNRVnilOobnHjkQPTJYZCujalEODlpIQba1veNMER7zeBTt1uTMvD5oM1l1CYzblMJ5zgwjSA2aHQQpZeSM+HIOqbZmRsOsSHghm2Hk9Fr8qc8k4CbpncciF66XbLtyAnglwCrlH3NzlWIAWsMIQeXfZiRAkqlUpmdMEky00hp1TcIC3HUlDBdGfTRCQwaH0UhBoIbygpzEJOZxwJc5KBIANztzzZDEJ3HRYn+lsoNHFLgkgEEraQ8Tkek23P67Hxj0hDG4ZGklUb3Gn753sbP1ovMj+clDXQIPjUtENH/gxs3uby4TImGVEatBtZSD5z1Ex2GsnU0tS2pEoOqjYZVeUi89V3ayT2+c1TyzuyCyXrDOkx5/f1vsHn0iB/84C95+NY3mNx6nUcvz5gd3OOtUPMH79ylO3/O/Ztz3OIFi7MTnC14/OwRn332Ef/7v1Q8/eIL3n//6zS+5Fcf/oKHX/uAd7/5dZrLM46fPGJ1ueDG0Wvs37B88emvOH56yuHRLe4/eJ3JvXu0zQW3Hz7E7+zwar3i8M4B9964x9PTE1598hlvfe87lPfvM9vd4eX5GVqXeOe5urikKBVqOuP1g9vcnt3gk48fc3F2xtXlmrpds3f5K6JbEGKXSr8DLjoa34hPEB0aiwqgTJ6n63sLrBLQwitxstvVmsu1Y316RVGUKGuY1hPRuEZxcHMfYw9lbojE4NEefLfg0Uc/42y5IHRSGRCRhjMheF6enhEwTKdTrJHk4NHREevNhuMXr0R7cdUSAtzY3ReGlm8IXSCWOvkvhrIsBcTqBQJMz6RI5mPL3sua9em1AfjKPxzvx7wHh30qG6NvAhLlRCV4SfKE6457lCBa0TND83eFFKwL+JiAt5j2Sm9z1JCEQUoWY4g9eJD/U4okcyD7PUZS0nvoW9A3y5QnTuWQw/7KOocq5u7kCcCIKXhOZ3EPt4TULEzr5D+lYN75vvHiAHZKCXnPqIR0gKTqDTWwtFCiUZ7Zx/k8yH/P7OCIJ6jQAzuKgEnBaMxAY8hlvxKEqDTu4/I+RZESY/k7TPIXZV57ZnRqYCbDpfAootuwvjwVjb/MqoxpfoLvQS01BuhHQGheUXZnBz+Z0YWhLFgK4cOwr/J49fM22PCA+D8mjtf5IHc26HkrkeYarfWtJOnoz3xW+5BBcblvH3ySajKiiRhjX/KcASGZZwE8tcqJ3rQfEnCUpakkmZz3W0oO6lFFSrqcy9IjVhr+pYUU0+eG4Ieg3Bh8EB8VLf63D7J+M/vLB0/rwSrRoXTe4eIoZiAOaz2dOT4DejGv4gweiT3wXvRZe5BcqbTHB+A5EhIIOyS3ldFYXVAUFRFhZGZQzmhNR8TO59iiwF1twCCyYb5lpRbUTnHTa0yn0E6zOr/i+WefcGNiMMB0VvLt735AMd3h5OVLDg5ucvxiiYqaYFTfdC4n5AW4U/38+zS21gSMsSgiWkW8ayGmBp5pLWZGlgKMJgHfYWjcmn0+lVi8uW9CGueQg7VsO1SKBVVeW2P/R9au92ks1fA92aIEsv85NFnMiX8BaPNcjoC+MMxNRKUKISOJY++HdaA0PkQ2TZvsmJRm+8TUzmtaiEKO5Vp0Fl2KV7PdKfTAGM+sySxBYkxuKhUhVQ7Y1OBRa41Tgc53EBKQl5UQRutw/Nk9KCyhtoxtiBR9EkQluYrQnzEq2Yk+2ZXA2eyfRhdQMWKjgrKmtQWBVsY5yS6G4JlOKyaTCVHnZmbpPjMZhKHZZ9aEF7Aub6f8HOMKAfnZdRY+DIDXl8C0ZN8VkabbUBcFKMO626CQikDj0tmBgFHGCCNQlqRIv6h+bRbpZ0kyMMkEyTMmUMs5rNYpVhtsbs9eH9m73u7161DhQmryRQDlsbag8y711PD4KOxkpSGX/OQqoMzelbMnEd2Sb0M6q1w6K4XtnGKNII2sVbqXyFB9mT83hJCalqq+KaNCQHyT2a0KTJSzN/iuTygXeth34g6lau783HK8pJ4VY71qiYMNiuidaNFqQyfCzBhbElMSWqXEcKFLNFBYKK2idclm/xbg9N91jZMC19/72z7n+mvXk5r5ui4TpfrfyfFcAuXV4EvJz2WlhhgooqbpGtbNkqo2Qd5AyAAAIABJREFULBYrXBsIbWAyKQRPsB11Xco8Ky/xmVLokOLN5GuElAw3Gfhn6NeSbVT2LehtYmC9blLSQBZZf/ppUM7j1mtOF5doWzCdzYUNTkws3igNK3/L9TsN0mqtqKw4sLn7Y0ybVIWYMmvIxlMyoSo3A/M+OZJDuKG0oqgqfBSTFZKkvvw09DT+3Dkv6HSYKo0ta1zn+ejVGSeLn/DLx8954/Vfc+/ggHkpGqfSHGrB8eUVT16d8PTylDZ0RK3wVkp9sr5NBhRUlIPd2BQsIA6jZLs97aqFIFos3okWl3fClHVtKw6/tSg0Rc4uiZcpzGCtadqWSV339PicIZWDOIMjOh3m4nislitWixWzekoI8l0FctIVZcmu3UGXJn2fRhpQidC36KIEWrfm7MrTeM/GWZad5WJdEN2S+/cO0H7Gs2enmKjl4LQFi+UV80nJtC4xhcUUlslkwstPPqVpNtx57Q2ODg75/NOP2axX+LbBmIIbewfM53tobSiNOKe2MFJCoS06KEI0aFMR0JJFl2HCmBJbSElBVIZ6MkkJgMjZ5SuCbzFIhz7nPZUpaJVhb3+HiamYmEI62xtNYSvqaoLfbFhfXlCZktn+DleLV6zWC5btmnXX8OrsJWeXJ2jjEmPRpOYOimpXgV7TMuP5lSPYknffe4uvvfmOJA0CvXO+Wm6oqpLsQI8PahUjGeXRyUm8vLzg1fOnIjjuIypEfNQUpebBw9fZv3mDCBwd3UJZzcvjF5y8OpZSSueTFk5mRIlMRAjiZMUQULYYlXnIlRvPRKRBysXFVSodsBhjWaw23Lp1i9lsxpMnT/DesV5vgNjrAuXM9TjL7JwT56+0ojVrkhSIB6JP+oG6D8A0kdShRBhFIblKWhzv4Fz/uilEfzESiS4QTXICTWbkaXK6Y1w2l3WcMotrrO21nU0cmABjZyWmvZud9ByU5ferJMUgDDkpb9SoBOglJ0mJ86KTDMMYqM1jOQYCMkics8+iHZbAVSONhGJyOpQaAQjZlkAPrpDGYLDhAwgZQ0zJNSABS8Iq2i4LVCqXaqvt78mJrD7AyE5OSAd5XpcZokhjncY7Oz6SySYFPEM2XykpQYn5Jui/atTZepshNdY3zI5cTMkuhXQP1oBBUaRmLGMNrPE1Bjb6gy2BwEVVUU1KhIVpWevbrPe+QzP/GjNb8qfvKuZnz3lw+wafH7/Asss3v/kB1pRAoC40h7slr93b5Y07e+jmkjsHFdqds1yc8/g3n/Fv/vqv+OLZY27uz/neH38LrSf8+V/8cx7cf8B/+d/+dxzdu0+gwBRT3njzDc4vTpnt1TTnT3n65BVdp3j25Nd8/ug2H3zwbd68f5e3/+g/om03LFdXVAcH1Dd2sD7gMKyoWMaCdu0p5zcJzuPChqqc0LYL1qsFu6ri7GzNZPchP/jsisU6YC+esL/+hAJHR0dUXrrOtxtWmxV9VIYA9jqV58MA3qTV1s+ACmIbdudzvvXW+zz9zWNevXpF0JrNpmNVrLm8OAegrqskdSJr+MH9B5S2Zt227DQNvttwtbiU5F8xZbPZpEC1o+kcPgWrTbvG+466smw2Lc4FvItM9if4ylKSktBB1r0yamQDR38frd/8ZH0H7ZF9iXGQVEJl0Hb7kkByYD1dT0DkdZ47v2+9l7G8xyj4Gr0/7+VxKWZfxpsC4QymCYCUfLD0Xq30FiCdA+0cSI2fOduz8Z7N93W9uc749yJD8JBL2FV2u2OuXiGBWVEC0ZQ4FTZt1sfNrKc81tv2/vrY5LEdgw3XpW3y2F0P0rf/Pf5usEnyI7+v/7zEgPuqID+mZlUwVKd0mw2+7aQix6cSS2u2NBvz2PYJtf7eRBuuqCrsbAdvRUc+pBKKYU1nYDpuldAPAFX4cmA3Pn97vyP7tQwg7Og9Y/bt+PXxGu3HKaRkTDqfcxCfO7L0iQElVTXB57M/J+JUL5MUyeDWAFBJQ5/YJzJ7wA4AqQDLZ7T3Lo2BzI1KYMEwJtJzIe8TayXZLXJFmhhdqijShKYdJEH6+UsyBjH2lXlFIc11e6Auvacq6629lJmyPVAkmLGcu+nojjHSpSRv3haSeBIQ0cdINIq6nqALKzFLALdpcd0aXcxowwVBzQihQkdPt1zw5Ne/5t7NOT503L59SFkWdOsVlQsUG8dUl6x8IOiU0IqqZ7ASGaoRUBhTiAxdFIDKj7Umcys1pQXQGhA1SZIoSVpnXe08/9I7xQjYnwGjjL/GXK48JKvIazQvW7UtO8AYKGHM/FRpLGOfvMTa/qSTZIwA8C66PgmU94A2RpiG6bsiUh2R5yonD8qi6IkJ2XbkvZD10ttm0Cse79UhMUCSSos9e1wSakKY6EFlMankhkjkOCcMZfFWG1CpcRTbNj5LaWSASuyO7/dZyAzGFEM5l3sv5C/PFQyJ8KHotcOzjxpSQh0GyS5iwLmOzrW4LskhRA+prD4nP1X6vLzjc2wwLC31JTLAddDrq0Cx3i4x7D1ri37dhZCIGT7Q+hZtdGIA0q8V71PM54Mwa5UwpRWh16KNClQUv3t8ZfudvwuE8Sn7KDW4ZIg/dIa4EtNRGrwatC0EkNOprw5K7LEW3ACl+nMsx8VKqdTkD7KsuEqND5UymKD681DM5uBPdSON5ryvev1SrSnLsr/nPhkVPdYU8l0kFrHSoBLj2tg+oSJjSj8eDEV7aGX6vghSzRcFW0j6t9572k2D6wJKbyirinqiUNGIXe+rn8QHUST7uulQfPVaGa+X7Vj0y2vquu/yVZ+R/z5+Pf/5VbI/1797/J78uti21HxbvIREYLQUVnNz7waHNw/Y293Faktwka7taNs2JbUiZWmZTCdYq1DWU5QFhdIIUdxgrZLGeXG4X58qLcbzH+O2z5VtqNI6EYuGGFlrkXeqypKYeuy0TZN0bD1laSkKy6wqf+u4/k6DtAB9NkcLrJrPt6gky0ViO8QQ0aWI3JOAiqDEuusk1owPiSkWiD4IRTyGJGSebFcEHQc8PEaPW4tMQF1P2Xg43qx5+fljfvLkGZUxFCpiIpTWYsqSzlo6Y2gqg8sauUEKA3IjI5PkDkKU8nHQlMbK5HUe7xyrZo1rWozSuLaTrI+2RB/xnTQLUzGzscSBM0Z+Vw67BHgYTdc2KfASfbbOSWlV7jTquq6XOxBnTjKgKMkyOe9oG1CFFdadLajrmtXVAh8Dm7Zh02wwxjCdTtIZrOl8wMcWH85ZXKxxbUR3r6jMIZP5LqfnV7RdS2kLisLiXMfV4gLUDp2TEoPF0ye4GJjv7vDi2Quiizx8421+/oufUU6mvP7gDablDKMsdS1M2qpQTCqddHghoolRo4wlxvRaEv01KoBzeBcwpU0AribScbl+RVVorJ0QmxblPL5rab2jiIHTi1OmugBi0i4R3ZKqnFJMC2FCTCyLxRlN2+J8YFLVXFxcsG6X7NhW2GA4opayWRUtnW/p0Dw97XiJ5tPzEx40LYXucD6xOY3mxt4OPvo+UCJmVlAC60hrHHFyLs7PuDw5RiNgvzZiiIrC8vCN16lKK9o9yTt89eIFq9UlxiqEKRPSGvQJlFK9w6i0SQFd1mgRPZjc0CTEwGYj2jjT6ZS6rkFB1zVcXl6wWFzRdVk7J7Iz36GqK05OTsTBKAsmkxpCZNM2OO/Zmc2JVrHUAW/AZSdNjnJI7BbZ4B1eCXjr0/iIHrMwb6X0ocPaAp2Csi1nOmnOSFnPUAbTe1Op6c3g4G0HmOPXxjq1Y0dL8MttMFc+fnivvC7geM9aJh3O6QDLayE7tOP3Ar0Tcj3Iyg5KzuZmBxmgC93We9M0iRM/3DE+lb6WtkjPkhoTJuZ2HxSmXUZfuitjmdnvWTcuO+TJ/SGXq8cYRBQ+BQiJKkH08pmZyUJO1PV2VyWtu7A1JuPgnBRMZABs/Lz5zzEolLPlLmkaKZVfT8E1gdPTs8FZTeyi6+yPHkSJOjHLwJiCspxQqglaBZpYspw+pD38Q6Ka8PcfKt7ypxxUBRu3xuxNWDctp6fnzGczHr71Fk20rNYbzl48pTCG3TpysFuwPPNMi4LjJ894+eIV/9V//d9QGM/tmzex5RT1zff5F3/+F6ybNX9vd587d+9zerVgfnCH+eERL16+4LXbB6i2429+9BP2b9+jqiL/6vt/wdk3f5933nufnZuvMZtvWCw7mp0a2wQqXRKLksn+LTrnJK+iW6qpRfnIctEAkePnr7hq4LNl5F98fErXrjhY/R1z/wptnTRyQdH6juOzV5wvl9iUZJPlpPo160eOfM+6i5HcNK+0lr39Obu7Oyx3dnjx9DlRa5qmIyTGhVYS1Dgva0lbzcXFFWXlSFAqMYEjUIBStC4QmxZjkhZq1Lx2/z5FUbC4OqcoKppNx2q9lmaT0tWCxN8Wrci0ll3nEvtGp2TI4FCOr7GdyM7idRCTkelKGzIBE6ofmy853nFIwnzJriQHymjd+zmDA97H5cP78nhxzUHneglcAnzGDNT0M5XY9Hlur+uODrYq3yu9E032d/TQTKrXBe0Z/KEP0nOyahvMYwiCSWupt2H5eUfA1Wh+fltgkn8+tg3bdn9bb3H8/kG3MjegGbFK+7mUs6hnhpBBjxR0pyBTa1l33nmU7/AXV4T1WgCDxAC7fg9f9YzBe6wSsHiyu4MqCkk2Z73yMNhDiMlv1V/53LANZI+/UwCiFOzHHDOkNfsV95o/d5w4yCtFQZ/cDSHglXSezomIoJBqjRRDEJX4EHmPIa8Liz0BaQzazRlwlXVKX94bkt+eg8IQRJc/J9sz4zprKnvvcd725eSRzFJXSTrM9mdqs1725d2ROHSxZwQYoXqWV0hSG03joSz7sctnKOQktO5LRpXanp8hwaF7cLmvHolxS95EAMRIYS1FUbKzu8v5yaWwjaJn2a652qwwesqmbbG2ozCWwjmOP/6MizdeZ+UWvP76XWazGR/9/EP+6IMPWFxc8OTlc9xU46LCG3lWnZZqr/+fRtCnRmkKARFFt5IEWKY1pyBitvdWAuZQCpPYfGNA6voe173tE1BPjTR+UYptOzO25zqPlrg3vTxAXs+kNa9HCfMEnmbTp5I/zwDGl2UpIxAScy8lOHPTW+cGABQGezHsQ3p/0BhDm0hEIOXG/V6NQ6Ipr6XBBxUAddDbVMnvVLSuwdqhQiMiRK3czFEqSvSWLSMO5I4QY4r5Y69vvm0XdOpLknewrIeQ9ouPnj4YSHvUke2/IQYvM5psd9d1nJ2e9kQoa+zoWIn9gShMeCnV7+dKjW3el23gV/n0w9LZBtqyD5vPdVMUeDfYROeF2FWqAmMtVVml8VGJSJIbKQkwls9sWXclkZCqFovteEnLc+o4gKfGCBs1s9Gz5rXVJslWyco2CmxR0nURowt8WkuRlGhEkje5qlgaodvenxknKXOTsYx1ZB9e7sckoD+hpYgtHo/52AfKflSfgEu+TlkKUcplSYWcFE3v67qubwQ3PgNijH1vJKVMkojQg69FktQLsb9/HwOda0Sv3OQKjzBiY6eTIFf+BKlO6SukVP6+5AOOpULHz5rioK2meqP1lc8RPXpP7/uMjtnt6pJhTK+v2esA79h3740LUFhLmeRBqrJiOqmpqgnGGDbrNRpDVc9wIdK0HcvVptfKN+aCsrCYQlFPC/ZmFRNrQUOFpbIlkdg351Q++5PZvkpV3ji5ZBP5RubV9z+TyiXxHStgMpkSolT+NnEjdrdzBB9pWs9vu37nQdo2ijalMlp0r0g09hEzRikDKuA6Txc8Vilx/AhYLUehUQLb5C6o0rQmsQgivUB8v1hiTOULgcpavOsIKlJOKpRWdE1LqxTrKM6c9gEbGioiyjswBlUYipxpU7LhVBLNRtELoUcUm4slTUQA2k6E6DsnYuvRaMlURZ0yKJqYjJ5WKasn0ZXo3lSFlA4gUgcxgRxagU5OW3RSMpjBE0sh7OS0UWxd0XlP5z0oMTYhKHwn7EtlFHVVowN0IeAJrJt1DwrFANZUWFMQg6PdnDObzfng62/yr7//mLOTFe1OjQ+Wrlsym80wRrS3FJqmdbx4dUIMnouLC7QtmU2nKB+4ujxnZ2fGfD7n4OZNdndvUBc1e/NdNpsGlYWbSwtIsO7j0AjKhYAmpuyrGJoQU2dFJcxjVKTzS5runJ1JzfTGlJvTXU6aM5quo/Ut/vKSWguw3G0a5mUtot5orIFpUdE2HbpQ3Jgd4Og4Pr/inTtvY63l8yefYGJIjeM0mgLvClwItH7CorGcXTlaWxOqKUU1ITqVMp4j7ZRkzOkNb8i7Y+ToCWt806zw3Rp5VEVMHXXLQmN0YPF/Mfdmz7Zd13nfbzZr7e4099wWDQEQIACSEikSaqgwih0nqbKtih1XpeyHVJ78n+XFD6lKpZJKrKScyHFclqImEimKFAmQAIj+XtzmdLtba80mD2PMudY+APPMXRIv7rn77L3WXHOO5hvf+MbVM0KS6biNm/H08WNi6HDO4G2L91Jd7/dbGt+yWq3Y9V2taBvE+fm2pdE9WAXlg/y5XC45Pj5mt9vJ8AEghF4Y22Ega0DjnRMZjyBDKFzbslwuuLq4qjp+fd/jbINbtISaJCloidh2Z4UxHkvubY22WVplxCpjS6vxmdLSIK+SyOpmkaJQyBhPZYNipW2qgHJT8GRMBNEq9eHQjYOgSoXSx9a0EsuNwV8F8jRYEg0kFCDPGAo7qXzB4fdMAYJfWS3VH98EMsvfp2DINCAq11kCsPJ9B4CmGO16jwLWakW+fIoGh2YyhZ3SxpojpQXsgGGQ8mjfS9tVeWwKzpTPKgnal91/iSeKnh9Qq/YllYMSZE/gmAw5jq2UBwB9lgr94X66CfhkTSr037Ns2MY3zGwr9iHBtTljd+dbhNVzvLZM/CcPesyzR9x//UUuw8CDkyMslh/85Q/Y7jY8eO4eQ7J85d4tjhYznDUsXA9xjfeOq+tL3nv/F5ydnfHGG9/g3bd/wr/53/8tjW958aWX+f5/9H2++vrrvPOzn/HZp5/z2mtf5e7zb7De7NiEhvnREYvjaxZHc+7du00ftrz68j2ePP4Q4wyvf/03sBjuv/o65ERYd5wcHxNiJiYwrpUFt2BN4sNf/pxnn3/Gqy+/TEjQPHiVP/2Td/i823O6f59b8RNJTomoOCub7Y5HT5/iZ0sJkGOQdUxgvD3YqyPIVb9WW4Qzl5s1f/ZX/y9ps2cYOm1j8zhtgZ/NGpaLVS1mhDjw8PFnYKQ9dL/vGIZe7ZNnuVphjKFpWgXwYdft+cW778sAk7jX4aZW9zu4xtLnWFknOQsLu7Lky/5KUYHGMVGeJp3TvXVzon05g7nu4/oJlONfdd2m4FZNkL/4fYXVUt4zfcnWvgniyHkaWYDluw1FU7ey5/X8l5fV7y657vj7rtqEAmhUUCFntQsFyBjP6XStDu/LYswh+8MyufYSvGuC9IV1mkgGmBt2eMp+vQl0FrthyvtuJN43//vmtcs9SrI23rub3JNI9piSsNV3cmDbs8rgxN2W/mqNTRkcwkpK8mClPVlAEknChaWWU0lCHc5l/NGS+fExtmlUiqokbl8EGm5iD+P1UOP06d6bJn71T7446LJ81tQH3gR/pz8veuoxyrRoed46KGiayGfI+bAggP7edDBPAVdlWJO8T+yFgBUpjtPOMeoHycrY02NgdC9l0Y0seqpMAKaURX4iJB2yaj2kSAhRpZ8SrnX1WlNShpD6vDI8yFoBHIdhX1nMRfc+pZEBWdYhpVzBiFIIk24ZkREIUYfxaHxg9RkVUgEZjIJtq9Njzr2jsY4+RNbdwMVuwDYBZzZE33I8X+JSZHd5zW6zw85EG/bk+Bbb6ytMiHz7m1/nh++/wzptyNZRIAcxGQp1auxh0C6eurcUrJicFax0Z02Z+kVD2VmLt74ynYFJTKi7o4AOCkjV+57kp9P332TWp5RrHCaFKlP1clMBeKZnRskjJh+CMK4UtQtgXtjBdsJCVYAracznva22PjPpPijyWQpaWGuZzWYa00eyysoYXfICkE2LURW4rX+HOpLAovFutQjif7X1fASdStxbgB25/6wFh+JCnJHhbiVtJhdJg6S6n9LBYqx0ksVJXGeMlaHE+rPCeAYt4JQYIxtlm8peGJLqm9e4XpnFFTAeu1RGbKPE1yMrta7AdE/dsH3Tn5f3pSyglTm2GJcxSdZKdFp1v2vSVFiwbSPDzWOEKVO2FABiSjTeUTTUDabq61rrxjaYCXprjKngofe+7oGcpRtB9nRDVvAzxYFEIGaRFnLeqixJ1twu4psGa02VyBOMxyqO4+r3W32GJXee+nXvmgrYloGn5ZpL3nWTCWpMATIzxllaa2sHUHFvzvvK9C3+MIYojE/d713fi36sKwUslXvSfeWcGc9/lA5TciaGgfXVJavVipCTroPITRrrRaovF5a2UVMjhfScSu5oqpxfdbxqD6wpZAF5Lrnsjxo73txzxQ+X98vv2uLPcjl74xpOY9ObsWvxiUyuu1zbfDaT92RDCJHr9VrB6Iaj7JjPW3Z9x67v6fZ9BWqttczmM8KTgbPjBWfHLbfvHpOyY9PtMFjaBtrW1di5dKsMw6Bndtxnpds3RumKHvWlJeaaqS0UmS/Lvuvls/qBy6trDJLj/arXrzdImzMzZCKpyVna4insEQEdqy5iViq89SShTlK0JEplxoJY/iL0l2NtD4Hyh/ybsL4kwGqsIzeGPgayifjWwWC1ZVwYuaRITybsAiYJk8bODFaHXhX6vvezyhCTgV/Sshu3A72yZqUFINA4bfWOgHXsh6FWeL0D58A3YiBdM8M1jpAS88WcEIQJ6Bqvog7KrHWi4bAohkWDjhhlLXqdAhgbuNpeM5/NwUgLVVKw1mRD3/X4RiZ9zpGAf6bsyda3RNPjnGfoI13osCZx5+wWIV3jZj2LVUNKe2LoODlacHS05Got0yfnbctyseLZk3fYrK9YLhbEPmB9Q7ts8Vi6bsc33vg6c9eyT4G2lSQ4xAFnMm3TAk4GFxgB5I01nN465Wg1xzsBcoZB2ne8b1m0M5KZMV8saBrH7vqK7e6ChW94cOseD47v8vjiguvNmlnj8Tje/MortKbhk48/4qUX7nFydMz19QYbApbM0WLJPkVuLY5Z73ec+RPuzE+5Wq9xydI4S2Mitlvx6btrht2Kk5MFVzHz4b7ncmtYmCUr5rS+ZYiFgi97VQc0y1kwUwOJALDFfipgen19xRD2sm+0/c1jaRtPTgPORAmmB9HNfPzoEaKhmvFNq0yCTLM6whoJkpwTrcTG+TGpVJ8sz0EM8W4vOsxbBWcXiwXX62t809L4Gbv9DmOUGRWiDKdThzBfLJjNWvb7HevNmrad0XhPHgJDBD8/FrkDMiZK21NSNmU06gRCEt1q9b3CuimJugaERqbmGjs6GsgiOQK1NYVyqtTGFHB0DJxyHbowJuMjoPkFRzRh8WAmP5sEBKL1VVod5botyhnOKFiPAhymBpWjOf1VCX39aQUGbv5bcUxM1uamxmwJIsqU6JvfZ/TmSgJamA6Km1S4c3zvoQMfL0au1TsJ8GKOlKEFUJJtTcbLs51Urw1FB+qLoFYB0yXhNQeBWln1AnqUNav6lgjwbI2RYQWMbWrGmLFDo3wPX85ozqqdTEo4LMu2YeYNkYF9OiXf/i77s+9ibMvfe9Nzdv1LXn7lOULb0gFhu8bbhtY7mHk+eO8dnj695K3f+X3uHS2JKXDx5CmPPn6PN994jee/8jwvffUFrjZ7jlZL3vrt3+NvfvhDfvTjn9AsjvjH//Tvc+f+86xO7vPjv/0J/9e/+/d85623eO3Vr/PiSyuGzVMCme99/3usLzY8e/IMt/DY1LFwWy4ev0vAcXp0h+0+0N6+T2wa9n2gH3qWy2OwDucb4n7N2z/7W+L2grPFnGZxn59fbvj5+Z7F/j1u9+9yatdanLQ1MD+/uGC/23OyPMYaYfJIsawkzOWMSzGgakk73bfGMqTAfthz/+wWtA5yJA7a0poTcehYD3v6fo/zDY1vSGkQSpZJhD4Q414AFWuIaeB6fYW1jvmspes7hiCDeYaQ6BkIYcAaSTJCGjg6WtJ4K1Ok9TyJTqbYIGNVxzAWYDAD0s5stH0wJ2FuTwPfguqUIJvys5IwTgAz2bqm7u9DcFHb/e04IEz2rATjKRUAatSHHQG0G+zH8rlIm62hDOoyoy2y41mtNqYmAmOhXcAipwnmIVOlfN44OX1kDtaCvN5POYejvmvZH1ObrYCMJmgc7CsdflXvtbRtqnUrazEBF2+ChoffRQUK67rpHU0TnQOQu9qzqWyD/4LvKc+zFKIK89QYAYtCjLWl9erynG63oVUfaZMSJfzIRoZxvUv7rlGHGY1lsTqhOb5Fcq3oROveykVjc8JCLbtvypgtoLGd7K/p/d/sSohxHBBUgTKjQGsFddTH676a7nOZUK4af072V/XnOVOERVPOIsVWbf54beWaorITQ4zMF0usfkb5HRlgq2XXWkyU7SXXIG22FRQooFoWph8aAyYiWRl/maQ6hZkuBp06LtcZYsAPTsEYbTE3hhB6HS4s7yGCCZKcikyPUZ3csfhR/rsy3Cbnyqh0dGbc50bPST8MmJCZz+fCynMWrAzccQbsckGee3ZXe3KM7KPhou9p2hbSNbnPGDtwYhcMIXBxcc5b3/9tMo5u39PvO56dP+XpesPyaEZcXymAIuJiRfYhE2uLcYkP9Iqhvofqu40OCCr7yujwU2slD8o5k6sSQtY2eQEaCns0l32W1WaSqy7uGLOZGqOM+1IAG9miQthwFSREWYVSOKlgrCvP2NbC83ifpbamwCimDizLCEu3nhNr68yBhBJByiadMDwr0zpDSONAwQLSmHpWjYK4hVEuerRGbXRp1ffWj/5K3YZJktDbaUyd9Qz1rwS3AAAgAElEQVSaYse0kGCM5jp5tC/WYLMwanVZqzxEsf9t26pshAwPNsYwaBElZyFYGWUNOyc4RcyjvEuNdzFV91bsVClSCKFE7MRok0e27Gj3il2bxu3TwpTsrUNfPfUpRf9duoBCBYycG2Nw7xy+znmQwnBMWYsCWfe3dKRmhNQUo/pC5+Rcea/SOrlYM33ewpa12rKcSoclRbYuqVYvZDl0WCv5uxDeGpE9SQGjP3fOgZJtbsoTFfCzdFFXTXqNo4qTGQvGVofDle08lUoqg1RVbtOYytgOUaTLrG6KYvNNAudlSF0BGZPaxH7oca4R+YYCclpbs03Ji5LmErbahGLvfWtpfMN2uwUybePp91ts04LNeBpi6iS394LRbPZDZfUaW1r8NTKa+lGo3yk2IOt5ovrJg7yOkb1efkd0XSc5mxn3rlUN18KUL/FODdOKTalfMALBpeui+BbBzoodyWy3O7wX5v8QLzDXhu1uLTbfWASJNhBhP3TEAJ6G1nmOB0Pf77m6uialzG63Y7Vc8cKD+yyXM2JMhCGIDyyyoXpIp2dxSgCRxzoW8WKQQZnHqyNiTHIeyOQs0gu/6vXrDdKCOC4rwu6SzKtDS1EqmiYDEmwUdhRGnwcFgafqDxm0tQ1wxtcAXFhdsexSLBZnxLiEJEOtjNEhNA78zBL2GR+C0O4BomhuSiUjkDsRPY9DxDjRs/F5L5VFZGhJxmDaBm8tyVnVW9HJq1lYNSDVl1Z1ZY2TapKxWgmxjnY2JxvwVqoixqHDH7SdhZLURUIfsFYOejb2UC+rFe2ULvZ8+uwR7aJl0cxYNIaMF7AqBVLKDKFnl8H6Bmctx8en9eA7dyRB/iyymp/SDR2Pnl7w+ePHLOanWBu5Xm9wNnO0WjKbzThKmRgTy9WSd997j8uLc6xN9D00fo4zM7p+wObAYtZyfHxC3A2cHs0JQyDHQBh6lkcrZm0L1giLOAcssJjPaRzMGq9TD8G7trI3k/GYdk67WBBtph8GdsOOIQ/suz1PwwUpJVbLJfO2gSExb1uOZkvm7YyT+RE5RBqE2h66wO07d3l0/oihHwhd4GR+TCax32/w3tKoE9+sBx59ANtn8OrXX+adTz5ie7SkC46VP+b+yW28nTHQQw7qdMv/a4KWdbq2gxRL1XaSgOXI+vJSB00V9qLDJEu7uMXZ3RdYLY6BLdmKvvH5s8ek1OFcC0ixwZSzZMGYTI6iu9kPPd46de4SqPT9wHK5VEDjHJB92biGruvJwNnZKffvPeDtn70t7TTlHCJGrmlaTk5O6IaOi+tL2f/OYb0nZfDzBtt4Oe3ZkrIEpTkFbCO2Iam+qknCUFOoDZk26hQpkKEexhUWk0aVWZMtM2XYaNtglvNXNMwkaZIGoDLps1QU5XfVROm5rYyTYu9UdkEwDQUiJsFlsW1p4li1D1PtJZR2+8NkXF5fxjwq+6QM/Chc0aRfWIKFpMCz/MIIgKI2C1MYyqYmIbIeGvBoVbeAnMXx18sQLOxg307bd4txKU76YOJwwav0PGTjpIW+XF+eXo8kHCmX4UJjlbtKJGQp5mUFrjTeZgQi9DotZKNsucLSA2zRrqva13l8jtOgqDAtajCia57AZsfq6IjFYolJMgV9405ZPP+bmNkRv3Mn8O2jjvlVxC4aPn38iH1IxDAwaz337h4xdJmPPv2Ui6uOzfYaP5+Rhy37y6c01pNjYHV0i3/2z/9b/vzP/5T11TWhD6zXO5ZHJ3zjW9/i7v0H/OLdd/l3f/zHfP8//gO++93v8mf/z1/wzk/e5ff/4PvcPbvF3edfIqXAcn6Ec5nr7YaXvvIcq+MZu/0a1y7p+i37zZpu38LpGSRoik6wMxB73n/nx8TNBalfs91c0c5e5PEmMXORNjzmxPXMbSLlSEQG1zy+Oufx00d4E2jNgMmtagAKUCF4iKy/Lf4OsV0xZgmWU6Dv9+zXl9x98UVefPkVzp88Y3V6StvOCbsd+92Gi8tnXF+vWW93DKEnRWE+911XmbIpR4YhaMtbZLmcc3R0TLyQYT3GWryCEfPZghQjjZOCVxlLlS00XrT1JQaIuMZXEEwS6AxG2gmpzNQ0IlwaSI6/kTUGUOBTjUplb033udG9fWPvy9AdkXtJCcrQv8KMqSYzC1dS9LInyfzEDtWfe9FhS7mcdUk4x4T0ht2yoh3N5D3CdNdhXvW95byOcWAxEtUO6xdYkxWQ8FC4dtVGCihRtIELSCy2R9a4gi/W1s/WhaBoFIqdKkjFaBduMnMKQFJ/bowU4Grwr8BljKiZ0QSuWqXJfxdbWoYQFakPORuFlQpFFki+30aDt9Liv95v2F5eSi3Ce2IciAiQ5qynJEnFVpbnUSGnnIjZkds5Zj6TtSjJXp6w8Dgs+o2b5dCXleR+9MVfbCUfC32pAiolSdT+k7onzOSxlL0vIFEYC6JZPwuDdUa74KBAEeUXp+B6uaYQA1Hfb6y014aswA/TgkPZIzpPQdfVmvE5lXt0VsgWMcZatA/qU7134r4UVI5KSdx3+wpkhBDo+xJfzTDECh4GLXxIUVjOZYyRGKSt2bRWh+rJuoUo0g3DMNR7Kn7URgUZSsF8qh1Z/16YarKaNksMZtuF7seMdZ5EYrPfcuf4mJwChB0mzWnmR6SQePLoIXG3I263fPLBJ/ztD37Eer/hcn/NMzuQfGYIAiQJWCNr47UtVWqjptopaakubMkC7o3nKUZtMU5RJCpM6dxT5nuWz5NJ8gU0HeO9qIAPhSlva+Ja91IB8OS4jwBAKeSQpYPU+4YSIsWoUmZlY48nkZxFlk0KyVkNYYYagpZ405AtSIeIdPrlJIOQamw8iW2rhm2SeSk1BlTXlFX2o2yaanftBODR/y0yYsaYusY5mxoXix/PIl9YwJJcfN9BRoTzcv9Ffqe8UhxjvUJukdMtYOx8seD27TtsNhvOr0SLfkhCYJEisMyhwRtM48Svm3hgn2sMm5P46NHi1GspbOJpYU2whvJewTiqRA9TEGsChE3+7WZcDwgLNQn+0TQNwxAotOKcBV8AKcC0E11OvPhGHX8h15i0eJqjdGPYUXqplCjLvBIVrMV5L3GHFv2stu4X0LMY31xPniHmSMLi2xVgsWmPGYCYVFqv7MNyTuzB+dLTNtpko6QLK0SzYo+ECKJnwRSwV2KcGMfhfcUvFwCy6DMbnWdUnqsUbOVcNc6RLKCgeEoRGW9otONE4yhhEMo9GZS9KtdfYoiUE0lnkuRkyc4wxEHyZcSmudZpXttILu4sy+WS7b6DbiAZw5BKVFh2ZD4AZqcA//jvJYJEz285reZg8OXBGUsltxn3YfW7Jd9CgGprxzx3/B3GfA+Dw9F6X4sc5EwMieBkWGFMMv8ohb0SvmQ/lKF9MQh4bJ0TWUPnsVZG8D59tmF9fUGMmRAN5+fnzNo18/kJ7WyOc4bNZidayA4yRQqmV0KkDjjMpYgmuIFBipjiJjJeizpt41nM73Lvzl26fq829stfv+YgbTkU2uJbsAijRsAUAxyFVopuDGtlIiWIgVCGSSyC3WXDZDEpIY/SAVkTBzl6tjJDkiYRpcXDzSw2wzDIZ1RdxhwrMGNTxieLs9La442yL5y0VRMl8B/6Xgydl2AhhoCZSaukdWIEXeNxrlHGjISZ1hkdfgbGim6sVSaiAB6xOrGqkZJK1dIS4qiDU9bEWSOT4TNsuy27fovTiDT4jKnRijjOEAbSMNDqcAp5JW2HQVpxmiXtrOXJ+SeYmDi7dY8QArvtlsVizmwuAwhmsxkYw0cff8yHH3wkGjVhIKXArF3wjW98g3Y+4+MP3uVosSQMgXYmLfCb6zVgmLUt8/lMWEfqeGPfsZi3rJattqk6vGsIIRJj4OpKmJm+EUaEbxpSTOz3e/bDhi7vuL664M6dU3KG9W7LdpdosuP86pI4C5zeOmW722Is9Pu9DC9rPF0YaBrPUeN49OQJ88ax6zacXz1hPm9wncWlGSenJ9x/ecnDCDN3wv4icHzvHvPZFcv2NndPz+rmF8Ze1FQjyZ7TlW9nC46O5pyfX2Nr+x36jOHi8lxBESsSHxhwDfOjU1YnZ2TbMGRojWO/27C7vmDuPd4YvDIKiu5WmYy57/b03UCICb/wNYiTQRi26v7EMJBiYAiB2VFbg0hrDBcXF4QYcMaPDjcXzRfHMAxs1hsB1r3o5g5BWvkWixV25uizJjMK4JlcmKdaTQVhVivjqjrd8qeVBAyorfilQltYP5JDld+zJTWryU/OAprEXJI/U/1hYb8cgqS5sj4LAJiNBBHl94xeI0VzKKOsOnGVpUJbNdDMGPhN5RGAyffeAAtrUjv5efl+M96ftMaOztSqHSi6RlOmVwVQtDtgRA7ygaNVM62sBWrgVhLyKUBTWdoTIGKawFcAnfF+5Z7ke6f3aOuwgMPPKb9Q16T8rtq+4oOm9wuFySC+IifqPU7ZD+VZlGR1+r0jkJUhZlq/YO5X5DQjm5Z9aAl332S7eJ4XXeCfvLagvfyEBy/c53KzZXlyi6UxzL3j8tkTjE/ce/AaJ3ee59nFOYtlQ9+tGXZXDMOOs7MjjM0Y4xmCYbE4Ybvd8eMf/ZBdt+cb3/423/2932dxfMzLL7/C8fEJb//dT/nG61+nu77i//w//ph33/0pf/AHv8tXX/kKs+WSPsP89JT29Iw7D17ANQuaAfohcH15Tui2uGZODnP6QYpjLnbkDG//7Q/48O2f8MqLd1nOX2Q/NLz3eM8PfvmE9OQXnOYrlq0hB0OIkC1sc+Ljx0/YdgONNdgk0KBXRk7RbZ4CU2Pgp88yJaLNdPs9i2bGvdt3WbRzbr32GkcnJywWK7rtlhA69vuemDLr7YbNZgs5E4bI5nrLdruh73bstluGvpd9gEi3uBzp+h3dfi8dIa10qGy315ANbXsiZ6V1mMZiHFVGJZEggUnatlfaZfUslU09ZV5UJkPW1jY1HIYx2RptwpjcZKjJTrFHpiQ/9UwUUIo6NGEK9umHqnSLnjUtmJb9XgsmSecJ1O6AL9qim+wh1G58IeA/SPYn57Ky4Uf2GJP3yNZQu5YzpTgzLayNcHcBXOQyRtbToZ0t12UKIJFL8e1QC7bcF4y+Jk5ZPPXKp9ejn+um7NVyDYfJUvE543DGsheM+kAO3guJUD4D6clI+z2mD9p+ObI8cRLX3mxbljUdWWI5InMCZq3E0TZXgF2SXFtBm+ITDtg0jACTm8T5VhOem0nl1Ncd7h35nOJDktoCKWDLIpf9bu2ofVm6sEafIF17ZShhzpkUYmX6TEHjomlazk5Kib7vMcawmM0lN3FWJQLGux31l2UdfY2v5Vw55zWxc1hb9O+KxFBWtlmiH6IAVXE8r5FE4xu9XjOytWpMNLLFcMI4bLyH2aFUSWGjkxUcVlCYLAWPVttRa2yTJCcrhdy2nVE0e9Pk/FojvtPPGuarFd2mAwwmJRZty9Fiid32tDQa41qa1vPs6VM+++hTLi+uGbqB1nmun51jZp67J7dY7zbsUiQgwFGNSxI1fkHPWwyxtseWOBBQsGnCUKz2RJ5TAc3LlHhXrNHN/ZyL7ZlqZ45s1OnPhK3Iwb9ltVVJpZ9C1yMd6spCNNQhqCP0ZbRLbsBr7J5BgGRlj1YdS3L9XueUQVgvXve/EYZ4YdfmnGUGS+Or/a+/a/M4aEq2OKU/oEqSaGwlcgnSlTkMAymm4o3qGZkCcYUEUECfCRSEqjVQuIDjCYtVwkD+TfL0GKJIR1jDZnPNbrerBTKToXFehr8ZIwUrJPf2TSMzKyYSBwUEvBkHFv/rvdP8exqHF8Avj8U+xD8VSYExHuYLNi/nsTV/WuQ80MJOiZhkyHfKhUEeKwM2W5ECTIA3DtfY+mz1MckgPd0nTrvnaug88V9ysxKHueLTmQ5JG3VpS8FKCkQqR2dkv9mmZbff12dZ7j2TlY04xv/FJ8j/y55JGoNghBxjoQ7yqvGGFSGjEnxIx8Z4nanGHNNYyFSfXvdySgfXowkcKSeatq16yORcZyRN853pqwzKygqGmixFzVQGWeo9Sc4Q6bdb3HJBo53ExghI21xcEWyiT9I9GpXl5ZyDqCcml1x4LIaGUlwxJV4oPloxI63xyLVK90lGWaOTeymyKaacT/UZU3nCaexUi1BaoPPG463DGaMkQR0Cqbherqs02ocS+8t8xzJ7SoiGVjt8ttstKQZCGPDe087mbLY7YnL0g+H8co33mZnPpCEQQif73RSbJ8+6aRrBQ7IW+U1kMV8ylPDcOIxxRCKmtaSsZ8hYrGu0wPflr19zkDaDKYwmnchezLVRA1ziTUSjpGhlFD3DovuqnyZgxpRmj1FjI8GDVHeTVqLHRAc0kK8O1OIXc1GST4nY9XTdHm8s3lgBjrMaLAwmQXbFZulkw2xI1olerbdYLyxElxLNYs58scBYrWSnTFKxbGN1inISrZpMJCMD0spEQYA8SQiSJgmFRVn0eATMlTYNb8dhKylF1rtr9sOOedsQ+sjcgM+tHlBX/7R2DEiLYTRZzm/oBsLxEYtFw3q95cUHL+Bcy/X1NQBHR8f1cDrvpWKe4fU3X+fR5w/5/NFDrPVkBWBfev5FmpzZ7DpiTLiZBMqzWasDg1QHTAGVrt/hTaadWU6OjxiGhPMN1nuR0DAe61qcb/GzGUPKxBBIw8DQ77nar7nO1zIMLUolddft6Ls9CysSC7/4/JfYxnF9cQ1W2s+3sWfWztgMe/b7LcenR8S4x2RHu5xhGtidX9PmzLD1XHy2Y3e5JnSOh598yNz2WLNm111xOsscz+cVnNJUA3JEqIe5JnJ9t2NLEIOU1bjnLOzaNHB+/hjIWNfURMk5x2q1ZLmccXqyohv2NE3Ds6efsdleSlWx6MggBgZlQIBU5Lte5BG6vsfPvVaVsgQDWbShU0r0XYf1DYvZjL43zJqGzWZD311grCQrfd+Tsra9ptLyPmAMrJZLUkxEG+l7GXAWTZLii4UUEpBwxlB03EjCUBO6gwyNm7ZGZtBiiCReJZlyWuyxBmFll/drIlfappPqycV4WMVOSTSWboLl1brl4vvGNpsYohQRlN17U3+vsCD8xAEegCMcBmQ3K+s3X4eDCA6T+5tApzEqpGAsogtb2IlfvJYKjE1eXzZ511pbNYrk/w6ZvtPrGVtJDsHlkYUwauQViz8NWEsBzxphKOYSBE6uffpZ5WcF3qn/dgP0zpP7LmfC2sM9Vv78/wMUxn8D51tWq1vMzAwTDT2O7fwFZs99jyHe4vefdzyXnnHcZobccXrrNiEb/uov/5Sls9y5dcqtB2fY9ojj9oQhDTx99Cl3bp9hwp7FzDF015w/27Fc3eFnP32HlDL/4T/8e95883X+4OTvMdDiZ8d88vEjrs/PeeH+Pf63f/2/8vH77/DOOz9nvljw3be+xfn5Je+/+z6//dZbPP/iC2TbCivdLcnZM5+3GLtje7WnbQyzxYwQBvbbPYvFnNR3bLfXnD/8EIZrZvaM45MHXO9OePvpnM+3PcfbTzia99gcdbBhwBJ5ev6U3WZNgyEH0Y103hENlTFbwEd0T08T5lzbUxNNNnz9ldd59StfY7fZ4J0nBENKlvnyiH5wZDvHuxnHp5F+2LPdXAsg/0B85ub6kidPHvPg/v36nFNK7LqOl7/2Mrvtjt1+r4lDIg4DDz9/yuXVNc2sxR8vyN6RcpBhHBSmiqMAI2HSljcF8UzZR/YQABR7NZ7v4uPrni2gzARku7k/p2e57P8CUNy0MXVQx+RzMIfvnSY10/M3fc9BYWby84NrmZzJoG2N2HG4xwiqqY8srDVGyYOq96k2qHyuFMxE81eApLF1uAB6oF0NWYAIwwR0mLym61NaMn8lmMjhq9jZCcIuPuvG+6brdOMTqq8Zd0q5pkNNYP0AsBJLujTAeosdAjYlCXeRSfXeOYYYDq69rJv3nmHo688Xi0UdYgUywMcao8XIcS+WltOx1XS8zlx0xpMM8KwTrCff+2V7qKzNdG1LUkcWkKquffWD1O8XNpt8n72RE9jJXrv5vOv1ZFP9TAEQpLPEVGkQ+XkBZ9S3agHEO0/rnRaOjbR5mwzGSWw89S/6ucKytxgrWsEC3nusGwd5iVzQ6I/lv7PmWzpAWO9n2k5cmOEFKCxdeTFGzWsUFCn2wWizjwIVXvUuc05Yd8Mem6xaxjI46PZzD/jkyTkmJrw1LOdzLKLjm2aGFAQInLUtu/2Gjz/5jN/8zj1u3Trj7/9n/yn/9o8DubW8+Z3f4v/+qx9wffWIa93pVp+jnYA6dd9YS+tGTUJrR0BeBVIxB7HKCFIVzd4vnr+b+v1lK+XD/QK/cj+Pdg15TjB2R+QEyNkIaSzSV2OsgJfxwoK2uqdjGW5nDoseRaLh4Hyn0b6XbofSmWqNDNcu4KSqiugAb6P7W89UdWCTgoxien0IGCOFFAGmbAX+DtdM4uUC9CkCN8pnFUIRhTQyWf+cyUY6qUxl/csQchA2ct9vR7mtLOtTfJfR4VJt09A5h/eeoOtTzvdYSBoHUxaAqsT1U4mC8pDKvY0s/lI0/GKsX5/LxN7dtMfVrhvBPIqWdE7UrhDvfN1LirDI9ZksBDPf0DQC4g59qIPgCvhtssU7i/UWUonFRUYla8dajAnvnQ4/dTLUW59HKfRJziV5a5kl4nLCuxk5L7UjIkCSwpe3FuIYZxWQtg4AVZ8nmMkI8k/zgnqujLI6J3HHzRjkYMiWncRQk7jmIHYqwRnyTPuuJ4SkQ9tlTxV7LzIzo+50wZlqkSuLVnDWZj8qiC1EP+l29HQ7sLS4hUh/euNFKmIIGOdr0Saj0lWTGDHnXDhYquWcD+KoGhelpIWaiYycnkPrRp3yMY4aQeBxXeQ7nRFcr2pjYyRvNmOhq/WNxgpJiIhGC2I5EkLg6OhImN3G1mJ446dSEUYliTIgRB4hbmb2XS+xhDEM+z3bviPmRA49jz9/RNjNuX3UcP/2KbshsL3e0fpZxRnJmWQtg28ga8HDZ+J+y269xVoPxjNfLFidLGhnLX0f6btQiWE1rviS1683SGsMOUdyRA4/aXJAGDVptRXDWW3DUUq4zRKcFe1Cia0tWQ+1xSkIY0UHENW5MBYc2BSrYyuLGBQMzkZ+5uetHLDGY7CEXScuIRsGEqkfpJqoVaeUkwI+mfm8xRtL8khbQdPQeE+IEdc2RCsbKpN0iIgEPClFkX+oDBkN7pBkk1qRElACIxqJwrxzB8y7MWGTzy6bzlgBXZ+cP2M+m+NNw3boaBGQyOJorAz5Knpy1ooxcc7hrejZ5CSDm9brLc46zs5OCUPPZrOlaVqaZq7tAXKDUdtQFqslftZKNa9pMc5wfX3F5eWVGvtWBngNe1Zmxq2TU3LO7IcOZyAMA1frDY7IfNHSNK1cq5V2xDAkhkGA9Fu3bjPESMjQx0FEt1NiCAPrMLDLIqZ/vb4kx8hsNqNtG5poWC2XfPT5Z8yaOaZt2G43ohEzZNb9Dodlu9nSMbDeX9M0cx5ePuXR1RMeXzyhmXeE6Lh+2HH1/o5fvhNYLC2nL99m3WWu9pGz0xkzNyeGRKnckKO2ECVyttp2akgh0eUeaz0yEsuQiViTWe/WPH32uQweS2XCacabzGLesFlf0PdLnE3gLOv9FV2/UR1EVANGjmZKYiTbthWmmLWEmFRk29dz2lgLKbPd7yBDJLFczOn6nr7vsN6zWV+TEYHwru+0xQ+axikzXCZaeu+0pVX2bEyJbA37HFgYcI0T8K0mD6UYU1hEkqk6Ow7ukhY/XVeEoVzOgwRZRh28lXbYwpJhhMtLsC4JljpzJywNa6ys88RBjU5fqulOizfirIv/mgIhwkrAHrZ6fhkQejNIuwkG3HxJsKaC7OqYi+01+RDsKe0oMEkqJpDC9LvhELwx1uCyG4M/DajIpYW6tL7xhc/4svuq/w2qs6cdE3YEMIwyZQq4XhJ/7T5CdvXhNU+vexp8mJJYlLUpwdnBjyVZ40vWpbymgeGXJWYggc9ifsRivsKlRDKefT5muP8WYf4qLx0v+S9eh9mnnzE7avnFL9/lm9/+Lp8/esLVsydc9Vs2lyuS/yoheW6d3WWz3vD2T/6W5czz0ovPcXp8xMNPPmNxsuLqcs2syXz29DFDv+X22Rm/9Z3fgWbOctbyN++/z7/5oz8idtcM3RUPH27AdnzzO9/hO7/9HWbNiv/lf/yf+Vf/3b/i9773Pb79u2/h5y37faCdN1xdXPDs8hnWOVazBpo5ITuybZgtT8lxYHt9yctfeZF4tmDY7FgPDR9vPE8uN/hwydJuaJpG7I+J5NSz7zY8+exjmij7CG/wMy8tYaX4eqMwYIwwOgujLhlLDoE2Jb752pu88eJrNG5O5yKb/Z5FY9ltOvxMWllTSthWwBEwxFbYPtZYWmfAZK62G5K1+GacNnx69zaLxZK+79nv96qNmMkp8td/8yMuLp/imhVutZB4IIkumcQeIptiTbFZZgRslHGfkurSZjDKpjrY0ymrf/4iGDoOtxr/7eZZruwV/bsz2oVxY58Lq4F6Hqd27ybIaoyhUp0Yz3O1MpME/gtJwjS5L2fPKns6l0Q7fun9lCsetQNLEqK6cGZk8wg4IOwICsEYeW9l1hSbVa5rso5fBBYUDphMf85ZNW/Leyf3Vn4/5Vz0Z8Z1MKOfoDyfG7ZsCjzKV6s/KYlaHp9hvWYna2JjptvsYLPDpqTMtxFYrP5JcYDp/ZW1N2R842V4CpkUBvDShVbtK4eJXrm3uikZ2T3lXkrSOjHJB3+W9Z6+bhYT6tRpmNhtvZ2MsGNLQsl4vVVPMyaiGYealL1eJH0KS85aU/fVlOWVldGbc5mNMOgz1zgBVPNSgAtMidedctEKgCggUAgB53XATS7dQQ5j0CL9KP0yhFCfkbA+ne7rTBmy5HVaeuMN4BYAACAASURBVAGoD+MHyc0KEJbJdQiQ2Cpb9UzT4WOoey3lqB0n5YzkWmjK2YAzLE/P8MsVab3GOcvl5SVz41ji6KIM8O2GHY0OQXv89Bl3n3+Oxltu3z7B+syf/sWfsT0/597REYvLx2xCgEZi5gK0jEWBrEMf3eQ8SOEnly1Z4jjtnKng34H1ErCnSIiIloKZTJMfCxH1/TcKVmX/OjvR/FWgUMx+xjhDiqiEQxxBnlzA7lIoUMapUxA/yfC4MkSu8b7uxVLMPnzeAtzL3i0SBNqlEsdh3Fbj4NoiDnUwUQHfC3CYlFk9tesgtkHYlZRA7QuvAlxW+04BZcVWWBXbKTGr+Ef53eKjhHosg5hySszbGQ9eeECMkcurKyCQCaIrqp0WhQ1soGIFkk+U7ogvgsllgC4K1ss/F3swSsUYU9jp5X2FlVvuUPZb2ZvTrqybe+ZmTGlU5gXQIqsCY1lyeWt91VPvh55cQFsnQ4+M5jEGlZpzpgLXgqXI32PQTresALCVfYijDqtyOrtk+preR07S/1+Yw2h80riWtpnTp63uq9HXinTZuOZjXpTU/iRkOGKuOfQ0LnFK6OPGZ1SwF7GfZQDszTX+VeD5+FlRz67F2cOzbm2xzaMkkVVZnKlW8ehTmBTQxLdkxVCGMDDEhHNLur4T6RuEZBWSMDyTGfO66b1l7Rqv9zSJhaZxWLk3U/wyY7wkMV2JN2/49bK2mlvXOGziW0b/qtidtcyamRQBg/ilIg3QNi1hEOnOopee0thVoodqvHbGs1R018WHwmw+Z0gdKQzE1MtATpMJQ08ePM/feZ6vvnSPjz76gG69JoZeCjMhMGt1iNsgGIdvHDPvIHfEuBW5zmaBxWOz5frZM64uNxgczjsZQvirMdpfb5DWGIOzjYKMauANquOnAsRGJhMahL2JJsFOteca6+T9+pmCGWkdPWe8BoMGi1Vwt2ieUDQjcyYNMtyjdQ39MEgrjJRicVZA2uXtU/qtUPJtTLgkQHHVmNUpT8ZJFam0yPmZF9avlaSlbZs6gTQqkFY1ME0iE2tgKzdldECW2Ec95xpQjGFDymNQ6JxqDGlgatRAlIql5IeWx0+f0riGe3efw+ZAdjK10iG6u841zM1chxdNABgi1jbM5wuePHnK+cU5t+/cp/GW9fWOGBN3bp/RNguMTXR9T8qw3e6qREM3dNimwTWNSE6QiCZz594Dum4gGrBEQgz09LS+kRaq0JNSZLGcM/eO5axVoF4mdfZ9L8GSshbB0s5a2sWCRbMUAzl0PDl/ynUf2DvRZutDx+bqmtxYFss5OSWePn7CfrfDOMtiNmO3lmFX/W5LipGTo2N22x2JgfXmEjuL/PXPfsL5xUNSHtgOkc024JoVr71yh5/+3c84P7/ga7/7TT4dnvFst+HOZsN+u8Ud97JvRW1TAqJcdJmzipdDDAPGi/kU3aUEJtF1Gy6uLghxwEZTWxC8d6yOT8E5Lq4uwXqIkf1mTRr2+KIu6MZgqBjgEAJD15FiYqaU/xjEcFrnaHzDYrFg1s748JOPwBjW2y39EOh2O2G2hp75fEGKIsGRswCSwzCwXDbEPlRQr0xBdr7BOsfx6QnN2QlJhzck5FlJdU5ZTkVXK1OrpQdBsFb+zMRw25IkIWeYNGosyhkrWmumalpNq45DaQNVJzZ1/iNwMAKz4pwt1nrqdFfKOU4H7KuSSNwMDr4sQJu2Xt4EOYujnQbU0yzXWCMFrUnyJB+cDpLmnMZgqTpeDbiKoySNTChgnICpa1ubesyYkEzZcF96D5pMTEERxUz005j8zGhrnqVI1pTXNBCbBiQ1kCrPdfJMSkIOo9asXJcmIHlsvbn5bA6Ap7IGZa0ytL7hpFnSGo91mZ4j8snX6E6/wSJn/uEbc25vf85s5cFbutTz4x/+FR9/+BE57njz9ZeJOTH3jt31E7zJ3Ll9l5deeZlPP/g5P3/35yxXC+6fHbOcN+y2V1xdPiT2VxwvZzx59FABgcTMDLz0/Cn/8l/+N2QL/9P/8N/z4x/9kK+9/jr/8B/9ISeLOT/46x/x53/yJ5jQ8fjpZ/zFX3V86ztv8eC52wy54afvfcS267n74CX8Ysl8tsIZaIwhN5ZuiDx+8oz7t+7RHp/y9jsf8MOffMj7aw+bK+7s3qf1AzmL3pZrDAOWjz57wrrb4bMMEGybOXbWMCizSPTHJPUvmlkCdiA6kSmR+8wC+M1XXuP1r3yV9VXH5dUV+9CLVvkwsM1rmvkMa6DvOi4vznGu4fWvfR1zK/Pk2TNSTnTDntzOuXP/eS0mSYEshsC+63G+rTpmTos+OYo+eTY9fXTkpiURwUmi6TSytercc84HA6PqGTZlWJ3EGwntPCrnr8RPWZLNkuBOgbFfVQgZv4cKWsmez+p/zEFy74wyItWeTAHLQ+B3tIeiQZfGNrcbr5tJ5/TnJUZzGk8VEP7QNpahp+N3lvNbAL+sAWZiHCBTNOqsSgsI68x80cYwMlmnmoo3i2RTG16ea7VfX3Jv5Z6d0XbLaivkf8Y1Fbsz3tOhnYHCphwLZWPhatpRIOfDpozpAvF6i9n3NNZiEIKB91509RT4ER3Pw+uWAlzCemHkWgVqs5Nkv0jNlGFl5VoKC8ZO7n0EKdB9VLTdJ3ZU33+zffjmv5eX04Ey4+9FvQ4Fsw/AXnSwjVRTR8mdCRhdz5O0UY+MU6f6j6PfrgB3Pizalec33S9WJSxQgKMUjgWYDTWGQNeyxk9SptTYYTx3JY4oia0ETRZrMyFGkYlRZmHM2p6uDPVRSkP8nDwCZeDmwlQb92I5b/UZaByUNJYq+0QS7MLQNMhgIm099DP8YkncbTFGugiSt+yGwD7vaZNls2915kDDs6fPeP/dX/DN33wT+sDZrWMW3rKYWfp+y1HbchUjQzISz2Z5wEFjVrFvpnZVlvORdSNMAd2RnRnqM3POTlrI9blaQ5Hsk/37xcLNze6nm+8zmZEJpu8pkgpWzxAKABWsSeovI4heCvIGlKUoBajalpzlebqin6u+Y2xdN9WvFV80vX6Q/LRcUzknZY+WQVUl77A6pCrrvTrNcQu5IcY0xmwTsMgZK7KBmKrRKTGcrHXOoukZS7uzgtWp+ChjFGROQmPJIvN3dLTkeLng6fk5IQ4IKUzmbVgsISfAVdWxlBKNkedi8jjQ+TDGLzZ/fN4w+kzdbvX8VxIOY/xetEtLbAxTmYyxW2z6OvRxI/s5Rjlv8/kco7MYMNIanmIkBMVOYpL9E4zM0MnQ+AbnZMCRFIIVozHSnZZKbGJVVzgmUI3mlArGUtjoYwxSWbQ3hkkllfFzdiyIOOdlPyq4UWQUjJ5ZM1kb8d9FPmKUgKMQ5W7YxKw5tFxDKb5Mhk+idqJQxHXfxhgPWLdl/aexihRnBCA+sA2T55ViwjYyPDXnwlYtxJyyPyRHiDkLeSrJmif1T05aXbjerrHOsjpaiU4+Y66aNERIBWBFi6Icxn/l9aXDm9WmlHt2zsmgyTz+W84aITlT45Z84zMO8mLFK6pEHzBrW5q2EUZwKxItw9CRcsR7z5QMU8DtKmNDKQQq+J1kGJsU5hzGjITGrtuTjAL6mkNaYD/0JLvi1u1bLFctq6M5/soTomrNJ9EDNkYYv0ElT4r28mzZIvrAc3KKrC/P2e+3WONYrVbEGNlsN2pvvvz1aw3SVgNfACgjAG0JyE22NcgNKdKo1qtBf6e01aAkCHUAzommZc6l6osGaGgwFAWcmYi9B5JqZjrRpVEdnqhsxiFEkoP2eCXOASQQLYlVzkjqpBobzum9yMMUMDURkzRdYKgJRdXbMaZOSizGudxfSfadVoaT6u0UZyfrJGxkDJgSMKAVXUzVjCqTrxOJFBOPHj/CWc+8nbNcHdG6RtcoSiWXROOasTqiguBeGT/dELC+4c6d2+y6npAytpVhT32MnKxW7PuO/b7DOcvJyQkxZXa7gcXqmJSkrclniwmJo7MjFsvM9WZNzgaXhDnbdXtCEp3ZFITlOVjLvh/wztA2ftQPyhnry5TazHw5Y3VyC2PneNfQDx3nl49JaSDbnpB61t2WXb+nsTMMQsFvvGcxn1XmcMyJfr8nA4um5fbpGecXl4Q00Pc9t48XvPHG1/mbn2x5dr0lRsv2IvDLy095bv6Ay0eXgKO7usItMmRPDI6QBOgiRoyynUGDABImB9GIih3bzZbV8gjrvLCArCQZfejouo6uG8hekgSLJTee1eqEk+Nb4KJM1yXLenaDFEB0UJQ85yjtpSFQJgkvZnPRdGlbbWdJzJzDORlE9+TpE9lPOZODGHMJwOQaTDYsFkuu19eQRYNNHJc4q2wMs6ZlwLBcrcg5C9jurejrWETj2eg5EZssLyMBwjiVSs6KtQbrx4m8JOEdm5KGZzmr5UwI1qjsdA0GhQV6CJ4IY1tsi9ghDWr1cqImKVAeo1Top6DqGGkrKyWMTIBpUlfs05icj+8pL7EfClKoTSxBSs7KjtaBGeXXCoAiIvuj0y32dvqashlqNKoGSWFMCfY1sKuAjtpqNGEVpy6FkxF0LUyQw6AHUIBW/02v1xpUV9gcAs5mdODj4Ci5l/Ql61aCjxgF3Dc2a9Jq1FbL/ZVLGgNlTUB0LdMkwJkCRHUfmMla54TFsvRzFo1OyY0tvX1AfO57hOaYt+4u+Fp7xfrhU26/+hXe+/RTTpdHPH74OZ8/fsjpSYtvLa2bc/v2GReX17z907/j9u37vPa1r/Pcg/v8+Ec/5MMPP2DmX+b22V3u3vXs+w137pzw6NOHbK8v+WzoObtzwtXVQ3KElC2bIfHeh+9h25a/9w/+Ea+/8W263Za/+Ms/4cOP3+EP//Ef8l/91/+M6BqMW9DOjnl2ueHBi29g56c0swXnn3/GyfEJje/wKwFsnjx6SOMMd+8+x/vvvE++/QZvf/KQ3eYJ880vWZpzsi+s1Igns9nsePr5Yw0wRfAnG0cyVgYDZmH+mSR+V86KTNkuPoKcmON58yuv8huvfoP19QZnZKiOM5bZckXoOkI/EHrRRu870ZptGkPXiZbubDZjdXxCFzIPH32kCk1ZEx+xzynB+nqjZ1Vsj/NeWmqT2Ao/83JOvVxr3WVq7iURSvX9BShME7Aw5ZIIGNlPxtTAtAzqKJpwheFWAbFYSiXlDJRugsLgK8mJHoADIE2BNsqgQQVy9e0uo+CwgjVq99DzVJK79CVn8Oa5r0CnnkGTQbR7Vd/bgCk4mhwuMukA+CufL6agyAQUwEy+pwxHKv4HhOHlbAEbUrVzOddVOwBZiq0rhRxrvljAqc+NYsMmibhVhuekg7o8I2sK+/GQ7VLedZAF6csUX1j2TlLJpArEZHGTKcCwpdtvFITK9dNSCMQ0CIFCgbfD5yQ6gdbIEChvPWY2wzVeVtqKv7dlyITG5dmUglkhVUye180F41ewlKf7U9e7PDvnHSQZcqWrfeDvZM2F8VhiCBQwykYLj1nBBbSwWsEQ2cqV/TW5LjmzVJbSyNQcGcnybCYP2SAfqOdWc0xqATdHCmP3YD2kriDsPMpelhiqJPuFBReRNuZyzlrbjDESev8KUExU1MZX1XSXfCEo6y/lXAsVlQloTZWVqOZj8lGldb4UhEtXmDfSRRmM7NeYIx988gn3Tk45m88YUiRlS4oGGzOGxLs/fYdXv/o8+8sLPvrle9w6O+E3fuu7mNvP8/Yf/WsWQPSZHBNdGJgv5qq3LMxUlUwGI5qvSW2dURtWMvmUyzqD84XZluuZBwjKFv4yAGf69yI3Ue5fraXqPmYh+JS1ywdWWjue0ngOi2Z1vacvl78qBbGcxs8EAYAs6DCpLOfXCHM0UrqvVHMySy45su5Gvc2pjIi3Y+Gs2u0aoqlXykhrtubL1lkhV6h8HvWcjcGxy0YH5mk8rN9X4sUSu6oZlUKLNUpoEf8UYsA4x/V2w3a/I8bIEKQVORkow8Sska470Yq3NO0cnxLtvMe4p3LvE2mTctZLUQVGKRMBtkZJhAL2CYBb9pH4pMLATBMQ+DDuH33NTX9ZCl9lPVJMDDExV+zCqn0r5kbmKUQGIr6RPDeEqAB3Zr4Q7COkqNPpDb12EnkFCeVJSMdFmnQyZSVqJPUP5Tupj0ILtbVbUfj9RfIpxUTODmNmZPZkVH/biFZpTKFAjjWXKmSPsmZCRJvabT3Xur/GotnEp5nig0pBOFZwsMQipTtzWgCtZlKfWSlEle8o4LDcf1TbrkD9BPSVPERb9EvnQtYh9U4ARxkWKUMErXXEsKfvGs5unbDTdMh6R8hUzdxihG/GV+V53Szal706SuMcxlPFPk2ZsRrcyR9pwjLX9TTWVruaS46YpSjdNkLya2fzGiMA0qkbB+msm8/p+15mPTStDC2P43WGYRAQO4q9c84LoSEKbmEMdH1HCAPGe5ndFAPGO1C/j4Xr60ue2i37bouhFDSkK9jZLB28YqrodgO7XaKZtSyOFoBlv9mzXa+BntViwZ1bp7TzVp5XyvR94Fe9fs1BWq2+IBsqJmmnRhOPMdTMtc21tqApkFkqJOiwoKzSCGChtCqpI7TWCeDlLMXUeGsZUqRt2jqQKDNhSxRgxWvinRNO9biKZqxU7YWOXTahaHUqpV6dj3NGALUoGpvZOWEf6ME2DqXBhxrQFedZK1QVCBiNjNP2LJnIOB4Wa1S0GzPKRqBjHIwQKn1jsdmw3mxELHm3IzcRPwGyUkykVoy2szr1Ul/WWoYhMF8sscay3m7oQ8R5YQtfXV3RtjIUbbVq+ODDD2nalqPVUlrsfEMG7tx9jhde/Cq+sTz8/BGu8XS7vbA2EXsTs7CdvfMYC/uuo79es1rOWS4XJLS1q1RqigFyhuXqCJJhu92xOLqNn824d/uMI9uwjYPuK8NsPse1DSll+hyIThx/Pwy0bsZsMafrxcE3xjJ3HmehmTUQEsumZWk9aduTugCtIQyJO0dnXL73OYuhoTk+5vbpGeHyU2zy5GQJccAQiUNHmVhZ9j45kIZA32148vgz0Ua99zzL1bFU2bWtr+t6wr7HaZqWcqzT58OgmjY5ytTonNhud2x2W0iBxlnV+U1qoIIK/Hsg0jQN3gsgK1qLifl8TtHXCWHQaxWtmaCOHU08UkocLRaklNh3e9qmpW1bOdOF8ds0dP0gDDiTSSax2W5oYwtB2qQkwULF/kdTUvK3lEphxmIsqvGqul1QkztjTQUtBQMQdodaEMq06FKBVBNFJuOxVW+pgCSUANyYevYgV6a8nBXNigqWPE00ra1g4ug8x6T48M9yv7kmShJXjkO4qhaWBmbTtpqse70CFmZMgpMm0OPfc03kxmoy9VlPu9XKOkzvIaVx2FFZ9zyBTafAtZn8bPwMozqzunaMFfoa7FfmCzWJLy2ltUiW9d8mhS9hoaNs4sNES01fZSGXoGtkRMlnDumwcm6N+LEQgmj16f0bayFklu2cs+NbtLYlmSO2s/usb/0O1/Nv8fzK8V9+q2X++bvcvnOb8/Waq92G2dDgG8drr7/Oq699BWcyIWS2XcQ1C3Zd4J1fvMfT83O+/a3f4Pe+/w+484u3+fCD94k85M03X+Hlr77G5589YjlbEoNIjpzdvUMIicbNIDlWC8u/+Of/gh/96O9o5ytCtPz0J2/zw7/+a17+2qv85//kn3J05wF9TETm7M2Ki5S5njX81Y9/yZuvPEfc7Lg/DHgv/vvq2TkPP/2M1175Ko8+fwqrB7zzqOHjxZzZ5ce05grjA41vcd6Qg9iezz75hDRELbKpbuNsDsaq1IWpgzmNQbow1DYREzPrOFmd8trzL/HdN3+DtBsweY8lsV1vyUbAV+esToONYMG3LRnxm++8+w5gOF4u2O33RNPijcNokS+lRB8GZu2MnCNXV5d433Dr1hmLxVICdJuZ37pNfvwI2zQkIsZ4YfdgIOtwvnoGbS2SWWuFuVQSTgPZlGKUZRwkNoKI45kuzNjpeYIyYR0DKUpRR+tQ1RYaULadqYl9uTahB0asswSdnmgoBTlzEGxnNN4xpur/G24E8xNbcZMdVDVljQALElplsQn6LQI4lCLQyGTLeSxITa9/ajernbYjS7ZtmskZ1xgzU7Xdqk0yh/bUlAU2puri3mRFledQAN2cswAgNz4LvdYC6BzIR+SR0SyfMf7b1G+MRb4oyUhpC43Sp+MN9N2Gq4tzCIHGu2pHc5DPHIZBO7jGVvfScfD/Mfdmz5IcV5rfz91jyeXeumvtVQAIgODWXJrNbg5nejSSbKbHNH+AXqR/UnqSjY0eZDJpuofNnQ0SIHYUal/umpkR4Ysejh+PyFug6ZVpBlTVvZmRsbif5Tvf+Q4gzLMgk8OTrQkxiAZ0br9MpDKzIdP+MoghjDU9z8ToY0IIOe5QhlbuRNH7qWBAvl+FLWvIxxTfFP0gawZhBhfGZ2asqZFXgFILe8LwTFm7PvtulaGweYrz5Llq/B0mwJ3GAHr98my0M0m09+u6pvOdsJady2BH9iskYlSAYgTgJksMY8hycBkoyjMkTI5XEolZO9vaX/KnMt0o+1vBN5OT2pKUawt1Bi2MEf/tEMaexeCy/ilmLNAUMG8SHOj61KK3gCmBqrIcHR/y9OQV+CHbMZF/w1gIhm7jMU3NommwsebJg6c8+PQzri0butDx45/9jN7N+eGPfsI//uLXnD34E1VTEQzUbSs2TZ9/jFkncQK0iCEZWd5WAExTjQxGta8a/xS7ovty8vo61uzWKyawMRcG8h7Pp2EysJHiSFaSoYxIcVIxUmNK7Cm5spxD6cjKFzadyq4DuLSI5vI6jcgeNsmU2QGSK2fpuyzHY6zDFiYBZe+J3EG+3pi/N8elxirIrN1hU6mQnBskHcQl5xuSgPGiwamAZ1Xi3JjZtzrwW8Bri0POMZdsMYnMoHbYqgZj6UMg+qDvAGzuzLNlXYYYsVVFhSWtN5IzlyGClPUg12DKvpwOdRS7Ne77qW1I2S6pxIisk/G4Izg2xsdXW/Ona2vKzo1JOkljXADC/q1dZjHrMb3I3UUSTR7CW2cGdIq+dA7qg25mDc44yFKLU0kPfW6aqyYMJuuJiq6tsoflHcXHqByddopYOc6smdE0M8z6FZtNKNfpQ6Byeei6HXOL6WYscbgY6TFbUuDUCPYyvd9qq1UWpcQeTkHjvE712U1yPH0OZCxmKlckNjyUZ1j+UyOd8ymHEO40z4gq1RG3i8CmXKpl6AdijKy7NZerS1KK7OwsOV+tJA/N7PWxOLgNxn6dbSrDTnX9lW0+BWjNmDel0U/kpz7ej/JzfU/uSjCmsOmdMeztXqOqmiItWjqVjAVT504Hw2Ixp21lVtLQe1zWix6GTtZULiDAWASWomVFjJFu08lQU7nBJaYaQsAY2PSez796zNmpxfue1WXHxeUaY2t2lzsYI/u0Cx0pWbrBE1JkEzybzLI+Pz1ls15z++YNjq/fZJ5zgiEOkKCpGv7c6y8apN02NJSqz5RRphvRWpuZq6mACorey/4I2XiIIZEAX/V5EjopXQ7MuAiThvsmU+HDpMqeEPeZp9tq8FXOWwMXK8ODUsggT24PILdjqFGOqfx8ev1ToEKAgfGxJSbtymbcCGIw4hjgZucrgsljEOpcveVMin5vSjkYEGfT9wObbkMi4mzCuobKOnwc8J3HDz3zdoGb78hGyKycneUOq9WK/YN9fNbB8oNnuVyiLVd11WCMo6lrjg6PaWcznjx5SN9tsCEyaxfcuHGDw+NjAa3tS84vLmTCdzBEZ9jZ3WX/YJ/lfE63WhP8muA7hhBpamF4YkfjaYwp52NMxdnJOX1/gveWg+ObYGZc37/ONw5v8+zJYwk6ncs6e4nLy0tSCKw2K0yCtp0zRC9UdldRUdM2M3xIOFuR4lAMwmq1whgroLaDYKFZ7tDPT2h2ZwzzGYuDPTbPvmAI0rYzBi1hYuSk6hl9h42ebv2S0J9y69Y9mkVF01pkiqkkR+vNhqHvso6SVMjxYnBfvnxJTD5HqxGTIl23ZjN0NEBlhGHgYyhJtIJxU/0urVxKwqiDMgAjyVAyRibAZqPrjOjHqNj7zu4Oi+WiOBNjDGbWYqzl8uKCTdcRTdbWwtB3HU3eoUM/4OqqMM6newIEwDCZaaWgqQYOY2FDtoJq0xbATxMLRnBUEhZN3kx5v9yHzDqdOrtskyCOrMuJ85om4lPGqmq2Ug7zNYE9098ljKnynyNLhQxYqH7WNqNqOshAgZ3xuCYPANCKMlCm2KrlVAkDHegmTAszXqcZmaXOudxumW/BNLFJaZSQiK9f7xZLpAROqTyLEEIZDqm+IMZYBjFNW6oNhhQUpM4/MRRGX4ojsy1N19LXnNP0IvTcqqq6ApDIJZcWKyPJgEuO2lpuH91kf/eYVxcDA7ucL9/h/PgnWDPnP3yz5Vb/kOOdPeaHO/z8/V9jq4rHjx9xen7KnTff5vb9d3jy8BGPnz3Cza9x9+49fvKz6/zh/T/y5OGX/NPP/5kf/vCHfOd7P+bo+j1i2vD5gy852JkTvaGuGw6vH7BZrzm/uGBv75j54hrdJtD7gZs37vCf/tO7GDfn2dNn/B//+/+G73v+/T/8R+7cf4NN7zm/jHz04BF9PfDFyw0vfMvTyz2+tbjG27eWLOqIiwNpgDh0vPeNt5lVLU+fnXEyu8cvnp1yYhfs9xtqKyCQZSD0iRQGXr56xZMXLyV5jOLD61nLzt4eJheNUi7OpuynRXPLYyLsNAu+9da7vHHrHstmhh1i1q2W/RmClwJf37O7uyNAp9UuGEcYxBfWtXSPDN6x6dasuwuGfkUKA33fAbKuLnphI5akK0KKBkOFaxu++Vc/4E+ff0L0ORk1jmrChiNNCiJsJ/nCjBwBDpuTZQWIyvq0tqxOBbNsWZPaAZBXcAIFh3XyN8aMxS0jySsJkgkTMEc+W0FE9gAAIABJREFUWgbx4HMyMA5eUkTEWiegXW5xVqpTsbdTgHOSTEwTJRmmpUF+TqicnLNJUjBHk7JJ0jW1uVf38rTYdHV/bycuct5j0jc5fmLLNpl8/5XRlL+0XIMxwsQZvN+61qvfb0rcKs8sbV1T/s78+JjcN10zY+I8xqbqzlJMDMEL09Q5rDFs1muC97RG2vYTEJNIDZESw9BnPfBYirbacqrMOFNXuOUC09Sij59BthCF4af3wOZ28KKif+XapvZTu07Ut+UL3HqeKiswfQ29dAWVAms+hg4+0rslRJAxybbJ4jMDjpTZ0JP9ZYzEQ4P3guddZW85V46nYIr3nipr5+k+HmMH0bnWcxmLn9KiKd8bmQK0IwigezvHJiVX4WulJcjXrWujqipU+3QK7MiAUJs7BPLvUUA1AxYECGM8EFPEaG+tftdkrxR2KAo4xQJOyDkLg6ydzanqCj/00v3lLOvNBvL92/QbnGtyK6/DbyJPHzxh/o1bvPnuu1x/4w3OukDoHT/7m7/jwcunXIYLhgxEqRmRfbOtlSonJ/sXZc05h7bq6/pVkGkaC1+1L1fjAP3d1KYZRnDdumxZy72bMMeZFG1MZqRl/zWNpVxpHR5zUy2oTGP2UsjWc88M4ZDE75lgCiC7FbsmEEgz6xaX8wKTYzApkMbR5+TPJvQw+f25IKgyfHJ8kV8wQN8P2VUImUhbio21dEMPadR8nrJHx2eZcw5XZb8gxZCUkhBCUsoFNCuse5u112MmsgRhntsYMM6JxF/lBLjeAg/kpY9LY0vJ3bfte5FXs7njNQOa+ndl0m6Ds9vdE9N/62sLeMv+WWNhjUL1PiUyWcXaTN7JjGMj7MvKjjJ0YmcCtqpxqD0Z05MY5XmNHSOCQ+QUsOQQamemcju6pg2GZNPED+tgL1ckXSqbW92Nw+SZMXHik/XYUjyV6y6yHnmLaMEB3RvIzBSNAeq6ZvrSGSzOOTZdl+OKEZ/RPGq654vxLXHCaAumAPsU4B0LPbIei7SHMlRTAkvuCMm+3cvw+BijdDInGezVDYPkednXpVQexJZdmkpmfJ18xtQ2jOvbbt3rrfdPdoNqv7vcOeKDL/dIn0sKQaZLYqjrmkU7p3ZVLhzp8DnFFGSukPr5UuBgjA+NNYXkpc8zxTzk0CD7ONu82WxOVYv8i8hZmEzoSNhkOF/1PK8N0VTMjCHSsA4b8JHzVcfR3oJuc8nJxYp2tqCPidV6TV1XxM0gMVRtuXPnFt944xvMW5HKXK1WXK576UDhz7/+okFaYw3JRnGOuV1AEgtTsgnVvvTBl0AoIzAELMko6AAp2axR4csmccaKKLgxpR2wqiZSBGRDbTL7MC+4qfi7zYkXIHq22dDI15rC2owhgHWYrHBtjXx2CFHYGjkJwoyAg3glNbQKLI0byeVFGScU72JMrejeYUQGISSRDFBcxGbj6NOArVyu0vhicCUiFcfi6blYB85XiZQO2Dm+iYkC6lRVJa1D/YaUEm0zo3aNMB6Bg4MD7ty5w6effkrtKtYpMZvPSDExaxtuXr/Bq1evePHqJbNZy/n5GQ8fPSZVDdZWHO7tc7i3S0VkMdvl2htHBCN0/xQTVW2p6yYH+4nFfM3q7DkpUKYQOx3k5KRlYBiGXHESI3N2fspm0xODJfoO4oJ5M6ehIoXExeWK3eWSZtbmtp+eLg48f/aCvcWOMJRTwloBc7uup3YtHZaz9YZ27gjGsRo6nr16gScxpIQP8PzLV3xab3j35iFu9yWfPXrKHz/6jABs+o6+7/C+hxQwRjXRxLkbEslvGPoLzk8fUleexSyAHeg3p2zWHa6Z0Sx2uVxd0PmBxlkwAmK4ylJXlt3dBdboRFdxV323YRg6qVwag4+BzvviwCJItSmNTmk09NJOMwwDTVPTti11BmkhMAypTAQ21mCcZdNtsNbSZY3bxXzObDYjpsTl6lIkSqJn6BKVE1BruZgLq0U1hDRozedTqfMNAZ1IaSpbGGbOiTCZth5pmKNMy2w4coKaZVfUyqQR0CRNAq8SYOUEPLcJB0LZWxLrqA6TbvUrjKmJU0wTBzpNwuX9yurZZmdpEDA61xw4TbStpkWtEUNIr51P/krGtitNxcZgUb9LAYESvGkene3oFAgxZhJQajJpTGZkmPFcyt/k/MZ4NHNMFKBIKi+h18V4P+QkSlVYK/4GI9OwJ8+1NH0q6MK4xqeJVYxjkDMNnEvyn9gKImIOvDR5wGT9bxLz2YLatqwvO3oaTus9+qO/ItU3+dtbib8/7qkfnWEPFzx+eUpdN5xfnrPpVuzv7/P2O+9yfr5i/+CYZBv+8MEHnJ5v+N73v8/f/vSnPPziJg+/esD6csXDLx+wv7/H4c1bhGgIq0v+8OE/c/vWMTv7h+xe28GaMyyGodtwfn7B2dklq3VHFwJ/99N/Q8Jy/627XHYXvPfNbxE2HZuLjtUq8eLsnPb6Iffevs3LT08ZouH5qzXfu7UP61cYYzh5dc6rl6/43pv3+OwPHzI7fJf/8tvnPNtUVOdfss85MxelkJgC3nd060s+e/AVm+Bz0Cbr2bUtbjnDG6mSRxMJRFLMWtQpsdvOuXF4g2/cfYvD5T51snSXHZu+wxgrQG2SvbZerTDOsVwuwEiFvzYVynS4tlzIM3Syt/3QE8KAyewIIiQjLcA+DITgWc5mLJa7tLMFgw80TUvlLPdu3eL48JDT81fUGJLJevgEQhAd8gKeGrb28wiJiA43GSyY7tu8ZSbrVPftGIjroAdj1QjoWs9yLkiiLzGRxRAU39sGDCYvV4Cg8Xus0yqZnH2l7JY4+ew0wZyAdNP9efXfGS+QvZuD65Kc58TfOAUZNALatnPT19eBg7Dt3yB/l5kMhGK0aZDlBPL9VsCksIPyPdLvUUBX7fv0O5VpcvUct4agXDn3bTs1TbquJPvT76hkmK7Pcxma2QwyM2c6zRpjaNpWnlX0eY9YTExE7wXYaWoW+wcsDg8ws1bakrNTSPneCMDnc7GKyf0bQc3XQa/AFESU2D1P+66qLd89LYzpd4O0GpNZSTEK8QL9L/tAWUu5zVsBHCTqmh6/gONfw9zy3ucEOpTiBVCkB9Q/CmFAffbrCfHUB8eYh6hOn6GCUkbbgw3OCHu5tLUnZWppHiH3RljoOr8gg4H567VwoCBCAb/IQ8dKh6Kur/G4xpqiTW/NmNQrUDzdcYXxnUGTok8LtPNZZnjK8YfB4wfPw9OXLPZuUYsCqdgQGyA6vvz8CTfuXuet9+6x8oGz1YqWhhtHRxxf2+fZy0s6LT5BIeqAKSy7NLkiZQIXQCJ3ZJX1NYldps/lasFnCqyNNnby5zT20/cV0Iat90sOl9nHIYGzZT3Ja2TM2StA39XC15T9mPI6wuQiks3M92xbdQ9JTMzEL0mXhzMWbW9UwNY6YaAGtM07rwtX5eeeme85RpZ7pwe2WS4jFpBX8+uEAMm2EuAcDCaaDPRKV6uzEu+r1q52DKaY8kDy0c7L0KF87hlzMJlFWlcVzlW4JBq5MQSRWbIG3Mi0lXWSygDl0U6Nz1CBJ/XFCnLpeqmq0b7JMV+36caYLZBK3mu31t3VAoExamsSDilSDN7TVDVD7qB0Nkvo5SHjVeWonSV6YR9XbtRkbuoar8BgVN3jMb5VuQpdMzp7Q89Vrnvb1xYAEyXlBWw+F5MMjXXEqmGoWvpuI/GIlZjb53hPAVmx62y9dEingqwuS1So353e4+nfRz1vGfgcUyIInWMLqNRcSAe/TbYIJq+RqYbtuP/G4qP49ewPXC6Qhiy7NF1TkDXDDT5IAdNlWbeh92zWG+aLJWpTo2oN59d0jVxdO1Nboy+9NnFE4gtUAXb7neO/p52ExhgqV2XiWS5kxkjbNBClSLhYLOTfKTfEI3iYq2uCD3TdppBftNgYvC8EoxSDzKQxer5OdH5jJHiVGpKB4gZDXVeE4IXIR94fWdbQuYYBy4VP7CSHBbwx0hnkI6ZuqNo5foi4aqDzcHbZ4X3CWMdi1jLbqdi7tmB/d8myafGD+HrfeYgwb2YT//n66y8apE0ICGQxOJNye7RIARis7vWyAEJ2EMJaiEDMLf7S4iggrYiRy+RSg+q2JQVZsjajVGEixoxs1JQDiHJ+U+eKbJZAdoqY0gpts6OxrhpbBdLItBsHDKWsC6ttJePm0Yn3o/8W4yAPd3tzGaPJlAboY2Dg0aBJ20goLATVglSttZTbFaUtNxBjYL3esF6taF3L3dv3ZCptEAaE95KM+uDZWexI+3/bYNqWZ0+fcX52xsHefm5RNVnzx/Lo0SMAjg72OTk74cXLpywWMwKW3fmSN+7d49ruNVkP3mPblrppWCzrSQJi6YdA360xOOa7+8ShwXdrUp58nWlG+CGw2fSySY0pbRx9f0n0BlIPIfDi+QsePnuCayt635McWFtTu8TBtV2evnjG8/ACWztmy7k4p+ip64bVsCYQeHlxwotXL5j1NThYLBYcHR7y6OkTfO8xVUPbLqkxbE4Sfu1pK8eLlyekQyfsFoT1GzOgRIqs1xucs8zaGmcjm/6c87OnuCpydrZk/6jhwedf8KcP/sTP/v5/YPf4uBhWa3PCl6B2jrZpOD46zGtKdVkhDB02RhzStl00OdE2IUuFJXhx5NbaInmgO2Wz2bBarxiGgX4YpP3bVFQVZXjEcndH2vu6TgbIkcowr/PzcxY7S4a+l3VbuVKwiBlQNklbqyToEE002dNeEytjipZUgiIeHkzIjpZsT0xJ+JkEtcI+kMFl+jLZ2et9SxIRixNmUqzJtkzAJm1cU+cllm5bn2h78EQJrvNeLMkWo92RoNJMzo3y/QqiRFImwCUJxpwjemGbOVcV2zK1aVMnnqy2IZkSrGRkBBjZOHq/riaasD2kS+1gCTKLDbOjfqverZTATIb/aKCeI/XxPmkSabJm08gQMTk51dfVCnbR7k7j+0pSqTYReM3WTgpjW0FN2mZHlVZBPddEDmgtxhna2RwfpcUpVIdc7n+f9ew+h67jH95siA8/5vCw5Zcf/ILnpwNHN4/54MM/UjnD93/wIw73Dnjw4EsWizlvvfkGzlnWm45f/PyXvP32u9y48yZHN27xyUcf8NHHf2Le1ty/fJs333yH6Adu3X+LJ4++5NPPvuTendt86923uTw/5/zkBGMrdhdzzi82tO2MqrYYU/E//y//Kx988BHWSNdANIZoAdfw5OWao7mlnS8Jbs1XLzZs+kTaDJxfvuTxg6+4cbTPyfMXzJslv3rh+O3LRPCvuHHyGw7tCyq7xrg5s2ZBVwW++Owp56sVyUjxwyBak7PdBR2DSL0kSRhikHu5M1tw5+gGtw+Omc0WuOToLzdgc6AdE8lEsJbQ9zmQE0D21ckJkKhyO2DlLPNZS1OJNrdxltq1GOPYbRq61Yr1ek3TtoQok6Glu9vh6jmz+ZKqaYj9QEjCmFvWDe+89Q6//vD3xGhxUYoZzkIMtgzcM26bzalxgNg7NwbQZgyZVQ9Rba0WY9Q+jPsw26HMUlJAogT0JdZRHKv8ouyTsvZTwuWBUVUOoqfs9RQnBawMXE3BC7VZ0730OlCXytdbY4jaUpnSiJgogF2MyAhgGDO2n149ttoM8TEjyAdsJZWa2RUAM3/f1B4UkMLCVAZh+kopFQbH9CTLVViRsBi7NvKVTZ7h9LVdLBqf5Xj+CghRwEsBcgQ0dhFSGOQZOkvKXWZKYjBO7WkGtnQfJWHyxASuqVkeHrA4PsbMF3gENJEp9+O8By10ltX0+uWU891aY+hshmyjM4iXCgC//RzKHU2jtM8Y45vJs8oM3dJqrAxAkTEwhqK1OQW9rg6L0v+aRsgDMY1J8PS7lEOT8p4ScGG7wLoF4ODGwU7ImpJHmc9jooEe0thyPL2HX/ezaXvy1f2wFQMwDqzScyq6xry+T1XD36eECdvnM5719prNdIrcgRgZ/EA0eY/FROUsQwicrS9Yzy5Ztrv0fkPXNyLDZi2vTjsevTznjnGsu4715TmpamjnDWEYqIZBGJXGgM3Xn3QNTXQxy9oZ96zqUhdJEb2PjAPItteHrt1xLU9Wdr7/+dlk+2JgHKTI659TG6myfwrUxqCa/pR1maKwWfV6pmSeKRtu+nuSDk4UIzGdzE7urowGaleBEaAvxUBlhHVZfAsS41pj8xRzycEKSzHHszFG2Yu6R4KlqgyVk7Zmk4Ttql1gotefbUoGAZVtGfNwLJNM+Z6RZZcJGiERUWmDiS+0ZuwmLfJjSYYfRTBGO2YdwRhi1rzUYZUKEFbVdB8oyC57VfZaHoDsbCEKjWtlyp4dtWi39uGf8Y1TsHAKtpU9l+N10YcdAWUfRha7zfbcGBiyTF1dVTibyRP6PI0thJTKOVIePrgFGht1vlpIGmMIxSb03ug525K3SHyTLUm2uyIh2VYNqV1gibmtXbozbFUJRpT3kGGUxCg2NyVM9lPGjvJY1kpbfAjhyrCsDEZm4NVaK7kwug7z3AozMqUL6SdfrAxzTWwXF215bwiiWSug+8SHTKSWBFMSJrEUvZwMnCcXEmOkqdv8TAPeB/q+Zzafl/zcZOb21ARNc8ztDpHXi5H695KD6bpWvWSFoye+cWpzlODlkrCRQWxXXTc462ibtpCuQpKCdggD1jnWfVeY5zF4mrqRGDoP6SbjAV3XZ/xAzqfrNngfqOsKbKIfOgROkLkQlZMcfrPZSHenFawoxohphEEfk7D8g4M+eRIBHwKvzs6YzxvB9jCcnJ3hMRwcHHC4uyMER98ToyVGK74sei5XGzZdTztrs0b8nwl8+EsHaRMYkyvGRrRkXJW1Hq1Mcdeap7Qk5k1QPqxBaiSZiM9tTK6qZcGnqOzzYsSJhhQkUSgM7pTQwUM6MdNwJbCwozGVj6RRG8vq+cjvxBDJt0plj6LtKLTuDLoyScqMAFGYseVwDHLHZKKE8BkAKZWk/D0KtCQ7sjhIZM0l/W6bW0lEFyzmxCck0YK62Kz55MvPmS+WHO4dEhgYegG/66oGhFWLg+cvX9Ct1/hBWul63xNDoKkrZu0c34tIux8G2rbh8OCAprZs1j0H1/Z59623uXP7Hu1sh+RauuiJ/YZ51o2SIErkxb3vc+U/UrkK2+4wb1pc8mzWl2KYfGCz6Viv1jRtQ103DENi0w+cX5zSrz3r1SXza3sYZ1iHXtjcKWArx+XFmpmr2KQk0gsGsKJV1206YUfOqsx08FxcrpjNa2ZNQ1ru4Ixl0c6Y1y2VrcE6TlPHxkU++/IZm83Ad757l3rX8cyJOLZovPYSBOUJw4vZTJgZBHCOEDuOj/doWycAaOpZzhz3795g3jhqZ2icuCxnE06DtiSAZq2DeXKyLgzdSGVlWnfKgZBRxhXigIe+xxqnckQ0dSstKV5YKj54YQKHAWcsfQokE0VrbWK4h2GgqiqqzLrdrNZEEpu+I11I+4DEdyKQPvgB5yzNbEbIjA2dMKlAmjFjoKztj8oAThoApzHxVuAxKbCaf6eDqBLSBmRzsKdtk5Ar43mP6pRZ3U8xjQ7PMjJnAVIMhBTKtOzSEl2iGbXfqZyTsma1CqkBu2WSgOc/taJ8NaEE1S40o+Z1cdY2gxgjaGwy6B1TpLZVYcuS7csIBotduxoIyBWkEdSYJqsTm6mBqinamuSAIIMgE3uodk4DhJhbmwoInoM9DRhM/v6twINcEFYg+2sAFA0oS/qvSXEaz1kBZRmcpJBABpuyZMJ0YJAkozL8Egw7ix2W8x0iDT7usp69Rzj6W7yZ8d7ilObRY9qlJzQtbrbgsI4c3zjixqvrbC437Oxc4+L8nLap+MXP/5Ef+sCdu/fAVnzwxz/xm1/9im9//4fcvXuLveObfP/Hf8OLpw95+Ogxs/kee9d2+Ff/+t/x+Wcf8+uf/yMf/ekD4tDx7tvvcnp+iXXw5p03cO0CnJQRfT9AU/Puu9/j8ZOnnFysoGo536yp2jmPH2741Ue/pto5xC0OefzqhC+fzPjW0ZKLp18waxN3bx7z5b/8AV9f57988IwutSwvP+UwPaJxvbBj4oD3PU+fP+WLh18Wto20LlqqeYud1QzIZPUqGdIQmbmKG4fH3L9xh/3lHmYwpE5YfrgKbI1zhsH6Iq1irWU+m2GsYdP3xCgDQwcGAdebioP5PqvVis16RdO0eCctlFXbgHE0rXYeSFdK128IoaMbPJfrDa5usFVF2zTYyrJo5/zgr37Ek4tzVt5DkqQHY7GVwSdfNOy17bbEGnmadp6+IMBMrpWo1rcUtZO0ZzIBHvL6VxZhzEN+jLUyqdqYohc4lkvGgrbaKGO3WY2kkdU+7sZc/Mhxjr5CVM3mWH5emHgT0ExfV0FOBdxGaC7bxwL8jYmzFrZksNpYRJomKaVtL4MR5ffyl/JvyRXk3GyOmfQ6Mw4xgaDU5mwzUfPJbn3/nwOjk9ogTWLV7hozstnyfRjj0a+TbdCYL9vr0fjKHzFCBGcrqvmCfrGQTq8kbKmQpG2wKn4FSRozkwwDbtZycPM67f41QtMgXPBY7pHaeI0/81PBlLg2Ts5XY+Rx7eoDmtpdPX/tmCggNuN9VkBIW9oxYwFV148mqnb6TEDWk1HtVQV5XVnnMaXRd1zJt5y1paOnJMFpjNGVUFFVNkspjL5xXO8KnhmKxIdRVpZcgTESqzmb9aInPl+bD3UeAwli8OP6y7mKqxxDLzIWtWr/MoItZa/q2tS9nv1sUFkIM1n9SSyIFm6Vta33VocSlWduVRdVnpFPiXo+o1+tsRqvBVmPQ/D0caByNUMK9H6DdQ021Dx48ISfVC0H+zukZEjec7B/nXfe/gafP32A9ZGQ7Z10+SQm0cgEYDOFHWgzuzKEkFWT8z1OKoMRRoDCUAq/IWWGqd6PYjuMALN5LSSNGZg8u3we23bPjjun2M1YbOyYN2abMSni+dwNZ0weYldJd4HaL5XXUrk7rC122iA66Bgj80dwVJXF1Y3EyznWTilJDmZdaXAVGzEBHdXOW0P0YeyqMwLS6952zpYYtcxtMEa6PBllvdQOV1VFVVcMg9/eQ0ZjQvnOylZiuzLjUddjyB20ScRos/40MhPGTWRCUma9VxWuEZatyXG1DJ0cGb+jpmcmc5ABY2uJcexOFFsy2jeja2ry76ldnP59ignoGinAKDlmLsPMZXyXdJYE+qEv/jLVeW3FSNICXAiiOWykY2IcAiadNSHHxCYD6mpnJObNvgUma3UkK0wLirrOlXAS83qWDpzRTltrqZuGITTF/4ShFya3dRIj6XHChN1f7Plom7b00c0IVKo0jTWTuRY5jzDIfJuUhDFNklxOGeL6p3Py7mCyzZ/YOHnfyKqX+KMk4SUXU3kc53IuCZKvWx2/BraqaOzYNTr4gRSEgLBarRmGIRfwJX5URvrUpkxJNnqvRvsz/mwE/Cd2Sf0LduuzV+MPUsIPg7BUrS1Fn2HosU1LVeUhfcjcps6PNsFVFS7m2RI+kCo5Lz94+q7DGpEMkdvnqOtW8oQQRYYsjRIiMgQwQYp4HzEmMWTSnthp6RyWrShDyvuhwfvA5WYFQboCLlZrnr08pTKGTd8RY8/e3h7Hh7s0tuLJs6dsNhtuXb9BCJHOd/RdR+8HsSXoELYryfLk9RcN0hqgyszqfuhpnJXKgQaoVh5AZRwxt97j8tpJZjQKyWaKOyQrbREOGcCFmbT8MWkHTLLgIpCMpTLiSJMZAxPYXoQKEIjREYaazfRrQPTd8qAP3ZxGg4MMekgwri3kY/uUyYBDFAtVAAKbGT62ciVAhSylAGhLhYI/xIRNeSxDCLgc5MtikTY3Zy2uMjmIy9eYp/tWTUtI8OryjN+8/zu+881vc+/6DSozZ7XeSOUgRVIYSBGGOMhxDEQT6cKG3nfsLneoqpbQwGw+o9/0zGdzYuw42N+HMHD/1m3euHuP3d1Dkm1ItqZyDbVtMThiMGANCUtKgRR7VLM1hoSzoqWLlwFjdVVT147T0zU+eGoahhg5uVzz4uQ5z58+IXUJv9nAMFDVToLgdcfgA5eXZ/gusnGByy6QGstl6ji9vGBWzTB9pG1nDF2Pj57YCb3++PgGy+UOz5+/wFCxurxgtb7ENA2DScS24a3v3eVR9RHLwTJbrvj8y0vC2zeFth8Taegh9RjXAuCqStagtTganDU8evqEN+/dZ3e5w7C+pDaeb77zBu2sYeg3dN0FPmygrkhJKPemrlDNQBBRbovBIfqUVdWCTfhhg7GuOCmLgShTDqmSPI8Em/UaMALqZcttK0iDp65rLgcZSlRbJ4bWGrpuDTlgWCzmRO+pmrro/nR9L9sgyvnFnPDZqsYu5vTOlP3iMtss5HVeOamcS4EjIQNrNWiI2CSSGwbDMAwYaxgHiWlgJG00hjiCnhJmZKsxJtFaiRX9tpxYWgU0hHGSeW0F4CfvP5sdljDMhRWaSNmRZRzGmLKvrRGWk+56H4XlO7JAhAGvyalDJ3grf0c+OZ22OrZgieOQwA80MNbhcQIAj7/TRCJHglhTlWBnBIpHIEz+nUrirfZNA7ZYwirGpF31covJtVuDL5R1YBQsmADU+pymrxLM5mNvoUFb7xNfoID49EDKoLFXPpBQxqKhJFL5HqmdJxlshLadcWP3Bk09p2PBZXiT4fin9PaY7x6t+Y/3LPGjjzm4+y4vVhe8853v8sEf/8jLFy843j/i2pt7MqW6cuzszAhx4Le//RWPH3/F0eExN48POTrYYzFvGAbP7ft3Id7n/pvv8OLVK548fMjvfv0b3vvmO9x7823+x8NjPv/ofTabDV2yPH15wv033sDOZiyXnlcvnvL0wZfsHtyi63pOTx7x2Refc+8bb3G2viDZBfP5jPPLr1guaxrOuL2/R2PmvHz0FL93i52dHW7eOuT80VcYWv7vT17wxRnMLx5xJ/yc+/ODAAAgAElEQVSRRdWBCaRghRG8vuThV1/Rx06YXEkKI03b0uztEGpH9B7jI2014/hwn73lNQ5295nXC/DyhGpX5wRvZJxaYwTXjMJIxUTqpkanO3svYMysaVgulyxmS9FfP67Er6UAVHQ9WJewfkPfr7BWEtlUSbGrqltMLdqci9mc2jnquqauG24f3eR/+u/+Pf/PL/6J5+tz6rrG5CQy+I3EEoQCCI1rTa4rBEkJQxB5KOdsjn8EzIjekDJIUoLunMD5NGopSmEmjHtO0k4UBMaIbTUTZlaagIFaiBi82CKn7axm5LYoACHDSgWgUZYm2S6O56lB7OuyMGq/iu5wAeLyYCGMxF7GYDIoG8MI8JfrmyS4I4BEwQKKv9gCVDPgFiM4V96sNs0aV46v7Bo9x5KQZvDxqqbbaEsnoF8Sf2Wc2lgg60XGOAH9yMDPBKCT5yAag+VZCcZRAPZK9U0xVIjtT7MZ7fUjbN3gz86wMeKHnkgelJaJC1UZSAntYs7s4JD58SGDEikKuGIg5Y63qhrtaRpBKYnbbFkL5X5MQD+15ynm650OzDEj0DquTVvICql8fvxzelz9L6SJFnmOLUwZv6S3fwII59MtA8GmSX5uD00ZvFKALWXAUZ5DLkBmsFXPR9dGGfpp4/SMy39SiPZZei2N+oXlpUVOpDU5SdHG1o6Q76EfAs6Ca2tIY0vzVGajtDIbU77eYCXJtIkwhHFgVCYUOCfT121Z85khnLK9uBITRITYYrP/bK7tsnPjBucXa6JfY4HGOfwQeXZ5SlVVHLW7xBSIRuyNS45Xj055/PSUd2/dZXY58OLxY5zZ8G9/9q948vwZ//TR+wRbSYcciWDEXhg912JnEphYppArIhHj2PprkgCGIjcRSVHY/bKeQCe3G11Q2cZkJVlhxJZ1pjY3E2ZypyAwriXNLScxFGksaCVMHpoIKkMAeVC00Rg55rboAY11bR5ODYambvL3xlLQF/8owKFNEuPXdUNVOsHGrk5Q0pTklqVLqsxcoawtYyxtOyNlPfmqqmQodI5hTe7+0/0QE1mGYCwYyG6O6ADLOs9IGO02KDMzZXstw2x1OKjkA9HI2nPOCbiW701IWVs3f17yLwOV4BLOWoa+L7MZYgbo0eeDxrrjvlXtaSGYZEAqx4oK0I5FmFG2ZruAs/2aArVboYI4JlkvzmBxubXbkyJUpsqkEllHTVUxeNHmNJUAkdZJRyEhStxQ1VTGZODeabCMDgCUNetKHmAVnEO6LJXpHIIfO1iS2mny3pD/iU5vlqczQjxq2wXGGPywoTKB9TDgk5cOnhByB8sIshb5IUmDSCkxZIDMWXkGus+mBVXV19UIBmRwphwzvSYXorZfboehsk5kb/LPNVbRrgmNvzabDTB2IlqTJdKyDitA3TQ535U1mVKSvaCna7PtkkWcZbxkKGWISaQjCJN9kbbW6HQdbeNbk98buS+6kiGnsgrYFh8mRVznRnCYHDsVrM3ALMshikipJQRPGHphN9tKMCSfQyHvCT6yGi6ZzWZUxtLHAdtKzF6GJKpPCSJ7oj5cYmPNd0PZI4nc0ZrtkrViE4yTQbPn64HKRkgVIQziN41hsxHAtWlajuct1w/3CMHz9NkLVmsZ1kYImOTpLjr6Tti6VSXdBUOOC/7c6y8apAWK4LjLgbBUouTJxpgwKWU6ct7QyjRwArZMqeK6OEJMuf1D9FcMyhTTSqR8Z4hJ2oONVHNt2bPToRsKIhRI4bWFP00upgFhGTTGpDVBjUFODqaBXsoAjh5j2g6lbTZqIEpFdvLwDaa00Oh9kio2SI+qwkcObYfOJ0vIbZNNLdV1PwysujUffvwhdUzcun6Dtm3wIbLarKmrBur8DDTfKFXSisXsGjFB112wc/067FhSSAyD5dbtN9jZucbBtSPaxQ6z5Q4+OpJ1VM1MHIaRdkq0VRVh0BoiKbd59X3P5uIc368xSAvMcrZkPp+VSlQ3dFxcPOP588c8evSY/tyzOr/AOWl7aU1D6GUognUVm3CODb2whl1LGAbWrHgZXrJoFswXS9bdmsEPXF5cMl8uaYzD+8im63hy8oiz05dcri5IwdNHz9mmg73bpB3P8vqcv/rpDZ791494+uqUFAIxyJCJ2jn6mJNAm0GjJIlWO1+y3N2nbufgGgIdVV1RtzW2BpxcQ0qBEHK9K5nMnEnYlAhdR9UYTPLUrs3sWmkzqo1IMGgw1tYNZnIePkaC75i1cypXiVPtPSlJO/Jyvov350UbUJNVbc8zRgLIvu9p2x2i92wuVzRNg6lkQJjslbHlMzUVfZsBlxhKgqagpLWuOAJX5RauFDIzNjshKwC/sQbrUgHd5JxGja/chYhJ2gYjWa6yAq62GClzdwym5KxDGsHNJFlaTmKzlIsxJUGVYPT/PyjTkxw1nkZAdwoISMFJ9mFKjHfSvG5Trn7PyKVTTUuyrRLLoiGysh/U9pRqvp7nxP79+evaDhauMgXGARo5ePZDue5pK+uUuboFemTwJU2P/9otvarjOD5bO0mijRO4qgBEmUmUMvinSQSakOYELUVpm9ydLbhx7ZjaVIRkOe1qNkfvcjq/z9xE/uFbO+w/+4hb794l2Ui37uhfJk5PTrm4WLGYV9y4cZNXL19y/949dhYz/t2//Xs++uQT/uW3v2Dv2gE/+vFPObp+G5siKXgeP1oxX8xp6oabt+9S2YZXT1/y/vt/pG1b9vZ3+au//jf4oePFs0ckU/HFlw9Y7B4wb1ps1dAullyuO/708YfUlWVvd87e7jU+/OgD6uU+O7ev8e37N3j7nXvsL1rayrJTO9isePrFBxztVPjzgQ9/9y88d3f5zYMTZnFg3v2OuXuBS4EUgkgRkHj24inPnj/FGCkgWSutjLPFHFdXbIYBGw177Q63D465fXSD2jXIUE+Dj5EaSDgwVU5QQ5ExAGESVNZiKoezhj54TEw0rqJtWmbzGbPZPA+QrKiqij72pOBYLm9wc/cGzazl7OyEp0/+RL9+Ke2UtqZpWnZ3drhYrQBD3c4wGHyIWB+p64rj/SP+9U9+xh8+/pAnr54TjWVIg/jinAzoejYKTGZ2YwFJYxwT/1wcJifrY2Ase8RNir36WdHungbk0zhmZNnr+t8GLvP35mRTfp9ZW3acsCv2cRskJaWi2RnzAAljNbYCMymmX7UXajMlPrJbbBR9ee+3bU4uA8k+n8oARAEWc7Euqj+YJL1ThkmMHgUjSiKedc713m4nyqM91u8zZgI8lgR1EkcmgLF7Qj4vviFmfVa1SRn5KwCiPkFTBrxRJAGmw4+mz7sAxtYy391lXrekusGv16w3a7qhz2y5gLGWxla0bUOzaKmXS8zODinrvCVGprXY3Am4VBiram/zVPUcv2GVpaMDP7aZZNO1IOA6pYW3/D6v8RxQv+5L9E/YBtDl4JP7ogn69vfr+SmwPo259djlmOqH45X9WhhvSTqFJntyjCtE9opoih+dyjmU2D8lUgYmuHKclBJ+kGfS1A23bt3l6fOnhDAUUE3BwJiyDuRr64PX/m1y3KUAR1Xyhix/EQRQMJY8vTvLXZBtVGGFltWK7lCyzVlcO8bvrzldPSAlT7JGmLPDCmMPqeqaZCKJQXKaYOk3kd/98n1uvfkmzXzO7uEBhMDe3h7//d//PQ+eP+WryxN8Jbe1aAqncfK6XlvKP4NRV3jUFc3AfO5qEPbpZH1GlUrSosLIJraInKwxOSY3CopLzmkQeQcFswW+jfnZjjHKdtwmQKDJACe5kF2mp2vMFZQdm2VnrICNKQkL1uT3ypfpWs85qpUSWQpCYBiCz8fS2FnhLGHhj/Y6D43SPZL3kHWq3yp7OCDAU0zbAwDLvga8H8r+0pzWZbk13RNb8ThG5AbzsabFMZ1NoECXtMSHHNtldqRG5saQrOjSBmMwrsK5Gp/Zvzr0S/2hfqNqcNd1lTsIU54wH3KO4fIeFhxiHEQ+yh9sz5hg6xqvFp/Ge27Ks7PIHnTWZuAz64JrhO/Ge7DJjHqZVSPAaMzFQCE2QKVoKgADtXPFFyaEDKYdPHVVyzU5Jzq4dT3GE1Ul6yQK/pGC2h0psDljcbUMIk4pkYKnbmqcnVNbwybJoGuJdQTodtYRk78SCozDN2W+y2jvh6GX/cEY/6ekQ+VGvVi1UqNtT6N9SCNIO+Y+2u0gg9l1xtB0TWsnqXaW6nA/9UloXicIqHSxZtY+KYlEV96vzlgW8wUgQDshjozUOF0Xr7+u+qyrQO7XvX96rZp/y3ofC6SlOJlGu6d7tq4qVHKjNoYhRcGkbIXIWAQMrhQw6romxF5y2CSYmMg5GIyrhSjlvRQqU85FEVDd+9E31lXNYrksLP3oY8bb6uybBJ+Yz2bUTrRrG5uoa0dses5W56ToCbED45jPdti7tgMkTs/OOF+viDGwaGc0dZ0ldTIuUVU0TS2FPsTv/7nXXzxIKwZKgwWpeoWYiFEWhZsEYykHGjEDIlYs7JiE58AQLErIUieRoiQOMghLjGXtnGgEKgiCIVmTKyZjYi+LOAOrGQywNiP3ExAi8fpC1wRj28jKYVxlpUqVwBAzKBSxmUWpn+n7fgsMKcLOGYkox82VAnWGOgQgqmEkUXpTjCQqMQcYxo0AkKsty90dzk7OeHV+ym8++BdenJ5w985daldTYbLmnsG1LSlIld9VFc456sZhbc3uzi6r9Yra1VictLGGmuv7NzjeO8bVNcY1BCzRZO3TRu/xpB0sevphzXp9jklexJ0TDJs1Xbch9JvcVmTo+57GNLn1JtF3G85OT3jw4CEffvAJc7Pk/GQF0bA72+FosU94klvoE/i+Yz6bM3QDla9phkTtLHu714ghcnJ2yqZfk2Li2u4e/TBwvjpnvdrQrTecnp2wubygshXWCvX/2cmKl9051647dhaBnYNLvv+3LV/8/jl9P+dic85mWGOoJIExGjAqYztS1zNu3LjL46dPOYoVO4sFzWyWixGBlDqcDdJeH8RYGyBZCGkAPCkOmezpCV7AARnsItW7nZ1dZrOWa7u7GGM4Oztj3s4wwNn5Gb4fWCzmLBYL6qrOya/DmcB6teH5i5e0TYOPAT9kXS+TmUaS67BZrem7DZtNR+UqXGvp+x4wzNqW9eYSnTLcLltCbQgOojEMvqeqKxH07wdc0xIZAxEdUiA+L1cbSYiumwKqYsCtzdMzk+rFiq0xbAOgzjDqyk0cmgRpoEww2f9j0KU+L8WRaRpym1Q2DPkNOW2xI9N0C9jMNkflByRgtVm/OqcFmshlEEAcvdgH7TK+moSNdm0sFI3fKS1PZZJ3UlmVaeiRtoLrYhmvnv+V+zb+J5/RyaAxRpmGPTkHfa+rJiw5tX0pjZONNWBUcDXbYZfvmQJK02uenieJMaGZgAMSoMgaQO8rMogypiiB5mSt6NpRa1s7x/H+TXbmC3zvuewaTto3WB3+gE1q+ddveN6rXtKGU3ZvHPLV44dEu5DAK3lu3jrm/r171HXNtb0DvnrwBZU13L13j+9+53tcPzjks08/4eL8BZ9+/jE3r9/mjbe/xa2jY15drFmFyKytuXnzJvzgh5y+eo51hv/8n/9P7t69y1//9V9z6433MLM9fv2rX/KLX/2e73/321zbP+Lo+k26wXJ/c5/LsxfMZi1np2dgDbauWDSOu3sL7Pkz7t24S2M3BD/w/OQZ5y8eMh9m/O4P7/PlkzWfdZ6h23A0PGLPvWJeDcQAIUpBow8rPvn8I3wcqLDYKK1m8/mcdj6TdthkuH14izdu3GF3thTZIp+om5reDzRNQ1vPcKYiGQsETPTEGLhcXdB3PZerS1wy7B0dCOPDORaLGSlE6qahbResVmtCE1gul9JaR0V0Dc9PB9y1Bd/7m7/jxp0lYfOK3//z7/nj737P+fkKS5enuhoWi7kwFzFQ2TxM0TKrG966vcvBzh7/7Te/4OOHX7DqV7mAJFIpwjYJ+JS1yxwTeQODrYTBL+s0t+2xzQzRxF4Zbxgy4BelkHrFBly1B1PW2xQ8G/fNNBHQycds7e9pEq0/I0pSZlJOjCexi9FWvqw/pkWYLUBObcC0sJVSgdc0WYhZpiUByY4/F7ZXBkGCJOKj7dL9PrZCjkUx8ccmd1sRBkqmkqTYp5mixhFS0JHCv9y/3F0FGfQrHxmfgd6n/Hd05kIIBRSS+xjL9ejQEZKC1KYAM6KFyJbvELuau71yemOcxR3u0oYldt3hVivCppP3pMRysWC+XBJbB00GK0KAJAWVFKIAx+VmZqdWAE1bjkUqHDVMpDCJTPanel1gtmLer00k9dmbEaAdf5WuvFVvdoYqda/8Gb9QniVip5ShrIXB6STxaXFkq2jJdkI/PlcFrsfCoH4mTFg3V4+p5xUmoJjEx0mKhzHS9R3GSIFrb3+fB4++YjPIs5TvmwB+uTCgevlX/bTeH5c7haaFjum9Kkl8zM82aZ4xBWbZKmzr5z0RosHVM9rjG/DsWZGsSTHiQ03vPRfrFzSzA4yrsSmINi0zPv3NB/zhzbv84G9/xHJ3l9OTl4QY2F0s2b92jWebc9HRdCbvu8CYGTLe38D2dU/A0SILFQPRpDIoNhLFZluz1R2gw1vL+jdi98i21WLzPUNsOTKXClLurAi5XXiMh/QeV64qAEOjuq8piTSBkcKT6DeS2c1Z2iZfK1YKhwpkmHxuBoSwFJOAeIFsR7XDiDG+SQpm5bXMGC9N750Cx3oMknR7JZuUQYBXIoqZFCXyMUoRPUkRTp7BkNdQ9ndRZmmoXUlmUjif7Hv5+nFolvbI6fVLoU59XqTORQYfEzhLsIaQuwWmg6HKfUX3se4PAGVIyzP0XodMUiRtpvtaQTy1ZVvduJM/x+8cbYmug5QS3WpFt5wxa+cYI8B98IPE9Rk0VolDh5CVZPC5x08GclrniL7H5m7Fceifgv9yv/ocO5PJFDbnC8bl68m5n3MVwzAUv15AfwWZ08hKjwa6vs+dhHIslS2pq7oUpWvXgpnaFlBd4xEAz8BzXodqT/V+63A266zso7xnCxM072PdV1M/E0LMwyylLV+BS81C1PfWdV3A2andUYA8Zr1nWf+WPmsFC9BvhfldbJEpA+OHrs8xUC68hIHS//F6yrdl06ZrT/eK3pupnba5EKqR49UYT64HYRFbAVOFfCmAa11VWGNlkPgQ82A6K3s/yyj5LF1CEkkeW0kxM5Jyp7b4IZKQNm2OYxTEjUrLzHm8s46qkuFkdV0Lg9nI/vXeF7mflPM44yzB93ibmLUzXKWM8EgIsoDlGfeEGOkGj6kqjI9Fn1g7r9pmzny+FL+TRN4sDuFrnoS8/qJBWk2mFcgRvT/yQp5QyqOEE4XerMBs1qmE7daDAiBEHXQgNHrRiJEFHGMk5aQ/RaRVGHVassiU4l5akXKLm/zOjgZ+akD1FCbONao3RAFWdfp5Gr1RBqomIrEAL7Dd1qtBkTHiRJWJogZFkyXIGj7WkvKkZk0y5D2xtJMZY0R/JhtK4yx1U7PcXXJxdsFZt+aTh1+y8QNv3XuTqq7xfS9BXgn+IjbmRCQm1ptL7t67w6PH8ryatiJaQ21nY+ujNfSDx/Y9lZsJs8UHonWkyuZziqzWKy4uTzHRUzvRl40hkkJPGAb5TpNompYQApfrS9HeCoEHjx7wxZcP+fCjT/jiwVfcO7rP8xcvSRFaU3N9cYAbDI1tqJBBWbH3GJ8Ilx2z4IibDmdEFDqEQL/pSCHSV6Jh0lQ1ofe4BDZAiKovI0Orzteei2HDD+7uUPkNq+4x+8eBt74xp/lTxA8XrFavGDYbopPATVtgIGJiwiRL7ebMmh3adoFrZiRkEq5ZdxgsjYKGuTUWI8Dmqr+g92tSGjBUhJQIfqDJk5IvLi7oT87AVnT9hvV6RfDiuPp5jzGGrhM9oCZ4Nn3Han2JNdIi0zSWqq6lAtbLELHaiv5SyuvQB1m7zkkrQeUcVU7GQxBZhdXFBbPlnHbe0q3XIlZfVfQIuBCEnihrxxlcU0kIVNniZE2aMs0znhe32bMynOt15o4OH1OAoOwhthMXcVzZMaVxX+q/1QbpcYseb1WNAuxJHWlm+pux4LKlN2jMCMiqTUHZHRNLmi92K5ktAd0Vu7sV6LEF0KqjxIzSDuX+pNGOTf5abBLmdTB4es/0ZTBlSFJMWQcwF6gMI2Cz9b35QoqeIGwNUfm6JF6D9a/TbizXWmLdq90T+vy3E3YQ5gBGgkct+ImfMWUdGAyNrZi1LRu/YQgVl+463PoRm+Ymx03gP7xTYx4/5OhwzoOvPqGe73J+2XHt2iG3bl2nbmfMFzvs7l4DEs+rF3z6ycc8efyU7//wh9x/421u3LzD2dkJH37wB149fsTZySk/+PFP2d3ZY+0Hnj95xsnLl6wvL/jud77NZr3mrbfe5tHjh/zy17/lRz/+CddvfYO//dkeTx98TNPU/Po3v+HuG6e89+0fcefWHU5mNZ0f6ANEv+L28Zv49Rk7qeJoZxd/cYqrI8kaqgrevH+LX/zX/4s/vP8nNu0NLvsLluEVe2aFrSM+QPLSlm5d5OGXX3BxfgolKTW4uqFezHB1hU2Go4PrfPPe21RUxAh9H7Cm4a033+Pw+gEXqwtWZ2uG9ZrT05cMfkPqNlyuLri8vMD7gPcD13Z2pVvESadAU9f4YeCNN9+knc35p3/8R4a+Z/9gj92dXYiGo1v32Ts6ZtWv+d3773P0/DpH+/vcuv83HN+8y+PHL/jkw/d59ewB3WYlnRGNDC5rZq3YvBRJ1uISzOoZ33vvO1yszjn/8gTT1FhbS4XfCqglRflIIirJQibQo+BJTq6tJsxGgsHcjSPrXkEJtvbJ1dcIjFFW+RSk2Nq7ZmzpnTLe9TUFnYo+5+R7lW2kCd5oN7cZg2J39LO2JJVWgzQ9hyvXNSYOKRtnchyZcsvypJSextZyGWKxPfRwtBsTm5C0syeDoVZnG2QbOLkvU91aHWKqtuQqkHf1ZZICqqnYvavnpjIQojeaB6+YEZDId6R8VhlVkCV1jPjUylh662iqGlfXtG2NCwIwh5RE/9E5Qtbfcxgo3a6jHRUQU1unXWavgbVCuihrxMex66o8tym4I+cf4/Q5jM+0MBaNcnaUYW23pqF/7T222uVDGSgzsqTNZGnl+56B7IxPjHtt4vt0rZfne2XNb4O/Etepdp5eX5yw3tQf676A8XdapJSYRMEg7ViyeVYCrFYX/PJX/41+GKSwVlXUzpW9U4A2M9qZhBY8Ui7QGkmMSVvXpDmPJqZTEFmpLWUAq1E7NF3juZhj9N7IgEa7aGmWc/r+IuswGy6GwFkc2JtbjHVEHNFI0cklR7zo+fX/+3Peee8d9g6vMVssiD7w6Scf8/zJE0wK4CAQRWIq6Q7cfnb5J6Pfn4AUes1y3ya5VL4WVOpjckzILc5qM0AG9FkrnQQ2x6EIoJsmh1NJP5OlBWyObyUXFr3KqqoLqUdOweaYTBj0andCjFlCUICWaIQFGtN0YPZIJIjE0l3gchuwy2tOpTaK3AqZgGQV7DRbYFaxBbnjNUUZQqdrOcQgWuxmBHRDBtiCD1LEyTMVtuK77NeCSVvPS9myZZ9NfF2GA9AaQoiZFJUYRU7yehTGpIOYqKwM/3J1JfvITrtEJrlvtj8a78u6sVvXr7reeXlMcors02MGC6+sp3HfjetV1qIumNGOppjwvccPPalpGUFVV+bJbMX6RgC/MlMhihyiFEkkt5UYxMqEez3nyTUrESJEWTs2pTJ3R0F3jaMlt7nq7/KQxxBzEUl8WjSJ4CMheoSeKvKUIUVsJZIdZgKYb8cM4z3UfErxEN1LIQOkGCmyVHUt9y+GUigW++zL81R/p3a7rqtyj41RsqCO8WPLRkr+68q9l/MKuQAiNsY62YPGQvAhF2ZUZzyW9VG6ifK+LF3lxcWkoqmrz0jWzJVukrKOt33V9ByNEWBT9+FI+NvOSxvVXI4ic6j3o/ee3Z3Z5DmHXLQJpJQlkDLTXnO/MTYQO9U0NcZQCoo60G2zWtP1Pd0wYIzIljlXUdmaqqomkhWxgLN+CMzmMyn8pEjwUnyWdYpI4qRI29QysG3IIHsK9MNAwlBVDTMbcXPpQk4p0bYzTAg57My2bpBZPbjXYzx9/UWDtLowUwZVpHohAzVSClsL2miLQK5aZv9SDD7yo8IiCD7IVDdUg1Ha1gT1zlom2eHr2UiSLou5zvRlrcaQQeNCU48+O5BYEiOTnVipOqesHZVBH00eNLjVFhfZXNkZhvj/tfemsZZd2X3fb+19zrnDm19VkayBLLJIimQ3rR7UVstS3LKQqC0LhpUJgoQgVpwAiRE7iZEPSZx8CKEYiOPEAeIvCRJYiAV4DBIhQpDYkicptiOpuzk0m80mWSySNY+vXr337rvDOWevfNjDOfeRbIdGxKoS97+7WK/uu8O+56y99lr/NSUjv3MKpKcw+r24POmlPaUdDzlfehsiXLH3RiDB4xmmrgnRhC5K3jatH6wmwmA0pHWOxeGM1jVcu3kdJ3D6sdMMypLG+cl7xvr07lbjgADHpUsXeOrck6ysrnLz9i2eOnsWU4BrgkpSCdk0PupRlgUGP204tjRoXEtdL5hOD33fkdCAXltHW8+p6znNYgHaUg0qJpOJH4pgfSRq5+4OFy9d5LXX3+LStcu04rg32eHSlfep5zOfITtYhVoZlhWbaxvs7e+xd28f4wRplFEx5HA+YzGdIQqroxUKEX+6h6ye+fTQtySwBSNbcvbJpxhVI773zvdw7Zz9OdydTGB9QlNPmOqcti3YHK2zWu0x39vl8vvv8MKpFynWNr1DH4xcweGaGlc7Cik4vn2C6MQbO0C0ZjaZYByUxoZDq/WyHYahYVoms33apsYV3phz6thYXw0kZMzy9Fnbs9ksla3NF4su0x5E97MAACAASURBVAKl3tv1yrNtMKZgNBwybEvGK6uMV8dc37mZIqQxA6iZuzAdEVyIiBfGMKiqSKWm16xtbTDeWOX98+cpi02f5SPQNrUvgw5XpRx6ktoG5eqbgmvQG+CkTcZFcDsgHIddJkAXSZdoPIWeThqMjFY1Eb8RXRbtsvEUlpYOM/97g2rXW8wba6FAKJIuIinI9GEyJUaXe2RhcB5b10WPuymppGT5qBM6v/JoRL7L8Fo2buj93JUP2djXy3TZAf3X9MmWj3JU4799dnPnkEedGInqdCHj9TKS1p8cVz363hrW1LWVcRqp1fg7XTKYOhLHR6+jXPSNSBf6iXe94/x6W1Wwvj93XTfJoZGQulwWFeurGxCy2Kessr/5LNPNp1gV+PEzyvqVt9mslAN1vPzaeU6fPsO5Zz7HfNqwub7N6uYmq2vbgaRpeOLsWba3ttm7e4c3vvM6xXCNFz7/ItvHTvL5F34f773zJhcvvM3h5JAf/rGvUY5HDMZDbl+bcuPmDbaPH+PkyVN87ge/yPGTpxiNRly7doPbt9/k2Wee5smnnmExPWAwWuGb33qFW3cPOfPYY2weW2drfZ0PLlxkcvsql5pDVtY2efLJ51kbOSb3bnP59i02trc5cew4rdQMyiF7M0fd3KLUGcOqoRBf4tk637OpLCx393a4fOkyIqV3pBqHrUqGa2OK0RDB8cjmMc6efIKxqZjOvVNXFkM2tk/x1HNf5ss//Hlefu11fvPX/h6mPWSyv8tiNsG2jll9SOtqbGFYW9/k8y+8wHC4xu7uPsYYLl+6xNraGjs7O9y4dYvJ5ICitKi23Lx1HW3h3sEe24+c4dgjT/LISsXVd9/jmlY88+xzPPf7nsCunAAz5q3FlIP5IXcP9qjrOcPhiOFwRFGVlJU/S0fjFUpbcHxrm5/82k8w/saA85cvItUQH1jyZLfFZ7H5KojOVuhPiU36KTiKanxvSwKpFIMf9Ai/oy0Ruj0Yy9E7m6vrb7qcSZv0UPghah6V5fJMFxy+tEcDWeODu10v125fLZe9Rr2UMjCFpRZXcU1Jx8epG8Fei+uDEPgOesUTh14viEBdN/S4m3S9+noraAO8nWhCT9AjmXeBaFgOeHndvFx10Blhqv1s0CNPCTIQ+/WmclnnegN4JJQJlsSlqsaSaqWfSQT++mEEcf6aWgz4RFhPGolBqzK0F1MQQ4Nv+SJtIH5M18+1y/BtU3lj/AJCdx7E66PBgdegnxMpzzIhER1YTfIeAm7922FC/7lIVEZHLDitShxsky4phH6usa2TCT05/S3veqA753yfegkDZHqElkggmnvyKIF96YIEvTOPQHYHW3tJrnqv6ZOdRVEguF7v55Cd5WKAIAZqwh4K9ztm9QAsmlmoNFJKAxJamRnpZ+l15d6mJ1Mxo0/xCTA9Xnr5u/XlVr2t4uXTpP3nS+U72ytlyad+oI7GzdDCsLq+wv7eHVyr1MbgrHJrNmFLt1lVP5zYlJYCh292U3Hn6m1+5//+J/z413+C8XhMPZszn84oFi3jwnLQLGit0qj3lYue/YNqGkYb5TfJX6ie1OAv9jdnR9r0rod0MiBGUpYooXWA9IgUa02w/3xyQHyvoiioKp8dWdoq3aPk+2pHBsYKSSTamcsDE1VJvboJ3y3qUsS3rxDBE2x1Pwjkd5sGCYh9dJum8dm9gaTRQCp6f7qzvaK9qhITiTQlHtlg/7kwdNMUoWdzb/94efctZfrBKhP0q4ZewRoy3KNdHWdFdOebS+dRvFY+YNUFILth3eJbk4V7r+KDcc75uS5l+FMHuY730akLOqALiAbN3fMrXNq7CmGGBRBaO/qvqD39rUt/jlasxecs+R3xk6M+CK2TisKirmU4HuFaf92ttb5Hbt2G4cChWlDEX3MbeqU2IdsyEKFN26RMUMWv27XOVzYqDIfDZBfEKjY0VPqkM2g5EaJrJdnpfj+PA6xYfFuPEGARw6IJ829qF2z8GKzzJG1sm0k4v6LvmvbdET3btp5oVVXqRe0vAXEQXG89oQKpabqMyNa1WFMgJgTRxLci8DMpdGlPRxLck5RNdw/DhhN8MMAnKnaVjYKk1g6+r7C/jm2wrRS/L4rCep3SNOm7LwfWljPdj5K0R9Hnmjp7pndGh+BJ7E1sjWALzxk0TbifQujH6jiczyitxYTAq6ivJFd1FLb0iZAxUCmhEl5MyKAP3FtpaZxva7JYLJjP56kdJOJnthiMT/wrfa/epm2IbZZsCKo7Y7zPVhZJblxrMWXB6sqIolCMtjixzKY1RQFIi5rCD1V2PvvcWKUoDNK6xLvFZNC6aVjUC1zTsHAxYP7ReKBJWoJDXASisVUFaYHlPl4SDzMkTf92QQh8GwKL0vSGSBiMjX1pvWKIvUlUe2V4ohjnDVHfH6lGxfdrdS6Y5OFwUPWZlND1FImby4hLDlMhQhsiNiYoXkGoikDU9EgIPxmQUGYRIkQSs0xc+mwn/pA3xoQsS69AFGjS1MrQb1bbkP5OZ1U5R+xhFDPRgqfir7n60hgRQa13aMRYnLSYQlADDYqYhqs716iBJ4+fZqWqEOcYjsYs1J/sqspgOOTgcMKVqxc58cgpvv3qa6yOBmxtH6MsxxRFhTU+dl9RMF5ZwRrDYuHLBZyAtg5XO18e0dRoW/uhZyE6sVgsmC9mqDa4uuXwcEKrC5zCbDHj9r09rly7wfkL73Ll1lUcLbYwLNyUi5fe4XDvNmZjlXNnnmV9tM5kb4/33n2b2jmscwyKAe28YWCHzFgwm8wZjVcAoWnBOsvKoOLgcIJgaBsHhY/kjO2IzfEmFZY5hrvtgCvXDTuN4GYLDmtLtTFgbTxmo9zj4vyAncMDisLL0sL57GtRxdJwa+cKk70dTj56grZ1HO7NGY3GDMcjChkwKPzesZVFCqWZNljwhKNzLBYL9u/t0cwXDAYVGGXWzmnUgVisqdhYWwmy5J3hNhxGrTqsht5M4uVbre/rOBwNWV0ZU9qCFqER74hU5dAPeXDOD/BralL/BVEk9II5bA5o1ZcWVVXhD5am4c712xRVRTGqmGlNY9S/3gaD1imqXsn6BIAwsTE4J02YVCoS+r+ZQIpG4yg4/tHoi+ResBM79oFIfppwKLngLBFKmDX1VoqlKfHQiJFdn3EfMuFFUROjkP5vG5zJSCUqBP2m3ZABfLS/TeSm8f+3PXI5HKASFWtYlUgYAtcje6ODskScJqOlXSJWrAlkSeQ0XXQ4ItFNeo/4mX3jsh+V/aiMsf7rNTkd0WCn61sZdGQki7XjlbtIsThvKOCNxxgA0HR1e+sMejkazeK9VSJxo9HZQD1FkTh6/1wLtOonCJ85cwZV5fL1q8Rs4PFgRFUMKQebGBlxu1phsfkcC3Oc3/+Y5Ue392kvX+XY84/jVh/hB7/0I7z5xneYNW/xuRe/wInjjxBJ9UXjmM1mVIWwfewYK2trzB3cuXOP3bu7TCvLE+ee5pGTJ7l86T0ODqe8+earbG8e47Ezj3Pu6XNsbh+jqAZMDuc0Tjjz+BOsrAx5663vcfv2FW5eu8iLL77AqZOP8YWv/AG2HjnNq9/8Hd5/602++ENf5uxTZxkOlCceP8H+vX3WBpYbV95F7BOoU+YHu0yssrU24uDWHc48+gSPnN3n8rX3GOsMa8rQH73x+6iqqFU5/+4FDiYTH2xRcEYx4wKzWiK2YHu0znOPP8vqygbzxlfFDKqKrROnWD9+llu7Df/oH5/n1Ve+xf7+DkMa2sWUycE9cH4waVWUjMarDAZD7uzscf3GeVZX1ynLClv4YQTXr19j794eg6rCDgoWrmG+mOHUMbs7Y3o4o57POX58k2Z+j927e3x79zpvv7mKHa6yMh6wvXUcozX37l6ibg6ZzacsFnOqwZDBoPYRehzl2gZlNWBcrPAjX/wqKFy+fZuFA7UgTrBiMbagbh01YUCMhoysniMrKqBx4FRoaYAnF3ybmeh84bO3tGvPEnVH34jXsMmNhDYN4m2u5Pj3dEVUNaKabBgVUosql/QtgZT1OlrjZqYX7KLL0A2MRBp6Gl8vqtB6By4SbhrIHk/+dqRFfCvRmOjWn9odfhn+KmwRiKpA0KkfbhEDSmACGe6vZ9zjhpAN17rkePczJhXteo7T0/uB1JNQHWJjOwDXI3LAk6fiXxkd5UieoRYRFyoSQoBIogPWcb79XofLmWjh53DeRyLHBzZtz2+WdM1UIzkcExcIwzM9OZTIEw1Dq+KAnbTm2L4snB3Kkix9+JzQRH45191fEZtIJsCf9QTS0tiUGRfJ+5gdqvgMT0sgccM1ii09Ylm/EghEE9sbaCKjIxHp7YDuzGtxQfZ7lXJhvXE9i4WfsB4HocXsxfDtE5Hgs57C+RWJmyis4QHf6tUns6RrIx1BbIxBrS8LthJaJPmbgZPufE/X3EtzesyLiXbvpTHoGdfUI/RcS1FYn3XkN4a/Jimbu6tsEoeffxGzvAIp4YygUlOOB2BLUF8qqrVjdjhnf2+f0VBgWFFKg3H7+AYxAlPH+VfeZGt9g6/8xI+yeew4f+DHfpTLly7y3cvvo9T4+quCNrZ4IMpMyIyPdhTRRytRGlJv6NhPWQSJiTHO30unpKQYAqkjjVBWA4zi7VbAaC+LOwTToh5B+rZSGEYnhtg6xG/PrszfWgtt6yuRNOopTUF0I4q2UW67isrC+OSNxjVBjxpPtLnWZ9cmckaT3neNt4K8L9qrCHCxWqIN+qfnZ7eRaJOQZCTp2hghlZ5b8Rm14uLQKF9N6ROKFFzrreOwDxvn91Pbtt537RFORoKfAMSsx5QlbYLtKNbLoovnZLACxQZN7w8NxVDYEpGKplbEFDgrXlY02r6R+NUUcGxdv22I/4wuIaKvS0l6NOp8m+z5jsTsk2t9LAdNO70pgf+oF3UoIfdy1tQzrK3S+zl1FGVB2/isTedVDoOq8ue/EUxpvE5svU+KiaX7oaUigFEq6yswUiUDinHh7A8V0qrq55q0sS+oTWeVTzqKGcSh3ZB4u0ZR1BivV4ohxpTEdgZR17pQrh4Hyblg27tgywiG1oUL7xpvS6Q91CT/whP/LhoI6d6lSguR1DrNFDa0XGhDCwWvx1UUU/jPLqxgpARjaBZ1GGjlKK1FnQQi0tI48YPYEWqnGBtJ21gVMfMJTQa0bTFFReuUIgwNa9UnkhSB6IzkUF+Xe9XfBej7SUdp//T9taTqNVV3RP7KE8M+kBHIKqzASlVSFQNsWdICO3d3QhW8MF/MMdWQOHDVu1uOwXCAUUNT+8QNbKhsD712i7KgDq15Dw+nPsM5fL9oT1ahF/J8XochhFA3C1SVorS0zYKiGKCuQZ2ks7utmzAUsfIBgWAfu9bLduFgXA198CZdK0urbViqJ8Zb19C62terS+v3jCjzxZzJ/gR1yqAafGgPRzzQJK1qOFSi4rNRSLpG2immJz69PfVDomP2Y7q+N+YIz/OH6nJfKxOExnVWLL3yYkjkjT+sfclvJJDLsuyUb7TZelkd0YkikB3+PY0vV2ldIm26DBGWFLD3QfxkXIffrKqdseRaFzI46BwIb4V2h2P4/DgIw7db8N8zHhSJiNKQpZuM5FCS4UCspV7Mw0COlqatqazvN3rzzg0GNTx24gSj4cgLp/FGoA0TrevFgrffeZvVtW0ePXmaN989z5nZjEdPnGJ1pAxXhiCWeeP70NVNQ9MobdsQS0PUhX68TU3deqK20BiNND6SQsugrFDnFeHkcJ/rO7e4ePUW5y9c5O7uLnVsP+AcNTWXr17i0qX3OD18muMbmxxf3+LunTvs7e4zXB3j2pbhyoDDWYNzvqXAfDHzg2TmU1zjWB2ve+cqRnNVU5BgZ3eXtdV1QKhbmBVD3rvecrC5xnpVs3vhHsdcxdr6mLXSYrX10y9j6UYwuUR9OfigLHCjAYq/PtZaXwZSh16sqrimoTSWsqhwpsZS0AaZmRxMuXblGoOiYjwaM5nPUPEp/IUtmDct1WjIoBpQlQVSWPb39nxkKxAE5aDypT517aejhijxbD6DskJNyXzh+8zOZnPG4yGmNLgmOGdFwWIx9+V4cRJtaDlgrfUkc2HZPzhgVtcMN1ahsMn5wPo+rL73kc+Sjz1qfJTT9/OyJnqokuQ9Herh0I0kQSwB09APOmwdOqPHdfohZAT4PjiBiKVnTKVej0cdzo40Ae90G6LzJylDzru6JOc1lixDbHfQZc5LytbvIpzRwaCXDSSxbKrfkywgvjaudYnE7DvNkMpm1IVm/bhklEbFFb9rP7st6cW+AblkXB5ZU8xMOeK4m7Qm7fTXEQc/9Y+KfR/7JLRPWukiw3SERrxlqoFGiUZZz2DRxBT1IVhTcGzzGIOyYjI9TOSHtZbhYOgDkMUKe26be+vnmAzPsGVm/PipNcY77/EDnz9HYxyC5YVnXuDYxha//fIr3Nm5y2OPnvYRWlqca1gsZswPa3bv7rO2scm5p5/h1Kk5u/d2+Y3f/EesjEc8+8wzPP3009w72OM7b3yP2zevc+GD8zzy6CnOPvUsKysr3N3d5eLFS6yurvLcC8/y7A88jRG4duUKiOMb3/htxmubPH7mLKvDEW9+59vUizmL+YxFPWdlZYXHTz/O5sZx/slvf4O9+Yw7t27zyNYmp089xrf+4T/m+Oaj7LhVbukJmnIH6w4R1yJp0JCXvyuXr3Ln9q1EaoFQVhWjlVXKcow1Q9ZXjrE63ub49gkaY2ivXqOwFYfTOXfeu8CxRxZYWnZvX0Fomc8nzKYTmqYO5ZPCeG2VwWBA0zTcvHXLE40YptMFhTEcTmYsmpbheOz3oSiz6SFGnTfqnTDdv8Pl+YTW1ZTlGBzMpnfZudHQGMNwNKSSFnSBGKEclIBvx2IstK5mf/8eB5M99g4nbG0dY228wspwxJde/ALj99/lrQvnqV3rp24bw6Im9T8GRdqwb3olg0LMtAxlx0n6Y2sQ0xFSEh2PfiZFF7xJGYAx8h/2a9oLcW8aWdqfEnUaMdvVO4FHXUsXSL5IPEU7put5lh5M5Jw35jURzj5wQdIFsQRwiWROtmEyc0A0lYL3e4YbCdnISFpDnE6f1FvUwUHPhHf13ylOpCYSEP01GPpfVqL9ZbryRCGcQT0dEzNN4tnnwrnja6I1ZbFEUjgadB8iY3vot61ZgvbeJ342gWLWnpmMJucsPi/pRzQFdVOWTng8LmU5aOeCTHWPRzlU1d79JJEWreuuhZEucOBitiIEPR5sp+DISe/s9NlyQQZS9VlHcLTapvsgQXiSTY2GsyXY0T0nNxG7wa6OezCdT33i5chneg7PX3GTbJf4XP/alA2GJ/ciQR6kLNyjLvsVfMlnkidD6BXYzfVI9gJ097BXVu73n399dFrjwXuUSBfpeoYGBwRr4leJ9k0gwJNf4m3AODws7hk7rCjGQ2aTQ7T2Nofvxyg0rqbVJpTjx31vMRRM78745m9+g+H6Ks9/4fM8evo0X/nqV3nrykVM4zADWIjzQ1w0ZnMndROubbTgohEW7mXaTl12nOmR9P45jpjsU5VVuKcm6Q2nnZCaYHs4IQTpe9cpEbHdSKaox5zzn9uGnqLB8iEOx40yIOBbAYT3bZsG6n7Fgu/j6veJDXaPX49AaMsVk6UExCSijfBc/1pChnG3r+M1SZnY4ns6F6ZMsuJtKtd7XhQtDYHcLlmpH2iUQOq60LMX5zAa91+XgORiAoFEvoB0lsWKwM42j7YzKTMXY9IZYIwNQ9ZMR7CHSgqDPxubpg3nsYQ2d0ERfAQRFvWtBB8lJhz0h8TFPdnPoD36u/57Hk2EcM4FfezlOHIObdNgCxN4iALBUJbeNrA2bIJ05oRMTSVxDqpK09YY6yvFXOs5Cmt9wlrslR0THCK/U4SM5TjjImZddxsrtJQICTB1XaPO+SFcGvvn+pL40XBE2858T3RvHGCM9YGU3pkQZ3849QRiURT+Nb1r6H2Lzl+Ke7BtW4yNfaNNOt+dKtaWGDzhDL71SIqFhPtkjaEgnNGhHVUR2jMEqQcRrAiDUcWidr4yVvzQuaaZJ2K0bX2VcFGUXt6DSAyGAwjDxGLblKooMEioGe/0Vt/fOkrc9n2zfnJNfG7XskM6zqnnS8VjZDQcs7V5jOFghLEls2bG3v4e09mMoiy7nvPOUQ0qwFezWOmucx3mGsUDPfELxveHLaylKEtf7a1BF6gLP1vGA+v7GAdyv22dJ7yDzebbfUIizVS7ihI8h9Y6B+oweC5BFGrXJJJVw/nmkyihWfgKQRvOlcJ6clklZFU3DYWxDIqSj4N96aWXPvaX9xt/7r/8cy+tn972RCidkje9/lP+gIoGuIShEWF4WMj4MMTBOk3apMCSYEaHQHpZF95A8mtRfPP2JqToEwgPEwTTc7+SooD+DJCgtCPxGYibYExa8f1rF4tQui4SysgIWSqk9UXlqiYc2vFQwZfWJgIjrNaXtLO0oZx22bLhwc656vXHEWI5GL0eV0EJOx/F9MPb/ICmtq799w1KF+eoD6ZMpzPEGorhkLIaYqIT5XzPzoPJhL2DKU898xxOhLfeeZtmsaBEcc0CdULTOKaHh9SL2vdBbVsWC58mXi8Wvn1B2IgiyspozPrGBoPhkMViCuoorSdPd3ZucOPWJd557x3ePn+e3d0DsBYp/HV0gm9CXdcc39rk1OlTzJjzwd1LvH/tEk3rmM4PUaeUpqBeLNBWmdYzmrZlOBiwf3eH+WTOynCENYamXjCbz2mbhrIsWDQ1h4dTRuMV9g/3WTS+0XR1cMDJStHFApnDwf6C8fY61/Yd71+d8/ijL/C5p17EmYI6ZIzhHG2zoCxgPj3k7p1bLBYL6qZhOBh6w6ltUx+URdPy/3zzZSZ7E0opwwAdb8ivjjd44fkXESPsTybMFjXDquTdt95i5/Zt/ywF1zQ+6oWEcgr/DjY02Z5PpyEKLzRtQ9s0/n6psre/z2R/QlmWnDv3NIpysHcQDtSQ8djUEOXZeIO0rRvKqqIaDZjNZ9iywoxLyo0VZFh4x584GMoPZCoLT9Im0g6IIeoYLewOoO4w8k4uqbwQTbvbO2V8mICICiLxkhoJ3q7UNv4qTruMh34fRnxGrNJl8vpNHB2Dbg2d+eKdBSMxH6V3zsDSARqdwfgd/EPxUO0/Lj39FZy6fklVchjimuLPwYmJ/ZDidYm9RKOj2UP6vPBefaOgT+T2/46f2f3oM8W8k9+9V7qHvc+KWQuml3WS/heM7s55jyxEcI4gyUh0gqJxETz24Lj5f66O19hYWePSxUvs7t9DDRTWMB6OWR2tUtqKpimYVCfZPf4VptUZvvbcCr+/uMnG/DYnn3kCLQYs5g3T2ZS1tXWefuY5tra2qec1H1x4n739e2xubzIejxGnvPGdt7l4+SrDUcXGxjpVVVKWBbu7uxweTDh+bIvJ5IDtE9uMRyU7O7cYjUbcuXWb+WyGa2usMdy5vcOd3busbayzubHBY48+gqPmlZdf5v33LnH54jW0hReef5Zjx7aZzWbcun6dxWLGiROP0KqwurbB9onjfPeNN3j+uecYDgbcPH+JJ556kb//3StcacZIe8Cw3kHaGTQLv9OMcDCZ8O6Fd6kXU7x+sf7araywfvwRxA5YHW7wxGNPMihGTCZT5qH/eKvK4XzGdD5jejhhb+cGbX2A0wX14QEiLbbw9/Txxx/n7Nkn2bu3hwhhQNiIM4+f5ewTT6IKg8HAB4ij8+wcrmnQxYJ6OoVWMTjadsZiNmV9ZYVhaVkdVbhmSmFbrNS4esZ0esC8mWGsBbEY8VOFvawpi2bB4WLBrK59UM1YBoMBW9sbHE522b23SzEYUAwGtM730IrZTSacy4koinvJSNCFpLM97o/+fo/PTYom7uclUrKrLji6L/vEbuzZloLUYX/4PH+vH5Tlvb/UuzLqk16m6UfrC59NFttYJf3S08tJdabXLqsR/6cLupiQAdKfJ2CM9BzzsKKYHZt0h0m6sFONpjP++9c5PN/aIukpE847Cd9FA+mTslLCdzBHrltsI9FdOwAb7rkSe1dGnZwIyf45FNaTzqb0b7+WKBdLWahH7l2SDyNHzsYYYOzJm/iSzGjL9m9IPPYiEkmiR4eZdM5z/553CRx+PV2GcdDf0Z7WZT8gnlGtauqfGLNp4/yDpN8NKRCS1hTOURfO5M4c0O77dNxmXB6RnAq/DqRAuC0sky3Jl0iXK1xHjRl7MUATiRAS6XN0doYvgbXpnsEyWZj+9OyAKEfRPRHo7KRecEckfZulM727zoJNZ6Wk+9K/NkdtAhCGhUWbhoODie9VKIZShIE1jMsBq4N1BnbMuKoYyCgRKDQwPZxw5cY1RpurHD/5KCsrq7zz1jtc373JbGCYG28PeZc92G1GU2/cTvZt0juRmPW6M7QKWZJz//HWWoqiYDAYhOsVdKjS6dwkJ90e9Hu1bwfFbFSTnhcTjxIzGiQp+n8iJvRBdaiD+WLOoq5pwv5rXesJtLBOU1iKqvRnXtRDRtJgJp+YE2XXc3cOH+hZqjjoZ/YTk5WOEKSEUu1oZUc5iIGqSO4G3zSRz9rNqUnueJBRQ7cnRen2cLDHl3RXJHh7cubQdD8jrZyCHYFsjzIhxidpudkhzeEB2jS4UG0W93Ai9wWf0VgUEAnLwGL1sxSTzAJ9YjueGUcTGpb3yIexZKuHf1trGA1Hvs2cuqA7isSRkOxoCVWPfvicifpZNbRlC+eR9T2hrSnCvfY2ddv68vomtD2IJ781NrURkfA9g0VwRNf4zyrLMpX4F0VBIV2CXCTSWucwVkF9/21Dd+1V/LLSuUqYaVSE/sjiM7gLawPp3FUIpvMy2VTxXnY+R+ypXNqCmJ4jEhJLxA8PjL6gMX6IdfRB4rUy4vfeoPLZm4Jfjy1LysJ6AtgYqir02w02e6LxFQAAEMdJREFUymBQIeJ9NGt9b2RrDEZCAAH/2YumZt40NK2LEr10neOe/Si7ri9f0S8Via1++EjZi7pnUA5YX11na3MLYysQQ+0WTGdT6sWCoixZX1/HFMYHA0I7h0FI5pNQNRUrxFzb0jTOczXqe+sOygoR//0L6/vNGgIRrr4OpAwZtYtFHXrUe9lvmsbr0PD+1vpsejGFbxtR+KCitUpV+gr30aDAQsiM9tX1hRGqaugzpyVeKygEBrZgPBoyHgzRVpnN5liEQVFinKJtwytXbl176aWX/sej1/GBzqQF8I17XTKAVTVExwip29HqUUS0KzUTP4nPtZGIDP1qorKlU3Tx30tTSU3sS+g8MSs+glIUNkzt9lmMbVAuxhbgfLS56B2UaUqs024YjvOqrW1rf+C7NhwMpM3ctg0xYhs3iLWWRr1R1n0Xg4g3LDVMCfSN5n2JSj+iDZ2hHKdcxghoJKY0RCk1ZCj3+9k61/rIZ9vSBIOwrZugePx18eelgjj29veoL32AVAPOPbFJKZLaURgr2NJy5epVRitv8eTTZ5kc7vPBu+8zvXuX0489ysZ2QzkY4wiRJrW0rkmRlUS4GKiKCmhpXcu9e3s06hiPV5i0Dfd277G7c4OrVy9y4YPv8e61K8xrQ1Wu4koblEyD4lPhm7bm26+9ytPPP8fw5AanHj1J+WblyzHqBm0ce7pHgeVgb5+ZW1AOlMViRlWVGFvS1L69xmw2Qwg9eJqGQVVxZ+8u5y+cp2l9M2vahuvX9vi7l++y5YSTY8P6ZstkfJWttU2GZc1gMCROvWyDsdW42k/M1NZPcRShKgucWBaLBW3dYhFaUSh85G19fZ07l2/6pJtovDiHOuX6teu+H35haLRlUA7Y2twiCkBsMB8PrXgwtE5Z1D7rbLyyQh0OZis+EryYzXHMib2frC3Y2tpif3/PD0wJDdpNaX2E0/nhZq3GiKI//FVBW8doZcB4a4vG+u9UGj9wZ14vMPiG/i71n7LEoRsaotuxnJS0w+Lei7okHMSGUEbaGWrL/Q59pkYieun3hO4cL7/HYtZt59jFAVfR0ZT4mUhyANPmiwdqcnYiidt5g3Fodt+x+xCB0jfw4ndxIfuIGFBKXnHSX+FNQrlPZ/Q5Ddc6RpTd8mdpWn8kErqIf/e2ywbmEhnLcoZr8uI+ZFBEI/wIQXDkPfvlwkcdfl/zJkRdGSso4rnTGTWGMgzbaLTpeqCH+xTsblzruHP7NrECoRXf32plNKIqSwwVgglE6oCVseWJMwNufucGP/jiU0ynDfcODphMJpSDkuFoxGIxx2GZHky4cP68f3y8wvbxbba2tnju+Rd49fU3eP3bb/D5F59ndWXEuXNPcerUSSb7B7xz/jw7d+9w6vEzbK6NOXfuLMPhOq+99j12dvY4feYkVTXi2PYWe7NDXnv9DRbTAx47foyVlQFf+sIXuXL5Ft96+XVWh0PG43P+XGgdJ048wmx2wIX332c8XOfJc88wWBnzuc99jjNnznDhwgWeOvsEd+7c4c69fe4cwtpizqaGrCX1w4gaddy+fYvpdBoyV/y1H1RDto9tUwyHzBbKcDCgGgxoGse8XiDNIjXwrwYF2sBseoA0La5pmdUHSF1Tln6TjMZjzp07R1VWOKfcvbvL3v4BbQikPfcDzzM9PGR//x4/+6/+K1y8fJnXXnmFGzeuemPSGtQUqPN57m3bok3LZHJAGcrPBsOSyWLOcFDR4KiocFLTuAbxVXTUdcPhdEo5qNL69w/2sa0im1sMV4aMR0OefuYpFijvX7tFIdY7QCLYIvQVbF1Xdn9E7mOW41HCxzthrpP3nlN4dB9F58S5+F5HCK74M+JtpGj0htJVF9fT01tHHc5IQkbnNe6npG9c10cwwpjlDNhYchhLWZezNH2AuE+UpqwuTUtOOjY6ZXH/d2oq6IswbChmFi6Rhr33IWmP+JhL6019V9s2lbqLHnmvyEP272kgEbsAnv8spxqynBoi6bykDeMXDdfFxfOHziHrX9/4ub6dFskOOSpjcQmqy8RAyjTWmPHcvU4lEEDatfGK1x36Wd0dAd0n7QRfUk6QNz/4ZZlE/hBBGEuOzfK5k95TSNO2uwzAjnCM/sbR0lA/sdyGVkS97G86uUrlpvTWCEfsCt9PHiRGX7v1G4M49yEbOCKuuWmaRGok8dGQEZuqsnpZwm28/33x6O1n9TZT67rqoWUirrvn/rVevj8qc9tvlWXboPusJB7pyYK/BoqCMaxurLNzc4dG2iBPyt7uPbaGvt1YzFRMQXeEOHLg9s3b/MY/+Ic4UdbGq5RiWV/b4J6dhArKThbirumCtb0sst7PIsb36bRFGP4U97MLOsEnf7jWZ6gaYylCL1ijpAzVKFfxv14Xh7C9gogneiOxHt4+TbJXVbRu0/fust7izBL/GZUdhGsptE0T1izhM5X5dOoDe4XFt3JxyVbsAnzdfoq2dGyvkTSeSGptQU+3RvlMvnEkPhMJ5EuaO2EEsf5sal2Yzh6qQ/y6/O+sxvBk2Ecd5d0LPnZrIEpcuL8xQ7eJ36F3ILhA9KSLCClIZ8OQ47IoqaP+DLquf8bEfRLvVcyAj3oOJPTQ9veuKAo/OT6s86iu+vC++miS9qN+7wMKXjYCxx2ylDX4aIETEEFUMEXsNQyxOiVeL2//hu8b9B4aq2UkBM67Ie6or45NQU1VX+Ye3rN/XjvnWxpaa7CmhGBLexLTz6sZGGFWL3BGcAiDyjLZ3/dthoJ944MM4cQI184GkteYgtIGeWrbdN+cc6EdQyeK/hL2/BB8hm8b5vS41lEWBaXxxJ3okSBWTBwxvizfuaAT8MStIwRAgn0m4hM7GvwALW9bLVeGd3LVpnvbtg2F+HsWdXxZVpRFyawJ+0aWk/j6Z/bS+X1ErtrAG/X9o76cp2sbLlhRWQbDAbPFAmtlqQ9wzIyPAR5Vx7AsEODg4ICirGibxrNRAvO5nz0jRQktiadTDdVA4qtarfgWCariW/CFqtz5fBF0WGyH1CbSObbZqMP7mOD/N01L4+k9FnVNYawnb8Vzgn5OUgh2RRuu9dnli9mUclCwtrri2xxo7NHtiWVnC+4eHobq4Y+G/NM29v2EiNwCJsDt+72WjIxPiONkuc14+JDlNuNhRZbdjIcRWW4zHlZk2c14GJHlNuNhRJbb37s4q6onjj74QJO0ACLyTVX9yv1eR0bGJ0GW24yHEVluMx5WZNnNeBiR5TbjYUWW3YyHEVluMx5GZLn97MH805+SkZGRkZGRkZGRkZGRkZGRkZGRkZHxu4VM0mZkZGRkZGRkZGRkZGRkZGRkZGRk3Ec8DCTth6adZWQ8BMhym/EwIsttxsOKLLsZDyOy3GY8rMiym/EwIsttxsOILLefMTzwPWkzMjIyMjIyMjIyMjIyMjIyMjIyMn4v42HIpM3IyMjIyMjIyMjIyMjIyMjIyMjI+D2LB5akFZGfEpG3ROS8iPwn93s9GRkRIvK4iPwDEfmuiLwhIv9BePwlEbkiIq+GPz/de82fDbL8loj84fu3+ozPOkTkfRF5PcjoN8Nj2yLy6yLyTvh7KzwuIvKXgux+W0S+fH9Xn/FZhIg819Orr4rInoj8maxzMx5EiMgvichNEflO77FPrGNF5BfC898RkV+4H98l47ODj5Hb/1pEvhdk81dEZDM8/qSITHu693/oveaHgo1xPsi23I/vk/HZwMfI7Se2DTLvkPFp42Nk92/25PZ9EXk1PJ517mcMD2S7AxGxwNvATwKXgW8AP6+q372vC8vIAETkJHBSVV8WkTXgW8C/CPwscKCq/82R538O+OvADwOngL8L/ICqtp/uyjMyPEkLfEVVb/ce+wvAjqr++WCcbqnqfxwM238P+Gngq8B/p6pfvR/rzsiAZB9cwcvjnyDr3IwHDCLyNeAA+GVVfTE89ol0rIhsA98EvgIo3s74IVW9ex++UsZnAB8jt18H/r6qNiLyXwEEuX0S+D/i8468z+8A/z7w28D/CfwlVf2/Pp1vkfFZw8fI7Ut8Atsg/DrzDhmfKj5Kdo/8/i8C91T1F7PO/ezhQc2k/WHgvKpeUNUF8DeAn7nPa8rIAEBVr6nqy+HnfeBN4PT3ecnPAH9DVeeq+h5wHi/jGRkPCn4G+Cvh57+CDzrEx39ZPX4L2AxBioyM+4V/HnhXVT/4Ps/JOjfjvkFVfxPYOfLwJ9Wxfxj4dVXdCcTsrwM/9bu/+ozPKj5KblX111S1Cf/8LeDM93uPILvrqvpb6rOAfplO1jMy/n/Hx+jbj8PH2QaZd8j41PH9ZDdkw/4sPqjwscg69/cuHlSS9jRwqffvy3x/Eiwj474gRLa+hI9eAfzpUBb2S7GckSzPGQ8WFPg1EfmWiPzb4bFHVfVa+Pk68Gj4OctuxoOGn2PZaM06N+NhwCfVsVmGMx40/JtAPzvrKRF5RUR+Q0T+YHjsNF5WI7LcZtwvfBLbIOvbjAcNfxC4oarv9B7LOvczhAeVpM3IeOAhIqvA/wr8GVXdA/574Gngi8A14C/ex+VlZHwc/jlV/TLwR4A/FcptEkIk9sHrg5PxmYeIVMAfA/6X8FDWuRkPHbKOzXjYICL/GdAAfzU8dA14QlW/BPyHwF8TkfX7tb6MjCPItkHGw46fZzkhIevczxgeVJL2CvB4799nwmMZGQ8ERKTEE7R/VVX/NwBVvaGqrao64H+iK6/N8pzxwEBVr4S/bwK/gpfTG7GNQfj7Znh6lt2MBwl/BHhZVW9A1rkZDxU+qY7NMpzxQEBE/g3gjwL/WggwEMrF74SfvwW8i+/teYXllghZbjM+dfwz2AZZ32Y8MBCRAviXgb8ZH8s697OHB5Wk/QbwrIg8FTJnfg741fu8powMIPWJ+cvAm6r63/Ye7/fq/JeAOK3xV4GfE5GBiDwFPAv8zqe13oyMCBFZCcPuEJEV4Ot4Of1VIE4P/wXgfw8//yrwx8XjR/AN7K+RkXF/sJRZkHVuxkOET6pj/w7wdRHZCqW6Xw+PZWR8ahCRnwL+I+CPqeph7/ETYYgjInIOr2MvBNndE5EfCbbyH6eT9YyMTwX/DLZB5h0yHiT8C8D3VDW1Mcg697OH4n4v4KMQpoj+abxBaoFfUtU37vOyMjIifgz414HXReTV8Nh/Cvy8iHwRX8b4PvDvAKjqGyLyt4Dv4svF/lSeMp5xn/Ao8Cv+HKcA/pqq/m0R+Qbwt0Tk3wI+wDerBz8l9KfxwxUOgT/x6S85IyMFFX6SoFcD/kLWuRkPGkTkrwN/CDguIpeB/xz483wCHauqOyLyX+DJA4BfVNX/r8NxMjI+MT5Gbv8sMAB+PdgNv6WqfxL4GvCLIlIDDviTPfn8d4H/GRjhe9jmKeMZv2v4GLn9Q5/UNsi8Q8anjY+SXVX9y3x49gJknfuZg4TKlYyMjIyMjIyMjIyMjIyMjIyMjIyMjPuAB7XdQUZGRkZGRkZGRkZGRkZGRkZGRkbGZwKZpM3IyMjIyMjIyMjIyMjIyMjIyMjIuI/IJG1GRkZGRkZGRkZGRkZGRkZGRkZGxn1EJmkzMjIyMjIyMjIyMjIyMjIyMjIyMu4jMkmbkZGRkZGRkZGRkZGRkZGRkZGRkXEfkUnajIyMjIyMjIyMjIyMjIyMjIyMjIz7iEzSZmRkZGRkZGRkZGRkZGRkZGRkZGTcR2SSNiMjIyMjIyMjIyMjIyMjIyMjIyPjPuL/BVGLcZsRfaemAAAAAElFTkSuQmCC\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ }
+ ],
+ "source": [
+ "#@title Image Selection (don't forget to execute the cell!) { display-mode: \"form\"}\n",
+ "selected_image = 'Image1' # @param ['Image1']\n",
+ "flip_image_horizontally = False #@param {type:\"boolean\"}\n",
+ "convert_image_to_grayscale = False #@param {type:\"boolean\"}\n",
+ "\n",
+ "image_path = IMAGES_FOR_TEST[selected_image]\n",
+ "image_np = load_image_into_numpy_array(image_path)\n",
+ "\n",
+ "# Flip horizontally\n",
+ "if(flip_image_horizontally):\n",
+ " image_np[0] = np.fliplr(image_np[0]).copy()\n",
+ "\n",
+ "# Convert image to grayscale\n",
+ "if(convert_image_to_grayscale):\n",
+ " image_np[0] = np.tile(\n",
+ " np.mean(image_np[0], 2, keepdims=True), (1, 1, 3)).astype(np.uint8)\n",
+ "\n",
+ "print('min:',np.min(image_np[0]), 'max:', np.max(image_np[0]))\n",
+ "plt.figure(figsize=(24,32))\n",
+ "plt.imshow(image_np[0])\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "dkkBAgGcX65P"
+ },
+ "source": [
+ "## Pre-processing an image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "97zIaKAhX-92",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "c630f46d-9bb5-4fd6-d59a-b346d547bbd5"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "(512, 1024)\n"
+ ]
+ }
+ ],
+ "source": [
+ "# get an input size of images on which an Instance Segmentation model is trained\n",
+ "hub_model_fn = hub_model.signatures[\"serving_default\"]\n",
+ "height=hub_model_fn.structured_input_signature[1]['inputs'].shape[1]\n",
+ "width = hub_model_fn.structured_input_signature[1]['inputs'].shape[2]\n",
+ "input_size = (height, width)\n",
+ "print(input_size)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "-K0V6KWiYYpD",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "6f27f7c1-11f4-42c1-b848-71dc44f6646d"
+ },
+ "outputs": [
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "TensorShape([1, 512, 1024, 3])"
+ ]
+ },
+ "metadata": {},
+ "execution_count": 15
+ }
+ ],
+ "source": [
+ "# apply pre-processing functions which were applied during training the model\n",
+ "image_np_cp = cv2.resize(image_np[0], input_size[::-1], interpolation = cv2.INTER_AREA)\n",
+ "image_np = build_inputs_for_segmentation(image_np_cp)\n",
+ "image_np = tf.expand_dims(image_np, axis=0)\n",
+ "image_np.get_shape()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "source": [
+ "You may notice that the image gets way darker. This is because the pre-processing normalizes the original image."
+ ],
+ "metadata": {
+ "id": "-O6fHWIh4C8r"
+ }
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "ga1lccBpdxpd",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 583
+ },
+ "outputId": "7356f5db-625b-4aa8-ac38-293e99fe14fc"
+ },
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABWMAAALACAYAAAD2e2C+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOy9edAl13ne9+vlrt86OwYz2AGCAAGQFDeRlLVQgkhLpiXZpWixrMROzMh2nJJVciIncRKXK39Ishw5LldZtC3LStlmtFiibFG2ZIoSV3HfQILEQgDEYAaY7dvv3t354z3Pd957MQABAgMQmvNU3brfvbf79OlzTn99+jnP+7xZ0zQkJCQkJCQkJCQkJCQkJCQkJCQkJCRcXuQvdgUSEhISEhISEhISEhISEhISEhISEq4EJDI2ISEhISEhISEhISEhISEhISEhIeEFQCJjExISEhISEhISEhISEhISEhISEhJeACQyNiEhISEhISEhISEhISEhISEhISHhBUAiYxMSEhISEhISEhISEhISEhISEhISXgAkMjYhISEhISEhISEhISEhISEhISEh4QXAZSFjsyx7W5ZlX86y7IEsy37mchwjISEhISEhISEhISEhISEhISEhIeGlhKxpmue3wCwrgPuAu4FTwMeBH2ma5ovP64ESEhISEhISEhISEhISEhISEhISEl5CuBzK2NcDDzRN85WmaSbAu4DvuwzHSUhISEhISEhISEhISEhISEhISEh4yaC8DGWeAB51n08Bb3i6HbIse37luXNoh9cQO90SaGE8dA5kgA6fuXf9PQXqsE0OzBa20XdV2KYM30/DMS+FNWitQlnC8KHnfooJCQkJCQkJCQkvIfj551MhBwrm55x+f4/GvdduG7+vXs3C783C/tpO2xQLx1V5jXupnr4uhfvs59j5JbbNFn7Tq+bJ5S3Ct4WO5Y+hc6zt76yALLf3BsgyyLMnN4UvNvsanxv3XeG2EXJitxTMN+/idr7Lte1i9y+eXgFF1zbXk04P6LiqdcL3LZ66JT1qYAfYBCa4J5tdYBy+0GOSusk189xQrBa20StzFfa/+3bAlVe5smr93WDPYqqMdvAd6g/oGzWDrAzjwf2k45fMPy4W4RB69MP9rUMDVBU0OqGFDi4LK0fH0nmqf307+F0Xi/OX0OK/Et/+euXAZAPqDWCDhISEhIQXBk3TLE7agMtDxj4jZFn2DuAdl/9IVwM3AQ9j05AesAQcAm7A7lb+zr44A9sGBtj0I8du9LpjiujNsDvxNtDFZiingXueok53Q34jlDPgHz0/p5mQkJCQkJCQkPANDC3YQ5w71pfYrsDml11gjcjcLLm/RVR6Wk0s1ojI2tQY09XG5sFLzDODmtOKyMrD9n3iPHeFeZJUvw+xOW8R6urZoYo4R5ZYoQh1EEVYME8VipUr3flPQzs19l3WC4fQuftjhnMtupCH8qYVlC3I80B2ZbC8DGUXsjaMa5jVUAdmrdWBdtvIWRXZd9VX1+y65uq65ilDE/eZf7wgdEsWfl8O+3WxR5OJK19dWobf1Q0aPu2wf+a6qQf5DVBMoVyG/jq8/CAcD73UYGqZO4FrgOuB20L1NlxvPBpafAt4HPOaexB4cAiPbQFfAR4DvhpeXw51FzkrglRDT+c+xB6npkTiVWSmzq0Jv4/Db+Ue5EPbOcP6KJ9AVkPVBQ5ArbG7G2qtQtV4qkBuY6Lbh04LOgX0M+jl0GsZQdq4vqxcPTaA8QSaERQTqEaQb0O1Ex4bXQc1hJac2ThaWoOtPain9nurB8ePwOaWjeGysLFYAL0SWqHzNW40vipgL7RRK3weTaBqwjitQkdgiwtZC8oeTDOYTWC6DUUF2W8Bvwv8RxISEhISXlxcDjL2Mew+L5wM382haZp3Au+Ey62M9TMjsLtXuLHTQN6zG/PBNTj9aFgtHBKXOfXSnbl05WptWa+OO0YbOAY8cYk6PQbjNow72DTpCS49GU9ISEhISEhISHjpQwSjGD6v4PTSNsnxSqKW0esdF6V6XiIJUdYnJmzGvBJQTJmXznnmp+2Oo/lt4/6WlA/iXHiJGCHmMVv4rOOPsbm2Pw5u/1CvrAPN1JVTBEK1gCbUIw8EWFNDUxkBlXegKaAOKliCCjYvoK6hEVk8NZJsOgvT8MLqpOm8quKbR0TiiMiFt1yTqslF5IlvF1em5hOPXIZt/Hbi6UtiYJ8krZ5j1NAJzTntwHQEwxUYjKHowF4PRrltNsSofY28lfB+IVSnD1zEnkpOA48An2vg4gzODWBnGyMmRapOQztMwvulVLJql2HYRrw6hHavYDSFahKH7QSYFcxLb2fu1RjhuJLDwdwiDes+VHk4dhZI2lYk4JsCqg6UnTC8wrUzHUG2ZSRvPYNRqPw0g0EBowo2KpiMjIzd79xtjAAWg6vFBC1+1NC0od4NJx6eE5sZDBvYuwBVxj4bn82gXUCpRYOp1TEHWpmN23GI7CxzqAoYVqEtXTRnUULRiqR9Bcwaa+tyCvWEJ1+XCQkJCQkvBi4HGftx4JYsy27ASNgfBn70MhznGcKTsQPiDX0A7EC5Coeuhle/Fi7+AYzOB0JWMTg94rK0brCaXcjuQEvCE+KsbR1T377ffS98IpR1O/AybBo0uVwNkJCQkJCQkJCQ8IJDJEmOkTVd5kklTcN9PLdkglKfStXaIhI+iyH9i8eUgEBiAjGGQbG3XydPjortkyLVk6RTVy/VWVLODkbrbbpzkTqx5sls5jTse9EdqxO+k0w0tEW+CtVe2CfUJ29Mtaq6Fb1wiMpevSWYZTBtYFYZWVuHejQ1VDPYqaA9gXYJo3EgqrrQ6rt2bCJpN2hMgZhngRjLIsfdVpNmsblG4SV+2nFl+2HuagZ1p5pMhCtuH2277LoEIqHbhN8vYF25B7MRnOpD+2rjJsss2gzsYqrXaei5AfaUdCQc/hzwEKaIfRjYGsFoAMUYqr7r9iXscUeKTR9s6Pk+PSpNmefsRzOYhRo1YfzsC8e7kPXtPV+CbM92bjJoWjY2TnTgRGb1GBPJ3ikwDgdph76cNTCoYW8KW9Pwdxv2zgJnsfGrTqvcSY5CC0n6KwmvX+zouM6QcGdqquwtEa6HrMFmbTgnMrcTOrUNzZ7VeaxG2yP6PRSh3BX2/wdkXSOY567vBlrL0M2haKCc2HUwntr47c1gb2bXSUJCQkLCi47nnYxtmmaWZdn/APxn7O7wy03TfOH5Ps4zRpZbGFJ9GFvj1V16116TTfJqmc7R4wxf9Sr44nnY3MHuhkexG7BuusvMzy5G2M37XNiuiwmBT2BrzyvAAeC92AxJmGJxPhfCe1LFJiQkJCQkJCT86UCOTbEPEQkbiKH8NTbP9MSqZ9lC3DnLRGK2jbFOvgyxeT5Kq2Q+sksQMVq4z9pmZaGMYAWwzzZKjikymFC3Tji3J4gx5jpmN7x7Y1CRVjXG4qldxDgqKk0sn1hNySl3Yerj+LHfsy7kbfs4njFnMFqHY9Q63yFUS9AER9Uy7NMEcrmUVDWD2Qw2B1DtYvP8HLIVuOoqyKp4yrvFvAMFoQgNA/Hw0nbo74bIARK2lZvaEvO8ucqU2nGEdZt3oNBjipr7PGwsw6FlON6Bl2PxeOth0xXgKuxJZZkYQ3gCU9a0gU4Gu8uwtwwXT8D9E2g+jj3mHMGCAD+HyW/EuWvNwatnV7C1BT3yzIBex9Sq1TrMTtr3uhQ05PaPs2Ll7BD1MitEkbXexTZvAWM17CB8cQHT/O4Ck9C+u8yPT11zdfhtRGR65TOh8aiFBm8L4q8focQkxbrWNcb8uF/EMtZT8rzo2t9FyDvS7cJ4DJOB2SXwmNVjNDGl8T4pvBcaZWL8L3+C+UskJCQkJLzYuCyesU3TvAd4z+Uo+1mjGUGzg00tdrCV+M3w/hiwRX1uj9FvN9A5ApM1yE7aquu+R5bicdaIClatfubYZPsIsA75SThw3DyBhhNbTqYfjuknxRvYXTERsQkJCQkJCQkJLy20wrtIzkAG7qtHpaDzkVTep1Wh/TAfu66y9bfPIqQcBoqLF/PmiVgfYy/SR2yVZ/O8LULl9pfUU/YEipufENlGEVBjIlHVYd4gVbkWtI+IIck8vRK4jxFPE6I55mMWuv4kH9rDYftOeJ9BM7QQdQqoW24fKZJ9u5chWVdtFgWjoakSpwXUPVMPjgemOmwKWO2Yp+wo+MqWVeiawpS3s5mRYuLH1ay9vqloVQUpSX00u5pCza8IePmEShAtwlXWuxJJe8g/1ieD6kPTMXcGyUBuZD6d8UkiRa6eVbVmocpXZTErxhNt2O5D8zjGbZ4LdVYTyzZhhg2LoStcQ3X/XLJYmYJodSAJ7/YENht4JINWyxTJ9SZUW/Z8lw8g27X+awZGvNdFWGfQmcC8Gn3ozs43Vo6RrzvYWGyFbc4Rx1NBjHb0fgw+eVhBTOCshZjVhc5UQ6ljpWT3Cya5q+tW6KXTZk9Qt8wDts6gGWP/Fy4wn5wvJzL6UtjK9mRx8CQkJCQkvBh40RJ4vXCYQjaC7vEw4dKEVXf8CqabNOfvh/5G4FprrGkm2E1Lbu4QJ8C64SlcJMyymsIyVVYXzYeIGaawHQLnXb00KUhISEhISEhISHhpQQSHR77w8gv4Ilj8Z79f4fZbVH+KqJHcUslk5RmrMmSlhStDZIy+F1MmBsxnWVKZPrZeTCHuO81vB8ybp3rSS/Xx9RQDOWO+7URUiRgWKzkJv6ltGowsE00oOE/dRnYIhfnENkHFWJTQ7sEkHL+eBM/SPTtO04JqaqHi0zLsl5kHbV1BPQg2B23Y7UFWwmwK03HwH+3Yd3kB3Y6JI5U3eBkjSpdD1caYOHFWRe/SMovkpJSdfaJbWtftq4RfEyLR2wm/aWi1bLtxBRurMOrD2RbcvGpWpXrSGYWifSq189hTi7SZDXNPTfYopeEovlNubuL/xWVqqKlbcleg50HlqTvCPFXHUxhvmN9C7RcRLobG0RgR46uEyyI3IY4zr05fSAi3XyEv2dV+3l9VFZ26bXRdilGHeVs6XUs6wca96/+HmHdvppu7OmhBo8O+OrtpQ7VB7MG9cP7+f4EWLFT/FvOEbEJCQkLCi40rgIydGBm7cjVMdqESuSpnfU0eH4fBOWz1Us0ygmIVsrCyWBQW1lTV5r0DQBZ8jTpADvUF2NnCbpgzTDV7VfjsydivF94LLCEhISEhISEh4YWHFKMwnxjLp4kfMx++3HX7+ORbnpzN3fcic0T8iNnyRKaYMWXs8ccTIyayFGw+qhBmn+jLE7u4vz1Rq/NWDgYRpvp+RmTUxMB5Q1SVJ4mnP0eRx95f1ms4W8TESSJ7dVyRuWr7QARnuSX1Astm1e1CNYZqANXQ1JQMQjk9U9hOdkN5Qytr3Amfg0q37sBmAa22EbrVINRxDYoudDrQy6E9tRh/ccllIP2mDWw3cD/QTKHIoBXsETqBjM0ymAQv1BVipLqI2V74LCGzyFiJpeVy0YPhBgyPAQchX4EHVkwYrJZ6IrRWz7XoaYzy7mFxf2dDK202ZvO6LwKFOMyWwrsEqUtEnlOCUnX/MGxTNTAJfrx7Dew2MKwtMRV7mLPtNjEBlvp/j/nFClUq+MrO+SNrHKrCU+YXGzxhKtJfhKnY7Yr5a9FLeP141XiG+etQJG7tyvXXnBSsuvYhSqRVr5JobeLJW7Hy/nwgKsc9W15iFPuijUJCQkJCwouBK4CMHUO+B8vrcHHNPrNLvJnpZv8Qtv57NRYCdRA4CsdugnbfJnTHDpv/0JnTcPZRqE8D54MVglcD9IiTzD32Z0TPGarzsh03KWsTEhISEhISEl4kNAvvnvgZMp+gyyfKkvINIpvlp+Q+3B8iybOoKIX5uaCPefcMGMz7U5bus7CoKBSJpOMpHDpkiNonlqW+u8i8V61sGnQ+nhhTBvqu224TeDTUKSfaPiiUvMbm63vYHP0EJniAecJKnrl19IsFmEwC0Tpb2EfQvhn2HKDP3fDZE3ijEP0mVWbou2oEgxIGF1wbimxfJhoASHHZttcwEGV5x0jeVsvIWTWZmlhR9rjmETfo7YLlR9tjv9vyJegdiU6+ynrxeeA+Iu87C59PETWou1iw/vkZzC5gql7laztM5EE1vHaJVqUjd7Btom3BDLOJaGT2uu9NgFm5zYjkqk50xrwyVfBkv2wERN5f6prRNToltohXkkt5q77VNSVBjz5r33NEtbrGjfdAVmN56FrAbevJWI1Fv7izSlywkAQ5jKH9feTtrMR63j5B7P25S9QnISEhIeGFxhVAxg6hPg+7u9BsEZMddNkP96BDvIkegs71sHYNLB22lezZBEa7cN8FGHwJpqfNs4geNmHwS8TyzPITwxXgGmw28sXncC6aGCxjk9Bt7AbfPN1OCQkJCQkJCQkJlxVSikJU0XmyU0pPEUHeqdOHUYvAk4Ju4PYRiamg8inRhNMTNx1XLlzaI3bR59Ixd/vGpiKoFLI9JOZRkFp1UdGr40n9p9cBIhnUYz+7/L6a9gmMxRPJpbj77VBmF8sWlWHiicPhXefpPUL7RLWsHnXkcyuCz5Or8q2Vt4CUsHX4e0BU3k5CGcvMK5rVT2H/vBOPkfVg9ZDZHTSVCTj2xtBuG/latmCcQT+zKrSyWFSfyN1LtCvxpnhBmM9B1cMePWR9OoL6HAwzePQwtPLYWnr6USYNKWRlRAGmktXIhnCcYdhJPKp4zzrsvE0MQlTzM4V8CrPAKJeBcKwKR5xr0UHiFhVeMn+ynqz3/queeB0RyVlcubpmesSxo+tX9hdtjPxsYdpgqcC1SKHrp8D0w/Jlrt1xRMbi9tM1IClxEcrZCttpIULbQVxUWSIKfDTGdX0uLoBIUb5oQ1KEfRMSEhISXmxcAWRsY2FAe9vm97QfnqKbl1Y5j2ITxXULYRo8aKQrma3cTifhdQEjQDVhVFiaN02H+aQBs/D3UZ4bGUsobyccawlYg6wPzSmiNUJCQkJCQkJCQsILi8WkrH5eKDWdz8LuvVjz+V33t1mc13mCR3Nab8bpFZneqxUiGeR9MvW3D3MWMeUJHZE9y0QbAhGXIra0vy+vZVZezQJbmC0HC4EdYjb6PpFA9WS2ylohEsciiFU3eYiKxRTR5dvGk3meVBu5MkT6af8O8CDzHp9gZHKP6MUZBBhZIIGbHDrt8OrASmHfVaVZpnXaZk/Qyu1dPqtqUi/Ulf2uF4mKU1YXya1CRO2YyO8FDUqdwVf3YGUJOuEJcEikH/sLZyhDil1gOIXJMJTpE4mpi8R7ehth1UMkbZlbGwwrqIfmfZoFO4n9fllMQgeRUJTq2qtFtUihxhAabKzKY9hbDGREBbYf/2pEUdTqDCnEdQzVU896XYy49USsX4jouH3UuSuubNkdSH2rxZBWPPbSErQ65n2ctSyJF4UlrpuEDnqSB7Rv19zavz+B6gnYOw6cISEhISHhxcMVQMaCEbKK69Fq6ApRRdDClo+XgAHMzsOuslIuMRfGlPds8tBocgrz/l7umPsO9VIWyMF/yJMVCs/iXNgL78eAq+ym3JwLx3oekBfQXYHBzrOsW0JCQkJCQkJCwqXhs7Dr5X1bYZ4UvZQf5WyhLO3jyVyf+AdXhognRW/5JGQ+rb33clU9fPIf2QsElV62Bo2izHxyJOw96wZ/1lY8TpaHubm3VlCWKqmCRa5mRJml/m6Isky1hVhAkVlqWx+ttuY+ixwXGVuYSnUmRaxUyINwLIk4CMcQuR2eLbKOkbFZaVmu2suw1IXlIvBxQfE6LaAI7GpRQzGFIkTVNaF9+lnkh/WoIi5SAmYJLPvhNSNGzotPHxGVsgWcvwgXWrBcRlpQPbpM1D+LjhSqyjQpDJjnsuXCII5STgyevxT/2Sogb2BSLqw9BFJxP3JxjajAlhoZ1/beO1lj1WcD02uJSNprTHnWWmdO2E5/SwfcJZo3aGyJUBUJHBTVWQuyArIa8jHkznM564fqtWx85EC+HM+hDmr2phXLzwqoCxtHtGFtPXoK+/WVCTCqTXGcF2E81TaeGoz8rkNnlQUcyGDvUdi7nUTGJiQkJLy4uDLI2AI4WcBD14SZxBRLqjXCbAbOAfdiXlU+nKUN3ImFQi3bq3stTLdg+jgWtiK0MGXtBnaH3CN6Hq0SV89vA77APkmbrQb7hEU1xdeCVLBjqD/yLPf9Guitwsu/DT7zPrLajtM0yQohISEhISEhIeG5QWSlEvLIK9KLBjzRKpWgJ2JFBMnjcuD2nWEEkfdD7RLZvO3w2SfSWmfelgBiMjAp/bzf6wr7maSyVWhfB+NdLG5dHqC7WCTZRag3sHn0Ejb/HUC9RFQUroQ6a14u0mzEvLTyHFGtKkJ4lzjHVp6G5fB7m0i0drFw8pNEoYHOL9gOlEfhwK1w/t5ALueYsvIwkQBW+3j14pp9bkpTABcl9JbNhiDLYebm0OIJB8DGHsz2XFstQXkYugfhaGlfi9c+HE5ll6g+XQ7Nt4Y9gijQr+ea70Jo3qNWfHMfPN6Hbt9a4mWhV8TdFqEHRMmvhsN/pQ17fdf009A0sscVd70amlPiZjms7TtplJAfhPJg5EUHDWyJiF4NB9kMBe2Ek4b5a8aPgcZ93yf6Ee9iUl7ZUiyOY5G/3t4C4hjTOD9HJGJHWH6RLJZXLEO7NOVpWVq/eBeSRRG5hqc0QeJ+JZDVuohfq9BlriGoJ/gesJbDjZ04Hlax8TBbKEP98NDNcOoHgfeSkJCQkPDi4cogY6mB83D4Vtjehb1TwMcwUlQZKJWOVMu6Vfjt8VBGmOAOOlAegNYtgdiF+VAziJletYKrSXILuB5LFnYb7avfwk0/+3e5/6f/BbNzvw71J5/h+UidcBbLefo8Y28TPvseqJb5hX/6TpZXOrzjx3/0+T9OQkJCQkJCQsIVA+8h+1TRTNnCu9LSQyShpAYUyVi430Xu+im+iMS2+16WADqWXEJ9Eq49jBRTEiSfICuQsU0XxmL/9HsLI8KeIGaFV7KkFSwBVxcjtZSIK8OS054L+3rrASkft4nE2iiUcTyci1eqiijFnfdVkN8G19wc4/GnGH/caeBkBodz2CngUzfBcBNqJSrzbVkCxyA/DO1D0FqHHbFdassSRhkMx/a5aEEdSMGstGxaeQmVmLU+sAy9g9BvmSoW9jleVqz6rIZD6BFF+YL7Ydvl8O6j36fh9+Ah270BDi3DTcC3An+eOHrUyqIqtRzwaeAPM/hIHz5/KzzeMgc4eqEr1dziJ79EFBMPmOdDfR46Dd0Z0CzDcCnkN8tg1gky3QYGNUwqIzyLJnRzZpdGOwsn0Jjp7QTzYyCDpQbaDZRN5Fc9ZqEcrX9MsKHXzQJ5mtnfHJwXrxd5zJHVAaosWijr8lSj6lKCKMiW/8MUG8YXmeeIdSm13Pt66F9Zxi4ReWuR+4tC+SlxPUKc9gTYKInmFAkJCQkJLxauDDK2msLj98Asg8kTGBn6VeJSpM9cuehFtBM+b2NE6hPmKZs5Y/79WZE3cVq0LBhhd8UD2MRxyGzz/Zz5l7tU25+B5pFncULy0fJTpa8P1732z3H7t/4gL7sGfvkfvJOdi18GzsNsyutf/S08/IVz7AzOL+ylyXTKxpmQkJCQkJCQ8MzhQ+Z9BiaxLrICyIlx5mKxpFxV6H7Llat4cEkiFWgeCME5awJlZRd5uYMxZ1LtKi7eh3orsZBUh4tJsvqhXJGXUsiGBGH5MTh4AjqHIV+F0RiKNeisQ2spiFB3YPsUjM5DtYuJDuQLK2WiZ6rWiEmWPBnsyesls1EoDkIr6DxnWQyjF3m2G96bBlYOQd6H8QhmAztGu2Wqx3YLru7BiS4c7cCh0E554xwfspB3qoFpZiH4s2XYrGGQw7iEWY6R2R1oavOObbfsXeSgSNV2ONUeMWeTd64Q/6zhIEe2rvs9NF3vMBzqmNC2F3r+INFUYhENpie+JjNqfVTAua6dDmvMWxprWB4m5reSz6wej0Q45m64NKHhRlkc8rMiEpbTxtqMzKwevLOE8naVmNTX278uu6Ehe+DFHGAaUj5fnsrUq8znLVxLV6bO0fv2qm5eWA5RFa3PepxaJ9rP9rFHRT1eqr38EC9Cew6J7glTnjz05RoyCecmO4udVUtWPdYASkhISEh4MXBlkLHNFLYfwKYTj2Nq0j3mPaO8gbvPCKvsmbvYdGUIzciUAPsqAt3x5F6P29/febWMvQ6cph48zOYffZEYd/Js8Ny9XF/2ym/mm9/6A7zm7h9ltnuelda76S9tUhQFp7fP0u+s8plP3MPm1hMc6B5jY/QEUHDoyHWcvOG1fPaTH4fqERZyrCYkJCQkJCQkXMHQ3M95pO4TqmJz5FepeaPkhYpnbmHzw00iy7Xo4appfOm2kUWBAs3F8mjO2zJiNOuFZFNtyAaQTYLfZRFewT+zrqAIMdd5F4oeFCsYkVhAnQdfy2BMmnXNLzOvnMg3NyXpkaMWgp+twu6eeWS229BqQdaY7+VsBerzMN4kGqE24feB89FsQXEAGslcs3h+TWMEJxV01oz0LfvQ6s+TXNqtwqb5M6CXwWrPkiVNp1Z+DvTaRpZ2Wkb6XYelbjiEZcPyybYKAhkbXlOg6lpXDogR9Vl7nmcWOagkXNJ9qAuVJ01DRUPHe7iKhBVXnll3tlqwvAYnl+DGwqp/mMgZPh3WMCVthj1JnevD1hEYlTBchekYqvB4xDi0i4bpBCNjlYbCk4simL1tsh6XFJZfYcrTYRbdKqZYWyrsXq/FRzkph/0jnYhQOSKIeNW6hRdiq01bbjvtKwJXTgoix/16RhP6asp8vWSFK4WrypK3r4TiegT1+ce89YM+69+BF3FP3b4TYNTApLHFhfEmZMrulpCQkJDwYiH7RvACzbLsBarED2IK10exmJAN5ifJl5qSeI+oE0SPIsW6aJlVdzuIk2CpHiDelWXY/lB4PTdl63PBz//GR7n7Ta9mdTLkh//ye9j82M9y53XHWVrr86sf/01a3MiMIYeW1rnr+DfxoVO/Bc0y3/19P8pf++n/ix/47l+i2v4FqB970c4hISEhISEhIeH5RbbwubnEd/pvkxgAACAASURBVPp+EcqI3sVYlQMY46K5ot/Hzx3bxDmlFLJSu3qmx8vsJOtsB2K1Y+HemVgkQpJXxTN3gYOwdD2U7ZBkqISyC0Vh33V60F02grGewWwM3XUrq9eF/hIshTmwwuC9PkDV8qHrOmU1YYURdLsYQbQfmg4MJzAcwc4u+6apeQFFG7pdGI9hFg66tASz0hUe5vRVFYi/Aq5atlBzrxj0IfPejlSep3JdaBNDwX1OMO8w4d0bCvdqXaJtRKSKMK1cGwYRL0thO1y5qrtIVj22jBbqNTMXhEwKy1X7rdeFw324aw1eAbwc84q9A3squdTIvhTEWf8ylmnjEeDhBs5tw95pmF6AZjPUxxOFW+6zd9eQQ1yPmGhMClA5VEjVuUfMo7WHPcax0Oa9UEHleoP4uCbCWxYJHYxZVr6wtttvh3m7Yo1fjReJw2VTLCcP1cetC+C1OyJj5eWrMQbzl7XWYvzjpdpDiwgSo3u1rmwfFhcYBg2creDhEZz+Mux9Gpr3Au8iISEhIeHyo2maS95qrzAy9juxu5RCnx5ifllcNgW+Op4szYgxQh3icqY3EtKypL8z+v27xJCvHeAj2PLmC98PrXaHN37v3+B7f+gn+f5rz/A3/9Jf5/OPPc756YSq2UFLubfe/mb+yt/8x9z5vS/nVes5RbfgwTH89E99mM/+1v/I4OKXmPdBS0hISEhISEj4RsVB5m2mIDJfYsrEaijDjped+Yw6IQx//zfN/xYNPCEyO2JhRguftdgvNm2JmAnIl+HmmIeuh/6KEakNFoLfaUO7C+0+rB+DcWUKVnL7fX3ZZXtnnkhqZ/P5vTLgcBa9L2ssVBxiIilC1feIqRhEeoZ8XU/KD7YXfsumkNdQdkImqSYSUF03N26wsOpZE6fq3Sx2h/fmVB3kr7kSPD1FwnmS2FvlZqHJD7v6KmeT7AEEDQ+Yt8qVGFpDqI2pHUXiLTpLiIhVvRRKLu5c5yC/2F447oR9V4pOB5a70OnCaguOZnAwi6P0lgxeBfzZzEa+qH2NgGdKxqo3zgP3AA8ADzZwCtho4MwQHtqErTCeGuXPEoGKO6hIcBGLXfe72l2WBXrNiN6nKs8/ti2HdylHRVaL4N0junYQ2lBkrNY+umFf+d2eJ5KgYP0ld4xuOD/VX8pW/69i5srQ+c0wAldk7yzs49daem57Eba6/tRuixgTx6F383jsNPzee6H5m9B424/nHmWZkJCQkPC18VRk7JVhU7APLRFuYqpYT7R6H9angmZtE2J6yj7z4WiKK9Ky9YQ47cniPuVh868a/9HXOOblw3Qy5nMf/PecP/VF7rnzVlrHTtLd26Y5u8UKR+l1+2xNz3Dq9OP82994N7/046/k//tIyZc//wBfuee/8KX/8q8Z7zzMvGFUQkJCQkJCQsLzDcnNFhfNvfeqiEpvP+WtoCR1zInZbPSbpHo5cZFc5Sg2etEIUkSsSFRvf9V2ZXqTSb1E9Po0612TNeYtU4K2li37fNaCvA3tjoXK141JILtrsHoCyiDlrCqYVdBfhqU2rLQg78BOA8MZjKf2+xioZuE1NX9O6sDQFdDqQlmYl6e46G1gNIXpDNp5UPiNYTaDMsx/J7DPDrZaFl7eEL0xpQ7UI0kPqILtgJppHH7sEBIxOXSApWyeaPJBaV4F6UP7V4hODt2F7RQOrn26GKnnkykN3fayDfDaDAmUVSfZ+Xq3CLkpqIyp+70gKmLVDkq+pPUCkY+jhTbMzSZgewL5BCZ9qDswbFs1+xhfeBpLW3wrptXu8sxJWEH8tbenHWT2VLVdwc4QdjegkXvbHjZutkIb6hKaEnMbixM8sNAeNfOcYRbK2Gb+khYJL6JWZcoyeYdoGyALY42LKWaEq8tPY2FRjdx1ZchOoMFO/Cyxr7SfT8KlPlR9CredFLA+qZksKjwBLCJX7dAKddC/L1+u7BS8RUOxCfUniL4PCQkJCQnfCLjCyNjzxLvepdSoz4QU9TMDHz+06KbfuG39b2HynpXmofUi3xQ3zz3CzuYZNjce546rXsH64WsZViWDCwPqpuLWm26hKrt86XN/yHt/82be9ycFD37xYS7e/0G2z/zJi1r3hISEhISEhJcCvJHms93va9k5KaTfMxoQ52BiycR+SJEqZkPE6RKRYhov7KcYZ5XdYp49KTHGr8X8vLDnvtNxFolZT9i6bENNbkRq3g5kbCuSrhlhHtmDugWVk8K1cks+VeeWhX46hFEFoxlMpkaeNrNA3M4s5L8uLUN8FurdaqDbsWPUuRFguwTNQmYkaQMMKphOQvM39n2ez4dKe6LIT5H3Sag8JpkSRDZ6da7sdKV9EKHmhcleeetTQHSJ5FrLbaPf9dl3keqpRE8aTo3bp7jE354oZWE//3jg1cje71XtsLjtwNXXD7vauPm6xsi5yoTLdds45aXQbTtY1gxpwteIQtJnixY22teIzgrbGcxqmCmhlOwFvH5F3w2JlgCL7h1qT617eJJbehglq5oy76sK8yRu7cr23qpq1yq065DYD0PmbSe6zI9biP2lOupcCleu+sgnUtNj4JQoeM/cb/7fgsaQvlcZPvBy0fcY5q8DedEywXwRXvxo2ISEhISEiCuMjP0qcC2WQOvU81SmZhFgd8VlnmwwJMgEaQb1yH33QhCyWqr3M0BDNZ1w+oHP8rJDd3H11a9iafV6PnzhN9kdb/NDb/4JlnpL/MN/9ov8b//Nh/Zr3FosPiEhISEhIeFPIZ5KP6fvL/WA3yxsJ/ZgtvB7xlMTBNpPMeeXMh+VRNEzG56hEWuzRGQpJH+TLK2D0UqSLooh8rHGY+ZJVBHL3tzyKPMGnrj9PaPilbCSzjn2pZlBNYGqMTK2U0JThallY5YDTW4EbVnDbgmdPhQtU7MuL8NoZLHieyMYz6AMMrumMQJ2D0dWVUFlu2xWBxnQTKFcMS/ZsgXjJoTQF9AurC57mIpWbdpqmVdtUdo+6ioRcxOiOlWcvEgrTyZ5Ilbvni9XwFkZul5cdhbq1HHlSYm5SyS5dAx/LFkKqOuVGGpRM+H3lwWDhprIMhHLfrhpH+8PqjKeql5t5ok5td+ixyhEonEC0wZG3XhVhFRr+1z4lqvW10PGyv3hKqyZzmFdtFvY8Jtz1FCdRaL7c2mHdymSNUYat/+MqALVwfUQUhAtMIbu90BI7/u7qj9abj+NSYjrKupnJdiahr8vut9Emh4k2hSs8GSnEpgnhGVxoX6Sulmdovqqz7X2o+ujQ7TO8P+O9S8sxxZMVEeNYY3nCQkJCQkJ34C4wshYxZEER/vndHfSXVRLoVruhHjX1kxBM0O5tp+FasNCs7gds8G/nKH+BSzdDZOjMHsImj++xLn0OHDwGEcOX8XKdoHu6h/95Gc4uHaEl9/0au594JM0TTNny/VkPN2DVUJCQkJCQsJLBzJALC7xm6wBvOxs5D77OZFYGBlf+hTyUql6BayXG4qREYE5IzIyHYwWOkSUqF1wZbQwklX7lK4MmLcT8LObNSKB3HLfS4KnTEJjounnpdgSneti3LLIY5Xp5Zli92oYL8N4jziH7EBemoWBNi+BujKlq5JflZ3QJRWUMyiDdLKawWwvNEduZbU6UAYpaFUFRg0YT2BaG/E7m1nirNrN70pMNduUlkSr7MJSYcfdCnNj2QH44eCJ2cV8Zr5scdVSqdZEQk3Npf2VnV5OZF5RKS9SDdHSfa/M9UqypAz1uCb36gPvZ6rPGtqF+61ziX0WfURnRFvgJeIQlPeo2qFrXHnjHy2wbbMS2qW5PMwK6PYtJ9VaeB0EbsISdt0OvJFnb03wVNDVV2CR/jOgtQKt62C6iRHj07DhMnZZivRU34tU1yOUT5ily0skvMhtP36klFWfiaBXX0tRrGOpL+UwAtGLFuYvSf+g4y0mdAxvHaExKCuCZeK6jMrcJpLwLeYJYdVJa0d+/Oja2SUuHqhMeTT7gAP9O4K4CHFeF0NCQkJCwjcSrsD/zJqtyYDHKzu6xGXaS0F3cS3XCyJkNcPTLMvNmPaX531MjmZnJzELhV0uB1qtFj/xE3+N737LLTyxV/A7HznHn3zgN7n4hd8nG1WUWY9hfYE/+vC/oyxzqire1S8Ocg6euIa3/vnv4q5H7uJ97/89njh75mmO9nREbCJqExISEhISXjqQPMzPf0TAimnRHGdCTFAq8nFCjMyZuTLFdCwTpX5iULxEUsyEV7G2mGfaDobtRegq84+kaOcxxkV2AWL3IJKxYvgWbafEkikOWYyMV91qPy+188yRty0oXdliHNuuXB9rrHPKoOhB3jNyVN83gSDNt8PvpVkEzEamqp3VMBrCdCdMR2vbp56aArboxtOfZVDM4iE7XSNgqWKir1Zux5tMoN227dp9aPXNI7bOI2mq+W/luk1NskQkq0SSQZx6a7gpUZX8RXdCN2goqgvlAyrFrZSV0l744VaG73quHuuuy1SXRdsBHz4Osas7oSxpMtTNWjtYDDHHfddz20mdKQF26P6sA8sr1h2Txl7TIVSBqGx2YNI2AXXRNY5+UJrt7gbGS4+AM8D9mIpVwtAV4Lrwvk68Cr8WGuBBLHnXVzAf2s8B58awNYTZADv4BvPJttR/siqQOlSX04D4r8N7rErZ7BNoidRU3+rS0SOc1oN2iJd+Ho47Zn7Maf1Ij4dezez/HUlVOw4Nqn6bYHJjXw/VT8nBpKLVmPbn4ttEZHXj3v3CAcQx5hc6YN6aQP/6ZmF/VoE7eP6o+ISEhISE5wNXIBmrOA7FHvnlbG/SswhPJPrYKz1c6M4+dJ91x/UT7Mrtq9ico2G/55eMveaGV1GWfS6cf4K3f88ree03Xc3muEPn0I1kvRmbN13L8ELFzrkh9372H7OxtckiEX1x4wyPfHWZsuyye/FRxuPxpQ+WkJCQkJCQ8KcM3v9ehKpYB59BZzG6R3HWmlstMiw5l0bttucS7+CMEENZYuNmRFZjQCSSJR/zNgMhDf1c3LdYwLb7fYQxKN4f1jMlqq+2EVOSud88eyKmzRPWnsVTuyzE7DfBQzbLwiZZNAqtZtBrWdItCN+FNssy85mtHSOZ12ZpUJRmM5CH+uSZEa9Zy9SuYJ9bzoS1bEF3ZnLMAuh2odc2+wJvQyCiUcmPlJhKIdhqGm/xKzJNTbXsulNN4dcFvCenusKraSVA9q5gLYx5FL8v0bdX0hbue+/nqceFElNKKjR9USmry6R2x9Rv6l4NIU8AioxU+wDNAGZjI2VnWFc3IhTDekBTmm0wbZj2oApi7ryA4RR2O9DvwKkSdorYRAeIHrLr4ZR64fu+O31P0spi9R6MiH0UeKSBU9uwuwuTITR72PrHFtFCwHu9emJcjxxqDzHFIly9clr94/8F+YRwi1YPCvvXb976Are9V2iLvNS2/l8c7ruJ21b/1rw99chtq/LVqIT3PvNj1DnZPckaQ2Sy/3fobax1Hfh/qzP3PlsCbnQnn5CQkJDwjYArkIy9iJGePeKdXzNGLZd6l32PRdOgGTbL8DEjIYxsPzPBopO7v8Pq7n9dqNdFnn1yiwVkBbSXWO51ecO3vJ1O9ygf/sAHec0bTtLqtThYw3e8rs1O/ztg/B1cPA0PfPY+7v3s/3HJ4jYvPMTmhbPcd+8jNPV9PDdla1LFJiQkJCQkvHQglgQi8+AtBfx8SWwCRHZAKlYxHfJZ9eyItzqY8OTY9sXMOJXbZ4rNnTJXvgxNxZRJtTtx5W4zL0vU3EtSRzGIY6LVlGRtKkNli1FRPLRYJsVjezLWM4l6dyxOVrr91caFze3IjEAVedgUpnDNyyCf7Jv/a1XBJBDDWQFFB6aKxa4gm0AnEOVZsDwQ0Vq0TYFLx+wKWgV0nFw0z2Kzyv5WxOmISLZOwndyuVCIvpws5Gd5KcJLSkA/TVcZlwqw6ix874lfTbMlQO5izCPEIaimEaHmCVYNK7/WIDJWaxAKaVeX1q4sqYIr4tqED0/3fP2QyIiKRBzDsLAXEIllvz6C8fRVAZVC6IOge3cI51fNPqDfhzNd6GbWNQczy55xdajiEkbE3ooZf4hPb7nDTTCe9XMYkXsWONPAhS2oN4jk68Xwt0+uJcWy2rdNDO33fqm+rffc5y7z0L8MkbHeIUQVVpIrjTVPzGofrc2IOG0T/73o8c6vv6i/pGqV0F7npOAA9a3WdLxdtv8XsxTKkY+zJ6b9uZbMXy9era0AAk/W6l/nDJj0Ib8xsPYVT76IEhISEhJeDFyBZKyW2K9lXpWgO6omv4sqj8Ubl7zJ9LePJfGu/z7UbJGInWBxPNcDx4nBP18/sqVjtO/6MX7sz3837/j+u6hHfWh9D7/1lZL8Bjh7EU59Gd52B/yZw7BSwv2vgV/52acrdY+m/vJzqldCQkJCQkLCSw2exPx64QnMZwLJxBRXvOh36KVjPsLJQxmDSkz7t0FkiFSPkNSKjMiESN0qptETxB33neKfC7ef9tGcEuYzVo2Iss0WFH3m1boZ9C6VUqmEvGUvSlfFHqxfDaMZ9A9arHpVBeKzgm4Tm+rYkiUCaxXBE3ZsVgZ1aNtWEclCwSv5WvAkVV1J5LnPs0D+YMrIRQvdC8y7gS0zT4wprDsP2w6JQ3BK1E3Ak4k7kVjLzE+9ZSMAkaDT3w0x7644Km2rrFeLzmMqoyCqItX9GlqyQPCErgg/n1CpQ/SN7WJaEa0RaE3Ch77rnDzxrKEu14wtLCpdpPNFmF6E7R4MrjNr3+XcNgO4GRv9m5jSdYARsodCESuYvcEgbCfZyDB8HmdQHoJpbusD+/bJ8nxV4N8ykXxVgildLrjt5XYiG4Mhsc9le+HdUTy8xQDMk/hetTogXo4z19aEzzuhjWUfobbWooMsJaQG92rbJaINRZ+YJa1PXJtSIGRN9J2VQtb3s3eAkU2C98PVvlo8WPRg3gzHq5bg4Mvg/LXAI0RWPyEhISHhxcQVSMZCNAnSXc2H5usO90weGhb32wWOETMG7xBnDjI+0rYZUZH7KPMGU1/PiuVBbnv73+H61/wgxWbOr//jn+f6YpXXveE1fM/3XsNnH4a3H4c3HIczffgn74Kf+cB9jM5+kcnmp2D1DbDzaWgUI6YkG7t8bbVuj/7KSb71R/4W/+c7vo13/ouP8su/8h4Y/bbbpiTLVrn+9tfzkz/zN1g/ciOf+PR5PvreX+Wej76bwc6Fpyw9ISEhISEh4aUIT5T6DERiL7xczMMvYCubj9gmsR3KauOPo+81t5Ms7yxRgufhTSchxlNvEI0eu+wnfu2dsJjxwX0YneUjocYYfZW78nzGqJn7ewqVzgds/teH0Z4l4wKLMy87UBRmPVDPYhlFy74vgaUOzMJ5FI2pY4cDmM6gaaC3au0yymB3ZrHk1QhGY2gyWDoI3RK2N80PtiichUEejhNSNdVZIHCDfLCuYNbYafZXoVNAkUdCliqo94p4quKufbIsiNmgRL4NXRMrEZNP4KVqTIjDSda+S0QibcuVL+J1SCTbwBhHkaS7oR4iugj7+Km8LIk1jT/m6uFVtYspKBadMTpEDr90754Ul/pR23llqeP295XH43Cea5C1ob8ETVhz6PRMEXsyVPkqbMTegnGFXeAu5g1GwLhVXYUt4BrsijiOkbaDHlwoYNiH6Upouz0iYSmidTe0vfrZp9OQdYTGjvc+Fcmpxyqvm/Ferf6Ry7e9iNFJKMPbZDQ8+TIWWkQlt/pe49g7schmQosQhTtXjb/GbbvJfECA/tWJJK4amAXJdVXDJINu6Pwimydem3DydfXkf2+Tyq7lGhiNgH8IPERU/AN8HPgU5v6bkJCQkPBC4golY3VX98Y/Cnd7quRdzwQVtpS/jIsjI5oaLXrMeuWHsIzNFJ4p7Fx+5md+ipe98XuYrN7Ab//JhO/6S3+WQy87TnMo58g1OW8cw8k+9FtQ9eDcBkzpMsrWGeQnKFZvp9q7BypJFmIs1IH1k9z+su/iK/ffx+7O/Uxmm9QFXH/zazlw6ATQp9U9wh2vupvZyZtYf3XJbY/1WKuPc/PJkzR5ztnzm3zyY/fysptfzXDnELsDOHO64ubb3sbNN9/B2See4JGvnmVz4wIXB5tU2w/C4LGvqxcSEhISEhISvhEgxkvSPW+ueCk7qKeCz8ojOZrKh/kkYFpAFjsjduepjuXnfd7M07N8JbBmytV8DQZnMYJXskSpYUfuO6+0FXPj4511PLFCUyNP63D8JoOmMiKWLGyam7SxmsJ4ChenUJeWPEvHq7EsTzXss0nTVmiK2gjXatdUtOQwHkCZw3DHCKAMsyPAedTmXcsQRWEx8XShlMK3Dd0l6OZYUrHajjMrjMjN8zjl9aHli6pZwdsViHf3CbakBpVIedt1te86T9j5pF/eVUx/61FAlsaqR+O2XXQek5J3mRjTr+E2IAqzfSi51I0ibeUb6vO6edcPsaHeztgTtn7NQvVW+bX5y05b1mVZDmUN2zmcl71BeB3EBMkHQhHL4W8l9pKwdxPzin0Ce1LZwpYtdicwGZmn7dylrrqpbfQuv1OdmyrjPYQhrr9Ileo9h73dg0hoWWVk7uWJ3YE7vncS0ZqLb5QsfCeVrhTQ3j5bazcAW1MYTaDYCecUGj0rbDGixq6zsoBRHtomj4seJXbtjCuYjqEOg7hqYFLDeNfY9byArLH/Czl2zTWTuP2+F0Nu/xeyoN6vRpAdh0bJqtXQKxhznMjYhISEhBcaVygZq0nxOnYDks/X4ozm61GoKoAnOOgDcXbRYMukflapibkeUJZCnZ7JsUs6nRVuvfXV/ORPvoMDx47wmcfgnR/r8vYfejtHD0GxAstr8OoSygxGjS2wrh2Ea1+9xnj3Rs6eLfno73964byHXH/LKyhaBdecuIO7/8xf5Q9+/yPc//lfZ3NrTJ1NOHzkOm56+Vuo83UmdY98epAPfGGLjXydk3e+gWOtG3nLG15L3m9x/4MP88CZX+fQkZu4/0sztvbOcursFne/9Q28/Pbv4/HHL/Dpz3yF+x94lNaFxxic/hDjxz/JcGeT+QepvvmiNWFiUT3TtkpISEhISEh44SH5npeCPRd4s1Fv/yQGRQvcYteejoi9FMSU+UX0UE7eBI9VRQ/l7iU7AjFv+lvlySTT5xAQ2xRYtSZ3f9dQ9aFpG0nbYP6w+bKpU6cZ7J6HWWCzmipEN5XsE9ZZD/IhVJlTD1ZQ70S/2HpmLFq1F/b3xpT6uwvtJcgCm5gt2eSyXLbEYcsd6NUwnFhZs9q2bfegnUd+2guhfZYoNZlXeirUW3qJLFZlX8apBF9ynPDWAZX77K2L1V0i66SU9T6v3spY9sdqCgW2yQ+2Q1RaihxVCDxE0tkrX0WmeisD722Kaxfvi+p4Nupw3hpmsi8WqRkUxpOpHTfr2PAZBu5+lNkuG+FUVrF0whcwI7friRH+E+zp5gzwMOZKsR32fRzYGsN0EBW4c/bNqr/vY59UTeeudZRq4TPEy/BSXr7qS9lZeC9VT9CrX7yaVpelXjmm6PXt7ceOV8kOgN0Gdhrr180J7O5Ac3bhhFtGtoKpVFsdu/ZmgawtCkuI18nCIsYUpjtW0Yxw7Ve2wJIF74wG+z3HrtlmRGSMtcog9h72L4q8gkamxBrwL8eI2DWijDchISEh4YXAFUrGKmTtTmwaobuzj4nxpk7PBlqmH7Ef1gbEpd89jHD1RCzEWd+z6JL8EDfc/M185rNmB/BV4N4h3PeFho8fhc4b4eBSw1VlxkHgVJNxP/DFNvxXPwQvW1+jYI0HvzziQ//8l+aKLoqSX/y197N+7CArS3DVErTf9Gf4pb/zKI99egNmX+EjH3wXg+qVDHvHObPbYedf/SqttQ5rh4/QXzvIF7sdhs2M49eVbO8sM1u6g3s3r2J1sMTa8hp3veowr359wdohuPbm47zyNVfxvj+esbe1x5nTb+Wh+77Ax37317Dp34PWPtnr4cbXwWgHtr8IF97Lc/ezS0hISEhISLg8kPxw/LRbPT3EXonN0SK6SEPvM/tcEqFKgqiMU4V77cD5h4hZhcQwgrEmmtspi9EutugvZlGx0FqQJ5Tj0qDXymylOeF6IOdCHeouDGVYKnZv6OpQurJbRtTsKJmZWC/F369YArADq7BxDuqRSSmByIqJSQsSwnoGTQndVTh8GNqBTaxGsLFrxBHB1qAsYSWDXhPdu3x6BlfN/SZZx/ZROP5G2EdKUZF8F4mk5RbRgULNIg6e8HnomkvwxOkukTP3iaJyt4+GhghVT+KKfNVQ0TY+cZnqIhWtzkXfq+l1Xt1Qrlf9HiB2n08s1g7livCusGF4IZRzCJoDMA7tM+kal09o6k1gq7Gnl+syuAlLLXzINcWuO40T4X07VHv/SlQ99Dizx7yQXSTrov+tHr1EgEL005VryJlQTp+YFO0MkagdhM8HiWpltZNXMutfRwvLXiZf2r2w317YZhr+t+hfi8bKKWcTMG1gNg79twfNDnGQw/4glMVI3YbpMnS6MOtAPTYida9r6vOsNqVrHVo1L9z+Y/tt/4KZhe8lx5YPhBhmmdC6CIFaAheRxTsYBX8SeCvwayQkJCQkvHC4wslYxauIFFUihudiVQDzS6hybnfqgrl4JTnY+zScaxi1+vR2Be/46z/GT/1Pfw8wqnIJePv18OZfhL/ytz7NH/zcP6LXPMHrXvcX+Kl/9g6eqAvObMDoIvzwnfCJsVkRzRZylV1/26v5X975n3jLbet0SotSa4D1q6A89hpufNNdvPa1d/B7v/Me/uJP/DDf9rrj9EdbvO6bPsR04//mwtYuF7NlyO7kP35yzGv+7N/izW/7Dv7du76Tl2c5eZbx4c9lvPO34d3veoLXfdMh2kstdicwG8EtN65y47Uv5/iBPh/73T/EgqKuA9bJsuPcdf2reOizf8L25grwRuCPv/6u38u1swAAIABJREFUSkhISEhISLiM8KaJXy8kZVNCr0uV5WO2v14o9tln9vFT5VPYIv6EeVNRiIyc2DmpYNexOd758LuPQ9cxdT6L32lhv+V+g5hBSiSM9s8u8ZuMUhWRNYP2qk0A6z07Rrc0knWq9utY2HOWQdGBpTULoc5KI2CP3wLXH4BJbiFX48xUslUVyeMMC6UeNeFVYRmeMqgbGHhyPoOqYyHV4olE0HnuaISRbKtYdDXMaxt8QqhFTDDWUcpMqThF0k7dS5JQKSx9OHpwrGAlbDNlnql0p0Roiv1AOSlpe+43vTwxW2JZszyRGGx697cT3yaSUMO2wFjS3fBaY38YNzWwDMPGBNdVx0bIJjCqoajgRAuOZvsc7j42sdRPXyI6ROxfHRru4gXPh2NLuSsskrFeoazHojAk2cQutQGxX7w1tB7Z1CYDd87el1fjCKLlwG74+03w378DPvjL8IXfD79th2PvVTAYhX0H7DP13T7MAiHbyWBWwmArjJdlsw3ZP0F1vrKGYZUdw7wXQtfsSdodKHsw68HE59LIQtkTS+RXLsFkj/kBoM9qaJ8NTA0gPwZZxxwOn9cxB+AHgHtIIpeEhISEFwZXKBkL8UalCb5XARDetcwMcYaxwFxeEjKW8tYHmllqoq4Z3HY4zkp4bzMfWrKIHDhCfujtlEe/i2FnjX/zfhi04NgxOLRmUShvvn2J8r4tplsPc6x9HyeLho0hLDVm5r+bwSP3wvF1OOkOdfiGV/GKb34b33nHUfoty8OwCzw4qXnXO++jv3QjxfjzfOqPfoHRhUf4D7/yIJ963110e7dw6MYWG1+9nm6/z+qhazh84pW8+k0nOXn7Kzl8os+995T8yq/+B1g9wbU3Xc1/94NXc2a2yoEjOYdbsFrBp3YKBo9nXHWo5Mjxo3zHD/w4G2dewQ03HmEyrfjd3/00p+75IqONcyH5RTe0nTIhJyQkJCQkJHzj4PmwEvL2Bpfbmki+tGL2fE4BkTId9503sHSWAxC2b9z3KtPHpS/OPb2BqOY2PeblpbK8ktRv4vbVIr9ir5XVyhuiBnnqbASbj4QpbhWUrT6/QfCIHe5BNbTymgb2NuFL52G6F/xpK7NOaLJAuAYVcLEH2TRYLojdxMqYTYHlYKXQh/YKtHrQahvhlBUwGVs4d5FbjD3EqfkQ2GhgHGLTW6U1g5StamYpG8fYusCIqOCU+tR3I6HZFx0oRIzK91T+pMrXO3Hd7hONSVHrp6xSWnoe3fN3fghkrgyJsr1Vsnj9Tjg/DdexK1PDbws4bjako9r4+GnHRBl5BitFzGSx+LRzANNPPoo9uZwFHm9gUENrZrmiGu20gxGaahO1h1eoqq18rjvZQngy3JPa3jq6cb95H2KprEu3vdpRInI993wUPjiCM18KdRbxO8O8HPJOsK0obGzXRWxPEd8HChgtw7ixhs1WoKhtIaIO3q6zxuwIMp1saIQG26bJzLKgmgWPaLWN+7sJEZwNIbmXMxXOutCshxOUAbL//6LG8b4gShrdgbwN+RLM/mvg/wEeI3pJJCQkJCRcLlzBZCzYrEQ3Kc3C/J3dk6KaaPub3NPBL9d6/zEdSzc5pXRVutgxcYbYwYf1Hbrqaq65+Xba7eOsXPVDrB67nS88Bp8/C9eswtYyTFrQaeDNrzvAqQ8VbFZTbr5mxsECil1YqmBtDU5twZc/t01xssXKwTadlVtpdfocuvG7WLnm23nszJR2p+RgO2MPeGiv4cP/+SFue/kh6ukWD3zu3cCMj7/vE3y8/3nK1ddz6GAfsiWKYp1W5zC9tRPc+S1/jqwDF8/v8fFPPcGv/6vfgvVbeNvb38DdbztB/7o+/QwOZNCpMvLzGbvnoFyFQ8vLfNO3v4mHP3+UE1e12dq+SL7yOEeOl1RcTbW1TjUZwegUpp4dkpCQkJCQkJDw3CD7ALFwYnSU+GbZfa/5ns8UJRZIRKmkfP5vqVcXCV0tzEthp4V9sVdK4S5WaxyOk2Ex3L5MiOSyGLwy+NDWprQbjokRW6p7IGuaEpqhZWdiBiwFN66vwu421Nv2+77ZqtgwxedvEH0se+admWku3EA+M7I2nwU/3lDvemYE1uiiMYZFy7wuZ3mYhucwLeB8AcMRtNvQbcM0t+bwTaxkWk0wSd1qzAphJYMqj9nrhaaxGP4iiw4NIgXFYUm0DNESQL61EIPdfJNo6PTCPkOMANRjiI4j7cYiKesToElHouGm7hsRhyTu9ylxinwAmg5UJWSVVbvVwFIGBwsbQZcSFx8ArgFOA/cR7XpzYKUdHAmqoJNQHVQPqZfVNj1ikjX5vuqSkTVEl3nLA2lYWGgPQT7EkuvKsUQiTx3DK5UfgS+cJqp15y6T3F4doGrF8xG5nGMMdieDshsv1/1jVaYUn03N87VVQxYapoZ979c8nHRWBGV5ZeXmeSBjQ6c34bm0ya28fSI2s32bnqu8njX9AkzG/qDMWlgysBKavpHORQHNt0LzGWhCdGaj/zkzjIJ/lCfT9AkJCQkJXy+ucDL2EcxcyId++Tv7DLuzq5mWiJ48w4VtF6Glaako/MwK5mN3KuJy9x4WGLSK3UjPAJDlJW986/fzt3/un3LsCNyUwbs/BO/+CHzH3fBD18Nje/DYEMpexivecpR//ct9ts6v84o7bmdYNex9taKzlHHNyZzf+zh84qMPsPP4QQa3HOD4HT/N4RO3snzsRk6PDvPDv7jL//4za7zlqoxOAxtPNFTbFzj3+Ijp7ja2tL8BZDD4ArPBl3ni8RPAmJ2NHXa2epw6fYE7v/2tPPzgDg997l6++rHfpW5+g+bCOp/+xEV+7t/ezY/8XbgLi2j6wAw+9YjNj88PoM4ajt0AF87dwPs/9DEe+epplo6/jv/5X34L//ZXd/jUR3e4+Ng5mq+0ofn10FZ+FpqQkJCQkJCQ8GwhAtORHvuRTRVGTIiwFZOmOaPPPSD2R/M/ySlbYVtBMsldbH4l00vZC3hbhGXi4r4I3aBa3Zd8ihFTvQbuuwKmp5lny0T4al7bC/VroJbtwiHgsO2y9RjRG1NaSp+dSmzXJPy9AsVh88rMg9ChKaDbCaRwsKCoWjCoYDKD7Q3g/tDWXTt21jVJZqY094EcrjtQBR/OjXBoNc8+whejmSkcxy3YDmQslalvycyOoSyiFmNIJAZbrlmVyMk3n4jT0cJ+6v4D2PR+iilHFbku1WiLee7MWyUI/rPn/pXqQl3QDl12tWuHwNFlufHXKz24OrP8a6vWwhwLVVyMz1sj5jbbDL1CBu0Clo7AhRo2p2ZRXO+FArQuUIadxPP3ifmTRbZCXKvoYo9ngf/fL0N2DFoHkZNIRSS/RejKXkIkeYZdWl4xK7G5LnURqhKdak1EfSLLZW+RIBG9uND9+hVQFaaSKXIoJkbGNhmM9mznojBv5U4neNBOg3fczJLrTeULK1l1wdygy4P3RK3rPHcV9r7UaoBlU6HnLRvj3QJmy8G/YgrFGsz+nv1dj2G6HYj0bWg+AfwTzD8jISEhIeH5QNY0lzvc6xlUIstexErcgN1Fv8ylydVDRKXq1URH+g3MO2xwiX2eDlqaXfxOSljNKhTTUwBf4Y3/7b/hR3/gu/iJ7zlqc70MPrYLH96A5iwst+C1V0M3g3/+Qfj73wP3f/gDnHn0ccb5Or/5wTFZ0/Dmb76WH/3hV3JhD8bdimmVUc0y8u6MG7OcVlAs1EC7BdtZZnOUScNf/vkZn/2d97D5wL+n2fh/Q/2uw2Y3DfAZ4CrgBsr+bRy87W7e8u13c//DF8l7Dd/2/dfy2XtmfOqPH+LOb+ryt//BzZwewF9Yg8OlCRPqGs408J++AH/wiYZ7P1jxhlcVDPZq8l7Dja/N+F+/Oaeu4X2PNPzsHzV86O/P4NwHYfoR4APAB/naZHlCQkJCQkJCwvMJnxNAzI63qZI5qFSsih+fEKWLXiI5I5p+djE2T1FXYo+mRNZIr8OhfBmLrrpjzDCPSLGKUr+JgfLSQZHGIStS0TICqWqgswRlYL+qMYy2QoIvkUdizHp2vM5JI53ITfU63gsJjDbZt1YoDsNySAq2M4L6DOTHoH8UDhwzb1uRZSVmfbA1hvHUVIWURm5B8Lt1IgiF8uuVY/0wg/35oppkCVMnSsU5IxJ7wV1hP5mURNLizcWByQmtIJKAslDwak0RrkvMWwqLKNSQEtftbYUV7q/mFkfdDfW6msigasgdh8MHYbVr1fqLwC0ZXIvN6I8w79DgIbnD+4BPYZKWC5jAd6ex960GtrYCT9qy19YW7I0CSTtkXtci8lLBgRJwdjDG14vL9Qi2hT2G+X4ZExO+Ve43kb1t1/4iY7WWoUtOXr5j91p2/deEemsf7+jh10eknJ5gY12ewk1tr1m4fuuxvapwDeZYgfWAuHAjexRVJixC7Kv190IPbBEjPhch5njPnaQWWQ5iA6NFNKhQp4T6MMSy5j2AJflKopeEhISEZ4OmaS7paH+FK2MhTi2eiriTmkBZA3QTk8+rJp3PhviTB5ngTZEI5R6E/DC0r4LRhGKrw6n74A9W4LbXw9VtuLUHR0toViya5UDX5gB/9fVwpoDDd95BtXID7//ojDd9W5dTD2yztrRMv4RqBb58vmC9AzesQl629qfpuxXcP4T/n733jpbkOK88f+nKVz3vut9rb9AGaHQTHiBAM/SERFLcETWipOEutZQo6hytzOrsao5GI41G0s6MVpwZGY50KK0MRSeSEh1IEE0QhiBMo9FAd6O9f6+fd+Ur3f4R8XVGPYAUSJBarCbvOdmvuiozMjIisiryxv3u98Q3YKUBm4fgx2+3+NX3ePyX5Vu5MDJK0X8dEW2y2SxTZ49y8fjTUH437/vZH+NVO0fIOiX++mtDhO0SExuzbN0K77sry2P7sizVN9KwLQ4/DRu2wt+fhlZbLSBv3QsHLBhdr7K5lvM2b7sFhnHIOhD0QdZVc+TbJix+7y1wdovDhz+9n7PP9tO5uJnI30Jn8UHicAq9dp8iRYoUKVKkSPEdIEyKkKnm3G6twaXI5tbaVpVJbAREMSsskMS3i/logYSxkyQ6ErNuZrAqoQjZCgkJI6pWKc/R5fWC1wvZfnALKuFWJ1Th+0QqHr1cgmZH+bFGIWQdtY8k1gq0/2umpDK8kwUnD76+TstWq/WFHu2H6SslK2USVlBfY7EC+T4lncz1qbBv21LHrdTVsdY6ZQlg56GQgYyr1IP1COL1SgVrZXVotQWulXSJBfRlIPZ0GLelLAakCyJNqHpWwjWbmzRbaCVT8Vg3twiabdSjwDIJgdhLwn8LkSrdLNYIYkcgRKh4lgqHJvtLGZLLV8hYkxsXMlYyZ8kQzBlDQNwg+nR98iSh/YZq13GVHWpgqbeP6uI8FBFrinPXwhTqyhORjMS6BSsdWGpAfUlF07ey4OT0MJI+E1Uxug1MQruK4gvrur3FU1faaIkkOZkp/o6M8my6LRAgidifNy7EcMu49hq9XzPSdqraFmNazhNDJ1Lh+6422G3Kc2KoPGGtSFXEy6jFieYKhCtaYa5PFut7JF6BuKovsKhsQ64x/tJYHdSAagHrUYMzpxupQ5KRbI5EeizfPTWSRZ8ARdaa8m5HHycCIPlO6xjnFeZZVhuKpHk6UqRIkeL7g5SMvbbk+u1gLtnW6I6nEW8u+dGSZA7fDTzUdKYfnAEoDUPLwcqMUOzbwPDENs6dqRJQZnYRjp6Hyg6w+pVAoJCDZhaaPlQc6HFg7xhcAJr5PqL+Mhs2ttm0rcD6SpFKxWZqCZZ8mJmHpqciZ8ZH9fpqB2ZbMLUMR05oa68mPJaLmLo8Sak4xOjGCplgnFZrlU5nhbjQwO5tUFl3gOvv+Bfs3FLGjeGOAAZi8HoyDI+phLyNq7BhXZHFeZ9DX19l6WLAxZkO1ZZNYLtsPl5namiMzrDLcJ/FDQcs9m+CEVdNL6ZQjkVtoJSH2ydg1wQ84/cTW21OXF6F3B6wjqFWcYWM7SXJLJrTfZkiRYoUKVKk+B8PJbq9Ws2YZJOMNTMGmfkFIKGmTJ/GHtSczpRI5o33RKGmE+dcMx4V1k3UpCYZmyEhY9cGj4u9gZC7g2ANA2VlDHrNp1aXGzsQlSBuKMKTUL137Ro1g5UtglNSJGjsge2Ao8kkywYvp1g9NPlke+CKx672fMVWRGx5AMpDKkt8FGoCLIZMDGFDEb2ZHGSKmpC0tBcnEPV0h4ibHLR0ScFJuG9JySDknfDcOaOrRG0qZGjeeE82SbIl5xZVah7FQ4n6VD4XHku6XIhS6aIOCUkoKSnWDr+1Og2TdHVfZJ+Y7nYwr0/8aSERT8t+fdB2lU2vk4EZF4YsFdf2UmP9iqgRWdT/90nsWTuRira/ZoHcgkxWc44raBktyTpEXhekc75RBqupBdOifo27y7vGV8pfaUNhh4WMF1GnPMZVpV000RnqQq7xl5ZauOg4SvUdZxOFrVykBfgNcAPViB1RrQp5GgEFZcmBVoCzQvf3SZskylII07yurMiFISFNW3orkJgFLxn7S1nyPSNkrOwjA65ufC4WKuYAFKl1ZJxXOkAG7gHgCIotT5EiRYoULwcpGcsCL74GLDMeM9OtZAGQWZHM8Fr6syW+M7ErsyV57WJ7vdh2P7ZzHVZpN2w5QDQ1g10ZZd11m7nj9bu4/Nkczd71LOMy04QLUzCfh5zOKDsVw8wqvCYP+7Vwdx3w4DKEGZd3vcUlDGH/tjIX5uCRU3B1FQpZON+G5xy4dxDGbZipwvIC5OahvACj60OCasx/+mjMg594lDveche9Iz3UmxYrVZ8L5+fphMP0XvcWdu/aR3kwz/MzSljxzvfCXlcJE67U4Cvn4BN/Bbfvsams1vjC353na7VVWu0lYiuLFRX4xpXLfPKed/CaH65w7xss3rVLe+iTRDYdAq4EMBHD2yxFQr/99bBypsWRv13BHigSO73KP+zaxHYzMIvjdCiVJlhpnlVZgK+lfk2RIkWKFClS/POHhaKefGPTLFCXyahJvkp8uMjt2ihmxzX2FZPOEt3x4mJDZRK6In2ERM4Hib+reD4KiyTlrJ22m9JAXbcwgppIOIWR1HMdH6XUi435bVsUb3qua1lQHtYcbqhklGGgyUlNlGYyEOr5rmtBPqfIq4wmi32dEyGfV+85jlLWVltaZGyrei6uKtIqbyviq6GtBQqWip4WtacbJ1VsW8l0WjxFM3FCvmVRNgqhrm8ZyFvdYkFxbigbzWMmzhIrYIFEhnf08S26lbGQJPLySXxPxa1CyFEzSVXb2FdcyUTk7JBw9iJVFQ5Pul3KCo33ApT6U9YTelCOFW1d5yUI88oyoFNWXHdQTiLyX+qMeBQldVjRTSmXkXEgU4BmDuK6PmddC6enUSJMsVuWMP6CLmBQFWz1KN7enwOe1/sL8SrXJX6wcyS3XllXRvpZ8uDNkDDFctv5AfhNaFchXqBb8e6qhosq0Mkm5K6F+ifnQLUG4QIEVbqT7Ek5BWgL2y8yZfFyFmJViFhRytdIZMHyHSCGwzLI5Phgzb6Sd0QUrrJ/w6iXeG7IIg26rCwJ013V74v/tIiOzO1HUYNs1bjeFClSfP+xdoUuxT9HpGTsNc+tCt0h7aJGMONgWiSmU6YplCRjyPHtydgMaoI+gqJK+8lU1rPlzW9k/aZ9bNvTy8h4jtiBM8/C1amI5WrIo4cD9ux5O27UYWDC5VV3wKnjMDEAK4swtQiLU7BhPTxchG/lwM1CLoCiB5U8HIrgmadh4xjUGzDdhNEJoK0fL2x4+Agc2AiXTsGlSxAUYGwLPPWtY1Tnm2zo34zFZY4/+zX6Rwbp6+2jdnWZH3vXXdx0R4W9B6C3bLHJ1lOKGJ6P4b45VZ9mA+rzSrk7Pg6duW8x/8z/ARxHvmjk6+bte7ZzXe4G7EslPp+F3BbY76gsrrtQGtc/PgTfXIQvlOFn7oQ/+yIcn9vAxrevo8dr8fzxzbQv/DHMXtKlLgCbuOuuu/nSfb/J8M+dp/6VD8Dk17+3YZMiRYoUKVKk+C7xYr75/19AiAthbEQRJlYFoJgsMx27SbgISSFzxTKKTZIQYvFclcw+HolMU8hXYdFMEqeFijM3mUAJCe6QhCebTJw2tbSKYGtzSwetTo2hUFLFOK6SQuayUFuBdhuCjj61cW2xDUELPFdlgA8CqLUUGZbJQK6gVIHLNV2mrTwv3bKyCFAnU96trRCqS+AvqHoVeyCjlbC5XhXi1G6qutSuQm4IcnbCYweoIKdaAI02lIrd3q8BSqDnB+CHyu+KFnQ6KqTczUKtpHhpifxGd58oMaH7aUh4cOkmk6GUPGoxie+s7C+erxaJ6tPMyzZo1NsnISYloVWvPkePHgJZ3bWSFEpIY7EtkIhyIYSFoJQhVyBZGxAeMAKGID8IvUVY58I2YDfq7zAvDRv0thf1RPOwvpyqDStZOLkBVqKE+3SB6lmI+1AcpOQ2FuK0g0rDcVZZqvo2ivGNdbvIuoRwmkKOimIV/VoP9Wskdkm3QYtEjdsCOhm1tXtgeVwtOgQNndgO8LLKZsAcF1mScVleD7VBqAuFrQdJFKikV0yjnjtEZl0i8cToMyoiFRdhj6jLJQqzh8Rm4DzJ4BNvB7lIGRyyqiANO4q6gcQfI6ePLZAs7oiCVthzjLIhUfTLKsE8sEmXeY4UKVL8oJASsf8jICVjgWRC65FMrteqZS2S2B+Z9WRQP0amMbpAZlevh817oVgmk8ly282vYXAiA7aLm8mw88ZexrYUwHFpNG2mrsC2GyE3bHH1csTMhQ437ChT7nNorYZ8/GOrPP3EKT51YA+l8TxnyvDwPKwrQ6sGzWnlvzrThuUV5Rtf6oOb9sGGfpjLwMlleOQoLF1BRef4PkuzU/zXI79HffkcPZUK77j353jmiSc4eexZlhYmOe2uEq3Msdrcj13fT2HXrWzYu5evfupLfPVzAYXhEo6T4U2vfx17bigwukFNyo6fgWYAw33w1gOwPAWrKzB9dRVlBC8z4wxYPWRzN7Cp3I+7GDI5X2f6dJHGeli8Ecr9cG4Snj0JJy6qOVAhB7/yAFQb4DdsRoY9/v0HXXLNA3ziq7/FJ7/wo8w8+B+B52B4P4fnHF73mn9D8/wxWD72AxhLKVKkSJEiRYpuCGMlYfM/aELWIAUpkhAJ0K10lUxHNoq0gMQWQOZ8Pt0GoDJvGSTxVBRTUYmgMg1JpT4FEg9YIWyF6ZOHrhZKHGAu+veQtJewcHUSQ019rjjWYdeintPhx00ds21ZymKgZkFUU2RlLGaZIlVEnbu6oL0vY8WOhZFqAz8HYQGa/RBqRZ2FUrW22qpulgt2RvnFxjFYjsrihN4nRqlr26EiYRt1aLVUpFK2riZ0DRtqWUXyLqxAq6NCyDsOlCrQsWA5UKqEuAPxHCrju455j2Ntr9ADziawMlrhq7uvVVdtFaGuazQDJUs1r3SBKWA2hMPXhoLpaJElga2PNzNgiWerCA6l64V3lyRfIkYU/n6QhHgU3k/2F2WuDAGJRJehlVFNIXWxHOXfOrAOejzodWDMgutRxGofL+2h0LRWjenOO2ZZqurrgYKd8L8R4E5AZxQ6NehcIhnSIjavG69l/WMtYSuJvKStBklu0TaJolhuU7F0FuG7iyJl5y11u4f6/dCBsAjBRr1IYSePg9IoYn0AykqjqP2NQ5QS20YdEPTBsjwriiTZUy1V6IHeAVWp2RIETVUJO2NkN5NoS8n4Jgy/WKuIlFpIWi0/Rvxm5btEvltcEgWumBubxrpm9rjAKN+0WpGGlMF3QL9OydgUKVKkeDlIyVggcXaXmYypVojX7Ccrj7JiKLMAMyNtEejFciYY2fMOxm7aiVsqAA6btu+hMqYmfF4GhtZrpWgES1VY9uG2XjjTb+HlbWbnPOaWOrTCmPqyz+xcm3UTFTqeTa0DzVXoLMRc8WOs0MKNLEoZ6B2BiZKaQ8dFuK4XhnNqktQag9EQqgV46rHzPP7oSdqdBaaeO0ncvsjGsT7c1hTnjt5PbW4V2/fJFDoMVfoZ3biLsW272HD9BCObBpl8DqbnasQNn/7+cU5fDCEfsRrYDIyAE4EVqunE+jJ0bDj9+GnOHD5D4uDvgTWEm93Oxp2vY/N1vVhuhoVlWFyNOfXYAufPrBIXAmZaJXpHRnGxGe+FPRshXoTJKszNW0RNi6srsL5cIdNXoTyQZ4adwDPQucjqbMDjx6vASVK/oxQpUqRIkeKfCvIw/0+p9pDYbXNuF6MCrG0UiSEe8pIXwCNhhoROEhmimbDLzD4e62PMhKySlUn2z+nXWRKz0rXekAEqjVI/ih6DhAUScqdNd54CBzWfCo2/Ihe0deIg1yhD4t49xdDFMteVRwJH2RJ0mZE6OomWrksUKTL3mrWBp8hUL6e3olLByn5xrMhUS7+OAk2OhsqPNqfbxtVl+x2YW1H7NVqqDNtVRG+nrt7vNKA5T7fMNAeMgVtUse4UIbQTAhTdRLGj6hKhkjSpabvit+okibFMX1fTwkBE1JLLt0iSyF7ed9dsMnSk3J41XSui6SIJz1YmsTAQztwkYx09HMy1DSFp5TMdwBe7ip/u+NByoWUlWkw5pcc/Drl7xb7VN/6ajsdZK+FGgxh8iZ6P9XWZQ18IUxGAS3Q9RvuLzYCsR8itZDqHQHIbiVUyJAnQRFgu40H8ZBsWtB2IctBwoRGpcQNJci/hKCVoMmOrsSNif/mK8T3wRyDSCe2sSC1WWDkolZQa3AWCUaU6J1b3QrsDdgcsrcZvR6rhYs2ku0PqocpBqdGDLISuWoyImhDr74U4VPdiLA1gKnFNXw2RD8uqgbDeGO95xr7SWeK3YaEylEgKuBQpUqRI8d0iJWOBJAZI4nhkYio/SvJLLL+04Zp9ZHVRrWJmSluxvS3Y3g1sfs09CMs3AAAgAElEQVQPcedrKpTKLu0W+C31W29nlE2WH6nfzFwWevpguAD35GF4HKKcy7FzDoePrJCL22TtiJ6Czb33bmeuYFFfgskrUJ2ES8cjhgdt1o9a9A7CDQdgwlVzhpVYLR5Hep57Y0/Mbs+HiQZXHz3E2ce+SKavRWRFeO4AGacPN15lavIYrj1OX2UDg/0VfKufA3e8ne37rmPL7l4G19kc/uYGotMuURRw++07cTM2K9UI+4pNqQTlvBZFOBD7MWcuzvDYlx5g4fQTRvt7YI/hFfez4+Y3MbGvl9DNwQIsnI6ZemqeSw9cYrlaJ+7r430/a4PrsXEoxw/dUmA8D187Z/HsKTh/Br74OGwbh8UGDJYznHW3EAcOLD8DnECF7dSN/k2RIkWKFClS/OBgevD/U50PXhi19EqAkCAFkpRJMr+0UbrCjSQEiPhOZkhUcCaxHJEYkAprJAyf/F8knBnUXDfW5KoNsWRq10kHrpmXmsc4YBUUISqkaChzY03Guh4Ui1DoVYm78r2K+et0tG1AG7JZsE0yyFIJEBxHq1AdsH3l6b9wWU1c7ayyV3BtRYD5bWg3wNfZoGxNHMWaZHaKkB+BTB/EFWVkWrC6PV6dXCLWltxogyiS0HSBkARQVRI7TnlyCvVxQ7qMy0bXZIxNeHexK5D8TEL+CnEqZYuXrXSjdIOZaEwISfQQkqRWsTEMLJLgPdRxoQ9LOei4EHqJk3GBxNn0pUI02PIEJUYXprDVihM6v91RbhJRh8RHV25TEZHLLSA5k6FbLWsObxF1yhCVizETpknQo1xgTle6oNtZbpsFVB9HFtQ99VqsIYSIl3NIEjdZaxHxu6yTtC1wRxMiWOoh9hpSzmg5yYslt7VcWxzDSgNaTX1sHvIFyGjpsbjiNVEPkn4IQVupX0Jf+TkHklhM2GLJvIFqyFgiA6A7aaE834qUGxLSVp51RcA0TUrGpkiRIsX3jpSM7YIYVMkMTCBxPssYUwy6Q9DE2Ohd3PRTH2Bwx25qSxEBDoUe2LBJRVYdPwHFfiUC8BwVDfPUZRgdhv4eGM6rn8H9wNAWyH4Afv59PYRXzlDMWrB5kC1bYUcZanlw2zCds2jh0LcB+jeA1wN7LTiFcvbxgMMdmF9WfrOPHQx4+FNH4MLnyHqrFHo9arPfAC7Rpp/5FZtnj03Sm72ByM1R6yxz8fmDDO/613zywQcZOzPLbZfv4h1vGCSfK+BlHNxMm9/69xuZasKVi3DlAjx9BOZrcOo89PZDlG/zld98K377FN0PRw2IAiyrQm7bAc4sgFeCoBc2vt7irRt2cuLJnZx4YobnDn6NP33/bwPrKY3cw/03/gS3/YjD7t3w6lvgnfeqEu/KwOUGfP1mj+PfXE/1rKPEH7SAi8A+lP/Syvdr8KRIkSJFihQpUnwHCKsmMkjxchTvx16UH+MoiYloie4kX0KcuMb/hTkSCCOoGSi7RxGmwnSFLYh9ncRUCBozeZmr/GfjjCZt0CpXbUuQcVFEjFbdRhJ3H2hbAylHM4dWrBSB2axK+CV+nxaKqA20Jy0BtBYhmEOZiPYpgiy2IXL01DsLxQJYQ1BrQ2+PIqACXZehQRUvLzy1SXpCwj+JQ0UvScCbkHclvYny8jm6STlpLs1rE9DtHuGS+JuK5HSKRLAs+dhEKSoJp6SOPl3BY7h0T1flEUS6TwhXSWAmtqAyNIQ41Dx6r61G2DhwC8oztmwU/Z0g2nbhsDegeOjnUJH/Isa9qv9GsepyAsXHhyImXyQhjkV4Dt1BiHJNpmeu2BUIhMD06Pbqlcj+fl3RCqrNa6g+HychyFdQj3ja2vgaYS6ksCiSPX1sjm4CXfpN1kWknqarQGC8H5DYJoAaNyXjMyxwdSfKokHOUn1YRoldS8AssGDBkguBmzzGtkgSpUmnmbe3yJml/aKWJm/lTZH6mtD2e454UmchWCVFihQpUnzv+P8ZGTsAjAHbwK5CPKNi1FklWUJ9MTjAGBOvuoPq9BTLVy9CKQOFChQmIMjApXMksSt11LKob5Rho375luj+NZXwNcDqwK495IYqRLHP5ckaDi6PPJhjZrvHnn02N+6H85dhdhqWl2B+GhZc6NkAI5tgx2Y4BuwE1lnwDs/iz38Gnv+jQeqHj3Hu0Of4pQd8MhO7uPVte3j127Zzz4/A+eMWgyMqMuy58xG/8z99jlrzOfbuH+VD/9sHqGTg8594hie+dYSLJ45y244befbK82zfNMaObRv51OeuIGEpmUyGjeMbec9PbufrjzzB2XM+PaWbWTjzNBEVGnGb2W2befTJQZ647xgzV86Qr7j81octcmOwOKeECzfcBu/cAWfm4cjJgA//YZ0gOEuiBEnwIz91K+//tQ8x128xc0KR1H4Hpmsw71uUboZbbhxk71t/iCvP38PslMvSTMT5s+e5+t8n+eLycRx3BK/nAMUNm/iPH7Z47hx86fMz1M7/O+LQHB8xKkWr/4J6pEiRIkWKFClSvHQIWyLMkukXK+ndHdQcUgLCRaZpqoVFtrmOhAkUolRYJkkeBomsUNgfM3JLVLFtwIOoYZQPSSIgYb7WPg64ijnDJ7FHEPbRArcHMjsgiJSKL+MoCwMnq3xo/QAW6ioMzHEhm9Heqpbyi42BXAyFAth5RdbaqOlhNADRRgivg7ZWvVou2B40fc0mejCgSd7ATiSYoPw8TUpRcigJn+2TEGQ5EjJWms6RepCQmeNGkwtHJeSckLMFuv1iJ3TZIjd1UY8QksdN/Gglp5LkkBMFrtgGr7mca48fLRIiWKLH13qs5vS168RhVg+MDqqmEwfjyyi+El31fwwxyhTiPIq7bKOemBaAS8BcDDM++DU97FpaSB1BLMpguU3k+ky1sbRtji4hJ44+kVg6DJAMabExKJDYrkrStmV93LSxv6k6lv4yFwjEisK0YJV6oNtUxotYRksfyG0nVgsWiSJWyPw53WAiepdjTFK9biW3vLgC9JD0/2V9jCTNk68TGcuQELByzWIJKyrdaw4uWXV/UYRQCWSIY2UhIuVYupCcpxS4HRcCk+FNkSJFihTfLV7xZGwmW2L3Te/k1bdtoeb3MrdSYWVliLm4hRtVKToN+ksNHnz4EO2Zh4ha01iOR9/eN/H62/eyYahEX1bNjvomNtOqrtBcWYSsC5kczy/2cvx0lWe/fJC+gR5Wmy069VVYnYXwEkpbCsmvrvwiiuIA9douQW6C7QduodzbC45DJpsjn7VpNR2mptScdHEVLl5SybXqNWg2wS9D21W+sZkIBjbDqK1+6/tteMtumNtaoH7WonNmiasrWViYw3KmICrzC780ytMrKkql01zg4Ce+xonjf0voXyFqbuBTuRF8a4pLl2LWeTZ3vXEvd7x+D0/va1BdbbC8rDy3bGsLg/2b2L59H9tvuIkoV+DKSkDHKdOp1WiHPi27SHl0E7HXy2QTyrv30h5YTzbnsO9GGO+Bc+thNYLXb4HyAEyfh+MnznLuG39CHMkDQFcvU/UrXFwa5PhJGNCJCzouRK6aZzdisB2XYKhCOVth051Q9ttkFleZDS3OPukyXi6zZ1uF4wF8/I8e5ty5Y5w/fZze0hCt5Vkq5CkXRsiuu4HjZ84Rxb2omfHTP9hBnCJFihQpUqT4ZwKXxDbAZNTW5hmwSTIxiT1Aju7kXNCd3clM2iNyRvGIFdmjGYcuFlrCEppx1YanK9BtgBoYx9trNhesslKjdu2bAa8M2V7I90OuXxcfgheoalqa9bO1ejdjg2criwEhzK4JezUxa/LXFdTEL/YgyiRBVJaum+8pWwLbVkmXIAndl83MwStdYNpcSlOLF6soGE0xoHDWomYU1aqQdmYIujSTkKhyDiGApRxRy4bG+2ZSL5PXkihxs0tNoi4g4clNm08hmGXIebpN8yrSvdQDBU9Fu8sItEgciF8qLJQMZhrFc8oIbcVQi1VutkjbsF0buqLilXoLcSyb9Idcf8u4JrlFzOsUwhSSIW8S5dJWpl20CNJlHyEmZX1DjpE6RMAIydiRvjUtDOQWMceQfC63nktym8YkRKjhAtKVcCwisbCWc4YkpK5p6SrjSiD1Ka1pAxm3az2IQd3roQU1G1oRBLryjtkhaHJWS4GtEsrbI0WKFClSfK94RZCxrpfDth067Rf6ehWKZd7yjv+F9/2rW1ho5jk/DdPTcD6AZgsyccxY3udK+36iSwFW/RS2l2P9G3+Mn3rvm9izcYD+bMTiUpuBSpZcxsZzII5jrs5W+Yen6tQaFzhWOsUNr30tlxZ8FiZXqV+YoVM/BP5x5UsViiohD9lh3MJ6eitjesKUJbT6aTk3sHn79WQzHm0fyhWXShnaVVhZjqge8zl91mJ52aHdtvD9iJA2+SBDM7Bp1SyoQqUXRnVYU8GF24fhi5uyTA5l8ckAvdCAC09P4tfrvOftmzn+TIznRjTmL/LEx/8S+CoQMH3lKp/7W4fFzhU2T2zgdbffxo++/V9w573beNX16/nyVx7js39/DADHGmNwYDubNu1ldNt12KUM687PM1+3qC8uMr5pnFPzAXZ5gnzPMPkhGLt7P86Cip5582tgM3A0hNkI7vDgDHDy6CJPP/wUtRN/8CK9r+KIrkw6PPSNGmcuZnj1az3sfoump0QRQaSUspalcjKEOVi3E3b2ZdliD3FqeYhscRs3b4a33x7xkftX+eMPfonFqwfxvCuMjtyJtTJJL32Mlfex7safYC5+nKK3jlb9HFOXr0A8+4MY2ilSpEiRIkWKVwyExTBJBmFJBJbx1/xcWJEcSqJWJLEYKJCwG2Y8dYkkJl3YMdcoG7oZIdlPYp8dFCtjkqxilmkSqSZb5Brn8pTy1NbyuzjU9gSeUghYHtixUrXGkqgrB96gSg4U+RDrmG0rA/kKFHshU4bCoCaOfLCaEIWqXCcDmYwiUwtWQv5IkwjfbBKm0iVCvEW2InZdEgIrAnznmsrzGsFqKh1Nq1wzrFwUirKvSa6aybkEWRI+W0ivbNKk11SpZpIvIcrEDULsEMyw+qxxzfIEJkPCtNI1LY/NHMGW8dockhjdLsJrzf9nesEuQCYHA2XFLY7QbZWbMbrjpUCsU7MovrxAovvOxZpT95TgMgz1skCkXC/QbhNxrAlbuQ7dHpatrYnrYIfK9SKKdP63Qd3k4o0r/WBaG5j2ASZBGpN4+Mo4kdtJCFFTjL52TJoKZQmSlDEAyW0v/r3mAgEkSllxtcM4XsZhZPx/lYQwFpuDyDiPmVtrrUA1IiFoJbsa+q+Z4E3ay0I1sI8yE7Zs1fDi7xzpi7UsCCz1nRHlUaPHHLApUqRIkeK7wSuCjB2e2EOh2M+Z5+5/wWf9vXl++5fuBiy2AbduST7767MxDz/vc/jJGr/2y2/l7p1vY7TS/YNwqRnzwBWfj3z0BB96925u3Jhhfa/68f+9//IgX/rsQ5x5/gJeNsdv/P6vcfRilqcORzzyiM+pq3fChSfh6kmYPYNaA87hbHsbQ3fcy0++4zqCQE1ylqoRjz8S4ndcZibBcqBUVD6wDQvmZptcvbCC67oUB/qxcYnaHc6cPkFpcBOZUpFMyWOmAgsNOL7bYmwcNg6oSKfcIOR78/gMAS70j0PrYSaf/BLvumGWxP2903X9fjzFYuezWLyZ85cf4MRQjYtXbmVvbRMT2wdp/EOVbz1+RO0cdYjiOq1wlaurdTZt8Vj2G8yuNMl7WT70i+/il379PpZrAeNb87z/xy3+w9OwMgcjtiJi3Rg227DeBuKYbUB88FMsf+nT36b3PWA91fMtZg4+wdDIVq5OrqNZc1nJWCzplfTNo7B1A+y4Dv70b+DjZxVRvaUYEzwP81fVgq21uclvv++rsPoZoIzv38TlK1cpcz3nvUGa/a/iwB1v470/9zbeuReef+gkP/0TFaj/W17oj5QiRYoUKVKk+OcBSaleQbEhFok5p3glmuxJTn/WRDEgwnaZbKCpcpW/wqYIPSVp3PtJMgiJPA6S2GUxGV1bjx5eKI00IUpZYViEJsuDVYHKesiVFNkaRNCuQVCDQo8iV7MFyPUpUjVCkaB9g9CxdPKtdnJ5nq0SHuAoj8pOoHOk1VQTFgtq68koyaSwdnndHGZWeyGQhIOGJLxclKbi1ynJiob1ljXKapOQoKbXqEvCEprkZZ/RdKLANMlhgZCxHeP/ouoVwk1Un1IXIbrkPeHIZWhIYi7zHEIMSp1NKwTh5IVwE9sE83Mh09B/i93blvXguUmusncDt6Lm7AN897BQd9BdKL/ZKipifgQ4acFJB1p5cPPQ7FGft1BR+cIJZmJo+WrYtH31zOTqNvIyKldVCajEqplXI1ipqn3abWi3IKjrgk3V7Vq3jibdJGjAC/taXMxEiC5jU8hXUZiK9YMcI2Rsj35PyGGfxAUkYxxvitVljIrBrvwVr+KCcV3yWCvEqRD0ch4p2zXKNXP6me3RojsZmXztyTiqo1SxYUdtkRggS1Y7MSJuoHr2pRhbpEiRIkWKb4dXBBlbKsI7f/J/Z/Lkv4RaFbLwxne+idWgj+lVl0O+xfUe/OHj8GePw9J54CloTn6DTvMYbl+ND773F7EzHo89t8xffuocDz1zntXVBp1OiGW5TKwb5Xd+9376vEXKmRqUy3z5r/8fasuTZDybseFd3GDFnMxBPRcQ2E1uum4PtfEJarUq1dVlVhcn6Rsa5Y7XreNVtw8R+FDJwKHD8NyhKheePMqem28jV3HI56DYoyYOrgulUp6xdTkK/bB1nU2uDG0ry/DFvTz5qSPUWj5WpoDVtxEr38OgDqtqZyAow7oSjL1/B5t/cxMPf9niyEPzNKcq9Lp38ePvvYlP/Pn9LJ0+TLj4DPCAbtkBVQgLxBwCqhw7dYL/+md/ynKwQK5nPU8/e5SA0wDceOP1DI6OMzQywI4NPTx63wlyUYbb77yJ7bt38+ihgKVTH+HC6WU+dug9zA59kNtutnjD9erneTqG+1fg0iSU2vCLN8LeD17l/DefBA4nHd67D+IBqMYQrYDdx2qryaW5E/T7Phfml2gW1+OuG2Lf2yC7Dd7bB7fnVVu+41/C/TE8chQe/ZRP68F/4D0//FpWjk7y0f9+EFYe4+d/9s/Zf8dGCn02n/7YKay2x7t/bB13vHqISgFmPPj9z8DBb1Vwb95B8A3Shd0UKVKkSJHiu4IpP/t+ooRivZZe5DOLJDOSmZlJPhOyVDL2SCYkk8HKGO8FL7KBYrOEORG2Q+SWZRQL4xqfleiWy4Uo0qIEXj8Mj0O9oUhOPMjpjK04io1ydPkB4HiQyStiU9o4CqDR0CyUpclVIAyg6KrkWJkcBCJJzECchVKfUrpFkdo331IJs3Ag1ol/6gHYWchkoaTZo4yuR9ZNyEZQnrBiKWC5EJcgKGryyVK+sJL4yhTqmmHe2p7yWtMJKZnTXevo5pWukyY1w7gxujmrP18gUTs6upuE1BU/WEm2Jd0vrhCiehWy1Cch34pr6ilOFVIXUfvGxtahOxReIIpLIYnFI0Ccz4SAhYQ4M20HTIWkDEnUX6sHCkXI5qGQg0Ebhp2kqTagMm+M0s1Jf6/wUN20BKzX75VJyFeh60QoaqaKCzzo7dUqV30NIRBZSZT+lSWVVypqQdzimjVz3EHxg2J5EKFutRW61apCqsYk/q9rgzCF2BRCdIDuXHjLxmsh75sk7h1SLzm+ZewvayMDev+6rqPsI/dDniSJ2JT+vGocu0k3ZGFNOaKwlvObHrcO3QruUJdhflW3dLvJmGxZyvfZyeg+ifXX4YC2X9DfT+EArOZgNk2CnCJFihQvB68IMjbrwr5bb2B4cDPxTJOb7/TYuG0ji1GOmRZMOHrBbwUyNbjtRth8K0we3sKZQ4s888Tf8H//zkFuvWUHmYIyReqENvVGQLvZJo4CpvwGN9+0izv3jbF7q0vN8/jSX36GMKrQ05tnz95tZG2bfUNwpdLmoeV5/KhOKV+mMjqIP1LhuWdqFMtjVHp66O11icKYxw62Of70HDMXl/EKBUbHIV+CkVHYfh3MXoUTz0G1GbC82uDy1DRLkxk2bOlnfGsvd97uUmlv4PyZgPklh6iQZ7BXrRjPLkGcV+0ztgGWVz3OXPaYmYdgxYcwR8v1eOKUQ30pQ9RZQeUvFaxNN2pRa85wcfpxrkzdgTtdY3F2EteB8cHb2b5lD1uu28P6zRu5OrPK7NV5Sp5HEAacfuoJtu/ajx1VCdvHqc5+ksf/dD9c2odXKhLFcHUDfP0I5HtgqAL/5mm48OB9tGZmwOrD8ga4+Z630Nd/PdXlgLMnTrK0fJFcoUKpVMGJ2tSWp3ByMa6VYcTN8DO7enB6YWcWKg4EAfzBx+CJExc5e26ambPTvKocUPLPMDpqMfq66xjNLLJ/xyjXbeinPOzRvtfj6cNL3P/AFF+57xlsLtPkGE+cipicbRCtzug4qRQpUqRIkSLFS4fIzCTbjRnyb5o4CtNmxtaa6k9I1KTCbNnAEAnjYmb8yRjbWkJY5G0Si14kMV0Uk07J4iSx7iI3tIzzmFLLODmflQenX5XrZjTRaSsy04mTuGo/hFJWhfVGDoQlRXRk9Tm8jK52pMJ/bc0Euja4HnhZdS5sCDoqKZadU8mwQlT9SkIAt8GxIVNUSteWq4hWywNPH2Nrm4JOGyztB+nY6ty+rchdz4WSnZCpgQ5LFq5ZSMWO0c1YSVi/JIuChBiSY8ykQjaKBMoaTd8mIW+z+nOTjDXta83Q9rU5dWV/Id4kpF032bXPpBzTGleGgG/sJ/UVQssc4vKeWZZJsOnmuXaLmMM4S+IfK3bA8pnUyVTbmrYJUn/Tu9bTphl5yOUg66lcZiIyFj58xWiOlwvhmvuAGRLhpkDuZLkUaWZbDxnXSu5c4ZaFc7dQaxG+B2FRCTXbQsSaxHRsnEBOZjqLyNgQMl6w1t5AtiIvhJkkrR8VnS//l/Ehylw5v6lAFXtpUXiLalfqJuNN1KygyFj5qquQqHqFeJZFC3E20cnSuupljlex9FhrrVAnsUJooRdbdMdUjQ6RDrrmfZuDaiW5R1OkSJEixXeNVwQZ69mwY/swfeUB/JmQLXs8Gq2QUjFkcJ3DMOp3pTcHO4bgrbfA9h1wsDDM3OwA0cE5vvjpL7O4ELF7/042bh/gVTeO0V4p4bdb+H6baq3JrQfWceetI+zcWuTiYhvHzeMVRugZGmbjzt1g20pcEHdori7RCFboGXKp9FbI95SZnewl62SorcDsTMDokMOJIzUmT1ylXW8wtGULI6MWYRjh2REZO6LZ9Jmf7TA3VWd1fpm51XkWrnp0AsgVs2zemWfr7mE6UQhTMWRccpYSCMtvc6kXsmVoTkYcfchn9plFgitTEKzSzgY8+/gq7bmj0D6FWlIFtzBO2G4Shw3dyipGJwjrVJuXmVteIVidpr6ySk9pmL277mH37uvZfeNu+keGOHt5jtXVKp6TwbEgF9fYOAa5bB43a5PrWca9UmX1XEhUUKb9tg9z52BgFMLFDl+8f4bs8mnIeFj5LZR7h7n9df+KofIGZqaXCa0S1pUcuXyWrJvHwaFeXaE/00vO69BbDtgzBs0GXDkPJxZDgtUWf/WJFSx/BStcZTC3AO0Vmv4AOzas487bxyh6EflsyNXLZ5icqdJpdlhYmubRr5/k/OmzKCfbx0ltCVKkSJEiRYqXA5ESCqvxYt6r8lokheb/10oGJeGVGcMuEsNrmZ/o9lX1SGZMooyVctayW/J5w3hf1K7i/5ox/i+yOTFhzANFsPrUfrb2V8RSxKaDXtyNwArB7VWSvqgFzVWusWaWBYGvyZtQmWQ6mi6zXLXhQGir8oJYSQadjCJrAxTRmq9AWIfGZUXWMgaVHuXXiquUra4Huayqn/hAOtpuwLFU+W0UCWOTtFNsJcSiqWqV12b4vhCFZhh2ne4wetPfNSIJzxYuXJSAIkgWokqITmHsZGjYxrlEXSocvgw9CU+XrhbizLwOU/Rs2l+KUtYcDhjXKOVL2ea1Ssi7eQu0jXN5a16bvrVSXki3hbCQYobfqSXXp6/JRvHpnqOITtOmV6qwgFKy9hvFfzd+sS8GcZqwSaL11/KA0ixSfWkuM+eVyTNbQCkHflYNfz+EqAFBG2V7nKOb/AxIHD1kXAjBaa4JQfdYNZNxycnX2kjLPmIDYa4hyb6yqCB9K18/kXGsCPojtCWA3pokVh1y3mWSBQ1pWHM8S4Ob40/Gr9mIZh1FBWt61WJ0jEtiaeCjsieHAfixNu3Vizc2ihW3X5jrJUWKFClSvHS8IshYC9g+AuMjDittm7/7ZszxMzXu2eXxnjuLWNrmauI6uHsC3rEZ5mI4fnmRx89XgSGc5qeozfTi1Pu4ccMW3vnm29nSA3kXOiE8PQ2bhmG1FnPoTJsHD07Sbs5TGd3GwI4DFDfcTGjZPHoVHpsMaDZWaXZCLC9HadBhYHiQ1792L4eeXOCZpxqcPe/z1rdVmL80TXt+gVw2w8ZN41QKMaeOtzn2VJuDX2iyvDzL3KU5OvMr0Ghi7dxKs1rn7IlZqqtQym1mcUX9pg2UIJOPuXxWTTIKvRZOB0bXwUoHLh31OfPpReLn7wOugjVLzAJtqw7R/ahfc/XrWp54N/Wr36KzekK/P32ttSMsLi1VWTp7Fr/psXPz3bzh3nu5cf9+tm7PYLsdTp8NaTYanL5ynm3bx/jV//NHGOqHP/n9TVxdV2bLra/j3te9kb5NYBdj2hZcnrLY9+aIsydjnntqjqmnP8WtB8ZYamSwPZfrduzl7tuvJ3QcKutKBMUyhTO9NNp12q0OrXqL1foCPcU82b5+gr5+vuxHnD0d8fcfjXnuvgacvgh8k1//wlvY++rruXpqlV+49a2MvPkN7Nu4m803xLS8MT7+mYd54Gsf48jhz6PW61OkSJEiReMj14MAACAASURBVIoU3z+sfYIXCCNgepv6JHG1L2ch1Eb5vYoFgWTkEW9DeS3kqWniKWiQsCBr1blCGYnMTchYIWxDiNvgL+rLMhk9U6aoWZ/5BX2+mi4zh5LVifxOS98yZXDL6i3XgdhRCbQs1ATYzUG2pBmsQBG4AHYD5i5A9W/AXwXnLtjzTiiWwMlr8lZLNMM4IamCDgSaWAk04+k4SgVbE8KahCwENZUUcscMoxeCK0ARSEKONVGMn5CN0j2Wsb+Z76xBkpxdiF6xEJBmFv59raeqQ+JaIYpBIchyJDYG0p3iC+oY5QiRKn6vYvlb5oXem1V9nNHVL/ArXctwdoxz5EnUsGv3k/UGuf6McrGIZbjmNVcvu+nzWbGyBs5lFBlrkdjaCl+3DMwC5/T/h1G2Bd8PCCEbo0Z7hGq2Gsnol5FlLssIanTb5YoW3dMizbarogXbDvgdCNskOedQou9rhZpkvrOmYPk6EAWqnFiOkdB9+VzGhOk7bLqRiG+tnE++Bl7Mc1iIV7EpEBK5TjImA2AOFego/g5lXmiTIWS02BMAzJN8XWVIvG2lfpCodOU+gES9K3WvkZDFtZoiZHHA1n5x2RCCq9B4ghQpUqRI8b3Dil8B4dlbdt8Uf/FbT+EAZy75/P6fP02jOce+XZt40517+eH98Avfgh1jsGc9XKrD/Q/BI3/w01x46K9xbYf//JGjvP41w2BnOXHe4da7IBdBwYaMo/xMHzkETzx+jicffYLHP/Pf8MMSlfFN5PtG8bwevvKND/FXBz0e+tY8546eYdv4eqJcP9lKloFRl3tug6W5mMefrvLsiTrZYo7Maoerp46xtDiL3d+D8/xZouaDxGEE8Q3E3Ee87qfw+naQr5TJ9eVptwJaq1XsMGTPvr1s2t6PY9n4nZjlasjR0zP09fazcVuBm++GX7kV2hbcfy7mI1/3efh3nwOnRm6oj9LYMJVKlotPfpFweRpqZ2Hlk2BFEDdYm9CrPLiX0W1vZfP6MfryEZvHN7Bp/WbCTsips2eZnDzP3NwMS9WAfbfdxd2vv5XteyboG/PY2w8HL7dYasdkcTj8qMel5ZCaH+HHMeVChq9/9giLJ++jOXM/Ufgotj1EzCoWLWzbxtUO/XEcE0UQRWGy+BzHRHGMbd1K794PURh9E3OPPkQc/QWBP08U1IAq7P4t7v3lewhbFg/84TO0j36UvT/+72h7fUxdOEt05DME9b8hDOaJIpk9pUiRIkWKFCm+PxApVg+J/Kz6bfY1GZLv1++xteYvKBYrD9fiqRy6GTdh5WQzlbVSP1NWB4qV6KDI3xESXZ/E4udJLBE0c+ZklBoVFNGZz0GhoLagrc5nubparibuXGVhINVwsuAV1HVks9piIFYMVICqQ2xr7ngVFq8q1WvPkLIqcCtgFZTNQVantA+1Z2zQhpyjzTljVUfXVcSs5SorhBZKNSvKUCGKhNQSstJ0eXD133HgjSjm734UsTWMIlql2USpVyQZEhlUvPtaz0uzG13jeCHXTK/WtSTxWuG18O5mPaQMh25evo+ENJ2hW2nYJFGrhi9ShhB+pnLXoXvYOWvKMNczZIi1uKa0tNCErHzuaFJWE4OWrSLphnqVvZkU30PCU/cB15Ek7yoBN6657O8W0l1TwFngOKrrC6i7Z0lfxlRS1WtLHcJNo/eVXFtSrnCj7VgLyQNotXROucD4NhGbi7VfMXKSNkk4fdE4aUDCFMuJfRQZKjmrxJ7DPEYWBIRIFUL22+XYk3vDPIc5lkVFLvdTS9dB/GolSZgkpCvqY0IS4lTKlfGX0cebqvIW3ZYe5qKEbVybXMNqDNM1tfgTW8qHOueqxSj/G+B/BDhIihQpUqT4zojj+EWDUF4Rytjpyxf5lQ9/lNfcvp/33ryP3/jX2/mjj81x5uQU9YbLnv07uXGHRTkP1Q6cOxXzyN89ycy5KxC2iK0Ml64sYUeDDIw5NIpqUtKoqQitVujzu39xGSso8+yjf8/Rxz+Lb/ey7+5bqPshy6stqvMNTk/FNFchrtapz19ita/MQLmfwV6HkQFYXoAwthgczLNjawbLtiltLVDpv46p00UuPXOI7LpxOvMHiJo1IAvO3azbsods3zCRG+HT4aZbxukpWhQyMWNjFcbW2Vw+b3HxQkSn0SGbtfDcmCiKWKzZ/P5xGB6GWs5i+16XQ7u24a9O4+YyuLjYsc2WPXfSVw6Jqod56pMf1UvEEerXuAf1qw7N1UvMnPkSPcHruOve1zI6Ooznxiw3m1Sry+zavYs3bXotlb4cf/JnX+Dq2c1sXTfC+q0e/+3LcP/f/QfmrhzBimFpHhqdmCCK1RzYtZmbXMGvTRMFc0CbKJwFAmIiolBNpv4xRByleu7/oj75F7Rr88BFupacL/8nnvjwnxOF0D6/Alzm4oM/R2B5NGt1WJ2EaJ4XzoZSpEiRIkWKFC8f5tM9dDNJJkT6t1bz9nIRr/kLCdshEw2RLebotjFwUOmGhumOOY6N4+S9Ct32CYaBp11UJvl2RhGjlTG9j6UvN9REZ0b5w9qOIkIdW72ObTVJtVBEa9RUpGnggNWBTlP5vcZt5SsbhImY1zR+jDvglJSi1s4o0jVqKzLViaFWV3PCwFdWBqEPgchHLSWp9FvgZpUM0Ym036WtYt2dZNcuS11pUiFGLd3ULZQTlIWafvYZf02yTDw1TZ9VIbjM/UyVqThJyDFCtMn/zSEWGcdhlCuvpewOSaIv8XIV0koIqoAk/HytkFoIXxkapk2CqQoWZa+0p2fU2aabFLONz81z6r+Oq6yBS0XwI9W9VgT5ohKhSHeJZalrbKLTLpMII18u6ijeT/jLFoo37NHnP0NidSq8tHnZnlGWdPeqcQ2gbJnRt47tqHWESkXdGlGohjvahSPS0fWOp1w9og50GlpRm9Wktk/SryskTHAGpegukZCm8tUi1tjipSoVlvHWIWGaTQh5K+NcjpPEYaadQkdf/CKJxLgmjaDrlydJInZNwB9Dra2Vqy5kY2hF0FiCjv6etjOKyQ71gTbK68KK1PdA7CgZNrZWz/rQrulrtSF29SLOJYgeB46QIkWKFCm+d7wiyNhmbZmDX/gcQX2ZbeUedk6MMTJUYSWymGnGfPlInZHxAk5ss9qC1RWYPn+FVjUDjBFHAYeffIr7dg+xNSxR6YGsr+xtWh2YXYo5/GydXdtLVJerrMzWyI7dxsSOXUzPTtH05wmaIY0O9BRg/UCWxf5eGivL9Aw0cciQcz3iQP3oV0oe4+s8MhmoNsEtl3B6+sj1D3LzW7Zx/kgPc2cnac2cw+nZCraDhY/jWDiWx97rKowNZ6kUYPMAlCsQrsDkpZhWw8f1XGUf5sTYFjx9FYYbUPAgE9qMbOlh/lKDjG1TKLmsH3PoH1lHGLrMn51jrRrWRNBZpbZ4ktnMIJXiGykUMjRaHZaWV/DbLUZHhjhw4HomNhf4zx/+OCefv4BLk5mrC3zufjh83+dYnnruu+jdb1+Xb48l/Oqhby+yWX2KmWe636pOTn4P50mRIkWKFClSfG8Q5kzYIh3GDyRslGPsC92GhS+VlBXqxmTxTJmiKTMURkvYENnPJ8k6ZfrNmpmZzDLR75uGorLIbWyxKWu0FBMUw7UkXlGg2LLQV1Vo1hWT5mTBzkImo4nYUBG1QQCRpwgRR9s/RJ4maUOVaMuO1GbF6thOAJ4mdTstReA6vmKkog50fGVL4GtpYRwrNsrRfreWPr8j/eOo94UVtJzu7pJmMhMlSdizgyKJLpGwbKIuNY1EpduEXDa7yfT3dNecI6abiHXoDgOP6O4yKUuGZp0kzFw+D0hCtM2hJuSYT+Ifa5KmZh1kOGEcbxnv2cb/hZCToScwFbPmtWvERtvbrsrvli+o6wpDNSTcjBI4mxy5aQHaRClVR0jcEl6uX6wghyJfB/V5SiT5piR63iHhF6XbpOs9FHErok0RYgv/HtrQ0QJxuTDHVf6xRPqv2DkEag0j1t67sSZJ4waJ/680iotikldIxqjZaB0SMlb6q0nSh6LKlQZejKEV6gvT/szmgoPpW9v0oRmoRZMO6jvDj6EeQ60FHc0021pT7FuKifYc7eOKKjS21P1dr6oFFM8Cz1dZzxozEDTUib1etShzjY1mzcVJJaVXZD9j4EcOSv/8PMqBOEWKFClSfK94RZCxENB84vN8ZfIKj5y2+aX3vpPy+jF2ri8w08nxex85w8+8ewsjmwqEGZtO4CvTcGsj0CGKpjn4+U9zkJ3ccNsAP3Egyx23W3gli9OzEYcvxFRKRSZ29XH+6AEy5YCerbdS7hmkWq/T29dhoL+HStFi5xbozQ4zXno1n/mHB6gPLNOoeQStHnqGFRFcykE+DwMD8NCjcHW2yWLk0X/3G/jpf9vLZz9m8eRnn+LymUfITIwwffEo2WKFnuFhhgc3sWXMYnRYJSS7a72aJ5/yIqw4pNH0cQoZnIxDPg/DfSr6bOkYLHViHAt2boGgUcSyHAaGs9x+h8v6fXD//SGnptaqUzqIKlYQRT6Xph6ktvxecvkCS/U2F85PQgyZjEcu71HMh0SOzbcOHeKBgxeYnvr0P9FYSJEiRYoUKVK88mGSo8IiteiWBr7YvvDCuOzvBFG2CsFaIGHDbJS6tWBsWRKzRDmPR8Kg9AFbSdgukbOtjUU22ReJyxcZJhC1oNFMrqlmgVfUqleU+iwUraBAK9QsDzK9Ku19qBW0nY4ib+2s8ojN5BVR6mjCNoiUZxUtpVq1LUXQtgPo2OqzjAV9o+qzsA2tNgRNqDcSItb1wPIhk1XkcaiZyQzaCiGAyNVkpKdsC65lTLe0MnYNaR0CLaubuGzppD85CypWt5frWtJUeCDxxsyirIEdujlwGWamSFnYPSE7c3rzjCGTpTtzvKheTe5elL5NYEi/lmFgGecUwlaGhSQdk3B1UUZKePvatQK5fjN83OTB1m4mga0TmJncdNvXecQcVT3RqpvODdJ8bf35Nl3tMi8fFgnxOoBqugJJcwnnvQ5F3c2jXB8WSO42aQKHxNo4ixo+caw+y1mwol02wqa6mGZeq11XUWa4WRJP1gaqT8xEWTWS8eHqBinqSi2iSNkluhODzdOtZq6QJG4TZbZ83dSB88BySxGxngs5TzPRcbfKOURlKG5XjRaQ77kYletDjBqqJB4CkqBQvj/lRlhRW9iEdhMlr63qltbmyf5GulcNIJEEy4A3F7IkssD0/cgDT6L0zilSpEiR4uXgFULGakw+Q+urF/jCPesZ6nhc/sY/8PyX/4o4jvmN0z/JBz/4Xg5cfyN/8uEvET7xHLQeAU6gfrx2wRc+QPvya1nM/zruG0fAgguX53nq2Xne9/5dfPoBYPdb2Tt+F889+jiTkwFXzq/SWy7ygf/1/WxbZ7FQgu3jFv13ZXnm7M2MTfQxvs5jvA/yTejEKsLDimEoDzs3AgxzcTZittlhfhU2boXFHfNc/sIDNI/+GRDTpJ+ms43pgf+Zh/a8m1tuyXDdNji8An/1GThyeI7FxTYTmyfYdL2aO2f188edd8HX/x4uXwpprgbs3JtlYqJMux6Rd2NKE/CeETg2e5b555/59u27Bl/4xKep1UNmVqpMbN7Lz//yr3LTHetx8gG/8wcnOPbUn9BsrJJ6rqZIkSJFihQpXoi1RKwwVSbRupbUNFWo325+Ycal95BIKMsoMlVMSiURlpCuHRQbM0/C0IlHrFBEBZJMUyYpLFlwTHNSSYEEinIq0B1zvkQSN1wFX8hgCbw2CWEjNj62oD2XnPJaDnoXoix08uBXwB/RpG6o2aqsCkOOHZLkW0CrCZGvwo1bS6oO/v/L3psH23ae5Z2/b621573PPvO999xButK9kmUNtoSFBxnbGJxgwMaEQKcDFFR1SHeTdlM0PVSlAiRFhU4PpBO6oDspkqYDgQLaBmxMYoNlbEuyLcmapTtouNO585n3vMb+4/3e833nWEKSLdlXznqq9r1nr72Gb1rT8z3v82YwGSDUlzUsDZrQnILNZSsXVCK6jrCfTTA1CNqiyDNWiRdFYmNgIlHUzk3JsiS1/lOWnQot/ZZl0BtDrSHHm56W3W/bLOCSFmkThUg2KV9Fqr60PrQbK7ihoQmIwCVkCnG52kb29zkc4abFTpFhpMOhZtdRP1dfebvbhxZ2+sb6rGLdlr/q/a77quBYU2ydu4hkVbk1tUtQbg62ebEc8U7t14W8NKF0i1Jp6oSsnrEdnE2uCny1OV4rhPZYbXuMAdJVLVutTYQvPYPQg3psbfYVpLtGuQhL04o9+2JIx6KCHa5aF7INYALjq7ZtdJjb5Tu8WRUF0p59HCk+wOX+U/sNJfjVU0Eva6quvoxL7Fa3FVM0gVuA5ZYj3FOks0ZDthPvqUVAYcnXsLATN9qDKrWNcNcchXol6CDJEdK1x87JqS7CDCuZ2kAIXvUHaeBmE7Sgfb4WusyXduvMQ4kSJUqU+EZwbZGxFGTDLU78i19k60c+ylaeU2TyoJk//Ck++esXOXHnd/I//fC72fsTH+FPHzjCw4+fYfNUHy6Ky/kNh2/j7/7YLMbAx5+CP72vzxfvv0g2ewtvfr9hbdXw7MMjkscf4LHjEyaTR5m5dYkjiz/LAQPzU2AwRAZ+/qOzXLgQkhaGah06TbhrSaLE+rk8g05X4baDhmeeT/idP13hs3+4n+G64dIpvfHpjXcDspOw9nnOP3crT9Vv5vLKHMOk4MSZTTa2tphMJmxsXCaOF2l3A+otESfc0IHf+erjPPP0kKDRJCgOce6RJ4iHI4LQcPqLDT5ZgzOnLsClEcz917D2b+yD9ovBADPs6S5QSde4GvfYGm/xv/yzn6LRKjCm4MqVEeNxj52KjhIlSpQoUaJECYW+1IcIeaD+Qhri6kPZkBfze90N/7dV3LPIBi6bkhKsVia3I25eGSzfekCVXlWESdF1lR3MvfX8pGP6HNfGsX5q6AmOPVRCtYoQIlV2ErEaDqwB2Q27jhK+WgdrpVC0IJ6X/7VNshrkdVEEEEBhzSOLofxeVGFo2clC6zViOyg9r8DwmNgobNdVJZk27VJRg2xa2kAtFLJcYsSpilI2a1syOBHFrpI0tbqQtHlh1Qs1GG3A1lU4F0KqScfynY4PhFCfgklX1LohUClgaKk6NQadZJKgrB0KudtGhpySY9o1Kqa+Ypt+ARcDfwGnflR3jVkcmoidsM+n61wDOFZTLRV8H1BV0M7iEkOpKleVk6qqVCWu5cnJkXkG461TxQ1nRUWS2lebMmpMRYTSTeOoOxX9Kl/YsMt15E/j3JxfK/hnw4zdvzox9BDnilWkS5R49a8Eyo0bK/ousILxkYhHjbFcZg3pb1W/KpGq/sNqHaDqa10e2orjrQdOOZsgfaanqJ6ualXh2xaoJYFWIPbWwarAlQhuFjLBsRnAJBbFOmMZ0yAVq9UgNWL+W6SQVm3BdJBoBX25r1bczxGi3tbKNO/3tlMDZD8CQKGzDMmuBqva3tLrtvp5LNjl5yhRokSJEl8/rjEyFsgzBqdOcPXhe0muej6gm1dYDHPeemCBH3zn9czNzdBanObIzbfx2FNjHvvCMiaLYfYG1kYyPb5Vg/Z1bW4Z7mGQwtWrMBlCkBqKLdhiGegx7I05v3yJJ1szVDsVZqcC9s8Y3nZjhUtNWE+gF0CnBgdnIYtgZQJPn5LvczMQpwHdep3JhqFWQKs1Qzj7VrK1p3BPUj1In+HM8YcgDOiPA4rGNGEYUa9XyOKEeNTn/GlDaEZAgglh8xlYfuxZhms51fl5Ljw7YfOFYwSVKtXpeVbXq3QPTDN7cD9RM2L5hXVRXbwkAiphl1qtClHMKFsh2TjJxtrT5PkryLBVokSJEiVKlCixrVStIGGxu7Mt7cbXM8GrXq/gMt4ECEGgRKyfyvyvgw3z3yY+wREPfvYn3+tWj61MkJIa4AgRLWcfR4m1cLJP30hUZZ1VhCrTOsQ4eWdVvhcgpIqyRzVRxRZaxjaOyLVB6bkq6jQmWlMmWYYv1zhurbsymOpFoMSOsohDKFbluLQgb8FoXeqS5Xb5tLVniCGwJp15A0wdkghGoRDBeWR9NEMJ4S4qEFSs+SfOSSJPIRnCxpasZ4yQVxlQt/YKTSMck/p9qrXBFE5Rqjx0z1tv1VuuhKcSqtpsmzg/WT8DfQsharW7Napcu1VFiL7/rM4bgOPrfTNULUPk7Uu72/fMzbwusnmUjLHNaZw9b8fr+ba3e9WHq0rWz0P2WsL3olXt+zzCgWszLQEXkSuGykZUIZsa+eRY+9NI5iDiMTvz8IE7FdWQtm0/SpxqP/h+w3q6qwq2xs7Lim8boae52hHocXRuRUlfVWD78z/b3sZGxioVsRKZGPF7TXL7rmY7OrQ+01kuNiKFvQZsF1zl1PYT1mw7FNYfOhIT4cCeS8kYwrEkJckG9rzX/W3PguAy09kKb78+Glu+Dk5uHNje7FMSsSVKvJ7QWac5uY+GoUS+JBvAMqVY7tsH1x4Za7H5Vx//mmXvufNWfuaHvpe9exepVOr81PfM8L3vCPmTEwVb9TV6V9bZaNT5y6/Cu26AvYfgPXsWeffbF3nqCXjoYbknJhsVCK+H7Gma7T0E0RJPnTjP8cs19l3X5rYbAq6fgaUQlg7CxRxO59Aw0AjkHsoETp2BpVmotaA7V2XfvgX2TEO7VlCZ7OH5wx9gY+0PcXfoHDjF6afvIw9qhI0Oh2+fYarTpm4SNq4a+v0Rzz3xPGsXLjLc7BOPDH8+NDC+TGOhS7c+Tbr1AovNdTp7DtC4bi/rQYu73znPZAhnT1RYfuxjvLjCQ8phCKiFdUZZn618ja38Mqxcfr27tESJEiVKlCjxbYVpYD+YKhQn7LLX+iVhN6mrzJSG677affm+iApNe++Trz70WUoljut2uZpPqqpMSc4eEibsG36qWaUef4i8cA1xhPICQp0pQZohxIfvwOkTwZ4qddsV1GeUlIxVBW6GUGUqB1TGz9cxwk7WaQyct/voyv5SZbnU9qELUQ7pAJKBLfOCSDgLrBK3JduYmn25bIl/ba0lScdU+phnYruwfhW2LkCzY31ukRfSoCHHiqwEMi8ceVoEsp/IMmIRUDNSjY1CGMHMspeRkd+0aZRXV/J2ZLumh/iJNhAbhUUc6Zbb5tHqtWwXa/coQduy+/FtinXYNJH5jA5fSwTqOrCt1DQFFJEIKGv2WErG6tSIblJjp92pFqfirfNaw+qnd2gvl4DTyFnTAm61VTtrl6nBSJxLV0ysV2yErWNFohELJcAL70ADnAfwDNJP4HhLJVr1UqG8pk+EK3lb9/at6mVwp4onXN9BvOqlw3/l0lNJGWgCSKowrsKg7VS4Wg8l4/X0zvdLhYt851wONnlfrSkdnyPq9HEMizXxjVY5cg0YxKJESlegGNtGtJNXQSpK+MISr0XNDoxcBlgeQ6HXJttI2SzEFz3lfYkSJb5+eDNvxk5MAnKv3YcJboVwDlOrQTgh3zoJ6YaNhtn9HFPijYhrlox9MWyuLvPkI5/l906f4G13f4g7b72Dgwt7+Ojb4CfeNssv/AocXw44uyoT4O+pwekJnMnhn34Q/mARPvtl+NL5Blz3Fjj9cX78oz/L9/7g9zFTgf/w2XMsVGvsaVRcEgJgbQuOrcCeaejPwCiDK0O4tAH3Pyn3v0Efbr4eDu+Fc+fGNKMa97zzVv78kaMURQ8XzxRBf43hlUvEmyvc8zax0irMNKtr0zx4f84f/fa/pf/8KbL+UBI5dOow1eTo7dfzoY98Lx/+ENzWhkYIZ1ZSfuxfXuB3f/HvE/eOIQFAvoHRFJKoAuAk0KcgoR8f45NfPvbN6bgSJUqUKFGixLchqlDvQqUhHqFvSI95tRhQ6wHf4xac5K7OTjLUl1SGCPuhxKsSHiq/U0dNzS+vvpAD5IlV266DPLdp9qllnDWCPrKP7X40m5TG02tdFhBGqoYzwFTlsPrEatarCkKPdXHUHchzpLJTs8B1tl30mOojOY+wiT2IH0XYSw2Qz4TM2ZYQXi/LilDCsLfqOPWP9a+stUXRl6tSOIKhJjjKpO5rF+GMhmKvevUL4dlZnDxS5aiqHlZhhPUsaNVgpg57bReMcOpX2OaOGeH46gJhD9WbVAk4ze2moe3gePuR/azj8tspYatDwfeUVUJYCWJtcqSZ6nuh3YVuJLvRqPoG4sM6iyM38f7WFHURcAAJYH89EeMEyWeALyKcdoKMmGmvjOeQkT4aCbduKsIFbts6qMOJkqN6Wq0ijeBnItO5jHm7jcpvM29bHXq+Gwm4IeP7A0d2H34yMJ9on2Kngnn3PtW1DhGPh5ZYjiIRuvlzV6Ht50kmhDvjipsQUHJVx0fbbJ8SDAxcqTlleB2XrW25AsMuVLvSfpqvS0Wuav86wgn7fVJY/1Z18TngoV+Fta9QokSJbwQBcj/aC9ERaH4HHDxif8sJA0Nreg5qdWqRweQTrm69meLJWRg9APkLvPoJ6RLXGt4wZOzSdXuZqnYoNgLStMux5ze40LtKc6ZGpTvND94GP/nT0zz4JDx0P/yT/wu+/29DtQ4rGzk//hs91vOMu9/V4B//Sp3e1i383Id+gBdGh/j0sZiLT63yvnv2cvRNEfv3sv1s+3gOJ3uwdgHqE7ipA1sVWDEFV85mLD/VY2trjSKeMFev86VnrjJOoFqtMdWqYabeRtE/aVN9TpDHkvNE0SqNxoTFWejsgUpkmF+QPAe//6+vkhVDZvZMc+t33M3f/Ft3c+dbQw4t1plrG14AfvJ//AKnH/sqm8uPcH7tK8SDi+x0rVf0gGfs3y/lIVuiRIkSJUqUKPFqsQxpA4pZdmbLeSPBV4O+GDLkWWr4Iuur7A52KoLVs3GKnQSn7wurHraacKeGaAincQRxC5cifhO4ilPJqiK2EPpehgAAIABJREFUa9dVCd4IR6yqbE/JZFXb6u9Khvr1UfZLy6Tbb9g28DWPmzimqoaL3e/b9fu4xGtqiaDtY7y62/j/2IZYa5sFlh0rMk8W6dknAFQOQdiWpGNRF5ptMVFNM9gYQssmDwsKS3Dadmka6Z4azsRUOdsFW+0u8A7gzbYqSoo1cYSqT7r6gucpnDBZf1OrYG167Pc6TkgNjuDVLraKy9l9MNuEagSZ2UmwNu0hrni9oIfSomrLDmw12t7hXivY4EFW7HcbaMt1yOhbwwlVu4jQ+N12u1MN4QVrQK0ikfgBkt+qWkBzyUXmZznM2Ej/zHgjwjh3gKlCov/TAiaFrDNtRDxaNRLxOI9zeA69hsiN1YcbcRRYzeFCDqsF9AyMrONAGIjAercTq+/2mtn1Q2TdopBlCVIuJa6Hxk5dFLBuYC03DDJIY2gm0u/G2lOEFanDZAy9vmHjLBBCowPVDjIgxjCcNSRXkEuHFlIT5s3ZQuq4145Rsls7NEdO9TMTeOIHYPQI5TtliRKvFBq3cD2SJHMB6nMwvUg0NUO1vUC1sYd6Y4lmvQr0xaokyAkI2YgTgjyhyIaQTiSqJJiFfB1JylfijYw3DBk76A358lcf49LaBuPrprhp8QZMLWYUDBitDgmLfXSqIUcOwNT7gKqNMOlB2ocirBImOQfaIW87EJDndX72F+6h39jLMA+h0eQLD2dsbeQcXgpZWqiw90ZodeC6DlQPAE2xvdrow8YqRMZw/sIVVlcvk6dDspkG43gNEwQ06nXCpC5PEttpWjUMrkEap+TjPotdaNfkZh6EsLhk+Ls/cQ/njq1TCZvcdPtNLB1aIMlSlq+knDq7waceeoYv3/tVrp56gWRrBZlzfqmbosZQlShRokSJEiVKvJbIxCM0fKnw/m8X+HHIuxOQvVi9NSWRpm5X4tX3mPWlc0pUKkmpalv/GdJ4/2uZNGa64W2Xe8dQ6WUNF5yusfGa2qmNcxq127Tb0F4S38rYMoyblyDXNPPKLur/fYTW0qRkgV1PVb56vI4rR1gXywAiMA2ozcgL6sQavtY7kqzLhLaK1qgzqUlYdpFANYVuS5KKhTVo1qBbFQuCLINBCPUKzFjLggKRjvo2nCFwM85Os2GrYq0HzC3QvA7Gq5D1gLEQXkkoRF0VKW4eS86yRJ0w5qHWgEoIQQJ1AxUj7grVANLIpnILJX9T3paI9AmQGFlet8msQKLCWy1ZZszOXFKqvdbe8EeRjhoVOm4Bx5A0eIsIHwdO+Kg0v46qGV4ZlMcb4whXHfGq164Ce3CWqxqh30FG4UIgy9XQIw/cPlTwqtr0LRxfrQYbKixWNbDy6jq1EdtjtXD66WncyE+97bUNNRfcLNv67W2htB5PyW7/SuCLcfWs9V0MfCds/wox8o5XB8YFxFXJeTcphFhOrQI3MTIuKrDNrOdVSENZXq+D6eAsG0bewVVs3sRNKGieL181nCN8z9XTcOrj0P8qQh1/O1/vS5R4rXAAwiWoLkH3MN32LNX6ApXGNGF3GqpVqDSIogaVSpOInCANKYqCjIw0l3lEMrFSD5KUbPtq+0adAC/h4w1Dxm6ubfHA2iM8/NxxDrz/NhoLB0mnWoSjFVYv9zl/x/vJBm2um4u4+w4YFtBbh0sXx8RXJ9x9R5ezV+BQFw5EEGL4B//t7XzhMXjqOciSLn/4/5znsQfHHNhnOHKkwZveFfK+/XXaMzX2LtYpWmJPcPYSXDoHtTAgHvcZ9NeJ4z6hqRIypNWsUqQJg60+YRRAtUMeB5CPgQr15gKt5gxT9Yg9bWiqxVUInZbhA99/N48vXGHQS5hZrHBx+QxnzrSJU1jf2uDf/dt7mbzwHEU8xKUL9V8QSpQoUaJEiRIlXm8ENoPQt7oc3wiUslIoLQWOQvGdMPV3s+s7u/bj02Eaq6zkpFJHup2SsUrz6ON5lR3KVaPLQnlwDAD2gFE/1sIm8NJyFBDEYJbk98Im3DJd2cY0oVDLg4r0ZRTC4h6Yn5cEW4MMzATMLMSrUKzLJ0g8T8lQ1D6BbRMTAANJ9kUFjGo3u9bztQ71tmSXzwuR+bUXoD0D/Z7EqE+1oFGDoAqtwLGCqmDN7S4XcG4NXfspgDyUJGJVhKjS5j3ITtthZQvVPle7aWy/7xP3hHgFsrE0e3WvFLsWQrsi4eUJ0BtCsglcADMPlQ4060LCdmuSd6JppDgDhGxTKlwJU3UQVsIwst2o0fG5ceuOcbmjNI+URsqruQXevlNEr3zZrjML3OGto6nbWjj/2ZcjY3XaQW12x4gqVt0VElxE/BzurOnjdOJq4tHAuSA3cYStb50LjoLQ6Qrl1NV9cYIIOc/jSE09U9U0TnXkGrkf40w2/JxsbXZOO4xwkf3b9q644aRCUl9njveb32Z+ysACIfInhXXGyKFRQK1wy4cJjFKZHwntfEukSczs9ySTcZqNxQqh0AZt4Lxxc1sRtT6o4eZLVEqtcyqbSHjo+S/CxX+JjKASJUoI9AplvUtMKPe/IIQwJDB3ENTfhGkfJljax+ziAq12l3qjQVSLyNKUJMtELp+PieMYk8XkWU5WFCTGEBaQFwF5bgjSnMyoxdHwry1ZiTcG3jBkrCLeHPLCHz/IC3/8oCwIIoLmNJfNb/DL3/9e7tq/SIbhqZE8sFw5eZIzX3yKX/31/5zPbhgO1dwNfRq46y1Q2wMXPpWTPv0Q58f3cr5Y4Su0gRlYupNbv+d2fvDv3Mr//EHDrz0MJ1+AjcsQTlL2LS0Rhhkba1eYDHvMTDc5dN0+qvWIq6trTC0tMhm0iLf6xJubEG1w27s/wD3veC/vfddbObgdsSW36DQr+Of/5lGeefABtpbPSCbZwSl+5O/9MvuOXM9kfInx8ScR2/vLyCPPiBIlSpQoUaJEiW8uLMGXvVFDVlW1qS9TqqlTJs7P9HMUp17VDExVhAkZ2P35eeojHAuoCtdpnHpV5WjgqLC6hB8atRRQyq2QF7x6S5JnBUia+aY1rKw2IKpBWIVxKoRrYbOst+uyXZZDklhWrw71hrA1E1uOMBUpZ2cRZqZ3Cncj4OhhYYGSBNKxyO4mE4htQq9GBxoNKZdWv2f3UQdSSxB3bDNMe9XLCumGPpDW3XEbdp2wEEYTr6m1XBri3/G6cQtnTtq2/2uzb+LcHyreNj6PruJfI025tsW2TUGxBZtngQUwbUiaMDUPgxSCTeTR/ILkVxnNQtGB6ZrkbErrwhFHSNS4cmhVnM2ncmKru0ZHXMBeA1Ehofmq/NQRqVoppfsrOFo/tL+t2eZQ0rGJZJVQojaxx51FiNMuLw+1EV2x69+IBOOueeUHZ5erBh6BbWK1L72KS2OX40hgLZcPFW+Cy7OmQ8E/g68CF3F6cCVpq7ad9tn19AqgxLbykMbbp3KXl235taywkyxWdXBaSLn1Dc1X36pLgM4J6GkwyIRsnaQShZnbg5hUcm8xwXm76iWqhpMSI7qffARswZZeogpbOWXvt3AuIn7uPp/xDuw5+cfA8X8Ea79H6U9ZosRuNJGppv3A9VCZE6ucdgfTnaNVb9NqTVFvt4mmWrSjiKgaQZAxGU8gTamFUKQZk9GE4fo6RQZ5GFFUqoRRnWo1ZFLkZBhSIokCMXrVKPFGxzVCxqr/1Ziv9Tx9GeQp+WCDz/yTP+I79t4I0/Pc0QxZ2YA756B59Ajt3hLPH4N33ABna/Al4J3A08DDz8PFy3DTzQH/8He+j9//rb08+/AXYeWTQAcunePEp8+yeWHE3UfeRn/V0CygMg3NRsS4v8h4vMpgKyCqNPnwB9/PrbdV6Q8GfP4L5zg3v5d9ty5y8MASNx09wAe/v8FitQbVGnlF7oPrwFNP5zz+6Bpf/PyXeOz/+00mw5E8OBc5sMan/uhj1OeXqEynwCdxjyuvddbiEiVKlChRokSJV4KLEPcldPw1gypJlR2LEPZMyVIQls4Pu4edz0Q1nNxRJZHKvIXe/77/qhLKGgjtb2OAKSE8AVL1TvUjk1JvWRWqNXmOy1M74d6S300IQSByyiy1RLZlQpptq3KtSQafzBo4auafeh36m0JeBrYOmwNRqVZqUKkLGRuG0GxJhth6G1Z7QqQWuYTyT4aioA2tt+p4LJI6QqhtSlr7OBN/unxgy4HUqdGEZgPac5LRdhQLKVupCLlL4LohaEvW93ZLzE5j4ySDGzgWcYwcv0jFXgCkDiaSchQBRBWXREv5bR0aKjNVO1k17NSua3rDRZcV3jq6LyWllNELkfdsP6lRgpBZBYwDCSFf3yuODrkya5mUKStguCXNZKxcMqiCmYFiUZwWiIVr3r8PqiHkkbwbbG3CYALdKeHNRymcTaFeFe9QTdtW96owjUuHphxdC6d0XUQoA1WiXm+bxldsqlJVVaYvB4P4wR5kZxj+/K71il1/J7h8WBVkOFxCCM8EmfpYQro6Q96VriIkb4/tlG3b/OIA54g8sV20jOPg9Xh6diuZrXSGkrmq5lUtfAsvTxbOmkCj/jOcilavFhcQ0XeWuStDNoIssa92yClNKMR6YYf+9v+xHRub8ilWbKNt2IppI/mJ5PxLmpKvyiyr8lWtnHv2b8PXjn1sY69twfr9MPo5SM7zyolYT5VfosS3HaaQcIzrgcPQmoFmB9Pu0t23j2arQbVWpVqr0aw3qEQRWQZpmhMnCfTHZGFIbgxxllGv1RhkMUmcMBlNGI9TwiwjMSMmYY6JDMPhkGywRr51heLy85CdhOIq5Tn27YFrhIzVp56vk1gsUiZXHuRPfuN/5eJzH+C7fvhHeOFin7/4k+PctLiH73jHLaz3oDuEY08mnFjJmf1AjStDWL0KZgTvuNXwH843WHrTUYb9Hue//AKkFyBv0G7Ns2fvQZaX4Y43wQtn4Mx5w/Qc1BdCquES+/dN0W3mvO/dLU48v8byco92tcZ/99H3sNBpUdCmP2ny0BcvcvLkczQ7XQ7fuMSHf+Ag587DX3zmMT7/mQdZPvkFJlunKAr/BQPGva8QxxHhmj/PWqJEiRIlSpQo8a1CDgygeCXPJcqAqVxLpYnqjxogDEPVW67+px1cMinfJVP1Zbp/vOVKJ1W8v1Xv5v/WwDk/6m+pt65SLVXJumOUDcTbt7aFZUWCuqhPG+BYP0vkZtawNKyIojSryDEqVQnTzy07EoRi+JjFkFsGJwyhPi2sTWAzF1Xqkn4+qolCllR+iypCYhYFdDris5oXQo5OYslwW6+JCWlvDIOeTRzVknUnE2GFaIsSNs2FAK7UoNGGZkeMLMMMKhlEVSGZQUjfSl1sDqoVaFZEkqn5t5RB9DNPTaxPQK7Ju4zsr1DTVBx5q92r3a370q6pe92Hdzwln/zXDe36hreesnyFVJ+Gd/wcly83hKIGRVv2HYbSREFFovNCG7Ga5zY5VGG7qgmVpuyrkkkTTFegYj1iCyBqQKcK7aokauqE0t1TgUt7pmeIugdHXnVaXtE7CDl6E3AAF97fsU3gi4JfLXwC1seLOZdoE6odg1oVqDL2jP1/C+EDD9l6KEG6ZX9ftdtv4nxzldNv4dS3qrbVzwgZHpo4S5N6GSP9o8NojMyTMILKRIZzmsknz8T5I4vtd6QCoZ1jCTIYbNnT1p7qBTKnUVhV8/ZlTS9dvo+Emv6u2kawhCxDRObbT2XCJcP+n8mBAiTpT2hHRJrKhEuAeChXIlvxMSSxKNyZQDiAIJVGYFq2HT0H42Mwfgg4zU6N88vhpQgipar1Oq8NoPt+lWKsEiVeFzSR82ARZ9xix26rS9Sep9pcoNU6QKUyT7XVIajWMNUKjSkxYA6MITDyjJERkGQZcZIySlLyvCCLh6RZSpxlmH5IRkGe52Rpwmi0gen3yfOR2BEUE9LeWYr4PMRXIdULwuClKlDiDYZrhIzdrfDUW3jBKyZo07M89plLrGyucnlqjtHqBk/+2Vd5751HObi/wmL7Fk48t8nxR1OeOT+i3ThLNHMXK+cMUxHculjj4wM4dOM8YXIz4wvvJh0/TZrMs3T4CLfcupdsBIcPwGAEl9ZEJd5tQ6M6S5TPcnABbj0KX7h/jfMXxxy5YZo77pgnH424eH7I2Wcv8aUHT3H/48+wd88Sb7/LcOPRGl96tMf9936JR++/1xqjZ7gnwgCCOVrdCXl6hdH68mvX7CVKlChRokSJEt8QXuxFXUlMP3UNOLas6X38TEqaS10dJzO7DyVjDY4l2+3z6hOuofeJvHLouv6Lv5LEvgcs7Hw2NcDEsim7/WR30U7GeLxzVdSnJpBsRMYqUbNCFLKhtR8wRhJ5VFuSfcdYdieKxNM1TS3zk4sCVW0OikwI1cCqYustMZpUH9awJuxgpyHsYAaYmpCo9Sa0GjATQTixpG4OnZYwU9lYWChTWPImEyYpiMQItdawKtfccteqjrbP7jV7TPWr7OLkhhoarVJELLGszJVvpatvKipnHHu/gcv+pFy6Dh9f7afDSXl1HQ6Bt6wlouSgLipXJVxNRax1ffdgg1W6htKcoR2qQUWcIoKKcGTK/6ZIIi8TynCIIlct30nYT7hVNFz0eQVRzRahWAgoyWpwhKQqWrUHYOe0RoAjZuu8OFn6WmC3o7Ii9j45ItBcRSgFtUc4i6hKLyEU4EJh62ocyXoZuFzARg6X7DyFkuIDoGMT3kwKGIbQy2XuYTIRkXW1kNMvLcT6gVBOh8Ay2mEh8wLJ2CYrX2MnWZrjDHJVJquy2MAuu4RjyMGZzer41A7xx7rOM6ldwHlb2V7h5L8XJzAcSiK93E81BtvXqO1UZergq9coPT/Xca63A2QEqc54zvbEg8AjwKmX6uZXAB0BehboSDa4TGH+NfbbPQlkiWsfcxDuhWiJoHqYwGQEQRNjxETZTM8TTc3Q6HTpTs9Sq9Wo1+uEYUgQGIKgYDIeUWQ5RVYwyRKyLCeZJMSTmGEck1EQD7eI4xFpkpHGmVgOGJHET0YrsLUK2VAmubMRDE5BcRE5V0t8u+EaIWNhpwKhjfPk0rCxV3KRjln+ymdZ/spnt5f8/n17uf9P7+X06T/hv/zoE/SziElynp/77p/gp3/5aS5sRVy/zzDHIQ4swFQXNvZfx+zsIdaHYzZWJrzppirvuQdmWxJt1moVzC8WXNmAqDAcPWA4shfePGOjSDZ7VKYN7/3IHn7znz/Plx47wfljz9B7/jgc2gP1WdpFzsnlFf6HXzrGV+9/kGT1WRgvIzeoaVx4XAOa7+SW77qTwepXOXb/byFzwyVKlChRokSJEtcafBsAdYpU5izFxZP7skiVOqpSSrdXKaTBxY37ErIEeWZUUkKJ1ra3j5pXDnAujaoLzL3lSv4qwawkrxIZobdug52kL7JekYmsbpTJatWGEJiTTNSqIIq1uG+fwq2krhiDGVupYCDsWxRBrWaTghixDdhBMqey/+Y01FpQbYqVQZwJoVutiCpOtykMjCfQqECzClORPHKuh9C0jGPUFBlmdco9iit3rcRT12te/fhNpvBtd1NcNiUN+1dFqiYR0u7Qrkh2LVeWzx9SalXgq201XFuHlyVnTSBh4ArjcemBNnfLihM1B4vZaW5R9Q7jh/Vn3qH96YncNqESoAHCcfe9362+fMcoVuO2BlAz7u1IeT21AFWVaA7ssU0xNrJMXRt69qNdsWT39XpBPVF9rCO2AZvImZciXrOXbR0MQtBeAZ5HVK2bhbRpFziMUIVXDCzncHEMo4vAGIIG1K+HuoH+CGKbpKrZFkeO7KI9mHqt6mkO0hB9XFi/jpeBLfBpdvKdoa3EiJ1Kb71cDW3h1TOhZyuml7UWsJed9gDgOEs9xgrCTm/ZUdYKpcLpBdtq6kPd8Arga47XcQp/jQDA7rTHTk2xjozngc8CL9gCfD0IvP9riPuvf8ZMbBn1OlxmhC/xrYLZ+b/5bmjfQjB/gPriLPUI6vU61Yrct8MoEisaDAQFGRmD8YAwNFQqIWmaMpmkmLyw08YpgzQlTWKS8Zjh1hZJkTAaXCYdbsEwk4SV2QWcibNeBXVmpsS3O64NMraxB478jPhOra3C2jPIzaKC3HoXkanJ08gN6NXgMnn+JBtrcOSGIxw/dozzzz4FxPzVv/8Nrn/7R6je8FbuPQ3f8X64vSrPqTfcAfd+ts7sHXXueRN8z51wPIVTJ+GZxy/z+MOn+cJnn+RjH/tx3nyoyUxDTpl7z8EDf3U/D37uc/z2L50jmRzk8Lt+lG4zpZd9GU6fBRNw9mSNZTMF3EnWejPkNyM3rFO4PKpVTBCx9/Z9fPDH7uHMEy2O3f8V4P7XoNFLlChRokSJEiVeayiTptgd4bSBy8itejfVA6oBYgPn46qUl8oq1ZTTz0Xuv1S1cQSt5jPXbfTlpstOFS0Ic6cB4OpmqS9ETW//SodF7JSy1b11LOIuxGpYOvFsF609V6Zpy+1nsADFHqBm7RA0FNEPRje2/DUpR/eIHDsLhPDtj0RFa4ywi+2W+MemqXjBhsBkC4abQhq9AGz1hcRttUTa2QvdIQN7OFWWGpzKz899toEjbgvkvXIaebRVHmjF65Ka3W+TnZmmNHuSGnqqA4Z2Y2j318QxpMrh60fLYHDJuqw353ZsvHV+UFI4S+Uz0aGrosJp26s6rG05jO3+YmKF0DW7TszX2GsWRhS0vq6ksMPFVMA0ZHtaOH4sgyISpwo9HYyWAzl+dMCNvgqiKm21oR7KrjZwBPI8QsKqCvf1RIS8xRXstEw4gBCxm+xMsDVC3vYOIG6M+4AngMcMbA1hYwjLXThakSYcAyPl8ELIt2D4eRimCNHZlQNGEWR2QiDTuaGz9vcFZAyptFg5wg1b2ABprNtxEwYB8jqqtgFqV6FzOzX79152OqWouayOSY3Y941mfZvrGi7j2NjAOJR1zl0Hy0uwbJPmEVlfjFAU9RFykAJrhwKMr0Cm1xGdlNKTQFniFCFoHwGe4uu3wwtwzsW2LNsVBKeQ7SBk8Rs18WOJNzZC4AiwBI39mJnrmJ47RGtqH/WpDtV2DWNyokgI1izLKArY3NykKAqKPCfPcyLrB4sJCMOAtEgpSAkCMCZjMNliNO6TjwdiAn7+PL1sBQobE1CkyAVJbzqF9ynxnwquDTLWhEDbGuyoX1iI3Cw2sVboyJ3v1aJgEqfc9+iYF84s88wzn+b5E58ACi5f+HNGj6QMBhepTd5G4+hh9r494Lp5+M4FwyczePQPP8X9o5P89vRltooBkamwuTZh0Au4+eBbuH4Gpmqwuj7m3q9c5mOfP8Hzxz9PMniYpNgAlomCdxM16tA9CpvP2ftkTEYMnBTfg1zrN8IlqogoihrrJ5/mY//noww2zgEnvtHWLlGiRIkSJUqU+BbBJ2d3P9fpS8kIF8YKO+N9X+6FpW+399fbHV2lx/GDqZXSUoWZb5Xl6/xUfWu831/ErgBwzKKyjDmOaVFpqB4rguIg8sxr7IuakiR+LLOSGTUggcEGhG+GybT4QCZ9iWcH5xcZNnZy2tmmyDM1lVI6sj63bclQa6re74hK12yy7TkQ2JDjsLCkUwDxlpA+ha1jOi2WCtXAZnQPLSFlrKGqtVwIqxLnH2pmI9teRU38Y9XyobD7MBnU6kIwT0Uwzl2ceZKLhUJc2HxqgahxlcSt48LIx5otKYcgsfuPhDXNM8m0hLE2EPLTtuhvCEWHbTVkgTTH9girITy65pkzUCjRqvMIVmJbtBH+qo6Qf6o0tgRs0cMJDBu48PgC0ikwXRE5tww0AugEIozuFeJAoc7MLb55ZCzsdKWIkJg+dTvMkPQ3i/b7ZUS4OnFV403AkoFeDTZD6IfbUxqEgXT/uu3+NIFgUQ44ye2r5BUY9iCvQ6UL7dshuw4G84jTSB1hqEOICjB9SM7iXFA0E1gPabQpHHmbIJculRxrFjKNwt+PI15DnJRZmXNV3yphG3nb+mRtFTlfRrqNEf/lVgT9XAyGjf2kgZRXLyc6ATKYg0nXyrUzmDQg2YBkzbb2wFbiEvCMrfSrJYN0RkVHlm9BEHt/60TWmFIRW+KbA/XDOQAsQtiFRptqZ4lac5qw1iasN6mEbbKiIIknmHFBpR4xGsaMRiMmkwlZnjMej4jCiKIomIzHMEnFuScwhGFByoioUlCMe6S9VbL+Mnl+EbKe3GPTkczebacP1NCTEv8p49ogY7MUNlZgnECsU+t6g3ils3PTOOchH3WSZJonn1jj8sWrXLn8PCurJwGYpGusXHiKZBxRjRscqlzHxTsCqjFcWkk59egDHH/w0wyunga2qNHjXW8/xIG5OaYPLnHjWw4z1w65eGWTx09c5dNfeJb7P/0l1i49i2S5mwB9+ivPkFf20Zy/nuFmx5ZTFSCXbFZeP0PwIttSgyJgvHqMZ1ZP4nx9SpQoUaJEiRJ/LTxrzRLXKl6qc3bnEni59X0kvPyL/ivNDP6NQplEdexUSaiSFtvpgnCkraZDV2WuqoiVuWkjLI31iEw2YViFYC9MEkjXcDHP2H3r8bRNR/ajqY1UjdxCnqdVluerjrdw5q8aFq1yP1Xb9XGE8wJOXKDl9z0GErYToxFJ5qNcbSVs7HfQsrsPrQdu4JqtVjiiVYuY2+IpYakiYj1Ux/6tj+jbnHwhpJf6Aet7spJj+j6vXaeiazVl3fYItp86LkeRlk3VvqoeniAclpJmavWp1W972wTiW1vvCE+eTUQYaay1QjOSxF51AzPGiTY1SdcscBBRnKrA8/WCVlfdoHWKQqP41dYhQLjQGVvGMc6ETc+GPcAogs1IBKkD+xkbSCvizdsvhIA1uQyTygCSofWStXxlVJf5A9OGVkXskPMC4jaYOgRVCGNJmjZSUby8wjm7C+0rJU4zdvpEKH+phCteAyjfqWNEO0fHl87Z+HYI6rWs38cIIZxYX+XN0G2v0f/qPuB3QFS3LHchYdGmZQusAzu1FV2m+uK9AAAgAElEQVRFwqNf7Q1TB7yeHH5D+DNAmmJNmeUSJV4rqHTdXpArkmgyrFQJwxqBaZNn+wmCfZiwS16rE3amCJpVwigkMEYs2ZOExMCkyKilFcbjEePxiDhOyPOMLM/IgpQiy5iMBjAcQBhgyAnyMVl+mbwSk4/WyHpXYXQJudmUY77ES+PaIGMnAzj3CHIHUY+bdV76Ydm/++jT0g1IrNUmeiOIKk2i6BD16m0sH1smHQ7trHoDigHV9vVko4StC8/xWL/LgY98H+dCeG4F/uN9Yx753V+hElym3pglTw+xYCb81Id/gHe//+3ceNvNFK2C4TjmU184wZ/d+wxPPfEsl574EkW+ij+rePaJz9E9+Db23Hgnp08dpsifQ05MtbDfwE2D6/x1HRfn9YS3fokSJa5tqKyhnO0sUeJbihZyGn49QTUlSuyAPnO+mt+V7NBnVRUXaNYftVzQrEABzj0Tu2wLl+ymijCLMcK6DO3vyzBuy99FyE7Wp+rtz7ddiBDiRUOF2zibBmWWtnDU2Rjn3qkyQFW3afk1Dj/HhUHP4+wbwMk+NdORp3DOsWWYYTubUbUtib0qNWhPQaPl6hPa4s6FNpU9zkazZ1yiL58gbdliHUHi1lPLmkUNx+GnSFi4wrchbiHMobUuoIqzDu7i7Ds1XH2AexToIO/lvl3mFMKUztnm1IxdbTALktOFRCLRK0uwZ0pEkJMUtmKIQhFKdq0AGFuM2dCZa+wBbgKOItHzOlL95FqvB6q7vk/jejxF7Fh11E0hb3E9ZOT0kPxVOvqUn9bfNhHHi3kkudcohDi0I7AjJOt4ERF9p9Je/YG018IB2fE4hvU1YCQcfFCH2TfD8kUo1FrgCk6Oq1yi2rSqOH0dkfaOcToibQBVy6rIXE9zP6FcaBthlw0G2H2qDey2OhZnG6ICfT1d/YCA3ceqAFcGMNmwYdJXbIHVX3aFVz9JpT4gvlfIFO6mq9EDuV3ms9YlSny90Ak9O2thljBmEcwcJpyBTgszvYfm1Az1Roda1GQ0SqlX6gTAJB7RT2GUppg0JyAg1fCJNMeMJzIdORlQFJZ7KcTAOu0PYTKSSJB0A8IKRTwmG1yF+AkS1nAZ/kqUeHlcG2QsA+Bz9u+Xu0jXkPndNjJPuoHcgR5ldxaBD/83f8GPfehufvgeQxAEpMXd/KN/NuTXfv0qrHyO8dplDr35P+OOd3+Qj/wX7+FddwYcA44/D7ODFj/7q3/O3/sRePzEhH/3xxPu2tPlgz9jWJgLtp9ivven/3eOfenP2LqwTGFugfwCzoBIcYpm83r27Z8nvvNHuPz0J0jHp2z5FWrfPwDWYfr9coz1+3B39hIlSlz7mAV+HvjfKDNflijxLcTGy69SosQrw1/3bNpC2LSz3rIAUYZqQtoJwsTFONWqEpxqvKpq1CZOdDCPS2CmcfY6WV8HbpN1DvyAxMEvP4U8A19im9Vj3pZJ5ZxrOM2k1quDM2FNEWJGY/uncFmKVOo359V1jFBrGtlW4JKmjb1jqZkrYpTavA6Gq1AM2Zax1m4W2wICsTJoz0OtKWxkiESaakIvbYIuO303Vc1YuMPRttWwXqKAUzjqm9AI9xiuVddmi7wmauAUi0rKKdTDtmWrPo1TOdaR8PXc+z7lHX8s21fmoDELC4EU1RTiNKHWsSOEeJw0XDWU0wVRvyr/N7B/9xAbAIB7+Na9/KngN8Xpu2tIvdrICNIg9hmsmwQyag2Oq/STmWUIxefr4Qv7TxRBPIF0E5JVic4/qzmSfXnwijhcDFpI3+kciSaaC3HWBFsId6lWzyrI07mXHKfM1ldBnQfRwmsH6Bj0cxa+mPOJlkMlz7qPCBf9oQnsghfZNgZ6OUyOQ3EGmfTpIQN0BXgceIhXB98ne+IVaAU3qaNp6spkRCVeC1SQM/8IcANU90F7ETM/z+LsHM12nWo9giwjateZxClZVlCr1mCjT1CkZGkiBkH1iOEkI0tS8jgjTTOKaARhBRNUSIAoCslzyJOYYmg9SUZX5b41uIxcsdSrZJNvXsRNiW8nXCNkLLz8RXo/OxIW8ALOHEe3z4Aqzc4Sv/YH/y9vOno7CwsVTgEPPAnP/9lT3PcfvwKbjwKGj/7Sv+a73nGUm4/MMrcY8n98Cr784CnqYcB77ryO226tsDYD4eGQ7/rBOrcthDQ7htjAyVMX+Ad//5/y1OOfZrR1mSLT6dC5ryk5wOrqFZJnn+Lo7d/J2pk7SeNEHOdfNP1sH/pftX+XMyslSryREE11Wfqhn+T8xx4gG36VV590sESJEiVKvHGg7NsiLrOVxq6rY6aaiGo8slJLyqoog9NhpwWA7gNvv8oIapLbG6G+14b4q6mlSkTV7FKZmdxuo151yhCBo7aUfdqLI3StrNTUREU6s0+2TxNRCPXV6kDVuFq+pqtzY8EetwJhE2b2wsKNEi+upqv1lvPADIFuDdqhyB+btnmURFNRnjaxEqFqx6cOChkuL5vmYdPtsU2gCcGUt9bq+MSYNkMFZ0OghKq6QOijvDaBbqvBb5rcXvejw0DJuBqkBYwmsNG0OaRs1etekYyRKqkTcRenPG3h3paGyJTAvP3/AC/ubPzNgnaXujGo4HQVNxUA0iQLuFhJVfKqwDTAjW51Kz1RwMY6FGNZsQghaENo7KmhIvUeTr2sUEKzj1O/qhC8wk7tjE4C6JgLcL4KGvWvp5T2rZ+4a7cVdm6Xa5IvtbCAr5Uvxzh2Wm0tfEX37ldpTdA+HMPwiiViz9uFusG9SILsV0uWqt1ejDOhAEfC+g1RErElXg0OAEsQzkGjA9NdprvztJstmrUG3cY+qE+ThHXGpoqp1AmKgCLPSbOUQTKimVTI85CiyJjEGb1ej2w8oshSsiIjTRLydEKRppBlFEEBWRNMSGGAMCMdhRRbGzC4CvlzwEnIx5D5J52fILREiVePa4iMfRnUb4S0Cama4qgvlY+C5txBDr31w+xfeg9RI8AE4s//wAV4/PPnOP38gGZlH2+9+4d4/998J7fdMsWeGQgzsavqUGVxKuCWo3D0IKzmUGsF3HBjwOF5eOTEJudPP8ljj97HFz//GUiXcVOffeSR52uDf+L+VfoXn6Jz17s4csttXHh+jdULFxGlxG5kkF6xf5fWBCVKXKuomYh2tcHc3kUGwwmb/YBRto947QpF3qdMUFCiRIkS1wJUKunH8L4WUAZQKTElTpWhKbzvbXaye+BYGmUNuwhZWvHWUc9FjcNvs80ImhkI94iPJAbqM/Y5uYOQp3NgpkVtqlUPA0hSmzhWDUwzMSA1Rh6G47qYk1KDoi7kaaUL1Q7UWlDrQGrzNBQGor3CfuUGCstEBnUwkV2GzaRUFUI3bMn+wo6U2xioVhypubu6LZzHpt99WgXf21WrpE2rKlT1AfUjXAuE3PKFferpWXj7DLzt1ZVBj6lBedpVhbeOCol1H5ofTv/3j2GJuiCULlIdszZDDUdEGu97FSEl1TlBeeUu8kZy2P7dQdSmWuxvBXafeXpWJjiTizEus4bKXNTRdAtngBHY3zSSPwRqkXjJ5tYCOC3cgaKODMdE50v8xlRFqhKclsAPpiGvsFPYWcWpq7Nd26hfbNUu133qZWL3+M1wYnm1r9BtlNvR/e1uRD8nlvJCWhc9ToJMlAw2IDmPaI23cIbJMWJX0OfVw5ee+wM/piSmSrw6VIFZCOagtQD1o9SrS9Trc1Q6HSrdNp1ml3o1IgoyGlELGg1CE1JkEEYByThhkmSMxhNGwxF5kpEXOXmekucTRr0e+WhEkSZQZGTJEJIx5CkUmSSTNFZ2bgqoJBQTI0Ts5DxwDIkvKCcWSry2eOOQse0bYJhAehEXsPK1mDt8G2/5yC9w/CFD7XDBXTcYblqES2M4fXWL/mSBxT1/gx/9O/+Yt761TdgUDUHTwDtvghtn9jMzA3fdLiE/w03II5iZzgmLMb/3iWN8/pO/xfGH/j1y02ngplv9h/1dGK9QrDxBvn6Fu95+M1FxidULx3lxMhac2VWJEiWuNbSqIQaYqba4rruXt77zXVy4vMWpi3WWV6fhsc+xOH2RLA1J42mGwyGTtPSQLVGiRInXH2bX3wahp1T+piSEv84rIWd3P3f6NJnGsSulpCyfn+Cq4x1LFa+pt68QZyugylJwLIsqcNtsk61BE6p16A0klL85C5MACksQm6awULU6ZIW1dq1CP4E0tmnnbXnDQOLhK0C6ZRWogTwEV1vQmoX2tKhXtxIY5fLSSlXCRbMmJLGwYDQgatlmKyDNpVy1DoQNKXfRgklVMiypC8JuqFjYT0ANO9WkSnxqs2qzKzHVxbk/aBOrqtEgJJg6CilppkpHL78YfRxZW7H7VaWtP5yUIFN/TxVD+9YHqffdiGsDiC1hrQKNuhttWgwdZeDEuapJ7CJEa8seXtOw7QHejDOY+FZjgov3y3AuxTqyq7ig31WkyTcRunAVIV+VkNWofZ22qBuxFR4iuarSHPqWazEhVKYg2gPZKuTq5euTpOCI1R6YTHLi5eA8ERKE+Z7D2Rb4JL3myqvYQvrKV7VV9f0UdByAjFv/9VG/V3Ed608O+Jcsf/wr+T8u5JyPe5BcQWxUruKY29S25jciGtAC63W1RImXgg7OyE78BWACTBBgTBe4Bap3ECy9FTN3AzNTHWY6DTqdOq2owKQpSTxgNFyjN4gpEogLwySHWq0gjicMB2OGgxGTQZ+RqZMhZGyWDig2N2E8kXtUbLPzJUMo7ExLrWNv1wWYHKpDGMVQrAAX2GlDVKLEa4c3Dhm7ch/uQfcA7na98yayf7bJd9+xjz/7RMYtlZCbF2DhevjE34LfjH6Mhx64mcvLF1lOu8zbPWwhmTlvuQ1ql2E6ECN5gE4TugYmq0Pe+6E/YuPRf0g2vuQd0bcRGALPvUQFciajDf7yD/5v/saP/leMh6eAU/Y3TctZqmBLlLjWUQ0NP//+w4SFodGZZe7ADdzzvveRcYhw9jDNvYc4dATgv+fi8TM8ft9D/Na/+A0+efw+krx8WC1RokSJ1w+a7sePIfahaq46OzPmvNhkmc9s8CL7VAJWA8bH3m9qNAouHFiZH806rv6sDW9dNX30M/mMcWSsOmraemYpDDckBHmb+O3jnDinIKzAOHWSyyIWpVwxwsn2lN7SMtQhU+axgGFfLAk2rgjRG7ZhohpFX8anrNYI4sTbXw1qU9DqimI2rzrLXJ9p3E1Y9nFcet37XZtSP+C48TEudl0R4hS0sHOIaDi68uG+2Fm7CdQJTVjOaUSx0cX5w/pDaQvHMKo9gpZTlY6p7dVIRFlRBJMJVKtuRMzZIvdwo1ZHguYUUy5Re/MtiGGGqmKvJWhzZLh8V9pM4FIYd4DncWYZ+xDDp0dxSb32AGdwxHQTGR4amd8PZN/jDPIVxMp0GqI5KUCurhp6YCXnR8BQTo+0j2Q+0wRdAS7nsnbCht23kqH+m7Wqn3WsJ3b/eropsQpO4qvb6fFi3KtmD0f8buCIYLVnVi8LTR53aQDFul1Z/Zt1oG4Bf8nXp4otUeLVootckW6B7nXQXiToLDA9v5coHBOGVSqVJlOtOer1NlFkqFRqNJtywmajDcgmMI5I0xGT8YDROGMwTCHqE0UwHo0YDvqkg02o12VGJk5gMpRMfqNY9rE9i6Jy9MDeWyLIYkh7kJ5ClOR9yoTMJV5PvHHIWGLEPShAnoCO4m7pFxES9M0cmLmZD78Fzl0O2VqF+4/Dcgq33QntGw03mpvZP7iR73y34UpN9jQLYBOv7puDioEkg0+egOuvh2OPnecTv/8gG4/9Itlk5VWUOYDgLq67/Q7Gg4tcfu5B4CwPfPpfkcRrOPXrPHJTLBN1lShxrSPJCv7VfWdFbxUsE1WO0/z4FymoYMIqQaVCxYaUJZOYZDBmvLrGVJ7Ro7yllyhRosTrA/VJVXWqb/qpj7tqyKhEp6pYX2p/vuljhmNhdBJ95P2mpKSSosoyqhpWQ3iVgVH2RTPyaPC5MpAgrF2B0G417+OzhMry6L7wjpFBdhHyEVSmJe56kEExwBGp2k7KKPryT2WKUkhqQuYGAaRj5JlcQ5JT2/a6P9gmqYMQKjVotSRuPErEG2wylHXihlgXqApQpaDalVpVl593m2feYYerqkMVIsNOjtgTZjHAEa46JIy3TJM4qY2Aqmp9D1qwMkx2eoVqGTUthHaNZtgKXXWLGJKJvP/XI6gEO12GVQiJLbISspo3KkJGhppbzAC32kM1+NbZEbwUtDyatg6kea7iuvg8kk7qEeRM0LOqgO085YMCzhbibtEwznt2j/19O0wfEY6zF4ouTC5DOoRqQ5wyRuu4U0b7egpHyq7bwqhSuoojPP0EXTpHo2NsiJt/6XrrqFq6yU5bAn+eXqP9w10fcJ2qvrZDdtoV6D4nCaytW1VfH5f5S6lvpfgvUdpplfjmIAH60NjHwTveTmNmP2GlS7XaolbLIS/IMyCPyPOAOE6I4zH9/lUiUopJj3S8xXCwyWCwyiRLyDLICkOWjumNR2SjAfmwD701MNbOskCscgCIxYqgsMnSt3X2fcjUZkfl7BqKUQrlSry+uIbJ2AC5I7Zwfjb6INxE5n31Did3vOvf9rc5cOd3EzQMH3gLPH0OkopEQ2XAbfvghmaDfgzDFqwbuHBVnlE7U9BowsoFMCnMdGBfF44/sc59f/kVvnLv75KNzlOlSYYhe5mbV602zfT0UcbZETCz5MUEwkXIrtDfuoi7U4PLA1qiRIlrHQVwte9TqiNY3Xyp1W0wqtlO0VKiRIkSJV4P7DZmVEJSWRHYSZr6ZqDgaC8/9NY3lKx42/jGo6rz80lbJWN373d3inX/OAHODVNZQeN9dDk4qZzGP6s8Treve8fri8wvm0DRF7XQNmupLI6+fGq5fYYq9KqRQx7bOO81HLGtMkHfINVKBYtUEp7EAyFhkxzyzOb7smxkXJe8EAOgEUIjcAmvtDsnyLuzJsxSlaFCq6XklO/NqapX5Zg3cSJqHQL+Og1ve893FGw5lN/S33z2VPMaaRIwfzhYDr5QEs0++ueh84cdVCFvQHXWOTFosVTwq4RsBTiIvBFN2d+q7OTvrjUoLaLlGyKUYI6QySr87OG6v4FTv64hNMqGcfm24hQ2xjBpQmrE+WIKiCsyf9CoQL0KVwsYWzmu0cbybJO3bQZquLG0ipsg8HPu+YL6Bm7cKcHqk/sqeE/tfoZ2O5UH62noW1orIaunk9oc6OVG51P8SYAxMBmLaj1dQSS96ryrzryJ/f4C5btniW8eYmANsjMMNq6n0uzQ6swSBAFFAUWeU2QFaRoTpzFZNiJJE8ajHOI+JD3yZEASD4hH66RZSlHIiZEHOcloC0Y9mPRkxoUNe1y94vTBbOJiCPQE0g+lHWyJbwmucTK2gzxirOHIWHUxV5cgJW0Xue39P8SB77yT5T7cdQTSNgyNzIDmE7hxFupzsJHCn6/LqfjwGVi+XLB3b87+uYKnH4thXHDT/oBbl3o88JmneeAzn2b5+J8yN7uPeCNlnPf/GjK2xv79i+zddzOLe9/FE8/0GW6OGQ4KCBcgGyOPGPpolSJPhfoUWIYxlyjxxkULF7PYAwr7Dllsv9qWKFGiRInXCh7pBzgWQwlClTMqIarkaY5LgaSMm892gGNOVD6pQeI+a+eTvLszh5tdH2VrEu93n7D107JXcHJMDczW9VUJ66/rp1XXqT+tp7UTyEaQaVp4ZYe0XMo8KfM5wpHFNt4/kMQn5BkUl5Fn15Hdrmn3oQperQviyZeO5IG8lokMNB7D/8/em8fqkpznfb/q7dvPfte5M3c4K4dDUiIJkxIpUmGgyHGkwE5EAZEU0zESBYkhAY6zwEGQfxwH0T9yEiCC4AUJJCNwoCUCJDmirAUSKZq0NCJFckacfZ+7nf18W++VP956T9U5c4fLSOScuezn4sP5bn/d1dXV1dXdTz3v88YxxCVER5AOoL0IVQKF8aIka3wCsAJ5HQhznh1ykngNxc66XpggS5lKfezu40nU2/DIxypFbcrY1WPXNY0qXxPgXFBWGWwXqnPDRF96ah1BXLl6l6k08caGP5QYebJYDQ5DNdJ3IWH8GqavxSsnfFb8Yt8IDV63qVMIah+subJUmlO632IjzXmsnG1huoT9vl93FEnCrqgVP9m1DPILkO5AHck2x+c8TJwVst96vsNzrwnY6uA3tX8ukcc/df/QT+gvYfCXW3Pqe9goalOgl+kgWC9HJiaU6LdI1rK8hcUUyh1EyHQTf/FUeDPbG8CT3/hJ6tDhL4wK2Ifyy+y93AfT0hv0MekmTdNg6xbbtDR1TVHPqIoZRb5kPs2p59vQHEK7gGYu/iGN3uP7EPeEsC33oZq6/e27v3rP3wa7TZeTp8NZwxkmY2vkqSvHT33r44i6IOkdbwls8qGPxFy8B37rD+D6D8IyEcuQqA9/+FUo3gmbPbk5b56D77bwL78Ev/u5hl5vwVp/xuH1p+nZkicnq/zk7/+/VK/+c2xxnZXJJv/FT/4sP/9P/2ume0tuDwM8ws/93P/GD/zwx3hhP+e77/0pmsUO0IBRm/p7Xd33kYAckEeshDdO6NWhQ4ezj48BfxVxNvsVOuuRDh06dPhWIUUYCheOyAJ5tpq435XpUvNQZS70/xO8KaP6sCrJGZpJqivlgNd7xoJn7EIJpXtJPCZR1QZA66GyTA02VzZR9X8TfNYgZQ4z5FnxoiMZa1EanPB7VRpLla66PzgZcqnTg8oQhmatapMwcWW4yI9qF6/WvXZqvzmSzyEMjA+lfhbaobxA2xZi12bla7KPMpPl40vQRjAzMC9hbeyrradlH5nrVD2DesmWeEZviCdeQzte5b4JtgffJfQ1o8WTsrnbboy3UdBgGN2n+s7q6VTuXhOPzfHdJhRkazdx1ghmDUZDWO1LNfoIuTjG2+aOkZ4Y5hU7cC2v6d8y5M3oMeBDweGdRawB3+O+30Q4Rp3W1qkDleHs4qcA9KqIrLzXJSsist5bwJ4BM3Cn+AimCWyP4OoAHtqCp3fhyVt4uwolTVPkfOv51+FjgfS7AvGA6OEvmz33d+k+R3gitY9cRmunDlr7ZBts28PPqdRAYf2EQmL8Sde5j1sA1venEXB9CtULSNb3Od7MVieZEsR34XHE4q9Dh28nWuBpONhlb/kie9deJr3/Q1AntFVJW+ZQFNh6H5ZLyJewWIjVDqr0fhkvLR8jBi0X3f8PkAswRiYcajp0OOs4w2QsyMUWEp8Nctf7PeDDeCOpEXCT3/9cwf1TuGDh0QE8P4Dr+/D0K5K74CW39QbwUQu/eQ32B3DfgzEXNwb84j/6x1Q3vgLFEUncY3X4EPd87O9y6coWD913D//tT3+Y//gnv58kann15Vv86Cd/nt1XP4O1a2AmRFj+xt/6u3x1/gjP/ss5zzzzKvf8lfdz7Qv/iuLoAGwMXIHVVRhMJJvg9Sfcsd1ABpoOHTq8PfHXuPzDP86DP/bXefSdFb/4yU8ye/5/h+Wvv9UV69ChQ4c7DKp2mXMyFj3Be5+qgnUZLFcZmv6mrJiqQUPiUhWeBMtCY8iEk56pyqpo3LGyc0pyzvEyOU1lpHHMStpu4O0KNOmO1nEOvApcd/ymSj7VQiHDp37SdgllovpMrczTEO84qm1jXRnhMVeuvmt4pnHLHYdaGyiBrMS2Hr+SzA0Ma5F81pXYFhwfUyKqiX4fxiO3ywqq3NXPwbhqKHeNq5LGs6ukco3X2+pmwXeC3zX0XGP/U7ykVHnlAT4fmpK54Tu+vkmFDhQ5wpIq5z7GE8UG3120u6VS78kI+ql37S0Q0lF7491494YjPJ0/QkL8zwfV6SNErBKZbwfkyGlcBx5GtJvbCG2ovLXmadOeeHzVJjBOYaXv3CAszOcw2YSihMURPLsDa5dgbR0e7sNTL+G9VpU4r9zfBdLIGT7BSOEqdR7vHXuAvFxqTqAEYY2X+CDPLbwlgfrGTtz2S+T17xV3sFOgsTAt5HqJYhj24Spe0K6TBNNS/GGrQlSB9Zfczo9cQTo2Vu7/LyBige59s8NbiX0oHof9Papna1i/CHkBsykUR1Dsgs3d5wj4KreXkM+RC0gnFvSeZ06t16HD2cUZJmP1KUofQvUJR+9ct/BPSHJH++qT2/TO7fCeD27x5HUhWvNGbApsDu+2UurBHH7lcXhlT+5vWyszvvT5pxm0OR/+vo/wzvtXefD+IYPBeVYvjhhPRmysTVhZGdAfDYkNbKyt8zP/4JMcTT9ORA9LRmEh3nw/2cYqe7OanXnCYGWNKInwd/oY8srFHa3A+DzMr4EtgmPs0KHD2w9Pc/Tkv+CFX/o3TDehuLkH1Vff6kp16NChwx0IJRhPL6uD7xojrurXUBkaxgGHyrHTZapcLsO7dIbJrULDUQ2ahpPSNyVuN/GUkrJ/oROoZgfSpGAaXqxWC8r0KB0Vso1xsL3qIpVI1WPU7TReOozHHoFJ/XIbktkpJGNIRhLbXRdg1XsytHXQ7+rBt8YJK4Rq7vxmwyRnCYzOw+gCjFYgiWCeC3sWR1C4ehvjXwm0KZTM1OZSS4LTPp1p8Jty6yt4lWsoSFa73CpYX9/tdT/qWhEqKlVBqadK+fgBPumSqiTBO6+FFscud4yxJ3ulHo7F09wa3T5B3BG23CEN8FH3yjGfdSwRDnKNk820Dtzjvh8gTabUfosIR6sGKisR+rYW79hFKsnQ+pG879lcHOLsVJKkP1/DYAvSITx0EZ67LtwnOSL4PiY6Ec7SuMptIfMLMcJpKg7w2dV0jmPqKqxzM+qxoAJ3TeKlw8eufpYwXUA7gyoStbhxGeEtYCZCztLA8gDKA2gOoNmHVllh9Y5e4Gcc9Np8Dk/vd+jwVsHZ59SvwfTz0L5bJuCKfWhuQrONj1LR0I5N20cAACAASURBVILbIbzPd+jw9sQZJmNVeaCmSkFqTCwiVR8gdzN5krrxzOMcPbzGxpUtri/lPhYl0B/BsIRVA7NDuLENf/wqZFO4dA7KeJ8nPvdp7t2Y8LHv/z4++MF7eOAhw3w+Y7G/j21LIrvgiWd2efDedUwWs7I+4m9/8qMcFDB0D3w3C8tnv1Dy2v6S7Z1Dbm3v0EZAkkLUQLsnx1FYqGXq2wwiLIf4O3mHDh3enniO2bMvMns25uVuYqVDhw4dvk1QCePtCFo1gwzXVZYt9Ittg2XK7CmRocSperiG8e6nzSOVfA2Tb4GP4lKWUIlTzW6un1CWGVJyYZixkrAqEQ3NKaNT38P2SYJtlHiFY9NLsw7RAGwkyb5oJIIr6kPch6wHVRlw1qpEDn1nlwgJpApZJWMNVCpB1HNUA1vQW4XJeUl7XzeyXt1CmkDRBESsO47SulBu44jTNmiWyJOkoS1A2AWUCAubTxnAHkKkqQ1B+CpScJINDJtaFa8q+J0Gv+tcwASfGEzz9mrTqZNDAzbxu1XezuC10mlQjQGehA21YCr/2PCtf8JA4qxAec9tvNRGacIYmb4YIcdxC9F7LvD0Sx0keGtryRFnY/mMYhFh14cIMeoSp99qJD/cWg/esQG7RzC1YmNMiTSyKmNneKa4RRp7E3gGPzeiWcSU+I/cgah/xI6bPWgs9CIYJycdSozb1wJRB+ZHCKnqzqotoDqAnRah3tUj+pqr3E3XOlO81FvV+mGHnSNRmN3zaYezAKfvL56ENhELm/YQ6c/7dNm0Onyn4AyTsWG8z+1wM/hugPvgiX8GD94gzr6HK3cb5sYwX0C+gPsfgk9V8NgX4eZz8KMfhYNXIa4tNw+uMXvmF/jg3/5fuO+BLW7kOb/yS8/xZ198jD//zd+kKlMmlx7hoe/6Lv7vn/1hti5NKK1liOX5l+HKVkTSg8dfa3jm2Wv8yRef5smvPsvzTz3JuXfcTd0fwzCD2T7yxHZBEhg0u9jiEPE/6WYpO3R4+2MCZgXsK3QPEh06dOjwrUJIL2lCqzeCyhl1O1WnhkpY9UxVEiPBKztV7qZh+qF1gRpHzt06SuSGpqDq33qEd/80eDZGKbU1hNVRyefC1VtZQD1WZQZLV4ZqCiuERUyCsnU7FTbo8ekxVAjxM4H4AkQT2aZx7GGcCoFU19DUsrxVY0xNcKZ2DUr2zF29n3fHoHUEn44eX9e2gsrI34MlRBkMBpAlwqaBEMRRLLvbb8SiIXXkeVEI0WUiWOl5GakKq/TxOgIyI2Saio5rd0rU33PolqtwGrxDQ4VnObXLqX1BiygbVZA4RWwMB66sA3w3UgL20G2vLhO18BG1I2fXECHmAbBvTgp/9a8exj4i4lxDetJOUHw/2OasQXtxhETp7+CbfwdvgKHOE7eQgGTNmWVKGDh7iamRiObqJhzO4bABHkT4yhtuY3cZLCPnFnAVvvteeGoJr22CzYDfdoWfR6wBfg3p7riKfBT4I1fWuvu74KTAXtOdLBG/hMN9+SEeQLbmhxI9QXqS4lZMcNseJ21MdHJDW0zHCNVOq4eGGj3gtgfpCTvIu+aU7tm0w9mBy8JYffatrkiHDm8ZjLVv/aBsjAkqEcTrALe/aZjbLJcHyzj7IBev/B2ee/on+I0o4rnrkF+Hv/F++L++Atu7MDTwsQ+A3Ycvf2qb5x97jt3Xfp+qNLz41K9yuPcMddvSNA1NJaEhJoqJ4pj3/vg/oKkzjl59nv0/+yWa9h4+/on/gNVzI37t5/9nmmZO3TS0TUvbNJg4wjatC/nSOesEiXfRJ8JXODkf3KFDh7cj1h799xg/8O/w6h98Go4+BfaNkv116NChQ4dvPZRl07h265apF2mYGl19W8GTqBXeq07tBdSbVb1pS3w8srp76u9Kuqpibc39pgyfPheGal1VBan5pBKsQ4RqUx2F2g5M8LpIlWbq7yrbjPFyP0cMMXDt4Bw600cg2hI17GgkCVTKJdRzhBK84bY9cvVbcfsJ07vfQggj1WqqaeY6IqIY4omkNdmvuUuWm2sSa85FfOD9gdTRjCFdgwsX4MbTUKkc8Zpbz1lGmJ6sa1aclUID8ViyOZ3P4NFM8oy96Ipe4L1oY18MS7wsVVW3yucXCN+s6lf1ml3BK2bvQ/ajTbfjfldFpBK/664Z1qWZ0gdgMILMimDE9GG8Ll6ya8ADeBeEBXABT8nFSFj/KnAJSXX8ATzPF04hnBWEZLL2rkNkeuBF9/suQiM+g7dqqIGx9eYg+gaVz6G+jiRN3wfuhuSSWBQ0ryD2Aq7BzBiy7xVR9n2Z5Mj6Yg3LTwFfQC6ly0iuq30ggfRueOR/gqf+IRRK7g4RK+cKL19euu85sLSSsO5mA6WRkM0tvIeEQU7aFNiew9FUConWRBVuG5eoL7RgUX9qba1d93eOn2VQ04cZ8Czwr+giMP+yoG17GRlD9T4wc7+X+LFX3Z9nyPn5WhOHHTp0uFNhrb3tnOgZVMbaU39D6Oz6o8BnODmgSQxSUz7F9vX/k7/5P/yH/J2fGvDIZkThkss+eDfcdVHI2HsH8KVdOKgbkpUVPvzwD/LnX/0TnnuqYDE/4jRsW9O08Mzv/wK2NVSLGeXhTWDGv/ndKVk/YT69xekbnb0tv1ojd3bNBhgmjejQocPbFfNX/4zy8AYstsGeVvZfQB6c89ts2aFDhw4d/vIRSiRDv1h9/jptDGqC5WGIr9JGytZp+qAgQdUJaVyJV4xqJh99rtXIr5C0zPHx0XqPMAhDo/HsKfLsqKpb8PI6JXvzYH0lmjV2Wo9JzU/7eIusoUgyzVC2t06V2iq5m+MZyBxhj7QctSdQ1Z0qjBuEwcwRomgbr0jWdr0G9pbb5zbCUu0jzKXaNgzBrkF5DnYOoHoO7EtIWt7XEIryHLAJ9pzbh7ZDBa1jXI9W4eW7pNlfrmBuoTViMLpfiPFo20Kz8Fx4EkHSg40RrBnPaVd4clY5cO0G6kW7xIsZa4SQ7btTPsHPAWi3TMSOd1FJtHrtXkVmU7EOHUyE7lZP2BIhMDU6fuB60Dl3djbcsnCK4axBe/Ua0jyBSzERPmC5wlNeOTBrYZbD5QHcY+R0vWZhvgt2D+mKhfxtdC5G2WhnRWH3oLoGk4twM4dFC9UQ4ddeRHQyzwDvQZJ2HQrR+/LPiQ0eY1cZtShQcXgoZAfpY9bICWmNF+qrtLnFO3sQQRw7AXkLUerW0es3bDk986pOP23XomPUkVS+e8/8JmGAMX3uxTAmZsIqDzJkyJARfcZkbBAnQxIbExMRpTAapcRpK0S6u/raqqWqSoqyYG85o6WiZE7JlCV7HHDEnB0qDvFGHHDyXrNArnC9T3To0OFOwBkkY78WXErL6BFon8THBIXYpyz+hF/+1V/nQ3ffwwMPX6Feu4v5XTHtyHB+JJPjmxZ2F3D9xjNMX36ejaTP4d5L1OXi9bsNMHvlK6eWHHHrlSfexLFogoMOHTrcKagOr1EdXnuDX8/q61CHDh063KlQFdnpCf43o076RskMZeVM8F33P8WzNilCm6mJ6D4+85MSKuFLt1oRgFeX6gt/EqxfB8v1YxBqThOEqd2Bkr97osCzID5+Gusflq1+tqoyDpOEaUy21l2Te6lPrBpwlvjotwIhiZauPdRYVaWFqugdyG8WmejkVYQt02RElxDy1tlCRIlLEuakihYpp+jBfu2sCq2z97WBh2srPgFVC6kRNYWJoNeTauWuOpU7dX08966nJXOHsBI0u/4NLYVVGK3JxRxRaKdQK+/vLA+qCPIYqokcra6uZ0XD+DeQ3nQXoi1ewbsqqBj3LCb0ipF6rSJNrHa6JULf77RyuqrY++e2Fhal9KhxAolrY6s5rKYcJ8ayc7eRumo4wTQ5tK9A817YX8KsESUyPYRojRFPhIeRRj4CuwsHvwO8Ez93oz4L4Lv2acF7hdh96CVxnPvO9bll5S7dCowbL2zhknUZ8Uc+3kmYLV5nAU6TtUrUxgjNHVr7dfjayBgkK6z1LrDZe4QhD5PYFRK7wqR9mFEyYsUMGUdDRsmA3jAjswlJnJBkKcNRikkMkXFTd5Gc0qZuKcqG/XxOQ0VlZpRmysLuslMfsjDb1C6HTN02wuXaiLZNaOqGql7Q2n2s2aO1JdZI2ZHrh0UF03zJvFgwLw/ZqZ/m9ve+Dh06nCW8zcjYnoQepRtQPAp8mdveYNo5PPvj/Dc/9XG4+gmyD3yC9/3IiAcejPjeS4YH1qG2La9cs3z18/8PL/zOL/MZCuRR5eDbe0gdOnT4DsGNt7oCf4kIE9106NChw1nGWzFOKUunib5UyTrDh7KCiApKThK2b4QwFVOMJz01gdjp/StpCt6aYYRQXkP3XZOSLfGmqDcRharGYK/iM1RFeN/KipPSz9DvVm0dmmA9lYEq/dZzv83d76rpDIlf8Gnqewg9dwtv3XAVMQYdAgOxJEj6UBXQqnEncjw2kQxPN63YMAwS6BmpVtmT+pkGkiH0Y5hPhdTtjb27gqoeR3hmU7nvkTuES4hFgeZhUwcMJfo2gYcQxnQXL2wu3aGZYLsD+d72IW9hz0iLjYyQrmuINcHdwL3uDCsRmyB09U1E7HnZVe8swiDHAHJmdxEKcRt4sYFrNfT7cMnxjRmwNHB9H24NIRlAmoLVjVWMrr4HOu9xCTkXSq5/Ga5/zOWrayFecZbIatlqgS+69VtX3syVt4Wc87B7Kgk7w/OhKtSeA5X1wvcEySBfLjiZMc4ZHbdzUWWbDOpYfJGP11Ef6jDaSll/ZfhHbievID2hw9dDHGXE0SWurLyXD1z4OB+98BP07AZZmxA3Yk/NWCYAJhlMJjBeE3vrJIE4E3vtupF5nsxArw+jHmRxRBpHxPEatYE4PYdxQQT5DLIIYgPWiuo7TmR+rClhNoejI8n/XRmx764T6CXS74nh5j48ee1Vnr/1Is/ufok/2P8ZWnuAErLmtoIQf8+x1rqnenviV7+VwRrjFL/urwmMI23w14blWDQ4W3638ps9HXnSocN3Js6gZ+zXwl1gHoDs/VC8ADyGzJC/YcmAmP6bCIz5KIbzRMYCX6ZpX6BtCon/6dChQ4evCX3zup2iPcNLHRT6wgx3jh90jLz+vRt4GpGNdOjQoUOHbz0ShGob46WTam/wRs+xamq6iljlrCAOnFfwxE+DsE0xPre9Zp4aIOzhBYTcCWOxx3gfRPVEVEli6JeoxFHi6jFyHz2OUC6qil2tm5qrKsH0KnLfUUuEdyHOqIpL+CxauOMaw8plCRWf7gE7EF+FlQuwviWr3cyFXOjFMIwhb2B2JLYFK26dBi/hvOSKDznvC3gi9p3IrbJwzf3bbvmKa84rweGr9a+SeQvXpIfu8B9CXn96cO4cnIvgnJGeMMGrXkeu6MQVrQLdGbLuZbfbswiL9OKbiLvpY8BnkRxaO1aaMHGETotwmnOcyLQWVeBijuSMUwXzCDn46/jucD++i1WIh+wGcBXMJtgY+HP3UW3ODXyk/55brpfFJj5XniaLy4HPcbIbq4ds0UrfamqY9KBaQq4FqzmxcRVeg9FE1NnLhWxzfL2WeC+FcKInx3tWT4DfBP414q38nYow9R2ctJRRJCTRBj/w3X+fH3z3j/Dw5iXuGUTc24+ggMgY4tgpsN2wZjToIPV7AaAG64Yso+sXePtxkAt0gLc6cfNSpnCpJhJOOk8kSHI5Vz4z/PCvwRPbUBxYqiNLtd9y65XXYP8G5EeYdsFaMqbXG2Ijg6WhT02eH9LYgrIume4V7Mx3OGTJgpKChoaEiIbY9IniDQ62LhJfuhezcg4z3iDe7JEkUNawLOBoAbMDuLU3ZTqfQbPgoD9jOozJIyibijzfYVrfYHb0Eou9p6D9HHKRncX3pHX8NRfjM/l16PDN423gGXu7pFwhhsBERqPyBjICfT0S1SkT2gbbguUxIHMTl2r53qFDhw5vhD6YKzz40R+kzgtm2y+x/cK/xj/ZK04Tsbj/DzDpBbKt9zDINphv36RavIaoFN6ON3X1H/sSr2+DDh06dOjwrUGYVT3DyzHVMza0N1BEbl0lcFN80LpmXdcXzQEytoeZh3K3XMnSOT4iIkZ0lkNEivgq3l5AQ2PP4UOos6AcZRrA+86q72XvVL1AWDA9rtATt49PYaWq251gHW2zAcxfcfXflTpHjc/DtnTViiPIYle9GLYmnhAZcNKcFTzZpsrWFYSoXXefIXKbrBHS7i48S3q6DHWYUG5aVbZ9hCyMwC7g4AjSMaymUowaPzSuenOEcN1wn8uuiLNqUQD+zNYIGXsLOSXqG7th5DRMkR5aAYXx4tOihlLF2hO8WlW5ywzfnXaRczRGzs9FV+hzYK/j88yFeep28F1anT70HKqCtsX3kdItm+IdOrR7tsikwCCDfAHNDbdDg3QSZdda199Ssd0oES/j4+xxqq63QeHgFema1O7z7gDOIvp4B+TQbDlMNadjgU7ohB7YTbC+2JnEZI6/bJ1ztaxjiEmjIXEcUzVLqragpcEyY2X9Li5sPMQjF7+Hv/nhT3D/6nnW05SxdZdpJqSqicFoJjx1ilC/kPAUGDDhEKa+G3oYafBdh7gjjp1czNSVOQmaJBFO/jgoTe27F6KcnTew3IO8EOJ5NDZcvXoRc3UDTA1RS5LEREkMLdjaErWWXltj4xaLZXPZcrmpqIuGtmppqwY7TDBYzDiCCyn1KMP0+pBm2CRlHkW0TozdJlDG0FRwtB8zX0zIbcP1qGE7NeyVcGvfsn9YsW+XLJe7FLNbNNF/Qs42i9kOy8Mdyt0DmG5DfRNalaKDZ7K1ATUZWosMlqE10C5eMR7h3bPVz1wZbI1I0ciR0PonRQYTPbkZPkIk5NT6+GSfav0zdyf0rRc8djj7OENk7NeDzvKNxceJQ755A+vDr79Khw4dvoOhL3huoibuYUb3MFy9ytHyaepSX0ZPI1yWQnIV6hlgiOI+/cllVkaXacpV2nQTm91FO70F5UvQHvD28o+u6OxcOnTo0OHbCX051BdJlVkp2am2BafuRcfsX4oP/df1QlnVAZ7EDL0oE7w5qppv6kutWiSo9K9x6ytjoLH3SsYqmdLidY0hoaL1VdVvSDRpHHh4DEP3Ub/MFnnODz1zkf02quDNgYswWIG4B7kVs1CLxAjHxkd6D1LvMqF51pTfDaucumVKyipPtIsIvvbxxB2u+ntunREnHSBC0ncVz127ZroYw8R4GougWqofXkEUpecRem/ASXrrrKKHpzhifO/oB78ZfO6rJY7njFx+K81Jp9bKmhRLN1KCNoJoCNHYWbGCvxR0rqOHnz9YCSqm5Ls2qqqaa7xCtgbuQ3LL7eMvtVi3MRKTnsfiP8GaxJuzKkxW6xSCyRBGzgM5A0oXNF4l4ukcTSAagK0kLr7OxachXhfWsH4Wb4PyVkHPWhR8tDGVIGvxavrT3rdhcsSImDXiaEyS9IhTQ2RiHzbfpkQ2kXD7tsZYaN0JNyQkUYa1LXUrF3FkLDbuM5lc5crWo7z3yke4f+su1kxE3EBZwWHlLsFUPqmSsBqK7/paW4qjiUXcJNq5kKdRBE0up4YaIgvpANJGhqQ2EtvgKpf/N3OZdElT6K+L40qUOBIY2W/bQD2HZgptIV1m1sB0CnkFtrL08obB8pAoKSCuaU1D09YUbUHdVDRNTdLGxOiYZ6BuibDYEmzdYuuauBkSRRlZ1mdoBqxmW8SRwSRg+zDogxnIxw6ka0YRlNOEMk9YNLDWwJqF7SUMRjDagCRvOZpNWI42adMxg2TOqDigmh9QH01ppnvY/AZNcZNicZP54gjT5BhjMXFCFFlam9M2OU1dQb0uXhHu3hMnR9imwOjEYdQnijNsbcE2mKghMlC3C6yV+0XLhNgx6q2NJAez6YMpJZFljfMw0dkzvU+qn0mJvy8eIfdUndjsSNkOb4wzRMberqOG/lgrYNbBTGSU4yadsrVDhw5/uYiQF1enNUlSzMYFlod77Lzwp0x3ngIK8fCywTQ4LVGSgYkw8RqDzb9Gvvc8TfkChpLMzBikMxYrGdX4IZrJVdrXbsHB/wflU0gW6dMZuTt06NChQwfwEizwqeLDiAwlPML7Ug9hklQ5q4xTg08FP8frDpVkVTZRU0NtuWVHeFqvRjSMZVCfAZ6NNG77Qzxjpeqi3JWl9gnKZo4QaeIR/kW3cstXXRz5ttsudeXDSTugA7xcscfJJGVI+eYemFyQcvYtHNWe3dSilFhTDjwU8OGqq7/pblRFq3qRV5FXlRmeXQxVkiVC2qkouI8XMCvpq3y3hXgV3j2GJPJcoAo81UhCv19CVLG3jYk8Y9A6riBq3i38dK86n46RZlbd9QJpoheAOAWskF7K99nMEWVq25wGOxpJ6pF4Q6xY6SPnqELa/LLbgaqXz+PnE9Q1A07aXeo8hHKLBXLp3HQHo90yjTxf0wyguQLRFen2Bj8fYjkZqt5mUGdgV+SS3cfPT1SI9cFiCs0e9AcQ7cHB7/H1I0i/lVDyVQ9EaXS9yHRWA7zXR+hSqqRXK36nJqEX3cUg3WI4WmE4GRAnCcbJUE1d0jSWpqmp65KiaLBWVfSynzyfCtFGTBzFkK2xMrjMhfEV7p5cpl1YZq2lLQ11DkkBvRqGmfi+jvrOygIhY5tGksmVpfDhjbUsazd3kgiBmy8s80MLlZtjGRlGm+L/WjRQNC2zQnxjy0LI1nE/YnMfhgNDlol/LPh6LeaWovD+tDmwt2yoyoZyXjPfW5AfPkHEHrCgtkuKecHeco95e0TBgiF9eiSYY3l+TUrjunNLQ0mfLbJ0wuraOS6/ei+PXFml14uIVyLMhmFwJaa/Id2y6UNjIEphNIBRJR9bQlRJtxz2YNWA2Y5I0x5HWNpshBmsECeXxXc3hjyHJj+kONrh4NoLvHLzOaJ8TmwaokFMkqTUtaUsC8p8KUn6xmMsEQZDf9SnKRoiazHGYOKYuN+nzQtMa4mTHklsWZY7NK1M7tX06Tmn26ZpqacLomSANUtss8Asl9iiom1brC2xdoG1U2Glj28QytIfIgPIITIIfKPJPzt8J+KMeMbGrhKnbxoT5A41Ah5FhptbwBN08u8OHTp86zDAh8SsIQ+QKo2pYfQILK9L3FK8BuUNLr//Y5jhZSZbV/nPfvqT/PIv/iHP/tH/yu5zv36q7KtgfgjufT8sZzDbhtk1xNjsFURKs/ttOs4OHTp06HD2oYSlsnahKlVVOeEzdIsnU9cQ101VqarLqLKCKtlUhlEVqaq3XHVlvBHCMpXsBZ+0Sx1NNVz6pvuMEL9XNU9cwYd8lnjBxYcgux8Gm3D4B/j7Y+S+3+XKaoGXkFRWWwiFp14EMUQrkF4QadqwJ2ajeSnJvMauOGs8LxTjvUFz5LUjRSJiH8Hzxcr1XnW/6SODRthqM6RB1dXO4H532Er0XfbVPbbhHUAygdUNeA9wr/EJuWbAX3HfV5Go+xBvBzI2hL7VlcDvIlTGCCGaHwH+CG9k8QfA4zg+HeE79YoogaWV0O1jX940MMTridrQqlha3TnUsWMgpFIcSzc5VrgmeF5fBZ2FW659ocBbFMzxovNQ2L2Dn/sInTvCMtUbVKOf1VKzdvs5YbFp/W8RMH0a/vi/RzxjK7690PEgw8uMQwNURXxqWREsT0iiVYxJiUxCL+7R7/cZ9Mb0+yNGkxUuXrqEMbK9MYZ+0oe6Ji9zjmaHPPfsc8yLQ+q6oLUica2LGTUlrUYAxOe47+oj3H/+Id69+R4eSD7Iud46WZQdT2clNQwNDBMhY4scaisK2KaGgxxqR4wWjSWvG4hrSC1tbDnYmVHs5sS1IYsSxr0x9HPy2lDULQ1T0U42jSs0IWXMYNhj0MvoZ6lUglq8AFoZHOoa8jnky5Z5k/N4/iKHy2sc1je4xSvkXKfhiIacxtm2HDKnPh6jR0F7S/uv0Ccjc9TikoQxCUMm0TqXe5d539p7GPY26I036K+fY/Ou86zeZWANWjdjsnUOVnswymSYZQ0G6xBlokSf9eG1I5jNLPkUXtuFl3fh6NCwnElbFjlYY2nrivxgnxvVPtFSGrmhJUn6LBYLrDXEUUKfmsP5IVVdQQu9pEfS79PWLbZuRQE8SIiJyeIeg2wMLCmKKRGWJOqRs0YvmRPZFttCnSSM+1tYk2NNQRzH1PWMa9vbHB3uUi92OZhtU9Vg21r8IpIGijnMbsHiJjIAvIifhevwnYwz7hn7RjN3Oif6Eff3j4Gv0Em+O3To8K1BCtwNl65y33seYdjr8/hvfBZ4EjbeJeTr7p8BG2Aed9PiDfA8t74aY6I+O/GQn/3yn3K4/3sU813kTU5NzBLgPNgcXnsRJu+ACw9g3rmK3X8JXvkNKLeQV5An+PY/RHfo0KFDh7MHpZlAXuxOq8zUsy5U4KiOUEP2B3iCNbQ0UOJVEcbjJ3hy9nTA+xR5Ho8QFlLtAxq856z61GrdNBGKWieobDRG7nsLvNR0AHwAVt8LybpIwKJHod1D6LeZq+MaXtb6vY5wXZFY9CaT7E5xH3oDGI5EWloYkZtNYgkb19uzNsPQFa1SU3Uv6iFKyXe49Q5cte9D2NB+sJ2Kj9WJQd0eVFE7RFjGdVG9bmYwSKR6xrkuJOfk/ysRPGjgP3LFDGQzWleE8rd69t6u0LqnwEeR6ek5wj0+hvSOl5AUcyoOzYzPg9Tg7Xpj4Pqa8FsArfOZnc/F7c4qoanq2AgvFjeyfqsWkxHSjTVKObSW3HDf95FuPnfLV5BHvwmiI1InjVCpq4R+jrdMVpPfQ3x/VJW0zpXoHMzpltP5lfoy8PeA3+Hb9xypCcjAXwhh0qzQD1YlxNqIOmniomGjhGS4QX8wotfr0zaG4XhMHMVEaUa2skJpGohjDIa4lUOf5zmLoxlH+0fM53MhYW3rZKyh7KcKlQAAIABJREFUT6hjtJttdg7GGNvS5HOOlq9wLlmnF/VJ4oxhPMHUDVlryVpDamPaKibLUqI4omwayqphvpxSVkvqOqeqC+btkqUtWFoJo180UyJrSElJowGlyZ10G2pyKmKwYIiIbUbChF6USMJx0zA0GTERhojWWkrmLGhYtJZ5Cwvb8hV7jbK9RcMeNYdYWiwGS+rOB073aoLzIB05IiFzRicNCTUNORYoMEQctofczC2v7TVEww3S5YDsICV71bBME3JTU9JQtzFpb8io32fQz0iyjKSXkYxGxP0+UX/AaHWL8WqfURYLwb0myuNsCE0ip2p+CEf7OUVRM1pZpV8PYFRT1wVFtaDXH5NcMGLbYFuquOaSuUzbtDRFTT4vMMYQNS2xMWT9McNBD9sYIpOQxRlFk2NtDrHBJBktMWmyhW1q2qYljnvYNsPSEEUtWZYQxYZzG1eZzxfMZ0ccLLc5nM04nM85nB5RL2/AYCKSaJPCfN/17UPkZrH9l3e5dbhjcEbIWH3wC92sNyF7EEbvg40fgpefhuqLdNYEHTp0+NahBWawvM70ekSZZMhTdA7lqxynyKiehPYQaJxdQUG91N8jrh/dQnIC69y6mpbdDZP3EN3zb9MygvgCxCmWJUyvQXsNL8G4jE+oclr11KFDhw4dvnMQJs5SU9MUL9ODk66a6vmqrI3G0zvZHyU+OZc6c4a+jhknlW0q31RZnt6PVNYXqmJVIqjZp1TWp8qgNTwBrFLSIZ4N7XHMSp1/H0wuyv+XNZj7ob0kE5p2CVkNyUCkajaG8QQmI1jNoJcKmzarJZa9n8Ak8WHprfGh4Vt4Ya4m0VK3g3W8A0SGkGtb7lCUg76C9ytN3CHtIOyh5lRyiZ9Mz/lPpmBHYvvZG8BGJMmq4PVuCBoxv8An51pxv6mzwZ2ECDm+ywi36XJsAf6U1G65ugUc4VM7qwXwIPGCV3CkbR/KBuoKWvU70G4M3qO34vXJliq80Du0rVB3DxWpKy+pJ3APH4EfI/1DSdjQbjnFz02oHYImDgsvdYUerCpqdU5mNIB73wUvfxLa30IMHW7XyldcBbQib1a9p8Srenqcdik+nfQo9JJNgo8YrSa9HiZOaayhrFsik2CNoTVQNjW7B/vM84wocRSlNfSjjLosyZdLlmVOkiREUY/WRuLLWlQ0lPK8fXzMKcv5Tbbrhmo+pyi22Y5XSE1CZAzDpEfPuKxUlfislq0lSgwmgtI2tE1DVVU0TUltc2btEdN2Tm5zSlsAhpKFEK2kpIxoaLG0tDS05LSOWTcYDAkRK2RuiqF1AfSJa7OWloIlJaXT+FpKWvY5oj2W4hf4e4VOrOk4rJ1GeRexbWiIKIiIiLC0VMeSchm8lnZMVd4CRkS5IY5aN3+RUrUtta1pWwvRkCztkcQxUWKIoj5RuoJJV4jSNQZr7+DcxirjfsowjRiMIB60GCJMGxNHKW2TUVUNbQsmi6ktYC3WNkQktEVD07j2sNBmfSFL2xoTlwyHEEUZpqmJMfSyCeNRRhRFxFFEEseUtRjftpGhNTKVFUURTV3T1DVRElHXEEcpSRyTxQbiiDjK6PeGDIYT4mnCcKVguFiSHE6Z7TQkaU2VZZRJSm1SWERyr6F152b6Jq+xDncqzhAZq/EbAGMYvhfWPgQbH4Wtj8D1G2Lu0wliO3To8C1DA9yCg1tsHzx58qfZ0/57+cXgB50gCpNahdlrVSqxCum9mK3vJ3rfj9AWDezmcPga7P053Po0oobNkdere9z2YTbZDh06dOhwZyEkJjRrkI75IUsEnuyYcFK1Cp4AWcFHkCXu/7XbRknVPFi/cr+pUk1TeatCNUZkn+Bjr5U9UqnfGsJwaqixBc5DdFV+t0un6ouc6WIkceJmDcwKmBGvM2KNJ3D5nZLsqHY/D1Y9+YSrZh/Pwl1AmMpz+ChcFd8O8ITrDM9LTBG7gA08Tz3HqxRV4arR1ponBryoT7NnaWLuTbxfaevKGLgmmQgROzR+lZHx1dYodaXcVfM7QwjJTTz3l/H2VsJ+PahR3QAxtjBIT7sHMXaqkOlrTQ+nrsjW+rRVrWvnxroAejeP0UYuV5ZaHIdzGUpu6mUYzmsYl8LEJQnTfFsnrAZ07kRPki4HOXmbeAWteieEfUuTuSlRPMT3WS3D4udcQg7VIom/HlyH3Z+GxQE04XULvnfdi3hn7OGtT74Z6LgVmiyrnFgbLbQoCD1hdV01SU4giomShKwnifmqqqaqWrLMUpYlcRzTti3z2Zz+oE8cxZhIKMy+SciiiLqqKduSNEuJIiHw6hqqsqW1cywzZBwrgJSq2KYqCmZHhxTssh31iSxYW9KLSsa9IU2dU1VLYmIWFDTBPzkSIU5rCvbZZ8aS2kUEGFLssZQ6IWFCQkJN7SwDlrxevTwmdpEILS0x8XEXarFuO51m0M+bJ0i0K90eOkE2ZGZXoAg9OZTo1feUEuhR5jHlcak6mbcKnMOsPMxifI5+2iMxEU0D9BoikxDTI0vG9IYr9Mc9kl5MG7WSv8NAnCT0sh5VPXNpO+Q+Ynojyl6NbStoCrJeAybD0GJaaIqWdtCSJhFxYjFRSWoiDCkNhsYarF6zVknvmtZAEmXSzzA0rSVJI6KkT5RlVM2McTaiXzVEwzXSdkoaVeSjIfPhgIWJadoaWzWSqc1amUg89kfu0OHMeMb2rH9Cugrxfw5/9Yfg8gZUc/iF3wL+GWJRcP0trWuHDh06vGm88x/B1R+FC5fhj2/Ay38Ciz9DAvA+g7wV6hO7qpD0TaEjZDt06NDhbCBMlvW1cOxSeZv/K6OnIboT4G5E46dmllt4+k0xw7N7IM/FSq4OEUpv6H7v48lcTfdUB+srIbLOSWXqOj5NfBGUEypcNaY7D/6v8tBcjmX1Pjm+soStLTFZLBqorBgw9tcks0uanXRYOG1DqySZqhaV27iCJ6ZsUE39vYfP/tR3fzVSVBWO+ldvtSogO21pqTnBQneFIfL6kgRlKD8+46RIcAxchmjkz2ZTQz+CzQQ+xEkzih7+TAuNAe9DeONLeOJWKew7Gdqkz+OTfIHkSPsjJA4pR94SnwX2LOQWxkaSCjVIlzssxaIgTsBYqK/hz7WqWhXKE4I8mqkgPIH+gxJWbQwcTcHuILzTAngNuZQ1Mj9BLtGTlqieG7V439kwgdcML4CP8HMdSvLWrgwlf+tgnw3Cr+bA40/DrccQ/9gbHBvoEiPCAY3I0g779cY1Xee0qlVJ1Tr4G3pSx6e2yXw94gkmjknSlDTVRk9I0pQkTqibmiTxk1IGQ3/Qp2nkakmShH6/D0VBnVeUy5zZbIei3KW1FZaKmrk7/tOE8xBvqzAIGrJCiGodB6tvsH063B46M3E3ftBUKJGfIVf4FRiOSAZ9hqMeJH3iDHqDPqPRCnle0xRgW7mHJUmfmoIobol0vE0S4rYlsRFZMmSyNmbQGxIBZZUzGY+Jk4S03ycZDmnyGusYb2MNSV8Ic6oG00b0eiskfRgM+6Rxgq0t17dfJc4sZRQzb2PynVcp5oeQNNikZnf3JjdffIpytkdbTCE/hPlXkH51O6l7hzsZZ9wzNoLhfwoPfAT+rQ/C3xvB/ziAz/wJvPobwK8iyQeGSNDKtbe0th06dOjAff8V2POw8zxM/+kbrKTKogVwH7yUw/wWLC/A878F1WPAk8BTuLjJYNtjXYcrY+Q+h3R2LR06dOjwjcKgnnk+ORS8XpkSZvHWVOUlng3URFahijOEhvCHE2fKnphgfWVY1AIgZA1HeLmbxU/KKWlacDI5jkovw0zkfYRMXUNeehf47FOauEvJBc1YNMcTqYrwOGrZr8kk/jtrYHnkVK6qttX9O3Xtxjuhf172O2zFQqBoILPQtlBV0BtBFnsx3RyvDlziiSgVARM0fYXkRjmHz9UV8izqBXoB8XkFCWDpB+UoL6SHepo7T/GErSPiGCA5w1RtO5LlphUB8DGxNgKG0mQAGyNxTaiNrDIC1lNPLmrku/LKqivUQxq7w9DUZO6M3NHK2BB6mnYQ6nAJfAHhPnfwTgB6KhPjT2+OKGOtm1toVYm6hvS5PaRBNU/dLXyktxail+A+FLegGIvlxAmhZw8ZJpRQLZBHttNiuMItC4Tgxyx8g4+iV/7PIn33wC3T4UT7pF4nagetxG8OXHmHZFN6qYX2CcSy4KZrNS00zEoWIuxdejGEiQN11kQV9UrIKisMnpzVyR+CRnUNm4ReEUJNxEkiIfl1gW0sxDAcDRn0B/TTAYtygSkNTV1TVUvms0OWiwV1WWCrnLbdxXIQ1FVNd1XqrFBFsPprK/QqDPPUdETsm4dmr3uB19tYwMkIkRiWhjo3TA8MGFE/YxKiqI+1K1i7hgziEYYWiwXWMclF2LwbkxjitiJqLLQ92qgly0b0syGD3oCqrFhWS+qmprEyOJgko98f0h/0SRKIe0NoxWCi1xuxeWGD1dUNBoMRiUnI85z5/i65aSnjhHi2R20rTGuIWsPaaI2j/phmcUhrIszWRexyG9pwErPDdzrOCBnbQrWAmwfwp9vw6fPw1V+Da38I888hRKzecbKvXVSHDt8E1oEHkUCdz+Gfvzp0+LrY/5wYvhX7X2OlMHToMmRrxKMevVVY1DXYXeS1okHeAvTB8TT0IcYir24tXZRAhw4dOnw9qArstAonJBTAK72UMFCVlBKy6rsaeqoqQxjSZ0o2qFQtjD/WkE2VaIbKVWVkRpyMczZ4RsYEZSTB/8EzlGHMvEZUuJjnZBWSNahLSYZ1fNzKCKmf7BCSnqtGFJTlfO/aBqrSEbFJsL1jM00P0jW4eAmqIdSRsF9NDCZyVbVgExjE0Dcno5uHHNuzn/Bb1U8P7/6j2Z00YlbJUiVwNX59z5Wtc57Kg+t8qSoNlURbIoynCpB1HW1SzUOmHp2aEEpzlQWiP+sOm0QiYEN6WzdfIPTYxP2mAb9K7xfu+2vu7ybCQZ8PesKdDD0lyqkrUR32dBUj9xBFbG7dtLWzLKiUqTVgNcpaeTj9rlH1oXVByUmVdOpI3RlYzaWnczC1q5CqaPWjw4PuT7lL3Hb6ahsH22t99VLVoSlk7HUdvUwn+KFq7vbVppCNYLIJhyrv1p1rhz1NMkZBoWmwTBW1YXh8aEHQnirDnPp/QMoatSuR69+2Da2JaSJo2xYTgYkiojgiSzIwDUSGBksbt9R1S1NXlGVBXuTU5Zwqn2Hryp3gJXJlab11tuY0GavTHW8UKfzWRxDfOQhtdb6BVa1vffkb0R6bMPfxF6aezwHUI9hfBQONbTEWsJlMWUZjimSFRbxO01iqpqJtQQSLJZiYMh2wSHpEEZh4jCEDE5NEhr1rK/TWzpMOJsRxSr7Yo7RTMaxoISoKbBJhTEtkWpI4YnnzGZr5y1DvY0sD7Q4dEdshxBkiY5+GmzXs3YTJHJ7+XZg9CdEUWg19ChUNHTq8eWwiWo77gY8BjyJBAypq6NDh62L/89/ASqdm2qMpxmyT1Cqd2MO/PsRIeOrtyFiNn6sheQTIoL71But26NChQ4cTKs0T7IqmTQ9lkGoJowRjhn/u1IRYcDI5lZIPYRkh+6IMje4/FBWoulVJUCV6lVoKCYMo2F6PRx/f82AffXzIrRImpS83SiU+uw2PNSSXA8bTJEJ+nEi804BtoK2gLYNtVbrnMh6ZFNJVWFmBQwt1K355eQNRJMrayEAae65HD0cTJIHwKOEt7rRcNCTSlIzV05wF/1/iw8wLPIMHnly1+BxGJf5WrPy2ct3aZTTXUYVP+KX1UjIsINushaoVVWyDkLI1sDC+9XJ8L9DD0p6guZ6ed4eyRGj7HM9d38kI+XGl/RvgItIec2Qqu0XaRa/iAwulcTyrFd7PBnMxMdC4y8O4rm5VXK7dPg8qoerTxF0Z7hHvOD+P9hmdk9H+4w0//ZCiJ1ofE8PLv8FbgirpquJ5ZenhpBVCH2/tPEfm+RPEC6NtoZcEK2unjoJlOo6FY0xIxir0ItMLMiRcdcwynBxz1aNWydxEyFhj3MdvYiNoWktNSxIlxElC0s9ompKqbWnLAhu1LBdLmnJJVS5ZFgtss4R6JmPUcbSAKvp7JKkQ0U09xbZz/Jjeka1vH+gFVCHvTreBRfo/eulof45pGNIwpmSdkxdpjPJLNSn18ezIAIybjbMF3OrD+BL01jHRANvMIV3I7ExtxRMlzTBUGFuQZhHFzhPQXAcOIdc+92YT5XW4E3FGyNga+G35WgGfioAfg+yvQzaB2X+J3Ibnb1kNO9wZ0MieHwI+jvhvvRd51noMocZ26W7NHb4ZGHmID/B6K24DfBb2b1Lvf56jr34f8ApiT7Agiu4GDrA2kgcHC7fvhQNY+y4xnbv1BCeThnXo0KFDhzfGaaVWqGI9Pd4mwTpKl6mnt9oKKAVmgu+nLQn0r3onDt0nNEBVclbZvDCLT1iXBs9U9k/VS5kcFzN/QjGUAgWU21CGqpzTycEcQRtbqE4nhwlhg2UhCzmT/UcDyDI4amA2g/kCFqX4w45GUEXCePVjIY8inLGnk0EdSXWP37VPP/rroRnjc40p9zxzn3WEuFJi68CVUyBx/moJqU1RB/8/OnUaNDOUigqz4PC1S+X4EHdt1mGwnwaOJNeMf/c3wpepxETzhIV56XUXkavWNbf8CtJ0U07qHO9UaOR9gRz3CCFiNdJ/iKdojtzyiRHR9Y3W8Z0RJCNHwTUQWRilMKsg2nTEKlDNkACkEu8NrJVogRUw65BkkDpJ7kL7jQ4jQ/c35C31/2H0vh6U9jc4OWezwM/pIPs+0W/B96e+a5TQ0nkHOJjDbB+KqauIdlBlb3UcUoSKQ722b5dwKPR/PQ2V+OqshI5bOv66bUwEcSw6g96IOIncqBZTlhWttVhrqUq5SpqmoW2F8K0OZohxaI4fLEL2WsfpEUmyydZFSYp7uPcyy9lrePPoDnc2dKJQL5w9JOL6G91cJy1yqDLYvxu4jD0egbbxVkJ9t8cSy4KCXSSKsRPOdHhjnNH7dwvpw/BjH4Z/fwU+0alhO/zF8SHgw8APILYEl5GHX5Dh88PI89MDiM196BLUoYPCmJiL932EZjgi6/dZGY149+WHuHr1InVrOZzm3HiloGbEQVEyLQrqouC5l56n3T+AfBf4J8BLQMEPfuIn+O9+5v/gfeuWv//PP82nv/wCzz31DPVn/wVe66H4Ae79Wz9OvHqe5/5hD8qfpbvJd+jQocPtEJKsmqFHx8s+J1/cwxh1EOYuTHClalotK8fL3XC/H+DlcyFREZISqn08rXBV24Sa19sMFHjCN8w2pZ6yWkYYy98E24TSPjiZBSs8niNgeeqWoseiDqX6QqsM6WkVWh/qORz04HAGHLrdjiHpQ51J2HQVwbSQJssSSBM5lNcOxUaBFpIY6lrIGosobLMe9HqQpJCmPrvVCp7jDpWx2jTKWKoYeR1vP3CIV7cmSPx/DyF5J678Bm+5O8GTaLnb7jzwDqlDnMJKJu4MlZXqjBEPU42ED6Fa5rC6St1rNVYRDnno/l5w1YQ736IA5DRdct/D472MXA1j5HS8ihdMpwg3uWaktx7hidrKSHfKXUR73TpuP4Z0DPWe4/jAn5SQSFUYSAZg5s66QC9j5TP1kp/h1dngLxe9DMO8eLrPBG/HqsSw8kKau+94YsKtv40QsDeRXFX7wHwXlteFkD2elbCuECWUTo8NSl4pUxyOnzruhZNOYaUVOskULlOjZcTuxBpndwJ1vaA24XgDVRJRxQaKAppGvGXTlKjXY7K5RRZHGAMNNdQ10+mCpmmOadhebBmPR2xsneNd7/8uVjc3+MzvfYo/f/yIjozt8I2hPPX9BeT9TUei8B0ttOzQ3zomocPXxhkjY/Ux4z5onoQ/ugkvdVLuDn9x/DTwEeCdyAOdvmLpszfAu/DPNAvgy4hKdvHtrmyHtxwPbK3Q7w1Z1pbnb95kyAoFS2oqrG05uPUUNkmI4phpnLB46XGe+MpAQhGriGZxN3fffx8PvOt+rj58le9612Xa2RTKQmbyWaAvs5ev3se7r6yynsHHv+c+aqY0+0/x7LG53WXkdexF4Al2fusfY7Ie1F+gSybQoUOHDl8LahegBGjoCwsn44bD9D/hd40jDoPGl3hz0gYhNMKnBdXrhWaj+imC9cd4X1kN5Q3jnTU+Xl/olNSNgnIJ1u0FZSrLoxYHpzNTEewzxZPSoYVBHJSt7anUYagGVtlgCmZVGKo0gzwG24KxQp4a4zIrOSPVBOgZKXIArA/hqOcs0g0UrTNadXYHIOUksWyzgShS1d73dv6uFV6cp56zK2495ZkmnOTP1/D51AZIF1IiV5tKQ9lj4ALEq0LEZhH0ItfD3OnRFlMBgPai0NE4DBxXhFMBEfKGpMm+CnzQ952O0CxDodYO+4j27HlEObyH59YvIN1HT1MCJE40aSLJIRcDsSPx61rUrk3i7AzCS0YLKMDuib1Ba6BKnHes8pRqTxqeuFV8Eq/QSlpVszqHcxo61OScvCz1slUbVLXq0OjtOW4moIIkgrQHaR+aCV7hr6SnWq7oWBlez3rg4cRWONETNpAywuHkk1tHDGCFeLVGJlPaYPKrdeOdceOxdYZxNoE2EYuV1pCkfXqjEZO1VXqpXIjWtuLZWVjSbIRtWoxt6ccxURyRJjF1G/Hcsy9w9IXHuHHtS0iGkA4d3gxOew536PAXwxkiY0cQX4bsIViuQvs0PHcEz3VUWIc3D7V3+neBD+AezPC56EPHI50fniFzx4f4tEmd9vA7C0lkSOKIxPkNGCI2Nh+lNil7O9f5/9l77yhLzvO881fhVtXNnePkjMBBBkEQDGCOkknalGVKZ6Xds8daeWXrSDS90sqy15KPbcmSz8o2VxKlFZdBEmnKoiRwGUFgCYAgiQwMMMAkTO6eTre7b76V9o+33q7qQSQlAkOgnjP39L1z61Z9VfVV1fs93/M+b7d5dtPya5n3BgUclnCKa1QnewxafQx/QF1sq0h7ZY2h8TGmp8YZcaUvXrVzjPbaFM1zIxzbmI3Vwi4mcJbWEyrX2NyGHDly5MhxMbKVbi5m6Z6tmMtz/R5SX0X1YlU6Tcufa5FFZU2UwNTl3OTzxan/Kru0M79XgtjL/D9sLiKmryKbyVGlnpTpMS56Za0Ush65kKYXm5l1qtRU2wmbmaMsVWaBVYViHbx6wvckvys4onK1TCGIsjyvg7BgnpOm/YfJrkWI52WUFA+zLGE8iwiperHYOMtnq+DZI+WqVbWYFUqrDFXbMkxqS5At8gUpqVYmJWiTU2Qk/L2fEHphnJzNxH3INjbrCu3MqrOkapL9volSV3peNdOqZ3R55ROyehyyPS1GYq9zJFq1WAShfdKrc5zEopiUv/TjRJBppNMtptaSSm4Fpg1xIWM5pZeLXprd9K4RmmyugaUkf7axWScSvTSzItTsZQmb51GybiVZdl7Xqcy+VoJrAp04IWND8Yl2iuDVgAkhQWMHok4iDuhnVpAtavh8Z0MblVXIZu1RLrrXGlrFLvmdEW0mouMo+R6ZuDFNDMPEsGxMy8Es2BhRjFMqUSxVqFZqGEZIHEVEcaKwBVzHIQ5DYt+HMCLEIBz06fTWWVo9z9LCCaLoLM/pN5ojR44cLzEuITJ2FxSvgpFr4PSXEC/F5svdqBw/4igA2xFbAq1Sa5DaOWm8biNx/TQSjpwAriS1IMtaQeV4ZcGwEr9/AMPAcTyeXNAyzQamVSRw+lx10z/BNHfxrW98gW7vk5kcNouCW8DepGo4zfFTpzlx+k6++lcyhgSIgpg4UsVUiRve9XZ+8sPv4Rd/5u8xiEIOjE9SvNrA6rf5wm9rJL9AWgo6WwwmR44cOXI8P5QEVcpKaa4WKd31bJ6xzwZlR1RB2s6sTys/qeTNREgOLWkeA3Uw1HIgywQq61hIniuqVgOJXLKKXmVxslCCVFW8anSpr6xPpFYvCkjZHDezLn0+6Xtdr5K1qnrzZDuGkTBZybKRDYUaDE2CNwalCSFjo+TZ5ThCpOou6N8BaVGs7GZ195XIsW35XklVl9QqAFLvTS3WlS3spetVcbJy6hEpy6nC4mz9M4Xy7drOCdIgck5qlIUO9C1oqQw2Egte0xb/0jhO1K9GeoSz9Z7U/MJO3muSd4HUSKKWOVwq+n0lkbEXX4l6tXTYzEUGSCb+U8ATiCp2KYZSQr5GsXRPLcOnWvaBKSQ5RuKAkdTeMZD5gmAg3cx0pfjXJhVrNp1OmVx1Esn2JUj7aIXUukCZdDuzzgAJ8XzSy1Wrt8FmBWzWihVS4reNdJBVoBFL4bxucn+xbHDKYE1CzYW+B/4q9FvQa0C4RmrUrB0f0jgza+eS/U4noiw2W6doz9QdDtO/RtJoP7lHbZC0oViVEEMcY1Zq2LZNoVCg4Di4jotdsHEKZWzbxSKm57coxAZxBEHkQwGiwCIKfPqDDmvLSwQBxFETYt0/LdWcI0eOHJcGLhEydhzKvwjRU3D63/JMn8QcOX4weIg1wdNI1lnpou91SAUSTgwh8dNrkJihDOwFHgEezyyb45WDDSIWmN66j9/89MP88gd/hdXlHvXxXVz/3p/l479bZrpcwMVkvfU6Zt/+TgZP/e/Q7lMbeSf/7m9+mw9cZlAvpnHxX3wX3GkZnN13J2DDHf/lDp7+7p3Al4DD3P+1hzk4exmDjwz48h1f4i03v5X7v3svn/rjT4K1H9xZ8I+Bfypp4S4wXwMMIDrxUh6mHDly5PgRhPqsZj8XSQlJlU4q0/J8UAZEWZcWkn+sjItGCA7CIh4EymA4kiJcG4HKkLBExEnhmgwrZ8ewNA/NDoRqMqlER9ZEUrWVKp9bImVoHIRsUPJZidNsTrSSK9nvQZ5cWi1It5VV5+q2VQqoufqutCPsgTsElTF5hUDR2cyeKbMB0EyWAAAgAElEQVRo8ew1eYdIySr1xRwldYTQokea1qR8uJHZDSXJrOS0aBOzLg5k2qMjIeWbPDZXqx+Q1ktTPl+NXFWU7ALDQuDZVsrHDRKHhV5iYtqPk10z0uaqBlmbVCSNVYeQjK4pxJJ2ODkcw4hDwysRWWfS7P8FCJVWQQ5/MXldRnoqAiN1NO4ZcAw5dllXY52WUCGqbYMfSs06vy/kbGwmNgURz5wggLRPD0iNaJVF1oLpalyq8x/qnaANgNSnItsZVPUKqcOKqq/1MiZZpzL0a8i8/Srir+r7yTYCsEORZoc2BB7Y49B3ILQgbJDarKhatEeqktXJoaycV3XaWegkky6jUvTkoo1abFbdJmr8OPGDKA9huy6GaWJZFiOjo3i2TWwYhFFM2A+xsbExMGOxkyCwOXfuLN1uG8OJwQ6Imw3isANxN7M/6iKsMvwB+WguR44clwouDTLWLIP/NASPkiaH58jx/cNAArLXkWavlYGHSDOCtibLanaQCiSyQ53XIsOgAmnA5wLHkWAwx48iNHXq2YOwK97807zlQz/Huw+6lL7wvxD6ESWnyOTYEPetWKwdNRgvwXU7YuKTvwm9U1C8Fnf29bzhCo+lisGfff4ID3/jLP/5j27l8//xe/zDn9rCj/29WV73DvjN26DnnwCOoINic+Y6jIkrCMOQU3MnGPi3cP7kaR6+5x4Iu9BbSMzIFHMQbeGVpYPJkSNHjh8WsmouZVYgTWRWm4Ksp2w2t1gH8sr+TSE5NFtgagZGZ6BSg5ILdQPPq2IWPEynSHl4ioJjEYUmYWxiuQXCJOyOY4gigzAWAigIwA9iwvYqrK9BpwndFqx0YL0NjTY024g+UAkPtVuosNmjUaWjmnOfJVYTw1PTFB9GfYVA0Jd0YWwolMRnkoKQJcWq2A+EFoSGyD3xM0aegfi7lmpQKYkPrAp8NbVbm6XN1CZnOZwiKU+s/q/KRSeb2Tgt/WR9E6SkqxJgXVLBcfmiw6Hr1e6h+5BVz2YLI2Uftyq0HkKCTCXNyvIn6kp2eOhIrTHLkJdjJIJbQ3a7dNFuhQiPVkeIRq0vZia70k2WV/cEFVi+EqGHfQ45zXo8qgjvuIKMFCcQs6YVRBV7zpBTtY5cJSpOriPkbCMWMlyv8k0D4KSPBokWKHRkDsVO5m1MN7l7hOmyG0Spk2xAuUYVjMJmD4keqeJ1jdSbuEw6B5K1Y1WRupLCkKqys2J1nWTQcgSYifS6l1ynsXQ8VZV3WjBowGAZGeko4ar3Sh0dZSeXsprkmLSwV0zam8nsgFLnHVLDNzV1rgAjUK2IdLkXYLslDBMKBZuC49Drdun2A8IwJI5iDMPENgwwbaIwoN9ZIo7XGfTbxGFEHNiSdRA02Cx7V6Vv1uQiN57LkSPHpYNLg4ylD8ED4hOb3yRz/IBwkaBrC6KGLSO9aRm4n3TYtSXzGw3IstZFNuIztZNUe2ICs0ihgA55ksuPLjYnwJl2kfHLf5ylp04yNvt6dh28mbAcs7RS5Morh9i6pcrxkzH3PBBx+vg6kzWDoG8RrT8CoQ/xCsHgSU6ehu174cz5Lnfcv8oDT8GTD97G0ze+lZNnZjl7QcbXgX8SeBIJgGOmtu9gbGZGCkcUDGIDuu0Oq0tL0sCocFH7uzKINpz8VpkjR44czwklDTTnN1uERp8D2SI12f9TZjCp6mTY4I7AxBSUtoOzFdxtOLOTOOOj2LUSVtmhbxeoFMv4kU13YBBaPoYFkR8SDQLiQYco6IMJsWkRFTxC2yNyHWLTwXIcqu4kUbuF4fcx/B7ts0385SYsrMLKKoRNmF+AgZ/436jGr5jZR/V4VQsCO/M5YXBiIzHFVJmqEtLI8yV2wCzJvmODXQarIinPcUL2xBGYMZiRpJjYJnguOHZKSmUJzazNbdYyIKsGdNnMlmVtei92a9DdHCYlvYLMelWgpx6x2QJIShJDmmmt29PAL0uKabuy3JMeOl0u2bZhQDkhBiMjscYypDfpZtzMz5Vbg1QVq0Stk7yvkHLAqjl8pSJ7+pts5sPV3VRF0Q6bazsUSTPcdC5A669lNZkm0oVNCwaBuGiEapsqmfJYNnilxAfYBj+CMIDYJ7XG0Lp42mcg7RNK2LZIuc2sM4ryk2rH7Ge+s0gJ2uw2dB1kdlyFnhtksCmNtx3o96TBUR/CNvSb0FmF7gr4Swgr3HuWlWQNb7MXjjLN2dGTTg1o4/XsNJHRUiKHNyoyoWPVISzLhI8BhAPi2JA1xBCFIYN2m7DnE0Wh2BYYYDIgJiYM+wT9pWT9yUEL7eR9lhWPMu91n3KxV44cOS4tXBpkbLQM3ElOceX4fqEhgoUQqDuQQl1jyKO3hZCn9yAm/wPgjWyucVwgjW2ytUH3Jb9dREKVWrKNLlIkQDORcvwoIDvqUhjYxWGu+ODH+c5//RxmsJtBr8n31ir8+q8c4qMf3c8t7yzy+19scviJDmcPn6RWtWgsbSWKEoVR72k6Zz/Nn3zhY/yrf9SjGHdZL8An/6ZBu/1pvnN0hHNfvYG7vxsxORpg2Rdwy/P02+I3u3/vBNu3jRAZBtXpaSz7YvJ1C9IDNS8TcJK02JyMzZEjR47ngBKMEan7pn4OEWosy3TobxKSwa6CtQXDGsZwJjBHroKbboKJaeL6CGFliFI1pF6OKXkxrh2yfCGm6kCjEbByoU3nzFGp7tPrixpt6QKEYZKW7EJ9HMpiXWAM1XGmhpiehUHNw/JKWCWTs7Mu8VpItNIkbqwT9zrwrW9DY1GIlsCFeJXUpkAZG6X81GJAX8mzMA7F5DSKhDGMwoSvsEQpGwQQRKmybuCD3QPbBSuRtEZajCv5vWeJAg/SrOA+Kauo6UnK+2oQlSVCY1JuR1k3dZFQ5ayydeqgoKI8Pb39zHqyrg5B5rcqJlbORkV7GhCqJbxyTsqOXlxpS5dR8Z0Dlgejhc1uCTVS4a6uMrzopaRrkZSXHkLsCEaT34+yWbv9SoWJKF97yOm8QOr7WkKOURuYQSg5FTyDcPNdJGtfu6G+CrGolMOEJLdM6AbQ74LfI+XrfLAiKLqpBTGhWE4MYDMJqn91AiLbR/pJQzTrX/uomgArV6li0iwzrx7FWSJXlbV28r0W7NISKy4ygWLb0vi5XiK9X4f+EjQXoLsA/gWI5xEyVlesO5IlWrVAV9Yztkea8q9WBM1MwwNE550cfaOMaU4R28PgVMEtE/eaG0W3sG1C38cwXYIgwh/0CVYbme1GQiajqlc/aav2jucLhrOzKmqxQLreHDly5HiZcWmQsZsc8nPkeHGoIIHYDoQ4rZCmJYUkaUmIwX8TUccuIbHKr7JZWWCzuQ4ySEBXS94fQ0KLYSQ49oFvkvNhPzrYkfxVn1XJW3QK41x/wxCPeD3u+NxnefDOP+c9/+IT9Lfv5agxTO+7j/GXv/azED8OTNBilL/81jDEt4J5I8Q1+u0Bf/kb/4kv/sZ/JeYCxDaffnAa4p3c/enH4TP/GuI5zvAYP/Ef/j0F76N85p99HPgExXqdnlPi+FrAli17KTjuM5t+McyCKJdy5MiRI8dzIDtdaiBP+IvhkLIgY8BWMHaCtw8uvxyuOsjQ7hnGtg0xPW4Q9CEcQGOlz5En51g9fJTV9XVYWYALJ6GbMCJhD/wkh8adFMld0AFCKA+JdDIModtBpowLxHj0jSKHAYolqIzA1A748E+zb59F6A/RXBticQXiSgVWe3BhHQ6dguX7INY4WpnNrMmkDaaXqGGTxcyyFNOys8shbFMYgleEQQj+IBG/FcG1wXVEcQcpyRkjRqlZH0zrolOQNehXPly9WUtsZC5vQLOMu6QceUiqgtV1qj1BOVmukWy3nLyUoVOppPrUqrhPfWUnEX5e27RKKhrUfc36dWbfx5v31Y/hpC9uDcofKw1UROLKESSu1GysrN1tDzl76kZcQuLOLbz6SnduJS2Pdx4pyKvc+xkk820JmbLWWF+jIy1lp9QdyBxDuy/esiEyT+JrmZIBct6TftwfwGIymeAOyyVRK8JSk7SQWzabH9J+rrJnkuXUklW5Tp1USG4Lm8h+lQKrmqSdvN+4dpNllkhFrbqDNTb3y14bokD8FXpdaK1CuJAczfOkHXzjB6SycU3pz86i6AyIflZStEM6ewLqbGzYw9jDE4yNDRHEJr2+T6vZhKAHkS/qet+HyhCh7RIHftJmPRFqtttOznDWd/bFQH1L9KaRNQbpsJn9zpEjR46XHpcIGZsjx/eHfUhpjJsQxasmImrQZiKP7g4Sm1xDmrzy/wI/hhTmqrLZJUkf82rxvhW4BYmDjpBmH3WS7y6Q67kvfXikKiiFw8Ted3HlO36eN9wMf1bqssxpMPq4JfjK725l25TFE48VId4LPM5v/dY/54a3vJMzocXltoVhlHnivMn3jsf8zC0xH/7wZzl+fJ6R8Rl+/mO3ccPNLqOeS3FjVNpleHYWwyzwCzf/Kh9/7B9z7vROPvuZs/zB//Z1BoPbqDjrLC2ez7RzDultmeDTJe3gOXLkyJHjBZAdbKusrA+MgbUdyq+BG95B5Zrd7Ly8yv79LvVRj4dOFDm3VODMfI+5u48SHz9GPH+KcG0J+m0whkUlGvlgdiHuQbEMxXFRpfV7sG13krXbkeJcJpJGXChAMZk6LsTQWYP58wn3MA+Dk9B+GP6iwanhOvHkLuLp3bhbZwivniQOYuJmSHj5Ljg0AYcehpVF5FlRTfZVGc2kitQGSxOKqtU3ITLF3NRxwUuSvrs96A4SPiapdt5fE8I1SMiZMASvKnnelpluLlvoKEuiXlyFXjOiVQpqI8+0LNEKqbI1K24rsVnRmjVSVaZOWcssUaYKV+WflTBbS/72SGWpqqLVmmjZ/VNrhIvTx/U7WzLD+77Y7RbMzS6WyuPpI1wFuiVS7lnj0kqy3CpCONZ59RGyDeAUUoh3kpS4XgJOk562YSTSUgdU5d41ggoiWFlJinQlVgSx9g/1Fi6QEpuqzg7kEo+yc+UqCFVOTwvJZX2R9VrQ9102FwArXvTZyiyrfrHKc2o7s6rxNpsV5fVkmQCZSGl3YX0OaEHcFnXsRrWvZrKCrARcG6+zJVnfhWwBLz0A2ktVnmuxYQwxvAevPInn1nFtFzMKGXTX6bebxM0m+OtgRMkEkQ3NBnGnJduO9AQskzLZapb7fFAlrRYmVOOKrGG0QSopzonYHDlyvPzIydgcPzLwkEBsAiFYtXZCDSFFNc7WrDhIxwMe8ohuI+Tt15DH+x7EekC1MRosa4mMIrANuCH5/UryXRHxlC0iAfLSD2unc/wdIEQC0M0DctsZoljazuochME8pjdEfXKWt19tsGWfS3sdzi0VkBl+gxNzFbzjwyyZMfMnH4J4jbMrLY4v+txlv55OVwLFQX/A4UcfxSgcoBSfxPLXgREw6tzw7pDqdI2T9jauftM2Dj4NnZk2i5P7+Nbjb+PJe36PXms+084kON2oGAE4lgyAc+TIkSPH94mkItTo62HbFThjO6mM72bqpiuZOTjG8PYC3hCcfAhWHz1NZ7FPb30Aq204fQYWz8CgCWUHLB88L/FQLULgQ30E3KLcowMDGksQrkF/BXoNwJVCM7YF/jjQSdL52+AvA3UhcgEMH84fpt+dgU4Iqy1YWyDas5/KhItVcVnxi9DZKRXUT3swd4o0r1/TjLN+uHoMpBgOBVeMMeNIVLBRJNLOGFnGSH4X+PKKLbE40GpGtrm5GlI2f165GuVQLvZ9zQZqOhOecVLYlPKt61UlovIuyrppapPyLrrObEEuhQZ8mnmtNTJ1XZWL2j8AbwQGdvIUznp3ZlPPtfhYkuYewAY5u2rAoC8Z5I4FJUuabBqpHa2DPPE1Bi2Txq5aIyrj7Puqg49oI5XzLCN8pWo3PeRYDkg1mwC9MOH84uS06WWhIWGWmNdiE4qkn4XdZL2q1FCbDL2kstn9WaJW+5ma18Lmvp71jw3T7W00Xvuan1m/+su6mc8q/jeTv70AOiswWIWoCXFTPGKjJSQeHmQaC+nFlvWL1Q1mL8CLswwMOWjGEDglDLeKZXkYlSlMp0psOfQGAQw69DqrBN0G+CsyWxH32ej5YSgTQ5t2WHXNF8uPXwjKamf3SX+vB12vuIwFWI4cOXK8DMjJ2BzPAQ33Lo1ZwzJSw/gqRNG6gLRwCagbRc7FPSDemAvVuDubSAOpTdnfkO7hCGm9Ta0P2kfiJq3ieiMyl/oYqfvcvuQ7j5yMvbThI7qSbMBlYkQQdSKevD9m0D2J6Y1SHnkd123rcarvcviJde59cAUJ9w3+4ktH+cr938VwI56+/VOMT0YUvXVsq8vRB4dZXpGgtLU+4C8+/X/xla+9i0HrGH77PLAFzC38z+abmDq4nbvvg3/wQbh2h8fo3hK9d7yVlT+9jJOPfOoiMhbSQDjpxcUS2KUf9kHLkSNHjlcQTClIVRiC8lacA/8D5i2vpbxzgvFJl31bAnYN9WibXU6cMbn9v5vw4BFRk3nASB3CjqhY3SKMjEJgQ7kiQUbLkEJWQ6OALfnPmHD6CPSPQ3gOiS5GkGndEJleXiaNRmIwt2JNvYbYsInaTejOQbUISz1YOI3/dAX6RTx7Am+8TKfk0J8dA+cglErEq8uJ/YHGbhnfxU1VrwzxlXRdebVboogNIwgtkXNigRELURslUsIoYZeMgnxHnLJj2VpoGylHcUp82SRV3RHyS4teKRGVJU6fzRQ1Iq3opGpZJanUHnc0WbcWQzKe42+flLBV9k4Pl1bXGgArA2iu4ZoQDNeJbCe1JFBhnYrx1OIg4ZIiXwSKQQECC3ot4ewLLnimHAo9bCqElByaVLPoJU2pZpqc1Ti/0qGno46MAxZIbVYPIOKMEInwCsjxyjqJ2kA/EWBGgOVK947VwxWZX9A6dSBzKxuXSzJoiNpiW9BXr1f1NNMTly04p9JmtSBQSw5VXOu1oXyhugOouhZSwnWQeWVtXPvJAdFrQNUmJmKCu96BtTnwG3IPC9cguJAcwRapalTrFOiGO6QXojZOCUwlSruZ/y+CNY1hT0J5CLNWpeCYxHFMFET0eh0G3TZxvwm9JQhXEAmLSuF1BqWdhOjZ6nnfL0maJZJVzaseInqjcTe3fRNjniNHjhwvPXIyNsezQE20tJbpy+/p+z6k8NY44rM1hGaQ2dzi3EwwuI/5eJ1VJGhbQIY76ySTxGwO6J4gjdd3IkQvbBZyqB19hByNHck61cZsCnGZC4CHfni7nuPvBFPI2V1NPleolIeZGhvm/FNtgsFTBKvrHPneAm/6mT38jz91Fbd/9k/43le/ijgTxywe+S0Wj6Rr/I9/dAfvuPXNDBfgnifgf/r73+LksUWkp52nfeHPSXMfvwYRfOKX09/f8asAr6Ow+71417yd5hdu4pkB4WuQlLIFNq7DnVeCW5cLIUeOHDlyvAgMwfD7YP87MN75Hg5ePkR5RESgjZWIL/7Oafjet8UUtl6BqSGo9KSqT6cFjx4Rr1SvLJ+PJ/k4o30ol8VQsmKDG4IZQ8kEuwJ2GZYsWFeWTqOTHkLEdjY3MzrLxOveRn+lxcpdd0NnHqxVcBJT1JUQbjvKhcM3Ur3uWq780DUcesLFmR0nmrFpFWz4+pcgbiFRklr0NBDWqCrtNm0IYuj0pZy8HyTZvRYUbFH82qWEpYrFbFO5jSjZN89LgqQ48cRM5IcaSAGbqrN7ljRJa4r1klfWJ0qrXGUJK4fNKd91NntylpGZ8VEkWFOCSj0BLq7ipGpC5W40O1u3o+rY4zF89Rh87ndZowDv+Sdw/RXCAu40ZLvazjrpnGlWxBekJeSoSjdxbSgYibA24aoNQzapPLTyy2XpudQyu/FqUsaqfcMkEglpgv0qcDdpNYASKReqalkls8cL0g2aMdjDsNZFhOHJgewFyfxBmKhm1V9YBwMqBNWCcOqDoARsVqGaJeqbyOWtDVkiVa8mgtIN7tBFBhIDpB+OkRK02qfUUUAHJnodbbQzFp61sQCNM7D4FITzyUrWkXuPFuxSTw1trF6AF9ctCNggSzfMaz1gCIwxsKYwxsdwy2VM0yAmIKCHP+jAagOaaxCtJTuf+GhvmLtlK5VdjB+EHFUW/eLfqkJW90eZcZ1F0XFuTsjmyJHjpUdOxuZAHkxXA1fB1v0423cxvWUnbq3G3PwqzZMPwqO/j5TAeukeVg7iy6rDBxVAPAxcB2ynzAiTrNshNzkHeMyf457eGSAt5KUCiPJF63YRD9giYlXwDtI5YnUm0tqdy6Rx/wwSN80hoYWJkLkfAv47+aP80oTOfuts+y7A48L8It++52767Q7tdpvLr/sJDt78UUa3j/ET7yxQ9X8c06zynS//IpsrkZjAa5gpVRjzJHNzbRk+e9tvUC2EeBhYhNz5RMiJ0wPWmiG1EQs7gE4Pjjz2Tf76T/4xmNfza//qJ1laOc8ffOIDPHvvaSDDDi2Vq0FkblOQI0eOHC+MKhjXw8//K2a372JsdJjSUJGFc3D0M7fRO/Y40eJZaAfg1YVs9euieL33Tqk+HrSkCNf4AWiti6xusgrtFZy9E0zu383e/a/BrU/R6vXp9HoMgpDhkVEefPAQcWcFO+rSt016lKGzCIOWEJeHDsGFoxC0oVqGq95Ia/xGgngOti3DymEwffBPis1Bdw0Yhce+TGtuB4cWfo43/vyHWVwqsEqN0q1XsLDahCcOQUtJBhdRuSIet04FxreCZYMfQkMrCyX2A1Fiz2OVhZy1YymqMwiFiO4sgfEAjN8AoSPkbM8R31k/kII8g2Ty0HJEgWvb0A6haEluvjJnWpVelbFKcGar1MPmwllZBaKNELEa7KnITT01lXsKST1lteiXKhOVg9KCZC3gq8A3H4THvgx8Thpwx9/Ag6+HLT8H/+bNUDJStWKWFPNJCTwlgBNVZBjJabeTAlJBAAMDerY0dZQ03X4YmEWmkmeRbKxX25O/i9iQnSd1gtAMuBZCL8bJe62RtUJa+0p5+Y4PK31oNiEuSN06OzMCDv3EqrRDKp7U+RNIz2EhadA5Ui+zGjJQyVpXxJn32hcbpDWwssXudP1VUl7wHGKIq9eG+iNn+5gOWAaI/Lc5EPVp6zy0zyVq/PVkw+oXG5O6FGs+IKTyW+2wak4bJEc0Sv5vC5R2QnkE2yti2wX6gU+/25JJKCMk7q9DYw6CVYjUaqBFerH/MDIuVTKc9S/JGvDqgdbZHT0BWiZPnZnzUVyOHDleWuRk7IuGPnWzM4oekm5xaaTyvzCkgry0vQxGCdwylEYpVK+l6O2kMLuP0rbtTF0+RrXiMtadYnGLw9H1ZThpAkeRkDF8vg39rbCfNEtskjQ+t5CYZwl4EOhhcxNFHhocZ39hiuF4lMsMeDQ+s1GDU22VyHzW7CQfOAF8HgkRrkeCX5LPWr8zWwAA5KwPk9q/G0hsvwuJn7K1SXO83DDAOQCFMYgayQS8lHLbut3lplu38ef/992Egcn4xDCXXzHN9G6TU2fhyBMnOHf8YSSIzCIGLvCJ3/89vvKlCYIQTpyFyWmpf1JAsjefXoCVtYC+X8GrX88Nr309Rx/9a448+iVM0+Cqq7eyb5fFcLnH1bt8du6+kdvvOMTaelYp1WBz1YcQequS/5gjR44cr1hUkYHyKGzfgTUxQWlkmNHxUcpFE9MQTs9I0o9tU+pImcnnICG+Ilxse5bCGw9SciuEvYjFUwss3XYXraNHCFfmobsiPq1OCIVIKn0ffVLS8ycnoDQJgwaFmUm2bruO8YlhyhWHU48cwa972CWbhfYag5Uu1vAWInsE3zJortpY03vxu116rQ7h0iqYLoxMyrb8LhxfgaGCpP97ReiO0zsfEXVdKG8XMrS5Dv3Hod+AqA8swSAgXmrTe+BTnLh9nLFd1zLijdFte4zddIDV9WWCM3NSOAyQqlIDeZmh+L1GtuRsu2Vwk8I5pgVuFcZLYsNgm+DFMCiCH0HLhpYDgQkUwHHAsqSdJmJvENtS9AskBzw0Ew4mTjOe1XdTVamQKg81vNT5UyU8IeVZVHGo/pwl5NGuPMshhNjagQRoSpC5mXVm/WkhLQzfjIXMbnwH0z5MYaROf2WOkjuMXQyIvbMUWzGNgYGvorsgs66ssjfL7fQg6ELXhMCBwBU+3LbTXdLdcRDqLJsQ/mocsGUPZWLFu8lBVI+ZjspCUuGpH0PPF3F3aEotunBd7E0NJ7HeN+WSipVAVzsA7WdtoAZ2NenK2gDY7P6hBG4POXE6CFF16xoyQIiQW9s2njmpoP1UJwTUfiDrm6z1stYSyxC/J4UC+z3od6E3D/3lxH9aVahq3KCNUWmtNlA7sI+McLKeHYmtiV2HQgXcCoXSDLHtYFgmsRkTb/hx9KU94Tr4C4k6X2XEWkL5hzVeVpl7tnIayE0lK6NXewIHTJNKuUixWMD3m6w2TiH0fo4cOXK8dHg1Ptt/AGguSrbmaQ3x/lrmUiFjTVPi33CTz7mGdR5YoxAXEwf6YTBqUBjFKE9jjVyOU69THB6lWqtTn/KoezDhehTdbZw68h4Gc+dh0EHKj67/3bcfGXrtQo6uh8QsBcQXSlO1HMRmICBmHz5n/XPYsce0M8aV1R08sH6GNdIYSeN4tffSAggGQuzeTnoGdydtaCEhzApyhhtImKJFe3WutU8al+1NjkrGiirHyw4DapcDPvRVFSDmFZVSn+mJmO7aUaIooGBF1EoDZmddvnn7Eo89dITFc+oFoNGwRujzfP7zf8ZF+ZjPDnMUw3s7FSfiobs/ybmn78a2ba67doI4OIsRzrNne5mDV07z7XufZG3j0tLiAtkLOoL2Cgxyyj9HjhyvFLhCCJYrOOUKpYKHY49RsCexnS1w8CD29u3UtsywZccsIzULyzCEjDUT0ZgFrilcYIAIM6Pk1lxwwC1JjazlC+GwKCoAACAASURBVB16Z9r0W09RGjbpeqM02wVCO3mquxZmyaEWBFSu3oU3O0JYNHn68QeoXbmDbTffxLYd26lEEX5hlE63QdMPmW+0WDq1wJ7XT1AcqgM2Z053KQ6NEbkBftgm6IWYng2lGpQNorVFKI+DM5ZUGDJh1cA3egm3UIdiDM0KxPOkJUqT+/+gAWe/wbEvH2DiIzPUZ8ZYiEymr52he2SWoNmE9jJpqrGdELAO9LqJH2yiVDURgnYjZAzAtySfvmgI6QrgeqKsHVSFyHUKcvC10pSRFJhU8khZxrVEDqomqVppNSteU0noxWRXVtymAr0WsJTYPkQTULdlnSqbfDTZ7ghpgfhsFnM2m1nb5EvNtKIP5XAOamcwjHXs3hbmGvOUhyaobxujul+aeqQP6wXwtWCYbiPrG5p9BRC2Ez1iWQ6/WxSyUAdjGlMq56buv8rDaZNfLZ6xFkKd1ZGY3CH11i2SugSYyDlRMla7Sz8E35Zu6SUWFCYycWNbiV9stliEzl1osYkOmDPgDksWVNglPUHZPqXCTBWBOqTcZxMZbJwlVWLPJtvR/pL1nIWUu9TPSgL3YljzYaEnNzQ64DdFaR92YLAgatRYfWHVPVcltd3MZ/XyyJKxaqKczIyYVSFivUnwalDyKBRrxFFEFIWEQV/i0X5f2tNXBe4ymz1IskW/fljIVgdUIrlAKmm2sNwKpcokxeIwBcejYEdUizbt1hJrjRXinIzNkSPHS4ycjH1R8JAgeDH5PIwkDu0EHuf7q/L4w0OlCgXHYHkxOxVfBLaAdZmkwAV+krpWlFnVToc4aNDrnqTXqOCtGQQDm6mZCu0iGEUDP6wwvX8/Z47dQDS3LOkwPP533n4PeCvyyK4jR9gFrkDsAapIrPM24I+Bw6zzKOtcSYnbg+NcMVPknduv4Zq77uKv2RyseaQhiYsobjtIyLAC/BUSOlyVbG8Mmcg+hUxmW0h8pZ6zaiumGUIxkkI2R1ouKsclAAOMXfuIj/0VNLN9do17v3En996+AtEXADh36gKP3neKbQf28se//xfUyrDz4DUcvvcriGShipz1C8k61MXtBSYmomXizp9z26f/fOO/TNPgsstHuOPu21g69zSDlS5f/7OTNDc6jk0arS+Tjk5dWF4HKydjc+TI8aMMI/lngLETdlxP4brXM3PTLVw7tZ+tYwUmxmF8CrATIipRUXpJzZlsXSgXIWmUkLGRLHLvoq0GlOi8aw9nP/ovefoEPPLIInd96ylWnjwKh56CeonSjVdy69vfxi1vMdhfgtUnjvNT/+C/se8DH8EpDXG2EbN4wcAubsGpzVCKoNsM4Mgi73qfx+Q+h9Ue3PWdMhdOQuQ6BJ7NnOlRnvIwQggaa3TOr8Lea6X1fR8aqzA3J63vD2B5BXprsBZIga7hLbD46c07FEfw6Gcw3/VOirNXMDkEV18O5w/O0l45C+cWkOfHKNCCeBW6XSiOQtARv9hBH8IWG6nKiwGc3AnTe6FSAyeRfGq104IBhaSIpIkUNdP0f9cQI9QWEoD1EwI2MMQsFdLHmab2F9hs+KnSR/XnVKK2TCpyi4GldXj6DyH+RbCH5LdaG2gPqfGqEmwqs2yT1vIpJu1ORIKeAwfeAK91ryQ4vkjnvM/KnM3CUwZeocPlu6u8/UM3c6FmYHZijlkGF0qk6t6s0lGFh8pHkSyXFDCwbSEEK2Ya76rsI8j8xGGzYPjVBAeYRmJ2jcHVvUITyzukfrIhYp1qIiO10JP/K8VynOdrUHSkK1qJbXLRkZpXvnKIIH0iucFUpqDkiIC+v55s+CTpIANkMNDP/O2TWrQ2EUXHCqIqUUVHItDEIFXU6sDkqWS99WRn5+LErSqE9QVYOgrMIz1DNwypMa2m6WfNkRVatEuraWgH7SDxrQPsAXMHlCbkJuy6YJoYYYhdsnFsC7/fZ73RhZWVpDCXngVV5cJLP22gNxe9UWieZQGMIerbruS617+Ny664nqmRWe66/a8I185y4cxDxDRe4rbmyJEjR07Gvkio6TiIi+kY8qh/iM1eki8fJkoGv/7rP8011+zmoz/7O3zv9Dph7CBPexfCC7BWkvQxzaUyS6KS7cZS5jUI6HOcVafPyScrbN8+QVg28IGxIQN/aDdLSwcY9PVhe3HV9789AuCDSAaP1kPI2jcBvAHYT505Yk6zziodrsWGs0e5f2mOn736vZw7fCdP99sbPlKawnRxRpoiBu5F4p+twC1I4Ke2ZUvJek6T1vokWXYieRWAy5LvczL20oBhmBy8+f2cbHyPtRUlY5ORWXwM4pMbyx554l5OHG3z3z61RqtzgHByhJbrAe9FHMu85HUQMcrQPLIsssMmTTB8JkwDrpiyufe2JosnmjhGzL2nINgQ2VtI1K5eXQoX5hZ59ehicuTI8YrD2NsZeu272Pnj7+PdbxphsmZhmTZ+UGC5adNZsqiUoFiBSkXqZkEiOothtQtrTZkXjsyEjA2hVICSK0TLtCeCzgrCYagHp9bmmQVu3g7/cHaU3jtey1J4PefnQmLXZGjI4g0lA68Av3c//MHdFdhzC/fddRj3SJvK5DQT0+N4U2VOHTlOY7FBvx3AlqtxnBLDQN0F/3XwpXm4MA+9pkF1yqN9fIHhXVW8nTU69k1w9AmoD0HNEJsCbDEhX1iAufPyUIht8W91psD9ceh/hc1Kswbfve3LbFvwuO5tb+ZbX1ggDlxKE7N0xnfB4j3I80RlqqvQuA/oStWijdJRkBI3DZg/BIYHZhFKZVisiXo3RNYV2GJdEAOeC0PlRGEYQq8Hs+XUhD+rQlVCUplzTSnSVO2sj6zW2FHBW4W0QtPIEIx+DEpeWnNWkdjkbigVC5nve8k6smrEGhQ8mKzDj2+DL/7qJ1h57E6GnDZvftsb2PmxX+DQI0c48fgDfPLf/nM+8i/+He+ubedY6PHYAizMwFwJgoKotb2CZI5HqhBWctaUumfDVeGpNUpX0YDGlgWE+x4jTRx/NU/Baly9ihybCiKHeQyJy48lf+eRe4QKqm0Dlvvyf54JlSE5/rEpQvCgD61liOYRwrSNnKfEPtQwoOJAayC2yXRI+5Ka1J5BTpIOUvRyGidVjOvlZSa/aSE3pGEwqhCfzazXQ078qaRNA4Rh9hfACsBog+PBwCa1IVDW/+KYM2s7oBeYOuqCXGwOIi7YCVTBHIXaKNSHoVbDKzgYkY8RR1h2TG/tAq35E8TdZeK4BdEKQuKqNCUbs74UHqyqhfZJY+OMF4nhMTSxlR/7mX/KL/+v13GmV+Lhww2+8bnP8+0v/jahP0cUabW1HDly5HhpkZOxzwvNPaoj2swDCAkzR1qr89KwKHjPu2+mtXCGo/fP80//2ftZLW7ljz57Dw88cBy6Z4FRiKt4tWHGt0/zznfdwrV7d1P2Siws9fjX//keOksxcT9k0OmwcuE027eM0V03CYFqwaA0UsYq9JHIee1v1V5NNXo20lJjaEhrLGgCjSpRoYtJTITEK1dSxIoiWr1VbjvzGAt+nyYyCFNFrNpA+aQDtCYpAiTu0VqbNdLST2cz32nGGaRJPhFCT6s1vsWrU8VwaaEAxiTTO2aYL9msPQtxalhjVLe9jajfxx/UCAYl+r0YjA6dxhOYxhmEEO2wOZ9MidiLr38NBNXs69kRx9DpwtpKTLsR43hZIlZ/f4pUYqEoJoHvpTEJlCNHjhwvjGEY24N17Zt44+uuZGxyK9XZLVR3bKNed6kOGziWOCBZbszj8wHnnl5mcLiF59ost5fwWw2CXhs/6OEPIgZ9iOKY2IoxPBfHtnBdG9ct4Bkmw2WPq3bvZufMFvwwptXsUHNcRmo2U9PQCkUp57kmFdekR4GZgpA0tg1HYzh9Fg41QvqWw/Ce17K2NmBiZprx6QnckkdjvU8/sglbXaKnT8GNlxFaNscX4dQijG+H3VdCZRg6LYPZbTEPRzUmdhaojZlMzBS4UN1GoeDS68WsLFSkiJi9AxYn4WgZHvkaUBVV7OgkrLShdCsMnoLgPPJ8KOHPN3C6i+y6wmDFrzHcNZjrVjl9rASLPjKlXEOin04iM9YoJSZNildCI4S4klhbFaFTh/6SVD9S1ihyknR/Q8xQB8vCjmOB5UHTEcLWMFORXt8XA8/AhF4E3Q50e6LQNUyxQYgNMfwNgqSugSMSUhNRvvp9CJPIa6wuAZtP6iGrPExSHoEaqb2BzsJrobB++tuJWbi8BgcseMMbruGh9SNcOPYw37r964xtn6bXaNJdXuVM4yn+9Hc+xjU3v5mFXpHTC1C45R8x/OYyrRGLrpXEhdkwQInYMlQ9GDLTppikGsVsYnVMmo+3gkz+z/DqHLhpbQYv+TuS/N2BxOdF5JQ6QN1IE9YHQNFOphgMIWcHfuIKgliZxAEpH6nkaQdoQ9yHxprEZ2G279SSlatOR1UacfJ/Y/L7DcPfmDStTm02VoG6XGYbKlkVuY4gIaDuSIRkNRYC8DsQdcCMIOohI5kWqRmzjlRUru0lG1W638n8fwmsCbnOHFcK7kU2uI4Y64YRvtHF8oWN9lcXCP1HibqLYouwMQrq8/KNhy8SLGwIJzzAgNins77AvV/5Iv/H6W/T9NdYWlng3PET9LvHieOLZ4xy5MiR46XDq/GZ/iKgTz8DeXLWgS1ImnIPCYsGz/nrvz00moTUhOj5sf+y7Zw+9jBPPrrIBz/wfmZ3DPOavZMszS9w6tgcbrHGnh2zbNm9k+1X7uTmN+1gz9gIO2Zn6PkOv/Vn36W7FBCHMdHAp9taI+z59AYxIVAux1TGh7AKJikt+oOhjEwIjyRrKZPWaVhHhgxKnhYQBYuqArQwbocBPTYetUlmW0Qj8nli+TQXkDhIwxKlzVSE4ZDWf8hCLQaOIWljVeTxvEBaCDWLbCba+cw+5bgUUMKwDjC7tcqTJTX0ysCog7UL0x6DoIlhBWCugNGEqEHQPQTRqe9zm9rLDFJ/Py3ztjnQa6+1abYj1tQU7hnrWXmW9VeQHtb+PtuVI0eOHC8hDAe8Ccb276dam8TZdhmFm97FdW++lplRk2LCPK2vwfJcn9Dv0O92WGkOOPFIgwunzrK+vAwhzPfWGKzME7VXpUBMbAqbQghWCEM1rIqHXfQouC6uYVMplQg7Ft2uS+TDhcUVXMdhZNhmR8ukHzmMVirUPIeKY9F3RFVrmJK6vBTA6QDcasxlO1x6xX0cO9VgdGyCaqVKbxDQaoVEVgnTdKDbwauUMSyTTggrAxiNYcs2qNek2bOTBivLRcp1EZqWqwZBf4RCAOtrEY2OR2wURVbrFkSy98gpRLa5TQxGIwuMEVI9ZZLI3eoQdxrErsHYbIn6APoLRU7XSlCZhHYv8ZFUuk8LU2qsqdWrNGqCNNbz5KAEyHaNCjhlsBLpYBxJBaRuU9rkFMErScEuEyAWcnUQSlGD0IYoOX/tQUKuJmnVAzuZjY+kWpJV3Px87AKrvhRZMwNpR80SGwRNfcqahhaQAFFFe93k/1WJmxyCagn2FuGqCoxEsG/fdpYfm6Fx+hCHHz/EZHMVK7RoN9usLS9y/zf/Gmewxmq3QGPBZGftKuzLrsYsFAmq4lO6we+ofaUtFrteQZqVba7Gqdma77q7a8lujL3wVfeKhWbJqZK4RFpPYgqJzwtIHL5KYl9iJFMLvnS3qCDWBL12YvNqpo4Xmwq7QeoZ2xd7AgzkklGLVbUhHZD6I+tvVd2qyo4SqWuA9skewrTrdnukBcCyhemyB8APpNpY2BUylgGyh8rgZitjZCtmKL3vJr9JrnnTg8o0WNNiQ+DppImfMNRyTYfROnHQhs4qUeM08CSp9+zLjexYGdKCXdkTGTHornL0kXs4+oiF6KfV0zZHjhw5Xl7kZOyzIms0pRUFDOCTvDQzf8PIw0SrHCw/79KmCf2gx6MnQx56YJFHH/l/2D4ZcuNr38jI67bwX06dYGbrML/0Cx/hjW+8iakdI/zN1/+Sj//hF3n7m2/ljbe8lYIxwECmfo3Ax4oNmssduqHBII7xmwZbt89SKI4jhNAzyaUXix1Ika4phBjdgRzpBYQEvTdZrpns+U+SWodp7BIhZ2YKtQhoch5xsn2IzX74WqDXStbRIc38eTZESMJNi3Re+dloMZI2ryD2US3SRMBLIUR5dcMAcxyz+G4O7LO5r/Isi1hTxPYVrB79EyR817OmMoSL1rfR55+v3yvtP4LkqF0AGmAUIe5s/DaOI9pzp1kddDnjw5kXLXSdII3Wc+TIkeMSg1nAsExMbxJz5v287jd/myuvKTIxmlgOdaFYhIIVgx9zdiniyMMXePrp45w+c4yFhQV44ilYmoNOUj5zcgesLUGvA9jgDgmrokZCW4YIJ8YJy0V8zyGybcyuy/njDrQbDPoGS0uLBEEf04Ci4+B5Y8zseA0jkxOMjnvMjMbsnzJxXIMAA8eEgzvgwA6bTs/m7Mkid1TqNH2btUbI0mKLZgBGcQh7dAprepmp0SpFy2B8EuqTQleUYthZFf9aO4bBzXDsFKw0hJQbqYuotNc2sTEIAp+4CXSNhBB5VI7rahWCMsSL0D6EZGjZYO6BaD8MVliZn+ehB2LqkzAxZrAyVoDyCOx8Kxy5G/oN5NkxlPweUjJDzVM19u0gLJJW4UoeokZR8vlHkwR6PxaSKOhL6XrThVIVRodk+RDoBZLn3WomBcAM8eohBCwoVkX5irWhIMVIimMaTlr4y4yTR3CYvla7MFEWr1oVBipZpoRaYm+7wTdrylXi0GCOwGW74NZZuKkqXFTU7zA2NsT09BRPPHmIU8fOYBomhmFgWRZhGHLv3Q8DAcWKxf7VP6X/1E5s3yWcNlmuJ6dP7RUsJAO8IIdU408tPqWHaoBM4yr5WEMiiRlge+ZsvZqQqX+GSZrhplrPHUjv7SJjhHtiiejKhpzu1cVE7DkElaLUmwojMG0ol6WLxZpdn7U6VY80vVTaCDPuZhqg9hjZwUYJ6X8jmff1pHFqct1D7A3WEAZZT6wmQykzr8JTC1GtBj0IBhB1k8Yq8Wog16ydWdnGDzOvJC/QLIIzDfv2yORIHAprbRtyk+6tQmcJ1s/A8pNEsY52LjUTNpUd6wSSCqk0e7VMekx0LL1OeqO4NLJbc+TI8epFTsY+JwzEMn4FmQV8ipfspl0eSvzBbDFCO7fCcxFARc/guoNFTh+5i8Zii21bJ/j3H3s/v/YvP8XSrja7927j//yVD3PLGz7M17/7BJ/6zCHKZZewU2RnbYqZ+jBBr835+78Exg3Q94l6fTqtDudcKBbLuE4J263ieUOY5jxCQf5gRGwRuIESu4kp0OUA8DQS68TA/cDnk2VVk6x1OAdInNMmVcT2kUyeDmmYkAwBNizHqsiZ1ESeFYSMfaE9aPPi9IcBqd1Bbv9+icC+kfLW97D/7/88O8cLlJxnWSY4B8FdPHOyQ6/zISS6XuSFSdgsXOBacK6F8HbswgLVrb/E6vHfIY7mgT5RGHL3N77O6kpzI35vPf9KkR4/CxzmuacHcuTIkePlgAlU4QP/hpvecStXX7eHySmLkckCA0OErBaw1IQjD8OZU02OnjjH4e98i/joI0Rrc8TdhlQL756FeJ0NtdeFVmYbbuLc4kgZ+oIlt+lmR9SbYYRd97CB5cUzhIMOk5Oz2HYPz7OJopBWa5FWd5WAZS7MeYBFGAYcvOJ6Rmam8Oo1+iuw5zIYqsC4B7v2w+v3unznBDx4zOfhRkCj16PfiXHGRtm2//3suRx65ST7PYb5Liychp2jsGdCptm9KoxvkebPH4GKJfW0+qGIPLdu8zi/Cr3KMBSugq/+pKQPd+tSgHX2RlgeBiOAWg32HYRD52H9PlbWetz3xBof2VVnagLW925l/KYpWn5Ab7FDvPgIhAtyTBkhZX76pMaWSg8qmaEJ4l3AhjhRzg6Np//dQ459qydGnJaVkp4q3iOWImFOUWJbK2Gw6l4yzxlDGMqoZEOcWxDPCK1cH8SwuiakbNmDgg12WQKvrAo2WxBMZ+E1hVxHPYnvlFuBG26EX5qGXQVp8lkr5quf+yxm8zy1WoH3f+i93HPb3ey/4iDbd+xkeGSEj//hfyKO15ganWXPzn2M2U0mmt/i1LnrMPu7Wbsi2W2d401200ma4CPx5Qyp3CPp1Rtk4xBSP2EMIWVfOEZ4ZUId+OdJi+SqTOUnEa/YR5CRyTrC9ZdIu4BBwl+2wLMS4jWAaCC3jaxCeuN91jNiGhlkqH3BYtIA1e0ofNITCyn/qf1R0/WyxbsgZeCVT9RJBN2BkEw9rmxHtklz/NTOSvdYG6fy7ESeUt4iMvBiSSZN7CqUa+BY4JgUymX88w/CuUdg/j6IH02OdMSlkcavJ6WafFZZcoxcIRXkihlG2q33NgAPA494o4pIkx9ulmuOHDlyvDByMvZZMQ1cB3yFZ7qEvgSwoDo+guHatHtLEssVC9SGi4yPFSEaYA16WAOfihmzt27TO7PGgXEPswB/+fmv8Z73TrB1zGJqCCamJjl/9in2bh+lPnEV41u28d17/j+uuvYtOLVxnjyzItPG+BCtiweRbbO6fB5rfBrbKNDv9jk3N6Bf3ALVvdBcAM5937vWB4rWKBEhZyKft4y9jocbDzEIWkwirryJbz414Abksaq+rB2SAU2yzDpwHAnS1BtWi27pGVtLlmuTBrOXQkiR4+8KDtSuorb9Zt71wbfzxussSs4QrcE4j11wWJ+HwbN6R6zx/KYSLVLNSpU0Dey5MbnjfQxPvY8nv3Mc/DWIO4TxgNa508SJ1+tovcq1e3YwXr9AwZYh2ItXu2i+ZW5TkCNHjksA7m68q9/G2E23cst1oxS372N6yyhDo0VCG7p9WFqClUW4cD7gyCP30FtepbfapL20QvD0ETh/BLrLELYTE8dV5H6rpptrpKwGbMgNHRdqVSESuj1otoguhHRGyphTMxhhhyiwMIwCnX4bI5JBexwFhOGAMAxwHIeC4xIEAYeeegjjqDAoW2Z2YnuXsXPWpTQKBdugYML1W2DnsM01++vccbjKkxdgdWDRt23cEehaMok8YcCKC6OjMN+G5afhhp2yB3EgHPKuvRD24NxhCJc7FBoNdl4xw/KpZXqNJjTPAt+EKz8G41dCaQz6fThak+pQBQ/6szA+AQdeSzA2TGc14NTZpPhZzeSqqx08r8Cdc7fQ+p4DRx8jVdBl83gGpM73Iakppp0uY1TBroDjQGsNuo6YaRomVIvgu+AnzLIRStpzHIFliAeEMw2mBbaZmHeSZBEH4n9ZSiwKlIyNgChZv6Jggh0l1ZkQRWyP1PNKCViPjfq1z/mALUF5An5iArbZsqoohqIJc/PzjJgdpreNceCqa4jXIoIYuv02TsviA+/9EPMX5igWi0yMj9FqrTK0fIJRZ5q93gSNk1XOWkkBr8R5LI5FjWnYaayq1JJmchWT9+1kN+ZJY98CMjKxnrEjr1zolEATOSbzyLHoI2OFbyLWZqqKDRAVuhq8WUCxDgzk+BctCCrQHyRZ/6F00Y1LIZvdnnCepWHomf8/e28eLdt113d+9plrrlt3nt48j5IlPUmWZFmDB3nAgI3tQJqGNkMDph3SaSDQWawsQhZxx+lOQndWmGKcBAgdOmCEYQVLNrYlWdZga3pPb353eHe+t+rWeKrOsPuPffatek+S9TRgyVZ91zqr5jPX3r/93d/f96duxS2f4V4HKrPnN1Gy4YhuxryD4ggH6Ra+cOmqaZ1k0XYI+nZP0S1N4gBhTlmNRL3+BZqY1XdOIr3e2jHJVoan6cL4pPJssGywXGXzkk2+1yoTnvwqbN4P9dMgF5Iz/3ed66fJ1N7iWzbd9l+flF4DO+iWZnZBZEhP7OXEvR9l265JUqmYP/vjLxKtnyf0G4TtNoFfJep0iOIYeYXWWs/2vFkI5z6+u6BjEyd5XuOlx4qvPqu4j+9d9MnYKzCC0lBqZ6ZeSu87iDhUAZsIMVob7DkyjmG0MAUYRPhhjCskWRcGXBhMS9Y3A4pFl7YMefiJFX72xv3smh5kuDRAKmPyt1/+FpFV5OjNOW7atYtvnXyI7bu38dTJGb5w/wOoDqmlfL9khCreEGDIDpYIsI2IVm2d7ECRtNyJU10nqsWs1lcJ429PUF1xaMAcESEREkFbZhk0i8g4ohW32IuKR1xUatb1KLfeNoJ1oIqkTDfLZwU1K64VqTphpXcuVAdlAap51JPVOtbv47sRLrYzwMETdzAxmiE7eJjBbTdy1313cPNRA9cWLKzA0oOSxx8+R3m9V1mlE9r0XfHiyBancdNDBH6dankZwx7GcjI4bopSaZjCUI5ImtSbamA9d+o0Xu4mCqM3AedAXgAqyLhD0ExSSjHIptPs3rmD2XPz+IG8RldoDZ3A2DfC6KOPPt4gOEXM/BSTx48zPL4D9/AdZI/fwo4jBUby4KWUPeilJUl5xWd5oc7aYpOVmSqzF89BYwOadajVoFGBTg3CKkRVui7svQUSk5gEUIOeCMw4Gf9oz1JDMSyNOmFrA990kbmIuBNhGoJAhsRhDHGMEJIoNvH9Jo7jkE6nEYbB4vIszZUVOpVNzNvvxclkMONBjDDDyJhLzoDhNAykDYqDLhJVnX2momxMMwOQtxTnMiBgwILYg7VNxRVvyoRIkirjeGwImk249OAMjacvEFbOI49+DNlpw9p5uPQlYAF3504ib4IwcCBfhFNPQ2dTqWOdIaAM2e2QzhMGkkoFOm1IuYLxUUE6DYNHpgnn1vAvbEB0iSsZT+gq6nrJD9GzBEAVZBmis1D9W3Ut4gI4k5C9FTIGdIRSNwdRQpzqakqGIo/DSBGvAjANlS8uI/UYJduyDPVZKKEdKkUwQn3u2Oram0IpcFPJYTg9h6BTzNN0yVhNtunZ+hKMTsOx3XDQUwSegVJwFxAcXIj3RQAAIABJREFUOH4dYnOOwmCKifEp9h87yOLiEmG7gykiTtx8I/MLS4RRgGlK1sqLhM0yaX+JyfYCe1dLBNYgZc/Az6K67o46dJ1qr7NitBpWO9v31v1aTd7voCg1n67rwVsBukaWFmBr21+tmz+JUhBn6Toca8tWnT1np5TeJA7VbZhKvKFFCEGgrkkYKGJ2C/rCiMRaQp907YHWC5Mr3QL0Rey1b9UTBPqvZXPlpIEBW4MbB3WvenTtNqQA21H3vIGa7JBaKKQV7XpjvceRBZFR3suOB/kM+B3VZsa+er5ah7AMjVnkwqPQfhQ1MfN6VcDQJ+hqYlUTx3oCSMPoWfRv9J/b7PksA2YWNzNKcXQfu2+7lRs/cDfjk0PE7Salh1bxLQN/cw2/tkkcGUhZJw5iZKxZc+0FoZc+UdbHq4H2OemTrX28cvTJWGAreci4How7Qa5D9F94w/5QnSadZll1lGszvOPjd5JqnmfhzBrPPtFgs2NQygvsnCSbh7QXYY2b2GnJaiPmUstGtvJs276LsYkhVjYqfOOhRzk3v8GmL7nrgx8izrpgCL756Nf5kz/4XYoDuxFIglAQCpMo41DMeaTdmLzboZSBpdYspak02Ynd5DvQOmvxyIVH2PSrr+hMPRytsxc4IQSzG4sc9UrMyIjnO60t/9hhlD55FNiOIMTEBS4Q8ixJYVFUypLWL+qbWdsa9A7fdFeuHYI81NxVn4z97oKwU3iui2UNMTB4hB/+h/+ed92eZ7poMmBfWfSijEREEX/6x3/Fxuwi3dn2IWAJISKE4SBljG3ZyT0sMG0Tv9licPIWBsduoLY2T73yWazUYVLFgwwMjnP0+A0cvGEXfpxnZsEin7X5i3/7r4iZIjIiDOsycajTuzyUnqMItHFTKUoTU/yn/1alGUVbYooudKD5IpMcRlFVsO6jjz76+E7DTuO4DubQYdL738etv/iPufltghjYbEGjI7EsCMOY9fWIp74RcebkMusrc/gbl2FtDjIhdJpqCRqqCJSD8hyNdInO3oiit0BLCCLptV0BTpLPGwiwM0rtFQNrC/hWmmAgoFMIMQjBsoiDgDgMiaKI2HSxLIHnuUgZkslk2NyssHHmKfwLZxndsYvQlvjV3dQr2ziQL7HHM7FNpZAdMuDe3TA8BqfW4cwS5Adhp6lilzTKVKaRcIaxqQikcgRNU9XiKhVU1n5w8VvUH/4irDzC+ol7CUUKVp+FR34bgMzENP5CSHhxHo5tg8XT4D8HQyNQ+ghcmIFqGTwTmcnRaoIIJZ4tyLrKE3N6V5bOxDiLme1QnaVr/qSVc1m6VYM0OaJlpjGwjiXLOOEsTngGo6Xd/Q8Su3fTzu6lNZhVLHyckKiWqchYSMifMCFek+tquapEfRwq2WEtUeLmHdVVhyi2LGolxJMDVkqt0zDUic3R9e7M9NwqNt1UcL0uvXTA2g3HjsPHjigNsL7jbJSy+eOf+ElOP/4AnfUFHNNm2/5dGJakUdnExmTv4R2MbZtmo1JmdX2J0PCJow5euMRQ6GFXS8joJk4VHZachFKKu5yeNn/QlqO6Fn2Tbs9v0S1MpTPb63T1V9/L0NdD24U1k8cMKqrSuUFzqNoRedT5qqHOrS5vV0ZxmNiJE4YAzwVhKotUpPJubhrQNpMNaT+JRLkRaQJf/2U00ap5Qv0X0RdWk7XaK00PPPRARFsbGHQLfNGzDk3G6kplunyIMJNJiFgVr4t6yVgtMUnuHiHUkh8GK60mQtIppRyQIbRbaiaoVoaly9A+DfJZVOWO1zr27SWE9UFqiW/vay0u0BNDvVJjfTJ619NjwCxcDGMUIz3OwLZjHLrtfXzgEzcxcUDQrEkuPmtQLE6w2dkgjKRS65ttpB2rCxqHyfb1RdfmIH0yrY9XCs02tF/ui/TvrT5eDH0yFlDkzJ0w8Y9g9x6o/zU88Zk3bnc6i7TmFrde/ufPPsjtxzOUyzGX2iYfunuau24cIWpssrK4zOJmlXfdfJjt4wVSboqPvMPipuPXs16vsrRaY3BqB3t22vyzT/8iu4/fg3A8/t57fhSAT33qp/m5n/8J1psWngePfH2Rh79+mWdPzWCFIfkMDA/bbNtZZHURUikHGVk0NzvMs8b2xRzz7Rbr8tq1fRu0aVgFCu44YWOe0Bxgj5TsRnABSYqu2GEN+EskdULWgbN0g1OBunJZVBOovfW1albXBYauj2wf370Qlsfwe3+NT/74x3nn9RMcmzbJGeJFMxBjoBmEzK+W2Xj00wRt7XPcRmlNAnLDtzC04wdpVNa44+Z7CHDwDZMb7rmRf/OPf4WZMw8x89xjwB6gTmfzL+hsPsjmzDCXvjnL/Z+dAvMYZuZO9t72XlrN38Ws30KtPsH0HT/K/MNrRO1nUEW8Hug5EAesoa3SCy880F0gpiH+0gs/m94F67m3rnlcH3308cbAcuED/5zv+7GPcOy6MaYmBAt1QeRBO1DD2Noa/N79DebmZikvXETOPKsG/o6hSFezDRUf2o1E7RhAWAMjUUu+gIjVBWd89ZllQdaDlKVSbk0TrAgsDzwXozSMuXc/REcJ6nUiaREEEfVaHcu2cEwTCwkyoFwpUygWAIGUTdYqNRwchqb3IEYmsSxo1la51GqyvDLPucs72LH3CNv2WowNq4liDziYhrwJmTTMVyBdgG22KlI6CAxlYSijTJ18YHkBSmkopGGtqY741h//PnYe2MOpv97Jgeu3Mf+NgGYQoyIg2DhzBswhSFfgkYcgOAk8A/YuGM7BjcehWYOwCUGK+lrI6qxFKquEqtntsH0cyjfuZrGehvv/Jjm/WjqaRrGa2p1zA2UIZaJc/Z8BvsIdwA8h+X5UHhlAk1PMtZ/n/ku/w69d+hV8rgcxqSYOn02YJxmpgkNmCG6mR2qYpHMGPgSdpEP0oJFTufydCKIy3VwnS90PqQxkUirnvJic6Fyyu6ts+cGynhyel+ywwxbnc+M+uG0SjtEVLOo7sA1M7xpB+EfZmElTqaxQyLi0hgcIgzbrSyssra0xNrWPyMmw2YoZcjJgmThFG9w6Q6HDvqwkyKuaZwuCLRt6zbd5yTnsVclmkisggeOoGHcImEbZdukE7bcCQtSl1MssKs5fRl3mJupczqHOZ4PuXeKgzmUFdc58oC0gFMotWQDNGFpJ5V0zDa4DHVep3eOEs4vayXdqdP0RLNSMS4fuIEPbtuobyKd7sVp0a8T2ViOzuNJP4QJqEBPSvW89uhylD7gmRC5EeUiNQHNDtbEiVqa4oNTjnquqkw0Uu8SsKcH3odWA8iysPg/MA8+i/vPdIrOvHgaq7ei1QdGSYv08lxyMrqyrdc/aiPfqu7y3QFcBrEHITTG1992MTx5hdNsuth/dwYdvUHUB//KxBn/5JyvI1bOE1QqGkLgZh3Y9JKqrmg0vju+wJWEf36XQk5R6skBPNPTRx6vDy5KxQojfBz4ArEgpjyTvlYD/gipieQn4qJSyLIQQwL8G3odq1X9MSvnk382uv144hNIvNCGqwTskbBrwxBu9X134VRgeHWN0uI0dLTBil1ld3OBbZwO+8UyHdBTzY+/fTru6zMWFC8wtNPirP/8W0zvh4PHdjI5P8JEPv5+xfe/BSI8QNZ5jcW6NkZ034ngZqutlfuvT/zdvu/km9uzbz8/86GGarT0IKTlzssLKsk8nrjA8bkInRAbgkqE6XGDv/mk6lwLWl1Ze0TGdD+v8QXyJE4Tsa7SY9vKMDOxiR/k863QnmBvAQ8ljr9hBTzhD16FlM3l/B+rm8+haN9XoQlNy/abzuwEl3v39/5Bb334LNx4vMLR9kqmRQQppi7QprtBM9dbmAGj7LS5fOk0c69RXDdVxNjYu0258kSh6igfWn0CSJkbw9FdsmisPQ1hJfrfS8/sWsAAyRrIJ4SXCmsHFhz5Lp+Gz6Zk05+aILj9O1DlHdvpe7Mwg5ef/9dbWTcMn7VwGJLmsQxxLGs1kMsOaZO/eW9gxdTN/8zcDqEray2zpPbYNg+/1ydg++ujjOwAL3vETjN/4Dm68bi/m0DRjewZwCyaeCfuycLoKpy7Amed9Zk6dof78WToby8iW8szGDBPlqgkZC8obUKkotsMyFalq5cAo0JWeJT20EKrT7yRStCiG2jrEaUglik7hohnhuFNGik2sbBrLUYWoBCbtSNKslxHtNo5tkx9W/gABEWEcgFUiLSW1cpkgjBGmjVOtYgWCVDom6EjaoUndd1irTDK1vcC+gzAp1OC/5MDBArghhKZqrVsovmZDKGJoFJXJs2EosWfLhLEcPP0E5BYFhKMUd9yBNS0QX/ahHoMzCtf/EoweVSq2yhLMPAkn3g8jPwUDU4oFbrZUiXjHRuZd5k8+TiEaYWC0RG5sgP0jUEzBpR0CtuleM0s30tLskc7jD1ClUZ9A9X+KpLkJOIIiB/UwNA3sRPI/0GEXv82D7Ocbcj9PRMeBwz3bQBnk+l73utkpxXZFTZUJpver3QHDVanV0gSSqmgykZZaiWwxoFuNtZ5sRpNeleSwUsnnHaAARg4m7oGbxmG7o+YEMolfrE6AFghaAlwzhUGKcsMnrgTI0KY0OElpaJp0foyVpRqW47J9zwHm584yN3ueUw/+DYuLK+y47k5u+sFb2e+5pDww0tDJqm312mm11NnQ5hsUkiujRZfaVlfn9dA9m9/z6K3BlgKuQw04NacJikLUwtVqsuTomjlpEWoolD0IMdQFRKaqI6f5QscG21UiUsdM6ghKqPcONHRSkpbf6oBTD0g0n6gv2hUBKVcIO7f+FnqAEiQ7rpUoWizqkvjMSmXlIltqB+1ByA1DLa9YY4FqjIomuLaSAxueYpg9AZ0qLF+AuacgWoRoDjXRskm3ItmrGRUJVC6j9lOIkwPRcl7NNOvv6oPWVwkUba7NOvRJ0idS/ys7QAq7eIjCxFH2HruN6V23YhkZTMulsQ6f/n86VKpV5i/NsXHmLK6/Qhy1kO02Yb2NX/WJo1CR11ttHT3b7KOPa4G+f3pHoH308epxLcrYzwK/BXyu571fBh6QUv6mEOKXk9e/BNwH7E2Wm4F/lzy+yWCgwp0J1JR6QvHVN+GpP4XW197QvbsacQRnztcZygpGinlSjoEpQoYKBgd2OhSxSdkxs7M1FmY3EIbP5IRH2Kkxc+4Clv1Vtu2+nsBf49RTZ3nmsYeJOw3e8/cncbzthGHE4uXLDA7cw9hIntGxDFKmafmSlbkWmxst2n6HTDGLXzeIDRfXHCBdKjC9a5pGu0K5ssKS//LHotEi4nIc8SwwHQtaYYuKaZDLlKg0K8Qy3pp01sME3U1rq3X9Okle2wpgvZ7PehN39KT1y8Okm2i4nix9fOfgkh2YYN8Nt3Hi0E5uve19HDy4nz070mQyiQWd4AVEbC98CeWOz8LyDFJe7QMVA8NEoSQKnwMWKfvadA6q6yEqONUdbG/qiQeMgihgp0oUR/YxNLqTU49+Htz3EDJN2OhArQ7mTrLFw6QKJcpMAZfBTGOlUmQHWghgcvsI7XbAxXPLAIyNTjA8NEG2OMH2/XexspGlXXuK2L+kjsGyVMDdRx999PF3ghx2aZrBm++kVMoQHXw3g3uPMH5gnKlBMLPQ6cCpc5JWJeLk0iKzcz4Ll5psnDkFixehuanSz1Omaq9EEmoGkSLaJKotS3uQTqt84U5V5e/3Fk2VEuIekkBKiAL1KKNEcZn4jUolUZNCEreSNlJYSJRvbBQEEIQIYRBHMaaUEIRE7Q5hs0XQblObPacSVbMFDEcV7omRxJhEcY0wXkVKiyiMMJ0iqWnBmCMoGYnnqFDcYEXColDT/BKwhUqjNiSYuYSrsZXNrZeBjg2ylGXk+h2UxqF0wMZ1b8B7+88xY72HsDEEyzNQM+Doe2HvLVCeh6VZsLbBygKsb2APFckVJphoWqSjDjTbhK2QlGuStgWZHGBrb7veAaSOmNoo4rUCXGAXFxmlwQhqkvteYCdX6tY0UeYBd7BAkQ7TrJJmmYfIEDOEiqVsIClpj63eE6XE77dHMijihCyxwbYVaeu4yjMzUp6/OJbylYVuwSR9SDp/3elukgjFOWXAGoV7jsChAozakBJX1lnSzpRlA4TpYThFUvlpHC+NbdtYlonj2njZIs+fuoSNx1BhmN25LBdmZ1lbWWd9aY3bpg+xc9xi0FNc2GYNNsfVYXTocnl6WK+zvdI9+zGYLEOo++et1PPrY83RbRF0/K/rP2hlsfbT3Yeauta0mk461+4VIer8C1Qc6RrKJsR1klvKVBbUFuq/Kg2oadsBbR2g7QOuKDJ31c732hfojPvklr7C9jRI1uOjJhN6J9k1oRsAfgT1tsooiEK1Y8IB6YCRUd7MrqNsCDypGhxDJPthwPoC1GegfBKaT6KmhdZQcW7P5NcrQoruP0cr7PWBap8Heq5G3PNcnwBtRWArX1td5W7LN1xbMHhAhtTYUSb3387k7mNM792Hmx5FBgbtVpO1lXnWKmUqlU0aGyu0a8sQNYiiBu12gyBsYtiCOJTqJrjCT+LFLmIffQAirzyFDKBZpiuF76uo+3j98LJkrJTyK0KIHVe9/SHgncnzPwC+jCJjPwR8Tkopga8LIYpCiHEp5SJvGmjabgqVSFZGzaUWoXYRPv8fUJbwby489vgyO0cz3LS/hJuBXEbwtv0hJw5EZEQGwnXWlitsrPpM7YRbbh7hW8+0uTi7wNmzX+Djn9iNtfQkJ584yf/7ub9g1/YUJ971A5iWS7PuMzQ6xPG3HWFgoEgQhJQrm5QrknK5iu+3kFKQSpkEoYswBKa0yZSGKDnbCBqLVJdtlhau3aoAVNd3GngHks1OjUZYZ9vQDtp+jShSHWOI6vJ1TKJJ1d750xh1RXWW2tWErY6HdPbPy8NA3R+DqA67T8Z+p5ArjJNKDbFj/4188Mf/ET/3kQPkbGPLdu7F0GvdpdGQsN72WVi6SCxfLMgaQQ06LwIOqXRMFDUIOm2k/HZFC5QOSIgprPQYw9uPs+/ofk496mAV7yR2thGHHSALxkFcK0PKiIBtwCLpwgj54TEyg4AwmNw5RaPW3CJjp6emSWWL1EOTvcdvIriUozxn4q+ayMhPbux+ANBHH328jhAGODkyxQKGM0V2z9vZ84n/nb178wSBwBBKOTYxALUw4sJiyFNPhcycr7Mw/wxBo6KUm5cvQ31NEbFCQuiAneT/CqFSZMNQpdB6riom46XBX1UptFvysh6EV70WgGmp9WlEiQ+pIcGQRI2G+qJpKZ/FuAOWhXBshG0RhCG2ZSIwiIOYdsOnWt2kuXhJFSrvDBISI5w0hmkrhVncIoo3IIoI/Tahb1PMpBgeNBl0BCUBrgWnYsWpzErISEXm+AkBNCZgrACVBqyHcFlCfhxWNiAyPYoDHrkSDJ9IM3z7XRQKd7H0FYgfaSqCOS4g3vNxpIjg1Jdg4TwMHoSVZdhYw8vA+IDDsdQoMmrTJiRqtzHNNKUsZEUMDa181ZFUr5FlG4N1XGYZ5CneiUTpWw3egYFF+JKEoECpf0dZYy8bFJjlLLtY5wABk6h4SktWAdIQGkoBi1DkEigLA5Eo+1IpVTk+m1bXsRNBuw0ZU3nGaj5F8zea3OqtpaK7/w54HkzugQ/thLxURdYKoqvA3KqHLcC2wHA8nNwII+kBhiam8VIOtm1impJmR2ItNTEMk3RxmO27jvCVRx4lVRhlwsxx77u+n507Xao+eFW4vAzWLlizlXWENmqA7rDeRhGHWh07iopEcygy9q2IAlcaTNXpJrXrS99CnbdjwKN0CXVN4no96whRTY2UipD1cqopMoRqsqLkM0eCpf8emozVitU0XXmuHphcZWkKdH1nNbHaS9LquY92clDaXqN3EGOgwtR6CNWGUpCLnkphrVjN6qTSUMhDMQvNNsSBUpq3N9X3Lz0D5WeAU8mylqz41XikiuSMDiRn3aU7naBlxEFy8EkFtK3PtRy4VwVrKR8PK6tI5lhP2OgZFhthFPAyE4wcfh8HT9zFjj17SA9AeR06zZjmZpXl5bOsrc3SrDYIWz5xp4UpfHy/ThA0CKMWdsogboOUAil1gUJNIF97Ieo+3kIQBfAGVKPSbNIlY/vo4/XDq/WMHe0hWJdQMQMoIcBcz/fmk/feRGTsEeBG1Dz/b6Aa4zyKqvsj3nwzHd2Zu/Vyg+fP+py4cRcFz2MoGzGQDXEti8r8KYTfxJZw8llw4meJDYu0a7G8FrO+Pksul+KGQwc58puHKQ6N8diX/jtzS39CaOX41M//FLmccpG/NDfPr/z6v8LzhxgemGJwZIzRnRNkRJZsxoFMh1j4mHI7TbvF6N6dHBAVHvqzZ1/VEd5PyGHgUAxPrpyjRFcdEKJCdx1bt+hWnu9NLNFm/dpWSRfwMuhm/WjBxMsjAL7+qo6lj9cCwY/8L/+N73vXQd52OMfIgHrv5fBihSziGNrNBpWFp9WLF+C55NEGjnDv+/5nFhaXeO7ph/Frf/1ttrYBfA0Zd2itwcm/dTj5txlgN9OHbqbedFmdvQhkIPgtZr5ZS7ZRAmLuftdt3HBiHyELQA6/UaLd6qZHdVI7WAqy1KobDA4NsOvAQS4XBlicOYF/fgncnPJJ7KOPPvp4vZAahBt+kg/+019maFsWK6V4r6IlcHNKCbuxAA88BM+eWuXyzCIbszMw/zxsrisS1Ep637CSKI9MqEuwE/9Pk4QD9CGbA9NWRZ6Wn4a5r0JwDd4rmhTZSjFNplrDMPFfjJPJqsS0RsaqvTQtsCzymSyubRNGIVbGwzRVEai2iDAzHgOHbiQII1pBgL9eJyxuQqqIiAUNv47l+0SdKoG/Qau6iDAOIW8b4uCox36h6MbDQgXFlyO4vw6lnOIRJd1p3f/4BTi/Cu/4IViag4UqbJShPg/r0xBloFOD1WVF8PK2FO3pG4gakNomaK6ZMPl+xGAT6579BOP7YXmD9IBgagQ25yzyZogZdRCNMpaVZlJA4XIVntaquDF1vQhQhIoFnGaQS5xgnt9GKTLtLffNIoJ5uhHYS2OEmA9QJcNn+E2GeV7cA+JHIV6ny5rW1BmJR8EaBquklhYwkoeCm+yW2+N0YEFoKbZU88l6hl5/x6XLwmnhnQ8Mwh2H4J/cCdmEgE3Trful7Ts1JTMGtMYGyY0MMplX56IOrPkwW4altTYn3v02JtKCIrCMYN9N72b60L2MDWT48J0jtBGq4NYyfONpcMuQGYCGo3ZfF+/SVLgmYQfU7jKNcqxP8b1fsOuloP/pHdT/R6CsdwWKv0yj/m9LKFmNRF1ubW+g+c4mifA0sU3tdJSo3vWgWlfiUkMo4WktEWVKPT+U/G6LSAXFkGuGt073BtL2BPoGs+mm99GzrkbPgWkjXL0OjS0b5xAam4oddp3E0DaCnKX8sksZtYD6a/sNqC/AwuPg1iC4iBqOX0421OzZ0LWOefXBeyjaW7PU2g9Wl1hLivC9IHbXV6S33LIDRgqcLGQTe5J2oCxXtrTPI2QHruftH/sZpg4cAdcidCFVhFwWnn+yQWVhk8ZyBb+8jmw3iMM2YRwQWhB2QuIIpDQJQ3XN1SHHyUVpcOVF7qOPHsRzUJl7+e/10cdrwGsu4CWllEKIV9yCCSF+Cvip17r9a4OJCmvuS14vAf8V1XmAiv7WeNM1xPYgRv4Ih4d93nUTFLJ1Wv467c11mv4A85t1Vp061+8cxXQdRqYkqWLAeDUCI6AdBFgWTE0J5s9+nXReMHXoFnYevAPDHOauHe8mDA0QgkwuT1g/yfK6T7MS8zM/9jEunGvQbnjEsUu7AQy42HmbIJb4jTqjo7vwMxb5nJ1kIb46MnYFRYWfAt6DCrQadO3kdQig5y51t6kf9ZBMe2ppJzQNH3iea6tzCMplbhiPHfs+wrrYy0I9oHn511/VsfXx8jhwwwe5/e4P88mP3s749kkyWQfXEVcIn74dXuxrUROi9SbMnFUDcg6g/t+nr/pmADzHA3/1q0RRRKf9cl4bSfXuLejA823MnTlH7C9A5XlUEDmNmosaQd19f87tJ/Zx+MA4D37+L5k+dDMzyxb1cleJG6WnwBrBiAP8sI6FQ2ZgkDE7S2V0muHpEksXnSs8kN/cGEIlth5BDQJmUe2vQA05A7qykD766OM7iiPv5+B9P8DRe+9m+0SeVClDPi+wPWjE8LWvgt+EeqXO6vwiq+eeo7O6RNjchHYdwjqYiQpWCDAN8CzwkzZysAjbJxQZ6reg3YSRSZCB8g+tV2FzOalsfQ3QNoT4iYLSUkSw76vnKQvSVsKoRSAipbaKgCjEl4LQsCECN50GBEKY2LaDlzVxpIGMoNMJWWSRTiCJggAjbmM5Jp6bwXENTCsklBVWFy7w1CMRy8Mlzo/muHkvlATkJJRMCLJw+pyyPs0WIZ9Xrd+J++DmCMYy8LVFOP8E1J72YbNK49gwhRFBx0jEcBG0Q0FkgrSh5QOBIHXfLlJFieMJljuQ3V1kpASThqCwb4SLs5dprFfw2gFeOMmmDa25i/DUk6h+SZOxOjL6Gie4wH1U+GmUC6SKozoI4UHup5XqOX4IeOQlL1ENOA98ERV3HWGdIXk/5+VjLPIJVF+gU5ot5SUcmxALKJSUNiKX+D5kUV1pTDdFHLr8j2YpveSQhujOvPd6cm6H/+0+uHs3jMawMAvjE5B1FRHr0RXUQteqc09GqEx00RVCei6Mj8COQZe8LZBCUEs2f/3Nezh7sc7CQpPf+sICH7l3DMs12T4EP/dBeKwK5yKlTllH9YzLybaGULGviSJi99G1hHgr2RNcjSVU1HYqed5BjQtaqGtiocYQVZSfbBnw4yQrzuiWjWp21JLPwJCnrKoFqtmqxhDEypraD0EmRKlILK1D6DUU7q7UQRGum3SLe+kaVXpCQH8/ycLfInD1d0jCfiOdAAAgAElEQVTW6ybr0JwldLnNWFdqt1SD4HqqiJ2TVSnUlqXk1jWpGpPOJYiXgXXVTnMRWEDFWdc6zs0liwMMK7sQzGSiLQ1GoNrxLf9VXdUj0/Na/1H1I1x5Nyd6dClhYyWxn9GlbT2sqfs4cOxd7Nl3gjhV4uEvnWfPoTF27y+SMySPP95mYWaByvocfmMdwjqd0CcIQ+I4wg+hHYSEnQ5x2FaFAqVmwHWZ5xp9i4I++ujjjcSrJWOXtf2AEGIc1ReCmnab7vleYpT4Qkgpfxv4bYBXQ+ZeOxLHIOd21VlxCdW1b/R8pzfKe/MgnbWY3JvmvftyjA5cJpJVwrBFzk1haUdVGdKoN5hdaGKYIdmixb7DI9g7pggpEcVZIpHBc0uUxscojOzESWcBG8v10UlRUtrgjpAthlhpwZjpMTbiE7RNoshACoNCLoXlSdargpnLMZ7nkbJi7KjBZnqOqaJgsSqJXmG/FtGt4TmHir+1LYEeJuhYvDcdXc/JGnTTkFp0rZf0vG2LKwNtUI6w+6fHKeZdhNEkYwUMj+zATmcIhUF7WVIYOUh2//V424fpbGb4jd/4DWq17x4a7E0N4UDhOD/5Y+/luutu4uD+oxzYvwMnk2SfvsbRR7sNzUYbOvN0jeQ0Xd+r7FEpV83GOq86IDNMGD6GkRsgnfewiwXq9QbtTRuMAUy3SKZgUp29n5HBEQrZARYWNhgaPsTFM8/RqHQTB0wzTWSkiGNBIB0Mp4RrCkKjgysrDBQHKdv7qXEKOPfq9vfvHBZwF6orKKH0PgOo/bXoOr3pKumKFHllA4U++ujjVWFoD+6uE9xy6zHsiYMMHz7M+O6djIxDq63srpsrcHlVcvLkEp1yhU6lTHN5heb8aaivqzRYU0Kn2fUllEKRC7kBGHKVAWPYUen0A1OKkWxVwa8DsUqj7VTAryQTZtcIiVo3KGJCtlUbLFGsWWwkPICReM4mpKyRIpaSkJgYiR3bmMLEMEwQhiJmTAthGFiGTa5QwHE9DBEh4haOyAAhMjYhMhCWRdj28as+ZZqEvsQjx6FtgoIHgxL2mNAuwWoTmhUYzkE7gihxT2gAh8fBfifMbTdZW0ozMAzNADoheCklOPZ9dahGDOmiyu53ig7CU4XRScPuaZMdmRinGTIxafH8mRadCAYHC6R1gSorDU5Rqc+21HEhUKfELO+jxvuJGH/BOfeh/SD8ws/C2g3w+Nvhuc+84LI8jcpkaqCIxD1Ah5jT1HmANot8AaXQ0xrQfSCG2erwbavLjmZRrKQW3Wmj1d40795gUAvuHLr+VUI5TNz9Tji+A0bTivd3s5A2FP+l+VozOQZtlNEEMsl39JSrC/gGdAyBYQm8ZFNNqWLXQt5hfDSDbdmkvRjLFCqqsCCfVfl4lSiZO/AUDaS1yfpQ9Htt1KkY5kpLg7caCnQjhCzdsUJvZpwuiKaz4XThXu1mWpMQJqFFDGSEcrmQKFsC01Qi/TBIXFHW1Qqlq5oTbNSF0Sxwk+496SfvaaVrT/b9ln1GI1mHfk87DegRuN7hq20PWiiWuW2DW4SUA65UJsSeqVSx0lLtb5SwyZ1NCDaTHa6jmOJ2z0Z7/zgvBl2pbCBZUuCUFCuNqbYTJCMyoT1edUzd68OqTSR6oRWzPapcGah+Ik4q0hseVnoPu44cIj11AjczxlqzQexLRieLeJ7LxprPwswSM+d9GpvLtBsVgtgnjEJiKYllSBi2Cdptok6DOGgjQ1+RsVtq2DrdooV99NFHH28cXi0Z+3ngfwR+M3n88573PymE+GNU4a7NN9YvNo2q2loCcwLESZAnUYTsmx+ZtGTvzojrdsLl1Q2qjQ06YQc3k8GKW9hWhOdZxMSEXopM3mFwIs/+G3eTvu5GhDWG6kw1GdJCXfI2WylilAAHISRWKk8hBYUk4h0d0RUur7xNvDWDWtNAhAEpo4j0Bsi6BfZPF1h7vkr0omnhL48ARdcU6ToNxT2LDrR0GJHYvm/5wvqosGOZbkaQDhN0SGABWUMwKSR7iznGhtKkTEHR63D4yB5EJs9GJ2DObRKYbXZtq7PrlnFC+QH+5b/8DAYWmXQaiFlcaSL1FHof14x0bpDi8G6G972PT/zsz3Nwe4mc5khfByIWoOlL6s0OSJ0YukGXvn8hGauCs+59a9qDxFEHGeuKrt8GwoDcOKbr4jkFXIbweZpOYxBpeYi0gzeQozYnSHt5bDPL+oZPcXiAyF8jaGlVaApLeEgc5Qlop7HTJYQ0sQ0fuxFQGChg549DZkl5gdUv8koJzG1HjrCx2qBerkCn/Ip++9IYRo2c3WT5MEoBlUb9P9ZR57jNlf/aJur8WySjDvqEbB99vM4QBozspJRP4+y+leyJH+T2H3k3GVMpLgMbaoFkYz2kshywthxycU4yd/oMUXkRamWoVmF9UeXPG6jiSkEnKSqo0v0JhSJjS0VVRGbpMpx6BLYdg9yIyg1ubCrylA4ETUWmvhIyVh+PjJU9ARJSXuKlKFUKr0xIAp3OK0NwXaQJsQWRkERxhCGTPkFKiCWhVHI4Cdi2pRxh4jYyaGA4DjIMiKUgtkwcy8ZEQBjQbrQIWiFP+yZe1mPnoMmoqwjJcBjCBViqKh9KQ0IQgB9AowWHixDdAOakRXDBZGIUzs0rvnmgCGEbajW2ipVnctC2QDQ7hCs+jTUfOzvE7lGDbbYkqMUMpKFTrxGHJulskcZKh2a9RS1Mw/QUnNyka0zZQLDCftZ4JxE3vOgJ70D7vxPf+klEcA+idDOIL8Lza0RhmTZNNlDxWwcVw12HckpfUbvNowTA11D6jAFU7NkCeQjkhPqVlEnwlwQBmliFrrFqr9hOM6kh3Tz0LFtMne3B4CS87zqYNMEMVQ25TCHhspJVa5Gj3oS2xNLmDbLnUStVE+poyxlzWULOhMGSSybrUswqwl3vXiAUGZ9dBi+EVBbKeYhEtw6UieoFN1C95TRK/Kv1iW8l6Cggjzp+XS7qajFGC+VMEshEeCq64wVTqu91wkS3aSnyVQjVNASxuh86huIxg46yLKXOFpcYe1uW0WrYpAlSXYQiQF0szRL3Zu/r4l11uowydNl/fQPqtD8dB2uRqW4WbVv5VmZSioi1QjADtaFWO7HrkNCugdQS3TZdKQpXbbAXelSlHZM9tRijYJTUcy+tMhFAtadhklUq9T9Gs8fyqnVqhezWFeFKj1qp2vFIs9FgpQbIjR1l/9s/ShBJFlfKXF65QDY/xKFDJcLYZ362yrnT5xFBiJANZNggJCSUEkmMjAOiToOwWVPrjpMLG7XoSna07LiPPvro443Fy5KxQog/QhXrGhJCzAO/hiJh/0QI8QlgBvho8vUvAO9DxWRN4Mf/Dvb5FeA6YAqkB63PoZRX3yWzYIZFyoPxQpkLpy+yWG0QxhFpE1b9BUYGoTiWZWxigJ3bBrn5zhswU3tBjKPm06fpahQS6QRLdI3VveR7GVSEsYoKknWnrE2PtqMC5y7GhhxKeYOvPfwMtpnBNUPyBY877rqDJy59ET/4dgWQXhohKpnmInA9sD95v0m3a9d2YNAlazeTRdPLPiplTM8J92LAFLwjZeN7Hf789BniZ+FQMot9vLrA5fIpvv7Ms8kQ5b9i/CcQOFSZQLLBh+/7OG+/4VZgk1/5zDdp+w+DXHhVx/tWhBCC42//KB/9iX/Opz5cQOhBlx7tXAPkC56wFeTqWHezFrBR7iVdX8oxOEbR95oFVrKGgfEfpFGZpVU9zctO3kQRzM/Qaoe0ZIAafv5+su5dhJVJVi4nA19hEkY21abHeKaEaeqA1QIOQZTGsAyclMnASInUYAE/NLBMD6spGdthc/7IreDtBvuH4cEfQFUbvzYIw+DXH3iQ//BvHubLf/T/wYXPXfNvX2KNqAD7x5PlwIt8pw08gWprSnRJAF2eL5ssdVQCZ/NF1tFHH328KggBXgZ++nf4vvffwM6xPJ6nbDqngc2O5FIZvvplePbxNWpLcwT+BmQlPPmVZCCbVLaJ6iA7SXXvBuQSlbvrQSaj/Dy9rFJPhclAV+STwherEEYJgYqSKMaxYsbaa8qs8VrRrCvrAzsFTk6ptiwLLGW7pFS5YUIcqKJPIh1iOwLTtulEEAUhkR8RyxjLUnXtW60GUsZEUcT62jqu5yKjPBY+MgzJZk2kkODauCmLtJshjnyCEGzLZebSApgHaezNYO6B7UIwBqw70PFABDDqqMzixSZ86xloHoOLJ2H+yYiNbwV85B4POQLtWEVia2vK4aGZTU5dBG4aql9aoPXVM3DhKSZ+41NMpx2mDJOKYxD5ICsr2NKF+gh/8n/M8dAD36R1eB/W+ycJT2rv18vAZQwW+UlgN99+LrTzkX+A+aufwvr0JxG1b8KRf0tt4Q85y6P8IfBB4Cgq5R5Ub/o88CXgL7fWoqM8gC9CcAvw9yHaDpsRtE2dpay6bY8up6O7Sjf5eS+Hv5x8f0fyehTGdsEP3AJ3uRCtqx7HKUDKTrKt6Ua60I0x9eojukJFUNdjCCVvWELFl37CHw8bsNBR8wJFBxbXwRgGJwleIxI+7gxUFyUzHlz/AeU1GyUetkqjrM7bRrJ+nW6o9+mthjrdDLkQRaVVUPF+iNJZX4pgLUx8rtNd+i+Qak6o0gDXhkJa2VgvSui0lQWLX1UqZdnr9+rSnQSoQXYKGimIqskOaW816Pq/6opidvJ7re7WnrB6YkGz/R5XDmYs1M2lLUyHk89GgLql5PQ2XZ/ZpoTKBqyvJMoUkWQtaKa4zJWSXL3xXuGB9vhwUfmC06hJdV/5qqSzELWV9UzQ6Xpz13T81ptVqiuU6QPSWnO9rYiuvP1qJBlTRp6BycPsuuntTO0+xH/+zKeptpq4pUGyB2yefvIRqvUqzVaTTqfDUKqI68QIowNEWKZJFAbEQZ2ouQ6NiuoXkD0XYpMr76qrZ3v66KOPPr6zeFn6Q0r5917io3te5LsS+LnXulOvHQYqQcoCLqAG+Hp+/rsD4zuPsGNXiUFRw/N8pt0AQ0DatTh6cICjt4+SmbgOo3g9pjGBcAQqTGmhwjit6JOoKEAnQ2l96RBd4lWrA3WnqkmpOoo8EahObBBdHlSIGM9awm6PYYUxru0xtXMnpvWabYgBeAYVhN6RvNb6XJ1CtpzsXQcVchTpVlgFdcV7u1UvOfq1SHJ/o4NsqEAN4JEknnjskW8Qx3FXSWvfQiY7gGu3kStfBmIeeeCrPP23T7LILO1WMi1u5MCahM7zr8uxf09CWDBxN//u9/8pd95wmG2ZzIt859pXp1PSQqnSL/WASa+1Uq6ysrrxkr+HO1G/Oo8aWl2ma/gVsz7/H5Gyt5zHSyOTz/ALv/kPePwbD3FpZpWF+QLVsweSde1HReRfwcr/EIa9A0SIYU+zfWonT7o6Zd8GbifllrALJdycRUyW7VOC1YZBSzgQFTHHBIaIKaTy7Ln1ep4sfQn55U/BymPXdt5iySff+Xl8WtB5rSVBPoYafr+LrSyEl4TO1dOFGbRKYjB5bKAGBHmUt9nya9y3Pvp4q8Nm4GO/zKG738NdN+2j3SqQMSxKwOCQmn595DScOVXnzMk1Lj3zPGF9CbmxAkSwfRrqPjgRWElbWK9AtanIWdeFg3vUYFeSEJ91WNjoVrqXAVx3O8hIFZXZWEtIUgABZsJImLlkLH+NE0s6jDFNZeKZSig1I0l7jST4bUXMBj4sn0d6aexUEdexlEIuEXOZhmoHQyxMC1zLxkSydmkGv1GnY0GYsjClCZ6P6XgYhkEoQjzPJRaSTtSiE7WwPJ/NjXM8+XSRC7Ml3nt3jh1CMFWCeAA2DfiaVJxxXSqHhnANNk9B7eHniL/yZ6yt/xMmioLQgmYIS2tQ7cDmqvJCL22H0ihYH5imev0EjZnbueNmm0EDvBgGpkM+9+8fYHXmIlOT27GHIx79o9+htfl14vNDxOY+MH4C4l9HtbOKNJ/g27fgAC6X6Pyfv0rzT/+YzM88BHf9MNWvx3jnc/wipykxj42knaz5XwB/gyLMXhqPg/cBVZyy1+2/gyrlkKWbKqXZyt5YwUV1/DpvPVQH89474K4DcFdJCaObIuGSNuHo0LWNBjQHDKrn0nyag3LcPQOcnYOVWfiJ26Bsqc/chIt65BnYOQVTQypGbQMTu2DJ73D2kTprh0rYUxB5imD06dJVVbq95suXTPvehYuShLgoG4w8KlpboitMdU2YTm6dAZQjnRay2kA2USBHgC+gtqkcVqJkiCR9ul4QHVRYEtAdMoEiRUHdEMN0jWqrXDnX31u8okDXiWlP8lrXrtPuWdrSwEq2q6uNhcnrxKKVFt1iYes1WLkMlWVoLybtZgfkCsgNVOuuy5lFKJlKOXnUd7Q2wRhVz+1pSO2E4cFE9VIDvwbVSBnpRi0IWyqbgVbi82BdldXQy2ibPe9pBerV8bRuyJMRXrzO2vnHKM+c5qk//79oN5eAIu21Uc7OnSG7cxeG65ByXEoDWYpZGyuOiEKbluGyXi8TtpvEfhXZroIFwrVwHBNTmjTXl1FkbIeuL0QfffTRxxuL14c5e9Mgj+rtiqjGdp5uqsZ3DxELEJgWK/U233j6IsdGQ45OldixZ4SpI9OUxneRH3Ox0kPg5FHHplN8tYnRJioiANXjD9CdIdVRh66GoSMJbWOgZwodoIrfmmF9/TEmJn96K3vMMAy2bZuiOdehXm8jzQjPyyCM18fZKkyO4CSwFxXXhCiaeRUVo2sDf+2G1NvNX321deaPBNryhZ8BBMFVIW8k8JtLBEaXyN/orFLpbNDsjb5iH8KlV3GUbw1kh/ew49h9/MJPfpB3vu0gYwM50lffJtdAxCaZpERCjbENlBhAiwp6V1mu1lgrf7sU/LN0/zfaoa0bnMn45Qp5ddHxmzzw+d9jaeUcmxub+OUaKprVyXVtYIOJbUNYMkb6McXCGCODDratDty0THYcOYhISQLRIYigUq5x7Ogol9YELVMRsqEJsW0SWg71yOXo2w9xIfpfqT/zeTjzh9ewt5Laxd9V5Er8Si0KplC6px9KXu9ByZBGXuoHCSLUP1Z7mDVQ5zlFNxj3UCOOMbqj7vUXW1kfffTxkrCwR6Yp3vNBbtp3HaPX3Uh2aJpmPU+0sYzjFKi0HcplwVOXVzhzepW15RrVlTLB/FnYvKyKbFkm2LFKha1vKo9Yy4RUGgxLkaDptNpkFHftAIxE6a9LVsdRkoYaJrOftvp9FChbATMEwwGvqBiz4NpV/lgpJRFNpTAdBwKBFBFSGNhehgCBEALh2kTjOzAdF+IYGURYhoVhO2DGWLah7AgAw1IuokGrASsLkCnS9FI4bobCxAi2beM4BoYdE8kWQVwDYehegzhq0iCm5Uc06gEPPtThvhsGmEqZik+RqpWbuQir52M6syFLbZvKTAO/EUFmiJkLSonXllCpQqOsWsdmBGEDzBpEGWi3TWLXZGKfw527INdQXLjvx6zPn6VkWZRSHgYhjcoycXgBOA/2Kux6B1xsQdSmhOQOlKVA6mVOuSDGatZpXnqOBz/3PxFvhuwavpWp4U+SffwJrPDPuMAlHqPGnwJPoqbWvn1vGiaFgBIPygB1wJr51HN3WrjWSXZUk6/p5Ls5YAys4/DO/XDnLjhSUL6vFmBk1a3oCPWTiCvDjt7nvXo+zZNd7bSpJQ0rJqzZqnfLiySCMGAsB41BePb5Ms9GIW+7bphteRgtQTHdojJ/iYd+6fe48Z/9CO6BSRyhOLgRVPQwgBrR7Ege3yroDc+1hKRF14Jsiu6toaOstuhKSnTeX+JwqrShohv7BxEErcSiVIf8NlfALEC8nvCMlvJlFobK1I+10FL07JyGLnbRq+jWN5MmX4PkwLTXhb6/K6gkrI1knVpH0+tTuwpUalAtQ20N/AWIl+jGsKt0syH1eFD7JPh05bf6D1MCJsEbgfw0FCdVVbugqibP2rKbxBQlftymBaQTaXlHZUpccfX0D0TPok+yZrj1aE2PzLSSNkJGBmFkErZRV1mEELeI2hW8qEHasrFsAbGPJ9z/n733jpbsus47f+fGyuHl2DmggUbOAIlAgYRA0iTloURJ1FLwGkqWRvYo2FqaGY/HsmSPZjwjzxqJtpJlxbGVTImyaIkiJUoASeTU3QAanfv1y6ly3Xzmj3NP33qN2AQIAuD71qr1uivcunXDOft8+9vfJgg9vH6HdneT7toiUW+dxG+nc0mMTGKiQBDLtM8KZnp16AFF+6NJXo/4Yhvb2MY23my8C8hYvZCvoiaWcvr/s2SFLO8QawINUSQyDPqJTztsMbRjhF1X7Ofg4Z3MXrcLCrtA6FJeXbhzKbESoyJWPRFrEyLIuh/oIiyPrKQEsgnUAJokcpkwXGNwYjUMg9GxSVabC7T6BsK3sShSr+bodDp4/hs/5iGq9/rwwN6uoQKyNlvdfl6rsPlr2pukQ+SvE5HZEHi8nAVDCEnja/mGdz2mdl3Dvmvu4o77vp3v//b3YBhvzBDWT8sULdJ1P1kYN6jz7HQ7NFutV9hKDqWr0MutV7fVsICSa5FzHKX8tkzcSomcm8M0HAyjSNJ8gZF8m5HJGMbyCPM6LGOMMHTpdtdZXKpx6y3TVCoGlgk7dkxRLAaYhrrnhGEytmOSXtQhlmDYdfYfsMkXAKEazhTqFlYRhGsQImn2JQfHKozd/K0YrkmrcxIWHn3tg+g9/NrvuQgTpZnajVL53szlu89I1FKqS6ZfHyxh00aADpkSXwfsHd5x4/c2tvENwui+Kxm94T2MfegT3HrtrYzWTFqNmKNHenTmz1DOj5I4Lm0pOfLiGS6cOU8YehB70FlSnrAk4FiwnoAtlZ1AHCkFbLmojBctCwp5RbbGQRY6mEY6WceKXIs18yEVaWukRoiGBJGqk4QA01Ek7eXAMBRDIiSGAMM0lFWsCbbtksisbNZycphYCKl+jyEElu2AJTEtLo7DpmkShxF+31OdzKwCYd/H9wIMw0QIEMQQe4ReRHtTEgQRtuNQrVaRcUBiOEh8+lGb556L2DtTwhoTTKYZyCGgGkDZhyEk/hKYYUK+Xkbsu5K1JUGUh1YjYPFkl3j5AlFtBLkkkWsxQdemE43i+SamgKlJmCxCyYZ1L2JluUPS3mBy1wEqhTydZoMo2kCxPR1FbtjPkxce40gOAR9F6eNejy9pD1jxWiw98Zs4gF2qURuaJjEKsOcDnF55hgc7J/gjzr3+cylE5hOr83ODvX50YyTS/+vXTRSzWoDCLAwdgF3XwQd3w3UVmHRS2wET8mZWRW6TuZMP2hQMQpIRsC8nMQhQeQpTwsiw2sVSyiXHAqouDA/Bk48HLC35FOo9Zq/K47oCx4qI+y0WH3oaee6juBMQlZTAuyYU+apTnLoe7ZsJOjLQlg1tFEfZIiuMH7RVHVQwaxd6HWnq6M5LlNLc7yqFudT5d32CBzg5ob1eU1PgsA+mXj45ZB6xfbbKljUX2Ut3bo2MoG2RhTZB+nqPrKlFTGa1EQ+8rh8dCZsSmm1Vfu+1INkgqxHUkto+mQuxro7UV3oJdcNoJ+JRyO/CGN2DGJtG1IeJepvQW1OVBYHy0Ma2wbYQiY2MZObXLQfjeX3W9BkalEkMmuVqn4VBExB9Uw/6zlbUvoq04sFKEJGHEXuIUOIFAZ2gR7/fpd/v0O018JvLSK+Rntx07Z9I4lAn+HUD2UFVrF7X6n3bxja2sY23Fu8wMlYP6Bcjf1SpxQyKJDBRpOQZ1OJf+xBe6hz6NoezC9uxGR/zuGPPCD/4o7cxPH03Tm6YjJhokBkPDZPN7i5qoi2gJjNdMAZZ45xB91U9IepMqVbOgjp2HQqFIrt2f4IsJJQIYeDmRqhPefSMHpuGj9mB664aJQx6nL3QfsOHQSeSH0KpA4oo+4EOb0XZlomqQ9r2r/xaYTkOH/nen+MjH76fB25+48sJCXQCcI20/8vA83pI0Os5r9Oh13i5+16glp1LaM+owXYCl8JEjSLXjVaYGR2lUK0gq0Vmbr6aHZM7KBXGMc1hLBFjOJJ8sUahMoJdLlF1q2yuN3nu+eP89n/q8Y9/6A6mpot02wl3vPcAK51lEgaVYAXm5p/DKo6x/4oxfu5n9/Ef/kjy1FGftW7CzI0FRnaAWxTEiaTTT5hfNDl0U5XNfQ/waHU/0a/crFRsbwia3jZQY8h3Aj9F5gR4OdCrDK3W0KsXh63NHHTyyCGrOy0Bx1CrmG1sYxsvgWEgLg6GBu/9hz/BrR//PsqJsvmzXcmm77FwfpFnHn8cwynTDyWdngfrS7C8AgVXNYahp2p3AZK00eHIKFSrYArI55UiNgyVsjVAfdbrKiLVdrOMWBQor0EZQ+Ap4tRAsWL9EGwDpKHsBKK+6lIlLyPpYqKkbT5AAqaF7RYxLDtVboHj5AnDEJnEFFzVvMYw9aJc4lgGwhQIQ2Lq5jHEqgu31wO7lKo1IxJCfK+D4xRIkgQpBYHv05r3WFxYYHR0lFtvux1h5LFsB2E7RNJkZXmRhx6fwL/WJNlnMCTgoICRQ7BrwqBUdjnyIri7K/izZaJwH0Fb2T42nm1y8o+fhwd/GXHtB8GPkZ0ua5UhxLd8BGcox+ioYKYkuLAOt41C2+vy6N+doywEew/speubHHvmBVSVWDovBMvw/E+yE9Xs4VuBm8i4z1dDjKopeQG4C9gD2E//EhG/RM8wcT65wAt/8gIvHPks8H+//vPpuEp1PWgOGpGFnJrj0fyOGPi3C2IKdt8B77lN8sMzMG5ATQgssnovrabUv3EuVvTdkGGQv+SH602/EnSvgi8cVyXw1x1UJKrm2mKUWrNYhHq+xEpf8MRXlnjPoV00Y0EoLMZHKnDXt1A5WyNfAQ6CO6S+dwJVmr/EN2cqUjdQW0fd6o30YaV/W+nrgsy7NyCrvRlKt9OQauaxNIIAACAASURBVBsS8ENlNR1eYCvnZpHZiQIUINpE5Yw1y+spAvei8e9G+sUeLw0edbled2CnQSlLdLiToMKcwf6ww2RLNe1bq21W+zL1rYggaKhH2E1/sSDz8TDZeqOY6Y8to+IpvXFLHSVrB2LmOnJXXYM9OYUouDSe+GtorkCvATJC5MsY5VEMx0T6baLlk4qdlr1LVLGXlv3ru03vl/ZZ0Dd3J33foImuvksNoAZGVbHglonI2zQ7Dfpxn0QmtBtt2OyoeYYQRIjAB9m5ZF+0TtpAYCJJm0devAj0Mdq2LNjGNrbxjcE7jIzdj5pmHwZsKH0KzBugvQTJfyTrBukCHwC+wEsVo+8AjKzxHR/cyUc/cD133zmOZTkIkaCoyICs6ZZ2sdIkrVYGN8gmvHRSuzhha/LVSrehj5eeoHX0YZK1prVQkcffAbcxWJrsDNUwgpCoExF5Xa6+cQ9zy603hYwdxDky7VyOl9oSvLmoAD+NOhaPoa63la/bt70bYTsuv//UBW7bUWM0/0a9SRUEMFrY+pzWWHZQFVWT6aKqtdFkY+XlytwlKiqW5FF6+ipbbf0HQ7I8qhi/4G3wzPObdEKBY4H97KOM5CqMT+5hcu81xMUap148ju91KBYdbr/zVuL1LsJIMGyDB+7ewQ2Hr+PIM18i6Ld54J57ef93/lMWF9X4JKWk4XVA5jCtAm3p8jsPSf7irxfx+yWq42UmZ2FiGPJTQ+Q3JLt2mZRG4cAVsHe8wKfu2s8/OPILyKf+D+i+ukvfK8NAjbP/HJXgmmZrguZysQw8j0qQ6fZ6kI1P+toY7GsN2ZG3UXf/ZaistrGNbwrkGfvY9zH5rZ+g3nOxrCrje6ewejAzC90OPPl0wjNHN3jm2DE2ZA7ZDmF9A5bnIWooYlTmgbQ5iwzBMRU5OzoOtbpq3OJ70O8oKeDqqlLODtdV96J+Ny1fdRX71GiQdceOlb2BTr5YqA5HAPiK9G14SoUVXUYSKUYRvqYBiUW4OEdYqeIWq+QKVc3HIgwDaUiwIiwLTGFjGTaO42BbEU7ewXIsjJTQjgNBZBi45RI73ncHrdY6/X6fxuYKzYXz3HrPB3GcPIYwMRIo1UdwkoQwDHju2Se48tpbqRXymI5LLCWFyRIlq0+343JuwyYZVnYA+4DRGhh3qkN7ZhXm1kLmN3tUZRWrDUbLZuLAKM3SJzk4MUoUBjTaXS5s9rHOPsxob5wZRqgtjVO7WvmVXvC6tBvzXHvv++maFnPnT7Jw5EHgGbR20EBFdf8XcAMqknu95lJ/mZ7JG1CzhOYwXwR+LIl5+Od34UeS6HKjsxLKvtIkm9T1Tg32CfLIGgAMcDY3fgdcMwVj3Yhf+88Nfv7jw7iuuLhp2BrZAvzarz3G8GSdD73vAOMlXpuJvgQ5lBVBL4S5c7Bzp6rW0WnGUdSs58wUODBU4IbrR5i3BGUL7ryxyk3XXMcY1xCbFk/Nw98cAfdudT4s1GzZQxHfu7m0je67Fx0yCU0bdd6aqFNeY6vJmhZm6JXRbtTloiUUIUpQ6vtKmI+BuoZ0lXqUfglkLm5tMsZXWxnYqKWV5joXyVpzaGjBpx76dH9S7X3sofqbllHXmu48rMWhEWrp4ZDZrvrpviwGcL4B5gWQujlXc+CLtby3TGZEq3t96BWTke6QBYzD5EHs62/jjg/dRq5msrYScuHoInz58xAtQm6I/MQeDt77fu647TBHnn6ek88eYXE9ZaEjM92W1iTrVIQmgv30u7XXiLZS0HYBFlsT8Jo0hYu656QPSQ9CExkE9JMLqdI5SdWvIZDHrY5R23ktw6Uqc+dP0NtcJO7qgx6DmSAsNaAI30oJWX0BDCp1t7GNbWzjrcc7jIydR02zd8Dk7dCbhv46JEfIJgBtVj7PO05RZYJREfyrn7yBe++6jn27p3CcHFk7qsEOlnpyGzQi10SrLk3Rk3CDtNsFKtJYAY4DDUIZEElB3pggM+LKI9lFzEkMDmJcdJWvk5VzpLsscuRyJQrlEhuLgqFajUoud9Ed6M2Cnja1ZdjXd9rsAb+dfpvOyW/j9aHAoWtv5Md/9n/ijl116q6p1uJvAsQliyVtqSVIi69SXzAP2GitsLExv+X9OdQVbCKVMMGAkqmeN0P1uUtTCBEq7D3fhF4skYnEScBY7COdkJxdoTK2ydm5JidPzSMSj3LRous9SH+zy3B9jJHRCUbGi5w7Ocf09CFiaXFmDc6feAyv1wLyCHOCysQE7WWfjh/SPr1A8w8tlld7WLZF2SgyM27STSDs95HthGCzwnICjx+DxUAwOe1y/b/4CM//8O/TP6E76b5eXA28B/gwKtlzID1ar9XS5dVwFtVy41HUslRrWWwyY4lLV8CD9adBug/aV2zuDezLNrbxboCFKI5S+q4f5eoDVzF1YB+jO6cYzxuM5m36vsP6ep8nH13hqitmWVpbYX3xRVrPP4PMO4o07XZS4tVW9gNepBROwob9V0ClqJpiJYZSrPYDCEJV/69tBvwetGRKrErV1KXfgo5umihTfsBQalphpAKoWBG5oL47EuA44DuKmL2ciT2SYMUgJNbQKHa+hJPLYzsOiTARcYBlSQzDwDFNLMvCtixcxySXM0lsiYGFgYUpDMw4JrYMWt0WjcUFRvbuZnpqL61Oi1azQWj38DyfahnKhTyOyJOECZ7p0vF8upst4rhPnPRxsHHtPLZdxO/1OX/CZ2nO5kRtiL93W56aIzAF7LXg/hvh4SNQEhYjxSL7rlDOD0vzReLuFCtzHoudmNmZSa4+VGGmHfPsV/+GjVNfxLcSwvPfwiceuIc//vSXOfHkEmNWmYmZnRx7+CucPv4Iq80nGXTRrwHfQ1YG76PEfq+GEOXfX0WRjNNkXOlngT8FHgc6YZ8Z6ggE53m1BpqXYP03wTsPQz8LTh1CI9tlXWWt+SbtaqMFdVPwo3vh0DCUEpN+pULOEi+ZWS4NQz7xrQco5Gx25l8aW7wWdMyxcxY20kC3T1ZvFqBmzsNAMC1oRDBhCU73IDLANQVl16SISSLg0LgSB3/+UYivgbW8OuZDKE2znoW/GQjZPFsr91uoCLzJVoF0hYzOa6HitCFUlOCkD1uCt5K2C82pfFGgexZ76QcX0zdXUaGPQJGnG6ilgO6oVky/UAeZqWUqHpntqQ5V9PWpXeDm03+PkXGR2ilLJxW0LYJLtlzrpd/pRBC0IDoPRqgIyovqTv1mHU9pewKfLJ7ShG0RKvuovfcehq7ayei+OuUxiyNfXaHxzJP0jz4E4fNAGWtogvqBQ9x8935WV0MWT51m48xJCOJ0cWeDkGlFg06+DKpzNQnrpwd0UIlaRV3VmlrXnx0klvWZDtWBiAf7DaSGI8Y4I7N7GJnZxdjMLtYW5ol7PWJP+z+kFR6JRIbqpAskIo0xTUMQJT22Zn/eXCHRNraxjW28Ft5hZKzNRUv7xIFwEcI11KIfspmzy9tfEau9dLIyj/pwnjs+vJO/94Er2LmzTKmko03dqgoyecCgB4/O+es6mj6KcF0jTjyCZJGcOYoQZcJoHT86TdE9iBDKfV4Qo9S1ebKJ0EJcLN/Q+6gn+Ez1YGBhOTmcYokEl1J5lLHRAhPDMPd16L/z1uQuDVQp+wJb64i28aqwR7n+ppv4wAfv50MPPMCYefmLnMuBDvtANeWAgfi3vYbfXNjy/oIt2FG0aDfCiyFdwFaXqkuhm8Y1wiwEDCXgSawwRKxu0j9zmgsbCSsrK5giptcxWN1Yw7Cq5Id2kq9NMzG1lyCyOPLCCvNLq5w+M0e7sUwSaznEFBEGkTTxPZ9+d42+ZxHICKdUAMqMDOdZ98BwbErlhGpBdedubYKzDs64yZW37+DC4Q/hN2OSla++ytEbQtkOTKSPw8CtqIqCN4IApVdpAEdRNgOn2So/ycaYLADWy6xBHy/IKHTtGP1ydYHb2Ma7HTa5g9dTGZ6iNraT8t0f4crD+xmvu1QL4Npqfb664nHqzCZPP3qaTrvP0tIFVs6cIFxZVnYDCeD1FbkqpCJJLRvcHORKMDqm/A2Q0PcVaatJ1Tj1aJWJUrEGlnoe0iZdqXes7abdboTylrUs5S0o0+0IkXrJBtDtqs8lceo/qBfyrwMSiBIIQkQ9j5sv4bgupu3gJxbCkFjpwxaCOIwVkZGSe3G/gWFXMewCpsjhmAY4DsWiS79YpJgrMjY6QaFYJp8r0Gu2FPeQRJhCUsoX6IVdKsUCcejT3WjT7zSIaiMkVh4pcti5HF7cotsLaDYFjY7JXMtFVE3KtiptPzgKrR1gCANnxWD3FHR8EJZNSInQH6ex1qJcr7BjxyilVcmR1UfpnXsEbIdw9jBnj2zy5IOnWDvf4pabRthsr9HYWKDdOo8XZlUFLopMvQE1EmuqRPczz7oCZNBdCSLUTDGE4qUkioD9K+BLZBF3gtSdBXC4mZDnka8ljPCPK99icQ3kbgcxA2YF8nZGvuoSb52ZD1HX59wK0/kx9hQtahgkZXcL8SpRc7ju86VfO7yrjomaYaJLvkLj1cIXGxgrKZ7MizMaSRvxJOl3WhL6HsyrfnD0hZrFjBi6pjqWI3mwTTizAMurENchV1aUVZns3HwzQKdiNboozrSVPq95T62jLAOz6ec6ErrryjpCOsoFJW6qFw0LrBwEg8RpHxWqFMhc3CIyMlY32NLLKy041Tuo/WE1Aas5SJcs56zVt5LMAr+fbh+ygk5tyaHDokGfWUiZ5a4aty/KabUIyRnYkCZjQ6CoPL2MBIplxMRudl69m4l7r6EyO4ybk2wuRqy9eI7uiZOweA7wMKs7qM7sYHR2J5bpcurFY6zNn8VvrkDQV+O9QFUmSCethNCxmbjkr75ZtZLWJrPSg60U++BDH8xBEVKfiw24zDzDU7soj05h2nk6axs0V88T9tZT4jYCUQJhYAhDHcbERhhWOkIZyC2ZnUFCdhvb2MY23jq8Q8hYXWK/D1Xn4cLyn5E1f9FFKcu8Vt/Wtw/c9KFmZMsxOHjVGP/m336IA+XdmOICKiKok5GxOgLokBXsh0iZpmdlqjwTMXAMIbqESZtmsEEuvxfYiReusNF5jqJ7LTCMJTwsJIm8Tk2BQmUcBXlMdiIJSVjDwEGld8dQRGVGmhiOi12qYeTq5Go72bt3mPUlm7kvf/2dXd98CISoUK3+r8Dn8by/xvMe/0bv1NscAiyX6sQtfOonfpLv+Pi9DH+jdkWmsXN7GTZVqb4QICUUiya7d+Q4mpKx/VSJoBUWL0e5a2WsRjLwvuUYlhdXYXF1y2f0snPq4HsYnt3Hvmuu48arDkJ+iP/nV3+Vz/+3z0Lv+MAnqiRyD6ur63S7AWG/B2GEKYEoQpoVTDHE8FCesxcgN1Rncj/snYa1CGITCj1wN2HXFDzzrT9Nr5uj8/mn2dqcLG09bVuY7vUY1i0k8l7i5vt4qW7oa0GEWtmcRBGxL6C6+2oiVlzyV1sf6GD80jOgVbRV1Fi5jJKTaOX/Nrbx7oYwLQy3gG3VGPv7/yP7b76TQ7t2qpalI1ApSWxLMreW8OwzCfNn11g+e47F40c5+cKT0FyDVhP6PWUX4PvK8zWKVIvxXA5qZahXoVaDXBF6LWVJEKTKK9cGy4BOOp/LdKGtG7sIoRb8lpMyWqZSwxqmImJNU5GvoPxcowj6fWg3YH2FLOGpax1evaHiFoQRdDwYl7iug5PLgW0TRDamcHCNBMeIkVFMu9MhSXySxCQKTfrrL1If3YVdGcPM5bDtHG7BxXGmqA+NYJo5RkdGGUqG6NWHWF9ZwTItosDH93qIYhGIGRquImXEyvICrZUlRoem8I0CYWxTzJUwrRgjVsR2GCYcmx/GMQzcmiBvqDT41ftAuLDRVNx4rgDjVajNmhy6Yoq//q85RoZzjFYk/oLEXPocTrxCbfggu4aK/JffPMGFM00KrsAuOzz6+F8juwtgrDFosVRFtWOskwn09NGvkunU9AitnR2bKHuFOllhcgf4d8DfouoeNOYvVhK5FPlHtPk/iTjGa5Ls0TlY/xHgx6HwQaheCfW6Koc2pWI1pUjr2A3VJSvw4NzTvPDP7mK6UqDuGluaXWnu9gxKzVtD0UCQ2Rfo/kqDv/v1QKLSmSULelZagybVbNcT4EoYkbC4Ai/Ow/MBfP/7YdmEzQiafcUV7SAlih344I3wiw9BPoCZIuw04FC6399MTby0DEWi4qmN9FEkE5Jq+tEgMzT6qoTGSRg5CJEDXU2AuqheUKn/60UJs2bNIbvYN1G3TJvswvDSh75IdPW95kUh4w5TrpASmYeW5vo0U6+zGz5ZFzKdKdB8YB8liy6igrxiHtppMHvxCOmWdCm5KSLlxU2kxmXhQE4g8jmM3XvI3/8B7vgIjI1LvF7C+dMJLz7eJpg7jRX7iKFZwkYXe+d+JvfvZ2J8guNH1nn2y18gWp6DqAVRR43tZpyeDDtdgvfYaoenoe0RtCWBjjVzZHWOaWfeLSmRwdfgIpErihhmBbMwzt4brqPV7LM6P8/KiRdRAhov+4xRQpgupmlgCYnwY6QVkhASJwFRONjgTI8E29jGNrbx1uIdQMYaQB2c71FG3fE8cArVRkD3zHyH2REAWUMbhfu+5wq+7buu5YryDCp0XCCjfvRp0oqyDllY4gNPEvUfxet3kBLK5YryfeMQrjnCeF5HD9OUcj1KuR0oouQWEppEvEBXPktV3IV50QxgJ7BKi3kkMTUmUSSsVr5l5PCwZeOWqiyP7Mc7d4HJHYfZ247hy1/6uh29rweKRpVYGgxNjnDu3L3AvfzMz/wrfu7njnFZC8RvNhTHMW/4FMf/5J8yWit9wxUcLQmBsMFwIIGZoQqNdg+vGXHyWJs1MqsuuLxi/svBwvGH+MMXv8wf/oZIFcJCdfiWlxCJxVHkyLU0Nhv0/B4kAbYZY0UqsVQs2YzXCuwCvjQP/abahFWDkQjMAuSLUItU/P8j/z38lXcf/+XhEFo/NfBFu4FfhI/ew63/yGHyDsFSX/DVMdUL543j2fTxBIqU1fV7evzSq5QcWUfbQfVEJ31eS0zyqPFNl+DtR417S3A5JbDb2MY7EoLaDfey/x/+S+6/9ybWuwZOTlCvQdGCFx6C5SWPtc0mcytzLK6eJV5agbUN2NyAxQtKDiYAEUI5D0RKglcswq5pGBtW5GyvDY1FiGLVQTtJsjWz1yFzae8rr9ggUATr5ibgKqLMSBTZW8opEtZI7+1+ujgWKKsDL4LFM9BbRFlK2WTxjJaFJbxuyDj1s3WIkoDELZCzqliuRcEBx5D4fkytVqNYsEGGbK6usvjMecrXVxF2gQgHrwRGV0KcYMoIooiC6eCWc4SlEkmgSGzbtDGihG5jDcuCMAxx3IQdO8aIuh2iTpvEKCBcmyjqUyiPYOdjojAkiiOOP75IrzXM8u4SN85kUWxtCPZdD8trkB9V3Espr7jmD9xbp7MCc6cTums9HvjBL7Jzf4VqxWHl5Ab//l//c6687lqG6hVOPPIVnnzoc8jkGS5tXuuhUvxH1ZmkjyJYNQVeZqtm7XFUCj5CNfvSmENZHTzGVtvMS6/fBjNI7kFdTE+9npMJ/Fvo/Sr0roLFT6LmrVTpdtEgYBRFHxfAnOUff+ws/+R/nuCHfmCEvS/ZC7iRrNr8pXt5+WY82sBK96U3UE70z3dU7qKcU+/52zXYlDA8DkMT6tazJHhNOHcW6jdmDp8O6ur/8F44F0BrAaIZNZvuIiPRvxnQR62AdOu5Jorq01xmCXW8vPR1fV7HBSzsg9WiijQujiImhD6EulpPE6f5dGNlsqy8fjTSL/WzbWxpHFdKPz9KxhfqoLJCVkA4iTpxmujtpa+NkIU7gxX9WokLmQ+DNKCTS79UG9lqg+UC2FXI1dSP9qQiS20TChaM1qjcso8r7h7i/m+D3/o0rCwk+GttkqUleOppZj/0AfbeXGNoqsdnfuNhvHOnOTe3wUrjefzuBnFzXdnQBGn5f7IJgZ/ucB/FXPvpWSmh7k2dYNdEq+5NMmgGrRW0+qBDlpzXB0Az5qqpa3FkhuHJWfbu3cuF5XUWnn+e7uZ6+pmJgYMoIbaQpkWCRWwYWHmI8YhikyTR6tv+wOPr14lkG9vYxjZeCW9zMla3GrgZwtOqe+PFkHGEzGH9nQ9T+liygRBLqN9YJCMvtNu8Trtqn6AQ7WlqueMU7CuRDINZQxHWfRJxilC2aXQ96rkrcC0Dddz2ACMYCGwEFbELg2vJbAkKQIEiddRiaRZFxtbJUr4KUghVpWMJaq6DZ5ZxqH5dj9cbR5EtGVSgn3SQ1GiHY/zME4Jn5wRHn9O2ENt4Wbi7OHDFe/jtX/5BhioFDOPNoWJfq1RQv65TAoPvOT0HzaAKuSHoXWC93SWIEvoSevHWPqpbUcF1x7ly/2H2HTrM9Pg09foo+UqNfLlAkiiOIo6g3eiRGOBFPt1eh6DRoRU0WW5uML++ztz8Bv7GBrIfQ2wiDRfCBqqZ1dqWbzVdC6uWx/d7JH6IME1wXHxMJGA5Nm7eVs11N6EQpSV3FvimajYrJIgeFCRMCTh86x5O/NADHPk3nwV+iuK3jTDykTxXXrGLyWGXmQmDiglRAfb+LXzhx2Dh1VwNXhZdlITkCMoqZi19LKLGmEGjP8i0LHrs0EpY/R7dvAGycU/LRnS33Xr6+S6vRgNsYxvvTDgIc5Trf/rTTO0YpjoyTHFsFscymZ0V9AJYXpOcfy7gzFNH2FjaoL3RxN9cJV4+q/xg+55SnuaEUsMKwJBQd6AwDE4enBwU8opo9XrqEcUgI1U/PSgXCz1VhhrHkIh0be2ohb6b3qNJqmqtV1RtcCJVKSuoBXwcqG0aQDeCaAkVu2jJmC5x/VoU7xLiDQgSDFHEiD0sN8AULo5wydkOrpUj70qKBZdCsc6+HbNYB/di5koYTgFpunSCFnEY4uYKFGsjmKaNS0Dc7hNHASMVF9csIxO1j4aAZqNBr9fFME1KpRJzZ0/xTOMRRqb2MLX3ELmRYUw3JqaPDHvEUYSMBEtnQ/qNKp2NUe49DHkDhnIwPgrL52HuWXVoy0VYOwOtlkBKMGyDws4Ch/a5tDcEx47M83d/+gcYSZuc6dNrHufoU7+PTFbJKsYy6FT6BtnoPQHMoJSjWhvWRjXlegTFJd2Xfl4ADwKfAZ7mtQycfCQ/jGKgtGAihxq3X+08z6Z7cgH4hXQPDqZ/R9PPV9L3WhAXkXMxv/vrPi/Ot/jf/1mF/WQ0ThO1YhikgTRCdAsgBd2FweSVfXR1ZwYdd+j3TgNDBTBFVmkj6+CXwZEwaSuF61eehdNrKle8Iz0yfZT98bE1+NzvnuGKaytcddcwRztwZQF6xjdPFKrJ6WnUddgmU8nOoc5nFXXOdIMzXbTfBQoVFacFgRLpU4fKsDrecQTtc6iTqH0O9EVRIcsDL5AFl7r1hl4KSdQlqEMUJ90RvUzTxTxtMhtU7SSgvWpl+p5BCw7tUauH3gR14dqowLWt7fd0BCtQV15OyekdS/1gN61KsC3IOTA6QafpcuzzXS58boXVx44QWjlksYqoDzNy3320CxWefXwVlk8hn3oGegt0L5ykbxhIfwPprShFbOKT+fdrTb2f7os2jRhNf8CgqlUfzFezAdCJ90FoItcGo4JVrmBYLp1mgyefeAJ/c1Xxw3YJo1Sgmh/CKbpEMsQL+hBJ8rkcoe8R+D6mA1E7gqgPkZdeMdoGQT+2sY1tbOOtxduYjM2hJpqa+rfUdRwRarE/2LzqjUMAV+2pIxNJux+w3Ozhv4XRz5ljmzz3yBK8fxdZQZKmmAbNiAYdlVQoKIQBZg3TzJOZGymPHYHEwMExTQwxjCIhQ1SufQxBHiGKGMyi3MB0plMAZayLhPAoKhrR5koZ/ZUAiRC4eQvLccnlC+SLOXJ5ZU/39sSgP6VCkvrxer1VPvdbf8Dp1Q26xx55yfu2kUKMcfsdd/ORj32EW6+c+cbswss85/kQB/HF0lg/jBU3AEQYFEvXsH92lImxIcbGhsjlbeIIkjiHaZSZnt7J5I7djI2MUy5VSUwbyzJJogQZQywNWs0+pmPhBQGNVovORovaVI7TC4sYL5ymHcyRFKeoFYYZqQ8zM1PhxIsLROE19HrLLC9v0l1eA/oYYhTHSAjCLnZsIgwHQ1pEIl3qCfOiN2PQBcfIqoNlnPIkpuI/4gjONmExKRDt2kHxI99Lz38vpfsqDN1lYE4q4VpVqLvdNKF6C/S+F56uwMm/fK0j7qMWyYtktgEnUWr+gQ7qFxsJghq3imT+14PlbINKWb3k0uTrpVS7hZoPdqSvPfdaO7uNbbxjIPbfQnX3YQ7s2cXVD9zF0FAZ17YQQK8D/XbI6kab+QsNzr3gsXnuPL31dYJGCxrrsLqq5F9RBGG6wLRs1YyrXIKJEbBcVeqdxKrpltdLPWR9SCJFxiaxirdk6tcXBGqQEYBIlbaWqSwOnNR2QKTKV9dM1+eBUtzGESQpkSvT+zsI0kW9JhRM1LiiWYjLVcZKkn4fxwVBnyjqQNSk3zKxKzWMQoUw7pMkPpZVJJezyBeHWN9YpLuyQakyxPSePVhumcCPsIWNa4KwTUxCiDySKMCyTXK2gzBNZJIQ+B5B2FHetLaDZVnkDZPNjSVMy6JUKZIruXRbDXqdFkmSML1rP0iTfisiDgIc22LjQI2CIyiZMOlCfxJ6Ddhcilj3Y2zhUK0IlYCzBbW6Qb/T48WjJ3jh8WdZPH+UasFgfflZfO8C3Yts00sxaFepq6UDFLFVJ+tNFABfQI3Uu4BhBFDncZr8FTFfRJG6r3FiUMlHMBjB5CpCMw/xc2TVVSGZj2QOGAXz6nQq8FDK6SZKXKCZqrTc2SqAVVbN55KYxRfhYTvgP9yU8L+9T1ByxEWjG03zXEoFBekx0GTspU7mL/eLMBpWEgAAIABJREFUNAZpI5FuwzQzqswVMGqrHdD9oWJgpAy+gNBVn9kEuuktUXFg7748uydsZhzlgRqLbNb8ZoDmP3WzuE0y3eQmmVxES1Mk2XUcAUKJ30GkxHgZcnnVj9AfrELXOeBS+kEtt5WocKVL5p6SJyNGtT+szVbhp7549M73yTQ0+nl9McYo8rdHZnUwyGvqkEdX/PsxakGq4yuZbjQV7QhLdShzCmp8d1wo5KBagkKNuBnQWezRaXcoT45y5WGXqckyo0M1miPDPPh3EY0zZ4iP/y2sPQnJporCJBDrH9Ij82vYJLsbzHRHR6iO7ac2sY+NtVU6y6eRsb7D/PTzg81bk4HPa5GRNvQdjANT5awEGUuCfp+w38cLYhxhUahUcYtV8tUa1UINkbOIiPGjgCSICL0uUSiRMiAOAuKwh4zbIDtkpsA6dt1e621jG9t46/E2I2N1uUKMmvmGUZRBP/23HqTPvNIGvvZvNgTX7B8iCSQLG22aYQ//tRL4byKee3SDimmw+WP7qBX3IURGqG51UCL920XKECmVgbowKgjRRalNdBuBMgY1HOEylM8B16GiBF3yoWtzhtLnNdktBt6TkBnDg0r3aoexjBQWhsAt2BhujnwpR6XuUq/BkvfSquy3B16Jae8Sdk/y5L//BVTO/etVxP7Ox+jk9XznJz7GD/3Qx96U7V2qhh282i8lXQfTFJduJQoSEq8NvirRFHaBUr6IbTuYpsPk1Ee5587DXH/NPq6+ah+1Wl5ZKfoBYeDjExNh4eZU8eLmxiZe20OEkWrgYtiIJKIgCpgixJcxPUNy1ZV7sHMuS0stVuqb5Kem2L/vWg4fOsjtt43wmc+dwe/5rKxs8PgTL+I1niOJ1xCiihn5GEEHkwIisZGxIBJKZiGlSSQhkIqUMS3lKSilqj7209bDuQI0OvDUCTh+Bpa8CuXv+xShhNw+1aR6tQ8lB8bSPjouqvyx/T3Qz8PJx3gFBwAdjC8BfwM8iVLDrqPGgw0y0nUENWbookKt4Ei74l5UteqxRxOzlzbn0mpYnYDSy7TdKOpgjsyQbRvbeAfCsKBUp1hwse/5BDve/1Huv3cvwyWIemmfrFiycDLi9Nk28xfOszR/itaaB+vr0G2rR7uREaoiUSxEGEFBKAXsaB3GRsALoNtTA0mcKCI1Sj1kiRR5KnXMkS6Qg5RUdVLvTjNV3NqW8pKN07JZIdPMkKEIV6+vPD1BEQSxkaprIWvmomO+wSalNpcFCUkvwCqEyNgkwQTPpN9JcJJpTCnp+TFB0Mf3CiRxQL6Q4/mTL9C6sMHMjt3M7ttNrVIl7Pl47Q69zRZWZYiCU8A0QkzhE0kLAxvHdoiTmH6nA9KjVK3h2AWMxGSkWqfT6RD112mvnsMwIk4++QQba6s4+SI7v3MSQ+QJwy5e2GZzNeZ8o8hs3aLoGEyaMLwPWhvQXI25cM7nwFUOO3aqQ24Ykno94S/+0xyPffEvOHf0EUga5MZGmTvzMF5PS/peHrrOZ4WsxY9ERYK19G+Ccvr+AvBedMW1QZdhPkOHvyDm2cs6QRYGO3D4FkIzgmRdXQ8XCXjNdI2DdSO410OUS5OpGxA/DHIJlfxzuFisb7tQKKlrM46h47F8LOEXfj3h+2802TMEBVNFqhu8/Cxxad1Typ2+JjQRqLehn9NKXB+1YqmyVT4RAFfthckELkQZV9ftq0acV8/A1McmcCTYCVxvKxq6S9YDCt7dzbx05b5EnelxMmGpJKsr0uYmNTJlrCFSJ9U0Z2QKcIrq3ulHKlF/kZVPH4ayfiapkHlODKFCG32D6Ne0LkbvoHZa0itpbSugZdWDvafK6fOaTS6TKWUHzZsHK/YF0JfQjVWFwsUrSV+BWhhjgchDcUiN5cUSVCswUlPbWl+GXgfhCCr33MJND8CdewQ3VE2+YsJjf9MmXngOFv6KTGus2WrNWPdQ8VaLzFhjIJkuZhjdcS37br6eY88cpbd+gjjW79dzSp5MkqxZZ/07tB3O4J2qRUgCZEjc6xKnjSdNs0B+eJr60AjVyjC1yjD5QoGABGkZSFPQb/eYO3WcKIwVEes3iYNNMr8IyPwhQrZjyW1sYxvfCLzNyNgaqjhlKf13BTVw63I2HzVDvvlIEsn/95en1H+0J7rDW9or5vzKGj/7e5/hX//AT5NzButndD9bXVx2Fmji+R36Xg8riinV70eYaUDLXlTopo3ddauCWvpX2xtohzCXLKwZJD1qwDmybGgeVb8jUKHmDGBhk8UehYLKyO6o5LjlCofPrQaE78jKD91fV3fz3Mal+L0vfpob9u/5ujaWGOxy/Hpx5PgmaxvngQsgDPZc+3H+u+/4Aa46fC3lUpmRnEnFBRmG9Dp9zp1duvhZScpLWBBHEYmUNJsNon5EvVrBsW0CP6CUszAlxL7E7yp/wbNneqwsdMDrMpzzGB+bZqxgEbdjnvwybC542I6DY1QZqY8SXn0N7V6PIOzS7DaxgCjyMRwQQhJFKtCNUwHbPLC8odQzFooDyXlwahl6EpwavLAMj/05tJ9BDaMfgJ0/Ds15WH8QbrgfWhGcsCA04TYUpfk7vwtH1lFVoT/Ay4x5PvDHwO8Bn3+Vo19HjROzZP7WevwANe5sosaxXaixqY0aV7SHmJaSlNiqVdJXQwVVsjoL/CKvR6O1jW28LTG6G+NTv84nv/t2iq6FY6XLVA9aLVhahjOnE5YWT3HuwnG683PE8wvQiBQZG6dsgGWq+lwzSVWqMdRnoVBQ3oFGrMxINWwH1pdS8lVma2K8VBkrlcwvilQ5ZxyrOl+EkuXbdmb1rBmKOICldVhrKIIXA9zBYu9Up5grQ3c3WQVPh4yJ0GrJy4OMYG5Tks9Jiq6EMGJ6pMbweI1ibQjfM3n6sSdZbZ5k0Y1p765z9y0fIrmhhFMo47oVXAt66+c4+vhjvHD0CPfefjVj7/t2TLdEEphEKXng+R5ev8fG+jqVeo3a8CSOW4BIQr1OfXaWTrdPzw+xiOicPsHS/HGcapFi9HFkSSDx6fU9Lswt8IX/5nLDe6fZO1NkR06NoHfdDNNTDidOOlg5Vfc+VAdDxvzVn6/z2U//It7a0xCdB9ZYOPPqhgEaCWrkPQ5chTqF66gaAxcVPTbJ7AluQ43Sc8T8Bif4VS412Xk92E/ENBGbEPwKcIAsJq2k/94J7jUw/e1QqkGUpNdQD1Zvh/YaRMeAL6F8yZsQvAfkjWCNZU2OiJBPwz/4MvzsrXD/pLrqhl5hz8ps5cR0iuCVEA88ICO0Y9QuOOkvGrRCGrQcdVGpSkfAig0NoT63sAbPPwe9BK6bgQtdWGwob+idU7Boqv279jWP9bsTNmrFcQiVSNgg85GdTV9voK7tDRTXH6DsU618RtZKE3WRd8EcBXtM5atAEeJ+j0zFOkmmXSmhTp4++S7qxOrwRBsPF9OHfs5J36ddWbT7nEF28el8s5X+oDzZRegDDS+1KPDTN2uFuI6J0jcLobyrotTz2/fVWGxZUKrC5DByyGb+RINff2iTZ2/J812fmmR4BxhnHoHVr6Asp3Tj6JBMxrvOVjPbIhmZGgEe5HIkmATtHutLF0jic6hYT4/nWoWqiVn9wy9OJCk0yw1ZKiP9jYkPwsYpFKiPT5PLjzA6MUWxUsV0C7i1EYpWkVpthEqlynNPfJmjG6t0N85BuEpmbRgNfM+gMnYb29jGNt56vD3IWGMYKh9UnordOdRAnyezyX+OrHXlWzBgDrZMl0DeVnKyqKsigMuooLscLJ+H3/mXCT/z3RvkHG0nsAD0kMk8CIEQ2hl+P64zjGMXEKwjjMPpTuuGOVq56qAmPT3h6OgBsvKRDiqcuQBsELFClwXKXI1glbXOIk/PL/K+/T/GY+d/i7wluHbmfen37USQQwiDUq6K1/eIY0m5XOWm66/m8199mjB6p0xyOq1dQoV0Y6jj2OFrWYK8W1EdnuSH/8UfcPXENDVDvCpR+nqVHK+U79DuyC+njn0lbG5u4vkV6iP3cPu9n+Sf/MQDRJ5Lp+PRXFilNF4kbJsE/YBeu49h2OTzeQzDQAhBzjUxLRMpwfM9Is+nUiyTcywkkjiOqVQL9FoRSRyCEFhuifPnFmi0WrhOianhPbhOkU6/Q3/lHCJZoRf0CYMcnX6ML1ysXI6ku0YctJFRn9i0kH4MUYQIfSQWxG2S9ixRf5YocWg2wRpKbcQ64HeBIRibhplDcDAHhavg2B/Dmf8I/BHMd2H270PlRnjsL+Ge+5XVgW6nsAGEw8CjKG5zy8kIgGPArwAPoxonvhq0c1uEGnd0L259b1XIVigFMmJ2PX2tQuYdq/UwhfQ53RAsQB2BGqo1y/MMdgzfxjbe9rj3u7nxAx/i2tvuoDoxTqVsYZiCJIH2puTx52JW186zsrjA/Jk5otV5ouV5kk5XqVtjqf5KqcjWXF75tRbz4KYL3CSEoK+8YDHAixXBKoQiV2MvZR9QkrIoXSSn9i7KDxZwtU2UUKWyRl69N5Fg5VRX7Si1JfBTpbqVV+StaaXbs1X9sOmoz9TzqmlYe51sMa5dPr+GkqRY2QB2vRjfgrHhCiY5ZCIQpsXwzH4+vuc6Hnnozzh98ihnj6/TvvDH3P9d38PIWJ1eT9LtbTIzUWF5uMzpOKK7fIpSvIHhDhEaeaRpYlkWGAZRtUKlWqUfhTi2haWJEKuIS5GYLpg9LAvu+75PEpEQI9mIOoguxJ6PDANMGbGx8DRHHg3otaawbxhiF8pGZmpIEO2HhTl1CB/925O8eOQk60vrHLrlas4/12N9rgv+wsscEN388KXBaohKsfuozgHjqNH3TPr8MoqS+R9QEdAaaoT9d2TtwEwUqfi//NJv8qef/UO++Pk/f8n3GJhcU76P9tQVNHpzrM/95/SVdVRcNUVmUTABYgZyVSiNgesoa55Qwt4ESgmEd8DKA/CVTwMPQnwCOAru94E1AnlHeWTWBc/+PvzIU3DLDfDDH4U7ebkqmqwCJ3U83lIhrqGLpbVMQWs1IGvrqqUiejsOmRGD/g7tTmkBZaGIVZ9U3jAEE3tgYQFw4dypiBNHPKLVDX7wJ6aRBZOGhD+x4cNctnb8HQedih1C/Vadzl1HHUetmF1Inx8i4zOrqOEslNAT6viHAoSjlNI9F1gF01W22kWgLSFpkoUjg3Jp7Q6gxZyQEa0vlzfSw5kWXLbTbXRRXKCDuj11xX6P7Mby0/c2UWN8o6d8wP0mxM104zqRYYGTjrG2q+w6vLS7a7OrfovrKs/usq0+v/wcWDGT936QxJzki3/W4fH/9+dZm/8MeBfIKgH1d+lx+OWSPYM9NyR4DzN35AiLxx08bxUZddm6XpdkBhOp2vXiwRpUxF4iNRa2OllOGWGqijXbcfFjVanWi1F2BcUiVq7E7h17cByX5uY6Dz34p/Q2noFQU/eX9jIY9Cvfxja2sY1vDN4eZKxpQ1KCsI0amJuoMEf7ynwDrOsHx+YogX740gqKNxlxCJvLkv/69FPcffUNjFdDIk7iUAahm9doxVkNw9AesLC1C7lGh2zi84ETeME6Xa/NUPkahDBYai8y17jARstnpFLE91oYIubg3j08ePxz7JocISBg0ZsnZh6KEswaknG6eOSRKkAVUC7a9AyTxHKxihXqE1MYxrO8dRnHKmqJEJH1ALbS53xy9SswrCq91VMon8tLT6YmejrpY4KslHosfc8q6vp8fUqUdxtGZg5x9a3v52P3XUut4GC+Tob00uJzndfX2m8pM+314GrI4vWTsBrdVgO3PMnMgTK333kX0yOTzJ1ZJe52caXEMQzCICEKY5JE1ZxFkc6QSxwnRyJMTNvAsEwwBIZlEMUJcRTh+z5lo0KQePSDPr1uB7tcJe52yVkmU+MjjE5fQeBYtPo2YWRTLpqEpxNWGhb9sIsnN+j3PLUo90OIExIjUIG37SJlAYwAvAbe6hlWTlV58pEDbC6qHjrtWPXeiU7C+LfB1DTsqEHOgJtzUL4bnBiO/7J6T+MYGCNwaA+Mm9CO4IklOPoILD0DK8+jqtOWLz2aIepeeQQ4zWs71/koYlQrHbQtgZ5qtI5e66m1tkiX2+kFQIJa/RRQ8hG9EtKKBp1cmkUlkbbJ2G28zVEfw57dz4Gb7mPq5luZPXQV47M7cPLqam93oNWIWF3sc+Tp03QXTtFdvkBv/oIq+W+2FOEpJRhJSghYUHBhpIK1dydJIkm8PjQ2lcG0TOdeaSkSFqUapd9Pm3YFivSSAz59UaqMlaldUZIqZ4VQzwehUuAaJtBOm6H0IfJTdVa6yBWpl6FhZUSskU/FURYkuvxI1wbrjta6WDwmc/V8HZBqV8Mwodn2CIKEzW5IseEzdaBCdXovh6+/jbGxMV489hRLS6ssLZwnVx2iNrobK8lTLsDuQ23iOGDXVJV+38dKOhhOHtcuEmNgmCa2aWIkYJg2pmEhhAmmiWHYmLFBvgCOa2OaIYsry5RrdYrVGs2+hxV5xLE6xrZl0myusjR3HCE8igWX8YMFHCEYdiCpQdeDL33xGCeePUVjeYOrDuyltTrPyqkuxKtkHcw1ka11mXrWdSB3pyLS5XlgnhBFbGk+aRgV2bTSRw4VNXVQ08JfsNW9RpvWfOlvPs/cuZe3DZMIGu4I3dYF+v1Nsk7nDpkvsATzeqjdAMOHYWQUdhdgLPVJ3wBjB0yPQni8wdIz51C08SQgIHlKJSWSD0NtB9g1cAR+D86fgCACsw6zd8KkqX7Xy0HHIy/3fKr7u9h6zCCrBNP9nDTNpAndhKynu/6/1uNpYlfXewwDfh4644rPLxdhdkbgSpuVF8v4CJJQfUfbVunQWdSs+G6Fpsr+f/beO0qy6zrv/d1QOXRXde7pnpxnMIOcCYAgCGaIUaIpmZZkSo+SLMqinmXLomWbS5b8JFmyLL2nRCXKpiRSpEiCJEiCJEAiEWmAAWYwubtnOofqrpxuOO+Pfc/c6uEAA4AAMSB6r1Wru6pu1b117gn7fPvb39aidSWkf64gJNNeQsnVIoJ31ghnEBMhqjddYAr8mGjH2nqYBECop0Svt7EE3jxhko12S/R2oBKcMKiXdZbzojvHIqsV3XRCp0VYEU67PFo6f0ZfaPC8HPwI3xepGdeFagnay1K5VdXkw0ZUwMlIApJROU750KiLDrjfFFa58oPsBgU1R4oclo+D1aR22GJ63mDROsPciW8gvl3nPlsHcTqBUbPjNY02d2yKVRmnVcVp6QY8n+kG0+dQQaPpEMe5OwNffodSoHwUPp7nQtvEc00cv4yvoNmo47Sb9GFTLS1Rq1SYOHmIWuEpcOcJR2OTEAjWf72O5y8T02rN1mzN1uw57OIAYw0l0bu2rp1ZfKWvaLU5XlAQ4+U3Xyn+8etPsblvC/1dUVxVImrkMYx+hEmwidAF1CyyJOFiZoEyQRVQxjKO71NtFanWm/RlT9B2z7DSWKDpelhmg1Mrpzk0f4qZpTr712+jXqkTM9Ps2XItp+YfIdudJ5HKEoumUbTI5TYQYwjFOlo0zjq3pgnphM9CLI3vZMGrkcz3EbHMVfqfL4/pBLA8Ei9vIC6bBmOHwWiTGbgFOz5IffHziPNx7j3VLrROLAuU1IwRiA1gROMYxgR4k/i1BVDae3pV6jC8cLMSbNp5OW+64/1cvSONYVwYJj2f9mun1JY2H0kpixurN0Wd0lnP15q1GsnuIXJDCXbt3ozbgma1hlOvE4/HMX0b32nhe6I9hWHg46N8AWcN08S2okQiNratiMSi2FEb5YHr+TiuS9vxabkOjXaTerNGV1c3hucQMyCVSrBp8ybqXXFKdRPfhfU9ELegegScUoE2Fq1aA6/ZFn1FJwAd6jVhB0XiAnZ4Hq1yhYXpFR47AOWKxKwipkiIVZ+CxOtAOcL6ANhhQXYfRIdg4RCUJqGxDK0lWH8rcAqmKzBxDCb/Efgy5/FBG+LIWwqoQHta/l7Q2sg2v1NOxkLAAp2WprlDunqFjWxJ9XvaGe/UF0sQiq1pwbY2EiTpRVDkNbmCNbsIzY4RH1hHbOteui97HZe+6xfZPRpFGQYtH+pNRbXpMj/TZmG6xuzEEuNPPYaanoDCAqwUwI4Ks1WpQEXIgIQlRVoyKchlsPrzqGqg09qoQaMicgJmoP1qIBv9ekMmkrYupBdIgygk398NAFgvmKlNU6KtViAY40rwCMOHZk2+x3fFj0vFIKKkWg6G5AWbkQCQjYKKiXCja4CrtQI1whFBmFAeqAShxrReX3UY77m9CaUUlWqDSrUBhRLxQhkVj5NJZti2cSsjw+uI0aLhH2X6zCTxTC9963cxmB8Cy2XUtOjKZ+nJ5zgzsUijVCESbRKPx3A8AywT0wBbGcStCL4usGjbmKaJZfnYVhzTjFOvFzh66CmG129kZEuUetvFdBW2YWBZFpYdwXXrFJfG8TyXiNXD7o0bGYhC2pblaaUfpqdmKRRWiFkmWzZt5MD8GKq9DF4FonlwsmC2gBp4RTRlz4ymsdMbiA28l9qpw/jtBoa5SCK7gUZpnDnlnq0ZlEK8Jg+BOj3gDPAo8K1z2thHVoPPffZT570HhhHBinQzR4320jP4jon4ZrOEQHsD6IaeG2D0ChjeIIzpXYir6wLHwByG/AA0p+rMlaYFqLWvkytwjsHi16CVhOjlkNoObg94UdwFg6kqfEbBey+DdFLW4PP2GX3d53ldA7I+ssLYrAZjdXvovDPjnM+d+/7ZADTS6wcQsLAWgUwUEkkY6LLYMmQxnomhbDBVmL1+OvicVmj/YTOtNO8iIdY5RJjtdPD6EgKpZRA8cwphttYRH7IaqLR4uubVQaAf1AiYcQTZNYLEgWCqdE8jgKrWctUXoWNB04ir34VwYjKEtY4rSLcuEyLtOt6cJVR90wmKOsZUIMQeFaGik08AxjrQKoO/DEorEfuCKMfSEE8HZT5qEgxz6uBVRZP5rLxAwNWuV4ITzoBXpHxkjDJz6AJ75zetXaODZfpCddDn3Ln4+eyDPFbP43pAar+vcyRq0NcDvw1eDbBwXBPPsDGtJF69RbNSoF5K06oWwW3h1goU5qc4eeRRaI4Rag12ZmB0XreWxoI1MHbN1mzNXgm7OMBYrwH+DLLsnn6lr+YVNeXDF36zxr+8dIGrd2wgZb4eATK0grwWJ9Kq7xAm8wi4qEiC81WwFXOVCl8/foJ7H2zzq++5ms0jfZhGkt/+P39PNgtdWYOurM2m0V5u3/lvSEcriFtzCT9982XoPJqdu7YCt7LD1B5LlR4G0QubgUeMZWLdO6m4ceqtFvGuPP0pg3YD6i8bXmkg6cq7EW/mCBI/12ZL+yQG6RneTyJhMvvkJM9v0Z0BeiE2Cjt+kvjWPUTtCGp5ifJ9d0Pri6DuRzy114Bl93DTDTfw7z943XMe1unmdG5udIpeZ32Cc4/Xz8+XLnghO/s9bZvuTD893WlAsVJu4fo+vu9SKpUxPJO218ZVPso06O5OkEwl8XwPp+3geh49uTSRuIWvIhhGP3E7gd/2qNebtD2fxcVlWq0Wbc/BtRQtXJrtKo1ikbkzDtNz0PWG/ezcF2P3iJTOe8d++E//CCfrEexiHsv1MJQL7SpUF5BthS1UoEg/pDcBPZDfQzu/gSkb/N1Q9aF3E1zxTvjWPJz4f6H1DMR+X1IYlQFbgW19YH4CPvO/YcseGNgBnz8BvA/ZZX8P4azzTpyAbAb6RsC4CcYSL0bKMTBdESOOON26B1SR+SUFrO94zSUsz6E37YqwWIS+VhcZ+1ci8+PdL/YC12zNXh4zbejfwo7//P+x89JL2ZrvgqqQQl1X0ajD5AwcfHqJ6YmTVGZPw/wYjI1DbSWoZO2A1y2sU8OXIdM/GNDo0oLeeC6to0cF+FRK0lOddgDAesJmdT3wWhLFcXWKabAZVgjDqtkSYNEwCChOkE4IqIvibDVO14VWQ+j5tOR8saRU9LYCcRnPlocdAycKLROqLTltIouMcSe4hhoYGTDTYLtBPFQXd9KUsirim+hg6flMJ5KHk1W7VmPyscdJRbvwXJfR0Q28+f0/z84bj/CZv/0kBx5+mGTPILve/UEMw8MnSt21IRUnP5jlmYMHWFyY4qrXRVB2GstMYhqWbPxdiCYj2FELMx6l2XSxLJeIncA0o0xMHGH61CFSMZehoS4gSbtZREUiEEtgGd3EYjEqlTIri2dwXcWBfRu4YQN0JwxSJuzJwJtuu43Z7UWqC0ucODHJd+76Gs1CA+K7MUY3oiZPQLJXNBVXLHSmQGrDDQxc/4vsuOGtfPs33kd1bp54ZoT9b/8sj332dmqNedooXARf0pKZEUSZ9UkEy+r0qJ6PRePDdPXcxsLUXxP6WkeDe6kz4FLA7fCmt8NAl8S9N3Tg8BPA18E9AAdzQHI7vG87DH0kFIGdL8F/+xvgv0NhE1RuhfpPQmXT2YCAOweffBds2AG92e/1Kzq5f+eCsiarV53zYbkaa4sQQj0R5BKLrIZ+RjvOlQz+jyEasgkTHolBsQ2DNvQnIHZ5uBpGCMV6nkJCkDecc72vZtNtdAzxvAvAY8jvn0G07VNIWz9D0IuU7BprChwfmVt0faYm0qG/BNwE7Ti0k8EXWVIjztU1iyeDk3jITVoITqTxyBbi5i8iN/aG4Pj54LUWAsbqfU4VAW21jqye7jqp0osIwKvlCjSnpG2Cr2m3nYWlgiB0thcSGZEnmFuSwo2qEZy0gOyhtd6CzvjS701w4ewmbbrmiPbddDhilu8PtNSAbmeRVz2ydIUIvc+1gTaouvzOICAvcG4SSOARpVpMUp3pYurEQ8IkVro2QYWzWuWrRq8GhUHmJB3g78woWLM1W7M1+8HYRQLG1oD7ea2mfp/PfukT93JPYRd//LPvIWQTdCpF6WIXHuFCKaao8M+PHmLz9hEyuSSX7hgH1ckCAAAgAElEQVTmbXuGwK7ielHWx7fyWx+4EsMsYBopDCOLYZSI2RrgrSGFEtYji5kO2f4lYYQxAlyP0BhsDOrEmSbVt4+qk6LZjEA1zq5tBhUH6i9L3bUMwuGIIqlrZb6XvVcDvgMNk9NHLMxIPjj2uRbcGKJFuRmoQ/MEHP5rGkf3ErvtZrbesY13/9272Kneyu/+60N89yt3AX/A806nfJXan/3B7/CGW6654HGa+Xru5PJsk43uud3GS7SpaLrElEVURagWXQrNJrWWh2MYYFu4NkRiCUzVxvFqLBWLzCx4tJoOTtsnaiWZny5gGopIzCbXl8PusvFNA8fyaeBSqBYxzQiOEcEzEkxMLbG8sERteZlmtUJsdp5Eehej/THSI+GlZTZD12KE4liWanUevzgN7SWErhEUMMzdBNtvxdjYi4qadO+2iWVh9pvQ/wtQOgiFRbj/Ibjl9+DJv4Cp4/DlX4bM78PtBmxARscScOdpOPy3cOQoISPjvET/RvCJGcCB4lMYzjTxm99Ec/IylOPxwgMPwwg0rAUnNNvVC97TrNcuZKzqgnmdlTE0lUTvbPT2thw8zyEpsHHgLl4zTPU1u6gtfe1bGf7Qb/LGPaNEzCymb9Negmw3zM/D1KTLmYkKR44dpn3mGP7sGKzMC8BpGCIFoBCWqtuE7oxUyU5nIJcJ9pZKADjbChSeVkSCwHOFEXu2GJeCZlHAWK8tmki2ljXyAhqfFCLENIUFawcztuvK8Z2ThuvLOWxXZAmsKHgRWKoKQtKOy3NlB8BCW+j7ygH6oRGXaz/L9zNkA+1VwNN5vgNAHzLGCwh6UQweWmRR8w91NlVneSUx2zLpSceZOvIEi7PTjJ0a48TEFJfsu4x8/yinTx7h6//wd7z3XT+Hne3CivaS7dlCKhGjVilRLk7TLhxg7tEv8eSh0/QMbWVg4zaGd+6k2nQZyMRJJS2iiRi14hLlcotcro++/hx7I1uhegvRSByjLQRnCxvfUbS8Jo32EkpZRCNRWk6b5cIYD3zjXobeeyU7E1n6kVD8jdfC10olnnx4kuWZSd7yk/+OUxMTnJ48SalwRCQi2iZWsovYtlvoX7+H17/5DnpH1lNve3ziY79He0l4ne1ojFM7d+LFfguaf4Wj7mcBYb+aiNe3GwH87uU8yjXPYTYRPLppNZoszXyK1aBNBCkJ9gRQg2gOtt0C2+JnXVgV1O6940bY+nZY/hn45B+IXAM90h2MAKPv74WeZIYjmQ+h/h8DVg5C+2mY/p9gfRRiQ+Am8OfhK78KH/gd2HrVc6f3a77es/kq2Y7/dTlJkFUqFjzqhOHDTnBWA7o6DKJBYE2+bAN7o0InKAfva2GHTpVNLXFQA74A3MEPBxirrYrkrR0ibBcXgQRHEfBVewc2UG3KFAWEBMcZRFfDRVz5ncjNKwWvlQkbUiFujdY3WApeqwWPRcK4sFYE0UxXggvsTO7RqLlPQNcllL3XrNl08GP09XRufV1E5NaKg90NnimCtn4w/xUXoVSQed/XPVaL2DaDHz8X/Egv+EFavuSF7LEdQhar1v8/vw71izM9UjT4qvdk+sZoYZBOVmsnG7eINKYefUlozXVcc2dO3rkN7J/zvFNwZM3WbM3W7AdrFwcYi8eaiPZqW3iyzcJGvfDp1FztOWhwIkq4GdEpKQoDg/2b30xXukHU8silBumyhnFURZwYwyebfJQwLBtFvALtkejU+yHCiGwaGCGURkghIEs6+Ew9cI5MIcVYChW1ufzGfYwVTjBb6FQcewnM2AAkg81djTDRLops3M5ZiBW0Vu4L8pQuJDkRAeNKfuLjb+X4w9/hkS/dHYTRu6gfmWIhn+fI9X18YH+CX//lPXxlA/zJnzSBf0KcoB+uoEI0luDtP/HrXH3lLob6w+rYp56YonsgQ89w16rj9YbhfHa+TYOJsDn1e7onv+AiFUo04mIKGsUSU8tFHsfiir2jrBvJY1k5CotNHnv8UY4dO0SlWsBXTVAmjmPgek08r4Zl1rEMC8NQmKZJPBknGo1h2iMMj+7m+ptfT/dAF8uFIpVWleVKm5MTUyzOTVEtL9Oql7EMm2j7K1TLe3nqyfVctSXN9JlZvnmkwImTC5TGxvHLM+AsSyqvvQNr37sYuSRNLTvEUrKPyPo47TOSRqeSMPQeKD4KQ1tEieT0YZjbBaO3QXo9zB0Rt/vrwFcPQuU7MH8Qqk+AO0k4LJ51mm0hO48jQA3UAqoxQ/vp76L6boKVQSg/gmymIdx9PNd2Xet09QbPg1RkdIqyfu6wWlTN7PirnfWgiNDZnQ0d/2vqSQUpP/OyRH/WbM2e2yyb1Pv+LXs3jNK3aTfJbdtIxFK4TYO2A42mw2NPTVGolCktVSjPLtM4fhwWp6BeDqQDXEgkIJIBkpJzG0lCPgcYohu7sgLxWKjlGo8K87XVhpYDygMzYIcqX9I8VUuYtl7H+ud7wZwQ+BUxQ8Bf5chxvinPLQV2MEM7gUahGVDRqlXwG0BUQEHfAj8JKggYKwdhKXUy3DUvUIsqxpGAjOYhRsBcB+Yo0A9+EfxZZIZbRNZZLSlUJ2TUhxaJgx2BqG1BLEUED0vVadcXmToDJCw80yYaS1GrLFOvTNHfmyUaTRGLRkjE4jTcKsuFFcYOTRBXLpFIBder0VYeyWyeTD5KrquXRCyNaURIJ9OSSWw6NGtFTFzwXMrVItW6S3poBMsyUIaPpxSea2KaFtFYFEwDr9FkcWqcYyf2kjKyZAekRXqisGEkz+4rbJq7hhmfhKKjaDRrUJgEbw4a3VixFF35Xt789h+hd3AL06cO8+i3Pk+rMo0A21fj+32USja+FwW1B3DxOUabFYyOVn0KgTteSGhLypS1gRi+r31DbR6iP57D3PEmrF234xSHiQxZwlOrIcvAHJyYhGoMYlkksqgBrrb4CtShsgRO1ETlUvC2N8Pi5VAuQ8mB6buBLRDbDPnNtAz486dgJQ0/s+vZr78zURq+11/RxaQWkBXNOOdB0GYLiDeqyxUFyeIEgiGdar5nyZIRQ97fhvTyEqGgj17tdBErzRlMImrue1gNFL/aTHNAtdhYPxKaHiTMjSkjbbuCjHatD+vrolhaYBZWa0FsArMfVAXUxHmOqSM3TDd0ibCOlUNYFUxLGOiEwDnOSh6clb7WN9kILlQDwjqpsT/4Tl3US8eam4jWQi3wcWJm0KF6ZC51U9CwpPN7OqOgScgs1Re7RAhy1ggLqGqv+oUAqXqvqSFxDc6+lHY+h1SfVz/0++eeWyFtoEeVvs5z7dxRrEMbndUrkkSsOPFoD5XG5Iv7KWu2Zmu2Zi/SLhIwFp4NITAQuG8bslivIHG/H3Zz5mDpZI1DJ8fZs0WAoXAx0uLpmjmmF2ZhrxiGwdbh3QiosgxmDGhhG3rxqiCudqdyZ0OOpU2YBlhCvAhdvZPgeQ/ikQwHn69jaF0eN4jS2jbEkmzZuZvsvQusLv/wYi2A+aJ58AaC5ljo+B3aI9PsOghj6CZ+c5oLOxNB1XfDoX9DjNkTmskXAdOnvVBn6XCNJx/rI7YXrrwtx2xjL/y9BaVjQTfWDlGnR/jqDDSY0QzpwR28+0c/yPrRPMlE+F6z1sJtJ77nM+dKDFyItXHu8S+2tRTS/crFFRZn5vBdj95MFqc9SrncoN2qMj4+xcOPfocDBx6iXJY+aZtxPN9FnS02df6+alqb2b7rWvL9XUQTCeZm6xQKDQqFKuNjExQLszQaZZx2Azwbq34f84tNjh1rMHHpEGOHjzIzOUllaRavPCs6d90bSPZ0kxvehHnjm9h9ncGcgnpRCGzkoBXEXvJ7IDoh6Yx2DPIJmFuGK7ZDPAUzJZh+EI56sPAgLN4JPPR8W0/TOGaBU0EbSFqzd+Zu2HQH2OsRfYPA4hsktbhR5tlZ4ZppPxw81+ArhFQRPYfpXqDpJfp/fXyZUHlPAzpanM1ExulViNzDGhi7Zj9Ay/QQy/eSXz9K/u0fYMfGbfSkZd10q1CreDTbHqVqjScPjlMrz+FUVlDFFZifheUl0Wg1VJBRaUM6DVELTE/kBzIZEUFs1EVCwPPAClisliESA+2mFOXCD3RcA3asWwc70N4DJGLqhrIDCjm3ZQnr1Q0AXF8XUQ3WdeWLxrXyAoqiA41qoC+rAyY64KmL7JkIgKo1anU+rk0YYNE+htYj7AUjDUYK6An+t0BpqZMiqxEQDTyE67thBnK5JjR8SMUUsYiDQY1WHeZmo8QiJul0gmbVZeLkozi0UGYM5Vts37EHy/SIRKKYVoKVpSW2XzZEfGiE3OAwmWwPEdvGtmNYVpR4JInhORhuDddv0vDruE6dVq1KrdbGaDrEu3MYySgeClcZeL6BbRlYlo2FiembFJdmmTi1xGBXio0DqbMz20B/hk27UtRWHE5OnqZVWqJdGIfS6YA5B4aXw7KgvzfN0uQJjn33Gxz69hdIbLqBptuNapgov5dW2RGWNH3AdjRoo/DP1haa4IWXzvV1qapIHjKXQvFgIEGmxTBngL0Yyd0Y+WuglsTwDAwdlwu6zMQ0LBmQ74fYBs7W8fHdIFvZE+njupwU67rtGOXtsOziTq9A/e9hfkIkOfIeRLZw72GTRFxxVRouGQHTMM4rWfBc/orm5+kyQOd+ppMCgIKiA00L0pbkb3QmYWsI6ZmpNq2IQaInQtaCAYOzBb+KCowGdEUgHgm9fJ2uHw9adJBQ8OfVatpj70HY2VUEYF5G9n0+ImGwqKChoO1L8S1fZ7l3FhvQGFsC6AMrA/5KUO8uyWoipFZr0UCqdgM14p0OPtNAwFgtP9AJqGqas5YbAJnGdIBBb1G6g/e0Hq3+X6PNjaAggBUBKwFWGrxgrjTb4NUJ6bYNZB5sEBJ0NNWW4Md1yhy8GNM9/geZbaRvzPMhtXSGNi60t+sceaABWYME3V3DROwk7Wb5xVzwmq3Zmq3Z92UXERj7vaalw/cC/wPZYn8T+LNX8qJ+gHbo5CQf++NP8U+/9yFsW6draAC2U1lTp+lpvdcWsuo/w/OrgK5truN/vWDpSpctBIhpI55Jf/B+J1PXwXFclIoSiXRjpwaJZ11i0QMvUREvC4wuyL0RihPQWg6uLYO4a1pTSKdfag9L6+36iOOyyOrUGEUYKe0C+sD/E37/g48DW4BrweoXwfxYhkbN4si9iqd+HOZsg+/muuGyK+C+O8BNI0prxwlFp3RU+dVnif69rL/x5/gXt41gmqu3KXuu3/Ky5Me9YEZsYAqpCfPok49x5vgMw70DbN+5jUw+z2f++U4eefibjJ36Jihd4CAJ5HH9GsIKf+575HtjHD00xm8d0kVL9iObWa3hXCNkktt4S8s0ynNMTT/O1NFtsHQKGgVhsBl5SNwB11/BprfluPV90IrD5jgcr0BjDI79CZKDWIdWDcYPw00fhpN/DKoK138Mvv4EpFqCUbg5+O4dhNlpL8jaSGDjaaRe8zLCjF8HbIPx+5ExNsvZsTJwreyUT8yBOsH5nWHNeUkS5vmF+tZi2kGeQ7aTncW+MoRaZSeCNh5FxuU6ZFzr+cdAEmy/BS/RjLNma/acZhgYlo2x72YGbv8R3vyhD9LdhNICVGuKaErhVhQLU3UqlQor5SVWZk9AYVqKqrQaorHqtSQ11QiKZZkRGByBbAqUC8UlAU/bjoCrFuA0kCBhRCa+YkUKufjB5ttG0EjlChhrIOCrMuRvswHxuDBrIQBiCbQ2Ac8KAAZTwNd6S87peSJb4LXBbxKmwOoNew8hEGAj80aZcHM9iYznXmRe6Eb8iVOIvzIF/FQgpzAPdEn18LPHukjAU/Pn9Ho/QecGvl0PiMY4wCKJdQksyyYai5CIucS9Gt3dKeJulHqhyZc/86ckMgnarkEq1cfHf/OPSPguV11/FQN5uPern+eKN76dwW2Xk+gaotlUlJaWWJpfoSfXR9+WfhbOHKawME0qnSTfm6dYKNKuLGOrCHYkQntlDkOlafsWbd/Cw8Iz5LqUb6BaBsWlKc4ce5wNgz6VS/ZiBeBcJgvdOY+JxxfZnIsws3Kc+bH7g98NUKLtzLG0PMW3vviXPHXPg5QLk0RSFiM3vZ/T9xyhPT8tqFRjCdGZbATttx/RdPVZQPzsF28tyG+CK34b7vk8NP8C1FjwnkCG3hPjeEe+Bnt/lPYBBRvA6JauygZolGSpXErDptuDFcOFWgNmjxK6egEhLrEDoknAtVme6IPBj8Bdn4Zj34bjd0Put3AOxrhvAX5pVvHlj9okzyOLdK5m7LnWQO5F7lneN5D8sWHEI3ioKLWWhpIiuqHBWK0VuwD8188tE+2L8ra35XljRr5/APFaDwKHp2FDLwx0ywUOGzLCTEOgt1FEeKuOiIZdCFC+GM0mZPYOIKv+esRbuAuZERYQMLakpJ6y3xRZC6M36DdtxB2A0BUbli8zg/rGXobVWFxQUgKLUGNW05m7EHdEJwaWCUmVvcG5qoT8Fa0noaVWNeFf1yDNEW5DXMJtmf5sBWidgqYJzW7IbZLzVs0gKKbnucXgYuqEki0NQhKN1kLQYQOtHfvDahf6bXqvDKvRchmJNr1cvv96XN/j2/d/9eW6yDVbszVbs2e1ixaM3Qb8FFE+RJQZqnwUOMxri++0dBru/aTC/50lRL80jSzABQQUSSJuSwEBMg4jgGknS+XFpJUMAO9HgJkFQkmECcQtOh6892uIp6ElDKIMZRPYboplt5u20SA1EGP/xhHmT5zm8EzxPOd6AZYehI13wDMPBGwLA/GklpA20CHyFOKIxILrXkBAM+05ZRFnphOs0e2URdzbZwhLM0TBm4VaL9QeheXTeOO384tXD7DzNoPKEnDaAffTwAHEQVLIvUojG0aTF6a+djFYP2+86Wp+/xPvP7tfX2UXm8cfBPFTVpw9+65gaHQTi24cuxhnaM+NXBLvoh1LMnX4jwi5JysdH76QaQaX3mqdQfrdYPD5ZcI6wC0gBe1paJ+E0glQ24FLIbUb1t9K4sMWPZst+rcKkcgDnnKhPw3v3wN3/gd4+tMQ3w/RfbD0BNg+fPDfiE//pAfOPXDnJxEcw+O5a9s8pz0APAI8jowXM/jbAG4H/opQUfAXgT+HM38O3fvgxo/DA/83+POsZjOkEEB3Y/A8Rhg80qrCVsffrchYSRCmK/vI3HYG+HLwPVlkjroUeF1wT3Qe6zqEHdtG5qg1W7OXyeIp2Lyfd3z8HxgZ6CEWiVA7Cc0uYfAdPzHDgw8eRBULqIiCchG1uACNFYhGhcHqBDqtypU85UQCegdg57ZAULIJtZowZdt1YcnGA3a550mBMBdYXhQWYETJMe1AyLDVFgC1URbg1Y7KVOU4Ii9gBfRRwxAwFjtgmWkJgiI4Jbk+IyKIGBXClNBzk7ojyDyotaA1YuF2HNOH+AtaiHEUgZe0dvRRyL4ZmkkBmRND8h3tKniFAGy+BSlUozUHdfDm2VlgUzMNmG0Si1nk8nG6citYPTmU2aJ7MMn4yeO8631vZ2DdKLFkN08//R0aToxkMs7uK2/mkiuvpVhxaVtJFpeKLM+OYSlFabmIahbIpFwazQpHjh+jpydPNB6h2qgyM3+GTDpDLuHRrNRounGKi0s0KlVsI0K8d4Roph9lJWm7JrhNTh89SL67i/Ub93LtDvmJ2RTkY1VOPvJNLKdAc/kBztW/V40izYkDPDj+Nfx2hr6d72XLbf+OfbeN8um7/y3t+lEgCZ86AO5lSBDyKKLQ+RKy3xYOwtf+L/DSCFjUC8Yu6PkwlF2IxCCdhYYLTys4IVI8DAZdIGAVqgKM3w0bd0GmD5JZ8DZBLgnFMiwsgJoR3L5SAKcoXYVR4D3vhqNXw513wcObIfpzrOSv5OnFPsY/ejVbCbE7bRfSjC0FDweBr5/NNJ/w0j7xTm1kZesomUcUGQW//uF+lGHQb4eYnx985hIgsQVWmnB8Fk6fgkt3wuYsZGJhuCOJrNazwBsueHMufksg7XQP0sPnkXaBICnAAjsF2S0CTk+3YKWzQuy+4EPjwAi09PZA9y0IY7h+cLJc8H4UaXhNM9bEUy1WmyIs2qWBWI17NgmTFtcRJvykkL7dIFTkMxCcVHe6HFAZFl3w3hRs0uc1g8KIOSgVCWXkAkmbsxqoOqidQubfDNKjOim6awHq1TfAxmGMe+//i6BlfphB6zVbszW7WO2iAmP3AO/E4ErSZKgRweVxfD6LuIorvLZKsygF9brHL/3FA/zKuy5n67BBWC3zUULleO0RdJbzfLGWIgQPK4jX0QjOqyOzyeAaNiLu5EZgPYYRIRE3SSbS1Op5ysVpulIZeoY20zM8DTNPvvjLsvLyUGWhBaJD3BoE6yZsAx0W7xR81+pnWqrh2UyHtgEuoWvTraRG9jIzuwLjT4A3DaqK4Y2xfmsf5RWT+eNNmJsLznHuBlVzKaKEQFOJ589WfuVs73t/mcve8XaG4s/CVb3IwNhG3eORRyosF+sYEQvHnGG+0qA+dxftxoPUa6coLs+zOkBxIefUQsC/XmQ8RBEwIYH0taj0y1QE6l1SjFC1CIHbvHxWDSFszr0kt69n3a/GeN01MB+X/egzp+D6LZAPyGhRE35sGPzboNIFyS54/U1w0oe7vgHth4MM0FPIUHzR3clHGKdPI6y0JmHlWZ1GPAdcA5yCSBUGr4RpBf7XoToNz/wz+AVWzz02wlLtRYASrXutmeh6S6rvRQwZt5qGkkbmIk1V6WQu6+2wgQCv65GdjE6F1XIKa2Dsmr0cZtB/0zsZueGtbN+0k2zPAI4ZwYsYpHqFdPj4g0c5fXwcZ+4M2G2RIVguwMqydPGGFRR0VgKIDvdDVxckkyJ0Wl6GVl1kCeotKZCVToEZRQpuOQK6GipI7GgJw9aAcEx5YCopsJWIQyQiIHDLkVzvdkVoZvEExILv9Qyh3Bm+aMSmE1BrQbsMnpYEOreQirbONdcJr4EkArYGecDmJvA3yP/UENTkANAH9nbo/3EY3CtAszLAj4sY+GwVykfA/ybwbWQ+7iyF9Ny+jwq0cdstl+VCAzwHv1EhHlXEabOy4nNmfBzLMugbtFhZnMUz4jRaNgvLDkszp0mlu4hlcximTSzikIxGiNkZLBPKK9N0dWUZGBgmmUxgmhH6+gfZs38/nuvieh6Vag2n2GR5dopasUA8EqU7GsUwTexYlogVJ+oqGs0lZiYnOHT4ONt3bMPGwDOkOZqex3ve/Sbe9/4rOH7oSf7bx/8Kmoek3T0PVBNftXjde/4LW2+5ndzeQb745Sa1mk5Z9oKiamcQIHbsgm33gk2VwXsKWUsuw9x/HfYb30j7vmFwIiJr4XmiwaPjaBbiyh0AesHMg90Hfg4WxqXLj1wF5ZYoY7S0fixCMFcdP2HgBrg8YZNeGeDIdbdx+N//Fqr1T1C4i8oTaT7y0z/Jn/7nt7JjU8+qyz5XM/Zc60G8gQtRHEwgYQiFQo+KThEenU9mAFuj5tnVTMNlOuveNGCHAbUYLOcguRMmZ6BShb4uGM2H3qwWBNL5XDpE+Wo0HSo/glBMtOI0AFGIGhK78g153e2kA2dEYlsB7gqrmbAmYa0/LcirZUn1DdEYppTCEHBfS69qafrOLPpIx+f1zdOxId23s5xbZ1k6RTehHq0FxHIy78XNUMciboCyIZKGUoyQ0qslWlIdF2YgvlJnHQ29n9M/6LVo2u/sBK71TQPP79SmXbOL3yyIXE9PTx4Dn0ajSq00jpDFtEYJhEXgXp2ZqWv22rGLAozNYfAGDHbj8zaE8zQNHMHnUXy+SaiD/loz11V88Qsz/KubZtk6XEKc50nEkf5eUFEp0dYyTM7PZnxO02wWXZRHx921mJLOv4khi9hpZLFfd/YY2wLDtvHtKK5h0TZtEj39pHsHX/BvX2XxHES6oBRoWa4CjHWhs84F12C1C6w9p3MbRYOvnZRCC9gA9giYaZTvgR8BI0Y0uw4rlUElErxxi8GkA75R52h9knBz2GkBXdGMQNc+uWXtJfCWgSpk1gtLxG1CeZ6QqflKWz9XX38tl1+x92zR2IvVGg6cPDXNoafP8OB9cxSXCxjWCvXaNL7ZZPn0NHgHkMDCCzWdKt9DuMhrrULt8AZgQGRQGGWeJxVwWYdQdAYRsLAf2ESit5v1t8I1fXDGg8kKzLVgpQR9QYxBAcNxGNgOzRloPiNdZrEBS9+C5qNIhOr7NoXQaueQHUcnL0jrVJeD3x9UrFA6OTINzgQUHgF2ir4lK9A+RZh6nCXkA+mxJwUTpB01kKKLb2m5AV2bukFIO9HmIm2vuUCbOFvdhVpw3p0Ik/+Z77uF1mzNAIhEYdMeNg5uZOh172bkqtvYMTJI04D5GlSLDoValdqky+T4PMvzBWgG0kGLU1AuQaMJsXgwzOLyfyoG2QykUsJObTahVBIKmOuKrEmzLWAqHjht8Jpgax1XAr1X5H2t5+qrwCHw5K/rCtCrfHkNFcgN2DJfGQYoS4AyDVxETAF0acvvuOCG1e/4q4FbncGjxRq7kSCVrj2/iPgzJZEhSu6HfJ9oxLYUrPiQMaGWBGcJKhnEQ9QlfzLBOU3CgM+zM5x8H1pNj0rZw2m0SEUhGTVotWFhbpZsNkEikcFtQ8s3iKQSeIbH9PQ4/b19ZGkTjyex8MA3iNjgeS6VUhGlDHryPVi2jcIiGk3QPzREo9GgVq1Rb7RwWg6WaWFFIlgRE9Vu4DdLKENhxTwi+NTdJqXlec6cGaPONuJK7oBnWSR6B7jqsq2sH9rD7q0bOXKoyFe+UqZVmUN5blBMTXHTTdew8fWXMJfymHjwIdyGnkN1qvNc0I4vh06iLtpmwY5r2HTzW7nqnVcz3dXkwFMxagUPKk2oL8kNsXwJSmh3LgoqK10y2RfkOAVuWm9CYhSugpoDjhKgNhqHWApiQ5DoA2O+gWxWE3sAACAASURBVLfQQLUNyN4C5ePQWsBdmuDeLx7g4M/eQmK4h3wsVCy+UIq/5no/l+kRoj2HfkLvU8No+hgX8aB11QePcOgRPE8BEQuMBFTjUFiE6UVYKYr6SLYfEjY4PlRb8HQN4nkYtOX8uvjXq8XKiCeyhPTQBULPJAkkA//I8AWQL3kSq9FkRyNOmBjXhUwJmv2qVdc0squJpKng807wqCGgbac8q1YzMwl5HZ3ui04gjATnzbNatgBC10p3sq6OzzYNSMZDtm4nyzZmgtLl4zSwFEd6V2eWUT1ouQahtr6eHw1kcL2W2Z96ferMHl2zV49FicRypHOb6R98EwP9vViWot2u4VYnMdQktWqR4soKk7NjrN3fNXu12EUBxm7C4q8x8WjTQvEFKtyJlJg6/Upf3CtsyoOZb0B16Qkcr0XEOoJ4rM/2AcGCbPPZDxE7V1MxQqh/CVL1NoYAHRp8yqK1YhUNFF0YDGOcLU0AvlK08KgbHiSSlHAwurqJ53s7zqUv7gVMlOk82N0wNS/XbqYD7LUUnFtvKLQepQZmIWT56QVYM/Ug9Nh0anbgPRlvgEQ3palnKJ16CEhjRIfo3vJ60pu34fXDL2yCQxH43LEa9zGGuIznc3Q8jFiMyI534M/NoVaWUdVFfO84DL0bIzeAUV/GOnEvSj2B57RQvk7lfiWitSZ24hreckkXN217BU5/IVNhqygFk0t1/uYf7+Nv/urzLJ+ZQO5nCbmn49/nyXQVCE2v6KzaegaRsPChHIXuPaB6oJ2Ehg2xK8HcBv7gKqw/ZsJgTBL4h23YmIPDGXjiKNywVQqat3yYaMlZq0/A5Bfh+Of5PmQIzmcabD1GCCxrMKNTfwzOsoCdOEzdhVy9Tn2bBD4M2T5QB6HwCbRsSbiD0fmBRvC6Zsx2XodOwdNjU+su+ITUKX3ndZG+QwgwrL+/EHz3tQiA/Bu8tjcfa/ZSmGFHsXrXYb3r57n51veRMrPYgfZquksxs+wzearMM0fGoFKh3Wxg2gpPuTA3C4tnZJ6wE8HSa0iBrnwPdGUgHoCw9QoUi1CtCPgbtSFpw1JNJAM8R+QIjJYUyZSrQwq8BKiUcuV/1xVZAccVANdxIekHw9yASFy+w/Dlew0LaAfBJCAaAxxwK8L4f0FrkYa1NHIRqGQakUBnNgYMyHOlAy9HJee8+RNgdgdVzl04VYUrcpCLg7EOajeB/zlC3dnNCGyjM4Q8ns+Yr9YDrpgBMVN+W3m5wMpiinS6i1iqyUqlTn5wiGQ6heE5tKslvGgE3/PwsGnWZK7yPGg1fSqVCl2ZDBgGruvTarnY0SgJ0wYzRqPuYXgNeoZGyfT2YvgObtPFa5YwDQfTconZSWzDoVFbZHHulNRSMwNV3licoZ172dJn0R1TDO7awN//za+z7w1TzBy9l0ZpEs+pY1lx3nJ5lPg2m3+aKOM+8GeEgd4G+I+8wPv5Yi0Ob7mF6952BX9wpcFT1yf4yH+C40+bOE0DzDjUPUhZwsSuKEgaUDFQ86JM0X8pjGwGy4HGJOwZBnJwJkiaWAiKe/X0Qd86SA8rzpx0uecTyzTumYX5U1i7fgV/4jFU6QnwDmK4Tb6x6NMuwRW9sDNwSb/fZJ9zRTsgLF0Jq4FWRZgLonusFvrQ3HINQraApq8w24p16w3mv2swNQczSbjiRhjIQasFpQKcmYD0ZdBOw6gpq+CrQUdWt90Usu+bJFSa1iHageCYKlD3hSHdaEosygzKaRjxQE5bl4DQSiZawqAHqXrmINNOHxIr1wmAC0iMQifaaKarQQiqaqxTby207qxO7BlAAN7OmFSNsH6pBmxHgu/Wtbi0zEY1+PF6ircIgmJLhNoGSSQrMQqGC0Yd/DOE8mz64jVxRV947YL34rVha0zYV5uZZg/dfVex48r3c/N119CdjhGN2USiFv2pGKbbYuL4MR5//CH+4c6/wPNO89qk8a3Zq80uCjB2BZd3IOCr1kvqhNJe02YAG+FzY/fjjypu33rh4+0L5iZprVWtPZQE3oYIRXQRpmUXkYXcRgDgOUSncRrFl1niO+TYQIQRAJRSzDoeJcfCV0mseDfLxSlKhkkjGu04f5qwKM/ztEoNzApnWXJ+AA6RAvZDejOYGakCXX8E8ap0Kk8XRN8EbiHI634s+FLN2MkFj83ymhmHgathcVZKYeMDadbd+C6ufG+G3TfDxh2SSv7ZZ+Cfj3YDlwPXAffyvcrGMbpTvfz47ZcwPZ9jqWwyN1PkxLdNOD5O7rKtbLjyFi77mf/I1NQij37+06ycvh9ajyAu6Q/WzEiMt/+vT7F1d+psTP2iMlckD5ttwRvueP0vcOLEt/H9eaSERQ1x5+ee+3uelzUQsPI4YQ7aAuKpbwF7jwi61gtQ7EO2XpuBm+E/AKOG7C7+S/iNM1+Hz6yHvgV4T0yS+a+z4OE9Mv89XIBvH4H53wV1LyiNg7zkE6Iu/FckVKnrTPfVW0IdGBhAdg/HgK8j7NNrkcDNr0H7o6D2Ar8K/BEyprKEwZxO8HURmQeGkDnHBa5kdb6fZoFkgB3B/8vITkbTWerIyuEhkgWaIRJH7sPvB79vDZBdsxdrcUbv+Hn2/Ov/yKW5HI/fP0s2b9A7mKVSgQfumWZ8+hQri1M4S/OwUoWuODg1WJyGlSVhxdq2AKzxOPT0QD4vgOfcogCxZpDW0moBTZnklC3SBGkbykUBVX1fvku5wqQ1dRaIDWZC2K2NIGDbcESbVnkyWdbLQjf0ldALVUy+w7bBtsC1RYDTbUup8tY4sk6/kDQ/HfC0kKBYFOI2RPOS3VIItLrjI5C+HNz1gfxAGdwJmLoNrAehGIHSETA+BalPQncK2v2QficcuiOQg9HM2n8APsuzZQw9m3nBL7OBbAxaJcXSdBEYx051ke3qwm00aCgTW9nUSiUsw8ZxwIplcF2XaDSK67SpVIrMTU7R29eLaUdxfINGIy63PWJj2Rbdvd003SZ+y6NYqnB6YhxFk6G+PJlsllgzS1f3RiJ2A1/VadRrFFegLyfkYDti0tub4KtPt7l2a5Qt/TYR2+LQt/6Uv/zyE3zlK1/loS/+LZde93q68/3EbdiYaAJ3sxqE+UF414E+8B9+g//zXZNv/dTrOfMz8D//K/z14/Cpb1hw76B0kcWgyFyrDfEuYQnOgSrAZAIWN8OmIbhlCP6wX6Cl2VF4ei/88dehYMOVmyDbA//926B+8kswuAXrhi2kP3A5O3cbnHpgHyv3l1APzzP6a1up77F4pAnjp+FjG3lJ0EodbtQYnTa9qunXdK6H1XFMp9iGjwCQK0j/XACOTrnc+XdVfuKnu7nuBmjWYfIkfO1LcNNbIN0DZg4GW3DwGWgNg71eRsg6LpLN3gWsSgA8I799CtmJ5JA26UG89hPAksnZWp99UcjaYWb/rAV1DaA6iNvSRBoyTVhjsAuMS0CdRpyvZQTvdAnr/lqEqmidqPYwIQM3ReiWpIOLhLAYWIRQM0KX8rCD82nt2SFCFbMIcuN0bdhW0DhnS7/FwEhDchu0SuBVwNfB8WxwjKbv6upmurDzGhi7Zq9O27nvR7ny2h/hjW+9mUuuNtjSDckOvGPZSdP/+AZMs8XY7I/z2IF7cZxnePXVa1mz15pdFOvzDLL+1VnbMp/X6vC531V0T8Ptv/Hch66WJtCeQxS4GVntddLSMAKwSiVOxTACWpRxURRVg9PTJ9mU20ssmmKqPsH27JWYRpYqZeY8eGj8NG8bXUc+1n/2dKYt8namDZ7nYVoZsskBupKdzNhIcE1x5M4/X3MRj6lAWJ09cEDqObr3X0PvdXdQXV5k8Ut/hVdtQ6wPNl/DW3/5Kk5OK848fprmlz4LPESY+KSLh9SksX0Xlh6R9FBU0GY9JHoMjp02iB6Aj+wW32i5BBWSsHcjHNkB3sPnue4IbrPJ4sE/Z+PGdezIpYjtzpP6wC9w4EiU797zFCfvuZuV6QW2XLGfketvpWvnXuorP8LC1FFYOQH1I9A+wUtMjTyPZbCsvfzImyL09hpnY+sXgykl2blWFIjBUrHMv/jA/+L0mXvx/VnEET2KgHBaouKl2nTq7/EIdYC7wBuF5h6EXrEe8cbjgAkFSO4A6xqofAz4XeT2KXCq8I9vgU3/AyqXwbIHv/0MuH8IlZNQLoA/HZzSQsifvwn8PGHEqtO0w99NqFcGQScl9MtXWRl4krD4nXbcdXlfgi/VwIoGbTcDR2HbeyC+D57+JHAn1CrQ1w17L4OHvoaA4UtI4EfLlGiZExeZAyDQ7iDUotbs/1FCLpFmgSQJg0Ua6N2OgLV7kS3cOCJf0ATeAXwF2YWt2Zq9ADOjsO4NvPXDP0tuy6UYVheliMmlt/UyNwknxopMz55keuw4jYUp3JV5WJpHCl8lhW1aLEGrBomABTswBOmcgKILS9B2ZNzYtuQimwEPLmqJICKeoC4tBITVptEd3xVaGMgQbTcFTLWsgOHqCSPXVOC1JFip9ERgCLirwVgDKRSmXHAbcm2rim89X+sWoABTQGBzENolcMpgpWDjteBuEKQoMQLWKMzcDNVlaI8DDSgcAWsvjF4F+/YIgK0QTVtbM24XkU3WDDL+tXjjCzNXQc0DfFnyjXiTaHqZmGeQyWTw3RaGZ5HLZ7BUGsOO4zg+5foKiXgcz/NwHQff9+nu7cFXCkMpopEojhO0nVJYlo9tR0gmkxiWgR2PYNgWxcI0CpNGo0Hb80hnhmi3W7g0aTQaEMgLmwZETZNcMsPDX/sEkeUNVHYM0fAVV2+7gne+bifr8jGy+X6a7ShWPEOzCCunFOdfNH4QlgRloyYNFu+C1yXhj94Gv7Ibrh8w+M3rYOE+8McsmInDUgwcI8ScIoADrRVIDcCuEXnLMCRH67okbLwFZg0oJmG8AftcOLRtHdmb+xm+JcPOq00OnoZ6w8DLZzCviWPHLPq7DbozMkT+dBl+rBu6rZBD+GIsSsjk7FRF12FcLUMA4RDWWewJVlMULGTV1BSEZNbmmhsybM7BSgQMGy7bDaMbYboGjQL05GB4FCZsuO+RMT79v2e4bNc+rrgmzaV5k/UXqeaUzo05jEx1SaSIcxbxOjRGqoVSUkC/IbUMN9uwzhSN3mXgCSAbB0tBpYEguVpZTYOcKaQjpUBVEFehhNw47T72I3OiLlaiEXYd782xWtlpODjPubtqPex0B9CBdZ8wyUo72prUancc3wSqrsh6mL0imYYv65NXB78KSusuaPkXTa3VxBC957pYvPnzmc3Lnw34Uu4J1uwHZwbJ/mvp6coRcStMnjyOFR+mviFJb7dNLgXpJEyOwdgzTcaOrjA/X8D3j/DySP9pVW+9Z1qzNfv+7KIAYzu3/mt2jgW5TPOLcPQUPLkE+3ueTQ9WM1IGEDcmE7xWR1hj/YRFeYaACnX3FKXWSabKx8mmPPLxLKloFxFSpGPd2FYSZVgoq40WXLLIkWAPw4kWEUMLx4ulTIO6aWJYFp5nYKgEyXg3qUQO8YACmp+ZALtf9FOfj1mRAIXTwk8aPHIAE/wp3NIJGlMnaddSKNZBVwqzfxOpPddww80jXF60OLoux531Nq2ntoAzJ6hY0wG/hEzaAavGmUVA2kDrLmJTLrUxyx71pkUG8d1cD1TMgpEEHM+Ab51nrfcxVAOzPUHMXWE4NsC64TTbXr+fzdssUs0xnj40xkLlu0w9cZpm26ftx/DsDN0br8Fatw3b3QetM8wvTcLMSfDmeU65ihdpdmaY/J73s7PfIh0U3tZ3/hVPc1NQb0jW7unZGt944DSPfPfL0J4jnEFqyJ2JId7y8kt8EXEEeL0R2A9quzzoCR4dYdonwNuA7CzOIYErH2YfgLs/CU8/BBUfTo4D30AwTB9x7i9F6CHaOc8TVu3tNAvZzekacTqj3yfUr9c4KxAGNk4g7WUid1prtJqEd1yDH9oBiQLroVEL+mEe2ADeaVBjkLqKzFXvp/bMF/BrRcJdBsFnY6zeeeiHlhFZRti3bvDdmmrSS1jGuIEwavch5Up0dfYCYbUNH7gaAZx1BfiLyNb2BRevdQ9gb97P5bf+GCOX30Q8ncczINalGDuyzPT/z96bR1t2X/Wdn98Z73zvm4ea55JKUlVpKFuWZMmWJ8lgg8E2BqdpwEwhZNEraZImkHRWdxNIWJikOzRTQjCBJjg4NtiyLWN5kixZsyypVPP86tWb7n3vzuee4dd/7PN755UsySUZ2xJ+e62rerrDGX7nnN9v7+/+7u8+0uDS6UXmLp6ge+EYNBsCsHaa4NvQiYSJGvQg54kWYKUKXkEYr92+vIIgLdt3RRNWWamPrwUo1Vo0h7R5oJV8BwRt0GmNdhxLvW6YZntyrmw77Ak4q3TaXNAkqcyEgYC8UZRqxhpeXrq7VxQcp5ONnUvXeC9t8NcH3cIaGiWJN4M1IXrptg3aSnfjAtuhNw/uPAQOLFUgXBAgNrCh7YI+jzTxOoP4N3ci89fLb9SxqjCroR9BtxfSa/UIadPrdcj1clg6oVlfplQokSvl0JYiDGMcJyLo94niGAUUSiWiIEBZNsqyCFXaVE0laGXh2Arbd9FxgPI8qiMjWLpHr9MiCAMsQvq9FRINiY4Io5BBImdlI5fOtuHE4Uege5QzJ4bQVsLBbTsYH65yYO9WOpHDpx9aZF7luHjiHA9+9svmDL/DpoAC5GsQOoSnGzw4U+NjhxU37YA9G+HOCnzNgUujFu0jiHx5C1nGDSOwL73tKrU1yhykq4YN1RHxZheA4QSs7XDqRzfQ2F0m2eJQ6ovuerwIJA7OlMPBLTBWhMXTfY483CS8eIptP3KA/RM5pvIZXvZyy/vNlG5ayQ6v+b25z8xquraQ3EBkXSRtaBp6rW1vWc0ptmx3GE0bWEUWFMswXQZvAZZD6K3I/TFRgVMqYeZCg8XD/435zg2om7fgbh9hSMn2vuv+3BozuKQRJTJaux4yjn0yGdc+MpauEkWLYbI2xn0NzbRgwDbFNUYj1vTWNX6RyfOavqxp/ohU7oAiWZ7YuDH59ODyZBLYJle8FmmP1/xr9mdOVK/5G7ILkSaELgNvjZhwoKRLmTcCkZfK0SQQBSJ5s3oXrU1wG6Aoed6GX61mpKfWbd2+0QreEDlX4dAl7q2QBON0O7DQD1kc9AmDBsePaE48fYFz52eo10+QJKap9pWYAirS38VSKcjiiCzU6sMJYKWNVO3U/zKC0kaPZL1Z2Lq9fHtVgLHr9k0sBXJOLsHHn4H9tz//C6Zlp4u4Jjcg7ulWZII5C1yLeBBGh1GU4zvhac6357n//Bm2TJXZY21ji7eRmjpIbWwXMExAj+FSB42FpotPnnH7BqY3DJPoiES3sZSPQlHGoqUcLMtDax8Sl1zOJl8cBmsMki4QSbvT4laoP/XNz185om9nF8mkBcykF6fncpb2qXtonzoHHIDiCNbmPeSvuorNr9vCLRtgz244tm2Yx2tv5/RvvQW98oiUR0ZH0qZDplXAgNVmZmoYnCoUy8xdHDC6LcIt26utulwHvDyoIYknX9hClOri2X3a9fPY+QHj7m6u2TrB1Vs1w/EwD206xgOPP8LDX5wlDB0GuSnC4avZct1teEM3ki/eiVIWyyeeRg/+BvpPkMRniAaRdMZeXQi+tbRGYWILO9/1D5mybPJkgYXhHL0SB/6FdNReiWmg2QJtJzzy+CX++E8fhuChNVs2IU6brKCtwcsHE17ITC3aJHAQqv8a2ACD3ItjfA9AsAn5/D6+cY0ewCd/hywAWOsz5IGdwPuQ7tJHgAfB3g2JB3ptrzcLwYhr6ctEWoY4brr1muAWkLBvDpFfaKQ77CORicMqu/eypltFMtB2P1x4BHgE2IIq3IIOHoaBh9V6EyPf9wsMFusE554WRt5q3Z4RTTOJI9M0sJAeXJFMA7qZ/n8+/X41PcYlJDrKI7IUU+nvuwiQu5IOehFhze5EeDUXnn+Fvru2Nkpft1eP5ct4uw4w/M6f4O7/6X00ZhWWA8ViQqy63PvJIzTPnoKVGWgvwMVzEKXBsaUFMYpSWQAbGKpIcy43D4OBsGUHgfydROAkoAfi/Nt2ikwEoh8rCJ9oqyqVShKkN46TslwjLSzc5rIcg512++k0hY2apADtqtagA8oHCikTFjlWy5LtaFIBRpN8eblBfEoXsx0ob4V6Q8BgHYDq4ZbGGKitaMbke1ETgllJjFIGDkmSJ7ahPwfzBbJslGHG/y3wewgLvoZIBJm1+8rshXIhCRAECe2VPtCmvLJM3vdJ+iFHnznCxg2bmdhUwC/lsZRDOAhZXl5Ga025UiafzxEoRaLlFdsK2wLLUmgr7ZPm2QzaMWGSUCyXcJJh+v02gyDAUtDp1lG5GsqCOE7oB9KkygFirYn0gPPnT3Hx5BIFN6bsx/z0T7wf1/HZOFbm3bfs4cmzBS5aPg8+d4TPfewvX+b1+7syCyhDcUh0iZfOQrfCr39B8X09xftvU/zgEHi3wSNDcLwi/do4hkzvEatKOiM1KFakQZXBmzTZ7V9VUFOwqwB3HFRwcANfacLTy3DqIozXpUdqywZnSHPjSIKqhxz7TIN7/sNZOP0ptm3djH3rOEMbHVK15NW77krNYH194LSWx7tiSX7GeKyGSGnqQ0yaJURW3/Nk9VgxklLOAzUPcpOQU1BRWZ+pKaTJ2dFFePICLFhw0xbYNl3h7ESOz//VHzHXaTA+dhdj20ZwVIYhfjcB2bXKSyGZRKppWjaBcN5nkAhmkSynbUBb443MkoG1S6GMuTZaD4ZRYDRJPLKcc4i4CyPp+yaX75FdkCaC9BvFJFNlZJLfpnDIBAVrQVazX9MLeU2ua/VGMAMRp9832zd9hSMkEaV8yI9AkIdBD6KOkEislO6sTaNUk9g2lFtzombnr9YssIkwXuzY/i6O+9V43ut2JebHfeLBMoOgTtIfwtVtBk3FUj1g5uQCp04eY3E+pj5/iUuzR1luPs3LA2JdsKbBL6JsIZQpXSBJltBxiluYh9bKky7QiI6ceXjFb8iyLq/2BMi6vVpsHYx9rZgLX/8KzF+Af/XE2g98pDz37YinkEv/fS79e5gsx2xcTLPC5xnN3cJo7hZuGl/bYCeHsNAuAQ4eXcaJaPMIeWZoEXGJBjvZRF3/Fjn1Nqr8AzSagIAocbDJU6ptoU0b3V0hzg/D+NVwKW16lKvC+DTUr2CBLWwHqyLllqseutFB6pGVIF9EAJmdcNU7GHvDHnbdOsE77oYbCinMMwq/+YPwwftsgqcd6GoYGFHOjWRl2QDTUNsMI5uhuBk2DlPa6lGdlFGaBqZqUM3DzJyG4JIE1c83lRAEXR6//znabbiwbxuxbXMLMK87jA4/xluvf4y335ij/YE3cuL4Ml/42mn+6nN/yIkj/y+wH7bdQf7gndzyzrcTvfvtxE1oznR5+sGj8OC9EF9AELvPv/RYfhPbNKX4yR+2mbCzRhLGh/xuTxZaQ2cFvvRYm7/+xL088ul/s+ZT476/DtEwPcXLk8B4KVPAbcAvAreAPyySATZwP/DnL/HTv0CiqVuBw7zw2lxJD/3omvcMgPtm5EabBrbB5t+EhS60PwV8EHmkR9PXJMLuMFFem8sDhMuiyifTg38WiTSq6fvmSptaOda8b9r7ko7HJ4FTYEHp/f+J3uf/BdG5B+HrP0fpA1/Duu6XwPo4nPyTNb8z1BKHDB02z7KJbvalJ9NG5qD+muMZwcipwBvT73w5fW9jOhBlsgRVgLDmNK86MHbdT3tVmvPeX+L6u7+f99x+I2dOKHxfWHmDXot/+97/CvYKBPPQmYeFhRTItCUzV/ChlINBLA26KmnLmXoDrBXRjO0EYEdgx2k376JoqjqJsDBaTZg9D4OGALiVzZCLRdPVU2lPrAjitMpFpQCwkxPAkwT6PQjOkjXQ6iLPUAHcorSdJyeA6VpEJlrDnLWjb42oZDmQq8H4JugtQP8ChKcolnxilSPCFRD7xGMQriDP/jbkWT5KxqY32t8e8vzvAB5GIJghJNnyQHqOV24vFvo3u9DtaXKtFiOVEnGpSjdOePSpWcpunuGRSYqVUaq1KsuNBpbl4DiKUjFHLucQxzFoB2X5qCgiDgIcpbAtiyiKKBR8Kr0cecumVCpxvtmg14vodgMcXxNFkLPyxE4e23Lot0GPprBKoonbfYJ+RNHL4RYcIhVw/sLTuJtHKRdL+K7i1398M08BpyZr7Nizk2eOfsPpf5vNQRa2SVg8B9TBzsNfbIYmfPJMjq/lC/zqLfC/Afftg08Mw6dnkNxgnWzaPwwnL0LpzcDPZHtIgF4Cz7Xguoo0vlxrt5blxSbgevgYcP8cPPyo5p/fPAezT4HfgXIEjPIHv/JVWr+yn+RDu3hbeggVxLO4UuuSgYQ94I8Ow90bYP+orFRGjtQclllhFxC1Y1Ptbsx4uj2EALnZlRV7I5ko08b0d81YyPClEtz3CExNjfFDH7qFyaEP8/jXHmVax0wqATeNvOk3bS/xbbYOMlYB8tTPIccVIB7cZxBF+LX1LpvJxngCOR8z3ucBnU8LhyqilqL7iKsDUtQ0sWaDbfneaj7XSg+iQYatGJZsk6yrGul2TKGhoe6uFQw2YYRJiq9F4A3oasyEXYtkWYBRMraurSQ5lStKN784EY3l1TvIbBwyQNZoJpjSKOPNm8T3d6tB8ItZiAyCAZKff2yvpmNdt++saWZm72Nm9gjl4gY2T+9k51O78Is+y8sdLlyY58KlMzh+jl6zTa85z8vrt1IAaxw1vBW/5ON5Hq7j4kQO7eUSQXOOqL/CanwUmfRZiDykxlEyD38TmdFWWGfKrtuV2HcbX1m3K7WUBBovCuQ4zo/hkkcmhykEvDCLa4x4GEY80rDaXDKXUNwYpVyggOY8MV/lePsMs4MmQ6UxWgsBjldipdfmAWBHsQAAIABJREFUubNPMjLU5uqt+9lQ2sN2rsJhmLI6i73mNrKR3cWWBXER0FiuYnR6O7fddRcPfOSLJLEFViLB3pVYeQc4BQjqCG3CZKjW5tZhtWGXNwGFjfRVleWuYuEiJNuEYNtVcBQlDtrcWVg4AayAdyPVgzcSrbTpHDkKdEWkrDgO+Umo3cjQrR777lRsuRq+ouHhJbjnKTh5OBHnyBuHwTDoZTK6ZI3REcXU2IBhN6RxFPbe/CZufuf7SJKEf/8v/ynNY1+gwgy7dzlcd13E7dcq3rS/yK986M2s6M3c/9QcDz/zEE8+dw8P/csIJv4Z7/xHh/ipf7KBm7pX8/5PbubMMxHdM3W4cBiOPgTxs0gJ+skrvMGAa36Y4Vvewx1bFIliVefsxRgUGlmTwkSqYz1SUhZpd2nA8gVDcHnlalVLi0IKqw5Bvwp/9Pu/xmNf+1skGAdhfW9Fkg42mSCYsXFkUXy5rOE3Am8Ffijd5hBQEE27/wK8AwFL3wT89EtsZgXp6/bTCFEzQLCDTyH+sXHy3wg8xuX9Ff4Ucv8LlH4Yhlw4d4+oa3Ac2I8EDSPpKU6TkUi7XE7t8XgesLJEBnSaWj7DUl1Jv2yabpn6O0MBsRHNZReJbp6gU/dIBoeABkn/MY7/mz9l+O67yG2doHFyIxLhTJNxXzqIs2RqBPemxxOmY11JT/JqMv7Lk8jsp5CWJMX0/w2XxswntfQcFtLPasgcOZa+t27r9gLmuOQ+9E9591vey+aJndRPKbbtgovn4WsPzfH1J06C3YHlCxAsQ9gFPwfldNJzXaiUYfOU6LzOXYLnnpGKjrwHvmm6pQVAtS3RP/WBmRkYdIXxFDQhugTaPLxdcPKQxCnhQqdg7CArp4si8LTI5ERayldX5UZShqJVApR8J4jAj6DTSwGElOURR7J94rT87pWgscPgloXJVT8n6EhlGPI7obeR5kpCXKiLPEInhKUZiJvZceIg/okpufWQic7i5tuv4V/+9v/Ku17/M4ThDBLwPIWAt98o21MdLuP5HguzlzfVtCzFLW/dzzOPnqSx1FoFZU0rwZ6W/mb9IKIfamqlAne/+XpIQsIkoh/2yRUK+L6P4w7j2ArHdTl/7iKNxjLlcpXRsSkcLLBt4iQmGkRENvi5An6+gNIdgs4KUdSn1xrQ70aUPJugL7hl7AoG4/hCjIuATr/PM08/jVWeZs+N13PtgevYPjWE4/Uxa55KNaw84Lrrr0X/YpFfvf+jsHxJqJrfEfPICshPAoGwrs+cFV/pvjuoL9/FrzdtztwBr8/Dh8ah81Pw1cehqARcjbpQ/w3g2aPs3e7xk7ltq3tYaXWYWahz+tQxrr7lDSzHec7OLPDwp/8H9/7lf+FdH/hR3vjWt7F7725AVvJbR6F5u+Levx3jN39rO+eP96GjYWwbnPgin/q1hzl7zyi5j/0yh8jgrSu1AnIf5RCvxN0DDRseT+AaS7Y3L6PBpvQ3MXLnzqb7O0TGCN2JsEJ9oKxkBR1mVWCEqXRf84A9AtUKNC1wLXjg3sd48J7P0XvqL7n21g/ytecSlks9br8lz6NtmMrBuCur4nfLDNCdS/+eQu6Yswh+apQBKunfcwhIq5AxmU3/DoB2DO0BFHPCsI6jFIgNkQvjIQ/4SrpRQ1POIUi4qWwrpN+BjLZsplNnzc6NypJpJGYc5bVgrHGpqmT6r30yXLRFRlo1ykrF9HeGV1NCJgDj953OQdsDhsBOoNeDVgPai5BU01FaQXw8I3oxko6uR6a+20Gcz0u8OoBORXZRXg3Hs26vHjMr9Dydbp3jZ45ydtZDWYokTgijmCgagLLQiSFtXamNiRazO46ObQZB2qBTReTtCNuzcYZH0GGZuNMVrTxaZAmDHPgjWF4e2/XwbR/bcwiSHkHURaNh6TQk83w7pAXX7e+HrYOxryVLoN+GP/sI/OS79zNayyMLrlm9TevOUbLMZwOZAC7Qo83i8kXmF89x/Y6Y842nKHpbGCkdAIZQbKTqNkFZlKxtlIoDLHuSqu3iTe2lVJhh3N1Bic34bAI0nnoDih0AKBQWDnFiMUiUBHhWnlLJYWxswIZNG1Aq5VnqYI3Wyjcx7UAvluiIID1Xoy/0vNpuawKGpiFfZXqzy43XwNtq8OW2NK0+24anXMhNQJyziFXqOXkVgkGBBA/Km8HpQnlMShG6Lai57Hs9vGkbHCpCRUMjB0MK3Cgk6C9LOba+nO5mVTainSbR4BJeEabGimzYvoHS1ATHL8wyc/QBuidm6Ogubk8RrBxhrGIxNuqxYVOV/XvKFPMD9m5X3HGTy+JZl0dmvk7n6RXunRvhVOBTPzJCUtiBNbKNpJuHPSXo7YT+GegelY7UnOGbgZG7rzvA9TcdYsLLNGIVWX8YuRbpKSYS1yWxyFeFnbRllpJYazBIWzKVoVAUKYdXWhdn2wZv0HzxsRVOn3mW1soZsgW3SFqgRibkNZJ+3kCA8SsFFUoI6/N6BAi8Kn09z1LVAn8L5Kdh+TYESH0hctbarhx5cKYhPwqtr5AxVwPEfzbaY0YT9gLE90Pfg5UKDMrg7QJnE7AXOvel28+nhz7g8lndtBfumGPTSKg3l75pGtiZtiNBuqF8Om51suZb5kbw0gPMA1tBX0Vy+KO4G7egK3cRHYsJ5j5D5+zVRPYE7HsbPHsPGZ/FALI1MjpKiEQs5loZh9zoXxug5tr0d6MIJ8g0FushN1eLVZ1neuk5DiGByI1IefN6pnrdnme1MexrbuYt73wXxWiS1kWRC6gMweln5zl99Dzz585Bvw79jjA6EwQMdRyoVrGqVdzhGoGjoduGWINKU1CuDZ4j300SkQSwABJodkRzNuxLh8Ikddi9PDiuNNPqpwmTOBHN2dDUv6bPiQHZrHSytFO9TmWlOrS2SAPFsew/iSBoS6mr0qmkoAJtng29Zvsv13xQaeKm3wbmoaPAnQR7G1F9AJ1zkMwJtVH3wK+meuuRVME4jiwucQS6BNQgWubSxWU++dH7SJIzyBwUc/mEebl5bo5SPk+/sEyrm60BWsPs+UWC/mD1bCH1oBSUXEVxyCOJY7r9Hq5fIFfwiSKbxLWJbbl2tqNxlYdl2ziOy/DIKCsrTZJEZINs10JrKVmME1DKwsLDdXIkTkgw6FEo5KnUSmhrgGZAf9DDSSL8vMfQaI1aDYpGSjiJWVlpcvVNd3D7rfu5/pqdjFaLhLqeyjhlNg7kqnkKW0ahXwH9nWxiGCLz8knAA2cSvN0QFSD5DMytED/SY46b+Dwb0dc57N4A149A7RrIW9BXcKINjVROOKc0I2ukoPpBxMpKm2DpBI89qBnfsoey52MnAW/7/ndx1bXXUqtVV79fASoOjJYVbym7JO+bYH4uotmFJxcSHv6DEzRne8ydiehq+OOH4Y6tcPXElZ+1hSz1HeRxGsvB8RXRInZHZFTGEfehgayEbnpsO5HVdxZ46DQcX4A9h2SlM6lSg+GtbWtpMD8nzd1EIfgF2HX1GF58PZdGLC5eWmJsuc3chTZ//sePUq6M8abXb2BoY3lVPd7Uk3y7zRBDWwgQbNrgmNqXtav5BFkP0uX0+2s4/queSEvLK0nEm+ko6CbQMyHR5lTpJc1p0UXcAhtxJ+bI3BNToKPSgzUDnEpKrvYOtde8FDKABks0hTnGrHSfJjFuAFsjc23cL3MBDECbylau/usgemjKkvWkRNagURuQaH7Na5EMGTZOuLmbjEjGq8nWiuq+mJlJYL206HvL8nholI4Jw6b0F31FZh5aByiCNwZOTQhfykZrhQ5jdBwReuA4FpaTw7HzOE6VgdvFSYYgHhBGonvilUZx/CKen6NcrQEWgygkiENILAZWlUGwQDRoQLeDzP5t1mORdTO2Dsa+xqzXhT/9A3jPbeOM1ozzbTiMkHX5aQHLJLpBpOcIowYDp0m9N8fpuQWu37GB+c7DDOuEkdK1KMawOcCEX2Dcb+FwEGo9JH8/zL5hD2Gm1cjStcs4bEW8GrE4dhiEQryxHQWWR7HgUasGlCsmfRxLOX9yJUxFBdqGfgzdCHBBjZM18WqlTJ6+HJM1BrVx3HKOvdsd3nEd3OXAL5+HLz8H5y5qrJymOKQIaiXiQk1KJHM5+kspS68yDrkId3yapL5A3BRNmF1XORwahluQeNctwZfycNwa0O4uQmTaC5igz8IdmiAcRCw3BgznYHJslPHJYayCzcNfP0pz4Qyq1SVMoD6jWZg/i4pgfBj27nGplSw2DhXYesDDu3UIpznEX37hGH/95RM8cq/L/Y0yQX8Ktb+BGpqQZjATPnR2QHsc1BbopAxq1U6Tz0EqpxCxGsyqMa69eg+H9u944bK8tbpWESQDwQ50DCqUTcdWKssVy3ozSMAOIZekvddSApfBBtKr+6Jmdun78m9vEPOpz56ksTzP5ahnHylBn0NCne3IPRojCOeVZCPzyH28A/hR4D1kOqdk1V1G8nQ3YIETQNFNwdhZhM7yYhqyp+WwrH2QuwFaNTLsMUbYGbX0u0YOuQfhlyA8Be0dwD8HbzP4ebnUHY1EUoYsfoHLu46YGsD22iE7mY5VH6jC6E5ozqeN0EyhIOmGZ8mEaFmzUUMNmQJ9Ixz/CPZb/3d06TaiYyvAn9A89hBseQPsfAM8+1kyhq0ZxEmyiKeHzCkmvOqm12QKYcHWkP7KRnalRlbYaFjPOv3bhJUKYcLmkOhpL8LoNQj4uq0b4OTwN+xg/O4f4bbrbuLwl3rMzw3wHIWVCzn65FlmL54lal6AXiMFCC0ptVAx5AowNIIaGcapFQnmL0G7JxNhLg944Lvgeym4GkmiMkkgCGGpIbICxAKMWgpUGfyaNJOIYugPRFIgigSY7XfSADxOtQJT2pbnCUPXtkEVZbK1rRQE8ATEjRBEIuwBK/L72CAIJjgw0f/LNOXI2CTpYhGnMkL9MdlecQpWQlDnBa2KkQZlzgjE1XTCL8lY9ZvyShQ4FehpTp9Y4j/+248hIIOZS14ioIlBJYq8b9HuxeIqAFprThz+RtmSHtKVveTC0LC0WOoFAU6/i4uL5bloxyZRGnSE6yocx8eyHCzLpVarMj83JxqxOiTREZblEIUhUZigLB8HC+X5qDgkDtqUSiWGx6poK6DZDegNOng6pJTzGBqtUqpk+qGJ1vSDPq+//Q5uvn4TB7YOobXmbLuE5VwuWj8KDLtgFRR0v9Mtm0LkGmlgCKxN2IUb2ba1wLln/4hB9zScW4BzQxw+MEl52oENsFfBvmm582YTaBXhuVFQbglrzLms95Kk/xW+Cnn80Ye5pVBi9549bN+xkdvffjeu7xMnmmZfYzuAViRpMnm3D3veXKMHLITw8XMQPruPs8/kcIYizp2N+d3P9FFv8hgquEyVX/xMTWskg8OZ6ncXWYn8ngCkaiSr6Yg0nNPSgKqmxLXYhqxMR4HTC3DuFNiHZJVMyCRPNVleOyLjj4cJtBMII/EPXvf6Lbz55s08ft2dfPhf/TJJOCBqBnz6E08xNTbExqrNeNGlOpSjQbZifruDQpN7biL36PM/m0XuHIOTbkBWcCOhupz+bep2jHiSRpIWE8BiOrX0EiQ3tDGdEmPJ92jDiDWhTJPL5VQnU3nuKO2vmKofqSFpI5EY1NiEXimus4qvGMBVkV04c6Br+gCtXkTzWY7L9f1NgQ9aJqelBNqRONuem+a1A4jaoI2+x3z6ozpZGzkDefdJRS/IYPFXCwv1So/DOLjrYOz3iik0liqR0zGKPprwZajDP9+MpEce255A+zW0k0dboqStEw1hiA4HDJTCsnxQNrbl45SLxN4AP7FRUYIOekBIrjyMly/i5wrURseIBzGDKCIfJZC4dL0q3V6ToLMCSQOtzxHHl9BJU4Lp1Zl93b5XbR2MfY1ZFMIzX4V+9zhab0cp014dBMAwiJkNnKQfH2Wuf54LC8tcO3mQ/VOvZ/+U5JunN20nT5kMzdmKzXS6DQPomgnCABoml19MP0u15xAH5/wKLHVEu8q2018nQKSJI6OA5a95vZQpwIOhSdF11T1gGry3SYpbpz1Yox7ETwIWKA8c2LRH8Y5JeF/aearRgPosLB5LSJYHbM3lcCoTBBu3CYuoNgSX5gU1rFTBHmXTzTfSPHaexecuwrhPtwWdiqaXU+TJZKUYBNAwmWgDxkqqvFqK6DUiZuswW4c7X3cdxdI4DBp88t5Pc/JMyFZfqjjHx6Ua9aH74cmn4AtfCbl45iGq47Bxi83WrTmmp6d599U57tg9wkK7wtHTTb74xP189iv/jpNfXl4zdnuBbdJaeOIQsB9yNrgazh6DwVHQC+lZzEPh59kxtZc9E6wGrKtXwfg+aUda3YfOEnT6wnotFqBQRZxaJcStVguW2+kEY5LdoVwHx4dSTSp0X9J0KnWQk/t+YXHAfX/2n4m7z2f4PEkmqDCTvrYh9+WVZh6vBX4K+DFeUCVuFCHMbkYc7euB34XOx6FzDYITvhv4KoL3vcC58BngDAwuwEIficDsNZ83ELlUowdfR8a0hZBZdwKTaf+GLgTngTuQaCVJv3MfchsukckdGLA3MRf2OaQ0LZLaxp/6MHziKJy4F6I/JhNYAxnTJxGWcAosARLywKouIF36Xz0F2geuAxRc+BcQvQt6P4tcD1M2bRgaDlmzLQ9RhzuQDvYCov97bbp90ynD6FqH6QB1yMJeQwG+mL63Md12P93eDFLoeYorY2Cs2/eETe5l5+vexs//+I9w4TTkcBl4PeqdBl+45zxL9SNEjRloXALaUMjJs6RjcGLYvQdUTNxu0LlwQtCQQQCDfioX4KUCpZZotkRaGKqNOjSWRE/VH4W8n8kFOE4Wb8akciOOLKqWSkFK0+rbZG5GZfJNUuDW0hkgoBEQ2bLAswRNiEzPdmNr50rNlc+dqSkbvFEIOqkGLMgB5GB4I5S2gT0GrUiYwFYERQeclImfJLLYjFTBiWCmAe1TwCWY3CZyB1ExzezdDb1zEJ9Dippf2BYWF1h4mdLhYQLdQJNrdxgZHcGxFCpO8G2bKIpIegMiLyC2PWpDQ/h+Aa0twlASPMVSmTjuMxg0WZlfYnxkhPr8LEuLS4yNTzFWKJGrlIhLHouEtNstyqUCnZ7PUkfTDzp4YZ9YhVg+NDVcUoLTt7QmiAK2Tm+jWkzXKaXYUhZX/vkzWg9YWm3e9t2Y75bkNRijatX5xNfezXsOljn69a8j99e7mLwpYnJaGI1FZPaPgI4lJee8H6pqA6VtrJ5JEZgerTBcKeAVy1y4+FFioDw0xG3v/sHVbgL1ruaZ0wlDUzbxAHp9yXv84D45ujyiw/qPd8A//tMD/KdnDvCfH4z5uV/owJkn+e3FnTy3PMW//355TtQL+CwDxIOeQVanjUhK13i7d0zKcbfS9wFOx/BwAKMF2KIlAWBq2q4D9h6C+JCsrpC1YQrIWsT0EI9/ElkJW6EkyCs5yI3CNgvGY+jeaLPr6v2Uh8YoVcvcetvNfO6vf58//JOII2du5Bc/dHV6pRRlJZ6/sW8HfG88/6Hnva8R4aKjyGptUuxlhBHrkYkmdcjwSx/YkBYoVBwZwyUgSHPGqiQuvo1Mn+4Y9HzQriipoEEbivEAOAnqFij64uu2l1jtMep6ItvdbpCFTSY3bSQijWJImJ5II33fQS5YQKYZa1i65jcGnI2Avs4KvhoalkwFwCUoF6Qkax6YPQXhObLE9AqZTpWd7tA0su0id6JpkvpalG1aT6R/L5kCXCxKhSp2v4OOQ0xvvlduDkqVqA5N0419wlgRhyapHYmvREwUOQTEJCpCOS5OzqHg5yjZPo7rUvE8iCJs28bN5fAKJYgcKQqmB0mAY/sU/Aq+X0RXJ7HHbfrRPpZX5gmaF6F5FElBrSVyrdv3mq2Dsa9RO3H2S4xNukyM3oS4LD5S5quQh9oGdpC3t7KpUGPDpkUcexxx76Q0eILvR3EScX+aiMfhI+7YEJnMgXnPlLoYz8UEgwLQKAVbajCI0q63Cqrj4PlAociGjXtRKlXK0kMSWL1Uh0y3BtN3pbFmF2fbVdR+4vf5h//zMJ/8C8XRz52g88A9EHwqHYNhsAowOcr2ay2Gx2VqXQSOHYGlkxCdb8HC1zl75giJlzKNYgs1uhFtNyj4LqVijvlHjnD2v3kkncPQPQn9kE98cA9Hvm+MbTeXmJyArz8EJ78O9cPzsPR54CFWa5GUBfm9LB5/Epc2EzWPm2/YyS/99m9x9fYtnD7+JF/47B+wsT+g3YezHZhvSBy6fRfs2wd5Bzpp9r1+KebRL3eJolM4vmLfwQI79hS4ZqrAhrLDu67fSr3rc3ZF8Reff44Tx0/TaS9CMguL7TT7VsStbmXHT/wGM6cfJ0o6OK6iVq4wNnqQwzNFfvf3YKoHbzwIe66F0XEoGoGydK1SifSoKSIBoupln+EI3jsUQTUdBmV8SAeGNaiBMGkNePtSNrcMtSK0u/Dc2QTdP5kKgT3fDOII5N8L4dMQHX/pjXMT2O+HrR+Acx6EeTI1tufZPPA3CFHzBuS23wsEoos7/vOweDrtqfBCYKyx44hixOeR5l4RcA/w4fTzE4gW7OuBexHscAgZ7AT4BRiMAgdBfRB2W3C+C93ziHTiCbisiy9kemer4mdGpqAO8TL8Px+G4HGIniXrIuYjZf23IGHmk+lG1iZ/jBDa14D3QfdB8C7A0Huh8U+A/wj2MN7k1Rz6vw/y2P/xFXrzF9PBNNSUkfSAZ7hcNC2PIN+mSNNomxk2h+mYcS49BpdMK/ZU+vtd6e9NxFMho6asA7HrJvaDP/sz3HT3+yi2YO6ZFXJ+js5ghaePP8nCmWdJ2g2IBil7tA9Tw8Le9HLg2aKFOb8AK8sCRPoAOs0RlKFaE6A1CGG5JaxWENC1VIHh4ZQd6mTvB4EwXK2U7Rj0pRxVh6BSgW6nAElBmKPY8nkSy5oWpWKJsc0qXDSAdNYm4/IZThlkvLiYV8Q60rE0NlstOq4BV0FlL7jjkBQFnK5VYLgsOrolHzoxxD7lms/YlMfmrQl29wiDTot6vcOzJ1xuf+ttLNcrzJ9vM/vsCRnr4jSVos/EcBmbLqdPNAgCg3a8cosQ8llvJqGUj6gWXXy3hFMo0FlZIW63sBwbZ3iYYqlGoeATRgHLrRX6wJ4DO+guL3H++Ek+9Vdf5Yd/4ABjwxWqtRKNZpf6yjnGchtw3Tyg6ff7oBSOcnBCG1YC8mMdNowUuWrfTlCCX3cXYf68YuM2n9uvdZisZIvn6XTEzdTfQQAsHyj5HkN33sHKg39J0v3WQthXbo/SWDzLHRsC6os/DXwW7CdgdCvft8ehOizHfAQBF1+H5DvvsuHgD8jsvdeWFcDUUwD4rs3+7ZM8Or4dK19DkcmBWkC5qJi+ymZWyd0YaFh8ian/A3vg3dstBj9U4iPLr+O//9FpPvEXdaLuNXz4h0X2+flmvGOX1fosIJNrN2JKFWTZH0OmjQN5ONuDwIeeLSvXU0g+1njbQfo7k3KJEGyujjxlZsUbAGUPRlxoKRmjcaC/ovnIRwZs3Xsjo1smCFyYWWzTa61w6egX+R/nHudv/nqED//Zr/CGooNjCyCaquN/x4rYA+TafpwstTRAvHoHubfNCh+l5xYiXsk8cq1ryFg9l74XuFLJP5x+16RlTV8tEtmx7qUbWEZwyj7oS9Aupj8yuV0HBjaE1poNGldiQCbFajDQJSRPZJqFmcR6hwy1Nyc/SH9jGLEGdb8Qpwm7prBficDyYOBLVqFfh+QschcYtquRrTO6BoYcAhkCbPjb637Qur26TR4vTRRpatUKVb9I3qny1fPfWNlypaacAk5xC/1cjbDdISZJE+GIj6LTusx+X7IytpNq/cdUqxMU8mVcP4ftSTZnMOgRxQn9WHqx2thYTgE7LxUpdlRFhQlRFNMnptNxiChBbiMwLPr/vSVIjP+ygAC06zIG3yu2Dsa+Ru0P//woIdfx3neaYCtPVjA1QPLJOZSycVQRrDKmY7pmhZAncNlJqE8R6cMUWAA1DaqDLNhHyIKajQgTTrRQsoImw0bMyuMcS8C6JBICSz7NJuf6DrlCVRwJQmG1xt8kC+Q4UJuAmTqENkno0ZntcO+fdbjw9T7ByjyUi9DdgrhrFXA2wkiNGButM6XJ8VHIV6ChNDQGxAtLYC9KAJlUKPgWu193DdPjRQpuyEefPEy89DcQHYb4Aiydot+6kZP9zcw/UKRQrFOfbdFp1IjqTQguIS6ioTEpcv6AoB8Q6phWT/P08Tk2DJfo2D4nmjH9+RadjhClujaUezKR9/swUhMgVCOM2SiClWXNqdMxxSrYyiKfcwgY4KuAyGpRsTQbfMWbd8KWos1yX9FNIk4snqc1FxAP8tiJw2itwkplI70gRFkubmGYiAr9tkUSw3ABOnV44Alp0D3iwYFJqJbTMxuAMk0io/RfQ1VIY3hlJBFNLZkHXAS7nl5bQ7TemN5WVTKyZWpaQ3sWelW4sAD3P6bRusGLi7NLDpUwFIDkG75XIQP4BsB+SK6BxSmYUOJcG13255vpmBuQibY9K+etx6H1OYgfAZ54kUMztgYzJoTcLkiuhcF2xGlPHw9i4Ob0/8tkrA0Huc3GBJeZb4gcxGVSqw2ytfw8KdM2QUK4zyHhyoX0/3vQWUx3lEckHo4Bk+Bvg/IeGDsAJ87KuAKZXkOJjGGxA/QKhBYqPEn1XW+m9ZXjxMsJyclPspj8ONxxHepxhT5xNB3MNPKhkF6bm5GbwTDvDfu+m57Q59J9DqevApnYmglCTDOylBKPm+7HlPCZusKXSAKt2/eGKcX4uz7A5msOMOQVuHRmkUIux+mZU5w9dYz60adIOimt0neh6EG+Rn6ogJsrorFptVdS2YC2NN8KA7DjlEJlSympp4Sl6iooeLIdSLVf07VwrdaAwaGSAAAgAElEQVS4ZQJnnTXVCqPsM9uGfE4myCRJ51xbAGNtAFVTIWNqZOP0djdqjMZXWPsMmJrab+W5MOdh5l8P8jvAduV4DevXK4iOrrKwxydxIo+xqQLbt7pMT83QvXgB7Z6hllugWtvAto3QnBjHzdWYPXUO5h8ENaAfBywMeriERJHhyn3rphHsPQxjkiiGJKYfDdCuRbFcplobplCoEUcay/LJ53zAJkoCdBTQmJtn5tQxtk9CtVIiV6rQ6oVcmjmO5zjUhoawLAiTLoNBB52YMkUlJY4qojJSY+/uPdLKzILjrSZLSw2mN2+m4tu4lhJlVg2PnpChzxehOibDHSkoKYi9HDfc9k6++tQ9dLvLL3HW304L0ck8C5c+giTgVkBth0KeYw3F+CiUSrICucgK1AIqCq7PCx5m1MPXqvAkStF1bG47dIDxocrqrG6eACyFq7KUn9EhfTEruFBwFTqv+P6Sz+4fmODkTMwJF/7qKbhjJ0xXL/+N8YRNjZghOBrRHAMmmi4HFnJdSgl88SRUtsNkEUY0PKYFTG2n29ig5Eny0324ZMxVRab2/uUn+zh5xa4dPpGdFsYk0HMV03sdrp7ayFQlR9xXJPWdnH9qB83lBXqtJkk/4g9/6+P4P3k7u7aOrWq3GjflOwHIGiwzR5Y+rQN7yNpPjSJei4l4lpAxrpD1u2ogaeYYaQCXUzL27WUIHSmoGzRAXwTKoMtkvqsp2inKwehGenBGEyElnOqArJepuahr+6Ea7NPoLaxtyGq4MAawNQpLRh/WZBJ6GhoxLB1LGzoaGSYlgE2vD/EKxN0UwFnrmxURP8ok383OzMmYlM26rdtrxTS9cIHFrkUr0DjWy2WQplW2bAAnR648wtDEJgZ2kUGsoB+k2stWqtssvpHtQr5YRls5EssjiS3pjwp4tkuhKJJobm6QFj8pon6MRqW1fxrLtXCVj6UdLCy0img3h1iqz9FcXqQ3iETcWptKYSPQYvRLBmRNR9bt76utg7GvUfvb+xY4dHAZ3mk4AEaU2gRSBgUL0dSJWMAmwiIiTmY5t/QFnGSGWM1jOWfZVltEQJVFxEPIrdnOTjItTpXuz7iXJv+fWRRJBaRtC/aqFWjLxsnlwPZFZFQn3zzms2wolqF7EZRPYuXpzdV56NEG5ZLH2CgUp7YQnbPo9Dv0Ap++NY5dq+G41iogWERiactgMAFSAmS3sRyNlx9holbh2mu2sGmqhBV2qI4NM2g/QxKL9INrz6HsWZIZaJxRLLSPEcXPAlMoVcF1bJLcHixVwtIr2HTJOcvgxoQh9COLerdEwbY4fPo0Dz35LHFHGqGGwEBJI6xyV9aFnAvFEpSqMDQicbZKoFCAoSEolRwcx6Pd7zMIA/orLcL6AKcOu5MipVHFsqVZtnrUuUC3ERKHLjqOGVx8AOp1dFhEeaPkhzYxXFCMl2BzGa4alibhc0FabatgPO3rVCqJHhkBWZ1cB2EV1Lm8En1VNC0d9xNk1VKmTq2Q3kIvQkgdtCFy4cxswIOPLKL1Ei8NxvoyWN9Q7lFCgNjXIyX3gfy/3iK3+3D6lRoiqfpiFqbn4CIk0i7oFnT+Cng8/WwkPbczL3KoJip8DqyrkIjjTuBRMkc+Rhi4xo9Wsi/GkKgkjWeDvgTeeBCVyaIUo1+7qujQSA/40+kJGj2xFfly/k6c4lb8gkXn3HE5QVuDn0Bts3QbZQlxUgpkgKx5iENgQnSgw9M4V/8A6tGD0HiKZOYR5s78A6qHNmC367TPL0AwR1aPF6UnthW5qUwPZTOfmQTTKQS1N/IoReRmM7yhXvqvQcuNUO4iEimZfZq58u8GuFm316IpUD473/IeCtUNdJcHLC51UZ7PhQsnuXDyMP3ZM+AmwoBVNirnkhsdplosoJTFYBBCvyWBcRiIdl9/OQVLPQFiVSoXoLS0OHd9rEKBJBzI5N9Huh0mVrompve7Ivv/JErnDCUvK9ULDAfChDUdFS1EKkArAWmBDFy1yIqdX2zh1S/x2cs188x2wB9OPc1QFrlEg5U+o5HCLk/gxVAdLTKxwWN8vM5Cs00ULJKz5hmaqOH2jjI6sonumIdlByTRUdCxNIrsXA4eGbP9IkkUouNXCDxYEAQRzWaXOFkm8W2Gx8eoVIaoVobJ+QXCMKLfC/B8j5xXwrFzLK9cotNqsrK8xK4dI1SrNZRfohe2Cfs9wn6HoNsk0QP6/RXCsEusQzQxiU5ILIv88BjDU9NMT05KryAbOq1l6suLXLNjE75tY5HmQjWEXcG5tS0N1pOegLRlB3KOx8FDh3g8n3vB/pLfOYuQ6qEqsAHUdeAmHJuDwRRMFySZv4y4CovIMrcTma0nkBnfiHDBKrmRq3ZuXn3PLK+G350g+YzITtO1WqQfSnba5+4FTCnY58G+Q0Oca8HHTsGjZ8DtL3L1tMX2bcMZw5Is1DdmeOctMlEehbgYJjettAB7nk6LX8KEk4eXcSaK5CsOft6mpMRV6qePZaQEzzPnZla6syfbqILD8IhHdQS6WgmVwlcc2uewY6pK2ZJetNt2T7Hr4A2cOfocjYU5+v0O9/33+zhw/XasQoG940XcdB/LofTOreTk2C9XJf67sbUSDBNkrVd9RIFpgEQfE2TA9iWy1KpRmtfpeyAhhkKm30EvxTM9mYqjObLqfJ+MmWpQdBu5cEbDdSTdSZ1MBaBGhnf2kJu1Tib9mCDuUpfVirFVP9cwa1vpa61Mt3FnujE02tC9kKK/kAGpAYRNCD2y5JfR4XfJqoBM0s0kq5Ps96zw7RGheK2YGWwzRmbdW0/Qv1otTJqEL9yn8wrMAatGobgDp1CiVK0yOjZJO3bo9mOSpIsOBmDbWLhAgmUl2J6N75XB9om0TRBBFMWEUUysNbaTVgs7MZajcByHju6nd5QSeRTPxrM9PNvHsSwUA/ycj+U7+DmP5Tim1e+jYwe0mSzMSmeC7DB9resk/321dTD2NWqDSxAuN9F6AaWGkEtZJeux6iAAzHHQn2dFn6KsNuHoAp1ewP/3uYeIBg9RysGmCYttbyojgpcvtBg9BhwGfhZZ5IcR16hMlh7OLAihE0iJUA/RsWr1FbZvgzMEqpV2oX6JrgiQatCVhT00MgoTE6hiEd06xdVvvZODt27kwHUWK0vw1Ck4firh3NmEUtFm0wZFpZwxFGZOiDSfHYB2LRKnArV9+MMlxiY3cGDvPnZM5/CshMaCy3XX38x8sJN+vIJSAWPVYdzyRnrtgPbcRRpPdllqfBStF/C8XQzVDjGY2IXvJOSi8/j9J+g3PkOxIt16E2eIN9z5M3h+kb/+k9/h9/7gDwl74ueBONsrA6g0YaUDU1OwZQtsn1Scn9MEfen9su8amNwEo8MJST+CbkCrHxFc1ISHofMI9J0OhU1gT3ZwRxYZdWHOF2A1aB3j4Y98Qa5d/gDliduZ2PBzvP2GPFuqFlt9xbVpj7TdG6Sy1B7AA/dA83HYvA023ZDeYi0E7zJArKl68pG1xCXLE+SQpleQERdHEUnQIpfh+Xr1P9K3xapAY2We++/7MujTvPiCZEIiQ1tYa3sR5uVdwNu5nF+D1Hm+BZEs/TAvLt2zAHz2ee+1ECoPiDTq9elu/hnikBszoKrJZXwUujcDNwFXAb+DyKaausf96ams6oaRRXNpD5ytN4i2XnNYuk7z50ikMk8WmZAAjwCfRPRgDe/GSTfYh83voHLN29hyVZkn/q8/Bn1CfIBeIg9zOAGrSnyGrmtK3qoI23YP4KKTGRZPxjCogKqQDCIaX+5z16/lOXNpM88dduDMY2QcGHPTmBbFRvMiTPdjgN/byApBHSQLYHpMd8miqSS9KCnQzDmEInyOTJxtHYz9njblYPvjvGn/nSzO9rnQXKZULlPvNpk7c5iVmePCOnIdCDvQ7+EUcmzZvptcBPXFBq3mCioeoAeBgIxhE+pHwdqEs2ECCgWiQSobYDtgOyjXxa+W6c/NocO+LI4KyX4NQilXY5DeookgNp4jJQrdgXxuMNN4kOqzpnT96iRoSxqH9Qxj3ACxRlbopZz5v+tAtAecEGZwviLlEnEErQXpyogPYQHbGQXVwS3kKY3kGdk8TdCY5OJ5i9b5WSqFWU7Nfondby5Q0Vvwg+P0nids/kJPcn58F4OVOQbNS6/43FbaXeaWuvQHYNmKH/3gexmujlPOV7DR9IIuF5YX8X2PsfFhNk1NEcV1ipU81bFRtmzfTaE6TqQhn4/ZvmUDWg9Yqc+iLYtWq0UQQ6QjQh0xSCKsWpF9b3gHO/fdSD6X9l/UcLq+QL1+gff92E3k0jNyNEwq+MB1crx1BUdjePoUdDpQrMLIlM0Nb5jkz/LuS5zpd9JWEL2fAlBn7kxMbaNmbEjhuLLU9ZUstc9pmFKwR8lqYeokjGpPqNeoHT0PWzIewAA43IRKUeNakPQ1C5HmYNmi4ijJyzzvCLVe5SGyuQz/6Br4P+fhV//D/ezZ5vHvfv1udqkX3i/ICraosycwSkHVTchKFgE9B956o6SIS8DiSsBv/OID/NCPXMc73jjKjmuKnE3k3E9puKQ1jpJ0sq0UHYQpuhWw+vO0Gj7nc3nGbnUo2BZDSjHqwfAm+d7pAC5q8KYt7vrpH+KJLzzDsw89wuFH7iVaPM8n/uuj9FouEz96DdNI7ujZpuJrTXjDVnFrci8wVt+qmfRQNX2VkWs7RdagzDTwMqBrFxlbA0h301cbcTOPrEBDQaeGJMUBLIjriHRACbkgJnSJ12xkJf08THdc5P9n772jLbmu885fxZvTy/m9fq8jGt0A2GjkQDCBFClKFEVFimssWZQtUclWmJGlscdeXvaaNeJYY2uNKFm2hlSWKIoUGAyCyLmBBtANNDqHl/PN91Y+88ep0/UaaIBgsgii91p39et7b9WtOlV1zt7f/va35a0aq9TQiLfrjX9wCTnAiryq1AJc4mQastNqUUsmKi/eboPYbRXyeJSka60L62djSS7lqwYk4IxiPJhyxDRTxktRi0ubmBJ/Z6u+uKL8vpWBHQs54KphrPJlr/iE35OmZcDewdS+HVRKQ6RsGXSmhEm7owFN/JREelMCTCJ0LQRTQ4tSaIaNYRgQhIRuiGd4uKkANwA0kwgN3TCJ9DRh2sAURpIIRCa0AhGi4+K2GxgmDI+OMT4+QWNsG88cegRvYR7hqFVHxUSqki+DJJO4XNGV/d60K2Dsm9jWNpY5ee44u6YVSGGRgAyq7kXDDz1+/56zjFx1ltlFja9+UfD870PxbvilH4cP3x4hF/DXsioSqK0DH0CiR0MkfJRLJ4diGfpMCM24j4gOWQHlPg2tsh2cs9JpCF7v9rPAs2CuKrXxCGF9HvHAV2Fpk2e+GNJp7aM3fyPDI/Ded8Ld79EIA4MRG95mQWmL1/hHH4XNCM4vl7n3vtv58ue2s9EKcIMuK26dR5+b5/EjEe76Ku3FeaJ8gUL/NIXyCPmihZXu5eqDGfJpoLuHzRvu4KHPXsvy0nGGenN84J138u6fvJrRaY0jLzzK3/3FWU497dGXg2yxwtTua/nkf/6XZDI2Fb3JiFGli0yuN5CwkgecrkO/BdvGCtxx5zCZ3ZOs/uUTDKZdUpbBo0847N5XxkyZOEEXP3BYqQfkngiZOAbXhnDehZWTMH8KTmiQF7IkLhBb1fSa0H2c5oWneOjP/x8e/+vnufvWUd5zwGbiOhg8CCNWcik+9H7Q3ge6SwLAVuKXckB9Eo9ZSVZtxTwVBqZqyl5DlCxCYoBrLozvkOVmL5dMrFIBf7k3vh+V06SRqIKpeq+vIZ3WLfcSc8RtP4B3cCmPJbYccDVSy/XjJD7rN2JpZJ7iFmRDr4dImLYzJOtqf/x7T0o/PHsAaj8D/DGyJrOFJIJeR/JI+8icSNzLSgg4vg6iDCKDfAz3IGlFl8gt/DkShH2BpOhx69ik4dS/pXrmb6jd8yEo/mtofVoy/cQyNDNgHoDQgfBFZJg8QCKW5iAjkwvyff/d8Ln/CB/5KdDfAac34NCneODQ/0LQzEJ/Cc6rVhwqaFAtiyMkknyehO2hOgGrp8WLvxOQaM2q6CcGl6khr/mLJPeCirwuiuhesbeo9UxN8Y7f+g8snVpidW0TI5Wif6KH+7/0FaqnX4DNdTBtKJQga2OX0hR6cxQsaHcaGIZPsWhRzFrUrACR1wiLg3h5m8p4P2Ymg9A0QlvHCUxCM00oIIpCus0q+LHgoNKJJZA0PU2yMiCImbOOLJXIq77jnhQ5dFzotOMmXhEYaSjlAUsydbsbJJQr9Wx8CxYnkLQSCMUA+7qWBmMK0p6UJDDSkprmNyWKliug9Y3TbToM9GfQUzrNdp3Th59GX1ujveDizMJ0H7TWofv8A1Q7Jt0LT7EVSDA02FWEsx1IV4oUB3pZc3K01yNE95vvUixCaLShkIHekk4qm+aB+7/IgQM3M719J/lyHoFBPp8BAuq1FcpDFfpGhrmhkmfn1XtpVbtoUYSBwLBMtB07aG+sEIgIx/MhCDCFiReGiCAkigzGdu3jmpt/kJnt+8ghr96Lx+HCnEuj02GJpMXhRgittux3VilA2YY9OuRnJJOzGcBmVcoM2dY20FZBbLzOWf/PspPgr8JpDf9PBzi1tJ35a3vJp8DOwy275bfufQ7cd8EPGDI3WUQujQqGCgQcasKNBQkUvtIUZDVUgVY94szpWY4cOsSJ+QXmPvgT7Ns+yPa+REl5qz3qw3YDRgwpJ/iJu+Cm3e9ntg73PA/X7IWDlsTYXmkq1Xn/adjbDzvLSQtKVe8RIPOmqogo8rp0nvgr/vLw77Dtd36WGyZ+gb/4CrztdskYbmzCqRdDXpw0uGWnLBpb9iCdgfnzZzn85GH+avkMqdIIP/ebv8Jd+wfpG5T3yTGgY0HehN3FWDvV3MPozkn2X3cjf/gvfoJjX/oMWnMWPzBZr6f46Y+O0Q1trCY88hKc3gU3WjKt/e00C+lGluP/q1ZzwySNypQOsoksQDqCxD9VFKIYyBWk8lW1B0INmiKWIsggT/pigppEsUWFS1WSamATWQjYB1oexDxJqOPE26rqo7PIZP4ICYFNxJ+f3IDNVWAZtCnQUjIpZWhSR7y9CUFblldpa/IsRTp+acg7XvGsleptm0RWCiAVkx582TTysvNdSFLOlkbC3gq+/m62NMkF+lZN6UBA4luyZf9vZXD6e93kjOw4AX7exNCyCN2iVWsRhgJ0A81MYxAQuS4BEaahk4oD2Y4b4iOw7QytdpuMYWB4Ia6rkSvn6R0fBztN2wvBcfAam3jtLoHjggkpAiILhCbvtcWFFc6cOIHbbOJubBCGrkzMXxTZMUmIJuq93i3/D0lSkkrGoPE/eUyv2LfTroCxb2I7euIsX/hqhl//ufcgF9mti7CBRLtmMPUf4Yevr5EuneRYqs3C7XDsMfi+u+C6nZL88/UtQHodp5Bex/Z4/xGvRNRCDQJdJmrRIaNLdYJCUYPscFwbphyL17B8D1QmodIv2xs3N6AxD9EC6DnGp7dx3b5p7twDfRnQ0hBoGgKY0KCsyZs7AnwNRm0JH40NaUy+x+S6q/ppBQJNhOSEx6RpoyEIvV687hRrlkVVy1POGAyldfp0m1KPjmloEIHXNvixu27DcfaTTpkMD/TRP2GTymvMng6xjBqjw6B3wbZHSGf3k82mOAvkx8vs3d3PhedX6baTHJgKw6fHYGoyRaaniL6ywkA5RejbhEKj0ueQztkEWoDjO/jCo7QZMd6NGO4xsA+kGLuvQ18Ak0jHeRvwFWSzg9Nshc5DECGh7xH6/4wnn8tw7oLOPffrpP/yOrZNfoBd+2a47vY81++QpXuYstxvpS4lC3RdgoK+LwlakZDXPZWRnW11TQZM7RBqHcj1gJ6ByJaNECrEkook8b0BpHTot+W/jgZaxmZgqMzCyTKIBtIZ7UFeVSXiVYz/fw9JuXoFCb5uiz8b4DWnvdNIAukngH8JfA5JCv9GbDne5hlkBKQh6TAtEimEAkl/vAUIlqCjgz0QS0i24+3m4tNUjR1OIAHdMvJGWYJoMN5/Pv6NJrFgHPG4HEM+swtIgFI13FMgJ/K9yEFE8wjxNEx+EE4NQfcMaBcgk4+r2wZjakku/rHtkBmH8WH5gM89Hvv2eQiG4dFzMCVgtAeeKuH+zSOI0d3QMwS5gbgEr4kEVu8F/lV8jEvI6CZAwg6Z+JgVA1bNc4rJUCEBcWvx+8vxRVBNwSBhzb6yVHuARNLgir0VLJNKs3tqJ6uzEdPT42i2RbW6RqNWIxRxMwchwAuhZJHNpihnDOprm1hhhBGEGFGIH0XkMxZGxsYs5bGGhymWDISmISJBFAqcwKPu+XhBRKhBiI5j6YjIkJOqH8/IOvL/oSElQiwTQksya5s1JOgqJB3SsKQgu5aRx2rHXMlmEzotkkzMawGR2uU/NzU5iV8uLhUgVN7jsiZFgdI9aVKdFsJxaESnYPbPYOx9UNgBmg3ZDOXJPWilARyrQHddo16tsmS0CNZnWXvwU2jeBdLVVdJteG4OLjhQ3DiBH2pxKR/o2SJEEZHTYq0DQWDQrrt4zipeZCAYITu8g0zxGnRg/eXDiLD5eifwKotCGSN1/YhW28XMCrp+g5ZbJWyGpDMl8qkMpmGh6R42AYQmhjDJmHm0kkWzWsV3XALPRReC5dU1HBERoYHQMUKP0Gkiwi75Qoo73/XjXL1ziLGKQUbAgoCXnv4aRtdh3/QkgyQ1A4YOWkawdsFh5ewaYRhgp3OUJwfY1qvR0WTlRBq4+gMfwTUClo7c+4bP/9trGjILOYNk+cxB9AgcK+J5txA+O013YxPDfIjHPvJhtNFrqR+H6gHwS9CyZJ6yj6TIxNZgT1biVlvlCwBe3JB66tf1S3btH//DPTz50INcOPoERu8wizNTeBsjvJTLsvfg1ezJaKS2FHntMaW2qzr0kgn7BixmylLCed6Qvq7iMm01HQl3TQzJHnVKcl6Jeyn4p0TijaTzed7/y7+E030ad+hanluGd98M6QqMa1DKQq2gs5CFui19qgFbrn7733aAVtvF81YYHN/DVRMpjBK8HEHNg8GUBI2jWOlkGAiGDMrFLFMTE5Qzv8uf/e4fc/7ww9yzdgiHaeoXbuWOdx/g1lv3kAMKhhzjY/E4K/mIb9VeUaN0SeeLC8ioo0MCJz6LvHsc5Modt8xFjz/fJI4/QhBKscpDugIrJB3PVNW+6pBmkSgB5FF9jqWLokIf1YxLuRjnka5KDflQrmxAdR7E09A9B83zECqHTMkqxfTiQOl8q0y7i7yagyR3hgJiVQWRmq/LyKvYHxPp3LjBVzMeDYVAK2RYDYKi9mrxCeZJ4O/vJlMXQTVD+FbN4PJKyDYJMSPg2/NbV+y7ywqkMiMMTe+mPDAGqSKdSKPb6dLqdGWXF8vGtCDwA0JDRxAijIiIkNDQ8ERAGEQEXY9oY4N2o0bQ6iKw6RuaYGZvmtJ4higvaDoZjHqO5krA5rzP/JlN1hZOQ9BGE10Cr43fbRMFLkLzCdM6eHocYKvnfWtVk1ohMqD6ouhlcsPjlIoVbNsmFA7zF84jnCYEG7LPzXd9ouWtZooxdXm7Asa+ie38uRpPPTEPP6e0G1UNNCTiR0V0PcfesSJtTNYimJiCOz8EB6+F0f5v5Bd1kmY4DeRiDlyinhVrxMbelR/IplSWCZmshpYqxA1KVFf017ByL4xOYZZ6CWoNGaC6EehSRDOdzVEq5xnoS9oxKWe8l1e36FFk/2Iado1rFMcyuJrEhXMkarhQJESyCVZcqSvWZ6rWZ9Jk6YEGVw1jMHyRt+fG+0gbYFkahQzolkllfAdjO24BIXj62FFqjTV68hCUYcEDLZBxv6FDLgd7d6eY3FlG7+nDP/USvaUstabPZs0hVwB0gef7dBwXz40ozAn62lDJyuR7bsoiZ+YoezDQcCiuO+hIF28I6UOee9Xo38vKhvQlj6DBofNMTfjsOr2b82uDrO7ay77bK/RWLKwU1EpSwsDSpJat68kGCX4gx8IyIDJkD5tAg2YEjQD0lGzsFhqXVy+8CLNp0Dalo+2G4AqNlKEEtVJIZ3QCyYNQ4INOUu4O0smaAN4bX2HVEEppRb3CFpFg7ONIhuzJeLAWXv3V17RGPLiPIP3hbfEhnUTeqMpHTsWHvAzRLPhr0NMPtQqEKmA4hXzc+khm6hKJftlxklI7C6lb9jJxYFDfckLz8Y5U4kS91FxhknQIOyeBnvxeiDzwFkAci/UrG6D3Q/YGGLJhbRQC1RoljA8i7tzONMwtoQ1kMEZHCIZ3Is4cgjAPI72yg3z3CIgOSZ3fOS7VrVbUFTVoStwNEkpLRMKcVYCqkjBocilD+opdMTD7hkhP7KCYKtJJRwwO9OBFPnNzZ/GbmwjVWTcO1rPZDBnbwohC3I6DZRkYIsREEBGRsm0sXce2TLKZDMVMRBCGREEEocBPgaYHOJIIiR+BZluEuk5kRQg/JAhF3KwrlJOjiCtblE6siPVWVUbMMCSLVkNmxDRNasi6bSmSqKh5xOcRKvkPuAh/aOKNx+Aqnn9dHFMjVsOkrIFFQENsQuM5qA1JRlhhB6X+IcxMicjOo6fyYEZ4ok4UakRtjwvPvwhinQoROeRTvw50nZo8/djSuTxRGOA4Lep+DFe4At8DI58nU+6nMr6dXE8vTn0TTXv+0tPVDYm2fh0LAnADEGFI73AJ3QDX6xCKiDDQMBBksxa5tIUWRQSOD5FO2s6gaTqu3cRpNWi3GoSBCxq4no8nBCnTRotcAt/BstOMDUxw8I47GBkokk2BH4Scmt1g7tRhpian2b9zH3nkLJciTnRbUpv/xVZA0w/I2YL6/AajlTR2IYWVtsgAN7zrFtbOPcnSkTd4zb/tptg9+5ELK8AFqD6MOOESnJsjWO8AzzI3cXR2E4cAACAASURBVBdMOETHa3R+bJB6XqNjQUlIGaf6RoPNzSqu1+XWG3dfcl0VZLXW8HECgdZvkwNKFgStDV4+cojy2AzPPvQleocnKQ1PkN82Rb6UI23o2AYMZKF/y70Wh8D0pSS5URfgiaQQ/JWmIyt6pgvSS1a1KOo41eOpwFkNSKdt3vNDNzA7V6Ll6LxwbJmf/NDQRVGHQkpDy2pYBlQDWfrajHszpIsVSv1DDI+Ncted+yj1pmhr0HChq0mVfE9LVkMTyfg2MgZDPXkmP/ROlk+f5oWnDrE4d5aV2XvRzBzbpsYQB/fQ0y/dkA2SdGeVpCXAt8O21tkorHQNmZNWKdhO/LtKuT5FAqH5JNfpopcjpDLKJQ1Yt7oNNlycZBS3RH3WRboUa8hmradJtGVrwEIA801YrUt/y5mD1RWozyL9rrNI36bFq7JbqpLsVdZH4igqioICVJXml2rG0I98ngZApOKgS8kwbU08K70wFRFF8XuqcepW8Oe7zb6ZhpJbE43Kx93aJ2DrOGz997vx/K/Yt245TKufSt8QdqZCgIXnRTh+RCjAsm1sTaDrGq4T4Gsamhai6QIhIvwwkneGJgh9FxF0iYJQyvubNhu9gyzPg2uUsPrS6NkeckUbI9QQXsD6kk+n08Grr4BTJfQbRGFIGEWyOWgQO4ZCNT1VkbEK7LbGaYZknpkDkBpAS/ViZLKyjUApg55pI4INQr+AX58n6RB4Jcnwj2czyMC9l9fr8H0FjH0T29L5iBdTWyEtJeCuugD5COESRU38cJ05fFYcyAn47V+DxdNxU6s3ZBoS0EojvZQNkj6mly5iuhbLw4XQ7oCRjcHYDGjpWLdARLIO8LVsYAhjx24yYR+toy8johSkemX3hfo6zXqDzVaHKplLmjooR+zisSD9rcUto2Jp0Ksl7tHFzrtbthlEsgnUmW815dcRj8YWfqF0EK006Wwvng/9Izmuvu1Grn/XDwGCL/zZf6V55CGyG6tMDchkdrMrwdicDTsn4MaDZbbtHyboHaXx7CHKlWE2a5ssL9VIpzU816XrenQ6IY0mTB2DbB3sHlkiwW15GJjCqEPm2DLbH11mBimJelJInPBT8RVUfumlrqIAnuX87LOcny1y7xe302f8Oz75tVu57YYSwynJVKmZkI3AjqSjrxp6u4EklDU1yKYkGcrXwYh7ymlG0qBWdQkmvk7qeBrIUjQDWeW62Ypwqi6IJaQTqni/KpvwAtJjPhV/Vo2vzG6kRmwvl5UmUBdYxJs8Hb8+Bdo+eUDiL3jjfloU7+eLwK8Dt8U3xeeRxE2VnG/Gh7coB0I/DL13QGsGwjbSf38O+YjNxKe0h0SmeRWpXbsC3I/EHpeR/j8RklPycPxSdDYlfPZKKyAjEg+iTVjsQvlO0HKw+lVo/zdZJ8k0pG+F4Z+Gdwfw2AU4dhxOPhLvWzFYHaScyYuYmQKpEYPWDbfCfffBwnlo9sFUL6zVwF2MddFuQeo5NOJjVVlgxRgxkfOOmu9UoSfx+Tkk+hlK+mAICfB+vfKz1a/z+RX7XrLCvpuo3P79hJ7OUG8/PdkUm7UGjYVzUF+WdCqVq8gY9JcL6GZAu93C0gBCSUY1wBAGpmliamAZghQdsqaFF4WEWgh6RCptohs2jhfg+BGOA9lsGk/I9pqBgJYbEnW7iK4Xx8aBdNDDQC6kGV1Osmb8wxADpKFsABaGkE5L2QIjBC2FXvQRWAhXxCSJrZUoQiJKr1yCgy3zgx6zZNVvXQLEKkBX7S5Jezqba/RogpIOpyOAFiw+CO0G+o4RJiYOcHZuE7cbYY3lwI4wzDy9fTkmbI/DehpCjSqJUowGkNNA19B8gSYEhUIG3/UugjeaAZrIgtmHPb6PntFJBkenSNlpLqw+jRBbWbG6BIJ9BxH6CBGhG5LNrH5PnXqAdFlyadg2PU42ncbrdvG6bbpBm26rQF9/mXJ5gMgP8YKATDpDrlAgqAbkshbVtS6N+ipRJBgcHCTc3KDabOL6bUzfIQgiSn0TXHXrj3DtnfvJGzqegJrj8eBXn2N57ijX7xvh6l19hEFA1jDQNdmxuUfTmJ7MsNgcQBOwbdriy198msX8EOMTFXbvLJLXLd7zzp2ce3yUp60Uwv8WZSu+YVOJ0l6ktvhuZCL1D4Gj0FhFQo7DwBDBUhpqNfQnj9La6Gd2wGBbCoYieGAZXnxqgaeePszi8iyf+/Sv0WOb6FuQ+gDQ2l10L0IIizCCj/7oBzFFmy98/q+pnjnFuTOn2LVrOzffdjuLO/dSH9iOlU7TmzW4a1LH1DU07VLv7yLwqMG1l8nnwqWA685XvK/K6VUh6lZLp+ADt8J9T+7ioYde4sKRI/zrHxxiQYArYDmEZ32404YJA+YC+GIVZoZhfq1OO7TYtn0PP/vRaznU1mg2JDu0MiD5lqruQ7kfqkamX4OoF37lP/4czz77Y3zhL45x7x/eTSpcY+FClUefbXHdXWmuNQ0KuiYZtsjVeoqk78ErGa7fjDXil+J4buVFKl9+nEvZs0WkG9VFFh9tQ/q2dV027u0oLFPEg98maX3RG0uvqB5Xevy5Qn2XBBwJ4UIEC6F0ePsFLGpwuA3tEyCOAEdg5bMkvtY3a+vx6xswsR35PM3EbyjKr6KIDJGwaxWQq8BZLf6Ogti/W0w9Ld+Yaehomo0gQghVHQdJwh4Sqo4SCo4lg67Y96DpQAFdr2DZeYJAxwsj/EASU2w7QyabxTBkw67QCXBdC6FFCE0jCE38Wg1Dl/UMoe/g5bLgBYROg/ZchxfW1njp5RnM4iCZ0hA79x9kdMwmndaJwhAMnW6nTXt1iaA6D92VVxyfqlRUjbogSR5stTiFp6WlJEKji9New7Rs7GyWXKVCxuhDaBN0gr3Ujh4BcRTEGpdNCF2x76DpJKzmDyIT0BPAL77mFlfA2De9KfRHCXCqbEoeeIJG8wFOnbmPv3wiZEOXeObUtFR9fecfwbuuy7D/x1PIxfj1TENCj6NImYIC0i1SAHBifiTLw1KmjA+NuGttwdYYGZti8WwGt96A1mvpG0E+04edGWbz/JJs+KHZUl/PkanpqfF+to32kI+/H1cUvWbZlKr8ziI5lSqbrnKi6uxjBU0gaYL6SvaDARd/V5kg1uECQt/H73QY6s8yPnUz1+2Y5oZt8nvDwfO8eG6V2Zeli3RgEqa3QTYjWbga8A9/u8JzT61y402P05tN44606XZdshmTqekxyQ7S63S9CMfxaQ2AuykrE8xPKyjzBfmDmpDechGGGzC0LtsgTSDLzc4h4cujvJYr1kBwlLXwdxHt7RhuCT0N+ZgUvXUCaXUgjGvw8gEEFtgZ6RDrgBNjoepOUvn7rRbE4xgiy+DmgdV12Kj3kMrfiGS5zsXf7iLvQ+IzaiHBx+9DopQXgCdIwp/LmI50yquvGIBFGPgBSN0Js4eQkcfrrWVxPxri5prkSQDXXcCvAb8bv9dA+uxjyNjTgfBLcPJPkJX17wJ+CvhbLu3cO4Zk6Z5ASqFWgQe3HMPFR2mDpJ5OdVW73NOh+DllLnJMRCCHbuVfIdHdAeBn4CP/HKweWG7AvV+CM5+PWWVZZOpiDxLQVdTg+4E0/mMt/OcegXftAtrgfA3858D/BNz0G3DqGVg4RKIHoaIim+QpC0g0rQ0SrbOQREEQOZAXUfUO8oJNIJ9u1fLjir3V7e5b7+R9P/kxBvIajgPVNWjUIpxWQCafptvVibxAygcEAReefYpMT5b8SA+ZUg7TNAn9AKEFWCaYloNtg21qpEyTvnyGVtcnDAVGPO8UzBR+zsaLZL7MNNM0223qrQ4dN6CcS+OkLTpZh6ZehWYdmm2pDRv4EgksFeQaKAS4McVLF3JxNdLyM02+tP48V+8rU2t61Ofa1I+1t4xAjEy8VuxtAgUbxvrhpcUElQTkc5mVwp7ZIpgpyIUSxK4lXQOffxXRaA3qjxI9e46jh/fD5EGyE7spppt0nzlBUMqy2OmlW/KRfsUyWw9QAGFuCruYoTKwQbpWZWPhHK6b1BpP3nYb7XqXtdk1uq0qCwsptEyZQqlMreUkeLFegNQ0Q/uuI+U3aK+fZXPpCNffOsHZk4tkhEfRgqPxMhMhWZC2Dw/c/yLbtvczNFwhny1gmiZoDl4etKhEvpymWW3i+R3cWpvjx46xsnKSoNsmZRpMzcxw4cIKotuBZpVWdZOaA4Pbb2X3jT/Ajd//cc6saYz2ykT5aqvLy09/lhfv+weWX3qYh+//W274/p/lPe9+J7tTKQa3Xplijs3FTc7/j6MYvoGzdpZnz27yyL1dvv9j/4RdZdh220eY+acVTv+/rx0UfGcsjUycxkqgxhgYt8uB5dPINT3W1mQ7xd0u+uQgNQZ48o81rvll8HfLplLvnoF3Te/msatT3PtUhf/9//wCv/2L72WwnLu4yq8ALV3HMDQiAV87UqO3P8/I3hv595/8v/j1T/wSQghOnDjNqVNn+cyffIa3v//72H39LWzbc4DW+lW8/7pBUtY3Xoi/VeXvlfZ6PD8d6RPecQOUe69ic3WP1J1dhhOLcnX9ibfBf/g83HkQrh+F/21YrrilbC+9Q1l6MtvIA8M56M/J1bKNhNtyyBVV+VgnkCvjANK1KAG3XVdkzzU38vF/v84vHLyDz//eT3L/ZwZ518f/G+/7qZvZNppmtCBX1cl4vxeQEMJ2vnUwVim+h/F4DCD971Z83Kn4fBTxIoW8YxrxeztJWsOlgJwBnTIJWyOMd5AhbqwFIhe/dwHpX20gEd3PAc9swvmXQTwPPIDMdleBXikNIJWbSRiW/xh2GumgqtEfJ5E6AAnulpDPoGqD10COtHq9+VmhGgb9uRuo9PTQ6CyxtPEyCRdcVY2mSIR/r4BT37smQViYxMoPkCqVQQg21mu4XgiagZ3JYJom2WwW08pgGGmoGBipHELohJGcc8qtOvWNJdq1dSytgxcAhmJYpyAwCZZmCRYWcUKLpx/4IqTCuPIoArclE8FC3W9qFlargWLDqhRdPDFdXEVisFZPyQqoi5XFDmHkEnoGbtQhQ562FyI0DSwDa3IPQWcc0VqG9nlkeaaqkLxi31nbiexOfj2y9WWOS5sqvtqugLFveguRi+0kia5iE/g7njz0BKdnz7HuhozthtkTMnaqTMAn/hSOfQXSSy5/2uPz0btfa/9lJFo1iLyx9iJdsT6ky/PqfHjXk6VkeWKyDhKcbboQoG1Z9jUSZf1LnQHXSxO0s9BYl4FnoQhWGrx1mNqHWy7iWNol/dZVfyi1563mIaX2EJJcpOCbreVNCsr+em7VVmas6lMFEu75zKf+hmcfvIezL36N0ZLDyMS1aGIcT8DxDrx0aIExq8nMVbCxLCuLNtdhQ0jQcnIMDl5vs20qz/BAkc9+dpb51UUGB0L27IJtO0O8bovA7SC8AD2E+XFY8cC2Ib2kGiGIi+xTuyb7pRWCRLb0fUh/81R8RdNIX3STV7d6sXSTu6ZvYf9wnnIe2loC/SuGQlbIhuBhSsbugZB6boYhz1GFzLUOZA3JAgE4VZN/lzIJJGgip64ggqeOwZ//33M8/+gzrC1/FolCHkB+OwvsIGl9ezze+lEkonk3F+kQae3Sqq+tF7POq4GJ/w6bFug3IzVkfxMuK3GsMMM+ZKxZjF+V+HfOxIOq1AJUpZSOjBhVAlThhjsgdxNk3gbrDWQzsbPIWPVR5KM9j4wB4BWPTYQMW15GLrxLJC1+VcOHQRJtA8WcUCwBVcf33+PPb0YuJGW473dA6wV/BOiBaB8yeK4j7xwNWQxZRjI0anIgxBL4h2F5DO74OJz+Kpw6DM0nIDMZM24VUJw0HUw6B28t01HnqI5T1U0rNq1yYBSgq4BbBTqrsr0r9pa1yiSpnjKarXNsVvq21fUuS/UOoRZRHqwQtNZxAxOyKVKVLJ7ho2czWFaaMHQJtRDTANuI0EIfk4BKukCxkKGYtcHz6Cmkse00mXSeMAzoth0anTa1dgvX83CcKoEbYkQRWXT8sEPgB/jdDjSq0GhIZqwRL1iBC7VA6r+YSKC21BtPshFEUVxemwOhITohZ46uEnRCgqaa9EwgkPqymXxculJLggSdpP1vy4e5NTmZm2lJDdWjWMA7XvEiT36WyoNZIoFROojLBvddEPMgSmRrASN9NcbsDivGPNfd9EEGxgbI2AH9H/1NXnz8U7TXjuG3liGQAbVupYhEjtZKl1ZrDd9Xq7QAWqy9fIhAWBhGjqHd0+RLI9SXFzn/4pO4yycgKlCamKY4NEWuMslqYwPX7WDkfAZGbV56fgmn61MXsK5feuSRgLYHlSKYekiz2WB5fpFCLsP0jh3oumRidZrrLC6vYqfzlHv6GJ4Yp68Mc+eOsbK8wPnTOuvVFrXVdRqbDeodSI+Msu+OH+OaW9/NzI48cw04fgw2F04ze+x+lg99Ab/aZK3TwWk02Vg4yRf/c5meskGlkqc4OMOt7/4gIldGdDbYXHqWRr2LITxM0ySXKfPCI0+wNrOfVnaEqWv2cfrb9kC9EVNeR+yl6cW4TLsN+m6IfgqZRD2GhNbqtP/+DyH1ODTKiJ6dnLr9ABcKPWjjsW+naUzMjHBzMcdzT5zkfMvg+LqHFkTcujtNP3DLVAY/grUo4omH7kdoPjumB7n7ne/mNzQNEaPzUSS9mGcefYSOU8dzVom6Ne519nLdrlHGBouXOafXNqX610RCYG3kU6EUhlQB+eVgXg+oOvD0k0/zzJNnKPf9BKfmYWpcMmDR4MBN4OVgwZe9EDrAOw4anNvMMltL89AmrFShvu4SdHy27c5zeBCuMuTqf1GwKIhdD1O6IgC2rlHUNAqGza9+8g94/GvPc/jhwzz06V/iyFd2sPc9H2Lnze9gZGCUO66XhAvla2+tSflmrUMiVLRBAlCPkEgQzJOoDXSR+Kkfn9M55F00j/RTNcDshaAWb6SIoaqcbg2YBR5DYppzwHwIfBHWPw/NExA1SapuVKySRvo6FRInrj9+5Ulkk1RWKiRhn6omXKrpzta/4ZsDRrdmv5bi0VORiYG88v3xaC7GI6zma8UUffOabZYoZLcxNDbO/MJJWu1FLo1k1DVQ1+/NDz5fsdczC5hkaPxqCpVB0oVeMIsEYZsIB8PQMEwTO5Ulk+3BLPRhlAboGenFzOpEaAS+bI7ptAKszXVy9U38Zo1K2IYwJPAD3I5Lq7GJG+oIX4AXIKpVCcTqnnyl0pKl5PsykW7ZXJwlRQBhBxw1N2yt+lOIhAlWVgbVUSRJMGEoZaoMQyoXmHIOMlMWIooIPJ9sJkt2qB/L3IYRXkvUWmBzcxGntoHfWkfOlq/Tt+eKfQOWRaYOb0cCsePItSFALjKr8XdemxB0BYx905sCYFTBfBMhzjO38BizS2fZ6DTJDMHANDxzBhobcOpluPdRqC3AcSK+0BvR0xO3O8pDfxmmhiFhvU0gy2CuQ95kPSSd/rY2AoqPSEhSUacDxWKcyNHkXJJOpdD1jJykLCXYpLRSlPUShDlCV5NM2DCK105DArLZCpFhXdSBjavfL1HBfKXpyJgzRL5UEfTWbbaqKm3d7rVMZehN5By7XoPDzx/jhaPHqC2s02nCwbv2YWfG6LTbPHD/k+SiBoOVkIoNtQKkAlhZlaepZeQo5IsRphmwvuGyvCIbhwwP6eTyFhEhESF+ENHpCFbX4Myi1G21C5B2IO+D6IIZxo3BYsJjGemOqR6Mc8hpwkN+JpABwwaJVEAI5FMWP/JTdzI6lEfoUvvV3OKEK+kHy7i07+nWQig1jkLIdUoFIrohJS1E/JkDLKzB3IUOJ55d5MlzDQ4/dIKFMyfjPb8PWRzXRDqdR5He9Wz8XhaJfuZIZAws2bkCLu+DXU67axb8F5C+6x5kK+fjSOxRnZBN0oxLCfKW4/fS8Q3ycnzYTxOLzpFUpbRJcFHVnUKTerlRCYrXQvM+EGdIpH+8+PS2Et0umkBe0bPxeCghClUuoWi7OZS2oxxxlY6wJZizPQ2zG+BkuJhwWVNXVXWhzcUnq7g3SnhNxPvrxL/tQ5iBhSeAa8EZAG0UgpdAD0BXKRQVTikpCcXYUEuU2PKvAmFdEmBW/Q0J4q66BytF6SsO+Fvd0jP7MCoDOL7gwlJIX5/Baq3G6uY6jtumVLBp5dJAiGGZ5IsZPBuslIVhmBB66BZYhoYZz2omUjkgpcsGQEbGIpPJYdtpTNPGcQWRb2A5oIcBBA6mAZoI0MIACxNf6IjQQ4S+dLYtXT4bUZzGEmHMkg2lDIHvQlSMJ4sgcdID5N8Nh3ajJRtDBBroaRCxPBCa3HfvEMzFnRe1MJENEsjFuhU7jkIDMwO5vAwczDSYtix7qIxKyqgZlxYYUicXvYBu58jmbMxgjgCB70e4nS6wiNmp0WuU2DNxC41oN9HaSdZbS6SLFYpT+7GPj9Ktn9sCFOv43Qhdz6BVdiOyOanN6LQgjLByIU5jg0hY6LaHt3aWyBS46+foLp2F7hpgEbot3OYmOhm6zXVEdxXLr5MKIpr1xFFWYXwxJWV33FCeVjoFvu/iNjxa9Ra5tI6OjyY8Qr+D09TRiTANMIyIfMagWQ/oNLosz9UJ/AjD9mlV27huRKpQYGrfO5i+9gDjOyboyRushXDuxWXOvnCY00/fS2N+hZQA4YV01jaZczep16HUB4VKBit3mtWNDoVyAVPvEDqztDsRwyOTpDMlNMuhujaLVZpkeX6V1aPHwJyCYI7vfGmySrapJFod2RHJlg5PaRJ2TjM1Oslkz1nKOjQb8OJhwersOXAEdDfobmzH6fRc1A01gEIuzS7TwN47Tk/GZEUIPEO76MOVsob0Y8KQ/tF+HNejXOlnsK8fHYPoFSn3+maV6uIs67N5ctkKzWpArbrOjukR9u6buQikvpEzVvCcqklR26mU4OX2I5Ar6ZkzHvWNAFuDbiDYmF1lx3CeciFHW0jCuhlBRUtUmicrGjnboJKVyZpaFc6f2GRjdomFswbbb7mK4VGLvlKCSQYO1DtQd2DnuGx0GwpoOT4Pf/kY9ajA9J4DbB8eYuUllwefNzl++CjziyuUR68lpV9LytRIpSwqg0X6e6GqQSuSPQL2G6C9kQHbYqpaTfUHV/65ylcrGLSF5Kd2kbCiWuFryLBXwaCWJovqtFQsRbCVhbEEnA/hWAtePg6rF6Bahc0I3MeQCYI1pG9TQTp4RaSztx+KBdmEIm1DS5ffMcqJI9/pxCcUShatsxAfbQ3p0FVJZAm2es4u31rS2OPVQb8fj0od6UCqlmjKX3tz+0aRCAnCNvXWLK3uEl7Q4PKUmiuswLeGyZkxtNJEdprItOn6IaEQhEQIIQjCADMCP4iwzDTZygCVkSJmTkOz5BNR7IDTgHYtTbdewW12CF2fyI/w3QCn7WE3NvHCCLfbwWlU8X0XvDiovBjsatL/iqJYG9KWfwu1Qqi4JtzytyLJ+FLKTcQifkIDEW9P3C8AjVQqTTqdxjRMLN2gUulFy+Xlx6GHaPehpwZoWmt0jEU6ddXVsMmrKVhX7OubrMiSmNg0sgT2ABKfKMefn0cmmKvIebZxmf1Ie2uDsUaFVM7CTEloqN0Q4FchejPdmIrSbgMuIlojCA5x/OQxOp5O71CG7QciyLiUbDh9HuZPwvoF2QB9fhFWvgRrGuQs2D0J1++B4QGw9UE0bQp5k70NKW6Q2/K7DkkTL1CQm2FIIk23I3uKQKznZmgUcllMIx+DsSYSuXrFDWpsQ4RlhBtIPTwiKUKqI1k4moWp6aRjhqZqOP9KIHWrH5hD6m5FIu5lor4jZPyIYv9rybY6l3eaNWR1aF1ARpOkyyiC5RVYXdtgs96i3rWpuTbl0eso9I7TrM9zz598in3FNhUNChZMD4LfhNCBzQ7YpRjG8gIWVxtUqw38CHbsgJ07DYbHbMIgJNI0vECj2oCjZ+CRFyA3DNkC2P3ydgh9LpHkNZDTRomkWktpcsXKAgwj3UwVonlApOmM5/P8k9+6CzSD9QAaIZTiAVfjpHR3VaChQGr1t2rtlDYkmUuLvzhQiIHYAJYagnWnziPPCx74apW/+09H4qM5Eu/tLuCHkHzeJ5A1/Y+TdF3tIDUZ0kiUs4BkzvLNVaifQmK5Y8D740E6gVy3bKR/XiHpudAfD3A2/k4DiYnWuKgNe4lgnCJwqvV3CaiC0wfB22BsJ7R3QriAnNMVBqkisEv8daV/dQ4Jxi7EPyxImKEKBVb6rlsEN8wSiCEwtsO1+2H9WQiOgzkHDIJ7M4iR+IQ3SIIUJSWg2nu04pNXsgDjEO6C+b+B1Qj0QbCvAfcz4K7LB1JPxZIHXZIkTzXeT7Tlpc5Dhbld5NynCjHV06+QbfXZmz/YuGLfHus9cAtm/ziNdsT8kkfPQIb1zVUWl2dpNDfoK0C+kMGywbJMSgWboJCSTnwUovkRVl7HNjRMoSGEjomGIUIIPaJA0NNXJpfPo2kGjuMTBh0iLUAIqQGrRT6ZbB7fD/EIMDSBJgw5YYtIZrryWbnm+YFkVJgGOF3wO+A7gAZ+K85hBPHip0PoytdFTVBbArF2VgYIwpeArh/AyBQs12XZhOZJv0fEcIgiZ0DMwkhBcRy8tZidm4J0CYb3oLXPIPQQtDZGGkLHxsqNkSuPMDRoodUX8bSAZgtWOwJdX8DWMlQKATPbZ8ju3Maf/NYvslGDzOh1HPyJH8EuljEtCy8K5Axm5+i2DcxMheyuGxCs0Tn1FcL1WTTHJd0naC+ECC8kdB3WnnsQtz6PW92E7mZ8Il1aKw1aK+dA64dCBi1q4gZtWv7lQcn+AtS7ksQJoJsarVZbliqGkM2aGJpH6DfptE0M3yWXLZJKaxhRF000WJqfZfbMOudPtGjWW4yOgRcamPkSo3t3cPCdH2Xmmp30D2VIawI7HVJfeYn54w9yjxTNTQAAIABJREFU7oX7aFehpyhjMC+C9rq8RdICzG6X7vopvvz4KTChf8jgqr0pAi3H3l0z2MUsta6PaXQJuw1mH3+YI5/7EpRuksBT9J0uWzRIwKUOMA/ignzfrmBOT5P+8Z3c8vb3856rYMYQnD3u8Ue/+zka9x+C2iJO/VnK2g9Q1JO6LxvZIGsybTFzzRQA+RI0RVIPoQS7KrrB7XffgdOFbOSyuT6HgUFI8CoGt1OvU529QGSUcIMFDj1TZGbXDn5muMxMvkjWNjD110vRx75oTGJydXmcW/sSXExMv2I75cmfOuGQNgd52zUFhopgNOfRvTEgR1eDAVOKhalKIiX7VMrBTE6uzCcicDY2WH75ZV56uomR2c5q2mKgKFfoXqTfWVuD5WXYOyr9404Qcm61xb/5d/ewbd9V/PSH9/JPP/ZecuJufuW/XOCxL3ySl7/8X+nmryer/wIAuUqOHQdnOHhblnlN41QI5xyYiJVTbO2NN/na6jsa8Xkpb0K15tSR3sEs0sPY2qJGNQCL4gGOICGZpUhcgTPAM114vA73nQX+DPhq/MFWoskgGDshvQOMAujbQN8P+k0wrcmCxDKSihtjI4RI328lPqDAB68FzgkkeUBFFkowQoksqAaz34kKHqXGO/tt3u8/piUBWxC2qbdPUW+f+sc9pCv2XWIyyVB1ugROl6yZwoxAaBGhiAhCEF4XoacIaWCWPdKpDNk8WAWpwmTJnDxuA7rNHN1WDrcJrRp4LngOuF1Bru0SBF1a9Q02VmZpBE1ErRUDDSbgxLIGpuwBIMKYseZLX+1ioK7KklRQqM4jgKCz5T0DKMSsWkDTEFFA2rYpFAoUCyV6yj0MDg1S7wq6Thffa2Gk8xhGDtvqwTBLdOouEiicJenWciVO+vqmEI0MEoR9J3ArEiNT7CqQq7mDjMXPkVQsXN7ewmCsBmN/xNt/82b23j1MGAh+/zddgsd/GFa/zJvnpgxI6pbP43WfZPn0n7FzFG49eDfZ/Bh+uMgn7/kKthBsj7PqP/NhePQ0HHoCXnwEHvwDsG6Ek1VYiKDnKo27Bm7F0oaRKFMGCcrqSBBEqaw2SUASCcykM5IR2wFMS5bPaxr4rsA0AzStCt1ZWM1wWZvYA3YZNttSYE84EqzxYsptqpddYzZXD8ojW0HmrBWnTqmvbLXtQNuQ001hy/uuC/UaBCb0lcC25HfWkQ7r5R4QF/l4LXehkoKCKc+vVIaesUmucvfTZ47Qm387H/xAH8OjMHvOITj3DE+c8Nh0ZaXntRW4/WbQM7C8CYeeg48dhIUlyKTlvL2+DoOjYGdtMoUsjhNQdwLqXsRsGz59OD6o+de9SS5rik2sSJYKnlNMWYCbciP8/PgdaLpGY1N2bR4syF4qytTVVwVAaklRv6E6BvtAKgVNB87UYLIisctN4Jk5+Plfhbmv/Aah20DSUX8j3sPfI9HMSnxlngYOx++VkfddKT6SEnA1cBMSXv4W7AIycnkB+DdIXPdppN+uqhCUOJkCZPMkigAryDl7AKnfrfBLgXxsVHyqGK+q0v6zEJyB8/8CeEe83TkkOEy8vxRJRw5ATvTPIqm4cyQJGnUls1sOtjc+sCj+8Q/DrhkI1uDEQ/DXfwncCHvugLddLS/sV/4Y2iq6ADnOHZKSu7PIQGYtPrk14GPIazAAfADe/n55idZOwuEU3PfPoOcHoG8aVncgAXalEqfuSiVBoELOuNHYRbDVjAdbJ2HjqtRMwDeHwl+x71W78223MVAYp7Yp2Gg5+Eaa5aVFLpw+gV8/DeU0pWIKoeXxPY8gaBFg0u50aTebmEFAT2kU20phahFuEEDgokcGGTvL4FAf5bJJFEG73aFeq+M4Dm03oON1iTSXtAk5MyU7o+sagevitFzMyMPQAzlJroYy42caYOtyHTTCmE2hQSoDnZZkuJqmfKxbmxI4vcR18WR2NGWCE7M1oihpEJYvg12UbI1cGpbPy5pe4V66D68B1VUYrchtU0W00jAZM02wcoKgsYxhweQUnGvdyf6DN7J3xqa3/hc8+qWIXBbqtkz6DvXANW//CPnhu3jwSMjx2nma7fPQzuMtdTlxvMbO6XeQazVZajs0aicRqXfC2B604WEYKuEGKaL13RBmEO0qzcABoRhm0hpnX6MY3wDSETQukN95NWYqRdBYp3nh5EXQLCSuAahkKBgBRiDHLmoLuq4kJBcrgOlQrZ3Gc89TXcnRV+5DS+fIZLKU8zkGyiZ/+ufP4qy3yWpy30fnYcf+aa55x/v4yC/9J3ZMSgafAyz6Efd/7gxnnvwSyyefpLFav1gDEHgxOTrGTucbEoDcvg9WGxD5sLES8uBSB63SYexAm5SbZnPT4Md/8qO8cG6TjlmEsUnYcQA+74LzDIkG+3fClJCU6lx5BtnFE1J9A1z163v5wb2wfxQGdJmUPvvIY+zY5jHyz2/GGD/AX338t/mVq3XetV3uUenkqlVA+Whjhvy1ZaQ/qEIiDdhXkIfxuc8/zC/+6r/FjZzLJtrPz21yfm4THn7x4nuZUpn7/sef87H/9b/wozdMMtOXu8yWl1rTh/tWYHQEZoykzejlTHGgdOSqesf3FXj5GCzPO9RNjf/jF95GU5d39vSW81VF12eQq2YsQkIf8JEb4Idv2EvEXlaBY1Xpbt8voO7DD9pwoBcme+HUVXDOg41FWDyxzqnHn8c/eg8///s/yrXXzbAC5DSNX/3EJG9/7+/x4GNz/OHv/QEvPHYPorlGgMnDD+/ivTf9Agu2ybwDi2vwy47sT/H2tHRj3oil43MoknhvS0hvYp2klmeThMKhJMoskjq7FWLuZwD+KeT86MQ7eQr4fWD578H7/5CdUJUNAe9Bxje7IH2LbB7wYWQQ0RtfpD5N/qt8uI14k8eRbtjxeHc2MvFVbSIz6kvxvxfig6kjnUzlCF5hbr4x04EMGmUEG1wpt75il5qMSgPXo91pEhk6FcuglMvTDS0cz8dxfLSgRjvYIIwCdFPDNG+kOAJ5F7SYZ5LKQr4g7zjXhZojsVHPgU4bludStNspsvksFEsY/QUaqxuErheTTAKE40C3CW4b/n/23jzOkqu68/zeWF7EWzNf7pmVtZdKS5WWoiQhJIEEaEEgFmMDbcBtm7HbbdyNx/587LFn7Jnudptxt8cz07jd09Ptsd2DPQaDuw0YYTAgAZIQ2kpSSaUqVZVqzX17+3vxYrnzx4mbkVUqbcbYAtf5fPJTlfki4kXciLj3nN/5nd/pxdBqSrNkHaSvvGHnmESM+dnY60Nv+H8NOqbRnwuNMvPNOo3xKerVIRrNOsu1ZTy7guO6WK5NhEM9iFlu9ai3+uANQtBD8Bwbidsuaim/vG1FqsRvQcQeTaX4Ill9xgoCct8P/BUXLr891/7hgbFX/DjjN3+Qn/7JTeypbmZwNI8uKeY1/O//zuOpo/+BJ59q8cg3GvD5mzeILr82rZ+EPNs8za7iU0SdA0T9Y0xe+mZQ78ZxEhbXDvHY4W8xPq65+7ophvI7Ufoa/MJldJsfJ7lshs3D8CO/Bft2vJ9Sfj++P0210sNR2ziXeyrNs7KXNUDQp3M1h5ycVDL21iTeyzmyRydQVCtDuI4LybJki9cF1TNzxgokvk3S60OvLefQDcHtQ3GEoUv3MDFdppKWXNmIW1MgazY/R1b0PJSeaV+9kO2aQ/wrnTYZI/28yItLFDjpMYfyUEr3SWJ4/DuwafQOqsUbcIoO+67dTn6wykIEp6w8N97weh5fm2dhqctyF1ZX4JGvS7OrLaPwK++z+OCdr6PTX+X02VUee6LGvatw4xgMlBKiXkQcxESRkJz6Kc5UQabTl3/dz7Xz+d8p3wpN1pJg7K3Xc9vv/BtQitkWqILo5vkb9jMArOG/mJ5YhqnQiSAIIbEFKzgzB4ePwR8dgwf/5AzN+lG6/Tnm5keI+zHweoSFbfgUU4jr/SyChj6HTHgGtBtEnOgdCHN2CLmD6f6GRfpKXuVC+vXLSASwhjzi9fSQ24Hr02NVkIHwkQhxMh2MXvp9YwhOaF6bfnrMbvr5NuSBXUUiKvP988AX0sv8WQQEfhMZGLtChrPWSMdgmVQpjYx+u7Gk38Di5sTN/7vAITh2bwrAuIiKcAMWV7Cf7zP+YzkWnnsj8ckj0JxPx9cAnSYSOZoO0jii1WsaRQSs65c98AtwxV0weQvSZO0PoRuJhiB7EeG2xfQcDJfadAGGjCMD5yo3mzJYox9rMpLfTxUOF+3vwsaGp3DsMvVWQjuKibTIpChiet0Wc901CqUifqGA53n0+30sG1xlk8/labWXiYIIK++Rz+coegMkbRgaGGBosIzngaOg028ThgFaRwS9NkFkyXe5LpViER1G5KwI5Vpop0irV8fuhVJKEmgROI/jVCLAlZKCftrEwfagmIeVVQi7IkMQkDr+ZH1KugA2aEfqj4lZ55yFCp58FHJV8FIqiFOA0QI0Z6WsP1rNBs6ywSsKQ9YeAD0I4TBeZYjcZAEih2QRTh+Dyt4+VvsvaB5eRC/W2DOdsLgGHQ07trtM7/tJ8rtuZGbO4+Djj6D23kpUvZPhvbsYv+ZmclsrPPWNM3TjXUTTFmy9CTW4F21XSHIOURChWx5qaD/O8DV4ORd8l7i2Sjh7lOjsM1A/TrYi+ojU0jLkbErjo2y9+goO3fPfmBidwh8codsaY2R8mF5rlU5tifbqKmEPTpzqoRNNEqd+QSisR8cV32ZpqUunBuW8ol9p011bI1fw6fU0nVZM2YZ6s4OdVuX4wJvvuon97/wZrnrDbezapOgqAanPLgQ89dQqJw5+hifu/SKrZ04RdmUWbaR11+f0UkOqj44fhlIeuiqNrQLQS/CVT36ewYkqU7t2EvirTF0+wODRYXjahROHIR5GECYbAYi+V1bf8H+pcNj9rqt5/Ufey923QH0tYdRSbLMsRn3NX86cJeweZ9vOKd5y+yZ+7jv/hj1bRtYrcYyZVcL8ra3kjo9xLvu0nyT8l3ueZ2nlLEefPkC5HK1/9kqs12xw4rHv8O9+9t185ca3cNOdd/LuD7yXER+mVMZONaaBZq3DVz55iOkrJ7CvGWJgc2GdLLBxu5hzfdJh4BJfUdhTpLa7wOY8uJbCSq/drPRpGz3KCNC7sWgmQv7jo+Q7NTxTEP8r6cDKKThwGUzZ8jxu19BzYecm+MrDx/n2F7/MW37mo1yzeZicpziFtCI5qBQrVdh2wyS/ufNj/OknvsyZxZBOt0M+3+aPvtDhHW8q8tYhG2caHkngz++DbzXg9yvwU28TFfoXoWBAeu5DZCTT5xGXqYZ4A4Zn7SFYqCn2n0HcKC8d1yAR7kaiEbdwFngCuKcOX/s9WP08hDPp3gCT4P8iDL4dtlTkALtysKkgN/laJAFvSLMm59tE3JvF9CSbZPnfGKgvQXgcSTQvpydyDPFlTYdz8/P9QgD6+7YSrl2hXKiy1jzKq498Ntr59ZQbbWMvg4v35vvLUo59o0nYDYhWa3T9NQaKZSy/jJXzKXseSRxAEtOcP0N9aZbTz5+huu0qKkMTlCsDlIdhZFIA2UIJRicgb4m6QNiHTlPhDkvv0lbdpVWvogslvHJEonXqi2lsS+OoBJUkdAPN0uEj6LmDUDslJJd+67zz3yj2Z569jV1azO8Ge2lDx6Y7HxOsrFCzPKychVWqkMvnyXkeUQSdTkDYrhN3jQihWTXOVzBPpRSAH5QGf9+dTSKVuW9DAvdxZKXqIePUROb2R8mycSYef2Xz0z8AMDaH8kYp3fgRbrwWBnbcyPAl17HnmirbPCkxD4AmiuoWxZnuVqYiuDbfI9n86xz+zOfoLJzgXIfytWNhFHNmZoXtOx/HdiIs61Jy/pWAw+ra43TaTzM5brMp/x62DW+j5G1BvIouZdfihksGGN43xf5Lb2TLwH4caxcCpGxUu7c5V1vS6JwYGv65EKe2IXYgTOPJJN3NUqA8G2WlWii6zYVQskT30FFX9O7CvrCA7KrU4Jcn8fODoBxCLWdp2iuYacn8mCV0YzufjeViirQvic+5Xj0vdLBfYEpkSE01Z0tDawU8PYiTH6RYrXD93gp5T3F8Hp48YmHny5RGFHsqUlFq29BpgNeDiTJUbM1ae4nVWptavU/OgVuvhJ3bylQGHGKdENuKuJugFzSDZ4Qg7yJtreZ4dQpw50+vesPfYqDo+lSGh6nsnAbk7ve6EK1BvioY5flLhXkqXGR6avZTvb0EEgtOrcCBhxIe+kKb2fmvc+zAGP1uAWn6VEbEWfPI+3YaoYQuIXfaR4LGEoJEGkh4ikyzZTuZHuqGi9mFPGYv1bmkkh7mR5F51TR10IgjfyMSlbjIfHt+VXwemXvXEAd9nEySq4TgAStk0cSliOzBIplQL+nAtRAw5YvIQ7uYXrJpNtbfeImz6VitkqUgDG+mD1wDuSlpBNR5kOzdNs2x1iRju75vWbZptUjmTtPp70JvnxTB6aZRaovTi11F7o8pDDUX4CDRyUR6vGfF6Th7CpXMk7vleoIHPw39w6Da6XluRyQpOsgcBJn8gCIL0cxbZ5gk5vfuhoEzGrQX7aJl5lVyxI5NX0OxUCAJFSpOUDqRxoNBSKy7RLGF1iK0kgAoTc5TDA5WcG0bK0mwogjfBQounmdhOwnoCB3KXq4NnmdRLPmS57AU2GA7Nu1WnajfI4kTsFx6/Q69Vo2w2YOuDf2UGW6notoqJ5qtSaqOqCywXVlcdXSBmmdbyi/sPNg5oXLaCvAE0LV8ESr3UnDX8VIdsgh0HlQ57TGRlsg5HhSG5d/8AH5pgoGhzUxNj1Bv5mm4Dl1shiojXL5vF8VoBau5ilWuoHIOSgcUKmUKI5fRy1/BQrvMYhfaDowOVXFe92aK1RGojtAJNKXp7QxMFFH6KoI4IaRKP47ROsCympBrYjslHNclny9hFUpEA12Sylai6laapx+D2vNSsmKXwNsC86IJpKOAfh8GJrfQ77fo1yKCIMB3ikT0iMlhuxblgUHqyzWSWGMhjScHfOgEQg7ut2At1HQsCAoaFSas9WMCHRIGmrgrq3EQwmABhqslJi99A7d8+B+x9+qb2DQ9iePCagin52qcODHH0UNPc/TQl1hbmqHfydheyYtMZXEkPkSS5sQdT/gDSRdqM3WCRo+oo/n6PX9AcfJyVucOQbAEy7YsyAwgC9XJv43X60XsXK/kzf/kbq6/80auub7KVEWzFcWUpxhUULQVt75xD089Z5Erlil6Oa65fBpfvdAfOz9ZvtH3MNYHVrXm1KlZLNUi7nXpNptcumUXZ+fP0O0HL7tK6CSh3+mwePoYfa1oN1apz57GiuA97/oAl2+fZHLg3H2KeYeb94/gTxTJFW1WtPhBW+xUDiu1DcpY679rCwbyNqV8Jrpk6kESsian5sc0CTMhXw5ZBU06sg9sciWvE7mItGka9/QSWI2EbZ3UYWUlpNsJ2HPDDbRyBdFUtGQlHwL8ImjXZWhinKX376c1v4m5mTYHDtsszSuW14R8oRMYG4K3bYZuV0p+20jKdhNyXReyHAJZziGhbJNMAd5AB630euvAWQ1nEqgpkYTopvIQ/bQSmEQa4/b/vIG+/zF45iuwcC/i0BmnbR9sfR9suRMmLhOKdoLIU43IeFFG/DpT9mW0uZYQ9+tsOtA63X4YSapHK5CcQhzJiMy5q3Oxmejf1EIS3SYINfq7kqAyjR8uFDUZ8oJhURhf+nutsX3R/nYsAToQgY4Vum/T79VodQpYbhnLK2D7RRLXgsQmiSOSOKQfKeLEorOyTLMywmCjCuEwhUGboCquEiUoFKDopdBECQaGoNu26LQsKssOo1WYcmHYgpoDp4K09U0M7Y5maVNCMFukPb+T5dPztI89CMHzkJhYyGjXbexoY4T/zO9GiCfdRtvoXkAcJMQq7cmjLIJ+gGPbJIlN1A/R3Rb0OhukDwzwmt9wfCPz55CJxBi85h+COchEviv9dxtwMwICGOzBVIk3EPD1EYQJexoJ2F9cH/bFvvEH1HL4w1MUi0NUxi9h4v3/kvf+qGJiICtqNaRvN53Lu32I+zBYgpFrfbzb/wXt0xEzD32N1uIhXu3g/l1YHCWszLZJts3j+3uR8u6dwF/Taj2O1ktcvvMyPD6EYoqsjehfMZQvcuWmCfZtvw74KWTByZO2fUKcho3ZQYMAGVAkbdCzzpxNz0mJAxcCYSLKArYlFZexo9EKMjf0hey1pLkgbJ3+IARdSUnlx8Cfgvw4ruUThhbdMCMdmjIlM5Xkyfwms1ybqzLYjU5PQxnZ2xRnVuqlO8LGMTS7QAEpPdTC/vQj6MU2tnIo2kW2jUBkw6k5OPiMhdcvEnmKqapo0eVzELXA7nvkczaerTl25hSzs1LRoCJ45zWwbXMFZUc0Wx2WmjbxWgzPayZOwAeQ1960KTIqoX8budyRzZMMTY6uX19iS/zeacDgoFy7GU5NBoHGsZRynA6hHUKnC62WPBcHZuDBexMe+lQHQTvvQJ7ZTWQ6oCeRd20ROCiggyqA3g7xClnXrGEybvMOBO280A1DEls5MqAUzhUGVsgcux1hodbIHpwe8Ayizb0TiX5aiLPdhfX2yYYIajRip9JtLeS125xeUgJMgNoO+lD6N1NxYqXHCNNz/VJ67oNIP7JHkFU91kI1w06/bIZMeyxduFUOCkVypeuJc7uJkxA6T3Lue26yekXO1WTNQ9BBL5+idng7TJbhzCicWYEkLTVdX4ga6b75dLCfl/9XinKhfU8uMKjC3DIqegb3pz9A/9ERdPsQ0v94C5Svhe4jEJ1Nj1ciA2NNVtjIK5j5yCSJQjKm7kWN2It2YXNKkDgQK5tyqUjSA0KNlYClHCJlE4UQdGMsO8L3HZJEoSxwXEW5WMVzcxDHJP0I27XJ+S62I1mXOLaIQo1jW/g5F600nueimiFYikQlkMSE/RZR0CWJIyIcGu01OmvLhI0uxK5QHj0XlJ8++h6UUk3YsCe6r7kS6K78rrQssnGS6pFZwmJ1SwLKxnHaedcCr4DlV0iaiaAktgeWK+BcrGXecAfAr4g0QpBm38oTkIvB8fEHBhjbvJkdm0rMzE/Q9c7Sctps2baDvVftpbU0T3e+jju4g05SBL9B0RunPH0bx9emafRydGwHb5NPcWQAPbYfEiHK95qK8Z3b8HPbAE2zmdBa7ZI4AXHSIWyvkUSLWEELBxuLCo4awKrksEpTJEPbafZsWZiTBNwCqjyK3RwkDldIIk3YhcGp7dTri/SCHrG2qA5vpdNJCPsJlmUzMDZMvxsQ9nq4KmZzVTFSVcwta1bqmk5HblMHSHrgW9Bc0yy1I6w4U5KxPMXI9DC79uzmmjt/lFt+6B+xOZ/H1TCbaGbWAp47PMuJQ09y8qmvcPLZbxO1X+H8pcVnbbfkdlk5sFIw1vM8kkixeHqRr3z2/2Zy234WVzrQbUA0RariTrZIbdTlNhlqA/O9isTWxoz4RuzCUqiJYd72sR/ijVfsYbOCJRS7BtS6T66U4i237yfJl1hpR/Tjc1XYzrt0SM/OtJU8f7sYSZS3mw0G3Rq0Vmmv1Nm9eydewSdIQvpJzNrKKo16jeTFUO/UameO8tTCGZ5/8H5Wa+AWdhK99Qbyl1ap5G2UkgZilXKOd965bV04p5HASgJjtpyrqSYytT+G4mDYskZevkR2N4yrYpqtGo+7yAZWbAyzy9AfYj12j5RIOARA4EFpKgv8OhpWIik8WzkZMbtk4RfK7N67iyWl8PrSF2HVluLMjgeBCxUUd/7IXny1lxPPBXT/pI6tXE7MxZxtRHQizbWXuNyx22LQUSRK8s6nNoyl6WNgYjEzJkuIu3UA8fIGyerxWunnC8BCIvIKi7EAwI4NsSU+6novnDDBnVsi/H+Pop/+M+A/pt+e6kc5W2D0bfCGfw67SkIzNo9+iaw7cIjE2EY9qYhQkxcRlY9TZEpQm8j8t34b4jXEKTQiC99tg65/6BYQJwHt3qslSG1MfZh5rsD5/qJj53GcYSx8Em0R9OvodTLWRSmJ7w9LgAbofpqdBCKXbi8tZbQL4JVQxRK27WORYOmQRCW0lzRhZ5GgNUoSbIW+TWHYw2/aNNsW/miOiXHFwKBAE/4gDI4Ib6zXh/Iq7L0crvXhcgXzGh5qSD/UoA+NrmJx8zjNhXGWzgaop1eIak36y3V0rwW6gzyfphbAMFc3Et/M7G9WvvQnSVEPlU6KGpIooh+G6NgVX7HXFVzlHHDVyL2Z+LGAxNUFoAvKNP7rpRq352vb/iBZDsnCvQ4BAzYjk7ohKiZkLSZPIUDAQ8DXkVXrb2Y/oGCsDezkyn/6ae64+0ruukFy/ytk3E6jM1REHslWAs8+J0CcpeDEKXjzTviJz/5rvv1/vZXP//wfAH/893VBL2q2thnuDWLpf4yAURp5IB5gy+YrEbHK/cgD1UReqLPA/dy9/z1ITfY+ZDRm0qNudMgNhGnq39JCdBUhYvSjCOo0sX5OSSidWiMExCMnvboiIIgCEh3LHymm53OePftXMLgL/J3QLsL2fVAZAqeMCn18z0FrRRyf69IYwqApYTI5nRgo6XQZTtfiaEGGSuXBGSZbizfSZl/E2jV48kHY+9Z0iPpgr8H1m+HhVo75esjsco2vnR3GGdMc7UC95tFeuZKvPeHS60pTg3EffvpdOW69bi+XbBtmcLDLE089yLGjMceOw9oSvPX2tLFDo8+zh5v84Wfh9gh2BXBpKMX8f4iQ5y9D4E2DE363KkpX/coHuPTt7yRM4IF5KHvg5oW5YfJ2Bg4LkGkqBk7X4bNPwJkTMLEJnnsWPvX76YltBRaddOtfIWspZgb92vTH2PXyiLlAJ4GVW5Hnt4ogp6/QvoFU338U+E2ySMhIDRhccgX4HHANUlO3G5ELWEMe95Ppth9H3iWQAAAgAElEQVRBpGDqiNPeIkPF88g6ZiM483Q6MD4idesD75ImvMFZCZzX+yps1GknPeZ7gfekx/4xoBWQcV5GSTnLnHvHt4N/FdxyO9vfDisnApYfXYaZfUj04JKN+xiZdgJkDbEK0MrDf1yFjwxBeRsUNTQ/nQ5QnqxUw4jhdhBkeRu8+5dBj8KxGkTXwsE/geAISfgdWrMfgPhKJOzqgfXP4I6r4KHPw8zRdMBN4gjEQTANuYxDEpC1m7toF+3lLZ+SXXKI1GrcEX/d0TZFv4Tt++RzeUg0Ua8nvAHPQycWsbLwKiUc34EoIIpCgghcJy37DzTkIgJgsDyIsm1yqZZM3F8lChMCKyTotii5iiDStIIeiyt1VmaXiZYa0N6QnHSr4A7CwFhaKdYGtGgQOj6UfVBN0E2ZUwarsFaHdlPQQdLJWqUOexxCMSA3ZZHbPEir5sBKII0mlAXFCIplCH1AifD76KiAuTgoXOguoR//DtbEKu74FEMDu3Eu+2Eay4pm89tMXXcDq+EWovJdaP92AudG7NJm8kkTy8tRGd7KG304s6BZXIPlBtQiRTtI1RjyUBxK5R1XNO1GQhy0acw9y+59O6kMT9NYnWL5TAc9NwtxG/I2OHmK2y/D9nIkzRwcnIWRMjSWoT2HLnQYfd2t1NbWKBeLXHX1fp59/Mv0lp6lW1+Sap2pHQTRElG3gQpgsQ27r95Nd3WWHEu8/c48E6M+Txxo8eTBgCeeldukkVvSa0G7Dd14nZdDCFy62+f2D/5z3vzef8au3UOieaphOdE83dY8du8Rlo4/yomHv8qBz3/qb/Zg9+X7ARk8G679kSuwKjlmzqxy7BtHWXjgFAwVYHoLXPd+WLxfxo82kuCsI2/GFOIzXgJ8BUmurb3wO1/MTJ7PTncz03O5QP4TH2Nq0whjaIZR6365cbeeRfy2u26+FMj6ZRp9+/PNYGRbuXACvQBsVwpV3M5f/P4vsXDk29hxyINPPMofffWbvO71+4i6a3zi47/FH/8//5lGrXaBo5xr/X6P1f48AJ/83Z/juaMf4p0f/nk+fPM4vtYopbAREHGQNFFuwYirOYEsoZFSNBBxno18J5tMNd0Uia6QifOMptubNplG3z+f7rPQ0rzj4/Czvwz7pmA6PXJCprNaJJO7tyyYysO3NTz1ZI2zZ2B6eiuXXw5nO9DoQSeGobLEUA924EBPzveuIZHG2L3b43/9n8f45EPwwH0LtObX8Ojw5PQu7vxQkb0TNrsdCWufSn++hLhIHyaTFggRb+BJxH8dQLyLaTId2IMIu3ZWQy1AfLOSgMyBxzp2AEg3t6NdWnd9HJJPp0cwtgn4GEx+BP7VAOqNoJ9NvzjVF17vbzqMFGi10kFskUlTpVMypfRmmuT9dDroB0dgZTq9q2vpDuYEL9rfnRnOvEl/mDfMdHUTBF8ph/HqdWyZ3oZjO7SaDY489yRdYvQ6CHZ+SflFe+1ZTNbaL2G96ZWp6ItD6MToTluiHjtJeR4j+LaN40bEQZf67CoLs8/i+MM4/hAUq/gjl3DFVRZbd8HEdkV5UlwkyxMMdGwQ6o7M230tcfllFXn7FxWc1PBQGfKDUBzMUR2c4GDwQ5x62KczdwA6h8kCSkO3N4jV+enGjR1aHKRhqwM5DwY8HM/DzeWwbYdWrQc9JdVP670+emR61ZA1aDf6e0MC6toqW4DbK6AX0/PbOKf+oNhu4C7g3274m0kXziOr6EmkuuIAIp24yHlNXF61/YCBsR4Te9/D/h/9HX7qxxwKA0MU/OzxMhlkTfaoFZFF/y0WeLulMdHJGZibhZkZ2LsDbv/IjVzyhq38zvVtpOPma2cyLhQqvOktH8LzppEXtYG8WB9EANghsis18FkV+Hnkys2ogLhC0+nnTyNO+DuQieCLcvyokSKYk8jbeWl6nMx8R5pazbfk8GHKQrUCjdNroRJT1/0SzXXqc6hGC50MQOUGBrZsIlfYRL9W4vI9LtsuVYxMyJWVeKHikumPZAORlt4lOVuy55B+vSKTplwhSz7l0oO+CCCbz8HuCZjOiT5gswXLJ+HyPTA6UeXoiT6PPdviP//mk3R7NcJ+Qj+MafQcouQm4Dn6ep7ZbpPf/nyfT3zpKfbszPNjdw/w1v2v48M7SzSbPZZWlikWHbCb1Jci1mpAXQIWO73YM8B9ZGqa+fRueOklLb/g7F+53bHpRvZPvI7TWhqJ2VXIezLPm15TZlo3EFwbeK4PD83CNz8JnJR+MOtO64cREmvNgl8eFK2Hl7MYwW4vU/D4MNQHIXoxRd+XMFPZ/j6EYZogPnIReU0qyKNfQubcAjKgJmKcRKoVKkhU0CbrmhuSVZKU023biBN/EkmgxcgNC4AvQc8BPU7WNthcq6HHGFuGfB123AGHfxniT/vwzBpSEmEaV0HW/iKWL+ydha8d4PKf/Bmea+RYtm0kbD2anqT50h5ZuYqNRByG02MBfwkzPwK4MN6HpklzeGQzaYQ4P0YAfgFyoQBBlgNP3g/hSUBBPYA/ez/03oeUfhyG5M/hi6ehb7KS80iYabLDmiwa2thp9CIQe9FeuQWBlHZ3U3JS0IOllXkWV07j6ppglq68hBE9InxsxyKKNGEvYubkWfxd07iug2VBFPWJIgcdgYotHGwCImqtFkXPp+L7rC4uUluYY7VZp9XroMMQT2tIQsKwy8LCKeKZXtaZyVguh1cqUxoep1FvE0UKnXMhX4RiEToKnDy4BdGL9UfANhIiyHuXd6QrpbakU6XTor/QIJk7zcQOxdKsJu4pcIswvh+Kw+D5kPNhcAoGJ4Qxu7KIPvo0jI1AvEAcl4gSmN57GUtjm7l6+BJ23TTDwFCJmnMFoRVju+CVh7BHbHLhCEksU2JpEJaeb3PyyBxzx+YZfcPNTF2qcIYg8aFWg/4StLp9emtNdOM0nDrL2XwBZzQmiRR6uQVJXpqc0QffptONUTFgDaBu+2HQJ9Cry7B4Gk58jYVTWxnbsQ2/YPPtxx/G6y6jnZD8yBBDkzvYufdWWmObmD/yOLPHDtJtRTzzyGF0JAHdiVMdHKvLtrFE2pVaksQHaAbQCIWYkgCVMmzeOsI7/sn/yW3vuIGp0VGK+RJdZGaba8LJ2ToHHj1IZ/YQxx7/HKePPPndPdwbc3ExzC+uQqBY7TSzv7e6qFaAf83VdO9rQf9MqnEwQeY9GGVOB6wPgT4C+q8Rf/AVmHkEK8hUXgd2jVN61/V8/K6f59ADPYamWuzYI61UR8lcravJwNcYoRcEnF97JZa6Q2y7wGcbzbEV/+Iju5mq/AZPP3ecTvM4z594gt/+D3/MvgNzvOXOu/jZX/+fSMpbeOTeezh+8CFqq68MfF6ZmeWrf/zvefSeP+P+29/Ov/34rzMxMXbONj7yTMzGCb/wC5/ll37qJt5w9TRbOBdA1mSK7xuvx3RVCJA0dBoiUyKTJuiTtjRKEtpn5/jTT9i07ixz91tK65L5Ju8cpMdbQVbUFQ1b8vC2t1X5ehvu+S8nmKnBniHoOAIiOEhEMNuFxVPSH+G6n4K6J+cwasEPXwu3XjXC7OIQR45EfPpTZ/nheAvKtjmOuEGz6fePIo/GZ9JzGkGKjmrI/dyMeBimvdxSeu1HEZcrXE0voEfWxKGIkLh80IeBe74An/iY9KcwAKiahPK98O4y7K7ApQXU7aCPpoPokmkhVMkU2lpkZXaddPBjxB2ZSS/iBFlvY3PSwTAC/E4hb74BZC/a340Z6pVhGBoWoWEAmn4Kw+nvMY7jc/L0GbpBl07QJGQevU5WuOhvfn+YqQ81NQMb60VNhxPFOuEj1imba5ne6hqBm0d5JSgMUJzcTLu1Qpi4aJVHWQdZOb6VozumuPS6aa54PQxNSn7c6MJ32/BABA9oAWmLRWHta2SKWa3DkcNw6lDC6WcCwtPHid0qTO6HZCes1KH1HCSmRaVZRTaaIeCYXgBp/UDSExmChRqRcogtR3xBKw/5PEQFAWXoIyuoKQM1go8V1lNhliOVUzkP3FQgpzAGrQnomMyUIfi9NqU8X7kp4IeAdwNvPO8z47k9CdyLsKoOkiVyvnu2/A8AGGujrAGue/evceXVebZcdgmTV2yiNC1EuhzyY5yemCxPYhoW+QoGNVydS7PGI7ByJRydhc4mKFc8Nl82xT/+3Z/lL37jBI3Fo7xWFlSlbHzftKgyL+UW5GUyZdw9sn6kqwhUuQ/0w0AZ1Kh4L42nwLsa/EuQl38V4R1UQIewegZKO2TGaTwL1asEmD2vNYGnpITdisCNMdIt6AAKToStzqehXsB0DzTkKLBjdBNOdYjYL9LzfPycot9VNNpQy0HDllKqjVw/Q3TUWrJTXkcqNK1Uz8A2GE8P9JqmsxDhD9gkUUK/E4OfIykqVE5K/7xCKs6gIZfA5Ai4ljCpG80uzzxTY7lTYWrSZ/elOYYmSrTsSb7z0ElWltZoN7vUa6vEkS9jToOYJs0uNLshx87m+erDVb514Cyu7aKjCDvuctvrLaqDDqFtM7DZ58Y7Ety2hbMYsrQUE6+Jz3gYcXQbiOunyFyMFV6ZpXwoeoDHFNN2hZKV40wkibFWW5qGeaFgALYnMX4XWNJw33fgxAk424ITeWgNphUXXXmEWE1Pcgk4pkj1Kl7emumQ5RRcZcPTdrZ+vBpbQ5JZe5F1o408NKYWbiD9t7jh74X0d6MfZuoGc0gC7SwiB2ZqC42fZyj4ZqI5hDzuRk1AgR6EiV+EaIuA3dzPhStCD0N4HyxcAsk4qT5EQoYGGyXkIlmiSMv4BnMc/INnWKtpOLOQnoiZDUMyp9Qcc6M+q6hpQwuOxqBtaJvZs04WuYTITTZiGRpYgG9/E0rXYTubmXzvXubv+RRRMwe6CJ1vg7ob9AQyLz0EvbF0oDvpwM6RIdzmO83xL9pFe/UWh6mWoALL0fSCPpa28B2fnFWEnI2yHaIwRMcROrFwLBesSN4MZREFEa0gokdIpaLQOGgrQauYJLHRCURRRKACLB0RJiHzc6ep1dboRxFhPyKXy9Hr9ajXmrSXeugoeeFjHQdE7RqdxRniRMurEIZyEdVh6EVQKklGcPY5WGoKvbQ6Lc62XYZiBVxbFt8uIqoYxcRxTPNUSqCNkVK+lcMw+mbsyhBuuYo/spXK+BaSoE9UGSEsDzE4No6anqBQGmRs8yUktoPK59CFMv3cEKtxjr5TwvFtckVwB3PkB4BA4oN2XXPwdMCJx46xvNQiyufpxeAk4Cbp2+7C8BbQVZvWfIHnn9jEwJVl7MkqdiWPa8PWym7WZuZonD1Ba+Y0uFvRlovlFLAtG0ZdiEokuQaJP03iKBJngD4WcadDfXEON5gl7HTwC2Vcz0dbBdyhyyntLDFe2UK54mPNPkB3eZlmrUetJeyIRQfyfqqk1BPXKElEIQJg7/U3snv/NVx+3X7efOMb2T09iZ9zCYBlLVVXM2fOMn/2OAvHH6Z29gjzzx2jMfdKV+pXZgtPrUAOgiCUaTwB+hrdDAlXlyEMZE5fZ90Y38To97RAe8K8NhVMpnTb4qVJMQlZ348Ytu7Yy03v/Shbc2UmL3HYXMxCj41p1Q0KeOvsUoFIstJ8A6GsIuHRtpcZB6UUgyWXt71xF9ddOUbYv5x6/XoaoUVhYjOVqsVTZwd46vE6MyfbhKHNyNgEK0sLaP3Sa80QMf1ei6W5Ht+67yv86q+2ufn2d/D6m25l71ZRRlWIuzBmKd7/rqsYmBxgNb3WCWSVNep/hlBsPCNzzUaqwaRLTR8Es2Ib4bBSXvGv/7sB4oJicrv45Ua8J4+4YX3kjq8Ay4kU2sQJzM/adIJBKpt3MFyGKUcYvQPp9nVgZ0kqyY6U4fHTMDkpsm62SpVUPJvNjk3Fs7GdEeKKTU1Lo1sju2BYsEZeop/exxbymE6QSTnMIbim0YlV5ro98AdgZwUKLiwUYEVBO0oLCP78HvjyF2DlDOsO1dStsOfH4ZbtsN3F3apwRqF7FHE3umSPvkNGrltAfMdW+uXG/9uIhZiBriEkKYO5Fn1Qg9CcJOusmE9H9LtjUl20V2KGgGRmjhgDytp2nkJ+BMvyUViEYZt2d5HVxhGiqE8YJUSJKUneaEYy66If+to1oxkHmTbw+Z8bVqkhe6SyRnTRSQcd1SCYpxd2iP0qSa4MuSK23ae9EDITrNLtrtHq7WH3HovhKSgMpb1QfSgnEn9XbWkevoRIwtTaqWyfBhxFZDk4+TJOzgU9ItXHlZikdyk6hW/DKIJwTZgEsU6ntEhkq/odaK0KZrKubRyl1xKJqoCy0mxdXhhprgthHmEjGTpbCrbahRTXyacLUA60kw1nkgqJr6/WprfQxlrZ7xe7CymZ3Yw8B7uRtODEhm1WkFTig8A96f9fvSbsy9n3MRhbpjqxmcGRUQarw9z6vo9y0y0eE5MCkC0jVSp5lekv2WRSQgpxBoxDYymBMAtAvgytHXD0rHSxtR3I+z63/9ztPHP/Wzl6f0xj5hleG9oxFgbcE/OQLGy6UOgWJLNgNUCtgV6Rv6nXSTpY59DxMEn/G1jNNZRVBt+w5gqIdxEDJfHM2C6BXX+ZrGP9ubwEG2kGrZLUsdQyh/Ta4OjQtER5GRMugEWPSn+BqG4RdBfxrVF00yVsFOl1XBpl0bOqpmdjplxTjJIgEiduS84DB3ROozsRlmehtIXuQ7jaw9YuQbNLe6FNqTxEOGCBG6HcmKjsoO0cTqywY0XesgmbAu7G3YRev8f8UpHJTZqJcYeJTT6PPG/xMF2CTo32aov6jGmx9cKFvNb2ePTIMMdOPg90cEgY9CCXg6nxAXAgxKa6GdzQJvJiGsS02qD6cpcWEPfOSG8YeM70HXg5M+6KhcVAfgeOXSDUUqZWcKDTg3YPrB4kOQgGYKUG86uwWNN86R44+gzUlMK9BfQOBMs3Bx5GgMtlBD1+pdYjc5QvIZNqWXyF+5sopgccR6QDtqXHaZD5xobJM5HuM06WJCyTRUA63Wck3W6WLLMDWaRRYF3GYn2bJbKOu8OQr0B/G6IL/hgXxhpPCRF4eRuydg4g0U3LSg9meENG+8+EdxZQ5/i3GpJBcOowtoyTv554OUa3zcJpCgXN7KjJQuK+HG/2rDT1UQmUdkF7HrQpAwrJkOg88tTNwaGnYWIcdcV2ClfuRH3VI9PaaYGakxJsaxus/inCexkhW5bWNlyb4mLwctG+WwvDGMtJsC0LpaDX7WKhyDk+rh1i+6J8rRKb2IqxtMLW4lMoR+G6DjoJCZOIREUk2hUlOkuDlYjmZKLQKiEK+3QjTT8K6XXqBO06cZTQafVouA7tZpfmWod+4wJALEDcJ+416a5J2ZldLKFRJDGAIyBrzpIMYdAQZHVoGvJD0s3GLUjHHQdZ8/NlaIrHo3MO7cAm5ZnJIhmvgZfDGxmjNLqJgbFLmJiYpt9s0BsYpje+mU3jY7jhFXiORalUpB9FWHaM5dokbp4OHspysJUreuypRFHchXY3obYSs3gqoVPv4ng25fFRrLw0xEoC2dZ1YXAU/DGH7pBDo1NgaHSc2IMYDUHCSA7ygY2zFNJurKELw6hxsKwctuOhbQ+FB1YbTRmCBk6yRtDvoYM6YdAl5zi4bh7XK+D4RfoJaG+EwkQZp7qJolol6RzADYtY5AgCB60TurpP1A+x8jGuTghjsCwHN19gYusVvOnt7+SqN93K7v03sLucTtUxLIYJxxs9jhzrMnf0GCtnnmD57MMsnz7B2uwCQeOF+vmv2lyEXdDUNE5doIIrBjoR0fyCiNxpE6iaQvYumfp7quHBPOJhIOjoKLJkBOnjcyHnwoCxMVCGiS1bufHqtzGgYXRrgTGV8ZUgy0Ea0NGo13obDmUAR7NamRXLuAElZMk1ZnrVG77PVTsHkDVyM5ClMpd6cOYklJ0CwxPbyQ/lKRU8Ap6gW18mCl647ihgOA+7q3lWujFH1vqcOvEcf3TiOU6vdFjrKlp7t7Jv31Xkci4uMGRZ3HX75RyfrXPoVI1yuchA1SFOZQ1MWHt+itqkTB3OLek3xTjhhn183+LH3l6mmV6bwQ8NJzBHJmEPEtdbieR1ZmYhcYa58sa9TBegrNL0qs4U4UfyUBmGZ3dIgcvmODuWOZ+BPAxPW4xNV5mPZP9Ii3xHwZZiKKPGNELm3q2mx6hFcp5dRz4zVW4FsvqYxINBFy5Nq7Q6QDOEttLwQAJ/9TV44ltkQOyVsO89cOtPwN3yZ6uaNlM7QOZ3GTDWDKzpARBs2Mb0dTKDa8IfQ76LN/yt4oj+dncbRIOIE2w2MgSai/a9M0Xm0xrN2DI5t0zer1IpTdELI9AdEh0CLZqdtXT7jZ1ITIn4hdIhF+21aRv1UE0MYZ6DVLbCSel6GinftywRYdcBRNLZMOxZUOxBsYPyiygnIurUabaXaTWbBPEEYcNlfJvH8NY8Q5thaAS2eKIZO4nkdGYQeZWZUIqVkjHodyyW5xx0OIrIZGgsBVHkESd9sBwSy4Ggi+4tQRiiokTg4wiibkDSXgPrJDpagn4D4lbKONjQCEwrSGKUY6HsnDR27Sm0LqLRKBSWbeHYHrg5tHJAWyRhnySXkx6xQSJOWmhk8gy7FmQVMEG2mTwN1vFaM1P6vAnR/7sJEZM4v77GjOEppJT2S4hs0/fmmr4PwViFZdso9nHLB36Nt77vdm66KXssTLsXDxhwZOkbQTARo4Ro1socmTC+Id+B4B1vsuDhHbCyKA2LxkahOgof/NT/xhd//Te59+O/jU7+/mnZSjkIetRm3V3TOaRmJoF4FoIHoHAlMADJAsQnwL0JrCJ0TqAbD9OfOYM3OIhKFhClrgqiJ5s6C2oHTE4j7eSBwmayvq5mghOLYgmuYmSTckXmt9oKBI06SZQpvW50yM83KRSd5eF7fxGAnDPGUOUt1HMfwdu2j8LUMDpQLHjizI2S+Unrx0ggaktTUycF0uIIums18kNFXN+DROG1m7QbsLowS2P2FK/bs4eg49NrrtFpNFiNB/DLm1BBDhuXQrVANC3EoxG/yN1v387ZNahWgAjWagnHTs9Ta7VRyqZUKLKiuqANn+NcJLEd2hxbq2BESiNaLAfw7z8Phv7v2XB5Fa66GkZy4EzBXBcOn4U5nfWQNzin4blsyPu9pBk1TldZ7Nz1ek4WBvAiqHTBKcLJQBpSr/RgrAf+sOaz98CX/0KJdrVpMzuoCNaAn0A86EcQLYV3INqtF5AJflkzJz8M3IJUCXz9RbbdSCuBDGg1eYPHgdvS7c6QxZ/jyJy8j8z7z6WfG5E2yFgRE8hKO4XcojUysNZBAlcTXTZZfyXXfYFVOHEfIqZ2F1IB8XVemHBrIkJrB4H/lJ5jw4GHK+nBmkiQOZ3+vkgGqObhshtgehCqAeg3Ub18O83PPEbv0YNI6el2MlHyXnoRRis6fZt6/x9wCRSuhr2/Ao/9FoQPIChzCfhhZNGy0gE5IvtVEuKxiOe+0YDu25AH4WngGkgegn3/FAa3wX/7OLLYmZtn/n0JKZOLdtFepbWCLoPFiEIuR9yGbq9JrGO0Df04poRNoeARew5tS0PUQ0VtXFvjFRVF38H1QnzPxXd8WQEdUDZoy0TjDnYcY8WgE03QaDM2VqXkOXQbXcJml/mlOepLMS/Zg8RkMz0bIvALg8TaotftQ6BQ1XF0FApbVpVhaAL8ggQYXhX8qrAgLAuskbQcfQl8H0aGhdJ24BvQWpTv2bIXtMdgZZTx6V1Up/cwNVamvbxAu9ag04kYGq0yWBjBs8FWMUHQxLNgZLiE7xdptD162KKd2gW3oHEczcJpxcxMxOJsm+nJQcbveAN2HiIfaiEEbS3a6zkFg1BPQOehvANu3w/dJVitwfIZzcyTAf3v/CeuHCrjNELmlaI/MwMTTciV0LZDEINfGiAJEuJeBGdPUt1eorm8TNBtkhscZM/evSw//xyJ5ZAf20on6lHQNp7loZwBTj9/hOVDCwyPDTN0+Va22lXioEdr9QxBcxGCJrbXox9Brlhl02VX83O/+Ze86ZocI2WFi6zHDa15pgsHFgKe+uYp7LVDrJ45xNzJpzhy6F56ayvovw3lKwuoWqgdDvqhl5g3oxjmViA2qesmQg38dvr7ENKswtgGCuwkkhAdTTf7Jlnm19jGvB7AFRbuVkWxDQMVkQIzzEczy9eQZdbIEphUYExW6xGk2xgt0Z3Ikv1fkcd3P7I0Gnsu3eeG9PfzQU7Tg2nCh71vgJ/+81/gm3Pw9WNtnrj/EPmn/5KTD32OlVNPS6weZ8CZY8Ed2+Gqa7fw6Ik2R751dn0Ivv6FT3PfF/8r+eI0Tx1+kOnxMRxLGntFGj73mceYW4zYd8M+qu8YYZsSokADcRnMyZrzXUJiGCMGZqro4dx+7wlZkyujluQjK/ooaU9sLWMyBUwqkQPslWT7b/Rh+5VTvPvOKXYBbS3u0RnkwFdZ4Gnp5fkLN8kKb6vsOzfq+sbp2F7iyD1bi+FoG64pibxHIQV6N5M1220guOi3GpJ8Hh+U8yyRQWCL6fVbrriCY8CXEdera8jdP96E7lOs+yDKhg/+Ptx4vUhkBcCw9LAJ1tIHY4xzfTzTgMIwYausu7frN7pBVhEF5/p8I0hu2QO6VeheL5UHlNMRzZNxgV+LgMUPihkf1gDgDooxxkd2MlwdRWvNwSMHSZIFZCIzKaELtQ00oF5Adu++n1iA/xDNSK2ZoCsBcqAKYA8KqIMjPlQvEN+omRNAky7rz057AdqLaBwiawLyBShU0GHI/IF7mT9YhYEt5KZ3s/9muO2HFMVhWS595G2fUHCti8wNI/BV4N5T0Opb1NxNYIkv6dmIJKGROXZSXDjYihVJIVShAHEN1lYadForEIwS9uZgYQbqS9AxrJ8O6+IIuQJeqYDlSEJCA3EUEcdg2Q75SoHB0iAK6cWjqE8AACAASURBVMkTRdDrtegHAUG9Q9htQLhMVhJgKiEtMtZSnH62ct73v1ZMIV7D9cD/gLBiC+dts7Fyex5xcr6MNIn5Hp7Zy5Xh/F2YUuoVnsTlbL3iNn7jM/+KWycc2nmPhuvSdmTqNKpXmlSbjKzBpYEMN4K2kOW2bOQdUem+i1qyxp87BrMdOcAVe4TlcGimx0MPPMFff+ANfzsD8De0qd1w023b+bPf+yJC+VsFFkA/Bc0lcBU45VTfNQS1G3QNgetuAlUFPYPWZyCZArUJZRXShh19hMa4B/FgRhG3t4/QCq/n3JbxpfXzOtaHw3V47gjsugSGB2RcZ+b7/NL7/3vmD3+BoHn2Ra/rxQFahVIOtpPjmjv+D95w99u57Uc3MVKBESXO2dCGY4DIFAAZGTUEVjStR5fxhyu4hZxss9ZET+aJOxAvhNiWxt7u0Vpq0V3tMrJjDC5RYKv02IroCPQ0qAoUp2X+O/a8MAa6lubps5r2ap35pQ4nFxs8NjPDytc+RBIscW4osjFbZyKZC5ulpCm2QgKCvKcoNzVLXFg446XA7guPsE/R38Kfnv4OnaSM27cZicH3YK4ODz8N994Pj38R1HJE2LOIHAu2aRGzjdNv9YCPIUmnkwiIeBS4FYkunngVJ2UuxHjkH0Xm+PsRmWNjHoJl30oWRRit1/ci8sYgHn8OmRg8BEPMAzeDdRMUXenFEwWQtNJjGHlUo3myjLweRh/+z5CaOkNjGUJwx7cgOY0Q+D1kknoT8DPAbwDfQhJ0b0dw0c/x0r1S3gv77wa3nvDQr/Wg/atktNwygoA/kQ6QAmpgTzD+vmspvm6a5z/9BGrvZeizS3DyCBy/lwyMNZlM0/6uQSbMpmUgK7vhlnfA8wtw9n+B+heRd//1iMJbDgmLPymDYG0Fewr0fRCZbKmNhN0npexAAVEHadz2xvTzZ9KB+Tw/mCLxF+3vw97zu/ex64qr8L0qhw9p6M3Trs/RWDvN8vwz5FUACrqtJvXVJTzPoVgES/VRuo/v+wwUi+TzOTzXwYnBjdpUShb5vMLJKbTj4MQx/U6H+uoqteVl2q0Wy6srzM2vMHMmINEa/VIx+HAeCmOofBXyA2hdwimVULkcOC6OcujFiZRRJ1qyn5Yl9ca2C+URiF2RNOh3IehAYUA+8/y0XM3HcdrkvQDXCVlrReiDx1GqiBqYwLn0Kj76i+9n9UybuKsZGKzQ6ST0mk1U1CdnxXilmGKhQrPep74WYNsexYFhEmUTJtDtJ3zpM/cyfekeNl0yzqZdUmmRJAovB74Lzx+AXK8Brouu5PF2gSpBJQ8DJbmURx5Ne0g0NNHBDt/8Hyfx45CJ0WuY2vEevuVvgsK0AI1JCP8/e+8dbtlZ3fd/dju93nN7m3vv9KpR16hRJYEoBkQnrrFN3DCJf44hdhwbG5s4dp44+f0wtnGwg0sA6wGMRROgBpKQRhqV6X3m9n562+33x9rv3WdGI2kEI1txZj3PfW47Z5+93/3u913ru77ru3rHyfX2YleXaZ3di/P130RLD+PnBtBiMUy/hHfmHnzXoWtonLHdN9Fq6VSK85jRFLF0gYbXolmfJpkbJJrpp9JyGe3r49iTDzB/bB/+6iTWUA+vfvtHuPp1r+WqV63nilgSzwBLk739+8DBx1uszJylunCS+uIx9n7tsywdO0W9XMRLObDqh+StH8bSSFykYqTnMzNAumbrAYOms2QTQnqgMgXzIUtzBtnHrkPQMVXm/Ty4xLX/329ywy1v5vWFa7lzAI4I3s4goQektOdXEVxMsTkVmNh5ZiqfqSTIlFpRp4SBqjJXV6UkmM63ErJtPw3cASQ88Dwf13HxPAffsZlpunxjvsW/v26cdjNsvmTpsDOiU3Z9jtvhzVP1YivopNNJ3vMz/5G33/U+7rhhiD/5eomH7/k6o0Mxfv5X38qCqbFF05ieg8fOgJeFN49DLhp6g23Et1PFNlFCvX4z+Dx1uz1CN0xJdbWQYqAl4JQLT7bgmrjIianQOQak29ClQd6S/PnRKrRroFWhvALdO2FDFFIOPFWGzXmZSqqqvxach0YoYERwT3xfQvPJJiRN6LUkivA67k0diWAcD6oazGviBaiUgQKh5xCvpBi8vhQcg2NQ/NMm/PGYsC9wIJKDf3UC899n8LMm7iJhX1Al99dGXJ2gWTjR805enYACXw3EX5wnJIgpLozXcexjwfe5BuxbBv8pxDebRmKn7xFWHl62S2tqVoIEAIpvDxojaBpSUkgFz1NRkqracjlXpdok1J1V8mA+YUk4wftsXlnA02ULxVmSrPXOiRYgmUPLFkjF8hjRKLZtU6/XMU0Tt1bFsx1hyjoBQ9Z2g4BQtZv0QLMk+DfGpZQnPYKe20rhqmuYuEqjfzP0rofeERjXYEiTiGYMiZj2Ak/Z8HQVMu2gKqAIM2fh5IGAQOUhjcpbkshreR1yrw3wqz5ew8FtNWksnYKVOSjNw8o01KeQHVUFqS6YOXG6YiZaQpCxWCyJbkSwPXBq9UDuKYJpWRiYRCIR2qvL1GfPgjuFLIQKs1C6vBah0I7qT+QRAC7BeazwkhqBXlLTkXbnuxHH5RYk7u0UBVJWR875AAKZfxtZzC+NNKnvX1if8f8QZqzGbf/2f7Bt80a2jPexdSxHMw5FLZR97EMcvAhhAlPltpTyodpH1bJsEQKxnf2aokCPBisa3DogTsnBBswWYTgDE90xjM2buXf7X8GRX5KmVi/TdQctqC74323bhnnDG64kzNipZjptiI8GOiExAV3RgTH5G8OsZS+cabT2SWBOGoNoQWbQS8PdX4RrHRjrAX8MqkfgiX2Q2gTX5BD4+rmT2fcCUo8ha5jvS/lhKqqRSWZZMsw1MPxC1gmenzuyPr5v49g2xx7/EwxridzAR/mlt0hlXvQ5ZyLlpcA5DHQ/A7GRDEa3KeBqyYdoHG3ARNPBGBE3WIvpWFYSPx3DGDdCGnVwjdMtKFYg6cGGEShVoNSEpgtWUuPmKzUe35tmuh4nNZrlT3+8m59+bBcrracQ1/h8OsmF73Oneb7sESCyBW03Q4P1tJgUzQRrJ7RCKv1LdQ1yQxPsfvO/RcumaJw1aDTBjcKDz8DBz9tMn6ixsNykWe6Dig6+RmwdbPivGofPgvMXCMHGQ7C1RYSgsIqsy9P8YP3vFEatKvH7kLUVZJ1sB8efRIZxHAkYZ4P/dUobqxLLHNLPSiXGquA9LIwu7TXB61VnaCWPU0cC0AYSgCaRqDId/J5C6B7XBOcxFZz3R4Lr/jYS+T2OkI8eDa4tg/Tce5SwLu8cc4AyPGKwsCmOmY/AFksamvnzhJl/BfTXgw+MgnuC0lNZqismWAn8mVU4cxrmp1jTBjwnxFUbaRxJcUxB6u3QfgjqfwtPBG3D6ycIQd/DwG2QugJ6t0BtD6z8EdhHwVsFfjIYyFJwkx6Uy3IbweDdgoSRleB4JWTi/PNXH1y2fzl2YO9RCj1DTGzIk89CxYkQzxVo+3X8hRiG4QoIlEigaQVcr4Gpuxi+ieZ5tEsNXD2K5+t4lo+rGZiaT7PRxG07GLqHq/sYvofTaFBfLdJcKbFaqbC4XGVppYXrXsSqbGvgm2hmDCuRJ5bpot5s4paLUK/jDw3gt6WUDM0AMwGxjNQcGwZE0tBypCxF86HZlDUvGSeZy5AvpElHbMa6WvRl62QTNjXX4lj3AH5iA5VWnKeeeJTvfjmHRpJIJEUu30M0O0i9CqZvko5GiesmtgdmzKSrT6evN0WjqbO81Ka81GJusczY5m0MrM+SzGmsrICZFfkCW4d2w+bYwcNM9FjEMt3gxqmXIRYPdFhdkULrTgvObJoasSuiXP3+z2C6FVrFFWYmJ+H4F0Efgcx6yG8CI0nTMokYTeJRk4qfxy9shK4hfN/Dmavit4VP2Gy2WF4p4zZrlCsrJBJNIqZB1DJYmF8FP4kZyWGRpFHzSWVHSe7sYqC3l1vfsYeNG3eQH+jDTKY45EjauliE03M2x46c5PCRZ6isTFNfnWT++BOsHD5Kq1nFsxzJrl4KIBZCKZ8XcyNcTxqEeM8HAqn1/0LvRZZoJROuumv1IPtip2OnAaPQlShQiGZJpMNCRtW/WbWQVHjWLOL7ZQjFEtSOpA6pGLJtwoJD1Y6lU5HofDGoc+u3xOIIVKOUijQdfF2jZZokMakSw0/CuqTLx//mr2kuu5zef5CHv343h44+y4mm9xzpeiXcAx6VSoVvfumvOH10H4/efD3vfs9Pk3ZuIJ40iFv6Wo+ogSxcPwFP1OG4Lm5JL2Fj1qDGZa1oWrVzUZwv5fv6iFtxhrC4Oh7cMpBGW1dHQsBY6clGkN4IUqgt79kQBdsEPwHZnJTWlhuw99AMf/7xv+OGuz7Aq27Js2k0SgbZvduOSMN1GaHLliBgQ/tQtmSMmwjhZbYMc8ehtCKfdfOt0GeExIoewmnWQLyb84F5E6jMQGOvA1+qgVsOZtT1YH0IXpPDzehhUJjlXGBVfVkdB1eTywouQBEsVXCpGlQoZs8yYVmmOkYOcV80C4wMOAEphkjwj8vg3aU39TSomFgBqOoGG/gsCQHHVyuGYs5GCKnNUTQjiRnNkMv2gebjeTa+38bw29SKK7ScIq6n6m0VCu+w1izusr0CTNHbYY2BY4ksUTyZJJpMYuhRDMtD0+M4jiP0f8PGc9rgahBxQHNl4WplWMvi+D74dfDnoNQGJwLmEHELEjHozcJEN+S1sDL7pCdktfkpmNahFAEvJjKtpiVas4k4FNJQr0K1DJUiNCpw+y1QiAlJ8LALk0egelajPG8yuxSn2VqH70TANqDWAq8NLTtYYgLBF6cEjSa0XfxaGkjQNmJomoXrG/hOFLQIrmbi6zoOJrah47WL4M4R1t+q3VQlKtRupFKIqi9JJ7qmatFX+Kfp/WEiWNcQQijcHXyfCP6msCtVBlFCdph5JOV3GiE5lrgYbOZSnO0r17Q0sVQve169ndvf8U62beljpDss8Cgjy2CGcL9U+XyDULVCI1weY4RKMEo/SSd0CiHcZ+vAeFqIok0Lpj1oetATgfH+LNt/5J0c+eNfxflnAmPXDQ1y3RU7CNWaIkhDrgmwegkRKqWqZAEpqdOfuRf61gFJcDKwsA8KCUhug+h6IA9Hj8Lms0j21hL9sNYy+Edh6WEovBa0LOc77oYmzbKMAABVj5xugKaLO6yHZ7NW2a220QwhiK56up9vpYV9nHw6zaP3XMG18Vu4+foE6ez5mh/PY66GEYmiqWZMrgZRS4YuAor7igMmFlrKCoXHApKI78FSDRZXHYxqi7pbp7gUo+omSKQNeruhtw/27tUw0xEyuRjZdUl00+TCHI2Xbj4GjpvEIcIadVPr+SGOGCfRN8b4W2/nbFPn5AlozngYLZf7nvE5/g1oLiHBfRrYqosTGpE4OLYLGgfAVYn/U8haVgTt5kCh4SQyJfuR9e7FbAJ54BvIGqkFxxhEPPaNiC6tqtNT+l4F5J5phI5yhVBAWiXzFK2kggDGC+AsgHFjoPbRKRFVDY5/Nvj5bHCsZnCcPGG1fxcid3APglMuIYTR7wZj8k2EirM7uLaTiB+4NtldZNNS4VbQTWJ2ldUn0mjr8jDSDfM7YbEErRW5EUwHJzQX3IDNQJ3m5LS0Ps7nYfUwLJyC6iIhh0VxkXz5HEYxChmMgkF7Kg56TgbIeQpmUoQIdH9wYwaDAfBBWwTtiuDYdcQNGUYQdKUDqxB6VeC4DhFIX3z+uXDZLtsPZRFmjp+mWixiRSCTgVpRJxJNEbXz6LEsum3jeW0MTScai+PYPiY2lq+je1BtNmiWmxiOjx6L4Ec8YpZPu9mg0arQqpUwIibRWBTN9XCaNk69RaVYpVJqUq9fpANq+6JriIFlRjAjUfx6Ga9WgtUiencWWpJc0SMJ9FgWx9agHdCyWnUwNIxYDj0WQ0+0ae3fB/ogib4u+nrSZBrPsCF2goFImbTZpmzEcEb78HMpVisxzjxT4/gTe0l1j5DM9tNuWeTNPjzfxLI0zLiJYUXQTJtIRMc0fMyoRnWpRKkIlYqL4/j0r+sj3a1LM6mGEHONiLghlVWPpTNzDOdHSEZ1rKRc1poMo/SgEJ/NFEJvV8FEu/MuGqUqC0eeZX5xCea/D5xE9x20zBBurYxdThLNmkQzXdgb9mCO78BJdOE06jilkiSV2xU8o0Dbj1JbOEy9WaOQshjqNijWW7SqderWKoYVxyNDOpand2AL3d05dl61gTe98RqyMZ22AYsenChCya4yM1/lyKkS5YNHOLH3a9TLCzQbqywtH4dqSXR+NS5tTHIhR0nFR4q1p3J2zR+CjacoiiqpWuDC1FNDx7p+O31dI/RHs2SCcu7ORqGK2dpAtuAFZCuNB6/rrBnqvCS1I6pe027H35UpZqyGxAoqyQ/ngrdpBJ/rVIBUfOEKUDMglTC46a3v4NlvHaaxanLDaxz6No7xzGOPU11ZFgZ6x/B02tmTB1hanGJ2YYZdG4ZZN7qHnoH+tXGYWfZIWbCuoLNkCtu0s6BLMU0VOA3nkkoUjKRgJxXjKIw/jbhAGuKbd5khNAUhn8knxNK7Ee1mzwIrJjt3Czh8qsjDDxxn31e+xZV3vgvHD6eUBZR8yQFhQ29UyBDKhTI1YcU2CeWGSz6cmIP50y661WZ0IkbL1EhGIZKEgZhozKrXNxGQWsVtaqwrp8F+ugknzgRXUoD0FbDhrTChiTQyhBNLuTsqeREnFN9V4ZQaGJWUV4PtBxekgk6FjisNvE6pRBtwDOl463QhM32JkDZ0GYy99Ha+RqhaZBVC0CB8AoKGaprcIy2apWdogp5+i3gqSSSWJZnspbpq06jUaVUrOPVl7OZp7LqG6ykadKewymV75Zh6EBVZzQr0U32h4AO6pmOZBkR18H1cXUczDHRMPMMJsz6uSm0pcZjg2H5Lqo8iNppmkIxDKg5dSehPSrJP6WorEr7jSxgdB2IGZCyRXpGeNtCXgOUVWAx4Nl4TBgfgygIUIrDRhzNRqBZgYVHj2WWT/c9kqZouNhq+Z0A1AauOJPY9lTUqg1uRxl+kgCzu2vWo3VD6f3jBzuuuSeEpSRW1OyozO35Xu5DaudT/VSmqKk9WjKMXSPz+wKb0YjYgNSETCFAwjuxsqjM3yN1QZREzSNw8T1h7obJ250uWXHp7BYOxGlp0gv5Nb+ZTX/4dIpq2luNQe6jaG9f8S8IpZSMwgNKGXcvQ8vwlS+d+uuApbWAiDl0x+LYtMVLTg1Sfzgd/N86vfyZGpWbw8izC55eLnWsD+WF2jO5CQA01Knnw34Jc/Txoc+CfBvcZ0EZBL0D7FDz4Gbjz9yF/C7S2w9NfgOGjMP5B6LsJGIWEDsYK+MuSFcoMw57dMDcJB/433DIAJEBLnnNeliFMeMMQTSpNV/lCn5XKIrbbJkqo+1UnzF32IdujIoqXgq8LuSyLpx7k3k/v4/6vfYd7P7eZG65OEo2+yEPTBhakV4nRA1pChuwcarQyE6x86LQCYecEG2oVqJSbTM8u8pUvn6IwPMSWK0YZnYizbYOQB6tVm55+A3e9xq9826fUfIZLBzgp+PoZ+e4Z0Ax0stbmzfkL5wuYMYI5sIXUG0a4bz88/E2fuftd3CeVjmgayIGfkzXqA8BD0HwKnvlL6P9l8F4D9RoiS/ARwALtnWD+CdjzwHsRX2gT0pjwhRJOOvBWpK5jCvgSAlp+EVHPuAlZX1VjWvUIqvIztf57yFprIgmxLsIIRyH+U6zt1cwGe1W041gLwWsWEV9aVWuUgvffAuxAmnA9iGCLY0jk8Bjwh8CvBEO4AtwN2q+C1g3+N8D/DPDfCX1IswXOfsKowAxO5n6q90ZhaCPc9ma0W9+G/52nYO5MMAAng4s+gOgkBEBnbRZqKzB7BYIQqwiki7C1oUKcG8D1RLZuInFrnuW/3QlTXwLnKLLKPgL8HHA7ArJ+GmG+/k+ofgqqNeCjwbGSyMN1H4JGqxX8LkT2RNFJzucXXbbLdilNHM3a9HEapRU8zSOd05ib1YjEEiToJlkYQZtt4DTruF4bXdOImBkiNInhYOgWVa1GcaWIZ6fB14nqoFsu7XqN1fkZzhzbT3f3APnBPuKxBKZv4bZdKsUqjWr74hPsLUd0zGwbrW1TLzfwaitQX0GrVbFKFVzPR++KYuZSRLLdVI8cxS+WodnG0A384W4SVi+xVJqo7zC9/x60La8mNdJFT8bHPfpl9NKzVGlScWG2pWGNvRW3mSVpFNhx9SiPPnYMKxHHiuepVcEstsn3JMhkTfJpQAPL0jB0cF2HE6dKHD88TdvJoEe66BkbJpoU2RcfSHRLzz7NhHIRag2g5KLFhkh2p8kOQTsnwYplCJije6IXW8hDJg19BelLduJgCqMxRn78OqYeMYBFLLNCJAqVVg23ugrZfiIDm+i+60MkY0nKDZfq6gpVP4IfycPKUcysSSzTzfTZvwNgeHsvN1+V53vPHscyTWqVMs1Wi5YdYd363WzZcRPbdo5z86vjbCJIk3k+xZbP4hGHp+bOMDtzlKWZ42TbFSbv/xKN0irEDLSJHH6GAOUjkAl4GU3VsavS7Ao/WGXKC9nyhf+smRb5H/151k9cx/pkD/1BtDFASCjsPKUisr1mCPlpiorQqeDoIzucqtZcQcBUjUCxw4WIIaRjJ/icKWRLVj2fF5F5ldBEekxDbkdHWhuAatNmxfPRTYuyDZ/91N1ESPCLH/sd1m+GX3n3+9n73Qcors4jbasvbPVKiQOPPcC73vkAn/vc57h+x1uwvCgxTeMfDtv0Z3Ru26azJ8eaH6rgI3UuKmxVsY9yTRRYrQDq2WBs1pqi+TDliyyBksAf8OXZimji/sYJMcQW4p49GoxFnhDQvv87J/nKX+9F86d5z105tEyUZRdqGuzSpAh/rgVTddjSH8KNyrtQshNNP5BizULMhIjdJuUs8dhDwzR1j0wvTGzS2DUCY77coDjCVRoL5kjMF13bOqA9DTy2imS7PdCuhomr4T2pc5uFq+ooNcFqwcklCVk6SnRXUZFVEKkGXpEgFc6nXBcVdCrsr4RMzpomYpBkkYDfDz5AxWyXAdlLZyreUU+Ag9xc5UMr1mzwpGtRzEgfRqwfPTWC1buNm97zVl57p87AkKj6zC3AsUdg7tgqi6dmWTy1l6WVFrSLAaCnuNuKGXvZXjmm0lgxMAIpRbuBU9GouBpoMYykgWbo6LpLxHBousL81A0DL4IkU/CCzJIJbpJwdQU0DU2PoSWyWN095FKQjUizwhgiyLY+OBNNMf82isrdHGHVglpSfBOacVky2jaUy1BehmdmYVsEthRgm4bwbDbLMe534JN/B4ef6aKY7sLp2oC/OC3ZtPIhaFUCzcYWYTqM4GQ6wcYmsmB2NmZXbCS10yj2qzrrzjKCTvJg59qmUp2qOYvKRCuBImU/DDirmLp5JNb8IDLyXZzbYLoTMD6FEIOOBT8r6RGFSKld2OLlZry/gsHYHrbccRd3/NxH2YjGPOFwgkwh5bcosLVKWM6j+laq/bNEWMWlEpkvZmbHlwG80RKS2wICf24EjB2fBvuPYOkbP/wld5oO4IL3QhOgG0GjZoPfO7qo238IhgvGMLjXwj1/ChOHYOBGKLwN3vt7oN8I9EKyCHdcA488BbUgUwjivfoHoNIDmZ3AekjfAe1noPoXMH0v9O2GSPQ5p24Gz0UqJQ1FDaBuglN08G2fDLKWqKZpPuE9hXD664i2yvNucX4Fe2oPb37z3/ILP/cqPvHx3hcbWdDA7EPWHKXscLEWUBA0B269ARw9yUoxyfHj67DiGvl+SKdgaQG+9j2Yt+HVfbC5x+HT98zgti4laN9CwLc0ob7naeT+rZcLZZFwfryI3fnLLL39/dzbgqM3u7g1XXaGDj3gc+w3EPmVG4E/gtq/A/s6xAH9s+A1tkhl2R8Pft+C4IT3IWX5XyTcjS5kp5EE167gNP4uuBydMM14A/JgHg/ecwiZUEPIuhwL3qs6qihnW0VpTnBeecRvEzJpWO1/EJEVWECcdyVut4pEkE0EiH0bsticRdb1SPC364GPIQtGC6m9Owv+78CO/wjN98KxNvBJ4C3B/ysW/O/x4MPVyqchDv0UTDfQ/q6bkd/Yw8Jj62iyiGzLqi9xhaB7BOFmuoR0CFMaWqqkSqHSqn1wFfh9Gt/L0HgkC+69wWs2AnsQtHkJuIJwBf4oISs3iQjzbg5u4FGEDlwIbt4S8G7CzXgBEd293Mjisr1c5gHLcPrvOf3MNvLrd3Hllj7SKRE0j+oQ3biVuWaFSr0EGqRzGXBMXHcR2wdf8yEWwzDB1lyqrRp+NIrjx/CMOETiEEsJhdPxcJttbNuj4TjYvn/xs9tAmHaLCzjVNpVqE5pBd5lmBb9RprH/DAxsB9/FLS5ROTFH/M53421IkInb7Cgs48SbpAompuHTLrVpvP3H2Hb9mxjuTpBqHOPer+7lyRWflgvxnMmr7uwmZg+grdahuUK+NMsb7rwJt2sjjtZLu2bSsqAY9PmLRSAbgwMHp5mZq1KpaPT0bGbTtQV8Q6PRgqUirNYgmZdml8mBNfEUzAj0DUd493++nXhao61B04CuUWiVRP5saQaKCWjMwtwiVJNQKUifDc8Es78fc/MtELsCWodImnVy0XkqzRL4/XjE8fUe4pE+SrUixbkFmpVViCdIb9xK/fg05fm9lI+EIuYP3r+Xxx/bx47rU2zachcVP0Fbj5ItbOHDv/8+RjMxCrpGQWYUJ4GjZ6s89eAU+x/5ezy9wdzsKSaPPguHDuMrOQDPw29WBInqiOVeNlM6XGqvgrXiKaKEMocvE5nL0HXetONaakfmOFmzyXWPMYJss51WICwW3hCcnmLKqtBQhXGqoDiKALKx4DJU89HJVfiNZSJ7nAAAIABJREFU78DPvgW2R8VDVmRIJQmaR0DD01OwJQ639AQNrAg96v7g3P7bL32af/jeHNf97If5/C/k+MIXfo29Uxpf3Q99O+Av//6v+Pz//Cof+81PUlz45kWNywc+8AFeddvt/Kf/8ofctG0L2zZEmC7C3QfhPTtCRT6C61K9QQ0kB50irDdpIh7BmeD6k4RM2RbinhwHZqYhl4FsWtix981CPA/jCbgZ2Z2d4FiDwWcPBeOWJwxjN/X1Mza+gWefyTOBxgMH4XQV+gchPwpXBRoTTiZU01SMZRVLKUXBKR+u0KB/HbjRGJHWMNUlmJs+y8qsQXNpgK3vMnB0mcp5JDdfQrhLXTaUFmS+lB6D0t4VJAEdhbEPw67bpfJohND3a8nPMUswFsfgXClAJbmhAk1FfOzUvbA7/lcnjNE7tWgbHa/RgKQPVXUQSwaJkWDkLzcpvbRWJ2xfDOfWwkaRKDMBkS703m28+7d/lTe9NsrwoEYLjQlDYyAACmZb8IWjcPYYVCfrNFeWaDZXsZ0GvqfIMMrUKnaZ8fzKsSRrbE8XAVNtH9pVqJepNJpUkkk0y0QzDEzDRPOCBFKnqL+hg2+Bqwf7ZVBXbcage4yB7bcztGmM8W0ZdmyFkQlIF2SPKhI2iI90nNl6hMpSVB8RfHeCv0Wy0J+BnZtgfhVmV8J6x/Udx+kD3m7A7PvhO71w6iisLOiU5kZo5Hvw53fB/H6YvQ+JJ1Xpva8+iRBIhTCjpEpqFKiqdl9lnTUrnWUDEAKa6oqU3p+H7GADhGicUnWvIzvdWX6wLt/rgTcjTVk2EULg5xP0FNXvCNIVewkZDwVEKBKkWugLwfeXqwJe7BUIxqaR5i95zpRG+d6kuba0KixbaaxnCKtEZjhXQ6mDRA7I7VbdRTsfiOezTpKkhTgwiqC+iNyWCLD52ms4PNNLaYng06+CxBjEuyCWwNw0jPvUN/CLh8CfepFPjUvDG+8MRApyEq1F8J6rsLrr5iwjG9PB2dUI62iCwi5zArReYBj0AdizAY5My0h094GhJqEFbglKRRjvhnwAxGpJuPl6iDYh6iHuTx9oI5DtgY1DYK2COUzYTlSs1hD9VAPRfLN9qQJJxjTGenspzCeINw3iuOQxsXDW8g9RTJZw1nT1bS5me3Ool3+Lr37lp8D5ML//CR1N0y780ihow+HPa2n7i1UPUM9pHJZOgx7TsEzYuF6j3IRUDEpVODPnszLbwHEiaJoO9RVW7v8sXqt+ER9ysaYWQ9UFlOCCmkiIqDgmOUK6vRf8nEHc2zzifSbgEZ3GsVOc/svduDUjOOQLDIp6qPqBAtT/FLwBZCz/APh15AaeAb6CECgN4AvAp5CISHVcU+vgVkKcsAXsR9bVrQgWeB2C8zURQvAwsDM4h0HCHlIqclOdLFQ3P1XBoFgSCoeMIFGd6ggxGQyTHbw+jazbp4PhLhPK53hI461bkYqI6xHWr2JKTAWv+Ufgx4H3Bcf5azj5EHjrgG3B9T8cvH+bAZv74cRJ0RqLDsKwB6eeBq8OnMV3j1FtXovr9QYXcgQJJz0Evb6JsM2HUukjGAyluud2/Ky+AgDXXwo0JzYFF3c6+Ixe4G8QZqsfHG8SYcqOEDIE1gf/Pxp8XwlueCoYsEXObT1y2UCm4jDwJsKO4QXCstwKMnJngScR12r6n+VM/080jxPffQhLK3Dbx36R9eMwOdmgWKzj1W0SuW7y7hCe1yYai2HoCcqrNvVmEde2aWFiGBqO5mF4Lk7LpWi08Zoejp6kMLiRaMxEN3Xsdot6qUzdqVFve9J44WJsDRxrgV2Bsha0/fZCnU/fh6VTuMUptEgKejbRn4rRP+QwmFtiInKA+77zNBO7h+npH8DP9RPdvY6tVxYY7EmQaKxy8rohRkfGeXrvFCdOVXBHf4JGfASvcgqveBZveS/br9lANTdCzdBopOLMl4u0nShu06SmwdlJKDd6MNJd5PIQz2u0TI1oDKJRiLiCPRKUXrsuuIZI3UZSYEU1XFvDjolGrB7ESaUFqE1Bc1GaVjRLwpZd1WEmDlt3QTwC8UGNrkiUhWvvYP7JKcpzB6hXliG+CzIGvQmP4e4YVtSgFItgkaUcc7GLVeqzJ7FiVYyES3s5XH9836fZ1jg2N8Abf+on2bC9l+FBnWErwVWZGFFDp6bBPg+efBZOnz7KyYNPcODRb7Jydh+0yrTLVfzVmtwvJasW86Fin1vF8XKZznOdpiEEbbMQh/llBGJJRTE3D/De7gnO1k264+YayKdCOx/ZaRRwWELScqoqXNVrVBAPRf2uQkSdsGJcMUOr9TaP7p3jttcOMWYa5I1Q1bwz5NwBHJiDzx+a4+9X5/nEL+/iGk1b047Fh6/PwqlSjb6uOj/+jhQRAwq6yZ4B2JCWalfdsnjTW27mih1jHGx/hI/96I+zOD35gkPjOA57H32EX/7XP8XY1p185Fd/jVvG1otGcvD5Coju5txmZ/FgnJTE2ixyS/s514WdIsTdNWC0B+7/xjH275vGsHx+8hdvYb5scrIK9Ir7sRp85lJwTNWQSwmgNYDN1xR4b8+NvOu9I/Qm45w9OMOBOY/ItcPMjICnhy5ymRAOU8TUXkIu1XBwsleOwnX9Gt2e5KCeaPVxsqgxu2Dw/QNwphf6MtCfkPcvBO8vGHBlClYacPI6mPTWw9xvwbfeD0O7YcAQMpsG6Qj4UWgHE6bV7iClq4rVOmG3OKWhoSaX4rmo3xWZTGlCKAJmirDL2BwhWKtpnCs+q74uJui4bM81Ffu80KaqnvosSgcW0pCcIJIeJt2/nnXX3shP3RZnc6+OExF+3CTyDBRtON2AZFwSh65v0WqncBilVTuLa6tVqNOUMPHzdDO8bP/EFgcrA3pGRKldtYMgC3hjDlrgazq+ZmJraUhlwBRwNhKN0DbAt51gL3VFXNu0IJlB7xll467XseOKAYbXxxkc19myCfrjkLbkiVd7yvkiimp2djYdbyLrexXIaDCmQa8G7TxMpqBhhYzaDcjMjiG92t9lwMC18EAcvvYtjZYHfj4K0RHIpyDjw2QCmjHwlD5f526q1qLWef87Xw8WQqEYtYapkmF1DJWFUs5P57qXIty9ET0cQwffFpZbdAcYDlSqYE/x4t2+owhA8G+QZi3rgs9U5QzK46giUPYU8pSfRHbQOudmxzulGBQylUXStKde5Fx+cHsFgbEbkEHcDrwOiFNfNFg4ItNCYepKnUWVEim1CuUwKIlgheeoKaQeiAstn+fb+aBf5zTNE8p8u2jcemWeHfrrcW6IYKIDWyE+CNEMROOYo308FIepZ6E8qcDYFPGBCbrGJti5pUC/HjyoWgy0AWaWZ3ny4Azzs2eguXDBc7zmms2sGxshlO7vUMjSXNDGgrPsAa0AuTTk08Lc8S1wjovQszkKRlx0YlODEN8ZvC8O3XeCX0NcQiUgkAKrSxY4loDEWjGIgmTbLjTs4DHQRZK17UHThigeNj4GfnAvfeLoaOiY6OiY+Lj4+DgIfHMxMI3nHuT0qa9yz1fzbNi4kTfdcQ2FnjiR81mvSutp7Y28dH8oWGN0TaT5zDhkcoAVsLCLLmdPt5lfKuL199CM6xTdBvbi41zacmy1WJwfUXmEHT+VNpJabNRXAnnmtgVfSVjqxVtK0Tj8EgZkFsF1bwX3IWAnRHdD1xthdh/CgJ1D1r9V0K6V1/ongIcQb71zl1pPqL+1iOB/M8j0Gwv+X+ZcHE8RRocQ4LezwkIlr5WjrLRKVLTnB0NVRZJly4QSMoqOsguJdlSN3RxhRojgPGaQ5lzbgKsQwPho8Fl9wDsQQLoanMN2+dzatxD2xhCCuK3aMKfDOgN2R2FyGGIFobUUPDhdYY0b4q1Qf/Ip3EgS8oOwmkY2GdVcbyS4gCNIRKAEzaqErFS1dqjNVP1dDUwNeDUMXAluFho6VKYRhm0s+JxtCGquKCabgMOQHQCnCLVBQhFhpTGtJA8uMwiUXY3csQEk6Lwl+L2A2m/CztqryDTciIz8k0jn9sv24labO8LykYepLL2L7u4elhc8Kng4nk4slSfeKmHbNXTDJJ7IUW+kaLXqNB0fD19wLtfD9jyaLUBzMTzQIgkS0Siab9NuVGhVqhSXV1isNWg0PZznA75eqFJV09BNE68WBHeaKU05vaa0Om8Dnkt8OErz5F6qpTZLySIeZ5g/OMmmQgnLmMGM9pKzl7BW+vD1Hmx3FTfdxXKpRa3eptXyOHWwDNZ+/NY8Eb9MX7qXRHIQPdmDRgKn3SBl6ixVllheNlh2oKr3kS7EiMRE80yPyl6fjEoTC9cQtQXPB7sFbhv0uBBUDFX+G/zfd8QfdypQWYH6oo87ZxN1K0T0PLqvY2tSuue7AdM2AiR1YokudM2g3Szj+RqFdf3U4nnspkN5Zgq/XKKezOIZKcx4Gr8WpT7zMIY3i9+uQbQLWkXAI9u9jr6JnWx+7XVcf+M2NmzIM9QjQZMLzFRhptzm6aUiT++b4cyhx5k69H1mnn4Qu7oA7boMggJoTEJntea/PMQpVYGrEeITSgEGQmBJsQMbXJxj1ckQfCnnnMujXX0d3dEURq9F3gyrnpqEoVxnpVqCkFCoKqNUWw0VwkXOO20FcSkN1Uxc4zXbI4yaGongtGvIZ8cI3YJeYGsOTtZrPPr0Avc+bXPHVot0VAu0WH2+8t1V0ps2sPP6Ua4dtdZk5rtikI+J6xMD0oMF+gYLRIF3/PiP8eR3D3DiyFlW5p983uEpra6y77Hvc3xyhm2jg7zujtu58sYb1yAm5VpEO36GsABbxTN5zg1zDcSlUuzTCNJQy47B7KEzPPaPj6Kbk4znj7Hu+tvoGR9fG28lUWAHY75MqCCoirDT/VGGU1Ga5W4iBji2genrrMvL/88sy3NdyMDZEuhlkVN0PRgZgXwSInogIeHDggeFOPQkBHC2gS3EyeVgMQ6THjRMqGiSy/Bs+b1WFxnEHUmY0+C2a2BbfwpnZSdTg8NM5lNUe2W9aSyCNRKEV/7akonfIaMIhApN5xb6hUGk3fG73/F3hVconEcLjqMm3Bqb1iMEJ7LB6L78WoT/Mk1B/nrH7+rptpBZq2Zv8PTrMYhksPLDxHLriHWPYWWGmGtopF159SAdsr8atE3oH4LmFijk4/ibe8k7ER6OO0wfblNeXCAMMjoJMRphY6/L9s9nTdF09V1xUPxgp/ABPHBrAUArQb1PE/Rm0E0rim8UsCIJfNPFMxxc3wAthpntIt47RH58Oxt3rWPDFov+YZ2eIRjJSdOulBYqnZyvZ65M4VYQck/VkqER+E2AZkHKCskYbYQeN1MXv6rtQK4AVgKSKdHWT8TBMXX8eAI/ZeFou3BbLVnYa3HwaoQs2E5Wq3JUFdtVrVuRjr93Pndq8fM63qt3fKnmLNIcDBJgROWeaJ5kOtbWVF06RZoGOO2A7JeDhtJ0bQUjpIhmKWQX3I0AsX2E+oQXGm1V1jpDyMDtTOh4Ha9VquyqLsRDFvVO1u+ls1cQGPsapKb3zvBPs+Dug3kXJpR+WPCvTsfKJ8RbVONzNa0UNt8hxXTRph4IBXnZhBpKWWRavP0aGLj9x+jN/NgFbz/AR5Mm92XrnPrOM8E5jNC350fY9qa38cF/tYM9lug5AXi+z7f2w+/+5z9j6dtfwi1duITl5uv2sGlic8dIKJqDmnC9YNeACpiDIuI8MSY/44M9A5VTEJ+AzA7ouQNhv/XL1Wlx0N5LmNPOo3Lyvq/j+Qna9hA+DnW9TdOIMxzcnLYPDV/IO5oFjgYN22ex5FNfWaBu14ngEUcLhP8jWFgBR9YjQgsNjzY+q1x8HFCpfof9+x/lZ37mbdz9N7/NnptHGBg9z7PqPND5+/lLMQ2yXbCwJIshHqQSsFCGpfkWk0dXmVxaJrohz6zn01wqIzmtS60p9ELUFoUcXugzkwg/5HZEZ0BFci/RnkWmxW8CnwC6IL4DJjbDyseh/UGRHKYNfAmMDeBdB34cIUeqBywSvGYYQaMcBENUDINJZJ0dRhzdAmGUtki4Xo4G3xVGrcD3zrW7nzCprjrELSHR1SnEOVcV9+r1u4LzUlVlyeB4ik0B8FeIju67gduAP0eq+u8A7fXgP4igZiZwK2j94H8z+Ny7QNsC/lM2zBpwTIfbNPjWJkjY0N8SgTdNKSlXwSvR/NoXYfcbYHArlE8GiLhJKEx+NYISQ9itrPOpUluAUt5WG6rqs9wGtsN4EpwrYXkCw70Pt/49hK+0CaErOwgteQlBzW3otaDeA7UNyOZ38DnT5/92UyywGDJ1bkNw+gs9iQq7SiGPwhakxPQ4kvM4QJiCuWwvYK0pGotPcvCJfbzqHa8jmzGorFrYjQixeJ5YfQXf8/E8l3giSTSeplFbxfOCMM0F13XxfBfHdbBdnXjUJBaNY0VN7EaF+uoilVKJxaUVzq523JGOG6spJEoTIPI5plvo0RR6uoBXCmp/9IgkT9shrdHQNXJJk4VHv8hsu4GaAcl0lNJMhZJWIqKfxvWeYLa+wmpmAswMs7U8Dz+wj3ZNanef+tI9wDIkcuRHR+i54/W0YnuIJEeINR3cyhlivkljboHpaY+lZYv89l661oGZkL3cdaDdBisCuRxEEtBuiuZrswnJFkTjouSgmYF3EYXGsjBi3ab46dUi1BZdjIU6Cf0MWlca17PxDA1iCeIWZFOQz4Blg942hOmCRiSaYsNVr2XS76FSbbN08mnqex+C3TeRXH8lViKD50dg6kHaTgtiecitJ1qbJhZ32Xzla9hz509w14dupStgSxo+1FyfU7bHiVmXMyeLnHn6EFNHv8nkib2snjmKffa03DdTk5sb8YMKNy3cj/yX6emMAAXxt4ymxDHn9GVUXW8XuXjpsziQ1SSj3gZabsgcfLHLKPSi33Q7VV1nrFuAbOUfNwjxacVUDdL/EPxNKZmvEgafGcKCwU6vLkXo+Q4ULD72o/30Be9XWrRZwnjBDj779Ztg6YTPE993+NN/qHL1aJZExEAPfJJv3TfPXe99FW9/VZ4RJIbNIkPtEzYOVnIADvDvPv67fP3zT/PFv/4Wjz0wKSxt/3kCN9+nMnOWj3/stzkweZb/Z/16diSTpBIJErq+1vTlfFNcpDTCB1L91FTIm0D2h1rwv55g/OpnJ5l+4kHgXv7LY1F+53N/y56rx+khlD9Vq4dy2RTZpR6Mr5GQz55fkjHPdXczkYUbtgo4sDgnzfm6UrC8CEsnYXUR7LaQsQbjkNPluV8EpgPieMaQz14N7ufODKTT8HVbEjemDg0X5quS6FkJNCde0yW/X7FblEocU+Peu7r4xqNwehFqJXAnIdInWJwGVG1J+lALbtxkcHHV4GKViK5CUDrBWMVpULQ2JXHoEUpb6cHkyAY3ZNWXk6cejGgaSWIXgrt2OSn9wtaxUZ4T2UP4NCjvSCNkXmSRLs1JuflWHNIpoj0FYuk8RjxOsdTi7mdNrk/D9Ql4dXDUMtLvpJWGRFq0jS09TS6WZmt8GPI7eOCvV6ksHcMnCX4S0RWV89M0H98vgt8g9K0v2z+9rYATFWfD6gE/EkwhP/jeiZsAVKEugaVvJGlbCZKxLL6RwI36eFYLM54hOzpB3/gmNm/bzabdMDII+QJ05aBPEzxHsWIv1jp5pKoNyiIwpxJIjiSwfKSyaMqA4xWYWZVq5A15IZOWHMjkxe9qNiUZ7rQtms4mmq0GvuPLxLbr4M8itQaqoZYCX72O34PxOqd1pnoOjY73KBV35XB01q4kBFMyArpkNBlk39uSvVNgkWaBFwEvDokEssPdAs0D4D8k9xMLYaluQegqw4SSBKvI0ztKiI0Fa4eRBD8TfCWCe6+qilXyBMJUsBJAjXT8nkXi785M96WxVwgYayKh6K3n/nkFFo7Cu0/CV8dhyAoxF2UOMo16OTeAbXFuo66XAjMpv9khzFIoTFyZyubvGJUHz3rOUUL7Tx/YwK9/4Dfw/F8P1Tc17cLn5MNMs0X/plHG5zZwfDEB7nNL26/dOcTYkIGgRkuE6VkPKbb4Kux/HLwYXPVGCRCsd4G2C+iF+CcgrsQeFEqV5VxkspdzMwCiVtX2plltHOJbD03RMm7G7F9HYSTOcCAGVmmIVpxRhmYDWlGoV33mTrc5euJBvPYKE1hsI0WafhxcoljEsCgG0gkebbpokabJXsQ5vLjCjzrwt9z1gSi/93vv56Mfff25/1Y6F8+HnF+MBci8OQjdMSitwNEz0D0MZ1fgycNTfOf+vcS6hzl2T4Mv/OEhqs9+FRE2/afMlHYjwNhjF/jf6xAFrj0//MecBX4G+EXgPiiehYdvgKs2w/HboFQHvgf8BTijyPqq2AjLCPo0IO9lP/B6JMn1DOIgtxBPfxZZd/uRaasCzhphEnoYub815OHNIz5vHzKdcwi4ewJxxNvB35rBZxxCSJvV4G/SM0vYrl0ICbQX+GmkUn9vxzjYSG+sJxF/cBiYBuP7kHwflN8QHMsE7Scg/b+g9rPgngDtHyH9Yaj+WhzvVOC832LKuU8fhtkZEWVzVem/cuLvhfn1kNwAY2+BE5PBYJxCNi616agiUNXAQEXVKqytEyZdDhOGwrPAj8oNTV9LZORGRj74CU5/6hncxlMIFfm9yKq8GNzAPwA+BMf+DCkF6RRlu2yd9jqk9dld/GAFiwbihighkj/gB1Nb+r/N5s+e4pMf+TlededTDPZkcFqwUqmTyqbIO/0Yvk9leY5UyqTdztOqLFN1fHAcDMeXhCQejtNkbm6JbDZFVy5HzOii1WzS0jy8ZJRoXx5W5Y7olgCNABgQjQkJgCYUl3lOL6fEQB9+opuGnUI4OzXxBdwiREehPQm+gxWJ0T+2A2d2kvLiaVqNIoah82u/9yYac48yc2aGZ8/oXPPacQ7M1ZifmaFktyC2FW9jFGKB4/zQg4APsSxObJBlZ4wlp4dRM09XrEbTsPnzv7qb1kwKP74ObXgHNIvUS1kSGBgRcBxoNaUTcMsT/3d8J+inodEQrdcY4LgSUOiGsAyPnBbwxvNh605hzjVaDYrLq5yZW6J/fJ6px++mkDZ4+wd/iVQ/JLrAiEGrHeeKt3+YhSN/g1drkjNHuX5sjCuGtnFqapGT7SonSodhepyan5IPnTkO3T8JlXlIakTWD/LmN/4c7/ypAXYORMWV1zRMZFs43oYHpuHwQwu0i6dpFk+xMnuQ73/5j/FKDbA79vW+pNQNei6YjiCjqk+FAnwutQUqNLkBGN8MT04hzSSVNFzpJR7PQuR0tnfDUAryFuw/DZ+14ZQfHk8BUiqPF1gsYtBfiBHXwlY6ynI81xTXpg9pwbQdAREtZAtsEe5G64LjqWHMEra3bBEqHOnIvbufsKJNlfR3I9v5W96wnoGrh3jfrzzCZ9s38BYSXA1ousanP7mFRULV/WOIIlKWME+rzl1J0c8Ab3vXLt75+h388T3/mv/3FzdRL794w9YvfeYz3Hv33bznQx/mtz70Swz2dD+nrFVZlpC9p4iZZUJCCgQNrgjjmHVAljoSLWmQ2INtdq8dD0IeoR6M12lC5c1EcH3dQDoOO7fKZ17xan2Nq3QjMLot6BYOXLsRnI1wpgGnmpDKh5ilibhHW6xQcqGMqDRpiIu1EXidFeKgKx58fQmePAobNsGOjWEA+/X9sFyDrbulaGAiC/YsHNgPH/h5aETE3ZuzYflQcAIriEu0gNzMEqEWUA8yUVVvgblgQHzCLtAThPp5C8HxlgndnUjwWqsF9SISp6nZqR6gruAAl7qr3ivJNEKe+w/y3hQhP7tTt9FBboCiYKl62QyQBi0HyYKg+RELrBiaWcB1EzhODF2P09+TZPMGuCEZKoWBzLkkMt814MqeoB7Nhe+twmoDjMg6kpmbaLm7sO0GhhFH1yNo6KTSVSr1GnZzClqHkclzmSX7z2Oz4JelWmXtoVY6whCC+J3klLZopswfp1ZsQrofPdNNPD/KldfdzqadBdZPRNkyDrlxSESkAiEBxLQwynqpFkhusz08C1Y1+K4PDx2G+aK4Gv09sGUjOCnoTUIqDk0HyhV5KvqHpTHi7LIAtA0HGlVgqQU1A/ysdFItIQzVNVC1iewRqkryfFMomNqBFJtJZaxUnYYCLwO9QD0qJcSROJgp6U6maQLCOo5oO/pNQg2nbsmyxYL3ZHdAfQjsVfAVC2uCMM26FHzNIyu9j7CiBoFE2PKkshnKm6H0GuAvkKY1pwmVe9d33LkiYS29qq/vQ3ZEtZ5fOnuFgLHKpXhuOGrPwbG3wUPfhJuGBQdXpjIJmY53qr30YkHY8/Ns6mc1NZWP2Um063z35OFl+vqSFArPnwOJaJr4rJomjd09WFmC0jJoddi5A6KREAZ1KZPrc+ga1iEfhaUL6YzG0bQ2oSDnQcI2ngBl2NIAPy+vsd4K2k5ERzaKZBUUqNOZ4lWp3866tnlc9yke+eazHJ9sU7IjeMkc/SM3c+WO9Sy7SU5Mw3877HPi4Enq9VkMbYnBnhqH9qVpu22W5uc5+PBj1NxZ8tiYaFRpM0QXw4xgodOigk0VFwMHCwuLEWLMUKIhBQQvwb7EM/+wga/71/KG/5B9/pcpAqBqx3sxpkmiDR2svGSs5qeguAKP7p3i0UefZN++r6GZOubwm7B8ndxIL8XJ25AH+AyX5kFWRWkq4jrfIsjToayAuBy/Hnzv4geDgC5g6gHZiEyvJ6G8EZxbkPXxe8HrPol42hNIM657kUinBbwTaZT1QHCsYWSa1hHneCx4b4ywKUkZ2V/VPrIa/KzkCEAkEmYJ99sziHOtGpgMAO9C1uHp4FxVXkPZHyOA8zjCeP0jpI78NuQ2/Ezwukxw3qngtQ+C+whU/ytEfwHsXvCeAv9XoPpr4G0Fqm38p5tU/yaNd4sGXQfgyAk4/CPSnOzkAqBDAAAgAElEQVRxU1jCtVnYvgvcW6FyCKZ+Vy50cRkym+Dqm2RfcT9FWH5xH7IhtYKLUwWb6r7XkNBrEdlo3hz8/gAhh8kBboJaHPvEXiY/uxe3uTk43iJCcR4lLHJcBv47Mi8vN6c43xLAfwBehahTdHE+Ob8P+DHgf/BiKSi1BxYQUNdB7sbjl/aU/+WZZ+PVZvn2A0fYvHUL6XyKfE83zWaVqBUjopk4zSat5RWShk86blFLRGnVTKKGge/Z2LZLqVqjdPIY0ZF12FaUmlWjVKth+lGseBe5SJqN29O0dZdSsUx5qUw0IVI+PsIkra4+F4gFSHvzePUajWIWWbA6FqV2yLhr1hsceuxpEoU+qC1CQxzLymoU2+1Cz3p0bYxR2PEWtg/6pBfh+KzO8vL/z957h1l2XmW+vx1Ozqdyruqc1UHRkiVLlpOcZOwxYPCYGQODgYvBA8MzMMMdPBd8L/deMMkYc40BYznJBstBsiRbkmWrZYXOOVV1V06nTo473D/W/mqfbqm7JdlmhNF6nvN0ddU5++z97W9/31rvete7woTS0JGMEjJcLnSdgZ5BAulegt0DuMksc0tzHN73LLmFWVaWZmmUdNxiFawV3PIChYUY46Eo8Q6DeAbiKWG0uUEpxgmZUjbXNwSFFZEf6O6Hoi2xke3Kz+lhSA+KHxQKQ8yCHjNKqm+A5mQHp//uH6gv3kt2OIxzdgtdu29n8bBOIe/QqDnc9DqD4vhHmD98gMrUYT7z5++m4+ZfZ2jtrWzedgMOv0nDtag1itRyy9RL08TW7WDntTvZsCvLlusC3JHtYCRjEtOkVH0BUZs5ex6mJlosLSwSss4zO7mXyaPfZ+qpR3AKVbkI8Kvn4jHQDKg3oJLzNbNU/NJuqhLuh2HL0AzBSicCxL5UfGcYKZjZFoBkTWiJehr2XAOdDfjWPDw1L92XFlzZg1eQvScENCEUCtLb1UW7f6GmuOLOqBAHLi7j7MFvWanEsIaRlXASuSfb8FmqNhdTEUKIy6AYt29C0ov7piBlQKIbPn8SevrhmpjGjdkQf/uH19PqCF+Uo9+jaau7qMLfSvjcRmURfJWhBuLnt1I673lLgrftfpQ//f2P8Y1/+hoV6/wVh71aLvNPn/g4T3z1ET74K7/IL/3Czz7nPWqM1JQx2/5fxgcyVUTVQlyfXuC9v/tT3Pj+N7CyXGU6F+eWPT10IB6AiQBPrncNFaSmRpXYmvjSB7Ymx50BBoNyRgp/7PWIKVPIitUB9IchG4SYd/KKVxXSLlIOJIx4paqw1dL8FqMaEDPh+hEIh6A7JcezEbGt1iaY89gzT50EMwa7boLXvAHu6IAOD3cpB+DcBviGBntrcLKAzN8Y/iQMeie/gH+CKoFvIjd7p3dip9veV0BidIUnlPG6ogVhfQfMh6EyIfR/St6b4t7PP45gbJJgrJ9Yqpeeziynjz6Obed5cVJtafxovIGvQdY+KxX05XHq9binhRPDDKWwNQ09FMYIJwlqI/QO7GHPnVl2XhflmvUa16QgHoRJF77owlYNdmjiNWeRNSevwXINZnJw6EmYOwPR+EY23NBLcqSbW9/m8qoejf6IxPjnDIcjpx0unCgzuW+S/Q/+EcuFp7GdEq+Asv8rrIoEUaNIfHOpPp7ypFXQqFAf02teEyRkdDI2fA3XXdfJ+t0BRgY11iYhHZTca0C7eHY+X2TdLgRwqUqr+lz7WQU06HClSHLnepi0YbwGRy7AmcNCBtycgS06OAFoDcBsDxy3YMaC0wswfhbGj4K1Ao18H24wCq0a6I50GSt1QT0nyeOmapySw08eXQpWtzNjVXx46ZxW/F5PE9AIiHg3tmTiDdM7pAuNhkhJXHoMu4X0S9I9zlAQ6lFBnbGRmkC1lnTil8GqBJeKd6M+72jMQ8ztKBz8GZh8CzQfQBrZPI6wsdRdUfhYr3dcdX4KI1PX/sOxlwkYq/K3zzW3BfUT8IXPQ/INMLztue9pl4dUj9TlHgbwIccrNfJSxwFfpkADGi2wak3qhRJLF44zObVEPHgNHR1jV7pAijVYyNucOTbPxNQU+eUqtXwLKg32bdBxtRbJVIzrdu/kwoGnsHMXCLoVYbQ+r53Hb9t+GJl4l4xhBMRNOgFaCJlUqr5atT5T2QtFQwdo4brjTE5NMzk9S6G0iO0sceFkkaVygKZmYLTANJaw6jkWKkXGczmWqysEyNHVYTPUY7O1t4wZTmM5UIovMOR+n+OfaFK2XaoYOITZxDZGWEuZApOcwcFFw8TERCDsOoNYBHApoWFhcJrCC3gEVjh45iH+/qsW+7W1/Nr/9hPE4hFfbGXUe1u7zMmLMe+26Kan09IFJRsKy0WKuWWq1SWgSXDmXoyAjuY4SPjQQpBF+MEBWVVcdjmqTZNVJgTrEWTvDqSsPMlzJcV/QHsWAU/j4N4Hy5tA74TQHdBYRsr455FpNgJcg+yRzyLTdy3i0FqIgzuEpAgVuKraUSqaixKHdvAjPKX/qjpgtDfn8lQ7mPd+VhUqM8h8UMdWeQm879yCsGWbYG6F6Dug+DnkUUrh71EW4oxPeMdSjn4TnIfAfiO4m5HA9WsCyoq8qw4nAzj7ETbSYhoO9cD+o9CzHsxO6KxA7knoeivUkgLGMCIXY01DbgJO90mzPqcA7rx38hY+JbiFP+fadWLTELodWAPNpFdapTqUqbl1CLRtuG4vzeoi9K+B/CEBiDngDaJq2W15g/yKtZsSdbgZEePZyOUI+nUkudaJ3K+rA7IB5C6/Dn/qH/6hnPWPq7m4dpMn7v3/iL33P9G7fg/ReIB6NUSr5VJYWeHCyeMU5s6zbvsmdA1M08QJBDBdB7vRwrVtcBwSqQyxeIxQ0ETXLFwcXD2MqwNmi2SHieXWaFbr5Ftg1YWcadVFS9G+zP5TLTVxtZLnfF4SwLq+6KdrNagvHEdrhYhlo0TjfRQm5zh7KocRNHGDPZjpHqZzJrWlOYqLDYrLAWr2CKFkikAkRNDU6Nt1I81ICiOSJhCJs1yoU8gdprCQo1lvogWTEHUhYYnWgG5jlxapLHWhBTMYsYi47arKywQ3IEtzMAYxB+yGXLPr+dOOI0UA8YwAt2HP6Wo6YGgGmmFQWjGpL5dwaivkF/I88+g/0rlnJ4eeOMDc+XEcq0RX/68zsm0nyWQXi+cGWPzOecxgEiMSJdyRYfSanYyPn8FaKRJMxRi49iaufes6btiwhnXDcUaGRArL0rwcnw0TS3C0WGJx3mJ5tsj4sf3Uzj7B4vkj5KZOU815jMdwQPw0w4W015nAcoTx0XJlj1L6lM+dhj88s6CZh9w4sgi8lJh/EHEVeoGgd8MaOtSD0nGtPwzXd0B3GLZ0wFIAnCw0EzBjwuEnYWKOeCbGusE1dGnaqkS7svZQR3Fq1P8d/O1d+eBZfMilhdyfg/MwGIJ1aZ860N5OJND2PSEE4F0bFUk6S4ONKdEbDmnQNHVuGoozjazHqnGVqjIvIu5IP75urXI7TtiiDTjkyRDG8Yp0DI10xiCZ2cLr3/MTOOEgX/r0J7hSlYjrOKwsLLCyXOXeL34O163xrvf/AgndI1oj7kXHJWMG/hRrP7oK7ldcOHoeGkYH8cEONqyFvZMQTfpx0ox3rarvqaqVA5+1rMJwFWelgLCnYDGLALDdiGfZi7h2EcDSZdzVPWmDOS7SRzTwPWMVc6kCUgsBgTtDsKlTHjndgVNNIbV0p2FbXIgR9T5h5AfjEE3JfevxjlPXpEdxBejrgykXimWYSsH4hMiprCZP1GAqPQ0P0DVc6B+B2X1gLeIzaxVzp4VfneUAIV0kpqoxqOsiZLsKxl5CKf+xMB3I0j2whXCsC8OMUiiUcN0Xq7VotL1fzZj2ZkCKDRvwfw50gaOLlE84iWFGQIuhxfuJdg+wbVM/b7iph5HtEdKjJlZWnqkVDWZdaGjy/J4HkPCcJaRVQrkh+1Y2A9keMDIdZNJp1u1M85rdsDkFGa8KvhNYacLi7DIta5lGU8N1r4RKvGI/WnORh3IBeTCzSICptFDVaqkLVmIERDc2GCMWGyPRt5mOkbVs2jnE8PoAnX06iTSEg7LeqbXs+SJq95Kfbe9M1DqqzizIxe1OUGekeZUOYYnougPQ2wMTLakq0g2ZszFNgOFY0N+3tgZgIgRH4/B4EIrZDI1ijGbVwm44VHNp7FI/Tr0oeov1HFQmobkAdlIcMVftxsBqPxoVOyoYWamKq9KBCL7iubc5Og5o3prneKVRjg2tOv5zrkalCVbZB15177MBE7Qo1KuI/q/aTarIKt/j3duE6EiaYf+wOrJOZxHhcrsTgp0w9xpZAKgjqd52AlETIRzF8QEI1fnd8P72w7GXCRirdr4Wz1vw78I//y1siMH2ERhuS0tfurRd7oFoO9Sq/mu7w/Z8DFmz7XdK6mslX6Q8n6c4Nc3Zpx+k5lYYW9eD0OCe+10WUKq6zK7A2Smb/U8vcerAURqlFdxGFadU4r4HLlBolunt7+YX/z0cf/Rh3LCFk19+fmfdAE3bj7hQx69wtSCT9CwC3KripUF8IQehlruui0uJWrVBrZHDsg5w+Nh+njlwium5CrbTQSq5BoJhNCOAXitz5sQTlEuz1JmkZUzimEts2xFi/dYONozF2ZkpeN8ZxKZEecc0//yLLgdbUCNAiBSb2MIA65ljhgVP/NPFRcf0mpZqDGDSgU0TjToBZilSxr0qIHt86VGOL32fL3x/B+99zxsJhyMYCjBrv+EvAZN0234IRqCjH8pzUF7JUS3mUJ5YM/81BNSKITIcBuLGqvZkKnWgZsuLQYZV0dflTJX1DOLLErzxRRz/Rdr3EUA1CDwFuW9D9l0QuBWsAbA/j6x3St7JgMBOwAI3AlY3MkQV/C4fW/ApLyoqUHVzKlqo4Q+DKhtb9i5fAaZL3u8W2t6r1v0icD9CBelGmLIz+A0Ub0IkE2bA3AWxd0PxWWQRUdqySkpGNQED9DHvWElwngRrL0LjGEVu/XeQwLfThIgB5ytgRyAyCKE0HH0Q5rLQnYHublgYB80BrSbaO5E9UPsKMAGLJixqENzhDXATv59xDglxQ4hsQAC/eNRrj5h4Gxh9UDkO5RK+9oOyR4QdFdgqzQm7bQnQK7Z3zHOXnRavmEzDncCbgfcid+PybnkB0bvY6f0/x5Wfc9924sPoZ3jh8pD/Js11OXjf3zC0fRdGxyjReJbiUohay6aQzzM7PsGUXaVnsBc9AAEzjGMGcJt1HMdGs22CukFkcIhkOkEkGsIMugQDBjpRLNum3mwRCQeJWi2C6GBByxL2p+UIM/ZyViqD7/Ream2/c5pQGadWgfSODQSzXeQvzHHs0AWyQ1GS/T0kkxs5P+dgzy+ynKtTKUSxM6OEg1FAwzGDjFx3C4VciZZt0rQ1lnNl8qcOYDgGiY4+eka2UtYqtNwW6BG0iInTKOJUC9iNKJYTwdYQ6VZdfGXbkBI5wxSZsFgKCgUptbMt8cXLGmQHRTUp5PUGSOgiVdqyoBmFeG8XtdwIhUaFp59+jB2n8hx57HGmT30PU1tg010fJNPZRSDehZEdpauQp2f0GgKpLE4kyEC2j+X8EslQkVQszJqNN/Gun4uy3dTo0vwi2BlLmgrN113OTNpMXFiiXipQWJhmfP+DTD3+dZzygidua0gklIgI2IKDFkrg1rwAw2r4PIM6z18k8EOWLGhVoDDOS8d3Br2XhmQJ6o4XLGneDczCrgG4NgXdmwVgio9CqA+qIQKfC2M/9n3Mng4ywQ7BdLmYAal+bs95um0vxXhV1okf8vUiO9N9y5APOOiOQ3fWXP0OpRDnKTiuwl39SGymJN5fM+B7TwvIljzofcaTI111L2wEAN7DxUxUFzjiiEZgny7wWgd+EaxyS269+w6yvWn2732SfHGOUn6OVvMKK7Nd5lsPfZ3T504yfPNtjHVk6E8lCEXCq2DspS6rAjUVv6gd9qkB++bkGRzMwrXdECoAAb+BTN4b16ArrlUf8hy371Eq9a+aKCsGbgGou0ISDSMyw+qe1fEpIqoR86VggzINP31sIb0nVpqSD2jpYAUhocFwFBxNyA9nmnB8AV5vwGhAkjmBUWHlNzRoWNILxtX8+ZVGVLCuGYD6gDAfDwMP2FCtOdTnLbADUPGou0rNLYngAlHo7YTFsuAFq4RNv7RRbrzqmRpAUP90AHKK5amQ2vYR+nExE93oI9uzlXAwSK1SYnxyEmkY9ELiG+WYK5IQyCCqxmchfB1Hj72mBUGLooXSuC0LgjH0SIZgOEOqv49o9wa6R9fwxjel+YXboBqE8w7sa3p1hbrMqbQmObQjDuTrUKiAZUjzpKAjSYCxNdBcgmAgQV8f3HgDjNpQq0O5DK2GS7NZYX68wfTZC0yNH6VYWfIi1h+FRs0r9sJNsT6ryANtsapcroVABz2QQYsk0KNJIple+vs30rt2G33rh1i3DfpGpQLIDMoTrKoQLm0983x3WmFP7SrRal1tJwBeahp+UrE7CFsGZM0qeZ9XlI26LcmiTqDXgG0JmEvASD9YMaisiVPKiw+2lIe56V7qlQZ2o47WrOE2FnEWOnBKizi1Am7BxbVsL2fk7TBuwSMD1ET+wa0gUYcijSS56BlVcgSOtwK7liDMui4+hqU+156ea8iD6DTlPSZgOKC7ktxqqN3C8ybcBhJVZRAvYb2UQ8Q1P7MbxcdSYwhxzAT0rVDtg4YS1Z/Fj5zU7t9C1p4Msjsi58gZfI/hB1vHNfdH1VDgxZyEprlSv3wXwva6jL0ddv8UPPOT6nP+n9qv4kq5p0uv9lLC9fMdY3WMXLjvc//A7JmTNHLzJMMNwvFOrn/zT7J218Xam64LLi6TwDe/bdMquIymNe663UDzTtxuQn7KZdtNg8wtzBAKROhLD2KaJkYkRNmuMZ2fhUKbTo4OgR7Y/whs3XiFC72svRb4IIICxXDdFBKKzFBpfZ3HHtvHk0+dZzqnYUZ6MQwdbAu30mB0862cOH+C6dmzLM2dplyeYOMmh1tuS3DHHX1c33eH9x0XEHDmxEXf3KjDnWNweAlGrB5+ih28hdtZx6vR0FnkAl/lHk5zniYNTHQyZGlQZokcZRq4BJhihmO4qzy8q5mGxhNfn2HLtT0ku59n0ryEZKXripi2oUHDheUmzC7Cb773ozz75ENUGgcR9/4QF0MityPg+DTi7g8hK0MDWQR+mIzCFMK/+wPgBi4urvsRWRYRVvsp4JMw9CcQuhkqRZi9A5kSNYQC8Wew5i6RkKnlYfIbSP3hMWTtex1+baLlXY6SiFLpRYuLQdBlhKh5CllDVf4hh5cCv8K5vw9hpp4D/ivwK4ii//3Al5BH5lqkhDMP/K133G5k8XgMv5MHkD4Pej9YT0DxNu87Puid/x95/38bEl0tNuBr90Pn7bA1CQNNuOcU8AQMXQ/xITj+DWA/9N0MXdtFMf7xN4GjvP4YGJ8F+zyC9D7inVgeEertAL6Jj1grMPZXYfdd0JUAZxK+fQLsDyMU33aLAxvB+G2wP4TM1RdTcvZv0wzg7ciU2sGVKzIutpuRjb+A6Hlc3ZX3WrtxCvh9YC+v3KGrWt9Otr7mbXzgd/4HS7Ma4yfGmZkYZ2b8BEuzJxhdP0osmkBzYWF+H/m5syRCOvFwABObumWhhwMEw0ES0SBgYRhB5manOXp0H+nOMIOxFEuzRc6Pv4hqCOXd/wDEqRve8jrGdl1HZng75XAcqzRNs1qnWtdYIs7khRmadZtIKM62bds488wJ5udyNG2XrsEuZu75KK7VpGfzDex494eYKsPcbAnHdQmGAlTqEMpux+xIEewK0t2v0dkp+riBMGS6IJ6QwMV2oFyAp58SYkIgKDmlqSXYugnSWQhFhcwQjgiWWS9AaRrCLdj/jTKLh2eI549w7R23Mjd1mkqhjOaG2fSOW5g4o+G6QtolBh1xcGou2JDMaqzrg+2bYLBbtoUhPAzFlSX7AHBywaWQg0rOYXp5meXpg5w6dICzh54hd+ibUC4CLgQCkE7JBWJLgNGsw/kZGXil/qR6Wvyvd7NfmK1FkMn1SAHNk8gCtjEAd+6G4c0Q2SJZSW7jUnmxDcDsV75A6dAZYrVOlj/8foKGvuqst/dhUNwS8LVeL6e1dwB5HNYgu9B54FOPlLh3b5X//l972OX9PqDJ5+P4+VsV5CoeTQ1xQ0L4sNg0Uje0iAS2qi2Ix3NebZIVx+fhpIGHEe9ts3e8Bfw8sQIVVQV83nb52KfG+cyf/QKnD3/7BdwMsde8/0P85n/4ae561Z7VcVS4vtpLxvEL3QeR+d1CQuQZpMBoFnGPIkjV/RrEDVOs5TzC9D1qw/sDEu8qoAG8YN97VZFponvH+p4LpSZsD4hmYgUY1HzlikzbcdrbwKjiJZVjN/HTyHMWfPcUHH0WUmkYXSe+4nV9kDDkMw3Nk3O9ICzGbB8szUIk4EuFvqPbjxV1fCqEoiqcR6b95ybgaw9XefK3Z2HXGFyniz5GxjvRU4gLtQMJ5B9ANlzVB8ZEJtAC4hop2ncYmQQlYN95KDyJ+GFzCBNrheenzf/rNM2Ikei+iUoZ7PoKtFR33BciWeUBY6tPseLEh/ADACVi4j1hgYRsGkYQzBaEkujBDoKRAXpH9/A7n9zAbYMh1quvcOExGw7UYGlRsKBIRJiHoTBMTUKl4gFgYejshGwKEmEI6KJtXliShGIq5nLtWtg7DfuehlPH4NxRi/zh+3EnDkHlKLiHEd74KxIFL08zwRyDyDVo4V6S3WOEU52kuvq4edeNrF0XIzWsE+oFMjCUlWRxAh+ei3J1TpdKDqrcrPqdKnhX6x+8+B5HDlJkf7QAyw1RThrtlnVNMW/7EXTN1mCyCZ+chyOHxSezm5IIx4J8HoorUJx3saZs6oWjOKVFEaS1baiXBSi1mtAoQmMOWUlLyO6pJCAiMkKxCNghyc67uvhJSNNYeam1T6Gl7R2b2oUbVM2fDaSlaYAeBseAqiIXqj4pb4HtY7BBk42oC3/RV6UzajObRWL+Z1zgH4BPIcF8u6WQRf99CKFNCfzMIfjKUwhQ8QLul+s+7+19mTBjQXQsjyE6eZexB6VR0u1h+MqbIOU1w1B+rqJ+hy/z8UtNZc2VU6hu/6UjVVypMDU+xXe++mlqK7OEnBpJwyKMwWjfFpKxDi61xTIcmQEr1+CuHQFSMQPzktSJHhCttKeffYp9z5zie4/v48tf/BLd3T0s5BeolvPyAMDqWRmGy9oRr/HHSzLlfmwDDnJ+5mmOnXqaQ0cvUK7HqdRjVOtBLKBYKKLrDXp7Alx/ax/hyALn5x5l0+bz3PB+jdvXjhAIxAmF64TDZcTBUI7FcyEAx4XTRWG7rGMNd/MzDDBGkK3oREkzQidPcICjVChiouHQIkeeGk1a2FjYFHBfFMDgAg9+fJH4B5Nse21bYbBK0r7Ep0ApSJialGs9sxdi0QGy2QEqsxOIM6FuegJ4A3/8jT/ADcU4tu8kn/yt/xNpV9GeErgZuddzSNblcuZFnMQR8Pv5NFveBPx3hN4Z4l/E8ojfMQ38B5j5e9B+F9xxZEoMIkORBL4EFzKQ2QbhGHI5jyHrXhZZILuQIbS9Y0eQHUXVLKqaQlWnV0ZwyLz3mTl8z/9qAfG9CHb+USQv9DVEH1ZFH/PAUdCeguEvwNw5aJyCQAhu+j145p+h+iXkMQAKN4l0oNvuZ08ige7PI2DuQwhevtuQH3L/CGe2wMotSLj3KMzs97SeC8AxmB9BD68heMMo9e++GhG5XZILtP8K1r8dyv0wG0XguD4k/EwibTa+he/QusAyHP44GJ7TbKs+oFkubgdVAQ6D/YG2AX7FrmRDwFuRpzDDlRs9PteeBq4F/VUQ/m2ovo8Ki0zR5Dj+Ez2EEK4bSPCrsuzvQhRAXgFjr2ILR8mf7mHfiUn2bB6i1hyCcIpgqpfuNRvo6e3B1B3q1SWWy4foGuoirBkE0bCtKlahQCQQwAwEqFvip6biEVLpHkbHNlOvLeJo+nNWaDMbwkiGaTSjMDf3XOFYB+Qux1ml24No43SOwfIE6UyLaAxmzsPGW4aZP5sjP1tG13Xu/uV3kx3biB4boGIlqDOMEekAp4xmVYhbOimjQaGZp5xb4anp71E+fAJtYIjUmjWMrRtjrncQO5zA3LCT+MAoPXnQ3bMsnd7Hyr5nGdn5GmxjgHpFx2pFsWJRJqte8+oo5KqQTnuyBJqAsj3dMHlWEpmdnTASh7gLeh1aNlTKYHVIVVrLgboBRQtS10QJdo5ROTfAN48XSYZHiXaGiCajnCuAG4XOjJQfR7MQLENt0SKguWx/VZDrO6A/6PMpDDwgpwHH8zA9CyulAsW5BRbPTPDYgw9infgyVmUFq9kUnTVcCIYFSa5bML0sqLNdh+ryxfdOOf/gk71eTCz+Uj7zg1oY6DFhW1iYItuBbBQGM2CXYaUgZYvJHtodpyRwHbK7fPl1b+GodT/Vn/8l1h98nD/9yO/w6h2bV1mj6tLaTUG6iltyqR+eRNZOpeg3CPzGTTF+8poo/zgLzy7BrT2wrccHGhU3J4TH+sRvzLMF8VRr+JqvMcRr6sEP6dR63a6U1x4e3sJqcesquxR8zp5S07OBvA7v/6lhfvbN97D3qQk++tff49kHfgul/Xw52/u5v+E/fu0zvPqWW/jsvfeuFtYqUx0DOpAde4qLmVeqJYm6xqP4nb4vPU5Ah42ey3o/smdt8sZEpXAdLq4qjCCY5XxQ3l9CeryFgU2aDwaofh6q6h9vHNU+ptTm1dglDNgwAnpVHrlMRpoATuah5SU4RgaEB7WuXxhhNQOcUZEjuJCDoxdgqdvXES4joMS4971pZK7kgDWD8NM/Gea9rx/mzpDGTAiaBsR0yLlwXwEOLsDZM5D7NfwqXRXuaPjUa0UDzpBr348AACAASURBVCCTd8x7z0wvWCNQGfLOJuKN2I8DGNsJBHBtndL8eVzXEObcqtKy8kzg+Z3xBL7sgGK+emwKLQKBTkHjnYCUVbSKaMkOXC0AehDN8CL/UCepoWtYt+smfvE/B3lrT4AsMtp7XVh0JQFoNWH3sJyKo0kcF3TB6IBiQJJ563pgWIdpXZiy1QZ0xuHmLDz8NHznkSpfODLOyvg4K7l5yiuzVHPjUJ8GqwBuybt++OEKhL9iPzyzwBqH8hRuxcAOvovBsbu55vqb2HVHlMEhjWwSImFoepkktXaqKgiV9GuHeJQQnIIW27GmS6Nx9V6P570q3fJCTUeSiXsSUI7DnAPfmIXvnodmC8JRGF4DnSkIGkL87+iDG7JQLEK5ClXvBMZML2FqweKiwcqFzeTPbiR/ysFetCgtnqJVXcFpVqWastwPpSWo58Ep4rNkvaC9WgHSbbIC6kpL3siopItK07Vrsar3q3JZ1bW77nUkS4CWgGBayq5cQ5Bl+wlYiEEzA7MhcRj62m6a1faKIjhDFKi9E1zFnG7vvKFqYd4CdIsWlxYDpwP4K6ST9/1cEb+8ir2MwNgVBJj6Y+A3PGrzJW+pQe0sHPxr+MRWeOsgbGoTo3r+FmDPNeUkaW0v9RBp3t9tB5ZXYPbUERYmTrJ4/jhaeZ6wXSGgtdA1Ay3QydDW64hnuy86/tlJmdz9IQgNmXQmdcKh556ZpoFhagwODmAaUaKJNCt1g46wxcmpM5w6o7GyfL7trIXdnYmD0c6aqeLL6Fy15H6OVusR9h1cYXz6FMvFKVaK88wu1Kg1g7QsGcVYOMjwcAdLuTM42hIFa4KhtSHeHsoTC8LAUI3+7AqapuQllDMRxI9EnmsVR+VHw0ToJcIGdOJoBAiSZA27GOIIJfI4WLQoU6dCBYuWlwN6Hqnnq5jLV/d9hJ0zH2Bb49X+SljygsQwEL+YaX01U+91XNGcOjsLPT2QTsUIh5JoWpJ4dIh0xyil0jnyK5PAAo/vr/K22/u4dccYf9e7EXv+MXDVzK0iwCpcvQO9Kl8NA6/FWLMbLdKHteDA4lNI+v46xAtsb9j0IzYlbLYP+BmvDLeFrLfiq8kU8SIgqylNXWotxHHV8XFCNQSK+Nne7UPpxKqp106HqeIn4RVemMZn1F6OnFZBAOC/RYZtnNWmt2N/AAvzUsXvHhS5VKsl12qfh4nvQiuD0EUGgGlwZ7ynthNh3N6LUHxKCIWoF1g6B0tBmOyHeB9U49Lhz67CrgwczUKzCJEqbHo7HI+DfQZ3KYf1/UWv9EvNBRdYgEQGYjeDHoTpQ/gaDT0Im8nrskLNu8AHoRUDfQjSb4KNETj1ONRU0SbejbO9z7WBDq/YFa0XeAey1794NZQmMIftnqDWSnOMEp1YRBAmljqe6iauIf5GHnkM+hFw5CBC1nnFLmN2i/zEEZ78+/+DrR/5SxLZAE07TsMewIhG0GJxDN0mbOgEo1l0t4ldr9KwW0QTIUKtMHhJ/0g4RKlkUalU0THo6RpidqZCo1lDMy1iSakSAEDTcTVDKKCXSxSZEQgPQKQT7DyGaRKKpUgNDOPkIRMvEqDKzPkSS9N56k0LEkFIRnGzcdI9GYxwgvmiRr3VJKDpOGYQI+ww0tXFuXNHKU+doTG/hGsEsTQX09BoOQ7LhRqRkR2YiTSBjmEWchUcJ46maWj1HPbiCbTGLkyngn1+kWq+gp25lXo4DGEdsy44k66Lv2IYwtgIBKG7Ry4vGIRGXsbEAgIx6b3iuvJeCykxLlWh5ehoIZ1Yj8lAp4tbM3BaBqWmQWnBoS+lE4lqhGOQjMJgL2SGdDqAoQ7oDUvHYxfxNheA+SoslCCfd1iYXOTEuWMsnj1B/sQRike/C7lpKZXTQxBbS8/6HXSMbiOa6UHXdK67RidimgRdi2CrRhr4+EMTjB97isb5vaze2JfCjP1RsWnDSC7+EM8lq1kAmtTlGkHRB07rkDEEPbebYBXBziGaT+bquvPzyNb+rUILlqq4hWUmn/kOH/+Iw7G3vpk7fvo93OgdXv2jWD0qBHORXUbVEilXoLPt/erfWFhnJAhvqsBeA55dgFPTcN3ui4FGRVpUu6QiK6piyrr3ey+0I40v8bvaaMWFL0/Arh7oj8rxVeGNYvrGEBfG9r5TyTGseOcc1zSycRMn3sOrbogSMJMceKPJl/7hq1w4fYxGceZ5b1ejUmKhUmLv3r385m/8Bu/8wG+zdSBLRyyI611LJ777v+RdTwJxiaL4vaSaCGirxrCFzxiOIX6tcpnW4qf7283gYo8yCHRo4nbFEUCrX/PbfyrRpDPeZ1T7HAVMtKk1rmryNvDCmrDoc+qGsBR1TdaFQkkOmhiQexEw2+aOLqB0PA49A/4+aSLv1bzxwjuHgne/Ok3ojuskojpH98N3908Q7dK56+5h9iCqTNdEoBKDOQ0emobJo1A8ht9fUdUTDyAbcdEb5Jr3/+UlaJbwtQ9Ui7R/rSY0s3BkGEeP46DjuDZOrQGucs4vLcq+nCkoSvHjFSAbRjPimJE0jh6XZJDrghuDSADHNTHNCNFYls7+taT7uhjc3sf2m+PcNgAZU56JKe9sijWIhSEThc0GHLElCWHoMreyaZH+jnlff7IOJw/DyhxUV2xarQKPFnMcPzrPxOlpClMnaRUXcZp17FYJrbGA4+aQG69SAKrpzyv28jRLwAAXGit7mT66TKvwBBNHr+fWd9zFtusiDI74iaR2fVcFuKoknRKBs9te7WrJLv46pF4/SJtjtQ6HEVKY+vfOBCwPwZQDExrMFEQLPxUVlnePAUYUVkxYicFiVVzRbFIaLna6Gs0uWBwMMj8KM2tcFk+4zJwZpbTcRbVYodnIg5ESHVctChUXHzD10m9uFV88R0HToUtGROFHVtv72v+u9GJUWtT0cBNH2E5uQzYeIoI02xbYZ6CUBjcrJapKIVIdpomPKySBUQ1OxcG60zuPdjBW7eoepSage0ReA2pd0NgNTZVY+yJXx2+eay8jMBakDuRTwNvAGAIn9NwGayXIfxPueQQSr4LgCIx51dcvlHWkNm0VwF6U0XCh2WhQKJY4c3KZs08+zsr5gzRyZ+kf7qMVcNA0EzOSJNW/ja61GwmlhG3puiIAv7wiWbbhLo1IxnxBIF9vXwYtGGKmGiVRuUByqINAIs7iYpGFySOoTUzTIBGTAGf1YtT8vUq0XyxAubpErvgUe/fNcejkFE3bxgwEcNwgTcfFatUwjAad6RCbNnexPF+laS8TCefp6W0w1J8m5qm5infRbhqCYi0j9TrPZc4ppoBOgCApzEAPmiURkkmQEXbSy6PESWDRYJ5TWLRoYK3mVV+K8s4z059l/4Fr2bZlK2t2Z8GBltdcyUiC5on/25aAbAFvI9Y1GfPL3ULLhlIFZuYgFgNdcyUqJ0Qg4BKLj9BsiqKMZtg88s0L7OiKM9rloKUHYaEf3KQIzocciOuwUvZS/1cyVezQAPrQEzdDYg8Us4gbfSNSP/8vYMqzV9QTEPJ1GUGhbO9n1UNKddxYD4Sg3lZlTwRxXFWHPXWjg97n1e8qeJ1W8DvY1rjctJMFOMLVZV1KwJeBDyNTeV6OmbgZcqdZxTULB4QRq5lgnYELX0Lw7ziClE23HTOBoGKPAVMNOddESALiZ3JQNOFcUkqstJBk/PQLcOM2ODECHAAjD5mt0ma8eg9u6STWoSaYGbC7vA1vBZiD5izEtkPXnTD9eaSApYZfm5HwBkqxFp4FBsEYhsguyJYFBLooSFCh5SsO5Qu1ToT0fC0vPtxSU9xmCdxjuFaFpR2bSYyfoKdUWBXzUX1CpvG1YpeRabqCBN6R5x7+FbvEKkvTnHrw05x+z68wvGYd6WyMekNqXV1NxzVsTN0hmRqj2axRrVRotmrEAikCoQAtu0Wr2cQNmriuRa3eIhKMkIinudCwqDeq2G6TaMIHY52Wi1uzoHaFOnbdhHCScH+cRuE0gVCAZFcXQ+vX4LTC6KUJavOSwFueKmLGTELpCGZvByXLoWVVMJwquh7FajXRDQ1N09HNAJoJTbuB3axBrYJFA0IZXMOgYVksFyqYPRuIZrLosU6WlqtEYjFcLUQgnCSSzGKE4wK21lfQcovYKxXcWACnCVg6dhBaiVU5NhxHgt5MVnC9WsmhMFHBsaJELYOoKwwUq+WVsuvSS8OypXmqpkEkoZHtilOah/yCRWGxid2wGUxGiIUNMnHoj8GmfhgxDbrxO8FXgZIDCzacdWA5b7OyUGX+wjLnnznCqdOHWBo/Tm38GCxPEOvbTF8mRDYVw01uZs2e2+jbdD3xziFc3eDu14o/rvjL/cCjxhHyRhcVu04iFmD+zAHs1hUA9yvZjwKQjZlwZy/Mz4hAbjspT0P0b1Om0GnSFsRCXqcmS4IeJwfWFBgrQBYNgxga2/HElypNItUmtYALCxd48HP3MF0uUlmzDi3awbr1gyQiodWcuArT2iU3VWpRtcpQ4J0KetWwhHS4JQGVBOydgzMLMJATt6MzBsGQrI+qIFLlcGP4On9K97SIH0yn8AmPASDgwoUyDHcI0BdBjqvhtyoJIy6KUlxX59lEyB1mC6Kefl1Pb4J3vnkz17KZlVyAQ0/3kps9zsSpczSrBdxL2LLpVJJmo85f/PmfY667ntrujWwa6aOnv2+1iFuBqypXrQpF9bZrcbxzzHvn1cRnvKoxUZ7nWu+zKq6q44O67YJXBjL3k973xTU53oT3mYj3nhI+u1mxxC7tPu7iM81MDcIGdHhN2nQToqZoUGue8kXC+5wC2pUMhQl0RmEo6reIUJxLG7mHirhe9T6bRJrgmK7Lxx68wDMH5hneGmPPm2GzCT0VGAxC9waobgD9BBxJwVQAcnFoNkQztGnbYDaEklbyBmNeg6UGNM6CM+udhUoZ/GsGYw3QYhjBQfRAEBsHrCZOfRlcJaj7QiO2dgVO0YjV9CiamcAMZonEpVGkZkTQdBNHt7C81keRaIJsVy/rtu9kaGOGkWsCbNgpQOyiC+dsuOCA2YRaTipLdRPqDZisiqRvwBT+QjImcjlWEybnbA6cX+bcA2XKkzb1XItKeYnzc7NU5yaw8uNgHQeaBAh4eEJ7KqeJr6f2iu/8r8Fa1ZPMjZ9kbvxRYBw9mKJajZPbEqM7tY6RgTB6SEP3Yl1V+d6+Vqo1VOFLtL1HJaDasSfFu9TA1/Bpf2Ta2YJXsQCQ0eCGBJCQJNi+FhyYkryyY4qWf0CThEMyJMBspwYlXRIRvSGpGAjHYaoTprtgqk/jXEbDDXUSmEyjz9cpLoWwjJqXINEl0WRVvHJQhXaqXUPtiCrYV7A2+AQ+Bby2B/F623vVoBjysKJL+anmek2+1G7SBHcSGjmJjY2U+DOa5n+1wnvVJj6EZGwq20WOgU0IJqnYuQVktwiDqcuml/J+VeiBQkI2eh5HSmBfHMT+MgNjq4gM/B9C4PfAHoHm88w+Fw78J/jwr8HT74a/vkmS9i9korZrdKhNXyRh5SZbLZf5qTkO7H2cZx76IkZhkrhpkU1EMcnSMAwC8S7SA1u44a2/RCCLsGJcuQ+PPg437oGBPl70HhtNRNi0Zz2Ml+lev4s12++mc92/4+P/7dU4thSbaroQ3wwFehmId3UZc72H2gX2PQtPHarx9Ol5zHA/jQbYdRunaWOG6xCoomktgmaTQKLC8KbTvPHVaTojncjMO8dzAdh2CwB3IoVQz1z2vTGgkwh9Wo/fMLwFBiG62EWQDlJePn2Zc9hoF4lev/j4RNy8T/7xM0ztG+MT33oH1IWe79qQSnhOaBmKi5Bfgo5BMLshFJCN2m07UrvVGtIkwDBdDh6As+NzLOdzuG6dXP6fyeVLwPVoxu2E0lsoPjHDnyy1MDpCWI04Iq7aB/FNsP5WuC4EX3kSZj7L1SnvDYS+OU7r4HlEluA/IoXR/0JMWEV9sBDsN43c4DAih3U78pA9i+9pq2zUEEKpsfCpMHOIFx9GKgLSCFk4gNRiu8g6N+O977T3fQvIrvMEz78GvlApXgeJGoLeufcBn4BD70Xmqap3XIDsT4CVgeVjCOv1fuQW3IWIyYGccB04pwkgu3cBph34+hB8QoPpITiag+JB5Pk6A1TBOgqTW8DeCDwG5e/D4/8MO98HF056bX+fgvRnoPAwtL4GfAH4FhxZgZ5/D10/DfwX4AhyEsvAPUjt6RJ++RTAFFT3wUQPTDzkDWy71vGPQxndv6zdhbBiFejwQkqP2te240CZIkks9gSj3PWZ71P9lXfBdx7AxsVFHo39SE3Jo4jr8INk2f8tm9Vs8vFf+xC//tE/Yt323YR1DduJUanXcbQAppllw7rXM22VsZrLVGo5qlhYNtRLDVrNGoWFOeKZMLghHExaTo3zF87htmziMYi3IeNOsQ7Fuk+te/6TQq/nGRzpZ+pInqheoydpsWbtOzBT2znwtfs48uQBeW9LWA/pngjR/jEK8zUO5R4nke4jOXInIaOXoLdgV+s2933tEVLJUSLXjlEvV5k5fQamZsHScF0Dy9KoRjsJhbuwjSRO0ySQMghEBshufyeZbW8hng5j1yGU6aa5Q6NerhBxArRaUTQtSBRx+A2vQbGhe9X+TaguwuxJizOfP8LYW64hNhQl3AkdugTN4bgkRQMZqT6pF6FeF59GN8GOQcNosVIsoNl5GBilO26wexRuyEgdgHKTXNeXH59vueSLkK+5LE3XOHrgCN/5xleYvP8BiEZBa4JTR48Ms/19n+eDd4/x7uuDqyXWKgFSRAohLiBbmhJAGtu9jVJyGOu293Hr7n7+8r0byU2fgZdBfwZA6r3f/wsw+cfw3YLXOtyzTmBEhw0hCKcl26h5WgnzSxBJIFI2p8HtAG7G0aLMY3APHiDZ38W6td0c6zNwp8BxXY5+/escfeBhPrL13/Hpz36YV28YZlDXhenofbUC5NqbPCnXAi4ukb+UePEG4OZr4Ngw/P4j4hK8dY/LjiEIahrjSJ2QqYlEXB0hL6YQQC+BeKxF73fb8cmODpIj/+B2v7mY4kCcQYC9Nfi9moL4zFolfbbUhG8vwS39AhRnNPncMPAH/+MD5OwPcHpumQ+985eYOPwQzVqR9n4eN924m67OLJ++58v88a++h4dufDWvu/tuPvCbH2SNruOg4Woyhtd717Fa5Yenp+v9PIu4TkozWVkACZsX8ZtzqetIIfN80huPLL4cnGI193jXrthj5xA3LYsAnZu9YyWAiOurBqL541n1/jWRcdIAOyGeSB25rzMO9KcgqvnM5io+49X0rqOBBw7jg7+Wdx0ZV84jo0GvKx5SEGHhn3Vsvvjxv+DWn3g311y7lpUinMvCw3sh0+Fyy3WwR9P4yEZY2ghnfw7uc+H8CjxzL0zcV8e9fxzcRVY7GYI3emeRuKhdVO8la869DCwCbg9V2yQUiuDaFnaz5VVszfHSmtqoNEIXZriDcFyA2GTHOtK9o0QTnWjBEFW7Qb60RDyeIdPVQd9oJ2PbYc0eSCTlWXgYGPd6KWpVsGagvAhLBZdKTaQt5uakn0k0BkNDsHOXsLBnZ1wO7qvy1b//Ku7RJ2UDUtdj4HWELyBel0lrFVVQ3EjFEFHlga/Yvy4TluPDf/dFHv47SGV3cu0dn+Hnfncda8dMsgkNV9NW16ugdrHUjtn2am8w+Xyg2+o6rJb8Fhdjk6pB4AsJIi6xdUhzwxvGJKqbrgkLdrwijcdfr8MmA0jAVEJWpzCyP6gW7+GEVGQnx6AegeBJk8C5OJYTo7Q4jRvXBd3VG7BSE11YR6XHFvDLV9VaZ3FxVYBKq6kdq4qfelWCQerz3jHCKdH61AwRCG/p4ru5LcneW16qzWlBJQQL2z0df82XK6DtpnQhTsEMUBgD/gyJ4FT16SIion+zaJmEEaJsF16xaBRytyM7cJMXqiGr7GXUwKvdgsBvIKDSzZf/XAgi62HgZ+Hgh0S0/WrWrtux+jsXqrbLoafmOfDgp5g+9i3Kc/sZyGaIGhECAZNAOES8cy3pwa2MbLuVoS3XEe0NCWtSg4UleOxJePPtIgSuK8/yRdj0QoUvPXgGa/Fp1u6+g7E1o/RGawzu/HVa81+F1jzBINx0O3zqr2Fs5OrHXBqHfV+He09CuRXCcmI4JGjYBsFIBA0HnTqx1ALX39bDDesDbOxpoOkXCARdDE1DX72Oq2X2gsB7kEXsHAIT+FarQTYLmTq8k3fyP/WPkVrbhbaiiffkqVr/P7wXKBElwAwXmGSRIjkKVJjFYglxNl8I6BAkywDv5AL/iIPFjrV38D9/9QHe9Mug5yVLmluRJiNVT/9A16DqwIUmDAzDmmF/vlx6Sy0Xphbge/sdvvf4eR76xpeYHj9OrTCJuAIuhO5mw7af48mH38g/TsC9n8/x1AMz1A8dhHXbIT1KdmeazT9rEkvB0+8/x8oznwX+kCv3Q5cSIeG//TrSq30zF+fjfkSmOhKGvVcQv/5MKZu7SN+wLQjNYhpZ6TNIFJJGAsFZpBreQMDPQYhmZANJaXDiAqwoqt8+xONWHSE+h99xY633t5r3+70/wPXtQIYyiPTBmkWabV2H1J7/N9BqSBWGSoJ3Ism0boRdC/IHDaFPOYDliH4BT0L0HTCkQa0CFyYQlc8isFNOwPgW2K9GHNM88Bh0fRpKB6D+MPAl0N4O7msRTdiPet9pgPYGCLwbukNQMaH6aWjch2xuu5Fw7FK9hhBy81Z4RQ/2B7dfA+5GmLHKqblafu404roMI8GtepJNTEhcj/uGD/NE6Qx/+c1f4gH8Mijl7r/CvfgBTTPpedNvcd0b38qdr7uJQ89CLrdIMBgik06wcdDlyOPfZXFmL8XCMWrNMq5rEHChVc6zNHmSzt4EmBESyQwdnZ1MT82SX5mmUctRLxeZPu4HZmZIo2sowvy5Ko4DoIMZpffmW1lZyNNYmsMozrDr595BWIOezo309e0hb8aYO3uI4sJZVqZOcPrxh6ABA/0xurqSxGNZFhpBkqMb6d10HaN7Xs9SwWVicoZWyyFghggFQDPD6IEwjmuSmy9xbuIktVoZ13UJhxJUyw00LxjOJvtJRyKEoiF0zcR0TcY6K2Soork6pUqD7z35XWI9N5EPD1FPpEmOQGcfdA0IMaFZgW/8DaxbK4nQpUWXeNQm3WGAqeGGoGMNkIaObkjEoVERRu1KAapVqV6p5qRa3lpx0Qsub77F5a1bddbENToMAX11/AKKSRfmV8BtQi1fZW58hq9+5TucOHWAlcVpWvll3FJNmiEGQvSOreHvv/I3JNMx+kM6PaZ2kb6mSgq3qwA6yCp80oKW7ZJ0XV5l6PzfDxW4/xP/Owe+8qc/+vn7QiylwU9E4L/8IfzVV+Czj0icsRvZQ3cY8PqI1HmneyDk8S6XShBIgxGDYBKSoxB5A+jb0BhYZR7+sgtvbDXZXKtwzoFfPXaIfffeCx/9CzCCRGNhEm/+z2x97+/x8JsuPjXltbQHBKq8XnHLTHzgW/FpQt5nbUeYk98EPvUPyywvObz7XV3kLNg4COvjUq1QRu6dUkxSbE0vT0AU2SEVk1MV9ag13MEvu+/E769sITu1UgMteP86ruRg9xVgSxyGg/76XvQuOOQ6BMpV9i5Y/O2f/F988WP/LwrEufm23axbP0RxKc/eb3+XQkPD0QKkOzu555mz7MkGSF4S/6jy2fbGWercZ5BwVxGClLXP6yoSQrsIoOpc8lKJCVWTcxbZ6zq8vxfwe6+GELdpQY2zI8/JrjayQwPxSBa8MR/j4sKqEgKszrsC7qa8zynelZL1d733xRFvptF2TnXvnn6nJImerhCMuHDCleOlNIi6LgvFGp2BIKmAQcTQWNbgeAFOHHc4e8hhqN+gd0RjsB8GO6HPFYD52RY8XnD5pzMOB7/j4DwDHJuB408g6dUjiNO7gPDoV5CH70okl5ezpYBBAvEurKaNa+XBUW3wXgwQqyF3qw/IomlZ4skBuvv7iXavI9q1lmx2CC3ThZEyCCc0MnGXWsslFNFI9mgMrNO5YRCCpjQpUmzneRdOzcLJCTh1BM4dgvLiEk55hYhdomWUCbgBXM2koRuYbpjiwgSthf3YC4/Tah4Ee5BM90bS3WOAQTE3Q3nlAo3aAjKrVBDk4qcOSsjsLD/3cv9/9t47TI7zOvP9VeicJvTkgBnkSALMOYlUImWRlGSt5JVs2ZZl2fKuru+u1951uvK9DvLjuI8tr72WZFmyLFk5i8kSKSYQIAIHeTAAJoeeDtOpurvC/ePUh2owmaIoy/TiPE8/GHRXV1d99YXzvec977lorz7TDEwzQTg6xPi1/41Lb7yD171xkD2XQqcu85jCCVQJq+fbhb/ozlwpx6lC0CpVw0QmsZcZu1E5jS6yFpU92O/BfVOQ7IGNaXi9L++i8F61VzmNr6/uyU8/UYf9h2DiaVg45bFypIXnaRiaRth1qC8eg4VjUF4Bu4KslDmC1UTdlHqp8mWKlVBrawwV4sxyvjSmnoHOXsgkRS5A8w+zHQzDQfNcnIaHV61KdTK7KWCh9lYY7ISBcCCgriQLFF25hEBXZz3JYmUbslo2/QPuBH4HuESG+3ZkkfIlCzmFaOR6vwf8LRKQetaz+LdfwKvdmsCXkN4YRpb4516/14D6GYvpTxX4SaufX/kJjd0bX/ym2lOcACoWLC6scPixhznzxAOsnN5Lo3SOsFZCa4ITbmJEUxipTgbW7WT9ja+lY3CMWCZyXirg5DnIr8JlIy8fiAXIF8t8+f4nyE98lp/IbGZk3XpS6Shv/fD7uP9DE+SO57HtFkcPSSTvhcx14Qsfhb2HYSUP0YhGyRygZYfxPA9db5GK1+geqDK+McKG9RH6w31k+1pk02skYnUu1Ot4KWYgCNkQAb/hwPMeqQGmGSaeTkuq9l5EDn+YzgAAIABJREFUv5UWLaZpsYZHnTBRoph42Gg4eLjnU6teKujg4LJGDZcEHiXOLh7jjz/5P7j9536TWCZCJAydCajUYbkg6ZGRMPT2g9ES9YAXA1B0DTrSsG27xsTRDHbLodlQV+i3idmDHe1gJRPhK/vhxHSMphUG14LFc5A3aaU9CvO9lM5Cs1JEfnUDsr17IadGzdAfAG5D3OofcsqTQSCYo6pAqN1MexaBovAnCAJe/QS5gUVkt6OqOqhjRqE7A1ET5moif1vdj/iveaRJNvnnWUDmyUn/GsaRifQgF7J9XqrFkMWu5l+brzvOiP9bE8jcqgOrsrE/L89wO0KtOY6Qlc+bLlpEjSr0pAQlaEShkIXaY1DfBW4SIhlozCHM5h3SIM5HgLdCcheEClD4FJS+DYlhiF4OxXPgPQ7xq8EdBOtaBIF2wDsokYLaz0j+nOP4jewiy2tSGvt8OWAljn6xMNcrZYpBp7gRSZ4/TGIjW7M80gU3EWTSaIgrfw6bR8pH4JnjHLFzPIw4SBftFTbPJr//i5xJuBwdHCWVGMRtxYhGTbq6NNI9MLR+G7a9jGUt06hXMKJhaDUIhU16+/uJhZucmVrA6qzRm43TaBRJdsaJJg2i0QTexhK5XJnenm76+ztJZlxy56ZwXT9ZzbEoHT9Ey2qBVUPXINuxmZ6u9WQ61xNPj1BrVUn3rieW7CDTO0Is3c/UsaOs5WewzhWIGVWiIR2te5xW2SE/s8LEsVlcPURHtodsTz/N2hqVtRZmxMZxGsw8cwBrYRY3FseLxmlYVQjH8ewGrl0Dw6Hl1NE9MEMhDCNGxapSmzlA2isS9epsNZaZW0zhRC1whomPD0AFSjNQDQsA67UgZIskabpTY7DfxLahakGjCZW8LI1OAyop0Yvs6IZ42peGaULGEYJnz0aN0YTGLX0wmoKkKUtDA5my12yoOrKRaFbg2IEjTB0/wZmTJzj+zClKlWValSKUS1CrMHDZ9WzZcQXXXHkVl/WlMQ3ZZCmfskagZOh68OS8YJVuCKq6jOEdcYhFNAw0UsCVl2c4PBzl4I+iPz+f1Tx4qA4fug6uWYTlGXh4UtY6DUHKCg2paFSvQs0CMwLxiLB7PQsaDqzYkO6EhI1XmMD6wt/RqMaYe+PPM7n5SiLRMFvD8Ls7dnEukWb6quv4M6D2N39M4/g3Ofh7p3nn36/nNX/8Qa7vzbDtWa6LYjIGASlZek2CcKECVFXCjatDMiwiTY2bkzx+bI2//9gzdGwaY2k4Rn6dCRvgEk0IMg2E1HKcAHhVBd4gSNpRoG+CQCcwhcjuNhBgVQGvyi1SoLGB3EBSlxTomCG/VUY2vyGE0BHSdMLpJHvC8P6f+Qmu2L2NBx49g74yRbOxyNEj51iaW6Bed2nZHrZnk1tc4Hd+/l285cffwfVX7Gb3pnU4wL7pFomETm+3gYmsRXGCetVpAtaWsgtSZbmQPKT596HS+puIO1chkGtQCdnNtu8NEwC2y0icuogU2NpgiItYAApNKKzBUhG0LtGObkUCvV389o4BGzRx00yCJCYlU6AIGgpsTyN75RAyNhfx5UT8TFP1+ZTmZ5tasLiscetwHE0PtuBVpOs3yjUWp3Icf/IkeqTCpVds4/prtzGwXZi6GyMQ79LYtd2g0m1QuwnOzWfZO3ktZWs7+crtNCt5WoUV5mcsOPgxqL+aFd2bQB7HquI5TfDqBPzm79eUyIaJpocwU3HSPYNkBjaQ6NlILJ2ERAgzoxGKyVjP9EL/esj2QE8atvjag0qmdwHIt6Bmg2nA6JjH7BMujdOHqc4fouwU8fQGOhU8mjh44Bq0rAZeYwkaM0gPKFJdO0GruQCYtBotWs0G0vvaikJfwONv1728aK968xzs1hp2q8XZp/+C0uy3OfPYZt7ytg9w7fUZ1g2GyPoC2+0yBC/ZlGrcmgerLtg1/Ai9n6aQkrShFBdWXnwJpuZvtRZpGmzzoN4HpYjgHo9UIG7ASAJ6QzIvgqxtLURppQAU/DSgVL9fm8syqaxpOJZGGIOwOU5Vd3HWetFbTRxGIX8Wmkt+tkCdIA9GCcu0h7TttqtV3lYImWtq4JnQqIuMqRdG00x0UwLGhimhW7tZlz2vZ8j+21sFvgO5W8HtlYVuIxfqI2nI4tANrGkwG0awlY8jm38XAavmgA2SmlUjYNaq2jj1BHh7gBsR/diXZv9GwViAE0ivUzHr3QSJMYF5VWhMOPyTt8qWdJr6zWE274JelV31LFMDxPM8CoUKM7OLnDt5ghOPPUDu8FdwKjkMvUk0pUl3iEaJdPSSGdrK8M7L6du8lXA8IY6iB6VVqFRFNmDdkMgIvFxSYrVc5tC+feSP7+cN+TxNx6VpGrz5x67gwMf3kDuXw62fY2WxxeEjkMrAUH/w/UJBigydOgVf/DwcPh2iaYYY3xkhnIzRaLnE4k26e+tsX6fT1ddi/RaXzZsdegkRiI2/3JRkg4Aq+cLaCS6ghXXCnVGhKSzAWrPK6soSOR6lxhoGNk08dBw8bBwcbLzzNZte6hLn0qLCLJ4/6krVZR49/Dlmzv53RsYiRFOyx2iUIGyB1oJQCBJdkHUhEX9+eFNhjq4jm8VMBhLJGJ5j4bTaK0h1gZukUvX4yt46pxajlFphvGgKUt1CwS2XaUzmyD3s4VQaNAqHEDRQQ9xP5Wq2g2RhxLW9DcnnH+dCJa8fkqmglhIqi/qXmGp7X2m/dhAIVirhNp2APlJoO18n0mQF0HOyGS+pSNMKMv8d88+tsMQm0gRV/+8p/3yLyPweRWIDUxBULH4RsFpljQ37vzXjn+cSpLln/feeHQgJAzchIPBz5BBUJcgF0NLSsZIxCA3C8pcFbQiPyy5tpUcawuwHMwrWoDRoKCspo2yA5sMQeyOEhiF+M9Q+LDes9SNRPEUHXhTko3YXOHFZuEgiq32BQERXTVhqYXw5TvRFez6rIf5VDXHXny+sVUU28arcQw/SpT3O9xqmkSJc91HCnXmEBa/GHIGSkkrsuQihvzLWWjrO0uEOJvo3c93t72KoL0w4ohNLgKtrxDp6yPRsoFbLU6+uEYnq1BtVGlYVu9aERoVSLo+hebjNCoXVFXqHM6RSIVKxNOl0CDNh0tvTTV9fJ6ZeRzuffuKBZ1NfCkSnvXCE8vQSpjuMFgYjbRIOJensX4/nDOI2a3T0juPEelg7tp/G/BRWrUTUcPEcj/pahaUzZ5g/M0N3/zBGdy+RUIRQPE25UMRpuLQaFqXVOWhahNIdGPE0nmcS7ejG9WxM08B2bCzHpmVphLQYbihEhaj4xV6DbMiip7uTxRUdDQdcB7cFdh1alp9NZkCmG2zbTxLw77Feg2bTZ82VwK2BbYFVFrmCaEIkgzIhSHiQCsFgGAZTMN4pMV2V0m4BTQ8WHKg0oFZpsrq4zNTEHIeePsSZ05MsLM5QXFoGpwqNGjRraNEo63ddxY0338Jrr76EbgPylvj+euj806FYqtOwXCwtyhlLJ2tqRExoeTKL9iMgj1LjyXZDsn2//qO2FnDOg4PHIWHAriE4PBmgc5onN5PaBaX9InLsxaSyBy1J+2vVoJqHlgnNOkw34HOfxqvEOZG9hJCTotCKMb5nlFs7urB2d3Fm9x4mgfLKafKHjrE8vco/PrFG4VvfIt+3juXufnZdNXYeE1bzWogLa3dCoAOq9E5jBPU8TWTZ37UpQoEIe/fZrI94VItwuFZlbbbAlluGWLQ0Gjq4YZl/w8jzNlvQE4VVU/RPVVCsHWZRDNr2tFMFHisQU3nDim0a0iAWCYo4Kz3aGIF0XR6Rwtu2ZydDGzeR7Jti7ewpHn3oy0ydmGJ5YQnPCfxfx7b5zpc+QygcoZRfoVa6jP7RdRQacZxoiIQDGeO5MoSKSayYsu3ZFQ4Ckqq02nYCiwJW9bZjNYKC1Oel3/z3FeirfPa0+lwTUDpJAOZ6HpgOpD1xByP+b5kE7qbyYmz/e6sEXq9i17oESa7Kg1Z/q0TX4VDQ5g2fYRsCynU4cAa6G5DohmQCOnzd4ZgBvR0wOuLiWE2e+ucncCp1uhJJrt8u/OJOJCC0vUNI5GVgqpogu5SgXIdcBfILFRZOrJArT9AyDLxXNWAnWoqurf5+uQCkGmH+UzFCGOEoZjSJHkmgheMY0SiEIRyVwm6aBx09MDAEPZ1SRC5DMDYVDy/mSTHtdBeUuuDx2ir2ygmai/t9mYEm4oVZBArWobazSEm5prVGq+EQCieJRBLEIilwDRoW1JslAmES5Y21j7iL9u/H6lRzT1HNHWXhxCgdxhiV1QG2bx1k+/gYY8NJQklN5Ev/JVOUVZsgsmUBDU8cJMcfDzqB6LZGQH76F7Am71kv1bt1oE+DS9OQ8yQYVnQhp0kdLM/z52hkbu9A5rYWMKTJG5F1EA9r5MIauUWoFkCraditDIRTEHFA9yDcJ9WtK7NgTSMsWaWnrLRl2+smKOhYhTSV6rha4Zsifus0wdbB0NFCBmiiGeupalC2IZF/yggoEIH6ThH41uIB01hFefHbN42ffatB8Q3gTfrXOUOwkvnXqjh37ZesgQgX7QG+wkvF0/4Ng7EgVLMJJE/44whF7dkc7Sh4gzDxPf7fX97BQ/d08cG/hLu6IWxKiv35bY4HnufiuR6O0+LQweMc+O5XWD75FLHaPJHmEo7uYoR0oiGTSKKH9OBWutddxtC2m1h/y81omuZX+vVYs10mntHZuEljaPgHu1MPaNVKrB59BCgTMixs3WbZCXN3HD6y/s2cPAXumc8Cef7y4x6WDe+4V8M0dBoNh0MH4JvfgA//kZxz+2Up1m/opKOng6Wls1S8NTpGWlx1m87P3DLgg9VlBO36Qc3FLxeK9Mi1Cz5tX5ZaSNSbLEIDa8FZfY7vrDzCfv6OOAVSfjzfo4GHTRMXC+/7TsX1sGgwQbDQt3DdMzzwpRZ3vd1ldIMOMeiKQVf/hXPbNv/CXf/CNXUjbfdUa0KpDvmSgLLYZXCKyKzqgtaLZodZnSny3/6fFa54yyBOKc5idRDbuxHOFsFq0pwtsvy/zoKzAHwa0d1dReJSaqZW6S4aMpNch6SmK9f5X8HUpBMmEAiL4wtw+Zei5lDl+XpI16gSlO4FydJaQGb6LIIRfgVW5pBdyRpwM3AtcrtHgCeRHMQrEBWTO/3zfwXRbH0bMgda/useD/7ckeIjohfQdiPPMpW39yaE3aoWx6Z/f6rqBVyYnxoCLkcmcbXO4N+/U/VlCQ7Bsg3Rm2BgDDaPwreegHwCuh0YXA8rb5AbSdiQ+nGY/RlgGexpaK4D/jPwASgNQvwOGLwbTv8J1FRZ7CH/YvxR4lXAegh4i//ZEMIBgudLn7hor6yVkW6sqnQ/O1JuIzGGSWSU7yQoxGIjcYgvInqwR/D9tNpnzjtUUf+8ChxQ9Tsvuv8/uOVOPEFl/hSXXn4ne67tRjdNClWPhTxUG5Dq20konqVYbpEIL1JZOcfy7FlmJqbp7hFgES9OvZRnYWae7o4GqYEkmYEkodAg3b192C7YODRr1ovKidrNBo9++q9g5Co2XXMrl938WvqyW+ga2oCua3i2g91o0N03RmFsE6uTB1k6dUDSu8MxGqVVastF3IZG2OjHsS3KlQojo+Pk1zya9QYtp068Nw6jI6S6h4kkunAcg3iiA6tpYTVsavUGTQ8aNZtQKkbK1Ah1dmGP3IKpFTFCVTKhBOGOBGEvTTMUZ7kA2U7JFtIM0Y0d3wGzR6FaAdcQLLRWhURK9PDtqodreTgRDzcBZo/BWgjG+2GkA9YlZKx0ImNAAUuu5xNLkGk8X/WwKi752Tzf+sK3+fpn/kHAuniUWDoONKWqqSWKk7EdV3P5ta/npivGuWaDnHRiVRi3Y5mAOHHkzAon55sUQ8NkdkfozMBIWJawSaTYk+v5YS5NSBytH5ZkoEItX479wbvhnltgICuN2CIIrIZNMO6GyhGYOwNrhh+UjIquV6MFxTyUc7A6AUcdcdOp8dTQ15k8Osfp1nq273ov14QMujT5+t8D9n/6dZ4GvpHL86d/9Nd851f/Lx50drPpqjfxZ//0s1xtmsRMTYgNBMmLLr6kGDKvRn2GZAVhmCqZAX+vyJoHXRvT/PaH9nA78Kf74atfO8uXPvckrznwTh7OQzIKW7oCfeEnV+FoEfqGIZWC7Zq4Hr2Ie6LS3utIbPZqAkJxJ9L3FCCo+iUEqfZKAc9s+0xpmtb8cy7Z0KvDumSE979pG4+f3capo6cxWgfJJnTm1tznPPL7P/sJ9j3yEF/ecyXvfO/Pc9ut1xKORWk1odsPiKvvqETRBBcCy00CL3MTAQu5LUx0viRLliC+rpKj+gkgKAWit7ObNxHozXYSgKE9iK70YI/UIm3HGZYIAG+lvej4708jcfk3+NeD/5xshMqg3DMl9NXhf67WWLVbmfDvZTMQrsP8SfjwXrjqeti8EUZ65ZpG0jB8ZZLdlycpVNbzSzd8lnMHCxzI1Cnf81M0dB1d0whpAp6oIT8ah9FxMD3Aczl+3Oa+s2UOTu6n2Ky8ysFYFVp4JcwHaAwPzQyjeyHqTYfWWoWqUSDiC65HDA0zKrKE/WNSqC/rj9M60jdmESb2TmAkAvFuaHW4PN5qUc0dpFk9Ad4ssmI00TSZSEW2UZX6U/sFCw0DTe8hFBqjs3uI3r5uYqaB22iyNLfITL6C5yneuEqvbqfdXbR/f1bFcY7xza+9h29+bYiNm17P7Xe8j194x3bGd0aIJnV0XQ+KrcNz12qBJAJtG1WlPAo0EhDTINKG6pYJMMxeXlJhL1UQU41UxTONIhSuUU3wmFqPjJuiC/Oe/D2AJKP2aYEUTyUJ00k4PQLHWnD8aZifgeV5WDgNq2fBK1ShXMJxTciOQd8gWnQcbXkazZsHqnjeIp63gOfUCFS/VfhPFfxSzFi4YDyFPQFkbQ3PAUez8GwHNB0NDbwwNB1w8wiIuoCAE6egHoKF9UKVT2pBZUdFyO3w/21p8OR2aL4HwR4/gdBphxG5BL8RVb0xh7ZFfwjJcO32f/tfdtL+jYOxIIjK9xDq2W8A73ueYzTgBqDF41+uc+A7Lld9KMHv/Tjs6hVnB8SRmz+1xNSBCfZ9+++YOPA1ejrC9HSk6EglqYRGCOkxorE4yUwKYgMM7bqV0V1XMLrzUn/ChnIL5hYt7vv7I/zML11KIvWDC7BLcKSOiIF7JEJhqishHtwPt98LV9x2O6WixcG5Z6C5yMNfn8b1DPL08J/fdh0/9h++zKF9dVYVxpIJcWyyyOnZAl398NP/xePdt6UZ6w2jG6r+9itpSuvjq0hnvTAspMiQHuJIl5TnXJTXWr3JSfJ8he9xD8OY6FSxsWnQpIJGizDyLKMEde3+Zd1YB19dOXjHcfngb/0to5fcy+iGcUB6WbvzrL5ZrEKpBnYCui2IN0GzoWyLxIUXlesoVvwK0HoGtCRS3f4GGP1pNt1yDRuv28haTWfyGBSnwS7rYCdhSz+dm0GLQn7OgfuPg/09BNVT4bAKF/Le+oCfQEC2F6ne9sMwpcCg6Aov5kdayO5EeeMRglLDirnaizBKC8guZRGJwQwCn0TmsxzBLgDgzchc9yTwUQSs3YRouv4Fkh1wNfJg/sQD5xtIn+whELR9AVsF/qDtt0pIZaT2+9QR8PV42/38PvBzwKOIwgrAu4H9HXCohkzIUZi2pU3Wm+C9V06wegTy/wz8tfxQKQRlAxJvhtrPQvmToK0D4z+BMw58HmoH4fQHwBvzf7QIvB14PwLmr/gX9kX/YvMEWjwX7V/DFpENYxHZqD7b7kfw+yuRJVvNPStIKbY/RjYWLtJjMwSFWOIERYQUC8lEXIYi8rQv2g9mVrnEX//snQx//lN0DW9hacnlu/tWqVrQm03S1z3IruvezbmJTxI1I8QMAd+GhuPkChZNe5WZuSK3XDvKQG+U3t4WieQSTz51hH2HYXDdCNlshlPPnMBxXgKiVrTR1jRCToRYzCYRM9A0E9cFMx4jmb2MdG830fXrKfWMYFs2jmOiESYdSjDQN0zPyGa6e/rIdKTIr+XpHOjAaQFOD4Nj6yCq4Xouju3RaMDZnI1rhLFxKNfLeJYJaw3Mjghe2KF/0KCW6cEiSzUCRi+EOzW0BWgVwFkBTCH2G6FgWh3aLGxZqwaOCclOKbrS0SF9e9+XJlnL5cn2hrjz5y7n0l2wISTLRQoZN4rL30SWkBUbmjWINGFn1mP+TIMnvreXQ498j0Pf/jau1iSxbgg9EaFcXBbarQmks8Q6xnj/L/4qV18zipUyeXAJXtsPNw499zGMXDJC/y6PIQQwLBAwBb8FxG3QGhBvwTs6hA2s/zD25L0EGRvfjymMYQjYmIHubpk4TNqYIg04+cuwmoeuDIz3wMcn4doQZGOiF2HZUFmQ87VnWp95nK4eg2tefw+nZzUuHeB8hoyqSXIFcFV3J7/xof/CE7/1Qb6woPPgk8vcufvPSfzHX+QP3xrlnu0C3IEswwVkPjxSg74oZA1xKcb9Y9rl3zRgvinaeHdE4Slg1x7IjK3nyN3jfHcRbuuBMR9Ed/xbuHQQdgzA5ZrURF7xXz1I9QoVh95MUOCk6H8341+Dit9GEE9NMUwTyEqdQe5LFZsK+5+nkLXgTAiOF2GqBm8bhJ1jcOePv5XUwBiPPvIRio98h3qz9ZxMiMLCLPtX5pk48A3+5z8+ws2XXsL6dOSCY1qIO9VBoKe8gGy40wQFr3LI5tskYJzOEbhxamOvsAOXYA/rtB1f8+9bPcfDiDdr+G0z5h9XRbhE3Zyv53s+SUkBwuo6lK/e7/eLJ/3zdBJwkMYIGNWKoa5A3RgSa7f8tlexewMpvPzp90i7VP2aNB2IWzgPLNehUIHeDPzqZ/6Wh774EPse3scv/8r99K/bQby3m9F1Ce66AWbzUggqEoaQIaSw+qkF9j+2lwe//g3yk/f7gfqLxZ0Cc8Bp4lh1lisV6nPzpJphMhjkoiFMI4vT0tCBzpToXbqmX2QP6TNdyNSoZKEeAT5zP3zts0ssfvrDtFpPgFtG2l1D03cwMjCO59aYWThE0ENVql+MgezljG3YQW//ELNnZ2m2qkyeO0W+MI/n5ZGNgCoeobwx1fMu2r9/m+P05Mc5M/X3fPRvNH7hnZ/itjuu4/LrBxgcazvMQSa7dgK1mkzb8f+Y328U/mhxYWRM8bJUp38JEJT6+rPlaVR9sAgy13ma7B9OezBRhvmEbFe3+McnkNIoWzR4QxjOXg37r4JnSnDoiGyXa+Ym3IUuKM+BaRHp7KB740YGercwOAQOHsWCx/KZIpNf/zo4+wkYWMVnXW2FYDxFQQuD6ada+ZlknlWTO3BNIcMuWuCcRVYXVXn7n4GvAZeB80449yZpt3ECyMpGHNA0siABHLsCcpcB/3dwTUq+cAxZtCBg3MwAThq8ESQctMxLCVi9CsBYkGV4GfgTpCz7HxFMtRBwjkJ4rolVcjj4P8/yS5+dJNVRIpRYI9k8TJeToyvUJG1U0KuTbBtOkO7oJJnKkEjEiVQiOLaOZ4Rpmik277mX9VfuIdPXi24E3vTi2QqLMzXuecdmYnHjeeUQvl9bcWDOVvcKrt3AcOskQ5DLx7j8aoOlU1EOfiYDTOJFRzi9MsT9+3exftt7OT7xEPnlukhDAvEOm3v+o8f1VyfY0dPP0NhpBruqhH/ohTsHkV5ZveDdJgEkmiVO16Y4/BTiCU2AVguhEcXCo4sOQtiUWGONGtM0cXFxkXFSI2BKvDxzaNl/xYH79zCaGGfnrbKUquVXPU4dIYjEY5I1ngpLGhUuZGwwqlDXROfOsMFwmmiaDnpEdpg8A0sPsnKih1ZsC82QR+FbT9KyMqB3yoZmeZFywUSLhsALgVMC1iGzbxJxN08j6GUIGf3XIMGJ7W1X+69kan4MEzwAFRlS/1rIA1L/KtkCD7mNCjLn5pFb9PzvdiP0mYPAdxFwdYkLMxjw/z+IALBPAu9Fihx+mQB7n8eXP9VgyzUwH5WdGfW2kynh22eZr4lzXh3CRQJiOaSjOIiKisI2W/41p/C1aivAg/Cd14IZk9D8zACyFctB5RKYvBuyV0LxD6F1UO5/2zdh8nNgPQPcD5H3QP0S0YX1VsCpAz8JfErO4z0N/CKCQM/6jfYmAjQY/+L/1r+mV2uRiFenTSJr9vUEPhfIsHgQGeX9yOZcA55BRCaeQJSJlGy8UgO5Gg2HThKMMWBcRv/Oq/ibk7/LbP0sIL5BjouQ+ytnDo59gr/9649xxY13sW3HtZhuGE1rYTmQrzisVssUchXOnVqkurjMhk1Qrln09sWo1V3OnLboTFssLa5RWGni2U0mpzwiKZOOziSxUIbFWQ/XX7c1E4wk9PSPkJ9ZoVENNFH6No+QHkzRdEo49GA5HuGoRiQMiajHypJHPl9ncXmN5UKZbEcnkUgHaBFsz6BQs9FW17CaHqurBYqrVcx4nHA0RChiEDbDGFEHQ9fQNfGnKs0cK0tlnGIZb6kgumWOiZbw8ByHhXmDUkUjHtNwUzC/ClNTUF5Zo7FahNwyjdfswYwbUmvBR6bCUXnFMwLUag0BPkwPqqvQl1jljsu6uXJPP9fvhIGQVCtWjA4NHxxpwlIVlvICeBYXcyyeneYTU0c5vbBKYWmF8soq0dF+DNPFjEax7SbUG5LKYq2x4ZJLeN1P/hrve90ohUyYpKHRiwDrag9kEhAnunWNVTQeQcb19JTsC3pHoFiUpb9ShbUKFHRYsEC7+WfZVd/MMx/5TQT++gHZcFFkLXq5GcFxBHHUTsDsTICyhRBM4ZwHU3kBXPUKmE1ho5RbomPn1uCsA3OerO0qduwCp2tU+yuc7m7RcbZJqTNMZ0y/oOiWBpiahhky2R0yGRyEt9/aQ+6jb+HRgRBfPQxf2A+bNsOPXQk9vlSkYEmxAAAgAElEQVTeJmAsCmH9wqRGxX5UG0sHKBVg1oFnhuT5jekQi+lUeuGaTgH31zRRJIrgqyZpQpZZQVwRxSqqIy6LYnyqPbDi7qT99xWwqnRte9uuMYSIrbWDi7Z/nOd/NwsMalKbxIpBURNPun9PL28cv4G337mOX/2j7/LMwx+lMD/xnEfr2i5WrsGXPvZXOG97O8ZrX8uYeWE/7iJg7yaRTbYCLdX9zhDUSFX4QLbtERcJsmuV+pRKUG9PGOoiKKQFge5uB7L2KUJYBRkVah+szq3GXTteESUA9RXgbSHPbAiVVB4kR43wrILNBAlcEOgAgwARVTNwRxXQrJi3qQgUPHjmBMSdELWixvyJFfJH/4Lu4Z3c9Ia7KLWG+aVPPcYtN9zA7t09hMNwZnKRz3/4TymtHaNQXCSXy4GX56IslDKXIKurIhqPtS70dAbPKuGs5bAzSbC7cJo62IJXuQ44BlQ06bN5YP8cHNzf4JmH12DmJIXi0ywunSG3NE2rcYpAGFL46p6bYznXxPNU7QQ1EYKiu62WpqkdX+bUlE6jXsT1DKyGhefVCZiwitmnvqe45aoXX7R/z+Z5Do7j4DjwuW/9Ng891UE2283O0dt5/73vYng8RbJLl+5QQ7paO4FapbwZ2oVFpdQioxEwYVU1SSWUrTYKSi6wzYy2r3nPOg1ciCBoyBzYgWQGr0tA0ZBLm0Lm5k4C7VkPkS1IAZvTMLwTqjmYz0ZZm+2lvpqh0jIxnTBEDZyUTnIT7Ngp2u5OtYPZe1/H6YPXcvp0g/kzCxQm7kNIieqK1V34P6qGleuIL6Jp4vy5jmTsNOrgrBKUfSwhq8MiSlYFzoJnwezrwM4EC4VK4VYL3xAQ08HSQTfPy9YSQaYQVcRcaf2obO+ZMOQHgXcgIIWizbywvUrAWJBGVAjIpcDrkeU80XaMDjTx3BKlk99l/8mnILqKHqsSs09wQ1Yj2h8m2xdicChF1EhhxtKEogmi8QiaCTUrhJnopWtsFyM799A5MEQ4HmjVTs+CVdfp7gwzuj79it3dzGKdU+eCqovpuEYqajNj1cgXY2zsh7HeuIQCy01wQxQWKhx5YpHPGU+xutyCMAys07nthiipPo873thkzy6X8ZSKvP5rqAr2ID3yQuDHaUmNDA8Yope+/m64RQ6tFSBaTDPOKAMk0bGxsbCwKPhUzHbyumLEfn/7EJVXr/vfnuR7jz9C70AXu27dfd6hhABHNJHNcUiHqCGsdt0UrSLdgUgLmq7cW6XoYdeqeE7D1ylpAQWw9kPtOqhBU4dWI4LbNGXCDZkk15lYS01ahZb8gNcOvKYI6vKm/La9GqkWtR2ZGn8EpiYeCHYqSnK4HZSN+p+X/b+VHo6i9M0QgLVKBmA7UldqEj/t0bd2GeKN/vcOE+SqGsgEuUPOHR4VGdXGMlK5xVXJgXVk56jaV23tnwVqq1WrfZfSQ5D/mC/CUBLiPt1rCphoyC5xTIezSZh9GjLrwUwjXJqvAAtg52DNhd43g6bqBZ+GRhrcS4Bp8A5D6xRkrpbS4Y1J4DHgdchsbwFPIzoOw0hS+xRBH2+30899hhfth24lZPmfRTbcDYL4bpOgOylH50sIKfwYwtzJEiiW9aCxU9vNihelRR8trZeOxOXs7v8xtNXvMrV2iCYytC5qx75S5gEVpvY/SDScJBzppi87hlMAXI963aZVtymttXC8CLFkiu7+MNU6dHTG0PQGnlsntyLrQipmkIxHCYVNiLZw7RrNZpRMXz+atkRHpoNUdzfxwQGMaJJqYZ+AsRoQj5EY6EJPmhRrKzCv02OGSaZTOG4Iq2qxMFukuJqj2bRJpjJkOnswYp24epSmo9GsmTRaFmYDdK2BVakR0gAjjh4yiMXCRGIakbBGyNTRNYPM0ixlKphujZDn0SqtQCiBqXURMxoUTi9iRfqJhcOEQxq2Cy0HIlGdWGcI3CieK/ULbUv8ZiMOehwiMYjHIZEGwxEwNgKkM9AV6WLnpm62bkwz6rNlFVC05kHJhcUG5BtQqLmsLJRpVgoszcxw5uRJ9u19nEp5RUBuzUSPRzFMA8d1aNktH2mtQzhBsmeYdVu309kfwtK08/V9AY6tQn8MsnGhAzSQNb8JxHU/9liHhgFhkSwTGQsPBuNQ12H/UShWh3EHrkXffAduZUZEbR1DaF3JMFhNaNjQaEBrliD3p87zmkKrXi6mqyoKmmtSKU2hWyqfvgVUWv7m0AbdliUz50HRluMWkeCjWtsj/uVWXCpLK5w8+ziXj1/B8SULyzYY64lcINeilNfSQCYCG/oiWH1johe6CIsGdEZlpav439E10UBNtjWBYp62Jzm6gLUGtRa4QwKKlqviOsdDAqrpWpDgU/bPlUIARB1xLTQCfVLFe2v6txkmEIhSpGKn7eW1HWe2nVOpS0KQtafIBYo0FQlJ7YIZ/9pKsQihSA/j67K85Z44HUmLw0/dz9lD7U6Sf64WHH7sEXp6BujqHMTYtJPuTumb7WC1iqnHCeQdFB6gpBemq7Bah63ZoF1VYaQeglquSpJAKQC2/P+rYmbq827/O0n/XyXd4BEkUakaqisEyvZq7CsvXukEdxJIJsCFdW1KDThbAzcmDOiIHnTxdrlFdW3t2rmhtmMcAl3fQg1mVmB+Ca5dB9fsGcRc28O5sxFOTxzl7KE0zfJmtKaOtVriyN4FKqUljh8+ylPf+wZVZxb3OUUHLpqYGjFF0RRsJPHqKYhk8BoWzZZDNATJDGR7YagPRnR59itlmJz3yM2WeebwUY48vczxfTlYOAnlWXBXQCsSPFkFvEqOuNWwaCd1BZsYAVEbrVUapfbaHap3KIBFIWAKzVGpfErIo85FQPb/HJtdmmB2CUJGjOljFTKuy4ahJEM9UUb7B9gwtAEj0gGhGIRDQddrX8zUS0X3IlxYWRIujBYqUFbhliFJ0tW+T5RPjYC0BmlTftYi0BTPI/O8qrvdhayDrim1c9ZthEjIoDxiUF2NUpwXtQAzLJnEXhJiA9DdAXFC9A0N0LdugMEZl+nJQc70tpg9M0attIJjNUT7FR0cWwLooaiw49wQeCZSpAvRuW/U5AXIKjboN17Cv4N5xJOrAgegfjms+GJXSiC3ndBuEKQkqgVQ6fO0SzIqRySKpJToujANVq+B+tuBh5Fd3Qvrx76KwFhlM8AvAR9B8pOVTqLSeSkgoO2ngCcxmzUirolh6Oxet42NQykGBpNs2DFAeWWFhqPj6iahqIHtdeAlsnSNXs7Om95G91j6vDSB54kO3MRRGF8XZ9uWV7Yiw7GJFfY9EUgH9GfDZNNQLhYxct3s7jUZTCYg2y858tYc9ekZzk0/zace/zyZFGRHNa68KcRH/qyDJDYaJWSUTr+i1/ri1omARUogVKAB2xL9ZjxYzxjrOkaEwQ2UF6Az38M1oZ080uqhRoEGVUrUyWGfL2ijSJWrBM7eS7cMOv1oRHEp4HGa+576HKl1Lu/1dovz6Xtnaj8SR8a6mhtbCIaqqxfgubIZW1n0qJVKuI0iuEXEhQY4TSq6Qn/aY67soa3fCTm/xLNm0H1TltxDK9iTVdFA4RAyYSj3uIa4vcMI0vg64FaCuP6/sqm80DrSQGqWVp6tWjAcZAJba/tMFVJUBVfVTqODAJl6HbAL6T6q2yaAQdC3gaGDfbWQRfnfSFM8LQVW9DvA7gD+F8Ru8jCHofGwB2eeAq4Do092ONY8MpOqOaOdN+H3qjoiShcGLA/mXLhMF1HvFRcKZ2DrJugLSXucBc7kYGcctnbC9G3Q/HVYuRG4EbQ9smiwioCj34TKLeDcAuTA2QunPibXSY/IXJS/CJt/FlYrUmGOTyGM6C3IPPcd/1yKYzKD9B31QC6qh/4ozUYclwlkRlROTgx5ghlkTllBZJD/Eul2CrAdRzbuJjqbSLDJuJuau8ZJr8isd5ZWaYHLh36Chm5yZO3Q952tfNFeoi3uY2pfiIob58d/6hexnCjVukOr0QRDp96K0jW0kRhhEpEl4naNaFgC9b09JstLFeo1WLcuwfBoF2aiwmwuR2F5gXq0zubLtzL19CpbNg8xtu0Ksjtu4+T0DIun5mjW6lKcoL+PSLaLZshlsTjHzPIMW/QW3T0DRMNJ8gvLzJ2dxDTDhMMhxsbGiMW70RNdOEYUq6VhlE2ajTlCRplEJErFqNG0AEPHCEWJdsaIRk3i8RCRiIHueaRNi7hRJR62aaUi1OdO4RhpInqCuNbL0vGDaBtvJmqaZFIGug5dnRDtTxILJaExQNGfvmwbPBsiWXBtSd9NJSBjSqHMRFT0/64e1bicLee1HcEHuDxZFmY8ONmERs4Fy8GzmxRmz3Lu9FHmZ88xd26KhSOPQ2MNwin0ZBfR3j4cLYLVtGg162BqUC6jD2/GywxSazY454VoNjyqGlRNjU0uPDwNe3rF/z+qyexdsAXcuzcsY7oYgVUd0i50pqG4CFtjcHOnaD3/wcM2pWKFuGHQfefPkZuYwytoUIuAnYbxblgrC522XEIvP4Bb2g/2Oc6DsWqTFgLiJqzaz53eVV62wgJeaPp3kXV31ZP89JQmxysqoYvsGZTYtRLmDSEonEIbVfXBNf97Cc5nw1SWZjhx/yfxfvPneWKqwfRaCKcjzOUmhDTtPPClCD5t+0duBC67PvDxZgiKNeWR7ZUqE6vAN+WNt696Db8W7TASCv3CGpxrQjQml61YPj1IECyDrKRKPkABdJr/2ZL/GBRQGELm8XbXRwXdVCx6jYA8o+AbJSCU9H8/3fZbBf/87ezvMpCrgtaCZEzjPW/dysD2X+Nb39jFl2YPk89XwAseuK7B/OlJ9t/3AGErhvf2cV5zSZhw3MDzM/zaWcp620sxdHcgXeLwKjy2DD+fle80/WdwDtlzKmkG1e2qSLCk4kFckwCL2gW4yJqmQF8VnIwTbO4ViF1Btq4JJBdMXZsCZxVxTPcgbEO05eK6HjXTwPGB9pIFEwuw2CVFA/v0YN+sfkfddzsWopQ6nGf9vwScyMOBkxKb2DoI171jJ2960w6+ttfmd991F3u/9w225M/w7vd9kNXFBR746v0cf+YJFk4/xXMDK8H+6KJBUBvD1161HZxyBj2axfR03FCUzi4YXg9j62FjL2z0YG/d4dRUi6cerPHoA2epPPYx3NIJoIRp1nC8MTw9CXSheToeiwgho0QgPKLCAOppt4cVFDVHAbEJLkTK2vPE1czWXhxDjfwaFxT/AYLZ49WsG3zRXshaTp3JlQf5nX94kGFgW6KDN26/gbe/5e0kxrcQ6hkgHOpGN6OSNaQihBDg+iATUZILt6oVglQElZG6QgDUxpHJM875ia49m+RfMnWMkphxkLl/EVkLC/4xW4EOV9a6sgbr+qSgXtOSgOjqYcjNQrUJdgSqtmQzeRHojEN3H1zaB1s1ndV8lsNX3sX9n4P5kweprszilku4Tg0aFmgeXtiESIe/YJjg6cIAsDywLNGL1HvB6ARtWPbS3hrYh5GcxEW/Ic8C0yKC2+yV1KsRLgS9TS4csmoBUoXKVTVJCByZPsSpKEXh4BZY+DDYvwneF3gxTalXIRgL0jLv9/8eAF6DgBgziIzBfajWu2ZsK3fvuZL1G7rRqtOEog3imRBEkzTMIqVKkWrFolnXiPbs4Yp7f46BzdsJXyi1hGXBfffDTVdCuvOVv6PH7/sW3/iHf7jgvXQqxraNAxw/McW5sRGWa0VYPkl7cSwzDsNXw4OfjjHcE8HEQ2P+lb/Al2wJBE2LA59B6OYOLQtWZwXUXs8go/Sd/0ZvFrjEINkZIfqAyTwFSjSx8OgnqJBcI4jOfP8w0yaG+DUSXMs8T7HGPcAETW8rq54IwCvTCVhpyolUtZxUYYZuoGILwbGsQcvwKDWK2O4EwlhUz+jNYO7GNV0qxRqeZ0NlFZYKUC9z7hO7RDBWr0DlMDKSXYKtxx5ke5L1f/X27/vOX3HzCPyYOIFwmtJbUX6JEgpWM/gLZcnnkYbeibBd1yM5gv/kf/7rELsDevrEAX7ybig9jEyKbwMOwsgdkL0Z9j8F/DWU/r+WUJgJIW0ahfUheF0a/rIKbpuQ3XPMd6ZU5Y4wsG8enuiG4Thc78D+b8OD3UBKOkwXUPgETOyCE3fJInguAs6XwNgHqf8BpV8B78+AB4AlqP1vSN4G7qVQu0YunBGCymh/BSeHkC3ff0DUrz6FUIf9ytb8ln+RLTknv/ZCT+2i/QhsBhGJ6CCQecoiYhOTwEOIqu/jBCmYKuHtCaQn7GSY23kr5ew6hrQWi/XHeKb4D+w98mn/jBdB9x/MFDTxwgIP1szjzK+d4XND67nrDa+lWDRYXmziNBy2XnkvWusNNNdmKcz+M3s/+4f0DNis39THzbdcTW72UbAh21knnVzhgb1lTkxD024QS1fZegOke+NU7Cq5cpmecC+jO9fT2T+MgUW6I0O0ZyOP7zvE/OIC9bUK3dFucufmqC6X0bUw+eU8S4tn6ejtId3RQdgwmVmY49LrtpLsyFLIF4i1bOLRMl7hKM2z5+jouJnJQoVUKE5nNAGmyZGJCbLZXjKdWTDCuJEMsXCBlLGIac6y+/ULHJ3Os1g5xJkDByF7KQYNKqs2S4bBwAj09AIOGB7E/KZdXBbyZzjuZ743xFG3Ddi4Ea7aDP1RGScqTAZBlspZYMrXag9Z4OVg/tQKs9PTzM6cpJg7Q351mYZVpVHOwepROUGsBy0cwTSjWLaFU1uD4ioszUHfOP2j20iEY8ydOEjx6hv48ldqRLtNRnZE+PyqkEKfXINDOthdsDEsuKnlQq5HfO61jOhLDoVENEbrlyXtJALyNVaOsnswzR3XDXHbjZt40z1/Q3HmHBSikL0FikNwQwLjSpPoVZDN3s3CbXfT3Oen6hnIFL8DuCkO/30PDO2FpWdpTb4GWRqqwDcI8upfyP4RSFdg1BLETwVGw1yY194uMmcgjlHVf6UIgrM24hw1gYUa9hcm+fQHnuD12fW0Wp08srdB73URBrlwT6kynRST0vSffx1RfOtAvPwoARDXbs83+00hK2KWQOtudz9EW3CsLu9nkXl2jaCYiYUAoGkCsq+qJh1BXJiW//msf4wCdBV23UGwl1OxapUM1IHg345/f0qrVJUpUblOtn+8ibhFRpe8VwL+fAWu2wi/+V/v5Dfed44tm95PM/8tcFYwNBjPQHowQ4gZTu7/Jzy9zrGp1/Gaa7ewe2Pv+dluue03sgRQodr6hBGg027IWvQmAq3mpP+Kc2Hy0Blgqg65CtzZExQFs5AurLI/Nb/NLcR1CiNjZtpvnyySA4Z/fosgPtBe4KsC/N3T8OhDOZZXbEZ2DfKed8EGE7akYTwOv78XehOwJSRAvuXfu1LrSCDy/5r/tyqZCxdqLF4L7BqFu0cFygNJhlpswNiwiRFOUpqb5OTTC3zyz6o8/dTncJwX0oM1wdgOzglearXt/zOsXY24SbM8QmLd1WzcsZVL3rKRnTeLZKTrwXQTDlfg038yy8Q3v0v56Y8SpNv1Ew7t4dJLrubM9CnW1k7RbEzhUSIYxSBPNkUgGFkhGH0qVKGOU6F0lY2rRHPSBJ6bQtBUwQwF6vbAeXJUo+2cCrRd46LA1L9vmwVmq0UeeOpr/P5TX+fGcIpbNu7knrf9JAOvfadUWowYz92WtuvZqMiemoTbg69lgkhXhYAEOohEJFVayss0hYtkkTWpgcz3h4ATvq/0+n746R65rCbS4w/sgf3LcOwMnD4Bs8cgtwKdg9A3IpymdTEhw4XiML4L7rBh4dyl5JYuZXXJZfbUKezGGo5t4fpzqh0zsUsW7lpdQNlqEUhLtb7+nTAyAAnNR5E9OGCB/VVEU3ASmcW/KlfafA2cMKUtuwiGsxqiqo1V9FAxBdSiGfcbpj2WoxyCY2mYejsUo8CHX7B9X6VgLAQu2DIiyvsdlKBDNBzmA/e+m60beuhNQtq0aDaLOBGTZDJBMp3Atk1qZYdGxUXzUmSGdnDdu36RVLYPM6ydZ0nWgdMny5w6UubWGwZIZjT0V7DVPM9jdrJOeWECqvv9d+XHYxGTwe4o9913gM/83X/l9OljUF8BRAbzbW+Ge18P4YTGUHeDkN5E+5FvzGeR4RlBeqRcT7MBK4vy3wp5qieK8FfAXaBlgTMa7qRLgRVatHDw/PQujRoeM0jQ58UIHy9sOhGuZ3RgkL5YhuTClTxd78JlmSe+2+Sn7irw5a92sGJo58scrUPGlXw7WGZtwPZEqqTUkIM0HRoND88ugKdqxQoYG770Njq3bqWny+PUKQuv1oBGHbMzQvqurRTmYninDkHlFOKKzhOU39mMFKzrIqC9/ACz6StpSu1BTf4QSBIoioSiGKtsoBezMhK0OoUIq40jRbF+A/gSWKdhYQsULKj1IsWy+oDfBn4BFu6D5T8AFj0o+fzCnhDcrsFnLwc7KgK/c5rPUFUcmvacBGX+/5f9696JsGqdQ7BUg28PgLcJWYpscMd9scBtwCK0PgGzd4GTAE6AcxTKd/sSFMrJawF/DrWT4LXP7hNg7gbzV8H6IALQ3kmgPvc9pH+pXXZTfvNHPu4v2guZjRT26UZ8ohHgKCJLsB/J41BDSKX+iJwLJBkkSi8PMsVibh+zLJLzcn6i47OfucYmrqdAkdwF88hFe1Ebuhn0fpg5heg6P/9Ysss55j/7yzya/F3GN13z/7P33mF2ndW9/2eX08ucKWf6SBqVUbW6m2y5F4JtMOBcfoQQQnLhR3LzIyEhl1wCuSSkwEMqgSR0BwiEHzYQY2Pcu2xZLrKkURmNpNH0mTNzetv9/vHuV3tkbIohXEO0nuc8U87Z++zy7vdd67u+67vo6+tlYRyapoMWaiHe10Xv0Doy7R0cfeLTTE+fxDWqGIuwdTNgmJyYsBidBMuP9pu1Okeffha3UUdTGxQWU/RtPUEyspZk9yCxWIh4IsxkxWRyZJyZ6eN4lGhfsxtTTaJ7ccLoJNJxurRBugdXkM600yw3KVZnMU2HhmVhhUIMDHTwwG0HmTv4KG5+mu7rzkPLrEBTXZrVRSbLZepmmXI9gadGCWkaszmD9Vu24TaWcfjJhyg2Zhjo6iFSDuPM16g6BknVJoaLYokq+5Z26OyCVFyQU7VToEVFFb7ridLxLRth2zK4sBs2RCARCVh0cnYuIVKSY55gWRhNoS1rNT3GRwucGD1JfnEGw6wTTsVpLtSpNfIYlSUNO+NR3GSYankGr1bCq1egLjr36uluLrzoanbv3sL5OzsZGYPulTE2dsGGdvjMnJBGrRuQNmF9lwCBEjZ4jgBb24GOVr/YVTmbYYcHExYs37mGhfEj3PnQfhZyXbz7Qzdx19/ey8G7RiF3CIp56LwQp6ObRi/MGAqW6TeFieBTRRGo4ro+UD8Df3YZfHFRoGQKcCPigPYRxPY/jHR3AvhyVbRTziIyQq2IiUfWsktsYqke/NKGnCqB1GMEcYEa4m9XMRn9179A/+2/YWDdIGlPZRY4XoOYDu0RcUrmkt3X/V0t1QrNEYB+CkELTln+L+dLybac8+COWVgIw0BC7G8YoQXbr0MzDB+8HT5yFTRicKAhilniSuBdpQlK9T3/uNKIWNjyv6fbPzYZI/cSuEMSbJWSF5LVuRSM1Pz9Sjl9ebsaBHnuDfjdMfwDG/Ag2wY5DfKKwkAyxlMPfIRJ+w85cHCMvfcfoDL+DNXKBDPz0xRGRzhy/HNsPDVMs/BG8rsu45d2Lkfzj1dSIor+rYczAltowPY+0QQ55t8LCSP1IVYXWdJvsqQRWRiUlHABpZRBiIBPuNTqiIhBQVA4Zvz/S9a039/3TJ/UJkKkrgUoVeHrz3t87R+fYObgvXQvi7DjHX9Mp+oDxAqEdPjdLaIaWGIcur+9ZL6W/X3PeBD1oF0NiOAyFjfkfVfEvar476XCoMcUhusenUOrCYfqRJ0GkUiSleuuwvbKhDSXWEjnhef2AB5rN2xn1+U3Ekv187XP/28Ki/Ksz1lgItqyqOBSR1NN0gmFx++EsUNjzB4bY2H0ME7zOfLzozTLs4hRmyWsrsHzMti2xvCRr2GY07jOUmE7KeWl+L9L1MUhiFll2kcKY6QAFUUJEQmtoLOzA13T0BWVkBrCcDyMek3okfvyBpZj4mDhahYRDUqFHJZTwT1LY1ZSG1sQq12ToN78nP282VLAUo6oPAEEL0fHIh73m1WeOvECn/70n7P5a5/ilvN2s237RSy/5BJYu0IwNZeG/BJklZi9wdli2jJzqC/5fIKAMPUTQgcv3jyMCNO7EVVAiiekDeQhhxBrysXAljZoJqG8Bh6zYM8BUT1RacB8HuK9/hMXhpYe2JCGNTWFcg6mRlVG0iuoFB2aDYtms0GlXmF+Zg7XsKFuglMFLwVtK6C9H9o7oEURVT/4B7MiCpPboFlFeAQHEHNGEbEKvR1Oa1BXhGMns5byUV2amH6xEiCIE29DLBSy5AJFhO5XbSEdWY5963de9vq+esDYjpioQyv8uHo6MmVQoD2aZUX/KrZvX8OurWsY6I6heyWMWgXLNHC1MK4SxrUVrEoDw4sTa+8l0dZP1/qdtPYOoGoCiHE9yJVg9OgMZtOjvz9Gi6+79NPGw5498hRzCyfAFcpYmzbfTEumHxcPS7EJh02mpkYwrFE27YBfuiJG35DLRTtttm51/MN5tZQ51BGDWypFCbNMKMz7UkCUMWsVUet0BH/tcnHLFnPUUHHPKPuUCWSYJTP1xzMFiJFgGal4ikybTlNPoxxfAV6VQn6K/c/dgeu9jQoKBVtIpXVEhSSBTIhIkATEMG2YUDQFyDydb3KysMALJ09RbYZZqmMcaUtjaxFKZRvbcMAxQfdQIzrxzhTVOlh6CI80hPrAesY/a6mGNUigYfQqMo+guZVFsChIXRXjRT9/mJahVxQAACAASURBVMmuEFLAa4qAJDwqShqsZWCFoeNKsDJQklIGj4su2qoJmWugdFDDG9GE6PY4kEyJQVQCjijgDXJ2uCfDJ9k91RMHY9m+tm0EwilwFsCqQXG5f3CLiFE5DXYFEd1OiJM2JXu1BTgJzmcQUfU6As71NLjHETRaCba+IMBZZwjBEZlEgL4gQqBpzh6N8kacs1ereQhmn5QjqiIYsU8hhmftRZ/1kBJRKjHCuJiMcYRT9iKLlEgQYgM9DDNDN/20t6wk3b6SuqrTxloidgGMKarVCZrVUUEjPMe6eHmLJiDaAS0VKP0AeQ/Xxlw4xfijX4d6g/61u2nL9jM9U8G0LLRQCCWSZcV512E3ZpgdfYiJyWexFiF0DOKah1PzSGqQSkEoDKG4RzTrcPwFF8MxKS6WmD59klDZIJ1upTXTgkYrufki7ekUutuF40aJR2M4nofn4Td8UFA9l7AeIZFoIR5uZWHRRNciaJpOPKGih8KUxo5TLDYJt25EjaQJh3QU18BqljDNKrFIkkQ0ju45zE2exLUcwokEsUyC/o0XUJqNozdLxAyDVFShSQirVqauqDhYKKk0mayQP1dUMBzQwpCNQzQC6SQkdFjVD+vaYVNaADbSRKAigpeSASUb6prHwlSNWrGOWTdxTJuFuQrNWhnHNlBwUF2HeDiCpYcwlnRUVXQNRVNxm2WolcAUnrIST9LV3UZPbxuO6/L08yM8d0ol2b+KNdk4qSikuiF/DCxLyCj0KpD35VNdG4q+oPNKXcQ6Bf87K/45zNhwYgy0jhi15w+Te+FuzNwahi68mPiabtb8ajd6MsbR0QSeGoEpF/eQiTnyL5CbgC5H6JvsJABIm2XgP6DNCLLF8sJJ9PpHtSYw6ooJaCMimMghlpa0/76UXJNNK2Q2XAqlSlTRIhBylSKfjktz7yH23nCUZE8v17f3EQZMHWw10IGV2K4sBJZVgfJ/siQ+JS73GW1SCaYt1ffU8NmNUbCzkPGbMaX9w4+osDoEPf1CJkPXoCscVBuGl+xPelzyeCwCT0yyWQ1gvAFHG0CrAHyl19v0Py+VJyX0sxSCkZrg8lKy5HuldqusqHAQcWJrCCYaMFGFibLKBZuW061AX3svq9r6OZ1by3e/9lXamg5pT2NuapLjLzxDPJnFMyzmT/TwmtdfQ3skRFwJlKeklIIUb1KBeAS0iDjOkn8ckkEqpfpl8sEAKoaQ7ouHAm1XKSK3tCeDtIR/bxoIz0bKR0g2cYigD2yMAKpqADUPFgxYvbmDoZWbGRgIsaUPLEW4bbLxZc7vyptEeGOyRZOMlw0CfeCwElwHGRzL4nS5NkuJxhYgrUImDIUs9K4YgnIerzyPruokY2mato2quYSiUbLd67n0yl3s3LGDNavW8fkv/gemcY4V+9ImqS9TFHIPc3z/Apa2kZnZBeZPz1Ocmac6Nwn2KUAjosdJJjawWDNxvQU8L4eLRb0+RpDekD3j4WzlatkqTrJkRR2yqsYI6XFCoRi6LhqGq6pONNJDJtNGSFOFcowKtu1S08KYZhPHNnCcJpoawlE8XM1FxyWEjUcY289ouWcg/qXZLckxP2c/bxZBzAlrCCocJLQv5zGTgH9dxKVo1JiarVGYncCoGTw/e5oNpw6x89Jr6d+0lUhXGlpCYucyTHWX7EQumHJRkrJCcrKVGbL/BPhASrhE4SWRRDm/hoC0vwhYCTHSO+sw40AxBFpCqDO4gKsKJcFYBkJJaItDQlMwZ6LMTkCt4tBoREBRySklcGtgO+D56THXv9qxkAi4pNOQUkR2rt4Fi0NgbCKoYB5H3LGnwRiEQgacWFDyIn0dmZ+RWVWZLSwg+/yJkL2dQLtHFrlGElixBI7+8vKmrx4wti0mdB9+bDBWWDaZZGPXGnZfsJObf/lS9GYe1ath1OuYZgPXBkeJYlkqpueiqxBuW0Frzya6BjewfPtmwHdMLI9qzWV0wmL4mXnWrE5z/hW9P8WTFea6DkazxBP772Rq/iQAqqryml96F93dKzEdm3yjQkiv0DsYYkU8yQUXwEffH0JRlnZceGWsuIkJwWRRVYhFBJtFe5kR4b3o58s/21JEQGrpCBfTMqAwK8BYmxqOUxdRy1NADhyjScMrksMiStDYoIp3Jqv0yuBmFQgTIY6m6oST0NmtoJxYB85pbPcU5dqXOH7ijTSXx7HRcAyoRkXzYFsJmh7G/bOxLajkPSbmaswXTE5PL/D8iRGeHh7Gq8kUlTDNnaGcn6FRDGE2TDzXAM1GCWmieUISapEWLN0BLQXWrH+mnf7rVcSGXWrSK7UQhydXmp/UmogKgiOIBacbMdnlOMNSbR+CehXKU+C1IAQ3V4J2EbT8CpRv1/EWgaM2PG5Ddx2aOjTCMBmFyBCY4+DJUEhSflIE964AVKDpwPEWaE2Kh8WRonpSA2oGwUyt+dtI5usDCOB1pf/+pxBR9XqCEHMOUSrRhuBMRoGj4DjgFBEU4RkEMq34F2P2p3Shz9nP0ooEjWhOIxixJ/z/vdhkVtlGw8LCpUCVSQqESEQyLCfLRjPLsDdDJ8s4L/tLrNnyehYiYQoeeMUC5sIc7vwpLONeHOsQeDMv823nDKcE5CHlBojDD7DFp76N2XRo2CqXX/0GwkWXWrlBo6pQjcJA91rWXfBmwvEEcwtT5Iqz5IrQFYe+NPRlIJaCaAoSbSrtaxPMjDaxLA9NabIwPUF9cY6WdBvd2U40u5/SXJHB/gxGR4hqrQShJIbtEFJtNF0Fy8A161iNBo5lk4q3kEolCUciRCMRYroAEDWrTizTRWLT1aRasqArKG4d22ji2i6tmR7aUhkco87C7AmyvatRQirhtlb6t+3COtqLPX6YkFEg0+pQMVqoVeo0LIg4LqHONKEQOJZgwFYqoklXVyv0dMBgN6zMQMwnH2QJwm4XMUKnPH8mrXsYNY+wajN1bI7y4iJGvY7jWDSbJq5joqkOiuJgVcvEVJ2mqlP1AE0D10PxQHFtkUSzGuCFUCIJwul2tm5eSWuryqnx0zy693lmmzHWXNzChu4eLE0jlgXvKOi6YO72IqSJIo7QA1Z9OuAgwl854Y8PmfdbtGD0GBhuncbk8xSevZOmejljIzMsf+3bWXHDxcTWK5zeC8pDDk7Ro3myCf/wIQjXxfR/BYIy2PR3as2B8QGxJMgsjoYUlw6om/KCSoRSFiq92F0sEjA9sgRIeL//+c0E9ecdnM0S8ZbsP4aIRGVXZ/xjPlXgoWf2kMp28tqOPjqASARKngDtUILqP3kY0reUuy0RqAWlCFwPiQvLeEc2k8oqsKU1iJsURDVC1f98WodrLwoIQ6mwONUGAZFoaa2MbHpVIsCh8S9vB3DCgANFCIdhVRxa1YAgHCFQnZR8OAlMykS/VHeQ+5WQjPx91v9Mw4NpD1Y2ILcIJxZhcRF6B6HPg6H+dtYPtHOcbdx3191kSkXaoiEaU5OMnZ4kHt1DaWaG/zCjpNYMsCaVoSOeINneSiEkkicJIGzbzJ8eR9FTtLYkaWmNSRXPM2xRKamw9DpVgFxV5MA7W8S9M5bcR+ltseQ6yiEziyB2yzYEFsKTksxa2VtFArxlW/SRCycVbnjLOrra19GRhC5dFFfJKt4W4KApEkBZAnJZlmCYmvgMdyUoPF+qtCU9Pn3J/wx/+yQi7h/qg4HBjdSnZ6hbJgoKnlXHNUy0eJREWy87s+v4rd/7/1izso/81GnuueN2lkrOnbOlJmPbSRbnJlmce5jhp1YgggM5CYUIhZJ4rCcWWkFrrJvF2jPY3mHOliKQM4ScsORP+buHooRQlBSK0oKitKMoEcKhOLFoingsSTgSRlVVVFUlHImTSCTQFRUNDxWbiC32ZugahqFQr5voqipAJkXBtSx0on4MG8bFwj2DrMmnXbJ1fwFMFRkQRQEFD9eReMUvrsUROdMh/2+p5iO7x8i2cRZiLl2KqUwCt00do23qGOufvp+3n5pj1402neetIbG6g3hryl8YlED0Wqp5SDA2QaCi8TLD6Gc9uuRTLBOaKqLQ9LyVAgIdQxSgSt/PBlyfXRvVIRIHJQvZrFB3dEwF19XR9QiKF/ObeMlSIAOaGai2gN3u70QJwvowkG8BbwjyTTAkM1ZFOD4PAw2orQKjE5y4AGTlti1LTkoU4Yvw/DRQdkS51JQGm1SxmMQJWtIY0JCqJS9jrx4wduSVl1TqqspHbrqZ83dsItbZQqE5D00bx2hiNBVMK0002omOTUTV0fUk0eggV//yzejpKIT8B8ODJh5HJm2+93ANckf49V/dRF9v6qd2mkutWc+zf8+/8NT3vsrcuKA0qKrChz6wi3Q6zenpRUZPDvPIv32U935ikAsvXs1Aiwp886z9yGNXXvSkeS/6Zen7ngc33ggHDojGGVecD1/4hq/35n/We9HcKZ0QCbO+eJ+BZRFcBpFNBDAbMH9KHEuCEPFqSKyrdwOTsGiOcpx7zjT1lXOMlN945bxfBygwwwtMLG4m0zHIhmsU1HsuBGcfcJBq9Sk2rXuM25+4mI0Xt1KJCD2iUhhCXuAkJ/FQgWIJHn3Q4+677ufo8HMUpoahcMi/KnGWOljFR/6AYvIqaH09tO0UF7GSw2tEMEobWNEGY+kmxdwU1A4hpu4dwPnARbxqwVg4+6b8tJK5FQLZ1NOIKv2/RID2fw18Eo79GWImNxHim98DesCqwunL5E4kQjwGs98FVsCyjXDp+cJbP5IXFGjRqYuzWySCuI9TiEk6DQXJhp1B6L5Ugcv97R5FqAPejIicPeDPgY8j8qQesBf4IoKCtAgc9L/niP/SEff9ICIsWURIVNyHaAF16Ce5qufsVWDP+a8fxWxgBotJpnxMReFCNnLN5v8BXprnjjwJtUc5TI6erM5l29aTXQ7TNTj15Cinp/JEIl20dF9LbbEHo3YIMUbPAfnfZ2P3/dibVPZ/h1PTB3EiLtdc+d9YmLap5CtUSw0mnDKdHevYfmUPWy/cwl+97U1onkc0BqkOUbK/YbPw9ZS4wtBqnakNEEpAotsjucxmllY8NCyjTnXmNGuiRVAijM3kmRor0rW2i7ZMO/GIgqaUKVnTRNsy5OfGWczNkWmN07R0tHAfsbCGZooxteUdH2BhZpxKPkdEb4JmoymSVhElEYkTCUVwVMh0L2frRTtpXS6on3ZNpdddSc5ZRiijkEalPtvEmF7EaiqoWpShIVgzJBp2NYqi4On89bCpHfp8TdjMkuvoIcrVJvBV8/xYw7Y8iiWXhakGhYkJjh/ZRySsEgrraJpGrVml7hqYXh3LLDM+NYJRK1Oam6E8NwedPVBt4tbromFjIiJofk6UaKafZTsu4x//5v18+/6n2ffc8xza+wR0rCE2fpJGIUzE7OPgAWiJwNaVsGOZkGNdFoMjYTBV2LrELZSpUxAps24EsfVDczD56BPYw2O0tGS54ub3cPcff4QDyXlwXJRxle2vVxi8RmNhDh5+EvjbBixzRcFEN4JtUUVELiXEUvBdxPoYQuTyrkDEFbP+5075FzSGWLa2As8jIh9JtVx6ExzE0vQEgqIou1lFEXWWC/7fkqEjbWmpZLv/uQSB09QFfO1fGLVMvnHBdfyBopDzD8H1/cuKEpTxL20spSHAzssJcGQpayuLcDyEK1BCpD0H/O0lsCt1VqMEMSwIYP0AInhehVjpZfOsBMKDfTFHXuLZBkFaqxvoysCqMNx1N7zlOmhJie+X/c0k4Pi8v91q/7JItu5LERuWVkL2IW5rwRMVmZ97GIw8dLTApdvBVOCJGmQ0WBkFw/M4dWQvJw8Pn7XPo8eGOXpM/O/NO24DLmDTpW/gnR99PwzBRRnhZx6cWOS/D20h2vUO/uj338CfvO8KWhSFhSXXXZbvKwhwoYpILZ+egEgUVrSKz84TMFTnCbB907/OOuLZn0fc6/P8/Ul1zWnEcyWl+Fr96zg6CwsL0NUFW5ZBnybelx6bZB53KXB9Styzpcct2b8ybyG3Sfmvpe2YLMSwlpKLMnEge9g5QDsKPUMXUS/WKERV7NIJRo+/QCrZys7NN/Cbf/RX3LRVbH/H/Yf46Kfu8M/8nP1oZiAEnaTFUJSVDK1+M01boVyaY3T+WeCRl9h2qfhNlWA0hZD0uVhkHZFIlnA4QiqVRNN0QiEdPRTBsaNoOmiaiqZpQp5A19E0XcS/jkDG4gmdaDSOYcQwLRc8G9e1sC2TerWG5Qoao4qLSZWgA9PSWUZ2OP45t9Y1hFWdsCKSqfm5kyxtMviLaHEE6iExC3vJSwKRMiqVo09K4EjLA09YTZ544FZWP3Ar1267ijdc+zauuemtsFaHuAcREQ/QsuSLJKFalmO8qOfR/y3zEHKtOYKimVU+nLHMf/l1qBxBuDQFxJOR9MCswOwIFBfAsT1qhsF0scTUYhWz6PgLseVvOQvNIzCzDXKrIOTr78YQUFQfouH3RBccvRaevRbhSI0hjrCI6HO0FuxtMH+lqJQb9A80gpiyTyMWrLw8QzjTHOdgOxxsgZjfc2YzwinJESx0L2OvHjD2Fdg1Qx3sWrucLZu20btiK3r7csJtPazt7CIRSzF54iiVWgHbtWiN9BBPpUi0p4i2xVESOloiAqq/4Lpwx+Nw9NAErWmF113Zx0BmG8lk+Icexys1z3VplkqMnqhTLNnf936hUmHfyBH2js/zJ1GLnpTHiz1pC6GRdf8jsHMQNi0P3jOAmgt5C8amYUe3ICBXKvDh/w2f+9zfcPDuZ7n9n77Kg0/DzvNhczdceVELv/d3F3Lhjgf5vd+x6WmBf/oI1Cow7gkHJJ2Gv/4kXLxdlB4GJvvstbN0eNVLoqm960I/CboX40LfrAzY0E47QwydYRLIEjTpuP3kWN+3qNd3EU3s5Ma3qNx/+1vYPzJOoaoiALDf5Tu3f52RyVZalkMiBaFuqJdhfhZOj3nYNYfho4cYHX6CuX1foVE/hWU1BQ0IC+HCS47FEqvtgcZ+mAv7gU83Jt3Mfut2cuoAdrMGdhHh8l0O3IIA8f4TOsX9PNg0YuLrQASHVyOip28B/xMRzZQQXTqOA+9DoFx3y6gyBW0KDCbhsgx8cggsHaZc+I9ZsCbAyiPumWzlIBjUhLtEdHY8C/ZzCP1jKXy7yf/yC4BfBfVd4F0ktGp4GqHwto4gF/oJ4E2IqHoLYsBL+tJyxKwuTUOEk8cQy3MBwaatcM7+a9mLhSda6WCzsouNy9+I1reJplkmPpeGGmwM7aQvuRqjHeykqNhZPtiDakeYOjhKwaji0o7wJgxEKPtqkbT5+TZjYZJTX3w/jwBrV2+nuztDZaGAbTuUSx6WqROLbeUDX/gKjemPQf04caXB+dvgvM3LOT1e4sALRZ78bg7qHuE0hHQTx8nT1raRUFihWTjFyP7HUMp5+tasxXUzJFpaiSZtstEC4fIx8qde4L7b9jF0yXYy2QEM0+ax7zyJWXVI/cr/oNG5nFOnp7jksl0opYMUnnuE03v30fXW95HqjmDZDo2mAnYHNSNHwonRks5w0cXnY0c0iiVwS2DXBcPMW60JTUcXElqEbLSNRtlAV1wiOrTo0LMSsmHoU2B5CJLa2aXfUn4o78C+aVjeKRiKLRZMz3qcOHaS/HyeeqWOa3u0taaoN2oYhoEaUqnWihza9wSLYyOYc+PYtoXnarieK2irZZ++Go8LegUa6AlQokQzWfrW72RvSSWndmGZcRifAiOM1qwy7do8acLUMFz5elidCSp1HGBV1u8N+TJWRczy3Ql47M3wDvNi9o/fzeLjd3Dvn/4qZq0I938Hjql4l1/NwVyc4vUKtmnDaC2oyW5HAK17Ec78rL/j64AvdMKtFXi8IVCi1QjXqxUhxDqHQBtlE49h///L/PeOIHo9PohIiqvAB7rg70vweFNQdeqINTaCQEAlhiFLlST1VLJtk/7PpWh7L1CA4899my+/7zS7/vo+kopCrQKFIvybAjf2gKqL6zZPwE6VJf3tBNqxpxCxkQTUwohV94T4Ggz/Uhj+dpI0LNmOsvy919/fYX+fFxPUt1T8/aYJWD2SHStFjFwCIC4DbFDhWAaOlUTZ8rKE+C6NgJG7wb89i/4tGOfsviqSNKMS4N8mIoYMA90KxMNwqgu2boMVGWgJi/1l4tCow6FD87z7dReSm5rih9t+ju0b4U9v+TSEOvjDj/8L4UqaPV+8B7w6Ru5WDjwQ457ODVz/9i4qBKzeJEF1Zs0/nxbg/A3iug0ghpDHGQnhMxWdKQL28T2IuaANkS+QNXWyJVLdv17Sa0oi5JNbu2Ey61euqWLfUoN3kIAskudsRq0ctpLQLat4dQKAXT6/EiZL+u/J+Uvz70mMAGCJADe9Bh5yl/H43Ah77roN06hx8WteyzU3XM7uDeJzD0zCXfv28fy9H/8R7s85e3mz8Lx5Rkb/Gc8zcF2TwGsS+q5BiidB8PQmgXY0PY2qinrueDRJSI8SicRIJpNEYzEUB1RNR9VF/B+Jx9BVzWd5OtSMulhfXF+8wgZMEzwbT7FJRBI0zSqG2aBRq+HYTWyviY3pa8bOIZ4MmfKpI2a/XxCJgsJx5B2pK4AXAqVV/Mf7xYtphhAR+xBi7ogSKABLElvdf0kIXhasxDgDg5wFVY8BXxnewx0nXmDFlz7Mr114HZdech1D2y5CH+wPenovLU/4T5IkeCXmIqpf5jwYzUPZAE+Bcg9sUM5WWUoj5nWZrHsYmK5DvgilEtg22EaTZjlPaXaWxukiXi4H5nGEc/McgeL4A2A/Ans+BtN9MBgTYbkUHZeOAhCUHZ1EOEUu4jk8Kv5nvA1ORMQ2Tf81i8+3M/0j/Qgilpeegg7ND8LMb4gF6FLETW4lKA15Cfu5AmPj2nK6M6vYdcEqSvmjrM7qDKxcxqotV9G9aRNqNE04miAWTxIKR+gMraTFauJ6HjE9SSgSIRQLo8VCKP5FmZiDiTmDsYkCWksX2zel6WpVWJZVScejL8P8/MnNKc9gTh+mOV/ANBxcF9raBrl893vQ9QgesDg7yRN3f4OGaaGoJVRVFvQFpiKWnv/4VyifD8ZOMDzYthaeexQM1nHea96CMfJZPvVv8wwMmFx8CTx8D/y/v+ESj3iUq9AwhGzBKhVC1RievYGx8Ue49cs26SgMn9J4/4duYf/eh9l3aI79x+C2f4Dhi2HLpXDeReJYWplG414E8HQCGfg3bDhVlvopLiHTFBq5thDg8PBwcCgSiOvLyncpfP2TWY6cdZw5+xTJ9CAbL08xkb+CarWAxQvAOHvu+ycOHxwilkkSieRJJl1MQ6dWVSgW6thWjFxukcLCSYyFowgXcKmVCHLtS8xrivL2M+uscF+d2gjOmbNNIabym/yfrSzV3P0vY2/yf84jmh6eQASQ0mdZxG/VWAazBGa/qEuMNEVdLAnYqoimJBEXnvLAyQDPgFOH2gCQhWR7IP7LPsRyMAZOGRZWgSs7rDYRAKl0nNYglhELvNvB24jgx1yI6IDiIEDVVYjFYREBvG5ChH5HxfezHBGOyeXXRgC/Esh3+ZFqps/ZL7hpeKRwWEaBEM18mXAyRNemXVy/5iP0xLfTvW4dbkqw9ZoN6OqI0JZsJxZVOHzMxahPYdUMxEOVJIARztlPZK6NXc4x9eCXoTRL/+ptDGaXkS9b1Os1HDeCp0ZQI0Po7ZeT6siQjZ8inJzmxHiJ0eNNjp+AEycctBooZVATTZKtE7RGCiR1kyrT1Mw57GgYK9JCPNbNsvZ2okmPWu4Y40f2M3v4EHGjSMzIoRthTMNBaRSJEGFxfBizUURvmpgzz2DkTpCOmWzctIoVXRGUWIGm2STsKBSsEOVFFV0JoeLR3dcumlR6Iu40q+BGwAspWCaUqy6lXJ61y1MoVhwNl+2DsCoDy+PQrUO7cnav6iJiVqt6QZMeXMhNmczUitRLeaanS1RKFUzDwHVd9FAUNI9Gs4bRqKOpDocfuo/c5Cj1Yg637gd3EV98TFFFWY9jic5figcJlVAsiU2CSGsnnf3r2RBT2etkyVtxsBdBG6Kjo42qneDINGzbKeQkWnQBuBUQq0RY+8G1KgWEz92qQl8KfueyOF9u3MzdiTT1I49DcQRqjnC4HnsEs7SNuWwbXu0k3P91cUEkGNuFWDKe8S9WN2LZuLwGN9hibTxCUKIo0cNOhCJOiqBDkowCJbgqu2DJOvG0Dv0KbAM6FbjHEzcuiQj8FIKbZvoXY2ndvhTHkzorvYhlLwfWqRLzD+3n01/4C265+Z20RroI4/D8sRI3ZFsI69qZasAagWan5Y+dpT3IZam5gliJW/3LIk9PkoUgaKDSR6D5KQ+vFchXRTXBtk5o9W+q5NFJdqXUKM0SiHApBLJVFQMmq6KR24aEkPiTM2yaIPUVJdA9lf9rIIjOHQiPQMo0SJaw9PgTiMbQcdfjyFNHKMQdsqkImUyaC6/uIqsqPPHMHj732X9lZmyMwEIIyLcbMf/nCCq3TCzDJD9bBOb59uc/jm5GmBo+Cbh4ToXnD93L17+rc9Xb/+Ks41nKMpaSBR6+DjZn6+pWgLJP4mj45wGC6btnH6wahGRWABUlgk7cZQIWmQRN/Z65tOmgamJ/MQL3UFbtSX32CmK/S3vaSLaylP6T0gtS6iKOGEuyClDKWcgxJzmW0lM782hFYNmaTtZuXsPeB1ZzzRW7uf6G69m5YxOaH89/+0tf47E778RovDh2OGc/njlAGcuS9drSj5bcZsmBTiCe9BgQJaSnSMQ6iIRT6JqA6KOxKKqmoYZC6JEIjqf7vXd0UDQ8TcMwTeqWhWNZeK6LjYPmOSiug2vbaEoIxRPy7Zrmgafjuh6O7WLZLk3XxKaJi4l3hl4kaz5dxGj6fkLWz625AhiXc+6Z37xfHCJAGJFEGvBfvYg1Qs5Hsn2Khph5pzm7741cegf8kwAAIABJREFUSuW89WIFIRuomE2qZpNKeZGvPP0gj82M0/fEfaxs6+Hq199C97plJLrTgUjtq6SItoaYdyvATB1yFciXRcKwuQALfdCdhGxEsInlmivP/zxEOJ9vgF3zVZwVnXgoTjqSYt6dA2cavDEEEDrjf6uHeK6eguZfwfRuqG2Fma0By6/piEWbBQSJ6hkEIW+CoFYl5x/9VWD1QD0W6CWtRORSplXwlhHQXpeYtxectVC/REAA7QSL4svYzwEYK9R/Nm0apCu5nZXdO3jTTTuYn34CTW3Qmu0ks2YH2fWrUdWzUwLpRPb79ibvRa3kUc5XGJ+PMjHncHqixu6rPc7rz9CW/L7NfurmNXJYCyPkp+ZwHeHWZDv6ueVNv0dIF07iqfEcR55+VHyeJh4qHuqZ/u8KoLgQMmHmWZjJDHCyNcH+w0cxF+Cxb0BIaWNZz8WcfOLf+fKXFtl2EWzeCuNH4MAzwxw5OcV0TQyE/k6/j1rZ48QzLpYNDzwq3stEFW58/RB6eR/TU/D0CNz/TcG41TJdrNiRZXH6EH2xPJnkARLxGJ4X5oUXPDqyUKzBvCUzyTauV8KyxnGJUcchzymGOUoZESfI8iCTs53XV25NSs4BpspDTI8MsvESOPDMVhZmT1Jsin6wIwe/AQeziCdnkrMVvkr+ken+UdVe4jsaP+KRVvh+xuNqBCv2Ys5W4P4vZqsRl3kSgV2OIValhSWfmQcUE7SquB3zQEWGTCkR1XQj6iOedIQ3bZwEpQHxFVDugrALti6yBDyLuJ95cE5Drk7Qx7gVsYzKgjnH/9kG3t2IWfkm4BLgXwnc9wwiap7yP9+LWDFnEYvFNs4uhHT8Ez5n50xalGzrIH2ZjfRl1jOzUCdaWKQt0kXviiEu7r4QNZ0k3K7hJKHpCWZstk0nmdJxkjHm3CZ2bQrcKZq1OF4zjni4Xmr+OmevxEoHH8L0HBy7wbL2NIlYhnrDwTItjKaOYaTxyptxwk2iSpnho7PMzhYpLsL8NCwsQkYBrwiOZhJKzBDrO4FeMdAK00Qsg1BXP16im3iqm9ZwiqZd4fT4IU4eOkZuZJbODGhmGbcRA0+nNd0CSpJKcQ5Ul5bWNtzKOLq1QDoJ4UgbVKexauOoSoOoo0K1jGsNUFegqoOTzRBSVDRXodmwKOcMYh1xPFXBaCo0qh5hr8m6FS20hkQzoK3LoDMF3aoIVCIEGpA1FxYdWPDAdECxHTAsGvkaxbxBeXGeQm6ahfw8kUgEVVXRdB1V1WgaTarlIrVyAcwqJ595As9toId1opkMjUYTL6T5tEUfLlMU0YTR9SAUQg1FUGMpvHgMq26yIurhaS00pNCqaxIJ61RqOlPzcN1uoV8mq9wWELP6D4t3pv0pvenBchUu26Syr3oZj1hrsZwone09GOYa6hWd+rH9oHdTHdCgdBT2fk0AyVJKUNZQH0EsH+34Imt12JqGHh3URYE5yMIQ2TxCIkwhBLIlM9pnkEiCXpAVYM4E3RUA8HICiqIU900BSV9j3XCCHpgQRN1LhU/bEGDsFDDnYI4UuPNL/8zg2gvZObSTtnCKwlyTktNypvQ7iljF5an4srzU/K+S/TgqBMGr1HqVQKwMcHWgbgtN1y1xgdMvBeUyQMSCel3so40gVpJ9UST+LAtslyo8yu+fLDsMzzj0d4RYl1SwQ37ZuwfVit+rXYdUPOgDAsHlO1iHARX6o4GCfYiAjS0vrQAlPYziIk8fKmEbLqmWJGu2t1OeGWXvPd/hrq9+BmkdPT109a4kwjoUVmF4pylXhxkfeZzvtzp77/v69/331NR+1OdrNPiLMwxRSZSQoLYEzhdfdI3i/vvyfmqeeJ4AGhY8twAnj8OKdohkxRDNL7nfswQsVEkokgBoBCHLJz1uhbN1XSUYInvPyb8VAgk0WX0nY/Slj0uFgEUrm5rJR0VKXsjGYsh9eNDd18KazSvp2XgdN7/1rezasZyubIqG4/LMkQUevO02ju5/7CWu/zn78UyqTEqEQ97tLAEXOgQk0NQuNC2JpseJheO0pDLEwjHCuo6iuqghDU9VcBUVW1VwDF9P1lPwXAUbFbtZx2w0sJpNXNcFDUKKg+rauKYJhFC1EJqqElJdHCeCYRpYtonl2piegUcdMfqkUvTS1y96IzcbvJ9vsFkmYpKIkZZGpLm2+L+nEEmeVoJ1K4ZYVzIEeUqbQD9crnM/yDzE3PjYzAkemzlBAp3NSgaUNOtnNtO3doDuVV3E2lpQosqrAtWrA3kX5h2YLsF8ARYXoJKHRRMmmjDQIYpXTV00iVRDokJGUyDhgFICuwBe1U+lhEIkEwlaW23QPVDmCfquLK0YtxDx+pegPA3lWZiQqVEVsbosIgDUhxDltZJV20HApJeMdcfvnklwg5OArUFtEOpbRSMxpgnwn/2I0eGDsXJB/wGwzqvgtv0gU1DUGArnc8cdX2FwsGfJexf/yHvxlvxS8TxmqvDkXnjoK3s5f+c6LrxogLe9btVP88B/yAF5aJqN65V5bngYy7ZRlBBd3WHe8jbxkbuedvnu/iBPonqgei4urp/ZVVA9j6YBx0/D71wDO278Q8rR7bz9Vy7lL4HlCizX9jD8zev4Wk2Mp91XwbJu6FLhnb9xK3UvaETwZ2+GF56GO785x4Pf+oQQ3FeF91RzHfb81Z/z+fs8npsW24whGNirvLeRKbyLL310iORGuGL3SnaetxHXW841V3+S//6uJpmMuA9RwKFJnVHy3E4Tm30M8xDD3MNRIJic5OCUuY6fnMt1G1NHFvjnd97CH96lcOiCdnL5PorDXQiAQubi53np8vASgfD7S5nkcrwSXZw4opz95VTE/ovYx4DXIcoKrgPuIBDaPBP8eaC3Q7xDgK6fQET6coScQsgbLGigJIQW3ugKiChw3gDcr0D+OGI0diP0eb/JmYmXrwC/jyiciAKfF9/JQ4iJ/zqE+MzXECUSyxD6vt9ATMKnCfStHvQ/czOiEO8AYpy9wLly8XP2g20lb7zuY7zh5hvY/lqH3Vu/QDcG1UaZifl5Nm1djtkCThqMOJSLEOkGrRXUNPR3KAy5q+kaWE1u/HpGnr6S+tEHwb2bc2DsT9cahx5lLDdG06zwW7/5QaZma1SrNhgK6BEO7VfIn6xTm1pgbsJCCcMlW2BNn2hUoGmQL0BuwaU+XaczcTdHDkOlAEpUp2fdKtRwBl3VCVt1Ro+NcODZxynNVvE0cBIwOTlBynNJtPexcu1OqtUmhgqO5xFPJEi3tbK2JcLw03t5/O57KcxBVxaWr4Rst0IlH2f1+b+O1azilSzK+QFWrE9i2y6nFwscPTTCedsuwLRCKCp0JjTWX9/PpvWwMQVDYRF4gI8jesJFHkW4qWUTrIJHwgKlDsXFGuMTszx99Cl6WhLEFNAcl0gkgq7ruI6LbVp4jsvc1CxzExOU5qeoLEzieaIFRltvH8u3bOOFI0exTp/AMwwURTmrVQuOA4UiRrqJ1pNksZHjzk99iBPvuJVEW4S2TArcfhh/ilPD+3FiGTrbMtyI4EzIcvkOf1l3wW9McrbJVX+vB3MudLnwnhA8osCY6xHR43RtPJ/f/l/v5YQd5sDDY+x751ehMgcPN6FyGEojYicnEfKHOUS8MY9wEWT7eUUH73LRGe0tX4IDnijMKCNoJTpiqVL8bWQXKCmTbiGkzvMEDNxv50T+cAT4jAe7EZSfDNAKynYVb00vvFCBPYsBjrB0GZOIltSclR2Zqog1+tFp/vHT/8g7/p+38Y7L38TyzizPKQrrPI8eRTmjC6q9aLdNfL05f/dpgqqpSYTXZCKrs8T2XcBYFf59BF67U2irysSAVFjoaRUbOP6lXvTHbJt/c1s8sb8+/2/5PSVPMFptYO9YjaeervC7v91LWAnirgrwzWfAUqCrA67aJMjKnnK2Fzk6CvUErF8lwrcSZzfwEvrh4pwGNJX3fXA3n/zE4zxyzz4WnzzAFZefxz9+8Dc4efipM9dLUVXe9K538Z4Pf5jViGM6acD9j+/h3ddcIj6jKCh+6Z/rvrwv4gA5z9fqVcT5VxAxgywIl6zWpU3YuhHDMY7QbtUUcS114NgCvO8roldFKBVAUfJ8q4ihuQIxPJe0aDkjCyBpElXOBjcK/uclQ9ZAjB0pbSGbYktgJIcYF23+NgX/MykCUog8NtkkbtK/BnIcRRTIhKCRheqGZVzwxg/wpquSpMIKTc9jumbxhjfdhn16v/+N5+ynY/IuxxGzwiCBYKaIOFPJXtLpDMlkkkhEFEeHtBBhPUQ4rGHbNqZpYNo2iuWi+6xax3FwHMGCtW0DDxdVVbFMS2CLWKieBY5NtVLFdsHzRLs+nVYcClg0sDB9IFbWOsvWTpLR+6NAcufs/7bpiLnoYgTk3+r/3U0wn4cQ8yIE/bVkpcYCIjR9EBEFSk70UkmyH8Vq2DzpLfDkF/6A/i+0sHvZDv7wje/hvDe+Fm2TKONR5OryM2bKSh/IQDRZzFXh9CScHoN8zqNagGgRascglIREi0K2HTKrINYLiQxkotAswtQLUBsHvSH6LITTkIqGMeMpOKyDuoBYJV5OY9lGNJT5HvBB4DWI+WIMQcCSlkB4CxcDb0WIJfSdvStZZiHp0H3AJgUOReDZf4fa3wMfJqhmfRpxd/8YxhSRhezl5xWM7ebyX3knb3nv73HLoE4m85PTVZ84BE/tPcmJkWl6u7v5m7/ZTToVQv9ZX4X8oxSn9nP46AG+cvc4DcvlA3/9MX79ne8EhC/89X/6Y+771rfObHL0AchYEBmAuZOw89L38rlPH+Jjf3kvdReuMyBy6o8Id+k0EI7Th98DmTD8ycdhF6J5SIcB+47AP98Le+6A0mmhB6foAt+64d3w638OvesUvNgbUCRVUYFkWOfwWz+D9eAoT/qJiNFn4L7GJzl8z2f5+J2ABjftPsYtN5Z5428tJwPc+vfCiQOZeQ4TJUQrKhpZXiBPk+KZ4ilZHiSz0EV+WrCVR64xzm1H/447t/bhNLPEnHbWhr/EMfNazi4c6EVEQC/O5gWFF2ebdO1eCRDbgoig3sZ/aSBW2jAiGB1BrGYbEIHha4DfBWYnwYyA1QnnwdD/guJImvk70/Bv/vadiDlVCs6pO2BuGBb/FLxtiOW0hFAt6wb2IO5d2t/gb4EbEeHfjcCdCFT4SeDLwPWImXkcuBURNsiQropoxtWJoDQVEfSgSxBRcY4fqOR9zs4ZAMd4djZP74zL5VGNvpvfTH3/Psamx6mOn6SY7WbD7m7sZpj5HJwah6G1YPuk755BWF6FaQ1MJ0P75l00My24x7NQeB7sZxHj8Zz9NMyYn2Tyjs/ymbrLFVf9N9o6Bqk3NXRgaN0qhnMHODUlYIeIHiLRsZaWVa301R/j8UcgGoOBFbDjSmjrgYceg7Fjovt8x/lVDK1IrVQBS/D/Vm3YjLVOxyWE6oJdnmby9CyNUwfo7ppjYOUQZsWmulhj2plnXaafVMRj3WCE1Os3c+rAQUIhj66uEJ1tGn0tdXZfMocZa2G+rnJ4ZIq7vzvPscfuRNVjbLzm7XRHt9O5Xqc/q7AyI9hpniZKvKXCeR5fqtQTHc/NJoQ9CDWgOudy9PBzVPKLLE7PMH1yjMXpaRba03T29ZDt7UbTRYBcrVap1xqYpk29XGBhZor8xDFqUyPgeSzfsIlwSzvTMwXMyRzEk2y/9louuOxKyobDxoHVfO/fb+Wx790hDmxiP87UQVAUbNfjiv57ueXPv0lPawLaBsDQ2bXrMno3D9HTJTaR9Qs1hJjNo0XoisP6iEjHLTUboSD2OkU0U4ppArTVAbVYwDkxQuWpr/LZqcc57+ab6TLjgv7R3wVt7TDXHuwsj0CCDxAgiCCWqCYwbMGKArQvA+VDsOmjsMcUDtMgQf3+PAI5miAoZXQRwUQdEYOAcBjnEYzYHv9VQyyNyyDT28lnLz/MR7Qvc+Lwt6lVHhGOmqy2VgiiCcnMrQGPI1DLE0su1P//Pf59psSe4xO89/Lf4i9/7e/45bdcyg1v2oWBWD1b/FcaEeC2I0IuWWeiIcCyNv/zz/ufz/qXZ8R/v6BAXBeh0Sr/M1L8KeyfXp0AlCs5onzeDYnveGQCahZsXyXEoyL+ccwCkx6MPg8dqRS//5tJ1iBAU6kctwJ4624YLcOUAffnQOsQDZ5l8J4A3rVBxGqefzmlZqlkg9oEzKoaAtD923ddSO0dOyjaDuVanH9NnB3E/MOjj3Lltm0MIELPKPDYATGnSHv/P3yem37pdfQbdVZvW4VlvTQsYFhwaBwu6xOa0bIAXCEAtqP+MUodRClLoiKATdmMOoJIUz8bhRVr4A0XQIvooXxGkkCmCbOInHwM8TgUCYDVOALwTvn/l9xC6WnVCeQrSohxIsuHpfSxlD2oErBjJd+yhEip64hiLcnOLfjXc4wAiJZe/6L/94pujT/7tSTxkHjs7rx/kg+990HsE38Ezrkk6E9mkl+oI+5AN2LkxQjEPSLoWpRwKEIkESUZTRGNhlE1sG0bXdeoG3WqDcenwtuoHoQUjaQeA12nbpq4roLnhbAdC9uwsZpN7KaBbYuYUHWbKI6J49g0HBvHlyDwfOarhoGHjXcmAyaBWJkqkFmqOueIGa9+iyHm3h0EIoIy2k8SqBJ3+D9lMlgiCC4iJO1EjNLjiPkEfnxAVto0ZW6ffJS7/2Uf2z/fyW/95p9x4bVXMHBx79na7T9jk8l4y4JmBfIzMHvKoTBp4Fh5YokIqXQSNxGndhqUowJwDUUgERfbhC0IKRAOQTMEzSiYLhiookGG107Q8vNHOaJ7/d9f6lmLcqZperQl6CaZISjRlplAc8kutvqbjrwbxq5FNN1+xv/wmP/330MucXZZzUvYqw6MjUaTvP3dn2Lr+gSrz1vLqqE22tM/fLuXsyowV7V58FvzTC6UWTkQZtcvryEZj9HWGkbXf/bgV3N6mMLYAeYnTmJYLn/wwU/w2quvpy+dxnU9vvrFw9RqFTo6FWbGxTZf+Cbc/Tj09sCH/meM0l33M7NnkfmCuMfrr4O9uToTw3BBGlbthjEb5qdEMH7T6+GCa2HZJsiuEo0Asq2Qy8H8AhRmoG0VKHGYseHZ+zya7nOYxnGajYgot8opLC7Ms2UrXLY2xMbLd9Gh1Jh9ZprnHpym4ae3C/+HvfeOs+sq736/a+99+pk500dTpFGvlmXLRe4OtinGgMFxIAFCgknyCQESEvImuSH1vvfm8oYk5E1IQkIICdXwUmxjjLsxrnK3rC6NNCNNr6ef3df9Y+2lfSRkGxnbGKLn8zkfjU5de+1Vnue3fs/veS5gsUMiPtiFwKBix+O4HTAICUlj0kODaUK8SDP2eEF9DW9qLZGXAnOeaJIp3OCLuMUsgkH6ei/m0k3Xsf8+lR0Y59qtQC2b6qRThZfPdwKjXVD7eV5/MbsWuI7jJa3/G9sUsZf7QeBRFEtoGOXx+u1ADfxRmFzG9F/5OAsGHImSDLcCswdhugGcAdMeVO4EeRS8ZdGX/RyxSthNqJG5iDq7nEI5SB2o8Oogip6kleC0KN8qokRF4JsoxPggCg0eiT6jHa+nUK65Lqzxcozm0/azbQHDe77NtxMw0frLpFfkGXmwwsLEBL4skRofo2u+g9alSToHINMFLR1gJcAOYXZOaYEv1mHRtfALnSS6hxBJQVgexJ0fgtF7UGHnS127TtsxkyGBXWfyidu4f+Iwq7dcxebL343rhbR19rHunNeRa2lhfOQAwoJGoYfxME962QDrtj1Jw5mkHla59wG4+ApYuU4BNxOHIagaNGSSwEhhGik6u/opFAao2yENJ4TAxmoJaG3LUS2XWJgbp7QgEYkOsrk8hXaL9pYSvhTU0ybpjgF6Vxew3RlqYo7h6RKjOyV2ejvk92AbnZTd1cwcapBOtLN81UbecNllbDkrSUeLoC2tDnot4h2zggKoxmuKhSijFH9ZhUO7h5k4MsHE1Az12iKZTIJiaYbJsYPM7HuUteddiQy7qDt1/JrEqwfUq2Vcp4qR9CkvTFGdOkxjbhIpQ9r7B6kbUC4tYlcdyFhc/ZZ38IYrLuOSbVvxwpC2XCs9pqS3vYdvfPXfo4IrsTdcXnSZ2rebetWG2mMQ2Ox5ejtVI0VCrIaN6voea8CwD2vycGA/iBWwsueHb3+I2i26hYIJNIvyyQkYLiVIdfbxzo+9n3P7c3z3/h08dbjIil++hJGbb0EubgS3BpkzobFDdaqugKId/ylU4oUqAA59ewEbxFaVtgdqC3sWhWKliLXKcig0zCZGrCRxzqWHOgCdR21xEyigttuEniT1tiyfS9zJ+PZbcfbuU461rmCkHTbdTp0zbgAXdkF/CVq8+AzS9Wjs2MWRusfnqzkufeMltAyuYmIRtrYrBpEG+5ym5htAQ8KdLowdhs2tcFG/au4SjmdLaq++PwPvXwr/dS9ccRas7lJdsgIVDCdQu7wmHS+UVQrlln7lGSQ7oBSq7n1gGsaPgu1FrJ5e2NAPQ1nBsrQ41o2aLCwEmAlY1wKrs8p7NJuySLVqZNKKU2CbVSS13mA6aluaWK4gkU6QSSdI1D3+4DdvZvTQvPrSRJ7kWb/DliWrSWWz7EPNy/UoEnVf07htSyVpz2UxTMGbtpzLQ3t2slD74Yyw4uw8n/roX7Dqs79LtqtwDFJaR1xsUreb6O95/RtRH7vE9eWeG4OdC7DtXMimoWBE6wRqeLYQs2O1yrkT9cEgscyDlijQ/a2B30J0zUWUdMDRBixNQWiqduiCOVOuSqVtTccsX93HO6Lr0sCKE32mjPIM+4iZs1o2Tmvk5gxBe1q1/bP/9DR33HI/pcM3QqBLuZ22Uzddwq2F+AigSz1EB4aZwzKTBB4kkjkSyTTJRJKEZSKMBL4PoQwgASmh7pYhDAzDIHBDkskEiUQC00pQabj4wiAwDYIQ3IaL77gErqeA2cAl9BwM6SNkgC8DJAJJAhkthhKP4NgRQSN6FKO2a9EMrR1zGoh9rVsaNdpWEyWmoO5aErWm6f0+Ef3divLDRRKk3iOFypbJVyATKsjuMGpdnEatd6fKjw6RuKGPa1d4xnb4++9+mhVP38fapWdz7Xt/gzUXmmRaXx16rOZ320SZCiGkXaAK5UlYOFpiYWwSEfqIzlYypEAoEBYfzFqIMCW1BAS+gTAERkId9vsBeAFUbVhYDKFUj+SoGsSQ9ovZ80HeDsoh+jJQAO8SqKxWzlwHyg/SJ4zN2jT6TKgbqKahsQKm/xyVIfsD1N29G/gqOFdCacULou6vGTB2YM259HR3MtTbyvXvfC/nbzZobSLD6lPWZj/vxYaYHcDkYsC+Ix7TMwHppMvaFe1ceE7vi3zyFTIZQGMKe3ofi+NHqNcCLrriTfzCu97NmuWdeFWPJ/aXuPNbt1GZH8WyHFKmweVXns9Tj+/muV1leguCt77JYPr259i3W2KZ0NcBubVwcA/MJOCaq2HV62GhArU0XPgmuOQ62HYVdDRderIDmIHqUWhE+WElB+YXYO9uqLkjuI4qClMtQzgJnVnoXQJDg9DdlQbhUUyaLIRw2flQPArJKhx+zuWhO47Q8IJjcuUCnSKk7p5LiEcVE0EK85jul2h6vPyuSw0VrYCkG2nkEYlriME4Dbb5xFUrbGLp7RNbpLWKNGfiVG09cCVw/kv47GvRmleql2iaPGChCKhPR4+90fO9eXA9KFdgrEbpSEKVMDaB5RKyE+A+CYs2iE3KK5Z11ErYilokB1GAKsQRZQUFrBZRLvdOYk2aCrHTJKPnLFS4UUFtre9ChYXjxIxDXSVlChXhnrbT9qPb4sx2ys9kGElfzFXXr8Bqb8PPFKiXyrhCUA+j9MkEZFNQsSHhKx3xWgVKVZUmm2w16SqkKZU7MLMJgnwONxAw+gQvqCp/2k7RJI2pgwxPjRE4Nh09S8n1rSeXtugZXEm+rZ1C32awQtItaaxcgvauc+hc0kexMsrE0TF2bR+m68A8GQ+slMpacV2BbVgY2TzpXIrW9gKh72BUohKvQRXTypJISEyjQaVYJ5uqYWUKmJZLUK1z+GAJ04JqkKXqtJDI99OohdQaDcqVCocnoHXPUbLd7STbEmTaMwwu76Nr45lsWLeRi7esYfmAKsCj2YUNVPa5HSh9zlEJ01VISEgGPtgVxg9Ms+uJ55icnKDu1zGSJobZRigkVsoim0uQTCXwfY9yuYzvB7hVcGplXKeIG85RHh+nUZlHipBUoUC2s4tS4GLX6vjVBsm2HCtWbKSjtQuvWiWTzTF26BBOo0Eu//xZVUd2PYPbqIAzAgiO7HyKdNcQbFh97D22hHqUpt1LVMTrJN8liBmcOm16AkgFkMkm6VjexVVvHuKyNpjcM8z05AwzGwvwvXGVH+8VwWj65hNPoEuorUuXlO+bhYwLbSklwqtRqnEUla8teq+mlmaIEzc0nVCjfDqdSqNNIXElVdfAdV3u2/Ut3EceRx4ux8KmWsNBo58aCZUoiY6KqcRa81EbdK757DyN6rNsT36b829YxkSpijGS5fXtLcfykzRYqXX6QpSHNiVhzIMlgbqUKjFfTuuGdkb/70rCqnb46CE4c60i/mq1hl01yJmwPq08Aa0A0SZVfJUCMnnljlQkTIUQRAyZdAqyIazphP6kal+ZeF7oAlcJoCOpwN4Q5U1oRlUziKjjGe0n69tvRLdHF5vSZUT17wS+z/e+fROep0T1E6k0573tXQy2Fo6Rk7V3s6QDVixtJd9zGSl/HL9UZ+zAPpzSAivbengqcfJSz41ahR/cdCN33vBm8i0Sx17EFoJwyxUsbUuQTsfXqyXFKsQFy3QcG0rYvagqa9ddOGdQDZ909HCa7rc+b/CIi7jlicnd+vdOBK8hLiamvXhPxp697mMttVCTKgeuucigBhUj2QwdAAAgAElEQVS0DiSo6VKJPqdhwTwxaQpiUFYCi6Hk7nv3c9v/uZtnH74LvO0n7dvT9mKmR28KdUcKqDurj1FagTxCZDBMC+kHSrvVSmAlkhgYIA18HwhDpBAIIaM5J8AXBJ4kNCAUEle6NGwHw0oTGgIZhoRegO8F+J6P73kgA0LfJiREIgnxEceUk0FGx0jymLKwXqV0DAJxWcLT4PxPg+VRe0IPsZqoSSxnopmxyab/JywQGRB6ATQg8CHnqvIlOeLcSb32/ThiFQu4PHTgEXYcOMDS1DBGfhkbFpN0D/bR0bGcocEWsnk4obTSy2ZacqGB8gcdF/wK1IpQXYRaycGplEiaSYzAxAgMRKC0xAnACkAIJb3p++CGIVUzwKgFkBTYnqA47zA3sgjVCQgWiR2WUzVBzKh3o+94HLgZgiLUNsNEFxTOANtUS003x5/+odp9DJFfkoXZqyBsLh96ELgJwi5otLzgdH9NgLFCCK7+wCd425uv5JrN8fPN50U1lIOvyydpGrh2XFT1wwjAk+qapxvw7FMOux5u8N73DLJsaCmmCAhsDylDhDAwTBNhGK9KPCoDGzl5N7WJ55ifsTFbzuCfvv4fLGsHgeSpPVU+/FdPsPPOPyf0G6QEDBSyfOfmT/L2N3yE7z/wDCMlyXW/4eG5ESifh5+/GA5LaN8EW6+B3/hdtRicTNOseSyM+nBgEkZ2qULzNlCvQqMEnW1RQYOEKj6QNMH0YGIexsbhgds9HvrLOwBYMgBbz4Z/+yhs/ze4/3G4e9cst13zz0zxwwtMlgQGNRbYQwuCHGm6SDKICl50kYBmmv8rs2XNMja5h5smH0VyBoq9WEYtKdtRAKlWa9YzEY7vWc3lDYn5AD+qmcCHUIzKvhd570+LacBar/jihH9PwQSIbpC6aof2ei8A5tvh4TyMHoB3rlKVUnKofLZ/vxPq9wBZmPol1Ey5DpUgdxOq3+9BhdabgY8Cv49Ce5vlA/ZHjxPNR+nFrkKBr1tRcgePoGbNamIwtnSSz5+20/aj2iTB3HYqd3yJwlv/kA2XX066ZSl7v/8IvWvWkehKsxhCaRz8IoxPwZI+WLIEfFul+7R2Qt9KyLbA8L4shgHSqoJMEvGHftIX+TNoNiO77mJ8+GGu/K1PM9g5SDZboKO9nzVnXEo6LxAWhAgqZRjovh7PqTG8/2nmF/6a7Y/ci6wEmFKSyZvUhIEjBO0dbfQuX0IibODUEopRF7jgS6p2wOLEJHZlmta0YMvmfmq1HLNjixx6fA+3D8OKpZBv7yHRtoL2gQJ1J8QP8ohEN53L5zFz0DN4Lt3LLqV18ArOvWAbm3os+jIq7NUlUzypfLJpCfs8KFfBrUpMH6QX4tuwUKwyOryT79/yLUoLs7QWWthw1llqPxcJWgtdtGw5j9SmzczWalQaNm65omSj/BRB0KBRW2D/7kdhZgrR3kFqoJ9CoYCUEq/i4vshwjBo6+5gamKGrx86xHxxjL7BIW6/+Q4ac6PgqDVYCBPLUo6e56nNZOdDdzUVFpFUDu8mecH5LG2SDDs/q4p02MAN29SKnjvJHU8C16DIqy4KwH1YwrsHIeWn2L6Qor9D7Y4f/dD1XHRojHf+x03whjPh9p0w+QzqUO8kptOEqihA9mD0fKUEFz6o9r0l0es6TzuPLiKuzEW97wAqeWMQ5d5oFPIq4DbU1rUWdRZ9IICFGiyt4dz4DcUWac5Jz6OiL5dYzFMVKVc06Vun43L1Gs2eIIra6nD/HfyjM8bQ6ndyxXlv4dfP3kqS41k2Ot6ZA/YKWJeGMzerJi9KGJZK4zUVMZK7UcpGC8Qapqk8bLCU7EQa5ak9NQn5HKT7FMSTBy7uUE3TGqO6oFO/gDP7weqPGZzDKK8tSZzu3oFqg85mhDj1XXcXTddE03t8mgKyqJaDKVQbNClnPOrGAirOmZcekq+iQZ6WlgR/+sdn0CUEAbGCpgf0dMDGtWtYe9l/0TH/eaYPTPO90a9waHQ3rRMVfPf5Cux4wD7+x//6DnL0+zD2IMIwufYLE/z+5V2cO2jgRdev+2YBdR4wR6zmuRT41DMQtsL6fpUUquuyRgQqponvRU/UJ7qKQkDMgcoSs1htYn1GPew79GcE1HKK9N0W3a9i9Hp/UoHz3dFva89foOrO6RhKl3vRzNd89B1BqH4jKdSBZwlwQgiCkNFGg4+84zPY1ZtRE/a0vTRLoWajhr00h12LTeRBWsggIDBU1Oh7NUwjRBoCP4LOhBDIUBJIHyF8pZEchJgB+L6D4ziYhMggxMcilTKjQyWJGUDogmN7eL5NKmlFhd9CAgIgwIpUylWcqqPWBtFRDnHKgU53OG0/LWag1ohB1OhrLjap4TxNx2pBHQRigEgQ66dHZvqQDWCdA+kwLjc3Q6wo/ONahTl2O/fxJ5+5Dz6TZu36X+Dyyz/Mh27YzKoNCVJpxQjXoKx4ibwpecLffuQT1qTKyKuUYHIKjoxDtSYJAxMrkSaTz1No6yaVSSvWMET4m0EoBY4fUKlAseRRqduUnCpIgwCTYHaSYGQX1LejCl7PceqmYfTzULvSLGo3P4gqUnMT+B0wcyXM/AvQqjKEzjXU2/VJqEafHdRN7AP2C7CvBtkTffefAd8FesFvFrb4YRNS/uRPZoa2bpVf2/44naZ5bIC4xAoroPxHrwaGA8kUODakEpBKQjoJ2wQUIsZGIGHcg/tuhaW9kgvPh5QpECUY/uxd7P+v25g69BBDnRez8d3voe+ac1Uh+1fY/PoiEzf/EfNTM7Rv/Hm6t76TTFcSAdy3w+Pm2x7gH//kamSo3Li3roWv/xKkLknz7t9zuee5EKO3nUMHv8bv/uqvMzo5St8a+Kd/BStCpg0BZuTRnTjHdNK0ljf/zOfh6GFFGuzrUbR6PAg9cHyo2eA2wHfUY6oIc2WYWoCxKQgXOObpGY46CQoDGOqGla2wogz/OQ1O0xAbAH6VHrbRySp6GWQVD/EEN3GUb7JwrCaE5qdC7NS+MpZGRQgfBv4JlV6ubQtqI50hPp/XiUl6Q23u5VOZS5q/sRu1pL9GtGIN1CTSN+GUTacOTKJmsFZ+e4laI8sg8ztADRp/i/J406hgcU0NvvlVMN4BRjsIA4QE929Ro6YTdQ/zwAMoJ+5aVBLah6N2bgPWoO79C+m4CuJQSqfyrY0+2w98FhW96rDidOrRaXu5rAM4B7PtLfzFjddSGFrKgw+GZHMmDQOCpCAwYX4c9jwNQ2tg2SpwyjA9BrlW9UikJTueBBFC4NSoLxxi9sa3gZzklV5l/zubYSZoG7qIlRu2sXbT+VhtQ/T0r6WlLUu+YNHWDYk05HISxw45vMens+DSWTCpluY4sGcXE5OP4wQW+ZZuWlq7ODq6DywL22lg18vUypOU5g7ilRdIyBKdbUWMMMm+Aw7z0z5eSSJl7HjnWgpc/5sfwU710Tu4hmXLV7Ny1RLa8tCSN8ikDFIYtBoGvhAEIgbH6kDJhfkqFKcjRZkAbMdjYWKW0vwwjUqZeqXC/PQ0jz98L3193fT09NLR2UOpaOMEAX4YEBKQxqJWW6BWW8SxK6RMi1KtBqYglD7l8jymKQnDEO2vVqpFpIz4hKGEeo2hFRdx/rZLWbG8n7/5H+8mDDRXD0Bwwbb38oGP/jqON8+H3/eOY8/H78lC14VseuP7eNO738cnr1b9pVOxZ1GewrOo2fJ8JWRDlGv/hAcPj8Aly2GjqXafW6KU7HOAgVBSdn3e/LkRxm+9Hee5O2H81pN/6TpUtDaH2lLfgXKmulFBgImKFgMU9uOgwFkHta3VULHBTHQB/xZ95xUoxG4Y+Ep0oZdY8GdZ+FJZieA6xFWUtIBpT9QZHjHhK4dCsUC5Nf9JvA0motfXAs9xPJlFCITZy8Ztl/O5B29kbfR0GSXs00nMDtW6nxr8nHDhW8Pw/lXQm4xBOhMFmBVRpOPdgSIUrBTqiL0BjIfKX84K1cwcHAOC51D+chvqO4Po9zQ7sw01BmaI5QR0mqmWFdCBu2b5QqxVStSVOvjW/D/d9mGpsOx1RizZpSEerZVarcHTh8u88ewuAl/5o+29fXxx7zhdLYKMGTNqidrgBJK5SsBHr7oBb2Ynm9b38gvvvZ73/doHcZ5HM1bb2l/8FHPP3cbCrrsAgdH2S3zmc7/NNddtox71WZq4qngCNWc0eDEi4Zc+AddeDL9yKWwS6vrT0fU7UV+liAFsP+pvL7qXz6B2w0L0nVPR80PR+6qoYd8sF5FFgbE5lId2hGMw3rGU4tGof7QSaZrj8+A041dr+VaB20aVFMuSLFzQpe7bLTvge3c8zb1/9ht4thY7+MnH2D99pkvxaf0TA3Wn9Aqg69nrAl4JwCSRSpOyUhgiCTKBHwgsM4VpWhiWCSkTP/BBKmZsEpN02kIQEIQ+ruth5fNYVgohDWQgsasOtWoJz1f6sH7YrPvbrAqqR52PWqw1R1zDbDWOFwA/bT8N9jpi3WhduEsfzDRrV+t1rw31otD0/l5i2r0L0gEmYaEB476KRp9GJbQf5uSlw38cE8LEMCwsU3DpeZ/i4iuv4OLL13LVJUDipYOxPmqP9lHbedGHySp4UzA1D0cmYe8wPLcbSvNl/Fod4brk2trI59KkUhaJpEEqOldJBiBDSdmHsUmHYr2CXS0jF+dgeC+wCHIc5D6U1KCWDTwVG0CBfe8GrlIOgJQqa50i8KuoXWaW6KgN+APg7WCerXys1ahNSCtTaragrrS5EyVuy2PEXqKJcrTKSDl90h5/TTBj2wyDDQnzGOAMP5x6shSQkcSjYSiBfcNQfWkItSxrJycIYPfTsG0L9HQK3IUS//y+z/CI9wji6FFy47Pk7EWenJnizq89Quq+AslOk49e8mtkf/FijNWvgIxBdQY5tZdyyWLp636b3MB6km1JBJK7n/L4yn99mmce/Apvv8Bly+oNfO37Y2wfr3Dtl4Hv2Ow4rCZpplzlL3/347z9A9N0dEYn+6njWcLNJoEwhKfGYC6itWSSsDgOe+ZhxlMnGiOLkDQgjGQJFssQeApc9WyoF6E2B14DnAaE2pmO9p8wVLR0gPEF9fk9Aay3IBdANVSLjg8UKTIPFLDYyQgPMs8z2JT5YQfolTcl+59lEJvkCRCadtG0SIbDD/OLX2orB4CPEKuh/QRNi21pALZZp+6UTTsg+m5qNbSXCMZOgbM7+vgmVJ0t5wgcSsN0B/AmCP8D8udC++vUTrlzN/gLqHDpyyj5gAoKyf0yqqqITh+6P/rSRVTJjV4UK/pE04lvzaZr6h6I/l/i+FXrtJ22l8NU8BHUHGanJKLHwGoLuetzO1lx+SpWnJNl+SYIzlZ7Yjqt1u6xo0oAf35GaR02PMHyQajWoVrLgD8EF/xfsOdBqOyDYITTlZ5ffgsDj/LEsxzCpe45bDlX0JgHp5iimMhg9/XS1ptHFgTpjMmGTQZJK0E+L+geXEL38hyVxjqQYBlJDBJMT59FzRPUGzaNWhWvOkOtNkNg15FODdMrgpFixXkSL1DcHTO/joH2HG2tBm0Fiw0rhqgYKbLpHK2ZHIVcipQJhql0znQqbx2oBgqAnZlRrAevHuLXQ1K+y8L8UYrlIuVqjbrjIrwKrl3HsW0CYO3mrSQTCYRlUWr4ONLBMCWW8BQrqRHiV2YwvQrJoE697mFJCAJBECqVzGzCxJUeduDRsG1kcRFy7UquprQIvsGH/ua9bNp6NkEIu3/54/zK27bSkk3RCGC4LNi4vJ8NK5ayb3SRlW/9Ww5/9w+Rx1LKAGwwU8xN1Nn1xBjPvmmADQhSIj461RXZX2iFN1AB2ToTkv3gmTBswNxIkc/88fe58V+uxi+keNIV7Ju16GwbINi8jqIxS0nOwsRJ9p8x4n25wvHy5ZXoNc10DVFJPnuJU4w6o4cdvec8YnHMHSgq49ujm90bwKG6Sh6ZjL5DJ/3IqAPy0e91Rp9xo+fegXKb6tF7zyIufqHlEa9EoWO79HdKpD/PyNG9fPTv7uRrv/U6WtMJcqhjTi1zpatSa63QNLDCguuXgm2pGEigWLEaCE0AFQFrLHh0Qa2P57ap7nSMmGunizhJYjmtXmJmrQbjwqg9jej3m9PmNWCq1Rtouk0Gcbq+9tM1m0q7XPXo/Rp0HhJx1YL56DZrLzQFVKbqHLp9nPNCyS6gQhsJsZozcnDIgxYJA1ZM4HngWXho+wiP3Pr3nHNON8var6VcnOWv/uZTuP7zsWJ7aO0+g+v+7A/YcNF6Duy4lOFdH8N1Bddf3cuqs4eYivpvDnUukCNOLC9EfVJ24dv7oWsVLO+GzohJqodGgmOZvMdkJGqoYfm0r8gmeTOG40yg3oAdw4oYYm6Etf1qCGaJmcgQD9dFH6YCWJFUBdN0dqWWudD3J0Dtghry07lvekxpSYm1Peq1NhNcKfmf/zjJzvs/z8SOW/HsvZw+4HwppuMFLcqR5HgRD80WsVAjRc+2BAIT34PQVyNeIElaSVzXRQoPTIOESJFOpQilRCAwDaUyHYQ+BoJ8MkMYBkjbJQgknutRr9ZwvAZh6CNl0HR8p6NVK2qbjhW1VqwGkXWqgM4rOW0/LaaViVuJC3Tlie9qHlgG5PshmQFdgkjoN+hMEa2hI5TsFJ3QOgOer5CAGdRarwXxXk6TMiAIAoIAnnjufzM88SVu/14fXx28jBs+8GtsODtDZx+nlLyq1+26hJKEuSJML8LoFMzshf0H4chYg4mxBapzC/iESCOBSGSwKw0cGZJ0kySSJgkXXN8khQFSUnEdFibm8CplZHUeSkcgnEcdvR1BHdE2q5SfivUCm0BcAO1JGBDR+Y6EWgL2/X/g3Yoq9vUwas5+ETgIwfth+grAUCd+S4g3fa0d1I26obMGVPuA3wI+F7V3jBcCj18TYGyC45jcJ7U2iFXSafr3JCYkZG2lKTW7aw+PP/59HrzzFiZ5ii5s2olOUb0q1SNHKR0BTxg8sNjBKkbpufxc2i699Me/sCazSwtURg/TsmQbhaGtJAoF6q7Hjl0T3PStB3nk/u8gizu47oYlbFjdzw/2zLPnSIU7D8bf0d8LW9Z7tHU+x+atDr29HAdgA1QasGM0AmmTCqh2Hdi5D6YWlZZHYMDMNOydgXJNVbwLA6U1GLqq+nG5zDEvMWiAXYKgQnx83SyudMKcaLjqMY+qZGvJOP0nDQh8bOpMM8cBZpnCx0atWa9+rVGV6CTZh1piDOILqnC8EMbLlc7bh0ptfwM/8SmoJW+1F3oyzPGUTEd/ekY31wV+IWsGufXO5YI7RbijE7qykDLV5Jbfh6qE6jpURLgTwgz4S8GpgdyDGn0ucUnnDdHFPo6KFlNE3Jqozf2oVeaFwPUTjzzqqAnx49bEPG2n7YVMhYVmoYNdBxIUc2AmBPUggRsYlIowNqIcwK4+BcTWypK5mYCBPpNaXVAsgR9CfoNKpcQ1kckcdJ0NXa6KTsu6oESzPvJpeznMt4uUZ4aVFmFKMp3Jkc710dq+jAwWvm3T6EjT2paiuyuJkRSYSUgkkyRbOynITgXoSKWtlSyo+2y7Hrbj4Dn9WG6d0PcIXJdGrU7dTtDaJkimVbpMMruSJW0ZWvMmLVnoMBVQpQHG5pCx4asaCZ4HtQDqvqTsSObnPOpVB7/uIGs2ll+htDhBqVKkUq8RmBYJfFynjuM6BEha2jogDAl8j0ajjuOUSJghQeDgNOoENR/DrUDQQPoOtmNjiSQBgiBK+yW0MEwLyzCwsPC91LHUHcN16F2xld6eDjJpk2LZIVFYyvJzrmDVkjwpA45UoacV8ga4foJ3vuMavnj0IWYP/gC3qlPdQpat3IBItDBx8AhVBhhFBWNaHzIFzDuqkNQL1dusVmGmCj294IsIWGoE7H92nsMjIY2lUE1AtyW4fHWWx6r9yPBMAiuk+p2DIE+QD2l2jDTxSm8/2i/TWIURNXaGWISzE2iLdLw8qXCOg8QVRBzgeuLXn/RVzOMS54Jr0wiWR4yo+aigJiTOKiYaVDYxkW0liiBSIwZjAfCoLU6w/ZZv8I0ewQWXbWFgWc+xVHQNcWiWsgY1UwaszCvwbCG6jDrHQza56DOeAYuGumTN8E43vZemLtSqCvo5HW9pPzYRXaKOs7ULpeE3DW3axMzZZl1biIFHonaXJDiBSmVNmJBJxC62i/Ld/brErjskCgnmF2uMPX0YV0qV8dbSS8fQVrotmJExGcuWkqcePsB99x/imWf24y1M0Ll2FXW7wqGjR3j2ueNuxHG24YyNbLvyerZd80aWLYUlbUNsWAWOB1deqlJx66jh5BDzFLUXnYn6eSGEgzXYsBYGu+JhoftWg9nNfaRV/J89DO15WN8XFwQzURIOuQQMpiFjxsfgJWDRUQBuZzKGxGo2zNZgc08Mi+k8t+Z7CMd7csnoN/UYcVFUg95M9L1Fm3tvO8R9N9/F/M5b8Gcee97+PG0/ijUr/griWaaDTc0j1zMViPRbCc1IOkCVlrTMhIoZIr/dskySqZTKsgglpmVBKJGhSRgaSGEQuC6BH+J5Prbj4Lg1/FDzrHWpaYhHr57JzcGwDqj0yNIw/mn7aTKJmus1Yi1qDb9nUT5UezekzgSzg+PDeX0KViHWcNGPBCQS6oCpJ4jVj1/pEt7F8l6KZTg6mmdk9yItbRm2HFzGyjVLGVy7gZUrowTTF/gOfQmaauUBdU+FD1MTsH8/7N1dZ3q8SGV+FuxipHWZQqQgkAIrmUQKSSjAF4JGXVALQ6TvUKss4EyNQqMI9iw0RlB3YRIFaM4Qz71TNS0ZMg9hh9qg2oGMgEoC5s6Bogd2ErWr7UB5DBLoBfs8mM8DpprimryvTVd6awCNNgiuBe6K2v3CNYVeE2Dsy20GIUOihP1YyN3f+Sb/+vU/xUJBX4PEDGPtT9aBCRnyH499mdc/9mXOe/t1nLnpLIz2POKlcribTIYBlbkS04fn2XT17yLygoZtM3p0ln/54j38n3/9GI1akQvPbOVtr1+FzOXJtf4w2rzpDPjwhwyufnsrQmgNmti8AI7Mwae/GxXYalN6RrUyjO2F0XGYLsOMDQtS1VfwfSVLcCyLQnu92qssE2uCQUxTgB8pXt/XdOAuUM5UCwY+NkeoHss67yCWYn71k3o8GnwF5cZpVWJ45bQUtwJvQemV/gTMOOHvBPGh7styyVni4lgQhxR6GdfOFMTusG6APnEJUOHVw/D4WdC2FJa2QCIE70aQc8T9CFSPQPUOGB9HRZl11Eq7FFXZcAgVUo8T18GtNv3WetT9P0R86n6i6RCwObVVt/20nbZXyiSIkOSy5TzwVJLlTsCFl5qsff16sq1weF/AD+4MCFzJW96jTuCqDUmt4pMYMgmkyuQuFFQ6vKxCaAIJgWFkCPs3QbAA5X2oxWA/p87qEQjDwDQ0jwyEofbOwPcJw9Opmn51hlJ1jkdH9kFYZMmKc1m5/nL6W1qYmU6T7eikpb2NxlyBrqUGhmWQzAlCQ2AJgTQEaQPaEzDdrthloUjgksAlTy8RDhdA0Vba7gP9UMjHKdBwfLX5BCqrxZWR5lcIRSkpNiQzE+DUJG4dPC8k8H1cr0y1PIfTKOE0ypQXZtWO6Tn4gYdp5AhkgOO7uL5CAkMfCBx8p0GjWqRen8U0fVy3Tq1WBtunI5UjCHwcz6Ph+1i+CaaFj8R1HRzDQGQsrESafDKJbVShOAJBjUQmz8Vv+UWmpmaoVuqUqpJD4xPcf8TGymbY1GWyri0G0lYMZPn4e9dwaPZ/cd9nf4XZg7Hu2NYLXsfkfJ6J8aMUxIU8LVQ2/0qiw2VguAqlEN6Yfv5CssMzcNdhuKZXMTVngKOpBNaqPr6y21CJHgPw630w3Afl8hKq2TzZM9dw5JHt2IuPEfrl5x9ME8SCcxrV8oW6yLKM8YF5lF83AOQt6A6gR8Yl5/cRC2LWUcSRWRQpRAOxzaYv1kcRVaaaXjNQccuApX5P+Or1aRQYvBqlChQQa2U1W2UWef9n+dhzo/ze3/02V7/jUpa1tJIHSiJekTTZiKjJKVT8ExAXWdLYtIgufTuQblMg+kMhnCegIeISOmliZmxzISiNa3vRbzZQMmhE/5ciBhG1ulOzaoN2l7WblST2FgTq1mjN2aKERRf8GhQy0JlQiZOu/h4PqvMwPl5FrGthsVTi6M6dPBOBsZ29AwyccwmmhHbPoeK57A48apbJpz9zJ3uf+DZpc5r3vOcXmdw/ye333c7w6KGT3IjodiZzvPW61/Gxv/wgz0TtP2cltK1UrzcXly5H16vTeDV+3wLMhkqiwM7D1WtgKBl7ezqYt4nJ1fr4Phu958gzIAYg2xfXlJNAJg3nrIPedarPda7TDHC4rmTrWhOxdqzbAHsekj0xSVs/9DzWoHkKVZDQR8m+6QJsdnSts8DyEBYaNk/uGuePb/gGOJ+MWnDaXrrpWEHPEj1zNHTucjzlUPvvOnjJoGZTEoFBGASk0gkMYWJYSbK5POl0Gt/3CYIAwzRVEOwn8EOp5HP8EAIfx3WpOw1kk5iIODZi9Uqh2bHNwZPebfWKpWH+58tfPW2vVQtQwoVaeqYHtQfkDGi1oDcHmXNAXEksIK5vcQVFdd2HCit1YUw9vC0ltdkbKFzk1QBjtflhlenaPfzD5+9hMHMRm9ZfzZvf/0He/a4EmWwaK2GRSBgIcXIZAz0rs0Qz0Yz2szIcnYbZySLV2TmoLyoZAE+lTks7JMBEFsyIImxCYBF60GjYOLUq/swkTO6L5NOmiYtqRyDqMZ1YLWFyKsSRA8D9IAeg+DvqdDYr1EaVQ8EE8gJwloPMA3+KupHjwNeA9ygSWJBT/pZWSNFLgEkMZlUKULsKVRPo+yhW7/NloPyMgrG1colfvvJMMsEsvdLlCmKIpUpcAEwTDHQq0UrUYb1903ba7v9NlnHkTKIAACAASURBVM98Aawfv7JXMDVGW3aItkvPU5UAgE9/4vN88q/+gVlnnxqswN4dZd51yUPYwM6TxK4rVllc/fYEQpxc2/LJKbjjKbjrFujrUyfDngfFMsxNgrcIoQZWdZ6V3iO04NUraLFWs0kZyQgq8zyF2j4n+UmpK4UoAOLVkgw4D3U08CqbPmQeIB78FV5ofXgJlj3Jc3WU+zqLWqUGUOAnUQN2o3ascvS8VgSzUQP1Diiugurb4CoTHr0SivMo198G/gH4OvCF6Ds/hHLKtAP3H8CnUSvtW4FPRs9vBN4JfAm4F7UCnImaDE/zw0zX08W4TttPwuaBu7C5ATk7zOJknbHaEH/+MfjWAzB7YJzifftgfJ7w2msoDLaQ6xYsXZ1ifgrWdYERMaUqdVWkMWPAwDKDqZYzOLp/CmfhIWAvmBdBcIhTBmMz3XT39rJ8aQ9pSy0oLYVWTEvw7PaHGBtfUCnnWhLl1U+BeI1YGImtw9ThxyjNHsSuTdK5/CzSE1kMYRIIQXffUlrae0m3tJNsKWC1tdHeAcv61CMvFHCh75Jmb0kgYahEAmtNvAJqfydqAT6xgt1iBRYXoLQA/hQEtQrSb2CZPpbl47oKWHX8GlOTY5RrC/iBhxCCVDqPlUrhBgFew6HhVvB9HyMIsMIIEbRnGd79JHMz4/jSY3BwCY4IsJ06tWoF3/bx0imQAt8H2/Gx8AkTCTzTwPMDJbFUb4HqHEw9c1yPtuYz3Pg3H0EYBkdm5hmeWuTss87n5rv2sNIaYkXXUlqJXfkyULcEX/79VVx9V5a7m7KPHtixj2TXRSw/83LOQPVfB3F1d1BuUxF15LeGk4fX5QqMTapdrIDiVxwotHDpW6/mndfCXZMwPAt0qTKQrb2dLOvv5IyNUHjPHfzjRRdx5LEXqMC+kzgOuZAoP1uqQdCOYp++PQe7ArjZVvHM/V4sez4NfBO1pZnRxf199H2bgV9BbcsnFvzuIj6rPFHRJAS+DfzFuXCpCX0PxQKdyegzX0Bt9S9EElm4k0+9/y6+e+ObueEbt/Lr2eNrHteImaoaGsmjcluafXoN2bSg+tgHphwYr8GGDoUNRxyXY4za5vjAjl7XLNg8avyMAZMSVgul/ZuPLt0iVszXbdSmYzWbuCBV8+tZVMbkugzYGTVmWqLvGY6usycF5wwBQ52MSDhcLrF/37OKEQjYtRkmxp7h2ws/z3f/5208fu83GD38A1ZuWcGKniE+8ke/RU9XL9/+xD9wy6M34/kvvMYPveWTdJ915TFe3xxquBRQnlI1uo4WFEihdVY1GTsdXe/jC3BTEc7aqLB4EzX8gqa+a6CO3tuI5QMClEf+wetjHdcjxDq4uk9LqPmo5Rs6gdmkYuM+5MGbEmos9HRBvgtGhDqiL0WPDlSqcS16VKPfvWenkrV405nqTEHP/wxKfePeEtz4/36B7/3dP4PcwU8qevnZNC0Wokcf0b/6LoccD1/oIxH1fstMkUzksCwLy7Qwk0nMZBLLsgh8gASGYeH7Pr7tEzg+YQBg4vtKdkAKgWVYeCHo8nrymNqwPobQIx5OTszQgh0NYjbvaftpsuWovMrlqHWhF9i0FLqWo8LVragFYQkKUdX6MzXUyVA/6raPovZMnVlsKHipnTjr/cUyxF8JG2s8zNjTj3DXM3/Jv3z8Sq5+529yyRvO59Ir++nqOPln9KzMoDBJ2QYyhOoi0IC02cfISJ7pqQQsLkIqq/SvDANa0pA0MJIGZtI8VrnSyCQwZRrf0rH/UyiB+cMcD7gmUcrvPgokHefU1t4nUWk/74LxHpBRCkqO+GSXXpj+IMpzuxO180wCvwB8ARoXwrSp3qtPWQ3iLKCuqMkHBKqezP8GvoE65X7+Pv2ptSLqpFtI6D0OwZfIcJbLpMsK5LFKrPPE6UfdxH1XQi2husyQywz3hg/yfuTLco51pLyEdNKgb6laiL96625+8MxOrOwk//f7z+SCc9/Ap798L9+990kelvEJ7IlWx2dGhPSgtp5pD47aMDIJe56FHXth934oFqG2CCIA6UNgg1+KhKP1fqE9IG2vQlaqRPV7Nx1IAhxmsBBUkJR4MRL3q2EnRh6vhF2FWrl7XuyNL48J4ohD3/tZ1ALyimTVnzhjdqBOow4QK74VUAviWtRy3kCtglliwXvNm0hzbFfzH4KHL4bse6HgQKmKqhLyoHodC7XIvgm4L3q+jhLDm45+R0eHEb2De5vaOobqHA1XvJwmgN9mxZlryXRlWKguMrX3KajdDcH0y/xbp+1nzqSH3PsHwDUsli9nRyrHnjd2smaLYHGxh7HJFMW9ezgyb7FqCDqXCIo56EpDowR+tKF0LYG2ZRD6ELqCIA9WSxdz1SXM7SxA8DDxufcpLBD2Am3pfjau2czqjWewdOMKfAyKDYcV73g/u2ZG2PX4PUwefBpDlviTP7mRrV2d7DpY4uNfehru/rjy5v6bmSmgJWngzR/FDyEMAhoNj50P3UUym6erp5elQyuZnBsnXehlw5az2XbpBazdDI8+BdWqT0BIPpckaUb3FY4Vmw5t8Go2jWKVfEsnwhT4YYjnh3hWgGU2qNWLlMoLlBcWkJ5FPp0mnVbMospiGel4hEFIKAN8aSMISVoGViqhZJA8F8exsZ0aAQGGL/G9BoFbx7VLzE8eZGZkP75nUxjoImWBbXuYQUDKMknmDOo1GyENTGGQki4Nt4YfpAmSLWAtgaM7Fb07OFmwm0YIwbdvvZ1ndu6h2mjwF3/0h2xYsoVpL8UDh1U2UHs/tGahKwEbpOCWQzBzrJCUAQxRXCiTzfoEVicgWInaUaZQu/ZjwEwN5hpwmwEdLXCVBQNNMfZuYPUa+ItBmIq2w7OARtXn3++fwxroYbpqsr4FxAb1+ptXC35Qggeeg3PXC/xV18PRJEw+8PyDZ4KYSNaHQhF7iYOKpxswKtXrD6ASRHpR2+8oscOlKaW6a/ejzjfPi7p3HAWgQoyKPh8B8Cngj59TpwXtqG22gdrSHyamQb6ISSkZefhB/vF1F/Pd93+LP3tbB2cNJOggltPQj2YhqSTKv380amY3cBExANqZhEEJ/8/d8IFtcFarOhqGWFLAQ3ki86gYQ0M8c9HrHSgyTZY4mUzDMjrnJ0sMG0EM2WiQUWvQ6rrOHuAJ5X3oxDQv+q21KKAyEEoZExR4uG35EAvveR9j//k1JsOAxtxBxrd/kdv+qc7o0zsI7DI9gxs45/Lf4bd+cS2T9S4eeXw39zxzN77/4mv7+L2fYPwcm9o71rKZuB68TtFNE/MBa6ghkkTFoYOouOpp4KE5GD4Er1sd68lqbN4klv/QlTq01q8uptYQ8cFROzEUpz00/f+aVKTwvID+dCRFF/VpBgXC767C+l5YIeKEsGFi/cckylPMAm4QSxNo4pQFVGz464fh7k9cz9iOx5FyltNA7MttemFrFvbwiaF6bQHxDFWLsGmkEVjH2K+BKQgcB2kY5IIAxw0xhAVCEPgBRhiqbUUKjCgxzzDTmIkERiKB6WRw3TrhsXusDzE0K1arDWu+vtnUfr2q6BVISys0q0yftteitaKoO7+6Epb3QKELjF5ItkG6HUQnMa+om/jsAOJTKhN16mcT67fohBdHYTIB8YFWd/T3y60be6KZxAd+HSJDApOSdLFq+3nuvr9m4fBS9jywmXOvuIHBs7oo9CTJ52KwWM9AGZFKQxOCLJT6oF6BRlWQzeRo7Rji6JE0QSgJAggDAyvVirBSWAmLZFLQ8BVOmzQMJBmcjkEY7QGZ4uS6iSGqE9tRdL4txCv5FD9a7xWBXwP70zC/Qmkz9BMXGm0I1M26FFXQ60jUlnHgb4DrwX+v8pUk8Yk9xBt9FiUNVRIg3w1cDVz3vC36qQZjE4BTgdJh6Nkcg7ESSYhHEnlMHzZLnODQRXxYoeeIPmFXp+QeU7KkvI8OfliY9Ue0IAjZvXuEfK6fTFsCWzrc9s0n+dbN3+Ho3sdYXvB484WtrBuc4jstVVLE8/RktuDAzvmQFWk4OAIHp1U63NgsjO6FyaMwP6filaBKLDngEet6NUtt/ARiX5WGZGAi6QZSZDBQAR4cr9j66tur8csXoBiaP4qO6ks0kzhK0biKzpfTAmT6dO4VNx06zaPcc4EKLaaiBgwQpxeJ6LkZ1IKqt4wqamZ4UD5TPeePoBbJDOrkbAWqlPNngNtQF70RFbHui35bq5uFqFUhIE55gDgh8OWyHN0D59DTt46OjgyZlreT7+4iMCXTi7OYrmTu0BRO1YRw4mX83dP2s2cS6sPAs/jzXZSG1/D0Y5287kLYuD7F5M+18fD0EmbnTApzkG+DNb2KvRcIMOpKFjZTUIfTvg92Xal+WF4Co2UZFM6B0k2owOEUgwQpSSdzdHcPse2yCyks7WUxlBiOz7xh4E+tJTRcSNjIHQ+xz0hwzurVnLs0ye8ZS/C2zPPovGRk17PMPnb3y999r1GzLIvunl5mJuYwBRhSYrg+wq5Qry5SdCrkcGgUp8CuUzzawdH9fUg/xbOPHmFxvkzge3T3ttNWyOO6AY7nYQuHwHcQrsCtu1SrNfoHVpHJFxCmRSAlvvCxwgqLixPMTI5yZPcu1p93AWZ7O0JkSaUzyFB9n+e5eIGLF/pgKl5fGAZ4fpV6vUGjWsWx64iEAN8jcGq4doV6eZZabR4XG5EIsRKCaqOO9EOENEiaKQgNaoFLIMOoImsSz5GEtos0imCFYNdOCtan23tpWXU2N978Pe665yG8wGPl8kEKWYtCtoWp0RIzxRKyq5uBBLQaakdpRRXbECKH2kOUimgwVyJsmUMGs5Top4Xj1eJHgCAPPUlYn4S6oQB1iPVMH9kFy1rg8mVxVmILMJQVDF2Q5vJewZEOlaV30zys74DBLPQvwtgY/PIG6Nj0c8wfHsV5ITC2gUKadhPL2y8S53rbYYygyajxUyiHdyF6XmdGnVDHjMnofVtQ9N/zgZuijivz/MtDFdhZiwVVtb9R5IWd25OYUy4x9uRjLBQ+zZeO5tm99UxWbbuabYNqLWvO+DwxqbkjuqQ2YsncdUDNgHoCerrhnn3Q6IXXL1OXpd2kGio+0E1vEI+BJEr6qxB1m/YWtMuleQ6aBWsQJ1TrpGr9XRpwTHF8iKFdtzoxszqM2lVBjaWUgLZUiv7uLhqR9xx6Nk5lhuLiFH2bN7P6wk46egY5a+tWNqzr4YmvP8pDd3yHYnWRH8Xc4hEeu/e7fKGnlave8wEGUzDlwUQZZkfgnLOjmhBEsgEogDYJVBzJP99W49DYHhbbO1m6ZiUbicFpgzgmax5KulSuZl7p+6rfp/ENDdGFEoZL0Ego/drWhHqvacYFt+YAz1EyLAOpGCrLoWJBLeuo71Nn9PfmHpVloGXtDGC8BI8fqnDvF/6Ng9t/gFs+XfDylbFmObBmUYsTrVnBEiBEyoBQaqDUIAw9QmkghUmtEuL7IISFECahMLAwITRAQhAGYIGQUs0qKUCYIJIIGR5joSPCaD/So9dqaofmbGv0TdPl9EOrORtN79dc+dPg7CtlwjD4hQ99iNZkkql5eGBnQOnJPSC3ozao2PKoAorb0kpOqGMVpJaiwsxlxJUCW1CLSHOWsTadHtARvaeDmOIfAXZCqDuvZRC0N/JygrFW9P2tJnS2tZG0kqQSJl05i0w6QZvZhiUtSn6ZeiOHmShBxWNxVFIdeYrFrrMJ6MTvTGO2qL2nWZ5JAGkBhRT0dsHcPHR3QcM2qQRpxudzBLarWJOmgTQswsBASqEU2Ij6QQgs08JItxIW1kNlDfhHUXntzRaiMALNhs+h5tipVB73gMcg/E+ovQGM/5+9Nw+z46rOvX+7xjP26dNza27Ng63R8ywbbIMxxGMYQiAfBLhJuOFJIAn5cm/ITXIvly9AILnJExJmTEIgXAw24NnGyLNkyZIla5ZaUqvn7tNnrDpVtb8/9tldR7IkS7axDdF6nqNu9Zmqdu3ae613vetd50EqGVf+OCgd2eoaYA3KYepH7S7PoHblmVC9CkZE3HNQ38a6ArC7MfhRN3jdUDhR5XB8nd4YVgNqIbLiE/lFwkZGqXluG24eM5mbVtZPA+F4xOAjASy3lSPfMEFcgZ1DjbEuSZmFcrZwejGDAjOjCkkUrq7b8RRk45ccLwuM9T2fyckCTz25gxve1orjwv59g3zxi9/h6We+SVs0wYV9SToydUb67yMqTJJGOWAns4EJeHgXDLfDjzfA8zvg4EFVdlrT1NI6sdBV0PR4A0jVCBrXjDoJQmYiMHFx8LCINZt+NflRBmoyXYAqSPgFmk7566+FhthZ02teEyAWlGvbgVrd6sTFa5PERWlppqlc0315j6JmxAzint6DwE6YSgAbUKDr9ahs1TkoGs4/AZ8DPoAqiksCnydGozUjJEINVAtqYX+1zMEwU7S2teLYXSxd+y6WrrqBJQvzZLsSDA+VGR6dIpWu44QL8SfPZ9IPCGpDTY0BztpZO5kdgtoegoFDPP3Acq5ZbLBolqB0lc0z9/YwVTAZGVIlmefMh8N+g+3lqlveySifyAghssEqQ30Mosx8rNnXE5QfhaAIhgtGCoIKp7NYJFJtZNtm0T5zAYvPW0YRwYRQd/qIhENWF6XqJHgl5KYtfOfxJ+nq7OL6pYv5vdtXwXtW8fX98MT3vsX2wd0crUIwPqCEEn+FTRgGiVQCEdRxHBPLNrFwoD1PuTiFqFeZHDqECIuk8jmCwmGOvLCFI/tb2PP8E4wNH8Wv1eiZ3cPMnh6q1SpT5RKT5SnqYQ0ntAhDiRcFBN4Ibe2zsBJJpGUQBAFRdZKRo4c5vG8PLzy2gcUrVlNPetQMA9d0cYRNJapR9X1qvsrwSoAoRNZ9PK/M5Pg49UoFGdSxkzZBUKbuVfAqRUqlESIRYqbdRnAbMTZZIGnY2JaNZTvISGmd1qOIwDCQVha8NHhDqC66oycdv0S+k9TcZfztv3yToSNTXHrxOtatXQco7dxSsUC9XGL5qk7WCLAFVP2AwwWPua0p2jvnk2yZTXVqt+pgWqggpgaRwT4G6UWGAlsoEBfUNpppUz7kdah6j0zT8fgoxnJtFlwzR6VdoQEI5i0ue3eej7bCo6WIRwuSLx8R/HZesCQQJD1wq6rC/47l53Fo3zb8fbOQw4dPfPKa0aqlp0RjqDTCp7faGg22R+N5He9r5PJ4MFbTO7ej8pkrUeyf7SgyyvHblMZNtONWImbOHjnxoZ+2RQGV+/+Kr90PD152C5f/3gpmX91FT97BsYxpfoH+qcHOhY23657seZS3MQEctODq1fC3/w61KizshXV2jB3XYRqE18MbEjf70nHXcfJ/0yCrZrbqwuQUMZNUx2lR0+dIlG6zKRvzTMRp4anGsWhwt4iabxLw6hUmJ/oZa/IcDNOiZVYfq1fexuIl85g3t5X2xnu2P/5jHrv7q2c0/I898AAv7N5Lfe01vLUVdvpJnh50ePzBiP+n2+XcrgRdCQuHmFgUBnBwPOCv/v55oqfu4dL3r+HWt8xnKbGWr2YEQwxh1YjZwnpc9Ot1GJPk2HDGB3YXIJWCrjT0OCr/QONYWqUKoUc86LHg3AwMBOBbSlM22ziAYalAhjYB3RJKPiztUo3BOhufNxnBlv4y375/N9u+/vEzGsez9nKseWFp1DJPs0ubA9pmwFYSSS1iIgGTMNRpFBev7DMNiAoL4bhEmBgIpIQglAgBMqw3gDID0wQh1MoiJEqqQIAkakgMNjN4VQpHIJG0EJNudOVf1HS8OlCTxGzZ5iZgr7U12DvCACGm++XIUI//LzdQbBgGN33oQ8zK5Nh6IM2Oe7Ikxu7EiTxC/wUqpRKTxRI2qtJllQureqFtLrgLUUDsYlRWr5kFeyrTahtu42catRgXQDamsk4+aZ3sDCrH+nJHW+MoSdfCdkwypkGbaTArYbB4Xh+ZZIZkwqW13STKpnCtNoS0qNTGKY47VGsjGEZEJgOt4S4ozKWeSVN1ExSzKn6wRNz1RXPDcxb0tMFgJ0yOQqkKQ1WB4TpE1QhJhLAEURQR+BF+rZHIDgVSCgQCQxiYrkvUsxzEhVAch/puYlVwfX8MEa8L1cbzY5xW2c30UY8DXwR/Aiaz4HZDKgN1G6TZyNHPArkS5cgMEUsjPNq4YqtgogVsKy6v0Ju8i9o8WhqHWuSUCek3Dhj7BPDwGPLurRSe+QeO8iARk8fgoJ0Xf4b2t38C/iT+m5goYz3aDx9ehl6gDRTlu4y6RBngN1DqE/NRfmUKAct+gHn4M9TH/oPZKB2hHajLXdEe3cscoZ07XuBfv/5vLOy7GBHBffdu5NOf/jpPPvXPgLqc//eFKj+9+YnTLo7fvAW2fxbWnwu7h2C0DFM6yabXc0mM6Dan9l9nnEeg5qoCY8sESAxggInpEiSPX+V+9B3AJ1DqM9mXeO0rMJ2N09feI5Y0el1sqnEA7SjA1COmaVvEvY+1cxWg3OftxNFmC2qGHAJuQS2iOmQ6BzWmj6B0YdOou+uLjc8TwGWo2TeCkk0Ald3KEvdMfrVsJR3db+fPv/hnrFgKEyMlKsWA7s40e/aPkhI2+aRD2baZ2T2fcME4Rxni6IHdVDnLjj1rL2VJ8EKikQF2bZ/khxtzXLnO4uoeg59fl6MwKujIQFdWOUwLZ8CoCYVJKHngWlBqpN2zSbBnwvgYtC5cRCbXywFfwP4vQ24+pGfDwR+gMtOn3kAuvuHdXPy2d7Dk+qt4SgqGheKr7waeF3BgBoTJi6GlD6IZsOle/u4fy/zd0oux3vYOblkBH+mDj37iNwg/+h4u/SH0f/xc/MMn7/T9q2ATY4N861/+khtv+wgZK40hTUJpYkxMsOKcFYyNjbDh5w8zMraF5bWrqFc9apND1ADbtGjL2NTsOoXRPYwN7sGfmKRamKRQLrDmkguwUzlMM4llJchYUJwapD4Z4od1giCgMDSEa9vMnDeX5WtX0t7TQz0KqXk1grCOZUGlOk6lVMb3VUlF6PnIKEASEAQ17HoRixApImrlKWpBDaTEtGzSuR5qpSp2lKfuVShNTjI5MsJktUqyJUO2t5NaaZTySJGo7qLW4xwx/FTnVFrdk/u2UDi4nfyCS8i1L2PN6gt5+5suRUroH4NCsYOM38plTTJWG7YP877P/5z7/vkWbvyjz+LMW81P/+6/wPI/hrAKuToBRQ4Cj4/D2iSszKid5H3AFk68pepkczIFtqt2tXTTc0kLVubVffnzh0r8eHedzoUprl2e4FOHwTPhmzerEmqRBW55P4m3X0P11+ac+OR1XOKhtjxdX2+gnFldCFJBgbBa5lBbs9zh8Z+rfcjvoRR/VqC213uBe1COsjZdv30suehVt/6f/wd3PH0/d7zrbu7/1CqWzs1Muzja5dHgXaZxCkMoT2J947kUyv8fBS6/EsYq8O3DsG6eAuNmEeufTmviEc9GiJUWMjSVaxLz3zSEVGt8T0isCKHLUOuNYwOVYh7xoFCFVXn1XbNQBCwan6VFlfT/R4D79j7G733plpitByQyWW79w79iNTEhuZ+GDB4TvJzE83j/Af5iXR9/ASQWXYfZuZby0CTPPHs5n/mjy7jh8tnTja/KwI4B+OkjE0QPXQxyPZem+vi9NnW+enya+500q2hq5Y184/wLxOGNBml18y0f1YT4vDlxHZXbeI8mqkmg4EMyreQLRAibDkHbbMjY6lrMBO4rQWcCuh0lvfyvz6l4fHU7vHeu+t6HpuA/7rqHn/7p35zxGJ61MzWBumP14mKjrmqOOLWhAUwN0AaomWA1vUfHGfoeSYBhKcarVDJ+QWOGmaZFIpEgkbDAMnFsE9cyCMKAwmSBqB4ShRLP9xpFGnW0XySmyxHUbE64CXzfJ5Kq4kIyiiLh6DZzA7y4AVGAim1ejzbWOnDMQyqPk0xh2w6mNJgaHEHFXqXX4bhePQuDgHedey4wl/SKm+n74Of44u5buNi4hYGnN/Cjb3+VT37hKywBrs/B2+bC5TeA0IKu3agwVicwz+jLiTNQCgSh7oGsH8v1a0HBToO8fNHElIAZjsGbzu9jxapeema00N6eJZduJ5OZi5Ap6n7IyPghJksBUtoEATgVh57eTkxnJW35Hvpmn0PvsjWYvSBcNUtHpaq0a+6kpKsdXAFZA6LF0JqBVCuM1SCTyeAXBaFfB185HZWSR2XKwLBNEpaFlUiDKVRj4ayAvAl9N8CRdbDlzSiB+0dQu4iuR9F9aE5kp1tjPQX8Hwi/AgNrYeADKMS9E4UZ/Bgl0K+bfWs7iHKOOqH2UejvVYd2LrF4uv56LXKe49iGp8fZGwKMDbZuxX/3ApxaiKj45JgicwIFUfNi4NZj/xaNjeM9+DBES9ALoUOS2/kTNvFVhjk63cz1PNTkVpw7CTtuIh0Uprt/TqECyLS7nI90vgdxhmLbUsLUEfj+t/6Zrc88QmHkAI4PH33Xl9l5cB/7Bg+w1oDP/+DvePKeR/n2l/6dLfUzuOGOgD8OP3sBZl0OuRaVXSl6xAkCvfdoD/JEmuKvg+kSvjTQgo1NRBGJh/LrD6EOtwO1Hf3qsGPzwNXAFShHYbzxt/Sp3nRm1rzuhJy6jPA1swi1YD1OHClqvafmFg0lVMigeew2cSpluPGahio4Pop/0YlyWCrAv6FU4aqNv98IfKbxua0odfVNxApyb0VFk/q7T8VFP11LgfE+rn/3as5bu4hVyxawYqnAENDupvFqEaWSh5t2qXkeJh7tOQvXhHKnRW3Epoz7BtBMPmtvbJsJtEIQIqqH6HJh21PQmoWuefCh2wX//S8CjmYMZs8z8ID1Ap7OwU4D6sMwMqxKOCsVGB6CsTE4unscbzIggcmbP/5O9my7gdEN91Lc8hPi2hLd2ubE9vgj95NfNIsL37OegoD7UCDI4ca7QoHyErs72Dlr7wAAIABJREFU4dx3Qv8U9MyAmb0E5YC7Npo80yG4NQ8fywoeuAG2XvQTvvH5u/j3L3yPY7Wdf/XsgR/fwaWXXEd39xwOHtjL2OgE0qyTbWnh8vVXMLK3B9NOIPwKtYlR2jt68C2Ba1mkEgkqXoiUMHB4L8Wj+/HqVVy5BsIAYUaYTkS5MEyA09gqApAB3e0tOMkMdiaDbLWpGD62YWIZUPNLVManGBk+gl+r4NoWBB6GlMgoIIrqWFJiGXV8PGr1KuXKFMlsFokkCEIIJJ5Xplqp4tWq+L5Hoj1NxnaRUlIqjlE9WkQGEaoe/lJUW6TDqP1jL/A0p1KUdxyX6998G7//wetZPL+HEMFQXfKjnz3OmoWzWLt6FhLJ5394kDDVzsBUF52z38q4MGjvEHTlwXFd3nrTOxkvDRIGHq05l+FBGOiHkQxs74B3disNzLsPw3gA/XOhvwY3OZA2YxDO74F6Xh1bc8yWQvmgv/kVGPUi5iyQrL3GpWhCVIbnxuAPDkCyBdavhhtTMDLZxv94zzfhh5+A4nGefHNVq85k6+5R+4nBWk3Eerl+4ARKLPcW4E+BPwDeCfzXxvN9qK32FIoKx9hdF8BDY/DZvSre8YEP/zosXwC//z9P/V6/CN+7nfc+6HDhuz7CtR/5Y26dp1KreZSfD7Fe6yzUrt9BzF8LgSuBznbYmITNJfizQfhwJ+StuOgRjmW5al5OARVDZBqnniQGY6scCx2VG6/Vl2cucdNtW8JzJdj4VEhvHi5dZU63NdUl+pOoVJiuL9Kafdseh+1PSEzkNKk5Y69gQfZG3gSMCzFNbJAo7+rVEGDy9v8Ma3I/7Svfwf1/+2bmzWglScwJfMqD+x7+Hl//+MdBSr72oz/l/IsvYEgo3pJu1iuJ68O0BIBmH2/eAa02tC+MQVibuAmh3xhrgQJsiyJmLQuY7qmhWcznOer1JhCacP5sOGrF0hEZ4H0Z2Chg+xgc2gh/fCnULaXIooki//DBzTzx8EbU2nQpcduwOnELOF2eeNZenmnajtZh1aCr7oqkGai6JFlz2Ztj9Ybw63TPCc2aRX1OZGIn0jjJFMlkls62GViWi2mamCb4vooJgiDA82oEoUcYVjAtl0TKIWNKAq9O3feRUuI4Dq5rY5oOtm3jJmzV9NKrUKtWqFQdar5O52SJRU5oOgetvBw1zl/PupNFwnp2v1pMWp2Bq0FlGL8qqE834YlZx798puuiLRQAXgSOUNn1FXb+1Z184IsKRHRrNXK1In+zDN5yCXSvhtRKEMsbH6MzQRpYO10w1kAtMDnUxpJq/J4Bu6AqIgJUyF5FXXF95c9ktAWwMJukrTPPovkzuHjdIi5c2cecRUtJ5nOYSRfDzmLUXahFhNUqnYVOqiWPIASBwLIMQpGlpXsRiXwXdj6L6aLoqw1pgo6mUxfHfb/+xQR6u8CxIZWATMJk83NZBo5UGR8rEVZCpOeBlESWRTWfxw4gNBpqIQlU2UIIpDsh/WbYcwlMVFW5EyXgX1Bx/AAnF7DXjfZOpwy4hupjswu122jgtUKs6xgB7yGWGfFQUc57gGXgXQnP3R5XHGmUvdn3OkWQ/4YAYw3fxzyqdCE0xdo80QvzKE+myWTo4ZcHkEek8rwSYFoW885bw2PbvsN4RW2ZmrWg8lTq8mX9gWmdIBuFu7fRQ985a2n9yFuOkT14KatWfAYOTPCzux7i+aee5OjeXYyP9DMxWWOkfwC7VmCpVeHcmQkWJioUWjyWtMPmUyDlL7JAHXi1H0afUI6Fr9PLzfVRmhL8inRBLVSZt26Z4KGyBC9v4des7QhIY5EGAmxC6jio9clBxRC/jEv+ic1GcTLegmp5PIkCVJrd1zNZ2U9ixw/Y645k+yjQ+RlUKKHh9QTHOqp6QWu+43UmQffZdRvvLxKHO1Mcy6V+GjWmNvAw8R1dQ/FC5qGAXQ8V3OsB0lHqy7P2GVey8tzlXHbhInDWseicXmb15ulpy+DaIbVajcAP8P2QcqlOrRxRLE5Rq3rYliDp2mQSFumki5tK41ZS+FSPYbqctbMWWxGNwMiwRHl4F1VzMYOjWSaFw4wstPYaJHMqw3wEFax22jCVhIIL+/eDqENlaIzRHXupTJapHhkjSvUSLlhGalaWllILUzu6wMxAoFNogjjYPN4S1Caq7DxS49790LcAdgkYkI1Uh17ebKDVghUtULgG8mloyYMtKE+Mk+5tYcy1ecCAizOwKjOb37rtGmbnuvji09dSf/B/gneGwpO/JFYpF9m5czPFUoG2rtlUKmWmpiaYnByhUpoka9kgfUxpIHAxzQjHNAgiCVJihCG1ahnTdsm0dZEyQqqVMhERkVFEliyyLR1YFsigjueXiRxIWTkIPYKaQVRNYdYqBDIkigKqfpV6tUKtOI5XKyItE8uM1EodhYShTxhFBEGN0lSBUnEKpEQGFTzPazBpDcx6iGMFkBaIbBK/4lCpOki/Sr06gQy6UNy/lY1HOwq60U6xrrc/8bqYcG3ee+sVLFs4kwPj4zzzzFamigGFusRJmNi2wd6CJJlpobXDoW+mxeruDHNNSHXCrjYQwiDT3kmyO4Et6nRmDRanBX0zYdwBq4G47S0rTf52oyF3ZUH+uO27uw/yiRcfZ6EMd26G0QCWLkyweH7EzJTBVzfCshzMmgvbIkgmINMCEw5sD11YezncmzxWRn3iuOHQyJ1G8cocW0t/woHjWCzgZKZryAeAO1GNvRbZ8OnZ8G8H4RqUwF4YKPxck9pORlr50VHYXY6PGxQCN3AarE0ZQWmAoyV46sffZ3J8gh15l3V//DF62vK0ERcDSZSfv59j2z/oJlxTFuSSqrZmR0GB7BflYUlODZ/WKW243aphMLHH4hLPSs321KQDDZHM5VgsvBGHT7f7WepAbq4gl4LZZswyovE5JanIFnWpmlNZAVSPwMM/vpsdj95NvjHMacCMRin520g0jlWnz+ooj+nVAGNlUCWYOkJ138/42t8HvOP972PuilUMlwL+4zM/4KD3Aju3PUZQGeXPPv1p1px/Dtn2LHWUh6a9PD1FNYRWlLAnhLEqpHMQ+LCpHxbMVtJ9mnNYIQbVdaw7SazKERHLhhioEK4ZqouANju+ThOobuA50dAZPjLIg//8EP/vFbfhuCo8DiN4bAgOH9xEeayfuI3Y8ayXM9EsPGsnNg2RawC2WZZAs07Cpr9DvBBq9KA5S6XuNGG4WHaaTLadVLYbN5nFtByiAEw3getmsC0LQ0QEUUgU+BjCwHUTpJJZHCdFFIaqAtkwsHOGKuMXAkOYmEZEGAQgJJYlMDEaR2hgRAZ1v0qE0Uid6O5Ousxarxb6nBzU3QHxnNKlr1pzVhe36/KGUwG3p2uNlUqGijV8zHNJDDuNnW4ByyaMIsIwRPqB6hBL8VX4/l+EeagVwiBeAQNkvUB9rMBgQ9PEBrot6OmCGW3Q2ovCmhRQEWPfoulxOqa5R2nU4t9KLGZtKO3zslTr0BSqkuIIpx+VZoHubIZli+axpLeb3rldzJs/g2XL++jpzJLt6FasUysBVhosB1wTMxOSbcmSqvlEkQBhYto2kZ0hkenATKZUGZ0+h4Y143Ingh0CCeUKVMvKVXcjQdaC1qRgKmFQNA0CUQXXwki4mGmXKOUiEwKZAKlJ7IXGYIxb6lFJNw2KB9yOaov6ROOx9bijkRxb1/JSptOpp5I50K0rF4PdBm6ygfU+jPIwfgT+8+r5+nlgLEJd5KbBOsUt8sYAYzEwp3PWpzA9qZtM2AZWNonYXoOcAQkTYRl0X7qY4GCCUkVNci2jXUEtG5OojLnubeWhCphv61tJ3zWXwwfXnNE5lKfKbH58Cz/5j28RFIeoTA4xdnSI8uQQKaDdgnRCkMxZ7Hl2E2MDh7BP4LC/pDXS3BObG/83iX0DiL2clyVNoFcOF+XSvBWYC5kUzCrDzp+DbG67e/qm9YwVU98gi0GATUBEJxER8nUr0Hh1LYsaO63U/WYUELu86TWawlJBBZ6vMhj7mpt2frSjVEbx8Xc0fpaI2QOSY8MW7VbrwFv31zVR46gzYVruYJxYpkDbLuLypWdQ3AitFrcXBYhrpu2ZZD9OYMLBtPMsXtBL34qbuHr9Jdz6jhUkckn8SoQIJIRQ8QOq1QrVWkjNi6gFIaYFTiLAMCVuwsWpORRaWki1tuHm27EqQ9Txm7guZ+2sNdsU032loxqlw5shamVwwObAsEO+HWYvN7ASIG2lFztkQ5ulNPKetRQztjpUo7p/mNLW50na0FKfwmzP4HZbFIo+QbmADGvKcfM0U0UHCicCxRJQtzh4sMy9Txzm6t6ZDCQFJQGGVITYDCp56KVgarYBK9epWzYM4GgJdm6ktWcRk+kOHjCzZC04V8Blly5m6YrFPPYDyYHig0y+sInq6Mk1RH+Zrb9/D5VamQt6esm1tlCt1hgfG2bwyAHmzJpJJpXBdEwkIV5QxTYTGA25HwsIvCp2Ik2m3cWwQybGxggCCDGIXBvHdhF2ROB7+LUSRi5BFLj4oSTyfEwBdeETBR71sIYf1BBRgAhrGJFHFEQEQaAA1zAkCOsEUZ1KeZLC+CilQgHXTELBolqrEIQ+ruPi2mkEEssURI5JZdwiKGeh5jSW8bmo6ob5qLVbV0HoguRTN7s0TYOli7vpHxrkoW27+OmmnYgpuP7ay8lmkgQSJmqCxbPbmNkNXS0KeAEQrZBtUU3t5vQ6OK1tOK6gI22wNKue202jyl/CgTGgokqaewTMtY+FBCpA1wzlppaIgaGihEMePN0v8csFOluSLOxKMQPJZzYG/PEVJn09BhWUruVeAXslPCtNyM5UpbUQa9BNcuxtqJFHHTRq3TI4ubtmNT3/UmUZ+ns3NH6fYcK78zA+CW/2oS+AiUDlQsuoLVrfpscvF988FB+T/vnkc5ypDWx9ioGtT/Mwaf7oigvJzlmGlW6jfX5u+ivrKLBSN9PSPDmBivfSNnQZMFCBn+wEay50ppUEnMa2I2ICR6nx3mxjODQPUr9Oh3QaAFxNzNpsthAFAna4sHSh8SIP0Gt8VxUQAXhS9WMrepJtD73AY/d9l6PbHqDXFozUJe2AFw4x6W2cjml8wAthpCCZOvw8I6e5bqoiBpuKrJ/QtZRemcr+J/nC3z5J1N3FKi+kf6zO5//mDjKtg+RyHudfeCG/84lPgGFMi1JpBqyGMKvEAGpFwngEw0XoycPkSMQz20O6ZlqkDYEpVOXhWKRKYTWTdjJSTdksEXMmm8OqSMKwDylbNeOicRwtjed1o5wWGuzjaonivm2E0S3TwH0hiPjpo2NMFLYTV7Y1+7v6bLR/q6H5s3bm1hwLHA+2wrHNvDQ01AxkWvFPkcA0kxgigWVncFOtdPT0kGvvxrZTRKFBuVglkBIpDPVAEgmbiDqGZeFYFqlklky2Bd+vEwQhUWSQTju4roNhmNT9EAKPWq1MPfCQUYBtukSWREiBEQqKpRT1RgNKpfCcIu6uHTSdA8QzuTkdpHtcaKKJBmb1c7/oRICNYaaxEm3gusgwJKoHSOlB1SNm9b7R7KUANmV1oBRBrQheAYIJsEaJp2Iza09Pu9MN2zWG14paOlLq84SpKsY0GDuO2quOvsTHab53MuUyO+GydGYvV1+4hqULF9Ezv4v23g7au9uVJovtqGAgaNxXVgLsJIZh4WZblf+NAcIC0wY3pfScTuPcTvSSENXmoTgJhXEoTUjFn6jVETUPUauBNwlWHiOVwGhvQTqKDSt1r+8pVPHBIVTX+nIRFbvrHTyL6r1zKSolHqGwhua4WTtA+vFK56Yg1mKywehQGrN+G4gxkBtQVcA/AC6GcEJJXtFO7L9KTpUSfUOAsZACYTMtOiWn/3mx6b1OvzM/k/mXvRe+fwA5bx6iM4thW8xav5L8j5LUh5RT003sI06hTnwKJfNwCNV1+mYEiz73UdpveNsZHb2UktGjh7jrq59jYs+DHC3WierQacJFyyEMBeUiDI7Bt58tccez35kufXrFFnKq/hZnaElUQDQfVYD1QSCvuht8oQYXfgu8p1BLx5mZiQpQ5gIWdQIMLAR5MqzE4wHqPP1G0FN4RSZQwOt6lCwBKDevg2Mn7hhq5g01XntmchivrZ2OUylRjmgRdbcVUKCnRN11mpdRRs0CvShplTXtgFmo8FWrsk2h1oTRxns9Tq55ViDWFjzekXu1SpwFVmIO+Zm38v0f/CX5FpicGmbPvuc559zzKE2WkHU1h70AJsqSumhBOikSM2BdB1guhBKmKnD4KPi2SZGIbGWSysB+pJwiFvU/a2fteNsDSIg64OAjQC87H09SSLRQexdceh2MDsPoOAwMweZeuNGEbARDHnTkYc/mfkpHBjCdFEvffhuLLjJo7Zb4Xp2v/X/98PRdML4VvP0ocGyUuD26Topo00FRgtKmZ9ld/Bt2z/8srBKQhCSCC6RymyYQ7AbulSArKOZBoQDPbIE/+Rg/+80b6bjmWhZcuJ7MDNiE4CrgilbBhvcL/ur99/D93/1dtvzjPyLlr+b9MTp8lJ/eeQfX3vx+UmELqXSGbKKF0ZEDmBZYjoXh2xQPVejq6iaZTpNMJkkmbSIREVDEL5bxq2WO7t+BVyniJlK09c6hnM4w4YcYmDhOgmRbjlo9IKj7SGnQgiC0LOr1Gn69iu9NYSWgs6MFYWYJ6mUG9+8irAWEgcSPJIFVY2TgBaqlKn5FMj6hfAM7J3DTBjKoMVryqBdqSF8Lp/koOHQmCq56G0qiQDOC9qHW+Tqx7t/JrVL1+IsvfZdHNj5GZDm0tc2iy5zP7RcspLtdwaEXaN23hunZsymKeF5KUg78t5ugYJgcRvmJLTT0OaUCZPNScmAX+GPKB9/cJ6Z1PWkc5XONI55EieNc3viMTSFszMA7fx1+/7KHGB5YxfC1ffz3KyWFIyN8eVsb7lElVfOHV8KnhcI2sxMS8cMpZEnGX3KqpljNWmUvpRVfIg4OT+WM6hy9zif3AqUa/O9N8JdXQe4w1A4pskqA2m6LxDGIxhS0aWUg7Q69oltZodCfedsN0HkbCy9/D5//7o2oyy2YLwRzhVrBjlemX9w4tLIJK3vgu99UjEyvAz6UVyleTYaqEpOaNOiqOfoaAnJR7NVhYEqolbOZv9dsJ63+a9ghoF9KOlHgcDsCAbzgB3z5z2/HnNxHb8JjYU+KbYfKLEJ5P/2N4+qTMIFk/5TkqbslX/n96yhPnJ4mvYXBKrebLd4QZXnqkvu/++QngU9O///Kd9/HLe94E7++XnmAKWJvTgOyGsbUhegekDLgEgu+64MjoXq0xvMPFrjosh5mJ8EyFUt4aw2uSjbUb0MIK7A0Cy3i2L610NDMjWDDAFwwA1rdY5RDp6EwzWOZBVy3ZiG5e/6abFJdt2EJj5Xr/NO7v0sUjhEDsM2d76qcvFT2rJ2+6Tup+e7QvrB+TnPMNcQPMZtWk4jSIFKYVoZcRysJK0EilSGZbqEllyPEolquEtYlAgcRBtRqFXxDqJJsM0Ui5eJYAscwMAOVSE6nMximi1fzSCTAcW2IJBW/SIAk4bqYpkG1WsV1E4QhSEsgU+A6CQK/TCQhXlCbAVXNhD2+LaAGn42m8xVN753k9EuxX4lNEdSmCAYPnuA5nQHUJbq/nOZH8NwRWPYTMHdDxzJgDQq00DIDLSgWn82L+8idyPTzWp6gDYXPtQFH1FXTsjf9qDXzpYTzksBSAatXzWPxkkXMnTOXvrlzOP/cCzA6c+CaCojVU0vq62OBlVICsMJWlW9uqDLR4pVjEAaQEDCzFYqjUChJ9vTD3m0BO/cOMXFkhNrgCPiHwVlGEDoEqWwMcBeBgoDDUsm0RlINEvcAX0Ct2ueiSnGuQkkWLmr8/mPipl7aJohFbl5J4xx9v7YCm4EDjQazKZRTmUZdxTJqH7iv8egEbkZhaXqnGzr+w6ftjQHGrloI990HSJWe+JMBuPfdMPnCsa+roDyNXPwn69wELf/Uy/3n38ma995IJ+riWtdCKqdC1zHUUOgOqRZqyLainLQKkDIsbvvwV8gsXHvGo/LAjw7x0A+eY++WF8hbAb91+WLaUxETg3uwLXh60KTv4lt42w3vY+fHf4N9k5N44Rshi7QOpoXHZ6EaIV2GKtzSfWCFio3+0YU/+A786zvgwCNn/E0OCpLsIEmeDCV89lGlizweZYJf4kVcFQNfC7wDFbG0oxyIrwPfRgG070LJPoBy01tQkdCpXPI3gunM7BBxfYUg1sIwm/6vuxkqXZ64lrKFmOXa7FxoM4iZsiXUojWFqovc0/h7c+nRS9nxi/IrNQFczbs/citXrl/Dynnd1EZ3M16ssm//LjY/t53WRIa6kSQKHAQuHb15OpdA1hQkaCQbRdxEJspD1AvjK2cyXOmmf+QKNj78Ln7yw++zb9sGxg5t4ayDf9ZebGXo6IC+X4NdB7FWX4A5pxu/rHQEL7sGMl0w5cCTj8DmCuxdDQkXDm6A2S2w+rr5uNY82vIRM/oEO56Fzf+8hYM/fQCGDkIwqsSbrEXQ3QUJR9XJehUoHoLKvxM7/xIFXU1CcQds+RnccAeYs6H9XMoLLuLRm2+jdmsbS7OC+QasM2DTTIhGUd3Fcil401K48w7G7vgnJhNJtixegvH2P+RnV69l/bqZnAP8DnDtpz/NfTfczH+74UPAAd6YbIxXZlEU8sAP72DJvOXkW1ppTUaYnRkS6SSmKfG8AkcHjlKamCDXlifVksIPPKrVKkJYZFybepDACwI6erqJopAjh3djJaBrxmwwwAvLZLBwnRQJN44qAq+AX5uiWitS9YtksAg9p9HspArVUfyKR1SvEvplDu4vUqkFRLqxNCDyytcP/IjyeIiUdZAdqJT4bBTMlSXuiqHb8ui6pQwxh1HzEU+x9gsBmVamduxj3cVX8Pab30u9mCKZOHnpUQTcBfyv2/8Hm+/9EZYDX0ZpuraiGx4pK47DrmF44QjsePwQLckcmaQuNo9NovzJNAqeOYACYwHaTTjXVEmJP+rrYrQ6yZ33PM33v7SPWz52MzcusXlhj8+ffG2SGd/aR2VsK/PPX8iFt6znvd9q5dO3f5KRjd+GsQdOPg4vx06n6Za+VHo488DyDvidj0H6hyAklFvhmcG4B80wp96u14J4a4LEf11H7cKnkf3+qeP4PLEe/sls9E723XUP7+l2MJjFwvf8NVfc+FY+do2iF9zfOKSVxPqvgljL9w9+F+7ZAF+7E9z3q5omnRKG+NQEjZJ2Ym9GqzIcDmC1AWtNNVzNsgNnYhnAmor41n1FZs9oYf0CwdIuaDWgd26AzEtmzZzB8vMvgc/+O/OjXibwGQlhz7DSw/3q336Wf/z0/8bzoVYaP+3vtm2TdRfNZsEobBmc4LnR8ku/SViIc3+LX7tlFpdfqMaslXh8tMJ/JzFvVEM3uhbPF7B+NpQMyK1NsmpFApGOSWltAm5NqXtsahJqNZjXDR0ihkV1el+r+gkDrpsDaUOtLMPEeEqx8dD6vimg3YZr29T7I2DDRvjA39eJou+hYBBNEXdRa1aBX3jnuv80ptMcOubQgbiOFbQghaYqJlH7h0bKkgjHJum6OG4CJ5HAsgVRGOIHEVGlQrXuK0kCbKyG0IXrJhCWibAtjISNVw6xXAsnaeC6CmS0AhX3CCFIZJNkLMXGlmGEIU0Kk6MgTQwBrowIagEVr0LNr+IHPgEW0fSc0Qudjp20yKRHrGKcQ810Lbfmcax2rtMYo07ivfN47ZrXypozgL+8ZgAdBsw/B9rmosL0DGoz1yGqpuRnUAtG6jQ/3CLuYN6B2lNTEDgqr6n3mVMBsV0opGFhLsklVyxm9forWbD8HNp6ZmImMohMDmy7oRcgwFKN6JACDBPSGfDr4IdKH8FtAP7JFDgvd6d6sXUAGRMmhis88OPDbL//OwSBSxTVIBoDNoHfCXtmwL4ZYORBXAiyD2SbYitFP0X1g3kGlZrU2eIXUOU3n0FVbs9B4S0LUf1impmJr4YwD8T1LsOoXb5Zq6K5/Oj4hMgoCgNaCSwgrqg4sZmf+tSnXqUDfvn2pT//7Kc+dOEHId8JM9MwIwuXL4C3XQeXXg8PdILcA3OugK6LoC8GcoQhEK7A9bK0XtSLnXcRDdb1kTsPsXu4xCbvKLM41ikYRl3inaglfrkwmLv2erIXLMDtbjnBUZ7cHrj7MZ5/ZjNL5uV51x99lEVdErM6wsChYWp1SM9ZxYorr+Wca65m14Ej7D24H89/PVrcL0VN4I8BvwbcAFwF4nJIXQzBKqAPjFbIOMo7QqiBmxRwXQI2fgtG95/xNydR/nwvssGv8jmCR4WI7QTs4eX0eX29bQGwCsXuWdb4/1yUuxeitEweRAmpjQM3qkGQAupaRffltGb8RZkOK7RC2hRqgx8hlhvQD+2EVjhWAmCi8SjQKLIjrpssEWe1a03fM4ICUAsoQHew8RhqfH6z6Mrp2KvnkNhOns7eN3HJZWtZt24Oi+ZkmdeVwo1MJB5ChiQdl2pFIJMzaGvLMntGktacTSYhSFgCx1SNIExD4QaGUL9LEyq2QeRaJNIOqWQLbqqLdLYL00wzcmQfZ5tBnLUXmeyBcBlkZrLsrQvpnp/EtuHANpi1HGanoHW8xk/+YS+FnT71yKQ9ZfP+5XDlXLA6DUSLSRRajI8KBg+AkBa9czrpW7UEp2c2YWsPXiIHZqOUvOxBuQD+QYgO8OJ7TAIuRC1QC6E6BqWjMLabaN/jVB67m+G77qT/h/dw9KdbqYQ5qCehGsLECKRD2PosDA8RVcoEUwXq/fspHdrDwf4BtgxXkXO66UqnOCeXY/WyRTx4X4Ug0BnpXy2LQtU8pFyr4EchYVQnlUphOw6WZWBaBo5pE0YBnl8llAGRCAj8OjIIsG0T27HIZnPYbhooa4RJAAAgAElEQVTTTjN7zkJy7b0k0nmcVCtuKgumwDDBMiWGETE+uI+J0X5qpRFSLqSckMgv45WGmRjZT2F0gLGRIqWJMrVCjYliQHg8kV+C9CH0QE77p72owDGFcqj1HjKMAmefQnWA2oBywLehssCDqOt78jVdCoOSyDG8cyM9Hb0sXbyS6y6dS1fewTyJ7n8QSD73fwts/P6XmDy0CRnVGdwzj+SCWXipJL5QwNc3dkJNQKtZ594nh+lMtJDIJYnSJkUpuLJNkalA7VKT+hHCeB3GQpgw1ZpvBHDPMDw7nKB7bp4ZM3O0d7Zz1VXtpHIGRkowq9fEbUkzsvtpasUq9TDNjHM68DvzeGMvUNz5zBnPpTOyE+nhaXJJHwpdvuwaWP070PkWBcSODsDBA7AjUJf4EArlapbpO94SYOYN8jfl+C99v4391izDKwsEj5zkXj6tStwQGXp4lQq1SpHi2EGObnuILY/czV73ekaFSYsFfW4M8+i+LDaQsUEkIcxA/yAUDDAtSFoxcGupQ8dpem8aFVtLYIWA+ULpCDsnGMrTNRMFILalDLY8t5OIKrWozpGBCX7wpS9QmiiRaWtjycUrqU3O5lBhkCP+BDKMeGFvngfvvoMN9/+Ew/v3EPhnJv4VAVOex2//wSeY0ZOnMriHw4WX8kMk1CuMH9zC9t37OVhLs25hD0khjimu1h4vxPVhOtUuBAwasOsQ+DVBX7sgJwQJocbfa/hOnlBkrhYH5jqQFjEcpXVy040xrAtIGpARx9ZeZYnhPO2Bm6h72W7cA/3Ahmf3ctf/+S4UniNmM9ooH7+Mmui/evvP62f6RtcNo3RFoQZgNb2wE9PoBbMTjAyGmcK2U5iWieskMS0bYZpYloVpqkoQN6Fek0ynSDhJXFsBu6Zp4LgubjJJIpnGtlwc1yThuqSTKRwSCGFhGza24WBIi9CQIAwMYSKEwI8ioigikhFSQj0Kqft1/HpA1asT+AFhpGN+nS7Qi5mOBZtZwYJjU0ZaCEWnDtKodEcrsYyUFih5rUxvDL/cjFhoVO3acOtaWHo+JBeg9ruFKLxP86eaZaK1vqVW1Xsppqx+fVO4XJuCkbpqDPqc+tMxogqpxlefC6zsbuP8c2dy8eVLufLay5mzagWtc2aTaGvDdFII12kEmKaSGLNT4DhKqsC2VUetMFBdw6I6RCVVoukmXhUwNpRKbubgEXhyMzzx2ARP3b+NysTfI6NtILejELdD6kxlP0S7INwKwVMQ3g/hXSDvBH6Cqi0aIBavlKh5pgXs3wK0KbAvlYNgMao15zyUD/lqW7McY7NEjZYKOZFp1LGAwoAG+dSnPvkXJ3rlG4MZOz4JP7gH+rtVChtg4SqY0a523ftmQ1SAWXNOyMYXhsHsd6wg6oAoVHMRYNHFV7Nh9DAHn9rELpSfGKHuhSHUxC8C7W6CWd0zePzoTtKjF+CWu3DTp9YpAyVPsO9AgWqtRPeMNJdfcB3r33kbu76xg8PPVqn5gtaONoxUmnp5nKP7NxM6iZge95qYjdrAVoK1GuyrwLlRjaPWDmhkaZAoHE1rcevDrKG6IBSAcBGKrXiicoWTm95ORglpozxd3FPHY5BTEx7eOJYmzkzmUGWWM1Gr9BRq8egg3qBmAUtQA9rI7Fg05GRNiFIv1n77hVlzWwk4VmfJRF1kvVtokBRivsEUsUttEyvkaZ7DJGqx8Yj7D2snSpfh6KyS1kPSbSYqxFlhmo7jpbV+ftFmWQk62uezcvVMZnXZpM0qYXUCy8gSBiGJZIbe3gRjUzbpdJq2fIrOzhdrwMmmn3op12cZApZhkM3mWLhoOQQuoWcwuG87E+NbiaLX0sE6a29480ZhZCPMuB6nMkZSGuBmGdoPu56D5AhYo5Lifo9UJoFfikiacMkSBYkVyzB1GI7sg7oHySykEx2YM/KIYgEncDB9B3xD6TWFPtTGVOdIeZBTd/jVQUNBKfiPHIaR5xl7ymQMCYYLiZlqSexbDEkXapMwdwH0LYJKBYaHYXICqhsYLR5h9MhBOOcodpdDMG8+V7S185u/eRN33jnJM09UGR0OUKH9r5YVShNU/CqVukfScUilc0SRj4wiDCGoVKfw6xFSGLTkW6hHNWqlGoTQ0pKnpbUNJBhhRKubIZfvwkm0EJkWhjQwhMAPayAlwpBIGVEpDVOZGsIUAW5rN7asU6tMUBofZ3hwiGqpQrGomsBZkWpu8yLzTjRDtFPqo/YSvWcMoxx0XTVxpgwbpSNmmVmWrVpDrrWDkYFhRDSDWDv8WJuswXODkiceH6RQDcE2Cbwaz3zjftbceink2yi60NUJT0/BpWmYm4w4XKpwwcou6q5J4CjA+RDqnko2Plur3UZSEVCeKsOiNjjHhGQID09C1JIi2+4yv8Nm6TldpFzoL0DKNnnzpSl6e1NUds/mwIEp9j7xAl3z8ixYNxu5cznBjsUM79516iHRW/KrZVphyEBVBS7ugVkrG2feAUMCdlaVWzgP5Uu2cOrKwHFgewT3jTLjirm02AcRz5qqGlFPj2b34Yy3wDLFPQ9R3AO7TYcd9k0sPseh1GtitieZvepCOrICx4o/fhZwXi+ks7B1K2wtgGHDAhNyDQQxQewWa9hEtxsygCXGi9panNB8CcUIJgYh1wJpF1JNIUcScB2DlvkOz2/xsUSdibLP0cMFyhNlyuWQYk0iXJM3XfkOvnRoG16xxuxaxD3f/S4BzxHLNp2ZhVHE9oFhinaGBYv6eNMFy3iif+NLvEvC+A4evXsH217Yx5KhgMX2GHPnraKts5VMzj6mG4COwyaJ73gtC0I9btvXqM2b9l591Fi3usoL7Wh6XoO9EXH9lgZ/mz1X3SJJE9U0V1F/hu4hs/moZNveIej/eeNomrU6U01/e7VvuP/MpvtIaPBVQ+YpFIzehiCDEGkMoxVppREYmIaFZZkIIkzLwDQFhgGWaSEMcJwECTeFaTk4rosjHAxpIoREGAInmcBOJLBcF9sSSOnh2Aa25SBDQRSFIARCGkShpB41sDchEIaJ7aYIogghJURg2BLLSWLVIwwjxLQjHCuFjFykDAmjKlIa6GZZYDZ6RTjEM1E3LZbEMZeezbplHcR75+tB6mnWuf3lvQdcoM1UzTctHdbrJl7txIxYHRrr8FSgLkdIvByciF/louJ+3cGxRb1emnESt8CxzNg0yoOZLWBlBhYv62Xh+YuYv2YJi1efD215SLWAmYS6pTJJYWNXMhr6sKaMj0VIJV8gIjXXamWohYhqVr3WcE6fGyZVI9NSSXJ0uEqxHFCqBEyUa/QfPMqmrTW2PXuUwsBTqBr0M5kbLzWXfODnKPg6BUYXtOSg7dfBn4TaZpjaCWxHAVqvB/Gx2SZQV3bklMfyxgBjg1H4p9849m8X/DV84C3woTVw7w0oFudJzABWQL2sxO6dhlNz3p+u59HkZqpPCX6GZDYam1Y/LQSXGQYXdc9gydtu5fPf/zH5Z9aQ6uhg1rJuhNHomHicSamA2DCUfOPfnmfJjD7e9KbzWHb+PKLA59mNO9m1eQ+uYXHJFRfxr99/go0bfk5ZwE/GX8sl0wK6FAWcf1Op/06gB8wSmGkQS1CkTlDEzqcgehTqT6LuB0uqm7gewZ0hDL8ftTF+7oyORG+vqjFvfZrxn+XEBO/Xx3Rq63gKOqjBWISimvcAa1FsniOoYNJDNYsKgeuAFcBNKKasjRp4lDD1OahqzSqKDPSqJBX14nUiGFArnGndVVA7id7QU40D060naqi7JEmsVaQLwHS9he7Zq11Zr+nzm5t1VYh1X/cQZ7wjXo728GttluGRd/eTTc2nM58inTAZGxvATLQShiFBYBGRZeHatcybKXBPkMNp3laam2uACtrrHkyNSQb2QVQJyVgpZnbN56JL38mD9+2nWjn9EsOz9p/Aot3gDcBAD89+aYSuq1bSec1aBPDwNySPOICTRCxYydwVsHo9zFwGz0Rwk4CORh31ts1w7hpYeYWkfxds+JHPkceehbFtSpIgAjIZME3gAMjNxFrQJ7IyL2YJ2SjPNolC6YpQ2QrfbnQ/zXbCgnXwkY/AdTdDphV+9F31XHcezAoc3gzeQR44vImdt3+Yzeuv4yvtBt+48wN8+N2CH37PJazf/WqO8BvG6n6NibFBJkghRAsiklTLSst1dOwoUpqkkjnmmX2MjR2mMKV0smZ2zSfTkSGMBIYhSCYdMKH+/7P35mF2lWW6929Ne+2x5rlSQ+YBEkiAEGaQQCND2hkUnJrP02qr3U2ftluPbbdf99G2OdqtR21UHFBxQEBE5pkgZCJkTqgklUpS87znNa91/nj3yq6EBJIQIGqe69pXUlV7r73G933e+7mf+3ZNbCvA8VwSiQSmmxGLRSnA80yUIE9Uc1Blj4hsErgu2bFuhvrS9Pa9niPZxysLuOEi8vVEjHi8g1v+4VZaGmW2vbSF9c+/xLfvfIT/9fF3UVURhyBAVmRkWTCONg3BJ3/nsntkJ05iMVQYMP4UsBnFMMgNBmRcSNRJNEwTTPMaS8aoTrH0EoliRMyys2T4HbACgUE6ATzrCx/ZuAJxFdYPQF2FMOuoDAQhpb+7h5jTwrl1tfzdmfC/N8PeXmiugTkXwLLZkLj+ep54YDUP3f0ED273+dfbrqDtbcupj0ncdcstwiXjcDG14/V44nCPtotYhB7w4twKwd0Cked+2LdHrI0eRKBjYX/+q1XYM+Ctcxl+Rz//fv83yCeHKHYPi7RpLQeTBY4PUywfkmez9bvXsBW4lzjR1HQ+ee9abj5Tpj6lgKyQUWTqJfH10xNw5TL4r92wISO0SVeU0jcDMSxOFagwSrs7yqvfzVNPbRrY7MCzj8PSxbBgGsysPfi9EpCQJD75riUA9I8V2LF1mKJXKmE7Dhg53nfD+/jNo9/D7NvJ6disO0Ea+Z/4H/+Dz37sz3n/Rz7Av939WmBsOSa7N7G6exPv/h5c+dl7uOaaZVxxbi1RWcVTxZoqJGckKBemVcQSpH2m2E54jkPwNMTlpzaqh8JZoQYslL2LfQRvMNyWRFmBWpryu/BfqfS5IAgo2j53PeTw4OOhAVDdIe9UpmxZ5VQH04mM8IrXIGQIUoSCnZKcRJEkJEkGBRRVgJCy4kPERkFF0X0iEYhEVPRoFM8FLRIjosdRVaWkl6kiSxq6rKBGVSKxCEpEJZAVFFkV0Kbs43k+LsqBVQuAiydKzkGA4wconkQsEhf3nKziBQZxNSGOQY6AEsF1TVSlGt9zcG2bglnAdZMEXiCYili4uKUmQMEODjApd4VMNSgLFxmh602Wt4a4ciLm76MNSWiOBOF69sQCvzICywziiNutgvJtF1ZwQq3LkH4f8pdCEltIVm7gYIuYcOCpKv1+FAEjJMDXyivnqcq/EoKXOBOYocOcBRoXXruA1qUXUTX3DGjooDxJqggXLBOIga+WKlKh1FMJw7FNcL1y21LWEm0A2QwYEiQay86mRxGWAV1b4I7fDPDS1jQ93ZMM79kH/BSBJ4xzbJP3oVrRr9URezvggPpO4cJ5HpCugr2XwroLwf8YojO5j7deRsPitZKykwOMPVy8+C9waQ6hoHx0ETlUv0OCuVItVzGH39FFLyV8EbE8/GzkDNquvIRCUxW/W/k8a0ZeJvfPH2PN/ct414c/wSUffddhWayjedjVa/LA3Tv59A1nU9usosUlfM/lJ5+6BGlsF7MWJIhW1rP4i5+hPxbj1w+u4941YjGyqLWdsUKO/vTRgFESZV2Yo3MGLMcPofI9MFOGpHrACDR+FvzNl+EDErRIoE8tbl0NL6bhklXATUDeQYBov4Y1D4C/h+PhsYYE81axCwe+LhStPjmYsdcgJAdmI5KAsxAggo14oDsp86q3II7kHQj5h0rgx6XPh0cYBZaV/j/lPkqW3uLwSuz0uCNMBg9FAz1Eu2dYd7N4JbgKZV2ikHYflH72D9lWCFKHZcKQ5xmWCscoa52GOitjiBkowx9W9TRBRK2gqUqiXtLxDbDiEtFoEss1CYijVDeTbJzB7JYjE97DMwllz91w8VHIwmQaRocDxkbHiSgRfNcBLwNRk9qGZYyPbMEo9r4ZB3wq/mDCBmudAEqLs9ElWHoTbPyRRdsClZazVPpGITcCbVFoCuCx7TC0QJidLFgAlX8NT/wObv/GMPaEjVJwS/W7TvAdVFWlYdo0htauxA/C0lkF5cLN0STiNqJI1UbZCVVGjBEFyI3Cpsfg00/BRe8SdMKGThjZCxdcDDNPh1QDjO2GPS+CmcezxKdrgc//6EPMf0clX77+jxOMLUeRgcFtpCpaqartwCqMABJ+YGHZOdJpg/qGFhoam4hoGlXVdXge2J6Ha7v4houZM6iqjpGMqwRyBMs1UYsFLCuH7VtUxBWSNRWYCYVCPkvPnh7yhTGGB12Kr6sTN5xDD3e/KIhVSjgnWYf8TeK1SrURDd6+TOi9LZ5+Gmdd2MLtX/4Zf/mFr7Oraz1Gfow/e/tlvPPDN2NJLazZlqP78RewiwXire34Ui/meADk2L4pT2w0j6zKxKrjOHmJ7w3C4FhAm+tySRAwLAnOUjNCazTEKWM23P0L+LM/g3n1pSxAhcWlFmk7Ct85DZ4eNllyhceFF4oF4OcXgXm6aMEOuU7x06Fh5jlc8tGzmMhIfHS6gqPOZVVbEw9nm8l/9WaC/GEWOmEf9okkgzQiasqbEd2Dyc3Q1gupUldLLyId6iu9ZiOQslqOirA+/N7NCG0LDu74C91NwtAQt9LrShaLmLntfPPaOr4jJ5Ha30vVuZ/is1+YR2utRDYH6Qzgwcx2uP9J2G3C+R8q2+mETWPJ0mEa4iwwi1dmX0eKeuAyHS6+STT/HaqmkS9tt2HK7xzbYGxoN07gC1JWZQXNi06n8zSNaEJiOyLLOlHhAv/xwwf4+k8eOu5tPPH19/P0N2T06kYaP/If/Ntnr2F2dYIU4vmYRjkzHUTcPm0ITGAqwBo2r4d2sBbi/HeU/h5CpAZiFAlpBKENEpRJHyEIHB6jW/pZL23/BSdgxQWPku1+BC83gJiz6jhY2zrs9gqtyE6BsccfIb/cQswFlaV/OxBXWQCRErpofVU1oYWpCllMFAVJEi3+qqqi6wniiRTxeApXjRJVo+h6lGg0ih7VUVWViBZBUcWd4bouiqIQBAGOXTYGk1FKurIuqq4ge4Ls5cZUVNQyLK+B6bokJY2YGuDqCpm0WKdrepSUHgdcYeFjGZi2Qby6gsz4GJZj4QUuihLBzedR5IAgMPD8UQTCV6BcXoCDGbBvlUbsmx1RoBnmvAP690J+P2LSOXHChi5Q8KFnFBa5kFARg0iSg0HVkIfkIC5L6FntIipDYTHylZLyZRuettKrBbwhoUm/t7Sp0OJ0HrAcmNUIM+anuOTG64lcfi5yw1yIt5a+JJS1KAE4UlTstKKWv9v1xDODWxrsXCgWxMt1Qa2CaFT4QhwrGliqDWQsncF9PQz3PI8w0trDsUsLdgIfRSi1NyJaZO5HnJkjxUNAE1izYMsZws+rAUEurFTgqdvAvau0nbuP6dDeijhJwNiwyWdKL9KXboWrr5zyHo/xH/wIY/0Wpn3xG2Wr0ikhSeVajVb6+ewVbyNZU03lV79BsXs/lmMSqYhz+kXnEUk10q3YdPfu4PG9G9B9l7gFmZ37eO7nDyFJ81l83Qwq6mMHbqv718FEbx7dNPjQ9Z3UTtPQdJnxvh0889N/ZWTLDuoSRVI1MSoqdF767++wcOZM2v5qHpddl+NjX/gGPeOj2O5rcUFjLFt2Hl/4wi2Um2+EToUHFEoeSIosHsvD2UD5LMbSYkxE4Pa7YMej96DlLBbUzuHD0bOYJkm4nnApbZhyJyyqhvuXBXygc5j8ntug+BQwAP4IIhE59mpYOI6lUDHwKBAwRllh9LUcBN+ceB/CZCuJ2NsqyjX4dsRIqiNSt1qEMHMdZRO0DyHSyAQHN7NR7pkyEZJ5Q4ic43UXbALKEgA+4sFQEDNF6PI6SPks25STx6lOpeHOmZSvcSjSFuq92pSbwWQO7icMU+VxxLRSpCxvcBQmLCdlWMiqTbwuiSv5mHgoqRRtnW2sWrOeZKqKpmQFnXXyQeZcUyM84qn1PgswApCLEBRBt3wqcTFjBTwjjSlliMV9YvEIqZoqcrkoxsnxgJyKkyZcYBWYFaQ3JzHzCvLCxTgVGoPr9jHxWDdmbidnfOovcOQYfWMw2AUVTXB1pcjXxmIBOzc55Lb0omsRonWN2LUNRGkiWRGnqi5OU1uUsdEJbONpKKYRSZOBGG9ezYJ9agSIxDlcdNWAVrJ38S3wsuCMw8ZnBfPByEFFHWgJSNXAtOnQ2Q6JVsbW72TX0B1s/Z8fZg7QrqssO/tCzvs/d7P6H24g8E6OHos3IoIgoFgYw7ELeJ7FzPmLRQJnO6iSQjSuk80WcDyX+mgUNZDxPQc7KJLLF8j27WJoVCMW14nFIniuQ6GYxvcMZBysvEQxXcQpOhQNh7FcAddzsKyyOdfxhc0rJ7pKxGqntNA6IF8wQRnBe63JcR6XXvE2PvP3N1CnSDy3FyJJmVQyxmlLzqC/P091so5UNMPbzp/HooYGXFlHy6V5eV6e5/fmyWztwR7sKX1XP8bIWlQ1TyReQ7Z/EdkCBAWXGi2gtbmGiCLTJok9HUfk/aEh7OYAtCIskWBOyaB4RrsgqrxsC3nkq3QgA4YLBaVEmpFgUi4rrZvAtx6AxlqF685R6KyEGg18WWJuLMX82RfykhI5PETtcmIr21LpIN+BWB9tBS46A6Kng7MFHuuBJ7OwjfJk14dIg2ZQrv++2qW0jvLmCpUuDhc6ZUet14wA1zJwsWH/73CzW/neviR6BFxXx/WTqMkmPvZPX+Ts6iR7dozx///5Wm74ypUs61CpSpRBwbBhPfBhMg9eKFb6GiFJJR6Q+sqsyChtd4pPMX1Zm11DaYzBbmbMbqJn7xDGhMFLK3fy4/98N9u2bacRsYh/+GhOwVGG63m43vGz33zXxnfBHRuk/1df4avrf8S5Kz7GWVf8OYvmKgc6djXE8xR28srAgA8vZiCvweAo9A+UoKiSj1ZtDDLzBCEqVM5UKAOxYbNrKIzlT/k5BM2D0vvTwD074fk1A2z++cNkunbjGx54IQgb9u+GJITB0ivL0c+Dp+KVkUSsl5KU1xshyBRWAAVpJCitMzxPh0BH8nV0PUIgqSiqTlxP0VDbQDSRIBKNoelRJD2K64KiKGiqJsy6fAk5kJACH2QFVQLfdQn8AMUDFAXf9/FcDxsPWVWRJQVNLkkgKiB5Pr7viQ7Z0l4qilpifUeIxWRM0wHZB0nFtsH1TRzXxXVd/EKeQt7A8y2CwMGVfAJ/HC/IIe7GYcSMMEGZfgnlO/jEs0NP3rCBYej/LWIhFK5tT1zkgV0O/NdayA7ApYth0QWI27Kecl04QFSRwkpPDg5oLoY4fggPVHCwZk24zK7ggKe1rYtxL5xL2hBs2KXAebOh/fQWmpYuQr/0UqTGJiQ9VYIWpoqoK0I39QApyuMAlVcuMWHdEjPTs0VFQZchWgXRlDgwpwiOAxWhxeJrhCRqIg0tcNrcOrZtXsC+/Wkwn+TYgVgQ93stwgBdB/nj4L8DkUxsAb7GK5MIDzHbZSH4IWyKwSJJQDXNEpypw+7LIa0hQN31x7FfxxMzEGXGUGh4L2L9E5qSHz5OEjAWXnGSChJs7BI86BBi/c1vcDd1MTnvKio/djlSLHKAcRlqBB0a9TOmEUtVcMkL3QzrazEKBnIqyazpS9hvjPDy/t3s2Pcy/flxagDLDyj6ETzqUKPqAYC3aPls2mTQ1x8h7kJTrcr8uSJd6u3awPbfP8qa+x9C689S3QHJZp3mplpeenoVV93YRG1NlGJGDCBZ8ygGklgjTdMXcc01B8szhMdruMIHSlHKbTuHHn+osZR2ID0MuxQd1YRZHSqzS+8vSCAfcuqrNLi6Hm54l8zjd/Wx7+UdHOxSd+wRjkMpYmQxMHEPQH5H4sy8+TEDQeuYGqFgWkj7WEC5Ytt6yHsP/ewhEc6jacp9Ccc9NoQ1fQ8xae+jDLCGy8NwYh8v/RxKCISC7+HnQ55HCKhOcvDs4iGWiRZlMFqlLHgbgrG50vtCMNae8vpDBElcfGwKvkXWd1ELBpW2T2VNLbGaZhLJOlIVCVIlOtPUdGlqnWiq4EXYiCEjcCjFhqgX4Msu1TGLopUj642DOYadz+DjgvRWt1iciuMKXS75MLwR168EcPrbsEckbEuC6jOYdq5E7nmLic05iEnMni46mEYykB+HvTtgHRZ4HlsLAbkxDW+iiFKlENWiZAo2vmGiV1ZQ2dBIfXtA7dxZTPRXY42U9LLVNiEYFUwinusU4rl/tWc87OhwgSoISkUdKSJYLm4GJgbFWyQJNB38GKmKBqo6OojKEnUV9QQ7dtMkSfRloK0CUhK0NzVy8dVXseZzHQReH2+9RtQbF65r4rpm6f82EjKB5yLhEYvX4ctRJFlFiSXwPA/ZAzWIEPUT5DITeMUinqfguRqebWHaeXzPQgpcXFWimM6Rz7rkiz4550TNyofbTihV4yHmCoeylc/U9xw5zrjgEpavuI7lV1xEBMgrwqinUlbQUrU0tNbRNK+ejnqX+TNqCWyHyckelOIkly2p4fm1T+MO7cXPhPIJPmd16HjxLD2DA2xd5VDVshAlolIdl2lt0pBlAb7JiILauAeaDANFWDcgvGfrVKiVxQx5VkrwPHry0F8ErQUkJUXW1pg0OCA2m0Msuye8gEe7HVY+8hId9RFalXa0+lqCNglJhiHTw5zI0nnhZYxsXEW2/5COiRNlbC0h1hLhem+o9P8xYI0LLXmI74fHx4X261RD+SJltKsFsf44NOWNg1yvUXleJ5n7e/CLR5EfhMzZI8sRuLgAACAASURBVP3tmMMDoxfH6GXHYPi7CMgJ1GQDL903BydSwUj3JOseXE/r4jSRiy5l7pwWGtrEmjwK5GywjAAvG5CXJDxFQgrA8wICfNSIhKrJIAdMjOTADVA1FT0ZRyPAxUeWJRRVEaCubRIYBopto0RUkF2Gsxa5Yob6+goWX3QRBen3FApFVj+3mWeeWU8QuJTUZ6hGjMYnU9YQuDZmz0Y29kgYfi1jk0UGZynMX/ZO2hp0IgkJD1GWMYH9JuzIwZocpJMwlIehSUAtdQ3LUOGAvzVg//ZdVHoD6BQoEyYkojV1VEyfjaWA6YDtlrp0XSGliA+S4xFMFpjIj/PU7jTrX9rL/kc2lvZiqj9CaCoVGg/2US6dnByrlz+MCFep4QMbAt0HqHyU4fMCZZOoUC/VJQg0CECRNXQ9iRKJousJEvEKEhXVKJqOEokgqRFkSUNRAiRJEjOO76MEknAbCiQQjyWB5yP5ATISgQ+SHyAFAv5VZBlVUdEUGVWTkDQJ2fWwLRvXdZFkCVWSxPPugx94yJKK74Fru9iBjW1Z2K6B6xi4toFbzOA6eYJArJMEpDtKwARi/TXOK1mxfwpRop7KEfDHKecJRcjvecO+1QUyPmwahQcmYawIXTlI5WBuB9S3Q7IZoVAYik2HIGzYxhAOBUOljYY8rhBlC6UO4hzQVXeTYu6PIOC7FmCJDOe3wOwFCWpObyI1rx05GQPTBTsLkglKVFTyJK0khRETXx5I4uUhuswkH3xX6CPhgCukCCVVAj0C8biQoLRcsApgVIjfK4cwHeHApSjmwXHFRzxforU+RmdzPcN1LQz2NSC0Wo91QjaAXQgz13MgmA/KfLHG8KcDGxH6RYd2A/UhTF+fhtHLIR0V16gKgWqnW8BcDOZVCE+fNwOMrUGQ+hYj1ka9CPJKDvjJET91koCxh2ZYOnz9doHg++PgCAZehaqhqEl6//ErxFYsIdJSh6cpGAHES11O4bn2lBJAKYNemWDx+29ke20lubSJ60XISDI7Nj/K890vsXdi8MCQn9bj0HkaZ1z9Yc67YQ6BJJG3PXrHbH7w8wmuOK+as5dEmTM7KdoaTJMXfnsHK3/5E/ZvyNAKdNZLVKWqmDV/Pj+/YxWL92/BtLI8v3Lr0Z+SyhlQNfMVvw61llJHceXCKnFMg89eD1x/7Svek5DF6xWflSW+/6UGPjZwFr/s6yGff306VHJpX1KkMLGRS20bUV5BcH5rI0TOwjkAA6EL+yRwJ3ALYsjUjrCBI0TYqx4erBOUB+2j1ioIBxKPsj5jEbFC6qLsJ6tR7qEI+Tbh58JmrQRlaD+cVcIEaJCySvlUC8gQjA17MEKnN6EEfKD1+CD1mz/sMB2TvSP9THMMciNZYhVZAsdj1ulnoAYSFYf0JYZn49ArGqaaJVIHSgCGXVoY4BMoNm6kiOGO4GT2URzsZqJ/lGJ+gsD3UBUV94+Y9fdHGSlV9J+abyQ4uAHctNB8kj/EkvN0uofjZF/ugFkXsXSJzqABvSMBhZzPyOMOT+yepDhpo7gqNe0tTKg6WjRGLK7D4BDmYDdOlYocaSNWLTFryQy6ts9mpLtLiFzpnSVFkyiQB3UO+DsgyJb0zkLG/eGiNMa4Jd09JQJ6Ctwp3R9BIHq3iirNqXpOnz6dlkyOc5fMxl+yGGPSY6TbxF6oY6kStXFY0a5wW/XbyE38Dt8dOsJ3/3HFnq6NACiySk2qkZY5s6moqwJNx5NkXDdHICvE9CRVddVEesGxCuDb+LaJaeTwPAvXdcDzUVUNDQXDdU4gEHukyFKmcB67BEs0muKmW97P8ssuAUcAo/VNoBHg5yBnKlS3VrJ0/nTO7EjgBQGPrFrDrm1b0HWNcy65hImPvAfHCp9NCajgI1cupnt4lK2rH2HVludY/oHPUTetiWRco65B1Al8QA9EFnBHQRgv9Q/C6rWwpFN41AWInpn20pa3ToIxAclWkCrqGDeiDE2CExNzw4QHk45HIWfx7fsmiK38MbtjdXx79B08dXoVy1cE6CmZvskiO198gXf/1efY/OP/ZOfDv8Eq5IX4+IkMGUGznESojKym3Lh211a4f6uoPRc5fLdomDYtolzbnRp1ELkoybyfvJP1p92GvTv7+jq9D8Xxjzts8G3c7CR3/PvHKLeD2tz7pTvY8Z6fc9k7ruaD74kxNyIOa6IQMDYS0Gq5jLgyKj6BF+A4MmgeqSqVaFJGjsCmrhEkwyWRSlLXESeJTzGwUCIysVgE2/HpHx0l3deHOT5GsrYSNWnhej4RFBYsW0zjnDZ2ZwZ5adVqnn569YE970OklKchssG33v70cBHQ9eSddD15J/dIMtd+awdXXFRLe6uEgaBD/B6JFzIRnhtIMByFogyOBH4KsbZNAo7HyIjL7t/m+dl//haMRxFnoGQqJyvUn3EO8264mWJVJUMTEhkDCjYEBUppbQAZG7b0Q89L4G1GVA4CxGo+9E8Im4dDPvQY4kwb/OmwE09ETNXaDXNZjzLxI2wfhDL4rXOwNJrorlGUKHo8TjJZQ6qqilgiSTSaxHXB8AIk20P1HbyCQzQqGKue6+J7HrqqIKMglQgpilrS2JQkVFUtAayyKJAoQvpA0SPoJUBW11UUF3LZLIEh9MgVRcUwfBzXxjItXAvsoodRyGE6OVzXxXVNHMfEcQxcOzQvDkU6AsSAGZJZppg+/0lFEqQ60KrByvBWyH887sKTXRDrgpm/hk90woVXwawrQL+CAxwCqiirKIXL4yJiaAiFrOOU2bHhbRz60dWBXyNGmEYEhjhbgiUxWHo+xE9rQpnVCA0JGNpH4McJZEloG+kR0JOgxpEiCaRkhQC7PBccTyCl6UkCySeQ5ZIWjozkeaBEkCJxiEgQi5ZQQIvAMCGdJ6hMEEREJ4CsykhI5QWtB5lhSOcgb4EtQVUUlnRGcIereWRoNq77e47DcRO4D/FMnAmBKlqGgmqwlgFfAj4NbOKV2MI48O/gLoLJZphUBbLdhiDcGh3Q/2FEa08oLfNGhopIfFZwEDVaAoKnX/VTJ1lEgOvgvbdAsgGGxuGBR0AdRr3sSirPvpiKvMv6m35O5+cvJ7X8dLIZ2Dkm5lbTE+1gnbNgZgxiCmi6zOJL6/j9A3V0j/cwktvNaN9annt5DbbrHGgJakTils/9jEtWXEPbItF63GXCk4/0sPahnfzov9+OJB/cjvz4//0aq371DHs3TBJHXOpUcytVZ/4Z3mX/wJo9P+a2f3hBqGUey7w9NAmDb73B0W23/SUrVrSxYsXrA2PD2nKaAiYeMUTDa2gjddJEE2LH+hCYpBtHqIEtoAxuPg9cenzb96f+p4jILI82QkmCbsrSA1Zpv/oRieIuym0+oTVCGKFvcJhgHspYVSijxuG2LcoWFSVtDEYoA7Nh61aG4xuAT+4oZPJseGYNly1YioxEV7fErXfm+MePrKAoS0ccQENtskNjqhmF4goQIQAivsNYz2q+9q9fwSzYNLVMp3P6MmSvgNZ4NqY1l+fXPvoGHeWpeENi7M14HgIgClYCNqxjdO8y5HPaqe9sZ3QfvFeFdU0wPGyw4ck+WPcwKArV8+Yy/9rlfOVv4BN/P5+sq9J5RpTzL76aTCFAjkpE4kJW6qxlMLn7GkbG6mDHE6BKIJ8GznyR+J27GIbHYHw/TO5E9CyHhZpDw0GMHyUEx5OgKB3+vb/5NhPpNP1pnSUrziczAvpAH86uXXQ/u4G9//wZ5tbr1OvQENe5tf82br28i10r/zTA2DA832U008/jj9wrchMtiVQ9k3MWziKZkIkmdaKpJMnqagrZgPx4nvTwEH3DEyQjUJfSqE7GQa3i5YyLY53c47imRfm7v3uUeTNOY88YPLgBCmNQ1QxpwwHX4d9ums/X10BGFtBJjx/wV1+8j//zd+/mzHPO4qfrTeGbciAE03zl1mfZ2jXAqmefhRGLJ/55P4uuvZ7l11/Ne1rqKakMMBRAlwV7VkPWBF2Bizvgry8Qa6Uwwv8unwGnz4BnArD7N5AZnkd3po0nWoSf53274dGndrDhB3fhb9jCD5/7ChefOwdv3OHtf7mB7z1tcdW721l6SRs3XPF++neOs/yz3+KST93Mt26+DnZnD48LlcjsQHnNfzThAc8e4W/lZK6sWHRoWAhc60hdeS1QtaiOT/EVPvOTXzF+axbuOsp9O1zUc3j/wNcdB0OaO+75AtLezdQVv0Ti5pLfuWfR5BeoSuYZT2fo37uXiZFRGlraOP+KS4jpCj4ii5pzbgcxWUFVJCQJor5CpChhFbMURtL0p/exdcMWHrj3IV5c/SLXXXshS5dfTlVLI66s0LVrP/95y79gGsZhr+VUEvNJH4HPg5+az4OSdIjEU4Jg8Y0EH/gOXIS4h3zKymF7gO/2wL1PQfDJUgEwPBldgKiYjG64h3zX1/mnz+3nvx9RyEcRaK+LIGAN2oICl3URpZVJyvNT6Htgl/5vIrjrIeHhlG7U0UWorHqkyE15X5ypcnxiVR4KewWERJBoPEU0VoGeqECNRfEVGcv1cPMmqhoVBHrbxTJdVCAIVJSIhqJpQvfZtMjjEZRoE8loEkkFTY8QTcaIqlFUXSGiKUQ1+SDh4sAXe2S6Hr7vYxgGuVwW03QpWgaO6+KV5M+z2SFMM4PjFHEBq1jA80Mq5QBlY+Nw7RRQJr/88Xb3vHpMQDDxlh9+SEvaDHxyL1zyfbj2PvjM5aC+D8G6rEEAq02Im2IYMXSEVimhrEE75U6RUCOlSnwu1gDTdaEiME2G9haYtQiS84GZKWjSIWoSTPZS6C9gmHlcz0JXwHSjaLEk0eo6UtNnQdM0MEwwDSgakJ/EGh2iUChSdAISta2oVQn0punoVY1QUQ2kBCir+RBN4vb2MrKnG9MCWa+g87x5B8/vGjTNhvgkjA3D7h4IHJjRIaPJzZjae3j66Ufw/CGO/SLuQ7BfnwEuAy9cQSsI750PIsaEQ7EoA+Eg+lXYeSMUzhOF4jqE3kOlDuk2KHwGwUx9o/1XViNm4aeBH4hf6Yhrnjvih04WMFYDZkHzdFi6FP7xA1DfDFtG4ZEJiGtQHEBa9SPYfCeBr3FPfhUzfmDSvkchcel8/ChYvlgb+jZk94E3A4iBVJrp555/Nlvv3sqaDY8znu3BcV10oCFRxbmzz+bz3/xn2macTqpawQ9g7U6456c/xZnMsnR6C7LCgSpBYWKcDff8iq/efgdmfz91MZjTJlPfUsu8C89iW98YNy1fwS7X47KFEqOFgG0jKW799N/zT9/7JkPjr9X2P8QU6uSbFjbQP5jnvp9t5W0XnU1Vo8r8hRfy2LPPcs3y5TjO8aV5IaNXIYKLcaBZvhkN7SCvyrcytsJYM+Sml3DKLcAOxOT5UeAvECuUbuBSIXES4gghHnnU0Yd4UD9P2bZjaoQJplx6bzhpO0APYjKfpKyxFLJSi1N2itLn45QsRDgYWA0/U6DszBguG0KTgnA7h2shzVOecf54W2kC3+e5Bx5j7llLqW7rwMrneW5zljNnJ4knVQzKAGvoeXqkCBuyXERlccvah1n1wlM89cyTjBcmGBwawvcChh2Hi2MJBnv2UVNfTzwepSnZwHB+lOCkeFZOxckTJnjjMLSbLT9rpm5pC1XtlYyocNU3oLBvO5M798DGfigUoPM0UjPamLNEolWBW/42ycvjMFiUaK6H+LBEsShaOy0PIiosXT6Xmkialf/7u5BvBake1BRUJUCromLGNNzKTor7G2B0M2JMClcxYZnycPftq2ifBQHpdQ/z8she7NFbuKyzga2P/4KhLS+yqOUMZqQ8PE2MxmlJYoUqsfKTt1Fs/Bn9v/7yiT/NJ30EouDrFAjGd7J17T4UWUJWJCRFwbMdfM/Fc108RwCuRQcGMi4juTzIJo7jcghKedKFqsr8xV/Mo8tWqFYtbjxL51kXzo9AzlfpCxSekCSGx2GitiSwI0ks+LOPEp/WxCQyO0vG1Ur72QSuhT+wBYBf/HIthpwi2byQfK4XTJmO0+KcfmkVOUnk088PwbYJkLNQmQDHhFmV8K4zBRArSbDfhr0OtMahSRLyCVED7toN1vZfkVx+I1q8je2Ozxf/fjv9L91PZv96/HQfFdd+kWm1TdQqMkG1xp1fnc+3VrnYapFtO3tonhbl4X//G/TCB6k/bREzLv8Ke1vvxt+yCcYnDj5ZTQiGq4tY5xgcnB4cb7iI9PRMRJ3a5tjESrfB+Nh+vvjSeWR6B8VD/HpigjenLz/Yy57tt3P7lx/h3u+DRzUt01qYt2A68+fOQUtE0HBpaKmlfU4HhqqQMYq4roOiaQSBQsEJRZglzGKa0f5+XNNAllzsmEPnghncPO3/430fej+j4+MMBbU88cJuurt2MPbCC1iGecQh06esvRqW0d/oqK1KcPrsVla+uIvgGMWlg8A/4N1Wjjxsfwi+9yE47ceC1WUhAI5/A/a9Ewb2gJ/lyBIoAC6mMcJ3bjuPaOaDnHbGxVB7Btt2iq9A0aAqCUE95FUIeg58TuS/GmVrsdBzweRPk7F4vHHo/H6k+yPUILEpa8uHXXshm1ZUlnxfmG5hWcgFi0COENEUNAKMooEaTYAk4Xm+EG1TFQLPR1YD4ol4aVkVCM8VRSHwA2RFQZIlipZJvmggyQqKJKFIEgRgGja24+HaHp5jI6kWhUIRy3KQZQ3TdSnaHrblY9semEUcz8YJXCzXxfVcPD/UFzYQ6Iw+5dhCEsxUsbNTcTJEAOzy4HdjMPwInDUIC+dB62yoXIgo8ISmmUUE1hfWs0M2bAdlLc2QeF8DtR3wtgugcaKkX52AYgQsCyKWiZSZBEsCIwGmgep6SIEHgY8SgORGCIpF3IEBlEIOyfXxLQffNFA8C684jpnJMZEx6e/vR0rVkGo2qOqElrMbSrWS0k5Goqht7dSnWjGzDoWcxdCWfmqbG4hURA5IKklAsgL0GNQ1C3+wsYEEDXvAUA2eXTkHzw9lEY81BoEfAReCq4pHpEYS57V4PXgtCCGeew7z2V8DnZBthzWt8OeI/Ccqifbwuz4O/rMI7OT14BXnIDowkoiT8jJlTCaMAYRx2DLgr8G+ECbaXvVrTxIwVod3vhPOXAAzZ4CfZ+jJX8LWfUS3D5F0R1D8KJLXCFo90ow4Z1h1yKk59PV7bPrNehJNUabPbqe+OkVFQugDHdq5NXthDamnoxhFG83M0xRVaZ42jwXzzuS6K5ezcNkyVE1lMm2ze0ealc+sxtm7jml11SycXpIMkMAxHDJDo7y48kGkzH46aqN01tYwvS1KtLGKnSNZ1u7Zy8aXNnFuHVxz3TXs2T/BxG83sKV7F5Z9NMyTUIL+zQ0JiEUUprVVEVElXBsSlVWcu/RcZp13A3s3PoaRHT7m7YbS0iYmNt4BV/kk/kkELj0ETg84jaWf9yIywEoEENtKuXcvDxUJIbp7XKK3cWAOwhGjijLFpIayTm1okNVfeg0hRqU0YvURJqMa5SQxFGwLK60yYtDQCK9AOfGZCuCGWk1hdTYUiwsr23+8YOtrRQDsGeilblo7sUQFMS3GYN8os9t11KSKQ9kj/rUkNySgkC+yb/8gq+97kDWb17Jp22Y2b9tyQH3XAyYKWbr6djOrsQFXlckXC8RUlWk1FYznixTtPwjuy6l4UyIN7AF7MfntW1Cd3UR7K0BbzIb1/dC7A8b6IGsjt84k0TkdYjF2d/Xw07zCZRc1Iid1hocgZwpTVhmQLfGvaYKnJJCr25BnX4q/ZwTUpNCtsgMYLuLWRvGIQ7wTGt4O413gDSLGqeMvtrm5cXLdW9nz6EPEW6axd9M6Yv4ky6+7mMqoSlYu8/WTwNVL5yPlr+OBsVEmn/7+CTm7f3AR+OAWKWRfm73lB2C7AfYBCZuTPWQCdMakKHZSgahEJg5nqlApQQqZSiATwJIOiOHSPxAwIqs0Nnfywm6Lyskc8zt1PvOZT5OpmU7X1s288AsBxvbtN4k2NFPd1IRfVDB6MhRtibyhkaTUV6KDE4eEBw0paK2C6UloTok9dDyYGM+yq3eMPfY4zXWdzG1M4RoOq3+yDmfiRcY3nEl3yyxYOo1uP0Vq5kxqmzUiRYvIjNk8s3YSxfKZP7+G/STp3fkIE/n9aPE8NS0NTJsWI8iPkO3bT21dPYvecyP+0gvp37ie9Y89VD5dBiKFCQvG1cA0DRZPg8f2Q+BRkissR7iADCuMLgfjBGGEpMHTa6FGh2cGjh6nyoFjWnTn1wq2yPEyoaKI9c5q3qS+fBOzOMDA3gEG9gIkGdlXx/jAy/Rs30IkoRPVZGK6Tu36l1ArqrAdn0BSiVVWk0ik8DwXWZaJaFE8TEYGB8lnJjELWZAyJFDQZI3Ag/7BETJ+hD2DAwz19mLufW1Wj4tQrOtD9Ci80aHHojS3NSOt3/U6jf7C8KE4CD1Pwd3fgMp3gjECgy/CGhsmnyvpSb52BIFLX/866kkS69+DsmUJ1bGbyLgSviKLRbpdIXTtrFrwailLboV6ZQnK+p1wwEb8j0SK682NV7tBQvA11A8P/SxCcFbQHTzXxxbWWqgR8dA7iklE0fAkBU1SkBUVWZZRFQ01oqNoCpKiIEkaiiojTTGhzxVzeF6A5/m4jotr2wTIyJKMIoHvB9i2h2V52JaHY5moER/TtPD8gHgshWXaOK6D6/o4jk/EK7lpSDKyIiMHMp4kQSBTpmQ4lGVQQpm4UJ7haCK8D/0pr1PxRsQk0OVCZhxGNsPLw9DWBe1boLENkgpU+FDtgOSAZCMuj4a4dWspc6JC+eM4aA1QcwbM6IK0LbrzZQVsA+TxcYKihaeOIQdVOEUIUFAUBUUTpveSb4NVxJkcx8+PYhQMXNMmsF2iEQXPLyB5LrriY7o+GDbGeBrkASKJXdQ0ucjJatBjgrQYjRGpAklzQYlQmDRwiyVtZVcoIcgxIVerqBAtAbSqr+CaGq11KjXRNia8XhzfotxhcLSRB9YBj0NwLgSNYghIAX4TWOeUzMi2IPCZqVjaCLARzHmwp1VUJesQ8M1MGdqnweBysEzgxWPcLxAXdBHCzbTE9CSCmGmHEfjMIPAIZfnIMeAuCIrgnPuqWz85wFgpCp+8ES5bIFaD//ULhu+9nWBigCpZIlqnIfM+pJYrCeachXtFkmtHbforZZ7o38cPfvAgDTPquOLqgEXzm1AbVIpFlb5+k+Y6nepqkSXPmKPTMauZpubZSH0DNLTUc+bFV3Pu8rfzjvdfCkChYNGzZ5ynH9/Jxkfv4NwOhzOm17BgTt2B3TXSWYZ7eunatYELZtQys62NxsYGIvEYeV3h92u38OKuQSr0KJfXm5x30TUkN+9m5T0v8M27fnqUJ6WCg/1U35zQgIaqGNeumIeVgaItbsGoonHpe/4nvx3ch5Gd5Fhb0kNV0Ry5khKpRICCjVxqFzkZANnfll4hrOYirsE54s9xwFkITh7YB/o8mFDEYuKYd78e+ACCNh8qekcRTYtpxIPdS1n7dRDx0E+WviwEX8NVjEnZLCtBWYpAoqxbEv49TCSnqo4fCdw7Ga7LWx+jdp7h0WEqKmupaGgkPzrApFlP4MXwEProtRExWR1aQgkAPwhwLRezmKN3/wDPPrOan3/j79g+4ZJxyxZqKqUCq+eyaWAf71y8mL2ZItuGhlEViebaCkzXOQXGnoopMYF4htMwvJH08DgkY3B2I7y4GsxBob+eaCSy4Bzq5jTgBOM8//BGVqmVLJteSbxRpxCA0Q+VtSDpghGLBOMZGBmGSb+FqktuZqL/VxCLiZvdsJAzHkXVAOIQ7YC6j0H2TvAcxHj1+lAS38iTWf0oLyTmE5ENzj1nLtd88P3oEfGkhZaCOeDt0yF6+TL2qzNZt+NRjLFBAvfUs/JHE1IET6njqd0+rYt1pJTMiCvkOPoQWdNMhIfFrIWwdY/Hnn0eRkKjo1rn+U1pktU+f/uXKZbceiubcx6P/uZe9j/3IGOjE9hWlIRaR0VDM4ZpYfalGR336e2F2CzBsq2shvYUSEVojkLKKJA0i+zfL8CaogP7943R39XHWKaP1LwEMS1CRSHL9u/8GoxuhtbvxtZ60RraSJ7WwRkLO9B16N/v0fP7HfzqwX48q5maWTXcuQV2v/gEE2NbsZQ8Sn0zH7r2OiwbsrldtKVkPnHDhwg0jecffZBdmzeTHeoT52u89ApjGrAwAh+fCV39wm0ZyilAmNZppZMZK/0uS7l7dmpKMALU18H8CogNHJspqcPrb/6KIRSjQs+lNz3yjI/kGR/Zy8YjvieKolcQb2ylvqGBIPDR1AipRAq9Umcyk2F0eISx/l5In5gWymtrJVabATsKbwJEIyv4epxyMf9EhA1WP3z/FmiqA3MzpP+b49WhGOVp2Pt71OHpdFx1MXmnBl+Ogq5BPCZYWF4jeJOI3D+NuEFDBCU8NgWRpYX2w6fy4xMXYUHQoewKH/ZUhteAkvZrgBN46HoR2zCRZRU9qqNGUwSyhRqBSCRCNBJDj8WRZUCScGwJIuD7Hn7g43keoyPjGIaNbQuw1SvpiEuyhCzJeK4QHbPtQACyjo2qKniehyQpWEkfz3YJJIcAD9+TkNCQUJFlFVUVhmMuWol4FCJyHmIA0yj1aSAGW59yIQAO3z0UukNFKTOKw8+eiiOFRhn+hvJZDu+6I5Wvi4jV8jgwMgbqGNRsE9SsRRFoTkJbFcxqhFQnJGpA9UuSRTLCDBPKS/GS6oZUJ3amcRjcrJDaVAIws+AHo7jKKJYko+q1eF4cWYug6jpKLEkQOPiOh2sYmEGawM0wOTKJZVgoSKRSKaJJHTUapSIRQ9IiIMUxTJfi0AgjpkfVEhlZjUAkVl64RkFTVBRFxfcTwuvOELJ6iiI08Q+wjkq3ZTwKVUmflO7QWtlG0ZqJY3sITZljKfKbiDaZHwK1ka8SFwAAIABJREFU4NWAoQm4xAWCTnArERIAI7wSh+oCZz0MXisSwlASohbRwZN/N9gmBBs59mKajDDleicw/zB/NxAmYXtLx5BHHPt9iATq1XGzkwOMTSWgtlJkunuiUPsRFv3wI4LaXXfwWy2gB4lnno9wwSzo2GRj/ss+gngld37pa9yet0GegTRrOsH+x/jbT1zK17/+8QOff89Hrmf2ORfxvS9+jZs/+AnOuqSVps7Ygb/fe+86Nj+/imL387x7SRMJ3aN5xlzqFp4lJAqAPTteYsuaJ1hy4TXc+NGPE6tMkJ4Y56VnVqG7cP7bl9K5cIQ5z67n2XVP0P+uT9Dtw/PHVP3vLL3e/JBkUfGIxspwsCTJfPtTC9n52ysY2GUiet6OPjTEtsJT0EycmTTSRj3/l628AWJfxxlRRBmmCvFQhT8jnsHNKrw8CM6X4OU7OMDdP66QgMsRgOwexA0fRdBU9iL0r/KUJ+KQ/7UbUXHJIqaJqZZRp5LDNype7NpI1s0zc34bmP2Mjc7HUUBS4bmX4arFUJd4pbVbqGDx8roenvzVt9j4+8fYtbUL0xPpVAUiEVApq/1qlCT5HryPOYuXoc9fwPNdXWwe3IJhnAKXTsWhYSN4UDMBH8w8bF0JxR6IVUHTHKQlF9MyvZ66Gsj2dMO2jTS97W38x2YJS4Z0BhbMBTUKcdHpx8gIbH5ZGLLWNse57MoFfPup03Cq6qC+HalpDnXzYXIMnP4A9ruQz0PwXcT4dCLYQy7QCx1/zYIli2icMY2/+V6Bb3w6iaOXGxtDO4xzOuCX76/jlrl7eeimM8h0bzkB+3AqToqIt+B3vo8tAwrpOmidBu118LQkZsxFiM60kEwRECEagxsXAgth5OIGRhwYNuCuOHz9e2OcXXkZW7du54Z3f5KXhh181QPijK3fB0o1zR0J6ufAbxBZwUJgoQIvJmHvNnjm3vvZ+NS9bFt594HdXHjBlVx1w838r3/4BPsRipSjm8ah2A9EmX/xOZz93vO48G3w8S/BZRfDlfMgMtNg/nv/kZkfvQmztY2XFZjbCv96362s37GG+1c+zSMPP82FSxdy9qyZVEUiDAyNML9aoShB1dVX483dypeX1OEfzvCxGxgswMATYmJqR5A8PoIwQd6ISD8kxAKoCZG4RRDdeKs5uPg8BnynS5zsQxQS3pSYBP7lLfjeYwoTzzLJ7R8ht//N+cZL/zOK9YzLIz90ODoO6fHHQP8Id/3iWDQqjjGGPnSCNuTgGjvp/k0nRL4JrVdAap5Y/2eLJT5CBSIrCz0TQqArNJeaoNyVdipObEyVOwsp+SblrDi0fEbIfFiQHh9GUuJE9DiKqqC6lMBWH8/zUaM6ni3h+gG+72GQJj05xtjkEIViDkVRyKbTIGvgK2CDpAlY5IAXqRtKJUggy2iJBC4FEtEYUT1WYghGcWwZz/NBVfDyJrKigC/hOg5mMV8iHYUdr2ZpmyEMGKW8lpzq5xHefwZlwkxootxY+r+NWAdmEffmqTXgkWI2cDUwnTIBxkbUBHcgLLqPFKFUetiM3ouYLn9pAxOgTUDNHrh+FbxvEczphPppiKQ0ibiElYjLbiAWeTEgDWYU0sOQM8R6MpkX77MDsHwfGEWNghYFVQM8ISNm2OLfolUSV0kLMDcVl6irq6GmpY1oRS1aQieZTOIqCbRoBVKimkRDHXKk5EjqcvDCVQW5EiqPhg/oQHoIhnp9srZF28KF9L3YTG50M/AgQgv2WCJAkOKWgVsH2bmiJhYujIkB7wOeECfvoKhCJC6IC9WIyE1URC7TeBo4Z0NmDiLhOZZwERIKN3J4MDYKnI9g3X4Z+C5lfdqnEF5DRwamTw4wtrMa5jeS1qD/dMjOkvCi0OfA7lEYsKC3B9rboaMd4hL0NEv89o5eBtcWmH/xChIKZH2PVLKCmbPOZNeuHtLyNjautPjxl1v58OeuRZIkGlISy05vJPWlz7HotEriSRU7kBg2PX76zYdgaD3TI31MO0snVqGy8Pz3UD1rAZImwK41D9/P0O4uKhIpzrvyJvTpMzHSRVzHo6Opk+S0mUTbGgmiEaxP5hlbeTef/PK3eXHXXhIRjb84bzE/W7eZyeJrlPHV2eL1JkcAB4rARVcYU6ilKogkSfzgR5/g53em+Pznjg2MjSLM7RIkGcUgh09BhukzPore+xWwTgYw9gKEA967EU/+rYiHqQi8C/bdDn9TA7GZ8IGvIaQL/hrRJ3e8MYKYQLsRQ7uGkCToKv3sIPRJKhAjkowY3bOUdRhD84FQEO7UZPxGRTozxoaNz9FUPx1jLEs0kiJeGaO9HQLtlXNa16DBpq07efbn/4+9Mw+T6yrP/O/crfalq/e9W619t2zZkmVLxmu8gAFjtjAJcUhwQjLDDNnDJCFAJiGEAJkJgYkBAyYm4A0bG7DlRV4kW7K17y31olbvW1V17ffeM3+cuqqWLNkWAVtM+n2efrq7uvpW1b33nPOd93u/9/syxZ5nmBmdwDeZYR3qKmZQYyNBxTm4RCUL+89A64FdJI4dxTbj5LMOzi9DNfEc3mTkUQu+BNEMei34dahqgZp2zJZOYs0J/O2QqBM0zl9Mw+qP8dyPTjD5qX+kdskyOm99DysuVVVAdk59r66GdVeqNcBnCUIBDTbcAv3TxJtN5v2qIFgDux8FIwq115tccUWMR24Ikzo+eyR4Cg4dVSs9wvnOU7L7SxzI3sLRXQ1oo/fQoj/K+9/RzIIu/6mWg6A6b2um4PZV4P7OZ9jx4Lc49tzZPKbm8EuH7Ank8W9w4shv8lvrm+hM+EgKxSdmqNR86KiU5TFbkCqqPnE6YIYE2bECW7dNs3mvzQ3r41w1349mlGhadwMrll5KbWc1UpbY8+Q4d/z5jbx7YwPr69Um5wv74dkxCLgQjxb4/AdvITV5lEJuCt0Is3Tjr3HTe9/JlWu6uHRBLVVCnNJCZf0hWL4eCiv49asW88ErBKYG970fLmmG6SH4l+fAlQX+5PZFZNrb+PoPR9nyiffzgafuJqRlaKgr8Xsfu5WrFs4jGgihCcGClkY0ISgJmEgLugcCdH7pa5z8wt+QP9796nOYQ5GqLmoH6uWbF6CGZn35sRXA9WuhTkBxCB45ocjbvShi1vPI7+H1/Xnm8ItFCxXifDPc8od5OnKSdajt8BzOQPHT4KTB+ijMS8AJHUpeKXweJWHzfDgmyo953Xf85b8nmYu1f57wzq9HS3jevbNJWsVoSU9i6BhIDRzpkrdtHDsPM6ppl+vkOHFiFLIlpF0EaQMOrlPAcW1cVyKEAU4RhKvqrs0gMlNQ70Po5Q71eTCD+ENhfIEArnTRDQvL0hHCoZCfwTEMilJSsl1KhTw+XYKr4RQt7GKYCrnsqX995c/pKc40Ks2VPZsMr/oxzen+L55vDFQs5YpUqibncCbiqF5OHw3AqgVQXQNYoEXLd1dJVa//WQp29MHwNMxky4Z/rtqR96P6/p3g7FrlEmpXPgjsHgJDB7+ESAaV4EygSFnP+a98qWUKeg/As90wPKOqesJCqVB1yupaC6pqIRIDvw8KWRibhKFpSOaUohaUGjegQzwkaXOmKOpB/DMuVtClpr2GRHM9ZqIOraoas7YOEYmBT4Ke4zRhmTjt22ujADPJElNTkkwmhuXzo2smKpC4HHX/Jjl/G6wvAL0g/0XRJFWUrR8sKF0BvA/4CarNGqgGX+8DNqgTFy2/ZJbKlN0ioNAAycs4fzLWw2dR0eVHz3h89tn6HZQ04H1Uxq5nHXl2XBBkrGvqvOgzGAHSfij4yy49mjqnBRPizRCKqhvTRj0nQ4RsKYlpj9O5sI6BoSHSIz0MOZPkRrqps6fxTfcyfvgZJg9dTLyrDsMyiIQMliytJRyD6RycGBhl23PPEEseozaUotpnUB1NEJt3CfGuBViJBI5tM917guLoADXRGPGuFhILO9B8fvJ2kpxdwBc3iXe2YiWiaD4LOxam35lg08oobeE4U9N5dg4Mky+dTS1koIa+D4gQrV1JtG7+m3cRZsEuQmpUcmLYpq1TJ1FdibRbW6q5/qa3MZ7+JF/4m7tQN1sYNV1945zHNNCIY+Fi4yDJUmJCpjGn8wjnQimtaETlzMr+wLwX5em6G3gYjpfU5WnxoSLf7ahdTQLl/3o+KKEmqBNUmnX1oELnImr29rKcsvyzt4B7WXtvYM9QUaDNLca/SKRnshw62sPb1o5QnB7EjgXRwj5qYwKfrjbemaJNX884vQefpudED2NDJ6ijn2XvXsueB19gZGgaw1V3mReKBVBacy/01FEBxCSQL+SJFktkLBvHmbu+czgbJIqOmgQZBaqUxLW5HrQwhgaxhEGsStmWFfGhVdWw6VbJ9i/XI0SYmhpYHoRjBuR0sE0V3GGpmCadgyOHBfElEaZDGoW4YCIP9bWgW5BPC9JjcOigTkGsx1q0ECMxRXbr96hsMCSV1rLnieIQhdHnKEyGIX2UH9/3ORYvvpOqpouoD6gts1e8F5QQsWH9gtXUXz/D4doAP3ngO//x0zyHtxSJ2lZWXv5eli2IEY7o9A0W2LwvT3MsynSnoDoGMqieGwfqqsENQbeEZAaCPki6OoOZIPWNLkvbfLTX6EjbZTI4n3i4iZIRRooCi67cwOrLWxgsGHx7c5ZccozHn3+ZeDzO0vnNbOzqIrHyFtZ25WiIS2K6Re28taxYvZz2+ij+qHFqTzAJDNklmBiCzqs4GqrjoIArBCxshSELxqehf9Di+j/+DdKLWzk4VOCVrb1MnniFV44dY6gwxVQySLhjI0FfEEtXzV80XcVnAaAuBIvnG1TP28R9X/8/Z3cBkFT2BwUq9vSeK1MCtTC1A40FiDgwlVaP16EG2Owqr7lCjbcG9QFYU6NKMN0RsIoqPFwCfcclTQXF0S4BjjLncHo6xmD6ETAlevhOnKoQTPqVRA2Linfn7JJ5L04XzC6bn8PPC572ECrVfhoVa4gZ1Hn3krzltJtTwC1ICq5LqeAiLBvpaLgFG9tOQ6lYbkrpRdYaHjEkT2WRDIQwEZaOa1tYZhhNNxC6VISs7sMwNIThIlwX17GxbXANidBNhC6wNAPT0hC+AAIXp6RjGwaa6cOVYTRN4NglSnaBYjGtZI+n5BuekZ/X2MvbE3vdVswzzo3X0Q4q6toLZR99YWEpsNYHb6+HtQuhpgMCVahhbnGqlYrMQV0KgmFIFxTBaQTBlpCchvEU9KTh8QHYI1VRyGx4s0EBGE3DYBLiUQhJKKYg0w0ZG3I5dTsK1QuekgNbe2BbCsbKVewmiuuyAF/ZNrnZhropiOpglGAyC+N5SNnqzimg5FoxDTQXsmkXBz/CF8eKNVDVtohgcxdapAotHEWLxcFXTn6UbHBnlAq85KpNguaDuL/c4Os1IEBKgc80aW+qxlm1mPHJKK4MMjKqo/iK45zqtfOGjeXHgOeAz4Hzu5AJgKlDSAMnBJlbwV1IxTv2Gogvh0Rc8cC1VFxmPH8KjfL+qOMNvoezYR+K8wqhVLJnOz8eJ7QBeJo30jfjgiBjHWCfhGGhzpkn5I9aEDMhLyEQAX8JtCSkCpKJURtZLKCXJsiO7iK8ejlVsgc7NUYxe5xqY5yl1SE6oy5GqZvRQ0NEWhPoloFhQHVCvfbYlMOhw6Ps/PGPuW1lgMZ4iFCkEbMqRv2KyzDq6nANk2Imy/ixowSkQ01bF3ULVmHWqfL1kp2hJFOEYwZWXRxNV6fVdR0OH3+J6y/yk25IsHP3IJ981qtTCqHujhnURBqY9dhymhcupXlhy2nnyFuafpEQqJLU1CRMDrs0NJz+ipqAFStX8rHmDv7p3w5TOvlfwU6Atgvsc5OxGgILgzxZJC4lXCZlipnxozhvjdnXWeD5tnrYhNpKlT1cBw9ArwlGAjWwRoBnUQOvBXUN30iA5jXJGkF5wXrlK1MoKXuYSvAHaqfklUXNXpSZ9fc5vBnI5Yv0nxxjrO8wVa1thOMhZDRMMOIjO5lhPJ1kYmycA7v7Ofji3SSH9uGz06xtW8gtG64msOsYB4+MkJku0IHKG1aj9sOPoxb4DGph1amEaEiHfCE5R7XP4XWQBKZA1CACMWS0BlJ5dDuvsuo6pEcL5HMOrulyxVV1DGxZQ7AxRnW9Ch8KPhjXIG1AJqcsltI5GB6FPXvBHwPfvBC5kuTkfklnA7hpgcyo/cWhV6AYvgJ/WwyzPgdbt6F0BV6jwJ+VFrAhewCvXHH381/jmW0L8FWFWNNch9sSIySEstV3ldKw3R+j+eIrWdTVyED3Ho4c76GUz8HZSrjncBYYXEjeiNHqDlZdeSfzO6ooWIIDfVke3TJFvC3KhrjaPHnCk1qgMwGWhAkkTx/up7O+GumGsWIRli6FphqIWOCUNPoKNYRTBrYPrIDFhptWsHCezo8fP8kjj50kNT2J0beV4PJGAs15EkY9m977ETZd6WNhk0ENFUd2iVqVw6iooteFE4UCDB2m6ZaP0BuN82IJ1gShMwp7Do/Qd9AhPx1m4699gB2lHDuPDDNwqA9IsmXffgKRKGGzlWB4BSkBplDbdilRfs+2qrbtaNOYZ8zjxYXLSU9NksmMq93hueCFIydQIUkt6sB5YGgcxoswNV3x0jm1KM3hLUWtCdfElVr5xIRq8FACVgGDUCyokTsPleafm/HOQGorlIYQiVXgWwM+DUphpYRkmooQwqs2m03GzknBfzHwGnd5exyvSZWnLLWoTFgB9TfXxXVLuKWi6joacMAWUPCaFJfUcYSB0AwQfkSZjBXCQkoboZvoPhMzaFEUEsuKYBg6uuGCYaFh4kqB64JhGLhFBylAaBqWZWEYPnTdRNcMTGHi2DaFgoZtmtgBG6RE03SKpSLkspSkjSzlQXrdn73slpeo9jJenj3D7PvNI63PpAPn4EFDsSkJE672w40JuGk5sB61XQ9QseidAtLKliInoSYOdQboQdDrQTdBjEFpDCbGIZpV/q67S5XiELP8etWo3iGmBQXTYtwIkBIBkjmT8aTFRNokmbFwHdD8qpoyr8GzLuz3w5SwcQp5IAlyGh8O/vLU0zKtJGBeTyrVg6fSWnCGsjWTC5EiFLMg9TC+WB2Rxg7i85YjqlvAHwLLD36/8owvSdxcHqdQwM6kcWYKuLaGa4TQWxNomolumBiGhW6B0CschyxPkYYQRIIWkUSApsY4eSdMOBJj5+4IE1MBCrlXcN0+lG54morHcYnXji2PAF8GboVcu7pontWDswEKF4OTU+eLRgibZV98FHUTBhEEPQAiDm4U3FgcGV8M04up9OU5n0TGGLC1/H+3UvFQOBMx4FdQnM7rr74XBBlrA41CjRFLKjrMAVqRNAKGgONJ6OmD/uPQdwi6D42T2/p16H2SkDvAlqHnWLOwlc6rFtDQWEdDTS0N/gEc8mS1IGPZDB1Snur26ZH9J3szTJ3MsnZxiOZqm5r6NiJdFxFYfTmgbrZcaobJoRFSyW6a5i8n3rmAYHND+e8SgyQBM0k0mlAd6cqQrs1Az3Ns+vBaskMhuo/PjmAvRkVNm1FOwx6NPwncxpW3t7DxXZVnZ1CXO8QvHroJsSbBVct9yvj8DFhANBwl/vl/Z/IPwBkFQq0w6nngvBo2DqlyZz1PqZ/FZjtbyJx3x71fFLzSfw9eJtXLxN4K93wJwh+e9Zz7UddsGcrcGc7ewmk2XNRAPoGaQjOcvrt5rfMxJ0N5q+HYNs889F1E2MAQJYLFIvmTNew7tIXHH7mf5x9/lAWNcOlqQYMjkaNw+PHtZJ/fzg3r5nP9hnay/36EPGosjaI01g+h9OVnXuGbgPnAfZzuIDyHObwaE4APYTUQ6JxPdudRsB2MsEk0KBnvg97NA6THxhHxAkMjV3LtHZcSa4JQRK1CtwMvm/CcC92TqnTqxHEY7ofxk8AQVK8Aa0oy+YjL0/frYEDTJph/G5SmYWd2KbmeNLk9w6ijHqNSXjf4qnctUDIBeep3tba+Gl7Ti6XAy3zzr/+Q+75+L4tu+CO+9pV302joBIBkUfDcFqjNdLOwuYqNK67k/dt3sfqGWxjYswM5NXqWY8/h1ainUqb71mMmb3BwIEqoFuqaoFAq0RpKE6uV3NEErVFAVnRVC4GF5Y7YH/3rP6V540e5bOMmfu062FXmVQoSbFeyp8emMS6J+CU1Mbj9QzrNwA+3fpXue+5FLH43n/2zm6mLwORkjk/975/ylb9+NwnLOEURpFEphzRqq9FUfnwsB73pAohu/ujTTeh1YSxgh1Tv8TufuIsjR8aZd/PVvLLlOl7YcohscpSQM0Ea+OGPnuBP7vwNPvaedwCqJcQKWW5WBrxsw45RGJ6R2BJaauDyz34D/9Gf8Pyz/4T87KNv7AQXUYvQEOqytwyq3V8VKjAvMCfAulCgpcDcq8LIAiqwjqB4nCfhZVQh5mrmLtk5kevF3v524C8hdg3EmmHSRK1VGSqEgdefYQ6/WHiWBA7qGgjU3es1vrFRVJsPxRiUqIiYAuqpmULldz0KTgEMHVFufmT4w+jChy5MdF3Htm0sS8cXMPCHTGZm8hQyDpoQGIYfDD8+PYxW7s5r6ErQhdARwsDQfRhmOWnpuuCAgU7REeTRyTsZbNvGKTrYpRKOXUDaDkKzkK4A6X3eAhXVrpz1mKd7nMMbRQglpbqjCS5ZBq2LUSUCrajtvFe+PgMUQY5AqRteeRpsB8J+qIpD9RKIdYAWBrMFGtrhd5sh9jQ80K92/6DW+dXAJh1WtUDtChBN7ZRqLsL2X8TMTAtZ0Y7tb8Nf244RB3zKAiGbguoD0HgUODLK+KH9IB8A7qXA2Kkrn0Ql1aKoiDpMxaCiWPko6EBMqmFQ0kx8kQTVjR3Q2oE04mAGysazechmIZejlMoxNZJheKiHqfERspkceVsj3NhCNNhIVXUbNQ3tVHfoyJjytT2VE0iB39CpTkCkCiJdsH5TPX299TyxZQVf+e5GDu3cSSZ1AOVvNINatHpQ3NdrKWW9pMOPgPeB0wRFoWKSEDDhhwkNFaykIR+GrK/SjCUIvhDE4gKjGrKdkDvRSn5nI9x7McpqcjcVWv2NYhzlDfsycEn5apyJalST9s+8zmdUeF0yVgjRiuowVI86/V+TUn5JCJEAvofS+/YC75VSTgnFRn4JxSFkgQ9LKV95rdcYycBnPw0hPyzdoJa99DgkuyWpAwXMgV769t9LKncYTU+yuK6VTW0p/AtyxBdGaYtspLbrUpYubqG6LoEVraKltgW91gVLIhEI3cK0TNwcyBIYZWPiKy4Nc/GilaR6/5SGjhB60EBYldOSG4fkcJLkyCA1C9ZRs3AhVkB5a0gpyZzcT2H0IFIW8besOU3Sbduw+RGXrz32EmnHpXBqP/Pe8tdalK/EVhQRWwO0Q/Q2FjcHWVxfOUcegflmQDcgnnhtdXrcgs03wXsfhUNPA73tEDsJqbUgX90R1ivICAE1RMji0kuGlzlI5oLJ2XuBl4efoCiyn5R/n4EjaRCe+bqH51EZkh+gSNnIGccdQU0+w+X/y6DScSdRBWQDVEpO5nChwwV2ZCH87JNsf+Ypjo3MkETDdooYhQI+GwZOwviIJIbyFywCDUehpreHtFS2exLlYySptGo726YpUBfFH7AY6hufI2Ln8DooQLSTQPtGlq3uYuf2nay7fTVdG7vIh+DFb00QaGiiY1kbdV2SmgbIGpBOQjwPNY1qO7AGqHHh8AyIEjQ0QaIakp2w72VYtBwMBPtDOhM5eM+H4LJOaCjAHd+G0r13E5ycwueMMsWjvFYZXTgQZu89h/CvMDgUgpcduNaEv9v0LSKHj7GKHKtYQoZuujnAUQbZywTPUI/NJDODu9l1z29x7cO/z7Ir7uK2d17Jb74nRoMBDTX1RCN+hAC/ATvuv4fNLx/lR48/xT1//8dv4nX5ZYVXuXEhoIU1i7q491MxHANGTDjaN8qTW5+i8JV/ZP9v/gHRkIMc3cfJXY/R2NXCgsXtLFmyiMvWbiQUXMlFi6pYulCF7u8rV2I9nYffGyziPPwgE+48LmlfzrrFXWy+7wA/uPcHTM0UWPnO3+aG636FpTXTzEwOoWXyNNfHKQhx2tkJo+bzAmrO70UJNTJpmJqIgHUNn1yxhvY7/462Gz7AwkbY0AyOzJE8voU9X/0m+4wmSlzM4rfdyMp3vIPv7X6Ooa0/4Yfr1pG58h00ReCJx+DZAHQ1w0WroMeGwjTkBwqcGEyS7KhjcmCMZY0Xcd0HPs9f/uujav/wRm3bXJQV2z4UrxFH7Tk8EUg9KqwBZV3gR4nfL3R0oj7H99/qN/JzgBdU58vf/UBQgysawB6Fn9rknldbRk9fN2c3fy58HlK7wbgeojdDStnFKRWU13/dU8ZKlLprzqbgFwsXdZ5nEyWecjRQ/tmTNATKXz6MUBVGIITp82NgoOsS6bhIR6IbIMwAmhlA00xQ/bZUwyJd9UUJh8OE/DoaOoap4wupWAc0hNAxDF3RpS5IR+A6JWzyOEUHt+TgFB31upqFJiwM2yOWi/gxMDQfwm+QTxXKPrbeQM5QSViny599lLkM2PlhPXBjAG5fBW1rwLcC5YfegVq/CiiSaRR1iqeg9xC8+AI85qi7qDEP7eOwdC80jUNVQtlkElHHuG09/MpS+LtpCFeD3gJGCCwLjA7QrrwUan8dGfhVEAZLHY0RoTMtdNBUpb3nkBwvX37HgVGnhsPZDbz09CXsv+9/cnD3Drp7H0Hyz4Ai1PKopdxT43qt36pRy3SZ5wUbRvuP4Og2M9JmfrSOROMyNJ8E3Q86TI5nGB0aIDU1ST5fIJedIJ+fwXHySLfE+MA4SaOHzPRJnPw0PrmGUBuIEKeJuBMJdSsLs/JYSzu87xborA/x1e+v46UdIXoPZ1Ek7CWomo1jqJrQ10IRRSnGoLgJUvNVoOUmdqmCAAAgAElEQVSjXKTggDsNPAITOZj2w4EW1TtDLCBflaC4RIdrIdEFVUvAadIZDbfDfQ/C1D+j/GnPtwNpEtXV/Vlg+Vn+bqBo878E7kb1ADo33ogy1gY+IaV8RQgRAV4WQjyO6r+6WUr5t0KIPwH+BPhj4EbUrb8AuAz4Svn7OZEeGmLqvk9C0Ef/3hgZs4TuRjByJjUZCLvTNLSPqS7iElrrZmhq1zDcOqpi7SxfczX1i+qpigfxBXwI04ffF4CAQJyhHh4cgakJ6FqkOkZbloYet7C6ajAihpJga0oR6+YgNTFKvpDHF6uhtqMRMxBA6JWDJvuPUpwcxQpHEVY13gLtAsJn8Tt/8lv8+b/cT2//yKx3cRlqSD2LqjEKcsrkQkThyhC19Rq1s967htrOeoYGP0sY8EatDoR4bSI2n4OpCZeDe5Nc9fYI/iLsOuZArh7k54G7gJ+e9j9ekU8dARqpZpIivWSYwL6AAsRBOK337Fj5d0+pKsH5Lqo74NWo6c/zlBoBPg38IUrxXDXrGP0o0vUoasgVqeS59pePP5d1/2WCLWHfwDiu6zKdKZ7K2xuU3TFdEEV1V5iojdDLDkw4DuOoq38blYYzBirPn+L0DVMVMJTOk8oV58KxObwBtIEdpjg2QN9jn8dJ2/jiS6iZZxGtkzzRESLaYFHTrFPbAIlaiDWWw30bnkJZZySBw3nYtV8ymXGJRDXCEUFtFJoboLYahCaINZaY+OpT7OyVzH9HK29/z1L+5T2w5T6XkcJuxtnBQQqnHPjOdg87rmDn0TiL1gY4dmg/D9z7LNtXdVHz397G6KNJHn3kAcKMUwcIJrCYoAHBO7mWrWznpDuAnU8xmU+xd+s/EuEQwdK7iRVroJTBzgqyKZvjO7M0dUW5bNkiGqMRVoWr+Mv/9XFy+bm599wIoGa0C2GV9mPqAUIhjc8fgJs7oKOmnvYVl7Dn8Yc4fP938SWCBEJ56gMWfYcOU9vYiS/YRkdIsPpdNzNvcQv1QRVxPZ6CbfcMsDOls6e+Cmt+NeNjR9mzdRo72096wiGTtWlsnkd9YxOHdzzJb171Tp4f6mFobBgr1sBT++G6Lmgq5189N0nPUTJNuVmxhJJbhNIJZsZG6Lv/AaIZjTV/8T5CBsSWdFCTuYJo1eVc9yvruP/vv4/FSRrbq/mDf7yTuz6xhT0PP0ByqsCyD3wMpxTGqjYo+XSOjsBICsIhMAMZDvQew93/PPMSYZrr27m4uprQRevIPrsLmTkPhbM963sRxepZqHDFc0b6QJsyuz3+S2KVNAHsfKvfxM+ABtS5n014l1Bkgo8yGatDsw+iDiyWKvc/AaVDaneRRN2PczgbMiBfUl0r8wEIXgqFmOrsQwZ19lwqqkWLOTL2zcCZrZIcFP3kEeReS/ry774gRjCEPxDE5/ejawYOLtKVSNdFShdNEyBsEBLDMhAaGKaBrmvoug5Y2NJFQ/1ezJUo6TYaAk2o3i62q53i5l0Jmi7RTQ1hGoigjqVZ2I7EdR18YZPp1BS24yJ0iYEgoOnkRQlkHnV/ZVATq0fcerv92XZ1czgXNJSUbQWwvhYu7YTWS8C/HLTFKP/zWipuFyEqVjwScgUYK6nduoHSMeYdCKfAMNRT/aAqhR2wSqolQ7QJjOUglqI2az5UcNG8AELtYMSQspK/rCpPGQZq9vB6HHjWSkE04nGLzk0Wky0RJscvZniqmueH1vDDL24hM70NlyO4VGYjm0oqwmvzLQBHQiY7gzY+DP5ugon95LICLViNHogTqq5DBuL4Ey7SihAp5PH55qNZAnQXdBtH2AgrjC8YIRiuwhcGEeaUn6gARYwGVA884ZFLNpRykJqUjI2O4rg5NC1VvlI9VGqH3siK5FlC3gXsAedKmNgIegKKRjmhMQj8BOQ42C7YnqdrHIph3GIMJq8jHV2L3lKFnCfUhY1XQf4ayKWAz72B93Lm+5oG/gLlHXvbGX/3rvCNVEwknj3n0V6XjJVSDqHkEUgp00KIg0AzSgp4Vflpd6Ncav+4/Pi3pKox3CaEiAshGsvHOSuc1CThY98jEgzjTjRgRiEeThAO+AkGDAIRl5Af7EII6fiIxvw0tcYIhtuoblzGwksvp7p11o1wDgyOw4kxyCShw1WWMqYBuqkRSFT+WflgSPKZIsV8Ht00CMWjhKrip2wIpOviFgvkJ4bQijZGNKhMRspIZR16R0r4m2rRLJOm+iALOuMUMdi1K0sufwAV0V4H1IO5GCLNKlkwX5lIn2lJ4BUuzC7lfC245c/iSmX1MLsM9D+CYs5letSmmHS45krIdEt2PeIqsaf/vWD3gX0UNegUbDwPNQsfBhq2qijhwtjmKYyhBpeHJJXC8AZUKu1FFBnrEbTeVbCBR1FWBS6wGBWwDaBUsQMonYyOmuqnUFmhXuYW219ODKdfvbE9myOmQC24+1EjIo9KwcxHLZ7JWc87c0zrwMk5InYObxRWO8gQ9vQIo8N7IHI1WaGRE9BUJWhaFcDnh1gVRGMQCKogSpNQdODRXshn80wi2JUSdB9wyGVtmtp9hCyLWI3EzBeYOTKMdEq4/RZVR3oZ2j3BQDFDqamaG0WOgJzhOIMco/tU8sEr+jwTtmPzw+ee5n23XM7ETJa+vlGe91fz5/9jHTPOArqPxHjuyHaupglJCj95ErhUE2ScBEVSjJXZoemhJ9n9Ug5RjHD5wlX4W/y44RDZtCSVLRGpldTVRGn0m9T0Sf5VN5hGjclfEjrpzYUZB3tSdbd4y1FgKpPi2UPD/PsTSVa+uwVfIk7XyqVEr1iMLQvkgj6KgRB6xiB1corRwSKj0wYlv2DlhhX4DRgbmCHT08fTU2P89HujDBdrEOuWEmmPMd37Mt37xigWZjAtPzV1ddQ31hMJWxzZd4Ta6mrCVVVowzPkSzrHBmFtM1RFKgYaevm7t9UoADN5l5l0HtxjgMPM/leY8EfIHFrFlOGj6A/gb2kjEA1w6e3v5/C2/UTrEzS3+Vi/4goe/uZlHO/uI79rD/PeZRMOSKqqIOS3GT6ZIZ0W6AmNXDbFxNQE+uQg4eomEkaehAGLLltP73SKmWMDFMfO8073PGL7qSxQXiC5JgajfrACUJyCgeKrg0w/p1cavxXwQWhJDbLgkj14vgqYCwBeS4kApzdfG0cFEzZQEqqEM5VTHbI7URPvKGjTnB5m+oUy+J71WGdLE9U1Caygnxde2PGL/0wXHAZV2WQxCuYCKo2joCIn8cixs3kEzuEXDwNFN0XKX6Hy7z5AA91E6DpC0xGahtA1QKv4XLoOQipbJE2Arms4rotAIIQGZV9Y6SoGTWg6ru2CqzxiwcVxbJA+BJp6SUDXJUIINM3ANH2YmkWuUMSVGlIK3BkXR3MQro2m2QjXQZBHniJiPc3jbIrt9fw05wAVf9hlBlwXh5ULYOFyCC1BbbJaqZS1e/B6YSfV42YAQgGI5yqtlrISJooQTkMsoJp/mpbiz21H+bP7EyhqoLX8PUxZXeNJRIsIYSHKL/96NpMBIKBDYxtqXqeOmVIdjf1rOb6jnmP740yPhbFnXjm1pArUkuCZd3gfDU3F9DOZHO7ICPrRQ4ynShihGnzRemqlRrC6ESOYIGyGMZwCidoarIgfzSfAdEF3wPQp+fi5pjx91r7Vy504UJixGRnMcKT/JabsFIXgJNQOgTUGxSS4JtgGJGtRWdLZC1QQpfH1IqoCinfRVYfWTCtqfHhS5xyq0riHV9k8Fk0YqYKRjJKFtC2GiUZ1bCHAWAzcAjzAz+au/iCKEr0CRbnPhgAWAdeirsrL5zzKeXnGCiE6UGzTi0D9LIJ1eNa7aEaxTx4Gyo+dRsYKIX4b+G2AgK6xtCVNNAjhUApfSwO1MR3TlAjdxTAMSoBPM/AZOoY/Qk1jB/Mv30RtZxeaVm5Ndw56UpZjjoefB78GXU0QicLIFESCEPCpxlSz4TqS6akJfL4owSo/kQb/6ce0bQqjw5ilFIFYHaHa9lPFBq4Dh3qL/PN9Q3znrz6LdB1+51eX8qW/upJBJ8Y1N32RY8ejKBOTZ4AuqGqEy5rhfwLf5qz3g4VKSNiAfob37dlgo+Ktkg1x8z8WPnj2fdKVFDIlCtM5Pnh7Na50OdapoV9m4vwYaASmr4NpG+Sf4y0mGVQp9gZ0hhlhhOIpLeiFQzRNc/pAnip/acDNwL+hFs1h4GvnOMY/oQbcO1Gz81T5+UOo7b5EDQnPmG0O/xlQRDnTgPII/DDKNTqJKo6YRN0VZw77ceZs+udwHqjugrwPMlOAHxZtoCddhzzgYgc1LrkexobU+hEOKxJ213ZVXhSMSB5+Eb60fxhXM1TkOZ4Gvw11dfhMjYDl0vfUED07/g3Gx9H1xWzoaGP4RDdDD+7mngczLNZ7WOz004nDQpoYooduKgK7M1Gyc3zz4Vu45uObWXLjRt57/WV8aSu0xF1WXvNfWKxdwhc/tpxLCVGNSZAYPqYZ43EuYxG1LOH7vHjqeCcHtjJ6cifJbe/n1z92JzLhJz2jYRoBcmlBKeSQPzHIgb/7MjcUbSYQ9CLZxoW0Fl0IEBBthHQWihcCGXuCHT2v8L4vPcnEQ1v4ycUfp37ZYhaujvN/N/8fUgJ2D8DmbYP882/diZYTbHmim+7CS/hubuXSWsnzO122PHyEzZ/9HIgHQC6DpivQqnPE6kuMDw2SFQlyLU3sO7iHG2+9nczMDBMT/XTMb8PWNVZd/jbc6hHue+gQrQtcsmgMIkihPFzLegyiqLl7AhgYdRg8PoOqjgFI031wL3/w4X9Axhqw4jpOcozRgT6O/fZHuO2TnyERE9QkoE5A1x2fI93Xg+XPcdO1dex9HmqrJFF9hhPHDyJtgwP7DPonC0R1k4uvuJHVLQbhiGQ0Nc0Hb7mGh1eGOPzdJxi+b9vPfgnO5AbG07B+FVwThieegK9MQNapBIygdgYlzmYV/eahFjr+fgOlEzmO3PHT13/+hYakjoaGMU9QPFhSCosZ1N5xCSp0PWHDmK0IAT/KPuJ6IAn9mznd9rnegAlHlfCUccdtb+emW6+neel82tsvpVgsnsO3+/9njAE/gMzFqOJOz7PQKxX3JDFzePOhociZOOrmbqPSbVBDVS5CqVgCcjiOAxj4wiGEMBBCw7AAGyxNR9eUeUexkKcoBaLkglMin8/gs3z4ggGEaRKM+MF20DQHDQe74BAIBNB1A02rSAGLRQchVEMv27aRSBzHoVQqKJ9YUcJ2czj5GWwnhZRTVPTqBSpSDi9SyjJ3r70+AkCLgNsjsOlKaF4JsQWoW2QeiogNnvFPJqq/UhvQDg0n4MohcA+pqdRrqZ0DejMQ9BSyUtlPFh3wB6Cx3INdpkB4jcEcYHovhJYhoyvBrcPFQApF+Hu3zGt1lpn9c8CAW+cJcv90Cz/49o08c99LTO3ecOpZBRSbUE1Fsx9CqXilFiJXsJgZzTGU3I0T6CYQqiZW3Up7tkTLfAN/IIpp+SEYwKqPoIVFpU3O+WIWDZfPZhnuP8bOk5/nuJljqqsEXS40GIjhixHFGkiZiK0D4DwMFHAlSFcD2QlyI8guVNJlgAoXowMvoYRsDaozl6xDRV/TKLZp9hksoYR0XwGegv6bof8OYAEENHCiKJuBjwOfLL/O+UCiGo09AXyAs8uq1qEsLL99zqO8YTJWCBFG9ZD5uJQydVqjKimlEOK8Vm0p5dcoM1ptcVMu7vIRDFZRX9NBIVKFkTCQwgHHJRSKMTE6gWZECcabaV9yGfEly/mjP/s7duzq4+b3/T5/+6eXYJlnZyZzNvy0TyWMly2B9WV7h7oq6BmCog1L2irPtx3I5QXYceLtPqzAqyW3tl1kaOgoJ1Nx5i9ZS2DRUmzgHcDeb8PkQ35Kj9Yrg25g9OhBtnz9CN+4WzA2WkLRL/2oBl5fgBtM5bLroijqtle95CkYQMoGS6iBei6YqI67P/PAOgP2JOx8bhh/TGfJ+hp2vZDnO/f9EOOSNj75D+v51I9R46N9BbRqsOe7wEHAIY8aTsNMEiOEc0F2Iz2zkdYnUFPbE8D/Bl4AjvPaZuoplAfKcyhLby9zk0VNCn3l15lrxPWfAfNQSdMo8DbUfjSCKgUPoOzMj6GyVyEUUTvO6dmsOczhDcOoBbkXinuAVWAXGXl4K8H+GC3vvpqPB+C7HfDSAPTthcFhyM2AzweW5TJ5ZASe+AmEwmhdHYQuW0F1LMTE3hfp+94LiO4nsYtd3H7Th6izbY499h02d/93LpElOoAGgqxzrqNd+3VMOUmn3EYPXznVgNJzQZNULO+99NdHbr6ZD370o/zh575I2A/f+6ND6DuPE+h5hSqgjz7m00SCJoI0YHAIlx1UoXKAs1NbJZnnhfHvsP1vHmLjZe/luit/ldq6BI2lZk58cwsTzz1C/+67+fTN/4ttr3yXXQMvswhV4jNHyHqQMD2j/CsuEMSoZrW8mifSeRJOlJVVkIirCsGDQFsT3Hl9A8mvf4/LL4EHvn+cx5+a5lO/N4bYvRu37xWcyaOgJTE3fhZ7zzeQE5sx9vi59i/+gEt//1ZamwxCPnjx5Rl6Du5iz7NPcvLwAa655Vr8ErZtO8r9P93JYw/t4GiPTVfzeiK1dVB+D8tRc7lERRPVQFedwYJOa5YuYgzD5yfeEmZoYoTciwegkIKqCF/87v18+mPXMpWvZud2WHcpfOTd7WRlKxkJY0XYfmSQvu40SxoNrr96LRdH4QN/8yzHcxpX3HEtw3s1CmHYfnQ3+x7awvwrllMc8KsdZTsqDPl54At9oJ+Aah2u8sGP/ho+/T3YvLvynAvBS/YkHHz7I/yycouJO/+MTR/6EHc11dHWdTMzU/thPKlC0k8J2ClV0DBNRTw4juJ5FqDqFmejvwRdYaXmOKpKRXfu+SFdS+Ks3nQr4+PjrFu3jv37979pn/HCgQN8EkKfANkBWU+kEYRThjszvL7h2xx+ftBQEUMcNbt6hpXe2uQRIDaObSM0DYTAsW1sdErFEnaphDAqG2ZdCCxdp2RDOBrG57fQDQN/3I/PCGKYvrLC0UYP+RBlwarhtyk4RQzHRkdTdKkBUjpI2yWfz5PP59F1C7tUIptLMzY1RCmbgVIJnCLSmUTtCYtUCNcys4erDjjXMfENIQQ06KrfQXMHRJtRi+5sN4tzidYMYBGEC9AuYW0BnhuA3SVFr6VQucTBCViehKayCFsTEAopEUPNVtAnQCxCtQBqBuRO6NuLPPmXFPbr/NvJv2Ky8wbCK5dx9dsUbXg2cdwMFZdgm7KlrQQ9Dd/7Pux8aoKpniRKyrMT797xJF551F4zIiE8AvpoEkEKDQjqA9S1RXBrq3DsUdKvZBkYGqWmvp2ahiaaWhshF4fgz8F+xQdmyCEczoPI43Ac106D62BWwTWbkjS2LSDe0EVVfCUh6hksxjgwXMdjW1phnwk7amE4AU4C7GA5Z2Ergk43ocqAsKZyMRkJg9Xg/jvwGHCuNlWHUTvuu4ArIPchVMRWjbp4C8rPOd+GXptRd0w9sAG1uz8T4XM8rvCGyFghhIkiYu+RUnoN5EY8+wEhRCOVDkQnUfyDh5byY+eELgRV0TBWKIQe1ojWGEQiUYThR2p+rGgttS0+Eo3NJBoa8Yfi3PG7v83WrduZms7ywHd6OfJSHE0TBKpX0rziA3z+40vRNMEk0J2XPLq5xEc2mcxvEniWrwJoSIDjKpsJveyVqmsQCIDV6sP0a+wbdnli9xRPfeNfoLAHZB7X0cilwuS7/gchfyv+MR33edj+EqT6oTQqyi7HDwAv8fyRZzk58TR9Y5C1oZJhdYFGOBqGI6DdAH9jwkr/WU/VqTklqL9azXvW5/4cbY30CCxYW4VmCkyfYN4SixWLWinIagpDwJ3APcCoDvlOWPFlOPBOcFKEULd5gAgmggwuR1BOIDOv8ZpvLfyowdWCmubeATyM6lH7WnBQhOs+Ksb/nsFEltPNJubw/yvuuusu9PvvJ/OjH+FD5fA11JAsou6oUZQWI4MiaefC+zn87PBBOgX5IASXwvKb4NhXkdl5ZOrXceggPLQGtg/AwYOS/oMOqUyJsOaDgIb0a8SbE6TWrMGdSeOmxsk98DVGzRLF6V04qROQ87GQfvq2f4ajcpphTtAqs8RR9/U0GXo4RLPbjZ8oMdq5kfWk2cF+ShxDKQVnb6E8FPJ5Hn/wQfq6jzOYhNG+FExnacpl+K808QjDCJKsRqeGdmwayZDHROdXaeYLdJ+2bXGxKZSSvLLvUVLTA7z/ijsZe2E/Jw4/Qr5vG7fKDg5s/xbtHWtpbbqE1XueIZc/zJPIuXaKHpyTvJFOsG8O1rCw/XL++mNV/P6t1/FKNsHe3bB4CeQtVQyW0mAqqPGBywMsroKX3RJGLkttQwx9aiE1VS3YE+McO36Y7P4HkG4LGBFk0mHyeB/feraf9Rvn8Y53r+Y9qww++NVn6Dl6iOaEjz/8yG0E/D7Gp20INvKu37yDn37lb3n00iakVcM1SzS6UboKh0rTZhsIxgXVjbPvdok9M0pq/2N8/pt3s2vrXrq7exlOp+lcdhE1wRCFPBQysHU3NC3S6PRrLAFirqTzmgQ/eCLFc69k6IiA06nx0XctxzQEVa0GBxJQKEHBbkQOXMRPn+ymozPKDbe/E98Nl/G1O/7h7KfYq3P0uI4kr503LkkoOTDqwDMuzN8HN10F8+bD/73P+6hvPSS4+V9OlVn0/Rv48MZVvKe9lYjPx2/81ed4+Jt/Su+eZ9W1GZCKADBQ+8wCKqAwUEFFALgS2AOhQRWH75HgDuUrTSRceGHPBD3jP+Cx5we5++67iV0WwZ/1ke/55ezkHkaJ4np/pv8uQv77KLuxVai9gEDF72OoUX7hJKn+c0C5aiq6KUplkpptVJlGShe7oOMgkRLstE95xkqQeghwynazOrbfj99vgSxgFx2kruNIH8WCi2AGgcBnGNjYmLrAZ2iYmsA0NXRNQxea2skXwRUCR7oU7QLZbAbblZSKDsVcAc2W6EIgTA3NMkBGKeQlOD7UJDtNxQ/Xs7ILqs9EjrfW4+XCRS2wJgo3NMKGVRBqVkLJU+Up5bkNJZJW8DpsJlGFKjtgYgd0vwQvjsBTNnSjkvslVI6rBKRtWJpRApuqKgiFwdRAFqk0s0yjMsPShXwRkS5iDUDt7n9l7ws/ZP+9Uf69VhBCIrgWEVqP0baW9jUQbAI3AnkT9BJoY9B/CI7tKcLAcfp67yc5uh8yx1Dv8HSSPoXaUxrlL11StuRQC7DhShYNZaibKRKbzhGy4+jRBkLZEMVcGOnUqXN2XvXy54CAcCLMoovnc+PUO2kZ38fu8b3sGt1H+kV4Zc8Q/ro0ZuNhrI4ArYsKROoXYiXaWHl9H6klBiOxdnI72uFAF6SEskFyhoA+cJKQaobCxRBeBYskVM+DE/8FJhcCn0EthmcmMmT5aiaBbVQ0xYnyl2dLeb5wUHfMJ1EK3Pm8upH7a5Nxr3vahZLA3gUclFJ+Ydaffgj8OvC35e8PzXr894QQ96I6VSVfyy8WQApBIBLFH48SrA4Rqg9j6CYzRclUoUgpW6Br4XxE5zymfBa7fvJTHn/8R6TTKqPbe3SI3nL1lz/RQ3t/iM/83hL8piArYDBf5KUn9nKxOU1PWJTNPvzKKEQ3wHVw0ylqahOsXtZCbXUYTROYEZ2ihMPdR3nwvqfY8vCDUNgHsoBa5u+AZAf4I+o6vgxsp9K6NG5C+hYwmxiWdQwPh6H0CCuX1DAxlWdweAZTGBSlCSManFAE680haBAVqfzZYP4cWZsz5fGSV2dthABhQVVjmSUWEK/RWXVRK7likLQP3v4ueOIByI2gZpXqTShT481I+lVTM3xkKDCJwxBqKFy4y4yGqmWIo1oL+6kEAK8Hz9x5Dv9Zkc/nKThKFb6s/JiBmranUHdSbtaXRI2FuRB/DucPDYgqjxxfDVgJcEuQ3A56iFzRpfuAy48sQc9xwXCfJDnhULBtTE1guAa6ZhCN+WF+G9ljhyke78XueQybECoBNQE04TKBO9yLWzbfj1DxrRrH5QRD9LOLetoI4aOdThZwiBlSZHEYQXEFHlnlxcsAA319DPT1nfHJdCaoJQjkyJOiyBJqSDLAVNnsphXJaiIcJkvmtNI+l4npExTzabZHuygMTmKPv0Rsph+/1oo+MYJVP0PAl8AfbeJd160g4Ti8dKKXHXvPlV3/z4QLKXEoCEZ0upb7mL+olYEXS/QPzrC3mOeitdVEEaSK0F+AREiJQEPVEernSZassljWXE+dY+Ck2ug+Fuc7d32axMp3YQU78RV9LJvnZ9e2aV7cNkJ9wzgbb6olOTXBgnktXLd+CRcv62LfYIl4NMaVq8I0tc3jwb86zvZn99FZV8O7lnQSQc3tWVS04CnCS2JWTwM9AW4GTWj4LZOmeJxk1zxKmDAwQo0UpEYK/4+9N4+Tqy7z/d/fs9SpvaqX6jWdpJukswcSSCABBQQUQRAURryOqKgzo17HmdFZdO7oXMerv6vDzO/qjPty1RERQWSXAGEJhDVkXzpbJ53el+ral1NnuX9866Q6IQkhoCQxz+tVr3R3qk6d5bs8z+f5PJ+HXK5AbqRIQG2l6AhCCFoEZBVBWQ2Qd6NYbplGQ/YEOH9OIzFDBmSBCDzwTB99fSnGM4IDfTnq2lwqLXEi84M03HgRk/e9gFM6gvflPe5o9SJK1Qs6Vp+7CjBgwRObYcViiBkwvxO29548w+cUMyMUYs7KlTS860qWdM9lejDAkANzVl7Ikw+0yIZdYVsWYV2MdFPrkMt0Aelg+JBOx0JgCNxB+Ti6gKG8RR7kAO2E4VGT4a172Ns3zh133EEqmZLamaeoeSqvJ2z2buTgDyK5bEkk6uLd4DOMxT+cec1w4FAik41cfIT8u2NCReAiJAwF4EwAACAASURBVAte6LiePyBUUAJgmeC6OCjYwsGxTcySghDVBk1qEMeRWq/CFRj+EBXbxPAJLL+KX1XB50P4dFBVECqKK3BV2ZTFdV00VcOyTVzXQSgQiUawyiquXcF1K7iujm1JANd1FVy7TI3d6yC9KU8TM0utta/KK0e2l/L74xuPfqBBh+lRaE2AiFGTaTGQt8akxoKpqlngIG9vAZiA3CAc6IMNZdnbY5gaSayA3MfRobEOEs0QS0AoImEkRZegp5sEslB2IFeScgZ2BUrjMNi7nd6J7WzKw4g3VskigoNoHXvp2AfBVlDC4OgCXwWUCRjucenfWoHRXiQRbA9yHXqleS3fjmVGwaJSsbBtBbUxj2VlwC2iYqEqHJtF/BrN59dpaKvn/HMvoX2ykxnJmUwbbWbn9gMMjPUyPjZGITMGIzA5Bo0NNoHIOI5Px0mrML4fsu1Q2AmlAjgp5PrbD6TAbAVrVGpE5OrADiPnh9fG7FjmUhMB1JDofTvy3p5o1XIZqeB6N1Kmculr+vTxYOAXAh8ENgshNlT/9gUkCHuHEOKjyKKnP6n+34PIgvvdyHH8kVf7AldVMVrbCNU3EaiLEawPM57JsjM5wZaBFGPEuHrWDAJmnr09PXzp/e/naB5eKbmFkfX/Sqb0d+gqOCrkCwU23vcr/uLOJyWq6ItBohFi7bKDSbmI2NfD2cvP5WtfuI63nj+bYFDSifMu7N/2JOvv+HsoZQFDtpMTZwH/C3aoMCBkRBoH2qg12rSQi0JsKbhLIX892v4uPvy+xTzzYj93P7CbkBKgYqdxcyW5AuyD6YukiPOxwFiQslwur86QPea9d+XLtuS+UrRsLMcl6pdD4xWatIf9vvSCDnBlt+CzBSyPQP8Y0ofZKpBKFLdQ4DZ2Y1NGZZwyBzCZ5NgF/2+OOVRVeZErubey342kr4+9ead2xk4p+9SnPgXIwOfvkXM1hxxdA9TmtoZc/ovI0XfyzYkzdvKbCiTAr0O4RTYieekeIAV1BgU9zK6NFXb06KjCRZgOPttBsVxK5TyK48PwBQkHHAINYZJ7s6QyO1D0TZQrC5GjMwWk2I3c4BNI2Y0hZLhgAyUc6phgLU8xny5m04GfBpppYjoWZfKYwCgOOeR8UDl2GDGOzT8xzL8DkzgM4dJGA5vJM0KONCZhJvgAXXyHQfZQfIV3kC2luG3tN9kGXIlkUb7k7Oad4YvYve1xxgyN9vmXceP3f8h7yha3/eY2/vuX/oZsLg/uqcmoe2PMQ3dOhnuwjYzVxaa8TbiocM70EoUNY9x7xygrlzUQR+q77UxK/yndBu6Cs5jXABddDJ+L+hEWVCyFQrqD2386QudFZ1PfuZKgrfCxj85iQ2+Kdevz/OhHu/jcVY20TG/jA1ddyEevvxTTcbl9XYFrzp7Jkmk6mWwZRYuwZfVqFiQUzBs6adFgo5BruB+ZcKgAqRIUvMbBRieYfQTjIbovuJ5Hfr2WYDxIsCKosw0K2zezlUWUSlmyk0MsmtdMSFVJCPC58AAudz1rU6o0sXQ2vONc9WAMVUSG7QngxYde4Okd44wpBoYvyGA+yfjoOP4GOOsXn2X9jFtwhg4DY8vUmJUNyM2rhKQHvZq0gQs8uRk2b4G50+HdF0PfCBSKUuP0jB2fGT58uk77WbP4yNf/lcj0ecTDOttdmLShrIPjhiAYghkZ+LUKZwnocCHhQtKptgNHLq5+JJa4AQo+2GTCLQo84cjQHoHsPfI0MAjpdJqbbrrpzbr6N8y81kgAOgIX9wQS3f1IntHfICXK+jhUyuyM/WFMIANrj9LoUmtVZCIHelUQ1rWQ3rUOSpCDWIGiIPwCN2/J9ch0sQoFco7XssmqHj8ijyV8oBmUYhWE4+DYAsdVsYWOXXawAwKfT0VVVbSq/IErXHSh4o/F0IsFKhUT160QihmUMxnMQoFKuUSlUsI2bCxHxbY1rGIBSfzRqYHORSSEMomsoStWr9GLUT1Qr8CrZ8tOT7ORxRlW1YF0DRAeEOtSY7l4289UxEtD3vKQ7COVMyVoNcihdzIAzFDg3ChcuRT8C6ugr4F8VAUgCW4anDHI7IPdo5ArQ7ECoxn4HVJUQBJovZN5ArfwBJUe2Ntz+JUJjoZxvR4bAwIViJWkL6G6JkFDEAlpGD4VUQKC7qHAz4niSyqoIY3Fy1eymJW8zX0HycpeHtn7Gx7Y+FM29Y2zf9DCGXIY64OR7H7c3P5aL7vRMBS8ioSj4C7OJsg9Di8tQzoraThYn3S898+qfu61ShMczf4FCQZ3U2vZ9uo38VXBWNd1nz7GkS47wvtd4FOv+s1TrGHGbC75px/zyNrH+cf//F9suevlg8LxnsbTfd/64ZTTOPZNFkDYkjTtBmAODpRTQI9E0ctC7rH93rtdXGDD6vt51xM/5H3vvZFf/ORWCEBcwGf+7ONc+44r6e46G/gsNF8JjUsgr0qszpvs3k5fpJa4CyMHVxn8lQBXnXMTN3zwPCbtR7jrgZ1M2hlgG4zNh90zJG1+ASjH0W2rYEPJgYbjJWsewUwHUmlY9yjMXwCrHu1hcHiSv//nC/G/huOqQrarUi9DjsNeZIQeU6GwDKWyDz9rAI0DKAzzxrDh33g7gGyq9lZgAxI2KyA75g1wcgSlZ+xUMgu5NUx14VNIl68RqVTTgMypraMWQJyxM3b8JpAjyoF8EsxBZBC5BPQ6bDdL7sBu0BrRfBqa5kNXDLTSJIXJMZw0WGMKqZ6dBBpizJvWyJUfuIVp6Yv55q8+Qb50KMu/B+mLXg58F+n+hJBylEHAoZcyB0jTzJV8lG7m4yNEJxluJMIGNvIcDtuR26Una36s7P5uZM7bZIQv82OuZR5BVPaQ5lkKtDHODExyyLzmkWwDskx3bvXfoeTTVDCIXnYV7ff+GFQFFY33feYjrPhv17Jo6TWYo5txrT++QEeaF6ieDFZhaN8E93x/K7f+1UK0pjDp8QprY2XiyDW2Mw7L4hIyebJf8h5amuHyqHS1v/E43HtfH/t+fBd22Wbdf3weMe086i56D0V3Fv/85Yt4abPLju2CIQS3fe8LRAWkyvBIH4RnxNgdgWf3lvnuD0cpT18JfatZv72O//nYh/jaOyTuVeWpE0YqidWFoLmuehkFqRw7o2Mef/2pv+JXP/k+fX0pSk4ZS7i012nMmraSxmmziEbO4do26fcKpH5cuAj+kefYs3cUKxPhSa7gEmoqgy3Vr/mLv3gPiwdhwxh0z4G2ZuhJj/Di6G6ef+Z+MKszbSrO4ZmDnOSCKe2Zj9OSLmwchMmH4Jufg6//DHbsew0H+CO0qaS4z3+Sj191PX+1ZCVdqnpQ2mVvBh7YArPiYLuXwFgSUg+gf345VmsMlxwoA5DolR+YWuKWRi7Ws4DvgtUNziASubeA/6KGBZ2G2eCb4wkOVMqsyp9IwF1Gco8uRN6gP0Yd3TfTPFZsgFq7+ioxigA14MqjN3giMSrYHuVHgK3ipr2J4QW3BeTi5knxBDlEWs5xqGRTNLS1oukCVXUIh2KEQ41ouo5AYNkWVrXOR1PB51MRQsPvD8gmXrhglbBDDugGolSmODGKaoTA1RG2ju0Y+DUdBxUUFUVRKObGwM5Ur9lrB+ntxypywlrIiCGNBDT+uPyUVqBJB19IPkG/DcJCOpEu8lF6+D3IIGzqMKkAYQg3w7QOmNYndd9L1AgCy4E/XQBXLQNxBTLTGac2VDYjE5UqiKIslNaLVQynGvS9dt7y78fnagHa/NDWaDBr/mxmLe5kesd0mhOtxONhyNvgqrLZkMYb1m8IwKCOVv1cPjhnCRe3LWNH4RF2lp9mH5vZOA69B2BkOxQeQCoI2B5d41jWR22z2wwH663fzG6hAP8TCcE/ypHVgV9pJwUediBf5qaP/nf6173I4FA/tv3KYevaxz84C/kyn/3Ej/j8V6+n46wE3S1R7ln7D/z5jasYHvA62h888pQfXWx7mIcfvY3Lr97Ef/3kdzS0qmiGQkdbC2vXrmLNaBv3761jzTYNnqJWxjU1gvQavoFcCEaB0gRldxNPZB/iL294ij2jU52C7cA6WkIG1589/6AEwath6X4VfK9TrkBXoD4CK94mScLvvnEmZmUaxpRJaJYhn4Z44ghM2eqJCiRwHp8JI6NQMoEdoiqR+i5MBCOsoUwWu7p1RTgZeaZ5agIwSeSk7kOG9ycGxLae9xHq59zM1nt38varZrBzw7fZ13PvG3K2xzaVWqbV412eHhZAgj8mNcn7k9HakfGPSS2n7cW+AeQmHUMuxHs5SRbkM3YKmgIEwXah3AvF7YALXW8BrRG3lMNKDoGdxzIEQtNQFB+U8lhGCXtwM5W9T0BxE6X9y9m1Ncmg1o9qFymWs4d8k4ZcFT01szhyi/Oqviw8ZT0LHwUKDNDCh4izmTFeYB1r8RHh7cTposLtDNLHqzNk7wT+jDoWo3M3o9zNXgwsKtiEgSw5LiZKCIt7yR71OE8h14y/RQrhv+1Dn2Hm9TcgVBVKMHL/GiZf6mFiSy+35kNY6my2usM8a4+w5bU/mFPcVN5Q4fnXYYsufB/LLrmWlZd08pU715Md28VkIUAw0s08pJDGlhHoHYFoAirVxqyuAj/bBO9dAO9fDvPUFr4wcD3j9/wGnB7ckWfIrxnga7e/i/deWccFs3VWNMNPd8PHZyo4OvRlKzy0OkXBaeCJ7DgTyQmy/UmMtnbM0RJ92zdw13/+indecSNdqkIEGasJZC/WfBDqYlOvRiAQaAL69u5g6QVnE2uJk3OKnHPW2bS0higIwUhK8GwIOiJQr4LmQosF7YEA5ZZGoq1hJpDwUG8SChWI+mFhFCJNCovjEEgW+ekPHuS9V1/BxNAYQz1bwe2BhFVjwR7NBpA4QOgY7zmSFS3Yn4IfPiSjXM2ALa+g/5zc1k6tOfPrMR2Y1Q03fw4umi+bUgDggNMPziiIeqJqF18ElnS00llXT5OmkUKup9uSsDsPMzthfw/MveYqgnWCdXe+jPX0Fq55x/dJdS9kbW4c67efBW0blEs1l9Wrgo6Bez08+ChkpuI2LvDJm6FrGkxm4cUn4eGdkD49WKCzVp7HTMXG7e/lkQ07T+AILuA1pTM4LRHrk9o8oU9Pf0Oj5mmoSP/HU8z0Iwe+93+eAJiNfHZQ29O8ZllO9b1e6yQfCA2h+wg2xtCDBj5N4NMVonVRFEromoum6SiKhqr6cBwHV7iIauxvmzYIFaH6KBZcNDOI5ZRwHAfNCGJiIVwFRaig2aiagXAUHFf2scGIguuTzYsqQWSkUEZ6Wp4Iarl63t7PXlnqyRoRvTGmAIuAK9vgwk44vxuMbhCN1IpZvQplqA2BPLVbaAH7wdwJmUEYzUmI37tzKtCETOTOaAGljWo3TuTmrlSPWQR7P4xuh109ch9WKlI21nJkvstL0DYg0YQUh6JQdcgttoI8h98XpO4gQwTHcRHYBIMGkZifYNQHmgrlLKVMAdMsUbaLIFRUNYqrBHHVAIGAn4BPIIIgPDB6qlVJifZkDixQ/WH5PDQQipdUVmkNXUw80M4CZyl9PMHyxiGGOyc4sGycl68eYM1PwL4HSep7VdORrNj3IKOREtIj+hxvXnKijGwi9lbgH4BlyNTB0e2kiP0zE0meX/0Exf7+N+R4lYrJY0/dzU2Dl1DfliAc0HnrirP4+Mc+wiPP7GfjjkGK/auO9mkmksM882yWH/zoEd7zJyuYMTNGOGKwYsVyQpPgVNujr9lITbbGk1bz1nYvWWcin4uZx2WAZGWMZ9aPHWQDtaHRz3ZsIjT4VK5rmX9UPVjHli9VrzYaq75ejwmktlpdo/zdH3yl1oaigDaFJVspQ7kAofgrwdnrzod7Bax3kCxfC3DbsJlOEYGLg1VV8Tm+fMEf2g4Aq5BL4yZktqWHE1a2jS1lWveFLLjgAsw9deRS2ygXj+7dh2jERsPCxqKCjwABI4Dr2DiWhYqg4trYCBwENi4O49RSgdIEQTR86EKl4BY4edhNb5z9fgo53ljzCC8g3UBPukivvqqFVZjUVKHO2Bl77SZANaCYg8qA9A4BimMyS1Z2cEMNstuAKYMGBylkGa2L46uvw00nmNg1hstL5LJJCoweTOccviVVkPnonUhHM0etMnYMOdZ1ZM2Ji41BFJ06CkRwsclhUaaEhU0TEsz1ikuONgdGgJepIHCZBuyiyHwCtBPBxaCfIQJUiOFwFtUS3CPYOLK14v1IvCWUaCEQrMPesIcnnnyY4Wc2Yu08gNE3SlMpR8A20VwTDalCtKd6vkeHe08nMzlZAru8aaBoIc7uDFHORng+00S2qKJW4KlNNjO7VXyuYMIGnwnTwhANSzzp0V7onwOzY7BglkHnRa1M3JfAdXaCmaIyvp+161LMXxTF36lTl4CiLVOwigv7LRiYcDDLOdKZIoWiTcivE5y9gFzpbeQHRhjZ+gKZyo0kHQkA26oMDfzA4ABsHWyk/qpPMvnoz3HNCpOTJo8/8SLZZI6m1ul0nX0Wpl7Cn/MzLarg+iBdgZgGfgGjWRjLQbEEl89rJmNW0KJ+Wqg+pao3r4gqQ9YHMR80KAoH5iSYFtc4cMBCSZvUJYKkOoRsPjLG0Xu0hauv1+qsOa4EZMczcMPbob8PtvWcLEPp+KzM69uQPVaxIaA+DovOg6WLJYtCQUbr7iA4k7SIOOeoHVyArJQpIIN2x4WtBSnHm3bAKUKkCebGEnRFllFM3sz20W+TfL6PJv88rpm3jC1n38z+9bdjTuyC4oS8Bs8JUYDpMBZALtZTr2/vMIT80ByFd14OPUnYMwK5E9XQO3nMNnzE64LM1S22btjLCNYJPNoshzJtztgfxrx77gl9KtV/PSqGlzD0GK8eUH446WoqAOsJiApkwF6VJVAC8niqjqb7MYJBwpEgAb+OoasEfDqRgB9V2CiqiqoKVEWVXo4lvR0U2STcdgVCUVB1H7Zp4eg6iu1UGysJdEMD28axLQKGD83Rse1qozEhqDh+BCUc00+lqFKpyAZmrmvhUkER4LieTIMH9Xk/lzidu08IZJueGXXQ0QJ1bUBLVT4ggBwGUwMujyXrVS17rxHIDsHEBIwUJIHW41WHka37LpgFzfOQVectSOTUh6fLBVkY7YMd+2UDsE0luf9OlaHz6tamUSuAyFN7Qha15fho65KfIBoGilCxXZs8BeQ8OL5NVaueetTnwxcIADbFfJl0ahLhGgglS7mcIZdKUSjkKZSLlMsulhvEJoAjAuhGkFgkSCjuJ1TnJxYLEtBVHAGVikU2l6VSLGBnsvj1EInmLsLTo4iQUtXTlGunodZjqN2ECKCRQzNeIhIyiZDDavWRvNakNwvZZ4Adr3ZlJjIS6QQ6qn9rQ3aU34GkOb3qQd5gk5rAkuJ7e/X725D1W0e2kwKMNcfeWH6k41bYM/w71m3fRby5ibkz4sQN+PI//zNNd4+QvW0tu+57DrPseaAqiABGJIhlWjhWmVLZ4otfuY2WGbPxBWJ0+MDwweI6CASgIQjrVkNhI7UJPlVX3EvIHZwrniqkwRgmCi51msYlza2syu8nZ1q0+gO8PXp0iV3HBqssAVBFq24tU8BQ165pwCoKoByFyXq4Td2njmCaDuGYPL7jSunc9LhLIOhSKuURLqiKhq77+dTFkIkIdpmQe6h6XNsA149dZYOUkAvPyQmk7Ua6wX1Il/gAr4vy3ngJjU3Tmds8SXJ+idV3fIdC/shlTgKFCK2gRSm6Jlk7TVhpoiHYgF0xMe08PlSKroklVCpCoeg4lMlT0xECBR2NOEFhEBAWRXeyKsRx+pjHyitzcsd3ZeR5ashkqiczBDV2bBEJbI1yOrtPZ+z3bpoGhTSyVKfK7h96DpgG4VkQbwWjJEsdKqbcTEIR6pQIddNmodZFmNj1KLAHt1rq4TmVGjW/1ts1y8iVcVn1fcNIIt1+pDMbR45x2QJlHBcTFR91RNnNOAdIM4lNPdLxnTqXj5ZoWUWOfcBnkSmyGYRYSCM6Cb7LMOPk8CG4EJU+7CNKHtjIgr7vITuThrM5Krv2MfnUXm772mfI2xaNSEa7D5nPnoF082wkiLuhep1lXr2Q6tS2PCdLimhv7z5m7dtLS0jh5ku6ycVmUdqWZHTXED94osCXEyGiQEB38bsa08MQ8AE5UFOQtGDUgYoh6D5fZZ0vjmsb4Co4tk3v5j08vyFE0vTT1OrSnGhkQIGCBfstgW0YFDMZAkEIx8LoeoSWtnqSTU30b3iOoZdX46/ApANlDcpVMNYGNmwt89iGOlo/9i38e19mcnCSoQmVn9++inrLIJLopH32OWhRmy2rthDSoTEGjuvimA5OxmXniGDruCDkV7h52TSCelWPFlnD0xUF4UDQgmZqLt1ZQYM5f/pWBoE9+xz8CLSGRjItCrYXu+8+yk1vRU7uE+lFKgQYOiy/FOLbQPv5ydyttWaagHoDxkq1RehEMr8CucH7FbnxO2VIp2X9qk/I4LRKMWrH4C3IcE0g19VdyAB+TVrqIpZtGBmGK1fCMg1KrfMQwS/Q99XVvPDLe7kibXNz+6d44q1/yUPJPMPWw5Qq68A8LPnv6cmYHPpcb18F61vhnUvhkx+H5zbJYGL3OBRObSbowPg4Rt002tpb6MJHEluWj79mczi5Pc7T0aaCsZ6H7MkSTNXi8HRkPaBVoZaJMJALmcee8iAyqSurKCGEGgQ9BLgoRpBgIEwkHCEU9WMYPgxdJ+DzEdF1/IEgDg4uLioqpu2gCHBdueoGdFV+s+pD1X04fgs/FhWfQtk0yPliaFoIx7Rx7AqumqeUA8uywAVVU7EtG4UCZskgJ1yyuQK4PhzXxnEqqAq4to5LkVob1KnzdGqTuak6KKcCjeXo5pFZYj5oaoRoC4hWpHyAV5LiNS/0CkO9Hj4eWc5za3KQGofhJAyValBZBJgu4IognHceRJYhmyC2I51VBekIV1k0Bw7ApiF4tiThN++u+5CVMc3IZdcj7laQ8Z4XuZeqP0+Vtz3cokodEV8Dhhak4piMinFMK4NlFajYx95YvXvWDDQEA4RiEVynwthQkkpxL/7AMOAwMTFKcnyCTK5ApmiSSZfJmuDYGjh+UIPE65porK+jqSFGR1sdjcEAtiLIF4oMDPZTyI/iOEUSDe0snO/SFZmNbhgoqo+DtHEA4igohJiJzUtAhQAWsxQD59IKZsWlNwjlIV5FzrUAPI6MopuRpTyzgFuRxLoHqTXrejULUKOf2Lx+yoUL/BJ4CAmFjxz1nScFGPv7sr/983dx5Q1/zZ/9zb9x3QXSN/zUdU28fdEKPjzxOV58+j6sigtiGiJ4NW/52w+xd10vo1ufJLfrV8A01uz3kV8P84fgiovkcWcZ4O+C9/wL3LkSSqPIWddMrWLCs4OSa13IQXIb8AKNFFgxu42fbP4ev/nu99jwXIBgbPYxr0fVZUfe4Z3Q1Am6/9D/r0xCOQ2ZcrWzYJRaVcax7DgB29wwFCYBEwKuy/iLKR68/ycYpkJX0xy6F19B/SUa158rb8GtX0TOiVEg4+LikCZ7sOnLyVH8eCQzkZP79Zu/vJVnf93HCz/NMDH5DHLhOPJy6+IwTB8XnHUxZqnErgNDzGj2Y5UzFK0CjlMgRYmwEqYhEkXVNIYmkozhq27IAII47QR1DRUL1y4TQKNI5bQCZI+nc+TJYE3IfF0ImbcOUnMr49RcwhCy9+KZ9hBn7MRM6pIdzpCXWeG9UOiFnjh0dkKpBNkUTA6DnWX/yw8T6upk4VktrGMXUGNug2Rse4kEz2HwZPWV6jdcQq3V00j1vXGgnzy/5kluZgVB4iSYy8VkWIBGlhzP0M+/sYkcteI6pXp8r/fCVKsgiXxPA+cDkGISnW5amVH9fBMhmqhnC31s48jzyWt7cR8wc2+STP9qfvjA19CQhUVtSIe8hGQzRKhtpYuRLlo/0tX7Pqdz0erRKJNvgo0/zo4dIb649tP82yUwnk6TKg6Dbx+lnMU318+lki5QGkvjX9zFqnFong5zm+DRD0lZzK+vgrERmNupILqvgF1jsktrZRD3kau4Z9vNUCxSF8zzmYfv5wOzBE+NwoFhlZXnx9jyop9gRKOxXaVrMfxJGxTFfB5bN5Mf3PV2WkKCDlHrhw1yPowNPkt6215ov4WHX17Lv9y6njvu3cZkcR+R+Z3sL9TjboOKUGhsX8z3t0HKhkLZYeS5CdL5HB0JPwtmh1h2VYxqvxg0ZIDX6N2jatQ1NQnvcaYagPsHdtO/9mFyz/fCvjKchwTmjgbGjiFjkuOJYw43x4FtW2DVEzAxemoAsQCzoohfvg330gcgZcqbHOa1A9IOMroP2zDUAw/8HbAEFgagKQyhRmARlAQblRZSRhefQ667c5DPay1yDXppo2wofeUVcIUqn3eoBc5/l58Dq7/DY7+9hQf+49e89Kyg58G/57LrPs9/bVzJb5/5NTz97RoK4MUM70bGiIdfU88QDD0K8xX46hfg5W1w22/gJ6tf+308iWzVmqc5r9jN/GXdpCnhnEa+8OlvXk25SW0yhqilekHOGo/u7e3UHh1yamMsdcoxgqCG0BMt1Mcb8Qf8VVzXIhoM4jcMfD4do9rMWsVBrY4bVTVQXBfHkWBwLBRA1VSEACFs/H4NNI2K61J2HOrb6rAsm3KxRDFXJp22AA27ILBLDjYZSppFsVDEcR18Ph+apmObZfKqTtEqgxWvlg6VcYVL5RDqhscEg4PNy/BzZHrHqRA5Hd1CwAwVrl8CKxdBo8dabUA+Vg+I9ZoXekGWVf3ZGx4j8vdcBsZzMgHm9fJYALwtBp++EbTLkPBNE9LJ9cxDUXNgFsG05J31qsS81IAHw3hs25bqyyPqTCJ9yWEk5ni0utm6xgRzuucxo6ODqKGBHmf33l56ereyYe9Tx7xnbvVUe6IqrwAAIABJREFUk0CDoqK7UBofZ99wirLl4LgVFLfMjp276B3JMlCyDqGgJdQwM4xGmlvaGe8f5uVUjslUkjFziDiNGIqCImxsTPwaBIM+Es0z2LSoxJUCFl80i0ij7xWIYxmTHnaziqeZYBiXMnXATHy84wqbTV0Oj3e4stL/VXNg70Fqe98sf1UB5wpwlyLb9l7Dq9OdrgaWIDfMXuDfeWO8e0/v6OgXcVqDsQBrHv6/bH7hST4fuJ7v/+KTzGyrRzGj/MWVV/PhK5bRvbSVlhkNoIQJ1WtsnpzJ+i31PPPwRQwndcrxBNtTcGDSYee+Ile/JUBzk0JLAP73NCg8Dc99EQbvQs5mbyHQkIPBQE7inICMH/mwtzFBgfVDSb73yf/gWw+t5ZN/9T+46QMfPuTcvd6OnvaYEDKp3nSWZKtaeciOFHn5hS3YWRsqCvFYhCVvmYeIc1zVNJ7T7rpgZmSlq+Y/0hshFILbv/EdRnr3M629jqsuv4BzO1rZu6WHTU8/wPQ5c4i60zlX6FTq4db3I8fzFGZ2klqu8uTg2/x+LWGmKZaHSWVlj8ZGJYqhqFjCZqRypHRPlnxmnK72TlaccwOT45NkMwUm83lSeYN8NkPY8KM6RexSGq3KtvYE7lXRzKz2ZjK5MUrFPJVK8bQDYk8la0eCN/OQ8zlATWooQy3v5kMqkp0BYs/YiZkN9iA1JeKp1gH6HKiPglOAid2Q3wn2dqCJsyOLKE+s46HhTYD0ax2kUzlGjcHtKbF52lZe43VPmqAVeB+yKKeAdDANKoTo525uZRYJptNMC7NpRWMfT7OTEfYh54PHcfH86KPxNyaAu4Hvo9OHzcuM0kea83AZA4YpsIsSNwD/h6PPKRcJxjY+8wvahKCXmrvmOaKLqJEhvO10GOlMdwDnVF8PI5vvHU0a4Yy9ERZkcNcEd/x/P2P5OR9g+blR2uM5nlujs+bxl2gw2lk0r47OxRFGiuAmoCUIbVVN+3cDiYtgcxJ271N57z9cw9D2hfQ/eye9q74iv2Lkt+C4pDMO33rXPH6hd1OILcQ/fSnXXPtOzl7gxzEU/PWCWDM0CNgu4EDvTnb/6l6e/8d/oiUoaFBkECaAPUPgRhrpXGwT64JmVXDO1fPpUUy2fPVO/vzW79J6VgP1MQirLj+6a5I5C2Pkh/vY+9w6BtdvYt7Z5zPZP8ljPRPs7JnNnmsupzlhkEzl+M2D+/jFX85j1CfBgOmH3TUPlx0ExkaHKO/ppXnFOYy93IszoENE5aj87jpqyPKJgKk2kNtVZewjndkjZVlOJtubxb3+EchUQYswkhW1lhMjRbYBS1R4RxTm21CfA9Iw2QfWKLgxrGIDfaU+FnVfzENCMBMZNpwP9DdBx1sh6sKioPT2fMgeK7au0HntXIynLoSepxh/9jssu97lr7/5MT46dzlXJzr4eEM3PP4lEOnaQlYGrkIC8Q8edr45E/5pNdy7AcZMGMrCjcDkDNiRgv43quv0H876gNEtvTy2e4AszmsaygoaCbpIMk7loOjkGfvDmldm6mmjKtSad3mIm1X92aDGhI2CkuAgi9YREA4RiEQJR2PUJZqIBuvRVInYOQ6oVFA0F10BXRHoVTBWUxUMXSViGCiKBraDIgT+QBBd13AcgSIUdJ+OroEpHAwhCCoKjiMwXBWfT8Ef8BFt0CkUDEo5h0rRBlMHNY8eMBBCoKo+TLOM4wiEHkAzQmjFLKBScQU4lrxeBdlwyfVKcW1qwLUnhugB0B7c89rK208m04HOMLy3A665SDJWxQzkYhnkoD7pQQdSOezDnoPpObTjMG0XjExCYlL+SUU2uTorAVo3co1sQWL6UxlkavX72qB1JkzPQmuffJtJ7SnsRUJxBjBLg/PrYdn5oM4ENwK2DZYFVgrSQ9C3F+7cAY8hfV3Pm09NZBndP4nfikBbGF99kGkd5xCPTaetsYWxPdvoSfeSsY4M57rAemDLWAp9Moe2vQ/HFbIw2nVRcRGmScZ2XrHCJe082WKZ7QdGqCPItFgns2fMY0n95XR2L0SICmY5T3JygmI2g1UuI1zBcF+SjY89T2VihI7u6bR0dqBqFrY1ilsKks5U2Ly/xO1rUkzsM7EKoDXBuddYdCxoZk5cI/GuDOs2pul/GMrHTAqPAfdWB8B/qwJMAunEXAB8CVkLt+8YxygDzRBYAV3Xw+SHIfkolB5FNnF/PaZxLNTrtAdj89lJ8tk8oPKdbzVw0w0Xc+HybhZcPJPRgTa65sSYNjNwcM76oj5ag3XMjUfIFhwijT5UDVxbYLoaqaxAUSAah9YofGgWzPggPBeFZ39ObRZOTcJ5CMzBrpBLsNnLeH6CX63egFtaQH3dLBqa6w85d0/N5pC/CdCrmZ1iCcbGK2zfuou4EiESjBANhXCqMgniOJt72RXI9rsURiYI1AcJJIL4p2SAMmmL3j0FguUsjpmjUhph354eHsxsxc4VSA6MkEnmWfPAr3nXwk+wOxdj/Qg0/SmM/QDcPu9qBGFcmpDbwdDxnd4palIlJpsbwrQK2E4aA5dlC+agOTa5TJrQUBmCfsKxCIGAgd+ngqUwrbGNlqYEieZGNMfEr4Ouy+o5US6j6xpB3cCnRWls0hFjY0wU8yAcmsMJAqpD0S2Rd4tkKJ0BYt9Eq0fGYh5E5s1nFQnEpqjlb/o4dchDZ+xkMxsYBjEb3EYkuOJBim5Vn9CsNpvsrwK3ZSL4mKz0kLdHyVZGD6Z1vGJMGzk2PYkCr9wpRE3zuKn6mQgSuLwS6UR6xASdCin6GCCJQpIwPiI0YDGBSpZWDu2p4G2fxpS/HX6lKeB+bFaQoA6XbYwSBTQCNBMjTh06BziXAptxOHCUu5YBHi9M0EaN+WsDjc3tTF+whPZLlhPePIxv8xbEjg1Ahhg14DgOXFz9bCeyFef9nIphzrHME4yfsjr5QrLBSPYPuYv7CBoR2hsb+PUd22k2bLIDQ+zeuJN8WrB8Npw7V6W+TiE3DLPjEDTAcKXYUAxoDYGmwFxH8Fs7Sld4Fm56Pr2PzAJ3N1gZQJI6J3p7mCAJwT6CI5tZW3qR0PTzaVmwjGkLOmgpw4gG9z4+wuonNpMfeog7vxwk/ukP0jmthYALmgm3/fCXvDxSZExvILsnxa4VUZbO9FNc3MCOGWfxzJ3/gRFuwF/fjj8xk5d+u4ZLFr2fjhkhlNEEvWsHmJzYj2tXcGyLbA6GxyCdyVIwizTPrEcIQaR6l7xWBYPARAHSGVkpnyxZOKEmZs/rZngiT3zBFXReNhvdV+S5h7995FvuiTi/HjLV+g2yLL87IVtdj2dk12YTGSfV+WDcllTgk8DiDc1cccsnuGd1D+a2tZDtlforR3KjNA4lpR1uOrA4Cm/rgLPnQUIF1QS7AFYWsj3gRMBqoeI47Ext5V+N2VzrM1ipQZOAt1aJfH4kXyfIQblDRhXB3IV+2s6+jHRmgtzgnex67h6efvwi3nPRQi7tmMaXz7uCb6QPkB1/CLLb5KLlLdgzgJXAs1Ouz3FhJA8v5GtMsjxwfhdEJyAwCLtOhCr95lkFqJQqZEuvfSC7OBRIYR8ismug0Y6GjqBM8ZgB/hl7Y8xb2Tyqoyc34AkpeWJgIQ62+FWj4K+T2q0K6LoPXyxMOBokFA4RCgUJ+/womg8hVBRUFNVEVR18Chiqihbwg+Kgagq6phDQqt9puygIDJ+GpmnYFiiKgt+vommgIXAUcBUvEBc4toptKViOSsAfpuRzKWQrpCaKuJqCcFTpZykuqqbhKnlsp4hZyeHYBZyKhWOZ4FZQVOR5OAIcgXMQkJ0KvnoLlOfNec2/Tr2YsAlYHoYLEnB5B8QbQNRRa6bl4fDH6jmqUHNoVeACCMeh+2IQwzB7BJQx6FCgux5EPZJxG6HmBk09loFcm6MQDcp4L4T0f6E2YlNIH6QBWG5DIgH6IhAd1eNW2TmlJLQPg78PluchX4RKETIZSI9PkCq6JPcNsydpoAW3owodu2KSzY6QK01gOsde34pA0XLAOjTS9Hx7r5WdV6Hm+bE2LrZbgUoFhwqB/CjRQISOpm6md7YRb4wSiGjoARvTLGGXKlh5GyvrYogyTkklM1xCOJNkckl69z9LKaOSSjk8sONp+vcUKUy4uBV5P7emHEZa8vjiClbAxO3XJfX4mOPWQjbNCiBpFPOlPrumyj22cDUSdXoKjtqKd0TeJcWAQEK+fMBkFNIefeNEvXtvfh7ZTnsw9uCs1Pfz4H0vsmzpLK68ej7T4vWUHMkCLVcgm5fa9fU6JNpVlrTXaKUOUHYF+1yD4nY5QVQfRPxwjQ6t74RECwxugb6N4BapJfFiSDQmC5iubHfLuYBCoZLhid0DfOCyT9LW3PWKM/fw3KOZ5ULJcalg4o9pRIJBAqEQZQv0KvLzaoCs64BVsBnYnCHX30O4uYG6mS20LoyDDwp5h/GxCn37i4TTg+hKBaHm2Ne/nS3P7yVUsFBsF0U1yD5yHwuuuJLV++M8mFGIfXo6478B1yent4Jc0zzljNObBSjQiZIqjAJldEXQEWvg/HPm45YLTAwOEchmKYf8tLS10dBQRywaQJgq4Vg7gUgdesCPWRfC0MGnKmgI7HIRR9MIB4PEQmFisQbGs0VypoGuusyIxzAYQ3XKuE4ZS1in4r57WlgjssS5jVpS1nOLBLXeft48n+DMozpjJ2oOkJSikUSrgKwHxhbBzYBVqAp/p4AiKgECqAyWtmGRP+ineiGnV2bl+bZeKtFAju366r860h/2I9f2q5DYxSTSPUqgkadEjhIjFGkhSJg4QRTaUFiMVLJJIsHRXPW7PSmEqaGD52O7wN04nEuYDjS2kWEvJdrx0UicGG30McZKHGxMJrCO2ld1Ew4DSJmQyep1dU7v5LzrbsK9dCWj/o2o4ybBHT3oZPBzaHuMLqT7142s9t6GZAWfNvubEpL/OlMceM2AQPwPDMYKQqEAXTOaeOiO9QgzhTU5hDl6gPrpc2lpKFIfsRCWyvhEmmu6Yig+lbQLg65kEioONGrQ2AgPj0C0MUS6vR2MhXJeVCblHDloY1AYo9C3kRf67oeGdzP/0jK2cz6JRCtr3SR337WeDU+shdILrPrGPrrefjnn1jfTpjn096b5zS/vZUyvh65zoLCPxy6dxzVtOhd1hLl15nwe/PEnwW6G+gWIzmW4635D85cu56zO+TS6c3hhTYJcfoJwKEx9PI4QDv279lMxc/iCMGdpJxVHEHSgaNrsyVSwQwa9fsGoCROTDplsnoiqk5g5m0svv4TVT7yAO38lSy67FL89xnMcBYz1fNnXQwbc3APNEQnGlsuyyaBpywkUAZp1KLonDRgbjMVZdv2NPDj4GGb/ThjtPXpXZ52jd13RgQWN8JZueMsC6FwITr+8/nJRanfn0+DkZMCox2ByG9+JtVEUGjGhslCVShKeOiZIIsMkcs3c67qITIbErOUM7d9HbuBRGHmBZx99ifmxes5vms/HZszj0ZUfY/PLNpP7i1DsrWnQNCDB2B5kjezUzNcoNSBiD3BdA8TqIByF7CYYyfxROCwuDllGp/xFpiRVmvDhR5CnyAH+OGr93myzqHkiXrMTryzfh6QqxoAQKGHwBVEDITSfhs+nEQwGCEZDhMMGhuFDRaAKBV038Pn8+HQdRS+jKy4+IfCrKprfD6qNogpURUHBRSgC4YBAoGkqmqbiVEBVBYEAqBoIoeAIsBXZw0W4gKPiOFA0IeDzU1JAcRQmkzquJsAWuI6NbVu4jsCsZCmVU5QKSWwzg1XJy6AdULRqFylh4wq7+ndvQk4FqL2Uttdx6tQzgaz4uCoOF7fB/GnUQFivhBhqoqtTOyd7f/fMA1GrWlrGfJhpwsw8XLELSWWtIIdTA9Kp9aREOew41WGn+SGgy6XyIPduipWQPnHUgXwJXANEO1KPJlZ9gwn+ErQU4J0ZeGcSyMr88Og4bO9LsW53io39MJiE4b2QtaWe+NHu2fEuz95tM+Fg014dMBFYuIfAj0Usxouj+FOC6dYszNIEgXAdHbPb6V7Yhi8EwhRUsg7FEYsDu/YwOTZOaqzE+MgB+vr389S6x8ikTNJZizV7nseamu1NQX8/9JORkkthSODHKRxPEqG3euXPyJvrU6uyFCpUloD1blkGzgGOLEQ7gNRkKsivagECc8CIQykA5fXI2rjXSpsKI9MJR09i/hGAsUGE1obeejNXXfdRZp7TSAmXJp+gaYV8R++Qy3+tgkuXQucMqI9AYMpM9goh5irAgqr8iAnJAWjogPNUmL0Ezn8crrkGCi8hvaUQ8HngMiQ//LsaPNWJHAQbgRGEEHz9Zx+mra3tNV9ZXQLqEjEWr/gwAKmdNsVxF0sDawK0OIjAocNXUB2LVXMKkBvIsfaxu0n1P4Nfq6Nj5iLeHf0QdMH6ZwuYpsvV1zTSe9sB1rz0FGu3PMemQvpgUxOPjh/RSnzly//G+tEBdvriCP0uXAsQBRTy+HEpI4PuNKe3H6ciQbhBLCo41Ecb+MQNt9A+LY5VLtEYq0dYDjt6e9HLKn47SlhrRfNb+Hw6Eb9ONB4jpEE6kyYbKRCLBgjFApQ0KJUrWELFqA+yM/0sSiVEY7SZppiGZmlMjpnUORUSPlh/pqrqTbGPA+8EZiMLKErUqj29bcVLToTfpHM8Y6eZOYNIGtPUppgTciPQLFkP5Taj4uJjkFFeBGquuycPGUSOzRZkVn8qEOtHApCtSD9yKus7hSytnYtc48tozKGFAQYZqJaHJnFoV2/hPGcaLe5jNPAkD+EwXP18qfp9HdVjesUmUxMaZSRw+3P2cCV1fIKF/CPrcEmTJY3srupwIfMwSFNgkDXHuG0TwGpkD4jPAgvnzIJrrqLU9V7+3X2ROnJcSK0E3PPDvQRjKxKY7qzes78DXnr1p3VqWCwBuDA5RW+okJSvP6glKWZ2s2/j85T29uKMPAulfiDPxPg2/vJfu+k6dzmNTTFW/fSX3HTXzUxviRDAJSPks91agvWTgsEBuHgx7N4PFTUG7YtlTeL+n0Lp6E0WmLiHbXfew+i6FWQH/pOHb/3/caxHqNX5jLDz8RwXhCssOqvMzV++nUl/Gwg/DIzC9l/zRecTOLckmGa4aHm76ggdgOQB3OTvANCdItOjGrPPaaH1h/+br37lOySifloawtz/4IM88oOvE2iso2lmB/27lvCWxIcwEhrP787xrbsGWPS2eSw/x2VJXPBWzeRjP3mKT3/gYpYuXUb9O87lpevyfOMXj+HkHDKlYwToGeTke70ygyNZ+Trc9gF9+ZPKGRzcsYu/W3QpkjJwgiemI/Uxfvfn0HQjiE5wt0NuECZKkM1CMQWWH4INoIUASzZVZIT/W1ZYbcX4dliGD4YQB9vvvES10taFWXmLZUt+x4o/fRsNiUvp96WgfCvJ9b/inroo25VuGpZp3DN/Dl+Y9e98p+dG+NaFMJND2WTvRZJ+Ds+tTFCjeW3vgcuvhcuugSUPwhd+C8VTW3/yxMwFcpR5rooBeTUSSU6qgXza2lSg0VPj9CCkKFAHagT0IBgaAb+fSCRCOBzC7wdN0/DrfnRNpppVzSAaihGKBAlEVCJhsEwLYTqoloPmN9BUEKrAVVwsy0ILa/g0gabKvqmaJnEfTQW1SkxVNdl02zSrcv6WPHXHdamY4DdAMaHiU6iPBjFzGYTl4pgWhXKOXCrF6NgAmfQIpdwIMk1dxgNWLdPzuhyoelYywsghUzYecO3BcqduICiQXMe5zdDShexF0wAHM+ye0+g5pLIk61DzQNrDf55Kqk4gk1PHe1IqUi3CPVSO9khmAaYjiyIIIpcMD+g1qGHlWvW6moDpoIWhLQZtYbgsBewD53fwmZ/BQ2Ow5yiP9URXIhsZj3agYPH/2HvvMLuu6u7/c9rtZXrXaEYaSTPqkmV1I9tyrxgwYKqpKQ4hjRLeN7/wvoQkJCSBBF5KgNANxrgA7pZt2ZKsbvUyKtN7ub2ce9rvj32P7liWZAuMbWGt57mPZq7O3HvK3muv/V3f9V0qAxhkcV6UaoqRJ53qJ/b4/bzw1H5mLl3M4rWreZt6B7NaFZAdFCS8ERUlEkUfi9HZ2cmB3XsZ6O9n29BWYmacAsa5z9MAJwaj55VEGAfuBd4HaU3c+KgkAvPRa0APIPZIPzzD3w4Ax8DugfwC4U5qgdpakG+FIxlwvoSogTsfuwzRWeN7Zz3iDxSMjQAPQ7CJSz/k5bKPK3R+009G38QDT9azr38G73tPmBbEXOrrPMq/fvLf+Kq6gWjtu5i95FpWXHc5P/4lNFbD6qVw0zpY086pCaxoAog1CqB6IKLCGhVO/BTuvB8eO4a4ux9ATLbngaMZ4DsIIDbOrLZZbNywkZqamlfnqmfIhFsEG1ZyJ/UZrGDA0zth9SIIB8Bb56G2vZ2G6Sa9+zoZHT8hBqAMmWyKgm5jGBpf+qfPMNr7AjPL/NyybC4PPPs8Ky+/larmNmKKzN/98D+4Zd1NfPHTH2XmugV8tx+++13I213IdJ7qHTBVsuXCzNO9vFnY9DPIquhC1qxaxOJV7Ug+GY9Xw2P5Uf0BHNXHJVfcRHl5AwF/FFVSGZ0YYGxyjHhWJ2uNU1dXR6CiglA2jT8RxzOawMAkWlODNxRicnQMSZaYX1vG9HAYbz5GNt3PuKmDAnVeKNfFnupi3v61sQbg6wgReBkBMLnJ26lKTSriuSS4KE9w0V4t60d41wClXfR0KEyDkTFgFOxDWEySK3oEL6Xew0VIgAAl5qvbtyCKCNI0RMwqMufCh7utMhzEeJ/PlVQywSDd3McgW7FRgFYk5qEiWToyQRpp4yZkqtlPNTF2YLAXESq5lbQeRGwaRPgwHTGHDGAPoBFnMXt5FxCmiih1BKjlN2zgQTrx4XApnBOMpfiZ2ynmy08Ok7p/I3c5W7iZAh2Iee0U74NbwpWjJKugFe/THODLwIMI+f8L3s6kIf86WW19I++84wM8eDV89P88yZ4jY/ilHF1Pf5o5ZQmUoQOMHrdYsfJqtnp97NGhvyfBz378HLOiOnfesJzbmpt5RoewB2bOhPoPzOWmq2eA5TA6+Nc8+/P72PCD/wZeYM2t7yYarSI7Ockzv/nJqfOY6N3Jhq9djW1mOX2Tu+mrb+US58+47m//Py65/N1sGvknsqM9qIqP6iUrWHVHBc4MDwcODpPe+jOmz7mV0b7j5NIDCDqixD9/8eeEg48S9Zp8/4df4Huf/iCyBLIs8ee3XcOerkkayv1UR/2oqkYoqJK3U5yM78Vz6EFO2Gt4b8s6miOVaAEv93x4PRstDz95ZguDu59Hw0M+EeLakMKc5QtRf/kNfvS+v8TInRaRvRZ4+xtO08NEPIdXsJ09U3+7KuDSavj+h6HyEwhPKuTJCM+DoF2UjSl2T5AUyA1B+gQQgFAQrEn6M/28vwvu6JjD+zWNleJoViH83j7gqEfl6i/dglbm5ebWMn761Rn84pk/5ht/fzV7vvtX7L/nP5FnfxbjP2/llhkBrp+3jFv+tQ++MBciKeFgNUSw0ohwgA+d5VqPAspTYD0K3z0IN0swEYR+G46+gRr9veZmcRGIfS0tjogIXEphGLHn9wMh0KIo/ii+UJTyigqiUR+qqiDLMl6fgqoKWQFFUVAUBQ2VbC6LbTtIUuQUxibZRdahaQm5AhlkDVBVvFqRzK5BIADeoJAQVBTweACpqAVqgClBIi6aX5s6mAWHfD5LbHKUdCrN+MQkhw52kpN1vAp4FAdVtUmn4uTzCczCOKLKKY/YMbg1TC4Y6wpLmYjoxQVioeSgFEptWAuUWiBfWGN2fAgm/FARQiy7PkrBq0tJdbsldyACVVcIdioQy5Tff1szEbh3HAZHYV9CxJiHOXObqDKgMQC1s0FuRgzfUwLgxYOCiOHs4ukuzh5HuJhxoB8kHd49DfpzMKK/VPFdQiXKEqYtuhrZV0Yml6fn+E6M3JPgnK1GrGRJoBObCgr4KTF+y2UJ1RsB1Y8/UM7sjktYs+Jmlq5dzPR50/A1Kkg2xHsMYiMpxsdGiE3G6Dl6kl17d/PMzqfot7owbAP7fBd+dwPwsqBRCtHi9yqwvwjG5aArYhxEgcxyyDQAW+FUx4qpFof8qKgGaSlefCUwU4Gj14CzDzHv9p/jHKoRdJIlCCGzaQjKxt1n/Ys/IDDWB3wQmAuEQZoHvjB2uYJ/JnzoffDIxg5yOZOhvkkefrDAgrnlOIbMrs486UQ30E941jSMupkMFGMMy4b8Dji5BzJ/DnYG4mnImVBTCTUOeBybSBhmzJGpq4C/vByuXQKTEoRC0CvBCxXwfJsFIz0I2qyGqtVS31j/Uk77b2m5jIRpQLSSUn3pGUxVoL0FfB6hjSZ7NBZf3oZkVRKf1Dm+7Si//vL3WHzz1bQ2B3AkD2OdDu/8s7s49PRDxLs7GegfJg0sftettM5bgC5JBFfMpK1pGXPmTaessZz3BuBH8yG/53HUngcJTzmlqYmpP1SzsDmZH6CyN0w04qd9aSv5eIpEPEt8MsnYyBiXrJ2FLxLF5w+jqh4qPCbesiAFo4BlWciagiWBPxBCkTVUUyEQCBCorCCh59iw9wXmNNTTVlVBpVcll04RH04SMk1yDozlhU9viFThD0ZA9TDUd5T0RSXZ34t1AFcgvFCA0j6zQGm8u2GTG065cvoXn8dF+90tgRh5keLvi8DbBHIE8iY4CSCHhHFq2XGmvFKIoMCDgBBmIQDGCMJ3JylBvb7iz26/Sm/xdxE/HiNNHoMCl1DO80ySw2GUPNvp5jD/yjL81KEQopJ5NJLFQ5gEEVIcobTNmPr5NiV27gRi3nTi8N8Y3AUcIE0DBVYQYDlreIYXCJClHJEXvRfOKlfgIAqQtgLlYxO07tiHhX6qUtctFXaBWJetmy+ep7snEN1g4Wr+Rx40AAAgAElEQVTEnP8PLvC5nTgLU1SSoaxc7DTt1ybVNzJwmN/c/Tlq675AtHEOlZMa/YcP4Wu6nrdev4DD+7p46NlttL2lCtuZjqJCfY2P91zbwX997i+oVVLMW34ZRqCBgWE/3ohEQ1Bj5gwNbMjWR7g0fBXXLa7gns07GOzcyqDRiaG/uCmGYxkUMhNnPMdCZpJHH97B8MRPOHJ8mCtaypl/7Xymz5iOUVlPYZ6H+VGJAV8Qe1o7ps/AUXKI2ScBlfT1jTNvZiVzZrSx7fG9PLlzP5etmc9Vly8h5PexcJaPQ6MmL5w0sIwkdd4k9U0BxnWNsZRBR818to0EGPZDY7XE2qCPRQU4mU5ztH+c8mglZTVtTHjDHEgV6OwaoGLdXGK7jlMYS0650N/bo3x5K/PArCjsHHsdzuN3QIiXAm+zoCYGPMkp/UqpAaTmouzH6VsvpciOVYUESPIE9thxYnl4vCdBqqaNI5Fa7qTU4DATh+PHJCLtfq5pgkvqZBqjGuH5YfBeh5F/FCN/HArf4omvj7L6A1dz+WVz+X9lDdz7jq+yb889jE/uBmfUpUIJs4BHz3Bd+wagVwbLhFRezP/2NqjRIH0UBi4saoVbqSwjwIzfTUnzgvbwF5i5zbySiEjEj0BZKsAbIlBeTiAYJRCMEI1GCfi8KIqMLIOiOXg0D7IjgyOB4SArJqqiIcsOBbMAORtNLjbwUiRkr4zmK0pDWyKKt62iVGuxJ5gDYINhChWS2ATkCzb5vE0uZ5NOGRiGjZkvUMjmSCfHyWbSxONxYvEYeiGNKUs4WBgYyHIBXU9hGmkc262nc2vr3F30VCFDacq9cGuJoBStuBGLO+q14j08c7OnN5rZiP6JegyGTgh26YxWgWWAeB56AQwd0ECOQmQ+AgtrQjAKqk77QIMX375X0PD8lLmsgJh46ZOgZYQE9/rTPtIPlFXAnBpob4L5S0CZjwD4NF4sqeAU3/NT0sLKIYLWBIK4eRLYB7EeIa95JmKsg0WOfoYGTxCKNBIIhJnRNJOyQAVmIUEiNcTxvq1nvTyHUsPp8lCQkDdIyBsioASwJB82Gorqx8rKSJKDbYmXqklgg79GQQ4FCNTXUjtaTm4ig8frJWfk0H9LhrbkeFFkFUWV0U2X2nQmv+uywA8jiI/TgTaBhlcC4x7IVAE3AT+gRFoB8SAiQEVJRNdlLhsSNFTA6FrR7Z4hSrIDHkTkvwIhQ+rWytUgBqBbR/cHqxnrpbRlDALvAS4VJZlFZn5cguEAXLEKhienMzg+STIVZ8+eFGnLgoLKiZNpNEXCsPzUt7dStWAauRowFUhnYbIbjgxC29vFt3X3iExIcxNUjUBVGTRNc9AqoLESrp0pmO4jiCWiE2iaBupVKigdDIzU4/WGWDCv4/wcwMuYZRZ1md0uK0U7HfRUFGgpqiIYJsiaSnNHDVDDtAUDDJ0cZ9MDj2MoPlbcspbyunJGewzWv+s2Yn2djPT2MjSpM2fJaoKNTWiVlQS8Ae6cv5jExARGziLdG2PFjHJmL4GjD+/HYSchwF9cHN5wZIjfkw3qY+zrVbANEydio6R1LFMmX7AwCiayrCEpMpKmIHs8+KQw3nAA0zIoFHQKmQxGwUCywaNoRMMhqiprMDAZmhjj+JGDLO6ooy7ixWMX0LN5bEsn4NhYDqRMsW40RKqIlNViqBpjfUfPS0/mzWgen8hqnw/GEEB4ouWIvY1BqZzZbTngLnJ68b1Y8f2LMgUX7dUxV/HVhVqbwVsvyjesSSjEAeNUnOFuQF0ZLRChvA9RHNGGCCtUBFQ0hogLVaAaiVY8+GlAI4lMFpscY8AwfcSAHAHWMo8WttJPgQwmJxjD4VfUMIsA04hQSx0NLEJouFmk0Ivf5/ZZcPsmu8pnPkoxqisxcA0wTh6HOCeIUU0ZYZRTDcdWI/LlLsfkTJZGsBtqJsZoPrCLsuI5uK0vFEoKbDZizrtV3O499SHivmJamMcQSfYLC6qYYtmzdE+XJYgEIZ18zcDY+HgvW574LpGZN1LQ/Ni5UZIjx6mYvpKFi1rwGnEObzaJdT/HZF8z6YkgXkVm1cpWPntgC0+VTyOmNLJkZQ2DXTlqmr3IYYUyFcqLMoMLa9pYtmgaxyJzuPuZ+0iN93C+dSX793ey/9A9YA1w9Z038ZYFM1i6ahHHk0l25+NUBMNYoSjl81fA8A7weNDCVfgDEZIjk8THJ5BboKa8jk1P7eOHv7qfZC5DRX0D4UiIqpoAe7rG2HUiyZzmEFYAnGwEw1vJjPbZlDW08cK4RK/HYb5PYnkI6jzQUhahqX4aVqiScEULRMIMx/o4umknnjnzkY+Pw1Qw9vU0TYYKz/mJ373eVgcsApbpkDsOdgIcDZwI2DMgOwPyETA1cV1eSdQ3S8XSa38E4kMwfhgmO8ET4Hi8QFzzMyp5mRkuYxXCn1WZ0JiBymZY1wphFY5lIFsFzSuvw1ZtJvs3YMVeoPfJILuaPDRoFkvq2kisuhM1a3CwU2MgvwWkCRGEzEQELD0IcrBbGQ3QPykKL1wbsiGiifK65jAkBJB1oZRgBZCoQMaHxiQKeUzyWOTOyGu7aG8cc9OeDiIyqACpFkmtRvZHCJdFCYUi+P1BvD4VVRGarrICKDYSCrIkI9kStm2hKjYeBRQJHEuU/ysqOJqEI0k4kolpi/21YTrYtoNtyCiSjaxaZHIGXo+DYwsyVC5jMz6kkMtb5HSHvF5sfoSBqefRs2nS8VFsyyAenySVSqJoEpqjYJkGpm0AOUwji2NnwZ4q3O0CUC6w6soUuLVJAUr0jiLz/kU7jwKlTlSvEgvsNbKjiH49sQLYSViVLzaSdUCyilLkueKd8ENlLwQGITAbPK2gzUTcHhcbcUua3HDZ3aj5KDEBzoaQuU0bC+LvgrXQ7Ajew8KijLEkC/mKoCZ6Cs1ohIZm8HQgNorRM3y++7j8iABYRwSOWYRP7gPrOOSOwKFhGLPPpiDkoDOMPrafQn4cKqpEj5lQFYWCB8M4NztWjCSFMr+H6TU1VJfXUR6px+OpImcqmJaDZTlIkopl6cRjkwSH/cjRcoLREL6ogq/cT8T2gx+GT4xQW1tLdUUNsclJ8mROU6J9eXMsCQkVWXKF2l9OIicJ7AW7BczpQjckKhXba3gheQ2i4dcJxG6iqB2hzoVAs8BSyxFBvBdAgplesBbCZFpkBtiNGDxRhIjZbaBdAVSB4wfLKWo5pxEP9OznfIGCse62pxGhyvi10n+5k6ooTnoiCYYFZQr86Y1wIF/BzqEgmx/sZ8+mLQQsD8nhBBWRGYzEYsxe5Kd+mcVJVcbph4lBCTLgi8JeB965BnoK0HUYhguw8+vwlrfKLPXB0Y3wp7eAVxNxTbiIglYhpA7+dmklfP5+vvJTaGqEFQt/t7vgnBaghssdHBtsS7AeJUlCkqQXobEvYaO6eimAZdmsfccVNM1t4gsf+mu+98XPEwl8mctvn0bLcg+GYfDIjic5um8v7fUL+Y+v38N3vvYV4tkNVDfP4Zab3s5zv3mU0RGbaEMDH/63a7hrLXyj1uQIVrF6wIeCjn2hRGyvgnWlh+k6Nsyvjz3PW6jmLesuo33xfNRIkKjHg1eyUYr3o6A7eLwyXs2Lx6OR0XUykwny2TymbeErC6GU+TmxZwcHtm3CjPcyt3k+ZiZNcjJLLp1DCWjIBYMQEPFK5DMO9dEqNF+EcV0n9qrvbC6k3dIrMAmqmmSS4w7p+NmvS+LFSc02hEfyIdbOPKWkWgBRZVKgpOqkIsoNvQjg5qJdtFfHUpSYEQVQHfB6wApDoRcwTxW6pSkVsNUiSvFfoNjECtGUSkMAnsOIwpxdwDuBeXi5lFrgj4GtpDnABMcoIKpdRwGNKOt5N7eyj0cocBIx3k1gP8cokGAtXhRmMIMydEwG6GOCkjqaieBvuLwQF4StpMRqMhBRwOeANKP8C6PcjoCdM0jEAQWHZcXzP3GOu/cIEJ7sZt1kN/WI3LfbTCyIICjYiPkbRqz1GUqArFV83yke+3+Azxa/8w/ISwIOyK5oxGtnlqnz0Dc+DZWNYCaRU/2ULfwkcVPmpndczfplrcybP4+nl8xkIFaG4/dz1z+vxJIUdu7owQl3cd2NV7Hv8eMElEb6I0HSJlyzADxOUZHQ46FjyXw0j+hCLUkSqqpimibO6YHXmcw+IV7AlmcDNDbVYHl8PPH8JvY7M8neuIjyihouXXMV/U/sJ1m5kHC4nrb2ZTz/4zuID3XSdaKS3RVV9Bw/zmjPc/z4fodn+wIsX72Y9797Fs9u2sNwb5wvffQ9pByHo0PQ1NrG1740iy/vhGM9FuO6hGYrWItF4u+Ky1axftUqHhyHjAFLy2B8zz7GfvUk8p/8BzYHgN7f49M7D4vlYdvAG1DG4Azm9hG6FcHGknMwtKvonKxit10FjiRFjxGXBN3kgfqA0LeUymHmchhOihI8H9AwF7yNjA8e57HRJBuWXc4wIkHWWA23XyG+3gYeHYJv9UBdC7z3O+vZ9oulPPHt24hv+ztqvDm++9Wv843/foDGO7/KfX87k4XrP8YT7Yv5yjP/APpvhPBhGBGM/D1wD2Ix6ObMjutZYN9emBaCRY2QS8LxAqQvDC9XgcYsAtRKVaQIESPFiJPgCJNvIrrIhWhuTU4QwXprRfLUo0Wq8fl8RCMRAoEQmubBNLMU0HFkD6qsgaWg6zl8mhePoqEoCh6PF1WWURyQTVEjpMmAZZFzLPRCGsd0MA2bQsFC1y1UfNhGFtNMUzBjYJrYioJp2hTSBj5CFAo2tiOLbt9+FTI6pm1i2CZmwUKlgCybaD7Q8Agg17awHB1Z1jGsFKI+PYmIeFyQFcSMd0FVty2wTUkA0O1MMTWx4CAilQuDDXsm6wf6LXg8A6sOiWLwCgRmNtXkGHgHYe4mmF0PTU1QPhvkdpCqgYBQh8ECKUupMVAZIvCtQPjC8FlOxA2gy4BLYN5SmKfyYkDXjyBZ1p3nRbokZ7csP1O88D3g9EOuH471wcO8ODf2UnOAQyRTh0ieQa79XBZCYYbsp6mpjnnt82ht7mBaYwehUAsZEwqGTqGQJZON4Qt5iE8MUcglSA1XM/+yxSjlChTzqKhQXR9m8YK5ZONZ9IdlTrKXwvnSE/Q8BiYGXl6cZDiXbQDLA6nLYLhKPJsosMALW65FzKdtiNa7HcBqKJ8LzQ2ic2YbJfDej9AI8s6EY9Oh+0bgu+AEit3YZgILxNiBEvFczyJ2EUOcvS4PpFcUWP6eTZKk8ziJCEIM99viZ1kFbYqomZsk8iJ2bSuh+V3Q/Qmh6WI5UHAcxgybL3zpIcxMBidTYPxkikcf/wKSejly/Y3Ys96J+ZT3VA2CXA61X4BP3SGq9g7sg+37YfAI3HYdXLUaZlXDnm0wbw7MqoMZxYmcorThBaHZ6hSlojy/Q63+WBriOWiKgk+DniMJBk8kSI7HGBnoYfHiS2jpaCQyo/Q3p3/dqRvvOPzk28+y8JLpzF/UTH4yx4/+7l+wgitpWbqQK95ewZzmdm5obGRaoBLHCnFiIkP/0BZ6jRQjkkyFqjJqmkx3fFyxdDn/tfUxTODO97+Ph37yExYAb0NmI/apjtNvNqUpBQlFUfDLHhqUcj75/k/SOr+ZSE0Zst/HeGwcD0LXSNE0vI5CPp0hmUiQ13NMa23AspPc+9Mf88LOzaxZNRPLEtki07RJJbMYpoPpWETKKmhsnIHH28BwQieZSDA6OsAvdz7+Kl2NRC3NBIlw8pz6KReOebwqLbNrWXpJlN3bh+k8JETz2pthYBxSRV8aBi5FuO82hLtxEH64BjHXDUrl3AqlDus6wiWnEWXTYXwsJ8z/elHTpYt20X4XcwOVFUCVEJly9iPqNV561NTEwlsp9T9YhIhdjiESB08isIa/AS7DRx1VwHXASbKcJEY3RxHgbQLw4uN9zMFmHjvYyTE6i+1PxFyoROISvMzjZiQ0hjjGEXawCxG6uFVbCqI6a4ySYhyI9UMvvhLARxHbMwsRJ1/DO0hQ4CS9ZBmimzEewX7Z5loqYh7/iJI0QxlintcgAFhXNoEp93BKbvNUMeVWBLz1K8R8/4MySXppVvg1MRkkT5F1YCApPv7x59sYHNfZtmUnc9vbuOG2VUSrvUQC0OaRmbXia9xx1zrefmMHays1to85tJdJBDWJNLBfhmP9EPCD5qT5yv/+NXvv/iRVZFizfBn/9stf8bE7P07P4T2kUwlMLchQb9fLXr8sNfN/v/hZ/vpTHwfL4qEDSb71vQfYf3yAOatXE5CS7PrpvzN27CCS7MU2hW6s7F2E4rsEO/0jLKuAJLci+TtQWhej9T1GIZehumUWN9/1KZ7auIVQZZDyaa00z1vBl2+u5DeIsXqFLOHIIta0EaW1sgN/tBlWtYI8dICPv+dv+fjWH/PExz7FyQcfAPsNsBZ5EOH+OCUi3Ou/XXmpRRAdDf8GkdFy2aRNiCTYHgt6LXE9LnEtibguC+FgLQlyEoQVWBiF+gaomQkNl0GvA3YT+GZA7TJCQfjnINyilZQFdgEvZGB/CspqIK/DZY7DGiwGTZ3r1n6FweP3Yef3InsDVN/1F1z9wTsoeAa5594/hXmdUF1U/c4UiRITwAHEXnXDOa5fRrSLt+0LAzgv2jJauLxsGTdd+yecmLAwszHiE/3sPbqDn/MLrDcRYeSNby5dsJaSgqUPmAtaNXijSP4QmqpSVVGBz+tF01QikSCWZeEgocgagWCguFhL2LaNUShQFQoR8IaxHZl0oUAmk6agpzAsnYJVIJ83MXULy3QwTYeMbqIqPgI+Ba/HBiVL0OcQ8tioMlimAqaPkCeMZKkYBQmCKhHFgymB7hiY+Qw6kLNMMnqOifgoSt4kr09SMJNYVgqMFKYRw7HTCIcxQqlTlYZwHJMIh2MW78skJRDkD9tcGdiphJjTTUaQIaMSRGW4XoYlIZgWgcpKmN4IUgvCVzcigrxmipTb4oe44Kqr8OCWZ0kIn366z5NO+/d8CcjuoxtHBLz9iCDyKThyDLYPw89sUQ32Sgv+3dj0fNotqkC9pHDLW25i8bxFzJw9h7LaJhyChMMhIpEg4YgHzedD8nvAqyKpEnK5XCIBFhUDJg73cGjXEZ57dhd3/+g+OjlA4bzlClxaUxDxQDyImzT6MldeCSwB6SGo0sQmvbL4ETFTVHWpNgRlqFSgUYZ6WRzjoZTTKCDAvAkg6YgNx9GCEIUOSBCSwauUjpkExh0EpXkvIrP57zhO8ozD9QJixs4GbkZ0JKsCqkHSXjwLNcTzKkfIQWwEEpB7Gu7/hChjDEngSBLjHhnJq2DGZfzechauWsrjm3ZhZPbD0Fcg9UuwQojN7HzsdBuT34rzvWfmYJZ7SUoweQTUejjYKYS8y26EiQb41k6oDcHtq+HyCvAVz/GUiktxktuIuMxl3ZwvLhvxCRDWU3yK1Y0BQmUaRj7Czg1xFA9YtsFL2wqWbKpUyerlcwl4A/TvSbDx4c1c8ZF3oPprGBgY50t/80NG4iM8ZqQIqD4cRyGV08nrCbKOKUpbDbE57qHA1r5+fvn5Z7j5M2tepJ2SwSaP8E8RSiWfbxazcLAsE9Oy6DFMvvH4D6jfGmF2awtr1q7GF/GhaVFsWwbLQkLC6/FQUVGO7UTQZIO9mzfiI8fc2c1IkkZBN/D5/PgDQULhBsrKapBkL6rPixLwkcpJ6MkMI+O9nDj+aoKmDnHGSBMv/j618PnCNM2r0bK4BdU3TnXUIlcDSRuGPJCbsqjmEKHQDGAhYr/Sg9CKdJscuYVBruKTq3GZQrAM3d6nQbwUiMJFMPaivWrmzkENJFcEIwa8WDJD+OQXh+/diHGZQnTudnskuI3VJeBnwD4KXMkE9TyBQoYc2VONAkuyBwV2c5IFTDKHGCFESOIqMwVxyGPgMIHElZTTTgdt6Nx9SqPWrdJyyQje4rm5eXU3iKlB6Io5wI0IAPkk/QT9S6jzrWU41kcz/SxiDzpd50wfmYjZ+PcI7dcZiDWsQEnOwY3HXR1bFzR2zd0yzSr+uxwx5586x/decPa6JfNtcHRc+oljjePFJhMb4cjezYzuvptDT0dZdNVHaFt5E9vKJPRgA3OronSUe5iUoalCIqSCKUPcFs3t491ZOuMGkymDsvo1aNXXIHuzpGo7eGY4wtwbPkW04yjjo31MTg4wnHsaJzYMRoqztWG0nVG2v3CU79+zi0BUY/O+44yMDKJJBp5ciumNHRzyteEEEkhRibnBJXT1biWn92PjgZkfga6f4hjDOAUbO1FJ24IFjJzYyeTANh799ucYHR+nff1tzG5o54blYQZVOHpc4rnBSR4c6GPohROsfM9VXNEaoZUU/+/+p3i2M0ds8TKClgfUGo4dyJCOT4ga0DeCubKQcGaQr7Ec5k2HK6+E//oOjCbPb7f525oHsR+EkkD0/OJ7bXUQy8BYSjiicQMyTql03+WNuI1Zsgh8SXWg4IDHFqh5Vof+CRg+CZd8hOXeKjrkEBHN5pvPbuVbs2bTXVfFXSGRfJoBeL1QpQoG/vUatMoSflml4Ci86x9vZ//zqxk70U+YA2x/7H6e3rMZBx0GB4Qzjlpio1qH+FAX71lSPO/nKS0CU81GALEXmHUzyj5tiDtbFzF9uYMkGRhGjvXJdaw99m6OHNjHoYFd7Eo8Q4yzSLVctNfIFEoKv65gp4Rbti9JguTiAHo+j21ZaKqKLMvIsoSNBJKNYUsYeUOARY6Dqetk41kUOYGu60zGJzGyOraZwXYcbEnFVlTsfAFHUgTLFQWf38LjSPgk0GQNvyyINhIKiqLh8UaQtBCyFiDo9RNu8NJSIxMMg+p3UCWTrAUTEw6D/RkO7DpKYmgYveAq5IOiKFiGhHMqmgpRYsG6mxG3EVeh+P6bJ4HwSq806IiKl+m2WC4awlAZhepaoB1RCVBHqSTd7U7r3mI3yHMBm6kdW2Ve+ii0KccmgT4Eg8B9bF5EFq0K8UhPb5DqgjKloYBjwlgP7JuEZ23Ywfk1fXb3oudjJjDmWDx8YBtHB3uYv7+FZZdfQ8O0eXg8QWxDQXa8qN4AUkSGgPxSdNwBxsHKWSiSQtDjf8VLtI9yyn2NNFbOJVg1FztQgS17sEyJZApicYNEeoxsdhjMEUTmcASxO5h65XFgLzjfhcStoNWLez8P0FSwVXGYC1IFEZivjNhkuCCVQakMD0k8x2aveMbuxr67eIweh8J48Y19CDDyCOdixl4AYKwPofZ2CUi3gLT2pRnyqd2gJMRNWofIKByE7Em4H1iDGPu6DUfzMJLLkhycJKpVMn3+DG689QZ27wkyPHCMQrwP4fDjwAkwZqDvj3Pg+FKoi0BUgaEMHktmYCyAMxShQqun3w6x7TmFgJPDMzpGdLGfOXOqCIQ8Z02gnMumut7Tj/eq4uVaMKIRjGg4jp+Wjgai0QBa8JWCvBLTZ1Szb+tB9m05yOHtx7nlI+vpH+zn4P7t/OrXv8KwCnQnz5zNcGXCQQCug4k4+x/axA1/ufxF1zKMSCgYlIgPCd5MS4gwG4csBfb2HKQLlaHxQQzVorYywozWeZSVVeH3BynIFqokoWkKOA5jg92kJ8aoKotSW1NOvqAjkScQLMcfiBIIlBEtq0XVAhgOpAydWGac2HiCkfExBuPnyiKdv+lkf0s57jeeRYIa9bVBGmojTAx24/fZ1NVp5NMGE1mwp6xmJsLtDyJAoN0I9ptBiRkLYk5IiIWzgPAo6eLfdiMAWhmLgfNaWi/aRXulZqLiRcLCOMMYc5t1uQpjACFtKY3tVShtAnFIHILBwd2MpnpwEIBiP9CNTZIcC+mhCTHO3fYSbiWIg80oKVKkCCPRiMQQDn2ItTiC28NABqbjo4wqymnjeZIM4GCQowS8aoiIwEcpuHSXf614Xp3AYqAOhSMMUBVeRVXtasarkyjyGNV6C3NyR8glxjiZe+GskjkGQmM2TCnGrkGA165+rduwzL1mdzmeuuZWIub9PAQc/gcFxipesAq8Pgk4N4IOA+PkYglqIz4Wz63l2bt/TPcBKHjmM8k80lEfRqSZ8mCISk2MYcsj/nXjaBmYHoDkKIzHVKYtmsaN8RuIeAtUNNcybEmUty8jMm0aVnoYa6KHGTVl2PFhEvFx+sbHyKZijI6MYmTTYLijNs+hQ3uwtArq2+eyY/NTyIFpdMxq49KOWqbX17OlcS6MjaGqvaxbeyV13V5OnDxGz9AwUtNanP6NYHSBPQrpY9xw3cc4dEBi/+7N9B7cBECqdz/J3iZyk3PJNtaX9hA2bBqD0f3jlPtlPIE0DzzwGL1pL/aYjt8bwQlXcWLDZtLDA4Au9IAvbRbCdKnXYYV3sxovtyzKMpRXELr+egq7d1PoPP7alMnLCCZVPaI6cRZiIE0gJrmbn04Uz8XVKnR5Ee7uWKPkBF2dk4wGSjWabyZNvpnkK2bhNzVClsNSPyipNPuTEzgBiSbTx/XRANMkiekq+BWhoTirSBvrsuFoQWLBFbOpr55NvDtFxmlja7aTge1bYWS4dE0+R4CxjQgAIUgJ+7pw8+tntRhZOo1+NvZupMXyEtD8hLwRqqqnsdaeT5PdSn20Cc9wkG1dO0kwgEmOC4r++wdnrlr7lN8du9hJy8bGQdfzmEYBXZYx8nkUTcVBKmrjSxj5vABjAdtw1y4vum6STKQQArG6KF1VfUhBHxgmsiwhS+Dx+JEUP7asYCsK3oCXslqZaI1MKKzg92rIWhDT9uLIfmSPn1CdRmO1RCAk+vOpNiQLouw8W/ARDUZJK2I34DhTkSyXlmdNebnIYJqSHIHD+cFzbx5zMVIZke8aL/bWMXWoMEUxguZF+LsKRGB6OjI2tVEAlBqAuY8ijwAyxsRxuRRkJiE1Col+yMdBsYUMetgL09tFEy9pOqVSq4TqE1IAACAASURBVNOBGrcrbNFySejW4SCltlHnY7+NC88DXRPDJONx4qNjZAN+OiZ1pje1kKmrIRHzEa4JEzIj+MuCqJoHCQVkGQcHy7DIDGfIpbMoElSWhWltaSQ50k9Mj5G3zzZmA5RVLaS1aQmL562gZdZclEAER1awTJtUymYskadrLEnXWJyRyRFS8dk4yWHIJEAXussCKU0iIrz9UFgvpk0CsYlwJSRcKWaVUhVOlpJur1l8z2WHuD3ylOJxaQeyFozFQR8BpwtRy3cUIYGwD4F+nd3ewGCsK07dhOhH3C6yUm5w4E4Kl3/t6vlaiGCoFZGxPgmZcfixAX+vQa0EGROeH4O9I8OM7jxKhaee6dcG+c7/3M7ffPl2Hn2km/FDz0BmF5b+FI69jVOZp1wzdNUhoqtOCiMKBaaRVOZx5Dc3Q2Mb9Hoh1cs3vv8M8Tsa+cyn1zN7djWq9lK++tk5qyVzJbensm7ciXUmoFWSJBasmVU68FwHI8gtjg2O3+RXD/2YB//nXq5YvJ74UZ0fffN+fr3hPo7EtqHKKk5xwbOLHzq1P9zUzIulp0h0b8SxP4EiqyApZByLw4ghmaGYWEAM1zebXMFUS2Kyd6iHfff1UAfcdtvbmds+n7qaRgo+HyFNRQX0TJp9O7ZSW15FpLIC1ecnHkuhWzq+YBlefwS/P4Rh2CgeP4WcRTql098Xo+9wP/0T8d8z9/LC5ThLwPT6EEs6KqlzTHZ0jlMT9lBRH+J4Twynm5fE4FsQ4M9eRPk2iLlQiwBgXLahCxR5EH69gPDpRxBzYYJssWXRRbtor7bF8TsWCuopfGDqLDUpMV+zSHglH+trP8n1f/QWFv9xC4oMW/8Bvnjvxziy7zuAYJyCxrCsckxVuLSQ5hbEuHctiIgvXaB3FFCQCSOzFJMMDiFEVVg5EjZlyFQgUY2KTBvXEucXpJlkmFIc7EFAbzICCHUrgqey0HchQoCf4OVf6CdUlqe1vYnOtulEfOAfu4OOvnGa9z3Ht/v+jIw5iXOOdOAjiNgtgIib3e/MIRLsKiI+cxmy8OIl14vQ4nXbDgQR8dsFj29IMvjKIDsOzuuVTlUAH4oWoPdID+tvWMPVb/kwV979b/gDQSaHushufpK+QgVW440Q9J+SmtiCeI4K4JchWg5vuSRARRiSAWh/C3zg1vcQkmHcsHkwlidraMyfV0NHRS3tzkLyhZvwaBKH+ka5Z/N+ThzczlOPbWCiuxM7NoQkydiWwfGDGxkaOs5Sz6c5suVprnr3/+X6m97J7deI9eAXz61E6hvA07WJD73/esb1ddz/wM/47x/8GLW8HCewGKtQwDFPQGwrf/XhX7K9ey4PPtLML7/y7+gFg+6tTxAbjtMXr+Xb/34bc2ZKrGurYK5ewaHqRezbsIndVTaRVjj0+NPItYvpfeFebK8PVl5Gzw//A0aPCiA27EH6xGU4//A4HHl1E7gvazIlttC55A0HYjCehQkP9Q/cx+R932DiO/8Je3/PLEYDMYEvRQykWsQmPgY8PMwpEuVihGNwtYpc3MdtEONqA57a00igBPCMliNXrKBszs2sn3kZg4U8+/rGGdJtlixohJYZIA9xYGyEz1h1JOe3coeqMl2WmCnBTEls1g87sM+CwwlYXwVrV4BnRZhHnJV4Fn4D+XN/jvPUo+K0smnIOyK7PIigXv2BmwV0x3u466dvZzpV1NLAjLL5rFt0OzPmLaJhbiPV7U20DqxjsvtrHHDuJ80AF8HY18Nc9KuAiAACiJXVAruAY+awdAUHi7yl4DgOtmniZPKCseRIYNlQyFAq7naZpDZunQ5SABQNJB8oKrLmQQ14wauhyRoezY8vXI3lCWF6JJyAj2BdA9Mv8bJgtUTLTKHlnHQgmYRsGvJZMBRRwWyakCmAlYRJEyYNyFkyAc0vmL2OjW2JaMey8jhOBhFxuLqTbrQzFai9OB7PZW61lg/w9hbJjx6ojcLySZhTgEgS1HbwREAyilDJVNarqwXr5n+zlBoZZMAeEhLx1n4wBmGwG7oGoXNMwHCjlIq2ZwEfmgHR60FdidAC66AE8Lg4jQvGuqXFEgwgyAavtU1YeSYTAxx87G4W7jrAgo65tM1swa9J1NVV0Darg/qG6YRCVWh4wevBwCGr5+jt7kG10yiyybTmKt52wzo8T2c4MnaSofw4jgN6wcS2bBzHRpEVVE8rrctu55K167ny6nYuWyZkJqYClhlg+xA83Q2PHoKD+yC/H+yTBozEQBoA5zBwCOy9YPrBlgXA2oXQQSujxGSeiim6jSqGKU05GRH0u8CshQDfj1pCgN9JIer+nkB0zTjM+VS7voHB2P8NXAfSolIdPogbEqCUvWgWh/GPlCikojuIoKD3FF8/A24DwoLIEe+DsBYkrhRIptJs3wOBd0LH9ZBdNB0r/QF86vt59DM2E8dALAQngccpqTs/jhBTOgFWAuJZiFcjuC+dGEaMH/1IolL/Pre+40rWvaPht7oTp7PYoVQiqZzh/15kUzPwZzGrAJMnHA49u52efcfI5ofo69zN4z/4Pht330tPbCdtksJV826gq6uLE+khOou5mUWIGLQbtwi2+LWKFzPUhiMpLK5aQ1/tMN3Dj1FHKY8nASsRDubNDMa65iD8wzcfuA9Fup+Iz88nbnkr0xqimJkM+USKuupyauuaMW0N3XRQwwpVZVVIkk9ko2SDobHjyKafRNygtz/GeFcXu0Z3ktDPU8X7TWT1MtSWBfCWeTmw5SlO7LM45NdBA+ccacheBInENVdS/2mEt4gi0kmLiu+78zVV/Dsb0LGJXQyoLtrvxY6Q4uhZ/3eqR4jKVXym4n/42IZ1jNYG2RSDdZWw4nNQ1+2DfUFcdMTP+1kz91Y+/LbVvP8f6gjYFquABQgswkGskPVwijUrPL9CBQ3cwiDdOMVthslhfkkrBwmyGIFyXMpSnsMhR5ocAQTZzJVuchPUU3WwJorfm0Mk+D5HFg8Q6/w1I8lJbr3+Z4z6wGhWcdrqCEx7O297dhYbuz9DT/KJc97F5xFB8F8isJdo8fryxXOqQ1S3nc1cEHkewjfchlj3LmhzbMjEKK3mrwe8HEbzLWDlO7/JYCbDQw9vRtIPA/CDDXvYtsfmkYePkdt9kOq6JD5UwIuMqJTqRDw/tzpbAq6eBVe1iV9kBHt2+4kh/vpDX+fDd34QOdSIXBFizII/+69+/uq2apbOqORva5bxA2cIX3wuR8p8dA82Em2cx8nNv8DIpXDQyEvNLPjAD7j8vTNZu0J875cNYMEKmk50k+z9IYvXtKMoCseOboPcOMZ9N7Pun/bTv/lBTvz6K8AIXcNdzGqs5H/96Z1843Of5R++9X02bd/P8ZM59m/YTZvzVubIYs4cMOFAJ1QtXc2sFonFtUnW/+vnaWiZz+6uPjqH41hKNcYj+0DPwJwKeOssnI/eDfrrALLbvPIeM7oOO7dxrKDDn/w9XHoDrFz1+zw7MdEvBf4ZQVMaQuAkI4i9hozY5JkIB+Fu4EOIzV05pXKZYYSugBdoqIXPPMFf0co0yce4afL5gT749l04iVHqWxewa+F3sC6ZCXv6YawLXT7E5x+axo7LVvHOqgreVzzFGNCfg7gOd9SIpNFG4BnEjmVFRy1vv/en5ByHr+Sy9N24BPYOvj4s6DeA9TBOL+PsiO/nnmd/jvScWLFUJDRHIuOY5939+6K9GubSGFxtkCZKivYqMA52N+g2ju4FyjBPTa7i6px1NUXc5xeltFYpiAmtg6ZAMIikluFBJaBqBDwe8PkgWIHqr8NfXkXDSoW3/qnElWGYXZTGlIql2XoxETIowagEaUMwGtNpMDPgkcHnhWAU6puhrgFi0wIUUvM5cngHemYCIz+CgO+GEKuPy+67yHz9bS2DIM3sK/4uFYAxkMZB2gZzgKt98BfroP568CxCKGOe3nzLQQSaPQjfPQxsgbE9cHAINsbh1w4cc0QceiaZcwWYPAnv/SXMO4TArySENEyQF5PmZEqatW4S77WQ4jmDubH19vH9HNp0gMrnVVoC5cxsm8Om0GYUTxAJBR95Cp4QjjeE4ouimD6aa8PUVZVTV1vP7e/9JB/8xz9Hkh2MNIwOwpe/tYE9W7eTi42zaPYcbvr4h5ixxktdvUyNVJxfp1kAWFcHy2vhhhXwiwxs7ITDvSrZVDWSrxqnsAhSDvQ5cL8EPXKpC/BTCOCqFpFUraBEPs8hnq1BSZzYVTxw5ScmEWu+cwSxQ9gEHEKAjy6C+8rtDQjGhoHvg3cJyEXxDjcppiAG60LgFgS1LABci5hpWxA+LIsQcXwrorvOM8DDcOwaSIThaBo2PAFSv4KRm4bXU0O0RjzwUDMojsTAQYnWcpA0pfggFIQy07toulal4QoFJbeInV/+KEYGCGjQ4oMjd4MdB+LIio/5Sx7i+g90sOjSstLMPA+B2LMd9rIg7NQPOO0p53M6j/7sGa6Yv5oDu17gsUce4Xj/CeRElv6xI9SGali98nYe3vAYI5O9ODj0ORaPn9zEVZe9nUubGknKCf7n21/lc//132x+YQdf+d43T31+A9CCjK4KNdxwmY9IhQ99WCypbrJHpkQWuGglsx0H23FI5LJ878nH8XpVFlZXsayhkfJoOZlcHkmTkVQfXiUggFhJwx8IUNNYQXtHM08/8iRjowPEJnLEevsxCxcX8nNZfYNKY12UiL+KzScsTBOcNK9onp4+fnUEOy+JWMuDxZ/HEE2QjiNA3Kmh/cUw/9U018G6mTkPpXZKUILGooino1AShIFT+mRKAPwRUYptGKBq4A8WO/z4RAdsJVA83oJAEAIRCFaIrxgehnQWVD/qzNmEPAqaKiF5IFom/iSZMEgmCvi0AqGKKIokY2QKDHQOUzO7ieTJQey8ScXMForVP1RVQXMTbNkEtdXQ1AB1ldB3FNrnQyEF/Yc6efw7Hy1ezyvzsMFqD++7bzXRaX427ZXY1wOXv6vYdVbSkQji4Wq8FR0sXHcjl1/Zwdqrwiy999fs7fprynKHWVa8s2WUSGOCXNCEiGQywNgpxqirQevgkKMbmRx+JoF3IvF3zOIR/DzIJhJEECDDKCIezlKSeXKfmivv5SBCoj/Cj4TEyYljfPGfLsOQr8V2HDANpLyPbKKCRD6MKKPpPuu9ceOwbwO3IyKBqRUhweKr7Cx3XKJU9ZsAPkkjD5BiyylRzAvV3NrqkoVmt6OPjWLEJl+D7x9FVnbROKeZ5x//GUbiOIoxBv5ldGeDXHN5GVddUsVPd8znvn/9E07e/An2sB4dgadJwEgWjibhbbUwJsHG/Xke3pzjeK8COz+CmR8mk5dRe/2ERi5FGw+R9Gv0jU1yZUsvI4cO8rMNPRzcfYBp8zo4vH0Tx7t6SOVMEkPdIBWQVRnTkUhYKt/++GzqW0JEZIFnTx6EajzEQ+UkaUb6/9k77zg5z+ref98+fWZ3tmt3VXbVu2RbsuQqd2yDC9h0ExxCcPiEhAQSg++H3NxLCXAhEHoxBGPTbTCmuQn3rt61Wknb+/SZt7/3j2dGuzLuuTZyrs7H41lNeectz/s85/zO7/yOJCHJMu3zujj9/At57N672fbNO1h9zQpOvfqL/Pg9b+fz//jPnP+mNxNqmsP37/oWsdmr6N2bZbxnhFBIaKDJEhwpwgNT8MaLgKiMnIQ9QRS7cxMFZYCrz5zPwroELZ7CGx6/hvL+e8GahMcHwPYETuFwfKb9RLMggGuugXWnQjoOK1ph94jo1vtyLQZ0qfDXjfCRUVjhixu3lqtpRnRUficiaEsj/OsY0wwJl2mKfAWBqRSqr40jlp3GJMyZD2/+S04P5rJOCrPM0LlHnsede3dg73sAp/9JgkQAyf2g+0wmytyJxOky7BmdYGKkDxot/Kl+Hr6zn55Fq/j1hvX8GDHbJg3YqIs+GW9H+BwVROVcFJivqiSBCTnGRV/5CX9XqrBtz6/h0c8LqYLtiGzFEY7vFBMHTpHgnz8B/3kHjB2FyxeD0g7zLgFVgcwuOLgZdu6GHRWxnTQCqTpBnZ2g+v8g8I5N4LWCy5MxymtpMmI1r/lttRryBsTNNcm051BDRmYCBAmma0ktxM1Z8w5ADMDojM/G0ZLthJPNJOqbScfrMZQQhmGgxzWUuTLnXqqyKKXToarocYl0AlKKILOPIx61vIuK8EmaDKhvAC8BlSKkIqBX4YSSDbkimDaUii79QxmmSnkcL890e9MaCFsTKj1p/1ULnvVcw2R6gdsrMPUY3ODBggzU2YihmOZ4wKXGWLXAPwoH7oX78/CIDQ/5YnRWeP45wwV+CoQnobgXTqsm6qTVCPCk5kTWmiXU1hMDLEWQMP+cFgClIMB2HaaKU+zdvx1ZUZEkgezI+Piygi4p1Oth3rDuLTR1rqFtwVya57QQmyujRMW9qISgNR7w9x9ZR7GwBN91iIYjpFtDhBIyuvL8/c9qSZCQBEsDMCPQMAuekSW29oMdgkAV2ZKgG4YSiDWtnyqIyjRemEMwR2os2dqkrzMtTV1r9jKGCGNctwrEfhUR8R+tbuzlA7FwwoCxMrRcDp2tyLMj+I+fC04cHHWaElxjdhqI+bMDUU5TQXgZaUQ8JSFmxoOIlbQO4VDugfsdodVcMGF0L4R78rhBHFlvZmQ/9PqQjEF9CHaVwCpCYjFUVChlZChGIBfBjYDXCLGgAUmB6AKQW6DgOYjcyyRNLbNZdcobueD8M1mySiHVyLHrU86CKoOmg1SLJF+mvUQs90+A38AHu2Txhzt+gdaXIbBlWtKz6B0bY9nZC1imLyYSi3HasrOxO10WuovIuyYTBZc/3n4rvVP9VHQbVbJwCThweIR0cg5XX/B2fn/PbZQRAGvGr7C3sIu+fQW8ok9IVY6TWamRBsIv51j+PzM3COibEDT3ZkXDbWwh8MF1AjRNQVF0FC2CokaQVQ1Z07Bck4pdYjJbZCpTIJspMVgZwz65mL+gSQSUCznGRiRGcqKi6eVarXpltPpcj5i2iohpugchMT7I8YxEsYAp+CfkNZKAEAoqEtIx7S3/mLI5QAhD0ZH8qmcj+6haCMmTcT0H26/gYSJaHChIyNUF1q9CpjIqBoYuxrGmaYSMCMl4C64eR41FMVJRAg3qmwUmKsnTLntNjs+ntkxMq8hbePhoBAS4VcW3OBouEUyiBITRkVGqXpnQaVdQ0JAUA8+I4cgqpuuBoqAZYSTDQNMMUEIEioGMjIOPZISQQ1HkcBJJA3NyEq9iIisGzqwOEqqCrkrIKugxoV1eKrpYJYcW1SWdiCJJMmbFYaR/kpaOJszBCVzbQ53VyrADLSFoqYOmJmhphVgd1KchnoTmRTB3HkyOgGN00LrkHYzu/zm+9+JsJwlQNZn6FSl+evvD3PvkABMVhd2brmFhWlwrPVRHY+tl1C9fwsKzF1G/qo6xhoAr330W3/hagmIfhCSD1vAmpMqDRIPSMUyiJvMTEBBgIyEdwy9qzqtKBZnRaiVIDxKXE2+/mI6GGAu33c9hesjhHitWrFmtYqimWz6zgmgPPiuJsNyJcvPBh3DxEWhIGOEcjCDu1hcXDHIR9/ETCGB2DiLXa1T3vyZFFWZaemqm1YK0BmAZNhN6FF8xeLzyem7cV3VqagGKA+mOZsphlYImY469EnWzl2MWkpQhFLI586xu9m6f4tC+SS596zvxjCgHhvIUBkYZPzCONdzH8FiZ4RzEoh7f/skjjAQBE75KwdUpNcDw+F6e2ZvhmUMh6le8kwlnAfMbG1jZouNunIWcbGR4cJL+Iz1se+phAnOULZU8ZjZDcXKCwYkx+o4cJZfJ4PpAuUBDTKEiB5hWnsn9v+PpHe2sT84lmkhSBE6JQec8Gak7yu5UCz+85wEuPf0U5sybzaaLz+Wxe+8md/huKnYXsYVncf7738+2X/4CV/09sY4ljBTDnLl8PoZyDoefPMThZ8pkEfNiUYaiAc0GVHTIqzAuqVw+v4GwV2Z5Wx3z6xPU+z5XX3slT+1MkbcmiTYmOVjaCvJhGM9A5vkbT5wQ9tRTkJ2ClgaBdLwS9MxAgJAdAfTaMCdAPieJpMt491TR6CWIMpdGBLAoMQ3E1jpfG4iuzH4KGudBPAxeHCnSwcoizA1BXV0Upb2D3V0XErh1DA2OEz54iMmjWzjiD1Ke2A7DfwQ3BCEfbAnbLTBiTXCdUc94xWIiXwS9CLZCxo6TGxpgfP8+vrFgIddKEoYCE47NnYP9PB6MU0zNpiPWyrsQY2P38BD50hRHtTLeilOISRDReij3GbDOqerhBnAoEJNbLWcZRZRANPZDewl0F+pLsKAdFp0GRh1k28HfBWYjqA40ypAdhJUL4OAkHJl8hRf6tbcTFDv+b2oz6To1GmBNFyRDrZZsGpysCQbVGPw1MGRG9yNiiJU3BISRw2mMSD26nkJRUkCcSHoW4UQj0WQ9zZ1hFswzaEmq1IcVlGZYcwp0Ro+vfrEQMWxNbaSmPKJTVaksQTkPTh4KOcipgOfhWC75gks+41Ap2YwPFenv7cMq5/C9Wu17TQu2JlZ6Mh3waloFGAwEs3X2biirom9hqiYjE2e67LHWRbY6vPwKjNpw1Du+SvKFrA942AElA/o+WPk0SAbisrcgLreFWGOGgUkYMSHr/dmIscdZ7S60fJd86U8JBR2puTTXtTOnfQ6L1p7KvNXdNHY2k2hIoMSnma6SAoYm0TW/DuGPv7gdI0HY07ND0QXDh0ZFNGg7HINCNVni+FCu5V/qmVb9qE0dNdDbZFq1pDad1FRCSoigfQqRRXHGEVnK3yFqTgZ4dlT/cu2EAGM1LUzj+o/hbjqNyiYo/C0CfS5Qi9KOkY/Qma5ACBCD9TeIbMIqxAl/CBE1TSBmyfnAA3C7K74yxwFvBIr7cmidLdihRnbf67LFU2gyJGbLYFtQmoSmM8Fpg9JOjqHoU6Pg7oPudlBTkFwHaodFYfMwcA8RQ2X5ssv5m7//IpedI9hMwDGMoDwJIRW02g3+XN25XoF5riAJKLIAk6QqvVuemdXxwSlbPPrAXZgHD/DGq9/FtX91Hektp3DZu1YTjU+Hz+uvE823ShU4OlDhvVuf5LEdD+I9WSaFGJ8/vOXHXHfN+7npA//KI/fchocISIuSSV7bS+/2HM6UhyHJeNVLWmtkZCHC4hNiEJ7gFvjguYEge/gKMiqqYqDrUTQjgRoJ4UkWQ6NDHD7aS99IkYmMzfhkhiO8fhzf19IUWSRFbBdM02NwYBB7eJCpGdiVJIMRUjDLf1quKWthVFVDlVVc18ZwXQq+w5HAwwDmIVNCJotEAYndssQYUJFAk0CW5KoUjYocaDiUCALRGVZkGYPqf1U6vQTSMR4hEATVaeNZk8eMf4pFT7wQBEGVOljd4rH6Ko4TuZSQCILab4jUcFgykCSVIJBxAx+HKaBEEIDvJ4mqSbQgQJI9AtUjEq0HW8W0SxTtKUwmgBAyOiqqAD8DDxnQ0AhLKRLxJvRImEgkTl2ima65G7FS8wh3tJPqbiVIwZJTIRIX106RxPTZLENcAiuYbnIt9kuAES7gBOL9jAIdEpQDmArAkyAWCN9KkqASQFmq/hsxV1WAKUlss8aDDVfPmR+AFICtVJs4VWVhdAUyUhwLAfNNAUYg9leryhZlAwhQiUgqC4GmQDQYMCUNV24hAchuE04AWRUez8CKKNSLjlecs0BspxRA0Ye6uWJcZX3QO9tYeemnue/w7/ArLw2MDdyAI0dKfPxj3+do3wO0ztH49VVnEF4coVx2MGJpOtdcSuM5adJdNhmtzP0jIa77aITbfyUT9IEsRVkYezuj1jY0b2atsdCdrDlxSlUz1mF6qZYBnQpxhlB4GNiA0n0WseWbWLUzzIT3XXzyWNXwWKtenxo4W+PB1MIXG/gpFnWEuJJm2ggzyFY85iNg1BDTrW5rLR5ePPR+COF6Lan+5rzqGKlp8jbxp9Vmtb9VRB55lHE2hWbTajSxvZKhckImYl6qBaLEM6SgmDJNLUnMhgR6LMLgqw7GQuC7VCb38t7rzuI3KZvh8Sn+5uMfYsCDO+7o4dHfbSVyYCeh+DJGxmP0HSqxdJbD3974PWxJwqhLEm9u4iEFJrffSjkzSKR+Flf91XXsi/wr126UeMN6mUkl4PY/lOnt3UrPU/fwix98AUmSSKWizO9sZPXCNu554AHyxeKx+TUWVmnTXMZcKJUnmXzia3yk0s5N4Su4oiVJXIcru2FQAkop7vvjfG782rdZMred+V2dXHbZ+Xz1U/9GPvsQA4fWkTxyLm//4te58f5HeHjLVtJjRVZe+Q+sv2A59W9ezTN/2MfXP/o7JiUJD1Aj0KRDbz8orphHknH4h8WiLtINhBLBuC1x3bVvQNuwgn7Zp6UtzaHSV/B7f0fI14mWy0yOj/55kKn6FNgO2LZ4fj47eEg8ns9UprMkz4UthxFgbMSDz03CZaCsqkdydDw1I95fj9AaKSAc4CTTYtAHgV0QnRMnWteAGuqC7kuhuQG3rgM7cTYbgEvMEt22iWGb/GAcvlPs57FnnkD+42Za0nNJnTMPOeJQjJRAtUCJgeNCIQsT+zmjbR0PoYkJbiIHahPE4vi5LBNPPM4Nbe0sUnUMWeJRq8BHDj8D7jbovoTWaCOflFQeBD5xqIcHh3agRvoIOtYQllTa5RgHQm3QOCimyFUejHgCyVfsaQwsGsCT350GKg7ugWWbhKMqJSG0GORmaJVgjgYE8KthuHwl3N0jJN1ylZMY00l7ltVE+WpaqDXaTgFeUhxT8waq6Vk5gaa3oihNSFIdktSA1thGqrGRWKIOTYuBFCKVSmDEI8jxELNWwnkXwopG0Xrm2VZT/sshQB7dq0rcBGL4Ox5s8+FQX8Bkn0+x32NywsfOQ6XkUC6ZWPkKQbGAWclRyI8zNLiPoJJhauiFkAAAIABJREFUGhWqeTTPVeh+0l4N8xC+6I8GoWJDOAtr4lXS3BymsUIdMUyrpVD1TRAaAOVlKPo4wNNA3gJ7EOY9DdEQKGWQSoihbwNjEPSDcxB2ZGHYOXGTQ4qsEgnHCcdCbFywidWLz2LJaWewdP1cWudKhCIvvo2ZJjAPH9v28T1xckXMKiMrKuWyREWCvAyDFci4UJZFYUYoAnlH9FAt5WByGEF/nkTctN4MoU9fmu60PVNG2kMA4UOIYM3yEZ7+QUSN62bglv/qaTtmJwQOtmLFIp66/VQeBb46BT/ahVjga1FvVaf7mIjuAGL2ezMCnP4V8BUE9exOBBW51tW0FdgE3Ae91WB4QRhYBuxYR0N7C1qkjqHeIaygnSVIRGPwRBcUK6I/hb4TIQfRCcTA3gLWEDR/C077Nuz7MfTd8hj0nwvAuy74OldedQUXnvvcx5vuqv5Ry6Y38jJ0B57fJoYE67a5DgYKENEhFofUzM4qChipKFe985/Y/JNv8ei2bbSsOZ1rPrDuebcbCcHi7hCP7dvGBRdcwH333UcZMXZ/+Pvvs3r1anp7exkBTgN8FLpWrOVHTz0KwN3yIfb01zHJ9Hg/IQbe68h8x8UtWbimixFE0LwQsqfioRJOtxFONWA7Fcx8meKkSn5K5XBmiq2ZrX/uXT9hbVYaFrbCEztgTjNM+dCfPf4zdU0hznhTO7+9uRfXOX4ZbF1zFd1d61jYMJuefU9g9e6lPL6LTO4gBvAYzdhqPZ6SAAxC8RCzFAlVl4hEVFKxGLZq4PoBnm3hukXypRzRSIxUQojOWaaJ6wUEyKiGgaqqeJ6H67rYtl1twjmzBAswQFZlFEVBVUFRVFzXx/U8UFzMYhECGVnV0CPVFdL1QPKRFAlVDWFZFrbt4jgeLh7RkPjtwA/I53OIQkgPy7KYnMjgui7RZJxYPEo0GsU0TVAMVCWNqszGxcRFsGDlmnyAi5B/kVRQdVxVwsViyisy6jrk3AyRkIYWGGhZaGkHJQdyUQCtqII4FI+BGhbuuhuI6tpyEQoTgj1q22BXILBg4Vwh0VeyBIFKjUEuKxwuvdoIMhYB0xLTs6pDShJ+kY0AdUFUqFgWVMqQy4ntIkGxAEcPQHu7UDJAEYCvqooOq4oCsaRIxqku+J7om9ITgiey4rhUFepS1fj+EAQOrFkKTXWwJSNej8UgVo1xC3mxD+kGSKqQSsCalRrnLZ/FI9+VcV6CILcPTEwU+Yc3f5fx4V9jME7+CNx4STv/yg04bCPdlmJuU4Jf3zXMXbvuIRkxWHnBpfz9l1NVwFlnt+8THfsIHuPI/Gmuu4Rgh7sIMDONqPp9TAxbCkAPNrN4iChrUZ5OIh84g1Tb5+gY2s2A9wyDjB/DVWqjvtY7tRa+1F63gV+ynSEOcxfXcAE/YxSN6VKaBqbRFIeXquR6GOF63ItQt++qfrtU3VoNzHd4bs33lcBI/igwxtXKEn7m7cZ6gSZiJ7zpdWhNs5i9vBM9ZNDV3IJV38AdjzzNqx0+WOU8P/nUFfRs/xxTQ0dxJ44yUoRLFkPjX67mineu5vpW+Jcn4A933suDn/8hjU0aztBdkGync/E5nPPG83FdFePi89n+1F6eeGw/3/vKA8yftYTN7WnKbRHeN0/ioxdF+OnTp9ObCSE176Qh3srXvvlBzj9rKQk8nHIPf/3uv2Dzw9vIVDz+7m2L2fbkPgr9toixgWDHZ3hycyfRxsWcdYZIoDQB7z9rDW9a2cXcOV3sm3ovbd1tLOtcxBdu/j/ceMPHGLzzsxS2/5ZEYgeX/MvdnNmZRcnv58vf+BE7nriIt56isnLRQuZ+eCFd1WYXzYj77BPAukYINGaw1aHPFs1sv/oE7Oof46JLm1jZHaJYLMJ/fBGcDJf91fXccNe/sGlNm8ipvJZ5A12Hm78KTz4GjzwJDzz5yre1FIGu1APf408xjixCR65md4Fz12ERdC8GrkaICxoI6tsEYjGpAZLt4u/r3/LPfPDKG+mesak+4FbgfwJf23wrPPRLeOh308otb7iQlg99gIH5bwLgE7+R+F8T/RDsgnYDkopoPnT3zZTeuQa3ewWYBdi5A0iAMiH0a5rD8PUfsGnuOmhVoTEPi7LgNoCRJTB7scML+BnQlwpBoYybf4wfBQGbgZ6FG3hf/adg33tEZjIDlEKweC0cegoytsCLEtUDS1b/rgtgbAKC34MVgZwEb/kux+hE2b0wsQV+eTucvREuvgI+9KOXrg180v4/sf+qbE8CwcrqALkVKd3F2nPOpKW5jUQ8iVHN1psOWLbw4VChqRWau6HrFHhbs1jDX4gftR/hA/Sb0Hek6otUoDIBU4fAzYKVr2AVJykXh8hms6guSJ4MngKuSqk4QSk/RTE3SVAcYLo1qMN0qfNMwcqT9lpYD/ClcbgrCzePwBrAsBBZ9wRUi/yEtEAjNM+GrgloNl/e70wh6qhzATTshAtHoWMuhJch8C1VfMg6Cjsfg383BZ54olpn60L+4qr/wbtuuormlEropXSnfwGzczBwsMyTDw0zMdxPQIBqhDDiSZItS1HTIMXAi0IuBoOqYA5nXRFflYowNSjOH3uqj16gPIUAEWNAh5ChSyAeaY5JUBy7QB6ISGIS+AnwDQQg+//2njxhMDFJkugALpLgxyoEGabr+mbuZUBVrwHhABmIWfEQ0/IFdQgnYhRxvmtZjF9C7ALoXgTX3QQ/eXAxTfVhImGTgfA+Hn9oFqedAi2NsGkjPHEQYlEIpuDQQUTE6It90pqgoxUe/h+Q2/IJGL4VRW7gn/7ys6xf1UIqsZenf9/DsrM2YITk49ipx8SIFQjSAU/ctRtdVUm3Jpi95pU1+QJItwpJw/4ecDWINIJuwFgfNHZMM2Uj0RA33PROrvvbywiHI8RT9UjPpZB83P4e/74uh7mo829IGs3cfPPNfO4zn6G5ehk++P4P8xfXf+DYNm1FxpSVY3nOGsauIFhGJ9tKvQSrWPiZPCXXouSWCQURDC1EsrmN2Uu7CcV1zIqNH6jsP3AYFxPPq5xcwl/AhqdgMi9AnD3DQmx/cgZwZQDShEXPT/vwnT8FFLrmr2VO5zIM20YtmewYO4SqJ0gvvBQjncb1Qti5PFY+h1kqYBkWviw6vQbFEuFyGU01IADP81AUH1WKYjoBI5lxstkJXMfBMCKEIjEiCuBZyLIMEngqlBVVJPKCAN/zcT0X3QbZEcXanmcjSR6B50EQoCgyZqWC4zjYlke54mIYBvFEHEWW8TyPuvp6giDA8318z0dVFHw8PFlG1hSS6SRuNSAPuS6GESEcjuD7HoHn41qBeN+zcQKLwPcJ1ADb9ZBkSew/VJNrGoEc4LkBigaeZ+N5Kj4GpiqhSw4KDlIAigkVE2SjWoqeC7jtY0N0b0yy/OwYyxdBSQJbhXgC6qMC2IyHgAgE1aaXni1ATyUQTRWa4lCuCFkaXYN8RTwbimDf1ori/Oo+ux5MTYpnTYHu2RBRhQsdiYv1JRQBvVoJ4QJ1ElQMsP2qupkkfsOVBXhsuRAOU73G0H8ESmXo7QXDgMWL4cB+AeSGwxCYAlCOhcW2ZFlkgNW4mPNlJMbHYNOFP+GZRz7DQP8LN6gCCOkGl6xax5bBEFFHYBZbCDC5jYAyE2PN/Oann2LVtTey++D9ZI72sOeuw/CljwOwQDuFa0JXELYk7rc/i884BmIJNji++mekek7bEfhInunktINwlU6nl1j5MJLZRYDCCm8xRY5SYJxBxJJeqyxSq78xUwan5jYMAU9SZDO/5OOs5hdkeYCdSJxOcKz+rAkhQu8jnK4X19gOqp/6MqKkbRnTjfrCCHek1g/gWekS1Oov6pgo3n4MdDZj0/t6BWSLHpFygrPO+zjvuaiFH//wK9z58J1Ui+Vfk11QPI/lp16EGrqUmz70MR687iOsOb2OVV3Ch5m/EvbumkeUFlbOTbNT+iZezgY3THjOMq5fJ/G/v7+PgdE8TaE8P/j6RiY9g6NZhWKuev0kCRsZU4kgJefy5ps+zMKFTYyM2dy6fYyD93+afUeGWX/aKWzYeDqtCxQaly6h+KutHN7cA3Id+DIP3/a/2frbm/l2ehUf/vKnuWyJTkdSoi4c4QOf+RZf+e7v6Ns3xsfe83au3HQVn4p8mlFGKQ4d5O4PrOCh+++ho3Uee/dJqEE3aknmsSKEGyTef5WYE6AqMqPAhbNgrSYazAwBXw1Eddh9vx7kmQd7mep9Bkse5w/f70WniB8P4196LeFYmbF1p/BoIsIbNz/J5kvfSqHnNQwJXRf+40tQnoCRjCgrWD8Htg5A8WXq4B9BTCwSQjA4g7jVny1tHEJkV/YhmgCvBs6qfv8A09VsQgdF3MwtiLjj7AbSXTGs/ARL7/9PuONHkKzgGJAbA6cVyGdF7fJiBKB78dt526lv5F9mnweIWKj77CvZ0DmbR7/xNoiZUHagmMUfyfEN3yO1cC5rMn1suaMEsy3wJoXzUpkQjFPLhgkVWhzoGoX57ZDpZTRX4OY5C/goMLt7OU/OmceUdw3rZJVOoCfSDA2nCdrfhAvd74ZzbgCjAbZvhJ5hwRbSEfvfAMw+C9Z9HTQPhodIJhPMWbaQTUj8UIox/sy98NQtcOpquPhqGDwCh3bA21JwS06UrJy0k/ayTULQfxrQQs0kGuayZt0GIvFmtEgMLRzCiOgk6yIYYRVNl1A18AyQo6CEhWblyrnQrUO9Dnq4CsRK05VRe4CDGZjKiMT9eE70rXRtUUGbLQminVcWJeteySfiTxCYk7jWJJ47geqWUV0Fx/apVFyyBQ/fKeOZefBqGZkxhCdUYVqkWed4lvBJey3MAQ47cH0/fPYWWHsUWk9D9CtKIy5LPUhdwNlwURTi+0A/ILiBZV5aCrqCwAf/HfjOJMQKkNoPi1TB/XN8GLPhiQoc8Y+X7j5RbF5qI+suvpIzLzyTN1+ykGS9iqpIz9l064XMKkAxEzDa79K79wmGj/bQf7SP/QcGsEwZRU8QjSVJ1TfQNKtIvH0RUjKGG1ExNej3oN+B/oKIm+xd4B1xIDsO1k6w7gH7ccTCLahBcB54l0LhPNgZESddQbisNalT9gFbgd8i6BdTvBrJkRMGjAXhyyxTEA7QfqbnnlpiaGbnp/1MA63zEBlaj5o0nZhRRxClNsuAdcBW6F0I+5bDuhb4RWcdctgmpJo0z7J58gcjTDSnWdEQYn1cyB6lDdBXCdBmV45jonBmErY9HpDfXeHi9StYvVBGksIsbF6AoY9Qzo5hj6ns06MkmmdR15SgvulZHJmqLE7T7DoqGR+nooq7eGY51YtYrewzRLW/TAxS1ayKoUEpV6Zn/wSO1EFDk4RhgKzINLamaWxNv+Rr4/kBW/YUyRfFRTHCOu/+uzeRzSXYvWucAz09xIDFLZtYsPh02hbNpeBCTIFKyaZSNKvqk9MKOBJizL9Ow8/X1Hzbxy05+I5NvpRDiqZJJBN0LptNqimMp8lYsoyaaKC9eyV/fOh+Roqjf+7dPmFt1alziMZkrHKeyb4JsnlRuu7VfB/EuCy7ASMZ+zmn3kAGyQihheqob1tORwB6NEpduhUjlKTiQ6WQoZwbp5AZATdPIZulXC5g2nks2SASiSDLCoEHsq4SDYUIFPCDCmXLwqwUiSAh6wahwEdVVJAkXNehVC6h6mE0XUOSJaHAKin4Ql8ASZKQZbDtCsViBscsk0qkcT0XP/BxPJN8aRLDShKOhHGBfD5PIplElmVkSQZZQlZkfB9c2wcpQK5x2wMfPwiQDY2Ka4EPvuPhWBau706DroAf+FiOgywLxi4AsoyHh+/L+FVxH88P8AKfQAEnULE9Dc1VkH0BfMpVeQJJFoz9qcEMe38zgp6JcsqNi8S8EkyrxvqmYJ/6VdkCyxESB3JVczawQdariqGSiPV9RchXKNXPGMxo7yWJxjixCMiBkCOIGdOFDbIiEmK1F3xf/H7BFo6/ooDvgmeJebvmsGkKRGUwZPBlSMQgn4NwSAQGfYcEs7Y5DVFDlBYfOQzNTYLVm4gIkDlAVPIGtlgPlp69mt7DDQy8BDErXVc5ffVcQvdpFGfgZ0G1e4/nTlHI3c27L/oYX91SYLI3SyVvkSPAA0LxJqINi9lz6HsMUMGqnrtaM6/aWgXTZf1JxDmeheCk1orzRPuKPWj+Mgx/BZLWSYRWFjAHizwDDDLGtDugIMDPhcyinjoipAiF2rjb+gM9QY5xfO4kx3so00meFnKM8DDTnFatujdNTIvpvLgFCNduJwLX6UXgPBoiLxzjuZWIpGO/GNCNxRvQcAiQEcyM1535FazyJHsOTpB6+0qcssPk4BgQCKqHPQFeDnHlXx1rbUzT1FyPGdhU8hUKxYC0D/M0cb5XReDBeAPFVp+u06J8/Kb3s/uoyZhfx5YH9rBx5RqKUgue3oKtjLJ10OWs5RGaYzIVG7YgYrHDQxkOHpkisHSy2Rieo9KYggWtEXrqVrD67Dizm+J0zmuj4hbwgwZSiSZaGycZnjDBiFPKD1LKDjE+OMYd35mPdd5aZrXVY+Fy2jnreXr3YcZLBoM5m/ZUksbO2QyNT1DOZcn37eaH39zJW9+6mkhDM+GNFxA0KqQikA6L+cBmuvcEEhi6GKNJhA8mAU+XYHfJZ9wI0XTmMvKFQcr391DwQshrz4dEK5rRjx3rYNwJ0Tx/BaphPM/Zf5XM92HXATGhVWyBlrzl7yD8EOzZDgMHXvKmlCveBGYF7867xU1bQkxIzyaeeQigtgGRLapHxF8DiJMaQdzYNoJ6XOsHaQNyHFU28Et59j74S9i1E1ZWM1vNCKyllj3SgJYoV686hyvnncoCI35sF9bEU1zVvohHl10Jo7+CigUllyBrs+voPt7VvoAuPcoWMwbZPMR1sd18BUwfSsOQ82DUhPEpmLcYoi6TqsvPM9sYSS1nZyiMTZhTaeByRP/jByaOwuHN0DwfoqcSn3U50dQSRoISJBqhOQtyRRxrFOi+Crouh9QsKByCZAeyUY8aq2cCcA89ALvuh+1bIR+HU3UY7IeeIRi24HRZoAxjwXNLR5y0kwaIm6UNVVtEpD5KtC5MIp2gLrIURUuhhVKEEo3M7ZqPHoqgGyqhsEJdo+ipigaowu/T4sJ3jOlQp0N7WrxuAflArOGFgkj8V0wYKsP4sEh2FwswUQiQ8x6K6xH4vpD+s8ExbXzbRXJcLH8S38rhOXkcq0jg2Fi2j225WKaNazm4dhnHzuM5WfCnEJNOhWmhJR/hOaiISaZWHnzSXguzgB4H/rMXplTYUIJuFZFxr44nwkAnJAuwwhHNc4vDArqb4MWntJo07ACAB2oFwhUhl1AvXqJQfb+mzHmimISMToTFazdx9nlncMaZS2hsib2k79oWmGWo5C2yAwO4bh6rYlMueOTGXKZGe8kOD1GcyuDZJrYbxw90HMnHIYvjH8Qoe5h6nLwcZoIkE0OQsSVypkV5YgiG90F2CKwxRHRxjBo7Y09koATeMGTWQzAb5AjYMlQqiDP/awQTcxsCVHxlVhUefF47ocDYODBbA85GzEs1ubFnd7KTEOdlFqLEfy0iEptiupOHhDiPDgKQPQ34DewYhnQAV0gSke4oZt7CdhyaZqns+PkRei4Ps7g7xPI4DLUIgDi5GJwY9PSDOiYm8mgMcgehO2Xx7msu5S1XX43v+zz6x72U+4YpZSpYJZvs40+TmmPT1tWCKicJReJoIRlJrqo9ShLzVs1i7FAFK+8RWAGuGSBHJGRNEp2sZ1hNQaYGNtTYObWySM0QtHmAwpjFSN84u7btQlJaiMU0DONlpisQ+rPFis8f7jvAxFQZQzForWvhyvdt4Laf9HJg/xgBYtI469Sr6OpaAlEouxBVYGpqgsmJsap8uvCBayDEiap/8kqsjmqp9Kuwbc/xcMoObqlETs4QTnsY8QQt89swLY9cySZf8DFd0PQUg4VxRouv58Ywr66dsrGbphaVqbF+tpUmGJkCU0MM0Opc7VYfzwcfVGwTW1LQ62dRN99g8ewlaGGDUCSKb+lYeNhmHrOUITfeR3msB6fYQ9kuYZfKeLKDrASomoEU6MiSiqfoKKqE5AcCvHIq6F7kWGMiSZax7QpmpUyxWCEUVVFUFU2WkWVFoH2ehCxJyHKAogY4vgBCy+U80XACSRJAq6wAioUf+CiKgu/72LZNEIAkKSBJyFXWpeMHuK4nGptJHoosge8SBC6BFJDJTKGrOoEX4FQqIIGqqCiKgqzIuJ6Hbdvid4LqkqSquIGHGyjgSrhugEuAj0eglClmM8Iz0S30mIksGShIqIpglSaioBkWw0/uIzSuMPneRUQS1WaYLpgmeGYVAJXBrR6LHhGvSQhmbDEjAFZNmQZlpQACF1xfyBe40nSzbEWBusR0zkwKplmdtUZiriey2o4jJBJylui+q1WBIccUUkWSDJoqQOBaM8MAweyVhyCVBNeCoaMCUJFccUzFImRGBRicSkI0ArYkAFnXAmwwQhKzT6sj/puXBqDIUkAiVmF+dxdHQjqlvAn5IzM+UUKW9rBq1jBL5zdSykEoMZe+nITliZ12Opp44sDtx5qV6oiEWw2QNKvPLmIdqPUOnouoqsgxzaLN00OU3RjSGtDawW2iM1iEjsMRJngUq9pPRidNCiOc4FJrIQvppFntQNcWYNuPUw5ybAPuAzYxTBqXxfiMcA8KYXzCBLWSF+qqzzObgry4DVcfW6vHIyFywN1UtYRnXNuZEvIaAvM5A+dYYrKmsPT6sJrOrolZHuHxB+/n6OgpTE3YVHI+GCEILQJpGJwhcGpO2QvZKyvLjIdCGIqH55dZvmABmplHyYfQyhGciBhjyWSSrAHzV8ANK9/Ld34zzu8ePMrT2w+xL7OGxoYWZs/vpl8p89OHi5y3OEZno8yUC3eOQ0SGnbv303vgAMlEI5NjJrYdpSlhcObiFIOTb8SQp0hIOXRzgu2P9JCdLOFZKulUnKliCb0hiTll4pQyBPZu7v3hV8lOvJV09yKoi/O+922kqXM5fiRBz4SJ7lVonL2A5qkyk4MD5Mf7+dzn7qaxs56N165l/oXnINfBvAQ06CJcqCkgKwj/rb8iwNhlGizXxSg/bILXaNC4upmGZStwjx7BOjqIHI4Re+v7yG/N0BzaTTSSIpvR8MYy+JIqRNnc1zCFPjpDOygZh8Xnw6AuGmm8HDB243qCYg7v9/eA3ApyDmRLTKq1iuBal9lxpht1+QjpsyEEmp1iehJrY1qHpA/IhKGiQbkEjz0iYhIFIZeWBJ6qftYFHAUWreAd7es5Oznv2H76CP3wBVoUFp4LB38FZVtk4HIuo1sfoCtWhxyOo7YtxB3aAVpSSP4UHHBVULIi4+dX4EgWNngwK0o+7LM5t43NySYIFBYFsDFQSAYytzs2j47vhiOPEV53LmbbdUT0LurQGCELs1YJ4fNMHwzkxHG3nI/UchEyFbRyFrtuFZ4SoVAe52kzS3nbT6HnQZjqE5NakIWhAvTmYUSFK6Kw1YYdDvScpGWctJpJgIEeiqPrOqqWQpZXEY1dRN3cNPWdCVo7m2lP16GFdCRNRVIUVE1HQkKXIWLArHkQqoPAgEAVeZREUiS+k0BjIPyQXlfIlJUCGHBgZEywYMt5URkrD4JfDnDsANdyMUwHObCRJIew7ONWAjyrSOCY4NtYbhHfruA5JTy7guc4mKaJY9rYpg2+hecWcd08npuHYBKRnq4JVsLxYGxNRPQkIPtamgP8PAfubvDzUB+DVBrkJGKIWohB1QRt7XDeOPQPT6uvjPDS0vrWjOcS09DXiWq6rBPRYqRjs1mx4RxOOa2LRV0vDMR6HnhOgO/45HM2uUmPzFCB/i27cdwRHK+C5zr4lo+uyUR0qE8mcfwwE8Uogd5SZciYZAt5zPx+JkyDkUqIAa8Fc19FNIAJsggxtHsQpSzZF9irA8A4BHvAzMDIqQjvSEVEI1uBOxCA4ysnEuiqRFiVKNvPj3idUGAsAGGQ/gmCA8AzCGAkyQxqEsK52QlsQLBiVyDO/eIZj/sRFJM9CJ0ngAI8VRbMoU9rMHcD7LvHYKA/Tme0Dvwt3Hz3LHLROj58ucQGSdwYLTHonAtPXQpNbXB2C5ybhrVIzFTFk2WZMzYtZbhnKUf29LD7qT+QCuUpHHmIPb0qe/6YZO3Gq+lcG0ULy8dJAzR1hUWzHj9geEeJVDpEJKWixmfUm1Wtxjiqyg+TfI7TGARwcE8vTz/wDI/f+yAd2mq8BQ0iFfgCNqOPzzHLlQO29Drc+tkbGRk/yML0Iq5d9jbc3fCFf3sL2/ZvO/bZG750KXPmCDS4ufpTD/fcz2P7fksXIhivBeYhjgdmX8+mAe8Abkf47P+vzfUcKqU8U739kLJJpRfiVGRGh2Hbzgwjhwdw8nkM3+ZT//KPDHov0MjipJFsCBFpMhgsRHh8V/XFl6lxU6kkCNQ08fZGplKNJAHFCZAcMF1xb6qmhFFxSIcX43v1JCsxvCBC2TFxyFIsl9A0Hz2iE1JDVHwZ3w6qYvAqYKPrCqFQCNd1MU2TkaGdWHaZZHoB9dEoEhKyKwBFIRJrUANJXLeEokRoqOvAC6ewrDJGSKNsORAYzG5dCqgYVT3aeDyB54mZRVJkUETcWLZMwbRVFFTVwDVdvMDH9X0s02JqKkcoFBPNrEwLVQVDBVUNkDUZ13WxTEswS2vMWFXFVzR8fPBkTBcBxlolyPdx8OiTqEsniLSupXF8Pk3zVkIU6sOCOZqIQmruLEo9TzIwkOHznw94y7Uga1CyJMZzopHz/HkQTYEchtQ0+QjbgZEc7NkGDfXQ3Ax1DYAlAFfHEexUpVVo0mrydPkv4mOUAwhJQvdVlURcX84BrgBGKwWYGodUK7gx4Usg3sYwqt9BNEk0VXAdoVc7lRO6t7IZ8VjUAAAgAElEQVQEYUNUPIwPw9NPwcgIDAzAX98A2QkYPiy+39QsNhwLi3MTCiGWp+cSLX0Om8xMcv0H38mP9v6IoYMt3PXjbXzyttNmfCKM48zhlFP+jdt/9SG++p/LGXXgZz+CzBQQj+LOauYwYk3yEVhEBuGQNiJgzgjimDMIMHYUeAuCbDaCmD9nIxJbdWwhEQRQVoDZSIRpIMU7GOUAu8nhs5QuPim/F9ZcS3bXXhRcQg1xBg4dJI1PasYRfJoR3s8qriHNZu6nHp8CdZj4TNdpNFXvn5dfWeAjCpnuRbgl1wIXI4p9FIRzX2vuVUuwRKuPsxEVcCngm7weihIlRAq9APhgTsEzX+Dfbz2bnr0uGAthzjLYdxg6V4O0FA7fh4DdX8hqrdlent3/6z+yYv0ZbNi0husvv4Tr/unz9E1tYKu9kb88SwQ4LWthng8XScLT+fm3bmGIJNffdD03LQVpGex49yrunlrBt75gMRjITAF7xwK+8G34SQwGbv86aWeUS276PadugLoGCQfQVYV3nzOfuyYFKNqUOcoFF72DhqYWyuUSvu+zYOVaFi1fz9MP3c/hfdXUrb2Lp+++lfrBC+m67L188j+eIVEfI6hv4nAO7vrpzzBSyzjr7Vfgei633ngp8HluPzQf5+gavr5W4tMIXDAViHsoKokQRA2g4gR87knhM8pzJVJzxD1WKcNZ5zWh22W+873DkB2GVdfQsbyRM86W2OzV84HTzsS04LdbSjz8oe9DIg7N9TD4Z0r05jPwllNgw8VgvryQ1f6rG8UfySj8/rOw+Tb41Q74zYB4vR4Rb9gI8HRp9YvDCGKNibg5ayVdGaonGXEjjwKqB6t8Mec+Uf3+3QhiyAXVz8SpLqpRpA/+imaljnqmfe9yEPAlBz6bycPjt0M2K9pFmwjR8ls+x6HOxUROv4S2//NJ+latAa1NJD6OsQGqnY+DOpiKw0d/C29aAJs6oTsCwdfBLrHPUvh4Oc3H3Tj07ob6eWjXfoxT6eIZJEaBUQKQ5sKG70Dlbui7A37+XUHfit2GZpeoX/2PdLS0sJ+A/NhO8vt/Adu+BwdHIOnAuYgJ8MFBAXRHdPhgM3S0w8IpmDMJXzjRIYiT9tqZDqxk7rLL6V60lI6OOUSjbaQbG5Aj0rR+VFiMdLdaZaqGxDAz5Kp/FRVNXPUwpGNwZnXrPsJ3OwLcG0A2A14JNFP4V+YU+CUhjeWagpjuWj5e2QJ3SDQr8CyRGfdKeAUTu1zBdW0CXNyqgFLglfHsPLgVPLuEa9l4tmC+KmTRKQNFTCY5Jip+nMlMR8wqwmOq1ZaetNfKflmG7fuheADe54DeynSZrwsUxFCwFbHOrkD4uTUI6r+TScC81DxWzlnHaRdcwaKVC2lJRkXz4mdx/YJjwzSglIXJwYDikRKHBw9SLo1jl6awpoYIxUBRFYyQjhFTicVidMyN4/gG+ZLMvv4MbQs2oISbKVgq+3cdYfvOfRw+PMDg0CHEYvs4omR+7GUeUab62PJfOCvPbxIwvyVEZ9rg8Z7nF+U84cDYBPBrHf52GA4NIGKjapB5jH5Ua+g1Vn2oiOjl/Qg6ymcQgGwIAXw/hKCfxIG7wStC/kb41Ruh76IwWw6FuOXWeqTYNp75xU8xrPnMO/1Kzm6Aw5Lwb1QDbjlTsJvCyvFNEJ5tTXOgftYcFm94B7/92R9wJnpx82PYxUPceeQJGh6Zz+pzzmL5+lP/9MsytC2Nsvvx/QCsXL/4T0CiF4utgwD690M2L5MvW/QP9NO5op5Q7MXRplrubWbju/HBQe794e+ojG8l7jj0T/Twb5s/xVcv/TL5TIbzl2ziTWdczZlXvIk9z0QYOWzT2mYwZ9H0NlSEH5tFXMoakFzkvwcYqyAaZfz+Vdr+bkyOOBbdvZOUpR5mD+RpfnA7lS9+iceHBig6BdygjBTkKXg5vJPiD89tEtAIuqxQGLHZv31aMK7p4hTJDTEOfnjgT77WBrx7nmAffqGKJcSSc1FibZQUmD1bMCiHDnv09XsoKNQ1Kihh0FQVWWsgkE/FNVJY4TQNio7DKBIBBCoyIUKxFAq+0FpFJdYwByNZjyrLmE6AYpqoioskRdFCEZLpJKoawveEXIAg94gi1MD38X0fVY1hGAEYYcqqzqG+IULREBHDQJFksrliVfoAwuEIhmFQKpl4nolm6OjhEKgG8UgCyyqTz03SP7CTjtlrMbQwmqwhhWWammfhOi6e76GHxATt2B5uILp41xj9ge9PM2NdoSPtSz4oJo6rgpbCSM8h1pVmcqzCwhUX07lkIW1daVItIKuicrVcgoEeuOwdjUT/4l1MjpS57ZYevvXOB1h8yXnMPm0uLd3w0CPQ0ChYEXZeSBAqisjSWqbQiZ2/oNoQKyqqHvL/l703j5PrKO+9v3WW3nu6Z9fMaDSakbVbi1fJliVsY+zgDTAkJFwTQsILgQRy3yRcSEhI3lxIQm6IE7iQAAmBEHBYjNmCjXdseZcXydp3aUazL7332arq/aO6NZKxjW1sMCTP5zP2qKeX0+fUqXrq9/ye368EgQYtIBmD3buhf5nRa7VofBFpknevZohIyRbDutUNAy7bNvvmqoTCjDFSLE9BmDKbBK9ujkVoI1swO2ukjTIZ81zHgv5+kJHplikWYNEymJ42XaizNXjkMQMEx1xz3A6mJU9guhJUBP4Y1J+nSUqAzzYe5Z//8l56V11EbMXphbuhofW86//5Jv7SGP/n09v47n8W+egNm3j0tlnqcxF28UnE4c+cTCqaPshNtmeIOcYa80tapfHzBQwRLYmRgE9g9uzTjJKiyBYmMQ46g9isI4PFuXyEEj5PcIC3qI9w5qOf5X/0fZRFPRciOlvpS7dz6f7Lcb2tZNnPdzHFv++xi/W08Y9cwfu5nbe+969YseFyjvmSaDRi14M+h/duZ/jwzcC/PL+T9wyxG/gbjHHP+zG2Ir0Y4BV+VIWoD7NGLsasJ9/CkO1e2eFgqt0zNJPgrTe8j6jnQlhxtRnU+gikV0B2AOzXwsGbMVf3hQOuzxXjk0/RMdzNkf2LuHF2O5M7jrPlyrVs2TA/zl7dbu6P70eaT3xymPZL3sq1K1K85Tyzzd2DKSS8KS64f2OCTLwhrzF5kLmPv4ei2I+sTxHrXsdd9z3B+65ZTzkm2IGZFkpl6ItDIgbDlkWyq5NLLtzA3n37eWrvXvY+/ihvvf5djOx9giN7T4HbvQPMHRbsujXOa9/1XmbqPgdP+MyeOEiMDmrTx1i5LE3Hgja+zFLgMI997gNMb7uN0p99g6suhlunYTaEXAYqeaOffWwOnjioOPDlKd7xpx309zn4mDG2Zb0hZ07OJsmuWIJdH6Q2axOWLOaehKEuI+GyLgcbXp3k/q3v5A3WrzMqI+7av5+PXXzxS3r9nldojCbqnd83+i8vJso1uPK9ZhKtnsLSnsFoxg1hqkFF5oUjYV5XpfmxU5gbuggMYya1X78Olq01k9/ZjecMYeo7RzAEkxVACpIefJocZzRa/3wMe/9P3389B0a3E+lpzKj05klycWB2in+aKHLlnM+dMYuV+XVEEwWIeSCyMOlBKgOppGmnIIIpCZ85ArdPwQfOh7N6IT4GTgliJ6DSAee+myWxxawnyfd4+t3ZmNUTr4a2Nlj6EFz6Tki9CukMUcNsuUYoUTryAHzzBkjVoEvOgxZ247z+j9fAyrNg/wnYdT8cmYZaDd5vwagNd0Yw/rMHm5ZhtowhFotZxW4OM0ntJ7aY+u94ejiYHWec9sH1LFq8lMHBJXQsHMSJ5Uil8iSTWYSAuqhihQl05BJGEI8at4bdID84kEyZYR+LmRqGjsBRJhfZ3vjECkaSYCqE0nGoTENUMW3iaQnZyJjBepHJGWxAORYy7hKRQPllwsgHFWDhQVTE1jWUDlESHMcGaRN44FVDIt/HDqs4so6t60R+iSgKCaMAJT1cmv0ipzJfm7qWDaQZGucpxNydr/xy7S9SHAc+rGH8C7B5ISxrg54kxLsa2sFzMDxrlpEyZu5YheFDNHmVrxysw8Jkol2YO8PDjKkf7+CzOrmKTee8ii2XX8ZrXn8FmZ4Ysbj1zI53GqrTMDniUZqdpTo3QTg3Q316ilq1jF+vEnkeqXSCfCpFNpslm8uRz+ap1TyKpRIlf5ZKpFh/cYyBxXFcDV60mHvCPr6/VXLndwKOf2EK47b1yonmXXv+cpflSzrozGd54vizExFecWCsI+BcILUFMy6ewIzupvyAQ8MBhXmCRabx+AHMHdCH6Q+sYygAu4E/wMg+HIDRbfB+AR9PwYqUhRiEPZfFOPrDNqYP7OfongS3fN3jgt+OMyAEClOI60rM16ieK2wHbMfBibVw7pZzGd2bZ2TvdibHHyEsT1ObPoo/fYyxXTtZfs6l9K3uw3ENICIwbus9S7oIK4rZkZDWQQfRGOnPV2Qg3wnL4t04znmEXpyOQRcn8eNffcv3HuXhB/fTk0rz2jdcSW9/DK9cZHT3E8zKMhJJpBRCxblq/a+AmyRvxfEii6Xn9DK8tYZyBHbq9Pdtyio0276b9b7k8zifPy+R4uX7LiGaEprDkSIECjOHSZYmCZRkvFYhIkIT8twtoEnMBBxnngXWXPgV8xY7EnMTtWFuriSGsyWYF2Yew/DeKhh45efDhs2yLVZuGmKmVGZyuMih7Q2Gjwt+VKdaeeYNXgm4ewbkKbdQridB6+IY2T4D2rkWZDosshWolS1U2oBythYI3yLTkqc1vgw31UJrPIuwplFoZCSQocC2HIgqVGrTlKpT6FDixAAVIrXEFsb8qrNzIZZjk4pn0FKgFGiE0XhFoJRZ8o1mq0AIG43CjiXo6O7Fdh0sJZFhQBR6hEGI49g4jkMiEcdxBFpHKBUShhZoTTwWAxmgozphWCXyKiQcF8uKIZTAtm20Mjq1GohChbAslNIEoWEChGGI1TDwklKhlI9GoyyFQqGtGMlMnpb2RXQsWErfYAeLzlhG36JWehfFcNuNnmvMhSCAgwcEC4dsuvoydPckuNZzuLs+RCVyqVUCctkYa86Cjl4jCzAzacytnIYet1ImYY/FjKZspWoA0iNHoThhGKYrV0EiDkRGf9YWhi3r1RqSAIEhLg0tNxIEutHmWvehUoDSLIgAZB3mQoinIJc3QK/0jKmYiozurJU3HcC2MMfoOKawprXZq05NGffffCusycGxfdCRN527iYRh1Tq2+Q6Bb4zBUg2d3ecbAQHfvu9faNn7AMGprpPA7MxRbvnBR1ipP8QlVw6hfJ8//dBOHn/oH8hWjtLmrkKlsszWzNzenFHqzCeoDmbpbnoFxzB79QCT7OYw2MWexvPacMjjcJw5+jpW4OhBRKCwywXOZBkFjrCHCiMUeSSos3jmm1T9CTonVvIfpX9lItxOhjhXcRGvoYU/4y5G8WihwLUc4GI8Zu/fwSPTCwn6NzJ9AqaKVXCX0dn9S0xNNMX7X7igYYTBaQLg88AFGB+g8zGzcIwYDjbN9icHM9suAt6CIef9kJevwPeThwaqhpWnLJBzQIhfHgVrDNtaSGb9uRSPfxXGHoDqDCTXgrsOop2gn01V7cVtMpU6jJMq4bal2DcySuBF7H4yIPntOr2tMX7lYotpLShqwBYs6MqzcWmac/sd0jG4y4OhOHRbEFqCXA46LJjyoFzSqEqE0mNASDh3mKl7/obtB7/I6sE4nWkQkWTbk/vpcwUdXW0oJ8bQqrPZfeAg2qsx2NnOkclpvvP1f+PIoX0/8p11ZQT/yB2M77iCNdesYOJYjcfuPsaqpXlSqTxOpElFitdd+RpuveNf8asFRnc/yC2feB/v2fQ3fOlhn4Nlwfo1LbhxODdu5ptDbYqoNMED98fZ15tmQXuMS9fAqphZ4esZQeo8lzYJeyeh3YHX9cO9Luw+CmMp6OuxiHdnufVIFpkFtTbB0D98imPfHUPu/D6MvzyskmcMrU0l7blimTCAnrRgcRJedTl87wE4PmEm+2NzJlU6FfNrkj3ApDYW8+mQy7wjX9Njp46ZtIoYOrIDOasD7DTFQJq/ZyF92ZvJX3ghvcBjX38/ajKAXgenr4XNWLQ0PrRSr/LJO77O/tFHqdaPQ8KfP6ZGAdBUBhSVW2/CDxSt172Zsz74Tnb//SeoHh+DjIKSbaQS/LiZXGc8KFdBJqBgwQ1PwaUWXNYOA10gqpA5h85YL9p2eEqO44/dAd3X0ua2kUNwHI1kn5EbqMzCuR9mZes6Nth9OGR4WEm2HX+AUrZmNBaueT1M3AWHJo10godJkC+/Gpa+FjL9EP8mdCyExWcZvR1/BMbKUDgKO6oG4P4ZxnLaOCu7nMUDW+hbfTZTs0W2HX2Iuw7cyo6Xpf/tv0o0rOhj/Szo66EllyeZTGPFbXIdvbS1dtOaN5WgKNKEEbjSwnEgUgIdaiNmpS1EAMKZz3FcuyH7FDOSfcI2+/GUZQqd3ZjbugCgYVaCKAEl0BVQfqOnzCgJoAOTn0W1sLE98qnXSgTlGZSsgw4QykcGFWRYQ0USqRvdbY6D0B5CB4iwhAoqoOpoVSMKCgSBTxgqZBRhowhProWn7pab5jHNxySn2Mn+d/wUoykl/u0qHDoBi6ehz4XWo2BJI2k+UzXczKZMUBIz5pZgxlwZs2P+cUJNL29YCLsVt/XVLOpdiXIUERFhGDA1fICo8iBEP9r5YuPQ4wyy6sy1DCzpJ5dLEFUqOLPtEBPGGC9pCC6RFxH6Ab5Xp1YIqRUColoRVStQq5YoF6col2bxakWErKNljKCcopRKk0incaw4tVqFUqnAxMwcJ5zLiLku2bTABlI4rMVBnA9L2hVz58X4p7/6XaqT/xeCH/z0T+nTIiWgNQ6Le2BFf5bOXIZsugXbeXZC5CsOjLUwWP2SS2DsKEw/hrkD3MbPqaKpBzAjewCzizuOyS4XY6rSj9BoHWr89AC7YfYQfP4AfHQQuhwYaIGLzhUcv6ifue5jxBMtWFMKC1P4foHdyyfDti2WrV5CzEoSSZ9C6QSlAzOUx48yPDdHeWwaoVpx0tDW1UEikz6pEdvV145XkhRPmI2Jbsy94nlsrIWAlnZoac8TiyXx673Yaet5vfapbbu56Uu30O46tCT76F2mODGyk5HDT1HRAbqRvbbE47z59b9OFE9ybP9+SpPHSbZDR7dLS5tN6hm0E5rLSVMfJc68gcsvQjS/38sTHeD0oBe2gISpuTJhpcLJHokfaVtpRYgECLfxFwt0GnTTecJlnqOcwNw4CfM8QmApZhnJYSocPY1NgcTsMo5idiDFxuc3GaaFxu9jL/0peAnCsgQrVi9m5Pg0R/dMMDVseA5iKaj2gCB4ZiCgAjxcPP2xllaL1m6bzAKwlJFTs1MWVsIiHYN4G/MbOl+QsOPk3C6SyTTE0zh22aRWgSasS5TvocICViVN4NiUC5PEhYPWPlqG6ChAokhnWnBdG6U0CoHSZtQZay2N0gpLWAjLQmujUqm1hbBitLX3oFH4tTJRYCrzUkpiQYx4GKKUMuZWQiNVSORrLK2ILNA6wrI08XgSC42wMNrXWoAQCMsyDppKG+MqrYlkRBSGgCSKImzbHJNSijAMQIdoO46yBDgWyXQLLfluWjsG6epZQbajhWzGIZMEO2X21sI2iU+10qg+upBtcTh/Syt7d6/AdVLEEhoh4IzlhvE6MqM5fthoq7pxge0alm0qZRJ5zzNyQ0pDtQbFabCzkHaNhIEjTGIuFcyMGcMG1zHAablggNdkysgQaGN8zdQYFGc0XlnT0yeIAgENXXgnwcnah6UhkTJyBNWq+V5SQ3uHYcbKhlhtEJrjS2cg1wonDhqWbSze0KIVNPR+zTqhtPnu7gtcwHYcvZvU0T3EaKGhOglAoTjKD3/4TwTxjVz/3kuQURv33bGD40e+yCadYEE2h0q2MIcp3USYmcZjfs5v2mQ17zK78ZiPWb57gSUIWsiRxqGVPG2xTipDA+hFqyHRZYCYY7MM7j+PqgpxOE6NGnsImK4doVTvJCsSHHb3UF+QZaFYzobgDNonp/gy97IHGMVnL0e4mEG+//hjHDsSp211P0er7USlGk5kEY/3Yvhee/hJ3GXqmOacAvPGSquBVqwGGDsfNma23YCZkdswM+wJbMaRLzGX9KUIz+xE9KlquCGURrGyE8QHrkDkB9CFw+AF0LUI2s6Cgm/aDHSz/elUndgXu9GcxonXSbYm6CJGe187xw7MMfP1nfT2tPHWCxdTtG2OFup4x6ZZsXwhK5YJenKmMLOrBK3azBE6Dt15aLegGEIkHbDbOe+cjbiOojBXYN/e7/LwtgMkyzHS/VkGujoJqmVGKgLXTtOzsIUtl17Gd/7tyyQjQTpumOZbf3j7ySM+TR03LKFmdjH86J1c9RtLEbUUj4c2UyXB0tZuXDuBq202X7SBO+/9d/ygTm12lN23/CP7tl6PHulEeVkOxEICy+HqIUEmDXvbNLiKYEZxHM1YACtWwJADAwISSQiWGKysrcPIiWxqhQMK9h6DooZWZe7Zx2tmjCY7W1nx7nfT6xxhvFswvSOi8NRPmZkSw7SptXXB8OTpOrZndkNQhNkAsg4M9UI6cbrRwjO9X9P8oILppoN5MDbb+HsNczP7zE9yyjzWXo/hRw6jUpo0KA8LV1zMqkt/i7Wh5snBz6BqR6ACVluWAeY3Yb5f5we3f81oK6d8k44VTzne5uco4JF7mE628si1v8Yvvekyxr/+A6ojT8D0FNSTjTcEYiFMlKEegp2DSgy+fQImq5BYC7obBtKQWEtcxKiqKSbCneDdDWodMe2SFlmEBkoPQXkES7eSGvodVmLY/oH0edKb5bHaPmP2mG+FLb8G+xRM3AFTMyAdWHQOnP1GkJ0wOgsnJiDfBstXQq4F5rphwSSUImOoMvyz5qDGaHM7ObflLJateh1WxWWRPUA4VWC8cCczlJH/DYo9j2i0s7pJ4vE4MTeJZedw0ivpHVxCe3s76UwKkRJkEklidgrbSlCvGsNYYYFtC7QWSATKAi00aEOOFw1nHAtTqI/FTF6USIIdAzvZ6GaV89r8gYCYNDqgQRGiMsiayfGabHgZmDzPFLdDLCXR0sOrl/CrJVRURak6WnpGhiCso6VEC4ewGkDSRckQIatYskQYlFGyilI1wqCI73toJUCBTYRFgEY0bDybGweYV50/lTDzQsdd0zHw5TPQ/K8SO4GpCnRWzA65m3mfgzpGDqml8Vgzv+3CLC9NT4ka8zJVp9bbTo0mlvCy9AhYSazEcvoHL0An4ijLQWsb19lHbVJSL+6kWpnBLISNlwibLrefvkULaevI4loRlalp0kES4jYkwMoqyjMBYdknqNep18qEnkJHEhXWIKhRr1Ypl+Yozk5SK82gQ2Ow6zgujuMiXBcpoe7XqdQqzJRrTHZcTOjrk94LArNXSPXBqj6LaHOGf//G1VRrd8Hsvfwsx3kCaIvBwhys7YfOdodYDJyGqfazxSsOjG3GO7dA8hG4EczITWDmoJB5sdFJDFC7DPNNRjEJlA1chZGRGMMkV/+AKY25wHEQfwN8HHQLdDjwhk6LRR/ayNLcRlqfp8be843FK3vpGrqWpRdezC2f/j/o8CFaEg7ppOSRe2/kxLFDbLzsMpaedSZWtgFsCEGixSbRYjZruuH6qhudo81rqp/hTj31ejuxONl8nJFhiDecdk+NUzViZSRpdeZoFXvYfXgHN/zBEY5zkAqTJDl1UhAkUnGu+e11CGGx9Y6QbVsDZEVx/kbj7P70MdekbGcxl6nWeKyHXxwwtsYLsXx5ISFAXE66/d1c9HsXMT0HR25/mIltjyH0IZT8DE29oebN7rAJy12GjrURKA3EG90tZQzfqlltTWPqdr+GUbrpevbDOOlO9FzHehfwbeBTvFxn4ycJSwgWpVv56uNPMnpoXqMs/i7IrIqRnI4x/TSWr22LU+43jVbmvssDORfiLaZVPRFBabvi2AHN5sttEh1QqUG9Avjm/sklQOfTyNwSHBpgWwCypvAK09hUyUQDZCpT7NzxIJl4iC08ZFShODtGpe4htcRFEoYh+d40CIGS2rBsiTCSrIZSKaMI13FQkYWOYsRtlwgPX9cII0ktNItWIgoJwxDf94kiA9JHUYQv6yTsDBXfsIrj2TwL9HLS+XYsJ45sVo+0qZBpKZHKDBCv7hFFEVI2hZV0471NREHD6kgmEU4MIWxSiRypTAdOqoNUSythJKiWoVKETENXXQvDOB5aAtmsadsPPKhJQf+KXvr7DSNsdBoGW6E6B4f2aLberUjFbdI5oysbT8IZS08HPN0ELFsCQbcBZVr7oNWC6aoBbOs1OHIYerqgPW/MIOy4kQ9oazPH4/swM210XcdPKOamAtaen6AlZVrffN+Yd8Uds2mIu2b8xBw4NgYH9sH4CXj1ZeZ7ag2dnbBgAYxPGdA4iuCizZCOGyApigyD1/MgnYZ8BohDt9fQjn2BMQT0YHE7GQwVTDcuc8QDP7get+vbXPeGa/neV9fR0QFny2Wc4XUgZ2Yx/EgzH9aZN+tqln1c5h3dfeZV0DyaKVSMX2Ej07QSikW4C86k/6PXQw70kIZYEvHgReTfJjmnFifPVio8xSiwpeUa1iTOQdtZbmj7MvqyAYjHKI6e4D++8Bv8KpKbMeDoR1FsZSEP8hj75w5i3+8QP+OXqU2WKVVHkeoA84I6z5Quv7B4CqMhth/4EBDHO3kenimWNn7eiuDjZPgcVUaIXnnbf/+eH31MHyUKM8yVPPT634ftn4KpXTB8C7zmU/BkFmbSEDaVg5smJT/ZmuEHPsm44mN//mo+nBT88KbbOHDzNzmUWcEjf/ZhwtYUe3eO8Onf/Cr/sv8D1BIusxiw0Z+AT+yAM8+Azedp1i2KSCPIJizyOQc32cO3/vMLdKi3D7QAACAASURBVLVluOP2u7n66jez7ds38EQguXzLBv74f72bc644n7tui+hzBGf2WPzJH/8BhWInD93+FfbsuvNHT9PT/y19jt//l4hjV7JmaCP2WxZw4+e/yVkXn0e+t5N0VuBVBk5jWESR5PLLP8A3vvVRLl3Yw/WfK7DgoTZ+/b0WXYOCIcuFtlX8xXUuO5Tg9hnYPQfT7eBbpgcmg+F/n5k3m8udGkbqcNVaWOtAn4BPAstWwf4ROHQALj9b8HvvGeKm3/4LbnzwSu7YctGLlw54MdEOrErDNdfBX/wbzJbNzWRZsOEqGL4Pju6Hh4rw6KfmMY1ny1/aMcNvnHliWhazi27qwgaYyc3D6Mi6GPS6D9gBCwoRU3XJIxJDBJmGS4sOv4rLRlvy93/125T+v8+gTwxDlD3988MAtj8EC+vz+52GSsFp1asYMD7D/cMTvPl4jellae590wc5wY2or38MAzfloRBnvvdgAUjXVBODVrhzJxyXcM1q+N9bILmQEaYgeBSqN8NQFvSdjOs642wwn73jSzCwhsTAuSxVEcuEze1o9tQnOTx+DyxPwuhe8Nuh9QpYvRFOXA+7H4FqHt56r1mstr4f7v0H06n4ngbrJuyBpWdCTwEWd0B8B9x6/4sYFC8uzAa/WdQ2lJPvMs7B2XspPDLHb7ib6F7byeqBjbxNdeLdXuAm/RCFn6BI918jGkCsWATtS+lbtIjujjypFkEm0UhScNAa6lWbOBksO4ls2tUnEsgoie85RJEpDNuJGDgWUmoSDTkoLUFJQSxlZFpSGUimId0CaPBD0+EwnoA+C2Y1jNbg+H44MQzK0/Pd/w4gQYUmN/c9QNXxfY+gXkP6PvgRfs0jCCtIXYKoQkz6ZoqxXGS5gqyB0gFS1kFWCOqTBH6RKKzgECEjD8eK41gOWvoksAnQSFSjyxFzIKeVrAWnA7XP7xoIkUfQg9JPvQTX9Bc7BNbJLmUT+pT/AlpTYX45KGNm2eaS0ZTmcmn6PGoizCzc2nhOkwoVYnLeJuVhnmtoEUedhLxe2lDoqIo3fYi4XEnGbiOdydDVMciZQ+uYHFnO4b338uQj30Dz2MlvLhDY8TioEDvycYM6sjTHpNKEkUuoNNL2qZTH0PUqRD6CiEQib/a4kSTyPcqFOcqFOeYmpylMjlKcGGW8OI6nA0LUSeJGgNk3zBID+zFmihsJdSe2MOc6xbzkF0BmI8xM9RLNngHs4mfFHl8I9HdAfx/0tULCqRAGAVEwi478Z33dKxaMvQzYfiHc+D7g7zGoXRUzghcBV2MqzzPMG6Y1E6QjmJ7Ad2B2hD5GLCYALoEFvwPvfoPR4A4wE/W+OVjfYSpnL0ckY9Dfm+U3P/whtt/zBEeefJix/Y9DeYQn7/gsu7d+lQUDZ7L56ndw9uvPx3afdmniUC1AcRh6l8w/rJVhUqWzxjwGxWmisq3tcO6rDED7TO2qdcxpa9Wat132Ue5/6jsMz+1EAjt52JjrcHoT+urFW3jTZf8vIHhoDP79h7dz4w0f42vf+CEf+9c/Z/XydtqfxoyNYy5hiOk+KmEu2R6eWbb85y0EkEfgvCx1rPex8a2v5zXv28hZZ8J3HoClF51Da3Y9K5Yq/vDXfoeWik//ghjLLuwgMQCBcpidtji+J2THp7/XQPMDDIT4EQw3q7mEWAad0tZz4w0BZtVIYC6oj7mgp+UFzUbc32t8xivo6sbA7rS46KzF3PrlOKOnFM+8D0DqN9N0X5Lh8Cmjfe2aTj7zT69l+coOLHWQg48f4Juf2MMD22FQQXsEsZSZSCemYd+9X+Wpm+7gkiv/hTMGoFCBQglsbVzuAw0yBLqhUoF6Q4vfUQKv0IGcbSUTQbdYwcq1G9h9/3eIiSq25TOezjM9PcP08bupFY4iRIpc/+sIHIsIiVASm8ZirjSWkjguICWObYHlUKjNEXdsUukUMbeDZNKmWqwSBJJyqY5WNvFM3LBfYwJXSXAMI8GLJJFUaCdBNXJIuHFsxwYBjuMQ1k3C6jX6/cMwJAp9ZGQ0iQSpRlrSpBQ1NjKqhq4A8Q6k50MUknAN+BpvgXQOEplGK75jzBhi7dDeadrJDhyH6SLk83DBpeYtZ+egMA7TI7CwC5b0C+bW23h1oycW1aAwC+NjBpDt6YZcDiIbdtwPk0VwU1BLmuR+ctSAtokEnLkWurrMiQ5C6OgBkTTJvxM3UhbdC6GtG5SysO0EfT1Q9czzXWkMwRwMq0PaDVmCBJy5DtasNeZhAOU5Y441NgqVOTOGjo/A3oPwR38CyYZxd7EAXsmsBVqaPS8CKqGRUni+0YQcLYrY1OBZFPJ+93Ww6Wp4vKFHG1Fgb3gbh8P59qaI+aY6zenJZwYzlXiYJTwNvB1YRDshi9iGxxkd15B/4zk4b1psgJK9ULlhB9G9R2mVLrReQkI79NW72ETEk+zls3P/my1nv503XX4Dez6/kxP/+M9E0QyuDjmPS1nBpXTzfdp5kJuB17CVjShWMsU9/DVroyuxetuZC5KUSxlgNRQuAfkt4GvP/0Q+S9Qxfj4/BH4X+C0M4PpckUDzhxT5PfdKPqUn+aNo2098HC9PJDHKv48BAXryScJ/fwuL33UXU8cupzplgdoBB47AkjMhn4S9HuaMvDRbjlTCIdcSN81UDrT191EngcgsInBtdh6CHQfjWJkFbBKCQxgfooINf7gaZlbAuIId+47yOxvX44iNrH3dr3LBG3+JO0f+hvszCbwAyms28/u37udL//Y4/a0LcRd34gAbBZz7ahttwUhJcv3npmjt2MwH//5yetxDXLt5848etPFaPC3+/Neu4JJr381Vb/soF5y1lsHlA6Rb4wQEFNxOLv3lD7Ltnq8yfGAb5u66j0eYZkF/nGuuge++45+5/83XcvlgD1uqJfjsR3jbrutQA2egOjs5mIWP/08Yy8BhDeuFyS2/fwScGrSm4JGjcJ8Nb1wGf3S+MaJ7y+ehdSlcfpEx3dsK7DwItcJaev7uMcY/eBHaq/BTiXGgUof0XZD3YAHQk4XzNsBf3QjlU3KPptzAs4XNPI1fYXZ645glqgVOcwF0Go8lMDd0npMdeedcczlzA108+NSj5rm9sC5jvIZtYXF88zt583tHufX+78H2A6cfQzINb3wXfOuzoGZNjjWGAXWbfa/ZxudHwNZbUZet5ODhw3zjDW18SW3g9/f8Muz8BDDYOEjdeEETmLUaX+5Vptf2/+6Br5Th2LUQ64TZGBweh03LYOpRCB8EJwtd66BfQfU2att/wPbKILs2fgW17wfIaBhW9cPtH4RCGRa9GRa83ZyYS78GGx8F/yEIvwh/+RdwfBTyLfC3m2DJ58E+BNU9sGc/6L3w14/A/VPmcH9KrQBXkOVVXVeQcXPcdeJmvsMsEthHgY9HDzG39Q1cPvYeFrSvJpbJ8cubP4D/6B/zUH0/B39OJLp+emEBeRKxQXKdLaTaM0g7R7w1SYKI0J+mPgeeU8a223HsHK6dJkpkiKIMjpXGdRM4JBpk94xpi8IhQhCFEi0FUhv/F8sG2xUIbeNVDJO/XDJ1B1+a4rduaC7bcTiaA69q8qnpYdBzoHwFUmJpSSQN4SHwJV5NgpZIWSHwqoT1Cl51hmphnMCfRUYlbKo4kYfWdVABMlBEoUbboFVEFPhUK9NEXhEpa2gVkLBtcraNEBqtI9yGUW5VhXg6QiJxySAJGntwxbzi/guT8RlY/m7aBy8m0d3HA1/cwiuRJPNKCIFLnnVccs7rWdSzhFyujSqSRFSlToSnQqRfozCxHZSH0BKkRkQ+db+MLyPqkYaKh5IOXqhQUZO95COjACV9XOqNup8kaoCPkoiAgABFhCBOmjgOFkZiLuLEye32S2LfpufA+zp33HoziAGEuwonezFDZy4mHasShoKcNUhBNV1+JFpbROU6VCpExQpeoYKXqphNkY6QShOEVUIvBBlhC4Vraxw3Iu7EEdhIJZBWK26slUy8gKMsZiYq7CTAQ532vfSpv8kpPrArYkkvLB4y1lCdmFVuEWZ16+qF8uq3U5FbqO35Hsax4dnBz5crejqhtx06Whwcpx3pJ9CBMAwcWXjW171iwVgX2LAC3n4V/OvfM9+mE8dgPLuB/cMkZUT36kUcu+8bbNy8mTUX9LJyE2QXQmY1xpVcYoDbBJCGZA7OSJoqRYjRIRzKGSD2JAMOsw2tBZAUkH+xWgWNEMKwFmOJBEvPXkl7ZyvHuvv4j098mFppjGRiisCb4VvTE2zfcSGXve46BlYsR2Ssk6+PxSAdVxzaUWbR8gyxhI1Spk02lYa5aZiejpj2q7S3tpBOC1JxyLrgZvgRtirA3d+9n+/cdA+LXXhq5zcoF49haVORiTfaIk+durO4rFvdx6++ZyNCwMTeIpvPupQrvrSEbGIhK5ZkyDT0YrWGO6ZhtJETCwzp/dTJpMIvxtJg2zE2XvoBlj76RSYKx5l7Sd+9i3I1x7Fhh4Jn2G9aOUwVHQo7Na97Xx/dCUl7xiLbluDxbbDjW0eYPDxGrVgAfREnW1yEgHgOOnNQtc0FaLa/gUmA24A1mFmukRAnNxpzoUBDpdGuzRQGpW/ueSaBwIFKCkb6YPtXQP87sI1XghVN56Ju1l9zNvsPH6BWf1obgwfj+ysU2jzYiMETQnCcMm25B2lpiTF2uEh5tkS+FfoWQrbNeGQkG5W6jjY4/5oLWbx8CVuWgh8D1QIiDkHVAH2xhsmTThug0fMarVZaYCUEiSy4vgBPMjNV4eD2L+HXyrS0L2blq96OHhmnrWMhIiqAYxNPpNDlOtQ9Qt+jXi/j4GGpCCFDVOQTswSOZZinWgR4oU+pOEq9OoeUIYkwSShrYKcQVppASkTDFExGEtdy0YRYWuEgUNhIGRKGPhoHIQS2Y2HbNjE3hpUGr1wmk82gVYooDKjWCqiwCcc1a8CmndJ2UqSyvaTaF9HZ2U1bLkcmGcOJg5My5y/UEFTAaTcaYdiQsaCoGmmqDT09EEZwYsSYVnVnjFRArQquLVi1Fg4cgOHDQMPIq7UDZg7Brv/YiSwV2XD9JhYuMJqrpRIM74FCm9FBijmQsIycwOzkvK5rrQLVWdO6FIXG1DqRgkwehCOoF2BMwlwFoobBV1u7aakTVkM/VoGogCXMjy1gdHT++C0HoqphapSGq5R3zVEo93GsJChMQ2kK7NCAsdmsYduOD2vylTKjx57/jnZ+XvaZeQaAzHEcvvCFL9Bz9rncdv+D/PMNf41Uii1iPUuZYUSPndSLbULuDaLJaVe+jgFg88BSXNbzZhLs4zYm2OrM8ierP0DmtzcgSg4TX97GF4b/jkIJVh0tsLYco5XNoJchZAcZ+2zOkDMMMsc2PUPi8OMMfeuTFAqCpQvPIdHdgtXlkuiM89BXdjJZ3U8LI7QxzBySHDCIpkNXuG3ij1D2G5CqHcJp4BioUcxk189LIWTY5Inf1HjXj2L6EcxKb2ESlXnGVZNRnIie4I049LCAGwm5jzlqrzyeLCfFFbQHfpmp73+W5OLzcDuuofDgOIzdBGf9KaTWw5EJ8Kd4qcqyCzrzLOpu5Ysf/xoZ2c1vvWkTSgd8/N+2kRCaJQug4zUdXDd0GXnHolA0RerFWdNptyuAO7/7be743D9SL5eA3ey664so/yDnbPwIn/2qR8dCl3WLHN62PseWlrWkYil622L4Ej7/JKxcKTi4f4I7btnJrq/8HQmhUceu5ryNm7jxa1/jXe94B6XSfJEjqR38Bh+qGX6tyuP33sH4pMPUovUcf+Ru2no6ae3vpSMV5+hwlUrl1E255OaP/TVrLzvAxqvfy6MrWnhyt8NADjbkHeheQX3X38KBADrOoPzqv8VSFq4WBAp2enB4BHp7zDw3WYR3bIGvHYatBfjwo3DxubCwD6wsDFfhE0UIFGxIwzlnxvmn7BKGPvXP7PvHG5je9vBPfC1/bGiMU+Ejw1CODKA6U4fRp6BcN1ovT4+cA70J2PM0wFgxr/Z0qt6UdcrfmyZaTTC22VhT4GQ352bH4a7SFIfHDpoHsmC7jY2WELQ4cf7XhddzRmwhX6rd3GhLNh/Xlkjxjavfyh92L2R47rhh1HWuYWM8Tw5Bxfe5f2oE/uHPDdBcC/GcOX7vS49yw1VruHLzUqwP/zL/81duxZS4Tj3gOea7oWJAHFSvSeimbPjVv4B3XwvLe2D5bwBVyIWg5oA6iBHoaoFiCQqzqPJuAr4KCxPGCO3hG6A+Bqs/BD1XYSFYCIw5acL0WnBbYOx7RmB9w2rSGzezauDN7I+1URUW0dQo3HQzPFWGsVlok2aDVsC00r3MoOx26mzwUiy3Bjir5zz2j9/BUS2pAlVCviv3URj5HOvnLmRVdgvpni4u73sb2akHyBYf5QCHqPIytRT/XIQAWsDKYrktZNvzxKwMKqYoe1WkrhPqBMqJoWzbaAQ7Atv1UbHISGNJUFoQoUEoXEuhlETqkEgGSBVRDwJ8LcB2STRkRxylEMpCaZfxY5JE2gGlCYMIqRUqlNh2AjsWR7g2wRxUSx6lWY+ZsSqhJ/H9ECkjhJIIIfHqNULPI/IDkJHxUNCSSPpUSjNE1WmUKqFlGR1WUFGAVnVU5CODkEgH+IGPlhJLSoKggqN8LB2gMcCV0grHFljCNvODDbbWuFphI9EEDfjZnF+LHD4JFCVeiEfH1HSVgQ0Wr33nKvzq19h9xx9SLxx5OQbBz0EsIWV30JrtYGFfL4ODC8kv6CTXlqW1PcWiRXkWdy0kk8zguHE8FJaO8NB4oaZeiNi/bSMjo8eYnZ2mPFMmrHvI+CyWDkii0YkqMTtGFEaEQUgMgVQhqIhY6KOqsyjpoVWEUoq4kkTKcG1DJB4BYYOfb/qyHKCLgGlcVLPvARuTJWoMuWFV47GmVMLexu/PPieFRFEIHIeoQBge4Nj2NK6tkH6NuioBKVKiDyEEriVp62jDjceJJVPEUhm0ZRHDAlfgxiChk3RkkyBDhPaxhIdtO0R+iAwDgjDEdZXRWfbreNUaU9USQQNzeqYQlsvCde9m2YoFtHZCTcGIgGEPjtnQETMrnB9AX38L8Zbl1Jdl2f94Bn/qZpS3i5+Gp40pQUF7C+QzDinXJpBGYF5jG9nA50C7XrFgLMDSNrhiNfzrlcDjQDeklsOZF0HXQaNrmLI13efArjHFpRdq1m2EpWshE4N2Aa740fzq1KhhNvJ5+0f/9kyD+FSN/xerD5rvypNMpHHsGEvPupBju+9F1mepF8eZHJ9gbHSC1lQMvzxFx9Ih2vrMzaCikKDmMTdapLM7jpURaGmdLJRpC7xQceR4FR1mGPGmcS1Jb2ueM9YknxGN9SqS6eEaYWGUcukwSlZP0uufKS684EIufc0mzljTxe7dFcb2TLB81QIu2ryOmRndMP9pnj/NbY8dZ2Smetr5bF6P5+oY+3kLDYSWRVYIMvASg7ECryaYK4Boh/42o0+qJRQjwcCmOMVhKEyWKIwe4MhDLkcfDCmMNAQkW/uNonSzh+JU0V678f8FQA7cHLR0gbMWVLcBiaIyJC8w4KHAMMlliAFfm2BsBIw03rtkGfXq+hugUIVKFqr3Y5p0f3aRyWUYWj3I6OhOgrAx8lyL+FkdtHYkkMtCZGfI4te3Yy+MmHqyiBJ1vOIRU5yrSVRd48QgmYDILyODKo5O40njaH/G2gEGlgyQbzcLYrLRGuljugQjzDnVoXGqdh3DuFTSeOAQWRTGDjB7+CmmxmeZGHkYr+ogaWfBopVIuxvXHyAoTzA+tp/i7HHqFYkMFMiISnUaixJC+2axDzxcGxxcLOGgXJDKo1Qcx/MMIGAhiaiBlHhBEcvJQxgiIyOFYJSEm1CBwLZspCWQMkRraUy7XIcoiowsQRQhlWoYiGkQEkHIPJW6OYs2UFWRhFiGRLaNZLqVWDwDwjEsUgyA6QfgNllKDYwwagzpeAoyjjFsKBRgdtZotsa1ATrr0gCULY2elnrJmHHFHXDbNCcOlth3zy6CiSl612+iayXMTQbMFcCNx/DrDbnyGJQVRHWo+Q3zLxdmp4zZw8RoRLGgyORsegct4nGBY4FfAr8OFc/M0cmkAeSlAtEAk/3IaN+izd+EhNlp49AqJbR3me9tRUbaoCWrqdVgdNwY1ntFaMs0NNJiDeM4YWQUlY7xQmlGAYr604C+RCLH4v6zeO3rr+P723bwnzffzNbvfAeAY6KOT8BI40o3SfRN381mSMx04QJDpBkiyWIy5GhDLL0EnCIiqNHWfQH7xH6qR0aYvGc3Txy9iToGvu+ilRIxsvVViLYVuNnltKUk56ZC9uz7LhNzx3hy7j9Zw8VM6xl6h3rpvmA5sx0aVfHoKW6mOqPIPvxlCpj7dBGwCclttTvodDbitrbjdbUyVynhlesENU3kJXgpXWUOYu6I84ErMIBs6rleoMdYSpoFtOABbXSzjTIH+CkxEX9sNKvemlN17qoH78LtWYmVW4zTv5lo+DZzw+QWw+A5sHcbBjyawbQ/vbhIZoboXdDPsoVZ9j+mSKZdzhjsBFfiWmUev3U7MubiCJs+N0EMo2oVSCiWFfv3zXHL8f3c9+3vs/uB+3jVtddy4tAMk6PDHH70Th67762MPZWGapLZyKKgPDae3UO5JijOVrl32zjjpT5aC4JCTSOEZtMSh1lg9MRett4Na647D+K9YIWgGgXBZ9ktTY4eYrp4C12Daxmem+JErUxLpcZ5Z69l/PgItcrpG4wDDz6I8AQLO5fQlS+jKhFBRSO6XHKb11H+3idRk4eheIRw8UEef2oR5XjATCTxSVMLYixpNTqzT8Ug1wvLI9OR5SkYjsy6V5iN2LNDMRO4OKU6G9e4nLnQ5XwrzfSqaxk9dJBZEUONHYeBtbDzASjOvOjr+pwhNYyfMv5LEUxMzP+76RTbxPkF4FiwqhuOzZjWlKZ4X3DKc5rPb3RLn9Yt3Oz8b3YN+5g8KAX9GuJjhyntazBja/Dk+Aj3jx1mU88QABf2rCZcbXN4NuCgECzGzGtJx+WNQ6u4L5lmeG6MKKjDwFouzLWStyzKnkf7iWFmdj3BnjseYfboKDIMueNb3+a283q5bPViXv/qM/mP172e7Xd9jXrZh5MNtXM0ex7MIprBbB1j5hzefBh6dsBlQ7BhNTAMCceIJ+sJiEpm4UllTXsKnSBmAQXBfph52JwbW0NtAkYehL6NdAhB1W6j6jhkxQClVWtQ/SloaUGkLzQCMOVRGN8D+w8YK4KmWZqD0cz9KcQYESKRpye3FJWGFdO7UdEkY9qnABymjFN7gqof4NUk3e7ZpFQfA/YaSk6VqejQSWDkv2Y07IpEC8LOI5w0UiuiICDyQ4TQIH1iySQkEgjHBSnRdohWIRpjYqUtiRQRKIElQKEIIwsdKGxt4fsevgIcB9tJIyQoIpQlUKFNrSyJV2JGizOSCB2howjLjmPZcTQ2VRFQr9SolGqUZkpEoSSIIpRW2AgsIfFrNSLfQ0Z+A4w14FioAvzqDCKYQ6sSyAoyqDTy3iYY6xNqD8/zEMoQGKTycVBYzSz6aQYuQjR7FAUWFhaioaTeMOHFJmElcWwXXwkC2ex0/PFRKx8kCEZJd+QZuvA6Dj34EerPTtD7hYqM04obS2K7cWKxBPHkWjJOL23Zbhb29jI4OEjH4n5au9po78rSOwAtSWMEJ2yDHyFNB15Qk2jPx9NQZxYPj8CyCWwfJSUoH6ENs9WyYkSORAqJFBZaKYSWCNfHkQIZlSGSaCWxowihIiwENiHGzthscgxOYqFIA0UcAlJo8pglqDm75zFgbBKzHE1hlqkJTEb23NNoDXQNwikq05nGY03BhBxptx3XjRNzJclskkQyRTKVItOSIdeZI5ZrAQeEpbGwSDY2tVrWUbJIFIbUwjo1v8RcYY7J6TmOHTvC0ZETHJuZYSIMnrtpxbFZ90vnsHGxSy4DnjZEDq/xHesaxhvO8NmUS64lh1zQQjWwKRzRVCe6qc/thP+fvPMOk+Mq0/3vVOjqPD09OWmkGYWRZEu25Cg5yNgYB8DGsIsNXBYbdmEvi0l7wQtLWha8a/JiWIJhsVmwAeOAI85YloNsWTnHkUajyaGnQ+Vz/zjVGhkcccB77/c8oxl1qK6qrjrnO+/3fu/L7pd6+byk0FB+GOmEKmgjJb5vAx5SashQO2yu/WzxugZj24ETmiD9S3BPBrECOt8j+afj4CwkMdEOKPBv33kX09IgMBJQFGB7II1pFTLzOZDT51r8qLZzyP2RxmoVRni5agZW1mTG0V188lvXcP03/5GdT61ieP8u4mKUvl1ruPGaLWx44ljOeOvfsuySdyJ0jcJ4kYP7RhCVMoWDaUhCwjRIW4Zi5jVDqIes3WYjSgFPrFzH2ESJhT0nMGthG3oETIeRwY5hwHEnLyOdnMvG22/gse23YnhlhBBYUjJw2K4rymF1i099+fO84cw3UCr5/OKXh2ByDx2tHRTdJtasD2ls1elsgXidYsb+5to7ObjzwGFDl2qXlYEaOP7SEv0vFJrQEEIjCP3nVQ30A5dbf/+lw+p3z9J5+OeFSBJPuMTjHukkLF0OxwmoF6rdedCRbAng1z+HJ28+CLuvA5ED7V1gHK12ZjbK1K6IkvHYgVr31qFQiKOAc9XvVAv0JFWq7g5BZRCmBkHuhQkJYQKsFNhVn69qB5yPelNVEDKPuoE3vgd2Hgu7OiD4OtM+6q996EKS0ENGy9NeH1rapObTx3DCWTMom+OU3DEWZduJywIPXrEe96F9HNzpM3sxZA3ImlD2FKA3uLsXa9YhUotm0z+lmJjpBBCT7KhITC3SfpaSWAw0C6Zcge1FILerADNQ90o2Dft2wRP3/ZYnb/7MEedpHqbRQWN9EzEjj18u0Lt1nKfvvwMZbkHQQNzMkkpYTBZ6kQwB3hGKR0eWoo65ggAAIABJREFUQf40ilHVMHCLDI/vpTa2gMAXuI6LbSvdV5UQCDRdJ1ebxYjFcD0P27YJwgBDN7DtCna5gl0qYQC2lAR+mcAvMJ02VM0JoqlHmITCouxDSqbx9SyelqbsG4hxZaIlNQVWGzHwimCGSvvaQbGNa5sgK6FQgvEJdS5Hx2DTU3Dem8HToWArMpEVh3RcgZ8CZfKwfet+JgsbsZhg/27YMgCHBkoEgaSlJY/mKk+SiqOkDWxbAbFGVE3q74eZLTAxaHOo3yGeSFFTZxFJm+GWlMuoZSpN2nRadTIEfmTFIBU7L5FWBRbPhqkpZQZWUwuxODS3RSzqIljJFKm2FJ4H5QK4LpgJaO9WUgvJlPqsoxYLzMksB1bXse/pWlRq9uKimoodGXW1nZxz5j8xIUyu/fpXuO/22w4/91l5DxKJjmQRSpImxbS6WfUbrzJkaxCsoJXFopPAaOd6Yy3n/PV3eVtyIW/Z5lA6OMbPP/lJhktbMfBoRRGlaoAJJujjTubQitHagVi4GGPxPC6c/Tb2fukgmzY/xFo28je8ny/s+W+Wvul83vzGeWwOBKdesBijcBQbH17Ir9/xayaEwWrp4hHwBiRzcJifzNBwzEK0t87hqR1waPswo/v2MHHgCYJgJZ77ynGgDgB/j1LYPhPoIsR4Xh3CEhlKfBD4IGfzRXr5OtsPg9x/2XBRk0tVizyDQql2MbHmYYzOs0ic8TGm/vsm2LcHMW822jkrCHb+CIL5KH2pXTz71ffCUdfyJjrbF3NcT4al8y7m1zev4cDoOEOlIoaY4KrLriFwBbqZIFvfxgUbPsFSS7Kj6HPLngrXfm09gyv/A7+wkdZZXVz1q5v41bf+i/tu/gU7tmzlrm9dxzFLl2ENpTk4EPC534/wT185n637ddY9vp/N9z3FZz/618gDgtNb67n0U2eS1M/iMeCaL3yBm77xr9x/w8mQmgtmCRwF7FeesyQ9Rcw4xOJ5Myj2tLBv83bGhsfQGpoYP7QZ155Ci6WiUxUgZMiu9U9w9cf/mtNPew9HN5xGR74RkYox9x+OY+Oq+dgFG0og//B7vp25EJwxpe3W2sUFf1vHG+KCxqQar26XcN5sJWHQFMJXxmBiEnZvsRk4ZJPrqqO4Z4QNNTV0zarhknbBf7kJrPd/AmPpWbh3/ALeeRVc8RZY96Aa3F7pECjdGcd99kvGROU5B6P/T/iqMnbFcrhulTKJ+mNMQzJ9MyWpdpmqvKaqGStRdYM0amCLBO5kCHLrU/Dgzer9++B7Dz/EhsYsd110OUmhYwnBSV09NHX18Dvg3ahUqRrfbumEls4/PZZ4nE90z+HR79/A5z/8SR6+6SaCgX1w21Vc9YEzGeps4TP5LF+85UouP2EPe9Y/he8Oo+beI1ufUtFPFjWi1gEd8P3tsGECPnQCXNSpqpxaqCad8qQCZ41GNeG2vw/CQ7D3ahh5RFU1JLDpC2A3EyZPYv/bf8upCMaB/WaG7hn/i41/l8C951pK99/P6kuvIB6GhL0/hX2/Ud/VGag1cyE6p68hgS/X3MrMzqXU63PZ3bub3NSDbPEOsloGBMAObEaCNWwvbaJx+2n0sJzGeI7uxDFsmbqTwf+v7bymi29hUGFi1FZVZE3DMHSSKYuw4qKbJpYIScQU+ynAR8MGykjdAtNBauAHnnLUMgxc18H1dGKWRRA46JqGkBrBVJGKAXoYKOhSD8AAp6xjGAaaYWAEPr7vEHpS6VY6MDExgu87+L6L67r4tgAdTMMgZlr4vk0sCDBEQKj5oAX4vocXeOBVoDyMzgShN07gTRH4ymchcCtI30EGLq5vIwMfiab0b/VAmbUiEEJ1kKnQpk+fD1Lqh0kPGjECBBKBwMQ0TXLJPJOOYKxsM03Nf4FwV3FoTycr73sfNTNAj1XpUP8vlg6q6s9q7dWRXkBNbRvp2kZq65tpau/E0GohsAg9QaFi4o1JRm2f3kMeGzZDJqsIE6YFji6RFcnQmGRk2GFq/yB71j1MwCi6HhLT04CPWykTuhVCJ2CyWERHJ9R0pK6h65GJbhgqT42YhtCMw2wFXZPg6YT4eHh4uBEEr6viQHQFCCxihMTx0FFTT/Uqqo7meapEB1gKrAOeROnBP39UO7JmMq1+66KJFLlUmkwmi5U0MA2HbDpHriZDXUOGroWdkMlB6EdaIDp4PtK3CRyJXZ7EHStSKo5y4MB+du7cRW//Qdau3sDOiQkOei8kIyDQYyZv/AicV6+062NR4UIk1LQ8FMBvypCwo054ExI5wXFnzeXAjk/Tt2kbvY9dB+E3UZPKq3Pda0BGqHQklD62q0wDwVdS7Y7y9njOI5XP5gD1Gsdxxx0nn3rq2XXQpFS5z7+NqbShqeQz/kSBwoiDYWgYRgzTzHDiGTqBI6hNwuym6feXbPXTmHv2Nv2XGkeerZe9OamAkjAI2LXyD/zhttv4t299h2HUjdUW11jUkOCsd38Qs6aGbC5PY10zdTXdDIwXmCpMoWk6x599LvEW1cqqnMqVEczd96zHrwSce8oSsp1QmxYMT8CGPSGbN5V454VJmmo1enf0cuKCc0mE+2nJNJFP5fH9EitHd+DLEBPIaSbvWPF1Pvq1i5i3pJ1ASoYqUGtKYrqSYJBS3cK6EOgCgiCgqbmV0ZFhapD0MG0U4aBSwGqH1+s1iTmm60Q6G2dz6+O/YCaqwjTFszN6q36XzSiM82U36ok6qHuMX9zXzikLLFo0DU1pi/O0gDs3wZcvlchNAaGrKWdOESgHjqN1qBGK+n0X6k1tKEm/S1FltGqvwwjTXbE+iCrbNa10M+MJKA5AeCdqcTIPNdrbTN8EJRT5oqpbTHSiDgBDIQxW4P7voWxA+l7umfmzonl2M8ees4jHH11JYbtNUJKQEvCBFBdf8X8YcMfZNbSVtjkOqYHH2XG1DU/D/7pASZvceB1sWQu4MDMP+fmfZsbpb6HzjctZswoWngD9e2HLUy6H9h9g7pJOrLSB7YTs2+mwsCdONi2IxxUoN3BISfkmE1DXBAuPgi2PwtO3f5dN9/wL08lWgtqWJZz1/l8wMDyC7YeUx3oZ3/Y7RvbuwXdBhi5KVl5psybNOOlYDN0PcJxRykxhU45e83yhkYx3gp5C01VJoVQqIYM+wCCVamTJsWdRwqY4VcBxKqCrSUbXdDQh0In8FA8eVOwAAfG4gW37CBHD0BNYRhLfMCCVRk/nSOZnMnPWG6hv7aG2sY58g46RgcAQxJMKlKzpVPJ1oa7IPI6nPlfT1I9EFeFMU7X6Sx+SlnLOtW0FXA72QXu7kh0oToARl4yMS2rNkFwKrEaDkREwhGRkAFY/KujbB29+B8zqVkAnhjLSKgxBcRhGJ2HhYkikJYm0MtqadGC8IJicUBICPXMgngX0SM/1yIhIwnFTgfMagFS3ZslXxxozlflX7zp1zeTrIEgqFmylrKQScs1qvVycgvKUSgSaLLjhM9/liZt+Bbx4Q5SqtcYz+WyCmJXgN3cPcuXn3sXjj0yDsaezlAmmWM8OBEpPsiqzWJU49FDDx2LgPXSxhRii640c+9ZvEl4i0fbp7LrzLu7/+Tf5klyJIX2WIXkjSgL+p8AiYhxPHT0cSy8raRCfID3/QvibY+AyCC4bo+/hB1g7+SMe5EHeol3F/M+cTfO/LKQoobwdVl35FPuvX8Px/laWdp/D9UP/zq1TD3EfChi9GZ0V734fP/rPa5AJGJOSvhHJzr2SJ+4L+Om35lKY6H3R5/LFhI4CZS4CLnjR71ItnRPAI2i8j/C1IpK9cIjlIDogXIcCaC2oOwl6PgqP3gbcQ8fb3sycj36bB/71CXj0q1DqQ01Ee/7MD9W44opPc+WVX0VKyZe/fwuPr36S/fv7CLUcra1nkaybzfGLmrj8nTkWfknDGdmEu/N3lJ78MbL5PD79nX9k8THtJITDbb/ezm/+/SIKo31IqSNEHiEUwzCTztHVuQC9PsmhiSSelyZt5ele2EUybtCzcB4nLFvKiqVZMkKw3vG5c81avrD8JF4q2Cx0g8u/exvrDk3y8PotqiV39CDzjj6bhvYTmCjnMSYepHZ0NRN7HmftmvsQQuOWhx9mzvJl9CJ4TML3Fy5gZNtWyM/HfO9avHvvhnwWWtvQZ8zhV1+C2XFBo4CchGuAY4AuAXoJ5l4Dp50HvRtH6NtS4OJPzkIaMDoIrbbg693wjn54YkgyZEskLnzgNjB3wcSj0Hv7n/m9Pk805eH7n4IP/TsMv4R+JF08u4zBH4eFWt2CYg+kUTWGLKoH9CAqKfSBOfD5O7bz+I9/xj1XXqm+4iQQCqzjF9F63b+xccZZpDTlLOABD6KY8bUvcrerV87PfZ+bb7qJW9/5TvWEkWbRB/+Ot139DT4HPOl5/OBff8y1//Id1P03J9qZaqV8FsqPug1VrT9ObUdshOQDcGE3fPV4mNEPciNqJrCAU6L33A8bfgCZIbBKSoR9oKAoWU0Xw5LvglaHEIJmoJ6ATYwi0SDcAVOPw6afwK49YLiq/WUUVcVbA6xGCRK/hsvTFWIxF8w+n8v/7suU97s8+uSPWLPndzw2dD+3H7Er1bbxZjpwcQlwmUOeXeylSPAqGO78T4k6lFmXCbEURjyFlBIhIRu3iMehJp0glYyTTCYx4hkCYSkQNpaCRD2pZJaYlcY0k4q0Y1nohircOyWHeDyNF/p4gYsbuOArw1qB0nz1UYaxnqc8C6qhhQFaEIKvjGUDXKQI0XULw4hHprchYbRN3ykpVq/nYQGl0iRuxcF3XXTdJygVcZ0CvlfCDwJlTCul0poNlLyAGziECMDE0H2sIMAQqrOsekxhqIrx6FD0fZxQ4ksfHxtBGqmcBQClaVqjZ3HDCcpSES5edAgNTVP+DqH/iqiOvs5CQ42iFim9lmy8jmw+TyaeIZutJZPJkUnmEcIg0JPomkVCj4EPjhAEYUgQhBGo7iN9ifRDnNIkxYlRSuEUnnBJaDq+pyF1N1rrJDDwVeEgVAzqYrGI70NAGPUT6qTjSuCtWtnLpdN4nkfg++B7jEzuxcfBxaaCjY1PEgsLgxg6FnFsPAxsYlSwKNGM0k3NosDYJaiaGEyb4m5G+RM8+KLPY3VBH0MTtcxvOomWfAdWKo0RN5kRNzh2UROzZzcys6uZjjkzoKNJMUeq4RZxDh2iNNTHaP9O9m3tY/XDG3l82zYe27+TcSkjpvmLiS7M1IV8YO1VLO/QmRVXs88MpssJkxJuBq67CkxPGRm7upqqR4ZhsK9E77Y+Kmu+DfJWlBD7Kx9JDVbkoXumwkz0CG/3q6SbEH6xDgaK8lmhw9c1MxYirVTgb2qgLCFM6uROz+B4KdZuDBgeFzS26NSmoOCo4rsrpq2JEjFFGX4lgFh4BQDYP96YhOE949S1zOe0cw3GDuzgulvuxfZ9RpyQVYNlrJt+xc7AoKiZZLNZrnj3Jcw/7yJiySyeJ+gvq/YoE+UWr2lKRHjxMbMZGZb0jwhae9T90rd7D3f98jH27dqCN3AynTM6IQxp6+riDce/neUrjqV7wUxGyiGXHCzTVC/JpcHQNBpy3bR1qdtdQ1AXB0MIPKGmhZSYPj8BkZ5JqAZ+GT32NNPSXEP8uRyYVzcMEWd26mz2lB5gV/9W+kb2AQpkdVEA8pExw8pxRnYmk8PreRjJicA/os7JbuBx4FGUzPELRwNnvueLnHbyAk5baILRwYLZMWpMjZKEX/qS299lMzi8mdFSAX/rGWDrSke5RShEfhPKsC6Dolx8GZVvN1Kdr1RlQ6KQ8CoQ6wC2kvqr5gBeqCQJwiQq0d5RgXsr8Le1MCv6wquq4i7qxovarRGo2cLSoCYB8hJ4aisUHubPX3D/mdGzADmrBa9sMrXTJahEV11Fwo1lHjD+C1fzKXslJk8JueyMOi69fILErhIPrYKtg7OhLcHMmlpqrG6aUwsx8qfS3DWLzg6IrYDublg0H5YtMxgbb6WtSUc3oFASbNoYU4SSFkgmFWg41quMplIpaOtQzq9zjof6uos47tQljBc9CiPjEOjErDxarJ7u+XlA4tltFLvbsIcHkI6LphmYVpKatGBydAJkgCHAK04wNTSE7U/hUMIOChBUcJ0ydmWKYmGYdDpBTDeVideUTSAFGgJDGOi6gReTuDZI6VCpjLFh4wasuEUsrmNYBnrMJGbGCKUkDAO80EPqAaHuE1IGz0FPtWBZOlK3MGJJkokWHGERq8mTzjfT0jKf+pbZ6Pksek4n3ihI5iHQlGFXIqeAWENXOugC8E1l3uD5qtVYR0lFyKo0nqFeqwv1Pt2EbBYmJ5VWa6IOEpZATwmcgsa4B7U+tM4A3xPKjTcNu3dBQxvEsoqBqhvQZEBrk9I5myqDNMG0BJYyB8bUIB2qz03FYbikwNFEAlJJxYrVUfuBiAo5wRH7HhVdhKnISa4P5QrkW0G6qhBdnFKM3YQVHaOAiREoTSnWdSyjfC+EkY9uxBcfVWPHZ4bEcx2+8onv0LXwfWQyy7nvru8hOcB6dmDQQp5TGWPlYYVCCzUspFBDUCfQjYbPaXR//Fz0s5dAu0bhXwd4ZOeXePTgozwRHmAJ3uFm973A8cDfvemH1DTOJNOYQcxLkvjoN9ErFkyOqPHua6AfSKAREDDIAD7Xhd+j9bonmbnqFDqTpzG3tpn5T43R7h+iyFp+1f8HfuPu46noeH8NDBNw5723c9Z5K7AiiZGKB64dp3ZsCfOdN7NPW8lguOElndPniwC4G6WsvRf4MNMY0HOHWqrlgFMJuZ0W/otJ7qX8Coop/JkhN4FWgPSZUJRAP0xuhC3fgbM/CU/uZ+ipKZyrV7H84iWs3TKXcmmElycDEbK7L+COVQ6FYJC3nHMyiYTGXfeHPLH6aVo7TmX7pscZHa+nbtFbmFVTYWTEJTvrRBaedALvvaiTQlcrtdkYaUfQlK1DRAsHXTfI5upxx4rMmjEb07LYuXsd7Ndw/RRSxpG5ej577cfJGTpOIomXTpFBqC6BihEZws1GZQXTLNFkTQqnZBP4wbMelQx8bvzW55h16ps4+6SF/P6eP4DuECQzdHc38OGTLYS/nEPe0Ty94Q2E/72c9Xd+mc9+5ErOfu/FvO3j7+FsAdciVXmv0It/49kwdgzz3vE2UsvbefoOyRcufZQLPz6PM09sYLlQ118JuGcYHt0Py8+Ct7XArngNe2en+Lgl2C0g06DkVq4D/r4eJn4/yuBGB0yLzJdPZ07ziZTuTrL9y4/wp9nTy4yxAnzhR2rQeyntSC8GiAU1ePmobZuor81BrXYLTOMhlganNjKVMLCPTGpzgClxG2BQN9mIqoNXu/CPRy2Y89HjLxRVubVzDIOymeZWrQnCQfDL7L7pHm45dAUfvvFK5pkmH7n0QhZ1d/LJv/l3YAMKLItHB1EtiGdQo3TUuyB7oNwA94RQNwkXxOENx0WvyajXlQ/Avocg5ke60GUl6t7RA7M+hpU4jXRoMPrUPyPbZjKaW0ghvQApMzB5Izx5N+x+Aur7YZ2tctfWaPdWAQ+g0sPXeGGwVu7CmniK05/cw1EnziI3dgppu4Is9IG9/fDrZPTvSNQ7KDA5QIpOTqaPXYww8Nru+OsmpkD4oGUQho4gRNMMjKg/RtdjSKETaAaBZRAaINEQmrIpSuhghB5x4ZKKx0kmUngyIPBKeK4LvkNxYgQpffwwwHV9YqZJIEBKBaQ6ro8QmmK9OhVMXQc9IEQgpUBKHT0Wgh9GLcMOrmMjdA2kJHR93HKBICwTBhVFpQ0CHHuSwHeR0idwXZWn6RVkGDHtpE8YhEgCdD0gCEBS1T4UEFh4+ARo6AhE4Cn9/BCkFBDoONKPRLyUU596v1pRa0KnPT+b4ckBHFnVhXsJIUPC4C9FedIR7Zei1R6NjNUR+gJ2b4byFmVUSBHVEfPn0bJ0YpikSFBLysphJbJYyQwpq4aaXJ5EMotlZbCsDAQGnq6D0PClxHVcnMDDl8ojQ5MSIX004RNqHsKqkMyZWEEGGQZoIUwJW3mmBB7S93Dw0YWnJsFoj0xTx5AhgVQuCYFfQRfqm9V0HTcI0KTEFBLNCEjHkrgexKQghkHIFEqpFnx1xZAijomFRhxJmSKSFhQwuTT6nYn2oILCV0ZQufeLj+qg6xLKUfaNPcJkoYf62hZaGuvwZIzx4ZA+rYI9NUHfwQF0K4Gu66BBoAWMDfaydfN6du3dya79+xgoOxQmShTKZQph+BK/4TyGdjynNwsWxqbhiwMoSNUFxirwwFpwRNR9GElLiMP+5FpETX71JpQYkNYEIiURloFhqq7IMIBnuiI99z687sHYaqRQLFmpC2obTLwQGkZ9jBS0tQsSllqsWwYIOS3xpOtEVa/Xb5QnHfINNbTPnseZb347fQOjbN2+ncHxSaZcyYbeg/S6qk3csGLc8+C9zL/oHdS21uN54I2pwrSeUDqUQqgFenNTGt1Qz8UMGBqF/fuLHNqzD7+wn6f/AAeb+8nl88zvWcT8o5Zz1NKjmHNsBxM2zBuH+hykk1EFwomuaSKQ/Ag93mpdpIolDI9PccP9a7BdNWlUk8gJpt9Trc+93sDYRDzBRRf+FT/83Rpq0gEdDTlGBouEQ2X8cLqikycyIAsDKn4FE0kClVPOQcEf3ahifzfPhB+rNbIJYIpOzNaZNC2fS6ymlhPPP4cli7pYoiTGeKIMfauhdz3c7cPD92s440kwJGSjykOAWhzoqEw/ixqZ61FZ/mLUSKajXIKd6Gci2rE2Ig0LpnXWInZhUNXmmAMMCdhiqIT5vagbM2RansBkmiJsMJ37axp0dcDgeWodMOkw3Tv46ke2vYH8zEaSRpnAC6cvOg3Ihgw9uU8B1PXg9kJX7Ci62vdRHC+xaY1AX3AKTXM60bVmYrIN3+nATMwgnc3QVKckBmpyShqltkmj1U6QjUMgIFMWuKEOMUjVK3kQu6BYx2kNsrWQa1PAYp0BZqKNRF0bLZrEL07hlQVexaBcjpFIaZimQIZJUpk0ldoZBFNFDCNGIldLU73GyOAkvhegBT72+BDp7AiuO4Xtlyi7k9jFEUrFCYKgnyA4hOdppOK1mIaBxIGYwClXCDwf17WR4SQSC7AJwwqTk73EK/Xk6vNYyRSGlQAJmoQg9Al9iR8GGLE4pucTCA1hqotUN2KY8QRWpgYRJjFTTcTTbaRrOolnahHZGGaNwMhCol7p6MYsiKdBRo6z1QFEJ3osVHNDgNJ6ktVxSUyndkGomLRSgucoZrIRUwbWZgLGPNW9qhkKLPcig6+YAZoJ2bxqW0JToKihK41XTUJMgq+p/+uGei+aalfRhZJUGB1VjxuRRIWsKjaIiNUbachWH5NSMSZCCZ6rmK+FAmTiCmgdH1PbE1JVXEtlKO2BurzabyOpjtGxIfCLvFTxvedrKE7EMpQqKeywlVzziYwP9DFBEotWLLqAlfSizn2DOhxqiJRLjBwdNcdjzDqXZPY4CgOwbtcdtK7Nk0k0UGvVkGUTOqr41aZ10J2ZS+2yLlpXvAlDa6biltnVu4rxcIRuBkkUDsLGXtg9A8omKSNNG3XEga5EE42DSXL9BSqxDTzScB9T47uZZBfD7GZPpZ8NyMMM4CpEMTg0yODQ4OGhVX1dMVo4RNqYhc8fGQC+AjGESi6rQ+2JTDMdVOhMD9LTYaDmnFPwmCSkDYODZLiO8b+gJvskyIMQ9IHoUaCNPwSTG6BQhpaTcYrDTK79HbWXrkCfcyI4ozAygpqoDvDnWHtaJqRTggk3xqz2BnSvwPD+rVRG9jC3J8/czjSOhMef2MTM5tmcVF9HQmvAStfTOT/OLx9ciVOqkDeT5DKtaFFio+k6iUwNzjhU3Ap24FAsF6ivT9M5q4F840xaOxeSaGhlz85dHOjfwNDIQTbraaDIzmLI2t2DKMh/OuMRQrBg8SLcksPY0Ah9B57d6PLgzvU0z11A46weNaloCSZHB+k/uJd+ewFz5uWxvDy1Wo6eoTgb7voGm9Y9RbprMY0nS3xdUq5WV/wysu9hwOa4pjPoPjrJxIGQLbfsoGV9K62tDSzvUHu5cjfsGIJtRTj6BJiVgLhhksqZ2JrKbWIWHJyQ3PxIwEnBBOMPr4XNU+iZVlZ8/AQW1WmUw5Pp2Ptu7vvVTeAN84q5BXg+bNrz6q1kqiyCI6ULbKbdU6pufEkLli+jL+EzeaSDsw2EkA8tTkm2cuP69Vw2q5sFuRwaakzMALsGB3n0wH4ytQ3U17bRkTRpi09LecWjn2o0AU3JNHR0Q+8QEFI61Mue++/hv665gMvesZj5M1tJWgm2fuASfvnLDOVyHyrh01HJn9IhVDsZoE5iBmQahstwv656KycFvK2VdhKUKFHUJvDiMyFZVG0ZtgOeB+0dEF+ArAj8A7+HYCfonbhaDLcKLOkmjA7D1t3q4Dagcs86lIrO46hq1F+A4j9JiS2lHfxi48+ZYx6HZrfjth1Pe7YMK7+qkuEjwov0LdS6ZpwUjbgvooT2/25E2oCE6JqJaWromokudAzhoQm1UlSt+xJTQCwWwzCVpmciJpAiQAY2ng0l38UNHHzPVeY/rkvg+EjhI2WI5/oIK6FwARkShh6eF6DrGjIysCXyoxci6tfSIg1WTRBW89XAIwyipMvz8d0inl8E6SCkS+D7yLCidM4DjyBwkKFE4kWuYxBKL+JBhiCDw4C9ipBQQdNRjqzmcJ9QAcRKvACfMJKvrgr5AQhiRpzaTB0nHncSq1avZGRyAjd8va2anyeEQX72uaRmLyTRmCOR1sgPdmHYC4mFBUzKBPSxdnOJ0T2rKQ+sewkb15SEA3ESIkHWymDEk+hWnGQ8TsyIY2gWujCRoYzSpwApQjzpE4YeYeAQhAF+ICGQGFqACAMlM6EFaDENLTRVS54XIt2QIAiQvo/wQ3zfxtOxcoDKAAAgAElEQVQChJBRPq6hGwJNCISsOidAGIaEMkQLBVKAHvrooY+BR9yMYwhBEMSwAp9QSmxKCEJMdAxMYlgIIIyM1UHVAk1Unt2EAirFEY+7QC+q4PfSFF9U70bJHSFw9+CLCTyy2JZBwU6S258kmYjjJEylcaxpoEEoQibHB9l3YC/9Q4McGh17edZZIglGK6E2bQicYJroIVGmxvu3QVBRsnUeSu83jKYcKSXSrwp5vToFCQsFxVgWCF0i9Khjs8pODKO/n4fN+T8GjN1XAXxIIBmKhTi+JNugkW/SaGqIFiTWtDasLY84EbzCjNZXKGSERAo0hCZI5xtZev4l+OVxbv/tr9m0ZQfDJdg1NUkQjSMFx+X62+7h4s8OUtvQhGnGaG3RKfdHmFd0EQDk0mph7kjFit2+y+XAwZB0Mk5Lbgbb1+/FGRvBbevkuGNPIpVuoFzxGB0aBHRa8nnMmKZ0dyWMlBXbyjgC3A5DxciKRSe4+tSB/mE+9sUfQUVlsOKI52BaQ/Avr3P3p5FMJ3j/hy/mlse+y9I5dZx7/DzWPXEvNz+0nZLrR40nggX5Wg4ZOnYQsNHZTx3TsqnDqAGyI/o574jtq/xeo0iCPXUpDuinkzz5PI7/yjupma1AJB8oB1AYgZ8PwQM/h63fR1H9NAvEAvVBLdEGh1HYpoWiWxyP6kqLXAWEN/23LIHmospnwxBuRq0IEhxmFB4Wvg2i18VRooZWHKbiqu/hnSjQt2qfnmPaddg9YltVYZsGYMFblSDdtiJ4d/JCfo+vVLQ2p2lvS5IoT2JkBd5YpKkRQ3XePYi6QLuASUhPdbC3MMrGp+EP9whOP3YZLS3LsPQmpiYDdhYmaDJiGLpOQwbCjDq9U57yBMlZagyyA7AF5Jqg4sKkB04JSsMK/LPSoOcgTKl7NZGEgqdAtI5WQV0qS3EcxgdgoFfpgxox5WqvWVk8LYuUY2gxjVhjDqsRLDOLVgZZ8dB9nVw8g+eUsJ0yVmmSUc/AtnVgHMcuUC5pJOOtJFJZ0hZkGvL0H+ylMDJIuTiKsjOuY1oobwTHTymWayJHLJHGtqeIaZpytpUGjgOJVAO6UYPvOmjxGAgH3YxjWinMZAYtyKAl6tESzchEEyTiWDkNKwd6GuK1IAxVAIpVNWKjSU0jMqhCsUs1qTCKqgZrFawNosvQj6QCK2U1R2hSvd+yIC7AzajPSSbUWCnMqKjnKaasMNTnSKlMtdIZNfa5DlQqSmeqKorqRoUITajvSpiQSig2LBK8iMUrhRqvhaaek9HCX0q1v37E+C2XYXQIChNQW6MkFw4NQMpSxA3PgbFR2L0Nzr0AahrAsNS4XDoIntOHckZ5+aFpGmectYKb7nuMg6PjNHWdwfjATUAnDt04tALTyqFVXSsDSIo4Nak5NMy/HP/UZTibhui7+Ske3nMzF3f+NctP/ygNezuw9q/mD+jM1uOclj6Fpd0XI//hLVSMCewdkwxv2Mb9P7+KgEfJE5CfyiI2piHfAHVx8ulWFpZPoKPyBO/NXEDOa2GyWGJNeRXX9V7HVoqHuzJeKDU7Uk4yxOUAG8B/5RixfxwTqLYyA/gMahifZjaohe5z7/UI5wPnkcSlmQcpMxbxK5y/hBBQOAaV20C7HBhWE084CY89AGddCFOPIrf9gOLQ5zBOXIEeVAierICoAfGAEi33XxronUuV6WqeRIgcAo29W9ay6ZHbERocNT/D8qPaGR4c5+s/W8VR57bzjqNqsW3BQztD1vW73PLTm9m7u490TT3/8JF3cRgQFgLNMrCFy+5DO6OHBPPmtLNkxTIWnvhGepa8mQfXDfKbX93J7sfvYGLLH1BIUz/PBT4KTeOY449HuJLdW7c/JxgLHpODgwzs6AORBU0wvGcbjxccitkeLukUuI4gzOU45pyjufVLs3Emd7Btez8/+fkwe+vyZKw6UvlGHF9i6RLf2cZxwRDLYi5bTg/Y7+1l89olzGrxKTQalEK4awMMlCDdBDKhrrw2S6UBj0pYFMJeDx7f63LHdw5xh9MHGx+AsWGM+vmcry9hkTCxTjmBg/Pmcv+Dh5DuWjUBVsrKEKo8papRLyde7apDiEpVnuNyFFaSxGnvYLscZ9iN5BIEyj1FwMxCkk/n5vLGn3yNxWdLWufMI5dSPKaFwGMH9vOZe+8h19jGou5TObMpxam1qhizD/U7b8awavNkRdTpl83AUT2w//Fo8phianI7n/7Qzzhx3qdYsqSDnpZafvSjD/Hkk7PYue86yvZj4EyiRuZqkW4CNdJVrXsFkILNKdg1BI9NwPIUc+tgVM/QH+9muOuvgDz0GTC1DdxDYDWCfwh3ZB3unlthzgJE3YnI2CwggSZswsxiSLRCRYOnQpWzVt1mHgIe5i+qWXagvI9vbP0ybF3G2Us+xKKjl9O17GjEI19Dyioq/8yQeNjsZzd1vD5XNK9VqAWtkJKYYWLFDQzDQtdMjEBDaCA0XZlXSYklNFIJCzMeRxhxdELcwMGxbUrFcRxHGcJW57wgCDB8QAuQIiAMQkK/QhgIQll1hwGhC4SITJgQxCJmoUoUBTJUUnq+IGoTDwgDHxkGID2kLBM4RQg9dC3AD3y0MESGAWHgRhqxUVFNRoXzMDgMCgfVv/GREfIQRPSwgDAa63wCAgI0JDqqiT1ARKvkaTBXIxlL01bXySmnLqN3Vy+V8hCuM8jrV9zvyBAIYdI8cy4NizI0zDNpnROnJ3s8Kf1EagxBTledZd+6Btbc8HnKA1t48WazOhomOjFiWox4PI6IxdAMHcuKANRQEAYBtl1SibxUvbqBFJgBaKELgTJBDpyA0BDTjI6I8YmQ0dUt8UMf1/UJPB9Nhvi2jS89FKwO1QW0bhiKMRo5P3phQOBHIK+noYceRugREyHxVBzd0JFeSGD76FIwFdm4KZmCNDoWPi4ukjICD0mF6eaMFNOkNxO1/G9CjUgDqKH2xVv4TodNPwOlfgZLireV3APxqLjWj//qrt6NGEGynm1FQWBApwEzhDrWGSKyhHahsEup3ThxQCpfGxF1UcogJLBd1Hz36iQKFlAjJCkTNC1QQ40RNRgLVbORRJ2Qz3Wor8qevQoxvE8RAccclyc3D2D4Pm88vZGWmRkGpmB+Vi1KvYiJFP8j9LXKxnxdhQQqgplLWw7vnEglOOktH6Zp9jImRwaxSzZf+Me/YXTKYyCcxsV+9/VvMXX6W1l68pnElzaRbIXyMDjjkG0AkkoOLJ+d/rita56mOZ/gg9d8gmKUhxlCTRQb+0f5zmf/mQ1ffIix8T5atVl8+8ePseTMGpId0O/D7No/PYf9JUgaUJf4oycqY7D5+uc89IBpoOT1VuOzKz5337iL87ouYfGSmSw6YR7dC87nJ6vfSckdI43GUUaaq+66h/Z5XTC4m4Eb/5N7P/czvFCpxNzN87WdCXzamdQvY/H9n+LY7vif9BLsA34/Ah+ZBdLhmfNuM4ouUUSVvNpRQOmJKGDRQImoPBG97gSlZ2Kh5pZSM9TllKGz2wKH6lEX1VS0zajwQYZpCrONAl5XAMui/8ej54LotxVtoypXUEViquyRIpCNQf35kFsOK68Efswr3rr4LNGdiiNHxvnN7XcxZ26W/RuKVAqB2q9tqPXyLpTi+SXw/m/fAPehdDUIeejKv0OJm5soDluBGW+8npmzzyJJHSOor2jTZli3FZavUCZh5ZIijaRSSqJgqqRaF3INkOmAZBacEAYnVct5XCi9mUwW/Ej+QdfATEG6AeJxSNcoBma5DO02JP1aTAu0LBR9xSYdPQRDgyGjAxO01tVg1ddhGCAKBfRcjmbHpjK1kNr2eezcu5O6nh5iZoyxsTHSzbMIhibwFIUZxd+pQlcm0ESuZTbZli5S+Qb0WAzDHkf3AwhDYpYgVxvHMHQCKXF9H9su4fu2SpyJ41NPPFVPmGwmjDdgx5swcpBuhFQDGDkw0qrVI+o6UZPVswziIWrSjRtKVxUx/bKqv1wiCfF6WL0NarPqPvA8KBbVOa2rUyzYmIiITxFjNUA9PziodFsbGqC+HhxHAea2owy5PDeSHjBAtxT72fMiAJaISasDWgS0ekA8mqijCToI1I8fKIMx21bgu+tE7NK0YtvGDIg1gW+DJSCXg+Yc+BMKoHVKUJiEbErNmVGj/cu7gajuo8/3/+1zLDztHOpq2tm+YVt0bawGDASth8dzG3XLt0Z7MCP7dhYc/VfIfziHtZd+hDWVu8jPXsLl//Bb1Ze/DuK/rWMmx3I+s+noeQ+xU4+GJW2wFv77qncyUlhLPyPcC7wHKDOOy24sCjAWQMMZsPgY4jO6ueDqMvcM/SdPMMCT2Oxh2mewKfq7et++mBCoetWrXT4KgXtR5+4dwCcOP/NCZgfVKBNjG7s5ieuZ4GZGuJHhV35HX1SEEP4HmG8HOsH7LfAD2J4FdxB3coKH3ncxZ9z4QwY6L2Zr+wWQrlPz4UOXw7qrX9KnXX311fzkF7/lhMu+z8UXnc3O0TqgDRke4MMXnkhbzzzecP5b+I9vfIX3XnYFP946jghidLe20XX527juuq9yy613891v/5Qffu2zFCbHAPCcIn3bVz5j+NF1nXPO/isOFMrsPzBK3YyDfOa8buWsfDieC1yNzk4gueYb//Giju1A3wEG2YjZ2IM30gdeCsP2qalMsmddjgU9cHQTHJVP8cB/PM3qL53KxOafUey7l57PH+Bbq1by4N4Sd2ye4sIuhzW33Mfdu+q4/SuPMulWCIfXMnpgLg9uyvIxq4t9w/DtsyDVqKbFEeCXE3BODP4qylf+fhC2Pwb9966FO04F/YMQC0DfjzN0Pf/7A2/nQ19p4YKjLU7I1CC+cyNyNnDtlXDt1fD334PvfkgJcP8PjpSe5LIZF3Pd9y5jYvVDagGfRNUuJWRC1Ura2N3N3177Fd7aOYtff+ybgFqqn7V0KaKjkQ+dNYu9OyW3Psut3nTSqZx728N8v06NQ+g8ky4LQBnCH7Hi9Cz/9PkL+fyXlhMXgrVr38THf/kmfvDrjTi/+9/Ra2tQo+HzLFCdBtjYAD3w9EY4rg3mEud2erDpQbZ9GHJroP+rMDwEWz4OuW448z3AB8gi8CjjMEk9eYaZQzh3Jtj1kB9SLQCbgZtQVajXRUhgFfc8vYpHe8+ksetThOGLMZ5dyzQc8npb1bxGIQw03cIwDAQGhhnDisUxMIkbkE6nSKVSZDIJDCOBa5cZGx9nvFThsJRphFf6KLBUecPoGOjEDcW+EwJiugWBjYYegWBBVBA3EJrA0AWWEccgQGgSqflKv9EHXE8lYb7Se/WDMjJwkL5DsThB4DhI34cwIG4AKAat73s4pSI+NqAhpYhMeZSGiRAhhgFFx47E+ao8RWVWdqRSphFV7xVnRd3IWgTOKvEDHygzVfbYtTfgV9ffQBAo3VycFLw8zuFrFBIZFtn8s6PhZ3lgMRgXwjFvJd7dQtsci54FcOpiWLQIhlfNp48VwD0vcvtRUo0iqAQEGBpomo5tq4VrpaIW0EHgYBgmoesS+iEiNIjH46CDbsaIm3GIx4nHUwhdR+rRusMwcKamVLegAem0EicpTU1SmCziBxUCygQodrSOQY2fIpHIoMcs8MH3A0RoRj5tPiV3Eg0XHQ+dkHghfnjk0JH4+KSJYaJjElPsFIBQI5SCOA2kGSKFJIWiyjwbvqWj/BZaUDWvB+F57WGfLyRH1iNfBTPOZ4tMDeGc+ezuhZExWJ+EeEqt9VozoEvVxGH3qe5JWwMv6k5MS7WvZRng+VMgJ3i1wNhqA41hQColiMcEppAYgURK9fgLKSP9jwFjpyqQi0FM9yhO9HL9967kgfuPpXvBMTTUdXPqwk5G+/fT0pzg1DPm4zCtGwuvDyBWRq1OxQlw7TJ2qcBA/0GOXnY0sUQsoktJDhYCcu1H0TjnKLRsyA+XPc3+1eu48c47+Mlvb+DURpPGcIw//PYH/OoHX+OoE4/lXZ/6OsmWPDID0gVnG5itoNdMf/7+3i00NtViJhZTF4f9JQUSlacO8Y/vfxdTA1uRzhR1QEarMFHoxfW6qBNpOo2oHUfArl5YvxaWz4G+3opq7zU1arotls6B1QMut2x55uJfaZ88MzRgLgp4fD3Vk8vlKX78syv44X/+C3OXzMRMm4w93YCuqRakniXH8N/X/pyWrlmYVgz7oI8zNcwKJC6KIHrYHVerU21fpJGJZirOIsxzTyF29kJazqhF67YQlkKPqvfqpf8Eqx6D4qDq7qQThYcZKD3YYVQ2Ph84F1jOtEyAgRptl0P+bJjRClY9TEmlexj40J5QIHxoQFCjgNk9o+AEimlHCQVMdqJuokkUYFlGjW4a8GYU6DqtST6tRXskOFvVXKvqrgmhwGSyEP8EPNIPlVW8Usy954rxvv3E6+K0zWhnYXcHIwc2UqlMqTxpDdNY1SRwQ7Svf+J1dZBnCGxkY8i0gR3A5kOQiikQdeECmCwo8M4wFIsol4PRKaXzrkvVCu9HzE4zBjldgWg79irQriajqnsVDUoaOAbE88q4SZnjge7DwfXw0C8+iBfqzDnlw6x420LQBbEs5GaYJJt7sF0dVwqEBCNeR219O6Jsk/N8GnvO4hjPxUrEQEgcp8zE6CGCyUexjDbqZ8+lPFhhqjgE6QTx2hxNzR1k8m3Ut83ASmYoThZpq0tRGDlAYWyc4qTL7DknMWWXsQMfT4Yk7RL4Nq4ncQMDIWox0g2QbSGWb8KqEyTrIJVTALWVmgZi5RFyA0R/S6aZ9vGo+ByipAgMQ13f1ec91ORcVrtAUSijaCRs3qrYpjpK+L25VYGeLup+8AMF3NZH/eJBqL7PIFBmXsnI4E5KRfSqVMArKsmCUgTEg9KqjcVUl2YV5HUDJW+gA76jwHWiY3Mc9Xo3AnnzNQpYjVlgl6E0Bnv3QlsLHNwHvZsL9N7wM2a1vpdkUw4ZXTOBD4E8BnVD3/wy7iAVmtA4Y/mxrN1zA+ViQJu5hP7DzxaQR4BPJRQxrDH69K9N3U7r0yt5w//5Z+J2M2d87Ku0nLEc6qH8uQIrn/ou6aYcZ3zpl1iLYpgHchQe3sCWL/6UT/i/oaG4lyw2WeBilKTAVnahU6CRWdQzBnslInssxoJuFr77CnrvOEDdxBO0cYgEqhM2YLrNKWTauPuFopqMvlbL7HUcNmnns0xLAb1QqFzn/7J33mF2XeW5/61dT53eR6NRl1Ut25JlGRsX3LDBGIxjagg13MQJ5SYECBdCCiRcCISWkAsJ3aHZtBgbYyNcsC1Zki2NrC5N7+3Mqbutdf9Y+8xItmxMrjHi3vs9z3nmzD67rL322qu83/u9nwIe41ok2zD5Ixq4kunnawr9JJMQPACiC4yXg7wXRr8Gqhm4BHiIHT/uo+OCBra9sY6+YUGpAqXDV+Mfy0P+K7/W1Sq5aXZ++W94wUVbOf/qN9Bc183XP/d6AMaOn2D82FEcM+Lg7m9RGCtBIHhiwOb9f/o1ko3tdK/exA03/h7NqTo+/ZG3Mju9ABQ2GQnyMqCCXsR/5p//hWSmgRXrjyO9KZZsqCGR7Wb9ueezftMmdvz8Z9x7+12U8sWnlLOutpVzzr2K137knXzmPe/i8fvve+o+dfV8+IMf428/+gHmykWs/AwdSxMEzesp+yncZDOeykFYy2BB0ODCWhWw47NfIT+itSvD/BhH/udG3vrFNWz7g1fx8mtfyH3f/AkHfvF1SuPjhKWK1vs2ugkevBUrNUDXje/lru2TvOmROqhIKn6R0ATvnFp+piz+XsKijXB0AibunyIZNPGWPbv46sUfwS/uAYZBlZHbr+Y7//RVSi/dinWVYMUcfKIVvD9/Cwfe8gpo7OC812znsbmQ+/b0cOcfvebXetbPq52sSfskfdokcCXw3Xv2MHtkSP8WRyJVzTIMvnfFVbzj1q9x133fYVuuj/s/8G1M06RLCK5vbCe67XH++u/fwdhjj0P/9CkJ071KiZGBo6j6ZdpDOzYEd9/+NKziL/PFfz7Kvj0H+dEP34wQgr+4Dl550Soe/PCX+auLv0KlEKBnq23oiWN1SXlyDFs84OZg7kXw0Aeg5nWCs9AKA60CEql1zHV/kk5DcmzrPgpmBsQmQJLHZBFJ2rDYrUaQd78e5nqgMKUH5k+jB4kzFFcqzT7GQM//ACR0ng1urQbyBh86zd5XaK04MQ3hs0+W+X+VKQlSYpkWS5YuxRAGKoxwzEhLByjIz8ww2teHFIJyuUwYRihhEBoOYGKYFoZt45guhhEiQ0kolCbvWBaGaWCYAs8sYlk1mMLVbFsDwMMkREgBUlEqThP5ZfwwxA/1OcJKpBmxQuC6LhXPww89QCfYolIi8jxkGIGM8LDwoxJSBXHYuIsXqnl5Pgs9H1QqQhLonAnzfEUDMGKlkyoYq7DnBagNzbaM9UFBIghjQA4gQYSiEI3z2NFfIGWBMKrwX+M4/rZtFtgB4UHo+RzeEZuBewXjLjyaAClrKE6Pw6+luRwhCYkICUMPz/MIlIGoSIoUgZJOKG4IbFtQinxcoduGF4ZAAiHBtJOQrCGbtREmYBgYwsRyHCwLDCVw7KReFlYcgsCjXCrEz8hC4SKBgDIFpomkR7LskfAqpOw6bMdBCYESAguBqyRIECgsIixMrWus7wSIMDEw5tMhQ2SCtG0MZeJ6LQgmyRDRxEJGiCfjXFUCwTLgE8DH0MEHR3/tZ/fbMJNFy00ufbvg+nWQMkEZek3cp/S6eKIfeh8HQp20SwoNg7iA5UHCA7fow/Q0eqD5VWDsr4o+O73Noq+93IJ2UhCzmk1KuFZMYzJOjSo/3ZV/JyyThcET4wweOsCDP/0mQ32HKQUz9B/fT122lf6Ht3DNVetpbW0DmJe+/lUgbHWu9LyBtabWKBSWhWElafQbMSIDJTWtGiDVaJOyLRzXRKRgSW0dtckaRvNFBo700aFmiCowNDrGwRO9pMwKJx5+iExXJ4nmOtpWLMGshcnBGZhQtK5oAGDrBevIZJM6TMOOE9K4YJYVjh+SUYJUthHXdPFnJY8/8nPSHS6euYLlS3XhHCCThsYunWFeyZBiXguKLz+vHdOAfQdOsP3+x0+57Wq0+8mm0Avh384C8fTWWNvNys7zeMkFL2L5pi7qOmuQQlG3wmLb8suZbg/ZePYmlq9f4L1GXpnM+LAGcIAGYdFkJHSIRMs2EG1I0YzXuR7jki6M81dirG/DWaOPPwocGoDHtkvoP8j2nzTTezwLfkJrvVYjyQw02LkBzRxqQPeyXSwk0SoADtQsg/p6yNRrTUu/FHcxhmbT4UFhTgNGUQBuFoIKRFVmbC2YsQRBVBU3qzoh48n5PKLhoHv8BPpF8gCddDqOJ4//VlnaArBNjKANmb8Z+jth/GEIn7oYfS4ssagVI+HiJl3aulppWtxJomUQYy5AzlROdRVKdJ99Wjs1e2mCGUyVx6eWyAZczRInCcWyBgUNI9asVnrCJkwdml6VbvAkmFEcMh+H40upE6epGLgzHLASIBJaJsQ2dQi9m4ReHyaGTzAz0YcvU2x98f/ESAj9jFMG6dokEzNa7swCkiaUJ11Gp0tIX9G1qg03Ub2upFQKsd0kRqIJ20qQaWrDsUIWNdRgptJYyRTpTIZUXRvp2locy6TOKbC2u459M8OMzw4xMdLHWRuuoqZ5MZaCnF+BSgEbA0uCIw0CUlipBhL1NaTq02QbIN2oGcA4EFmx9o9YCJysDpHVYMF5R1v8RcVyLBYLy0kj3lcqXfcd3TEzwtDgqWODY0BxDmYnYHoCzlqn3xOI9bLFQgGiSMsMxCRgzXvwNWhaLOlzBkEMpHq6TI6jw1OCSA/YTrUNKFCRftaVkk7IZcTRdIHO5EB+Rr+fWQechP5dyoXrGybU1sOSVTbJy9fQ2++QLUK2Nm43IfFi/bnrZcOKpDA3xmx+EiNxcmbeMTQ7SFsR7TfqjK8+IXP4pRzDFZPL3v52Ol54IRVpce+3bqPxfpv6FYtpXrOcbOsS5MExdvXcyrH9Ozk4/DghPfMM6QTa219gNbVMMsgI+/BYj8tSP0F6UCL2NpH6b+2sPfRqJg+ZjOT/E4MKMywQ/220Omk1EBJ+9VTt+eQ7ldGpnu5Aa45fje6Gn/1cpUwdUINFEwbvw+UoGfbjse+pnqbfsE3pl8GwYNEVMPG4jikzO2DxVRQPjJA+u5N161eytgMO5uHo7k7G0qshn0a3pmdnSgaUpvpxa0MyTe3UTSyd/235xstYfe7VCKGoTE8hyx5IqPgwWByHkRHKxQJBIUfGacKrnOomrqgIYRjUpdK0t7Rx8MQR3HyZSAYU85Pkpzyuv/llXLDtIpZ1LaIxnWbi6DBHDx5manphYHnJS17CpnO3kahZyrZNG/l6fZcecKO5U67n+z47dv6SSqVM6JWpTBxBHFTIhrUEqTYMK4MXRLR1wKwNgyEcMBSFiTwyiN95GeKN9tA7Ok3qJxGO7OOVF2xlX+Yytt/+Aw48ekDvZ9ahkLhOhc4WwaaLEkxOGIz1Ckb2S9j1DZCvZ7ajkZEGGBsF04eo1sVua6J1Yw1/9p6XcfujGzhwcA8c/j7kDzP1wL/y8Oy9RHtsco/Xc8/AFpJLFzHXfhbTg7Dh4hrOEdDVUMei972Pr37yk/iVM8k9H5t6mu8ZEB2aY2oMlmA20J3UKvR8LCalCyFYW1tLzZqlzI0fZM9dD/PRa/6TN667mEWZeposhxet3EDhpjfxo0U/4YGH7oe7FxLaNdkWv9eUxap2AIEPczOnLap9zitYt+YcXrRl5fy29jowaxIcalyGMM5Cp5QtsRB7UhUtP41JkIegeGtIUFLYL7VpbIUGA1JGknq3mwlA2kl0yrp6apCamUSeiaCfcPj7MLcbJmd1JNIj6LhXj9/+IiBpgK+eQl+SUQlZjjhtEJMAACAASURBVJXES9Pgl/Xgezp73U3g1cNIH/TMwOxBfjdCyZ87s02DVNKiviGJa1uU8wWKuRnCME8UhaBCohjIkgiCIEApEIaNNDIIoaUNHDepQ42NAGnoEVooCKWBZRoIy8QybAgtDVsKAYZESp9ISlACpRSVUhGkj+fr5F6hgtCTWnbGNJGhQ6VcIog8UBJbGIShJAxDLT0QSZQBYSQRQk8EQ5SWW5AKlNR/owgIMIji/MUKWZVtQGFgxP9DdRFlxDpwCoWFwMSIOdX6mHAecFVIJCWvyJM1x3+3TKLH8SJURlAVDSn7VH0x1VDLp5uFVQHsk98p/V1hEsgQJ5JIP0QKD9CMaikMpGEiDC3DEglQQhIpRRBpQNwGbEMQCYEtLC1ngIVhOBgGOK6NsiXIEFtWME0D27LIpNKgJGFQIohMwsjA1aIJmNJEyYhQeDhOEtNKgq3nJ5Gv26GIwBYRtuEQRBIVP/2ICIWFxERgYBkGvpIoYYLQshZVHXGbZ+5ljHi/ZWjX91T8Of3IcSbZEroaunnVFjgrpQk2FWBGLczfSxKiSCEDRaUoSFsCM6mjB8tx9GJYrkBhBA3yP50TQwMU9R2bcWwHJX2K+QlKpRwqGAf1zHziCC1LOB2ZhIj5kEehRLwGVSjxzBETZxQY+3TFFEBrIxzcM8Ojuw+x6747CQPBRF8PE32PAIJ9PMGrb/o4q1d16EV51cF7JlBiYxMCcCBhg1IOKnSoSddqbVtV3UfQ0OrOH6MUyADquxezYeM5zG7uw/FnKM/lKKoR8kpiBCUGex7GHGgj29VN2+olWO2QO54n8iMaOmqxkgZXXLVVJ4PJg9OgGXmmDa7jcvbqs5kbSpFwLJCKofIQR3t6aFqzhbpFS1m61ESgI68WNUKyQS8MUwMCz/cxZZnlnXH26/372HPfz0+594inLqcUOiPemTS0NNct4YKNN/Df3/U6zHZBKQyJIklmhc1LLn4lZeroWLNo4YAoQBby+H2DJJTWjLGFjTIzeCqFbL4Eu3EVRkMn3qrzqHkvGDFbWSnoLcD2OfjpXvjODyX8shekozOwpRM6jGsvuvIsdI96IwvMC4me8FcdOmWgHhraoCaJ1tSPNVyteIwLfK0hW5iCiRGojEDbRXHodKBBnqhdZ2InAapGb4uzjcU9Iro3rNH7zKdxrOaYqWrUplkQ70yxQLxwwMiB3PRSsJeC3wlTR6nrSFOTEJrteJIpFrDdqkkU+bCCbVrYwsR+0kJCxkUtZG1Cw8S0HTpa25COhZFKYroO8mROdlXe58n99YIG+6mbSyNQmSQwFpHOQtKJw+QTJ7E3DQ2oBmGsU+poPCK09G9eBIbUg0fGhcamGCAPtQaqMPQ7aqfiBFHJmPlp6ORTqVqoaehgdvw4E70/BxOScfiGI6G+ST8jITX+61gwIaBytEwoA1KNWsI3nYIoMAhnHepUOw1dZxH4ZWrb2qDZYMXGc7Esh8gPKZXL1LV2EkmJ8nK4cpKMKuHPDjE90sPYwGNMTAyyYvM6LCdNIV9AeSVsM4kldLKCsmFiuVlqGgwydZCu0fIEdkZLIitLP4bqI6kOVNV2UNWxBl23UUyVNWOmqRGjtbGMK4ahGa1LV0I+D+UC+BVobtLKGUFRJ+Y+MQStnbquEwmobYBS/E4opc9bifVcVfyQIwmVsh74g4A4bI358JRUWuvGBj7IUAOotq3Lp6Tev1SA/Kzebtvx+SO99pPx9YTQ14qk9hCnMxqgrcnC4u4kS9dcyf33QjEGgbNNIH0QRoiwQ9SpvoT/kimlGBgaoVKWlMM5+guPnPTrBJwUDl9G+zVmWMjZDTAiBF0vvxQZwcCDPez+t3vY0L6IrVe/nnR9E/kT44jbenhi+nvszO3lOKOs0c0YF5dOTFZTpp7FHCdHD1M8FKfNqUFij1g4YTd8eRtrL/w9pksFhp84guAQA3jzyxmB9m1V/6+CstU2dibYLPAo8Hm03MNGdJmrDopnYwYhWQr8DRnup4Yf4VEkpJ/K85jgywdGQU1Dy0vAN2BOgmiClS+DgRxuOUdLBja0QaoI4foGwiMrCNyzKRSnkIWcztyuKugB5umekgI8Kt4MPlmm5MJdbr3sZZz3wus5frwPVVJks81IGVEqzNLY2kU27RB6M/Q88lMKc5J0UtDc2IntJimVKigZkXRc6jI1tDW2cqj3KJVygaG+EqODQ0hgzdptrFq2kVpDsG7tFlatupfi3Bye51EqFhEIbnjZjbz0FTez79gIi2yDZUtWc7DrEKO9uzl5aVUqFfnGrf9OTboGG5/y9FHK00ehLo+1ZBNuuoFI2ixerOV1J0O43xfYDW3IUUdLHM3bME9svw01doD/1fNODr2wk+JMjqGxPOWiR8JIYnS2UtfVTGONYNuLazg8AqlDYAnBwHe+CS1Xk2qvIbXCxvcgk4C6NRnq67Rky19/4NUUfxjg/XQ7BXmA8aMDyENf4eAhOPi9JNDNp+5+Ha1rL6Bp3Ur6ogLN9XBZTYYNRg01b/kg3/3OHQQDR1Heswfgnxd7OjC2NUV0dgtjyifMKaiAaHZIXttF46TJzH1jhGj/dS3QdckW2qcHGfnSj/jgD7/K5vbV1GXqyQCrgfdc8zoKps8Do4chO0q2roVax2XLimW8qasVgKGxCYbHT5UeEW4Gp6aJ7nqH1Ev+jJtfvJK3b9NjwXQA+ckcQ7MF+vJFpKxmVq0mNXmWaOgdEf4RSX+zzfKLIVMDGUf3RUcARdv8mFuLSQTMhsNMFn8Bxz4PXl777HqA3zJ51DAMhDA0SOiasU7Qk/oUYWjdofouvWAKPQifpl1evQ5mGmBfCnqXQu7QmTOQPE9mmYqEq0ilIsrFaXKT48yMj5ArTqF5qVXWSMjCCFZlJ1TAsHCsBMLPoGyTSHgIUyINhRU7oEMTkCa2kcCXEUrGEKaShJGWE9CopoFfKmnJKN/H94J5KSjDtlHSIvR9vEqRKPJBRZqXqszYga+0Li2A0jqzwjAJZYBhxIuCKJ7EqRBBhCHAtRxMCYEMUaoKyEKIiGFWQUSIgYGI2eg2Fg7iJE6eHsMW6slgIeX1/632zA44gYvraPDd86vOZD2TU1iESqEiDV2HsQiiZUUgdMIsJQSm5RAhUUID+qGywTQwTQdMhxALR9gI4aAMG8NIYBgCw9IAehBUMAyBJUwStouV1czmoGwQ+TaRXw0PZT5hFwQIkcK2ExiWTah8HNNAKAmBgS1CLFNzoaUEkPpeMObBWAyBDAVKGToXBSEp9BI8RM+zW+fr6XR1p/fdiu6nj/C7AMaupyOznuuWLWwpAqk46tEFSjYcdhRe2dcEKExCx0SmDQoFKORDvGIBysPotcnTzXgNIEO26WxS6RaQEjF1nHBmiCAfIP1f7TGMFEz52imghBmTK/V6FyRSiThF3+ntjAFjdae1YCdLpVvA6jrIXrmK7s46imNz3L/9NoIgT1WUqciDRNbMPChVmNRMK/Ok5JanY8EKiMW2T9r2mwZwlZ44B0U9tmc6Yt3Ak+leJ+2c8yBrQagMVLqeP/jXv+OXX/0Rxyo+2alhbnrtzWTasvT0HWTyxAibe6/DWg4rt3ZRnggYeXiOrkvryGRgeBCOHYaLLofBIzrsua4mzfot17D2D97B/p7HObh/P4sbfc7a8gquu34VKzc5eCwwzrIC0kJjgM0rMyxen6EhGwc6KYUaeggO33bKXYRoFuyTh5IzbWiJZIQvPNx1MN2n2P/4FOOTc9z4phXc/Jcvx02Bc7IgcXGcweN93HHPGH9CjEVKReBL9pHAy69g0VvOY8mfdlIXH1Jt6pGCq+6Gga+DlwLeb8GRa3VlHUNPVr8DvBXYjJYN8NDZHLYDO1lAPNai44GzWp4i44JV0cSJTAIMT4fIl8tQSWictzYJZgJ6j0D2YqhbA8EqzcYbHwH/cXBaoPZCmI1DBObnBcQ3Oxd/iuhyt4NwQKXQ6RuduMwTaO2GgHnB4LDa+6xaD01d8LPFvO6LL+b3z3XY3CJOeRUC9FCdofrOKkrS59vju1jc2MpKu4nF4iRNDiCHYpcf8JLGRh4+sp+Vm1dxzc0v5tbPfonZYyXC0pM6xiY0Ve7gSdvsePsoT2msxw8fYVV/PwabaEmCGUA50uHnECdlipmxphUDajHSEyotXeDnNTNShhoArG/UGqSVWI+UUK8H7BS4Ndo7OJuD0IeUA+dcDkbpsxw5kmM8yHPB+YKygHwI0wU4fAhauzX7UwUwNweda6FjSTcqBMOG3hP6+lEARU8RRnDdm9+O72m2ZxSGmJZFpVgkX84xkcuz+Nws4+M5jj2xg0e/8dTQ0nu++1rOve4hmrq24k0kcEONy7tV7dSEBirNhL63VI3uB90YbK5i8SG6rnwgEzeIKo+H+LfhUV3Oplbt6ApMfZ2MvQDGJhzNFAVIZ8FW+tEWYxSuthYa6iA3BmlLJ94yLC17YAJOJnZ2CsCPRx1fA+m1tdDaqt+tclk/98lJvXCwbZ0krAIonYyV0NPawJal24MMdAKuqUmtG1xTo9uKZcGKVZpZG3laR9Y0NXu4vg3q6/S5pqa0xMGyFbD2PJ3kzI7vfXQGZMM5JBcPUTp2x1Oe069rCsmOobtxqcGmC5/jz7h/iPbC22jnXQTcHoVcdtWr6EPR1Hohf3bNh+HWNtgLR762g12fup1uBrnpr77Eit3/xr0//BAn0HLYW1lHC3Uc517u526qeQjb0LIFPRwmIMey0iDicz+A9yu2tryW5R/Yxq28njJ76Scgz4L/qA0N9I6w4HcJOHMCAUP0UPDnwKuBN6Gn+6edLjyjFbiYAhfTzrvYwIXsZIgn8/1/wyZ92P1+eOE/QdgBvcNgtWJdfinHjAzR3dD6clifViy/ZTEzb15M3/FX8qM7IHfbNwh7fgbFR9CDi1bWe6opIM9H//Ab0LKSk2O9rzq7hvroCJdf8RbwA17++++lMDfFz+/4PP/9Yz/k1deuZHjoOD/92T384NbPcs2F53H9jb/Pqo0v4Kf37aQyM0s263LwwH4+/KG/RurVE6lkHU2NSyiIkPf8xZdobF9EZ1cznXUh+3oO0N7Zwarl3Wz/8U+wSFKZMxmb8JmbGydFN5//1Af41rb1vOHVb+F0oRk3XvIKnuh9gkee2KE3zD5Iq72UtqYWGlsWs1jA6lp4qA8+fp/Nkle+nL7Pf5byaXCjUMF4GdbULOa6P/tH5Ms+yCN37WJLpkImpahf1sZUWTGdgPt+CBe3wN+/1eKFH1oGvb1sbshy4fWLOKig92FY2amTxT64G4pb4ePX27z7ZVdyR2EXf9L4BkL/3vgZxCL3xfcxtnMdYzuXAT/i01+DT3M9pK+HtZfQ/sffxfvGuyg/+uP/cjN7Xm3LC8n/8Zv5RHCYGaV7jVTbCi746P38NXV84i1vo+fYMb6lFG8Sgn++4nVcPuPye5+/DT7yPb577btQXau4Nl54KKXg/l74j71w3VKuveWTvP2sc7m0sW3+9z/5249x+22nzrFTG65l9as+zKPvXo0QIk4opN+PL/TCdz/0A/b8x3fQyoHnxp/VLGjHPhv2iqtX8q+EY/8IrS8Bfxk8KDRHYK9SDAN5oad9FQXh5MPQ/zmojOpjf4qWhvotW026lpSbYnhySLOZT2duCtpWwzv/EpaeBQMDcN9P4dvvjXeo1peC11/0fBT7jLayX6A8VWBs6sSz2Lvad1fB2RJIm9C3qfguuSBHlADHsXAtW8/5EhYiAs9TzOWmKFdCyqVynOgrzslrmTiOjZOw5x35KnZia7OIokhvC1WcjOuklh9pKE/GrLtKpYxJhG0JbMfCSrixt1zohF2hBUphY+JaNqlUkkQiQT6fJ18pkg+LMdDiEhISxo5EK07cZWJg4uJRwCT20s/XSbXQv23q+G/fLNJsXHERoSyy++Cd8dZq2KXAwiWKBIZpYFkWkMCyEjiOg3lKfLiBaVo4jokO6QwxhAtRAsvKIC0b20xg20kStbUkrAQy9PC9MuUwIAwtHLeOKLIol2YJCUlkMogooRkXQBRGRFGElBLL0tq0pmWCEIShRaqmAZF0kX6JyC8RhhVsQoSKUNiYXoAVO7MCQoKY5aNlMSQuFml0qxhGwwEv51RpztPZKnRg7V50XMQZbfZlYF96yqZ0/OmK/58E7DCif2gKNTlKoaWZ2ZYm8s1JrBAq45MEU8Mgp3hm/nAIDNK/9xNgbcPJbKC5O0Nb09lMHJmjNOVximbQaUwqyFWgXKkgXBPHtiCRwMQi8iNMCcYz5O44I8BY6Sv69gwhZUQ6kyBVk6ZcLqNEgGkrEq5JpQheQVJrh9zyx9fS1DTH2L7NZL0kL1i/mpvfcTltG1vnz5moAh/PwnwfZqehoUGDt79xMFaAFQNhqJMyrJ1mdSUjyfFfHmT1qiV4E0XmpkfAh803Xknb+uUM9LyGqdFeTJpobTYYHx/m4++5iZUvuJILrr+SjuVL6ahbAKla26GuEfpGYPVarZMYhCnOv/Eq1q2y2fTSbrzgxSSVwnKSJFP2fDT66aqlvV6H8Uboid8L/uBOeu478pT9AjQz4Ew2h7MZHHb5/j33cvZnV5Jxsgz2jbP/ib28+8OfZdWS1/DuP7+Ja1963sJBJrQaWi9MP8ZFDNPK4dRyMm/+FBveWkt6iXPKdT5xAm69D8Y/BKOvhvD3gTUgloJaCTyArqwrgH+FS+PEPXkThiV0WuCtgukr4PitwOeg+6OQvQgqAhqzWoM0imA2njeEFQ1AuUmtx2kI8BTYTZDcCrYFYxMQ2NC4DMSDoH4CvgvBEKgLwOoE2QSyxMI8ocSCA7cZzfar9jchMHDSjY+hUQ8H3WCa0CNJCliUhe6r+PLnK6x+h2D5ixwaTjq0ylyr2p6j+3ng4KNsvuJC9t6/nUzXBhavOv+Ueo6IKJKbR1h69xzn3/d8iVKhiAxP0zlMoJEj9MPctFbQvNjmCVHL8M8mUd6px3jDo+QnpphUMFYAf0ZP+KTQ+rwTExqIS6ehNkbiTRuSCa01GsQePtMEO07EEakYwLM0+JY20SEt8TOsoLVnbEeD+kf6wF2eZu3yJOuSrRwvgEprIDFRA93r9XktQzMtiaCY0Ncz0WU4/jCctRTqasENI358zyEaWxbRsShF+2KLkWkLywLHTZFJJEi2NGPWWKzuqqeh5UIGjn2SsR3v0ajiSfYvn93O+dcnuPSVmzgxrh0CVqSBOSywanV7dJIaYKxNgXuSzIAVvwY5D8oVaKsFTzw1rLytEaJ6ze4tlTWQLU0NzOpgpYU80dX/i75OpjYxCTUpvW+mAa68Xj+jKsM18MFy9WTetrSsi+toMrhM6rHCjseMZFI/7zDU2sFRRFVCDXKxepgZjzHocQcVR7R2g70iBmdDrRlrJWJQNZa2yeU00OsILdtDRl+rubm6cIC2tgXQ2AzAL0Jxapzy9IKy6/+5DbJh29tQUZLdO+5EnTKtOzUUJ0S/9i1x3Qv0a/8eDvG3ra/j8tXXwYomeMs4n3/4L2mqXcr1b3svVjrixFfupjLyKJtI8MdsIEGRrzPI/eynBg2ibkZ3J3vRnv6DQI4yU6UxtnxyFJFswlru0PCZTl78J++hhVs5yC6OMMCBuEwNaDiiqr4SomE+gzNLy/xxdOrA+4Avov1GzyBB9Qw2RgtTPAicqL2WL/h9fK28/zkr5zNb3D4e+RCkN0PzDbCom7Cnh7lcO0fUCj7+ZUVxTwl5oB85cJQwt5tKeQRZfgCCKghbHQ2S6Kfn8RTRo6Ev8oKXfpi2zTfzvc+AVTzBOz/wbSj2w1QfsJE7fnmIletW84cf/gZXXXMWP/7xz1i+qIF3vvX3+cPX3kTCcQidFOMlxVRYR7Ylzc7d97H7l78giBYm1qXyLDNzfXzsf93Omk3LCLMpjk3M8fFb/oatF17CkUM9PPLIYxQjgDL3HztGzfAIV7zgHAzD4IGHH8I3Qj765U8znZvg6//4KUb6+ubP73Z3YOWGSKWTnHP+OnY8+Bjtjc2sXdpJy3JoEvp9GFdQ50c88fgvCYpa8sBJZdny2nez+zufozw7yYmjRzj/rG7efecOKovaWLmphms2vIDVQlEaChgcyvPYt/cwWruUYHyGRFOKBrcGLr8Kdu6knLexWMTfCPj5eXr8mpmBR07A+0J4+1rY1AyvTrmkj36Oj/zx1zl4/x0we/f8/Sy/7Eo23fh+tlxaYaYPfvYvH2PXj/8KHt/IWNCO6j/wnLe835Td0LiMm1rP4Y3vfjH+xAgATZjcQh0bEbzrYx/jzhP9fPAzX+J1b38DtmOz+brr+HRPD+88+2y+9Sdvo/4Nf8C17/hzAC7/p/ey++d3Ut/azk0f+Rzva99Km50CIIgiLvuHj9Lz8zthrE+H0y66nu9+/k/ZumUdVmphrv+Vh+ALP+5n8GtvIh8epzSXQPe+r0H3Hi3okXES3Yu2o9+nZ9GrSOCv4NEHoPNaeOUb4T+BSv+3iewsquNKJtiNnPkWJI9DVxa+gSYXTHFGeLpyhVnminPPvFNlCga2w1/t1t7R1jWw/CL4H9+BmRKMHYe+x2DHDxaOSdfBsvNg/3aQ/x9E+/UsQBLiUSbw5sBP4toJAsvBMqGYi/DCEmEUYGAQxg4HocAQJqah4c0grOAXFZZpYlnWSSxoOHklq9CJGEUUoWREJCVuKo0lJZbt4qaypFIpalIOQiiEEGRrUuBa+OUSpUKR3FSO3OwstmHgWBZuwqW2to6SkAglsUIDy3AxJdgxa9MnxEOSxMHAJkLSUb8YpRRhGOH5ERXfImRuXj32d9ES9cvpOPdtXHzBC7jnrh8zePgXMHc6veVfbQET9J04EjOsF7Zqvd0iIbXge5iGhWVbpFyd6CYIA4IgIIoi3Djk0hAmCpd0WrOylXCpKBOrAlnHwXRdrIROROf5JQK/TKVcIpfLERTKzM7kmMvNkJubpRLPGi1hYgsX10qACjENpXVCTyqtaVpkMlmwwVRpDCIMGTI3NUbk5VF+GVWpqsZGMVNa4EYQUiSMFIEIqVDBR1X55Eygo6aW8JRc4E+xLegA1x/+l57C82fmxk7MDR3PuE/CgIyIULNjUDhORQ4SzCUp9jlExRHk7HFk+Sg6A8OzBATDXfi5vYw+oeUGZFgFOJ7ZhGFhJdoQiQpRyiJMCojKWCRIxNKCQjx9Et4zAoxFKApzk0znJvFlhebmFpARpmVgORZKCQpzPgNzBcZyJfwZybkXnI3aIKhMFRnuH+Rw/xAjfonaukYaMi24lZCENLHrDOyaZ7h2BEakk6MYZgzEKg10BAWwUrG+3zMBtKeh3EYBBGWtxfkUcDeWlDh5s4qj7oQNBDA1MkXohWTcDJ1tLbhKixzKco7SdECyKUH7im5qGuooTy9D5gxGH7uHwd5jDB18lEXLmhjcVYPwPDo3rJm/jmnpBlyf1aCQvjeD5ctTpDKQNG0UMWByapGBhUj4EvG0zVzYPg4M7vsm+bG9T1fVZ7Qtqu+kElhMzvTxtW9+BccuUcxHTE3NMjAwQHez/xQQb/quHYR37aadFI9SwrI34l64jWWv2kri7DbSywVWSoebfl/Bvg9q0sPBKSg1ookJFjACag7Ig9EBmUXQICHbpZMkhECgdNZEGWiWZPNKcG6EYguk1mjQJmtCTTwAKKEZkV4ZxgcBpUPba2Lw30hAsh6ybTD2CBQG4iitpaC+hQZSl8bNOwPRY2i0wgRWsCBWU20UY2jUvSo91khVv34h/L+6VnDj+26Nj1EGnJ+k0GPyrdsr5Gcr3HJjzTwTturDrNpcsUjvyDhL8nDWknNpqGtkjiIeEps0o4U5+mYn2d93HDMlWFzfTBRIho5otDWT1MBpOe4bV73+QmYPjzH+yDEANt/yctZ3NJExLSrTJeqTo0z0H2duaIzyUDyB92YwgjyO0OLhUVyvpqHrvbZWs11dVzPfkxmtPpGwNaBqAJGty2FIsOOXLAw003NsENQsdHZBY7vWlzXQzOPq+9i2GEyltRBCK/5NaA1aw9AAoZIawDMU0AC+0H2AE4f0r98CHbUQFWF22mDVmhaSKRc3aVCq6MRfnR2QcARIg5kCtC3Vk1jbbuaFN1zJbbvWEMljnCxGkj96OxNPZBk7sQmndgEUtWMd3FRKg43VqIBKSbO1Exb4EgZmdDSzY0JrQvfJpopBzlAfJ2INZGHGiaVtzR42ACNcaIpSxgm50CzZhKGdYW5jrKkUs3HLcfuVIUhPM2NLQoPZgaWdFRCzLOLrl6XeT8XvgozZrn6sJVvxFbMTHkHFw/fyeJVZwsCjXPaJiiVUsYjhlTEbG+JwpJAoX8AQEQKJoSKMKMArllBCv3RCauVTpYyYaR8RhpMo5SFEDFVHkJ+GySP9qOIxnjuLGOp/CKX0Qr6B1czRh0OKLE2McXh+TxW3iD60r6YG7XvJEbC7sJPsYIKzd2XpOXKANesupGPtWtKr6mAccsWd1FXmaKOLBxgkImCSAhm8+fPm4nPWo8FKgMUsYpH9IjgvC7MmYp3A7k7SWbMVkT+CUoNMMzAP6RWqbYQFCYzq9zPJAjRBfyfwQeBtwFIWutRnbxITnw4gXTnEm2QT3WIbn1d7mJlPJPKbsvjs3izIfXqQeigLzR2Ec7MUd++nXM7jz1kgXUTbEqyVdWSTBUr93QRDD8Hgj046X4BeWjxZSw6IZinMzFAuKFZs2MKWs15A75776N9XwZx5glf8zZ+zqr2V5W1NrO1uZ0mdzUN+hfvuuYcd9/2QN7z5NTQ1rmLviXF6TkxgWRny5SGO9w9wvH9w/l62XvYyGpubCYM8e/bsYteBI2y9YAMXbVtP7pabGes/Rra+mc7us/jh939AXXM7betX07y8GcO2+fJ3HyPypjATFou6G6jPmSTcU2dgDzx4N7m5AGG10ndiiNe+9tX0jo7SZlGA9gAAIABJREFU84tvssTO8K1SDRduqCOwE2zr9Nn76NdQBZ14LJVK8MbX38BLtnRx123fZfuddzI8OMC3//b9iFU3Y9RvoMkbprYyTDC0j672Oq5+xY14bpKGDCTTNg/MOFxyy0Xs/Nuf0rd7mrs+cYChDWu44RLIW9qn6gvoLWmphADIGoKLu5r4sz+6mjvWt3LbvcvgkS8AMH38fg7+7J9x6t/DwK4dDPUPgVOEzgSybweJjiWI1mbKBx5+7ppePQsel+fQbNMiFdn4d/dpTRtLy8eswCABnNXQQEGa7BquMG4YtAPNqRRXrVjBP37qUzyuAlZt3EhAPBW8dydzh/tIBIqdf/8lkv9wHk7C5MT0FJ974Bf0fP8HFAb7aV26ivNveD0vWnce27ZspKO1nlIAX9kLT3zvH3ikZ5j9R/LkB/vjktaiIfsqCGvGFRKgJ3C/5gx9FvyHYWI8ZG9PheI/pFF1G3S4jSwjC/8J/T+HI1PwuA/3oHHf55WK//SmlEKpX3XPEqIKzMZuuUoApTmY3qe/JxpOzZJs1euEDSvOgwP3Pw0YW50QnyEVccaZ7lclEagKfhAQRaaeJ0pJKAOkkhhxWL8Rs0tRKgZitdvXFCbSsvDDENu2sEyh1+KGgWmYGDELyrUsPQ6hZQIdN4HjOtQ3NNLS1k5NfT3ppAtS6sRfKHKlGabCkFJUgCDCr1SIDIPQNAn8kCiUFPNlfF+Hy6MMIiQyXs3YwiRhmjjCxhYmiBDf8zUYKyNKUUBECfU7rjkclqeZPnYXuyv7yQ0dBa//Vx/0tCbJJhwUBuPlFAvJPgIkBeaYwSWDGQhMpfC8Aq6RQBgmGALTMHFEGtN0ME0X106hRFrrwgobsPH9AL9cwTQtLMdGeh6mEChTYDsm2WyCvJfSMyip8GVEQZWBCg4mSaHlJ0IpcUwwbYFtm9iuC6aDFAahXwZpYlkmAkEYKiInpVuzBGWEEBlatgBJhCIgoBTPWIUKkZQIUYwQ59ZAy29n0b1L8jS1R7xfPRq0bUcv2c/UFrZ0ncnStc8MUc6Ow8ihAOaGoTwJZgplBqjQIpgZRpWPQnQEHTf3bGe2Piif6NfsnqMQpsZhtr2JOlzSNjj2nO53AokIhU40+DR2RoCxkQyZK40xlRtlujRDqTyLa5pYtoNhOZQ9xVy+zHAux9jMHIXhEku3rCHVnEbVlhkdG6N3fIxUzqehxkS1NFOfiDAsE9NlPnHQKeCnlmpBehoITbgLYKyKNBtNBlDOS6wEOEldiYGn97NOqjkZ6BW4YZnzmpkqXszPx0I+ncXlIFAQKaIgwghMcsMz+IUAp8GmrbsJCgGh51MuFQjyIYkGi0Qmg5vOYCzpINdbofL4L5iYmsYvTKFKg4zs30NYiXCyGZo6FmnlGlOz5mqz+tKlUohXkTQ3OL+ioNoKAUyUYawEq1t1cJMloFgJ2b5vjMrodqgK3v+OWdZ1MYQkLMzwwMN3oeFll6ra4caNS2hqPhXZ9w+Oog7nqHG7Ge+owW27lK6XXUL32zVLcxaYGIKDQ/BNCfd9QWtL0gFciEaQpsGcg0Q9JGchWgeZZmiMoLECaRc8A5JCAz0lqdtfpk5LCEwsjZtPuIBxRjEoZAoN7pULcbi7CyjIzejM7IYEYxQmfgZqHLBhrpqHpxadbLcFMEFNoVddVRmjrN4fBfPxwmGcpCoLUR0LSKqFRj2y8f5VB0cnenHkA4sFHHV54LEK+SDi3A3wohUaCKtqh1Yt6SZpyjZghA5nLV5KwpbkvVl6+g4iwgxHRsc4PjjEiUPak1pfn8E2LKKSIAwDRFCkHEQa0UslWX395Qw8fJip/gLRyBhLXnoRHekVJGYduoYGaWwfR+x2iKTCHy8TBYEOffBntYSh0HVrxEx3i5hJaWmQ3DS1NqtrxWBkDBi6lg4rV8SJvAz93AIPZgYh3wv1SWjv0PVaKmtw14pBV7sBRKjPUR1rokrcvynw/IWkYErqclWCeBkgNEjbvQTcCCbzkpm5iK5lTdimwA+g5OnEYrVZncxKSkm+UsYr+0jlEIQGrYubaGjdwuz4FIF/UlxsbgfTh7o5+MBWGjd2I4IAUwWYBBimR9aRur81QNoS01EUsykSlkVZwoFRiWFI6lOKtmzEcOyx8n2DMBSYpiQyNaPBQGI7sQJGpHVnzLipmug1UVXLNZHUbao6LHq+rgcVweyMZsIGnv5USuCHsb62ntPF7ApNSjIMPVaU/XjdVX0Gnma3+r6u79nJEpViiXJxhuLcGJ5XplIsE87lkbkcFArQ3K4ReenD3Kx+oaXUf/0KBPmYphtq5BzvpBcpBIaoyvb8pm1k6DFdB5g4dCOwyNgNtDtnMVY8FYyN1ULnl6B16K5lV7EHNVShoZxgvCvJC7e9lbrmFsqlYbzhKQrhHlym8UnwIEew0P1bJ7orUegeOkBPPgtodmyJBKbRCG0+DNswYGPYNtn6xXQXuzkeZefJ+WUWGLvE32Pp7DPSeeiju+B/Q6vWXArzerr/Fav1jnGpyLBULKVH1TOSTnLMm2AyfB7SmwdjMHM/zNTCBRcjy0nkbKgzUWWyWneksR6zvR4704xRNmBmFjgZjH2mhB+S8ePHMGqfYHH3crrbQwrDWSb7EwhD0L3pbG7cuoy2pENh1sfLlcgmXOZmpjg8dIBi6TpGJmZ54lAf+4+OsmrFRqby0wyPDDM+Pj5/la7l57Jk5Roq5TH2PvYYU+U0y1oaWXnVFl5105V89d+L1GQayWQbaFrUQ6qxjVRNikpphp0PH+Kb397OxqUuZ63roHt1N7OGzkZ+svXs3YmdaMOyaxjs7eXCC7dRuefnDO5/hIO/WMrxgyso+itZ1FVHp1WEEw/p/gLdZzXaFVo2rOPxh385f84d//HvsMSBhknIH4PSMTLBYa675jw2n91GEvCaEgwUYMqHVS9axd5v9jB+YJLxgV3sfHEbN19Qy7hhMOzp92/OhJ4xcAvQYEJowPptayg0t9KfXEwfjzO9by8zfbvIT41ScC5icP8OoqEZrFQLtedsZvqeQ5iZeoRIPRetbMFcnvuXutZiQs6wr/cAHInpng74hPTOjLGytokmw2RDOsNL12+kLxTUGIoGQ7DKdVl+yy1sn54iZZtMBWV6Dz5Bed9xGM9RAfb863/w8EtfS0tTEz2jI/zL7d+j+NgxVi7p5NwrrubFb3wrr1/TSM4XHB0Y58SJXr75S8kvv/BvFMd7WegxW+NPU7xtIbx3ofc7+fuztEEoDCoO7PDhhgnY2KJ1zKJRmHkYeo/CLwpamuA4z+vKX+dSFTTQSGPXIqYqs/RN9P+fFaIwoT8ndur/O8+F+qVoZrEPwtUshyeNwcIwaN28manxEkGurIXds0lqF9XiexHl2RLkRqCcf8qx/29bSKRCPed60rtbTYglEFQTHwkhiCKJIQTCsDBMmyiKIM4ZYRsGpuNimXYMyELCtjENG8M0MWMmbSabpa29la7F3dQ2NgKSSrFEKV8gl5ulmC9SyOUpzBXwikWCSoVIGESmhTQkgRfgVXyiMCQiAuUTzJfYwBQGlrAQpkAKhYWiWClp/VEVUVLBqfksfkctrMww23svs73PzfkMK0ApE4F1SvyVokyZaSIUZhRhRFoLO2tkwbAwLItkIo0wLQzLxbJS2E4WZaQQposhTITS+tHlSgllgjQkoeeTTqcRhiCRcHDdGpAm5SAgMgShoSiVirodCYOksLGxCIMIJSQCgWUZmLaFFCahVPi+hyEtlNL3UPEDLNPCMFwwQzA8jBhzkISIuN34eBj4GHgEFFDopbNOlwi9aFZsBb1kr+X0vXkKPQp0oxm1T+4NXZLYho1hGxS8IvK3pFXctQJaV+h4pyynv5fpMeg9EEJxCPwR8Bo0IOWmUFLFLMcKPA8Ja6VU5KYrTBaaaWrIUCcElg22FScA4XcAjM0VZuibOqazj6UsBkcHcZWJkoIwUsxWQrxQs5ZK+TJTw0e550t3UhZpGls6uGTbeVx8ySUMHpqEikNUkZCxMB2B8aQ7XJCmVZCDcg6kAdlu/aillARl8GcFmU44sDsgXWOweIX+fWJYi9bXNor59hnmfFRF4mSTutVEmsGVmsc3xZOufUqJ4thISeT5lGfyZLIZZKGMrMQPsQGQDoVAMjyeJ2loGfCgogh8QaZeULc0SaatkWRdO5nGdjzPJ9/3BEN9AxzZdYDXvfuDhJaFkRG4jbpBRMDho0WOHy3w8hs6NFtXnFrWeS3fePuhGcVjB6Bnn+C1/w3WGpp+3T+c51WXfUlnovkdtf7xXkyRoMY0yTMWa26VUEoDTH/5d6+ko+NU2nzr2dvwR7IUp46w7S8+SPZ6E6tN11+k4AEJX/4KfO/vWEhcezFwHhqQ/QqwWUsMrLhGE2VHFMx4kJuD3Cws7oZWV3e4R0Qsb8GpAILnxbIclgaXfKn7IRFq8HfRUh1enUxqxuahnVA+jpbeewg4BGxUWns2JbSc2Fn/m73zDpOjvLL+r0LnPDlqRpoZZYFAKJBFFDljjI0x9tr+nBYw67AOuxjb6zXYxgFnvA7rNcYkYzAZAUJYSEJ5pJE0mpxDT4fpVN2Vvj/ebo3AiGADxrscPf20pqu6u6q66q37nnvuucXtPAphqLgK2Iuok/0WwrjlGMRGF4p/h0AJiCZSqShCCWEi2JLK4gYbYjsPtngsMSAKsAIYCLFzEC74gs3Ef0PAI87LQ108Viw4ghXzlxx8TUIiNp7iq1+8jompacb3R5kemSEUEsEUrfNnccLqlYxPjfPk/VvI2BmkZh8sXkJb88VI3lH6qCDx7R8xnpaocriocgSoKaslkYoQ86fIBQys8hSxsXGgm1R6gMEBA0dYxusSynNbEbuY1yDoEmS6bUO0WPouyTNqeUUpKkMt0JM2DhcEHOD0QlQSrxtJyEYhUGWzrw+qqoXtgaRA36BoyKdrgqNraBTCDbsgOL2RYZhVL8r808VEsooo0c8XhHK3eQFkpmG0X6O3I838xRVUhoR3aUgV+5GYhIFpmJzMsb9rP+NDQ1TVzsLpdDA6tJdV517C5kfbGe8fftH1MbTjbkY61hJe8W3yUyPkkxMYqXFIDTLTOsnioNeFYwlQDnqJKisU18siKD0DMfFxFN+TQNxoNWai9bdrrvdV8FpEA2+zijUbizHExDRYUcWsxiXs2PyXBVB5xK+ZYYaQ7QRi+S4i6Z/ziXVRpGcUpu/czdivH6OP35Okg61odCCGogZmaOdS44IhxBDThOh1uAdIso2s1s1HftcMzmPg6Qqkah/UgDRmkzVhujiBezsrA14JeeBfgfchPGRP4tWoFElkekqwmVFt2Ttpsg9wH0eRmfderh26i19PrDuk+/ObCQ24BzbeA/hAaYKqjwoPx8Gd2FofGr1ohBEk0sQrf9xLMLrxPnKDvTR97DZu/fi1FLLtCE9WlW+deyNnPH4j03Wz+OmjQxxTYzCvop7rr7ueljlV4HDxozueYX93P5qeR581SSIxTHykn9TE+MHv2LVzgGi6ivLaKmbNqefipctYtXQhsm1Tj0TYFeLRpx6is2M7qxbPZ+vuHez4w/203303j/zpTizLJNrYQuTyy7nmvVfwXE8a1en/i33RtTF0bQyArgN9HH/sKpobh7jl29djWecy3nM6DfMaaAzksN1VYI6CpRGbnOTiY499+QPU91PxKGLxKdew4OgzSZkWSVliQbnEMRWi+ecHesGsqUfq24c9vAd2hRnQTuWFjIcNQxLDaZtAK3ztPjC7Jer9kPTCgnPg4oVlrP3S8dzwxee5f9nRTO3ciZEepv/uM6DxSrDChCrbWHPJP3PPuEqm438g9tIKK2mmycNfg7G/7m2vBOn4COu053jm9kNKbwvQP5HkgnV/YOisq6lxeaj3KPy/Zg/fHDGpiciEPSBLEgpwWlk5Y3aOjeO9XPy+NTCaeNF3XHT++Yd8oYLiWMXNt3ydiy48EQDTNFk3CHf/+n7u+Nr1iJFWRkwcqhCBpp+Z7LlZ/H/Jgc/LjH/U6yRjAVBB88LqL8Pjx8KpXjAHYWQK2k1BwpZMutO8uCHIm4ggsAAHl3E2V3zsRn6//3Fu+PXnsd9IafRYD0xOgVIF5gjoYzA8Bn84tDuZhCMQ5Ip167j7Z7sYeXIjtG9HOu5cVt50JkO9KToe2wmP3Aqd60VDgHfwmmEWqVgwURTRyV6SJBRFxaV4MRVwulx4PB58fh8hf1g0cJIlnC4Vt+LCH/DidInyKFVVhTVBOEigIkwg7GdwoJe+A+IxNNhLNJpAwhJqRr2Ao0ilKJKC1+PFMAx8KlgUmDamDzndnUg4sS2DTFGULtpPmYCB8Rbddf9R0Tm58zBLTCBFgQJiYukGFByWjGnJyJYLp+pDUVwoqgNFVZFUFY/Hi4kLuyjNUFGYzmRIxFIQk1BRKa+ppiwcJuj34/X5iFR5mL1gIanpJP19ffT27sUj67hVG5fDRtMMYskktp5HtU1ABdPCsArolo1pFEdhI49pFzvKqaCbNpKloODGqUTANFHRsdGLOnoJi2lM8qLCj5l+2RmEHfc+hOL1KODs4pF56YjuQMTfCxCaq5dOKeqZTZWvGl+1h809O8jZU5gU/qKv05uNyBxgttjGE/nL/bCB0WGbfe0FKHQDXZCpx9JN8tUtKJVt2FMy5CSwB7GsUtnum7UfJrY1wcBIkPKgg4qgj4jDhwsDSzGwJQlJfpuTsUgQn57EMCx0FMZHh4lG4+h5A9u0SRsmScWgLzrOyMgYdvckpm1hIzEsSexbey/7/7Cbz3/2kyxb3YqrUkYyRMnuSxqsU8iIhp5mHqaGe7EKNrLqJZmpxVUN99/xGHZB4bRTTsVfr1BAwaFL5KdtRg5k0MaGcLaVQ3mV+MA0WFkdPZujkM/gN8JoGU2UhHs8EDxEz2cDOdEQWPEIT0CmINY/SDaTQZFlamprocZNrdWALdl4m8LiLCwHR5mMbGr85mc30zB/FS1zF9Lc2nzw41tmL6X6knpmfbaRU087hoiVoqmyjNa2EW64dCVHn7iSpWeu4ajzLwGKmipLJTalcPuP+3jP1Y0EAjOnxJPPQGdPHsO0aZ4thO+xaQunCqcvVfAkYG0c+tPQ0Z2AzH8ipomv+FO/DW82QryfsDp43xUf4KtfuplgncX+501+/Ktv8Ot7vnXYd3bpDowjj6D+3ZfiXyYjOQV91JeGVTeDfodI2GAjGIVViNqAZ4sf8K+weAXMrYUWoAvRdEdVYE4ZjJjQJwtNgx8Ry3oRA3EprHarECyaHmYyots7llB261kYG4RZc4SPZjoLSg6sckSQPI4gZE1gly7+3+Ccqd8tNebaCpwGzALpw+D+KGj3Fa0VOoFjEcF2DMw45JuEJUJeFUpPJATZ5EfE/F4EQVuy7Cpxb4sRNRSjUNgCTR/N8B+fcrPwKJUx4IriR40BPZZBJnGA48Mt+BQX/lCIs6+4gg+ecg2/vPsn3HXv79n55H4AGmrnkE9J/Ow793DKpcu48JMXUwhVkghW0njy2TTl65noSeLNuElUODm95gTqq+eiWB6iyTz+sSidiW3kJzL4VD8xxGR8y/33sPOxLeC7BKmsBbx+0T2KPLYBkmkimQYUCtghd7ETmY6UTIORFz60pgFWBuwBJCkGBLGJYBkT2JaKLCeQlUmQBjCtHLIURJIEI29ZYNslwjKHLM+oYkvLD752CA79W1bE37YFlmmzoVjOJRUvjYPr2sUSfNPEsm1GRPYG2zIZkiRM/eUz+VYhTvz5T2DbRXmuXSJgX7RF4knv40VNMV70fOh7SiPJITv7Dt5ShMMtNM1azc5dvwBsesa20zfRedj1JxCXew0zFtNp4Nuaycc+9TRPPvYThoa3k2Sc59FJYhJBOKK0FtfPMtMvsKSUzSPGzWUIms0JqCR5kKtZUTiNMvV9uBZeDj8A1zVXoG3MExvxkGYfNn38Y9KxAncCW4BvAGso1XC8BO4WaLwQNnxRSMLHgC0T8L4LmGmElQU24tu5jR+0vIt31XyGS3b9hByv4qn4hsCL+BWzYO6Dsc+Jl+2Sj80ZUOxI+2rxxV8iRUVNjms+tZDR5GfZ/8efkBjohfKjYfgudvMxasuXMHdlgFXH2CxSwC/LGNj0xhIE6mYxf84iIhUhLp4l8+8/68G0X1xFlCsM0rWnj80PbeeUy67m5lu+z7ErlnP1e6/giJVHUtPUwAUXXo563mWsWnEElJlseH4XejrDL2+/he99vJUXNveyf8cO7nt4O8lpjZDSQMQ3Sjwz/LJ79b3vPcPHP/MRTrjgNL55/PF88bY88889Djv6Ag9+60PY+TzgF7+9pwziL7ymo/XC+jvobd/IpvvWc/vD/4nDo2JK4FHg3jlg3LyMb/48xtd/MQ1qmus+vIVFH26j7exayo6Erd/L0HC6C+lMB33PwD9dDzsfgok94K6Dd0vQes86Hr/tZzz9X7+HM78Gj30QMhPE9Eru/robvaYB6k8FtRomngA80LoYmtqgpgHu+S8oJIpqk78vvvyZ/6Fr2zZ+8/kvvnjBwCj2Vf/CpeuW8cW58zkvEEAGrq9VuG33ATRZ5pLFrSxEhD5bdu3gx3+8A3bHil5RL4OaFpyX3ED3v19JVVmAjJmna2qQ0xcfh5bXKRQKiGu5CQ722i7VSvlf8nBTNEpiRjmUQ8wKXmpS9moYBOcTcNsZsEATKuv+bXDHTtHR1EYwo0Ks9pbdrm0gj8FG1uP7xkO4zQiflD/NbdavEMHoG2ATYCbBLLUmfvkdcxxzDr6P3MZP6q+gkNsC9fNxr76SC39wAUG3g1jeDw0J2LdO+CO9g9cNC6GP1PIaXo8XWVaRJAUDjWAwSCAcIBQJUVlVid/tQVKVYrMWm6nhCTLpDOmUqKrKZJI4XS68Ph/eQIC8lWewZ4Do+ATT8QSWJeN0OskX8hi6hYIq/slOTNMmmpxEsVWSTFNALxLFJWjYL1G82rxjWPHGwDrk2cSBiyx5HHiKZLmKih9VDqCqXlTVC6ofp6Ii2VLxJDIoGHnyuolu6WjoMJUkndQI+EM0zglTXl2N6nDgCZgEy1poWnAU6alxCqk4+XQMbaqfCpcbydLB1JFMQeoqloTDMMgb02SSCWRJFqIc0wS3isfpxJZkdFshrUHBymDZBhIaCipaUSVbgspMH4xRRFjnR1SHlWQrJ8PBxuGHQkWoY1+OGuxjH3hMTp69hms/9F4GU3k6Og6w9YXNbBpa+0b8UK8BDuq9Mk3emabdL0UUGE9EiQ3tR8SxI+JVYwopXsF/3H4Z85atAb/JgdEC3//cMBNbbqCQ2IjIDr4eCG9hXqEBVwkHhmIEHEHCcgW1R1ahunUsS0fTNFHBehi8LchYSysw3L6fpKYxbVtMxaKMxmMYpgmmTXQkjS5ZZPIahWxO1F0XYQI5w2Br5+N8+bsDLH9uKaeefDzN5TVYFugFHV3LY+kWi08+FofPixwSohDVqsS2QFJV5LBQHNZUVmPkFJyqOE2bZsvoeYlUCiqb3Uzlwmx/bheJh8dZc+aZmIaFZOpgm5gSaKk8o8OjuFQHrS0tyCE/kiK+z9RsUhMappZHkXUcDhu/04ttmGjZHJKqIPk94JTo6e4CE5bULgcP7HhyA5ueXs/+kf0cmaimLngi5UEXkmSSPJBEURyMHRglNRFlzrwlLG5bgqMwid9pMj09wd6eIeKpBLHxcdTEFIuv+hCSJNHU5MLQ89z+gy2cdmoN6iwVt694g7AhMd6LaRhYDQt44u576BzYSbaQxO110dp6BgeGO4jnBkmmu3l7tTt57ZAllcVl59GVfITnNj3Fv3/9C3zuhv9g43MbGejrJRIp54p3X4Pi8x8Uddo2dCbBOrIBvw2eiAfJBb8dh63rYP9dkNiDqBwOI9JVDoQKtR7kVeA+D5YsgcpyUQo+iSATQj5RNq0qQgFZpYhCswDQb4v4tuSXKSEUjMkJMTcJV0JaA49DqDRNN0heyBmgRSE1Bg4TWpfCuAuiVQh1ahjhX5GzBWuSQYzqk4jZ/tngmQdqUbCTS4JdUswWEDF/sVbY1sCIghThkFrw4r7rCDFGNYLAXY8weywRwjKCkJXE60nVwc8Nk6PPhpPeNzNcOQG/LJH1+0GSRTm618uSVccRCZez+Mj5HBhceJCM7ewbAGxyuTzb1u3Ht3MMX101odZmfIaDPVoDNdXV/L/3XEXZmStZ3daK6fbRP5ri6Uc3sWPtzxnp3ouemsavzkxWTD2NqXdB9k5IBoR/hFwkDuziiWIVuzg5lWKcYInad9ssqkREKCkOeqF4opSs2aXiQdOKy01m9IUlWMXX39rJ6aHf9sp0lo1tZl9xjdf6Se/g7YNsJs3Q0DCLai+mJ/oMOT2BZUo4WY5O+19MOizEWTyO0DNXI85yj5HnE4/+B8HRTsxCnBQFHIhKAC/iMory4qJaGdEHZhpBI5aGlTkcLBhlK1m2sJnmiUpaN4dw/+hMXKudDFWfTmJ7NYmNj2LzPCIr9XZvL/ny0BF+vLcgwstjgFm8xDNs2RysT11F4mvdtE/9Dtd0mlnUUfu7W5FuuANGNwFdSJhg5vCOPssytZFfS2ehLZ3Nd3v/wLbE4Un2vw4LEeNcHHETKbE0NjMdIOXisieLf5c0IK8P473D3PrBr9GdCpFNT0IhCrFBoI0//mkS386dJBI6JFpoPjGIPyST1w0yqSxDe14gZnvxlFVRHqtGScZR9Bcr16L9O8Gy0DIJtj39MJajmj07Ovhp7Oe8x/gElS3VNDVUoE8l+cGvHub9N5zH8qULiI8M89vH1pKWG3nvDVdiBhfyXHsnmx78L3p795PJxw+7T/n8AYbGkwxGg3jKlmHnHqDjniex4zvR86WxNguFCbASgIS/9XhaW4+gPBBk7d0/ZMbsYwamUSCWGGBL+/18/P0DmEoTtS/zAAAgAElEQVQVkfBcWmYt58Q1K5m7SKXtnKM4vbGeJ3tC5B5+Bne+DK9Zy5YoGMe4WDJHYbEXAmVCJPnFAsTywnv7CODnAwEOTFWDVglb9oCmgH85dvmRGFVHcum/rGSZZDDRM8l3Hz4HjzPNnAVLWDy/hhXzvHDhKm797L8w3Nf7us+FNwwSUAnOQACH4halSIfCtiGTZe/nv8CDn/40yplrOFuScEtwbmMNz3X38S/fu53wxqewbZuReJT9Q72HJWK9y89h0eqz+fSVZ1NdEWLjyBgbNj3P2v/5BbGpqaJqyc/B8qSDoyWIUcKBIGB9xfXKEEGblxmFLLz2+6+NmPLvguYxuFSCM2Jg7oSde2Fjh0im1FWD3wZnDnoTb+ntPQ30YVHBOH9O/xLJbiHvbOPKxV/gwd3fIp3vZ8Z3Eli4DDxe2Lr+dXzLqySDl5yNuehMMlqBQmIIzv4oHLsM58oFHOt1cMdnbqbHs4Tw3FW8+7e/4b+//gDZvo2Q+jue2/+AkJFx4MTtcuN0OpEVB5Kk4Pa7iUQqCIUDeHwe0uksZt4gl8+h5TV0Q8dIaWQzGTQtT76QJ2OkkWUZRVVRVRXTNsmms+S1PIauI+EA2cYyhaenIMQkJEtMdixMJCT0Q4wJ3sEbh4CrnNpgCwcmO7EP+sWX/PBgZj4koSIjH4waBaHmUAO4PCHc/gAeTwBbkrBtE8ssYOoGbtlGNU0sy8KwTFTVg6q4kFQ3hTxk8jaqaSOjgOTDpcoYXgcSQSQ5SMS2KWSTGHoGy9BweEDSbSRddPS1FTBdKiVBiSXbOGUHquJEdig4nX7wejDSDixNwdLBRsPExC7O80optFKVmAcR/1UhRrQhROQ0jFDAzkFQEHJxWTsiHfVyM0YLi/HkCOvaH6U3upWj5iyhxhPknGOWUK1Ms3Z4Fxnj9SbFXw8k4GwWU8MKSdyhXg69BYimJrAT+xFxoQ7IYGWwtV4eeHCYhVP11C/wUdbs5TNfcpKf+iL7OyZ4bt0Y+5+89nVsU2mOPhfV4UGRHUhYaPkDxe+eubFZdoroVJIhf4TFS+uQ/SoO2UQxCiiOl5VLAG8TMjaX1di98wDJfJZpWyedyzCVTWHZNliQGHm10nebiel+ntrQz8BwJ9OxCebX1VEXqsJhWdhaFtt2MrttHsEmBUfIhW3DVL+Jx+XG63HhDAluZE5rHWZewh+S0bMwnRwlOpEim7I44bT5xFSFnj372b9rC6vmHYk3EsY0NXQ9RzqrkYhP09NzgEgoRGN1Le6cG902sXQbQ7PJJbJYuQwyBroKatBkejpGNpvGliT6+npwJBUmR8dxqm5y8RzR4SgTPSNMjYwzlYxSSI4T8ar4Aiq6rbF341Yi4QhTw0NomRzZrMEp55yDnY2RiQ7TvXcbY+kMyVQaM6/hsw3mn3Q+am05kYiDhgYHmXyWJ594gWNWtDJ3fh2BEITLQLWSpKIJxnpUNv35AboHt5DS4iA76dmTZnRiNwW9j9daA/b2uzXJSHhxSNVIOOnpO0B0Ks78llX8+dl19A7sIxAMcuEll7FjTwcBV4iQP0JlfQ1JGyrrQ7idEDfghUfg3mHY+iQM3lf8eLX4kBBJlXKQjgTniRA5SwyeKpCyhAp2VBMeobYMWRu8bqiTRIjtRxAY48x0nDcR3q/IYjhweIsl6uoMYRuoBsUFZkIoZ/URaF4BviaY9kOhCpEmk2TBSexDGNA4mOEAw+AIg9NTtD7IgNwIlru4vKT09hctLceLXqgVxeV7gI0IhsWNSGLJiDvIOKLGQkbcMUqWBQDDKjs2mqSdFpFmg8ETFGokCTdQLsngCiIXGV+H6qSxbi7PvrCert4uMmkxqW9obgSviqwotMwL0N3Zhd0XJTgcpSaewq/7qGkrpylUwZz581hQsZT+9b2MZ/bQOdhL+1MbGXthK16/B0+kDpcjQHQqRcFMYJdIVGPvq5eQv1Y+8lVRcrV8B+/g74eCniYR76O59lRkyQlYqIpMW+NqDgx3U3gZpbSFGA6KQwYRIGCbrO1bzwLEGGcjArAS6aohiFe5uNxRXD6BGK4SiEvLBI5HiLCSiEZXY4zTkNlMa68L9z0mvo+uxlzZzNzqEFumTPLd28H6a0pz3z7IAn9GDJ15BBE9t7jMgQM5XIU9fyFj1/2CXNskhcl+JhLd1N57IzyTgY5qmNgC+4vlGqleKklxmVRDQQnQV7UUSXWwNdrBK9/BJcAHnjngjYDLK+4piRhoo2DGmCmFKLmAy3BYT7LS2XLgbzk8pGIxnv393TBnKX5/hOojy6mqnkP/SIC9O6LI3R04yyrorLHJryja+FsWqWSKiZ79ZG0HijYLvbmSap+Ep5iLkySJlrZ5jAyLyiaA0b5OInUOkqZMvxLAaZvUlvmpCzhJOyFnFxiaMFhQE8YXydI7EicVlylIHnA6McwEA4NdFAoxXjm5Hae7cw+hhkUcffrJLD+qmj1/Wke8f8sh6+hgOZEsP765y/G1rMZdNwdHUV0sq35sS8O2Xnwv0Y0sk/EuHri3C6giEl7A7KYRprRJFvRITFXNpn7WPE6udtI1HsGIJRh/ooPouIbt9+Gx65hdFmBZGGITkLVsehJ5HtqeIxQOM25LFOqbUeavxOyZIrjiVPx1C1EjC4nLtbiUWbQs9TJnkcGZrkWozjh4m2ie7Wf5UsgsXoL7+7fDeExkhf8OkBwq9WefQPf0JAMTozMLHFDRNg9/RRV9z64n+cSTPD9/Af5AkKXHHks1sDASJBb0cV82x5+27yXXfwBLO3xwUL7kBI4483xOP/10LjuyicfXbeKJfXt5/s/reP6PDx+6Vcw4c3uYuaYURCo/wExJUgCRtnIx08xLlHqL665EYJSSJKW/dcSI2wmMQEsnHK/BRbXg2AfPb4ddvdA5CrMqwe2FTEFk6N/CkKWSMmqopJla2sgwZcUZo4ekLbFcPQHloC3DIcddeUkzkL8JEsw7jtYzzkOacwx9yEROXUFq8YkYVbNQJYcoAHv4UWKBLiKyguvKMzjuXJmOhzKMtJdSje/glSABDsWBQ3HiVty4XR4URUWWFWRZwaGoqIoQQeiaTjyZQJUhlZ4mm8uI3g+GRTqTIadp5PUChVetvjBf1CDg76/P/78ECUlSUaSSur9EhJV6J0iltVBRhWUFKrKkikZekozicKI6XchuDz5vQNCbloFlqVguC8XlwjQtLNvGxEbCiVN143H7kF1ubEnBkmQkWUZRZBwoON0SluXAsmQ8RgrJAklSMGUnimqBpYFhFJWuNkg2tmWJJoLYKIpoKKfIKpLDicvtwFSgoMroGTAKBUzxzhcZuxUQXECpL6WXmWn1CGJkjxWXZYvrHkDon/o5fG4sk0/RM5aiZ6wTW8uxsLqRRn+EtmA1/Zl6xtLTTGs5cn9FcvzVIUPluVS6aqlnJqX4UowmIDmdE81gsRCRfwCIYJsFtv+5h6l4goYuJ3OWGCyqzOJyyrg8VSiO1xvzl+6NPtzOatxuHw6njKHrJOOj6Gb6EPGJTiKTZGhqioloA2WVIVxeGadso6qHrzp5W5Cx0eQ0j21sx8Yuen789ejq76W7v5dKn8R7TjmL2SEPATT8kWYm9/ei+JyEQ1UgwaaN3dRX19E4p4LqCgdmARYeVYOkCLFachCeeHgDBw7swTKyLD/uyySi44wPdDLSs4t4bIja1tlEJ0aYGJtgoH+Irq4D9Pftpqm5iaVHHYGcdJJKpTANWzBs+TyFXEZ0dLRUzGmDvr69OJ1uCnmDZ558An/QQUP9QiIN1URHoqx7eh3N4XKqyitQTYvEcBSjoGErJql8jPvvvJ2jFs1DwoEnUEkyneY9n/s0UlJn3+bN9Az/J2lHN5Zp0DEywehjz3Hp6ueIXHE6akUY1aXSfMQs/u3Gr3PVle/l/e+/jMXLZFpaod0n0Tc8xtPtG9jR9RCWnYZi17/+4Z+/MSfA3xVuTLucXdH9GGQBm+nUJJ//2vsOrjF/4SKOO2Ull15xJU55DvMWHc857z2XhjkQtCCbt9kat7jsEhkzL83ExBYi7k0g2IQQ8B1wLAVfBdRYEJOK/aANGMtAfAzqGkRDOdWEuW5RdNaMuPXMlYQtgYF4X0wSXIK3SogqNAkcATBVMGWQPFAfBExh25EvwNQuGO8HaiBUBpOllvMgFLLzQBoCu6X4ug5sALMCrEqh2A2EIS2B7p6xHnQ7QK4CU4LMfjAnEGYvI8CvECrYDxaPy07gbuBGhMFNibS+EDEHnQBOkOBPCrgUunbr/OjTGnOe9nGhG2okaJBkGggX+4nZuCWVKmq46utrGO7tJR/TkGWZ1WedCoqNx+ulLFTGd2/9FlbWIhNLM7C9h+bIMi750GoI1xOPQyECN1x7L90H7iGT24bT5WL17MuZc/RRuCPlRKc0ooMy0dwLFKwX+7u9g3fwfwcZLPsAPSOV5IuTWo/Hw2WXvIsf/upeorE4r0TelTL7PsS0OIYId6qZsR8oOQHnmdEgRRC6rklmqIEpoBuYj4wPCQN4HBML2MFuyO+BLb/Bu20vX7+ygbNXh1mXP4+uWz+Glc8yU5r7j5vkuAeREh0B3o8YTkMEcY8FsJ406Bpdzwn/8+8kt66n+9YfQcqGH14Guy+HR/fAV1aIDoFFLbJk34Vry5P826k3saThON77zL9hSTp5s8CLujyrbmRVFl2JmQOzrkOavRKqmkFxwJYNMHofZDZg0Y5hgK3vLZaZv1W+tB3QE6fl3V9g1cXnc9Z5s/jJXSYvfPMrGOOTNJxzGVIgTN4CXbcwDZPx8QmSY2NEArDQ52HNykY8qUrCQWERoygql1x2Jffe9Vt6ug8USQCZ5Ph+6hc0cMTJ5/GuMxchSRIaoNRG+LebruTexzMYmIQ8IZYtWMUTP/4c//HZf2XW8lP40LWfY+yU8xjY+SSjI8OMxQ4vRNi27j6mk0mOOPU0Pn/TpXy19w429r/UjqAWxXM69e/6Cvmck717XiDZ/hCQwumdj65NYBZiYlVJLlZpHIoJ4okJ4ol1bCva9VUv+gRHnfFpvvO1Sm5uPZet33qUoW/8CcMYgZom+suvYKhxMSda8OHNMKlYpAZjPLNuEHnZCs67HKg7gZ3Ni4jf8t803XgDRy4NEZIVnnnQ5s4v9WPfJHPuWX5++cE6JvQ6bnnKojttsbUg0z8BhZYTcYwm0bs38veopnB4vJz1/Z/xwK9/zcSmZ2YWRBwc89H3s+CUs/nBymPRsxrtt92GsXMnxzz8MJd6vTgkiRPmtnD3pz7KSVKAzp/dTLb/gKieeSkUJ8uu/Q6fOnU+pzd5mE6luPzD/0p6qB3+QjmdQky5FYTDto2YrgcR5jBBREDqLj47mJnKi07dM2RsKRtuMmPyLyNG6S3AV0Szyctb4aJKOKIL7vk1fCMDIxbMUWFRHUSjsDcBO97aXhJLWcDFrOEDvIsY3TzDZh5iIy8UNpDfZKOR4i+m+e2b35gvlyRw+XD803e47II2JNXFjzdmmfuDb7HntxtIP/IsmDauU65BYgI2ryPe9Tjf037OY59awy9To9zdOY6Z3/TGbM//YqhA0O3D5/HjdrsxDOGhLEk2kmSRz2ZISTaZaQemaTE9HcMw8mhaBkPPowB5U9Cvr51UfcdK4u8Hm2ltmmnt0EqdUgm5RimxJOPAixdV8QIuFMWNoqhIqonDYaM4bAxJx+t0UpAkLMsJlgtVlZBQyBsmBdMElwsVN26fG5fHg8vlxe3xoigKiiILwZMGhm1jWhaGkUdSvDjcIWTZjakXMAwNSGAbOeyCTt4wyGazGMWOwqqq4vF6kC1T6KwlE5ffi8vjRPO4SDsUkpMapp3DJo9NHhMxYpfSY4Xic5piA+/ioxNBxPYjik8VhFr2AKIe7LWc8+v2bmPf3m20qh6Wth7L+W2r2D8ap310iF7rAAX9JfHg3wpJRjrmSqyyAIdSEy+lT8cHIBUrNZ/xIFiSOlGSq6jkBvexf2CY/Y9GWWsnEDOEUrLyr9leGxjH66ogEnETqvQTCRzPjo0dxFO9FOzhg5+bMKL0xjW27wjS0FiJ1+/DHXChON7mZCxA/nV7gR0eNjCRsbnt4cdwAdVuF5888RicgWYc5T7CNVXggws+cBT7nxuhf/cweqGZhiNEPGrooGkQngXnX3Ix+7bMYetjj/LBOadiFaaomtXMKWdfwJJLz0AyZfITOXKZBGhpyhUD/6wwyAkefeAXNC9YQt704lDdBDxeysLlmDbEkkl0yebEM06kfe92KiIV5KYz7Nq6iXt3PctPvvZjTjyiFW9zmCurrmTHCztImpCyLOJjCX57+09ZcdKpzG5txciNMjis43CHqPN6aG5oZnjXOJNTCVCque5Lv+Loo3/I9N7NPLe/k/s6evn49VfyzRO30lwRJhR288HrV/DsH1uZGBjliQc30Nm5lPJWP/c+9jRPPXEPtr0D623g0fVGQ6EcJ0eT4w8cbmiSJfDLkJ/y0bTyJJaddAbHzhGx6D8/CA/cP070zl2YhdMBScTBbcAmROJuJXARcB1UOES3ey0O27KiI7tSTOrpAH7R94AEeOKwYvVM2S3Fj21EhMSHdkKUizavCSCqgi2JYaekLJuOQzwFcQmYDQPPIFiQIIL5WCpWdLogfBS4T4aJJGg7EVWiLcJKwSWD7CgSvgGwB6EwJbYhHYXyueCph0wY+CTwZURt4geA54APIcwdkwiC9j8RBOw/HfL3CcXtuQhRc/sCYnBdqnLd9bDnk3BRG5zhKf2GEMcijU0NCr+754/s2LaZ9Y88zc9v+il3/Ow3XHTlZbjdYV7Y1sH7P/x+gr4APfsG2bJhH+lcI+4yB/OaoDANd/8BegdvozxbzrmLb+CT3/8KtStl4hmJof0m7X+aZqhtkq0Huihk3iFj38H/XdhYxNlLSYnl8Tq4/ENH88eHLiKTfIycueew761C2K8EEaVTcYRIvgcRXpWoOhmRxypHhNrB4vvnIq79ECLA3AQcw3EEaOARVCz+55BvcwCNNJYr/Nco/GC3TfctBWzzRmY6CMaBnyAGp1Lp29uvluOV8GdEoN2OGFYDTNGQi7F4SEK1I0jv24CmbSKWG4PP9sJXG2GJExYtgOumoPloGO9hxps1Bk9/ivMrT2Ly5D+xo6aCjz5xFe3R7YhfphJueJLl57exejksQkJFwSlJyJKECfjt41DslWSw6dZtvncXjN/8RQqdjwAdb+HRGeXKcyJcceksqoG7GhRUd5j4pEZ3X4JYcgMXrM1y+slNnHtqE72jOt6QTTCYxjI7eP6Jb/Gj259gX2cnksONFKzm27d8Fcs0aWtbwFlnX8y8Vadz/+/upGPn82y694twyxWAsNmIInKdPp+BaToY7hvh2bt/yXzVwK1AXXKYJYNP867/+jbPPbuW395xJ7/41W9eYX8SDA/t54ffeRhPAHrHUlDuhalDVZZTGNkddN75GPbi42FoAwzfAYA2vR+wRRDiCuFpmE1hrBszfXh7BIDxjp/w+L7bWftjCXPB49z62VUs/8Iazu8xib/7hzRnFRYBTTKcvxTaKmQqnLWE7BqOkEUfuT1l8CgpPv+x37L7/CjXfOsCLvr4crgAurqaWFMNc3T4aAye+CUUdnVRWelAS8zm3vPgG7d/hm/f1sIXv+yC1NN/9Rnx18IlyXzY28zG3z3FxMYZArzq2n/jrBPP4vKF8/BFN/Kd5tPITEyxb/16/qmmhqWjozT5/XgBv8vBpk9fzcm5KTY+/ABseUl5vL8KTrmW2y+aR6TcxxMbNnDRqadS0PVXaWJWStVbCHK2pAqoQKSxqhGBaRCR2qpCTFRLdgYGLy75LSCI3mFEEPc0SFvhq20gPwxPp2AdsNkUWTEQvlhP7YTttmAI3mK+/Ek24CHMGi4mRCMnUE85c5nH0/yZh1GY4E0j1WYtRv7Qd/nM5Ut56JFN7Hv0j+Qf/j6bZbBNG2ybVHUtn49dw0RpyhEbhG+fx3nfPYIzb/0sVz1yK78+9RKEKuEf6x70VkMv5MhZFoaWI53TUFDQbYOCJchWU7IEOWXzEv/Wd/CPjVJFjcpMcsmFhwheqQy3M4Tq9oOkIssOVJcP3B4cHh8erx/J70P1eJAUFyYqtqXgc7txoyBhY9kGGTOP2+fH5/fjdrtQVHC4xVfagGGKrbCSCrbhxGF4cKu15CUFSc6DoqNpScBAt/LkCzm0bILhzDC6XUAGvKgk0pOEPWH8vjJ8oXJUA3ApOL1evKqE0+djalDBNNxYuCmQx0C834WoGKssHgmbF1PTAUQLxzZEoj6BsCh4Pa1QM8CUqtDQuIDjzz2Nq2pbkZUQu/cNcNN/3khPZhcpon/Db3mIAZnkpWYZtEdmmpG5X+YdWzugfzwMcptQHst+cPvBG0AKRAiH/WSMJIXEARh8HBFr/i03IhsYYSIWRzObkZxHUhkIM3/RAsaGyxkeqiBtbT+4djKb5uHtz1EerubY5W3UNjqF9ephoHz5y1/+GzbujcFNN930pmyEbdsYtk3WNOmMJZi/YClubwDbkggEy3lh7R7W3fsH1j1wJ2sfvJP+7gGkvJtM3GKkP07dnBBOl0x8aIyhnYPMDrWQ0XVWXXwWaz5yOaGqMiRVYjplI/sizDtuAesfWsuftm3mqfZ22jsPEMENtkohVyA1ncFSVGTVhdcfpqKqhnBzEDPlorKlgerZtbTWtvHQQ3dx4Znnoien+ebnP0fIG6BhaTO5TJTBzZtYvWI5VTV1JKMjdGx/nlQiw5rz3svcBcuprmkik4rSvuUJhoYHkJywaOUi6upa+MmD9/N0x16mdYNxy+LcU66hvKwKZ0DFo8LzT/eRTWlMjI3RsWcPd913O3t2P0o224X9BpLlbyfYOLFwYL9CK/NAuIKTL/ggwaaFnH7iXJbM9zHuhH/6EDx7T4zodhMj1QCVXmgs5m/6EfHsZ8HxPnCvBrlMDI6FAmgF4dVvx8F2CQWr2y0sBEgDMsgVUFkGhiQcDizEoOpDhM2Z4qoSgnw1JDGFjpZ4BEk0pR8cgcQ45AbB7EHM1i1gFqgLoWyZUNY6vaB6BLFrGuB1gq8SnIvB3wJKtdju6X7IPgj5MjA6gCeA24EzwAgW1Wwq4i61EcEar0ZUXf0ZwRREEcrYHoScqxsx8qrF1zYiBBhHIe42SQnWS1j7JIbHIaWCe4Fo7CMBKhJeZBwSBBQPDzzwBx544AHiAzFs26Z+zix84QAOvxtkE4fTx+hwlOHeSb504y0sWFyFw60gq9BcBWtOX8Hy0y/C37SU9WsH+NlPf8xTj3UyOpRn/hFtOAvVhI0IsgGT2e6/9vR7B+/gfwF03GolsiRR0DP0d4MvWIluThKLdx32XaJ9hnjuQQSJKQQVWiqr0jjoBHWwkLakAih1ky1pu8aBQZIUKudx1PyraR/dSopU0WFLlLznBoYx4yHaymbzs88pXH11A3XnLID6BgY2ORDuWoHiN8Xe6AP1lqCAGFK3IoZVR8bDqlE/ZddeQlAO4U/nqZyYpmfkTpQnepCH3Th8zTBLgWOPgdQR0B8Gvb34iRZyIY4a2054IMNxV1zBmo98hBOvvZqzr76Sk05byPLZHpp8Ki5VAVWmoEjkFAldkZAUiYKqYKgKLlXl+FqV00+ZQ3DFmewOrIHdd79lx6Z3f56OYQ3j5CP5xfcfZdWKxVS3zKZvLMXRRx9F7/ZdzG90ctLxjfSM25x20kKy2Qy7du5j67a9rF23i6nYNOVVdaw+5zI6d27CtiyWrTqWD153Pb/8/Z3sev5JYuN9eLxu3nvd9biReGrTbtY/386ZC2czK6TS059m354+jJENPL95N1bOZjid5d7OXvRdfyZTsDnQN0j73r2vuD+WbpAZHyPev4WyZgNfSCU1eOikyA92ALL9MPZ7mHwW9AlePCmxwdKxskksSQI1AFYY7MM1ubCLHnsmdmonPe1/4OlndzA4fR5X/XMD3flaHn80zX0/3Ma6x+IsXuRnfpWL+aqEV5ZQJHjg0T5+8N1NxPY8B1YT9WvmkWhs4JfflyiUS+zrkli3FyZl+MRx0Jd1MhbXie4bZPtQJU5JYfumMbau7wf7cB223xyEjp7P7M9cTa7Rz+bf3EN6dGZaW3Hx+ayeO4/jK2toUYO0lzuZnpwiMziKaVps8S1kSV0FhtvB70cnuW37Nl741c/J7tkFhUNtKUI0NS7hvp/eyNyGMn70/e/znZtvZmRo6DVsoYEYBRKIoMtEpAHSiIRTSf1eqj0oPXLMpP19vFiLlAIegfmTcI4JX87BGTIMJqFbgxFbfJ1W/IjJ4uPvQMSWUE0Z86jDiUmUScboZ5wBUkTpIon+hm2YA+RmsOtg9vGw4Djs2giD3/0MQ0/ei7Z/M2TiolFPsYmpbUEq4UDbtB40UZGH7cAy48TiKfr6p0jXNED/7pdXTL8DoNTbxCJvGmSNAnmzgGXr2LboYmwWjcT+98mI/u8i6K2jte4kqgJtaJqJbPrxUImLMC65moCnjlCoFn+wEm+whmCkhnB5DZHKOvyRCmpqGyivriFcWUNtVR3+sjD+cBB/2I/X50VVHbhcDtwuFYdbxu9RcKkWDtnE61JwBSQcLglFEZemrkEmo6HlNXKFHOlshnwug6braIZJwdQxrSy5bJxMZopkNkrSGqVAnAJJ8mSE3SBu3KoHr9ePqjqQbQnZEkaKlmnhV914ZRdOy4lpyeSKem676CTrQpCwJcMGF2JK3QosQjQILzUCDyJG+AFe2/BsImzRnXGDmppWQqEaKhpqmH1yLSecu5xLL7yY1SvOQM2X0Tm4SzRrfl0IQJFaluQmjrz6wxwx30lNaKbl5EuVsbc/At37DLIJBYIRcJSB5APLAaaEkc9i5HKi2iuXAzbzxiS2LAwjQy4zBikTnz9IOOilPOwjMaGhk6J0VG3bZjChu/EAACAASURBVCw+iaXJqKaL7Qf2ce2nbrjp5T71baOMfbNgA3nLpiuW5Nnd2+iJR6lo305zUxvD23rp2PosYwP7kc08XqeBK2fgD1eiSyrLTrkKq2ARm5xkcLiXd1/2HsqHaph/8pHUtM0+eHb4KoK4gj7K69wMTSXpG5skHo/icAXIT2cJuj14A0FMFCzbwkbC7fbi8wTJxDQkXBSyOmltmp6uLnyWTO+eXYzt3cOedc9QE6xmIjdJT1cnadPgQDRGec5kMjHJcHQcExfBsjryusX48ADTiV60bB7THSaXSjDQ24OVNJmKpUllNCwEF7Z/y3bqqstoLmvDJYM3VEZfXyfR8S5yeZ3e0T1YdpTX0kHuHxcFLA6vBCkLN9HUsBxbkjluxQK8XomxpMZD947y1GNNFKKKYDAbQzMmrkKEJUr0zwN7NhASA6VkCRLWzDMjyCp6i9s2InZWQfWBu2Imi1XSKrQw4/jlR7xnMgWyCySH+CyHVCQubMjbkMqCnio2avUDc8EbBqUJ1FngrREVowUF9AJoOpCFSATscsiVAzugsBHy45CfBIZAOkEQxtQLtS9rQT8OmI2QsZ2BIF73ItiWS4DfICRsXYjAfRkz1mTR4o4lEIF8H3A1ovrAKB6IYRgZhk3bwROAsqVwRAQ8inSw0NiHm+nJaaYmooRCHqpqa6lqqKKyvgrZ4SKTT+BSAiC7ME2FeW2zkZ0SecCSYTok4XCdQDIzRP/AEN3bRmjf00PL4mrkahfOiAMCNVTVL2cyO4o0uQX7TSFuHEAI1eHB6VBxSBaKQyKdmaSgvxlePW8cSu1CSq3HDodikhmLvwwKZOSikkHcQAu89UF1yW3kHbwSdCw7g20XKBRyPPfcgyxZfIYwj34FlKiePOKSLxkESMwQrmrx/xZi/AwiklAyYhysB5qQaCl2Bt9Nkj1mDxXaDpqpZoiBQ6puTAp9E+hlWew2Cd8Khdn+OqJxyFWFsBIyY/2NjOww0RJx/lav0jcMsoI8awVexYWRtNGiJaIliLg2UohBVkBnhguJA0p2mPK+B1g1WY7/2Fa8voWoySSppj7UbhV5bS8UfOA7GlaugksrwV8NHSpsuUPcOPQEUnwLQWDFRJB5nMzknJXQLKotSsR5qdi5dM2UyPNJU2xXWIHaWnDXtqLXtpIom8eU6wPsvn8LuURJH/3mobtjBxnVgz6viUx/B7XLZxGqVDgwMcb8hWG2r7UZmTLo6LfRXUFmtdUwMrgPTXIyPBFjKpZE102MQp7p6MhBhWLBsJiaztH+wnqmJgYIBMpoXbTq4Hjld7mQdLjnj5uonN3Ejo4upiaGOPn4Y/njHXdTbplomRxDPYOc0eSlYcESFJdy+B0pltpJkoXDlccf0TntuGNJxye4a9Oh/uV5IAraOGilHssvRZGMzengC+CPVFBX1YKmleMNOphOxBjpH4D8y4yEme107gEGRpBivyJRA7JvNRFXGY21XvZH3XQMy8wuh2X1M2+r8zk4oaWCE645nzwLoKqC9bvzDD0+Qdn76unKytRq8P/ZO+8wt8oz7f9Ok466RprePMW927hgbDAGbDqEDgkpJCQkm54NabuppG7CZvMt7CaQbOpC6C1gMGBjcAFs3Mf2uE3zdElT1KVTvj9eyWPAGEMgZHd9X5cue9RO0TnP+7z3ez/3c2kALmiA3oUenssm2fVsgmdyI6gd7bTvH4GyuhNtV/COobS6hnlnnM3zd9/LaCT6qtdSmzbT2TSBtoZGJjrdXH7WCjg0wKZkntiuPbzU2kEsnkLzaaxpbWXNg/cyvG8PxF9dYTN+9iyWXng5M2bU8+A99/D4I4+wY8uWE9i7Isl69H1UbNsSQUzBcwidVPE1J2MNRIsjcuao70sCr4DvIMxKwlnDMCcLIxloz0ErgnSNF96a5R30x3/7GGKUHeyjHA9RBkgRxYGBv+AkWaBA/3poTqidRNP0hUQVDyN2Drason396lc1mz4adjZD8ulHkRhFCgfAE8ZV1kh69zYcBngNi1CpgyHppC72eLAB07Yx7bEGtsUFXpkx042T+N8D25YxTScO2YsqlSLJeXTZg6LIeAJleP0leH1B3C4/3kAZLrcbp66juXRUp055OIzX78fhcRNweDFVGVOWhDmLDXLeRDFtZEshj4JtimFekiUU1cbCxrLAsCQMCywbLFkBhwPJ7UHKmkg2SLks5DJIkgRSHlsbxVJ0DNvGxsAii1WwHACZnFkilJOWiW0ZyMgoBamRKasoDh0jm8eWc8h4UXAhFbJlg/yR695R+NeNyI+rEbUPlUc9X1p4DHBi7WtNIGkZtMTaqd66k7zsI+9w0Fg/jhmzZqEaMpMaosh5P4P5CPsOtBAb6ieXP1FPdwci89eBMjLDEgNR6PCDGhD3cNElWEJk5j3DkLDdEC4HVwCyeUimxOJWPo6RiQCDYPQg1HHFGelfGxUsTDNFMpmhz1AwNBOX7sA2DQoUzKtidt/wINsPtGJkDdLJNxY1/q8nY4/G/auF2b2CQogA0/GQJIbiyDK+xI85eJAtf2nDkhT0UJgPfv39DA/kONh6iJbWl5lx9c+Yqc4nb0MilUeRLGQJfCENWXJiGxbRZA6HLVPrcDPTWYrPoVNTXkYgXEneVhnNJJFsCyOfIx1PMhoziPT3InWl6dy/l1/++79SFgjx4urVOKw8PhU2PPUk69c/T296mLaRYXrWb2SyN0heU4hhMhjrJJU12LOnhR3b12Fl9jJr+sWEykqwswbr/vIcqegwSiRCkLF+xBueeYCaKh8N08ZjOMFyeegeaWV/2xNveA7/N0HCiXAbPXapuUv3MG3yUs46/YPUlek4JNjcl+XJ5yL87OPbgVoRKULAZERUixb+fwnwVcAWC+I5A3wqyCbYWQS/nUIoYAuMTyaDSGrLweEXvqzDgFkI+BoQUwTP6UKU5wJ0RsFVIqwUPBoEVBFu0qZQsuYsQQIrIZAaQaqCcAA0ubCeYIltqFqBPMsJ1b/XFCTr6BDwMHA3QizmBWmusCpQpgATIB0D7ijs/3KEvcBkRMRvQ6hnfwd0AY8Dq4CzgPMZM7K5v/C5RkT13IuIHaxCjCBa4XMB2NcC3VvA/kf4p4VQ5QZMk2QqQT6TI5vI4cRBsNzJvEVzaZzUTFlNDT5vgGguTn7YRHf1IeFFlse8KRN5i0fbkxz6jcSWNRuJtrcwxV9N2C5hdv00Jo+bQMY06csZ+CprcY1MQt8/nrT5DvmNHYEM+JGViXj9Ffi9XoJaHndAo73rJSLRNgzz78vfsmiVLCOmfMVYczwy1o+EF4kc1hEPJAEZFQUD88hzIwWL9L/V5KTYf/VkMv/myJljjEh05EXa9vqJZ7qP+5l04XF0uVSRxM8wViCbZaw5QWXhfcW5fzMyU3DiwkMzEX4MHIy9SCK2hXLORD1y9YjmUk4akRIKPX0R7mx1clmtStbhYNJ8H5NPm8rah2H1La1khnfwnk6DVQ+q5kCSZFDdqAtuIiy7SbbmyUTiiMFmPCJiH+RoMvZo9AKP0ctzuUf4yW1dLH/8Z1RWN+KMh5l8yVzs36+DPeuhdRe2ZwbZ96dRL6hDXdQMT14MPS/AQC/kiq56L8G92wh0f4iA1QSX+hgMOYioMkOMkbFFEr1IRnYaYrgbr4jnS4GmGripIsje9/0XQwdv4fCWp8kktyJ+3XcL3fS1rOWhz2UYN78OLddGqT/IKTMl6htGcQRVdnTZGM+mmD4RJIebUFUllU319HSPdTiPDfay9rG7QVJQNZ2evhiPPvIM/Xu24/d5mT3vdFZc+iEU2wYJ5kwbT0528aGP3srS6y+n+9DLNPgtzr7owwx/7mZ6KTSok2U8TXX4xlXg7DiOClLWkWULd0mYcfPmM2lGjk9dcz0dra08/Ic/kRsqkq5xxpY9TgB2lpJSnQVnzmYoMYXxMyrpbGtl3RNPwVBeTCGzGbKZLBISRq4wBsUPYr/wUR55AS787h1ceOlVXHr1TD67V6alS6LsACwJgmaBxw0XnlHDhWfUYNtncdiC/9gKq1cOwY5taCNurCo/05o1/nmWuO+vngZyt8zOx2WG+7u4+4F7ocQNzeXQ97ezE1F1JzWhKhaFp/Dbry/HyhdGBwlwagz+8S42BMOUT5xIffMEPj5uFuZlWVIONy/sO4iuySgyxBNxDrTuJnLnHcdUPp6y4lQu+ty1bBkY4POf/zyxgbdSVFpczioavbgQZGyxNaITkWTZR73fQtx3BmJFvKiozQP9oD0MzSlY1A+ze6DjEDwLrEYsrBv83fWbGmSEjexlMdMZYQCDEXzYlOKgQtLJ2xaJv9aqQFbA54d5M5l704fY9sI2RlY/BS/ceeQtxTziVVsyc7D/BbRqoGoqct0CAjOWkOkaYsbMuTROa2D9s39g2LZOkrFvEcda2D+J/z1IpdN09vYQ9FYh2R6cDgWnw4/LpVHbOJ5AqAxfIEyJv5TK2mq8XjdO3YHqVFA1Jx7dgcupoDvFbZiXRX8VSwGnCl5VQTFBMlVk2cnoCORMMCybTMYkblpkDZmcKZE1xGu2qqO4ddwuP7bixTQNzEyGfDpBNjeEnfKBqWAaFlp6EEfGiWk7CrrtNHni5O08hmVgGFkwJCRNA0lBQcEpaZhmEtsWjcUsFDQ8yIVGqFaBjFUQ0b1IuNYh7At8iNxZQqhjxyNGgCHgMUR/7TeLhAYW+xhC3byZkYxMPGdj6joTZrjxl0B5VYjLrzgfO1jDf9/9W7ZuX0tkeDdv3KD1aBSjpBPbDtK+VWJLGEZt6B0PUQ3GKRAuiM0ey0JXHNJON1KNG9lX4FaiCazYEFYsByMDYG9D2BPsQsxKM4yp4F4Xld8SbCyi2cNE20WeJiMTwMuxJEOtfYfo6xsgf5zt/Z8iY4swMRkkxpqimi0HL/XHOKs/QQg3BiaZAZn8jji9XX04kjJTKiby5L/+hVBNPQlZYyBvcGBkgMpSGB8M0RQso7mimm9+6dM8fV+Q9r07yOcStG5eS2/HAYIV9YQqxgEGgXCYg+1t9PUNcPqSpWQzCYaGhrBR+MI//4jzP3sJd9xyO3s3bqFxmsaUuim8tHUlo+0xbEmmIVDNeRdcy+lXX4RrfDkLpk9FxiA1HCM7mmHSlNNYufphbvrSD6kdN5Xnnn6a1Q/cw5Zo/6tcPX6z9RnKTz2F5XGTTFrBXdGM5gu9Fz/JewIvF2NjkuChY77+qWu/yWXXnsfic2aCDJ/+Izz962c58MIgQrIJzCu8eVXh308D7wP5LNALTELeEH5FCR3RvKQo9SoIEMzDjMWiAOCGvCQUrXGgz4CWNMh52FknBLc+BGmxFPA0iDTaLjxXbOLSNwCHW8V2yuZCwCPCUTEcZM3CIAPoDlBtcKvCbaEvCJHnwHgA+HXhy78ILAd5AZSVgFJQ4FpVMPR9SJUCfwJuP+ok2gjP2NmIyP9RxKhwB2IU+BJixDCAy8S5owHRtWwc8FvgwsJniqPLasAPyUa483Mw4VGY1whW/2G+/YPPsen3q8glMyDBgAz79t8Pf15J87RZXHDl+5l+1gqikX7RuEcxMSrBoQr+N3VogH+a9kPOsVVirCZJJ57YQgbYw+q/xNi1fQnVyy5h/IRGKlUfOpOJReexueUdJmMlJzhmUDdpEuUV5ZSFQzSU+2mYEKRlcz07t77Ilh3PvrPb/CtRRtGVTqIPm8Mcn4gFkCUNhyTjsDL0MtbXGazC2vFYP+cTGdLfDqTCdiXEMO0qbLM4FT2Jt46O6Ko3f9NxUPyti+Q+CEJ2GBHDdIS1dANVeJgGnMY0bmEiJh3AU+QYC8ogftEYSX5Jct+vieyrYu/vLuO3zMGeeSb1ZzWw4uPQ1QvZXAARYd8jSCrM/DYzl51L2FeF0WsT6SvjwPMPkB6KItLtjyOW5bp5436zAqLgwuRTbGLpRWdy/Wc+w8fu+wVSu8TAD+7DPfgyPpcCD27ike/8mjlXfYCJV50Nn9Dg4wfg8k/AIw8zZgiZhfV3woYH4B9+Ren2FYSm+skixp0EgmQv3jsqUF7wNDcQ+jwHsLEd7tkCU2fDd1f9M6t+dgW//+bTwBfeuXN5LJiD2PHHaV9bQ/9sD5ddfC5fXXEGlUtvwkpXoJY0MxxP0LHXYPmC5cxbeA6VjhA//NrPX/NFEpK/kVnzzsRXUkbrwW7q6mfy0IO/Y+aMaWRMmzU9Sc6s8uDRbMaVq7zvggn8/OOn0BufyfMvbmPFRR8jkxWl4eXA1JzBV361is8G5hMZfGMVhasqTLiymaaJMznnohXcfOXpOLUM+eE2zl82m0cf2nx8W9E3QipH145d/PeuPVSPn8U1F3+eL113BbW3imatLXYXf77vLh66+z50wuxa9QL5zKv38/Fvf4Lnb7+f3yz6Hevvq2TtIli5E077d1jSB9+5GWprxHWZAG7vga4QjJubo6Oqk/7v3UPgy5/CNXcxErAS+M63B9nRFkOanaFM30ts810YHWnoCPG3XDSZ+aFLcJ0ymbufuAfLPGq7bh2uWwL3bmDt//t3Dq5eg/fFl3m/W+eTcxcwSdFZvnErH7n2IsbVVBIOufnaBz/AdV/8/DGJo3v+5V+496c/BUSp44mjqC6CsehZdOAeRZC0RfVrcXRVEEun4xF3ZtE3tgXYCO7tsDgE3+uF+AF4qg/+C0HC/h3Xf/fRw2pW8j4mEydCmhgGo4ynlt8HZ3FHZiu/Sf+VFhflE6FxLpSWcv+lsyEZ57XXYxBBfBxL11zaAxXlGRzSPl665XcATA6cQpPTw68e/9t7IZ/ESfy9wyRNyjyMOqLh8+o4dA+aM0hpaRi3P0yotIba+gYmz57MuEqoLINQEPxuwCUIWPKi8db+LoiMQion5ukgerj4vBD0QXlYFHgl0jCagqGYQu8wpAxIZmE4LubospLGqcg4NCc+vwd3AFzOAE6tAlWFkT7oPXCQvkNBNCmJ3pdnJDtE2kphkkNFx60FQYJEJoFqZHB6/EiyA2wwEnEwMqRzcTL5RKHftYostOFCSISI/hlEpC8uioPImY+GA1EbsQiRV6sIW6vjQ0NjChNnL2bSzNk0TJlMoLSU+FAaKSmhOxRsh4tx9c00TbuE3tEyIltXIYQCwxyf+CwyUzmwO4i0WDzbB88FwV0GM86AmjoIh8HpgCfuh5FRcFaCtwSq6iHoheSAh1ibi47NIRg+JHwg6UVIAYrlGk5EtjUOUbr7zlR+W1gMHWdFcuRNRAb/J8nYY0KSqVx0BR+68mpUI82Lax9Hm+Jl0sRGkmYPfft307XrJfxWmqe2r+PBV9aQMw2aVLjinKtwzVpMZP8h6sZXMn7hApJyjs1rVxEZGmayArJiIlkJHMhI8T4mlQaZWdvArs2PYdkWdc2zaZw1j+nnno3m0LjmM9eTveFyzGyWf/3wF2k5tBsUjfMWnMt37vgpPduz+Kor8AZkPnLJh/nZj79PQ/MUFi2/hLMuPI/fPDSfNauf48xlHs6//Eq69+witb6X1miStqMO2xgdJNO9n2RwMvVNFQRLXnvbvsOnmb+fsptw2IdtGySOqjD3ak00VCzh29/7IvMWV1FW6edQT44rvtzG4U0vER+YDOqpUCKJ+fpBRC47F7gF9CaQQsJHJltgFCwKVlEjYBfjQfHOczJmVeDkSMctIwWJPqACJFMQpS51TOcwHxFKhiSRXvcguM4hC55vh4wGTic0Fshitwuc0lj/XAXAAqNQ/5sDRg5BthukBFSfC7lFYKQRZWjPi436pkMgAGlZBHQdobrNZsG+UnzGXAf8BOETuxUxMqwD/XNAEoyzwJiCIHm/XTiYqYhsdaDwUIF/F+eUxxE8gIEYcTIUHMUNMLv4+YVwxsdLGDc/ydZ7niOfyoIELr/OuKnVKIabzoOHSSeTDGQsZkyp5fndKVS7lEpfI56AWBXNA3kcII3ne09dwCPrr+dgd5qvf6CCbZc9RHw0yozJHr7z3RoiSdi+Mk774a20HLzn7Vx+x4dtQK6LXCqIggddD2A44UBnlLglg+fdvU9PBC7CBOVS6pw1pLJDSNYwOjkcSExyuRif7SJtZUghEZYDPG+NknrN1DNi5zEkhYkuLwpZjLwMiormFqYTsiyDJBXM8s0jscO2bcyCGXogEMDhdDKSSLB3YBDrGJPXosm9Q9ZwuRzIsoRpWYwkU7gBn9+HpuukcjnskRT9tkH27yZS/c+ECw8OdEaIvvmbCygWyxbP/NEql3ThNQkRLkbR2U+UETZSxS78zMZPK+UkiCNi4rHTPwPoA/subNZD64v09szmwZULyCo1pKNl4JgEuSm8keL0HYd8DsiNoDSAPAv2zGNPlx9VGcXOH8TI95JN1iOWPFKIYBkTx8Eo8EPgB4zVvRwbm22b/rvv5vnNe/n9xQ8R+vqXkZ/cgrFyA7GWL3POpM/jWTYBym3sLxikNj2F8xOfQF0yF27+Jq/y0bVHwLgZrrgd+bKPoV95PXVzhQbPYMyR0o1ogqkifrsyxLjhsYE8bNoOp1dITLuxiRumn89vL9uKMBR/N2udbTD7eeqPv8cy8vhmLKKqoZaBjVuZPKmOqSvm8fiatfzDJ37JVz+8hFn1r06Vg2U1TDt1BZs2b8DSLIaSQ3R0tnPmsvk8++Ia7l/5FzoOD3PqeVdjhKbh8ziQUmnWv/wCaw9ei2ym6evtp/1gK6c0NHGgr4dIKnnE1ezxe39DOv16Mra8uop/+ObXePCJ1ViGj0BJOZMaGlEUBUlyo0gh3GpRA/P245eiyJyxZB7d7Qf4/d4dRPqiXHzJecyefxafOfejLCmfyxWXXUlT2VLmnT4Rb4XKo08+Q1/rbmzLIhndwO41K1gwr5zlX7qVpnmzufn9sOspkHXB4Q3b8GQelpbDhn7oSufB2Q+sRj18GS2b4QN9BntvWUlv2zOUNAeoP2UZer6W5i88wIpmJ/PcfVx88fK3fZxvCRUwscKP2dbByv9+XJQrFRAMlPCtb/0nTZ9NcdcvfsFDd93F905bRM1TzzC3vJT5kyby4r/9jCs+dANcfRWLlp1JbVPjsZdRCuUBtmrDEDz8B6j2wc5d8LFvHv1GB2JUi1FU/osl5WpEhhdBJFNdCEftAGISGkJkO8XmNx7EXVlcCrUQXlJ3wrQULHXCR1+AwV54Mg3PISyk/o6J2CKyZPkzf6AaPzZJ4gzRjUTtqMoe623GF4cb5l5G6IqP4nCVYh7uZPDOmyBVlESMYRZCizAHoUjbiCBvvMDZiBgZMJI41Tj2kib++evn8uiWVn76wMNv+5hP4iT+dyOLLA1TWeHH5dFAdmJJKopHp7aumprqOqoqK/HrEh5dEKteP0cq4ZWiuaoLGjxgHQBignDNJmFgGFJe0dvFNAUBKKmgaRJuD/jzQAKyRh4zlabE7WN8vU4wBIESCZdD9F2RVZCUQhvFCAw11hHtKqG3s4kD+16mp7uN0eEoZiZBLptGUxxoqoaqqqiqilPVUGQZybYxPTrYGpKsYEsOsqlh3GgYqEjoBAiQo+eIVVTReCaByBBlROvFeeKwj2QHSxD9xqci8us9HCtrKKPON44plZOZOGMxU5vrGVdfTW1dBXXlfjSPhCWDbYsu5E5JRUkACR8O13xu+vFthGpt0nGb3kOwaT0c2riSXOoQomz2aFFRJYrjo3z/Nxq6DwwFkjJsOwS5BPSNgpWHzIioHNZUcHlBVcUjVCHh0GQiCZ3kgWbIlAgP2VchhyAU4ojxrhoRkUd4dVv0twqlcHZfa9Z1YjhJxhZgY7Mn0s7j7WkU2UNnrp59nQoNTRoldeWUT59APjZEsKEOa4fNyOHDlCATDMpkeg/S4/FhaU5UZ4rymmqmWwvJjIyyatWjRCKD6A4HAa+XeDJNPjmMS8pgup28tLeFGZVlSJkkaiaLnEyS6rVwGgrZlEn7/oO0dO6mviJMfeMEJsxZTEnZeBJlcToO9dC1YTf7u9tYOGcBaUOhJ56htLmeiVMXYpkqvT19uELlbDncSncm9TpuPhfPM9qTImWliEU6yKRP1OPj7SEEBNBIY9P7bnUzPUHEs6/urlceGs+cqUs554zLWbJsFqU1Ehtf7OHBR3vZ/oIF/fXgqwVvSMwTizPLicAycJ8qqpYME6xE4ZuL9iRWwUKxqI4vRkMZjpidFkUKslDP2jmQbZAtcDlFVV4J4uEpPBwIHrgGwQtvkKDEKwYBlw4+z9gmZcY0VA7AkAtkhVxQAvZCdhPwCoyWgG8aOGZC/Hqw+oA1kFcgtVRYGZhrIV3wnpXGi1UqZ0lhENiO6IWTR8zO94N5K6iXgFSOULheiSBk9wD7EHOK8YXXFiDmDmciLpoBxhoEW4iNpCXo8NI7avPyVo22hEUqWqByJNB1Fw1Nk5CdpdRPnYfqLcfpL8PrclLiqyAcSBALiICfKZxP3akzacY8encEULo9eKN59m20KcmHOWtFI/NXjMPMyTzy5/s4uGUf+/etI505cbLpxGGCHSEe20sPgySGwhz2VIHmw8imGR5+LzWbYtImAbJtoJombtuJJflRJANbAcnMErVtEogJR87OYR5jmDewSdgWvaZBTbiCdCaPYZvIKjgcDhRFQdNEgmJZliBnC7AsC8MwcDgcmJYFuSy6bR8pcS/Cr2qE3S7KPR6ymRyqQ0NWZGwb3IpGLpUm4Pbg8/kwkzl2j6ROKmLfAWjIuFDe1I/qaIw5BL8eWURi6UQkkKWYSBioKNTiw8SPikoAEUKOb5KQR5AVOcgkyWcOEBvcJgy0TRdYMYQ/yvHIWEfhPV28vQSuCaQmkCvAWgS2CmYI7ImQKyOdlhmreRhEeMRaiKSxFajAXdNM2QQfixY2sG51lsjBh8jEdrzhFpNAWyRCavQlfqL8jKvGT6SqsgznB8/D2R3At3wOQ7EtDN91HxXPZlAPDCNNPU14c674NDz9A7Gy2J0QeAAAIABJREFUCIjBrR32Rsiv9GCOJtD3XEXoshJ0t0y8sNdHF0MXhz4ZqCiBxVPBYYHHAXpAZ/LiGpZ89Wpe/o/15OJd8K42Ds0zPBilPzLMgCmjaFVI3h4mNYa4YI6fZ18qoW1vK0OjWXzBck6/5Bo2PvkQRi5PeVklF11wMS07NzGxaRwWKtGBLnoHB3hmbYJof4LBwTS2o55Kt8LcKXV43R5OOXUBVQEHuiwjz5zABz/5Idb+8Q5yhoEEuFSVC88/k77Du+lIv1qxMW3GZKbPmUlv3wDVdY1oaoCq8nKMdBJsGxsFj7eEhsYZaPIa8mYa+21cl4pDwx0Kks/l2b2zlfjIAMPRKLXlYQ7s6CZnQEd3N+nRBKNqL+0dEvqQTGZ0hJLqShLRGLl0gvToLnbs8OK451c0tCygunkajafM589ruqltcNMwI0SjAt1pkEctwkmb8gqbwfYkQaMXeaSHLVkviepqcocslK7dDK/vRTZUzvviN5g7p466lOsduhaOD0mWmX3OmWRli8jhLhJdPa95h4yNh6lTGrjg6qvJAI/+13/xx3/7OeY1V7N4zizmNDfzkYsvoD06wKrHHsPr9o8tHBZ5VB+C6MxDaQhuvAkWL4USF5TWw82j8ItfCKJgzMgFxJJHsZPAMGJSKBeeK3YZKGaPUcaWScoRNGHRO6vo4P0SnJmERcMwNy06y65Jwsu2mD//D+nna2Kziz40LDJkOEycAaDHfOuuCvoFH8SSdHJdvRDtILdtNaasYw/0QvS114NANTBdgUUO8KTFmY0hzvp4hGYrO5gAn8o5i+vwSr3EDrXTvbv3rzjqkziJdxp+xtRCFiJ/yjFGPP0tITxRVCmDy6kjO12genAFvATLQgRKAng8LtwOoaJUJNETRbI50ti6WDSgK1ASEK+pGiQTYl4syaJqNJEFR0YsJsuqEDgF3UKAhCljGRrhcqislfEHwO0RVgfF77elwnTVB5mQk2S9SqTZQVWdTMeBBgZ7+hkZ6GJ4OEImk8EyzSPiE9u0sa18gTiwQZJRHS6cLtBNG6wckmljW1rBe1Y6MscqesMWCdlBhM9qM2Mu4RLiV21CZHJdiJw5UfhbQias1REMjaehrIFJVc1MGNdEVShE0OvHret4XCqyDuk8pDM5EsPD7Nk5QnvbILFYFkUNMufs6ZSWylgZGJkC9ROhYzFEhwfo62lj6/0pRLfuPJorSLjpDKZOVPB5xD7mLfDboGYgYUJ3Cl4xBamuOcHhAkU4OgBgaRKmUwaHDtkcr1e+FussDUQOnz7q+aK53lsZ4AQboyh+goEgTs3CyGfJZbNkMlkyZjcnMj84ScYWYNs2r+zbyCvZBeAajxsvp6+KctoSGE3msCtDhOtqqJg7g+ZDM5i5fSoVIxmq/UNkY10c3Jsjp7qIpvuYt/h0JkycSkDx8sr6NeSyWfLZDIptEI0NiFsml0R2aGxt76LZ4yYx0M9Q2wEGt4cwfT5k2c3AwCDbXt5IZ7STZdPPYO6MyVRPa2bzS3sIKlV0Huxl3fqX2dHZxo9/dBvPPP8SPdEBJJ/E4qWXEe3uYM/+fbT29LBq2way1uvpkFxGJTnswAxniA50kEq9e8ZP4uaXaEBjGOs9J2Ojic1ivySJYKiMuTOXcskFl3DtNRcQrIXOzhj33tvBbbcdBppBXwIhTdw1/YgcdwFwDsgXgtsL6REwU2BlEe8rChCKA4GNuC+LNl0U3lfsdKLxqjFPRlgIBNwQ9gpe0o0IH8OIQtVpCKtVN9AiwezysTJfi4K+yB4rvZYksXlVAacQHooGOVnI9oKxFiL1UO8F10QwroPUVrCfgEwcMrr40tRvgEmgnAm+8aLU361CvgmSV4LdX9gBDXjRJv8NA6lSwZ4rgxeU5WB2IqqJdyF4jXOA08TpJopYupuJiI8JxnKANDCkwPoyGIa2CLT1OsUOp3uAHKrmIxSqx1kznglTZiA7SuiNmFgWePRSgv48waBEXhLnxQRcDpXG8RVs+F2KjGShkmPttmFcqVHed/ZiGudWs3pNK7f96HZMcxvvnlGaIF0SsZGCctsJ1KEHG3A6XdgnbIz+TkMYyoMTkyxZO8pITkLBCZKCrTjRNI1oaoA9mJiyhld1EMmlC65Gr0fGtmjPZWn2laHoGfL5NKaZweNxixVi3YXb5ca2bSRZEob4CDI2nU6TSadJpVJkkqkjQvOjh76A6qAmWEJdVTk9/f0gO5AVFUWWCbrd9EVi6E4XHtWJpchEMDFOqmL/amjYON9B97aCnpU0IomsII+KRgkl5GnCxMCNRjUKQUy2wQk0aRktPPYCzwpJxBGza/14H0QMAFMRGtwTOU5JdFnUa0GVIb8UjCUgjwOzTKyGkWOspEpirHXjEMUu6ZKcxlWWwutppuSUKYw/s5arr7c5FJ1OItJxXDIWRJrZmRvlG+u+Q/m6xcz78DXUXHsp4dGzYAUMfOk2kr/9HRWSjGRPQVrjgnlL4fIvwzM/OoqMLR5VAmPb42T37kB/qZHghGkEJ4bIBN1ICPKhaDVSHINMoLIUlpeKyUBX4ejKyzxc8KPz2fv0n4jtzWKluk7gvP41kImPpuhs6yZY0kQkHCUc9jCxJInX4yNXWsNoTiFtOLjm459lz0svkMvkaGps4qLlS/n3f3XQXFuNrGgc2KPTsnM75HTyaRksndade3gi4MHjcXDKtAbOOXsZfjNGuCRM1cLZVM+Ywl23/ZRULodPkqj1uPjEB6/imVV/Jm/upr1/zOhl+ozJnL50IX988FkmzzuDcLgCv8fPYE8XiVQjPrdOsKSUGbNPxee5i+FEL6aVO86xHxsOl05JZQUdHZ1k4n0YRhxFNnhl3VZ27byHnmiMoaRQFfbGdtK7fueRzzbMmU42mSKXLu53gs0rf8m2NS9QWn8J33qwhFsf6mTKqbVcNyHEdX6bn/Vlibcn8fdHqC2XkasbqfKnIdfGge4A7kvmYES3ILUPktv3HL2jUBn+DLhtWv8GnJWkKjiDARaecyE7t2/kUFv7696Ty2Z5ef1GFp+5hAXLllEyroGta5/nnp/9hLDfQ7AszPzaGr77z9/gGz/9AY+sfIY9O9vH/GJLgCmIkNMJISfMnwo/+tHYNhrL4Acz4OE/QdcgZIziVBtEflCMV52IlWxP4V/RFEUQshpH3W2IDLMBEQMj4iF3QfVWuMYBs1LgPgCrM/CXwle/m5bO7zBsoBeT8eQYwmB/4bljd4kQeCNNufOMizGkILl16+Gx75LYv+5Nt+8GSmVo0CGUFmnuMIKkrUCc9cH+JLZi88lPj2f72vX0bxn9mzelO4mTeEPIQWStCUkKYqGBBLYxCuYoWMOIq7jYdeNv4dZrAinsfBxdC+PyeVA9QVxlJfjCQdw+N7qu4dZBdxam2gZFhvHIDW4jdtfvFRmWpoFDFmIqWxLkXt6GRKZg4yd6dBH0gUMBj1MhEHAxrhFCVeDUixZrx0Ch+MDIKySGfNSOm0ZdbSPdhwbpPLCXrq5DDA4MkE6lMA0D0zCEHgcD286BomLbNoqq4XTJeGwJw8ggZyWMvEbeHsW0NSTyqNhF4S85xC+TYKyFY9E1vAgvMAGJq1F5FJsObDKSgkNx0xCYQX3DNKrLSqkMlaDrClY2SyaRIpVwksnoyLZNPA6xoTiHu/azfu0Ae/cdYjA2jMPvIdxgU+ICtwzjx8GMBTDEbHqHYMfLg2y9fwQRGfO4A26mnD6dsCJoUR3BUZQ3iL/7gU2j8LANaMLNT9YFGWsrovl4KleoSlYtkJNgHq9arLigMFw4EyWIGeSJkLESmsOHU6tGUSvRHBVUVwbxuiTSiSTxkQTRaIys2XtCi+InydjXoiMOJEiR5fNf+jcEC9RKVfUAmzZvpqwMPjfzM3z0s9ez4c6HuP3HXyTT/jIZRJ7SCVz54mYuP/diLn//dVzy3AqsfJysmWAo2cWuPXsYAWZPaKKpqoJqYENLKwORCJG+/WSGD7KnrYsZp19Mw7S5XPq+K7jnzh/x9Jrn2NyyG2/d0/zplS3c8qXbueB9Z3PZp37I4j99kHELJ/HxxdPFPEmGiWdcyvdvuZF1Lzx63MPVgpUEJ80gdIbNLGspO7Y8yd536dTaQBs2Mqn3mIYtQtRZOZwuPvnlH3DDlRczrq4Ch1OQ8+eeewetrXOAq8TbFyLkp22IqFsoxVfLQEvDyCAY8YIVQZZCJClsqugReywUZ6gGYzUEDrENIwk14yDsFMEIXp3Q1SKogwBwKsIH5jFESUIPIhCrcISMLZaPHglPEug2qBI4zoHhSdDVDHwBOp0Quhia58GB/4DMd8F6HLi08NkPA/PBbIbhESgLilIBxQv6DEiPFnbSDYQtuLOT3Fdq4AId6cPgqYXE5WC9v3DcICoHsojxvQtx0MX2kErh9RQifioIMjxKwVByApzaAus/Cep+klKSXfv2M7t2CvHRPB6vg4qycXQNS+zZHaFvUMJZNhGvBElJnJuReC9PPnAjZ519H0pVKZIfxskmz93xa55+bB6Zv+zgV2uvfoMf8t1EFjhAZriTDF7eO7MPm2LrpaINepJR0lhgQ8iooMGawhYGAVgWmsgV5dPZvnst9zLMyBvWNtoMxmI015bi0f2kMxl0nxfV6UTTdFTNSSZjkEyMIClipTqeSDE8PEoum8GwLPzhCtr7ul9nU5A3TbKSTdohExseIRQOoes6usuJ0+NDdwcY7e6jtaOXPW/qcnsSJwoFGccbp6dvGyOIwqZZwBSaUdF5hu3MZybLqGUOKv30EgHW8pbaFyHS1s2MqcmOBwdiGUx+k/cV4QTnZDj1eaQaD/ZuCfaMQPo5BBk8E0Ga7EBopiTEwFDMLpLAfJwlN7DsF3DFBZB1QncE7n0Utt/bR3b0xEtvbeDTrGfm79ez4sU7+N7TO5D2QzaWISN5wXExB7K/pfZnX8G/4CxYE39De1o34Mp0YWw+D3XhVXD7TeifOouJSLRJY1qD4uTAQNBCYcTvOVL42wtMQWL8d+6i9fbPMvTUbSd8PG8PBlv/spL96w7yi42b+N6NT/DQX55l3e5BuiOwbMUl3PP8y6xcvZlN//1Znj39fMLlZZy66BTG13jQJJ3Na9chqZAY6iPRdgAIgCtEuK6MG258H3t2byGVjhFNhDi0+km+d/fTXPPlf+S0884lH83i99aQy7SjO6G8ropAzQSmL1hGW9Rmw47+I3vauu8A/rIQV195BX19EcKaCbkkO/fsZ1VpkNNPmUxVVTnnX3wOU38zn22b1hAfeYtVGzL43R4mV9Sz6vnnsTMpVE1Gc2ns2rH6TT/evnXXsc9ypoW+fS38w/QfoS/5MVNOK4WciNPmUy0c3PgsXR27CHi9fOeXD9CaSPPKy3tI//H3pCtvp+QzN7J88sf5wHh436/gt5028g6bZMu7XyuvV1dQd9UFpFMZOp7eSW/Lvte9JxWNcM91V5D5+e18bMU5LJ8ykYdbW1leU81t//RPvPj009y5ejUzyLLivAUkkr3sWfP82BcUq4F+AaTg81+Bb33r9fuiSPCfF8K3n4L1r1qniCGSJg0xPnsY84t1Iu68YllmMdm0GbMtAJE17oJgL9xbCk2vwIEIPJGF/0ZUL/19JO5vGWmiZDl+1qQc9TiWi+DI19563rcL8OUhPCT+XoTIx12Mufj2ATnSLFE38ss7cnQN/X3ZuZ3E/2UoELqBkrozkL3lJJHBVUWm6wDWYB/EesBqAV5GzDj/RiIR28ZpZAn73ZRUleIpq8ZbWYvX68cX0CktU6iogHAQdHfBmqBg8zfmdYZITCxQZBuXBloQDEPCtAUhq6hibmwXmmirKgSDwrZAcoD6Ft3iVA2C5RAoA1/ATbi8FnewlLglk7RV7NEoZnoU0gqqCpqiospicpw1DAwTFNVEkkwMQwGPByufJxsfJZFN4qAXjTSOwqEV9V06Y3nWsWhGLy6mUcOVZFiFwZAjTGnJFCbPnUGZJ4QqSSSScbp3byIzPILb5aG0tJxJkyfjVQ1G4jY9fRG271rHmk0ZolY7eQxks5YXW6BuKlR5xQKUaoNLggUl0FBdwr/wYeBWIE5VI9x0C0xwji0dSoVj0RGVwllhkws6WDqYjrGGscm8IM/thA35rPAf5LU2Bce8oHirzU4Vxcm4CVcxf/J0/L5yUNxEk90kMiNI0REyVpTsSOyE4/hJMvYInMATiJpzH2PC7buAGAP9u1i4oAGnXMdNN3ySGz50Had/+iru/O1P6MlmyOVzVBc+sanlJcxkP5HD2/nu6pWcZpm4CuW4HiSGsHm6rZNE52F0hDIkHAxiSxJ/vO8BNhgm09t6OH3+Ii664gqwxYU294wVfOpb/8L3vTm8gRBut46RswiEVc5YsgjHqIdpDQv54Of/kQ3bthCNxI59qEfBVQ/BBeL/3X2jxBPvfv1RB+91oiFRLc8hZh2kac4srv/k97jp6rn4PG5UFfr64px66m10d18DniohkpqJ8E0NAdcAX4Nws7AjyWWFXZQthEtjVlwwJgMqzhmKllzHWiiRQAqAo9AYS5OgIQi6Kv7OIMoIDiOSPBeC67wcmIHYzRIEVzyCSMVDhV0yU8KgPBeBll+A/QxiAjAPpMugYg6Uq1BfBcH3wy4Z7N/B8HZI/gOUr4C+z4M1BdGk6zHgEnDMB085hGToisBQDmgH8yFgFBo/BqYHOjfJsKxejG5+sP0Q7wAC4NRAyxeIYkMMgkc4nGLV3QhivlFUx6YL/x856nxaiIh96g+BTiT9EGrlTgIl5fT19jGaGCRnH2bxqRewb+82drwSR1HDOFkGhfMUQQdO4dJ/1aisFr+llIRf/m4CvcPDDEmdr/nRilLmv5VcpLiK99ZRhWj781PeimW5jKBMoowtK4/NyCwgU7iYw3iR7DQt5kZKEZf8ttghWkYO00iGS6sa2ZEcZtvo6wkCG9gdO8zsedNprKxgdGiInGmBKiHJMqDi9eikU3GikQGGh6JkMhnKKypwOj1ksmkGYxFe27UmiItJjU2Ul/hwmhLhYJBAIIjT5cDpUPHoKkP9u+lIjNLNW1eRncQbI0Kc2Lt0X1iIHoDbOMAMVKbgoIM+woTx4MGLl3r2n1AadmwUu64eD1EES3Gc90le8P0a34IZGENe0vtk2JDBVjdAPi/MxWlBDBgbGGvB0Iu4Y5tBnQ1nGtz4TxZzGp1UyxANwcFh2PESdLZAUwh+sqmSZzfexstPfYD+u7+B6CJ7/JE2C2wD2g62snFRI/fO/xNTG75C7iMXMfKHmxn/ze2oU8fBltXwhZvBPD4bI4a9x8l98wXMR5bg+sF91M2BqCJCdTF8m7y6wNGFSIOjiBD+4bPhnicW8RwdiMHm3USSXO4gf7nvP7nyypnsXL+ZNY/fSt4cIXz+mXimLySXnsItd23lI1/4R0KhEspLfCiqwmUfuoLzzjub6toaBmIxLr3gEi6+/KMonhqQ3XzwotPoOnceO/b088S6Ls655CP8+pf3MkFLcnqFzGGXTmllmNF4D9HUKK8c7kexDZJxjXT61VevLuukB5N8/8tfwTRNps+ZyeTZC6mfcz59SjlDODASeXa2jTCcKfjBv1VYMDgwwNq1a7CzGbBtjJyFmR8jPc+89FzOuvw8sqkh/t/Xf058+NUTmI/ddhsOXec/b7zxmJvIbvoxrcmdPN/xfq77yflkY3vo3b+JeCrFjV//MVcuKcOWbZ7UErzwmxGmqwlumOOnYZxCVoX7PwZf+5ccyZRNqcOk/5hbeeeQGejn0IP30T17OpnowOten3DhRcy+4UYYTLL2324lvm03+668ks9cuJQ/bNrEz2++mRcefphLJkzgvmfvI+lUUXxHLfRMQVz4twFJeOwOWHDmsfdFUuC0H0O4FzHZeBWKPnUuxlq2FJt2qUc9HIg5TgtikSeGqDV4Bs7Kw+fKofIpeDYLB0zhiHKY/xEesW+EHYzpIcYhMqiihRKF54sFa0EERT3AX9/a5SCiRPhFxE9sI7KpCcByhL2YC0gM2Nz/1RzWqMi4ThKxJ/HeI4gkz2HCnBvxTqhGC7mQdFBUhXi6HPImct4kMpgn0hYhd3A9Vs8qsO591/dMlsCrQl15JWW143CFq9D9IbwOH2VeB5Uh8OjCU1QqVKXbhUl0PgNGXqQyyQR0HobIUJbRRBKn20nA58bjltHdIi4YgJoT96XqLBS3a0KN+XZg25DNQCIHWaeMt8FFk7mEFDp2Xzv5hAr2AGYuRy5vkrUtVFXBthVUVcGpawSDPgzDQNNUbNsinYxjJ7yMDrTgznRTTQwfY0W5xQZfvYyp8scwFbwzkZsXcv3kKhY7LUZdOrYvRL7ER29nO9FYP0MjI3T1Hqa7o4uI0UlcGUTTFCRsLAtMyyKfy5KxbEwMYCGKci3zp0vEdKFqHbAhkoeABuMkSDMC3Esx0lqqsHltQzBxxVqPJsT577UgWSgWUxVhHSEX+uM4Cy5eaR1Ur4Sh6+JrzRNJhJyINotZRKR+84pX08zTvu95yutnMLG2iobKCmYatexL9HDwUAdDo1nSx2/h8CqcJGMB4d7zWUTL9yIfXzT0nAMcwjRfpvtwJzLD3P/obznUtQV3AHbEIki2RG1pNcsXn8mK0loGDx6k1OuipmEKQ5m76LIsJIREXKPAvxsGGBKTVR3LyBCLJxjN53klmSQC7Ow/zPDm9bSmorRbIgt6umU7I7ffSqmrkog0gIlBPmfS1TbEvv17UTIa0dEYw3eM0B3po6/v4JseuayCoouj3fryVvp63v26r/d6cV2WZa659joyriHqJ4/jgmUzKQl4kSSJdet6+MMfDtDRsRiaKyHkEvfpPkSjqSWgLgLfRHHecilhLG0PMyY6gDFrHZMxiwIYW/K2AR1crjF/WFsRVgRSQanqVETpv1Vo0pUzITosVvl8TghqYsWoF5E8UtjkEGOeMW6EkHQwCaksJIYg14lgxBMcEUzEHoLcVNCmgTELms+Cnh5I7YXcnTDiAvdcyC4UVAGDwP2iUiU9F2KDkH9S9HQhijCoWQ6GB+Qy8M6UsLwaDrc4nrwJ6ZTw13GqYn+zGXHMeQlMvXBQebF/jBQOpFgJM4pYiA0wpiaWEUy2FoasRl4OMJD3MhCJI+VlVNWFJ1CJZUtU19ZgzDRw+koYLnxtOgdtaQ1drePW2/+A3+PAZatUGBJXnXcGB/1ljPQMQqEBb930aymvn4InoPH83d/4K6/Kt4K3PsueC5yBsOC9H2FL9+YaOh1xcouakqMv5DEUJw4pcniwqSBPpLCXfsug0rKoIkgkMUI8lzpybR7dqAkgb5lsbt1DOm8ws3kKQ8MRZEW8w7YgkzOxCmWdmqbh8XrRNI10Oksyk2Mgk33dmcmTx8jnsHJ5ZE1F0VRkSUGXHegmjOw9yMHRUSJG/g1tFE7i7cHCxnoXz+ko0ItBBTITcRIji0WUUrzU08gyoqxkhKGj3IpLEPnZm+ufi9f70UH9tbA4/iJMA9jLIFtN9lAbVtqGrAm5XaLjIZUIYuTAUXsmi+fVZVzx0SBTJ4UIyG7ijaDPgvZeeOFlGM2DFQKnB2YshTqfxPqDKgcOlOHyL+DSW79GDYNY2KSBqAUb9sHI6s2YPbsgvRcKV3wOiBl5tnZ38BPp31je1cy0mnJKvvpltEubkZ7dS/bZDSSirYR4I3FsAIkSRMw4gBLrgy0bSd96M67/z955h8lZnWf/d94yfWZne9NKq4a6kJAQCCEQooMxYGxwiW3AuOdz4pI4+VKcOI4dX3H73O2EOOAOGJtiEF2mCRVAvWv7rrZPL++85Xx/nBntCiQhbFMS676uuXZ2ylvntPu5n/u54l+IrQlgtKmrmS9f/0L5eWXBU4lh6gL8IWhedSZTepL0PfBak7ESp5TjhXt/jn/tpTTPXs6lb5vF/Xd8m60P/JS2xWupaZ3G1m3buPicy2mrjRAPGAjhMn/mVAYHBkmMZ3AdycK587j0wrOJNLaRlzrDoQDNIsjoNIldFaWuqZbpMxp54Zn1jPTtp28khWmlieASDhm0TY3SPG0WQ0+8wEjRD6FmyKs5WXdPH8lkmsTYmAoBCo2m+jpOXzSH3T0GrmvgSI28G2DugqUMHNhEIXMSyljNBH8NFMYAF8/1KLpH01CyHOS6+t3v5dIrLua0eTP49vd+iG1PbhsCpr2bmvYz8bnHz7OWVpKhjmd56sEUn3YepedwnEDdNBY317J6SQMyrOPXBHWN1cxYsoA10/1sfTLBoekG09fEKeUhW3CY1apx+YoG/E1f5Qtf+AKJROJV3veTgyy5OENpnBf3Q+rlqyu/lNQJSX1bDca11zGUy/Lopg20NkY4e8npXH/zzYRrarj/Bz/gq5//d0oNNfR2dE1sIIdqEGVR2bT5UNuMmvuMoFbO5eC0EBCshQ9cCTUW/PejLz2aip+jTrl0XnnDNqptBphQxo6Vd1DWHb3Thss1WDgAv8mrQl0VuXpL+WMnmrzHUV1aHsXxvolQCbNWtBAWR/fq3qS/WSau0h8KB3X1C0wQuzkm7HPegbq9mgNbB2Cne1SJxFM4hTcQBog4kdpqRChEoNZHQxskR8DRDdxyNxLXwS1FSQ3tIv86TKErZVbUXEEQ8Puprq4iEquiOhagsVanOqZqHBvlQlpHzOrLfIcwQC+p9h6NgY2B5g+imwb+oEBXrmtIqR5uecdCU121KGdqngyBJiV4LjiO8vrOFyGbgsEhSKQFOQtcYaAbBoah4WkenrDBKeKVbFzHwUZiGEF8QT+GGcTn8xEMBtA0HSk9NCEwTfDGq9FJAxmqsalmYn41hlrNHTNXTegII0pzZDp6LEAmaJIL+hnQJRgRMLJghhH4KZRssqUMKUZPfOKBKFrz6TT4BA2aumcacFCfGJlUvsIe1BWeg8EZRPWJPlJnoiBZCCgUYGhEcQiZ/NczAAAgAElEQVSICeGWKHMIngulInhJCfmCqsB2rDWICEDoavCaCDbXEJ0aJ1RdTe+LDu7Ii5DbjAqhnQgejn2Yjj0PISmimefS2NJAbUBnaKyIERx5qTbohDhFxtIO4mIwPsHRVVsqMdIQk2XOHmk2v/g4m1+cSNlqFCZtwQi1M+bQ3DaHnZYgEgnRtuBMli8/k2bPJZHJcHh4mJ5JE8aYELSZAToci95UmmJOp7v83pCVY6j7AFu6Dxz5/OE9O3h2z27amE4/PdjHUHJ1JlJ0rtt1kufuA2GoBZkD+158irHBN9ks6o8OgaYFuPqGKzDjOjWNIU6bGad/HEb7x7j33sP8x38kwPdWaBCK7CvLeMwrgEvBnANRVxlL20WwKxZ/lZ9J2bz7SC8yuXJWxThPAy0MsRh4BfCKytemJqCIpwoZK4Ciq15zbBjLq036DbU/D0Xy98GRwkUWE+lWJmq5b3uQs5QhudkEdjUT2a9+yKUgNwiMgXChNQLDZ6rzkvdD+l6ojoE5A+xLVAVKeXtZ9DsMxV7gt0xYHIZBmwc5XSl8fS3qQIJRpdgRBUUu+31g6uq6OFkwQyAsEA5otSDT5Y5XK5+IyYS0KoWKnVTqTlT8eV0gH8OWAcb8AfrG9tEQ0qmurqKxrZ2SA2YwRk2jQVVjA0mg6EHGhVFpEquexsYNj5EZyCHGJAt0P9/60btYrwfp2rQX8VCM+vo6lq65nraFq9AD7utMxr46zAYuAa4sP29FqT6OT8aWf1wEURe9oumAyQObjoGOhsDDxaFI6Yjm5nD5m41CZ77mI+AG2JgZIoVLVGi0BsLsK2RfVtRrV2cHmh5g6YKzCIaLuG4J2ypSzOUZTGdxHQfT5yNaVUUsGqNkWWTSBTL5Ein75SS10CSea+M5DsIwMPwB/KaJz/GQ+Tw9nX30wClN7P8AhKihRB5nEpWq6p8KkmhEsJHkieOnnjrOppGp5EjiHlFkBlBd1MmbUWj8fstyE6VsPR2sbkodW8t71oDnUVH4SvXVJNBOrFUnWmsQ9rUgfSu45EaTVSuhVkJvAR4uwObNedb/OAdekNbVIc6+VGPOWRAowuP3gDcAM9qaWHbLe2g47IFwsXyCRMBkdD9kxQOIg7/DSFeRLRXp2rcT2yriokiAW/t+hdVXh51fwZz3/xMRZxuR+57AW/8sxROGb3yoPIzZwCgGKRjtx/rl1yF5BUHZhrGyGmbXkkTF1yrJDZUkasFEPXcLaFgxm1nJcfoeCDPJWOc1gec4dG95hljNVBYsPo/2uaeDv549Tz9IsKqW6qZqEqk82YKLX5NE/eB6ghlT29jV0U+6dwzdgwtXr2Llktn46xoYtiVJIZgCBH0mnlmib6Sf05fOYqy/i76OneSLkqpQAFlbhz8EM09rZSSVpWO0xJioJzD9LNqDfXTs2MHhwUFGR4dob/FTF49TW+VDuCUCuKRGS2TSYXw+g2A4yOLTl7HxkQhjR5VNszHiNfhr64mEogQ85ZNn+gPooWZEdgApbRzXolDIUSgVKBZsJBqaaRIwTeavWEl9bTPp3jE2Pv48paLqOc1QmJo5Cwgv/TMKWjvJwRObXqZTnexOdbJ7J8xe9F5qp7QSjUfIDbzIcwNQW9XAcKpArDZKrSiwrTOPJgKQh5ExiDdL5s4XnLWqlsXnfpJvfPObrxkZq4z3JXSNHPPtUjJJ9uABoiGDpRedx64DB9l/6AA/e+wppseqOfOcVfji1ex4+hl+9+gmUtEAVm5SEGcccEHToLkBgg2gh5nwk6rMaSZlXL31AnASxyJjYcKMqgY1GifKG6oUJ/CY8HvKAWNKGHveTFihQTihHAt6UV1YHWrS0MGxyVhD7UasjCAbC9DlvunI2MmQkx4VlKfkR8jYP2ZZIpejFbYF1Hw9h1LHximXobDVJT55o5lTOIXXEi7ILKXcdkpD1Wi6Hzdikunzk88KHMfDc110F0zLQXc7QL72Yi4NQQADXddxHBekJOD3EY2GqK83qa7RiEbBF2JiIVxZfxsqOVP3QJpK2FTvQbDKIG8ZSKn64Ypoyi2b3XuiXGtFqHWr7qp1sq4OiHIZiyN9iuuqTFTHUWt3Kw/FgiRXkCQzksSoTSLhksm55C2bbLqIZaXxnBzSzoFbAruItErYpRKOY2P6SuCFFb1g+jBDATQhkAgMw8RHAJ8RwhN+ClJHw6YGlSMhmDDeermg1wKZR7glQoSIGTUI3Yf0JKV8hkxekrGg6AoMI4Q/ECLghfE7IawTrSJjISKnTSEmlK4qgtJKhXR13ZJALw5qNepiRpcSqV5NCxPX0kbN1TXKxchyMDQEssKxTHrYFuQzUEh4eMM25IZUJfVjzt9NMFcSrDqfmcvaOG1VLfEm2FsDpe65WKNNDKQdxrsSSG+QY88/JZBlsOspXDw83Ue1nIMv1gRaGCMYR/dHca3jeHu99Hqd1Kf+10IA/wjmTWreMsSkEboyXH8N2HDCrQxJm6He/Tz29c8dee3cc9Yw58qLefqZZxACtj7xBL/64Q/40p13Tdq9QPp1MkXB3lzhpEoBubh0cfBVnOPxIUQLQlTjuJKBBGS67sJOdb/yF/9Hw4dhNHP6mmnEomEEkrwF33nQ5vZ/foiBg02gX63C1aMohWcA+ALUvgPwgbRU5xoIgJZH9Rg+Jlb4FfIwi+qFJqthy5NqzYBANdT5lDDFC6sO3EURrQZKIasLSOchV1Ade1WNet9nHO05VfHgy0kVPshINR2v0FPResi54ASg8e9h0ALnqfJx/zXqS78F7gT5N/D82cClKP+DacBfQMIC3zUQugCKfwu2CdwN/KJ8jmtQ6uG5wHSIzIb0IDg9iniOt6nIliPA9UPVrPJ5AnYB5Ajk40APGA7EzoBiA1hxpcA9IqmqKDSSKHXsnvKFqOScBYBxidRMCmYLHcUWIsEOpoQFzS115PPw0KOb6O8KMmP+ctbSyF4HoibU1AWYduYyfv7vb+G+L2/huds7WSAaqX+LydK4pDscx/ju2Vx//Qe46C/OJWfW89Tv3pyVbyumAl9H3ZYGJpwcju9yKVAqtxokWVQjsI/5ySi1RAniI0OWMRIocixd3tdMYJYvSpu/msfTnXSiutn5/iBnn7aM7t3PkrNfToNmc3m6egaYPaOeocF+Bvr66Dh4kOeGBrj09DOojscxTB3Hcgnix7Yz5HMvH3A1oDUYoa4qSjgaQhg6NdF6pkRjpA8cpHP3Hp452Yt5Cm845nEp/WxlkD1HXusDLCwMhrmKIHEEBjYaaVpp5wr6CGGxHWXxchg1EayoBV4Zx/7tvzLqUcvue1A69CZUq6hD5SVPATGIEGMIpoH+Wc7+PxHOfSesmDrRvT0nlXXLtoOwczd0rTsAT22GhgX0L1nCcCHAWFIw2A35HJx3DcyaCS9uhHu/kiMqkrS2mSw8p5EbLod537yMdvNy6lzYcBg+unY+fYf2ASCQjAF3M8qWPQ8w47oHOAdVQ7EdxcccHyOovuPPUD3Adgz6iUoX1q2FdW/HvOoaan79LjRNkBKi7Dd9tMmDZIKMmHoaeGMh1rMQ5eP72udJ73j45+x4+Oeg+SF2OpBjYGAfRm8j8xes5JFn9lPnm0l9tAEhBLOXL6Nu/pkMDAzT13GAT1/5Lkwh2Nufp+9wgcuX1WAKwZZH9nH7bzaRy27jX/7PGgLWYqoj1SxZ/Vb+7p++jZsZwe9z8UUNPvDBmxjWVlBqO49ZV6zku58+jffOn0/Pvv3U15r87QensuatV/HN76znNz/5T/bvzmJH2tlWtZZFS9qZP8OHNbKIUCSKECGECKN+8aPUr72C6e+8hXOWn8+MLExphvoaSZVQ8wdPCEbGB9m5bzM7O3dwYM8gJS1ApLGFOU1N3Hfbb/je179Ounci60rTNOoXns47fvs0Z8UlP/xvwYZfn/w1P7DjOQ7sGOO5B8e5/WsAghWXfgTT38S2h9YxVGzn059fBe31PNYjqbHhxg+HkYbkybxLX1D8wenkfwj6Dw/yyKOPMfjIQ7z3O//Gmgsv55ILVvPed3yI3q4hPve+t3PpkoXov76HLQ9v5r7vfZnO7t0TGyjzspEIfPT9KugNqCjFrPLzNKpTqNi7zi0/jn9UqKV3Gyov5nnUbyDAhN6oDAPlV3vgkJoHzkdZYd9c3swLTKzoj4Ua4FwN4+dLcTbsQN6RhCeO8bk3gRGqhiI/lSrraIfLyaHc19qsTaI4+MdQo0ETivc+WffxUziF1x4JpPcIO+97BBWtibOZBlQg2Y8aqSusxRhqNnbsgNUfEyYmURHHHw5RyBbIJXOUMiVoNAhUQTAO5mTWcXK/VXleVrbqEmrDalYmBTgltc4uFBTxly5zeZ5UBKCjq1O2ikAAtKgSEL1UAZnKwdAYjIxKnCKk+iCb88gVHfKWxWjyMHYmQymTJJMcpugUyWeGcHPjiGyCQMYBy8IpFrGKBYolC4c0puHH9IfRY3nikSChUBDN0Ck5LpZTRAqBq0PKKdKH6rbjqLsVQ3XvLyf9SiCz4CYAFxsDz/XjszwSiTy7d/cwmOzFcpI0Rvy0tbUTGfIxPBrkIFuPe5+qmmHRpRAWE8cAanhBXVZ8iPI7gtplFzBnzXWcdYzbBmqumMzAcJ8i0Q2/ItYrGB6Gw92QOGRD9xDIJ1HhrWP4wEobki9w2tpr+MA749x8tUcADXE9wEo6xlbyxUf/hp996NdY2a+B3MDxB68sI10PMdL1CBvvjzJ/6WeINUxFCzRQNe10EgcfRXqvvI74Eydjb4Dq2arRJnnJtS4Bt8HvqZt6btPTXP/eK1m18nxEscjgQC+HOg8c9ZmM53J/apwqKd8QO6bb//vHnL9mGYlkka987UXSmf/9xWvOWXUmv/7NfcQiqtLzvZtGuelruyg8sA8rfznUNSsitrLe/wAYH4H62SqVyM6rDNNsQU2e7RITVRrjqPV3CtX+25kwoyr71pQL0aOF1LTYQNkTCKHUsI4Fuq+siLWhdwA8H0Qj0FCjVKag0iRKqHn8EEr7UAQGPHh6Kzg7gUEQ40A/eHUgFymP10X10Pgt6H0chu8HrgN+DG0fBOMz0JlF+ZfdVt64v3z8/wGlPVA6ALwPjI+DdzZ4HShTl/lQY0C4LMm1JBSHgRx4aUgaoIeUJYNbBHuqMkR3HLDHgReBC8BcApoOibxSxvICqhJPpZpvxR+2ktt6rEwEWX7zaR+Dh2C0FnoWghlTCuB0OsiitdXc+LkGmoDtCdiyFbqf6ODFR87mnz+5nm37f4TFc6xxPsu/rSxw5jdDxKqbiJxzFedfcRUNNX6SAWhb8nv+GF9DrAKuB96DWpJN7ugNjjfprwKmEMTE4iDyZUYCCpVBMsUwaQQCSe2k9zUUf78i0ETBK/F0ppvNqNs101/FmbE6UkGHq1adyaZ9B+k4fLTrX/dgDz9/5Bf85btuJJUaR7oezbUtXNJcT3V1DY7nkc2pCm5WNsVhK8GQd/SAq6FM4gMBA00TBCIh6hrqaGts4Imf3smOkVE63uiV4Sm8KuRxsI9h0TEKPI7EpYelBBgmzRhJVnE+q6hlDw4Dk+ia12esPYzqPAWqs+otPw+hSi1ewpo/v4FLP9DMRVME4yJEIghpH+wALBtynTDcA129cNpi+OtLofvyBaz70hwe3aBjf3WEDdsi9J8T49P/BJfMU/3p3l3ww69L3L2bSHn7yOxOc+ARjfu/6SdeX0dj41RaW2dS0xSjauYtTJk6RKORx5/oZ+O2BwnbFkWUG8vpqHHq5OpUJIBvwZQfQuo5yDwMPFV+716sdVtITn+YhoO3MtdnYDKRPJJgwgSlQpKrhJRGlNP1dv5wB8dXAa8EqZ0gLYZeOMjI9rvYZjSz4t03cfGSago0MAR4ps6MGMyLNuDNqj2y/jutOcjMxgCmEBwCwtPiLJhXw+N39/LbH/w3W3bvI2u5XL7qXk6/4dN07drE4P4XGHrueV7YvA2PnfzZEj+f+/h7aQN+s2ED//XACzyw7nc8uuEnvP0D8/jyVy8nmw8z2m/xy0cSdHUME/EbnDV9OiNzm2g76+2cf8NH+fMPv5VmACSaz4f0+ckY0NMF7Qbo6SJPbOvjulUzMQ1Be7yB05dfijjjIlxXOWkKTaBrGn938ZU4jotbts6qFNYYw+DHjuTPL/4pp527iiWzYePJXutgu/ItcioJ2pLn12+lZcYyrv3I+7nnBx/gHw59htXXX847Pnk6//D5FBuzB8nu+RnJ/fegzbmZ/ODrVDjmGMh1d5LvVVLQX/7VP7Prul2suP6d3LX+bj54+mK+mejjLddcw8evv5YrbmqmpsHgwXvuYeOPb1MbKLui6RrMipczhSZjCMV1aCg3k2OSoqtRxMi2Sa/tR7WsG4GrgGeAzagI9ji0VMEyP1wzrl5+HBXzOB/4RyC0VM2jLhyDzw4ce79VKHO/izzs32yAr7rqEAxgYfl4nfJjOio29dqK3E8IG9W/vlQZ+0ZhA4oabwaWo3jtSpLXKZzCmweqsLmKzmwvvza5FVUU9689BAYGYZyAQ146pAsFUqkUjUVws5DXQXMhVs/xA0gVFFENsKKwpJzZjvIkNcqTEc9WFv/pcTUvMX1KQet54Frl5NdylN+xIF2EdAZSKY/x8XHGRsbJ5/MUCgXy6TSDfV14pSJuKYuVH8MpZjG1IiYOPilxbHDyRWzLxnYcsuUDlY6JBvgdCKCjuwIhNAIIikWLgBfCIUQejtjvUT7FOBOWKS+HoT4RiEB1BF8oSNCTxJ3pdPc/w97BAbLeHoTYCxSQnoP3Cve7ugYWnwH14thEYxHIHCFGoLoNamer1wPH+HwIwIZ0edLhDyhRm5CQdGCwHzId4HSOwdjdIG/j+AW5isAv2HnfvfzNw3P5XGwtYum/cs0nYdEiaKmDy68VLLzkKm77h4Vsv/d+6PvMCc+34p+4b/sXEZqGRMNzBdI7udDenzAZK6DqRjDmqN/Cy/jWEvCfKAn1K8PEpIooupEjFIJgyMAfNNi85TlwHYqFArnS0TuRQEHKIy5Prx9MYDXTZzYTbwjSMzjMut/8jGL+DZwlvQ645ZZbuOGGG6irjSOAr925l988NETi6QJkz4c59aoiVz+qXf011F0GdbMUIWq5YJXAkSoqky+pjvfI6rGS3R1iIucSJpiv8o32RyEcU9E4p6CiapoAXYeCBWlLpTgUS2AGy+bUhhoQMkWIxI6cEhoqPtkFjPbA0ENQaIXAItCXqsJdxa0o1eteKL0Ie78Ei8IQWAGxEBwsAN+C8XdC6HyYNg0y74L0GeBUKoY9gHLVHkSphfMgomDOA20aEAE3og7I09T5+DyITVWWCE4OcsZEkTNpgTMIXr26lqE6sM+FUgbcjeDuAbmjfIIj5f328iom8mWvRzuLHNaxvVp6DwgefrTELVea1NTOoK45SHW9hgPMi0GwDbzpOo4dY/0Lf0cytxvJKD/iu0S6A0Q6VzIeSFHq2A6WiSE1dFcNxm8GCJT27pPAMtTap/YYn8tzLFVgMwZ1BKhBJ0/pCGX7cupKTnqmIQkLwdvnnMFQXxcHskn2CbiwZRa7x0fodnIMSI8wSinbGjTR4iFCNTFisRi6v5b62gE27txyZKue9MgW8tz9xEMsbm8lHA1gagK0EI7jULIsnJJKbLYKFo7jICcdlQGEdUFD0KC+vppgvAHdX0UhD3c/+AgHEwnGXOfUgud/GPrZSJEcir6baHSSSiEqjxRFOrDpw+NsLOYwlyZ0JErJN5WJqrKvLSRq+jsLmAFt57L0vCrWXqiz1FePzRyM+dUY08IcyEFtkwr2OVkYS8G6n0JpTwI3rBE6s4r3T4epUdA1gzrHwN0JVe+KM3OqwdyZkNdg80YYXN9L35Y87u5aPvbZeTz+oEfHvoPYhQ6CbhhrPMtIMUlufAC5F3KFAnqkCru2lamLVnHBirXk+vvIdnWT2raNXvazAY8sylH/xHCAQbh5KmitcLAG8ZOnylejhGkPEju8nsz7/46qf/wwjfNmMIK6F5WYWqXQhFnenB6povHKNQw/ZKix43WDBKmMf8676DKmzlrMT370IHse/wVfKYzx5PlruextF7OoGoIa6AhcTeOFLNSFQAhByRPkk1AKwYJZDTSymPT4Wvbe/y3SQ4MEAzpaYie9e59h+bJF7Pfn+e29v8BxFHvVM+TwzB6dG5aCE49z5XlLWBDW+c8vPob0n0Xvof107tvCwGCR++9+ktaFa5jStBpDzGBWVBA3PYY6enjyt8/y0fdewXPb+xgdzmHlfJhBHdvSCE4NE4tCk0+nYq2Xt4r0jI7QM1LLWbOD1EQn2MGQz6/mrfkC21/czsLlSwn6feSGMvTfvYmGhgwy9Tz5oZO1ygJKw+AdPbC71j5GBwUvbq7n/Ks/w4ubNrH1zifJ7G8llbqB5lYH201SGOkD6xdgv4FzV89Dlr3MS/kCB9f/jlIqTUxoXHXL9ezdvJP77riTuuppXHvRGVy48iwy/X0TZGw5mGzqMLcVfBVT68qKNIbq4CyUnHIc+rdA/yOTD2I/L19FeKgl+TrUBCpT3mgaWgRcmYe5UjW4Xah57yDliq/Add2q9PV+S/EvL928H5V76qLe3+GoYl9hVEfrRwmTKiRyxdv/DcabqQ5ZJZOopENjHFrGYalU7fDuN/jYTuEUJjCZeH1jW5CGwESg62DoHjo20rNwZQHX9WFZoOcgEAQzMmEhMBnSBWy1zrassuWgVApYqwiFIhQL6qHrKjhulVSdk7ytiFiBstNzXNA9GyEkCGUnmMrbFLIl8pkCyeQYydGEImNzObJjY2SGDuNYWZxShmJhDOFa+IWNKcCRAkt66A4IBJqhYzomNgIpNBAS4XrYto1TKqFpAl/AQJcC02ci7AC6E8ShcMRf18eEFuyYXbCUqqKZ6+E54LpC1fbwBbA9geUUcBhH9Vgnd/9rYrB0thoClK5aDQMVqLzLijFMiPlzTVaccSwbBQUBCE/dO91Q91UDNKkUzZ4FsuSBnQK5CbXSPRFhXMK1S+Tt3eQLCdjUxaP/2s7z1Y2EA00YTKNAnt4X7ofxp06wncmQuG5h0iU6+XKMf6JkbBQ4F2JnqRzoEi+5ZyOoEPHzL32DAEH8pjJ6ttwMwi1iu6BJgYGGEAJdkxiahqEJhkdO7J3l8brqPQDw+fycd941NDdVkUin2bqzk459T/DaJ+e8cVh13lquedt1XHTRRXie5JHN/dx53wAbn7LgcC00zFFSugyqIZ0HXAKBeRANQsYDt1x4yikXrbWL5c+WUx6O/PVP+h+O/gkZEApCVQDCbrmOi1BKVwEU82V1kKcidJEIBA1FbkpPDRYC9Z3KAjYJ9O2AwT2QGYTIXAhNB1+V6rwKIUjsA3czuE/C0FMw7Rzw10N0OZhpsL8IuacVkRqLQdVi8M+BwijkOlR6hqzUmWkrD0YSzGpVL0u4qgCWMMvDtlDqVj1SFg7b6pgjPnWujg62pkhafRREGsQwcBC8TSh1xc7f504rH5cJs14JRQnpCNlBwT7D4dASKDl1+HSTSLnnbw6CvxlKMwB0ekfXUelRN7GBxc4wI+MlMloKe2gbHYd6aF3egjACOG8Sw9GKO8ZaFHFyvEHN5qW9mknc34aPOrBBehaCYPkn7GJjc3S0Sn07ihrkXUA3ffiERhyNNjQKusEBt8hhr4SLEonXAa7nMOaWiGIQNEK01VfheQbb9u6m6Ez4D3mex85DB5haV4svFkP6DeySR65gUbJK2LaDKyGTsSmU4IjHre4HIdB8GkbUhx6rRg8EyRZL9A0Os2n3XnIvO/9TeDNCJ4oggMBAYpEmzdSmOYQCQfZ2rT/qsxIlICvhMY6HRZ5xEtQwhUYS1HKIMY7YGyJQ/eZrhxr80YVEmi7GF5lL/bK1nHV5NeddCct9ihLpKsHeBGzeAadZkC2qQFzeg+5OcDMSM+LRUAXBKsiWvbbaDDitGkKXhJjVAI2ey44Hs2x6eD+F3aClgyw+w6NtYQtVz48T7BtVnmEhiXRyFLMF8pkRHE2nuiaIPx7HrG8kNHMx8ZCPgehussUXyO9KsMvpZpwiQ0gCKMV7pWd9OSRQgLPD0NAK24vwk0XALgQeOkUCTi9Dv7iDphWrqBVVtM6tZZCJWpc2KqNCynJRS9NPw8ppjDymvc5kLFR6iVC8hqqmZhAlRg/tY4t/ClTP5ayLJPvGUtS1hKkOmYQlDFhgBJSqpuB6DAzlsLwcTcEQ0ZoGpsyaxZ6RBGGvyPSmJhadsYg+J8v0afUkRmsYGFe/ysaGZlw3wPbdg5w7q5GuJESKAep8UQZGLR55Yi+9ezYw1HOQqppWMpke+js303koTt/oCtrqQsye0kB3Rx89u1UgoufwMJ1dkE2HqI74qI/FcCyJGdeZWh9BaGWfNleSKLhs7y2xYKr/KDIWytnmjkVqYBd6sRbb8VMaSxHpOUDE7CfTfYhk39FZYCeEm4VgLUIPI7Md5RfHKWQO0rW3kTkLP4RWuovRgQ7SY7Mx51zAmadNodNqZGBPDaXEqyB+Xweke3voyGV5qrGJq69ew96NW9mxcSN3N93H1RcsZm5LC6c1N018oTwYOQ50dsL01nLiZjNqKhNFrWYLHMmwcrvAPcpR7OjsEo6kf1YKBBZRRv5FCFlwlgGLLfBJJc88hGIFy02YBGCOqw6zCxUIf2n7q8jYx1DZS1tRHVszKlNqN4rcrRxGiTeHHPV1QgsThbuOl3Nooy57SqjivdEkRN5MbPEpnMKbDAKJhot0bXQkhqFhmjpCd5BS4pQJViuvxmKMcsGtMqSrCNNSuah1vgRFR1J0PeXvakGhKBQZW1JrWaukHsUiWI5AF4qs1D2Ji0T3JEJ6ICW27ZDJFihkMhTSaVLJcQqZHPlcjlw6Q2ZsGCs9jmNlcOwMVmkcvVyZ2iufneQkKVcAACAASURBVK6BDwND09F1nQBBdAQ6BkKA59rYloZrlxC4eI6J4QpVH0OCwIddZpZMXqkgoVNWRxWhVEQruQjDQ2oSXQNHerhHBoWT7ZyaCPobaa6d0Ey/tOsfTsOhEY9K8ZemOj8tLYqCiXA0hUJ5z66nHAb0CmdStr4pFsBOgJccU4QFO1/FsZaURcPINnqeSNNDLSpHoQs1rt6HUqD9Pjj5leafIBmrA3NBf0BNcioR5yPwgE3Ap6hcSIFA0xTR2kIT9VVtBKsiHM7twij2M553SJdKjDGKbaNWeUmL40uk3zjouk5DYw133vFxQmH49YNbufVHD6FmTv/7IIQgGAjy3Vt/xqypjbieRzZv87bPriO3rQWSM8A3V5lqPoeaXM5BiaLHoJCGZAByAcgVVSVEO4u6tRaKnKwYhU9WyFZqJcBE8VoDtBqoCkFd2Z9Gd1XkTXiqiFduHCJBiARUVM+QoFmKY9IC4A8qO4OKuD8vISFh8OuQGQDxbzBtsVJZBV2IG8Ai2Pj3kL4N5PdAfgI2/hRq50KkCqLXQmIM5I+gsBM6amHRZTDbD5kpsK8VsqtV5FCiOsBA+QBMwC/VeeQKKj3EKBfacoBUFqxRVJ/WBNPq1ftZF8ZtSO4A60mwHkcJOP4gVOjpA8AUlE40qt5Ko0y+63x8/1FwDpjMXmgQcsokpgYtUYnTUEJJgCf9hjBoqp4HpRgFO43jbuPeB+5nwYXX4Y+0qgJjvwc0IfBeTbnFV4CHSo7uQ5Gf9S95vxLbnlxPDkBQzdzqOfiI0ZMYoGRpaEQwqCJEgDFGy26Ssmz7ppYW7SixyxYp+f7OTSBhBgZrpJ//16P6k2qgXQjOloLnkQyms4RtjZnxNoSXxwwFCAqNllgbneP7j1K4AvQNFSi5IUJRH4lMmnTJpeSZ2J6fggvJrI0nIviDEQRTEeEm0AVOSCdRY1IbzRJz8vT29/Dc3n1/tGt9Cq81dAJMx2QKgipchshS5K2rP8mM1iY+9Y3Vx/xWggpn4bKTTlawkKlUcSaCdUg6UB59bbySE/yrg9BNdMPALM8eS/ZyamZdw8LrbiI+0+CiCwTVNZKSEKx3YJ7n0TPksHefwxP3weGFQZJZgR6EOUth9tVQaq3C0lS2wHcsaAtAsw7LYxD7BAy7LvlB6NxQ5N4bOzH0f+Xc93+YZdddzrzz4bavQjJhEA4G0I0q9KCBa0MplSefTtPY2srM6bOpq2ugKl6P62tlPFtkIKPTYensC8chFQVcZlCiH/gEysWnEm88JkIoMqY4BfS/AvejVFIaJJLDdBH/wsPU9IVY+G8Xst5Q47QHuLI8jNpQzEHRlTTMlOzR3rgAytPPPMvmnXsRxf1IXFpqG5nS0ErRknzhV/s5+63tnDO7mnNME1OU47EChHQYPdjJpm178cVnEIo34ngOAsnUOli1ch7v+6dbuffRDYSCOrg5dF3DdT1WrTyfeFMVY7ue4InTrmbbRpeRwX4Gurcy0LGFd73zegBmzZjBX3xsNW952zWsu+8Bnl4PM8+4iI+9ZR6XX3YxHfv2UxhSrJ1PTyJDHgVsfMEo05qm0jjFZHorSNmAW/bG04ww4arppLzkcZYzElO3aa/phvyTJLISa9zmojlFHnv8WQb2DVBIjb2KK2yg15+LiMZwdn1l4mVnGC9xPw/+djm+TIl46+nUL/gzhL+WW649g6em5Nh2aD9Dz96Dik4fa8n3xiA/Ps6GW/+DteesQEqDxMhhHrj13xD//tfEdJ0qCT6/n5I1sfhIZ+EfvwILRiH8NtBrUDzqAtQ0JooavOug7SBM3X+iIzDUB6lFTb4OAJ5quNOAmx2V9LcB+DlqLlsR8aRRzfXzr3CSxfKjwgNXodr9NNTkYy8TGWIWirT9E4iCVmjwS1CuWt2oZf3xqIFRoFtAdXnseKj82imcwim8HBIXR1pYmQzCFfiNIOFIFJ9PrU3dssipUFBxJyEUoVqBU4JsVjIyJslkIOdIirZLsWQfIXIdR8N2dBJ5te63CorAdYCAYRA0JaZemQM56LpaG+G6FIt5rHSKzPg4yfFx0qmUkghlU6ST4+SSYzj5JG4pjefl0MukqTLWU51AxAwihKLnNKERCcZUNQTbwXVdXLdEKe9h2zlc16KYgQg6RTuL8LJINCzKlgoocrNSyurlXXAOvCSymIZMEl/WAny4uofngk0JlxQvD/gdCxUfxTUIsRoNWMyxg/f7OuDJjU55u/VohLBQyRVzmbApr9y6nFTEuZsFPaBsfTRNKZNTGUh3gndoBww9jCJjT24uILQWNP0MhHYZYCHlANLrw/O2gNyt/HRfB8PzNwcZW7nir8tA/S6I3aSUj49wDDFoNypnZ4IJb69vZ+nMpcxe3Io53seOXbvYuv8gPa6iN94c07+Twzve8x6+8t0f0D8s2LGun7vu+iW/u+9rb/RhvWaYP2c+mx/dgr/Jj9DgyRd6uPSjt2O92A3Ox6H+NEW+rkNNet8J4sMQ1ZQv7FgGxrPlZljJ9PJQmvsIHOnxJq9M7fLrZX/YIwxYENpqIa6B6UEwAI6hFKWFAuSy0NqkrAM8CfkCBLIw2AtmFYRbwKhTnbYf1ck6wMEucIbL+2lXg4ZRgIIHRQMiUVhUA30fgK5zgb8APgRj74DUtRCbB9U3Q3YelB4C+THY8WPQl0A4rmjNsZKad7tlda4RVAdw5LQNsA0Y2QMiCTIOBEBUqeJhTbPUYHBAQGk7cD/ILzDh//pHaftJ4F7gVlSy/rUvf3sH2MsAEWeXhG/9CvrH4NzVsOt3eZ795UsrMteh6Zdy01eX87ueEFufB88t8ez6L3LvluUsiLbS0Pjqj1QTGqtbF7Nt5CBJK/vKX3gV+Evg46i6bJMhUfdwjMm15nTaq67BsV00CtQH4myx1iPJANVY1CNJoGjXis5DYSeKbL1ACK6bs5ZUOsMLmSF+lOlComqCzIlXU1tdy22dB1lSPxVdN3B0jWQ2gxEIE0GjOhLj6ksu4Nt3dWA7R+dC7ujeztyGt3HW2r8m5m+huq2Gujadpikws1HxPhqyrHgUTEEcGTY9oYaVyy+5mI37TrhyPYU3FTSgiRwlYAyBhslSpmsBwukcrv95opzYDaoPl9vZxwxmcR4mMZawjhcBxRH8PhBwZL8vHfNnf+T7XPG2d/Olc9T/H/rqDg6M+4nHHe7+9K38+owltC+ezqKFLSxpgc//6BCHN/47+Y7b8aTGVd09rK2rY0Y54h+Q8Mtr76Nz0E/gvZczZSWsFKr1bUvAN/8Bkneuxy2WiLTFufD/ncVfvPMOBsI63Sl45kloroau1BCj/T0gDoMTpa66lrrGGLLeRgRheGA3XQdfxCq4hAJxhkb7KAw8j53cD94olY65E/ghashrRHnJHpsOR/mRxIHaOrjmerjnZ+BsAUbRUI65T49/n+gTBRZ+9Wyu+myY51BEui2VdY+VgvEe6N1jseHBHlz7jWNxqmJR2uYupPacy3j49q+w+5lHaQz7Oe9vLmTwvLn88KN/y96ZNZz/o3/h4hrYVVRB1Bq7xJ7tL/D85keJGnXURacgg4IDrktXH5T25LisZw8HejtYNHcaixYs5IMffAs/+MF9JHHp2v4Y2577PD/5mobnwZlnXcC09tlHHduhzk4+83f/wCc++8/84Od30zOY5Bvf+SEfueKrNLe1cHjgMN17lClHdchPtTaK7RRpj89GlnSVrolSIv/6FxBqgpppUDcdjOo44pgrhDRmyGb2mr9HaAKjsA1f5BBhs0QqP0TJGeBIVaqTwn7cnoPHzp/UNKJrLuC7n/4QF8yLEhU69xYET+7XWP9CglzfIA3taxilCm98J6R+XwXLHxk+H0ybypc/+nHOf89NXPWpv+G3X/8Sv8s7PHrHXUjb4r82bOR9Zy7DK5sUChMCi8F8J2gtKGtXUMToC6hI6zxUPa4LUA3mtuMdgIOSo8ZR6ZrlwjoxVMN9BmXnPPlyTW5iv486M4WalKZRyyhQLi0rUf6x9/EnQcbORfHYU1G3qBd1+/6LY4uDuwHdhq4uqJJqpnUKp3AKx4aHh0OBbGaEZLKH6mScYrKKYrGOgi2JBiAUhfp6JqxRyjVGslkYHIfB0QLdh0cYHBklMZojn7cpWC7FnIPhD2DoJj7dR1j3Ix2wpY4tNVwXso6B67plaxoHp5jFdR0008AXDiiDvGKKfCZLIZPDLhZxXRe7WMRzbIpOERybkizglk3jDAx8+DCEga4ZYEQIhcNqfe15OA7ohoFumOr/koWVy5J2U+RljhJ5IhTxY2GQwyBJFRMesZV1eo5jWWKmoTQCg0lIJEiHE9iuR8inETFqCfqaMYxqXOdEhKSOWo0pY7ympTeycPFFrOb4zjTZPIwkKuKnv6WK6dRO3CryqBGs0h/+dASeSEJJQMCAgAmups7HdsoWiF6WYxSAOgFqWXLJzay84a9oOFsjB/Tul3Rt89j9mI3T9wjW4K9xc8/x+6tjTw5vDjL2dXNTr4bG+dC4VIUejznhGEaQxk8t51QVyOULOMVhOvs3srXfQJQKZLJZ0q73P4qEhRBf/vLnueyKSwmjc+tdm3jonq9xcP9GPO91z/97XXDjjTfywVs+SKA+ABp841c7+dlvDmLtqQfnapg5HQxNFeuaAfwlmMsgWFJRF1VemCMLFpXrWf5byc8uorgDo/yeH5UTEFHPA34IGeoR86nKgppdNv7WIFWAYtmqoKoWon6V4mi75WNwlEVBJgPjneB2gr8RamuhKqK6QNlY3udOkP8MvV+AKUGICvBp6jADAhaHYelc2PINGPgyuIMgt4I7H4I6BBeB8JXTRIWyIQiWTxUTDjvK07ZUUGRyODSRJoAGRhi0OWDaylpheBDkGOQPQV8fuOuglAKZQKkyXk29uHbUAqQe+AkTC5WjEAEuQsXUFh17OyWUf25ckK6GYR/cdCU8+CTs22MTbqjni+vW8Zl3f4mm/BzOWryC9/zLCmYsCnDvDw/TM9iPphssu+DdtM9uxO+Hwz2v4jzKkMCoP4at/fG74CFU8ZTfAlcwMRjaqMs2yNGXPhYKIqQkb5XI5Ao0cAZFhimRJ0+q/GllJFdpAnkmRDRbpYTeFxlxHIac0pFYRUPTNCx/kP0utNdMJVW0saSNrfsJajpZ2UosfBpVLTOobZ/Fh897G7/9/ufo3D6hWZRS0jI7ziXvnkuz5icZ9GEHBAQg51fH4Qd0Bw5nYfcOmDcXauuhkC/yoXf8X3bsOIj8IyqQT+G1hocaoBMouZWNj2kMeuu4Y4vA9NnkT7wBSsBmJPeyjXNZylRWsoQX2cXEZPTVxrolTJS0C51Gy/yz+NAX3sNyoGraIgKNAXYacPvd0N2fZnz8EF0D9+CO/gw2ROnbGSQVCbI9EGLx9V9hwUWfYDR/GU/euYNN+0LETEjVqaHkHCDzuZVkLI3WRuh8Fp74ZSfJnk7S2cMkehZz5vvmsXShyYxZJvl2jY1FH1oJvAQ4/S5Pfe+XjPVtwPXGMGrD1NbU09DShpCSYj6NTRHTFORzRTKJEcbSnZQy2/GKSSQmhBdAbhfgHcle/hnwrth0bKfI0/nDTAEuBmrRMevb4VNfVwMZUEztZvDpTzLV3Y9WVsZW4u4LcckfXEff3TfR/qk7eMFUBSuTFmRyUEhAagxyAxbunl4VBXyDMNp9iOzYCKYZwLYtpDdAZ/+LfPuuR5m55Hy0ap29iSz/8WgnC1e2Y/oFOR2K/gCLz17LxRctJZHxGBwp0tvRgdD8fPRTH+Ud119He1M7119eQy4p6BwIwpRrec83P0auex9j7lb01iFKPXv4yne/xxmLl+KWbPpHDrBx/ePcfPMHmTlrNj+49fv86mc/4oLVy7lw2XKm/t9buPORp5hz+lIsJ8NAfy8AixcsIJPfy8j4YYS/SE5IDvZCYgSkK8lFBsnbOqkBjb6sYM6iGkJhgYNqMwFgYGgXoWCE6lgjQldGOGFfFa3V7dQHWmgNf52CbpCreLZPQiAU4oZPfYz9W7bQtecAh7v7y++UM1pe2hhrZuNf9j7u+MxclsyKUhMw0CWcY8BPDieZPmUxjdd9jNtvvQ2veRoYfa/dj+DVwrahfwCnZh4HB8fwjRzGdVz+8SN/zljnfgxfFZuf68GbuQx6dkMxi2PDvl1QSoBoQk1nQqjOrIAK8BeBNDz4bXjwvhMdgI6aZCXUF6d5MBs1fzqMEqKMogbQP2Za/D7UgOxH+SVNRf14nkBFsRajfkha+f+DHM/E/k0HfWELMmvhdR1f9b0S1R8uRwWq8ygxw1QUSbsZVUBschKtr/x3o1S35H+vWdwpnMIfCRJcV5JJ50iOJUmOJgiPDhOMhZFmGGmYVJcgGCwrY8tfcx3I52wy2SLZQpbx8RGGh4pYlocUglzKQcgCQghMzSAeDBEwA+ALIDUNq2jhOAIhBFK62HYRp1jALik7NtICu1RCeg7Sdo88HMfCdV103SASjWN7eUynGuGFMXCwS0UMT0NHw8DALwyk7SEMA003QHoIBJ708DxP2YxrOqYXxJQueXI4SHQ0BKJSjusIKn7w1Ry7OBYIJTM1ffgCIexglLQPdA+i9bWEMu1Y47NR3uQvRRTVw9WherMaZs2to/00Hau8X5OXq2PTwzByqGxi0LAcL6RUTX5U32iVn1fI2NEhSCdVJrFhqL+aUEOHi4RCTkXyX14A6viIvI+EtprOjI/SEDTPhLmnw4x2yeKFJpvuOJfOp+4glet/5W39gXhzkLGvG66GwJkQqFYTkiPz+woXnyReMw5ejkLSpeh5WBKyVp70eJHh3P9EM58YhjGLG25YxlVXvYX65uls3T3CYw/dwbZtj5PL/u9MiDn/squ57K1vY+Wqc0BK7nqqh3se7GLL01nILoTpC8Gnq9seBN4O4dUQqAUjA9n/z957h8lxVmnfvwpd1bkn5xlJoxwtWbacccIBY8A2aQnGsOS0L+EF9tvAsuwu+8LCsixLWsDkXdjFROcs2ZatnONoZjQaTU6duys+3x9PtVqWZSMbG8ugc119zdXT3dVV1VXnOec+97mPDWKCas+RgvQqlYdO9bJRq6/HEqCF5AKghSQIG9MhrkFUk8CuJcB2wPagELRRmAZEolILpSIFoGqSOatFwc1AbkjqvpabQH85aGdLokNDBNJzwNoH3APFCyBzKRhNEpDNIh1bmw5zktC6Bn5yHWRGQMtArSJdqF4DyjywrgKtSbJqi34giyAkOKxp8iH8oCsw0G0JKVISQU0FhUgfSTDfAG4fuEeBtVQ1eX+XJZCMZQ0Z4FeG7F0PPIosfj0FkQkhlbouRJ6Zk5hA9vEXIX8ABhvg8BI48Mh+xvYMYjLB1FgY37dwRI6CNcP4aIYp20EIhfaOJuqyF9G9dA31TQks26G373dBQyffjYm8hf0CgAwWkv13HzI5SHFsnBlpniqRrSHwfR/H9bA9l7DaiOp7Qf15BgMFO4CwNKSajkG1yjoF9BSmmAi2HQUaCRFKtePFm3D1ON2xRhzFRkuAmQqRTNZT1ziPaP0swvXtJNq76OpcTF/fHtIixMyudcf2b3qkRO/WSV722jkcVhTSVHNTAdgWiBwUjkKdIcX3D+w/wmPr7uW+e27H86Y5Yy81q6Sk8kr12EuJXvqnTr2C4wEbmWAWFhdTw0200scYTrDNZwvPm/E4Z73mRrpVCEW6aZp/Ftddcw3dVEflHHAEG3dNQH4C3RmjbB2FcAFyOcoFnbIZZ6JhIW8+K0p4aTf9mVmsuzfFyJjOTLd0aSEBdR4Y4Wb8yQlm9j/Cnh2D7FlXT1jz6OiKc9XlIZa/soFZiw3qWiAtYPcRmDoIuQNp0pu3M7L3V/juIbSYQUhdQjQWRTNCCN9H1XUUR6WUyVOaHqY8fQgrOwPWAPGaNoxYC0WSaGqBcnEEzyshkMMYduJRZxo4ei2ZbI46XFKA6Tk0zIyT+N/b8DSB07MfMXYfcoF9coBcB4Ryw8z0PUJ0d57Y3BiKUCnlpTTQ5AhMDcDE4TIM9waLzYtj5UKOcuF4HnaZyfF+7vnVbdzU2ElzVyszI2P86hf/S591Izdd3Em8RgrHLlvQTiRUx8SOvRwZ6iVdylDXtYSi0BmayFCTDrHt0bUcOjRJwayj/aw1GEsXo+2sYUFXHQsXdzG0ZQOXX30NLW3NjE9MsPplV7B1Uy/LVqxh9erl/PrOe3l87T3YhTytdSkazo5x92ObSYYVGhsaaOteCkBdTS3J2jridQW6O0x29E2SVmKoIoKqqZDScG2wCh7C8llzFkRVsB2fnCMIR1Q0LYSqhDk+pTNUg1AoiRpqoTWVYsjQKZzk7hIIysLC8Sx88cxBQMOsBbScdSkLXvlKzluWYnBGZf8YFPMemekRdq3fTQSfVCiMXRiBXBTsF1YF+lmZEFAsQtxisq8H1S8ghM/2B++DQgbNSDAy4YLZBErPsY9k0zDYD00tUBNFLnQ+sr7cjIyLHNi4HTbsfNpvR3q3osyma5CM2o7g3zuRZKQX4pbKIIOEePBdzUhq6BBSS3aRDqYviyuT8lgYpRqkno6mqhjz5+InwojS08cS84CLg0eFHxFB/nS1SL5HM/JnaEbK9E4gT1UNEqgd4iRh7TPvHHXdc1HNEI5tkRkckgHRS4wqdMbO2KmawMdTHEwzJDXOXY9y2SKfnSGXr0foOooRIu9U5ZQUBYQKIR1UVUFRFVQNdE1F+ALP9fB8H89zwVMRPrg4hFHRhQaKiqsqOE4J1xOoqga+j+daUqfVd/B8gScE5XIZX/gorkD1BJoA3/XwXBff91E1FdUwEPgonoIiNExdRfdBFQIUhZCmo6kamqajazpCOLiugxACX/i4rocvfBAqGiFCmAhsygic4N6vkA0qniDECXM+nnRWPRS/CMU8qu3iCYVMKIQmoKa+juhEFzPT85HFvWmenMTXIfPuJuSi0kpbR5jG9iq79UT910lgYrpI+qgUKq9fNptYQxID6Q/DyN6aivCQBeSnwc5KPELX5MP3QfXlzBopImsgf/XfZQqQhMhy8k47w6OgxuR1koqDjoJmgjWzH88e5dl65edifyJgrArUgP5pEHPkeR3kBDC2CGympX0Qz5ukJz3D+uPjb/ulB8Sa4QSmsYTamjfxnVs/iOt6bNg1wY9/s4N1D/xxShMoikI4luJjn/kSa5bNxfN80nmHD375CSY25GC0GSKXyNL1BuRPfwGofylBTaMIlgdjE8giUA3QwpNB2IoXqyhTV64jExprIBoOMFxV6qlW5hc4AqkBqEjN1KkcaAISCQiFpS+pXGYCuXjkTSAJSgb8AeBfwQlBRgUWgBmDOQocugjsKRA/Az4NY18F9SKoj1SlvVqAGgVer8Bd74L8Q2AelaRTFxkPUwPZc2UbwAxguWBqUPRkNSoahZAhh00ID1AkSBtBOnrfhoINY5XWum9zan3BCtID68gAvQV4DdLHfx/Yhmxz+1dkYjEK9FU0YjWq/E8l+NDvsGkorIeDu+FzjeD8Zh2MbQD285frj6IwRpmdjO7awEPv6WfOOYtY9cpGXn75GkZqSrTMnk04HmZkymLPwWc/m11BJZvz8F4QRohGLwIPn5uQcsgVAfcc8hSrgIcKhCVL27Zx3TKq6uDroNsqmhCoOMQwcPHwAzmARiTgOoqCEyz5JTQ0LUzK0Gk2dWZrCczWRZhty2hsXkLrnDXUdiRpnq/RMhua43I7AgnT5JENLltv+QjT8XaeOA6M3fbgYYb3388bXvNubF3eP2UCPWUPCmlwRkDdC6teDaMDWR78zcN8+q/e/UKc3DP2B7UyghFKjDztO2QdTME9LggNKwqLogn2lPKc5c9wJRk+wiq+xYNknxUlXyFakyKkaTTPnsP7bv0hrw3JDgcfGSQeQV6/BcAWPur4PiLKKGbCR4m1ke88F6ZB6An8ug7UNa9h4bIawk3glUMkvTZESUXJe+hpH8116C867P457Lx3N6OP34oZX4cx/1Msu/4yrn7LEi6fDzkFjgjocSFaFihph2132Oy/az8c/A+kZIuLKjoxvW5UPPL5DAgfYZVwi1nG+nrJTWzHyu2lwpdvbOsm2byM0ekMYTPCxOhjFItVZsADpWG6axpY3tjFRPYQv8JHwSM8fYQVX3gXC4ng4RDGZSmgPM2I0hgQKXvwyyHq3zyHsGlSSkNuQjC0v8jIHpf07lGY3sqLPcH5RMuNDbHltu/SMW8FXV2zEelx7rn1c2w+bPDyputZtLSdRCxCW7vGvTtmeOChdTz+6Fqaly1izpqr+PW997B+w3Y+/JlV/OV734WjaKx59et49zteywBpXn3FcqLKCsaLJdY/uIn6xiamHIsR32XNldfw/e9sxFFS+CJEIjELBQ3XB9cXhHSdV116PgD63EVoZje242CEQhiJOLVtzayYk+CxjVtIdrajN7ZixjWMqSas6RJ+wQLLYgWAgLTtk8m5NEVMWhoWAARJoQDhofoqKiE8VaGjuYm9psGJSJ+iKLiey29++hO8yQxeyUNRFRRFRdc1mQwH7fooGrPPuYxLb7iJ179+JdMK3NEHu/tg9IjLyMbtjO26jaaETmNtDNwDMHR6DfE6ZuN7KYwf9zwjn3iuhXf4Uai7+il9o+u3QG0znJ1EMkcbkOhdBEQKMjOwJQe7ngReVmKgSkwUnEsTKRuyHAmUHkIWyV9I85DB5E5gNWAo8mZfJeDiMDg2ZGyOVW8NZIG8IrV1mpmia8QuuYDsph78maeyYiuNctcg+7JWUWVzGcGjQg1oQJ6SlwO/ANYHr9Uj05F+niVJWAnRef7F6DVxculJMpMPgDMpkf0zdsb+CM3Hw6ZEPG5imiFUTcPxPfK5LNlsGmFEUSNxMhbUSbxSZoe6zM3jMZ1Y0SCSN6lN1VFIaSAKFAplDEMBVHxXkaCsUPF9LfvGegAAIABJREFUH9e2sQHHdnBw0TwtYOf6cmCwpqMpcoCXpmkIV4AQiOC54/u4rovt2Hieg9B1PEfgCRfLs6gJhTEA4Xm4roumy8Fduq6j6zqe71MulaQ0uhBYtoXrS04oQIQIHkXyuICLR7XhoDJ+WUUCnSoybo0ef1KFLf3G6BBKzTzsSJJ0wiBmCGrr64jHZyG5/VlkMl5ErvFSUkx6tmTwTTFqG3ViDZXRXE+VXukHjqbTZIeGAYN5VzZT3xklgvSFCaoRhEASHQpT4GblcmKokkvn+DIHDHkKWiKKazaC2gy+zjN7Ug3oAqOGYsFgvM9Dy8F4P8QTAk3xmRwucfDhf8Oznquw2bOzPxEwtg3YBitr5dUxwAmxoouMDN7C/l2nSt07/e1tb/9PbrrpDVx1hUJGhc9+4UHuu/1/2Lvxuy/2rr1glqhr5iNfvp0LF7dTH4W9Azku/tBDZO4fBOvl0HKW7CP6KbAUlBvA+CR0+FAqyoFThRwSiaxHlpPKVCVRjp8RoVPtuwxBpAYaFUi4QTXHBdMMQFYBBbcKYoZVaAhDOQ/pQRjzwDMhHAdPCZQPBMwESGqsHepiMNUCjEHp21Dqh7F/hcUGmK+B+CLINSABy4/CyJtg9K8gEexvQZGV9z3IGD12mTy8juAQ40BEAaGDHoJSDjI+6KYcKuYRHGvg58wAlKhwZA4hh3H5vwK+wbOTH2kA3oEEydciNc3+ESKTYP8ZeD8H3gVcCdyEjGj7XCRtdj6nVg07iWXB+RQQugy07eCtB6CeC1gZv4aVLZex6pxLSL9RoXYeDB122PJAlqXz5jFejqAmdNZc1BqoUZ6aqVqEeHIO7/j4Q/zie69isPfh57bvT2M6y4iSweIwb0fKFXQTxkFnjDwlKh6uHZQbCc+9mpnh3RSmjmCVikx6uxBkqEBMM1Sh7hIcO1aFehQiCEp4LOay5bew+uqLWHPLfDoWQq2iEAdiKOjBBgrBVm1kc0IlnPCC/9+yFNr2yVl6VVtP1jnCP215N689S+oVC2SQkdkJxT6IubDyPHjwV/DVr/w5W7b84nk9p2fs9LV6TJZSwzrGEEi3vSpew7f/+Wdc9rn38t/DW8hxlL/noyg8xqnro6hAI//fA/dy7VlLOVtRUBTJBE8jr7+KHHg9sm5nIFAYgngRU9do8muIrlqJ2XI2424dY26C7rOX8qudcMUiuLLbZOX/LmLLZrjvR0N8bd0hstseB2sdQjig1mDULeWt3/ser7pII1Uj/fjuAN/QLBCH4ftfhX0/XY+buQ28J5DohhwJ4RTHmepfx/R0mtqOWYRUFa8wyWTvrzmZiuHU0GFKeQU9UQNuOkjsq8Ft0XEZdKFAmAF0ZhNhDg4JHH6I4NWUuBxZBIo/w9lVAK1Ugh9+j7azP4oWbmHgCBzaCyPf+xxebjNyVek7xd/rD2u+L9i44xDTh/vxprLEIiuZuPvjXH3/N/joR97DF//l4+hAsq6V93/so/zN332MhA6f/Oy/cf6Kd9LR1k5YGyVjCb7/X1+no3sZP/33H/D1z/0n97/l9Zgpk5Hhfjb8+jY273mEpfO7WZaoQXQJPlbK8Omv3IMWi5HZvha8KAcnVHomfRY3VTkvI4OHWHf/JgoTHVxxyXnk02Ps3bGbzQ/1UXIdkkuaCS0I0QAcbYOpnjCF8TCaLa/vMRc0U6MzqgWaRNJcz2c8ncFN91LX0EEi1Q1C0L5kBdGtu2DoyTpCyZZGGrtnc+ixjQAYcZNEY5xUrIk1553Frm072L97n3xz01wGBgdYv3YrZvxKLjhbY8lsOGuhJHr+bKbMoaMZRo8OseuAjRRR3c6zak88HUy4MHXnU/79d98HUYSzLaSu0LVIBxMFV8B158Ce7ImfWiDfQBGpu4W8+RqRufJvkDFtHk6iIPH8m0A6yruAV8bhTTHYNAqTeZnPV9SPmpBBgR/s02nYqCdsh5nv/PBpX08hG7beiiQ2JJ5hW6ng0YU89FXIAvkMz0GRUFGhvpadO7aAXURkpiRSf8bO2B+xWcAEgnw+jxGxcV2bcskin3aI5gRmDfgq5MvgO7LbFAVwoezKDtRkUiOcTVBTA0aonmLRJZ8vYZXLQTSkIjwFK2vJD6kqviDQftXRNAN8geeWQNcxTPA9F9u20XUJqymKzOFNHSxLxy8KqTULlAt5sEp4bgnHL5G28njYiMAxz0zNECNKPJIgkUhgmpLhZTkWtmdT8C1cOcUFF5sSRcJBRBpCxSBEGofDyHV8GpmnTyPrei1IX1U1H0QJxibR6kfxtQi5ksNEjU4xm8a35FAvmai3I8XwikhWrBzyKh253P/dPRDpBebL5etEiYIiUC4VcLM28DI6LzKw2mROWBe8pyKz4COXksk05C1QEtUZ6YoKShhmd0DkcpiKXkBhZxQGH0WWt55uodOAeWC7FEenKWVVpgI01LPy+Nl+xPDPQdzOHyquOD3AWD1O3fV/y4KlS1kzv4WEBg11kIhC2IBcHvI5qaOZyTls2zHJwcFthGNRaqI1tIZa8KIaB3fdQ3ZwJ8pkL0PjA6w89yoyqcvpV66EYg2UVXk9NSHjlgkCUHYH8E5OvYf69LWQ2U5z1zv4r+++kq5ZCwGVRx4r8/FPfJDBwS3kMkf/aKumzbPPZfUlr+O91y2mJmZwz6Yh/ueunWQf+S7C/hKs7pA9+XciPdH7wLwU6mzIZaEsZIdPhaCBhsw/C1SlCqAqWVBBksKg1kFrCowAWRIuTA/KYVqKAYoJvgtqBPyyfF03wCvL6Y3lIlAGN468RsPSyQCQh9I4lNPAG5D56UHgNjnsr+9/IF4H9bNh7gdhhxv4kO+A2Aj5vwSWQzkEkzno2Qn5brisAc6Ly5i9gLwdhhTIhqAU0PVDQrYFFIVk7TqBnmwyLP9OuVCaAO4C61YQ48hA+9m0wN0QHNfLZFtk8zmgrIG+d0L5v0A0IJnss5G9Xd8mwFN0JO1DatcRQU6WmYf06FPAT07h+wXgdIF4A9IxfIk0O9lQzDNamiHacCkvvwAOT8DhgSL9/UcwoglmCjpqVKGh4dQOUwHOO1dj/pKlNC/8BO94W5gNdy9isLef6sSL38dM4GY++PmbUcYz9N61ltG9X+IjwLvRuRqDWmAO0EeUUNsy1rzi//KFjyaZyKzm8buO8osv7eXKsz/DRR/z6d08ycPf6iM9fQfzQ0uZ3zyXWd2dpC6qpfV6cE0dFZUUPrVEiEfrCCXj+PUargqOIhf/qWDPKg1+OvIXq3ghQVWFYlCBEbqA1wM/P/au8sw0t7/9vbzqjr8nObcVwwb7KNj9MKsF9LLNbz83zm1r/4zhkT1nNGL/hKymqZGLL7iKf/nE+3nfh9/Hzm1b2WXb3LF2LX6hwGE8fsYUtfyY/DO1Gyk6euv7ueGD13Dp2S1c0CgrT22L5hPSNMapYhmSU14dFB6CY2yEulqIqiaaJrCFTsSP0dLVzMJwO7Zfg+8pHHkgzbf+8wDl4S249m0Ui5BNJ3GcCDXNGjfd8g9ceH6M+iYTSwtjzNbwYgoTqoyDmIGNj8DOtTPs33CEmUP34xaPgqjoL00hm2ODu0ukEbl+MocsFEUDL8fJx8lAPt9PsTiEMq6h+C6OU+ZElkHH/LO49DUfwAt1sXXtbzi0+34yAxvJYXEHEm+ZDM5XJ9Idn8iOUEC2Uow8xOH1N3M4HmN0eIaxX/4Ur/DfPD8KinXIgK8VmUAcDfbueTDfZ/yxdbjJFImmOppSNeTWrUO4A/Qe2chd6x9i1tzVLG2IYYZUprM5vnvvei5evogFi+bhuR53334vn/6Pf2fe6ovxLJemuIfwD7JycT0LzzkXs/5Gwn/1buZ2dRBSpH7rCOCn2igOPw7OMHhZwOHWb/6U7ITF5/76dcwgU6RUBJrDRe789o9Ys3wRq5d10t6RoGe4jp2HsnTV1TNLUahH6ljanoIWh442OWyzFkiiYJ4whcOxXXr3T5CKmsRTHihFFKKce8ll3H/vBtgzyPEj9vIT05SzcqhXXX0difpWjEiSgf3buG9ylHLxOPb0lI3XYqDFYtQs0KAZvvWh99OzaSPRcIS3X/cuHhnbRzxRy4oVl7B+rMz4nr149ksMjH0aE8CDj0FtFj58M1AEsRW274Z3/jccyJ+snNSP9ErHBV6R4LEXWYV3kE7qD7k09gI0wMoOKI7KOK6AvK2nkRdzCRnzRvlDDK1+Xm0RcBHwHiSpoaJ3+HRWuY10ZDg7gyw1TSE9VA/PghkrfEhPIoJuhxeozeqMnbHT0GRspuJjWWUmZ7L4kQaSWZd82kKLloilIqRtOS+lMn+lZEG6BEVbJ6zHEEkVX8mh6D5m2EBVongeUnXV1ygmLdIzWVRboDiye0PHRcGXXaG6JgFa30MIHyEEhUIBVYOQLxAeFC0QjsAIGdJDex5GtA5fV3DKPqWSj4WFh4dHGQ8LhxJlYuTLJtNOhKiSRPc0HOFh4VEM+ho1PDRcYliEAYGGho6KThYHF7lW5JH+phHpbp86XjOIXkWClBphKhQmZ8aImSambqCrIaoCBxEkKOsh0QOD6uIi2WotSWgwITsF6xJSrtFU5buXIoeOT0z4YIeBy1k2y6DhhCpWxVf6SMpVyQDNkFITehgUH9QAn4iFobYWvBUqRLsp+P8Aw58GsQdJnTj59UNmEkomQs/gWABTCH87+FtBPM7Jxp29UHZagLHNTfV84C3X0trZyfzWWiIqROMQNWVVoVySOoCeB8Wyy/LuHEcmWwmHTeJmjFqthqKpMro8wtjBTga3rePhdePk3XkU3FVgnAWKBhOKPLeV/kIBUk79YV743p0X3s5bcyWrVr2cWQsuZ+Wa1ax7eCfbttzDoZ4+tm9+EN8f4fQVZvp9LczSRQt58+uuorUuQs+Y4LHHt/PoPY/gZ6+A+nYoRyXTYAZ4D8TOkmxWpQieDb4A35N/j+nAulS5/scLn7hIrxYGIwLJJMQVKTuAJytyfhncIjgq+CaEY0AZCvvAz0L9aqkZ6wgQgQyC8JG9S1Fka1kHoAf7FAJeBixBMnsfBnJQ/hYo1yPL7QLE1Uj/sxPYAf4PgRVg14BtQEEFDLD1CndK/rWQAFpFjUFFVvdk269s93CFnFJfUsHZDaWdYO9G0iU38fS+S0HmxJcjA/LHjnttGHkbzoXmpYAPhSiwGMSvkBSwGXmslIJHCHnC8xFkcm3IHpSLkFlonmcn8yLC8gsBmMLlZ+T8wxzJrmPdzi/RfuBDFHyTfM4jO1XAtzUUoeA5gnL+d2QPKmhhmL8cIvWCkiKwETQ1KxiGylPrhs/RFAMarmLOuctp1h3mtdVw+AmFO+78NlsKZTrwaUM2k+iAbetMTiXonJcknE0xtC/Mgo4Yb3z7IhZfrDCnLU/cnE0yn6JZ7yREC9FUA4svjWOcA5mQhHMiVJU8Kov/8QtphSBdEXI3qA44raSOSvC5nhHYO+pwfCIPIFyL6QMPMJP9JMkyJB3Z6Th7NqT7i/Rv6+OhR35MX/8mfP+PIyk/Y6dmWavIjpF+lm7tpZQr4wLTrs1t2x9iupQPmNg2D9NH+SmpbjPnX/0yFi6aRaOpodVew5prVzKnu5bGVFV+oNL8ayOv4aD8QwgJypoE/hNQ/TzRiMAwVGwhMJ0Qup0mPZ5j9GgeKz/ByJEhpgcHyY/3gbcRo3MNC89eyOzu2bR1RnnFFYvpWBBGhDUmclI652gvjI7C+FGHdN8hRgZ1juybZLzvIN7kvZI2CKh6HCOygHLOoerhVVRieGUrOJISKl34ZKl6+zRg4XtlfK98Ul9umEmSrV10rDiXueefQ7KxlVSnw9qfphkYOAwMMo0sb2eRdcNrkMPUa4Lzc7yIjEBQcmw2P/E4e0JbGJ8ZwJm4B4kePdf72ITQMtDboXYe1HSiR2pxtz8IXoHnDYxF4KQPg9KCrXlklUpQaZGbmmD40ADtnauZ8RRGBo6wa8dO7vjpz/jU//kA4bDO4cODrH/obr749S/T0dhMoVhi0aolUt9OqaGptoVFC5uJRxTiioIKlMpl+nr78Er9+MUj4FY1LAd7NnGot4spXnfM/zY21rF40Wx+/JWvYJVLNMXqCIfDhMNRyppO3jc5NCbb4ucDIybkQ2DWSA/sFyTLSI/4lDIzpGpS6LpOqVzm8SeeoKkuhhlZSl1DAwqweO5ckolOULpliw1bAYHnuniuvPds26aQzVAqlrEt+ZBmgNLC8jffwqols1mxZAFnN/rceecW9mzYTHmwh7kL53PBhYv55o98ptJjxKYGSbYtZ3K/9tKlUYTmBMFVDtmrDwcn4Ze7oHw3Mp7JQP8AbNvxdBs5AZ5dRLXXczB4+cUAOcvA9hz8ekxSQg8jXVIlAIDq0NuXEAgLUo//UmTI2Y4MUQvI0x59hs9BtcGsHvmLH49FPytzg3a7M3bG/oRMICi6FqriowoX17FwHQfXLlMu5FFmdPSwh+5GSSVUwmE5kNotQqEItqOgayEMwycSttA0FS+soGsGvitlClxXAUWlWHZwfAtcn1AohAhXBngJhKugqCq+KiUNFEdgGAa+cMEXEqD1BAgfVVHQVA3heWiaih7S0YUJPtiWhUAg8PFx8bBkPCnKqG6BMjZGIBdn40mZNhwMXDQsVCykQ3UQeAgUHKQ/0pD+pRkZowbqgidYIGInPFzXxhYulhkipWqEzQihaBzCKSh3yPdJfi/Si3nIyK6y1Si1tRotddBqQFyVg7Z8ICtgpw9r18Hhgy6gEWq5kJZoiKRelXU5Pi/0fNg6ApkiCAc0B9yQxGqUYM1QFUlqs2cU3CkhAcPjmLpPtaCr1qkBfwyUFMIpISuXvchF8+kHNb4QdlqAsa1Ndbz3kk5su4zj9AMCe7qa/KhIPAZFI6WotM7XOH9RFzoCVQiEX2LacVnZMIvhOosnCgPs2hLh8OgcyoUWSJqSrVfpi1UI0C0PeAS4+0U57ufDNC1EQ2MHkTC87sa3ceONbyHZUGZg+Cjf/t5vuOeOuynnN7zYu/mCW2trN5desIq3vHoVAOu2DfHYwxvoeWI3GP8IjZoE/fJAG5hvg7oohCwoebLKIgJG67He08olUplim6CqE+sgc7oImGFoikDYC2A1X4KxXhEoyU24LkRTEqz1BsEeBVZAvhTIm1RoVi7wAFUefjdVeYQo0qOmgfupSiT8C5Q0KF0Ckz6yhd9GlsEeDt57CFl67wIuAVIy8dqHJJJOAyMCpoXcZkhIcWxfyK9OBBotri2LI6NT4NwJ/IoTe8qfbBX/rCJLc+9Hgs07qJbnNnJsoERNDAZ7YHIfMjv8NdXVQ0ciiRGqKt97CDYUAyMMs5AU34Mc69Y7dWtGQgatwC50RvFKo/Qc+BZPbHwPrd0mqhEiXpdCVRRCKuRLHhMjz9z2rGigJ2HRxTDS55MezeNGB7GEwCcHwaTx39tUFaWhm3iTyZKltSTPbeLImkvY07uBvp6drM1luBl56kK4zGQK7NowRsZP4qBQk6ph1Vk1XPtWMAyIN8VpPD/OSrpxgANHZKtIxwqZQJSQbtVD/rxG8NcXwfDzYKFUFFlwCPnyutKEZKGXhLytbKT2z4QH+4dgrOjQPjvPdHY2VnYY362EEH309o1Rm2ylNR6jrAlqawts+tkAD9z2IJv6Pv/8nMc/JTPC4FQEoF9i2XBg45lp7ty0jslBm6EpOVHd9hxu71l/7D0CwQ5yOOiEozXEYnGScQVYzuvf8Re84pUXs/i4yvwkkrE0iMQKosgYpMLornTVCiTGUJ0AK1C8IlHDJxyRYKzn65RzI/TtHGDLum2I9F7QxjEjBqm6CEa8mdT513LZDddzzjmL6WiCJQYMuzAw5nGg30FRXHr2lDi4w+XA5gIT+x6nY1ULlp3GSPTjFofw7Ai+F0EzEsTr5lLO75daYOgoxFE1HeEXEUK2YWh04jOGdKgGKj4+M5yUPqeoaJpBLN7C/HOuovu8i6lb1EYkBNcuPpfp3j623rsbpzQISMzlMLAu2JKJZMgWkQBEpUDjonAEg3Wb72KnN8q0cwjpwE/VKsWsCiARAq0Rmm6A0GpCi5Zhzu8k1uQzfshC5PaDf5TnrQNKTEHWp1zOUp4JHft3djLN8L5enHOK7CxarF+/ncfuuZOtd91G9m1/RtbOs3XrZjY8+iAx10Pki0RjUZauOYem9vkUrFpwTNqiKiGqy6hVtujduZ+6mhlKaYfScTUrK99DLneIKWRxTAEamxtZvGIJRwZ6yWfz+I5ONBRmTp0go5psGtaYGIflzbLG2xOTYZJiyCQuXZKDROMhn/RMmkRC9ghaVpk9e7eSae1kwcI52K6OHlKY09JMbaoT3VyKW25FCsZXplBJy+fy5HNP5eaAiaLM56r/+3Fe0Z1ggeGjThf59Td/y/jRCbpTCc5ZNIemOQ3ohs5MZgQxtJ9U++JgcMcfov/++bDKrxncY8Ys8HTwxjDCArucY8TyGRkSPPSj58DMUZBBHcicJ/cM7/1D2PpJGJ6ETxowasufyKQ6TKFCfKgAxpXa9Is3s+8ZTUGmAjchC02LkCMMjiDXCA95/z2TVbTyKwOGKrqOp7oCKypouozHz9gZ+1MzISBt5/GFjSpsFL+M8Cw8t4BVNHCnoeg6uPkw9fUKiYSCroNiQdkCz1PQNA0TAyUSwwj7cha30BCOhlX28YVHKBzCMMIUiw4IQSgUksVSAb7vIdSgTVbT8X0fT1WIxmKUSyUU30NVPBTFxcFDCPnAc8F30RSBqmuYRggsgYogSL/RUAKmrIfAxkVBQ8PFxcVDQcXHRsVFwUXBxsPFw0NFHIMGbKr8pTLVlVij6mvkahRMjXHLWOUClmvh6woaEInEMWK1kGiWA2u8DFWWWqWV4Xj4NEE4plObhLYoJIM5OQVkvrjfg4cecBneV0LTPJILz6FBCx1L7U2qJB4FmRtuOgBTM6CUAh6uxMlRFTnIK6RKkL0wCNahEkzvR2apT0c+dIGdMu9xW5AefQYJZrw4hMXTAoydmSrwofd9ie27HuNQ71qedklS6lCiDYRmNzGvdR4IB9fKU85OMLh3EOFO8OQK8WWSFRsBNh/372Obn0AKVD78PB/RH85aW7v5zq37uPQSME2F3oEZPvlPj/CTr70Jx37hJ8CdLvaLX3yX884779jzL/yfN9PTMxfC74SFGowq0hMtBuXzsLINKEpZAgMoa5CfgWMdmZXCiorMxCslJguJ/eU4JpaqOhDOSL3XsB5g/Tb0BjOIGuZA3RwojMHcZdD1JigXoG8GhIW8Cyt0wUrH+l7gUWSk14YEVm0k0eS9yKJNPVJD9ZfA3wAXAl8KTsB5SNG+jwTP9eA4TI4NTsjpMCwLcxxCDt4SvmSkhxUwdPn2CPL5KDDWB0P3AX9xij9MEvkFZSR9QEPKm90I/Oi4900An4dtT4enxZFA8tXBMYeRBaz3ggRPFZl4nOp+Pa2ZwQ5uop3dXNCd46OfvoCHlihYMVh83lKueO8/UhtV2LQPJo+mGR3ofcYtKhpoKdh6APQStDakWLBqJaOqisUQFTbM721eCbHvs7SXv8ws5pIMw6yL4Ozb1/KZv/8kP/nWFzkHWAj0YjPupBHTRxgU81jWAJ2Xw+I5cKgXurtBi8jL/yDy53M7oaazOrCoklPZyFumBvn+GQG/DK5tNUga9DKUM1KWw7GhUAgIHarEAmdmYGQC3vwqeOsnLyf+kXX8xTdg41cuIXO4SqP+/Ou+yC3vfztv+8BrqE/CLWtuZ2jsWzgvYR/+opmmw/LzYP+AVMd/0bP2526+8HliZP3Tvu5SEQLp5LIr/5YbX38zH3hrRVvzqTyBOqrg6zTS7VtI4BWk+7GR/M15VIlecUWhq72L+sgUId3FQUOPR5i2IBwaRxQPAnmUpjdy7svfyCWveBkr3ggdCkyNKYwOw8M7ILMYhg/B9k1p7r27h8nRHsqjD+Db/cgq4Fl86J8/z6ZdRdY+0ElL8jqGtj9M/vB6dDdHKtXMlHIAIRKAgsDCtSu6XpPAGA49SKdqoqGQ0pYy4x1CMAUnDN0yzCSJunnUxlt57Z+9i7ZzFzMB/M2n4Of/CIvnv4x5l4TYd+99T/qch1SVWaZKr5r0JTw3E3xDGpdbOcgT5S0UnhP6kkS2XBwMns+H1LXw7r+GMsxfobB4JXQtUPj6Q5djbd8E00eRkOPzZO6MfBwXbm3esY2ew33YYYNtA8NkZtK4mSwr5q/mljfcRDQVR9N1bNtm2bJlXPPmd/OqG2/k9TdczX/88ucc3JthzM3RTx0LjvsqoUcotKzma5u38e8fej93fPvbT9qVKBL0rhIh5XCteurZ9cReYrEa5iycBUCtqbOyXUVT5PWuADc0ydVoNzJ8UI6hSjq187pRAt3YZCrGG2++iisuuJKRbJa9I0PM6ppFDdCxcB5diz36dmrgXYRsmTkVLUsFRdF5bzuMx+CeQzke//E+eh/4Ab43xt4Zm70/uI1/+sFtALzq0iu48ryL+MgX/gFYiQwuRk/pJ3tx7YT8pvAwACGzlqWXf429a2/FKkwiL6iDJ374mU1BOq47OX3AzDxQMOFVS0Hshkds2Y9vIh3zKDL+q9Rg6pGOY/qkW3vRLYYcX/BmZPm+omSWoVLW+t1W4ZUNIe+Ou5Cqx6dqiQao64TDW57Fh87YGfsjMYFguDhDR2YEhELI80g0NmIVkwgjGH6laZQjLumMStlRiJpyCLWig6mo2CiEIxpJzQQNXAXyeRer4OH5nmTGAqZpommVjEdCZpVhk6YZgAC6HOglQiEc18G2LDRdYKjg4qIoHr5bxCuXwHJxrTy54jiuUwDfReDi4SDw0VHQA3BBR8fAwMTEwgte9dApUqaAoISLhcA9ppqoo6Khox8nW1Ppfi1SZcc+2VwgA0WXWEGQSvukxj30Th1TSxGKdKDUqIhIGYZ+BFIDAAAgAElEQVQVcBPITFBDZn6V8lIBiDEwpLHjMOSSMKdOfmdl/+p1EOPD+NlBEolJLrg6RpepHOsoqEwn8IMtTnkwsBMmBwEHIhGIx0GPQSgiO44TJqSSkGuB4ngcjqwB1gCPI+Wpns72cLp0xZ8WYOzQcD+TU1/Dsn9HL41II4o57INH6OkLli7hI3wP4VZ+voqFYIkiaVknnf8ggFfyrIOd08QWn/8p3vqGl/GWm5bT2AgbN3n84Pv/j8fu+zHxbBbfPvkE4z8200NhLn7VX5Os60RRFIaHs1xy5Tc4cvhyMC+G6IVQVmAGtE9A/CaYlYLJUbAz4FgB+9oEzyGYCoRs8S8hBTbnIMHAPNWyUgyIQE0tNNdCQwSG+8COy8FWuDBrIeSmIBWFlC61TRwPsi6kizA6AKI32H4tMpBuQ7JH7wd+C7wR+CRyJ3cG/28HPgxcgZRuuQD4PrLg8Bbgm8F+hpGBbSPyTveDYxgAZkMhLN3UjICyIyVBEoocQlYPZBRJwu134OgG8L4L7g6kD/5dFkJKKUSQ+XIU2dP1BPDqYD9zwH2cnBiqBPt/MzLPiiCzxL7gHBxFZozH3nwKVpG6Idhme7BvfchzO0rQwSq3N8RCfts/wCMf/38seM/HuPENJp3dMKEqTAgIN0AqozKindyNzpoH2ZzUIy71QbkWmhqguT1G55w5TxqI8vyYDTxAz+1ZWgXMOUf+ntFGhZsueS8NR+bxb3e9jzcG74yTYbu3mX//4WX81Ss1ZrVBYZmcVrl7J+zdDL1H4M3/BKYiq5DBko2KzKUSQMyHX+yD2z/7EIc3340vfk7BJ2hTFSiKDyKM8BMgVIRwEf5k4OmlcIHnGXg+7PmyjRlrQkusppRspThzImhyL9jnMbT3Aj71ia8yMfkj3GdcbM/Y05rnwq4NEg1/STDKnpstu+wDXHHTx/iL6wBCRGK1xGJyINEE1TpYZZ4MVCdkt1N1/UWkS6rUzSsdO3Gka3GAsKKQMutJmT4h08ZRNXQUEklIXX0xZ59zJWgrOTyqM57Ocscd23j00RR1sWnSo2lyU2WsguA7Y/uJqC52YYb05BArz13MzpkN5O1BKi0be7ZaHOkH34tw9tXLWHHuArbe3Ur/lnUM7H8Y4Y8FRyCQab9Ftb2jIioyAwg8fNJentqa2RheF8K2yFgZyhSAKJ4dpjzpc2TiIP/8ya9ywRteweVvvw5rspd7ds9GaI2sXD6Xffee/Df4rA+/TRi8ri3FfQdiiI5ljNnj9IxvJEsO61kjRyGqE+QrC4gOLYth4VXy/wehZ9Ans0cQu05FuB1IiHGIZwRjtYUQOhuSNWClIRaCxiZYdCE8/ihM3Aml3zFhVwlRdgweXbeVmrhJR0SQj7ncf3AzrudQX1tLLFmPqrUxlfW4+YYbuP7aS4lrKtcs66IpUcAVIQqDPn16ls7GBIf7e+kZHKa9YxltqkKUFBJGraJWlfDFIegmA8xwiJffsIILrzqHtlltVFoS28MWLWYChWhVDl+RS+T5yNomityOHKZRXa9CIYOuuQvRdZ2C43FkKs2hwWFec9655IuT5Ar7wJtAVpRPbWCeEq8jctZrqdMNdqw7yiN33Mftt36G97zhRsL1rUTiceJhDXdmmm/819eoaYrQtTgY8xG6BLxN4L8UwNiTm2Nn2PPQR3DKs7jqtbewfM1y/vVTL392GxFUdVVOJ5uw4MO74bPvAmUTZDfBFuSlkeHJklIe8tZOBs87gvcM/UH3+KTWieQ8/BWyMFfpCOpG7mZF4uvpLIP8eXJI3sVjyN7Mvc9yP3QPYn+sinNn7IydgjlAMZ/H1LIYZhysDFZhGj1qYKoxTFNH0XU8FFwXPA3CJkQjENJACAXLCjr3fCj7Al3XsRSPkKGiCkEu7aLrYBghDNPE8yQQ7PuSu6nrYFkutmdLRqsv10hD06SeqVBB99B0HUMPo+kKnldkOjuN75cQQjJMPVxMQhiE0dHxKFOihIqKRgjQ0SCQMJAgRBkFJxh/HEH6HRkZ+ljYmKhoSD9VgQCgqiH7ZKvAtS6epmMbYQpRg3AZdF8jaqaIJnUK0wXQDoMXlvRgXKSjDiMddxZqu0g7USbSUDMNrTWSGesDjgMH94KVHQavB8WcxEzJAc8pnjzwtdIoXASaXNm161SksV2wi8GQtpzELwhB8zKItcUZalsNWz8NEz+A8kPIBP/0ttMCjHU9B7d4MpHdE82X1D3HwXmm7h0lCk1/D0pHleH4JMsh65H9J3vxNLZGEsnF/O3fXE9T16XMmT+Hohrnl3du4I5f3sGGJ+5icLCXFC5xoLujDt9Q2DExDbnTLTp7fsw0Qnzgz6+jpamGg5Nw/x6Lvp5HQXwQOpdCU0zi7R+ERa+A2Qsg7MPeMUjnpbSICIMog1fpdgzkU6hFepBppJdQqYKawYDp8gxkHUjXQlgAJdneHwpB53ywOoFQ0PYXXL62G7RKVILQMhyTfFGQSOh8pGbsDuQco8q4+UuQoOZSZFleCZ5PAw8hwc6vI9mjC4LXK6WwSidnA2BAyZFauYot9VfqU2BGqkTcZcB+H3aXofgwMng+zDMT6K4NztWvkHTby4Jj/A1ofwveV5G9q1nk7+IUkPegjUz5ovJEdwJvCs55GUnm2o1U8hbIqPaZulk7kAfSLI+VJ5Bs4kpffA8S3K1MlqrQ344zFwNXbaQYvYDLl2ls2Am7R2DOxRBWIR6DcMTDE0/uFdMNaJ0HJRcsV0pWiKATPJ+HdM7HslyyQpz6sIZTtiK33/Ef+InXE+66lliwCs87tx3dvQRl4kMc2P4dxtwyDpPo/p3s/e+r2LdqAYnOJE2aPF1aK8xZCslG+YtMU61W+sEpDSGHuu3Lu/z2y3/Hrsf2kx46iES3K6zDCshSgayiwadLyAupMpNevr885YF2FNUcI1lbj186UbenyOaNtzM2coSRI+uRGdoZzbTnbPapASUvJYvVLKRj7mX8+RvnogDN3eczd+lcuudWtbFtpDs43u1WBnBVOmcFEro0qeqdVpojjh8+V4EFj5WDDQ0trGOaUoNM96FkpzF0iERUxkdHyE1bTBw9zOTEKCHVwBSj2NkMjuWjhBKkRwcx1DJ40+BPkIrOQlPzyPtGA4qMDoyTamhl9ewO2haFGdsXJty0FLPFImv7MKkRbVxCOB5HV2cY710HWq0UKPfl0CeDTjxMfCCEj+Kq4CkIX6uMzgMcfL+E5YRxhSAz0svAho3sSupEJwdY+0MNr5QjOzxAGwlGyeOfgAZNAdstD3eqSC8uSraPvJcPYMTnQuGriKMcD5trUCjD8F7oORtC9Vx6lsLlZyusaIfJi022jNcwNp08bjs6xOagtl7ErJctIeNC0Wmk7LcRSkSodUoU9j5O4eg+EI9AvBW8VZBVIfdkCEVRVZo7upkaHcRxPBynzIF9O4hHQoQMBce1sByLlWev4rrrrqNz9iL2DpZ5Yvs21m3ZxoG+Xkwtxo1veSMd9REsVaOkKNSoYb70xS/S3VHHqlUrUJvi1KkKN7/2euo1j29+88vH9qECxrZS9cCaptLQUotnFXFti5ARRVHChBSd0DH1Y2kWMp4ZL0MkDtOTSC232iAsyoBVzmOVM2RzNn4rtCSTuI7Hrpkimw8OcuGFyzDrW/nt5hyHflkD1oMgqov1Oz/6UbpaWynlbL5+x2Fyu36KFm+lputCVq1ejVvQaCgqrIjGsVbOx1OyzJt3KbPmdtPYGqWcLvHjO37MwX293FO5dPwNIE4DtO73MeFjl8YBhf4D91Aq9CChv2cS4z/Zdl6Y3fu9rAw8akOhH86qBW8F9O+UNZHK3JeKFanWWSp9q/XB86N/4P0+zq5GFinOR6YBlbm+FYWxyp30TCX2SnOvhWxyexgZij5btYFiAcZGnuWHztgZ+yOzbCmHEUlhqmC6oNkWIc8lLAQh4eP7LkKoIBSEkJI7ZiC5BxANyXzd8kH1FRBg5cB1HZyyjVcuY2XLeJaD8MF1XHzhIwQIIXBdH8/z8BFoioqmaSSTKTRFxS2U8EsWCv8/e+8dJslVnn3/ToXOYXKe2Zmd2ZyDtCit8mqVQAEQIJJJxp+xjI2NeT/bGIN5X7CJhg+DMTZYCF5EkIQkJCEh7UraXa20OacJu5Njz0yn6orfH6dqexcJjEACIfa5rr5meqa7+lR11ann3M/93LeKQEdRXKnRppYIh8OYJQPHcXERcj0ldHQ1TESPouGSUD0QCooncE0b2zZwXBMHExuDJB4eOh5FPIqEsM6QOZAl9kBlsUA5P81R7kwqm6oG2os5lMIMbi5HsehQiGioQhDWdSKRGPmICmpMtnt6JeTCvMBpqQIB9Z0d1DTFiaXlZ/cPwVQJFE2O68g+MA0DvAq0SILG5dJcvIicVyOUxadcpCRBJAXNrVJOMqaBKmDKhoIBuTwE/p+eCVbet9dt6gT7epiKyS+V3pfpLHxp4hUBxr60UQnKCqj7Cyio8o551lrdRZ6K9/D7Y2YVZ/78VhLJxVTXXMyf/uUHOdU7zEimyLYdI9z9nfvZ9NCXKBkSJZtA4m1zUlGUqMJAYYpc9sVpEv3aofiCKr+FhDAWq6Rj7nJu2bgCVVXZsnOMezcdklWb+uVQ3yRX0SrUvhuWzIWuqMSlj0+A40lDKlUFqwhClxc5YVDS4LZIsyrPABQQFf4c5M94ng7GGExPgm5Cc0ImZJonHf+SzYAm14d5QzIOdV/WzA16u4OepkCr1kLiVvP950VkLm4igcW/RAKewaqrgAQdL0ae2gHL8yJ/25r/3qDDInANUKBkyAeWnCgrXDn+lAfFLDQ7EFJgJqBDppAobdj/3CKnQWkqkevhW0BUgt4D5mPILtg88CyIbwDfRZp9HXL9jU4gkVnTf27LjaUqYHUKHkEm4KNIk69flICmkRSeWf/zUv542pH430F/GwGekaUsBhkI7ATdFuP+/yxArYD0ZUTqYN8uULNQvRYqfKnNklGkUJykoiXN7EQWPJdQEtKt0H1Y6ut6/vyjafLmMTPrkM0Wfqm8+IsNhfKCYMtzd5GoD9ExbyFt17WjKVAzP0oy0UGs94+5U9tHYnKWOTkbLTtJ9sm97N5dT7o5wQUtigSemiFSBXOLZd+6oA5R8mDalOf++GSBPSMn2fbtz2GXDCoTlXQ0roak7ldxPVwECnFAxSOFSxwHhxKTKORQMMGTMiGukccq5ijke/GGT/gXytlxcP8WDu7f8ry/n4s/0BBRRKieBYsriQhBdeOFLFrzDv76r9YghDhdQDCRl3SgnxU0OQRgbFC3CuSp/ZSOCGerPAbbCd4f4AYBS8qxbTRdRY8oaIqOZnsUCiaOVcI1sxSms1hZg8LoYWaHThKORiga41jFWRRVI1nXhvAGKBWnwZtC06Yp5AZx3TNhYIuh48fovLyajvM7qG6F0RFoW9BGIqQy3haleLKGUHoxQo3hFEcYHziOqlfhuWHcUk4aSVCFhwrCIqapCNfFcWWbHnio2HgYeBSwPWkzo1gjTBzdzb5ChmrHZuTZabLZQcziMO2JGgQOmVIJw3JOm5vlgAnTYdOEX3yb/U1NtIKKaDDz+W5F2TEobYXEOmhX6GxKcvmSMOvqYfQqwfhzlYyeaAHa5VutEqJiOfrKd9Lw5vVonkAtSFPPkAbNOgxbY+SPPQf7fgQL30OkfjFqKozRN4JTLLNShRDE01VkxofBsvDcEtPZDKFoI64NZlEiTvUNDaxes5aV51/CgkKIqvZKnnpqK088cwAMla5Lr2Z1c5JIOoIS1agSER56bDM3XLmOjVeuR4lEiAu48ZpLaahJ8OT2TRzZdxxXVSgocQZmPeYnQfE7L1RNo23+QiZHRglHK6lWEkRikRc8qlNT04wYLmNenEWJEE5BkNchk4CiCeOTJoXZaUqFUSzLxHVdapMJhAdHT46xt3uEy1YvYOG6GrILLHoezOGaB8HLI9QwicUd3P7H72fNgvlkJ4rs8fawbXA/VriKSLKRhsgMO587iHGqRMpwWdDWxt6hPqoaKmhdPJdUS5LxkwYiFKb/ZB/mVAFEGJxnf8Pz6ZUUo5w48DAnDqSAa5Gw3W/P1fllCRtZyH9mL1yyENa1ws/2yZRPOiyWpQcN5KQaoUz3SiFzvBwyx3tZJRgEyeYV1FQohEPgWA79B/ZzHi5XA6uRHWNnsmBfTI+Ti0yftyOlCV5IPfkXho9QGIZ8nItz8YccWatI3LFQhY6wBa5pIVwHXYAuBJ5n4qGA0FAUBUUp52r4eqO2B6rioSoSqBWui2NaWEYJt2Rj5opYpiMLrKZcj3ieh+t6OI6NZdlyHaeCp0gDLysSkQBq0cTzBJ6nSTaOsFFUnWgsCa6N5Sm4WAgXVBFGVSNooRhxNYwIhUEIXNfFUoq4VgHXMrAdg4IniKCiEMIlTAlBiJJv3SX8tVoRgUsJudwNeGaB0mKJM3PbAHzIIYozkMth5kyySQ0U0FWBrmkoUQU3FJXasa6FJMMEXVcuECeeUBCqwHIlIWkiA2NF0HQ5X3YfkR3JhFvQq9O0LgJbK8vd+ep1ErrwZOeuEvd9eRSIKXLuK+Yh60o+1/QUZeJl0ZPoejwBsVWQK0EpYJK9EiuVMl5lYKwArgPxbQmyDFAGvE5r+5vIPusv/64G+aJCCA1Yxde//iUuuWQFlgdH8h7vu+OrFCfHSGo5tmy963nvmwAOHBpkThiur5TKGQP8vBLcyxCJCJQsSQl8mWPx0o38yQe+gxDguh7dT93No//7i8AxeIOQmc6zIN4Et7VCMirNhTxPOu+lKiHur+eMENiOL4xfDZE5kLcl888sgH0YIm0+GOtKyRTblhJYRQMGBERbYF4txCKyJcL2JOAbTkpgS9Wl+1+x4Btfp/1HFB/FRQKxjUha6rXATcA7kfqoCnLNKSi7JwWW1TXIDswEsArJDA3KXsFXESAMgS5uwJhNQ7wO4kIW7qYc+M4Wn7lbBywHPuZ/zh7kybQTCY6WkCDmG4BPAaZkHtdeD/210t+EG4Cvedh3c4ZBoYF0KhtFIrlRpJHefwE3woHXwW1X+6/9JalucGe9BKmT+ziy9+sQL9z7FWiOx5Fijysol+MS/nH9KtCJlC2YBG8v/Me/wXs+BAuXwfQMxCrg2V1wcOcgwwPPcOUH1/Pof27CcbNEK+FoL1gB9c4fZ7JSahQrwqEwm0f1ym6Qv2nEkadNA7CLEnseeIjk/hyrL/4WDSmBUATRpihL/2Epn/7oZrwn8uSenqB783E+/9TjPPK/J+jtriHyL1EuA4Y80CNQHZGnWYMrlScLwAkP7uv3+NmX4fgDx7C7/xawUBBsXHsNd330u3AZFETZjT5omQ2qtFNItYyQB1EPQi5s+h4UD2+n/8Bmnt16L6cmtuO9YoTvzsUrK0RZ5SO2mFjbh/jOM29kfkg9y8naQ55zAf9eo8x0DdisP29XFfjCvpD2n1+rI3zG9oNfwp5Hq+Pi9E0SSceI6goFYaF5NqqmEw5ZVKVd5l1dy6mTecyJGTK9J+ladAHJaBMjIyNomsLKVct5+MFR8lMTuFYG27bZ/OSdyJuEQsDhPfjQD4jUJmg7v4N0NdRdCW/ZUEOnUsNJVnCicDs7f+Sx+7E9bN+0Fb15Jamwim3kKMyksKYOUqQXSKNrVaQaUti2gWWYeIZLuBgnTCNQwiJHkUlgFtOeZXhomMzUca5/3fXMbZtHdnou4yP9GLlRLnMi/Oz4MMeGp1mErIdtQ5qhleOlKENFKHvvTnG68m4OwO4OOHkRd2ZXcqJ/Dj/9sOCPLoPHf7ic5w5UgrsCEjoMPYbWtojYDZcy3QbxKoi54OTBGIWuBVDK38RIrgF+fDX072TejTeSqJvP0S02U7u/K9tKANdx6N5fBgU1TaXrvMv5sz//R6p1l1OHnuFDH/4THnnoYaKpGiZtwTW3vo5LO2/l4StuZeveHvZueoojPb30HndYM6+JK9fMAwRv+/AX0D2LLX06kazHRXMhpAmWrlnDD57Zztr6jVjVUcbDS3hou8NlV6qywCAglkjx1r/4GHd/+d8ZG4kxd1kri1acfU/1PHkmP/foZqZnc6y8+AJaGttpbYOxkuD4FAwMgGGM4ORGcQtT6BFw/ffpwqM2bHIio+KaCiua4JPrXf7bOInpVgEx9MpOLnjo28ypk/pwqZooP/n4a7hqzz+y57lvMvD0V/n2lk9z5z/XUaWfjyI8MtajLOyqIdQaIjsnxdaszbbvdzMxbTKnsZnFnYvYPbUfSj3lquerJmaB7/2uB/HSxnuH4K9NeENUqsT1IZdkqv8zQCYDjwOQOVk1MqetQ6aJv3ZDo/AtZ35R4iVQ9TCv+Yunec8tceY1w9TINB/samXYKnACl0ZkqpiGn+OV/88RQc5UPcCPf53Rx8Ar8mpWFToX5+JXDtlTGUJ4ScZLDvGSScj1SOk6WjwOugEqKHqYcDiMEBKnc1xQdI/pjMQCbM/DEQ7kIJcrYJoOnqeCFcaxs5imTalkUirIBZ0aUvHwMM0SRtHABlRFwVQUbNtG1TQ828XzVEpOEdvxMC0X14ZwJI5q1RBxdcJaDs8rkMuPAwqeJ7BdFycWR0PFdj1s10WL68S0FEYui5PPoplg42L7fYoqaRxsTDw0FCIIbCYI+ZZdZ1JaghxY5efDJXBHEI6BUiqQKcVwBICHcB0iMY1iKolnJyQgy891LnolejbdzYjzetrHO7jwKsHaRVAZB9OCyWGPvl6wiilo7iS8upUFNRLWqETW3ALl90pg3IVnLTAc6TWs+Lq/WgiSKhSFlCjIHwcmPMm0KzpQKsgX5ovghpCL/cc4B8b+1uKjUPNaKeAziLy5B2WA09/BPwOf+90M70XGlVddy5e/8t9UV2hUVCQ42Gtw/+ZhvvCZj3PZshh94wd49tkdZ70nYPVYwBVp6FLg8ITMeVqBOWmFhlqV7554mSrt2eJv6XyvZW57NW95g1xwbHz73Wx53AD9z2UL/51APSRvhMs+BUbMJ8LY0DcLliZzd9sAw5XsWFWVAFQoCoUSRDUJFhkuzPpCK9G0/LyJISSeWIHMyOIw48C+PtCL/j0gLo2d47UQqwY0qBLQWicBW0OAnZA6KKdVG3XwcsjSe0C/+iiSyH0f8C7k6asjUa2gn3YMmSFeTNneG8raqxrltXyQ8MaRCW8E8kIaN/XsBeVBcO71/7cOqdu6EcKLwZ0P1pVIzDSGBIkn/OcXwcqLIWrD9v8G7wQSSP4X4EuAmYfiduSU2+oP6g3+YEaQaG8zUkh2D5LiewfPg0XiwCJ/bCuRdZUsEiB+mueTSOYhE/lA2mY5sj+sB/ghcp4IqHEBenOEMvvCA+6FO/MQXQGpDtiwTmoDpyvB00zuf+gRrLCF4htSWTZSzi/jH29VavLObWskHq+lr2+SAz0e+ZeA3dCABGKbkOuWG4BR+tnS/wPe07WZf/7W08xd20YiMGMRwCUx4he0sPSDjXzZuoBxK8xsWKWIBEnv2wUDM+A4sop5YBdMPTlDfs8gDpsw3R1YxV3EzFPMI89iHN571V2suvlGuEjusk2Z4DLhP8b9ryqNPN/v+zFkJuHN74TX3ArLnNVopWX0zryPvp/YfPxz13O859XEejoXv3Gobajp9/PQjncwLxkigQZqlApdQaFsI1CiTHzXkdNj0KplUF7vB5d9oOQSNBS8mPjej+D++x/nkQduo1AwSaqCS6++jPf81QeYmjCIKTrJdBXhiEY0YePkQ8xf0ElmtsDRI/u5/oYbMEomA32Hue+u+7DMMJ4XLPeDdoBqQEcoGonatcw973UsvXAhC9vktH+VLhf6uwuw7RQc3wo7v/YjRvY9DtY2LJqYEtKl0RMeIr0ILzsLrotjOUyPTKDFVfRkjHhtmpCuMXnsJJ4VQSeFprYQSUSYzs1gOUUMY5b77/kqb3rHR0hU1BGLagz0mWQ71nBF2yTn955g+5ZNRJBKOqeQCjUvXWQ5m1cWJB554OuQmaLwZA9P9iymvriRjX8M5h213PaBKmqql/LgTwTDP5xLVXOENUvhqrmQV2AsB4MzMNALngIp4VDfBKNUs+qG5axcU088FiNSOp99mSFmhvdgn8GQDcIqFTn89IP85Y7NKCJJff08PvnZR8jPnGLd+pV0LenCLMB3T8IFTXDpNXNwrmhC01T68PjxDx/mk5/4Z77/g6/heFP0Do1x8KRg0cIqzmtPMYOgAEQVlda3/QPvv62d+YtqGHJU7j4OV7dC7RmViZ8+tonKymEcEixasfJ54+0ZOMbE1CnsfAFv4jgTjTaViVZqw1ESVWDk4HB3JbmMSUpVeNuVywjrEo5KJiJctKqLB54cxSgqHBiBz25WsPUWQqvfi5cbwDxyiCduPsKOu+YSmRehyf/cWhuunLue1nVrWb5mHp97+HHWXXULVnGEb37mAY50D/ODLSVem4Y3dqr0LVrIW974XvZsu5+f7tjJHXfcxX999Vays7+/erF/UPHlSXhQSBesEDKBqUPmptOcNpjFRiYPk0iyQQXSX6GAlKzqf/6mf1ksSlzH6sTbGBsZ42k+QZGJs1+w4H2su/pmvvkPa0nEY1SGJFPObU7x5FAf37z2M2zd8VM2sYv3IjkPyovc9XGkLMGLtYxRoirRxiiLliymb+thZiazv+9c6XNxLl6CiCLUFEokTQ6NispaYvV1JBtqqaquQU1ITE5XBRFN/u6p/vRiwEQuT3Y2S3a2yGymyNjgJGNjeQozRUrZEnbOwXVNTEXDFSF0L0qJHJGojq5rKKqKqmmoqooixGmAM6RpuBENoUTQo0nSaYvc7Az5mVmKuSwGEUxzCq9YIoSNRgRV1dFDUcLhpM+VcnBccG0PbIepUh7FttBshTARDHI+kUDafFUTIYeJ56MJERqIMUGEAgksNMokgxByqo2fPo4+zULHINYAACAASURBVCDWgJqoJpWuYE5tmsEaaUoeLpkYuRkK/cMw/VOwn+YX67BOUujO0K3UM1mKc3A3EAHXBmPMZPieXbj2XdB2FVqplRrkkj2Y8i3KJNeJDPQcBLsIkZBvfCgkk9bzu47HR4DDHpy6F+w7wXsamc0LyZzzHH/rr2xiz6sEjBXAcmheCxWd5W/0TGE3QNYidyC5Xq/UEIQqr+NP3nUxN167jrbWGsaz8KUv3sfuXTsYG+rm6vPncWD3wwwO9CDsEl1IKCsomDpIudHmNMypi9BYUUWtgGL/BHHXpCqpEF9dw5aBDIOzjgQaX6r4LRUernnze7nqlpuI+N12M/0/IT/RBOq7ZSv9Mag4D5reBlVxyV4N63J8ji21YkbGoZCTFPhoDZgaOBpYHmQzoI6DFwbXZ06aBZ8EE+hW+5UahNSdmTZBHAMlK1sc5y2UtPqoJp+7SFauKqTuSWUEBguSQes6/pwRtMcHlW8FSS26Qn4O9yDtqdcCC5H76lCW49T85yblWTewvA+YsB4yuY1wGsh1vw0cAuckMsmdRq5zD4L+U7jyBpirQlGDvip44kJ/fHVI4PIE8BXonwK1Ddxp4G+Q7Nmi/0BB8rMbkWjqamSGPYxcqh/zd3YKmbI+iAQgVgCtoNVKDdo8EnmMAf/tj3fY39dA5uEiZDGs5G92iLKUaY//PJB5cP3jUUtZHLIDiUqO+cfpGJR2gJWFkgp9MZibdqFQpJSfxNxvgg1uHLwkqCFQo2AXwPX1CAb6oLY2RXtrGx2rVrGiTiHxYqkVLxA1lN2wg7bpSlws12DX1DCf+8wHuebyd3HB+mtpv9xPF0ICEVJRUUkQomcWZoU8VcaArU/DiZ0DuIPH8JxTTE30UBoexp0aIcYwSxmnhQmqKJBEYQPXsWjjPBIbkngheeqMA1MuzLpQqUrAv+RJ87qd++HUMRg6UiSMy+EtcZIR6M3oNFToLF0Zo24jzPv+eiaH80wVXxmOl+fidxE60Mzr//5DrGpO0RJLIMKLWdVcTzyknuEZW25eDyQHgvV8mLLO8Zk1l2FkBT6GvG6CetX/1HZ6fAB27R/hwe9+GzhMd6/FqVNDTE5KpoAJFAoFYpbHDAqaqiEUQHgUSyb5UpGJiWEy4xM0t7SRyefJlgqUbAOzFGhox5ETeopQci51De0kUpXEUtXUzVkF8WZGe/M8dNchNgmVFas6OXF0jJ5jQ0wODrPxrdfS8MbV9C+LsGdnFUP7T+KFBfFUmERcY3T4pH/TkWIiBdtAL4YoOiVETkFRVFwBSjSMqqhomko4oRJ1EoTcGIpwyeYtnn7iKeYt7qK5o476miqiFbWEYikSqsvcwR0cOpkj58lbyksbHi+ccHhAFuormHvhfLouWkLXpdK400sraIpCIqwzfhlsOlxNybCZ7R3nwtU1jAjBppMz9O7O0l5dx+iRMUa7B5gdPgjkOXXqJO1dnXiuwchIL0vOW82BJ3uZegEwFsCxTOx4BMKVlNJNWFWdNLTMIVpXgx6OUxeCdY2QN3L0uIJQRZykgHoBet7i4P4B/s+/fJ6+kz2sPH8Fy5ct59nnNvPatdcQD0Vk84sieOs7lrDzpyd4/P4RtM5OLppfhdlw5vEwyJsWRqabk2PPIKuYZ0c4GSNZ30huMsPYzCwnt2yiq2ke9Q0dJGvbCSvQXh/l8LhDX3+W/imHjlodTQVFqIT0FCvX6FRWxZhVQalQqLx+PdXzE5jT40xWd5Kub+SrH9/O3UIhRgg4xvZ9OxH2cXqHs2TGuigUMmSdcSzPA+biuAZbvvt5Bp78FvenFfYP1fGm89pZ2NLBxPApfvbIpzCKr+Sc/lycFUUP+jy4CzkBpymbvGrIiXmackXNQaaNcaRBdtBJ9iJj2NjPdufrFClh/pw4wO1f+hIr2tbR1dyOXVNzuj6vAagKoZpqrv34m5n/zHIGt23HefSLFPz/v1AHxc+H5+/SMDL9PPwix654grCjUhXzyFRKqXfr98nu5Fyci5chND1GOJEmVlVDrKKZ1s55tM1porG5hmRSwQv73a4CdA8UTzI0SyWXfN7Gyno4efAMBc/WcRyN3IxBZjxHfrqAnc+jKgI1lkBoUDBNUEvgRfFCCnpIR4RV4rEIuq6iCAXPc1GEgmt7OJYLHniWh+OpOCKMrYUwM6Ogh/AsHccuyXWbIlBVBVXTQdVPL9U9Aag2iqOdfl3Ic4mXKnwurI2Ch4eKgkD4SvAeRYQv3+RgnVbsdCkbMTedPpI+HSEaQ8QjROIhasMamRiYig98OibM7gN7G3J9/kL3XAHaCqisRaRC4MLYuN+Im4PCgIlrPgWcQETWoiVlbn4GLwwPqcioIAdbMCHsM2IVFRQ/QXd1H86wPTBdsCfAGeOXm8m8cuNVAsYqwLVQPR/iaXmOeLxArv4I0gFIhvj5fwMhdF8947dfd4zH0szrPI+mJTfzxtuuYtmSFnqHcjy9dQf/94ePMj54mNaKGeJddZw6eYLM9NRpvC0QPNaRF9iqBMxd0srcJc0k2ppZpFoM90zhFg1iusvyaAXxnT3s7Znl6KDBsFH4ZUN7ZYVayUWXXsa6C87Dshw2bz7MzGgO9Eqo7pJIUCNUr4a2NaDkZIEEVR4jVUj9VtcCpyRBM00DOwRKyGfJKpIR6CHZMUpKsgSdDKeZlGqjT0x1ZNWn5PmLeg+EIw29NAMUQ5pkeZ6s+DiW1DyJKKBZYJvgBaWhOGWWZiBGGEei6yqSMLoTCTg2IVnAgQCiDzafnm0D4ZVAiCUoPYX9104gGeQHkN1wvZxtzuULLIoi1CjQ4SMUlSE4uQBOKZLZSwipNrAVJivgdHUgMB6LIJPtscD+Ju8PupWyzkBYfmlEkClrUFqY9Qcaks/j9bI0lkeCpU8hAWHf9+u06VpgAW34j1HkvKAigdikP6YkEpBN+NsIbClTlJP+gGU8KjWEjVo4FQbNO8bMxAEKk6fkbvn6sJ4LWgJUH8h3kd9LZgxsK0yiqoK5K9qoTMnz7jeJlL+bEcqngEK5ha4bmx2b7yGUrcLORMGup27tQsIJDfWMBY0QUu5Z8WAwJ1tAEnmbqaOTDA3+kBBHqWKUamZpANZQxsNdoXD+ZTeSvqgBt0vq/Ix5MCrkN5f1yv53AikHMj4tzWAa0x4Vqke222Mk71CTUEjGFFTFpfvkEJaloIow5+IPKVTQ57BgRQvVyRAxNQS0c8ub3sqiORU0xSAlymzWQG4wUBANgNng/h4sqgPWQvAaB5m2xZDn5/PbtspRtGA6a3N05wgWJzjRn+LZnRPceefdNKVzOKZH0Sov8B0gO5Vh+MAhtLZ2StjYjoNdcnBtQa44y3RmhNnMEBU19YyNjDGbGaFkBKCeRSQRJRROoWu1hJKLqG9tIpJIo4WS6JrO9OQRJnpKTM7CVKmO4UyIvgMDDB88jhjcz8Y3rmPB2hZq5yQx40nikT1Yuk4yHSERFWRys3iqiXBKCNfEsl08x8EzLOkY7HnEQlGUaARF01BVgRLxCNtR8FSEUDDMAr0njhBLKFTXJaivrkRVVKxYDLummkRLHf39eTKO9yuY1ASlpBdrZ3NmhFFCaSrnLad21QoWXb2QBRe10tUpp/PAE6gGKMyB3WmdgeEJxp/ppfqWazAEmGMFTu0+RU3zXoaODzEx61KcnQAMJk8eoTC7jFhUwSpk0VI1CPHLofu2jnlkTZ2SY3Cou5vm2jhtnRXoukZKl3JJh8dKZEyBYsSYLjosSal01texctkSDgxOk+kf5NKLV7G8s4G9+4boOTlDZ7OgOhXGVQQb11Tz6H8cYNe+Ek2zRRpDs4x0xUnFNZIagEc4GsESRbLmEKPDY9TUVSNcFzwPoesk4knQomTtaUZmiiTiAss0cWwLz3MoTk1gFS0K2QyT03lOjueojKmonosiPFLJKMsXhZmYtugvWiSSGhtunIderzM5Xc3JxnqqkhU8+6l95IcmkFeJpDhGw1MUigbW+Djhxa3UVNiU7ARUrQInx+TgMBN9B9ianSRspxmsvZlCbhbPMTm49/7f4Hw5F7+TKCDz2EB1Jchb4/4jqEcFU8EEchJvR+ZzgdaMn3f9SqHPoqQHqWifw/gJgRJpJl3TwrKuFDfdfjsrKiqJWHB40kM3SkSrdPSoehr3XXjtcmraWxiunwPuQZxn9lLKzyAbpX9x2P4QB5GYcg+SH/CiwvFwiy4RXUNRxYun5J6Lc/EqDKFq6NEYicoq6hq7aGlup6m+gtrKGLFgbSqk8RMmmEUolGwK+RLTmSKFgkMhb1EsOhhFF8cWOJaHZTqUShaOZaAoKhHXQRUurmejKaAqGqoaRtdiKIogFAoTDkuGrOu4CEXgOp5c13vgWAKXMK4aw1ZDOMUcTiSB7Zjgmug4KKqKogTyW4rMKxRwPRdUgeIL3np4eALCRNDQcHEQONjYCFRUFH9aVfEI4aJhUZ5SLf/xfMckTwq7hjXCIYVaFU75GISiKLiKAHMMOZNl+PkWVFVPE69cTbpxKaWWKpRanXgEbAtME/IZyE7YBO208XSRysay18KZJogBr0rx5HoyFodIDCIR0EPg5eVwhebfQhwPvMLzxvQizyZ+lzIGrwIwVgAxUD4qreBVyobDp3u/Ayrjw8hboQwN4XNC/OeqRp1aCwLGmcR1wbbN03paL2domsa8zlV84m9/zIabIwjFZd/xHF/7QS/f/MSbEMlm1q1dzRUXLucfP3bH6feZlKUxQ0CLgLco0N4puPiPbqH9qsuhogbcMRDVUqTSnYbRcc772Q6eeqKXe588xTe7j6AKUcawfwv7/OuFgpo4jzUdaZY2wVTGYOPG/4Pj3ABLzpOg5f8F/hgaVkFXCEaPQ3WLTzpVIBwCMQOxSun9gC4B2LAOoTBEwxBph0wKjKxsZ1CboJhDgow+vz+2QDJaLd9XRQ9D+wUQnQVnGDBh6hSEDYhaYPpAa3ZWGjmhQlMIRvKQzSHnkcCaO9CQ1eQYvRZk8vk2ZFv+IBI8fbM/noBBEJhMBxIHQe9tYFEYUMTGgAeA+5HSrb8o2qQh4VYLRlWYr8BcDd7RAv/aAlNN4KWRfVdTSDJrEIHzUz2wUsB9QQbtU25ZLw8crf7jKqRZRQ6YgxSCfQeSensK7ANw3xv9jYty//HFSI3XMBKc3Qb8qPyy04lrGLkSTyJ7zFL+sQmYskcpd70+xdnSBcF6ewS8H8OxOjj2029C9iGoPiSJvn1IwHcUbAW0GGcXhAwQrkDTFfSk5AL/JqR0BVhAWUbYQYJKCX83q4CrkV1+z+76Btt3/Yj+f93IrY98kaZlaeLVKkJVQcCypBx6nw3dffBX74KBFe387LsK3/rG26k1S1yAx4VInnI1EjKfFgpaPEbF/W9HjccoejDhwn5bGuIpigTyk/6hLiCvr6VLofNq6FBieCOw6Scezz5t8Ja/jLBstcfYZJ53vPZ+MoUfYHs9nIs/gBDIti+9Eqrfyf/zhfdz+bIa5sdcPFc+digOTzsq67RyvSmA8Eqczr3xkOecytkar2d8FCHkOe/wfCDW88DFwzZdPM+mfwae2Zfnw9c/wqTzdzQmVpMMzSESOcB1yz9GbixJ39hhnsl86fQ2eg8c5J4vfIm3fOFfsC2LQqlAySmhxuPkcnkscxIzf5Lu/Sbxig6M3FHs0pAcn6LS2NVJXcM80vFKbCuMEvKYyGTpP9zN5PEfAs8CLij1iNRVHPVGcYRFJDRI0dvOY9sOseG65bQsquG6zvVYt61nakoWCu1Clr7paayJbtTiFMKYZnZWYBg2igIKLrgOWjyCnoijhnSEcHBck2g6hIfA8TxSbhPTUzuYmhxgsL+GizpXMTORwdI1ikJlvH4hs+IU1tkuqr8gYv5j9Fc/Z84KFUVrIFl/Ied/+Du89gbQ0lBQoN+TAGy1kLej85Hz4w8LLt37jzA09AAnP7mBKQ2msyUmj3TzyBffJU+EFW+BusXyI4a2o5fWk4o005yqYPvjT1OczPzSUV1xySXs3bWNZ7Y9wPf6B4hUJJjb9CEuXnU1lu2hCGipckkXYGLEYeeJHG1rYtx4/UVcce0lfP0EbPvO16itW8qcqrncdlsH3/vGs9x4+Rxes6oBIWSPSe3CBURsk5Cm8bOth+mavwg1lmRlpQLEaG6sxQ6ZxFIxnnjkSV73xutRSyU8yyZcV0OFXsHI0BSHuwdpmtPI//umd6Oq8srIF4qc2LWZo0OzzFphtHgl/eMTpDQdI5sjpDisXdXGsnqPv/veDLvHYPXravjiW8I8q8C+fJJDmSSqBoe+epj80ONIdo3Mvpvql1JXtYCpyZMsW9PJm67oYtpp4D823wS5HC31YZzJwwztvZ+m6WN84+4v/0aQ/bl4hYSLvNzHkRPyIsrGqmdGHolk7qPsU1CFzMd7+eUdqApoimBl62JuXPMGqi/5c/7uk8vw2i5j3cb38J9/vwoN6LccDk56HN8DhYERIlfWoM+JUaUqp9O/mkVV1Cy8EN79KJOveQP5I9spOmPUSav1F/z4AjLX243kDxzixcsU2JZDdqoAahWZGZ3Z7P/8nnNxLl7tYToOqqZRVVVN19zldDTFqalUSPvgXTwpcz3XgVIeRmahYOSZyk0zlpkim/UozEI+Z5PPmRi5Engauq4RjgCaim2DGnYJRT1i0TB6NEo0miYSThINJbDtIqGwihZR0TUFI2+g6CqqriN0zSck6VICMWbjhRLoJRMNj6IqMF2IEsFRbYSiYnsOwpHgrOc6lBwLsFFLNp5ZxHOK2NhE0H0SnuxwzFFA9atajt9a6+Bi4ga9QhQoW8acDf75lAVbGpnEFJcWXA6bKq4KEaERDUXJnl5EPx86jKWXsOCCO1n32kaGJxSmS1DSIWOAnZc+Ojk8PAwgS0OLybxlshPZAGxxNpEisLhxgUQFpFKQTEpgdnTCN04Pga4LHDcA/n4T3XidMnf4tx+vAjB2OSgfg9eHJIkuIJYE7vSARPE/RiA2HMho4gOxAoWImuB//c2neP2brqa9sxnT8vjJQ/D3f38Z3Seee9n34rOf/Szve9/70LQwvXn49y9/n8ce/DFH9zzAn97yp1zxtgvZ9txWPvlPHzr9nqCaEBiT3FQLGxpUljQnaF3eTtWCBqhQwZmEp7bB3GZIRwADDu+kcl4TK0r15IsT/KQbblmznFFPcHwmy4ET3S/7Pv86oaoqf/yBv2VOx3yO5+GefhPX+wEkPgDuYvkVNwALIKPByBhU1kI0CaomF93tKZjOgVUJ+TgUVZgogfE9cCdApEC7FhprJdOxMAO+GTzMlVR5NexrQ/uUZEWHhlpoqITpIvQMw4IFUN0E+RKMD0KsDiJhyE/A1JQsQi1ZAPEYTBkwnpOTkueDsIQhmvBdBU0oKcCtSCZoBxK/PHMdGNiG5854DhI5q0LOoTZSqePdSDTtfzICOALu56D3y9B3KwxeDPYqOYxjwDNd0B3YNQbXm+ofr5uQyfIA8NNgg8v9PwaUVV/n4XQ8jESKVWSG7iHpv1EkQpoB0lCtSSTy/f62H6C8tgv2OwksRso5NCEB7AeRGrJPUe6yeCEWfav/noCo2w7sRS4cbOAh4IqPg70ejvwrZB+Rx9hBsjgyYATyEKocS7QChgYnGeueoF3ITf0yNt4viwjyNG/3n5uUwdjgBqYhpXI7kWTlU2T4inc3z91wDxsX3M75629m4fuvJ7IYEJJNu0yFpiVQIeD8C+GmNS18/s8mufuapRT6e6n0P1NHTrfxFZfwms89hBqJkAP2T8H9fdDYCRtUSCgyAXD8wxgH5ocg1gRJAVkDeibhYD9869/jZOJw17338De3307JCCoJ5+IPIpYKNr7lXXzgji9iC43tGY1/PNDPsYMHOPHEw/DwE1z59o9ww5tvp2KdnOqDhoIgAofrEGWp7KBQERhznxmX88Ikowlgz6TJhy57glMDf4lTilFXs4GPfu3j/Oi+Zt56Wwe33tSB632GH2/XyR0WVG57hGe+XQZjB4oGD46OcW02QziSIJ6sQVFVZvMlOjqq2V3fQ7TJYMml17F64Uo233s3R3c/iVDGWHnNe2ipn4Om6ORyOSbGh5kYH2R2JktuJtB98Q0X3HG86V1M7DoAtCIiTehzbmQmrxKugab5Mg2YLkBmL5QMiKQTXPfWP+XglkeZ7D1AfrSHRDhOQsXXzHFBE2hE0KJhwokI0USUwSNHpPaKcEARaJEwiDRDA/3ksuNUVSXAMJjK5xmbnKL3cDeG/au6zWQ5uzXjRUbyPbzujpt440cu53heGnUYJhg6TOdBS8lbQg5571oAvOXDbTTcfDs7t9zGtX8zQ8P6JE11bVz1Z9fz06P/AkYPTNswtUt+RqyRlra5pMMWT937BVy9Ai0aR4RUnOzECw7rG1/5FK7rSi2jye38yR1f4TULu5gamuEzDx1gTVeEge79ZPM5CKdRih5fP9LA4hVzuXj9PO5YANrV72ZUETx8HK5cCF2r1zJVpXDEhoW6BHfmbain9mKPebrBh8//d348+1oSr1/Byls7AIirNlX1taSTlXz0I//E5RvXU1dfe9ZYVyyci+Y6jEyd/T24jsNI/3E+/P53U1tbQ2Y2z90PbMFrbSdjKEyM2RwbgdL0ITZvHyFRn+TN59WgCCnt3hKD1qiUqvmRNgjJVogvh5HvAxBt6eSCG97AP33wVg4LhXpdY++JLB2rF2NrDfQ/8ySxrE5n23wOTh95BdtwnItfKwIh7z3IpEX60rwwSb7qjPe0IpHOX7B+Fho0roc7LpqHfSTHjp/8kNJjF/CDB7ZQuyCGF9MYAHIZ+Lf/7zG2PnWExqoEC9JFjMkF9K7u5LwNc6mnvAQAObaqbd+GIyYcnIbeZ+HT74Pc8+VKisgUeABZPjvxaxwekAaqmjYM4vmctnNxLv4Qo2BNY2CgxKPUdCQIN4FaCUoSEtHy6xRN+r1U2DBrpZiwTbLZPibGp5kYdcjOeORzHrZhy64g10Xz2xbjiQiO5oJmk0xWkq6oIRxJEtJihNQoth0B1QEFqedfU4ljOuiKSkTXUT3QtASuKzBKNuGpONO2TTiskYtGmBICuziNaWaxCyaebRCPJ9CEhioEYeGSz+aZKY3ielK7ReCg+f1eGjpRoqioOICFiYOBg+XzYsscr0nkPBaoFJbDA0yYHIFQFWqkmnALGBG54jYjEgSVWYHDC0242azB3j29XP6nDbzxBohXyjz6oAmZw3BwM2ROOVj0AzPMjJl0H4cnZqE+CXNEucm1HbleHDDBmJF8wnBYMmNjMWhthCkbEkkJuBsVwNgMuL/J3Pi7Le/+noOxSUi0Q8dFEhULmGwBQ9ADidA8iURhpMhOoBcXDndxwaXXcd5r1nD5BY0s7lxIY1MtkViEsAvrL4MFyz9IJvt9pkbvfdn24s4772T9+vWYVoidew0+9okPcPzoPuqrKvj4//oE19+wkc986VNsfvpJbL/62kCZEXfM393uGehuqOL177iBiJhAq0j4zEADOueCroGjgKZApBJ6x9BHx4l4BQTQd7yHhtoEl1VVsO7yDdy5ZTemKdtwXikhhELL3PlEY3EOb+/hP/9hE577V7CwRdJejwG3ARXl9vCKCsh7kuSiKXJiqkqDZUlPqRkbSjY4SWAcxBhUVcHkFJQClnUBeRhiQBzUCNg2CFWuS1UXLBNQoLIJ5q+D5nYJ0jILpWkplVVRCU1xqGyR610zAXZJrtMcTc7pWlhuX4mCE5WsXSXjj0FD4plRyszXlP/3oAdBIFG5gAUb9ODuAp5AXgoj/GqM/hngkNSt8Sw4GYLSKvnRFUjW42ACjBXIbHMRkjq5FnmSAjwH/Cd+O1krMpvOI8VeTSRXKVgUrkU68E0g2xl2I1myqv+6Z4ALYbZSEma/QlnjNsDtViIB1wb/GDzr73tGfhfs8X+GkUD1Qv977UWyW5PIok5Wfp+U/Oez/vY9//gNhqDufJj7N7B1EtyDcifTyDtd1n+vK3fXSQKWhVkyGSnAoCPPuxcbCaQaQ52/+ai/K4EMQEAGDoCpPPKcbwfqcZg1He7reYiHp3ezfN+/celrbqF5/RVULWoh1aFREUgWqKBGFPQ5MTZ8678Y+rfHOPX9TXydp2kA1tHE/ORctJVR2U4D1CThyk7pnrl7FIYmYHoG2tthfBJSFVBdDaYKg90wchg8E951u2A6Dl/4p4/zyD33UDJeSiHrc/FKjKYb34zSWsvY9G7MkafB9tjxxCN8bMctuAXIlCCbN8jlshQnx1jw2g1cfXUbG+b7LUz4rAfKJPkg8fz5awLkZTuIvDQT/s9gcV0Cxk2XT/xdH6M9T5LN78NRBrntwn/lyz9ayCVXL+St73g7+6dVTg1b7Dzg4cVUNu8u8YG3R4nXCTRbhW+X9y+YXqKJBF5JZ7B/gMNHD7Ft6zO4nsrI8CyuEWJ2zMRZEEOpaCXevoaa2ij9QzmGju0E08YTgvaFrbR2tIInMHIWe5/adcaelYBuOUmH46Tqu1h64WqiXQuoSSWIKuAY0H9C3l866mBBs6Buvs4/Dy/DyDoU8yYuCogitlXCcW1wwXMs2ud2sXDJYpYsX8x/ff4rTPTswzKmQXXRw0lcLwSeQrGQZ//ug6iOwUxuimxuhpJR5OVt/YqB3goXfA4umkP3hQ08XgwTBZycvCebEVmMbUdOzQH/VgGWxxSGGxT2zlcpnVJJpFSWNAlWL0yy5D9vptkt0Nc/zexMlsu73sn9j+1CS6XpH+7HdRyormTNdW/CnBlj9z1fI4mcb89cqtj2GZO853Dvt79EZ7PCVRuu5u0bFpOOK/z3sV0c6TtFruAydriXhYvXMjM7yXMH+ugfznDB9deysiVJVwUoCOoaVXZsP8Qu8rzttvM4ClzaJpgaF2w/6ODaj7F30x7Wdb0Zbv1rAKoqK3h263MchfL3ygAAIABJREFU6OtjYOIkjus8T2KhsrGLVqWeZNFlRiinUwsAy/MQqoqma1Sl4tx45VpmIiGqHB1N88gYHvsPTTAxOsnIjOA/HoR3Xi8LAWEB8y34yHOQm/8nxGsy6M4Q0z4Y29ebZ9veWZ52I3REpRJRqiXGH93ewac//QClE3djTx7D9KbPAbGv5vCQNfggeQnaH4Lmxj5kGqhS1qn5RUQmFbQovCYKTz4wSGE4ymyuxID4Aa977iMIL0SiEQwVxvphZP8gAzu3MB7qoUcrUB1tYdlzaxBjNxNtWsr6NWGq0urpaVdEwtClQ30YipdAw/dgy27YvR1v73042BjItDcoBE5STiNfbLiex8jJaUzjXIH6XJwLGUWmp0Y4ceQoczvOIxapJhrWUFOUr1P/lZ4HyRTUOgJHSeOyhFRqGE2dRtUMPK/ETDGLZRk4rgRXHUfFdVRcoaM6IRAqmqYRj0QIh+JoaoRSycMRwTUp0IRAj0QIayoRXRBS5XtcVxB1NCKJEJpbZFTJkzNncEIargGm5VAyS1iugZezicfiIFSE5xFSPEJKGNf1sD2VEgYGBhphFFRspOGMjoJGCBWNEiUKCDSKxNAIYZ9uug3kLc+++/vIWKGEmzEwx4uU6hNYEVAVlwQeoySRUG6g+3dGmDms0X18/2+LPFrfQai+FtGepnouhItgHC9gn5z0R3A+a1fN4ZqbZQdpSchl/Ig/igGgdxQODkEuC7Ek5LOSSDA2CYUC9J2C0WMwe9SBU1lwep4/pt+j+D0GY2OgXgyJDdBcW9bDDB6nb9C9KOIxKiOjTBsOjgcBN3btxTex8brruOiS5VywuhodqU9hehBSoKEBlq+7hPG8S2kv5EdeWkA2lUpxww03cP1115OZUdj85BF+9sQ2nnz0QZauWMRl6y/mmiuv4cThnWzfuo3u47JdNxA5DjTy8H8fMOHQrMPQcBYnP0E6to9UYZZ0az3UtMLoKezJDLaZI+wonNjRw+DJUSaHM7RrEMpmCekOUVXF1UvURsKo6WpMp8TI1AsbVPx2QwWRpKopxYihc+j4IMe3/Az4M1Aqy4nZCiAs9T09FeJhyJmSXeopUo6gKiqZi0Vbasg6GSRG6IFiSrZ+MSd1Yk/rWiHBVTUiJQlKwf8ANGkMpqtycjErIVYlQValJP/vqSCissKj+FW7LFKguqRItq0uQI+BCIHnC4Datj8O5Pi0On8SdSXbVySlyLbjIGk/CYgkQPUB2bwBPI5s39+CBEd/1bAoz2+9kN8Pp3bA1mrY0AKNug+besD1yPb/JUgwdCtyZTrGGQTHOJICUZA7wxTyjE7KwdKKXDJH/TfuRlIfiv7PJmAIrCJM6bC7RvY31PtvPeaBZcsMe1aR88JJZAbsIRHMRs7uhwjYq/8/e+cdJ9dV3v3vuW36zO5sr9qm3VWXZXX3XjCudBxKgEAIgUBesBNCEgg1phkIhA+8LwEMoZrmbtmyLVuWZHVpVVZti7bvzuz0dsv7x5nRrGQ5r7HNi0n0fD7z2Z3dmXvPPffcc57nd37P7ymx6e3i6eYWSDizWEJW9gdKNbSugqo3wNQPgQFQE3JclCihUoQaKwWZeI5UMkcmDwXtpcEUlcjLDc25jBKZulQJvhS/UPyMigQgGmTvMZ0aZTg1SvSkwvQUdE9O0dHTSVdnPf7ueWgVVegBF4ZfRfNAzWWXoE34MAvVOAeaOHjs11RaPuxZNzwZJedyQ7WBWqMSaICAJjcRHAGZnM3OZzMM9W3E581SUenGpdSSGDyOHllCR2sHPR0ufvHzh3j0N/dzaPful9Ar5+zVbN0X30LcThLLjpDJHIA8dFy+CqWmiskntspncBYmo0NMRobKOoAB8NUFue7yG1hx07WsXtJKfaX8dwloLamhlCSe52pPlRRGSs9DSVsdIO84PLMxRySyk3juJFHLYvToEtJJF3Y+gGGHsNKztM+/nJ4FC+hq62V6yiE5e5z+HWlyU7M8sN1iae0QfjXIseMDNFYt5+KrFmApgnwqRSEWZ/v2/eRiGUZGTnL0xFFGx4aJTkWxLReqq5bI0BGO9FWTtx38VY3oXi+xoT2Y0SQu3aC6sY7amiC2LsjnLBwrgQzrS4uCjVxJKgnUhqntbKCmpQpXyIeVUUlFZd9UuKC2BmrD0Folp8LuhTXYzCfodzh+RCOXHQeRxClkcUyTXD6L5vLgDVQRCNbhaCHMvEkhnQKlgG2ZOLYURjPNAuMjgygUyGbj5At/4A2V4FKo7IKGxXDZdbBIMOqD7aPQWZQYUg2p3V4XhlY5nE75TwkAVRKB0xnBvEU65zfBmipYGdJZeOk8GoCjJxMMTyTwOSm06jFGkzmmJov+kJmH+oXoNQsI9PazosbNzl2bSSRfOCg40b+fxx55kEIuTfe8TnqWLiVXKODyeKmqriI1MkGg2k2gwgUuF4NJN+s1geqRLN/hSYfJiTgHd/ahEEd94yqqgQ4fDKVgAzYwRnR8mNnpVeTNHLpq0NhYQ3xTgt17+ygAo+MTBEMh/L5yTrivupKwJ4RaUBiI5GgJGQR1BaGohBvacXRdapPrGvOaatg8WABDxV+jkZ11cLRKnMyz5KxJps0r2DsNXZXQYkBYQF6HupWriO3vI3WwrJyZjGQZHkqxfRxmFYjM2iQsBQIBli8PsW+LTSweo8DkKzuGztmrz7KUC2CUrBTwxJGOj6/4mVnKqUBnOFO11dUsWtBJfHwr/YdTGOlaaoylLFzRjOPXSNuyFo+tQyYB2dgImcgBMpxklhgRRghZFqn6Hsw1TYyEdNI1XtwBP1UVUmcfvwJ+A5xauPZKqGuGjmZo9SKe20U0MshIPsEQcr4p1Yx9KebYDiMnZsmdA2PP2TkrmkUsNsOJ40eYGhmmMugh5PeSC2gIz+mfFEKmtYeCIBQDXQ2j6VDIa+h6AreeQlds8nkwCw5mHgqGC0VVMBEITUdVVdQiuKrrKqqiYuFCcRSp7erYCMdBUwS6IjBUBbfLQNVVbEug2aC5dLL1YeLZBGoqgfD4KcRj5GybnJ2j4KTRTBslbyGEIpOUUNAQ2GiYxSDVxkRBRSmKEwiho6KhFiM+R7hwbBUVGxULh1kUbGxOrxF+ujngCAp5m3gihZ30k9IARSFkaCDcRc3EKNILL6XmhlC0egx/NZmoi0JBQ0kLRB6sGDiT40z3j+LM9AM2eC+jrXE+69vlEUo+uYkMtTNA/wQcGJKF1k0Fgj6JvxQEpNIwdgJih7MU+mcg+QySePlSt7r++PYnBcaWGS4C6ADvX0LotRJEm6YsiFGq6EEKOIgmHmde0EUqn8G2HBRh4Pc08RcfuJOL11TR2lA+R8qR53EJGeStubyFuPt2Yvol9N/3yoGxbrebhQsXcs8995BOFdiwYS+/uPdhHnvkkwSCXt79vg9w3RXX4klHeeMl72DULJzSvasG4prAtEG3yx7IBLBzLMIvv/QLckDvst10r++h9+Zb8HcuQET3kevfx+yJI4Q6l/DIw3sZG57FQuGqKjcUbNK5AtND4/SfnKInFKaiuZlZyyKaSErCsVn4I+rJuhFqM6EGwZbBPFuOjgBbQPkBDKvSQWtBMiJjEoy1NXkvRUFWUSzIwxDUIK1BxgVRBZwRoBqULiAA07PIsVSiXBXzXrUKcAXBMEBJF4eZCrYhRcK9mpSOSmVloSJhSeafY0mA1NEgn4OCJQHdrCOrzWcFGMGinm1RZiZvgWZKjVkzJ9shNPC4y1UFDQM0N0RtSBezPEU1hIqALAqk+oB/QM5VL8dUYD8U/g/0nQ+X3AINRYbxxBTwPSg0y4nTmkQWBdvN6VIKgKQ+HESWgYogn9NZyhAjyB5YiqTylrQOBoGPI1W3PIAXcutlJyy0JPXmRBb6UtA3RyDWVRwTVcVTXI6cI8aKh3qS01ems2XKlhCd0ksUm2MAzX5Y/FHYOQ7TGyDXJ2/8KXZ+8YoiEFXTRKfSYEuJa+X31ClQi5fSdMbfS3LAvuLPUg03i9P1MhVkFqCLoo6ZY7Pt0P10HLqfJUoT6/xrqHr3zdT2riA0vw5/px9ftUZQUfDdej4961dwzdfew3f+93YeyQZ56qSK+omTzFTVUb8iRPNqlfbLIOGHZneOquoCQ/ks//7vo+x95KNkk5NIFvQ64CdcsPhjNF79FmanK/j4u+4gnTqnD/vfxVxuN26PBwXBDXd8k77McfaP/I6RoQOQgkUXN8EsPLVzq9xzKaGlKqg+D17dhdopaLu4my98+Ud0IsdzCact6UqV9F9L9RpUTpHRTzEBFADHIZR2MM0sCStP0obP/csUffv/nZnIw6AW+NKdz1HR9Rq8vttwYhZf+tQ9rLn9zQSCXrY9FmHZTUD6GYY3F0htryIyU8snP/49FNFB2N/DBee9ne//xwfIuTQODQzxyONP8eU7PkEsOopl5XF5XJx3yUp2PbmLQl4Hu8D00S08NT5Ofed8fMEKYtMRCtPH0RQfNQ3VLFu7kHnN1UwmZonFIoyNDyBTQAQIDSEUhKIglAW0LFxJ67JFuKtUfK4c0XED3VJprIZVC6C+WPgshYRzz1vjpqWtl5HjTeQfUpkY0cjEpzHTcaxMBttxMHSdQi7P6OAEhitIIOTD1D0IBA4muKQujYOGQxrbAd3rQbU92I7ckHSKWfq2haxgeebkeCqd6YVobtqc7wjQAtD2VlhyLaxZKhMqYjAdgeQMiGaIpaHG6+BXockStCpSM9ZGbkiNI6fwkzFIDcLNb4TbqmCpLnMxKLYm1BxAt7N88fOPcyQ1gRoMkIvnwfBCZIwjUQNX63nU3FjPreurGL7z7aT692HbLyzP8Ntf/IbHHtzAvJZm/uLv7iSRzNDb1cOVl1/Fs+316NUNzG9vpaN5HuJZcHlhMGtzPG9zuM9m8tkTHNu9i8Zwlro8NOsy2Ix6wTtnccjkMszEpqkPN9Ixv5nKmspiQoxg6/Y9hEIVzO9sO/V5T1jDH4JU1mZfXxTRU0mj38AtDDqWX4xt+MiYDkbRTz7aFyHU7KOizkcAQVVlJ4a1Hd0osPi8v2Z3P3gWQrgCqjVYez5Uq1XsPDHB6K4nyw3NZUlHkuw9CtsScGCPST4Pi5YZvOdDN/JvzwywbyxPJjnDOema/wFWVGA59XvJSlOAFzmxj1Bmydqnf7a7tYO33/hm3vm323Achw56aQ/czlvffyOBSwWKIX1slwsSJhTsk8gddj8AaeJk40MYh/ZRtaCDI8+qGLV1VHS0sHKximGoCEXIuFQgHavmXriqFzHyBtSPfYGZPfdyaPwQT6dS5JHe7kvdonIcGDz2aiDFnLNz9uqxWDzC0eMHmB7ppzpYS8Cr4fdq1FQVMwXPqK/p94DXBWG/QjZTjaIIQiEX1WGdcJUL0/SQTqmk4xq5pEnWzJLJZnAcRxbp0lSEiqwuJWxUjwfVUnGsApadl46OMBG2QLE1DNUAvThXFF2CioYqIsk83lQBVzxKZmqWnHDIixyWkyaLjZmVDCIVhRA+hCJQsFEBNzo6/mKRLlmpW1UMDLRitpeO0DTceS+K40bHIE8SQZ4sMtqeqyxYNgGai6wQTGWTONE6Zr2gujVaatwcDPqw8ouxLR3LcuNYu5CoSgeqZw3BzstYuCSMz6dgq5A0ITIMRzf0kZnZCewDsoi6m6gKtNGDnLKDlJNQZ5CbVjMj0H8MBodhIgLVlWAUA9xkFiYHoHAwBof2A19EFgN9OQW8/rj2JwXGSu6cwhRe8D0A3Q2S3jGFZASmKcPqKYA7UXgUx55k/4QceC7cNDT28t6PfYVbrg7gPWP3pPKMB9fKQM88CN8Mn77vlbuWO+64g0984hPy948/yiMPf52hoe209F7Plie+QoW3il2PPc6X//qvCJgF/swjA5rRnMSU1q9rZPt4ioePzKJTHoLDefjHEQlDOSMZKh7czfLP9PGbrxxDv+EKBk9M8tAPfsLe/p14bIdFC0KsvqCVlTe9BmIzFKZHsAsZ9NYuvvr1e/jhgXHiribefcub2J012b/5MWLTL7XAxss0bwinfQ2xnMIPPvkQezYNg3gXNBUFODuBNyAHigWJAkxGIBmG4/0QDkI2Cf/5MPQugMY2wCP15KhAsmkTYI8j/f0c0tHzALWg14PfC14dVBP8dZDJQ64g0yE1DbIWeHxQ3y6HpM8LFU3gr5cpUyagKpLhkgOyGXAHwBWQzlZyVh5fEVKvNpkEq5SCL+dcXG6pnaKoko2LCU4RrKULalqlvEJ8BjLjyDpYL1a277+ySuRztRXog295gRXQ0Qo/flK27zfApinofxYJdp7peXoAqwfyPcU/tCFhwQnKYGwVZZilHSlyuxFJ6b0D+Ask7DgN7If8n8GGA/DYb8D5UvG4LuASUB6EdyMRzCPAD5CytCV7sfsKQWSE3oIcZ9XIFW0YCTivBFruAvU/YPJuyO4t50nnOYUgpabyJCNZbB/sOQKJ35MmsRTJbvUWD6tRjktKuK4151WyuXLCpe90FS+ngNQx222P8LP4vehf+RVvQGVp2wU0L70VsfpizHm1KJUhFJ8X5zYPleJJFOGnoc3L+ps0yELGgqk47H0G7nsAjt73YzJTD+PwJI49STlSiiDBJIdn9v8Lm/s+zae+itRVPGf/bey9d9zBhz/xCVqAA4rC158eYM9zKnwduA4mx56TqNjOOV9qAX1NgJU3f4LPXPN2FoeqCAv5GM3dG1Mpq6+cTfO1pNRypn30zgiPbfgCR/t/DIBtT/K2eX9GMPQx7oukedffzeO1N/6Y+qYQ//rFG1j39FX8zXsC/Ognd/PnH7sT8RE5TscAj9LEouBf8r3DR+gIewgIGZhLpxk8VKDYvURnhnAcObY13UXb/PPYtzlBc/eFhBsX8tyzj0F9DTnCmOOTTB/5JVQtZv0ll9E1v5nKSo2+/QOYZo7JgaMM791WvJo6/FUdBOo68NW2UNW1nCUrVrN46TyWL5UFLAZOysyKUKi8pJXUbbqArlpJ6sov8fOmG6/nt49fx+atOxkcHEDXda698TqWLNPorBG0C/jk+xaT4E4c5DySo7zpUwIbUmkYn4HRKRg6CePjMHMSJodg6LBJZvtGcHYgw4FSHfJDSEf9MGeflDuRC0oalCq4YAN0t0OdV348CzSANw2eEdj5Y7j6cshGbWZGHWbRyHbIARNErh5PI/GT6xdB90K4VJRzMko2VWxlNAGPbLTwXHkla6+cj66YDCsr4OfvIhJLo6ohwksvpWIVXHDVbbhUg4N923ghW7RkGR6vl62bn+aDf/Z2Lrr+ndx2ay/LW6tZ1vI6vvPgIZIzUNsJF14qWb2Hds2wd+cYyclhdj17H621DvM7FvDTR+DKa6WMepcP3tsO/y7kPdm+dS933/W/+dznPoHhasCnVeIXLpKGyj/e+Xl8X3KfBsYW0gkSs3EmxmOECm7GR4KcsCCWUmisb+bgFMSiDsmITVhTufvzX6dn7RrWXbWO1Wuq+PrXvsHs0WEuvayDW1rge33w3GEQTdDaAmYUVnbDbP1R9tob5/TIdhxTwYr9M39zE/x4pY5hwZfbYYOAb/7sAzz8w14+/i4b7MeL3ykJk2Q4Z/9DLId0WIaRz3yKsp9e2oUr2tPPbeOZ7c+dIo8cZ4S0to0PLbiR7ppiYVwg6MD1d8PE7tVIHYRTBQ7YPn2UDz5+N3du/AU3/OOnmLRjbNqzhV2bOnnT25cTDnuer/vvAjoU+NmdLOMO0vfey6/e8AYe5IW3ms7ZOTtnL81sJ41pTkA2SzqWIjIVxB3yUtMBFcaZqfjShJDFupsaIFAZZjqmMeo1yWKSzWrg0lF0AyFMzKSJT/WjaRrBYABNEwingCoKuP0+sqYbw+XDwaZgSSRG1VSwBTkhcGsqmgCXH1Rd+mPZWaioqsUyBXY+AokoufwICdMkbs8icCMnNxMFhwg+quwKVJRT6ix+/BhoKEUPWAN8hoEqFEzLooBJDgs3KgbeU1VaZot9MA4sfl7PTAMqihFCq6gCN7R0w7peaK/3cOFtN3Jwr0P/sQzH+icZ27IZeALwUcjWMjm8n0P6AtyuIEJ3Yakqbg2wZyhvgbtpuEBntlOwFRnP9iD9eKP4vgFQCpDISRJdPiszS/0KeFTIZkHyEBNIv/DFFMB5ddurGoytMGpoDLSysLeemtA8Zq0UgxGLqZ2LYGkYQipFDWPpj+UoL8yLwXcigiuTQAWSNqiKwF/TRPeKFbztjefjdmvP2zU58/2zv92MHgrRvTz4il3Xm/7hi6y6/hryeZX9fQ6PPPQtuhZ28s73vZnrr1iPJ5XgR3d9jqcf3cj4+DjXVMCaJR68AZuUnSOZF6z/u7fhfWoPY//xAMeH57SfMhNOARIOPJMtsO5z97P4W5tIJtMcGYGltsM7PnI1bQtq8Nd5Ueb5wVHQ1WpweRHhNm6vqeSZf/ktDzx9jJ9vuJ+07ZBJxqmtqqa9uZWte3ae5er+cKYoCi7DxZETsySTG2QOtPJeCAo5h7iRgKEJqJDJQmQGpnwwfhL0JglsZp+DtmuKAKgGjW6Y7ZHsVdLFDjQp15cqvjdzEBeQLoBRnBFNU2YqWjnIBSFmSRkDrwvSuSK7VZVyvVlHShvkkLIC6TxE06WKgBKkTecgMyLlFGy/BOCdoqMpimztTFpKK7gN0Ipt0DUwNSgkIBeHTBwKs0icM4hk77/cueooZYZoJThfAK4EcQ14rpIYeD1QFUDqtrYV+7NQvC8BJLZ6XMC2PDIAr0dO0BOUqasq5SV0ATIUXQdcD3x7zsWYwJeRQo1pcKYpu7tFHQH7e/Dz22UHl4Dh/wqA9SKB1SXFppSqZJWKcWWRiKar2IT5yMBAALoC4RthuBU2/yWIAYmoz/HA9ZZ6/O2N1BjQ0SZZzi/GNGQCQDNymJcOqVKuzWYhwRA/pzNj5wJW5pzjlRQadGAVZcz+O47DBkw2juzAHz1O7/Zv023Mo2nRCkI9i4kHgrizNhOpIJFcLekneqnrlsxurRZ6WuHm8yDzVzfw5OYefvLrFfRtuOOMK3JO/XQchz8a2f6cvUwTQA1tb/s8Wb/D+MkNsPs/4XzwLFMIqipJx+FvP/sQ+zbew0zfRjnonoS+xUefJ0c+b9l5XPDB2/h47+00BCtxqWppOgfKpPSS3pWY04ozWwXw7S8d4+mtP+fQiV8CMDhkct0Vb+FjH7gfT8jiPe+9gXFbIVDbxE3r1jLyU5XM6P08sGsn+/Z8mvGTeTbs0JmJTEhA1YGvfPXXLFzQSFWljkutpT7s5WePKDy9JcXowAj3f7cLwxDMDMfZ9tDR0zJJNNVFc8uFXHl9G/XtS/DVtiJqa/n8X53HtkNuNj7Tx6PREyw8v4epmSlmo9N4fQa2MHHpLhRXJd66xYQb5tHU3oLP78PweNEDYXxNrVTV+dE0wWwUCpMwPhGThbb0INkCiJCcCk/1myhJPQgCwJWrBT0LF5DPd9AtBOEKHa9X4FKKGSaIU/5FSa93rhxKqwOWDwoGFGog3yUzJ8x8Ub81q2Cn1iG3lUpqv1CWrjl9964UeKRxk6NADJuTaJwIdJJwu8jogpwKaR1CLsiPQTIO6eUQUqAmoFDrh0ovaELmVwgk6LqieA5TwEWivEwaxXPGgB3Afgd2BCrg6tex4BIvC5a4qAtBd9M1fC/9eTK7fkyrtZ+L1v4zOx7dzKoLLsZjp0nPnGRwfPTMB4Y33PwaDh45zv69/QghWLpyNcf2P81vlCjBJmhrbKci1IAR9nHEgZG4LFIxFR1hfHA7M9EBWpa0oSQjDA8PEx/7BqncBQTCDbi8QQqWiqhaBzO7OX68nwceuFeCsU2dUNFIqKaZD//NW/n6v36T/tEIh0bz9DbqQJ46t4fKGg89oTDx2SnGshFScQ2zoNHdGCYkBMlqmIjZHNp/kje/4zbUijrcRpCpQYfc8Abs9DjjmU7uH4VwL8Ti0rfyCHh3SC6T6pLVDF/zTnY8/D1wt4E5S/xkHxv+fjX7/rWX8F+9n0uuWosQMO3Av31zkj2/HQB7bmHZlcCFyPSWxzkHyv4PsZHiTw3pMjZQrpkwQbmALeBRXNy95G+Z7jfZlIa9hNCsYjkFUVTbdhzMw/fB7G+ALajAZ5BzQBKIYrHJGWP4O59kXssCqmq7+Oruz1Lh+gxL16yisbOZmgp5vpIKnkCAKjfnll5xBZ/euJGnr7yShGWdA2TP2Tl7RS2PbceIjk0R8EyieQ2MsCAaDRGsOXv2oVPcrNQqQckIVNvAlQ7i9RXI5NPkrQKpfIF4ziLvmBguHcWlY2kCl8tEaCaoNkKA16eiIRCKii0U8jlQNXGKlWsiToXejijWhnGB4VEwvDqa24vqcyOUUpRm4xBHgrEFLCCFhZ8gLtwINEwEJhqa0NAVBV1V0TUNr+ZCFyqODgHVoSAs7IIJFnipIcc4GhYO5W3wOb0CDEFsAJ9eS0tFHbt8FRwfgGgGjnkEG/eCPyOoq/cQbmxksvtatm90Y06PYBguqjqqyefz5LJRUHWEZjA+cYJc5gBycgbwseoKwfxucaooYgl6cZC+WRop06gUdfc0F3g8YLglNmKWyGnCVfxGGIkj/OnOrq9aMNYAmupqWNK9iNqmWny+NhJphYLmhnnLoMElR/pcf76ArOfQDtddC0d/qjA7pJDNCFShYjo2XUuWc/F1N9BQF3hR7WhqrCSR9zFx8hW4KFXDaJ/PVZdcSGfzPKYn02zasIML165m1fqlrF2zhKXtdQxs/CWTe7ZjnzxKb0hwYW8LrR15bCVFLJWnozbI2K4jqBPjrG1UCVVW0n8wQqJgYyJZH3kkKKapMl1vaHAGZXCGFDAm4KoAtKybT93CLqmO7NVATaBoOhgecAep7+mkOhjAKBSYjMycuoxcPk8imaC7rp60z0csFiMxc/ZKwq+kOZaJmYizd+8J4vEeufg/AAAgAElEQVQjQD04rXKrx4V8qkvMaAcMDdxF9mjQL7VibQ/UdYLiKsJ5VvHxdSPHT0lk0ESChyUBzowMKMwCWDZSe7ggi1rZBbBNCa5OxOWEWxMAtyYB4XQBTFsCsIob0OUCIYScVBwhd3k0Veps5pU5wHAWGSUWFxQHwJZSB1hSYxZHfk93yQItuSGwS6XEQ8AtwK+RSN3LsQxlkcYIpU00ZlX49VXwIWTlZN2QTODHbgS7hvIc3IncHItT7NQA0h3OIN3eI0iq+1yum6/4ChQ74lnKegsGEm0+CaxF6g9kgB8VfxpAM0yebW+0aDpS57aHMsNKR+re1iEZsI2U86NTlNGg0rxfkmxUkBoRzgqY9x4Y/zHkBsAp6wfahoGiu/ALKefg/BdNm2sq8laWFtDSqZ1is0oy2XMSeU/VMjwT5yx9bm4XNCHjGgVZz2wGiOWTJPNJds/CNOOE85P4JvpIu31UO/Wo/hYUs43koIrtbUY3DBTdQdOzBANudE81/jadnpVwYmsvmeRxHOfVUwzwnL0M6wV3WwW1Ld3c7L2W7EWXs+/IbsZ3jMoBOQ4T0QyH8zF69SAH9x5g8tBh7PEx+f1ZqA7U0NDVRef7G3joR9/GSdpkInFm+4foWV+PLcQpRvdcrde5v5/t8dm//yAbNjwJZHnwN2Mc6H+aRPIIb7nyrRw71kd71zxWrV1O3xELQQf1Da2Eqkx2Df2c7/xS4+TkLiIzRykted1dt7Bk0Wqqag0EcPXVF5FzhRmdSnLkmX3knprkie0H2X9okMhEhK99bTG6lqC/f4K+PUeY+wSqmkFdwyLGGxTc4SqCdVWsumQFSk0b0d3HSWcTtHb1oKiC6YkT5JMJdMNAC1bS0NBIqL6ZYMtCelcslU55Lo1lZXH5/ATCQdyGg5nPEokYZDI2Ciput4KmQcEpF/MTSNZnSUu34MjpnADUBH148LGQ0wuglexsTORTVpp4SpuYvrN9IERZjuaFbS7IWyLEpZDtnEAOszxFnX8LvArkqyDtgFkPAR0CLkHAA9V+8AsJsJa+50bOcx7Ksi+TyJVoErnHNlP6W0BnxVW1rO6Bzhqo8kKLUUXydVfx6F33ktr3CIO/DnPoxEEKS1YwNjFONpvFjUIO+7Q5eGx8kunpGVLJJEJRiM/OEo3OcHxgkM3b9rHi9sUcPDrEwf4oqcdijOQrya1dxMiJCNl0itUXraCyopp0MsFw/zEe/8nvUEJZupYtxdH9HB+Y5eo33s6zPx8lOnaMmZkpAEKVQQyfjtvn4jXXXMe3vvJNYrMzRCIz0FgPKLhUFZeq4Nd1XCJENpFHUxUagjqOkL5kwRYoisB0Q/fSZjKmW64zjoOTOwG2C59STbcHAhXw4Em55Js2bJ+EmWHYcUQhlpLhx2tuex01AZX45AnuvfdnRBmjd98NjM9bxqOWiwefHGPvlikmRiaKdwTK5fHaiyNlFrlb/EfK2jpn//+s5EKUfOQm5LSS4jSEwY1OvRPAicexrBweQlRTQdqCnCPd4+gUfOceyExvRDcP00icq4Frka5qFgOPCHGgshZjOs10bpD9kWk8wwcxRmewpnNka5GZdcDgtMnoVIL4+CAXXrQEoalYvkrC85YzTwiO8tI1Y8/ZOTtnZzML284yOz1DXX2cQiZFIRvAKpQTSs/0WU7FRwVIxAuk0w6W5ULVQuiGiVAzWE4O086TK+QxbQvLtlBUh2DAhyIcHCxsbDQEii5QVNAUubutFGtmKKrMeFU0sNVinCYkflCwHCxbQdU8uLwBvIEw+XwcJ5GjQAIbB4GFQKDgxqeECLgr0V0+cgr4UfAqCoYAVTg4tsAtdDRHQXFshAaO5aWgOpiWQMvZCGcKC4sCZxP7KdZwsUZRkgO4xyqwQ36yU1UUcjoJYZMYSBKNJVD0LI6aJhEbx8n2gTWKXdDITqnk0m3YehDdU4E3UEU2nQCrlMcZBLz0dig0VUvuU5hyvcaSnzQNmDr4QzLxWXgg4JP9mLchmwM7R/G4CdnuP2EgFl5lYKyuGXg8PlRNxVOwmNfSQPfyLpJKiFlRzYRZx6S3ERZ3S6ZdhnJZZRMQ4GmE5itt3nxLgh9s10jHXSRsA114cPv8rL7kcl5zyy0vuk0XXbqAbbvyPLHpONJtz/JSqwNrbjcdV17HhQvaCBtejg9Msn/XJv7qg++nsytEyGdCZJyZPZupNJMsqfPQWqGydn0vjnuciekJMpE0PVVBHvm3X+N2mSxrc3HD4moeHIkxnlXICIGWKxApQEdQ4DFg3HLwFCQzMw3kBfgDkPF7yNa24q5uBycBzmSR6qLgOAUcGxrdOi0eg4OZMogSS8TJZtLcumQpsZZmRsbGGLJMYuk0dv4PB7Y4+Ty56TF2bt1HfHYUqADHLxnqHcjbMwVUS13XcADqAnJCbG0GrxtML/RcDaYqJV8KNmRycsLEoVz9xUI6dkXQ9ZQmVUECpQWQQ6EIiiIgnYWRiNSDVRVoDsJsVGq+prPgGFBRV2QmKZKpo1qyWJhpllMnrApZ/ZpM8VXcN3CKrFRdkXNQOicBX5dbMmNVDRQfTB0GtQ3UIDhBsN4LbOLlg7FQjs5LBa12wXQBvvl+eFclLPdApw4LArD1dkjWg70Xmf3VhlQbGAMqNBDtEBsBu/QA9yHZLiWJ8RxlFUgNiY4uAZ5ChsxVyOncBm4A/hdyGt+OdKVbgauefw3+4ktH9u3rgdcWT3cEeACJFbiKzZii7EHPLfxF8RhBylTUIKCF4byPwo4ozGyA1EGwZYdZOQszY+HkYCYpa429GCulZc8FUUvMtNJtVZDYR4m8XBqyZxKiC3M+Xyr6JZdIOaS7i/+fRiqo7QRGiGCNRLBHdgBwhbKYxp5FeJQJsgPjJPMXY5thsjmbZDrGlkof/gobvw+q6714A73k0iexrHNg7J+k+Q2ER0UoNo6Wx1nn4Lk4TMcV6/hS8z/yUFQl2f87nt1a1IGcgpHLMuzPx1mkB3GSkziF08PQRfMXccGtt1J5bSUH9z3CeP80U8eH2XnP7yi8499PsWFLj1pRTvY0RuzZbMuW7Xz4w3cyt7JqR0MH/3z7P/LY/h/i9VZh5qd5+gkby6ynrrYS1Rjgwac+wYOA3xWkNlyP2y8j+9vf9GEuvmw5vUvLG7g/firCj35zhAe+/FO83h6E8jss6zmymRk+9tFu4CQaWVzKXP6BQFFcBMOtFFzHSDoWARUWLGrhoYMZnnruOcYHDtDW3sTA8CFi48fJRKdBcWHUdVPTOI+u3gX0LF/JeZctZt+2EaZGh0klp/F4DCr8PjRhkcmkyeUFluXQ0OChslLF5yvK6SvlOoXDyOnLRuIbU47MuAg44BY8P/32ZVppiS3dvxfyouw5nynt/ZVKTIWQe2Ol4wGnxIMFSM8+/Pxzlpbx0rgpgazbc1AhIGBIcDZa/N8sMm+jBZkFU+WDxRfBkgBUKuBywPEK3nddB/3f9/LsY08zeWgXABNHDpNORInMRqk1AkSdAnkrf0pDdtOWuRU0HU4cOYzuDZNK2xzYf4zu5hbufWgHTz65m4N7BknkqtHf5kIzk/hDlVxz6600IEOQTU89xd0f/xiV1QVqwtPEChpPbBrmH77xfxjc9jPiU8M4DsTTJkG/gdsFhltl9XlrMHSD6fFBxgYOweIG5lZMEkIQ8FVSQ5yGChW/4WV/zOHkiI1XE/jcCp4qP9VhjWxSkMla2BrANLjOp8LfzQqfHEe/GLOJ5CBrK/xsFAa2wsCWKGOHhnH7grz3r9/N4o55HN+/g3vv/RlwEmtggpO7Z/lpwstPP7MNrzeBnh2kcIr26EKuXDqSGnkx5RS5JH/qgdk5exFmIR/W5cX3pViwaD581NsNbDy+kRgZUqykhpUkinFQMgq7d+S56yOjBHiCeka5EPgn5IjKAQoulola2qsWYxSm+FVsmM0z/awAgpEZnPEoiaoUqUoDt1djYMZix6FZhnfvZvn6RczG48TGU0QOzTDPcRjmHBh7zs7ZK2sOjl0gFongmCkZPBcKMr53QHOk7N8ZXwHTIROxmTyZYjZlks07pLM6ZsGHZTpYtgUOFPJ5spZFThOoah5N8cnjCQcbW2IHGohidqurWKzbcMlYP5eXwKyNbI9jQ86ETMYmnwNN8+Dxh6mobka3BL6cizQzFJw4wrFRUdCETo2rkcqKOtzBIHkNAgg8KuhYCCtPNmeimqBYNqppoqo2Dh5MS6dg+3AKOsLqRykCGmdPlE0A44jMAIy5MWsCWJMeCik/luXgmpzlxPEhYvEIufQYZJ9B6vSlMPMG0cNHgAvB346o6kD1hZFel49yemyQ5hqdgL8ktyDNTTluPYks9lkRhoYGsHQpA5krwGysiKckgXwSCSi8EmzJs5kiW6YaCE1H13Rsx8G2LWzLhEIauVK8/NTOVxUYO79rKddf+zbqW+oZPHyMydEZdm6foWNhE2m3zki+iUG7S2IyUKZ4lHCbXrj6GvjcO3N8+uPfYCIyjBH0UudrR3NV8dHPfZMLz+tkft0LNuF5dn4v7N54gI0/eBi4EpkOdWZp9Rdn1aEgT3zzi6TGBYeOjjEbi/L3X/0wbX4NVclBegIxuZXzlwnOn78CO72QfDKPuzIAvnpmDx0leXCSe743TDIG4xkYHMpx/vJDLFvl4ZqGVlBcPLl9L1v2wYERh2mkOuObffBcVgKFKRs+OQqz7/wit/7Nm7n4jvcALshGYSoCWROaqsk9/ji3doVxXbaEjz+w49R1KIBhW/hjx7i4zU/g8lVEX3cT//Sr3zG7axd27g8EuFgZmB1g5rFNlBkSyFnuduRTPQHChHWLoKMSwgrEJqHSLwFo3QUNXZAsBpwzCSkwPZCjrO9gI2cGOL3sYEmIsxQhFvVaT/3NlBICgxkYnwbRK1M7qyqgWshu9ftluJDOgZWUcWPaku8TGfAEZOq6cAMVYDZIoNYqtiHkg+qQ1ExJpSA2A23zIewBXZWPRGwRFLLgssAfhqmmOdfzsu8Bp6N7DrAPnHZY8TX42LXwpi64WcD3/bB1HcyEkWDwfyKf0wuBC4r361ONMJ1FIp6bKPORDgGbkemsrUj6QwMyHL8WybVxgIXI57GdMmC7EdjCWdMWdeCtwJ8j2bBByhVt+pApcOPFn1HkGjKveFqNMnJR6ovSdl5pHJTA/C4BFZ+FvrVw5Ocw8yP5ndEJJg6M8cBuiGpgvshqDqVTyABBDr8SzFPS2vEUm+OmvLDFeP72UWnSL2IY+JC9fwLZ+1PIR6EoQUwNcLzYJaWn7jF7PxzcDwdBoLCaK/G0zift8zNuZRlKDMP0Rig8r3rbOfsTNOMtizGua8SojmC27CT9oxyJw2McrX0UmhwyMcifsSwudYV5ra8ZDWhZuorEwHPEJw+e+n+IFrppZq1PcOmTR7jtrn/m6d/ej31wlGnkk/z8VKoXYznmArEAmVSazY88Tnp8gO//3T4exCaFQYH7uOu+e0/77NvXfYCb3vharnzvmhc8w/Zff5oHvvIVQHDtzffiCX2VsdGdPP6bNyN1T6Hd1co6/xJ+MHM/ABo+tEIlx48dRrELOGaeqbEou3ae5OSRXdjJAQxrkoN902i6iW3pICpQXZUsu/xiFq67hRvWdHLj+ZX0IzgRqEDM03FEA6Zp4Xc3kcnlSGSyWCJG+/waapolkOijOH+I8hQeo0xcLQg5F5jFdfFsersv10rKP6VjlyQIoAyyl/AVN3I++3/d/9IxXsiRLSlXWUjyWm3x5SA3mR7YAzkXHF8ml6WSptpAsR0rAJcJdUmwhqF1EXQqoDrQn7dJPfEYxsw0bkqrjcLggWcB8BhuVqxYzWQOhkaOMjE58Pz2Fwuwdvd0UVVfi1eJcTxqsujCW6ldeisT4zF+dfdnee6Ze3nLO6/hta97LYeH4fGsZAKfGLPJODmGhod45rPbSGQF3ur5VPkcOhdfTHQqTjI6xHcfGuEdVzUhF7L6U+f/2T3fZXTgELfdsOms/VddRMFNG8jm2L8/xvldXlb2BGmnitTYCEZjiHhe55HHp7BtB3XdbezpeT1/tgHaNDg5FqPJq+LRg7x3JaxYCV9LJfj04ynW3fJ6VndWU1sFk96y3zi/OUZP8BC5Z48jjv0DSWuG04tzxIs9XhoxAukXrAO+i9yiPKd98z/Cckg/zs9pE0GBNqa4lc38E+Dgp4NOIYvb2grcdRd87XMHgeW8HXgbkgoAcjQFgTwJBuw+Fh3p407gWrWG1xq9dOf3ceJbd7Jmy80sueCN7F27nGtu7eLCboNLutvg5jayQvCpj3yGR3/9K7Kjx/Hz0ot3nbNzds5e2GR8ZGJ4HRTFxMrmISuzWO2z7CoXcjJ2PtYfo2/gCOOTcWJTJuPjs6RiOXRVx+3x4PL58Bo+0ulZ8uk0SZHBrAzjCvoxdA8qGi43aMXi2kKT88tcRq7ukTF8wZKSTamsPHc2I8EFv9sNoSr8Si9OqB6a2tFIkk6lsPImwnRwu3243X6E4QJdw6tChabhEeAWDoZqYZoFVBOcXAE7mQEzSkrkyRcEiqmQ1TRcdhW1jkMrKZo4W5ZTMQfJzkBmBtfgDIoYxQrXUfCGQHPjdfnI2FFy2RiwB1mMu6TffgKYguT5ZMwE2bwb6d3NR6aZFsB1AUetAJOWJJCdQO6nhZH+aOkoWVWC2W63LEau+SCRgMQsOFmkC5CdRRKv/lBWDe4rUMPL8HTNp7dlCcl8kkh8msnxAdjzK2T1gbNV/f797FUBxqoiyHtuv4t5be2YjsLw8SlGJnMUTBPVZzE0M8Ezkz3EQkFZDtdHuXKEibwpLvjL98HKxXF27Onnvh98lc6udua1d1JZ18b85ddx9fnt1IY9z9OF/S/NBY1dday6Yg0P7vDC7NZTLLffx1ZdcgVvfNf7cDvw9OZNVFSEWbCglXC1i0JiltTQTpg8QMg6iVgxH44No2QsXBV1sGMrIjFDY0MlFe+6jebfPsN/PjxNJm8S0mFyAn7cl6WG4/TUebn4ih6+cvAI56s2jcDxDDyahg9eUcPieZUIw889P93JQAT2bdzOwkY31bf/Lbh7oDEBkQmcR7fyu9/t5ft7ptg6ItkIJXmmOgHNqkOHlsA6sY3I9CHMcAP/sv4iNje1sm33Lo4cO/p799H/27JIWKhUVqNsy86H6mbwjkGwHuaFZJVUp9hwUZyUTQG6Az4hAz2vDsEgiBm5Y3UqvRIk6JZG+vxlORd50FIFVyiX7C6BdTkpI7BLgeXNEDQkC1bzS9kEtwCPJTfwxvaDEQLVD34XeIrpDFYxlcFMyV02lw5uBfwaiLw8h8jLU2qW1IhNAZoBPR1wckru0lUF5XVFPwTWL4EHX8HbUSpvnkTSKMfgB2l5d76NxCO91XDMBbvqkOSVAhJnfQ4ZL6UFEmytQ6qWViCB1aVItuu9yO2EvcUvn4/kbnqRCqoLizdiLnwQKB7LKb99P3BZsc0lNquCnDviyKFlAMuQCGQF8v6byE4eQIKzChKdLLGvSrmzJnJI6sgNQD9SlEy/Aipq4KlRSG8C2ySfN5mJySUk9yKLP5amrJJaQqkIlwsJWpR4QlqxCX7KTNdi0sApsOPMHdEgsi2lV37O+UrsWh+SJVaBrEA+l9DrYLObTSijW7GFkIpEtik3T87Zn5xdeee9XHnRfFpaknzr6I/YP/gD1l7QgU+r4lff2ACDOex+BwJZphLDvLvtl3TVXIYdKrPR6t7VSsP6SqqFQHEc3v+ha/nO8ANsOgAo4P7zKlZ2uFheHGl+IfiP93yQ2FveTaFgUs/pzMzfZ8m+YP3r+cJnF3HH368/9bd4cpbv/fRuunItDIjDbHUGsBFY5Lm24zquuuJqXvvR1wAQ8oQxAz62RLK8fd0PcZzv07vsJi675mN85D3yeL3L/451V17Isxtu4+Hf/iVf+vLX6H3ba6hp2ssvvr0Ky8pR0bqIBWv/F+KHLhwexyROPD/Cvp3baO7qRHN7Mc0sbrOfzvo0e3YOE00kmLdwKSI9g8cVRNc9NM6bz20feiddzQGqAjoHcoKHt0IqYZEr2BRsFdXw09OpEMl6iGfcIBysAIykBFkb2oJlOfUSU9REbnG5KLPsp0rr4u8zYF6klTZ+SlbaDJprDtK1SyBd9xJXM87zwdm5+RMTyD2zM8HbKeS0XVN8X+IwuIrnnr8UIkIe/yCyoMUFyHwKk2LehQ4TZpJfbt7Lv939DM09K0inM9z3o68STh2kOTLDUmRdy7mMzIDfx1+/4x1sHDzBhscyZwVjhapy6fs/i8jmMaw8VX6diKmxI2nz3N4xjmw7SHedm9FYgs1PH2Ym4aVx2To6lsDRQcjULudffv4E9dV1HDp2nJGTEyRnMgwPj/PRj76H+1sN/vWf/4HPf+BSrn9qA3plHbN6NW//6Nd4/VvvZOOjP32Bu1Vsn5DrqqbAwhoXPzx5gpOVtcyKIFUO+GrrsRWFWLrAyajJLV/eiWlU4+h+lDQ0dsFsNMh+l+ALMzA/DEsEiPYVVF3v5s4PdRBUUmzfsJMHHtiCUJZw19bvs2efxrPPHCW28Uls+0wgttQ4HYQf7GKJ5VO6GO8q3s0d/GEDtf/e9jrgejQuRAOyfAoZdg78UVt1FtsOrKZMbe+C737qu6wdv4rxjwhew1O8getYwxqWaUs5rxv+9TvwzDNfIsDdXAp8GMm4n7vOdMxbRNK2GR4+yIVI5aqGqhp8DYtZsWcfNwK61siYWMboYAfLsiqOKjBMSKUcHDPF9NBxQk6Wmy69hG88+RT5c+L45+ycveLmOA5ZK0s8HceXTpFP54jNSIKSUwH4pN4oyDIeZhaSCYfIYJz0WJrkaIzIcIxcOoGSV7BthYyIY/p9BKorMBQFTTfwuQNYloaZF7LIdnHCsCjWdFGLoaQq429NkwxZVYVMRhY3taxiHFYoYGYzWLkUDllUXeAKBfFXBnG5bBRNnNpttm0bl+bBwsG0bSwrh5HP4HUcXI6FsPOoOKiqim075B2TeCpHOpXCthwcC1L5GGknQxjzlKrj862UW2miUKCVLCczk0zELGYySYZiE0znTbJ2HOl1TVDOd1Ipw6lBVC2I7tex0DA9XThZE2ELfCsXsiik4y/2VQgJCZSyNH0ObDkI0Xi5Vakc2HlIZWTdHSieTil5sq+0FRmxxnpa11zCvMXn09XZS5XPwHQkazqXX83x/mvIT+5l6MAOBg5sZm7xx9/XXhVgbChUzYJLLqOmNYRtZZh4xCKRSpCIRcnZBvF0LVGaMX0BiQaUaBRpJBAyC9wK9QshMXqAh77+DeKzM9i5JnyeAK2tXdxw2TKqKzwYmkTVHMrVyP+rdDyhQL4wSzxxEDJPgPMSkkyCIdq653PVBWtRCzC/uwmvx0vQp5AYneYn37mbdnWUnhqTUHslhCqhFkTOQYQqYcl5EB1D9+gEgn7mrZykYlMckTQJ+l2sXt/NoQcOcTheYHAshbozQqXlEPRAXVChJqgTi+TQs2k8nkY6Vy7i9Y7Kz+7dz1T/OFvve47rex6BZb2IXAJ7ZpLc6Ah9e/8ve+cdZsdZ3f/PlDtz+/a+q131Xq1mS7KEC+4dY1OMEwyY8gumGQghQExInGJwMIEECLgEY4o7Fi4ylixb1epdWpWVttfb78y9U35/vDO6K1sGYxvi5NF5ntVqd+e+d2buO+97zvd8z/f0caQrzVDOQgGWxCSaoxB1XQJ5sBIOethgeMiip9OkfiRIaxQCY8I0Rdt4pb2LTPYNok1vyPxiwwTglJ5/HaLlEC+HcAZqdVBMsTjKKoQ1MB2RDfeXDRfIFEUHeF1DAIMvIpCp2Qi8z0Q4dwkEoOd3SRrtT/ngrF++P0q40y4ILVhf99BxRWYsqELQBicFxVcgOge0CBgO5BJCYiEQEHqwmhcpK7L3swKSLZg5AQl0GYyMB7DJILngqAIHM4rgFqAQAncusO1t/CjAE+xDRMwXAG0wqMG6AnxLE8ULCRdSIYg1Q7oGIQPQB2xCPLsFoC4ArQGYFRUNtduBoZB308/GE9dAfPZjKXVWK0OAuKNdaG9SNEdEdD7NO+QiBBCree+b5FR6qS/KGveG9xtCjL7GsDd8gNJn7lNRiwiAVvN+9umobhSsyTDj47ClB+zjBFSXsnIIWqcXlz+d2d5p+5uoSgmAHS1J4H+Z3us0SgDEaPkCFTGdy71T9XlGkne5vuqC/3//ozI5PTBmkgfrDPj6v8skoIbIpFbGzpzMjNmTGR9Qmf2uxQySZP2hw3Q9sQ1zpMBRYy8BNYjzkiGIaCkg4VJYk2dN7l4OxdYyuPvAyZGvvvAm5k5Z5BHHJc6uibJ1wdmcOHqM4/vW8L73fJlJzVNOdq6XgKaKKuoqqk427JIoaYVGRh33h6yxsYxl545ldDG86RTYljqIIo1QUVXHzAmXc85VswCYXDWFcRMmUTdxIjFKeqqp/hHa23+O6+4glbUZGkrTf7iNj3zpvcxcUMMViRbWr4JsppekbRJvjHHTe6awf9/f0L7tXrqG21m1+wFcDiGeshCyUkV5WQzbNSnkBylaEJDyDCT7KaurYszMyZx3+XIObOkjm04RjkUYM2UcS8dVU4xKJE3oHxZlWqquoYZkFM2loiZAY5WEm5dwDOGjyrJghhSckqKO7+/4kib+zxJivwwg1oUQb7+9Wl7idJ+lv6WXUyrm8HOkr14qR4O5Faf5O4gdxG+0PkpOnqj3O1+13F/OKxBJZx+g9t/IyGWIb1pL4/atZHsyHDcydB7eyjAjxLzzXYjY1jRgbG09M8dPYs3mzRh1dYQqG4lVt5Ie7Djl/GRZ5sKrz6fOcTm8dRtPPPIkP7hvMxdcOA15TJSB9kqObNxIKj9CfXkYxzyL3gJcHIB4LWQjUVrVOWwZCXNudSXa3AyZZI4jJ9JYahipYOM4NoO9HWSsIjEjRzoAACAASURBVHa8DrduOifcFt5/ySQ62texe8dWfvS9B7j5YzegKd5VKz4MLvxlSQJdlWia04TbGKETqJIkgqrKCJDWFGgso1aPo1dLxEPQ4MDEKmiNKOR1iARLUHVjfROzZwSw7RyPPfMir2w8yMaNR5CkCiaOG0+yx6VHOsLenk247usEW26REjsWSn6CQilhexTB3jFPN8IZ+z12EJBxOOAFu3vx5P7faeZzNMpAHq9w6V99nTmLV+C8ZLJWW8UdH7qVdY+vZ9XAKtrTg7jfvpIXnvsXOg8+QgMn+AilpBSSDloDfOXDaCNZIoMpqvpn0Pjcr6lxXbTcAIX+3cwDzj3/c1jnXcLxOQ3sHQ7w3X9ZQ0ulSXNDhKYxY8kNdKE5MeactZRLbricu9e+hGu/OhV+xs7YGXurZrsWJ5LttHSPBTWApCp0HqvCKVZgmwpOhUS8QuABvg6SpkJYj6C5IeSijG2aWHkDyxLgpSKp6OEAUtEkgIyshohoUUJqGC0QRAvqBMO6IH0FPJmCgBhXkQVbNqB5TZpdD4T1gNjKOIRcHVOLYaTByjtIAY2g5BIJKISDAWRdQZUVVBRkRca2ZQqmSaGQxy5kkXMSQctBtS0cGwoFG8cqYJkGBdPAMvNIpujwbVlCX1FCoYhMClEFOfk1d9Kj+QTKIFqJEw0SVVWShSJOJsFgdweG2YttHESUkqYoeWhxhEc1CfQ2nHA9lhbHKeZxVRVUC9mFuikaMV2iynM16hAwi29DLvQMCvxCUsRnJmvCl9VVCIcgEIWijuee/N4uBm/SPKzJ7iTVf4jejjI0rYJ8PIYtiYomq1Cgo6cXu6OD5FAnp1Rrvwl7R4Cx5ZXl1MwZjxM0MBIGI5kMjp1HCwdwtTqOuxOxQnVQFhRetE/18mgRkgxTrgbb7mHfuvU8/dDPiIaCqJJCPF7F2HETWTStFmk0JdaFvCs6vCqvjgpcB8cu0tl5gnQmz/4DW+nqXA35Z3kzEgUNk6YwecYMZoxtxjRg8pQ2ivkMyYF+tq/bwb3/8QOWtCq4ZzVTVzGTkKUiVTYI9FBTYcJU6I+AbeLikNVioMg4MliaQllzA/HgQfoy0GvYTGhPsrAmTEPEpK4c6uoCGA06siOTcRSK0TBLLp3DkaMZ+o4PcPxgDwOrHiccdwkUctB5nNRQL3uOp0gb9kmccZoOY2tlFBnSIy7pEYeAKmEkLXqOJil0bWTygkrGto5hxrixSPEQnceG6RlMksm/nQU6nksvFUFJQKwMVZNOAltSEYy0YIRqQVC8ZlaOJLRhHY8alC4IMFZTEXS/RxHzK02pljGHWG985qtVevuT9CJG/eybIliuktekyUIAsZmcaO6lWlBIgj4EUVcwX5GEHkowJDRgZdnrHuiOyj1JQrNWxsv6yVDwqJKSx6jNSoJ1a+bByIFWDVIzSPXghnj7mg4XvftVjwBjY2ANwWEF7q6GSLkAmJEhEoZ0ErF+7wAOIyLfJgQxdgqiB1cKIQGTBqpkCM4Tu5fh/e73nbuKoEBFEYD6WYieXg2IfcJGgO4+49UHWH1ANkApci9SAmRHvGMqKFFSoaQP4CNFfqM1fz3Je8fWVMHs6+DQakhvwHaqyJsQjL9xMNaiVHjtSwj4arpQYolBiT3rJ5t8CWT/FjkIsCVKiRWbHnW87Y2VpxTepigpMZzhdvzvtpaxY7Fth+7jPUAUraaF+llzWXj5eXxozmzsbIEfPP0yjz7yGF0/fxmAA517xTw/OGqgIri7LY7tfvo1bKlJdTOpjQt1T0mCCQosWLCIjmSS3pFt3LDkVlqiQoP11RIao50SX5rjNX2gfo+VlcOESSpjWmfS030QXdEoj1dSUR8HYF7rfM5bfBE3fund7N03hG0NU5Rddh4Z5pyxFbiS5D3aFiKDlae/ZyP9PdtZv3ou45aPZdbE6Uye4CIe8Bx72geY0tfLxUvrWH3VbRQyRzm271me3/YTAPRAGVqokYraSVRWV5A0U+StFLbtEqTISDJFvL6RaWfNZPmFiwkwiJHLoseC1I6tpz4Mh4qiQWTnMCga6LqGHtIJx2UaWkTVREgS+47iiOYUkguOAzlHSOZEpVL5XBDxPPswlZ94CVAqDvlzm+Sdl59zL7gwZEOd8lrdN/86/HzY6awcsc5lEdfphw6+TxP3GmjGdQHClp1uLAukVIbg1heZ3tvFibzFgFUkhEEO0MqraNN1ZjoWWwb6aWloZM7EKUxvGceDq55l4tLlGJZEKFaDkRmiaGTxZ70EVISLzGlqI3/sEHu2b2N3+gWuXdzEuFCcCk3iWF8n2XQXxSlnoSkyTgjaJGiqBqtapcotY0caWstrqdMqyecN9h/uYLAniZGziUXLSGeS9CYMjEA50eap6C1zWbCghcfrylnV08eP/+Ne3nvztRAACZfASTAWwMV1HQzDYtq8Zoq6TI4SGO4A6Cot48rAhHgb1FfAVMR2nDcTDOYLuF0una7EHjNFbqBArWLRO2KyeXcHG7YeZN/+E+CCMeiiJhMo2ROk8gd4fTPAHUbsUg6lHauI4DlWeF+9iEDJ4LV1IWfs9WwnsPNkevcdbp2gE6Xh6inc8OHbaXSDbHJW8kv1fn628Ps88Px32D2QI5buRrl7OjuG/52g08FsRLuAkqkQqITPfoHkw79COthNVeNsWp97mGq1AjdvMJLfzznjZzHzmv9H5l1jsdtg3w6XR+44TGWgk/HjdRatcEgf2U1FvIGpM1qZsvz8U+PPM3bGztjbZo5r0ZM9TE/vJFRVA0UiFCnDsSQsM4JVEAG8FhQxs10AGYlIKEJYjRJUQ2haAFVWsKQiruTiSg6aJiO5NgE5QCCgo6tBAmoQVdPRgjrhiIYaEJqmckDIIIZC3t6oCTJVUBexfyDg+R4BsKvAjegUcyqZkSB2BpSigSY5BAMKEV0HTSGgquhqAE3TyOaL5DMZCrk0tgG2a6MaQgnfcorkizZ2IU/RzFEomjhWEdlysAomlmV48nYqJvLJkNYPg09dmUI4ahwrWoYZ0lH1EFpRRc6ZZPoHEKUI+xGJzjxQhxYdh6I3YtsVyMpspPgUiDfjxsuwc7JIChfyyK5FZSMUPHm/qFRSChwdbieTorl6QPPuY1D4sYokGrKH45DWwFFeneJ/o1YiapzefDD2EInjOrlshlQyQ3VFPY6k4No2tpHn0NF9cGILFI7xVqtw3hFgbEWFRKBW4pHH9vHQtx5A61/F+99zPhe87yqaL3w37/8N9K4H20ce4oiy6AwQAP08lydb4a9v/x7PP/kEAVVh4bRJ6I1tTJk3n+Xvfvdp33fEEA+GPsrvdF0X1zbIJTv5289+hJVrtjE4kjnt69+offbzX+ai81YIbbMgGPkcQ0f2sXP17/j0Z79CJ3BwCHYfS1A90MXctskoU2dBWRSpMAKd/VARwR00SG86yFdvW8khxHTS+3I8/k/Psh3hgs6u0fn45S20TWzgRHc7x44O0HHY4KNfuAw5FOXooaO8cO/9XPWJW7jpu7eSaz9C95oN3Ptfazh7/0GamusIBjWOHz/Gs47oAhxBuLiHB10aGwI0VqnU1csM9KTIGy5GzptIBZhYo9NcBdWTavnc3Z9jw4Ob+caPH+G5zbvffhDH6YbiKohfi1KUkAwoFGGgH+KSeHiLXhbMCnqlAXapsZ/tCs2SsAI8jVgFjgHHEb78LE5tYe8jXD4IK8hOpVpKH5iVQQlBTSXEQgJwMwtigdmzG2ZNgdo4DA7CuJshVAVyCIIODCbE22kIECOie3oznhi54WHaCqAq4pp0T9qgCCQNkEyIlYlNIZcX8gemCvlGMGcgJALeDmsBbkTUdZ4AfinugVUL6SXwrhvFhQwAB/PA3cDPEEzjZoRI11SE9vZW4DZE1OwipAI+hujXNYKgZTyN2AdOZ4LkB7cDKyhJBcTEOXCMkoxADeJzNBAT2+8f5nd4URHxWwohlLoaAer68V0ccVF4Y+sIQDrrjVFAIKddeGAs0KRAx/dh+285crTIPT+AKz7rNY57A+Yr4x3zhqvwfm9SIuzaiOnoyxwr3ndfL9LXVvSLSYLe7zu80y2MOi5DSaHD70B+BoT9v2Hf+O53yaQK3PaBTwBHGHn5CKvWPcLBe8dw2+Fj/PiVY6z+5dN0/erXpRdt9b5L0qmTVgIJ6dS54br8zfc/g3HTl5h++W0ng9DzzpmFVgnbDj7DNEUhfppz88fx3asIp5bMv9E5GI1V8Xf/vIGvfXEREysncONlH+aWOy4T40rifE3LYdlFD5Ho/S/CMYvxZ32GzU/9BWgKMWA6GpK0Atd9AbEYmMAGbr30fBYs/SZ1TRcg1K42cf9dD9C3O8kVT3+Df74tTlT7Nk8+9jO2PPtXgMvYxotpnTaDxunNmLZBdmgEW3JBkUhZNoFQFGyHbCJPVw9Mn1ENSjVpA3qTLqsSYr8oFiSx71eCqiroZaCXQVaFo5bQJVccQBFNpgoFyBdh2BB7jM+kB7FcRRABgoHIU71aHuLPbQoCFPVt0IJfJuHjlULe582Y38PXQLjLeUrgfmtUFDTMQqx5r5FncIEUWB1JBnauZAowefJUxofGcfxwH1t5hQ9cdgMLJ0zgeGaQ//zOnXzqM7ejhmNs3bGT/R372N8hNNUCwXIaJy/mxJ41OJZInVnFIp84+2yuvuVvcZQwweo68nuf4lsPLiM9OEDnppWcf+1HWf3MSrpTNid6DvCxBQvQGCXMI8HNU+DxtS6PH0gyPHiUeQvHIQehbsI8lix5N08/8ytWrjqKFa1n1tRGmme3oQS8CqF8kq0HXmTAtFEzJroMDUExuuuKOknLMjl8sJd3TW5BD2onbw2up8MbgsXTTr11NsLV+OuvPsv+LUcpCxTptYK47Y+BOUBNcx1z7v8p59x4C0dPfI+ta9cjSV08/KDBpse+xLEdv19CQTgGR7xP1kDsYP4uV6BUznQxQrZgN6dycM7YWzfp1FjYPfnPn93GTT2bL9zzLDcgZkBOS7Ivt4F5H5uH8HYmkXFS3DX4F0AfHwVufdUYrpuFwm7IO6z+1a9RNrZz8bhLuNR1GVd7HSfMbvYoO/mLe7eTmQt9YZfegkRZFSy67ma2/eZ+Vv1uCzuObKJ8ZB2f/PRVTJsxlpdXbfCepTN2xs7Y228ukKCQ6SUxqOFQwDVdBof6GNPaRn1DA70D5USD4GiCuBRwXAzDIKSFqK6sBVRCoSRZ08AqiKRdsLIMFZWAFkJVA5hAzrJRJLcUTHlbjhqASBTKy4U8QUAR8j4AWVe8pw8laAqEVZCLCvkhBYwWdMVr6k0JmJNVgVGBSzZhYqagmJaxsxJpO0fBKVCwLCzLIpVKiQZmRVN0BkfBoYiNie2l3G1UssikERyoHKU2J8JMwKHgOIyYFrZtkg/EkENhyhW/IvWo99UvXiJ9gjFLrqVi4kwSQxCrASUs5J1MGTID5aSOQa57BCc/hKTCdleE2LWUkul+H+wewM6Je6fLQjM2GhFAbNYQlV41cchp4Mina1H9h8zvuvJGqraTkH2ZQvZl+o7/kD5qKXmPvkf59tg7AowdyMN3/+ZXZA7v4ublcOfdawiFNRJBnW1J6HkSnCaEpxxAIAZ94vvsKfC122H7hi6ipsG81irc2rPoNQ2mjptE87gmxldzWvC8NvRajbGf/Oh+Vq5cyYsvryKTSmO+0XbnpzFV17nqy1/k4sVzmFodRwZMF3Zs3MET9/2Epx7+BScQuFQESI1Y/NPKQSau/kfOXlDLtItnMeGjV4LRC2s7OLHrIBs37GU/oto7T6lK3vLGacoa7Nh+lImzpjHxY59hXEzF3v0KhT2dFOQUMU1l4cK5kMmQeHoVRjqF6+QZPzGAJEns33eUTDKHm5Optd2TDTDSwBPAZZPrWTS/lXhTA4/8+0MMHYfBNBSCsHSxRFkU7GwfuQEJMp3Mv2gyD467mb272vnpC5u4/6nt2M7b5ZRsB/frYFyDUhSPmKMIwFLJAgEI6aD4wKlSwtosoCoMR0fg8R3grqZEEUojWqreCvIKUKYCI1AcpgS2+ZScV+tceMxKKSCadckaOLZgqB7bBUYKBpIgR6BqKoQqxCIOAkRtLhf6trIhdGYsw2PzWiK7ZhpioY+GIKhBIChOe7BXMH5r6kRwHtYFM3bEhvSgYArbU4AvIcTA3opFvTGuQzBdv4novWUiANp54IRg5TPiWDcMVhi4GhH59nv3bybwLQQamPHu69XAJQhJgWHgnxCTfYRS46xX25cQIn+zKUXTPrKY9t5vwPtdECFGeBCxG+QQgHDOOyaLqHB0vLEqvddkEZ91DIGE+pqyxxFA1W8RjN8cJc0Af4/w0Q8TsM7DbQIrDnWThTzFH2N7gXHekJWUdHZ8rUWff+5vN6r3u9H8lhbv/2lKmoppSuCr4V1ubtT3M/a/xMZ8EurGg1yEjb+ksW0MyaFtZNOl8ujPfPCDXuOgku727HNnsfSaFdx05zd5/of3MdzzKifjPInm5TO58uyv8cMrP4hlGLQsreNdf3s218z+AX22yUg+ydBIDweefZKXthzg6W0ygYo+bl8qGgbVAPPqJvDBv7iHQwGdEOJRPJ35lQC++UkCnw2pUGpm5/882oI63HBlkMvPX01HQWFXQuX6Ozv55qcaaImrIocmQVOjTiEpk0vs4+jmrzDofpAKFDQgVh7jR8/fxzc+sowTh3cR1spYPvUjrN73I7ZtvBNZvguxcFnALtI0sROxrH3hL+LMmXgTd1WsYPuqO1l81fVIIZu+RCdKMY8rBUB2cFwL0zLQdR0rl6F9+xaO7ttNNBjEKNho0QqqmiczKTGfssowwYByUkJE0cX6EYqI5KMagM6MaAap6VBVAUVLMEpDgdL99NnGOUrMWH9Lm8Lb1+vx7bA6FT5WKVi9b8t43ndfisBzCxjiddjAHkIrj4kTbH03ZjbLgUMjyGNrueMf7uSen/0b1csuwpw2DtvJs/2LtxGIRnnggUf49TMbQB8DZjdQpGgMngLEjrbOjS9gOw75np0g1zAxtp0+J8NhvYPn/nslV7//7zl84CD7f/s8S//+g6QR6QEZEVQNAfd9/2aee+q3hEIhbnj+FSa1ljOz8SxqyiWeXr2Hj1w5g4kTx3KwY4iLPvkd5M99jM3eY+64Lo88uZbFC+cxvrn0VBZyXciyhhqsYcr0NhRFPukCKS48lYHdxyBkwJcWnHpNMqI4pdG2OTC4jb7h34g8jj2JaNt86hcvpLyink3bDpBoWEb5hZUknruLx/9lJsXCGymI97tpZiitAL6UVR+lskEbAbc3IpyJrZyxt2iSRPmVn2PO4quZNGMSrVOE/Na+3xXYvvIXvPLwF/6spxP77neZetNNvI/XC2oLfKx+GZ9v+Cx/v+3jVCCdzK/vR7SXGc3Mqg3DxfVXQmMvUlkLzZKE3fsAbbP+kvGX3Qsz4d037KdqdgWLLq8nHoZUop9FSxbSesV8poyvZcs6WLBiAcc79/PR2/4S+4xEwRk7Y39SO9q3j3QuTXUqjTmcoa44HddyGRlI4DgStg3BigihaIiwpnPsUCe27eC4BSJ6kdjYcmQthKYH0YNh1GgllVVxgrqCLAtSlSbJWJaEg4Ssgh4UvlgsDtU1UFUlCFKqIqpbsSBreX1fVLEvDnmbt40gkKkWKAWhvFP0coq6ImQPFBVUS6Jo6SQGNRIDYVIDGplkgqKbJmvmSCYS5ItpKOTEgAULFYuCXcSxZSSCqNjolBHGJoRElNSrex4iYoIkemGImkSQycEKuqIZMkEFCYUQDRjMxyUHDINk88OdN3N2UzONqqhGlmTRELZDgrUWPPUSHFoLTqyMmBvnU7eA6zmZvg/mx6gGomg2D2gBwYr1d/aCJfxZyfJ6NZpQtPo5tVzvjdibrfZwEWDCn6bC4R0BxuYSCa5c1kTzVW2MqXaoratEkiRWbYPv/06Ul5+E7xWE79UDZedC23KYHbL511//N93dxymqEnpZmKbyqVx+0QXMnzkF7XSSEpKYCP6fisUin/70p9m+bScdHR0MDg6/pWsaO20SF3/gOt57xXsYU1ODIsu4tk1heIhDv3uSrt1bsTJZWoHFcYgrkLNhW8olU8hib+smi0U4ZtLQMJUnn9jP+j3H2NqfJ0OpzFBF4EJN3v9jLhSLNsmRBOWD/ejxBty5c7CTDkrBQndc0DSYPo1w9SBaLks4m0GvqWfXulcomBaSHCBdMHjv9HLQJfrTRV7an+EQ8JMtQ2w5XmBmWTcVkSjllTmCFSp6NMrECbWMDPdTME1kM4YUDBAopqlQhphRmeOWRVVEzMms2Z+kYzBDKvdWO9CZ4HbB0Pfo2nkDMvXURwBPp9VyBBNW8QSCFW9xtCTBVpUksA+B+T1KwnF437PAb8HVQK2GcROhW4GMC8UcYvL49ENfjNNbUZSACJCjYZHZch1xWFAWTFnJBasoFm9HEuCx7TEzw548gWHASBKMw9Aw1+v+mIBARGjg6rrYBAKuAGuDIXHekaBYxLAByys5lSDeCHkF0i7YPhr9x5qGiGnOQnisP0awPzsRkeF8Svqp+6DQgyCmNIE8C1pmQ285FDoRMdEvEImlGm9cBaHt6t17tiLILElem8SajGh/fbZ3Ps0IkNRErA8qyLqQoDCAkzQ8HbHf+FF4DMHUHfSur9G7hhMIMDaCAHobvL93I7pY+Jq3SQSi2YGI/f7gfdVhBKy18PwPYbjrDx1/qtkIDNlvQuMTt311hdHasX5Y6puC+DgmepfXh/jokghgxt8Ube/nkHfZae/4P4VM+hl7cxYArgSWTIBYdQCzup5DM77C0cA8dm95jiNbVgInSA6NYBqj9zKJdDJ5yljTLh3LgncvZeLMFdz1ua8z1N2JVTg187Hk7Et417WXc3nd2eTvuIdnf/JdRpJH2bm3g3+4oFokAqwajNoGEuFK3rtomFh5M02NJf6rDNRGdN4zcwzVsvwaHVh31BeUms05o44b7QbJo77gVBdLliSCQdhwvJLfrf4Na1Y9TPvBHC9N+keWL2hiwhgdR5L4wlfP5d//6VFeednGzKd46L7NvOfymbQ0lhFQZc6eVUYkJN7BUQLkaibwzQ9/m9/+ZhXPP7cWsXgAWBxvH+I/v7Wdu784i0hIZsGsKJ+/dSz/NeZWMm6WgFygorYRw8qhh2M4jk2xkMdJgWOYjAz3kRzsITfShxaOgRajsr4NLRQjO9yJrtaghaJIgSBaQKzzmgIBWewBWVdoo5sFME1orBABgIIAng3E0uj7PVkgYwnmrO1CRfhP5Wa+eVMkCL9NJxVArJcg7kkY4TulBm06jxWZ2BCg+/gJonqEytqakpCkAnpVFePf+2Emz4hiqQpyrJzY+PFc3XgbwfEt7B3qZe2mtejlH6S9o52Nm7ZiZXpYeOFl9BzdzXB3O9mR3tMCsQB6oIBl20hOkbLICJctHoMbq6C1UeH+v1/D1nW/JDE8QHl1mINpICiYN1Fv8keAj9/yIc49dzk9WYUTPYcxs1GOH+1g/Zq1YPUS1iAeDlBXFWPF0gW0TAgQFkohOI7DQ/f+nJbGOsa21JLIFCmLqKhaGCQVSZJQVREWWRbkHTAD0N0HW9Z2MdiRx+mcQCgs9NzUMGgxqKyA6/5yIZU1NvffDyT3MveSK5gwbyYz5kzknDE6zzyT5eyZDZwzIc5dL67AzP2a18+8jrZRTQNOpm984QQ/u+v/ruDdpUkIR+H5NzJlztjpLF6JOv9CZiy6jrbpU6geV0FkDIyVYPp5NheNu4wj55fx0KoR9j//HfLJnj/t+dy4jA/MncT15eWnJJJawq1c2XQtT3Q9QjNxynMq1mCCMeyljQKVCJ+mHuHvBGlDbZhD/LIrkX6bQl9yNk5kI8WHf0rMdQm6Jtp4ldyFVfzno0WO7PkuAW05zpTrqVgiU11XxvKpEZpj/by0eiVLVkzn14/8nM2vrCOVfkeq7Z6xM/Z/ytLOCJFiFDsXx3AUcrEYCWzM5AiGraBqUUJGHllTKTg2IyNpNFVDCzgEdZtIXCccjREOxwhHooTL49RWa2hBUQGQz0PA9vpqOcLfCgYhEBKs2LIyiIeETyZLAmNAFhIFiiy+JBcqo0IeyUWQqCQHZFtgBY7n9Mqy+JIQzbpdS8J1JFxHRXKipAbipJNJ8rZNIpcgnxrBzuZQbIuABG6+SMFyKLoODi6qpKG5IRQiQAGH1Mk4seRiBYEQkhxG0SPouo4qObgUvdoTGZeod5wCrs2D/xpi7dkqLTNgzlS4Ju5pzAMxB6bPga/tggMRGUWFcSGBe8QQ/pjPn1KAPhcSlgB0NR0iEcE0dmQPZ7YEWJ3Lgp0BCr5X++ey0RHK22vvCDA24FpctLSNCeObCHlU1c3D8MxeeH4Tgs4QoFRO7HU1nzkb5s0oUOgZpmPfFkbyg9gYOJrKuecs5+x5sxlTV32KvO/oMkj/4oeHh9m0aRM//elPMc23LvQ/Yfo0ll18Pte/7waWtc0EyaVYMDGTKQ6tX8vBdWtw+jsYHxUd4jQPSbFcAXxkgGODJu6OboxAita5YVZtOMH64yPsQbiSXiWimPCUugXHFJloJEhPdy+pzbuIpzPUzJuM0tSIms6JGxAOQ2UVViKF4tqosoykJtnWbRB1XCo1BVl1WNYSJFobp3ukiNFfIOAWOXwiTe/RNIdUicvnxWg8ayZlUY2ygERzRTVmwUQJFNDLq0Avh74jZHuPUejtpMm0WdES4cQJg9RInqIiUcDlzSeMPac7+xC968ZSpi9gzPwGCIjmXKopJAlcf3HzXmV5AexQHgaPAM9x+udrH7i14NaBNgEqKoEiZGQhGXBSP3Z08y5HBL6RsJAYUBQR6Dq2CCw1xasgKHqHO4LxWiyIZluav4i74BTBGBGasIUCWKYAYzXNK10ICCp/wBJMMAkvI+eK5QDqZwAAIABJREFUTaOQB8uTVYhVCB1aJwOp+QgpxDc61SVEPUErAjRtQ3Tn2k4pwp0DLKJUvbAZ8Zz6HW5DoM0BqdYbL4FomBZAAKtTEUzYvDfuVkQzr9EmI5DEGpAXgHwJWBcIsN2xwfXXZY/NJCmerm4Eit4GgIRAIWREek3zjjcQD1IVJaqpL1sQQoDOvmzBNuAFStSyP2j+ZDku3ijr4B5Q2PsrE/r/+IRE2hsxiGBFad4p+pc3mpjrA6h+HssPVlIIDNm/5X6Rp8+ay1PqT/16TbvO2J/WpsRAL4rPIOp3FPLmpl6E6wpwURiUSonOlhDG5IWksgrBwmHoWw+4ZNMDp4wZ0ONYxSyuU4LWQ2UaluPSe3SIEzvEQ9cyZhxNzW04usuOgzuYNnUpy2dcwjy3geve/yGk3iO80r6GrqMWR3a3YyUGqSivoaV1MnOn1iBNKyUEfJOAqKYwu65UDD46/+XPW//M/P/7Oa/RcsyMOsZ3Jv2Gc/5tUoGkCXu37WDtr+4F4PknV9BWdQETxkxEkiWuuGIyj/+sgldQsC2LJ3/9FCsWNNDaWIYkQ2sltI5bSF9vhkxmmN5cJ9de/3n0QDm5XJgjfUfpP7IW17EY6Enz7C924Xx+BgRkGmtlLigLs2p4KQMHNxNSTcrjARLpIWI11Rg5g1wqBY6Fm8+QTSUY7DpGrv8walkdargaRQuTSQ6RS/WiyC561EGPqUR0hVBIIhgo9RPMuVC0wTQcRpJFJo3RCCnSSWkCn9EIIDvQl4aMLV6jSlAdfi3g/X/FfH/P9/lcxBwpA9J9GY6v7WXKnHIK+7swAmEKLS5aU+3J0iklFqNs+QpaLqwROnKIIGpO1bs4uO8Qm3bu4cVVzxKO1LD/YDsHt7+CW0gSqa5C6y1HUcOUahpfa1kjdZI5p0p5mipVKtrqSRuTuJ8C7fvXABbxqsmkHchloD4skrL+FnXRBRcwdwnsGbZIH9pEzjQZSZskDIkZ58yhoOkYDoSCOgvnTaKqUkXzS8Ncl23rX6Sv673k8tNRQzIh1yGghpGlU9kMEsI/yeHipBwG9+yifV8fuyePp2dXBjluEa1TaZgYY2oclpw7nv6hItJjSaqrqqifOpvKmgr0QobcieN07tlFrVpJZVgWJUVv2PKIHcx3vvyz88uWbO9nH6z1NYrqEbIFA7yxUsUzdtL0KFrdBOqWXceEaXNoaNGJV4omuNXA2DYFrW0KsxZP4nB8ADe/jxO7XmSo8/Dbfy4yEJaYdtWlXNw2hhWUeq1KQENFHRfMWs7GrkeZUxWnPJCkp7CVGfEA0YxE2IGAGqa8dg4nejejOzrh2rFEr/4Q2V89gjU7iswx9O41orXAhPkMNo5hj5nghe1hcskN2APNWD1FQnqQ6toILW0Qc7rYuesZWsecx9PPPMWOHW9359wzdsbO2OmsgIllZbHNFEVbJj/SQ1p2MXNpDFdDC1dRLBZxZJm0ZZApFAnrYWIhFU2T0fQAoVCQSDRMLB6lulqnoV5owbqSqExVLK85qguGLeLxQFCAh6GQYL8qo9VblFcBbZKoaj2tnQ7r850VG8JFsIoylqGjR8I4ioJh2eTyObKpJIVsGsW1CSoKbkE0DBCwhISmqCiWjkQIG+NkvHfq24laS0cNYYUi2MEIAUlBdh0sbGzZ9QJpBb8bycsviuutA06EYazskcJUQTIcGwel6L1XTITZLuL40e23LWDAEpXDRUsA1AFFNOwqIiQKfPA6b4CTc8WBf3RzTr+e1OfjvjPsHQHGNjZWM3NqEyAYHpYLt26CbUcRsPlYSpFWAjgEgQXwsTGwNJfi189toaExztD+bkb6BzEVlVs+/CEaw8prSs/84M2/8GLRYtOmzVxyySVv+TokWUJVA/zVN77KlVdcQaseFeCGWyA73EfPtp38+G+/TPuBDuZUW1wyUeZAj8M9/ZB1xKW2eV9F4OV+m7tWJlFXPsIcSk0o/AJSlVJpchIhszle1xjX1sTOfe0Mrz1AU3M919x4DtI5CyCQRlIU3FgMOjs5vvIZwrhoAZ1fPvgy3zkKMyw4twwWLYDKeIHxkxoZawWwkzkudpKs317glWGH5y2XxKYU9/7ga0yuV+HIDtwjvZTVVKBGddTmRly9Cad3Owc37ubQhj10HXGpnRon1pujLu8gB1WGKJLNiyzTmzMb2MDwL+4mWfwAzqSbkVFJJ0Vpv+Z1NTwZiXlxRViC33XAwSP8/p5sa8A4Atta4KxzBfCpOjAwiGBCxhEfnI8WmF6QF4Kop1ObtcVCYhbFIiIXQM7CQAIiVSAHRffrTN6j70tCc6UmBloUhrOCYVteL65BCYMlCyBXD4DmCvar46FvrgtmCrJpSKWhqEGkIACdaCvs+1dwr0eIs/wh8zuqXAC8F2hH6FVs9O7ldIRm7KWIuGgXsN573SLEw9YNzipob/R+joFcBnIOrKUIRm09ggV7L68lxfjxVQz4AnAlaLUQdCHpQMj2smYZSu1+PWkKOwZVTeIeGn5/DygJE/rSMbWURPgsRC1/CiHS+pT39Yaoof5uOprT57ff+k8EIGuCE4HNvd4N/eMtg1CI8JmBFZQ6h1uUlks/9Jco6W+uQRCTB0b93aTUFzFBiSk7SEn64Iz96UzFa1DkeSYycPtkaBkSXclnNHsHVQGO6Fvj9oLTDtt6CzzV1cmPtv4jKcPA6N7L6bNLEuU1E0gOtlMwSuzYLT8/wJafi0Y5aiCALEnc+L5b+fCnbidXa3HN568gVjcJ3WwgS4Hzq+G8O+/guT0H+eLPH+emb/yA/hcfZsW51/CJL97D5YtK1zDafl8+2QddfenmVx/rz2ll1Lg+382l9Bh7pHhi3ngXzYSdLTKPySqOY/HL+z7JWXPuZumyTxNWJKqAiBpHUcuwrWHWPHcnQ184H8cZjySJpe+K9/2QIv/E7574MgfWfQs7dwufvPVaLrv2Ou74uc2v/64ZMzeM65oM9u8TuvPeOTou9CdgxoIFxLQcbjFJWSpKvLaWgb5hcCVimoRrmVimSS4xDJiEQ2FsRcEsmAyODJAeHiAxkiZSnqeqUaOyroyyMlEloXnXXrTFHpBJF9l9YJAF8xqoliViktfwEfGcF13IF1027wVFcQiHJWrKZeL83wRiT2c+OFsD9HR0ceTh53CHW2nM2ZiZAiN7jlB74bUUixYSEoYsMzCmmpwkIbsi4QouSPDU48/y0jOP0blvNQc3rS69iaLxwvMroadHZFIJ8Xosju379p/8/2AGXtm5hRbTIJPMoKgBbEt0rtRkmBBzeW4fVNa6aBWuWLdlkCUZPSRR36iwpG4RliRRP34ukZlXceMEhWFVoq8AZYpLfaXNcD/kR/s+xROcOHqczq5hZsxtJFEwqAhoaNKpIiAhVUglZV1oJE+07zGqc7t43wdu4kufaifjpmiwyphyzhzm1YhcbJ8SIFxRzYr3/iUd7YfZ/vyjpA7t4OVzl7F59S948YFu/jhBHAlR15FGlLOAWAU0hIBPGSXmbBixuecpOTSXAr/h1F3wjP0hk2onUz7jYt619HoaGqCuHsrjwg2uQKzHaRcGNJml769j+tyfsOpHd7Hye3+N/Tqs8DdtuoQ6SecrF3+EeeXVFBAueQ3i2a5ui3L2e9tY9rTEFYuiaNI+OnuP8SHtgzyz7ftEjCT1ZeNxL/sFPb9YhJE7SlnlHmYsNjjyvi+Quq+XCgpMB5ACuJ+8h9WJBu6+YwfjLlqOHhqPa8cwMjlsM0h1NfQNORzqSrB3/8s8/8yvzujEnrEz9mc2q5in4CSwgwqZRA+uXEQrprHVMLmCiWlWIWk6pmwzlDEoFEAmTCwcQUFHklRkOYAeCFAdh8YG0TBV8pkuRa9tgu9U8Tb6Ta+XDfe24GBREPjyadB1BcuxyRsFzKxFOpEmbQ0CBUKoBAkSRMVFEcwkRQVbw3JDGORJI/zBUGl4/LjVViVyMZ2UXk5YDhFxZRTHAc0WiLTrp4AlKlZIZGqgpx+eWQ9DBtQ1QkMFNIVg1z440u6KRuNt0slYM++9v88zMYFEHg4fguFh0G0oBkGqgXBUyG+ZlmAhF2xwDdsDY//Yms0YUIck9SBJeVzXwcX1WHv/c/aOAGNHW9qGW9rh6FMIv9VX+B1G4Bn9IHXBM/8N1UHYfzBF+77tjBQdKqsbmTBxHrPmnsOYiPSa7rvw2gDx0391J/fd9+BbPu9IZTlTli3gpz/+IdXlZYQUBQOvY3EqwYaHH+T7d3yD3w0WcByXZdPmcO6sVh779uOMcYVW21gvY5IzBfmukxJBb2YUIja05UUFN5QC1CzC4W0FIo54ViaNn8re3An6u4d5+qmXaTt6iLaZU4k0teAWg2TXrePAlgOMmT6extZm9rfDdBfOb4MpcVj5AmyWhvnosXU0ahLr1xe55rKpLBh/DDeYpb9bVGrnho/DhHfB4iVIc19CtwyP0pmD7c/wzL9/j+c3pGjvcik6cGQoRZfjSWtaokFYPQLwSfBWbA37fpOic1sPl935N0Q1Cd0GJweGA6gQjoEcBkOF8jAY/wH5x9/A0J3AB2HblyE2CQIVEApCPohAuEKjPhAVUibkjwqAdXyjcFYrwzC+Brq7hJarbUJTPRzcCyFP5zVa7o2hg1GATBL0EDh5AcaqHq0xZwph64AMRgYiCjim+NyHC9DZCU1joLYGmupgyzrolKC+BRobYeJiOFINloj7f79NAJYjnsVbEc+hv/ZdClyFSJb8FAHSZhGxzyTg7xAxkQ/g/i1wN7TOg/lRuL4bbrsH+tYhgNjjnD4uWg5cDtKHRMlCher1yHLBzUBWAdc/pwoh9h0PAgXoPg75HtAqRFlvwV/xyhFYaRFRi69Too22A3ch0M5+75yiiEla5A8k04a9Ae4HHvZunO+Qj37xKCr1mzQXcdu6ECoNkxHsFH+z80dWEBK8bYjQdR0CZC1S6qgZ8i7PZ+b7Z3ZGmuBPbzXAHQpcMx+i9Zyca9oJwUCTEwidCDjpqNku7HXhZy68mIMtgzksHhUzzXm9OeUy0LVN1EKNsrEhyNtgldXwH/f9lGULFnI4UcZvNvXx+L9/jxvmLOWFv/4239/7oZP759IrPkOhaHLoyXsISnDNjAu5ZtlCLlnw2nc9nfngqz/HRgP+Po8cTp2HOiWJbmXUa17NAvcb0PlNARbM/AA3Xt3Kg498AICXNudpeDrNTZcJCYWv3XM3cy+6kC986DoAnn5RrMdnL4C1AyBVQai8dH7f/LHJzdfarDhL5Qefkrn9o+0UgBASzagEg+pJhi6S0A4PxcC2LEzToW3qVNSAhOQUUO0MGDJqNELfQB+GY9K/K000Wk3ecsknExzbt5v66nrUSBQC5ZRZFqhQIwvYKYCQLokGwC2DobTJiNFLb6GeWgViXjmcgVgbhgtwbNhm/c5uBo5tZeqkCayYP4MJze9Ah/DPYFWN9UxePJd//ecPcOvt/0bjuediN1QzsLqHj3zl62i19VSPn8SQomLeci3ntOiMiQoJpCeeHmTzC8/Qtf/l1w5sF6BzB0QninI68417OB0JhdlVbVy0ZCLFbIR/u+OvGOofJpHTeOClo0SdKp7Y0E6y6yiBbD/zzm9m2dyFNNTUo5pFPvH39zFtyhziVQ2oZeXUV0UIItb7GCrXLK3nOy9K5F6FDT/528fJKy5N424hMzhIuKkWLfTalm4qIl+5PakimzV0n6jirr87xsIlU8koCuFGmXid2Gd6B2HMwrH84yOtJJB46f2b6T1UwM2prHzun7HtyZTaxL5Rm0+JY1NAZKl89egIYif0u/xmKaVyfA2qIHANogGYv4uesd9rcoy5F9/M7OtvpWUiBGIQi0KDKgqWYog4ZE8S1vfB2HqQIrDsuv/H+DHnc/fn5r6tp1M5aSZXr13HZaHwyQZ9JmJuSkC8uZbxl53Ddgmsl/dx/sI5XHr5cti1kOGdP6G2ahG0vgdCYeZvPAD7JYbWtPPsjC9zwV8+xPBvvoR8ZC2oETj3SfIzpnHi5Q7ajxznMzfA7Z/+b6o1BddRWTMMRGH3nlc49soz9HR0nwFiz9gZ+x8ww02Tsh0ixTDGkIpCABmFUHUYQ7UoWDkUHAIhjepgkPK6Gsor4pSXhYlWlBOJRKioCFJZrRCMCtkn3Sd1wehuV392U+OgSWB1g4WFVchRyCbJJAYxrDSG14BLRvWEBISmoRsMYFlg2VGKdgHTBQMJFfdV2G8OOIFiVqAPNZNosFD0AMFoJaFAiMp+m8SJCI7l77VjmThOgUbQq6FtLNTWCimj9AhsPA4P/xvkn+snNl6jcnEFhyiRhXzaUhVipx4siP43Rh56TIEfN40RmrqxkJB5kF2IVsBwTMHWcoh9/o8wuQY1fC7T5y2gvqGeoaEhjh/dTf/hnyBQqP8Ztuw7yvceAnYZsPbfIOM3Q9URyes+4IRgJDT8DTTFYdv6l9i6ZQeJ9DDBgEa4oY1ZM2bwnqtWIEsS0mnA2JP6dC7s2AGd3d3kjY63dN6XXnsN51/0bhbMm0tteTVBWTi9mutCzmDDL+5n/9MriSdMznG8yu3tR/ndQILPXDuHLz21GwwLNQCVVdDZA11uqWE7wHN5aHRP1TxrQ2DVoiBVyFZ2RKNMnj+f44e3kU/bJBNFUpEEWmslbn+aod49HO/s46XfnmDR3Cr0XIKda9byrAvnqJAchJeHYbUtGLiFUJiAJpE3Rnjk5eP05A0ShqCXjwW+/tUfMbX2UebEQtRUD7PkqvMJTZoKNRMgNJuz/l8Rt3olFWv2smGvSadTajyG9/E2AWPq6ylvbmJ9Tw+He/so/tHaBQ5u4SDZvkdZc998xl+4jNqWCKoqPvOeXqipgVgtBGphXScMHUXMqz9kXiTr/DdkL4Xwu6B1CRzuASsv5AV8INavjLNcOD4IUQ3qwgJfyQ5BSBMxmoToCBidD4M25BwPeLAFS9iVRemDGoCyKk8IXIZcESKamL9FU+jMFFWhWyPLYhGzk1AWg7IKoU1bNRYSSSgMQS4MrgJ8G/ge8IfA6G6EjEMR8YAWERdzAwLh24hgs/oM4/kIRuwS4DEEs7QHMZkbxDH9eVgvQcfdkHjR+/urS/5jwDTgixBpFLq9tgaZHpDKPN06A/RaATbYASiGhbZMmQphWcg/YIFrCgaZHIF0QMg3nPTYNUqdW54AHkWsx+2IB7Xeu27//E67ThvAswjtguMIaOQEYpP402bbHASB9wgCBl7knbZOqTlhBQKUyiKU8nq910ne2eW9v/lMWpl3UvHG/3aTUAJhrvzXB1jYGKA5COX5JPzwJuFVOKAZMLUbqo6A2kFJ9jAnEi/5ouggCiXWqAE8hEjMdQBFB07ONQ2q22q48bb3s7jpXH58z/dZ/bzQSNTCMpbh4tilQPGihXUULYmeYiVLFyyisqKCPcN5OoeOsnvbQySPBeka7CauRTj/rPO4/pM38NjKTjZsWIdTLGAALx5+hcyaSgbGNPLxa8/jdOn9IqV0xGju+Gjw1Tcf/vFH8eek90iflkDgVXKd5MMpiLk9dVEt1zKZBx8Rx21c/QtCUoqbLvsHAJrjOmPKSjU0jz70Vda/cDeVFTBkigqDXCJCbfX76R98hbZpYcprZWQZdFmiLRA5KRvk5YBO/qwo/H/23jtKjuu89v1V6Jy7J+cEYoABQBAkQZAAcxQlilSwkiVKtiX7WrJs2b5+fnddP8tXcrhO99H2si3Jkhz0rGwFkmJOEAlm5DAAZgBMztM5VX5/nK7pAQiSACnJtI1vrV4YzHR3VZ06dc539tnf3qzpF5UL1Yqo1oiGJOZzEprlwxdI0tQaxpfJ0dzUznJTN+nmZXJlDaOwiGXqKP4whfxmkuEwpmmSy+Up5FKU2oW8gBdRJhZAnEBTMkBffz8v7y3QsC6EP+VBRWy0aDrkipDPQtAvE08FSaa8JGrstvNheGhVeOFReOjbf4CSyRLDg8YcOjZRUjR62rkosY5EcwMVv0zJK1Pw+pi3dDZfvZaO/iippvM44E8hDMDXFaHznQOM3ncFzxx5iY7mEC0D10E8ySXvvoNdO5/hxfu+jxFvohJrgndtRN/QBI7D4X0jBJROUvEBljJn6uogNj4qU7UNknNnBj7wwydoS7RyaX83Lz90H9VSCTCwrQr5nM3bL/NDbz+lSis5S0PzKLx8Yg6OL+MJtfGpD93M3/3L/cSSzdx26410EuLQ4QLBpIeWNj8hGbpNg4h9+vw0PXKc5ZOjtPhUHhqeYnz4JP3dLWzeNLjyntkCLJahpQmaBzwkEt3EwyYXbW3m1ku8PPZsjgPPLvPCj+aITBep5os4poksWejOSdLldmjfhFIJY03t4qtf/QN+8IMHuPfeHyBmsXOJEerLFwvxFEiIlXIzQkx+NefHQYwGrlxBG4LdkUJoJLmlOW9epuw/a3R9+h66d1xHW4eXhqQwiW1Xob1WoppHtLBlg0+DwpgwoalqDlm80LsDJl+qscTfXIR/4RcY/NjH+I1giDD1CiE/KypVnDy+wA+/+zyzDuSLDiN7T/DMvJ9vDP4WMcmPv20dbL8BPhHiwf/5S4xOZRldKnIgM8n1g79JZacfGQ/4U/D5jfxIC/J8tQOrOURRgl1ZP5GYKKU9ehzWDcIPHtzFCz/+0WsCsQHEdsF5QggX4kJciHMIEwu9tpqxzDKm7sHSvdhWFEXyIileZEnBr6q0trcQCYcIhnyEI158qoRHslEcB9mURDl8Wmyo+2pknZW9SRmkV5Mb+CmFVEtuHS8UDQXNVLBtFVnxU3dZcCuzFGw1hKz4UCQVr6qgOCaSbqCYZcrEmSZLF86KpYqIDJI1g1oeJ7bQwmRDgmLAQQqodLS1UZwdQDcXQG2Gxk9ww+0RpEbAK0hnhldUhJU14SVWPQV2ZYpoMEJPW4IQdUX3PHXz2DyQ1sCcFAbmckhgFZojMJZiSTBjTaNmYt4uUZpT0efPar366mEvYFVe4NThOPlygFCokdb2a8FQWJreiW2N8u8xOr+lwNiJNPzwKMyfQiCNIUQu5RrsVCHRAu+5zmFqZISDu3dz/PAwlmbjk2y6+9cwMLievt7Wcziaw33338v42BHejF/4Le+4jTvufCfXXH01/e2dFB0d1QHZ1NGKeU698CyPPPwIwwePkjHEfn2LDItLOR6vVOnrirAmKsymZh1YMIU3nAP0h1S6mwIcPFVg3hKJzuorCyESoYt9kK6KVP+EZvLiZI7RUzkOZQ3MgoNvVmfqWJ4TS1OkS2VmpmYozFaw1vuYy5bZcyqzYujj1JikU4gHZnTJpqpKnHDAmC0wV7slzRJsjsOJqVHKy6co+KAoVWiNhdFP5ChEu7CkFAMxg7aGIDMtYeaOaCtm82Gg1SOxrreRTYkYiWAIA5nhaZt2n4qp+NElmYX8+WhqFrCqx5h5+Xt4ozIee4hgsH3F0dDUhIaqZMPxw1Bc4Pxy71EwXwI9BsY6BDLuUrJcmbJaODYUqzCbEbIEeIQurG4K7VYJyCxD70VAFTK6GGh0hB6sKoE/JABWPzXw1YIVzzO7hiUqNTMvnwAoVRWicSEY7jgCpAlGxWIdG7KLEEgClyOkB+aB51/jmkvUZRw6ECv2aO26J4DdCI1XB6Ene0ntfXMIo6sTtb91AtcDWajsg4oJM48gNGa12ve5xmIhoA94Byi3ihJMTCFibsxBaUoM9pYPws0Qqw3YVUQ7rDhEKhCJgVkVoIhXBm8AKlEo5MDKI6gcSwim7G6E1q2JQC5SiMzZpacDdf/xI7UPutoHjwJP1xr0tXQvfvLhglxlRHMHEWzLVsStCiCWnUUE/8dtahnR30q1v52tPPxCnGO0tdDfP0B3axt+xHJ/diFDqWwQDse55Y63s6PVS6cfYrlF+Aai0U2xAVOxIJcW5TeujpOHOttHQ9wvtytmEJUJY4iuelo44A166drWi1ePI60SqAo44n6vBttDtk1bXwdrO9fy/IkX0PNlJi0/TqTMLbdcih+FATZg4yfi7aFr7VWUv/UllufGoPZdU7l5zIMvo90bo7ND5bpNlxMOBFef1QqDVaeON68GZKEOskpn/A7qQGvtElf2U1xhEIV6v3YVrWygscnP+qFGOlq3MDt/kIWZYUaPJZjNOxwfyZGd28/uZ59eOc+xEy8wdgIkFBp9vfStG6Szfz2By9dT0Hu4bEOEpoS8cn4B6uHq3rrggCJDexvkZmxM3QFL6IrFLChnVAz8RCJJ0tkqCipeb4BESyfFhTlMG7w+P6nWFmKpZjyBMMFIkMYmPx1hcfElxAjkHi+gQCLkobMjyrMvH+dIqBGcCC0prxjKdciXRXm6RzbAqaJpBcqlHJ6Vrd7Xj3IZZqcrfO/79zF83w+J53I048FkARuLCilktRUjfhSjKcWET2LKKzPj9ZK1DLKLa+juCdPRIO6rC9K71kvhWrt6kWrSFAEcJCwkDEkmoMTwePzIXj9OwI8TjqCEQqgBL/6QSrKhrh35uhH1IA8mSO24EcI6WtyHFpKJxVW2X7+Fw8OHmXo6jVOw2b3zZXqa/FTKBiFbwpoZQ6nmUJzXAFrNM+eD19/uGj8+zP4XX+bFng5mjhzAtDys2XQJG7Zuwy5XCXh14g1hZE+csuOwmDOYr1QolW0MRyYWbmDs+H4ikTDL65qZ9nUxcWCR5LpWpLYOZCBuOfjOGPDL+SWmJyZ56cAUs4s6S3OCx7IajHX7tQQcPDjK4hJ4w610DoXY2AH7wxL6YppjDz8DZg+yDZQK2JlZsB6HgbuQFHWlLLBSmcc0V1eQnEtkqT/pq4X7FepM2SCiF0URI2ge0dM8iAnfHYliiCwrjdg1/lkagvwHCFmBcCN9V91AqrcTbwCCfmhUoVUSaxqZOgfZo0KrH4xl4TJuajoVrVQT9v8JnE9HE5u2Xc4d11zDRurjhls1rAOZJdiX8T/YAAAgAElEQVR9YJL7H7ifkuNQsmBhKc98/jjfD+8EM4RRsSjoi4TXd7P8zKNYWhBJ8ZE2xlkYfphyYYFAZyf2DXeQW5dg/xMKOU+U3svCaDIsGJCpCo+GbBo83ZBbnmBxbuRVT90tpgu+6jsuxIW4EG8mTKDiWJTsAl7bj9fwYBp+LLOMqoaRVQefTyIS8tCcCBIOevD6FTx+Ba9s45gaegkKkkm1CqoqoSX9RMJeFBUkX42h6QHV1c16lUTDQazDHUcAqasJgm9E2sC2BRipGWAYNlgOKhI+WUZFxoeKXQNlHUCSZVRJRnUkfJKM6vHgOEEUJ4ZhpRgnTwKLyGnnU0ZyMsjGIqFshkzMZlmWKAdkIo1R5MQApCsoapnk2mto6pFxEkK5oIk6HJJXoBR0sDMamBqxeICeXjFGu+bz7v2ygGUbZnTIZsGQIBIEb7BWAV6BQlEQsEploZlvrxSanu+kUsSxxskvH8ZUA6Sa+olHmwhFBsn6pzGqRRzrZ20M9hYCY0sWvDgC93wbQZWMUxeT0IF58LRA/2aHP2qw+Z9fuI+DB/aSzy4TC0Yoe/3cuO5iBtZtfN1j2Q4YhsPf/PUnWFxcfN33vyJkCUVRCAWC/Pnf3UNPYxseW6JYLmJ5JBSPipHLMXt0H9/809/la3snmcpX8SMIgz0qTFlwsKjh3HuQqwdhnwkvp+HAguh8lwO3NPj54NUt/OF4gcdsAf24eL3reC4r8PFmhaenLA5acGghy2996YGVavImwJl2WJid5jl7mgWEwPRvboCxE9OcXIDdc+IBecqEjYjkyuVLPLw3jwc4BgxIMOeI90YVuKgH3t4dJh4JIdkyzz83ybP3Psnw7JOMLIjE7JduitDS1ETJE2M3y1C7pR0eeEfcy8fftYXuLUMcPz7GY488TzCf4fKYD6JJ0pKPXZVTGLaNbVvnVvZjl2DhHxj73iQ++xeINN2BTw7Q3AAEhNaqYsLsk2C8kc2P56A6AycCwB3UKV3KqpfrlOKFybSoUNTD0OgTSWJjo9CH3PcyXLQGGqJC9zVvQNkLjkdo1Hg8AmC1EKCqpovdJsMAvwJ+D0SDwsHRdsRAHY+LBNhC6MXqljD56lgL83MwOQWtcSAP0m3gtAJ3c277EZch5Ac8wF9Qd3aSxbXyXgSjdQT4u9pnJASD9hbg4wg638MIVPAkYu0jgeQHbzOoJdC6wLoGPL8KqiEYZY4jAFVpCbSXAT/IF0FoDYRkIdNgmNAcFffY8Qhgtq0TCjXwQSpCRxSqURg9DOVDCD2Qe2vXVkE8MDiCGbvSP9xSSKP2piXgC4iC/1lET//3NwKxEJcD4jYFEIwVDXFLZql5XuBKr4szz3E68feCgt4biIuHeNsnP82H3n4njThEbIeHdu5jYipNWyLF9hZolk18OhiaiXQS7GNAVQwhc4hHIUtdJiJGnddl4/qcir+fRHTRs+4lGaDldY5Nn+Sfv/kQk4f2AzU2fsXEJ8mUZQnDtjGAqcMZtm6/ii2fupWrfvNTpI9Nc/FNl/K2u+7gnm99C4Cxcpld+0e550+/wz/fe4DdB59hefnQaYednxhm5/2nOKGO8PAf/sMrwFgXMLSp65y6rFgXVHXhFHD3+OsAp/sdrsCH20/dv7uy/K48+GqQNBGIccOOX+W79/9flCsZCtUCu47l+fsvHObA459jafwJJCT8gQgej3BfUAiwKXwXP//hT5Pa0I7UptC49ucYUiFwlkzaZftCHRS2JaGruHTSRq84qLKE1wdDSdAyMpkFFUuzyC7kySymMbUqnW0NnCoXMW2JZEcHW66/jrUbr2ZquUBjdzNbr2zjijgck8Sz6+puUfs35oOOVlhKj7Jzn85ioYVrtqUwZZlsVSJbcShXLLCKpBenmZRMJiIBpPXnDsamlxx2v5Dmb/7x/bwHMd601I4fBCQKRM0xepaew7MEe1A5jsQoDkkUfvCsSQiHTiR0bJZxVkDZcUTVTQeuDIOMj2YMVMooZPHQGlpPJNyMmmzEbm5G6+/H291FpCVBY2eIS7aJ52e1LFU0GkWS5dMWQR7AVGE57iX5vneyNuXDmwhCRKUtJtF+eQdPrRsg0DyKrOmk9+7hYd3h8M4J2j0emjLDjC48TzF7PgZFq5/qV4nqDLufeZLKVBZjeQnUFLe8/xd5/y99mKce2c/oQohmpZGGaJhmWaIp7mUovpaSCbNFi4fuPcLMyGGCAZMXfuzlwJEhChPjdEV2wCUdAHhRUF6xJCxz5NQYn/3S01xzyVqOTcyQagphOY549iSJpgg0hBxKZYMv3PMop0artKzroGmN4Jt2NsRpDOpw8iG46XN4oj3Y8/PYB/LI5Qx2cRinqmHlxwCNT33qU+fRdqtDRfS41RZ/DkJb6GHEQqIXIWyvI7awStRHG1dZ2kb0hA2ITPckb1ZC6D9VeAJ4+q9iQ1uYQEhBl0Ru2op4RsNA1hHb0AVbVH+tT8F8EYq2g6SVMArTMP7cT+R0Qtdt5X19HfwG9c1JFVwJZwwbnt1f4kdP7ePHz335tM8u68t87NkP8Dm2kzgxRiT0XcLGZXSHo9zYdi0lJYyz+6849jefJKn4CP/c+3C+fA8TJ2D8FEQTCpu3Kah+QQIwLdBzIFcdxg7kyS+lqRsXvDJc2P/CpveFuBA/nRCMS5NFY444MVRTxaP78eslAiEHf1AmHPORSkVIhTxEIjKyV8KWQVEstGKJTMkms+yAKaGqKs0tzSRTcYIhCSMs4fNL+AOgeKgbPp8lbKcGNuoCuFXPVPw5A6B9vTA1IU2Yz4FjGqiOhU+yCCs2VcmH13Ew0NDQsLFQHB2vDV5LJaDatRMIIJHErJQ5zjS9aLSdNtdpQAnJyeHPF5m3Fab8KpWkhMfrxdu3HktJEXTKbLhKoSSBZomqdY8EbRL4JVhSYTHgIBXzOHaIZHOINZvEGB1DQHxhxCzrAxYtGNFhsgreCLQnIZgQVcbuNWfzsLwMc1NgnLIg49pNn0+YiDF6L+V5Dbu8QCXRSzQYwhduw7ZzmBUDscL62a2G3zJg7K8Mw0P7EdW96xDbhzqC9lMAluG9d8NtHzD48mMLPPXjnZRm08g2mEmbjnVDXL42xcau16cs50rw8Etid+GNRLS7iY3bL+OLn/9LkqoPfTmH4ahYqhe/30dlIcOeR+7jy3/0GY6cMkk7Iu1LIEiE6ZpBURvwMrB4VOzjr0ekjw8iCHpT40UOfm2EpLNaYLkeo4AcC/DFj27l6f/3OQoFnWXRVCtRpLbfb4sxIwGETbh/n3gABtvhrg0g74cHEEyrGerdexGBT90IXN0MX03DtC4enLFTEI1WaOlsZaCvB0/Ey8TMNIZRJVCxWSjA/3mswLhUOE0PtgXY1hflw3f0sebnr0bqH2Sj/21s+Myv8BtP/Zjvfenr/GjvLDPlEL//oY/xo0OjHDt5hKXM3LnfJP1hjn1/kbndh7j5//4c4QbhdijLYkBz/hWRs7+RGAd+H4Gc3Fa7INcPR6JeS1sV/y5VBSDb2gVdXUJeIJ8RAOORWWhoFo6BAS9M+aFkgl5jypo1sFf2CNarqgq9WVkR12IYYnCSPcLV0e+FhrgAIB0ZoiEhYaB4INoESRUmZhEaujFQL4f8VxFA6ettBD2BqMZ3q/1AjKq9wF3An8EK9dmNhlr7SIjnevXY5kWMxJdC09vhV35PbFbcMwov6XBlEp7JC8FyjwyRKFQ3QiEiGLIsCqbykXvAbBDnMT8LDELPTRBbC5kizD4AhCBrwvQ08OPayzVijiAUBk4bd126ris1/jXg2wjeuoswTyMGp7dean0cAcACbKW+R2AiJkGXKetqxLqsywtmXW8wHnmc9tvewQAwZ8OhQ9OgazR6NYrzJ/iXr89geiM0+WXWmovEF2G89my7oKHL5oxRB9fcwiOo6Y8jqhZ+jCCmv1rPWz65yFfv+hthNFDbxFKBf2iHjYkBJooWXz91gh8Av/aua7jkyjbm8odZ/M44OLDnwAuYj1X4/L7/CcCffOYzfOUrX8V2bPbc+8e1jbHTj961w8+mDzfQ3LGGYPSV9Vse6gZcHurFBK5usQvKunOdq3vsAq0uB85lxbrt41ryhFe14ZmyXs0tUb76jV/kiZ7/RXkqw8ihg7x/26XYzjg4JjIeot5m/uLPn+fWO1L4Yyqjsw7/+M08X3nhCInRKt1rLsK/B8ZvgEsboC9w+jEk6uT+M6OMhuHzIXvCHDoF71sLzaEIR22Tr/3z9xg7epD88gzl4hJGNUfHunX4DJvOgUE2X3kbHWt6yQ+X8TcoBOPQIIm52l+7ZpftXgUqktioi/vDjE3uZnE+zPLcZWy7ugdLhbxRYSaXw6BKvlRkc9t6tly67ixn/ephTVuYz2h0IqRROqj3Wddo1Eb01QbgXVzPrTRzmAUGfZfzuP4YOSdPmBANzPEN5mjD5NLa95gIHf0G4CQ2MIuNyEf2A8ulURZKUJiH+WGJ/Tshh4RVW9icucBRFIXJ2VkaksmzyltEbIdjUwUSUQlPWUa2bbqTIUCit3OA9931Xj75yzfzd3/+ZZ56/B956pmXa9/jvAFtyHNLPE9NDTMxdYI4gxic5PmnD6DED7NtSysnp48zWVRoawxzc0/9M5YN+VKFL/7xJ7nzQx9m6NrtJC/q45tf+gb7n/o+awciiBIViK5T8KXOdFGAzGyOl+7fTyKWRFVDlNUAwwWNoYi4wzZwarbAB3/rAdo+/jHecVmQwW6x8ecDAg0QaCiAcxSWKmi5eYiGUN7xbtaF72D0O3dRzR7lzc+bOq90+1wd07Vj9Nf+347onYuIp6cfMVI41K3/1gBdiOx6gguALISiDdz40b9gQ2ccX5PIJ/uBzYgWKyI2E0fL4JmHqAUhH8TDUJktc2zkWR588Ws/sfP51mf/D5f396/83x13dCBji3XJPX/4YV7a+cArPityHIejJNiYei+dsZvhhxLX3j+M9ft/xOx3v86liDGhZ/N/JzV0F44ODRdBwxoYnYSJCfjg7WL5IAEFHxxfhK98eohyfuYVx1wd56KKdiEuxIV4c2HjUERHJYdiBJCrUbwmhKmSigZobE6Ram0lnmgUVVqOjG7JmFWTUi6PVi5g6VV8tUW3UypTXIihBkPEG1tobJKQEmJTSnXB2BpDwERs0miG8H4pVQUBzO8Bby1xNU1R+eoL1OUPziW0PJQWa9Weph/VkVElIWcY9sVwzLCoQLBNqlSpGhVs2wSPlwh+fGaVMhYVdAw8XMF6EkxyuhlMBSjgSCXMsIrcmUDpDaF0Qq8GkaYgRrFX6Mb3wMxxKMjg+CDdDi1JgTPlCnByBJwKkFhHKOmhxQ9xSRTKxhDjbAmRu5cLQgLJigg/nUBK+FxXEddrVoXfTrEKRhU4cRAyR3ljQI6NQLpmqBZeoFpoZlnZQay5DTVyEaaShGIQOMDPCpB9S4CxWeDow5A9gTAMcusPXQD7OPBu0Dth7sgSj3/ri8zOpdEWlwgqHhpaWvj079xNT08r0jlsM8zNlfjs5/dSKp0/Grvh7Vdy++03c9OV21G0MrYClqwgqYqg7lUqPPbNf2Tngw8wPG1yRUh0RtMSxVKnEN2+TN3aZwFRVhyrXbqboi4BzznCZsCldVvUOnrt54mcxi1f3cvJsvHKclXqC8RNwHofBGwoGeIc4sDoAhzNCCzKLYd1gdg24JY22LGllyvfcye5B+/jCp+HvacKPLJrGq8C64c20L79MtSBPloyeQLBAH3tDguzVb7/oxFOGZB3ap5OErznihbWr22jf1MffdsvRuofRDJKIDlIPj+sCXDDTYNM5Ewmnp1h7wM/xFuuEtPK2P4AcmMbS1MnVwCGVw8HjKMUp8o8+b8j3Prrn0QlJBZrfkeI5pkh6sqa5xkm8P/VbsR2YAsC2XLril1nNbkOICQaxaBj2VBugWgjpFrAU3NqtJzaJpst9FFyRUg21ngfNUNEn0/oxVg12r7uF4zZQk4YVHV3iwnCX5NLU/wC1JUk8PqFuHa2NnEotvhMxw0w8wWw/xYhQPxq4YK1btO/r3adC8CXEZ3aRnTmHcCtCGOvYcTa5kyUQkes5D8EvnfBkCpUDv5XN+wy4asliAWgyQdaERbGQJ8BqwqcBHsfpDvA3LdL6BQ0JGDLEPwrzB6HwnZouR5mnwZ7GFisQjkH+SYwJUG78iFWEtZxxEjkejz+LWJbw5UZDyBQeLcRarTGtyAQ64Z7Zodr/7oSuW4BhkadeVjlAiP2TYUFR+bGee7UIQZbhgjICk4sis8nU4kWqC5ncOwqVGDSrhB6z9tY+MYzLCzlVyohXFanhLg3LoPZ5XFZCHbzCKL3ve4IaL/yHfNZGEyU6PUE+QgDXIuPdRuux9+Xwu9fon9tKxMnFmhZ10rfzet5rqiRDHoZvPo93Din8Oh9X1hRpAKxKbR2KzQOeQn1hAgEG9m45R34fOGznpOr6wd1HpvLjnWftFpzruzVuNshbrjqm2KPXzzCHurDbrkIpRw0tgnQUgWQJGQZWrvuJpu/D49S5tprP8e7PtaNUZQJKBK9XR52LzaSD6jsHc7w9e/OcOM7B/mF915MPOjB5wdJhXBMJNaun1941XnLtfNxQWTHhrnpWvJoi+qFXBpGLGjrlLjOhF2POXQOdGB2J6hUimSKWW55/0e4ciBMT2OEeCJJxQ/bWv0EfRIBSSiqZGvXazti+NMRiWpJg4IuAEhteZJcpUC5NMtkrotIIoVumBQLBahCNJXioqYIm+LnVzQ3ObKbp7//r3RQLztzeYazq+5vAVFtE2i/CEtdT2Jhkbw/xkDinQR7O2gduAj7a3/PvdzLAHFuYh2y3I/T1EegDGp5hrD5XTQmUNs+SkFuIjn1GBmO08cOPIRZZpGdzlN8DZEWNFEHqF1j0JO2wyN/eIJr71bp3Hy6QpoH8FQ1/vULX2FLb5DW7kYiLQ08vpzlpnd/iB2XXsSlG9sYOTbG6J7DlJYUFKcR601CKzIKftlP2X51WRsLgxyj2FQpLp5i9OVH2PfcDL/167/K0eERHvu3nfxpLsfv/9kvszHkRdNhLq/ygf+2nf4N61nT1UxvKshFv3gnv3usSjB5ce2bJda0QDzUj8gOD9R+3wRyI47XQHM0rrnhOrYNtdEXFHnSvKYzuzTPxMw8737vGt52tZcHJ2QemoAbr4X/PQGP/NMIhx88IsT2jn4GpItRGofw6H2cHP5LtNwpfvrz5lpq1ANELwzXXinqu+euKYUPiEE0Img4hg7SVvAuQ/VJMI//lM/1rRut297Lmls/wfqL2wgnFcJeSEjCLNh9vjNAyYHFEWHmpQZEjlrOweHjRxh78WmqL/34TZ9LrLWV//Zv/8aBiSgYOutb/TTFHHa+UKS710ck5mVp2uR3PvxHjB45hOPo+IHfAR5DzCftiHS0n5tJXnEJ1iUqE5+9l+7P3MaDC/McY4KW2vsCHxii+M5BJrzwVBpSgwIoyKbhsAPVJchOw9jeWR786z+nUsicw7rkQlyI/yzhRcz8Fd4KlYGrw82XHRwM20YzTTTNJByOkIonaUg2kUi20tTeTCIioXrBRkLTHDJzzViaBZaJVi2hqD5Urw9JUWtXKVHICz3UUhWCNRk8qVYlKiOqM6salErCc0DSIGMK8lS1Kqo4Q2GIRCDVCM3tr8OQrSXKNqLaCh+oES/BZJhYJY7kaUSOhlBtB8WykXWLaqVCqVTAMk1Mx8E0NYI4eGQFW/bjCzgYFQOLRqQVtW0dsfJoRpbaSSQb8akqli1RMSHsg1RUEr4zOuhLsPeHQmbR8UFzFyTbhclYOg1HDteGxC6JSUXi0WGIhmFDq6iObkEAsxIiNw4GYOslcPklEA2ATxWSjQsJYFzk+IGie3PnqLPg3kyUgEkc60cUFiPYThc4DSAPiOSaUz+h47x2vCXA2HReGPNYDoIR685nBiKb9sPbr4FAepg9z7zM/MlhHFNHVSQSDQ1s2XYDGwc6iXjP7XK0Sp7j+x4WAqLnGrKMvyXGu++4i+u3X81gVy/l+TyO48G0ZGzdoKIV0ZZPsPuF55keOcraEHR4YY0mWIudcYmr2yP4OnvQvH7SOZ3dD+3jMLWycuo6d+7lpxFgSo8XWhwoGGIB6n6matq8NPXqZTEgkqa1Hmh0RK5ZBpo8MGYIQ6iKUbdNcHX3wsB7hkJcu7mJjZcPMnB5J8f2BrkolSIeimIVdIyFRQ6P5iiGT9FR1Iji49BImbJmkSvoLNXu44AH+qMetvYkuW1rHx1XXUy0qwVfNOyKn4BVBo8Bfi/JgS56+pboOJ7mxNw8AaArINMVDaImA4yUm1k0bSp6FbvyWtdewtLGWT5xL0cfX0PXjsuJ+9vFxZlu4hSivrd+lggi5pyzGSHPALsQ45eCoAe59d41nVOqoIYh4BPGW6pUe/kEEOrxC60V11Ap5BGfyxUgPS6Yrv5IvdzSdgSDVrcEw9dGJL9BWwxcXo8AY1GEmZVUW5WaNQqZKkEqIiYKu2YUFkhB5FphMGbGEBV+Z8spzySJzCM66QJ1t/c1iKrAyxDVfhnEOHYmEBtAaNbeBKlroLNDDInHEUByLA9zx6HnYjAUUUqqSBAKQNEEJw5KOxhpoDgNuXmRKQeG6LoBcjEozUH2Kw7Oiw6MSVCUhf5DlboECjpYhxDCuTPUSxmfRgpEQI3ilKtgTSGeULcRfra6sG8mXPjY3ZiBOu/X3fN6VW+yC3HOsf/5l4ilGml9XxuKZBMI+lG8DrbXgnQaVbVQFAVLDlAcvILY9gqLB44xf2pmpTTbfc7d++GW3Lv6sWkE3+s8agRWwgaerUJfMU+76aASpQEHbymLkteBOSplHdtx6OhZx+YtNxBTZAISbN2ygaQisbZbpQI8ev/9TEyMoQRl+rf10bapjXhrL42NG7ksMYRfefVNLmnVv85Zfoa6qP/qImKX7er2UxPIlYVBn2SArAqGQLVkUclZ+No82EgrZloO8P4P3sazLySZXyiSbNvEbC5EyJcglAyitHop5sTJNMc9XDYU5tI1KoMNUbyeejqyWrvXZfSuvjZp1XtM22F51kK2HDwySI6DVjIYX/DQ1yARiCkEoyGSER8+n4ovoBCOw2VXXMT69iCxoLICSLcEFZTaOZTcczBEiZgji/Ffqm20WbrD4uwJKoV5NKPAcl6nNDxG0OsHy8I0TORAGx2N3XREw7Sep0PwUmmS4YUnaaHOWHbnMFdKwt3kGQPmtaPMGUWm7QJBXUFHxZ9bJDE7T5RJFAwCVJBZpuj4aNaieMwQtmNiUKGCQ0qTScg+mknSRicd/l5sO4pPj9DFy8iUkbBXmOUexNgnATgOY48d5NKbm+AsYGzItimksxxO7yEzFSbV2MCx8Sls3cOmrRvxNUS5d9eLjBsmJXScszAyZUnGds5nFHWwsQkEW9C0DLZ1NtERB7OmIZSeHcUyq6SLC2gf/yiSUUDSlylml9m/dy/ZYIRUME5HvInk9TcheROUs3Mcmptkx7bLuOHOa4k0hhidLdDfGiHuA78iWDAiBoBGlFAP4f5eLt3Rx9ZNXaxpjuJXZfJAVZLw+ny0JeM0JSOsa1A4URL67X0O7BqDyQOHSI/uAwwoHQUqONIMltNMdX7vWa7x9aIRkTD4qattujUDrlroaqMuEHBhgNOdOl017yAQE4mZXePmR3shERY75ZohXD6VglgdGmsgM4bQif+vBbYlGrvoW7eVVNJH2AtNsrgbUUSqm0WkdzrQEBSSUZICZc1mPlNg//M/YvLIczi5zJs7j0suYeid7+Sd27axdLiMXrI5PqFDpwdfRMHnlalW4NCYxfC+h9E1wZZSgWsR49A4Yt4Uhqdpxuc0mg5D4PgkM/d/CWdiL1Gq+JBItt3OnKefJS3MbKlWQVQW1XXtXVAwIe6BqYUSJw9MsDT+EK9uQBFDmKCEgYO8lozBf6Rw59QLeeN/jVBkFb83QCoVJtXcSCTSQijYSiwWIRQW3h6OI0ylSwYsLmVIZ7Nk8jlOHT2AY5X4WVE+XGE5UFG9fvzhCKlUA62trTQ2pkjEo0QjQeIJP8mUhLdWYmQYEI35hZy5Y6NrQWRFiE5ZpkSpaGOaYu2sV8G2HHI5AXQ6kg2KjNfjR/JK2DZYhqiExRD4lllLkvx+CEcgHBUEq3O5HqsK1ZIAeE0dLGTw+FCCQXxmlJDqQzEtZMOCioHs8SIrCoam4RgajqYjIyHVSBqSrdRU1F2pH5MVPXUpBWocj9ePz5FQqg5GQaLgBacEUo2zZBYdJkYMCmUdKQB6KczMHMhlKC3oLBwvQbVAsCVKsNWDEoSKLGhOJmK17Rq6T5UFUB2PQ7wROhSBztgOaAoUm0GXoGrCQjOUlQrOm94EWK1eu4hlZGs9Jy20Eylw9lq3n3y8JcDYTBqxsklSpzSskmn0rIWPDpk8+U/P89B3fkAkUibilVAbEqxZv4G33fl+GlRFmBQhBgQ3RRP/d9CqDj6/hCxLwrkncx+vXeJ0eqg+lZ6tQ3z07R+go6kTTbew/MK/2TJMtHKFzNI8J158lOHDRyGb4foOyJZgjQptSYktQ34239RD8KrrkcNNLIzn+dvnhklXNBZMWDhjVnPLOHcDP++HiAUzhmiaEV5ZUrza3ATqJaE20OCBbBVKtrjq9R54whQasKsPG0TsfLf64JO3ttF1zRaCA33YIQvb7+CNRrkoliSS9PP4IwZPvzTG4aNjDHUHuXTDBn741CSzBY1q7fwagCv8sLXVx9YrWrj4ynXI114l+PoTpyCTFT9buhjdNLAiCZo7kvR3Rtk/V6QrEaIz5SWRCuNtDtMcTPBStsxMJk3V1DEsQcs/e6JcBp5hz71xLL9ETzwMngiOk171/lcZDWWQWkBqAnsvZ8+1DlGnOr8f8dy6tbc2UABfSGi7+mTxFSrCeCsQPn1JYdijwzkAACAASURBVEgQ8dYG2grkZyDWCv6omOhswLIE4KoCpiIO54sJHVq/LLRk3UnRHULU2iRjWmISSfogbYq+YJjgGBBrBvNuMLsQ+aI7Ur7WI7LzLL9bh6iLTwJ/Qh01cMNdC3UDvwnyFdAeFH5dpxD9utWBmZKoQNh+sTC2KyqCkRYMgr0AThjULsg9AE7IhPKkcKcPQ98n4dQ4TD0G058HPLZoFK9XvFa7ImGA+iKoTyNJk8jyEo6zjF3JIYfWgr8fS8uC9TA/q0H5pxUugLT8em+8EG8oDjy5i+Jshiu23EhbSwuqImPJCrKtolsS/oCCGvAR8PvJKBfTcrtKzu9lajnD0XyFJHX5ZXdn353HAtQ35+aAJUkWtMtaSJJE0B+kXC0jSzKKrCLJCppeRqpBhDY2D5kwkCkwYFtkkCmgETr0Ik1JlWxrjtmJZRwgFelnTdMVDAY8wn9vqJ0dQ+189EO3kAaqpRI7n3oUT9LDxmtvoqFzA91tlzHYcgUXcW6JxephwZUukFa9zFXvcxUhLbvm1i2BIUO2LIocKkWhY96WBKlio5QNEnhWyuVl0Uh86teupnvDNp55SaOcyfLgYyP09kFnj4e06kXxC0Bh/WCUrYMCtLMRw2CFurKJy8h1nyn3GqAO/4DY/MwuaAT9DrIikvFyVWNiDCQLvIpDY0uSkM8i2dhId08D265oIlw7ZtoRrDMkkZjKkjgPV/NZ0yBXcpBkC8nvgKMg2RJmxWRi9CWMyiJ4LXTDRJs+Qa5cFmaIUgCncQOXrV1PeyRI/Bzu1+rIsshJDjFEHXRVam3iKkxZtTbbAzy79DhHEazZFk0sKvQMcETIM8UBkxInmWfGgUszhwjRjIXFLPPkAGl5GC9pDEyaaMPwKxQsh2XdS5UIJaoo2Ji1++Nys11Ow8LhF6hmNiEmn3p4gKgs05BoYPrIj9AWNCqhKMfnx8iMTzF96i5ig5u4/8XnKUdDWAEHp+ogB9uwczk8sTDBoI+gIjM7OXbad5+5yQB1GQYLm6pdpSF8MZapo1tG7RNnX7AuzpxkceYkAOnlRZIJlc1DDXS2epja8xyTagMb1wzwkfVt0HYT0/MjPPvCAV56eYQd2y7jbe+/mMNH5nju0DQDrYP4AK+vgBquYNIF9s2gGfiTbXTs2Mptd23mEkUmZIsN0CkHVMlDQ6KJZEPTyjN+eT+s0W0aZzXMPcvYE89AcR94Y/jDEfT8HHZhHPt8vFhPa8EWRCaZRECBsKIBtbJlFar93q1DkqnXe3gRvdPNESXxPbEu4ahaqUKyBaJ+8XHNhEIJzCgk+sDOQOZJkBbAyfJWY4H9NCMe8NOViBMLQ1IReoCNiD68jBgPCw5YEvR1gFkErWyTy2kMjx9n785vsjR27M2dhD9E7623c8sf/AFXAmwIsetQhWNTGqmwl3WDQRIKnJgw2Lk/i2XvAyrUCGSsQ9z5bwP/hugRHnYR391H8+4Y21Sd5+7/LF0U6UFiXgoSWP9pdk33c2I/6D6It8HIrMjjB/pBNiEVAiM9w/TRvQi+7dkiiMhub0UIeeQQZWL/8QWh3CrO86A0XYj/wKEqHsKBKD1drazbvJG2trW0NK+jp/diunuj+AI+VNVD0PawVIGDR0cYOXWKk5NjPFL9Zyx9AdOsUtUcSoU8plnGcX564KwBWCio/gCRZIK29nba2ttJNSSIxoKEgh7CYQjFhLGzO6HFm9xvkHGcIDhijayXITOnsLQItuNgGaAXHRYzOrlcGsM0QVXwBVP4fDI+L/g8EqpHQZIkVK+EzysRDgvJvaZWCEXPfu5uOI5I820LymnILNqklxzKOYtq2US3JCzJi+T1E1S8oGvYFQPblPBKMh5ZwfRUMCoSkq4jOwqSZeFYFrZtksGmioyDUlsn+IEYSDFQwiBLBAwTb8nCSqukVShngKqNpDkYhsPCSBmzVECNyijJMMUlsOfBntFxxjNQyZBoa6a1B7o6oFIWEouuXWYOsak3UoRcTjBnNRvCMqQkMb74vBBtEBiJZkCkEzRPGfNNjz4xFDmCoiggzaIbBjizwNTPfN/1LQHGruRLAURmHECAOGUBWg39Mgw/NU5xYp6mRAkfFg3+KE1D27lixw5u3Z487escYNkRoKIMlMo2Tz6c46ZbY4TCrnriPOezp5dKxPn6P/wlMTVJNe/gGK4+nOCFeD0eGpMJntq3i2R2CbXGbrx/Cq5JQd+GOIPvHCD0Kx+FvAa+VhrbvPze71zNJQ89zd8e03jsDC+xBIJkGACm8oJ8OIIoaV2dDnpq/3fHE3fftQ1x/ePA39YMmtYiquqfLYuH4MwW2ARcG4Zrt0r0f+Qu1L4N4A/D8hKqalGqpgkPrWPN3bez5peKPP9XX+crT4zw109nuO7pZ5ioHdNA8AjuBloUmF8q8sMfHmbzxz+MHO6EUFDU7VOB6mLNdtUDe/YwvucIswdGMBdnGfLDF/7swyBrWKEQ8YuvJLPnJe752qM876jMt93IodlJ7KVRMF7Lhep+9n97hqN79tDwy5/FtjUEx0xDJPlniRgE3wv+W2D5j6izYM+MGeB7iHHsPYh1Q7V2Y/IQDgqTLjjd8ftM3Hb1sx9MQevF0D1YZzFaDsRjNXDBW9Of0cWiHkUkxJpVA2WlusmN4hEO2oYpKvAmjtX6Tw3hyE9ColP8jfXA4whK0a8hCKPnE/fWXq8WQ8DPA78MRERiLyMS+wiCRfW0A9kYJK6CPlk8xzM+GA0JIe+Nm0GyIb8M9jIUnQ9i77oGxrMwBU/9CfA0ogNKEgwqgpyQRYDnq0MJQN/7oG8H4ZhMJCBhMc7itz6CtfT8G2iAC/FfOabmZ/js3/8J/3TP37M8PcPy7DxaWSNkFFH8YbyKjNenkpUUqvEBWm+R6Vgb46HPfXtF4bABsYRz96rd1zKChJ5W/VR9USjVtZJCgTA/97af57sPfZ2YL0lHYy/Bxlaefv7fCJh+FFSyFDiOzq9nwUuZEGWygPPNRa54Aq5qqY9Bj37nO8yPTnHjjffRwOls1iTwta98ZUXSPYsYx6KIOevVwh3jzqZ/zhm/d4uH3TAR0gzFHFglCKqQaIJNKdDCMJyGkVOwvguKksqReZVLkVYWjKstfgioRHpVbnh7iNvWtuN5pWzmaVHhdG3a6VobuFq31VXtQ+09LlBr4RBSszQkYvh8KpalUMrBqeMTjByvoCoW7c0xpsbmCAZUHCOwcu0eoGLBvCZMN6seUdngnq4GpAtwYkznwOFJTKr0dbUTCYWYmlnGLoxD1AuSiTM3AyP7ob0dtbULT6KTyvwSvSmVVOj808AK9U2dLCsFTPQixvQTiL4aRYAh3Yh8w+2xLnSWr/1+LSK/OYLoSycYxcsoAUTJcBWY5FkyiHwmAijZxwghQNfDtfuhIwBfVzqhbvLmcNjeRca58xXXIgMBSSIVj3NQkTCLaQLFNClgLnuEubEETY3wO3fezpe//STz4aux+3+R+Hs+yMJnf5eNn/80N9y+kRtjad7e1IRt17Oqs+Xz1/hg2ICp2ttKuSqWqYIcB08EtPHXbX9LDbF162ZamlKUDYfq4l6SUR/RQP0JbGsaoK+ryuycQEEt4PCLBxjeeZCP3DwIQMcVn2TA/AWO+gbFyuipz9I5YPOBT2/HK0sYwGgR9i0JRgomdDXAmiahrAoCKl04nOPO9z7NnrEPYtlliK1FWf8/uPlXfpvn/vRmloafet1rOns4CO3WecRddRn3Wu1ntwf0c7pqsQuaurxyqJfT1rSU3vF7MDkHT7wIJ6dr3+NFPM15QIUFD8gB8F0OgUugeA+YB9/gtfzHi7APWpPQ3wOXSGKN4Y4/OURLm4DqiE3/qgm5TIGTJ4/zN9/6bZzFqTdPhrvhbq7beC2/t+pXVwz52TIkjh1G3LHZY6f419/+Iu7qKIgoVmtGjNdjCMuDKeAoj/ISC3T7rmRb95VcckKmYoFElA3SJby07hp2VfyMjwpy9HWN0NIicuy8DkMBOHgCntv5Lxx8+A9f4+TfjeDmrkM8YO9BJKdPvMlG+fcPlzN1If5rhGZUmM9MM//cND9+7mUAFMVHQ9NmbrrjajZdeilD6zdy5eAQA92wpmcAUW0B/PEnABidgPufqvBPf/X/MHLsO1TKM/w02bKLFPGbRRKVIsVikWqxihYz0EwLpebJ8rrKIlUoZoTPS2YRshkwHRtsE7mqUVpaZH7qJMVyAcOyAT+KGkNSPMgeH6FYE/5wmFAoQDjmJdEqqlmtc3h4dE0QDXLTMD4Oc9NV0osFyrkFKBYppSepFuex9CJ+fxjJqRvlYoKm6ZjVKpau41dVJBNU28ZnG/jR0HGoYqBTwbdSQxkHxwLTALNEoJwnUgwQUSIsq7A0C5XlKlq2TDlXwqwWwSPh84XpqLlyZWOQj/jIOSk4Vaa1TSYcgkJeMF87pDoO0oTwTlKpVQ0rkC7CQhgMj5i153XI5yG9APNjMD8Kjn4YAb68meiivXEd3W1dVH0lDuwfRaseBGecn/Xo9tYAY21Ei7tiayoio64IVuA2CY4/8feUFmdJJuOoVo5osoMPvutqrtqx7RU6sbpm8p0vDvPe9/cjWQqTJypEVQ1Zchs3jJggf8Crl5bUY2j7eq5797W8/NBe2OglEoyjyF4cWQILHMfCNIoU06MEqxV2dPuY9/t5drJKK3DFxTE23HEliQ/dBXIjUjQPdhXkZZS+FMdOSvgycG0AbuqRaWzs5otHFti/VOIlVrFsEGnGHkSSkau9ehGLnwqnLwrPxoCbRmBtLoB7ZvgVaG2MsP22Lai9A0ihBMhepAaJ3o9/FLlsIUfiSNEmCA+y+W6HO3kQc+wRjhdhe1gwO/O6AIPvuC1FtVokm9PIZk2+9lt/Rkdvgu5N61h79Q5QHEh4Id4KviTEYixnShyf1FishvmNu7cSaI0gmzUR1uXjxG6/jF9vDNN33x5+/0tPETRNSPSh2xJ6JQ+VqVe5k4fRx8vM/5mDo38CsXRzvU3d5fqqFvw0lGWoPAb8D+AD1PUczgwD+H7ta7YDl9a+1i8MLeJhUO0am6lG/VqNAVgIFpXmQDYn2F8NLeJG6ZpgxEo1KQIQP1crMH8SQnHB3pUjgLfWo6XT9Rf9AbBLAqxt64apF8GaY8W3ItcJznrEyChBqAuq3wJrFqEd8N85XeP7fCP0/7P33mGSneWZ9++EOpVDd1fnMN3TM6PJo5E0GuUsEAJhsyLYBrwYMDaLgTU2Tp/9XfY6LKzNt7YxeMEE2wQRJEASEoyE0miERpNzT+qens6xunKdfPaP95yunmQEEl7523muq6+Zrq469Z73vOF57+d+7gchw3oNhNpBi/vSHFL9eDXmwdkctMdAsWBhBoZ7YLMM3SFQU5BLQL+PsEyn4agEq98jkcu2MvXtZiGxoCCEaG5CTIpjUr0jAns9rL0Hbr9HojWcZnwozoEXTnFk+w703X+Bq7+ytLrL9n+nWYUiY9ue5vipQ4RdlXA4TDbdQLbjCmYXilRrNq6l0NPTQ9izCan9RNdu4b9JNT77dz+imq+hIlalOOIQmURsifsREIER0UR0ZwkYW6mVeWjbA1SqZWq1KnOlaeQRFcs2cfyV3sNDpQmHEgoSqVAT99/zVh7Z8S0Ozk9xcokUy4d+69f4yEf+K03U084DkwAkabEgZIpz09OX2vns159kSz9fAk5PwPAERB1YuRlaUyKjQMHj0edNTry4l8GDxxk4PEzjmrVc9ad3kGppIeZnM58P/KrA6zdK3LZWSMCE5LpW1/muV1137NwAWhvnKo0HkgpBsnTFf78BTEuQTkdobAyTzqjIKkzn44xPSGQaW2jvTNPRLjFTtIk3NKDE4oyWIBIGRYWwAmujMCHB9LxgCDSkRLsqOqQz0Nll8cwLI5z4/v9iT3kEOWRgt8RxpBJU0xCKQqoRrrmVxvYuUvEkEWTG8nNsWL+c9vbsBc/t37LaPJhFca+NCNAjeP5xxJgoA43I3E2Yr1FDQfgpgY0jqrHfR4z38GtE3/MreLaCMXiasRc/z/IrPo5qasjFCup8AY/vMsAuZpmiF7HdLiBc8f0IgFb3v7vHb0eNc7erk5yi6IeqL3SzZexwE5askvevF3gRzxzdywuDA7jav+CWOvAiWcziSXKf+grrP/NNNtzaRtWp8IXHznIRmWZui0gYtkfeFs/t6rYIs/MWY2UxulIUsRr7IJlBTSaYOZRAaPxcukqwkVrOtJZmfHqBHdt280t39hMLNRNT4ziux8n5KoWJUSYmF4im2qggXOvx0b0cPvQI8DsALOvuZHV6nOP/63Ow4T6WvfM3aFsfZmpM4oVJmO8XPsm0BOkI3N4kxubsrMXv/f0Mx198jsm5R5nJ72Z6oobj+m0uDeHs/xue/oMvoucu5Y+9XAvE+AOe8dIE6YAFO4R48o2IkXHK/1uQihP0QBCiHoLv/jFYqt/PA8AqxGoWQnjWaf96cZGyGI6B9T5gB9gPvsJ7+ne2TDMbb34TXSuuZGG6QjLVgKpIxOIxstkmZmdmKZtFRo7sYODpb4nPRDZBZBkhFfokcTwL1sB5xBFNRiQehQyo6kKre2h0jGd2PYH33B7x4iu0Bz76Vm65bitQ3x9USVocBRLwmR/Btx6uAMcJxkALFjf4f9e638GG2iT3z23niwjX8ErGMc0n+fCZ7/FfnDKdQGLdOtw/+Ve+cyBMrlmiWIXdj4EbgkQIlvXA8mYYGITjL+aZG73UHJWBDwFvQoSigiDACUQO2H98+4+dJ3bZXg1zHJO5mYM88s2TbHv4a4S1MBFNQ1H6aGpdR8eyNazevJlbtlzJsjaFZBze8boIN17x+wwP/CaDJ09z5MgeHnn8ISruwEXlf16JWYBpOdSqBsVCgcLEPGoohBNSCTc0ogJWTWQchYJqqIAXaLcpkC+KmizlAhQLHrptUqkUMWtVnFqV0uwshlXAditYloVRdLFq41gOuChEEg00dPejRhOE4wmypTbcijjjGo2CJRuOi3oE5zvJqgOaDnbFY27SZGZqjtzcJJXCOGp5jloph23UUDwJySnieB6e7YBnUynk8Cwd09Ax9Rohw6ACKJ6F7GeV9DJDijIaVSAgs+UQe18RKjrTNYkzFZlBCfJxqMhiPZSjMo1qHMoehqVTzRuc2DGP1NOI40m4piqkf9IrWXdbiP6NkExAVDq3FkawjrS2ilh0JAJqBKZlmHcFYG47UK1BKQ+lSfB2A/oORJbBK7HDTMydZDafwJNW41ouMhFf7Opi2pQ/P3ttgLHBScaBRbqNL/YlaSbhMyep5UaQXZNkJIbtpFl//b309q8ik45fcDlFkbnyyibm8yqqIpNsDtPcpqD6FJhIvIENN7+LYzt/iGP9ZDC2s62dm669nma9g7ASQfYkMWc8CVlC0Lttk+rMOKpdZL6gM1SwOWKLisAt1y4ju3kVSqYHMIT4peRSq5U58PwR9hVtPBvWtiW59751DDw9xEYsVqxsZtNdG6FWozw2xd4z8zw5WEBHuJuG320N1It7LWW62lx4OI4gmFeXkiOe9mDYlYgpqlgd9DzoBlKxiNacAUcToqRyDeQKkXIeuVKjaorI83pTHJwbkhpvuLaTzfesY25wiHKxRqStG2VmgkMD0wydqnDyQJ5JCcxYiO72NP0tCXLHTvGjnWOcGasiGR6zU6O4sesJpdrEHRkWSrKVpg0aayby3NL/NA8dM3Br8ziejIpL76qrOTs6jqUXEKX8AjPwrDHsuccQDtJmhPON35NBUqsHxKBZorEFkhUYvhQrdqkVgZf899ksFvXyUuAp4rGrQdoBgFLX63TwNQgdodYAIiIPAnj1DJEqoUYgnxfXcCwBJKiqYE5FVCHuHSTvBem+DhBSBRk5rPpTrR8KYajmhX5tfBnU4mDkwT0F1nWgNkI4A6E2KPw/iJPvCYSMweBP6IvAmhGkgLuBW4B2sZBbjki9CIWEDkzegMKwWGxb+oSWTlcH9EgihbUiifThKR0G9oqoYiUE7l6YPwbVAyExKQIg1vbba1Kvs9UFoZvhl9eKNrWshM4miycfPEj+0FNMnhzCOD2EUxx/mTd32S7buea5LmapzEOf+wJvescvccXKNUiVGpKiUq1UKRYquI5EQ0MMRYsTSyVojHbSft/7uPvIHLFdJ2gczYkUYupFvFzEml2MJtAVVVSBWvq9nkexLFZ113OxXXsx2uYugZ5cdNb2bgLHZnx8iCNnDnDzlvuYz1WYmZ3nd379ZgBuu+02li3r/DfvVWIJ25Q6zBEoTy3de87PwAh8zqXvKQIVU5zfbV2kjklAUwKaotAkw+6dIxzaP0puagI1tQY9Z9PZ3s6G1W042TakUBRJhp6OurxA0M5AFjURFeHYoE3nZyXIS14LGLFQLzYWo+6ySNTjx0v9aAnBap2zQA1JRKMSyYhEJARd3RIT4wmS6TixRARP8cg2txLPxCAkU6pCSRfZ0thCSr0MHDw8RjIVoX9llpY2kTUUkcGMKSSyTejVs1gzp0DVIdUAsTRyPIyazBKJN2HJNqZlUJifpVKrYpVrNGkh4qGfzg0c3F5h5oBOnLqqVBSxTncj+F9ZwMBjOzYD1MFpHRGkHUEs1+OAios3W8QzPchVidBL+g0b0WIJsEy8SpXCF7bjmiEUBNBapZ54XvGf8wZYnDdBsDkoGJcBipiYSyJyS6WsJEWhccV6lN1Raoix2Azc+eb7GSvAVNGjp28dk0MlzsxNI2HQ2bORX76hnVCLxuldQ+x54PFFmk0wPmyg5niormj3PPBi0WbK8hbHSaNdwXRTVI0FSvo4dUW1S9uxoTyrlrXQ0xRm7dpltKWbCIdiTM2ZHDw+hxoBr1jCKZsoBkxOQdnVqeVKlIrzDA5PoOs20UgD/Z0m5HbD6WO0vO59rO3dxE1too/bQ0ISpLsBojI89fQRFsbHWBgdZ9fjQ5wY3k++chjdmqYuIQC4FuhzVKbmftJw+jcsiuA1BkrNwc/S8tMWAja3ELNTQxwke6hv/EHoJAit+DO3aC+5XpCLsKjeT5D7hlsGy4OyKag6bj9I94A3hBjJr+GUc1mFeAs3v+mD9K25iua2DqJXS/S0xwgpEA9rNMfjlMtlqo7OmWv7OXz1RmQVFsxOrrp2MyvaRSHEgKoQSB2F8LOybDBNUQ17ZnaWoWMHGXj6MShfOpjw01hoKI3SF0daktIb+LYeAhQ+tAuOblcQK3sHUKMJi80Ixn1b1xr6Ymu5p5Biz55t/Mpvf5ize4/w3PYXmLIqyNxF6BfWMn/zFp6RuzkgQWcLNNSgaRwoQ6ZbkCTGpqEzDQ//6B+ZHHj+Ii3uRDA33oxgBiYQgP9RxCnplcyJy3bZXkvm4Tg6pYJO6RxQYY7YxCjDZw8wOLSd47u7aExKxKKghWUMPYunN2CUHSwrRrZlFVJeomaOYbuv7vzIm3nk0gTqVAOx6ARdsQhWJIOWqNHRJoDQkO0DsAhFu0VzEOtkXJzdcSBuK8QjUWplmQoqRqiCpkaxbQvLM/E8C9txsC0Xy/WoGga6rKAl0kTiKUzdRJUa0A2NXE4hk1ZJpyEUFudhVRG6uzVD+MFmBRaKUClXMGoVTL1MtTSPVi1gVCtYugmORMWqIYUVZGQky0OSFSLhGCFJQXVlHMND8cDFxKKGhY4rRMeQFoNF4pkK51dCrpioloJiKWCAFBJKf1I8REiWiLngJUOUqgY1w8GseYQ9v26NLOG6CoatYMnCRzMRobK0VMcmgowmNSykCWJRgWmossBDdF+as1yA3DzMz7owWfQLxrzSPUbHdnRspwpIyJKC51V4OSTNV9teO2CsSz14WIWGRtBUm2SohHdqD7ZRIoSMKkl4kWY2XH8Hja0XVzpTVZktt3Sw96B4sD3dKpl4nQGTSqd5/Vvu5fR+jdpPkH+SoiGam1vZ1LuOtNGCZXngSUiOh+uaaJpGSFaE2HNuHsmpcXJO50DO5iwC8nMaU1iySm00TySuI6lVTL3E7NAoP3riKGM6rGhJs2FlBx39vTz39T1sisqsuqaTN/6XO6FUZe7wIN/bfZZJ7SzVyWlGizauK7b54CB4vj5Z4LAstcBVzZ33vuBzecRhChtRWU218Yp53OEJ5Ph6pExKIHvoUJ2kcuI4C6NTzJniwBiJRWhRFdqaY9x1bRvtW68mpkjYlTJd12+G8WGOjuxn9ESO2TP7eG68xDSwtl1ma5fM+KjNi7OQjYZZ2RwlZ9fwYmFoz4Ds4k2U8IouUrqRrtVd3HdLN48OnEbRZ4SbrUVpaV3G1LQhUhBchADropURXJpvU9fECNLTLOqAbAwsSLRCkwnDn+Ll+dynEOuDjmCZVkUabakGRkxcWvGEZkqQQBdwPByEWLXniirl4ZA426k+8GrXBIBZmfaPDKpgicXiEA8LVrPh1mUNkAQA7CKqPYYUkCOiyIu0CpQMKEUBejR0QsGC8ijUzoK5HCIuhBMQ6YTCh4ApkF4EfijAZYr+z6XUIdoRuhevB97nd7Mh0owdIdxFVAVPEgtuaQpCFXAawIsIHdymJYeAiCf0IUef9DBrFnLagBdMpicyUFDE42umXjJ3xG9HI2QaIbUFWt4L77kDRqfKlOcLzL80weOf+T6c/iwYl53ky/YqmOex7YEH2Xzzjay7ahNJRaJieVTLNaqVktiHPBNJTRCNxchkG1Cyb+b2X9wHhRqMngu0OohVKwcsRJuoujYsXDxg0NrWQaVSplwunrMZaCGNpkwTU7NTtDV1YNoGR0f3c+jYS/zqL/02jpXk9JkR/uiP3nNBpsnLvm3qaftLdVPhXDA2eD0IPlmmWKdKGhQdKOgiJUxbqJHQFLIxD6NwmljHKo4ezvHQ9waZGhrg/l9uoaU1w6r+5dx+RxczVZ+ppUJPUz2TZJFNdV5bAzAu4Mst5dwFQGzAeg3etrVXswAAIABJREFUD0tq/y2x4H6D2o0SIgthvib+H9LEWpdUoKMDWtqSSIqC7dnki5BpaiKSUEEVxRlrNSiWoFIDowaaAycPLRCKKhQKNlesMFBTEVRFplhxkCIqJGyIesKLTYaRQnFCmQbCDVli0Sy10hTliUnKuTkolwmnOshQL4n0cm3gmRGm903TtKS//Hr0JBFLbxYRBHgUa5FBZyPG8XLEriskY20OMkTs6JNIlo2TLyLhkVs2htaSRFEVNClC7p9LGKZ9QYGw4LlJCPjN9b9jMVUPAbU1IIDfpckR3pLPyqpCx7o1JGNNKJEGsrEIGxsbeO8vv5tnjxXZe7rGHbe8me//4GHGSzkkWWHFpru5q1lmVIaJ2Tzm4WPnjAfNb8uEJUK+MmK73L5gnyuj7lTwzByeYVGuTC6+rqhhFDWCqQfJ4HXbv2sXVzWF6L26j+uuXU3Sv36uXOHgqRwtMZOOtIxn2CxMTvPSj48gUSM3Po3tuMzlCgwMDKG295OKF4ARGH8GdeIK2vRmbunsYNDv0wz1IiNfGpjgwJM/ZmbfTqq5Q8wyi4MLRJFI4zHFq5feF0Y4EXnqIZUwYsQGIk8eIkwVVFpVEL2dRPS+4X825v8/mOWBJxzM3IDUYS35Ho9Ff9DRRVUabJGGJN0N0l7hkDFNvUzma8uUcIzsupu49c2/QSIaJx5xWbMywYpO4Q9GJNELMlksYPKq1Vx7170oGpyYFaDjslbRm1D3WSuIHnNcUVVc1z2KBYvTZ45w8uAOxve8+Krdw/6nB+ls6aB1Zfs5r7sIjHzncTjxEuQORxEjtgaMk6REvySz0NBDtms52VSU9XmDnj1PsezOu9hTKvL89ieIAZ70Ftw3vo6Ze1aw7SmYiUN7SsgId2RBs0Tlc8OBmVGXrmVlhnZ8mfkzp85rbTOiaMJHEY6ojNhFqojqHyPUC+Zdtsv2/1fLUS3nqJaPMTkCB3689G8y0EtrUzcN6TaS8SYi8QhapRXTzr/qYGzZLmJVXJhJ44RSWNFGHKWMopbobLcJx1W0sIQWOAT4dVcAHJEJElHBjkA4LOE4Kno1QbUUpRAxcQwTS7JwPbAtG111kFQXXA/PczD0KnpumqipY5k1XFMnElPQjTiFQphCUqIhKRFPSETDEtEQqDYsFEA3PQzTY7ZsU6mWsYwKjlGlVi7h1KoYFR2zZmLrLnqlgBpXURUVzQuRkkPEVBVH1lBdFb3qEnLA9GrYmFjksCni+XSNuk/rU8RcUKoGYdMjbEmELdBMkBRQwyE0OSTqW2hR3LKFV7FxaxaJtABtPcsPkZpQLMNMHqo2xDTQwyLrS1HqgXNPFr57NCL8QwmoeVB2BDEhNwlzww6F4SrMHwKnzKtXPlAEdV1PQSKETAiXFIHycP2U8Gp934X22gBjbYQ/kwayHjTDf/oALJ8vEHnhNOP7XqKmGxRND82MkF5+NSvXxUgkFRwuvAkXUfTHbRRgbMb3szyftdDRIvHJj8K/fkKi9hN8qPDGNhpXdNIRakIvOui6jm2aWKZB0SjQ37uSSDSKq2gi/9yLs4cFDmKiIg4B2z65g6EHDrN2zeNcfdt6vJY0YwcP8tKz+3lsEG5U4O2/9UY6VnXwhff/DcNl+MCvLOeqX+iHVVkINZO9/l7e/wGLX80Ps/cjv887H5mjUrDJIpJeAghxqQXspEC+NCALTpz3niBRC2BVFLY0hiHbC8/uxOvtwtENqjsHSFZtvOuj0NIJXhIO72b39n2MDI7SCNwJ/NqbVtPd2oCEw8lTx2hV7iOTyuBZBkxPwOtu5L2NWZjKU10wmf7Y9zjpwXcnXb416aIBVwJvunkF999/LY333wblObyIKrS7mpoxnnoSrbeBzmyCN37oQ9z4+Y/RlQFThlGjxtPPf4cmrR8v3k1F7YK5Pef1jIfIZz/jt/oDiCNiMJJ8dHEIzs7D2SlPBLWBC4/hF7ExhDheDbgVJlUBMsQ2Q9qG1rhIeap69SOWjHD/Syok02IzCGuCoh/1qWeODrlxCOvgakI3NtUCiYivH+uBZNVZ0p5PW/P5HYsHUVWCaBqWpeqgg4rgoFQaYXQNzBwTpGjTFIQQVMGUVe4D6V7QpxCyDN9FaOmebyHgD4A3InzSoJrLMHW0ZpkAphVAi0HrNZCxYOIIjJyCzHJ46gqRUpYBWhxYOAP2Nx3co5O4HAcGIfbLoDUItNYGnkRQhBH3zzvgF38T3rIB3oTHLPDnf7GLF598AP30F37y87xsl+1nsIeeeBgrLvHJd3+EI9NlOjqqZBqiSJKDqqokVJWMLJPxwEOCd/4ZHKzA0weQlizmOuIIdxwYVZaTlwK96wvtw7/7xzz//BNs+8H3zmHyL+/u44O/8kE+/snf46m9DwMQkhWuSV/Bra9fzpprNp5bADJwSn8KXHYpGBvnXIDTRtTXU/AWmbRTSIwXYWIIGqKwbpnH8phw5E448M0HjtLWnSWRNHjvvdcxOnqCDRs2EImvZ3m7Su+tUCiLFTmfgv7UuW0pU0+thX+baxjEgoOiT64nfi9K55YGCvRcg0BncG/Okn8DXUVDh9wsGIaN54r7jsiQisKynhhnRqqcGaoAkG3PQEhGCgs5FqksGLFRTwDV9hws71nF3gO7ePjbX4W5I0SuvwovEcORXGxnHroaIVLxqzSuJJLsJplJ4nk2hckBarsfhZkq6C5qLMmqN7yN5dEY6Zf/iAHYt++L5E7+kE2w+NmAJfsiImmi7PdHUJs1hwAidYQs+SaEyzeAyX9jG+3D20j511sJHPztrxAFGsmwkq2UeYow9mLd36XF04Lg43bEPtHhPwON+rOPc27mkEQdygMRwF93dZorm7bS0bieO29az12/+X7i/WH2TXwXY+wo2tB+9j/5t+RqIzR39tLk3cqxAY/GrMet3VfQ/7sf4KMf+yau5xFBQIJlBDPvQpN8QNnjEGUoX+iIprL9NHZsZnDfU4gQeR1K3ve5D7Lv0fez5e538C9fvpPDCNXUZT1p3v7WNXz6bx5g9VvfwNjsFN948F/Zs/fXaG3MUNUNupYtY8uVV/B3//MvIbOesh7A6vDiZz5Bduw4H7vj71mLAMxdhDQHwJ98/G4+Z+f49PYdTDO9pLU1vEsWMfpZTSgFC/BKW/ITqGfHEeDXSv/9FUTaYgMswtMBSJtGLIgVfLEX6jlEtn+9Juq6sgHLt8t/XQXCEEqJaLmtQ/xNUFsD7naE0/FaM4Wmtj5++x++SdZPwW2Mw5Zu8VcHwBM9kgRCePREoScqaEuGI9hKplefJwHPoBHRayZg2x7lgsdkbpKHH/kEp3ZejC36s9snv/0OrO6PsfUtf7MYKPQQQOxZF953M+Tn8Vt1B+L5HRJt1uJsevvnkaKdTO1/gMPPfoLncfn2m+5d3A8kJI6F7scLtVBrhp47wDkD1hyUcqBHYbYImRrEQ6DlDT75d0+Rm7kYC+HXgXcjcgSClo4DjwOf4ud5mL9sl+0/hrnAENPzQ0z/O1UTNpwqI8UBSsUQZjlLaTZBdSFKMp3FDTUgaxoxH0QMHGEJQYZSfCdWCUMkw2KFXaumUJmLoqT6cM9qqPNxQvkYhj6GbVewXRfZ80g1JnBQUSUL1amiEMExKngWOJZNuWxTzqs0NWkk4vIiGFvMQbHikK/qjMzPY5fLVEoLVArzVIoVCgs5zLKBVTExaga2o1NbMNBUjcZImnA0gh4DPBdbAjui4OigOiGinoTN+PnCjL5NARoSPahGBalaRI42omhhQaZC4Ay2DZ4KhgZqQ4hEJoQWitK+GnQDaiVBGGtpF+7N8SMCS9gRgb410JuFFXHB17IQxW0df3kMfGxPFizb4dNw7FkovFCE/ceh+mG/na+2aYRZiUI3VcJ4jCKCwWUELlTk56Ul+9oAYwPvOsgd/L7DjLUHzXmJ6Phu5gvzTE/NUDYV2no7eO97foOuSIQIF4fGZKBVgrZO/yDjwaAOn/7UY7zu+uX8wl1rkSSJr7x0iP/xux/lqYe+ecmmbV3Wz8p0C/p8Db3m4NkVVNlD0lyolMEus1AsUdWLpDs7MeUMtu+k2sBjwLYcbK4WuXOkwrYnh8i2ShQXbGTCPPYXt6Ot7yVi2RTPHGLNGritO8nyN1yJsnkrhPoRDqUHmEjYhFV4pwJPSbDbHxe/gKhNdHJJ2ysIcuYNCJd22O/mVsTBHmBjTGjSfcVfFHdUYf+hef7xt7/On17pccN1V5KOxxk7OYE5dIb4M/tQwhqGa3No9xleOlajUnJoV6CzDRrCYc4cP0NuYZ4VGzr4p1/9JLe/525WX78Fz9Y5/Gefo7pQIJlIkG3poLUVbpmDWVu43BFE/PjTT51g99ER3rn7BW748PuxjxzDRSJ+591E3ngvqGXI51BGzrK1FV6a9zhlw4jfHzlzGNkaIRrSaGrtY2J+FNexz5tHg4hDzkvA3yGWhRTEYvA2hKcZAjp1RH7+OurJrj/BTOA5xNzdClUHnqnAddeCVIF4GWwFyirIIV822QTLEJoqMiI7Dl83UFFFxlk+D81tkMiKYocV/+scTwAINuKcIGv+76aQNgikEFwASUx8F3+z8ccqktDO6QpDyxUwPAnlcXBnAAPsbrAb/EE0DlyHIAEUgd3A//AbswX4c4RIYCC/5iBYw8sQJ+YlPqmGKNLVGIUXvwFGHLLL4MYVIpPwK7tg4UVwnoPqteAVFcQhqQ0B1UbFOmn74tNuDG6XWH0P/Omvwo1ReEiCH87Co+NlHr1vLQsLVUzj1Umju2yX7WI29IMfs1fKcOSXPkR3c5xSTsO1FCRs0HVURadWsZlUxT7WmQC1G4FWLSk0V0bEgvYCt7znQxRNlcf/9VMUFi489H7iz/4AUzYWc3/StyT4xbs+zJqu6xkfn+FPfucvuXLDdSzr76K5J0JIVhluTHMGEY4CkUR5qgRFHe5pueArLmkKYqeKcKE+rAEMj8PMjItVrtHdE6e7Ba5Ow5UboSrBV798gt0vHWdyfJi3ve2tJCMZ1nUnuHpjF+uOn0JpaaYlIhPtg0wT9KqIwq8X+T6JegGnIPsgKO9zfiGxQGohSGYuAqcs2GfAsgRs9PUSg0Jqi44idX6eu+T3IPnZtqBWk2hvayKelEmEBKzTABQaIZcPky9KVKslbB2ktAigFSqgeZCOi5qWtTJUMtDaoPH6tVu56a2r+O4PHmfk+POYZ4+LRTrpicU8FiPc2knzik2YZo3iyGHMM2dwT46AZoj3WKCZIa6+cjWR8FL125dnu9jLHCe44bzn3k6MK7iO00xgITONQS+DjCOAwj4UrkLjcWqcFo+O+xB5Kh1+PwbPpAsBZ7RQIMozWNiLGvkF/306deZzE3VVUd1/RoE0hQznFKE73xzAUuCKjfCHX/1T4p5HIqYyHIuwWoWJ6b08tfMfeGHf5ynXirg4zEye4Dv/8js89q0/JiVL3LhsBe/cdD3vwCPVHKalrQ0lleVPX9h7iW/1LuLShwlprbz5XX/EM9ueYqFQoDg8C5fwdJcndmIeO8Ht3e/l43+1g9mNrQwPHuUbn/8y669ZwT8/9ixb1vfyrce+ycHxOR7/py+zb/suzpwYpLOzk3w+T3fnIOFwGnjG74kJnvjhl+jveHCReSzRgEIzcFIkrpVrVM2f994ZRzy9PMLLCe4/mO0BhWAaMeOCkeMhVrCgPK3nvzdCnZLgIjzjtP//gK4Qpb5ilP025Py/x4B5X2PWjyxXTfBaEDpMMeDhV78bXoHdfP9Hufvdf0hvBpqaoCsCLaF6wAlgzoD9c1AagROHhmnr1Lj5rk56I9DdCKbPfD2qCl/MU3xmug65CdAkMAyHmZkS337u60wfGoSpV3ds2MDRH5V57E+meOOftyFJEi5w7Ai87u6lij0NiFogA0CElvQGbux7JzS3w7t6aN73n7nJu4IvPvfX/BrHmfCjlR4e/2Q+yH1nXk/f0Aqy7aCtgwM7RVZbVz/ccS00hKG2AEO5HAceey+WUbxIa7tYLFoEiPDUo8BnqTu9Wf89NyB2xhBijD2GoMr8/Aoa/Tzs/IzMy3bZXosmAQWmGRzfQ6kyh2kWaWhpJhVJkAxrZBpFNuoFO22UehrNkoupMUh1whVxSDS0MT2ZYXKiGZQIU+NjIJWRDYtwOCJkC7CxHQPb9xIVVFRJQ1U9bLvMQkGlVFHRFIExeJZDtVYjny+TzxeYnR6hNDdFNTdLLZ/HzpdwDBvXchd9z2Q4TUMmTXtzC9GQRMg0sSwLDwm9YuA4FcLeLGEmaPJv7eIFdceAh8E5SHOpj7ZUhoVYmlAHzC4IcLVkCYKY7WMTahSiLZBuh6Qk8Azdgbe9C+4Ji71iDsFZPKII7dlTLgw7UKz4GbyhOmkigiAvhMMw2wonG6EaD2OpMUSp15+HanUNS5JINnVw82330tO3imgyhWXZTI1NcmD/LibOHkQvDYB9hFczI+a1AcYGFIUzMzB8GEa/wYFHpjjlTaPWZtAtm/lChZVrruW667aydXWcsPJvFASR/Jqoip866Akn5P7XrWVZe3rxTZu7Wnnd6z+IXu7khW3/30UvpTkSquXh2TaOWQPPQlZkFEWmMZnGqlWxJE8USUnHuOLG27h+royn1zhWMjEQBRAGdI+SJYRJolXYnJa4dXWW7BtuhdJZKLskWtNcfe9WEqtaSa7oQoppIqccABdqZczpKZ79cZGQ7NAfBkv3Y/oS3NuT4apYiG8MzLIBgZcFkvYlBD6YBdaHVX7r/qv4748fYbRcpeqK/soAPQp0hj0akw4/GDDpuTZJ2YvxtV3zNGNRVivMyTKTnkt8tky+BCkJmmKQScL2nWfo62tk9c3X0Hjb1dwU20NrWoO5eSRDp6OlBXv9lRTnCxzZeYBjRRhyxYLQIAm25kgJ5kybp6fKjP9olHeZD7IsLdGxdjkJJQ4LEwzt3MnQ/iGO7JrmyYLHiA0Lbp0M5uHgeg6y5dBWmkeKRilrUWqui74QpEE4+Edv4BPAe4HV4GXBjMKRMuw3wC0hojCruQCMDQgUsxcZPKZ/adWH0m+HE3sh3whNGWjICPYBHhgW5BYgGYaqf2ZWFIhHxGUsX0cxloJIFrGKqiKNKoJwkh1JLIrhiH/kkERkyXPqqbaeJ9KCXT/iJOFXKZyCbAfE00KjVlYhlRKf02NAWAide/P+YCogTtAx/+d2FskjdCDOOr7kCCb1An0Bbcx/UNWyWMxNv0BC8wZQ40JWQJHh5Ldg9ofD6EcmYSwP46+HtTKsUGBWgSNhcS03J+hkjW285Q8kNq2Bdb2wtU0EIXb+/WfZt+sAVtlkemKcn1xC87JdtldmjmEysHsvf/XRj/APf/93uBWd2tQc1dIMETmBHW+ksdtDDqeo2TIZIL5mNfKdN1E5soMkgQMJuxDrfKIjzpa1G7n7yt/nzOl384Uv/yWTk2cXHcVyya+s5G+OtUGDXdaPOBU/TClfJIFLOtlAd28zzW29DFXgS5/878yNnFlkOdaAvClSg74Tg7/+678mnU5fcOA632kNflcQ076gC3kWatDYCq1pSGsSuqWRTcI3vvIExw6fwjZL1Bji7EgvitJA77I2rr8mTc1OEU1qzJRV4i1txBUIJ8GKgxYWK7En1X3kQHYgAJEC2IV6d1xQAdpAwDkztsAQHEvU6Sl6ULTghZOwcpkoKrBUTibQiq0iWGVBl4eoB7cMx8M1XBqXy8RDEq4kdhsLaExAJiIzJUlUzQpGTaVUTWCFNFQL3Co0NUAkJn6QhS8ST2okko10xG7mpYE+Tp8+zuj4SRacKcziNK3L+0m0tGNIGuVDOzGHh3Bz8yDrotFlQActorFl7VYi4aX6my/PDCwq2OQRa2sbArKKq1E2tm2lO2biSGGyhkly8jg1WSba0EY61Uxrupmka/P145+lpaeT+259FzcMQ3JqAUnVkLQoydkK8cGTKPZhQkyTpBmPlZTYQYRhVgMyGiEsZB/UHEdsAwHTI0gMDpQ/z5fNWGoeYq9MhWBCTlEqVZDKFcKtER55Yj9HTw5jWhVMq7L4Gdd1MGpFWmtFru9axm39y9l0580kjXl+vPcZZhdKLMzX6EZoWr68Y4ON55XJFTWSrZsw3UOU53YjmKAXAjRz06Pk5ydZyC3wzX/6ffrWb8SolJgb3Mvx4jAN665nrredQryJ9auSZP/zO3CqBQ4f24U5JVh9k1OnUJUQdc/JxTCqTE8tZf0t+Hfx71nQIgBHZc5Nkg/6IYDaIwh4cWmFBAvhlNQQA34BMQKWlt5LIyB8CzErC9RDK0FR1xn/8xoinBBf8jdDOFa4QBakLKIK9SFEHsPPl/LVgiBVdCLuPoCZa0CVKH2/+FH6b3szfV1ZWhKCjS+FoCSLjKxDe2F5H2gJkEMe+bzL9ieewXQMjg6s5xMfv4l2WRKulSQyJDwFioaQgjUWPCbHapRyM+QLM4zMD3P6kYeoTk2/MvJnCrqT0BRWiMghdp4W2mAHz27nqzs+wRv5WwC+8xB8/QGYW0rOXswv66CJMNnaONr4Y1QfKxF5+2+imA7qeAmDCW7GZjei7BvAQb5C4ZFp+nK3sfbtd1DKQjYLsQ7oa4NKEXqa4dTep3nwH76IpV9sLvQi2LlBeO5R4BEE2SMAbm9CsBU2I8bRPPVCKav832v8R4I3/+O09LL932seHg4eOpZbplSdZ2JmlOOnjxFWZXS7k6rTRHunKHYtSSLByHUFQcoyxY9pQiLuk6MUoW0qA7KsEIpEiCQkYg1ZQgt5VFPIEXmui4qMJym4qDi6iV4qUXA9apUQSshFckzkUAhV1VAljYVyGdc2qRTLFBfKFC2JUrlKWTeoGia1soFneLiWh2d7uK6DjYNnW6iVGqpaIB4NkfA8JElG0mLEmlRU26VimlTcAn2IHdZA4ESJc/orCFJWCes14likU2ClYO0qEZOs2aAXYGxGEAhcVRQTD4VEEE/2axp0JYUWrCbVSRIZRKacB4wqsE8ROFmQqRv2W2B4UPALqTV1gr1eo2SlKT+TQezrr37gyvUWMKwZ8jmPZZs6SPYkCMU9UqsbcDqaiOxbxvzZPirTWcrzzyI8zVee8fDaAGMlBGQ+OgoDDwNfYPS8YubRWJSVq/q57eYt9DZf5BrnXW6p461I0BiCO7YK7o/ngY1HYSzH6tVbKdyTZPLsXlwXpsfnqFUqiIFoEtUakSWNarVCKV8gpMlEImE0TSMejmKbBq7sIeEiJ2J0X3UN142OgiThjc3SGI+jaGEKC3kmx6eY8aClAuuzEplGiYInk5Qc5KhCpC1Fb3YlrFsJoRhE4ghn0a+GXSpiDA5z4ESVlrQQQe5HDOBEBFYmVbpiGi+FYYUhtv8xRGXgxX6UoCei8N4blrPjxBgvnbYZKZiLkyQtQVaBhrDM4xNw3YROW9zl5GyVY2WPGUxm/Me1ATGB05pIq89bMDs1y8rNy1h21Vq4YhUbJQ9qOp6uQ6VKtqeHhWgjlYkSw4PTGLJwg5OIaEqDJiJNZ3SYND1+MFgjm9vF1lUNOHKE5qFR4oUxJp/fxaFnT/DcniJ7qcsNLzUPcDwXt1oklkoSiUWwFJmyWWGh4uFgIiZzCRGVbhb/d6+FfDMMGlAqgXOxCLhvQYbcxcBYEKfUU4izwxqYjoAhQzUsImumLnRcTRf0qngGC0UxfhNRiHlCN1CvgWVBJA2k/OJtnjhAap7vMAOOLDYKX/IFF3ELqP5RxhXi4A5CkFyWxWZTLYnrO56QQXNcod0iqSCnwYqBfQa8gLEfrOAe4tzThaA5BaE2HfFgJXx0h3rGluI3LAOmCqYGVhjSCWhaDbGQiFDmPSFZ4Lygw2BRdOYMcC+CBBGcFz3I9Fo095l0tGi89b1wQwYyRZP9Ly6wzTzBnm8/wOkdOy79HC/bZfs52PTYKA//85f56B/+HookE3YhNzdPIi1j2BJmpoBr1ECNsVCykHvWEr32DiryDhKumCZ5BFG2BEyMHaK3K8L63hRtbRv5/jOfY6E8hl5c4pQENHggYUWZPzNIURklGk9CKspo4Swnp9tQxyNMOGl2fX8bQ4cOIOExXxNrXTiqkUilGGvvx7IvDSV5ntCpNk3xf0kGNSTWIdMVGlGS6TE8tIDmuUh4VFyX3rZmDh8dZfvTx4mrJtGGU8Qb2+jta+Sqq67gitUJLEuiUIOiKbbDKKBodZJC4LgtTT1nyetLJWACn2CpxqiDWE5OGDBti8DYwRyEpmZIxRXS6SbGFqDUJfa54PMmdRbsvAdlF5Ky2FsD9m0NMFwPx/ZIJEURpOD1GhALQ0yTCMkeTq1IreRABBw5SSwewqqCmwZVEwUTqiUImRBTIBMO0btuBVrDCrI9K2ieHGa8cpbRk8fJ9vcTSSUYHTlJdeAETM2BY9azjvwsbEmWSUdakSX15QjvnGMRVFxk5nEJExTHghnJYzpiosc0ClKYqqQgy00kFAVLa2cu1k4u1UqHA5ISRY6naOhYRaIEkfIMaihKKJIkVXFxpTC6rOFJs0ScFLAJmwFkpuimCYiAFiIiyaRcj6QlNiObIlEqdNHOS0xg4Cyyni9SrPicew8DR48NszAzTzRksiaWYm6+RLV26cqd3cDycIS+tla6rrqStrk5jp4a4Oh0nuMLc5fM3rrQVJAiuFKc0eFBXCeJIjlgTXCpYhLFQr1iyu4dD5JIyqRTDSQTESaGR4n1rWNqZpq9h49zQ28bnd3LybRliWejXL9uCzU9z/jEJHNzPwk4NC7Zhp+fBd6LQp3V6vrtCAo9BDM7KA0SzPJAMTiA4IP224iREEY4EA0IJ8aPUCwG2pcKWFSpc7BDoPkhK7PEIiNXioHcAF67uL4XR8B8SwXBfnaLIyQv4tSL0/X4P33UE42qQFEOIbdtov+OXyG6ZhXhKDT5sli2LN6jepArQdYWxXaNmrjA8KkB5hd01Ig2Wu9aAAAgAElEQVRIh0gj1raqA41hcBW/3oEtNP8VxeHkwAlOnzrETOEI8wf347k/46E0BKRk0i0JeuI2XVGFmBxeBGPHCsfZccrg8N6/paDAQ4/C975zqYvptOLSZM5jze/CaVoraL2zUzC5hzBzXE9d4mQWmOIlpg5YjJYlMr13kFsvyBJtDbCmDcZHYGjvKLt/+Cwv/eDrl/jeTv+Kp/2rfgd4CuH0yojT2j3AzQg29SDihBYAu8sQ4yZPXRDisl22y/bqmMhosClSs8LMF6KMTgyR0BJYjkTZUCjkFNKZEKGQgiQrKLKEZUCl7FAumRQWdFJxFzUso4YkQiGIxGRqVYVyBSzTxkMGVUUOhVAsG8d08JDwJAU8Gce0qBaLOIaBokp4so2KjayoyEoIiRDTC3kMs0YlX6ScL2PLUQzToFouUi1X0CtVPNNAcgRi7Hg2NiamY2HWLHTHJBrTSMkyiiqDKqEoFnEph04RFwONuktY5XwwVkIsykkitkJUAi0CcgzaV4CcESQqqwjuUbDHwDAhGvXrQFjg2IJQFpOgJtVlvMKIsFVGgpAkMI4hTewzsiz2uSRiFSy5ghjiOBBLQ6JDxchFuFS20KthHnl0/SyTowO0F26kOemS6dFoiKbRk2l0K4qixJm1XMrzB7i4SOhPb68NMNYEdrpQPAJ8+qJv6e3r4e67ruW+e69/xV/nAEUX/uGLL3LjHet5w5s209zyLLoOX/vMo5w4fBAYAWWK3v5biGZaOTs9SnFkhsaWRhoaG5AVQe6WEGXhZVkiFmsg0tjOlne8m74tJ7jzyG7uWb+eeFsnL/xoO1/87Jf4qu5xO9Cru8wPz3D4rz7DNR/5T4TTChKGQNi6ekBpQ0yGYKrEcCZmMXbuowRUCnU9vDDQ2AxTk3OYFry/TWJ4zENx6nGDoFCJqkAsAq5Z489e182DMfjq8xMMIA6m0xa8YHnEijp54Gtfe54rUxLXrwzxBwdMHE/EflcgJk0nELFgvgg78/Ceq0I092fw0gk4dRKvtwvJlZCKJRgZgUQD+770EEOHh6iU4a5+sE6CVIOUC/ki3LYc+ufg8KzI9N+/ABxewCzuI+6VWb/hSmojJey8RQQxFYKF5fx6bDqwD8gUS6yPurQ3JLCXd/LUUZuKO4NzTvWpfxa94LbBwmo/vzU4EKyg7qQvWQTu8P89R6D8PJuhXvHgY4IZa8mQKED5jGCjhlOQToqU1EJJLGrZGNgVEf3PF8FyYcVVUFIEk9ZzRG0yRYKIJgoy2P4AD/lZq4YJk8OCUev5r7W0IDYOByRNqDL0bRC3aflKDoYpSNlRVWjXzhUR8zTp/wT5olXqA1FCrKAB4hHcc+Dx7vFfTyAGUSciJTskAOrjwI0piEtQc2HQBLcbiK0GaXX9fPS4/68v/KemYcuHWrn/Y618wPOPcbbN9sOz3PVLT8L4B8G77Nhetv8zZrsO//TEI3z43rewMqmi50dYvX4V+XwNVXWglqNjZZKTx+eQmzYQXqNhJf8ct+hR9XzAELAkmQc+9fs8AIQjUd7/of+XljUeRTPBmT0FwV46j6Zy7e3ryIQzNKXbWLF+Myu2rGTf4Al+NL2Lx76zh9vW3MTyTBftfTIhbB49tROAruXtbNi6hbf96ieIJ5eoii7RDwyY9jM6TE2J9UQNQzoLfVFoDzs0qy6hjMzH/3gn+bKJ6XkUzBr/+Om3sfGaq+nv3MTNG1dzzevjmJJEzfaomSJIEw8JFkLnkvsJuHEBhy2Q14e6M+NxYbw80HddKsHvAQeAAzlocOGdbR5fOWhx8Mkn2NCX4j3vegNdXSqTIYmwB82S+L4KviYsQv7nrAH9GvQq0O4KVoUu1SGcsCR0uoOiTlbQfhVU2aayMIdRXcBxLBTHpSHcRDwKYUVCDlBfQ3xnpQSVChQz0JSGu9q6uCfSxYx3I19/9ARVx6JUnaZUKokNFOtcv7UKhMAKO+w9NMLd1ywXyPBPYT1Kmhk5wbRbpG/xmUgUrALbBv+Wsx78GI9TeITxMJGYLXtUhkUffBCh75rddRR712PkEM55A9BMhGvZiEErqehdJJXX4ZX34ZKngIFDK0KIHDoaN9ChZdis20zNHCGNzUF2McBhPsDbeTefx6S0ePuBru35Ji15/Wtf/BcKs7OsX9tJ3xWrefdbb2Ho0A94ZpuEJ4EsSXiuSAuUEeWlDg6eIDFyhtsUlcJ8ASXaSi46y76F/EXFCC40BUiC0oMbWsfpPd9CRHkvDcReaCl+/f3vpHP5Or7w1e28uP8pIj1phk/v4+gzj1F8wzspGiqD0wbX3HIj2x78HoMjz/GZf/wS3/vONoZPzQg9ziULyP9ZxltQHRTErGlC9HgVwYjB/13hXK9PQ6TmGNSLs3Yj7iZKPT0nixgRZYTTskBdpsBFOChd1MvCNQMrILtGRKunTnNOISbPAdcA+QZgPXinODc1/aezAFKWECPhBoRIVqvf8ph/5wHTfwJBkPCiKa79xT9mdk0vdiaMBrQlxJ2W/J7KyrDidnHHZ6Zh+LhEW4OCHPLo6Gzh1lu3LrZjpgyTZbixS/CKW+Ngx2GhRaK7N8l3vryHZx96EKdy4Ge6TwBJUZCzKuq1GpvSV9K7MEfKtnCRkaU53EB6bM7jd99nsyOhUjv7v9l77zBJzure/1Ohc56cw+5s1GyWVlplhAQSSQRjMLbxJRjbGNuADReu/dgYrrH5wTXGJIMB/8CYIGGEkJCQBMrSBq025zS7k2NPT8eqrvDeP96q7Z7dVcIEcb3nefqZ6e7qynXe837P93yP8gw3qAPcTy8ztAGlSJj0hz6MUmiCof8kUvoaLwMaFI2kEHQg+D6CaUCwG2M2w+F7HE4qKkvbFNoVWNIn6O0U/Mabv8ue7Q8/y5EkkaIrO4F7kWCrP1+IAn+OFJRroxYIJ5FVd2HkFboSCd6OIkHdXx+7KFdw0V68JpDebx4TE8epQBHy+RYmJxJUiibDw1kOpeM0NDSSzMRJZSK0NOjokQC5uSLTE7MMHT+FbRsEg2FUVUacoViIaDSKpoNwqxjFCmalgutIMSxN1Sg6DsJxUVxHtpzM5QgEg6gaOFTRsXFMB9sVVIWgYtjk83kKuTzFhRK2rWFjYJQLmOUCjlXGpkIAFQ0FsLExsHHQHAhUNKiAjo1JAYN5YsyxlCpJZKylIqfljcjRbrEFvaVWktbSRESQahXKESg5EA9CvEHKNNhBqd+dnYagBgs5SWxwkVVmJjAl5PYcJDDrj75hZEX00nCtsimGTATOIlmxxbKUW7QtSRyrlgW/KFastDxV8xBnjn8Jd8+VLL9qDU3dDZBQyJnQ0deCnTcoZSfheDuymuFc5OmF24sDjHWRgpBsf8ZFfu/t/4uNm679uWxOA9KK4Lav/SML1rt5/Rs7ePcbZfnSn7zpFlz3Zfjcm0BQ4+De/Wx/5HEuaW8mGAxi2zalUgktFEJHh0AERVHQjSqGUQI9RKSjj3QwwLb5GZzHtoGZ56bXbOGbtz3JncC905Ccsblszxi/M/8lLnv91XS/ZAusvBTUJGdLoSghb10dLdNMeNkq4GmGkIVjZ4tb5mDV8jBLlqUYGOhiz549HHza4dSUvMhvb4S783DYguPTJp/+0N00C0HRFdT37vYnuiYyj7sP2JoXKHurWAJem1HoFCCKgqVNkErCvhzsmJYPT7S5AXdqivlHn8TGYXh4mL7BtTStWg0bN0NXN9dnkvQ98hjb7ryPU2dA2PIoxxRYqcPeY5JVlUAW8xwAjpThR0cLLD2xm6i6lybHQTiCqboz9WyWA56cLhGfLtOlzNDvRpghRZ4kRRaotTD7CbinYOIQXNEAZwpwPEutxZWnDwASJfhW3U+fzUrA/ci46z1gbIHTT0HlODhliDRC60bIFSQAW3EhfwTCDVAMQsWQJQG7JpB+qASiKlmrK1dAlwJxb8KPLhmuAOEArFkn31u2zFi5Kji6zEKd1U3UJNjra8iGw7KxuyOkXEB+hpogou8Dm73/LeTN2IZEIPwGxo3UCCkR4DXehTCQz7zfY8PPFIzA1iZQ8sAucP8RxEEk/WMTcm7miyLHkSKXn4bta2FlsubMPnoa7vnI+zh4+7+BYYP4ZbN6LtpFq5lTtfjmez5I+6cVMskAR7Y9zL5TB+noWEMi007KdEkN9FKySwxXHMyUwtKP3cgTH36YsZLFDmBU0RhY9zuMnfwJ5cIYplHhy//8N2wQNusDLq9ogv5uOHoEYlEJij49Do/853YsFBRFQVW/haIpuK5ACIGiwpMDEf79K3ez9pKNgASOAVRVRdVUdD2Erkkkr4oMOyaHpc/WdYgloD8DTf01aCSryL+f+PtP8M+f/QaXXf6XHHjkMd713jfx+rdcR2+PQAvpvPZVazAN0IRK0cM1ijmH7LxN+7qQlIH2zqHfP92HSnxXdG4DAt/1aCwObgTS7fhSAyDDzZcAYw7kXBgyK+x4bTdGucyT8RjHv7ac2x59nB1TCkSgL1PbHz9F1w20Rrx88hh87z7o7ILXbZIAJWhnNXRNanqmJpCIQVO8Sm5ihFKxSKpllnJbD1Y5TG9fjEoZygYYFmiWTKgFQ5IdTFgm4VDl8bYDr75xOfc9uJ9Tu3dTeeBfpOaCn6H0pa0EEFGporD1wX1UVne+YDD2C5/8Dv/xzS/zyc++lz6ka98cfymbMq/EbOsjeHiKXGUne5xdfIpdvJf1OBgcZJ7vMckCUtlxHgnKDlJT+RzF4CA7MVDIVO6nHZ1VBLiLCsNY5BF8gX8FYG5KZR6FWWAWh8uBHC4LOOT4Z6axiHnnvg0J+C5mf0jTqHXvver6K6iUSyxbmmHl5jSuDs3Nfay55BqcWJjLli5hz7aHOD10FIHfhAwO3nUPu+7fiWa3Ykd6cKzNrGMle7j7Wc5kCJRWlOXvQoz9BxRPgV1Aij+c4oVBG1n+6tPHSbdGiGgOn/7BF7g0qLNt5xm+eMfTfPG73yeaz9LWEGXTegm2zQ2n6Ar3s75rKdMnprn22kHGTg2jmiZLmjPsOjjBJL98Tuz5VqXWrKP+nNSnVuqXPYO86kkkb7QJCW5lkUdTAR6jBh/52eNj56zLT9/AWdbtxG97693rveIg0lLaimXgxpDeKg38DnAbPwvD8XpkAdAaZJjlh0iV2p7gIKHpKby8d2KQjt5XMrJ2LVosTHsH9LTU9JIjdUcCkurR2wzdN0pW/x2bliNCDay6tOPsfvR5jV7rTUeuc6wEH/7wX3DNVZfyoY+8G8ZO8bPYlf/yL7zyzW/ij1SFeyZUHvrKR5k8tIN4cYGXpVSeLLjkHahUx3nwwJU43AGi6xnWpgKDNPEUbUyRtm14aivc9XGYOHp2qQ2v+RQ7Tozy2MEnmGAbfxpcSZe2kjGzl88+9klau99P36YgXcshX7J562/ew/Ej/0at28aF7DByDuuzpv179Trg74GNLB6VdCQMolBLEgSRIhSd3meH+XVp+iWoMbdLz7HsRbtovzorY2Oy4OY4caJCZWSceKyNUKqFeDpOWFfQgwqBkEosHmPJ8iW0t3XR0tLCsiV9aDoYVYt8ocDExASnjh5lyizhWlVsw2R2LodtgFA1WbOv6YTCIRQtKLUzHYd4PCTZrTg4mkMYQSQYREVB2DbF4iyuIwhGw0SUAOPHRzCrU9iugYOJQ4kiOQIIBDZlD4RQCBAgRJgIYcI4zFIhi0EODXG2BaaN9GRtSFTjfG/q0/xsVps2paLDWBZGR+BMEew4iCikdFl5a86D5kCxAEKXeAW6jFknq3DMgqIJrgVXt0GHUmvH2ScXJU+tdiWPJzLk4RZGBeZLkM1Ccdpnev0irQqMMPrQK/iO/WlOHH89b3lXM69aC3Mrgpw+vZRdT7byxWPjMD8iWXH/RXtxgLE24N5OjfJ2vq1bP0h7e+uiUMyCRY05nq8pCqgo/NU//S2rB5awol8n6FUoBQO+wljddkzB/GyFUnQWoTZgK0J2pHd0LFz0qIYeCqIHIqiOjaspaMEAajRMItiJo4QpK6DNzvC2VsgkwhTyDo4JL7m0h3SDS2F4npnHdtM8X4GOTinQFAxKIdZ4Bc6cYGHPAY7sOMh+5KQ4DCxT4boU/LQIj52q0jKdY9lek8MLLhM5+aA1K7AiAX3tAUwEpYrNzpMO+5A3fVSFV6VgZgGWdKVpbghyZmKao9PQLuQye714YEdR0Ab0ChjQYWQaxioyKGwHhobmyU+WScZD9PTGefzxWbbvfIpM+1F6B1NsvHyQUDxGa1OKSzcMcvLgASoOLO9r4KbBNtoaw+zcd4gjwwbH5uSUREeG0AsuHHFdNFx8pTu/gNAvYjs3V5LS4JaMwsCyLn50ap59U0WGhUDDwMTBOltw6gfmVXBGYfqdsOZ/Q9DXc1KQQbUml1MD8Fpk34vRug36FN0LVfY6yGT3HeCOQLHTYzbkXMp5mHBUQu1gDFk4OQVN0Ym/UU7Gq16dmuuLInptyx0Hhmcg1ApqXFL+VUXqxzpeuUDBACUipQycgNfSIiilCCwhnaeie0xbW5Ych0OSHVu2wQ1QiysN5MTeOw1ndWJV72byL0AAefF89KEZGWsWqcWc6br1usAYuH8DLFSlRsHxkPTI4952/DnNarjsRnj162DtWljmNb45eGaej/zpnRwu38vEoe1UKhdDwl+K+TPFi/aMZpsmt3/xS/R0ttKZivLYrid49wdfQXP3AI4a4sSRYRrSDZQti9lKnGWXvR2hbeUIFvsBVdf4nd//A1zrFZzZfT977/gqa5wqq5pkY5FkUDZcSTbKREogDC0OXJNxKQYhp8GIYvPAHqmDFVAhnQxy8+tupbWjnUgsumh/XaRvmLVlMBTVIOSVEHU2g+rKJI2mwu5p+NFt91GenSMV0qkS5D1/8FI2bLiOd729mZu3XEvxHYMsWd5Fa5uO6YBZBjWgEQnK8teq7mkfGirCa2CgeqiBTU3R0WeL+bqt9XUK1br/6xtr1RcuS65CrYg5BPQ2QkZAVA+Q/tNPMvfT/6C9v51r3vFO2lWF2TmYSUEpU8ve4603pNQkDNIN0PlSKS8TSsBEXhCOCAzUs/k6f5sAiTikGwRly+DEiUM0Zmeolk0S0Q6CS6IIV6HqgGlCXJf+Ww9JAFxRa0XbBRMqZYWxOYWpiXly4xMwVKh1Jjt3YIzHiS/p5b1vuopMIsILtfCKCKt6VvJqbqHMvSwFGpsaCW5chf7mDajbDRpHNtA89AQ8vZd1f/x3hGIhxInHCX3/47x7/f9HuLONamuIcotkQWijoFZAqTgopxZwOtPMH7sLzmynixSvYwuVTAtWIIBTzHGw/E88Ikr0kmI17exlmmnm0XCIAcexUIAUKhkUKjhntTUvZD7ANTeXZ2zkNMV8gCtedT2nz0yx99hpzoyeQInH+ND730NTKsbBrc3Mnhrmmg2XUz2wnZHsFI+XJwhRJeQqtDeuZM3q67jy0tfzzW99i3z+IDJjWW8WiBnE2LehMoqMoib4WZ3p+IGvMHM8ia5V+Phv38Erb/1r1HAX7cklPH74m2iVg0wFXYaHnubQ0QO8/W0fp7fvRuZnXe5+aCu7D54halVpiYaIR+Is6ewgNzOLWX1mmYZfnp0LTD8bD8+/8R0WyxpUvPd1Oi7PaucuEwXh80vnkUGMXzIZQwY0fvY5hJzqvgpJJxiGRVVY51sEyZscQBIsliJhX52aNIqPi/oEBBM5F+hougFt4CqKG65mIhCgI6kQj0BDXW+Nc4s6dz21gGHDhg0pZovwlre9nGg4wMCSmpiHeo7mW/06+uMgwiHiL9uE0fRZPvbhd+GcmZGdW57LFCCgcMXXvsH1117HYDxBRcB1HeBe/3qORpqY3H4PPStXsnP/KSjJOgPHPcKzs5AUoJUkIam5bhnwo0/y7cmTxK0qGwnSwTq0N1xL4nSY9E/WIR7dxo/sMSJOnoo4hOM2Evnpn9H/G6Dn4N6nDU7t/HuM0hku/GwqyHthilrdg29vQN4Dq6gp+5p1f/PUWg+mkFc/i7zSQaTG2Yvh+Xt+Vs/VuGgX7cVrDoIKhhhm2jTIOmNQjsGshqq4BNQAATWMpkc4cuowiUScZCJJS0s7HW0dRMJRAnoATdPo6G4npCsk4lFSqRRV22JmOsv09CzTM7PMTGWZnp7CrLq4qISCQeLlIJFgCF3TEIqDhYoTUb1G3gZV08Y0Leyqi1W2QJTRz0pW2ggEKjZVJDgrqAAqAo0qKg4aJiouBRxMVARx5Kjk9zUAGbvG4SyeUjMpUQARDKtEvmSQXYCiDYE82GUZt6PAQtHTiA3JCl3HlZVhsSQsWwqrAlDSwPFaIIWR0MA8MhWVQSb3GpD+o4qEScpI7EHLQCQE3b3gDkPe/GXx7wXCqTC17/M8MfUDhh+OENMvxWreghJdgnBSMij/OcklvDjAWBevrOfMeV/pWoCOliV0d7aQOGfiYAopIuxUoC0hQdbnbwq33HwNjd5E9tkslUrT2dXD6PguWjSFsOISUkDVdRQUsIOoQYFAQ0FDUzRCeoh4JEEqEMbVowQ1HRyb69eO41bmmRNFqqpNZ1yg6QEUglB1EVNT5KYnyc7aKIEwjX2tlDVwTw2TO3GGiTPjTCCH8VYFlquSgHjGhuiCC3mTWMDEjkB/WCZitIrsmhqOgK5KbdYNcUhmEowWLQoLxlkCjS0EjisZkWGgLyy3NWnIUGPckqGDrsAJQ5bUjztyshwEnpoyacekJxGkvSNKMBxhbirH7OQM+QmFHoq4Da2SqekKDhtQ8Opdg44Uo75kRStapETpdIUHx0tnHYWv7tqIDED9yflzmQv0BQXdmrzDsmfXVh821N88ZajcCZOboeCzBKreWfcfmYBHOch7sVJCbqlHlZ6oHqA9a0Ie7O4KIudgr0lCIwQToFhQmgUlDFZWytQ6IQm+2q7MKFFFnugkNTKHC4UFqUUrBGTCkPYyU44nZVApSx1ZJVA7zEBAfmcJCWQ6yGtetWSzgkhSAi1CQNlvwuWTSkp43XNYLMboox7+XGgYeRM1Im8Oh5qObKBuWV8Y82EB97mywwQlpMteIbtO+HYVXH81vOxGeNX1klW177TLqZFD7Nq5jR/+8G7gx7wY+DwX7aLV24n9B3EqBi3XXEXH0rXEGlsIxGLYps3k5DSrGpswLQXDjTHfsJ7o4FLGD53kZK6IqqpsuWYNI8OCuaEEGjCoSzkAXZX+wc5B0AbHlHI0q5oh3QmVEGRVWTSZbOjFDC5BC6VIZSK8/KZbSaUyADiOy/S8STodQtfkM+d7xYmZIrm5BbKT05Tnp0gn08SicSKRKGpnPwtzFUozJsGEhqqr2FVYvnQljdFuNg30oLX0oqhgCyhW5aMf1KXvMXSvjF8BVBXLi7V8XVgfdPR0/FGpwR31TNf6Fj6+VIFfTl7PlPX/9wHa3gjMCpizdV7xmlczmqyQ7mlm1XXXM+1CKgLRYC3561u9Fm0AKffS0SeXO1mGXLmKZZXIGQ3oQQmAK0rtuFQBomozOzvD7Mhhqtlx3IpJON7Hqk3tKI7U37Kr3rFZ3ljgrcP24p+iAbNzgpMn88xMz2AUslBxvDqwsDxiW4FUAxSLJPv6GNh4Fdet7CT6woImaSnoWdPP9a+4ha33/BQVi6w9yanSbhpnHKarBgHHYVYUmQYOuLOknAjjbok8gqhwSLnNOE6EilNEUEJzVcJulIiIE9E6iCR7ORM8xhwnmMdk2bJXonZ0QlDHzS8Qd0YYPrqdTDXFy5OX0p+pcjSVI+84OFU5NJtHn6Y7HCUdVNkxd4gAXagX4MbW8yPREszOlJgZH2bbE3tZmCoQSzdwzY3XUlWDdPb1cTD6FKZwqaIQbO3i6pY4C6LMPDYBokyecmlI9NOzYpCrXruZO+58hHx+mJo6/gw1VmcFigfr9uZnZ1gYuQNn85Vbx3eDO0hj2wCWUaA8dxqscQxNo5AvMzJeYenSraSDKuVylHWrLuPo8ZMItUpOtRldqFAS4tc4x+YrBfuBSoAaFO8/uT4odqGj9Nvx+eSMAFL+oL7ZWYxa0OOv3+9e4Hi/W+ItH0AKzkxzIRC5C1gP3IiUJUhTY7Ia1JJPfsOVKjJCmkUhQAuicwv2yiupDq6CVIRIXCEalD7SYrGEiyLkOrPzYNuSLVVUoHtpL6kwtNWp0jyTKQqkg7JEta2ziavSL+XyG1/DgZ/cRX54zIvhntnCmQwDL38pt956KxviCXqQwG9LBHqWrWIhu0D+xH5wDBTNhw4EMpv/XHelThpFNqR0HTi9iyHvnBmKznXhZZiNHWjJNrqKAXj0Ck64TyNnFxowQ2X0LpSnr2V2yuKnjz1EcfYphDh3uz6bVfd+e+6z24OsvbgKzrbHrAEqi/WK/fRhxvvf1//6+Uz0f1n26+svLtp/P3NxyFMSLljzuFbAIzi6aATQPOgyW5gkoEt2aybdTn/HEpLxJPFYnEQiga4HiEXDBMMh1ECQltYmYqk0qcYU6cYEiUQUIUaZmc1RKJYwjQqmpRAOhAnqOpoKASVA1ZQNv6qWgeVUsatVrIpFtWSCMFGxUXC8RmTSj0iWrD8iSLqBz9WSKaEqAQQJ5DQ8ihwVff5MHBmRLKZiQK1eKIkei6JHdLSAbMrl2LKZme2FMGbZA01VqeoovJ4zehAammQ/BdVz4X5i0WIxlOBzu3yvOAmUXBnj+o3JMzHIigrMZc/d2V+oGdn9TGb3M3lYBUaheYJo4xI5bzL3gfivs2LhRQPG1k+pFlskHOfm695CayZGKLA4jCm5MFGGkTF45UqvbO95mqJAf+K5lwNYtmKAdCLFxz7wTVYFVRqFRUK4aDEVXQkQEDbCtalWbXRAQyOmxYknQoRDIYg30NjWQdeKFTS0N7H7obsRhRF0y2DixCniXU20rFtBqH8JFTPP6YceYef2GRTH5dLBJFMnHXAAACAASURBVKMjE1gGuKpOTg14CrLQrUlm7Pi8vJCrFdgYhK6MQqpVQQAzC4LdpwU/mYCxCQtFgY4A/NEyjd9e28m+oSL37pni7ryN4QoeHVmQQnhI9aJUCkIarBmvTSHKwLCA2Vm5H3PIh2cSOLEAW4AWXSWVSHD9SzLs23WGoVPznDghONY/xNjUcSqOwAoq3FaFlRqcGctx13iOBk3wzj+9ge4ek3THFLd//wSGu7gp2zKkhmIe+SD7lfLnmorUN7ljVtB0aJRYUbINLvwon1v+Ngc7/wJ4I5Kv4BeZ+vyqqEzfFLyTxWq5F5uD8kSN1iOV/vq9+3xsRtKJt0fgz3TSK1Sp3zIC5Sy4dkB6yUYh3zvAuCJPcLt3AvzoPCwvyNgkzJagqQVWp2B6FqjKxm6mCbopxbJ174lXAzKz5QqwZeUEti2B17kZaO+EeNzTSCwiY8aSd/HrcWmfgFJB0rD9uNlBknxWIOcsPhFgmJrXiSJjzwKyGutzSDRY0UHMA98F/ic4IVRdJdAMoY/AJy6DS1PguC75QoV/ubfKg7f//xx76P9c8MpetF+wXYzAn7cZgRClth4++I73UCzMkitnscwqpUoFy7QIagHcUJwTVUHmd29m5qt3cnrnEUIKDAxo3P3De/np1gcZzkMgBm4JcgbMLcBJB4qOpzCegFs2Qkc7BHQpQdLvqLzvA1dhdv0R1fR67GScVuqYpZbL7sNzrN/YRlSz0WybhCIzMtv2jvHA44d56CcPMbHvYVavXkdXdz9d3d384yffTvHajVDVaGtIE4pFCeoKXc2wpLER0wGtKoFXRRVEdBfdtlGEgmFB0RK0RoOAgmV7JChqU1Y/beYDrH6g6Rch+OYv68Mj/vT2XJ1Q/zP/82XIpjYPCIW/29jMyKY/ZgKpc7XVgU1LoEs9K1F9VhqhPnhUka5YEzDmwpFxizMTWbJzw0z1bKahQQaUQggqrkvJNMlOOEwen2Xo0GGMsT1UnCC5iRnmnRYue9mlhFUVRyjYpmS/BpHyMrbu/fUqH8olmJmAfbtPMTc+AnZW+tYmFa2jA0IxHMtFHdyCcvIk/Ws3c9PNv73o2r9Q63r5ctJrUxxe+WlmiqOMjz6CNvoEW+5r5UGmiBNnCp2jOPzt599KB55GJfCD3e9nYPcrMNAZ5RQ2w8TQaaWXDmUl3dFL6GQQO5dnAcFh5Wlef/MAWlsKAqAYTaxo/AxLP/MRYjmVjpW30r1xLS9fJaV7yKqEtDCf+tQf0NXagp4JcFtuhI7ozQQCnRc8Hj8Cbe4cxN62n/1bd1P6P1+kr72bN73xOq77yz9mKmcwc2KI7Xt38tC+J1FVlf78GH/10Q+x4dJ1qKpMYHzjq48zPqsQbWrn8hszhCJVajJHA8DD/DKc5tYfffy8z4KhNuKxLmKhZv75Mx8mojexsncF/+N17+IzX/wyY6VjTM8vcHT+xV5V8mxgn42MDP3WV75mpx+7+QDrLPLpPVdGwH/Sk9S4QylkmbmFjCCjSG8zTw2g9WozwXvve6BVyOZMx5ENnRZHqwFkIfsHkPBbiJqf89PSOtK/hJDhUh5JjjiNxhplA5PLNsO6NcRWddIahoawlB4QQmr0xfwzJuTRZR1IZOKEBKTCoIXhwHEpe9vxPMBY3ypCSmoFRJA//cN/4BPlYfbbWewTz8wCVkIhWteu439863bezWJWlg0EmxKk+vtoGriUU2f241ywKZhXAhbiHAxUnrFWHJqpPdcJpIDADlUj3NhE7oSGux5WX9tK4J//F5bxu8hkiYPCPHP8Mae/8WVMd4EHTr/tGY4khQToI8DWc77TgJuQQOwyavernwCAWjvHejDWh0mKyPvlmZtnXrSLdtH+q2ZjsUAt4SatnqpVLecBAXmN0elxsqNThEJhQsEg0WiIeDxDKBQlkUjR0tLCqtWraWtvp7mpmY7WBvqWdNCQSXP40ElOD40yOzdPuWKDCwFFIxIKEdZ19GAIRVFQhIMWAsWxcc0q1UoFVdjYCFxF4AoHCwOHqgfK+jSEKheKK2LIGo1u5EjmA59VfLj1QvJNvkxBM5n2Tto603S0wIkILJiyWs6sIluxeH1mrCoUK/L/ikcgCEZqquy+jImGhDES3hYM5BjnN1TMI4thSw4YpuyjoxZBy4M2NQMn9v4M1/nnYS7wFMw8RXnmuepcXrg9JxirKEoYKe0V8pb/nhDibxRF6Qe+gwTcnwZ+VwhRVRQlBHwDqfI4B7xJCHH62bfiT2fOt6aWNF/4979E1c7/PpuFiTnI5TivccnP07QghOJg2DoP3vdj1g6uZv2GDdiaIBxPEVItQugygLJtNAd0TScYjsv3ehA3EEaEE8Q3buGKjg7OPLWN0zu3Mjp9mh0PzrL7gbsxAgo3JxX+/gNbWHHJIDMTszz12JPkJqC9Q2cmK3j6iIw83pqBtAlTZfgB8OYodGagpSnAsp4GDNNgZKyMWbLIILPuzUBXE7xkZYgbr76cU8dOcd1V/bzhLTfw8Pd/xN9sneek6Z5tS7AV2Da1uAs1SJcVQfIWzztXyGBxqGLw1P7DhMNxsgtlQjFY0gqH9lk8NQdHDTilyCzO2y5Psao9jNAUntg6yXf/8yGuv3YNL13Tzz8eO8EHD0LUkTffODVlYX9yfiELI4HXfqQzGpmRCl8jz7D8ha0IfB14AHivt1aPzaIgm6VW6/YkFZKLGnlkkN5bty4bidK2Ign5U2DdBfe8msa/DtB4DfS5YOTgxCNQnAfXEsz8YQmuiUJFkyf2CuQT5yMCGpJGEZCi2ZOzsDwpk0flvNQYDMcls0u4snGYibyfhcd89ZulKwrE4hDuk+sKBiEcpRYrQq3ngM9wBXlhvH0428DYBi6n5n1N77eXU6sVBrgdSWTdJk8hm0NwpgxTk3iKxcA6lr22kd/8FvylJkHlGeDp8Tlu7X8rrrsVV9Q107hoF+1FahOHD/HI1DS/9Zt/QMqN4LoOQoP1awbYs38P3Z2dtDQ3MVWYo+3md6HffxRl51EUgjQC40d3MXLygCSTlyARlIHPfFXmOfLAmhQsj8OBfTKR1twMehhUx+WeL32bjW9tpW29Q5DrFu2bIlziRg6l0sznvnE73/7W3fQ19FPMGbQtWUsy3cq1nZdy/Tt/j97WCIlYBD2UZPi4wrKODhRFwUZlwVCw8kAMQjHpf0AGaqeHS9z742Pcfe8DxMKtVC3BQnmKrfd9AF3XFtXxR5FTVd/1ONQ4bbCY+y6QAV+EGum+/ndQg2B8rVnfBQWQnV37ArLZYy/STaW9L32d2vow92wTrrrPHKAk4L59sPfRezh9ZDsL2WE29f0DOC1ML1SZHJ5j6NAwX/7kx8hlDyDEDK7jQ81NmLkJRh/7V277/vXcdMsyGpsSlCsSoDYn5blMNskkqYlkJximPLejux6hooxA0IF2Bbo3sul1f46SbOfg0YP0tq8ltj7IDZe08abLul9oKdF5Fmtr4X2zR/n8unVUDh+mCZsiY+SAHeSYQUIRCrL5kF9afQ/Qw70yWYrAwJM4IktA7EEvKSzdrxBEkECwTgju+vxSjiMD4CYUuohy1C0xistXZv6JuccV1iBHbCfUzt+t/CzB8hwjR2exYs1s3PiX/M9730175nwOCNTymmo0AyETy9jDoYf2chiFvY/30tjUgpnNMzR6EsuWYJrrutx5/+28+vWvpKuzm9bOJgBufPOV7D1usf+oxUN7oVL109gacjz71QEspfIkpfKU905QrJ7h6eO72PWp7+C6fsL4V21JFjMIz7V6XRxfcOTcUu4KNe3YAPLqRpF34HMxa/yp6gzSo8bq9mcBmWUeoqYNuoD0PhoSePM5+74Vvf1pRibtT1Hf/OvtSEZsklqO2wcRS9Qmz35DwBzS17vAGkXltsYwesxkdY/J8svh0CMw9ROY7YcVq6AlI/cwioz3xi0ozMLq1Sopj34bBy4feOHJmVwVsjmwRwThmSJvuPaDtDrL+PGJf3rG3/R/7GPc8L738R5qBVNQq1jYnIDBzQOcWvpmNn70fTjOuVG+CYoDS3T4B+Bt9adTAdIsJUCfd45OIMEIF7jPKXD/6Of4rR1/wstXNHP15gRv/fgr+I+/DmEU5ZVrQeMPeQd3nfooh87TEa43n+l87lkLIj3ab7BYjbFIDeax615V7xX2lplD1rE8yIvjebxoF+3/ZRPU/Lta95n/7JXrlhxmtDyEUo4SIEpUSdAUa0YnhOuoWLbCT+66C13XCQQUdF1g2zahUAwLDVuo6GGBbRjEwmGiAZ1ISEfXw4RCIQIBnUBAxXHkuOfEXNwGF/QOFnILFIsLlMsLmBWVWYreHgYR2BSeZVxzkKNZhVocHEJ6mlFqbS4vaOUyAcskrnuNv6KS4GEooNuSHFANghUA05Z4gmGCUCDaJMerMrV42+dkZZBQRh8y1vZTpf5Zf1qHvdOw70kYuh/ENmD0x+D+8TNfyl9jez7MWBO4QQhRVBQlADyuKMq9wPuBTwshvqMoyr8A7wC+6P2dF0IMKIryZuATwJuefRNZLoQzt3a00Lt8GV/87h4u3zJIX0uI5joIvy8NbTGwOyRF+hdligKartOzpBdj5iSHd+5g/Phxrn3Zy1hxySCOG8FyNAQajmlCMAC6i8BEYKA6oAgVVJVQOAypZro3Xk3bkjXgGgQe20Vp+27ODI1QmIfXfmEfVyd1tqzu5Np3vo2TD25lYWac8nSJkhdzVgoQcqX7CCBLFcdmoFCxCelZRoZcLNPFtiGmQTwNAwnZNASzyvZte/jMUYPstjyZ0FEunVvgnWtiLBRMjs9V+f6sDEMvFAqUkaDohayM5BscNuDEYYcptYhZdQkL6J6FG1MQ8rLzC0IGoB2ZDI0xhUKlREKX3fK2PXaCXVuHGRmBN6XAKIOmKTS0adxxymZK1PgMSWTQWh+yrUTGap1hSGdgIQsnDUmhr7ckcvKdRnbWPh/Sc5EchM8hXUcGws3Q1SnjccfTDNBsuFyDXbackRM8Zx1+AOYHY0FgAIZUTv9Agp+X/AYYGbAMyM9BOa8w9+4odKsS251Bavv7+gx+V5ic938CaJPs1ngM3KrsvJ1pgJAu2a+GIRmxigpV4QEKHjXBdSVTVtEkmzaiyq6JXQ0w2uldXJtava5/Afxnz9eS9RETH5z1vWwZOSsoeDfJ/cjkvyP3mzEFDgHmVvmF+iZ443r+/NUJbtoktWeCwB/+/XH27LyHwvC3sO1j3gov0jMv2q+HlfI5PvKO3+QbX/kSyd4+pgo2qYY4uflZAkENLaQSDGmMGhZX3ngLlpbg/oe3oaNw2Yb1TJwZZuejB5hE6jeZQo6gNrLtR9qCkAOtnRAJyGceW2qDRxzB0PbvYCiC5Tdcd7aAtuzAvNBoamoiFdW46pI1xF4dob+nh4oQNLc2k0kmCNkuIhMmolQRjkPZqiJElVhSJxRVUUIKKRfGyjBtw0zWZvzwPJ/8u79jfm4OxdFIKK2s6l1Cz4pVNHW2kmwSfPUrP0QVKZrbu+kbWMbQUTh55gytfXG6VjQuaofim1974CKnsnmkf9A5X4BGo5ZN9nNF/ucqsqPrld7yYe+c+JU2fqFz/fZ91RjD++uDCmUFblkGyamVxKZz7D84zCNf/jq7Du0mtzBL1SxhlA1y2REcu8T5YJOKsAMc+89v05l5J31rVxCLe9N2VUrNRAJyvwNBSMVkwq2hGbTpE1DcA84ZMAQcPcKhe7+P0r4CM9ZITG9gWV8bS1tjNKovDHYxqUkE+b9UFAUtEOA3/vqb7Pj3z3Hsnn9jGTIL70tD+K0xn6A2CspGcAKFWqlaNxK26ECgI5hDDmsz3vJJ12YpNXXFBgqsxqUVyWB+UMhlx4ARY5I/O/Yhxq1p2hFs6FvLB/71o3SkIgSf5bg1kLIOfgMBIRAIpifGKC0UaGvo5d1/+OcEUzEmJyd49N77WL60g9tv+w4/euBhMt0DLBChd/BqbK2V6Xmdb92zjfmFdmTENEpN/fNXaeKcdwLh/qr3CWoNjeLIu61MjYvuF+uDvJPqxfktFmsk+fVS9YCtec46nslS3isCtBCkmyitpGmml00IikAejRwJquSYxcTGQqNChAoaKioaKg6CBaq4hLBJUKBCrV1dLdLsR8K0PkfSlwyrIH2af8f4d+4U8rnKE2K3aCBn6nTrQdyszvhuiAi49DJoaYRkTOp7Bz0ZGNWrjHOaIKgraGr987z4TIi6vxXvjJw7zTpzOMvIaIGAWaI4OQGFAno4Cpcuh53nA5nxr97OG6/fwlt1HbXu2HxI3d+PSUvhkaKGK9qQgGc9m/gDkPgDSL9GnsbVyN5r8/7ejgCVs5ULeeCK1b+FWXTJjowwHF7N3Lzgu3fMoT2m0pJKM9jwF5yyvs28uZtpHL7Mf1Aly/OTDal/dhJIwsUGzpcZiCJHl/rGCz6rwh+NskgvNsmv3k9ctIv2382eax4ppVIEVSzKFEQRo5wnQgodHcVVwNaJahHi4QQRLUU01kwgoFE2TbBt1HCQeDhORNcJqRoB1dOvci0cW6AJHceuAg66oqPrOk4Iosko6KAHNEzbpmjNeIiCwMUhzIW5sRXkiOMLD4SQI2wvcrRVuVBlcRXpi05BoZ/IfBNN6XYyIZVCUJGNYzXQk558mA6OWkM3wlFoT8KaZK14tn48KSHjuyFkyvQa5Kgb9L6/FBmTN8eBfpidhuL013EKP+LFUS3QgRzLNWRcN4E8yz+7PScYK4TwhXqgJowkgBuAt3iffx34CBKMvdX7H+B7wOcURVG89TyD+ZnjmnX097BqcA3rN2whFosTCyoEzqk3jAbkq96qyNIZXIipng7dz8FUTaOpuZupaISjE1McGZujHE6Qm55gYHCQtu4+YrE0wqniuOA6LrZjoikOjqrgujJYdF2BEgwTbmohkmnCcRwGlQhFTac9GSMyN8tTZ+Z4JCQw1CBdK2fpWb2GbQ/MM5QvckzIh2jClnGIH7SddKHPhpgpyGYtsjkIByAShFRS3r6XLGkhFtWxLItUVzuFvcc4ms0jyBMGzLyDZggSmsYrBuL85FSeBVec96D6D5wvR19/YVuQ4Qgu5Ipw2lM08TmlQzpMOzVOQQwYHi2hFEBTDVoawxw6aWJYZWLhMskmhas2rWZ0eIKp6XlKhqBO+hQusA8AK1PQGYBkSIKxrYkQpaJNuuAwOi8fG99xlag1hbmwWcgOx3cCA+Cug8oWT17D4zEomtcY1fB0BbwbcyNyY8M+GumX0CWBKFQUKk/DXAzG+qDvcmhql41aRESBoCZPkj+/8BW4fcapL6ioyLLlZBSCrmROaYrUaolFQdNk1gohg/NS1islEBDLyN33gVNF8Vi0lvxdVINUExRK4JaRj6tadyPUXwifvlb/8udJAum3TiJB2F3I0UEgESUsKO4GysQ7u1l+60ouuyHNa65UyYRctm4zuHv313ngrhGGjmyF+R3PeMVeXOYH2i+GQeSi/arNsW2O7d7B0fFZ1jT30tqYAE1nydJectksIyePsay/h3ylSmf/Ei6ruszbAk1VGRzcyJEjQ2x/9AB7kaXqYaSHKiMn9Try2Y/okgllVUF4df0xAaWJCUpTE8gurBoaCtlShcmpBaypCdIZnaZ4go2rl9LQkMSNBIgnIsQiEeJaiGpCQXGCWKaNUrSZm13g5LFJQlGVhpY08WSGH97/AzQRJRVpZWquQDiSoa83STIcoSncSn9XHw2dTcQzMQiafOPO77FhzctobmmluQFUG8yiiWOEz4Kr9YIv9aCAzyKL1n3uywjUA65u3UthMQigIYNBn7RfP774wa3PnzC8c21SA4ItIbVdc1mXsb372f34kxzbu5vJ4WMUssMcPnmIsuG3IXsm86FGk9Lkbo7u3Y8TjrFybRdqQDZl08Iy6BXegShIHx8MCshPQ3kG9ILMvs0VKeZnCTT1kEhmmF8ooOs9xIKhC5SlPbv55/hC1nHlRlZab4Bkhex3vsMktWjOpAaF+aqbJ5DDQAtBVkQb6fm917IEySXze4vPeetwS5A4Jtj11NewnerZ4vEiLkFkrFFGDiN+C6UFYTFUOkIjsOqqq9j86lsYWHdheYJzj1GLaqjBxZCTY7uoms6ydat5xatuwQlpDI2NUDZNwmGd/YdOMX/wMBw8TJEQ3ceHCETaMKoRjh7Yj1U5BRTRAilSLVcTNnXKhSEMcwSbiYujwtlpRQj5FPvTRl/dzqQmClJvftTnP7G+RqwGlEkQ9+CvImkceoAGgkRJA2VMDAxcDPBeKmF6ibOWRgaAVgK0ECZNnDhtNCMoARVUDKIIimSpYmDjUMXG9NqnqAhcNIooCDRPBbSMhF5DyNSB1JW9HI1uBCFcYoCOgoNCDJc4BhZlJLhYxqZAhQpFbEoojOCQN09ROvwk48UJcrsbaKQL59rVOJ1xrBad5ECdRrYi5QueT9fj+pj6XJ8oBJQs2chFlB0cs4Qwi1AuEVA04o1tFOtZpdEovPQG3viSa7ips5WBum34YWK9jRxf4Me3n0aI1Ug4tX4Wsgv0cXlbPICUwvLls0oAARRUL+xUaKSB5kteQoeVYEnDBB19KxkhyNCRSYrVMmsH+0jElxHJpVkw5WrPMHr2Dszg4bzPaRmkh+tCsgv81B/URiIfePXhCZ/v7EsTTCOZ06ef1xYv2kW7aL9sk40hhef1HbeCSxWNEBo6AREEVyegakSDUfRwFF1XUVSNgGPj6oqMul1wXdvzgSouCsJ1sR2HillGWFUU1wEhsAMCw7KwLQfLrGKKKjYuVSxcTATmoupl33xVa1/iRq87Ap9gUF8ltvgYDSAPZo5AZYFYpUTATKCoshmX5VFsHVUSvISHGzhVCMYgFoNEQK4lwmJSRJRaHN4KizAdWdsgGbNqGJROKFwJT+wVzDsvlgSVCkoItWmARKQf25rAKJ/GWTjM+bJHz8+el2asoigaUopgAPg8Ek7JCSH86GgUScrB+zsCIISwFUVZQBIqZs9Z57uAd11oe7FYjJUbNrBm/RbWDG7h2iuX09V4Phh7IaviDZwOhJWfHxirqTotrcuZaWhi/9A4h6bn2P/jRxjZ+Sg3vPoWNl17DcuXrUQRCsJWcJwqjmMRDKoIXUdVVRQhZQzQddA0bNelVDJZsnE98XiUid42xg7uZ6p8gKdLJR46OkXqa/fx/r99P5PZbRzMuhwCXhlROWK6zLqczS6fAJp0OQmfWZCAdCQAyYxCR1uA0yMOvX3dJBMhCgWDlTdt4ZKfjjE9bzAq5AXdeqxMBlidDvG2yxuYmjPZX6gya58/DfPjufqMB0iguFlTCKkKectlEpkB8Xs3PZ2X7/2yqTiwY+8M2UadZT1hlq5u5cBElmDEornZobHJ5YZXbebI7qfYvqPAPduts8RMH+Mr1+2TBkR1uKQNMrosxU8kFNLJCJmiwYoZl21lwa5qTTp/RDx7f9aa/QBYL1t/j1WoIaGe3owJuBXvaD266U3IavthP9hykK6pbjp8XOqw7A1C7wpIR0BkZK8vLSQFs8/OMVTvxPney0cXVNntvCMoJ6iOJgk+wZCMg21bPgv+PHMuC6WCx4R15Ha0mJzs+/0SqqZknAc0aErJUgRD9XT5/Eo+H83wUzQ+/akeBfEB2QJwEClJsM/73XIkEWDWg8X1R4glr2Bgyzp+87Mp3qtAccHk/n0lPnbbMIe/8Cfn05tfxKYoKqoaQFWjWJavnHPR/tubcPjxzsNEWjt5yYYBRubKrL1kJU88+ACnjx9neU83plEl1djA4IZBkq2NqJrGqsHNDB4bJdFwL9uyORTk1M8v7HUVyZ5UA+DaUisWRwZKtgIRDcoFECWBcG0qigQK5gplpoYnqAyfRNM0EqEQ7W1RoEokEcDVqlQtl4ptoydVTGFQdV3sKuzff4wnHtlBJBJh5erlXLJmkG9/4bMkQm0s69+Mobr8zm+9kYH+NtLxKNWiQ3m+IPXHzQrjU5PsfOohNq29jqamEG0dnvrK0SDRgIbO4iY0sFiuwH/fTM31+N/5kgXAonHDB2NBuiwfrPBrFvzcke/OfA5eGRlfzDlQsBzcYhmlWsByBfk8nDnm8L1/vZOT279Oce5CQj7PZr44N4DO8b1PoCTiLF/bJeViYhJ4NYRkPrtVMCpgOZ5Wl5GXzjwchBgolotIRAhlkmRaWpgencZ0lskx8gXumcriWo9F1gMrf/eVtF2xnDsfeZS9UyXm3TJ5LApIgDWKvEdbkcUPxXSaZaEWXt52Cbd8/vOoinIWqrCQKpsqoE6C+z2bb089TGHiNAnDOMuQ9YvO/aRuBl9zU6FEkBta0rzy936PTb//++d5Xf/+qAfaXSCcgmAUUBRCoRDhcJhwJE5HTw9XvGwzl1+9gYncHG5cYXPwJnYfOIk741CcO0D2iNSNzB5+1NujKBJciRGNNdHQspmBTX9FYjbE6In7mJ76KQvWTyjWBe/19+Wzffb/lkWosQZ9gRF/ChlBQvMai5tj+bGUX4IDEEIlRBybCC49RGlFpZEs/cAN6CwnRguSbblAlXlc5sF7RUgra+hQX89q5SUgkp6WE54OWsnbTx9A05BTm7L3crEp4FJGYKMRQSGO6+2f7IYdRzJq5J0rCCAI4fNh5X2oSrYyDhp5dAq4jGMzjsEIGlnKVJihjE6eQPUo1pMVpgljEGCA6xg9HsNe0UHj6jDJmEoVUBQdVdVQAyqKpqDoCmoAFP/B9h6Ker/oh3Hnd9uGbBlCWoR0qErFzKHrAsWpErQESSdy1pOhqWgtTbT+xZ/zwfYUS4I1IocPBCwGY+eYPDjEI5/fB+JaPI9Rt2cFKW47B9wBfIgan+ekAqIFhyAuKgElypK29cws20AxuIRoj2DVlQ2M3DdL/tgxZs8Mc7QKA5kgjfkEphFltipnFD4buA+FCuJsSuB88xMB2dy7aAAAIABJREFUvUiZijZqSYX6FKLPXvBlCRwk0Oyf6TlkAe9RLiwCd9Eu2kV7cZg/8ZZ0uCo2EEYlTJQwKmnCepBoJIYWDhEIBohpMRxcyqaJaRoYlTLYVcIBgeZ5QlXVUBWNfLmIUy5jGkVMq4SD7VVzaV6R6QIVKlQp42KgYV4Qw/DVzlPIOMyv4Cohea8N1PTIF5uf/DTAKhIwF4iaC6h2QsbGmsQDXF3CWULzYmsbnCIk4hCJ1eL0OLVUKdQaVMaQbQ7rY3bfYkBfCNKtUH0LHP7+KuaH+14kwVAJ1Am09vU0Nq2iUhrAnm7HWTjNM2n3Ppc9LzBWCOEA6xVFSSOHv5UveEvnr/PLwJcBFEU5e3rD4TBvf/vvM5Zv4YH7hrjnh7t4445rLoDcX9hi3qtOi/nnYsFwhKuuvxVO7WbkxAzjTDAEPDYreOzf7mHtjiN88qPvZlX3asqWjWlZCNtmajJHNBolHosSj0ZlWbimUa1WMQ0D2zYplXSa+vtp6umhe80m1t1c4NEf3M7hPfvYPlLgf3/0i5yeKFI14Nqwyoff0MED903yf9l773i5rvLe+7vb9Dkzc3rVkXTUZVnFktxxNwYM2DgOJBTTAlySXMhNuXATwk1yU8kb8iYBkhv8YggETDPYxr3JRcWWrd51dI50ep8+e88u6/1j7a05kmVLMjax/NHz+Yx0ZnaZPWuvvdazfs/v+T0bpx0OuPAepHs4VoWDVXlTE8CiMnR01XPVTcvpGRhlIjfEyLQgHI4weXgPq5Im/QkYLMhj8kh3YDxrUbmvj+/+0VV8/hf7+fHusVOmiBZ5uR0Fls2r44J0mG3bxgm7En8bRibejPj79SBxyt3+9y64aBG/9ZHLYHEP194+RnHiGFNjfRzYv4eXNj5NSyLNmrmLOLBlD8PIgURHMnH7kG5PEsmG/egiaElFiYQFRgi0cJgfPpxDR9DcAO+8UiW50UPXIO9Bb0mSNM/MtiOHskXIIcUG2sDplE8GRf8zV24vAJWAlJ/AL/Py8tMeA/ff4Z4q3PyH0NAFeQPmJeDYIagGtC2orVcUpM9XlF8Vyci4vCLk4rxUgaojBz1HBthkAS9H6kjW18vPLb8it6H4AE5weZoEZj1dgjkNESi4kAsYCEPIVYzKidmFrn8zAoVugUTf/wzpZ5aRz+ciYCu+3FtVnnD5f+cTfxbiN96jcDGyX3/kixt54N6fwPDXzvguvVmsLtlMQ30bLS0dPL/1oeNaQOftvH3/f/826fIfsWLBH/PAd3+Abo3hOSWikRBH+w8zd+kKSqUCkUiGFcsvRmgqza2d3Hr7+5g/t55fe/cdbBKCHmRaz3V+6LsuDkZC6ou6UQnYVU1wijJbIXohaKqKWwmj6wquAS3t9cxpryd+7So2PPgU+YpCfaaBBQuWkE7oWFUYHc7y6DMv8OTjz/PwxvuYGJ2gjgzjvMhlC3+d5YtXoVtFrn1HC/+Z+gkhTyUaUpnOj2M5JaYP7WG4WsXVFBKZRuYv6WZRcwvr1A5UHmGw6FD2wsc55GViOISOOyknPzkB7yhY0AdaWIGbHEc6oQGTVedErtJsc6jpaQXHl5Gj9vH0Wf/vGDA6BjteHONfvvJNRjb9DZ7z+lRUrVk/HNtAqtDEsuU3UTTBCUO5CqWyZDrHNXBtP6GsqOC1NoNmQ9QCoZK45UYq+w5THDxCxQmxft01zJ8forHh5Uy305lBrR74K1lqwQI+MjRIuuPf+MHIdzjEJmLIKSBQqAnm6n/953/hsutvINbSxE8UhXpkFL8JObdryCkl1QLh39b56m/v5Rvvfz8bf/QjBpA1ygPFRckvlJrwxwCTGF/kWj6x5ZvUdTedcI2z9YOhVjgiWDAsXQTb2iEajfG269/Fbe97Nx3dacJJlWyhzEBljA0bnmLX/sPMGCF2TRQ4OjxDaXq2zFbgHQUe0sf4yGd+nU/+7hXMnQMvPgc7H1jC7g3Xs3ljhIPcg8AlhOyzM9T6qep/luWtLMQTxi8VigQp25B+Uh3SxwoqzFeQLTFKbZkXiF0AVGgHfg+p1tnE4EmLTAfJCZG8kGCROvf49rWQei9kbgno1zWQz4Ljq4vjuJrpb5hAjjJ1HOHnTDOIg0MXXegkyVJAQWMe84gQoeqDygYqWbLHGfYgcHCYIscURSp4dNHFBdzCOHuZwKWCRoQlXEyYi1EwcUhgMsOMTBclho6B8+gvsB6FIRSOfLaOKXRS4R4y9d0kL2wlOS9BaiHEV0LsGk45GJxuzeXmZCKY4YDnCKaLJp5rUhrsZfixh2s7djQw9/IVHLryqhOOf+XF52+y5KYJPn3/R/jqpf8DIR5HPhXBM1aSYrUA70T6nBchMdBvA6UGpggxTTtN6Wvg2Le4+fofcWR8mtbF63GmYU68kWhEQThjWMXDXH3DauZfcAd9Bzv5wpNfP34lbYR4JwnmMM0GXokhG0cm2i5AjiLBLOJwYrhniBN1Yk1q3GAXyYZ9yt/vvJ2383bumAzIeSgUiRLzojSq7SRiKZo7umlobMAwDDxFkHdK9Pcd4sDkNsYnBrEo42D6AjsGBmEcP0Dr4eD6MKuLg4lJlQrieBAHf79TWww5g9bD8ZDfbN5m4BOfmhlbAQbBHidWnKZlOk9jE+RT8qCYLuUJ9AgUbFlwywUKDrS3w9wOGarMIqfTOBKLCMpclpEzfgAdnDwF7UMm0Pb557QauyUye2ZpCm+wzYC7FXvn1tctbHZGYGxgQoisoihPApcCaUVRdJ8d20ltBhlCSoANKoqiI/2dqdOdu3V+J13d3SxadCGXvPf36eyOUKfbJIVHRFFOYDJUebkaT2AKtQ2zF29nu/g42TRNobkTGuasJ924k0TkpRN69YFDA/zW577C6tYuPvGx21i+YhFeXYTsDBJ41ULoKliOhaVYvt6aLksPuIDroQgBkTBu3KZl5Tr0+k5KY9Pc8+wTjNguJqBaHr927yh/uDTGdc1VlmerdHbXMXEsx8S0YKosuRgp4KAHB3uzbP76VhYaDomEy5gFvQWVm8cm+PdjFQ6XIKHDLZ0wnoVny7CvChsF/M9vvkBdyeJGBR72gcArkA/4DLUoyzByEQTSLf3p0QK/GCxiujXu6MlSAnlgSIUPLoTrP/xrzFm9GKW7UWqvJiBc0Gls7qDxbdeizvsou77zffZuvB8PmZU0g3yQw0itv73A9Rc28tkr2klbDi9s7WVqooonwHWrlBzBXg8mxiGc9VhQgaVpaPV1U7dxNgGXfuBLwH+Tb0PI0WYy+GUl0CuwuAOeAcYDUf5gaaBQq8MdVPv1P/oxPDUBTbdA6wdgbAd4P/Nv6DxqubEBnctf7RpJn9EDlBxwhRTZ1gOWaxUcEzwbtKjUhHWE1InFBdeCUEQyr1xNsmJVId+rBkyMgeVJ3UJUZN9X/RthIlHxgC5dRa68Db9jbEWSiieoZSNayJHW96nVpjDxjyzkwY8bzGQUth9VeOhglR//0SX0H52C4rlXoKujcyHFYo6Bob2MjB56awGxJ8vynbfXZPfcfy99pRx/+alPseGBn1LfkKapuRlLd1FcB9fxqHom49ODxDLdoKjoiSYWr7yO737rOxzY8CUObu3n8C44WoVwFZZ70FOCbX1Q0CAdltrPRgjcLrjkXR8mteZGDuSOgt6KGg6hqSoV4ZG3KvQO9LFi6RK6FrbzwKZn+ce//ALFfB7H8TArFsvUpbytYwnzrnsvqy+7DD2ukorWYWgqmu6w48ntWDmLSCiMiMdIpBLMaZmPFlMgJPCEYPMzQ/zh7/0Nu/ZswWOMQr6C8C7govWXMTJ4A9dcugZPSWHr2vH4zqnAgdmQTOBsBp9HqMnhBPhJwAgN+HUg8ZYqckiqAKYDji3lHbITMJ1z6esdYN+2bWz/2deBUWzHoWI6zExl8ZzXlpZ0etvLnu0b+MqfruWTv3cDMwUF05+vSmVfddIfwyseNK77AE3tBsIZYtvD/07pn/4Fb/5cQvOXkkjF2P69r3LDqj8nHlp01r7QmeyvKApCCK7d8H7WHr6JHc8+x5//1YfYQC0lzohF+dnTG5jfswAnkWRQUehCyj4mqYGwCtJZH1ekP9OCwvu/+lVWXHMN3/zsZ9mJZM8ayHs2jJxhf23Vx7nj7b9P1x1JEh318ppmXeMY8r7P8d/HkO04hZxOkw0QS4JZKfPsEw9yw9WXkZ0cYjo/hZ7OMFCKsGX/OLtf6OPo1pewnBR2JQ/2qYpnRNC5mndc+hmW9MyjGlKYBlLLoGEcMhP1JDbeyBKGMegjxAwhTCl7gXQrEmgkSLKfPAVkKn32nBQ26EB6bk/47wNeTLAECSHvRgBUBXWV8/72NDV4OpD7kJzSFcBnkQH+ZiSgX8dr8fmzUmA7r9SUBEykoyRcZJhgM4h+/7pWAi2gN0FsFcwzmMsX6araiLLAmJC8/MawB1EFo84AR8EwpV4yEUjpHsL1s40swBK0FD1cx8MTAgMDnSTNdNLAOjxG/YRWyeUXaKgk/bREWY9alr4zENgIygiG2ckG8tVNiIkY855dRXTLPLSQoBpxGYrZzFBP6ztWkLwxReimWoucMnDlQrEEwoRKbpzsxDCVqSGs6WG2b3mKg727T9j/xnfeyh1/8icovijtK/nZQphM5C7hmH6YBx5cwV1fqEeIMDLUOAXsOvEAA/kgL0QSIbZwHK/dTButN13ENX/3Ze4dVLn2/3knHwurrExFedoFpU9hycJLmTqyirY5BrdeGeG5//dJ9N46dr1rJ//20BfZ7G5hnCm+RTbw6k9hC5GjVzcSekjJG4uC7OM20kkOzjCNnH0M/32gmj0MfBPZt88sT++8nbfz9mYzqbA9RS/VGZPx4iTpvg665syjLpUkFo+ixcOkMzGSsTg5PULVKRMnjEmJMiYuOQQChyriePCm5GdLCMTLysm+sgW8qcBPjlFjwgZhxAEkGNp4wpE20jNaDChEbIv6YpG6qTyqnkB1NIwERGNSSiqElOqygLgO8TBUDNghZJZ2WoFGRcbLOpGjXoCKTCFJZEEGlUD6aRNAqQrFPEwcAntwP+SOvpabck7YacFYRVGaANsHYqNIQuPfAk8iA9A/AO5ACmoC3Ou/3+Rvf+LV9WKllasl9FSGhRdfz+olbSSbVOoMhaQiu900cmoLJCZfzYQA05Xp1WdbMHjGkR3ANmFupna8osjFbM+65cw7soqmvj1w6NDx46yqzbHBMexsmdDPHmL5oX30LGhiybzF6EYMVQthCw/HlW6Uqwo8VWDoOo4jcG0HVYVQJISTs0m1NpNpbCKtR3AySfbs383YyBjT0zl68w73j1bRqy52RVAZs+gIwajuM1uRDNRxQKu6aJNlhgxQS5B1YMJ0KR606StB2ded21WAq9pDzIy75CZdBoHnpsp0KjXMOe6fU0d+NheJvM+GyVygYntU7RNVgIPUyEsbFQbyglIVxnWNay69kIVz24g1ZSCT9rUPbDTXIZTLY5sG0eZ5DBUi7BiushfZHyr+axqJ/DcC2akKGw/M8PaOJGZZ0JcVFDyFlc0GDQmLTEne32FH/uZSRbpEBc6W+W4jnadHgNXgLTlJJkSRFbKiSIQkPwuKbkKOhI4JI71Ih34WzJCD4lYgDCIOmaUwbUptLgTS1wuYsQa1bD5fq6VSkunItp9TZfhPeLEIdgWEDeYYiJhMZ1Y0qSEbDsvK67oigVyrIlOeXU9WS9Q0SQTxZosuJqlVd5hdrCvkX98AsnLLdr+5OpF+aYCCVIFWWHoJrLpC5cJLwnQugOeeOMTjm/Yxtf8F9u3ejeeeW85pJBJhxUVrCEU0jhwokcta2LZ1+gPPJWtGhjxPvUI5b2dok4ODHHxhK+Zv/RbdS5aheRbFcomXtr7EJXqCSCqNYhjMFGcIT9aRiNVhqCEisQa6lq2hPPMuhHGYeGuOanESc+woVt7mcAmmKlDvV13RUtC4QKXpkncRnncdlcgSihbobhkDgatqKK6HOTONWy6gKC56LEJDY4qOplbCjV0kY0kiYYOu2ByS6TSZ5kbS9QaRugSJcAjDUFD0MBAhk/FA6FQqgsN9wxx6cAPxdJJwLEqxVGbj8zsYGRgjqdSTiqVYvOpC8iJNY2cnwjMoVaB9jkG84cSSRydrC87WfA34RSo1ae0yJ0pbz5Y7qDCLo+RB3obhARgaPsbI0cMMHd6DOTlFueIxOZFlZOAYg/u3wkmshDfOLCqT+xl+4QdMj16Pk1BwNXA8WdDS0MFQpQ6krsLSpStIpkPkJ8PghvDGJ2DRUlyhYfYeotK/l4xToe4NLXaqkFyYIVmfQa9X+aT2ZXb9fIwH+x6mpOe4YuVaupdfQDgcxlVUIsB8JNQWJDMF/4tZryrQ0tHBkmuu4/o/+F9876t/S9x1qQMgxM28k+hnFrN27XUsW7aE0NLaj5ztAp6cDhf0lSS+jIXmZ6YLQalY4KWde8nPjDM2OogejxOp38tQDsaHpihMDCMnuxlOVfpTJhWGqYxNkz3SQrYvRlMrdCQhciE0uilS2Uvoe3wcrbAN1RlAMM4042Qxj6vB2VhYCB+iPBejX77GxgnLDT8F8njRrQDAqs56adSe/Bl/u6xGWI9gAdJ7uhS4CulaxXn5GHE6CyQqVGwUOycF9clAxfYx34BPVEBOesPIgLwrv9VbCFUNpkxCqOBEwU6CSPgDlF+8wl9XK4GsUxy0oOJgcCERMArIwalaaypD0THUGIRSEPOgqsp0Jc0PO6mqrNDq2vL7LBUMF4wqws4ws/dONjoD4ERY6YQJGcuhksDICuKuBW6IiDaKUq7g0Ij+du04eBpcmoOsI2CakJ0WTI5mGTzay8RAH3Z+EqcwwrHhI4zNjB8/7h2f/jQ3v+82Lu14ea3u2c9hPneYQ/u/xSOb9tCXjbL7pW6m+1f5d3MVskLXLDC2E0lEVZC6sXvxGVMKsICmD36I2HszDC1pZ2gKWhbVEQtD1oB2F1rC0BWKU+yJs7hL0Hv/0xzc/zxG1mTeZJrb6j+Cmp1hs/0SezCPC1QImMVkhprDm6CmJRZCOuZQUxcP8i6gVg6xiIQdDiJzBCd5k+Tgnrfzdt5eswlcXIpuHtcdwbUUlCGP8FQELWwgwhqeajKVG8XypLyNiopBCA0DDw0PDw8H4ZeK9VCo+IBsDS84/ZrSohbaMZCzbIha+csitVDRiZYBdSnMvRXsNEJvxY3GEJqK5imEZdwPQwMvVFMqjAF2GDINEE/L5WFVgSkPpitwqATtETh2BEYKMvTUOheWd0C3JuENCznDFpGZuNUy2EUQ1V7w3rpZA2fCjG0Dvu3rxqrAD4UQ9yuKshf4gaIo/wdJLLzT3/9O4D8URTmMxMo+cCYXks9m8fQw3SvXs6hdpawoJ/goBWqy/qfDVwWQM+VCNHSG+gaBQ3Z0yuLoaJHs+DRt1y4gpCrMLsA7d/Vclg1ezP5jx9jYewzTO/GBGCkW+NGjG9i4K8EV6+dSf1uK9vY4qqFiey5CKKgCHOHiCI94yMBzHIQrt+m6huPa1DWmaaxvZFH3PObM62LLYw/Su2sPfYf6mZgY54GjJgo+QJqtcHWn1D7tRU7p0/5vqkM+aIdtyNk1R2JsuIYfmh5smoJ3LDDozglGcGVUQodjfnp7CuluHKWmkppB4m1VauUWytRqS80GY1Vk4YCLUnKnY1VwdI15CxYTVnWpNxKPQF0UFA/Nc/A8KA1OES0VyBZsjpYEu5ERlECly0I+tC06jIyW+M6kSdflrUwUPA4VYAyF+SEDI1IlbQnSjnR/ysBh0y/4dmZd5BQ95mmgEZw8FHPIZV2wsIjK/0pFsAIIIATdCugu5CswMoSMqiucsEwchuIzcsG96s8g1AzOBHgTIILCC1X/lJb8Ks8GuwwlDdSo9Mk1RTr7Apmq7NmgeJCfBKO55joiZITLAJSKZMm6RQnUugLcMIRCoASLBL9gGElkByz7Pz1EjfSbR+aNPolE7KOyqZhEMk38vNCGdQqX3wHvew9cXBVs7jvII/c9yeP3PQYDP3lNd+a/0mKxGK3tbVxy+cX09u3EeEWhxXPc6hUZ8jwPxv5S5uSL5PqO8dKuPVy8ZhX5qUFG9m5n/85tdPcsp2vpMkKxMPlCkbHxCbwGnUQkjoGBk2hC63w7rdHFtCwcREweIXfYY3qkyvSUgmVCfUohmvCIt0HbxQZzr/p1cskLKdtpbAHCK6Oq4KkGnuORn8mimhUq+SKFQpGWTJIbLr2SlkQzLZkWknUxRFjHcqpUqjZlcwbHsrAtqEvVkaxrYGLUwQ5bVMoe4yMVNm/ay0//8zs0t7STrm8mW6xwbHo/a5ddysJVl9OVruemG9/LsJimjImiKRCC9m4VEa5BNsEIORtsmS1Z7c76bLZ0gYXUWbVsOfREFBAIJmxBwbTI52YolMrMmFWObIPD+7dxcOez7NvyEBT7f0U94dQmKgPYA/dzZPcE7avq0WIGVUfqiGuqDJhpKkR1hUVzuzBNm0I1JoEgTQE9glt2KI/0EzagRZUshTfcGqClYQ6fWPtl+qoHmXq2ylRohNve+S6mDHndMaRfkeTUPl3Ef2Wo+R3JhYu49gt/zLfu+k+qwkCP6TQkEtzMR+n+/NWEF7+6mEKgcx9YwKhWkTBboEoa2PN7DlPI5ZkeG8LOjQBxSM33hdUD0DDwRE40BYFKgZEjOxnenmZiXj09K1TiHjTPgZ5MnO7ocrYM2JiHMpi5fRTd/QiKlKmSx2MGD4vK8Wx5+5wEa9qQd3k2e9imtkwMMoZk4a0aWBVYTTVXQfIPVyGlKt6OzFD/ZU3WNxTglsDNgplBtvhshyZHDSwrI0G0UVmw1YzA4IS/vR6UZjDa5PGeJsHTCjJSHkGyOxzVF+V3ZdXVsJCFHyoGlFSoKDI9qez4EZcIRCOQ8eTc66kyIhNotbh+k4aRTnGAgVvNWIcKbHEGGUfhFlpYrStoWj2GCJPGJO2asKePajGJaekk3t5wvG2E/0/V8+WvCpDPwdRElpGho4weO4wozKDmjjE2PUrOKqFqGs0LF3H75z7PlUuXMO+kuznbPHeSsbGN/OKBv+KuH8PI0R7M0irgQn+PTuRdDywOnSFJSh0D7qP2+CkqdC+k6RMLiV0FwwoUk9AcgYoma2t069DeCpGqR1l3WBDP8nf/+VNGj+1krpumdHiAixJXsL/4I4btXYxgHlcxdjh5jCgj+3WFWpli/JvgIPtxwJ5IUKtdHvSnQ0hK7w7O23k7b28V03BxqVJGqBZWtYjtWrgVFROPsldE9SzUsEbEjaE5HpowUNBRCeOIQIfQRmCCkkaICb9Gj+rPSjN+uPaVA7RV5MgTZIoF5WYCIZUSvALrPwHKQmi9AmwPocURkXoi9QapiH+sJac+pU5OY8eLc0WkBGJdSsYLFaDkwUQBRsdlQfkXHq0yOlSkisXydUkKl8fIpVWawlDRIav7GRgVyBWgXATPPYBfjuotaacFY4UQO4HVp/j8CLD+FJ+bwO1nfSVFQWMkxppVnZSQPkSAo+pwfDIXnL4QqOtB3zAk5rwcjA1cqVM5/2XgkfuPcv8997L92W+w9ugB5id0oied47p338Tcnh5eeHAr23J7/QfnRBsaLXL3vbu5+97d/MnnPsllV6yms6cN3XPQLRfHEaBo6LEIYFKtVqlWbcouCE2jobWJxtZWoi1pulJLaVjYQWlykvFDBxB/8QWeHvFwbNlGm4HNg6duiyCFrxPpTGSRftolSAQ9jzxHM/D0lhIhpOu8GPhAC+yYgamyLLxxGOlaBLIDL/rt2Ipkt8zXYKMr/aPcSddhA+MC7uwVZIE5KtyoOjy0YTM3Rq+kvqcBUVdFUWy5WjQjKIUQet8w7NnM8kaFIxd08ItnDrCWGinPBTYCH26GEQuemnL54hNDNCCvYwyPF3cUafP3LyMHpg9oMupy2G+/124/RS4VQ8iEOQ9IgJ6ReZR7jkBZQS4p58MaYEsW9gaVdUvIXhlA2L6NCpxHYauA9i9CJKxQGAVziprCQQhJC3Zkn7csKIf8wnV+Aa9wSBbvSkYh3gjpNEx1So1Yx5WLesuSz1QhC8URKO+XlxZrAiVaY0KLqt8BStRCbEuQTnGwBtb85vge0kl2kej5HGYJ8wqIenCjxqf+Aa5pF3RY8P0Dgi9e9zYK0zVmxblm69av4/prrsTMHeHZhzaRL5RPf9C5aHlxPpvudbKpiQl+98N3sGnHLvRQlESyjttuvZWsmaNSnEGLhgiHQlRL0+QMBU80kIjVY2ka5XCSQqgRN6yS6mhn/rJ3cVEmQV0iIudJR0czTETIwwqHOUob1TKg5QiFFBwngqZpqJqH53g4pkN5NMvB4kuMHx7GsUwacHELY4xXZjCLdaSbGmlo68IJR5moVHFsh91bttLVNYd5sSZuvfX9TFr7cEWJEGHmaGsgYpJKR+hZ0knn3B5Wr/tTjGgCTQtjaCHaV8CcUCOKj7Q61JKRA93MYJYNsAeokfHxPwvKIgayBiFkIcQZR7BvECIOaAbYjsfogMXhXbt45K47ObL9SeRs8GYzgW0V+PHX/o1P/t0naE63o6EQSQEOVMpSq6u5WY7hBw+OsX/fJETaoE6DQzuhaT7qwpUsXHcznU2tPpv0V2SaQtPfLOazA3dSAhq6PL7GIW6jiwuJESi6ng5i7EZqz5c0aI0bvO/6/817Om9g7pXthN5z5pcTsKhP9X0OkhU72zk8Sprmte+jWw1x+LufAkqQ24Vs7WZknzn11UsF0D5gJ9nDPRx7YhEtnWG2mbBunWBeB1ywTqHx46t56UdRDu2MMTM+fLzvj1DT2D+37SZkztYPXmG7yatXIDYIyu9Fgd8GPo30O1+PuELAdjQIoRCjxmrM+99b9f8eQY42c5H+3DZqztgYki07DCRANEC1GYhAJYrseYG6cRCwD2rXddb9AAAgAElEQVQIBKJbDtAC6hxQYqDqcuDLjflR+Ih/tVm5rxIDtaUm/KcrJ1bZiwi5pk7B+9x38xgVNvESn+JBnq6ESXA5MkEU5EphCPNolKkHx0iIW463Df6V5UuQH4dKXsYidF1HaCq2Y2GNjlDc9jCWkMBArL6eL23bzdtCKm2naf1y+Vvs3PtD/s/XwZ4E+B3gHbP22Y5UDgzsEqh2ySD/AyedLgL8ALbOgagJC6P4pXWgQciQQALYacOejTZH7x4i9tz3+I+pO7lDXMkV2uVMWUMMTj3KUXaSpsCtSPJtP6cibgwgE2onkCJuAV3IpHZPg5I5QXKwhP7l3z9D9p3zdt7O21vHXAwMklqGtvouVq68hPqmDqKJNKCRLRQp5iYoZCfJTo4xMtIns2WFQKDJQu+E8TyZG5SKR6grzcMTKgoqGjqjHCJPH1Wyr3gVx9VvkONeUKBWoabQHhQyPxEbGwT3J7AxhWhcT3zZSuasbufKTmgtwr4xwZEJOSe4jeBEwFYVqh5k5kE8JIuFC1HD7DRX/kTXgYGvD5I/+hCwk83cyou3Xc2K68P0rIRMK7Q2QXYaRifhyBBM7oNCeRMyg+CtaWelGftGmR6K0bP2Bi5YfilLlV9e31VX4aL5Nb3M2VZGdtDMKY6LA//tA/P5wLs/w0TxwyxKauivcCFdPfP4weZHuPjyFUxOTbzq9fzjN/+Tb3zvRzS1pvnGX/0+HclWQp6KY3sUs0XCMQ3D0NFUFapVGhoaaE6lSOkaTi6LEFAtmTihKPFlK/ndv/9nrtzwBCOH9zDS38/mAyZ7kG5jHIkBtodkSv60J92EPchULhPYj1zczFMlQNovpFgyyAc2jHTR9o5ASMBV3XV88N0LSMxpwEk1ce/zA/zpnc8wjq8VAuQUSEVAlGGVkIDuBPJe9iPdjSKSGOkB4x48WvL4/tMDhLf8mDuu7OaP3r+azIduRXGnwRNokSjpJXNRtH10ZPq4cX6OhmKUr+yokD0pGPTjUcnidJAus410mZchyZlj1LL8VwJ7XclrmHzVO3emthP4Q+DrSNjbkVoA33sMKluBORBbB+vmyxHQ9PyWW+xfQcBRnd1hhay+9Xie0Wyautt0Gt4u5cxirVAoyWgRU5BaAFVbFt+aykF7AqJRCOm+vKsJ0YRsk7EsZHOSCRs1/CLBwMAAOBXpZGeugPYumJ4BJQzhpCzqpY5I4ghTSKLC7NyEgIL2XWQNgiPIAl1l5I2fNYYm1it0v0fjc9dBKgf3/fRZnnrwfo5t+w+KM6/PHfmvsI9/7mMk4hq7e1/gFz95mlL5jdKS/C+0aBiWzpFBhqp7+v3P2xnbQ89tYMW8OXS1zaNqzhAvOeBY2Pkp4pk6ciUTKx8jqtvoKYVUOkF9WxuJVBzFNvHKeUxFYVR3GXNcFDTyw9OENAvVcLF1ldY5jYQEGI4CVQVHK4IQaHoITTFobG3k2o9+nEQkhF0o8MBd3+ead13H2MQ42akstuXwpf/xx4za07goRESMLCVS1TDXXnYNt95yO1/68u+wd/sWutrnsGD+MmKkqGuvI5SpJ9SYJNkdoiUcQlcUP8YPrlGrQTqb4RpAGC41TdjAaQyKHCnUdLDcWZ+VkMPQeBFGRivseHIjLz57D0O7X2Jm6CieC45tY5VPzWx805hnwvDfs3/T5aikmTM/zrQDluvLxvjmONDW3oZZKXPsSDOseAf074Qj2+HoXrhiAVHVO20w+/W2OLC2HSl9BLQTZyEarchW/wXyvhnUGM51SOAkg4zjBaC7DkTCOp/+2u1EtTDaWf6YAM6abUGpnYD9NhvPsrc/wMjux0/hj1pIT+PlQGyQHxPCoY1jJNhLqLSMulIPF89diNBg430eX3vmBX747Of5zaY/pkNJMBYZ4zk2UWSaIbzXmLHzZrE00vv6DDKC+8wvca4q9Ugm7KeBi/GL9L5OJpB+sTxngMYHQfIysmDYLmoiaQHQFkam+wTc7gTS8w0coyISVg90nQLP2kX2nxlqyaIF/zUIXk6ey1UhVwYxiHwSGvxXDJSQTF3CkhVYnah8H8R+NWTAdNwFxQX9Dv7Ki/I7TpoXeJIw7UiPcAjJ7BwCQlQJk/eKMHMLpKAkoGCCMyNTRRUHdAGFGShODlMcH8Y81o+x6yVSwuMqoGv1zVz9oT/j6pBCRHm1QmACuIv9O3/Ojo07sKcjyJVKCyfW9z6IBLkDa4JdcbnrbLsQ1C/DbyyCZBle6oWnx6BlLnx3C1RnIBWCK66AD/ZApzHDw+zgH6e/QkSUWX/JzVy/8CNoukLdf0xywAmxF3icGoTaCFyoG/zTolVsPaxzd3WABxlE6iQMIVdfi4EL/P4Q9KFB/zdV/fveD9zNqcsgn7fzdt7ObZP6M67rkcuWOHTkGHUzFslUI/UNzXhCIxRtJKUlCetNCBFjYnqEcilP1SpRwsGhjEWBKnnUUhUhBCoJDJIkSfuSBa9uAZM/8KlnkDOSjpzNyshRqdXftwYIBvPSN2H627y42eBnLxr8Xw0ckcJx29DEArqUa+m88maqySh5T2F8CpZ2+uo5mhw3ha81FYlKxqxRBUU5hCwmswVIormXooswwoLsoPQekoZk3VZysP1FcIqBaNVb094UYKyqKCxbsZpFi5dinAaFnb25TE0DLjZrm6JIIOpUdhL/8ITzKkAyrhOJJqjPJNCVV9acFahURR0LF12Ms+8FstlXjm4WS2WKZSiVK/zD13/AdevXs3DpYpo72qnmKoRUA8MX9xSqim3blM0KlmVStS0am5upIHAUBUWFZFMbCy9YQ3tLB9MLRlDCW3D2DTFgu5SRsdoZBywhXcIuJDBqA80aZAzoN+Htc6IsT8WYEDrhnWN4SLCyPaoyf36UmYkSqy9axPJLFtN+3UpCmXaUcB3X9wwjmhr467/5GeN+29cLOGLBjKhpkujIB//i1joquso9g1k8pDtah3TqZiwXrAp79w6x+UG4rHEuybkNaKUqSs5BqXiQgVDMozkT4pIlHdyW7eW+UcHRWauVyqxFqYfkMQR8VZDtENTj7VfgN5a2MDyQZaTweizCbaSa7jeQksqrQXRBeSeSP1wGtVM27jZgNIYcAnXQ66DDkGKuxyaR7p6OdMzHwDLw9g1RvqcJZ7Ad6wpQLSlDQAUYAbVLZrEJRYpoF0yp5SI8+bntr3SFK7VkPU8WqPEcufRIRKEhI/kWVUem9JoOoMljs1lw0+D5OrTHM7ACcb8g3+Ff/d83g0T7J6iF5nxaW/ct0LPSZdmcCupELz/89++zd9dejvYdoTx5bvKAIpEIt9/2PiJR6D18hL0v7adYOreX0q9oqgbRjMwzfuvOi/8l9vPvfo/47bfRefFa8pNDeKaHbTvYtoUiLKpFB8dSUdQQsWSGxroQWlcrVasB13Yxy1XMUgXLymHZBSpWGdt1mB7sZ2yon4NHjnH1e99OR+ci6hL1RPQwnvAwHIGqh0DTiRhhlFgSWxG4jkdMVWnp7uHh557lqaceRxUqB8b7aIo2sbB7ARddtJaiahHyNLrnzCeUSdDTlqG1q5XGliba2lqJGwbRRAjFCEFYh6SEYIVSA1eDDNvZ1e5nM2ADkHa2OzYbhwsSPweGPHLZMtmZCZ7b+hzD/dsoFsqUSzYTg8OMDh2iODmGda4VBHQLHHzs52SiCgsWXksyDRFTan07/tgaTUBKaHS6rVx62Xspu1cx2r2L/PA+7Kk+GpsvIGLEzlpT85exwK+yNOgfHeXel14g3OxhL74ckmFMBEN4qDg0o5FAp5/aFJNHxv7WUOsTFUWhrj72Mv3XM72e2RYAsUHS/GywHwDbxLNfKah26vRAX6bZB49dIoygFQ5S6VtI75MLWbIGXtj+Ix7Y+DOGRvfyi9I/s0RfTtkeZYBpTB+IPRfVYaXVIXOlrkCCk48g/SCYLTlwJhZkXt2OBGNX88qyFr+MyXElCAf4ICdFpDfdhxQA6/G3C2ryBbNrUQfJoMHVBRD/7BSSCTjOvo3572f8/YLqp8H+OoiA1xkUDQjL44Q/ago/B8Dz5GJFUQC/EESw3dMgEidtXEpESROx16NxKQpRAkZswJnSMNHLWfb90wHU6+dRDMFMrsh4/1E621rQDA3HExQLNlODx1CmckRKRVx7ioXIJKjurMqyA2HivFrNDoEQDlsfuJu77zvAExsBtRH+pB2UiCTDBlVIqKNWehFgLdidJ57uI9D0brjsEuiKg5WVymHVGYjMhVwfjO7YT13lAF9633sYenKGpx67n4d33E3ZK9CJQnpOlMi6JKLOo/7gVczfc4SWrEGJbce/pgQc9lz+fmyAMVfhEAV0wDnOZ98Px0tOhpFOfw4JKMeRCPI4EgB/uVLjeTtv5+2tYAoqKrqqE4nE0cMxPDQqps3k5Ay26yA8gXBcqqZFoQwVM0LJqVLBpoyHRwmXAi6TICz/rDkcQrhE8KjgcPrMy8C/hprCoEatuPokctR6BCn7UyNDCqAEniwMnKzK2UoeMYZGPwPKQbK7D2FnLseMLKYiUjS3xkhEFVl/BolBhDSJM9h1kBsHOabX+/8XcFyBaUK5JAlhpRxE4zLjV9UFruvVmGNvAgsll5HouImu5QuoejDZN8XEwWNQ3oVMAa6e7hQvszcFGAuwbNliehbMO77YChzt2c1/8rzuIl2Ys3HMAnfrVfdR5euVzPUgly+zYcNmWjItDMaSZLPjvKqTKcAsV7nvoY1Uyy7jZZOlpkVzXZKUHkMzpCSvLsB1BaZZxXFsKlYFPR7Dtjw0VSNk6Hh6mFRzN8l0G5m2+QjHQdeSvDg8xOFslpwFY74n34B0ZkE+QlEFMprkchajGkuaI8yLx3AmKhw1TbrCGgvakiy+bh6DA2Uuu24d89avgGWLQG8BxaCntY2mFoOnvvccD49OI2wXD1kYK0jYcpCPWgGIRXTiukoC+egF3IEC0l2xgcHxAk8/fxQSW2hc0UNadUkpVRrTcVTHRvUcIoZCe1Mda2IKT6uv/mAGiW+q/50Bu8pCxqiNRBhVfz2XpS5yOAtCAx3+FfisBlGQSGnvBFgJjjuXPXG5uiiYSKe83j+fjVwMJGGml+oLo1QHZyA9HzsZwdAVtBCYNihV0HQfH1Nl6oDiyYqG4bAs+CKUWsoAyEIMmj9IRsJQ3yCZxYWy7N/FigRzXQ/sAnhREEEuQ5DFp1JbswwjZQk8ZFgrgfQ/fVKIEoK6TrjgBoeexkmap/vZtftJHvvpneSyU6/jffjVWjqdZv78HlatXsbGnc9ycM9h+g4Pn/7Ac9IUWeGmqp0HYt8A275xE2uWL2PJgvm4lo1jVmUco+RRnBmiMFNGT7XhOYJMfSutzWHiRgrHkcz4UhWK2SLFQpRCwcAybSKGQcFxKM9kGTl0hLGjh6hLZjD0EJ7hIRwHx/FQdQPFCKEqCooRpWzbuKaNoQrCsTqKFYuRsXE0YG7PPJY3LWfNirVcddN1OBEXz3PRQiGMeBwtFsOILyJeFyVWFyYergFpAummuLwcbJqdJqX779VZxwWQ2OzPCiWbXKHE1MwEQ9Pj9Pa6TEwUGB8f5tHH7iO39ylc8xwDXl/Bxvc+yeQF8zHta4k1geVjL7Ytx/dYHYSjkEjUkUmtowz0L1rE4JG9jO/bRlNmMYYePWsga3YBiNdqLmBZFpXxcepCMVSndvcTCFQ8GlBoRkIXGWrF1YICmyo1vkaSE2GwM7VTAZxi1ncFmmw1Ec6ztyi1tlKAEFOoZj/l4YPse2QlUculf88zjAw/jUKR/YWnqDCBwGYG67gcx2xTiPmVlc/eyf/VWhqpW3Sh/1KQANShVzvolBZCekNXALcgdWJPldH2y1ptsRoUGQs4+mNIx2aC2ogVjFIBjD97pRKMXPh/e9Rg/uB9kFIa0BUcZI8OPNWgGkIG2ZN0ZG8vzrouRV7P8cWp6mtIaT5b1pPaqYonQVqhSOdO6SaiNjCfpdRaMvhuKQOhM4lqTvP43Q+jWSupRgyK+TxH+3dy3Q3XEEtEcYWgUCgxOtBPcWwQJz+JoMIiJFxdPzlBfMdWJDP61OY4RfIzW3nykY08+niBnYebIXQJvE09jgHM2psTn8UV1FY1wGqoux063wHLbYgZYJkSiDXHZcZeAki6JRrtURZaFt96aCNPPvsLdvY/BkA7aeL1YZgLSqNKdO0yuqdvpNMsgFkDYyvAMc/jrqlRoKYQEQOqOFSZ9EMpgYJik9/G+/37+Tx+4YRXbJvzdt7O27luHgJPzgqagScUbNvGdYqUiiWqjg2ugnAFVcelWAaPDHooiaGahLGRgo51CJHCExau48naQp4s71VFII7PIUEw6OUW8LYC/dhgBgn8nWnkDPAMcCUnSoTi71uPnNXlTFRFMI3LNFlxhOzQGBSmIT6MGu8kGrmCkKbJmjXImS6sgR4CLQ5WFPS2ZpT8CkTZBbMRV9eo2DLjV9clAaxsScjEKgvIH5PFbN4kphpJQolF1M25nYaFdbQfHWei7SBO/jnGhxIUJg9gFUc5Gy2/NwUYq6oaa9cuYvnybqCmrHQ6S76hV3Vq8zxBseKxe38vv/uZ93LtmgtQnQoKmu8sn94efnoLDz+9hbaWRv78C59hXls9Gh6uq6ATBgRVr4quqdSnksyMTVEu5UklM6RauzGrJrYWw9UNQuk41932ad713iyP3vNtHn/sUZ4+5tHrerhI128H0r/ZA+wJnlvgzn1F3usJbr9Q5YO3rWbgSC/zuuuYu34x8Y/egXSs66lF7DUQDp5uEG6o5w9+42q23/Uoh8azTCG5EIIaFX4CKRXw0/5pbGTW+uUa9Aro9aTaWieS+TJQgh/3Vvhu7xPEeYK1jXD1kjTv/9ANRHo9qqOTVAt5hOdw4ICgeIa+TAQpS7C59rNxBfzF88fO7ARnbQ8gh68e4DLgQfnejsmcWfdR5LJiuRwBPwP8B3AAgqVbzTHvQXqlM2DdB/2j8OV/InTvXJpXGITCcKReMoyFLUmLoTCMT8KMCukUtDVLKTHXlKfX/FG2WpWRqkhUfhZKQFMcEmXIZSXIq1oy3SASk7rBXkDO8Em9qEiseSuSFAxSQzbsfxZYBEKtsP4P4Z1LsuT2PsPG+37A/Q/99A1o/1+dKYrC+vWXcsfHPsa993+Nx+5/gVzuLaoRC0AYnDCMToB3Ho19I2zj81sQmseH3nEN5fIIZqXEzMw4A4d2MLhvH3OWrGPRumvo6pqDIzI0awJNV3AicqTIJRPkc1FCUymqpo3eGKI5k6Bn8QIWr1mBCRhCxTNNLBssx0FYVSLhEIloDC1moGsGjqVQrCoUvSLj41Pc9LZ3cNnii4i7Co2NrSiNaUIN9STaWgk3SmkgdVZKarCWdpHzQQCcBeGvYPiYDQwGx86uRyOQmIOsvS5QhHypnkcW2HZghuef38HjD36fXfd9GyHOXT7h6W03M8U++sY9lnermJNQtXzn2oBEPbQmZZCtPw+JBKyxuzm8p4FnnCW0RTvRFAWPswMxAyg7gG9eCysxBVzR3c3cj34CE5kdI2c5hVvQKaGT9Pdb8QrnCJgcJhJciXP2ALHDiXUHZgP7QeKHclx757WB+DGk5xTyrzVEFoUBSoXt7HqgyvMPyHJca1nAJqbRSXOMfTivIpWhsQCPSTzezIE+HSki8G5kunYEKeUwG0A+83mjBak2+yf+32+UvEaQSC7o8N8NI5+Qnf6WGLCOmrJewMMPFK2DEFOgRhyMdiZ+1S5qK5ogVWg22liiJrQyJo9V0qC0gReIXgQ0kgwnAsZQK3oWaNHqoEVk4BQFvJK8FMWRAC0g+3YACDcR1NRWcbHdSf7ywOdR/7aBJBlixBhnjDUr56HRjvAgPz7OgYM7GD/wNEwN0ImE3huAYmETh48cZqX9QRntP4keK4RLMb+bTU9ey/c2KBwZU4ELwP1H+KEBFiiHQdFl9pasCrF/1hnmI9clQv6eu1RW9ijMr0L/GCzphHIWRvqlSsv7PwEr10LTxRexsv5Cdnz/GH//3d+hMHWUer/FF7KelNFSa5ILYd7IDXQ703Do307dcaipv65E8ovHgSIlJDtqP5KUoSClLhy/T7yV56jzdt7OG9jYmBS9EpPZAhVvmLCuoWsquh4GdDQ3hOeolKserlJPU+NcovFm9EgGS9FlwgMOrlPFskxKuRLVYhHXrKBhMurux2YGIfLANIINCOEhhEAIAT4YXETODmHkDGJRm5EVapqxCnI5383LZYDakWjGCuTIdmKu0D7I74N8FKHNY/LI8xTWx4i6CmkFkgq4iqw1qScgtgDSt/dQfq4Ha/eHEL15lMYYJQWmChKPcKpQqcr/vbyNeOku8N482trm9BZGZ/Yx2t/CH9x9Jeve30RHsokcV/Cdr/5Ptvz4L+h/4V+RM8KZ2ZsCjE01NrO0cw71Sg3My/DLMTHeKHv0sYN8+65/5uc/vwubMo9t34onxBnpd5xso+NT/O4X/o4VTa188EO/xtXXXUkqncRBx3A0XA8cR1AqOowN5XEawzQ2QLFokkqn0TUNVVNwqKJFOrjpM7/P2z78SY70HeEbX/2/HOgdwiyUySC12k6+wlHgzkMlftxb5jJlmHet0em5qoPY6vnIdPla4QT5dw72bef5ezbw71/9GXcXHCq2hDhtpGpS4GYExVTWhKQP2OvBHgU+0AnXz21jc9blr3eMcwz49ShEXBiqSn0mBTgyBT/dlOX3t96DoSi0eB6r6jXuWBdDjYla9a7TWBnpygW7avwyy6wztYeRGmNPAJ8DWiB8gfRWj9VLfS+QjfUVZIcnidSaChzXgCPeCrzN3/lF4AWyX2hH+6JB7D2gh2FyJ3iTEK2HuiuAPnB8ir+SgEQKClUJQqsKZJKQK4LtSUkyr+JHwzyIq5DMyMK9o6NgeaBGobMJRi4CW5Z0lqvmB4Ef+j8TZD2TAU6scjAX1lwDn/ot+OAauPPb/8AT9z/MU4/ufL0b/Vduv3nb+4inDO789l/z9OM7cey3uIZqZyOkUrB375sqZeStZAd37cUQgs9/9uPoUYWtLz7P6NBhlNIULWkdXZ1kenwne7ZGSCQz1LVliIeN4xN5zADSKmokAfqFmLlBVM8k0dRBumsxFdORRQH82xf1EyxVBZnv7oCm6kRTSWKhKBfceBulunqS7Z20xHSa6yCpKHh+SqymSIZmUCQggB0C5y5QwjZn/R329wlkCQI1RajBGkHd9QqyQFV+SjA1doiDew+w44UXefhH30PkxvFcD9f1cBz7LQ7ESju4eTsThf+Pjn/5BOWyIqVmNKn+MD0NqgqRiGznsVGZpRzW46xbF+PSdZA2OGuZgjRy9jE5UcnxbMxG8sH2IKeJQBlyLtLXS3N6kLeK7B9pat7J2VoA8INchExTK2qhIyGeOElk/s7ZewkGtdqWGrPLOw0zSZkZnmEnI0QIYxAhTgOTjL5qRWQAh92cDZD5qzUFWA78M9IxMECtAz0F1XfyWtpxLXAz8EfIseH1liWYbTU+a5P/bcFo5Wu3HudhO8hRbnYV0wQ1BmtgASN2BNnL4v6+Ef99GdnrKv4rSDUq1/YLJ8BIQsHXiyLuX1uwvD5FboGYAXcCSIPVBEL3g6YmkJKrXEUHLxih8c8dKHPLUVzDoRPYyzSjTKOhUIdg6v9n773j5Drrs+/vKdNndmd7k3a16tXqluXeYtzABkx5DYTAax7AQPKGBwgvIRBDKAkECIHkwTYBDMYBgw249yJZsmWrt5W02iJtn51eT3/+uOfsrGxJlmxLlsNen89a693Zc86cc885v/u6r991dW1HzhXBEyQ1MISxcxv7ckkUKlpVD2Lsh8dL0PBrWH8tnFV7xGHaxlc40PtDPvxtSO25DMu4AOgEaT2Eb2DJpxXmzYRp4/Bvy8HJlMq+XC6eLl+1EDg/g0/8DU1fCTLrMshUwf5dIog2VAPnXg0tXvj/LwdrFHZvHuHKLy9jmp5nDlFUAjzGMO0sIRKsE29gQJzaQFms8Gpw5xivsDihgLC34JXXagpTmML/YAhexEYhhUE8k0eVJHySl6A3hE+NEiCIjAdb9rLovOuZvSJCTaNKICCh+CDSAKEIVFVBxwyHWglUxynXbw4jBZtCysHJOwRMBwYtul+EA5t62LP+Sfbot7GdXnJoGIjelCaODDB1dVU2goboQtRWLydjHSaiyY9TPxZxrG4e/9b9bHjxQlpWt7BkBZx7DQQl8VwIlrf/oZsh/5dQSMqMDkUxPVDMQi4rCNmRHIwPgRYDz5gOzm24JglnDJwMxG/kh29XUGQJSQrhcBGGHscy9nGyx3tGkLGR6hC19VXC9xKhCZyskjndyJcgmYW2eihakElrxEcy9BzYxsYnNjJ+YCvVTkGUVPZrf8g6jkNJ09k3NspPf/8nNuzexeXnLePaiy/H8svopk2pZFNXU09VuI5QKIRHVdE0DVmWcXw+vLIHPF5KqorHE8QfitJRVc//95Vmdr24ib6dWxjc8RKjhzQGEGVfpwRzIyIfYFSDZNHBj4Ui2UgNdUjTWxEfTQeoB13DGO/jW5/9KQfjcWIDY4wnS0Rs+PiqFqbVR8haMl99rLJ6HQRWAq31UK3CYg16R+FPMZhTSDJkOEhi6xwuz7LcPTqIGtK0oGSZwicOKMVtjBdzUIDCCZz2G69q4Zo11Rze1IVlQdP57dQ0R3C2xfngraOUjFM1uTER6+2fBq4R71KPiLuhWc77jmqw1gfP8MrsmOuBtAZPJSm7+CII2XlAB/T7yNwFhREwLgOnCdGZFgLFiziB2yHng4E5EL0ULEukGAJ4vRAKiPZWywbVA56y12/pIBy+G+o+CDUNYAUgp4rWgWk1UKyCbA7y64BfIBh4qXyISY7spLsYrl1t8LY1EpfOMnn83p/zp98+ys6d3ZjWCUqbz0CoqsJ7r7+QAz37iSVTZAsDN4UAACAASURBVPKp/4FE7FG8/bwSBOUpIvYUwrZt+voP8bkvf5W//7u/oa6xibFDfWzvGmJ/UsfX3UPnLItz1DBdDevweS+mrraGgF+USLYEkiLh8UKwxoPjawbLwjFMpEIRJWBiW5ZoxJYkdKOAYpjYjo0jy1hKNYbkw+dTCIYDzKpehB2MoHpUVFXG8ggqwKFCrFqIAs1DxY7AXcKDcpvSpL+ZHIPj6oQsQNNBKxnk8wWG4yPs6NpJ77ZtDO3pwtRBK2XJpjOkEklyI4eFAfafGezMbvI9/83mde9n8ZIgqDIWEI4AHsgXoFCAUh7GYmCYYBQlHENC8ZRtJU9ynxLi+npf7YXHgasV1BHP8hwv8/k/zt86CFrLpcAMxJPwZEjlSQ3dE9/rVMYlVCyTxJ5em3+5iViPjCAmNDbisW+TwaGIjkOOIkUMFIrYyK9KxAqcqWTOO4G1iMCiFgSB6Qd7B5g/RZzLkzv2GkQJdB0V8v9UzQMsJmtM3eAtD5UlItcb1rUlKCEKNpsKCeuqZRUqI1RHkHHZSdsLUInZDSJqu+FJRyEjKM0g6CUwxycdXbK8nRnlY0hQIVRdQtgWfytHhKTUcY/bEn2islkODnDv2O4Um4n34KBjYxACvDho5Z9mge2bNzBH04jWt5IaOsyB4hApq0gTgsZ2VeYK4HWKJLM/pMpeg8qRZKysXoNjq6QO3oFlfh6hxcqAtR7uc1j8TlgdgnoT0Wm1HY60RvwP4Hflc9/LgrWfQAkEyWUg4ofdYzBnOtSFoSoACyVQUvDoI/dz6+3/gazluLH9q0Qz1YykDrGLHxDAj+IoldMxAFv37GBH/8tTwo6OY1d/Z+rndgpTmMKpQltgLS2NC2htW0Brx1rCzSqKF2SPjOLz4ZU8+FBQZBnJo1AzI0pNs4I/JAsFqQIen+h09fvLArUx0AtiHi97IFuEUgqKSciOgGcUckMa41aQQk0D1aOXs4iXGKOXMUbJI54aHsS92kQ8hVy+LY8Q7dUg7lqTjGAmliEn12xHh42llci/lGAsFeBAPkq0FRpnQ31YONzZQI0PQgroQYlQnfhZIQ3pJPjGIRmDlAIFCXQcRI/3GTjHdoroE8+mAvAslc6Xk5snnxFkrN+nEg6KUl+ikopsc2IFt+OA6UAmY6DIEK167ZpaTYNELEPPwWGsBg+9wwnGxlKMDI+zd9dzdO3YTmyk7zVv/2jI6Bo7D3QzFBvF0rL4lCBzF3QSrYuiBn0E5ABhbwCf6kGRwB/woaiimLJtG0n2YCIjSzKqRyUcCLL8vOnU1VfTMb2OfTUqicd3UhrP4DdMZkiwNAyBai8pZOI6BIs6pmmTGkmS6B+gNhQFbxCkKuxCDuPgFmIvbmakWCRbMFEdOLsGLu0MEfX76Ynr+Kjwiu5kO22Lktb1gOu3IFUs4fPIrG70EclpVPm8pDUbu2BOrNpMLmEcyjEDukNp2KSel1lKHQWdYbhwZR3vfvc0DrWNYY8labqykUC0lqGexGkIMdGAhxETlDowp4kVd6tcNPuK0O4VA9d2iS8LorKo1QtugQ7iB+2Ida0o5MF4CYw8op6fC7IufFltCUJ1II+BUYDsIFi6ILdtB2RH2IgZpXJDnSLaB4oJ4TcoxUqkHkogN7dQc4OE3CjCemUZgopYDMoOICKwdyMuTGjSW7ZBDoF/Flx2PVy/KE9naIj+rTu499572L7lAPHkWze4oCoSZvaM6ciyTP/hAUZjyTf7kE4fpLeCZ+FbH9lMlscfe5obP/wBVG+A2tom/FV1pPsPUdB0StYgwdAukkWbcFUz+sy51NZH8fvFc0+RwKtKBEMSkjckMlxMC8sXQMJCsi1kJBQk8loJUzcwLRsLGckfQvKoyD4ZT0DGV1uHToVMsxEjwC3IJnccuPdu9xluT/peBooOZDWdgdEEul2CUABTlsiXivSPDhEfSJBP5ynmi8THh9netYP+rVuJ7Z3covrnDB+YGYzEDrqeWM+ShRcQqA7hyBAKgamAbUAu4zDQ72CaEg4SlgmSAXmt3PV8ksyW64r5euBGG9VRGTNurvjxVLHueEtTceh0tYLH+hsLyDoOwwmHhoBEfbDyStd31l0AcDWB7hgX6jZX/XjycBAN7DoVz/o0omnRmeQfZk34vJ1spNWZAj8iVu06hKvrdIThVIaJtmz7j5zsO5MQQV3nc2Sf0KmCOxakif9zj9eNFHQNU+xJf+E+B4McuQQ1WQvtErEalcSCUnmb7tKGZ9Lr3aWBarEtWwM7M+lvXQK4VN5upvxVLB+HGwrrF8chyZXJk13et1MUbVCUE10nCFmXnLVw0HEoESwfjRskpwO9g/uIRKqRChrZwwcZMrMoWNRy5GdYbNVEZzPO8/0QaoY51ZWTLp+FGgkRWZElvf48HDMEDIPTBgdipDfXMlzjIx8wwTjAy5timRSohSThrbcYGRKXYckyiEZETkJIgRUtgih+4Omnuf/Be3lu48PMJcqy8EWoWhALP/XIBAmhOOXpcNkFolgyKehnIAEwhSlM4QyGQkCeRn14ATNaVzB30bk0zAGCYHtA9opMIskCqfy4sQKiaUE3BAdl6GWtgWWCbVIsGozHFQxdBlkhWOXB0CGfgMyYwVhfFicWh8IYuWwP4/YOLHLY2EiTnqJu95pLxkJlObGE0Fa1Ip5SBSpTexNBh7rLiseEBNMXt6J5fajVgCLqTt0R23Q750KAVwVNFXk0FqLDy5IgWILMGMg2UNAxx5IcKe84U2HxWhfx4QwhY32IEmLyqXYdmF5+8Z3yfywHTMPENE1syyBnwM7dacIBD2cvrUf1yEjHjvI8Ao7jYNtgWSaxcYvu3QfY/Ogf2UOUR554nuHEIAU7wVj8EHG9iHWKlGHxVJbfP7qR3z+6kb/77Ie4/NI1tLS24dh+JNXAkRwUFJqbG7EsE00z0MuKPI+NaOWRLWR86KZF25KlNM6dw+wVq9BL30fbsBMtlqLaMfCEHKbPDLO80Ucw5DA0mOBgn0zPYy8hxwZY/YUQNC5GkjTs1BDGtk3cePF0ipkYvf1Zdu7VuPgslfqwxYGDwzz3Uow2r0RckcW1sR0e1W3iIxVNwDTgbVFQIhCu9lJbEyFxMEZtfZjumM5z/TlGAc0pF8mSMHB2oSOG+giv/rG8cjrMnxHBt7iNOYvmw3NbobmG4UMRnrh7mNMnzPwZkAWrFsZnIEa6AVYeMtXC7NX9GMq2cMl+xoGUzJEfT1eHVsYYYpZ3GPgxqDXiJq9Z0LIQfPMg0wejuwXxakmI7kFbrK7FRiAShWgNBFTY1QXBdvCV0qjjm0n/9GrsCxS8nZVka8cArQvy9wN3IPpNy6pcestH6YXQTOi4CX7zCXD0QZ545G6+ccstvPAWdyaQZYnO6a38P++4ii9+6wevSxV/MlB9PmRZQS8WOX0PpKPsR9OgmDtN+/8zhgNO0ebBx57l/MXzaJs5j9VXSsTHfs2+uMHQeIbRxzfTsW0LtQ3T0W0LTT6LtpbqcisUeBSx0BL2l4knR8GqDVRCj2yhlvebEUyrXASa4o7j84HHLwpHd+ruBpW4mOz/qiAWeVyXKtmBgCPiCxzHwWPbmI5DynY4MBrnsYc3UCqNMHvmNPw+mZGRQe575E8ceOwF8uMppnAsRAEDq5in995vkv/AHdS3BohEZRSfuMdreRhPw4sbbebNUwiGxD2/ZMLQOOiN4PjenI6jaoS34k5EPWAibNSXciTh65KTky0rhPdqhfo6HkzgEHDfPpuLp8uvIGOhYo/hEk358jHp9pE1x2uFq/o+EbgN8G/Mnd0NH3vjtnj0fbQCtyBoU3fpJUqFxD75/cuISdo/ALM5vTZlXkCaMFspIY4/QSUzYbLpio24M6rlvwyUj971h80jpq5JKhkArmbaJWNtBJmaRpDYrgGHu32DI7OvI+Xvx6hQpAZihd/dZgMwA+wQeOtEMSYBWhq0OJUQMBWhh3JHf+WYHDQc8oSpeAy6QclDhWEa+/bjGU6QGt5NHItOoLN85FBZjJuwnvnWJpxMPdIXVkyca4kwwfalLP2377H5KiiMgW02A+8GnuXBX5/F44M+gufrOJt/Bc7kgNfyrFBWkFUJv09mNCZxsBfapsOSxbB6BTx8DwQDcMEch1wuxz9++3Ns2byZCF5WMQufBgUzQ4kUNXiIylG8kk+chrJ6pKNtAe2pueKyTWEKU5jCCcFHTrfIlSzyRYeClqeoyxiqjOnIeByZgEdG0yS0Iug5iJfALIi5eSEHo+OQjTkUkxqFVIZ4LkXQ5yMQ8ROuC9IyI4psQyIGqdEC6YGDjI88h2PtRLd3UbB3YKNjv0yZL1FZ3oOK+3meI6MouxGLoTOpdEadyOxTlmUu+Oi5xKIhzDDU1EPTXJFHU6OIp45c3n+BilVZCWF3pktQsqGUBidtIw8lYMv2M7wb050NuWfvxEO7JuOMIGNNKk04rodFHFHilG3aJwp1GzFwto/AL//zcZ6+/4/07f4pIK7XmmWX8+kP38J7b171ct/4YyJfNOk9nGb9g/fR3bODXbu2svG5dWApFBwL2xFTg9M5HL7zgzv51x/+mlAgwFO/+RUtbRG8agDd8AhliE/D63GQbAkJFUlVsWUFw5EpmuAvmdiyg+zxUT93KZ/+l5/wof4utj33DA/c8zse2t3LSE+CWDnN4q/nwSd/8+/IPT0Y+7owH9uF+t7zwWeiVHmoWnoua1qyDOx4gXkLTD78sQ7kzvn85O9/zp49MXx+lb2fmwYLZ0LWZMuOOGu/s5stk96TBDAKC0bBlEocpsT7HIj3Jajzw4UNcGUI7j0M7SGo8sNtR/FsPpHr4POJ1nrcGLNz3waSl337Ynyi+3QL3n8P7AVlJ1jloAYtAL0O2M8hGNgmkH3CfGvAhlwQoYZ1kURMDhZUfqQhZrNvB/17oFwL/rKlQMQHkRDUt0O4BiRNmGGbJShloSoiPLEcG8aHwchCMgEtyxu5+tA1mEgcGIDMYWjoACTYeRvk/oAwyDoH0X85SGXWWQcXfwSuewd84lwR6vOOd32Rhx96EOst3q0V8QWZO6sBm+JpJWIBrr/lG8w65xL++eL3IS74m3EyozAWgsSbQeP8eeJ3t/6Sqo+/h2WrFmJGw9z45c/BQBonr4Mso01vprq+DcWxMPNpTKon8sDdosvNobYRP3TpA0kBS4FSuffcnvT6ikJQwE/F9dD1f3W9N119X9IUC0GGAaPjJRLpIbRillw6ycGuLsx0nHhigMOHDvDCU89Azs11kcqBAzbOVCjcq8CLUCCGgGf5z289wrs+fglXvWcuFlAVgpwDNU1wziUKWl50RRi6CKLd9iLccDGnLgnpBI6+HjG+9iLW8pYhUnwbqIwxH4KiGkP4zI6Xf9da/mrn+GSyF1gsSSw6R3lFDTjZ8zZE2f4IUW/OAPb3w9AbYE3mfs5UBD15tJHtepX6kSiecPzr8eBD0JgXAncjCMFTseq8CngHcClHvxLD8BqCxmYB30VUOK/HEuNkUfGMrUXMQgrlr1VUlLEuyewqYy0EQeqlYsySQ4ykQUS95kN46VYhRlkfgrYcBvYjCqjq8nY8iNG4EzHK3btuFHEdDyFWvHcgbCFWIOQNcxDyBFcpu0vsSzdFYIDkAbtEhRw2ESvoUJmWu3dyDS8W1aj4qWhn3Un6EOBL7GUAiZ3l+ZDrt9xR3oJn0uujwMChrxKM56mjQsYCzAvAo4vhd73wo4/Axl+7xPBF8KKE3gT6NSXgv8rnlPL5XAnez+BZvIoFl7Xzn/8EOyQPPQMQsuDKKkFPX3c+tCuQSqVobW1F0zTaEGYa01HZfPA/OMQheummhIbPzqPohriMqjhdVsCPVfVaXbKnMIUp/HmiwIjxB0YPPsiGnhDSQ7NAWgi0Ewh00tG+iui0+fiqFHwBEaSNKmo1qxxaZQKqx8IfLGEbWfylFMlECs2IoHgbkaQo7bNg/hLw+6oIqCspjqwgta9AYucuRjbfTx/3s4/9FCctC7+8DjE4kjrMIZ5Ou4EXEffxGiodP9s5fm+kA+zIiS7baANEZkBznajZooinmns39yKefK4JQUmDfAr6DkPP02A/PwBD94L1ec5Ii4IJXIqIp29EvLuyAO8kcUaQsVBxa3K9Yl0PIhADIg1sePEAzz7zAs/+6VZyOowOJUnFZSz77Vxz882sXe2ho7qGOmfGqxKxjuMw2GewZ/tzdO3ayrYt+xjpOczBxEHGMqPkDdHA9GZxSLZtY9uQzRe46Qtf4tLz53PB+Ws4/4KLCRLAMBQcK4BjAZaDZYnkPMUBRVHAAlu3MSwdTdLwKDJWXT2t557HNTOms2RoEE8syeCBLrq6dnHHgQTWR/6NKy+ay+L5TWSzadRH7iMwrQlPJASNjUg1dTTmRpBkB6OxhZ996S727EvQ2uBn1aomPFe8B9rrkRyZRSs1npo9yMc++18M5DW8iCK7PQwdYYmDOuxPODyIUKK0aWJCX8xAxoIXc1B8HcH0139wBYtXNWOl82Qe76P6Gog/miN2T5oaKpOw0/MRd4AesC4GvgHMBSMi/J0dhwndmS3BPsoWBa4ioghv98NhH2yLHH3zJvAb0GMQfz901kAphxDgAkOjYnM+FVQJClmINInwLwkIeEH1llerNIl4VqKQg2AYfBHw6bDlFig8gLgjtyLmDK4QxAd0wic+BdeeB8tnmThWmrdd9X5eemkz5luYiVUlmYgaoGiUONA3IqYvp5GIBXjmJ88wtDXIt566k6/9r1spDjwBxb7Tegz4vGDnoPQ6PpRTOCk4ts39f3iSbTt3M/fsGWTj9Sxs7iTSXo2heClVhbE1CS1bQk/kMN1cLkk8O10VrEFZGU+lLdtA3P9cGsBd09WoNATZiHuz4YhiSQH8kiiaSiUNw7awZYd8NkUxlyCfy5BIpti+v59d+7cTO9hH+tAIxUIBxzQwTQ2tVMTOWlNWeq8JYwRnnUNo1tuJPfosdtd3efq3CbqHP8DS1e0sXgSbXywSjzssXxmkFIBsXoSp65ZDJpZjzAjSjELVm3D0rsJiHqKekxClax4xDlPl710fsyom+khoRhT0tZyYdZUESLL0CqrQHXYuyQQVx00F6NpiMdBzcoPz5dZKfuBsf4ALAiHG0wZ32VkyRxnwLgVWOEHX2FfHOcDbgPcAHwL+BdjEayFGj49l5X1MvhI24u7hIEjE8EltcRqC+jyHE2iFfANRQIxFMd+ooqJT9pZ/m6ei8k0hRmwB8f46EaMVKhqj/vK/MtCGoCml8s+i5de7o8+DMO5wz9VkYzYNUWA1ll/bh7hzz0IQ7mEqDtxtVLSpHvE7NQKOVA6+0srbTSKWNrKIyaMbMOBWwT4kgkBgwtvZbWt1J/ExIFUmYjsQI2E1Mgvx4EGbeI5UbGxs7C5b2FpdUznvkgQeCf7CCx3/AI+eK/O17/jgkCSO+zmg3wEnAZiozKC2aS1X3/YFDF8bGSmC4/Ny3xAsmw5NVaLtV5NE6rfRCOufeJxr/ukrlEqCjLio4Xr+bvbNRM6pR2rzoW0u0LdxFz/q+wg7uI+ZxUVMK8wX/PgMSG3VSSembJmmMIUpnCwsHEo4jgHObsTScgfFwiCH+3KE/VXU1zRQU++nqhF0C6QiaAXIZEV+gupRME1Z+MT6vFTVNlNb20C0rhZNg8EB8HlAVSRkWRImNuEg6eZmxprnEx95CnOCUTsx2Iinm4542kHFxsC1czqmZELugOCHae/0oHuF/SE65EqQ8FXyClw7S3eO4kU8PeM2FHTR3eXkAC0JVoLXqjQ99fACl9B5+eeZvriDmfO8rF1o4OG9JLMWvb0Oj/zK5OBLH8O2hnhlONCROCPI2MrKdKVBSDMhlTYZG86we8N68sTYsbePrVt2sX3dOppnfYily+fT1lSDV17GedddxFkLVaqUsu/9URAbzFMq5slnkxzYe4Bd3QMM7NvKQO8+9vYMoGU1xkpxSnbx6Bt4E2DbNlt27cG004ylswzGc/zF2gupq2tE9apYpg2OgWNLOI6E44BkgyPbYIJjOti2haSo2KqXcH0zM2uiVE1vQR0Zpy4IGEnW7U2wYVM3igx53eKseXXE9+1H6+5DDQWpa44SranG394OkkS+oDPQfYgZ7REWnD2XhZetROpcA7482AaRGoMLF3tZoCoTMvg84LFg2HDIW0KJMkh58m+LFsGCIUrMnAUlS0zCxjj5ubukFHBSAxSLJv3PF1h0RQfdO/Zw+Pk8a6nFIcxh4oxQYPS0aJ6LCHPne4DLwTwLEq0iUIEMBIJQXyUK0JKrLShPX9NA0W2mPAb2lh3FImB8APRyjoQqiZB0SQZ/UCiGQwFQZNFaLCG8WiRJhMAEQuJhgAPVIbByMPwCZB5EiDk8iJmza/vaCNHZcMWVcN1lsKApRjHew+0PrePpp5/BMM7UG+mrwyUPZMfGtC20gvWmuNbEench2V4GL23mqvddw6YdDQx0PQ/7nz59BxGoE62Of4ahSW8mRodj5Et5DNXAaEtTFwhjqQqSP4zXlihaGplcHMtxiIy34IlWE1YV/HJFIes2ybqT6smemSUqHrCOI+7Butsj7tjopoGul8jnMpQKeWy9RKlkk0jGSWaSJNIJskNxzGKGUjFPNpeld3CU/sE+UoOjFKdsB95AaNiyjOlvgumXw/B6xnc/RU6rxtavJRRsw0YmWuuIe3k1eA3IpEDXHUrjOWKWj8wJkrGuV7ur8HwjICEI1dlUtIXl2CGKVNwzJYSKNoqgn2rKX69XpzY5i8Bd7pxMSfXtHWJs4OR8wMNUVOND5ffSqKpM8/vZlSpyvKfGZCrs9aMJQRDOLn/dgDjbGxA5yW8ErgQuQlBxk+GeTQvBZjUg6PQT84efjzA8qOP0Wmi4C1NC3ypTWYpyYwZdJawJjGMzAujIhGCCvHXherq60Sh1CGLatQFwJSfu99VUlh7cfgR3NuT6xLrUZqi8Pddv1h1TrsmbK2UJilV2rxdMoxzk5b4HqLRUusFgJpVVdQ8yfjwEyE96J+6eZCqut9WIEbAUWIhDFQ4i8utIb78w4NnXg/nwM6jXXATA/gyMGNBYJ3S9K+YLj/PDIxJ3PABWN5Doh8RTuBPxUM08Whe8i5WXLOWQJOFNQz4DwyloVSGTE8SE2ShG/KNPPsRj997Dxo0bAVhIGytrlrJk3oWwxgttEhRsQj0eOvoimMSw00WRu1vOPduf3kt3Zv9RRs0UpjCFKbwa3OVW19pNxbJVCoUIjpbAQzV+r59wqExOKmW7akuEl9uGjW4YFEs6BcOiJlpLVVs1jW1BqhogGBRCKo8q5u+aDOmcguWpIZ1biJ1bCYUY2EO8LAHxuHB7FE52GUqN1FO97Gqa2hQsFTwhqItARK4Y87jaLfcJ5p6hLOD3gT8CkQBEaiFfVY2VrRaPpzMSwmpIK8jYSg2B1jqmrYG53lloRRie69BoW2xf/pfs2DXCYO8hCoOPHnNrZwwZ6wAZ3SJeMEgXNVJaiYM9eTZv7OdnX/4GcBBfEAJBD83NrZxzxQ/4xEdquXC1KJuOQGPlW62kUcwXKOoldm0YIx0fYejQfn57x2/YNLyJsG2gIlZ8z2Ts2DPIjj2D/PH+5wl/LcLqNWcTrqsBnwfJMJEkFQlZBHbYDpJkgQmKZYNuIfmEEatX8RH2BpBUmaLjpdrMMcPIcvaGw3RpGve90EvfcIrFX7qaxHiK/Vu7MYsF5s2pZ/nyuVjnX4ppSGR37SBUDVde1kzHtRcSvuR69LwPT6EbqZTFzubRkyVmSQ77JBh3hDm0twjdRVF+LkWs07tZse4UqIlyKStBm1PRJ5zMpOVQ/yHaqhQiHpue/QrzUuey80CSg/sSvJNZ1NDBFvaymVHWUyBzEjer14fvA8NgvgeS70DcisYgosD8KnhcB8f1GQMUP6zPgzOKqBTnlrfzsilLApxNYPZB9krIl0CxxI3Qr4jwLkUSNXpdA2RK4OigKGWNhgwNDeIm2N0Ptc0QlGFsL+y7HdH95tbtmfJtNCgRWSax5Gr4xicd2pUSQ8M7eOyJB/jUp75/qk/kKYUiSyg4qI6NZhZPSbPn8eDeEwV6Gesf4cefPMhvdv8WbfVaUk+spDC6Fzt9FB+PU3E0wTYxsSuOnYb9TWEycskCO5/Zh3ROAhWJ5oZxamrrmTHNg6VYZLQUsVycqkPTRH9Q0IcqyfilSW5GDpg46I4DZT9XbIeY45QbVYW/q6HZmJYjUv5Mg1I2QS4+xuihPsZHh0mkE2imycBQP4cGetm/fy+57tcWdjSFk0cpOU5pcADPyk9hPLYHhp+jlB5mh15FtP5qVqyN0NbuwXFADUHYC54YpMZBsjRitk3KhmknmGCZRRAvbyQZ60e0C4O4x7WU9+MuDrgEmYMgc15O+53IPo71M3fb7nFMpr28QP+ePYwPnJxJZA2iZokgyFg/osllWLb5o/NqUaNvJGSOVKt+AEF31VCpsNwz67pAu63qx1rudo0j/Iiz9nlgOa/0unAj2kwEjd5c/vfVyVgfcDZC03tyOp7XB5dqFfFVEhIGosBxKXoFcY4MRAU6iEk/IOOlg4qXrPukdkeVqw52GzxNKu54rs7Ii6AN/VQaOGXESHSXHAwqnq7lNBQkKlPlcn8rKhPXXvaBNyAMwx0bzLLSFL18TF4EqesavmlU3PtkPPgJECbJKzvH3Am1ivjMzgZWIshYsf0I0hGOhGJP+r5NFM3biXARyYLJowdzbEjprFwT4H1ykFqPzIrZEj/6CjwZhuHbQc9uA741cW6rOxYz44IbaAmJ+YNuCfcFOw17EsKKpbkGlJkOo6OjfPe73+XJJ5+cOI4rWMby0Fxo9QkhcRVQK+Or9zKXejQUjOEsmb3jeGr86JrGhrFH2Zx/9hijZwpTmMIUThQm4lk4gkU1hnaIUj5MKeugFRDL8gAAIABJREFUZz1IYQ8SMrIi4fWIasU0TUzdwNJ1LMfGV1dNdIaPtvkwoxPq64QVob9syZjRYGAEBpujqIEljMauI9k7jFk0ceg75e/QG/XTdF4H/iqDcAiqqxQaGwWPIEkV6yE3ZtKNj3T5naoqqLGgpQG0mWANzSBfaD+DyVgT2MjQliewZRk1uoz2JSHmNCq0+CQ6Z0tc+Ncqe/lHbv9liSfve4Gue9Yfc2tnBBlrIpyQ1m8e5lf/ZxM7f/kQjvMHBFXn4hauvula3v/x5Vy/4MTN/dfd/zT/9f3buWvD75hFA/VVEbw+hdHYGDYmJ6eBePORzmb5y7/9AgCf+vQn+exn/4ZQOIxqqiJ5z9LAKmKW6yHHsjENi2yxhFf1Inl9KLIf1fRT0ziNptY2lqw8l/Muew+bn3iQbevWMdJzgJ/99B5u+uhVZONjbH4xyUO/GuIrbbUc+NY/s2tvjt1dcM0iaGuaTjgQRRseYusPfsDyL30G/7QO8v0DbPnd7fyuqIEj6p9xmPCQzSC8nUCUmW56n4uzvLDAIxTSszV4GiHMPFGc/clPMnNOI2YiwXmlOyn86E9oW/vwU00HF9DJci7iM8RI8hRPcjP/LgiK04L/Bg4C50G5LQzdA3EH0eY2XfxcQcxEB34BegKhNrmIY35sDXCGYOBtIP0IqpeBvwj+EoTK/cilEuRzUCwJJZxHhYZamH8WKEFhoN1e7oJ76ZuQuA9x0WaVD00DUZKn4aZq/uG9Cp87V+x+ZOxuvvC//w93/3bjKTlrpxPT68ME0NB0nZ7TLO7zlr+OjMoq4tjbeO+Cufztr37FuX93Iz9eeTVDN9WeYrWqBFSBEgb5dEaqTGEyHAe2b4yxfWOMthlhzj6/jfpmP7UNnTT4WpCkMGYpRXJsCKe2HiNSDV4xhtx2U82GUioPZgGjVKCQyzGSzBL0qRhmnlwxST43TokSuZzweO068BLP370HPWG+WpfNFE4Hxp/Aa3ax8sbNbF3fSimfgsIueOEveTb1deoi11PdsIhcFtSk8CDLZsE0JM5e1YFii1a4E+0ib3z1l7xuuMV5AxWS9lTC1R6qCMIpgcjoOQcoDR1GS8aP89dHRxDh3uN6a96TzXJP9nQvUmxBKGPfO+lnq8tf3wKuAjYj3vVChB61D+FFeqwU4LcD1yE8Yl9t0LhndQDhbX5iRPRlCBfUmSf06jcO5Z4kRpCZQw3ivNhUSGXXgKKEqF77GKMfmWpaJ6wCXOVTsvzvciohan6EzMPVfIMgRF1SPIAgrGuoKGMjVPSozqTv3QCu+VSWESgfW/m8ewPgDwkp/MT+ZCrXrZ5yohcVP+HJJLzQpJtUcZBXKqPcBWkvop4/C3HN6iZecfTxPsYhRtjIKsfhI3cf5IVffJOR3se46+8/yg9b/povLavhqjYPNSr0fAGufBIe605Tqfgl6hZIdL4Tuh1QTNAOwuh2sIZhxnJYswpWtcMKTaNu1iwKhSPFFYu4lI6hpcII8e2IC18EyZTwozLAHm575q8JPPNjVnMD63iAR9jJYRJHfU9TmMIUpnDi0BBiqlEcdrG1+3m2ds9BlubiUZezYMW51DQ0EAiF8XoDqH6F2novM5tbCaitmCEwVaibBnWtoPrLm6wCTxjqqsTy5/TpkF4EYys9LOu8jDt/AAd67iB5GmztCv3Psefb7ezZfxdnrTifpWc1Ub0KWhorvR+uFZosDp0AFSuccSDsgXAU6mdAehxKRbDeaJelNxqlbzCy/h5GXryYp//4WR6+uYMlazws6oRzAsKC6e8/6ON9113IDbvmHnMzZwQZu78nyQfPuY58bB+pRBHHyQKX0b7yMpZecx7X3AAzaGJaXYTGWgldEiWE2/DjQrdh4NAwW9a/xO6n72Q0PsLI4TEGeseoBgZJMJRLoeQlZMzTSL6dGtz169+waeMLvOvKK/irj92MPxjE0DWKuoSiadiWhW1LoCpYGhQtHRsJVA+oCsWSQckBVVJR65pYdMHlNM+YSXK4l3xiH/lCAWyTjCLxmOGw6yf7CWoGBQ0yNsxKgP/JF5gTS+Fp7uBLP9/BXedvo7kmzHjXALf9oZ+4bjOfytp/NxU1zHxgI6JsbERoPrchys6UDWMmbNJF6ZpClJQzEXalx7pyKmLF3stqJGkeaqhE7XkW3/vOz0gdUmikHZVWVDrRiVLHdN7NStq5hB/wRbay7zSppHchjJ+/CkwDp75c7brxJSZYITg8CmaeikrjBcTkylWmOIjbWATwi/+NgfNtKF0HyY9CQ1qQ2n4FIn6oaoRcGrI5cBSobYVYDOIx0EvC1iD2PShuFYfBYkSXY7k699bLLPnnKv7lEpkljTYjh/fzk3/6JPduPEjfoWN4hLxFEPAqLO+sZ3t/HNOw3pQQR3caFkb4LF96PTTOgdt+BvvjcMcXv8iCK9fzyX/+MbfeuZmxr9+EtvP5N2DPASoBI2Wofui4EDLjIpV5Cm86RgcLPHF/L88/+XNUj4fGzhZmLJvDwuUraZc7URJgGSalIoylMuSKcYpaGq2Yo6+ni3wiTj5RJDdmYcZtZEl4qNu2iW1bODhYtollGWh6CT1tntn++X9mMPIFtv/qv/Fe/nmc3Y+g7XwQGIbeH/LEV9dx4IG/4OIv/m8UP2zbXMAxYcn8IEs7oaEGZK8gDFs4fkv46WgXf7V9VKKFQKaAjINCaEIjeLJwaagUgkzSy9uXEHe9xnkrqB3YQuLgiW9zEEG5beXEwkVPHXy8UrHqKjdV4DYqmcjua13l5bHshKoR0ybXG/VYZ32y6/QmYD2VqI7j42KEZdXpjobUEbc1ZcIGoB6hVlWoqEbzQA6HNAXSOEjIE6pZECvUMUTN5p77IBWqHyrnu4XK+fcjzmuIiqLZtS9w1bmuUlYr/9ydurrLF+7iqAR4hTG4YUAwBJoiTFQlCwwTMeInx8q5o14qf+/2njmoWMxG8JXuq4JUdL1RBAH7F+XvC+V3cjRIiMo0cXiEr5x1A88nu4inhoAc3H4rw2O/52trPspzV1zJv/7VEoomGPbHESazApd96L/pfOcF+OZCzIT+btDjEDRgdBhWfRgubIT4ixtZ+bGbKBaLk/Yv08Bs5nWspWX+LCHlLQvCrVwGPTFEmiHy2GwhSz87uZd+CmTJTa0+TmEKU3hD8PLKYBSwsJ0EujFM144ULW0LCFfV4/WG8YeryETCBMIh/KEgsgamDTkdEmmx5hZQRSOc1w/ekGiGMG1IpmFwQCK3H/oSXjL6a6X5JKAV6maAnoJsH6+6wGob8Ojfsn9diEN+lccDfrzq/0KedwVVnc3UzfTROB1qOmBOK8ytE2RlLbBGgkVBOLwI1pmQ3ytCgd8afXc9oKdht8aL//5X9Dw+lw2z63lkmsKas2H2DAl/GPzH8dk6I8hYLRenZ9sWUJrwNL+Hy2+CDu8KWmYuZtpZc1iwGFokofLoScOB5+Hy86DGAx7TplTQeP6FDWzfu4fenn76D/SR2vc8o7kUhYKOVrLQAQ2LOiVMVAmSszLkKJSt6N+aSCQSFAt5PJJEsmSyatXZLJg/j2lNNZhAqVTCsWxs28FxQFFkHJjw8XQccJAwHRlb8iBHG6lVfUTqGiikasiXhpCrpyFHHZIM4Y9puM6lSQn2JMHTnydv9xLsTxDWiux4ch17bA8H+zLsS+ksVOCyBdMIqioPbetjlQTROmjwQr0Fz40KRcncoExrUGbbuCnW722IOTDoVJSCMhx3ndoHNHhk3janlqBqgx2ilPGw74/bOTicJaLVESSIhA+VEA6iMauaVtYoa/mI8xnm2OtYxyZ20HsKrxyIgnsvIvUY0M6G8engHALyoLaCb5GIF6QdUXw3AlXQKkOmRzCqdJa3Faxs2gT2gfEoZPzgXAcNFqgO2BaoMgQCYNngyOIG0VwDSQ+M98HII5DbSKVDMcGEKs4/B6ZfJPHJS1RWTYPBPS/w3FMPcf+TL7GnN4f5Fg7m8XrA73UYSxcp6RbWm5Tu7qbaR4FLL4XLroTGeVAowO13wujwAAeeeYqGn/wbl3/gM7z0zo9zONRI6vk/vc49+4EWkFrEhM4qil7AhiiM7xEPmym86TANm0xKJ5MSCx+pfI5EOsVw7yi19bXg2JimiaZDrlBE03OYZhFT14jHR9AKBfS8gZ7jZKykpvC64QdfHSy/kPrOdqoaPIQjEJYEVZItQLZ3gNTDDx7XDsQxCxR6/sDMy79DurAWbXQUxu4HfYzM4BYOvZBj03+V8M6/gkQuysxpUVa0B5kdhZAXvPKZkZ9WQidHBpu92IyjkyNv5RnKZDGKChIKquLgCWTpiECVpOMBTAKorMXDMmRqTmqfbgN6AHEOJvthJoDOxe0MHKg7KTL2eFTm6cVchC3By+HSnJ2vvgmX3zMQq4FFTmAhxo39c91/FSoOcceHDCxB2DycbrhnRYwB91hdVasH8ebdqMMiJlbZg9slTtMIeYEbMmIhaGW3cHKVp+6Xe1685e27Va275GAhpp5ugJhJxbkVxHnuQpDGHQhFrYcJl2U3cdFT/ltbA8mgovJ1tUlJKqTuZGsLYdghUSTAkb7Krhuwr7z3ZQga2ebVx74XkPQSD+x6jiQxTGyxwf0xDCfGgjZY1FnDeNrgjh99l77eJ4BBVDnAytmfZeHbzseZ3cKhhAh4qfJCqBZ8ElzaAee3wLbH7uPpP93Lnj17jti3ispKLqA+2Iy3yi9Y47LYeCxxiK6BbQxRQhJxOyQocgb3xU5hClP4HwEbl2Z0kCkVtzI+liObrkdRIwSC06hrasSTC4LXjywH8Hq95PIq6YyHYI2PaBSqDPCVoJgrO5anYbDfYtcOjcJoF5nMM1hW9+s4zjxoo2B5QGoDZxxRrR6ngswcppQRT64UHuC3ML4b3/5qIvUqVbUQqG9jb3Q6TZEOakNzkTugsQNaWmF2E1w3A2ashQ0pePDF13H4pw0aODEorqMweim2p4ZcxmH0QJGxvTma2gKE60LkMsc+b2cEGStTonH6bDwN7yC88Ctc/w+wKgRhpWImbDgwWrTpHrR49skiS+dLWFIRO5sjPhTnt7++i/sffZiBoUEREiFLpG3niHLQL1czr2kBM6PNbO/ZQ6xwkLe65KdY0tjw0mY2vLSZd77rPVx71dWoSxfQUFeNqqjYto1t2yDLKKoHSZIxTEMUWYqCJIliTLNNTNWPL+LHH6qlqqGG5OHteKf5qUmGaa3LMd+2CAR8JCwLJ19kd05HGoekmSQaStIcgKee2kQ26RBLSXijXhYXddbMaMD2eVm3rY/FXpjVpuALQCxtY4w6zPXA6qYg09rCrN+bZYFjE7RMcoaFUbAnMmgtGXQvyKWKAXRp0rnwArWKzOIZ1ciFAazSAnIJePLWxygUoA4fAUIoBPASwMTCwUZCpkZp4v3Wp5glLyLkBBh3CowxjnlKx4cD/A4Ig+6H8SZEe98I+AyILoD8KGIS1Qg0iCK2XhHmsLk+REFu8YqVtwxYm6AwCIWzIDQdfDKoJjgeUHzgLSeZyBK0VIOjQjIP2YcQ9WgrgqzpEZv0NMK08+H8Dzh8tENnfCzGs48/yO9/cyebDx7ZVP9Wg0eS8KsOsmzTPXJioSOnCq6PnRe49N2w9BKJ6jaoDjls3wwvdcNQbzf33/JNvn71lWhXvRfFU8Pe3j1oo6/1wasgplct4J0HkRohPzEOQ8QEfVSkuU3hjEN2PEt2PEvv1p43+1Cm8HJIMt7m6TSEfPiUauTITLj+Zmaet4qm2X4aGqFeFvq64QQMP7+N3uE447s3QiFdTkN/GRwN0k8TMtIY9Z1kO9eijz2EuGvEyAzF2HTr87CmSMP8FSyfPp+V0xqIIqibM2X5WadAhgFMnsBkN1mGGLNH2ZQfY6Dbi0/1UB22mN4coz4MQckVtak43IQ6Een1itSAY6KcNY+PI8O8FMQjb96Kenq3VbHnqTf63Z4OLOF1GT1IVAaISUWI+aolUAnRQm9wMkSsgrCmmAsnSam/MXDJRrscVeeglT1PXaJU/NZ1GrYACQl5gqxNIHTRWcTITCOUxK66Fo4MynInYm6EifsadySWqChs3TCvHBVvWncBvwWhN3UVuAWxDccLpk+ks9olcFx1ryq2IZUJYqec0HoE1aqUj1HIVlx6VubIDkQ/oh12DS/3tT82hKOtxV5GK8StBSRh2kVzec+V81izNMqWzbv516/fgqFr+CQfDYF2rr/sa0TPl9nvhf5+yKThkjkg10NtDfy/Sx3i3d388Ze/4A9/+OMr9q2gsopziKhh4bLkioItiCUG6R7eRQxrIhptClOYwhROHVyTJB8VF+4S0Ec2UyBLFRDG700iMRs1FMHxBlHVOqK1QRzJL55DPh/VtSIDJuwTYdyaJVwq7YRDtldjcKAbvbgXsfgW4kRtgypwgBTkUkKgI00XtScZTnw53wAeh5HH0UbE00hISJYAK0E5G2ptWAMzV8OKJVCzQGIhYTxNFsnWcR48yaN+82AAB8DsQo8HMQtZ0rJG/IU0drgapboGPX7suuiMIGOjHYv59saXmFEnSoycJBp/Eg4EcWgCTAfUkRINvTEuVDbR96jKg5vXsWvzJra+tJU9WmGiMHCA+FFUbWeF38VffeQDrLp8Af/4Tz+g6+kfYRn/c1ZB773nbu69524URebFxx+ivb2dYDBEMVtAVxQkC3BsJCxx4S0LWXaQZBmjXDzbigdb9qMQoeasVkKz0lw0s5dZ05rwl5IsX7OEdCLBYw8/yyf+sJ+hJJztgQV+idtjDsQcpgNnN/j4zg2d/O4X+7n/ga1kHdFFFWyA5pk1xJI2G55P4ACLp0tcceE8zr1oLZf2H8Qs5UiOj3Kgd4z8Eym2IXjBhWG4aAF8/UVYZIvSdNOk958HuksmP3zwIPMueZjFV7aQsmfxqz43/7eVVuZTxUxUmpAxUfBgAmo5d2C152IWe1azunAnf8NXGOJ0BCT9HOxB0N2JlAdCHmjWYfAZ4HIgAEpIcLK7HLAjiCmMSME9apNfCWFNexUUN4K3AchCtR90s9yYZkAwC5Eq2PM0dN8LbAfeBawDRiqba/syfOxyh8/PMzCL+/n+V77EA09tZkf3sfzm3iqQmR7wkTFNxotnhsbJBvIKLLgGGjp8SKh0rMrxta/BT++AR9ZZ7OqP88VlV/MPj/6SuTe+A6n+PLbe3FROTz5Z1ADNILdA4zlgWRAKQUAHczsnMrmewhSmcCSUUIS53/s937xiAYtrgxPCrDxHlrMjQLYWklcvo/fy33PL+/8RY/1dEDt2h8bOH36Tlkvfyczli+h6IYogh8p1j2PB898gtu8iCt53M+3DCycy3l2K6WQwOaIIhK3FSUOSJj2lHKoYJ+LsAOJo9FOgj6gnxuE2uPOX0NoE5y2GtzcLF/UKWWICtyL0lNcCq074ECY38rv0oYQgaMOAvBa6njv5t3ZmwPWBfY0IcmRq0wn7NbnOuwnEVOsXCAOq46Ma+ASi5f3NmIi4RgATHvjkqJCXrprUi6AgQ4CKgopMEKEPTSOklm791YiYqMbKr69FVKkVklPMcCjv2SVZXfVtDnFnKFEhSnMIgn1yoBhUouiKiPPu6r3D5d+5nzSz8uWtArkKim7vDeXjUqmEhkk4+Cacar3ld+J+ZhoRNmDLyn/hmh4cD15El88SRGnpetFKssxtv9/AytpaNj/yCB+86qqJv5nvX8yNHR/hcz+S6JFBiv9f9s47Tq6zPvffU+ZMn53Zqm2Sdler3mxJtuWOXLExxtgBAgSIgUto4QYIoSeBUG9IuAQIl0BwwIBjG2KDu40tW5ZVLMnqWpWVtved3mfOOfeP95ydkey1VkaSZTzP5zMfaWZPeU97z+993uf3/OCAA44chZgPXDmQFJOgYbBg7VomJ1/aEsNyvEexT53Nf0chmHHQgod6XlysrIIKKqjg9MOJiGbsvtqqGQMIW59BwCSbP8rwkEH97DW0tM6naXYNDXOFLbjDCQEv1NbCrBqo8UOVB5F4pUIyrnLsaIiffOdtPLfhMuLxJ4D/ptz65ZRhDovPacMe8dHvEK/LB+DoA3AUiXtxIjzqJxBu/q8xjH0LY2wdku9qQuddxbzVF5HKGExORhnOnOjEXsI5QcYG/KCERMJP3BQzry4JtAxIEwb7tiV48Befp+vgNgbH+skW8uiKRKGQo5jPk88XZjRD+/f//nFWXbwIPA4uf/vneGLzz8j/CZGxNnTd4Pq3vYuF7Y2su/xS/upDHwdU9LyOXAC5CEWPilsHBRnTlFF1UZFPlmUUSRJhp1qFL+Sn2ldLU0M74UMH6QtPoiizOf/a2+H+zxE3TZ6ZgE1hcQVWApfOhQvnS1R5VSQTnjcFJ2iaoAzDlofDLJ7t5C/fUsvD903wk16To3/YTV/PYea0VHH+BSvo7Kxl9vwmhhNP49phkitCOAEPvwBXGqLkhALciiBkRxFBnq0d+Og/baThn1/Ab6rMAmaxiNksp42lzKIDH34rXJWQymUAVeBqdHOD+50s2H0t38t+h5/w/bNw1Z5BeMh+W3xVfeDVEcUweoFa8DXArSbcsQ2SGiK8tZ28X+YJ0GG0H1y10OyC7AiYHlCyUEhC9whsXA9Zy3qQtcBDTGVruargw0/AezugOtvFs394gj9/39eIx2Jks9N3Luc66huqaZ1dT/euLgayWYqvki3B8fgwcBiDJ4jqNmliD86E3++7/gIWr4I77jd59pl+vvvOjzP/TW9j9Sc+Q8/fdBO/8yb0sb2ntlu5Ecw5QIPoCAwJqjVolsE8CNJr9zpXUMGrgupqfCuW859vWkKrR5uqJmvrImzHRh1BTHkQZMcCh0rsx5/hnr/20PPYgzA5DbFlbMSQVqK7lkLTrTDyCzCOj2eU9kU45y7Aiwj1baXbK4Wtp8smdaIjcXavv4fRw31ERyfJpTM0tM/htg/8Df0jMQYnIihBD2p9PU2tXmoCWpm35C7gMGmzm/9M3sGDm3PMbdZZs0TQXFe/G5Z54AK/KBb04qlGAziIIKpmTsaeCFsTaKNaAv/ZNi/9o6EA/xcRff0RqEGMf07ZuiSOIARPbTjhBi6mVGX5bENBkIQmCqU0oHGE0tXOTTGx1Us6RSQkFFyIgfQ+SkWx8ohYzEQcWRYRu9k2ATZhbT/t5b6taUo2D+U+viYlQrjRWq/G+l5bto2ktZzlgJzziVixEICc5YyrKeB0gmRCxkQQyeU2DDZTKXokm6p1YNPQ4q9rgDdwvLZrJnAi7FqnSg8E/LB2DRvuzPDthz/Cnu33Ti27BLj5xk4+/G/vRZKE8cO1QWhaBI9pUO+AFSGQBvYxZ871RCLTl2GWkWlgLo56p5hvtvntPFQrTtpcbhqyokBwxYSpggoqOLNQgTp8rGbpoktomjUHt8dBa1M1kmGQSKYYCU/SH0viDTTjCdXgqXHiD0J9DVSFwOMU7jOFNPRG4VAe0lkYGxNWnqkUjE/Ajh5I590I8nclosDnGOf2tJOd7/x7SlkprzUUgPXoqc1EtvwfXtjeiGFehaEufulMNwvnBBmLDA4ZFAPUPGgJSPUmOLp7L73bN3HoSBdH9q4nHBkmmU1OJfWcKlra/TiqXQyk8/TEExivRnWes4Sx8QkKuTTxVJ7BiSTnX7CE5YsWE3B4MNIFChkXk5ksHqcLn8+D4lAwdAPD0DHQ0WUZU9KQkFBVFWewiur5i0inI+SyBVJjaZb4vHSn0mQMA0WGN7cKM+b5TU7cLo1tu4dYekGQebOaGMoaPL/5ALe/90YeuHcLEyOT7EVoWwo6DEwUeCxXxDNYZCS8j7ikcCSZ47l+kwFDBH01CrR5IJoXYW0aSEuwug7WhyFQFER+L9ATy5GP5WjHwWrm0slq5nIBjSzDQw0yMpIqibjZj9iBFU9LpozH7aOj3sV7Yu+kPu3nW4VvnOFuIYcI3u8ALoVimzg4fEAM5FTZ0ypRCoPjlFQNJ8IE2YBGmUBAwucETQWtGjAglYRcGEY3Q/IhsRskRIHltFh9/hq48QPw9oUwzw27tu/hN3f8isGhs6EYPjPwB7yEqj3IkszgwDhZHQrGueIevQUaVkHtlzD2fZXne0GtguagaF2wJYSnPoWnJo/DhGRc5/Chbo4+8wiSo4rr/uxDPNr9CSLb74WBR2e+W2c1SDUizdEAzKJwiK/ywrE06OfG2amggtcENC8rz7+Av/jYXzHf68SUpONK8dgOkRIlh0nb0bEoSVxYW0Xg9huZXLeIePQYP/vlfZiHdkK63CokR6JrM7m0hrLiYvSJuyB/PBm7eOVSFi1fPKXDs1Ozy2ElhUxRQTZOXM40YSAKfU89SvfePRw+dBCl9wDhcJx4Ko1Dk1lUH2X9v3+erqEUiQKsWtnCsfFJ9gVUGtsCrLxkDi0LLkCSunlu5zZ+/tCT7OpN0j0I3X44thjO+xx466BGhaBaeu3ZhQ11JFTqGRw6hJ56ngBLCc5bgCRJdG+eYM8fujkwcg/vff8XqJ0bQgsef0zlPrF25rL9NlUkkKhDKEy7Xu4KnyMIACsQFNksxBHmKKXZnwIilGSLpwQNMZUgI6bFsy+/OKJlToQb/qs1CLEts3U0YAUStYhjsc0rbL+GAsJUI4sTDRkvgsa1Vam23trW2joQT9SYta2A9fFxvNbUXr7cvdYuJmbDtjTwWdtwIs6vUrZ8HSUi1RT7zclg+oU1gZkHpxfcmpU1k6Q00C13ThbbkDDxUdLh2pM3rQhK2Ie4VZwcX0Ls5aAhCubdDXDtlcy++ko+tXAld//fb9K1+wkmJ0qFX2+97cO8+dZb8M/yTbWqXoHznFDdCrEi7Hr8PjbffxeDg4Mvu98iRTaziTlHmlhYO5v6Rb4pS15XdT3++g60PoUx9IpTbAUVVHAGICF6TptsaCSHTP/YOOm8Sm0wRMhfheb+VZ8XAAAgAElEQVT0gsOJy+/Ek4+QiOQYH+snTw+qZrBvazNOVxCH4sPUNXRDpqhLFIs6+UKedHoIQ89SKGTI5tLEJtLohUOIScNdiEnGc6FawEzwWu+Nc2DmMPKQzyeAAsjbLM/dl8Y5QcYaRUgNZzHiSTJjYSZGJpncH+Hg5mfZvelBjsR3n5b9ePygO2E8nGfnsaMU9dci6z5zROJpInsPsufAEcbHLycbTdLW2EqdO4RW7WJyMk7GncMEQtVCs6IXi+iGgeyQkXQJ0zQpYqBgotVUI4d8SPEMcmacN6xYgtrXw3gshlbIsswrgjPDVBiNQ+/AJOve0Ez7vBCZjERDJMhbb1lJpG+MzRsKPHc4woqQi8PxHOGMyY6MSWEsTXb0GP05OJITYWNn2yxiEzGyuQymJkLjHELpEwFWOEWwVivJdGoymVSRccCDi2ZCLGcB7ZzPLJYTpJ2pYNeJiCxtw7I8pdi4CE6nymptFZ6sxk/5PuMkLX+xMwUdeBjwQ7YdJpchgv4suHOirX1A0UHJyctu9Et1siY4QLoIaqrAr4hJD3cQpCxkI5COGCTW67BbhXpJRL4DYm1PCyy+Et72lwZLMhMc3j3AH57YwOOPbT6D5+DMwaEqeL1O3F4Hfr+LWCzNyPDMKj6fPewA95VQdRvwVR5/Fnwe8C6BoBu8NdV4qcPvS1GrDrJnGIqFBMeO7WLvXXkuuukaOi55Ez3pBBMDexFpLyeDE2S3GLhJsii3rmTBYVV9Gy1UyNgKKpgBJFlm6erVuHzVXHvNddx+880EEMnHeV6c7m+TUnZldzupuA2YffVKcqxkPJ3lfwZM4iOj6OkeykvmpPv3kU6CevPV4GyGYhGMkrRx4ZJW5i9qAUrleqCk97P/PZkGQQIME1IFGDw0zM71m9m88VEWmCnCBZM8EKrScCY1fvfAQySz4Pd5iWSbObSnC9ltkFheTVPdcprna0hSmq6+Hn5+3zYyVoGGcWC0E0KfhUAOBhMWfVVt+Z1LoOHCZdaTj7ewZUsPyeEtzKKJlokIIZwceGCA9b98nv29P+CNjdfhf9N5aMHaFx2LiQh+7fryzrLfUepBWwz5c52MDSKSxq8HOpgqEz+TaWOV0g1g29glOUVDYZseL6f69yIKfJx8924EjXi2vTrtVkewXfRUBNUYoKRyBVs1apJGJ0WENCEcuKcCxwJiBtt2IYZSQSwDMVEuIwbgbgRhbVKaArCfPLPsI1nL2fGdPWVjT9eAeFJM628qpUJeOmIQG4VCHCQHSC5QHODURMZL0e47ynsbvazdUim13/rFJmQXW2fJdrPI82Jl+XRwILyBL2hfSfSGm5n95qtYNRTnS8/fSTxe0qS6gfMvupm2JdcwERVxqymJfbokcaafOrKDjb+7hwf/+79Pul8Dg356OdI3QE1bkLq8l0IPGDJkMk4mND+9yIyhz2AKoYIKKqjgVKAAbmTmIhFCIYAiNWCYGmOT48TiaSLxKiQ5g9vrB1UlbwqF7PhQikgsSTydQPTr44jcqRCCw7CLZYJ4Fw0i3r0pxMu8H5FxexgYOqtHXUE5MkA3GAO8XNrROUHG5hMm23/ZS+8Lz7P7yd/TP3r3mdmRE1QNcoUMG3buEgOX1wF0Xee+B57ivgee4uq1l/HJ932I1Z31ZGKjpBJhRvNJAgFBUObzBQqFAh7JQ66YI63nwSyiWEWiNLeKVuWi/bwOPvWNz3HRo79l/9bn6d7Vxc4u06osnMbphEVzYCieYGzrZqq9Pt5yw3KUgSN86IMX4+ts4KPffpBfXNrCp57pZziWw49IxHomIboUSYJLZJk7P30r37vrae7asJe7xoRLXB0iGJww4Zf98GcyrJrloqnBS+SFcYaBC2nhMpYwh5XM4SK8zKXk2QW4wXQhRplJMJ2Ay8T0mpjjkOoxGSoM00M/l7CMh3ie7Fmpm3y3iOPjy5liipuA2Sb8zl7GVkooCNOG0PHHBoJY84Pji1DrgKoMqAHwKOAMwsEJ6Inp8GwEqIWhMn2DDJ0fhOXXmcyJ5+ja+3v+4oNfoetw3xk87jMHSYKaah9LF7bQ03OE7oMxsvlzlGDsmYSebkDmx18wSIeBD8C180GSqpCkW1D9eaqXfZ1Pf0TH54JHnoixefMLfP+Wr/KNzf/IPi7nV09GMfSvnGRn1qxtStS+RKkGfy3k02DGINoLx84NH90KKjjX4fK4+dn69cx3u/FRIl29lPRudtKyTXLYmrYMYpJRtpaxy+w4NRdr3/NpNj7zArGJFBTLA+sY5Psp9vRD8DYo/g4yu6b+2tIOzXPF/8vTwU0sz3BmXgJLkWFRPXjf/D4MvYb4sTHqCtuZGM0Q0k0ac3m2btnHnUPwoQtruKJeY/1T+xmPwdKF0KqkYbAX0ziIKTVRFdRo64T925giAVUZWlR4+gX4bY/I5LjtLdDqEQnaHczmUv1dHNiS4Fv/OEDXrqdp4GlagDfTRoQkMcZ5G5D9wt+Sdn4G7+K3I6svpoy0suOXrWuSA0x/HdKsBZjn9KtOBi4BbgLeRqnYk8SL4oATYefnpxA3morIeh/mJWuBvjxyiDs3i4hHfmG14+XhQjiqVp/Krk5o2qnpfmXMsgnrLGKoKgENwqEdkyzSVLq/fXIiGIySZYBjRCmgoFKgauru0RBPsfNF+xNHaWctpSmRqnZZYps0z1GaTHcgnkb7rowheoJyb8Go9d1Vto7D+u5B9DQ5iyfXIVQjKrfmspC13VFtnX7G2r4Pmxa36WMHJY3wHOBmROZbwNpLgRd7xp442WRDRdiN/Obv7sFx5Ry2j25n7aWXHreMAnQgMTBk8uxug9SgzDuus86MaZLLwKbNOh/5y9sYGZneS/v4/apcyHkkimHC0XH0g42MP6OTKyrsHx/gmck9/BvGazIZtoIKKjiXoSB6yk40luCmHrcUxK+FyBWLZIwk6UKU/vEj9I9vLFvHCbhQCWAe5/D/CKUXdgAxZe9B9NY1iN43jeix64HtwCFEhkYFrw7sN2Er4i26c9olzwkydrRnFz/58hoMXUcvnrmBf3hSWG32jLqQWhdibp3JnO6fFtZvfY7tB/Zy5Q038bHbb2Rh43x8mg+3JpNDJZnLkYynMAydbDZFNpVElVVqausZ7OlGczvwVQUJ1TZR37qQt77/k1x+zTH2btnCFz/zTQ5g6Qpy8NQRuL4vTnM1+F0Rtj7zHF/8+zfgmF3PVecHufvdbezYdJR1OYMYYCiwtBbWXLwIR1DF6XexZPZC9m14iljfwFSC1v2UNAU27jPg98NptNEMjcASGmhgHg6WUKQNhVZkyXt89ZJJICy+7jdz9EsH2ckOnpM2MWT2kzKOECdGnDQFslY93bOF/wE2Al8D0pCUYbyIkK0GKBV0aKHkG2YijB908bc3gvYluLodAglwegQZm8/Chp0w8gMo3muPxMrCZxX4InzyHbCuOUZ6+ABX3fQJkqlTNpM7J7Cw3s/5y+aTzhb5w8Y9pAyDc8Iedlr8GlgPyndA/wr//f0IWx+Hj/4D/K8bd+HSZiHUUIcpqot45ztytC0AV0Oep+77PV/51GVc8+eX8fVt7+Cz582AjNXmQlECIwrGOAz0wLwY+MJQrLzIK6hgJmhfs5r3/PM36NC0qWTn8gjD1qFh/W5rGE/U1OUQ7zlbMycr8K7lcFD1ECueSPoAqQF49qOw/EuQnQOZcWwlRKlI0fGwKTtbi3cqaFkAt37qeq59/xU8cG+cw1+7gexIFykKdPjgHVUQTIQ5moNUHK5cI2pP6pJMehI2Pngvyy9ZzYVrM3ypo4N36d0YjwBBcF0osQY3P/9chnDARFkGd2mwoAVa6iBdnWKt+yBPfuwP+PvDrEMU51wBLKYXJ8Juxgs8wF4OfPFzVD/4CDc/+fMZHZsTCLmdNIYCDJ3TZOz/Aa5B6A1VhPrlScQVvRSRFD4N7Ox7e6woI/g9E3ECTMRNOCPsBV5AxCVuZlrosQ1BJZ8qDMSd3cBMvWYdiInqz5Hhx0gcQEM4MW1BJI82kUWcuwmgHUERj2MToUmG2c8h9mBikMTLAM3sQtCRXkQ8VkOJ5LSVpkHrdy+lFNVJbHOEEnWZp2RYUmttI02pBxi1/h9EkKY11nr2k20rp+ynPWu13QVSEVz1oCqgqGJzyVGmjFOnytfZhLKMQW6quJ199q5BXDObqrYnl2bqPy1be5F/E+bL//Z9vt/z06m/BYEWnKygAaXmFh7/2WMs6w3zrr97J1j73P1CnId+t4ev/fObSKcTM9qnioeQ3MH1rbfTMkshcIWCci00rlMwU9CavICLexdy3R3XcNv4bUSNkyu6K6igggpODolSn18kS4wcElEzzkjuGLAfkxgmKYTyqmgt70C82Zopkkf0+w4EmRdB9PP2712UMlM0xHuiULb/bmvblamms49ZCAVdMwScaJpGwOciNbZn2jXOCTLWNHTy2Zm9YP8YjI7AvFnQ2eiis3MF3Yr6urtNi7pOLB7juWeeIjx4mMsuWsXVl67loqXLyFPA51SRfW4kdPS8ieTScKgamqJR19yA5tRwujxoTgfpXB6n5sJdP5cFlwT4+o8auee+33N47z4GBofpNmBLDuonoUExmU+Bw3uHmNw5QLEo4VFdaD6TtVfPoqa5ler6BpTRXkwjS17PkItE2TI8QfeBCfZEM/RYx+CjVLIgJMMtHZDPwd447IyahICFLKeDlbSwmCYW4yIApknRzGKispMdHDQPM2aGSZBlgBGi5jEGGKKbYQqk0UiiU8CBjguoooYGZuHDQ44ULhR20csY8TNwpQqIzvWHwE2i/03qiAFDCNExhxGjKSg5oJnAUWheQsP8IAs7wGX136pTdPd5xST8r0kyGxXIOcDjKKnnPaC0wbsvgzY3bFu/jf/4wdeJJ1Jn4BjPLGpCQS696DxCjiwDPaP0DYdJ68ZrwDUnD4yA8SsgRSEHA6N+7ty4mtGRDbz96r0s63SCVEeo+r+oCn6Ni9U9ODDZtz9B+PBjHN5QgytwLdf+011s+M7HyURepjS2Wg+6ClIAHI2gpoQK21+A6MlVThVUUIHlFilNH1LZZCuId5dd2seOQezEZdt4xk5E1iWQVGDxJTAyBP0nqsJMKKbhWDdkAiC1gynIWJ8EXknsJ4ogPuza7/DSRKxdSX06okVWQFMcVNWqXHmDm3mz/5mx7VsZ3raZrk0PcjgFsz0NLJhXzYpFJgV6CAV9+Gc3416+mHt+cT+tdRupWWpwcV2KX/+NH/3taUxNh3oTnRzt7zLxmWCEoLoe5neI99EsZ5hRcyPLFtQxOZlEzRZoRpBzfowpuwEZmIdOIhvGlRjFNE26duTQ/CqBapW62tI1KSesDUByqKjuV6us1MthEYJ27gRuRGgNbfa0EbjaWq5u+k04KRVyziAuts35eREnb0Z6iAKCgB1B0KNDCBJzZrOctv7zVCEhsqdmKqPQKZInjs6dJBkkarV0IyK6CgEuFKCGNCM48KBNTYnEKTJGknH6MNgKVKFQR5xhdlJNEgc11r1jF1G17ygV8bTZ2lHbEVqj5ENrIuI3e+yjIQbvEUpkrW2BYPtn2ctkKE3nZBBn1GbZLTLY4QPND5EIuB1gGFZBL41SsTG7SFh+ansSxSnnWz9CY9XG8a4WSeuIbBdcu68qv052i8MI2uCbgLbz8+xOHSOZEnHFBcCKxVey5PxLWLnuIibDs/n5T39HSspSXQ+ZBNz5o9/x7JZNbN+/mVRq5mW2XHiopRmnpuENKji9IkNKsmbFlISKM+bG46hDOutmGRVUUMGfLuxCVDoiyyKMiUYpQyNGKQK0I64kpShxkrLpeOCotbzd59tGSzZkxHug/P1r5z5VcNbhbqCq/nwuXnsZHR0BTAlkQ+fu/3xq2lXOCTL2bCGRtOYcQg462urpUeTX5a1qGAajA/2MDvSTjMXJpTOEh8PMXdBO0F9FMOAln8ug6xqGpqAqTpwuF7KvBsWhoMgOFFmlYIoMf8nlJdDs5dLWJsKxKB01IY4cOkx63x4iaZ10znLPkk227hglPBGl6NBQ6+roSsLlHTLtnSEWLusk3i8z3tdLVpcZiRa4f9NeXBMQSR8/52NDAepkmDsrhKIUGIimaaOWOXRSy2ychMhgcIwjZEiTI4+OxFM8xU72McIkWfKYJPCQxcCgFg0VDRk3UEAnT4IwTiQ8yPhRcVidpnTKuqJTQRHYCsyB7AKQ5lHq4GOIztYuDqEjzpBQSSgrdLydUJeDYtw6ZzLki9B/GNJPh9HjPqhyQN6Swrgd+OcozL/eYJVzkIEXBtj06OM89PD0Hci5CMXhIFjlo7GuGq+mki7o9I1GGBiPvoae9xyY2xDDxQyZQpDdw4KUb245htN1gAWtT+P23A6so7VFxcFOFizV2fHsIYb27kMJncdV73o7m392N5nkZii8lG+QwpTSWguCrxqcefDmwIhBbHrD8QoqqKCEYlEnGU2+5GSPZH1sEsnure1E5/IyPnlK+jq7v0oD7sXn4TryAtn+aRoQ2QdSC4IE8gMJkUQtiRDdpn9OhvKSPtNBB3RVYna7gznt19I7u4WDdY2kFRndgPalTXR0VtFQk2J0ZAMht4m3xosZzOHqTiMfSOHSoLle4s86fBiLmRqiPJTUabkEvEWQVagPwMJamKNALRmi+QGaL7iBeXsj6OE8fgpTCdsSMopwuKeBNH7yKMkYbOqnMOIg5XShN7qoq3VPXRebPsM6bl2CwjnHzcwFLgSuBM5DKDjLyydVWZ+TQKF0w81HMPQR61872WZGfGoRMTGcEKa+SgEye5np4M/2Ij1V2I6qM788JiZZTA4jO1tImBn254/xAuJwbVsQ05oeMYmio1AkhUyEMBMcI8JebCv9Kpy4MKaKodhGIwbinNh+sHbhLfspLnC8S7FtTmJnJZVbHtjEKgiG3MXxZexsT1p7EF8o+247ufpBcYOiifLaimYZQ9v7cXE8EZBC9DLC2dp2qA0iNFnVZUdgTyTFy77b1irl/VsKodc+ikjO/D3A2B+EDYKk0OGoYk1HBysueiNLrljHireuZnQINh0+RijkIa8XefrhHdz3m9+zs2sjw/EDM7vkFpy4qKcOTZZQPcIKfyqT13JokDMKbm8ISTqTcXwFFVTw+oPdv2YQkc3JUD4LWhHBvLaRQ1YyeLwSFyzvxON1IxsGD/16umLrrzMyNlfQkQyDgCYzvwPWK5UX8Pad+9i+cx8AX/7CZ7ju8otZ1D4XhwyyUyaXy6PIKm6fG0l1UKSIjgKSgqq6yKEjyToSBtF4ikWXruWiK64gOtBH5sv/m81Hk4zkC/QYJn0GKE+NUSXDuJlnl5lkHFDyQ9R4a+mY20awrY5gtQShFoqjMj/5wV5uUSXqJIm8CvuLBuGy9o8a8OBB+Ow1nSwsxuk51stqVtFMKxpeJknwPAfp4SDDjBAjRp4CXRxhlCQ6BkGcLKCZZSwiSAMqQUxghAHypEkRYSebGSNGkhgODAoYDFopkWce90AqAKl2SpqpGEydCdu2wAr8peW4bvTDUpOJF0w0RcJfI1FIwtiYyfrvFiA6BLNaIFANuw1gEqUpyLx1Xj72OYPYLx7hjv/+FfsO7D0rR3i6IMsSvmCApUvn4XeqPP7I40zkTtEG75yBCSwA+jGlanLKn5OouYR7tn+X4fAmPvv2p9Eckyjy59A8q6hp+SuuXJvl8NE0I/274JEgzls+gjb7b5Hj38UYP7HgheVrZ3iF3M3rhlk+0JOQHofxHtg3M2+2U0N5TfMKKvjTQC6bZ3hoAtM0j1PB2ij/bdK0aBNJEB42AWrbF9iOlQYgmYIra1q1guj+NgY2Mg02gbkKoROdi6iiW4JdIf2VwH5ai0ChWCBtGmQkaFY0kCTkjgXUNXXyiY++n0IBHAo45BSYh2iLeiC+ByaOYBzZyDVVUP88aINAswlzEih1wqbIMMCUob4aZnnA74YGn+gFaxA0VUKRcV28EN9vh9BJoVgFo8TwRcNreai5OYZMHmlwBP0LD9H5gTUc6PeQiPnh/JapYysnyQFyxSKJ7Izz9M8S3oIgYlcgru1MYZdoK6P7DQQh9WZEQdCdwCbEPK99kqeFfacWEXepAdXXgisCPd9gpv26TVeeKuxaYzOFeMNJQBuu4NvpNwYZHP8Bk5T0pRl0Uoyi0oRJgiyTpIjixKSLCZ4jyeOI53IOrcxnFkEUSt6tdnqpXfjLLk/mRSicUoiTaytbbT9YJ0LdrJb9vWht06acvZTIWxAXziZOywfvaUo9hpUea9oq3DyYlnXVVEqrbSlhe8dOIsj1JFLZXhsRemx7S0rZZ4ISGeu2tmJHoUlgP/AtRB3vUWtZm66erXr465oVuG//G/zzV+Nua8Tjg7r5cOtHbyaXhN6+OJ/54Fc4ktpA1jj17DM3Durxo8h5TFXDcEjIsiQuunUjqW6Nhtpm5KNKRURWQQUVVFDBH49MF/G+Qdb/boTrlrYwb+l86qp8eLTpg6vXFRn74+//AUmFdbctYFEtKLKdElQpUAPwtW9+h298619Yung+v/jxt1kwbyHJZIpsJk+2WCRLlqJeRJJVFIeMq1hEcQKSQSoZ56EHH+Rody/XXn8Nl1x2Id+++7d0PbWer99xL09u34sBPArUW9Ihe+7nx0dgw9E9XPtgD9/5/i1IF62BtExgsJ8bgHe/cx5z5zUSnczx659s4SepkjOZjnAs+8wTzzMXjU4CAPSyn0k20csQz/ICxzBpQGIO1SxmDW/lCxRR8OJlFtU8zJ1E6KOXLkZIkCJHgDqqaKCKBi7jA3ipIcphJulmhD6GGLPLaxE+4+TSz4DHgG/DlCqjFpFA5kaExnGQYrBwPs1FmcLeOM+9MM5FV3dQPxv2DcGTmyPw5PfB8TEYCIGeRXjLjHDzBxez7s+8zDELvOmLnyWTjmGar50I1ePSWDV/NlVBH32HjrJ3aILJ1zzntxkwYXIQftXGwXdsI7DqRzwz/jTfvfVmvvrJg9x6fg2toSYU5X20dm5DC82FkRpiY2G+83fP8dmfrGLjj1tZ/+8nkqC1wKUQnG8JdjSQ3dDuBmkPxKLCOu+0wvbQO6cNGSuo4JSRTqfoPtJF3DTx8vLB1UMTUO+BBVZVLxeCjrG1FLadp4To7Sfy0NwBk022Qm869CE0ay5AIoJE7CRtOREvFS6aCA7jp8APHvx3eia6qK/SePbWf6UR+Nlzz/HTnQf46mf+F2scwi2rqpCAyS3w+A+hKw3DJtIEtNnFfsesg+sWDVQVCLjgvE7oXQBNAWj1lgqdFRA01HC2wAdu/hfMtMFSTK5DqO86gHk008ZyJGYTYBdwkHiil/XPfoIrfjXEypqQYMAt2ELQci/f4vAwyd2lImjnBj6IsCc4VYwjKnNZHrJpxI3mQbBlO6x/QXTLMU5i+9prbW8UQUaeB0vqYVYEemb+svUjXNXONLLAGCawm/tH97Idk26wJttFeZP16PyaQYoMcTlwFW4uZh4DDBAnj4mIsuYBi1AIUo24w0cQ71A/goa076sU4sa2qxwkESfVhfD4b7T+lqP0xMetjw9hDFBub2ATrwlrnRFKJLBt9mDbFeSs9WVRHEDPg8tp/V8G3aZS7XVsy4So9UlPJcx6rS01Uuo/dOuInJT6rKj1bw+C038SeBBLiGudaz/wVuBe6+ykgrUUb34/NRddzZKFLhqqS2dozRLL3mCywIHUo+jGKyu0PMAxfmPcgd7l571D72F59Vyar/SI09QkDrKYhZFhMQlUQQUVVFBBBacDejHB5PhTfOTTUd77vnew7tILKRSn51NeV2TsvoPf5eghjUsnFrCmVWLx++7k4ANfIXbo4Ve7aecEdF1HBw4dOcbtH/088xfP5p233cDKJUtQTDcYdkoT4t9iDkUCWZIIyC6uuHgtq5afR2PjLBRDx+v10jR/Pje9YRVzqxXCowN0zpnDo1uOIOWzrGvy8Mv9UQzgmGHy24kU4S8/yrf+qxNPZBDneDf/9L+vYiI5yu8fP8qBY3HCGZGMF+d4Cj1kmrjJkyTGQXZh4iBMlghpanGwggV00k4jTTgIkmCCPRwkzBgyaYrE8OPBjYt6ZGppIYGGm2q8VGPiwoufARKMM4SDAn/GVehkyZEkSZwMOvsYITHz6henAAMxAPoq8E6EOqYOoWhwIUJcByhz4EYJxSXhK3jwNM8iGITeMAytP0rhl91gvh0KfjBtTVAQ53sbOW+tD8/AVj75+b8lk3ntELEhfy1et4RDLbD76CCqqpBN58iZr3kmluOeNz2L+fjtHNh2JaHOZSy85hF++MMv8LvQTlpahpi/eAG3vOEHfHKOmwfvGufxn/WhH9zJRHQ56bl/BRd2wpYPlTatuMAzB2qrwO2Fog7ZJLToEO0C46VsDf4I+D8B+X2Q23B6t1tBBecAMuk8fceEMtYuMDmdEvW6KtCUkuM3iGBMRlAvmbLfC0DQAQk3qJoLoaWdrthMFEHIiDr1yQikIiCFpg/2bErIe8LvBrAH2DOhs3vfdjY//AOGk/0MOPvJ13kY1Zt5x43rcH3oTfQc28NI92a+8bNfc21gDiu7ozQeGifdNUFzOIM/bZLOQU8BZumwrAhVNdicMZggGWI+qD0NbXFQlgBtMLu2pKxTo1C7BxbldeabsBpYiyBjtwH7GWIuGW4mhoRJHpkcoBYLHLvtX2n8h3fgv2bpS54HBRFX5IyjUHxymrP1asJObZ8pfgJsQLDeDx2/mQYECR7m+Pm5k74yB4B+BGvrBZpgx29B+80ptEvcb9lTWuPUkUJoVf0AmDjQ8SCejP2UaNAGhO44jMkynMzGB3jIkEGjSDWCkFyBbQQRxmSYJJN4yaAwF0GyOhB3kO39YO/dh3hm7YIuAcSJngSOWOskEWfEdsQt19Xb/7eVtbMRNKeEoEVtIjZmbb0/i7UAACAASURBVMPyr3VqopNJTYAnCA6XWDQdo6SkLdeFC8MOCQU3cD6i/rNutTRk/T9vHeEAYuqnF+EJm7RaYB85lGyIFWsZO2YfiQ7zLw98k59//kacVW7yMuQM6DoE6+/dSfe+QwwP7UU3XnkMquHCRzUHzd38OvlzUpl13Bi7jGd/uIFLbruU3+1/hLufv4/+aD9xPfKK91NBBRVUUEEFL4ZBUT/Igw/+ku7dO4lHpq+N9boiYxPJw4wMTDDZBx3NEtffcBGpPecTO3QApspDVZBKZ9i6fTe9I324NJX+/kHaW5tp65iHz+VBUhRMDGTDQDZUJBNkQ6K+ehYNNQqa02FVHXHgra1n1erVzG6uJ5WYpLWpiWL1LmJjI9SYCVr6omhZMHQoFnQe2zfCWx7ezmwtRUDPsPSK83j0rm729E7y/EBmKtXJHjPYSfsiuDdJUUAljgsfIVwE8GMgEyKAA8iQwcBFDhMfDgpoJAjjxUsdDThwIqPRQhtRdHQkchTpppcC40TpJ08Uzaqsq5OjSAaDPBI6bswpz7/TjzxiGLGBUlqbrbDIAR6QZ1G7QMIpg1ZQcVbJhOpgfzeMHo1iDgxD7RUQVkXqmmZCc4Dr3+Tn/A6J5J4wOzc+c0Zaf7ohyzLVs+qpDzSg5+Ik4+PEkpmTr/iahGUpMLaVxGQWMz+Jr3Ud49LbGB+LcTiq0D1RT8cVq6hdItG0ZgzfVjfJpzczPAmBzg4WXhOja4v9BAEoYHqgWMRRU49ZKFAcioIRhvgIpE9zYTqjHswjnKmno4IKXk0Uc3liQxMYFhn7UjARvXhIK+nebHpNLvtIMEXoyhL4JVBVkGVbrzYdGWs7wwofy1jcJJ4wICQft69ySNP8brfp+SN7ePK5J9j7+GNgjsB5CgRmUYi62fzkFmgzIDoCfYfpmjyI5myk0BenozdFdkAQNA1Wi7cAK4F5/VAVoSQAtA5YVkXBsY5RmBwHcxy8VwIp8KTBNQzB7XCrKVZroPT+7wUSZDhEgQ4chHDisipThjDpf+5R/GOX4adExpYfuwIks5ApJDkDKQGvEC6EPYHP+n4qZGw1QtNZW/pJQ/B9zYgLolMSWaaYARlr+5Lmre32QGQzwtt+5ihwIhmrII61FkH2vnKpon0/2OYMDkTRrghCW5qn5HfqRhCtIMSSbQQIWeeraG3FiThls3HipohOlBwTVr0AndKTar9bC9YnY63pQZCwbusYy8v3pSkpX20HY5totXXb9rmwL44HQYVmKFkaZK0jKyJo0QCYTtBN0GOg1gnT1IJ9/ex92tu2s2Z0JAo4KVkR2PWfHdZebAX/GDBofY6WtVpDELcN1r92jF7e/2QLWQ4O7uOh//k58+ZczJzWNhYurSFXhNhkge6uY2zb9SgzuCGnRT31XCRdRnv9Eqprq6ltDCAj43P7kAoS/lyAUDbE3uwmpu+xK6igggoqqOCVIsnIyGHy8TgFfXrv4NcVGQsw2Jvk4M5J1lxYw3vXwdH7V9G7tY9krOfVbto5h9HBKD/56X082vw0N16zjL981/tpb5+NW1MpFPJkTFBwoRsmhYJwg9KcLlEVumhQLEo4fdUsOn8tK7RLcQfdFJGoO281h/bvY+fm57lwYAjvSJZiushkweDxAtz1o//hshVNrL5gPk3NtQwOjtGbzHCU490m7XDVLmelIaGh4sXJLOqpoREPISZIM8QkB+iiiEIrC2ihldUsBXRGGSJHnhAhfPjxUUUttWTJEGaUXroZZBNJshjEMclSALazeapwQRoRhHqt9k3wx4SRJ8OjlMhYP6VquBqyUkdbNSgRQ9iEqRKBOjj2qM7EYAHUIjRrENPBLCBVGbgvC/C310OLHmNTdLpB/rkFRVVx+3y0L1+ET/LQd+gQo5N/yqbnCmJglwF9N8ljXRz4j8do/9JGEhO1RAeiTOzq5Xv74Q2LId9YT+hSD8mtffT0mqy8WqejWaHrn3yIp8VKWcwYEE7gXBrCNHWKw13CT3goAtHTpV2SQQlC6hjiyaiggj89GNkc2aFh9Jfp+G27zjyCXiu3BLBL87gQNEmaUlmfAJZ+Ta4CZTboh16mJUUE9QThWJFwTMdExsGLqbwCpZpOZtl3WyvXCowe2kDvnvUo43F0DSiqkNRhIi7mVZ7bjJKXkSNOCnuy7I4PU2uWyJsIgh4KA9sRVHJywCqeJIHqAcmua2AxNgvjcHgnJA+Bow20Yagag+o+8O6AvwaeQBBCB6wjTiAKBqUp0kYvSxHKvmpEDske9jH3BBK7nPxWgHAEEqmXObVnHQHg8wiS8lSrir3V+pTBh/AHaEScPJEYIy7KbmbAgdr+qDLizD6EMIoKv9xKL0Iewf3aMFGBKkwWIzGEhPGi+OlkNHR507OU3FFlxBT2UQSFGbf2XQNUI9GMxDgGdUjUU4WXOiBO0ZpYt11cZ+FHJUOGNAki1NGOTBAxIV6gRKSqiBNtl8DyW1uwh1s2mW0n8hcpPfkKJa267ciqU7pLbbrzMCaj1rbnI5GkNBETFvvNq1CQgKSQnKOAXk4C28Ss7eQqpopM0hgI1WuqbOkxsaXjplJt+lgta30AcXtdhIhYVKtlAwhXDHt90zT5h098gkXL/5p1V7+Fj3/sPKqrqmhvVTlSGyFhnhrBfyLamMvtyru5at51OC6QkBaLU7f2jRdDEK5uuJp5LQuQoin6GUCvmMZWUEEFFVRw2pEinD76sku87sjYh578GgOjD/KWm15gbhN85itvYellAT77tl+82k07Z9E/GOFHdzzD//uvZ/i7T9/ANZetYlHLIgZGisztWILqcGGaYvim6zl0XccwiqRyOVSXSpXXh9PtQVU9qKgsXnYxnQvO58orb+Lwm29iz29/TWroENHoODs3ZLh3EELtHjqHMtzxkS/zy51wyBLznZhRV0AEf3VABzW004wPH0VSHKOHJEcAL3OYSxtteAkRZA511BJhiCI6nSzGR5AJBhlnjCMcIsYEYYYokiRLiklGrPIGQo9QRAxL8lY7HJSMA5KUCNkzh6cRjmcpYCGQBc2AEDh7oZhPkU4XSBVkdh2pIvOfQ3CkA7gAdlmOaQE/1Qv83PhBWOGED9/+Me68884z2urThfbFy1hx2ZUMxXrZ/MQe0uHRV7tJZxgFhFefjTxmsZ/uv58Dc++gZs11dL73QjbfD5vvF7aIckGDZcvY/aODOOMtNHZ6gUsRZH4rMAf0CZisI7ntELjyYEyAGoG+oshNPB1Q6mDOQ9D/Vij0nqaNVnA6YBdeqeiCTgPyCRjbB6bxokRjGzKCphmkNHlno1xfJyHeKbbn4hRq6mDBEtj/xIyalJqIEJ+MkqJuSltZjn0Ims8uZ/UcwhvT/l4FfPUvPsZlb7qS7+25g0PXfRd+kRMKWUYAUL90DfMaZjHrQIaNH/wVRZjyUv8VcD3CZqBg7asWQd8dAYImXJiiVM9IAWkCQipcEEeYUL4NaoMIXkukt+Cthosi0F8QOU0LgXYE4daDEH0eFotSC6hIzOevCLLgRefALgrlQhDAQ2eiZuErhobos08TfNZnJ8KmwObh7EBmRsgj7sylwHsQutNTQ4rjtccGOYoMkWPIshUowfZQPhkZm0Jc73Ji0E6x34ogFyfB0krbZKwfNwGiDBDFxEeKOsJAkRQm+631gkh4CTJCH3mKuAigsgqhp7UJV5WSCtmgRGXaJfmGrO/NiJNuuznHrO9Ojr8YNrGqUiqcZvcOoxi8QJ4BXLyTks7YZS1jk70O0T7FAZIMuiomRvVhbI9Y0b4a7OmgPBM8iFCa23YD08GLIF5XAsso0cHWXqesIvLWUb7Ue+bA7u9xYPev+dm/X0L//ru4+/ef5Yn1j51kzyeHAxdes74UtEcQjHKLaIzmhapZblr2rkThbs68cUYFFVRQQQUVvBivOzIWYHRogn/90n/w6e+9m06/m5svvwDu28qX3n45hVzlhTwdTBN+escG7r5nGz6Xi5VzTT79ua/ROLsTNBd6HhR0DEOnaOjoqo4u6UzGCyTTGQJVJoqiIpkyOiZ43cxb/QYagx0MdW1m75bH6NjwJDHgnh19PLZviFwG8kUR4Hk5Xk2hWr9diIN5tONAJkaUBBEcuGilnVqamSCBjIYTp6U7iHGUYaL0kiGGTpEsJiZpMsSJkyCJm8OMMkGeOPqUVsEeMIMI3ezxSx4xCBxAhLZnpyTcOPAL4I1AFbjdGC06Lzy8CbMwgOFwYfjbGVWWkUkMQk0NhIJwZAyYhHk5Zl1e5GMrQ3zx//2cLfsPn5VWvxI0LbySC2/+Eg3OBI/f/2Mi0X6ee/wRomNDZJIZ0F9ZkYfXPkwY/CLRyM/J7lxL03v+kSuulshnoWePwfZnwhDpZqzbQ85QEYSuCUobSJ3CJzZQDTkdpDR4MjDeA4XTZSWgiAHgQDcUTja0q+Bso7wPq+B0wMDD9F6xIN5bTdMsY6dY2wR5ed36bB6KkhPcJ9JV06PKWUBzFhhBkKwmx5NaC05ox2oEX3H3joN87QNfB30P+asMEoucTATcsMYU5dET1orzwB2vIf3CMYYe3zGVqG3/+RbgbQhixuuB4FyVwDffitJwAbKzA4VGIA6yDrIBUh6kYSTpIEx2YfYdgS3dsAMkW9Y4DmSgpijoq6DV5pV4ON9/DVHvGtaPfJEGBMdrSK0sd34K6bG3oC2tP+782FpDOxAeOHaAybHBqb8vBSQJ8pIo8lPjBs0DMQN2nXGbyUZgTVlL/0jYswMFBEFllH2PME1HkEdQmMMIwtGu8GVTnq8MQ5TS3+2mOSgfkLSSRyFGD0FKkxK29vTEZyeDOEM+BH1dQDxDCURcttvap11roIjg5GpxouCnEXFKJKvuwASjSOhTViIqJmlS5C0/Vg2AHJKofGm1LIy4I7WyFuqIqHAIMQVjMsSTFMjjJ0CIG5EIWuu4KOlQc5So0PICYZYfLBci04aTQaCBJA+jkMdNK1NPhNkPZkychbEwVC0CrR48TkjYldxsNt6DuCGSyHiYi7jiL/fGXoogYJsolRKz1feKdSYCCNG1EzE5Mj3CZLJPcvkb19Dbf3pmQxQceKyCvjRREpengRRIKchncvRwEP3lq9ZVUEEFFVRQwRnD65KMTaSiPPTsPSz5rzbazl+Ot6We69aex9b3foaND/2K0YEjr3YTz1mMjycYH0+gyJCJwo7tu7lA89PSNo+8Q0LPKmCK+XFFkjCAeDRJMRMjPB6lvrYW2eNEciggybicXkKtHaiajMPt4s/jfvzPr6dvOEE4nJ9ytgogwtEMpTGEE2hAZjFzCRAiS5YCWaoIEidNjAQKk4CMisY4A2TJ4MYP5CgSo0CKLBlrTtwgTppRkgyiMUaaJPq08+UnqnRt59azhyJiZLoNWAhqJ/gk3M11FJMmKBqS20fkyT9AIgiyFxIGYtAwyuxWByuXOWjymDz78P2M9J9bqkVJklnzhr/GV+fC3zgPX8NcDj/7GxKRcZLRMQw9TT41vSH2ny4CiCGP5T9T6EePxUmnIzieddMTPZ+ifwHhYhPelhoaF6gUXV6Gj4wgBoQ6mJYUTfZAqBFSKVF52Q3EUqCfHq2k1rEK54KrSTx0D2JoXMG5hAoRe/rxUnYANuzftZf4m2Kt60C84+xl7URm8SLSwBeYcVvqm3xUNfiIFCClgls6nshyn7C8G0FoGTrsTklweA8Ui7DPA9UhaJYhoUNBxlMb5J23fYgHnttBYs8RjENR5sL/Z++8wyS5ynP/q9S5pyfntLNBu9pd7SqtUBaKiCAkMFgE24hsm8s1BmO4Bptr4F64JBMumHTBWERhCSGUUAblsKvNaTZP2skznbvCuX+cOtO9OUqzi+p9nn56pru66qSqOvWe93s/rp4LS+c209ZUjYdH4y97aYh41NRCdZMHuV2yMLFxaOiGgn+HNQ0wdQQl3DzoTQ3oVTFoOAfOnISn18CGvVLQZ8HkNOQcEAYk5sVJXvUuIk2vJpJrpP6LZ9DINko4hJpTxN93DZzXDtEDKXDlaakBuekRirmyr9ckoInyQqxwwCxC7mU5cVqBc5ExNhaSrDt+ApQqJOemc+AqzEyEtlpGVgYaauNByoHrqsW+yvFe0zNIAl1BkeLCP0I4eS66FiYyvXNmvGoV75V3J5UoTwXyu5SdWEeQaukByi6pRX+bZqCGKCYNdDHBBkYAAwMLA32GHo0j6U3w0BFYhEhS7R9V2Q/kkPrvSjuCLDBJkR0IRokggGqi1BDCIEyLXxJFtipbghDlzAiTlIlapXqVtgcaLhq9SJOHJPqM9UAROccrIGfM1eBGpH8sDliGzJYnjIrjWjPvOqEZh1vLr3+4or2Vu+88JL+pvrMpXz+qkCYWYf//rN86hzYCcBFimvWb1h5yi2OBgUHUiFEdq8WoQXZ2Esku+5kSXRdKRZs0Q4FnbIAAAQIEmDW8IsnYXCnDs9se4KffnM+KN1ucc3WUiy9I8hd/+z/JjQ/y3B+LjI2nwT49/DNnA64HW4fg4cdWYoaShGIJahpq0cw4mgea62HhyXQCk1km9k7gOEViS0yMUhQ9HMEMRzGcEuFwmNrO+dQ3tzCnq5vwj0Z4/vldbN4+TX8uzZSukyoJNEfMTDctdOowmEOYLnrIUaBIAQODZjqw6WeKKdJMkaCGFLX008sYQ1RTRQydMAYChwJ5PCzyGIzgsBOHrZxOiaA2AHHwJtDcPHXLFuBNtSNcDc92mfjxvwHvAyzI+GkXYhMsntvKBXMMdvXuZOsTD5OeOrS59GxA0w0Wn38Lc87tpqg7bFzXy8O/uRXhqQDUVyrilB/YlFZ8CmGvZPL+lTx1/9uh5xr0xRdQU+PQsayFnVsnGNmyHhlaHALP8SVhjVDVCLmdoNkQ9WBvFpyT8XCSwOq4kPglbyd9z8EzmAcI8KeG49UwKjI2QplYEoAt5OmoF0HXo1BVc7jdVBTEorWtmvrmKjIOTJplfZ3KJK/8HtVE0EZyFu3VKeZdcRFCe45ssURmTZbM5CDcZECTByGDSFc1N772Fu7/xq/I9u4mZhpc0lnDP12kkTq/HbobELbDC3dsIx0HpwpGTY+6+5+hlHyGUHctiTM78CbAihvodQmorQXaccfGffFlC8WuZUQW9qEV+/Cm9+IMgxWHSR3G01AQGnRHmfzIX1Pdsxht2yDhLy4kyW5KmBht9fA/zzxi29sAbh68clxLn/rDJy73qtxMfjuGNSiJl8rmowFY7Jci5v9/AmSsMikuIW+fSma6D9QHioxVIfLTMONRWuV/9q/HXZQSksY9mAVBFhDxTqJ6FVXTVf6xyzDYN4mrQ9nzWLmgZpA05l5kuP0EZXMFm3JgfhURTBpop8hWptAxsQhTRYoMRSw8IsiWt9DQ0TCxiM1ocKN+W0wgFzqTlM+wLDCMTR8uBSK0AXXU0IE08mjxf6d8/12/lJa/X5WMq97/PoE0DqkGPFx2Y7OJMG3+vqcpp9gy/RaJgbYAzBbQwlIooSk6W7Wacn6V7xomUWQvS8ED+1hHWH7payt+FfZLrGxImvw2U1T+KJLKf7n0pwYGruEyHhknEc5RF2vEckOyuWNSMFwoOkxlc0wyjBeQsQECBAgQYJbwiiRjFX6z9dsMPjzKSOHN6PZbuGCpxhlf+x53PrKWT/7rrdD7JQLt0OHxkzsf5id3PkxzUzU//t7fcM4512OEQzjCQz045ApFRidHSU9McvY555DL58EuERUelikfOUtGCM2sJbzgQt7xqR9w9vpnWfn8Izx+33+wJFHNhrVZdvUVZxy5FlJLG3XU04BDkTxpsqQpUCBChAs4hwnG6aOP9awhgomBTQ0mSQwcHNKUKFAgQ5oIMdYDfTiMvEwmAycXz8GEQDx5PrvfeC1n9MTwshp7tkwhdSGjwDqkK6ADV13JRVdGOVPv5eIz/wzcU0+16LkOP/rie7nqnZ8g1dzJzi0rEWIdgcPlIPJx52rgLg5sj5/B9p/hbdcZo4ZHfrYMGaypwv8WAdWgGxCOQ9YFS0C8BJFR2L0FSicjmcXryT6aIvvobSdhXwECnB44EQ9eFTIfR9IwGWBKQCYN4TCEa1JQ33V0e4rNpTsWZ25M0jSDSBqngFQlbkMSUu1I4RjIu0QKuHh+M1u++34c3s8dBfjNvXfy8w//JfxcEWM249p2Xv8fCyAnPSNf21nP5377SShE2H3Pzxn+5r2IXbA9B09kYOWgDBf/HLAJWFQ/zps7x8mOwrzrIXxTO1yYBM4nlN8Gd9xD+vbnWX07XHgpGDHIjMGe3bDoBph3BqzeCXe+IPjf94/y0X6HN7YIluKylSmSeEQ5lyjXHbKV9p/dNTS3U1VTexTtK4mm80Kw3oaJl+yW5CBJPkWZH13ZDoo+KthlJNtWoCIWXbl9VkIgSbtaZMB5q/8+wonCRZKlTez7IBIDxoe+gU4n7bwVjR+BNLbaByr5GpSJVtUNLrJqWf9VoKyMLR2wlxDQxlLfJTVHmhStjDDOKCVGkWYREcIMoZEmjcUumrkKebZPItiCPKOa0GaWU7KAIEEDAhNBE2WDhAY0wkiyXTrbCnYiPUCWI1OL1SEVrgm/VaJAHIwwGBqTokCv/SLnswzNj/aSZ7aD7KM4aAkI9UAiAqYmJe+FAghlvKXMmsvQkNeAdv+IDfv1j4kcOh3+UZqRifLUEpGOpI5NvwWU3Uo/Lx9KlLi7dDsPjPyWt95/MZ9p/Q491kKYAO3NGmwQ9O4Z4pG+dTzPFpwgeVeAAAECBJglvKLJWIBVL/6Ovr517NjyIv/tQ59h8Tkh3vWmM7jgsk/w3bv/lge+9EbGd74428U85TE8MsVfvOdbhEM/5L1vv5Y/v+lqmruXki1CLArJpIHuRTAtk7Bh4BhldQ6AoesYpj8cwzEWLL+UjoXLuPzSy3nmF7/m3t5VjFDkvZxDFSmG2Y1HCQ+XfrbRwyJ66ECgk2WSrewiQ5YMeepIkCeLh+MnEihiEGOMNOPYjAIeDrtxyJ7WRN8acD9A4Y6H2Hx1O8KKUhoPAdciH8M3INOmLKRneTv/tXIXv+x9HtwdzD7BaQEtvOnvf0Dfjm3s2vgYezf9EoDHb/84upHBcUogZrucpwpGgN9z+H5Tip0n2DcVUBUQBWH54YtZSJagOgvhYSh6J2cNas47Ib8Rhj53EnYWIMDpgUrV3rFCkbEJyjq3mAfZXWAkwYyEIXxkmwLdNPnzX/2G1IpOisgzXiUuSiCXSesohyIr9FHW4OGX5XVhuOC6a3j7g09z45KzcB3/rp0E/inK2VsLnDMoiO8d4f3XfIbHhEY2n8P1+R7bKyfxKQH/C0mKXTgOySl4zoO/+ynMeXaQ6PdHKe59mu19NvF0gVROEmHGszCowaAH/S5MPgKLb+4kUmNTXxikew88/osfMq90E69afClveMMv+OaD53FV3RVctfDth2wnl7IuEGD+uQtoXdl6yO07kLRYGIhpMLcV6m0ZKWT5DfbIEEycsD22Uk9OI2msTk66MEDlbgJ/39OUCVmVWm4aOaJr/R+0IdOyff2ED58F7gVuhn2Sy8VRqvB+XH6BQRUaaRx//hajbAel+m3EL7kKvPc1oYQpu9zmkeNO3TFLgDMTdA81dDNBH+OMMMEQW7AxgG4MlhJHQ8MGctgYpGnGRPbNOGVbgAJl4wQTqX518EhTYj1FMkzzGCHiNLMA+HOUX6tAJ8dqouxE51VIB+dzKRuL5GXN3T3gCqoRLOev0OhA9k0SOU6amTEQEAYUp8AeBzYDgyASwBy/B4oV5Q0BFgbSS7qBsidzvV/KiP9eQ9ksKYQkb/dPWKi8fZUL7ssLjWpSzKOLNuoJ9ZhMFbYzNbKdzvqrufz+y9m6exsFu0iaicCmIECAAAECzBpe8WRsqZRjdHQXz794N9/6TpJ/+vRbOev8uSyPhHjP1TUkh/6Rpx+8jXVP3T7bRT2l4XmCkdFpYJrf3vcEu/oHaeto4s3Xv55EGNrb6sjXJUln05jRGLouHwFdbDQP36PSxkHDLjhgghWJ0TpnMQvPHia2chB76040BBolqkj6mo0wc+ihjhpKOEwxQYECJXIUyVOkgI2D8MkoB48iWZKEsCmRw2EcyOKQO0iwkkkjOlWUkD7CIVKYpIAEOTYx+yRmJUrgDSA2f5ZC/QcgtRQxGUY+QAEI0ENQFaI+GWVs7R8ZevIOXr7gsYNDD3cTjs+luq6LTc88xtTYFjIjG2V52U0xN8nL7cZ76sNDPvh1I/VFh7Jt8Diw7ZLMOFtqQHockkUwM5AdkJn6TgRGGJb+A4w8CJmVzHjbBgjwCkDlssexQiW/UeYjISDmCUb2OIQbDCzHor4qxugR9qNrGlcubaWuKoKGJFDU/kEWcLsL9QbUaKg0NzT521aGjcc1sGIxjM65nPfer7B+4/1kwgXC85u47LIuIoO3Ma8nwbJ5DfD4Vn65pg/DdrE4uH5SmT9t8OBXniR4bsvAlb0ul0y7WPMLNLaClYdIASJ54HxIhkATFlVegnDrfCLLu2BkCG1wlGjGJpPvo1AYx0iZNH2wkXNDn6Fj0RJCl5WTdqk7XeXEV1AOX2/stEjVHzr92hSSWAoDKQHDEzKxF0LyXvMWQGiMI6ehPyLmIgnZqF+6+TATF3Ss8JCmAAkwDDnAPA4yUJVC0kWSi1BOd+UTdmED3AlwTjzJUgF4GpnkTZGxyjs2ggzEF2Rm/lOWGtOUbSVKSPI2VvHZDuTdMIs05VGpsCqVs4Dvi2r7W0ufWA0PDxsTlyokrRnBIEWUEHV00IANhGcI60nKNK/j7zVPgWF2spdGmkjQhUkDJmE0CmjswkD3S63IWw+NFCEuR8Oi3PeKFC9V1Fgm4TTQMZjvbxPdb39F//+E/N8rICOkBoBllO0VoExRC7+dPeqRZGzMr5EiYxVlm2Jfb2t1PgnKQ0uJLUYpgnhbngAAIABJREFUx+S8XFjBpayIn8clLefR0VRF9YoGrJwHVg/YcG3qJqrDz7K5tJ5Jxl7m0gUIECBAgABlvOLJWIBiKUvfwBr6B7JcckUt4ahDY2M3r+oMMXHdzWDrZEf2MFl0mRpcj+cExNDhsHLddtZu2k5DPbQka2hubiRVm6KuuY7pzCjVoSZCIRNN00B4CM/Dc0oI18YVGnahBIaLFYZYvJa2BWcTTz1Ejq1sY5Q2TBJUYRFGQ6eVNgSCDFnSjOHgIND8iaGgQAkPBx3P9xWTTyAWIUwELjqTh3h60ohj+KGBGjphEoRoxKWRHL2chKeukwwXhv8Tsb4LanUwliBVLTagySReSQdvvJ/89ufIbnt6lsqpAVVo0ThGaA5meC6xqio2P/MbXGcPZZ+4vbNUvtMFSSQ9IOCQqeb2RwywpHecrsnYX9PPgT4xcGLFMZIQnw/1N8COd0Nm3YntL0CA0wjKt1I5MR7N9gqV26sZhoWkyHIZDxE2MF2TVCx8RDJW02B5rU44pM2o2VRYtyJMpgTkHdB1qPL5R+UNWaBMzSn1W4MV4rV/+WHCzyQZDGfRF3ZzxZz57ApvpqO2njPbuhHpAqmNg2i2i4EkYyv9byvJsAH/+2VIs5VSGsIC4kugrgEiDlgaUoZ3UzvJiElSmODEoP0siC1B27INo3c79sZ+nOkBirkJ9DhEr9e4cOI91CwF/azyMRX/qCa+qlyq31K1EKuUae4HdVeykHfU8GS5fpYJC03fkvOE0UI5/buLDBqvPs59CeQ8RewrA95nDVZRoCCJ2xFkLQ3kaMwBKTAyINKcjMXRIrAS2aZVyD5RakqVkEuOF3lfUxT5FLIlbCThquEvL7aGyScMCltyjCEtPib8XzscuGwu85mpvcg5noOg4BO/MSQZG0Un6s8Dm1X4P2HkWWH7vxIUyBNCoJGnyAi72USCPFGaCdGGTgqLEhGKyD6pR/ZLEQihkSDEJX7pVMKuEGWTBaVkzfifJ5GUqYYkV0v+thlm5nuEmaGidUvW2mv0962uUsrQQZ4JOh5VfhvHKScwU8n+NMoU8cGkCGpxw/PbfQ+yn19OnMU5XB97A69tuwIWItcychCZqoUMvKX7bdSNtaCnTbZwcpKGBQgQIECAAMeDgIytgGAbH/3oBznn3Nfyvvd/nSWvnkNzWOOma97Chee+mft3THHfVy4kPbzVF48FfrKHgu3AwBD87ae/RWMMLjx/AR/79HvJTDokox7RcCtxo4GCY4IZxnE9Sk6JYiGNqYElPAxDI+dEKEbb8Mw4/WT4Pqu5kRDdtBPCokQBi3lMMoGDg4nHFBNEqMUigoVGlkkK5AkTIkKMBDUIItTTiolLnlGG2H3wejCEzYT/qBImjMCgQI4icqLrcrgcsbOGLZ+D+Dqo/jxyKj0CuCBMcPbw/K+/CmNbZrGAEeBCwnPPxxntIz34AunBF2axPKcjBLAWOAv5MLnpKH6jtHd+GKUIQb5fsh7OOOw5QWe31HnQ9Ql48D7KGrgAAV458GmvoyZkHfZVlrmUQ60BTE2jpiOMLYApD+0obzd1lPO0K91cmHLiqVdb8JsJSIah3ZfOKktRFfCs0gABhE345wvhLRfewqYcbJ0S9GRBdLyOpqYotU0x6hte4EzTZKtuMyoAIWbCzg8WrmwDL/jHWAV8LQPz75Sh65c3w+KLoOqfNej6azQ9gUYaxA4YCUPtNUTEcqo3T9C7/VaYfoaJ864AJCHa844D20Tp/xQUL6k+UznljwTXr8sEStcIhgsbNkD+pOSW1JEjaRhJZd14AvsykKQd+3pDHRI5ZLqlZmRrjCKp88WQW8nJ0jkWgReBrcjxVo0kZqspc8b7h74rMwUZ2C+rsgtYChjvaiPxqmouvWElj/oln0L20cGsQ6RZj1LGAoSYQmcngnEk/V0P1GJhUoOvh0Y6pdYjSesiwl/q30YfnegYCApksdBI+nNQQRFFpGpkkYrVaiQJWvJbQLUClOlogaQztyB1vh6wAqmcrkKOxDT7mjckKI/iCvlz+GowE5DLgSuQc7Ao8j6d3afFY8jrh79si4m8jpiUFx9UKfdHZVLALPA8cOtBtnspkSRJ3EvIjlfcdxEp+M7BGcuaGd27gB07e1/mkgUIECBAgAD7IiBjD4LVLz7ARz9yPobVxN+88UNErVZyrsUPv/06Vr7vWb7z+fv5xVdvB++Xs13U0wIjObjniV4evvFfSAiY26Jz3bVX8/4PfRIz1UTJsynmXPIZB8MAIg6ep+PkdIxSgarGVjpq5tIWaae/0MfDlGhlJ0VkWqIU/cxH+OoKgY3AZZhRNPYi2OsrYjU/1Evz9S2ar549MDVEJfJUY3EDN3Ib9zHGIDCKYIB9p6WnILJ3Q+5Z4J+RM9EN4G6EoV7QsiBmy56gHRmG9xCFjY/6cZ6nIKF92mADsj1fC9xzmO1CSMXVKCDAdSE7DeyAkAWlvnJ06vEiXg9d58CLbwaRPfL2AQL8icGhHPh76ID3MionYS5S11aprg0Z0NwNE5MQ8RN5HR5Sy2r6+1G6OaV7VApVA3hdSorjFVoppwpSRJhKZxny3xcA7VG5BHTbky7XvfUdmBM2azcPoSU6+Nm6DThrnuLZe+/iPf/3Z4xRDnduQZK8q5AUkI4kfXqQajsHmeTrfwFf3AvGXaA/JLhU/xzLVmgsWR7l3LOaKKYTdF73BHXxRpb0nIem3YoYQ/JSx4BKBV+BfT1FD4c4sMCA9mbYOgaTBSgIeGAKnBNeo9eAh/zS3eC/4of9xclFAtkjE8jIFOVHWg98GtlDJwcCeBS5lLjc/0wtThxsZqUjZw9T/jYp5MzmGSD01Z1gauyhTFPalHOU7d8t0qYgipReO0CWFCVSyDSne4GrqaONBsoUsYUczTGkXcAwQ2yil00M4ZBjN51008QyLuEyTGLAGB4vUmKKCAv8faWQ5G7GL41Sp+5PpE4DTyHPlhAwD0msT/m1qqecJkvNoRzK6bSmkGd6THrBeyWorobxfumrMQOVzKtMf7dR1kVHmDE2OiIqbQsUzftyo4oUSZGUTZJAzmuUXNoBtsITY49yK9+fhdIFCBAgQIAAZQRk7EHguja53CRQ4DeP/pBlZ1zGpRfeQMjUWBJJ8RfvvISWng5+fe8N9P/+b/CKgSfi4SAA2/GwM3nyQKEP7AefYXrs01R1RrngytdT3zCPiNUgOSIkP+e5HqabR3NGuey8s8hO7OX7d9/KFFCLN6NpcPCoBUJY1BMhgcUAk4A7E0i2b2mO7WmpSJFtbPXtD4S/R/XUdyqTiDaIYeD7yKn1CLBHhhmK2Sz3OHKKb4NrH2njAEeEolySyIe1PRw8jNREqnpAjuFBpOJGk8989vSJif2tG2G6Hp7/oE/EBpEDAV5hEJDJuYiQQDOOTF3sv4UiYxXxoQG2kJfr0RGb/r2jDI4fQc2lRcHqoeDvXdErKgR82IM9HnQaUKfLz5RwTIWLV9I0+xPKBjJ5VUMIlp6ns3MsTGfYItbk8fHb7uPDqRTLli1i6U3X8fej/dx6++NcfflCFvW0EiXMmnuf4Kalc6nqaCLUUkdkfjsJbR4mEQQFxsU6+n7xMzavGmNHn83oFDxHni0vwAM7itQ9WsJ1TObf/T0uXLSE8xacQbewuPAjn+WC6687bNMcTBkrKl7FErhuDEOrBTF+yLt7AdjpSc/Y6ZKkxTxkX504QkjKsRuZaEn5h+6HRsByoT9POe3V8ULNa5SUUKVeUqmwQsAjyDnEybVmuguZMGoxshaKiFVNWfCPriHbOEKZaFXpp5oAveDNWFAoYh0OLQSWJgxpHHbjEabAIA4FYhi041INJLDQiSEJ1BokbawcmDNAFps8JRzqidJBK9V0oNOFTgtynuig42DNLIHofsmHUGYJkpitXGVR5GoOSWlO+q1jIYlclWjNoKw3V+KAKWaSsGkxiNZDJCLD1TQdkgkYLyHHlCpPpQuvSwnQiBDBxcJGRznr7pvw72BQiz0FYDUcIubspUVSi5IwomU3hyyyAv7Ki3Ah49mMBbkIAgQIECDALCMgYw+LApt3v0g4FqVnfg+rV3WxdGkn55/VSqqjlXz4VawWv2PrqlWM9vdzzLKMVyAcYKIAG7YPMTk4RFUbZLwQZ59TZNGi84mEonjCBSHwPHBxwJ1m3rw2Lhhfzh+ff5zte3eR8VNygZxCTgCW//hqoTPtZ7412dcdC8r+cOr3BnK+phbN94eNzXb24M78Qj24HB3UFHl26E8HGQg6hpweT8xaScrIMRv5df+0kQNtApJXQ+YO8IY5kAw1YCbcMoJ8IByFcAJyaSgdb3ytBpGLgVbIDcFUkOwwwCsTAkGx4CFcScaqBDfHQpMpclT91tAgHpKWj57uYIsjkGFGFBJzcNBnlJ+KBioAYy70l6DN55QqfVMjBynrwdS9BhA1Nbq6NH7/exsRE1SVdDbn6hkbKbBtcAqhO0SjISJoLFnYzqUXLyERryNmRLng7CU0dbcQaquBRY2g9SCZkxxCVDNYWM+G1jF6d5UYxuG5vl307S6wY4vLU/48a+0LzzOyfZritMx6P6frTGrq28hzUOoSKJOxyg5CfaY8RfNFsO0QBglCjM/Qk/vfMW1gTMDYS3Ybq0WyrQ1IvXJlrwhgCHRDJuTC5cC0a8eDIpK1ylFOVQZl+u1OXoo57kb/1Y9cSlQQ+72rvw3KhKxSvKrgfgfZ98PI2liUo9T3hwP0k2YXfdQRQmOCAjY2Uq2txoWDhUmt/6lSrtrI9ing4JAHYmjEiGERofxo5fjfaJiEARvXb2N5XqnA/yRlHao68x2/hiq9XiV5qpZr8v5vlLmJRVnDLiT5aiUgHpML3zqQjIJm+Yk61bGUQ683U6o82szCjLomVfaDx4GxYZXnVhZ4Fth+kLZ/qbGLXrbb22hJN5GIhdCmNdlMcWTBLdANE2OmrQIECBAgQIDZQUDGHgXWbHqK3l3r2TUwxue+/H5a2hs5P2Vx0S0af/yzn/GVj32de3/yc2x7tZ+1NMCRkHZgcxrYBBu2/Jo3vDFL3QeamD9/CcWijeZ56AhcDFxKxOqjLFk4jw9e/ha+fPe/M1EsUPRcNE+qIQaBQUoo1UYdzEyJVQ5i9VDpUE7soDJNL0I+EExzYJiig8fgTOqOY4MKbFP+WbOHnbN69AAvNYZAL8Lcb8HWNZBNg9ifKbDAqAE3AVoKScxmoLYExc2QOx7Fkx8EXfc1GPso2H844ZoECHA6w8naiFoxQ0ocyyQrhKTfhijr1DwNOpsgG7XIGnWM93UdnhILx6BlHkLTZrKal5A00hAw6fNILbEykaISFh0O+xNampDcxt7ePFuGi1hEuemW/8tZ15zJff/xJe77zY9Y19+LZoUYjsaZqK8nMvcM3vT6W9C0WjQ05F1xF1KhL7PSa5pL67vfTMstFlcKDc+ewPjpD/iv7w/y2xfz/Npnj4ftEret38Iv1m9BAJvu/i86qwUt3VfT4dfKtEwM00SJlCuTiOUpp8dSlNZ0FvIFHV1YVPltl+HYlw41DTRNw/OORyqrCDlf3XhQPAVDMSRpW095lnMiyCAtbEaRI0VDqjBBRrN88yQc40C4SO/YR5BOqLAvwRelrIpVUIpmhzL96FR8F0FSmBEO7Vw+ATxMlmfJcj1Si6zsKkJIK41mHJoxiNCGPIMkDSzIIturQAmHCQTDZOlkAoMqkhjIWamJ9N6t9/e8kiL9aBhEZmwBpJWARoNfqjBlctRBGjhULqukkfSzh1xkt4EpBCaCajTm+e3n+Y1kgB6FVBXEdQjroNX6x8pR1szrCHR0NFLAGDKSLYEcZfuPxJLfTpWLNZWLHVPA3Rydk/3Jxo/ED+ibHKJuUzfLjTb0PRpaVEdr0rDHbZyoS8w0aaIqmBkHCBAgQIBZhSbE7IeSapo2+4U4Cui6gWkavPudf8+73/Vh5p7TQlUUdhQd7n8xw3/71DZ47DJwA9XfsSKs6/R0tnLv/T8lHG/FyRVxc1nUFHs6m8URkKippdpr4Klb7+Sxh+7jt8/fw6GCNhPICbkKvbSQU9wCcoKoHpQTSDLWIMIgHttOYhheC2WdSYAALzm0EJz/Mxh/Gnq/XPFFCmlVcSFUVUOyGbBgehjmvwjbnoWpI+VoPxh6gL8EvoQc6afFpTxAgJcEVijM1+96jDect4i22qqZz49Ws6jolyEkVZIBpgX0lsA2YPtuwao/7ObJW7oPvZNYE1bPa3jomX+nKRYhhcoVL4PMhZAEV412bFpKD0nTVeMrDj34/TgsTgpu++V2/vjHIX7+nQuJ6xrf+toL/OdP7ubFdZ/lq5/9KSufvIuRya20LG3gs9/8NnVmE6GZNGUZZIKoSRTBBbtIZ0cY3tXHmrue44KO11A9/y1YrYtwawzY4fC7f/4Ajz3xII/sHWY9oOs6um6gG7pcBK26jHf/44d4+7tu4II6WYfKq1OBMu3p+W2+oR/+61tf5ldf+DjHey0LAx3zmmie28zj968+rn3ImcrbkB6tCzhQf6ioSa3i/URtCjJIHaP0xZf05Dakf+2vOZZooMNBkaSKhlSL4ucC9yHHlyJbFSrV20XKBgqKkNWQI2iUmdSUTCMJ1W8hVbf74za/hsP+9+P+7+JI+vRO4J20cwVnE+ZmpHp1HNiNYC0ZNiLIMMAkG5lkKxBF4yJexbmsQJ51JnJEqNRja8ixA40sET/NlUsajfkYvKqidJUuz3F/H3GgDfQG8IrIJYS8f4wfk2Y1U2Ro49No1DGjIzbmQ3UEmqrA0mH3EExOSLuqmSilSaAfj7UUeYJe+mmnbIwAB3OVLfeNQo7ySPwt8HHkUstsQEenigRfMz9MCynmdC6kurOLTz/+DW4Xv2HSm8QRFQnOAgQIECBAgJcQQoiDTtQCZewxwPNcSiWXu+79OZu2rOOiFW/kE598O+2pGDcuTjLvCwv44i/uYs0dn2J8x1OzXdzTCiXPY+fgMO+85aNcefE8mlJxWuobufjK63FJYLoC4TjomgMJl7NvvoJ5r13OTWO3sOuFfu740a2sGtjK9graU+psyolCVGKBKHAuMcYokpVGCGwEWimhI6jlxPIYachp9FnAZmZbERvgFQVRgs2fhfiF0PkF2P0J+bnRCdpicGIQa2TmATERgXxGJvM6LgwC/0lAxL50ULZ3Y7NdkABHhKZptLa1EYlEjkiNHaA09V9GxUulC2qxYFKDpKmRCh9hz4Usom8DOSHIIO9FKpi9Fqna3J9QqcRGG3ICzqmI4FVlq0bq8iwgrsGrqiBpadx8TQsrltTy09U6r14Kes98LnrrO/jYly/movlnceX1Z1Kyc4QTFrVGA+Y+6YBiSF/UFsqGAcuIhku0dBZIvHWK6mgDZrwZIxzDsoA5Ic7/l08yf+L9vK1QYnwYHv/p/2PNuudY37+N3UBp/Hlu//d/5qm7vknKArD4y0/8A5df9Wo6kOeVTjnJE0ApB07x2Hzlq4DqEDRUG3QsPxs3XodmmRSLubLA8ZjhIa+tTyNTSZ3jt5OayRwhNVwKeUluQmZMe46j4FLHkfRo2n9NIUnYVUfz46OGDO4vRy21I31FB5Hu9n/LwU0XFAUd8n+fR6oz1ZyulS5azUVoNZeijX6eYZGjj3KLVfaoCdShMZcY9cQYYoS9yL5M+Mc4G2gh5Hu9bkeZXxQZZJI1bKGPNgxKlKgizFt5FTqLSNGJ1LdblGOtPJQ3rBzhJXRsQizDYDtTbGeSPXSxHG0mdZbq55D/W1+Za1oy+ZZngasccjWitGL52RPkrLck7QiMxRAKSUPjYgmyjt8YSseq/IGncZggzyQlyoYICqpECi4H2hRIIwZJcH8eOXJnCx4enmZzYTxKjV3P5MgIj4+v43fO3UwwUWE7FiBAgAABAsweAjL2ONA/uIux8TGmxzx6Omq44roV9CzqoOXcJL25K4nl/5y1j4fYs/ax2S7qaQMB5IslHn/yeexsP/WpOPN7Ojn3oiXE4vMIhU2EIfUSwrNJNVVT215Ll+imp2kMLZdh0cAOdubHGNvTz/YNmxkqZpnab8Kl0hTkEdiImXQVGSCERwRJfFjo5PD2SQRxLFAJDAocOoFEgAAvCaZWg1cFyQYwLwfnGd+yIA20QaIFbBvsSWAM0oPgHK+9Sh6pngpwshBGaph3UX7gPZQHZoBTDBqEw1F0/Qhk2WGgU3Z1dpE2BRENDCH9Y43DMakAXhEt108Yb4ZAUa6QasK3P9Gl7leKiqvEkCvvgdWGvDcql0tDg0afsO1uiVFdG2P7VrlzPRampqOVC66ZRzugdzdycKgl0gOnoqYJZgJiiXIZS8j7dSKm0XjWEpqBkAf2GNSWJjlj2XyW791NvxDsenEdfXt2sal3tV8ng7Ne81bmLyzS0RaeCX1XAeAakBt3KGaOnqRpMSNccO75dHY0UVMTpnHhmfRnbEbGRhjs30Ftaz2Tg+N47vEwshPAOmCH3z5dSPoyfLgfyYokKEtI81Qwkaq2lWmYlL5UJdY0kbS7hkwGeXIpNTUfcv2jqTlSHngQuByYT1khC+V+Us6oSjlrV3yWJElU1CLcAi6CAlLZeTDto4mkN1NECVFDO5PswJ7x9o8AZ6BTQwRwsFmLSSsatXiUsMmwiywttJCiiTBVdHE2GsspU8klJC2Z9kuQAGKYVOPhos3ossMY5DHJIugHUmgzBgBqLFpAGLSw9ApWJXWFv/8mTKowqaloLUCY4DlQsqFoSFm8V3lFUMm7pKmKwMHDmemjQ+muBQdeQ/D3lkPOCNYepN1fbuhC0OBlSHouuVKJnDPKAIOzXKoAAQIECBCgjFOGjN1/5fpUR6GYYeXGe/joR4b4/Fc+wjta3kBVKsV7LoPa6v/O75rncMeOtRQyJ6KxfGXimdVysjRvzyQ33PgU87pjaFYdZjgMhoZecPDsDCXToxgWRJZW8+al78XMe9gjk6y571Fu++6PeHKsn41uhtzU9EzOVJWtei0HJisaRgpKmoFWTPZSYgypbVCTz6MZoyqU7ngDFAMEOGGk/wiZTRD7ArjrwduGHMk9kKiGTFrKwIqboLQN7OOSbwV4CZBC5xo9zs+9DJmKK04IST7sG74rr0qn073zTxoCSiX3qLxCD0ZmqHtMnH1JKxdwfO7FO2I0ug2MzuR9VwJXte/KkG9FsrhIIrYXSFmS8lNXhK2OvGfO0QUN00VMXccIGYiQQUFASANdg3gYrl0iKSfDLZJzbdJeDE/zPVSP2CIHolKj6iHvq2PIY8wsUOgQaoCL3vMWLuIt8ndC8NsvfJ0H7vsdz6x/kR1APltgYkeR4c1ZaAv7i7Jlss4ERvummD7KrFw6sDCU5G1vejuLL74Eo7oGzDBPPPcCjrOKybER5iw5g3XjL1DMHc9ilyJjR/zaXwIsQ3p9VyqL94OGHEDT/k+HKr9U6cgUGatchQvIlvWQNGgUqVV96a4sLnLONez/ryMTPt0F3AScSbmPVSltf7sQkjC1KVtNCATCHUGMP0qJwoxdwf4tryHp7BA6IaLoVLOUKH04jCPw/ON2EqKKGB4OOV6gCgOIY2BgESONRZJumuhBEuXtSO25g4yHSgNrkB1gAAuBamLMQVCNNFXYC5gkaCNBCIcBTDKU/WkdyqYMpkzOZxgykkUoKcEY0mhLuUOX/BomgTg4GUhnQa8GKwymIX1kZ8y7yvd+DQ0NfUYzeygcTps9BDx1hN+/fPAQ9iheqYaYiNCoJ9G8U6VsAQIECBAgwCniGZvUTGGiMXmaagg1TePiSy/nznseocbPgrF6QPCDP0zy7Xc2IrzTs16nAnRN4/WvX8AV117L0nPOo7tjHlYeMAw8Q8czwHRkDmgLnQg6ZsQkVlWLbpfYs3Y1n7r+Bn6dK1E4xqGu0meEkA8MSmxy8gL2AgR4qbH/EoKGjFtdBjEL2p6BoX4ZlxxE7Z0SWBaaywNtX+Qju97FY15mJtT2tUiyYrhi2wZSlLCZOuYUQwFeCoTCEW59cjOXL2imMXF8mbrV2ZpBUjqKJN24F/ZkYOeO3fz2mq7D7sMKhXhwfJy2eJwaJH2XRt6/Isj7WsZ/3z9TOv52e5H0TpOQarfnsiX+6o0/Z05PO2+/dg7vf1MPPxmB19dDoynvlwWkNc+DD5UYGhJc9/owZ1dBSuO48pbbSEoygiTIKtUDR7SBEAI1v/U8jy987DssvfkqllywiB5NY5BySLqGJJH+7n3/m6cfuouho7SZagUmNY2enoW86dobufndf8FQMcJkZorhkT3c+4ff8+AvfkI2fXwJQMv4ADJwvgPZGpdw0BZVQuMzkWTsJLIBZyAqNgSZ2HPA38ik3BoZ4E3MxmxHB/4FeAuSvlSUo1qUUE6qinpUYzqGrMG4/52BNHn4APteMzVkv91DI2fRSJEEa3iaVf7va4BuoJse4pyJIMwY62jmSnTyCKaACWwEJt3o1PsleNI/gtLrhikbMlQjvX/PBhw/JqsA3As0+q9qJPm+AM2Pz5JXgASQkl6xsUVyf6USOI5Uvc4k/coiOzxFeSCo9LG7gDgYdZBsg8k9yLPaRpKxW4FnyfIi46xmCJjnH9nk6BdSBPBj4D2cGoRnTTjByF/fjn73Jpgy6DNdlg98mEmO0z0kQIAAAQIEOE6c0p6xXZxBiiqe5Gl0ZEqYJhoI++FYGV+/4BEmg8amfZf6Zx1CCFa98DxXX76Cn/76UbqaY3Q1atx8eZwfX/oNcqu+jJjePtvFPC3hCcGjj+3khVU/Z868h7jhTYt5z1veh3AT2I6J7ZiUnByu6+J6Ak/ohLUwXkbg5NNMFYZoXBbnPXYItwilaZfp3Xk2e/Ix5HBZqW3/e3XmBK6Y+yKGbKOAnD6Vsf+IFcwkyylosDsrveSCJ5NTBkP2Hr7Q/3Gu925iF0/SxzY84A/AeUia5Fl/2wkg90R2AAAgAElEQVQyJOiihU4GeXS2ijwTDny8Zhd/SnBch5OxyO0HJhNB6u3qayFrwmjYQNJJeznUCooQsHUvpNqgxo9qj1MOoFbiycow8Ix/PJWdvhlJaoU1ePzxPv7xy8/wb59/Hfl0mHwxxPfuh+6rIGnI3wi/NAuA1hUW07ZgMiEJM1VKFTUSYl8/ykNBkWMqoPpY1LWapqFp2szf7/3YzURrkkT8z+oPUq5dGx9ktP/oY1pGAEcIevds54e3/T/WPHUnl77xgyTausgbHh0tLRjtc6BvJ6RPJI3nr5G+pSuAi5AEXJSyRrSiIg6wxa+cq8wABpCLcKa/kY5Uvj6JjOFJI2feEaTS8nkOa7BkAk0QrgdnCtwsYEC9Afo4RPJQR3l+pVStdUiqMO9/5yLnYZVH8oBHmElXRQI5LksoZ9N9b1dFJJFeokyDCuQixvP+9pUoqzql1jqLzi/81qhD0t0aUEOOEONAiGmyNDMNJNGoQbAQixxgsZ4tPM4zDJJlBVCHIIJAQ6eOGDUsJUarXwt59mkz9+UzKY++fuSZ3ua3klreEEiiNgVOEUppqK2VfTUxDbEOyKXBTSMJWcvfjzrLlM7VBD0M4TBoaRAqq8K+15DKJGnKvuNosQrYwKkxT64FztaARJHdhV8SHS8R1po5B3gCDhIbFyBAgAABArz8OCXI2IgVZY6eYLgI1ehczRyaaSJMBA2daXK4gEaIIhq9NHE/65jEPYl5708M2WyG1atW8t1vf5V3/NXNLFg0jwX1Bre89Sp+PfUcQ1t0yPXOdjFPS0xPF5meLpLNpjGtHIWxKi5dsZzOti4SVc24lobnCYTwcF0XpwS6ZTKdnmBsYhTbKBLxPMwYYHkkDTlvjblQcMC0YSonJ+0Z2EdjVjlNDfiqfaEm6wFON9jAVDnuN8ApAw3IiBIPlrZzFss5l2ocGniaEaYpi9xSSLLBwaVAGo1RZFhqhtl4FA6uBWUI15Ns6HFC2+/vEJKQqrNgMgxW2ATmIDWAhyBjEQwMjTNdZ2GHQzMElENZcdtUsX1JwA4HzjDLlgImkrDQgEgyytz57cRjtbzw2HM4WpLOM8+k2ypTTFAmkItJjdG+KX71w5XEGSCmVWNZ1ZBIYes6Zj6LJpBh0zW1LFzWTDxpkQjB0lpYMw4De13SGUEsYvKqxRA2mPF0P+Y21TSa2xsq2mffhEQC3+M9P4lTOnqVuVqILJSKDIzu5dnpYZzE71h0wUV0nnUWkZDOecvOZbPr0H9CZOwYsB45OxlAunI2IFvEA84Hox4iUcliVkpBEUiqUr2XkDUfRlKQe5C08oC/r0mkT215DGtI6tcF4iYko2CEIRaGUkRyvvEoGA4YcYiakgzLOTBahElPjqUpJOXrUFY7q0D7ylbv82u7AUk/q2R2IMdlkXL/ZSgn9FI2BjUV2xxssTgK6ITx0MiTZz1y/jfqlyUDtJIhxiQhIr6SVTHdDhoeMM1GhlhFL5vYi0CeVzXEiJIkTK2fPM/wa2f6ba6ulDpyySPrf6b7NYkiOzHivwryXYTAdcBwIaTLc0fTIRwDz4OCCa6NXKSJUDZkiADVoCclGesoPbEy6fBmXsK3aaj2f3kwK4L942zUZx7weyTReSogBrRpGlosRqxnOSF7HbmhtQwTBAEFCBAgQIBTB6cEGYvpMMe0sYvQjsm7OJtqqrB8E/ssRYoYhDDQ0ZnAZQ87WUuasVPoEdDzXL7+pU/T1NVEorqKM1ob+djbFtC77gaeyhWZ2rKLQEd4/JicKPLoAzt59IEf8rG/eS2XX3Q+nZ1nEmtvQzcNdKGheS7CccCzSU+OMzTQz3Q2h1aCeAwiCQjVa7TvFdQVgCJEcjBQgkENhjzY6xIE/R4FTpWFkABHgkp3ciroVQIcDhry0XstsIkNLKeRerpZw8hMYpQkMqhVUTsFRigwjiRncszGo2bA6SsIsEsIcfB5iToLHeETGELytran/hZ4rsB1PKaLJQq2Q8l2mHZd8rpBvqiTHc0i+/rQScKEgLGRUaaKNeQrwtlLyHGjRotSp5Y82JKHMxKAJsXyOQ8GbKi3oG1OHW97Vy3r16Z56rHn6e5p48qrzqRLA8tnZHTKGs1JYPNQmtv//UmK3ko0oxPindDQgWaaeOOjIAReNEmhaS43hOtobLForoLuWniwH55d6zEwIKhLgdEMjSlosiB5NJLag7S7QiWBpAg9Wwgms3lc7+D9pgERHUJRC7vkYjue9O/d7xgDJcH047+nFBJUdzaSHh/m4qXLKQ31079l/bEXfB8M+K8nkNr4diRxNwW8D8xlEG+B+iQMV6ZuMylT5jlk7xhIYnAKST2OACuRelU5R9U1aS+q+cnjanzv4KYwdCUhZELck3mhiEFDAvamwaiCsOf7HhcgPwVTRSh68jqhCHuBT9gi29Gm7I46jhT3Pol0yVVUZcR/n/JroM4AtT/D37be/zvFgVdDDaUQt3DwKJBjkrK9bh+SkL2EPHky6LgYfqItyOOS9V1hd/MHVtNLhgIwH4tqQtSQop4GEszBooCghMcQOgWYScwV9Wvf6NfW9D8bqOi3ikRdAEKTrHdUl19FLIjH5W8LBXBCCFdpjRP+ODeAKqAGtChoFtgFf7FIxTXpqOU0D4FL2TX4WNIQTiFNF47O4OOlRxR/wcmI0HDG63AyBYaHHmMjL8VT2OmW9SRAgAABApwqODXI2PxeljDle4KZLOAcNCZwKeHiYmLKcDlklvtaotzCUr7DJsYYneXCH4j/8aG/Y+Wjj/OrX/2YrhqNr/6fG/nxd/P8n489h/RmCnCi+PK37+HL376HWCzCN37waS656NVUxRKI6SKGC+Q8hnq3sHnlU2QzUjDiCLCLQFFQdKCQg2IJxjyo7oSWMBSmYGgI7j51OP4AAU4QdchH3uxsFyTAEVB52fkPNvGPLGYpca7jOe5EqrdiQAv730lcNIaCx8FZhhDgTI8jnLaDWhUITSMDDAjI2JC3YdqBnZMwXYRs1mN6tMjQnlE2P7+ZgY07GN28AyYmoaoGSEHRAR7gcEuGmgbxFExZMC6gy1e7TiFVth1qO3xy2IWxMYGIQVGDYQeenYTerRpvPAPm1EFkjs1n/uFXfO9Lb2bF4mZCSHKuMtO6qvEcoO28Dq7u/RTP5SAUBsOUtFIUyNmyGpkCPPY01DbIbYQhdX0D/YBjkYhCehI+92NYcTVccQbMix9f3ygf0UqqCyGT3xVKNk/f80eKU5l9ctgrJAxYUQXnXTOfTRsG2bZzgoGMpNH2Rwb4/cMP8PuHHwDgH/7+U5gnPW/Aev+l8AgUL4Ph62H4HUiiVqVoCyH1qCAJ2J1IEnAvcgzpyNn1vk6a1TFoa4aqEIRLUNgJq1wIxaClHkiBaUKqWr6HQtA4KSPphS3HFHGYH4WeaShNgOPJxSavojSmX9oUkgidRrbrOn+ba5AGDUlgKZJo3eXvI+6/epB3txHkgtWg//c+AuEKmIDNLoqE0bG4Aviuv88kUpE7lyYaSOACBhowB8EG0mxiO1u4gxxP+8d+DSYr6KaJs5ign2G2M8xO5rGQIlO4eCT99FjyCAn/l0rdPOjXMozU5xaQI3S33y+LgLng1csK2DYU8mCUAAtMFywPijkkhV3t93uUGe2wa4ARkR2WbvVtCpT5VsbfPozrl6SasqnF/mr9/eEAdxymvWcDCaDLdWHDBuifYu/EXl7kpSJio0ilcXAHDhAgQIAAx4ZTg4zFooswOeTKtLyd1aGjoQMm0whcNFw0TEzqWMx8ahiAU5CMhTyrN23nU1+5j3/9yHXMjelcdf0b2KnN51cfPX+2C/cnhXy+yCf++5f58If7uObKKzl36fnkxovkx3Yw3t/LyK4tMmGJAbrwo7yQuQ+Eb0QnXJjKwHQWhAehWvizJOzpg922nCYHCHDawkqC1wKeAVYaStsJgspPXSgtWyPwEPeyouZC/m3po6x+/Fr6vRIjSOLhRuBR5KM6yPtmM+8gwwYyrJqNor/iITyPdas2UhtrpLVZIxzRIeJQirqEIhHikTiNwByfIxOWPBOduFTGFoXOpBth2m3lkdc08MjDce770krY+3MY05A3LDiSg7mmaSw7aw5ZYvSmIVQFi5HUz/5kygSwYazAb765hdH/z957h0l2lee+vx1rV+7qnGZ68mhGE5VGAUkwQiOBycKACQJ8bI4vPr5gH4frgBMc2+fxOT42vjYG44C5GGyiQMgWykijNAqTc4fpnu7pUN1duWrXDuv+sfbu6hmNBlBgeqDe56lneirsWrX22mt/613v937bVzE9dYqhUyc4cPwId/73X2Paj/DUf+zhj//vz9D5mjeTMo2FMk+JRcerIUmsdqTmL4okdHZFJTm80DZA6JJ49U14482gBgpMVZGbDX90sxQB+kLekwUQiUox4CsBH0lJ3n3PAwwfvo/i2Hc4dXieW6/MMtcFx4/Asfwi4kYH2iDTt4Zdazcwl53iyd27mZ8THJ6FnC0pzQ6kqnIx9Xpy9BBed5qem67nzPcf54fCMmSHzrzYG1YiI5kq0msUpFr2OJIWexOS7Isjtag9SNXlyaCFO5DFpK5CUp+7kd6xDY17rgLFU/KcKELGSXXgyCwM5gC1cV6VgOEWoUNHODTDv/3GeYSzR+6it5zVb8WgRd+NwduIEnMFx+s1CjTsB6aDHpgI/m8jT1Wotj2fiDr0k/1DBD42s9iMBt/nI4n4NUALK3CZp8o8OnXy3MMphplhnhwOceA6YBVR1pMmjUWNCUaYYJRZVqBzkmOMYuMCWynTw2tR0ZBE+ANB/zvBL2oNztXiQd4enMMWqWw1EuDZcifDrwayZR3KFbA9BCYVysQoI7d9YkGv1oLeCMvgWZyte5Wa5HCTwoaFfl7kSHxe+ME5+H0uMFwvAkygVdVh9fVQ2U/ajHHhsocvFYImEdtEE0000cRLxRIhY1XqaNKzC58SY0Sx0EiikkZhNTJUCj2OTDLEiSyV5r8Agsnxk9x71z/xgV27GFgDy7sT7LhqFf/e/S6Y+Y/AbL+JlwshBNmZeb797Yc5fPAU69c+zoc/+GbKuQny81kqxSKGJhcUwpeBoxZkbfuLrf2UIJRS5XvjPgykIaPAMh9GZ892+2qiiaUPFWgF3wDfk6tpzwe9F7w5EE0zjqWIkJjQgCIVRmvjHBzfx2/f8Sf85aN/z6HJY5SRVevPLZhV4iD1JaVP+umC53s8cPdXOPr84yxbuYZ1W7ez862vo80QRHQdk6C+eaBUXWAyA9bIQyGBgoOKGdVZe90qXvPr7+D0zFoe2T/D6b37KO5/mgsv/CMo9NIVMTnjqNQcGCvC2oS0FFCRKePPlmBTHEwNehMat93Swf13P0mhkEcoDpet30R7UuOu/+9LOLMT/MJH38TKjVvoa48vqEvD5jvA+NQU/+vP/5wYEGM5BjFcjqJzGYnLrkaxkpTGJyDRyv/1tgHm6ybf2WtjJlVWDMj6AMWiy4mjc/zSW9swkxolD2ZqEI3JQmI1GyZz8KbOgCT8Ec5NqIqdq3ocmCzz9FP/yMjhJ8gOHWb+5AkOj7jMtoJdgln7bHVszYUTs+A8eoSoZVCvlZnICtZk4PWbIZJRseI6qpOAWA8YaYQapWzn6V8TZUU8xUa6qb62F+JJTDUGaFSp4DplKSf1bIRXx3XA6EozM5ll6MBxRk5MkElBNB2HSIKJcQPczWAth4gJ2ij9azx03UHXDHS9hTOFOKWiwHODEmhqN9RiMGvB9HE4/XngA0h6dQRJDJ6t3vUFnE/QW/fl49WGjyRV73Lg+qva6ak4zO2bxEFSjKGeV6fhWR2e4xxSIftiZXMrwBHARSqjr0bOp2eQRKQ8fpk6eWbJM45PFycBO7g+BRGkAYDc4PB4jjPk0JmhSA2PdqCTFgZwqONQD/xmoYighk8ZlVaUBUMAjYal0OLSWTmkzUBdSpCdMoTWI74Pqi9VBn4EhWUYXIfcygssDPDl+zU5fogYoGhyNwQVOdIdYA6PItXgEzoNunZRmPwCjAF3IePjV1r//XLQBlyhKCixOEQTUnr/qqFJxDbRRBNNNPHSsETYTLmHK+lWgUOdCCoqDg1nKZCBgyw+EEdDf9FQPEwFCj2RfvwhQnF+kkN77uHB7x3iHW1r6OiIsW0gSvf29zHz/cfxyk0y9pXEM3uO8MyeI7S17WbD5jbs8RkmpqdBASuio6o+vi/AFwvqDd8POCoBqhoQs8ECz65AMgatEVnbVq2AqMtFbF00PWVfDsJF/A+znrOQV3yTBH8JUHQwl4EnZPUbVUClJtU1SqG5fljC8JBEqwIMVqe469Rd/Oq7P8XDzz3EPFNMkOMIjQrz4akssQ8dkwgx7OYs9WOH8H2ee+pBhjp72FjM0r6sm0TCoktViCAjkSww5QdatMUshxtslghP+jqis6E3w4137uIwuyg/eAq94wFGbZX86T1QmZU7jOdAt9Jklt9Ai6JSMmBeQKEuE5HTBPSLkD7p6+Lyub6EwVtu7eaJux8iklDo6Olk85WbyZ0e5rF7H2P1shR/+KnfoIUGXRSW/jGCv3P5Cnf/y8NBIc11OI6GW/oWcAuZGzyItzJ/7CRkOnjTjgwjOYNP/9tposszbFljoPgwl62w5/GDvOXW27C9KIOzJY4NHiWZThJTdEoVhZGs4HVvXUVcU17gaXnulLY4QrSB2ZlphqdmeGL4NLu/8zm03CmqMxWyp2BiGuamwDIhYkFXTIoODQN0Q27izuZOyFPkgxqFvhWwcotCpkfFSupUhUVrWzu61YmnJsgWZ6iIGnrUxIyn0K9ch59pw9LTaIaOHS0wn82RsjyiBuiKil1XMWPtDA2fJN5fQu2cZ1mPR6ozjohmSJxMUS/2Yltr8axWtNgqtt1oEjM9TF3FMGKMzKXJZWP49RY0pRNH68Ev9aKOd6IMG5SO/CM2BRRyqJwGcijuahRRBr+C51aolGzy00G9p4sEH3jSgeF+E8uB+igMzjeS+03k+JVXS+D/iyRpKzR8tRdDBK+1BJ9NA7uCz3jI6zMDqFRwqFLHJofAJEsLcZIYqPi04KIhMPFxqTNInmmkvjSFjkGUDMvowsOlzCwFZsjSQhoDAnfWyaAF0eBh0NDnQsPn15bPKcFsryjy4bnS4Nl1wTdR6CTCdiSdHA9+lSt7SotKmwL13K0UHxllFXGpUA2eXUzGLu47Fn2yjiz19iUuhlP5hZFSTNZpacSZY+D4FNGZuNiNaqKJJppooolzsETIWI8iPnmghkmGXSjUUSggKdoR5FIirKnqLdjgnx86aNeBN44Mdi6OlUHNrvLx33g/W3d8get7t3Fld5QP/eZb+PvDv81s077xVcHsbJ73vPv3sIBrN6S4YnUHum3j2TVwPTzHxa64uK5cZLh18BW54Aprd6gKzBeg4kFMhVgCNq+DDadhrgSnbXj2ov7KSxsGLPgNXggqMtFyDDkLNPEjQjdhYAvkZ6F9JZhp2P8QOE+xtDQsTZwPY4RbifM87D7IxJ9cz528jw28jk/wTQSNCueLFbJt9JMkw8nmLHXR8Pr3/RfueOtbeM/NDVsiAZSE4J8R/LUrmHalhyYgJ8XpivTLcQtw5giIdt7Q28f/3LaSJHDrzgGWb/15Drz1bXz7t34Xnv9XqBVe8N1tq9Zz6+99mpgZoUUHPS7n0lFgHUGpIA3uCOwnXQAF1pgKX/3Me2VbBdTrLp2dH2Hzz7ydy3fdQFlIEiaFVBSWAVtR6EQSYx2plex41x5ct8xsYZSZ008ztfsIChnyT9yPQKCICIydRilfiTNcIP+tr1C48jbu+4cRKOfAm0Lxv0Gs9hzfP9jHV+86wP5P3wjcDLSC0InGPH5t7kus0wwSP8S5EMEPGhKCL3zjKxx75mv0WY+RmBQceR7G52WEqAArgPW9sHYDRNqgrR06u6G9E1pTELegVJH1koQrC9g/+bTg6QddSnmXtv4KHZ0T6IZUj04FHqqIwIbCg5IGIgqxTujfprLn+z633bqOTVs20ztwLS4WFVFBdepkdqR478619LblEUoNV5TA6mf89GmGJkeZd5LE+zdz7cZNJNR2NN9AdT1azH5itJMiQhKFKQXKQpAkg8aNPM4ehgSYiqTrwEefexTTfgJR2Utp7ln2Pj7EPX8jmBxctGlwkXBwaJBUH3S+Hu75qkzed5Bz341IFWSYeB8BbkNqQ13g3nOOFRYI+31gG5IK1ZH60wJyTt0IaERJEmcFLj3YzFBnmjImUfroxGSGvTgU8GijzmpU+vExMEiT5jI2YXEZCg4GRXqZ5O95mNvUX2Alm1F9H6nPLSBncHvRrwhNFuJIOUA7iJjcsIkEuwS+B7UylMPZP6RILRquyGFpMw+cOlRrMKeCqC3qQQ+wEWi46FRobJYvtnpwg7/DzRiQatijSIOMJYdIH8Svw/6LDxPZ+mscKPl8+WK3qYkmmmiiiSbOwRIhY13y1CkALg45HiXFSnQMZEAxjNwLhzCBJo2F+aJ0rAPegzTCiYsFH4fDfOWuvdREO6+7cRn/zw3wjTf8DbMPfhaOf+Uitu0nGzXgseNF9g6XWJcQ7Lq5D1GuUJ4vU3IlGSv8wHJLk8ICaHifoUuRkutCvS4XUZHWQAmjwxU5ePQEnPZ/MKm4VBBqL85XdOTHhTXIQD7H2f0WOqZlaQT6PjJ1sKmKfYnwBORK0L0BWrpkiuPKtTD+TOA5d7Eb2MSFEG5ARJB3vwPALCqX08PvcQOfYjdhwmqcRnm2aUYoU2E7/40DfB73BWYGTbxaUDSN9Xe8hV9631t5zZZtZ70mgGx1gk8+8HZqkVF8y5EnN4JkhBxklcmcgJIHQqNYeyfD/D1rkQRUPg2TKwzo3gza+dNuuzt13vuONJbWSOfWaCgHQV7608ExdV4YCA7PwOce0rj3+L/QFjPRTIM88Ow8JJJw8rjH/mdcfvHOCK2KggH0dcLX/gyOEuezX0tw9PQ1fOrrD/IzikZVkUrcwyVwIz5rO+Os2SF48B1Xskk3UbwgRQUf+B+kW1rY2A07e6/iv4kpsHQ6e1QKQ0fY+w9fpI2znTUvhApwVPj8ya9uwpkYx8tWOTAqODYGERfWtMPb1kPvKtmlhg66Jj1rDUsKD/MlKJehUpE2BpUCZLPw6IPyfalW6FsJs5MweUaeRteHUkkmJaQSkEjIQqJzw7KWkpiBLD7OHDz/2EnOjOXoWj0BCQMDm96uNJdf3sbk0aMM7p+hkndxawot8SkyGXj7+m66utaRUE0OlL/DI/ftJj9borunl7prMDd7ivVrNrDz+rfRb7yZU+I4Z8pDVOvzrM1s41olji3KlOw55qZHSKdcYulR9GQFUhk+uPkjfOxnnuH7D5/inm9koQaFChRKULWhPQOeLseOV4Lpw1D25XD2kRRj2P8vVzX53F5YEe3kprevoP9rT/O4kMe3kDHN9cjLJ/Tb/k/khvkz5zmWglTFrkaSrumgjYGhA5HgNQ0bC4MIKXwEg5xBR1CnxlGmyKKSJE4KD4c6JSw0YvQrW1gRvwpt03UwmoX5eahVUY0tfKi+HsNvAa0m7Swq14KqgyiDmEVuwelAN5Ji7gC6kBHtHCgt0NUHcV32ajkOI5MN413hB7+uSEMvLOSvEh54Do0rPjR5CLWwgc8qYbHks3HuHOECfwJ89QefvouDWhbEQax3/yXUdOInDi+sIptoookmmmhiqWCJkLE+Hl6wC+vjcgZBChkWhBVBw6qwRlDI68La2FejZuZLg8e9d3+OuFFlZf9HaV0Jr3/DJtTJXo4ev9ht+8mG6wmKvuCkD9Vn5lnf4dMdg5YWkyp1aVFQl6GquqjSg+dJghakcrYGYELFBi8Ppi49/y7rhZVVKFchW5HFS5YKWjh7QQRLI90/3B45V5cZlkCI0dByzLP0Ut8uGagJMLsgkoT2HojEpUQrbsLVnXBsBqaaJN2lgDCJNAZ8k93c2H4zbxz4OP/j2ccRiAXF0gCylI+LT5UcozyIR1D06aJf+T8dUBCkVJ+YoWMYZ4dXct7zqWgzoMxC23ro2AbaVqj9Kfh56f+oIk+2MHDMOjkaRFNEhYSlQ8tqUM9PR1qqwoqIioCFQlvaor8F4PiwvwY3WOCpUpPnIImph58vMzjjc91VSdZ3pLCCmmG2gFRMEpVWj4p/rXHWqNJUSCUUBgBtbIzZ5+eYmtpIZgO0apDxoDcji3dlgoJdUcsgw/m9KDUNNvQZfOqDbaCBFQOnsJbZa++kXdfOG7yee5wiMDIzwne+9adYxVOcGaoyfRqKZei3oLcH2tugpQ1a26SVpqo2MsA9D4o5KM5JEeJ8VjpI1CqQm5OdGU9I69ZKAYqz4CnyNyoR6G6DZAs4FajmoDIMtXlJYiZNuGKtwrt23UI8lsaKpzCTCU76/wZll/745ayxtjGwIoHbPUalPkbVmcRx83hAJtFCQjMo2N8l5Y7T0zJBWzLF6vWdtItr+O7uf8AUHi1aghIH8e1xlNoZTNdmuWISpQ1P8XAMje62JJo5hKnmUKmjmGlipklfxmLragP7OrA8sCy5x+cEFuRKUER+/hQ8MgzDZXlvjyApRAfp27o4ESxFg+wzgNOElSBkmbEu5Dw2S0PxP+7BmOtR0Ryu2hnhxFN1/JLAB55HFpJbHnw2jSRVB1lwVj17XCEVsR3Iy0wP2lEPxk8a2Aro1FFwKVLnOGWOIFiDSoY4Lhkm0NHwOUOB05pgQ/c1PDa1j1ExztpkF6+9/lbYoOFOeAg3hrFqFdZlt8DQNJWD48w/8TxdsRa0FWtQKibuRI3h+mEGWIlJKui1SNBiV25WOHkoJQBLer9aMcikoWxDvQxeIfgVYc+FLtWazJSxIhA1aZgQhJ6xGnKdFTnL9uZcdSzBaw7wFHACGactNeiA0b0SZcv7oGzB8SfJTx1n9GI3rM7bTMIAACAASURBVIkmmmiiiSbOwZIhY0VAxioIHAoIijRCpcVLCp0GrXRpmB6eOPYkgye2UyjIIPG129sZ+34/R+P9UD59sZv3Ew1PwFwd5k6VwVexWzViaPRnEgilSrnsYdtSNKgocvHleY3qzsKXhKyiBrZcdXBUME2IG5AJioJlVJgqSY+yH5QAHm4rtAT/z7G4hvErAwuwFEhqMB40KExIWxxs/7hRpkEuQUN9IZB9kAweHkszyL9koMfB6pbWBMnAKdKvSd+N5TEY12VB5yaWPEIbAhd4jiES2gDXWYLL6eMEU9RwcDn7Zu5RY5bDyMX8j1LmqImXAyHALZYoVetUHY+40dgwVggyLywjsLXvhM4rQLwLpv5WmpVqkYANPAVVBVdtKAt95EumrkPLcpmqfB4YyDijxtnb1clF/xdAVTQEdXUfZmuCZ596hD1HMvjRLn5mV3LBY7Zkw0zOZWTfQwjhM6XEKZjtzPet57lpj+VphdakypNj0NIK+fETZPfv59nvRnjOup7e3ijRmEZSk3o/BTmeYxfoSwXIJOCNVyx+NgNXXv0in3ghxibHef7QExx+9EvY01VmJiA7LdWvKwegfwCSrZLTssI9/+C+X61A3QPfkQTsfBYKs+A44NhQLQUbs6bMoinmpGuEHpF7X9EIJHQwVajbkoQtT8nPmmloS5ts3dTBTdu3omiSnvSFj2rPUys6ZPQ5ol6eaCKFkkzhKAlqfpRiuUa5pmPoUVzHoVg6hDM/R1r3IZ4mE4+wqW0bg+PbaU11YakpJurDmL5KWrPwMWjBxHULqH4OzcuhOgXqldPUmEHVHCJWFMw8MTPJQF8n2rUuUQSmn0c3FFRNp1LR0WN1ihMOozWP4QSMVSRpbyBJ11rwrxF0bR1JnEaQMZAZ/L8cvG4gSdJa8N6QUpwFJh2H+WqJ3s0Rlg861B1B1m6kyod7GO00Cnmdl+QHNsiRtBB/aMHnuoPn+iCoWeFRxuEoFUpAjDQdtOHTQQsKGlUKCOq6TtfKbeyb3Uu1PsUx/yiJ6rNoqoJnTmNENDq62vGXp0lZOjXbZfroaYrlMcyIguo61JUR9nOSOBnSxDHQMfGRJKmQrfRmodaCrEqrywFomKCGfrIEvRpuebsskLGKJgNZf3H0F/rTChQiKJgL16a/6NXFPv91ZJx7D9L6ZClumEcBK9YKvZvhyBTO6efJlYc5c7Eb1kQTTTTRRBPnYImQsR5SMyK9yKpUENg0qJswFJDeR7L+aZGlo379wdB1n3jUpQWN1/UpPLV6K8rAmxCH/+5iN+2nBgfGfA6M+WiqyyfvWIVqjqHMFvFzsmCHroFtS9JV1+VaV/hyoeVU5eu6D5ojC3zN1qQipiUBK3qgfAieE5JcDRe55yIkYtuBa4LnnkZW8dVUBdcXrwhR6gCrDNhowT8Vzg6Ydc6+chZfXa82SbuY/1ORKpQwwLdpuEKrL/xoEz8KrCS09ILRAWYUPBtUR7LzXvX8ZbKbWJLwOftO+MTUQ0xN7eZjvJc/5bsMk8VFMHjeT7/S2zxNXAhCCMbGs4xOl1hXdIi3NuhQDTAUDeJdUB1Dnps60AteClo2Q3wV+HE4/r/hlINfdwksRxdUqJqqo7SvQLyIMlZFkhHl4G8XOd/30CCnDBU2xxukmFf3GRtx+Ll3vYfbr/4I73z7nfQH7/V8GJzx+MKjc/zVB96I77mgrSPZvYvf/c5fcM/dBX5uh8Xrtkd5xz/bvOf1JsdmnmJu8O/45u98mqL3FLe+bQ0rV8WICJddEQtNUSh4LvOuy6pIBKEoeJ7A8yW/ZDuL7oOBYammqaAERTcRqIqy4AcbMRR8RUEEBLOhyH+fePQ/+e69/4JRLPP4g1BwIKXBthis2QjxNrlX1ZIJNl8Dy6JKGcZGg6wZD9yatB/AldabvifPp+NBLi/PjQZgQDwO3Z1ScXtiCCpD4FflqY7oUNeg7zKNy6/t4PIrb8H3UlRrgwiRx8ChC5X5uEK5doLDUxPgtaFreQwNdEUDu52InqBYqVLySjhZlWPPCzwdMEqczA6yfqfNrdd9CFSTmqcwOT/D1vbXoMVcXL9MrWaTn78bxy5ilwtkp4Yp5UaoKApmyqJvWYrL19lYqfX0J3vpX9sPvsvJp5/DUFSSqTQdehxdn+XIxCz1cplVXfBwVhLYIOOgWjDuLNk1TAXj0QtGv4skQGeQm6+DNKwH2mjYFuWB6arNZHaORDrGhhUV8nWfkQlJwJ6g4WeqITcwxjg7M2jxdbgOGXsYwfEVpCvxMqR9klwY1QGBjc8EsBqFZaymm148LFxq2BSpouEZGiu2buX5w3GO25PEp/ex/+/2kUBFR9ARS3Pd8a3UvlziiuuvIZFMkrta51v/cR+JY4dRPI+6Pc9ppsiwjOV4tJKjbWGLOlTIloCV8qr1TCg7UKzKggdqDHQLXAcZUYqgh4XsGdeDmi0Ho3CD31cPzkYd0FDQUWk42IazVyiFCcwSOAH8DUvXoisDpKs2jM/AxHGKzl7mOUPuYjesiSaaaKKJJs7BEiFjXfIoFJHed3J3uoIMs6LIcE5HBhbhfvkUi72Oljrue2Qfs7/1We795kc5fhSi6W1cdZPDniYZ+2OH5wt+/xtHaNUF67o1btpu4uaqeDaUyo1CXhDEuB4YnoxlbS8gVKPQloFaVS7wqtOwog/6ijBZhZN1zkuOrEIqRTzgPuQIbgV2dUV5z/YOPn3vKMfE2Wl9LwVzwOk6tNbhVmA3DQ/KxUSshUxv7kOG79NIFcqribAC8rXAvuD7Qs+2oGZwEy8XyTQMrILWtWC2Q30OjCwoZ+DwFMw3SbpLDVXksrwIPI/LtTzKe9nOU4zzPQ5d4JMhBXdpZJJc0hCCmX37iZoOycx5PF1VVZqHlhXwNwO3yOfddvC3AjtB2QHtJ+DM49TQXjAfKwpYlkVNVc57RoNyPVjBvzL5+JxjIDMzQrLl1OAY77jyY5TtHKvGD3D54JPAGkrAvuNw97e+zV//wXslEUsHeDMUz3yRT7whhZf7Ijt/57/iL7+Dwp9dwXePfJP8QVk0VfgeD/zBDTz8hY+jaDrm9Gf5lT3jrOo2eeZf/4X//NQnGR4awgY+80CN7+yp88DvpNjyywfJOhE0A8qTo+BavOldlxFLp7jvgTzlWonLNvRQrdTIT0wz9Jl1PAAcKUC1CL/VDxPA9MwhZo8+hnsakp5MCoib0rM13QOJFojFIZaEeAsUC7LeYWkOijPyflQrSZ/YWjBlhtkznseCHaevSOsHKymn3mwWjh4GYUImIjdyCRSzb/55eN2uO1iz/np8P84Xv/hx/vZvaxw6JIJNUT8gmUOyLNzeXXz2Fl3VQkirUAXk7LAPTXsf99//Pa67fiNCPcPmrg1E2MZc8SB7nruPO974/yKEtzBmhRAIBFtvhTe8tZf/vnM7CmuAGrXSCMWZE7jlGpqrUbFdcvlp0HV0HYyUx8brYeMGOPjnUJmEYk32fw55vy8Hj1Dh7y16RJDq2JbgtRFkv8eATcBBJP3YU7Oxsw4tZOjrF/TMQWqiQewOI+fIOJLIDRPxz4fQP7lKQPQiN8g3Bc93Awo1wGQZOr+ChsEaNFYA7ajorAiPbqQg3Q8bbuKrb/p1Dh/bx/D4KQQeuq5hxVMkk0naM2lc10EY3ajRBCu3tJGd8ahkK5TnptDtKh/gdlbQEVCiftBjLcGvCjIF83NyF6FWhjODIPZC22vl5mtMh8OnwBtCRnotSAMHDYQKrglqqJi1aVDiskdUGiutsO88GrHZHNKe4Fd4+THqq4kVwLLebnjz7bBjB9o/3o0+ceaCxnZNNNFEE000cTGwRMhYgYJYqGOhoCGDSoOzjeYFMjidZpBxClQuVoN/ZOTnjjB09MvMio+SSkBfV5JlfR3sudgN+ymF6wnmfTg45TNVs7miFdZ0tWJEHDytiFOViy0hpFqGqlR8FKoyOO2OQEsM3JisrFyag5kajFdlELsqAqYt/dJs5IJkNbA1CUdtGK5LAtInUIIoAs1w2LkWlo3BsapMvXupCBfkdS7svVpHera10bBXiPDK6elChWvIb6eRWyt9yCs8VOUaSFLYMiDrQa5pcfky0AJqGxgZSKTAiIM9D14dEi6MiaUraWniggg3LQx8vsEEb8QkQoEU51eBSTRJ2B8rhJDFEhfShhdBUSHSDr4GosrCFpkZBe1ypFulISs+AcL1Fhwdw4euKEQiYCvnP7MeLFRED9Wx1jnvUZGbgirw9accvvtglF943QcZffARlg09zvC/D/KVff9KvvdW3vKht7BqoAs3vhPqDwVtdkFYOLZMG/nit0e4/9A+cKv0dwzgx9KUgpJIvr+T3/7gTpLLB/i7u3fwlZ9/G1HDJz9+Gq8mE9GngInpKaaOTlJlB5U9D1COrUZNtlJ79jEQHo+MPY2WypBVWnBHDnD4yS7i/WtIrd7AG3/xLrJGC9bKAdZvWwl9cCIP07M+5RmfuSlJZbXGJTE6m2sU6arWAkLPh9y8tCIozElrgXwVKkVJxtp2cJp0WZxrvgjpKGguRCKS1I0nYX5cbtIKV1ofCBOsBHT2ws7Xw8Zdt9HXvYOZCbjry3/FZ79cYWhIUHtRbcG5Z/kHXc8yTr7vuT8iZ7bS02awZcVOFEXlrq/v5W8/8zWq1cYdPtYKa29W+KMP3UlHr0FbZwXVn+TogYNE9ATCLeHZOVRXw/c10DRU1QJFx3M91IiOYdioiQrL1tmM22BPQ9qTLSkH4zGHjAMMGnXr1EW/RgSvtXN28S+CEVewoZL1yZsFhObTHYfLk7C7KOnGaWS81Q1czgu9ThcjtDEoIVPtnwNeg4xPoihBTQoPQRkFDx2BRicKacBCwUWhgNRgWmDGYGsP/fV1HBw/wEh2GBcbXREc12BKVzF1nbgQ3Dq0ji19K1i2upenjz+LZVv01VNsYRsb2YSFhXJWvlCeBauB0PjBrcpfIGrydacIpQLUwvcNIKnmc/OMwt4Oc5AWGzUoC1raMO/QoqE0zgMPA/ciN9CX8l0lBaROPI7/mZ8j6zgkZ08R4/wewk000UQTTTRxMbFEyFgHBx8VuY+ro9BwygtZg5C28YA8ZzhD5RJSxrr1PIXcMEOjDt1xg7XLDMazab6R2Ajl40HaUBM/TjgCcjVBwRbEfLA1n4wliEUVTEWlansyJdKTo05VoOhD2YVoFeI10GNgGqAbUK/LNXZEldacXQJ6VqwmWygwOzOD60kP27JoqFQVoDMK7ZZPzbaxPFiRgKICxyovL+CtApPIxVCodAhVqTM0fAjLwftKsJAS+0ph8WILGpYERSRJ7ATviQBpRZLfdXEpad6XIBIDEOkGz5AdqhGYIOuyo8MBcakibsriJXNLWZvz6iDcVFGAYaocZJo4DptReQJ/YdNDR26wTLO0F80/qXgxv0oUVRqGKmHhnCBPIdYKugeUQElK1s9XEJ6/kAJvEPhsKnL4v5gTsIecX6M05v1zN+PCDbD/fHaOwUmN9tYY1227hr2PGvSXpomXpqmOHCK5bR0tH6jS3tdH/9Z3IvK9eE4F33HQVZPX3bidoew7iWU209LSztve/36uubGLA5nXcGyFR6mYpr/neq649XKqvoVTOsX4I8+B6ABKdHfL9hiAZZi4isXXHqtSPXOSnu09xPv7OPwkYKpoRhRFMXBKVbBtlq0yGdiaILPc5F//8DugJ1h9y61s3LISEIydnmVyvEpxTnZEJgmtGWktZMak5SaKzH6p16TgMJeHehHsIthV6QvrhjcppD2nokp7AtsFoUjPWF0DxZWfreTkMc0IRBRJyHb2w8AaSHWCY9c4c+Y4g0dLfPvbBzl48OxsnFcKTx14kkirSerKJHW6GDsKzzz5MM/tOQVIJfDqtRbrNsXYvjPFa64y8H2XultgZmiU6bExrEga01DRVR/PFmi6CaqOqukoGAhNlfZNqoNKgfVbplFKAtUHbRZaLOlNnHdAq8vxGHrFhjRh6IkcFiJcXFArT8Oiw/PlfmKp4mCqkIhCXwtEivJ4VeR8N4jc7A2L3p0PoZrWQBKOCRq3RKlKDYpk4aBQRyVQhC8UEw6vyhgISw6KDovYqh6SfZ0kW9J49RqWqZNxy8zWCozm5uT3tKxAU1VqVQ+nIsjV5zCEwgBdpGhBIRK0vhL8Kp2GGKUGupCDTYS/rl3+bRegXANRQEZ5ZvArZ4L/qzIGUMPaG4u1r+GMoC08EyLc2B8DngX2sPQN4izALOSgsB+PPHvxOIIcT0000UQTTTSxlLAkyFhBjRIyvGkPLOSVBRv5fPDwgkWlfH6KcaoL9v6XBuq2z+OPTHPnW7vYttbAUVKYAz9L/dhfgFv8wQdo4lWBL2DfDOybyXF5F9y4UiUWiyCUGq7j4zrgKmBEoGpD1gGjAJaAVBtoJkTj4DmwTAuKuHiyWvL7b7+F4ZEhHnrqSXYXXeI1m5wnR3KoWFrVotCf8CkUqgydgp7lkDBBq7w8ziyHJFjjyKvGQioGNiJtCxYH3EMv43suhHOJoGLwCL8vQ6NEX0SFrLv0A/0lj+7NkFgGlaAUuGXJBZgelzsKlzoycWhL/FSSsdBI7wX4PrPciMpr0TiERgEHH8m5r0NueNTP+vT5qLkmXmm4yM0+69zLTdHAbAFdDQhZPSjh3odMtI4BbwIs8DVZQBJ51kIvzSgQiyyq13MOHAGzPrQq8nJXCd0vgyYAvu8zP1/hk18+xRtu6OBjd/SR/VqEGU1lBQR+sTpbWhI4jmCmq5fXvv3DuHyYerGCXaoR11z+8ZMd/PvYu+hLwOWtYHMLvcBT5Q/x3NyHGBuC226Asg7P3PM8c499hUxmK556I54/QiSxG4BeYG1/L62rO/njL8xQo8bOq1Ms276CyQNbIJ3g+jdsRdcN7rv7ILQnueOPr2PDpnbsM7N893ceopJ3adW7Wdb3JgDGDh5ndHCWuTnoj0F7O7R3QCYD0SSoRvBAOgKMnoRSCTRP+sJXS1CvgGlBNCprJqUzUiFrOwHRF4FYSnJjhax8TRdyyo0Z0ru2tQVWr4b+1TA4AuPZR7B5hENH4d4nXs4ouzD27a+ycnWV9M4yef9+7rnrMxzeX0dVoaXFYPnlCu95Xyu3v76bjf0DjDyzm5n5GSrlEn7NlmM4ViQWjxKPRymUy0TiBqapYKgaqmKiR+Komoam+mh6hO3XzKCVBBEPIjZ0dsqCZ4UiZOehqoFwZMzlKXImmgVK4mwLg5AAzNOIXSLIMV+pyWwlMyLPaecYCxUm5oHjyCwklxcnY2tI9W1P8N4WZKykADpaoIDtJiRFNSpAJw2XWZAGU60gonKXHRfRmaJjxQCXr9uEV7DJpDNsLE8zPDvC3aU5ANatHaC3r59Cscaq1HqeLu5jyJnB9DRuZCMqLYCNShkDD1VpRRHJ4DsLAZPtgqsCJmjbQIuDOw+lU0id+WVBrxWCHlnBQqSlmjQ8aMNsQ5CaYKuhwA+eDc/JPqSC+MQPGHdLASoKChk81mNxjC8xywP4jF7shjXRRBNNNNHEOVgSZGy4d6sgg3LZrCoyENKRoZNOSOUIYBiHS42+zOey/NqHb+e2Q9/msvQqNnW28/bf/X3u+uXPUZu/1H7NTyYOTcHhKR+FCh+9IUG76eLaNrYpyLuwIyZrH9k25IvghHIOV9ZO0CLg2iAqCt3Lomy6+QZe895385ZagaPP7Oa+r3+Jh47PUpyt048MmVvLgqLnUsy6HHLh0SG5CHm54sVQhVoHXos85jg/3ov+QrSPgqQe4kBchbgFeypSGdvEy0B7OygW5GbhzBCsXw0ZC1JzUByTUu9LGafn5aMJBHAYH58If8Ut/AYPMk2FMvAokmzIE6b7KhhswOUU4pK7e15aKAmoCEiej4xN9sh/SSGTsiHQctFQq+ngKbieJJn0RQ9DkYrDCeX894iqDYMTEO2VZHB4xHBjTgMmJnIMDHyMO//wYyQyCZ4aq6Id2csbXIc2IEqc14hV8NCfMXemwBXveBu3fHJncCRJCdeAhxWFK5ZBF5KaCnFdDK6NAf1ynn8SWHfjNv7g6c/zq6vgkAL7puDkaGOy/8D18L7rNKCbT9z399y6RuHmVfDnb30HKIs8Un/5JgBOKfCNxwWf/2YL90+e4Pf/GnovU9i8Sb7v5KFDnJmepiig5MBkHnpXQDQjBYJWUmazOK4syGXpUKjLYp2iJu2HzCjEolL56vqSDHQccOugK9JzdtkqKOdgfESqYHFl4U/fl/YEK9bKDJp8Fdq7pWXwd/4dHnnkwmPo5aJ/NQysg/Z2l+zEIf76H2DoBGzYkOTAvteDojM9PMzs6QmeOT7KfLGIUC10PUY0EbgM6xF836BSNtCtBIoiiXzHc3F0F+wyds3B9x2SKZdcVTAyDTNV6FkHm7fD4HGIF2DNali9Bh67D4pFeQ60hBRzlipQtiV1GG4ih77HCeSmbdQFvwztSajUpWJZAdYEv7eE/PwZZHGpXciRej4kkHOig/ThDj1RK0AElQQWkqL1aLj8V5DRVNiq4F/fhLIH33uUZx67m28/9xCPntyLhcIAPcyR5xRlngu+e/UTD3JceQq3qnDzjW9gu76dodHjPHP4+/xXPsVKujGJkiLD7dzEmqSOXgtShtChMi4rzClJ6Ve7eRNMT0AupE3DcmmhNngZ8soPKW09aH8YCSqEdnAGBomg38JPVIAjwB9zdgHWpYwsnQzrWzkYuR3XdThW/2umxdjFblYTTTTRRBNNvABLgox1kDf/VmANPnAGLyBiNakDCd7p4lOhwjj78Zi7SO196XARYpDJQ3X60pDuUnjfLrgvolxiGt+fbIjg8e/7KrSqgmVxjTdc0Uq0kKNWc6nVfBQN8jnwXKmYjcQD+y41qHquKsRbWyEaw7daMKKtrLmxHTPRQ8dD3+Pgnmc5PZQlocpF2ukajAs4ibweXuks8n3BcWtAKMa5WBo5i4VSFJhILtv3oVJdKJzdxMtCHdIWtLWixNIIw4foPJCFymnJFDTxE4MyMIjN53iMn6Wdp8mzJ0jIzLL4Ghe4DPLzb/yfVOt5/vX+T1ycBv8UIPTEfAEUFbQU+Cr4/wHiJDgrIPcQJH8BomtB2FA7ApSoaVI5GNZE1wBLhVQqENaeB/n5Mk8/eIQdP7ceU1UxYCGKUoF/+9pu/vR/fRO/w+TO2zrZeFkCQ1NQfm0z8cfvQN+2DiURh8/fA6XDTI38G7P/dAhj916uuf9jqLrGvnG4/yRovbB8OSiRhr9nlEYGdUgEbwbWxhSc5QqGBusVWNYBtdSirlFAUxSEgI9eq5CypHoyp0nLjXN/bh/wvi1w2zKNVRr85XsVDAtaZBUs8pVZYqLKQBx6u6G3E1LtEE1DOiRiS1IBW85BYQbKc9Lv1a5DLZBWViryvmRFZWGuWg1cF2IxSGVgcFR6xns+6C5oKmiGJHs3XgcrN0PehmwJKgrccBm854MaK9bAb37y1bsDX3kzrN8abHrG4c//CmJGD+lYO9+762FJVAoXVNBME9OMoSoKmqKiqTqe5+HZDr6oIzTQIlHqDqiah2q44Nl4tkzqx60zOT3L+HHBwIDc/2tNQfYwdKdASUBEk+dg1XqYL0uP3nIJjCgkklCvQnlGEn6TNGyUIsixdXIejINwvSr3Muw8lLIQj0qbibSQ2lUPKeV44jxjBmTccRWymGoi+I4ZJJErt0SU4FurNMwTWpBXkIOvOviajebEpberOAOVCXh4lk2ZDN07bubdW64iEs2g2CZDpwZ55PRR9p7Zy53o3Pmmn6W7pY/R54+Rn5rAjFZwaxBRl/G0f4Y9ZPFQiDHJCBP8UfKXSFtrwG4HfwVoNTDawcpAMgOGDr4Nfp3GFndYayOFtFcw5W/xK4EH1GKn3pDErSNwFjyqw3lnGPh1uCTWWwoKK9nARz7+W9y4+VrSIg0FwZs/XcQ/dS8PiqcvdhObaKKJJppo4iwsCTLWRgZCaUDHB6bxApc0HwewEagI6vhUqVPlKHIH/dJDjdlsjlK5SqsWZVkraLHN0lDLy17sxjWxCNMlnxJQcXxSYzbr2hRSaYt4VCBElVhcesUqgUFgNCbVGo4qF6Plqk25VsN0XFwzhhJrpXvtFq72XNrbWnn6yeeoDJ7A830qriwOVuHV8XgMvdcELJSdgCBDFhlov1LfawTHDz1qbWT6oE2DiI0H7w2rGrvApN8o9NXES4CiQmq5HJQRHWJJzJYu7OoUeDNQH4H5QpPx/gmDA+TwOUyOtej0o1Enzj7KC7klgXgfQZXR6f3UnTry6qxf4MhNvFQYilROvhAKaBZoCrgTUM2DcRLscVkJnRZAA20zcBBfyPOrIc+hgrzfGNaLk7GF7Cx7vnsf4l1r0AwVEznnKsBXvv4EX/3agwyeOMSvfuxDXL6qhc5UEAbGEvD+t8G65VCuwneegbJKujZN8cxehudcJv+P4Opb3oOV7GNNmyT5WlU5r4fNCbhQ6fOJvB8kgESY/xy0J7a4ftDiHlKgPy3/vpBlTQToSSr0BBnca7vkd4az21XXXIE/8jgzJVjeB+1tEE3ILG3dgtycLEhfnIe5M1CclSrZag2KZRZKFDiO3Cz0fKjVpYpWVSGWlAW7Bs9AKQcpBRJx2eZUJyxfDf1rYeAymM6BOiftjCIxaE0ZLJsKHVNfYajAOrhsbRerOhwsdR7VMthxDaieS62QY+jAPAndxNR1dENDFT7VSh0zCpgaim/ieh75+TpO3UNTob1LpWq7aIbAjCioqkq9Aroi0PDQvDoRDVp7IBkH04Thp8Hw5e3IMCFfgvWbpGXB+JQkUXHkWFYNUOJQKDc8ZcMiUgpS+Hm4CJ2j0NEinb3KOXk7i+jQ5kHZl/lzc7x4QUMVSU/GkbzkaeARZFZeB2ChBq+GWvQIgTYXUHCFR813SC6USJ3EqT/Pqf0nEP9pmQAAIABJREFUmOlQqSgevhDEzDmSLui5aTpqBbYD1yDoGx2no6AScxSylTquV8USOka6j7nCOqqegxqxSMVjrE/q6Amk1F4xQWkHpSLVuIoqCxbYLthesIMfoVGYKyRnw9k/VAsYwf+dRQ9Jwdpo5JB9mEYWN9sNHOLSsI/SFI3/ct2HuPqym+htXYE35jFycJxebz1dxiGoLyZjw1Fmc/FM9HXkrNWMfJtoookmflqxZMjYGeQypIzAI4tLEoFJuNT0cBGoePgUkSb9l2qi5cj0COuL/bTRL33gum9Hy87hFZpk7FJDBRit+ozuz/PhHQZ96RiRqEoyVsdu93GFWFj8RWNQKgZ+Z8Jnbi5HoVDAqlYRioktNMxUG6uuvpGONatxMwmevKeAn8+hFmwiVZ8ojdD4lQzPzj1WctFz7Uiy9HwUXVhQw+eHD1fjSL/KiAKGkAqLanD80PMwQqN6cuhpeJqmm+XLgqpDzxaIyJLfihnF1KLU6yWENwaVQZiuNeP+nzC4waMKPE+WLaS5lgQHKC+UmQnJvDpw3zOfR17VFk0y9tWBhuRbz/+iGZCxtuRHrESQKx94QCoRMN8M4kEIKtKHhDoEtIn+4n6YpewMe+/5FnXvF0liSJWu7zM8kePT//AQJw4dYNO6GP/7E+9COct4VoGPvFFOysdHYfNKOKXS54LNHM/a3+e+3/w+yicG2HjTDm5eHyXd03bOMRoI3SjPw7ee971BC86CSqNk0g+D0GtUQ+HNt+2iNvg9np3U6Wp3seJyivSCjO9KGcp5yGVhchxqBdCCFPhCOSjWpTQsB5wSVIMbVCwOyXbQNJnZUq1CmwHpFqiZ0L0G1myDTDe094OegkgCIhGZTeMYBoql0pqGQr7hk7oYIY32o9wTVVMh0m7QeVuay5evYSAxT1TksawIZlQhO10iNz+PFdVQVBOhaAih4tcFpUKNiCKIoGEIgfBdsnM25aKPokI0qVIs1YhYAoSKJjTqZQdXyOGs+tCahs42iFpg16DmSUuCqA7pFOQn4abXQmxKZhbNAnU3qF8rZP8rFem7G1KKFgulqyj4cPyU9OhVq1ArShI3HoH2ulQ0n/khxks86NsC0r/+UeB2pNeohYFUlIalRRPIvL0IAg9H+BS8GskFE6gZXPcgwycrHJrrpGi7eLU6SVOjo5pFBzIovBWVTXhEHn0EzepiWWsfLUC27hNVoyRTCRLltVT8CimrhfZMG529Jk65Sr2Sx1QzMsisI71I3KKs5OcpUA1UAERoGC9Aw6wqIGLDomPUaShiw2hTo4bGLDIeTAD7gfu5NIhYFZ2E2sbHd/0ysVgMToO/RzD0rdPEjA5ajH6segu1BRlPBDm7/CjR7SsNPfjuZlDWRBNNNPHTiiVBxjrIhWQRmAB6F/R7DYSEUBGZcn0pFwP/P9/4Aka/zvor3omOwms++DEe++djjD6x52I3rYkL4J+ecoB5lrUY3HlNByvaq0zNlKnZLqYp3zM/B+WyXDxYeFTsMnXfxdA0qEHF9RD4iFg7V972bnbcsJOHv/ZFDux+ilp2lnVIq4JJ5ELl1UIGGY4XgGMXeF8LsBypQp/gh6Nu2oHbg4ozz9VgxJN+bpuRpSR8ZKDfRcMdeh6aVh0vF5oGG9dBRSZbCiVGrVRDjByB5AiInMw5bOInFvsAlTzLyNNCQ5GeRG6Q7Cdc9rn/P3tvHmbHVd95f05V3aq6++29JbWk1r5LXrGNbbyCMcEYQiAJJGSZl5CNyc7MJPM+rxkmEJ5MBrIyYTIhDMsbJsQsZnkNMRhsDF5l2ZK1q9XdUu99+/bdaz3vH6eqryRLtgAbSVDf57nP7b63qu6pU+dUnfM939/3h+qVCV4OnJpk7TSIKB1RU0B/DrquAe6H8gbI11HGEj3ANdAu4UtlQxEfL6ZPXnAAJBfB/Q4NQoZRtNJi3WHzre/nmuuv5U/f+WZ+7Y0bn0+ixpmSANavgr98D3z9z8F3sFH36xXAH7zvLfSzmtcvv5n/dOJjZy2CFr1SnD+RejbodBJQnu/2OqqatxXhuwMDPFkY5rkjR7DT0NerknC125Cpw4lRGD8Bo1OqSp2qesaFQNFVSSU1XYXF+4HqS4vAil545Wvg3k+p22qWyKYgBzffDt0rQcvDsSmoPwZZU5GVU2WYzsHiYo12De55N/z3D8KU13n+xeeaRT0np76P+uq9PMc171nPvW/8z+jaN4DHQOgYNEBY9PXnKRQtDHOefXsb6IBlmXiZLgo5m8XyArU5B114dOU0fBmqphbCfKVFswxd3VDIhBh+CBGpPT4F330E7roV0oNKIRxqsGEn/L+fhsYMrOmCddvh2WfAbYBXg8V5ZfEUaErgGTjqriTpaDwN1KK4gWrLDeDgSTU26dEUAW7oIGog3Bef1MQmBBqqPXeh6r4HyJFGHTmHGvXkUOSlBfi41KlTp4zDCjLRETTSeNzOdm7/08/B98bhwT2wq4+/v/+dXO8EbMeOWuYM0EC2j9Ge2Mu/ofxYx6PrXEe1sZ5FGFyE5UeVQvU2drLDvhXSW9UAs1EBz4H541HNBHSW8YmOAh2zlFPvIHFKwNi8JF4abyJxlm4tXwa+gVLGXgroZjU38O/QZ1LqlLKQutzgduM6vv3Afobqt/Mq+vgasT1PnE72QiIZ9SZIkCDBTzouCjLWpeMtNoYaAq2lEyjkoAZQDmrA8mUubT3P9P5vU5t8FTpqAHjrFsFYD0mmz0sEk1WPv3tolpSQ3LYzw6ohjaDtUi23yWSVRYEbaJR6e+hbuRI7l6PZbtNuO+D7UaZXgYEB1nKufe0vsuPq21mYGuXovgMMT01Rnpum2ijz2jtvZ/bYKI8dnuTQZJk3rxPsOSwZ9ZUC5Af18drP2dU4Z6KCIks3cP7JG1rAWAB6E56RMBr9Thki8xE12Z0HCimYDWEqkcT+8BCoLDRGCcMuYthphO/iZyRS+tC6lO+aCc4X+wCHLv6K1/IfuZcZHOqoPj+I6ofJFPDlxUm/xpRfZ72RO+ObFIiN4KbAzZDyS/QbMBlYhGEXihqSgANuiKOp6xVTKBLQpfIsfSG3EQlMtqDHhvu/d5QPfvhBfum3/4B3vSbHpiHrnGrWJSYwBQzo8HN/B/f/d6wTTzEIXIYiw/Zxkr+Yvpd/3PAwvzD0Du781ddyzTtecc7DvRhmUNTQKRayVFAknI4KHz+HK8PzfisEHCn50iNP0XR9brh8C7nLi2Szs0xPzDE33eTocag8C0dasOB3xqCxv24cEWJYShnr+ypHk49a2JAL8K2H4UgFenzFYfua8pnNdsGyYSgtU7fc6hx4DWhUYX4UhAe1uhJD57Lwzt8AraQsFAoZRVTWW5Ar2PR0Zzh5skylogIesnlIp1OcnPPIDnRRGOinq3c1jWaVmlwg25Nhw+ZNaKKM4BiKOu4CMY0TttHFcixzJRs39zK8No1gECGGQVwFDBMGh5GyjECiaZP43lHc5hSt6hzVhSp+rUV3f5bubovKyAj5TBHNMAjcgFdfWeFbjyglbDYHpRwsXwG3Xg5H9sLJE4pgnAvBdZQydrECBR2kBkTtepkGdqCuf+xbGn2Ni5oX+Kh+4QlYoUOmoL4MGnFSw3MriuM1BxEZatioBKcmYGNHV5io1XVF/9tAg4CQFi0WWIhaq48kiEr4CkQzBb94ObxrG/Ipn58v/i/snxpCbOyHwwIu85XHBWATcgdwywEIquC3QU6BPDLJN5/4n+x+9hNchbJPWM4B1UhyKehdA4f3wcIR4ABor1VlkXo0oItbrxm9V6LWLVGEbSMqexynpBObxQlahMDDwBf4/hYCLjwCoKFukHF2NkCsErzixvWMP1Ol8uzLYAuSIEGCBAkS/BC4KMhYUAOsFGpluE1HEWFwepDNFGql9lJWxgZukzDwlqz2N/VDV+bF9kpwscAPYaEVoAFPjbmcLAsKImAgqzIEGxZohsHwlm3oqTSeJ3HbPoHrEfoumtDRhAo81bQAM1PE0HUyuSxatovy0cPkRzPMTmjIpoPmO6zvydBtpzg8P83xyBfth3H+PF9aLkT1vSnOP1RNF5DR4YSvyunTcV8rovq5JcC2lH+f53TCPxP8EJAh1MpQ6COVN0gXTPymS3twAKYMmG1c6BIm+BHABSZocx/7uQp4CsEYEgf1fD3z2dlPHpeAysvhX/kTCtd38QLvLCMsAZgQKpsCzW+QNUAYKRV3TQ1FAkkIVJj3LB1CKlYKvtjtUkqYmWnx8f9zH8cPLVDo3cDbbu1n0yqNYuY8KFIBpDR42/Us7v8KJ0+McZg5fBR9k8cnE9Q4cbTGfXNf4OAnDrDxuc3szFzPa37vBjJ5a4n+adGhhc6FeanOryFgWfRZrF6MLNnPG34Ix1pw4tg+3MUpMoZGIdNLKpOnZ6ifTJfDwPKAA3P7aYxKXAHd3TAxq/a3o3N0UDY7Oir5lG5D3oT5Bsy3oHFcqTklyqbbzIFpwdwMFOeUb+zKVTCfgukxqDTBa3WehWEI1bLKw7Rtaxcr1wxRSq/lnz/xRRbmJbrmY5stypGXrZ5ShGyxGDK/CGKmzWBtnu2bQsZ8Bzvfotgr6UmDYCfwiLKnCVqQ6kcXOxEsQ2gpLPNRLNEAPQTdQpG2EyBPqismeoENuK1xUprEMlPkuzcTeoukNQczbGEDtqZRr3osLriUJ2DNaujvh1yUVKu/H7Zcpkjk0kjkJ6yDJ1XbNiwIolVhIZSVQ9YGvQGaA61TfOQt1Pghi+LafBQZa5uKxG6n1Lgidx4DI9Wm5NLfGTrJRDukZYZIZ01sIBzg0KZJnTpEJKyHoInDDE8wfN8nWdzjU895DE9dReH4PNyxFfrXqI7goLjxIEDM+uRCYCAFw5ryZnjYh1IfhalB9GcVDazoUledddACM0VNe5Q6j9ASM6zpegei2lIDKSQdx/7YfqAdtbhY8hL7x0YZ6tCBkDYNyrQ4CjyIGvNdSot2HlHug9h9x0c1mhBShknDmGCUhy5kERMkSJAgQYLn4aIgYzVUMFAKtWYbJ3+wUMOEOKAyRIVKH7gwxXxJ4XlqsGpZsCwPWdNGDTMTwuRSQQgcnHAZ02HABm2VStpiF9Pke/vZuOtq0G1cN8R3A0I/wHEcdN1E0yN1bOiClAgjjZ1PsSJTIK2nMFIWaAbziw51X7J8sJc1VoZPfb3CUeksuX+BGqy7vHx+qxKlXDpfaKjwzgqxf1+HRLCid1NAPqPyUjgi8Yp9SRCGMDkC0kYYEl1rEtRqELag2obZ1oUuYYIfESq0+AxP8y4MlqOxiGSR8KxJbXLYNC/pWJOLEL6vXtbpH8cxETIUELhoQUslM0yZwEkIDoCeAxZBtPFE5z4ak3j6ebCTUobsf3Q3X/74vZhGF2/9rTdx81YNXfs+aE1NwK3DtO+7moWJOcaO70EyjYsixdaiRivPLT7Fnn97isw3SrymOE3plTZrV66gK1Mklc/jF3VS51LiRgii54B+ymdm9NLPsc+54AWSY+WQxvRh9Nok0AbNJkgtJzsgKWo+htfEmZnkyXaNvJnnsi2r2Hcc9h85RKPZQoTqt5sB5A3ImGBkwdNhxlHE6qk+QqYNXQNgZ1To/cIM9K+EdFol7EJT3qgARiRGlJrKk+Y0oNRXYvX6LRSsWzg+eR9TxyR+04fAp9ZUybCErgjZYlegxo9hi2q5xfZtc4xOwdotGYqpPmzZA2wHNoEch3AeuBpD3ImimqeARyAsRwsAIVL2gfc0TnMMJKTs1Wj2FgK/RRB4CGFSGliLWz+OaMwimw4p00Yzs7T9BpVqyPw87HwFlIrKA7ZRhq4uGN4KhV7oXg7PPgmptCK5rTZ09aqFAxmiktVpkDIg50LoKY/YOJdaFmWBlKGjkjVQOawsXVkVaBrowfmR95LOdrE/r1hyHfboOBAHp+wTEhJGKnULQYqQHA5Z5nmCvgc9ZpllXmvTnf0ZwnoTnkijFRyMBfDmwBoEw/fRjju4PrTX2sjlOnoe0uMg+kw00Via/yy5iQZtaIxA91oa4mkqPE2TIsO5bkR9DGU6FQL9dNSu0Ll7RBnplhJWtemM0CQOLSZx2IOyu7nUII0UQVcvQVEg3ejamkAbwgxUzQmmSazgEiRIkCDBxYWLiowFRfr4qAFYrKyI13Wf5NIcJJwNczOSY0ckW7aJaNC1ERUEeKk4NCWI0QrgeAOO74cbhuEVuzZy3W13sf26O2k4Bq22SxDRpbVaDdPMYpoaejS7FpqabvouGIbB0Kbt9A2tYWjTVo4fPgA9ffQtH2RZT5E3LM5x7DvHWHD8pSnCFuA4P7hlwUsJgUqOctLtZELO0ZkaxP5/AshY8NiMCv9M8BLA9+CJrwNfp8nLkqc7wSWGL+JzLWmG0PjsORb6jjH7Iy7Vjz9SnofhPT9+RyBIU6BVE0gvg6EXVQi+lSHwvgqt3ZC9E3gWsofBWg6wFAgN0UK1HdnPngOh7/PXv/omxOAu7nrL1bzr5wdfNMz/XBj40O/SvOEO+t7yae6TH8AmIIty1jyK0uFVgHJY4d6Fv+OLr/47fuGyN3PnK97Eiltfy9VvLKGnIh2iOIX+Ekt/seOMwsXjvoDTrQvOB74nmTzQwGxPo/uzaKKJQ4l87ypCLFrtJl5tnO033ULFfpgNO+7g137/fwNww6uv5InvPcVCQ3mlH/dgfR6GekAvwN4D0DpDLhgAxT7YdS3UFyCTU6RgowoH98LYBDh1kBZY3WDlFa+mu9Ddq6wN8rkU6VQGTc+xbRdQVWtoaRum58AwFNFrZZRC186CkYe2hH/8JLRz8N4rtnHditsRvB315L0OYdhg7AT+JKrJBWAfiG+DnVaMsLSAMfyJLzG2xyfwYGiTILdlHXZuCGexl9aCAd0Fxh5/BkvU6e7JUdi2EfIrWB5WWd6YgtGjYAjcRUllEaZmIV+C3hXQ3Q+9fbB/H+QK0NsPK9fA/LwKz3caUFmAQ0eh2lKlN6Qi/eP1jLjNWbqyMQhRi9/oyhrB9ZTq1gm+v6ghQYeqVE0ysgmhSSfpVRawyJCnhKSLIoIhJN3Y7MCmyQCf4jn20EIJjh+sfVRF9H34k9gfVpZkU8A6FF2aRo3bDqHGSnl0drEWC4M0s6ykQ6cC4EzA6N/C2veiazq9bKGXu6HhKX8GFlEU9Q7ULMpEjb4K0Zk1onOK+2AZJddVozMPnyOEfPn7qLuLCcX+fq658w3UN+qkdDADVHV4kNoMRsOHR50XO0yCBAkSJEjwI8VFQcZWgE+e8Vk8MDp1UBX7pv044JvffABdFPnrj/wu3f1grxyCwQ0wlZCxlzIeHYM9M/v5ytM1Pvqxu+jq6kJoDYQfEAD9A/2EoY6UioA1DJsw9AhChzDyTPMlaFaa4ooVbO8tMTt7gtrcAkfGZhi+6lp+L6uz+5mTPDNa5RAqKc/d3ZAS8M8vZ9av80A/KtFLDeUVGyvaVfoLpd0QqMmKnFYhpQkSJHh5MA2EdLOBPG+jwWc4QYBcUqtfSmGolxIG0ln67Od7DwkEOWzaCGQqTdvOsw8IVg2Afwzc70D9cTjmq/CZrs6+Swm8hCLnXkj+JzSdrb/556wZXs/GrcN8rwZvzP/gybRW/dQGfv7I7zO+tcA/O3/LBKNoKLonjaJ8LJRycRZ4bO+XOHjga8h/tgjeLVjBABuGr+fau9/NTf9+K/mMyjeocrifXq44fWuc6/z7RRi41BeOMH5sL055hq7eYe544//N1Tt2Yug6VS/gcLnGni/8MV7OpJ43OCxhg4Cbf/qXacoiz33zm+QyoDWh6cJCC0rdShXbOuOZ1VWCrdvgjjvh/q+DZkPgQ7umTuLqG9XCo+aBs6D8VEMHfGULTLYbrNQcuN8hFM/xtp+xcW5ts7gQMl+BugeDg9DTr8hNx4FqE3q6IZdTicPQ+simJfAUiiJfFV0NC0X/PQs8jurxITAMuNAegeZBqLgw4rNKA2FDakbiT4/QCkbZ87TgoW/AlnUPsHZNG1KSOd2h1buAYR/AaUiCZojpgmFLjo7C5DQsLsLiVGRTkAORgutvhIV5VX7Hh8E1yuJzbkoRy7kSSEMR0cJT5KuOohHjpHClKMmcpkEqBX4KnEVFxuooAvcHa+exYUFXVHel6L0YfV5Hp4yhm+jpDH4xjTETgrcCuBu0mxkK30+ZE7ikuJJrkaxEebE20dAIWURnGQITQYVtPEA/LgGSFAGCY0wDWUK2RSVZi+pnUAH5b7Dvp+ipFgip4cv7MebXKBNjdGBArdT4QJiOiPZ5VIaBSRQZr6N6bKyUFUCOgBZVmkycd33liVLXoXr9mTO2Hy3yWZtdW1fTdacglaIjbN4LJ/bDXBJ0mCBBggQJLkJcFGRsrIL4ScLJ6ZPsPfQsAKYOa7ZsYMMVl3H4Kxe4YAl+KHgh+C2PsZOTfOD97+PmK69n+/bNDK9bgeu28TxwPIkfKD2G0DUVo4emlK5SI/QDDAGmYWLYkCv0kRJpXLuO25jDNwrsvLKPzZcb7D85xRefOoAIQxW+ep6wUM6EFmrq9lLBQKk8RlDDc5vTI3VjXzYNqJziB5cgQYKXHiGwmwVcMtzCq/gC/0yTgBA1T10GzHH+ftAJzg9Np03LbVOyi6d9riEoAGVNEC6W8ccfZT7924ThE2CUFWNneJ0Y/VRn3zisWheQzSoXgbNBL6wgv/OnuflNt2NTpLuUQdMUJVM6/ZDnDd02yA8VeMtH72LDU2v42qNf5N7vfYImauEtSl6+RMe0fQfLd8i2a/jAIeocbTd4tD3Fv+zvImXAGtHLldZmttz8FlbekcUq6UssWpxW6AdR82q6QabUh5lfzYr1N7F+y7VsWb+FTDqHpmloKcl63WLmsjs4cvIAlapk9ESFDSuL2IVBzEyJVApWrwV/FmwBVgqCyJLzzGpfNgilPJTnlQeqkIpHbzqQy0B/8a2k0+A4kyxUduNVGtx3n2R8FK65TPDmX9mE76eRMkUYGmQyQ5QKBbpXZljmWPihQyaziJ12MVIObbdBSRax7ZBUKqbobQQh0EDKkGZ9Ajs9gK4PglgGfIdg8ssEzTqeBy08ctoiKVlF81vQCtBDEAGEgUo8NjoS4IUBYQU2DoBZg+aIigSSrsSwApoNNVZJGco31zBhYRZGJ+Gh41B6Dn5Zg1WrVc46UtC9Asw2NJqQFtB2VL0V8rBqEJwa1GegXoN2GHn2ou5XTUB6ioTNFiDfpRpJswmNNrQiD99NKNXp4vm2bwBWAqtRRPYalC61gOo1NmAiEGSsBiu7HLRsDhZTEBjKIkgeZTd1pvCRgGSMdWzGWIr9i3S+uY1glMAP0MLr6G7PIMMWGh4hKYzICgHAxMBER9NSimQtlsDNoAVFoELAPMgqqvfZqryBpyqaADWzqqB6afzuoO4GsYM/QEgKDQP9PMZkJmrZvUnHnDX2pI19an/0I7sw9Gk5FYTVjYhOy2/7PPftp3HN9bTCJAQrQYIECRJcfLgoyNifRNTr88zMj4JQE44Vy5ezdu0aDl/ogiX4oSGlpNlq8dWvfgl3ZpHFygx1ZyfLBvsoFHpAkwg3JAwgkAFhIAnCyJlMCkQYIIQgFAIpBaaVIyVMfMNm1mmgFwfp7+mikM3Q39fFSLmCXJyn6TissKHdVpOXNioQTdCZhEvUBEUnzh6s2t9LNXRWOXlV8JtPxyvWo+NOZkS/t0jiFZsgwcuNMZpo1LkMne2s4wAnWKS5NIUuoKbViaPwS4d6o0aj1XhejL1A3ZuFBBoNZPkobWsCUtG2GkSGlKfYVcooWFqgo8jYtAVCxI6qp99FC70DXHXXW9i0dS2yoZNNQcZQVEyeH4yMBdBNncvfsZn1GzaTH7AoG2McePg4VSYI8dCiksSJlnpRodkLKA/jmdoI+54dIVBr0GxngKa9i8X5InMij92dRQqTNlVy5LHT3WSKXXSt7MUyQLNUgswXg6FrDC/rQd95PSvX7mLd5isY6M0u1VJKF/SlU6zdeA2PP7SahmsxNbUAK4u4nosMfExNkX09TeVdGvjQrCpf0zO1f319kMnCzIxS+4JSfTY90LOQta7DNnMIOYWZzkEwwXxznkMTiwRhk5/9tVsRRprQ15Ta2GphZXvJGHmK2KieWQHahLKNKWqYRhdChERprKKSxFplkzA8hpQN1JJopD32TaSbQzqCgCZSd0ELlWTVAtGjIzIm+BlkmMfNNZFS0l0UDKwRtMoN9CAgaNQJ6nVwQ4IADFtZJwgDmi1I51ROsCNjquS3boVCChUyY0P3yhSZdkhlPsCfB7+lim5b0FeEpgGioewLan4nD5NPRP35yu1CSqWOlagxj+sqpXEDeNVlO2mP11icr0Qt8Nzo2BMMAIOoZerYfCNeTo5HMja21qDXquDpAlN4CBH1QblIFZ1ZdJr4+Eywijo+bSSSNL1AH1K3QLcRMg9iHTb78JnGo45NH2k0EJnoZSpyVQSgpSG1CsIpyC4Dp41oVRUTrveBzEJgQRhLW+LrPxrVXDX6zEEpfTPReWmAxMQkdV53B0GH7I1Hdqd+d2EgdImeD1QJXFWU0A84vPsAxuZeqkHii54gQYIECS4+JGTshUK4CN5EnDSZPrvAqkzXi+6W4NLCA08+xANPPkRfby+/++7f4rV33omVMtGEi1tr0m57+AEEobIxIAhU0gYZ4jjgBy6WaSgPglSIleli3Y6rqC8ssNh2WLt5G+8pWXzxvoeZGhvnrmWC0eMhqwyNMSH4RijRgpArpJpe+MD3UGq4UTqqk5eKiJljKV84vXR8n4l+I4savreibRMkSPDy4ziT/Dmf4h/4E/6az7CbQ4RIxoFdKL3UsQtcxh8nVKsV6rWq4nfOgASVrUpGus9yC0oGoKlVqnL0mgNsA50ACx2Njv7MlCDoQREqtdOOv3p1iff8wY0cmYKBZSqsO6exlP/91MRF3w8FGD4lAAAgAElEQVTi+3juOviZ6+7iNb90E+9f+2d8PPwnZoMZFsOANSi19SaUxrAI7CemEtXp1aLfX2SaZ9tf4+nPfg3rswBDuPQxxm52sItVa29l/TU3c8tv3MFACexloOdPL8/ZgqIN4OaNOmx8J7quYxgGEvXMsaPvNaGxa3Ad9y/bwXjFZbY8BQwze2IPrYXjpIG5Bai3wWkqP3eJUmqeuXDZPQiZIiyU1bNUAu0AQh/Ffms5NHaStW5l67pfBJ7mj7Y9wHd3P8qfvXcvofx9MvaKqHQvDC1S6b4QhAjIF48CnwCOoNLe3oC+8m3o9GOhk+MI8BgqHe4UqmXk0BlEZx0ml3HZrYdRT+s4ddwhoAKVfTC7D2ZaapVXk+CDrEoO7Q4YXAfWAfjaN+FrPhwdgd4i9A5AZhAGri7i1B2MIzVOzit7gTBUxKplKdsCWVQ2Dost1W77UJRhC3BCqDtQn4TFMqxdp5TIhKruR4XgQ3/2/zD9N89y7P7v4Hlff9F6Veiio+92iM0BOqsiacBCD0NsZ5EJp0yfE2AFBVQ/3MYunsbGZx9zfJ4Gr+MgTRbwkKzBATyCxe8AAoO1oN8N4V4a7KHCSVbxSiS9CG07pNaBbkBzBBmMQ8NHtPOwrh+yvWi1AtrRCpRWQWYleCbUXagej8o/DRxE5aHoRS1/N1Eq3X4iB17ipMEpMujn0QbVsUfO8vmFNZFLF02GX9GP0FD8u4DQlExOz9EYmGeynfgUJEiQIEGCiw8JGXsRYKYGuSwMnWXiluDHA7Nzc9zzX9/P+z7wQX7z3/8Ob37jm1i2rJe5uQqtmosXhKAb+AYEbqBkH7rylK3VqoShRIY62H1YNti5XnRdI5exaAeC3qHjeEFAkLZZsb7O//WWW9m0oQeHBf7+zz/F/FFwHSUYuBo1PRuDlyR1jwF0oybbbRRZ0E9HAaujRF8+aqpT4eJINpYgwU8SfAL+Ix/gNjawnPXcF8VhPIMizVah7gmgaIcUSkuV4PtHy3Vpe883f7BQ99+xV1yL17MOunWoBND9NtCvBYYUJ7QJCGGtZnAH+hI9NA8c92F8BHw/Q4cw6sBH3WP1ImRMyIgOnfbDoh39og7kB/P8l/l7+N0n/zP/46N/ykc+9X4OocjYVwI76Xh92tHLR1Fd64CtwBV0Ap5nOMkoExwDHuUZvjuyj8zo3/GVz+nkgZwAU6hnyjQwHr2/0DPsgx/8IL/9278NdJLEnopVO16DM1HFqStJ6/TYt2jX9pHJwfisCn0PXZUbsRaeI5Ij9t5xIFdUhKILuHWYPAb+sA5mD7ACRXwup09/K6+94i5e+dkKtrWKl3YorgHrgc0oAu549Pla1JMaYDlwA4rqjMPN43D8uCx9KFbLQ13xVwP7oPgGKKRhbRbEfLTNAjKY4bH/+d9YOeewbAj+9mPwN38IG5ZDcTX0rgG7L4NRWI9IVyg4x5l+ro0NpKxIDK4BabAk6D7UZyPynE4A/BzwCDAlISvhw3kUARd93wKeOXmI9//Fm3n7O6/i7rs7ZGwapX09HQLFmpvRucZLB+tQJKsR/Z8DqtCcJWiNcYAT5OUGLD0Feg+4JYZYTR6dYWbZwiGe4Qm66KWXlcAyKN6M3ngY/Kj12jlo3YgdZujiUXx8DHaAvkwZ6/s1kPvweAhJEyvMw5VvV9drFDg2D71dUA+gXVeZ0Kih2tlTwO7o+hai8i8DtkU1kYlqLAAMdIxoyefShGnAYC7KEdiFijr0TAbf8VbaqR5K89++0EVMkCBBggQJnoeEjL0IkM/AwEoYGL7QJUnwcsLzPDzP495/+T889djjrFu5hl/52bdj22ksyyIULo7bxG0HIHU0XQdC0EykJkHTMW0DgYcIA6XAkSnSfau56c43Up06yeTh5zi673E+/YWHWb0sw45NGX7uF27ju19/lP0H6xyaUGP4E6hp2EuBADV9iZ3CTNTU5lRrghQdFS6ckSU4QYIEPxLM47GXMfpJcSclvkplSTV4qspQabgudEqWSxhaAFqwRB51oe6BReD3gZ9f/Yf4KY+ykNwnPe7WhsmIbgzSHS9YXdEl/SgKJYeizOY1KBRA0wqcTU2poQjYHhsyurI1iJMoxmrSsyljJWo7wfO9Wj06RGy8r9AEZtakZ6fJL/zRL3HV61/J7vvhrz7zDh5ulSmjCH6dTqqfOFLCjY7Xio43AFhIJJIRwEGiS5/uwGdzoCjEOFS9gqIYrWjfOKrjbO3U95VaT5yxTfze1beJHqdKe6ZOBZgc93HqIT15mJtRybFagUradS5fZV1TCdXMlAqTNzylYNV8OL4bHi5+mG0bHmH1ss3RWU/jiDyBvpIu/XpglpPN/WiYLMvsiGopNvQxUJS2Hp1pTJ7G1HYK5XWqcfpVbUTbpVDJul4dfe7SaTM6qqfPoEYEFTo1HT+963Q0zcDiQTBzkB6Mvqvjl08iW/NomYBj45LKHNTmYNNlcPUboHsAcsN5SqsGSfUWCDwBIotRGKLuHmFxAbIG5GzlmLAwC7at2nipAI1q515kRmewC7giDaWSKqUb1U4bSCOZeuZjBJdvo7tvF+sv+wuO7vkPSOkvkbHKmiC+u2l0SFf7lL/D6MhxC3KBUSRTSFlnpb0MMywoL4pUDopdaOVryQVVLGp0cRRYwGQQk36gCxoTiKA/ui4LEOhAlhRZNFIE1NDXbEa0UirTmVej03PqIA/Dt76r/m7NgpyD6qySEDuzEJzg9CWTQRQ5Gyt7CyjzkK7oGjeJ9fYODdxL2axGgzAeYLaJDLbBCjM8+MRB9h8Zv4CFS5AgQYIECc6OhIy90BBgG1AsqEy5CX78cXxkhImTE4wMjrJiYBmbVm1gcGCQ7v4SASHSEMhAItAJCNBTaRAhaAJN6PiOTxCCkBKkIJUpMFAo0d3Tg6ZBu11lamya6UWHVc0Ma7dvo7o4T80d4+hcmUm3Q56+EOJoyBdL7iOjbSSKMIj1NbGSRfkdquP50StJ3JUgwY8eHjBOHZ0UWynwOvs1POI8SlMuogmdtelljLem8KS/1EezKMrmwgahXlpwQw8vPJ0IBHUP3ALsyF0GQNkP8S2f20mhRymYAjpKQD9UIdiHG7DQgBMtl+MLTSYfHcNvz3O2ZS0NsELo0kFGPx4vhL2Y7i1ePDsTEnX90zyfyE2VYH1pI0NrN7IyIxnlrWgTC1gTc5zc+8CSh3h4yr5tFA3UREVprIo+N1FUmKKoFEk7QIciDKJtYkqygXqWeXSeLbF6NXbEjMt/qq1BJGRFN0vkCiZpTGY9qFWUN2zWhraryuyEL7x4qAmlxgsBy1RBLUgVvd+eh4N7noF2jUblEFoIXrvCop/HZyVd2YCtW9cwu/AQQQBm1xy53BApkcd1HeqNeebGR9BMjZTZQtOaLCw0yQ9kSOfSZOwVlMxuYnUj1JDyOB77MTiAJtpR7ZWibRboUPM6MA1yHDgCrREwB5WkWsSO8hmcRptW/QTF/m6EiNNveiAdoE61PEZ7/iSFnhJrL1uLPz9BO6gxV5WU1kfFyllYhS58YVGenMUuZLCyveSXHaF8SHntpqxomKOBnlIJwWLr5Jhqjl1xo1RYZEKo1xVp7kbtwJJQmziE21ykb1kfd7/pdfzl3j/G931sFBV5ytWL6iEXHzH6O3aS9aJt0tGJqBYqEBRlBl3qymMhDCFlRWSmh4ZAoNHCp0ENkxS9aBi+iUj1KH9XX1NeDNJHw0TQjURDhFX1XVCBsAak0OhHxjWgoaTAmgYygOpRaJUhWIx6RhjVkA0MIMngM41OEY08ipBNc2ayrTZ1XJov0NIvbviepFYOkMMa+CoZh5YSDK22OPb5xzkxdvBCFzFC3IeSJ2qCBAkSJEjI2AsOiZow2AbYKUi0SD8ZcF2H0bGj/Jf/9l/56VvfxG033sa1fdchrAx2xkS6Pn4Y4GNg2CY6PhKPwPdxfB/HUdNDYVtouo6XMjG6+xm6/Br6lg8xeXQvqaBKscfGtVew7bobaTR3c2TsSSrjrRckQ0+d8MSq1xcaNmqoNuyhVFy9xCkhFCKBAhZKg5M4dyVIcOFQBjQ8uoXDB4p/zK+Wf5Oj3iJ5zeTG7sv4/NQ3qfr+Uv/toZOHO3kynR/qzSa1RgPP9egyFDUTCoEUgjYdZ8qiofH6krIamEcpPuuogVkLpcqsNmHvGJwchamxBicPjnDws5+ChadQV+Z0CAlGAJrecfyMc60bvLBfbLx4djacqpg9m7rWzsOuNwj+4Q0fYfFp2Pu17/FXH3iS0RY0vQb10DvNP9zBxCfDQUI0AiQui3hL1jZ5FIUY++Sm6TxHmnTIV5fTydn4+bIMnTxi6Tdj5884/VAVcIKATMGma0WaYxUXtxVSW+joIeMURS8ELUom5XjQk4d2S3FkeqjKPLkHKhMj7OsZIS1hZhymFsHRYPnwv/CfNv46c5MPUm1UaDUeZMum15L1h5hfGOXoyEM8ft+DpLqgq1uRlLv3wLbbTJat38qKgZsomTtQvTOL8nX9JA35r+TFTjTWo+wG5qL3k4ThCTw3jZQ2un4CTYwjGIPyQWShgrSXgViOrvsgNlMvt5g5eoxi/+VQ2ERMzUskhC6z5RPMnTjACm8Vb/2dGzny2LeZHGkxXfMpDFq02z6OlkJLmdQWWhw7dILB4dUMbxpk7VUa5X0hpgdaCkVIW6ohBiEsNlT9x4rsMGoXpqaSdtUdtfAQJ0CNtcLuIjhtj3Wrdf7kj1bztx8Q+L5qO88nY62opcVEbD668nHK05CO0cZaNPqBBSynjEZbtT6/BmmLFo/hMU8blylGmaKGQ0ieHFeykQK3g51WrbnWwvDnUX1YACtIkaM1+i0MMqTIIKIWa7AJxAbQu+GanSB9OHEc5stQ3wtyho4JQ7ykkovOqYTDOCYpTIrR5/HyioeMaOwqizQu4dFZq+ox8tQs1+wYUPcnoUj+9VcIZk58ldmTT1zoItK5+6R46WLTEiRIkCDBpYyEjL2AiImuEuBLcKWJorNmSKa9Pzn43Dc+z+e++XnSdpp//MjH2bpqA5Zl0ghbdBk+kzNVPC9EYGAYBj09Oer1Ou12mzjLb6gbSF3D1lPkuvoobVhHq1amOjfF53ef4Npt67j8l69k+GfewtM3/Q6PoNRJZ8JCKZFer4MeqAnrGCoFRKx+PRWF6BUHVcahtLFaKdaTREF2jMMlrL1IkODHA3PAg7LBH06/jSoVdHTGghb/+8SXloKe4xzkY6hnVA9J0r3zxfEnZ/m2vo+ZCdh2+WYKhkExm6NUKJ7mXaqjFq845f1UhAa4JdhegkdXwyMPVzn2+HMw/SHONUbwJVR8SJsdAsvnxYlY6NjInIkU6j5foUOIvlCqn8IueOXOa7j2d2fZf0/A+/7l53jgyOeX6IcaMMAv8Bb+mgonyLGHx/gMe/hXHkJRSlr0m1Oo9hdbGsTe41b0iuszftYEqGfbdexg6JQMaj6dRcK4HLOz4xRNgx0DPfzxP/4TCwvzSwpLOL9RWC4HtgXNJpyYhO4ChBIcR9kXZLMwvAI2bNPYuMnmox9pUpuEUIOBXkla1NGpMjVxkueenmJ4sMqze8Y4sLvJoadDijqsGYy0jE2V6+2mnUUGel9J2rwKeBrYgHqyloEKJXEFyqO2FNXMjqhmRlisPMa/fvqD1Odgw4Ysw2tSlPoa2LrL3AFo1AQEJtt3vBWj5za6ezfRnTmI8p5dE521B1g05mcZ3jrM0Posx558kiNPHkYXDta6PHlL46o7/oDy+DcwUg1Edz+9PbvwMiXShkA2NdrtPEPrqrSmJLIFvX1gCJgbhZqrSlxCtbmYeDdQQlRTgKWrz3UTNFeR4D7QXYTxk/+GfrjAptWvW7pWcRK8DmIitoQiYWMjjXgpINbmllEpDmNlbA8lZtT+VhqyXZAvUai8k88F/8jjfJV/x1XsMv8A3Q+ZDJ/k87yP9RzGr/n4tBGE3M5fEvIdJBUgg8Gr+A+8lxvJ8hZ2Aq8CsmANQTYPfVmVve/gURg7BMxB8S4l3/ZGwd+H6hH+0nkJDLJLNgVadB2307FeaAFTHGCO45cwGbvvwLf5td9Zx107ZslvyyCyUK+2+fkbPsSRo4+i5lUXGhKls0+MuhIkSJAggYJ+zz33XOgy8N73vvfCF+ICIF/q45a7fouBvPIdmxyv8umPHwB5lCSQ+ycPfuDz9DO7+eL99zE+c5J1GzfQ3Z9H83V0dCQ6aBpC6BiGiWnZ6FoKTei0Wi0c1wFd4IqQAAMtlSaTL5ItdlMuN5g8PsHckRE2Lc/wwNFpmt7p6UiydNI8OFIN0U8Ae3i+p2SM2JmsFe3noQjcaTqT9rwOPRY85atJcrLMkCDBhUcIlGlzDVdik2UiolpbKI/SNcBktG0crDvE2bSYCc7E3MwUzz27m92Pf5fLbngFm5avpDuXI6VpSyHX5/USyvO1KKAvBTMLaZ4qryS9/W5ahxaRTgOlp+2gf+UabvrpX6KQUfvHkQunhu2Hp/zG2XCuz8uo+3tsSXMuCAFCCIQmyG/Sufr1V/Ca17ydK/rfztef+AJSurQRjFMlIM2O37kcZ9tNlLmF/NR36aWBjaSByttuoRYH5qNXNSqLi3rOxJRSnQ7R+kvXvY/L7rievq0qaVUckB7QcdEcGZlhviYZrQr+9vd+hcrkJGEQfF/xSa9/NSwfhGYDzAw06tCKXqMjoNvg+dBqS6yekJYmqTWVBYWdhY1rAnqzHpYrGN/X5ND36hx7ok19OiSnQ3caevrA1sEIQbjguC5po002PYdu1qNaeRqoIcR1CPGzCOFGZ2kDN6LaybcguB+tPUGx4LFhe56VGwvkSzbpgo1h+KRTPhkh2b3nBF3LrsYu5BXrqc0jREjHY7aGYS1HN2u4zhjjR57DtB0KeY9M2gMa1BtHCSkjTAlGDtN8Oy1vj7oCoYerBYTNKkKGpAwo5KFegcWyqsfAUzmphFBR+YaAQEZnlYZSEeyMsoSQoXq5EjbthL7VGmlrkfrkCT758ftxg3ApN94dxG08jSItV6GEEBadZeVcVK8jwJN03IpDBF0IWghyIHPg2+AEiPaX0TlMPwE92JTCXejSwWeaBocYYgU1HEZp811ahDzLF9jLcebJ4dODz9+zhyE2cRU3IliO6rk2SE0xzpetVsx/Yw4qh8GLGOigeUrr70UtaQygyONapBF3o9YfRu/ThBzgOZ5kkXmO4XEx6Ed/UAgkO3Mb6N/UT87I0Hy2wnv+5l3U2tPIs6ffS5AgQYIECX4kuOeee957ts8TZewFRBDA7GxIuEJgGgJbtyC3Cqovpl9J8OMIKSVHjqkM527oYdom1161ja3rLqdUKNF2ferNKl7ooRsGBgahH+AGLq7noQlJOmMhhTqWpuvoZg7TTuOEBm1X0A7amMtXc8MVc+w/NMHEdJVa9PuxY5pNJ59wBTV8V/pbNYSPU3vA6eGcp1oTxB5+AjVR8sLEniBBgosNNTwmKDPct4HN/dfyiX0fW5qum6ic61N0wrVjaschWS58ISxWyuQHu9l++/Ws7u0nZ6dJ6caLKlPPRLx9Btg/CnXdYtsre/H1bh565nU0n6vA/Nhp+4QhtB1FWumnHCQOTIZz2w14dNJHnQ3x4tsLqWLj40jAFILMStiwciPLh2B5yeHdxm9S95sEEz3IfSt55uAJimM9nGhqTFc1SvTTSzf5rjS+6XJg+mk0wqWg6xRKoxhTT/XovJqcvti38YZd9KwaPK1cp3rGtgG/3WDkuaMcPnSAmZHjS1t8PwuGmg66AVJXlgVtF5ymSm5/9BBML4JuwcAQbLxGsn3bG+gqlKlWF0jnPfY+PUFlQjJ6xGPvbnCqLTwXNAMMW6lrc9Mq5FqGioczDvjc5YxhWw59soluztF05kAvkM3mUJYEAYo89FE99kkCdw+BN06xW2CndTKZEEIfP9TQQqX61FMGwgzRzCZCPEMYzuH7c7QWDiMDDc9dxHUWcbwUXV3r0bRJ3NYs+a40hf5uUkED6bfwXINGcwozlUPTMuhGCiiTMiW6FOhopLQu6BsjqCsLWmEo4tqP/DLsNFjZiGiVqm0jwfUhiLx6LUvta2jKogOURYRJBdqHmJuf4vqekO/Oge6d2XZjc4N4dFOj41gc4jOBw37qjNDP7Qi0aLsFtZ1Ig5FVhretBkiLAbaSYx02LYQ8SJMmAXOsYyslhghI08Ringq9rKKf4/i02McYkzhM0KYVec6qHpdWEvkw8hqtuuDHvdCCYOSUntGPWlLvp6P2jZdO4lFdgIp3MJFUCKkwwwLe0ojt0l0ulxLKUydwZxeYmWvxxOceo9IaJ5SX7jklSJAgQYIfbyRk7AVE4Evm5tuEYRoLSKVM6FoONe1SHg8leAlw8OABjo8cZeLI9XT96gArVqwlY6cJPJfQU+maBRq6lLh+gCBEaBq6riM1SRC4hFH+Yd20KQwWqFtdNEWBqVbI627ZRZem8WjtCCNtl1bYUQ7FGaqbqClcFjVdyaAm2Q06Gazd6Ls4s3WcqMuMvk8JFbJZjlnbBAkSXFR4kgNsH7iOd+38db66/wuUwwrThFSBnSh6oonq+2XUfSDOYJ7g7EjZJjtvuIbf/LN7uFp0IcTZadjYkTJWy57teymh3Ib/7zC4PXDDLYKaofPYV2+lWX4c5h84bZ9AQsNV913tlIPGC2mner+eCYdOaqdT9yPar4C6v5+68MYp38eINZnmKZ9le2HLrRYfuvVPmfXg5OOw/zMNPtL8X3zrsYNM16rM1EZZT5puhlnXtwqj1KbZHKHPb7FC+PSmBKVciqmpJn6g2mY5+u06pwf/rr2pn67h7GnnEZfZjvZrVGc4+Oj9fOmT/3COGnlx+B44LrQDSHnQdKHlQL0Gx45BOAmuBkNl+EVg1+bfYMeWfbjBYdqey6f/5is89KUqo4dc6hWlBm2haLM40dmZdZ0r6AwNN1m/bppiSsPOLVCrlpEpG8sK0PVNCHECGEWpP6vU6vfj1h7Hqc0gjJCUpVGddWgshJhdJhYpfD9D4FlIXPqW6wjxBO1mmlZrkYXJSQKnRqO6SG2xRrUpWb9+L4YBuq7Rv6yHvnU78RcmCJoVpPSYLVdIpXQs0yZjZ4Fnsa0QXVgYQuBa3eiDWbyZEH/WxwugFdkT6CnI5CEU4LRVPQe+IlqdBviB+sxMRdwkqu2HgPDB1Hw0MUejdpC71wqONYHFMxXdHh3jJIcOtV8CCjiMUeUgs1TpYwdiyZl4AciCyIJVgEwBGjVgLUVyFLGQHAaeoynmCEixTl4D5LExyZChi0mu5o0M8xAHOMBuxtjNHC08oIZkFsEG1Vpl1Gt1EyYb0NAgLIA2COFzUZm7UST8StRdOjaI0lE9t0pniXwOSCNpL3kpB2jRmPHSnHxoCLLo5C0wam0mR0/wwGe/QsLDJkiQIEGCixkJGXsB4XoOx47vww924WHiGlno3QrjCRmbABzX496vP8i9X3+QW266jTe/8We47Zbbsevguh6eF+AARTtLLq/0Hrqu0/Zq+AQIYYAQ+IYalItsnvwygWu6+P4gl91WYtnKHg4+8BBfnII5ebonZC8db8A4MUbs2RcrkOI8w0PR/+3o+ziXb08GqhKeSYxiEyS4aHHv3o/xzP4v8k8DH+LXZt7DRDBNC3gUeD2wF+U0WEOpZZPu/MLYecsV3Hzdldz4AkQsqHvlAupee66tGh6869/g1htgoKSIk0dcCGW8FHY6ZAiBE/E3pyBeaHshxPf5UxF7i6fpeMrGSumY7jnzuOdS1sboNaD3Oth1XYaf+/C7CerwLx8e56N/9hAPND/IozzMqyqXc3n3Frb9xlsZGhnBNkYpXGmx69cvZ3TTJ5AzISmvk15plNNrI7sdUn2d8/LpDKtiu4K9/z977x0l13XfeX7ui5W7Oic0uhFJAAQBkCAYxSyKClQyPZZk2ZbHM/YojbzjM7vrXa+OZFu2R9q1Jc945FmPLVmSR1QWJZISM0VKYgBBECByRjfQOVWueunuH/e9rm4QAGl71gDE9zmnTldXeOG++6pefe/3fn87f8zhfT95ja09P5MTKp/XdWGqBFOTqkF8Q32fru+Blath9QaYmJEEQRvHTyWYL7XR130V7/+Vd7Km5z72vvACe547znM71fvOlyr5oX8/yJvuXkHnUJJ6dRij7mHQQr3uMnpqPwODjwBPA1Mol+QJvvIP36ExeYJOW3DFliTP/9Th8B4Xz4fr74aBgRx2SqDpEs/zmJ+vUqk8jWlFblCpZuPQQJiSTBpKpVl830PXDQzTAm7EbC9itquSf8uX11GhRSbRsG7SGASmQRZoMdtpWXEXR4ZfYtQ7TGFGxROk09CSUW7gch2qRXAq4JegPg2mo4RYpwa2AQVfzb4JCAvW2ZBJm2TbM0jbpOMOm+zYLE7BoW1JSzo05+wY4f0CStCUzFHARbKRmxGsRgmaNZpzg3IgcmBkwe4A5zBIG+hEsBnJVtrTOaUgF04APyDFajrIEDADnKSTu+nkFm7iGHVepIeX2MAsPqMYtICWUAG5ZqAao6yD6IBMFlrbYaYI9IC+Cowe8AxePSO/K9zuKDwqj4pbcLDp4VZ8dvMKGcbDfbz06MHm7doA79l2A8mNKyDXxQ2b7+LzI1+Lf07FxMTExFy0xGLsBcRx6xw7thvfW0+AhUikaFm+jsIuLZ4DGrOE5174OXv2vcLn/uI/8clP/iGXX3YZre1Z9WPI8RC+QAbNS07f9dGFaP4o1n20FJi2TYsxiKULOjtWMTS0jQ1X3Urhi/83u07XmFqkslRo/tAt0HS/BjR/lEeFuyrh/YDmDyIbKLtQjq+EY2IuairAfn+OT0z+r6T9adpQzkGAJ1kqDE3QnAwbl5o8O5WZIrW58nmFWFCfk200nZ0uTdlqHHhhFB7cA//brZBMwZyAE9Hs87asUmptUJYAACAASURBVJ3OwK3D5DB4q9VU9+hSIqqxvriI0ZlblzvLY4mzvDZazrn2zjrH4xHNZlF39DS84yO9vOn991ANDrLjARg+eIyJkZc5+ePvkXHr2OsKJBMpAq3I3uVwsAgTrpLT8uG2q4FCDdWqGkKo/hkVgPLCdogGDo8eP8ypkROvsbXnZ+8BNW0+16WiCQwTWlrUrTQH+QS0tUIqY9C+vBNNT3LqeJGnnniWpx/5MsK12HhZD0ktBXbze/d8fPiD9zG4vBst2E+p+mkq3jy1WpG5YoWZYoNly3sQooHqUVPAdq7ZmOHLX85w3/Nl/nZrg7QtGR+FUgXublF9wkBHFwLDNOhqszAtE0SALx2q1Sqe7hNoAiuZxNINTFP1JE3T8DwPyTI0MYf69k8Ck0iuQjk2O4AXQYxTKx6lUTpNPjfE/FyduYl5KiXIabD2Mshm1KDC5BToZbAz4FXBL0Jdh+Ks6jnplIpxsG1IJ8GVUKur/8HF9WvU/SpFZrkTlwZnGygQqF7eivLN+qhPOI0AHZ8kgi6awxFRT5prRgdomlKLZSJs8wlgFIEPlTTHxRhf4kt8mworMLmcgGuoIynSj0sCA5giwfXcyRwtaOjMAo9B0AtiGWT7YM0quL0dxgQM18HVYObtkFoJehZ8Pcx4iIYlogJkKdQ5kUBFF6SAOoIykjoGCSy0S/oHoYvHLEV0cggMhsdO8v0nvoeMv6FiYmJiYi5iLuXv3kseGQRUq0WklErAsgx6l3VQEiLWYmOWUKvVqNVUOMA3v3UfywZXs2rVGt7+5pvB8qjXqriOg+v7WKYZFn/RMQwNWzPwfJcg8JESTMtUjiY7gaUb5NvzXH3jTXQMjzEyMsPRw2PMo35QS5RPwqH5I15DXdJHRWAi38yZU1drQMmLXXQxMRc7AVAn4KQ/wVY0cpjkEJzAoQK0o0TCKD+2jJIuNqHKBsUsZbZcZrZaWXCPnq9QVnQRFk3/FwF8fx/s2D2Bb2pcd2UnXRmoh8W4dB+mpyAItMWq5gL1qs+pwzW4LUGAWCLGRmLkuYjywRfHGESf74v35XzFv6L3/GMQGmTbTbLtJlLmSLwF1mzKMTvdRnm6nQE/4FRtH7WWaY7OSvaMw36nWUysEt48QBNJ8skb0URTqI5KF8novgTHh8pcg3rRXXhdVz80aqqA1OvBREVBCA2ErqbVm4aaOh8E0LdMOTfNDDhGQN2rIpli50tH+dnTh/CqY0xN6lTqDXTNp1ZSOvu5j5EGpGlrWY5IdlKvz6JpaUxLkgk0NJLYSRkKscr9qGTnIyALLO91CDYI9IROzyBsuCqgVJKYNriygS10dD3skTromkAIgYFJQwo8x0NDx9QtbNtG0wS+HxAEklq1CvI4gTcFzKHpPjCPwAaRQkoTpzGFaQUYhgVJGzQP6TvYSZ9cF7S1QLYNbKHEV1eH6gkQKXCFOm7SBzsLQQPsRFQsLuyTMnR2a4AWgPAR0iORNem3faqajx0s7rtRLmsGNZ8nEi+zqHJQEtXru8K/UTiLTjOn1VSZCrlO8DRwquBWUEMqdZAmOamzDcGDlKkj0bFZSRsZLHTGKFFhmhEmGabGNA10NCSdtAMJcEMRtTcPq8M5SiUP0hZkB0BkIbBUpomGEmUXgjmi4YiEet9CZQAAF4EFCGrUaJzXj31xIwnwZJ3DO/fRmzM4te8Qz1deiqXYmJiYmJiLmliMvYAEQUCtVloQY3XboL83y2Ht/G6amDc2Dz/8EFa6nXUbNrFh7QraWrIkTQPdtggaDpaVxDJNAgRCNzA1Hcep43s+QRCoilpBgJQBmmGQamlnw7Y3sbz7IMcTBykdHqMOdFhgpkwaaZtjp8sLl/aRgLBQoGvRtkWX/hrKTTcfxNmSMTGXCh6go9FNli4sTjK+UP4lj0GaNMcoUELJFQPAEdSASzyA2GS+XGK+UlkoDfR6sIFyzefIWIOvPlrk9L5pbrgixbt+uZMK6nM0QAlO8yUIHC+saLSUetXhxKFJpBxALhrYjfxyZ75jsVjRoPmZfubnuh/uS/T6YNFrzrxiked4/MzXnC0vVwhYvgGWb+gBekBuAw+0F3cwUzvATP0weutGpAxwiw6NYplJb4oGLhKJpSfp77oTXUssfB9FGcfR9teR1Bylm/mL9KfBtVnKRZeGU6de5jWxgdaccnIioK1DTZ136sqhmc4pp6xvQU0EVGplpJxg//6T7N49yubVYOMzfHycknv+aALVOAbYfSB0qoGkJiFjpLBtk4Rmk0r45LXo6LWhhMYqUKPmlli7yufyfgvDtukZCtgqXCplD8OS1NwGicDGwkTXlX/UEGHusBDYuoXnOEgh0TRVIFRtU0AQBHiuBxxBBrPIoIiUDr5bROg1hJhDyizTE8MkUxmSCZ1UpgWJjpkwyHfbpBIJOtp9Uh0BohTgzElyHoyPqG2I4jB0HRJ5CCpgGWE/8lWGrB+oGf3RqIbAx9Ag0Zaho8WlmPQxl1QSNVHiZAvNVHwX5YL1sciGrtjucKGRK9ZEebGjZRjQ0gNuJ5THwZ+AwAS9DiJJGxp3y2v4uXwFL2iwgQwbGMDGQsehwSwzTHCIg9gINDKkaaDO/Dp4RQjK0JpUH7y2C4anVp1tgZJQFYEDTVWUE1IJs0uu2KLhdSPc5oBmST5BnfolLcYmLItlbW2cPnqITFsns6fGOcyJC71ZMTExMTEx5yUWYy8gvu8yOTGCH6jsT2nCsi514Xk+90pMjFOZYdcLT/Du9z7JL//yr/JvPvQ+rlh/GYVyDc8TeDQI8PClj19v4DgVPEeCr6YTCsNAWAaBqVNtNOjuWYleKGIlRnFQl+c3DMKN13Wz9sYruOPDPwapfqY0aObIRpf4EVEV7RSQ0aESKDdLTEzMxU1UuuVneLyTQa5mgJ/wA2qoPM4O2vh7bucuvk0VjzHgMWArsItLNWnw/x+cyTnc2cLreq1cdOf5g2Xe+cn91B55iAe//0HuvnvlgpjooWYbNDTItYFwZsB99byDcnmOfXuepB78KqnX8Kie+dEcZam6NKNoQMlQ0QTtaMp/gzOLIf3jcGW4DHH2bVmSZGDC1ddfDVwNwE07PsWTD8FPHzjGU997kqcmPgecRNDATmS4Yus9mHaKgGbb6TTjCWaBsaJHw1u61i033ogTTJDs3MlLP37tfcgBaweguxdOFWD1EMzNweQ0FKtQLoCdVlPuaajCUsgi4DJXgqd2wg06dPgq8uPAa63QyiBW3w66heeWcL0Cuq1j4IIJnuNRrXikOvKob+ceYBC4Fawf0zEgaLXzpA2wOwwS2TpOrUGl2uDUSAGdKkJKWvItanW6AULi45NqaUNSoVqtUqzU8Q01ud5M6CSSJgIBoopuLcetz1GZ+inz04fRkxLLthBBimd+PAsS1l/VxcZtfQihk+3tINuThqBLiY5eCcwaumyQLngYadDqoFnQkof6PEy1QVVTLlkfqM5DqQpVHxJGGF8gXTTPI2Ek6Ow18NeXGCs6zO5b3KBpoBcWkmSnUMnYnYBNL28OH++mOXSQADKgZ8CfC5X+ABI5ddFjGGq5pVnI58HQEEJi+NfzJ7XjUDuthFOyEGa0dlAnz5XkuZ8EBjnWkeNymsPeKBU6JeEYsG8GTlahYYBMQqOo3LBGhubPujNDo0zUmR2dDUnVKcNhFgsN8xIu4LVmYJDP/OaHGZ/z6LxlJendkxd6k2JiYmJiYl6TWIy9gNRrDfa8+Aqe62KhprN15M868zAm5qxIKbn//m/z6CMPsGXLVXzi4/+BzWvWUal71FwH13dp1Av4jguBDkLDMAx8AW7DRXoeqXyKXN9yAr9O19wMfV1weBJeOgarrruRX37Xn/Ar/20NDx8IKNSW/hivoz5Esqgf5stboac3w+CGVXSvXMlXvvVzDh+buIAtFBMT81p0oibi7g3/f5hXOCqm+Uby/+DXal9gXlbYxTTv5Qd8R/t1/ih4nJ9zcqHI19UoCeMAZysp9QakrqZRv962qAD37YTH9mZYs2UT9//XK+jpVM7OSDoRqM/cigFDQ5DvbcVJJ18188AtzTO142lk8P5XrSfFUpH1TIxFt3M9DwtewH8WEwEc8uH2qDIkSjqqoiSy17oMuvEOuOam5Xz0U+/HCd6Fg894UTJT1Vkz1EY+p1ELl+ejYjVqqDacCyQHD+6jWllqfz01P0+6M0/3xqu4XH+Jzt4+updtJpntY2RkL8ePbWdqh0f1dJg0aoX1mkxICMgYMHC5EmfNBHzmMzAxoVy5y8xWrt32TkzzJu6643FK84LvfF/ygt/c99fCTpusvXUIw9LxGnOI2jSGXgfPo1LXaAhbhdTSgxLeckRpuldtvYaRYzuZPjVKLt2DV/GwjASJVIqk5SED0A0N27Yx7AT1Sh3LtFTucaAkbTuVRrdMUtIjMNQ1q5QNJJJMPo0gAfhowsE0PTq6bY6fqFMq1gmCBldvhY7ufoThMzc5Qlv3ULh9UsUKWBp4dXDLBFWPekVFEfiOin7ItoBrQDYX7p6jnu/tg8oElIqQSIBvgueBVg2oV+vUXRjoFNgdOo0lVgcDJa4mwvv9ZzweRRFEPTKttpUa+DOg2SqiwECJsHNTUK+B9CCdAV+E5lsLWjrAzcFoHmoNlV3hD0GjDvjomseQcyWCKQSd4TEEKEKyBYw2OFEAowX0Tsj54DowXQR2gJ+G4AqwWmgOQUTi65kCazScHrl9bdLkSFKkWdDs0sJY3k/2479F+uHtPPv9r/PC9mcu9CbFxMTExMS8JrEYeyEJAtxCGRlIkkCLBqnUhd6omEuNRqNOo1Fn1+5d/OV/+QKd+TY+eO+9DA4uRxM2jqdj6hqBJpBSOaUCP1DFTaTEqbpITyCsDO3LV3DV7W/i5CM/Y7oYsPv4Hl544At0GRJdNFPIfNSP+o4Ok56eDIODK1i3dj3t7SnS2QSGbfHDhx6mULo0L+xjYt5IlFk6G6OBx5ic5ofOo/zRxt/jvtMP8bOZF5mmxlfkc/QRcA0tbKeACwyjBmNW8zrcfW8QfOnRoEqGJOeSFsse7JqDuSqcrsNQn8b7rrDp7xN4mqBOs7hXBZh1YMyBwIDGzBRe9Sxz6YMKsrGfFMHCZ3XE2bZisX9uIbf2jNcs/r8BFKowXVDOTzNoFnI0zEXvEWBoaqFaAoQFWEqktMLnVp6xnsiB+3rGoy0bLNuAnAGk8IF8K9RdFRsQFRkLUOWUkjQzc30ZcGj/firlpd9Pp2eGySbSSF1gdiWZcSUJDIx0lkx/B+lGirn9FaJWTeegpw+6e6BaBa8BbgPqdXWMupbB/hNKL5unxhPPv8Qd156mc8sqNlW3sn90O/tfDJ2zrwPTFvSt0dF1kLKK785wcuQ0qRYdzTKxU21kU0Oob+kZmsMBNinrSvIdFVzZYL5SJ/A0TD/ACOMGEtk0vpS4mkbV85CaTs330YWOJgzQNHTLRDNt/MCn7jeQ0ieRsEhlEuQ6OxGaA9RBTCOlw+lRB11KkqYqctYz1EEyvVplGcs6Stz0QIS5vbIFxBjUJUEVnAZ4ruoQIoxIdpzw2JsqmiCZAVmFhAm2Bomkypf1ggDLB1sYOKZLUvMxREBySYsKmp5pUPN8ol4Tha9UgNPAbmaR1AAHHxeXgWCQZO0a4GbociGZVm+vlqD0DLgvQiMFlQ4oDqpiXFanEnGLZRUzIgyQAuH5GLShhrYTIEyQDTCyYNgQeDA5Ab05FUVgSRVH4NRVZgMSZBncZNihFif6QzMYxKd5hkWfEAEaOuIfnfZ88TB78CSP/S9fwB2e5sUTz7Nv6tiF3qSYmJiYmJjXJBZjLyTSh0YBZIAFZA1VdTd2xsb8U5iZmeHxJx4FYLC3h1LhStKpNO3dHQhbwwsCPM9H0wSNhhNeegcEDRfHByFMsm3drNmylc0joxyZrNMIqhzd9RTrttzMFXKY0bkqrisRmkFPNsfg8jTLV7Szav1GrtxyHZl8DsdpcOLIYXbtOUGxFJfviom52KmFt8WUqPGwt53fSv87jporGWWY40zygNzH3bSzEp0xlEwxjnLW9qGKfZVRnqw3co6sJCBYyJ98NfNVyUQVplzYcUSSSgk2DgrevVpdACi/nJJT5lDtiQThg9RB83xEcLYpxXWQIyQJVPzRwvY0j8fiS4wzkyXPhlMPKBd8mB/H6uzElTZVR1CugemHzl2hxDFBs7hjIqwj5Lo+2JDI66TDFkkK6NRDg6MHMhTczH/i9Y8OZGxI2c390MNblATqR/sbSI7s3k21XFqyjImJabycS7Yri2/rTE/UkePTOCRJpetIbVHRNAGJjMqJzefBNMF1lYnUaahaTulWmC/D5AyUqbPjwAE2Xn2UoM0iPdBNbhmsbaQxDBsEuH4dGdRwPUnDUQZKTQgEEssWdAwKNqzzMQzQcLFNh6ovcISObacwEjmSVpZmaEh0dEFnkFyuhNQF82PT4AfoWoChCTTNxNLVNYKUPhouelJNy9c1gRHVMZDqb+D7iFoFyxBksknSuQzpbGd45MsgKmimhtsQ5FIa6SQ0fJ1MWwtCtKhBXakTyACoIXCU4IoF+PgNiVcLY1ClMp1qhmrballpjUJTplQroWbr2zqkNCXSSl0J7oHvowUCzwRXBshAntHHo3zdxSnH0VT9InOMU+YUDQ5h8gyzBFTDvqTKo90M7pASTaWjIiiCkwTBfmreY5g8gSSNoAu9NIhgJaLjOoTMg1MEGmB0KidtMI8Sfm0QNRANtSNRIbrAV0p0QoIfOokDF9x6uPk+UFWi7aLj3jy7oXlmRo+JRa/VEejnPL8uZrqw6SxpzO88hZM1aBgm0rRe+40xMTExMTEXmFiMvaB4wCnAVzVOk7B+FeiX7uB0zEXCf/qrL9CZa2Xz6nX82ec+i5VN0fAa1Bo17ISOO++iIdDQaDR8DEzcQEM3snT1Xc57PtjOzOQMXq2AlQr4rf/zb1n3o89x/PAhJqcaGJl2Nm+5hq6ODnLZHKlcG2Y2j6kbjBw/xO7n7uPkcBXXeyPLMTExly6R4/Ufnv0Um7iebu7kD/g6ZSSHmOEy4H3AX6BkgAmUCHsbsBPly3sjD8UY6CRZKggsFL8KYPdwwLEZya3bNO77usO/vdPgjtXNS7LI0+YCoyjxZ4UNOQtektA5sJZ6vpNXJ9O6wBQplkotC65QlsozZ14Enq341tyUz65nSoinvsvV730P3et76ewTiGUCKSWuEJSE4JjQVM150Sw2FgCjJxrIBixPpzDCZXuo/lEFxmrgG8rx2CZUQufrlYUWy9HhzPWFLFuBmpDdF7anH74h8H12P/oo7vTMkmWNH3Fo6UvQ3d3N9PgJ6sWAo+M/Z+SAwYYNrUyfKFAvN9eYSEEypYRYz1c5uOkUpBLKnVlzYGYeanMqy7TguMxWX+HY8VFe2Xucg+OCT316iL7+AaQhmS6dwqsfZm7OZXhScnwMbMPEkB7dywxWXWZy5y1lEkhMJC3dGQa6rw1bsz3c+6PhUU2GLRHJ+Xky1o1krG30txZQZ2ghfE8qbCmBGgaYQeWnWuGyQwdxoCMDn8DxqBSrZFryaFYL6Ama82YkuqmTyLeyfk0F9IYqGmoYyh4tZvH9Ap4/jWHoQCK8FomKaTVwaj6Nmtoay4RkEgypdMe5KSgWVH2qRAYMXZ1PCQG5MDHAToKQAW7NwanVSHQmqQcq2nUp0RBEFAQSDVlYwDA7+QE7eIXTQAcLnlVSwA3omNwAXK56nlZBDj8A7ndo8DTHwyMCdXRmyLIfAw19+mUEq1DhMOPg3YjEIeAoMI3AUNkXMg/6BoRbRmgt6lh29cAGAYcCZZP3q9BoQBDFKJRonumLz3yNplc8cktHj6lPAB0bjUtTwLyNHn7p8tu59wufJ9iiceQb20nd/x0e+96fX+hNi4mJiYmJOS+xGHsR4dVg/vDrn7IWE3M+potzPPHyc9z09jfzrnf8KnfffSdvuvVqGt4svt/Aqwe4rodHBcMAUzMxTBs/nSHTu4y+1To2dXJmA4Tgxrf8GquvHOb08GkaRgJLt5F2CkdLEtQ9uvMGI8PDPPLYT/nM57+J68Vl6GJiLkVslOhgA//AKTQOs5UePss2vst2VhDQS4oc7VzPCLtQzloPeBC4HRjhjR1ZUMdnhgYZEguP+Shh9Rt7YFuHxtZklV/6vT08+Omr6MgtlR+TNMXYAZSc1kBJLkkXAi9HEJw7ATbKfo3SI71wGXVUSue5clkjSW3xxaFpG7T3t3Ll5z/MjtlJvv/Ut/j6/Q+xbts1jJ04xODQEBs3X8NV226lPwurhZKaJPDEGBz5WZEOC7auTJ11ne2LKoFFfr1/CmWUJzSDkg8XRzCAasuqA+WJAE7tg8YZwwUj0KN3s/GK9eza9SzLhsALIJNLcdNt17D7o4/iTKkp9UJAfw84FZh04PQEbB+FqQpkUzBfgi99DYpjgANzE/CN/wwPffVvaIxInGmJ50n+4/v2I/oPgAA5JaERQC8kOlVNqJlhB3xoaXPYtGWG993yNBq/izq7ngZeQYmq16L86T0or7q36P+xsGWiEps2TUleonpGa9hykYCboCnW6cAMiIMQDKMxS7ZrFYgt4bKSqF56kGaafArahgAdGZTx/RkMBNCJoSUwNB/kLNQL1BwHTwhyuTJQRcMnaaqo1O3PQl83tGTVjP7D+1UsrhmG1xuGEsJNE9Jp9ZqECbqp4yMpl4vkB/JIXweHRWfjmUQlSW2U9PolJphkjGaCrI9KlX0LKQz+HHUWVcB7Do58jSm5mzkq1IEWVOxHBrBIIOgFfils69PAc+G6nuM4RXZSYBLJMqL+L2j1Na6hA8u+F9reAas7VIe2BSQ0kC5488qZuyT7Nir8FcY/YNAMIDGJinYp0Vm9p0qdOo1zts7FzDAjvHLsaa741F/yo/0/4+/nXuRALS7gFRMTExNz8ROLsRcRtRocOaRG+WNi/rlIwA8CavUaP/npwxw4vJMHHx7idz76Pjqz7XgE1HyXBh6VYoFkIotp2uiBhqaFU9ZkCp80ALrRTsKskDIKVMo+ugW+KZGmIJnLMD4zzpe+8jV+eP+Pcdy4jE9MzKWKi7o46AMSSPZzFDtr8VtrPsB3X97J9sDBp0GKWd7OMkpMcgKHcvi+3SiZYQjlfJzmjRdZIBF4izIYpz0Y9ZTn8O7lsOtwhZ9P1vjcv15DW1bH0F8tQWqo9syjxO4wPhPLBCsh0I1zy5Y6URqkklx0mnEUJWDtwnYqoiXVwve1LFpWpkWwfJ3PV/YfZKa6iwP7nqS+92U+8UefYmz/zTz55A/5yTNf5B2fuoXP/Pkn+MA972TTmmv55n17eenwXm7YdgMt61bwo+c8nv76z/idj21ipODwDw8Mc/2a1aSzWTas1Vk2AN9+Gvq6oDw+T6XgINq6uOEmyCRVnMHEPOht8MrzsCwNd25p7mfAq4XcKBV0BpipQKEYUJsM8wRefdDwaxX80iRtGejJC5KZDJqd5ODxHXglb8FYKADbhn17wbRVDm53F0zNw/S8En2zPSA6wDRAN6DmwYc/vIm58dMc3DPFY0+A4we0dED/MrhiNdx8nWCqJilVYH4Odr8C1ZoSGNta6owc2UPf0APoxuFwj69HSc9rUZ7NaeAISg7PofycDkqqjsTXKLghKnE2jxom6ADaUJ7O3kU9xwNmVUaGoYOeQ2hdNIVbM3xtVDBKQ4gsC9K6ZqKLqFflEcJGSg+EDmYR6fnIwEHKIhR83Ao0KqqW1/QU5DMqBzhpK7OCbaq2100VZVCpQSXMl7UTqq6V4zlIXYTpvoJ6Edwy5/F+RqEgHpJxHqXCMB4i3EsbWAWs4jIM7gGWI/gJShQ/DvIkLVTwCNBRMrhBGzpXodEJnAB+yBx1HGqYlGlFYzseu/DYi7dECs6HrSWYQlZ/hKg1IHezOvl1B7QaGDVIalDJQZAIj0H0SeuFx92jmRUb7Wdj0X0f0GlQw6F+zta5mLEwMYsCZ0eJodpy1tYPUgxmOLEgRsfExMTExFycxGLsRYJEZfIncqih/YWL5piYfz5j4yOMjY9w4uRhhlZ30dfWzeDAMtpb8+A6VAtlLM3C1k0lHwQCYYCGDnr088VGExamphG4DsJUfdbHZWJ6jKcef4ZHH3uKPXv3X8A9jYmJ+ecS0KzBnQLGKbJHjnMomKQHyQgwHmYUXkeeK8ljUeUlykhgFiUD5VGiRJiO+Ib6RtPQ0KXFjAeHDk/gpmysnjwZoD7nEjQCWtMGt29uPev7oyuAqKhVVGrHAwjAtNTn7/mISvhEknA0UTl629mORyTPLMayoaUd/NMCoafBSaDNG9y0dhXTCcHLTzzGc3tO0W/B9kd+TN7VmN8q8cs59j19nDs3byOjmezeW+L++x9g20aTsXKCXc9PcNNla3j8sccY3m+zZX0f2GsZnYTySYlXkXS1B/zg/kfoyXXT2dVLfqibo8cku/dU8ft02KIyeSMh1lzUVnLRrQ7UPahUHIrTU8hzdEbfbSCdKsv6O+nIBWRyGTw0du45jowMhn5zAviJYSUApltg2QBMjsLMHBSqGre9pR3T6sO2DHThU6vUefNt/UxOlOjuKuBTw7KhvQMGBmDjesEt1yeZnjMozElmJj3W9NUo1NVqWzM+aa2I4GmUGzaKJ2hBCaHF8FZCibGEr7Fp9qIozTlysNYW3bfDFrTDZUa9wQnfm0Vo0TIjITZqiQbKKZp91eNC6AihL1m/EOF0fF1HGALNU73dK6soVOkrUVXTVG6sDFR/b21XkQ+Grp5DhAYGoXJlLUu9r1H30XQdw0igeTqVKYE7Rzi0fDaCcLtdYDcv4zBFM7jAAPppp5vVCDYBL1PiRXQOkOI0hK2WRWCRIEU/6tMziYtDkRIWh3EXDUuVgIBecpgM0MBjglGg1eikT+8g06igUQevBO44JDxYbA7QkQAAIABJREFUbkJJwHgAhgspAW4WHEtVjcOhGQSy8InBUqesSzOyQJ0tJRyqXJqD6CmyZN1OEnPtDGb6WKbt42gww4nzisuLi5jFxMTExMRcGGIx9iIgkCr/KtMCV90CupGjWQIlJuZ/HvPzRT73p18E4EO/eS/3vPU2vPkq5fky2UQW3U6haSADDUMXGIbANqMfURIhfDTdQ+g+uuUjcSnMldi+fTu//x//jErlEkmJjAqSnLUATkxMTOiFw0Z55/aWT/J7L3+GX6VZUGoCyVc5zWe5kh4qHKHMHErwKKPkmW2oPFlJU9J5IyA9iVf22FkM+NL397JufRf3vivPoAd/9myVmzfY3Lnp3JOmIyLppiLDNpXgNpQYq5/nCs6TYEpVcymSxbKoY5M62/aGf8+m7waA1DTuWreeE3PrGW63eVGrkBEgByDV1oVhr2FgAyQSkm9+61ucPDzBd/7ua9x//3O0pi1SgcPMgUmmCt/hkS9nsO2VXGal+fX35fh//uT/4rFjGW7edA9f/NkavvcgpLQMvX0Bb7ojoKPjE6xrfxv3vP2tfOyPb+en33Jwjk8gUgmgf8G7adAUYiNJCprxDpYOuCXGR/dxLq+257oEns/69VcgvTq2pVGtVfFLqNGFOgthyHM1cGfBSkK3DdtWgh/A6SmYKdr84f++jdXiHVjCRlIBRpnkKPkgTe/mLHes92hfJsimwLYEti5I005/axZaA1hVhetPU0TiSEAKOrU0aoq7RAmnlfCoHkKdlQ3UGVpBCbYTKOF0sRga7oQsArWwMFeShcgCOQWiStOPHYmy3UAXCC8sWlVWDlcZOWDbEFISyApB4KGbcwhRAlFDSifcntMIAVLW1bYKH80IlLIqWmjU5jGERJhqzZ1dSmANQlV91WVQHge3Br4DekodVxlG3qYzKlu2XvGxDYOUnUWWDAonBWI8ynE9GwFgElDA4bscpkFAM9YggUY762lhNZIyDT7LaUpk8MPzSQAWWQyytCO5nYAZJC9S5iRHUI7XTkQoCEuOApv067hOy+OIKfY6D/FFAtamNrE6dSPMjajjJyTYK0E4cE0SagaMG2D7kJbQSEFgg2OEx6x5zdYcWmmEN52mMzYSY2tM4zF3ic5fyNFLl7aOrsRm2toy5NwdmN4IKvf4XETDVPHvrJiYmJiYC0csxl4EHB+HbB7MNLTkNET+d6H+t+DuudCbFvMLzN9/+Tt89SvfRUPw2T/493R2ZujubqVarTJfLqM7OraWIm1bKBlgDtcfo+YUyCcTDB89yuOP/YifPP0Me06UCC6lfI0rlqt5jUfHL/SWxMRclPjAJCqqYAAlNUwBJ4HfQE1q/q+obNjPsZs3ofOHmHwcFwclEwE8iZremyD6FHlj8OgTT3LHO97L2HQHP7/vj7lqwwpmqvDbj8Dn7snRnXntZZRQ6Z89wPEK+Dp0JyCTgny7KiB1LsarqtK8bjSF1sjzGGXIRmWLoqn8HspX6bE0puA08BNH8t+/MM5VCZ2Zwy30d94IwP4TMD6dQHmh4d6rv8xz7vN0pSC/Hk6WJ6i4dYKagzFXZ3TPQT70r36fp578CnZPC/AecryJrOUykEqTAPbtqdCXshhst1A9sc51a9fS4fXzyY89z/CxV1iz7Ra623oAJS0uLgi2uGmD8PkJVLGtWjDNz19+/JzfVwcOjVB5ZJYP/MbtlBsGgcxSGnV44S93LhlJkAHsfRGy7dDeD606jM/Dcy8pIXzT1Z2sE99HCT47gBeAEl10kevOEnRdSVLTEeTDI1ADpsE5oPZCt8DoATrI4QHlUCCNZk7NouIF9rA0GdejmQU6CzwPvERz4yNBNqnUTMcLxWUNfKmqkNUAQ4AuVacxaRosLaGeKwTQEAQzEr8Ivi9I9FjQ8JmfDDhyFLb++nJEzlDBrlggCyCiFFYJzgxYLdhmM8c0HVZvq+nQmIF8i3LBenX1lW0AMxNQr6jFJhLKzKBpKvUAwC+DU/JxRZWSW2fnUxN0TCqX/tLhj8gn3iyANs0o/8BRJsJnW4FeBB/gSiyuRTJJhY/yVwRsJYr70FGxDr+pjiG7gb9hP1BAYgGrw2UJ+sPjN8EyHKyb3gqrrkamKtT/y0HuZYKVbf2w7kaVW2G4kG9TavT+nbD3TbCvCCPz4eGuQ8MFNzq7M2GPXzzsVaEpqkcD5hmajmiYJwjnNVx6dDPIYHoz+cs2woo8tWc0irXKa7zrbHMAYmJiYmJi/mWJxdiLgN0vTdHb2sqyVSlsIWBgIxRbOEuZ5JiY/2lIKfF9iQ984W/v4+++9SBtmSQr21L85kc+isDECAz8hOD4vmPMTB7j1PABDu7fzQ8ffJm5hsPc/ByF4iUmxAIcGY/DmWNiXgcFlCEwh5IQxlAevHUtV/LVgXu5Y8+nGCfgpfCH7R/TxheYZ4YADeXCPI0SQkKdhRl+8R2yteI8tckTPPm1v2Tdqj5eGBY8ewI+eTO0p8SCOf9MlE9NSTqTKDF2GpitQZsFrQk45oFTBv8c9XakhIlRaE0qp2AULRtNTgd1HDI0JYkkTWlCW7o4Tp3w+faPSuz860/Qce8nue6ujXzsE6sBGOyH9//2Hdz2zmsA+NCfXsl7SytIJEDTNX7tI7/Duts6yGRt8sVVmB0Gn/7rj7Fzf4W9J5V69vE/+zhpJH35JA//FHY9+jzDZhJnupvL3rySd33g73nr21aRT2c5+kOL0osNkt0JUj1Naa1C0w1bpJkAGu1rOzBfgZGjE+z4wQ8I/LN//leGYfZZF/tDJ6n7WaYmHY4fL5+1wyaTUKuqbNfMDDx+P5wchlQGelrVmoUQwDpgWXhkwRYBUsjwOSN08AZI6YJZUFsvNJXbHgUviChSoIIaIvFRcv1wuOc6TSHwUVTvkSiRcGP4fC68hVPU9TLYHphZoBWkDtKDoAxil3LACgtEGqSl1i9L6vmcByKJZniIdIBupiFpQjqB0VIhPXmM6eFRcstT6ElBIAIsy2RJsq8JIBDCAgykTENqBOwGmi6xDMimVWRB4EK1qrJkpyZVAbX2TrCyYKeUeZQAdB1OHlU5sy0tNi297WxuSVJ9bgzjdBWJOgcsQFuQ8BthmxQoMcqTYYtmUANRH0TD5B00+AkHOMCjSxyky4ANKLn1u5xghgkq9CMZBCTLEdoakvbViFoJwR4cjlPCZRxYMTGGM/Uko3O7mGIOC5upsf3481+hd3cvGasHTUjVtiuXwayE2VEoz6q9MPTQpRyp5QmaXnBJs5TdmWX8ohgD5Zh1CS5Jj+gABuvoY5UxhMjloC5oBEUcihd602JiYmJiYl6TWIy9CHhp5y42b8wztGqIViFYu20Vh8fSlGMxNuZfiBOnxoAxkobG6XyK/IOPYEody0xiZXI0fJfi/ASzM2OMjQ3z0p7Dl3YGZPXSrBocE/MvzTxKjE3Q9FydADo9wc1Vmw/mruWhyiuM+mVsAq7H42ps9uAyGhbAqaNkoyjBsIemJPCLSm//ANfcche7XjjM7ucPYnSvYmD1FaxpU0ISgOPDWA08DxoNqFRdZueKVKtV/HSKSsJixtDxyi57xhukCThtBxyuVJgbTuJWyudcf7UErV7TRxnlx0YTl6OJzCx6LBLPz5QpW2zBxl6Dqes3snVLC9s259h8uXLCtiRg45oOVi/vAAHdl2fpIIsFiADuedsgK1Yqh+7WrQbChMs2DpHphn4Vtcm124ZImJDUwTsuuf2ONhKaxfIVCSwB775nG+s2WVi65IZCQG9uI5dd08JAbzNUwQn/Wqh+FQmxUTyGB5RKHrOTFYpjo5zr2yuoQ2PWwymMIxt1xk8GHD109vgdx1N5uqYGTh3GRlWRrkTizLiHDGKRX1ecQ4gXQioBdAnREYwKMtVRZ6QW3l9DMwN0HlU27yRwFHUkO4BraGbLplgQY0UddB/0NM0M2AAlUG4Jl2/R9BrXIWgoR63mg24jZAGRrijFX0tCqgtLK9K+4af41WcZOyXRUoJkJqCzS61DSkBKAhkgZAUpDSCBFtm4hUo+8Fy1WNeHwAndsWXwXeWKFWoxWBZIR42vWhYcOgkDfZAYtMn39pMvaZyyplXRNRYPNvg0YxsARnE5wCjNAag+UixjiBKH2ctRXmGKY8C1QDe9ZMjiUuAwJ8lxApcKWUxslpGmBQ2h4hz8EUpUcZlGUMZAqh440I2R6CE9DQNJHWuwAzObIxEk0Q/40D+kqpg5dbW584AbZo+4TqhrLy7QZYf7FJ3VNRaCjiOH9UIaeEBUdC0qgnepkSJBq50nl80jUzr+VJGCU6L0C/3tEhMTExPzi0Isxl4E/Pz5R7jrziFuCIboEoKb3jLE3PNpyscv9JbFvNGoeQFHpsv8xX/7ChbNCY0xMTFvTOZQP9tNYDB87BSQrExx5Ynt/NHa93Dq5BTP1Y5zCJ/dFLmNNnQE0+GP/Kio1yxKFriMprQUJRv+ojG0ag1vvudX+Ni7P0VHW46PfPQ9/OtfumLh+ZrjM1Px2THpopspZuYE45MOJ49N4k1O0tvbhZXPUk3YnBqtcGRynmrdw3M8po+dwMob1GdPn3XdUqrMTNOX2EIgaRbvioSoSJ4Bpec4KHdsllcfj5W9Gr99T4a+DZ/kbcugL9mMobCB7hQLQbSR5y4AhAZ3vam5jr62ZkGk3i51AxjqbK7zmisFV1+5hbA2ExJ491ubeQzvfHcbvPv2hf8jAckJ9yn0by58f/lAWUJBwuRslbmpEngO50N6AaXRSaReZeyow9G9r369BIoVWNstaGkFz5fMTEFLB2TSkM5IGn4FS0+hCQ2JROIhlkhekTM2ksujEmSL1xL9NcLb4myKBMq7ubg1VqOiCUbC5XUB70K5c5M0k3RfD2VUqyZQAq0Pmg3aosn+LaOoEIho2GYFidYS3desYualPRwdKSPtgO5+QWenVEJrEBAEHr7voQkXAg1Iouk58NQnhk84ZuqDdNUt8KBehZSq+6USP+tgGeCbaia/bcPhYTDWQH+QpnNgDebBOVyhipNmlrRw1EPqqFKkx6mxiwLqPOgFlpMj4AoO8G0ewOdU+NxlJOlhEEGBU+xgBy5DpFlJih4sqqxgniEsdmHJVzCdF5jDpoZK+O0nQZ467toezGVb6a5souelzXDnCuiz0bw6xjePwtUb4MBROD0BehKmfHBS4FegXFQKtIxSoSNRXlv0fzT0Ev1fDVsges4B/LB/XnqYZLBzLVjtGchJnD1TzNRLzMdXrjExMTExlwCxGHsRcHDn/+D0yZsoV28hk4abt8BzeeU+iom5UJz/52pMTMwbhdMoWcZACRRtwFFG+T39IV649l7+bHYjX6l5/GdO8P8CX6CVzRQoUeXpRcsRKLnoOEqQsFACbe1fdG/+ZfjZww/xs4cfAuBHD73IVVddBTSlsMd3TPHkjpP4xX38m999P342QWtfit+/+3Lg8jOW1sEhBjkK7Jyq8emPnML9zsdVJaOzIhk+OcHqDRYGiSX11KOUTFCyTPT/2Qp3RdjAMg3+3epXP1dFTYT2UX2jgpr4nAyfj7yV0fIXe3kFTc9l5O3zaJakimTHxfm2i2mg+k4GJQXO00z/bKeZIzsPTNRh78H9HDzwynn2VOG7MHEA2peVVVDy5NlfV3Dgllvz5NsCnt1dIJ2Hm29X0+eT6TKPH/tbbh36DdJWnoA6FY5gMI+OREdHJ41ytiY49xGoo47A6xFRI+/nNuBBlODmLmqdqFDX6yV9jvuL6UUFkCxO620B7Tdo37qby099D88bxU7p4CXAsKlVi5Qrc2BAPpMNpVcPk5Oge6/KyUgmQRpKs80ug/6UKpTmC+Uq92Wo54aaZJcG+axBvquX/r63MfbsC0w5exfcrk0i4bIOVDhKmWeocAToBG7C4GamOcA3eWe4l1uAm7G4ll/mezzED5nm5bC1u/kQOhWmOMDf8Ax7eIZrgevQuJY0y7mL5vC2QT/f56G/ejcVlIxtADykjlAejdUkMX6wGkhCx0q487fgxRE4Mg2jJZhzIZEBWaM5tDJBM1QmEvEjN2yULeyjPnk9ouETHfmqeJJLgU5ypLv60Fd1w3KoP1ughhtLsTExMTExlwSxGHuRkExAOqUuny5rh2znHZArQvHxC71pMTExMTFvcOooR2wHSixoBTS3xr/9/n/gN8sJrqTCdag673/CMDdhsI0UL1CljoomsFETqBso6aYDuB14iF9Ad6xlke3r5ZsPPMialStBCOoBvFABvQGr13ZwzWUtEFxGJmExYKGmNAvVPibqeiAquWMB/RKMfIIP/sFdPL7qr5l69O+o7fzBq1YdBJLtu7az5cYMvQO9QDMn00ZJfzbNKduRC5VwfZGEEyFgiRa4eFJ0VGIrEj9WsDDTHHi1jJhYtL7Fj7soYdWTks9/IyDbKVi3QuMtK9U6oqgBQXOCtQjX7wGnK1A2IGMrKSqKJ4hqyBcbcHpshPHxE69qrzOplOC7X4U7/xWUZ1Dq8BkIYFkWRo8VmJ0DR8KmFTB5GF5+CqYmCxzb/aekfzdNvqufQrnEM49/lx9990W8qouhC5I5DQyLhC5YsxJuuRmGj8JsAZYPGmzYaDAzX+MbXxWkbVg1BJuvhP6V0NEBuYyJRT5sEQt1Rq1ADZ9E/s5Z1BkWFRMLi2kt5MyCEuuKqLPcDJezFdgUvn4aOBy+J5rWPxke3cjpawJXoZy5WYQoAMOkMx6NhkHDDzg+PEVLNsl8yWW2APkstOVsdCMR9owU2DXQK2iah22DV1OJCBjgp6FRh4ahnLG2CcyrrQAIBAgTNt8IXRs20N79ZgL9brb/+Gl+MuWzBrhr0fFrumKVA/gYgpfC5zcB7XSwC5NfY4QZVPLu1eS5mWV8gPs5RJk76Oa7DNFFis/wPU5QwcDhNuCXwlYJCNhDlXEeRSIJAA3t/2PvzaNtu+o6389cze736dvbd7ltWgKBJCTBSARNECgsARmWpYLFQ+uVpVWvXuF74zkchaW+Z6mllmWJUlKKOgBROgkhAulz0920t29O35/d7736+f6Ya561z80JJAHMPZf1GWOPc87ea69mrrn2Wfs7v/P7463s4DbmmcRda90RdLJrxCxttnECk31QWYEv/zcQTRUYHQxA9AZwb4BgLt5rXXZvNWnPNQySEn46KdqLO3fAHJLlF3fzS5499NATFBBBBmlBOwwI5WX33yQlJSUl5TIlFWMvEZZWYXYBto1D3oLylW8if3qOzsOpGJuSkpKS8trio77iz6AcYhkgg2SlNstRSozkt/IvC4dZXPkmU/g8S4SPyTuAL6CENi3YOV3rbKNcYbro0uXCrkOHeesHfpI3HDqEMAwqQEfAqK1yMIcyFn0ZC0leiTNG4mXTUkKEkkuaKIFGCjBNg5HRHvZefQPBMw/QoYxK5E2QUnL23CmardcTMr4WG6CFVi3yXpwnS7ydpoTVEK4wwRRQDeC8q1by1ONVevotrrm2xC6UD68Rr2MwXod22l4suOrX9Lb0a9qz15EwGcKefYKhkmB7TxJ7YJD0wR6UzKSTVJtAzlK1jAok/asNtKXK5q1VYP7sGZYunPi25y6KoLYM9Rp4eub3BoGapSI8fy7CN9W+HxmDKAP9+SwDe3u56pojWPkOOQuypWEOHngDj+0+yjPfXGRp0sGKlWnbgOnzUGtAby88+TwUnzc4dtxgaCDgkQfVTPRnx+GFc7DvANzwBji032RLXwHI4XQEME4ur73nMt7xFnoaftL6IUqs1XEDFVRZvcl42RJq6OU4yhEboK7Q7kzZC4ClqmvJEAIBtovnPIrn+Xhenf7SBUwzxDBNAjeg3YYgdJBC0tNr0t/Xh2H2YhjxkIBUPaPZirNhQzBMMISKvMgZ4NVVnTHDBisDDV+d99CGIAI/gOEDMLR7L+XRKwlliU8dO8ZKvc6WrnPXPWCgs3hXCNbCHd4MPE+bJzE4j/qMuhYTScjvs8I8Nd7OEQ4hmGaBF8gQsISFjwucQHmG91CghwHa7MFiEGnnwMghZA7BCCV/jnE5g8EFAp6nHO+RwKTEEGLXzRD0qTzeoQIcexiiCVRpvzy4ByBaIrnaeuLzq69qm/VXoi5hBkmgiOoB6z9FNgeD5Mn6knC1hXPc4/naOZrBxhnPKSkpKSkplxqpGHuJcOZCk6ePV9k23ocFDFx1hIEzp5l5+LXes5QUUNKLLgqRkpLy/UaEEr0mUZ8GuoRQL3CMJrdlivxw/7UcHVzms+dPc9b3aBHyEeBJYA4l/4CSPrQ3b4kkybLD5RNZsPvgIX7sQx+mLASVANoCQhP25dY7UQUvnqDeLZskE4nVJ7B2zQ739TNdGgNzFMKLZRTJ7PnTdFqtda7ViESU1cJsd0SBjpFwJMxFsDfO5WxFcN4DN4S/f7rN6NYMhcMlttowI5Q0l4/30UXdWOp1d4vL+nh0NIKWBY2u9y5EgjddLxgXap2r8fFqSXApbo+ReDsOSkbszap12qh+utafJASepLHssXL+HLWpM9/irK1rQlot8CIS+20XQsDIFptnzgYs1ySmATsDyG+Bbdvz7No/xhtvuYnevjw9uQJFa5zSG3qZadzD7KkWF4470AIzq47fC5R794Y3w4lpcFoRJ09FXH8VLC1BvQ0XFuHkHBycAisLvT0RW/o6gIfvq6JMuXwTJZHbJNmgfSiXbD5uNX2lad+yTgs2UGeziYo1OI8S93pQUruOIeguJuar6lphE2xB4E/gtOZpNerko15ENsQPVLxpowmWH1AqQ7mQIQxKBG4G7BBhhAjDhzCk1ZLUG+D7avciA+wM2Flo2iBM9TAM1W62rWILAh9cH4pjMLB9H70jhwhlxOfPPcNex9ng7kX7wn2gxSo+s3GrHAH+hDp/Gy95CNiGySIOf06DOynxz9hBi0Ue5TkWgAMYbKVEjSIz5Jg2DHYYg/SLHfTzJrayCwq9IAoq95U8BKv0y5P08wiIJjJ2xwuRBWM3bHsviBAKERwZhJkGVFrgNYBl1e5rn5ptVIhMt/DePfyhqwA0UVe6vjoFddZHiGwGLKCfAhk3wF+qUJvxOFE/S1OmYmxKSkpKyuYgFWMvEe7+5v0EuRHuvP2nyACHt+WY2JZl4/IcKSn/lBio0j2TJI6KlJSU70eWULKMSRJXEAELtRd4Kufx8aPP8tDthzh79iQV4GPAR1ETpR/qWo8WASNgFvgRlDvrchl/tG2LUk+eJWC1KhnIwJYeVarJIREOL0aQ+BW1GdPq+ikkWAGcfuEcy80C9F8FyxcJjFISnHoG0aytCZ2QSDF61r2LktdK8fM5lOhZNGB7JnbjAuMZuDOjfJLvvmsLNR8uzMPsdiXZDQJbUBPXcyRxAibrC3r5KD+fzu4sogT6YrwvoYAjmWQdVVR/20binjVJcmAlepK1Wp8VL7OKEtR6JBQDmK4BUxOwPAed+kana0NWGtDWgbUXYZiCd/z4Vur/c4FmrYMfgbMAbhn67Qz5oQJTs1OM7j5I26qx5Fdp1Wvc+Lob+MahOY6dXSSIoPcwlG2QLagtwD2PQrYHxsagNwNnFqD/CNgt6HRin6sFZyZh7KTB9QdUlmu5pxeVdGoAO0imqpeAK1FyYgkl3N0dt6BDEkoxHJ9JJ35N55BaqJ46SJJF6qM8yM24Q7bAOgXMUyhF2HYBiw4nL1QZHISVChw/CU4ARw5CuwbT53zu/coE//IDMLq1SL6nQLaUhSDAkBIpoRWovk4IORNsXcPMUuKr58WhC1kVX+C5ULehrwjjY1exfeR6HEcJlUWSfqUc4do5qk9ug1lczgN7UHEqZ1H91Qb+A/AneDSBj2DxH3kzf8RDtKkxhgp2uI5etnMzg9wC5vVQKkG+oNRiABHnK7RdqFZIhhn2A6OQeQ+CrLJKZ4CSBXUL9m2FK4fgtgxwPXz5QTg7Ab4bH9X++Bi6O2pEcgXrTxoX1YOm4vOZjfN6s1QwNpUz1kK1+XaGybQ8mp1J5lZnkDS5vOZYpKSkpKRczqRi7CXCyvmvMveCC/wUo8BNB2DpIPzja71jKSlEwDnSG9yUlBRQfrkaKp0SlMQzj8NMZZpb3/e7fGn03/E73hf4g6nPI4D7UAmUh4GPkzga9VTh4XiZy2mox281WD57irOnzxNZgxzatYXRnq1rdc1fSbEcfaNmoLScnVvg7Xdcwb3zFzj6Qt8G75DACWyaZFgv5lpdf3e3dxj/3V0oS++ngdKGjgD7d8XF2w21bBMl64x1rUe/B5KyT9qVuJVkArUu4KUdsjq2ohIvn0FFYuhlIpTv73j8e+wtXMuQ1bEOVrzdxRAWPah2JE89fC+rS7MbtNVLE7gqsuClamsFjsnttwuu2AenzsCjJ+GOHbD76gF2XLWHVrvJ/MoZyuUtIHPU5k9gOWd4xxtNRsMR/vgPF6lMQ02oNpXx7HIhYFGo6flSrn8AHDsJK8/B3PMhzakmP/tzt5DJDMc72upqbRclyk6TCHPaW/0LXa1rosTXGkqoexz4e5SkbcateiH+qe8DcqihmE78/Db1fqGm8oehRa7kMbEEzz4HX78Xpk7Djp3qPOUL8KGfzTO4FTzfw1vxGCn0srri0XEjHA9WVqC3CL0lsPPgmLEXN1RHkI/jbe0Q6h2oN2ClKbj+hl+md/gqGgEcr0AkEx+vdm6v94Rrz3WLPuDdwM+jknJ3AD8G/BGwF5UZ+wNs5R/4Oq8nxyg3MGLdDDvfj00JsxFC01NV4LDB9cD3IGtCNqdcxJELRgCRVvqzQBHcOE7AM6BjQicLPULZfZc78FwGvCz07oOREWW3ryzH5zeKz0k1Pq95Xjzck0UNheTRRctUOME8Lt6mKtoq0Nf5AKEDZr/N4Rtfx+cffQgvupz+k6SkpKSkXM6kYuwlQhS6uF6bmqvcEMM2DFnDwC3AA6TTw1NeW1IhNiUlReGhEiTnUV/piyiBJT+9AAAgAElEQVTPnO+3+LMXPsXr8we43SjQM/wD/PrS13kWJQFsBe4E7kHdfBgkgqB2UF4utJt1FqbPki8UyOf7MfNFfBLp5eWIsdpN6qPau4bKnTVN8KSNLA9gDI8RTW707gCfaF2baq+cluPK6AJDiT/y4ggF/YhQcQBGfNdooGS8XpS0Q9d7IEks3Sgztvu57vxYLeLavLiQmI5oCFAeTwmsBDDvww/koCnUMhkSf6htgIwiVuYcjt93D9WFVybG+k2IOmzYMaWUTJ5bouN4mDbsPQB92wRbdvXghXD+/ByIiNz5k4yOBQhy3PeNL3PVvl4efajCI99sQBy3evF/V32391L/df0A5qfBbcHqvOSnfmaITOb6eEcfi1tK+689lGe5TUhABNhsQ8126SfJFC2hruJ+JEO0WWT1wlEEdQp9RbKlHoh8hJSYwiaTKQM7EKygBN8IyIJYJQjbNJoejVV4+EE4cV5lux56XZ5bbx6kr28HhcJWDhwOKZdfwGvPE3gNnHaHZjsiCJTwHPpQrUKxCBkbpA2OA+2G6od5C7IF6KxCEKr3tAMY3/UOCuUdvHDiBX79N/8LQeCTRfUlDz1AoL3W2i9eQU/3l/ERxSkJ+KiBpzsY50oGGKWfiHfTYx6kkNtJobQLeg7GyQ8ORC0QLbCLIIP4IVXeQrOtDkDWUEMZOv24K9BDSmUTDyJYDcBYVifbd2CpAdUGOK5ahk58ri+giqzVgPehPm212KznIGgJMyCJmmjgskq0FmayOVDF+wRbitsZ2HIFhaEtGEWfSc7TIY0pSElJSUnZHKRi7CWE76tCXj2jUBJQtIeg5xaoP0gqxqb806MT/zaoXJKSkvJ9iyTJ6lxGiRt9QEn6PFp7HKO2wM07buOK0Zv45NLXmUVN+S0A16F8d23UJ4sWYy+3TxnPaVNfnmfPVTdi5ocolZPK5hvFE2yEdquGKOlEZ71GgC9BFkpY/UMv6WjzpXogkk9yXdoH1HkzSIRTnekK6tNfC6LaweyipB8TdS5LKEE3Q1KbXU/81v89urlYmL34Nf2+HKp/6fXpvFzt1N2CEss6EcwHSgyuAc0A3AjKmXjfAwjbIc2lOvMnj+HUV7/FHryYyAPpwoY6lYTKSp1QgshAsRdGdoIs2LQ9kDWfvr4inUYHp9xECpe5+RmihsvDD1Z49unvLB253VSPhTnJow83uea63QwM2Kgr7RxKvs+jWmIVX7YJMAjJEWIipQOyiowEfgBWboCsKGJRAgbxuZnl1WdA1ui3JYWcBaHARGCJLEamF4udJAEAdRJ/ch0pVPvNTcDCHHgZQf+YweErc+zYMURP725yGYmUswjqmKZLFAqM2BEshEpA6HQglKq2V4iKInBbKkPWzUIuB46nzodpQscU9PQfYaXVzxPPHOXzf/mngBoA0SJ/fHZJhifagIdNBxG3XoSSqofipW9kK69nP1vjuIY94gchdx30D8BIDvpKYPmQEVA2VIUxIw4Akb7KVQiBdpzZKh3Wx0TA+qsmgjCAWtwJfU81Sq0OtRo4vqpuZrqq0hkV4BQqL/hOtV2y8br0sIgWY33U1aViC1rUCDfZgLuB+uwZKIxQHhhDlEss185wlknaayX8UlJSUlJSLm1SMfYSwmnBuWcjdg8LsoYg1zcE190K9/0WyMvtq2rKpU+RpGxPSkpKSkKImuD6DOpGIov6crwdeJgpxsYK3Lbvan7yGZs/CH2eRQlmPwbciOBRJHPxurQv7HJCOj6i0uH2AwdZEIIc6x2k3/b9KJmoiZK69CT0DkoE7xmAUn8Ru9j/0mJsoB7Y64t26TJNufhho86hLgUkUeeyGb+WR/032AI8H79ngETqEfG+zpNk0OroAbqW0T492fVc99/dz+Xi5eskQrKFikToEPsYhcoSNVHi7Mk2zLXgwCj0CahUoTLnEdankeEKvMKJ2GZGCYIvlZ9RzkM2D3UHZmZgEEmtssy2vWNcsftKdu7ciRU4ZPMZAiPg+pvfykff/zmate/eNOogkLz3PV/hz//yg7zth6/BMFaAz6CmoI+gAiSq1OUgoRgkoh9XugTB3Ugvh9exWamG9O15BzuMAuXYu5zhFsLcPYRRBpd+grCIhcAELGES0kMfexHsQQ3JPIN24+ZyHlu3TiL9Fa7YLWiGcGIZHn2sxZ6hMzTqq2zff5bdW7cTBC0sM0ehOASmSWGwzXIrom0qcdW0QFrxwEJbRUeEHWUMbUjwcqpwV8aCXBEaGYiE5HP3B3z23qQHdsdzJHQnKLfop0ke+Jv4mbcA1wNjZHgfH8BmWLWp2AnZXTA4DDuzsDvuhEEGhA2imJhPM4AZ9+p5oH8YFsowEd9XyawaNVhLcNbDJVKp2S0gmwHPhooLS21otJVtOJ+J7cAGROPAm4AT8Ua7j1wjSEonqqEZSZsqdYJNNi8hg/Jl25kyuC6VmfM88PzdPMoE3iY7lpSUlJSU719SMfYSorrS4N7PPc5tt1xPv2WybajIvpt3cuZ+Lr9vqimbgJdf6CQlJeX7D50mbaAmQg+TyACfefwTPLz8GL/1mSXaP3OAr1QWOA38PoJPGO+jGD3Iw0xyjuTfmy4gtfJPfBzfC1qew2xtmUBKRoR4RRmxkNRD70PdqL0Aa6VpLKB3GAp9Raxs/0uuY3kWKnMwvGP9TPvurFYdhdBB6T7amapLP+nlibd7KP5dO1b1BOig66HjGLrRgrtFIjfpZUKUn6+KyqXVeKgE03PAAZRLUfcVA9huwX4rKbK0pQzShH/4BhzaAkUbipFHc34aGb3yAe3eXnCrG78mJczPQ6YEHR8qq3DvffDPf3YPg4NjeJEgV85Rn60zt7RMLlPiQz/4K/xa5m6a3+V05OUa3POND1Lqfxe33PQx4FdRwmgelR+6h4IYxCeLhyAUDpZdBNsll69SLk1RW36SM2EOoix5bHxnicFRsKxtCGnhBCofI2Pb5GwLseZVHkLJ8qfibZYR5hbs4iG2bjvNz/z8Hay4BmeWTvL4Vx9l/1VFdu0ps30siyWXcZ0KZkaCZUCgcmKXl1Q8QRjC0DbIFcA0lCAbOLB9GxihGmhwHMhmVbavEarfH5+u8aW/+GW++XefXmujOlxUoMpC9aY2qsc22YnD1ahM7J1xyx1kF+/lX2BxFxhFyBdhqA+OlOGwUKNPQ6gqhOeB6TYs1KFegdIojJRgOKt08X0oUdXZBq1xdcHNCJirwswCVELUk9r/DhRMsKTq4EN9EARQvQDtVSX+mg7I1bjtc/FxLaNiCgZRIm+NjQNDbCRZqjhxgMXmIUuGfWwhaxV49Nw3ON+coIKbflVKSUlJSdlUpGLsJUStuco3n/kyYXQNYFIoZti2a5CzQqQ3GCkpKSkplxwSpUO48WMLSncIIh9v/gyf/v9+mp/4vd+m87/+nPo99zCP5I+iB3lr3x6G5Bi/Vzu6ti6fiwWTzUuEwJUGJhtnp347DJTEJSU82IA//+tjHNjZw51v28MCyjEY+G3azcpLrmN6fonphWUGdgytuWI1FuvzW3X0gC7zZJFMbNZO1D6U2K4zZDU6RqGEkv+0zJW0hfrbi7dxcXs48TZc1rtmdcX0HEpWskn6RxaQ8UoaehkBRhauPgLFDAgXmis+q7Ozr0qMHd4xSMvtwGI7MVBqhHJsLtfAlZApwy13wP79IwwM9pK1QWDheBGu6+MEFR6Z/DpB+N3P5pTA5/+ujs1jvPna34V8GSEawDCSPYSs8PiDZykMjDK0Y5wo65MzDUyRB8MiyuTJG3MUsj6CNgQROdul3ljGMDMUigPkczkyliBrGmSESvcVzJAU9dJT34sIMYTEJ7AnEJzGbTo4C1Mc3AMH9w0zMDCMZfahet0yUdAhIsIQNlZW0qqrulRtDwZsqMcJCKELnQY4BaVPBqGKMPBDJdwaHuSbEf/plz7Cc889T+gnURA2sUl17Rk9PJFHfWItEuERxbmxPwy8jR1cy+vJcBNs2wejFvRZSuV3BItf+yazPMdE5hRnO9Mca4HTDhBugOF72FaO0qRFNmtADkwbtkdwZbSVt4ibMW74ccQ+A3b0QDUL5yNYbSllv15V8QZuA2wL/JL6MMj3QmFU5XG4NYjqcf6sBFEAeRXKDZ1BXVltEj+8vuLtruO3cDGJ1q7SzYGFyRD9FIoFDg+8iRHnMJNzJzCqr/STNiUlJSUl5bUjFWMvITpug3MTjxBFampVzjYZGci9xnuVkpKSkpLy0midykAJdgZKHPPbDb7+4Oe47qc/xI1X30Kj5fK3D93HU0xyRI4xVBzmHf238sUL9yORa1PpLweiMMT3vDVB85WinaMZYiGzCcJRJZYKwGIdok5AJvJesvTO7MwcszNzXHn9EFKoej86/3Wj/bq4eBckEQFaatNFvkCdK501C0riuTiKQC+nvX7Zrm3rPNooPs7yRe+BpDhcFp1wqcTXIokw7Ma/Z4CSBWMjKoO/7UOj4zEzM0X0KsTYbKmMlYvA3LggULGszoNvwuAA9IyAYbuYhiRr27RaDYQlyeQzuKHLs+eOEYTfmynUZ89EPPTAFPfe/WVuf6dECFBnpAi0uDC7yqjZS19gUG0sMzaUJWvZEEXU2w4ELpmsjWkJIiPANnM4QQ4pLIRpYsgII5SYho0ldLrvEpIIseaT1qXp1HR4w8oTBiv4bh2vscroEGSsAEMEGCJCSovACzDMKNYIDUxTzcAPPRUTYZrQaakZ+8IFpwkdAzK640nlmjUB4YNcgoeOfRXnotOtBx8SZNcrZUBSo8kCVQRwDYIrOcJ242bI7oGdvVAKWDSmOdE6xvICNM9+A6/zHD6n8JmhRSJ9hqjBie7kfd1CF9jCU+YCq8MWpSGDreYIO+VuZedezMKshMUInDq0oySmLJOF3hKUh8ANQBgqo0G2VNCuWQRvAPUJoV2/bZKU6u45CCoMWRLhIDaZLxYMDIoUIZIMlLZg5wZZmJvk1X3apqSkpKSkvDakYuwlROg3qS4cQ8oQAeQsGMurzP7NM16dkpKSkvL9RgslNoyi8jt7UILEM8A9H/wj7viNj3Do39/Ko++9k6bX4i9qR3lb/638j9v+Lw7P/XNqXoPoMspGDz0Xr7o+cEFKSRQRC2UCiSQKJUEQEIYBMj5+w0hkIwkcNOGdt++jXJB0Gg16gLnjEK06DGXCF5k2NROnTzN55iyhfxVkkhgBfT+hoxD0793Fu7rJoIoZ6frrWorzSMRVLcFpEVV2/dQT2rUgpYVYs+vvIdYXNtPir45NMFAO1AWpJsTvFTAikn6mUzADGW8zgkYnYmG1xcmzz68Ncr8S/DBHGLQ2LOAlBAz0wflpVUepbxQWqnBh5hxWoY/+0SuYnDzLUF8PPf1F2q7N088+h2FKhPG9KQNw7Ok6/+FXXuDRdwwjjA4q2KKBwT46+SqytA3LHmHimcfp7xugZGaIPIeluQmyMsCwCgjDwrCylPN9ZPK9hFFAEPi0aqv4BFjFPoqlEhITFSgShxITovzLVaCKEMvkc/047iqGGWIYkC3C1Ow0I16bLeMuplXCaTSwcjaGVQAjgwwFtpAU80qMtUyV2yuk6gOdFrRMIAsZE8wQevLQdAAX2lMbt432hG7cCySwjSlWeZ5ZLGA3RXrFWzCzP4ocGibY4+CdX+boxN/xG1O/zOOoKIPbgB8FbkblYXskDv8BlMxrxc8vowIDJpnlk+Gn+fr9n2YvcBdv4f2ln0X86x8l15fDGBiApTyszMMFqS7AfAkGBsHKQrUFvgWFIWj2QLMAZqAyGjwnPso2yZWRJRlSgUQmVnur4082EwKDDAXqqw3MXItm6DJRXUSm35ZSUlJSUjYRqRh7SRGgvsaqm4m8DVv70nHelJSUlJRLHxd4CiUBDaGEsl3AH/JFKh/N8c4dd/HsLx5j7HevpeG1+MqF+/mxuR/nzE+c5K4vv4uHFx5ZW1cvSir4zmrOv3bITpNwYXLdc74rOfW0S2kwiygI2p7HC0en+PwXv8SDD93L5ORJhHA4dOAWcrkMwgwJZAenGXB+4hiOs4wQjjIESpCRRMqXFh8uPPUoE7u3Q/iutQJGEtZqjWshVYuvFkkxr4Ak31UXz3JQortNEmmgRdao631aaDXj5XXsQTH+uxw/56KkO+2n9FF9hvhvfYPaQkVhnHPhqap672C/0p70fjbjbbsSqh2YPAnN5QUWTj9N5dhX1ZTvV0hAjsiwNrxTjkL4/F9BfgCyY3B2WmWa7s3C8GiGwUHJr37sE0yegxtv3c1Nt+5luH+Yd/+bEe7/22XOPf3d79n7r4Kf/3cSw1jEAwTzGDzOBCP8izt/m4wYxJVNdt3QT631DBlRI0uLHE2qrSaBaTIgMmwdHMXCwhY2vtmm5dd57qmjIAP277uS3iuG4/YJMXHje1TdQ0ySnhCwOF/lwukmZ08og8EjD0OpsMqBK+rc+pZxsraHmRFEuLjVFs2GpKcEuVEI2yoiNV+EMAN+A0r9YGchkuCGSqgPTOhE0PBUP9joitCDBS/2JSdXhIuLDbwdeBMfpWffXTC6myjy+dRf/QS/Fz7EM3KBDPDvgZ8CdpBEeuRgnbs/RPXtbNwq2+LnI+A9wD2ognjf4Jt8vHk/vb9p8HF+ne0/8kPwzqug1g/PSbXyQQHXxAfQ6IeWhLk5CPKQHVK24VB71z0SH/tI1950D8eoK1siaeIRbjIRUyCwyHJs8X6MpbNUpcFzTBNtsuNISUlJSfn+JhVjLzmSG4nAheZK6opNSUlJSdkc+MAMSj8oo8rIhEiej/6R6uwEd/3NGb744S/wf3/5V3nwzH087zX42JffxY2rBgX2ci9ngZcWVTYLCwsV7rn7IX76ttuoonxqbgSFVsR1b76SrWNlXKfDxz9zlNXVFWr1Kr7fQQjJQHkBS0CzWWNpYYrFmofrNImklj5fJu4kUWcKz4V8Prnh07JMdzEtUK49FyW2jsav6yRJE5WuSfxcByU+6b+1a9aI36/lHj1N20cVUfLjh44YyMZtk0GJtXr/us+9RIm0uzNK/AyBjKW22yKJPfCAZgjtJUkmjAiaFVqVBZDey2+zLgaG+1k8W0/U6y6EgCNXQdWDzCCM7oW5GpybboJ1jHpzkQ+8/820/ZB9B65gfHwLp1+Yws4I3vtLb8aNcnztwUeYWFyiVYVgHjjDKzq93bzxx+DmH4DxffD4cTV7vVBYpbfvaeomzNc9tve+lW39r2N/5jYwr8c26xhymcL2I7jhBJgSX4ZM1paIQp+tPUNkLQsr08vNN9wGGOTz5dgVG8Z9ZycGw8AJlLQoUA2mEoJ7+0vs3R9SLMHCvIslwJDQrIc8eWyBsbGA3ozE9QKWph3mTkiyDtihErzbbTU7X0bgeXGO8AhkcxAGsDSpinq1JLRtVQhuoybsLlSXEJLkql4AVugnywfYTW7fuxC7d3ImeoKPH/1F/j44gaTOLURcB9yOKlhok1w/2s0doa6NPEl0R3csiO73u1CfkfuQLBBSj0J+iz9k10Of4tqZK/nB2z8JbxRqpQHKWjsFzHfAc6GQVRXrvCzIvHoQkQjiRrxHOighgrXicRFaNnZfos0uVbKotq0T8N/5G26XryNHjr/iG3GvTElJSUlJ2RykYuwlh1j3q0xtsSkpKSkpmwSJEshWUILEAMqbVWWFec/lvimLfzv0r3n7/jvxvICjkw/x1YVHuIm9lHDoRxWL2uxfqT3PZ3GpwteWHqCJknzsjM07r9nLzl1lxkdHCQKDW28L1qbtA0gh2H/FPtqdkKWlFfrPnKb03AnOzbfpeK9QMok6hL6D66pzoTNauwVY/Rwkco12wwYk58EgQS8nSSao63V2587qbQUoocpF3XRqj2p3vmy3E7a7iJc+4gzQa4CdUYLaKolgn4tf1/ttCrANaLcaVKrLvFpZP8JDmoHa0YuMtUKoWeNBC8rDsP+AYHduC1/9yiKnzq5iZVxGR3ZT7hF0mnPMXGjRblQoly16Bnx8E7btMejfMc7czCqNHhcvA74NmYwSU502OFUY3AKWoabqZzJw7aEcfVYPOXqBIVzOMnCkyuiYR70eF0LzoNzjg1XFs05QsPqxrCyBqCOFQcHIY+AhcLDyBXKMEGHiBiFB1CISWQyRxRAepmkyOFBADasoT3OIg4GBiP+WsorvT2CZWYQRIaM6wrDI5wfo7TMJ/YDVFZfxcdWchpC02h6VCti2pFyQFCyDyI9jUD1VsCuQcXyFBBHHpxZ6IVsApwOuA44DfgBB9NKDOBmSwYeLziRgUaVChw55c5Dret6DtWcHx72j3Lf493yl/iAt4AhwEDiMcu5rR6xGe1L19aDjNbrzkbuXz6HiP7KorO0q4HABf/UCc+48j/X/MdcY7yEz3gs9NiyiLibTVheC50IkQGZB5lDSbkRyNQlUYIIWZH3UJ1FSvAsy66JLNgNbGeXazEGOjL+dm+wxrtxygIq3yvwjs5vqOL63qNzmRHxPSUlJSbkUScXYS47kK48wwcp/i0VTUlJSUlIuMXxgCSWaGcAbUE7LOk0e4Cjvmj7JO676UYqFEk9MPsxzSLKcpYCaylt57Xb9u0qEml6v6ctnePftr+OGu95KaWgfljXID/0zgzAChEAYBlg2LQHzqwFzc6tMnDjLib/9NMvf+AwdbwOL5rchDCWdtqQEhLEUZLC+troWMHS1eX1jqF1+elmfRIgNUMKXjhyQXe/vXqd2IwbxesqsF3O1Q1c7CLX4anS9X/+dIcmV9VAyk45HMFDRDYaAfF7QFlCprDK3MPeK20zTaC/j0VY2vA2a3i5AzoC+Idi9x2T3NXv4wudrNFstBscatNrPUi4WOLXyPE4zYtv2Efq3lVmZO0+z3WHUDth98GpOZp9jruzS2A2dASiVlRC7ugCLp2HfzQY5S2IEkmIBfulDRQ6XtzFs7EVyNTU+xz8+6HD+gse5kzA2DoRxHq8dIcw5jhw4RzbbwOUBqhhkGMWmiKCAoIhJAZMebCtHqSSAcZT6t0pyxqtAgCTEp0mOIQTLKD/qGTx3CpErYQqDMKxjGT3Y1gAZy8Q0KxSL0LsbfBcCD/IFqK1Ab9ZgKJehbzjLUk8F15cEAbgua9ZqI1L5sIGv2t0ugOuBX4fOMggLwnDD0wSoU6gHJBIEOkBjCo82AT2ZYXbu+QX88ZCvPfRxPnv6LzkJ3AFcj3L698Td4eKhkSxJQIDyBa+nO6NZXwOQXDcFVA5tA1huzXHvP36YPZXd9L7taqz9A1DOqB2oF6ETQKMRq7859W6RR10xOnxEC3J6a3pIxI9fzwK5FznRL3X2so/bcz/CD131C/xQaRnxljLfbDxE3yO/x0oqPsYYqB6lhfiUlJSUlEuRVIy9pDBRwfrqC5MfQK35mu5QSkpKSkrKKyZAiQoTKBHiAMr91R8F/Pb/uIV/+9nPcvUNO7juM/08xipPoOSfnSjB7ZUnfF76VGotfu03P4X7m5/iyBsOc+Caw5iFceaXA0SmQO/QOHsPXEcuZ1HOZshYJtuKWSrXX4P92JdflUrtupKV1ZDybnMtGsBgfXqkFj4LKOnGQJ0zLWtoWcfqer9GC+66GFfA+qJgupyQRRJzoCdTe/HrPfF+dEhyNvW2dPoorI8+2I1yYFe7lmlHUHehVpUsLyxz5oljnHro6CtvtBiv1SII/RdXNEPtnDUIzirMrMDD9wU8dv5+ygNw5f4Sb3/LAL1WHyG9PHJ0gmefn8ZxquCUyIVgWSZWKcfO0V7qKyWssIEMXIauMAjDCMu0sA7aTBzpMNI7gBU4+I0Wc1OSuRMr7Ny3wvDgceAYvUxBxaM2A4tVaIXghco56rWhFMCuDx9j62iBopUhSxWLAZQvcxAYQ1195fhstknmxfcDe+KDbgMGgiI5dqHk+PPANDBPsTQULxdg2Vl1hqRDp11hYX6F5WXIWjA+CCM7oOaClYPBgRL5/gHIZOjdVqMlQjohhDUImuqE+x1oLUNrHjrzKlO2YKgO5LVUXm/zW9jpNy7gpR2kFvcj6AHeVrbhB0d5+vf/M3d3nuVp4Ebg3ah+apAMIlwscS2TFKTbiIud3znUNdD9eg9wRdzqLeDBp97GoaX/nV13fAD+9AY15eDjwJIH1RVoBWBk4hBpXbTNQn2XyK8dn3p0d2Q73pcczgbHciljk8XyczSnmwSlJsV2jlEGeQ9v5c/4B4JNFbrwvSLk8hnWTElJSbl8ScXYS4ossB19K9duwsRZdY+VkpKS8k/GHTfD0iocO/5a70nKJiZECRS6mNMISmyoAX/9i7/INUfu4E9+9W6u/7UbCaJgzU17K/AISoy4nPCBU6g6PHt7S1y5c4zM4D7aT8yzsDLP6uoS00sLNKvL1OdnadVWaLQq1Nw2q6vLr2qbHcdlbnGJMW+MvA0YyRTqbpFT11bX50oLnNpF240WXyERbLUAZV30mkEirurnW/FrDko6ynWtQ++LllO0wKvRgqyBkpoEqs90gJU6LCwrSXGlMkN78TisnHwZrbQxZhhiONHGVeQE9O8DtwaDQwPc8LrdzDbnmelZpJSxyWf6ufLQDbitKp3qIllpUMibhNEkXhQgLElvj6BXGOwoL1EOPFwXsm6EHcJAf4aegRKNmQ7mbAXLkmQtye4tYAbQqAkqpkt/3wTg89bbJK9/Ayw14fQJdf/YaoCTg/27YbAHDL9Du+pQXYFstkZpsEWu3EH50XtQfvYZlMA6Gp+JlfhvF6I2QtggysBeYA7wiMIOXrsGWERhQKfdZHVpiSCEYrmEYZoM9Q8wfWGVTB4MyyISJlbWRZgCz21Sn3OoVTxWJkKsDkQOrK6CbILdo06wuwwnLsTOXw8KJegpQpCFSgtanTiiYYPTpfNc1xfwSuT9aWAXQ7zB34mclfxv0SeZ4gLbgDejxFHt5rZQ8SsXf4HqRcnVelBBDxx0R3es9SDqomMAACAASURBVK31XWltXYIkB7kv3rY5/xd4z8+SefzT6sNjPAujZSgOQM1RobqRAV6ESl7OknjI9RWtr9oe1BWnr0CXNpsnFkaVJBtiF7soyiIzS7PYJyNMUaTIAeBuNlcCbkpKSkrK9zOpGHsJYWQLFLcfAkN99QkD6OhSxCkpKSn/VMwsQONyk8JSXgtCEvdid27o1NQU+fBJdhQf41fe/1H+7KufYGppigZJATCTzSMSvFxclIR19MIsU+IJrOIE56fq1JtVvMCHTIFOu0G7VsVtN3G81gYV4F/B9nyHpfoCgRxbKyLUXZRLC6ARSoorocTMIuvzLrUwK7vea3U9p7NmdYmxCCW6F0iKHOnYgxZJ5AHx89pxq4Vfvb7u5bpzbHU+rJaYbMBrQGUBsmWYWpimXl9W1Z1eJVHkIb3wRbGL2RyMb4HyoGqwgUGDXMnkya+1EV7EeN84e8evJ5sb4sQzTxO6TbaNFcnny7Tbq9imjWlGGIZDxllivODQj8RxQdqAC0U/IN9us6sIRhBiGiAMCAVYDWiZkmVXEroehgE5C4aLgt5ei2LHx22DFwlCUzAyGJG3wQgkViDJh2CEISKEwG3SaZ+g1AdCVJHBPJEzh1H0EEJ7mF31cAP8tknoZslml6BQR1gSGUQE1SZG7zBBCO2WZHnRJZMzyRVNhGlgiIiBfoHrShzPwAksTCMgkBI/8Ik6AXPHfRZOQsEE6arzaTgQWkAbZBscF1o1aK6C9FWObC4Pdgd1PN/unK79pnt3BDi0kQywiy2d7Tx77JOcDWYZx+VqlFvf6OpvcSjAiwYptCu8QCLaXryMRt/WX2y6DlFirkB5lstAGKwiLzwHf/y38BvvgEEbduRheByWl8EScXasVBbhdVeqQF1FumVyJIENLpKIedY7dC9leoAiFhkzgzFgULYGyfRkoaXPTEpKSkpKyubhZYuxQggTeByYkVLeJYTYDfw16n7hCeAnpZSeECILfBIVr7QCvFdKeeG7vueXIblymZ3XvxHDMFXUvh/SqLz6LxIpKSkpr4oXzrzWe5ByGdFG3Qx48e87UI7Is7NnML/0J/zCf/0sx089j9fxWGgucIJkynzI5hEKXi5TwNSZaTgz/T3fVsdtMbs8TcTVGIg1cag7VVILn1USN1+32KTF1e4iYAaJyNpdpKs7K1ZPmNbr78S/V+NlciTxBt0lh7oLjV0cUeCTiLF6WzpPNnKguSpphAEXpiepNWqvut0AZOQgg+BFCl+hAHv3Qf+ATRlBoShoe20euK/CFTuhrzDKzrFr6YiQC5MVirkCO7ZuI58fotVaoFwU2IZPq17FDz0G+vuhT+D7AjeQeB0whMCUgsNb+1VLRwEy8vBClz5hIFyB04C6CAi8GuWsJF80yJRNtpd8jDJYJYHVaxD4EaEDkQt4kI0gkhA6Bq7rsrL8AqbhYxoheA3CRgvbiBAihzBCDNEGESBaEKwoN3C2dwoG4tpRAYR1CLI9hEGGwLeIZIFMPouVKSClh+879A3A3Ay0Xcg6kDcMQkJ8M8Rrw/IELDwDxaIqwOY2wZbgChAdFVUggMCFTkN1At8Hw1YFzsxofb/oRvflcN0z+lmHEEnZ3EEuGOMrz/03JB32AFeiHP2QXDM2Ly7eBapv6jiOiOT6eFG/IhkQ6RZrdXyIHuzQmACLC/A/PwE/fhXYW2F7AbaMwERbbTmK99DXV2H3VtokgSEm6mpRV50kYoHN8xmrPoMcHLNJVI7oGx9ClgV+M6KV5sWmpKSkpGwyXokz9t8Ax1EDkwC/CfyOlPKvhRD/HfhZ4I/inxUp5T4hxPvi5d77Xdzny5axsS186IM/TyZjEgILCw0e+NrJNKcgJSUlJWVT00JJAquoG49tQJUmX3Sewf65D/H/fvh3+NK2B/jI5z4C8bJjqOnBaVjGq2d1tcKxJ5/i/fJHyKAmMHdHAWjxM0RNTM+S1ODW1ef1HUjQ9T6dA6vjDLR/Mkci3mbjh67f7sSvd+KfJVTpp56u9wfxa91CLCihy+9aRotqZtdP2wZhhZx+YZHJk2doVL7DzESzDcaL77/yedi9R7Bvx0680KLthyxXVglR41jHZ33mZcQO3sqNdxr0W6MMZw4CV6OuhBrQUqISp8lQxCRHIpIFKClPt94OYA7JaeAYUEKQRxIho1meeuBPaXouoRvSaYQETdixA4a2RJSDiMV5WJwFJNjxCctaEAiftgsry7B04jRlU4makYBSXwcz1yGXV+KoZaGTCgi1Gt4AmhAFKp92/pnzZHNZegeHuPktN4BdZn76PNXqPPW2QxBAoSTwfZ/5OQ9cGBwDK1Jiq2VBexmimlrn6hyUy8AQSA+WV5PIC+mrmWO1WAjuuOv7xUZoh7dC92zl8TYB0V9ippjj/5x4jO2oz58hVPxAQBKBEKA+ny6eDF8mcWxnv1W/igmI62+hrsMc3+pLWQXCL8HbXPhP/w9ccZMKl33BhKarGgxYL+Mq16/yvNfjrek9ayNpIGnRYvPMQJgFnuN5dnn3cv3k7fSN9tF+EubOt3iSE0RpREFKSkpKyibiZYmxQohtwJ3Ax4BfEkII4HbgJ+JF/hz4VZQY+874d4DPAH8ghBBSporit2OoR/DuN5tYZnxT2TgDx38f5Ga5TUpJSUlJSdkYiZIDTqKcskPAMCH/hQeY+19/ytWDP8AnrjvKTz91A6Bqub+6pNQUjTs7zcqXP4/V+Y/4toE0EhFJi6daBNI5mNot2+121TJhh0T00sKUFpX0OiERU8+TuGx1HEEelYdZQklFWj7SgpR2E2qRWP9+Md3bbwB2GcbHIViA8MmvEi2efWWNdREtTxVSvZhCHvbsBCMcZM/ucZzIxZia5IP/yqddr3L46hyBGARxgN35XRhrPmLi1sij3Ys5roiPeCMPZXeK7haUmHtn1/ICISRXvfHDIO8D/yhB/VGe+NpJhACMLEZukLHDdzK8cwbHaRFEUB7YgeBtSEaQGEThNIah1+gj6WAYW0CAEAbqll9lwuajBnnZAWMHiKuBBjYVhqIqA9EkiDqG0QSjCeTx/XmiSJDLCYJA0l/uY2XeY3a2RXUOBnthag7qi6qF+reAuwTnl+GLEzBqwBvHIBfA8qKSsjtAMQIr7hytEFwDogyYL3symZ7Cr74GDQHm6izNiioz9zrUIMEyqk+Px+/ScQXaVd5Nd8G7b4Xeag7V/3X8gb4W+lBTDteTQ9WUmIavnoOlPXBgFIZL4NaVGu5qGbj7iqt2rblEImfrIwk3LEZ2qbIHOEgv2/1+qvMTuA8H1Fo1Vmvn6V336ZGSkpKSknLp83Kdsb8L/B+ogV9Q9wlVKaW+TZ0Gtsa/b0XNwkNKGQghavHy6Xeqb4NlwGBOIIALdZiorULwKJvnNiklJSUlJeVbE6DqPLuoqexHcHm+9VWa0mGfexM3cA3PcpIOTupz+k4JOwTtWSpTbcyxInbBhCwULCgIkCIRW7XwqWUaXfRIkmS3ahE2uujhkwhLulxQgWSidL0FM3Pgu3BwF/QWlWxS6tpVneLpdq0XkmiCoGtbej+0IOsDhgAr9FmZO0/YqUHof2dN5w0QRR2UDzIhCKBegeWlGoWBAiInyeVMdm0d5e6nmlQq53Gcb7Dnjg9gC5uIkBCJuU50lYi18IeXJyAJbJSQq86GABCCTHYvkEXaWxCiTNM/RUdKAmsAkb8S03odZmkrRq5DKC3s3EHgJtQtfYSSGnVQhHZTDl60Xyr52Vjzcg7HDw9wMHEwOQy4IJtIOU999QssLy3jeQ2yRUnHhVajw+JcSGUOBoqQNcF3oFKDoK5iCWaX4Ow8zISwNwQRKAfs+VBlGbsBeIGKWnB98Ly4qJupjmij1uzOSU5I0pBHEDSjCebjsoEOSWzASWAete183Gpb0deLTi321/qj3t5L5cWKrkfUtayW6HPx7+swi1C8GupNOPEolC249n3QX4TFeE8j7XzVV2CISuBejteYZy3/d+08ypeMdvjW9KOk8e8k4CBHcjW/PFaBh5hgMfwa09UZtnSuIQwEp/xJTnEMueF/jO7AlUsBgfp0bJN+v0tJSUn5/ubbirFCiLuARSnlE0KIt3y3NiyE+Dng575b69vsFPvHGRjdsxY/f3zW5YXZCjDxWu5WSkpKSkrKdx0tCTSB64BjHGexHbDUrjFEH+ZLShkpr4wAIZtkvQDDU+7B0FYygCAWtCTkJZhGXHs9VrO0GAvx1PD49+5M1+7iWtpNC2o9OhPWAVoB+C3otJMZ1RIlDzkk4pTOhe2WKJyu9esZ8trNp4XiThvaFYfG7BJTJ54g8Du8aqFDAHkTwxxGsMzFYqwMwXOg4/i0HF9FNQQRoWtw9hRYhUXKvc/SvHWWyuIC7U6bIAzI2hmkhEw2QzaXJZfLIrDwPAcZhRiGQGJhmBlMU2BZkMsZGIZEIBFCC41JLqiUEVJmESKDMMcQ2Z1YPQKrJ4NRGIbMPmAErB4sK8Iii5rfXiTxQY+i5PhuMbaXRLrUCajdQp+WC+14XbDmyRAOyAV87wvUqm1836HXUMtKLOp1ycICbDusUiA6LVhdgsYijAcwX4OZmnI7DwG2gGWhXB5jQKUFOVs5lF0fwkgNKlimEvc3EmN1X01e6+5tOUawWGGRc6hoixpQ7t/OiJlnenmOEIFHm+D/Z++9wyS56nvvT4Wu6hwmh52wOWlXq1VAIAlFkhAGvSI5YmNhLhdjXxvMNea9xuHaPPZ9sY2zfY0BCzBRAskCgQAJSUhC0qLNeWcn5+mezqHS+8epmu5d7UpCK7ESOp/n6Wc6VJ86XXXOTM+3vuf7w17xmYq2TP9YZE8Zo4GoGuyp9bYyjmiKxNCMBdFp+qib3dUgFBEtzD8JMwY0fh4yYQgroDkiu2Fljy7CQ3yc5pEMjkLgL27g4a1ccPnJMPw2zoUgMfrZswwsM8dJb4Fs7RCDtROEiDLDMhOczQkfOMxfTLQmZEskEonk5cqzccZeAfycoig3Ir5bJIFPAmlFUXTfHbsKcfkV/+cAMKkoio74Rrd0eqOe5/0r8K8AiqK87P8abXn1z3PZW35lJR72vkfmuO/hufPbKYlEIpFIXkBs4AeIREObYxzm2IpAJ3l+0DWF116URNE1SghX8iJiVXPZATtQUcOicFKQBRuIQ4H0FgbwmoKTTXPBs+ZvExTj0jzhVA3chMkkDG4X4nsE4YAMnIqtObTCZ8kpS6fPtIza8wJh1qMKzIx4jD05xZGHH2XXt76AVS0/9wMWUmFDnHhHL0a4zukLuwwTenoVOnr6SKWHKFZLTIzPsPvxEyzmYVN/F+vXhDk09QW+8Zl/4eTRaQr5Km1dwlU7MDzA4OphhtdtQfN0ZmdGaNSKhE0dhwzRZA/xhEkmAxvWhgmH6xiqi75yfUJHiGHCR2xbJTQ9hqo6qNo821/pkensIWSuwnUzKMocIuYgTtOJ+4h/JtoQSWTBovkKQrxrLeMWlGMz8Dwd0PCwTz0pipAZFRRQDFB6aOu+Esd6lGJ2DsVRGd7cQU9nPzMT8xyfGWf9EJQKMDMOIwegOgXd68X4XPJ7mdRA06DswjhinByYgroDA73g2KAaYChgOqLHZxJjgyiNpvQXhKY0gE76STLFIiOIom9LwAWvupVXJjcS+8+/41p0JjjAIZY4iMcFiupfLsrged1AduXiRbCvdpplwlaybv29B1MuKOKl05T8Tx/vCoCdg6XvIkTVcSh2w3EXOhRIuJBzm5b2lZm0ADzstzLo96gClPBWcosdcvykkiiItOdz5bnP0TIuD1ACfvgstn6xRb15wLkVF5RIJBLJzwbPKMZ6nvcR4CMAvjP2Q57n/aKiKF8B3gp8EXgX8A3/LXf6jx/xX/++zIt9Zn7p+jX8xtsvAOCEBYe/+REmvnX7ee6VRCKRSCQvLDlOFR/O5LfajMiQfcqVXcmzJo7IoxzAP97NyEyh7fkErtfAP1fx788CRVsUbLcbUPeLJjVsqFli+TjA/DzUa9DbB+UapDMQi0LEAK8G4xOgGdDZ7cuKJjTqoggTMfBs4XS1XIimWSkE36iKeICYCfms2L/luMwdnWZ+5GGyY0+SHdmFtbTrnLL2FU0h3hHG9Vxc96lLm82ISfdQJ/WGw8iJSdB1OjqH6Og4waYLYPOWFD3dae795qfY9egEYb1BX7dC77oImtmNmcjQ0OHkyFGWJscYPTqPa1Xp7FLpGhqkxyhTKFQ4uH+ag7t0orE8iWiF9kyDzRtCmGacQrWB5UIqluLEiWnyRY94Msy6dXGOn/RILI3TqE9RLH2PVLtKMil8maqq0dmZYX5+CZwQkUgnff2XAjv8s12n6YlO+6OhikgULjKdm2J0fpzZhVmy+RooJqYRoz3TTdiMs3FwCx2pXnB1Hnzws+wbm6Veg07P4ILVN/Klr97J9MwiA1vh+CJ870fw2D6Yn4HrVoGnQ80XnQcV2HQBnBiDSlHIiRf6w6HUgHJJiNumBp4LtiNk87P9w9GaQdxytoEwGdZh4bHENBmETP29b/85+xWNcerkgTds/+/02hbdR+9AuepjsHoVTEzhPvEw2dyTpNnEUbLMssw1DKCiI2aNBaxiiWMs+TJozj/Cc/4R1/wj3EkzA3n9Kf20/K3nARdm5uCe++DWa2FUg6wOed+yvRI6EkOU9zjkH7Ulfw9T1DhJlQIL6MzgreTdSiQSiUQi+enxbDNjz8T/BL6oKMr/Bp4EPuU//yngNkVRjiPifd55bl382WfgwjfQ3reOsKHhuB7f/PZxpiYW8GzpDZJIJBLJzy5Pd6W2h2Ha6OEgjzKFdMs+N8JAz8oCZbvlWd/M+BQXnof4cqgh5JygSFYfYGvgKkI0c8K+wOWC64LjN1RPgeNAJCoEspABIQ1UFXImpHQRidAdEe3GVbDCUHOgpkPag1pMRCh0GayEadYdKLRDRoN8L9RcsFyV6XVt5AuXU85tYvroZfz770yDdwwhYP3k6JpKf18arAae/VTPoIeD7ZUpVBZRzTRmKI5phtDDaV77hrWkkxmKy1UO7p+k4Fmke0xWbW1nx6WXMzO/xOzsJHMT49hlhekTZfKLNRTHpVJ0mFuYYXS8SLVuk1+uEg2r2KpFPGLTlnR5rM+ivauBqjvE4zprV+tMLDSYmPZoy0RJt3fxH1+YZvVGj0rVZnLapq8XcCBsQiyikEzVyC43aNRF2ah4oszq1bvRwg4oLjjQ0x4hHl1LJJQgGtKIJVxypXFOTh7n+OQo+UoVA4dCXaNY1SlXxkgkdPal92DqERp1haWlk+SXK9gNmMvbWHc/wcR0CVyPkAFzx+HBXTC9KMZZRwzG9gM5EUcQQoyJigM5Ryy76wau2gbtEdBsyJVEVmylBssV4QU9WzKowuk5rhpBPEMP6/DIssT0SvBAwa5TA4764//Y+LcJeS6ak6f7wKfpHOsgXWmQKGdJsArtnf8viSN3Yz15Jx7DcP0vsP/I56ioS1z2jr8g/vhRjLlFOjSdSleS7933QSzPZSC0ibXmdh4rfZkIwjO5RJL1vAE4AZyEdAwufTc8vgdKj0J1Hqa+D+o1oITADYnJtlKOL0iC7kKIsDmasQw2Bg6uCMWQC+UlEolEIjlP/ERirOd59wP3+/dHgMvOsE0NeNvz0LeXDa973esZHl5Nw4bFvMv37/4m8zMz57tbEolEIpGcN1RUwnqSzV1v4tjsvdiulGN/YrQIRPtOyad8NuWiAtNsiGaJnU6EoKq0KFqnCzkNQE+cWiiptUBQGoiEhSiW9ts2aZZSqrU8D82q8sHrFYTDt+hvW0chQYyaHaNUHiKW7EBIdmfLj3xmNE2hoy2GVShiWU8dc67r0bAcDAVUNUTUTNOZ7sR19jKwqgvV05keXWJ2royjQzhjkuxKYITD2HaVpbllJkeXyM3D4rQoaqYDeQNQK4SmK3gKWDYoHpTqEDEhmYCOSZc1axtEopBKguNUmZ33GB2FSlVl/YYQB49BrBfQQ9RVg7l8meycqGemKh7RWAMtLHJurUaVRmOKwyNTqGEhbJoaXH5Jgv7uOGGtRNZyCC/PUyjPk12YpZbPUa55GCY4dajVFPJ5i2KxxsTEDJYlnM6eKkR4DdBx2LNnhMJyg1QY2gwRYzG9CKUKxGNgaFAoQMgVgr0O5KpQtYU3Vyysh8EBSGiQXxDnI6SJqI1yQ4yLM4mLZ8psbcqzCnF9NYp7nIYrxqMNdA7voN1IkT96hCPMsVG1CHsuJa/G1PzjROeTxDHw0HAxOKrXyKoWDTxGqRBR62RVB1dRIRRB0WKoSoWomiKuraMItKGwSu1kSNvKDxDzrQGUiaCELgU3Ia5KRGKw4RpYSMPIcShMQeVHYoAYUdBq4DqIo91aYs+gmfXb9AVr6GiEAOWMMSASiUQikUheeM7FGSs5VxSFkBHhj3/7rfT29rFYcPnhgTrfue1/Ua0Uz3fvJBKJRCI5b0wzQiMS4rdeuYu/++4OssVRHPcnTzd8WROJo/auBpSV4kCBUBoIs2cTZwNppwSMApsQss7ZSqt5CDEsinAWBu0Gdds1RCX6zGltVPx+BaLs2fqi+20HC7FdxBJvDwjrUFREBi6u+jSf6plRVZV0Osrx2XFqjad+F/NcFatm0hntQjE76ctsYsvAxXylfBfLSxVU1yOfXaZUFTWX4okImqqy/4kfMDM+w4n9LsePwdFjzTZ1FSJ+1SY9Cql2yLRDfk4IlKoBkSRU6tDdDk4VyjmH8bEitg3TU2A3GiyXl0h3KazdqrBqOI2qdnHo0AEOPAFHjsDkNJgx2LYTwjGwdJhZhB/9GCwPwmHo6YK1W4v0Rorkq0tMjo1RytdJhaOEdJdMVCdfs3AcMMLQHjXp6xlkfHyU8XGLfN7DdaFoQToF7SlIJT2Wl4scPwFdKQj3wqph0P3/QlwPKg3Q0xBVQa2C5cB0ASp2U0bUgEwSTFeIswqimJenQtXjrMvtg+zWsxLfiF7bTbgmLgTkgMte+16u6bqYJ/76E9xa/hp/ctHNJO0Gn/7hp1BMlTARDFfHdTwW9SxfvuO3aQDJiMIxZy+Ze9/PENBPHO/Pf5sCY2RxCbGWTq6hiMc2NNptqFYb5BGJsCZQUTXsaBLF2Ypac4WL3XBh5w7IpaGwD3gMNBfi7WJiYNEs7lYjKNIlfgYzMCjUlsBFoU6VKmd3E0skEolEInnhkGLseSTdNcwt//NrRJOd5Mvw5N5p/vgPPke93njmN0skEolE8jPOYnGEP75jO1/+s/u57Vt/xtcf+Jfz3aWXFIlUkrVbN2IrykqxIO2Z3uQTFPDS8B2t/vNBomjMfxzIPXn/uSCbM/iCGfL3ayOKMKUR7tao/7rBMwhlNAuGOQhxOLgfyE4m+DkMNjDBcylJFKAoCvFwmFKxTO0M38dUVcE0VA4e3s0Vr34HfT3rxKfS4Zt3PkK5ZGE3IJ2AwTVg6HOMj82TnfbY8xCcHIfs8qlt2i4UAyWxDrkcjJ2AUyouzML4MXj8oaf2+eLLYc36BulIgb//uy66koOY+qso13YyO/kunnwMTh6GUk5sf/LR02q5GxDpgVgbtPXB1CScOLKPWgVqNQ9dh7ZkiWhUZPyiQ6EODQ96ey7k12++n3t+/F6+9d3vs3Bgkpk5mFwAewwGBuDS1yhcdnGCHdsVwoZKRPOozy+j+IPR8aBkg14GSwE3Apo/iBqK6GcUMW7qRSHUVioQjggR17HF5zmbjSEY86eKtcFsqMHGIRLTGVITcAx4FfClf/tNDl13PR+Z/hptvd9D/60bGGi/jJs/dyuv+etNqKoCT+Th0TwDvzzIH8RFU8occK/LiY8O0VkMkcCkzF7a8XgCOMJucuyhjsdt2Cw4D5FzHiaDmEcpIO5Oc2/+fXQDg3h0NIZgbD3c9wQUj7cMHMCr0yx9d4JmWbwgfbYNMTODWdkBRHBYoMYx6YqVSCQSieQ8IcXY80h7MszvvW098YjGkROwf98MJ/f9K64jxViJRCKRSMDGcaf403/7Z4aj13DT+gv4r2MfON+deskQjaUYGNiy4og9XfQ8U2xB6+PASxf3H+cQko9HU4yt+M/biIRKw28jkEMthE6qIGIHbE6VSoMvoqcXWAoWW+NvH9w3aArCrcXeGg0olxS/t88k754dXVPp6+ygWlJpeAgVumVHug6xOOx+qMoFO2wK9hLZ2jI2BSzLplzxqFQgHYZIXEEJeeTzHnv2w7FRqDzLIvJnKn3reWd+/vB+6OmxqVsFlufBsStkszPs3/MdPvFxmBwTRdEC5c3zTnMh16E2C3M5KJ6Aow+A4wiHq+uKfOGQLmIqVN947LnwqhthYGOdgjrG1EKRmaxNoQqmAW0JaKyGUBoKeY/HflRmwxro6ooRikTRkjEuW1dh5LiHVYDcFJg2dAyCasLivNiPpYhzbfunoeJA1PPjCTTIZaFcP1NxriatntGWo+k/WwDFpl/xWA/8ANgCjLkOEwcn2fPhr/HvX/8Km3ZuoziXorYpTMkwiKsK2rqMyI/IhPjBxx6gcuAoqUKeq1Ztp25diPOhm6j3hZj63f9OAjGUdux8NZ2//CHe+8E38+G1v87wDZdh3biW0BTs/di72Dc3wQgG17OWzlf/KtGEDn1peM2rYe8E1ExWsgUcIJuHWg2SBhTGxEGjDSHrRhEzR2v5qQM6LioNHCnGSiQSiURynpBi7Hniwp0X84Y3vpENq+I0gF1P7uX+732fSuHk+e6aRCKRSCQvEjygzr4T34HuOkkzikgvfbq66ZKAcCROR99qUERMgcPTy5SB4Bls4yHkm7D/OJByAh2otc0ETSHWPW1fgcAbQwhrIU4VfVszbVsfW34bQQGyAMV/LtBIK3WoNcB2XaDAuSy8VhSFRNjErSsi8eA0MTZkmrT19NA3oBNLRCg3coxOjZJbrlGuuHgqxDIqnT0ZnvlO4QAAIABJREFUOoYSOFaRfCnPxEmbYkmImM83xQJMTbocOGIR0z3CmQbTM0V2/QiO7HsWDXjg1qBeg3peiOvPhtSPId2xxJp1X2VycQQlVCGdAScqCrc5HRDzLdXHDjukYmCGGxiaBhWXtf0QbUAlC3EP3IrIrVUUIRi7inCzBlEXFuApoOoiIsG2IBQSMQ/PJL8HCbE2YgwrKyEdZagWGbbS7GAYm1HCiP3aJYvCvhzX//UvoEVClJfBaNepIwRhFw/Lc4loEO+No+9xUU9M8OTiIebtHOmNqzDWZij5nyFirCU9+ApW3XANXe3XsP6Nryc91Mv4WI1ue5BNt/w8o4/cx9zJGbpu+SXi/Teiqjp0G7BzAPqHYCkKVQUwxMHIFaFcAy0QlyuIGZv0f9ZpJj+7/lHQ8dCwZECBRCKRSCTnDSnGngeiyTZufsc7+dCHPwSex1SuzD333Mldt3/hfHdNIpFIJJIXHQ5PsHvuCRRShNmJxx4sirgrpZ4kZ8KMxulYNYRDc4l2a0xBIIh6NItkeTTFUrflMQh5JxDFGv5NQXjw0v42bsstKAQWPDZpCrutUnog3rY+tv39aC3vb3XPOgjZyQOWy1C2QNFsYIxziikAQqqCEuw8currRjhO7+qtXH3DLP2rMmSLOfYdfoT5WZtCCZIZjf41UdZu3czg8CqK2ZMsLh1jfiL7nPv0bJhbgHvv92hPgRaFmVk4tP8F3SW7H4SF2RnS6z7BxNwyiZRHJAKVgijUpoWEg1VpwPiIyLs19BqKVcea9+hsh3YV7E5h7lyeFQ5npyre4+giC7ZKy9g0hPO2HgPPhlDGF2Wfpr5fEEig0hxTykqSbAmWl1jXGKCgXQHOqHB6qxGi0XZiPQPkFgoku5MYoRDJGNRtcENg5xqUjhdROwtc/I71qFGbJfJ89om/IuwuM8gyCTLUxF5oS11JoveVhIZN3njB+2j7xVdz4IFH+drvfJqrt7yG19/x+xz5TDczt99D8v/+ATwETNUh7ECnC32r4GgEMSMT4qBk85CvgR5GXA5ZhJUk2AjNWVKneZFCw0U7a8auRCKRSCSSFx4pxp4Hbv3EPVx37faVvLS3v/WTHN7zNeDQ+eyWRCKRSCQvajL0cBUfQKfGo/wNUzx2vrv0oiYW1Rnsi2ErQoZpLeB1OnmEp9RGFNmK0xRJT3elBomUSc5eKivIcw3csqfku9J01QbbttIqzjo0hV/L/wxBbIGHELnyVWhYoK24A88BT8GuhXE95VQV2VeuQkaS9vad7D3yKTyvhlOtU5xZoicOdhXWrFnNlddcxtCmV4OpU1g8QWmuDfjWufXrGcjl4ckDsGM7uHlYLvDsA4LPgWrF5sj+3ErGcKUE85NQKvpadggiKtRysOcB0CuQ2O6x+0EI10Apg26Lwlw1DVT/yoFmi/FS85oO6TTQnoCoAY0aKP4gKRXBeAZDdHBhoPnIAspADWby0LsJujNw8PPcBXxi8Fd46+veTuMvruSN/e/hT770P1h74UVYBizOQls3RGNRlMYSd/cNs6n3/fT9wdvouOv3+F33g/xj/81YdNIAZv299m3aSHLDBkIRnXf/9S2wC771w1G+bt3O5/fczmP1a1gVvoLt8V7xhhRwx31wdAxGL4HvPATLS0AS3C1wXBHRBPUG2N3+nmYRMQVR//PF/J91YAoxe0LYWJR5GgVbIpFIJBLJC4oUY3+KGLE0l//KX/Kua9eycVWIbLbGp790mJMHPkc1P3q+uyeRSCQSyYuaPKPcz4e4IfJ51MY6cE4CCyuvJxG5pDLwR2AYkGlTCCM8cmGaX/xaXbHQjBlwadZcByHd1BByjuE/1yqUBu1oNItqtRbxCl4PRNzWGIMz+VcDkTYoOBY4IoP3g5DRqgjPnwbks6B4EDGf2t5Piuu65MtZXNsVHQghlGAAA7SITjSUpFCpU6pXsJQKkXid4dWQ6IDufgfDqGPXHaLRbiJxj0hbSRzgEi9Yusa6jWne+YFB7vrSXlwFFidg8uALs69WLAtm5iGmg1UXYmw+B+NHwCuJQ6jqUC1CowQ/fhKmpsDNQkyFmAbJEOgaJJNQWoRGVbheGxVQbXEKHOA4cGIC1vRAOg1zJVhahlLt6TNjWzEBZaXIlQuUwcpCbCvhjn7WA5cB5an7+eJX9vOVh/J4lUlUfhHTgM4EJAqgd4CyVCA8b3HDJ3ZjWhmsUJLCd1ySr1FJxC/ECHUQxqSfV/EfPMqad6zDuXgNI/+lsOZScMfHyEzPcSFiPIcBpz7C/N4v8ukLv8A7fuezRN9+BXRfCmET/tACxwGtH8I/ByemoJoFxwI3CBDZAvT5nzb4nEn/swal9hQ8PJxzcJBLJBKJRCI5N6QY+1Mi0b6G4Quu5t23XMeanjj5fIPde8f5xtf+mdLyOK4jr05LJBKJRPJ0ONQpcJLD9ucpeEfgNGeXhdC7JALTgI6M+LJn0owbOBOKv00gggaxBUH2q1+3acUsGkg/QfImnOp0DZ5zT3uPc9ot2Few39ZIArXlfqsYG+wz0EpDihAF65Wf5OicGRePqlUG3W1WjQoEVB3UkIKuaIQ0hbjqoYehq0MVeacmJOMOmmKB7eDZdcLhOJ2rhtn+hm0c+MZBnPqzlQ1/MjoyGV550Q6+9O/7UAyPugv1n0KssmtDJQdVW2S3ug7oijgXXpnmSXb8VfVLUKsIN6yhwpouCMeFA9ati/Y8W5g9ly0oe0ILd4EsMLMAbWFob/PHx1mKmrVyusDfHEF+IrJXBKdO0o7yetbhMULGSqNkDXLZ/QxiEsHBCEEmAWoWlMP7YGQRdcQileyH/k4UM4STr8NtJ1ku7qH+o7WY1nYGP3Ir13ANXVdewOTyKHd9+R4+fN1vUR6fxJlZWCmzpQCWO0e1sof6vjJzd3wJc2o9xqX9dFy3AVIp3FoI2tpRd7wCjhwXKjcqeA7CSptBXHoJPl9IfEZiCMdsA6jgYmOdQ6E7iUQikUgk54b8K/xTIJbuYu0FV3Ldjb/Gr1y3hqhmcPDQDHd/+xEe+t6/0Gg8D/89SCQSiUTyssDjgPX35N1dqDQw6CFIOa3S6pOVGAa0pYOSPad+6QsE0IBmaZ9m0ayg9E8g6QTCaasjFk4VXgPRK3DBtgqv0MyCtWiuKg8KdrW+v9VBG2yncKoQq/u3WEQ4YyvPgxLveR41p4YX8tfHF1s+pw6K5uG5NulkiDbTpifuMdQXJRYVztyQ5qK6Quay60U81yPZ3s5Vb30FRiL0gnzzjqVUOjqj9CZ78WyFSBhSHSqpVU8nvz9PuKBXdco5UF2VSEglrIESqOgtQb+6Aa4LhQIsFKFogxmHVLuQCMsVkf/qOEKMzXni8Nf9ZspAtgD5AlT9KNQVIfZseRk0Xdj2KZsGUn4cKEG1QKqic3PiOiqKgU47nXQxDKwmRLShYriQioBRAuWHJ+ChA3i792Hd+x3Kxw5h5U7A7CGcv/k2TvY+nHvvR3n0JMlfvYKbfvVdxCIah/d8lzvv/FNKk0eYPfYkpblxIn5vmCpi5WdwjRkG1mfIH76fpR88Rv7RUdHxRBJPj+N1d8H1m2F8D9TLNGdEOyKeIHD9Bp9RRwiyGcQlFwcXiwaKLIP4nAguTUkkEolE8tyRztifAq/91T/m7W9+Le+4ejUAowc8vvaZT/PPn/nT89wziUQikUheWrSKBwm2Mcz/YC9/hMckpztlX8wEGZYvZAkyTQHTF/9O92MGhbUC4RROdbTWaQqqAVVEf4OK9IEoq9HMcg1kitY4BLelnaDwVhmRARrs20YIbyXEouqI34czLaQOMmQDkbetDSz72S9Vf3o8HKeGZ3t+aGnzlVAIXLXKbHmCDZsyxONTmCGXyy8a5o5jS8yMQ1vNpqPdIpVKM79UYmp+hEKlxNXb13DbFo3qfoTF83nk2l+Kseaieb5+16fJRF0ufQXEkikW5jr4xz889vzu7DRiYYMda7tYLE6xem2Seg0eemAZr8BTIhkGNoFiQXlRFBx7x2thdR8YCpw4AotFqFTBLj+15FQwpkxTCLrlsij6lSsIV7QW5GScAY1mewAeGgohmsEbBSgskIiv5eqf+yfe/tXbma1/k8uB64AJSijHbbROjxgQawP+5M3wpQdxPvofTM9/ikO7xdyIAVuB9wL1459l9Phn2fcpIfkeBKaBi4CHt2zhgN+vVwJHAPXWb0HxIKl1G7hx396VSaMA2A4sZNHqayCyCa/XBuV24EoUYjRL6QUzsej3JiA4guJyh4P7PGTGKpya4/FyIYkYTdXz3RGJRCKRvISRYuwLiBmJ89F/28MtV3Yy1BWhUrb58ueO8jd//15GRved7+5JJBKJRPKSpsAIR/k0t7T9Ez8ofIgFe8/57tKz5nkoNfWM6Ag5ptVtGoifDZpCZ9TftuTfCsCQ/1odIZ6GaYqvhv98BCGq5hBJlBfQjEII3IgNmoJvqzsx6EdQ6931X5v1287QNJEGjtxACK7594MoBVUH9XlwnIZ6ILrJo2TbuP4KdsKsCLKZDPT1GHQl2jmZU/DIUGu4zOULLJVgx8XdKFqCSqUGeo1LB7bToR5nbO4okXqdD/63m5jPzzG3vMDRqWmOZ3O4HjhLYI0AvWD2gjsDjGpseWcfG9ddzqGHjrDvu3thpqWzKihRuO5muHhriZReZnYMbBNecfX1JNIhjp+Y5j3/O8Mdn8mTnXJxn2ftKD0AHWtsyizT2x3CqRUpF1zM8KnbaTpsugisHJSy4Bbg4igYy6B3CXGzZxhMG1wNlhfhyKzwcNZojrsU0NkO6YQYgzX8MeWC8zTxpyqirShifEfR0FZ8234YR34OjDGU8Da+qVzNgzxMhRnW+O//3J//GooRZjUKG5UQW//oU8Rna2idOv3zQmwFMY/ifn8jiKjgVYh5sBkxT+aBcX+7sP+zHfjhxF9heQ3WFGz2Dg+xBdDZDJ2XwNU3QUGBtTdD34V44w4L3m4yXIVBlBa5GjGDGjQvqbiIGRPMnAYWDfLn7Iv1ePkJsSDOokQikUgk54YUY18gtl54Ib/8G+/l9VcOM9StsrxQ5InHR/ns5z7O8ZF9VKqF891FiUQikUhe0niUqLGfA5WvsqHjrbQ1NnAk+5Xz3a0XDYH4enocATTFUJdmHEEVIU9FaTpcDZoiaIimwzXQvgyE6DSPEFIT/uOzFQoLFk6rp70evNZOs2BTaxutK96Dol6qB44HyznIL0O1/CwOytMQjStkOhTKxTye4za1LV+MNSOgmRZLpRzLSxYFU0XxTIq5JKUSzM2W0EN1wlEXrV6m4i3RnooTD6+nale46RVrydmLZGtLLGQXmFqYwQ5VKBXL5KaKdG1YzdjEAexcFaMSQu9W6A/NoQ1XSF8bolG06O2OE4ua4Llkszn6uyET8ujPmGzoSTM7P8vqtElHV4SMkqQ9lMArFCnmw9h2lIWlOh1rtrK6/TK6Y2swgHEWeHL/Qxw/eJSJJ2fEQQ7U7gB/MBhphXUXmrQZJlqoSjKjsnptN1ZxkVK+TL3iYWinHteQDju2gl6EhVGYHwGtAk8chXwdetshX4HCSVDLonBXmKaTFb8rNUBRIZUyyERD2BNl0nHI18B9GpNnEHWhEBTKcvzxbyJGq4vj7cUtzqDv2smm7b/O7pFlFhZnmAOGAXd5ARsxPjOo6J//N6ALpdZYGSZBdEbrxw+eM/xbAuEIryJkzJDfAxtQnTxRIOlC98SEP0diUOyAtuPQloCL10FbJ/xwgoZXxyPk79Gi6VQNYgsCX3pAg+DSho2H/E/kuSLDHSQSiURy7kgx9nnHZMOG1bz+xhv5jfe9j6QLy7kqe3aPcOed3+MHP/zP891BiUQieekSBEa6z7Sh5OVBA495xmrfZcD4E8xwhpJ7gqnlH5/vjr0IUFD8uvGtma6cdl9BSDSBOOTBSkGhIG3SQDhYTU7NgQ2KfsX8bRcQOaAJD/p8i6zKU6drkPXaoCm0Bs9naEYQBGJy4OwNtmsVdh0PZmctcovQqJzbL4ZoWCOT0ikXsrhlp6lvBf3TwPXqzOVmWZorMWuW0LU45WKYhg0zM2VSCZ14OIJaLbBUHsFUTDRXoV4qsHPjZZS1CiUnj1UpUFiYoh4uULCWWSrk2Lz1Kh5/KITTKBGNGOzdc4RkdYq23jrrehIs1XIM9IdoT4dRHYepk1CbhYgDmbDOmtVRVrVBkhIpxwGtgZ32uPaaMJ6exFWSHD62TMfmLrb2bWMwdTEmGvucE9i9IzQiE+QXwKuD6UFIFZ/Z80RerqWBloSBbTqDMQNqDmFTo6enjbxbp7JcR3VtUnFIZcT7IhHo7lTZutHFmgU1D3kDcnlYmoOQC24Wai4sTvoFvDg1MiN4XPHPt2nqZNrC5LJlknGoPYOqGIxXl2CMB3mqwaUEBYcR7NoBOPgq4m+5hZ78gywtH2PKHmcdsMbvQwLoxkV/6G6IDkG0Z2UsthazayXwrAajUwU6/c/T6jSP0yzB1bny7ho4BSgtw9a1sHUVFB148hFCnufPcNdvLQIr4iw0Z3TrkVDxUFaKHUpZUSKRSCSS84MUY59PFA1VHeL//J+/501vug7P9aiUXb5zzxi33/6ffPWOvzjfPZRIJJKXNoE6JOseSnxUVNZzAQ+P/webhl/Du664i4/fPYj3PCWIvnQxUTBWhM9A9AxEzjmaQir+80HV+qBgFzQF0WDBs9bSjkpT0mpDOGOPVUC34C3t4v2niz2BQ1Hx22zNrg1EqSDOIEgJsGgKtAZNV62HWJ5+8HAOt6qiN85tHX4satKeDjM1O483gchgaEGzwSnVWJgZY2pykqXFKrFYB9FYCjOlkJ326G9vY2PfarzleWazhxg5fpTJ0TEaFYXNf7geJRZBsSysqoVSVVEbcVJqlM7IEBcoV5HZGsUMKYRVk/nD/0jMHKenK00s1sWuQyVmR3LUIzniBpgOeDaELKhlS0zUS5hAbu4YhakGE8eXKOnQt20tXV1tGLqO0lhm9Oh/8d1D91P30ni0s1waxVOL9HbbmDeBvQyDfdDTAR0psG3QwzA3AxNjHtOjJRbDJYb6E3SlE9TLdXrTXVjLZUJujb5uqFdBDcHWTTrXX2VgeTXuftTl8SOwf06c/51pSGngNSCiQdaFCcSv9yiwmlMLuJWBWgMqDYeK06CzExbmIWSIPN+zrZgPLiAEY8vDoPkvkBjVNhZV7zCFxrvoKr+aN4V/iS2pLm5b+iCTuEQQYmnSvynkoJJb+VsUollw7vSyacEcqNDMRTZoxnMEvQiCBE4dxSUIV2BtP7zpTVDW8R69B2XmY3TjolADlv1bD80ZVaMZMBKUx2t6doNUWYlEIpFIJOcHKcY+T6RWbeXiX/g4t/3uFXRkEoyeqHDPXeP8w9/9BVNL91Ouzp7vLkokEslLn6Byj0Ti4+Kwn2/i4PHk+DGOTu3iWu2L/Mj5IGXGz7n9mH+bP+eWftqsAvpXlnerNKWYME2RNRBaoRlXYABTCNEp4d86aAqiLk2JR0X48YYRObPbEuB64gvmEk2HbYxm+SDb308gFAdSEQiBOBCFLeARYD3CLVht+SwrBZl0uOgVHSyM2YzvPrevtYZaI2RZ7HsAnDMse4+HIRm2cOxl9LBGpTJPtbpIuBTmyku3MDU5R6eRJl5XefzL/0a6I0mPZ5M2a0xN1finD7yLZCc0XDhwyKNa9eju8Ghrh0ynxvHV/0GhXsWIaEQSIXRm0E2VSrVApWRjlxpQgnoDIjEYaBfHqKtXxwxDtWazqgcShkbY0FC6FabzHqtTGjHDoFbXCdeqxGse5YUC5WyR+bkpNNOFiIcagc4o2DpkLEjXIWP7InQWlAY4IRgXwas4jTKLkxX23T/DO395PV2DEWJFi1K1xI5LwWnA6mGbVLfNow/CXAUyEbiqDzJtUM5BbhlmK/5FAre5zN9DiPtBrEVAXw+E1TrZ6ToxA/JL4FkQNTjr34YQzcX7YUBdkfuDBOIUEUzmCfNH1Pjbb3+A5A2/xfD6W/jg7XH+yn0/62iwGjE+BUmaBcAWVwIAzjYCg7TWKmJeBBnKrcXvOFMb+noYvg4+cBO4OnzhJPOPHuQA81zDNhR1HXgx8Gr+O8MtrQQSdHALPrOKgib/CZRIJBKJ5Dwi/w4/D7zz127lhpv+H9as30lXR5qHn5zlvu//kG98/jOcnNpHzZrD9aR6IJFIJBLJC4Hjl8Jy3Aold56DyiN0sZU8GllOnlPbdc5apP3FTaIDJd6xIraevvQ7w6luWRMhuAbO1aCSfSC+6jTF2iBeIERzJb+JEJYiCtiKcDFaNIW0MkIiCiINgmNab9mH5m9jAaNzFnfemePwgx/hje94D5e/4nLWdQivn0UzuqBhQTKlUk5ooJ9bFa/sgsvIQRdngTNGoUQTEEnZNJw8IUPDNKLooRCmabJQKDM8OMjJh6vc9fUj7J+rY4aX2TkIvTGXrz/iYdpltm6E9gyoVciOw8RJ8FSIRGHz2pPML7v0DCps3KbiKHUsS6Gmg6669MagXQddh0hIIa2HqOoNGhWHcklk55ZdiGR6ibhlCnNZzJrN2J4Zam6Wcl2lVquA5ZGJQKTDI6E72BboJoTCEI6CbkBvCowQ2FWwS+I4ezVIanDFDli7sY96scjEWJGxadi3Z4r5MZtG2SKdhrZuWMxBIg0FBzQDKgtQzUPIt4Qu5YXQ6+ow2hBL8zv8MTKLGKNpmm7SEJCIgWmI/oRjYswkY9Ae8Tc6A8GYD8aZcKoGo1vcFHrQsIizl3+3H+N1e77D5mGI/dr13PzZ93DIvpMZJsgAvYBHFYWo38vFFZfr2YIyWvOWW6M5gvkX9E+jVfAFrrgabrwZ1hvwI7COfYOlsa+zD7ia4ZaWDYR3N7hUEfQmuAwT/PRwCeFi4JzSk+eKAqwjcf1bWH/pOi7bniABPHQMRu6/i7n7ZDybRCKRSCRnQoqxzxE1FCbas5VLN3fylltu4bWvfT0pz2PP7pPcc88j3Hf/t3ly7zfPdzclEolEInkZUcNljllvF+vZSEckhRnuYCb3+HNuMfCSvdRIdHWS7Gw/JTM2iAfwEG7WQAgKnINBvmuFpsTTKukEZYG0lvaC4xMkVaqI6vZTNuTLzZxZ2/OYncrSn0zSlgqRSDfdgYFQbLX0wXEhV3F45KsPsf4Vb2b9JbCO5jLu4BK36/garOJiu+cmmxezHo7DSsGu04nGIRKzqFZzuLZFKBwmFNLxUDmwP4fTkWLsUJnD+xd4fBHAIq2YdG9O0bd5iBhJugcLpON5QpFldF1hsaJStUDFJR6OUAlDJhGipzOME9YJhUPomoKueWiGg2PZOE4VxbUwXYVGbZF6tcrCosPxY5AegppjUC83GB2HpVmoTxapekUcFTraQbEgokLYBD0lCmapKoQUkRUbi0CbCnYd8iWoLYOqCxE1qUJvG/QmNLI1WFKhLQ4jTxQZHRPvWd0LHZ0iOqBYgUPHYGIc6jlolKCugZ2H5SpEFSFG5xHRBEMRcBRYqDSjKwL/6UrhN39A2/7ENA3RztloFUnFHAiCC2r+KzaQJorLxezlO8yhzjxESQ9zyc5+tm1/C4XpOvn8wxSqB7EBfeVSQ9tKu/BUaTN43FrUK0h5DV4PpNTguRVBN3khXHQpvHILhD14fIITo49wsrAHExXMjeBGwVHBS9IUY22aEu/pM1fs0UZ9HtJ+FBQ1zPbX3ETshrex41UbufFVSbqA9sNwIB3ioDfDrvvvP+c9SSQSiUTys4YUY58Dmh4i1jHEujd/jE//2WvpjZuoDYfSQpU//9Mv8+Ajn2Vu/vD57qZEIpFIJC8zloEC0EeJK9jQ80Yu7DX5ysM/x8st32Lt+gHWru3HoCmIBpJM4MALsmHD/ntcmu7XwJ0XCLY6TdE2EJZMhGsxcLcGuZkFB57Iw9JxUBTQVMB2uPOL+9my/UIuvyjNNTvFfj2l6eMrI86SBqzpDfHb7+/ivr+4lkRHN+E2VtIx8y190oB6HWrlBuXKuclL1WWo58/+ejwO0bDF8tICtuXiJKCmu1QqFe79ao4fLOQZyChsv0Tj8XtdFFUh3NbOpldu4/ff999QlJ1kC3uZm/0xI/sepVMHPWTieSqu69HV3UfNVUl1ttMz2AehGChtgILjOhSsOuX8MtncGNXSHLpdIlfbSyM3weRIge//l8PVb4PJiTyLE1Xu+x7kCiHCaYdUh0Jnl4puqoSKHp4FrqtgemCGoFH3cBpQbUAsoVCpetglj3rWpZJz6OyEZAQUQ4FFhYXlKVRgyFC4+QqPr3wCxutCFwwtwiWvhw3DMLUIX78dRn4MPcvgWpArw1ShJfrCVzJzwIXdENdhdkS4fIv4hbv8sViuQF0Rhb7mp4Ug66kiGuNsBE5qDSF6KiuXAQIrbQPI0E4b70LnO9h8kkf45sQkX/uXKubf/iFX3L+NuT23c3jkg1StOjE8NMKIklunCqxnI3DlqqfdVxEyajCPyih06mHY8mHYegn0gbfgYv3DXXxl6TBVyrxHSaBmroRiHOoOuIbfl6AkX+A1Dy4lBcEkLioWFhbzeOfoi9UJRTv4vTs+TmXepDcEFwPdwKWbYH7TW3n8jTt5y9Zt2PUqslyYRCKRSCRNpBj7HPiF932Ud//m7/PK1TqGrpKdhQe++wTvvfUXyNoTOO5L0UMjkUgkEsnPAgoKES5NXwKFVYxla3TxlyzyR7gsn+/O/dQYWnMZ/asvWYkoCAputWZUBuJsKwZiGTY0vXWtkk5rpqVCs6BRwBgw4UK8Bj1D4LqghSCR0njVxVehWgquApMWpENiabrR0l6ZZvGuHk3l4ZN/R0PXsFSRtRm4cIPF2DpgahAOq5ixVv/hT47rPb2olyBOylKpZ0ssLkL/mgiRthRaIkxH5xK3vvsG4vE0M4tVyPyYTRsGicVTOJFeTh6SI8BOAAAgAElEQVSwGd7cRVvyDWRir2R991V847Z/JtIzwKp1F7F127VMLexhuO1SzFDaV8+bdk9NgYwBmU6oJo+CW2VbeCvrL3mcsHeEtQ//gMnF21A6wRy8jNXD7UQGinQNdfP4Y9+nu3uAjRsuZl3/Tk5MjKHrJuFIjEgkgVOrkc8vYNsWhhGhMxOmsTxHeX6M/OQB5g48DPU83R3t9PR0QUwHPYzp2lSLeZ44eJRD/rnTXBhvQH8HJAbBVSGtwMwo5DxxXgO3tg0Md0I6DEcnYBLYPQqDGbj6YnjoCah5Qoz1EMJsviAe6x7YNRidB+o848z2aHW4m4hRm/If1/3ex1G4lX/gM/wmNb7EBD32J/nP3zrE5b/7Mbqvfw9dE29D+bO3ISq8VYBdwKn5r60Ekm/6tH4s00ysrdEspLcZGGpbC7/8Dbh8LeQMuAfcTS7/X+l/8bCzzCYuYpgPgN0PjSzY04hgh40tLQU9qSHEWbvleZMyBic4R3k0vQr1wndwgaaRHBTntjVioRO4rGeY3/7aEv/33ZsozI+dy94kEolEIvmZQoqxz5JYqo23f/hvedP2DjZs2ED/gImhe3zjnj186xtf5pEH7yXbmFrJrZNIJBKJRHI+cPCY5JHSP+EpCRStk/VDH2VdZAcn5z/JTPaO893Bnwq9PQl6uxOoNAtvBUuig/uBEBtIfqc/thESVQkYoFkBHk6NKsB/fs6/061DTycYihDNQiqEdQVDUUD3ow0UsSzdoCmsRmkuGgewFIW4GaLMqQXHAjHPQ+SbNkwIJwySmUCIemGwbbBtFc0wiMQhmYpi2Q1OnJjGAXYdPcjmdTsZHr4IpxKlVF9ES3VhtvcxMXYEVc9QVTQadgW1PsvQxotwDINIJI2mddDVdhlGKIminuHrecsy/FXGEI7noKgGMbZRJ4+XiNI2CGkX0kYHsc4thFIJBhKrmcpG6OkYor97BxGth7W9m1AUFVXV0DQNz3RpizZwPQ9VVTFCGq5ZJpOp0TNcZfWOMXBnMAwVwzBAq4CSQKMDdX4RfeKv8ZQ9gEtfFN4wDJdvh8Qw7Nyhc8VlBpdeUeHRu2H0EMxONZ2kDQdqtnCvasDmHSmG+gxqTp2u9gKVZWi0eBwaDoQikI5CtuHHW3giuuJsBPEZHmK7xCmpw0VE7msgE5skuYU/4Efs4CS/j8VH7UcY/tL7ee26n+P9234P/vITUK/B7hHcB35Efv7vmUFEf6QIggua+477ewvqT9Zb9mz777sSIPUB4h2rUNoTcOA4PHA3rB2A7jTe7jkOW1V68dhoRFDi/X48QZHmioAizSPptezJ9u8LWdvFpYIr5uu5UCrgHd7D+IjLJYPQFn3qxZ2oofLqLSa3hQYprPjaJRKJRCKRSDH2GUmzcfN6rr7hCm666XVcuzGDqWssZYvc8dWH+N59D/DwA3dz8sS+891RiUQikUgkAFRZsH8M6ES9IdJumFDnlXiRKYxog7HJu1e2NAiTooMFJs9fd18AujM63Wl9JUEyEF9bl1NbwHIDJqZgYACSuhBHg7JGQVZskB/b6jt9SkSnB5UsqA2I+JGVYR0UD1QPVAViGZiedskXa+QrWQ4f38V1b76WrkwSU2m6bgPhDJpLy4PcT6XlBqJ9zwP3jL7E58DT1DTyVB2bEHatglWHeq1BuW6zuFBmaHUH8fZO9GgGzYjR1tvJ7P4RShWX5cUGQz1tdPXnmC6UKDeqdKYjhNv7qNdrZEsVDo8cpFxrEDLCuK6D5TSIJyOEw1Fs18F2bEKmSU+6F0X1cF2b+doMCVPFVhqopk2qS5zDeChNLNJBXTU5MTFFxVKxVIOGblBV4hCOo6BiuQ5LdoF0KE1YV9Fbz6qW9vMrVOhcA2TFScUGxoEYeHGoQcmO4vnv1TyI2tCfhnAatKjHqm6XaAwqk1BYFOMtkAgtgBCk20Q8wfaL1jMw2MnE3DJRZ4JjuxYo5Oor3XJcUEMQiUPYEDm3QbTG2QhOZxAP0Ew6Dt4VZKy6KLjoDLGVLAoqB8mzmzl2jWWpVBUSXi/bQgk2XHw9sa4h6GtH+2GJyP79mPUxVBao0owDsWhmHC/79w2EYJumFzfcTyTaR9dyHsVNQyMJRQ3m/wsmJvj/2XvvKDmu+0z7qdDd1Xl68mAiBhkgEQiCGYwmKYoibSXalG0FS1pbYR20+63TWX9eS7aO9dle7TpIVqAlmbJFWaJJiSZliQQpkRRAkMh5MMBgMDl1zl3h++NWTQ9IAKQoAiCB+5zTZ0JXuFVd3X3vW+99fwTWUrEbmDz8AoZlsi66gvWBVaDoUK6AU3EvWq80nkn9nQILi5R5x+tgY2GfKRr5tWMWcNKDjAzXuLxVRw2pr/iMUBwIVGDTdb/Erm1Vxkde+Hn3KpFIJBLJRYEUY8+IghFJEPKv5t5fvJ8/++zHCQDlssnMbI4Xdx/hNz72GSi+CI50w0okEolE8uZiTvywdJzpXVSXrmPJ8nfR1b2c8Ylt1Kwk4BAkQg8rmWXs505QfDPREYf2WF189RyxFeoRBRVgugw/3AN3dEC/Lpx9nnsvgJB4vCnWnkjqnaV5B61pkkqlmN0Leh7UMpRKEAtA2RYFvTQN+lbD1mcshoZnGZ08wP/91qf52jMPcNPGNXRHwvMise5t2xHykVkD04FaoP5/x/1JVRSNKhdsCrmfo4DXQoX3TGKs5qfqaGSSVYpFyKQqFGsKphnmhutX09dxDarTQLFo4W8MkJod5djBWRwzwv3vvxs9EiM/lSRbrtC1fCmFco1sLU1udpbM4CATqRzhaIJitUS+lKanv5W29k6K1TKFaoVYY4IbYjehYpGvZphKj9ETNaE2RLGUxhcA1Q+lnA89aFKszPDolsdRNB8lq0QtoNJi+MAGv+ajbJcZyAyxKr6cRQGDqM+HrvtwHIdSsYxpWjiOKMSl6TF0TUPTqmjqMI5dAmUW0zpO3qwRNhRqNciVROSAVgbdBtWx8OkW65er7L3MZuAoaAPgFMFWwNZFNO7iJkjE4MorN9LWt4bwsZMYS45QHNvKTLaCZrlSsHvx+g2IGGAowg96tkRoL5/Vc1WL/9QQV7mC8H57CcQixVVhJWto5Suc4K/I8l0cdk7vYveWj/LBLR38+l/+M303rSN42zVEG64nNvoAZJ/A1HaSch3hFQfyDsw44n1gAQHHocm2WWXWgFU4kZtw2m6AwnHIP4GZG8AG/DwMtGEVgmQmA+w5+Chr8HNH2+0s810DY0Wo1sCuUvfkxhFnw3uXerdivDMgbsvYmNhvSFnCMrYzyonjOWZX+WmIq0S0U2/a2CZkRxXu/9CnwJlhanIfVu3nLx0mkUgkEslbHSnGngF/MMpHPn+QT70jQV+rDxDdtW9+5xDfevDzbPnhPwkrhkQikUgkkjctRWeMJypvg6cv57bb/pBVS97DzSsGePpwP6adIcMsO3jyQjfzDac1Ds0xITfp1HNZa4iJwo2IAkqdUVj1ixClrkX6EVOrT0fBXb9zwf+OHj3KmjVrACHERIHFCOkng5hAnQFagaSzUDhz+NAt1/BHf/RHfPoznyHittXz8ZnANgeefArCJnz4HiGb1Uwh8KpubmhuDpKDM6T2Drze0yUaV+Gs4aPpqQypEQUtAPG4yrrLbyOa6GUubZFI9NHeuga/FgVLwTTzPPavjzEwmUT1h1m3eTP9fTewbOmtVJwic0zQonQx6aRIF2YpzE5za0s3U5OTjIyPMDo1jKGbtDb6MeIJ1JAPRdMx1BDj2WlOTA9zaODHPLDrAbY9k2PssEllAoJt8D8/8/+wcnUDmza3MJnL8dS3Z8mbJoQUcVKnoWE5+KIwsxPogPfctY7N161l3carMPN5/u5zX2LHziFSObh+M6xbv4JVy1ezcvEq+tp6qMym0eN+jHiAj3z8I2jFP+QL302za8DiJyb8w3fhfR+Bjohwg0aA2++DnlVw1dXwxc9CRIOGAER16GqB9vYQDeEIZt5ieuAo6zf0c+XVuwn6QN8Lx4BsDvIF8Xo0t0NZE57dudf4Ms8L/WjURUw/dTEWRM5qAIijEeP3eQf/gygjDPM0T/Exxvmb3/8F3qM08z/o4wpnOVz/e3DVB9FWx2gOIC7UErQVYUkOmAGKVdH45DRs3UKVb5OZ/Xuys59mCT1AjeNkmKTCjSwFjjK+798ZBlIofIw78RlXA42QPYiwLlfdn5EFF68X9rEwMbrqNirPDBNMM/0az9jZcSybsW272dt6Fb5aI2uXnPp8OAjvuQ3GZmDo+C9xck5n39OfeUP2LZFIJBLJWxkpxp6G2++4g7/4y8/R1t1Ea1wjk1I4cijJx//oD5gZeZHU7EkcKcRKJBKJRPIWwQEG2L79KUpWM//vt28m9ZGvMnDor8lmtl7oxp0TvvPoC2TVDja/YxNt1D1yVYTTNYCbvSpiXCkBo1MwOlbi5OFRDu7czm23bybsV9n13I954ZF/QXFmqVCjiEIjcWbIYmJTLJfn+0UaQvoZoZ4HG0JMoPYDixCCcAEhHTmOw/NfeZbP/uhzlHpWkw1GMbp68be1YYYD/HT7j6Cm0be4le2L19LV6Vaf90PUEM5KpQBOLo9Vev0CU7wTaikonkWMnU5XGRwB3YKupRpTYylSWYXpbBF/tBHbVyYSXERUWwSOwu9/+h+5e+920slZli7bxMmZFzm2fxeTJ49RyKXo7VxNVlPQIgaJlkZymkVPWyeJeJDG9hilYppq1cbMllArJn5/iLHAEHtO7OL42D6KpQF++MM8mSMmtRQ4NpRmYPVGiCQKjI1Ae+ditGiKeMikuUehpTnEibEC8eYQjc0NXHNrO+nkFGOlYb7xvZNU/uVpfuG6NgqVaYyYg+LAnkOwf2CIpf3TLOnbTmFSITVl0dKl09Sq4bNNjm1LMzltoSCKoP3Lv8Ham8HfCsGICrTw7cfmsPImDQ2wYgWs7ITWZpWAoTKVNBlJVrD3DRJrdgi3JNj66EO8uHuOoRkYc6/dg8OwoktEXlRSYClC/G99ldfXkyTriEJWQsj0hkMLl6gBVRRM4CgKCh2EuId7WU8bDkM0OBmiFPkOj6Ptfong0QBRQ6NFgYgNIduHYqvkrCqYDtO2Tcm28Vsml5PDRydR2ing8ElG6cThWjrYSII8R3gYkx6gp6GXVVf/Fj42ohSaYNaBoA6lGsIJ690+SVMv1uXdzvBCSrwzoGGjYb0i3fX1YVsWP33s+3TFG2kNraS9J0ZrXfFGUYR3xcrAnddeRmOwzCee/jIwzc9ZPkwikUgkkrc0UoydRwHfEt71i9fx9jt+ga7ECqIBjd07B9i/9zDbtu5g5/anoDIiYwkkkjPiuTNagCuo17oOIhwZGYRTA6AfMaQOIIbpDjAB7AWG3OUlEonkjaJMLrefoWMJ/vP7JsW5XuzaUuAE4rPn4uKlbc+QKcyy/8CW+YJCnuPUE0kXUgXmMjCXrDE7Psfo0DHGJvYQ0BVOHDrI0V0/RXFyWFjUUAgTJE0JFYcAwgnreQ197ja9aeHevlTqDt2FrtmZqaN8b/ZRqsM7KfsN/E3N6PEG7ICPk8f2EvQpZIbi5KZ7aG2EigK6DkE/ZMowNwUzY7NMnhh83ecrHoNiRZQ4OhMTkw7FIqgmLFoWZW5mBi2bJl8pUyosYWbmJIGmGA2N7WhE6etbT9hIkE6Ok5wZ5wePPMqePQOMj01RK5dpbDxOVdXQggbRhhjBcIREvBlVt3GUPAGjjBHW0II+LHQmRqs0dQSYyJ9kMjPBbDJFctDEKjEfsxBMwC23b6Sntx3HMUilJ9F0lXIOCuMORsgkGnfQFJOAAqtWtKGUExw6so+hzAzjUymmZytMZyoUTfAHoGZBvlQhW1Go+Hw0r15CllmmczMk81liAYcsNqbiFtSy4cQoPP0cTBch0uCgFMv85yM2VhEa/UKg01VoikcJGH4OHJnh0KhNXhmkI5smpJeYGp3iZNJhosR8vmmhAvkilApQyEDYdVqfTVp0EF5RT550TpnG790+8Kbye0tnEX7bOUS/poSfCk0kaaIASifovVT0Kl32UtRilUChikGVKDUMwE8A0Am5peoSmIRJARM8zyzHgTIOGhXWYtFCK01omKRIUqYb6Igto6nzeuJL7oS5BnGR2iVQw9RzYP2IWx4F938LE2tt6oJsAAhgomK9QUKog8VU8nmee97CDtxKqPEdtF4VxFNjTQvmUhCOQH8ijGkv5qob72fHT7+IZf7cqbUSiUQikbxlkWIsgKKh+KI0Nl/Hb/7mp7h63SpGB4qMzqV4+NEtPLPl+2zf9sSFbqVE8ianC2gC2oCVwAfwXBhikDCH8ErlEJ30O93nYohUQgvYB3wL2AIcQQwcbISAWzh/hyKRSC5SBpkYKfE3f3iSOO/HiC1Hi6fJZH7CxVble+DgTxk4+FP+46HXv439+79/hmcc0hQxEZ/uQcQ3gOczXCi4gpfCKfC5DxXxyT4JDDHBAWuC+fLuI6/c4+hh2PPj138sr0Y0pOAE4Gxuvekp8cCBqwpBThyfxKfX8AVssnMjVEsKASdCc7SdsO5HJ0pL03I0DH785Jf59lce5MCJErPz9xpPnHY/sTC0N0JPr49QQwB/OEC5pvDic7P0LgdfM5QUOHYSrDSoMSAIThaa++GW269i1fLV5DI6jz3+NVTToTAOpXGHnF2msx3KZoV8pYh/ObTE2pn0H2NaVwhoNum5HOPTFqUyxCKgqKJoVjjho3VxMze/7e3s/MlB9m3dzszJNCFDp2bY2FpdjK2V4Yc/gj1HIBR3yCUzbH8SClkhoq/rhWIRsIMoZojx4RkGTzoE/MfQyscJ6WWqZYeSc2oerKqIjOBcEvJzImQgr4rYijPhCbGePOnMC68g+iGekxRE/8RGuEyngRSwEdEHSSI8utOgvBdTXwSGwSYrhlYrgpNHoYCQjus3m0OATRyNMiWGyZHlKWZ5njGq6CxG5wFUHFrJM8scY6SB67Um/O03wuK7IbEaJqehVhAhyo4nruqId5T3zvNOhBuoPH/0jrhIKGPhYHKWE/Yz4VBiDz/duYdsZYyIsZQrlm0gGgNNB9sWYuzSXvD7oM9u5V33/yb7dj5EKT/Ny/3KEolEIpFcKkgxFlBCrRj99/AHd/8yy7q6iDX76TKqLL/54yQPP4N5tjlrEokEMXj5HkKI9SMGCBGEu3UUOICYGBtGiK9R93dvEAFiQLQeWAXcB/wdcBViQLQD+O75ORSJRHIRM+s+9pLBzyfe90kM49389ee/BPwtUhh47XhCa9F9jLt/LxRjwY1CeNk6NYRc5bjPvRkmKy908J4Ja0HNo29+aYyAD5raYMlqBdN4jr6eTUT0CDEjQk+Xg6H0Mjqxh6d//Bgffv9fvea2ZAviMTBSQ5yt+kyRqYVJDAqwCWLtYtJWYQzWbwCrNMje7SPsfmmMp57ZRW4UKAtZLr9L3OoEOEaKF7/z+Cv2P76jBEAwCpYPAhGIhiEcrBINmqxashx7JsDQgePsTw8yNlZj6LAQ3hayb5t4vOI82lAwobUTioUppk6CVYAbOkFRypgFMBrAaIIV46KnMOSu22VAswpaVbijLUPkBluvUVv0PKIvaxH1q9EbGkUQN5htRAhCr/tcEtgF9lbmSo8wVkrT5i4h1lQQtyi8BOQqMMMc8K/AM8Bu4J3A/yHEUrqIsAh4mh+zBx3Rk9oE0P7HcPld0NcPUymY2g8ZDYqasIejIPpUfkRfKuL+r0Y9rsC7aDXqRctqnIvPuv0HHuPEiRdoiEzyvg8qNLcKAXb1UuZNuh0tBv/9w8v53F/cQqn8EzBH3/B2SCQSiUTyVuCSF2Pf8auf5vY77+PmtY30dIcJBv08+uiT/M6n/pjZsf3YNTmFRiI5M0uBzcCfAB0I58jCghFe6Zh2hJtk4fS/DPXJhV5d7woiufAw8B2EwHsfcBfwUXefWxHDmXNokZJIJBc5DrCFb3zzMnpX3c5H/vwPeOBPVGzr3zitLVPymvE+yT2UBb87p/n9zSDEAmgWqD+DWbCGMCiWJiCVg6WrTdbcupp4rIHZyUGmxo7Tu2wZD3z9YR74wsPnptEOsBvi90KsD5xmSI7D7h/vZGjQ5vEfFiiVoVZ9tQ2dnnIeqiWR+4kC4wcqbH3sGF/5zCf46Kf66Gguc+XaLnZvG2VRB+SqUCpBdWHKkKcZLji31RocPgnHDkFAcajVhKit2JB3oFYU0mHAEZmwCxX7kgU1DfQQ6HnQKxA1hUP2TCyMKBB4Ba2q1MvbeTeGvSzZVsRN5GZEv8Ryf18M6m1wcwfNySEadm9B46toJKmLukV3Hc8r3k0TjXyIBPfTTJVOQoQJcwwfUwgHbgfX0ACsRlMuh+BiWHEDtLfWNdaeHpg8Cam8UKFf0Xaoxy4s/NsriyfE2QoO52p0UyjO8Wd/2U/T8sfZfO1qetvdti9ooqor/OMXP8/nP/cxnv+xFGMlEolEcmlySYuxN9zyX3jHHbdy0+bF9Dbr5NI2Dz74AI//4DFOnjgAztmSwySSS5EW6jW0Y8ByYB2ikz+O8DrVqA+/PRdGHuFGM6h7omaoe6PsBet57pSrEYMZ3HV1RP3vDYi82XsQA6l/R9RYTr7xhyuRSC5i5ijkBpg63sPRp0P47KupsguHPGJq8unREbeQXqe+ddHzcnH1zSK2vhrNTY3YxSoiSufVCeD6Cy0oFR3GT+bJZYropMilshSLRQqVUQaPHmBq6hxGYFQhvRdIQXMH9PYaHDyWZ/CIRSZjvurqZ8NxTnUDm1Uo5U0yczM8/h2L2+5dy1W39pKcnuXkcJnLlrURCOrMjM+xa0eZSgkaWqC9Dw5uhUVdUC1ANglVE148Di2amCdTBVCFKBuJgqZANAC2CubCi8jVH22fG01gCdE2dPZTNO8HdY+MU/seBvV+i01dQdYRrfOCNRA7NxZBWyeaL4zWoEE6gLjBvNB3GwRfGDQDxdbRqioxbGKo7vYUsS16EOJtBYMQosRdFzgdkAhCQodGDcJR0H1wIg+ptHvHYxbRF/NcuF60k03d6/1yz7dDGYvKOZoF4Dg2ydQwX//yN6B8Dz33X3/Kh4CiAI7CNRtbuOneD5NVG9n39JfPSVskEolEInkzc0mKsarqIxJp5+57PsCNV69mWbePYtnm+Wd38rV/+jo7dj9/oZsokbyJUIFuxMdFF6JMi4UYQPQiBg4T7vMLc9dM6k7XLHAUMWAwqZdI8abReQUmFqYJLkeIuCV33VFgCXAZsAwhzDoI0SQODCNyaVO8dYb/EonkwlFGYYDcbIR9TxZQ6CCub8B0quStHXAG75gnb0guLiKREBnj7MsoCDHJdoTs5ZV9AqiUbMqlChVfEbOSR3UqjJ0cI5Wcec1T6F8vmQFQitDWrNDTG+eJnUlOjv98Quyrsf3ZJFfdobNxZQfrr15C1TrBZWsbaWkNMDcDqcwcJ49XCcZsmruBra6eaENRgaoDA9Nixn2TCkULnACEEpDQIGpAYwzCIdA9nRPQfKD4wdahaol4AoWzvye9Sft1+VFd8HBe9vDwthpACLIqYAv7rj8gwmv9cYisgnQL9eJZnsjrAy0gqpRZ3s3mHKJfk0P0bTrd7eruOp6gGgBbgZgqkhKaVCgEoaKKExKsgGKBM4IQdINum33ukXoCrCcoe78LwbmMSZlzeX0oPPnEf7CoJcq6y3q47LLu+n12xHuoqw2uv+0upos+9j39r8iirRKJRCK51LgkxdhQuIWrr/tdfutD64nHQ2QLDnsHyrzvN26mXJZuWIlE4LlEwsD/RIwI0gjhNY/Idm1DCKHeR4knqnpDnjl3+WPAw4hBhidlNCxYxyur4TllvaJf3nZ1hJDrINwnhvtYAbwX+BV3X99w91NCCrISieTVsHgWi+2UaQbezk2Jj1OwruG55P9CZF2/EumIvThJJVMU8mcXqAyf+GYs1hBfU24dKE1X2XBVJ+2tbURDEeKREJ2dbTz34lZ01X/Wbb5RKAroukos0UtqqkB2tvbqK/2c7Duwi45VZT74sd/BUL9EqZTBzPtYd/l6miJDPPDFEwydLDKdBGw4euDUYm4ASQvylvjWrpZgbD+s7oBfvRmam6HYBeUaDE2K5f1BVwvVoGKKW75Fzl7i0/OK1vHhEECZF1q9bFWvKJbnWlUR/RODevwSYtmjFlRtoSrPr+utkwcOQnkU0WfxITLwg4j+TMzdh7Xg4fVr3BlCSgHa4tAdgLgDR0w4dBKm5qBsCSG4UqQeU1CPIZi/MLHc570LVkjWJWoUOZfXhw9I841vPMFzz81xdOCvUVRQFOWUpW5cB8WJGF9VNuI4z/LyV0kikUgkkouZS1CMjbG4bxXfeehjRCIGE5Pw1Jbn+MTH3ymFWIlknijwIUQmLIjBRAOQQAxcPEHURLhevXxYz/ExhxgaZREC7gxCTF3kbvMK4NeoVzFOA9sRWbBjiKl3M+5+vKGbgnDHdlIvAHbS3XcfsBr4AvA3wB8A3+TU5EKJRCI5HRXETaMH2TI7SJzLWM77GeDPEDJP/cZOB/VPOcnFRSpdoVi1UYLglE6/TCAOhgFGCRoiEOvUsQ0H26dz87vuYnX/taiqn0xxjnwpz7K1t3DzO8OUgn62fHvfuWt8FKoazIxYjO7bR7V4fr77nn84yeiuF7A+egC/WiaZrVHIOKjWYRKJJjriJvkMFHTxLQ+nCqM6omexMgLvWQ/f2wZzJiwKQawH5obAb4kog05E78CquEZTB0wTAkH39q4JZ9IXfYhlqngT+8vEKRE4pZiVl3YcQwiyPuou17D7iAr7br4M03mRn1CocOpMINz14ohSaUeASUT0ku62xKE+m6jsPjwh1gbHgpoFx49DvBPiPhg8ARNJmE6Kk2l5WbAB6sW58tTFWMXdZoa6OCvE2pMUGOZcjnmq7v5yTIwOcX+ZZ9sAACAASURBVPcVW/na41fQ1nmq9TwMXHP1FXzxqYf45Nv6qFVlnQ6JRCKRXDpccmLsfffdy/vf/0FiMTGl59uPb+Ghf/seuezcBW6ZRPJmYBFwByKWYC2iq1xADDBUxIChQL1AheX+P4cYHdTcv1uA26k7XivuMiHEQKcJIex6GbERxIBiqbtdbz/fQgyd8u7/cohCF7PuusOIuATPXRtFCL2/iSgsNgH8KdLLJpFIzo4NlKg5e8mSw+FyNvF7HODLFJmaX8q7DdWITKm+2FA0CzRwlDMvk2iESAxSc9C1QqdzWTuxljixpgTrem/ENEIUyhWyJuj+IP54IxtubsA0Os+pGLt+/SJaux1UJihOVLCq58dhaFYditkamYkMiTjoik25AlNjFuNDKaINJg1ZyEzCHTfDkR0wlxdFukB8a8cC0BIUMQutfhizYboE+TEhxAYR77mF82Q0R/Q0YjGIxEGJisJenKEW1MLU1BqeV7VCgCyib+FH9EUqiHe2QX12jur+PyA2oPggGoOaKYJvLW820EIRVEX0c65CRDtNI8TZgLufKnWBVHX3H3DbYokoBE0FLQRV3c118EOiBbQ0WN4toZjbVt+CbXnRC9qCtsBC12kK5zx8fjlAiErNx47BrzM8tJxQxCC6oNKaAjRFdG5aFUVVz/LGk0gkEonkIuSSEmPXLNnIXb9wJ3fffRuO4zBwssiPn9/Ktm2yKrtEInJYrwTegfCghBADEA3R0bcRA4gy4qOj6D7v5bbOIaoPtyPE3A28tmRFz73R7T48LIQIO4kYdBTd348jhN+S+9NrZ8ptXxgRX7AOIca+AGxFDIYkEonkbMxRxSKLTYDldHA5c/hIuypPkXr9csnFhaYpqLqDop855KalQaelHXwBk2XrEvQu76GxtZmGhgSVgkXRmiVfMSmVqzQm4kTDnURjYXx2B7fe+VOe3fEMtWzlDb8/eMX6Hrp6bYYGJnAmbUI6BHQxjf9c4nP3UyvY1FSI+CDsU8HxMT1bprNVFAGrVkQGbLMBag38NuSqQhgN+MCvwcQcGDrEgqLHkRuHxqj4X1gX3+wKIoJVUYRoHoqCEQHHBP0sZmBPknR9p27vpYZDEYUa9YJaFmJGTyPiXe7JuCbiRauJLYQMCJrg2OIAsTk1fEFF9E28GUF5929vHwuLhXlirL5gXw7ofqgpUFXECSIM1bSoGEfFbU/UXc/bnped4Qmv3pF7bRT24SLOOfXFCnTAh+04zBS389xTx4iEfazeED9lqaAPeuIarT03M3nyBWpleZtLIpFIJJcGl5QY+6n3f4YbN14pqsPa8OWHT3Bwz3bI7L7QTZNILjAB4MPAvQj3hkeRugjrTeXzOvUF6vlk3jS7KxCCbvQNaJMGfGDB3zZC8P17YD/CHTsOTCEmLzrAQYToeh+wCRFf8Ajwy8C/c8Y5jBKJRDJPmho7eY6dvJu/Y4w9vMjXsVwFLXuBWyc5N6j40XwWWriKeYYXuacpzPJ+jeaeNJtuXsminpUYvjCVTJFHnn6Q/r41+IxGHF+cto5u2pXF+AnR2d/Htx5/jPXvWs7czkmcGSGW2baFbds4jgOKyNR0HCEFi9/BsexX1pVCCJKaqqCoCtddvYyOVpMTL20nHIauZqhVYTx5btPTG+MKrY1gVRxyGehfqtDRadDU1MjgvlFsYFmneHz9QVjWCEsSYJuwbw7Sjsh+LVmwd1REP2xsErmw6SkIahCOQCIqbvMOApoOjg9qOvgiKlrIpjAFufTZ2+rJkt58HQsLqLp1pbxZPiDe4W4OwimUgLyw8Ppt6G6EZB7SXlqtwSuFUC+DNoroI1Xc5738VpP6DW8NIcraoJjgD8FcBgpRCMbACcH+bZBNU58t1OruyytR5m3TWbAfD3v+GExq57R8lyDg7lO4j//Pnz5GQ1Rl9YZNr1hS1f1c986v8/S37mN6+Jlz3jKJRCKRSN4MXCJirAa0c8Mvr6BvWRP5Mmw76vC1z76N5Oz4hW6cRHKBUREFtlqpT2uDeu3hIjCCmNjnZap5UQUBoBm4EyHEegW6zgWKu68/dvddAP4NeAjhgC0j3LE/ctu7Gfgdd91/Br4LvO8ctU0ikVyM/Dt/yobgB7nf+AEPpm690M2RnCs0sHQ/ZqmGOX1622oDEIuGCTfqGNkUumkyPXycdHqWidGjLF99HX39HVQrBuOTOY7u3Yu+NkKr0YdmBzmS38cPvvUAJSdE2TEoo/D83id58sf/wcjUMAQ1VqxcweDhQUKan47mFgpmnt1f20X5RFl85cWAOBgqLF0U5dfvXcmSpRFW9OVJjk/RE4X2BpgbAaUC8QAcnDh3p+2aq5fQ2xnhnx/YTQ64aa3DHTdprL8/jlIeY98uh47mEHfeEifsTDC0C8bHoFiG+zZDZk4IrroJqZqQEScmwdEg3AZdBoTCEM7VowpKVahUwKrCzIyNYkGlBLmzBDl70qfqvo5h5kMHUOYFUS+qYAJxI7dKXSQ1mY8rsGdgZASaglAsQXHOfd5ztnruV0/u9Fy1DnWR1CsE5rXCW87NgVU08CWgsw9UFY4OwIP/DPYWcFa67etGxD3l3fV10b75/S4MdvDiC8RZrKKeh/CmGUTkgwnkGeGrZOhB3Cg/Fb8O3/h0M3fv8PHk8DlvmEQikUgkbwouCTG2paWZL33xmyzqbCdbVtg7OMUffPYrZLIpHEdW7pRcysSBGzlVQK0gCmPVEPEAOeoZZ16+WitwN8Lt4UcMCAzOnRALdZHY5/7U3DZcAWwBngQOu+0bdNsfAH7DbWM/8G7gYc6tV0gikVws2KSZrhygxVjJn9//A/6/732AdGHqlGW8ScLSd/8WRQGCEAo1UNSLYJ1+AndLDJqaIZwAJ+MwdPwgre29+FBpjLTRvWgVOAH8foPWZoXpqRGe3foIa/pvpLttGdNjO/iLL32bzTeup29xF6Mjad63+T42ty+nUi0SVg3y4TSja4dBcTD8fkbHjnHd7yVwyiZOzaFYymHoJXSnQHvC4PZr+tHLJSKKRs50iAehXIDDY3ByCiwHmlsglXRnt7+B3Pn2OD7mOLhripwlvmXLWRg6WuTJJ4ZZ0euwZBn4QxWy5RShKKSz4tu3uQUaWqHmgM8GpQRYUCoLYc4XAp8P8hb4LCgpYPsgVINYHBqb/MTjfk4czaMYopZV7SzH9/KiYUKM1VDmBcwg9ZvRQeqzgLy+j0U949UCcwiG/VD1hFWvPNjCjFbPbatyam6ru415QVZxH1XEWVTF9L1MCcZmhM15VSfc+074/vfAnEXEH4Spy8xwajKusuC5uhTtuPut4pyn8qbemXdwmOPA3iLPboHN7n2tQzuq5MoOizYG6AyAqm5CxFGdw2J3EolEIpG8SbgExFgNw4hx59tuJGAoDE7D/uMZdj77fajJSuuSS5kmYDlwC/UERG9gkaFeMGsO4XAoInLU2hFi7CrEYOBCoSGybTsRgxs/IpvtIHU37xZEFu5ihHD8i8AB4ATi+CQSieRsmKTtowxXnmFt8ddYE/lFjtZ+wnT18CuWVFlYIkfylkEBX6OKzwij6aKIF6cR9uIJUSwqGALDD3atSECFUChBPNhBItHLzGwKXcsR8PlQrBzZmSTTRiNKJcOJvc/y0k9fwCqn6etpo5DL89tv+xStiSZMu4xu1RguHSXQ1IpFDUWDQKUNrS1O1B/DUA0yhWHswhB+tURDSKO1WSU7nKNUsKlW0vjDMDcFcwVIFkUNqMYG6vcyF6DroHs6ngpGCAJ+keFq2BBLQCgaJxhpR1NjDBzdjxHUiceiVEplNNNibLLA5EQVE3GbdDoDR4ctfFqeuA+MKGBaWAWbRIuKL2rTHINFi8RzoSLUslAuQ7kKpRok/KBpIsogX4JIsC5haoDmB8Wv4KgqllOPHTib09OTO6HuP9XmhVPP9eoNiaJ42ar1LS+MZHIF00wI7JC7jifGeuKjdxGZ7p516kW2Fjpkvdbh7strqU9sTtchokOrActXQGgD5ANgG9QTcD3h1cepUVLeRbzw5rP4vfoq5+uNwTvTXiauycC+WbY/PcbmWzvFEmWolhRqimjZ4pWb6T42ycgxKcZKJBKJ5OLnohdjfXqISKgFIyjytY6NV3lxXxLGXrjQTZNILiAqQky9zX3EEV1hLxe2ipj6NosQNY8j3K9rgXsuQHtfjU2Itg0Df41wxs4Bu4G/RThorwHei8ibfRCRNyuRSCRnJ8cgh4ojHHr0KP9tyT9hODFeSE2Qr2WAU+UWkILsWw1FhVhvCNWIgK8iJlScxhwba4NA2Mbvs4mEIBEN0hSO0pDoIhRdQjzaw769P0ClTGtjFKdcJGLnyYztZPbYdvY++33CVHjx6b28pEFXn59S2cTBpmhmSBdHGZ86Rq6QpOZUwacQ9QWIxVroi6+iI7yIjLWDkeFJGsJBQjoU09OkZ05Sq5TIlguoEZgegpp7EdqOcJvaL7soVRWiYQgFEV/9OrQugqYENEag2YJll8Oi/jZauzfjV5bxj187SUtLhBUrFjM3PsMX/vdBpnI1KojrvwwcnYV0EQJViIWhsR0STdDYBO29Oh1LazTGHBb3weQMhAMwU4DkNGQqUFYgokHAgVpBRA+0JUBVwLHcAAAFijWLTKmK4hNFyqoOmGe5G+ITh4jjtvPUuTEL38E6oq9TRuSrKu5PT9j04gyKUPUDbYgb2wvjCbzlvIxWk3purOewnb/6WFhYS/wedJf3QWcLtBgQUyEShab3Q/U4lIsId2yNupDsp+7Grbnb9PpzC/epUUU5D2Js2T2OAOLGfY1DO4dpUXfw3z4txNiWNj8RE6IBcSZuvedtpMvTPHTsgXPeOolEIpFILjQXvRh765U389H7Pj7/908ee4av/fW/XcAWSSRvBvqBG4DbEc5RDZGTNoeIIhgC9rp/K8DlwK8hBh5vVvyIY/kC8CzwQ+AbwHaEs3cG+EPgs8BzSDFWIpG8dirAC3zp2G/yu1f/Nv/l2vfwy49eM/+sg5A+OhCfmnLezVsHn8/P9ZvvolqtUpvP33wl8UWQyk1SOgGzcxCMmmRTRRpiAbq7VtMV28T4on3s3v1Ddj79IosiMUyzDJZDqeCQOVHll6+FoA41E2YrJt976pMYmp9aKU8mOUa5nKNYSJFO58lmyrS1qwSMOJMrV9PZ083MyBCHX9xBc0KlIa6h6xZ9fd10dC0iOpNjYiDD4LNQcguQqQq0GzCcqwu0aNDTC31tkDCgmhMGTA0IFCBqgh6BkVE4MT5ApTTA1KDCU/sdDGuKRt8xRopQdMR170PIlzPu5rNF2H0Mov1w7XKINfkIG0HSZp6N1zgUUjA2Avu2Q6QMyVlRp6oErIhBMCDEYs2GiCEeWR2KtpAf4yGoVkxOjpvM5sXfnR1Q8iESlk5DBCFxev7WuhhrI248pxEiZhgxNJp1/++JiZ4T1YsTCCJmDvmpi7h+To1ryiNE0aK7bFSc/PmYAvfFmBdyfdQzX92ZO00a9CgiLn9Uga42yOxwxdgl7np+9+Fl23rH5e3DpO6g1SlTl33PLd7ZLgIhoJ9ZcoxwEFEsFtqWnLrGe2+D0hg89KVz3jiJRCKRSC44F70YGw00sCi2GIBpG/KlFyH/yAVulURyoVkObATWIQYaeYQYO4IYUs0iBicxhOP0LoT74zRzHd80KAt+XoGIL9gA/Dli6HES2AZcDdyHGDRtOf/NlEgkb1kK7OJf9v9fVg1s4DP+L/Ln1U9Rcm2UDuLT89xXKZe8keg+H5tuuI19u3egRk6IiSKnccY2xxQ0HMwK6JZCNNFCFYPZTJXQ+DRdsQD9K68kmZlk/PgxhkdSTIzYNDYqNDaqdLYbnBgsY+hiGn7FtPnJI08SNFSwLcqFGrWyRSRsoVQs1IzDxCGLmi/DxEu7CIUPUM5UOTlogi0yVaNRWL5yhJaOcaJxm6YGqKTAdgOMLRtGZsFceFFaoohWeQYaA9AWg5gOJRvsCEQbIdACsUZxTRfzkPI7tCtg1UR8QNQR4mkcITEqwLV9MDAjIhLSqsIV13SxaLFBSyJAQ0hlbmgvqVlQyyKKYHkXPL8VKAjjZ3cYNqyDZBqyOdHmRAxCAYj6oc2AXBlUC0oF4fbNVoSDlqpw1Z6JJDCNCFhqR/R4gjiE5gXLEvV8fB/16KaFhba8KADD/TvpHnkY0T/yIgJgvhAXIeo59wHqTlmTV2bGemJqDVQT4o3QqEBEEbsMOaBboMQR8nevuw2vCJjndfXcsF5ufgDm/cs6FSys85qb7yCOewLIUarpHBmDpR0iRuMUFFCUOOLG+tHz2EaJRCKRSM4/F7UY2794IyvWrqN7bSsATx6AgYkc2LMXuGUSyYVmIyJH1StUMYkYqswAUwghdjGiYu9lCEfsm1mIfTlRxAAkCHwIOIQYEGwDrkIULRtGirESieRnwSbPaOEAtUKOdt3ket7GPl5kihFAFvF6K6KoGon2bhxlB45iovlfGRmrKNDW2I9fm6ZSzeEDQqFGwuFumhr7aY33AxGawqtZvcRBL7Ww/8jz9K5ppS0RpyUeRsHP4Pg4Ub+B4fNhWibDk8cJBnWCQYOgL8jM1CSpmROMHU9yYjBHtQCrVurg2Fi1MrpaEiWlTKi5kaa7tlXQYtDWAcv6YLQipu17VE5zUVYrkKpCpQxlE4IqmA5oeZg0ITgrsnG9ZWfHIVsTBcFwhNTnBRuVEXKjWQTFcn2hmsbKa2+mkDlOspRFsSvksjByHCiCoUA+BZkyNIcgHgC7AOMzoOkiFzaXh0IOrAT4FOGQNcqg2qDY4jXBFstVi5AsnPk1HqHub20FGoCG+XgALze24P6MUM919YRNL57Av2BLJvVh1MKMBC/hFuoFvbx9eDm0lQVnTlmwnCn2pyig1oRy3Ei9vlihDKZXMDUsTub8/ry8Wk8U9rbpuXdVRCEtZb4l5w8bIXaXKKTG2f7wJH0fbUUzXln01RfuJtx5F4WxQWSxVYlEIpFczFzUYuy1m97OVbdspmtTAoDv/miKfUfPPAVNIrn4URFC5XWIYlfeoGAEIcImEUKsgxAtVyMm3r4V8SPcsb8NfA94EdiDGOysRwizEolE8rNRIckYSb5r7uO3+DxFChTJkiPzM23Hm2AsIw0uILqKGjHwGVEq1RK2VcGnnbZ+F63Nl1Eq76ZczaEDmhahoamXjo7V9HasxyZCRImwum8p/YtuJdz7LZb1r6HZ6CKiNYGjMZw/QkOggZA/iGlX2PrS0xiGQWMiTltLgsHBPTz75BPsHdzD1uM5ADbd0kZ3b4xoREezpigpWaoVB0wHrWhx+GCNqUGH5hZwSnDCfm0SVsURQm0q/bInJl/76SsgJMUoMDYtZMuAApGARsfam3npJ2nGxqeZKCdJTcPAYRGhEACxsAqxZmgIw+gR2HsIli8HIwCFEszOwqJGsCzw+9z3S1lk4Qb8EPHBZBkyOUi9ihjrlexsQ8iYYSxi1AhgoVBDoYZwcHrCqyduQt256sUK+Ki7Tj28uAE41R/viaIV96A9ITbnrr9wPVcAdhQw5yCQAT0Olg5FU1RlqybcM+6jXjjM248nzHr7tBa028u0VeeP9vxSASpkZ2Z58qsHeOf7mwicRowNNy2mZ927OTT2t+e9hRKJRCKRnE8uajH2Q79+D9fecOX833v+4cNMHNt+AVskkVxo4sB/RbhdgwjhdQIx+ppCOGMLwO8APe4yFwP3IHJyv0N9sqJEIpG8PiwghcUX+X3eq3+cDcrV/H3tz36mbYQQITAvIqMNLhRabwvGHVdApUC+kKdYq2Jpp19Wj3dTrAySroKiOoyfPA6hNegNJsGaScRnEkbHDwT9UW6/7CNixQUJOr2RtfN/+1S4ddOvn7KPTWs2MTGp8dKeKqJwJjSt+zVuu+serlx7GXCU/3j4f1OzClhmhdzEDFdtOsQzPyiSnrNITvAzmQm9slU/jzBnIXoSnqbbHIL1PTYv7DrJbLGdPfun2frvR7myA54/BrmKkBF7gRuvgHhMtGGxDbsPgxoCowHCFahYMDwDZg7yRREv8NNBWKvCNS2wdgWUM+BURf7s2Ugi3msTiPfdWmyupMS1nCBCAoUQwhWrIyKa8tSn91eoC5qe4FlF9Kn8iGinCEIkDVKXqYPUM2S9aAKLelSBF2fgXXQWUBM24cxe+OxxuPU2aF8C2yZhpArVZrd9Hj7qgq6XY+ttL0c9M1agY2JjX7BCg3OlGR7c9xX+xryayHyEQ53Llif4r7+xhk88oeA40hkrkUgkkouXi1qMjTSDEVUoW/BiEkrWMURpDYnkUiVEPf+1iBhAHEOIsVVgFaKwQhzx8fBWiiY4GwoiJ/eTiOJkDcAK4D0IgVYikUh+djKUeMJ8kFX6FXwm+k3+NPdBzNNIW94n6ULhqwjspC7JwOkdmZJzx5r+ft793vtQKjpW0caunvkVKJgFsoUaxQLEoyrdi9Zzw+qbKdQMfvSfD7BuzTUs77wGfyAuCropyvwEdyG3OVQUi2x1jtHRQXZueZpf+cAnUXwRyjWVQtmmMWxy43XX0NumcePGOH/y+//CF//qHyimj+CoN4CpYKtNOKofX8Cid2kP7Ss2cfjA45jWEC2tiIvtNBqWjpjc3qTCqF2fzP5GOyRDMei/XKW3uYeo00S5M0O69wUKExC0RARqaxA2rIGbNodJpqpMjNUoKnD5WlG8K5MCXYFAAAwDymXR1gpC9M2rYib/XAZqJQgHoVEFRs/cLgshkR5DSJdVd1vPAMvIkCBLAyr9DNOCToA4GipCxi0iZtrEEOJnASF0FhEnvAC0uFuNUS/ppyOE0Br1iAMvSqBEPT5AcdcLit99KnRcD8s6oLERgkFo74HLDThWgrQCjlc4zItaWCjseu5Ywz16L5ggTIUKNewLeAMoC/wIqIkwCAvsKmiGeE27W+HtV4vfpRYrkUgkkouZi1KM1XQfa6+6i0i8AUWDYtHh4eerFMpVzkf9UInkzYuOGDDoiA7xFGIwUUKIkyvc5y9G/IjwtYr7ezdwC1KMlUgkrxcbhwyzDNn78VWf4DeiH+Px4iOMWqeWdfe5j9KC/3niktiO5LzTDYkVCVb1r+TEoRPglFGxz/hiOE4RXTPRVJWqaWBbUYZHhilULIrJEYYGHJSaQSiUwDKrDA/up1gsEwkYNETCNDRGOXjwEAcHRhkaGmX8+BC9i2K0d69EM+JUalA0TExznFTyOD5/knvfuZRCSaWny6FcmWBmNMV3v72PG69fzGWr2qjlaxw8eIBSLYujicJXZ3LG2gipMOOc2+tNNQL4FrVj6QZ+v00kGKAhomBHHbpNke06XYM9E9B5vEatapPMwlQali8VUmKtAjVTCLI1N9u2WhWH1hmEFj/4bMjMgWaLLFvrNdzJ8MTnCeohA0ICtUkDQSxGqGEDASwMVEIUCTBEM3M0ECCGTpQmFFqpF+fKIW52e+KodzPby5ydQzhtm9296tQdrN7Dy7l3A0z0fiAMeZ84wJwJRcu10XuxCbxsX17/pua2w8ujFeKwQ5EDjJE+XYW684IP0HGcDA99YTd3/tI6evobKWUg2u4uoUMk6Ifwr0DhCbBTF6itEolEIpGcWy5KMdbnC3D7vfcTb2jCAjIlkyd+OEaxKCcCSi5lGhAFuaKITnoSEUtgIZyylyEq2L4GFtaqeEuhItwtIJLjNlzAtrxO/NRnTUokkgtODZNJ+yTTlYf4y8hXOFo+TMkqMcfM/DJeyuSZJBBpADu/RDvCNFyVoGdDL02JVl6Y+gmOnUVVame0J1t2AV2z8Pl8mE6ESsXPgSMHcXAwdMilxplpHEevFilU8ry050fkZ5JEgyGaEzHaFjWy/fntHNifYmwsT61S4viBZyjlZjDCTaDqROIGudIko6OHGZsc4o67LyM5kaWrN4Zfg3x6mn27jnLVqnYiio/JfIo9e3ZQqhVQ/JBxc1NVwK9DQBdFsuIBMIKiOFY2C4GqkOscxFeKA6iK+FqvuBdjOAA+TXzd1Gpg2mDZIq/15adIB3yGeC4Yj5HoW0Mg2ISp1QjoEAqAFYBFDZC3YSgJE6OQ8FdJhAELUjmwfRANgl0TRcp0S4ixpQqUa6J9y1qgu1EcX6oIPp9Y3v4Z+iQphGc0hAhkmkZ4W/0I6TQF6JQIIXpHIabpZppmIIFCM92AH40AGjYaVXzk0QihEcRHGNHX0hBxBWMICXgV4ob3QherTj3/1RVYHQ0qMeGAnQD8JkyXYa7qVk/TQNHFA1HgDafMqaXVqu7PAg5z1JhkjhGeZpLpC+aLFcfoOGW+/dXtLF/VQXdvI6Z3MbpTCFQtQO+K9zN2cDvVohRjJRKJRHJxclGKsUbQz+/+9/fSrGnkgZP5IkceeAiqsniX5FLmNuATiIHAMCKaII3IOXsfpxaiOAsKYgRT4C2uIIQQguxbjE7EJ/fRC90QiUQCwu0aBfqo8TtzH+CT/AlLWMlX+Vsc90OyTL12+vkvnCOZRwHNp3HNJ9fzrre9i76+KyhZJscGd1IpjKGaeTTr9K9RrpijaitogQgBowXLCjA8dIJYLMyVV22gpWMZia5NWHqETD5HPjXB3PgY5XyBQrXI8MQoazZewbt/dR3BQICju15g5epl7Nl1jPTxcaKBEDfceC2G3sWR7GH27p/mllt/jW1bvkmiqYd1l/VTaC3yvz52JdGITnJkhOTMNPlSkXCjjS8EWbeGXBDoT8DiDvjeXrhpMaxZC/FW+NHjMDkM4xZUFehXhdAa1IW/86h78Bv6oCMurtmxSZgrQLYI2VI9HxbAp0CTBu3LoVRVWL26h7vu/BDLlvwCL2UeQVNqGDgMnoCOpRCsIO4FA1uOw2Xt0BcDPQClInS0guED2wIzD5hgWuJGRgVYd704Lg1XVPaLKe5hDTHZ5zUyhTiOKWAx4qt1EbAEIdQ6ofSKzgAAIABJREFUiH1EEV+5JeAwMIED/P/svXmUXNd93/l5e21dVb039oUASBAguAkkLYkiKYmkYo2i5XibiZdoxjmJHY99EttjZ6yJJz45nng7Hsf2xCfxdhxHXmTLsmTJlLVYEleR4gKSABoEGuhu9N5d1bXX2+/8ceuhGiBIgNh6wf3wPKKq+tWrW1Xv3br3e3+/728SmCSPFGsLnecWsSmQZZBtyMXvIc73kD2DjJBNMpQSi4LkFTp2AyFo0yUITMSMIauiuTGU0mjCANMEwwazFzQHAg/hJV62LeQZ7AIlBCeIeZ0ZTvFppvhVzo/Qv7F0jX1fHX+ScvsB7J7b6Os5f690xuYX//3j/OK/yTMxdoObqFAoFArFDWJDirE6MhHIRK4Lt2iB9zfIwZBCcTPyIPAh4D2d+88hbQoGgQ8j40Eug2TOkEPOikLWsSDrcm5GuJ6YYONY+SoUG4QGcBToBf6e3+aRgcf42s4v8YHvfPc5QRa6Ip/e2VS+zg3iILzrscPcevtetvUO8sjD30OjvszizCyV0ihu4wxvfK1MdcElfovI2GYT6sse7VadTNGkMVdh/NgoxYFeDt5xiAO7H8Y2+gALURzk0EP/gjiOqDdnmJx8kc//918jkw9wWoNYQQ+O6eI1JkhbFYweQV/WYutIEfJ5+jcXefd7v4vtO4Y5fP+97Nuxix5slk6+xplvv8CLr4RMTmuYZgyFiD0HoBnBcy/Ln+QDW6AVwBNHO40PYeks1EqwpQipAIZDcDKwfx/ctg9GT8DxU9A6JeM4Gz6Qgs1bYGSXtBeIItCEPI+HCtuZHK/QbLU4dHc/hz74v1HcfZD8ll3ktu2iiM7o0Vd57rmTnD4Cwyk4PQ7zFxTaqlegGsHgCLR8WG5CXxFGtkFjGaIGNOvdpPyeorRQDZuQS4FTgLYA4x3GW8RIUfI08v3EyJ/WBt18of7OY1nk8u0g8AAaw2wiwxAGGXRMNCJ0HHQCNDzAZYHvUKJJBY8qUhYN0RHoaGhk0SggI237MOgji0kBHQsTAwcbFk3iUlJuK8KMklb0QJiS/g3EQImYKRY4yxkCphGUEWQQHCVkjogZIo6xUg5dLUygjwrj+NQvuodjwfc/Bv9vXg55FAqFQqHYiGxIMRZW1BX1YLoWAqdQ8SiKm5cfQvqjJgmJEbAbaUuQepvnrcDoPD3JtU2qf6xbHGQ8yzpjXdpDKBQbm6RcTwvQqTLXeJ1vnf0K//fOX+PPZ36TSX/6vOXgpBdWXCf6oLAlQ/9whpGBNHWrzgOH9nPwwH0MFTdRXWpRK5fxGlXcUplTz4/RqrjEbzFMFAJK46NUSjVCIcgVBBnbwQwNqvN1jr0yxgPvbjKY7UUzYiItwLLh2e98mdnxF5kaPcKRfxjnyeeXyObOYOgW9UaFdNqk2fSJQ0iZDl/7+9cgYxEToGltdmy18euTtGaPcerlDDMnT9Ksuyw2YsZrEBqguYANfgCljrp/piILI5mRFBQ3DQIxLEzB4hKMe+DHYDZh1oe5MugB9Ofh4fukp6tXh6VpqM/Ln52GB7keGB4xOXTfJqqLNtmihuvHvH6kzv73CXSrQBBlOTteQ1g1xkZfJ3JnOXRPnu29vXz6KzMs+90POUVnaJGCW26Fnl7IZuVj7RpoWVmgy+9YKIwAZgBxKO/bafBa0sLAvcJwzxgZITuBFGJzSFMnAznc0ZHXaoFuJr2LwMHEJoVNGrDRyAD6uWFRXvOxRZs+AnzAxUZQwWOJBtP0kiOLg43AIiADuDSJcIjJ4JABMYhm5DA0DbwaMEaNeUJiTEx6KNCiwTJVFilRo8UCMQtIl9oIOIY0pCoh7RdWf9imAxkE5Y45MF3r3Q6aBikHdOsx0GOIX1mNhioUCoVCcV3ZgGKshvyhl9TaMF2OkUMQheJmQ0dGUXwXMvkuRkaIDyPF2B1v/1Toin+JnZmOVBzWvShoIWNdFAqF4togY+JizrqTNP2v86/2/EemCu/jxcbLjLbP0OqYPa++ILLBcMDIWqR60gz2DtC3b4ih7T0MDKfoLwjGTo8ylOslQwa3HrDcmKa5tEi7tEjp7ASzJ0oElwgZXDozT7sN6UKa/t4ijm2QdRzKlRqnjr3B6OjL6Hsd0rkeAuGzPH2a8dPP8Oq3n+bYC69z4niTM/EyEWcvenwNeI1jYIJpyejPzcMwOCCFKUOqgPhtWGhL4ZAIBlIQexB63fNqsSmFTlmcCio+tFowvwiLZVii6y5aqoGow8E9sG0rDAzJKNj5eVheguUSNH0ZtappEMUGg1uGWCqViY0YP4qZnWjTarWYm5nGaGjY6SHyQynm5+bxvDpDO7P0ZNOQ1skLi025FBnHIR23MD0PJxtR6IX+bfKD8FvgLcsCXkKHuCPGDhigh9IfVmjS2sCNwQukr+2V4iHFyhZSjE1KnCYaoYW0K9Ax0HGIsAnQsc+tUqeR4wkbDQuwSesW6TgAkaQQ5YB5XLLUiChQQMckxMenhSAmQqDTg24MQHEPFPeg9/VJ34ZWBepZ4sYEkV9HD4CojzjU8AOPZmTSRuCS9ENSZF5Aft/Vzne+uiSFymygRL3kUl2IKGyRcc/J+Zsk/2zZ+QHGJ6cpzykxVqFQKBQbjw0nxmoYGLoUWARQqcL4xce9CsVNgAU8ipxGgAxBOIW0LbiER2wSRLuyUFRSE0KFdCkUCsWbSPJwitTZEb/O37zxK/zovb/D7dVn+YPTv8rR+PR5QmxS51xx5eiGhr5Jp7C/j2333MJH3vPdfODBj5ELbbzlGmPjx5gf/1Nmz9aYmX6GibNjHL7/XvyFOpOvHeelr3+LZunSrzM1Cr19MLw9x4H9+2kuefQXHdrNgKmxV/jcn/4O0Q8ZbN91KyKO+LM//U8c3JLizIkaX3qyecnvWdCxPA07WxtOvY2TTgrYpsGH74HQgqk5KM1yTupNIaM5S8BnXjx//XSHLlP7fSFHAsKAvXdJywJTh8wSHL4fKmV44zhMzEmB1rBAT+u04yytaJpGO6DZAgwQoskLT34JPb2Jhz/4g+zaeRftwGaxDkuuzfiZSTYVQu4+OMBtB7ayZ/MmcE/wnRfnmZysUatBIYZIAy/sWCK0wdZlsS5Ng94MaIYUZzVNtrvmSjH2akmsCjxgKzKEI0Reo73yLZImTS/DpChi4KBjoZ2rqhmtOEoEpoAwhMjvHDUL6KQo4rAfgBY1Wni0CDHJYpIix2ay6b1w//vgPXfB/iIMOxAIePlRisfGYbYClQgaFj3lRZzKCXprLzDLc7QIWO6Yo9Q623Ln39W3RckglwgMoMmJl+sc3d3k3Z/IAxB1LhKzo8b+0+//IEH8Ck/81Wq0VaFQKBSK68uGE2O3bdnKBx58HE3T8IGlEM6qquOKmxYLGRWb7dwXSJe0S0wLdeTcIdnNoBtSoSGF2hilIigUCsVFqALHCQl4msbLP8F33/3P+LMf/jt+9I9v5xW6a1yCrvCjXO3fOVbG5KGfOcgj976XTYMH6cncgiEMSidLtOwCtpllcGgfP/T9/5a///JneGPsRfRUg1/5hac4fGAItxxw4jKLIR6tQaEOM8uLjC/8HVv6Yf8d7+LeLYdYrpdYrE2hBxW85UnKi5O8/PzfMZqDo2fi6/JT6QJjAv7667BlM0Tx+WunFeR5eLHXnozPf3yhBMf/CLRORowQUuyEThSq6O6fzbdZyD/Fv/3k7/LZ//E5Xnv9y5imYOzIq5x45Qw4RYYKBXLb0tx61204eomxsVFOj/r8rz/xMIPDDnFcZ7H1KmY4w1ItZGpWtj/b8YNNVEPTgnYV2i4EOmzbBX1bLHqKFoGvU5ppELpyf4Mrx0XKhEmBPZduhKxBYo+fQZo+bMXEIkMGA6fzrCyQAs0Ey4K+PBRz0Pag3oJyvfNtBJ2j1WngUmOZmAircyQNBx0TohCWZ+FECqJtsNAnv4SZRZnaTwhuE8wcuC0ir02dkCfxOYL0/F3svGKJ88+L1aUjVHf43b/4Ncaqx/nCJ34LkAXcdA3MTtLS934EZk+ixFiFQqFQbEg2nBiby2bZuX07IN9cWIPq1Oq2SaFYPSzgfchpRTIJ2MolL/0MUrNdGQHbKfKL2Tns2+a7CaS8kOO84mBJFQwbOVu4UWjI8J8cMl8PkJOCde+1oFAo1iAC2eNOENOOXyM49Wnmyqf5+b2/y6+c+fecCEvnzJOWkBJPkRvbLa57TEj1OvzIB/8XCv078FspGkst0MC0UgR6jK5rCOEzvLmfO+48jNA9nnnui/yTj97F8efHmTtVRVymUio6//ObMHsqYtiGsDaP61u0q0127bkHx4zxqpO054+zb8swn//aPDNz12/VMgYWYtAXoceB4QFYWOr+/a1e+cLHBRBEXFbWS6sOL/5jzJd2fpbl9jyFwT5OjpWZn5thfqnJUq3JVPkv+eKXnsT2p6BVxqsGVGswe2aChcmIcrmOYbW5Y29INgeDQ9IrNp+V4q8XyKb4NpRdOXLZNAK33AtW3zBR2iA0PNo05LqxCbF1iYZfggA5zMnRXXPOIPOKRjApUiBDAYMUaXowyKBhyL11B6w0GCY4DvT2Qk8anAB0E1ptcAV07AgEghCPiICICNDRsMjQj2UOQ2YACgVIW6DrUqn2fSjVpdmvboJtQ2RA0GY5bHEcn6PAKDCLLE+a2PuvnZGOi2xRCBQIo4ggbJ37a1oq0ufImuAYO4B3A8/c0JYqFAqFQnG92XBibNpKMVzoB+Tg0m16VOcvXq1Todj4GEhf2CTeIwT6WOmrfFGSCngJYsXjBpdpU6BdcJDOcVazcs15zfGRiXsKhUJx7RHIaNc5KlB9Fb9ZZ/v2H+CRwiNYjZd5xRujjpQnNKTrZBEZ0XghOWTvvfqV0NcWpmawf2APUd925vw6bnOBVDaFqekIEREEEGsxGGkGhrcyXNqJaRcYHM5yJA7xNZ/sIDQXL+/1AqAVQlCDhTkwzWUyWQ1DD9myS2Nq7ChBo0rp7Bh2GLM4D83Gdf0I8ICWJ7PiUzdgVB9F0g7h6SdfYdvwCFt2buOVY2WmZir09mbQtJDJE6cpnT7NpkF5bjeaYEVw9uQiYRhSrbhk87C9H1IpGB6RuqMBhD4EvhSHPRe8GLJ9sGO3xuDuHHoqB0aMZnjSJ1ZALK4+BT8pzpWmO9SxkOu4PaRIkcHslBwztSyaSLycYhlG7KRkKK9td/wcdDA74mwmBbEpq5GJFBo9WMSkiQhwEcSAhkUBw+mFfBEyNli63HRNirG1pvwCohgMaeTfjH3KscscHiVkNGy9s7U77yMZ+qy+LUoiDQukkUaLlTkB5gXnr6lB/+A+dt72TxgfVWKsQqFQKDYWG0+MNR2GU31oaHhAtV6nPDez2s1SKFaJlVOLJOyleOmnRZxfSSGmq98KpCLwtiP6xGXtAlqd7UYjkNprdeWDDVQcmkKxjtCTvOn15Y/SBmao0AhfZvb0y/z2vr8lZ/TRLs3zStQgRPZGBjJvoc6b16sGkV2nEmNXEAJNMOsxmW2DlJyIMA7IZvtJpVKEoYYfCXxi/NhCs/P09G9l5633UKmM4+QF/TsNLC3izGWKsU3kT0kuhuNjcOJ0lcFe2L/boHx6jIkzR6gsVanPV+krgJAa23VXwEJkka3q23jMXmtefHKRHd9zO7fcNgRfOsKp0w0+9qHt2ELnixMVchnIaVDyYK4O+xwYO9aQXrACRBtmJyHfB8ObIaVJe9XIl4Ks24L2sizStWWrxqE7LXryI0SYEDcxYpegLUXoIJRa5dVgIuXBxJ4gWU6WoqwUYjVMYjTQUiCSCM8ItLhTZc0B3QA/BF+T37thQC4HcQCNEC20gBw5smRJ49KkQRstGTdle6E/B44GZgROR5B1XWg0OmKsLltpGCyJkEXhUcPFo1vGOBmyRXRrr14yqemGkBQj6BQzFGXCQBBHoRTEdQ3TMuXnr8GeA3fywU/08Pu//H+tYpsVCoVCobj2bDgxNmNk2JzaAsjBhzc/S+nIS6vbKIVi1YiAKWDzO3takkmWpPYnxU2SvL2Q9ecZG3PBLGQaeHp12qJQKN45W/sgbcOJ2dVuyTsmqdbuAT/zxsf5yV2f4n9s/iw/8cpjfAMZDVtBCimDndsru6szN7i964U4jplbmmOo6eK2WrRaNWCEMAyJNQPNNDBNm6brEUY6Q8M7+J8+8n24lVkGBr7N2MnXOHPiGO/kxyyXgoMDMDcnhcQwgudeiqjMHGP/uyx2DAj8Xo3nXhL0boVoERrXWSRdvvQu14WpySlaDRnLPVeDbz17jJQmz99GFW4fhp152JyGO+/K8KffbFNpCkzgZAvKFdi9G7Zug6EC3HWfFGFPn4ITL8LObXDXuzRGtvWTKW5jaalBhIfAxXM95lyoBjLytnQVSXAm0kWpZ8X9JEHIBJq45Ik69wXELnKWYYBmS7HVsjohuiGEBoSmDPW0NBn+u9wG4XSOmEYu02RI0UMqiYu3++WxCjl5oqUjsIVUqOfmZNW1OO620pSVzQLkgo6LjN5u0403TaJiDeTwbZm1NXRrLsPxJ2OOv/Y0rSBg+NYR7nr8DkY6thMP3AvFXvj9X17ddioUCoVCca3ZeGJsocjmW2/vjj5qczB9ZFXbpFCsHjowjLzUS8iSDv2XfloSlpWUFk5uJwKsz9oazV8Ri8Brq90IhUJxucxVu9Gx65AYKZAsEPNHM7/Pd8rP8anNf0h57ic5GTeoIbvVMnSSoaWokpBGiimlCw98k+IY0GNFvHL0BPfvvBUtcrFsnbnFCZbmqqSyOXp6++nfvI16vY6mBWiGhWX1Y6Ta5Pu2sPegxb59u1h4/e+oL0F8GbnuNQ9eWQArBLcsow3NWJ6e1adDMhlBOg22BffughP98MYs+BtQUW9Xp2jGXdujqXnI6JCzYDGAlyZh1zDcswc0y+V9BwRnJuHMtDy3622YOQNhCaJh+KoPpZIcudx/GG4/1Ec6l0bTLVrLNbzmApERoYcheisk40A8AEuLULrCCniJpXxyfTnI/KFeuuJsSIQgQkNgnCvpZXHOBMDzIajKqFjTBMeElg9mIMM7jU7UrKYh3/ks4KJhd145Kzc7BL3jvZDPwiP7QMvCXEu+pJORrxUnrrY+MSYxNgKTFjKy/sLo104c7VUVObtenB2b5Q9//TP8/O89jljQCdwQ/9V5uHcI0LA0yGoWsAs4y9UbUigUCoVCsTbYcGKs6VjkBuTwKQLi0ANP+UIqblaSaYaOnN5fhkXBxQ6R+MSGyHnE1QqxBrAJmEeGcVxvkrnieVUsSsCxG/DiCoXimuCv/0l4hBRLJrwZzDDkveadfGzgI/xt7Vledcfxkd1sUkwocftOnrv6KcZrh2LBYe/uPJOTE9yxXMWyHAq5NI12m9LSLD1hH046RRj6xLHAMHR0XcewDARZCvmtZLN59HAZMw3aJazUEyIBdV/+stphd32y7gFtQaoOWUdqacUCDOkQ9kNJg6VpEAFrqaLSVVFb8ohWRKQ2fcjldG7babLJjzk2E1GuChbm4XQpxnWh7XbLejZicFqQ0SAaguMnpd3AlmGD3bekSWdiYkLiICb0QuKoRShijEBAAJoPRFCOYPoKP9PkOuvEuZJFJgRlOo/LNWjp3aR1/gNNRsQKQ54AIdJSwDCkV2ysSXNh25CbaYJhg5b0YRpyTLZic9KyClvWgWwahoqwOS/DjEXUGYsZYGjdCFxCPBHhASE6Ad0188QdI/G+1VmbMma5PsdTr/41haFPENah0fRo1rqDTB3QtRQYD0L0WWQMsEKhUCgU658NJ8bqpoadkSNq6eQUs3rVghSKtUQvF/VxvRRJnl6S5n8txFMD2IYMAQu5/lG2Ft0ZM3RuLAAnrvMLKxQKxfk0kEJeKVrkC6Xf5Sdv/y9MBEvMuNOUCXCRCQlmZ7+ky/VRYuxKeosO+/YUWF6coV1pkB9w6OvJEPkBUdgkDtLEoYvvt3CcLIZhYlg6VsrCizP05bcRiyZeM0NPsYhbaeGKkCi4PFXPQ/4sBshSkG5H6TJ8SPkwWJd2nz1F2FOA9D4pNIYNIAJdN9AMGyE0NF3HMEziWI5XtU56lx+EeJ5LHMbSf3aNibjLJbm4APJcDYFURue2XQ4iDFmsx9TKgtFjcKqzXw9S8AQZKZ6KwY0hduDsBAwMQnHIZHg4R7laRhidEneRQNMi4kh68YoQwjq0qzDnSUOmK0FHisOJLUEP3QjZZJKkdeYRslyXQKCBZqFhgBBSlNUNWcDLcmSxLjeUwqzViUk1LLmPZoMocF6ZML1T5CufhWIP9OVhpB96dKgFEIVShNUFQgshjhBehBaFeMLDJSJAP2fvn7wXIY9+Toy9FmvpV0fixNuVhhvBAq+XvkjgR7S9CC8C3e4571m6kSE/9FHqC19GREqMVSgUCsXGYMOJsWEY0Wx6pHE6j6xm6XaFYp2RhIgk1gRBZ1t5OV2LkbwPPHsNjnO5JOP6peSBY8D4DWyAQqFQSDxksFuIoEKLnmP/nK3s5YfZxxGO8mWk5hayNiPZ1grlco0Tx9s89OhDBK153EaEZho4uOzbsQMvCAjbVbxGld7eHkwrSzqTp3dwgNenZunP57HtIqJ/mB/88Z/mhee/yOjzp5g4snTpF++wgBQWB5EJ1CBHnM3ONj0DvTNQNCE7BN/3cY1IF2DY9A72kxq8j7Zvk833s2XHbuaWZrEF2KaDwObV10/xzW98mcWpCu1SJN111hBJ3pkGvNeAkzE0FkK+9Q91wghu3wlNC06uqKNbpyvgghQI59vgH4XiABw+DLfv8ijPz8lrwADNkEGhpglRE9pNaFfAW4KpMahfZQJcBhmfmhTxiujGrvYDJhExbVwaVHFIY5KK09JmQNMhlQbDhFgHX4dsTp4Yti4bjiHftZOSwqvfD1GnbJ9mSaHWNMHUoJiDTYPy35wGRRuKWTBT4HrQbBG5IUFLx8TFCj10fDxczM57sDtbUvAvCfpe/QKASSGCXmCMZHVBCJg8BZu3ZykeAMsGTeta0uR7M/zYL3+c3/s/fpbqGrsGFAqFQqG4UjacGGtaBpm8TIByAV8rgr5rzUUTKBRrEhMoIGeYK1npEat39qmyfq6rN1Ws+Bvgm6vTFoVCcQE3oNz8GqON7FZdYBxBmTNs1W/hX6Z+AdH6FV4gVN6wl6BUgxdGA0qtZ3hwIWJk+3byg8M4hSzNhovhpLFti5CQZrNFOq3jBwEzc7MslUo8e+w1hgcHeM+7H2TX9v04sUE0/zUmjnztHbWjRXf90kCaAQ0gxTAzB44t/WNjB05+XcjIRcNnLr1AoferWLrGsmUw71gYZohjgmNqmLqGMx9wb7tJIx/TcKBqwvQ8aLH8+V0rJlwCeCaSa7cCqEby39NTMqP+7RJq2p0D9IYy098tQcUGLwYjD1bHQiIQYBpgBNCowcw0BJOwUIHmFaxaGEhpMBFie5BDmyxdz2Y54HFwMNExqFJnnCXG0RlikBw9ZEWWYrMPU7PQsIA01Drx75rW8YwFQk+KtbG2orvzpW9FaIGbgXQRentgOAvDDoxHMDoNY4vy+aZBEAqIYpyUjRY6OFoW89yKuTzvLDgnzMJaGaqZyJaFyMXwbqs0DbbdAtmchq53rHU7hICR0fjuD8Gf/KIceioUCoVCsRHYcGKsrgvsTgXOGBDFQdixX5UiViguB5mDB0OcX857pU6S1I1YT3V03hQcryJjFYq1Q+LMuAbzsK8Tic1kGzgK9BHgikUGghd4iIM0GOM49fME2UJnm1yF9q5Folj6j1YWWyycXUCPLdx2RH64j0DT0a0UmmYgYp1sNkutVqfZ9IgjyFgO2VQOQ3fw3AAttsimC2zfvYVD9+9icvIMtQWILyOxKvkuk9suUiTdAQz3gWkDBphZWdPJAHQBcSsi8ptEMcQdcbW3IK2RXV0GVYo2BGUIQogiCFrgi+5rrQbJEMC74PGVxeaSj+1ybJ4F0ofXDyBsQbUMy478vGxdRk2GPriutEltVmFpCcoLEDdgIoTqFXwYFlJ4TQTYZJPyq/yeku/WpgeLLHVcRlnurEm36cGmB5sBkSEtNBxMbGycuI80OXQMNHR0zcTBJBagoaNhEBN27AQMdGGDOwCtvPRgsJFRskIHL4B2G7w2hDE6BuigWRphpBMQdz5v65w9QWKAYHZu9yMPWWc1e9iY832v8sizJkDTZDSscZEKY7ELtGBTCkw93Xm+yhlQKBQKxfpnw4mxiBgRu0BaVg4t9ML2XUqMVdykxMi8Rplod0kSV4+tdEO3oCu8ihX7rMtAthiYQQqxKu5MoVg19I5/IgaEiTygd4rf3DwJ+gFyeFIF2qJEGHyVj/MoB6kgiDhGi+XOvimgDyXGnoeAqA3lhSrEBq12AAZYvb0YQkcXBgSCtOMw15ynUqpgmQ4jxRwjI1uwLItG0yMMQdMNRrYPcye34RkLtJotAldIr9bLPB1jpD2Bj1zT1G3AlMGQ57LVhdTbQh+CJsS+FBmDEBxXam46YOnyp7a0AK0AXCH9hhOv2tXE5PyEGbi6+PYYcCPwWtCsQ6sIcY+0YPVCKcQ261CtQm0BystQWYbAhWlxvhB8uSSuTHmkCJtEyBp0LQtAEBABDilyxMTM06YNpGmfK/bVixR1c0AWkzw5ihQxMdAxMISNIEdI2CkDZhIQoqOjYaLjEAfLaJUYZ9HBWcij1/uhx5T2B+jSoiCOMQwH9BgsQRRAoMXEgIF5zht2pW+sTjfaV2ctiLFJ61IkhQiEgLYPtgPGBYX0RBvCpRg3aCDCPuS7UfGxAGgdYVusdo+gUCgUF+OtRwZJV3+tHBDXKxtOjG37LeaX59m6fSe9QN4wsGz7hhRsVyjWHi7wJ8CPIKeGl2ClGDtN19gtKX0cISell2+pt8bwgP+HKy/1oVAorgm5YUgNgp6DuacAAVYgLffPAAAgAElEQVQ/WJugtYTsZDa+IJsMU8vI3jogps6X+V4e5F5GeIrn+JPOPvOdTdFFIMXY8fEpZqZnyRfyFAeK9I9sI+tkMDSTVrNJbXYRM4qwLZ1as8XwcIG+bZsIg5hK28fMOkQth1RhhJGdGnv8Nkv+czQrLmEDwrl31q4AOAIcOfXW+2hIEa/Yud8GmmX5K5XYtYM8L5KklSarP2kRnXZc7PGrOaYHtNoyQjLTwzmv+uoyNOrg1mB6Cpoz0iO24sql1Ssd37tISW8L56f2Z5BynwUYCEJ86tTYy242Y7AFuYDSRzdJqImUFuUxQprUsIg7JbUADGqkaNPGI8AnwiXEI+4UG5btMWYsbp05xL7vvJ+U+VPwwAiYPZApgDcLGRPNzshXNSJSNphmChuTLAZZutGwSVSvCZxmrXhQByv+7fphCQFvTAtu3ynIZ85Pu4p8WJ51+fxnn6RZuwPZWyoxFoBUv+wA/bViWKJQKBQSDR2BgRy9nJ9mpAO5jhwboBMA4Rr4hVoNNpwYu7y0wGsvPMXWQzswNI1UOkumb1D9bCtuUlrALwGPc1libNR5So7uLCMZ0ces/izwqgmA/87Fp5IKheLGsAeMbXIimclCPQNbR6B5BqaeRcaY9SI7o419ra7sUtvImP0Q+AzPcReb+SiPsshXeJrz5YcssjfzubkxDNhxG6QCjYVyzPh8k8HRUbSeXoqhSaS3ODF2mt5Nm8jke+gdHGbfrbcSBm0s28ZJGei6gRaCFvnYuSypwWEe2LGDvYffxdLSOItzE0yfOsXxr1WIWuKahRYKpJ15dcX9xRW3eYvb6/5n+CIYyKs+BViG/IgrbShVwWtC0JZRxI1lGK3CrCdzWyKuvkRvSDel36IbFesgE/8dUmRJYRPSIOA1pLXIrcio2hSygFsi5saAS0yJOlk07HOp+SE6ETYxGtAgpkWnvgWyp3MIqFClHi2SqrhQCkGkIFeAXE6+WJiS9gXCh9AlrWVI42B0jtVEDt0Knc8mh7TNuNBWYnVocTGPqzAI+Z2f+yN+7pc+yh13bz3vb+kB2HQozbvOfBDnz77K6seFryHai2zMHkGhUKx3xNtYj8VAPSngeJP36RtOjA1jg2aQBjQZTWDrZLOWEmMVNykCmdg4DWxDChxvgU03nEIDPogMp3gSOjlwV2jpmKyImayu0exJ4K+RU5Wbu+NXKFaXGDDBDWXOcbqf/Y99lHa7xvjTt8Dxl5BRU4mro5Q3NvqkM1n3qgAVAsZYAjQ+wEGyjPEqbU509l0LqeprgSiG8VnYkhK0fah6Ia8cmyZtjePt1skM9tPfXyAMIwxNI45DlpaWyOVSmFqIEAAGvYN96KaARp2o1cTEJI5iLC1NLjVAX882hvNnmZkcY3GqzNLYtWl/koyScLN+pwEyFn6TDbjQroBrQa0OXgP8JrQbMLkEU4EUsK92IaJTauvcbQM5BLLprkXHaMSYhGSpETCBy4vI3JrFzn5G5ziDyMJtI8BuwEQwiKCAhk1ARISOQEMQIQXScuc4s8AccDuwAw0rRob/LjakPUGlJavBRZ2xVCwgMgG7EzUtziUuWUghWScxAbh6wfrakvTj25Dj0yZxHPH8d56ntPgQob9V+ix3iA3Qcxp3vNfhoYcf5Znnxjh79vgqtHstcrP2GAqFYr2zsUf0l8+GE2ODSKPp6whklEls66SyG+5tKhTvkClkHMkKMbYPGWUx07nvIGcWSejNA0ir2ZeQ+mVi7vKOx35rIZYnRjot/hVq8KpQrBYd2ULPAKas2FMtw+YtpO00schA/g7IlaQAoWVB1yAKIDxLV1IwWGvywrVCIGPHasA0TRq47OFeDhvb0cQSpbh0kxg4XB5CwEIZUjnpLWpqoGkmC+NzxJGgP2yz9cA+am1wbAuNmHqthmloaJqPEDq67rB5504QGrFmEgmdKLJp0sa2YwrFLIXCdoaGB8hvNSmMTZM1XZYXFmjWIVqFLyNrS2/NmnvjX/t6ECPPedOSPrCNGggTSiVo1aDVgnoLzjZlNPG1sh5LLBeSNegkhlUKszomFhYOMSnq+Mzjchrp4HSh63waKcZuRi4lZZCOTwMIUgg84nPr2RFSgK109p1CWpBEwD5CvKDC6MTT7MlqmMKQldCMFBhCFvQKY4g0aUqs6cRoRGiITjuSZW8TuYy1Nkc9AySr/IIGk3NnaLfbb7I/FYBhwaY9cN89dzExvpmzZ1ehuQqFQqFQXGM2nErpeW1KpQVA0EIjdizShfQln6dQbGxeB/YCe7oPHQZ2Av8NOVJPAz3IsIoQ2IcMSrsFeLXznKT2wjsa2SdVS1YTDzn1eXGV26FQ3KxoyE7mFkjvRVYxaqJbAjI2L/1//xUiHXp6Yfc+mDLAtNBSGWi1EOUFiNvIvmRjF3BJeisX0In4c57nX6T/Ne+LJonbX+SzHVFH0WWyAb0a3FJM8dDjh3nqKy+x9OophpaHuP2uQ6TsPMIKQYtBNyiVKngtj8AL0XSbA3d/F8WeDI7VQyqVp9ksMT+3SCvUEU6Wwd4RbHeQA5v3cfDeEtrjE3z1L/+K0ZcDqiUhlxxjOpG2159d/VKQ/fbEjXm9G0UbWPYhbMhM/OU5WKpBxYey6No4XAu8zlZDmjilOo+HyIjSPA5ZsvRQRHq+NijToPE2bT/b2b6NFGK3Ide9jc5x5+haBlxMTzwD7KDC3sZ3+IMnvsCvzv8Gxa37oK8XMg7YKenV4PuABnYKXbPRsIg746x8py31zvtICnmtPWzkoDMCPDyW0VMBVur8vUxACAECDmzO8q28deObqlAoFArFdWDjibHtGqV5mci3GRgxNbLOagtBCsVq8/vIIfrD3Ye+gQxM+AjwdOcxDxmG8BRydrIZeBR4DTmqT0JH1h1/DHx2tRuhUNzECFn52R6AsAmuz5b77ue7fv4XcGODZz71c5SPvwjlcahthe276b3zfgYPHWZwpJcXfvnf4M+NdQqV+EipYeNKki26RZtSwG80/ivv4U4+wSdJ8wd8jm59xcvlaqrdrwfiPLR6W7z8/FdJaTHzLcHsqRLZz36aw+/7KE5/ES1Oo/lpigMppiuzCN2mb2gTlSUX04BYM8DqwUxpHLirH69ZJ3Q9nFSOhhsQhSFB1KadW+CjP7aVx2svUS2PMTs1xUv/EDBxEtz29X+vx95hQbH1gpmS4mHYltGwc0swI+TCxPUiAJ6hO7zRgYPAHbTZRZs+SlTReBrBcS7/Gmoixdd5pIicQ0bCBnQF0osdK0WGffo+/nP+kzg/8MMwtwzzJfkhmIBtS7sC35e2GlEbQYDZeQ2vc2wD2Y+s3WUrF9nKDNLhtsRbmU+EruDss00+85v/gaOnvn7jmqhQKBQKxXVkw4mxvu9SrcjkIQ3Y1K9x960az69usxSKVaaNTIQ7ChyQD/nImcD+zu2jyJlCsXP/G8iQjqS0cIt1WMRLAKPIN/Py6jZFobipGQRRgGAG2A6bbqPk53nmv/0Ncb1GveFBzxC022BnIDVIo24QnFpiabaB877vY9DR0bwGU68/C68uQlxlIyfse0hPSR3QCXiFk5SocZj3Akd5gQaj7yBhe1113VdAswlhAA0tYkQDfPBijxeOnMaxv8bwrltxerfhOgH9opd2K8Zx0hgiQ2WpgR+6aLrAsDRsS0czTUyzgJGJsXSbTE4QRQI3qNNuLRMHvWT6D9IzfAtbD8bcdrBFq9pAxCGGoZNJ5SFwCUMd14dqvc7C/Chu28N1I6pexOx8iaAGgQ9eDO1xLmuNId6gX2bKhsiFagDzNRgTcvQScX3XgS/8yE/StRqwEIQISvCWUbEXo0FXRE4kRpOul+tb0SaiGgdkmiG8NgmGCZoFoYDYhVhatAgh8BfKuEGLiJgUJkUyVGnjIgiQcaeli7y/tYFPdxoa0ZWq34wGOJFBIQUpswgMI2VuhUKhUCjWLxtOjHUDj4Vq6VyuWCEPWzevcqMUilUnESWf4JwYK5AzhUlkxYk3OveTyjAzSHO2Hla/9tYVUUWG9H4D6bNwocObQqG4Uegjt6KltxFNvQGBAblB3DjNzKtvwMJZyMZI42rAzLHr8K3oA5tpxWlmJ2JyO+/CLGQw/Rr2cg1/9nZYngT/nUok64eYbgX0GuBSZZE2W+hnF700EfjUOX0R/9xrEQWb1Gy82uMkPx3XWz8MQ7kFgGVKR4JUHLNUqnN89ATLVY/CSJPMdhsjZaJrDmYqjYg0Gg0PoQkMExAaUSzA77htiphIuGhaiB4FaG6NoDxPdWEK214mlY1J9TigB2CHRF5E5MeYegBBSBDo+D4EfkgYCMJAEIWCOBSICLDAtHUMy8RoChwToiAi8GKcFGRzFoahIWJBox7gNSHypPB8rbxTVwObriiZeLUGPixF0PBgwZXy3GpQ582R50kM5yDyXPaQa9TNtzhGwPnfj0cn5Z63v66maXOEJbLBLH0nJzEG+sCxOj7aEUQxIgwR7TbNxWXagU9ICATY6OhotBCUkUK2x1p12I7pxiLDyrKEHVcCGa2sgW5o5IZN9uzbwWi9xEwUUK4rMVahUCgU65sNJ8bW3TZj5XkE8uc9lYZi/2q3SqFYCzyHjCT4MWTiqy7Drv4M+Od0Z94Nuj1Dq7OtO9rACeA/IQXotTkVUSg2PgZGKoN99/vQ+u+k9YXPQzMAPSWjvRDgViEypOlmDBhFHvzhd2MNDXF2MmT+L5oICjSbPqbfIl/czPL+DxEdexEWR4GTINazLHVplpBdtIPPn/Ms/zN3cQeCAXz+kNab4oNNZMzw1QigiVh2tb1nIrXcqF7YB86G0mVnACmqjY4vcXZ8iS1bFrmnMEJVmIxs2klKOHiNFqFoUOzNY2gGIopoVJYhLEnVM/YgbEl7jahBu1WjMjPP2IlvIrRpDLuFbmucmRBMz0F1EdrlFQ26hKJt9EOm36S3P0dhd0h/L3gNn1rJpW8Ydu7MkE4ZRH7E6bEq5UloLUIrgso7CHnUkcJWtAaiak1kwk1IV5JLA4vLUBJQFW8fPboa2Mhz6k5AoLOMwSQwgcBAP+fknCw+RITnffURUpy91Md/hCoZPLaQxTl9O6a/hTiTIpqvI5LqYlFI3GozOT/HEk0qNKlTwcfHQzAHnGY95A0kg82unVziuxwJWZAPQLc1CodsvuuR97KkZali8PTRF25sUxUKhUKhuMZo4kZVG3i7RmjaNW1EX18fCwsLGIbBCQFfmZjgf9+181q+hEKxTskBHwd+Axnf0aGInGmESIH2WoVErRr/DukTO886fhMKxTonDRzi/t/6HBN/++fM/ePngHl4+MdhKYCFOZg/AQSg94BhQzoL7/kwW+55mNZEmfb0Ird97F4e+36YLcHUFCxPxZz6+rO0jz5PVBoHUYKpz9P1Utm4aMhkhTTwbobYT47XOc0TrD3xai2gIWtS9tOtyp7tMbht0y2k8iPg2PhGjEuaRS/Ca0X4tRYzp1+jTQtx0fNJdAQjccGjb3royhsturdXJqVczWvszcGmNHzrWlbBugLyGuQ0mFnx0SaRsVe7gHC9GQD2o3OQfWznXQQYNGlwD/3MMIlFTBoNg5AjPMkEPkvI5eEUskBXqXN/JRd85eSBDwBFdNrIkcwLneddeNaJi9xey59h96rcixx4Bsg0rGn+6m+f4PHHHydrr9h7xQUw97JgbLLO0y9/m5/7D4/dyEYrFAqFQnHFCCEummO84SJjLySjwYCmIUWoJmt9iKJ4O3Kg78V57Ed58P493LWvh0O7ZMVam270zcUoAU+dhO+cbHB09A3mn/kGovQUeBu0CsZboGWyZB75GK2vjyHaMdJ3Cxk6tBvZI1SQIRzJB7puLpkYOVX5JPA8MpZs3TReodiAeMBRjv7mz+CVOzYh1t1w/AQ0axAEkMqA+xrEBexbHyL78A8wsm8bC+UMYa9OKtuDH8Gf/c4kbisknU9xz6Ob+afvuZPPf2aQo19/ieCFvwB9BOIprm+pn9VHIEcybeBpykzS4v1sImael4mZvszjJMLXWsBG9t7Xoz0CKfUsde5rIZSqEYvtSXRjFjSNWIMYnVAI4kggohg/bp2LdLzhiPNvX6tfsbMtmL+Ky2PHphwCg0Y7ply5dPm4RHJL61CwYdMmmJ2Gmg9LF7wpwdoXYkEOj14h5g0meJgBHr3nwzzy4CeojJq88uR/Jt2KGaYPiwz38ih7KVFlngqTHKBIC48yFWY5i0+bCm1y9DBCHyEVRlmkRCijuYEScceAQF73G2OpKbkqo87txABC44k/XiBdX+K7/9nARZ/Zt0+DTVkWjOINa61CoVAoFNeLDS/GpoE+LOB24AhdBzbFWkdPFcjseZgPvXsTRcvAIQ3aVqzDj3LHbVvYuy3DrhFwmlBMg9XNcqKyLL3HdB36BqXW2LsN9t3aYvzQDpZvH0LU9hMEZRoRvDEBx196lWb5NASXO51dX2y65U623/EI4eY0r/W28CO/G0oVIT+kNDKEaJFrYxRoIcfZGm+2O7impb09ZN3izyA9YssoawKFYrWRvieN8W8COmiOfKjsQ9jJ47b6IT8EFBjct409D+9h/HQaw9bo35Wi2GezaTMcfz5Fa3yO1sQ8U6klsrcNU6/pCJEFvQ/Z0chEfrlpyE5tY8gXK4k6W4mQiDYncNhJPwF1HFxOX8Yx1oLopSF/bnqRItf1CthMpJ9zdyJw2y4bXbi/EDeW2xU/34sQCILw8g4ykAEjgkwKenvAEBAI+Wt9sSjutXBOXoqQxE+2zWtMsKk+zs6pecLyLuJogBYtFhDoNOghRYuAJm1a1HiJgJCQFnUqePQQcKj3Y6SDFFFjhpgyOxDoyOHSWWS86Hr4XN45nQvxnDOsAZiMH68ydaqGjEGWuC60mxC34fiJE6SzeTRv4/XrCoVCobj52JBirBCCyPXR0w5pXaePFJgPQ/gGSoxdy+hg5OkfyGCbGk7/LgY/8rP8n//uPm7JWuTpmPrHnQIIkcBvxZycaMGwgWNpnb8HjL7ept3USDkmd9ybxrZTHB7UuG84g3F4H+J79qHxvbSA2QD+9mvwF//lD5ka/TJ+/Wm8AFkVOWyzEZI/031D3PXwx3jk4z/Gqae+xumBImGzSew3kc5tSC0zC2xH+sZ2aylcGRoyL8/mOouxDWTjnwd+9locUKFQXFOm5D9Cg3ACeBcyX0EDX4PhHVj53ey4Yy8P3JPmW18M2bzdZXCXydYDNrfs1bCtYU7XFpl9YZ4jf7HMi1sOImo1KFfBGYZaSLfTySOHNxvbtiACykR8hRL/kv0cJKaHgCmiN/1qXdjdrvZSlYH8prYDm5Dp26ucPa+4BPPlC5PrL44GWDpsLYIIIZWDXB+cfQPK0cYZhR/jLMHJf2TxZMBuHkOg4RPToIxLiRQRLcq0WaDBWZ6kTYDAsmzyuTy3+DYfHPop/EaTVxp/jEYNiAmQBfvKl3j99U/SC+mdLcvCYo2lcvW8vdw2LC2ANw9f+MsX2b19G6Z1eeeiQqFQKBRrmY0pxoYR808dYfiBO8gUsgyYadj9YTjzpxCsVm1WxSUxirD5l/iTL/4gh/fmGXAuvlulAr4HS0s+p04u8/df+ku2bBnGJI1Xj6gsneDpJ/6aTCrN9l37uO+hj3PwgQ+S63XoKcLwFghzcrKQAvZY8NMfgp/+0Cc50/gkLyzCt0bh0z/761ROfw7cZ27ox3A9+MhvP8En3ncX92Vdfv2VrdyS+zzj9lMscSvwI90dm8i6V48B36Gb23klxMgZxdv9/ZrwR8iI2Cev1QEVCsV1QSAXt1b0qWIUJnXu/tQ32PPgewkrEZTGmP7sPzDdt5MT972L3Kc2c/gw/MSDB4iXD/Cpr8LJZ6ZoPPEU4dhLECflrSLk4kz1Yi++IRFIy4Lf4jgfZpgdjHAf0zzD+V3sWouu24TMV3KRPzM3zze28cnosNmRImwmD6YBoQuN2sZbGjnJG5zkDeAPOcydHOZ+9nOALHeQAgLa+NRpMsednGWBFgfvfg//+sd/kcrz8NW/q/PS/Bd5lTOkaPMUchh2cxAiR+FpZBrVrbxWmuau5TPA3ef2KhQhk4bTJTh4yyALpTlOnj21Ok1WKBQKheIasiHF2BiYIaIPgQVYtsW+Q/s5M20TbOyCy+uSj/yrT/Ohh+/g/Xc5YA6wdWuOlCWrVoQCzozDN59t8eyzx3jm679H5D+LEBFRJAj8iEazjmWagCaLcUc+rWYdXdM4UnqVrxx7AuePs+i6hm6AYQJ6mvv3v593HXqQ97z7/ezf3UN6q8bWLAw48NAQ/NQX/n/2zjs8rurM/5977/QZadSrbUm23HsFG9s0Y0zZAIFAQkgIEFI2CdmQZTdkN2WT7Kbthk2WZCHJLyFsQuhgSoAQbAO2MbZxk1xlS1ZvM9L0esvvj6NBNhiwcbfP53nmkWbmzr3nTjn3nO953+97K7Hs9bQNJrnvaYtV955POn56xe64C4r43PLV3DqljpF5CsmUk7JRc0hHHySb3AA8ArwI/Abhq4z4Ab2OKOpVwtEJsseNVoRa/BCirMUp2UiJRHJYmGz735vY9UApmlaKFZjIJ777OdJ51bS0x1h+9bdweCdzzo1zGbdkDAtmWDS9WYplloDpQ0TGpxFJ7yBE2e6TdjYnAwtYSYBSFMYByxA9ZN8hti0vKmbVLx7kirs+T3N3x2Ef41gkMyjAFMQnpQEjgSZOfqSu5NhQWwA2FdoGYbAFCpzgtIOpiSJUp4pP8fGggV00sR8HTlSUocJrFhYmJjoGOjomT2/bzC+/8TBGChIxk6QeI0XobXuCs4d+xLJMPsIzVsdiEIvgQVspCmRSaTa+sYPps6fS3h0lmDr9M9YkEolEIjkjxdisnuWlN19m5NRavH4fDqfK9PPz6Vylkj17lpxPYVzUTZjO4mVXMKYIpi5cyMSxVdSP0FCB9m6d5pYmmvftZu+eTQSDWfa2ZGnZ303L7tVgtXC4U8KkniSSPFTMjZ1sKEtr2142bV9DRYmLubMXMX7KeMZMrKHcDxWji8lQTFVCDBHPL7qbnT0xduzt5K1n/8z7h32ebPyMnzmdZZ+8imtnTqDSo2BpEMuqeKvcROKdJNNdiHikNPA9YBYiVmmaCM1QGX6bcwVvT2p4VRZYjZAY9gNtQ//3I6fyEsmphMqwWXQWMdlO8X4JyqlgGyl6gDygiz2rTXRHHoG+GJH9q0B7i83LX6VzTx3e/GmkWuoxs06w+0UhMDJAOTjc4DQhenaJsQBxDEzEOz8OGIMdL9DCwavQiVSKP738LJ/52Kfo2bGdpi2beTnQ/oH7P7Dau8KRRTnaEZ+sk2H3Gjfi29GP8OGUnP7E0qAqkLEgkoWsAZoGqGe2EAuQIk3qcEwYUgn6eoIfvN0ZTwnCGyvnZWUw3LscjN2pMemcUipKC+jsChMPxU5oSyUSiUQiOR6ckWJsJpvhL6ue57rrr6eqqhqHS2HWIievuJSzKP3nVENFUVyMGleDWytg/kVX8Nk7/4X5I4SNYNaEaFqnty/AWxt7eWPdm7y5bhUbXnsakYR5rMnS2rud1t7trN4kHrny3FtZfMEFzI/PoqDCRllFLT6fkzIPXHeuAud+jdc74G9rG0g2N5Gmj57eGPFIFDKn1sDanjeWqQs+wue/fif1CO+xEBBQwfJDJNlFJhtFTIU7gZ8ClwBLEN1CHUQdiGn90EMnPKrcGmpbeujgCeBx4AlEjI1EIjl1UBAirDH01waqE3zFkPCA0QVWhuH4ykOt7GQQXrJB3lq+7eCnjC10rYeu9aXA5VC3CJJRsOtgOsAYKt6lecBtnrXqXhJoRsjfNWjkYSOFne4DYu6iiTg/+MN9PPubR8jzFbM5lDgsMfZAVA5fjLUj8i5y0kvum+JD5Dj0crZFBJ65DB4wXMsAGZMzz5tAcpQoiEFlLirWzvD1IOcfezAOl40Z540g1QvKUF0QiUQikUhOdxTLOvlOYoqiHJdGrF+/nrlz55JClPb5RH09Xfv2HY9DST4QP07XdJ5r+Suzip0U2UUxLoA4FoEkNLYP8IXv/ICe53+PETuZDnIqUMa//eQ1Lr20nmlTRSSPQEFRxLBxJ/DVu1fzt6eehN33nKzGHpKRf/c7bvrYMr5/UyU9CgxYIpF3f9xiwyvw58/VEetrfY9XOxERqON527rgEJEKx5ZDdQFZ4DPADqALWd5FIjmV8SCktgN+p/mj4bI/w+qnIfgcpHYg+hQdESl7DCLaHWMh/6MQWA9s4mx1H7Uj3s0Dda+ZwGxKmcF47mAN5iH62TuXfoSlk2ew7J7vHbe21QH+ofbZEBGylQhx9pfH7agSieTUxA5UABMRvYATseieAiw+9akLePDBO97eOle4NxWFdBh6e2Dd+k3ccsfsk9F4iUQikUiOGMuyDimmnJGRse8ktwar8BVEoZ81J7dBZxUl/PNPfsjVH/07ar02Cksd2IcWvbMGvLwJvnfn52nZuw7d6CUci2GmT3aVVBPo46ffX8AvfmyjoLSSBVd/m7s+t4zaChd5brHVOOCRb84jcuc0uuNf54vf2UnTC18j0d94MhsPQOemPbyYPx53RSWLl8CgBQ274Y1XBln1rZ+TirxfIbs0wnHQBswHvoCo6HU8BdlBYDnwMqKCWB9CjA0jhBsZWiORnJrYEQbT1cAIhH3IbiAN0VZYfiVkJoM5gJDjcvYuLoQw6weOohhLphmC9yL6i7PXFP5QZ94AdBCkgQ18hVoeoYued6RR37fqJX6/esUxb48DKEfILDoiM8OBkOurEFeZN475USUSyamPjvD5zyBi+bMMi7EDvDPzKZ2CVBwcMcivFPfzzorZq0QikUjOdM74y5mJiLnLA9zzL8WW3YreJsXY44uPkup6rv3yF5ha4Gb++QsZM6ocv1082xyAjRs28/LTD9PaE2Jn4ytEw90cH0ZB6bIAACAASURBVDuCD4tJLBogBkRiUbLP3Eu85TlKS2oZUz+Vqz96FdUjwJ/nID/PQWGhj29/1sngku+ysy3A2t1x3vi/+xHepicunUrVHMy74Wdces5sCkfUMJBN8Z9ffJZxF15C864utr6wkmToKT44KTRnu/Am4nN5EhHLVA9MBmZw+OJsfGh/CaB96NbGwQV2UsA+RNLq4NC2Jz9qXyKRfBAGEIOySjwTr+W6T+Tx9J+2Edm9Hfq2Q2oXIo8gihhy+BFCrB1xhY4g+pIStLJJOOvnUTaygM4Xfk42cqjyU4c4viUNiA6FEEFN9pGmnCBTsZOHRdMB16REJk0iIwTaKsTyV+7drET0xqkjPK4dKETEvYUQn3ya4cjYnqH9HpkxgkQiOTOwEONi59D9DBAb+pvmne7CNjuoms7mxgC1lLB9yz7eXCeXciQSyWmA9xxGzFpAXvVIWpp2k9ryezCkzYpkmDNajA0NDhKPxXD4fBQBI+dNYGB/GQNtJ7tlZxJD/k6KA7zVTJ1cis9RTM2YaXzi1s+zoATsKugGhOImDZu20NiZYOWKVTz2/34HZuBkn8AHkk3HadvxCm07wOUdy9gJ5+L2FTK63s64UfWUlxThz9f46KISrEXXsq0LijeFsbe2krJ20RdK0NefJNGzi+MiMiqVlI6ppKjES5Hbxawlt3PZIgfxdJIn13Tw3K8fZ35QJdC+n643X0TESx0u3QyLpqOAacA5DAsrDsTUO1eoJ8O7k2WjQ/uIAXsQUXB7EMKrRCI5vTGBJDgs1OJSKi+6HNubE6D7FQjo4DMg2gyWgSjZVA6OqqGXBkDfObQfB4qjBK1gPK7yWmxV01HzetEMg0RPB0K0lQs0R0oWEWu2gwiT8FKNkxi2gzxkISeHix48J8Y6OZR74/szESHoaoi45xjiU9cYznHoRCzPDXyYE5JIJGcABqJXsBA9w4Fjx4P7eZsNLMVgY2MXUSPJjm272Lt394lusEQikRwRKhqjpyxl+qVXU1Bfj/7qZvraV5OK9qBn4hjGkS51S85EzmgxdsP6dZSUFDNj1myqgKWzIL5G+MdKjhVuVNWD6qlEmfIV/vvJG5hRmUcRQz5PgG6YDMZMtu5LcsUlt5FJN8FpWkotFW+i4a0mvnL7/wFlfOPOX3DV1cuYdY4bTbOhqgrTKhWmX+nn7it/Tjvw8Io0f3y0iZ2/uxmLXVhWFssC07SGBIojFBgUDUVVUBVxw3kdy+68lWXXzOC8Eovlf7XYsT/L1sYWnnjsRbAe5Y3HHz0GZ982dHtu6H4Bwvcr5/kVQMQ8hXi/qukSieQMpGMbsYHf8ePSSyGQB/jBVQNTl8L6f4FsBBQPKDVo1ZdgZtNYsa0Q2jK0g070jheJdrzFLqbivf7TlFVU4Y7F2PW7e4B1HHmMpgSEvLEXCBNnCsVcTSn3s/sgD1kLsax2oPi6/wiPowDfRpRZfAXYxnCUrB8huRy4NCeRSM5m0ohew0RMR4WhHBaYJiiKuAGkMzrrt7WzuWEF7qyO23mky0QSiURy4lBQceHjjjtuYcr8akwXuJLz2dZ+G+27XyXY20g0IusYSc7wAl7e+nzu+NxX+Pe7fgDAmhDc+93v8cjPf8bZWuTj6HAg4myst+/n1/09N376cr74uQXU+e243XY0VRH1si3Y1g2//vULrHjhOVobHySZSHDm+H8qOOxObHYbLreXL961nI/fOJnR1T48Q+NEE8jqFindJJhNEcNkfTus3JbgoT/vg7/8K+hbOaIYoen/w5UfX8w1y+r42BgAOzannail0RjUuetLf2X/hu8TDTSg6zqWcTyFUZVhuwKL966SLpFIzmwUwAf268FqBKMPrBBoCTAugNHzYdQ01LJx/Psvx/DQbffR8MzTwKuI4l8pRI/pAu1CUBrEZFwtxnTNhkgbWDsRcZWSD4MCVKIwCSfzmcuv2EjwAHsglYN78DyESY3+rj29GwdQi1ieCyCWW4uA4qH9pRHWBLs4JmXbJBLJac9CRN+fi5ANAe1cdtGVfP8b9zFrybAYGw6lePB/t7Jgzhi0tElD42Y+ffeyk9ZyiUQiORycLi+qpqDix27OZvElc9m8+SXa2xs4UItSET3h2Vv54MznrCzgleiMkR5IvS0VuQywlS2C+j7YK2v4vj8KjP84pE2I9MFAIyKx0MLmn0DJ2Mv47t3nU+4bw+jaSsaUevEOecIORmFfa5jHn1rHxjefYu+enfT17CeZONNiYSwy2RSZLKRSSR554J9YuyKf4tLRVIycx7WfuZHKWgXVqaDbNDJOLxkL5tbCzEI319W54NbvY5ph0qQJI6KFTIaTtkBMiP1DNxXQCmZSNbKU8govaS+s3g+7dpvsa2hgxyv3sXfLJuIDOzCyJyL6+EwR1iUSydFhAQnIvoSwFFDBUQoj/w72vwWGgzHllXztzloe+KOTtuYdQK7YYZrhvsQAMwRWAosUFqGh+0mExOdAROIXIuIuk0DXiTzR0xYLCGKxjQwpdlJDBhvD5XLe2ZsnEVYDOYuBQy1huxj+RCyE4JqrlV7BcFm1BCKvQgqxEolEkEEs3eT8YrNAithgkrbtSWZd7AJDoau5m4593Vxx7Th8WQ82N0QcBSe15RKJRHI4pFO5uXgKjTfYsL6JULiXd2YIv9ugRXK2cEaLsVbSxEykMNJRVIePfJtC8cjxFExYREiKsYfE5h+Fr2QUo+vK2JWeR6p3PyYRwAHuembOqGVE/WxGTLiMq69ZSJGiYGfYjr9xRydNTZ1s29bM00+vpmnry5hKAlQD7EWQTWF3g9uj4nOpWKaJQhbV1FF0AysN2TgYlpi05Sz+taH25SZ1h3aWOgm4yrAXV+EdWcPejkb2vr4ep3sEJbVx1KoaKsc4UO0KhgU4LAynn5r8Msq9BRSN8OOZcB75HlDtYjiaRUxkc+cOwm/PB3gtoY1nExAOZti5s4eOti2sbk2ya7dB+/YddK9Zjowck0gkJwcD6Bj63wUooIyB8hiYHpR4Fluel8Y9UDCxHm/FIvo702R3vjj0kmJwV8PgAMPFXAzI5hbyVM7wYctxJw0EMNEJMB4oG3q89xDb5jxeXYj4tZwYe2AEhwdxjbYPbZ8G8gEvQqRNIuLdggiLAolEIhEEEcs3UYbjwRR6+ztYu/F1ruISFCA+mGKwPcLs8/LJJMDmU/CF7Cet1RKJRHLk6Bj0093T/55bnHRNQ3JSOONnNdlEiESgFV/VZKr9MG5iFWNnj2fDcx/82rMOxY6v/lImnH8jN39yET/85yfoHViBHt6OO8+OOuLjfPW7N7NkwWiqfeIlFqDrJmndIJDJ8PMHVrH6xeU0N6xBUeNYZhn46sDhBCOFPd5HUaVJdbWN+kon2WQKhxrDkYlhj8bReyDSCsmsEF0HEamOuaibiAqtpngut45+4mMzFcCG2+ciU7kA7+zLqL3qarY++V2szS+QzqToTG/nF/f9ENx+yCiQNaAgA6XTKBx/EUU1Uykp1KgZAzNHQXU+uBXwqyrlioYLcFsWKBC3oBuLuGXRlTXpa4EtawdpWPUWOx+7E5R2sN75LhxoHSCRSCTHi0N59ylAGjIBaNkJF9wIezvZv72Lu5dbZAotpt98J3Y1w5rl/cT+exZ6Ng2lM7GqL4F1/4Ho5d/Zr5mInj+DlPY+PCbCGGcAqEKhEngF65BRqxGGi3sNIMRVO2KRMIpYKHQw/MloQzcVIcJGEH61g8fxfCQSyenIofwSLfZ0bOJ3L3yPH5oXo2gqdpsLp5nP4O4wjtEaWVMhHj89605IJBKJRHIgZ7wYu6NhF08+8jSf/tpkPMDoMpg8Gjac7IaditR+iosuv5FpM8/hgftb6NrciB7O58ILb+GBh/+FinwVm6a+7eEEIg7qlXWdPPToJh7633swzA1YWgFa3kj8FeMY7OjFSgQh1oum9nHbkhLGFWdwWIOEw2E6AzB7tJ+qFBR2Ac0H11XVENE4GxHFRIpNkZyaP7RNF/AWJ1iQVUrQvJfyWNuv+EXCzerlz7DlpmpRceDef4RZs8FWDIEgtDRCUwPsbYS2fbBqOYMv/oBBQ6FZEcXkHq8CpQBwqTBxMkrFdNA1GBgAnw1LjwNJ7GaUUbEm9DcT6H0WmZiFG4NkESKs9iBr2FqEVN3xztZLJBLJMUBFyHATebvwCiZCgqsC2oEOMJ6BFRkonoJRM4VYO5jJIH/90hZoa0NLJbnmF128tauZ0GAEM9JLaF0UaYFy/NkN7MHCByxAlEg7lF9ZGHFdfhb4B0RhLh1xlVGG/jcQwqwPUdpRA5qBJqQ1gUQiORJCWOZOeroGKasooGZWBfYihY/OvI2W5ArCZoLEKVDvRCKRSCSSo+WMLuAF4M/zMm3yZF5duw5FUWhLw6qNu7h54bWIqYicJogkxOlQcz7FHhdem4sQtfzoP+ZQm2cyotjNuAmjcGjCTD+chJZAlief2cyGl56kvXUPff0B+nvtaEUaSs63IJxFT5vgiFJZDZcuLObCSSmefnI3Lc0DKIZBnRMWmRpz0hbTUw5IzcdylmLlFWC5vSgG6D6NaO8b9IR3soUBQiOgLQDdKSHGbuDExX96LvpHpl14Ld+8oJDvdSnse/pXhNf/FXPfTrHBhBHg9YFph2wWjAQYcbDi4EyJWWoeIoczH2EE6wQ8GhS6obgcHH4xI06mwJ3i/EkaF7h15ltJitN9ZDeaKH7o0hR+t8nipXtAL12Af/ZiJn38cpaUgE9xYWKRIE2/BZ17YfcGgz1r22Hbp0/QuyWRSM5MNERsZCEwDkbNxls7jYpJk1n8UZ2POh3ElTSbe5P8+OcZePM3oIyAEXNRr7iBilE6mWCM1P5e4lu2U2w9Q8w9Dk/dOApHlbDv5zcD3Rxe6SjJ0aIiLkuLES6+LYfYxg58HFGQaxei7Fohw1GwToTlQa4UT3Rou+Qh9iWRSCSCMsSAWB/6vwkVi/KicezrWIvTaUdVFdLJDLteb+Kqm5fR3tMhl+okEslphYbo6dyI+KkUQoFSOD4ahgMFExX97UxZOZ4+2ZyVBbwAwtE4rV09b98vcUJtYR7OuqWkW1vAPMunCq4ycNdhYyp+n5/RxfmMLC2gfGwVSxfWUplnx5ObXaWhoaGZxn3tbNzdwqrVm9j55qsk00kUdx55FWNIZjJYmTCWEcdMWtTPWoSvOEvNiCyzZhpUlQcoHdlJBgW/x8cIIqgbQ6hRAy8aqjICysaBzQ4ooDkg3Y9PN/FiYlccdNSW0ZIIEEmlTqhvbNUVn+LcZR9hzoJzcU4x2H7bD0i++iJ07R7eqKlDNCg3UtQQs1gHohfOaRgwbH6rAXYLBg3YN5TYaQC6AfY0kR477U6TfHTchonZKiJpg3aLgS4Fz8c+w4SRc6ifPIO6CxcwrQDsylD1agsUC1LlUOI1GHD3knR9gcSWP2FlZJqvRHL2oAKXgbcULB0S3cArH3JfFqKTSgHdkG7CjDhJ9Tjp21HArsr5eKZ4KZxocnV/kuiMfex8w6SrB6ztG8kkC9CjnRh9g1iJKIG2NvD3oZoB4pkJCGnvQPsDG2IlS2QJSI4tJiL6dQCxRjgCsdB5oOChA28A5yM+iVqEXO5FfDoa4hsxiLj2xJCflEQi+SDKEJkUKqJn0YFBLNJoDhuKKuauTqeD6Ysmo7kcUoiVSCSnHblRc3bor3XA48cDEwvrHXtXEeKvDEM8tTjjxVgAy7JIpOK4nR7cqkqJr5CKC26k/c9/wEydzdMFB86iKXhrllDoKmR0oZPLFp3DRQsnMX2O2MICsrpJOpkl0h7l6Ydf56WVK1mz+RWgCzQX5I9GLa7DX+Qj0dCEkeoSkaBaFdMuXEJVtUZ5Xi9Fni34C+GixdWYWYuygjKSwVZ625KkUwbRLHgUoMwDsRBKaBCblgc9b5E0W4AokxUfevkYovuSDJDCjojrVRmeuueKXx0roVbRbDj8ZZzz9Z9yy7RyRnrT3N/ag/7UT+GdvlXv7OEMhjWLCMP1CnyIbN44QqxVTDCSMPDu7+PmodtBaBqa04mvtJgRq+/hunI/s+ziPYghdN5w7nAmZPIhf5pGXUUVfVW/ortnE9menViZnCJ8RG8ImqccIxEGK41cbZNITnUcQDnY74KiaaCnIPkGWLsYls+OpB8wEVJbEuiH3h0ke1fRuWUknU+P4fnJxUy4uYJzr7dxy0d8dH7ic/z5P1voeWg35qoXCTSUQWQtpGOg1gFFEH6dxI79JJr6htpjIYaNuXiCOoT1wdl8zT6+rAFmAPWIyNYUw77sFsL71QOUA6OH7rsR1x0Lcc1pZvj6K5FIJO9PCTAWkSaWASxM9pChnSzW2wY4qIAb7JoDFQ1TygkSieQ0wkRM+d/P7fpYVnvR3z7qMLniq7L3PLU4420KAIpKCvnRvf/CDVfcRp6vgEDa4qEOi3+dV0Fs4L2r2p35nMelH/0sn/rczdy49MDHlbd9YZNAS/MALzy2mW/86Efo0QAYAwiZz4UyehmWokC0HfpeRSQ7ZsBuh5IZFFZOJNHTjcPoZ9LoBL//8SfxWyGikU7a+/cRSsVIbO8nvj6CtSHOfIajbDyI6JtcO0IIu/+XET50cYTEkEVE8ngRHVkrwmO2l2NT4sU3chLn3dvIn5bCX50Kj61+nacWLz4Gez4KauupvfgS/uk3v6QeyKCQUUQHG0PovnEgakIwAnoE0ilIZCAcg7a3LPoe/QmR1+7n0Emp740tv5bazzSz/4E70SMvATuP9dlJJJJjymJQnoK5hWKlJoroUMMAX0D0qkfWD3wwPmAc8C3cX1pGQaETtbeXzseeg9DPEcPNONCGGDAqwChgDLBiaB9uxCS9CtHLNxyHdkreSSVwNeI6uwUIvM+2LsQn5EF8nQaRZSMlEsnhMhOYjLhW9CP69w6KiuL09e1C1VQOzOv82NxbWbt9FV1JeR2QSCRnJsfLukBycjlrbQoAwqEw3/nWT7hk/rXk+Qrw2hUWjAC7di3wV0Qsx9lCHg53LZfe8g989YZzqK+rpqBQOagol2VBxrB44tEtPPbs39i2bRvR/m70lA0sBXChaNXkTziHWE8YI9ENmQ7AjrNmLnq4BSPcCQNdaOWVKNk48VCWbRH4u0/9km9/4xrmTq2j1qvQ3tGCd4qXgpo0xtI43YFetFAE76BJJghNbZAXgHxLrJ/7EUM2sX4+jG3ofgYhRIYRBb92AC8ifPA+VPymfRmVJZ/g/gsVrtsN+37zXULPPfDe2+dChI62Fy1FaA/vCokV+K+7kXGf/QJXKgr7EOeW+zFriI5cQQTdeoCkGwwVnBqUOcE1Q0F/zUsE/+G3Sf0v6q+czbjrq2jYrmCpKzl0NVyJRHLq8AMo+CTM8MMSYK4iOsYfDj2tfgesW8DaBHzpGB43gTjQV0k9NId+rRaUCnAWgTLngKjc3Mq9hUiOP3CBtARsk6FiIXQ/CUboGLZP8l70A48AkxDxyD7E9fRQpBFircqxy0aRSCRnC12IHmYkItZ+G6JHyQcs3jlzLZuziO989jqKSpJ87LrrTmxTJRKJ5ARwMsdRuRoAeYhwCZn/evw5K8RYQzfpbu1DzwobY4cKNXYYc+617F6/l2jvmSrGaqh51XjHLOAjS+qpcim4FDd2RzGTzruAObOq8fucgLBy6A8kiUYSBAej7Grp5vWNXezpjNEThnhEB70NLAfOvDJ8FZUYzjxQQxRXjqSoZBxtrU14iitIpnswwgqYClk9jamB6XCQtJzsa93H4ytb2dMVpi5vgImjKnG64mR9EVJ5KcJk8HpV+kIWPQGLyiQUY8OGG7vDgT1PxePyQLAPUklMxFAuxLAHSy783kJ0KJMQomQvYup/JNGy5y+q57rrFzDKZ9H08r107XwBy2gVeZz9iNlnrqh4LgchZwhzNLiAovd4bsJkJk0az/yayrcPk0s9UBDn7Bpqgq6IIOWMAk4F3DbId8L+AbARQrwrh8IJNddTMLqWUeOhuhTy1KWEvTW0deuE1nwPM9WGkL8lEsmpyURwToaCWpRqGH0hjC4Ehx1CX4Y1zwM7qiCdD/ZCSHxrSJRtROQYHA0mItG9HWswi84e0ErAXQuWHTEBzxlp53qy7NAtRwzMToh3gBl7x3OS44WO8I9tQ1xLHEANh/5G5K65Mu1NIpEcORGE/UwjYoRuQ/jIVsO7pFhob+tjRHU1Pl/5iWykRCKRnBVYiDFgEmk3daI4K8RYADIwGAySqKzE4/FSqijMuHQJge4/EX0vPeq0wo7m9uHy+vDne8lzgIIDe8VUihZ+li9+fTFTfCp+m4h81bOQTiYJDcQwTIN0Jsve5iiBYIz9HQGeX7WJlC0fw12At2QE8UgMUhtRHWNwFVWQP3Is/V0dWKpFRf1kJs+aR+bN9aSzfaQ1DUXVcOQVY1oKpmaCY0gmTNh48Y1uNu0OMKUoxK1Xz2ZUtQ2f18RmRQlqWfDaCWUhGtRxxcCJDZviwbS5MfJt2MpKUawMesginkmxR4NORSFjWqjmkG+qptKNxYBlMQoNX8YgV2YrzuF1MFWjx3DNtZO4/fZ6diYsMqvuwUq3CXurfERQaBahJbgQumQfIiBMZzhMyOTIQ4ZM3r0UpQAelcKLLmb62DpmuKBzaLOcZ27ucBmGvXOddjBVUG2imVUe2LO/k+zgfkQJlneioOZPwX/u3zP6gnOZczHMrActAi//JchLD2yC175zBCcjkUhODheBsxqKQBkL506HC3vAUw17b4GmBIRNyA74MPXx0PE9sB4F63mwVgMdHP2Ci4XoZ7rBcEBsH7xtSONFLB8l3uO1g6LI5qAdYcAih4YnkjZEdEQxwie2DRn5KpFIjiVJxPVBR/Q2FYhCXiMP2so0IZUEMx0n0BdHs2knvKUSiURypmMxHBaRq98uOb6cPWIs8Mc/3M/HbvgkCxdfDMDSZbB7BezfeJIbdizQaimdfTlTL7qU2264jGvGg2NorDLsC2xhWWAa0NcBW9fuoHewj/7YII072sBVQNnI0Riah+4BOHfpuTQ2NtLf2w3pEGhT8NfXY7ncdLTuJ7tvCziKqCqqZuGCyxg7fgH33vMNEpEUHl8e4889n1AoRF9vB/pgNyK+xoHdNZKBSISXtq7lr2uD/PK717B49mhGVkUI9IdJ6TqFM0MU+aKkn4FuUlRYKWwJGNgPFYVJmD2OQDzKtl2baCyFPTYnfUmTUDRDGigq9uIwstgzBrotH333IB7dpAgxpR84jLf0x88/x6IJE2iKW0xdD2RSUG0ICwENESpkIGL4o4hF/YKhx8yhA8WHnotyZJpG59DtQDwqXJDPTd+9i9GlIwggJscjLXFYhzIcnRRD/LjzFCh0iMdUwG5BMRZr//kf6Wtdfehjay58V73Ozf/kZvwUsFkihu1/nrXY+ejv4a93HcGJSCSSk4MCfAf0UhgBtn+G23pgRiVk+qD4VdCmwKOfgOYGiD6K0F5910P6ekjvAa4B9nDskpQyiCgolWGX70re3+4kBWw6RseXHClRhFTeixyUSySS40EacfHxAxcgPLoOXnjLpGHjenjs2e/hdsOmTZvg7hPeUIlEIjlrkBlPJ4azSoz9f394hJoxk98WYyfXQNGkO2DLaGj+9klu3ZFgZ8Inf8D5SxawZF4d8/0AGqrDhd3pwuMGuzq8tWVBd2ucho272d7QwNbtm0ja/Kxf+ximaaegeDyVk5cx9dwr6Ag4CYQtpl01nXiwj76eQUKJNI66KUwYXUY8ESLU3UJ2/xbE9MzPaytfo6Gpi3MXXozDVoynbD4lBW4uPO8K7r/vXhKGDzx+SDQBk0gOhrHMEODCSvfxzR8+yCWLJ3PDFdMZM6KG/v5OkqV+snYnli3AthXQnAHVA+FqaLB3s2dfP20DFq19EO2HLClMC0xLAc2FOpDEn5dHRUk50ydPZ9yy0Yw2baTSaULRPvZs2cnmlt0EYofwIHSWYT//NaZ76ygGusii0IqFDjZw1M+j6jNP8nvEJLXJgjUW1JrQawmht9+C3RZELDAtxLK+lYDUbkh1QaIfwv2iqnl/HwQGITgI6JAMQyoK8SjsQugXDtBG11D4P6v5RGE5RYhJ8j4LdsdglAtK7CLyFUTZGyfCniH3I1eBWAJ+9wrEkm9xyKjYgvOxzfgTt/+bi5mVQi6JAa1ZaP/1ZYQ2vPGhv7USieREUQl8GfDCTTDpGrg7AedUg0sDawQsugqmBqH8WejPh8F/hZ98HLgPYaMeroP0CqHc8h3gqWPYvg6EEKsheqpCRI8mnalORQyEJC6RSCTHBxVRzGskYtR68PjU6YJzFoDDcRKaJpFIJGcxolqQGAfKRfljz1klxsbjCUKhLsKh/eQX1FJlg6kLRrO7byK7fn2yW/f+1C25hTnTJrBojA8NjaJJixhVW0VNZQHVwvaVeDhDOpomHYzQ0LyT1o79tHd1sq+tg1gkS3/PAIH+fvoHAqgVE+kJ9mDpblJGFSPmljBo5jN3ioNRRRbpfDt/WGGRKqzGm85S5bPR29NMVo+QNhW0ogqMoAqqRjoaINiSZU9JKYpmYXO5SRoKW3ZsJ6OqWHYnWIXABMrHzGSwexuZWAciCN4kFImzbtM+QpEoFRVRFs3Lo7y4mvwiG2GtkJQji55ViaXSbO/vZ0VrhmAyQyQNMROMgxbQLTB10A1MM4FlDuIvHGDKxNkU5xfh0DTSmZGUessYO3UOYcskqJm89Kdfvx1BXOCz8cOv1jGi0M7GVnhibwKrfS2QgSlzqV1wOd8qqGYsIvC1FBiPWNNvBPosIdJeB6QV0YE5sYhbWfYbfrx6DH82QUE6AZZBZyJBMJkinkxRhUk2m6bbyLAzGqDxD3eLCNmREyk4dylfL6miimEfvzSAUwTNmkDIgl4DvBr4FSFxZBE/dAdghYNsuPdnpCN9vHvNayqlNedxzpeqYXQnjwAAIABJREFUSacgmgGvHQqTKX5518MEd+7CSkWO4bdaIpEceyqBecBHYKyD2TPhkkmw2AMuG6gKoILLC8UqnL8QoikIZqE1CPHPws4e2LfdDk+XQTYfrL9HTJTXAS9x9OvlxgF/DcSykVM0TPpQn5LIAbhEIjm+ZIZuJkOj27dRFHAOzXWSlggSkEgkEsnxJ2ddACKEQkOM2tMM1+uRfHjOKjEWoK2jmW07NrBoQS0FwLRpfvZ2l7Hr10UcXvL6CcJVjK+omBGjSinSYOo1N7Jk4WyunlqAmTQxsmkMUycbHaAzmKU/EKCvI0g0EEFNxtjUuIGdTTvY07yXhqa9B+9bteO0+8nqWaysg0RKx7J56QxmuWiWkwtm24lZ8ER7Pvldo3FoNjxGkD0b21AcFnaPHW/FGCJhFTQNsgnMeJbAQBcmGSwjRTyRoGHHNjSPAyOj4fAUUl4/G3dVKbHeNWQy/Qc1qb0rSHtPEGchOAvqqK/Kx+90MZAuJlUUBUNhcFBlc4vKtt6haNP3wjLAssgkM0SsOJFQAptiw+/LI8/jBYpw2/MYY9hIOd30uWxsW/ki/X092PKKqJ0+l89fZmdAUVi3oZO/rGkE10pwZqgcO4d5ky7mk4h6rz0BMLMw1g02TXyDbFnhyXthGXiAdATCgxbtwQx2bxlV/gpq86C+GGJx2O2EnmJIOmGqDWwKbLUgFu6h8cFvgt3CVTeJkXMv5waGk3vdQLECmmPYbDsFDJig68KmosAmnnMoIs1roDdC+8u/5VBlzLzVc6idcx4XXw5d+8BmQDoGPS0Z3rz/YSzrFPp9SCSSQ+ADpoO6BBxTKL0YzpsEF5eI6HkYLrikK4AHRs8AvQ9CzXCDBv3zoDgJzpEQDCj0b3RjhpZAejKiqEocETo7MPT/0ZArFWAAJYhJ+JF6ukgkEonk9MZi2O9LlKA1ANUSQuyBpAyIyVqOEolEcsLI5a3lctpyRcMlR89ZJ8Y+u2IlQSvBogUfA0Ta5mBtIQ+rF4C5nJPukKGoaJqKUnMRU6+8mm/8241c6QFlaN3ByJoEm6OEA21EEoMEY2Eau3p5+NHHaN7TQCjY88HHsAzS/T1giMhU08wSiadp3dLFuimVVBt+Fioq11wKxfapbF7louGlP2IGGsBbjj9vNFU1Y2nsCIKeBiWDqlnkF+bT29NHsn8feiRIIl1LZU0toWAv1RVV3PQPd/DYE4++d7tMSAfht79uAVpQNAe2wiqywTawhsNfFUXj8Cpi2bFpPspLqnHZ3dg1GzabDcvScDqdBIMBrGSMUf4KrrnuMzz52J8oPudKlt11DwArDYO1u/9M82s/g2VhqExxTfF0bvSeh2VB2IJnVlp09cO4cQoFPtFZDQ5ANASzPwFVFjy9zeL+51O89sweSmZMZsZiB3POUbhoKmzcA+EY2DxQWQdKEUwEgpZJJGnASmCsSs3oiSyYt5QKhOh6YPXqAoR0YR96zGuD3l4YsEGgGFwKFAF7uy3WNOiIKmPvRGXcJy5mwQ2Xc44H9Kki4nflZpPvPJjE4mVk8RyJ5FRnGtg+A+4boBIu/wFc6YBzDpi4GojI/cGh+xWAoxRKSy2ungvtz8C5PoWOWbD8Y/DQ7RB/FazWSuBWMG4Fvg88A2zm2FwzLaAEFBuKEsIy24/BPiUSiURy+hBBLPT5sXATNyBfFZP+A0klIB4+Cc2TSCSSsxyd4QCwsxMFRVHAAguLYxEXfNaJsYNtYTq3DUdljgCmj5nEzB/8lq3feQEzexK/Xvk12GZ/jpaHbifP60Wz23A6xcpDrCXMQN8gHd1dPPHS4zz+7OMMhAawLDAsk2w2i2keplhmmRBvRXyBkmQzvexv2kFA38UfflrOcw/VMf2Chdx+M9x4PtTHg2z64UqwuiDWzuCeJkItO6CqGpunlJKiMkoKSonFEiTbmtBjAyiagstro7dhG05/EXGHlxf/8jLNu/eQjmuI+M73j6qyjAzZYKswvQXAg6rVsfSz/86mtU/Q1/IGxHJRv15EVJgXSIPqBLsNnE5SsRCalkE34mTTFm6tAJ/Lh+4NkkmHMBMRSnwlLLn955w3t56b54o9/uCen7B94zMQ6YH/Z8F0eLohTcCdpHyeh3v+CGte6aYoHxbMrmJEBby2HkIZ8JbCrj6gGN58dTNrfvYW6CbB3n4aOicT2zmC+LnwtxfEqv+U2bBgFsxlyC1r7ZOs+803RfWsxXdx1fjL+C4iXqBx6IydCOuBFMM1wxzA+Qq4y8U2+lBRLy+w/smNPPOvTx/inVaA/2HmlPksmini01yIlIT4jkcI/OrzB4nhEonkVOU+KJkAM0G5Cz4Wg2kl4PMNb6EhalbnHlIAYwASTRn2PraFiV+fTnWZi1FB0O6Bj38N/vfb8GIjRO8CdgO2u8D6IuitwCWISfTRirLd1C69mfE3fImXbh13lPuSSCQSyemDBfQA/YBCJlXEUz+3uOrTUFx+8JbRPgi0nIQmSiQSieSI8DBc6/z0JVdsuIyR1ZOZOmkB4ZCLzY2/JZHcj8jq+PDmOWedGGtZEIlF+NumFSyeuhCH3UFVqcZNV3lo/J6CeTJSX2xzuOm2y1hy+XzyCuspLynCZtMw0iaxvgSvvvY6zz/zJO3trSRSSTp6Oujp7yWbPZrG5gROHdOIMdi7D0t3kU2ZJP0FxO2wqh06WqFpnRPUarBHIWtg4cCy3JASP7CkM0vUkcQ00liZEDjAcmhkundgJu3objeR/jZ292wkHe7BTA3wwT9LFXCCVYaovg04/Zhlk9i67i3CXdshdWAUcE6SjAEmmCpkVfSUjYFoEksfRLVcKIoDw55BMcGbX4ojk0c6maZA8XPDkomMG1uOYoPXgYHBFejqLii3RHPehODO39G5o5vkjP+gcX2QubM9zJniZEE9DOjQ3mXQGlDwB1RuXASvrIKGxlaMzAZQ56IWOiks1LAbWV59PUQkbDBhQgE1I13YhyIANgCN3TGMDR0wxckVl1xI/fgJBBBdwYF+LZmhT1IZuq8pouNTxaINdoSX7R6gO9uAnnz83W+1ojD9jsWMm1ZBmSZO1QP8+L+ivLg8hJV5t6WBRCI5lfAC10JJGeTbyXfCIj9MKYIC58Fpnso7/gJE94fpWdFDsrMTo38yeh4YiolLTTNuD9ySsbNIsZH4b/j2csi84IJWOyhOqH4A+pohswJ49ijOIUYymSEY8AKTgb2c7sM3iURyJpNL1MyNwFIcvwwiBTGqsyHGurljnkl9ZJacM6GejvDq/z3LeZdfQH5ZAfYDLliV5TB2zMlpoUQikUgOnzQHx47aEVfJk5yH/gEoeKmnvHIiNRMmMvPCuYyqd+OzOSny+in2lPDWJo3m//wbiWQSEQonxdgjIhwO8/Typzln/FwcdgcFHlg0RkErWUS2dwNkT4w3psfr45wFF+HLm8c1H72CpUtn4LUs0oks+5s76OroZv/e/ax69VX+8vIz9PUfhgXBEWNgmQlSg61oagne4lGMKM5nwWjwKvBmFPbqRWg150HSjZKMYpkZLM3ENFWsWJyUYRBOJ9BsCtjtYClgmRjpFNicGNkkydAg8XAj7z1w1EBxgbsKl0dDTwTRE4f6Yut071sDyVYwkgjn1AzDifsKNruHfK+LdCaDricYCFtEoyHy3T5sih3F6cRSbdjsbsBONuvC7allSm0JleUeEobJU8EoMasV7CHRcySADkjrW+k1nLz+ShedTRGuvqSahTPcVOdbrH3NJBiAeBw8fihzwcaVvTTvGgTFBHcB3soyKmvcFBSYNGzK4HarlI2xGFUHZUNnuLq7nc3tnRA2cV76EZZMnMikoqK334G8ob/KAe+mgugKHAe8IxbDtcrXbYE9rf0IWfbd1C6spLzcgw/RSWaB9avX0rBx0/t+eyQSySmA4gH3NTDZh5oH/jKYH4NSFzgP4yqvpMEKpgi2rMFonQtuJ1FDpy2wi+KIjfH2ciZU5JOYabB8vItMSmWwVaO5Ow8yHwG1FchH9Dr9wFaEMHEk6MR79tOz4XWEecJ+ziyhQSKRnFkcL8e8nMALYkSmIZbJc0vvuZGdDzEBzPlumwe83uL0s5Yabr9uGGzfvplkah4WBQdtlZcHJaVu3N4pJOM7OdWn9RKJRHK2crr0zna8WNgBOw6cFLgmUFk8mzE185g1cylTzlPwexWcgB7ReX1DCxY2hlWZ1g997LNSjA30BvjV9+/lW1+8G5/Hi1dRmajY8Mz4KZl1X8YMvHZ8G6A5cNg1xtRP4N7fLWdsJWiKiZnVSelZOvcF+fMTz/HyihdZvfq549sWDDDjEGnG8DsoLxvBoknT+ZcF4LCJ5NOgNZLuxO1kdzyPFt6NmelBN4Kkoino7SHdnyGtqpDnxVZQgRYewIxHIW8Ult2NGQ5Cqo/3nFirTuz2POyualIV11BUYRBr+RuRtjc46MudDkH7FlDaxVBVzUNRS1GUIIqSAstAUTTy/DVMGVtFb18/nV1dDA4k6e4N47DcmFkocLuw4cM0TQxLxbD7cY+YidtpwwH0Z3X+e9MOcKTF+DcINIDd5cWwsuzfG+Vfv7wSw11GraeY8UX5pBLw6/szOIucVI9SqRkrigxseGY9rdtToE2DkhFUjqmnfooDr0cn+5aHgpEFlExVqBsL0xBD0eVrXua1hnWohQWUfPlhLlVVJjK8spTzjU0ifsA5U207whvWhRieG4ghuwH88X9SNK48VCS1iqL6qChUKHCI4b1pQYcOqdjPIPnXD/WtkkgkJwo7aKVQeRX8nYLbK4L557SDbZ54+n3RoSAvH62ykFcaH8BquIpMxkOPkeL1rX+h2+bgoqmzGZ+qJb3c4muhSsx/sLNB1fjVMyqZX4FhqwHbraDfCMoq4KtgdXCkyUmxPa8R27MDmIAsDSCRSE5tctPMA2tNHy05sTU3PcsgRnUOhotcuYBCRK5UGDFSTzC8AJaLnhV1IU4/NEzsNJv7gcwhL2F2RwlVNZ+jZffdmMbRFpKUSCQSyYngVKy9qKBQoNVgUIRl5ZFn5lFQVIvfV4Y962JwX5rYBBeGBlkDejoy3P9/zxIczBWcdBzV8c9KMTZHeP9GCjzzcOSX47Yr3H/fZP7j5jw2v3J8j+td9o988+Yr+Mer5mKzi6FXZ3MP2zY18Ojjf+KxZ58gnUkfvgfsMULxFxNNJmnY2cWPHi7gn66HfxsNt9UqPL/UwS9/dhXR7Q3EOraS6lgDHSt5Oy3LBMJ2dGsc+RUj8BUWogP9b72Cpffwvv6wU/+T22+5iDturOem36o0/Nck0sG979hIAU1Ezhb66vDkFVNQUkVFTT21tX7yvDbS4SjxYIiaCjcFLhsdfd309PfhwcmoqjLcdg3LUtF1HV1PoaFgmjYsm43JSzU8ucX3zCCs/QLs6RUBXrvFw5//7XZW/+lxtrzwMIOtt4H3P0kkxxJHDIUD2ChzK8yYBFcthd//DULRt8DKgq0OpbKQWecppFPQ06ZRWVrAhDkwdgSUucUwezeQeOSPsHUV7royPqWIITeI52MIaSM7dN819AnYERGxLnh7ncZADOMbgeTmr0DLine/947pMHIl18/KY1yBeF3GgM8/CLu6DutrI5FITipfBOWn4FNgKlyuw006XHIFKOphvHwN8NYAvvYkf/9qN+pLLWx9agUBW4hf/uGfuf+O73P3H+/E48nj91/7I5fl6ex7sI1Kv51LF/5/9s47zI6rvP+fabeXvXd71e5q1ZslS+5dttwxhphiEkhw6IEEAj8goSUkgZCQ4BQgdLBxginGBncbWbZlW1a36kraXW3vu7fXmTm/P8693pWQbbmp4Pk8z31278zcuWdm7pw553ve833ncuu1sPEuiD0GbHJDYB3ouyDVBan1wEdexrGkkTWcG1l7OTg4OJyqvPrEHUfiQg6pB5hp3YFsmenItIsm0khKR9aX5SjZGesxiae0XZrTqy6NABqCAtPcTqb4l5hWK8ZRvdVwIMj1l67j291fIHe6hF45ODg4OJxSGOi0U8cVF76XrFZD31ScDdvvpX/oVnYNe4nsOYMle25h/gXvpL5WQ/jArPfyob/6CP/xxUnGRodQjTRm5pWX4Q0rxgoh+ONPfJYvfv4fufbqG1BQaK5U8AbXgDEExe2v+XdGKqv4xu0/p6lhDh0NleiGQdYUPLShi9/+/Ls8+8T9jI2Pks1lEeK1buS9CIoOnkbmzltBJBDCzozy9DMJ/s1ayY0XG7S3qrzZC8q7NR56ooPdT6sk4gngNmTDz4X0LIxCVpAenySXmEKkEwhrGNkg9CNH8GdHSRmgXsXCi89nn7eVT949Sef33kkh3s+RjVwfoZpFhMItBF0VNDTVEamNEIhUEAhX0lHXwIHuHYwODxGfTKKbFUx53MQSBTJpHZfLSyGVI1DhR9ddYMl4UasIQvgx3PXMq1DwagqbgTttC+KHoL4ARWjqaONf//oHrFxchzF4KVMTFgNbR/ngZ65m4aI6RmJw/wFobNWJuKBWg2jO5CffP0RsOoZsKKtoVp557dC5pcDgYZto2MMZS2B5GFoUyFk2f75vnM6BHOiVeBeu4H0oRJmJhC0gde/ypDSQIqyvdBXKTmIq8uZWBezMQdbaBwyV1qilPXRQ2XYW134zQEtAwVNK9pU3i+z5xtdIHe567X5jDg4OrwNfBt81UOeCa+CTi+BKD6y0QT0qBbVA3t/lGqDM+AQYbSEq1nnRWg0EzcxtitA8ZqJv07is2EKHsZJ4Yor1v/gv7jz8LGsWXklzVQfewQO89YwrWXWOytYLYeO0Qvw2BZ5wQaEVXG8G12JId4K4Dan8vhQm0if8xI2fBzQXzZ4Q+9MTr7m84uDg4HB8FJkJXCgi28saM+lZPUDlrO0zs7ZVkG1N2d6ULcBya3Ca0ydCNozsL5jAAIamgCrbvgYz8yV0TaM6EEBVnBkUDq8STxMgIDd4skvi4OBwgjGx6Gecu3Z8C1tpJlc0KLIFQQGESTx9iF3d9/HTHy3j3PPn0toRoKoOFi924fFksc0CwtKAauRU6pf/rH3DirEAm7fuYWxcnjgFlUYXrDr3QiZHR+l8+rUTY6sXrGZeazPnLOvgiksvptpQsAsFRgbHuPfxZ1m/fgvPPP4wPQd2vWbf+bJQFHB5qaqqwa+5EfkUk/0jPK1VUu2rJ5ULEG2Di1tAnBkgZDShqmfSN3UD5vhehF0Aw4XurcJMFLHSk1iZJORTSAnRhfypze7maoAPRIBc73q6Y1uIT0+Q7N5w1DZhgpEWolUdVFY2Uh320zZ/HuHqEIqukc8X6O85xP5dzzA2NkQmnSMxFsAwDHL5HMIGqlpBqXw+SswuKqiaoGgKVMMgHKkhYICqwuFMgocn+0DPyAH6hsX4667k8ksuIQK0z29lzqqLKGQmuWhdE7U1HgZjsHm3QqACaiPgjcB0sUDvli2IbBFcYbSQj3A4gGIrZFJFUgmLqoiHhhrpLRsGTNtiy+Z7KIoJaG5AW3YRrcgmaar08iNvczHrbJab3xqy6Z5GxlV4AbsA69dDKpkqXYcaZHM2Aywn4D+L887RcOul9GcCem2LxKH7sXLjr9EPzMHB4bVFASohcD5UzEdrhqbL4Tw/LPJDVJupH5SjPlV2E3y+U9sMWsCANgOSkOtM457SCbiDEIHQWJZl/jmkjCA7d+8l5Jtg1+DT7Bneh7/g5bLqs1lRFUTxQ9awcF3r5slqhfR+L/R6IVcPaitkLSjWAZuAQV48qiz72p6ul8BraDRHA6SsCbxeN4YOCibZtEVltILRdIHe6dnD3mV37iBykOt0ETocHBxOXQQzsuNsj9iy3YC7tK6IbLGJo7YrT5UsC7GUPhPmyOH8Uxkd2dKV/QY75kakQQnObJGPgZhWWdIWQFMdMdbhVWKX5xo6ODi80RAIMuTJxLqQQYNepEYiQ1gse5p46jk2Pb6e5OggCxbUMG9RBSOFIrl8HJdLweUKkkpW8EoHPt/QYiwFSMVjxONThMNVNClw/U2XUVCn6dzyUygmXsXOFRRFp7o6wqqrb+amay/nvZcvAyCbzTI+PM6ObXv52y98hcnDm7Gtk+iiURpQ9/tcuGzIZ3LkJofpNndwd0qwe6CB5ddrvKnew7XzFeY0RAnNP5vfDv8D08/eTi7Vh2VkMSrdWKk+RCGG7KCWjylZ+hJz1pfqgBfEIIfvvre0zdEPQxeKOoeqxjOpikaJRIPUNIaobq7C7XOTTqcYnxhkx2MbOHTgd2Qz0wB0z9qD1x3AZdkorghoNrawsQoCxauQsxT8AQ91LVXPZxsfnR5kZ/fTUAGEQTvnMnxr/uL5WIT61ihLz1uDP7yUJcvcVHigawD6eqCpEVoXgbsZDllFxNAWFMWHEqnG3VRN09xaJsZVUikboVgoGkRCEDJk8zplFWHDrRAYQFu+Ds9Z1wKyCZ1AiqyVzMRNlIWV2VJ3EZgqLXMDuazNb76dQkzayIPqoOw7phhn4/efzzLfjO3BWFHwxISFLbby8hPwODg4nBg04AyoaoSmAJ7FcO6F0BaHkIm8+WdhA5YA2wZdhdn918hZpX8KQD+kfjWI1+fBWFkFCz1kp6epbmkhaDQQv2cfH3j7JXxuy2NsHB7ArQdYHP8g7TvbWJLViVhFlv6tm/51MHQ/2PdB4rAio2RHPwzxy0D5OxCPI4eXcpwKU2jdHp3GhgBu20VddYiABzSyTAylWTCvmqeGkvTHs4QCfhLJNLYoR6jNAcY4FY7BwcHhD4Hy3CcT2bIzkMPshdJLY6bFdqzEXsxaVu4UVjJjcXCqi7HlCN8oUEvsgE62xSK8YGaqR3YM7BGNc1cFMXRHjHV4lRRGT3YJHP5gKYc/vNQyh1ODaWTfxMdMKvQMwu6i87lf0vdcLXsbWpm/eCH9HotYLIbPHyIcjpLPRClaryyJ1xtbjAW+8k9/zbat9/LDH0mj2DNa4cCq1XDO1+GJD/DKGy4hgsEl9PQ/hsfQj4hO+tnd/8f/3va/PHTfw6+y9K8RKlABA5Od2MUIqZhg+PAAsJ991hPwQAT1O3P571vexRfernFeM6w7Q+Win8/l6Q1f5KkHetjy4Hayg/eDHgZ7DlheYH/pC45l6JQHRkqvY6PoBt5IHYbhRXN5yBVMntuxm9u//TfYVpbjuTbFfIbDe7YwvaaJgEvHcLnImSk8RBBGDRV1dSw7c9YHBn8Hz3wSqoA4LMhVcTFtz6++ZAWsXqGi46ceWaW2LoZbvgQVKqxCyspPT3pwnX01IX8Ub2UtlXNruOxtbp57FIj66aiDhlZo0uQYzAjwiG1jbz0ITQU62qu4btkKlJJKXE7dMPuGVZHxA1XM+MgGmfGPLQJThTT89vMghoEJpEheB1TgP6+eujfPZy4QQzbX926y+Pyfpx1twcHhlCYE3A8VGlwDvnfCW/dCx0LwH8NHPg0cAmL9sKwGKn3H2KUBrIKqz6+Qs200UL6m0PHdz0EHmM8dYO69O5ioWMh7372MyxUYHTd5bP96RpbmWbOgnfd01FCxX+HWIcidB0O3wAfiwF8BzwD5BaDdURpR+h5wlzyOk0xFKMg5K5cx3hbAK0zcxRzuXJKzazQefbqbvmmL2qooP/z6J3nPx7/G6EQMOUTWjZxtkMAZvHJwcHj1FEuv4wkGUZlpB5etCcqCa1motTj1BdjZlGbNEQH28f1/P0g6G+QtC+qf3yIcgbALRK10WXNwcHA4tShbxLiZMQgD2VsPMDO7AWSdrSF7+SYOJxOr9MohlZfy8zQHPEkW6Byq5NDYApqW3IgoViM0HVWBuXNWcqhvD6b58gWUN/xjbHwCevZP0r/xARrPuYKopnHxqnq+8JV1fPkiF8LO83JHMK7+y1tZe9nlXN3hlkKsopBMTtPV08lnvvwlOrfvZ3J04vU5oFeAYhj4W9rIFSySU4dJjI3DeBcwCcIGRcOe9LH/37by2Wf/hAuvX8jN7w5wFdC2BmojTRhtAZ7+dwXid4BVdjgtE2Am2YAfOepwrApHBaJccMU7SCTTjIyPE7M8jBTGGN7zOFZyGNsuYlvl8PEXRweqfT5uPPMsGgN+dGFjWUX8IbB0Dd1Vg+GbiYq9G3gqJyBmS4WzArpSv+S23X08UlgCviCWomNbFuQS6KE6FJdOQVNIqwqa5cMbasDnqsQbiDL3R+ehqRpuzSDo0kiEFc6phSobogpUuqChFBW7KZ3kb3sOYqUELF3Lqvln89elggWQTdNybtzysZWbrOUqX2UmbkJHxmvtJA/cgRztoXTeRwCL1rk5Vq2SnrTF0mfIbofDnwHhqLEODqcm54H2l7BEgzcpLGiHtRNwxRLwGTxfnwnkIMsv+2HnELhH4R1rwKUdaV3w8/UQjMLqFXJARlmggA72BKRz4JurkPjtFOaAj4ptnyMQdVOnK0wOWgw8VWTOmQaes/x4q10YKGzbBmdcBC4bCv2wSoeJf4T/SMD9exT4b2RiRO2tYJ4F6RuBD3HsQTsPM8m8ssja7ehZFq+eg8Nj/N2d92FZBRbUBuiogI5gHtUq8HjeptuEsFUkMXaIm89ro29Eo3eiyJbunfzRijpa61oYSye44+lD/PWNF/DzJ3fRPTL90l/s4ODg8Iqxj/p/9nTrsgh7ukVgxZBhBQFgPw/2/xsLJ/6Yt/BnM5tEkM4LGhzpgO7g4OBwKlDO0nC05ZZACrJlka88o6FcVztRs68lClLb8DEzzHmseegKCuL3zvsL2ZckscwDDHXejpkfRi+0YNrLqF/ZjDaoYb6C7skbXow1TejuHeY/f3Ab/7D6UlyaRlPQxVWLa9jyF59m48++R3z0pU29jUAt1QvX8cdrm1h19RUsWbyIRVWCQtxkb1cnO3dv46mnH+PZJ58lMR7Htk6dkWoFBdVlkM8VyWfTmNlJMLuQ4mm5svCQG6mge8tGVC1s2ovBAAAgAElEQVSFoXVgntvIvEaFta0uAiLCoYtWMJnrxZ4IQ7YbbB05ui8n0CuKQsfq6xk88Dsy8aPPqY5uhGiZey5zO1aQN23qEnGmzTyHew+QyCfJp8aO63hUoN6l09ZYz/y2VlYumYvb78bUNBRFQ9NUhKXh0v0Ymvf5z63PJdiWz8jitgAuyIeGybOVSW0a3HVguCCXgYH94GuCopA/okIRpt2wuB238BIYtXCNuaC1Hi2gElPyJHITfCkK9aoUYG2kK8l+E56L5Rg8OAZRi7qVa2npOItyHIA261UePytX3+5Zx1x+6aXXwBg8uMVGMMmRFYqcAjen3mbJXLltEOhOw+5EAgrbOL0iKRwc3ijUgLoE3OdBI6gd0FQJZxch5IGiAl1pGMiCpsJYBTzSB72DsLoBkhqYR83q3Le9k5GxSZ68r0C0Yj6XXFPDnBqdSACMy6RXn8t0oas6+tIQOrLecWVsfP4itQd6MEUKZXkYlkapbIW8ALcGlSEIa5BMwU0+aO6A9C3ws4NgPhmFAx5I+4CbkYN0XcBzs0pXHoIqt25en0ZqvmgyNBUvfYXNdFKh12sRUG0GcoIcoGXy/OKhrUwNTxFLaUwkZR3ZOzVB2jZI5HLYtmB37wjJrDOY5eDgcKI5un48HTv1CeQsLjeQIlHYRcbsP2ILRQcrL0gcNhF2COnz59S5Dg4OpxrHqoPLQmx5nc1Mn/t0rLNPXcpmPQVeyRyRF7oWJpCgmCsAKQrCRzo/jpmrRYhXdv3e8GIsQP/IGLfe/nPe/+nP0tTcRsTr58ywhz/+7JcYP7iXfc9sIDV9bCFQ81VTHfFT17aCjis/xpc+tRKvW8MsmiSnMxza0ct9jz/II489xIYNp4gtwVEIBLZVpGhZWKYJZgY5nb1MedQmSXH4KQ49Ps3kYJacCPLhCwMsrNGYM8/g4evaeWJ4HanOGqzRWsjXgegBcxDsLIqq0LToUqaGD5BJTJWiL8tRTm4MVy1LVq2lrr4Jze2hzjYZT40x3N+NggsZMn6sBpeOYWgYmoJbg4BusDTkZc2yhSxdsYyKqijTySya5kV1e3EbHnTTh9fnxe+dMVd8dqqLztSQVErbAb8XhAA7BmqP9CHwuCA1AeZT4KqHXAHSGRhPySR6Le3k0znyO4bktNwbzodKG9U9TrjqEGcE5aTWPLK5OQX0WzCRg+oYjFfDgsXnMqdlxazrc+SVMJCVSjkCFqQIWxZsy8m8BnoLPHhv8tj1idHInOoQyxrlai+wdVDwRF8BGZng4OBw6rEU9FUQaoJ5EK2BeSE4o2RNkAGeHYX1A+ASMD4XtvaAlobwpZDRpRibLwgyOUFFUCE/0c+mB3awe3cfvpZLsOvWctGZQRbWq4Sulvv1NQTk0HIZC7yGirdChW29mKMhRL6A6hM0+/wcmnChV6sEq2QdFTkMNxThQj9MvAO2JiDlhozqY8pog4kPgz0F1nqwJoFhZqZsmcxUYrNTF74+jCbyjB5jhnA6W+DOB3f+3vLN/UMwSyu4d/OB17F0Dg4ODi9GOZvA0csEJ6L+fPVkkK1jkC3dcfLZKZLTeYKRmfZ6IV3k8DOjiGKQF+4bODg4OJxqzJ4FJjj2rDCH14pjxSf/Pi/nuViWd+Uzx9YsikaBfDLniLGvFrNY5FPvv5zPfeU2Vp1zOS5V4Z11oH3tTu784Tf55b/9FccKbq656P/xLx+/lnetWwSAEAIhBOP9ozx57wbe8VfvwbZPbQ8QYdmkJmMEKqrQFQWsoyuGckKBNOR7KE5NMWb18qOvjtPTfR1/ekWEd5+jcM/1ClerS9j66EImtscg/TQkn4DhByExhW25WP/Tn4GrEVxuyO9FTkMdBSLoxgLa5q9EGDo5tch4YpK7fns3md37ZHiWMR+Ku48qmwJaHS1t1bRXulhYobOmqREr7Ed3B7ANN3HTjRqpJBII4g8GCFZE0c026ucFCVbPugU3/TN0/k4WKQDUnQMpExI5CLdBcDUoSfArsCgCHg94vWBp0J+CpYA1BElb3qNjwLI5kOyiou8Qf7ZSOj26S68QUvNd7YaV7dDYAJ/8P7hKgfOPkZOgHG6vA4ooNbdL25UjYmeP+mR29zHyzQePfdHbvsvcisWsKl1ZC3jwf4vc838nMZGcg4PDS/ApCFwFC4EPwR8fhBsMWH6GXDsGbNgIP74TGACWAXOgfQUEqmChIrutnd0mTzyT40PvCPC+960F0ce2nd+g0PMT7r79UfpTiznrUg83N5UqmKuP6t4nQPgEXKWjHLwS780wetcmhpbfxdyLr6Tjo4tQI2456UooiJVyZmkkCe074ZdBGPo4PPIR+OcdOnzuHGm2PbkaRtcC70Q+bwsc+dw91YUEBwcHh5OFghxa9zAjvJaH7U1kGECGU3/mUxpZVsnB7VM8+JNDvPVji5/PozA1Nsn//ct3UbImGqojZzg4ODg4vCJeTc+iqrqdpuZL8XtA7dJe+gPHwBFjS9gCHnxmnMh/fJ439e3gzW//FABXL4CVn/8T3vex69mRguQgLK6EpTWyc6l6wlQE5VR3Ydv0b9/Jf972Ax576il6Dh4+5YVYcEmhU/fg1j1k/QEIBmcFR5ZjMWel586nYKoHYfjY/VuD73StZM+OhXztQ3DbWoifr7Ktu4L3/Mtl5O67F9JJnh+XsDZAbjGEm6H1Oui8G4jirplLeMESzECAqeQ0O5/4KXu23EM2mwHLpNzIVJQltF20jmVN9SSHe9i84W4uXFLBlVddypyWFgJeH1Mjw+QVG93tRzF85IsCt+XBNjWyuSKZiQk8RKg3wri8HqBkyHBwCCYnoRbYDSSegnFgWIC9B95yNex+EvY9IgXalTEIuiAp5CyphwAlBw1ABzN31xi4DsL8q1/4husZh28/C9Y0dJlSR1l+jO10ZMzAf90Nu/rgMx+DC5mJIbNKV2oMmGQz8AWOVc1c9YEI89Z4MJm51Obhr8Chn71ACR0cHE4eBnA7+FZCNag10PBDuPJGWNY8s1UbEG0ClgATUPN3kDwI2Qz0xKC+AgwF5rfotNX6URR48pkpdu+fQCGBH5Ut919PPP5xspMfpOOvgixAOn0bs4sTBmu7Te6OIv7Pu1H8ClXzlhJ57xz0L0WJf3Ev2e9b0BSg/j8WMD4mnwC6AQ0rYZ4K4km4dgguAb64CvbGIdVZCaMXA7tKX3Q/8DPg0df39Do4ODiccryYf6APOc8qjrR40ZBRBC3IVmAOOcKVRAqw5Yma5ZlupzLlyCPJhq2/YTQ1wFs/NvMcKBaKDPaOMi+8kkOpDJOF40l45uDg4ODg8NphZLPow8PsGeujWJidSPP4ccTYWWTzNo8/3Uk690viiTjvetPN+KJtNFUEiYSDNBUgXwshDdzFLIef209UnWDcKjA+Nca2rc+yr+cAm3ftoG9oiFQydbIP6TjQARcksyRdKYSq4PKFKOhzwOznyKQAQ3JbkL+z6XES2Qk64wOkJyZorLyAP7sW5kQU4jUaDY0eDpt92HaSmQZlEUQfZIsoU61ULryIhroafNVNeKvnEM8m2PPYT+jvfIpMYvKosgqEGGWqZyP7JgIUUjGKpCmwEM3TCEYtOVtlMjuJompUBasJRyLkixmsnImmaeiqG9XlRbNcKKqCosqj2wDE06ZMWBZFJgew8zLvVR+gFcAahtgUjJV8ZRO2jJINqTDPgKoi7EUm2B4AmgCjEtIjqBPSl/UYAa8AZKZhYBMwAsHCkTOCj3XFGhqg4IJmjpx4ppa+YxSYIIc0Qvh9mps11LDKKDOpvbLFQTB7X+SbHRwcTjwBYD5wNkQraF0NF/8JXOKGni4IKHB+ldzSAFrmw6IJ2PcTSA1DMQXCgmIGRsJwaLvJgZ376d3/Oz765b9gyQof6cTZ6OJD7Ni+hbH0MOnYAIe2PsF3/rmelvo2vF4/bfUGN11QKpIKaqOC62odQtB322E8povKG6JM/izO8FObCJ7VRsUlLYzem+OH9/6axjNXsvisBTQul+VsaIfqCNgZm/N3jdIarCS2wMXUW7xs+Z8m6VRQbALqTsI5fzEakQKH0/l3cHB4PXmxeB0LGUZgzdrWLr3PI1u2ZS/C8gyDcoKY04tcIUE8dWSeCcsymc5M8Bdffi/f+9UoGzZ1n6TSOTg4ODi8UYllD1MsZkkWEtjP51p6eThi7FF09cZIJLcSm+qiPVRJy9KLCVc1E/KHiQoL02UTTxYYGJzk2Y1b0WMTZAoZ+of7eOTh+ziUmjhGRrZTGAWwLYjFSDOO6nKjunwQmAvxKRAZZOOu3MArh2BbkBmmkIkxmZomGU/xo1AzS+Y2UlOnMzhl4U4lUOx+ZIOx/GUKkMJQ0gRcLpoXrKGlsZJARQWKL8DQ+DidOx4kGx89RmGLwASxvhgxDBTVhcsdoKjXU6CSrBnAsoqMThfxujQqq30Eg5V4bQ+peBLdcONxBQj4KxAE0HX58zeBB4GYhVQJIkjl1FDBElAQ0lNAGYRiUgYcgAxI8JcEWZ8GZlF+fhgZbrocMGxICZQJGavwQs1gKw7pPQrB8HxadB81s9eVPlfOGesFVrbB3HopxpZjJ2Zvc3gaBo+pFahAiPnVKgGfjKfICuibhnghg4ygcHBwOHWoBNZBoAF1hcGci+DGy+BNOnzzNjg8ATUTUBEFFPA2QPMi2OeRtgA+N9QbUKNA1yQ89PQUT967hV1P/Jgl15zLwqo5NLbNZ/lqN7sPdLN8SQdVVbW4jXE2/SbNs7U2NW2trFlRyYUrITYBkUoI1Kj4L5c1TmZfGtoFrDbIfytPMZVBq3fhnl9JfGOW3v2HCba0S5vwEpE5QB0Up+HC9izJtMXoAuhcCFtup1RZFph5fpwq+Jh5CDg4ODicDIrIQSGFmWQweWSrTi2tzyHr0HLCGDg9rV5sbLNAYgiCtQJVV3D5DOasauLN77yYR3b8nA2bTnYZHRwcHBzeaKQKY6QKx5dg/oVwxNhjMD5l8tDjEzz0+Cf465vezKUXX8+K1VcSNmPE83n6x/o5ONDFoZ49/Phnd5DNncYdM5GBggkjQfITMYjUQUUVtCyCPRNg9SJVxzJHOzMNQSFOYaKbHRsS/Ln4W0LLolhWin3f2QzKAHKCqoJUKgtAM1VzzmfFupuoMyxGDg9g5DL4anzs2HmIfP7FfEsVoAKoRfc2EqjpoLq5Hl+gEsVVQTabp3dgmnDYQ3VTHcLQ8OlRbBFCV1TCPj+t1Q2YwQhev5RGC0JwO4KEiuxnVyP7/w0+qC1CMS/n/xpD4EnLw+hDqqJDVinsDDiEjIYNIdu9VYDyFIxPoBx+cTGWNKj9bs746Ne5pKmDxbNWJZDxyP7S+zBwcbWUxcv2BCozQizAE48Ltm45VqPbC8ol/FGrh8qIvDIVCL6xHg4Pv8hpd3BwOAkowCJQvwJnQPAL0LgM5k8BNfDhd8M9u+ELj8DlNwIu6FSgWAfqp+GWi2C5F+oFuC3BvXdYPPDARg4+9yiF1A5uuexG2i/8e5rbVlHhUTi4/yF+/OutLJvfQWwwxpe//ACPbrmLZRfcwMIlUX7RCffdbnPtOxTOXaqwwq2gqrDwz5fI+tCApjObaFryflIpnezdKq2f8/PtD37mmEcnXKDXqrz5fe0k7obdKUjuBvaBfNZsB359Yk71cXPwZBfAwcHhDY+NFFvVWe8zyGgAP7J1dzrMzjs+8knY/IMC533EhS8iaJ7fzDc33ion7DmpDhwcHBwcTlMcMfYl+K9f38u3f/sgmmagIJNz2UJg2xamZVMo/gFk8FQU0D1QKMD4CMQTEKkCowYUD9jjYPe8yA7SYPXByC/pW2+gPLYQCgpwJ4vf+mGGtvyO2OG9yMahCqQZGdhN7H6Ti6+4gmkDCopFNj7J9JMPIcwMcipoE6hBsDcgW1thYDlEFxKoqaO2upKOhkqWLgsSjFZhuAO4bQuTalyhKJZeSSLrRsFCMzWMgAfh8RAzTQIeZrVhiyT3/xrLmpTqZhKpcHrzEC5FvmoGmFPgysliVCN9YUdL2zYBlyKtDbuQpq1NwE+eg23288m3XpACqDGN1jefiycSOmJVBS8+sexY+931ncfofHjz7y03fDXMu/x2DK+XALLJbgt49NbtjO8+2hbCwcHh5PJV8LxDhsB/FD4/B671wFw3HEbGzF68CM6dD+GSqetWYF4U3vyncIZLGhx4LTg0XeDfP9FGIh7Htlz4A4v50YOP092ns+G+H/DoL77JWz69leZoCz5Arw/zqX99Czf03ICuGmSmsvQ/0seG7/47m564hGDLKhqbF7Dh66C3MVNJ/SWg+1B3gT7w4kcXF9BrwnID9lvwi3vhW78pr/048PBreTIdHBwc/sA4ekpkBtnWPh0jYF+YqfgQf/tP5/Er36/wXdUMixX5zNkOCyZWsYxD7GLjyS6mg4ODg4PDy8IRY1+CfLFIvljk+QRUf4gIG4oJECpYOuRzMGVCsQBeD1BbGmBPIx1GjzUMbYEYR8R+zfxzbyBaO4en79zB4LOVZKc0ZLhoEin/uRC2Sj5fpGdwjKn9G1DMOJpiIcwuZPTsNKCAmA+AXr8Gd+Uygv52WltXYNpF3Bp4/QYuXzWW4qZgKeRsQcGyMTx+UF0UbRu3GyxFoaBY5IWF0DQKyHyzAEJYiPHHoDUuo2EXB2DnGIyapUBgARETRochnZYRYMuQUbSNpdNRdnFYXir+pAFvOhMO7IT9WSnOvgCDwIAA24R+j5e8dmQ2vrJmXG5aa8zoHi9oe5DfjF3c9XvLDUNlXrufnCEjbjXAKwRm788RqRcT3B0cHE4si8DVATW1aCvh3WfD+WFoVkBX5HiQG9jWD9t64YMXAQosBOpUEG45bhQECjbYeUEuE8c2lrJg9Xmsu+4C/vsfPkw8YVEUEZac+wGuf3sTd23ViUahuV7hzEYXwTZAQCoCrnwt7u8bLJxTS3VrFWrA4ut3qbz9UoWmStAFsopXFVzzQW984aO788EcsSysWeOhX4UfZmF9FvLxNPATYD3Q//qeYgcHB4c/OP6whFgAUxTpzB0gNx7HTteiKh6ELdj089+wIlhP7uzL2LXJEWMdHBwcHE4vjkuMVRTlMFJJswBTCLFaUZQoMs1xKzJI521CiGlFURTgVuAa5BDtnwohtr32RXd47bDAjiFlP49UBXNCLhdeUFRKJqpyGTlmsrKWkwaUJswXDqIZB9GDAhgjPjQKVtnQWAdPtRQrVRV0F6OHB0n278LKjnBk9rkMUozNUj1nDUbD2bgrFxIKVdPQ0EIyOYkmTIJ+L+hhTAG2JSiYJi63QVV1FZXVUSKVAbxeyOdkdKrhduEJuNE8pcMCaTMwuQ2iKWgMQk0DWGOQKTVoXQaEmkDV5R0TMmB+BaQSoKlga5DRoBCHehVqBHh0WLwUBjpBzaJos2wKRkqncA6Qhn1J6QihqODTNdQXkFhfSoA9kk7g98VVQ4c5raDpUkM2ARcCkXoSzGP59Do4OJx4FFCvhlA7tLkx1sI1jdCuy0GkArIq0oBsEQaTsHcYbBXqgtDuByFgPA+2DpoCQV0l2nQmGbGKBSsu4ZprL+K/v/B2bNtizQXv4prrrmXhEjffeqJAKKoRs3XUBMzrkFVeyK3D0hDXXreS2sYWXEEfSZGmZzxIuijHogoKeDU5dKlHwBX5/SMTAsZzsH7jbqbGTepci0k3B3m2T+HQ+BTYncAvkfXXqeYX6+Dg4OBworERxEkxPTRMfaIBn5Bi7ANbfksk2khWi7/0ThwcHBwcHE4xXk5k7KVCiIlZ7z8DPCqE+KqiKJ8pvf80cDUwr/Q6G/hW6a/DKYsNlC9tBNnFzwM5SMeQ8p8LmdXbKK3LI+VFa+a9YoNIsPe5ndDVIz/ny0B2EIoxUCNQPR8melBdoHm9xPbskdmrZgmxquZCCIEQgJJi9TX/ioqBbVoIQyUdnyCTjREJ+KmtrsbWAxQUE9XMYRct6hsqWbJoLnM76qiuCaLrguR0nkw6j65DtD4APunOIA/fgqFtUF8EvQlEOxS2y8hXHxANwqLrgT5IpsEnYNEZ0LsbXB7QfaD4YN8W0FzgtsGvA60wbEAWNM8su4FNwDCIDwC98FgnrN8pt7lch8hs89eXyUw8RC/STOtIdBe0L4SoIctSvpKwF5l1zMHB4eRSqm9dfwNNlejnQeT98iFagRxESSBrzCqgvQnO9sGPngLTA9ctgrVz5Z62TsKSCmj2Q3ulxhlXfo7YZJ4l8+tYUWuCAorm5rw1dfy/9y9gHzDSN0Y+H0Qzwty2scinPmmyMqpTa+jU1mr85Fu3sP5J6OxOMp4eY9HZQYIBKZtmkY4Kw0JG5VYeNXIkBBRMwdMDRXZtvoOx/Ulq8h9jybuWktxgY+/aA/wQ6fdyIlHlAKEQcqaILO0JLoODg4ODw4txYM9z1Iw00mJWQk7wP6O/Ymzf5CvIX+3g4ODg4PDaU+76HG8v4tXYFNwAXFL6/8fAY0gx9gbgJ0IIATyjKEqFoij1QggnPdBpwTTSkyA8a1k5a6tA2g24KMVkISUBS6p8zWdBfx+MjYA+BRUXQ7wbRAq8QahbiRGMYBp+7Hgce98mEHs52vPqrJu+wejUNIMDXegYpIuwdP5cKvw+xsaGiE2nCPiriFQEqKgKoBte4pkR/EqWqgqdlTdchtdl4AtAICKLP2np9PT1IkSe2qblR/7wbQH9tvQL0MahaZc8rEOlw4ukof134ImCVYR8Cno3Q08cFnRARQXYLmgOQyYNmil9ZjNPwWQGADUqpWwVpNEj8nSmHgezCPjBWA23qHK71wu/F66/ArzKjLvCAL/vOubg4HCyaAQ+Dgt8cDOsWgvfABqYsSypnrV1swcaG+DqG2ES8M8azAkw85DXNJX3fuRyHrq3l407ernzl/+LbdmsuPk22i6+BAPpvtLzm08QuOg6ItGr2fTf3+Pt3/46FYs/zJlr38nnP7uYc6Kw8nxoOSfAhOlntVtG3oKsLgeAqRS4DcAjl5nIYbzecfjGQzY/+MjfcMMVazn3ukUcHq7gf74J5rZumHwI2Zw4kVTjirQSXnQm8ZEBikM9iNwkMnHlH7A9kYODg8Npxhe2f5a/2aDy3uBi6MlRzDvtVwcHBweHU4eXG8pxvGKsAB5SFEUA/yOE+A5QO0tgHQFqS/83cqTR20BpmSPGnjaYyI4oSH1fQUbBepA/hULpr4r8CVmgFMETAKX0OTUCwSgkNoMIoGh1aP4QmsdDqLIec3yC+NQ41JwHUzvAnMn6Gvb7aKlrZcWcBRzoGiCVTFM084QqotRVtxOLWeSKGVw6+L1u+gdHUXNDeGu8NLTUs2xVPaKg4PFL71XLAn9Yo6GpCRsBHik3e0ulx0bOiPUAIykYM2XoWRZpJ6Dr4KuDp3bCdBzSJnQmpUFidgB8Y1BQoTcFNRaMCkgIcBdhXMBhMF3SNrYZiG2Ewv1Qfx94V8PQKPSNyUhdF8drQ3BsBLCHF86hqyoQUOWVcwMpE56bBstpzTo4nAJEQV8G0ZtgtYtrV8O182ChDUUFXArsHYN79goS+20uu0ZlUa1CsxvQoM+GqTFwp+GCNlhaBbEEdGUgHIG7fz7Is/f9msT0BBWNjXzhew+zfNVy5jVX0DOa4n0330F/31amf7ubbU98D2ENYloVvPdNc1l0ZphPfPRJwvkUn/jMKlavrqFaU9AUWXeV50gMApVeKQoXkQ2AJkpDejmLTFeGWt2k2vDjq46QaQ5gfhNE8mHktIETUBl5ougtl2N294ApsIoR0tNuApXtJIQXM1cExY0voJEbPIydG5TWNXiRz788TgpvBwcHhxPLoLCIF23wKChv8XCX+1fc+sN/ZOfmZ1nIEu7jaWxHnnVwcHBwOE04XjH2AiHEoKIoNcDDiqLsn71SCCFKQu1xoyjK+4H3v5zPOJwoBEd2NFVkXJPBTJyTVdrOA2iy/xwfBDsJvirw1UM+CyIH3ha0UCv+YCXZQh7LtLEsUwq43mrpxTqLXD5Le2sl0dYONKOatK7j8RnoLqgIBwgFIFt0YxYLiFwBVEEoHKKqMkhVVYRQyE0urSCELEIxq6AqEIn6UTRQtJkIszwwJZBDBVVAsgiTFvSVDk8DFAumJuDgNBimXD5iSQuDRBbcWXkatgI1SHeAYRs2DMIuE3qhGIHeJJyhyeDbXCds6oXVN0K2CzJDUrxQxasTY20Bu0chlX/hK1u+cjpgFaBryBFjHRxODVaB9iaINDP/ErikHS7wyQjX3UmwErBlT5IHHptgeVMLKatk710iqMDhacFQb57EwCjVlSECAT9un4uphM2+bTsZ6tpGIZ/E5XfT2PF+2ls1qkMKhekCvtoKmpdexGjvM/TsfxKAG9/+Ca5auwxFS7P1dz+DTIaOFQppcQbLl9QS8sE40DMJB8fAng+h2VkGkfXtpAUpTaGjXoNzziKRCtG3p0ifz0aMHYTCU8CBE3OahYYoeEG4gCx2IUFhshfdrEDksnK6gmJiFyppnn8B2cQQU2OHMAs2FMZBTPDCYqy7tM6pVB0cHBxeS3JA18Funtu+jeXrzuTCdRex+eFfoWw+TD0+VJya18HBwcHh5eFGqlyCE5+t4rjEWCHEYOnvmKIodwFnAaNl+wFFUeqZyRc/iAwALNNUWnb0Pr8DfAfg5Qq5Dicam5lIILX0sng+KRd+sFQY2gqYEF2KEpqL2L+75GxQj1HdTkW0kkRvN7HpMUgMI+M3y9LgDNOJGKrXQ2NHB8GqNiayWbzuArYoYJkmkZCNG5VUUhBLpPEF3TTXVtFY6ycS9oMFxYKMiLVtyOfB44FAqGTxyswPPw702MhfbwCZtGvckhaqtaWXJweHdsKQgHqkCKuUij9Zet+B/ExnaacxE36wFzbK93kV9gzAtQaEClK8uK0fVswHHkBavLqP/4qYQtobaupM7DLI4yAh394AACAASURBVN2yBxLHrElUBAa5WWc8lxccOigcMdbB4aQTBfVG8H4QmmHddXCZH5bYkFPg8XEY2SvY+fgEux7dzke+30ptWMGtyvs+mYMWA3rSgoHDWR54bi9NLQ3ctK6FJRGDwTFBPrkdwxijmM0yNdBD78E0c1sDVPk0aiJ+Pn/r2/jeT87i8bu+SmLiEG5/JV+99dNE/RGeePR3WKP/RSBcxW/ub2agWMG7mmuZ65MZPO8ZhHu2wDVzoVGR/rYhRbqQW8BADqZ0lbUX+VjlvZm//1YvTz2UgIIA7kVWlr2v8znWAQH5PNbhTmAKyCEKJuZYL4mxBmQFLqdG5Ghn0cVfZCqWJ71rDyKbwJrqhKIAO4t8Bh5defqQDwebl+8c5eDg4ODwYmx6aiNVmQDLP7kK6oucGWrE421nymMTLlQRz01jWs7MBQcHBweH48OPlIFOSTFWURQ/oAohkqX/1wF/D9wDvAf4aunv3aWP3AP8haIo/4fMORJ3/GL/UIgDQWbyeJvMdEYVpFjrBdtAmCbYMaASpmKongk8SxaA0gdj/ZAaAMah9yDlFFJlltUtpkqrRi1YLFmtsfGJPMV4kdhkkYn8KAOxEUyzKCNsCxYej07XIVg2fw7uwELqWyBYCaYFRRMMSzoNuHQpXs4mB4wCwgQyyBxWE0iL3EjpUEMaVFfAnCmwhLQv8COtDXSkmeNSpJHjKFJ5qAQ+64JNRYgL8gnYeScUJ6D3Mdg1ApMa2HuBbmQ0bYjj7rMfSsOkCYsqZiUGQ4oyezshdcyapBqD+bTOPv6MYP/uPLbliAUODieXzVDXBueA8i9wWREaLJhUYPM0LA3DxueyDMeCrLh2DU3LYIUmq6KJJPzlj2HNeXDJHIV/WFXBoH0l19z0C7IpL9dcGOIdV2jc8dvPseGBLnY9vZ9DO3ew99Gfcu4ZbyURqSVrg5kDU00glDzh2sVc/8kd1AYUPvXVZ/j+jzeg6QZ/f0c3N6wJ0Fo1U+9EgfZlsHiZfP+LFFxjwLWlxIWbgCefAysGl62D/9wK0/4W8I9DYRPw/5idxPH1wQXqmSBGQEwix4g9yMq6iJwe0YsUYssd+cM88ONbgRAuf5RFa/+I7slLyXU/jj38TOkzA0eVfbr010AKszrywWK9zsfn4ODg8IfPFnZh5XW+1Ak8vIm5qoeW991E83v+lMUPxvjyD9/GjoMnOgmkg4ODg8PpylTpdTI4nsjYWuAuRaae14E7hBAPKIqyGbhTUZRbkD2Yt5W2vw+4Bpn+KAP82WteaoeThI1UKQ1kGGclIMBbAZ4KmO6CeVdDMgu9+4BxCJ8FuSQiP4lVVGhqX04y3EB2pJV8734obqEsxqruMFWrPso7P7CaQLSK0ZjCk89mGOydopDL4Pa4aWpr4aa3NFHhEYgsxMYE6bhNOlugqd5LfQPPKwS6Jr0MTQsyGVB9oLrlt+nI+N4a4EINlFXIfnU5TXlD6f8eIGbBtpg81pI3IwWkwWsFUKFItTdUlP3yROl07S1CXoqctgo5P4gGqN8tN/EpoKws7Scu91tOdPNCVgVCwLZRuVGNV+q3s7e1bZtd2/aTSh5LjZ0Euo7YPpfP0nVoD5blCAUODieHGuBWaKmF8xU6Lod/b4TzNAiq0B+D7XsEj983yEhC5ZwlHj7x9lpMDZ5MQZMOC/3wT++AH+6Hbz6sUK3CF98Gd339CjIeLzmXyvpJhfogRIKVnH/Jat75ntWMTugUrCCFaZv2ZpWKWrj5xnm8dd3fYYgMoRqVTWPQ1/1r7LH7Mdxv5y1nGtRHFLqKcE8KHo9B30GY3A/ZEZj/T/BhHyxUZN0kBFh5uGoxuFLw1LPwnQwMTyuQKCLFy9dxMMjVBN52CFTByKj0csFGWt0rSB9YN1LWziAFWgMpniaBLYBOMRvg0GMFCtYEdr4HOYJWtu05FgFgjtyvD7AGIX/4dTtMBwcHhzcK8e4h7v2jz3HFh6+k5parEHOiaFGFyxpDfOuROjgYYWZgzMHBwcHB4cSgMBOyeDy8pBgrhOgGVhxj+SSw9hjLBfCR4/x+h9MOGxk1JJCSogc0DXxhdP/ZqJEWrHQXVj4JWBCtgXETl+6mrrKWdCZLMV8g7xoqRc7mSvvVcLvDnHPu5bS3RAgGDSr9Nq6cTqYqjFn0obsMKms8LGhW8bsURBGyEUE2bZMvWAQDKpGA3Jsya3aomQfThHQG4imb0ZhJwGNQW6ng98hYXyxkPzxeejUg++ruUhE3WTAfCMtDxkaKqIXS+qKYCarKI+/EUfH8nVjMQs+zYLaB2wJCcCANmZ1gTcr9iJwMjXdx7BtTpk4T7Nmzk+aWWurm1KIJlYGU1Be8OvhVm3j3IcxM5hh7cCFVgRmsYp74cC/CdnwKHBxOPGFQ5oPnIqhxs/AMWHs2nOuSUfTdRdg3bLF7V579naOsu7yBq87zMq/exSSQ0GEsL21JzquG85IwbIBHgI1CdyxCdRNUhmUdlLNh5/5e8mkTPdRKW2slVl7g1iGZgvEUjByG6aQfr9fNW5fAoAKhQB1VzatZfu5bqAnr2DoMJWDTGOwMwHAtFLpBHYau/9/efcfHdZaJHv+9Z/qojUa9WcV2LLfYih2XVOP0EEJIQrJJYFnKcj+7uUB2b7iU3UuSDwsfuMACy3JhQxJC2BAgpqSw6TEmBOK4Je5FliXLsnodafqc9/7xHlmyrLA4sSVjPd/PR5HmzOjonXHmmfc85znP2wTlVVDgNX+vMQqWB4IJ0/P20BC0vwCJo0CmE1jPqU/GKsyZsiDYYUhZEOsDPYAJ9CnGql8zmECeYmzqpJ2vgHN/Bm1bxIdaMJdOdDv7eStFmHphP6gcyM+FWFSSsUIIcQr0J4b4+b5nuCT7VnIqy6DSTP5DQTeF3ipyKCciyVghhBBTyAUn3bv8z13AS4hxbMzBay8QAp1EWS7cJefiUmm0jpJxMpLugnwy8RjeYD4FeWFS0XayfF6SngSxTLOzPwuvP0xR6VzWXrCUPL+XAh+UF1ksKvJhirOPp8EkSosUFLnAdoEal4QFMmnTOzYRB1zm0v2egRTb9/cRzskhuNRP0O82O+vCFEENYZKxhZikahYm2boNU8Dmw7zLRo/TY8Cghv4M7MLkOxXmnTXulEgqBgdfhUw3xCLQlwUdwzCywclHmEwrQ4w1gjjhVdcmWdvWvJWi/MV43fmAj4O9adLaRWHQYm6uJtlxGJ2MT7KHPEwL53GvYypFousoaEnGCjG13EAtWBdCXjlUwtK5cM1sk8Z7rRUOJ2D3UZuDB2IMxwa59oIaLl8RQNuQGoBZubA7BtsGYHEYVlaDvwbcFkQ0PL8HlrtgWRDmZMPuOBxuO0LLoRH6Ym5uuXqE2rJSlO2hpSPD0S6L5j0JdjYN4PYm+djlJeQXwaL61UTsRVz7wSvAY0Lk0Tgc6ICRMrDzgDDYHujcCp4iwGsuKtjUB+eVQbwLOg/Bnh6wnwLig5gm289w6pZccTnfLUyfmRJIW5Aehmib83dGOH7xrQwmkMcwFbEuTEC2MUE+6ezPi/mQSDN23luP+xqvFAiB0uDxY4UK0O5edCQbUsOn6LkKIcTMNEiMX/MG92Y8+GwX3nH31YUXUBPax46BXdM2PiGEEDPP6Do+J3O9sSRjxTs0ACMt6JFh4q2dmHTi6AFtkrKyUvqzComkFG9s3053eztXX3clw4UJnn/zEWcf+cw7/xYuv/UTNKzIJelXRDCHwVlv8VdH/ycf/R9YOwlS7RwTKwV9vdDXBy4/FBbCQI+mpaOPP259Fk8kRG3ZKkqKyswxd5Mz5NGrVUd7v2aPG0QlJiFrYY7JSzDH9UPAy9q0BVyAqZz1AxcD/+78rgeYZX58uRu2t8N9FrizQDtPQmPS2yemnseec5eGFasrKAqnIdOJds9iqPUILk8hdkGO6Vvgd8Z4giKg/vhN6TT09ppms0KIKVQO3A7Wp03Hl+sgyw95O0Evgxf2QaAY7IDCHXKTWxIm7POQBQwk4GPfh299WHN5KawOKZ6OQW8cVgVM8jWk4IbbYf0G2LUBbrsWGvzwky9dxxO/PcLff/EVfnzvl/jGtx+ltGIuvQNR/NkFfOIDIXYdDdHc5cRTBf/nrlVE0bSi6VWKRg17NXRGoOczmHgYxsS4F+D1i2EwF1xJOHoYbi6F5hHYtBW+/S0groFHgV9igu2pEsYEvzgmZezDBEUfJjAOM5ZInSzmjVbMejCfQD3O9gAmGZvBRGivs8+0s8/UhP2lwHKDLwyFIQL+EGlfAwlvCRz4ySl8vkIIMfPYmBOO6x58ivdUXE997djc9s5PfJCiMjf/8I1fTd8AhRBCzDhvZ/ULScaKU6Afc+Cb4ViJp1OmetGKd9HS1ot2eVh58cUM9UUpzM+lxe8hfP7f0LfpJ1xy0ye59n1Xce11dQSzFD6XOWwOnMQIkkAyAckY+HwQ9Jv8YsYGnwta2uHZP2zj5d++wB9+9V3Q1bz7qq+weFGZGXIa07m5EVOaGmPsStQC54/81rkvjMlpHnae9gimivYOTL7zEPAG8AgmQQvm2L8Q+Bp4vwoVz8H1t8DDv4SWP3MBcQvIU7Bhz35CC84nXFKBAi5eWoXHbeFxQzplQ+d2SEYm2cPogjJjlNuLp6CCVJcl68sIMaXuh9xVMBu4Bz4C3FILy2rNW/F918MTL8PuXYps5eXb31hAcYGbAUxMW7wQPvPwIAGPh3k1Wdx1Iyg/+MZdHbAaaFgJUQ09Kbj6HrjhfbBscSmvPXY93fFLKc8v5IUNR3nilSaWn7+CVCZIcb5FyoL9MQgGoGsYdjfCb57OcPdnXDz6rGJfGpYsg45K0IuBeeCZBw3VYIVMOrQkAHcuhzceg++th2e2AIMZ4D7Mmp/7T+HrmcPYZQkhzKfI6KUMo9txbnuc27FJ9hMGqwI8dZCVjTsniK1tbFvhyV1ImnJ0bAgiTdDzG8wHwWiiNgHUmH3nBVCz5pEXDJEfDpGblYXbdR5bC8vQWx+AxOApfO5CCDGzaDRf3vo9KnvmUD+u0KC4AZb0LuXq393Hs5vu5bT2JBdCCCHeAUnGilPAZrIqI4WX6spKknaWWROrPIe5lUEyKQu3PZvUZXcwUFvDsjXXMGd+HaFcD6ixadNkxZ2jedPRv2ZrGMlAd6dNPJIkk0jgdluUhLNQ2iKcB1ZAs+tgB2/+cQM7Xn2e4aEOIEo6PWwWs1KYCtjRRbSjmERsEpOgHb3iv995rB+zdsuQM5CM8zXsPLYT0/bgZUyiFswx+h4gBHMXQ3kasm+BlQXwq8c4tuiXzVtPGy0FeRrm1q/Ak1tMfzxNgd9NTtCNZZn70ynt9EWc7NxMmtHF0o79Gynwedyk3nLJMCHEqeUFrgLfHCjII3s2XL8cbhmCRYXg8kK7hv4EREbA71UsWulhabELl0sRtU24uP5cOFzgp/GIoqvXZk+HIpFS1IZgVt5YqPL7TXG/JwOXr4XKcuhPuNnf4qZ6fhb+IDQsDBGJ1fDUlhi/fj1AbTUUF0GBCcn0dEFPL1SVW3QMQdNR6PfB7DAUXw2XLoS6MigNQ1kujIxAfBjau9McfK2XZ9cd4rUmNwNdcdA7gaeBZsaC69tlYaYxPkzk9GMqYXMxz3o02ZrCBPUEJlhP/LwarZYtwbTeyTFn83xh8ARQlgt0FpnUPFbecQ7LijLUuc5FDy/k0Y2DNL32JoOtpmm4KzyLTKQftydMIK8Qjzcb7QmCJ0ggGOTcxe8iUZhN187n6Tu0ibd3Hl0IIf47FuYk1RBna0JyINnBxmf2UxM8xOqbagFw+2BefRl/c8flPLf5PrQ+O5+7EEKIv3ySjBWnkYXf76O0tJi01rjIMLfaRWRIkeMtoiTnUqJLF1JWXUi4xENKg/dP5ARH645SYFoSZJyr7ONw5EiSRCSKlYmh3D500kVOjgtfQBMZTrBt82vs3ryB9sZtzh56OZaYVJhq1y7Gju1HnO1djM1ho5g2hBmgHZOQ9TmP15hLdQcx1bBDmB6yo1LAQfO7VeeCLgO1GlYUQsFmoMlcEtzbP0wqnAceFxNZmGrh+ec0kEimiKczKAXuiQ91J0BNdglu1HneY1yWIjfgZkSdrVN1Ic4kCpMkfD8E87FqIW853FgE5/vB5dL0RqE3oBhOQDAINVUWFy+zKLVM6rIrBUeG4Zw8WFrlZ9t+m1d3aLpHFJv3DDEvL8PSChe1c3LxM9a/yGvBpWsgx4LDrbDjKPTnQNVsmF0XIlyQw0t7+zjco/Hlgttvw0CS2lk+PClFyKuoXqroGoDBQRs7C/KVxYJL4cYqWB4wXQrcwIsp6OyE5jdHePZHv+P3r+8lmVKYwPgK8CbvrE/s6Kk6D5avCG/BfOaUx2ntK2B40E9mCEhFnb+XxCRlB8b9vgtUNmjFWIsBF9lFDcQGhsmkYqaZt52NTgTQrjyUqwBPsIralVVcstjLqmLwuVfQ+2t4M/AyzW/u5khkgGgihhrZh2VrPIkomYxFzO3C5fLg9gaYNauOVNUc7JRNbLCfWN/+d/haCCHEZBRmkqo4e2d4CV7f8AbF3tksu6IWT44pMsjPC7JkfjlKjbUvE0IIIc40kowVp4lGE2ff/iMsWVmP1+9n/54hrliZT0EIUoUWdpkFlJnDZS+0pWGWB/xqbBmWsb1BTJtaKj9AGpIjEOnVDPRDf3s/Kp3A77PwBb0caOsEZZO0UzQebuKrX7ybkUgbx1WGaswZc0uhaixozpg8SRkm0doJtGIqXsFkQkaLgHsxCdnR9rjjB/onir20BvdljNWhzsX0md0NmdYM69dvZ/5lDYSL8k54/uY/ilK3F9zese1wXF2rGr0y9wQdwPbj+ur6PG6qy8J0KSX1WUKcdn5M8+k7IM8icA0UfwrmdUBXAloHbQYszewlbhaUQtFV4NGw1G9+2wu0DsDru+EP/fD+NbBsvsWFC0wM+No9W/hB4zA1NTk8+NM1zFHmQ35ImTUIGwfh6hxYUw31pXD3w1BZDEsDUJ3j4vF/LsJWsG4DfPuhFPsOtfH8t2ZxwVw3F54DGsV3NoI/EsefhOxDAT44F5Z5FTnadFgtBdaE4MUd8NKWI7z86q2YS/d7OXYJwDtiOa+jAoL4qtdQ/YH/x88/l83dP4/yh+d2MPDib+Dow5ggnjpxFyobvKsh4cEE+z4sd4alN3ycnf/1Hwy07QG7Ezo3kyEIzMadexGVt9ewe5+bkYDmjy6YXwT//F7w37CWLR1r+aeXkrz00U+jk4dJJgbp69ll/r3r5tAdKiAQCpPx+yksKKHk3Bvx5s9l10/vROthzt5kiRBiemQwFQVnMw9/PPo4ru29fHDjjVSstVCWouVAD794aKNUxQohhDijSTJWnELjz767QOfxi698nln/9jlK6hewYf3vWXHejcyb66KwEHIKzCH1CKbPYbYylbGjlVzj9QP9NsRHc6mDMNwPHZ02Lc2HiQ/3kYoOkYwOMpTsYGh4mIPtRznUcpCe3euJRUeYWH306gudFGZ1s+jSXIpu+wLdO+8n3dRqCqjSmNxBcsKvDWMKDQoxlbAWY2u4JBkrsvICKzD5zx6OFWXtbYFACgoy5jmwBErmQ8lC6GxK8d3vf4nr679OXdGSE17dWAo2H4KVdZBSkNSQ4zn+TayUIqc0RLrLTeaEpHCEjO6kR0PYSXi7vW4KKwtRLmvSnIUQ4lS6GqyvQ62CO2FFHdy+EepXm5j3m0dbeOL3AzSsPo9/uQ0qfSfuYV4R1F0EaPjX5yGrFC5YDucDT99/EXt7NdvbFF//LtxwK5wXgjKvWU+wNN+8931AlRd++CHweeGJrfCxlyDLDd//MNx4ITSc4+ULv65hWcODVCxdxeXXLOTLH3dRkAXZkTcYOKhpcy2jco2P9GJoHIA3G6GkDq4oh3I31PtygVuBpzCV+e9UGabvdQdQB+d+mOBFl1F5aTbPW3DgR08x+Nv1kPodJsk6WcVpNmgPJF4B5gEtQBI7Xc5rj9xBJhlnrHWAjQnuO0lH9nLohz+l7v3PoX31HD0a5Ac/y/Dke1yU10NWEcxb4WHPB+6h+5lvkGh/DtM8fBc0/x5bFTPirWZHZwvnLF9FVU0d1RdfweorD/DIXR8kMbQNdM8k4xVCCPGnvLb995x/+wKa9r5BMBRg7vJSPvK1NXzhcSUJWSGEEGcsScaKU2j8hMcFhEjGdvDUk89Q15niwqsb+MF3fszCC5azrKGKSxblMSdgKmE1Y4e9KUz9ahpTFRbXEIlC1PkajJuOgG4L8sKa9o3t+D02ls6g00nam3fy5o7N9PT3ERkZIhmdbDErePK5B/Bk99Gw9m5uXnUTj+f8go6DrWPH4RMTsWAKuxKY9oMjmMW9XJjEqnYG76xAzgHn/nEJlS//CP7xVriuAngS8MISHzQWwXNo4gMd2OnJs6IuBXlZELPN65FIgScM2S6OZa+VUlSWlhPb5zvWrnY8pTRBNZY293i9VFTPwrImLaUVQpwyV4K6CgLlsByuOhfeUw2X5Yy1GrnmwiJmzcqjKWnim3uSti3DGtptqPHCu5eAJwDuIZtPPhIhGh3iilW5XLYoj/oQbNgFf+gYxK9s5izI55pFJt6OrlUYScH5Hji/GnzXQKOCrSNwYFOS5tY0qy8KEB65lKF4Ea6Aogfo64aVK+ZQ7IdFtR6e2ASvbGinu3OIdDzF1/7vQr71uRbSrhwirjDwt8ALMGlEOhmLCNauwhUMEdm1HiiF1i6GX9nBzn4PvT+J0L7jJXTydeAIb33pfxwTqNOY4O1xfk6RTkz+WQEZ0BnsRIKOV/6J2N4GLM9sRpqz2dQeJJA7jDdgY7lz6WtMkYp0MNafVoEdA/ogDpnDIxyJHmCgeTHhOUuZf94qFlx1E82HKuhvexOObnuHr5MQQswUZhWJdCZBd99hPvI/PsFn//EuljYsIhQOcd/fPcz3H7+Xtq6m6R6oEEIIcQJJxopTzLmeFi/mQLef3ZtfZcjO4srbFnB0MMbghjfobW0j1VGFtaCavAI/tsdFQoHtdtbQykDcNpWy0TSko2DHMce2aXD5wOsB2wfBHD8kY8RjMfq7Omg+uJ3mxu0kEpOtlD1mb+PrbN1ewpHDH2FFdT3PBgN0aCZfYHtUguPXwEo63+0J3zXmClk/x1Wcrl9vLm31VUPoZSjyQ2GeSawAuH0u1IS86LEUt7bRiQTtnXFGYm40XnICPrxek05QChSK2qo6jvgCk6Y+Uklo2gMVtZBRMISb6rowliULeAlxel0M3pVQ6Ie1sDAE5+ZBbZG5NwPUz86hogL+2AouF/QOw0AEhoZgyVywLBNiRtLw4m6oq4DSLLCTMDCs6RrJELVtfD6N35MG7aZjWJPRNr6EZtsOm/JSi0Seot0LPWkoTENeCBbkQ7EFh7pgy2HN9i0xcvIOUHbOAuq0h9ICGNRgZ6CsophZ+VBRCqV7obHdpj+aJpBKo2PQdyBDl7bpCfiBZZj+L/28vd6oo312S1CuEJYnBygGvNDfRmIkTUdHnI5kNwxvwzSzGR736z5c3mwKamroOdiEnR7GBHEFoQoqZ1XhsmMc3tfH4gvOoWn/EYZ7OyA5eZXqcMtzDLc0AfXgmstQrITeaBcZOwXBYvNhFe/GBH43Y8neqGl0HukjEjlIJNLDwNAgPleA3Io6Cn2aTMDFUKQJIoNv43USQoiZZrT6QWPbcX72i5+zYE4dmUya+nOXcMtNt/P4S9+RZKwQQogzkuvee++d7jFw3333Tf8gxClSBmRjkrFp8zXcwlBvD9u7qnnfXX/N7nX38/q6J1j/fAu+7AUks7PpSrtpj8JwBkZi0DsAfb0wNGK+2ynwuSGUB6EQFOSCxwcJbREuLGOod5DmffvYsvF3bN72X2Qyf14H1GCgiKzgOVSvqOPFnz1Ed9uRk1vcOup8vdVVUIMcn9ztg02vwFNPw4HDYL8EnkIYzMCr2y2yV5/HBy6/illFJSfsKh5Ps21LBy1NB4mMxNAosrw5uDLgjoErDdoF+9thz5YXGeg9esI+lApjpz9J0WJoTkJrXFFZZvGr+79OMv6nk9dCiHfi8xC6ABYC34TLDsF8BZWFJnyMntcJumFOAbgs2NgIz26Gdc/ADWtMgtZjgZWAaz8N6ULIy4VFxYobL/KzbG2I7JIA29syfOexCDe/38+8+QHq5wepqYa//0KCoWwLlWdRmAtpG/bYsCsDRzJwiQesbDja6mb3ph5+dc8XSWdfyU0X+7nqAujQMDIMfQPQ0Q/dI3Dnu2Hxu3JpWFbM7OpSmlsUt80Ps3dvFv+5TmMC5H9iLivIvI3XzQvUAj5Sfc0kOhoxZ7kGMKWm3RDdDonXQe/nuEQsgKuIYNFSLv27z9Cy8YBT/RoFLGj4OLd+4n+ycPlatr3ay1eeeohdTV66OiMw3PgnxtQH9IJVRdm8SlKJQVJW3PSV6OuETAfoIUxC1oVJ/ibNeIkCIxDtJ93dTvvBXnKLyimuqyC3NI+jfc3Q1YH0kBVCiP+Od8LtJL999WU6ugZ516U3U9tg8fCPH6CtrW1aRieEEEIA3HvvvfdNtl2dCb10lFKjF31LwzQhxKhCJCYIIY4ncUEIMZ7EBCHERBIXhBATTVdcqNZaF012xxmRjAVQSm3WWi+f7nEIIc4MEhOEEBNJXBBCjCcxQQgxkcQFIcREZ2JckFV7hBBCCCGEEEIIIYQQYgpIMlYIIYQQQgghhBBCCCGmwJmUjL1/ugcghDijSEwQQkwkcUEIMZ7EBCHERBIXhBATnXFx4YzpGSuEEEIIIYQQQgghhBBnszOpMlYIIYQQQgghhBBCCCHOWtOejFVKXa2U2qeUalRKfXa6xyOEmBpKqSql1Hql1G6l1C6l1Kec7WGl1AtKqQPO93xnu1JK/ZsTK7Yrpc6b3mcghDgdlFIupdQ2pdTT51kF8wAABKdJREFUzu1apdRG573/M6WU19nuc243OvfXTOe4hRCnh1IqpJRap5Taq5Tao5RaLXMFIWYupdQ/OMcOO5VSjyml/DJXEGJmUUo9pJTqUkrtHLftpOcGSqkPOY8/oJT60FQ+h2lNxiqlXMB3gWuABcBtSqkF0zkmIcSUSQP/S2u9AFgF3Om8/z8LvKS1ngu85NwGEyfmOl8fB7439UMWQkyBTwF7xt3+KvBNrfUcoB/4qLP9o0C/s/2bzuOEEGefbwPPaq3rgSWY+CBzBSFmIKVUBfBJYLnWehHgAv4KmSsIMdM8DFw9YdtJzQ2UUmHgHmAlsAK4ZzSBOxWmuzJ2BdCotW7SWieBnwLvneYxCSGmgNa6XWu91fk5gjm4qsDEgB85D/sRcIPz83uBR7TxGhBSSpVN8bCFEKeRUqoSeDfwgHNbAWuBdc5DJsaE0VixDrjMebwQ4iyhlMoDLgEeBNBaJ7XWA8hcQYiZzA0ElFJuIAi0I3MFIWYUrfXvgL4Jm092bnAV8ILWuk9r3Q+8wIkJ3tNmupOxFUDruNtHnG1CiBnEuWSoAdgIlGit2527OoAS52eJF0Kc/b4F/G/Adm4XAANa67Rze/z7/lhMcO4fdB4vhDh71ALdwA+d9iUPKKWykLmCEDOS1roN+DpwGJOEHQS2IHMFIcTJzw2mdc4w3clYIcQMp5TKBn4B3KW1Hhp/n9ZaA3paBiaEmFJKqeuALq31lukeixDijOEGzgO+p7VuAEYYu+wQkLmCEDOJcwnxezEnasqBLKawkk0I8ZfhL2FuMN3J2DagatztSmebEGIGUEp5MInYR7XWv3Q2d45eUuh873K2S7wQ4ux2IXC9UqoZ07ZoLaZXZMi5FBGOf98fiwnO/XlA71QOWAhx2h0BjmitNzq312GSszJXEGJmuhw4pLXu1lqngF9i5g8yVxBCnOzcYFrnDNOdjN0EzHVWP/Rimm8/Oc1jEkJMAadf04PAHq31v46760lgdCXDDwFPjNv+185qiKuAwXGXIQgh/sJprT+nta7UWtdg5gMva63vANYDNzsPmxgTRmPFzc7jz+gz4EKIk6O17gBalVLznE2XAbuRuYIQM9VhYJVSKugcS4zGBJkrCCFOdm7wHHClUirfqbq/0tk2JdR0xyKl1LWYHnEu4CGt9ZemdUBCiCmhlLoIeAXYwVh/yM9j+sb+HJgFtAC3aK37nAnXv2MuRYoCH9Zab57ygQshTjul1Brgbq31dUqpOkylbBjYBnxAa51QSvmBH2P6TfcBf6W1bpquMQshTg+l1FLMon5eoAn4MKagROYKQsxASqn7gFuBNGZe8DFMn0eZKwgxQyilHgPWAIVAJ3AP8GtOcm6glPoIJgcB8CWt9Q+n7DlMdzJWCCGEEEIIIYQQQgghZoLpblMghBBCCCGEEEIIIYQQM4IkY4UQQgghhBBCCCGEEGIKSDJWCCGEEEIIIYQQQgghpoAkY4UQQgghhBBCCCGEEGIKSDJWCCGEEEIIIYQQQgghpoAkY4UQQgghhBBCCCGEEGIKSDJWCCGEEEIIIYQQQgghpoAkY4UQQgghhBBCCCGEEGIK/H9efx2BOTISvgAAAABJRU5ErkJggg==\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ }
+ ],
+ "source": [
+ "# display pre-processed image\n",
+ "plt.figure(figsize=(24,32))\n",
+ "plt.imshow(image_np[0])\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "FTHsFjR6HNwb"
+ },
+ "source": [
+ "## Doing the inference\n",
+ "\n",
+ "To do the inference we just need to call our TF Hub loaded model."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Gb_siXKcnnGC",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "3c4d3952-74d8-49c8-98c6-70966ff241e8"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "dict_keys(['image_info', 'detection_scores', 'num_detections', 'detection_masks', 'detection_boxes', 'detection_classes'])\n"
+ ]
+ }
+ ],
+ "source": [
+ "# running inference\n",
+ "results = hub_model_fn(image_np)\n",
+ "\n",
+ "# different object detection models have additional results\n",
+ "# all of them are explained in the documentation\n",
+ "result = {key:value.numpy() for key,value in results.items()}\n",
+ "print(result.keys())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "IZ5VYaBoeeFM"
+ },
+ "source": [
+ "## Visualizing the results\n",
+ "\n",
+ "Here is where we will need the TensorFlow Object Detection API to show the squares from the inference step (and the keypoints when available).\n",
+ "\n",
+ "the full documentation of this method can be seen [here](https://github.com/tensorflow/models/blob/master/research/object_detection/utils/visualization_utils.py)\n",
+ "\n",
+ "Here you can, for example, set `min_score_thresh` to other values (between 0 and 1) to allow more detections in or to filter out more detections."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "PMzURFjxxqF7"
+ },
+ "outputs": [],
+ "source": [
+ "# selecting parameters for visualization\n",
+ "label_id_offset = 0\n",
+ "min_score_thresh =0.6\n",
+ "use_normalized_coordinates=True\n",
+ "\n",
+ "if use_normalized_coordinates:\n",
+ " # Normalizing detection boxes\n",
+ " result['detection_boxes'][0][:,[0,2]] /= height\n",
+ " result['detection_boxes'][0][:,[1,3]] /= width"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "FILNrrDy0kUg",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 583
+ },
+ "outputId": "5ba415a2-ddaa-4b26-ec58-041387751498"
+ },
+ "outputs": [
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ ""
+ ],
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABWMAAALACAYAAAD2e2C+AAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADh0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uMy4yLjIsIGh0dHA6Ly9tYXRwbG90bGliLm9yZy+WH4yJAAAgAElEQVR4nOy9za5ty5Ie9EVkjjHX2mufe6+vyhjxI8tgBDQseiA69JDo0QUewC0egGdxgzZPYIk3sOQekkFAqVzYZWzjMlXnnrP3mnOMzAwa8ZMxxlz73Ft23fK1GHG0z1przjHyJzL+MzKSRAQXXHDBBRdccMEFF1xwwQUXXHDBBRdccMEFF/x2gf9VD+CCCy644IILLrjgggsuuOCCCy644IILLrjg/w9wBWMvuOCCCy644IILLrjgggsuuOCCCy644IIL/gLgCsZecMEFF1xwwQUXXHDBBRdccMEFF1xwwQUX/AXAFYy94IILLrjgggsuuOCCCy644IILLrjgggsu+AuAKxh7wQUXXHDBBRdccMEFF1xwwQUXXHDBBRdc8BcAVzD2ggsuuOCCCy644IILLrjgggsuuOCCCy644C8AfivBWCL6r4jofyei3yei/+G30ccFF1xwwQUXXHDBBRdccMEFF1xwwQUXXHDBv05AIvLn2yBRAfB/APgvAfwRgL8L4L8Vkf/1z7WjCy644IILLrjgggsuuOCCCy644IILLrjggn+N4LeRGfufAvh9EfkDEdkA/E8A/uvfQj8XXHDBBRdccMEFF1xwwQUXXHDBBRdccMEF/9pA/S20+W8D+Ifp7z8C8J/91AtcScrCQMrSfc7XJZD+iC+J6KdaxcvtFaWuICoYY4CI9B0iEAjfep3S/0UEkkajmcR0fFjsCYG2SQSBYIyO+/0dkB7jJWK8vL6hlAUC4P71R4gMAKLTP2Qqz/FOEOzbBpE2B0ACyEc4O0zoJx5IM6Ljw545TURP7zsm/ONzN0QEEbF1otkWk69mvPQ0NLKWz518Y+D+2Ddpgig1o09/i3p83Hmlf033P4Xaw5dk8/roeUq/nL+Pfk5feHs4fP/B/J4me161bw75GzDfp6dP5YNvnnt9HoHx3Dd6/wjXKhNo8uA34eOVcnr5NSvym8FHjPCtJk7PPuNw4k/g/C0f0vfHXRw/lY9b/bXj+TbdU6z1tznpXwB+E4b75ndJZoQwRmIa+vVL+tNsMR8TmfroMLh/SfjWUAUxH3nmgPht9A4ZA5ChY+QCKgwiRh5woFGVDjBE3xsDT6dlPiLOXwc/tU7nptM6PbGM6+tSAGb7+zyoj8DWvwukD8jowBh/hgnkpp7tErKBMhdgWQAm4wRKzyY5+OfFIk86+NdJPTo8Sadv48ezAg5ZQ78Jvr/BN1lO/Ble+w3H+OcBhJMKPXEXmT7+WN/9OlD7R9/T1zO/0uE55MdAIffdXp0v/mZCTOTMKh/3/fHbpzc+1DuGm3jhY4U3dez5/dzDBzZD7tP13zfG8u0JfDDTA9FlP4BOPz+mzl/PD843HzxDE2FuF8+hnCyhNPZ4lo44euqDAGZWSWT+DrP+EwlxCgLA9vMjkZoxMARoDWh92N+CMQTdZKrIMB8GyQ+RE09Nf0Lc13lCzZQ54SsEHqYMdRtXwu8Se17icxz4aeI8r+gBd5TXTP/5Os9xHfF+HIecxjG/+xYQsbYN03E+hngbOCDqhJv0Rfr9G/0ZrsSEQm8b9scd+/uPkPY4YSbh/kQUPyWvn747iwP5aHTTV/GxBc2WChxoxZ41otV1yX08808pRdfH1srxnelsyAATB00QEcYYSf4aT/ka2TqLyIFOxXiTmWMoFPOWGIckRMQcQMffD+g76omPdP6v07Pe17G1n4KsFyft+Jh83uef/vtRLiUbxNch8TMdeC+/4fGP09Ak/mf4nP36H47vNKjUcLZrJs9/yH9nVSDPWM5rQukzAoF4yu0zRG+5D5ocKOOIU/lAFuSRMB37ciqaeHU9LCEP8vpm3B3lX0KbIyWr5vFMkVk263CnDI+4UEaY9Z/fOeM4S5gp1nUuQwTACII4jMj5z9+057O++YhtDtSQGPJb/PMRv/rLjo99b+i9f9jEbyMY+xsBEf1NAH8TAHgh/KW/9gaY8ViIsffNhCajtwESU1hM6gCJo5YAIQhnI0Wf+ct/+a/i3/wrfw2/93t/FV++PlCYQfZvqRWvt5eT4SBhwPpit9bRxkAfamwEkZnCcCITUeOEmAEMbPsDP3z5U/zRP/j7qEWwrAXLbcWn15/hr/xb/x7q+oZt3/FHf/D3sD1+RG8NrTf01lFLQa0LiBhjCECawEys/uiXL7/C93/yT9HaBoGAV8boAwNKZAzCIMFSKrgwUBhMhGHGFADIGKo0/G83dmM+ymRDBsAEWhcUIsgYQdRjdF0LR9gQELGLbkBYx8MEYjYjMREtAUKEkRQbEWuwlhH4LrbeYkzEmYmMzYbSFAoTWASDJwMUKhCzQkWAMQaKB0VNQQ7SNHF2EcYwBv8ATCAxyHo2N8Fo9CAMbcxDBmIDwMav4x4gmcYDAxiURbsc5dVJHjMXEEYouTESHqMNw7WtCxNN4/ngEIjhiVOw34wjYvSR8aF4Y9tgcEUxRI0YJjIcK4wYvwtn2AYJKybdOKKkeLL+jF8Ygp7GzkffLOkox5WPE6YEIuhDwVrwME02ruZGyHEdsmGeg99Z4ev85vNJrfpigIQgNIIZ2OhgWG+FOYmmgW6bOkf6nwbf/JuflWP8E5STheHKGWZMutOWnxnRkq43E8OlSXH5FEr02D6Z3HhyJojArguzYUQqn87j97nPNuKl4B/9zjA4hQjOEEaxzVmdZGAMAUFUBtFR/ROm/JfRw7BQzvEHaeLX6UQAIZm2TA46Bs5N95hBziDjUydilaEiojxihCJkZvgQtPsDX371PdrjARodt9sNt+8+o7y+gOqCcGrdYBGgjw55vEMeD8j7HeO+ofc+jctJrsGXTDzpXqA6RoarZLBZLGo/TX7PRspHBvs07PXJ9XYD3W6Qlxvqz96A9QUoZHKSoSulE3EaI1b9M2SgjYb+qzv6D18gX74A+wMY3eQZKQ7Fx6KjGENifG4wHljB9UetWF5esPz85+Bf/hK9LhAuUAn+TG+HucqkKvngmcMGqPcLla1HSEY1TCdnBzEFc7zfMIoBOPP53+postk1DKYCJp5CMuNhjlr5Jch06hvXd85rYQyfmnqyTDPdQ+l+2g00W3FvUWA6KF6f/J3ap8SPapeoHHPnAEIHI96dKcGUT4HXJBxC2p3kDBHQu5gj73MpAPHT2nZRacoHHNlciVFKib/BnL77JhYxxplePBDBarcFCCQmKMfnyWxmUptaXJcJVL8zY4wRfJNtyowviZZ1dpxxkCwVdl2CFPwgVrtCVMew2ZKOc9dZ5z5zsEvGyfkCFKekuBxytPcK8dQfBrqO3qbaqb2PQD+zr4l9X6r6A06LJnC6jYW5oJQC4qK/U4GIJo24/IfjyvtmBpvN43RBNjYmDQTdXm4ACKVULOuKt7dXrLVimBZfC/DptuJWCa83ws++I/StoTWVqUSE/bFjgNCG4N4EP3wVvN877tuO+2PDD+8PPLY79sdX7NtXbO+aVDJsMy87z/67QPVNH11xnRWsrz3Zs2K27BjhhzhuhAQi2oYg+YMyINLRe0ummNqhoWsJ5ouU+a9UFK66cclmm7Hy2wBhDFW2rW3atul+GdrX6A1m0B05l2H6klBrwd7nRidzwbqu6HtX3W48ye7jJv9mmLHqPkPv7oIo4SnOgRkkHMZLxgfMhh7ViSDBlx//GH/8h/8b/tH/8new/fHfB41d8W72h8vcxFDxq9hascnGMYZpgaO9d9ZnIaYk6Tgjk7C9RVBvBevbDb/4xS/RR0MfA2Po90tlLOuKulbUWwEYk2eYQVyx1IpaKkopYCbsTTeluVbUwhh710CXyZLXlxsKM2QIWtux7xtEBkrRNVLZKxhjoPeG1jYwMwoX1FKxLguYSMcpM07QWkPvw3xtwrosKLWAmSFENj4O/4lgPrrJ07bvhh/TnaxyzOl4mu2K5957MokJtVQ08aCy8aT7cI4voqQnBMP4auFqOoKMfmsEmSszhvSDvhPje/c/PTANk73TxlI8Oj9HgNq+d1ucQRhDZozFdLSusbZbuMZciQgoRf13l+ljoLXdfD+B9K6yYwDd1rIPld8DaqPD+Cb8LlI56j4XE6MwQGS6g2aAWRdJUKigtTbnVGr4JEMErQ20fUMYzDT5u7DJdONdNl8rfAH3NwgYfajdoIa8xhJo2gWjD1Dy3ISm3iSSkDnOpypP8+YSlCf2fcpwGRGbsgULnRg2PyymAoTOdp4fFksbxhPFbKO82aG+s1gsTW3afd+DRk3qG811jNGw9QaIrjWBQELobQ/d0UfD3jvKIEgf6uOMEXGI0V0eGC0OgMX17sQ7MNAtpiPmKxYuAKkN0fuO23pT+tBlgYCD7f7wH/xjfAt+G8HYfwTg301//zv22QFE5G8B+FsAsLxWORj8zGCp8B0sKmUKcmdMRzrUMxX7DtDnhAnv21dsfQNXAtUSwQgyYhBypcKopWDbNhWgKvnD8YY5ZeEsWx/u1LlhLhpJioDord7w3eefg1hQK2NZFyy3F7S2g/gBEuDzdz/HD9IgeGjNCGP+ZVkAEPbWDV/WJxM+vX1G6zu27V2D1tUIHVMIDghqKeooM6MQo/tuH5QAYycF09Hz+Q1RZi6m1WmpEdAle44hFlAytIfOFTNWzLkgDVyXqg7A6B4sUQVOxrCOXyYXUNomMwUzs4wZAHYhCMT6M7QtIsVBKCuyzKVg/Hg1AiWxuyjqFrlTF25geidpPf3ODCYnjniWLOAkHEqVTZnm4Mv0qA+dWE8Uzuw0inRMk0adKH0Np1kYgU1fbzKEUfrM1+3gMsH4zX/NgTobpzuzhzdpPhP2dnKMxel59p1RGn3hGIh+fpDm/Bz1SPih49OT5mKZJv4cd4EHms0ccI7D8hz7zHSbQpLy9ELwmYQGS8E4t7Zs3TwoXEAH44tSo+chZhgWCHU+zdnqRJk2zvideJjLOR3aj944v20dzp/JsKIT2oIFJDUQfRkP+ngouNIRGm04XqOdNKK0spiB5yBSEAhMKcfx4DB6j75p4bKFQz7rKyf+ozx+bTMMNTeu4LKB0udprJMJ4XrAN89kmKG5bRi7bqLQsqK+fsL6+gm0VMCcDV0G022e8rTtkG2HtH5c5+B1BH/7plfiIt2k8w0AymNGyNwM6gDI4fMxUnDWHD1eb6DbC/DyAqwrUIrqIoJuzh7WyPHGEJgDvzeM+x3YN9DoB1rIwfzDxkaIRwvgxDeTsZgLyu2G8ukTytsbpC7hvE/ZaG8lHeVZNU5Tcuo74+fwN45sHXoqy1Tv7BzIPQyfjjKXJo8c5E4YxZMGxZ2Bw+zmGCQN8ihf/bPneUamzQfz9XcsrBX87cHEiZdjGxn951ZjI4cIPCQCgh8FBacsJ/8xW4os8zxZ7+PYZymZdwGicphvDmBEe+l9DyqGYkn/jkHbM8zNnGnTUEzkeTNEYq2m/MkO0kHbBG7C7gVQSt7clw9/jw6SHRpBciI1GlWBBo9GEOIgh30qbm9kvp7ZoZnHg0b8WbjkTTLRzAZxORM07OMZEFG9ScMDGWLyp9jUfKNn5F1oc1BV7orb2eS14ghSfJNcbdVhTDUwQMPogOYGArFuiDKAAguUj4Fts0BGKWi9gRkYdcUwdIzCKDwAURt3eQy0faDtAIhRCuGxCbYu2NrAow18vXe0vWPfd+z7jtZ2jNFMj+jG85CBMbrOIeyqaRkKLHAYwRnXRxpQUCe3xxL75/AAT6yBaOCE1H+rpaLUqnrVfLtM08V1atBtkqFGF30MwHTEiDXQtdcDIw2tbzrn0WydB0bvGKOH7vFgAIKHBMK6Qm6HMbEeZmybBTrsXdaNPKdVlVcjHHmN7g4MoWl/CMVGhesUWAAYRHYKsZhqGBBpEAgYQ+0c931cvoslckzCnzphMrRyjWeTJvkz7VrH8bQ5nFv9AZttkoFuCpPp96zP9LVlKViWglLVRgAT3LBl0s2N4pt3Y2CAIujuwU6YXne/v2oExmhP+ZmZUIr1YZsMfWgAp5SCpS4WkPWApp6E1UCjRIKCjrGg1oqlLhGAbTJUTgzBQNdkKgsQZx+TXAeRJWfY3qjKREQQFwSUbpsJtg6lFFBrzglmwFmC1VnH+xIO0ZNEggjyCzEgTfkLglGKZsUf5DCSn+mb2hRL6MlfzIS61APfO8TpZZjtxdlvIlujAXSz80azgN2kjxH0SNZmBxWODS31gyTWzjePOnwzLjkf4X+4vUwAWxAuDCeBb2C5VuHCsamjvDb1dCECKkNGj0B7h/lFhi/XKUyswWMa6NaHB6MLCFyKJiWIADzQLNEgYjik/bhuc7novC7SweybxTOpKTwVMvqtNWQDCKilaHzIcEeFQsx7XImIUImAwqABk1uCwQB1wuAZOyPIgY49OJ9toVpTqJJU3+ozBZAKHh2QFR7ABgjDgu3q91gAeEB5zuS2ruvQwPa+Q2hAugBDZatuQBw3GsawBLsxUIom5InYxp3F4dj0ffes4fAJT7ZQgt9GMPbvAvgPiOivQYOw/w2A/+4n3yDokQRXBuwCEgARyq1YxpJCt4Ag2/FLEsIwZhVSQwogdAwM0sxO38GHOcEaDe8oi+5+fX77jO+//1Pse7MdLV2ovBsukBB2wDTwnNCHB2AEqGXBzz7/HCIDX+9fMaSDWLC3hvcvP4BBeHn5hF/+8vewbe+2UwyI+G65Lg2bsJqZucCy3vDzv/R7eH98xfvjC3bZQQwMRuxsDmgGnPqpZEpvZlBiSAjMcK5JImNICbZpsLqo4ScdEDe4TTCooaRzry7c0roKAWBfnwFgzOCtq2ErW0DzCwTRss5lBl2s3eQYEhBCOXUd7wRzJ5tf7Xgz6ISsj+xAIAxmH7D6HlNYH1zTML5s7AeFavlSYfhY30jvhAVDKaidhLyvG1ESXHQcgw2S0u+RkRGBMGvKDL9wzsNZ85c9w8uzTqwvR7MZgod1AU6OMhIeJj4cc55BR4d+p7I4zh1Pcw2lmx1Fmc+RPW7bFHCnbQbqZ7jX6UX8d8PLNFicfgHCzASegbzDIOdYpu0ZMiTUnfOdr4+IZSQov8ZnPmvimaF1JLETTPqIT8w5KjzLwWRDLxsinp00s1vMeKWjgxsSOQV3AyeYmUaOz5yn5UYXJT5I3Ac35I9rMScc7Jzec4rNhRPCybD35ucTL04Bih+Kdt34USPQg+U2o/hpxmMaG9OkJUMPMuO4fPbMFW9v+j4nI9Rwb0kRIcAia28MjH0D9h1FBHVZUW43LK9vWG6vUINRjT7NNlKDe7QO2e6Q+wbZZzDWaZooBQpghmUI3MQ3aX2muTHXNZHhxFEytAkAOG8QMHhdwC8WiL3dgLoC5BlhvpbZDRSAiu5sD6jDdW/A/Q7aHmDpINYAR2RuHBxM/Z/TLoOA4qrIjDBboLIuWF4/YXl7Q3n9hM51juXAcxMPeT2ddA48PKkjZNDUNTTHJukTlxuY+jDeONA9Ys1y4AogdewST/sYYP3773NdM3if1iblZyZdJ2TE3M44yW/5+H1cRKy2XkjpRGXieCK4CTA3eih17Wtrjro5IXMITun2TubN0zBjAyXP1+gyy6igUfL1MXkCSmNyH8fpImkkl0GRnUwxB8ynnjDqcsp1jgfGjoHV2fd8z0t5eWCID61rMGy2QQB6Dn5SgUifjcrc/HwOyOpnvTd4YJEtg2RmpCoNl1LUCRex0zaWreIZomn9XJ6zZ6QKzC6fNsU8eWP2fPqMIiPWJR6iXZEeuKWDjtT+RCzwRQLIMHPB7MpkHniyBsCWNaRtY3g/OPgcAoCELclA0NmSSKC2dyJ8DGhG3hgDNBrGaCgM8AupY8yMwYrnLoRtF3z/gzqVvQkKaxCESkXbOx47cH8M3LeG3na01iHSURhoNu9SKkpdLA1ohF0wg6eOSZkBGBGIWQS9q7+lwSzfNJvrWosHvVhLJST5vZSCl5dX1PUGLlX9lpxMY/0xuywYaL1hjB29aZZubw2PfUO3ALOf7po2hp52JAyABggSGzsEoJJnknkW9KQ1GA52ACDWQJRlUm1N0LoFULgAFlg92HwYoScmB5WDbDhs7Jv9EYHEkFEj5CKxoBRbaxKACSw8/STnI5/jUbCBcD41eORtl935JEforiT3nCe9zZCZ5AHOnmxA/Xq9LahLiWzf4icpDR/VAkf7vmP0gU+fXrHeFsgAWu9obcfCFbd1wVIrCjP2bUMfDSCl55eXW+Cg9x2jzyDXslZ8+vQGZkbvHa01vN/fMdos1VFKQX1ZsfAKLgWlFs2eM/4efaBtG3prcZJFs1oJhQuWqslY66JZuaVoxrRn78KCsZGdR9MOPQdX970lW9aCdJ5xbmvTW7NYCunp3K6Zw5OXgG3bLVGto3Kx+Ij5VTTlZMREyPqRuc6FCEutuL2uuK2rPc8ohaOcBGTiSGPTM4DYQk7omHofIJmBMdDDMoslsmr7GBpwLwVsP5UVGXVddL08C36YzaPGlf5jwt52dIsJjTYwRlNRZ3K7i0T2KjGhlOVAk1JUX/nJhaVULHaSQWCn04xRxbKGe+/Yxx66c287Cist1VJQqVhQe9qTtRSUWlNWvfGQBU1bnGBR/LTW0Jrq/FIYy1JnHIsIXBi3dcW6rtMutg2Y1hv2prEyGR681zbZaZYZjIFiySq6MVFRXtcpm4du4PVuAc2ha66n8yzmBcFtXacNwy6Tp/1eRgeanVgweqtlCfuksurPYqfNe+9mQ5u86wPvX3/U0+ZDNxjRgVIIA0Npf9swhC2DWvNHVd7M0yB+gklPqQP7GCjHHfpvwp97MFZEGhH99wD+ZwAFwP8oIn/vp96hUnH7xS9PjhHCuhXS04kOfHoMgkihd8ZkIkh9gdwqUC1lv29G3AN7H/jxa8fL7cUIccHb25sGY3sDiWaWOuMDQC0cJpozycN2iocdkXy5rajLGgKg3iraH/9TvL9/RWsdpQj6/sB+/wLpDV++PtAHwGVBJbLdIInyF7HTZYq0mOG1LC9GmITvv/7pdBizokN2CHUHfcZc3OlwYxTRhvmhqKWagNBdOIKgZCVsRg/DjknBnQA3fDSFewZKZ8B6OnzAdKco1lNO9DsD4ZbhTD5ecxRbV6NiekzTkLZ/ORjUAZA7Ztb+SIJtxMhw8CmTZ5JGPp3nHB7IoDvUfHjHXdMpO6fzKPNPW0MKo9uNvDwOLkfnwIcRBg89cY3ZRaecJfeW3YGUqezL4b35Qg5onkFSfwkbh65y1x8+f0K+H8NPKzSdPh14CjhoL86zuXQCXOkCyLv86pR+cNwy/RdrdZp4DvyBRPmV5vHneNgmH8EO8yoZnGg3B299BP76xNOT3DytROEynTq4QuO0CpZgINMF+KD15wVznOQAk7dPgO9euvOq6B7zTUqBX0We0T2f1iYb67O9GSxOeNQBpPW3oSe5FQarPTun5u9wBEo9K4/N4JxZNyU5QYj3vEk/xiaAHbGZ60xEVtLhSBM5aDN5fzKkbujkMQu2xwPtfse430F7U4NsWVDXG5b1Nuc8BNQHigBjVwdUtl2Dla2hmHEu8FIQKssOVHLA6cyki3lNZB/me1iHmLEH250OVEcLCIMY9PYG+fwZtN5Ay6Kldoy3D0IqtUqA1jDcGsbXO+RXX8CPTefuMmD4ZuAMQZIR2Nw8mGN2GvHNDCGgfn4DffcZePsMWVYMlwfe4Pl0OLKTdGz7QD9yfusks8+i8ezsQvX2SdJo/9kgdGal3MccxBAtC1WY9Bgo5LCmp23Ipzkh8EGHoIVvWodRnWkmzfT8We89HWPLgTqoI3jGm9kz7GU94ugoMDd/8C8AlH5mntXP1PbJ2lDHWsoC5Re3V+zUjc046/+D1joERbW92CBK6+bZlIeNw/guy5no5jB/XRcN4FBau8N8PVhtgRJf16XWkMX7vusbWdbCzRaKj6PEAKxUwBwIBgAWzbrSY/wVwAC5w0MMPQ5/lLyA6mzXJ1rea+p9Xxd3TPuwcgfCYTvpAIdNvYRFqEdLLevNso9qKViWFb77O0QDGF3TthDhNFF54o44iFCtPIZn1QECaR2b7MFbw47Oc+GgE8MiInvY7DMtCQVXPDovW0smwmgNbX9goRuWZcGn1wXrwqhMoaeWKni9ActCWCqhD2DdGMuPnoVbMEZBH4I2BMu2g34UjFowasG6MO5fBdsmGH1KCCErXWWJH4VLHAX11WNeUKvxqXS4/FDdIKjm9NZ6Q11uGCLoXZNpMNT5h0BPQgzdDPDMp9Ya9tGMJjp6tzIGY9PgOtSp7n3e66GBzLnhAT+SbcEDETFBm+14YIw9SFIDUhRBSOWLgf5o6G4fmU4aWS4ic6/bEVXp2k4EspVZKEWzgeN96diHBUe2eQqSiAwf9hkB7f4DHvsGFA0g9zFCboUvATwLC7hsysfbbc7OiWeB7N8n/8yTnZ7A0B5Sy4KQShMd5Nm8jLBjmWZQ2gOdzAUvtxuYCdv9Yeta8Pm7N6xl0bKAbcPeO7gQXm5LZPbf73c8HlvIp5eXG15eXgAo3X358hXb9rAEMW330+snrMssjUDE2NuONjoejx2jC/b7prRAhGWpuC1rlFMotYAX3dSN5C4/+i9WtqADbZ8bF83qVfimh8jRtmVmzYZ3Gx+MWsukRyhfuUwjOyJf62L4tCUhisxEDWKZPeqlvESP3Wuwu0c8pHU9kt662pttDOyPhq/3rxYA1SBmsUBpZEqa7tHglo1pWbBU/ac6sCAn/gDA1rYgUBmCbd/RejsEed/fH4pP25zY9x21LiguN00mzwAuY60V5XazbNe5iTssiO4/NWDb0LutWbeEN9kA6YcgOFvMScukFPjGCjOjckV5KRbEm9mYOcN1bzu2x2YbS2bfjMnvALCsK7xEJDGj1Ipqm3iKYqstzlraq7eGx/YAmsrJbdvQ9y1xt9mYPIOty7LOjS6zE8POE9W3W9egrTkXWG6GB6PvUhi322pJiGon6IaiBjRdNn5DRjsAACAASURBVMnQjbRmOIdojKpaWQf2TXvOZZ0spjUE0pomxFnWu8sw1ZOM9eWT8oLb6wMYUH2h+H5ogL/ZiYje0EXL1LTRI/AvrcNPzxQMMMRKC/200flbqRkrIn8bwN/+jV9ggrxq5Nt35zzu7QZpGJWuxH3nAghjUACAVYAOADsJdnQMdKzLTYWG7XDsVudn7z3qPi3LgloLbrcbtn1HKYzWu10AMkBl0QtS5jxDsDoDv7zcUJd11vhoK271FTvveOwbmBjbvuOxfT8DNDKPpswzKTjMTY9ZqIs8BlAwULni0/IJrTbc248YtknOJsDFDepv+HIgd6xmoGYYjiNbLrJCra1wPhA1Ip8atTZVj+vuEXkbMneVs+PltmTy+WydjR6ito73PwOfOsx0LPw8ovCTPWA3MGv72TgFiEMOpPU7bZKH9sgMTCEPHFnb4m87cvTLQ/AptaJGEU3HOL7iyFYiO5aUdx7no3TElbiA/WgtJszgvOOGTs+bIifM+n/65jSQTs8CmGHtILecwSSzb8LhKOd81uiPPl7F7LjLISM3OdekhmVc00PWskjIEXZ+svEM+JgOJnAaO1CJ3ZPHGeZTk09ytozPpdpxquGIIMy6zcmAOgSBgzz46OQ6bcF4K2VNPRvIM+gF8rpsc909axjCM2AjsF3bmdlyIC2y7D036mj2lR/Oz4MsfBBO/cSTpOdyP270T7RPHqfUxqGfPM78LCsmRkJhiqQ8saF2J5blNOefN3vi89N7qsdG1Fieych+vEmzV+SI1XDQZisxev2EoFkR/q0MYN+BfcPYtT7Sy9srbq8vqLcbuFpobsx6ZxgDozWMvWk2bG8Q23x0ccRenx1HqeWjUXqh4PW8JsBZpkwYThTOH4e5a2YZWJ3Bpa6g5QZZFqsFZs95IOdJtKmc6a2h7w+0xzuwvYNFM5n8eeJjVnuSJCh20edsUo1g13OFAFkWLJ8/o3x6A60rOiUsiWeEzHp5wWeh6pPEO0azJ279iVyPzBCcM5eQ5vHk2IpvrGqrozsv0awDPOwItB8ZC32qEkO6oCanTJVxDAXA8zo/B2aP4LYcp3XIeJkvu/H60fam41Ys6EqQEy3oMDwQK4fvMo689plvOB4ztc790bkF+NF0t6KIipa/cjvipF+f8cOpxRD4ptYIs5brlINKoxaQc6qRYyYbM8NORcfnGnBym8fnYvKNMieoPjgItkRLhmF1uiwLM44snqiYCeBBMTUiQttH1NEPlUZkNRiLva3O/N62A230roHjpc6ahhog1tr5KaQ07XR4puwMlM9kY4HXOlW8EkQYpSiTDDvbz1WPW3I4vBL2RQRDRkOcrxLvt6CwbjIJaTJF5Rr2bIdoDdLEzyDCsAAieIFv1EYgXpRqCs16qB44ZpBlf6XAvGViejmd+33DbXnxj0AM3JaCylZspncNqO5Ff8pA4Y51vaEPwWYBzloKHlayoO2b+i5BtzoXDxR2C/gY9oPfZikMk2OwOojGtmM07H3D3hoID4CqUke3LFYL6mkd2oGBPktExUbECKr0TESK7FeBDArahAikDT1GawEfpfM92IEIqfamyws7exh9ThspfJjiAaQp1wgmv6J2o8yLe8TWVhQnKsQZbexGD4zW7fi4eEbdjknlpqbZLrGCxN0rAKHUBfXlBXcgysl5pjhOsjnLMTHc+hrmE1CRIeYnW1Mbvfe5TylHXai2J2uCj65MyCaQ2lDERdePlR9DLvvxc9E315dbBGf31lBZMzHXRTfF3t/ftXY8gNtSUQpjbw3bQwPWXBhvb58iWxQA3t+/WhBU5/3y8mIlETQoTqIZpo/Hhta2WBOQBS1Lxefv3izLVW0YD0g3C/bI147eZ9DNa1C7binuB0Bl5bqsM4CYNrjcJi6l6Ka72wKCw30AImK1TXsK/LpOkFiXc5CUy7x1guzZZVlA0OzMdVk1AcHm2SyY5nfGzBjOJIYcbPS/PSDXx47397sG2GRuvob9b2MTEdRlylZmxq1OWgh7gozCRG2g7oHBkP9i9Kpya9+3ZMdZHVskG9k2NHQtFqyr6yR/xu7ssXrZzU6DBAZFM49zIB5qCodc1A0Z23xgwrpWQBiLLGZ3OF+bnnC5ZRtS27aFn+ou5xAC9YG6LrqhZTSz1iX0GkiMTpNtaPJ2b3sE8pHwQ7CylFZukxY6bNAQaVa5Z3e11vD1/R4EETWUzTZjC66WUrBgmVnXXoJAhsboyOJ1Llc8EE0UHj3TLFfqgVvfnB0AuJRpN5BgDALViqVqaTIiQJqf7hho0jTD3YKxfQj6Y4cHF+rivCcu6fAt+Fd2gVeGCDyZdzuLertxCoTFm50wOoiEeZyd2BSjG1mC27ponRNyQhwh8FtveH/cVbEBACSOARCpJpjDMHRa38ogddaPge5Ee5HfPgRLvaHWBfeH6nASWIr4DoGmke+7XpxCpMckNCOAwkj0i63iuCpbkX8ueHt9w/71gS57HHNBoErnn2/ae/bbVFB7+nV89rRQHgCcxkbWuCKz17w82YWZJki4fhabmgZ7skkTzt1BmX6BKybP5vUYgT9ElOgHeJo4Yb5ni+oPJj/EDaLk7KRX3Ll158/RMRkah3emQ5MMwISlyEyJcbijP1lg4nced4yPKSHP1jWmJu4wYuL8MIaMnA8ExwF9Uxnp2IwmZGJx4t9X2i8xm+3qIzGxyEDEqe8cqPLfgwrjO6Mh8rC7AfOci8ihlqjHH30eOgZKuLUAQmQOnNCAtLbiAfpzsJhiiCwxActy9Kwcp6fDa0c8HLwBbVXiQUpOdXr2hMMsPvMf2VABYDuU6hz5g8/zl0lypII79/qcBXgQCNOYsjYPGauSjwJmmeJztTGdcZTG99Su65Y8NnoOwMyf9LTYB57wDpJRCZo4PGbjPo/zI7ab303eFHNcxAWNCDAE3TJiZduA3lHrguXlBbyuoFqnMB0d6N0CsTtkb3Y99g6MEc5r4Nn7DiEmB5ryDal8/JZO4/5If3ietzdF6VNRTZUup6Hnts4IOxCzOq2jNfTHjn5/gFoD+TE3H+pBLk4a+ImliAwnqgXy8gpaV0gts45q2CZZAfmYsqw+40SCZ2ewa0pL9+snecnhvXMfH8FZFmRdCdEg9SwbneSr6fJDprZ9Ntd6/vJT+IuxJOfJ/0bGz+lZ7ctkOjItnA1BX9aj7eKOw+wzOXJAOBsh3Q7PZnDd5hpnMn0EVw46yf9nbz9dvIZwbg56zccRX0ychOxNY5xrk8enT48wAz9emQjOpO8nbbgMExzOoQksIy3PK13IgnnSwXHphX0yjUXNNQlsRf9kjq6vsx8BPAQDWOIIs17e5COcTnLq2Whr0pluBFjQR8Qc/h5HfkXUF9Gx+rj1M/FgETGoa+1QvyREZzI3RjVDlewodQEVzXKsRTPgugw8Hu8QSTI4AgeMQZqVQ+ZbMBcMquFo6z+di7opDOYRdAFYMKUzRDr6AGrrKJYJiEVDiERzk7IwUKpuGreu61qqoK4MUMHY1DGfG+J5LecGtNOnjrWgSDr+m2h7+IVExkMaHB1xTLqPZoFXz67VLC6xEgzavz0Pu+RU+tQjQRmuqpNseLLkMn84yac1T7ZD0Kcd+yXKp2bsvSyjgcis07Y8aC9JGc6NGXH5bN9PvcmaPKR/xKVNGkjrceSZrO692r48N5XNdCJmcKmodY0+p1xFyHQJ3jIcnmzQg41zkMnpd5dZ3vZBX8UiRbMeTAopbQE4JgLS8W/QcbMrTrwYPgWiJTQseBh3lQAR1CKiCOAwMUotWJYKXjSA7SU/RGxjpShf11q1zTEw+kNpJTL9imVrS2Sq+6WrfdhF22Og7TNrU+uAWqJKShxxE1TEjlr72tj4A5UjJQcl/8PbcJinAJxGB0RqorukM9M6z448wGU01wd60xhG2C/E9rdeCNjGsBILbpJm/zqv/bxUDIBlSupge7M2JPEHZkA7dOIQO9Xqn4+gJ0p4m7aWnoITJoDKxK8bPDLMF5pBNUl8IiI6f7f/bEwuw738DkcbfrmejcXK4qjO04nN8h6+Bi5fbBPJjvKL1UmKlSnp1ErUPGctGzApwIK8piFNoQ/RjVUh0juaTD+J+IkBzxpWGeWb6WOwL57SqQdJRXmjtR5zz5eL5wu7lmUBD4bXcPXa2LGh5xulyW4kWwG209K+eX+whUOfSJQlpJQoIfGMYZtwMHfmRoRdMmbmUSejd3DU7hXTgb0PjOWmR699zumujnM5zQy/E8FYyMw+IVM+s+69Zze4aU6HGi4AwmBSBa9ReeUjiRojy8sax926H18z821AsLVd63LojQtmKGjaMTFpDToCuB6PDQGayeN99t3SqIfeukZUUcuimT5MdgRQ0KVj7xtau6O3Bx73B3oXrMsNL56yTYzW7NiOHTGotaINxZnfJ/3plfG+v6PtHV1aEJIiQXfeB1HUJfoWRFBFzjPEVOS+DnTc7bBljGeffYDkgNk6Hh0N1VZnYZ2DtOY72e9H1c/wsgxJiRgtTUMstZn7/kAzZIcsnIHcX2i+iTtOuHNjYCqz6dqEaei1cr18QThZ2o4K7TQe8sDFDILOsoHOAWmU+V03bJLxE8FYTDzZCzgETuKbrKDp1O449C32fXaic6r+YScvjTVVHH767hC4lkRmJ3uhZOcrt2k87wUJ4O5bDgoAIXzF5sqkxbmDJo+Eq+OwIxUU7/DB2HfMKMnYi8Uwmm1gXx/Vp+okyalDw4W+5jvix+/miqW3rO9jkJAmudDsn2K+uX1xayqckdlOnmlq+yPI9HqggbSQ2RkIeeD0RKFo52v6efD/CQ+OiXP5HjmN03dRzxD4zDz+rclNzym9nwwAd8Dk6A5mdOkjk+ZAMxcOMjC2hvblK8b7O6R3FALW24rldgNq1aP+GHpKwurDUuuAB2L3BvZMj8MYE+UQUg3mKZ+OWDnR0k+Bix6ausZXX2umK01FRgDGrG3m2Qg44QwerIZmdG0bxuOBcd9Q0+3Vgfx4WD8InfWxd6CZyAJwLeB1Bd7eIMtiTqmEnHanasTFQ0fIjrrqzoEpHU8YPbyeNkFkYpxOeDgO+8SDyVZyx9bbnZsbph1Osl0y72Vi/Fbv9Dynb47Nnj/8/UEPHHwgafzOH8feZnbN/Puj3601vWgBAE4B0+fg+RSSkbEFz37iJ0EbayTnfqcVcNZjfpLpI8w6jR2Dyz4vnP5OcgOeXXvk0ziWzTTnajLpW2xs7GBjNUfedP+U5zogPQbq6RHHEkoimBlYyGNPdpYcv/O19rH23kHD18nkhdN6yLEwHHSdBHoZDUkE7/TinB63arujqGXH/KZ6cyATTfgJlsJsR1Ld6S/wurOFvTzB1FFuIwr0pu/39x9t3n7RVIGXW9CgBjSI62ULuKLwYoHXjsGMTh5Y8uP1OyKwbc743jbsbWCpWkLt9fUVmsWt89n3ARagFg3GUiNsrWk5hwIsa8HevC7gSJlskzY0g8uzSb1W6wwoubyMzTc7Wi+GDz+G2u3orfSOgYHRNjsO7GfPhmYTe0kJwE6TybzAi33NNJvaJWZwgft/mW+S/APsuL0HYFxmBg1IBN+UPhJfumpwfjA+dB7QMcyLzNwl09OPZtQbn8jwS42MjmlmcHtgRLubtWZTtsHMnLR+mOz+jlE0M3a5HVjFx3iWfyI+h4Qzlxfxu3885xqzT7z7EThOCTOIlb/TS7G8BIANmZCCXJj3LZjMZSY9gm6bF601FLJNEmtHj3w3rR9rR55LYT1Sv+/YtgcA4HZ7Qa01nXYzX9+OpjNpLVAtp1GxLKtdmK0DbaNh23ddT/MVhl3OzcyoVLVUgWXb1mKXXCUcHf1LitNOHqwaIrPEBs2Nz7iwGnQqRQMgNtHSZeSpY8HUOZPWOXDXW8NmcRbduNBM08IanRgCtCFxqZqKgIFS+DQ+7duPv+vvtk5W65Yts98QABBZvd8RGfJ5I3aMgW1/mFxXPURMoDJ1CUXpH784nGydDRdjYFmWdHIClvBmZQpGR3v4UX7F176b/HVapsk3bv+yXQJHVWXmbX32y1wuwu76abueyvbL4noXw6dthvHEH1OLGBKR1uqF6xfjHTBAQ+u+a53ggSYDbCdW9t5srazmMVw/2uVwplcPG0YCyxS1OrVtj8Bt1PsF43a7BS9paYwyvyctN9K9NNHQchfeD2PKNS/ZkmWe0xQA0yeqW3qKGxKRboD6RglUXoSGcH2WsuPV/tbNZGEJe0FPAWjssdu6YyBOnmGEqJybIR/A70QwVgDblfYPdELuO03JIE8BQAAAjcgk85qrfqqjN61Z4gJOhqDHMUwt8LzvO74+HpoGvaxYFi3uvdQVry8vuisNwrpocfDHtuGxPfDYNrS2oz9UEEo3Q80ZvACABoDX5QWfbt/h/vgV9u1HvN+/4P39K/b9DqCj8oLXlxe8vryhsGbFzqkymApu6ys+f/cdAC06vm9adL6UF/ylz4D80PGr+4Ze7RB+MtzVwM1H25Khe1CyYTY9OUcYEjeT+mdZOOZMqY8d+KOw1zdmWFbk2O/cSZ2fxXHT5F/47ijnZ7yNFNhhWEDDJSJsLmZIHHd55zwiWEcUNUe7HSUIHIopnMRrguwcnhyPgxNqRqZpq0KAH72bhfdtIyI7jYEo30lWo8xM2/mMjQ2YNyCCppPkgizvorpxN40wx3MOc3oLjl1z0uBHvNKOIo5CMsPMJwquRwQJ3VAFUhB10gGeaO74HmDlvcz4ENF60kM8qG2uWzqO6/Vo4ts+Zr3lM0wh5VwFipHaWKOnNK6gXSsbkL4QOL34cfaJ7zPeJH5HOKN5aK5wZh+kx9L9LafhicbZfnKSw+iGlpIoOviDM/MROA1EH0ehgQ/fDqOTkAtwkltz0cQ0vH4TiMBietzJyAOf3woleeF6gdKS8+FTYPsbIGcEJ6fU383TyHjzdisIXdT42374AvlyB3rHUgrKuqC+vILLYoY4gKHHTVvrGFvD2DbQ1kC7Z4xm/p0lO7LocNn5hGORJ3rJkB2vXJYmr3/IZlEeJQEqFyzrYuLENhzJMuDwTKP+oewduH/F+NUPwNc76r77SL5JK25LeKZRzurydzVBh0DLAnp9wfKzn6OvqwXl3UaZtdvMTX4e4m9IJ/r9x7LmwI6Hz+kgY/PnvmnzPA6XFcfRevDVA3jJx556UxnmIHuO/9ffDvMMvT9Hc7Yx/Lmw5fyyKMz5zQDQsy45b6B+Uy6ISxXNLjmM/ydkmmYCeX09dbT85ngcZC/F84doVcAwyk5jf8LFzJzTlZhHKL3t2LgDTnNNmUJyno8H0pzOjg5sBKOCT5MTCdWfY5gjPjwAqfMbQ7TsSca9iN9rlDJEMv36HMgczoZ9n6UJjpes6fz3fdeLZGrFsq4ovOjt1PbM3AC2NXP8EsIpOy7NxA+n9S+lJvnLANWIYWjlIj2WqEHnkexX3QDb+6whKlaiqBBr2RgRdTaByMAZzABa1A7UWrAMaTwnAMaQ7ru0WsNOBmTo5lsccYdoWYVSgFIsY6mDRkddCJ7uMoTQOvDlDrxTB79T1HN8fwCPDWiN0H61Y2DX49z7jm3f8HjcNXMXiIuTZqbasLqRVvtvDAzRkga9t8Nt7COc7h7yVIbW5DMJffQDNSThZomtoVlOti8gXTDIruU1XRuLl1rygGtsPmGeyOmjR0buZG8rmWbOd/YBIDPT0Xd9vSyCCNAf/dC3Uf/BVwpItwOS07H9Xdjr1duFdqQBMk1C0BMx7AH9akF92PtEkRnbX95we/lOyxik9chw8N8+EIvhvYme9iSrVzztyqxvUiNTAB3ai5InfWZnEkMzzO0otd+GXlCAuHRw+n9MNANIMrBvDeuy4GbH+h/bjm3bMMZAqYTPnz/r/TB94P7+jvvjHY/tAS5asvBnP/sZmBn7vuP9/R37tgMyUGvFuqx4e/sOt2WFX+y77w1fvnzF46HlNVrvWnt0WVALo5aCt89vcZLW/aJ91zq0XQb2x33WRXYaMpnrQShfn9D9DPQ+SzpGEMn5b8ykNi6zjW6XPEEQJQ8iMGt0XGudR8WXanEAAm6AvB3rqO67Xjzll96GLTB006o1PYGs9Zvnv721oAcP9jlflmSbaWyFsa7rzFJelsmnFmxfap0bOzYW1X1e2mRoEtxwf0tJkvkRePPP9ZRDQbHaq6UUPfpeKC7SKjwvIvP6zGLzlD7iwrf79gB6x/1+t+ZnpmgGLX+p67quN7x+WqZMCH/espN7x/3xiHI8o3c0X4e8/nmTcKm4lVWDuMx4+fx2YHPT1pE53nvH4/7VWDfZOAC41Li4a1mWWKusvxUvgm3bY82VDlo8Q+R6V2v1nnWztqM2e2sNvXU00aBxDvgSac1cjeUVlKKXkNUy9VQuodOTHIr62iK43VbMU0yaMayllMz2Y4CMdwbUpxldS51wLeGTu21yqJF/gt+JYCwA8N/YQL94Ps71m8BH03MF8UP5A/y98g+1btNnY49sgMYL5hi64ZkQGA6L65HXowGb+8suRuYtVaYjjPdhBosLn053DPyIjf75Magis8VJ3MnAsHHL0CM6NzfwAg9n1f9tODhlJ1fr17197HN+enD16PTCnwWeG//2M/8SIP94gfzBC0gYfi8siWY8AVZmgoC542Xdsn9O4ZgzKDIP1LDgpzG6IeFT87o1+qWFqs1iE6jx4O2HITrfjnbZnGYCYh6AXWBFHog1gzEp7hgXjpmdmQEIYgbe/NiNZT9yQdG/B4kFQmJ1Q5UyMo25UUfWtxph2saQEbW4mEo4qN+G2a4YEsJNTmvm/DQdGON1y9D7KAvpo27OWUp6NKbE34cBeNYS6aJGSCMQmRHu4zkZ6h58EaXDM0QNL1trASzwJXDDaBpqCI9Af5g8MgXssrCYYTaDyp7dNfET2X9ZUdP8G6d5uCMS2HPH1c2AOBFheLWdlAgYuLxN9KfP+/uGnyd/4GhI5P6faV6hy7zl2eXv+Zkn0RQBkeM3+RIcEb/hVOsZxdgNM/nVLgPUB3hvoPsDBKCsN/C6orzcsHx6BfwIrnRFWO96nFYaSPTCEzJn/pyZRhElybLEBN5Rkh8cLX6SHYYjTPyaH2gtTkoje38EXSJ4X5ggxWlYQhcedeNAl4Z9PCDbA/39Hdh3sG9Ha9RkBmbckEy0mDNCspPjmKjrAn55Ab19wrjd0IY7qTKPUxIAmTh6XvNnGeIBgvM3H8YQaTr2Pq6D1CKKzw5qVuwTyXLQZVCgMdrRD+jwvtcTnHopvXR8HIAfA7f1zTry8NqBmhKTn2ypnNWZEPMUiLXnn4OwJ163r5TmvL4vg8iLVPp65qzgmGmSyuanil4MRMwgKXH/L4ZfiGc2ms2RiW1OflzO5/FEBaETQeqgZwxGTdSgxck/3p4eJ9fu1UeT9LcewafIarVaeKxb1tI7vJ7nmFoqHM1u5b9mhtExQ1VsveJykXCy7QZo481SK2rlWLsmeukNYWZMufPk674sCxYskYXGrHVE5/xmYAFEs+6xMYjf4HxmM79kS3Wq11B3etIM2OCzocfhPWNokpzh0zJbs0pnMJa6wP0PPa48b9lmIsjQDMkIuAjZBSwl6f0GoQrPyHYnNbjf1sBr8FbPYhoNextgumHbG7g0LEJabsUSSbS+4Lu2ycUymBnggb4PDGEQVTB0U8JrB8rYwVa31B3jNpoGpD3QJ8CQBkEDYd6WzS6PibRGLQEjxI1A6xdPizFdwzD5xuW3y/yDEGxp8VXPRZYV0aGOuD7vl8FpMJuqJ+7sSltagHvalHpMDlwWc+JDCiA2ZA7mmyeheKaiJwJIlB1wGzHrpm4Xo/kRdr+wZiZRuJxPG3AmtzXIrMPoAEAdUhbIywqtS6wbtL5BGoIijTnjGT4365YYM3vOZ08U9xD4CRxyGe1WgORmxWrWztNsxGlDmqBHqLkA0JrYYI8XEjCApRbTJcPKEgDruqAWwkDD+/sGJr3npdYbuDC2bcNXuxWeAbx9+oRf/OIXACEuMno8HuhdA6Gfv/uM27oCIMu+3PD1y3sE7scYWNYFy1pxe1k1w7NUvZUegAwNcG2PhwUL7fSrbRKpjKsadAdFgMs3aVymEPRYflzoRmQiwWUWzXrBY9YiDVuA3KrTwKRfQtVM1mbV1VrHvu0W2PsVvEYxBKiL1gZ1nV9Lwbbvc7yewWgyfV1XZCBMWe0s76cN3Cb3TZM+Ugb4EOzbXYNpQ/WVyusgUFDRQCNb9iWTylEP4t7W9WSbHa2h3jpG77Yxo3h8f39Pl+aN8DNm4FjXgb20pOmxWhfcbi/4/LOfhYwApmXdW48sX5fjbdeLuvbH7gt2iAO57cdccFtXVLu/aF4UVoz/RpQH0kvG9AK4R7+HzcRm1JQU2yjMWNYFXPXCuc+vbwcfSTBwvz/QhuoyTxLMyQEehCymi263FZ58IuIZq9NGJyJs247Hox3tTJffxKjLgnW9xaZA6H8LOvfWIATs2457f8B36dZ1tYszrY4vtD+/iBQQiAdsh1103CX4LU68km1cQCKbnUgzY5HlP2B11y1h40PjXuF3JhiLm4A+fXugf1Zw9hrYsWH/yWf/VUJSbQcH61+mvZObk+A3bz2P68/2/L94n78TsIhbUadJHZ1Kv209vF9Xbi4wB6I2mSo0Mzi/gQ+NdZFl3cWnpnhOh1LNsTg7iv4VWfaFK94SY3crzw0jH7g5+DmI5w77adMinHvMIEzOoJwBGJ7PuoYldUIhLkBnpvZE49Hxi7wl8mWZljjZF3I4Anx05g+rRnPO7ghgSKr5e7A/T5g9QuwyJ2PZ+z9zQHQe85rPTQdDnl4bQ5KjhVnD+icE+mHch+fcSJnrl756Hi1RvEP+liCO6U9p9XHAelIEuQ8Uz3r72mYK2R147hRwF31Gg/wf4fcbcJjbsyPxQYxsBhNiHI6BU6MeOfyp7j9yaOBTF+wYuQAAIABJREFUTWMQb4tCjswkJzVEZXQ0qxOL3tXAWVaUdQVbtqatmvYbRe67BlfsH6lHeihB4NiJLg+c+EzX+cRFznzFAa/p+HNqx2l4xuo5AptRcxJp0yDRvAd9gqLE5tQaZG8gz2agQGwa9TT23YhNg52Ozpj0TKWg3m6g1xfI7YZBUxYL7MiaF7ZIDvpPsejZIPOl/9hQs1URpMtgEh4PDQHuqD19EaxF81kAoOm8qHzhQBAdMPcTYA7TOVviIzgO+cyPR57XZvwYpb+cR3XmTUn/zhmhB4k09SQcl0n8GJGc0UvAvOQQqosoHvdMLkEEWCWPx2k3/X6YwyTZzPYUa3fEaVAhYQ7ceS5wYQ+c55Fpx9rO2a/+jM9pyl19gYlApWBonQB71497HjNhgurIg/T6XWRgWRamZ6rImMGmqZPHYS08u8SP37qN5U6lb1pwpFjPTb1sisw2/QSPZv1qPI+A4TJI5/a4P8IRc7wq3bMdIZ7t5c0LzXwtVi+2TJvKHPoZBPZMZj0VFYFhmmd45ma/HvHXu788k43npb2pfb04SeyIugayHtuGUlcQFcDKMugJSr2ERvu0jSyMyCAaXeIm6aBrRZjSCGlNwx6ZeEanY26okyqNuBxsbuBPXTg3K13dJ/tlRluyuaB0DLHTaXN9dH49GYY6J8UjoYhJlVAHWY45DZegnaDqENzumDMK6wV0BKdD61EMn4Ev/eeBcqfBWnLwkeJ0gPM1c42jszrmxCfDM/LmZohLG5cVAthRfaB/euD29nNgWSFNAxaU36MZ7AlfR+R0sW+g/3ABrPPY4QN7P3jO1zDbFhEElvjPccHMKFRQ3E4gCr7LWWfTtkaM2zdzSmGsyxo23r5rlh5Bsz9r0exGD0zuFtTJAVERwfv73eTVQG+7BohKAS86tmVd5mlF8SzM+wyMyvTBqm2+1PVm8lRLEgJ6kZ/PzfnZE7nE8ZkuXLXEyLABuRS1A2Vujrr8d/xo2xrkZGYsnDM1dV3GmCclIwjpSwvNXPbMRybCbZlLLaIlHXYLjhdiu/RK0vuqC3xjBrDgvq8lWbY3yhw3Fwhe4BeQARo0VpnnJ0olcDP6sNqhlikLmbVkMTcyJ2/p2nkgEdAx3KDr6XcSKb9QrOeUMTr54ZmTNLA3rTG6bQ/tk3Ueenxd39WL47RcRq0Vy20JNspJWDLmWux7A0jrRjvShbReeNbBSiNq5zIzqulk/XzKDeeg3nfNBIeWYliWBVN+TVlZSwXq8SSs041/piU9eozHgWhuKLqdsK7rNGuYrYRNjySh3nf4hZ0E3QKdF80BtdpFqsyQ4ht59rToOJvTMJHawVro1fQRtDyZXSqs5QjUVgmXhlQPk0BPYkDizqa8MR7lhzDx9RH8TgRjJ8srgeHH84CdwIHDQgrO6zo/t0dVQVa8vr7NHdXk9DuhuJBMFhUAimLVzqx+5MOfz0N4zoI6GsRqgM80fTf05g7LNBqf5h9jcGNtHqnqJny8T5GB1vdkTACg8zHYZOwbsBHcUgpebi/oo2OTDXtvaI9jZth5eL/bQIcfCu5k2Oef+xT8cBeQ4klgHtOn1FjwVmqb7As9ODaZcvhlIXNJkGkkGxH+8UiNzkBEmoLxRuYOIkTQ7JDRdMBIMviAgxCNQIR97xmSHwbd8rMhFnEyxo6sOnHw/JCvh0AFeTgp0Jfikj7IYeyH8cg08A4u7Mk/9ayFCErDByaHjObzXM/wUfDhN3nvp+G5zafvyZzBKT2RzQH9ZP42A2XPZwkorbN9AN9pDucEH1BS+jA7NOdp5DHp56e196dmhG42Jf7VNHd85ofhhutBp87sjSf6dcOGDvP09pTmPtJFc+hhvJyJfT6a2pwfaFLBgWvnPNOakhncY3TIvmN/v2M8NjWeakG5reDbCq7VXR41mEWAbnX3ut42ija0wDrmemTj6zx8X/8PJ2OfHDZkPlzTJ43qyMgzh+86h6F3+PbYZw6HSu96Edm2gfZm+fxTTvvyTvLI8naOnVO/5AJKoAGUFw3EtnXRjK00sSCfDyb7Lb4PXnMn1+kez+/OgNahoE/gcr4lhx/fsos+HpJNJPO5dftR5v1T+/JnkXFTH2q3WXbNpmN9fVqEcCYObUwqjnfnd8cx5Q0EpTcKBxX+0wjlvHFy6IOSvnQdCYFH8igU2cd6gWhS8E/xSzyT5XIMQj78Pd6V8+yzjMs623QG+VQSTTpPxxt+XFsDId2KO3uN1GrH+o8Omb7pgUV3xtx21aO1Ehc2kRwzc+IiD8d1cnZEBkYXROkFm7gfOxXP7DUS0WGro63HYNPMBHafwwAzwFQxutVgtPH04XVLYWUqgE6kQUzyY7Ups9b4k6noZUm82HFbG5CI1u+E6yyTbgKQl47KG/oAWDxDvkOzipo51QXCxU4e6TjAFiyysg7MBbUoIh6PB5blZrd0s5XGItSiwQE9jQTFsSiOdcwemG2IwHS2MYnsHgPfnLDjtBixaa58xxiUN+w93KxZpwzWzNzhmdtTR/Iky6DVsHxI9KSkyzJSe6d1IHY37fKb2GggAuKkF8WJrGkvaRBoQAAetnlPWnsSALFYvVfL7jMZMC+oc94rRofzUie9XMpkiGeaY/JVPm0BYtTqwZBoNuhe70gZtik7ZXk20sQYvVYCRsOXz78AlRuEfvRejvo65qO+q/eVN6wJTroUm+tzXbP8yC/gpDcIXpLN2X1m3s7NCnY6IYpLrN1e0tqN1he5fTIvuyMi3G56ObZnz7Wm/LNYwK0wRTZs75qpWGrBaiUOAGDfN63/anKZQVhvmvk6a3YqfoYFkNreI5MUUL4utVpgXIPytS4xX2Ce2hAZcZFYDm7J0HkPx9XBvrWNnuIng0yH5BIEhvW6LAhtQ3NDLesKDw5rHWuBlsYwju0dRLnciIB5UbtTBCKkQe1umYtoJl/ncXDfnMvJLesha5UwCuIZhh4DL8xIN75j33cLyLoOMl1gOPD+os4u7FSLE36yy2ITYDnWJ61294+3A6N3gvOsz1tPkPTcp9njm9WZJdKSC8XqEUdAUTRrvhS2TTOK8nnOpKNLqrHt+iDZAiLoWbbynBPBSn+wB5kpSs3MDWNg3+UQ3Pa6q273+ikoJgQeh8xSL8MydI/0S3qayOZaiupL59Goc20ykJmtJrHia1hZDbGMchHL9me37LwGMGv9c/t7DMW9n+oZQ/QkUNToHka73hYQpxhZN1vyHRuwuRJgGyzmd9lJKTY776cu7crwOxGMBTCJrAHj77wg3zZ7DnK6sx1Ge/CrCuNZV7Zg5Rd89/pL/Cd/4z/H/gDQrTQAa6S894593/G4P7A/tnBW9UJVwuunNyvuXVDAuL3eTFjvyvijg4G47dTrawCYxkedRan72PHP/t9/Aoig1hXr+ob7+xc8Hl/Q+wOEDs8ymIaZHUPggsoVr6+v4Mp4fb1hXRf86Q/f44cf7zb2jjbe8f/8yf+N1jfdKSHFhZs1gEbrR9OMA/e3XpdX/OLlDf/GL36J//iv/4f44cfv8Yf9j/BP/uSf4Z//n38CVMbwWkm+Bk5oZru7JzczCHx5k/KWKWDntyfIzsbh2fSd6Xs+XRABeDkBFz72ISMdmxkzi6MK8F98b3MwhFhae36fCVG7MF/IEn2ObnYpQTND+9HZEj9OlDxMqBoUwTwyDtcL2QH8OOMkcOM0Z/7KM07p4ERSUeN/2sLPx6lz9mf+eQ5qZWMnjT79Pn9Mw3I6moGjcLimQhhj1oTyFv0zr+J5Dh7PY/qZwqbBono7yxMELYXxKnPQZ7y4cM7zz5DxcQ5SnAPex0HkZyQUj68dT4vh+O7hbznM7SP4VuZapgHyv/NYk3PumTi579i1TTQ+c55t59WdoORgR9aFWdFhA+ZxuoOenHxKWX06AB/n2cj/eA3FIxYnfjryV84oPq1bHqPPJcm5g7eCvPZ8oGed9pQFk/7J+h8Y+4b2wxf0u8r5Ugvq6w310yuoVk2JgFi2kdJv33agDcjetaZqazFvwTwKmJACIPI8Y3Qf0cvMrDjO7TB1ovlAwm12spDwpY6/GUddSzKAh93uChubo92K8j8eGPd34Ms7+P6IDdJha+bZKbnWvM8/15jLATIGEDeGLyv49oq23tDZj7g5TrKO8/XLf2UsTmGUDePYOkl2tsuNGbhTaT54BNsAc6PO3SohgOI46Elmn9ZanR+3MaaTOPGhRytj0y61FbI8Gfaw584lK4K/DWbdOvvO1skvosxOovPSCMU4efCgi2xQkXkZm+omoxKvyfD7BXg6YR/AUb+NxLuZ5Y2KYix94kuQaN+zLnVWIccFFkqYgfbRfV2TTkQqyyAIuXUQfQf6Rrzj81B+mPTmF8PGEJlQqEzbLqbPaY3cHhILhJTICGTW+orD7mBwx00EZmNr4KNY1o8nHxS7uVmP5pfILGxN22AgjoT6jL3GHNsaQnK5CYpyAkzT7hZ48gSDuGItN5Wzhi9mAUSTEWpdcHt5xdevXyP7tveOdVmiXIQHkj3oqriscMpV25gs279qRpfosWbNRHZ6FGyWnae16zoKaTmDpS6odUUfunJMBVhWfa7PeqbzCGjFUhcIWxafKP+KdGz7jlq0xmUpFY/3H1ErozCwLp/xshaUojQ5REBc0NrQM4VCKGUB08CdNuyWqey3ufc+MFqzI+4I2SFW02t4bWYSrfNppaasIHfowtGHld3QMk869w4NPHd4hvQQPTUEkQjOTIUqoBTcgdEDyLKejIkW163Ga0RsF8bMzOtqNKbZzKwJLpPLUMtqKm7KmhnI4Sg3QTHPmcFMXEClRnARsHsozrxKSNmQOt4ZmODwZ0QEKMDywhY4WFBr0Yt7LIAuY5a6YRooIHz9/Cco5YY2GT4LlRBjH1mdAUlc6N0pI2wxr+IzZY0K0CEyL/F0m2QgfBJxmhfBQrrZUJjRRC/uK9D68lFijRBlUyLbkWA1vjXTzrP6vn79GglRt9sNb29vgAU839/fcb/f8fLygk+fPsWR+n3fcX9/11qzMuy7W7pfptqFXxvev37F4/E4oGipN7y+vlr2bdHNE5droifg3t/vwddR45MBGTMjMGq3ctEatHVRqk7yP2rB9h4+KTmNYMpTpQmdtxg3eODQ//VuF436RpZtEHh91FprHMX3y7aKJXWtdZ1BVuaokasCl9DiAjRN9Gou11Lgz9dyjI629ZgnwY/iS8iiUqsF+/QJz2Yudimb+yvF66pGWTWVPW3fFRc2d994u7/f010tem9D1q3B8zaGyrppwrRgNSPZM5t9s8F1SmtN40i96eaAqJ5qzWWdHa+/3dBaw21dcVtveqy+WDxi0Wz5bG8AGgBthk8tS9CsZnoqpSIeCyG8vLxoANM3JkrB58+f8enTJ/illtu26T/TWZ6Y+P71C3pXfd6HZtgXL81ROMonqAwsKSFx4sI3QJQmUjDEecjWcq0qvf1CPWbG3nrE8nrrSrc0bHOErLZum3KMBC8vL3oxpm2gjNGjlrSf4hhF9UfrO7amJ+yLn9xhzXLmWszuBFgGtPSxlf6AJoz4nKIEyAfwOxGMzca1LmJRYezK3R02txMFcVFGdoGy++1yn6Rh9DuAhtvyio6O/bHhy5cf8f7+RRszA0LrcbIdP7DU6m0Di5pcTQRl21FqxevtBbBCwdlQV6Xg9RZ1t1XMKFUCv+Ht9edY1xt+/vNf4q//+/8R/vAPfx//+J/8X/j++3+G3vphIkQq+NZFb0EtXFCq3pL39csD33//I963O/r4/5h7tyVJcuRK8CgAM3ePyEtVX4fNZsvIiOz8/wfsX6yMDHfI2SWXMxw2q1lVWZkR7mYGQPdBL1Az98ju5b6Ud2dFhLubGS4KheqB6tGKTHJCMZUzvn3+NT6//oh1u0JEQorumMrOIMw5Y6YJ0zyh/YcNH9+9QybCd9uf8N//69/hf/tP/xG//5u/wm9//0v83flv0Ynxcr3hVivW2rD+jyzOjZ5QWtrrm4DTbpb+Ark4/G2zHAEjB9HCM5ktVYkd3DCgxPgZSe8juCUHBlX5JWWLxgzPfgBY7trrJ+oAocNOyY7tF+MmeN+Pem1+flSwB+Nld9XOQR3p/49GEBjpAwAkZQTwDeMvedlp5vE9f6SP+RGoMRAiwU7amTnIzkgdsGvjupZxGSt/fAA3Ckf1bX+i9BmDP9fc8H3L5LlmmBzH77E8H19mjD++5m7MHt0hXPPomV9fX9KGeGdSHSpGzT4e8+sv9uc9Kry2b9P9PY99YzeUrF1DZrumK9q9dnMuF2PAZ4cHHB7kuwKbk6R3OnaYdJz+onl9dO2xjW98916U/Do3Drz/1kepFt1qRds21Ncr+vWG3DvSVDA9PWF+fgZPYoxHQ69vDX3bgAak1j0y1gz/mGr97+j5X/Ty0/Ov6BOPclEAAGkcqjEzyqFxEjGg65eAtm3otxv66w243oC+r6hLOr9WwMDBTb1HrJQa9XwDQFNBnk+gD+/QzmegTMo1RUBWXcJyoOuHWofXcZ3af3fy4oK+12nmUNh/KQB2rOu5694W1/MRYHwTSH8Akvvvys/Ye1MeY+wFZa9eHrxCi6LTo88ZUVWs/x+Ojzl6AjpbtNd9aptxv9mrUPLoC+uL8fkyLJJFUx2JkFKH+2K7sWdtdnf9EbOWWhvRSQKWGOArP6V/FWq8yTw6H4gY73d2BY8DEvb5HKAOCEicEPXaAKCGjB0PSO0r8rc8zUvMJdsXhuXDUEDMZkdt4KYRmGNaye9JyTgv4ziMf+IYbR5B0nvGNCkHKoSnbZpmTGVWPlmNomnCz5mINepkOMPmyEmzu4ItE6xoKCWbzzEHlrpONCPlCy6nd0hZBJlZwOlEhJOCNpIWqQ4cNwfaktr0RIQ5TxpZKs+udRyEio2nYGWtgHKssvLj2XgRyTrugiigkICqJRfkJONTNIU354J5OmkBEfI1kpPJdBLfIEk0laxdkV9iSX8VsHnG5XTCqZxxngo+PCf88j1hLjJqEq9C6F1ASKKC6ZTwb58afvw84fPLhJdU8ErCKZsToVXSVFPdb5mxXm/CjMMdqTXUVsC8ucR1tfVSsnlSeetjLwMzWpfIr95lfZeUx3OIkFLRoBCZz80cagBMkgZeZtL1YEV4ow7S56v53rvxQBuwRMhUBFQ2uQcPsF+dc+H3RZjbvYni9ogtIe1r1zTrWlvwMcYacnAxCdXF6aRFeAwEU8Bh798Y9QOjschcJ7UDapXI5ipFsFI+gewQ1FIi1C4y/ZH84G7QgBjK531jqZMhPJXJe84sI5dzEQ7O/tj38ehCvY5ActaVxecFAC2bJDKkTTDfs7WG0+kEALv9/nSSg5fb7YZ1XTHPsxTt0kjA19dXiTAHMJWCb775BjlLVPb1enXgMueM9+/fSzCURuvVWvH5ekWvzX2PkjPeffxW0s11foiyAD21YVk3vNSG1irqVv0gaZqL82BbEaSUxyGnjbkdBBtXJYZUje/2jnVZwAaCmQ/EHaWM4lgCno00fwPdYjBYb1VT8jlEu45/BELdNlnP4bDVD8LIIghp+GfFDnql7QasWaS4H/Sav6s6F7puBqgoHKhSGLDp3tEdZDQbEBhR0inpmg70Aw4YT7O0xWSf5DqLDu1KT8AI0bXGUVqbcOsGsNuon+Z5cr2QsthUSSkxnp6eRVbYNJJQuKSsILQWIVuWBb0J3cVV15Af0vQOhu5TSn0wn6xolRzKpHzx/lvEqQGsrRvwLWtxWzf89Em4gc/ns2NOgB5WKb88AXj37oz0QYBuAZfl8Ky1JvyxG1Bbw6ZR4rbvGaCfUsL5fMLl8qR+puj+Woc9XzWKvbeKRqLXXl+70ooUyQagjJITpqIArOoq6LPsQLd3BcHXVTSlzkvORcdODn8IohKTYhGdGeu6yiFCF975jo5Wm+65BZfzWYqNKzVRIs0yKScw2Nfro9fPAozdv1SZBCJHGh/5X7aI5XdJ8RDH5ADUQDa72/UVBKAuG7ZlwVqXB6BG2KA19L1xw1JX1N4wTyes2yYOcRrVcD3SSE+35cp9inTnDq6MPGVM0wm9MT79+Al//3f/J3748U9YbjcxvMoMcMc0zcilKF8Go20NrBMuSmeB8Thxr0DvUrWWCOjAPJ1xnp8AZizbVdLB1PvLSJgA/Mf/8Ds8/eId8jcnlPczbl++x3J9wcobvv34jKenE/q2YltuKARZkPOM58sFaTrjX9sX3L5b0atGTQy6Px8XG07QcI5d5ew8hb2zRYe/x62C02g/icP7MnfmKPndVLOStktSndQo6GGmyIwpi641h3H/2jk+3teQJEvWWhqSYE6Mt/vYU5Oc0Xay+zA88G88X6GcIYjWBRzH867ttq99pV/HCKTjd2I/yBxXe7bevx/+HtcxEhK6zoOBpIwB0gDsPJjmzPrtrA1kxjFczhxIJRp9jMMEeEQ398MIBCLNR32X67UH+tx7UDTCI0O2d9FcPoZjjXBYE/tIaLtdjGCj8O/wvDu5Cq0yvck6toe5tG/GLhEdvyGyjjAOD63r/ZPDvca6lOttDEbb79uMMBBff+3nS1ek0U6Md2KDAA6R+zasdoG2ya6Vv4YsOhBN9i+Ac9oBKwrnb6qn5t/vkKJVsOIFDbys4G1FWzfUZQHXimmaUOYZeZqBrFERNmad0WpFV8Mw1QreNnDdBATQfcr9LRx0wB4pH8Z21AlhZA8a2t896sbjy6Jqx6GarvUu3IaoBOqTpPtoxWQvGCfIrabfruB1BW8bKBx6mRHvI04ytq0qZ5lV6lXOP/mOOsAd4JRB0wn09Ax6egKmSRxhaA1yBcEIDLBybo1FetdrS1cagNjos8kdYawN25b2YxzTxxR44Bp0m+004xgpVgonddAUBfB0NrneojXMeRdKnSQpPwBYuLNghTTCUGuUiR/2pBBpy1A5Oh4ORmoVCNjpo0KaiW5RwOrUVPtUXo1GFGpKCRV22CA2kEVVejO0f4wu2T0sdkPSyMqxK3WVibGXGXgmqY8qhibntg+zXLsvamXAOO3sCgJ71J7cfxQ8s3GKUXQ2BjuhsDVGQX5kKt2xHs4oHKSJ8iXgpc2d8u1ZB7VPdnCT3OkHLBWfEimoOvYiczbdEe+s8y/PKWWSoilpAkiiaCQ6ZVKOQELdVrS6iF3LDbVuItkqp0nlimCAlEQZml6xvX/odHNAswJ3VuQn3kfeap0hOe2QCsxauIu7RGs6QJYSzqcLTqdnzNMZpZyCBeNTPnhDmf0+3St8qzqzta3jPbhipQ8GPlrEY04B+Aa5CJLZ4P6+cXBnJBg4T2Dq4ofMBWUS4KFWoBAwFcKkfI+12j4m0dxTJpymhO1U0MFY1hVTzmCNHEWQBAYhlxlCWdlRe0duCWiqRRmuS4U31egMBi+mnB2K89w1OnYXWQ89aMOe4iafSrABoYD5WH8iR4PawK41MDYWp0vJOP9CCjXJeBgtge3lTYNzTA93o8tQ/Rz1pmdWQLgxcy4o6o1btNekb+y35eRzTqRr3aJe9bs7P0sPU2AAKjOgMjZNMy6nM+b5hBr3y90Ii15zL4bG/ELHjwOAO/ppP7WqfGdwUg2XVH96W8NeQPBgKFkHyjuse0xrTdbqzi8QQ8oLR2pkvAE9FnkJojsgtWq2UAkFhixKz7JpprKnIGi14nVZXCeTRkIWTZu34kpbrQ6WCWCnFBxEyLlgms9Iz+OQLWWDmeFy02p3/S+HjRYJajzFQ/7igaPv956Bo3fVtHk7tBIR6Z5+XaZJ7mEHDLZ/R52SKdjqGiHf5936urPVSSdX324GZmlxIytcZ2Cv7VspZS+wZ8X2Ell2CTmfZykzpmnsgba8Og9uazn0tEPfPaBsJ7ObPdvGjAaIax2xQ5CcBORkZkALutlh/wBjDZCVvbApSN4UQ3IA2tLi9T+9dQXbk/LJSmQol7G2hrxLQTgPPAOBksqD0v/YEHTufrAnMgCnu7C2AFD5nHdApBX9qj2m8I7imkR6Xc4AMrgw5lkmorauhdaMpsDoh+S6dV0Ar+0ktC+jABrhdJpVX+s1zJDzCnabx2gGADh4PGSy+/oFGDxr5k6wi5quZ7GbRH83SFE/O+wESVaxRKifkLPwr4uu1yjarY590+ktyPXyW6+fDxgbPLuDfh7viZXsAE38rxfk8dvZSRID6FhuV5QyodYVW9X0/TTuECAz2KIS/nrh4WitIZcCrrLAEiU/IRkpUECDkqDTWFwGfnRmUBfFv9QV1+sXvLx8Rt1uaF2qD5bpBOodeSpAIrQuKVtVU7/yNKHV5n8rDAwRSquQy3KCOp8l9LqukBQ6aVBKhAnAb/7qV/j4179A/sUFbWn4cXvB1Dds1NH6jJIy1uWGbVlwmc4AdaQ5Y7484fL+W6ztO3x//QHrlw190xnYZy6PVzQoXDmqqcz7KI4x+VEIRppOHN+j/MTIhOPr+NYdE8Lh25TYaj/ga4vI7x0fmsgX+nA9hzPKREg8jBp5D25gyN51NO6PEVi2YQzDSx8un9I+gva4P7JpwsPLNkN34r8Cgr35ick/Ywc6j3sN1zNeY5Fvw9Q73vfB70R3DfHxcKd1XDQc3/39DNCwscauvf+el0XiWTODMXB8mRXhf0SFaHIUxsUddcZxUMawULBMxojbcNm6u29H+JPMYD6ORXzug8E/fuTrmzBOFcysp313d8s+zmF0aOjhHPolu8bc94sx+nW8x25E31gfNre7G5sRd1i3sp7Jtq/xQO/2cKiZO7hVtGUBX2/gbRNwdatAl+imlLOCOSOSGGYA1g3cKrhXyciomwC7qv+9N74M7ylijhK/G6cH3x/D9GAiHn33jSdZBVhuFaV1C1FSw1gm1Tl0a0VfF/C6CXiia5q1MUNUeBjWuzbY2rCb2spJQJqA6QQ6X4D5JOCsOSNRd9gD39QRexngYJjb/1zaXE/4cV64A41nRBmuW4+gAAAgAElEQVTmsd8dsxIkGpQ9xRywoiFiJ9irh8MoS+yAFmYCSbRGt6rn2PNXMoDUD7t0iEKWlid4oUafF95RYbA729bVUWDDfwY+RddrOrR2T1GF5Dq327hoY5PLATuNxX7c4vAyRnEcBb6SFezSOgLuzI7rLILMALUYAUmK+BFI06uTy5xRMfihsYGxEKe6ch02DuNgvJApNIgjE55ts0BdM3cMdEnIZRogFoKDFHRbyiOHJGm/rUp2ygWeh2y2jEeYjMg8V99EKHnCPE0AFTBlT9sjEueLQfJ7yhId2yu6ElEJoAmkZGOlTpJXQh7t2G99rNFOBUR5zxFo86bjaiCpAZ+dioPJIMCKzKSUcJpPOJ3eYZrOKGV22o/RX22zgYoq160qx58WD2XfI1QdOdAqfSk07DkrcigRc2lEzLnMSgaJ8MDKXgGSrDgiSYcuU8bpPOF8mnCaMqYEiZwlwpSAeRK1m2BtF3GbC/B00kjZibAtExKfUBJhq+KrkKY+d2ZgknnrYOTe0VoCtWQbls7TiI4CkR8GGBWBARtyYNPQenWdayBEc+B0X3TI5sAAHN+tO3uQAIGQSx4AFiSSNzK3JOPvtQMIW8Mka5ehQGwbyf6StSBy6uqWrdwMYPpYdIYWsnMASiKzpknc88ETapcOndabrGvbCxgGGthXB+eyjGVF5Q3oG2pfAK4OwHioaTDPoq2olMYBRLWvKWCDfWQ4YhZWXBS++91ZGqN/gZZkzGWgB7L2YX+Y6XVXgu/SI/BVimQbBb7SaZq8NowVvGvmh2QDV+H36k04K6F6ImeL6jQqwu6yOQpfSSsTiU4tOSMp+JtIdC+I9SBSAMrexV/w6EuNzLQ9SY4Wh7XQDSSj0X8ZJrMRZJy68J4gcYwWDGn4bdTqIF2TkcfTAC3zDZgsME0PqlT52t469phBtYNW9V4d3LVCPViCc7QfDpQ22vmkBsZSMjvYrWifR3l0Ur1HbkJ5oWQDEXlkx9p7YhNpGj8G1ZXIVVLxZKV10WyYRAMshtgGmYVyx+lHOoM0Ctn8XB97E2tdc60KrZgc0mg2TTAXE0lmF5vP4H6S6sKcnPOY0aXAlILuskk2eFa49osSgawoAhHKVFCSHE5wGxyvR3vJxlE+0j1Hx70ksW0KJIPCjmVZOVutcFw3nWvrmxkeCMdCVSZyNfpo69uDmAKdlO37Zit2f591/6ZxEOrKxOTIxGFkAUSX1Q6AjTLE5IEhe0VrMt47qGPvlD58/XzA2PCKxgWrFPoJUNjOPK21izHn15kRqtwV1DvW6ytOH98DU0LvGVwZQPW7xRM9EyrOkJMbPRmsdUWmBO7hJNWdQF1UKqzWRo/yU6NLFIYZixW1LkDfkEmKBZzPJ+SUsW4LXq+v+OGnT1iWG+Zpwul0QfWok6GEo0M2DAWJjgUYy3rDul1hPHEpE86ccPrdBR9//y1O5wv+r//6t0h1xcenC/B8wb/98CNutwWswPOvf/Ub/PjTTzg/Fbz78C2++cVvUfuMrd7w0790LN9ViaZRwnl2yxJDEY7p8bHez7kuhhi6dXhR/EnB8AXBo2sOl/oChSpmqxpoX9xVSFYZgPk7pHKoJ65hYzYAwoq/+ImeKaxEe+UQPo9OyvDlye9pjx7zS6E9w9DfQSO7fofUDgzuGTcWu5UoIzBbipkZAvLPjTREQ2j8vXsahXUE4XqKEEiAMA7XK2AZjLWvg+SPX0SBzJ+CmRd+MZmxfo4IJuz7hjFmx8hA+9x83z+jX61LEOOij7+9k+P59xG24xXbZw7/sf8DALGZtZ7bkxDWRlwnFs1NvqnGrAGKso2vy0I8Qaa7WT+EzgOuI0JT3OAIN73r71tPAHR8jm9zHAcb84e39X7cz7v+DJu2vrG7DrvvRfB/p70AaKSlWNLCkdoqeF3RPn8BbqsrzmwqBeYUiKEFX9/i5NdtQ2pNjL62otdNHJswHqbjPNpg10kKv9J+DKIexXHeaXd5cJnGHIU2uGyS6TCN6uwdaATJb22g1uDE/Ar8ce9o64b2cgWvK0hTqH06/cE82qkGWKuSqsnUkeZJv2N7NIFQwGUGnc7A6QzkOdgVPHSFAQocBY3iw/1dj1QMjmGUcV9fOoAjvlXv+eAAx7Nx+pCsuBbinudGb7ANDNjctdN/UR2apLgSkWTdUKHdvU22DTwy0DQCvAYA+vOU59npYmjvlpNOoPFRCsiQvG8GBIoKtag2yR7KRZwh63NsB5gHv6QaJBRTxlyZ6/5MCqJ65Ky0SzL0Bj+eRbs4T7kCtw5YJgGvzGE30ATAjtbJo6zsgK0PZxewSuFx/EdsmtgegPNqKz9f1DMpkUeEgwRILeUEo0GQ/cCi7sgBItJ5BXeUJO6CFzLJkkprEcMMoHt6NI1x2ulRgtF3dRwLe4heAxIozQAKOhrKfPK+OqgdgGNxiPbPMNkEyxOlAA+5bTAwHXY5s21Z2p6RJkmlhaWC0wAkREwTWhMuUWD1fd6icQwQ5x5tIwM2ZlCRatbNBZ0d+MgaFWX2pekxgqRRRs7p3jtGJWnWjK7s0VuUk6fbTyXj+WnG09MTLqcJlznj+UQ4F8a7M+M0A3Mh1MrYMvt5GAOgM3A5ZbResDZG4Y7X2xnLWrHUFVvtqOsqwSO1olEPByWM3iYQX1yHmn3qhwdJ912LDLZV17um8gsYK86vAAtbrWM96XiQpqSyAXqsPJEuGVHfkHARJuGVRLJDiSQUAl0KxRwP0Y3PMumhaG0NCYPOxCvGa3sSWQGeoaWbRju6jaUy25pEeNXWQlbF0GfHbK4CBXKjnATfhroezvWGpV3x+fYdtuWK9voFy/d/ArdNdDxhHDDB9k3s7WNdH6pCx4pOpIepJOeZJByMtqcZZUxKAHeSCEi4RvPITNcjzGi1jSrzlJDzJBkwZAfRe91imQCW4m8p2JYCT0S4KSds0WjX8/kMQCLz1lV00TzPeHp+ctq2uq54fX11n+jpfMHHj994ZGKtFesqfLHy+yqczaYnp1n5KUe9kdbke7dbG7yt3EHKwz1NEl1YSnZuVk+p13kqeVCmWOTlPJ10nmQgu3mQplsoeXStT6jLl6yp220ZoB3GYYDxu5p/GAN2DNwGBNw22cg5KU91GutcFgim0+TRyCYL3M3nkkyNqvyfQPBNu9HmsAO1ndkD1PzFCdOcff5tvcvhT8aUy84WCpLvY2MF3uz5rQldQK0rlmWMi9kMIKDk4tGzTmOSEkrJSGnCPJ8EV7EoX9Xz3j8AtW5Yl1VleBvAqvmkgHIgj3ZJxGvGPE+Y8oTL+eKZTMSSud3BbocajYBwv1bUKqNgz5H5y7q+9TAjJZwv553ftG2b2s8CZrc2DuSZGVvdhmNAAmRO04x50gPY3pGL0B3JjUVq13XFtq7Y1s0P1nc+O4BUZH7LVAR7InIbzKKSWe2LbdtERyAeEKhlkRJO59n9B9a+JIsuVJnMSFqki1HXDUu7wYqfTWXCNBdcTlK7AwwHxc3OedvD/zmBsTv0JCwINZhg3GW7a8wZYt+MYA4B7ERSaAa+//Q9TpdvkFCEbwxy0jTCsPUWHJyS0J7eG15fF5xPJ72eQMpb5umfMJnTLT8u8mCU5pzx/PyMy+WML18+Y11+wrpe8Xq94V//dMVtXTQdQ0iVP374iDlPSKmo4c22Q+rGbMZIcn9CdsuMks74+PwtvrwAta/oTw38y4rPAP7LP/w3fP/6Cb/79S/x218WfPdH4LqtaI0xzULJcH39gvl0xre//i2++d0fcDq9A4hQtwXvn2f84be/xncT4U/vv8eVO/DPGdSSLqm3Xnsn0MbL/6JBbh5BoSEOASjRgXenVA/e/WO3GEaacYQfHi0OBjQiaN8yhnKX8Rjv2IZxg+Mbw+H2Puw+k5aYCz6AjgAwH8Zo117v4ttLPQJIvl/Zppqw28QeR0Ien6mtpX2rwiyFYflKu8I3YmTq1567u5rCJqofpWBsjwv1ChpubGzZeO74LKsjZpcfoG8XsgOcNXTS4asRxPj/+orAY5Tvt+ec9+DvnTzGNfK4VbvT9Qcg3SP5uHO8rd/uAZt1v2vqeLruhl9foaHx/47XX3Jl7HsEZo99PgLR+7//gqcbsLpcQa838LqhrxWoVcj79BnuwC3KYU4ZPFVQKZr62oC1Ilc9de9ykJjdkIQbGdaORHYodD8ib6/8qJ8eXXFYC1+7k+s4NaxipG9vQN2ATEBipCQyUZcFdVmwvV7RrtfAszWcxeMcmVGYKEG2bh4tZXgFcqYEOp0wv38PPD2BTycg6heEKBxWbbBTqMdR4p3ezRbRZjovGIMAHGCx6z0aKq5fQoieAWLROt24Dm2woc5DT/GYv6yO0I4Cx/6nSkKK2Ew4z6NAU2fT/SMZH2qQZ7I0ruIRX3EP3Wr1sXGzmvd6xX1/s/Es8kTbk5OknIMVeNW0vp0t5GuYfN+2yGRJS50GnZA/c/Tboy2t7dwdIDOZ6J2RjFIBEv3BoS8SvVh293FdbtymvQf+YtqDfmTp9THbxSZR5YQSpumk3IQ2xwO4tIJQ8UyGmYQ7UMFTs6t8T6WElIq/z8RS7dsiU3jss426c7r2NCJshW5FwXcDtuLGAwPVGsxjlL4LEDkx0PM4ALfR670DechIjFzyvca6A3H+kIpH1xhgF87g3QG1ooY5CT/rLkrV6VKsKQZgj+klKh5BKc+2tFoCZUJvbaQAKwNtA8OKzlnkV9ZIO4m2mkFaDKoYp2KyNukBj0bJZo3akeI1s1RKJ4mhO58Sni8J336Y8FQS5gJMxSJeCc8nwpTlvq0yWKtMsJ4afH4F1grUDjQicD3j5Ua4rcCtdizrirosWNdVftfIUKkoX4G8aQTRfv5HNFQsbhfG2lWErW1dgW63DMBSJt4KE4/IvxgoYbKoX8a2rQ6A+0GZXtu6FF3Z6uaZGy7/OXsUuFUZH1HjwudpMsbMaHXz50Yt7TyULJ0zuy1hXyjWQBuQ2d/yWvsoCkMYoOT4Jx+8Ll/wz//83/D3/8f/jvXzj+DrK3B9RfvyA5jXnWhbG6N97LrD/BG9L0nOPHImB4vYHWrrv64fW59EPp6217guVnumbhXn5ycBZrYNjSuMXkECEuQg0NKkc0ooyg9rKdWn0wmlFPTWsNxu6K3h3fOzUKWAcLvesG4bpqngpHyhJWcsy4rXTYp0C9gy4XSaBVhMCVctAmb/UjKu1xOen997MUMDvaw4kQEzzHCZK+WEy/kZEsSuEbMloTV2cNJtmCQg97auuPUBUrpM856+oOieYIClpMfnsZdqGriDTbng+fnZ+cJBGGn2qmsMbI42oIF1YJY07d6VfkUEqdWOjavbSlagyQ8WSSL2Ta8BRic1sjxytqJ45D4NeVQulEpmtHNbm0YqjoKHDhKqJMthSPJ2Wb9Gejn02UVBxKK8xOz9JiLVEwOsjpHXzYtVSc+22rBtqx9AiAxMrn8s2vp8edJDVHmvhZoIrZocWaHMDYCshetVCtEZCOxWlvrspRTkUjDNE+Z5ct2YkhTWvC2LpvD3cR0Lp/W6rvj85bMWZJN9eqsbzqezHHhqNsY8zW7Pml7urPp0q2jrClbAGgzcXjfZt4oVpiuYzhfwPCuYGwDrzqitYllXcOtYq+w5RfdVIglyOZ+lYB4p3cs0TUOfkXB+19qwVSmetlxvY1/QtcEqVykRpqkovcMA5609vhIYQBdKkqrgN9Hg8v6a9/mzAGPtxHi8zImHG/z6xbuXuQIeJ8oD1KFEyi/VsW0LhHsIQsDbqp4aGOQmit05izoPA1kVRkrCA5PITjXYieOjg2qKEG40j9+JxPkT8vCMH9YFP/70J6zrK1rbQCnhfJ5RphNKmTGXIn1kcywkhcEm9QgueTQAyUlroiKFy84rXp4a+km5WQB8vn0G/alhWX7C737xDSgXoHZ0NKnWTYT09ARKGV9eXvHrj7/Gl9dXrOsN6/ULvvvj/8Ty+hl1eUUBY0oA/6qjf2L0F4ms6QQ3giTCIsCLO0eS1YlJw5DfAZ+68/NQ4gZfsg1ElKgQjXOH+2AsCTeudtdi4ENmO4R/8VnREOcgA3sZ1Z9kaYrm2Fuaic4r2HkMd3exMfDvBkNp+B7uBMqr+xXj+2O8ZX3IHwPofnxy4w7yg89GH2k3DqPp+zsex2cHeOHt70ZQfYwH1DAdKSUuW/edGPOYhhGwe0Xr056F0X87+XSbP3h9rAgpYRgKIqe7W+0BB9dXj/o83iVAOJn9rceAy/0ryOlhbsQ4di2C41OjMT9euloeHDbgcJ0fPDwAMjV+GaYbvW3xQCDI6t1nA28Y6yF87gcz3kQK/z3ezzyKMS4PlvBONrgfvxNGMQJzzhM7nh9nrnH3dPt+fQWuq6TcNw4HfGZI6bNrQ+NV1hURYM42swCYXVKKuHVx8DmMZlgr4xCD7qSp73SuzeHoQJQRHPSC9fh48BD1pN+Kx4pF2McIkOhVPRFPvQNJok/qsqCuK9ptkT7a/awtD4DR4cyokxvSOEEMpgxQQc8T0vMZ9HwGnSb0wQShgwdvqzkekvYfjh0VAEPQLww4T685nvvDjRExHtedtbl3hkWUguEpcSNe9Chz0LT+5PaAR3GZfoqAWJhDB74YIEhaZwIpsJC1+AQhVvi28WdmKXigKZhJI1Ci8wcAOVXU3oKByp5dArXb3F7SPS3eYweAsaSG5TQ5DQCERdLHE2BQE0AqadRWyhMSQdOcNdokkRaRUv7KkLrpYxUOvwH29LQxj0nP74LF4G0mL/AT78sZ+75RUp5KBYTNuYZ9rnUVAC9ckcsMouxzJ467RPvlXKxHITUQyjMZnf0oxgmJtOgUALCl6HKIXpK1YGnkZj/bXm7glET/E5CsqnR4DsSpM95gA4+skOejwpHGLSvjaMWTxpBaFJ4/IYlTn3N2GUsG7iPoLAfboGM36TqQyyybaNjyWjxKZXcUsBrzZHrWfkrRMGkXAeBuhwza4ixrLdu+aPqWR/SaAPgUti2ZI6tkP6hUtHCac2cC60p4fWHQ1FEnoSVYM6OtjLYSitRm8YI7ZlUxCJudEbIUHJM2y6cS5dmkYJtGtFU1Miy1WwpHtZH6yXIQOWwSRrEIKdMHLPuC6NiR7usAy/AARO6c62vofaNxc3OtWyBBGuDNtjqgDbK08bGOkwKOcb9LSWSbNcKs80hXtkaMdT34g2HyEOzLTGIrij8wwCEDk60/YlOazk1Kpd5dhgGyRBIYqFQIaMRAr1i//ITrH/8n+PYJWK/gdRG7gQCjY7F1NF50+FvbmWzflpRiAkBMHnkHWysk+t0AWiL5XtOIbutTt6xPAripDvGiaApOmyY8+AuJpJI9eESXn5XPUwr1QIslPaHViuvtpqBvx/k0e5Rhq1Lgu1bxxS/nsxxo6JpflgXLusiemDPKVHA6nV3XCvDS8OXLF9SqVILuu8shy/l8wTRltzVlPQtIJ3O5gbUw0G6vMXtHAVSTIaNIsLlyH4SFO9O4MT0bk7vS9Aitod1fxH1T36C7vdGDLBrIGPlODUS0/SBREooN37dM5lUgDBTMRsOh0a69BZ8K7h95bRyGH9y5rk0jSM9sv3iQCZWLrJQfdnBj62sAhbqvhSym2it4s4OOYQDTYU8aBx4yH1KEbdJ2WF/gMkAgwaMao3U56EmkMZgG3Pdhp4vdzt4vy3IZfTXgOO/aw4BSlLGD61aPoreGl5cN8zS5HI1M8652V0KxcdPvTPPsesg47UsVjEp0cgfzqnJ6oLbQdp3PZ7WdpV/bVp0qxmh3JBiRfd22FvmwGFOZRjFUAp75CU0Lfhm/stx789mr3Q6DFIfzsQPyPLltK09g1yVVD9HWdQUgRb9szG1csvaPdb+yNeGcweCx77zx+lmAsXcvNhPg8CaA/a5gSofUaBqAi39TizutdUFtKzIJEbCfmOq9zeyIFfJswswi82IKqqSSn6jwrl0UhAbATumSTkwmTc3mjm25ofeKnAjz6YRpekKZLpJiBDgJM4tmcs5adzYO8ytCLtxRgDpH7zPSOXmRGADY+orPrw29LjjnjA+XJ+RSxMDojHVdcD7NSDljub7ix+//hGVZ0eoK3q7g9Yq2SDRX7h3vzif0Cdh6R9XUxvYKrTwtDetsjtIYoqhMSedrRDzDnQsppMG4I6Yd/vy9mPj7OodQWbkftt34gcY2IrcfzlUEYg5Y4/29zODaNfYt2Yb3199zBI4habQ2YPGkej+G2nwcB4PtfoEAZQCxx+ftW/34LW+sbeX+bMI+cpLDfyNY+lb07Q4EtI2TfBrdAdr1TzetR1PiY0U+fLAonzfnwjoThXTXaziHZWwJMR3kYu/ovvWo44cRGDSZPEZfxtkfIGiUXL/60IYHvQ6Owp9/7XXe8UUP22oO0uE+JBJh0VUE05l/STtwnJ5Dz752j7CmsZdRa+teDt+6Pn5Mu9/sl8M76gDKCXG/3cC3BdiqpOKzyhCOsqypigwwVlDJogUsYkZT+1l/woyPu/uM9ppBJM17EFF+6G28eAcF2jiF9+M1X5sFVt3GppgB9NpQlxWpC2BNkFTCto4CZXZn7wfGs4/HMSM6G2MfCPNCWrQrnU+geQLKSEfmsFlQmFTbxdpBToMm9Dncg68UfkZgNoCxvnEl2fMoHvhADecHYKy+R2mAsYSRzu8ggI0zs3KXS8MH+CVtKHnyCC0HuZL0jHrX4i3qGCcZIOHDKwqg5mC42uE2QVhjjX9WnCvfKVP2/T+Cej4ucbZ1LlOK0aMWRQEYeEKk9loAygzcsecacGzvdDZ+PvK5NIPCNAalAAqQAGl+cGyjSCFilUijf/Q7+n4sQBRBPJHNFPo9oi7j/aXAwV7GJOInwbg3Wx98nja+XmDG9w2zbzpIgw7MZkJT2i4OK805gkexMOjMGVhlR7xpJ+suZqEvlj571CBxLySfI3JnKisIFwGuwEqsTmakqZChDgcPBE0r11F1GQlNJSNCspGHz2H8/pg7Dj0L+sfky77DY86jLLh1wtD1L/UrkveBXLbBpMBkR+IE1jUmQJhU5mZO6F34XRcwOhN6lm0iK2AmNBxSvC+TRd7pfmV8giw9KgkoGSiZkLM4pI2kzd38FQU5jDakGwcmsxRsVICbWWlcBtymNsSQAZkzCvca/oEVfcLuYF6fjxCR6fIJ8Sc01bz1jq50dFBAzeWJCImTP0t0uoytjI/IROeuNVbli51NJer82j6NYVscQVmyPkWLJLTb+TphHJWiE7zPfjm5enGNycK13q6vwPoCUoo82WP2toyJNoC9S+DvuzZ0m44Y8CI6rPsP2MdMwPJh1SRfX48PUW2e7JFW8T7qTgepFBiOUcEARsSyRW4C4/CNlKIiWyam0aTAU9uN/7L35t8BgGmenEqEoDKkEZAiywamJY9sZMbgq0zJ68/ItV0j8AwQHzu7Ad1GJScgF4X9bm83HG0Neb6s/2R6nhF0ahxpOyhJLnfcIo3M+Hn0bZ1/1jR+AOT9UJQwDiRpHFYgERBwT/MHmDF4XiFmLXQsWuu+vzPgh4RxzuthfIxagvx9pTwiBicC+oh67NzRdz7moKL0wyTVb35AnhKqyv44mIHoEAVMk9oiqcALo/oBqwKFQr8wDgdjJL+Y9g0p5RFpb2vQ5CtE+4rM6MGGFa0NUa+7oAtgHPT6fMP7JvscvL1EJlujDab7o5yM9S0/LVsEoQ2ugmg8e8yTrXcFzFUH2fxH1UVEXkSUoUFMqls9SKgzGjeABsVPZ3ZQlcK9DFj14Ahm3+NM/cZI6D0NiFltGJR0b7x+FmDsvePUXWHrO7Ydh2vkfYdR2Ywgc+rM6Wc0NCz1hmW94jJL1cN1g066LjOtKtt7CwLex31dwY/FKu3QzYZ5nASZsbpz4KRlIkManQCtpJkK5qngdJpwPj8h0wVMSU+b1zEKvWtVUUu3G06BjySRbg4NXVSR9PNXDXkr4NZRw2JZtdL2D58+4d35ouluEz6/fMGPnz7h93/9VzifT/j++x/x//z3v0WZJswl4VSA53NBXQjL2pFbw8fzGUwZS1mxfljR0bH9E7A2QmVCB2FhOf1ysySuJI5KB74oTZHb9h8lg8jkYmzs9tMMOdeH9jHdmR3hkQejRDSWv3cPEA2FYj8fgUhyh6FQrbBKNBxiH0TuWA1f2t0nPnqAr1GxjZ5EYwbBMHLhP7Zy1/V939zA260+3uHFw2H2njxqufy1twbU0O7uZBzbN0Ql3n8YZfadO3oJ27DDOvTxc4vz/nl68RhDop1h6oGP2M9hHPcIjps++trL5GfI03h2lOW3Jdgbu38U73/ZaVc+bB5BNPbyfC9R+0fKe9FQs3vcv3bKcXe7PzdOvhxdlg+tGTvp7qI4ljaeEUYfonX/bJMu6ctIN2czbOM3H+gX1vYQRG5aq+g3AWL77QYsa+CEDkauq8bg+HEDbYy+JpScQDnLSqwWuqQFJtqRcCe0MqyXOEaPXuYkkvYBgJ6043Do8IZM7h/ixvP+sXu5qrWKc7ttsGiTViXNzXgdYw8e6ougk/1j5lEA1IoZEYFyxnS5oJwvQCkD4Abti3btequAQRrPE9B3/9w9+Iq9roj60n73KvDydyJG94PIMUZh8PxdBjkXqRvO9r8YgQsILYMZQPpPIk2kXVmLKmXK7khwF4M1EQsQS8MKAwScseJC5FGLBLBFdCZwyigg9MQ+JxYdCEgbos7IOXvEigkc81hn5mRlGgV2oMa88XuZUW1jZ0U7JK1bUs+SVuC1gwEDoIdjv3f04+EXQ5y3UqYwp2OevTfkA60OhhX8GHQ4gPmxslIEdLGo1w7uBjSr7HYgNSClAfrmLI5a4+YVqqF2sdmrXbeIQUFpzqoBYR1CxSXj0tUpNvBDIuCaDqbtTzaPcU9UJw0dFCK2+SC7wyaJMfLxgMiiwIqmeCqFA01SaExBaqMCsJdEvLLyH1DVyEEAACAASURBVAd7Q20He7qndOoe0LXIzF7X2DWmybpywgrP6ABiVT6CM64jJI4/yH2PoROHLvBd7WCOmi1jbbT9yMDHzh0NOtaslCFJKUOUExU5SaHhLmpuUjlsXfqZknDIpqTeDgO1MQyrJhJbfiqEeSY0kjrYzDNa3YCtevFZwhhiky1VGmhMmn6rtj0RBF+JFhyDFOg3/kUfT7JoJJXxLsVqAAPDRBezAml2D5tDDrJhojcAXNPn6gseopoIyaOzLEKQ0c1Elm+YDaYynSJwepD/MbcGWNkh46CBkaIxU3iGypNF4EHsCpMfAzQiT6Q3pzUZ1yQAvYEVJnaho8NU84ZC9QhrYJLMc6SVizZMBK3iVp8d4ID2Lw3gjeAHR4kJneCHZZYBYc+SyunKnZwG4GbR05fLxfXB9XoFM+N0OmFWruBtXTTqTVK4T2elNtBouNvrq+8HRdP4L5cLDIDd1g3L7Ya2NRAlzKcT5vNJo0ZHBF2kNaitotXgzzcgE2GeC0qeBh+oawZ4v44yY/0UWTB+Xll3kuGbnQvY50bNlHFIqHNANuEU7t+93bavCAdqUb7l5LLWWsOyLFqksDvVBxEpaKlAd5b1k23fJvJiabbH5lAHiJnvaAvWdR0yrv+Mm5OZnRrC1prZH9ZPK+gmY0ujsJrt8QZ2I9ARKBpc+3iucKaq3mBWntPBZc0shz5lmuT+yq+cdRxyEZvLIqsNeGxt4AVVgf5NqTOEXqH5/Y233SKm4zj6QQQZ9YMssGmeD5QmQz5sLBflD3aQNwWe2yTUJBGsbDmBaPYxt38mo6013G43EFkEcRl9AKTWDBkdQXf9lrJleUmEeG+S9VFbkywrHtlVKSVMRehEInVT0YNA7gxuHZvSSlS2g86qfL8j6lsok7LMU86yF9ZNDu+EyNbtK5GxwQFu9tY4PMJetx5ePwsw9u61AxLM8B0nNYBv83fXEYCMDGFikgsE6d/w8voFc77gPJ/0zoNd0hyKGHL/8PQS8bRWgR+3L8bJ/hHIMgOVWUKnbVG/f/8BTH+DWhcwNzBIowkYw7SQe0r/wok/i9FhvBQ5BeJ7zqjf/IT0vOFpTvjNx1+icsbn1xf88P2/YetXcK8oRHiaJvziwweUIsoCldHqiuenM1qr2LaE8+WEHz59wpcvr6L4ueHd5QzKBSUXLLcF1x9/wu/+5g8AA8u64svLF7z+9Q3vpxkznnD+/B7/5X/8o1IXwFM3BzCgXmQf4zneH+A60MepShibYSiPis87UEjvlSjCovJK/vcwi4dY7eXs6GQ/+s79d2X+Yzugwct6qHvHseugkz/EGkxuBAHxhDm2he1Bo5dx3727Rj7ZATZ2D73Gjcvd/n0/Nm+dct93bji0ca09Ulh8uNYdEvdoAtj2oF3393oAbNg7JlsP+nHHg2xjkYKDHFrrWb9m1Ae5fCRXb8vR2zL2l734MLvy3r6L9216q13708777+8c7cN47q6zKpQpeQG2rz3XKsYSkTtm/p03wLg7Z8I+j8L8xmsUSGJXLzYXBAW+dN+Jp9PHJyYAvWqK0FaxfXkB367gbRPHyL9tjulejuxOctqrLdJUfkpiiKfeNTK23xX5+AtW5N0rHgwcR+rtjID7JzH2q+2rbTFHXI0x01PUlcGQvn6v+4PdcUI/jEMAlJCZ0EDIU0G+nFCeT6DTCZz29x3HK2EUwhe8OAvu94S3Dtti++yQ99j2fb9GgZvYjuM1yY0+AStyGg6MtAnuzHAHUkkOTNg+mtMwQsV5KDtezj0QQL7uGJaKa6A0lC4h9Jjh944jEQ33h2On+7tFlTrwZcZ3njCV4vaXOEjaSnWsDDjVQYjK2MdEbCrdVy1KNqQz79pqkX62f7GlXtJRFe1Xsj6fIYLWAKEmMRuBIGtY53qiDO7NZ1ui8jBsPci66GCvISDVwA/yRrZmGIyOxkGKjoSR+hIAtkGosUKqfniRyQKUSEnntrauenPo/7EPctAv4z7xt8FbS34P0cTG5Xco9KT3NxvbXkltCiK4XjS5kmjQhFJmieQNvILeK7Mt9fl2PxnXfQRtCnL7li4YEUHS5pKLcsQOjlHhRTbgMe18EgZ8PQ6QQWWKCJQKpnlWHsKCkgjnU8bTDFxOhA8X4a+WyB7GaWY8PwsYlBKhJGAixuQgH6N1YOuE1gmV5cwvUUfKhNQJlICNGzgR8pRR+iRp2koNJxSwBKGNDHKg002w9dU8ok59b9SukW47TuQOKDUG9wZwTOmGAsfkTr5Vt94Fd4RFyppFEm1jPwDSV9mlJ4sMshYVk3eiPSV0AdJmeF8NLLVVY3Nol3VuMOM2W1am7zl2QBBuAULb9rpTora6R173JsDQtq0CpORJ56T7+t9rqKP/sH+JXyC60q7ndgCryagewnF3GmuF+1j7e70v/zHdpUkhSCztsjHxw5gkxcAMTKIMrHUR8I4Snp+f0ZoAZswCtp7PZzALwPX59TNSIpzm2TkhhXfzixb1WnE6nfD09ORRtK01fP/99wKQsaRMz/OMD++evHBXg9x/WTZs2+p2hwFK05QwlwllOmGaJkzTycHwzl0AH6VStGJ01mYbX2AfCWxgqI2lHVwNCgN5fqsGXrKD1HH/jRjIQ5qYsA57ayhaYMy+//79e0xTcRB3WVddX10j46V9WffXxhKc1bfqbdi2Dcuy7DJeYr9KEe7W2M6UEk4nA8EHkGs6fV1XhKNvf/96vUKKzcncMI+inK5v9f4lZ6HD0DGfpoLL5YS5CB9pd+7oAuievG2bULv0sadvy4LbcvP9NAW/QSL+k1IMJQVppZ+n00nlt8OiUmVsRhS4jaEApAOkXpYVrdWQAQQ4yOr7oPDIliJ7Uq1SOJHURhIKhT0Hr2FZx2ADKzxn+yrCuE/TtAPQDbC1eTc6HpurMk9eaPF0PrmebWp/9dZwvV6xLoKt3XBTqoOEpKBvygayShDL8/nJ22s6tWmRutYa6tawts3bl1LCNE8+XoSk3OzTbn3ZgUVvTelQNfim3/tl8fXzAWOPwIS97f+NO9DeERHnVYTc0zspfgNgdAU8K3KSKJNEkLBtFpAl66mILeJmaQOATkaoLm//5WFQJDUqbEHHTXTgWkNBAGJUPV/e43pL2NZFjV7pRwKhpOzcM4bOeTi7KypRNHYyCwbWX3zC/JTwdJ7x/pzwyw8f8PTxN1i3hk+/+hG31x+wLi/CX0sJ4Iw/fvdvqNuKdV1we33F87snnJ/eYT5PeH5+wu9/X/AP//hPeHl5AfeGbd0ASKXv53cXvHv/HrfbC9rWsK4blttVDuK5o5w65r8G5tqw/UDAInPTwmja6Bj4Kgb0vVx4RIMbOWocmLNCw9EzI9AiQszhsisfub/mvEcD+hHw6uH8GBtF7MURCDZfS4w+HqI8fMLwDASZ2dtE/qhdX0bbjGJjrB3c/bZrr8s8hzHV5j0CAHfXHvzaB+19+KI9jHAEYh1HewDqmfFuL8FsRjTPvq9hkwBGCoEavMPRsuOYxy2P97CXZpgMv8w/OHxRr390qv0IqIzydi9XoxV7oP/wPP1gdz2LK9u9P48A4cf32zkuzCAKUWK0T6nZCQSOxjbtxsJ1eOfdc94CxHdrKjgfgC/xMADj97s58r/5rr02DnFxxvUrQBa73iEyA0rGoimNzOiDRqSQcETV9Yp2e0XaNlDYnH3N7doRHEzd5Ek3myQCLVFAXQwSc7CkTeSSzeC7sX3rFcd+zJP+19e57b13Vz98d/Rx1zt93njCeG+vC5gkkqaZ00wRIDbHAPDUUXuSmw0SmWIFLQzMz0go5wn5koFTAnLe8cRmGIg3+EOJkha10X19N657g3TfU/nNdJB0MR3W3GFTAGB8o2xptG7fyEkeqYC7VeRrO7kTYdF9ZPdLBHR4mmScFmZWQIQgQKRx1enA+FrtsEJRdh1zR7LCpgRwYgc3bS7JfoHsgylljaSTKOMe5M7G0rhjDRiVvVdGQyIhikaTsXMTWvYQALStemSrg1a7/TbpfEMng9BY11AS5yjy6JmNYpzvFvDXPLLLXIn7vRZBTmyeTN7NlmCydGS553CaUghl1YhT7iA0kJ5u2z5ogQNdM6rkEeztl3FMWsBOT4Z1gphDJBZziPCUuevBNpY5segY67N8WVRs8rYn0gIYOgQGyJjtzDa2JGOekoHbg3uUw3yx6vCYGjkKII3CLxH8k/c04iXteQ9bewyiWoMp2C0WwRnX2LjGfo4Dw5TSnjsakMOFGIFtjjQN0JaSRR8RjFyN2wBPeu8SOUhZItsJ6JtE/tTU0YjRa8F2A65zwrYKXzJ3AS0vZ8LrrWMuHaVIEa9idAWk6dEUC7MJ1cFPLw2vC+O6Ma614/VVq19vFVtXR7RW4WVuDak3dHVKDZSRthso18G9hXVjByMiR+b0y+ALuANbLxw3fx7FgyART0fg35aQgxeaYu33oj0hhfiVPchCx7q2AZJ3Rm2jmvvYOxXgLkWA2RQ4cd3GVT1se7leW62fQX5yNpedMOxX6zXGRqJy2kGaNs1Iypk6TTNWDW7qWijNIiJN/+iy1qF+Yz8P25Q925tz9Etsj4p6xD6j/Rsm03XT7BiIvm7cwQos24FI76zZpRLZKACe7AelFCzLDcuyoZSCeZ4BAK+vElCEruDsaRzELMtV9rCUcT4/4fn5PUqWOV9uN2zbhmkWjtmny8Uj6YRKsGFZBEBt3D1yU+Z/cmDKdDkgxbhuyw2ffvqMkvPwX9LIEiSd/5wS5nl2/TVN090+aaBoHEv7OQ6lATtNP6aRG+C7v05AJAPe4jq0Z5Y8OEGNQikWwHS9SUavoVzmqjsTmU2re68Cc7EIsTx37JuxSn20Ve15A5Ac9pnp/axRsYUI0zzBbKoEjQrViF4gHLoqcFjbAI1vNwHf5mmWvbo13Tuzb/VWxNQs0wQpzC6F71Tn9+ELdpZo5FGoTHhVbW7kn9FpGC+/tHue510UbykZkx5AvHsHBzqNO35zAFwiPtd1xe128zlCGpGvVphyLrPWW2KPbLUoZCLyYMNaK263m+qzsdaZgfPlvCtYFv+ZnIJlPLd19Xm2vYGIUFV2k+J25/MFRBmtNi0iNvkDjVqASGT+uq1S/ykcNjioT4R5nnG+SCaYPFtqHJQyobWKulU/ZJnn2VWhHfiYvjMuaWbRPSnfH27Y6+cDxoYXu5lt5+0QB8y7rD93PgsNI3m8E35n9L6g9wXMG0oCGgfjDEVHc2+I3YMD1kJxri3ywwZ/RGWGxhEpfxD7exF0maYZ1RF5MZz3ztEI17bUQ6+WS4SchGC89YaGCn7acHoHfHx3xnkumKnjl7/6NT784tdYN8Y0nfHy04xtewGapPj88OOPeL3dsK0Ltk0MKn65IZUvYAbev3+H2+srltsr1kXIz2/qGE8l4TRPyNOE1jraJor0ti4ok1QBrK3h1jZg7qBnALMOhfGfrQS+hTE0SeAYvxwkJM6LO7M6+8yARRDbxuRG8F5sCOGP8J4Z9jG188+9Iri2l0WVHX2YNFnd42CUxXYMoCk8m49gxui3/ddBVeh3zfo/tmZ3m6OxRcFrPvQx3IPvWnN/p909j4/1VkXn8jDTPKIVOIwGgwf4Zrew7gIPI/e8vTYk+rvpgJiMGMedjmPFR3kcHx1Bvfg6GklvfTWCM+Oa2Ah++Hu8nxcV2umtcYUZeBzSft8CQPdt4ze+cz/gd/ejMPT6n/snUWgj7a61VeOfswGix63gsazdtw9Krn4Y0WA4HJ0Ef35o1l4ucb/2GeJo1Yq2Lmi3BWjVOV2Hk7h78G7/8Tbofz0yCt1JuS16wp9Lb8vYfhweHxTYZw8a8Be/du3x59lnd9++/5Pe/DTMG48FvxvH8VyiUQAB0AIkDOTTjHI+I5/PoGmWCMrQRt/XWTkCQ7BUlLfQu9DP/Zo11Wxr7z7qbhirD7zVXXGa8Vwa/fT+7p30rsU7vKgldT2EjryLtmZsX4LaNaEHvlY4CrqPRdyz4vjtslgEAbi30g5z7Yemrqz2n7PrDlLbp2vm7ADljN+NIMUb7G/TO2acx3noNt5EQNMCESmPyNqjbWfjYdfbujk22N61ajR4HBFK49coDIfbkOtS3znV6R96YddEoYfwe2na60EGo14e9jd2wLXdR4A/gCCAqfzLuo/Io3tTLuBAc2HRxvHA3dYEICDZACQSUi4iL6yRcDBOtyHjFiEH5Wq3dH9zHqV4kHaO5H0vGJJG1NHQ+3LfoS8IsU6Bg61+kKJAs86Nz6EBwwGhcnDW3wHQBTAlwKMxOUakdeUfVYe+KTjC6sTbYUoi4REkjX4ipd/YuGHbJpSSsGxJ6RpEn5RMWFtCyYwpM0omTDlhnpVHVvECq7hu9AprZXy5ddzWjmXrWDZxvKs64r313e/dIuOs3UEZmk5x/UAW3SVy3XlkOZo+YQVjWWXm3koiEKn/oNyKYxp4gEPj6647uhcA9K/D9PfQHtJGj0YDhn4gkQmJAOxonZQWQAN6yKK+yFPIM0iKohlNgw6PHcoMZRysbns76FryzJmhb82OokSYTmeU+R02izgXSQdzc90MUnoN5z58w5K6U0009gNGWDsP9nXrx+FjlwuGRLzurlNaFJJtWHxD5VSHcUwmZJX73jpa6wfOR/YD61wy5nmS7yr4xtz1cMZATcZWm4ORki0iEbRgSSU34MlophgCuhhIk1LSVGfjpu1YDQSzg4nW0GDUMFD5k8kVwEnogmSY9cCtD/tVQYFwSEY+nru1pDUH4r4Xgz88SMzT3EUeTe/bwYpxkjICD67vEwLIJRp7ge89BghDUu5LKV6MKm5+3LuPv+lN/56tQh6RvDIE+z7HSFH7vGnAQqNxDwHIRFeXJIXVTN8INQrQe0JP3YH3+CwD8WTthwwcyNi1VkVP6YFhIkJuaUSK6z4/ipjCcR4b0yKBtshKldEm0akpXG993tNsTqi6t6VE2LY62jvIIn3uXfYo2K8+Z3L43iNlQLfsBKOkIc30yG6HmZ1pv9ddG4fPb20fMgkA2YsUW9E2WwN9XdWOkCNxC3JIypGMnPSQN0HPU3TddLRmnLI6Tgq4SxfVjuvyd+9t7LcsIHmZTD+QH0T4YQfGTyKgdztwfxuIBX4mYKwMSNhQrVK0K/eozGWTVe2ie58qWvsGEcADwhNTitHbFbW9ovUnlJTQW/PnmLLxQgbEuqGGCLAIROjJfUeTKFaS9Clyxkr4TxO2rpuP7Kn6Xu9atGuWk+S+oXnhCFsUxpejaRm1AaS8sQxMpeD0NOO6XNFoA/3ihm/eP+OXHz9iKhnLbcHHb3+N9x8/4Lp0XBfhqHnCRUK6rwte//gdtrqhstLY54Ivrwtq+xHrsqDWiu+/+xd8/uknrOsCMLDWKqcFKWGZMtZaAbaqehVbXVF6BtYVjCSn9/MJ0wczQtUsJ6B/TsBKoh+SukqyzoJs6AIN1auZxQin3N1QZO7KHWcG2TDkbDnb/Yb7GGfM3rNIy8E1NXwjc2TVabkDNILjJh4NDBzxTU7dCzMEo6zsbmOPwcGAhIzFsGfMaVEHam+W7U0i3Yxt3RyNLopps8HJNt5VJ6S2cSXaKVbfrO7G1W7JGmmlnF0whR2/tL8H4hq393UpxmcwWXT82BBt7AyziaAMMyMj8FDxGNG9RIzGiUySqyjC0A/H16MT2/EZjbW+++5+xPZA7p5kY3cIEFvruuzudh7JdbSThwH051/RwNo9/zAOx3XBuzH1AdTnw//gcIXdI5EtBtZiGRwv3D8XQzbefJG5gfH6+3uN902m4E6YPJ78GwC0uNFwvHvraMviHLFZ05BtLwh2qLYnKTcqtEgS9BRdvsRR5+gGasYOh4ZEoDiOUZzlt4DY/e+Px2Q/7ffr3943w/LR8+S9oU32+nh/n9GSocHNWTZOVd8v7H39ZglGvy3zcpqRz2ek0xMwndC1MMuYD9s1dE8Ket3mhr4iO/FwzhyT6ABFMPXRCLvm5Xhn8k4O2TWwQAAp8khBucICXdPOILTCWePZ7qRZ2/0ZrP8nT4WH65cwZ0SQA2nRa4nGoahx7zrwYvt5h7eVCW7geyv1ecnnIaZrS3ZNr1XBMAA8ioyYgEpxoOiYAq1Xj4SIGVEyNxlAAxu/abf5CqDcbsYJEkrWnQ9+HDTScLpMhygYNEAL+cMdtIM9sAPtbV5MDlWWhO8uwwFpBb0t8tJ4NG3nSxqhKi0JlC/K9wuQ8zPaM8ltFgUdFIglksg/r0LPDGQoZ2LRLC5Nb2VxcJpWxh77vFA9sGa6xEgZQDhLj/QWDhqTCgNkT40Fe8SBGtG7Fg3rdyArctYPMjCAauaQPQQBB1JKThfVewcTIbmNYvdTWywldE4oIbsOzBAMbERwo4vtmlNB12rSIsbVp98cPRuEuAeZLZYUyE6poLeKUjYI52jBVuV5OYkjudaCuQjokAkoiXE5EaZiEbqMkuF7S2dg7YSXDVg3xrZ1rMuGdVnRavWq5L1WLRrHQ13oK5HqKSR1fK0TaexdOt5dOQEBzeJLqu/UnmaXAbH3zfKVtSV7aU6muzmsJXLZZmbnzAWTF/YaelZHmk2HG4CjTrwvTQPPVG5sqonU4bdcQIl0HNyESdNYTSHaOt2HKwy6Plmz5M8dz7bvdl1PVlgLIJT5jPPlW6zzE9BWoFVQmoG+CqVEU2qBXHTC9N+DdPW7vZ7HWMb3bX/264I95zZ0WDfaI3gBH3ubAQnnls+HnwdfgyVLKjP3jtoagIzTSdKILYIypYQpZY+S3DTzlMDIOTlAW2uVoqEK6p2mGafzSTmrodydG5gliEqAxaJp9JNXqrcih2Cg1YZ1XbGuG+wALecsae4pgZHCXKtMJ/m9QyP8uaOBULfmkcMi0hbgZdzXCSA7AFHxZQZCoboYuQ/AI1/tkMC4RqcyYXB9CzhsAPU4DIr6Z3Hbu2PP69paQ6sCqlflnW2toaNJgUgFvk6nE2zbtGJp1mbTcXGfsHRx2/tj1KzNv6TZj0JfbasopYDBqHUTDlkiP6grU4aUyZV7TNMsXNyBvzbqAB8jLTLIvWFdb0JT0JoXX69mCzE0Wt644ZNmQszoHSofoiNKyhLEBtF5vXewApitNX3+oKuwtSRRxkJvwixRn0anYRz3pst8XLXP0aZnZtRtg4bsiw3Vuh42JC1mx67XjOPbwUmdF4kohc+B+TFGsSEBipPbqmUS2yLHQwYSnTaioiUYEYlEVTGj9rrTsc7f7JqIJMpZD2FaG/Qd3BlbrXo6PNYjM2PSulPzNDm3tK3Z1iRqWQ7/5YBrUzoQAezvfR97/SzAWCA6dWa4yF9BZR9Al50XqPc4OEIqUvbudX3B6+0LzvMzzqePqAvUyNpvLBF0sQmote39DQzOEVG4xt9BoxhDH/eIvbE2W4GJaTqh5Bnz1LFuC7hV5W8SvovL6QRQwdYqluWKT59+wLK9AmCUnPHx+RukP1RsfcVUMv7wV7/D+6cLPrx7ByDhxx+v+Od/WUF/+hG1N9RtwdM04en9E0ohLLcr/u9//HswOlIC8lyAPKOkE263V/zx87/in/7hH7BtC1pvYnTmjPfP77GsN+UhMiPvpMqu4XyeAHTcthUgxvO795jOT0CexKhrDR0bbsuC9sxoz8qRq4dMvAHb/0rmU7tTFywiMXIYgDlLBDCypOWZW3mQ/957MMbNXRpSw0Tq1MAX+vGaKGVRVqI82r3NmXQpCIaI7GOBP+uN+4thuf/ElL4NDtGej8wvD3Lr73ungyFlblqX0589+OHmq/8+nGP+mo553CsHr0YK4W5NR4ONzLjW5/m15OkZ4cbez65pJgB2FajNyHcIgroUtLDn6r0f6ROGOT2xpfD3JTrnjln2K6+99L35rd0AyzgcgV3r926e7x6hvVBLwCKC9jpqbM6PXvfArzmUb7/PQb5c1gI+8TUQmjB4HPdjMWCy3SA8aOtDgJGOs6ij4wDF/hUjCHbvh++K6ycyaNWtuXdgWYCb/KOt+R5mwM2u33GYMObyfL4gZeFxui2LHCD2EXl0BEDv2/n/5/V1OY1G21fv8me/c/+cO7B49w1b73w3BmaYHl8EcSZOpxlpykAu4JTBODicjFAVWQXVApV0oTmg7jL+9f663qPB/j6c0DfG99GQEY309aDHbSfxwyaTZd26OtQ50XtmKrqdaivIQA5xThppFAxZ9VzZT3traG2DH2VYYQ2LNNTd4sg5xwrONOUhyznL+rZ5srRfHunKtr/FAzazAUzvMrNzN9vLnk2kld5bw6YpZz5vvQnQkJSGoFsUDgEkhRua2gGJCCVUKm6aMq+unu0ODsQYeDWazEAA7yVqM0b7mI55FEFBYVz1dqT8eXkGMzQizMByAHnYLwAw5dkjmHwMwRhUE+ScvAbOJuXANUU9jpfID2bFTlJeRu2nyVite1ATgKcfW5neUXjMviugITOjbc33ctMx9wffY4z80C5EwcMcXWpj7NXLt9sIxyDufAkHuGIAgM64FZ4ZBxTCu2qvnK3YUPJxMTt2f3Bl6YwxtbVr9PGIutz1OeynIt9Z3xQAeGuM1BtKEXkTrsk2UpBJgPKpiEI7X549M2+pGxpnPJ0mlASUJHQG61rRO6EhoXIGU0Enq3GRUSZJoW61ojKjTBNStyr1HdwYlCbIYUnXYBIDhrVLJQfHndUXFj70AQooQIUQUcculUNCyeZPI3ttPnU8W2tort/LOOvUV2tdACIlhwDDeQcF2Eruww2zWg4FKRWUyaLBE4zibkRcYkQ1A06TMGwl0yxSiA1swDNUnmhU9Q6cjQ4GaVuYjTNWxmQ+P+M3f/jPoL5iefkeiRtSmdHrFbfPP2D5/IOAtMl0rnXs3gGxtXi0wgzIiXtvTnm3hsz+k3HE7n3VBArOqJZQHWN+DnRdgEbAVFKQftuWASol4bm07zw9PWEqE9Z1xevt6qDg8+WCds4SjwAAIABJREFUaZqRSFK5jZs154yPHz4MgIoZt9sN6yqFRUvJOJ2eMWsdmiE7DS8vL1iXBYsXLJqcR/P9+/dOm2By2llSordWBejdhOJjqxVrXbBW2ZtPZcLTfMb7yxMsujhRwjwVAaR4+JpAQqLuYyU/skYHNqx1O+hKOJgnAJUAltJ+5WlVwNLwD5PWRHIgOE0Tnt+9Q9HozjuXE/t1ZmugbptydnbUVnG7Xn186ro5cAeSTGMpYkUBbMu7v61fFn2bc8bz87P7k601t+Wkz5sUQKwaJQ7GVpXz1dY5i7bzWhIk/LUgAQ3P5zN2+1DOePf+g8ti9BQsErR1Rt1WBWsF2H15Ec5iA+wBCGCvsm90FFkPWlPOuFwuuyhhtwEDMF2rgO3ruuzwq3FYDJy1+JzZIXkqTrHR1H6yQ2wr7tWqAOwjw9v6JmvWrjfQ3GTf2mdyEKkw1rYKqG3URIDPLZQ6J9v9zmfVEezUArVLdkZdV6y9o+Ss1BMWzS1F1cSGmjAX0TlJ7V3jfBaKAunLYsXZdJ7kwGDIHABwB+Zp1j7nHcj8tejYnwcYqwrZBbUfFfTROab9b6ag7Xa2wQEIiXUg7li2Fa/LDaV8cCB2B54x+5W8VxmwPdJPgtTAl9Z11Nrx7vlZhRR+CgrgAJQMgy+npJuHkEOf5zOuXMVoVg60l+sLXq8LbtuCra6Yy4R3zx/A7zbwuxU1f8H7yzv89uNv8Hx5h4kYn378hIyCy/mCp+cnrPWKp6cnnPIFtZ7w6fv/he9+uKI1oW74+M0zvnwSZZNSwnma0Jnx6XvglTqmRCB+hpRgBagUPL97j3mecJ5PuFwuOL//iL/5T/8Z//ov3+Ff//l/YH35Dok6kDJymTCfLjidLvj47a+QcsGyLLhdf8IPP/6Il9crXpYbvtyuWPvmY1x+y+KgAcAC8HfJi7iwsbtDwRo1VjxiAfLxsdhXSqQFL+BK16THUkbIIvCC2I0qr2FOA7n1HlDi3fd2Lx4/5LMEjh8MabNvPbiJKlzjkdw5osNFPIhwWEcjemDflv1aircYxXOkTVJujkd18weHIo/ghbccKflvWK/0hh7wNj8GgPhwBXO38JLRIh6fS6XvcAVrC5iM0sfBAAcAHHA79OfQ4R0I+Ubfh/E9bmFgj7XVNBJgxpt+9w58jL/vaQB85p0MTP4NB5tDW3gcfpF/9eHrGPn7tfePQKoPQARzyf8DBzS0feOqx88E84h+5kBt4U71PWh3fB0/+ep3g9GzB3l1U2sd2DbgekO/3sCrRKMgZZhWUg020mZiO8Ite22YcgYoITk1wYNZCQ6njwmOevCNtRmu+1q/7dtvYatvzf3/y9y7NUmOK+mBnwMgGRGZWZe+ndsczcikkcz2ff//+z6u7a7Z2mhNo9kzmjnT53RXV2ZGBEkAvg9+AciIrG7J9qGjrboqI0kQBBwO9w/un78lK/fu3YMuvXNn0WRfwnbvAbGb59SCwJACNIVQE7Wg+I1Iab+7B7a+9e/wy95PL21kPJVhKK/cE/rLRP0zbeZGREtlhjUaoFsaTtOifXc1xK2NAHVIiDzF36NidNHLUtRoF40stEIcth/ankBgkEa1Sop4d3hpjqCm/QW0IiBU2SruqE43vlprtzkVUICiL4wjxTfgXNjmvPgYMgOlIOdVgdjqjhgIoEoIhaC54LqXV1TOoJAlwp0CECJCJJwOwst2uVyw5twO32UylcfXbE4bePnDpYCi7WOkUe/tQEzGbBuhCY0u3mtz0z1+CM0akazj6FFBDG9XmVF0LJszHYNw7rYCMB2A6kZ2aAcIDLBGkbshwQBidP5TS7d2Da4cgkQaqay6OMa6eaeURpQaUCrcGTNZsRTZhvGbXvcZgEW4isMo35YqYLlH26ozbEC0RJJGWS9VojFbuyqZvkdx907kxbZiSpqu2UBlk2lrw/pocwZsU4KJOiC538sBBcpDi2YnOyAJG1kABMgMmk5N1Ara2LummDANA4YUMQ4BiYDjQSKrAyU8PQQcD6oXNAX1dByFL7YAzxfGuErqdA5JMg2ZsaoMm11qlaYl6jOhcAFrqnAkqwLeeFIr2IHxEIBcCoYEAA18qKXjtAQjqu6yyFcfMBNUGS1YxXRWUII39gR5Nh2g0fmR5IiF9DCgNnoBgurYEEB2mEFArRJphbKKHimMWgms1TEKFgkgISgw3uaYGQio4JrB1Yrm9Vy2ED0EpRHw/aizGhyI7dtlmB9ca8XHP/4tPnzzNahIAecaCdeXZ3z/p/+CP//j/4XrD38CjLZgs721iPuYopZpqULrYAty/0L6Y+GMm0+X2WT7TR9xJbyxixwiDYRSM8Zp9HlKFBBdrwBcGCuvWsRJxiln4X+1SEBmxuvLCwIFTHHAeHzAOA6Y51nAryoAi4F2YKCsK+Z5UZ9EZOj9+3ceBUtECtAuXjTIDhpPDw94/+79JmpTClsVLxxlNAchBKEg0eEJFBCIMSbCkCY8BgH9QghIIQHEiLHxXJYuOlN0ZJRDRUAPRESOhiFqYU9CLs1GMt3Qc8Iys0df2vsbaAw0XbWuKyqAtVRcr1d8fn5G29G3HwKBYtDioMF91zgI53WMCREDpsNBdaTI3ZAGDzywvphuaTyo7WlWxPF6vfpeuNGTRCo/tluzRmBGP7QMiTA+nJxO0aIxZe/qIz5lzJZlAdB4U2vRA0BqBzmiP5Q2SykxrDiY9etwMD9FlrlEnkYsy4J5XXyfZmYEVFApyCpL/SFfL6NJeZQHTbG3edPlBmb2dWN9rJWRrwUrzw5GW6S2Z4fUVsTOCnP53DBvCn6VUpzX2T4SoZtcBmOMUiir89XtXZ27lwvm6+LR88P1KnsnbeskjEMCaaQ7EbCsa8t+h1D+rEtW+gr4YaWD7KafQsDQcdwyM4rZfmrj2GGBAd8WwFc7Sp3b1dA+vw4wdmN3aMi3GrECeLECcjY5/Sk1ufMpP6vdvwm2MwOKsJaCeV2FgyXoggLcGEDXjnzdfeeAn2xtW0Jp+X1eJR3IwBozEt0v9urc8v9gF5EsvGFIWNaIZZ2x5lVI+OuCnGWiT4cTHo8nlNMVdczAGPFwnPDH3/8OD09fIcYJL59f8PAUEccDOA6IlHCIRzkFiBEcKgpLBVJiSasbk1STXBepuDdDNuPpOOJ4/BqH8Yi8ruAihcIQA06PTxjHSRZ4GjE9vgfRgMPxhPdffYX6mDClAVBDLeeKwzRKuD2LEftweodhOOE6X3G+XHFdZixlxbwuWHJGqYxKykuyVsy0IBsvxwzUF5aNns2Y0jQe29zB7gi2KKbQVX0GUOsuJkpO5EnbcaePtw5R87X3TvfeSberejCEm1x4/95oDtwc7N1aNueTTS7vP7o17OMCGTNzK+6AaDdAH9yfb93k7T2/JDquf07fZg8Eyp8uDcvf14zLNp63Ddu1sqVYBI6BC+5bmqIF2uBTA/Bu+A/69+5M+Vt+WrrzL7vHvu+c3P0DOhDNdGBrbaePsL/mfoffEole78rPtzrQQQtAxucLYN1bkYDb/t5ZO7uJ3uhzlVvV1DoKpH3aQhT7zvfLYe+kwNruu6L+nBlBd16w62BHzdFNjYEYpIYsLSvqsoJKSz80B8nXUO/4d/1oj2UvaFB1rVuUoUc1buQGHXiwG5a7ioZ9H72/gnfteBu/bL3fi0zu+3dPbXwJzO8BmP043WunP6AloPENk8hSizTymgo+T/oU1x+bNpk365/9vbp30sbamu8uRrMn2j0GRvayaRZD2z9CbCBOa8/Wcfelfc+tjU00BDew1g7VNu16F8ROsfZJDxGp6+sGQ1Lj2aOUiDa8xh7pqPuwHPbpbOwfzu29ZV60sIvtjYCCVOjAxu1c1VI05bmlkDmI4mtRIwyVI8RBHmgKcaweZRNTwrKuW9vBCguRUVd1E90Bpz7zG3FVO3Wzl5L2M3TYRgMgamVkniG6yFuVa7nNVUQCd4C+c6Rpi+ZACT/alm8cZCoqNJoLJrAWyJJMAOHmlDOFFtnY62qAuzGRrxptBnV/mwyKTnLZYSAK5SyMH9cyXgxcb+u/djIj4G+kewYUdG+BVvy2wwDeYFG2Zto8y3oQ509TSfWQ37Y5cdDJKYEagLqdQzv88MMJe6pOf+w2IwO6G0dji5AUarZGYUM+lgLS9/tVqRlrYYASQBF8LkhJOGRTFB7OdWUkfTcj56jMWAowLxVrZpRCKIWRi0QOOSBCpBRjnV9FBKNes/2cqKoeqa5Lmh3YbDPScYiREKB8hJ2cm/3I3LIh3LwCfAzkXL7TQbD9XsFajwxnlMrCSRoIHFrELlwnqKzXisKit0peUWoGVgvSgeqC0JS3zmfR1HWQQR+qorlIxouDsfZu9tTg8mB7jchrdV3e7Zz+N+s4hGkEpXegqoEUERiGE47XCx6eP2F+/iuwvPi+5ELdq+TS9DYIcjDsptx2r/aB9vm0LgUzO5oNVe1ydnltelPtKjIATfW+6nCuEoErOkUkViLWBNYxQD2mhKRpz5UrLtcrcl4BAsZx9NRjjxDNBaRgWdQIP0AKHlmq/rJmAOyRoTG1A0075DSgTNqVPcX07qApz4VtHRmgRbBIcrbxqNBisFXG0OwYVs5N1S2BCniIziNsz57nontz238sUjBqRkI3SbJcO7DddT3g4FRMSbWNPsd8bbZ1aofCtl/L/sOlO2zlCiDDbXAVEajclmQHZEJBkVIDuM1m6SNDPVKx85Nq7daIbqhS6V5tldwiI2255mQZDrQbG+mnUyR0JleMEn3cg7Vue6pcFJXHnIuOv+o/oh2NhfLEkshGoIAwKODv1D+M0D0P0PlVGRYZXSTbglTfubHW7EL47wTQNzk2m8EOyw07EVkWPVZLkcMuu9Z1Fnumix/0d7Jjc2eHd6UU0KqFw/Z7ospiIgIdyLMLKIRNRgVQN/z99g520ECh0V6EqDqEJVvEI1khvlYP9jvVgbZH+ozURWab/JndCwa4ktsXb31+FWAs7b/o9m41TyEmnS5aM8jtfqbOIeoBj+4iUduSBpAXFfIERhF+v80g6en9zffYGAHkzmQTlXXNiFF4M24cGkbH8ULbDqryiar0LsuMy/WMZV0RB0KkgHEYcZxOOD5NuJzOiIEwpgnffviA3//294jjA64r8NPnGe8eT2JUhQCKCcN0AmJUw1CI5A/TCK4RJSe8vljVu4KSV4AJQxrx+PSEh4cnfHj6CufzK5bLC2peJF3idMI4nSCk1QHgiM8/PiPnjGk6Ih6kvxSAZV3w8vyCGBPWVZyiXBmn4xGnhxG5FCzzLOkZJeM8X3G+XrGsKzIXdxQu0wW5SGROfmWsteCynCU1nC3tf2+IyTu786NKuHeot/JIW7HpJNT4G5vReCO97ZmtQfnLjTFt1oyr/frsDJ9mn7RIxc2l3nz3HmrgublJW2Xmj+gadIW7HwvbgDZOtjw07N/T276fsn7v09++AXjI1j/55r1fS3eRZzMCAO9zoFuult7JEgPYXQHlgTTd016cuvkW4Juak+UmPG/a7zdoewLQGaw382LfmLC0u1yvdUZvbxyYU3Frined8GeQ92V/Wrc1mNHeiHAjH5t34a083crA7b0bkI5uZnMH5sJlu73lrk16Qyy8gb5NvnNRN35dO+ZUbW+7v7H6t7UCuYDnGXVdhQ9wr09UHxkI1gv5fl5yych6Ai8ejBnp3bP3+5WtRTeG7/fY5nzf1g2Yu2mfN9/9EnD+fv8aD+dbn7dA1i/93r5vDjTangDdyy2NmAArUMC79dYcb24GOXfPZHhxxvbc7c+k+moPNvgyC2gLQGW8dbfpGSZyA3BPAWAP9t53KqTfC7xS+26+DMChpmC8D2Kr9lF/hFaIq+2XRtHRBkHGzB1oBWRtL2YFMfxglG7laGfRbd7V5ZoIgZvTaYCiHbpK0aMGxrL+CSAYWkZW6bbTr9setD12W1Ck1+cm0633TbGp/Hg7nUGgO72lPwL9uhLuP1UVnZFPmkYtRSJMP1fP4JH5kkjQ2roDpULj0ubSHOXOmfP3sfEnic5xW4IiIkUQidMk1A6SEbYpZKaH5BbB2d59B06TAPwWdePvGSyH3eAhi3AljcwxHlVN6Xa9VNue2NlU7dPvA1JYhHzMm4iZ7t8fVfVRVm0vtvuqJuN0YLOvL3Tv2NM0dBPU6Yu2U5s9s91znQvTSMbVJ2EGuEjghRQGMucXyJWBUpW2JCGvUK5CwjBErDliiozDFHAYNSWVK9YCLBm4roxc7E/FqsWSSrEIoG4AXQ9A14JFVKvc+3tC+73dV0weRQRMXpqu5MLdfLWIsl5/yRjJO7RiLLAlaUPWbE6bDWo6zwqByYFFER+xVI38ygjEyGURepeyNrmhTs5Vt3uRJe7ehUzWjcahoLPiPYVZaFKo7UFuiJteM2DURrVl3jEzamBQDGBiWTtg0HTE8O4rnL7+PX76839FyWfRBb4bmuhrSxvfWCP8uemgXodv1ka3Tfthml1TG/DcVkOT/E2bKhEWZWzrKsWk4yOPChoaX40PmhnDOCEKCTKWZRV/F/DIQQAe2VhKQSJCigPSMCDFBO5+X4utP2AYItKQMI7CW1u4oqxCOUAheJS4gVJAiyxNKSEaGFsanYjJPFfjtdZxqQAHlr+p7TvsAG3VqERyLlcbZ+l7Rs7twNJ5P0vxse3HvQegbO0031CwFFtyIttNj1mGcLM/WddNq5tAoMY1rRuURWECMn95zUhDArPgCTkXX0eyhoO/C2CHXHBwMSjQVqsVbDKeUi1OVSTtnqm2cYZSKpmvxEAIDfcBoFHXsfuOMUo4v46V6Ah7Lqn/slrBds3abPoOmOer8MuGgBgThlh8vxAu36j0kNHfN+z0ZakyZpIRVJWv1t5NC4kNyfWuHexREO7zCCAlzRiBTSk7yNxoKqgVv4OMec4FVrDMgPHeJ2Rmpy7oM3gKCopGXdfSirjJ+Oq+2a0ZE1O3mzr9YqAwVC5rUZmy9aDzIKCzybPyvlrmVJHAvFKEhkkKf7b1IP0hMNr7bekslfIyiM3Tde/m86sAY28+sj83Ndwb5xujypYx3Eg2Ix/oUojZ2OAqljzjOr+g1hVpeEDFsgFdG0iqgsfGyyZcYLnseKf0SsA2l6KCoakEaJMMiHHUQtXFkPA9WS2Dkgsu1wuWdcU0HYQ0GmLMLlxxGf87aCl4/3TEd998xH/+D/8Jh4f3eF2AZZmxrgVzBEjT6VIaECgil4w1F6zLjKfH90hJCo5dzi/4p3/8f7DOn5EiYRoHPDw94t/97d8jpgMojEhxBE0vWNZ/xrxmlHXFeX7B+48TKCZkJizPP2EInyWFUBcPoyCmgMoRCCPWKos/BOG4GSfhQUwJmMYDLpcrmCsO0wmPxwXPzy+okBRDAPj26SukcUThiiWvuPzxjH/767/i+fqK5VNB/qEgRvKiFYCkDtk8UGibvszZdnk04/fWAdMXctEz7OQWCNga7YDuj5vvvrQsXRQgi7kp6dvrulM+3I+EswgJudaiuTcxvhvelm3zvFkPdn1viG3e8w4g8z/6caV76z3t+vj27+300YxrK+plJ7a0H4PQFwHUDcOe0g+JGz7VnQnq0mK917xNha/YMlJuxvnOnGkj+vN+TrbjvL3dHN1Nl/03zVDmXsLvAmq7p/oXvxRs76/jHfhgP/ppOQQ0F5C7G/vOpxOngnVet7r39uH9vc0o8DbVULx9l3ai39a7GP0wx6RbD5t7t82grivK9Yr88gIqDDZj3J3EO2utmxPpq5tKuje1VcGbta9XbcYbm3/vNV3/77e00eaAZHf//llvyYWc8Icb3dL3o+2Rb+vFnwNf7/XHniAjq+CUgkoxJYSYFJDt5Ilve2F96w3m/pnec2q6p71d929uJASs91v6NgwICJs7dvaP3Bc2UR/dr11vkDfRpEo+hbViOAvvpVy2A2K7tqvaUObUDBoF0wCqLhKVAfegugFwN6XbZ8xRqWgOvx1KeNHFfnmFqNWzydtqvGfASsF5bY1nzJ5jabKtqi+AWpSCgAAtWCVGv4Ii3uvGl5tLwXW+Imn0RJ9mqZ0UG75aUYiCGFJLKy7UzXk/Mc3ZMxDRfrktNqV7jgGbMN50m2XCbtA0nXKbxVX05xSl+vgQI2rJyJACPvs11NRec0IjJS1So6nTXCUqUK/wAhwhgaKAtr0z37cVAvk8pDR6eiUAVI1cMlvG5CNn9nEqxaJOuOPNN1mT5xStxB4owgI8rC/GC0fdXLuVQITYDykFidDVNvriJD2QvC00E7yv5lBa0eB+7+1tU2gh46pgqu2hUalqgI7TmuVgiQMjhKRjwqgkwEXUVG3EwSezQrNvEzlFRanixE/DiMMp4OFAOA4EYqBwxOuVMa8C+IwjAYsWPmErxCrjE0JA4CDF9WrWyNGAGIxLHUCpWvOhi5amBC3J52Nle0fOBeuyyNzEBuxLxgjrO5dWpV0BpmbnEKjKmAq3psjCYRwArJKFVxS0qRVryT6+rbq76Lp1uYoO4qLXiB7jWkAdiGpryDnvFYxhLZAEtEJI0Ehv8ynsoMqWs1F7QPm0DajkomufVJ/WFvDDROhTZGsVHuYKOwwDgIpACenwgKfvfo+fvv8DPs8/AYum1xpoobZZrVW8CLOviTqbtb2zrOtwK9fyG5d5H6NaYKzUzBp8wgTOApCFSaINGaKfjddSsD7RxSA5tDYOR+aK8+WKEAhDSjgeDiAAeVkEmAHw9Pgoe0QpuF6vTtUTU8R0mIRbHgFlldTonIVHeBgGnE4jxnFELVXSxKv47uWaUUAASUkuicZNDtYcDgfnsmWV4VU5UHUAZM+FyGgcgkf/mfFhGRrGRxojOn8/qF7rosRFSjBNk9uORdPU94Fnvjdzxbo26qKi2SXX69V9Q4t6FJs7KJ+pFaMTXWNcuTFGpBgwpAEHTQM3mqaYWtSh0BF0h6fmI4SoNBmDjl/T4+t6dR5Z/9PJYNA+WESm7S9Ch9DuEf5tMZwqNJq5SG2GrPzLFhFaqwDnza5g58E3Oo0+i8H+pGHAFOW5isX62q21YhgHZOWQZWPY06j/mgsqz1iWBVKUccA0jb4/kAaeESVM44hpGr3d/gC/WoaxgdOVFURtVAeBDEiNvo+lQexnO7iwwlTS/8ZxW+2ArtYNVYSte+sPEUkxrBib3UwC8OaShRKD4JG+nLNzCxs95TAMSvkgEa9BMaAY0yZ6uChd1ZpXLGujabJ9xoFt5eFNiTCkiqEUzMrTKzaB/U8+uRRUPRwQuoJGvyD2TNxE+t77/DrAWN790zasnXKozj0QNjeakeZuhwpuAABrR3ZOScFfr3i9fMbD6XDbFWsiKDgQthGJfSjyjcEKoHdSrXJe/w5OyE+yWGutwjkEuJP47cfvEMOA18srlnLF8t0n2aTU+UkVeBhH/Oarj/jDb3+DvFZ8+ukZNJxwOp3wN78f8f0//xe8/PUTCAWnhyd8+PbvkBFEgEvB47v3mOdZgErOACqOhwGHacDD4xO++d3f4W/+7u+x5KoLFDjPV4TpgFNKOEwjXl/PePrwUQiq04j/+//8B/zww79IZcmY8O7dOzx/Yjy9f4+Hd0/4zW9/j8PhEcwVl8sZP336hNfXVxzGARSaYTmkAUOSRXR+uaAuK8aQJBWMIqZhwmWekRDwMB7xmw/fIj4PeIkXzE9XMDL4z8OGT9EcM6rcuOzugQOdcdzksvOs1fiwCKC9o/vWp1b24g7cPXpT2+/NhXrrIO+vbREnDZgJvZy6IwB7Cbgz0rVnTrZxjNm9rRIz3e3nW/166/NzgJ4Yr3UzPvC3k773IME9EOqLz0fvCvaOZicr+lVnylvnm+ZRg7Y3dipYqyp3J9kOwnUuLTWgA9gBO7yLBN73vwPgtEtA9zz79OPSnOBOou48wzTpL/l8abzdodi9iEXptGVl47q56k6v7j/vZpzuvQCjgafdnNjfb8m0OxoO0rHLDnzN3Xa7Lgvq9Yp6nVFyQeRetgRssfTeewcorQ/d+1nb3ZWtkMDbwrJfmz0o8D/z2cre7R64X4vmTP/StfnWZ28T/JI+9pEXvj5iQhgPoNMJPBxBwwikBO4CdG8OgqiNm4OEvPm1/71lFr/TN3TyY9+YN3v3xk5v0Haub8ek6ab29ZdlQ2TconDa9/f+ThFY89oBcLs1WaT4UJNruWZdm5xH5ZOUPrboCtfuN6nrEvGkZWssA12iTSwynKEACCEoV3Q1XrWuqVYMp0WoeOSb788sUewhtvfv9PY8WzVsi2CzMTPdRg7OMTOGgZTjllBK1jHZr8k+Um+74IXHvy9yFdAiHe1ay59hmFMMNG5Yub9JJhEQUvC93aghKDSaCoA2Udgh9M5SxDAeMJhjb84e70FmAMjCgwmLYGn63kBW+1Q2cNzelQAUlWU9Jmd1prXKtAc22Dqyjds7Yk8QvWvsYsUBoj5yUaMPWQFzsnREatQOqpOHJHx/Nn/3MunaeDcAPmgqdV9groEwxeeYiEDrKnJFLforqqzYwZIk/jCYBQwaBrFVjNOwlgKKjKIHDAw5zJGCLnLvOA5Snb3IwcYYJwwhIFFECgEJQK7AmivmXHG5Zi0gKTzCBJJMEDabSIvGFItEF8uor9PQSDKiDpPMh4ChBbVKllxeGtczcytWBfJ4NV97tWaUopGppOOj15skUAhCdVYZKSR8fDri7//97/CPf/o3/OtfPiPXWUDdsqCWFdwBMARoqmpUjmoBLEqR5+sLIPZ62fVgBQeTOdPPdujUiigFCJAgIG5u68N0VBUBtOIwFoko9mbjV5bB4abbtSsxNsCJWcAbQgA0qvP3//l/RalnXH78N+TLC5CzVJBPo8zzPIPLCt+3KgORdsYKfF20MfAvG3DjvrLeq3Jta1h0fGzbQ7UDPCAlAb0sNbrUirIsGMfRbY5lXaWwUUoIQTgjuTAOhwlTfH/mAAAgAElEQVTjMDkoZGBRjBGPj4+NF7IUvDy/IK8CgMcQMU4ThnGEiHzF6/lV9LrOTwqEDx/fQejwgMJwgMs4M8/ns3NMGnC8Zqn+HqNUajdQrx/L6Xh0G5bBUgyxVJS8YqnFlh+CgqIWfBLs8Ie29iDB6Ba3HwEQFbg8Ro/AtMONvK7tEEqpFWTGrCingLilVC/0VEtBXldcPSK2ZfaN06HTE/Bx6fX3OI6IIUl0Yog4Ho4eCGMy33OpAsC6Lv5zyXLglvV9AynXbQfI2VhE5a5NQ4s8JTROUhqCBpG1AqhGa2F8ugZoFwUU+73h+fnZ91hAqWDCzlfTdSP2hFiWIQYMo1BKWpaDtVs6fu6qkfuv59cb29t+Nh7lGCPiIMEJ4NKKsJIUTltXAT/zugoWxEWjc1t2kPEWA1De3YAQE4Yh3GStc220HTbedthltpNjN2QUAA1EJ5Iike1dpQhaZUZZF6y1ipxr4KPJrXBJK390jBiG0eXQ+iBrVOarLIuuXWk7AFiXRWhIghzWCFVGw0VijJLdnaWN8/mCcdTaCqqj3vr8OsBYAHvP5p7j5VsK6WR1ziV1i7Zt7P2mJEMmYecZr6+f8XD4Wo3zxpnlz2KWkyz3TjSixNJA3IHa9bAChTWkPFKXAg1ffH5SqsIYQtB0r6Ah0AnH8YhMMy50BlBQUZAQMaYBh+GI9w8POB7fA3TA83kGoyCOQIgZqAWHkcBLAdcFka6IYUUpYlynwKhlwTqfkULFEBiRGDEOGA8POD6+x+npAy6rpGHkzFiWjJfPzwgUsJSKv/zlB1wuV8zzgsenFxyOJ0wT8Ph4EqFMA07HE4bDEdPhiJRGLNcVP/7wz7ogBKzNWUK/4yBg6+U8g3NFigGHdMDjvGJdRoyjnKJdLlesyyoVRCsjgDCEhNN4ALgihIrrUlA/VvArwBfyk3jZ5DsOUdwCOYzOgSf4yeOyrBvgpT9tbxhdt8n1suROVRPwPvbWPr0MOmgKM/LapnMPkGgAsihtdvmnZiS6o2b33DTjv7xxLEh6DN6+588BWvv32wMzZih7e92oGIC5w6I2/UTf1g2YSZvLd5gFLFLOxmJvpOidyi/Z/DxCqyrNbhiZvaj/mQBB+lf1mTub9GfApS2YeQtquom9+fs+ML538Ls2Nhbf/vm4++zt89++5l5/NvMCQl9h3J67XT/t/9tnbAHrbpW/LYtm5GxEm27+ffNuts677zdF1rRNk+26LCjzjLoubnR6toeNQzdfzTDDRjf4abqCEaaf7oH1RF+WJzs5/9LHjONtu9t15QAeN1m6d43dew+8bT/v+//F7r2p/7b9333XPykQMAzgwwH1cEQ6HkFD8qJL2Eli39N+jmQofRF5/21/3+Fp3fJj1xf9r/1Y7s4UCfAW/fb2rDvv6+bKHSd40ya70W0N9/PGraHNIDDUstI9iTtZ9YVVuz3QO9plB3X7UVXOxe16l6yD/v6qIKysJemvpF8bMCUdtF3P0pHvLFvV5V3Uvn5fwfC8TwpSjMw4Lv0Kidho76etsTxDIo6p2YhQRxwMLnv915zRahsEd+uJ5H2NW88AWdLoa4nMCRoZa3apTpTy7LfDU6NAaNHGpmcKV1zy3ObP5MPn3dL3JHKSIDxrsWRcLkU59xq0ZiAZabSxRRe15tviEEAmdg6gFij0iOOgkaG6MkMEuCi3pzpiuajz1hyiPlvF34cJVSonSeosafRMiF2ao42gCrsOVrZ9XmVXstts3uRjKbD9XtUAdJk3ZkKkQdJ6h44aipsU+ux41DY27ZWivIjq5YZgexGAQKgd4F9rCyYx3UmlYBgnGUu1jnkRQJ24RXsz26G4HCigAMNAGDNhjoSilcbXtaDmDKuny2q35JKdp1n26qA6RC9UepoGLqntqvIvtTeyDIFUGEQLOoDrSrL7VDtZkLX8YeyrMrKCquYL/Pjygv/6Txk/vczIpSJXbtHIarRFaoc1pk+sOjoRgVJUnleJJhU57g/ERFaC6wxbJxoJurELm7La7MY7O2pj47ptldqcmnY2Get0ilsa+p38OyJNER++/R2ul/8Fz09f4/ryE7AuSMMB0/EBXDJe//IveP3z/yuZBfZoty30724PZN3zZE02/bJ9114OdIMsFeuaMUyj+MUgwaGVJ9rAUwPd+2KIRVOcrep8LUV0KBGGw4SokeAWVU3UeFuJyAEVAxOl8JH8nitjvlwa0EOEYRwxTUeMQ8IQA6YYcL7OuMwrLldpS4ppMcxu7aM0e1C2/450jOTgJGtmrvkOtelssvRoPRjjirxqkTq1C5mqZ2W5SNm+0dl1VbM6bF+TaMhBADaNznUqEP14FKj6PNKXgGHQwJ7NsyzaXN5B6AhasSQH2fT9TEaWWaJBmeGFEo03X/rQcXmSAXsi24EIYbjVp+M4NtsejX7CuKJrVZqX7mDLeWlDKzxlY84axppSkuhMCK7R92nDWc2SwWCUgb0N5nt6rQIwwn4n4G0r1BacFjNoxCqRFG4chriZX2b2ImghBNXfq+sDo/4xjmspskagISEmYDq0sbIxvOlzZSwlA7wKRzx1fozSg/ZRqETk/e91goHnzKzzzk7NAB9P2yuAISRgHMQ2VBk2/l/W9SPzxFhzxjKvDUQmgmWzUiCkIQEgDMGKcMqaW9ftPX3AZy3yDNsTUooIASIHRM2mfePzKwFjm3eycVbvOV5s5r9usu7BtLbEfpB0BnOQvHEGuBacz6+oH1ZIwYa2CHxhQzk1Qvs9MaMoP1W54ajoQKTKUgRkk5qpkZRsnHNC+m6VgBECmArWKHy2OBTQUMG0COl4SDhOB7x/fMLxcMK7x/cYD0csOWLOBUNU4S0zCAWHKWE9i1ExJEakAlRJ9A0hIK9XrPMZlKRi4zROSEPEeHhEHB6QK+H1dRZDtTCW64rL5YxxkOja5+dXzOcr5vMFl9czTg8njFPCdJA0qBgT0hhxenwAUUQpFZf5jO//7d+QhhHv3r3D8dsHUBpBSbh2QoigmVDLCoSIFIDD8UGJ0zVFY85SJVZTG5gZMWRMcQDGCURSES+flLPEikh0vobxtvj87UTMvu6XTQMPDRDRkH819rh5UQDzvSabX252PrpkphsAo92xx3z6/tzrtd3bHM7uZPzOXff0w/40bQNEoD/VtGvFAO3f3IyrL/W7uY/NULN37ifBlGH/EgRomhv3X9/9sL5ow0S2AKD5Q8yMELu2HJwQh8f4qdzLt3cwFbafJ2yHwPUb91d8oc+4He8vKfQtbMxvyE5/tRrKRP03asbf/7iR+FYfNnL89vvJRf6/u230MufOg0lNKxnv11J3z/4xDV7Y9mkDLN7pV2+suQx1MrcBelhP59eMumRwLmhxK3o/tZZ7+dJdvHMw21h3gtutzZ1hvR/qL4y9Gej9GNwbm/2nd54Aupmn7so3uvClud58ub2+NwB393yxx53vC0CQi5SAcQSPB/A4eHEK2kx+Z5O8sdz2z7VVcYfJ9eZ6i9Tqn+hX8e0732nh7u86d7hXYr1W9ue3dGy9g1nTV/lm4kQON73c/Yv3w+ZKvNlU0hNPywN39Aa3oykFiSDGLthTiwF4lOJGJ3ZteLTLhoi6KcN+RzTQ19+b4DbmFlBgva66I+h7PaM5S9RCA5ghNQm64IEeqDZZdnxJ17ZRWZmCYZCC3F16LwkgySyRsq3KdNAqvwxoMZu+sIc2ACotsnnlCpBG5TWJAMiKQmmESNWiOABWzArQatGv3unqgCYDzWF9c2nQMSJGQEQINvY2XYQKifqS4QuIbNEr1ddQXrMC+hKxyB7dY/Nr8kAuaqVkT2sEG1DNrVdsTn2/mht46IdrwSbOCrL4zAO+xpTrT+1/ilEId7g5+L5jc+36Xdt+070LusN5sK4nqHhZoRCTPQhnncmWgcVJK9Qyk0QbBtnxQyTlCSSX10Di41IAjpVQC2FdAy7FIsPleTEIEFi4BxvaXJust3GQZ8NtDaN+YgABIcgBhHAeR5VteNQUU8foguYYG5+wjaPJONBsvghCVfm5zDP+9fsZFaRcygaoiw9I0YpCwde7jK3KmM4z6wGOADKd9ab2cSCRl63tdGuxcDdOmy/1OrdlfE11bSlNihe5JgKgtAZstozocgfPiACODYh4fIevfvsfMJ6+wnx+Bq8LhsMJ4+GIslwR04DLj9+jLleAVXabyQnbBBq4au/Q6fjeT7prQiign023iBbytWD2i74ThYCgKtpsIyKJZKweCQmkIenhixwU5FwkGlWjLQFodKP4jwThi6Vo2Q0BuS6opSDFiGlISCkKBcLxQdOtCSgFl2WRqFE9pCGSdWWAF0AOSJnOt3875YkPnYyH8WnaeJqutXTyLYYhBwJmb/qe0e/THUDYpkYG2CLrfQ/XaHrT+YRWPDomOdTiwMJTDdsuewqSdjgFBaekF7KH9bZCKQW5ZAh/sn6nsmCHTMyMWMVZ46793ibw6GKyKPku6wOQiGkrrgc5ZBNATfT2mhcZ6u7g3XlOq0S9MkN1uACmIUTJiq4BTvlDja7GnuOHZVQ3774BTmtflMv24IJcBCAOyh8r6fgBMSrFRpTxbNymbS/jVF2HWhSttcuVwIFRoAfIGj1rXkoMUeyenVzaehWtGAAFPatGqbrssegjsz3tICV0h6fui6SIUMNmDdVOKYrs2ZiJnASS/gWN4PaAlyB6gNQfIEDWUgwa8EWwIpJ2wGOesK1VkbGxrUlADiG4HX+VnPVdFCUIZi+26Oq3Pr8SMLb/6MbmSrX/DWQRewhzp8X7EXIwTJUybPM0UINwns+Y1ytiEKoCB7B0EzTjvjnDAQOAQgEZWTefFtZuHyZLFxMjyzclA2C4KRuwbi5BQNMVC16OfwFRAE+MnBfES8KyFDw+nvC7b3+Dv/3jH5HGA4bhgNfXGS+vZxyPRzydHjQ0WqtCHh/w6XshEB+HEVxX8Cqpd2kIOF/PmOdX1CK8Xx+//g5xGEFxQK4Rf/7zX/HVB8Lh8KCCayH+suMNIWIpkgaQ5xXX8wXvPzyCAcyL8Ml8oK8xHB+Q14p1XnC9nPH6/IyQEmoF0vCAh6++xvH4gFoZ53nFnCMCgKJGYhxG1FJwvVxl40wHfP3dt3h5PuM6L2qIAynOCIFwGCfkWvB8eQVOBfSg6v6fCbZDVCJEO6UlbJ11AJYSIEo2t43KTm/cMCJN46uoRWXF0C9Ctyn0rofFX/XPU+WLZrDKfWoMfyHNtwfW1B2EddAVUbPb3CgDWC1Z8nt9V3tDZWyfr2vUnts7CN017c/tZmmfqtxNm2+1H5YaBqIN9tbbn6DuGf799lm3I2d975rQH1hB1/08SOQUd+uZmwOOPn1cx9vuN8PHjER7NmPDIeNy4RsBacRee9X7ANp23EQ1Neu4Tw2VW25lqX9XS7/bD1p/gGHyzLv777V5v69tMtnftj20yWn3YvZEs8i9ybbR0e769mzytcsKPNh4bvrOTbisV4E2cGrbh/RTiTRATh2IZUWdV4TCkjJt6WO0Xf03cr1t9mYMLUrH3mlvvNn3zXTaj143jncWxFvAeZ/GtdNcXX93ezXt5+/nP8yM/ROaw9YDI926pnZv74h4P6w1Un7UYQANAyiNiOMEDoRqBft6GwK3mQtvHyz0MCV5Wl6ndPUa9nRje06bR5sXamPgcisXmw1jfTGAgHezK/eaIdqvLfmlReGIw9Hd6/7GvYO4tg/1ETv+emgS4P21d4TqI71PTLi6me9SdE16NfPWflCD1h3z7mHmCEj0jR3E73RPv0f24JqmohNoo4etXYECCV4sB2pcVzHbxYRjN7RlfTYapFqh4A7bwMt1VW3M0Dvjaqeo8xWDpfoJpyQFQrE9lvU+nUsJEGjFfVLsZ14duQqN9vNZQl7XzlbWee9kyVIymbX9UhFiQkoDCMB5Fc5D0j2KK3sBWpFrq9Qg/RancWi/4yZXbRDk2lokeyznjGW5atpl8KgarnCqAoJx6mrEFgegbG2E7VZiYGoB14BCweWolz1zFKVpBoWkBzcBFYy1ZqAa8NzrO5Fq4daUrDOv6k7KjRhJnUxJM5ZxaPeTL9e2H/a6trdXbgILjEeWIgJJOuYwjnBuakjEayQBU2IIGIcBITBSJAWXGDGwUBQExjQQhgQkIkRElALkSsiVAAQFgwasJSPUjFwyxppQzI9SRZBzbm5QIBSN2LZ9vR1CAsIjmQCuCDX69+yUBX2dA6GvoBAQgnIua9R640xmlaFBpcX2TN0xq6z5SKwYscy1rLWOw4bZDx8s4p/VTiDjwfT+GbBSNCqx2boO+toe4PaJldvj5gubzUZC1mJS1pkEbo/qrtFkI+jeoe06Z6bKrejXjvovRLz/+m/w9PUfwCwclZSEP3O9vGAYBnz603/D/NP3qHmG20adXS7P62SYtouQ1LZtXLKqQ3qfHoS8ZjncrhUUJQp1ayTI+ATdD3MRztAYpBj2uoosDikhaWGtZb46r+PxcMThcMCapdDWssxgZkzTJJmdwwiGpHsvlwuguv/9wyM+vHuHh+NRq90H30sYwLoW5EIgijgeJ4+i9mJbuaVpewQk88bWGsexRf6GcMNtavvnxhatFVEp/iSFGmAuaptCSaKbTnFe7g48G1JffKrnwpbnlFIwL7MXwqu1gNcKJOheUXG9zo7h9HyqDsCF4OnsotN5A8g5Fy61EIpahXtX7AV5blAAuqcIsHF18FpNMTbbvuvHMA5NLkMrvhSMfzRNwjnqkb/Bx8AOhEtphcAqC7hZckHmrBHNcpjofKahB7/J94Zpmtpe2Fa4vEfRtHzouy4Zl+vV9xBbI4ZfyR7Zsp9ijDidjl6ELiQ5TD6ejt34VceljAt3WWU9ZV0fwv3bqDpNlwj3vETsDsPovkIxO72TpXmexe+xYDlqdqhhb0SEaTrI4UmMGEflxNW59KJkepi55oxLvsIiUodh8FE07tZxGJCS2WZiWwgHs9pezDhfLx6Fy5VRqmTISx0k2SfNdzQ6GWJGpIAAic4vuagcVKenMN7aL/lEvxIwljYK5a0Oywa2dRLYb1BjxQx+E2S/p2u/VszlipfrC949iKGS8+oL1k4sVlXwtnEJFw3pqY0opABTZPCN0CI4GBUhFIRgyg0asbAj1WbG68OPWA5nAW6qnMwMccD7h/e4vv4Zf/jdd/jtd9/idDxiOj0hpAMqzcgcwTXj+bXgcJiQxgN+en7G9HTC17/5HcpyRuGA77//KwDgMB0wDe9wGgYcv/kGrMbE4fQe0/GEEBIoJgzTiHlenZvj+O4dTq8fML9+liqGxHj34UEjWsVQucxXDNOIw/FRFn06ArmCS0UaJ3zz4SOevvoNrtcrpumApw8fkUtGCgVpGnA6DQhfvcP5dcXr8zNeXn/Ccr3gMI0YTgNGihgOB/zmb/+A95eKl+cZP/74gucfvscxPgD1CqpXxDjhNDzjulwx5wWv6xnpd4z6YwDOcgoq1k5v+HVCtgNyYkziXEdxbvpLTc42ztzPoRCdA7QPzaeNMv6lHwNDb8Gc2q+X/heqDAHuigbcttyDG20bt3XiTbVK1Pue7RrtT2CBfqTbT6xz0/sYYO4KH93pp31Pbd3f7cc9APON3piRvAeQTZvswZq+Y3clgLDhTLMvtxgQbd7PiiS0LvV6km9+BmTOiQnNtqEbOfslny9F4NrvyZ73M9duge1uU2Lq3q/pxjYI3P1RZ1KUut1+Z0q3BkDvrHohKcbPyEL/dG6Tvn//IM4RVQAlAzkD8xXlekVZM1BuKUJ6kIDuSvOdPnQgmD0bd/5t773pp/55m63oy59fFOH8/9PnzjCjn0/RU7zRoe7Mwhzc/ZoVIYlDBKcRw3RAOkyIcVAxotuH9u/LTQL9kdj9wLsv9id82F5jc7pdw3ZgoDFAFUDHJdgcNele4bqbe5fWjf1z2w/WKAEDZb+sF0z+BXiziMvtSzO3nyUFTqSuVgZFQgUpD6f26k5Ue2UGF8aQOtDIIkEUTIGCHp0CAWC8dzs7r9OHqMWdOwe5NeKDdf+MFGAUCTKHUVO+AZvkmpvToEOpe79+EQioBRYZ2lmh8JWoY0CswQEgdZYZsIPJmgVkzXIoQEpj5dGfWtxDO9BREDDW3FIlW/o/IYYRLYKWO7u0gTgeKSetOexDQ0TQSuWWbj4wYFWOrR2pQaD/VsBdWEUDiBMikhZqhBbYVW5RdYxiCAha6MVsgEAR43RASoMUpwlSmMfXPTeKgI5qTv507wL9mSLBiyWh34/aXsPMzgcbSIrxVm78cbIEyB1dKWIC1fG0W7MytlZwSOS1cQhSVGDE1uMbun0TdUwNPPOIJ2bn+KUYEUJCDEMHxKqIhqgOa0JKAZEYX398wHEKGIeAw0g4RCARYxyAwyhyNQRGmBgxAUgB66bwVpCUzBRRSkDKhKwFNy0KSiLqFKyoUvCIEFC18ruBk1avzhzyXFavRi6ACIBS1Alf3clnlqJBAj5VTYNuxbNE3/kwwOKhVGDVJKC7PMCWQu7zWqRojxXCEk7B3p+IALTglEZtiV8Y/HmuM7hqQb3+w2C0AjMMO6hZtTiyUnoA6rcWBakbZ6Xd12lEVADXuQhwrHqoaOalRCFTA+a4geRYdX4KIx4/4v3v/ogf8wXLcwby0uzuNzbGQEbdYnaujr8Fmuy479vPQcZO75VCf/A/xu+MKsB+4YohDnJYllcwCKfTgwffrKuMzTiNHuH446dPyCUjBims9fDwgKzp2+fXsxTAixGHccLhdEAcBxyHEWMawMyY5wWf52ubQzW2ruuCXCSLdp0LoJkLQlEokZVGf2AFfno73SgMmSVN24pm9XQGvf1gqecNpGIF33TcYDzELWu0TVXTLXvQNGn/TD+FGHE8ntqaItpEcFpEqktdFUqYHnQ2Ts11zViWRQsdJX+PBlQbR7RFlJpupc14mb03DAPGcdTn9hRIpJQ0oa2pzie0/Wqe5w24K0FWAJS2IMWIIbUo8qh6dhgGMyuaXUXNVmPu3ytvuG2FaqfidT1v1kDOq9PolFr83QX8jHh8OOnhU/B9uI+iDRQ2IPXlfAaRFCGttTglh7Xp+xjETxqGAdPh0PVJ7TduEbt5zVjWBeuqOqoUCVrTNW/PYDZZHzGOAwzY9oNM9ID6iuv1itfz2XGGaRwd0CQiXzODtm9F7DzThIUv2t79er06PY2aWRiGhHGchCYzBBAXPDycxAbpDlaW64I1Z1QAy/WKWQvvBfUpLFpYDheiY2JmK8lBrdkAb+M7vwow1k79yP9tYb29wX4nUsWVSaMDMFvfTj3Nce+NFzmnLXh9/QkPh0eMaZR0I8+YI/87l4pQGYEkHb6vtuZcU7Iby+ZQLTqj45dltMnRd1mnM9ZRFx8IHLOn7BAFIc9PyvnxzUdMKaEsGeeXV9QakA6McUr45vgOgGzMaZC0hOnxiOX1FWn6CggHXC9nHA4JOWdM0xFPT494fjljKRUxjZiGA4bxhDmvEv6eM87XKy7nV5QiVSMfn97j41ff4BMLx9fxeISlNS3LgnmZcRqf8OHDRxxPDwgx4eXzKxgBMU2Yjid8/d13+On5J9RPP4IZmOcr0jDh+dMFTBcx8McjhnFCGhOGPIGIcTo9Ig5SkRchAiHh+AAcDgM+fjzh+8eETz88Y70+g/Oz8LUg4DJMuK4X4MpYy4r1PaOOAH2WMS/oZMY+4guLY9bJVIyhAZsGqlQNhafOiGDe+Fw2//Lr7hp8GVBxGTcnrfv5/mePCGgn1MmQx3dO4wYQbO77poUe0ND3sncVo9fevRGtt2imLp2ye+/95im/0LWtDv4+Aq8durQ3awPSAnz9bXoAmqjTLbfjR7t7bJ7Yh4t8Drf6yH7epZNtetd3mLaDi27ON381mXsLhN2/2/bZvEm74cqevvRzn3205VsgnznA/6MAXZNl2s5xB8iy/18cwO0jOpn1rtHdvgJww3QnMZvWQLSbTXQ/2Vi0dwbY01rk2fJ9LQVYM+q8oL6egSw8TKRpXHhjrDyHg3kzn9sT8p/XFVv5vfOeuD+n+/u7J7Yequxv9VA3Zz8jBi2SsrXX98UjjmkLTTNDImW6VHNz6Gw57d/nnswSSYphHCbQdEQYJiANqASJ9gudvupfiJs07kVo/8pFOUq5Kfvdxeb0wy10c1xb5ElLe2cQJMXQUvhC01/+nB6UVMfdZNP/tscqx1rPzQVIQctu3C36grt5QRWM0WwrvhEhe05L7SqlOdO1MmIg5/FkNjtP/h1ACEnTTLvhh//cg1/yrL4wapPRtpJ9T7b9jy31zNY1IQ2jAoLqmFIQ/lL1ogRg0n5qx2WrY+3Ddj9lndvgTiKh9PYnNS5OocESO6NURiWltqKos9+AUMAiUFID9NwU4W5fM6cqeepiK0K1Xadmz7ABpoH8HAzeHhCVw5UdOGlTLjReFgko0X+k/QcUnApC9SV9HzwyVsSKPXKEhlEPHiNCateUwhjHBujZ3LW0cfkqpV3UCbM7ewY19/ubrQ9zmGJI220d0PGDO5alCtecACmM0Z3Z4M65F+YiApeKGho9xP5QRbphHH0tSrFF0GztpSYHNg8KVtvPOsmBNP02DMrFGBSkNsBdCycxBLAMhPPrFeAJBMIYA2IColIsVgZykUJJuQDLysgrVC8ExABkrAARaq4oWepM5Fw8RTUE8uhAnzd1uCgEibgNEYwGWFh0FhiIbDx9Eu1WlY+22WXUjUlQRgmWR3Tgi1VAt0lumQF2HCFtVKeugAI4Aes6+7zYgYbZdqUWBcLZ9a1EHYuuz17EpztQ03VSa9E0Z+oOi5vcyGsYwFYxjKMfjFTnzbaIvOx2ubyHtC81SWQ4lpJ9b7Co1Yysc0RqE3URjSiaFQYRhkR49/u/xfL6DKoV8/MPAJut09lo3WJykIjaGPv+omun1lZ8jDRqliokSr4wCsN5iZ0jGfwV08AAACAASURBVLZnmc1MClzJOhnSIBGvtYKIMQ4jUpLDnHUVUDKlJFGJUUCY6/XqPJopJRyOB9GRIOS84sfPn/D+6R2WZYZVT5+XWceLwMSIlbCWVewCSL2ZMUSNLEyIY9B9oY2PAXT2Tr0tbiBsSzu//TNNk4NfgKztNWcAloUbNMWcXf9tgHuzrTpb1ALPfCbdH2r9MYDT9k3e6DeZS8umsM84jpimyZ+Tc5t7K7Jkkaf7VH330ZhvQM3t+IXGmarYivO9kkRxxiiR9xQCxjjieDx2xbZk7Ym8SB/XZelS/BmlLMj56q61zYUBxU2/bLNbA0mwHWkgW8kF4zRiSIP30aJR11UOo0pt75qVKgIgDaYKvpf7nqL7igUSGkjd1mAfjS02R17zxh4HkY8xkYDR4zjpvEfQQHrYBx2T4mNjh7xmv0k7ixcxJf2/A/dq143DhCHp2Jg+QItGZmYvvGb7MzPc7pKDZ5HLFI2PXvqeFaCtejDIKBLZXE29sfDzcjucrsr1PQwDOArYyqzn7pDDZpFFlsKRaDaB9X3v3937/CrA2P2nbSb26YzeJkc3xpM5Cjt3zNuUv8lTIebrK0qewaMAixav2j/bNyRi5ByQkolROzFHhCopIXuWPVrJpaEpdpSB0SJLgHW8IE8XWC1SSUtLznGSgoRVH44jECTMuZSKeV5BcUGhiIEIKY6QtClxaIYh4DAl/HXNUkisEsZDxDhGOYEaBiGpL2KYAAU5VAwkofLrMiOvK5ZcMF9eZXBrwTUm5LzIBjeOIERYKk6oFbFWjOOE08MTxukAooDDkXE6TcglIKQJgKTsDlGqgM6Xs4TzW5QHgDCccXp4BLgixoDx4RGnh0cMhwSEgOvMuF6L1GGJhMMU8e2371EK4xUrltcLQhoxplFO4bnicapgYqzHgnICOEZcf1hReEWlAqrwRDd298aMNRfKDv+h5rTvIqDM//Mscfea1Mi+I+v7n98CTL70sQ1K/Xz4miH799tKwJ/dvfdt+9S9FPlG40ALPMYAN0uXWxt7QNYM196p/XL/bNtozb8FwOjF7jxvh6HNp7XaxqqBF+5kb0ej+6492+agvQ5th32jm+w5m8f2HbrzTh1DGu16z+ZYkL/LTbtvfPr52G8Y/dja5monhvs2+pNm3Gnj3tz7O3SRdb9AFN783MPCtr/n7cVdalTXY1mvN4No5gNADngToKlCWFfwsgJr9qi3fs7d7XOjspedLVjgTll3zy/SDXz3n79g9b/RXLfH2gnv7TXN+dt+109kd9jD/drb6b/ufv/Q7Xf33qe3G5qukGiKkCLiMICmSQp2EfneLsZ6BXqdse+fGhbtAGl7RdEoDJG/7by6juvl3f4iU1GsRbGwGUvmAKK6yXDgakfNxV4cdojddHNLq90cVHd7V4GIf+jkzsdjP7b292aIelncHpa72OzE1Sl3ukgoi5Dy5zugYS2TRsvZ2qM7YGxznoDGGynAhvSupWmLkxHThKDASqUq0SUhqjEt17C32XrTHCr52udG31XSGpUTUCeYNNW56U7hFg4k/GoGYcqAtdFtBj0JV75WQd/MDbODJRQktVtAT42gAxSUac5sCBHEVXAq3ccROlkkgCgKtQc0NdrGw+ayA5elXeP47ceMNOorCUhs0Xzo5kQLbQgYEgFqYDal3Ty3f26+DwoiuV7RyBWbL9LIGbNVbKMIJEBx6MBYe3aMFrlj880qWxIxZfPs/oCBqgawEG36YDpxS/uictvZNFs91/HNdW23XnW2iNliLHrIDm4KFCjRNVIzo8aMQgA4gGLEumSsQ8KaohZpsyg0HXUitfFsDqqDjV4FHGYHEioHVBbfB5r2T0SaCpsd5LHq0i26KyAlGXtL86y5AK00nwMIBpgaGGnjK4cG8r5Vx74BGVX9nk6mmAGuLXOEWzCPREglEDWwx8FPLn6/zGltcs9y4MEKflXll2zXACADmrICkRGVg0S4dsCSSb5cKzyZRAATefE8i3jPOW8O3KxYTSXlWKZ2+AezGZUapzIkwyc0oiPzfasoOnm1EHD8+B2evvk9sMzI1xcUrVpv9zQ7b2fHqS3gNDpmN5LtBT4F8ndloRLWWi2IGnUH6qihHIr1xxAsVbt61kTsABLrUwjGF9vSz3196sFWjAlrXpEV7F7WBdd5Fm5REk5LidBuPtAAo5/SSL4ohaZjDLLHdHusyU8PjMrYbe1yiwa0cXKue/19H+lIEH3eUwQwWwRhu6anKdi5KjDAtXRyb+33XO8OslOnB2qL6gahHc76z9UD1AD4u5PqTM/A6d7vnp/SuFctKrjZdLaP97qidnoi1ojUPcPWd384bgf1zHrg56n1siZLJVCxWd/OZ793cL/uIfuvUOqIHFRmjzxOyVLzJ+S8YllX5LwqNYTOBVUEjhtbzfZ3AY51PNEBs2aTRNKx0gj5aFtD4y32d+neyeRE5N50hoHy7bCUCIhR9iXHdQL774Ao+1O1QvZysEUEOZQOopvs0NBkwXhgHdQWIXUZdL0GBYXVHgrMHeDbopaRzaKEyorKrirDWqtjgiEE1/d+uAjZ3wIZlZMWo+syVZq/wP1fdz+/EjC2xQEAEIVvjlXv0DWEC82zs9+1llTXo4E8zcHowdp1PmOdL6jjSSdRquUSmfkDD0euaBUa5YRWN+ok4cl2irtqRJSd7oBYwrjHM5bHF4QoxCoEOx2JSCFgHEYMg5wWCQlwxDiMmI5HFGIgJhQGgqV1zSvWQuBzEQOnMj58PODD+wMeTyNejiM+zzMQJ3x494QYCvI64zov+OuPn1G0cNlaFsxrAVPC09OEumYs6wVUACoZKSZwXvDpL3/G6+tnHI8nrQ5ovBsFjITxMGAaJoQ4YlkLwBmPT4/4wx++w/PzFc+vV/z4w1/x8vwjDuMAQsXry6saSbaZBqwl43x8wOnhAafHRzw8PuJwmnA8RlQGrtcFnz9fUXJFCsDjKeI33z3hfLlgvUacnytSIDDEICMEPB3f4eHhqOAsgN8N+O//249Y50+S/hQ2ISGi8EIzygE0XsGN4HVAixoiPThJfgVv/uWSfrMybcNrPHJmsNvpkj/3BpTpntM58+bQuQMCS/XtokTuKA1rqDeq9paSKU1Tsuzj8+VPD5rIptce2yKX7n96IPCtq3qOXb4zV5u+uAdmv++MpMq7d+5Ai66F1jr5j0YSbgC8y3jfiZ6upHOogMY12I+NAxLdmNlcy8+6oXXtbqtKd0Zyr0fvfPaAUg+SdFft7unYSv057dpm4Ox40NyEtSFqd/Xv2J5p178lARZ118l1N0bbzQPmO237uvuXrcXtsiNvKq8rMC/AsmrAjxHIs7qQ2889IHafptbG4P6/b956tzD6d5IhDGhLvl8X23Hkbj5u1Ex/FTdgis2x28wddyPd7920GWt37+t+lOzyNib7A4MtuO7LFG2tsXDNDQlxHBCmCTUlFEKXtmRgAWvfOk1gekmJnzdRbX4vb5yZ0GVVuBHrLUo7AkC2NeiGKTQK1fpBFbUSct1NbjfG2qC0wwxiaaOBBHAD0lLbzQGguM064K7PVngIls5tm8DOoe2dJAMjQmjRAb2sm1HMWe5vPHGm9xjkwEv/jNj+bX3rxqBqijOpAKQN7509oqXsSyVk4SGroQMQKDZr1NS5jUewvak5AEXpHhiq8wMhxKFlQhm4GwTUbM3JnAUQostrkzvWAin9/m/RtfC93D5qu7qsSbo6s4BYrfZIu6eW4lG+fboq6/OJCKPx6dl9xnWLJk+8P0BQ/U46l4wWzSnyIWCY4jpgALkUAX0ZwiOJCkAK6qRhG43rexH3urkqcKodYQDURaSChPcttPGvlZUjcECKA6qROaLpY+PCBdQfiADF4Kn2qC36tj/8Neff17j2ewMCqs9i4AGhKp90bOAGOv1NsXt3th65E++6R2UzrxkCsjNiYqXmYoAraq7gQIgcNSJ4wBgjqqb1Q/c6OagBYiAki1bQv9dSMY0BBRL9fV0ItRIQE4gDQg0SGVxXSc9WECSvAi6smuZvQE8MEqk9etV6ib5a1iuul6vQhTDLM3rgh4unnveRyQ7WaJQkr+InNd2m1AhVuTs1Gk7MA/IUZMQEq1rf2yExEpZFI3gV7OssR31GgBymybwG1QFsUbcMfa7cHyI0hdzA2AYKAgZ6q6wwAazR107R0QHS9ocZKwWNKmUgSHvRZFb3QagMVa5gKyhHDSxzzUTyZ3r/DT789u9A64rz8/co+bqJrG+6ufuu27dJ9YLteX5gYjabfW/sM6xUNCkq6YnoCyvcx6aAoanjmnI9X66QCMlBUpoBT/9PKSGmQeguVskKraXieDhgGAbfx+d1wTxfvdBeGkesNWPtKGxs31TxAaUknK/BeKIjova31IpVuU17cLMHAU1XWuq4c3OmtNGn/cdT66sWaFJ92iTSEJFmH1sbPVjVdA75HBn1ooG+ZltYFGywfZ1bUcKcM3KR9Znzgn7/KetrB9QpjQ0pOB6DR4yS2ULUR5u2YmUeCcyQvcd0pNpTlbNTIvRRtHsAvLeV7GDI6ABMNi3SOiYLxJDxnEYbsA4ohB1yQ/e7ZjNU1UPLskhUfK26DguGYUFKA47Ho0QPHw6YDkfM1wsIErHPUL5vLahmQLPxqJZSsCyLtg+f/6jBgfJ+IqfJbRWZd6Hi7A5zwDfjZqn/FkFca21rjiSj2zJ4CKSHwzZ3ZpNJlH8p+nc1HbaC+0Mlk3uNKLf9VqgABBz3yGldA7VUiSbO2Sn0nAZEbTTvnx0ChwAQ66F4kj6sK7KupVwL6pzBpUIy0TUgIBoeGHxd7HmYxcbq6Ore+PwqwNhbf0+MBnPgBUgysnMG/KRY73bDjmADBRRB3Ll/ggxM1X+uPGNeX7CuR0zDk4TjK7+JpRoVHVAmQgwsRp7XnEXbMHWDmNLUbdyMnz78MwCZsCmMSDEgxUGiPlPE40lIwtNwQEwDQIS8LFrNsWJeVkzjCQAjpgHT8Yh1yUixoi4rcllQS0aKEZ/+suCnvz6rwSybdgiEz+cV8+UZKeopMUeEOEAMdXEwrufPqAsjr1oUKySkAbheX4TzNSYEZOTlFdWq1RXG48MDpsMB4yRA7OPTE3KpWJcVy5zxj//0V12AFVwyIgEpBczzih9++DN++vQX4RghKfBwOoz4+PTvMNEILBecfwq4XM7IHx7w9HjEv/ubB/zpTz/i03nGdal4fQ24roSffvyMZc04nE4IqHiMAwoT1lWM5mUWzpKv3r/Hf/yP/wn/8PG/4f/4h/8df/mXV5Sf2gIhBEQkNx59Mt8CJe6gFe7QoJ2wEynj5R0wZf9NX5jgbezFHGAx1G7B2t3VqgDBDA4BctzcLu5WCDbACcyJo24YGEBL45LNUMn13Silu3rHDYguPUy+ZygNXDNq+3xY5lZvbNtgu6Q1d/vpCuM0c7A7VezBqX66t8O0OQ/aurDdOPU3aN/tnbl7unWm5zRr/bNbG9BhHTJbtT8JlGt6w7kDVUJwA8yvvfvet5GPduLM+j798G/72f3w1lqBGM05b9OY+lkBdxQz+gWzvT/jdoK3sto60IwiP0RzJ627tOxus77QdiZsffWOnn+PAi4ZNa/gdfW9inRgfB820d8tTuZ2ctuDpW+Bk1/86Dv0xnd73yYDb4Osm57t+vk/cc/m73ZE9UuaaqfcHU+3G7vbFuxk29puSzAgphHpcER4fAIfD+AQxZnrFrKsebppk/fP6U697SmBSOhzSH5vHGobw1zBNoYWWrLTeeswASDWtF9xAs3Ik/TV7jIiBS1V27KkVgEWqRYcPJUMNO7SoGGtiJ3jg9Y6w4F6leVGcStUZZE55E51Pz/35lAGIYBiEnAMYZNWaMOgHuQG4DLjPTgY2m4wp3LThutTORBxxx66tzIhUqPG8QgdyTvr3gVaQEjtUVNRLICEBHVK+xTFCQmUNIVY+ir+cItKKVVA1TZm96PEA7UUeUBBEgbAVZww9s4AAIYQEFIE9bQC9tYEf37v7DvoQ+0wYaPXjJOY5DnCvatzSuZwSGEi63kAoWG7Gm1WgVwymCU90SIgJZI0eBRkqRWlrkiUkKJERwYiFM4oVpilVlCM7lTKepQiKqxciDLuLTKLKGAoyTlErZ8N1AhQpFXvbfLTz4HbCnV7yGFympS6jIh8XW6dcOHps4IwzND3yiBo5E8Rzz5EmU8gONBhzxR+0tLkiNFx/WqkcRBKLwpROXgDKLDwNsMAzxFDShjTgMN0wGkccUgRQyShKYjAkNqfLEGuiJHw4d2A8QBcLsD5GjCmgM8LsGaS4l6ZQZck0aBseVMV83wBxQVRq6WbzQMIgGLcmAAcHCCQRnrrmgwROUSs6yIgQ69H2J0vaYFkrI/HR49O5ZplPRlIXAu4FBTlbl3WxdeM+VKAgevGmRxxPCaN8s2wg1eTFAnOWWVuCQihdmswiXlcJbtQsFxtX+WOySSONHJbDjmWZUblisCARb6n1Gwjj2rWIagADsOAXDJq97sUBXBCp6dKtTWmK4Ag48edaURCrTKvK66nB+Svv8bw/Btcz5+BmgFwe3ZnB+1tS2bj+VZNYb/vdL7ojiKR0blimMQvE65hqVpPtci+qUC3gZclZ8zXK8ZhxDgMsMJBXCoeHk5SEAjA68uL0OWlhDQMOB2PiFGySA2kr1w8UCoqAJbX7KCaRQWmKIcbwm0dfQzqumCZFfgzfZ3+P+bebMmVZLkWWx5DJoCqPXWTPBzuNZpJJr3pA/T/fyCZ0UyUrmiXEnkOe9p71wAgMyPC9eBDRKKwu5tmemi07a4qIJEZg4eH+wr35VkA3x3I2g+MapUUdfNDzR48n8+SYl0rivqJAeTrf5pnj0ptTQD+qP66AJhVCk82i3JcdR82yRW9aMWNQjB92A+pDQCNes+oma6dnkfA2UMWeKnUDTkOUbu6PxkIvm3b8JnIwfW6aCQ5AH2WpZc7cK3jBrUBouMIw/6qalEKSw3A484A1gC8QDrmQ7Q7a2G4VrFtqxwMGRZl39aMCwe2Q0SK0TeOlDOmlBVMJAfM7ZkxBqxl9RT82gqeXp7l8DMIWJhC1OKHCuTqYW0IPfKeAZ9nA1VtLRmIaj+Fs1z2n6sB1ZDocdN9OSaE3IFUywQ5HAbubD3MYsDXBQFopaLxNtjuJi97ntpAhKxodo+u7Xud2MuM5XrFWTlkSQ9JaOivHb5P04R06LDmOJc27sIF/SpAbulzGaJyAk+THN7kCQlq82u7tq04J63pq3UrfqiKQQ6ICGnKvi+/lbv96w8BxvqKgS75MKHzn0kaFxiS0k8EsnQA1i1IFZGf9MFAE3N4LF3N3RkAjMoVz5czYnzB95/eIUVCZXMwtGmhc6yI0DMCSeqQLKzmRlfjipf3P4I1vDpFwvvToxAWq+F5OhwQk1Sbo0CYZy10pbwTpWzI0wEUZJMvZcWcMyjICc3L8zOWZcPf/tePCDFj3SquLwtSALhtMC4jWdQdjJmnCWma0VrFVhdcVz3RZckBaXXD9fwZZV0QA/Ddd5+wXK9YlhXrIkpouV7x/uNHzKcTKB8QpwnPLy94eX0VMIECHp/fIecJMSQ0SFXJpmDD6eGEWje0xliXBefzC0AN0yQb05wnnA4zphiAtqEuFXXdwOsMrozXp1XG+PWMda1eie+nvzyDWwG3hpgyvvv0HU4PE37++Rf8+OOPeHn+jHW7YJom1K3gv/3zP+P59QW1rAjHBj62GzxHBGt0mEdY5FsL6ka/69hT38ZYHfybRXvr8I/PGU8v70bIaVj8uBkMvfBrx89vn3a3N2/62EEvUW5javJg/I7wizn4N7caAbgQo1zaGD1RjIfv0U6Jjc62NkZapmDD4HYPLR8BO2v7aLDTnek3J7l/sn/G0M5+BYau7V/S8A7GB1PY9rz9/Mrcj5GYvPu8d3+UJYsY8p7Jq/EbWbjX+m/dW8CH3s79N8eRG6Jnuw/f+4m3hws732l836tsdtDC2393/fUbNytMp46G7NO3m/z+e9K9fuBw+xx3d8b1qHNivLwhJXCq4KIFRNiyMZo6QvvNeIxisd/HVKnfB3721whGyv2/fa0B3F0v9bl1GdbN1EArcYZHfTToFN4DvR1UHts3XrvXgffbeF/mv3Wt94GtDRFpUiD2cATmSdJGLbrQsujGNtjaH/TDOK4uH/ppUMc5DM+2e+4i2Yb7BXS5Jpt3DJlAqmfMCBSbJ/gzxbRjiSJkAXeTPto4wqCgUqSun++N9U63tsHtMt07ABBEJFVjPZJiiIz0Da+PY39mt+2Cjj2NscLD+Nz+9JdhoXRL19LlLpjRTEo3QBbRSEM6+bimSedXgQkIIGH7SdQsJjvEtCihvvdCMod0rddawUEO8G39MKDUAr2NVQElP9gZqk6Rjofzn6E7t30pSLstMsls4ejzZlWeuyPkQLYLEWlRNHuurjeNFjeHvK8/OxTrhSmMk9YjwkJAoLaTmxBin30CoCB8z0Idir/IyQE4BZS6orYNVJVHdNvUxgbAmxbUIoCFj1OiazaNKA4IKah/QAClrns9JZtR2zb4BAE5HwToVT1smSi2JiwCNZD0tXHPlBsBd5OfEEI/QB72ZZv3QAHEhKRAI9B5aq16MxGQ8+yHJkZB0O0i48W19+TgVYA2AQ1jjFrtXSOxQ8A0zVpkNyPnhNNxwjwHpAxQVH0fGYhAC8B1g4A4Zv9UxrpIvUpuLJFWgCv8GIB5SjD8SXRjxRxICyYXrMvV1wXrnHDtqf/gHh1qt2aVAUYExQkpJMQ8K5DRI5L9pvpcZgZFIEfhN1xrQS0rWtlEJiIhMAMhYg5RU1IBsM3naEOKvARAwG6alCbE7M4m/ltjBJS+rvSgLGpEJhgIIXlKbQiEyrXTDmhf9jzfEYOWRsoWDSjfSeh8h9A1nQiIhQQ8BGsUucjD6HtECqA4aUoxYOFzZqPtbL9AODw8ILY/IW1nXH78EfX1qwCy7mur3sDt6z7VlbXX1kirxj8pIDkj7wq2ttYU9DQ9Lvvhuq6wCM6UEopSVIAI03HG1irW11eZSSK8f/9eOWqFi3JZFv8s5wkhWhFnrY7eZH2lmDxyT/S4AFq1baiaIUUgRBKw6DDNXgirKNAHlfvz5aJBCuMuLwcfhM65K7iBcCxbBGJSbMG+a1QpIYrNYDkkbr+C5OyJCESH3f471vSyvY/BPqW+36jO3rbNx7vrIQH5HI/hoRC6gmdm14yRhCMgezodd4e1BrL77k2EUurOFYkxOFA9FukyW6agqC7qMjbqUANHR4Bcxp6RkAFC55SHgXzShjba+2YLq756eXnRva0XafRI0aB2S58+2GGnHVDUUlBRdUyhLutQfLWZXmQH0cfXLUAtayPL+NQmB846KilE12XcGGWrqKV5XxqaUwd0Ww1+wGgcwuNhs/liYi/CeYBLqWqnmP7r93TKDQVsD/MBU+6ctzFGn2ub76rg/tjv0ccygLofgkjBQusbo9PerNuG88UKqvXshvFl4z/ljH44fRM4Ukdqm04Vde/1xwBj3/BumrNyY5AzQO0GmJFvDP+Azi+0uytsA3PHnAjLtuKyLgAkvR2RdhsJjVaUb7gE49la8rPQm+tiqGkRrtgoVQgfTxI5aul4c55AMXs/Y0xI+QhWo5QYmA8zwrZhW+R0qFo6pQpcTFKls2lEFrciabID6BZjQs4JrKdQ8/GIaZpFWOKEGRV1W3F+fsL59QVEBdt6RaubpoBs2JYzuErxspwC6CCng4fpgDQLqLwuC1qVVJsQEtbrBa02pDy5MwN1NO304nq94nK5YCsrmJRAfZpxmGccjkfk6QBQlGrCrWK7nrGtK0AB1RwVFqMiTxloQC2MWsQgESJlIMYJh+mENb9iub5iW6+4qoFT6goh7gY43VkgNAJh91/fBoa6SBumQW/k8a10mrEzghy/66UyeYMp3HnC/b+7cb+/bA+EkG46o6HVn+ntFa9OolwxWE63zQUAYk+n4eGe1npz5GUMaQ+4vLnnCA6z/zQnpffHdkkagIM98Lq7P/X3cfv+r+BEb4Enm119kkeijWBG1y80AEKsbXQH/wagugX4+v383cFR2Pfx18Zz//t9edwDyPtH3pele08b2r+7xATy/kD35932ZpQfed9pOkh+jvNzu9burj2yqBXya3aOTEpouUnaYCkScevGpIK839IVO1kxg2C/h9mzb5ekfe9eu38X4Ikb3XPzgQwX7abgPwMSm0F0265f052/886DUdwbbEAqkaZHzRPCYRZ6gij7ocvVrWiNaLLLkD5r+Lyvyz24ThC1Yn0bx/+NjNlP9XLJ9xs5hNn1UyfiTVaFohwGNLm25HFt0ChGez05ADtgcnqTm4cAjbwQj21sQdGXfmi+c9V761nBUzXCSy0IECDL6R3erEftt8l3k9Q+d9aCSaorcOkLCBqbidb6uIgQ9/UqqlAra5Ma2wbGanEbCoTQkgMjYO6Vv83Z0vE2qiVmaKqajgMBFq01zmZlceajOgQGxppDQCDlKsxKawWY80pkkZkjh6WMAZEUqRH+y/EggyC1PmQczEnuOmlYCIOeu93/BZvZR3iMusP+BUv/C1GLMsEdevi3bvcOkshp+x0KKG+bfFsDMsxIYa8IrrRdjdHaBkn5JuQwKUWEHb5YH9QpbKP8iKMVNMKGQhB5swPTYVMikFIpMIJmlUUFZkIMChCIDLtzqeMc1OPustOdTutX0nXlla2JHLi/fY1p5AYEmK5ySgvSVM4ABFnKCBA7roHQSPbGEITXLwQ7FAS22n2fbWs7Z7Q1SN2JZryUkEJLjRUcAMDsweZq0WiGQECKAc0jvDvNh9l5bHzGb8DYXgiKQgQ3PeAJGj0/ACKkdmVTfSq0C0qj0SoKJRRawXEDKShQuSGy0CtYcWYe5UR1Awa9rUnW+lzhjgUHxMTgliBRtQCgXpfDowAAIABJREFUAEBMiEEipiaE4RCMEbjomHDvqy9jQqbuOwrngFqO3MBcQdzLL0J9UtkTEzg1P0AwW1JWmh5aUU+3t+ftfmKMGpcZTScGv/sTQn5Aiy8OSI5a5b49hZ0hMaqaUfcMnob+bRFp4psLDUT/ck/9t0J33QOwTA6JyBVgzFPuay/AOYKC0PGQdHaRcwPUbe8e+YhFzjrQY4W+rUK7yboVZDLTvPm8wdtPNEQMo5uv/Roblf7/pnNO1NOkbyl9fGYYXtDLAWXs7WNACtjBCoiaTatrl+0Zg5w4wKrtts/HA2pvywBU7cWDOlAHeCq82zkDcGe2ggHwRmHQ56/bnBY0N8paL9opbRi5ewlif8B5dlvnBe8C3m006uC5vTIkMtuQ7hBFxzMka66hoWoAh8klKOoBHPe9U/sUvJqqWbJCw8O657wFozsYOwKDBibbITaz0MaMfncM40EQEI1+bZhr2Y8buOo9dO8mmxcDPNF1GZEdgOm+xn3dG7BKRKDWhHs99ENf67jJlEXYBvXtWH+vdsirsnVLtzDacdC9gUieEZpO7mgj8T6bq9OK2PZ9ywcvr3Et/JrL88cAYwHszHjtnbXbNjrnYbS/of+zzVE5kqDvDwEU6qTE3eZGCFix4cpXVNpAKSGEzkERWkCj6hPSPJ1N07wo4nz4iopNMRRChHBtTXnCYZpwOj3goGCsPZvJjDQCoOlEFBGCRLIcHx6RthUUItZtw7JeARQENXQfTg+o2wZWPhSuK5Z1Q4wBKSakOGE6zpgORyBklA3I84yckiySGDFNhLJesJy/4np9xpQkWiGFhJxEQW/bhhAT5injeJgBBEzHR+TpgDwdEFPCcj2jbCLAB72mtYZaCmJIfvJgp2bLtuD5+SteXp/FMQuMSBE5JkkpmU9I80nGpTa0sqIuZ2zbsyiKEPH4/gOYGSnOeDjOSDHjcn7BsspJzuv5VSsRFsSYMMUM4oblfEZJC07HI4g0mi1ErUpogsJmFe4BA9/N+moazXlg71zYptu3PtaIbn57Pb11Yvtd0Bcy9t/vcq2t4aGJ7smON7JLad9wf87glGFvmABw47R/YxgLc6J5sLN+RfGYYpaCd9a4m1EYdIBYIr154+3HSCXZVHqvOsAxGnemT+xwxt30mzaPpg76hgKT55vBHdrFY0PHa26mxR+5FyR/hv09OrP3QLYdILt7Atl2jsHsHlvwq8DYbwFmnsR0c91oJt6Ljbjn7FuzWC64+extn8047e1/e83NQ3fGrd0kDkb7r37/5jOXTgoIObvzg1pAV5Y0I3OOw/6eb4jyB2BqvwaH56pR2+UAO7m5BbV+6zWuid0hpa8S+Of2twE/t+PxbSAYPn17gH8/xb+nvbevDk73gXC5CwFxmqRg12EGzZNQCdw+Ro1iaaLd42bcv6GdR92Mm3EYi4NZVMCunzs9oPuN/s6t75cEMS4JI6WI3nuMqFTd53ryZlMZdYY5jlKUhv1ac+KsW13/AFassTHAiRG5RxDek7mdMap86602rMxIGmVkqelju5pGR5pzBUB5waoWWwogUqoWnxqLimMQa3RsJXVmLa3YHJE+Hm0oGtKNxR59RCS0AmyRVXbtuA1CDowNHJ3n6Yb6JaLG5HPDgDvIkQTEq+44NeUzjEhpRsoNeYIDACNFijmpO0fT5kJlQUyvcV1Q59WMAUxjuqHqnjegXwcmOkhgVjjBg4AhwEEkpRcISe2/hPoGeEe/B5mdFfzRJvutNWxlBbhzs9qeLo5j9egYU18SfSPgaowZISQAGiUdotB4UEAtkuZvbYhpQgoTUs7OxcdsnNJNuUV7SjKcAkMc4ZwnAQGweERf0OgmqVIvoIwFVFgETkzJo7hlzgQ4ica7Zw6tjr85paZTLEW21s5drVIJ330ZqKWi2jscwVTAKYFbADUCKCGGhkTCYdwaYds6z30pFSkFp1doPOgj1TcCOFTBIhmSrTbuWa1p4EZTvl1yXuEuZzreulZ7JFGPLDKbrtsF5PoJ+o7pR+H9l30/ajX7QITMjBIyypbRWNpUtoLQJLCEW9SUaLO92IEFoaUhz6yQtZmkWFhTwLNFpCmAuA3eqq3BoD6fcB9aP1or4BrdnQUkKq7ZQUSIiMkiDM13UaoQln+BtdiWAiLQiPOQSO2T5tag7w/DIQjpnHTNgW4zDvtBUPs3VMI2fwLFg6wJkuwvczH6YU+31dyZ3716EIrrWpN1DEALQ2kaGKCA2mQdi7wJJdU0TXoAZhHuuifoOmhNrrHgoGW5atq7RKnb+z21WdazpeQLpUB0HbQsi+ptTeVO6odbRon2v9QKLk0PJatG+7LybCakLACvRR7KgQJ7xsDOLgQ6HQEpQOifwPVMbVqYkvr6Agf9bu3FvMiiQvdAJsBCvxPSoKu10JS28/ZAFTrv1r4qC3n3udtHMN5sC0KAzrPS1lTRIZ6KrkYvBcKUJpEt7VetjFnnfozCdTtD9Unj6msagPBmq94xbtla645L3e01NTp2Ea59wYKIkFOH1SwS0+w6s8+qU6TIW2UTukkiaJbOOOf9EEBwJHmeBe/FGDHNE0ACRrfGTvGwsz8J3q9q9AK1gYNYwLU1jZSNap9AuFlj3ydDINdHAib3yGDRQ9BDjf2epU6d/B11z40JMQSkltW+Fb5XAcN7VhnQ2930oDluQgVh68WimO2ZMQp2VoxDmTuXsWcyUd358zEMfLc5Iuek61DnvjHWdfNseG9bqyDhb3Ig3+01BkJSmi+1A771+kOAscyDDwEAkGJNiYQLK0I4KAisgKwkuTUOqHND/RtJK+jkNhgKeMlmIpVh1ZBoDRVC1tt4xZK+4Ifjf8ecTw44UQPef/5bnN/9jDYJHwqqRbFBhUA2W0P3Ywg4HR/w8cNH5amR54cQlHA4YN2kOFcwfipmLMuKmAXcTDEDYcL7jw94ePcOiDP+8pe/gMoVkRg5kfDNJFEeYEYB5JQhJYSUgZhxfP8By7airFegBqzLqxA7bwuu5zPOZ4kWzaFhjkBZF1yuV+SUQZiwrgUpyQKvreFyvWA+vcN2vSBuFXOpeDgd1dmWxf7dp79GYUkfKNuG63JFY2ifA5gr/uPP/4rPn3/Eslx9T345v4BiwHR6BPIJW9XT55iR0gGndMC6nLFeL7heLvj3f/0XhJAwzUdcT+8wP5wwTQnHeUY4ycnxp48nLNcrnp6A7RoxRcL1umHRqp+Hd+/w8fE7ABE/vfzwVhYHZ3k0G3SvGH7XTYgAzzXYgQ62aAmBepGWAWa8ubuJMN/FAN58j/e/upGlnaDxUzOMgbtPt2e7jebO8D61e/zubqzUiPMthLtBB3f0xkiem7vR/he7z/5596A9qKM7Gr33Wnv7Nw0/+/X29G6O4M1v41i++XjAQW5xvW6a9nd4lBm32cnv730eDNxvAR8Ottxr1G1Xgd19/rMvacvAF9l78w35ojdt3bdx11J3SN6+fgtQvjfHwzvUo79G8OHN6fw4eYOgOwCpjfRT8ZSBGYjMWJbNARC2fYv6fXet+pZMew9k3xrH9VvXc+saq689v9HNxbuH+I8wtNne+31ScqspbZxICn/ourdIoP14/5pWevsZs6Qn2/3tgBYQJy6khHA4AIcDOGU0+rYRtHsCdTm257izx/uIV2aIowG4c3nLvWkXMu31RY/Ysb2DPTJHbCErKkDiyMSAbZc2rm0cZEcc5C6j/oybrWSndwcwxCgXXHrUybHoNUBpCjxVFg4UjdEuIxAvgEt/duCqTgftUv47qChOiIMww3crGlolFMuuN+fe9qfWo4s6sNVlUJw4AWbp9uYMwLhDZSKFNFOBOC/uYYDwkFYog8AIMWjxVaOX0EIkJrrq+ObQnUUiQts6DZdESkZkrSFgEbthSNOU7Ki012PeiXE8lbYiRDAENBw1iDuk6vSPQ2GvlAQQNHPE5gkK2pWy9SIZRullDiTMpdTVREGiEweai6ZZX00jIVnt2dYKStmwlRU5RkDTOcnCO0kLpcUMis25fYnFUY5pApwXWlJ2DdwEJD1cIrgkUjFFud7A7EBWSV0i1Boqrufr4GRqyqenZJoDGsBQHlISByxq6iYIWHW8WCZVF6P+sxxsXZ/c+M06G4uAjTLMg94hlVMKrFl4I8Clzqr6VjlFzFPE40PE+1PAYQJSAurKQApImTBNwGGaVK4YzITaAIoSSVQqMF2ApUWcLyx8sQwwB9R1RasaWU4AuDhg2bgpJ6ctoy4/FmluumgEZtkFq0dgjjqNeEi3JniaeEoawUwANUZLEXWaUFpFaQ0pC/hTy1UeoNyyVsBoPJChGIBmhxOiUwIAjrquWgNjVtoM5f9W/2AEzUlpKQCAqxR0toMARkPMGVH3IOOIDSFKRqXqBwk8WVGK8NXb4XJjBgyEV3TUYptZ19x4GAZuaFyg+fXogz3+SpBoc8GjmQMua8XWJOXY9pPByuv+ktlA6oePF477x26vZ4BrRdsUqIaUfudGejAge2vjisp1B6QSBBgLgANsBEnRNmBl21bknDRgSqL4q0Ux6mFMSgmn04Petwp133YZ1qDQGeSclDdWRnndNgf0iISP1A7Mpln4mscDR4ZQW4x7qL2C7SfUbUrLKqTAQBRqlqSFiXwMCA5GWkHigM6BCe7Rg6xtNqBRDlsrXl9fAfToSvs3HqbCQD+nXyNvq6Waj1GWALytNNk+EHZrbN1WB2P9e86rKrjJTq9BuEWt78y844k1eqoYyUVM+iLPNsB3nuc+/oN9YgXLG3dAj8Eo66by1RyUJ+VeNZ/Yx00jtrOmzIck1+YpgQcyRNuXnSd9eL82PbhhdMD4fEatRQ5Bo9kWcMAzanEtigExJGQIVQxBeFCLRSCDUdZV91Lhu42B+vqRjcgjkAWHtgyOLHts7NkzBPnusix+qEFmv4UCK5Jn3NpEwtu6K6KWssiigaCQwww7cNhqxXVZpD8GAOuBs81pzrmvNeULL7ViK9UPJkrZsCzXHaWDCqPod5u/2A8gjqejH2BIQbKMRduytnEPk9uMPNm3rz8EGHsLUCQ0MXrBCKFi+vuId/MjUp6R0oQYJzTIADauKFRxXq54PT9hq5sYagByTDhMB5wOJxznGY+Hg262RXelAIQkRkNt2KqFWMuEv376AQ1FNkAIrcGYPmppfT5tzHoqlwAElLKCQLhcrsglY54nTHmSU7EiirfVgkoFoTBinpFzxrI2PDwGHE9HzMcJz+eKy9cfsVxf8Pr6iufnZ8yHCQ+nB5xODzg+PqKsV+eZWrcN//v/9k/YlgWnecJ/+dP3IGq4vrzger2grFecpglEK6ackFPEXz4/Y54PiOYwpIz4LuNyXdC2DXmasW0rKgg5M3JOWJYVl/OCddtAFPD56ysoHfT0mzEdHvFwOmFbV6zXK75+/YyffvoBDKFaADSqBISH95/wD//4P6BhQlkW3aybGOYcEOYHHKYjplPB8d17OeHUqnnl+TO+bhuIEkKekeMMCg3LesHz81d8/vwZvG2ItUjY+4WxhgRqjIChWq9KoxdoY97VkAog3GTsdsll+Ik0AAVfbPFbbCLdGCq4AeLEXScA5HpZNw5vyD791a8angUMQOpo5JABF/vX7h17HPbfv/cyp2wEZHdjIhd1ZdRuSjNZlIODU2Oqlxoa1g/YqWl/whgJ0Z0av3tv4xCRvG/nWxBstEF3ZiX1e9ob/kQmn+OxTeJk9qcwq2SpfvIIBOogRkzRHRCPhrxFdIe+d6MHb+TiLWA7Cq/MMuwZ37j/r74Gx9Gex8P9XaxH05xws95uV4S8twf4rT17Y+7XgeQ7Y4Zv94t3a/DtdR1g2UdZc7N0ObgBA51ncyr92apTFCXZ9bfxHkzeRZFCokP8uOE35sZElXt3buR8WES8/9wcehuL3iJ76+1c+W935sNGimvXpeLO7Z0Oj9qAyVH7zbkK+zflvRRBKQkwPk2I8wykLL57rbqHW6t0VnwN2fxpKwlDlEo/Xe/rS9PRlG9uHDevnqrrw50W9BS2W211u6atyi5ADgiaDJtR2heTRjQZhyRLm8LNGJq+krUv/km4scBu/XDnvSQgRwHUxm+4898aKjefR9Kb7I+GAkA9SvJtsUruUeS38jToUuPGt+ucp0x1ktPfoEdxGCWAFcFghtNHAUDKygOqeibCnDWNbGEGyKIVabde+4EA+37NIIl6HLjaDMwFdSAuhY5M2D4Y0+QRkx5dqCmhNuY+LD5OHcz3NaJOM4W4kyfA0vb64Bqg5SNCEs1s79amVBAhiJ0YIub5ODzL1pNQY1UFg8wpCw7GDuMVCBzj8EzSyNIE5lkzZ7QFOl4SrShAS0pZ7KrBBpE10qkJiA1c7RGosn4GOgXl8FQP12XMxkWi6WZ0qe/jOOqPFAJizmCWPk3zrBG6EkmbScAz4YgOzh89ghzM7KmwBiK80brcKaN2NuTtda1JAZiYlIoAyDFiyjNSygiUACYsC3ChCq6EwyzRslwYGze0KhywDImEbq2hVMbrueG6bCiNUZBQa0YpFcsqFdTXsokDrY6z7P29crbrWJX9QEAdbAahgYld16l9XTTNnEJACsq3S52WwObOIvMKa0Xz1rBCwKYIW34yvjEGABVMQG1S3BghInADuKKVMM64/BeHg2+2grbD3irlONw2NAqIIItFiwXJ4Y2B9WhmoYu8NC9CrZHaFBCjrXGgtaXvSyDXKQwIRQzU1aVu/1vzWAEysHwse6PwR/biWxZZh91BXQjSj0CEyBDyYOf5h4Bmd2ywcedgs/FtvrvBuLMNamsorQllS6vKZSt9DiFohqUV7yIFfUTflFKBKJmnWYsRlSLgExFpxXrhHC6lYNk2iTSMWogR4ue/Pj9hKwK6xRARc8Y0ZeGNpaDZGwVlW7HUpqnyoneSRkce5kllZSgopKnT1hc/oBz2dYvGdx5TMUykyJ/a9HKPirqZnMnBYtDDgUixy+vwL4TgEYZ2QDrn7LryFhjuPh+7f7IVOTiz6a5VUt8lClXB01pRBluvR5/2VeX6WV82pzGEriPJDlTJszy0ZTBWfY+CVLB4jNxtjbGuRcA3PRR2AJ/bUKtCVwqRRgZr9jJJAXY51NJHtz4mzvfs0b6CU/W+yZc67YVRuxi9ifY9RqQUdzanyEBESsH3WhGVpvrNCmSK/SKHNBuK2rFRbYDqusoORjv/+5RnqEBJhK3qnBwScpY9p9ZNwMZ1RVDZqyy+fYwRh8MJ02FSucKbuY0xYJ6nvkezcPVbgcXVDvBUVihEAdVtLajMTsejyqjgQNdl1QMhVaVNomxLKQoGdzkY91tKCVIwVf0zkufGELFtBVurGqVdnfbF5Ov1fBbMT7nxWyta/KsfggYKzpN7PwhPXn8IMDaGhBwnbLjIKL4rCMyIBBymhL//uz/h4+MnUEhgRDBnVAK4bSAuADGeXp6RAaxlRUwJj6cTHo8PeDg+4Hg8IQbGx3cnlOWKbV0xzRMqIl6vBZfrisvrGW0K2BqjVFH+tW4ItVfFI9hmr9ulhiEbCXPKCYd5Rq+aaSTMoqDWdUNsRrIM51zhQGCsIgfcEGPCdZGquXmKOL1/RLk+Y1svGm4vp0LGVvTx40csTRyPuhZ8+fIV//7f/0UKYb17wMuBhFS8VSQCDqcJx+MBcxZlUMoGbk3SraaMaZqRpxkg0mBgcUZDk2p7ISWAAkqLiNMDchDutek0Yz6csK7Ct/Tx00esNeG6FJyvF/z084/Y2qaE6HLKMJNEv8omWbFtF+eVYhJTQiByPZGNCWlOmI5ivBEDpVyxXM6Y5hmnh0dczht++elnXC7PWK4vOM4RTBNoFoWDdMBrIUwpYC4NkSYAS5/kgaxfp9vBFXuzY05mANl3+Bb5cFBjF1Fnxsfg+NvvN1/evX8PoNhHS337JX3pXotFZd3gUHeab2PBb97vvtzNZ/d+HzEoA4vMAaLb76mJNqTiAsp39o329fuO0bej+QlVxrj7Gr9z88kbcMsEYxwDEx0zuHic71EseHcGqo7kMPjU399FuboBJJdZoZ5u/9N417FTLoPsHRnabH+Mc3gDPH7zxfa/HklpqFuXaR0YfQT7d8ygGcf7N54HGyvuaU36rN04eu/2d9496U7fviXrt98xXqpqRzB62orawJtUZyY1XM0pGseXx7Qt6vceAbl7z33zvjs0I3A6RlvrJBDdLNFBZ/g8j5J8e9V93eJTzvv7eXe5p01aC4WzS9v2DTn7LT1n/dy1g3TPjRlhnhHmCRzjkM7e14o5yGA17s2QB2SfUe4o+fctmdzPVz+4U5BpGKDdOO70FXvbzVneyQWN67t/t7WGQLcyMYwH9/7gTR+6PnMKqNvv2brUaD0BKMVmCWxHi/tbguGR2eT3gDvXAEkBCHvOm32rR2uOc9sB8MF5sQM7e7w6UUHHEb639jEXMDKo2IVeJEv1aLC0cHTn18fO9XAv+hGMk1TnL2jqum1p8rWhAI+OI5zH9EbvEWA8n7tNSp1IKxJixVpuxMh/2p5BkKhkgs6ZmSfauNsoNCsYaeQqYaD1GPWPReZRTIiUfL8j35yp/6MePRhsX7PsdwouI0bFQRTkQFLbGMzBVSkhQAFzAIhg7tHgzMN+rOtdhrJHbDFs/7SIraBgyjiQe5ep7zG98JHbb9YunQwvkqIxiDEmieCzMVQwIcDA2A7U39f91HXooFB8+fha7G2JocucFFWBAgpCs5BSkkOrQBBaN6MskeS/WvuhFLNwwVYSjlnmHqXamLDVgKVIKrIdGDUHWqrLm0dNDpF41pdR30USnSOZBOSpqcQqI6RUSwaYuJHBo3EhcmJDWHVN2BAFHqLmO/DCkcUhniZ44TDlgM25DXJgcsiAghDQ+48H76LjkkrdTVYFJHrZgHfjgbQDKtE5DSVoQTOzNUd9MoydpOWLRmeQgCRB6ms4f/TOHLD1OQg4NwlyqlX8PuHL6YEdNmNk1gaLLOcMGBXLILb+pTcyfeelBpyN5XibplFslVkCaMjNSeV2Fl1qVCbdntVCUoOulPRtcoq6EIDr5erFzQSEEb+eqwBXW9lQtp4BkPMkkdEs0XqtFWzrpqq77w3jMJSyuVz0g8gO/BnQ6nsO70FToINLTfWBVLzXAsjQ7AaGH/5xA1DqwEk82Crco7NHgIoBlHXdgWd73d+jau1v2xNosEdI9ZCviKEfMg8SSWop7aPta69t27Btm8xJtIJpXccbgG1b/g0TGOxgIFqRNyZIcbqAxhG5ZZd/Ur1strPrHR2rWirsYBdBDhQtypUtkv3G3jAwuVYaMKE+3+P8VqmEuPMvPAITEMoUZlRqOh5hnymgqzOE7nTFuI80FuA5glpAI3bQvK/b5hQEJqNbbUpvI/81wPsdIyGRBDJGWNFBQi1CFwmWcWLl1Ld2GB++RUozA4mDHCbUoEB+PygmzTAhWxcaXSqR7n1NhUBAs6h9ch/NXrcHCwZY22F3GiJ6AZlnD7j0fVs58EO3S1gPi+xAR7jV1ZOgAEp26DoA+Hdefwgwds4HHKaTgrGM8Cj8LVMIeDhk/Nc//QM+fPgrlCYpaoyMawVauYLaihQqppAxBUKpG3LO+PTxIz68e4/j4YSUJ2zbBd99OKJtC+q2YZoPuGwMfHlBKYwSEw6nRyy1Ya0Nq1YJ3MIK4zgCWKuRimLIeppOQSIV8jRhnmYPvXaODy24sG4bSJW62Q16Pi+/N+FcCjHj9TWhMeOBIg7HGedpRoiiPGIQ43G5rmiFcTgccb5cQdywbSt++ekHfP35z3j/8IA1NTx9jShcMeWE03HG48MDjqcZ8xRxvlxwXa6SThWjVledEHMWw3hriHoaPs0Za22gkEAhI+QDUjiCWkUg4PT+HY6nE64XBWO/e4efvxRc1xVfn5/w+fPPoCDpfDEF5JQxx4ScZgQA19dXbFvD4fgIxAA565K0LzQo124Ex4w0S0RvDsC6SOTBw8MJ7z++x3/8+Sf8/NPPuF6eAN7w/YdHcDwgUhBusMN7tOcVlCcgTvhy/opqYKw5Rd1WNLu+GwoMjICtvPbA0mjOy9t33ieLeulgbTdSbwzy4ed4YnkPPBqNPv+92yeDnaROL/W/b+81vvzkyH5HH6rf+zIw8U0fuy8BH8bxxsOY+7dGJG68x2jo6/9pnL9bS3FwrNRfun3wtzvEw/yOz9+NU3cudo+9d7vBWGe8nQsbFhr74nKqBv+tc6KAIIABMO03Gw+Y7Lm3EXXfaOzgH9p49yhkjM9Cj5Az48E4+/ZAo7SAuRsQ5kjdgg/9Pub870Vid99hXPs9bibiDih4218Azic5RqS11qTcdCloywYeKG24z5ivWd41dN+mcU1/C5ztXxia/+2WD1eMc2D6YX+jUY/t7n07NG9438Z2Ws9FT6UUcJwmBAq4XC5Yyoa9Nrw1yH+H/A2tI4JEzMQEmjLifADlhGYRBFCDCv2gBrt+U2/Prl8M8JiTvu/rvrkjRciwnm7X8DCXLhl6Lx+REZAjONjo3zMQxvaQ4Vq/sVyof45t6IDVjh9Y72mfmZPbtQKB1WCnYNaQ0ieagBiYQNDUWPZxkc/J8lvvrzWzibT/Hmk67E0WpTwCUMwMqwUxOp1QvUEh6ThblI1UNHfwm4afdhcHITqYIY6m0A9I5NQIxkYYoQ9ZpHRjEMWuMxDAbIDvzsywhkJAyj1Y1JpEETEAdv0x6gYDg2zKTJ4JQE9x7vJj0Tb7Qij+kwKiFpp1Z4eMAkDAWJBwCXb5ar0B2hdo0aIemGCgh/Bm+oGi/gsKdvqYA6Ba+jgxQFz3qacqIsbPOFZct/mNKQ5tA8iKKVF3CP1++orU12prBjiQj5vI4d6GIcJuXM0xM05jQBxmVlDe9lnTJbYF9vZrTKiDe+ztHeVotEOIJNLSZC4GwhQjSMpTIOWEKUfkKSBGIAXGPBNyZKQoUbAWrepdawCUrqWPAAAgAElEQVTQVN4lDCQn4Twt3NCKFPqNJD8DWMEYceAFUpSIrF5YyXTDOFe+iGXcmtkDWkiPAE69Xc0OQVX3kMn2sK4j93UM1hIjwdZ6H/SIIAHrQSjm5B4i117zw1vKqGXb2QCi63W9KOhsXJ42n61WBUcJMcr8WuugtpONDREQa1EdbQBOt3vuHk6S3NvMwsABzewT7geMzsFMFr0l88to2MQZlWKX494y+hhuPwgYSzmrvr6/c+9AIdzspi7stH+G/i0cmA2FGbEZs1TXeVa8xwD2nu5u3Jg8tIGR84RACZHkgO5yPoMg/m+eJ9G3xq3JQrnXmvitlvIsgVSMjSvqVrCVTbJJVTfGqIUZPTpyX0xoBOVMl1nqtx0cWkTp+F2L6i1NdGBNyaPok4OwveiV/T7qKQOpxnaNINSqIKet014UTUFszWQwihbjD7Z901YD2RyCd9kh1gbjzfZzjxubwPhb7TMi8sLHrTUHamUclSPdriM5XI0xKgeqiJaBogEBlER31iLcuUkzLTpXsOibUooXeGuN0WoVDCYEIAoPuIF6UP0fY5Jo5CGC1aTeQNrx1VKUDALu11DotDSVga2WThk4FDezMY/RniOHNrYXDQtND30IFHTt6KGBRcJ7PzVKuNaG0izQRnT5lIVXOcWEHBNCEKCamVGqrIuyyfdjNH2orQwEMEFKxeiaDQAhSaEuBKmtw2mXlexZII1ddrdtU33PDpqaDT0eWHnvaYxelnEW6pCqintfKLNaqA11O8zsFcP3aq2qoyw62QJNRBNSiOI/MIPu+Evj6w8Bxr5/eIfvP3zCc/kZBMIpHjHnjDllvHt4xF/91d/i4cMHVE7gEPH+0xE/fC14+vFnXJ6/YFku+PjxI/7uT3+NnERZVG6YU8Kybfj6/ISnpydczhM+fXyPh4dHnF/P+Ld//xHPLxcs2wYg4O//6m+wbhXXZcX1esV22LCUK+q2yb9a0QCcjg94fHjEu4d36l9I5b/lcgU3QjU03RQalEy7VLVRNToCjLJtoNpAQRD1GlZUbli3Fa+vE75+mZWDJip/mHAMhZiwXK74+uULfvzxLwAYtSwo24J1uSBnQkyEra745ekzvvv4Ea+vr+BacToeJEo2T+DzFeuyaXg6oCYTamOkKaFBK+yB8OHj9/jpl89oLSDlB7z7/u/w5eUVXJoA1PNHUEpIhw2BGk6ZcT40fH35BT/88gNqfcWcIuZ5Qs6ThHdTQI4JkSvq5QUhJDVyzDSQDS1FAYlzOuDpZcXLywKiKxIVYFulGiEWbO0Lfvzpz9iWZ0wpIKcHlK0iUMZGERyOOBy+w99+yHh4/IDL9YzjMeKf8BMAU9PRDRd5T9KzxnTO7rB1OX5jZAxX3otssw3N3Cb7nLnebG7sm5q93oCtv/Iy0m+tsYwORNy2tysRM3TkGb9yc3Ne7/TvLdjViz44ZDEaeqNRBgMbxrYNP3V+SA3G3UPUWPZmcYNHeFE/eTYFa07M/mURJ8Ocm4PgfR2fCb+ezIViMw5uBmHXH+mrpe3Z3IjTbQ6BgSdvAXhuzTf2zjGnO5+O0ciw2g2k3ss+nuTvSGGEt5vZOHY2k/1m+vzdnAyggbV5GD/2x789GR8B8i6b/R4jCNtXnzl4b9cH95vdtIPc8O/OyrgehzYB4NawrisA0VFcN2CroLWAriva5YoIEv1FrBjF2zXaLO2XrP1Dd4a+/lpUiX0WdtNga2NcT+M47dOz3wI7/f1fW/r32rGTb4IUySPgbz59xP/4D3+Hd4cj/vXPf8Y//cv/i0bUuz2AIKNM+aze0XFDs0ExIqSEeDwino6Ij0e0nDo3O4IJAEY5wXDvcDMFu3XGfb3Bos5MdwwtNpB0H9Fy42DejJu0hsVI9X5XWKo7bvruThSar0JL4zOusq6T0NelXOj6aK+BenuCfd+u1UMT76v1TYHWGKXwqTSz+OTYIYRTNuhTK49j2yMmLGqOiEBJDWoFSAzIYU3pV1WsXQ2goHyoITpoBpsvEp5AcUbEjgpR+AfH5xpYI7cc1gNb1IcNlESTMIJX7jVHBYaC6LjGqLnh5nAbh+dQWZntYpL+jpaGr++wd95uZUIkqA0Owz6CN6cZ4+GXVV+3QkCWhtnJHyQdUyIhm89TgDo8QWSTeSzAAqBBKSOiFsICEJLTNWR15C0124toaRtsz6zNooBJ0trVEWuNMUF4HC2yVSJieoo034xPjEFt6L72wi7yy/SsOXDs89dl3mS4A62CWdla17ka7HuG0tvq3EBBiRH46PMs/4yQoB8JwO2cUR7YwXZ4m90Rhc5BFFlPMeFwmBGiTGDKCd9/OODdQ8ZhIswJ+PgQkARbQE6MrHdvTatSM3w+W4MExoBxWiKWNeK6AmuVmhaXK+FyJuhMKeeqAn3bul/ztWlBFPg+ZfMYNHsuhSCcoFXSoYW6oLkDbM64FVoDeoGgxox5ElBBjUHRCwP3CkHktoE99Z4jdduWOg8oANVnG1hiZ2A6kIHejqI0CdBIMrXRyApcufXEEjmmMm4Fl6LyaUofJEqsVou6Nk5QuY+k9IqzT8TKl9vXebOoPR8TBasVmLF93tS+FSy0Qy9bDzbWMUbxebVw2Jy1JofdhIe9edhc7vlA96LV/NphzdfG2EpFyLYXqV1EJHVlLHJOM0Ttvikl5aM0MFGyI7etYG2b6EAKwhkbI7ZWsF6vQG1IKSJPE/LxIE/U/eS6bW6XhRAwH4/4ePykHZK2r+uKbRXwjCBjNs+zAn6dK3YERNd1hfEmG7+sjYlF8gIiS1nnigCkoFynUwcdAYuuJJUFKKhdHcS7LQrJzF580NfnAF7VWrFtmz+glYIy2MKjo8PGr1qV+zhp4TPlA00KlHaNBR8XG9fT6bSTkxHAZDC2dd0BkinK8zcNpLteLqI7FRCFZU44TQo7+G0AqXGLBj3MAqOnoSv1AgUM49aQFNwum6TDV66wIlql8K6IlI2rRfX2Z8LXGxEhcEBU+2TKE/Ipqx7uvlMpltpfhY5DlrhTspStdE5okHMUGxcrESnvteVYZ4SkNzGaBwidg91zKxWXy4Ks7Z6nCWUrYDQECshZqHzq1lBLByCD8tUzN5TliiVcRSai0IekLLJba8XLy4tE7WqhPJ8js99St81IO92KyBgr5UPTMS8KcNuc2vdCCDgej37vaJgDy9oTChGzs7vu2tjsPLOVCSFk55bnRohJggOD6oNxff1akNMfAowNajCgiAL5X/6n/xkPD49gRNQWcVkJp5jx8y+v+PHnV5QqRM1tfUZoF0yp4f3jCUDD5bLg+eUVF02Vt0HMMeLz5wuev74iavW4r1+fwCyp+zlNOD0cUV4W8LoBxDjkLITqU/P0mxAijqcHHA5H2InisixYlgXruuIwzSBLf1OgDdTTl0IUknYKCQ0BMR/w+vIE5s2dijlEOVUB5HQgTUhEeP/hI777/hOu5xcs11fEFPD47oh3jx/w8vwZ23rFej3jyxdGnjLevXtECITL9RVrXdBQsZYVX5+ewHgAUcblfEVZNtRSMM1STTbGiJwCruczCMDhcECaJlyuF/z8+TOW0nC6rKhxwnx6h+MhS1RIIXz++oRtW5Ei8JAI/+3/+Gecn37EHDfg4YCHw4zDdEAMSfg0qxgfDMZWN0RmlMsTOGRQnDGdvgPlhL/5/gHffzzi/SnjP35a8POXC15fXnB9eQZfv+DxdEBbX/HydEXczvj7v/lrzLrBvr68Agw8fviIx4+f8P7T9/j56wu+/PIVl9cnHObsstgao6wNFLk7pfoanVb7xaq73i4xs0U6ELa/j/h9AsC1GwcADkaKgg5WGGy4sxnvAMMOc8yAQnfRYZEMzNXvv2/r4KjftN7uv+v9m76aA9tBMPJxazdXkl/T3+S+iatR2IZNq7/2UXS4o9R6VNlN1ICPrwIeA6m+p9YMoyBXdm5ovBmf/horZ0sX9sDD29bdkiwMnw/An42hD+1wzfgdgN3Y9PYaeKvdHplqTF5lI6+QE1R2Y48s15RFMtw4hv7tP/uzrK88/s5dAu/tP7torgEg3QO+cocOHHbH4O2KG182xmH/tgNl3Qmwyqv+fNzKHfpnZtMZuA+ZoQDlX1xX8LKIh0bCi+pUNIMDvnNAtEseEOTK5LcPWXbtuzMcfbR+77jt58C+aT9NwsaV8e372BckmuGXL1/x8vIKAnC5Lq5HmA1s6LP1hoaEBw2lazeGIaYoCC1AOsyID0fQNKORFAFtkNT0oDLLu7GoGHmIeXeNRQwFPZXv4+CRSyMXtTdPHZUmDnBwUO+mT+Mb7jz3z2LMOjZyIEmqZ9l5ryBclGR6Qz1go0cAEII6fhDH2fjTRr0kPGhDZeBdO4Prgd5PyQwyUJNiQsyzHgTFPoJDpIKrCgiQUBurc+ON2GOLLAVOhI9PCp8UjUIjBT5CtKgc42QlTcPXe2n6nUU/WmSrcH4ZkL5fwz6GYB/jfliqeoPEqbN7Ry3C1AE23at94QjtVYgRMSVM06QRS6obPa2deh9AbsR7lCO6jLYh7c9E02TNi4ewtIX0pzm+1rfGFk1iOkmjQ6EpiEHqHog+kihQi0Cy5xpIAJc/kztSWzaisTosel8/elbATQCh6PNF3hexf2NKnaZA/8e2XrQhIQTEKSEGebdsRddEj+YiInfcx3k3yRRcqqc6g2TNNQelAC+8q0LdmCXCyNo22Pmu3lmiiowz1peXyp+nkmrYs/sJBkqAkO136qC+zZetMdOGBCtWltzpzjk57ViggHmKmOaAD+8Jj8eABMZxaghNAMS6NFAkHOcsB/gsNTxiYGxVop9AEajARAAlUvABmFIA5gkxZC2217TgjPDmofYIYQKBJ0Icq23ZOhzk9Hy9Ks9s1cOV0sGlZgcF+p0mEaukB1WiEiwa0wARGjaZbnsYCNkagRLcdgbfFF5hkUEDYn2vFrGBNYcGu93S0A3Uksi7CiCiaaR0AKFgwVY3rNvikWmkYNthnhCTHHQ0VnC0ViDD9Q9zUZBWPQhSfQHRCQQ9ANK9S/RJU9ok22c6zYzZD522QcaqAmAuQIk48ILp4YD1a0arK9D0QK7pWA97iv0aQkDZtr2FTGqb39g9jQXYW68NU7qFLNij0cS21bVK/TCIKA52Xj/ID0kyBmoVfmPeVhS13eaUpUgigOvlAguKCCFgyhl5mlRXib55+vqEUoUKkBvjMB9Ed+eEKWccD0e3LQQo21DKmL6dPBMBYOQcTIgUS9CoYyLfkwEBYoPa0su6ujE1RrQaqGujv62rrxlmiQyF7jMpR0zT1As0haD8l32OWmM/uGb13yyTBVBbWHlUG7c3Ea4jKFVqQdk2bFsBbig4/P4qL9OcvU1WFMwPXlXMJLN3xvEEX3sd+GakGLGVIvM0gJhSVK/icrl2LnWifZE11Uc5JeerJSLkLAB/CAHTdHAfXHwF5dB1Pc9gYqUZ0HXHUjht24oWO5QDZPJIeFmn0fj6aYj6DQkhRxBVgI2bVmRH6iM1LSzW1PYJKEUoOEttWJcOpAcSWp2s9XxqqwjKnQxi4bApwiHLRHpAwgCSxN8QYSkGfrobgxAClqXADhAZBSEAKRJiCkiJMOfokdjOY5uT7tuiy7da3Q/hYV79oAWMFBPSNCkHd48w98MGjWK2Iltj1DmR0jioLIcpI4Nc5oRbmFBLxaacueIL6t4NoICxrQuATnlicxLiXhfevv4YYGxMCCkDi0zc337/JxweH7FshOtVOFTRAC4FVDccYsbp3RFlWbFdVlzPF3z58oTDYRoc5iEcmRmFG+Y543Q8YZ4Sttrw5fkV1CSdZpqyputEbFvE9bWCdcHFkMARWHlxQukQJPrrej1jWVaUUhCI9MSeEDWdoeqkWdpKqRU1BKTMSGnG4TAD/ICyrXKKQRGRNJq2FaCoQZ4krL+WTRdxj5qTCq2yOZcqRvM8T7KYzXjVwKDLsmDbNhxPBxAYtRVQAB4eH+UEZhJA1isDQhR/Wa5IeUatC8q6Yo3A5ekErptGpQSU60EA3BBQY8S//9uPuDx/RWobHqaEGB7x/vEROc1gBrZ1Q6Wtn9RASNBNF8cp4+PHGY+PJ5yOCTEwluuCH//yA748veJ6OaMur3g3NxA25AjEY0RAxmGKyFkXwMOMZSl4eT3j6+uC/+fffsTL61fUsgHXBjo34B9VGNUwtuqj/TXCEbLwKroRbadod5EnDLfaOZ362QBM9A/EuZHgIwUH7F5qyLN6Ab0KrW8/3WHQtrJfM3jH3uUOf+yBqDuNvdcv36w6wGbW7s5huLnFLfBGwz8HPWgPwt62wpSybVgGuN25yj8nsjb36xyEIoWbiN50fxzhfd/6yZddbMPYwcbel/F7t2PxVnxGR+UGtPDvvn3PrekB8CA14mTDIwjnHvvmapEhxkc13lZO+cY1IeNnc7prloEvNnc2FjsQ3Jzy4YJ94+906k43w21k9PDZm/XLu7E3/r9b0PO3nsxsgIhcnbaKdlnQrivYoyasJ+Qg9dso195/buy8SGZM3wOFv9kmvyMGUBx3xsZ0wNAKA1NuXmP0hi2HbgTZPX59tFj108YQHikAlYMEFxoswjcL7W1DerV3mTCNUCAgkhTsmmbw8Yiak1ZzhZ9qA2IAW7GHHoUbujE/9LnzQopDzaqDbU682Brp/A5zZQUNdoWhkvVMrxlBO8jmXBW8FRVkKYICzkk0ooKBtcEi84JVIzbDv1kUVPP0XuHIg4O4rVYXAQaE+wqkUV7B+2Ry6eMBBflMLaqzkFNWYHbIBGqmLLkX45K7eZqgP8N0rnUe5jwnByoRJsRcVYXaPYboZI2ubKqPfE+iAAzRjsxQORJQ0VKRXT/t9sGupwygEDDWuN+E6kDS/8fx6mCsRdqmyRUiCAIOW1lz0jT7fhAUXFbG/sm+oTaBURmwcZlF3fPaMMYKyHK/x5iC14yXEsMBH/c+SKSHZlwwO7AZjFcNvRCdYAbB+fws+oxBypftsJb301d5AxAscg9oTbLHgs4dW9EMP23SefRdvu+9tao9ZmOlPw1H6xHwwSNpXbfQeI3Mt4GGNk769J6ibZ8MQHTfbhVsHvUk9R8Osri8kMu3R9xgcDaDrcFu15mf0/VnP/jcFSgZZFaK3wTULWK5EjIBnGQM2spazR3ISSjhoPqPCIgNKBWo3PWY9FHqe8QIhDLsuyQT7EtRU8zZqmmb/nSAv9sHJjuNWSN8Ca0Zz2JVkA2g0KO2mVn4YAOBFGwiZjSCRjAH1bb9IE9XKZgZke3+sj5vjv8HO1WoR/IADMqhvn2/276m3kaQqQ2HYiMYICDnSbl22a9l7DkQjduz1iacqGQgFtBa9O8wAHZ02A5oxKnoyRoiP1XXHQhaPFiODizy1oFsFt0kwR0CttWUgJDleY13a0tA7r4wLN14d8A6jO/oI7hN0hq46j+Wtgfu9onZtHJgZFkEnUcyxh79WeumBbbN5hmiEYkwxexmbisVjQWwkcLc0SPO67bJ5824Qtlp/pJWcJd+y3Mul7McdOi/SOSF/UwHjwdmIbRh/lkPIYLv7YYntEEvjHv2bvz6iAIgBVc7OCXYn3zPgNOcM24DFcZ9wEdeVaPJZ4h9j7F7TimDUx7Wd//c7rttRYvd2VrQQwNLS+fmB1etVaBVORBo8OulqOXS5c4PEHskaEtJ9TohKRUjzJZTKh1ZD1JokEBKr9PHq7FGsXMFGlBZ2i5rmftc2j7JagdZ/6MckJFOCUFkdpqM9ol8/dr//RDd9zXhS0aTg6mtbGi1KIje9b5RF1SJTMBWjMdbqC4bG/esaMRSKtbVgHoGU5H9ks3uTQAqWlNlUSQwRQprdVxCTQnRNV7bo7dFIlhVh1XJniINJeXGoBjAHmQk1AjTlHXPozf0HYDgSRuEuoD8EGHYQ2kPrPoBrfnuYlDp+jKe4M5N3GsXSL9E1s1mlklJRG7bjTocXKUY/S5LbP/6Q4CxFIYIASJMhwMoZKQcMIEQKUHpO5Aj4XSakaeEy8sVr9srSq14enpCrSfMc0bKEfOc9YRSFmVrFYd5wuF4wDxNwLKqEpMTtJQnMNg5fqTymWWYiWNQQ+dzqcobsq6rpN40Fs6YaIYxq49hFAVFI1MqqhkbFJDzhHnKssGXos4Dg1sRsA/wSFtuDdfrFWVZ0ErRNBhGbWdcLxes1wu2RbhPD4cDrNIksxJmt4ZtK1h0Q4BGWMSc8PDwIJUl5wNCip4m4QqeIRytkVAiI1EFyhVtFe4wBoGqEJ3HmMCV8Pr1BVRXzJFAaUJKEe8ePggVQa0gJpSwj1KRjZF1UyXMU8CcgHVZcXktqMuKH3/4AYWrLFY0SYdoEdNBaAzEeAVqWbBtjHUreHm94un1ipfnFS+/LCj1GdOUkOuEeM17MLY1GXPdy0yxGDg4ehO2Gd2CJ93B2W+Ie+BDFYUbFrz/iv3i6av9dFT3/25U0hDRpdf6pvwG1KH9lXfBmCG6cbSud56U9YFgjgDzPSNg6OvNO+ac7T+7be/+mTIGdy7ZPdfk6U5T+1120JT/ztS7yTefwYxs8p/3Xl0e9g1/a4Dev8fvBeNuryHStg4pz7cPlo1JCPfNuFeTT9Lq7Zrxvv59kaumOmGQWtmITRyDS4U3wRo43tfkeXgS3o6SXnv/7Zvvjg97+3nnSjSdY2bP0AZ70LAudqPcWAp1KV9du25o1xVNDXQaxttBAX+GxQ6+XRH27r0R+L3ycPu93/rO2zX+/9/LdaP2yx3AARTqmmi04Gz85X9mtPp9Vd+GGEBTAk0TwnwEHU9AiuAYBJBlIDLAQ8EX7KIMJYKGRrGhDhh6G5kVhOkHPn4/7+jQowEIaiONiF+xBwjVE3BdECylmmxeZD8TzKYhcPKokB5SrY5bLRqZbU6NRt6wjKSsUZsYMwxZ95gxhr7PA1GP1AP1okchRI3MkTENWtSEfc61/YOMjaAg2efUdS0DSsckYLR8T5wKnx+y+englG8+3nyb825XWl/snkS1jy8JLyhRN9z9Ozrn4pxYEafo7dyPmc1nn3Hjx5PK7nUYix5R6oCAjYHex5wbEzPfL1yPapVklgKxzKx0ThHska0Gfg8y68w9N+0YerF7Gao0bKK3toyINMH4agEI2R3BeW7Z78AatcuQyus9FTYGUroJoHJPu3ZRHYfaxps7oBVvK7m4PU47OeiyA5Wrmy7D3rc53/ffQJi+dvt37Gekcb3JuiB9nu2xpA6d3cSAWBtf42W08R9thm7OcJfdYa5pHHe9R2PGVgjXq5THbRloiVBXoSVgkByYMXlRohAgxVmaFoXT90JrCCS2ujFyAEJl0A+oR2MZsIMlnwd0W4V1nnwsGJBD4wChQtHIVbLDFQLYeHnlGRyjgrFKdaEOPuv9Qz8agAWrSIQTezO5qy1vHRtpMwTgQxz6ZntcYwD9gG/M6hmj/EZwx2hAWmMkPwSXxV6UJ9Lmr9phGhS0URC2/7u1rqwHdleWaNphzyOykdFjEx1bdZ89+thAr+5ryNrcWpUsR00R1iVx9zXujXc/h2/7ch90tUOm59H3l/19b4uiWijK/rnj3msAroGxgNC5ub7nDjRawaGm6fpWFyDGqBziSiGgwGPl2ue4VokQ13EMOcFqyoi4my7tUXxEHYRjyGHHzo63jXO3p9GN7O3BWeahsBYbF7hxm0qBMwOY5XMe5l7+tkA0u6dlA8UYdgAuUS9ytfONB2qEXgAsoFU4XYcdCFobJcrXZNGwlX6QYu2tA9hVSvH5sedUja4MIYCiFmNiSbEnpbMJRKLX9FAkmt6FRVauWrBQ7SuSw81SK0opsh/raRGh8/LbHgtth2WKmL4zXet6e9izWDMLxsM3+7Uffks0q+93IfqctdJQG7CtRddEUB1NMNUnzWhDwTfhTU0h+R4XLIuFRcdbI7gFUNBTF7WTGQxzHCXTRW19NhoZiVZuWltA+i99CSb7ujZTHAvc7TMebW07sCp/qOz3NeF8wYH0QKbry+DtljFstSk9Z18nLr8U+j7uq1NelmXm6lXHpxnmdl/tAfiDgLHgCmJZOK0xfv56xla+4vjwDu8+fALXAxYOoDTh+AA8PD6gtoq1Mq6lASngcn3BPAUcpog5TXg4HjEfZhh4uiwLkqY8vZ4vuFyuaKVIWn6eEdKMtQDny4brsoqj0pSyPsqp1+l4wnVZsGqI8/F0RNsqUAW4TTkiBMK6bliXgsvrq4CvpXqYeJ6EHH5bN7QqBO+GnMcAgBh1W2BpXuCmUbGEdV1wfXlBXc8AFz8dIG748uUztm0BoeFwnPDx40dcrwu2V6n0+Pz0LELEsrGU2tCKVJY8HA44nU6YphnzPINCwLZuYBaOkJwnfPr0CTElvH/3Xq8/4nQ4IuYMBAFjS9nweErYtgXrckVZnnE8RrQ2gwjIOeMwn8AghFhl8y/RlYyclChZeJjAmPD8esUvP33G8/OGy3nFtryi8BX/5R//hNPxgO284v/+v/4Z6fTXOM3vcDg+oOErXl6e9N8zvnx9wtPzK87LBZfPK87/54I8V1CUtrcj4fi/ijJqLGmFMQ1cbugG4w48ADyit8vym18GZ2e0UnRDAdwgNIPcHdlgqYOwq3SN2Mn74MjKgzAWoNi5dWqAqInlm4K3zyoz9i4PG2h3DcHj+/dfBlTu76FOWe+ob6bdeBuu9S7YxkC7zzWTQ8Yj7sETH6lhAkmdLmZL+yU38EaTGuTmm/cBt9dAFbKnowztto1yKI3TWxZ2intvxu/bD0AdfwOA5Pv3XkTKPYrQHUJAI2G7fDEBpKm/IAVYICealaVybFPjApoiA2a/jzn1ACNYtRxmUCtgjjIUSqRP7gB1Q8EiE/mm5/u+6CSM4/HGcB/ltvNqjZ/v5cl+5/5Y//jXZXm8wp29UpFYTk63tWB7PUvRrtYdOkDTtbhHspgT3nxRDwcRQzO+5TRyhS8AACAASURBVKj82us/A6qOY/NbzyLaV2XttiDjdzzKGgdw01kl/zlG55kOsDXTf6gh3MPRAEib0jwhHmeEeQbNJ9DpsXP9BalUbmnRzfTIEIniHdT+dLG4MzaskRbQg+8R2NoLlF7e+U9TSjunwSNzWdZJY0aMeQCHTOMPutvWqvFl+ZN5UHMMVEJjSXsFLOLHnD5CHECA2qpSRIkTFWMEDTMkOrDt3gtp0qhV4RjtMY9Apwjow9Z4MEC5AaiqO7rs76kdDDgaHLjGSNSXVgiS8s9heH4wGVUAE03b2J3SUYatpJB/x8a8qSeAIYphXNeREIjBZA679W1nBfi8EQGlbu5QtsaauiZRtcPV6tRH/7vPtEVfd+fdNLu8KmpZ8Mvnn1BrwbvH9/j08TtIpp5Fsg58e9z33ltwxA56W2kQ/l+VBY02Q+2AR/R5VnCsAYzaOUB1yqWAivOwDPKsjpzJpDqCpGmxwm0pEcgmy1A7ZrQxEo1gJZxuw20etVlMD5tTHHbgxaAPrNfU6Tt60am+jjvlx//H3ruFWrdsZ6Ffq6re+xhjzv//12Vv405izsnGEDRgUBQxKGpABMHggzckIl5eBBEvoOiTl6MRo2AQwRsa44M+iAgSUEElD7IhMYnByNkczW1n773u/1rzNsbovVdVOw/tUtXHnP/aO+cYXQ/pi3/NOcel9+rVW7Vq7Wutfe1i7+Zed1ibO9uHVQdYJhHDx9BbW31neDHrWsm8gejovuP3CWqNdfrO4yYuLBnEa86YFxnZujKurxIICioFICZ5XuYsD0N0dRxIrQ2SDFqQVB5iYRjrMViybC0zqpSKWljBSgFyN3amgg/G9Wo2s4FkrPZj9fUpiSRU7USms6W6UA4NljJASZ9AZ5c2sFiTb1jsY+EoNr9MQF1ba83xb5lqBtLIebA5r63Vnv+zZdhxOwdbVl0DqvK6YF7PsOaNrRLCbAmltVBZrCxAU7Ym0QAQjOvV7rdAQMtWsh+M2kaDTGZl5lKQSwGQUUru7klsvUhAWU5Y7u5RzycgZxDYGynBRK6zAbsH4JLbVhxvniUZ3UmSxstxGDV4ym3sFGD9FgKFroM6w3i2zaeMMWCadogxaAJP1Sy5lmRlVaxTGpC0ERfp3mhVruu6IsaI/bTDNE0YxxGrNnAyWVjOi5fAp0jYTZPyZlNbl5VcNkqpyHntfLsGGgdtrk2AZnPK/PScrz63HfAq64o31ShCIdCDqxW7aef6oioFF6tREaIkMIjuVNktZfMMci6evJVzdloYrl3md1cKHqKUoJfcGlYRyIEsy1w04JQVqARLmb74GYInBLcB4NmLdv9Cb5TdriilYNXGsQBw1jmr3GjEWDGZEJsuTKnxltZapYmbLUBmUAhd9icc07E1Xs3eKhk5Z6GJsEQ33StKzW5fug6PVuYePLvXbJVhSPq4BXCcaAciCchW7TlTy4qcGeucMc9ZwVh7FqoXdJFSsEzk4tm9IOGuFZoAnR8SOhNW2bI1W7mCVwjdBMwuZVSS74p9mSR72dWB7CNFm8IL9ZQE9GrRAA9L1v7t7T1204RBqUMBoTDqgU/jIQ5BKs1Ej5I/ewPn7ep9FvMQIyZNyEw8gAcDwrcNv0rOYgaVqk3+xGcWzEptDIbQSAQB9yUY3/i2X3V8IsDYnBcsyxmAPMSH4wMsUkkVuHr9gHfe/gBDjBiHAceHBxxPR/z0z/wMPnr5HvYJ+BXf8s24unoGgLAsGSGMyGsVRD0m5FhxOgu36+l0wv3dLZIatmvOyPdHPFsK1nlGyWtDz8myNOAE3PM8Y1lXPDw8iABVUXLn8wl3t3eYTycAjGmacDwecXX9DMMwIJnRFSWCmvOK5XxCGhKCppmVKqUnMSTEIFwar73+AhwiTscRMTDuPswIlDBpZ8NIwOHZlUTf8oLz8QH3d3caKSjCiVqBcTdgvz/g6uoaRMG5YYYkAPHDwwNubm6kA2WtmHZ7XF09wzBOKAh4/fVP4TMs2cABLFy5ywwLzMQQ8XB7i9PpiPl8xLycJEtW+Z7EsPsispVT1uoRReOAiTFiN+5xODBSYbx8/z3k+U74nFBBVHH17A3kteJmOeLu5iOEGLEUwrsf3iO/9yGW+R7vfu5tvPMzX8T7772NZZ6xWmo8iwKw1HwEQrxO+Dp8BgChlop1WRECC2cJWnaN+6j9ceF89mAbPfowvKFIDw6ZM22vWAzGjCKH9dRQMW4rMWqT2ei9h+7nBragghhzrZTSlKnDCZf4wsfd7OW7HwPsbN7pruFOm9rY1e/+ibnb/NJO8tb3fB/Wr/8/XnntXzh+/o5nP/5j+Kb/68/jfjkjWwaQAidsLW2swYp+xwowvXwfAsj0DrVlhG2yuXopUvFtmU4tC+gS0LWqCzMIA1kzDR2u6eVLQ9Z+B9T5liYiPK/I5xmcC5CLZMRqJYVFuWV5kq8nM2Ya8OMrztf9VwOkfqXjqQzap+ZvqxOevi49+uvxdy6/uu3Yrs616y97T4GgSg7uCiZqjvWFHtG5RCTpYB+jUBMcDoj7HeI0AsMEHgbl19SyqmpApZWll4tz6i/uzLTRUf+C32fnQHble0/qROUyrbXgvCydQdeBPQheZi6lr9Dl052PnpYNO1PQDFAGAMvM0XUTY1IQzp6V0S+YA+QUvHouglUFyAWEp6w4JYeUVposuxnMtj7U6aktw9aeb/DqpxYoK5oxVLm6wyLBFeFYhQMI1degfdnWq30vxAHjJF2ypapqQCnN8aLNHFhZb8sq659h7ZxA/7sqvzSiBgaEZ08cme6c2GZj2ASFpABZjA5w+6bfbeAGnkHlw8CXGC2QpYDThTGShgmffvMXye/arMx4Y6G0ID3w2eufJ/dt2hoFLTO6l18bV9OVekZM04TXXnsdNVd8eHODWllKX7XxFqlwEKDPWr4bgjrCdm8GWuhUXYKnrPLQAPdOvxI3QFM/3zfQaPy3+l5oAKhJjGXjCG9lbo9rY2M1q8+6Q8uzbHNi68PO1/aCFqS057OZYbtW7fY1bt2jLWvX6RlATW6cT1kzdogQNeNs3EUgEgoDnCuWDCQCovonIAIH1tMaVcvWPjTwKQRgGiPOa0UqAUMCxhEIlREio2bprl0rYQmry5/r42C3GoBaUVw+ffOUa1lJONuEbuXWgwxdYgFAzvlt57Bn3wP6BhwZjACWDMhaMoDq6490XfQ9GPThIteWJUjo91j275YL3WJrXsaSYZRkgYCUAhgCWpHJJySDz8rvTVcBLB3KwYgpSDafnjdnSXyR+4ooNTvQQbr/me1FIB2CNsZKEblIE7EGotgNZtByQrj7CPRwCzKu2M1D2Tygx+9b1UoQShJpDqaXiBFh2CkYm0BpAIWIQFVpMTo6IbKKEsAa+xFJ2fUwNGC11oLTfIJXaLBUXcpzkbnYHfbYjaPsUblgOZ+wzDOMP/Xq+tp7xpRScX884Xw+KyWQ8KGPw6TVqTKn65pRNeEMJLaklXcL+Dh6Nav9E3BTwTXd506nk1dZmD6woJ9U4aTN37msnlkv2aZpowOXZcE8Lw7KC/Aofq9T/FAD49xyCY0agxnauIldTpNReHR2eXYKLynTh4KWWRsmeVahymKtFeuyIBehC/CgDtdu/fV8wCZjpGJFgtkMW97XEKPPQaMMgYOxUkVsHPuMdW1NygzY82AxtUz3FrMVOTe+0BQihhiwG6VhlNMe6DMw/vas1c5mG0lmdcVaCpbjUcvn5Ts+v75XGWjb2zTQJlQEb3poRNAVMOCGiEAcxKThgMjNJmA0ADiYrWA2FGugRGmShDiirUfdieTvCqAWVKrS1NL2cbtOFZB+iAEpAeMw+TlkzjOWedZ9TtZ5XtcG4HsTtdXlbhhGjNMIZpHzmMyusCBCdp2fS8Gy3GujSRWlWiXwSLSR6RgjxiFiJOGzdTOOWXlk5dxFxVF6LFCT0Vccnwgw9uF0xs3DERjEaHjjxRVub++xLgvu+R7j4QFjEtCucsW6nHB6+BDrfETNCypJpGt3/QwhJNS7BwABXLPwBaHio5t7AIybmxvcP9xjNw2Y9jtIJEujJsuMWlcRmpJRDdkOQm5txkOIEUlBLGlMQFjXBcsyC4/QbgRXARd2+x3GcdiUKu6mwSPftknkLFETsHH3yIqpteDm5lYaGZSCYRwwjANQlSsIAIgwanRrnc94/+X7QF0xDsJrdJiucTydhMpgWTDPMz79xhvYHfbKbSIjq1xlrGmPECNub+9Q0opxGDEOI95+93387Be/iLvbj7DOJ4nAohmzXIX7pZQsvEfOddoEPKpAVlYuImJ1ZlSJx4RymLEuZxAFnM5nkG1GmmVzc/uAL33xLay3FfNbMyJnvB3fwZpXnM9HLMsRp3fvcH54wDyf9btoCx+anQAAhVGXVvoDVSvzWoSDNgzelqR3fxp95gXAYQYH+QceOTuPTBKdfz9/t1n2Trin/qM5gL3f3p/YHOoGhLTNyKKa/fea+6E/3ZFom/CTWTR8cf8XQzHnwvEOIv9bbORm3ftYO+eOgYuN1s7VZQrvduB967z5C8f/umPcX+Prd6/jHbrFPS9YUSUbQ8u/TCZks7RvcWfcsYJfhC0utgVIAThop76SO8byoxmJm893G6BxzwUvXcM2kRydkWAGk0X2S0HNGWVdUc4L6LwIzUuVDs5k99Cu7sayNRByudbxul+p91LRwANbQZcZrz3Y+nHg7ce9twViH7+/mZKeqxH05Ofb9cgNF0Azx2oFqhTA+z3p/x1c0KxXNn1m9rQ+CwoKIkwjeBiBYQBNe8RxRBiSALNByrLhGdvmOJu3zR3Q1RxuGbP83ua96aFeozXnnYAe9NHzd+It4K98Esu8Ite1G5MY0zEAlQSAiJ6JDgSqLugCLvXroskFUXC+S98PdD5Jx9hEkrqf6oj0QCfg5WIBqp/1/gNie3J6PWZCFZ9HuMuo7U8h0EZuY5fl2gcr5Zmz3nNPb2D3ofLkgJNm+HN1zkFrclPrqtcroCBd16s5Dep4SwBYA7EETOPOs2ue2JX9CDGCYnMUG4grTk6I0ed+k+GMZhPYOMwMse+bnLmtAOUOtr2bJIvNOqdvTAx7Jjqvxn8cDDByr6txBfedxj3bspNb7u5PRF3lD9WDWHbVth5sUDJwadxVcX9/r3MSkZL9TG0fULkOjdPGXD8/pcsLi6x4Mo5x/aEBD26nmKZ1U6zdY19uyB0dEVcS/mmSoDAFEmd8Xdv6qMJBSbomTUt0kuJz1x5ps1l8HA58hU4GzAgjPY9+NrSqpV6uSP+WbtODgBN6vyEmTSQJAHUBnxCFpiWIE1mCgHYpxY0VVkrVXhlVuQ7hz4eC2lzMmGcFICFrVzqHSzmsSJ5mgQ/yvM5nIY214IZNUguGWvZvC2aWXp8B4NLb1wRi1k7dlpnWAq2yVlQmdQ/mklG5+F5Qu7mtuYBrdpkaUgQHap/vAhlcG1etAQboytuNu7tNXr9ejM7JziV6mFG95Njo7XJewCXLWUpQSWkAQaM5sKZ8UmIr+6aW1XNVujodD0EAVkWPSM/Jts8w+V5MAJilo3pbONJ0OOQZ891LfPjelzEf7y94mLsFWNta8Yy7mJCGEUSjG2GDVyNKVSgTIQyj7P8RSENCTFF+D7pOdR5NfuyyVUGtGCSAVpVf156Xg3HKQ5tSQkpRgni14nQ6O3A/TROuOv+CiDCfzwqwVgwpYZomhLBvcudZobaqAOPJD7rmGkXSE9l76ntZliN1197SATQwlrn5SgL+RNSanV7B1i3a0sMwSIKW0RNcBhVDENoKazpXSla5I1hjw9LJBkHGMIyjrxnLTBbAV/CSZc16DQ3GgSQ7k1qQNcSAq6srgLQRU20VHbLe2RtUGbVCLgrG6bhyzh78a/4q+Ty2IJNm5iqvtnD6ykadUuNOJwJybtQWxgVrTb9sPzSQt5SMshYErXo2kDuXVZrMadNkWQK1G1tEhGFGQoFZcnU7ICoAXKrgKGUtWObZWtjAKDsEt5Kq/TUXcI2qX0SqhAqAEUR4FNhs+51Ur3RLv/NyJPtWqjKrVml76rLbBHYe1XkkTR1DsExo5XRG8xmk/5FSG+j2k/U6lv3u9q75l5oNa/K/rhmgDPMjbUlJUEn0rnFJm05IKTqtp8lQIHYe5XVdhcqi8xEBwbT6ZELLYrdnOaQkDWg72+Op4xMBxs4547QsgDbts9TsAuFdOT7cIsYJsA2nrljXWZD0aQJFws1pweG8YBzFCUo62QwryVkxDgNKtTJ0aVQljViKGnQFkYAUAmoIMnnBNnN0D56QSFB2I2cmRef3+yuEJSGvC2rOGLuyAlOA4zB46vmQBqQ04HQ6SekEm0MO2GY9z2fEVRWKbhwlG7cqIcWIEEeZy2XB8TyD6gqiEUlazIqwlurRgNN+j6urPayRhVEFxBix2+2w2+9xc3MrdAr1AXcPR7z17ku8/e7buL+/xXo+odbsi5MLsLxsUW8CWgdB962UVwfKG6JcYWaEEhFSiDgfdq5slmUFOkOIK1AqYVkZ+a6ivFeQSLJxVs2wzmUB58W/41QC3aI0bhL5u9M2BCAYQXpBqNLciPuyyY3D3o6PywyVD9PlC/ZFP6ttGu5IwLJluH3UjFc8Lp93ReivNgPejAJzmptZj6ZiewfoKxyX4OwrD+p/bRAHudEGswI7VQ//DPqP2C/Mlzf+C8f/hiOAsEPCECJCbessgCENM0wf9HIsMtn7edxe7uSpl11ds+6c2Wv9Zy5lR8+t+tRACgdju/8/OthKBwWE5XVFXTN4WVGXFVQKyLqauyw2YMTG4yO6XPsXf/Lm98dj6sFY02nb09Erv/v4Ck+9R9s/9Zr/f5aYG8B2djbd032ia4zlj5ukHC1oiaBkxgyI0wQMCsiOOwFitZQRnvUJbErG9cIW6iK0OdpmofVz2M0BzHDtXsRWP9s7Wy2rjpcZaSQZlfaZoKBIn21yOXebue/A3j5I0TSm3Zt9U87Zxwb1NG2Urr/16mZD+yBkDev2rDYsK2ekOA6MoCBZA+LteXpZIrXsmAbu230EaMcYAeW8mt0cTSvHTL7Wqj03ZoSg5agkVSKkzo2cS7Mz1G4mZqViaeM1R9bAnMsd2sdpxpvvrbKPEbUgqlO8XO7r+rOwcDWWUgXMoNaMzT5vmeTkgQJSAIw8m80aZZKPR143gEFKIMWJBksg3Mq/G6BkEkJul8rzMmBaJoPJzgXAwwvybQeUOpkyR6eWgrme4Vk0FMCsZaS+PlVOyDKT5FTGmyvoUEA/9b43mLrwqev0iH6ggbP2vGTeSpGO6aH7rGB2FUGBJnvncdlw21fsdzVuFVyxRdRpgV6oqI2L8ITs9e/buqHH1UKmW2VtRM140isql3GnUP2fyUIuFWPScQdn5vBHWTQTN+i9WvmolwnXbjyq12WtCrflUJWxMxjYzsiZwcpPIHSMjN4eAMQ5l/JtdM/MJloCZ4b796ajgyAGLjooyjDuUAuc1roC1CgrxB8g1LKiZslgtCBKVT3ZN9mCSZU51zqAqjRPtQqIWjVIK+NWm4P6+4Gsz1ocFOGOP7kW4adktiYz0PGgW1O1+VjQ6p1cXEhJX5MMSwnypRSVv5R9D6yVnQqo927kNC3j1+WIACwnHO9vcPvhe8jzSUkkTa83nSPjUB+ZogQLxgnjuEcIO1njqBiGIHuLBg6YSPuliJ4dEpS7VeQwmFKgbm2i0wXcss5bJaZqgU7XhyiZawb6rZoF2ZfMp5gckGycqq1hov0DsAXW9VFLk8vggcGgesPOs5EvbuvbKElsD5Uu8cZ9eVmBoSKla0CqhBpfqsxJ9ax6qP5IkR4FUL2CRM/dUyKEvtSaGUDcBLnMX7exiFxWH4N3rzf95/5cleCLf4+AoTWuQzcXNs4QGFGzWY32g7TiOWfZP5qFpEPWNV2KBXAkWCPKCj5OuSa1YOHmaD64jUXmqQ+SyHrOhSGoVPXrW5M9aUQbEFjAbTu3ZTLbwI3SyGKQQoXACFRVRljpMFX+WPZtAZxJciJqBWqriu1tmn7le/+m3i7s7HZTBcw6HqNkqNXnyXAgeKCo+HeyZkHb/jWOSQKAKUjShQL21hAM3OgELmW+18nM7PrV1rlVLMr7YvuxVmA1G1XnXL9jdjlRUD+28RbHQO5PQq+dFQSu6oM4hQ1EdoZkcnKJbmyPTwQYu1bGXNqE3p1O0nEuEjITXn70Hl5cP0dKE5gCmFcUVEzXV8A4opaCL9884Ehv4/lhj9emAYf9iP1+wnlZcH86idIZR0yHaxQmpGHnjkMIEmkIRNIdGIQUCA/HhwbIVUZMEYU1nZ4EAT+dz8K/ioBhd8Cz199AuH/A8f4Oy/ksaPu6yMJIESkm6baoYOx+L5tSXjNOmL0DoymeGLT51rJ4R+lxGDCzZekG7HZ7pGmH4/EB85pxPs9IxFiHgkALcl6RolAslJpRa8HtzUd4/bVnqjgko9WEPqWIw9UVGITj6Yz7hw/ws1/6Mr701rtCXF4LCBW1K0vhmXH8r0I10faGpvTN2RanQUsQje/5wiSbBkmpL1U67VW0jpUANoqKtZNhM8ws85M2i7ZfvKZEjbNws0SIVOFJ2Ywt7kqEkAbFXbi7R/h5+2O7QW7BDocn1Pno/It2XsLWcUUHapi9bx22L665tf2bQ8Kwfa+p3sv7eHw05+/Jd5+47+3dtvPYfdj3iOCOZrvpy7FfHKoIt03JvuJNfHXH+QxoAzw8eyabc38cj8AqwQE8e9Ymr1bg7u7x+Z46x8/n0Y9jmoDdrr3X3xsA7PdSS2jHwwOQu+yH62vxqi7vLUZ5zy9Z8HA+Ya1ZKCbErjZXE1vgv2XAAsqlyvqqP0/hGdoac+a0miMTLiWlvdc762YgAf6sArUobA9k2GFGYuUqurJk5GVGPc/AmkFLRvAoePUMjH6r3dCKGIBA1C9n+UTzIt0wuDwu18BGj/m99zNB8PSxVxz9OS7v28ZGl+9fXOryHLaeN6CIOrSdzefDKhBdbeBAVENYsmIkKBfGCRgH0DggjTuEMSEMAxAHcNTIbYvmtAH288yPXoJnSXXGb5vmHrDd6vDNuZ5UTdu9BuqE7fZ7lQN10FQ25VlpJp+flLz0u3Y3cJkh3ZqM2d4auj3SjL+ndE+X3cUwjKO91/258b91n6m1wBpDERn3Y1BQHAgcLuSq/eJanuS+UcXwZbLO18IZtlkLJA54ikmNYmk61HcrlvnQxhLOe0jCY2kyCEauBOHXBmJI2O12G8ercYDbkHtHEiCWbCMCO4821YqqjSuYgVrVYe72OXZuZBtO3yE9uR3a/7PKqUgBFQIwG3gkfm8PLFjGkAa4CEhpFEeNxeErmmnXnrEEzCzwb+WPHRmCOHFyk6AQpNqhW2fcObo+Xwri1WB8jipnIShn3AAibXJrtlin+wOgpbaSZZpS1OZfjZrBxKeB6YScDZSS9RVIGpuZzUkgUBSgz5q81I19KA5/sXVWq3Zj1hkzcfSLw2IIug6kvFeytAxUqb6W7TsO2LpCbU1Z2M7/hO1KndMpY+ohBtrso4yougMAVyBEecCBQRWetbcfAgIxIklpey2SHRmjZAzGFJCClJo6AKZgQK6QuWQSLsICTKM4tEMSLtmwakNkAhAlcDNWwpoZuSSsa8/hSK5jjI+fmaXJjtEZKBBTsKU1MfCjlIJlXWGUNFLOXbQJVluLtaxS7m6Zo1WeU10XlCz+kvG9Mwsgu64FlvxiCTDcyW/V5lWVK0pZscwPWPPcZDRoZ3gHDu2eNeBbs6/NXj/XuoKhYEepDop6wAlNBgVQzlpyb03BCmouWLNkcYYQME6To+9t/25Nm4o6FSZtweXXfAlN7jnd4+H2IzzcfABez5A6Z7ivYlnHgQghJcQwIqYBaZgw7q4xjHsMaa++XAVRhqNNIISkDZaqVIzGAKRgYKwGcjS71/3HAPVPJcMPAag6rhCtiZNw25L68MMgmWvzPHuZ8fPn0hslaUXq8XSSkvksFamHwwG73eRcouezVmBqlW1KSdeNgEspibz13KM5S6apyZplxFuFqOzxVTODIwyMZWwpvEyHA9K0ygCnWemzLLvVwOGimd4NPDYe8x7sagAuIAlgwyCNyShYUK3po55XU76nWkrH10DsLQenV56hownReSSQPrO+EqXpRclmHvVnkspea4ymz5pBnlELNnoHse/XVYIuRZ+p7cM5r5IYVwoqyMvMQRIMyqUq3UDwDM/K9pwSIgUMKSImyXxd1wrmFX2QYl2SZHtys7ikqrigltbYzA7pRVT83jgIpYLpk5QGwWZYGhyqVkApspCrVn6VWrTlqBh1MZiJzm1Ds7VE2vyQWtBA5AWNOogIwYPD9mzRHRVOt2HZwl7FIv5YKSMQGCHtME2DUEsE0YYWgE4+S7IPNA5+qb4zWS62foZBg1XmbrI3QqxVsuQtY7thE/DMVumlILZejQ1sHoaEISWvdsw5d83uQ1uDKtNWTRQBf/9VxycCjM0lYy2rMVniWM6ITLi5ucP7Lz/CWjK+9ms+jTff+BSmcY/b2w8xzzOO5zNOyyKZsMOA9z94D+W0x4tPfwqf+T8/AxoHvPfBS8zzimfPXsfDacYwHvAsTVjnI0pm5CwP8vnzFxiGhFqqLKTDAXMu0igkBQwREGORfEMMkBRkAFhL9c6vwzAhxhPO5xOOD7dY14wQEsZpwvWz5xjGAbtpwjhEzOcV77//IeZlQS0VaRiQRuF4NYHd7UacHu6xZiF+HkYBVoXTgkAx4frF6zjOwlvz+rNnePnyA5QpoSrvaSXG9fUVmGVh7FLC6eGI48MRlRkpjXj+4jVMux1KJfzsF76Et956B2+//Q4+uvkIx/MDiAjrT84ot0WTLurGUA3B4Q0RfjWg3b21zR5ZMz9gn/b3AeB8XuFRczIaBeVkDBIpDUG65VkTKzMS+lKccO1QUAAAIABJREFUR8dT+IR86eJFNQak3hqlZsQhCXeNN9DYAimPwdfLc34MOGI/zYfXlMHH2Iy+sHnjqRt9/Hqfj2bK6as7Hp+/v1f73csEO8NALuNeDIzYvxmbLRoo5/kKwOUrgKlXzcDP+fjrfx34y39ZrvPTPw187ddu3/+DfxD4l/9SwMh33mlg5rvvAt/wDY/n9Cd/Evglv+R/1ui+8vHyJfB1XycA6p/+08Bf+2vtvb/wF4C/+Tfb3//4HwPf+Z3t79/7e4F/82/a35/7HPCrfzXwsz8L/NJf2l7/1m8F/vN/9j/nWvDWeosHyhJ0hRrjtZGTyIbYRcIVoK2lOkWJHRsACIwNgtnewKOn3hk1l2/1XKVAV6pqmSBmGOrvpWSAKzhnlPMJ5eEoQGzlRujM5dHj9qzP/oZehdxdHFtQ8+cm0Zef/mpX9qMxdC7+VzpfAwbavF9mQwA+xSILqpYpRkTlj4SWAxuXdYiEkAhpnIA0gsYRYRxBwyhlbO5At0fhII3+3pgV2lz2z0oeiTkcyh+I4HLqAzWZslL6YFdo4Fn/rC7/FoOWMMTkoJBkCdROikXvyVVb0HI78W1e7T5qNSBPm2XA8B7qvtJKt83JaedoC426dWMNbwBIiXTOmzVZraENESICBnPebO67Nb8Z/RP7TT9XTzU26PW7NF9lxEgCpMToVUS90e2AC6RkMcCCMQIsRRKuOtISTrNJfHjGGaZ7ugAilukAhFBgfLORIGAXsgBIFCRwHsyBFH1nGXrM2124Aig1w9wBZsu2I78v4R8cN983fUaVNqJSaxEAGupwqx7O6gwB0pAlKDB6Pi/uHAPqAFrZJAWAomchO2WIgYWgxvvnYzP90Z6rcKpZg7gBQ9rBqEQse0zkVwyeSMLL6CXrRFqGLt8wOCgEK/MNTn3g42Onw4M0FqsAZ6QqmfQpiS23KnAhp7byXFnuIQQHXsQpbI24yABfpe8QOg+VFZV1mzNpBkPdOiTffwQ4slJ3OQT0GF1+Qgje7Ro284aLaUdswTHV9grJZ8r0DyBNhKL2ZhAqtAgECaaMI7RJMRAjIUYCCmMagFFjZMzymRTVzmfRWpUhgfFAuL2ryIWwFiCtErCoqAhRs2UTUBhYc8C8MNZSkYbRzWWujJJXDYIWARsGyDrVZilEhHWVTM+SpVHVojyBtQoYK45/gXHWO9ClNrsEDVrg2cDQSAZKyJxK6TYL7QJb8EqCDaf17OCaVR2KjyI0Lbv9HmEhXxeVGRXFy5mBdi35adn+FjAx/0ezHK2Uu6mP5n8YqCYwtSaTi+aLMWLlWTPvAioCTsuKGLtsR7S9UMAp46G1S1njNT1UppZcsKwZJa86htDGXoEUR6RhQhonjNMe03SFYdghpgmBElIaEEk5TKmAYnE9wCzVjqCKapl61GU96zAYEuCQNSDgu+sB6u09dqAtpcHp8kotKHPBPJ9BBG/IFWPEsiw4Ho8CroaIcRxxfX298XnO5zNyzliWWSpdhwGHw17ob1SvAALQGDergZH2+XGcvLt7N+lC3aN7qmTlBaxFuGaZBTepxc5X3TYahlEzXauWvxcHr0xeTHYBYJ5nAaZy9rkntM9IAlef9dx0voFUSalRbD20AKPI8zajsTZ9nbQU/cI8kIBH6vZnebbFM4ilKfvxePbgEpH5oGaT9IAmtXFYhm8gedaHg1cq9WO3TGgiePNN+b1K35vKG3uhFKlirlXxEUE5EeMAATqbzdw4d8WWARGmELvnZDQQDEtvymVFmaWxutmtgNpASMi5ohbovYm95DgCk2bu25phX68gwXFkrq3ZcGeb6QiqjkOeoOixiISSz1t8oQvsMFccj0fts7Q4UDlOk9NfpjTg7vYOpaxgzpjGiKJBc/OpAkh4ow3EDR0vsdpNy7JIk71aUe7vUZgxjjvnaWf9ntCEJKWfsH3SaE+Cy9rptKostGZs5/OMHHMXLLHgcZOdcRxhAQVpFGjBoq1evTw+EWCs9GtkjBAF94V33sPXvP46MgQIe3i4wZe//IB1fsCbr72B1w4TXru+wvPjgOM5Y84Vc65IBDy/OuDq2TM8rAEvP3iJj25u8XDO4Lhi3F8rEfAR8+mMEoBSZoxDwhgDnl3tMS+rRBMQ8Nrz15DLIgY3MUKoGMc9nGuDpRvxmAKWNePueMbp/laNigUgIe4W3hI5xzqPyMuERRd1xYI1r2J8MKMW6UwetFsxIM7c7XIWha9ZYcs8u6E8n2bc3N5gWc6IRHjzU5/GaZ2R64rTfMZuHJzDVng6ogC6MYkhUgoKV3z5nXdRcsF8t+KjH/8QX/jSF3E8HrFmic4SGOXE4NKySx00VcUDwHVOn/HwWApr99neRVHH0bNbWxq5nHNzCb2Qvt6Bo09jjbq8N0DCq6GS2p1P2CoYMA6/yzEA3QbUj5C6zaaprFZy3RwI3aE007cDNDond3tVenIcG6NNrBR5pZsje6+VPFoo5KmJozbHfk/bTD4j0JZ705E+OpXdW+doWyqPXV1l+uMAqTaH3Wf+wT8A/sk/2X7wW78V+Dt/55XneXTU2rJDnxKgUuT9fNGo4I03gP/wH+T37/s+Gcv/yuNP/kngh35Isna1xAqla1b0u36XgKuf/SzwD/8h8Nt/O/CX/hLwIz8CfNd3Ab/tt8nvv/k3A3/iT8j7f+SPAH/4DwPf8R1yv//8nwP/+l8DP/7jMk/f8R3AH/2j4K//DEpQp8KQN3VKt5l92MifLCUpmzI90qKUUnmwMQpcpyh3ZPfeZq2Ex3JjRlHTRjZOMzypM0YYy/mMUAuQV5TTGbQUWftV/pHx+BkCdBGAaEubtsuJ9dr+nb7TdneTqgf8fLDzWClyZ712OsrOQO0S3XW3OutVRoEBKnXziVesRbu2f0suyp2O5f7bml0QUwJ2e6TdhKANfRiSSRNikIaWKYIpAEGoCnqlIqcusFLc3ty2YV1mkm7umLSxQBRHfHN/qn96TIlru4rJavv4xUzy9jr9YX+FTi58X6DGwSZY5zYwtWlKwwAiQXjbZIarLTALiKkIbXYCsixQqEFtWZgtu8aeFwFAJb/u5tx6ygpGAZDIsmzk86VaM7uWMdN4mhvfWtvTG0DV/+2fo4BcsnYFl3sizRAyI7hWy0is/gw3oDdZsFYGRpr90DLmbCxmx6h9ow/J1m3oM+r652gOi2bIEZGXv9qcGxDv6z9I1g1Rc7xY37eVFShKto9mk4pqCL5fWxaTlwmy7OWnhUFdcNM7NbM4nXU+OR7V4tnkAKdQSjWgv3ZyQ5oRRApGSiaWyQi2fG4MMAJyzSg5S1+Gjofa/m/nHkJCrWOTD9qC4ZbhRBSR4oAhjohxEAc2Cp0FGXeuAhLSXV64HaVjuDTakMZGZmcGz2YjkAMl28yZHkgNwkXZZT3D3WYB0lOS70cO6LuPi3/B6LPVpOxa1uAQk/rJtuZs37Czaxa4gucsA4JRFpBma1kGdwQQuOo/WQtxJK3Og18jkkI/lVCLmhABGCJAUcaZIhADJJmCGUsWgJUiMIwBvAKVgMRAGoFag5mgKLVgXiRDfS2MXFbU0vNRd9l1IUA4wOFgS8nFdU+gAI4JNVtWkjrp1Jxr6JoLuv5bA8PGkSt/j8qJKllWuQpPcCRCqJKVBTZOVrUZWDiohQ+1duu3JRtQSAArQNu0m4Nnxn0NskxuQmVb52IbLWtp8qcyLRmyxbuco1oJsIA8ZA3wWBoBxXEEBwJV4XSUc3d2hff2IPlctLY9uqZBwltbezgmgocBPAyia0uBlkRJwGPc4cXzT2HaP8cwHkBBst0tgBjQMlUJ0ExlzXRVHZyYsdYVqMK9an6XJX3I8GLbEwkAR8B4VnUsQtsgczyOE6Zx8gy9ok3DhPNV9HHJRRsBiY4eUsKkCVBE5ACtZdFN0+TNtwADaWfxuUEb0Maeo+lbsSekUVitLRsbuhe4CgiEMY26tqPyVCZgpM5mCbDydAIwThLAluz8PtBn+4fs15MmlRgI1WfGEmklgdvtF/YNy/0KELYiryuGcWzUoZC9J2e4vW37WC3Gh6t2oTWg0mBmKY3DNqWEiIjB1RVLo0oWShXJCC6b8Qk/fHG7gHX8fZamBQOD8pnDsQP2W7T9TMZphhUhJqWdACHXCqrVe/BI43J9lhTALAEfk7vzuoAQEKiAgoB0fTb+kAbEIBzGwzBimvY4PJPm4us843S6w7qewBZ0tT0i2roIINQGXkMpEVQxivuSJVCIpoNMV26WlGwwQi8J5dAGOeayzmc3GhnSLMv2/1oqpL8RS5Kj2mqWXQpdHy+evYbdYcRuLxSe7H6W8ihXoRs121z498W+MBnZHQ7galzbQqFpgV2rmqjuFwvYHkKCNdkjYs1Al3MOQ/IscKMhLTnLuNi4ilsCRqllUxVFJDzY0MZmagHgVccnAozlyqhKU1CZ8f7NDcaUQLUiRAJKxnJegZKxGwJef3EAEeP66oDjXHFzN+PutCBChLgyEMYdlnwDRhIAlRmtHEAya1bLgEqSOXA+HZErAASkGPDseofKCcu6CnkvBUy7HSpLJ7dlXrUMQYQ00gzWSEqMAdM4YTmfWqkSM0oRXlMioA5ixchmZA5+lSYxECJ5EIkRO8+oNYNiRF4ryrqoUxEkqluE6zaMAwpV7HYT5tk2fd34QE7mH7WZTc2M+bjg/O493nrvA5yXFcv9iuMXHnBze4NsCjPAm2a4lkVz9ritWlmk1DtyZvCieZOmM/rP2WYbtqWOof+b+jPCNwQ7VwM+n5Cz5h/4OUDYlJLbOSW6y6hdZkAbdtsAH2fFmp1gyru9Zkbno+wzNrePmlm/6WjYnIHNfOrZQpuCdhfdJWTDa0p187nL77WZ6Qfo72++fQHIbs9kY5RRcntgJjHdWG1WL8ezudjFn+0sDABf+ALwn/6TvPkH/gDwgz8I/Lt/B/zdvwv8oT8k6R8/8RPAv/237STf8i3Ab/yN8vs/+2cCaNrxfd8HvHgB/OJfDPyO3wH8o38k3wcE9Px7f0/SPX75Lwd+028Cfv2vl/d+4AeeHn+tcg4DS1MSsPOJjLCf8/GN3ygUBOez3Pfl8cM/DHzpS8Cv+lXAt32bXPu//3fgv/03EYrPfQ44nYBPfxr4tb9WvvNjPwb81E+1c3z+88B77wHvvy9z+tnPAm+8gUCEXRpxrkJR4g5Jpw9axiRUNLfPcptR2RwP+UXXgq8PXYSqR1z6OpHfZCvapx6JKW/0BDNaU46SUddVnvOaxYnpFIdt6G0FtsOGRnbx/trU3g/YftBxbLM2Lg66+Nnf3+XnPCuK22do8343IPttoy+2J77ElOVDbSfYPM8n1MFmzyACQpTmW9OEoM0tK4DA7EaP62TSMn6fx26GFXWW+eR2fnVkHEzzIat8VcA4Zi27owfe2mgbSNYmA42zVPe09rcGICpvJtS/7/tn/0Tkbwnwtut4sO5Vk1oJwrAmXqo0qBSQkqyzfK0unRLsaHsj6VhrLagkNsx2X9d1VNu8uhNunyQpf5eySgGeVi0dc/5SB+Rk7iVjrfGbmjHbQEqfNB8IEQGrAp3dvmKNvSgElFqa82Njf2J1sL1XioD8JlP6k0KvL8jHzTq/MYpzaY+FfdDtfkqRjMoYJeulH5ftxUQBVAkcilARGEADzRRlcX8qMTIxiFrQwJpX2R4bQnQ5trmTTHT5jgCq6thWBjE18FafrQiHgDF2CEAd9LlV5DVrqXoUm5bF4TGbOlhWZrGMxKp8e8Jbx9CsLlWEhC5j1IAJo78yZ07B1GDkpbbeKanpFoBKWMoCLhCQNkmiAVcCuJXBllKQtW9Czhmlss8PAgMZHT0EQMV0QtW9QeTAgFpxTBuwJnMZlB7B7B7S75i9IrpJ1nqzl5kEWHUeWwMtqmb6sy0Jy6wnBTzMdlVNTA3Ys/3JAcoOmIwGTHZ6yigIGiBk8sYIqmfAAKpcOwUgE1ogCIwQCcY6PFRpFGWNEocYsGiGGAEYh4iFCaVyV0oMlRW119HAoxA0Q9OqqezO1Q6tumZjjAhevVABbiWkTbPDbXf7x1zBoUqTMB0AB3bdqeiOZEm7zq3yjFjGVn2dAzIT+vAI4svC7kPl3IIk8gQQbD5J9rRooANkT5FM64pKFSFUEEIna3KiGAd/5mspIKqISejpKlqwirqxmnHCREDqApIiiog5brLzYxywctFMSNLrSmZkHEbs9i9wuP40pukaMe1UR2kVCkm4N6iulQCYzrFl+0F8zooMa2IJMrBdgwYsOuQpH8T342LPS4MVCJ6dZ5UVvgYVI3AbIMCD5V4Srb8bAGSZoJbRaOeoFZ5taZ/dVtFATZHqafxEpEEe03XcjDidFeMvdZ+QOr9a9/c+CIkie66sq1Z1YfoiUFSOZMUJggX5NNCnPWV6o9B6v9hKCkrBYVmEKUWRsa6Zk4q0z3VloQcwShcGeyMk00nSXE0A/pxXWDDCnm9RugDWfXjDW6sXCjHqns1O65dsrRahigCMvoxcVgQPZ9ch0mCUmm9DbroLZYnuZ0zcbEDR4CKrBFiTJ4oaxGOCUGUM3l/HplmCeSPGQbLK97sDKqT5YckrTqdbnI63WJcT8rJgXRYZo6muqkFd3bNY9YeZRB7w8b2XfX01eWPZuzuah1zMbmh717ycbQsHA15RAjRbIKUI5qhywEKVAtPr1pQueLNX0oAkBepFz0cmDVnZ7VOhQsj+zC51u9iosd0Zt73fkmay6Yog+6fw8ra9H4CueUssAEipoCy+bPLSJwSycxOjw8QeH58QMLZ2Bhzjgw/vEEG43o0YU8BAwBgirncTXjy7wovrPSpnPB8OmHNEjA8I4YxaVgQEnM4rht0OadxjxwG7XcW6LjjPZ4iTIlHLMi8YBuF6WtYVLz/8EClp+vQu4PnVDjRMeDidcXtXQJCM0lwq1izd1eI0atmc8U0owfSYUA57nI538A7PJCU3y3KWSBcFDGOSVH1IRFkIxGdRVLqQRF8XF9ZaKgIJj0scBlQwpmnUVG3g5nSPYRzF8VFUfxynjaG3nDJiOeN8POP2/Xu8/4Pv4ae++GWc14yiCsQNYFvkG7BV/w6k+wUBVhKmRkPp/Su9dO8Q9sTidnhplhmEQFvY3Wf6zzNsYZhhVtp3ujFfOqLQzYam1HYKuxD1kSR5cbuM1PDtoqH9e/6vU36kCtsdQB8Tt5t7Yq32ykW9yc2VbCxs92tGlXy5cxi3429zGJ58fTMYBtABBPacbXxPfT3YRowG1zSQjdx4tnlh3j5bG7//vHwPj58KAMnu/O7vBv7Fv5DMz+/8TuD+XrJX/9gfE4D1gw+A3/N7gG/+ZuBrvkbA1R/5kXaO7/keAUp/za+RTNHv/m4BfAEBVL/ru2Q8v+/3CRj7cceyAG+/LdQBluV3OgG/5bcIFcI0SRrKO+/IfT57Bjx//vHn7I8//sfl5/vvA9/7vW3O/mccMcoY//7fB25vBfD9q38V+C//BfjUpxD/64/haphwM88oakwIN5qdoBdszUDTdUr9Jy5E1Ncqkb/ef86dRvQyZd/t1q0bOLzRH81AYTdgZR9aEUrRZl0ZKGYstzmtpUXAL/WMD8PWS780dO0SXcq5rRMz6PRzPhE2OeST0OvG3gDppuGx/nSL2DIztuN2g4MUMGlXbfN/cVD3OXYd8TGHKE2ENCCMI8I4+P5nwSv28cKfHZkD3OFHvUFljcDMUenLvW3sZrALzY3OF7ODP52WasCHlaEB3kzDwSfV23UDzmEDRl42lLGjd85Y/98vW3uel8958yx9L+j/qQyBYKCFyzdzd4fiXJRSEKgCHB7pXgKB7JqeokNazRDAJDyGiRKmNCIQ4eF0Urulbgz7ykUz3KR82GwdyU7on2sHfvhkALUDa2xsUUvqQYTixPEyRnMq/bl0jgfMSFfQ3B0Soi5TVta8NdSSubU5Ur6wddVHoKCwGA0oUiuIWiti7UulzUEPNiiI6FkZnHX2FmA7wECiRgPUZKLqHLUn2qbLrkm9dOlz0CVIQbn4VbcFzbZCfzrT2fI811Uqs2KsACJyNnkkzWyTeSpVOrrXWjCkARRkREKXrECyNucKWt4cNaNTYBrNOGQFTtdF+PdM9hW0YKpgKpIcURehkWKRe+LJbTOzZZmlq/yyzKqrmqPGao8w2KktcineXKlqto0AsSOGYZBx6vwYV16ILHKi0TbT9ZIVSMglQ4B1qDMumcwxRC2flgUrTj+BS3GZBUiXtIFwgiF7V3XVYJGAFNuz9IY39o/ENhPzvtsTiJSCgMEdl7/pTQFdpNiSNF5mEiZruYpuV0B2SHoflUAIoESYo2ypIRAOuwmEgnnOyLq2RVepzPuGHRToj2DODtI0QCoI0KhzFtPoz16CNKvPaXUA3p5/UIAzwIDyEAgrlJtW1yUBiNzmOACSGW9DJKnuBIuq9OCgKSB9LjTYehIaBHbwT5ty9k48AynVLvvawPS2oltmvew1ay0Yh1Feh5Syg+C9QqTbfBW+aLb17SeVsXsGsQUEKnJVPlSdwxAjclmRSOQrDQnjuBM6gt0B+6s3MaXXEOOEGAcHMGyvBmdQULAcLGuWZD3A79VAVJXfYM2buuBHt1fbmJu9KBmTgIIoIUpXdG0KbRmXbf0qcBSilzZDZXvOs+vwcRSe0h6InefZq0AAcmA6xYjkz8gaQ1fvKO/7OyTzNSZr7q33bSXStaAU0RVyHgF+gy0aWPXCliopdxm3tg/KXIns76Y9TuejUHMBmMadyLvpxhQFm9HvMgHDMCCh08es/K2UXN/Jvm7RHbEZogZOJZBRnGJBskWzx99lS5J9JJeidCFtTG77M2MYJi9BdxqGTq+nOPhcejM0W2fK70swO1DGMwyjZ1iW2hqD2ZKWZmEiFzUXjNOEpDYs14q1VrAC3ESMEJMGMSVwKrQ7UtkTQ1LAddQgnuw+dRXqyGEYMY477HYHUEwaZGOs+YSHu5c43t/g4e4GH334EgSh3RTcB04F6X5SV6XT7Kj2f5MLQINKLHq+VOPCLk614YEuCLbWz7ucx2pMGAhBqj30OilG7K8OAKwJmcpDLag1oNSAcRi1OrrRacCWt7pBbDzdtSKXgvMy+6Zh9rXIoYxt9B4pMgEtdq3B5pLlNZaqokpCPep2e9XeUiH6GnPdAQXc65YTuadIYV9/Tx+fCDAWBG3kA9TMeOfHTsjfnPHmpw54/bDHbjfgjefPMY0Jp+M9bm4/xDRdYX8FTPvn+MxnvhZX1ye8/+57WJcVSy546633kOIAJCCvMz79i17HBy9v8XA841xWpDTh/PCA1998HS9eXCOCcDydnNAeNeNwGMEJOC2EZc1IIeD27t430sLAecliIDBjHKJEi3NGAGO/G7GbxuZIQPMMiixiThU7LY8AtIznfML93Z2TMTdeu4BxHHB9dcDhcMB+2oOUQ+bL776Nd955SwjGS0HW5l7DtEOMCftJygZubm5wd3eHu5d3+OiHbrCcT8jK44FcO4UFSc/WzIZArUOcAwmhGSZAi0zbfRowAzSHevPI6bGDasflaw2MfEJwLr7evmqLsvt0df8UICAdRsTDiPHN1uhIzA8l4koMWDMhIikLIcuuUSNUL9g7zTJOW4T96L4CJ+rFPV+CKa/4pAKjaEaIOaXdPKAHdD7mmnK9/jw9sHXxdZ2Xpw51B1uTER2nnatunpOW2XZz1YO2zWDZvncRB23Hr/yV8vM3/IaWqfr7fz/wr/6VAJ0//dPAt3878E//KfDv/z3wxS8C//E/An/xL8o/QLJJe87Yz38e+J2/Uzhjr67kHNrg4yseP/zDkpEKSLn/4SBl/p/9rFz/279dwOGv/3qZ0z/7Z7d8r/87j6/7OpkfAPhzf054ZX/0R/1t5oplXmR762XWZEVlqIkk64bayZQehEfLefPsXaJfsZ+9SpfUi3XkHbIBQMtNUAp4zajnM/g8oy4Lai7iOXbg5fbiHdjkxuLFPfTAkOvEzgQi8vt+DKs8no+POy4N8afehwKe9versko2Y+oG9wh0BrbP+YnPtq6wAsBwiojTqIEJLZmzuTFwiGgTRWYG1toy/SxibuV2nlWqGS9yPnLAxcFbLYP0LAS7AebuATQnwV8koHWBF6PbCkg9c6k7rBTb9gjdkt3Bs7I50jmx6XlKtrcZNU2WuWr1DIRX0wGF2sJflgFkTiAUlPSsHQNUjCKhO6QsTewVe88aGzBJ8a2U2hGGGBEpCBhZVqHzsHmzc4jL5Pdvc7yuxkfXrr3RJZ1T3Ac9h2GUTCG20jCdQDb6CXt0AipX2P6s2df+zFrgIyjwVe25adBRuEaHzbMgsq7HDcavYARSAJcZUiTeHJWUkgY7jCZCnDdzOBkAKzBXzWHUsj930NH0zQbU7/i1o4IJdl2jtDA9XbliMaeNCEMAQoqNTgKaAQahDokpYdrtvKxT9myRJwEmAioX3D88+D4vASsGZ3N0GcM4tWRrGBgrGUL2uwfjq5R4Eykw6k4gg2gB0VF4SWvGkm01kpYDB0Q/J7zaykCJEBIqAmLUhkLjiDVnAe+4ehZN0sw29Fm0EBt/LWWjo2IMsFIqAz3EYZWMsXU1h6/fj8i2BnkuMIqOoMrF7FgN/uv3hnFASkOTSVVfITBSYAzRqF9svbDwiYIQEUGoGAfCbqfU9wQsqzR0GRIhDUGoUAgoJFV31r4t6P8YYudnpTQ4z5Ipz64nRe5yJuTCWNaK22PGWoWCIIaKOAIDBWBlzHPBUsSxFjowzcq2xnMGYpoxQXKeJQtncwiDZzKaw5wSofLqWVNBzUwial270Q4CYHRLZFmIJKsVWpZarfEOQa8bvOlc2+G7rHoDuqnNn2TAFngTLkdImowZH28rqV9BJWsVAyDUeVH1AaPUgtOyCO9wTIghICsQJ2BhURUpGb4WaIsp6vclkGQ8mT3gUkGoTM59uywPuH/niwP9AAAgAElEQVTry5jfv8VyLHjtzW/A9eE1DOMOIQ0AEoYwIYaEEEQ/uOokwKAHUsBK8uYXCMdohaS5M0IAEghVS/ArS6ZvO3jzz8LItWYF+CLGaQeAFdgrGIyvHsKXKjyyku2+s6a3na4YxxHjOMI4IXMpOJ/PUpqvAOA0TTgcDt5oiyg6FcqqwQA5rewNMQlnbug4VlEKal2RCyPGIDslQYHYIlhAiOgl1sBmWfsCMhp9gjQgNPnSPb4yWPk+QxAw9tnzK6zrinVZsK4FiZLrYkYBUkTJFcsqtIcEOOWLyHVsgCVhy8erQF6K0fdKk3mbUztKhevTlBLSNOL6+oAQA6zhWQO6jJe02QUcAkpugYu1ZtyvR7V5dOEBvs9SsOZqSTMhL+h/guhZkzIXXbQgSNF9LRcBE4XFQNaxlLJbBQaUxSNgnBKAhP3+CtO0xzjuxH5LI4Zhh2m6wm7cOVVIIAiAG4LeAmPNewxhwH7c47A7YBxHvPXuW8jrKvtSEUBR23TK3rIW5QwXgz0ESGUTScZxpKQgp+iTXLUSoBbM84zz+YR5XqRRpQYpo9sYskcJj6tmjQdNHlT6MSiQeXV1hTc+9bqCrBWrcn4zZ6x1RTmtQknggZu27wfjn09xsw8CEA74ok1yITpvXTOE07/hIYZh5VyUn13k0hr2GZ1njBHFKmuYBbcrxQMvAJoNFsgp8nq7y3wyt10/Bsr5RICxMQp/EQBxXvcv8PCBlCHlT814hoCv3e0xxEEsAw5Y1oJyf8TxlEHxhP3VNZ49f4b5dMZ8PuHD99/D4dk1CIScV3zhCx8i14Jp2uGN11+gvmB8qS6oYcRpAcpyxm63wzjtxMCJETcPFffHB5zOZ5QMUGBMgyieUoSqIKuyMUM+O1+NCPh+N2FZVkfPJdIl3SFDkIYUQRt8RC1hub+9AUH4K3bTiMPVDtPu4JvIsi546523cTqfcZpn3D884Dyfm6PMAKps9Os84+HlLX7mB76Ah4c75HWVhXSWhjSsBh8T3FmRc1hZo/D1GEF40qYr+qgU3NQsnk30ito+YEAboUfhWvS647fcZHh1wqxD8rm1o3N5O4mybBaIA22LGQClgGE3gq5GpOsDsBtQ921DYCLUEDHEKOCtLSooJ2rnsG0WlpZkSGGoNv9Cl+HjDoiBi6qwYSUl21V66YBvsmO71/qyDb9GD2R0iIk5Yk9l823/Jp3PHpZpDgN317k8jxmhPXj2FKIkxqh+/wlU9Sk52Iy3DeLxl3/gB4C//beB7/9+4Y393Oe27z/1na/mta/091dz/Kk/tY0Q2H288YbQBgDAm2/+3M/783XYPf7W3yqg8v29UDMAwF/5K1g++w14b73HGhig6qLD6mT2p7GMN9lfSzd/pnPgYCa7zInuEP9LnRX/Tgfg9UPGdv3YyQ2MNJDNr1WqZMGuK8KahWOssmeyCpWMgYQ9oNbWSwjxQuDbwq+dgG8yNVlK83Gxrs2x7jMZfQ32CFc/BnX06oUOvmy8YDr0VUYB2XSa8+DXwfY7qk+t1M+fFx49DrBqRQFHIlhLjAYDVTvA3TQjLtY71zaHzJBSUiJASfEly4zcSZbvsJaEaYYPt6tI+ZvdUN8VvgGPNtXs/9kzIR8sQbKq7Ghld/2ktvI6+ZPUke9uiPqM6W1GrD0Fusg6blm7ciLLyLQGFlxahF6y24rLVK1iOFcDC2Br1J6fZJmB2TMGAcIo7oE/18oFa56RSwRCkoydzR7NwoUIckCOuePG68bfnm9/7+iEkBwsDFaRY9X7vi4ebzadNdD+rg1IE1tNAInWWKNlclUFhJgXBz+YGbWsInfdWB8FRLiI/uhAPMvkYW4l5IjRyzSHNEomIAOVGGGQ8Vh39DWvkiETCFwIzOI4VLXnxEns92+ZlahOv40lgAB1QiMFTeRv6xoAYrJrM4CAytmBbVNzuRQHOiIFkSnNgl6WrHQakj1bV7OTuieloGmgAAoDEmmQ0+0/W18yusLSEVqS6sR+GncjiKKcS/VMUP4maX6TFIAh1VkaSAhJKDZCwrKeBDzQdTIO4pymEHF1fY3D4YBSNGOqVCAklwebZClplAxSDtCMKVKwSxrkiC6wEs0mzzFExERodbBBOXwV0IfYTeM4ICmQ0YIokulqmXLrOntlXQAp76E49ALERZQVWINk10ovNpHFzLLW7o6MIwlP7DAQ1J/GEICrIFyNrLqsVNGDVbZOlCI+0jqrHBGQEmGaBlBmrBmoawWCcE4PuwHPr0dwZcynjFrg4I2oW6ssY83AlvmW5sOiP83qFMo7cp0qcZeWGcuAdrdXoCNIJrHdn4tlpw8pyLXyyphn4b0VIMbMgtBVEjbrZKONNMPawljqzcCzq6rxEFb3ZjIzVs3Q4zog1OKl+nKLAtBVpd8IUTL0hihUIhylGbT0NVmVP1lky+ytcZi0s7w2tOOKNoURhCi8x6hAXbCc7/AT//eP4v3/5/PINx/izedv4LCfMKad8jVHUEiaEaqgXoWX7Nvkmt5stANBbAXWigTL5q0ZXCXDzTk7emPRSsJZbK2UgnM6k3LAkjpISRuhGVVBKUVBGFlj4uuLjpbmWiPSOGAtGetZ6AqlMlX4KPf7PSTrXXSkALAZUDqESAHjMGwaWwnfJUSfrwVLXSUY1/l4MQh3PkyqKTWgF5LB7rrcZLvbU43H1fcx3wVs+uWVZZldSodR+EnFxlWbQitXmIED9ngNL+TTlZFX6STPlcVfNtnXZ8sswZrCRZ+BAnQhSrb1WlGqBErO51kCmUr9kKLMfwwJKUr1sgHZ0OfM2ojQcAmqFcMgMhFIggwxBF9fjQopuJ96Pp9EZ1fWJLbi4CAA2buCBm5ZA93R5lIoeICI2tmDwzCqRTnKs0oDxmGHIUqzqmGQRLpxmDAkCQaGFBHigBAHxDBqlYoGGLVxXWbJZremaEwBHBIQRwS9piUcMLNwXpPMVUGFNR83mam6HxViFCLkQKhZMl2tYVlWCp6sfMCkDzYF6f0wTpNnf7ZAd+PYNV0kCadiR+WyYllmTNOANETsjBOfR1jFzzTtVWJFL65rdhq5Wgvm46L4k6yPqHy/BHLAVrh2t8CoNCcUHykN5JiOVeEsy6KqJWAcEoZJA/4kujqGgDQNDVPSaqZq4LTaSjlnqcJZVxwOBxi4/0rHC58QMBYwJxMAEeJhRKWA04OUwWUQXl6dwSHiqlSkIWCIAwgSSeJa8SIdkENFTYRw2AMgkEVRWKKixLIJT0ot8Oabn7KrAzTgPFdUXjCkgpQSVshGl4YJzJI+ziSRKtlU4Wn05nQYx4lFQkMQoLlQ52T4opHvBA2VEhFS3OH6mUSqCOQlEb4g8or74xH3Dw+Y1xXzukqTsLU1FXLaB2bwDNQPCct9xvn2jJwXd+oCet4odmXaH+YMMkO7/nXPrFnTarXo29y/3GfLkV/LLRa0jeGrkhO2C7TYswMV3H4n0JYjlgiUAuJuRHrtCrRLoGlAjcGSV/x78txC5zQrP5fqXtvY4WCNli0ZD5gaSeJU1zYfF0CIgZYy9uYYbkCIVwCmlz+3D65tvY9ntt+Qt+duj2H7zR73vARaSN/YAEduK/vkA6aabdydKDzpkl/IRD8vLejw2PEGAHzTNwGvvy5UAJ//PFCfQHu/muP7v194ZEMA/syfefz+936vZMheXwsFwVcjx9/2bcJVa8c3fqP8TAn4Zb/s/9s4fz6Pjz4C/tbfAn7drwMeHoD/8T+A3/27gb/xN4CbG1QwFmqk6ADgltiF9Pmy4W5BgCAoAKF/mlaq3jAWW28GHnWOziOhfJpHzHSFg5I6FiqsmbEr6rJK1ULd5rj06+apc29u53LVdQK+zRh+fL7LcztgfHlJVxztIrbUtvm3Blj34+l0wFOnffL+VL8/Ckg84XQ+cU/BuNEdeGZvHPTElDy6x6f3CNMH7dtNp5HzzzWHxqoWbE/r5A/iHHWD1rO04JnrM5XXNsTmfHRoZkfV0Xas/gVfBV7ZIHqyB1C70W5BYjwGY9HuVK5d26u+T/p1JZujHxldPIR68ZMIyJpdJVlj2mzG170Yp5Yd0u633ZdnpXMLBG8fbVtrTYS64J5+ti8Vk5t6Iiu9O2fTGnAd5N2KicBBwMvCApwRtcYXbf3p/ZFlmTaONtrolXZPFkQw8LHZFSYz3YjVuHC50IcidmFEKZrxayLm26AF/xuX2UYudOzWGMW24RAH51I0sMC+ExgIUcoFSbNbOPWOWktCsABEKUWq0chafZBWVyV31ARIiB7Q7rk8rYlWislLs8ma1cAy4oOzxtjzi6FlSROiZolrl3bWDFuyhloChMSUYJlDxmt72DfHMgZxxsCSFHHYH7Cb9pKAoUEOayxoY7Nrsdl5zBiG5JlizJqtHJIDxoDcUyTlqVO/30DDGBJCHHQNNMczKC+tZBBDS+kt0GJl/Dq22OkH1U8lZ5xOjHUFzokwDUEddfayTmZp1pUCMA3i2Mco4Ox8VsCdAyoHZADrXLEWQqnSWXzNjFp7AICQAkCJMRDAse1ZFCSzOAIYSMA7oenQ98l0iv5UGS4FkOre5nBz2wg196MIQAeC8U7HGNT3snts/kibq/a70DcIeB2JMWfhGCzFAiCW+alKtFt6zQ4GiIWWgDYNjCHZ9AQg6jNjCXgkEnBBMtsDwKmVnUPBcJMhBbFElVCTzSAUesmysxT4tT1F1lAAcwRHybANQANvdH3WZcXycIsPv/QzuP3CF8EPZySKmiQ0IcTJA1nChZmabu/8gKbc9DHpvhto8KaSAHtmsCT22D6tmlz3ctO1zaJs+5HInHJzBmvop7ywqluHISmQqhl1lZUypNG2LPPs5f5gYBonB1Ytg710WZtVqRekYVF0ENWuXbgIQJZbwykiKd+2YGCKCTG1rFY1gjayKVz3tpe1CjBf54A/X5h/RiQBIpMb/3zdnKM9Nt6sK4bgAFxEhxjnamQNkOo6aiXx7HyyQxqQQpQKns4OMGqA3FWHUCCtKFIO+lI29kBLcOjWkfntel+llI1eaDIhMhMCYTftZA9TeUNHfwJmFLYGcWo7RXm20lA0q37RZpdK9RMoIrACzzFimHbYT9cYxz3GYUIaJANTKkrknw4IjfKorRHfz7n9oyo6xGpsAEZKAZLFLgFx4Y0PumLESqlqn4Er1py9uaUtz6rBxp6eCyxUBbZvGoVH0Gdp4LuPVWnqgurryprZqzKXrEpFT958jma79xUdgFa7RJNpRkyip6Dy1WlaFJbMYACgKnZFjLrPB8i+T5YJLZ4k1+pNyF20gjSOTUqRJFQK2kRW8T2zJQmC8w1p1H3GsvDXzu/4eIjgkwHGWt0GRAkMVxO4EmouOH0UkJcZX3p2xP2p4NnVjGcvRhwqME6MEJRzh58jUMY4EELaScp7kdIOLgt204g1V4zDoF0GB7zx+hs4nU5YlgWcIu7v7nE6zYiRMI4J45Lx/MUzhDAgDgEhJuSSHfUmMiVmfDPkRjnQDPEQRSAkckWuyIOWBIXUQE4iwuFwwDyfVUCCdH3VcoRaK+5u7zHPK9baqAEap5o0kKilghdGeIhILyfs9/8ve2/ya9+2nYV9YxZr7X3Or7r33et7/Ww/Y1wILDsiihIFWbEwogF04gZIadGzhETSgV56+QOQQAhQGhEdOtCJaNAgSJFQiNJIhBJL2LFBNjZ5xa1+9dl7r7XmnCONUcy59jnnvocl4DW83jv3d84uVjGLMcf45je+cYPT6a1k3XpwY46S2TKb/H2HbsdCDV2fx1/TP1n9D7Y1Q+bQDjhjXVDMZ+nBsBnIbsCvWZHjqs5j4OXn1+fy+E9DWIJWCA2Ixwnx9oDwwS0QSQFyO/X4TDrRCD5hzSlUH6czfKN+HixVZcEKOmuIxkMb+K31dn7ouGYGPchAJVuEodv5Y0COrru4f7U/q3WYO4/U+9Jaga7ukffjobfX7uYffDZSUXTpEx791Wsf+MrpeDj1+msB2d/+beDVK5ED+Jmfkfb58R+Xn1evgN/8TeB0EsD2Z3+2f+/jj4Gf/mkp1PWv/hXw9/8+8I/+kZzjr/7Vfo6XL+Ucf/tvCzj58z8P/Lk/J/f9+ef7+3j3TrRg//gfB37rtwTU/LN/tn/mk0/k31Lk84AwY+31H+T4vd8ToPTVq/7aV18Bv/Eb8vtP/mTXe/3N35QI5pvfBL71LbnnP/bH5Npv3sg9AgISf/KJtNM//IciT3C5iC7tX/yLwjwGZAHX3D8rCDEszX47HQgZHUago5ODwwEMfS7jk8jciX7cvwrujZWdLcEwtmGOokgUoBSgFNRtU91I+Fwgv2e+d04LHPza6tXI+1ebAINtHBmt472O/3ZWkDHV+hP7b1dTozMpdatHJzWj23v0W370uD/vePfP+Hrvt6Gdub/LzAhJnpVJdpclVt5BefeOkelqY2psb7OvDz9M17+ydh8dovt6mjwMTe5OlvdzX+v8/I4m6xl0/e2LYdeMHW/RGMv2fJ29bJu9bRdgEthPa/dvbWGOYRu6pyvxEICrAYI+R2qzQnTj50cQ1b/gz2zyQwLMDMCxXspSTn2soWdkeBuBd+Pf4EcP3q76s7sJBjcpsGjKjAxlCfZgy4CqESCxANROOtojZmMsyvetcrqxGSy10oFUY9fQ3ldxFqjerwTrfRwHlUjoPqLNzd43Bjra+SU414Jzg60Z56cAjQLuWVDtvcbyvaz56OZ3CXu0M7ait48yWibRRiUI25DBSDEpIFmkYA2atxVACnKSCzJVT2U0IFb8aLKgNUVl8kg/TZq6W2uVon4xIGlbSMXrDIAcEAWE0DDlWckFESEJgGksUdL2slRyIkKeZ2lfMyeO+smvMQRkTY8lkrZIIaOk4JkVaZ5l3BC5RidDNjlKqdjWVaTLorAmA0QTUhhQEoS3RqqnKEXDoAVBam0eIMY0DfqeLMVNuM8r0V60jX9l7ULsCRSQ83VAQafSKtZVUsRzCqiHDAwzTwJYBSojoW0RAc21Yk9UgQZhaBODA3A5F5Qq4GwDsJUGCqnbPxJWbSZSAgTBa2WpyYwBCFlSa5X+ghb6yuJbFaNJJZMLGXxmdIbuWpqAlDr/TL/aut1BWr2XJo48nPUehGXGDLQqc7ZVYVm5nDyZrIvqa/rSw74GohYwb4D2kwzPYRNaf2lsTD5hcAewtDHIr+ebIZZWDfFTbJvaJFa4sbO1DKxiZl1n5DOlVpdsCByUuc/KvpQzbnXDenmHd199D1/97u9g/fwlEgEpz4g5IgSJqd2eUEAKCsaSMRkHn87BGI2euCGEBDItbI1tSUEfsS/NbaXbTPIz6jgyYog0VFMgUKvBCUhSqs6roMCkaKuCoUBscvvaakNRDexAhBQTjscbsW2aDTCu+6Q2CxDmbKQhk6J1aR4DZm0TLaeMnPMAxkbVZmdfF93PcH/AGMW8i5FHP7JV9XFhNj/s5okPvdq6rECzVG84mOkAXWOkPGlhNNOhN7C7a91KpkZDZfmZomx++XglUukKsceHg7AJt01S1OHP1VCaEOtMt9qebfSfaq3eb0Ftno1zAwutrVl/TykixyRrBunoqg3NdYsh1+UGmF40kcxdCmBUcGEAATFI1nJOE+Z8ADXpw5Qz5sMRx8NTzNMROc+I04Qpd4mKvrmrBgi2qd39pNFHsLGsQjEgLcoXY4QVwJS2k2wXJ5NQFMa7zvt123C5LMIS9+sM/gVsg5d8/cxp0nE6ZNgEA49NmkLmvPmETFCWbvR2F81ycvuyD0poly1tOvujnxqmoHI2Mi9KLW5nbdzU0tzmNRamtfmF8oxwnXomcr+MW/f/t7YiojPZxS+RcUgxwfTkbW2hEDBn0abl1jDXDcvS2edfd/xQgLFWzAO4A4WAp8+/Aa4BkRlUVrx7+SV+97cWtPYe6fAWT79VcDtNePrkiNubA26PRzQwfuJHPsZhOmDZgLu7BqCgbifU5YRv/vgfxau7FTdPnuB4e4NtqwgVmCEOdzndYVkvWM5ntFZl8Q4B0xczjjdHPH/+DD/5R76F/+/3/y0u5wtalcmSVHtGds0aoLoZZsBCSqCmTp3q1R0ORxwPB9wcb/D09gZpSiiqibKsBa/fvcdyOYveSG1opeCD5x8gT5IGWLZVUgRKxboVnC8XtGo0bjFqXCvyFzPSKQMh4Bs/8ikuyx34XcG2XrThZXHzBQv3nXzb6WOwp9iNwZoFNFZxr7WmVYR1gXVD4yfEntnGgw7ZEIBfH2qsyIPvIfpEf81CEHPUKRDS7Qx6cUQ4zsCUsSYpEhGYds8ynqm0imSpx+ZLsgVPYgBCIC1OIE8UidxijtVy+/18zfMBO+N2Dcg+9nljz+gLu/a6930Wg9IDUmmxpp/3MMyBWTVUj6uzPnjcA2KBqzEwvHH1EiBOJb7feNhfcf/nn/pT8u8v/3LXjP1bf0te/wt/QaQLAOAv/2Xg7/7d/r2/8leAP/2nBVz9lV+R137pl4B//s/l97/xN+T1X/1V4E/8CXnt135NdGZ/7Mc6WmLHn/kz8u+f/JPAr/+6gL1/7a/Jjx2mGfvyJfALvyDn+HfVjP21XwP+6T/dv/b3/p78AMDv/A7wd/6OsFl/8Rfltb/5N4G/9Jfk93/xL4A//+eFCfyP/7G89g/+gRQvAzqoCwhYa+cAYM60Oy+wMSTv7sH8/Zi04BXcX/Pd/eGzZi16oNjn+LW9Go97gKcBFGwACINLQV0X8LKAlxWoXftVvmNOfp/Pj20QWHvsf9+Pie+/JHcZBL1VvQm+mgs0/Hd/6ZEcak6pNrK8THRvCo791B3AEci+modDNDSCPnJ+mcNMw650jKCcgJxAOaMSAZpq5rqaV+1ga4v1wX5dut9ueztBPcJHD2DHMWOp6a3p50iYA12/mkBV9AjlJN1umotrADz7NfoY6S4mewrZHnztr1l7mxPYH8UASDjY2NmE1T9L462h/+27/8O1WUFG+6x1JV+/Yjbb21G4hKIVRiBuSGNQxOyB+HVPNq4CgtC+70bAWACH5mNtB56qbI4HWg0IKYlOLVRywTOhxvWKHEC1YHREcizgEKCOhn7cFwiy1XGaD64NZv1m63WrPStqnDfRtOjU4Q9WrIp631u/210ZcLh/fuvbrncrwKGk03e28AAy6hks8LV+MtakB4Mu2WDgb0aMAnz2TR2AeZbgXtuZVHLEmDPQVFSXcoLGrq7HJ19NMXoRHADuu8YQukYbNIB2wCV4H9Wm/UlyhylMwhiNEQxhjZrWqEk6xKGoFZcFpOxZqQw+2HwNcgVoUULFxmDaPPBvtWFd7jDlBIoJHCJiStJLRQpAtm3F1ghIBshGLwjCLCmnW2ngJvcpz2JVzSVQF1/9rvvZLMAwRdGDbIrOaUt72wkbT6UQvP+kIFnRFbu1ouMHOBwl+066NaKUihQIKRJyJOTQU7FljskzVa1AXZmxLA1brYgp4njMOMwJ22ZzmIGgtpYlQq+qFNMseYwZpUD4XjqAY2BQBUY7uZvbulaOOryK96A1AWS3ErFuOjdh+qpNWLGJkLMw/UwWoRcC0iKdZoEb61gH1trQ2GRpZH6O874N/dw0tRatgpQ1ec9u23qh+rAGtlYFTmy+iQ2vfRxq7GTMz15USc7jlc2HtHNm0YO0DZW17uM6XZ1g3LsUgHcvv4Nv/+v/F69+//exfPszTATkNCHljDRPIARNVSeX3EgUpEgXuBMYba30LrQNAyPr9NcCNl2GRPoDBq4xw8AeInR/Tm0PsxWtgts8kyVoreJ4exR9ZwKYK2olZeRHpDSh1orz+eTg35OnTyUW1GPbNk9pbq1hmibcHI+Ys0iHVBagq5SCzaVJgv8YszDnnu5casVWm4J7el+tgWpzOy2ZCgKEQdvZbfxgb3czJEFYtp75wK5hav09+ruNm+roFt90AuAyOLXouBukhlprWE6Lt/eshZIGFwZSOv2k12LEkFTTtutaW3sY3sAAiG2TJXhhMxtjLpuI7tvp5dyeE5GP81YrmmYxNzDWpaJsVce8immpD9iPhpwyYshIMSPnGTkdcJhVUiDOAEXEKCBlzhMO00GKmYWgoH/21PkQIihFZ56bzQZMYgYO8NmmqZGt1NX0n0AkDNnatLwN69qziYZtVV+IZTMnxgSEhKqFy5bLgssi4LfZvJyzj0/X+R18pKTYjh3MHTvy9UNvsJFMZTP/FISYCHTN5JwTkpIV72/Ci4G0jYjT6aQZ6brREbse//FwlM/qWKjbBmRoNlC3y7YJsm2bbzDYMcqIGDt+nmb3W2IixLQfa40b1q06qzunBYf54G3IBATVpfV5+shB3x/o+Pd/HD79Ef6x/+6ngPlLcMk4/8v/CttyAV9OaKf3OL97jVIEFAqBMN/e4NlPLCASh+F4nPGtTz/FH/mRD/HpR9/ARx9+iH/zb76HOR9QlgXb5YT5cIv52QdYmywwt8+f4t2bd1hOJ5RtRYBIIrx9+w6nuzucz3cwXad5nvHkyS0+/uQjLOeT6HHpQspcJXWriNF9cnuLacporeF8OeNyOUuKSEqYcsLN7RExTv7sMUU1gCuWy4Lz+YJXr17v9V9Kw/F4QE4JTA1ffP4FLkuRypasFHL9kUp6DdPvHUCVQCzC9oyG9+9e4uXLL/D559+DOA9hZ4h3IID/ux8f9xizQzBhu37jbo+f7yoIfQxQuR6P3/d9XAVfZI4fgeaMcDNhevEEfMzgGNAsfQKMBBJ2UwY++q8ZFIDlXxPO/3cERdndM2PUn1uf2YJFk5cAwLAt/P1zj47k1z3LNQhurz0MzA7OqTlSNL57fU7WigBNd1z75x6CWnua6RW4dNWve+DoAWNqoAZRd7bkzQedh/vPaed96DV5gu/8T/8zyvMPhYU6HvMMfPRR//t8FtDTjttb4MWL/Xe2bc9u/UHO8fSpsF8fs6XTJOf43vfuSyZ89JFcoyqnQJkAACAASURBVNZ+jqdPgWfPHj7XQ8eXXwLL8vj7n3wizNn37/trH3wgzGE7vvpKmK92fPyxVvYYjrdv9238wQc4/Pa/xKf//X8L2918fKnBI+MY+prqf5izrvPMKoo7fjI2MT00zvfXG3eW9SuSAlgrWiloy4LtfAbWAq9EYpsR+kUrNgTsN0ps8W5tD/44ADTMLLa3+gRwp/FrD2WRix3cg1xXTbGfW/4qd5lu2n/HoAnCfu7WVq7sPKGn8NOuMf1b3G0FgSUbQag1YAoIc0KYJoRpBs0z0jyLHQoE0CNg7Nf4Jt0m7NcR+0q3h90mWyqet5l6ikNimgfFI6pp/5M/93dpAbsEdqot2jqDxQLbMDTWNZhvz2Lr0q5f7XMELd5h1wJGrriHIUQAgmqSTZ3BwPDNXagdNi1dsutYLOzA1BisydUU2tHXJHg9TkdMSdKxz9viQZyNKwtw+obGOK7ga4G8NF6bzI/XggoGHOpZKO7GqDamzjUeQGFCU8CCrCwG6fi3/tUAF5r6Ke1h9mxI349Rxixj0DE2v0AUjO37UghCWRW6WR1CdG1+Ad+GdE6FSGOMMF4goG2Hpm2jgUsT7UnbVKjV3hef1UCaEAQkiSFqqq22jwaCPs95AOqh1zCXQdlNcKBQtdNCVHanBPilKROFyG2LWkoETddNKTuYL2xFm7/KxhrTEoYx3byAVtBiXELRDNqOOU7O9AVFtXmsfro8U4gBlo0ehvXGx3iwsa1jho1hLNXibUwY4F+rFWwRWzLlCQjCPmrKeAwBAmSSbF5YISSiiJSFKcssRA7ihnnKGIHrWgoaVwnoQ3LwNaS5M6xNR1QBGdOiHVmKEkwDMTByBCbV0osROEzAh89lfrVCWBcghIbDFGDudY6EnMSmme3JKThg2Bpwt2hxLQVLGIRa+xynaONJ3KCtsPC6mlyDAJTC2IoAtQzGQfgTuplFKFUYt6VpbU3pPGj2vWanySG1PRjL1mUNLFgHSHWjNaVXN+SsL7tOsgI/zICBoM1YX1GBVoZp7vh8ArCum5zfAVgtoMTj6LZ1SgqsySaQaSNKNe9Wm2RGlgJGz8w0YLUWTTU2l5oGUHZg2FKQQjNVdRuN2UmAgibSZ7aWlFJQ1gu2ty/x3d/8DSyvX4IvZ+TK2BIw5xkxChs2q/SIMSTnnHSLXkAuiY/HTeBgBD8PAxgBjAKRFdzQ6hmV71DqglpXgCtyEpmGxp2NBq4OUFEIWtiy61iODFTRkyXl2Jo+ZZY2KQXb1kGpeZ69oNdyuXixQ7GBwYEr60fW9txqQalVmbQRSTMMbD1iMKDMfvNHqvqdvfiPMGwjyU8IQeQjhixICvB+tvFuYJPF4laUzf0iZk/Z7vI03YcS4LpvQvWNSH3KYX12BmI14Lv7jH0jgvtaayNCWdCeOm6LJ8g3GWqrKhvA7s+OWIDdw9hetRZfcx2wTVqoL+qGq7a/riYotaGUppIjTVicZvtbQ6sbSAs95jjhMN/gcLzFNM3IaUZW2YGQpFBdShHTlF3/fSd5qI/TmBFaz/aTzXHT/2bVW1eZSXSGqbRNQakblvWCul2wnN/jcr7D5fQeb1+9xOcvP8fd6YR13YBG4FakL1nW5zwdtEjfplIytS+3BNVAJl0bZE1jj+EFpLSi5uYrQEckKR4Fir5GhMAABRALI3aaMw7HGTdPniDlKFnjYJj+OQXV3FXN96hgdimb9F0TeY9SZS7YvDViWr8vIKfs2V/j5oeNeyISzeNhHoYQUNbiBR+Zqtrz4CxxUjvv+sc2osy/b+J7Br2nzqoO+Cf/yz/DVy9fPRj0/VAwY0XsvUH2+xmbV6ATAfIwHyHipwKkrmvD6WVCREKagZAK3pwv+PaXr7DViq01LOWC0+mEKUbMhwm1VZRlwbJuWGtFDBV1XVHLCqBhniec7k6YpoRaZ5S6iWHWtLIYI7Z18aqrIpauRQcAtBgRKOBwPGJbVxk8RHjx/IXswgFSie28YC1nSePICbdPjljXFXfvTzjdnXE6nbGupeNU2sHLZcGZzyi14O60YCtd90YmuOyw88qIrzO4BB2U4kQQAYfDDZ4+fY5lWXB399b1seQgH6gGnO184l2I2A8P3Ghks5gN3QOpI7D4IHAHOLPWX9MF/vo+9kAvrCA1ACl4EZ/cgG4m4JhRZqk03Qga8AzXHuK44W78Xw/HvEPUeXIvogeM5v97GPII2OgG42ve/8Fe17Zv46UUAPB+8DC9f0efwUJ554uYl6gGZHQuwR1a8lSnEWS+34gKHND91wCXUXjseAiEtse/3w4s4OX3AzCPR2Gwft2R89d/5rFzfPObX39eAPjRH338vRh/sHM8dIxg8WPH8+fy89jxgxQNe6yNx7l4ZScchPf3+8cNc7H5404XANdLsv/yOILtPB5JPzhn+hxj/X93+LhWcNnQ1lVAWJd5ESdigAJ8Hvj9DEF5uwbXB/vUg4yxQYZfuLcXgfbX3J8OZp93O6wP2QnuZ7ie+4z9ue3v0YEGOsPO758NxJJvjIChFF2wCr/k/RlSEk3FGAEK4DmDpizayCnBikzdtw4jA3rc6Nm38wi89s/0J+zPNjzr1XPaO4PpvNdeYXxrGAc9MOmAkgOALKxgCfzZ7ae19c72D4F572rajW0BM+EB5f4Z+hokN6yAjKY+BgVwW2NEimhxYN36euhPNLSeP7CnANsnHLAL8vy1FSybMHiqMluvwetAXYoJDnho+9mn/VlNhmCY8yTsHChIaMVC/Z5294zdtQmatTL2rs8jwMBrAK7ZKFglWyP19iEBhSTQD/66NpV2JHtQaOwIRFtbAzpEDG/PMRiIounhP1FBH/cvzMnvj+HjkPS6CJoyq23EgOra6TzRIiojWFdrUZAXrp/Wms2CIQC7AvwABhMj0aChquNI2qgXq4oh6vU6AO6xeJBA3d2rPot3LcYQ8M2eV14d7UlT2YBuwwim1wtPkeSdj9ZrBQjzTO6tKngdQkL0dHldT5x1pMyhIM+ayL4vNjOSwxCa8qjtEbWoGEftK6gcxZCSSZJ6GrXImIz9ipgzYtSK5tz6xoDNJ4IHsw7qRDG9x4lxPESEKHq7c2ZMSfoxJmBKhJQCpkSAgpxzJORswTe7f2j9URtAsWFrUthLAGkp3GVAqQAcpIxSqH2U/U9WsH1rwFJEb7Y2SVGei2i7ypQkKQxWGVuV8VkrK/itsVCTNHRA7N62VQeqDGSRcymBBXsg0wLnNnxebriqTq7pXcLBzofB2NVZz2ajbDOEoFlAnsbS74+NGciMraxSULQWoBbUumLZVmViSZpubUNBxGG8E9v1dHPMqpVZuq0BxRo7NvXxUxSm/XJ3wvL2LU6ffxfnL78AyorIDSFFTFPElLJWlQ/Iggx28Alm08QO2dwgsvhDNrGtfDGT9CE4wAqmxhjRarcltRVE1cA0/6+2IoxCXVNE07v7h5Z1KbE6oTQpMihalxGsRCgp2kRISRh3I1gDFpsRc0QMkrFQWda5UiQjNcWka5KAQNM0ywaM7v60WkXL0wDMzUDw4HYppeigpsia2JiEj4edv9mEfdg38zo5xs7BHMBkYJEHUArk2hwgf78xS5ZtR299Xo1+ga8rzDq/uxSCZ47YJAF046x/X0BjkQSwe94xX1lZ1tT7vwy6saT97ZJXmmXVWaW6Ti5VXaIe9xIZmzwAiJBNAAXr5wPmdARRAoWISQvixRBhxR7n+YCcJ6Q8IafJNbyNhSl4D/v1fN3S+eiSAK1nNkGZqax2qbYKMhkgsRxY1gXresG2Ldi2M9q24Xy+w3I+4XI64e27tzifL7gsC7Z1Q6sQZnprvnHTdO0VZmpAmqCxjLSrby5cPUf3RuCSRfY5NaaSCadj2rudWAhr3H09s58pJuQpGfFX5DWVUGgAq/TTItgUma8Hr18UKeqmJLrtZHODbWzIzYyF2QDzzeHzXbJkxG+ISfVjwZ4NbTGH6yvXioLm12isWeEgILD3eTBtS2urR44fCjBWFtTmdZTEZw1AmhCIMKUIxjt1FmVoXt6K08MbY50b3t+cUJYLTucz3p8uQGtY7y54dnuLb3zwAXJIWM4nrOuCtRS8rhfEOEnlRBKx/juuSDnhwLNMBpJqhNM0YZoy0Bh5TrDdJ2ceZICQtXrbhMvljFIrck6YJqlOKJUHC5ZlwXndkGLEPM/IOeKynHE+nXB3OuNyXjSm6k6oTYpaKi6XRQp2aTBihg+tAStAp4DwJsF2M8QgimhzSBMON0/x/EXFui5YlgvECbBWHwGMHszcA0N0ze8hrQZcA2tsfPfrGE7jsWOD7s6sIfp18D1eRyceCAjHCen5EThOaFNytop93Ca0BVfyplsP0ZcNpmeiIZMFlfpfDpJW1gsNaZrD8OSEsQ172z7UHg+zBXs/fP825N0/dgNj0N7vZ3+tsZs12hueRIAYJt7JB9gIsMDcuGDuCbmxBnoF1MeP6+ffg+3Xo2F4wO9z3j88/kMcPcAArubxCLCSva8ftHWcrmcN7I17vfsYBnnvjq6BfEikIYtr66yYUiS9R4HYPnQHMAwkOscYRhx1m/QwyDfc8wO//eCH2YD7z7R7NtyfDbt7uvIDzOaTFV0Y+4Q7sOHxnQfe+1uTVKwEoGuREQWEOQsQq8FaO2RQTKAYQNEcV3QPz8N8Gpqe9hfD3i6MY+F6w2b4ipy1P8Tusw9tDIyDeVyLDPyxb9izUghXJ2JhBMOKbJCbxtH+drOrttReDVLggh0YUGZgIAe0xIm/GlniOMh1QvAiQXLFBorkqXCCx4V9e4Iwps6b9Y/G7FB951YH9ihsI1jPG6QQkbTP2Bcjh8I2fW0cWGZHNxDetuMaZtW5GwC6Yp0PdqP3mXeiO9Ljl5wfM7o5+p3mJ+52IRBAJlM0zH1o04xjl4GB+WWBiNyTB6m8bxefPyF43xrjUXQVhw2j0KUKpD3lMwKQRxgHKwwACMUAv3UieVdZIiklbFsA1wKQ+ZyyrhOz90PT6sWgIExtCmhMiApINQdHWe8/Sjinz5WUnWRAPhQ08N66MqF9XnZj0RqEhYsuW5FidN1LuT1L09d2ZZsT5gfBsXbvAQWXowbWorGnTNAgPuHOZPkoo27PWAFovb6xdHTlQaAEkGwqdKICK4suuGcKHSNBmf0S7IsmMFqUSuGeuRUUFJJ7tTaww1PQ9cFDZKRISAmIkZGSbjCwMnmT7ElPSQdwBSYFaaOyjJmBogEyAygNKAyEAiwVqBtQNNhtpHXBm8gQGJOWmVAaoxRGEwlalAYsG2PdGtbSsGyiWRtDZ2QLSNmwlYpSG9ZFPW+1xa0VxCj2oTGjFWUIKuOOtYiWM9HQQJ5BoRNXx35pDVvZ0Mqm35HvAdDiQraBoO1rMQMD27qYJVFfRgBms53d7+mD3tiAslHAWNcL6rZJenWrqG3DslxQ2ibsUPdZdP0gUuBYWZIOBqut0fWhKfABBWOrEqAYhCkk1Fpwef0G55evcP78M8RSELX9YxZdZmPcExGSPo8xwjDYACKS+QCz6WKdyjgz3P8YfRFLHlemsBa+AoQtKEB59TlMuiYYcGk/Lt9CJsfS40FmxrZJxkiMaaeHKRJGBQTClBJySioJQ1LASnWdZXPLZC5kDIq2tQKvpitpKwcPm1r+2ORZVvZ+ZUZg3umSX29K28aggbEAXCLGtk6C+yfDpl9UyR7zXyFrQmCxCS5np8xYVmeJmUWv23u4r7G+UeGu0LCwAu5Dyz00XxvN6k059/UUrOniZie17VzrmVxPXDY5BMyuRclIrW+kNL13Af9NCzmoZJBuWKuG9zzd4Ob4AikdkNKEm3lGIClAK+0akFNyzW/XqR3YrzIFq09tG8Xc5Kc6yDcWfcPQj4xaN6AWtFZQm7Bhz8sZy3LGtl5QtzNqqTjdnbCcz1guF7x9+w7n8wXruqr0gGh6NxapS4AQUhV925gkFR+h244rv9fwHF+TbG7y2LcK+pOC8aw2WsfUCISHaKx0uZixVaNKFxRl7fv44E4yJLCq8esmcAz7jZZAoNZ1qfu86pvK15to22bFuaJswquPQ4EQVCc2EMk8H7AP28SyDT4CufQNM2QzFgQOVkiTvdbQ1+E4PxRg7IjME6SAFbM4/dwYIQLT7TsspzuU5QIuBWVbsdaC+h7gUwbFt3jNFd9tjN/G7yMFQmTg42fP8K3Lgp/7qZ/DF19+AWbRyvnutz/Hp9/8CTQm0QSBFKSYQkZWbYz2RKplTjnjcDhAMFFD04PKFciu8jRNuL19IvcMWfSON0e8efNW2Lir7L6lFMFaWXorBV999RKXywXrumFdq+uuwSd2wOFwwPE4Y1kX4A3jdD77gk1N2oxbQ3ydQW9i73C2wEL/boQ83+DFRwe8O52wrp+j1jbEQDZYbbe/T7iRwXXN6rHvmWg3hsX16xig14eDGnIhBxPusc88qNU1JpBokcQAniLw0VPgyQFsov2QIMrblDs7ojvEtlsTcTjMuivZn5OugiPTYPJ0DphjZTf18LM9BNz0Z+Hd39ff37elfRbd8qiT4k8z3IY4gJ1x4Z93b07+tp725ZYbdk/zwH17h11HUsPFaWihkY310Deu26ezhh4aR7sG+MPjP/ghO+mjzdq929EyfWUMY+FghNmXXkQH4/7P8InBFg3Xu55PfV7bNfsuJ2oDV2HHSlqyjnsTnUcf5p3Z11lwPF5zmJP7zaiH5/E9sGFgf5IHVPc/9+j59J66A9xbyr7TGb/9Fmj4bl8uxCHxKuT9JA4adL+MQEGlB+LcCzgFSenFPIk9JpIAxlKSyXa17z9kD0u7bXcHZriuvDfYvwfmv2iiqgNGA/t/bLVhjRlft48aY8Mqy47tKmYneNaLA6raEJao7Xb7SruK/FnI5QKkzfV9A4T0MKfWdMesSRw4NaaonZdJU7kGdngAAtQ/MK1Ba89xzNh/WRghFhAZeBFoAAb1Ga3vbRNZfg/3zq2PqUErudPf3yZnrgUrgqnPx36C4bn1PmzDevQ7vFq93hO3nkJibRCVLYq2/64Fr33KdUC3r3s9k8iCk9agaZJS1TfYNaiD6n3OC7vCxjD544keJUEYupL+20VFGu/ZxwxoKqYwzqEpw9rlCtTKd23zWMB9rWAfpUBYLQSONm61uIhpJWoQrJCKgC6xp9Qb2GGyBjZhgxVtGcZaSglWIBWMofiLFPnwPh/AL0vPZd4DAEFZphFAEIxT3+r3FULUsdz76jprwOxRZ+MIYyrrcxlgQdx9GRrxO7dVXTuUhwDW/OQQpGCM3Witm3/Zxj4boKG+L5MAJKQAdAxRgQ8pctaasMYssM9ZGLcCRGwC7oNROaCyaeQCcw6YEkAN4AIpaESMyIxtLZhiUr1dsT+RRN2bAE8J1VYDgTFPAQ2MTYGku1NDmqLPoVqAdWtYtoZSROsYLOCrMF2lf0ojbJVwWVnrai4gEmmLw5yQY8C6bRIzbYx1qy6PNs2TBtAX981DiOBWsW0LlmURIJIH9h+gzHCJN8mmfyDUWoSNtixuxQhAI0m9NxkCY3e5TW+Msi3aWAIGFJWcIJJnT9MBRFZ0aByH9jujbiu25YxSVwnqI2ErF2x1RWmSQk3Kwu5ZGl1XtmgxJAOgko67bVsc+CBYjCX3XrYLyps3WL78EtvrN0ilIkfJLoxJdEuZ4IXpQLLx59LraiujE2RkEwY6VththLyi8JPaVwHLW1tRthNKvaDWFaZv3NomtgLKgEaPX6tU/ALQK8JLmjXr+CAhVRFrIW5hB6eUcDjMrrN8Pl9AJDqyOSXkFJFTBgEo24Z12VCVBZdiwjTl3RoGAFwr1nUV8B+sdjZ1aYAbsaSyQSCszp4ybeBzkwzaKNePcYBrSMb1rthYM4mXfrTYiTIyFDsgLKZN2aiAjsMOvBIFKbA4jHtmxrv377Gsm2/MCUs0o3EvwtV2cbFKhpTq9o24a28ag3maZvRNX91gNCZnNNa7rCoxilGqilNQDEKGmyYdX7LJI9JECm7XhqVsSrSSzeBAwmqNMSOmCTfzMzx58gHm+Sj6rzm7T3zdx2MsIuQ9BfTMl9C+2IGxLGn2EYzWTLeUNd1exrlIlBRw27CuF1yWM07nO6xlQSkrSimo64pt3XC6u2C5LNiWTbKqVW6hVgYjaoY5AUgIDYhIAiwLAiKbtqRFzWJnVft6roXjWcyR8HSpx0ECNJKPIYAQk2T3hKhgemOXSBGsRtejJlqr0D5OKTkzV/pfxB9LK2hFClM2lXDYthVWpJRImaw2ZiweIlkrY4zIOaC27q+BJXPBfDWwasmWbjsYskFgbWLF/ZhH9rmcrzaRK12XVVxnbrJhoxsxNs9+6MHY6TDjcHME47U04JMjtmVFRBRa+JSx3d4ivXuL89s3uLx+hbrJTmFjRiUWzUQNCJkZ2BikA3sKhJ/51k8hp4RtXVCWC5a7tzi/e4Pp+ATIGefLGYfjDW5unoEb4f37E87nt5gmlmJbN7dYlgu27YR1kUY/X1Z8+sk38PTpATknLOsFd6cL3r1/h9PpPT7//DMEijjePAE34HKWhcV2xQOJHm1KE2IiTFRBapCNFUJEmOaI2ydHxCXgdD6LnooWF2gr4fDdG0whopbmA9SCyg4cAOCGVoDChA8/+ibW0xmX83tZ6AJglSgluOniyHtgbOw5C6h7wBNjgqWnFJ3IPQDd//vQ4RIFHu/cZ5MGfR0EUArgKQA3M9LNAfHJEWUOqOYm66QcdyENamzMGJIk++fVsYaxj0cAxkAH2Hk1fVcXJnt910r3Av4/2PFwu9G9vxiWhvd9DgdhBrBmXJDtY18DEu9v4f77thTwg+/29x47xuqZ/h0Lrnl4iD88/qMcliVQa92BDg9/GABZyloHOC3FAwBQ5YMU6N548WDoB5xP47h1vpbuOKNUhCI70sEANAqoqP6d62PcUHAwzXZiH/j87vpXIOIDH370+379r2lb/gPMA3fi7QXxzJDyJGCmgivC+lFgyhz3EICYgDSBQ0LMSQoTJGUnkYC7UFZGHAArt6Uwm9CfycE8W8dV8LbuvzD8st8cNGDQ+IukOqNhvPDVNce9vvtA/jjezEk1MLIHsHa/mkTla5SxMph1o0zZIbVWT2EcWS1w8EedWx7YtTAwT4tOqN0G1PkzqQ3YxkB3ImPMuo5ZkQWGVF6vGrh3QNMOZ8tRB4M7iGVAalSA1hbGBKAJOct0xwmemkeAVvCWTmXAwTK7sgVpIZh2Y98ktj7gxugpvsC6tEEjVkBkthT6EexmnSssaXK1yF35UqLsyEC62Y59m/a2UZabB6/WfdcBGwTIUFZmLbJZbwFx457m7sFnSl70Q9yQeg98J4YH4swNUz4gocHdERlYHqzkXXVuedim6bJaJ0d0C/X5E2lxKGkgALJRDVt7CaIjy02lB8RvK5q9Zg3SKiOmjBQTQpKMrbJtrh1KQQLrGKDMVUtPVHQLpgdqeUdqEkilL6ICMwam6jNLm1kgKZp/RO4VCrur9Y1mZjNVPPSnbZRIWqfGbDun2gCKpm8Esz0M1zbWD4PBAvJ6xgd7SncgYZRPwZj2CpirL2pyA3tvVUGvaYZtNxEI61pcCzKEgFIFYKSUJFtvDoiZkCZJXgBJunNtQC1i1w5JxliEgLBBCelNgZRIAYcUwQAq976+UZn5dZFxfTqb9qSyWyfCFCNiZZSVtcBWxVoaGgJSzpgmRp6B6Rhxd6q4u2vYtg3L2rCWhONhBjdCQ0RTYRQmqa69vn0rgPQUNf3UQMqmoApQuGFZLhqkJwdirYg6G4ipjK0UA+LNQZnX0gdbqZJWWzcwFy9olFRDlZlRc+oZNUTKohRwlEBgyhDd6+isSkNlCRbos2rVVrRWAKpY1jMuyxnLurhNhAIkzeUjbIjK+7VsAFdEAogaks6R1hhbKWikYFGtqOc7nD/7DOXuPVA3RNU7Jd2cEbmMpvGirBFVvQhhxkuBpl70yj03t2MNIqXCrQgo1RYwVrS6oLVV5BiWt2BepL18DS+6tvS1dHhaqKegGz7CGCcAMUsF+9a0eE8Tjdbj8QYxRteeZGbklHCYDyplQChlw93pBIICMjnhdprd35WxL9+3An02t6c0KQMzuI7rum2o69qBSBawfIoTUoq6Xpu/ONj8oMbd1vwGXM6L+yu7BCcdA42lgJVJqjAPG74DmNSLEhEO86xjvS+xpGs4V5W2CSJPVErFsqlUg4JpwvLPLn9jhcPGw7cjdR218VHKJtITCs5F9TdrKzifV2xr6dJPclPm6WmBwerXTCEjzwfkadLs5gkhZiCKBEGkgHk6YJ4mTGnGlGbkfJC11+1txx+sH6zY1ejfs7fTkCWqY7KxMvJbQ6ta+K0I47WygrHrgvVyh21dsKkMCZpsBJ0vJ5zPd8peL2i1qJZ4EPCwCPgaYkaEyE5UWVxRWnG/MAfJhqGghTMN27Db3Q0echu0m18sGychRqSQZG1KATGKlExjiE0l0Yef5xlTnhFT9CxuCQtM/59xPsvGmbVzKRtAhGmafI4FgjDXk8oq+fwQcLa2hk0lQ8zXrK1i5VWlK6RGkkiO6jgFKd6kD0/AMc99k0DntV1jXVfc3d3tYgSTOIgxIieRrWDf2AJ8d9jm8ddgXz8UYKw72P6npNW0WrGVDfVUAYpA3RDQemopROMhTQk4RhCa6KPabiCJ9lYpBefljK1sOJ1OON29QwCwnE/q4FYQV4R8RJ4KUp5xeHKL0/kOd+9f4+7tGxlotSBH290x4ykMjlo2vH37Fu/vLric77AuFxX4JxwOB6RImOeM82mVnVmQ6HdQ0N0LcYIIypwQZAwA4bKsWL78CqfzGW9evxF69VcTaIMwY81IEtxZoCC7Ik2BjqozrumgmKaEjz75FG9fv8TbNy9959GOkY1qRru5TpvdW+8/ZqCUCtO/YR6Zsg8Deg8x21prjtD5eBgWuDYgagAAIABJREFUJHsGBEKYE/LtAfT8iDZnUIpg1Z0Bsy8k3YEeX6CdIPPwKA/MF+rgK7oRgAHCNDyLXWcMsK+edywGND77Q4e1Zf9+u/cdo+J//dHvr3HvR0vpGUERB/SHRebxw9qUZDCiM1e8TewfhjLW9unrj4FuQG+rB8Gxq/uLn38PH/6Pf937X7piMIC9IfW27js8u3OjDQE/YfujP4f64kMfm2Ob0TBox7EKwygImP+f/1PZLbAhsgfq/ErDfQyvG1759lf/G1x+8T8Ftg0/8tf/B1DZdu3ATXdizenfiuuihiYBM6WEkCTdkWIQZ9qilfEeaAAYHpjD4fXLnc7QY/ObiIaNIsDYSe5IYlj0DVDj3iIUyFGza3DTmUh8n4U/MqAiGNw2YNvAa0HbCqg2V0MdN35s/O/OBcZ+/msbPDKPr+/H55Tr+w2T+5Hj60Dc0R6P13qIJfzYOfyVYMBIAuUJlARcjZrmbptQ9qwhBGG+Bk3JtcJGwULNITjwf439pyAD9jayg30CZoTdPfZUqns2G3DQz/qRNYjOujlY1WnfMWp5WBvI3M/+r90q2UNYfygIK7/uMwdYnVXLctmDtn6zXYCbOjDjgCWp5ta9hUn8Iu9PgreVsaqNlRg0vVD6QdjJY/GP4Y7d+awr99RZNpav9hsNOpvDeiTatKmnd+va2tml5H3XGTdAKJ01y82sXAcSHhq3nqKo/saYKdGBWnl/wyAHADgz2TTFwEAJ/Xrsfdy1bC2w7vhGz6YZ78fsPmF4ZPuHCFWDFkA2oJoWgoHZmhBQS1+bUp6AdbWlAwxhPnrTswT6SQFWZmEdzYejFNRiRiudcWsz0gB6O0oru3MaGEvBAi3yeSp9rcVwYNp+UTfNCCYpUwctSwoy7ihYlXUdf6yFZ30jSytl08AQ9KfvGpGAgdjaljrmUsri90MnK+tmROucsJSy246ga9G6lT07S/05OXfYreXBZQ86SMytuZyDjqKdfxy14Ja0HQA0BWP3rogEmgE5RRQSQgPIWGERgSQolPTnJKmemvLKACZjLWo8ESlIYWCVf0s67iQjjDEFIEe47ALAovlKSlLQTYGtKJgfxGA1u2f9Tw7977HvUiDMmXGcVB+QhNnWqrDVpEYIAGLMh4g8JZTK2Kpwarj2ol7HOWPKAaVUlCJAA1GQwioghJARo4EdVTQWwLDU9m1bUesm6fUx4ubmBnMV0AvQeZSS+/atNmzLitSK+1BQiYNoVeljQNIiR61JhfZai8SR2gdEAZhm8SHBIGixs2qxqQGn0dwdsdlqF8zOy0+GsFergk2iXZpilvR36utVU/++jXYPQI2hA3LUZMO0VgF1GgNcUaE6+ucz6uUELqUXUAXpZknQzAiZGz0TNCFNAp5FChjqJKqN6Wu9gRutFpTtjMormBes5YRWL2AuEKas/Tv4QWoFdllEOo8MCLN7E6CrYp4mgBmr1nIRuZ/oMj3n8xk5Z5coiCTFsoTJLEWF5mlCTlnkUBT4LwqoCus1Iubkm84hkKfIG0N59NeEUDywTlVvnhtjayvW1XzdTsqyzcau1Y3dml5Us9ay1IgkjT/nrC0nNs42iEGW/WoOmukp68aubqraeI4xgiKwlQ2FiqSNMwPK+t5KMSUjSVXX9TiGqM8Ol3tJcS9/QCqBARJgmqihNYlrrDDczc2MdjiAm+qWMlBLj6VjitKOgZBCQEqTg6sxZeQ8Y5oOiGnSuZyE1at+rumn2xjl1tTWNv8But9ta4YxhG0eMxooaL/XDVtZUcoqdSpsM6DI67UJM/p8d4fL+Q7bsiizuAJVrllawbqsaG1Da7aBLtfhBinSTgBHy1yQNaMiIDagKFlGnktY2MyahTL6w2rNycYnAWQ6vprpJBuKpqEbXfYkT1HaMUrmRxEDD0uMgWoDhySbjwTL8gqYkLU4ndyEkXtA5BkFhIoQkm4KRVlL1S6ZnTHpCe8b6nFmUwaypTAwM9ayYd3Mz1K7SLGfF1LIzwl5zMhpclDZxq6MQ7Gl67Z1uRLa28zRTj90/FCAsWOQBEDlCRq4bKjrBqwXICTUbUUroreabm9l4YsBacoIt2dhwpYNDRdQqcgcMOcJUz5gXTfd/dpQyoaYAhhCDYdIpyJjxlYZHMUxPZ9OWE53oheEhoCGdCsSBiEmHI43SCli2zas24a7uzucTxelm8vEq1XSVWLOyFPGcukpfrY4V02ldKfGvBrtvHXdcD6fcDqfcbq7gN5H0PuAUFUDTp0P3y3SMJfBujA3TztnAEyMGAKePHsO5oZSNrx/91oDeu0T3vfJ1zLe7NzcNTv6q/fBgf4n7T5p1xwFwPtOk4drMsnmhHB7QHpxCzw9AFFSpJjZWVDuCJABKcNd+UTuAdl4Vzx+BpZaOASDFh5Y8DmcxL//Bzz2wO6jn9p9wAKv+4BLD4jNKRrfM/NgiwkcnLBArLfaHlwaos57d9aBwN11huDQnpMwjDWiqxHx73aE03vc/u//q2tWPQg+Dc8gwWZPRR4+tWsMDkD5+FNQragvvmEnUukKmRcpJhEp14CxloLKsiPNJIyZ6bd/A6ExwrogvnnVwVi5GRiAPLYqDf+tTdrx9Eu/Iq+2itv/45+BlmX3vCMYCxCwFfC6gbeK2AgpROSDpBbFnIAInOuGgoYWsBsTwH2w8R7gqcVerl8n2PzV85hT3x8X9ujdq5b/2L3LeWUSPwbIj7/vNnhszDNLZMcVqBVtW8FbBUpVDUgdgw+0/UOz6RpAHcfZdTuMAK+BL3aOR1mu3NvuHiA1XsuRlMePe/1Cdg6zCSw6d5rmHHIWMHbKQBY2W1C9Oya4bbaUI2GoCGvG7CzYMX23BeNvu4e8biP7G2I1PE548LjqawDMBhgycox4cnODddtwuiwAeoq3t53ZOm9Pguimqls9bkqip+rDXDju7Ea5vmx8lmpAT7saH/JVS4XdtY2+aU6v2RaQrS89MB56WO7NAl4vKgRAvQMDoKIyUN2qkG1ioD+r9wPrve5T1/oKKO8Z6yVGkzBoGHXsbJztWUDB0+gZjFa9IzpoafqmdrvOjuwOtmkBsra7Oc22dtmmOZEyG4kcPCfsGdF2HZOZAGmhIebOCgNcC82aXvpQA0IilX3qz0GkG4P6k1JWrbMu60IK6nSWG6Ez6OR7pZS+ompfVi1uIwFLBYKAjgLClb7+6lT3vtZApQeZDAOpSZmZMSQ/N9kwYGV0U/BAShvNAUZWXUeCgMw5ZlgmmM0hkIFGnXEegum/Wu8oqUBTsHcbvAoGCfMqSQoxN4Ca+3wGRrIiiDFlQPsyxPgIGNvHQQg0sK4UkIAxAw2QIjQ28E3v3NjNGjSSj0vxiAJpOrVdjxgcSOyOjynTn5SA1XwkQEgW0va9GAzB2EIJSYPJmBKoybiy86QUME8iTZAiOqClptDqLcbQNzfFlu+JDQxhw1bu65nJFjRlSsZAyFGuw9AYuA3PCPP3RLM2JUIsQCtSDAxm5kLAlANaFsBWwFxoYaeGwLZJQOAWdF0R6aTaKqRehvahMoVj7GxAgHshZk0jjVEYlQ1tYFUVZ9wRBaSsc1xBGwHbSg8v3Jb1DeSqrEJb+/f2VV8bYgnLjvANUBBaI8Q4IWW5SitltxzU1lBqlfkAdKmbBFj6uwAdkjzdBUVEBqNtG9Z3b1HWVceutqkpDuh9Ew0+E6nciQNa1PWyrUF0oDmTrRSUsqCUM1pbwLSi1RNqWwHIxgppNs7OJyM3m72tzd6SWxi1RezSJJ56rK9B51SrVQsZdhtkgJeZ4xRks1HWBLGVW9lQixXhmqTezXBjBjTyFZAHdFbg3k9sXvldQH5jcttmToDF+JYgbrbQNGKpkS4fHcgPA+HII5pa3Rcz22VrlNgnLWzXJMW80f7ehVlYte8DSlVwX9vXYprmNoMdwCQorZnbro1s2Q5haEaw+Owk4G6KMyJl16MhikAGiFRDO2XEJPrhKQYtrjWLXxsTYsyY0qRgbIQxJY1AZqOVWeYCg0BM3h/NSHNQ2+n9W7Uvxa7XuoJIdF+3smLZFsGulNW6rQvKtmFZFxTFf07v3mNZzijb5nIOWokbDFYmrKbpc2eY98w8aZaotRtCIIQGMDJCJWwbdtKL6jXu5hPrZBbXpM+HmAR4DQq8ChNWCprZOMuTZBnkaQKYvGgiBZEtIBCkqJXiUjoGI+IgZwVfq0KwmgvqWxiHiVmLDY7EwD73YhgKYLoPRt7HIj/E4NqAGDsxRtuj1urzk5lkjtscgm2Qdt8fzDsfYrwXZpaNPMgc2mNf948fCjC2VhFjN7mIbdnQlg1YN/Cyoq0XlNpQtg3ghptnz3C4eaKFQMQ5ak+/AtqKsixYASTe8ATAh7fP8dGH30DdKrjJIE05AjEhz+IYl60AvCHdJmwcsS0Fd29f4/VXnyGFpmL3EQkRz25vcbg5YJoPmI5PsZYVb968xfv3J6zbhm29AE0q+InNqTifzzgAmOZJd6lIKmO25ju6ZEZV9bv6wVjPC969fY9lWVFXYP7iCGattDewaRuLwfYFzwwGACZLLzWHmJDnGc/oQwSKON+9w1bXrqV6xTrpi4kFTd2hsOCtOx/yXVuEeupp3x24F5iPT9z6oLbPufEAoSVCen6L9PwW8dkRC9mEZXdmLTgFa/DW7xwgcsNkger9oxstWbQ04DNnyYADaAqYte8QLHcnev+6TGb2trrPXLOgUs8/Lk571wRjYZD+D3uA2JdgcxHsXsYWNWuMwfkZAAewn6XbGwbU8PceMscSmi7YHTH2swzsRn+Ofi/71t8ffO8vvjoPPCi6HlMj2LM/IXvALl9jb0OApdBJyjj/J/85kKSIH7ghVMAAwhAiDmlGpCTpmCHizCecljtNh6xoYFx+/j+TVMGXX+LJr/9fQNl8Ftj4cDBraAR/zxv/qmGGYBuAFuqR1wszcpiwsQRQgRI+evEhbg83mLKkamyh4fXlDndlwYU3SXjUS3l1VnTne9eE5nwN7SsL4WO7gD2oHsf1Hpi0eetdBEA2WfiBk16zQq/PJQt4QSsreC2oyyZAbG3mP5mL1QMOv2x/5ofA5uEhduNrvJ8RZPQNp7GdBmd4d/7x3OjgltnP6zZ4FCy3MW0FFHx8q/tJGuTnjJAn0GECpizs2JyAFrR4X/MrV30AVjtmp5S2hjBlYTaDTVvGHZihBR98dgY6yNmH4+DoD1EaWwGE3jIEIKWA5y+e4f37E+4uCypkDgyPvxunthkpzSX3uRXd6YYEPrhygutVm1djw6gDbwVUfE308cS9+AfgAS6BwEGZ5rpWGdBttmo0A15Mk7USN4RS1iyShMFbysZq3dYGtVX7Vrff9D5th9/f1jWMlI3BlprO4CBFUNqozQXWwhWtj9kG1y4138Guavc3gtie6dAGf0bXF1tlmuqKuq304Glg3e/GmKxFfc4EX+Bkrqk9a4yQRPvMigf5j457DzRDAFAxsifHNFDTOzObZMGWjBsFY4kQ6+b9ZoCBgavCABIpiFqU8VEqLssChCi6e9KS/fkpdPZ/Yx+DRFIt3CuCJw1MYxQ/skIrWKuvp+l3MUYkMKgN6a02rzzwl4C2oIFi9o1L/QhsUjsvvEkBKFZfylgwzIyYo65vPQi09iWIBEdSVhSBPZ3cUgxtvJMBpDGhtobpgG6zYD6CSmpw2/m8pH6ezZkQM1KaEaAAb4iS6RaTXz/puK0qKQZI4axt23YBnKX3ppQRHBiSNkh5AiyzjQKmacaUBOBuzA6OhxiQYlYGMDnzE2iIISDPCcdDxGEOyKlqpp98JAQgRsJhEmJpCoTAjBghRb4SAVWA5MaSZVCYseq8VoOArTXUFlCaZZdUJCJUlnEnjF+1LcoEX5bNg+8UCIcMVBbWdGXCuoq9CETIUQCCWoFaCDU0bGtBToRASdhyrYpvGoSJyikBXLxfaxUZjMM8AQxlLa4ACzgQYsTN7Q0ul4vaIyn0IkxrZcNW66OElLWAVakKuOgGnGfxhB2bHhjtrY5Mey8YocR8ErVSFvQrU07WviTAOUW4jAtE05EaDxrpWjzNjDULo7OUIkBQ3dAqI7UKbBvq5YJ3X34J2lYBNoJsDMnsFsBt4yJF36TbpRj1JIWtDOAXnd6+8WW2rbWqQOyKZX2PWs9gLACtAK0IsblvJHFW8ucLg+TDGNcY4Nq4IUTyOBDK4K+1+pw7Ho8AKYO/SGx6OM6YsmTQLJczSikIISLnCdMs6e21SBxv0nuRxK7GgYlnIJoQsfraZezC65+uEavjrIq8SHQAbNhchIFk+ujBpp2lShupRHwPXx9ZgT1duykEYEjDNmKW23GP6QGdNGCwZJEpu3HKGRNmpJzBLAW9zA8WXyHoutHtq+hz6qYU231BJRdFP3Qri9oiKwLHqG3TAk5AjgfkdMCUDpjzLeZ8wDQdEfOMmDPSdECeMqYsciwxBoQ0dZut0jsG/klBLxUt1CIr5puB2GuE7mWSpP1tAxMmh6NrfK0blssJaBtqXbFtK7ZtQWtVWLLbivPpDtu64rxcRI6AGefTSfrAfIQqF2omAxwMgBVfsIv26PpEDTlmtdEERkSoDSFG1JoxpQ2l1F7okkizKXohUPPEQiSYDmxMIhcRVIc+hICUA3JOrp8aQxS98ZQwzROk2Ch0HF6zi2U8ruuq2IvGl75pINeY54OQHgOBedrPL26IFF3zWoozNq3hBAd0qTMeYBvh06QZOinikNUBUMC3top13RSglva+LJc+KhprwbGOuUx59s9TiLi5udUx3XROkT+z68E/cvxQgLG8FfC6AgeAW8Xr73xHUm0gS1cAMMcJL26f4Xg8It8eUVOUKojrhlZW0OWCGIWhdri5xTeOhJ/9iW/hk298jOfPXoieS1nx1cvPcPlyxesvvsKUbnA4PsV88xS3Tz/A4emHWEvBtlyQeMOP//iP4dmzZ1i2Fe/evcMcAm6eHXBzMyHniNNlwb/99ndx9+49ylYwzZM2fNXgvwDcsCxnpBxxc3vEk9tbvH13Evo/yhAgiNHbNmHTHY9HgIHT+Ywvv3qF8/mM8Cbh8PLghQPG0ILZdFBJWBIdydkBH+OOXNmEZfzhi2eI5WN8+7PvYisV0B2jbd388/cBjv6XDMaBQROUzs4NXBqaTjCP6Mhtt1Zmvo+wNA2GA5PvnIVIiPOEp5+8QHt2QJuiALGtg5oWnEqb6P0Bu2vYb8EWVNs9Hg4Jp4bX2wDy7IK6ESwd2+QxluoPckigt2eM7VlR1wvEjiEI6gLqtkgOv/fbcvP7yH08DKfZOczYPfQpdnDRrvMwOFdNONDHK/R75o71c9AP3H6PH4+xEQG4YxQ0NbKBUT/4AKf/8pdRakNbVlADcgugQmibiI8jAevdHRiE+XiLm6fP8eknP42Xr77A+7uXWJc72WFdGG1tWI8f4NV/8St48b/9E0npguiYISh7VLzX3mbc+9nYKn7PrfUtaDwwRxXIohAkCGXgy7u3eH16D2O6hTmDckQLqnbZ7KJDSo6efdy4aPfGN2Dg5QhU+jf8u8M5jJ0yAB3AuMkwPtHDffbQPcjtCyumrivauqItK9rpDC6lD311OAUX4Q5ED+z873utB8DPEaS25/S5eLX54vPcrqdtuJPoGOesgYMP3NOj49tBpj7dbITFqhuaLCy0SAFgDWpqAVvRJ2b0blHn0O149dsDyIFU79M6rEn9pnZj+/r+HbzbjXeFwHQB9EBPP9N84wJ48/6MN+9+VxzlYdqMTO/Rflpq8mZp1uN1oTbXz9NtMXBf1sdY8t1+yaIXRzttIGfo/QnvavuWfg+amjyAl14dntH16kbHWieih64WkNG++u/1YUVZ2PvRntdu0YojKbCgwLh1o8mWeNsGks/ywCIYT0l9daCr9hnbdgxcJV3b9CABLlakRdZz0xgWRmDy+RzR+97Wd1vB7Ps94gWsCBjQteJg35JFFSlIwaScJ2xr8H5iJuQ8OeAtwM42nKH/N0VlmQRd/QZbSTmBVZ+TzM8JARwaEBPS8QaIGU+ff4AQggR2DJSyChiUoxd/YX32bdsklfMwA5ilbaIVlpJ+31AQtA+j3d/g54lmLWTjuzGWZQGoui8aSACxwA2kQaA/NQPEhJxnT+FlbmggHObj/vldf1LG7DTNwvI2z46sqrX0SdTAmJTdarSaFBNCzML2V+avpxPqcxlBotY6jH2xfZGsCI+ygoMA/VKdOqOKei2IoH6lPKgHhgBiAKZp8mczptkIEICAlDJSnpDTAZGa+vH6WQRhNDpgzBqAJpdjkMrk8uyVWaSIGmFZGSiMFJuAmJFERxSsjDkCh4AYgYkAakDZerwhKaqEqOuD6dqCgYkCqvoUhSuy1OcSBi0CVpUfDsSIoYFbwDQlYcMFIAQp1lyLMF9bYyQwtiIuiRDuNUU+iUxOmIKAfltDQx2K54wZCQms+tjbVlCrgBLDNAcgUnPMq4A4vkaI7RJ/O4JRNY0WKKVh23qRuEAJMQgI5UQYVm1lwP/2DXhYXEaDj0UDkWeIXdTWyKN1sNfmoq15EovJZo350pZnwZBaI+tyRikLuBZQrUgcga1ge/UKl88+Q1wWpGjZABq3qb4sqAIhgpExTRk5ScFrGp4LALgUSUV3AIIdzKxNQGBgQaCiAFwCU3N9U4alzA/n5IFMMsSzou0KBGWFFxRtO9EgBeBFtmpruJxOMsdyxnSYEVPCskrqeC0Ft7dPMc8HALKunu5Ovl7O84ycc29/hmTGOoIJ9/ukOGTwezX7byzd8XMpJtxMRx17sg70zXcrbLfBdMQN6GZmLMvlKrOv+zNEKtmiNnrn70RjAHb/s6purmdMLCu2unUwrVatXt83HNV6oHsfQSXp1FnUsdMUVE1JJCLyFDGFCIaA3TE+lfmgzz3lA2bdfBIQMSNSlvFNCfN0FBmCnJVIkJGTgLCmj04x+LwjIhHGNh9qDLXADqCLPN2OoutHa1XmUdvQagHXTTVc1S6UglZXvHv3Gtt6QS2rFAHcBJhdtxXLsohOM8R+chXwDtqa5tcGCgiJfN6b5A0D2GpBDj0rgyAF5RhZbYQWdQSDOYDniFqqkO10c5kATKMdpCDauvMMK4Abc9xtOMi6L/bO1mDWNhMwc5W11djGOlfzNPV4E+I72HjqRezY58i7d+8GH4Dd9zK/43A44HA4uF1ghkqqqe+yrb7xRspkrUVAYCEuAIEuaK3oRmASqZIYARIfOKcZNzcH7XfNTtJ1pZSixfxWfy6AcaKTYAha7OtwOCKGg8+7XRG+q+OHAowlZgTntAOhVMRkFHogUcbt8w/EcUwJCxoud2fUZQWXDcwbwragFsYxRnzjcMQv/MRP4cnNLVKecVoLzucztrvXePXyJe7ev8eTJ8/w4Uc/ipunL5DnW8Q04/WbN7hc7kDcRKtoukElAkLE8eYGOQQcb49oreD1m/f4zuef46uXL9G26tUd05RkeDap1s21+eDYthV5njGtMxiMFQ1lXb26KbOcowJYlwtKqXj79h1KKZhf3yCedKegVRGM1wEQyAJjGZSy+dVDRlnleypkj30DNg3sbz74GId3d2h3J9lFrNuuKI/31QAyOgtNJ/OOzQlZuARs7Q5DiD1AfwjccBaXGsimf4c5I93MyB88QXtykCqRzOAK0YoipcLzmHpvgIX8x40DZGzBbfIYaNp/HwpU9cbYnt2GbAe797q6++cyx74HxVdnH4zP/vXxtftB671rafszMUbNU/Y/hzQpuevdueV+++f6ee3x5USk44owjikDaDqzx79NvaWdjTI+p1/EmHb7z/iTfM2zYxib42fNWTEd48dYhAaLSEqQ6Sc1tK3g2e1zHNMBsQa8/M5n0m7E4I3RgujtcZOCAR+8+BD/P3Pv1iPZkaSJfWbufiIiM6uKZJPdmt0BeoCFhAEEPS6wgAAB+g/S/9WD/oFehBWg0ezsTHdPs0lW5SXiHL+YHszM3U9EJNkjvTCIYmVFnotfzc0+M/ss5wvWt884rxmtFAjLSHVjxue//494+D//DyznF6TTgmxGrBsSuz1CatDM43Cn8yoHurLhvFWWrrQkjQQhQXUDLxCYLZWvWmSF0G5eXAluNr4eJSXX16gloPM2tZswojs8Ws5xDTdSr5XJ9wE6vC83MESHjp3T3RS0rWi2RRF4sT0mMm+qdMMFwMixv/PZrZc7QOhNhOd7/bhznUc3jnGang0X49eOsfvjce/dulOvPLMEUCJQCgr6HCyHdQdG+0kz3DbXEnOGzn2dgAY/490W9iVyOy63kb63/b7Xd1eLVGgqt5T34d475s8ulRBOFzSNoZuG8v4e9BYyse0ty9MlPSf8nPToS8AMrza9RxrQYxlt3mZDFLRrq8AicCxzo59/PDjQvHGeZrtr7aQT9HcYF+koyAl7r+oXI22Nu0NTizbECYzcR6xf75c+jgbm9uyg6Z7Bt+trUOsEaLqZt133jctVM2XgoS1NBGyvb+Rjar2lMa/3HECDH26sj5HW6PPBcHI0Dkt/r8vDrvswgcgjkDAp8dAMDLW4DChyWgR/z1hbBDLeNOMQtsrsMaZuhJc8KvgyaTSpn6UCYOGoYzJFB48lJX3XOI8i2/u68UdBs7xI5Wkzg6oCYETbPwb4Ow+bqCHlc040eP18eXixrTE9hBCXniqsBTjSTk9zjtXOc0c0AQ++7mT3jJ4K7rqebiJEDoiU+tyL3a+zzB1gcSOPRMFgDskidqutUiDSOIt9vXh0tYMkZPQHfm5rESfV4JzzlSwFXIEac4A0la8KkjsYq1QEIoIQYRG6mvafkiAF5XldYkBkYAlAjArMRiacFsISCZEEJBXHFGx0GgiMSBaJR7ryPKVeZAxhbspHmyIjFuB1BXIR5OpOd5UbiYIVe9Fiaq0KSh6FWUw8IEVCacMxRmJCo+nbmYGwEAIxNhGcN7EoyNLnQe2xV1YEAAAgAElEQVQr14kaBBWlurwY55w+mpTTtlU17kmL0xAZsDfLaZoDVSYdQiaZhzu2Do13ek9dKg2QbbLhiEb7MTINYMXUZp5YLYbUdrZFqUUj6GtGLStaXpWT2pyOEOD80w84//gX5OfPII/EbgKi2sEMAQOk6zAkrTUAVpkqZncR6/oAtCJ89XdLQ6sbIAUkFYGUPznGYBGvBVWsALTVn69tw9azxwTEQd0QHkUXrEjlHT3M1FArwuRBBLpejqdTp6oAFEwNISAdT5aVyjifz/1ZMUYcDoeu3/l5U4r1rTVEDhbNOs5cjbjUdH6tqD6BrzH2iHDXzZoIigOXxi3sclKpH1p3BLF1MHBAii4v3dF6G0DlDqfJAjP7au8gSFY9fohOQS4bnPJFs+dbt8263JY20QFyPy9rLSh5A0A9U2FdBYG1yFuIyc4tBjhiSQcsywFxeUBcTjgsR43EjUpHk2Lq/PcpJnCIEFKu5fn8FhFUaeo06rRJ6lCV1qa+eySxW6yAKWQq9UxfqKVYZOsFb5dX1HKBtAySCinq5Ck5d17iy/lNC3GVDbVkc5YrwF2s8LzrSe7wFNODGGR83n7oq6wfahv1M9CLpIWo1wYOFikeFPA1CiQFijWYgCODY0Dk1PeG0o4ZyB6AECNiSkjLcOJCFEhPMXTqAoLbmLXrqDAnvTqt1JPXgo650j4R1ml9enS3Ow2caqln0cIydCzrTER6VGyzqNiuZw1QBk1EszxMf0nB7B/Tx7ygogggDVgteNIl8/nSKw/0/ROinqleEK5Vd3aIRT+rw0EjeRveXt92sr9OBVGvP78KMPb6E4jgfm9Nm2csT09AjMrHlldFuLNWxiYTDkEaHg4Lvnt6wtPxqIslBHCMuOSC9XxBKxVLWPDh4wc8PH3E4fiEkI4AgtILiIbtL8uCtBzhfCAxaiW382XD5fyC55cveP7yRYFAN3B7CLIDZq5w68LM24bD4YjjcQGg1TGzqCHmvCwaYSQ4X3SDr5cN/CUgvDGQjWe2lR7eTkRIcUwjubGhmnYXsq6YdOVfABEDMQkIccHp49cojVDaM2re9oaU9erGgO0b0AUHdYMuxYSayiAvZ4J6qd17jW5o3v24bDwsSE8nxKcj+PGIlrgfBGRGrZ61s9IzojB60WkHmYgmQmXq89Xf2bBL5fXuzWM5t9hJy/3LGai92yH/l/fv3rUyDIURXfXOOOF2XmB39jZBJp7Cd96JYZQblnJjP08PtEgFAegKbHm/mTftnQ3O/Y1y8//dPP2Vn5voQ5koN/qamW6wyewz3QQtN1AVRCEkMAIIXz09aBpfYEuTjBACOB6Rjgu4FUQ0nFKEHI9AK/jxy2cUW3NEhJIeIB9/g9qA0/kFfIxdsZXOHzUpCDTW365/N5M0TSJs7kmrXfZUOD+4AqFNnHDjftqBi7s3ixnrP79tRxuIduM/5vH2ATLfB4DuL9R3XjziAgUqK1HrSJOu1biesJOF/T007Zd3ZNIMMDnQPLf9XcB1Am/m72/BRJhiedXvK0fG/ld7B9nddgNdmsjUFvJc1KQgLMek4VszKObrBebZnvs/z5O9pBtHLkT+yn37bh/suf1xXfjsxweTpLQv7ft5zfWX3X037Ckg2b9vvt8fOS7YnZV+xvSxngSu7SwMVwbt/tKvryHvoU/MZ2yfURqKeL9O3IifxoWAUaDgehgmEHuSUT3y1K7lvjSog32BA9iAutHhaS9cTedeadax3qXz9uZp2zmQIg7crA1zlWb9DGoEA0W9SIs7vyjYWM0jOmQbEVkEmzlziXZt8D57+8nngdmMKNNWOYLJojgmKdP1juARd1dT3KeBQFZcpO+p3RC6wR1sIjSdPaSkGp5o9EUUsWIWej759bvniANFTp0wGsQ2J+RcrqQgBbMXa1OQV6QBrGs+pQQ2skgyHYvMUB5ylXvkNZw2AGGsVY47o1qPqGARqWqE91g/GXPv/Jdqv1pm0LS2R4Ep0bRE8l0h4xlTtBqRg2GuqPr+RtcP3T4hplH4blpbiqVJf0vXOfv+cnDkvmPewXrflx2UYQcJ7JlQfTNGRoy2ZxjgoLQIUQTHhRCNx3VJgtORsERBDArSBgDHhbAEQiSlMDBa8K5Hmp2OQGo46lAQZuVBA6sVpF2tOCaTRtM6zQEwAgH0PBGI+U6CDqqlMMNkj1Ij1CYojVEsalYjNfX7VmkU9g0MgQIqY+/omvN91doctOFbj7o+qPuiWtRigDJOmE0hoqCjU/H4PmptBwyOc9nsklnu+VryMTG9wjNMDAvt65eAHXVcP4LsWgW/xl4eF+l3tWaN0ssrWs5opQLNAmVaQXl5QX17RbPgIN1f1XQlLUYXAtmf+SyyDdGb6nqCFzarE0DcNPrZhpGtaJ0Wa4LZ8tZbIkCCRhrbHurD52dUj7xsO0BR9whAYs45lwUms/UMm84m28vudHPwjIiMdsyi5i2Kz3+nYsHB+pFR0KyCfQdEeaRis8lUX3vdEdaphfaOzM6BSaSkdi47+v1jrVGfFJuDK9vHHeNdDvqUtTYynDrtzFhlDvAKLNBL2EAx9GubkPoj+1mhRY20cJ5FWMsYZ4IWSwpGrcIcFYM4nnA8PmI5PiGkE5a0IMWIlAJSsEJbRNCCZ5bRZSvQsYQdJZCdRw7o34KxI7tA+8p9PasqJkqhU5Ri4LI+4/XlM3I+o5UV0gqkVJS1IOfcaX9yzihVsQ+nAmm9FbqGh/NzX5jV6SA8GFFFlzu9VLZqJgEPHSeY0xnmGPcCdZCe6VE2dQxwYIQUcVyOdqb4c1XP9wyLZVnARvrd+prU87yZ4HFcZD43yagUdJtK1698C3ptgv5hpVFqJiO9+J2LTGZGomluRXYO0WCOcCINrmnGyQ7ZZ1Uxhc41S8S9P85xjXbl+G801opAC3xZ4UnbdXYc+Lxx53h+38a7VvjG59cHxtLw6PZAeCLwwxFZCOu6dV4NMc8gk6YLHUnw6XDAb7/6Ctu6KoByOOJ4OqHiJ5QqSPGA43LAV199jcPxEcQRmhkkOC4JiXWxLscTAifk7aztMG/T9z/8Bc+ff8Tr2zOkFpwOCcUKAbBFk0D0oGcKakBA0/G3dYM8VJwOCWgFZdusdthYPOqJKthKQckFpVQcvj+hFqukJ1qFMmdF2D0trysGNmZM1AETgUwclOMQGNU1CUUED1//Brk1TUsoGfc+0iYvBDAJ7qZpQ6ZgevrVcjj0tAwG67nYg9EIu4Pc5toFJQjKoft0wvLVB8THBSXBay51cLEXAzFJN9SsvqTGN+IRG2yRFLy7WvVn0Sjj6QnshsxksJhaCVfwxxDvDZv+bBHcowRwyoERrTopiQL06hlX43QvutiFnjdw9oTOV46Dundq91z93TiMvT1zn8kVB1MWh4E53rpXH68F01Aox7+AuUk+qruRfAdwmp9/PT49QnbiwOvrdp5PMbOOCdJIlfxVPd9UKgQrUIG//ZtvcEiW1rEccTgetCJwIeQWIOUNC1V8/XTCV8eAgIqXLz/hsmWNBLEDI//u3yMLQP/5jzh9+wmNRNPtpPWId23bRNMwdb+11iPi/ICb9yZPhp4WYGIrNgA7LccaGAqBjsl1PKPvDacnkOme67U4Az7XUa/A/iy+BVz3h5dHkvm/u9k7fd9f7R56K1woZtWJ8TFpGMnVOrTDuUeq+TDbNdcFzBxQHvsBcBBgHrPrtTd/d/3zHui5AnnvrPc5ze29d/R10MdqejbZuRoTJC2QqByxISXXgLoi2Pto4z+9qPd2ePH3hs57/WUegMo9GXb9nPHDcEx1qeTGFHxN7tvpO6cvkbvyY0QnjUj/Senyt05n6NzG/Zib48v3E+2fBNDEaS6TaYUOes936DM6LANiLVLRrFgUQwEaTeWWPrfNOJFdH5i6Oh9jU59aNyoBpxZyp6XrDGONakRs6OlhbgzR1G8APTtm1hs8Hd7/yTyKLowTCyYoWBVhGSnyXoBjBs46QAlN73NAdlfhfDwZ6FWjbY6aR0bQ2CukkTUi0uXAKMAiUO7OYYxrai+Nde1AjXUqRKMs8HmxqIrxcQ5ABwHs3HLj3t6h/Qq94BZYK4ATCClFcCA4+6KmuY7Ik75OpwjmftL6JLAVBfN/i743hNgjk6RaJWnyoIAFQSzzRGcBbBHMc4EnhtMhMJqMCF/VZROGbNV2qT1kQEkVKIel7QchkFMjTOO4L7ynkT4tAaExyKrJOzjq15dS+9olO0PGGtPINGoNTtMBCsqdyYIABe96JA00MotkjI+4fWBrZTTXjVnWNQXRgBR2weaQrYnmwJ3apOulEKVps8gdtKZ0AixYAuHhoFywMQiWBXh6AKJRDsRAoKpAbXIw1lKNHcQWjziY9idZP2fHejRDvQBamM/kRWAgBptDkQ5ElA3gaAAfgBjUwK8CtE2jamtT+ohcKkoJqBLtO1tTLcPDd5gjwhLQmq3D1pSpQiqIgvY1JdSpeJv2SfvXgClqTQNjUgpAU1DJixRHi250gEALNtadc9JB3ybD+TbOC8CL5rV+BsqOfkCjo9uYd/CsZPfnjPNCnRK6nvwbrZ5eq/K01ryi5mxzYydjrmivL5DLRXlx2c8mLYAGUQ7TJXJfX4FEMzhMdBCNs1xHrWgRW9O7lIrAxsUCZZiBlHTvl9Ig1c4QOzsaA4lCP9P1aFVASRmV3IJkswVdzpptB+VS7kXO/Llt4pdk0qJ30GI9uRY413anZAGhzEBbKUgxYlkWxJgQQtAI4KZ8wtV4vEMICDHqORRGsSi2s3nO0JOrdeM2fYpJubOhUXUzkAuQ6bimt3hx1a4Tz0FBBIKC44HHuenFQuegsVILxi432qKJ89u58w0d7E9X0HZEHHNik70PCCEhcEAMCUtajLvfzyXN3Agh4Xh4wPH4gHR4BMcDkhXjUh5ZqAOxNaO6GLRRTTwjeBRMa1WjW7u1Ilo4DoZ96Nk/zg4HeOfTuBmnrYKxF1wuzzifv2BdX5XuY7ug5Ya6jSjpUqqaGbbOilF0+V6lYLoCHCci5VRnl0MaBa6F4k2PCaFrqALNel0W5cNVKgzj7nXaGHLeYZNntWHj0jOIUop4ePyAxbJbPLKzAf2cTzGZHSxWDNLWdo+83xeIYzaKM1u/CAEBsddP8E/JeWczVnu2n3McAnLeFNthBnqWh3Gzi3LhAkCgOPQiIuSsQHg1+0jXgq7nQLpuXE+DCFIMfV+G4FlsI8LXsSvvu9IX1Ulv8iKb3Ne/7hme9NR5L93iP/75VYCxluQFQLf2QWFyACpcKwc8Pz+jcYSAEQ8LojygrhvqlrHlFQ9SkZjxEBIeDke8vmUkshBmEfzNd7/BZ8q4nJNywyAgpSMqArSYb8NyfELOZyWzPx4QOKG1DWxe83/+l3/Gj9//K8p2BqHi8XTS9FfzAF7OFwCEJS3o3GMhAJZudL6ccXgNeHj8qEK9FoQYkGLsEw0i5FKxlYraBMKsqRqlQKQOBSHaiIlViG6+uGF8H37gS//Z4W2BkmQLOfmxRo8djgd88+23OD4c8K//5b9gO5+H0e9Cl+bDwJ7mB53Aws2deFnXdl/ogPKs7PWJm4+IpmbRISJ+9YTl20+okVHYbrlvS5ty6NT1dwAg/58pX8EMKsJecZ/pYsQUDeorFehg8WzRzn0xQ16aK3pXDdiHIQ5Fw/52vleTzrhOLb7mJ9wBkP2Z+8Ed/Hi2rzya+O5gzh2ZBMk0Jt6vfiajD+0Ygqtn7QzBXdv275qHZ4Yl5lbt7333pbvrXG3gPmaiBwANYMQPbk2bMY8lBP/+62/w1eMTTikikeCbrx4AQFNAY8LxdAKQAF4Qlwd897vfYbs84+X5M16fP+PL5y/IteDHn57x+fkVX55f0KSi5IK3H19Q/+FPoFXA3zwAiSBBC1/0qG4Sz/646hffzPX1p68JmX72X4R5DOf53s/9viCcfefr+3o+3/n3HClyb153bb35hb1roK6+zVxLHwvR5HUrFbgUyNsGbBlU6hiHrrPYyvDbabTsFiTuPbptoUy/86ilCcTdOXx+xpnwSx/BJNMhCL8w9/P7ZiNao/gsbzUSEEl5KYlAYYBkeuVf1655TgXz/N5KhfeA+/fafC1qPQNkfjeZAeYOoj6P/coxAsJzS4E5Gu/GYSQmTx0UMeNoXvuarjveKfvB1rGZwGv9jjSSi6gfACPSfTpjDWD037viGWLogBpgpWEmY8iBv3l0PcLBQYjOHzan6MsAoHD1hDlqR4Fgl5Hjv+6U9raT9HWL+Yl0e07tpYLPnyn9gm44qiEw+FwPywleyX5E/97Zp2M20IWfiEUy8ZA/blCaMjB/fz0ubDoPkVN02FqczsV+tvjc0JgnohExO1YqmdOomZGsBhARgYXRakOM1h4RSK3YjI+WDCCCA3wcEAINQJcIXlV9DwiMqLp5/Hq0U20osqEi65xQsEg+u29WhWyuai2TcmNO8KAFuJrxfxI80uX2gPMIxZKzFvehME4i8gIgZHPu/dP7Qt8L1g+YQSyi54iBne6MiDH2veXt7RFKY1Y0rTIqeBBiBFt6sngkrUUb1OL0AWakhahrDg6E2FjbelFaFIZIGGuKlU8SRGanAGRV3HUhMZhSH+JWBVIbHk5sdAHA6aAjEEjNkSXpc2pRkLAFwhIU+IQIOBlyZpydycavQcZut/fNVeSdszoQYQmMYwJyU5ANjXFatM/MQC4EpW5niHJbIEajQFGxhhAEl00XU4qMZQnYMvD61gxcFaQUsV5CXwu6jxpKYQAVVbLuB9Hotpo3s7ksHbvVMbfk0dPOcdmwbQpkno4nZANwAbL9OChMahHjJ3UKJE9V129aX3sq3j0Se+jEAKHuvgM8ktiWsNkFXujHI17FwONeIMZsBhEFiUvOkLKBatUq8Y019LkJpFVcXj7j8vwTtvUFVarKrWxUGgQwa1aoVlFnBOdbFk2nb1ljEz24x3vNEAVumRATY+AQo4Ns8nyJERELmhRoOAQjiqbEa0ShAmfVHUgYkj0SjzDu+RVikZDwc8h0BeYOwHIcNgdDeSKXQ9L1kjXo6XI+AyKIKeLhdOpnpYjSs+Rt6yA6M+OQFsTjCI7yOSuWss2Tg6efJ9P57zpGa8C6bfZcva5uoyihA7vO3VxbhZAWVAv2RzmePbqWsfCi+9fPKD/bTGZSIcu+bX3t1eoXkIk2B6i84GYFGFhzxrquKLlA4IXdFnz48ISvP32N4+EBy/KA4/ERHE84LAeVocGpCoZTKlgGhrZRMzJ0gIy+wQ6BZuB5a0a9BgNQmxVPtf3pThNAzElt7QagAmh8evGwWrHlFblsqDWjlA1bXtHqisv5FS8vz3h9fgZEEGCZPYaxNJAWTe8A3dAZHPxzgaBbe9JXbZ2GJSAtSekCDsu0dQgIyre+HA4I0RyYpEBnLUoPosDpqMmynIBty6oHMEOYUIPrtgymCAYGgEjq3GutgYUBUQ74lFI/I50Dv9WqQYRd79Ngga1svcAc83AyK8c79b3BIfSAgVYrZFls70oHQl1Giwha3uw9UxEwO69TSp1WpIsDkwXcQtdhW624XDaTJ830BrPpTVglL67Zed4BuEQS6ZnhrWnQgb/HI7DZ92LP5Hrf9vtVgLH7j3r2AzMaESoxJC662byqI0cgnbAsDwp0rhccww/49HDE1x++wscPXyPXz2gVeHt5w7ZVJfCOR6QjIzbB8fiE3AKWw4JD0uiJ9bzieDqAIKhlw/OXvyAEQl7PeP7yI/78x3/Cdjmbh5nx+vKi3BpRCfjXt2et+PZwQjocEJcDHk8PiEkX1rqt2HJB+fIF65aN7FjDyZto9Vo3WogIcU3g7xdkrEbE3GMQh/UphFwKCrXOq+Hcaf0AEqA1/Y5tYTTzEjVLh1auLALHBcvTJ8R/97f4p//nH1Fr3psz1GGQAba6USymkLUKTUdTZdyrO85GHDAbpxOnExOQIpaPj1g+PYA+ntBisBByMQNjVPEdxmsP9u/t9I+4EQfXaZpxU9GuPXdXI/kzXJO6MtZNcI/vXGPWFu02nwtff5ZHA/ltBPRCYVeCZPagepTOz7Vb+hLZX+PKY2+OfrsDX+4/V6agoQk4gJsobuDaeNP8zXQUXd2rFuf8ztt3+zfXz8LV9/PH10drrXu8ZN/pO20Z3ZAmWP/Df4f2t3+Hb58+4pvHR+TLBT+9ZAANa1nx9vyGXKpyFjXB4+MHaAol4/hwVPNFNPXqeDjgm68+4vF4xOPpgLytWDNbil3Del7x05/+go8BiJ9OiEtCgcy5alPbZ1BD+RB9n4/f+Nzoz2ogU3d0GBLSr6V+pY2LG60O0sgA80cUzxXocucz/34uSLWby1kO+PadwLZdl+Z16l+Jmdqm4DRRD3ErFeV8AW1FNcr9AAHwiDMfWlu/qHsPJtGuOvJ1o27Wn7WzN/Vqk/v4DoDn+v47z7wdjflVO/CSpoe6cj8eYmnbMYJTAi9HyJLs50WVXpoVw+k5VzKpv2/6ft7z91r987L29l1dskxr5vrZ9554850uNDuwaCh+ctv+eey8EJl7vu2CG9nBzqvnxihpASzvi591zp/LQKfC8T3g7+9Arq9J8Tu8G1ZL19mRprNBU7Bpt37ncSM7c8je3CNmd7QPgp1IdKOtAwd+z3j/AL1u18p4Dl39PJ1zIs5Y0HUdf4Fyk7lcckezhcaRRxLFbvh4NKw7p+99ejE0Gca92iwu59yAH9Fo8zgPUBNAa+o4I88akC4/mblrN7D1pOc39X0r0MgT/zBz53fr7YAbSSq7R3TuPKYY1ZjtPl+zpWgRlhhD5wGWKcLjFpC1KEOLxHIgnBv1ArJNGopxc7qHK1DohqWIz510MEDPYlVOmBRUAwUVzU1TOdkcoZqOGiwgQHbv0fZpX7T42ViQO12zzxv1NWSZ9D1iRrlfLRqSXMfUgILmBi1U53fDFdKg8QWqtzvQrUDvkLtqUDJYAJYKjsFALhqVzW2spIoV0zKwZMrm9HmutSnuFJx7XkGlwMouk4JGuj4cyKi/pSf/kKUR16ZRuykodUFgQQx6vzZJsLAWG1Q/nY0PtJCgB+yOUZ32ODQqFiIjetUyD5mA4wHgAhA3LbRnY1VFsK3QIAwSXLaC13PByxsPAM6AxlKhelNrWM9bP9OEG4QEaQmgRkAjqAc7g5mQkhYCKnlDbcq/GTjq3pBdEvEIHmlNuf/ezvBIQ99TTi8wdJyguj3pXpFpH6YQjUbDwKEJzHLdY29D6N9ka3XWJzzYpjUYpYPtC7aiPQ7USkXNG1rJCnA0A/IYgNi6qQXnv/xXrG8/opQNIEKAAQjEnaO5wfiLoVQDWugp6+SKFjQiseJ1TAq+BEYKrBHeKJad6QXuFKwDKU0FQVCIIKJ8zgItatvAEBhXJBhigJCIqqRSLVKcyM4PFZpOoaZ7w2W82dUxop+ANOSkHp8NW8nYtoxqEbIHD66Cch8TmnHgOvitdAZe/R0glG6femSwniuBRxTe7KwfATaml1iErfR16WnpPIAde68JDXjxX3J5F2bHqC0iUb1BTOdtUoZ8sQWWUgJbVKdGo4+CceqEM1Dext2TaZaT4KFWrOcN21YM82jIP37BthV8/Fjw8QOwHI44pAWPjx8Q46L7hgLYqRVljIOPoXNAo+k6Vh7U0mWnXutRsbVHq2s9GeltB6C8w6Q4RbOIdhHbH65TQbGLzy+fcblcUJsGzry8vuDt7TPW9YKSlR+WBQAHiKWpAwyaAM0QBxjr2VLRfs9G4xBj0n3pbSUCs9g4B/VQ9fHQccqlKK1ArUq/EpSygWLAkpTX1W0JaYJSGg7HNlg7SGWWKSu9SJbjCyEEo1lQag7/+XA4DI7XNoqeOqCalgUEBXGXmqaipWIO4DIKaVnUaYixOxGcQzaEoPt+kqOuezeXZXD6gopSssoFk8sOes9ObxPBYGYtcglfb7anjb5GoMX7tpy7k1v3IGE2AUVE9wsFhJRG8do2+G393e9bPvr5FYKxXkk0AjGixYhLdmGghoZUNsJ88/wI8Hg44dPTBzycHiBCeHz8gPWy6nFmwns5PuJwfISAkLNGhV7WC2hTnq1aCop5+dAKmBvyuuHL5x/xw/f/irJd8HBcVBGtDbV5OmLXvZUXJgSkZcHpdEJMixUYAGKLmgpRdHHX0lAt6tILVQHmKXiNoJcAyqa8uqrgctU0dTXwLB2nHwAAauuLV0TAMSIaYtMV7+7NsyrPhqKFGPH44SM+fvUVnp+/oGwrPJJmWP/a1u7dg1d4hdO0dN6P2XgFZqPGv2mWQg2EQ0R4OiJ+fFB+2BiGZ3RSsvvP/anWV2sbWV/Rm0p2FlHfGP3vq/U36fU3n78uqs2UcgNq98jTlMo8fa/t/ZknTsDXvXZcA7i/tPF3bb0yvvV54+fdu3YG+d2Ru7705me/fzz3r2vte1f93N1d4Xnnun0M3fSDCOR4hDw+gQLj7XLB+eUNW97QILiUhsv5ommTdt95FTg3YXh5RasZIhVMWs01kKac1ZJxPB7x4eOCH376jPW330H+h/8e7f/6z1ifX4ADY3lcdA4YAxvrjZzmWcYhg0nwY1r/6CvOIwqGrJn1tNvjYjb0HViyaKbujXx/Tf5bP4pRTsLl564FTVPVFyXcMym1AVVAtY2iHzIpM+98dnvTuy/XK9n3qnTl6bp1dxecfUezZfVX9BXTo25MX7kP3F7fTSZ7HIhFjKAYgBhAUbnVyQtWybw+3n/6vf00HxH+uQHxrp57DcLugLz+MHJJdfP2nwN4rz8CNVbExmT/rtuxnFqMcdoMKoRbZ5d+73yR84tHy2WmVr0a41mGj6gOpRAY779p3Y0svT5jvX135LaMVD4dZD8TJkXyyvnihSP8NgWtG/jOqpiB3NFekx1XW8uLkO775sbj1bNptE31HO8b9ftu+45hBMCcUERwqiBMffJrr05a27B8UbUAACAASURBVN7zee3PdZ5S6fNGIkY9Abgudu1cBTDSwP2dPVV27yjt4wnX+0qP3vW0bC8GF4jU6DRAwIEl6QCg65AytXuW582qDlvk6bSxvdiMGsQjaleziNxo8oH0xe7Rc+56d81MwNTQDHRv0Ohfj3TxyBUBNDq3th69w8xobT4zRr/2eo02XAPolKqgGH1GN9imc8R5+3Qc9Fm1iqGVus+1Irwb2maQ8nBrujOnVatFASgvJrHihI3sbPJ9pn0nEKgJWhCtNu4FZqZIK/bCJHYSHhYtdhWCj76Yk1Kb54l6AgUzA2mhJdd/KPRAYaM9CjpW1kMF6ebdRf3ZZGvWHTvG2IoAQdSQw35HJeW7ZRCaAeNNAKmCbW0AN8RIRk2h4LOI91uB88CCUgWlKOiltAcy0RIIpKnjIkZClgISA8B8/bYxnsQMQ4WHHWfjLKIrrxhtG9EYe18XXuhNizXayp4KLLuM4m6PqTyrfqaJRxgOZ47s/gZIDGw0YFwMpHDgyQSO7pNmxfSa8lVKzbr/pSkvNrMVbK3I2xlvX35EyW8QqQjR+aABDppurIEr+uzmlAeOskvTIkbIYLR+Liiwgl5XgSCYaK7hIKmDt0yEwAGtWRo2CNwEpRWlgXHNlcyRBCNkYLMHzdbanZGkzgOnSPHvyKlhxOQr20I227laBlWcMh4c8KkOPvna72tI7bpiha469ZzL8MkOcQAKuNKDnFbHNlVwZwvps0dE7ZBpCtjqczTbVRewyhCjLIHLPLEzd2QQ+LoboKb09VhrtYJUFd2oN4FIfiYYB67QnHVjRRVFo9NFKi6XFYGfEYhxWI5I6RE5r2AOSMkArEkp6kC2BXJpPacK5TFuVsS8YASoke1FSyVvtZ+PrieIwEC8YsBrUX7gnI3XVakPam0d3Ht5e8Xb+ax0A6Xgsl6Q82r7Sosd98UAF+VOZWPyIkxnBMZacKwopojD6WROhSEriZsCtSEohViIgDkBci0afAd1rEktgHDHyYgcU5o1WBil0ZDjHaLY6XrzH+wiWV0H7NGfJvfbdL+eg6GvFz+rO/dxG3qk62Kuj7Rax2HV14GgB+BhCrizg4WJjM5h6JO+lq+fM/o51jH8dzZmZP0IMYLpKsOa/JHS215rRbU5L6V0+TBsZrddfv7zqwFj+5ImTYugkMCHA8KyYK2vuthscUNGFCRDEFLD4/GITx8+4Hg4Ys0Zx4cnaIDU4EFLyxFpWSAgrD88QyC4vL2hlGxE7Yy8niHSNC3mwHh7+4IvP/2ALz/9gOMh4OnxAXkrWNuqaZ6knmapehiHdMDTx494eHzCcTlizZ5aYZVU2cLk7XgpWVNbBo8Loa0Afw6gt9CFkW+YHnnh6qxo4Yk5naV5IQrxQlcCVaXMEGxtGN5AP5CqeZGYGMvxiE+/+Q1KK3htFbV4apoqBr6Th+eBJoNzbIB5Y/t3+oNNuIzoFo4B8fGA5asn0MMBsgQVjGj9eqdN0Lc4sDoMptmO8007nV27disf1n1jem7i+Fxbd7e/uQ9oDSV/NsrRmoLDrtGOBsC9OzuPypVg0a/G+6YZ3SnJv/SR/j/vkwwbyt47IuG8Ddf9vPfU22t2UVM0P/H9593r68+/15s9Do+9YTbGRqa52Rmij0+QuEAA5Frx4/kZ63lVxQSESxG04nyz5oHelCeKQ0QugvPrhmok70BDpKoFC1gP4K+//oR1XSF/89+gfPyAwz/838iXC+J2NK65SbF8Z4RuwMXdfZOxD5ke4ACAzdKcdg2XF7dv2wM5tw6Wa4dBv+fmJJr/QdOzp7ZNW+aXPt5DiJHVlwYpDWTpSLPp35XyIST2a3K3D273j/RhtLXTz/t5n+/bt+uZiMrergT8cv/mPjp49O6N/qvr34vLeVbw1YBYsQgWBMABjx1NiBkCCgzeUe4w3tXl8pWsgAzw8V6rb/e3g3f7iO3ewem+e2vu9nd7Qe3zcM2/8J5cHb9vvVd9mUznBeY+mmHvckVsfd6sp+nnMZZu7E3yyNMSvG3X/dp9dJ/uZEPfu7PRMO0dYCcrZ6VWdTINw5rPdE/hHmAAQXpKnvS/xYSLTA8kjC70/XHzxTzX+/GagSmCRlNBLFqM0AGLvl/mJWDda6J6l49ZPy8wX+tr3rxiO84v2j1/t++mcRe/svMqTnoM7eVonwMfYwr9lfP+6A7p1iAWQukVr714TNeJRMEhiEa3tVr6iTLL3T3wrOB2awKwUgC4buDGcSlbj94iglUo565bzTJR1RnNFGEOve3OkycgUKugoDqtFyYRGMCl5HcQMS5bib3dzThjRz/8tQPu1b7CxlTXTim1G5uBpiIqRCA0IC3TM7XPDEC0KRpJCC3g5kXcYnIOuwHG9r93Y062FcgiCsf3gBfo6ovKl5IBXbFHuXoYxBIJaQFCIEg16i3bd61CuW1h/LtN0JicDhQkCo468MrQYDv9mTqAOX9utFxbRw46R1IGnEMEQnNnDYEEKKTPF5Yu4tQcaahFwJQgTQvEQUqPBI5BgUGRBio+LhU1ly7r8qb2VmCjTJsADmaNimzigJvLaAZoZNq507nLBChnrX6vnLEEpY4Y0U8mB+AZWQYmwca2p6m6g43hBYW1AJ3vEe+XKDehZe50Ldmz6USfX4vqlrZMjVPTimcVBZlQc+fB9QJqkIqaV6yvP+H17TOkrRoZHZRNQx0kZFXWm+kGVTHrrCC5srU2MFUQst4bAlI0xwAD0XmIQwBZ8S4HM2Dbmg2cjSGgViM5EHVISK6+e/sZNoOxba6ODulkbH2f9Xz8IQ+aiPYDRimBzoroBL6WWqwAWPF6LUbrQpF6DZnZtnXuy5GZwMbbrBHGMDmgfKaDIkbF2yQ7HHSNjBTi4IKF7+HWbfxaxjuZzcnjUsQcBxrFOAp3KfWEXUUYa1Ww2wNadDyj1govwOVtH4Y2G4hlWbE2dpETVJMxR2EtuLy9KRh7OGJZHjSyFk7BkCZswGWmynUFvBpazXAeY6ds1OWs7dAzsU6Uj4BIGQFz0rBtG2pd0Wxv1JJxvryh5IxWFODMW0EpGaVkrFvGed06V2itdQB5UECaWTOLye17aeY0Uv2IY7T2eWGtgFyU/5djAKeIcEjK8Up+VpnTyviG43LQ1HugZ1mfz+d+7jVoxKtOoq2N2oxP1vSUrjL6GWN74qro37VN6VGqMUbjRx4ZNV5QaxT40rYHoyIi6wPAPdoWCDuba0QxD5ynr0NrrbjuYvLLi4oSYNQc4wz3PrZWu80nFuntz4YYpzs5r6zaZZ7hwqz9BQ0aBB8fHzPf555lJeYYG0VjqY/fcMi///lVgLGurDB0LV3WC6RUxCoIRTeQ1Ix0WHA4nhBPB5QK1bzDG+T0L4gh4nQ8IkTG29uLOTp1s4AZl3WDECNXJSgKKeB4DHh7/YLz6wuIqwrluoEgyBzw/Z9f8eXlM7bLGelwwN/93e/xpz/9AbloahUH9eCu66rpQ5zwzbe/xX/793+Px8cHfPn8Bf/4j/8VpenBr4unIUWrSBsjnr980WqBMQEC1Lri8IcHnN8uKHUFg1Bbwbatpjypgtuc76QDdJOpZRtJaKRlsHlYHLVft7UfitIqtqrpCrFFBAkQDvj4zddAJMTDgr/88Y8qJBt6VUgOAdM2BjyagIywnoryT1WCFPQN3reYHYAhBoTjgvB4wPLdR9QlojEg1TYelGR8yOpmHsvBENt/OSCAeYX1v9zDHiYqBwpXxjx1XX7unbb6SjOl6dn9mn5P68/Tj6a6TLETNgcW+QDqwnC8dih6biiE9wAIzOb27ccVvRFNNMyV62HsBqRf44bk7vn7f+37av+cDXz4oXh12e7d0u+79+lG6Hugieyv3X1ttiHdud4VXodnz//pf0I7nCC14cv6hqUBKUQcjFC/1qpKGWm1agLh9OFbPDx+wuH4iFI2/PT9n5AvLyj5Yl7YFc/nDbWtAGla4JISPjw9IRPhu999i58uL6q4Ntg8j3G5jpYQAfK2gUvuxvfAAKgrOw6I+ly7YTQMCEwHjgzStv3A+zmkz5Hqutw0jK6Yjvn2Kzzyq6/8/a/7OpsjFrSPcwr0zQLsN2tKuHGp1QrJBW3N+rfxbDuXmdxpX18Optw4AHn7ken//hmAzr1I2f4mGuPt/yaaeOGmW3cRE9M9o3iaK9x+/f7vmz4RKahDBAoaGat5rAKK1FOkiAzNumpS8/nbveBqjieFbP69TPM2JdtrhM6kkF3fL32ur/bx1NF7xeHGJX61G2fTL2kesyFL7o27j9+QiJNB6evS3+Tv6Gno3gLB9dTQfHcX8+N50q/SF47hmKS8PbSDHbslRl0J9P9frw/HGneOlt0YWOsbgGCOhH4eacRELZ4aOzol3TCZOjtv32vZLFNvx4bZjYWudzdWNUVd07S5c9y11gBLx9+Nswz5qMcrIZAVHyMvhCJ9MhTIBXoOpgOyGMbSvJxcRmuxE5miO2bAc4rAnfrTz/Zp0JmDArGkOoPTSfmYx5j6YFUzVr39c8Sy1AHUMI096h+NEByCfJbxrUJlhY0NgdCk9D3gIMUQFgyOM7faAJnmPjvA6FHQ0jZ4sayFAOIEoFl0X0YKqWdZ+RorNWtBG5oaLkN3coNqcNHqODMIjUeDxBpIGKAXAeAQrxiChqLg0a/OETdANE/PHoY5WQEUP34EtY+1smoCBOmUA0zD6I0hIqRFDXurJB6C8nUGS+92/bfmZpyFukpTVCBIRPD5yxs+pWPndw4kOByA00I4BOCQCMnaFEBYmLHYkLJHOl8fNNdH49UcJyZ8OAbEQiiisWJbFURRSoRyEKwFaAZiiwR8/Mh4PQvWC6MUBXICi9pbAJpRj2hEttpeGt1Mfa8pBUdD3lZkgkVLacRVJUKOmmb74WnB6+uK19eLnSFK/4BObzLi7dxmqFWj40QE8SGq7BBBqWRR0hqJ1yx4BRYdS8xIrWcaT6MUQWw0Xcp8ATAsslIM3KogA2S5OwwUlGbPaJhkuEbsNtR8Qc0bIBVVilZzb6oBMQQtv+Hy+U/46Y//gJxfsXBDiBpJnCKbU6tBUEAVEBSUqkCK/jGqDmoIsSk/cQIi68/Hg0ZFHhLhcIg4HNK0hByQ7Dw7fQH1+ZJm1BsBJBp01fVe0/cYgNCke5lep/Je31Ntb3mEqNurwQBdfWbTCFpL6w9Rqf9qqwYSCUJkLDGZnm3UgCWbbsAIFPocpKT2gAL/JrurZTBY9Lanp8MyzbwmQ2sNYOmOp5wzetCRne8dLyGlLEhJ+Y+rYShKfWIZvmCNAoVAlFRes4tJZVOKqYNrRKQFmKD6RLa17meLiEXSSkPZMnJWsPayZs32rT6ntuZTwrIseHw4arR7Lbic3/D8+Ucc0hGtZpSyIpcVy+FJ59CjilsDUDvAXWu1TMPc72utQhltAgInhKhrTCOYLeW+5V4srZSMt/MF23ZGKStK2bCuK758/oy8blbcGZbSr2n5XaGZ1CMACMYrGmNASsqNyzzCwjgOYB0csByO8KKbHCPAZEX/Wo8YLy33PcykgK1G+AqYz3h8fERMsWMsy3IYwG/QPalR7CoUnEt4nHG69mvV8WnSEAyraSKoTbBe1u48ch0qxulMihFxSYMTWxpaaT2zO0y6jDoONKvgfLkoNcBy6PpDpzoQlW1xSXCKzWt8Q+eiANWdD0BruYPBKgLcOa9zGFM0CgE9H1KIU0Gt8fxSfa4FtWR1LEAdWvq96V3mGHEKGyJd47sMsckh01rrRf/8mp+zV34VYKymfYyVXppgqxukZODCyg3TKta8Ibyd8fRU8fDwUSe1HUGvv8f29E94vVwQBIjQSc9VPUd100iAouwDYNYCXa8vP6LVipgiIhO+fP4RZdsgVdPt0iHhm09fI3zzG6SU8O133+Lp4ycQMWpt+Jc//AHn9WJeDAIa4dPXX+H5+QUvr2/Ytg3LcUF9O/fqbr4AIzMWOWBZIhjqpW9n4MOfP+Ev+AyRCrQKYsZhSZBW7YBQAVFNeKuRIf2QDsxIMdrhraqZAGbMOWfHZPTKZERDjRJoNgBQBZ8+fI3TcgJVwk8/fd8VPE3XiD0CBXCPgs4hsQLeD8cPKMumhNfPn9ENY5/3EHD69An8eICcIrK55puYt0eM98rC+AZlmKuxchuJtfuIydLJGgR6JPLe+nNjzeDi6XFDNnRzErs77fEjFWlKBekgw7hVQD2d0PEbgacEDuPobmTrZAgOYG4ACu992NJxPDVFMZdZuR4Gfh+W0ZQONMzRZn+Fw2ffdOis+dz9Wz/vgVTTFbY+xu/G8TT+vrElauvzJdO1zIx0OIDXgrpV5cgTIOcCNj6fJQJxecTh9AEfv/ktvvr6O6QU8P3TR/zw53/Bl5/+jPPLTwhxwceHR9RW8fL8jOfXM1qzaJfHB7z+r/8LHv/3/w1Y37BPg/U0vGrcX54CZf3wSl+2Lojd4aDyRou5cE/XEi+og7H+PDqnQyJXgBrk/mzNYzkfwnrx4CPyNXVt0+2e1WlNpmfJlMZClgZnh6tGl3nKmf3ZMnDZgG0D1gzJ29Qe/OKa0yrZ+z11e9FQ/W9X0nTQ09hPu35OAzC37Zc+w+ifx+eX75sjOGJKWtVbLW2EQ+pd2ANC1716fz/1PdfbaWlFM8jciyBOsrO1fjbNPJf+DH/bvB/v9e3dedp3YDf3988K82JPz/ulZ6txtHuNza8rXQ4/j3Ux7xnZ3WP/u5Jr6nScXtghI2hVaZA6O2TMtcvowfl8/dz9O7rD7M4S8EjC1tuisA5sb9Y2ImU0rd37ewUyQnBPZpP16xbM37fSgS+gIUbn5NV/z5lBvvb2e0XbMoP+DFJZujvn2+69fh68+5na7X10bsYmUIDNDYT5+ebMZi8+Y3NKgFJ0iUdsWDSWHcgiFdvWerVhwFSj5nM/HBzOATf3oEd32Tpx4yfGgFLbzb5TA0OBP5A69F2/iTH2lEMiLUoGDqgiKBaJyxwVOARApFFTmkotXQ9ttWpbwqhArMtxRIB5mxQwMDndARzuxT6UgocRohq+PcoM5nyf5VjPRmMFfCYHvWBEL5OtIedqnAv4TAvBF5BmtdgYNSvKC7Iow7753VljMsF4P0Ni5ZV0ANl+V6UCrJGIx9OhF+6ptUIpBc2ADowUYRGk+rqPH09gAgJ7ZW4rplSNl7M1rfSlyDwk8vAv2jP+LXqeAKjSkGtDrkCuCsSes4JDvThQiKhVQYAmQK26AwQCMBAX4HSKkI1RcsO2FgUzrJgPs4A4QFox3UH6mg4xGA+wgpEpKTBWS8Frzoh8xLIEEB3x/Pxm811H1KFY5GltHfSPVh9ERHC5vKE55QREgZWyKfBmkeLVqnqDgBoqOEZ0rkNBj6ASkxm5bNjWDaWs+k6pKDWDzL7jEJAOCwLMgQRBaxnFaAg8Uvb89gqRAoGmYmeBMu+JoKBC1hXb57/g8vlPKC/f4zGJRoFGtdmIgJiC6ZwbaquWV8kARXBYQEhYAil4GwhLBA6HgCUyDjHguEQsS0KMwex73x5KfVInPXDeRixjnzcBDssCr0qfazazj4YOOzsBJxkKc/QEilNUmkZtV6idpdJCiwJ6pp9AULYMW4J2mBlwCh3jkiukKv1Yl+Nmh0Ma6uZFrMiiBhtOhyMWKwI0wFWT2ZZRsNtiZjfq2TFc2B5gIdDCZcoXrO08xAUeoQdP77f17DQVam+Q9WUET5FRRfSsV+j7l0PqernIcEAxM4Q21NqQYtAsAwO2S1GgL+cNeVtRy4bHx0WpK7hgvZzx8vw9iD6CkAGjGwhxMZodxT5azUpBIg25Vlxen9Hqpt8XLZqWloAYE0JYOhZRrNhWq4JcN2xbRt4y1u2MtRe38sjXTfmPawPaSFEXKK0Gw6kcdNSbW7AEIGj0MiUGIoOMvzwY/uJCsxHAhwUxROMxVaA2QZ2OIpOTG3omhBBQQtCaO62CiLFtqzoAIEofsVl0LZvjDZ6pPNmGpGda8DUsltafokZje7Q+CE0Ix7yh5mJnN8MDynLOuFwuyv9KQ5NXnUqMcoGRYrJgQ7ONlwVoDWk57M86H2dR+h/VZ/RdA+ykm78VJE5TpoH9ngillH6mKg1oxXpZ0e1P19VsamIcReK0GGzD8XgwJz+hloaULINCho6lwQdtUMuYc8X5Yj0q1s+LET2/r+Vw/flVgLEuDHzJp+MRTFrtDZrN0bk90ARcK7hsZjgziCOKAOct4xQXLIcjtq0a+Td1ovzj6QCBFkd4eXlGWS+qRDJjXd/AEDyejjgsC06nB50gFpCRVRMHHE8PCsaK4Lvf/U7Dzd0AqrC0DjavPixMHHq4t4ZKDp6qIE8xouQKPEfgC6GsemBpmogbe37aEAZPRhybzsLklfvV2qpbU5WMK2uCCT2d0PyDphRMhpeYMlobKCR889vfoaLh/PoCqcot5O5cMuNLmEyZdaLxBcvyhMOikayvr89IKaJkHbNlSVgeT+CnE+QQURNQWbTipytlu7bvo0wADNxj+vlqcYF2UXkG8EjrkQI3hmmHDWx8ZPxmbsMEu/R/D6/LaOfcYlfSgb1BoYedKgb6u6k913b0ZGTuIkW7UB/9vFsIaQLY9OF6Tbdnxe+96tw0Bv7+/btoYAk32ruO5mi7+Df21b6d90EQ+Znf2Wdk86JbI1MXpF8mt6Pi19O4npuAqnjulKU7SDdqxSKxIIzPf/kj1rcX/PjnPyAy4/X1GW+vn7Gen5G3FdIawqZuULIqKE2sQq8QwlcfgA8nCFYzCMbcdrqSm1GdJMNOsTXlq1gKpxdFCSNC0B0biRlBqPMfNSK0XcBB6xaZOwralFIyUjBt8km5i1pxI0nTe9xI0irve8BlABp0b+nou6x4jKb3qYEtIua5aUBtkDUD6wrZNCrW00X9QdcgnMh+Hd8zOuXOfuuRcT9npPp9fUb0uxlw9OiMAV55O+7vhZ9ztngfxz3Dyan0BAkIxhGruYSWJ+jzSj2l6713TVLU4QSXiuh3uhzYN2kaF+v79P11f13BmSPS9g0Z1tx+/ub+3xmbO8P33pj6PP+MtNm/R26/o/2v9t/trpvaLT54Q3ETv9HWDHvleRn3t518pbEn4cMls3hT+XvnXBlDTtP5ANCM0MCjNYeh1nUOtZLh+80VYH9/cA61eVD6uyfHpeznyw1mN1zENWQfmnlfXYGxajQAno6pL2f7t61j+97/1j1ue76f+/tK2NfvcyBWcLUW7XovHuNce+TRbp7SSAp2NzP7tCUere4GgMsK/6MOpNkJB7DxbZqx53PuAKwtihHhq2DPfKJogSIyHZkMCBsRHl7Uxquom72xO6/YdAE/5zWVz0BYH2cmhKgVtT2qtLqxQ8DMM7uXE+jvmSNOnFKhpxJj6if5XtMoSufbdTBWAVka1BsYLhyx89+dEtNU9LnoqZLArvCIV0P3lHsAaFV2a2P+OFDT/42xh1ur6BGcAEIkpKQgbCBBVGwAtSjgrRFOI4JZgzIASQ7CMJqI6gE09AKPAJ415J+ThXNbrQOawktqG2xmtFNl5Kq8rwJCbcCWBesqCiIzwFGJ1UIkHBAQmBS4rTAZiLHfenSUjWcRc4LonOasa6n2CLuKlxdBSmqMPz094PX1DQV63ZY3fYdUq/FhWYNeWduM7svlAl8hylPvlB1qT1VLv22tYWsryCkWfB2zAu++mHMpqGVDyStqWTVyyKPHIZAi2ErAwhp5WUWQy6rgUzWQqWhEl0a1Gj+0rW8NOBTgcgFdnhG2F8R6BnNRx5FEUANaWwGudk5b8STSTAImIFJA5NiTaxSMJRwi43iIOC4Rx0PqgUfOKalS1mQtKUilchYgAxab6SBgBTgBt1ehGZttyDM22r9Zzdcq9aqbCl2dceZEqa1iSD3ar20iLFEdSF7UTUFdO3MAIBIkKHgjotK5VuXoFTs3GvScUxpLL3YkXfexAe+yiQMQeQJuyPed2nADkEK3a8Q4uDVYVYuL+ZzB7mGTfy6DtXB367qnFkFU96qwlZps6Ou6p7B7e1jl1pY3bHlDrhlbLmjN/pSKVoruR3PMZSZcgjpQa8sQNJweFmyXZPqBRsYfTycdz1rQakYumwLxonV23t6+oBq4q3+qAqYUwBQ1UroBtRWUmpVuQEbxqS2vWEvRrGIZILW0NqhauoNOIEL6PVtQCQMhJKRD0oKhJmNi1PNLaVEC4pJsSw+9oKFpAF2jXjTNx1ZIQNV0tisdUikChjGmS5hxPB4hSeBhNQRRbmXbU5gwgVYKiogCr3a2CgQxMApPBU/tTOkUjsx97c0O3pzz0F0FKBZpq1QSK/K2jb0fAhga5Q8a3NAzwBojg/mAsYvRo7XncdSfK0TyTgdzXTfG2IPZUrTMhW7L6w+lFHMGtu4UdCum1mLF7TWL3fXLzvcdhgPb27WnzfRzqZquuR87143e+/xqwNjJCjXUPlgFZTPaWgOCHXRSIduqKQqk5Ma5Aa+XFQ/pgI+PURVRHmkdZEpQa0CtBev5DJJiHgXB5fyGJRAeHk54eHjAw+ODIfa5K1uXLePhdFIh1ho+fPyIXq0dhJwLLpczipFAl6r8kn0hN1ewvV2aqowtQF4Y9RnIVblL1LuuUrE223SueMNI0V25Yw0l1+IE6AqoGiyw0H8A/Rl6uon0RPpu4DiC7yBBKcqD+fj0AVvOqFWwrReQp77OoEQghJBUyQ0RIR6QlgeEYF6+ZcHh4QRaVxATDqcj4tMD6iGhBgVixTTB2Q6bjXoHT1zmjCtmQ1P2d3ZDgQwnkA6MCDCRcNtnoBFwK2JsuFk19UjY6w22/+6usS/j8fP1IzKI9hf3H2X6cT6k9+/wSKdhkM7f37ZlPNsN1+t0Y1elbg2HX/p0o/7qlbT7F/o3sxG9j5SS3d/jPLgz/h2kuH2noE8rbkY6BNSPnwBiUANQBS03UGmQ6oU0gBRDN95iYEQWlMszz6x1vAAAIABJREFUXrYzXp9/AJp6hpVXLw9n0kYWiRR3UdSlNiQANZL5OIbhJGLRNuI9uu6VaZ4QUy7Gb1XxBCiwVXJWJ4oDJ4EYT/GI2IJGuxHhUjdkNDSSXjwP8767VmAx1ptPTC0FdS2Q6pVPFYyVw6J3h5Gzdws20v4gszFv3v8+t6TGmJVtlq2gXTJky0AuQKvTWBGuwZ19D/6/fa6dFn/NzrgB8PpmeGfP/8xnKHD3ZJCNp0VvUIwGxo7iXeJnbz8z3n+3r7zdb2WGt6939N07JsUKXcm///t3ZOgV2PlzI+UyZH7GzylE9959/8LrF03f93un1jli+f/j484iN5R6f/zneQ/a++e9i2mtqvrKO1aN7ngcevZQ6vs5R9YGvVCDL70dZNejG5oCy8SgIaXJK0iA3hlvMTlrBlHfG0Oh3/eHpjb4/f6M6Zzo77hSkq/OlfkemvaGO5r9jLwGY5sIxAs63gXYqNMrmVLZn8ekhXMCO7dgu941trRUbo9H2z73qEcrcgQA1AAHmndOpK6z7fugciJ2HZMMLFTDzAHk2xTCfT8FzqfmBVhcbhMAKVOmg7U+RNcXUzeC5uwtPwtBY63PEc49uojG+TF0KAdxx/7xfisVhPXVUkND0JTmCitQ0kxnhq6JJqK2CFPXH+DRyPN6sGg+wch2ktZAXnFd1CEslpvuf/dRvF5/pr82Me68vka1anSIHn3YBQSaNJSqYOzg+Nfx0qJnZhwH3akpEKK1gshHb+++fFf3648f7yEohy2E0EhtHfUhEaoo1ihQ+yYXwWUVxIXRQLv+pwAr7iTIuaGUmafPHOJ97KtG77VqkczBxqwYl2SxdOSGw2HB4bDgdDxiWxVAUQe7aIEej5RtFTkroOOVxGNKeLk893XXrOhPP05h1AhVo1trzmjQDgeL3MYkD8jkpEbnZrS6QZqlt9raLbVACoCQdQyroLQNpRbksiEXTcn2yEeXgwoEolM44fUL8Poj6PKM2Db4IdAalJJARNtqk9pEn0mBDOwXmxMH/glLCjguoQOxyzKlaYOUv7+vKWhsgKiDzOdZ11brS0h5Sk3mw4v16Vni5wBoRIC7rHIZ0h17GHu+B2HIWLKuY3rjKEQwNJiqiUa2B3cAghA4QuCcvk2LdrFALBMscECLGiDlZxyTRiX2M1yUEkp8yxCsfgj3A2gU7htUHNJa35GdokFUmrZauk4FwjgLpq1P7M7ScdA32788XTdgPneM2glkQ1Wl9T+lZtRSDEQt3TEmzQI7akHeVOa0pungl/Vo1IwMqYRWSW8g3TelrNiyRojXVpBzxevLF5T1oqnkZk91rUJYqSZEs3ubFGxrQcNwxJSWsdYKkAa7EcECsgblQ8+MEqBzPnNUecaEw3LE8fGIEFKf2xDUkclmY8WUAIwzDK1NNRMEzunq/0HE+Ewn/bnrrEN31YA5PQsiR3AMnVcXMocXOa2EfudOPwcePdIcomSXDsaC1IHEIAh7fQDZcca6PJmz3kKp2PoaqINKTYyXtTk/qxVRjNQLqYsBny4r/JyeAVh/lusUWmBtjEvX8Q8HeFFLjxDmjgGOs9l1GOeUdR1XWkMjAmrre0GkQgHpKUK9yyqj9ggG1ptjuNThxHA9dK9h3v/8KsBYVQ9c4RG85Q0MtoOsgqNWf1xiRDoElFZQXi+QRiAEUFxwPGT8UDYcKOC3X32HmA56qNuiTCnh5XnFup5R84qnU0LLKvRy2XB5e8aHb3+DmBZspeDz93/Ctq54fXkDAVjSgrQs+P3vfw9BQy7KrVG2jHQ6ggLjdXvGtinp87Zl5LyZt580JShbOhYFE6AVUgQPP32FL+cVazVBs62QqmH4RQDny2bSA5GJsKTUPddAtZ/VQ8IQUIi6CJyYeB5vkwdE6jH1wg9EDi7CDkCYIlxRAHzzzXdgYTx//ozXly8IxODYT07EJWE5nLAcTkjLERwjUnrQBb1kxA+fcPzmIxZpoECIMeCCggxRL+nER8fT6u3BnTQt6ncNbFcg9rQAZOPnCr2mqehgtCaTGrw3DPfK59wINV70sB8gb1/Q/d5h4Hl1Qz2A3WiFjfv74eu34Kwf5veAhn7FJNCkG1jdUDEjdjx1MnqJNM1rPGka2f2nj/oEDAyJM/rfn+CKj9tFDLgBP5YeXRnE3ufRd/++7UiLJ0G5AxGwf8DUepluJwByesTb//g/g8BouUHWAlzU4ytNoykeH054PJ2wpKRpGcZLUwDEZUFMC9bzGV9++B5Zs+Xx8lbAPRKkIp83iAhODw92uDWUlzeU1zM4F1AMXZHU7lCPMupdsmVRLRqLhNBKQ86lG2qAFVVYEiiYQi4FgQOWwPgYHvDvHr/FkRdEimhE+OPzv+KlXXCRjK0b06YDi/7QIyi9TdakWtUTvb2ega2aU0nHuaDCq3rH40EBwmlKegqoG73TWmgixrlmZaamSGXJBW0rqG8X4LwCrVkl6TDJvXnRTav+xri8b2yONSi7v3F1/7zC3jFbr547e1rd9pCba+Z97XtVBDtZNdrlxjtGAYEY1dEQCCEykIIBAzZG03q5Vl68MwI1zOh6Q+5bO+T19EyzKDG7zPrQ3XnONcAzrtmP8M230/wIrjis7rxn7+y51xwaxkg/OCcqC/ufp0/6mO85cOen7Xq1+/bemto5muzHYYROeyR4sc59ARH/jGzGsdY8jWDM5xiTIXscDGsWOTkNEqnhMzu8xfY74CCCKaXm3CNWA5tpKi46nesDUPN1P84wnwsyDsBu6NsYqsHR0GD1B67kZU8FtTURphff20cataHcoWJ9DCHerBdvpxo5wZxAgPRNMOa3Vi1gRZZ+6tlLXtwjhGhjKjZvljpue4D8mf5OKKckW4Sdc5V1JwwTpI3xdB176A+6xlopAAUQJ3hVeEJVQMFoTZqIpX4bn6tFDLJxLUptQKmoZetyItcLlOPfinfYVvazo7WCwEd17pvcb7UAcA7Va31M/64GPMxyWQ1Fsuha3n2/2ytoSPEEgLpRp/SNo3CYR8a6wRZZwXKYgYkGSDci0ekNcsl9LZRSsCwLpLFFpBXw4QBqviYVqFOdO9xZ73p2xyWhZC0uQ/CtVXt/dN4FxcRTrUAIglKVmo2jBoEwa+GsaGir1SpCYjUEFwISKeBGcIbksX7/qo8b0011BAYhV8FWKqpWTdJ5s75ta0XO5tRhxlYIObv8JhQDbEMgxEQgFlAQbBuA6sCaZt6hr+eKbRsZR8vxiFrNOZ4320G+eAhMEZ8+fcD5siJcNFr6808/KkVVilgOhB9++LHTfsQY8fHjR3z58gImjcJqVLBupa+zUsWiryxqrGVs+ayZnRyQqkbSVd/37JQaFURNC2oSo4ItKlOg0QHKgwqI8riTzlFQ5EFtEgOgmqh9bCsNtRW0fEb58z8i//jPaOsbSCrAQWlfSFDLBiCidOYZsvMuIhBhCfqHqCESIRIQmfH4cMTjY0JKGpzgur7YWAtP9gERArTwUWvS/zADpa/86WPbQe1f5ca8YxKZbl16tLGIRTljBA2pDjsU6BCUJqL7B13uYrhGmJUv1g8q4qTrS3TMUgr4f9l7t1DdtuQ87KsaY8z5/2utvfe5dJ++qVstIltKiFAix1gKinEuxLEMyUMgLzHOgww2gtjWQwgm5CH4wcJPQWDIcyAgRxCBIIgksmVHUeJLIqulCMdWR5Zaarf69Lnsvfa6/HPOMUbloarGGPNfa59zutOYg/BsTu+11j//Oce1RtVXVV/NFzNiDI3+bs0b8paxFf1vtK9V5wPYCi9qozS1X6MnpQUweDRzLVU5K4mR4oQUJ4TELbOpt35Q1oEWBSm26aZpwjTPqsuZjMq5NNoHDgGmgtsjo4JUVgwXFeAUcLy6AoUTarnDAuVhVWDQNreBnCRVz+JSoUQy2p7r6+cIYNRckbeMsCy4vb2BA/JbVoqDdTsh5w2lVFw/f46a105jUB3wMn1mKDIKCGpxfVb/n6JyWXvaH9vQBwMJQ9Lxdd0NErQgGkeANNI5TDM4TSDuegCRnjkhqLzwbGjF6Myx6kUpHdAzWhmI2kz3y2lYfTo39/f32LYNtWaklHA4HFrxXwabzNMlFJmNfkYlt3AFU4SgF9Rk05GKiBUkLEqlUvRsKjA+2dyLaRHJLiOAyDKgzW6JrNQpiSY9K6w/McaW7b7en3BaFt3GVWtAdUDUZJXprF5kcZ5neAG6MbW/WlZqzsWcXz1AsZSCdVnMIcU27mJzbYFTMSiXcZrAPNt56/cdIANWknPBuur4i+h6YnKnvLfI6Agse36kK9B5VoB7pNF51fWxAGOdalqdpgSaZ1BlBK4AZ6x5wcTKkyogTPGAbbtTo1Uqyrag3t9igYK3FBP+0Pf/a7h+cYdtWSGFcHm8wOn2BhAl9gVP4ASs99eodcFrz55g2xb83ttv4/n1Nd6/fo5AgikxjscLXByvsFXl3AnMyNuG25c3mKaIq6srUCC8+957uDst8KIGBMJWC9YtGxm7iqinxyvMKeGCD/jM+hmc4oYlFJyM/qCgINeKWhyRJyPuV+kRg6e3mxVoyg98oRhdAIN0UKtHI2irREzJh4eN6wLJJaNVbSbzwlet0ke1ogjj6tnrmI4XmK8vcPPyWosKxIiYJhyOR1TzRiNYKmxkO8wvENbXkecICRWVCu6rhowX1GaEOcDAw+EyYk8dpfOqom4XjimUgIOu/h0O1IYrsIbqB+oRwGjf7orwGILeV6offLX9TceUhs9dz9O/eZ/0gKuNu1OpEqhZFGRz424ZaeBFv9yYeuwagROPwfZqitkN9PacEYjtxm7n4jUlanjvWYzEONp7BGMkwW1v01+bx8k/crfsvie7n9275Ma4q0mvGoeGA73yHhlWV/9Xie09LUeNwrKuKPcrjhcXePL0Ck8uLvHk8rJRafTq0QoMHo9HHK+eYJ1mUN2MI8yN5IznL17g+uUNbm7ukLPg9uYOaUo4HCbIVnD6oT+K9JXfRPzNfzx0xtv3sD/EjDRwUdVcEWNS0BOaJkeAGnM56/Zh4GI64HA84q0nb+CQAxIxai24XxecTvcg0khdEKO6cm1vSSBsyMikBkHfMdwoXaYYkE8r6rqhbhkpJoRp8tB9TUErzteojiQ3NsQiItr/zHonAwVa5NGyaZGKTSNhad0ATy2zseuRFw+X2eNOl2bdn92Lpvg8+OAVB+y4Bh86dfSODiI8jDh7+L3H1/v55X2tqFp0PBhYFxk16pnApOC+smB1HrL2Hjl72zkIPfys51Lv2e45AOQ882D4nB75qT9p6M+wyoaenrXb7hraWAYZPkbJ4Ow7+3bbs8+nTPzu8ZmD9PRfPLV0J/9k97DROerPFzMs1NFxPve6t/rzVF5VU0y3u60pyyOf1vn1YQphKzDlxywZV6zAgATbBNT8IXZey24PebqfF17yte68bgqm2fqxisStn4/uUzOPpQJSINVoGewKHNWoNPBXC3t5FChpFJFaoDArAxJ6Srnvv/N96vvTAYPCniLHHXT301J6antz0KoFou9pvPcGDBgfISDIeYVhmwAUbNSxIQU9vYAXayGJMVrUDVJP7XMuMxVN2g6v5O5gbS6KcrFFu3KIiPPR9AKdgzRNlgJeDRgoyPm+RRcyGcdyBrKPU0tjdJoRbYNylwfkbdOsN5PvIWgW27ouyJsGMFQR4wFUYLhU5QrV/5SLclvv1SiHFmYJzTDVcARAeVfJqBSU1oNVT724BBGwnG7VCK1GCxZ6xDYTgFIblcRGEadTbAa0SLFCUqWtHyaPklEQ7HA4IpeCZVUgNedVDWbqdBLRqjYTCIEKtm3Re4RQtoznd+8rf2rUyu4xRqSqRaqqOUqfXwueW/ovEWFOEwITpomtkJLvHz0YGIR5Aqakaeaql5ldQFrEa6cTfpOX2hSMYEU+1S4JWsjYuClFCPUEXF0SjkfgtAieX1dsJUACW1GsziF/OmUs64bTaQWgUbJi4z7PkxWkES2mauXdpVbLSiLM84QUGWsAlmVFzgUl3yMvKyI0Nf9wuMA0P8XN/YQlZ9zfvEQtG6Yp4TgnLd5VM7b1Hs8uP4EXMysoV3T9BTauaqNDcCc5oOfvMR6VS9T4OwOC6pmSjfot2pizKmno9HFCBEZSgMulE3sqOjcnQi7ZnEdoafEaqBNAWCGnG5yu3wY2K+Bs+yMXXT8qr1fkSuCgezAmy3ZMEygmUAiYUsScAuYp4uKQ8OTJJVIUpTNxMK9J0Uf0Vv+Pu3UgFQpsm4xy1F4CgYQVazMeDY1M7TQgYgfuFCer5C5WX0EsU0Dfn0LEFE0OinNxu3w2OQ9zWLDye6Y4KYgmBEjEnJ4gHg9K1cARMU7NgSVVbC12G5vamvfI54JiafiFNhTakOUeRRasy8mcUYTCWuzJI/gJDCnFnIIEJntX8eg7VkCSde/6mRUNPKoiWO5vcX/7ststHCyTTiAkqKzjXiAQ0vNBLKNXxxyoCMhSVf+fCPEQcMSEvC4o24acTbYTI5Kq9Q4qE4AQGdsieP/5S6R0Qoq6xpw/udaKJWesiz6v5A1SN5TtFlSd8qZ2Xm0vzlnE9gTQQlFttSkYz0jM7Z7QIpcLiAkxBKQ0WUCN8rsiBFBV2iCQniMcgkZQOsAPQpWCAuMbJo9GVzmQJSNwGqJvIwgBfuATEaZ51szFJgEIx+OxFYCKkXt6v+lked0af+nqiiPgm1/1L6DNdWAgxMmieNXxOqW57UeP7NxFpVqRPXdsKxXK1goZusNaiqDkgnVdMc9zB3CT/nsRFIfQwKAJMFDVaQ9ylcbzX0Vwc38yB4DuTW6Z2y5BOjAK0qJ5fvY2maOz2/bduiqn9/2p4Pb+1L7Ptj9LA4QVUJ2mqfPX+nPNkeIyp9SC+7sT7re1gct2o9aUiQbO21M+yIL7WICx52bWthVQLWCokh9hSk5MkGkGHa6U9H/dAOMMOr13iXh1i2u6x+987Wt447XfxifefAuXVxfwAjZpnhEigyFIU8JyMq4cZhwvjljXE9ZNOXguDgfMcwQFXdDPb2/x3vNrPL+9VV6JIliXxZRW9Zzc3d/j+st3zavARKhZF1y1QzlQwKff+iyePXkCOUR8Td5BBXC7rNiyem7V2xrUiOaAvGWzQ/Sghx0uahMZuMGjksedtNwQMDeMlOKy85Gp7jlE8JAvemqgiAMjpSjXTkoTXnvjEzgcr8yucQNNjSXlneUGOKrSRJiPM2IkYBKUSq1fZ9Tl2C1achvYUjZ2uRQec2fm7ogHeni/Gz42H2287BHknslXrU3pUSTkwNEgEBogIP33bre7cJTdIm9jL0NqyPAs8meJKy0jt2oXDKOuvFN2/LnDGuDh+61YnpzvPAdhNKWgtbe1kR7M1ONXs0LRmaIeWNi2xvbPbdEhtbdt7NpADdfn5BHj/THQqH8P1jYHPvQB+TPfge3zX2ztq1n5xUIMuLy6wOXxiHmaIADWLY+z773GHQh5UcL4bVk1M57UK/rkyZV62ecJFxcXeP/5NdZFCeSXBbh8cmHphwTaCgoJOAZ4dV3Tas/mWmyULdorhla0y4tHMIBSegXbw2HGaxdP8drxiVYDJgGxpRxJxtV8qTKB1Caopthlq8oaQ8CaN6yoyCgoVFBIvb86a4waAEwJNTBkTmCO4MBtbjW1UDq+JVqMwlxyrShf6yYswt/2kkfEYtlAuWg4UD1TJM4XhhUCPF8bD6PKTS5A+p57xcL/IGCrb5tzVG/4l7zvjTBmkCVj+/b7dL8E+i/O+a3imDWSJBo/bAxKARRTK5bjzxupWsbIrD6SnklQO7WB3tzX39Cf7jCxp7S/++97gJJM0EsbGpel8oGYwDjTLnMfRnP1/dkaRR3Q9D63sX4AgFPff4CBbF1yjV1TQNVABPFnna9JB2vFj+d+PohmiYwGrIhYJGXvRYscZ0a09o4FDVoK2Pl4Pdgf4xrXqEEfefI5svYwnDvP+jssYcB5fqnz2bZ3DvHpcsaz1eZaht/3c+Lp7qrzSBt/scXiY8NNXbF0TnYginaFRn1apZQhJdaKl45Lx35u7TC+UNUBLIp/N8CDXAEBdo6OfKa1CihNIAtL1GrIVoysarEg/7tfpRSNHAUBlQyEtBNMfL7VKPHx3UWC2uet94JueBCBqyJyJSzYBMi8tEjmxskKUae+KDdmlQoKsaek+nstVbvtGXufBwPknMHkIJ3OZSmrppzWiloyYopWAX7VAk0QAMEihxO2LaOUE7Zt0Wrc24p5OiCGBA4RbJyaurw9ekp53AgVedEK4+u6KGAD9Mhel0G1YuTLIwqY4lHBPurUCU41pMPjYwF1zkLHuUgvxFZa+rw6V5ynT2PGzGaoFZtoUaacc49It+iqYkaq61fblgEDvzlEZCGkqFyGMWqVe6nU+qLFvyq2LEAFKDpdARBtze9KnX0EpU/OfrLVj1PWVNgKYErKFVuroJjgEzEeU1He21wFIAPBAYCBLWuGoFC0TDxWuyorN+ScEuZ5AkiwrgV3J3U8F1unGo3uVBA6XzrOBTlXnNYTnhwvsW4rqigFQEoTcgxaLf50j4uLS9zfqyNiWzf80699DYA7Gez8Jmop0cUr2LdxUX06RnOcC1qUmy+6anzKfj52/dv06UE2YtjfCnaTk7COH6vIACAo2LY7XD9/G7LeIaA0G6k5W+x5HAJS0L0W4oSUJswp4TBNmFLCHBMO84Q5RUwp4jBrZBiztdHPVm8fAPYzUKSPix7AyhntEfy1qIwrnYKm2z9ukwhAApZ9psI4v3pWEHoWYB8XIkI14I9ZgTR3hLIIEqmsCxwwxwnPLt9ACgeQBEAipvgEMSREjggUjT+UdzqUR2r7HJC1z+lLtpxRpKAio2JDrosWm1oWo8hQmjC36ZkZqNB1L1qUrtSMra7KVWt9FxRUqhqIQRWF0fUsFoADyDm7gcZ7rQxeDHWG6jyRInnqNLAzJ8Ay8exMChDcSUGRFUwFEkSp3YRQiVAsG0WXqTrntlWpOET0PDjRvQJcTecklKoUiVp3ooBQ7Fzs28nnGNbzWqFrEASQIBrlAxv9Dwc2Kgg0J4ae5WIBbEF14zgpB2xKNq9adBIEk0ukIC2pXtGK/vo5SxUkZBGcG7huIApG/6K99KwS1/MEAmzU9MmRm73pVhYp6lkY6Ri7bgLN8KZBZkipzTGjW0kjocXe7fvTM2Y6LODntlgtIm5rmTlgmgLm2beVR/gqGJtSanNSRaOeCcBiEeohBNDpBHd+eFsDcxufRoXk4gRjYJz2d9ssczxniCg43Chf2pqwQu1GVTCledDnYFhZaGfNsmxaGC0r5QIE7ezo+rCtHc+ioYDj8diicHu0tvRzoenxvuEevz4WYCzQ4wxBFfHJNwARBBiJe1VARGIC0gQ+3CPQC2DbQKWAqyDnCrq6Qw4bruUlvnL9j5EvbyxNSCu2ZSdYhyBuAct6i1xvINgwEWHjBS/nl1hkUcB1ZlQGtlxwOi24O9xglVWjuggoydKDTYcvIeM2Lc2TRKLh4tImRAXA7XQDSoItLrjm56DAyHPFdlmQjaJAjUoCyNLBqJjXrRp5+AgQAsd3DmAZ0vfcYLQ1rwvD/rXznoeDqvrzLF1GKzkKuIqmTphyraBIxBQjYpzhwEixCGCGg56w9H9TvFC1urt5phyeY/IooX0cZjd29RoVe9+kXXPuymAzqAeAwu298XBWhXl3x9lP59ewiZzk57EvyHCnDCmqomoFajc4HYDoj9l3ZpeE23Sx0STfp3OPF43GEPZGef/soWBw8MR1QbL7H7t2piftQS47D3dveIAp2R/Pn+4FxPZvokcnh87Q2FdFyz7WV1PZQADKm59E+dTnUD75aT3QxJU7YJonHOYZySLPNLKodIMP3ROc1xV1UxC3Vul4jEVQpzTh4iha1V4EL1/eYFm0sieYUaUgz0fwa29A3vl6A2w8QjScRbx5tBmIzJPth6bzhDGoKkDl4yqW9rRuG65zQeSIKU0gAbJk9eiBmrFAav804vPIAVtMrkbiVBfcytaMfTUqGYh60ElTWEjRdGsDGdefVAFKRakbAE3FZE8Hx7AmNWdVDZaqHLG0VVDV1K5XHnMfwZjc3b6TCw7QPbJ+hoN/nA//zFCj3etlQHvOn9gcYnj8mXvg+PH2wOQbsaVhk3r3xf5jI9angdz+wSUPx1LOPt9/4M4CByZtbrv0RrdI9k9sgNIwLjQifeOLmoHqAnKQl+3Zj8i19usDq2xQlPx7g5J4/nUbl12kbRfh+/tcXpsM3M+Xp9QbKNsARjTgyyPVxrb0ddDXgv/nHvzHoqsf+30E+P0W5vHclGY8kfW7QiyQyiPUPSJpPHcDXID6vh3f+di6FUtv7Pupj6+DgR0sd/Df8miJQJWBENsSaPqNssjBNYwGttq564WefPJ2Thpfl80AcB624cwxEMQdvH1cqS2vGJOJvWKRfoLMBBRq+laI0XS0YhWB96CwePSttb3rRN4fv9fGrWVCjWuEtaqzRRPV6rLGjG9USMkookug1KJpjYMsHE5Z26M9GriDsQ4En607i3arUuDc3cTah1ozStbCMkohoFkakAqyaEqF9jSrKNdNAdysaay1FAATpHHHOq8wtF++HwVAtar3VlSyr1t7Z3Po1b4fbNwqT3B+O51fbvQQ+zUaGodgGzRf1q5Dk3JPxpDszDYwHUCuxc5qixAkQTHbQapyh5K1iwz0CRwRYkBKESEIpomQEhCDoFZCzrqgiIBIogFPIoBRFzBr9q47gzHM+2PSeDe3O71PWldhp4DXP3X5WRyMhQZe1ar7JwQFhDVTUox/WWkOtk25AsXoK9RZzFoVvVghH+PHzGXDZhyWJKJAf3EtqrY5BHTN3q8LruQSJW+arBMnePEZAhTsPqhOVQoh5w3vP3+B4/FSx4dgUQLUxktlQG02jssEj/Bqe8dGHH+mAAAgAElEQVTPAtOBOt9yX4d9zfn3+txAaosoa/KzHW0mo0CQbUW+u8XpxbtINYO9GoDAsjHR9g2zOjRC1OrwKUQFvKeEyUDZ4zxhShEpBqQUOrA8LJTRziFGW8u+B3S4uNkYlUgDXxkgjnBe43GdKSjT/xwc9Bz09Q62aFGqUdGplt0horo5B40mFj+zoPs6csQcZ1xOl3jz6lOIfAGGgrGBLxq/txY1s0jD1leNgHT9lWxfmCKAKoJcrcAaNF28VqUzKJaWXqsCqmrPm81WFfDKdUOWjC0vKHXRyGrLhcySkeuGrWasZcP9do9aNs2SggAczalm+gfEHNI6ZsHOTDHbhcUCl0iL4TIp/3MBo3JC5hm3YNxNSTMFasW6AlVmgCLYaDbI+Gstgx/ESj0i5iyRWgDx4pcEUzBAVJVfmBhMFqFMBLBbbv38dcCOgFaQUTgghtgKYRW2FH+4QxUDr65GMyp/ua59YQaL4i3SCqkJ2JxyvrJ2nOpUgQoEKvouCW29ksnCWrO3fLfG27k5nCfVqDabbSfQeki0z6Zjw30aR7kDzq5HUkUtJgVFzBltOgO1Ddv2Wa0VCGL2ApvzbB+R2v5HBIo9CKC1yxTbpgPXAinSudph2TW+d0EtcA6DTNIxHjllq9nYvaDfaCeJaGR8MCq2DspKa1Zwagc7d73o2HiNOIoHMboNwFwbZYGrX15sTWztYrTZzuTj+fWxAGNH1Y1DwbM/8Osf+p2LNz/489/BN/A77/5fH70Rq/37iVffMn9+vPHh4CUQDt93+NBXFVzjBa7x4qO3bnct538QYPobE2hRz48EO7BNsc61Ys0ayQfjlhVB43sV48AiC6EHB9RtQyBGYfOQ+aJMBGFBpoJ0nJSyoWTUVVOClGtUwR8GEJNFctQMYNWoBQYCBIHE+EfM2BPX2mrrl/MP2nEBLwzSuG27Bdw2pUf6YtgkHPXvML1XDyFTynaBPD4m/Qyns/cMtw0Gkj0YbizbbW5UY6cTQKeC2yE6QjbeTxdi7ZXe3gdgCFp/+ztHBdnuox6hOqajjs1yBeo8enD8bPhgNxYNmBgMEB1yFdI9lgNNQFF7trWrOlw1jIrYfOEh+PWqa7RR2wEBF9qDNkcEhID1+/5V1Msn3bMIPygYF8cjknEwFz3NQDAvn0WdC6RFYYOAkAKEkqUSqpf3xYtreyXjMB1w+NSMGCJeXF/j5u7ODumK5VOfxvrkCQ6/8D+hDGu61gpKqY97U0BtvZC0MR7HtOYCy7IBA7hf7vH1bcO7HJGCpnJeHI44phnHOCNKUK+yjdEUVQH3wr9RGDSpgrLKhufrS9znbDQyttwILWKtgwnS2tq4AEsFSkHdMpQHT6PZFPgJDXhCFSAYD5VxHNUlayRPO0Bc6pS2Dtp6aUSmw1obD0pfdW5A0Ai89KXSfxnW2vCc3e+PAE8QB1V8oUnfn/2mh98bnv2qqzmaWBVmDkGt7KB8sTVoBB5bivV48jYRARiAfv6uPajmyuJ529pnbTyoyQEHa21D73rZjMmhHc3w9D/uv2AcYd34AsZpGeQXqI95a9do1Hbg0J/iEQwPxlvGKOau+HX5Nbbf7x/bov/vxlCF7o8RhKzVCgl4a2iM7PRlRX3MiAwo6BVoSym7dS6PzNd4qZNp7wStcL5oB5AEVbTIEuAJsy7HXXEeKWSkpXGP7eiUHA5IjGcMD+3GcF+/d4x8sNajhmhjpztZFfDYbnKDxtHFcSx8z3thJT0rWgxse0ZfYy5Hwo5/cNd2+6uml2vKdSkbiIB1dQPCI+smbZ/xuLV+UU9/rzKOkQ+o0SxBdikjakBoISOzU8FBOQ/JMyfW3CKGNFITGn1btAjQlpX2AuS0F7FzFVdYhJG0/TACSL34lq1dUuM+j5GjOuKNh1XnVil2iGPb7lUqlFrRTzW21M3NqBwI0zQjpUPLyNLithoJWe0/AqlRzgRIxrblVmjWASxIUEOaBMrhCqMcs/VkxV3EhBI3vkZtLFWl6IlpQkwzpnlqe9/Xbggqe1OMOB4vMKVk9EEEQLNgct36+hYDqSOjVs14yZs5ZgNjSpOlVAbMEzDPyn87sSCwGoQ3t5ptOCXBPDFkEkyT6p4QQWZGgKAUQgGhBEbEq0HYvax85CKd38iEyfpUSsX9WiEcjf5M9bBtq8rFaOnnhwMDG5BPSjm3bRHbVrAsG5YlI8SEaVKgizmgIGBZVmwbwEFBgpyzRVoXy07MWMqiazkwpmnWtRwici24vbvFspYW7RxE9LtMoBAgINze3ak+Ag3OqbVCaDE6jWC6AlsqsoK4ZduarUJmJxXj3vQIKiKLni7qlHAsQGycPcKfhqj/YSZUrlhk5F68W0E3Cogg5Ns7lOfvobx4D7MUCEpzBhYB4NXPLbNhTrMBWFGjYdOEKWok7DwnzFNAMlnCwc54B537MkDTpF0NsxT6bkp0+yio4G59HNUiBVeMD1sjfuyTsViXZjew9OwgADuHSa3VChFBwTUmrHkFBQM9CQg84+nxGZ4cnuLJ4Rmepk+CMYEQNMCqqgcjkGa6hqDFlFphSRqLZFmUuUX/NuCKGILSZKTiVAImtwQF2ehZXHXWM6Q0mS9SIZShEfyqR255w916h2U74X67xbvv/y7W5VblZS0KIkrXbSznQSP7arXMi4EASADUCkZt6zjE6JySECGsNWMpK7Kok2XbCEQXyptcKqgUgEWBcQCQiq2cUMqCXDS7QWRVYNmjw5u+ZoXgmBADIca57S8/013vUFtJGi8wgcDTrPy60QpeMTf+0EDBzlgFhavZdp7FTKR7I3E0XahvMEZoZ3MpxpsvBFTqvPgIWhSR0gD2a2o7itj562t1bz/AbMacNRSuGF84QQvKFaCl+rtzL6bQ6KHY1lmMvfAUBz3X2EDJbdtGgbHLcnF6hLWsBsYSwHr2jlmLwcBuDtyKfPn6dpQyECFOqXGndiNR51nPtM14YP2cDDt7g5lxOBwax3OMEWGeW3ude7/rIBV3d3co2wbm0rJFa6MVIqRpboX5PKBhmiZ4dG4IoTuRHZwGjMe3dsxFukxzvnqXpXFKcBnIVgjtVdfHAowFHj/0//n10a93/61vfPANH6A7PbgegAP9yrv7dogEgCHC2a51+PlieH4QYP4mmtQb1l74TdwLANurPxr+1oAsqAJNj9xUxT0eHdA454z1yzLF909hJ9rW9PF2w16L6T20+RAoUf85d+hjYFDHGvfGoR7iBfvxewXKNAAWHwiCio+b9Ibz+E40HOQ8sk/O5tELrxH3VEBQF5jn1753r75qm9ez+ZkPuP03/70BKNLHTSHh4rUDEgVMnJDChIvjBWIIqCVjThExWHQhacpCHTnCiCBy6ABZrTgtK7ZNjchcMwITnjx9AmHllq5SkZesPuw4YfuR/0DPrS/9MvjL/whgwros2JxckIAesdmBkT6y0g4WYV138/ESWy0ouUJKxakoZ97l4SnmiyPmOKGWjGmaQWDUCiQOahBDi1V84tkbuDhe4OXtNV7cXeN2Y1yGSTm7lV3J0mpVXlQDT8UOQgdhpWbULUNyQXCgdpjKYtG2+mZCgXRFp3hE1iPrYXRG7Kb7zLwc9sguMnLcLfL42ncFxyuU7oHdMa0Gvc/YP6s5L/Ah++sDrv1+GvvGAAfgMCNr6WONVN7RE3hfaJAxD/fUBxwHD6427tLHUJF5VZjOhSGJZ2qIpnf5fhmMukZZci6LzlN+dufRrlW9Y6NMIf9MWns1UsXBNjPoRHaT5UDTeb9HcLeP4iAX20hqClsBlJtNpK3bZsDRaNSS8cjBjN7uvXfFN4Z9hB4R7cDZ/brra8ZTq0f5OmItOwNbCHktIOOmdK6t1g7RKLdCANG5JtAjJrZta+efg1QjwM3B08L6MtpHW+znRD9b21hBAKkFlUsD1UGutPtZonv4gSHk/PXwd48gtjuoOgDuBTMAGLjR83wgwLaeFOguOm5qmte2OiBAzb3t47oiMt5/AsiiBxXw0WgPdbq7oaBZX2rsmeEYLP2PFVQNHLWgLAdkrpin2baArn9ibY+7tMSeI8zKMx2TZoy1+dJsELJ91GACGc9BbnPmRBspReOqDXCUySPN2LJDxoHw4pVSK9aitATrtjagdIpJjTQz7HTda2ESQA07IrJaCxXLsmLNGWmakdJsqeNkDgy0te1Gll+n5c70mGBFO2ITHx745sWYNBorYp6jFS1ZsJzuEaPy0MUQGo8kjEKi1qIZC+KR1LkVfAMFcKhYtxUpRqRk/1kErlRgXQR5rUhTxIm0IrS2RZ1wlQBhIEyE40SYQsTEwDEBRyIkAiJZdCI++BIB7u7uFCSJCtgNm1MNZgBHqkhMWIixZGATA9+qYNsE9/cFQsUirSK21TLVRVOVl3XFPMeWqk1msoYhy0NqhJSMWgu2VQs4HebJgDXl2Vw3i0wn5SkOxHYsBcyz4ObmhOOcEFNELQrk1qIc+8eLA1bj3M+Dk2tdN1QBogiSR9zFhCiMUhmn043xskOdLNRlbhVL+/bIKlJnhKZa92grjb5UuTOw4Q/zoLrVWPSTwVboWc+F8vJ93L/9FZy+/ltI9+9BuIAsHJrAYIFxUdu65YA5TbrOYsLxcERKASEyYgqI9rM+Q6w4JGnBsKZHizlshnPHaGMenJ3o4jwGkwn2iTqW0AAWL9xzHnDgZ7Vz57Y3ExpAdW5DaLHHilSnlrI8xwPefPo5vH7xJo7xAjMfMfOVho3bnCiYpxygDDYnULctBN3pCAdgmVUuGhhFCKBg9EOkhIya7l0NACp21lu74ZGXbUE1uV+rF/8qKHnBs3lBKQsk3+OLx9eBbJsKBdG4t133YXiRQgWXihUALrVonZs2j9DzJybklEBpBkICQlIeYQrqXK5e3LFiy8WCVyoyFxQLEtC53FBkRS4L1u0et3cvseUTtnXBti7I60ntVPLzVZClAKJgvVXsAKi2tgUOLXqRQEBVmjfnxuXAyCJ67kBpJdgcQRyc5z50u1PU5khxauNFIC2u3lRKL0Yq7eypRvfm2ZCA2T8G+G5FKSp8neqe4BbYo0CxgZtWqL0ahY/qMuw9tGwTA+Z9vkSLdOWcUe7v2/5RZ+eEFgjscpR7QTymoBkWU8Ll5WXPpoTa5ByUIkYLSiqlElnGxrpuuL29ayC5mL12nOdB3zYHNfQ9Hol6eck7Xc9pZkSkZYNs24ZcqIHDeVmMd7aaQ3Lu4xcCnlxdDfqdFoxfN6Ug8CCBdcvdmVN17RP3ugsuA8egh8vYqVFKVX3H+ZkBdZDlrRez67zyYReccH59PMBYAnYOv39+fXNXx2H+GV8f1UTX68Ob+EF3fLMd/BbBjVd8vUfo9BtapWjBg8Pe+cZ2oCn598Tc0QN4OY7lUJxDPT7S9sdWy2Chohua3qrRmPN2u6Rtoh/AubFMHumk1z5Y39v3cEydJdR/a8rOaDy3vtAOcBgVS2mdQWuHDIcrgF3Uqnd0zDTtH2I3tNJ6PtwgQP7UZ7B89/cY2aCOdeKAi8MRF/GA6OlK04wnl5caZVEKTqd7bKdNlV5ybp/SojEgQJyUKJ2CRR+FCYcLwrplbHnTgi3rBqEV0+GAy6dXuD+dkLdNHRqRgUnFs3z390CePAX98t+FFxDpl/MVdaBAbzCHARMQuR0kCKwRDZMa7blklJzxYr3BXT0hkFakTaTRHqUKpkq44hkX8xGH+YDr5RaHecZpucfdeo8Xyw1uqUCTpTSmrJhBDxFNEbTDSqpGoHCtQMlaeCtboQVT1IalAAyKoADKITWAZ+Plysjwl0FB7ovI0wMf7BWocsNOo0I07GE6G/eudLvS7EqLt3uE4HYA6Dnlgez3wpjqc+68eOxq73WFLjAoRqX1mRIoWoSsecxhiofv3sGEAOresTO85ME7x3/P2zzKAX02mROo9bJ3vo+Srh7btPXMQeLvwdnf2oLx9eNydgTEHUxtoPWYJTC0Rsa+oRtEDlidjc0DEHxoXAf43VkHWxeiUcuikHMZFGr4+1samK8Nc/SJRqxC+liQVBf2w7v7eI3zMQKuIlUjfUzhrYNDoqsUKl9G6Uk8rpye8ivQzAFqxnCPBBrHyKMeFITgneNCo1z624g6ULsf+4f70XnOFfBwhGx/BmlaLAHUjei2A4a0YcCLRvR5bo9qS7tCEAwIcfPf4Hejgiml7J4z9kBgkS2l9HnyM5IIZPzMBBhtVGi82cGcleIKgBnrEK1eXQfgmYmscAfb2ApSYMA5cBsYy1qcqyow5BF7XogL1ItcAGJAXDJjHgp4mdHZnAqcBv/H0PuBAmcs1ARYIa1qIyRqBDrHHgCL4NI9z8RIaWqypwqQ89aMU1ILExQYa1mtYEhW4xdOaaAFaTxV06PbIIIYJ/td07cVwA8t2k674oa0AVoxYooBU4ygEHTMhDDFCfN0AAe9j9npDizKGABqaVQRxBFzmsEcjO5CAeNWGyIoD2GtFcIW6YqKUgTzLIgMRBZMEUhHjYadEuGQgDkBMwMTAxPpvxFkhjo9WKvnF5Ea1Q0kbXNrZycIkUV5D0DIUN7QvFblkxRdx4djxJaBXDyqXbBmwrYBtYYGGsbEtj5J6eFrj3oG7Hm27EIIECPiFqnq+iBbc0LY8gaxaC5mxjQlVKtoHjaN/PNIrVJU387b1iLjgkeQejQpOcWL0YBQBEu24nSbFoJtjnrXb3QOnVeyFOVU1ErctTsgScFJXadQflNRbmYFE918kKb+EVRWRA5IRPj6134XL7/xVSwv30OUfRaGrmurFM8KTKUUkCbCnKL9x0gpYJonpCkhpaS1P9qeE4ts9jNcrzBkCrTo893CIqPdItP/HZzU9dNFgsoBYTG+6Q76+ilEpPs8cOgOQmAwZAZAk7rjTCAIkjGlCXM64nJ6ireefgcO8QIRChoxSNehAzKm93sblQ3CixKaJmX6H5l8llzh0csEjRZkYViUhJ0FHv2bzTFkVBnkUbuWwWoDWKqg5moFwwqybCh5RZVscjThMF+C5yOYtAaPO896XZIxvwWa9SDO66zPhhVG4hDA04SVEyonVApKFQICSB1+0tQs0ey1WlBRsCJjo4osRWvjlKyBGzVjLhsunn4KRTbkvCBvahtV4xKvVhOisNPjdPockdLWPofU9WSBFYZyealFmQRogHatxskb9CxT8RAtC0nnLdr54EW/iAh1o5b5ZUeGAepi2S1AyepwEXOSbmUxSpUMyhuK0Sx5xk8pBbX0tUzAI3QlXQ9RcFn51Imopdy7Q5OIcTTnR+MuhTs3dN5rrbsoTzG6oL5NyThgtZMeLerBGy735/nQnuft8z453ZGuV6X3y3b+Bu7283nEaAM/LdJ0pnkHOquTXR3NMeq7T6dT+76vvxi06KYAmFJy7Uw5rkMAzxPcHhBR559n9rgd4qCwFxxzoFbXTARRgWfbctBo+cSpBRW4njdmyD12fTzAWHzwwf/NXpIFN//gBiKC6dMTDl9Q6oCbL92gLnsQ6vhdR6RPpsce8y1fd79xh/x+BgXC1Q9ctQOprhU3v3LT7gvHgMvvu2y/55cZd//wrv2eXk84/oGjPvMf3iG/7Arp5b98iXBh0TAAbr/nT6Km47e1H7+frsP/8j+ClqUblexRrdgZtvW9sDPydtCOHQR66xnYqE9tRubo5WnKjx0aLgw/LBpuNOFc8UAzvmQQmniwgXZQkAz3tW8Pvw8G+tjzff/2hun5dR6dq3/bP4v5Yam2cQ4GlQBi46V9oweg66tHzpU/P1BVqJ5HxOa3Po3tM59Dee0NEJTbbwoTDmnGxaQRsQGMFAIu5gMO84y8bS3VQqD2ILe1Y/Nuh0iIE7xwHpkiwFadNcYJuR6whgWUTxp5xAHTdIfbcIdl27BJ6dViL68gn/4M+Iv/Auh3v/JIf/fzp8CYGaEAQKbQGW8TLE1FsdkIYaBQRa0aoVWlYJHOa3kqhBoq1lwx0QaqgngKKFKw1YxT3aC1eNVpYIGQbZ3voiWN7xW1AltxK6w7IORsHZIrX9I3QNsI1Bbzw5iRcXwe+2TcAf1ntxn8da4AueLd1/j43fOfXv2mV13noObwwf5nol2XOhCr863hUMoTCwMDwGxzPrzLxnC37XwUH+nIDmg+a3P7/FXtfrzHj/zF96p9bhPQ93KXMw9l0NBu69suGnTXXgNpXiHfdiumC90P6Qv1H3fv3L9C0LoFAin/lxujvp79dp/v3YPNCD5rdUv/2g3Cw5XnkaIqNczZUAWVeooa+fjAzhFvsD+3bwycR+brW0eg+8PPOact6Ia7vUn2n+/Q0GFwH+LzXbn2PuuH1I9Dt4p359p+vtxQ0GkYx/PhWegGmQpAQ4WseGkdiid5C70Ne77HDkQoBcHgQnRwfnDO7PecnUE2Ni1CxKKCPDpUv1v7GA8GH3Le0w1IN0AdOFSHihljBqhp5XCrZ9B0JD8TOz9t27eWxqvRgty+4/3wCKfx/G6gZQOPtBp9M4zI0509StjmpdEI1JbmW2tFmrTYF4gUdGgRK4QWeeSFc0x/Iw5wMNaLrnVnR7D5C40uAdBU9W3VaJzWVpAV0NoAMZCDGE4n2gvLMILRS8D7R0CaU0uN7nyHOqchKAdwYCAFwRQJlxfAHH3c9O+BgMSEiQmJBJ75vdMkXrFvfetrSup4Jvo61P1CII1ABRAhmBjYoh77iqF4IRTNlGN4lKXYWvYzwUCTqM4GQIGTUg2EtertLos8ykxEIEUdRA2QJQPiCC2CCrAMnqqp+1xlKISpzigOnbhJj9q+Ngho+yOYriUScZyPWFZCNolaa2lAi+/lStn4+Q0MjaFFpAMaKarV1xkg5cevojUJUDNge9tlTpWKGowrkQg4nXD33tex3b6A5BOINX1aZ8r6yEBkddKnGBFSxDxPOKSEKSakFDDPE6YpIaWIGAOYocXvXHadaee6Jvr4uEPDgUXVsagBFk1e+17biXhpvwSQrn0OzclF1GVeb4ufU7Bn988BKHelcyMLY05HHKdLXM1PcUwXCJjMUQkUqzPjNBRCAnUaa1u13oqDUK6JmoPUQNuW5mxdCVwRRPUybWFBrZoBU6tSzKjcVodH66MPsYhyLxvfqhb12rT4l2SIFHDNCFULJhIp5zZDg4jEU/ylc4z61ieT50qj5IXeGIEJEeYUhHLlCptjipJmXxkgCxJIUadBQUWQjAi1FzhEcMkgKRb5HxFJKWJEsnKBGq1P2VbUbUPNGzKyFr604BOlv+mcyW7nuIAqpVhtD8ALLvXzwHUT6L6yiREK4AGM1XWje8+d0gWx6c002LY6LbroalRw0/cqZUG2VxdbB9KoCLkXrbK1DwGYRwogakCkAoO1cf4CQGECZTJqkdAceEDncPfzx3nRzwFQkQCi3M5IjxZtfLJnOofbRn0Pa7sdzuVgTkpXbav2s5qDd6S06lG9qpM42KkF0rQIZHt305f2gQa9H/a80UkoTpk1tL9UoxrsAQXkssfkCFtku5hsJaehcLyoaqFPz6hznUDsO6XW3Ts/6PpYgLEuPutWIafHG82X3DfSh1x1rXjv596DiODpDz5tYOyLv/0C2/sbUIB6r8bHJ/+jT35bwFjJ0p754m+/wP0/ugfNhKt/5QoI2qbtnQ3v/PQ74AuGZEF8GnH44gF8yZBVsHxl0c8vGfVUcfzuI6bPTOBLxvNfeI7ldxbQTKi3FYcvHECRIJuALwPe/WN/CeXJZ/5/9+P35SWCN37ylxCfv9uUqRB86TsAsDvp7N/9IaVeKH/keNj777UrzfYlv7/ZYaNAcQ6dVy1rOzAcVBsFT/d0oSk80l7SH9uUmeFv/XvWgZ3uTe2AGa/z6KZXNvjBPWZ8inqYxgOA4NHFXaF3RV/MkHWB/aAaGLohvPu7POz/rkVEqGnC8gf/RZRnrwNQQPIwX+DJfImL6YgIRt42PcRJgdRaKpZl0WqL5rV2tw6T8YLFSZvCAfPFU2x5Q63mebQUVSZN9U/hiDQdEZY7pHTAxeEKgoIXL1/i+vYlXt7fYK0bPPaBLi8hf/iHQO+/pwAbHG7xA9nWsQ2gG4gWJgUHY7vFpd8JgdWjPDwrwnj8YPxLibAByFiA9aSfrRrdR8xAJEhWRTp4igexVSceDj9pr1Waglxg5HG7dBjfQ76cG0hnf/NjU3y6TTPy9Xu+piDDvniw18el4ZtV2jpyL+l5xOcO6BsO/L71vQP97w+UhodNMDBs//tjbdxBo7Y11TDXCt1qdUcFYUdeKtEoSN8cPt5j287fKcPf9hLmFdfQdzew6OzjR74EtzY8skr3n+7BSmjGTI84BXA2DjQOiI3XA1Du7PIR9Z8tbloNivO7Hjzr/Jk+QtR+dRktptzL+E035t2IACxqud+zb3d/tsN1HoHebxlcE+19TqvTW+i8YsKdakPauKGdV+fzNxq3exD14XkJk+VEo7HSn+EG9d6Y2V+ailxMLjTYWs+74f4q1Thc+1zt9yu1sWiy8pGrP9I/dyNpnHMdoGqGg0+0i1aPiHp4agq8OMnemaGf0dAnB0RdnjpAJKJ8ch4x01tr+8e+44ZZjKF9bwRbOXBLKyWg/euAvY99jBEpJaP31vNI50TsjKvIZjS2tF2njKMAhbqc19giGS3F1mkXHLxx3rk8AsOoIAqNw1K5NXu2hw+jz3EegE8/mz1SWddcRIozQkwQkBV7qtbmPZAk8KhETW3tKgd10NUKt+zWmWjF7HV1aqLa5kCNwgqIGnCH+QBKEzx9WIHzCAd9/QytEMQYcHF52amuDM8JJAaoMQILUhDMCTjOwGtPCYmBnHUvBtZORAqYSGtddBn40WwsIk37fPQzHx8fD9LorIvECAG4z4L7FVg25R8ORAgRlp0uSFF9tKUIcF+AGhuvMceCKgEihCIE2oClGMUGoAlf3Au9VBDqtjVnpPeOmRGTUU2Qr83c9PI0TSh1A0vTLVYAACAASURBVGf9HluENBMZpYaDaC5g9V9fy4KKJ1IQTgnrtijFQd4asObFET2KnAgI0XgP27rXv3sBsNB0JI1YzHkDQIjs53q1CNys4HDOuL1+gbv334Zstwgodl5YJhixOjRIkJitSNcMCoyr4xFzShpZlgIuLpSvMTIb3UdR1Q1oTn6VHWj7UteCU7m4I8WBRWoyuDm6HwMt7KEeEclBi+A63QrvaJdkJzs9EvX8mdUdSnaFkBCDUpFNYVIAXx+iJl3NYHH+7qA8k+RZFO3Nrd6Fyu0Ct6/UIVWVw9tULy24R16WECJFI11rbtGVgRNiDAOvKFrfYDzMvY8VFVq8S0SjsWteUfMdVP4qEKVUDx1wC03e9SAjT5rUCF9zRHBQvuZ1xnF6BubZKAoieJrB0wRpYKy0uYYouIkaQFLBXMCUEFMB5QUbrdoyOzNAc1tDmkmXIWVDXk9YtxNQDTj1Wh3e92oUH82+NAfiSBNIUDntmTZGm1Vla4aEtDhOndNaSqvtUr24XnDgUACnHBn0F5+nWgNq2VCYIaTroUJAeTObTPdg4x4344Z2+0LXcS0V27ZqFpVH35bcqCG0wGFuZ6Ry1a8D9Y5mAExpaoMRY4+i9fnaNpVTXoyzBdW4TkDAuq5tf22bZqFopkgHIIPpHxpZ69QBCjgS1OHqVykFxYDmWqsWFJRqS1YDEHPObc+6jqIBTtz+m6Zp2PsyBCigP3twyI5Rrl6ssQHJ5hhrTmwRUGDE1KllRCryVtveryIoWR2ifmav6wZAzKnyMN94vD4WYCygh/ftr97iGz/1OPfp5//S55He+GigKR8ZX/gvv/Dg75/9Tz8LAFj/6Yqv/tdf/dYb+8h1+u0TvvbffO2Vn7/8P1/i3Z95V9vxY5/Fza/c4PnPP8dv/+Xfxhf+iy/g/b/xPl7+Hy8BBr7wn38Bb//3b+Pu/77DV37iK/jif/VFAMDVH7rC6//u6/jKX9bouBf/6wvc/IMbfMd/9vlva19+P16eHu3AhFfl7LajDFsdJgjVe+o4JJtw3IWb78552mcgk6UtQXkz25+JXPNEN40/4Kr98Nk94yNcDlBpWx+Ff4Bdzx97xge9awQn9vf1aBq9j5kfSTnV/u+jY3T8effebmg+3oKPcIlAQsDdv/0ntcARGCkkvP7sDVxMR7AQKGsqhXKHZax5w/39PU7eKo5Is3KkZYumCUF5yY7HI5TbbcLTp2/g5uYFXjx/B3d3tyjrpgdorSBOSIcrhDThMF+gphm1FJSaEeIRV09ew/16j+u7l3jn+j1N/YSm0mw/8u+jfscX2sh5ZEwnsxc7191D5zcOo+VGvBke51GCpvZiXDr+91aYiTSiSNOv+hRN0wGvPX0GIsLz62ssy6l5B8EEsRRDLlYww5TTpnTrNDXFVl/VTcUOVLkhvgdJ3bt6fvk94z7c34BuVJ3tyXMAtnuHH75otwPOQc0zcKj1xefqHHh97A0j4Nvu8wgeAmIET1rJRQyMdRCn9Y7OHym7tj16dcRjp6x6m89BSjnr/+OR82fAZl8I1ivgMM04HmasueDly5uHz9kP+Pkf2vMf90yPczjKVrhtPczBRwEqRpm2l10NBAA6Y2gXjhax8sEe9L3EHJ8qw+fUl3Hrpv+iETGjlG3twHhWyP57Lpvb3O/PiwdzImRBqB8M8o/fPd/H3j4FQACEiH5OdENp90QBHu4OvZpSbZF6cH7DZigEZKNAacUZHm1zL1Lm0Wu9GI8aWNXSX3dNq8UAbI96tKjA1i+/r69HopHv0IGfcVWevcN0GCJqTk/vD0Gdid4fZsZWatNlHFw61zEcPBRZrdgVOsAhWhUc0HV9MR8MguvOAI3ASS0ySSQbILAaOBVwOFxi3C9jYRFfy/N8REoHhBhxd3cN58gUAbZthRjXJkSNuxjNILVoVoCQpgTiAOYJAkI1io5aq1bQ9hRMA1l8KlgIHIM9u7bU/OlwhK/JtmY4aAQtwcC92taY9y1njZX04m4hRNMTtSgmh6TtJkb2M5K1Grim1FfMKWBKhCko5+PVMSBFQmRgPqjDd4qEeQISq1EdSQv8Bi5g0f2Ta+do7jrpR9cvP+wimAFODMSCKEAMjBSAUoC1ALmigQohAE8uCVcXjJIDjhMjZzXkU6o4XjJevjS9B4wX1wF3MSmlQM7IeW06ShUF4DlE1XUgTacU6DOqIoJKJ0Vaad4/e/r0WQNCi4PoJqdKo/nphj8N25JqxfH4FNN0gVyzOReUskSg+tq6bS0qsZ+BfLamigJ0tu+7OLKoQ9FVQztZIAAq1vtrPF9+C9t6h1CLgt4hqJ5rfKeRGfOk1AQXx4SLyxlpusDxcInj4QLzNMMopxsg6O/ioNy+DmOpX8K5fdkcBt0R/GBNmc63/4P9ZH+PweAb8kg14/+0iOCU0u47za1gFFzLclJ5PBQslmqRfyZ3NXJVC2bdb7eQTEh0AFMEjKYAAoRCVqCNG2+tg+allgaiO7jqyq2QcrHWrfOZBg4AaYFMbVkZKGPgd8F52TUK2xZX43TU9lej+CgQ3NUTSl5R8oatLKiyQUQ5YcG6hnJRPtgqAqYAW8ou+ZT/mNmmo4KKZu7FGpDqgqutgMmKH4aENM8I09EystQ7FOOEyMHA64hgBeAcrC1UsZaMUldIWbFsamvlolzNUrP6LEMAmBCJEaYZjYvEdJVmT7rFPmZFwKIYBf07tkY8ylkjR4vdz6gIYHLyD13bgTXCFO3MqVitgKSUDaXmVgyvlVAWi+yF60ap7estrFjXzuVazYnSLBsipBCtYJpR0sSIq8tjA2M5RD1jSbMJilGqOOUTGe7QnZoV65qxrlmHzg7WbRsyNmzPMXs9AN2eU0xtPRQRzIfJaHbYQNKu1yjtivK7blvG5u+Dnsu5Ko1SssKHLVrXaF/SNOFwdOex6Ra2/td11ajpKshbboCqUg9tO2DW9b1gYHeMEYfDofXRz+uxrkIVwbqtKCVjXTcsy6kVaNR5N9nv8ohhaz2CKer5YVe1TBymaGvS9IMPACs+JmCsxzn1663/+C2kt7qgjU+1qevXV7z9373d/j5/54xP/oefBAC88z+8g9NvnXbPufqBK7z2x14D8O1TMB675u+Y8bkf/xwA4N2ffRen//f0Id+wS87+BV5p893+2i1O/0Sf+/X/9uu4/P5LfOo/+dT+pi99CfjTf1p//qt/Ffjjf7x/9mf+DPD3//7+/h/9UeDP//mP1tZv1/VjPwb80i8Bz54Bf+tvNa8SvvpV4Ed+pN/3vd8L/PW/3n//O38H+LN/tv/+J/4E8BM/oT//qT8F/Nqv9c9+9meB7/zO9qsS4dtRPaJHEDOQudVy5zOjrqWzDIevYM+JNOI44zJTjid/m0UnDoAGXHgPBpnrKK78tOaah6rfhEGwAo27Tnrfuumqf9ob6q682L2WAvIY6KvRNh1k6AeeK/DS/yEFHEZd67GIwn7tn3l+X6uUiOpBRc0oPZcbvRE+ntT+VD7xKZz+pe9HATBxwsXhiKvjJSIllDVDiBAp4HicMU8RaVKKkdv7BcuyaVEIAMuyIKWA29sbEAHH4wHbsli7GcAJ22nB7f1LkFQc5hkhqFIQRJOFsh0oMST1zCeG1Aw+3SFywBwTpjghxgl3pzvcL/dYy0OZEuOMmj26QueREPYiZBjLUpxGw5ToMvA1NnXMFQ8dbDXmPUnPn9eVwkCsXLG14vbuhLu7kx6OQ/qKmPGHlvLlYKrxo5GCv35gDRCOrakORXXF3udZGkYxriGNWqMHe/Jx+doBhMfi2R7cPSiE7Z0PUc7dZx1EOwN5BjDrIcSyf66c/aRKAYNCBKcEpKRcw5GBZJEjZ99sjdi9YgC068i16/uMzr7j/entGB/vxul5TOXYnTFacgd0o0dxLssJ67ogtygcX37+3HPw58GQPQCbuynT+3Ler52MJmpvUBE8ysf+vT1u52vJ2zA4EcSNQF/aZ2voDLTvLelRLP6ABqAOgOt+FXkEuSBQtPTdvv7GCsEC2u37thvO9w7t6WZ8n/l89/+N6/xV/2rfR8ebS3UeDzf/zMdqPAvPAVPyvzV4UiM4/cwgM+hNBlUJzZhqc+CjKPtxZHK+OBv8xu1IaLIJYjLU10rV7Op2hvp+U4OwWn+8fV7tuc+LAFJUzpPzDBIeRlpQ4/0Vi+ivXuAiab+aMy0EBLFCXYOcqm1RDee7GfyAWAHAPoN1MACTcbI1YBlqBJLtjVJya5sDElqoszRnc60ZEO+b8iqm4yXm+UINUAGm+Yialau21oIYDOi1tXp5+QTskXOWJlzsjAEFUNDiO8WB6MA2dg5+M6hqJCYREDlgSvq8Wqvx1CYcDppx54Wd5sOMFFKPZOaAwBXRDTFQA+MIjlsEA5lND4jBCoM6GEKA9SMw4XgR8Ik3ogLEUDEvNeAwE+ak/4VYG5Sg6y5YVoHSE0xMSMyYgn6fYLHLogVi907wb+3qcs+oOHT1IGdBLoJStFBYMGYPjwarVSBrAQfG5VM1qO/ui0b1FsLNNaEUdSTkXJC3CILyvNdAylErsMhJXavriXeyXtOXs+07QN3yUJ5PrsaxiLbHtJhip3FxLnKXnUSEmCYAVnjG1iWDQDEhSgCHqJXIvRVUMVPXnbvTBPCMpsCCXBgi5sKjToMGEYATuNnOshtzkoI0HfHam5/Dm5//g1je+S2Uu/dA62KRwwEpTDgcZ7z5iddxOB5xOEyYDxNSSkgxKWUB96rmwwtAgcG1Kr9mk6keqabgxauA2AdOWbjMN4DDXqT897HtJwEMxLRnhoCu4vezvVStmq4AVWPV3eljAgWWahWQZKxWRFGji1ckWGQ6EQJC00kJ6pxRig19o6/xWnMDflskJSydvArqpjyhJGTZPrXJ2n0QgZ8jYdiLAg42jnbkePGmaglmVQR3smGpK7JTFZAHXRKcQNePT5MQKmJs33uGjmdZ1jZaFaUCa16xCkAhatp5JvBKKKQF8SoUoFfZ51kSJlOtOBux8jJziE3ehBjABCRmCEVArMipOUhDjMax6/p+7YEkNr+VBJM1V8wRA/KoauNZdXAW+l6lgrN5aGe4r5U+bmL7zNdy8gCaUpDrZvzqSotQ6wbm2p6HnJESWwT2hGA232m5Ry4bAglm1iJXYmtSaW27jna6vcF1Kc3Z4ZGWni1ezcnuZ4faVwHT5BiaO3e6jsZMlmHTddNiYLiCqRukZuUrd7BW0Li29YxmK6ZokeMhInFETLPJMt831KiMNJpW5ehWMiQb/UNWaj49E7VYqEbduwxGA6a9qJZfPhdNplTBsi7INfuCaDZn2wMQi7K3sYRgniYAE9zx44XEG+4jaNlAknVf1AqUsqJkxXrcScQhQEiQktV+aTbj49fHAox9zPQ9/ZMTtnc38JHx7F9/BgC4//I9bn/tFuvXVjz94ae4//I97r98j+e/8BzP/ugzzJ+fwUeGbIIXv/gCAFCuX1297LHr5ks32N7ZQInw7N949pEBXJ4Z82fn9vO3+7r6gSvk9zPqUrG9veHwXQccvuuA6a1pb67c3QG/+qv68/Pn+4f84A8Cb70F3N4CP/mT+rff+71ve1sfvX7zN4Gf+in9+ed/HviN3wDeeKMbUn/v7wE//dPa9j/354Bf+RXgF38R+Ct/BfgLfwH4m38T+JmfAX7914Ef/3H9+ed+TvvzF/8i8OUvA9ME/JE/Avy1vwYsiwK9X/4y8KM/quk1Q2pRO5JFGul4P/ZGw2xcm/7LGCFEg1U9Khp7gxhAq5Y4XjI+p7XKlUQX/n6zv6R/c/ckQb9fzu/oz/G0A3+K3k7NdAX2CtO5rds+d7sd0sCRFo059P0cGDl70vDMvfHewdSzJ+7GYRzPRxpqjcyf/hzypz8HefIMkRmXx0scpwMiJ+QtA1UVPQ6s1TBLgWw6TrkUrHlrdBHrtiGGRcnYibBtW4s68kiKhU9a+TioEqIKBAEUwWFCSBcQ986Spkdoca/ciitN6YAnRyDFCfM04/qkkabjNc9HnE4LxFLQ9vM1jEdT5GkAs23+pNNd+Ig2AKgpJI9I6TYFDryzKbN26HuRAzMgHGRpEV6Dt1CGYhy9H57K4+3sTfDI1Coe4b5fR+NufnUk5dky8R9l6P/wwYO1OwoN+6LYv4+dG/7ZuPf2LcUjb+37jKwNgqG/xCCOmkYZtbKtBKcnGPb4A3mw//2VEZlD4SmVErRr+AiiPiYzzofosat9ry3JQckyQ8bh4bY6CMM6f2y2PqBP+7fv2tsksst52vf//Hv7qytbDkA9wAnHLQn0fXE2fvrZ0CuddHtenwBdq4N8dGOlVq2ds3u/V6H2c+vxRdGkQDNO9nJkv7/6z9SMyLNPLdoL1qcxC6IP7348aVg4bS31HzoQMo5GG/v+yyAFGkigUf/U/k7wbBdqcmUEYR9s0AYukN3bi1o1fMfOPT3TqKexe1q9RZLonDlAp19QTjIe2kEmBny++7hTMyjRz3yL+nWqHxe3fj95Wn0Vq1NlxoqDJ8O86e/a1mD80y0FuN1nxh11MNjpXZT3NLZ5V9oFgCW2NR9CgnOuejK5g7EUGMfjE8Q4G1hn4C6r4ebAmILqOoZTUlkYYlIOT+gZDgdILRI1W7FNn/cQY+OjRA0QFKPg1kglavuBEENAMpqDGBOqCKZpMh1TxzjGiLxVFItsHFMiPeItGI88BwXskkX0ukwAALKIXdctaoEV59L/QBoRG4KNLRO2XOCZniRmxJK0gkYiCry7iuWAxUeRmN/0ZZtU+wA4/7LLPiWD0BtTFJRsenqtSAmYMyEQIRfgtOoiD0SQAKSYUSpBAiGAUUqw9O2ufzN3Sindi4KA0ICPWovJLm0DmRDUbSE7OhRVnXzdcjPqm9ZEmsLfHT+6jzgAlHtUGpPSJGiRH0s9dpDReQqh8+nFH7WqukfxWd+gjh9/rur2NkZxwvHp6/j0F78Xt8eI5fnvYbt5D4kTpsOMw+GIi4srvPnmm0gpICZCjNrmaLLAQbmdrjLogx4AEkIw50rnS/7m1oifSd2O8OAPEVLqIOqOjCoCyRmVh+9AYfWWtt6KlTHIAjlQpQOmJj+AipIZG/TclLphM7lBQOdzrq63kjPS2ZqSvlbsudW4UotH5QopGFtJwVgwpA2TtYn6uaOyNyL42SkAB1cCdT1qRKUYvYFGmN/WFatkZFG+UrII3ZYVIkZPtDsLnDd2OMMbJaTZoEP9AQ6bFu/yMWcFYKudV9XWNw/nCcPlnsq5Kc0adchs0YsB4D1FF9o5I4NdOey3CuVdbZcBhkYzxkY7AzE6J+MZHuU4i7auaxNwRbvbG+K8yL3gZ2BqDjcqhICKrDw+KJuAWRSstrOxVn12jCpD+HQyR4dFLaPvLeUpHSgIbaEp2EhwceRzqYNi/PSlg8u1rg0AdFCfg2WLNHuwg84hJSSJqFVp+cqcUUoe9nNfEyJKlQQoAN05ttF0VSIbJ3N2+gQ2qsLBXoIAJZZ2voO66SFGg+S4BfuaOdPxIAYIMwHB9KKmj7mOY1kvRTnbleqhmrNH2lzzYJu7fQug1X8ZHdjMhMAVmRi5ZICcp1xxhMo+Sx9sCX0swNhRCPt1++u3oEiIr0U8/aGnICLc/T93uP7frwECXv93Xke9q7j55Ru8/z+/j6c//BRP/vATAEC5K3jxv734ljSL+99QgJcPjGc//OzDxu+f2fX0B5/+f+y9edSuWVUf+NvnnOd5v+HeW7fqVmExQwkyKIgGRGlx4YAxa2mUIHYTujuJUcMyxqFdSoxpoyK24kjQ1SIqatQVXdoatBm0EwaNMwJGBoViKCgoarq37vS97/Occ3b/sYdznvd7b1UJCNVpzlrfvd/3vs9wxn32/p29fxt1XTHdMuH8fz2Pw8cdYrhmwHx2RrpaTz9uuw14//vbTbfcIqBnCMANN4hnLAB86EPAi1983FK0Z/Qg7vXXAydPfuQNuPlm4GUvk98/8IHj3//BHwA//MPy+7d+K/DSl4pn73d+p9T7N34D+PmfB1Yr4Lu/G3jrW4FXvAJ4/vObZ+9jHwt81VcJGPve9wKve52Auv/8n0uIjhlPREoIrRsgAED55ghqxLpJBQcidGP0hdn9e3dQhwnwnhfPgbHavm8glHgmGm5jAFozxHlRj2Pv5StN2oW16tf3RlW7gL2u9pm9v3nxtXstLJWv1B362cILrK/Zjiq3U+y2DW+1pPvO7unD0Ftf5Ac+BPn6ByCAsBpWONw/xBBk05mmCZZZu3LAlLNkwd2owKWISblxAKDMGWtSwxICzsopooWIaD8wA2xKv4QhxjEhDvsY9k/BwiRqlWy6R5s18maCcPAEDOOAvWEPwzBib1wBAbhzLovN8WDvBKYLF1FyhR6nujJulnvbeMnBvNaPvZptkEBn7lM3L5cjpv9SuyZ0J8cpOSm9nVgGXXdGIC9Zsds416Lckjo/W+hyN0m4n5N6Qr4Ir9Ra0fZca+3zeaMG4naLrlSaorxUSnos0dplGeP76+ux+9t9bYGT6y3UXWEKU18sYQzFASGN4JhUaQ5+cNB7gizfd7xNzdu9v6brFW/o8T7yeb+zjXRsfffXLQBdl7edLKKuL3rNy/9v1/cGUv//sdsXdVleZ/LWQUdqnx8vuwUe919rP1ofNuCV1VAxudn6mrq/fcVy+6sB2L2hrIqm8mNWB1ttDVsmWlU0+8fqs/qlZoCY+bXJe81D3vrb6hy696Dbu4LTiaB79nGP2W4R+TP6lrV902SAUXP0XIOkwyUeMG4ugikiJlV3Dfwkq397n4Op+mpXyME+Js2rlQRMQWj18jbqvCZ0kSq6ZmGHUoBFKACkXi/RAVsDlMRDTIVCbToJGfVC6WaJNizGCKrNoCTNCB01C7NwSy851WKKyvOpIxla2D5YvJdkfilPns85VmAxAVw0YZfwocY4YBhXEINUeeBtn9L5QsaRirjYT8yDeW/vhIw1i/cTh+TyG9DQ60BKBShgLNKgoZAJAcF53kMInmE5dyGKpVSs9vaci5JqFM5QgoAVMQKVHWAINu+0nlbX2MmKlAaAM6jI6FhilTgIDYF5jrGOcYyNnxds9BdtToMk4/r6KCLtwfB8HTMZ66JgUS6MWmw/ZwyDgjkQHUl4+cQbmAlIDsZ8lAsBpFRfEUCKjMiEEASwQIHyPEtJkZCievpl8dQdBzGwQwHmLDpDSgErAqa4ASMhV0ImAnN0yibh6YXr8tzpFDG265gz2ilZ3w+8WIcmf0yqmFEufJXcyZLQRA9DeH1tzbpOFjAkqXelAiaNMfP9sK2DqDJD5njA4vAHesiv68EO8gEGxQHj/knc72GPxKX9hKM7T2F97gMYIrC/L1QEB3sncOrUVWDOkFRj2QHfKg9caki2PZsuD/k/xNTokLokScBxvUm8Mdv+bjuhyMu2r5hnqvV7v49Yv/fRAX4oZN93+iMbTzc0RLkWAcJqBTig0ozMFYUKKiKS748MQkWkqECt2InLTPe6/1R9BzNmzihooC9xQJ1ZXUfF25aCxlCwcMxW0nBmGAAsh0nevtC0VWYJhc7KlVoqY67AUZkwc0HW5FjMG+HKhsy5WhmRBMyiYOCoqVwily23RFAQikJAGAZQksSwFCOy73kVMepxitocFdzyaNi6ZuMwT0hxQBn3kZS+hkzhDe3IPVDUAypzKuCtubHUKUQQRrXnRZcOYanvs6Tt8LW12NNh2lg/dZveE1wukMtrskNPVAEHI0ClIisTsHniBhDmmbv3ib4UNQFaKUXsS9MrgiQnk6UkuMFqtXITwcLzAfgBc62yB7R5KfQ9uWS9TvaacQXRJQKQ8wwLnw8xItGAlBLALdlnrdkPt8wGMd5hoDhNAHFRPQxuk4lcIKQhWce3uvihZKONdB/eWjHn3OlecM9jA2QjkcsXHX0kpRoCou6lQ9NlbLzV07UUi7LV6CFIcsWSs+tuAeLtHWPnmZ9anW0uhhCABKRBsAQbD0++pty1Te/ZXe4TYGxv8Fu5/p9ej9WDVh/zulz3ldd9zN95bwoz4+KbLuL237gdAHDLz4pH63DdgAd9u3LGfs/3CBBp5Zu/WX4OD4E77hAg8+5fArzgBcCLXtQ+++VfBp797N7Kbd/tNE6vUJ76VAGGAeBLvgR49avv/b33tvziL8oPAHzxF0tbfud3GtChbN4EUQyFo4ccXBD+KKBpUU157YEGUyZ8znZd4l6G8NthoJgp13adKD3Ns6bP3myCrxR2FgdmLJ5tQ0HUKmHGZPMskl8WHLkMOAF933+Ebh1uZXfcus4MPyfWX4AD2xBp6yPZ80k9keTK416NvTFvRlz3VAcAGNvSza7pukQrKgrOGAZcc+JqDHFAyQWbaUKuBUOScNHMVYBNy4gNgIJsNJ58AVFCHFmy+YoCGlDYToZNcSCEWkBzRSThoT08GBHHfVQQ5mmDPK9RyoRaNijTGrnMwjEDiLGsZQgJZ06dQQojPjTuSVghAYcHp3ApnkNGATtZO/Ud4n3soKcqtq7kALBEANDxsaWwxLKWSnVTdLD4PNnJZ7dh1VI9vJfNCA9Jw1IFCE+pn/+mfKuh4x5HXdsIiKwUFtuKGTdwpdPx0SZv9/cVyq5Dg94YkOY0OWFtNRB6G+ALy4rsfmeP6Ox4d++5Bq4IcQAlQh0ItIoogrP4PBDDBDv6qI3l9gGJtEgUlzYpbHxlzvAVqtkMSfh9vbDqDwb0g1Ybf/5WH7lQ8MptbUPHD3h2AadNEW4NZVhfha1rqcnjrfHtKuwPMyN4Ifn6F9Z2vxlFvfRtJ/PtvsW7ernI7dXucamPEhBGvTS8iuqhaOHvC0WWlae0yVbyny2+0t6A9lB6csPcjOk2vsu5tZhjW+NlXo1u7ENEsHWjK8e+R7dkVrU7gDPl2JJzBBIOT1io5LE51hv37G3oZw8R+5yTa8STEawg3WKtbd2tRwAAIABJREFUW9/ZOjSjBotrWvPtXaQcixFpGJ3/rdaKlAakIblcNiDCPNEAlsND429V70/3Ng1tHsfQwHHzYgIJEBxDdM9UO+gBlILGZU93NGfPKMXpGgZJzw1WwGIYRozjHgy0NUCcFSgW2gPxDiVKSzllY2n7EYUW8gcDkiXZkoHc0v6g4bIA54ohRKS450YgEakxKYB6jBGrUTNtM4Q2QUPfrcVUtF9Y5xYIc51AiAjREpIE32vEGJ7FOy80zyR5p8xJBqnOUIV2gAjjMMDkSG+oUhCvqmEVsRoJMRICMWKAeNupwpNLhSaNRkoBwxCwNxLA1UOCScOuwSxJmEpFSpbsDB/VYmIyABgYWFehShgSsAJhytAkpUI5CQ4YBwDEoMjYbEjbUoUfNSas1wWrERgHQqkD1oVw/iJjvQH29gZcDoT1esY8FT0ogMxJabIa9aWTr5IwZkm+wq7LG7c7u8wn10/MyytnASiizmfm6JF4qihjHAaXte4QAgJIwIM+hLbPSxGUgxhoc6sJcLUjVA+XfZkACMLGxEgnrsWpEHDq6jMImwdhoBmBIWASE2ZkEBWAi1APQOqmGmyPowgg0QOgkPXGECySCD2uLX3Yb4n6bxN/bZ+Ae9ctKVj6340SRW7dMVkJTvvCbFyuMwxQz7mglBl2MClbbhEv8SCHSJUyNmbbMCOXLAemSvVh/O4GfNVacXS0Fm84TejEBNQocqoqMWydGZwZXMR26OlAGIwpN4ePECIIymNNjRrG7Cci8mRDVe2QwmLDZi7ItaDUAkC8G2Xe2UGqejJa0iVUIEDtAY1uMH1PfyoBHMTOaVznZtNWoVvTejKpJ6qO45gSRkqIpIdRIeFoGpFCalOLJQIBKm9jGDCkUfaHENy7koKBeVFNejmM6HVTn3Cqe9o3AvAGTx5lTi+ms1MILbmt3am/Fy4611uSxaYnyNwKJEmxIkbUogc8NGCOQjdRalZqnYzTp0/j8tFFXD66iM20xl3nL2BWIDClAfv7qx3zm3wPS0n0AeNdHcex8eKjYQ2iIwmQOU3Gqyoe9tO0UVkott/Fi5cwjkPj1RaOG1TlYxeOc5FVq9W40GXNICilo3Nxm72qziF7mSXCtnWeUlrUNxj9RATSkLBarXDixIn23C4xV1WO2s167dyx7d2QRGA6bquVgM0pJgyrEVF1iV7eWN4Ae4850JRSpN4XJn1ecF56r6/22Wq1p0BwQIHkRjE+6bsxN+8jYCywEEyfKMfLrb90K+LJiAd+0wNx84tuxvVfez2O/voIl992uV30vd8LfNEXAc94hvz9kz8JfOmXikAdx90PtsIMPOUpQgPw6Z8uNACf8Rnidfq7vyteqQDwnOeIF+uZM8Ab3tD4Xj/e5bd+C5gm8cB9ylOEouAJT/CvGYBRv9ZakRCwQsBIhMNAuBoJZ8uES7XiMjE2avQ5WMgiVLrgPCiLjP5Fxxdaj9MwsPTa7L/ywBF9n37ugqB5HO4qBtz2rzRFw3a7JYggnaFqIbYBJX/o1vNNF4Xe18DRZWKEK4FJrR94cdEVQV805Yv8nfIQ6/V7KhwIR5/7RagHJzCmAScOTiKFhDxn5JJVYWHhrmE9BY3J9/NIhHEccXT5Mphj81wqwOlrrkWICVOecf6OW0EwDyHxOJENUlT8mjPSuJJwomlGGALmzWXkvEHOM3KexJuNqzseTlm5x1TpDwi4+sRVODeMuKTjcunSZefikx6qYO4yzNIS+GgckTbm2rMdoGAZSWUTEc9WMRL1um7zYlVYfX70I8vL56KynPjHBNhp62K0jgMk9hd3Srh9Rzg+1QwkNQW2V94bFtIgBVNut8HTXUDssfXna3L7Wvls6QG3BaTuaLX3Ydcvqk8aRLJ4r4R2JXBIQEigNCjpdUO0jILFADPzvmJmzHqK2ysjkiW9V6jsXu8Z7OiaThneUY7doH3f7x28aPGiBCIM4ygebhpa1GTyrnrYI3WOE3s/yn8mq1gjExrwautid3uOe1D4WCuPapNsNocXl7W2K7ho+4nvIj5XeWGEcncvGM49bvLUAMs0SMKBgbl5yqN5WLTKtJZwMA8rRm9eWD26ZaP/KxecAaJoBmLzmm6ArQEL7X5bf3JvVGDT32rXKRhZS0VMBqbK+ytbOFv/Xu4MeuEzk2uC85yx2Q02MEaVQozkmbnbnm7GjACXhCGJh21o7kTdXNA9twVFCzhQGaGfqtzqTeZ6qetTkj9FxNTPpI7aIRBg0QAKYATdb+J2yGZIyudmodsaCh0CSEEEcs7uKEYb+tBSXSOdYG8Jh8RLNc+TeOFbeKAtS7a9c18OjCBAUYxJwHNSGIDZgVhS7zOYQcwsSYoIAix3hp0dXjAzps0GaViJx6v3pc17uXYYhQMT0CzUujRa2Cp8SxR9p1+4YhiGkPzZIQTsjQdi4Ku3sR8XWIIgqmr8t4OAlFawJHK2xlNcIaUoHJ0xLsSa7LetHoEChhQguRmlP4YhYlwRYlQJxYSiof3ik8QYksz1CGBvCNiLjFUkJCIEjohhOZM/6kXblAJhrlV8AZgwpAAKImPSINzEApgS6hxQM2kYNECazIwLY3PEmNZAYeDSpmBTAuYs3l4APPyciAV0Ej4OD1EXvcDGJKHWGTULeBujzC0xzKvLgUZYDuQshr89Ry0LQPX3EMm9x8GNW9n29uZR26KpAkVUlAYmVAETm23BKBq1xbVF6pmccblHkgiOK6EigWrCMB4iBqElifkyuGyAMoN5AnEGuEAgWA2FNgm945ASIaoThsVMkK9vk8kyBjanmj632PNtbXWgX9ub2jX9AbXJTAuDL0o1wty8oc0bjSujZElgZYvKDxWNVs1qV1XWVPEsraWIPl6EciIp4KKOlbi8FvDVAKCcJVlT1bErqKhBLMZSKwKCcNjOGUUTHBkPJkHkVC5ZQqdz0ag7lSsqb8Uz3/QDcxBqkRXB5Yo6rxAhRdurzVaVcfUICQRwhHORppRke7LcJqQejIDMb86oGeAywTxQBdhOmJ0eAhrBIfMnpYQxDpAkhTJPAkXlzpV3DCmhotGFSNRA0oMI8VC0g7MQjYc2eoI3mRsyR2JMeoC5kmll9eQguiDFtoe4TGi2JWCcqHaoavqJ9tGgIJx6bgtdRBaaBiJQyW6pEovHZgkBdj4+DCNyzhhXKxQUTGXCmTSg1IySC3IRb2PjvAbEeWmaJpc3ljirdrq6A4OdDnzsYJ00IVgccOrUKWVDsqgKCIhsB0Ekc2meM0quWK/XaivIqhGKF5F3KY160Cr6kukJkgwseSIskycm+6ryO1cFLCUBmMjwPE+Y1oSjS5fdxiSlPUhR6Y90vqz2Vq7LG2Cdc278riom10dHKEXWpPGUR/XSjUMSj3jtP2uDJQlMKeHg4AB9cZ5aVVkoBEybCeujjcoBVjoKpUzYYTtZuU+AsVKWtTz3unM48YQTOPzUQ//s4LEHAAN3vf4u3PmqO7F5/wbDdQNOPeUUKBDO//F5TB+ahFhXH3f0riPc/p9uXzy7Xmqg2MU3XsTmAxtQJFzzJdfgwhsuYLplQhgCrv6SqzvulLsv8+0z7vqvwlM73aJk4Jlxx2/fITr0XsDVT78aZ3/vLM695hzm22bEExGnv+A0wl7AicefAEXC+T88jztfcSemD04Yrh9w6nNOAQQcPv4Q8SAinhKg5OIbLmK+Y15W4pprgE/qEnqdOQM85CH3qv4ABMi8cEHoDX78x4H1WrhXb7utXfPMZwKf9VnA/n5voX/8y/XXA69/PfALvyB/v+xlwOnTwAMeAHzbtyGANOkBY8WEk0y4OiZcHRPuNww4jYhbp4A7a8YdXHEzFxyZYg6IYIL+AttooMpVUxiuBJi6po9mCJqgJb9iC5qipVdRD3i1X5ohwWjgixhUWqcQXG2yzQZAO0Bkwuetn4EBq8WzW73c7l981jdryyRdPH93bxhY1S4yqGN5Xeuh1oZm8AOMSz93GeXE+xDPr3F49OytNwXMb384EITTahxHDGFwTin7X5QZ0lArU3LlDZZp28MVWBTN1d4eiEQh3ByNou50oHRUjiJAjIMQEyiMoJBAIaLkA9S6khAlDy+xTNwKBNSqXMMtPPJT33EJR6feB6oF1972dEzry7KJonka96rmrnFzBc8+4wZ1uwKugH7lipijPwuAK5JtHK5c3FNBjRFiBkIFDxV/VV+L9/HbgH4udMBo35/9Z7tBULS2cxu/Kxaxuq8IxPae8M0g6gDVxRpsxoknO6O+343X8cqLgrvvydpuhyrU5rwoIEFCxoYEpAgonxj1S6P/lVr/DMMAZjHstmW4hQE146d7ljXz7jp18Tx9iHvYmoLfnuej2AsUf4SahCzenhaxt+1Va5+JjOzDFreAY62DcfPJWq5tRDtj0ADX/nYD9vr+bIKRj3WN/63G4gKKV+3QQlPhURPSP31bmOE0MNbWJZDd+jPou8Dsni592V5DFiLM3l/9Wmjz2F9AzYAyMLYvBly4h4OG7/Xtdq9Ze15oxrG9Roryn3FxLx5bh8H7vQNKvP8auG7eoQaYmM3POulMSXfWVmp9DEiIMLOA5uL0GbpxWHqIySBV2DERc+ex7QAFuzwPPo5GK0LHOBdlPAhMjUutliWA6F50RF3/x8U14hEpIfopRfUoylotrTG3MXNeWdcFqKMwYNU3qlA/US+TzW4lhJQwjitAE9548s1ujhCMyy/qfAqoKL5vWvSQG1kWxqnevbUYRzk72Cyepzb+JDich1aKJ695i7sXs8+LBqjU2mgdiNvcE11QZQl01xW00PUJdi7zIHNTf0g9hGTSsdn4YJAY6/PsXle25zGg3smyTqYs83YIAm4GlXO16OFSWM7vkivGSBgiYQjAKuq9JD8StbqlxH2Uim/T1mfs0J0CCdTOjEqj42Jm5CKe/rFb27UwVpqTozJQs/iDUFHtsUp7A8EPxauOjYD3yuEJBmtyXWJIIirLxG4Z7Mkin6ByqwlaORCC8ClAEhjaoY2NvbXFwA4ZkqrUo0v9xnQRW4tEpHyY7UDU1oFWwXUKAkkbVL7JWXqQSKTKYEjoMUIEpQRUCZ22PS5UG5d+j2oOIH2uC1uzTAbvNWNB9uodWlmnK7K3WfeALf3C9Fe3VGyzXXiXQ+0c7vrUPNk0hNsSGDqvNHyRs0VDVsC8BpXpBcyMucyo6j1tc7Sw9EyFyJJpXiMXoQKY1ANevPEFQJ8VnBM6EJHdPfg011nZxKRnAgvPZM6TAMoMkTm519P7RJemXXS6mu1f3Vf5WARLA/hkjhFikmRDMUbkYt6CUH7MgEBjmwu694reJKNUwWBzZqnGXSrAaiCJGJxrXYCxBBdSABHGnOyMUt4BgoCiSn9he6bhMTr+UQ8vKQTdn4ICdhEpjfBhh+yJAHy/iTFJr27r/mRgvyZp03rbfA1TbHQ2CKh1tl7Q9W4OILbGgfV6jTmLJ2ogSCRL0YNHhob+F03+J3JktIiPYMkkV94H7h3d0WUs1mhn11Td65kZmKF8tyQHGd36Fiqg6nPDwMhxjMDA3jeGddiBktjG0T1Eqx4iscqUSGI/G7Cuw7ewJWMEOASJMkktUWbz9C1deyrmqjQ0sO+lTnaoYIe1Bk6beI1j9GTTFs3j66ba4UlRgF0OfjfrjT+XlHbCllly6itdx+pYYHzOpJQv7JFRV7b/7hNgLEMUoHgQsXqwAEL5jox8Ni+u279hH/FExPrda0w3T5I06yEr4XYFMH1owua9ktXcngPAP+uLfV/XVb6PKohvnbF57wa0+ttpJv4cAPEwIh7Kwt/cJJ8dPu4QJ590EpfffhnzrQKi7n3yHq56qtR9/5H7CAcBm5s22Lx/g3gQsXfDnicvO/Hp4qZdLhWsHrzCfJs8Y7y/ery+6U3Ap+zwUj17Fvibv5HfH/MY4NSpe27MxYvAH/+xeMgCwKd8Svvumc+8dx3ysS5veYvU+Q1vkL/f+EYBka+9Fvi2b0NiwqoCIxFOUcQnccD1GHC/MOD+ccQBB5xGwa3M2K/AEYDbmTFD5WVoG4dtdE11WpYGGpoBzS4MXH3pUYJuf+0B2F6oLoxedrjO711gDugUnu6Uyy1P260JSiZP+MzN07DPJ/62vX7fKL+9BmCJrf7+8e/f8bGoxIfTd/sf3qve2Lf3yR/eMz7ehQAk4Nb53bgJb+sUik6p9GtpsV62DyZ6b0K/pn+XGzrd31vX76wiNWPYqixrpn9+p1aYAUydUdPfvFWPY5KDl0/tFZYeoIeGmFFMoCECg6TF7g2O/v3bJ+WL37u+WxiI1thjndKGozONdl63uN/qRB0kaXq1pdPuP2da3F9LBkEOBJqMpMWw9u1rXdnXzUC6ZgwGUy71+21G8P651vf9vOtnXD9eiyd0X3jduacpEG/6/l3uCQlyo9NkuijjEQ1s7gwUhofCmuJuJv32oUMI0cHY1m+l6zvyd1pP+hgSaQ7yVl9blxa62zwyuk5hdM+0ZBXUtW/R6Q2cNGN/MaeqP6e1of1YiPKSHmR7XEMnXpb7LtDeHTqjrTKDKiOIa4U8kdu09a1WwafmoW2RLz2ALPnQWwKMpewjnyXB55FpFj4u3LiA3XizQwPGgss8GJjSSzDrNzaDswOvtWEGxtogNtCprWdpNwMs45piwhATsiVU4u692n7xXI1+CMqVgWBckKz0DjY2NpMlIY4Dpwq4VK0Lu8FEvkZrFeAELMBpiMrLh+Ve4DxvLBEhnFi8R6lKGLO2lJlRqXGSWiIZyR0jYJ8d3gIK6gEdENdGoJgrGQu0Id6HAcurrB3AeqookVATEFJQPj2lrCxASFKnaiCgpCAQIDYJIBshDL0BaDy3u+T9R1hsG/B9VEW9gJ3a/0YTZtGnrHKMCUW9ytnGsVThPQzk1wxJgGzJQi7zOEQJr6fKyLnJPuauYi6HFYY0gJEAO6xrCc+We3PwQxNb4+06Nj2+M9olYV5VedHkQdiSnZa3IgCa4LWnNIHLV/PmEyBWJaMCKymqJyQxkJVS2mwQ5QO1+2ol39PlgK31iWUxt4MQKx2G5m12EPDYBNDnQ3fITj+xv7flvu18/jtZ2+TwVA4/JEdCNY9/BU+AqkBq08nsMD2EIHz6XMGlgFHAhZVb1S9GzVmp0dqhinugVjnEzmUWLz4FZMUrsoGxOWcFYuWHmJVSVqMsiEBc2zhWA4GKA7vUTq/gh73UZDL0gKi7ROWNdqDOwVrbNZYE0AE1AmIdkdKAUhOiJYgjKDWAclsbGKX7omtBgRShlnnTR0jKXJLD1FJULyaC8MuqzDYpV5POBR1vBpiDRx3Efr1B+jFzVuql5N67RBF6MiFgK5seJAAs0LyqjefY5iMRdA6ZfCLEQfrADnu5VpAmb4whOZWa8K+3vV76wYQv4ejoEuY8+eFiAMQTtojQk31HOYwhnKZCISCyWtZ9QvM2bTRNtgYNqOx1iFqNakDoM8TbW+RFLhkM6F7Ynml6QtVnCIVK9O/6vDBcq3u/2jW1AjzXtv+wJLIjEq/eWqvKN5loYxpEl9V5G1ME1YAhDU6pJBQP1fupFg3/16rYnk1MwmGr7THqBjaHqxiFb1Y6Tda3PaN0Ol6tyPMsSThrFgqKcVDO7xZFJ7pu0+S9D2sAaQSIHZb31DO7yn0CjC05o8wzDh5zgIPHHNztteP9RjzwGx+487trv/zaj7guZ77szId13+pBqyvWqy93d83qgff8jHgYj13DzMCXfwXw/B8FPvMz5ajYtNjXvU5oC0IQuoGnPa3zwoH8bq7WeiKPxz4W+MM/bNf0m6VdC+iR9L1U4Jjbe5vmcvx5wnzcrjX+yRAaJULT0Nv3X/u14rH78pcDD30o8Ku/KtQKr3gFAGCfGVczcAYBj4j7eCgRTlPEYSUcTLLxXtwcYTNnFDDyaoXCGefAOIJspkzkAYiBWzCi29rcKc9ulLXTKSICxeRmhRnwatNplywF6jEDtQecaMnHBLITcvOEgfK3yfN5l8K0jSB8onyifAwL6enzNM8gSEhPA0c6kGjrvsUp444l0rCXDvzq1tKVKAlcGbQ6kECA7SXNuOjvFWyBFCTYqo8Dqcfbv+vgpW83kQEYaqKEICBsGoExIYyDkAmmCKS4AFrcwOvkCDPj8uXL3qJj8kWv2Vb2jsk299osaNrZ8bJ8/jYgZoCSKTjm2cF+SW/kLhXN488V8cZbc6Wzvrv7LGSSYoRlouWtui1a5eCZ2UEdEGuIwxIt68Z7W8jaXNjdb30bbQ4urzSwnRbz3N7DRssAOKe1zWl0oKL3tz9HQvh42bDFW6U072DC0rPclODlmmrPaQYdeTvMy94MYrvXAABiaiDxYh1v0y600rzal8Y9gK31uTD74aDFcrkDBsCZd39A875cXLhsd+8RzYyldyeZlySw4Oft1m0PTrVHd16fRMpf3mSQZUveLsyM2ZJNXmF82swSfY31Pkkyg24eGcjR+rOFXatHdKAGWNSqYFnUNVcA835JBqy1hpYixlcpBQzhbexqphhP8+hhNjoMASdDKZJsIwrYW7ii5uJJQAYWA75yo5BgbkadXWeegNCxTzH6+NWcARCKr1XGoMaZg1vKn2u8fPM8eXirdWTJRQ77Y0JMpP0E98ZxyRRkrKdcQGPAmALSIOGlpaoXV9A1WQWBpcgYh4gUzAMWCA7idXrih1mOeXhuf28dq3+EECSRFxh7KYIJONpU1KJ8jD4GAiy5dysLaM1csZkY4yig45ia92qILWxbOJeL9+U0ZwW6lSoDBUZKHUloO2KSwz6wgH0pReHiLEWS3qAtwRQjhhS9/xhAqRIaKzJCKIGkyBUiHppnoj2PdW0ImKUerWhbDitIwJCQ/BiTzNVOjgco328AhnGU+TrPmOsGlC8DeQ3USXgg9P1sLwgK8sA8UY3WpltxW/u/1X2hQ+yYA837vHna+XeLf0nnR+PHhcmE0PZ/n1cm342WwKgngtlcMu9slwlBQtqHPXHCmjYbzNOkUXERMHoIBZcAaocDgCYzE2Bpk2fMyi0JABSDUJNon4QYEFhli+5nkiuRQRzAqEhEAOQExealqCgCaBancqEW7eh9qmNNLXIBEK88i/YRr0BLwNhsUOH+hoNqDCDPG4ALBoxKT8BIISIQI6Ci5AkcZL6weqImBwSF5sDmhukDtec/Lo0P1KItZL20hGXsOIBocDJ+RksQNcow+jXiw1jBMSKgyLpS+S8c77YXFA1bNwoYktFkqW0M4uVq8ntWigFikQt7+yOIlOyFBUCNKWEcVhiHUaPMKmrt5oMfhDIqKuZ5xnp9GcJTLXIKlTHnCaVmCX8PEVNJKrMqNpsJ6/UEwMLuYxtrS+7V6Vm9vbDklCWMo4LGaOuoFgE4AVJv8qp0d20P5FpQioKtuo5jihhXKz/UlXdJokwHJjlgb2/Pn0WVwUEloMqtzeW17PEskQ8lS66UooDlMIwIOl6SgI4UBE8IRMjzhCEOC/litDE9/2xRTtl5nhdyKgShDxqS6CMxRqQUWiS86gAhRKc9KQoqV+3Dkgvy0ZHrCTEErFZ78ENqne8xyo+990rlPgHGekjUJ8qHV4iAN78ZuO5hYpjfcgvwiEcAX/M18t3BAXDjjcBXfzXwrGctwcwXvQj46Z+W31//euGZfelLgeu6RGZPf7qAmwDwlV8pAO+ZM8Bf//XODXhnec1r5F5AqBAA4Nw5oRcApG5veIPw1D7pScL/+rjHCffr6dPAv//3wn/7j/6RUC9cuiS//8zPCCD7qldJ229XSoonP1me8chHyp9xDw8dDnGGgWtqxV4uGENCCgkpBZQAnBr2ESLjgAn7ecLBMOCDKPgQCs4XxqTYs4VTBDP+LdSTW3Cru/TzlvFby9IwBHxztGf0nkX+/xbC0ysyIuY65Y4Z3H0mtsTCmrM3y9efWHufKB+nYt4csp52A5ZAg7MWp74WbtjPdQANULmybHKFFOaNa3cuX+rv5R3fb1dwWYNWJ11q26DQ8To1GXD88XKqG4ZBqQkSMETUIYCSgooQw8ChLgODtvph14n6PRYzDLZ6gEiMC6BXlHcZ6KEbI+7+RdfJ233UhaX1FQHQFOrtLcglsPy14EmFhlf23rEM7kDWduoN9KBwM0a7yIYFkLkU0UsO2tbnV+rq1ld9Y47tFDIPHAy1+dKus1wK1IE4dueuGXj3c5KxG2jXJ14B8BMldhlub4NtnqHWumZ4L+djPz/tPqgBtXudXAEMYkt2JWN+d0Cs1L3xPhIFFPVUM/CsFokDJ67i+RAkWRSpAVdq8TZZPc24dxDbE0FK++uiHljILiJbUU2HAKn3sd4W+zBi43yl5Z5+d2ucDe0lBqv3jAPAsPcLxZPN46qGiVLOwUEsFiM4RumVnAvmIgkpPeyVW39XFrDWPBFDCA6ScPc++V/aEYIlm5I5NiQBWlJMyrEoGZUbH6wjTIiUHBQyjj2QJEqt7hXWvhNDSrkJFbyMISBFMdIKWxio8DWPe3vuuWTc3JYrQDybwpYcYJ0jygFLx9eVhNQSYgCGwAiUMERgTIRx6GQNC6fk3gCM+0HBNcbhijCqV+wYAGLGQMsEQn+XhSGAagGjMJArYyqM9VxQEBU0l64YIkA5IGcgW164ILtLCoR4mJALI0VCisCYVGcW1h5UAJPkooKmWsIwCChR1fsw14pQBcS1iAFwBycRQIFQc3X+dCsNSO30aQO0FzKLfR3aYVgt2b2vHODUd1u0TbW1pHIugATIYPMSr7AdzLwcfc/S4ZznipIlIWyZLyPly6C6BpUJKBmcJVeCeXkRDSCOCvCojsUmdRjEtbW1a30PDi77iBa/7wIgzM/ezZKOzsvGwaWeySHuPIgNUEkJyQFxVhClurwzapUYAoZhwP7hAdIw4Py5s7gwZ6E0YPVWJACRPBmbgVJRZb9ldJ9KdduuqPZDIUigBgSAo5CAZ+2uAAAgAElEQVQQuEIOeqvyHutBHtmcMU9CUumaBZyl1k7YOKtHYTQPUNsPezqWTq9rh/jo5LIdcHZ7gT5GEputsdlMSEMH8gFAGrAahdc6BgJDDiJSGhCTcH1D90uZ6BUxDZ4sstNIUaskUQOAFEcHuCSHhMxvmxRyEFcFbKWkVGymrDMKK7+oUiYFjbJ35wUKYC5NT4M4U0U9ZGAGVnv7WAUDNisKC28rWOTklC+DYnSKBYDBG0aKg+85YhxU17mJkreBiYVztc4oZVavaqMHU/odnVsxCpcrAOzv78uBXy3aXyJDbA+0uZlz9oNDAH6AaQmyADlIsH0TBN0vNblnJMSQMIIAHl0vsVLmsngfw7xsbf6we/BajgAibodSAPaGEZTEEznpHrh/cKDSRYD/kmfXc5g1ERize7kzKuos9AS1FnCpmMPc2QDkXrC9jbi3t9d0FtPXlFqhzBnrzaaTKQL4Nzkj8ywG9Q5P0aPJmCEZKYlajg1AvXKbbCvThM3GxoI8wdmucp8AY6V8bBSD/27L6asAPY3AmTPAz/4sMCunbEoCrn7rtwK33nrlZzz84eJh+nmft/z8/vdvv/+rfwV81VcBq9W2FXz35TGPEaD3SuVRjxIA+Vd+pX129dXCgwsAh4fA53zO8vuHPlSuARr9wpkzy2uuEpqHRyLhQUg4QcCKC4oaT3ICJGEDBwiOutSUwFyRGBhAeA9mTMxumwqdE6sC1YBQ+b+F8LkNCdk3GS3xCLiBJiYCZUNrRlkz5rsXmHHopQN9uo3WzdjF3ts4+6zU/oL7cNmUI/zSTd8PRsVjT302nnLmyxbf3zndgv/r5hcDAD732q/Ao08+6eNRzZ2lcsUv3fQCTHWNhxw8Cl/8Sf/rx7tKf6vya+/7EZzPd/rfz3nId2A/KnUKZ/yH934fMit1StjD//yQ70SggLec/yP80R2/4/c98eqn4wmnn9Y9WeaeHUDwsX+1bCkJi6987RhI47csnuNKGus9O/CvBSzSrd32hX7Yg8KaRMJrs4WhuXRg3K3MbKGcnUeqvTyoB0vQ09tQQcMgFmjoEkExO9iw07Nem8Kq2W2v/AZ8LEHaY94v3JljDgZ0jbYxOQYoinG+/Zk9l7Z/d/nXwBiiZa2PeQd4p1v97BXBZXLfG7Q1NG0ou9lg33VyeGH4HBt/XlxzvPSAYi+TtwxbUDehuyrpO5oBE5zrEHHp1WzzoGqyJg+29qFcgkNbOJGPSTO+7+3Wb+GrveneAAjbA80TzLx3TLn3PlC8wZ5ypT5t4GFV4yz4a0uxRDttnlgiCufwhHizmacVzDxgoGVs1o5ZgLx6JTevDOs4A4GbEdlAB4nuFO+JYonk9MbtsRMQTx7roZUdYOurjQgChlrG6OPAdt8HXlGdfyLeGH0iNpAdpTSZSQgS5t4/h1iNYfIQTvIw1uV73atVk35ZgrkYJDmKJU+ykGTWAfY+MA9jSkhJwmxjEKM5hAju6DFER4POicb9Fj0KQ8bZPBmtz40X0DPdG4csmZcLQIiyniggDaMmd1PO0SDja1NCm+oHZ270wQ4EuaNXsP5qh4USdMwYYkCKUO5BVn5UKCevJE+R71npCMQ7rYAwByDZlHQZtZQHH83CTCjMyJWRUTEzkFn8QXIF5mrAibSvVlI+YwAKpnpAnc5PMLmxPoxmXBOmmbFZV0wb4V80XsBBk48aBzV5iL/MQ9N/zfOOq3Ap9/QmDk3pRwIq5QUgabyGBtgaV6eMnwD8s8lgVTB6mcLVWrzdh5aUitHWOOkaAqAJYhw4rhlUMkKdAJ4QNZuSRO4EMMmBBdtTSI5aAKG6CNAksqrrtO3W+qJR8phHq9knvd4ROqCQ/Xbyfjd0yT0hYbuPHvuq12TzIle5TUGT+KRl/4ElcVR/OEFtPTGA9XqDfOkSLl+6iGlae5I16vbY7j8BXHWvMi5pbZTvX3BZre3jgEAVjeNCHhgYIiOJ9X21m2dyPYUIAhChSZC4tb9A9hvS/pF3tsNm4ThW8AzqBduFXnPfTq1wCITaRafWWjCV7NtVCAQuFZEZxCPCIHQCOcteHXIBU5DQcveGZSC3PowksrYl/bU5JGMTVS8rLPsOM2niKxt2cpnaVV4AUptYJNEHFKnjwefFvGFdY5LDQmgt6pHs9SkOHVDdeVuXnuvUJjlQY0aNCTlGWA5OqxdhA3GeMHBSue91MdVakdVDnbRDZvXcr74XJYzDAAM/TTdhb7v03TAMGMZB50jTA8DKs4pOByADOaG8xAW8WcaSJd2/AAguoocAMl26vSmQ71Vy6ChjEEMDwBuQqvtPnZHnLFyqVi+S+cG1OC9wL+OiUyiI3DCw2TxdJcF0dVDa6mn66mazcVnkBxnabzFExLKk1DIeYX/PtGnJF9WTt49+TKm/fyn/iAgcJbqizxNwpXKfAGM7efaJ8tEoITQv1L584Rfe872f+Znyc6XyBV/w4dXp/vcHnr2dXGlHubtrrr/+np9xeHj8GmZci4BrELGCyOeJzLDWsDAAIwIqyWlnCRGlkCrThLtCwaUqIQxVQzZqFe6fYx5TPYqzZYSYUJR9W9USUo4nPw1lV0Lco3XLQ+nK4WE9GNRvvO2j495y7boL81m89/JbF0+MlPDok5+1E9j5WJbCGX9+9ndRUXAinT4Gxh6Vi/izs68GADzq5BM/6mDsTZffjvPzHf73ww8/DYfpqnt1L4PxF+f+M47KRazLpf/PgLFTXeNvLrwBf37297AXD3AiXY0bL70Zn37V5+ERJ56AIaxw48U348/OvhoP2H8EKhfcunkfnnD6aXjE4RPwofV78cZzr8GjTj4R77j4F3jA3g149Mkn4Z0X34RHn3zSwrhuxqkuEG6quYEiC5Cp+7cvHdwEB2B3XNU2fey8ZtddYjirB4ArrOYdumXQdqiwrXveAqb8d75yLa2eHlYfCBxIQieNWuaK7dpdRPSJMXR3ni3bfy89hFtPH3t+P45+Iy0budVgWnxIO4Z2eYMZP0AvDxXnM5nc1737nbc63LEJn3dbHq89eNHXiBuYYWPbAJ4eAOvnmSlz7Zqd48WmSLd6yaMqLMaw+veMwNGVULeWO8OH69Iw002m9Yhf23rl7mfRdhv7frH1Wr1t7fCi9rf7d3YwWvxwo+1xoQMjd/dZm5FtD2wAomG/PYBpbW7vWc4h9zbR54phbB7eChLW6slsekCEIetLuNG4e4d48YhXqLw/ILnRCTN2GjrReEcdKLCkRwb0ANVpDtoau3f7tekg1I28gqQ6PxpETM77J93X5pqvFSWDE64/4ZGLrGDowlDR0VHQNJBlyG6h+cJ1yAo2LeeaeMVGxJAQNVM3Ka+uG0J6vXmLh6AyNLQkZe4ZCWiWdgOSoodeyt99X3DjZTYD0vtf1xFJ/W1OElPj7oU9y+Zrm49SaT1cIfkVAV5PrgLIqo+1hlJLtvYYxUM0ECOSgK6JGCmo56/KqjbnP3J97t7MMdZ2ZmbkSh6YRxr6a/KNIEBVKfCxN9tQcUGU0v4GM0KWJF+bibGeGJtNwTzNntCJK2MYos5y1n2JfQxaNFvXHQqyuXHdfdnrC7Ua53Cbm70Hew/Myr2Ng9peYOMoc7CAl8zM4EI+UmYT9GAFhdYOoQwS/lEqE0KdAc4gYuWijfITB/HCrgTiqqzVLSETG1cpY4sfv42nvt3bbnK2HQAf7y/b01skRw8Dbel6Og5kz1BAhhkt+3mMXd/rY5Smo584DKj3egHPEzbTBtNmLZyZzhmpbdH7lmoK+z5qY+DJj20sOjCXQA6qS78EGRdrk+27Vk3lSUmIQgfAyZ/Xg6cUTH50B6Mafu7zVeWB6HUMRae9+4Wev+mcJof9XawevLofVZVzpRSkUiQBHOw6S3gXETg4taAn7NX/CwjDwB4Z4APWqXht7VgCY+OXhT+LaQluA+RRJ2bLSzt0hTM3ANj6iwAK7PJVQNlZ+oqSPEtSrwmHL2ftD+2lKgCihPALAC18tvpwdCBzkXkKEBaJKGMAuLhsMTnhWz4Ldc3s60X6ptRGWyTPED5XCkKzImZJq0ufbJRtbpJ6azMjglGotORSZPuM1KHWAiY4yOlezuYATbCNXfdwAdYrif9fVZsuoDmLGD7CbLqrCBmuVeelfNYOk6PahoTknLbiEU8g4XEPVelFOnosE2Gmj7EentcqEYZOeUGL/1tyNOk1jg0ila3ZWyLPLEW5rHv9sZPPZDQTwQ+er1TuE2CsrMEI1LhQjvy7HTfQciUvLu3F/5UKLX5jX/QmIe6NmmJv3WmydAKdAHBKwDDci6d+uOUjV6z+ey4rBIwISARUIqTBuECMWJkwqqJUA2PNjIMUwVMB1YwSRpwrM84DmCBqk2j4S+PJsl4bkTqjnc6iXeZFBJiFq1Tf+LeH0/bveyquJFGnSBGUq4cBLpolsD3M6prrjBsv/SX+z3d9KwZaIbNkiTyMV+GHH/97IJCEcXBLrBcpIVITI7nOwsfVtxEBKUiiubluwFsr057BzJh5mWxvoJX0DRf9Tu4tnDHVtV4zCjdPnVo9eO6+b88w702pV0QK97wmrV6/88GX4i/v+n0kknu+6ZE/gUee+Ix7vL9yxVzXLpAqqtctkRiS220nEIawwlRbm/tCCBi0T6U/CsqH0bZ7Khfms3jxjd8EAPiC+30DPvXU5+D73v4c/Mx7vhP/5KHfhTPjA/HSd/8bEAK+/P7PxVG5iJ95z3fiJ2/8FjzvUS8DAJxIp/HcG16I57/t2Sic8aHNTXjJu5+HF3zqy5sp0ykmzfsAcBWYt9aPGm+7intUtE/kFltA3Trq5yJ11+z0IlOFRbinWtbtcTVimjbtvs4AcQ+Qeyi7W2ItlH9DFOWOYxSeLueGbEqgbWF9SF/fhu3P+3fZ982jpQHgXs9eY9yx52zvhb0hu70/X7Fw85YxEBq9jDWh1r/Hx6hd2s6v9P2d06LNs0V9VSO2Pm/XC6gvSTXgCrG9cBso6g8MujfCwNr2nc9+937oDVnLELt8xrK97JeIwmqZcTvHTnkWl/Yot1UtkZFcZ54Utg76ubOcA5Y4K2K7mNLbulSAxMYVi2P91a5t4EhFCzXlyogcFTwjDd9rYYHsyjMWbfR6O8C3PHyx0Lu+Ln124oV0YLU7AhBjM4itHiKjqnMLWiW4yJ7u3ncxIlSbzzp+nEExtoQ5LDOOOAAIMLvBvF/AyhmINl8dgLD9UUP/Fwcp3dwyQM6MGyLj8lPZ4HyEBogAsLQtDkqqNxJBOZtIr1AwMw0INIDC4MBab6AYsO2ARpXQUzvY0hZ66GbfDvEy0QzOlGTOBYAqCWgBC000rtuemkTeV7rkJt2kUa/ZiLaOxTuTQKicBYjVOM2YCJqkG3mewOrRZpQ7FLwHxQjWEOQWui39Z1z/gNBEBESAtTepghioxKiBUbJ5E2mIc2VQBIZIOFix5HMkYC8SRqU3yEzCGUvAVk/g77IQsYfUVwYyhOMWIKwGQkbFNDNqkdpUSMKtUuV6ARoFhM0FyFkBcARUBOTMmKaA9XrG0aZgmhjzNCMax6uOX+gA/UBymGmGui5F318MGHEQnltvGfAZqNPV7V71eu1nb+wNcejBbXcY4bYBM+acFwaCrAUGKCnAWjrdqMk88WytwgdbM1AmIB8BeSOALEwnCQhpQEgBoQYEzkAtkvGbM7gKjzNpezoRoy+yvX8xwt41MfT7QUWpyhGuegypXmL9XTXcf6GLdL9uhx3bmrEs9qYberUM4HP6iYI8ZweWJOJC+T1r1fvM5idvl+2NLXw5iPzWNR8CoWaFzYk05FF5tXW6EAcHsZSSFtC62r4VUkRlBay4gik5NycgicSK7h/MQKjFgU7YM2ILq4bu51UpKKKhszo9qwJRsH2PWWVNZwsGQmCH5QGWKBOyEy3W/g4mzaH0BY2nvFQFgHWD8+RKZGBXc7yQA6aKaZpQzG5kln2zb6fSvlhhAEwkHN0K2g5DUhta9TTCEij1yBj76SPAKtjsWqpgKmASABVUHKBEZUwlI3dcpRJRYVElwDgImM466Ydh1NfL9cM4gJJyu0P0G/veFt1mMy3oB0otmDpO1B4gNewAqE6vY/2VusRbFCNSihLTQubVSU3n0T5p7wjgonKIhbcdtSKkNn45ixdsTEJBsJcGIAWvg1EJ2Tg6wA6xi2utyoktnLul1GNttzL0bRsGhCg4S0LCahgXdCgMpSvpOODX6zVyNg7h6P1o7Y2RsFqtunGN2N/fQ6+zWIRVUaoD4WaH8sgyNkp70CoiXOQhWKLY3ZYecB8BY4c04vTmmVjffBm33/FBXDr7ASBnYC7yfy2IwfI6FdRpwmo1YhxGEAjTZqN8PKKExRRbllUlzhdtprpxF4PwnlAg1HnG0V13gadJ3K9j1HAj3TiDTOQQBSyupaDMGTxvgJqxSlFQe5bOnnPGPMtGYCd45R8/C9N3fdffXSfG8Z6v+f9xWXNBQcUIUeIrqWVFBVyKcDlFYBUGDClhMwu4ElPEfoo4JCDxiBvLZXygTrgrQgnwbTtvUIMZtNulN45sc6pcMZfcDF81/MFN2Voa6VdezPaOXZ+5hyARUtrFnwf88k3fjz85+0oMtMILH/cqvOTdz8PbL/zp4prX3vZrTgUAAM94wDfgiz7pOf73r7zvB/And75icc8Tr/5i/LOHfQ8A4Mfe8fXHPG//4f2fi79//T8BwPiutzwTFzQcPtGAFz7u1VjFfbzx3Gvxc+/5t6iq6v7+7b+JP7zj5QCA//0x/xF/dvbVeOUtP+fP/LX3/Qh+/f0/hkgDXvi4V2IvHuLNd70eP/Puf+PXPPXaZ+B/evC3301vSqko+I6/+jJcyufwaac+F//ihh8EgAUIfXflPZffgh/5m69zIPit5/8I3/LmzwcAfOMjXoxHnXwiLuZz+I6/+lI3RK9bPRj/7jG/iue/7dm4c/rgsWc+9tTn4F9+8o/6339+9nfxi+/9Xv/7i+73HDzjgd9wr+r3kZRHnvgM/NinvwaA9Mcbzv7esWvOzbfiW978+cg84xW3/BzefNfr8aOP/y9INIAySQKEjuS/P8jyQgZkNQNq9yo7vgZ8zXV37DocWXyP4yvNjYIYME/iVQFiTNNmNwBn4MbiyceeuvU+VUA75ZYJCEMExog6DsCovLGBDCXxzPaAAkQLObOs2xKQpcXncn/ZAm52g2e7JdFS+vXYLZl192GWK0cDLK85NnuaaO5KgyEWntYKNJkx0q5pfb1EYxuYc6UDt+NtuNJcWBazD83jblffkYJzVl8z5noPgUWVFQQgCLjTdi8ZoEC0mEvNOFzWWYyT2gBUU7R3NH7XAUf/+dbVAKED2qwBzRhnBdeoewbr55JYIvg9/n9s71p6bjWjUN6+o48BIIg9HWK0VSG6ZS6SBCQKj2gihuZsRgwRJ/YPxCAKFiqXFqAFdSCAGYnzPGHKFZtcsFEPmZmD+d6LrOCupqwh0x1o0a+VPpTV+6/B7sBibnMDWO0NCuRIkXh4A5ykz5u3cK0KOMcRMawABE020+aNGcJyaHB8ToQwOEAr3jgRwzAoCGdcs+zGL1dIiCtYM4Db/KQ2pw0U6363Pmnz0GDTju/Yl7nWBwSmqh7C0KQfBrBpQhBahtQyDOAXXUKSDpEehATd2hpHHcAgnf+lCj/qkAhjIqwSkAIbZTjGAVilgHEgHKyAE3tCp5CIsNLrwYw4BESSzwcS6oK7k6MfzRIgXlh7FDBX1iQo4v1aphnzzKgcEMIAEFAqMOWCaQYoiAcUhYoYK3KumPOg/IoyK0MC9g9HxBUhHIlnp4FvFYz1eqNUBb2st325SVbLdG9roIF0Otu3ukuWiAFO4uTQ9p6ghzBwj3o7HPD7SfwALdwXFFS/VQoFilJHA0jNRliMG6MqDyzKBJ6PUPNFUJ0R3OvTOLABYgJxAAUJLZaEZ0rOyxWEaoQFWg/bI3ixXbWdo9sZjJpNP5A1Zt7PFSXrLuXyTipl/6cYnfaFSHmbF/Kdfe9qFSFsNhtP3gViFANJlF8SbOMuwieq/BeamJZ7wN7UH9I1u6z7oaBJn1RfggFmFbkUcC4ozEopEIQ7NrKGrWsbSaeO62+tVAW+CpF6ccq+dvJg38HXWspWcsQqXnoARp+cwlMMn9cQGaogrCSWWnsyJp+XITR7ESxe1AXgCdquiHmeugMLwUtiHJBSQkyD08DEFDGOI1Ial/O20wkqMyhFNDqOgoVDE4tOO46j7wsgQqkF66MjCVFXOUmaxIwYMhZs+2JATIMnVTMVIA2StCzGAIo2NwWYS2lAKXPrTO2SCAl3h4Lvxt1sURdQbmfhqJYfSVIqnNXTNPleJAnENDSexUkqakTJnvKPExFyKTgZm96Qc/ZDaVtr0zRhvV77OqyFMZVZo40qZuOX1frs7+/DEouHEBCSjpnSKwzDCnEv4rDLfyDJCRsgnHPBPGfMOWOTN2BLgF4kIRcXoT4YhqHbgw1E1v04RqQuGdfh4QlE5WT3JJ7MkoBT5fo0T+CylEuuL2p7xnFEVJmSUsL+/n4bSzQg3pJ8tYNXkRvTlHG5NOqpGEWPa9E1JEkBh8H1uMODQ113uj5rQcnF94e7U/nvE2AshYh8NGF94Tymc+cQNlkERyWgBpQqp1uWEa+EilIYmzoDulADop8+ikgKcgJr2YQDIQQVuCxeL+vNrMTU+zhxVcR0dBnzegPOmlkuJQVjA6IK5xiTctbo6frmCHUuyFxECMSICDGUScMqJGNiBNLq49TDnygXwbgLMwoFHKYVEkfUPEsCBghJ/VwLEsmp8amUUEoGDcpNVgkPrgEB+9jniHfWI1wwHjuWJV673x1UcWUD/reVnR5nC8DiuHdS3TJetpUGO+EKaoiYGW8KiYTKheW7TZmAeL0GikhhxDMf+I24mM8hkhhHv3LTD+BtF/4UB/EU/tnDvgcve8+/w+tu/3V8aHMT/vGDn4eXvPtf412X/hKZZ0RKeO4NP4REA64arsW6XMJL3vU83Hz0TmSecTJdja9+2PMBAPdbPRi3bd6PX77p+3E+34HPv+5/xKnhDH7z5hfjJ2/8FnzFA74ejzzxBHzNw78fL3nX88CoePxVT8XTrnsWAODq4X548jX/AKeH6/BLN70AAPD59/sqfNqp/wHiQbqH3/7AS/DGu14LQsBzb/gh/PrNP443nnstLuRz+JqHvQD/4abvw53TLcfmzQP2bsCzHvS/4ese/n/g5R/4Kbz78n/DT7/7X+O5N7zQlYVL+S68tAN5+/K0656FTzn59/D1n/wj+Kl3PQ9TPcLDDj4V//ABzwUAPGj/kXjLXX+IV37o5zHzBs958HfgPZffij+981V40Tu/Ac94wL/En559Fd547jUgEP7FDT+I19z6a7jx4pvxE+/8Zjz3hh/Cyz/4U/hvd/0+Eo34uht+AP/xfS/En559Nc7Nt+KfPvR7QET4/dt/E284+/+AQPi6G37A+V7vqZwcrsE3PeIn8PPv/W78wR3/CW8699rF94ECKgg/deO3I/OE8/MdGMM+nnvDD+L+ew/H6eE6XL/3MADAL7z3e/GYk0/GU699xsKrt5/RMl/JTxG3Dy8WZYctefwegoGiBmxdCayFndRvf771KssO6zralcBKsn+klQ2w6p7K7UH+r8kAVSoQI2hM4GEAhiQEgaQn8h1GRtjRtq3+caPO9ZjjdXeZcQ/FqrkNaAcH5XogyMKbpV3G02ng+nYd+tKDZcs37ZgA1sdawyUmSf4HWb23QGo4INKub56gzbtvu4cawLc0mI8Dkc3j17KsN/Bs+d42L61d201th3SlLr04e+MdgAD3tnfo95EaD69dYvMv6NhR12fNiA6LOb/dxrsD+q8EAPWHkUsAUe9bgGeqeFtzfHsNPs7syrYYtA0w6OdS84K1Ovc8kYv6soQ4RwB7acAqjdhfjRhHcQoYYsQYA/YSsCLx4qUQMK5GAV9Z5FpYeI+x2xJGIcEKrkwlI5eKOUvCmKNcsC4V67lgPVdjnte1BOdBJTJP1taPNhbk69Hml/WneSt1gJTWtZ9jgSKYLCN11wZqv9fKatAlUJBrG2+uAb3kgCwICzBA+i16vUIIEjmz5VlNIA09rqjEWA2DeH25vhU1jFw86Xow1p5r7bd5tVx3u+apIGsEOYQbUvIsyQCBIoG5CBgIAX3MGwokHmW9t5+0zTzTLRS1Or9iSgGhVpi3bCVCXCWkAEQIqJAoYH8ISIHBueLixar8tjOmgbA/RiSqGEfxhpKV0W8aV2rrR6no/kYk3rqrBKCoVyMT9saI/X2VYQWYKoltFQQDvbyWTNrDQFgNESmSJAErFbkA40CY5hm5REwZmCbxGCtlFm5CDSNOKTWjvvYHut38VUU5Z+FvbIev0WUwIGI0wLKT65ohCT1uenxRoJPVacPmLtSbSmgbDHSMIQindxPRLoZCjEJ5EqPkkK8G7FMLANa5XWp22jUR5dUTPrknLgNUK8AZzBkoxSQmhAJDdzrdk2SvJB9H+b95Y7LWMTiMK/KDC6OUWcFNKNjUvOZiSAjqGFIV5IO224CmyiYj27wtKttLztpeBaRIvJ1rzV5361CLuGWwhJq7l6sBjz6Y0r4QvT9ML5C+kwSEPZkPsxww2P5BFDDlLFzNqmoF/d0OdIwGxo8EmJGLJRIjDHEAxgDO2puBRPZq9KbLSxDSAsVhn2OlFKSUHKgVbljdD3XPGAax7cyD0Pe7br6KV7mAmz4etXlmFhQBfYcCwgDxhk8eLVErMM+z6jlmo/b6G+v6N6546ZvMjXOUgh4fGpANYFiNWK1WCoLP4JKBKIegAQG5FASQA20pJVjyTUmMlTFNk+qDbW6XkmGHZ0RoHrks9g6bfgTRPdoBoHhiiqPf4Hqu2O3FW7oaB6w3a+kLCNaUUlQAjzFNs3pgtv0jl6JgYPD9chgHH3bdJxMAACAASURBVDP72dsTz86ooLStT2bGZpp8zULHvyhoWGpBnjKAebFP1loWHPV2YGJ9Zbzqq/09BAoYY0Suwkdba0XJW/NKJYS8Vz19CyMm6t679IImIozjiCEllwXGB266Ww/cWqLGzWbj67qNf6NQss+h8yp2tqHoUMH5Ynu9sXbv9ENg3ce5LpOdERGG0aJc2DHKXeU+AcYyV1y4cBfWF86DNxvEqqTZXD1rbSU5EY5BMknnPKNoFkSAENPggs0CEAM14V5rcQHjZpUmiyCIN+14eAIMQl5vwFkmimow4EKyweoDxAU7Io0r1HkS1D5n2fhC1HoGce12IS8lvPKVoAvnXaj0YQbOVt96By2wA8r941/Bjbt+c4AZm7qBBUIYBwmnsA5YPqT7rRlNtkl4n9lmhmZU91PLHrsLILSBiCm1JFj2PgLKwx+B/JjHHZ8cH6XyJ1/4hTh9+QL2QsBBHECVMKsQYq6eWTQG9WQmwsWakYlQgoSEbWrFOS44yxkXeYPL3p1iqbZTMjPsm8G06HJXgrHUunR/anIrwH1QiLoxsPf2t/lkcqqE3msIaIKrN7AA5TP7reOe1Q85ePTi7xPpauzHQ1wu53Fuvg0VFbdu3odVOABAuGo4g5H2vP13zbcjUkKiEdeOD8Tp4ToP8a9ccW6+DQBwajgDMONt6oV7VC4gknih//XFP8eFfA43nHg8HnXiiaI4ALhmvB6PPfXZXrf7xQdjri3M//57Nyy+f//RO3Dz0Tsw0Ii75ttQeMa5+Va84+JfAABOpmuczH/Z5tNgSFtm3uBiPoe3nv9j/NEd/zcCBXzS6qG4/76AjrvKKuzjIJ7Eo08+GVHl0Yl0elG3MezhquEMAOBCPoujchEzb/C2C3+C/+Uh/xbvvPgmvZLwKSeeiL84+1/w1xf/HG+/8GdgVNx0+e34wPpdWIV93DXfjswZd04fxDsvtvP2vXCodSTQ4hz+7ssYVnjsqc/Gk6/+B7iQz+JSuevYNQTCVcO1KDwj8wTeVJybbkfen3HNeD0O41X4i3P/GZUL1vUSPrR5L27d3IS/d/XTG6enLhBTfHsw6/hmjnv8GzC5Qy5n/XMs/+6fsQAlu7Vs6xksnJYNWmuycccTjwFou67ZqoR/xESgGCQT6SD0BMIZa9ygnSGtW4TJAeaudl3V+Ar1WfbzdluWhsfxti2v97/66rGBQfohtZ3Nkhbs7pvOOu3qYPU0+dqPdasvtd2z69ftubBdHEg+1qrt3c48dXpD1b5uusZ2pxy/rv9sG1Dn5Vi2q5a1sX71brB+7q6irX4mmyj9jtJ+DLhzCJosEVJ/7/FCx9q0u/goUfdeQgMQue1ti9ba3N8ez67dcn83Bg6oW+nnVTPYGygohlekiEQkmdxTxGocsT+ssD+usL8asVrtYRxGpBgxBEIixqjga+GqTqfNK873YBgdAAEU5PAempwmEHLJ4j2oRtQmzziaM9ZzwdFUcDTNmKsAOgzqeFC1J/t+RKNo2D6IbZ/b3GmGlgHK3qdBOCeJt6J/qPWhePuEhe7d1pLOKWt2L5hJ9iXSEEKgGYSii5oca/OaNIQ8EmtWb712kZBK3inJ3LoJQ/C2catdZ5Sb/tzXzTwW5fcY9VrjiutmUoAlCrNPBaiJYdkuex8Dzr8XAiHqj4C2UO9eBTWj8MEOidw7dowyxecMBQEJhQm5Kq0GtZZKO69Ar/ZRLyoniRCZMQTLtSDg1BBJqB6IUAIB2cwgQhkYtGGUXJFJ+AoLayIlVYtLgQA15tzJLBnCeQApCBg0cUqVjRro1rnp1VWJbIXWQlmiWfouBPEGB+l+os/gWgzX0FFn/1e1dQcht416O3wzo74dhpg8NtCkupx1gNRfqnChuBn7QYqMsnloQ4BX6CECC50B1wyUDNQZxBkEsYE8dL8TjyZP2nj2w9tALN8NDDAx+6qj4AlB+V5DEs9wA2AtvFzfYY4jBoq1CrF2TVUwVuw3q4v0cVnsTU7RBiyp24wChtl1EGYN5Rfhov1fBSgnGxLtY+sKbjoWB/GwBEnCzGr2OXUULiQgmz2HtVm9/ilymoGk0pfUk7d2CaBDQHK5ZusMLstLLQjMKFkBt5ytd8FRwL1hFAcxLjZOQnEjXt16eGYzUmlkpP81eqra2IhXZwgBNQroazzmljjRoI2WMLqNKUN4UheH0upFz2iHjYGKRloAgSNSSL5v2x5oNDERwZOD/b/svXm0b9tV1/lZzd6/3+nuva/N69OQlkCgQhcJAQkokAAmpYRGDBRKiKSQYRAjJQWFFpRlQhFx0KRAGZYCMgBHBlJaIlZZohQShSCQQPqGl5fktbc75/fbe681648559r7d869Ly9lgm/UYI9x7j3n1+y99tqrmfM7v/M7RaQBlArM2/mq3muz44EQunmeVtrYdTKBMlxbbkjbN3QoGNCfaPt7EJNVcj1SmwOOz+iciERJNibm4TsHQoOSQKxOjQdMgttZwQu4SVvPPEtoud8vg5qIEGNHTJFU06KQ4Szn4Eob1UDG4M9rMU6b/EUSLc7otgChab/6vbjdXmslxsI0GRs/+v6m9+ugKmgAU1mm89hwk6OtKSFSTVN59idCa6v3pxZODYSg60fzN60flfHu7WWnP2pbQ+Z1fO5b2Vm/RSyQFFjM9Wvby348LsDYcZp46KEPw+aYWIQokVJH6jSZWNCkzlTMhAQ594zDAHUEEQU/Qw9Rl7si2uGaUhaAStkOTcPGIwspRaZpYpomchc5ODxnA0AoJxMiRYe7RdjDJEgpOngtOrBar5iCamFutwNJhJQhRK3yWktRkGexOeTv+17iO9+Ba7l71T4pBUYTFff5Yt9paQa+EOuLLcrXGA8hIl2vOla2CcYuk84dQp8bILvLxtFIVfVz+vu+KdsmXUqBViUyEcfRVOPciRJbECqVupNWKALEwPpwfwZjfUZF2HzV13/8wNgQ+Nm//OqPz7n/f3CEKsj/8VtnXj8pVygyEQjsp3N84a1fQwyRX7zvx/i5P3g9x+XyfI4Q+Oq7X8NP8z/zpod+CaCxVP+rC5/P197znbz8id/F33nHf8v7jn8PofIP3vs9ALzotm/gWUef1c71Hx7+l+TQc5C0OFaO116mqlSOyyVAAc3TR5GJk3IFoEkEjDLw8/f+IAAH6Xy7xkvvfNU1r1Fk4vL0EP/ofd9HANZxn0095h++72+yjgc8/+Y/xcsOX83XP+l/uOb3r3eISAM2b997Cl92+zfxHx7+Zf7lh//RjibvR3Ns64af+4PXt3vbz0ftvc+48U/yGTf+yY/6nN7HX3Tb19HHNR/avJf/dPFX2vtTHdnUq7z0zlexjgf85iP/J2+/8tf53973N3jNM36CVdrngeFefvYPfoDjcpnfvfSr/N7lN3FSLvPsc3/M8gyDOviPAu5c771rfXYnCLRIwfXARgt3NSdniQnMARQ/xzJYFpYg1Kk1ennt5aEfj96hC1PldONPn099gpAUlMWBipgayLPTP26Tz2blGcdQAzWye8FF+/U4C9b7tZZM1mv9vYOZ6A2boRNPGS7uuKohf43m0MxN3TzserPsQnTkCdkBdU7bPDvAEfNe2vpr8czmsbZgv5x6f3YZd2HCHXDJL9xuzJ7E4v2608/XB0ZCdGdxB/o9ZRQv9IOF1ueAgvqtE2SulI3u2cLiPPbvzOY63S7ZGe+798nOc54diuve2ikZhNAM47lXFhVow5w025zPnaapE9zYiJgOajOc/cvm0GMOr52riBDF/FwCfU6sw4qDLnOw6jg4OODc0aGBr5qllVOnwEJUgGscR2KIlGliGCdOhhOCmE1UKuM0WNqy6fOljpAyMWa6rNpnXe7Vdo2aTrwaRkoZzFYtjLXwwKXLXN6OHE/CUAOVMo/HsOz4CAZkeY86K31pRur/8/ca+1kW/dPICWeLhTmotaMb2UAUtaOXOvU6HaThSl41PIraln5+EZi8yFCYAWJasa5I9tTBeRQ1Bhdh1qetIlbJHKii7TG5CxF2HULxlHKbB8FBZogmKRDmGzGgRhdYd667znVK9ZO56QzOTCNnb2OjOS6uExByipYym+kSxCjkJOytEl22Il1Z2FuB1EgalJUbQ0fWLYO+M1kCFuxIW4seZWp+bA4Hqm2JzgGK/Ug0sMNy+XOK5ApTiHQJWMF2a2zHqXJStLVVqgKsREoR+r6jSCBOllIdhJw7aq2Mzgbzfc+IFzGGeXjacyiWnqqv2ypkxegCJo9h+5EsKq43ZtYpG6VNkaop4WLgloOqzUmvQg3q8zko3OZNLfq+6PokUokiBJShp/7fiJRRATWUhBSJWsgtRmrdEqSClPZZqv6Ig7ELEGGGpnzmL3bQxf6r9+jjeE73149Jy2h1dnHOnRb1c1CslkVfGTu2zQlp4KH3ajXWa1iA1J7W7p/T4lX6VwBlDDvL2f1jX/9FQTkRUUkDK9SUs8lhWX9TK5OBvpVFMad5SW3BJwF9PjEwmnSi791FPJ9B555qzDogK7rPl9lOE7Nr5rXQisZFZd3HFOmswJCDpylEUpdnGRYjiZUy7TLDxTVck/n3gpTKOA5Mo6aY11pVLmFS/ELAsIZ5bVaCsafFV2oo1Fh2+jiBSpBgoHxcrD0GlE1lQozlLKJFsmOlAdqa4S32XIMV9JzHoGYSJFIUJGjVkiqCmM2sGQk2fiOEkFl1Kouy9C1qKS2whwjDUChlalkiIpqCP8k4B3AobU0XYKwjQ5h9uKU8zkx6iO3ZKvOdVpQqhoj0u4xXkcqwLEwoQhmnnc8UEVtn5nnocjeO9ygr1LIPCOSub3J7nhW0PCcoYXEcFSfDxkAptbFqXRbNf1pfo3/nnNvP6doBs8zC0m+DzWYzj4Va2W63DMPQ+tylh3Kazx08OGFrlLNQXXZI58DU2jXamu2M5lIKfb+a/T0UI8yWqeLPywF/t1Nn0psHQ5It4YVx0jz9qRSKLEH8s8fjAoyt44BcuaypN7qCEkqlTpMCslS6bkXssoaFJ6Wfy1SRMlBqZVMnuvU+MffE3DFsB7ouWTQEY666/ocb94mU7WFvtozjw+yt1uwdnoP1HleuXKVMkxoS9pOSPuxp0k1tMw4qNj0V6lQYh4HUF3LXk3NHSCDTLioeuoSkYJuXTciuA4sANCxmx1KybdF9pJbmsNwoK3LTTfClX4bEoBtRzkiXmWLYYQdFc8wcb62L9s3H0mPVRdDKmMB2ILzxjRTc6LCIDGLaXml21MWN6EQw8WiNOgldn5nK0KJyf3Q8fo7/9d3fwVsv/RoH+Tyv/eRf4vXv+Gbee/xWburv4H989hv573/3pTww3Lvzna+666/ylXd9O5MMvPq3voBRtvzmI/8Xb7v8G7zuOb/Etz717yLAw8MH+e9+98sB+Gcf/Pv8sw/+RDvHy+76Nj77pi9vf1+PwXFxvJ/v+J0vBeDLbn8ln3rh83bef9eV/8T3v/2bgBlCWMd9/vYn/3Ni2E2DuN7x7qu/w+ve9o0Iwiue/LeIIfGj7/p2AL75E76fpx9+2qP24fWOoW74a7/9YiYZFq8K3/a0N/A7l36VN37ghz7qcx6kc7z2Of8CZ74GHv3eHsvx8PAh/ro9p5fc8SoFUBfHO66+mde//ZsB+OaFhq0f/+6BN/JLH/qHvO45/5Lvfsuf4Xk3vohPufB5/M23fjWgsi8pdNQ6oCjS7tO+Fiv2Ix1nvtOWSGcZLF4UWe4IO8jRWYfDUplTPKUr5jjQ2XYu053aWurgx+7ldo+AFvXJmZAyEs2zzp6OPLdt52thBvh2+kF2cKiP0gl3R215nSWSY2/EuZ+ud4UGbjPviaef1Q7E1va4a+1Py+P09YI1KZx59Xq4vrdjBxzUF+x7S8DSRlO49urkwOx8rdDuwXdTPR79vtyc3BmjBE63RD8zf2oXNL7+Vfyb3sOxgV2n7socx2vdZ1gwGnZa/SiDzNem+dk/thEZFv9e887MrnCQf5mW35iO/lHUUI/mDq9D5nC94mC94mBvj3N7exweHHCwXrPu1/Rdp3aKaF2AqydXefjkEmMpjNPIdtyq3jIKwJSqznuXTF9QPLVzduzcqclRKxHnoNqwyp7JdN2Km2++lb31nn2+KOCbEhcmlS24crzlgeMrjCjjcL5BHZ8OxC6D4/7k4+JZh4WuruAACVj1GWUKO1uzMV9jm8kO9Lmzc+rBcK1n7Otico3B1O18TuoMWgQULI+u3ebXNBmCZOSLaZoIQI5aNdnZdzk6oOGZDWJAjTrSfd+Zv6DObym1sbUCcyqi953BAsw7yMLJLJVtHZqT6c4cZh+npFqBm81coLM56+g9h1rJKRGTKtOkpGn+XvNbtVGF7Rb6qHWCcgiEFOiyNK3WSKCPkWyBjceeF/OxOZqrGmjp0dFAhUqgFtsXgimoGqkjBtjfD+zvJ7YDbLYwTMJqlck2Vk82wlRhqpWxVoZxMnmKWQqhimsMzj6GShHYzib+t60dZdZoLTKxFR0jyeqG5JwYBpMLOJXCevbetZ0O3CoYYDFoNPsLA/pijFSbT85clqIpt8oynZgtWQXw6mQAqyhwS4ik1Fl5M60KL16Y0UBHaqGWkVoGpAxExKQXNNDgc/XMzra8RWeO4sVr5rnin0s50/czWNJ1Wce2ZaTi9449hKhp+C0FuBTl9Luud61MowMyDlqHNr6a/Ris9YuU/iVYtgxNtSJbLO1CD5wbOB8mlYcQDRZZLKv5777RtRUgoNJSwEihjvrMUwvG6OhMOVOqqByNgcHTVHRcgWXYmo1ha65KWihr3mlRWjTOGZVCHQuFyQxTWlBppxCizEW1XHPVWdWxy0RRLKKIIBTT113YL02P3ZnfIEklvLQGSiSOpvtu8jExKiDf9b3pyiZSiqQ+kcMKQ29VM7cWnErnoBs2+j1G6M/O98WmjYs/vsqwU1DJQEnmopoxhFYfqGmFD3PxS7+2SwSUUuj6TIz7phu7nA/avnHSonm+t+sQmfeG7TBwsjlpAKmCmgtglUiXs2nt5gWQqrr0sevaey1wUUrba3z+iIhpc+s4HsdRwdNJkMmywsMJpWiguHrRT9tL+75v8ybnTN+t6PrONJfn8VBrbUBtSolxHBcyECPb7Va1W1NakAB37f6+n+8JtJDWer2en0MIFhxQneRpmhjHkQmhlImJymazbWRKgC5lzVAJidz1dJ3KRylw37FareZizAuJA/9x32OaJspQrI/n9jebw9ecoGOsMx3ZPvT0UskxMZVJZTPi9Xff8FgZRx/PIx6dl73nfBa6YWskqowK0FUrkpL6FXnVk3KGUhmPj6nbDTIN1Gkk9ytImditSKu1VprGOswMtzKNbeBLKVZV0zfkCqIaKl3u6FJmKpWyPaEMG8qwtWqkUaNIUhnHjVKWxwkZi+lxqomXcmbV92w3JzqIXv51TN/3PwGw/uOfS3znO5BgulemckspyPGGOo2QXIxY+0ie/wK4SVOZCcyaM2YQuLMoKcP588Q+W8U5XURqLUbPngsahLBI8/TzGuLvkWI/NOKnmkSlGr380mWduO99D/Edv88cjWk8Jv3Xix90HeuDPV28rfLoat0x1Ynjr/w6jv/SX/v4DbI/Oq57hCp8/xf8Fpv7389/uvRv+Zn3v5Y7957KA9t7edrhc3nJna/izvVT+b7f+3O87+T3SKHjjvVT+MDmXRQZ6cKq6YL6IQj3nrwdQXj2uT/Gi2778/zM+1/XTMlJRu7bvAuAP37Ly3j+TV+OILz+7a9iHfc5yOfbuV5217fx9KPnUqVw78k7+In3fDcXpwc4l2/kA5t38cqnvJanHHwye+mID27ezevf/ir6uKaLPQ9sP8C3Pf0N9HHN711+E//k3r/LnXtPbSbcUb6Bv/TUv3tdwG9bjrlv826+/+2v5CjfQCA0APrW1d0878YX8+Lb/8JH7GMR4d6Td/Bz976ed1/9HW5e3cEfnLyDP3v3d3BxvJ9f/OCPAXDb6kmc1CtcHB8A4Pue/U/5Vx/+Kf7V/T8NwJ3rp/Lw+CFuXz+Fr777Ndy191Tu397Lmx7+F/zifT/GnXufgC8aF/pbedVT/hdCCPzyh3+KX3vwfycQ+MtP+5Ed1uyjHVMd+cDmnfzwO19NpbKOB3xo+17+8lN/mLv2n0EOmfs27+Z1b3sFF7pbECpXpou8+mk/yu3rJzPUDZemh7hj/RS++y1/mk05Zi8d8sHte3jtJ/8LfmX1c/yG/BJ1O2iZZbO0Qgg7gKf3IZwGca59eKrW7DiDszSLOTpae2ORPoTvBWevuXzN9cxOGxVLg2v+/AKkkvmV9tuM91nRLhqoGVY9se8InRXs6vtm2DpvMzAbgUtoagkeLwHIamv+NQsjt7aF5R8797HzDLyP/Ab8Yw7GLj4QvfiOdtBOKpHiN7t8yNOAuvizamlntbHwGlR7CtibGWdzH+/edAst7tynuxxh+XDMCVi28cwYDKee7an7Of330oFaHinsGmwi7pw503N5Q36daCDf/B1P9W4slfmM9ofMf7dTpoXdETB3D79wG+v4PIw741/c+ZNF+HnRFcs+a6ncC/B7OWucnbbTzzsg86nr7NzN4rwLgHC+UiBIYN1n9lcrjvYPuHB4nguH5zk8OORw/5C+7zk5OWYcN4zjhu3mhO1mw3bYGnto0kBJUFaX6qQVZSdZ0a4ilfVqbU6xMuS8e4M5qOpoocCEFUYZrHBEELjh/Dm63NN1K3K3R1rtq3SSmPM7DFy8eokHLl/lyjAyABOJEFJjcDg71CaoBYh29Us1YK59qyzBXZBJP5dxLWER0xO0/k1x1uxdrj/L574E332IqZPWEUNuzlIbpoJmWRmoHNx5TqmdJUYtGqPjP7Zgj49cVwhtxFwRZQ2m2ADWMmnV45zmwnGzUyYtSCHW6LADECyBioU2rZQmVRBjojPtxeCamSkxeupw8GJlysZJln0XY2C1SuSkcuHrLrCXhb110II1ARIT+73pGYpLVSgYlwKs+8i5VWKdAl2c8x7+cwO1j+3QtcMBlE0VNlUYirAZhbHNe92vx1KpITJNsB0UpNpsYTPAZhvYjNB10XSINSiyHaHGyFTh5GRk3Np+UQWRwjSNbV+SKozDoBXCrXmOH3o18+p2iLXfuynnrgE3wzDqec0XVPBhbP26yy5zbW79jPtrXe7aWAWIKTftbw3mCdM4UKaBWkbKpIF7l7uqouSfGHRvFBF95owkKQQZoZxQNsdECpFCkAnKljpuqUXPqxIFZoMEZ07Pz067ZbZhdH+YgVBBmMZRCy/5OE6Rvb09clI2bLI9tBVWM1DFjzmoN+83tRSkTHghbgdL1Ff39s3rOqD2kTiYHxFjBzuo1HRLHXRpUnUyP2vBGMnKxJWqrLaZ/TzbhDt2oT1r39eLKHg0jCPjWFqf6fohEFXXuohn+5cWfGpV26XMVee9iGUVkGK2i1jxLAO7zLbwUeRtarti9P6dWYu1aJGhMk2M09DGaK0KrFbDTVqxRcMGvCvEpf6MMSjBdbpDA/e8kHlKmdz1kLLhO9rSGGfGPgEkhKanHWIk5aRBhhiafJADlP4snKF7Ldb2MiguTd7SpBxasVwNorm0hrImtchW02THAWGdw3796GnOKMt3ee9hEXytBpxWKZQyM+t97unYRDO/fVzZfqK2g7FgS6HrugYG6jnENFy1rV5YasfKq9WNK/vOXBBuGicrMrX0edRmKWbTxZTUnjk1/p0R2/c9XdfpmigesHKCntpiTpBQALRa8dFqwHNqkgiTFRwrLSiZLGtE/S/fq5t9XhdZXmKauNNcaAwR0yoGTE931rDW/ccBbkTtkpTTmXm+BGxd57k9R4LJOZiGbIAuzev8r/zf/w8XH7l4zY33ccGMpVZkswEEibbQFo0ChhCac6obp1WfXGwXIUaLUE66qadE3ssahbXbjjEQug5BKGU20P29lDqCJKpFxEMUYtbBHFKGlGEwcWPTAIpmzNZYCUk3AgFKmbQIw6CfO7Ua2EInzSoKBItYzpXbuOeJyPnzauiKwG23w9HR7Gz5piHSCnNES9dKOdGve7petcw0JUS5BT4ZtKKjghPRNMuIsS3ePkFdukDApApGq5w3Mq1XajxMAzWq0xff9Q4YB4o7b/ZsNFXONzKbwJHmKH7MjkuX4A1v0N9f8AJ43vN233/f++BnfkZ/f+lL4alPnd/7yZ+ED3xg9/PPfz589md/DBv4GI5//I/h/e+HgwP4i39xRhEeegj+3t+bP3f77fC1Xzv//c53wj/5J/Pfn/RJ8CVfor//g38AH/7w/N4rXgHnZ8AT4KbVHTzr6DP5wlvtnEfwxP1nctfe0wB43k0v5hnDZ7TPP/PoMx/1Nlx64O79p3PP/jN55rnP3FnUPunc8/X/85/NPfvPRET4glu/ik052TnPYb4AaCrQ3fvP4AU3v5QHrdjWs889n6cefApH3Y16rb1n8MJbv4pNObbvRJ64/4l0sSeGxKXxoZ1z76WDR72HVdrnnv1n8oW3fg1jHc68f9v6yY/6fT9CCNy1/zSed9OLuWvv6dY/z+OZR5/BcbnEtm6u+b31TvsCTz96LjmsuG39RO7e1/Pcur6bTzr/fE7K1Z3vHi4A7VtXd/PMo8/UTTM89mU/x4579p/JH7/lZVyZLtq9wJMOPol12gdUW/hP3PpnmYzS38cV9+w/kxgiq7THUXcDAM+/6U9xeXoEgOfwgllawgyGufDT3Gfgmz7td3/vuqzZYPuCr5HN3QkN5Jlxtus7pNcCYnf/NiCR651j+bqcfT3QNmkFh6qxb2bJmWBGiGrfXO86skhDny+3wB7a9drOGRafCWfvcTbfT13nDDDm55ifVbuy7Hy1PYXlVRpI0x6Yn/os2Cmy1L5MCz1LrfIri0YHQmNi7YC6fhmZncmdRgLOcpgdz7Dj/O3cwek20gbqzvtuU22LrAAAIABJREFU7O8WPzrb7/5dB2BbX9jll4b1EsR0Q9ffDTvPYz7v7r2eeuZh0YHemR6w1Q8sP433xRl29s6ZF41efk7mSxC8aTLf2+xeL/6dW87Ou9d67+yzQsRsQpUguOHgiKODffb31hztHXDh6AJHRxfo+zUhRo6Pjzm+epVh2lCmgamMnGxPGJwB6wHtoGnlSETEnApnYtWg2mRmE0qZVE5LTNnR0qlVz7KApUTmpCw5RJiGE0ItiDkVqRTy+oCuWxFSJkmlrteUouy6i5utaskGZvaUyJke8meiQMXs1C7X2zaVBbMDLaW1daksPjcvKjvvB5oj7yySWcfWvmcGphi45SPAx77hZLSCOl653W3g5jCJPRdUAxPwtM0d0AZwJpVgNvlkqeBJQVmHVpBKZCLHnhoyJppANZCNdp156fD2uGMGVfX0TB/Ui6dUcb1D90W0kItI1VTdEIgU6JS5VVJsMjvR2LJeR0JweYZgOrGRFDUtdzFdH22GfFyO5cibqqYcV3Nbij+3oE52McmCHfAEAxSMODNOMFpaf0yRWEHEWXSqsVuKjtVqveUF8hrQwGJ/B50HLnWRxIp0eg/p52qt4IBgrQp8BSw4ASQd60sQVtd8vYrqGoaFHNxCKqQ59H7Pyz3AxrvPC+8fEQOnsLVHoOroVBHdCeqkAKwUQF+TMmF0ZJx8433dmmZ/ziHqhc3ifdcCEMb2t0rsbsN4cR8FKGQGVMtEmaaWco31IWWZuaD9U4sDY5U5/fr0PmZ7YLNH5r813X9exLwOzDy8du2MYMxg/7ctbw6uLzro7M7drmxzWxmHO2uTXdNFVVpQPWBkX2kgT1A+brt3EUc+XCvU5Ql13kcwyS/rT3xstIep4NWOSSCtr7RSfCIlUUxDKqQAKRpwaIBXLST7XQE1sUJNlSJBF+uqDN8QLA2/SSMYGFp103f9XGXhzmNQzV/LgGg25UQgq2zXwr7RcaSg2O6z9GDnPNcVvIssRoXKZhj2UZOyk8W0akOIO7ZpdGJb46mZjEqwdQYrLOf7mgcnojOzNSBhw0BHTPQggRlFSfGZ06Dyrp01A7gz21KZ99Nk5xWZ7XK/oDc82LOJc7A2d5l8ZmzMki91sYfPdoKz3GngqbJkZX42zPKgMeimFVp/WiFi5oBwcr1d0DW5aJBb5Z5Ms3camYxNHE+ttzoNDCRPLglka3TwuR0a1ub7ZrB7cTC2lEKYFuuK9XXTjo2R3Mahjv/Qzqv9Wk2fZ2nPX+94nICxAptBl8BoulSuzWJ6eS39cqHjJLYsEaOCf7Wqvuy0pQtr5oq7sqjWGNrA9I0vxcTeag9InBxf1ciQCP06EXJHShm6nlKvKDO3FggjqRaQUTfhKOSUbZMxnZbJ47677kn1wmSSwB1pMb2YWgmHR/DMZyF33W0+oG1CMqfPRGYDLJrIfMqZ3GVW6xWrvRV97sgpkWPCpXQCrpkSF4uhpxO41owNsGLRDfHIdqWWgXEc2QxbTsrEZjswPuEJlFtvU1Hm970H2Z40naOYsciIQyL2fzjFfhNgHBUsXR4hwBOfqFbnYzkeeQT+6l/V37/3e8+Cse985/z+M56xC8a+8Y3wG78B0zS343u+5w8HjL16FT6oACM/8APw678OT3gCvPKV2gcPPwy/+Zva9nvu0ft88pO1bU98IjzwAPzrfw2veQ086Ul6rhe9CJ71LH3/B34A3vMeOHdOgd6v+Aq9z5MTuOPO1ozb1k/iz9z1rdds4hfc+tX/Wbf4p+/8S4/6fgiBL739FR/xPJ9/61d+hHN84zXfu2vvade9t0c7Ykj8qTv+4kf9vWsdz7vxRXDj2defdPDsa37+oeGDnFTVvQ3AZ9/05dy6uqcBoX48cf9ZPHH/Wde97nPOv4DnnH/B/+d2f/FtX3/d91LIvOQ6mrvL44tu+7prvyFmGkVaYQ4Rd3Lc+D4dnXRn5iwgtAs7zEAsMDMhFw7HtQCx09HQ0yCw/s68L52CiOaI/BxFb8bXoqXN6RIIoZKDpm5VM9JCsKJdyfYuu0zjTobFXbatcQYpZyPgrNvtQMmulaBGnITTn58dU1kYp4/FmT/LILXo+OzptHNdz2BxEMeNrmhgSYoa4qtlke4430Yz1ATAtK38mg6I+d35X+6gtsqnMo+l08eZlCtZjjjTto0+FmYjdglMzqw6/beawa4f88BpaOMEa+vs+s1Iy3wmaW1p++tuy5mrmcx97AZ4c3DtbtrtLcE3oY3z5b3MwQ89f2UBhLXPzu1jJmO0OIk04MzH9eI5ytwmCaFVFRO/rfaI5zkQ0LHQxUSfE4frNffc+gTOnztkz4pwrft9+vUeFTjZbvjQAx9muHoJkUKImlZaqRAt4yp3iKhsSRAtOhTMeYni6fUwWXaVTAMxCDFnpnEkiND1K8o4aMHaIOQYSd2avbUWxZRarMiOsjzGcYtsr7InVQuLdStqjKz7jhviITElhnFiO1ZKs/h8PfXnqmuE+HyyIL4DH24XOxijfzoAhOquMn/Gx3pYfn65+lqRFx/281w2W1NANTh9BXBG9zwGnPcvCJRJ10X12O3voLUdYlI9xZiAuZLzAtKz3+tusRSZ9xQCSIjqs9eCTBtk2hBkj9AdEEJHFeUa2mPDfe/lHBG772BZYBKKET3c+TdAOgZLnRYk6twPXqjF9H5D6EjJZmOwZxO1iFctkRh353JKgS5rYa8uQIri8PfO2vPxP+Z1qZof5kzlEJyJph/r85LlNrMkoznoCSEWGEc9Twiw1yW6DpV2K0YuifYsg0CVNrb1suovRlnuu7Q9SUfK7KT7PXgqvq/d4nVEbD9yHUofCL72VC8wJdIACUIwMNr2I13wlG1Y5r23WvEoMaIOJkMg1cZB1fVinhkGCIRqoOuATIMCshQdy1UzSanFtHNtDlbfA6Fpe9rjcxIPi32kVlc7ndPnVZpvoc+JfsULmEk1ILaYbxxCA3JiDI0x7HfTQB8Dch1vWc61pQUy7+32e3uetD2jAdC2dzlTdFf7fqm5qRMtSjWQUZz7tDNCloZQCDTmb2kEq10xkxSiZlQQTM9XsxGmaU7DdpkFPyI6r1PUjIdqc8P329gyG2Jr+24gbgZjl+w+BQh9bKOELgJe5CrERM6L7xTXDvU0/EopzGCdBMopcFR3I2VI5poJoSyyABJbqQ3/kDaabV20eSxTUcmZZjbqnHGmdQi7/oCOrzmoISJ0mWYzz0aE7V8xkyMQ5kBFzrkBdL6XxLiw43y0nPIhavFMmVmWxue62N7T9kJCA7ZBx2TXd+0+nRnrxbBEhK5T6C6ZhIIbV5uTE5VCcZupSfNYEMKDTHbtnLum298yOuyn6aQufIlaZSGbMus2e2BxmiamcYTgLGC9VvJskJhakfQlwBwMMF3q6zpLtdTKdruZWbCiRRa3W81EiKf6JmASKXR45lbX5bYuCbRij0vdbylFgyfmE06jahjHFHf7xCb5UqYAZi3qjNk2IbQMcEKwPYnrHo8LMDYE1USqVZAimkrpAYwQCEErL0rQSGqVSsyZ3PeUIJRh25wtRJi2wlgG+rzWTqm6cEyemuKTFEiik3Bv/5DtNFGuilGagXVAQoJoIsSEtinkWpArBdlW8jq3NCS2hYHAwJZxu9VNEWChVxRCbMi9U6vdoAspw3/9Z5C+s/lkG2GdF5AuBbqc9KfvWK9X7K/3SFkjksnSp4LpoOh1PM3DjRCvBBpQOy5amphGN32yT0bzljoCE0Shz5G9vcQNwDCOnGwnrmxHHrl8RfV/nWJvqQjWGESsUqPvqkCdqu/YcO+9u+CoD44PfQhuWVSrPw2ePJpxuXT4rwG67Lz/sz+rv997L9x116Of77Fc+6M5fvmX4SUvuf77P/zD8J3fqb//238Lr3sd/OAPwtOfDvffD9/6rcr43d+Ht74VXvxi+Pmfh3/zb2aQ95u+Cb7xG+FpynTle78XfuVX4N//+sfmHv7o+JgeIsJr3/YXeMhYwILwvb/3tXzDk/4mn3Xjl/wXbt3H5kiWclQavFgWU1JTUnWzVwec6sUNzzInr3m48S7u0M+Hsohm9PcsALk4zeK90xHq9ltzInfP4697vYrFft6MkBASXR/pVx2p65hSYCJQkzkVZogsWjHvD34N2T1vy7Lwdi5sUP3/LBg3t/fsvQQzUhwk3OmzXURut59OgY9n1tDFGuxwzJL57ECealpqf6iRVqjGFqnGZHAgqd1DsAIVft92zmULHKJpfVKFftWxt7fHsNkwDKO1aVc+YAnMX+t/hyTdyPZbbZ8JO91v7y8KwTTHfX4eepgD7sU0zBCvdS4kQUvZmhkti1PSOkTm7l/qmzlQFkLBx8FSL8vHdKmCa4rO352fdYNlFyBuaJ1ejSViyJIZtcrqqHN/nxpj3mfF2794UXUPaTdYbYoHhMO9NU+4cAO3nL/AzRdu4NzeOVJWYGOcJu677wNcunyZglYH7jotCIKliR4fbxR+MPbiYM5AnzM5JvoYkNhpgSeTxpKQgITq5qsDVmTi0skj1Dqxv7qADFe4eukiVYT9vQP6wwvcdNMFai1cvXQZ6kgOExISFdhOcPmhDcPxJQ4Oz3P+xls4PgmsVoF139NHGB98hCulKqht9CgfHzGmGagQLC3QtSyDrU82UELaGefLIwatOu6js9Z6Ks2xPXLcMZ9/bD5LaPqd8/ql5AtnkQes2JYBvqAp4/MYDUzjQM4dOfcazCruMC/BEO3/GJyX6wCJrbFB0xWtDDAxJMbNFU4e+gMu3/sWCHDwhKewOvcE8t55wuockrQaeRBpdrfriLY5UEwOJThz0yRFmH0AXatMDiFjLEjT6e16cp91rEohBZCq9zgFYRgEmSZyUKBGU9hEGVcpqDJprVSTWZgVM/9wjiUZJWcFUzQBMlBCYrCaGjFW9vf0voZJx89QAgQhRegEVp0mTZaiBWsuXy5o1qzJ0dk8U3DPAP2oGozVmJkhCFOZW6cjYRHoEvWdpFWOn1lezsRykDHgPhpN75S29qvdokxaYQpxlikISqiJCd0IbAxuN5e0HSGScwQZleHqRaBlmiUW0IJXenlBZFKwtW5hOoFpQx1PCIy6nsoEZdRzNaDM/KJAa7cHQpihTHBA2gI2MQRy16kWbDZty0aYmYHh4qnGkzNyXWZA70FMIsDnq2ZmGtBlsgWKSTqbMTTgNHqxwJ11xrc1fwazzRQdiZHlHiekNDNZlxIIuz3gwGBoYI3vMTOgpNfRAnPB9nLt65w83KLg3SgVSqWIyhkM48QwDUzGQA0mb5K7zrACA3ryXJCpTHOhrKgon+qBLmQAY4ytXSEEpFrdm0VfFQQJopKN4jei8yhVwGokYMCYtPuOxBS06F6sGJCwMO90noyjMiXHaWQ0RmNOHdicEhHVIo1Z9UurZhrXopliqWZyp8S1MlUCRUHppBjQ/OytjQaeqswDsxZoKYxlWjApYRoXxZJ9n1us3Tl5EUbzR9IMdDfQsOt2zNuDgwPcBm3sS8FsHZ1r4zDugOFigcNiWqvbcZgxIQMmZ8DU7bjYwEbXe1/trdmPsekDa7x9lpWo47Qg2OnzmmyNGsddfdeUEkWW9p8GOfu+JyXFnwC6VT9nFSzdAExP1rVqpVLqZHIus68xmWPU565p5Pp7TjI82J8zRGOIpP3DVhTRr4VoAbNxHJmGkZNhtJSa0NqlpqGCiykluk7Z+zEEYtcvfBb9b5y88KIswNti8lDOFvb1X/Wou2z69zE3CbyUk9ke1997HxdgbJvktaKMWFt8zJAMIUCtKiUQA+NgjNOu0+ppMTFuNnhKXawVubohH61IVnJ0HAYE1ygR9yyJORNSYjtOGg9NCVJpKRT9yg1DQfb2VDfIWDnb9T6bRx4myIRIYTtNTCfHMA5IUR0M8wUXVCbfRFzbBdXI/eTnUJ/4RAWUU9QoqG1GXZdYr/dZ9R2rnFn1HetOQVN11ph1Dxsd2zeeeSvJeWaXKpMha5Q+ZVJeE/O6aeZmE9geS2HYbtkeX0Smq9QQCHU0cFlYdT197jncE9brzP1f9CVMb34zvPMdLEWtYwh0nS0QDiqIRutjCgzx1CB9zWvgcz4HvuzL4NM/XcHHr/gK2G7huc9VRico0/M//kd9bj/xE/Dd3z2f43Wvgx//ce2LX/s1+P7v13R9P17xCgUvj470HPkxTIfv/E746Z+e//7hH4Yv/uKP/L2PdHzhFyprF+Brvgb+/b//zz/n6eMNb4Cf+in9/QUvgG/5FmUD/9HxuDxCCHz703/cDLr5OMw3/Bdq0cf+0CXKwJhmCM9HM1gWBh4GuKkDfRYk2D3/7EzM/9orIVCXxoMZTmEBOj3quU+Dju2OdoGDlJJGpJsRtWyDtipEkBAYRShSkdgTrKijuC7Vte6uFV6g9V2ttaVnLtsWPTrL4sPXOhrAd8032bFX5GxK/E5vmBGzrKK6/OyyjTuGFfO9tHM2UGjuxGJe9ZyOOLtkgjlGp27mzLP1zgvzd4dhnIuMhLCTmn29Y2m0nb63Bjpep2PdZQwBqxY9N8f8ZDTFyoGNYM6zp64GC+xaRpE5tZ5VoyZUxamnHuSdwdWz96LXMT0tFs8i7Pbz3MrdOXEtgNrT98PyqzvXhUk0O7IxWqWSRHY08aI76gvHytsp5uB6emFeZY6OjnjqXXdzfu+AddfT5cw4bHnggQc5Pjk26YEKMZs2b6ZLiePLFxmnUVlLVdhb75HrRETUQSwTh+uO/b0Ve3sHhDSn9IkIKfdcvXoF6nmVtwqq5nl484BU1RSt6yvko2OQQpcze4cXCP0hMg2k1USdjgEhygYZB04eeoij8zczbh7m4pX7kfEqN9/2ZMaxkKQjnz/HplTuu3jM1bEw1UpOsyyA913uVhjuPTv27bkECDNrhugsPytMMk2M41UODg5tHAW1DcMixdqeuzI79fq1Wmr1onqyPzQP8swsFwOKkcYq8ZR8Sm3gtn+nUilSyFLMZq+NiefjOYZAjkkz7ppWuI6pFEFzEpQUcvzIBykX74VLH2A13U8KhZP3P8SwvsDhTXdzePenUFNq0gUzSMPCqfd5vVg3G+iMgT/KCg5BgYMuW5ZaUF3aftXRd4G+g70VdCuHNyshQu4Dq1UmAVTYXwct6BW0qFcHWsArhD90IBYa/oUAm2FiFE04HgtcPRGqge7jpEGBEDJTCZwMwlACwyRsBxhGtC5IUmBdpkCZIE5qEzjgUCZlGCqwo8ivFjsrTKNqvc7+0qKdC/De07tnUM+APVs3x3HbdB2dIRVTasGv2rIZpZ23WHo+mC54kMae1ikXSUmr0kudKENlHK7OBQmlkpTqaD+VGsQ0T62AVxmIMkLZQhmoZaCPpr1aC0iZAWTsXA2IrgYXGpM8BIRIFZVI8e+lvmd/tWr6uV7Z3tOv9b6KgTDTLNVX5//rNC0CJb4fgbTnEhYwqo8iPXdIp1LtHaSFpk/pt6aSDou1Jvg/y0CfVpgPxvostu60TNTF4ZkqowF+LeCtC6uCOkmDb10QQomWgm+SBTZ+3J5JITT2ad/3SDDAVoQyFQPAqwXMVNdTuyrs9F1KkdVqPZO8bA1u4KEFJYKYCRBVo9gBPtf3rLUqpoKvYXM20ThOnJwcG8CuILuUQuo6Ojzwi2GiuuZK1fsWn19WIC9mG2kWwNtsNprlVPX1JFpQEVT2cRqVCJZzT04decgtO0X1aBXqXkqdpRSgQnS/3vYJt+Uc/Pf9pi6AWN+/SilcuXKl9bUyIa1o1KQa0KvVipw9aEnTJfa+dS3ztl8RjOym+2JK0UgN2j9FKuM0ar+1wEPcadMwbG2NK6SsoN84jZRxUhA+RNbrtd6bAZIIdCmRQtb6R15QywmBQQOjXrwKFKjVZ6AgsUsRLO0ub5OISoiu1+umW0uIxJzp+l4zQHzNdVPDpInqVG1Zk3a9WivbYct4fHUuZma6xNhY8j7u+1739pzZ29trPpGEedzhhETtUTtHZbRreREyRNcTnzse/EgpsVr1JgGkz3q7Hdpao3NWAzBTqVqY3gKAjUW9IGWePh4fYKwZJepY1DYwleVgLJhxUjmNnOlzxzSqtlZMmdV6zUnwoioVKRPT5oRNSuR1Ja1WhBwNqI3Eqjqm+n11DoZx1IUvgNjiNJWRMGWLtq/oujUSVJw8xUBe7TOVggwnMG6Yhg3TtIVxi0wjtU6kLirGsPD61ckQWK+RZ32iRtKfcCscHtiCArnr6Dplva67zHqt+q856SDJTXR6FgwPzA6KA6Ee9Y+hMy0ti3KECKQGxua81v9TR8odqVur7k/VBTBIoQzCNCXK5PpExRb2QEpwPh2wueUWru7vs7WJFYUWMfHCJDN4oP/vh0QJkcvLMfGrv6oMVYBv+AZNt3/72+GHfgje9jb4uq+DzQZ+7ufg279dmaGf8inw8pcr4xNUouCFL9SFaH8fPv/z4eJF+NEf1fdf9CL4xE+E1Wqmq13vEIG/8TfgF39R/37lK+G7vgt+5EeUefr1X6+v/9APwbvfrQDvd33XLvLyaMfBATzlKfr7ev3YvvPRHK9+tWrGPvgg/K2/pf30whfCnXeyg0j90fG4Om7sb/sv3YSP6+HpIs2Yxv4Ou7pEfri8CsyA0ZJx5RH85TGn2TAb46eBVFnwZj8CEDszNndfP80gOw3KnV0KbNWOpm2UjAFrGrGSrBL4Ym1agl1+v83xXzgwYXkJ5PSvWDD3DB7mRpldZHmSBoTOcb4ZaD19XJsdfPb1Rzt2nv1OYxet3kWG2+MNQffF3c/vXvvacOJ87VKK9VM801nXu79rHTMLR6/ie5+Ps7g4uT+j9pnWxhnY0b4v5mRi4OsuyLlkxXq/hDN3eu02z/diDkJ7duy8vrhDTvfiaSC2Gd9SdYz7Z004NiCo7JqCy6uc2et61p0GoA9WPSsrDtFlTzlLZvPYOcLMAnJpJVBjerVecdOFC3QhgVTG7YYHH3qYzeaEcRoodcKLmiroV9luTgjAXt9p9eo6sV51rFbn6bueLkW2Vy+qTRaDgS2VmHoIWthrLJD6A9WZKxPbSQupdn1HjsYm3Y6giaFIjGylYxoFaqTGFbEzZ2gzcXL5Kg/fdy/7tSgrqFszPAIn63369RFdTNQauOXokO0wAQOXR7OLCQS8MrOOvyD6LFTCy5wyQItireyxzQ67fldZo0rWD4Sga1QIJg2wGMMO2wszOxsHHGptNmkDits6uWDG43asDyUDomrVokE2PXPJkCpTAAkjx8fH1DIpSGGFfSREK+IRW+vcQQ44VlSI5Zju+AN00/2EdAU5yExjYT9CWhX6cIV1ucRY95hiBHLbX8TWYhrjdV4rnIVcJmV3OcDVWMolUoJokaYYGjAkCzvaCVZSBKkTVVSaITtOXcSkD7Q/s4E+Mcx9+PE8Tq+FYv06FS1WNNlPJRgA7gAUEBIVZbRVoYFTdhb1lawojJNqanW2WGhpuX5lkUqdAuTYYgyl1FbZ3jYLYzPXGYxNs69SSiGZjnALYHmQy64TggNBwYC3YmC7ApP6zLW6eCCQU54ZesGYqEGL0SGTpTirPIHzVFW6Ra8tdbJ0ZGXNigGy1AmpoxXvmtDsg9lGaJIHy7Y3wE3vIxDMLtNe1HkZmwRBTpGu6+c9Lbikgvnxxh4bpxGxKvcOHnthLA0awqwPbO2R0PYz3wPnePsyILoAVE+97iuGfd0Ks1mGgA8C3y8NyNRAdWEctkzTMF9jIeUzZ+tEgmWDOCAbo2o5i4E0LUguc9GmuCwo6mtEdB3YedyUpsVa5+b6mFlIJ3nhqca2NxZnW8sW8w9EWcl2aYsBIEjTJ60WNJCyDJTp+BU88G08TjHUIdg5UkKMWlsRYuwIODNyYipT65cyFUoqzT4JIhYjDqipFcgpKdPdMiLEAngpKQPbn8U4jQQrxo4Vemys12lCs/MdAwnUODNbQXN6/PktAcalLe/gXhthQYAVpRTGcWxgndv4GvjROVZNemIurir2+mwPx+QMV5smQDDdWB/HKc2FpFLSAHkptTE7de6CxNzGXkDnpXJ59N62lv0kaFA2G1DtczCGOdARoBH4XNt19rXmQrq+Rio4b2uoAEXHTql1YSuExu5udgGh6QLvSDK0+aPyM2HpZ4jqgfv8G8ex7aXYM5VAGytBjRqyrbXLQqF+jsmK2TljOAAnm5MFqB6tD2bpiFKqZelYYCUHQDOGdNwJk8loNBLodY7HBxgLqilafdmYxZB94pdSNEs+BLpVr58VTSdb7+2BhFYJcBpBtidsNyeUEDStv9MCPqk5+Fo5LWYtjDJNE5NvWjFA1Qk1lULMgT6v6bp9hqqaT6nLrPrMlePLlDpSt4W6VUA2DAMUZctK6nCxaj9EBFnvIbfcQn3WJ9pmVUgIfaeb3mq1ZrVes7+/x16OdG0hru7C48Zksj3GK825OpQv4irKvTLD1yaUmmpa6TAqCOtVMGNMRNMS0cBKpK73GTF2j7hm0KDGgS10ezly7uCQ0veMZkh6K6NYes/CudNnDAchM5xKAeVd71Id1BC0iNZtt8Gb3wx/5+/o+y99qRbr+smfVD3Ul71Mwdebb57B2M/5HPgrf2U+5xd9EfT9DMa+5CXw5V/+2AfpG94A990Hn/qp8Lmfq6DJL/yC/u9g7G/+prbz5psf+3n/MI6Xv1xB41/7Nf37s7S4Fm99Kzzjme1jJweRD9/V6z3UCjfdBHffDb/1WzqGb7tNJSN++7f1C3fdpezkt7xF/37yk6HrFDBfHjkrWB4C8eEHyfd/kOt7BteERxav7QIB45M+AelXhO2G/B5lF1+Qm9mXIwTh4m0TxdaQUiZWXd80dGKMbDaqR9N16uzHFDUSG3RNGseBlHIzrmtZOJELwDDGMEeXc9ZAjRVdcJFyr9KJCAeHe7ieGOi5rx6foDqEic5ScPzzalhGhsMDymoFUukTB77aAAAgAElEQVTe9vun+uN0r+2aqbALJJ0Bka7xSBzwEPOwRYT99R4xqGbTZruloUDMZr7/bVed29K8deFYLs1LY2vK2UY0I2kJ9sjZr5ztiXncLM9grt3piyzaPxtLer2dj5xq53y/1wLpfDP3v5cMUHcgQ46qjZ4zMXfUbGCs6YCdOS+ycyc7rZHdTy4x1dA+6DIHyzGwcBZab+1sXd7qnUf0aEDr9frjIx27IPzufOcaf+18wn0tOc3A3B0P7mgpuBx2zqdfcxDE0yev3c7Tx/L+ZtbmvL95ACK6A27zyE7YCltVZkdUMFYrQbXmFtrKELTgaErz2DUDkxawYMdY3e290+PAO22eazMbVq77DE+/dPZ88+s+dgMKZK6TpvrnqFWTD/sVR3trDtdr9tcrjg4OWa9W9H1Pv1qpAdzsHD1XZA7KCLT0b3U8IEQtJDIOA2XQSuJdTqTYU6qep6LBkaQlyjk4OGC/78kJTq4+wnp/xcHRDaxW+ySEq0ErbhcRhqlyvN1ydP6QlNcgke32RFMGQ6FKYqhbQlTtWhJURiR2umeiANVQIA3VwLRECL1mKNUtmxG2x8dMFx9kfbBPXG+Z6sjV1T79LZnU7xMRbjjY5+rJCUOZOBlHxqrgg9TSGKwxLFkazliZn7sCsDTHJYpq06VQKSEhWaUEQkwGzubGyPfBoHukggyTuBYf5kxpZmtzlprTE2YQpc77T7Dz6l6r4MA0bhmngf39ALkHEUb9GifHl6mlKmspAhKUicPMdXRnMFqbBH3unWzpuUhMx4RVIXQrrlwe2Ntf0a874h5EjglyApKQqCCiiN8zc/Fdn8M2sV2/VCt1295ghY4wUMQlYIsxpVy+QwTKJHruIExWqKpM7sCLgrXZCvWGQBfVR/h4YbHXygS4xqfwQF9Lvw2w6rUoS6kwTJqeXYoRTII+sxghZ113JgMnk6VVu9xEtDkfjdLq4CwomB1tnVTNTN/hTu2roiCJzpF5D5IqpD41DcNpmmYQSS8AEszCUb9USjE2uQFsZWCaBkal90IHXd/NTOU2X9xHcz1OwbN/nH0aa6FOA9O4hToSg4KfUouy72UkSNEfHMx3G3JRnMz2hoiywtWXE9NCNi8zaGpyzsnYaVrRPMW0sAddCmehDSuFMo063+3aSME1dIMZIyHOvnEDqwS8mF+QBRgfpGnbBgIheWCzWTM2IBbP1PetoEX3gmUFJKsFE2Ns2Zl1GhtzeWkf+Lhe7nshBnz59OI/bqdXRLVld/qdMzaTA2ZCVC1OYx86o1vQ+RAtOyWlBYglcyX4MBt1C9vSANOysGXbXmn7oz+XIq1QmBYcZM6IQChltLEnluLuQKw0gHsZvAAhZ9vhjWXpRDmwwOI4Nt8oBF2XscyXEOa0fF2zAoREzpFozywETI83NDlLs5ja91oKuT+/sMsm9iKKpZSZ3b5kBdvRdbmBldW0XlXTVKVpqsuOtEJctExvHQNTm08EtUs8bR/bX4lzCrsAucsEJ1LbHPHHrFJCyeZlZ9e0zDvX3TZQ1KUn3NcoY5l1TDEbye1NUQ3q5d4d0jyNfAwGY/s6noNAqUVB9nHSNTgqCbFK1dd9xw1QS94FgS1DQEFmY5db8TataeQyGfPUBCihtMzJUuo8VlCpUQmiGVU2T6gesNdPpRjbvBZ7/mWacB+3rWuLtbMYU3jJ3g+ePdbWGl1nokmNhBg1g2bBMr/W8bgAY2OKxD7NUYxJGSlzIQsT1a1FF5cg9KvM9mRQfdcQODp3xMUrF5mYCCRi3qfUylhG6smx6m70PbFfserWrAj0KTFVnYyTjMg0KoMTNY5yXpFSx2q1x97BIZsrA5s6sr9e06eOdacyCCebY7YPPUC5/37qOFkBgYCk1CbCjltShfoJn4A85zkq7k8l5cjequeWG8+z2lu3SZYIRJmaoyGS5jU9OMKvg3Z/3dOlzGbUKDRWbTGlnhA6QorNuAB1CoNpvk2iC3CsgSSFmCZlEZhxk7sexhU16WROVKgBqVOLLFDhhnPnmY4OGVYdx+Oc2hKTRsFNLnxe8AWOYmRzGoz9lm+BP/En4NM+Tf//+39fQcGP9hChea7XYr+efv8xAAW8+c0KEPt3luf98R//6Nv4h3HUqhIN3/Ed+vdLXqL3/umfvqMZ+67nHPKDf/tOuOnTlXn85/6cgt23fqqe40u/Db75m+ETXq5f+PN/G77gC+DT7O+/9hPKtv3ir5+vCwrq/taHICWOfv4fcuOPvJY5oCDNBtPDAaQZahG59qMJBP7gdW9kvOfJdO96O7d9w3cBgRdt/hueO34+EuHffcMjPDJd4dLFR7j44IM85e67uXT1mNyvWO/t8/bffxsHe/vcdtvt3Hb7HewfHnL//Q8SozAOJ7z//e/jhhtuIlnhlatXrrJer+lzRy2F7XZDqZX1asXJyQknmy033XwTDz/yMMMw6Pp0eI4AbIeRYdhSp4HnPe/ZjNOJ6WlVpFTe9B9/l6FE9o9u5LZ77qEgDOPYjLTVas17P/ezefgpT4LNhtu/5M8TikUF3ci1/msMdGYgJgRNkXHpFU9DaVDU3OX6ino1dH2HWKpVGSee+/RPpF+tuHx8zO+/6x1q/ChkZGsGzfiK5uwWmQ1Umayib6kw6WeDgTTumLNo+w7kZdpwOi5cm8kNZWO3efsXDlfTN/UhV5nBgYUhpHaXG73NzG3jsPXLoueaE477FtI2a/98NKOiFK3EHrMZHEkjqqFfEboe+o6Ys2VtxMVVtJ0toFWdBRF2NAxmoHbZg/4sQQI75/R72pljzQFcnLf9LnNhrHbPM0jnJrBjEWHRt/7ZnXs6fSyCE7v3vvjdx7atEx51FuZ78Oc3c0UwsGUe1/MTl1NFWdzls5bbxXZY2w3OYT7nNY4GJFk7Vfo2mi6XPrjtYNqC3vVt/kpj+LqBqGdyJsXcVncKwJ2g+d4QB4S91WEHtPfxeYaF7sZlM3T9Z+eBnRpM+pl23z6JWnOqVYlXA/SG9QG33XCBG46OOHd0xLmjcxx0a1ZdpsuZrs9AZ2PNgKuQzrTDnVbFW6QZ3I1NtOibUgp33Hknm5OrHF+9wsVLF7l6suH4+IRVShwe7nPDhQucO38je13PuDnmrb/7QfbWNxNiZGtAILEnJi3YFYuw2YzcdevdrNfnKKNw6eL9DNsrpFpaNlPulPVRpolxKOytDwhBHfJWAAMFTss0UerEWCCuDjm8uWctE/WB9yLHI2G8iqRLbFeH1As3k1drupQ42FtzYX/NZrvhytWRk0Egd7royUSpHTFmwoJdMmsmGiC4PaHv98gpIzYWVB/PwK+QtddbAZBATuvGTlQnN4AUCrrGyyKzQSUHVNdXQQYlEoSYQYRo48YDp8FAIN3HdAHf1MJ9932Au+7siHuaSVCngUBkb70GrDK1A6AhIUStVl7VJu2iprROoimbOcCFozWH4QDZbKmjMA0bji9NRCb21okLNx4xpsrF+gjqNScmFXs1oFsd0iLFiIEzY8/NzJTdMVTGl6ZaKs03RG0ntlaEFFUXMOh60GVYdYm9labNpgg5CjlCT6GPgVUKdJHGmA1n5u3H59hdB2fAaZUUdMlVlB1bgQ6GCbZDpU6FoQarCzLP1z4L6x4gcuWKNCBQgCqBSaVImSoNyNfvR/Vbgo7rFAMhmS6hjVdsj0oxUstELVPTHZzlMpSBllJi9NT7Whm2W4oUHe+sGwNV51KBAuM4KshXRg1ITEXX/Gh7lQMCAJ7Saimzm80xQSbTjq2Mw4mCr1Ip08C42RAY6bIBwbVYwSZlxDr4XkVcTpMZ07BnVGdAzVlokxXXWq/XrNdrcq/SdQ4EBn0UWoRKROuKjJoJKl7cp4zNz9NRgAK0JhmSLGU+REsbFzENaZldMjFbxseTM0tltmGAxnz14wzTUTWgEJtn3Xqfw6Pz7O8f0uWeSxcfQsrAYPIrakwpUOgBAbfn3LbzseE2x2lShc8DB6+SAfm1ul6nsgpVikCDeaUWhKo6rH2GEOeie2ByBZatY3UGdJ2dZbx8v62iQZxaS7PVQtD1M+fcWM4AUjQtvrGmQ9qxt2N0VqbWc1gWaFsyEf3ecg6Nvh9CoF8pa5hxxPWTx2loKdvia7wE0/3W8eiYgkgBRqBXZqNlc5Sp0K9W9P2K1Xqlmed1tkOzkRn8mbT+XwCyIQTGcWQYhkai8RG7JAN4+r4zWH2uR8sISdn0Ry3boeu8eNR8fQeRpZ3TpQi02Jez8mutjJst2+3WSEJdY6gWKwy3HbVoZbYsIQ8yZSMTxS4Rg9pPTqQRPNhUd5jbPnJCCIzWD96WkFwywH1wfd4pKaDar7TAmQaNI13f0/U9rVCcj1k8K0R1uLuuaxrUU1UfOoi07A0RGpvaA7Rd1mzxzuQrutzhhAk9Z9/WsK5U8209WKnyDUvWed/3be3154OtTQrUZm64cMH0/5cZGr6W6r1tNtsGtosIwzS1sZUMkI1xlju93vG4AGMBYt+RRSnofakM00g1o6Rb9ZTJozOFzUbZBmIP7crVE1KXGE9G2BZSrYxhshQAoFQ2V67SrUZW6z261YqcOrbHx5qa3/fsr9ZcvFy0+huBEBJx/4DV/jkGgYsXH2aaCnfcchP7/YoU4NLxVabjLdMjlxkfeoR65aounF1HK3xgQv0xJucMUL/4i5T1aaDJjTfcwLlzh+zvrehjYCwTCVG9J6/W5mh99fYZEGuT4Nxe5gk3nWO96vjghx/h4klBubYeOzb9JJkX9+wLg9jgCgJhJJRKGYG8wr38FDskduTYQapEKsN2ZBot2lnFItiJ/lOfS3f+AuGf/VOQSLfX68A3nY5Mx4V+zT3757k9ZVbjlt+OHW//eAyst7xFWawAr3/92cJcv/ALKoMA8M//OXzmZ37kcz7vebNcASjb9vF+vPCF2u5f/3X4jM9Qjdwf+zF405s+9tf6vM9TSQSAr/xKOH9er+UpIo/hFBrV3I0kLdexZmjtLG7u7c/gC8BqvU+8ckKoWlV4GI/50H33UiRweHSe2++4QxnlAR586EHuf/ABUu7ociSmnttuv9Mib5H1OrO33mMYBku3Uk2iHNXBW+/vc3junLYhKNs2mvGdu071QCURUqbPge3JRBlHELh08TK1BvpuxcH+HjEGJtfFCRGJDnQsjgZ0zUBSA5PUamj95ZHNVa+MXC2A5FrdNLCrAZLQooLDZmsa1oGQIu+99/2UWhkmLSihDM5oBWfd3LcExLA8l6WxFfWeXFOqVLRYgBVqWFa3DViKkXhWwOJxL8AwMZCHMLd/B3RbnHN5l6eB/ms5rYH5nKePJZh5+jt+31MpM6iVouk1KRhLVEZs6NeqE5vTqZucr+6pvTlnApqKtQSeG/uoOTCLvlg2atnOBYgsAsu4WDuNzGOrGbTXBB+v1Uth8S87z/BRAcxFMOEaXzTHbWFQ2nOuVrhCDEDdvYI04ysRWyXcxrQOOo5OF+tyJwzUwXZGcysKsmj3kgXbjPDFeaSBTGqAezXcYAClzx/X4mvPddmL/l/Uf1ymYGfcL/pNUOPUU7T0e2nRZgU6Q9jNXCGc7r9ryfksBpmotSGnAyIY+Brg/P4+d9xyK7fecANPuPEmbjx/gVXucZJUKSNlGhRITZEYe0LucWO31Eqpc7ETT3GMYgFley79AnSpZSSQLBuqQ6RjNRWO+g7OnafedjvjVNgebyBA1/ecu/FGzt10C+/5f9l7k1jbtiwt7xtzzlXsvc85t3rxXsSLIjMIIBNlCoScBkHD2BhSyEp3wMoGSiSLlilEISPkhjuQNEAyJKZouAFCogNIYNHCyEqDRANh2SmwqFKAE2cRxYt33y3OOXvvtdYs3BhjzrX2ufe+SECZEUK5Is67Z5+991pzzTWLMf7xj3/89E/z0x//LIzXvLg90Z2zZlH0Adc5pvOZZUnEVBj6A96r5n7what0w4t5Zo5HUkqEruN8PjOMI93YsRPH6XzCOY/3xtZBiFZxPM2zsfogi8eHgf69L7KkmdPxE8rxjhgXHl29z+3HH7GPwtXjZ7x+/jF9KTwZe+J+5PZ8y5QCMReKK/iQOB7vqDp/1eGxR25HYp6PLGKAq3O4GGz+2J5TpK17zvThto5v13eWxbbdVTDGSL1WIqalkTFiNB27qkFIaYEBEawaswJUw9Dz3V/+MsGbFEGbA2Lr7aaQigGdBW2zF0sRtvsdQiBIZh8ST3eJ5z/zDeL9C4JLPHp0wxe++4scj2fOxzs+Ov8Un/mw8CTsGMuR43Jm6d9nkpFsgYKglr+yk2jLk8UTPF3XqySCbCpZb2oniKg93Xkd2yQFKa8eQzBWaIqFwy7zeOcZnH5u74PC2rKKMXwnHB4YRAhe04OXVFQ/tmS8h8M+4KPj7pip2sIUS4FH+yMlrIiPZu2NPnEfYUqirPEpGbBSsxo8ONWdzLE0Tc+6RNdhOS8Ly6KZlTVg3AoaYprEuWZXrYw+CqbhOGuBNAsCVaZgHwLJ1tBsEgxg2u1Z509vNuI0TdQAp+7xHcu0FoJWSQLNRvSScb3DZdU5LkZzkebxrT+YNIeYNmoRb6nnSnKqQXQfOoIbGPeergsGjHktRmODVyrgmBaO05kUo+5jKWp6vxGnaIEds0sqm3Ljf4I8kO+zf9t/thklOo9D8Bc7ei5l3ZHeAXYoi9bRDT3vfeZzfPjFX84cF+7v73j58dd58dFXyctikh/rWCt1oVtbSLUvYo5r/Rm7yvZ6W8vFoQGGxQA9BTQ7vOuowi4uFwZvT9KCEfOyWAGhTVZMqUElRzlPjR3rbLx4Yy6L6DW74Fb73vzvui7qfWqRXB98A+JjrPr21ZayQk1dv7mebLqmBuEtZXyOnG1fyjlBLvQy4II3/UxF2n2v+sgxGVCWVMvZFSGTW/Cy/qS8cLyfmgRRSgl3r+zQrlOy2W63s4CdY9kA8hUYr4zbdcyVVstmO962tShEpLGWJ8sCjEnT72t2hovCHGf61ON9MFwkXwQGKvt2BbM1ENL7DueGiqRDgb7rNoCpBkqHYWj2z3maOZ/OjaXvnWeeZ87xTCVr5JzpfGiAIFi2ARbY9MFA45VJPJjea92TnPlvuh4WzscTyIYFHFVCIM4LyxKZzmcKlnVe/RtZ+zaEoAGeGpzwjsENXO0PG/a0jSVjLaeokicVwF7iwmSg8SofEBgtW7PO1FpwTJeuQkmZ3hjytYBZMj3r+tyjsbbrSVbXQvuoFjBzzhG8ww8j47DXa4iOyaonDViAfd1TPu34jgBjK0W/pvXoRLcFyKHFt6ogughlmdEB5fEm6FtK1u85rfCrFR+twqb32inTQud7XC8EFyihp6Do/ZxmXadCR+h6xmFPGHaIBEbxHIYrnQxx5ng8k1PCl0L85sekly8px1NLv6HU5Cd0IItcRPJKF5Dg6bvA4yePuLo+KFvNoqVjP5rQsjpOMc5taXduBWObwemEw2FHSpHzlHj86MDhkefV7cRpWsgpgvdI0XTpLnj2+5FxHOj6AfB8/WsfKxBtgG9KkRB6auGR6uQAyiyJkRwjTeTcNmtXCuO44/rqhnNR1qiK2zuQwpNu4IOrJ7w/XvHZfqR7+RyfM+PDcfo3/gb8g3+g5/3zf14LTh0Oyjz9vb8X/syfgXlWLdi/+BfhK1/R7z17pgzQP/pHVU/2H/5D+OQT+HN/TsHI62v4S39Jz/Fn/6xad6eTFuL6q38V/sJfgONxbcff+lvwr/+1/v7H/pgWwPrn/xz+8B9eP/MDPwB/4A/o73/iT2iK/uPHKqnwDrDhjeMnfkLbA/Av/6X+++rVKn/w5S/Dn/pTWtjsD/0hbcNXvqIFy/Z7vZ/Pf16v+bt/N/yzf6Z99vt/v7bhj/wR+NznFBgF+NEf1escDm805T/46HuVLvg9v0dlEPpe2wxrgbXmq78paH0hY2FRzkvAgzV9t2Quh04zQdtLH3oDIWDsPfN0JOdEN+y5efSYx48fQ7EUN3GQEyKZ++NR2U+y4nh1k7p9fcsyTc140+ig43A4tKhfjbrmWTfT41E/JyUz9sqazymSc0RK4fXtLcpc7RS4bcUPKuPDvXF/BdY0dmPDb6h1yrxoDBtdM7t+rwyFNONKBudaykzDTh9ivqybHCLczZOuA9v+NyNpfWZmrOZCMq9HgVjVT5SyRmkxUKW0BviWQtbA1WLGVaEx/y5BWzbO+NYcNve8RfG3qF519NdzXDIyzSp/6zR+C2grD54NK4h5ARJ4hxhrQrxHup7iA8VV4fvtWS9BDO8dQ99rKlzKF3cqGyS6GsjtTt+xFMnmgbepZsDBQwmDi/sUedPAKOuStzJE6vcv4MQG2qxg8OW8b9+qe4s5ANvUoYubyLkN3lZYo173giGhDU3pAdhr7d/eY+iCRvRrld+NE6MgqzQDct2XL8/xsI8qoL2914rTtL5l1RVTJ/hhQ6XN6Xr7iAY/tqmKFW3Qt415KMq43rY1W0p/BWNX8H3rHF+m/z5kLq8zKhvQAL4Uxm7g5nDFzf7A05sbPnjyhEeHK/bjnt04qv5qdZJKITpYlol5OlNOBScnlmKMq6zB32pMV2DbO9d0MetzCcFz2O0Z+0GDTykbo6Oj70ZStiq3JtXkS2QYqzMmnO5P3J9+lttXLylAP14bo2Kg7zrEi6bDFdUOO08T49UOyJzPd0zniS54xv0BFzw5LQxDRymvtehHF+h61er3osGmeZkpTkHFtPQsJ8/x9UslKQSVZzjHjHvyBfJwRbp/zenuJaPbITHR5cy4G4k5EUom5sS+cxys6Eh2niKOnPIF+OoES6tMbU5KLiDeimZokZlMRJ2lNU2vzhv9zmLrnjnQqWYxXK4LyZhFYqmGmrap33TOt3GswQzfHFqKaEXmRfd+oVhgyhiRTX5ooyXuvFXF1vVT5545k6jkhxZ8m+j7wj4kdm7i0fWeu3jHcp559eqlyqPFxPH1HR9//JxlWnj07BkzPeelx12/pnv0ZVK4UhmHOq9aUEnntXdB6z8ET5Z15uec0OClpU6bE7nEAiUr2B9EC1k5rQLvghCzyhlkIFBwRR3Quuz+PC3QX6CjrvnaB35dJMhixfqc6t1SoKMw9OCzNK1NBGOcCd5nBSAdDJ1wdXDk28ScCy4WS1Sr67DaPlkyrrhmxImr4KA1pKwZD8oy03HYqrDnzGJBzxYos4JdWAqybBz8QsFlBSSq3qbY2uycyuKJOFJSGTyfVlBBnCPHpbH0lmkzd3KhJE2/lZKBZIB7nbdrNkQFPp35lG4TiIilUCFM8Q4fHH3o8N41/dRa5A8DQbMBscrWXzhPR+I8k7P6gMqKXdmhCI3xWtcG1Qu34EdZAcvKOqvB9JWF9mAk1X1ns44UKSTEQGJ9vt7Wiwoq1eec0sKLl59wOv2kSkYsJ5bzPct8Nm3bQlEVUftZ7ZeV1aZ/v2ilrPYx5meUykBsNnFue1VNX9asgBVwW2K0QKMyTGNKLfvpogCqqD1TzdI6bopkYsqkVPPjtChes7pylResc9DGsqzZVjknYszG6NXsjC2gWbO7VPezAotizE4DknNBxOO9+h/F1mS1KZzapGL7gBhw5W39jhlVVU9kVwEw3RNqxpcXxYW8k41+rNocyzxRQsC5QCrKpiylUFJhnuc37LGHsgTKlqyvi9niev5MwXdW9Mx7fXad+g/O7CJnc6YbgoH1lzagMskrKK9jbpJ6H/pspcBsxaranskK7CKqH3zYa/Z3NmC44kd1HYsxUoON6gtU5q2C/cs8r8BjGxJ1z3UGqGJkAbVvXbcWfdOgt87Hri/0KTPshtV2tDHYNKvtOJ/Pq+3Gqodbx3j93Tun7GaUYdraITDudpaloOMn+EBJ0TSAVxmI0BkYTZ3OLXf0DVu+3nP1VASrA7BpfymFZZnsmZQ236X6daL7BhXQFvXVymauvev4jgBjC6a3IlzoKtQHqnpqlqoElJTJLulgMZ2RWLJaL86Az1Q0FNuMRshRqzimmCidaqwlYyCcpxMJZa91445hPFCcp2SNXO6HHaHreH0+M08TeZ4I5yPL84/I97ewqMRBm3g6K9qieOEIO6HrA7vdyM3ja/q+116wPhj6gc40pEopRBbWh04bkDVa5p3Q94HzdCLnyM31DbvgWUZPzoljnAk4+q6j7zuGITCOga73HK52hG7gm9/4mFo8um4OlZlQUF9WvG3oRY3DljIpdYMFyTCEjn0/MuBITg15L47Beb5485gvXb3He8OeR144vvgG3hV6QQtX/eAPrv20LPr6R35kBRF/1++Cv/23YZpUh/S3/Tb9W00bORxUH/Xv/30tADbPqhX7Iz8CT55cnuN8VhZzPcc/+SfwjW/oZ7btqH/77b9dgdq+X/8G8PLl+vuLF/reg0XuWx7n83rOX/Nr3rz2b/7N8Ft+C/z4j8PdHXzpS/C936vtBmX/jiP803+qrOtf/av1Hn74h/X9H/oh/ferX9W/39+r7MOv/JX/bu38+RzPn8M/+keqrzvPCpL87M/C3/t78Pt+3wqWbRx82IB4VDBg/TuwASSEjoEx70kl8eR5YhlmuueF6/yMe3nNFiLwls4gAkMfmOYzWYR+GLm6usKHoGlWKVNEwa1liZxPR+bprJFjHwBNr6MUzudz05cSEaZpou/7ZlwBDH3PPM2kFHEinJdJNeyc6kKrmL0xYync3d+TsjpjUtPmsurFrf2zAQ6lpgxpij+yRrRru7YgUQVhum6PyGyA8azGZL6M5r/NGi527wWYy9L+lotq8+SLD7I6Bwa6KsCkxgNbMNXWvRbCMuNXqqFl5xQLvKn3rOl8ba/Yjg8DdvW8WzhSLu9LreY3AFTKRi7B1uBi6/mbHbMyqz7tuDCkjQ2Ld+AD4gMSOmVUtWj+Oh8qSNVYG9A0yt7Worc3oN7fKmGwTad727+61q9OCe0WpE3OSwbmm32zznM+pQXDtqUAACAASURBVJ/KxVftdtv563NYP70xlteG2jt1k9TfdU+tjvhlb1Vwtc6TS2i2NEdHmbLrO00Lim0frPNsvafNtcrKXK+GaH0WrqyVctf2lU2/lPVPm55t913Hep2B9Tw293Rj3rIL30RoqqNZr9cA2c31qqG/js/1vfpTr9uJow+efdfz3s0Tnj5+wpPrRzx7/Jj3bm7ouw4nCkxouv5MTddb4sLt/T3zdG7M71jiWp17M6OttfTB0201x9DCGMQr8riDAnOMVohGpadK8YR+MP3ATqs8e2/dqY7daZopaWE3DhQnnKaZzvQGVWMPZZqJOq6dfV+d2oUQHMM4ErpAKYm+C8RYtAis14I9ZVSgQ1OZdf9xXoE6iTMvTke6rmPoe5wMpCxIf2CJmSU6Su6IYc8pFsaYNAtj6PA5MyyBMXgeDR3zlJlLTVV2FEntGVYgswEItpiK0/lTpOr0pWoMappynQW2flOD987hXMfDozpmImKMQQUAVodNbF9ax2Up6+hClDyR4sqwEhGCLyv4w+Xaqc6Wb5kVyViy3vafjALhnYvsXOHgE4Ez465nOfYs53tev37FaNXKl+nM6f6er/70v8VJIruO81S49oLsH2l/+YOOi7Z3aCfXlMVaYdt5TMvO7jVnixutbPpcNL1SpNCJsMSC8ypN4C0b5XLl3bLoN333C3S8K7vhskX63+2/yUCB+oEalO2DIEmZs1bHhQr8qwmjUg/OqwswDsJ5zsQI0sPcOVIE1TMWY2+vdoYIxm7FfEpZQS2ptooz+wQyiWWJOq9TXkGWmimE1cOwfac55k6Q4hTcdXoj3iaLiCNltTPFgNJkrMlad6ClOG/7uVSgNUPbm+taXwOzZd0yqm667dnahzqnHMrGD32v7Fwnlu2BSUYVA3BUA5asxbGXeWI6H0lpUfsJBWNX+2pjY9TsMXGobMFmry3vGDsV3HjHONsGG9vU0jeoWR6ugr71zaJMu+PdLbcv78hppuSImJwDZS0g3vq0roGs64jiiu2JtPe223Rt69Y2XcEfuWALtsEvNYVeU8KrpJfbnGtLwKp2ztYqSlkByWqjq0ZqMjBKGhh7MaZQsDPXTIR6HrEgWql6qDoWa3AiRghhZXumJZlOqgWRReVmPOpTKZgtSA32uTrfofiCSG4p+ylFRBSUVbtF0+IxH8Y50WLgzkZJKZSSbMwopCVOx0cLmEtNT19ZixdPwPaOGKP1h46HCsY+lDZoWJSoZIXbPKO6Xjkbx7IBfCsbU7WVDeS17EBdBvT7S17W9UVAM5sqML7W/qlt0vVoZbQG7wmuFi3cnCMmXKa146I/6t5qGroK/tIAb6o2KoKn0LK/bRI67+h8v85d81Hqc61HveZ2r25ZCLJm3hUDUaserN0KSJVLMrJTznQh2Dgwn09WrWyb/rYFr2D0yoJeZ1FjMbfn7NQ3rm013eQm51TZvMXGplcdYlIiG6DsfZUW/XRP7TsCjK2bl/oNqivlglUk8x7BE5e5OUE51s1KkKCRfuaFLI7iHKvYfbG04Kw6Q2Ygn6cT4pVmHFNkmieOxyMyjFqxd9ghvuP+fGIcB6QTiit8/aOPyCz0S6Q/Hbn/qZ9k+ebPUuappVSuDKiN1s2DhxCC5+r6wM3NDcPY65pvhlrwgaGl5Nl3dWVhWwEO2yhFCr3X79+fZk6nEzEWOu+UoTo65imx6weePLpmvxvpes/r+1tevXiBE+Hm8dZoXh2/kqrsciGVhA9hZXNZJKFGWJ05hg5H7x37bmDvO+ag7NggwuMw8J98/stcx8CI0EshBWEQT985LQ71d//upw+WvldpgW91/OW//O73uk7B2IfHj/3Ytz7vH/yD+vOu40//6W99jrcdv/E3fut7h0//zK/7dd/6HB9++OZnNqlC5KTA8DgqkJrsNWjfh6BA0jgqIL4s+jmAYdD3//E/ht/5OxX4/R2/Q1myP/ZjTfO3pQ1Wfc8NOKT4waY9F1NHcOIhZ27yUz4ffzm5FN77vxbys9f4byYeLb+Wf9H9n8qEoDa7auUl+r7n+YsjuEDoBkLXc3f7muP9HaDgZtf3nM8zxfRtcsr0vaYSxyVyOp0QJ9zc3BjjpnB/DJoiEwIxZ0LX8eiRMm6neeLx06ek589Z5pnghHEYyDEynSfmWSOFt3dnjqeMHxKpFJwZACqarxvW4LeMNmG325Em08TZoif2foNtxCLZ4unDHsEry2y6u/hOad9bO14BV3Oi7VNp9TDVeDNDuO6arXhQA4TM0DRDxFXn3wxAsVzcugFia3ktNiNAGDqkCDlGchQkq0C92rJ6Hc2OXrXbGoiE2tYrO6MaDH5z72U1nspGd1U2LI4K3FUw8I3+XjXLLvrUgNxV2N32Ku8pISBWQLGm0tZr+cYKg/M8UWqK3KJ6StJ07bbt4+Jvpd3LpUu8fqaOEf3bloWR67PcfHf9BpvzrG3e9kXtq23a10Pg9V3Hw3PVteEhI7M6f7WF+tnNu7nCdyuwu3Uw1n5Y71LMYdSCK9aHshr4DXy6uO83b+YhK6DeyNYApigwUa+x+SDbp1U5LQq+SCtKU4oYDJseXL3QwsFFVoZK66MavLn8Th3bamS67VtA3hixNP1GqWAzhc45bsYdT66u+a4PPsdXvusrHA43muaIgpZa8EnPM53PnO5fMZ2PnOczx2Xh/nhiMa1FUmTcjSzz0hzF6gDVEVl6D11H8M6034HsmCcHWasqa0qf9pSCtoF+3BO6gS4M9F1gd7hSvc4idAhu7NmPPakk5tOJV/f3pCLEqCmdqQDOq6xNN9CHXrXaugHvBnKO+BAY/E6LgkkhF8f5rPfnpBBCZ8El1djXlPRsTLjC60+esxt7glNZqpIWTvHI8XhPToWb9z5P7kfmORLuT9zdnQh9oOsCfZgZfOBzTx8Rn7/m5Zw4xowEz5yWNnZLUdbGynTSKu1OHGKCkwrgmh3qBd9ZEbVSqNXttQaBs5TQ7gKUSSk2R68CCXUmr8/zQfqrvd8cJIzZV0EplEHWN5CqtHnnjD12ERSp6YIiJFmQonqsLhQejcLTMXHdLZTlCObkOe+4vb1lOZ4Jocc7xwfvv8+/+Bc/ye5wRdf3xJzZPd2TTz+FlAjdB0R/QynuYu8Q51UTtzn4yvhvnkLRvqrpoc4pm7Tznq6HYUTHhdPzjZ3+DF7ZpSuEa7DXhbjmg5n+lj3jF+Iom39TySpRkAvHOZKdkIojRjUnUymE3lNcYZ4TwQXOS9L1RYRS92tRgPr2PrLbdexn0YCGE5ap53aeiDnjnNqUi9moyugz8Ml8NF/9mZzJrWCUAofe1qjFyBUNwDBWo7LQ1I4VpAWQXSWhBC3uliRSgqcsqYEXuRSO08ScImH2bQ/JBmJIyWShZRlowUdHKZrWXZKBhw7NKjJQEWj7YSpW2ND+WnD4zuO8gnR919PvRiwEpfuboHM+ay2DlGaW84m0LJS0WFaVrg8VSBRqsBMDJgxoa8CgZq1ss2W2gKUOd9ujG8p4OS7rOtVIQBv2GRhreWtnsIKPDlGZMiLeWcGhDZRbxOotmI51BdtEWosAY/FRLICald5dz1LtNgzU9qsWxmLXS9b21e4ykMs7nb+ScSUjScdulYVQGyG3PVtW6oO9rf/zZrtibUgxgbNiX+I3BZjEsuaELqgvkMzfSXlDlMG3faGyB2v7K5NQ2aSOZYnEokCqAoCq7b4Waat6ywnEwM6gBbnishCL3l/KiTzrPqMEBF3L8bV4nCO4YM+87keq27o/HOgHlQpIJRP8qqm62+1YYlxXSFkD45UFX5+gc1ZYMD3IwrExUIHdZVkQtLCYD1WPt+qoqv3uS7nQdq2sz0poyzkznSdqQK7qusaUSEV9QWWNQ6xSKYv2U2OBewNe65okru1ddY5ogS6verImATFbELyOoZoBttrYq558znFlotp9OuGCOVrlMra+YO3rOl78xme5+KlAf0os88KcZgtqxyYx0cbgeWrzS5nKWuS+XlPQta/6XbUeRDLd7iXqebftyNkY4daHXdeZVNbaX76rDGYb0qUwTeqXiQjixdqcyEayav5mUV3odx3fEWCs7jF1EbHgjvMXD9OHzja86h8oACHO4fuObtfhPCRfoCwKElpluZRSE+onL8Rz5j4Wdvs9RTx+GBnQgT6nTImJFITx6oo0z3zyyccs90eGrmO/3zFIROKRu9tvIrNWjMStUTLfB6QLZJsg2u51kxj2PftQ2B126/2LVk0U8RRLDasVUGMKqudawVmL3gUndN5xteuIy6S6S4eRZ08e88knn5BSou96PvfeY8bxwGlaeH032cBwdC6ons28cDwdETdYUS0dnItgEYKqB+ltINeKj2kD0Ji7X7Rduz7w+LDjo+WMM2BpmY54X7jygTELkiOf+/wXOX/ykaYp/dLx7T9+/P+Av/Y/wr/5N8qq/et/XaUaclZm6w/8gAKuz5/D932fyg788T+uA/Vf/SuVQhBRVuw46jn/5t9UAD3nt15yu9Ft/lixiHY4PN8ff0MDlx4KFDjnebx7wm+9/u184cVXwAqjBgcpTqSc6PcjV4crikScdxzPJ6Z5UbCiJJYUmaczIrp5uxC4vz8SU+Tu7o4YI10IlFw4Hk90IRC6jpgSX/3617i+fsTTp+8h0muBsEOmGyOPbp6BOF68eI6UyDA4zqeTGsehR0ohzkkrvHpvOYq1L7Ia4161cWqkFeAwdtyfMzEtpJwUjGjfW6GclY1neJ8iS83oWrvfQDjbaKpx0FgY9lzqxlYZSMWkDhrjTwSplUerEW4ORpUecN7YoXXjd9JYJ601lSnqFAgoVoTD94EUIz44Y2wUSIm+65ruFlmNhpqaVXIhLvNGTgYFh7fGBBjoVvuurm4P9cjeXLAeRntXF8jGp/e44PEhkJ1XVmwISO9JHvC2V6gIZjMSS9Hoe455zRwxPaaUV5kCS1JvTtBDYPZtQK3+njcRfafMZZHLz60+UwNBto5Una5Q8OIuUvq3fbBe14yk8hBA3ugFNmdFz5sfACsb1Lp+2Rpo43V7XqCl9lVHwa0FLctm3NXgoyvbfbtBKgY+PgSK6/1WZ+XN8fC2oxTVqdq+bncnqzNXTG2wmQBSGSjVoa26ctvDHMtSWkBHJOOc6nnVebI1pMWszLr0lrywcscEJJOrrr6rAFkmFDj4wOc/81m+8sUv8t6TZ1xf3TD0e7p+17QScUJK95xPr5imM6fzidu715xP98Q0E3MkZZiW2dgjGS+F+ZzJxYIDxaE1yTVl0TutFk/K6qIWcEFBxGWZlLHaDXbvVUN0IRMp58gyO07W94f7K0I/4nxPjgvj7pEF7UbGfsf1oyfc3t1zf3/PfZyJRavX+xB49PQp4+5RK1tTvGOJmePtHcM4stvt8V2H6xKdGoYs53t1lDLkIjgfOAy9anF7YZADH3zhu3BemUZLKoz7K1IMDLtrnPfsdnvOp5nzdM9pjtydTnxmvKHvetJ4YHed6UvhfsnMr+85nxYQNLWvVEaW2rC1+Cw5qHNWatESh+RKONCn6X2watLm7JRMybVora7lXmj6r4A5PCopIQYd1oASQC6p+k8NilWAtphTWvW3zWY2reMpnugYCKHHSYdIMDCgFrpT1qEYoAyWwusTO5/48Crw+SsYvYLhU/S8+PibSJoYh55f9pWvcPviNbvdQXX1xPG1r37EdJoYh4Fnz54SyHTpBdPkISfivicxKARWLH2e0vwBLYiZFNQWMRypmJSzsWSDY+idFhkD0lzwe5UV917BJ6+GN7loOKb4h+vAt/+wHUO1Lm396jsP3pERug76Du7PCfGQjYW1RAE8S9S4/5L03ylq/8Wp8LnPwmkq3B6VKZ6SmL9i+1qzgbQmiJON7rGtBVJbue06VVbTrL6ut6CzsQNj1HRsa2eDM2zh1H1Z1/UKhqhsHo35LdQUcbW3VMO42iaZUqIxbtexUZd0qB6XXkvIVgx6/bsG3oTcgAPdK0LX6xx03qqne5NPUBtscI5lvmee7plPd6T5SMmLArBZ0/hXeajS2PROVgZYsWtVrcpqL1ww+7Yp4g18NZtpEyxtdn4FWiyjwnuvaz1i/0IqiSwecR3eBUpe6sij9przFqQhUYsLKdevBkNV3vCCZSz1vkp9cOS0ZitdWK12L9WOTGbHLVbJHila9HH7cT2lYrtmtxfb96sdoWC/a7txyaUVAFW7RItWVcAVEQ5SH361HWzdKdtn6IxhLwp82Tig2bxVMmlrCzpSEUoqlGnBOc9up+tYjFoEr7TxCN4F9qJZEGlZmOazFbDSPT6EQIyBJUaV/rHCY8F31VTEpoWucaxZTQUt/rfMmXlZ1n0JMHF8vNNCWLUQn/eujUVY9UzruKuM1JSSFj6355FjogudgYoKSMaUOJ81iydvbbmkTNQInKkBYD3/PM92DxrQrvOg+Tol44OnF99svJwzXbFAzX5TsLUoWaYWYK17+mmeGsBcwcyY4ip/J2pvrIERKEWLggXTmtXgQ70hHeU5pot7ySatEWNknmdSA3i1rbU4Wu3n3bhbZUSq/ECxYLBTEPlq3Ov6VYrp55sMRk4GnCemeWqs2ylYsbYWRNF+7Loeb8BxrbHU+ULXb2zejZ8wz7NKcJrftSyRvAWsS2kyOG3siLfghg7Vod/R99kA9Ev2bX3Wbzu+I8DYUiDZQih189l0UO2wnKJVjLQIWbRoSopaYS1FJKuhWFFz3ffVQfRdZwamTbKuw4cOVwrRWGOMB9z+Gn99w/2r58S7O8TSzXb9wmf6jjgfuT+/huWs6RvUtNbqYOqD881hgSjSeCv7/Uhf0yMoYIUEnMah8ALBW9W+kvFOheCDpbYpOKMbjEbNocTEYJUA7+/uOOx7TUExzY8UI13wDOOO3W7HJ5+8ZBwPiMDr27vm5eWSkaJtyTlpJB9laERRrRgZeopPzKXXCZG1Ih6lkFyiK4VyuCL9lz9I/vG/oxHrXDiT+LlXL3nybGQUx3yMPHr2AffHM8kPvyhj7ZeOb3H82l8Lv/uvqSzEn/yTVmjOju/7vrVY2X4Pf+WvqN5uPT74QIFagJ0FGn70Ry+ZxN/zPcjP/KS9eAdQ0fAP4ZfF71f2CmYDFa/ApCgwOQwjd1Ycb+x7ftVXfgVXhyt8egT3epocI/M0EZcFJzvGccer29ecjyeC6R7hwBtgMM8T5/OJQqHvx1bMQMQT48T5dDYNZc80L5RyJuVI6HZcXT/m8ZNnzPNCspSPlBNLWpimiRwTY+94fHOF9yq8rkWtFnKMdMOOfuhVbwxpBalyNYg2QCwUXrx6STqfGju16kyKrShUYHGzSdc+z/a61FK7GB+wbJithrStr/VTtervaqeWDYizMdxsba/suWKGcWWcqN1qqSFVhwlaFVvnrJiVKBfAbSKk8+mknnNx4AtSPBhTr3pbCs5Yn3lwpVfWWR1PziEVjCgVyMyrx5NXM7tG0mmv7QbfJcZKhXNFP+wqa09wXYcMvYKxQeUJcj3nFocvl1H7Wrkc4Obqmmhi9ud5VkO9VRzetrP+7fLcFy3dgLWlfdheNcy1tPO9cZqNk/gQ+N32xxv9U/ubTSYIVXfMvfObm5t71zsP2mjumGz26XzZR28UDMtF9fmaM1DeuN6/N7us+sushvY7PypSJ0SFsNf2tHlbdRCrw1r1xraMYdde53LZp83ha/dR5/r642QFap1AEOGq7/js0ye8d/OEZ9dPef/pB1ztVac1dL3qk2bV2YpxZpnPHO9fkuJEjAtzjEznE/OsEku1YrOgDBtxekdLXqzvayaO7QHO0QV1nnPOpMWyGYLpKqMZETA3x7n2XQVjqgNWSuF4uoPzPaCsMWUPJZzskH6POM/VwTP2I4fDnlf3J07LZJqdHS4M5OwJrqfrtJBHCChrKN1xdXOjzEgWRDzDeICcmeMtJU5InBh3I6dpJsWZsky8eP4Rn/3Sl+nGA+I0y2M66b6BOOYyULqOm/euGUJgiZlpjjivDKHD4aAyOfPClIU5H7kviZzlAoyHYmwRc1T8Wum8SFGd0hDoxDOIMOSEy4VUIImQfcdSkqX/FsSYJsnWEHWAa8EQwcn2WayfqZtWbVYql3NDZPMDBh5D1WVs52/pytK+B+Db1lToHVx3wmfGxMCMS6mBYMuyECQzdh27wwF0aKld7OFXff/3UkpWCYmh0/EbzwS5Y3Q98bwjyjVFAkgg0+PxSFndLr1HY/cZocM5oIjKhi2JRQS8kF1Rxs2upuyan2FEllKjjOI2O/Amw+PbchjzLBemmIgIsRhAFTNkiLmQiuoL5wwlYhIcmVwCMUJMQsqQsjDHZAnlqrv6/NXMsqh9sFg2n/MOsjRJkxA8OZn0jIFWJasWavN9ck259Wi/6b4kovrT+vzVvig5kfOG9VzvttpZBqg5kZbdo4CIa+zsBgQYcCAiZCtUUzE01dzUjBnnPBRv61ndKevmXD3IS3tERAsnqvyRAih93zfwo+pSVowg58jxeOR8/4I0Hclx0pT+EvGsc67OTbUV7W+y2jstE8bpNYKRCHRLEgNaaH1X998KpoDZSyW38VsZlqUBIdIwAwzg7fsbrh9/hmE84H3gk29+lRLPluVWq7lnvV9Blb2qvEMDXLL55JkakMo1ylc2etdIW2vqs9/un6XtsfrfLnRkO2fZcNjt08SYmONiQP4KqIvN9Xot73zTwdxeO2XaPpaWxWR5tuvf6k+ooqPa8afTqY1bHSo2VpqvYaBYTEAy2cj12VXGZ91HK3M0l5UoMC8qdVHIiA0YcWwKHGZc8QS7PqVrhchKKU0Sztm12ICmtQfJxdi1Gg7djzvTybdHh0oBaTDBGygfyaWFmi/BWNugnBVYrT6F2uQZ1WwWOh8Yr29sbujYjilu0uSrzbSOl7P5mPMysywq01T163HCMs32rGTNQs4rl7vKFKzAsTRSiXOOvu8Zh6HZuIL6dH3QIGvKiXlZVBbP+kafcdYsgjrONsB1HcnFNK6990pMwuRy+o4QNDO9SQgVyLsdKZr+dilKoLQAbM5ZpQZKMSC7KJjufOMjqWmg+v44aVmvgx/anOt6zZrcklGWqD61FCgipKJEwmjZDQ8BYRHNHqvM5ZXRus7n6ottg0U1KyjGbOtLtdJNjiklWsGzd3sy3xlgLAD2kGr1s+Y3Vge4GoVU56BoGn2pCDRUQKDN9FxACuJtEet6XQpzgSSq0Wd6X64ThmGPjFeUoWfJhWU6U5aJkBNDgMchcZWP3E135NMdJcdm9DQHVq1DS+XXFBbnhLxhutXoTJ286/9sg6E6gIUcF3ZDR3CCk0KNSla3xImyQpLoJMxFtSefPb2hC2slvdNpAnH0fdCBa7q15zny+vVRr9/AlPZQqM64gGmiOYJ04DMeFW+fpsySY5sE3nmkC/jv+hI+dGCTfhH46utXfOnJM4beUzzk0BGub/AVvPul49t7vPce/OBv0N9/4Ac+/bO/6Td96/O94xx1aS91g2t/04UslI5H5Rk3+Rlu44CLePrgGULPOO64uX7MR94TUabPB8/eYxxHzl3PbNc4nyfmaSJFTY/tOk9KL1nOJ5UgGDo1SM1AKUW1A/uuY7cbGoPusN/TB43edkGLbJUixJQtWJS4urqmHwbmWas+VsMtpdSMVO88wzAQl6Oa/MWKDgJDr9Fb55ym2TWd5rq0SfMqS9FIHmmTcFUtwPqxCqBsfmRjUeeSm55rNXpbKme7aFkrshZYi/xUa1o2FVvrx4wxW59xM0mqw3hpJDYd1XaLuspXo6Ng6bvOqT4jKKPKdHLFQZW4aW0olXm54ViJUFxa2SVFHVlnqUHkQsnCqvZtrNt3HZu3mqOxuX5L1xFjNXhNt5IuNCBWi3gJoqH8t7rOW5ChHtk0ut7FuvxW7a3HNl2/MmQf3FX7rTpb1qjN9y4/+7aLrh9vKMzbG3Tx/uUn3gDEN+8/dIoeAqTN8bWTbg2jB5/cNL3NLH2nXay88a3t96v8ysP2PrxGbeJlv9f+Km98bnWCVyPbfNiL79Yn1T5vc6nZU6bB/0aqWNk6WuUSwC9FK6KHjv0wcn048MHjZ3z4mfd4dPWY68MjrvaP6brQ0uLm+UxcVGdwns/M05Fpumspb7Fl2NhPTmZQJ7t+aVWrV4ev4IwRqD/rztGKwSZlmuELuBXEXgF//UaVFKn9OS8atMsxcX3zSBmppg+mlYn3WmDRe0IXQDr8+cQUI7F4XOjxnWZFhK7D+xMlZWVYmBNQq2WLC/RBGbjHV2fm+1fk5UTZ76BE0nJiun3B+dXHDN334EJPKqoHdyoQF2WI+j6QUqTvBnznyQVjF5ljZlWwD/s9V6eF1+fI/TRxmX658p/Z9CfFnGYBT2GXE7scGfOZ/jbq+hkCqR+YDo+59Y65iNrYuSDBpIhsHHm/zTBYoYrViaLN3TZ3yuUaV1k8uo05C2hqVtk2PbICCo1lX0r1k8il0HvhehCe7GHnF1xZWXTBBwVg4xnfaR/u9jvmebH1BT7z/nvGcNLXS5wpKeHDGVduSfEjkkwsckX2e/Bdyw6qe1pzqJ2z7lglcIrRwJZFoAjZgZNClVzPeSNvQu2P1bZqE/cdy9S/cwDpP/BovkXbSGraua3Z5i/FUj8nDWRSfVnLhhLIWSwAItyfk6UjC4VkzFOHOC0onEpSv5IKtCnQkKVoVk3d1VoGY11bV1mOZo/Ymr4uuNs+LrYtrLZTLqYna+CZAknqgzYA3lLGEchxJSUp4KQyB4KlrBt9UmWUq32G7WsOjUqsj1xEM8ZczW50un5UCSfIljGkRVXjMhFPd8ynV0icVeKlJISsfi3rvrrdN5CaMl77orKT9V8fNlJ41qeXmu1sDISNDXQxRsX+v7FJLMPFhY6u27G/ecbNk/fp+p2u2bcvyTPkpCxM0Vs2FttGBsCwglLBX6fyPyWzWSNtXNQ2t5zeXQAAIABJREFUP5g+755P1heIymyR2rxttnz1s7fgbrvlS1vmbRk3SrSo2S31dVZsY2v3iNTSbZeA0tY3YCXAXQTy691s9kt5y2fr9y8Mt5LJSUy3ts44o55b19YeVjO/Bij0ebU+YvVNCigwX/teWPedUkxewTX7u7J7nWEyzjlSySbRIW1fwL6LPZ78MPvMgMN6rRwKxQC9Cuz54nFSmk55BUm3Ug8UZVnOFQSsoKcIueqMbuZabs8aKrUvb/p++wwrUFp38oIy6HU+WmAoZ8WU2njT7KpqDzQgv2xsp7KSQ8pmL6tPSOe09ZXY2CiCC2615YQLqYIKJEdW0k+hEKtUk21ldZ0pxsIV5y7GcLPjpFDKKrnUZIDsd88Dvd1SNWtLYzaL2OdqAMlWHV/HJBuZM1v7Symqc4xrYxVqIUjbzz/FVfsOAWNNE0eEzjRZYq7afqYnEjV9SR6kDyiJKZMoK8DpV/3ZKqhTQNNbneiGmWApAlE3bu/3XF+/R7i64RQj3/zkm8jxnpBnRhYOOfJZ5yjne8r9a9LxfpNSa6Z+LpqG2gVcFzQFN3iCd+Sw0pOdD4iF5kRq2oFQWR8q4G5U7OnEB595hCuRuMxM00ylStPAa2XMikCKifvjiadPHhvdXPVgzueJZYkgwv7qoF6Mg2k6c3d32yIcDctxWHViNQCdaApIFxxChyua0iWWarUsczMu64Y2DgNj6JmWSC6ZxQk/++oFXz/fM3SBR0Ngigv7J08Yr65a/+zu75BqLGw3JmgLw+VOWLj8kL7YvpTtx0Q4X18/2Oh/6fjFOko/kG4eUQfcyvQSwqJjal8e8cX0q7XKZp0fInS+5zCOXO8PPLq+4dnT9/lnXc8ZEO/ob64oOErTa4KX85kjQuo64rinlEDsXnJcjhznCZcmvAttI93tBw6HPYcnTzns95SceP36jqubR3ShU6C2H+mHgYLqB4o4Xr96ifeeufOcvTBFiL2yYibvcdc3SJ7JvRB3O26nM3MYSeKZSyFdXROePMJdX5HHkSXOeB8oZiQkX0jDYLrY6Pi9eUSZ5zYdsq2lpToAUqOUTguKeE9+9Ih87km+EGUyB7GZR+Ra3KJswfLVINViNasjUMxIrsZCXQNqJoCIWPrp+n4t7Nd0ARBVlXBqqGOGvLJU1u0wkYnVYNrtARO1x3RtRSOzWeprwdXbEShRvdi1Ur056SmbcZWRly8Qq66LA1fKClBfDOR2hrYPSL3OhoUndo/OB1zwSAgQAtL5Bi6rsV42p96AD9a/tepobcft3Z0auei+WD/3NsZGbeem2e1ZrDqROg+bxNfmu9VYfduKKeZcWVdetLE6sbmUC+UNPffD8zxwvOw+HtovDx2Tek/VSLoA+Tdnu1jvC61I0Qab2/wjb/RB8xntP6tPvjpm5cG5ajsuAahqHNbPm/Hq1mvWiu/rs6v3WVrwxLy39n39tTTjv32mmIVh7Ot6nnrl1rKiTHJXHTdU3xUDCgTYh473rh/x/tNnfP79z/LdH34X14cDRRwpKeNNvLIv4rJwd/uK8+nYmLEpTogrVjG6auAV08GthWB0HjbjPSlQo+CiAsJerP6dMwZbWQM3oEEq7xwldBRf1ge2cawLNYXdAepIpRiZTkfmSesFFMFA1MjOOUbfNQAgyMjjmx1d33OaFk5zJoSecbenH3c47xn6kRwXnR8lEVMiLlHnrA+EYSAJxOnI6fXHpPMt1zeP8AjpfM/txz9Hvn/JGAJzLkzTmX4/ME8nzqcjzvdcPXrK6TwRU9T0WufNqcmaQicOnGc37tjvZnbHGaZJ52nNbjDHtTobdQxVNlUQOKSFZ1PkZpo4nI+416+QLPj9gfzoMbfDyFe7HbdOWEwWACtiVKW1WpBPNkDVRkdRfaFM8N0638qaDtxsZlvnnHiC12Jwzpsea1mBDee8JSO0xUnvO2ZuRs971473rwqhTFA0dVNE8KHnvQ8+y+n2hTKWRRh2o+5zUUGd3X6gH3qT7tK0U8i4suDKPYc0UcrEyWdmF8gc2nqg4IhYETe3WSOKBSekrSsxRQQN5HkrTpU6kxXOhRQT0jk8lfu+2rub5eHti/cvwiEoYaQLocKFpFJYxGwEEWVdGjBZIrgiWvMq6xqQitZkzqXggsBcSElvcIpC3zllcE2FNEeo8gGlEClNp1dT+VXzuALjVV8YBMlCyhoIqvu2bLSHmxRTWXdoNV11frc9qKaXo+O8KkesAQ97Xfd+d8mydeLIokXwirM5U4sUCY2pLtUHlrrPWCCwDh8HoesuwFj9u66xmuYblaF3PjFPRySeIZ9xVbu4tlPcamds5zPoddt+ZACssWFrFlntO814cg0oFgNaygNwufZYG8fNJqjPRRDX4UJHPx44XD/l6QdfoN/dkFJmur/D+x6C6uvroltpvAU2NSuKpNW+sbmZNraMgkxc9gW1EFFdv9b3L+6hrMHhYveT6xizPhMBH1SKJqVCzMnki+oEXsG2XBIP+QFmQVwAfl0Iaz9t7MFKOpE6JzcyMcqOtKJy9toJjSjn/FpYvB6u3ZseKavWeB3jTnSMzstCXBaWJRMTCBpkUE/fU4oVL0tWN6jZW8Vs6mKar6t9J+15KHOyWKZfSYkUlQXr7R5XGQLtc+39FUQVHPO8NIDPOSWoxZza2lzxmlKg5MScEsX2Umf7zTAOre8qGJtLVlkD75s8UG8a90PXM5oMSjGwsu96LEFCgVQDQCv7teqr1sJXQPtblWXr7H7rGlOflTN5qZUB6tY50W8CTpsx8fDaFcCsOqu16GBMWrskhCpzoGtnlbv0JtW2ZfUC7V4qyOudZ5kXYomqNx8TOa660/Myr/aJc+Sc6PuaXa2Brso0rrWmvOnl1lU4b+4jpUhMUesKGPbkvNfMON19EcQyVqspuQLftWBgzprfbh4zWEA4xrcXjtse3xFgbAGK18hvMhZTLpGc1oXNeVmzL0p1IuwXKaS84Lwi8H0YWI7rBuHsHMsccV0HIWja1rTgOmEcdzx7+j6ffe9Dht3Ix88/4Ruf3DKUGf/6q1z5E5/dF27KU75xNxNPEy4X8B3iIt60qwSNkHRDj/ReQQOB0vkVHAL6YUeYZtWIbfumsw1AuJ8W/KwFhHJK3N2eGAfHNCXujgufefqE3aCFjFJKpJLZDT3BOw4ycnO4YuwHUlFQ24eOvjvxmWdPGPd7+iB88N57LPPCk0c3PLq5JiZBJHA+L0zTzDQvZhSA91o5MeXKUVQjMJIZh5EYF5ZlYo6J4L0Z2ongPI/3PZ/EI6ek4chP5jP/z8/8DOn9yH/6xS9S4kxx4SLT93/47/87PvvRRwpe9B3Z9+QiLElZjkuMJlithnyOC6WgBSLigljKWq6VHSkECVpcIhfmLvA//W9/l+WX2LjfluPuv/5h7n7ov3nzjQK//u98QnfWRevVp53kLUD6J33P//I93wPAr/s3n/AruCM7x4//F/8Z5/1/DsD/uzGQPvX4hQLqbU34v9/wjHQt+0Qv/vNznPqer/+v/zuX8Nr2ePtJ/r83G/XzuNi36/hWHfG2tm82irf186cdKfHhb/318OqlFsjIG3TyHV99AyyEC2O0CCry13dQg3Re9fO2xRAzaZNW9O4x0Bx3AWqaYbv227+0ZXJIa5S+ak4Ea5oP5aEis37+nQZFlRpor8vFHPr5zyZ569R7yIzbvHMBWztX2/nmeVswrgKVUp2QrRv86W17+91vx1ne/FWfkRMhhK4Vf6ne5aeNxGoAwxbMVcevsTQ27Nu3takUTflq7zunqh4WZCkoqKlB5Qq/VkcTcxYLvQg3+z0fPH2P7/3SL+ML73/IzdU1/TAyL1BcZ+2K5Djxja9+xHk+M88T83SkebkCgmrOpo2Dk8mbJU/36JJSS28NgxVNQR2eLriVtSHreFHJgg437qBYOlnR8b3KfFjApKjNqAwNoRhQqkHkkdHkeFJamLJqz57nM8PxyLC7ph/2dMMeAXbDaGl1E3M643Jk8I5hvyOQCV4I05l5WciWBhi8J+CI00IBnr7/Ptc7x/Hlx+wOjznenXj+4jU//VP/lsdXV5ynCXrBu8jx7pYcT5zOJ7xX6airq4PpnGVKcaQlssxnZdbhcH7P0O24OmSul0x59UrXjMYeWVNfc1HmSfAeL0K3TOxOd3z4tW/w5dMdH5TIMwq7nLWgyK1nernjk9cfMTz5As93B25Dz50PzMdIogbvMiqBtzINa8J1TWE0ZMtSYcXAuKRpoWKMKamFXLwWEvMDQzeYTViYl0iMKkvho1digfMMXbAMuoxn4b2x8KzPHDR5/mI25ywMwzWkSJwcKS14J3RdYCnKdJ6XhX7YUcQTcyF0plnnBSQRimPnF0pI4LJm6nivfe4aH2tdl43B47ugAdEC+8NAFxydd/SdcLWHfQ+HEfaDcDMIewc7p7Ih3rmWX/eddIgIvWBFjDTZ3zlYisnGA0jhdonM0TEvjmmC8wJzhKgFqpmWTEqOZTEZA6vcPrmCuKQFi8T8KREN/Hjt25zF0khXZlYFGfDGGHMBl90qc3cBfMSmcQnQdyoZoq+zMd6zATWXzMeUM3OMtD2kUHdb/UvR8T2dJ3LSjEMlzmoNkeKCzhY7pYK3QfdsievOlBMSLG3Y2IXeGHLVBCilQMqkZSKeT0ieWU5HChFPQkQLlImhQZUbVmxuVmak+lbSwD/vQrNl+t6KUOeVI6aqxzVbaLV9tE01wGhgaY0I2bHdz50VBwxdzzA+pu93dMOe4fCIZ+9/CM7z4uOPePH8axDPqnWLEphysj10bZRd4C2D9sEeXPdU3TtqWnJ54xTN+swriaHUdPCsDFYNDPj2jeprqyZ6ZLYCrZTUgP8aNBdjL26Dt7WNVT5MRKU4NOBTxzIWHDAw13BeiZtaD2Ap+LS/FTIpacAidKGZO5W80likG+Cr1jZoIK2DYTfSjyM57Tidz1Q9XMmFkR3F9EBrYawUYwPNnfNWbCpf9HNBwd+cMyxadAlbZ06nIwgNnNQiX0FxIgMC5zkyDAPBanWUUhjHEVHBBBCdS2M/0HUdfegZh7GtL9hQbWn4OROzPr9oAN+8zMwGIlftWkSLClb906aPbGNOsx1UHqULOq86k2cDDWapNvDKcPZIS/kHKzZo4KKCjgoyLstCjJGUM6mUlumjgVHd/4W1j6osXAO9+54QfCvemlNGnBW5cp7z6dhs1Jq5Pi1Lq38xjuPGaredqjTKlZECTPrS1pJiAGuTLG33FBuIu9h4qXJF0zxTCoSgxbW1sJrO/XqezgiLXReAcWXRmilynif1A4sRdopKTtXre+9NB7aC9XZPorUMgneM3uO63vaXrczg5fEtwVgR+cvADwEflVK+3/72FPjrwHcD/xb44VLKC9HR+T8D/xVwBP7bUspPfKtrtGvZLlVQjZ81AqmbnLObLGIMrraiKuNjiUmZExYFyfaQwapKBo90PRI6coLdsKffX9MNI2dRwfVnN3tkOfJTeSa/+Bq76TlPbzwfXF8TvGdeFuY4seSZKWskR5xGW8VBGHtLhSqaPudMI2izaPehI0hQxoe4thEX0XaWXMw0FBye++PEbjyw2w1aSRBlo57PE6fTmeAD17sd5MySlEV8vH9N6Dr6fsT7wNVhz26/t8lyYolHhnEkeC3K9erFC3VCdjuePHrC4fqK0/HM61e3nM8TRTLe00AJreAndL2nnz1Dt05MDb2By5mbceR4H5itknGh8LVXz+kkcxgd333zhB0amWiDctzj+1Gjvgnubl+ZaLfDuUCQNbJIyTjUOE6Lii/vdnvVf5JsqUiJNC/ERaUUJHTf2fjTf+yHyAYI2RylmJH27/lw3gFwFJuHb7Th23G887o/TwD24bm+XffxH+uRi0WRhQpxxmoUPgAEHxqFaqyrMVGLceCcasJ2geKcspWd029sKv/SAkfb820ebwVMGzC3HtvTbMfQRTobNapvH9oUhGzRdfvuYbfHeU0jvLu7b8DBG/OrsWLaH94AYNdX5Q3Si8hD0NRc0wI1Fflt2G+9Lyeb/ipq+KVaSEtcq3D6EOBVR5YLTbN6eY12VzhjBazrfbZ0wtrczY1Ue0T9ts2oKGuxu7fN8XoaNcDXNm4rUq8fetCH1WrcdNYWiCkltcJnQTqqFNL2Ws1AFIGccCUTEEYf+PBzX+DD9z/Hs8dPeXrzmN24Yzde4bodLgzsguN0PnM6HTmd7jmf7jmd7k2iJaLOdUGzXBUsb46Wgav6fNSQDz6AZEs5xhwNdRAdRdkiMVO8b6mm2qlBA7DmZXpfmfV6l9lAlWiOatd1kBaquymigEWKsYEoLqn+l/PGji8TKd9agZKZXcn0gxaaCKFjtxPcnCjTLbFTA78f98SUcSHQLyaXM6OBdg+d7zje3uPnCCUQhhtkOLC8PuO7A48/+G6++MUvEvbXWiwsLtze3vH00RMeP/0A8b06BDlD1v4NXphP95xZVCqhG9l1HckJ45jo+xMlo6mDrCmMygjRMexL4SZOyO1LwutPGF485+bFK268cNP3XA8Do/NkMpIhTWd2n3zMcI483z/i+e6Kn9vt+fq4ZxaU/VRArCBYBXEqsJPMlm7z02xjLWyLBrNKqeXx2rzOGZakjq5Luq4qQUEosbTCJrFoYG3wmtH17MbxuF8YSqQskWCA3ZZBlhErSuRYzCGjCCEMhDDgQ88yJ8Q5xnHHNJ+ZpjOffOMb3B1PfPDZD7l6es1Ozjh3j7grshXukbYuayZK07ataa7OUqYL6gQKSHF0vpnXeCAUGLyjQwMrW4C3roupOvuFdm+/mIeuhBrq011ViTXiICcrWkQFFTK+U26RixCKxy1WwBThcPCcp6w6k94jxbPEqAyynElxJkWPCzZWSqYWnCtgkiMK7FZmU2VrN8DBQI6STR8Uq/zOKulTCT661SiKlsqaQdNSsQ0Brb5o3UfX9VvbqAxVDdzgPMUKylKK3quJ6UqtUSKizHrfGXi77ktdMOabrNkC3gElkZaJ+XhPXlSTOsczHQnHDCZHoM/LrZkj0OaFMidVCsJ7ZUp6H+i6frUvBJNCQANtFZQ2Cm/RrsDVwkWgYI6oL1/366bjL2h/mFRC6PeM457d4ZphuGnrRF7O/NxP/WtiSsznI/F8h+RFr2s+eE5lY8td3h8GelJKAwVbkeqN3bUN7ikwhO0il3tvfcJS+6+NB6cAWc06sTERl8R5mjaM2DovlKjF5rpqT2nWb223uNKkGCpAV4HZdo+1x6W+NkJTXf8b09AyU8jGMFTGeDxHavEmQWvhVFm1nFSWLS0q4+aD6bsaO7qUWW2RvI73+vxLlehyqhcqzpM7/UxJqvUZejFbXNvpxem8zHoftQBUvcvgvRZH3OiGaz8Ze1gcXqztuRDjBBj7sfz/zL1JrDVblt/1W3vviDjNbb72ddn5VWZWpqvcYSNTgI0smQkMbAkLJEYIIXlSSIwQnjH1BCYGWXgEnoBhYMHAWFgYmwEYA8aUjClXZVVmvsx8+dqvuc05JyJ2w2CtvSPOfd/LLNmWceh97957mojYO3az1n/9139pBnPX6XqdY2aKE9FF5tNMF7zuDdZfOkZr4DCp3nvJeKcZwl3fNYDVO5Un6a24cJxnBR6ltKGpgHRkHJUcV3V8qbavq/unBpEQUdtpecIatPEOMfJhqeuWVJZ1PisALEWa1m+yZ1TnQowKQOrPRAh+0YEWG4fUPZQG4Op8KRacWc211ZpCVuA0p9iuuwaVQfewLnRWnM2brqzDi9dx5r3JsejMyRR2KRmIK3iv9aKcWwJwcZ712ZoNMsdZx6DNd2dZ5cqZFpyN6WHY1BloSjEVQM+mq6yA7WjFAas/U1BN8y87fifM2P8c+E+Av7h67c8A/2Mp5c+KyJ+xv/8D4F8Bvm3//jngz9vP38FRGiUbMe3GKoAsNJq1vQ3YZzCD24yOkuuAF8SMTcEhYQDfUXxAfE/X93TbCyT0gEeK4xQTP/npT3j96YfEu4+R+xfsQ+bC9wziON7fcbq/ZxonUo6aPiIg3uFCoBs8vu8poTrdQpLaunVTy7kDjbQPFBZujfp0uj2OU6YPuvA1Joh3DL0OUCdYJcIZUDCbUohxYjw5QhhUuHiaOBwP5CwEK0yEqBMS9p5h6OgHr+mCRY1zqVadc2ZOWZ86rUC4GXpS7JnmiYhVrM6QJXMxDGzEc9DAFSIwpcjn9/f89qef8GzYMgzbc6CjHyB0lJhaf1gQtjlPtEhEaVFcpYvTqtGXZNOyLBIXsQhjXjbM7vPP2f/G95Y0Hu/xXqOuGjmbmOaRGuFMMZFytLGW4Yc/oLx+tbA6msMuhO1A2PTEP/DPMP/+PwilsP3Lfwk5Hs7BHFeNs8XAWw/0hxv88tkF4Ggf+bK/Hxw6ZcxMLiDTd4CA/+gnXP43/wtrAONNgMhyvOnNN13cwInVOKfA0/wOwSL8TjxPf2NmJx3DMLDbbBi6zsCCCoicAxoF+H8fP2YMgU2MfPflS5w4no2jXrVkLv/Pv8PVZWcpE5kYC9vt1gysCpKoplA2pnnwywa2VLTXjWDZhCz13DlefP45+/1FS/nJKbUxKaBFlk4nNkNgGDxD77i/H+n6jnEcuXl9S4qZZ8+f0XUDNT0/5WTFX1SNZrPZ8tlbT7m/2EOM7P7yX8Llmr5xjvUsxuMC0og49hdXCjykyOF4D+S2qVAeFF8yRkDOeeVEWMER+Rlj0DbafPWI9Oyt1byt0U8z+sXuq0k7WcQ5Z8IPvrcCHhdwbJkfywVLaRduTskyXqSd4eFwrcb38ff/s0zf/MV6ttXYt3Vm7d3aeRqQJ6tLr/qu7k3Oewie4qQFBhbHX8+55qGW1SnXz/QMXH0IyK5ABFaff9jYGigsDydiu7COubrend0Q5+OrGnVnL63ee9O9VKfmi6ByoawATH3f2nzeijOnaLlMWZ2HZrQu4OobjhVQ/bOO87HAYumuzlPH0fJjOWde96Vdr45IVs+zzYfVPKtzspRs86N+s7TvQuM0P1h5a2E6m8MpIqKVa3W7Wo3poumIvROud3se7S55dvWYt56+xeOrx1zsLthvd/R9j7iOnOF4OJFT5HC84zSeOI1HTqcj83Sy1L7cmAbNGSoL28iJEAyQy7FA1srqIsv415vNuFKoTF1tr29/lzavda7WbNTzR11aX677uxZpq+y38XQEBGcpnurfBHtWiVKVyKvBLkLXD4TgVX6qFGIaSeM9c9fR769tDClzrO9Vz67N96IOaJYAYUu33xA2lwzbiSdvf5WLq0fsLy6YcmYeT8xJ2F48ZthdcDpNzNOI74YGcPvg6XxPHwRXEmQt/KHO25oBU2w9KA/WmEzImV2KvHW4Yzfdsckz297z7qMLns+RS+8YHHSCpoBT8CWxn45koM+RbRrxZaIEz4sucMQxS2XUzTa2PV7Cav6dzxHMkXIr7TYtKGaV52Vh1bRxVUzPD5V/UZ0JHSUpJfCObe95fuXYu4lOEk50jagOr45VczJxIB7ne0uprmmfyiY+HkcEZS1tvOc0jozzzDTN9P2Woe8IknAcSOmGuL3UMVrO9xjVdBYQZfyqfqkjBEfw0HkhhIIPqxluOFdd1xfV97XN+LPXtn9Sx7JFirbNiq3MKdNCACVbMR1bz0xmw3tR+5/WYct+4hYbxElhuxHmW/ULEGk6pgoYOAWwatBTFlbnmvlVQQQxmYMmt+QEyavUWGNYPiz8WF2Bh0e1RXRpX+wg1crOTde0rmNtvapyLmlGrBBV7dWCZdiYj6xpx7Q11BpKjBMljsTxwHy8p6SJkiIlzxRXFKR+YAdIkRUga9eyvdVbRXnnvbKJvVUzb6t2tdVMFxQUePwSZ6KCS3VPVD1r7YuCQxvlGDY7dvsrttsL+s0e5zr9fE7E+UQ83hFjIqWZkmZcSTauUvMDz+zklVtS/1HO07Lr+Fp+17G5+sa5nXIGfurrKoGTVG6lDpDVPldlWLz3dcA2Te91OnrVnizUAkl1rC5FiGrWSC0etx5/Iqs5ZPcoWEC2+jQGTjW2rF9AwFIwxi3tGpWhWUADIj41bdIqbYFJfdQibc7GQqHaBEk1oU1CrMowlNV9ViZuyTT5EjH/QcHe1O65jiFJqmveMsNEjGG5FKiq47JYYUVv63z9fb/dNdZoSloArj2zjOIqWVmwKSmIGI2hnI39WyelPhOVnKkeja8FwiyrK+fSAMdm/9WhWioRYZGtSNFA1V6fo+512QhryxrH6nnXcVplR9QH03ccDu8LpdOpW5moVV9fZSxkeY6snn1cGKvrImMPjyZj4DTok7vOQFENlnnvW4A4l0KeKltb9whXtMhdxQhTyQiWzWNkC1dJL1QmubN925k0jQLvDZy2NtSxPs+ztqmuFyLIvARsnXN09RnZYuK9I4SOrlMd/5yXbIlcbc4vOX4uGFtK+Z9F5Hc9ePlPAn/Mfv8vgL+BgrF/EviLRe/ub4nIIxF5t5Ty0597HbTFeV0Ywx44YsL/KpJkDvzitGQzxLNpqWVZKvzhPOJ7XL8j+4ESeqTfsNle4vsN0xRJc2IQz83hnt/+0fe4//QD4qsfs5tuuN4/5qLf4BLcvHrN8fZAmjVK6/uAm5X1EPqeftsh4sjeqePtTMNR77a1NUVLJWAFMmln69Apy6RxDsR1nMZIyY7tEHRACWwGx3YYEKtep2k0kRA6hs3ANM5aqW8+cHHZMU0j4zhyd3dDCD1x2gNqsPjg2e639ENHLpnXLz4nzYV5jm2wOQOGi2nt6AYcoPTkvOH2/rYZiJW5tLl+xPDZC7pyT8w1Pu64myY++OxzvvnoGVe+O3NWcwhk50BUO8uFbpks6MbKWY+yVP0zx8kZW1qKGn5iAPmI5/PttmXp9h99zNO/+tcWoK0f6Dc7NtsLvPPc399xd7glWsRrntQBOsUJIVP+5v9E/u3fIt5h+eF+AAAgAElEQVTfa7TPUlNwwubpY4Yne46/+u8pGAvs/7M/h//sY9286uZgguKNkeWWod+OClrJz5rOC2Cwdn7fdLT3zRqQ8c8BF3Q/+j6P//x/pPfxJZf6snN+8YMrHxlYlNjVSerLwLfjH2BTtnjxbMKGy90l15dXXF9e8uzRI672e7qmU2QA9mo6lQI/vLxiDIH9HPmXPvwI5z13h4ETAXLh0V//G+yf7tj0gVISd/cTT58+JwRPShNQcL5TxtM0cZpHhm4wjU6Y5omcMsNmw9BrSqQC94Fu2OBDx2/95m/y9rvv0XU9pRTirIU9+l7ThO/v73n54iVPn+x4fD1weeH56KMb9pdbXr16zfd/+4dMI3z39/0y+/01IlqJfIqzMs/GkTkXHj1+yjT0DYy9/E//Y0KuhlpuG/xiNFplegDT7nrv3d+lMi2nA599/hGFqOnLLTq+2rjN2Ukp2qDU94LvV85kroOKEjy5H2xt9sSvvc/0nV+iYHqSNoYbs92epVdbsEXhJSWGv/E/6OYYI26yqKXo/GhMorqR2qZH2zL0xDkrU3/Nc1wGjzHmUubzX/33GxgL1VEu5BxXWqfL987mQPvdnQFmBdEgolegprhFw4gaUWYxqtYTTkRaOmSDKlZOaP27fvbhaw+PClq0OdkcCWnOfD3GcVyi2kL73ALYlDMD60331NqwcmDexOo9PwwYWn3uTWDsgsGvAgHnLaWlIra2Vqbt+b0WWX6HykhdfY2Hz3rVG+v1sdQ21ue0fmtpQzv12XdNr7ghFjbOi+53pVhRqzr+WcC0xXqowNRiSy33YXMuRsQt4GUyh9ujWTxDF3iy3fOV5+/w3vN3+NrbX2W7vaDqV4p4+m5DypnTOHF/d8/pdMdputcAZcrKcMgrVkMRA84sDc+MXeccwVkqpThSjlbZPFNyBFnKIJDMJmIZ7+sZvR7btYNzY3vXzWLR7VsHBMzDISd1eMfphIjQ0dl3KiAnBqBELTBkTAjvoAvX+DAQJOAoHMeZNB8Y750W3YoGshToQ08fdK+JUdMZQz+o5qhocNwPF+wvC/vLR3jvuLl9zXj7mphHCoEnz97Ck7l/+SGn04lhu1cmSZwprqcPjr3XFOq8CkaHTgOMWHCxmC0Nas86cbhU2MWZZ+OJr796wbM+c7Hp2V9suXae7ctX9PNEyEm1uKVQRANrXcls4z3dMbJJI32Z8UNPkD0vQ8+dOE5J19SCKABkIFKde1BZh84AbG8OpTpN1H73BpCvrWsDSXS+JlwrzVLa+Oid43obeLIX/JQJKHtJGtBatcwd4gO4oECs7+mGJY1R0HR7mdXRdqFnGDpu7u60kNAucP34LTabrRZOiSem+QXi3mUmtzlVtUppc6wWWdJ+6AP0A3gpdEE1k9dGVQFi0RRioWiRyweG29oRf9PxcM3+x37Udc08nnrnucCUFHjJxkLNa+3xXHCibNFiciNzqlq5JvkqKmeRc8aFwn4fuL2PiBgL01K6K9jkimvrdL0TLbL8xf1M0/yXzy0BTy3wWlKppEuWYNlifyyAwLIW63VXdnydhyaxpkDH6j4EJf6kGUmz2lorgFTJa2IkEtVj1HTaYnM/4oDpeE+aDuTpSJ6OSJkRyyqksk5r+9FzrlbX2gP6KEUYhl5Tvl2tS1BsfRRdd0qh2kO1Leux9bBoaNWTbDZbUmkS9YV0fobQc3H5mP3FI4bNHh9UrzmnmVwS83RijqP5YVYbwNa/bMHBihcr07wGARZbWdtavvjaCqxOKWl/WeaKsmo523+0XUuH6tKVGthYx0HFN0pRQlHXBYLZJXNSrcxSVMdV70XsPJFUMg4NrjkDYhUYNXa99/w827DaMU039cH8byOt+p/OnYOxzli7DsMlpDFfF3kA1+yQh/dR+zgmJTjNMZrch9mqxo5uEg0i5CSkEslplR0lqveeXNbAXSnkGElxkb0Q51tBdQVWsu4rjSkrbZ3S/9Rv2m639J0yO6dxYo5TI/6VrDq2p/HANI/M80S1NSuIHnPS8eu8AaP6jKod1IXQ5gEYJutUzsDZ+Eg5tyBSsQGsMggJjLXajM6C1fGZG4BaZVkoiw2GE4a+bxkq1S6q9+i8axIl62c1z3Obz8oirsELIc/ZbJtM3c+CtW8B+GHb97i+1yyJXAjet1ooTpR0WAHgnHPL3qrFDptGq82NjM75WicJFnkOPVxj59Z50gqc2aIduq75wCkl0ulkwLIR7woksy80CBHYVanLUoMuKmXkXKCUXs9jbOOccwO833T8w2rGvr0CWD8C3rbfvwL8aPW5H9trPxeMlWROh4VEShBjOWpFS++UWZSzsjgXhL9QKxuLKPtjPE0M3aBAbNcpE3Z/TfEDu/0lu90FoR/48YcfgKjQeJ5mPvn+/8382U8px1f4cuRqt+edp495tPGUOPL5i4nbu8TF/orrqz358JJua4uHFCZR9kLoe5yElfu6migouBNStMID2Ga4sLsKOiC9OGWOiJ4jG0tu02+bELMVWyenGQzsmOaEMFphGFE2Z4o4EYaup3/yHHGe4+FIvL0HER5dX7PbKnv2/nDks09fAg4vRgvvtD2+RToLQiBT8F1Pv8lshh1zHNGKyIBzfPIv/jHyaWa4u+WUVccrizAj3OfM3/3hD+i/8XXuxtPSP6eRKc5I0QUv5mgrlFiEMLfBXxd455uyESULaZ4XYfuug85zOyc+evSUX/sjf4xsi1NMmbtxBE54EY34Hu+ZP/4YQqDre8Q7bm5vl6s5papfPboi/2v/Ouk3f5P5r/z3nE4Hjod7k1wQJHhSjItjCMRZ0+LEW9TQS4uSYZttXULOANUHG/3POx4y0do8kwX8WVhWa5iqgsJL367goJ973cp60hSSZq8s3zejpc8Dvzz/Ch5P7zr2w4a3nzznK+98hYvdjmFQrTRNdLIvmWPtW3qT1GHRbvdNzsQ8jwR/yWbYkFLk7vYFu92erlNw9tGjay4urpUpejjw0ScfczqdjC2t/VW1wlJKnNKJl69e0Pc9fd8T+g1XV9dsNsq2rZHDzz77TFMhnGO/3yFS2O02bPcbkITzHaUEUhLmCH1/ibiBVNTg8t61FKCuGxhjsgIrSxtTSpDiYvRXAMOKe7R0qgKFRJLEaTziJTBPqrfTqvJWXauSNRputmJBUzNr/1c2xjJoVqlW73yV8Q/9YXsYVnyrOGDA5YFUahEhdeAVZMkkJpJTlq7zOn6nP/ovQyl0H3yf7d//NW2fDYVS1KDfb3cGasyaSmqeX+uHGrGnrIdJs50L+mzX2l9eHLksY7kO3Qq46X2U1ub1h8oKZZOgKULS9bhhg+t7mli+LEHExpG3G2uzbjWHq0FVDSEefObNfy/zt62WK3CqOvXqRzkzmtW4qW2rkgpV+60etRJyPeebDP3zvjpfc+rvb5qv9fP1/psvb6/VfdI+vGoX7VPnt1POrrcE9vR/tbDIcm+s+uf8GstbFQRovCn7zAI3LMwafX19j3VsNUZfPYsIXpZUTkppoKxWupXlvjBD0f6ujlEpNOZlHffSmOx67qpN1iFcbfe89fgpv/yt7/Ctr36LftgiLlAQPMHGhTq7r199zuFwYBxVE/Y0nTS9y4ZVZSFpj4jWSxFTxJcKXFQwX7MRUjpwvHtFnk+QNLOn78LSq2YsV8aPGtntCS5gm6yfxDIYxJwxQAGECsb6Zd3K6N8X+yt9JkUZJ95HS6fVAjQk1fIvOarNRQQS2/0V292V2gtOC4FMd5/x8uYlYbMH50EcUdFHPv7oI07HE9dPHzNPE1PKzDGRpszcTyA9OakcgpOey/01235LzomuH0hx5uLqGbuLzOX1c0J/Is0nth6GLhCnSfNNSgGTgOr7npITx8M9uUQ66ZpWq4gjkHgynnjneMe3bl/wrTwR2LIJA7t+i3jP1I2klPFJU5o9TsE068cyT3Aa6Q53PDm8wt++xl094vLRU148fs4PSlTJqZp+auSBEALedziUud11Q8tA0WdUC2+sYKGyImDkdLYetZ2qFESUQnAVMu9der7ztseNrxCJVgRu0TpEtNAlEug3l9o/3UDfDYT9JTmqFu94vGOOIxeP3qLvN4SuV+mKiyNf3V7T9QNP3/5qsxnkNHF7eM1w+Alu+xVyuKTUKvcVhBVnxemEIIXgC0MQNh2tzmU8waZXkHYzwLavc0hBZR44e2eBh3+ajiLEVIhJfQEt5yAMg+rCKlbgNfBBoogWtIoR8IFgjMAYI84FnW8TpN5qViS1K6ppE+OsUhgpGiCRzlLNU5rNDq5Vv2uK6bJ31kMDZQXvvMrKGVFDWPadGjByToPxy16w7DHKAtN/OSfSPH3B4kbE1uqE5NjO3U7iAOdxIeBDp75gzsScyHliHu/oXSbPJ3KcKHmilBkpqjMrFQi0lO9szDTtf5sXq3ZXlt12u6uvrtpkaeWrebrus8ZOewDKNrCoMjJtTaoz3fuOYbPn6bN36LeXIF7njvf03nO8m4hTJM1R9WGNPVzPsEgE1mwbbA8vpo/aGERUYoFzShoq1Gy62MaDZg5VW9P2Feff6B1VW2KaZ+Y4N5C67kctYCqQkxYmikn1y1NRokA2cFNEASUJHqSz+/Qt5d5536ymxo5dgWx1vK/tjWw6rQ9Z4etBWCWraoZgs9vafmza3cHAzjpiiq7TuSx9tbb51gDrwKCAXNGgzOl0YjaN2DpcUtIaOrlkUpo5Hk6M06npayvYtuQHZHtmbe45ZaTmWPB+RoyFXKip6wr6dl2nGY/eczgeefX6pWrXB83YHLpOdZhFCVU+eLZ+Sxc7pnlU3WqbGiIgwTOOoxYPLtL0qE+nkWmaGj7gfJ0LweQjo4H00sDgdfAUMwW992y32wZgAmw2mzNGbAUVtV9US3aapyY9UKCtU9NkYDMQnGcYhi/M2xBUwqHrurOgxW63Q+3tWrNnGU51rJ2mkZv7O/zRLyBxnSxlkYDxnQV7vGOz2y62tHN4MRDb5nMqyZisBu7HrIVSS7XPHeM0tTFbwfdkY8R5z2a71bnjHL3XdqeUm2wBKAs6xrkFG2YrSlcZsJC5u7tt/VXB9BYE+BkYyj9yAa9SShGRL7/Clxwi8qeBPw1A39NSps0bLTmD0ch9FywSqvoNPuhiVtrmVPXhvDrAwMXjd5DdnjFlppQZLq/ZXT6mFOE4jbz6+COSKZHOxxvy7SfMn33ARiLDLrMpPW9vOi42DucLt6fE4TDyzltvMcfM7d0NdzevcX1Pt90Qhh4XPNM4MhkSXtPRPO6s7RpRyeA0slXBprq018U0hMCmH9j5wm4A51TXtpRMRpnCORX6TheGWj3ONydbAY8QhDiPOAf9sKEfNjjnubi8QH2iQimOw91r5qji5FeXF8xzFToX1XSp1U6p4sWdDWygFIYhcHc8KnuhOqeusNn1pF3Pi5uTabroJD2Wwocx83999BEfvr5p/eOHgeId0dJ2xCZsja5V5bC6q65ca1Q5ohB8V/XiyXnm1d09v/7t7/Kjr36d43RqU2Kz6Xn3rScMXW5jTyRwdfmEsN2TpWeMhU8/+ZiPP/2IGOe2+Ny8fKWL3le/jvypP8Wjv/ZXkdcd06RadPSORI0S65FypiQTyPaC5EyJKk5dN7ZijI628bXy5mbonEU724xqxhW1N1aG4RoYOTPMrU/PD93S27QuD99505JiQKlfnk1pmzDt/t+Pv49tvsAXx7YbeLy/5tmjJzy7fsyTq0d0fb+w2hcoYYkkr9yxB7fWjjN2GzB0HRsTjz8dj8RciLlQZgUYpjlzc3dSAf2UkAL90JsGjzDPkX67JcbIzauXvHz1yiKOUIogfuD9b/9uxjiTYyLOE94Ju+0Of6GaNiJwOB7YDB1D5zneH+iGgZTgNBaOE/SPtuA7DSLlCvg4xHm6Tpm4Pvi2WQHMsRBnZVOoTphfnlCpGmaJKjjvnWM+jCSZmeO0AitQzNQ2Q+dd6/MG1lsQBkt1RoT05AnHP/AHFZAtQAggDucvcewR6UECRQaNUpuxrNiJsWBIlDwyj5k4j4Qu0Q1QwfX0la9zuH7C7m/9TUQWhmWMkdd3t8voLXaP1Yg0ILlOBt0XHzirQFyBZgBxmmFWmRZDmKhA7BqEbON67RxVNNV0YulVK1a8FgRQILucMW7apcvy90Nwc6nmW6D2QV45ZmKuR23/z/S9VwzbRg3N5LjSj6rGduvY2lvrpn+J3MCDVWIBgM9B0/ppWKR5GttkxaHS72GPwu69Gmare9EP2drlVgxSu+aSJrSct1CNP/tsrhF9Wd1dvcbqFxv/YmOkgf25LM7NWa99sQ+lLI+rrFgPxQD7qle3ZtxS18GVAbwGG7OgqaXNAV1nlAhMR5xoBd/nj5/wra+/z3tvvctbj59zuX1ECFt81+O8I6XMzc2NMl3jxDwduD/dmxGfVPe0WDCHareYUV/TLoNnGPpm6Oec6Lq+7Qc5RQUJ4mRggxa46tygDo9zBhYumRqV7UFZJ2Yrw867ao+sn3CxxU31OS3CtARGqpPorIK7zb/C3H4X6/slVb1QiMzTyP3da+Zx5HR/x+XlNaHf4IaeEDru748cbz9DXMB1A37YM6fM5dWeq6sLun7gdo68vj9yf38gpsx+d4XvehBIWZ11VZvQtNNUErEULh89w4cOLwEpI/thy64r9FLwmw3jdCTNEZcVVogpcXs48urmXqs1dx1SMr4UNsDz1zd88+41Xz/e8o3Ta7ZMSBoJ05ZuX7j+hW/zav+Y8bPPOL74lJJPqu8ZEyUlIjOBzDydOB6PvDocOYpnf/2I8Pgp++fvMr37DT4NOyZxtlII3htYn8H1ndlGAXFdkwHC7Dq157IFYY3xaAzartcxQ2Wh4ExSMfJk8HzrrR3PtoluesF0uKXfDDjX40LQQknAOi3JhZ7t5VMDqPS14sCFgX4Dg+wJ/QbEkbLQ93v2l885Hu+Y5hMf/fRHPH32NiIdwxB492ngbn7NiWdM7oLoOoauY84qERKcpQCL2uzbQYHYEMrKJ4DQ6e2kDDHDhkLnhLAsLWfH/69A7GoBrauzavBpm50Hl3Vsex+sMFIhJn0tJphmx+GUOZ4iUymUojJq2VihIkX9lpQYx2RsSQXk6p6vgEsi5YQ3lmXbOsVIEiz7ywI8KVifawPMBnJAFisYWRREr8XBSmHJ3iQ34ETqGGu+2dqezYgo6NrkY3BK/C01NbraB1YR3auEhrig5y6q23k83lHSCHnGoYBEiiN5npA0t/2o2HwqmD/a/ChjpYdOmfq+yuMZzGaCvyILe3S124MxZevfDZi2NbxtV7ZXNHtu1kBcCxA5YX/xmP3FNdvtBbjA7et7Ntstm63Hi+Pu9jXTeCTGUfGAklpwtR413Z8qEWA2VAsS5yX7s7TvaDudKOAupvMqBYJ4K4C13HsNMioILM0Uqazfru8peFLSlPKkarpUWywVy9LxlSUsuAJuxVBue+AKCK33VTXRW6DZ9tuUIrWoqbLPbR+z74pNgJqVEo20RRuD4LKzcbIEcUH9rBrIyhnKFJlzYZxGYw665ovVz+jltHOaDqqNHosDUE32xa639a/uvVnnQj8MiFdGbM6ZzioBtowX8WeyH0q6V0azeKHrvJ7DbIwU88rvLvpZxAqDT5xOhdtbJQNW5qh3wYD6YkNfi0LpPSjjtC+Obb9Fept5Zs/sjLwjwDxPq6Km2v+zFb1KKXE8niimf67FNrXIZV2njgZanhEOSlGmqP1T/1Cft+8C2z7wkCRQU/iT6fRqpmRhKYaumXPjOHI8HhvoWM+RUrZsUNfGq3PVhxf6vmPT92Y+Sxtrqjlc9XajjQO1q3MpHI7HpmnsQ6DveyvQZZnPhpGoj+sJQ9BMaRsL1XWKKbdznwUlUuL+7u7Mt06WLeUsg6sLvWI24vDBNY12tps2hpPZuDVwkGxQT+NIqoVIv+T4hwVjPxaTHxCRd4FP7PWfAF9bfe6r9toXjlLKXwD+AoDbX5QaoagpdtgGUWKmdLq42GxSSr735OTM6NeJUwejdx7XDSTxuE4Nod3lNSLC6XTk/v6OcTrQd17TNg43pNefEvJMH4SNd1y4wpOLHpHIac4cp8j+Ys8cZ27vD9ze32uagGCCx5oW5UNALMIpopEF29+WtqMbeUZWjCx7sqWqv6nY8KZ37DvwLrbNU8WzV85Wzo2d4pzSwkPnV/RzZT05HzTq0lV2lmm6mbFbiqPvxRZ7xzwXRAJoIiOILkzzrKLS4gSPJ6O07CbiLqUxYUrOdMHTd93inBoboAAnyXxyPHIzjUsHVZkHaGnGupeeA69I9QNtUhfT/IyReU6Nzp5K5qe/+IvcvvUWbDdcbkIzHrabjq+884jOZyseoqy/rtviw45uc4nrNzx/dk3+eyfGcSTOSX/WNIRSGLdb4i//Hvyv/322xzskONgG5jSdUdN1H60Q41J5NbuMs6h8/WDdxBaFuQoaLMZM270qBGIbnVRr8MGxBk8WkORNxrox5tp1oZpcphm/eqe2q0bhzo0hCkh2vJO/xUV+zN7t2XQDT6+f8M7T51zvL9lvtxZx7NoCWqu11sW+3u8CijQMYt3CZji04bTSPNJ0RN1wxMDKoR+4v7trDk9KiV4G06ypgBMcj0fuD/dM02jgQqHg8K6jH3rVwOm0gqJFLyzSacX9vKPrVKA+pYR3HafTbJVTxQwDq+5t5oizQmfiwJHM+Vwa7cW3qFwGlAW0ABQqhwK4ghNPHzbshsfM88ictfBJ/XQ10Np32yyViv9QNlvmb35H+1Mcebej7C9BFGwU1+HcBvwjClsKujFrgcOonyE1o760xVHARUpxpDgBkdAXcIXS9eSrK8bv/jLDD74HpgdcDc9lU6+OV2njg2rcyLKuFntPGc+5GXv1yDGqNpulppAX/bAvZ3LSAB0x0XzpAxKCVc9emMbL81sG6mJ82qJWjcr1feXzjfzhrTgnrGs/nL+/kkM4v3vanFqBavaN5lzWNeYLYOoXzlfHzPK6fkVaH519t6zabvtfs5zWd9PWm+UZfvFJSHMu6rvOtMqyOZ81MLpcSloxCh40pazGxRogP8tYsJuTuu6UJahaL2RhsgcnX3516B5VO6sVz6h61tak6rzXtVbWlaexgGkFDquDLJXNK3QSeHJ5xePLK54+eso7z9/j+eNnXOyv2O0u6IctOWJ7fGKaRo7HG2IcNYV2HjlOJ2KaaYCE3fcyn8H7QF9lRErmcPuarld2RTEQV6gOci0I4ZRtnxKxPgwzZCsQqqmzy/Oru1LVcBPLxnjIzNJhpgGpFrSw0SKs9xZ7VXQOttRNu4ZbVc2tT06LhiUiIyVrkbHd5SN8t1Ed0aEj55k5TeQ50vWDFRkrtrQktvsLHpXCMGw5TVp0KxnLzIlTWzfXVE/VLhezNbXY1Uxwwm4IbH1G0ol+03M8HXR1DR4vVYrAJFMsRVlKwefCLifevXvJVw63vD2fuMqRQFK2cta95fblS/a//Hvx77zN/Y9+zPGDHzLEES8F8RBc4NNPf8o4HokpsQmOTddRSuJ4uEE+LzwaBm53j8k+EJ3HD1u1Mes6IB7nO0S8FigKCuSXppVZnXibc22u6x7ijGGapc6BTO/h3SvHdTcxlBnSbGCWVYAWHXuCZXzUwAHFPhPUDnAa7M+ukCUpmBgGwJFJjPOM7zr6vGl+iIqA2HjqHEMpxPhK80KGp6TiqcWerANIozm/xc7hUM1kB52H3kOwZTLnora9nK06X7pX/ZM/5As/qv3a/BizlRDHNENMNYimtlvXZ0IERGuB5IqMClSpt9rUSlaoe51DQcucYttvgBUja8maqKwqZYtZyWADEtX3sfTrkkjJinsVk86zLKRcNOenFDSFuqgOdsoG8AhnzxqpxSQXm1ptVd1vc17YgE6qzJEWa3NOQHzdfagsWwVvkxb7KhYwy1WZt86WlRFv+1O1BUW8pU93hK7DefUpm7/Q9sJit7uyK1Y+ydnwa8+/7l/LW+37Bioijr7fsNmqXJzzHTFnyJGuDzgHMU5M44nxdCSliWJ9tBBflmeJraUqgVN/VsmA/MX7sEfTJNxWtqUg4JauW/Fvqb6RUNmuSyNTslTl1b+1EaN9Inh7xjU7o0Wpbc6cjREySF7sKBvHax1kTZlemLExlQZWt0CjsZ/1vvPKRq0+/OKHOefwK3+ssporKAsagKXo+KxawFqQvd5/sYyixacTEXIqpr+aFtKDGMsyJvtMbkGVnAwsNBsuxqj2HmVlr1vAAs3uSjkjMuta4sMqvV+sDdW/tDZ6h0hXZxilFOY4LYF9AbxYHxXIpd2HbhaWtTC75qM0hriTxiKuxc3XfbI8w4Xx2vpdROuIVN8EoOku233Os7Jc7XNi46bJQNj5qqRFZSqvCQ8Vg9CftPt5aAvX79XrVdKMyFIssY5TJZ5VMN+u24VWGyp03dncKWhB5JoFg2hwqLjc1uRSMGmLQiypFcV0ftGbb1r5qJ9b5RDW97/oJSv5cf0d0JpBZeVLFfLiN7d1wiRuMFkcrB/LOfD98PiHBWP/O+DfAv6s/fxvV6//uyLyX6GFu16X34FeLKJOw2Lo2tJgjrCYCruzThSvTm4RUTZFqTR7NVxd6MneU8QTup4wKNvjeH/H4f6W4+EW0kkvdbiF+1dwvCEEIYhj8HAxCFf7nphmjqfIcZrZ7rZ89MkNN7e3HMYTftOZ5mAkR8GfDSK7Z2fp2iv6f6E6CJWts2xc6wXXu8IQCn1QQ6AKVEsIVpW2GlxmuAShMybKsO21sFddmL2zCSgImSJiC5O3aIljGM7F7GMC5wZUv1IrDMaYOZ1GStGBKc7jilZrVU0th0h10JSV1wXH0AX9uz1H/ZcEbuaRoxUeAy30lXXmq1GiM82M62WzVUdNfxcrvhTnmWkciVHBWPGO7Aqff/MXmH3H4B27i02bFH0XePhvvGsAACAASURBVHy9U02ufoOIIxWluRcyQyfsLgYurzd88MGOHDeUXDgcjtyPE9OkjtacM+P777P94Ad0UceG3/YwFsbVs18MEW2LVpe07dwtxo20RZlm3NQT1PeX6SOrxfVLptgb35CV8bS6FOd/L32+NufK6n1s8RLWm3yhMJQtPnt88byT32fwPZebPY8vHvHu83d4++lThk7lOirjSZlVK0ulud7L3Fq/+7BNa6MbDGA1Azvm0qJo9RxdF0i3WpFWq3CrCHeMkVwy3nmmaeJ4PHI6nc7bLjVq5nXxx4PTDXsNIjsnhKCf886Rkjp603xknjR1bjMMi4Zcez4WYcyabulMQ6/2ym7YakpPSqSSgFVhE5sj3jYK5zxDf81X3vsFbm5e8PJV4TC+tpYog2MpTFHnmhpEFCibLenJU6ZvfhvsG4jD4cDtKLIBtyW7HbhrCj0UQUg4kjJCLSpdl/pmgCC4sEUilOSI+YR3GQkZXCH7jvH9b9P/5ANkHJfNXZZn2VJpHgzi9RDXtbeOUWXmnRWvAHWujFlTF+svgo5vGHm23ktQ40KC15Sy4C0Yt27tF+fa+XhfnEQ9t31bOJv762uvfz48Ht5/DTDU977wtXL2A75kxr3xeuX8tfaXLI7yF95ft/PL+rr5e/LQxz+7UgUt9XxKk2xFVqz/GpO1zs/VOddZBD/7WNbF9SvrPml+Tf2rtW8595ue3RuBc6mrYDX+lhZTINk+yOp7wZm2te+42l7w9edv8d7Tt3n3+bs8e/4eXjq02JEjIcQ4EueJeZ4YxwOH451lqETbXydSScpbbjabNdK2au89fdCionGeON7fQclq+BbVA2zftdSu4DVgk4uygqT2QbLK3dWRoTRN/bq+6dyvu5MFK88ek3EwVxIhdR1Y5pOda/XF5XnYfZY6rixjoa6zZZGxOeSEC4EN0PU7hqGnlJly1DRVyTNSFjZTToXt/oqLC5SFdjzS9z3HUQN+PnjIGgQX55DsW8HWnBPTPBLnkd45tp1nECgpE5xr2pHee9I0kdI9DthuBvLrBEnwudDHxOV04u37lzyfTlznSF8yoUAsmrVQCtx+9im7iz3d9SO6Ycd8SsSXH5NPtzBP5OS4O5woORKCY7/b0vcbpgwljribSRl2uzty6EmhQ/bXyOVj8H2TohLxFLFisc5XN+jMARTzhHW9MGkOS+d1phnnJDG4wlUPb+8zm3JUfb2SccGAWKfOOmiadAX0ISuAZpqVul44nBcDRiu3TUEqcVqN2TshhB4vDu87KgujmI/TBY+fXuNixOGIrqcUCyJkIDtSisRUSFkYOl2fghS8g+CE3hkYWyClQvEqq+Okjt9z+3C9pjxcZ9709z/W48Ga2u6lOqiKIikYIZ5pVumCVOe16PbpPY2VlNrmpH/nVM7Wy3J2nbrn0PywCrbUPbaCGcr6WwomiXrwSFG5gZyVdNNsyaTAnphwbE5LjqNKXdAWf9U/lcZSLGVhhRXEFKLKyn4x/6j6OeJxYVDwwqmWrhO9XpVuKwA54qgFnuzeWsDMnI9c/5ImLyJlYVoGr6yy0Kl8iKx8wrpGljdUBV92wy/upVhLa5+cBczr54qyI0MXGDY7rh89I6OVyeN4wvuO7a6nEBnHxOl4NNdXi3MtYbY6ppKxlcvqtdx0IYsxjt9gMja7fQ3Iiq92ggCpgUDVrmvXbydcfKGWYp8XoGvpMGkZMhUWrZm1Z3ZA3X9KvVo5GytiNn4FSCsIWvskZ6XSpxQNT6h2ft2+GxxPZTOLQCyxPtV27rXNUot4rcHDauOIqN+j2qLLs05Ja0Asfa3z0s0zMSrQ2O571Q9Ve7NYen0FUsV8PIULsjEQi9oSRjDRIEsGtLiU97qn6jpjxe+MdLZYkrVtvp3Hd1Zcyq7tmr+wjAehFjtH9XDj4tOXUkyqYLEfRFgKnsliv1Zy3cPgmojgjBVbA4eFJchUWaTTNLW265jTfS3lRXqjMmcrMPkwKBHC0vb1/VTboh4VMJ7n+cz3rc+jrqsmyrgCgYM9N2tDZWzb4RA2w7CMgZzpfAeukFwiStbg9UqaT6UXSiPkAVa81NnzPdchXgcX1hiGd5VdrX2eW9Ctjsdk82cBfb13ppy6PG/x4PlHBGNF5L9Ei3U9E5EfA/8hCsL+1yLy7wA/BP4N+/hfAf5V4HvAAfi3f97523VqWnJR8FUjcbYJmKUi9jnXBZIIpWmk6IqZzTnPTifU4+snhGFLdsLHn3/C4dWNGoV5oov3TK8/waUZl2dwEfE9pSR63/Hs6oLd4Hn56sDN/cz9MeFS5tXnLzhME9lpTHaaJsT1dJsOt+mJ42iaJhmXHSnPDMOm6VwCtnlHctIKt8qvqwNCQa2u9/SdJ7jMHGNbXESUJu9daay7rvNcbvf0Q0fXmW6L900HBSnKMEsmOt0Kh0mboBWYKBmSmEFRwMmEcx1eOvrdnuvrS2Lac3vb89FPPmpGn3OiuiVBgaacCzhHMjC29MpJmlJS40oqG7cwxsRkumYAn6XIzge2mz0yQ5qVCSdmqOumnRsDKM0TMReSFcUY55H9fq8LTorMMWqqTe/phw1Pnz1pxkJKmcNxAsn0OZBSUbA5JXDCy5sXgCOVwO2rG776lXd4/uwJkPj81cQPf/Qhr16/Rjzc377m7tVr3Gcv6XcDb7/7Ln6zZe46DtY2fRxmCNnmlMlItg0lGYgsrCKwywR2C5q7nj0G4lUjfGXs/IyjPPQ+66urCFHd7KCajfVTUs/QNtmmNVmWePHX4re5zk8RoA8bnl8/5e0nz3n32ds8vXoEWJS65BWI+LB51YA9B0mKWETyQVNzNaKWV8hp5jTC7eGkAGsX8OJIOXN7d8ujR9e20CeGrmd/dcUclQUep4lPPn7BeDqpdpc5PFjhhNB15Bi1vmkuxJi4u79lHCc2mw1D3yMOhs7TeUuJLAr6juPENE64IlxsdxoZRxBjZokVEVMmkDKF1gU5vvbWN/h4ytzcvSbOBwoRH6pDuTCFnPN03Y7ry6/yJ/7En+RHP/ot/v6v/13+9t/51D63esplMW6FopJarjC//03mb3+XBkYQQHqK35L914j+KVk2ZDzFCul5ZgIneg5gGlx2GasArcVM1JAbbOwIOQrH+3uGncN3RXMZV2PtnM1W01PM6CpL5LdCNGdfLmqs5JwpqSDzzFrcSFKGyiCok7TUsa7jreo+1bYIYuLyoh6kaZ0jgusCxVx3KYIr6qhXMOiM7W8Tqqz+NWPhZ8zrdeT84fEmULEFdOoWUM6XlXq99vk3XfRLnPpai6o5ZKsznTlnb/j+YnQuQN+yAq1PWo3Fqon24H37XY0kWkFHJZPq6pXtOhX4e9g/y+/n97sAyovRLDQo8Ow2FlbN0l25LNkF9dmqUbuMWQ3iLixZ72sQZrmmbhA0g97Xllnnl5zZhoHHV9e8+/wdfunbv5u3Hz9n0+1wrkdMCzOlyGk8cfPiBYf7W+J0Iueoe9r9zeJYqbevhbWKSg1V3dWaPgcgzqSXis72Pnitfpvm5vyVNt+KZqTkubEShy4ARfeFlDgdT+yvrk1bvZgOZ2xrm3dehX3esH+sWVfO1blUJXC033LOTV6nagBXZomutd5gi2JsNGXYOmf7blkyV8bxCK/VRttfZIbttRbsCo6SIhJPdKKpkXMs3B9GUrljPN5wuL/l/v7A8+dv6X1nHVeqNZhsT652MNzcvOD25gWn0z3f+vo3GHxioBDFClFE06BMkc8+/BGvXt9Tdpc8e3TBr/9wIpbCME5sjgee3bzg3fGWyxTpSrVIHV2BnFVbTW5f8/2/9te5/L2/h+tf+i7b97/By//9/+D2+7/B/Yc/4tOPPuXJxZ7Huw3b4HApMSa4KSMv08zHY+Tjn3yflzlyAKLzMFxy9Z0/RHjyHrIbrJBLaXMg54gXnRtr1rlfgVp1rcjGqtwMHpHMvks8GjLvXcJ1OFCmg9q0obexKmAMXHFdAzscgh/E2n6e5eN8R+c7fLdhno7MsxZ4dCJ0fc80npR9HFTfW7wSFlSXRrUVOb0gja8Yb2/Yf+2C2e0pvjegMJOLI+aCz45UHNOc6bbQ97rrDh0GxBVigfs5sguO4oVOQ6NfNBH/KTiygUcpZ2LRfaLrPLFkUtKCRdMM05QMjBViyva+2XlFlY5iwvRaI9MpMo6TptWSdS01u7mUQsyZmKyQTfDkpLqIpVSAIDbAHWhOuR5CSlqINbqZlJQYQ4xNkxIWMAZbh5wVWfbeMpdyUtuu7R2a+bjsLfq/LhgLrtCkFObOmz51JiA4Jsgz5NF8HsuKFFHWdzGtxKzs2FZ4udnRlpHXJDksWN/19F1P33dApvO+7Usa+6p2/WKHLz7Cm4+Fh1JXyHqe80PMr/FBgdj9xRX9ZstPf/ohJWvBvs1WONy/bozAUgpBvCXMWsBNKiEkUVJURn3tXwqVNaw2rhX0eoN9osw5QAqZpPqYIZh0GZzGE1GiFfcpVO9radByPpVX1JcaO3JtWxXVvEyov56Sav6WogX53Apk1cBPBcddw0RqFy+ZbeZbWy2W+qx06M7NjgWIBtitbREtbiYmm6EYQQWcgFVBMRo4tz7q385JA+yqTbloZy4BgMq6HIaBzWazsn8X0LhQcE7rsJxOR16/frXYgejcmeeJnKWt78mKu1UQT7tH5/w8TXoXssqcFGOJVxmC4EirugDeh1bHowKJFOi2Ki9TMyn1cZyzUHNKGiCVpa/rsJymkRQzOUcq6S6EDueWOhH1/irofdbnoj2q2sL6mYv9Hi4ulkGGhga9ERnv7+8Xnx3aOWOMJo8QSSkaaLnY2eKkMVqrnmw9KsC6JvU55xo7VwPsy5pRn8s8zav0fpXyWN/3MAxtDFVMsP6+2XT6rFuQRfsqpmjXNRsPtVFzqUXGYrsvwKRYlv4VFiKj2LUrYA2V9V3lQPSfYjjz2XlTSjSZ6J+xVv5cMLaU8m9+yVt//A2fLcCv/rxzvuloLo2YroUZv9mMaIxWLGbkt8HsvRpROYLvcP2A317SP37G6Dz3pxPzNDLev6ZLR5gP5NM9p9efUeYb1WD0HulUGPvSO57tBt663OPiRDxGxtsjp8PE0G+YU1YNwD5A8ESB0AfoOpIX6DuYtPp6pjCVgsuqCVMPrR5qG4gsDmcFFXqEfejZhYAz50e8TSYR+l7YbALD0NP3A13njVWgfZZKVHq86Y1hujPrLNclpe/sCZrBU/sZXMiUMnOcJ6Z8Uj2iAtM0IxKRUgtt6OLU9Z1G9qPqv1Eyr77zu4kXVzz67AU/vbtX0KIIvohW/TuNxHFhxv4/P/iQeLjnq1dXXG22lJy0D+qCk2EeJyvSlYhzJIgjRaXl42A8HSklc7+/4Df+hT+O7wZC6BgFfvTpizYnXt8e+LV/8AHiEyH0RtwpPH78iMsnT7WQSMp89skLNl1PnGZevXil1RNTz2bY8O67Gy6uBj76yU84XD3i+PKW433ko+//hIvne9K4LHhJMogCep66Sa0iz6xAjbw2Zs5hBqgbLFT/+wzcWLCMs8+/8Th7vV57HTW111bGqn5tDQ694dw2wIIPXAw7vv7O1/jK2+9wud0zdD2V7VJW96sL2AKmrtPmK3i/1uCtm3S797aQrgBsL0zzyOnujg8//pynj5+y318QQsdmnuiCp1TtwyIcD0d+8Pd+yDhr0Qdsg9ACH3V90ut1fc/11SXPnj1iPJ2IMTFNkXHqCL4zMXjhdDrx6OpCo4AFkEAXOsbTyDTOeOfY7TYmaWBMHYTge5LJoFAKmJQGqIbSr/zBP8L3tlf86Cff5ycff8DdeLtgjiYWLwbOTtOJl69+yt/63/42nS9QPCEMzLZWLdCmGjfx/V/g+N1fMifVgx+AAaQnhUcUuabIBUkumP0jsvTQIsKNd4FD05pbBdrlIoiBz1oWWHBBWSWlOMjCPJ5IKRF6XYvuf+WP0v/WP6D/7e81wE9Ex4EW0VBWQRsR1fkpCiyrsZEaOyJPM+V4JM/L+pNTRlr6Emc/63xrRpd1mnPOnBpH6HtKCMru96qdlVF2XxXoH/rBNJ8iMa0Lc1SQaLn/xbhbTbMvcbZretfilHw5+FlPVI3jtTP68JONVfMlx8JUtv6RN9/il7GzHl5t+fnmNWsBbFdOzdm3lnUMtwJF7ZStL8WyU2wR+p2AGEufru/TGrxq3zlDVs6/W43R5pSsWlqW71QD2Ttv+/eS7lXZvWKLZck6br0Iu82Gb3/jfb7x3td4/uQ5jy8faxAAR3BC2PTMGW5vX3A63HE43HE4HJjzpJJHlKWAQWWdilUoNmkPLaC3aeNCnT3VDI2yhAV3F5cIpQEfbd+iru8FJCCScMbQbc8xF06HI7vLq8YaOuv1Zjzb1ap3gyypeTkzHk9Lyreggbw3jUWp6YSFcRyp+qTFWaq8+AZeqHNozEeTHEIyMZ64v4uMpyOPnjo220seDRtKyaSYuTmckCJkMjmOlOiJxwPHVy94+eJz5t/1C/TdDnwgZZhjJNrPnCObvid0PdePn7Lb75nHE9eXVwRGpGRCH/j044+YxyN9PyAJ7j77hOP9LcfbzzmFLV9/+y0++vGPOXzwfcLLj9kPiX7TUdPqiyuMqI0iRXBZ2Ewn/Gcfcfpf7/jwH/wWj//5P8z07AlTfB/ZXfOVd+65ev1TZDwypYn7DD9OEx/Eic9T4kVJvI5HPMLeecgQj6+R158RLp9qgUKW1E1yJs0zRlaysW+yYEnaPPcutBqSSEGIXHcz710Wnu0yj/oZ0kTlD+U0suuu9DkqRIK4AKWyZjDnVvWFa+BFGbimp+mBDo7TK+4Pd8zTzDvvvEecZkRsjM2F29uXDJstw7DD+4EshX67YU4HjrefED//PvL4m8pMz87S0nUtSVHHVEqFnDRT7WRao9UiI2cutp6YMrvO4brSmED/tB2C7gvOOZz5RV5UvikCRMEHKFHHhnMCSeWVhh5cKNwfYBuEcYZ5NgZT73F+oM9a5CYEryyp5iAvAK36DwtTsaYHt6Anaueq9vA5mNJ1qnWYS6F0gTJHsunTlmRSC9ZSZdQ5gndkyXgH222vGQBlKbxY7VezjgghaFEfc9a8DxQGkvMKjGVdf3OcyPNIihMpzphGDTnNuBwpeUZyQhWzihUc1H+kRPC18FKH8yovF7qBbhjoO2Xei4GWOSVzLZd0/5S0ZgKVHFLK+R7Gel1d1vu8+kS12/R3nYslzoyHO6bTkU8/+pBpnlVaL3TE6Ug/bJRhbNJ7oWVRKKgX59RYr8WK9ygwrqtFTMUKLK+YpTUz8YGpsaT7e7vm0h7nHL4skmLRAHTVblVbr6X/i0NcwQev4yQbzWFtA4ggxauUWZCFKZhy69S13F2TyLCOVKDX4aSsxs6qOFJF6yitun0do4tuq75f71u7JjHbeKz2obNia4rMLeBV7cTFPqpB29QCtSknxlHrMbgVyLdcb5FQEAMta7/HnFqmccr1+4tt6rH09Xr1nFfAWAVkS9Oz9a3od7WZrS9EGi6EZU7Ue4oxI5LwQceP+hyew/1dK+y0BiJxNU1dWl0YJdt19rx0rQhdv1q3lUGqAfiF1XsGaNp6VV+PMWpmhg9NMuJ0PKmGqY2Toe/pu0CZRlJepByCyR0t4GbNHNa5oq7QeQHCeZ4NkNfCaZrOrwWtqnSCOLH78ZwxpX2na8+KsVykgHTNhM5loQzWo527qOayQ4H5mEYOxwNFjOVrgQuVBtF540OnuvIhtHMqg7spN+sYi9rHKSYN2OWaNbiwfGs71n1W7L6Dc3Rdj9Vba76nAvMP6o08OP6RC3j9YztKAUutKIZ6q7GkBkroQksrihkSGqmpFUTF7em2e6TfUroNU3ZMcYKkTnfvCi7dUqZbynQPZcQF3wZ2t93QSeJqO3C53+K953QokDxpEo6nGTZbsgdMixbv8YOn220I24Es6OTznuKtqvBZ+oQezlWnr5z5cxnb/H0Hli4/TjN9KPRembJ9H9jsAl23VDEUh0Vv1ikQS2pOoZhehW1adr26OJ8xDuW8dIoavpHD4cTl5ZUCLKJFF0IIlGiKpqKLeBc6Zj+p04UNRO/wfcfVZuDT+4OmcIkjIORYKGOkxCXt5ZNXrxlefk48Hvn2kydsfMCjjJiYIvM4Mx9HcpwtdShrtDRplHguCefg9uvv8/L9X+C+63FzZMIxJrg/HVubc9EiCKUIMWdzBTxT8hxH4XiamMcjr27u6DohHI/MaWY8nXjx6nP6YWCz6ZmOWkxi8yt/mO75M/a//T1ubu843ByZjlNrW2gLvj4D75YNQB9LRSFtWqwAiUJZNExXBs4yh3TeVGBticJXo89O/XBBeMOf7dTrzz5EC9bXL9WMFbZ5z9vpq4g4ng1v8Wz7lLceP+Nr77zHxW5vC6KwGBOgaZ//H3tv8mtJtp33/XYTzWluk11lVtV79fg6kpJJUZQoWZIJC4IkAgJswJ3gkQFrIkBDDT3wwGMNBehfEKCJR9TAA0GWDLiBbYGARJGUyEeRVfWqsqoy8zbnnIjYzfJg7R0R52bWk2CQZsFQANncc8+JE7Fj77XX+ta3vjXjI6xLnepSqVm09X1Y51fhuTo+D7HltmkIOWnjmZTYbbakMBUHNTEcJzYbZSFUsfTj6aQZLaOOlW9saQ5jix6QbjRd3+G9YzjcElPU8rWY8d6gZY2qdXMaBp4+3qlQfNIMr3PKOMqS8W1D17XFZyobQxb2bUvICQk6R7/7xS3//KMw39v19TO++50f0voWk4Tf+eRfEVOas69lCyybXGKYbviNf/0vaBrLMNwXxzQXYB1wjvHnflHt0eUlud0i4jB2C2aH2D3JXhLdFWK2GijQkExH7XitT7HolqFdt+cmFMXOyxzxGpS5bzDZoOWiLdZrMJsFDaRDUGfGt1jfaEaylBJKSR7lWra4clbmCGzOTqv+FEmZdxIihDw75PqeVMDYBbR7+G+lEtd5WhkLxnuwvsjlFGYzD5IapbxYpDgiedFXmjd9uzjVlMtfwFVZrcu3wcqHDPJ/21GBzVnHs55VZNZVnUH0eamZ4mScf49ZvWd5dR3sFPixOHbz9lccy7W9qWzTB3f3jlfqsygO/fqdkqHo6Npaojo7SKh0BlCzP2dDVp/3+obmZ1Rt8wyLlOCkfnYZy8q2qK/lmiStp53BVT3s/Lp+16yHvJ4fWUppY2GMALu249HlBU+urnj+5BkfPvuA64tHdG2PyYLEI9l6ItoR9jCOnE5HpjARwsgwDaptmvMcY1tTSvDr3VqLK/dfq33W821+enV8y7XNbkkd5yVkKsGqg+zBJi37K8G9b1ourx6ttMTLN2TB+HN9PKQGtmgQYysAZOhWAUbdJ+vPdVzXY5+TEMYJ7z3JKiHANcX5NqDas9pQdR3ozl2Ei52/ef0F1hq6fof3DZmM48A4ngjDRB4jQSJpPGIk0bee8XTEZYcQVEMvjlpTIFm7hSeDOF8a+Hm2/ZarTY+LIGkiSCBMJ7wxNKXibAgTN3e3nLKQ254XL77H8fYN8eY116cjz/otnbHY8pxyXTN1ipsMOeDiieaUSC9Hfu8f3TH5huvn7/PoWx8R3txAA/d3N9wc7/l8OPIJgS8z3MXIXRgZ4lgkCIo0hhjsNEKKBQhT21C7Hat9T7PtAC0VtHZJ2Nbn752hb+Hx1vBsk3m8Sex8wkoqQEYzzzfXqIxZnasWg7hV+GcKeaHadZkXINVyGaOBV/ANYdLg1PlmXshtp4nB4/HE8Tiwv7ii3Wxpmg7nRsJ45Ivf/L948bMdzeX7iN+BGJrWlmZdWu2x3wi7Xui9zj3FCQ1GFBT2fkkizRUNs5PE/6fHWwmO1XXUpBFIYfuZOWCuDZAMBkmZlAswKqVSJgsxQpgybW+X2j5rcW6xtbZqVTszJ0tzXuq4JBVAP1Ud+Nr5XOdF3f28t4SgCXBramJHARU3SyVodVsFqmabVhaQ5qyWPVIKw1eTVqU6o+ogoqXZwziUhkSVpNCVa1XfP4QR0gQxkFMgx4CkidqcSlJACkhfbRGC+jpqMPCtgsLahMjjik/lfYtvu0KWSaV6qOxD9Y8+3LNGvfW1ZV9fbPvZsUqMU+KXGgNUDVEFqhfyirNmlmVAVO7KGT/HzxZZAJoUSaHEnnPTM8ip6qbL/BxnfweQGYxTH/LBhC5gSwXQtZIvVcmK2nSoxKFVt3IBYmslRmncVVh/YqrLWf2QVdJd6hzJpSq4JASKZkKdh3V+K0EFIMFc/aE2wVq/Oi8QYgEmc2GM1nlQe8y4lclQ3EAlDsu95YSEZY0bo4zEbGqDNsUGRJb7MVCa9WmJe9t2UHVziy+BsKqOXuRCFmBWzxtLT5gUtd/FuoGUEWbQFZGiu75UR0lK1Ao1spBjwEpeyDvlvdY5JFtwCq7JzGAXRBzeaVPmKl/gnSe2nhjCDBgu8Yc+5xQjoVQqC4Lz1YYZMCoz471WNWvDZ4PLeQZsqw1bM2KXknqdHyEu8gBVdmsMAZPNyg4x2yOAYRgWbXyzVARUn8i5qtHNDCQbaqPJSi6poLLFO1cYpwrUWmNmSZNcbOA0BbX/1Zc1i2yYMaYwgitZUJ+lc061cyXPpsgYi/X6vDA6N+oclFz1vfXz2RiycdrQtPT1iCUpU+9Lq0eVLJV9xjdK9Kwxl1DILsVupVSTpQsmMa3seV2b83iutuV3Hd8MMFZAWZSVli5F24HZGXLW45sW4xzTFFQjyTlsoywB127wmz3iWoKxTOOAyRmbMzYFzHAPww1MR2waMRJnoATAO8Nl43i027DbdAiGKWRyhBgyxyGoTpfTgMB4q2DspsdtOmzb6DVVbylnzWqpjOOZUzR3lTTLpK9BXkbAujkzllF9q75rtBN75+m2nrnTPbqZzILgZTyrgWfe8NbBbzGUcxB4VmBxFtjqhhzRTn6mMDUNeEfbKBNvwQAAIABJREFUNoQcdMMuTmDTtvhp1CzRqsTBGWjbBq/1CLqQAJLq3JkVa/cwjnx+c0sOgcu24bn39Ea94zBFwjAQQ1CWTlanwcQ432fKiZAyX+4v+Ozpc05TxIrXLJ8VhtWGW0EUNf4li2o9SRzDpNIH42lkmKKyoiUXRy3w1Zsbri72iHSMRaDbffc7+DRiv/iYIBP3N0dyXG6ugq8VLHO2dvEtG8oM1K/XR30a9b/yoAx/iewfAv9vHQt+cP7xs18X42hW56yWfPlnfn8FJQTo85bL/ISn+QM23YanF4/nRl2PLi4XJpGsPz1HEquzLhc3B2IzwFHGyTrVZTsbMHV81qPQNp4xD6SYsFg2m54YRgj6PI+HE97vSnCgNmjbt7ppWov3qr3kbd38LbbRjrxN09H1Gw1UTcY4zVC3TYcxukmEELUxYF/Kb6kyLEJMQedU02lyowT0xjiattUgskwfaz3vHe7YxKVspml6nj39AINlGke+eP2Sm+FmJftg6s4FAjENvPzyU5z35BxmIXoRIXc9+fFj4kc/hTaGKH9sh7hrxF6R7RXJXRPNDqFBcJqEwi1xrGQoIKwhYyQVy7Z49QvQtrJLxkBlyqK2p8QVpJBxVpCmOv/L3KggfokGVvO0jGUZg7pBSxLVrUwZKkt2NWGWhBYzeDR/6ercVoo9LMx2KqvZWbRNtIL2FVhaA1Q55jql11N9sdDmfA3M63v+wNcEPOt7WF/5W0aljtlai2oJluuSL6PMzF2oc2l1TW99x9yp+B3fd3ZHb59jOX99/2KDHnzb2WeECnrKW9+zlOStWCblnLMdmicQ8zfVObqA1cx2V1hf4+r+RBnYeTVP5q7FnJc9z2tAVhf14B6rg1qvc35SJbCtoEZjDE/3ez56/0Pef/6CF0/e42p7TeNbYswcj/fk6YCzDWIcCbgfTpyGkSSatQ8pMIWpgHAGE6ay35eJatTxFrOSBRGZR20OrGYnVMc9S2Z+MsYsQ20Wi7AkJM3ZfLTWsNm1mLnZBrPvUxmCayXz8/VTikeNwbZ2fv/89FbPdTlnCXAK48RZO7Pol4RJ2YuyasEtwaKb79NIRiRyPNzQ9xtqM1VQJqA3uUi4BPIE5ETTePa7re5NVkv2h+FIHI/YpiUH7YgecjPPJYPQt57GWlzTEiUTwwFSpO161ScvJXnHw5FTnLDtwObihvfubrAp8NhZnrqGTsCWpFSuNtqW52SKH5AmvYb7W+4/+Zjm8jFt39P3HREDzz/k2G750nzB759OfClwFMMoGtTZsivUdZnKPDBrn7Pam3lOyByUz5aj+tAlIG+sY9caLreGFxeGJ52wa4TWghFbpAPqfLFY32hnZcnYWoa6SorPhwUry7Wpc6zXr4C77i/KmjQ43yowUgJInyKH+yPTNGGdpe37hcmdI6ebz5H7zzBth+0MudkV1qLR7uAIjYfWG5oGrBi8k3mvaJyldVpHY1cVAO86fnI1wh/uMfuULM84iUoThKSNJ1P5twKzOTFLVmh5tcxyBdXO6z0tZcwAS+8BfZyzHFhhxKbCMM+znmphma18hfIJQGPRueIEBcJSjjMDLBebD/WjRW84KZudcj8xRQX9y8+KHqWlZ4SgzVxLFVRKkLObO3RrbxJleUsKpWIrLLqw8/0sVT1niT5jSj+E0nDJOYz1yohte1zTKiM4R6SQBGZ/e7Z9KmNVB/Ydu+3K39HvPPOtdOXMvvz5utbz18P72rDMYK2O8VoDN+dMLB3K56ZOMSiYW8dXqqdhyt5sCui++J3Z1Hm0VE/V5zF7RKU6LRfpgyy1c/qiQaugfPXrFr/bLCeZx6dufHX/m6+FCq4V9nF1u0RU+qrs+VCArnm4ZHmfWa657oqzSyurbu85aWLKSQElXZHIW8egMu9dpgDOqUi1zYBwWYfyoDS9elFQSTSmyBEo01jJF8ygsnPL+arEYs5rcp5BqBILGWMaBS5LxaLJmZxqU82i61nAcHuWBC4SgVXjudp3MZgislbjcVld0zyDc4Zs59Jza6HxfgYC1+xVvXe1e1FAjJbNKwmn2gxLiEljzMbT5AZn7cqOaXMzP8fOcvZvZQ/7otVrMLiyRzm3sDF9AY+zqP44RvudrM91Lssj5GyQbFZ619WS17msZJLqE1qjgOzaT83Ft7KiOugpRW14WH3q0kNkboomFRRexnBdebdYCv0u5xytMdgaF4ue21qZk0P60UosUAmSVJJodS7rWFV7YzHGIWJmjHCpsqT4g4sUQb2mWRp0GaG5qna2iV9zfCPA2Ip+SzXkOSMzm8XQbTY03YZ+v8c4z/HLV9phtu1xmy3bi2t8v2dMMMU4d7zvGotJCRnuGD79HVw64H3RgBBIIWG86pU08cR3Hz3hxcWezjtC0A6NIU6cppG7ccLmDE1ZEDZjGke732IaTzbKVDHW4fsWcYZ00o1j1hIshzVV47M6KLboTqkRsI3HOIPzQu8dV1c9VzvVYzXFM6xlLjMVft5oSibOqOMrsGJ9LUwj1RHS6WKEGSCtwVR5MKgGk+XqYq9lttW4WdhuWu5T1sYhJSjpNxvipE0loiS0m2jRwe07rG/IpUGD+iKJ1nuCX0oqxHluQ+T05pYYRv7Ek0c8bjs6DNM4kMeRnBR0jXHCJdGx88XJFsddEr6Kwse3J44hsrts8MS5wdt8GNX9DHEqlRdahpjw5CkVfRPN5t3eveHm9l7BadS5krvE4aSZsvcePyJYzTjmPHF5uSXHTGw9lRvbWI8pgtXVea5aTnN2Es3yGYC0GFMxzJtz8YtqWFkf12IEH0b2xsyfOQssvuZY8sb8RAMCxacs/38vfptn8gHeNTy/esp33v82T66uudjtgOV9mmRBHboH519C9NWdFcel5FI1OeN96bx8fp8Psx9N0yDDgZwSzjs22y2Hu1fEcIKszu00ZLxT9v3lvuG9Jx9irZnB2LZpymZmEWvwXUvjmiIpoCtN/YWSXS4M2pS0dGO/gUdX/Zxp7PtGkwZxJEmmazvAEOME1tG2LU+ePOX29pZxmsgZfFeZC8taGafE5f6KF5sOt+v4/NVLpk9+mzGcSnmxBTFLg4Ys5Dwhos1ylC2kTk589ozpT/8ZNLTbgNmA3SP+Mck9Idk9yWxJdrMaY7MKYFPpfC6AQ3KZQw8DhXmOsZ6wGgwXRwgUQCFacjTEqPOhNcoqiRIXuYg6gUTZIzP4WvYVY5x2ag3FAUraAZ2U1F9fJYKgSg4soNG7gEUNzuyq8YUmdXBG2bBz4FKuT3TPqK9VdmO9dxEweXGEpdje+obqSi6Z8YeB0NvHmhn/rteXIHANyDIbksWZfufZZ5tyXuZdV+759777StebTS3J56zT63IPC+S2vq5qKRbg1K6/4Oz+zzHPCi+fj+Ia+FxeXzTb6ritg//6PbOjJrk0VamfzsWxWzO47FvPZrbZcm6fK65Zkw51xJzJdG3Lpm3ZuYbvv3ifH37/hzx/+j6ODoMGCFEGpnHkeDiAcSQRQhZCmJhC0IDDWhKJJHlmASZE7eyDRgdRqtRACfaKtEwdeqnjXoCONWO2auXWJMUcrMgSwIjUeV5AuzLP5t859T+EjGQzK1gbW5tvmAI8LI60q0nk+QpZ5q5ZflM8bUTySsdXn3UNXnW6awCe0A7CTdOw3+/1SmrCFUMIgdubV4hktlmTbpu+wzvougZn7zmcMrbvaLu2gFARSSPT8Y67L3/MzVefcXn9iMqWwnl2V49xvqFpPK0zTNPAxW5DShN3t7c4oN/0pGw43Z/I08R4OpDShBmPHP7F/80P7l/zbNvxyPXsTcKnVBrdGcTpn1yA2FyffQzc3Nxyc3/H5f6K9xrIP/pN7n/3X3HaPmb/V/4qp/0bXonh409+l0wCHJ3raFpH9FsmY8gGIkKIGb/b4FrVcXViZzkK0fbKKNlgSbyBJeNwqN9nrWXbOp5fOt6/NLy4EJqcabzuz0lMYduqnFfVPpxOt4hA4zuarlgRswS8i/ZoXZ2m2OrCXIsjN6+/wjrDbn+J6zZUJR4pYL1rIt61THnicHfD5fUjTfhmoW08Hzy/pgtf4u4spET79HtghdY7usYxhcQ0QvSGpuqQIjgneKsgrUPwBrwxJfgss/uPAHv9OsB3beuyCDELx5A4jZkpG0I2TMExjHneFlKGkNQfTlH1Y411WhmZFVy1FI3ZpEBYfV21PU0p3y1rOAWVMhuHlY9ZbEGudl8b+Wi5arXnS5VKtT8SVY6lJkRmT3wGNRKhyAIoxIP2Bljt5bPzUaq9vG80GSamys4z65vmWBiwI1omVdiNOaugVY378lI1ofNZ71AbEDmcAWPL3mY8TdPR9zv67Q7XahO98f6GFAOSC3PMOrxrFASURJgGFgLQ1+zzK+Ch+jO5ltYXZFD7oCyfUgBmSca54o9XYMxaZb+Z4rCFmMgxzbhBxQ5qX4c6E+fqifnaUgGa9ToVuJJZYmC5Fyk+mMzkolzIP5U0sQY/q49rUGYetkiKiCzPs1i3ELWSleo/UquksiZHS4JIQaWiu2qX/ai6y6bEgHoZS9l6fS7GQAwLaATM+pY1wdD4TGVXGrtqxlUacTrvwKMVd1nL4ddJTyWWLEBkSom2ball3VLuJ8S8Ir/ZOYFZP59SAq/N2W2jeqm2+CKVxNOw2NZxnJShbXR9mSJjUMvMT6fjrG2rUaFgkrLOVcIkIdYwU1uK32ULUcyJEFKapeVq8kUk4nPG54xLDhvijOmYIjfgnJvXp4jQzVVEKreAVD9D45lxVH137ffjEbR3TzIyz80xxjOwtPqYdRyt94r7GFv6ByiWYhtbmkf7klhaCEHbq+uZ2Z0lwzTNflMIgWE4YkyDEU2EeW8KmL/osXZtKvdf1+3CtHXOsdm05/NPSpq8rLdc1lAu54xVIkAWEHQYBkKICpx6VyQHIt770gBM9/eFSZzLHKzGCCh6zFIAlLX0QxStqk5pSeRVLdh5nTRFXgFz1tSwxotAkU2oiTq1HlMaSwXIIhnxruMbAcbWzUkH2mtX8cJW1IxQAV73V/i+x9xPbC4u2T55QbPZk1Lgyy9fLlkQY3h6dc308vcYXn3K+OYzfBpIZeFr1/ORME3s2o6n+54fPrrgB8+e6x6SEg2JI5CcII3Fdi1DhuyVlWB8g9tuCU5LJoxkXC6Gv2ruxICJqmmazoSS3SrgLw9HdCJ5CxuXuN40XO48V/stXaelGmISSRS8TZXNZYxS6QUNAqzV4EjtvF5rcTCXUKSW5pVgqnbvMTWQ0vfFnHFOfxFi5Dic8E2P8y2+8bjGailurTNKma71hM4RJouULLcF4pP3ePVX/lO2/+Dvc5hGck7EvCpVXx1d32H7DSlGfvfuwDgOfHhxwfPNhmfOYiRpGWGKTCnSGkvue07A6ynyoy9f8Tt/6Ve4212QTiPbrse3vQKoMZFlkQ3IOTPFAEbF49u2p99ccPn4PWIWwjgynSxpGujbluQMSZwa1AiH8UQ+ppJZaRjjRL65gdc3PLm6xvmmdPctz8IpRb4k+uZNBrMscH1GzFnQBRQ1y0M9c4IewiayZJkeHjXQnwGdt99Vf/PvcpzBQgk623LVXvLs0RP++Pd/hv12S1Mc4/U1VuZLrnWR8/etAubK6C73bCw0rtHmSaKsiTGcSiaK4rQ5hAUIATAlwG0cPL7aEYc7ri56Gt/TWCndZ4Uqni85YxiQmMFammaPlcQ0TDquzmGmsTxzZRZgrQrCi5Sy1E4jhnI7295zsdtyPB6QmNj2PZ++/IopGnzbc3F5sZTtoGUrd4cTx9MJEbCuxfmWpu/P5lPjG/rLC64fveD5z/+AN6c7Tv/rxBcvP+U0HLDegNh52qgGYOlY6WDynvu//CvgHGJbxOwR+wRxjxB7QXYXZLMhmhYxvnQJXnRrl+cmVFayvpRxEvB5xOUBKBrSq+f8dTNMYyKDdqruscaRjSdEQyOO+P2fh/ffZ/tP/yd9vyxA3UwBqMHzPJWU+Z6LBrDEhMSISbUT+nI1KWdsCf5zfgBUro6U1KlvvMM0DrxDnNViCDsLHa5AhPPz1LKsJZOels2dJYCVvEBwXdfOjmuMYV6nD6/xjLHwDkBWv1/H6K37+5r7nX9NNT/y1nuX4GQVjc2feteZzDvH5vxyHvxOHtqK9Tedp6GsXZr/rBmpFaxQJiRq/63F+WYuNVu+/xzgrYDM8h3L80oxzK+tS8hyDGfvX2v7PhyR83tc7q9qwhqBbdfyw+/+DB+9/yHPHz3FZ4OzDZv+ApM72rYl58j98cDheOB4OhGwhCRMMTCGiSS1+UgpgUdXpWqqaUMMX7UTS5CbcyqNrQzOaPOKWmJqsiY2c+lke/78dYyU6F/nrAUSpBpkLDp/uZJ6oAQPqY6CNuXIEdt0ChoKhDDNZYPOVU08Zq1AfWGdsNZ5p8t09QxEgUfnLJdXF0UzLRNjYJpGri4fLaBBKW2rXa9PxwOb7R5fnHQBbGNxJpOmE+PRQL+j2+zYbPe03QaMI+c3DCEyxcQUoyaN04CLgYuNp3/+jG2jTVJiyowxYcc7mtzQ0uKnhN92xKBAU4oTu6trEpq8Hu9vuPvyM8x0ogkTfYw8uz3xPbHsraUTaCRrFVaRC8pGMK4CVBpYHIfAq6++AuBqs+GDqz2MbzgB98byr8aJ3/kf/z63w8g0nDDDPY8eXbF7dIlJmXA8ciMTJ5MZctQy6zzRmEzvhKYxWNPq8zaL9rgCFq4E9SWJXYAza2HnAt994rhsJ5o48PnHr/nB935K92WjTKAUU5HTKtULVvj8889xxvD48WP6/bX643K+9Mw6w1AnpDGYUtbeeEOOkel4oN9cYkwJiNFYZhiPmLZl467Y77dMIeOs4+Lygv1uQ1MA+MNp4ubwbzCtp3n2EVhDKI1wTwE4CsMEvTd0rcErSkhOMicacs7aWNg8tILfrEMTGtrAynqLiaiEgQExwhSkNOjShLECGAo6uUYWfWCU4SbGMkWtMOr6RhnrsrBwdZ6p/cho+XIF65bnnXVuGI17anMXmdn4Zu6+LSJzTKf2StuVrsEXKIC+LZqiMRLHzHazpSnNGGtvDVmBmo1zykYvTkPKmRQDMQzk8YAzI4aEiLJ7ASXDSGVKVroexddfM8iXRLNrGrp+w353yfWjJ0piCRPD8Y7h7g0SgsZDXcfl1TUX+wuOxwOnwz0xFKDEQCnxA1liCWMLIE2xt+VJaGVDnkEY4Kyjea0600PK881zstw6IYepBjDzeay1+Kah63sa51UCJgZtbJallO6vfRVtolpjrLpVmRoLi8Yc8/PMaWlYVd9vit6pLcQxKoiqp3BGvV1nLc4Ycliqi7IIIZfEpymJXt9gszIKKzOz+rO1KVFGzy85q3RZlvkcdS9SHKUCvIqHtF1zBnxZl/HlXhQvqTGnlEdZfKVSSdZ4j/eq22y2WjIvmbkJUm1mVZ+bKY3qdK2b8nw8vlVAdxonxnGcAS6o+p3Cb/6X/zW//Z/9V++yGg9+rs/h3TZmjnO/Lsr4SeHtW+dcv/C272m+7q3/tkPO/vkDPdbR2de71+cxnA2Bv/o3/xuaglU1jcfaHdY2RWO3VLfMcYvaQWu1X09NAix6sjInNdc+csbQ+mZm6mJVGrNpGpWwYE3CYP6cAtfK6ha0wrGCt1lUqrJaG2NUl7fem9o/naN29vUXrLFWRlTwdakmX5qlxaiyhqnqyhYgt23bM2BWEwwqqyU5se2a4jvnWdrrXcc3AozFgNhiVH2Db7qi50rRUFXdvZvjEZuEzdMXXDx6hHGtOkLDEQeF9iy4HDj8/ie00xds5J5mYxlOHu91QvXe8ezDp/z4k0+5bAyPe8+Tfa8bZ1oehPOeKWlpu9u1+MsdJutmYLzHblpCcYqU9W2IkhHRktVmsyEYp10dVw6/io97MFbLTTRtg3WGTQvvXfdcX7Tsek/XGjKRYu/VmNbyPskFoGPeoJgzlqawR6R01tSBzlknbchh0SKiBq1VL8SULG2gMU3pUq7NgKggbmH8Om9wyRKTgq+1Y6n3nsmEM6DdeMOmsRzGsnCSbk4PjZGyGIRkhEGETw4Hxpi4HwbSbseToskrYonWcbSeu2Hiy8PA5yHx2Z/9ZY6bLakEXL7VspxU9HvzirWUc2IcBjAKroSQCCETksVaX8pRgjoWy/6IMdB2Hus3s47N/eGOJILPsGl7hlGB+JxWgHNhTigWuZQuzo1HpDaKUkeqagAtIGr5q25281+s5sHy42qJLZvTW/vJQ1CjlhqZ1Wvrs5Tvl+XHnBI/a/8k39l/hw+u3ufbLz7kYrfDFg3XuSzIrMIEmeEYCh6y3IYYMKsO42XsqzEr8Olbe4yxRkX8ZX1PwvXVBc4a2qaja31hveoaMWjmNoWJOI2IZOW6GqN2JSfGoMkbTNEfFINYTcRk8aQpq8ZYmSdZBEnKotDOk5bTaVKGgW0JUfjs5S3DkPBNS9f3WO/JiRm8yYc7Uo6AwwLeNXPTiXqEMHF/d09AaNKGjz76Ia8+/RSfM5+9/JgplzK5CmTgOPzin8T0O7JYwhShew5+A2ZHtldE84hst2TTIaZFcGq/TMnOPxD8n9muIkAEGfD5iM8HXD5h5EQWbQpUn/W/9ajz21pwXgGP1DONCWMa3O6a0y/9R7T/7P/AhFDWizCXh5XrUVOuG7fJxZnOqz+xZIweXNW8ha86v9ZzGmc1CDBGg0lny/iYlTzBGQdGGVm1nOrsi87B16X0SINWWa1Xg5mbfZ0Bi6sTvgs4fgjuzp+bh0nm89RS/3PDsi5bK6//JMC2mIf5/s+Gttqt5bqrdtpKeefcdq3s0FraQNbnfssj1udW/67M9eW3lc9UcP/y87o0rI5N/fccoDWzjTxnFuvYVMBOz18Z0qye5+r5SbGOM0hYtKSpjA7d67dNy/X+gmfXj/nw+Ye89+Q9LrYXbLstrW3xTUNOmTBN3N/fsN20hHBimE7cHA/gDElqh3L1l9aBscGw6TfKzqhlhiIrgGEVWmfVb5/nVind1KqR88Os9qo6HnVMKxCuNB9N9GSJpKJ/VvX65kpypMgbpep24xo7s6jqs6v7WAX6rTkfX6sdauZ7mq/PaDfcKQS6rqNte2WBxEQ26hsaSkklKtOQjXZcTjFB6XtgKMG6c0jOjMOJME0Mp4FHzuM7Dfz7Tcd12nF3f9RmRtax2ewQEaZJ7cw0ZUKCtmvZbRq6lDnev+F0uGFAkKtHPH30mK8++4TT4Y7GGJq243h3x+lwz3S6hzSw9xYXLPsgPA+ZpgY0tvhndpGaUeJOJmS1wWIs9/d3WGPZbFr2uw1CZiLz+RT4JGV+z44cMjx770N89x73h3vu7m/Jh6Pq34WgVSYF7G6NZ3KZm9/7HY5DZPP8wNW3f4ZkWqJU/caS4KMAKiKIOA3G0HV11Ro+vDTs2gZnPPlii2821YjiXIPzZplrVvVlnz3/EEOm73uc9ySrMYcWNdt5LBCWHPg8QIbGd3SbC2KYAE2Q1URpLSvebvdIVmZd0/QM4zgDSK7ptPeECBvjMC7w5ub3od8T22vEdfjWMMUyfwUaKxwHgRZap2wvMDijDD9TAJZv6qHegiwJmdJrwBih63SeWWcYRuE4ql1MWZQNG00B6aWsQV3T240jRYgRvLdMQyzy9WrDYhgBOetCr2BC6ape9Oidb2YgMcVYOrPn2WXWNb/sE4YKlGXiap9Ydi/9nWTRJkgi5CYQiz0NK1DTrDwjY1QbI5fzY5R1liSS8zh/bxJZ7REq/2EKqw4RVKtfE2umzlxj6fsN+6trNtsdfd/jm5bD/T3D/Q3D/Q1pPGGtAgr9Zsf+8hExjAzDiWEcZndJfWRATJH+X/yGObITZZCmFMlJf28NRRfzYUk889id7RkFkEwFAKkegGo2N7RdR9v1tG1HLM8sF5a/NajfZyoxouzhBay0lhKflX3FeqosXz2qxvssoViviwUQVpa2w9R4jUXyzFpDFkOIVVdWr93XuWhtIUgXCQEpurJSfSKdgLViyDlL470ywM1yLxijZBFTx2fxcYx16pZmAXfuB84J4xUTsTLsc+m1UedpxWgMmpxwRWfbzoD8ukKo7ivlPdbQGkvjPGa7VXtZQOQqSWHajtT1P9mI/PvjD+UQo4QiQigJsFgAzkoeM7StVhVXv0pEq31942kbrzHLnLwv68Uu+5HavawJnZxxVjV8jQOZZGYtW6egZo2dU64JK/XfvGtwnS9rT5vMzv6kFHtqF2Y2Aimq7UhkxiAlTlnFISnRdV290LKOpEi6aIVYTQhXMDalhPcqoRVKD6MQwqxVqyxpO7Puv44YA98YMFYZFc45fNfTbvcYY4mFSq5dqR1iHbiGdrsjGoOEiRgiYRr1PHFC4kgaD8Q3n9O6A1YmFQC3hq5xdNaw8ZYnuw1pv2Hbtex9gxEYxonON1jrMTZyCoFJMq5v2e0a3LbneGrVwWtbfNeqoFTZQJz6FYuT7x2+30AYS3OAer8U0WGrHfDUP6RtDFcXLdcXDbve0jZa2pBS3egp/5YgsASCC/YgM/CVUirdMKV05tOy2pQTUww0pqWWGqrWrVthdOtAnRmwnV9YAQa2gAwKWqgYuPMNruhfrqNka4TOG2wJanKpWRTzEKBZxKqtc4wTvBmVdeiB2LU01pGs4WQtX0wjr08jrw5HXonl7vn78zOwRhmnMS06Obhl2ltraFun+qPGzFk9axQYCykQwgBF27Mamdm5K8/dlI0qhkj6zncYv/VtBoEwBcJP//T8fcNf/MuYuxt1wKw9k6+osEEFbXSMF2dlvY5NfQD1hzWQMTtF56+/9UL9DjHIrzYQID1+yuEv/LUHYOxS+l1ckPm57t9E+ttESsLG/Qni7prb/RUvHz/hTdO+ZXxqxvbh/fyEq1z9VHVrKjgiIJlQ1tZkLb95sePbr4azk1tn2fQKwvZOARkpAAAgAElEQVRti0hS5lVxcuTBV9UyDoy6sKeSyY0FINAOvQqkOz9hfdBOyJJnoXqXLM54Guex1uN8Q85aljmOgdc3B7786oYQM13naZpFOkNLVROSR3W2raHJmfeHQI4LU0DH05FCJpwCxrVcXz7jwxffYbi943B7w1f3N6QPP4DGFUe4wbz3Aba/ANMi0ZHtJbgLstlpcy52ZOMRKvBa5krpJL5OLBkpTjgJKxNGBkw+FDD2hBXV566A0xrkWwOzK/73AgiugmfjGnAtMY3YmDCuwTx7H/v+t3BfvsQeDyVZssyt2R7OYJJqCKnmkxSt6gokr6bAbNKFmoExZ1dY8SPV0MTWSy1ga/233BkrIOgs8hBKA6m3gc3KGlD7m0vX1qW0W85N6/yZrzvOwMVl0OtFzGt87aYv/y4GRsHHr/+eemNzwmkJy+bTmQfnXObGenzOjd28z82mbWX76mfr7azPbupnzPp08/vt2SA+BFbr5f0EQ7V6j8gyX+q6qUFjzV1RA5USqNY5XoMnqp0t4IsDGuvYby95dv2IZ9ePee/xM54/ecFue0njO7zzaNoIYjxxGgfu7+8IqWWYRg7jwCkGrDgyyvxOcg4sW6NJo7Zpio2tzuN55Ypeoyz293wUyhjYs/evx9Msby12rkqYLHp+tTQdagAqRd9LP+9EkBhwvtGkbNYEiZbiGqpEwDL+zEG9mQNyi+SIMhmLRFO5Xlftt3U0pZmENaWreJ2EKOspF11ZJGvZbEp6TW45X5akTV+iNuSahqPajqbBO89msyHFjGHEhkTXtqQSoQgeyZYYTzjX0nUdLgReH+4JpzslEGy3DMcDh9sbwnhiv98RUyDFiWk8cTrdI2R67+kJXIbMLgmGhBghiYA1OEqlikGfScql8tZqAwyE7W5D37U03hNEeBUDn6fI5ylxX4IQS8Y1LXZzwbbfc3r9iikccVkbxpiswCHG0TUN43Rkev2SjKPptzRX7yGux9jayGMFzJgCUrHoKsYp0JqOXdfT+JZs6r61gAIxpsJAU+DeGMvF5WNEtLQ1iaF2aqk21paGTnOFWZ29dSJaT9vvsK6ZfWRNShSSg5SO3aZUYE2jBmZZZkDLFWC28QpMDcM94fAKksFsrnGupzb1VjtoGIPQeoN3ix3R8syz7fWbcZh6jUVjVyCKaqrmYvtqjJFNZeqdmRBSlqIpCziDrQV9RYfPGUvXeqqG3zRN9K3RAD/LnNhx1RYV/7iCBjFGnPVgMlZQllVhd1UwVlmJ5SHUfbPcWwXzqrcM9dpqCXUuJfnV3kkJ3rVayBSw1VZfo24DWaXQjKn+qAKHujzXgX3xN2q5rEC1cc44SiW32rO25+ryiovLa5quw1qI08h4OjCdjqRphNLDoO062rbDGBiGE9M0auXHrLO7fDd5WTc6CucxwzwupjbLqbJ4ZvX7d+27Zl6T9XlVP8o5S9d12oneqCTFMIyEmQAjGmdLjTtgpgyv96TZdzCzxEj1M2Yvrqy9emezP7T2K1aLL0vxNVf3ZW1JJUppLlXvM1cZlsKgTolYGIAz0w8zE52cLQSPMzU2U0Z8YVmfJ5RL1V1ZA2cuIAZb/ZIsc8UU1UdZPaIqOVABuvNzylzqvyYWzM+szBVbdDnnby+/W7um//74ozmksF2rJFImz2QCY9ZVfOobqpxLq9qtZmG2V79t7dPXNdiI+ksqH+KKnyRFOmQh9qitrD8uzdyk2OJZ37+w5xdbYuZ1UaswEBCn8zKJzNKducSDVfPZFR+ynkLnruieU9eiWdiy64qJeuSctfqSug9oszKxPzlG+0aAsQa0k2PX0W73bC6fkmMijQNpnJCmgbanvbik3e6J2fDlm9fYBDr4ql1hjrfk+1fEuy/weUKarBt/Sjgj7PuGDtgYwwWGy2dPqLIGh+PIZDPvPX5C2zZEEb66PzAidBc7dpeXnAS6tgHv8RsVPO+dmTOYElVjtGZJMYZm02G80XtY3a92dHNMoz71xsN+43j+dMflrsEQ9b60ZqXY1wq+yuzoS9nsMlkb3pa5PMWpAJ5K7W6K45+KDm7Xd6VxlTIX265VZ6c4A8oiLMxQSVh0s2u8Q0kDS/dEBRU104lTHaKm7XTSs4yFkUznVNtqgtL4ZwmY6iEIWO1aumk6xpiYcuJ1iJxu7/iy9VztdjjvGEX417dvuD8OTEmI2wtlqtUxsoYkwmkYkaSGpe2Wad80nkfXFzr/rCWLI5uW66ff4u7uxM3NS6bxhE8TNdO9ZHxKh00E5zzbzRY5Hjn+0l/g5j//L94x0Q03/93/8P92mfyhHSYL8o9+DUIifP9n+PK//0/+nT7nQubq14+899sDAHflz7/5w7vUn3jcNZ5fff8J/+3rr2ZYyQBt0yA+l46MjnEMhcUlUMp8KGvFGKuavysHMBwnximsStkHrHHMK9E6jG0LI1w1Zru+Y7PZ0RiHbRratiWJ5avXN7z88hWffPoFb94c1bkqTPJUyuUX56nuRI5NTPzc4cB9TGfgUNts8Vmw0WEGw2a748P3v8vx/sjr21teDyPjL/4pZLdDG015+u6SrnuM9ReEvOEQL4jmgmh6Et0539iAdtezJUKqHahXel+SMDLi5Q6XD9h0r8BsDhiWrrbl3Q/gr5VjK7IKfJmDT2O0KZZtWmJuGUMkZUO/NQw/96fo/+WvYX//R9gkUNhNlTlSQZiata9sWLNmxL7lAS5NJ2a7ZPRaq6MJzE3kBLVlC2Nief98j6sEy9nYrjHHswDB0XUbEAgpkobTMi7zB9fO9vk53vXa/P45cDx7eQWYrn8r83i85UfIwuh8+J3r+3/wIUU3akC7uh0toSxhQ16B31JDXXnwXBana359DgZXl19v8R2O0NexyNZlUu9yoNaM2fPnBlTpg3LUphxvnQPO57sIptyjNuQxtN6x7zb89Ec/4Lvf+g7XF9dsuh0Wj2tavGswxjKGkcPhnmk8Mo4nDqcjb04HphgIKRFyUo7hyq6pjt2iJ9Y4h7eOXJrTSEk6Vsczl73uwUAtvkgJdKte8rtkGMqgKWCVIjEEIKueG7qejPN4qqbyqvqHoutXpGSaqv1mszY3WgESplb5INQe6WuNNZFMCkeapseYdgZxrbNY09J41dJumgYvnuwVoNHSs4yYVBAyaBqt4AhhIoYJ7xsoQIN1FYjXsRSB4/EGYy0dO2VctFu2O73aGO/1OnxD43t8K2w3O968fknTaHIvTyOHm9c4CfTbDZ13fPXyM8bxpGbGGe7vb5A0MYUT94c7pJAR9hgupoiPgWwFsbVIQO/LrAADkoKYMQsRQ7ftubq8xOZMDpF7gd8dJ35sDa+twYwDFnh9+xpCJtod3/35X+Tf/Po/5zD9GJNGbIwYa8jGkKyh6VuuXMMxDYyvPuazaeDZ938et3+C7S6Kft5iSbLR6rUspVRRAq9evebu1HG139D3fWFRRmoCLcXA3f0dbdfT9RucV7C77S8UJE+JKQiziy4K+FrO0A5qh3QpoEU2Bt/vsG0/S93E0kBIAT1D0zqmceR0vOckifeev88Uy7hOytjsSqlkYxseX13w41cvsZLpek/neza90JQmXYLqq8bC1lMgT1eeAl01efr2svujPLSOSZhiIgoEnV5gKmtQGKPyPLVx1WK4tc+m6sxaYwrrlTnJYqyh7zuMjdzeHzkdjyoFYMxcUmqNssyxpbqwxlKy7BfK4FQANIRQOoIrM7U2E5rtWVWvEOY4x1GvyyxAg0EZoeWBKDPSaONhkQJ+abxTy39rXFcBfN0Wqx5m8QxzBbwKyFE1zY2UoN9hjTambqySbbq+5/LqKU8eP6ZpOnKOjMOB4/09cTxhjNB2HROJftOz2fa0red0uOf+7g1pUokE1WQ1pWkPYGxJjKTZ5i9mX/d772zRP7VzM5vKUF729Hfvs3nlZ1Two3ZX3+52Kt0yTZxOA2GaMHU/UWNYvq94bxUcNlXLtACO5R8twZfZoahrSqTuZYa5z0Wdg2uQv+xtUuStKpRqraPrWtVLTpk4RkLx5edYxNgCxiogG6I2fKt9Wvq+U8kA56m6ltV5kuIj1WZzUnwJY82s7WlEpYdmsLSMsXNFa1P0s7N0BPW5rKFbKSXoaX4+zvlSCfbAB6Ss4yK/NVfXzCC8HlXitmq9/oEcKcHtrf5/u4XKeKzHNMHhoP+/uNCm6/W4vS2Zn9XxrnP8YR/1OqyFq6vl9Rjh7m75uWlgv19+Hkc4Hpefu06vH+DmZgGJQM+7Yq7W+aNsU01cto2W4SMyS2zFGAkhcjweCSEUDeDqey3zwJZzzDqyVpuWd5uNEjBnf23xS1NZFyEs0iAW1SYKKWp1iQhdq9JfFZCtNqX6ck3TrGyxLXKegs0WcUtVW2XSS2XlluqqlDMhJVJSprCzlrbRWL1+r3NuXjP1+84qHFeJqCp58HXHNwKMFWMx+0vazY7d7pKULcN4T0Lw+y15f0V79YwomdMUkNNAPJ3oGosjkaY7pldv2MQjXZ6wbWKYImNQWMFby76zXDihA1oRON3zx374UwxD4ObunpdffUXjJ6a4p2k9ru9wFzuid9pwYDzy8vd/n8cvnpOdISTdmJgUNs0ipetqQcKLo5DGE+6B0LmQit6PwTUtSOB63/H+ky2P9x5DKOUKX5MpKpFxDa1DnBiGcQ42qhPQtqpXquCAUUdeVH4hhEDXdIgkxikwTBNN08+X2XlPyLohCFpW0viqv6cAi8HhnWb1c/ZEmyBGvG+LHpp2HZ1LAzE83ex5fXsimEykLNoHm3AS6JsWaxzj8YQAEQVwB4E3U0KGNwrylE1Mmhb3cz+L+aX/kKl069Pse2IIE62Fp9fXXF9dsLm65JOSHWx8w353icmZi4uddpo2HT/3p/8Dskl88qMf8envOmw4MIaR4zByOA3c3h64vx+R0pU1Z2E8nLi+voJNz/AHtDa+yccv/qM39IevF6T+ozokZ4xUo2dUq81r19kwqjzHMAZOp5HDceBwGDgcT6p1UxxwZ0rTAtdgrGqk1k6jekQ0y2uwJuGcEHPSIFFSSdBYNpsNXdeqVmI2DOPIMAXGKWCswTeOtmvp+64wZtR4L1dPcaotnem4uTvOgYpBu3g2onIIXgQbEy/e+4Cv3nuM+zO/gPnt3yLFSOM2bLdXPHnyLR4/ecH19RP6zY6QLb/+O6/47CYzRkt2JdKhACBZALcCE4sXKgkIICMuHWjkgEsnrAyQRmYwuZxmBQ2u/iwxY+EVzWH3mo00swusx7aX5NgxxRNyfMOmGxl+9heIz7/F7n//X1TKJanWlcxenrJgJWcYAybEuYlXTnG+gvkKrT7rM8dyBuIXFmcFXSlyI0r0L89OZB4zoTBaasfR1Yb8NuNWB0yycHd7N6cUTGHf2hVIuD5+UsZ1uYUaZDwAQ9cQ+TtPo2t8/vgDIPjrQMv1dc6l6fVbRVZYqgZnu92OGBOn0zCDuabqZNt6cevAgHdg6e8eh/w1v1Gd3nPQZS1H8PA+zNeM/7uO2pm1nuOtKoH52iqLaGGjPu62fPj8Bd96/oLvfusjrq9eEBNY6/G+wWI43b3hPkyEGJjCxBhGhjAxhsgYI0OYFMQ2Ws7czsG+lsNvu5a2aaBWfKSgSdxcA9FyfUkbudQ/jfczqJtnuQAKu6E0Eprngr6W5pmsp4nDQAoTOU7YxtfuJqheU4uRAKQiQZ1pnFvkLLzB+w3TGMjTqHp1OUEush4z60qTygYFU2q/ABBimPjq5ec8efqczjodpyJTVa9bIV1TJLOK/aCwqYXZdmhiVv0tci7nqOKBgnUeI0sDt9P9kRwh7AL760cY32LaBp87ehENwn2nkjxeSDny6PKSFCbGYSDHzPd/+o/T9T3eOcJ45NOPf4/dbof3juH+jvub19y9ec1wPJBCYNNv6YaAOR6Jb15xzBO9teSiC2y9JRutcHFSSkmt5W44qIxTjnzw/AVmGknWcu+Ef3Fzx8fGQNPSlCBtGAPHrz4l2S9w/WOi/bM8+fZP0TSWNx+fyARoNwwEBiLu6oKm27JLiTZFJjlx++N/ifRX+O01m6uneNcTgoLCSdAEmNEGL623nHzL//kbX3GYNvzgo0seX/S4JpJiKWvOE/uLvRIbSodkAU3c6YLHWCHlaQ7cSvYGa8/10bUruCijGMEar8/XJMbxxPF01GoppymA25uDkhiaFt9q81YTI5JUHss7p2vIaPdmyDzqMuP0FenVBG3LvezoO0fXgPeZbaPgS0xgW+XEV9u8suTfqEOAJAYpMg61gbL1wFTSMcUOZ7TJ0DQmTkEYg2hjLrHaUA609N4orjCNxa5apz0f+q3qGVadT6oWZp4bgWrYoclpa7VJTw2yKey9GEeVH8lyHlSXhFuVc6ldzFVORt9Tm/8ZgaZ1XHg/N73REnSjFYQFVDOgcnKyZogJmNKwULSc3TqnLFuzVOtY65SZ5ovMSNkfjDF4C13judhfcnl5zfWTp7z88ceEMJBCIIXAcDjw6NE12/0e33i+evkxcRw5jZEQT3PTptq8SjfdNLPJakMoyZnavMj7dZd2nZWa6DLz2jrzuX6C77B+T9M0RT6mpe97phBn3x1R4kXdp4yp/OAFFK0bUF5mpfpnFRyXc93UavOr5MD8nIvjUffBlBIxxzPfvAJDVZM1p1RA1oREyHEWYIHyDJumWbneotq2siQC6rzSOGVFyir350tzowoSC4KfafX1tXMw1piiw20sxmrCj9Xvhar3q2SV2thwZipKYf0Wn9eI4gUPfZ5auVITCOcsS6nqXn8wx2/8BvzCL+j//97fg7/5N89//6u/Cn/9r+v///E/hl/+5eV3v/zL8Ou/fv7+v/t34W/9rT+gi/t3PP7SX4Jf+zX43vfgt35ref2f/TP4839++flXfgX+4T9cfv4H/wD+xt9Yfv7bfxv+zt/R///SL8GPfqT/NwZ+/GN4+vTsa2vZfYyRKUbIi+6rNuTazOu1luUbI8XHt7RtyziOnE4njscTTaO2GGo4Vv1cBXdVJki1i+c1Yy3GO6wxNI0nR5UAaoDtfq97NkXSr8h7jONQ5hQzUa7GcTkltetV0/UBm1XJkYa+62cwVhNp+vuUMuM4Iuj9rpn6lZCx/qPDa4rMQpXP+smP+xsBxhrnkLZjyJl4POB8izStagV2Hc12z3AaiMX4e1uM1vE18fSGcHhNm6cZLzDWsttuFUjMEUumAXbG0ZFpjbBtLW9e32CtZ9P1fPStb+FEy6dySjRtw857LtsNN9PEfQh88N3v0mw3jDFipqC9J2YRboPJUkAcZY+KCLYxOAyHtuVU71c9eTWgYgtooA68SKIWHCxu1WrSUHVhih5GKTl0Tp0CLQFwpcmFNrtQDZqyURldQN43WONwDtq2BnmdBtuiwvMma0YTY3Sztx6w+rniuFgjc4ClYw85q5PTdRuO4X5ORmIcX/65v0j+n/8JzekzvRbr9d5Xe29KSfXoHNAY0rToKknZZJRCjzbEAvKf+2Xy8xf6e28xSa8NgRAj2/2Ofreh326x3i+BcBbiGMgG5O6Ic9rs68svD0zxnvvbG0ja8KtrGpqm4WK/570njzkOJ+7u7rg/HjmcBkKMvLm5IR1WWan/Px/yzXT8Qwz4vOzqKQs3twcO90dOhxOn8bQ4487T9zteXD2lbZv5T9N2NF67JxrrZ1YMFFevliVWh0OUQZ6yOlwxJmKqRnrp8Hg8aDOdu8OJcYq0rZZ8auJxlbRZgVcvXt3wncliX1xoJ4sVViRzOaYmhf7l+9c4Z7kJE1f3G64eHXi2vWJ/ec3+4prt7pK+72m8x1lDZ+CP/dQV7ad3fP4m8up0Qtx2WY5rGQ1Rtr5JCZsPGDni5ISXAZtHrKQC0kYqG1ZYOdorGqBZj6Y5n0ezv4523Z55nL4hlbKWLJlp9LRNQkxELq+4+7P/Mf3/9k+IRdLEoYFqStp1N4eETWlm1i0i7effv2ZGVIbAHDoIJQCyMwsvizZWEmuZC8Dme6YAiTIDh2mVdVc24Nm3ly+T1TjJyl69nfxY5AvOD5El+3sW7Jj1f86d8vPPr75hLei6Gq01OPmuEv+z6yxjmc/OjV6DwOFwmMHevttwcXHBaThxOBxKMGKXfMDqOlZXM1/4Qwan4WEA8nBcVs/7wT3VX9eg5DyMPB/n+ZoqkJkfsJDr++s5y3OWnOhtw+V+xwdPn/OzP/UDLvaXbLoNfdtj6eg6TxZ1BsfTPcPhlmkKhBgZU2SY1EeKOROKjpZfzd/W28J60aoTZQqU7tC1w28BABaQu2rlytlYOIyy1Sv7pwAU3pqzZ6sBbQl0EcQYbBLu727JYcI7S996vYZlOhQYtFxLARbsGfBuSpLLaHKYqovvQKxq91mDyQqIW2PJ5KL/Zenblu1H38P5tmilKlutBpyN8yWBLKr5L0Lj7QNZC2bdsBooawOtjG972n6jtt2JgrRzQ8rMNB5JOZDiwNX1U6xRjcamgTAOjNOb0iDSEUpTLgrQbLuOTb8nxcDxdOT21RdYMtZk4jRx8+pLTqeBVzc3xBCwztJCaUYWSHkgxsDBQJsjTWropKdtakM2mHJkiIG7YaBtWx49esHu29/h/uVLXg0nXsaJH5MZMtjjUUEY38DpiBHVMvRy4Lf+6a8ijcc6Q/PkgosnT7kLARcDPids7zF9r52wc6I1nnZ7ScQS8kj46hPEd9h2g7cNWJUEsM7hiqTUII6Xo5A//oqbYeJP/fS3eHKxRZw+0xAjznmarsP7Dms9RflLZQ5CxHpLLbsU0Rii32ypaVEFcNMMklRwYk4aWUfbdvjLxwqUFfAP39IWJmHbdjhrGI63jMMJjC2SFJkcAsZajscDr7/4nM3ukm3bc/jyd9k+/55quFuHeINYrW2QYl+a1pUu8plkNJ6qNuob4Z+V7TRmJWCELIQMCcsYIEQFu3LW38WgdrrtPcmWUU9ANoxTLOvCYJ0muE+niLKkteO3gkXlGRltzNt4jY2yCCOTjo1Ve0VhPNqVJqw2qdJnqwkdKV3f9ZZyKefW+tgKli0MTu+bUmYOtfqq/lFA3+D/H+bePNaS7Szv/q2hqvZwpu4+3X37jp4IxmACRmA+WwSiGGOiwCdAjsmgCIEi4I9EASkkBClSEhKHCCshAsU4REFJiIJJSEgYHEeOQBCwycAcPN1cD3e+t/tMe6iqNX1/vGtV1T7d9/rCZ4LX1e2zz9l7V61atWqt933e531eYymgISSiyzJqKVf8JmVJDUGdS/C4vAcMtmWROpDgm6zHKqNsuqrxIXB6dsrJ6Qnt6jRnRUhGxMHhEUkbzlZSnKtfb1CxJ/aKXiGEk+gEgM22rvd9BmMLGMLABra2yiohMgMTadwjGW2/KQ9HXt97xhZwpjBitRK253q9loy1xKAtaXMQKTECqWbCgFMaUggI7p0ZgIy2fLFFYArIpgH4T0n2sBFIlL+ZnJGFjmVZIN/6sVp8hBQVKmmMFiZ+SHl+DzrGuchcFEKBHlKxZV4PNksmDAxp0ErStstcmoJFMhmyDvYQlZbx0fm8wceBoevy+iGDj3y37POA9+GSsajzvc/rHmlkuCphWzIBuEkMspTTQL7W8kzy0Y/Cn//zu5OgquA//+eR4fmpWkoju/UetvGLvv8v/yVst/Cxj8Gf+TMvfIw/iPbTPw3f+73y+oMfJKcJjO//wA/AP/2n8rf3vAf+4T+EX/5l+PIvh/e+F77ruwRoXi7h534Ovvmb4V/9K3j0Ufh3/06+9+3fDl/8xfBN3yTH/Nt/G55/Hr7/+wetVpQSnyZC1/cZ9Ie+74eia2OGleBf1hhm9RxCpDYVdmnZW+yL3uukRYSB6r0UQfTO4fs4kCJSFM3YEIs2uOBNop8tax4pjutBDqDO53PGuaizj1dsUGG5yno7AqZFAs7nDIpN67IusmE+m2FLwS0t+4jSYKs0CUaknaCI0lqytYIQLoNvSbEESPQ9/bfSPjPAWKUw2egNMYGuSHUGZKs6R4cgS4ZLSsXmjLi+De05yq2ptEQh8/LLfL5AG03sE8l5rJKKsUtrmFtFYzXddovSArwcHO5zuFgKoyolvIKD5R6pDsTVht5H9vePaJMnqYjK6LoNkUBmtKms3WT0oKPaGEsMgXbicBeYRSUpORZTout72tYQgpViA/mzo4NSUjtGkCaNB5ObnZ2iKcggH1EYzaCHkXTKhYT0MP4SIdZ5kon2JVqqTqqsJ6e0FkdnshAro1BakpBKGkfR1Kibmu1GDRs4CvzRFaqmIWhJG3Iqgx+T/sYgVesKxb044UplPCch1SPTpMjClSuwty+syOIc5v+11lKF3GgRvXeTIiOTDdW5kIt1ddx+9mmcX9OtLoaIsETudNY7s4A4sUVQ/WK9HYp5fVraeg3/7J/J2H3xF8Mb3rD7/tNPw4//uLz+6q+GiTYtP/mT8MlP7n7+i75oNwL4+2jLE8/y3PPsIy9RZP3Xfx1u35bN9Mu+bNzE2xb+238bP7e3B69//fj7nTsSASzt5k34vM+T1//jf0i6RWlf+qWy+eS2A2qSWK02nG029L3HVHP2ZwthlGb5gPl8QVM3kgZqDaYS9llZ6KdpkoOhJir8g2NWNhAfPF3v6L1EyaWojGgP9n3HbDZj2XYsFls2rcMYzWI+z2BRFtAfQCW4dvuUw41nrufAaARO2+3lDFdXKGs4bySts48Vtt7j+OYjVM2Sxd4+88UCYyspZKh11pxKHC0NDxw3oBRt6FkHD0wZQaCSQ6UOFVtU2IocQWpR9JjksiRB7rRieKbKhajsJIiRnICxMEVJ408DA0VGoQBVCgTEkYcZZSsUkRgW+BCxKsqecXSV7uGXwyc/gVpdkBAHG+eFRuQFbEm5Eu2nMrAKYMZk3RmcbzUOj04MBQ+GlIjhMi5pwk79jXLsS/3Iy+hdDvUUTNzpIwz7yPsu/XcAACAASURBVI4nMGnFCB5n1y6kKNc6OboqqYaynhdWyL2w1rtZLdN9Ku30n+GY4xCUFksYGk2MIWvU+WE/G4KUatz7Rox4CsReugV3d3kYj0QBmtXue/d4rSbb1HB8NX5uAFiHP8saIfNX/tkBdwdjVnNl75Drh1e5fnTMgzdu8eDNB6lsnZ2lXCm9b3G+p+9a2u2GvmvpnacPgc7LmhPSqD8nBqIwY6wWXUWdKdbiIIecUim6rQUIn/Zx6tjt3ObCXsjoeCneorPDXbS4xmI92elKJT1UpGCKPl2aSJkI9JG1vob7zjiWwziPFaaJoq1IjBKgSoEYECZiMrk4iehSaq2kWKLX9H0vqXjNbNCYLJlNcj4BTwugoocHPzvOMTDgH3mN8t4JCJSZc671OQCTJGMIRQyOlAI9ET/fQ9dzjDLUtSLOPGG9Fi3wXvpgbNag1QpjLDE6SX1fndN3G4yGbruh76XQzvlqRe9dLnwRObk4J6zXqHZDkwIuCcBc7o/2AnANjnqInKzOiCrR6BmVbUjLQ870Kc+GDU/1jlXwTKtxd52w7VK2bWO/pu8Tdv+Aeu8KhzeOaQ6OWK8upJhXFM1abWu5RqWwtqFZ7hOiFLzpnMMFT+pbkg7oCgkCaCEKDEyxlDjdOPTtC46fep5lfZ/oeSupRyEJVCZnuZhhv41RMloalckFuqT8QhGeGZ7zVFhl+dEuD39+T2sDtmgfyt4vUvBZEsRUpOipmmYAf7SxeOcIQQpcGquYLUSXt7YQUktqzwlaEfWMWOsBCPQRXIjEpIt40CSIxF1r9QtlMPxBt3zWHZ8mJPBeCRCb8i6RZPvUeb+1RlFVKge1EyqC9yMbLysIMDyLqaSPi+Z0cZALOwmUEF92mty3lMgMZwngKq0hlDETcorNabYkkYUjg5+pLAl5fSjA4RDEyguEsSIpU/pprMn9kbVY5qOXkVKFQajz2hwnElZ5Xcxga1K5fojSWT6LScVwKbrahwi9IwZPXVcs5nssZgtmszkxJU7PT9huV2xXZ6R+jcFn6QsA8QcL+acU5KLcB+S6ra2Yz2fM5jO8d/RtN2oyEtFF7PcSIFLYkuP8vDRzLk3XGGMObmXf1hhhNuef6BEATjHbe+W+5zU7xQx8Uwr87LI0y0M+WFzD5B1utqyfuc9aa1SMuSDdJMib1wIKYK61YBR5vyt7NUR8HG3noTaJKmZZGg2QbDMP8guTARrBnsLiL/6Q/FSpaNeO/5U9tfzuo9+xWXX2oZUer/vSHcnjVopaln6InReU6HWX2g0pJSkMlfdSxfgchxAkxf4DH5BD/4k/Ian0P/VT8EM/BN/wDcIU7Tp417tGoHJvT4BHpeD975fPl/Zf/6v4m1rDt36rgJY/8zPj+//238L/+l/iQ37Lt4yM2qk0wOX2sz8LH/nI+Ps3fAM8+OALf/6ltuvXRz/40Ud35QYAPv5x+J3fkWv5oi+Ca9fEF/7v/13G4oMflO9dvSrHWS7hQx8SP7y0T3wCZtl/f9e7RLLh1a8GJFPYxIjN4H+VagkC5flYJKsG1ngSuZ4YZaI67fLalYZnJcRxLZ7+r7UmFdA0v69zQTuZ25NnK+NRpfkoRe6qJEGyYp/GLDuktfi4Ze/WRkuxu3KejH0VCRutBPwtPvjAei02btlP8yNY1oVdMof0oeB/RA3YfO36Hs/NbvvMAGMBi6T+KK1I2hBsQ6xqorEoH6m1xShFcJF+fY4/ewrdnmNiS1VBpXMF4uzoV1Ulot5O0pJro6hjYmkNe40lpsBm2+NjT90E9pZzDhZLFBofA+u+5+jokLoPoAwxKmbNnPXqTCaXNszqGTZlJmcMg1asygZgZQ2NtWy320vXO4p761yQYLPtOFslblydUdtqiDCNLbt4OvsGg/MiC7MuDvMkGqBKpcK86DV1LZOiiBErqQQucFOOChcnDhHGT5RohBoW9AQQ5dhGa5SW6LAsrhKpNUbAWKVVFocqY5OYGQ3GiO6IVtnoGa80Bk8KHmVLAaQcqcsMs5QSFnGwEoq0mKPM7lRWSoERg2Rez5nPGxSK3vlJyjGyGWiNSlnVLXqS23D63OOk4EihzRt3LnSWphttYtYIiLeYS5r5arshKCSi9eST8rmDgxdf2F+oXVzAX/krMjh/42/cDcZ+7GPyPghYOQVjf+In4Jd+SRbo0o/v+q7/32Ds0fM993+05fR6tVP9fKc5N2ravO99kmKxWMi5lZKN8cknJZ3i4EA2g6Mj+KzPkp/brWwo7363/L5ey2bxwAPy+/veB088IRvK2Rl87ufeDcbm+ZaA1XpL6wNVPePG9Rsc7h8wn9U0mQVbNhjyJlNKxZRNI+TNaNwKRjhLDyYM1HWNcgrvgxjvRgpz1XUja8dmxSJXEd1vHduuJ4YgTPp8/gI2qQTWOW49+QwLsyAdLIkxp8aWDQPojebJwyUXS9Gds4kMBkOg4eqNh4lKSwpeTiUNPmIqna8xYXXk+lFFInHRdmzOfDbR9GCo6bTFxAt0uMC4C2xqQQRa5BMxZBu16MoqFHFwbHXZyYqBjGyCSpscORft7TKnEmORk2KNq3wcbS1Ra0IKuahaQOWKzN2rX0t1eoa5uBDnxnsJvuQKIIlizE+QtZ1XTK58951BCzP/W4qX6QLQ5fUvl/YcDIzy+TQ5QyINunMyZ6cszcszjZ2NvNjmBQRRimH+lurKO3IIaXIVKe8jgiZQrkiVt/JJS38K8yKEu/s2bVOnIIQgDnF2Oku6XJp0ZLyjabjFBfxFgXN9rjadDbLSweE8E2BuHJWyS1IYSJeBh8GemvSjODsqj/NwpHHQys2f3I97/6KG30dDLW+dkx6Ic6RRaGNZNDNedutBHrn/Ee67dh9XD69hdTU43ylF+ral7Vb0/Zaub/Eu0nk/6MF2weciV6NVQA72Gq1pKsusqnK2jKxnfkA1Cni7e4/KOIzyFvleFgOhAPZJHMUCXYl9EPM5JiBrglIszmTdO1NbJh5nNp5LCm4pvpDti+w6qnwDnZcAkLKWFEIu+iMpwLkLUl3eksGaKHphSdJpt+0W13vqpqGZNRhjRY80CGNDWZF5ypDLMB4FcJYsgDgGjFGi/R1Fvig4qXy+Xa9Fb1ZrmuN6eDYICu+g67Y0ukJXhrqy2L0ZwbWsnaPvHPP5TILJeb5Zazh5/nnOT2/Tblao5NHWcnGxou87fAis1hvRzlcK53pOzk8Imw12u2aZIk74V2QcAOMlxTXlZ8D3jrPzUw4O9zEKoo9so+K5qHgqJJ7xns47ls0MYy0hRtZnK6L3olsZHCF6FlcOaPYX7B9f48r9D7FNERWkv1WM4vhnG0/bitl8j3q+JCUBHX3wnK0uaFsHweU9w2KVSAEYY+Qek+hj5GTtefTx57j/2gH7y7kEyquG3jkBYbUmZTB2kByADBYkVK6K40POXNtZNXabyApM102dgSoJNFhbYW0zAA3yr2Kxd0jdOLqug1w4LnpP8D2LvT3q42MKAWGpEm17QlTgVSLN5zl9WQqRdEHYoNowES1PZVO4G8n6Q2qiNjNCPBFwIeGDQoDshElgDZRiEilFSd3OcWEVEqkRELcAPcYqIa84Jc+9SoxFR+V7kt2UC6fF0caSzyi0UQMYW2RlrLUE7/K6GPN6VdZyNchQSI2ZApCN+27Ze8vSGRNYYzHaiu+XUgbFyJkDku0TkxMbJ9tQ5X2yfFbKa+VgJw7Br7xeGjm+1hptRXohKdFNTiFitWL/4JArR8fs7x+xtzjgYnPBnbNTuu2GzeoM5bdoldntGpHTMsL4ihnELMFxhc6FjKXS+mKxZLm/ZLPe0G3brMXo8/bpswTIpbKZE3Cz+HeXW7FxCttYKVBo6qrBWosx1aClmt1bUCIP1bXbCTDriVHIPkX3tNikhZFcQPQxKpNB/rKvZIRnx2ZUZU5lO16XjDWyn0+Wz8l7iYIYpJBXyZ4JabfyfMmYGklOkywq2XLHMUOxS8LKe3qWXBnA3QR2R3Ys20xaoZVBDUGN0QhQpTBTJlnpS+y+KWZQxkyNLwUELlqkIeZM3TjIvulsR4QoDMWd9uY3wyOPCLnoB34AvuAL4L77JNX+O75DwMi+F13Ur/xKuHVLSD4/+qPjMf7LfxH2aFVJ+v5//I+7YO2/+TeSHnzzpoCxL9ZSEt/zh35IQN5r1+T3W7fgTW8SEBSEKOWcaNHeuvXix5y2179+BGN/4ReEsfrpbLduCfD8gQ/ItfzQD8E/+kci2eB6qV8SLQkwVgIcJfunZPT5ErjIflSRBggx0XsHZJ85jMGK6bq4myFAzjoVO1UkV7Ima+5yWSfL32KMIh/j/UTTOYP83g+ZSnVdDwELneeuys+RzrJYWmtBQVMO6IWYA/eTDjD6FMV2ngY2h7EgYUhonTVybSE4loKe8UW3488IMDai4OAa9azB1DPO1o6kLCSDShpNYE+BTpEUtvj2lDatSRXoVFNpsAq8lV3bWMusaVivW5RzzEgczxuuzRsarfCdY7vdstoENmtHiCc8/dTzPHPjNovlgr39JYdX9jg+2me96Tjc2+ORhyqe2azp+g3zZDHWcrDYY6+ZkXIq1Kpr6bwnZWPbx8D5aiXi5mlcwHxM1KkwODXaKLa95/ZF5OBkzd4DVyYbQW4pawmFSO89PuRCUhlYnM/mQzTA5PQXsiNcIgo6FxYpYK2xxWnLkTY0qFy6IBulMafoxQhK56higqgNKEPdLKkrg6vAdT4zVosDKJpIPhbWDRAj2hq0NUQXqOdzXFjvuvgpZYfI5dQT0XyTAN9oiGkUqa7Y/r9fL5X8vCemQN00GGOYNTMWswUHiwMaW+eIKcRp0RalUbbGZkNW5ehy0ySCg6A1IRi8lw2kVEUVB1bGQitoast9N67yzPNwYS3tM8/Aww/LOf7m34S/9bc+jU/MS2j/+l/Lz+eek83rU0Rlfi+t2Ua+5D0nL/yBj3xENs4Xar/0SwIWA/zVvyqb53veA9/93aJt8+//vWyexkgKxY/8CPzmb8oYvuMd8r03vAG+6qvgr//1uw7fO4eJzQCCPfjQy3jl1SV1LULkGjB5whVtnLvbmLoUs46gGgzsCUssYwUA3nmZH0mOr01mUcdI17aEUNw70Rubz5phYR82rTy36t7xOb/9YcBAI4Zb73p634q2GOLc/PrLrhN8JLmA1oo+wPkmsOmhD9AsElcOloTQ49qe5bwhknIlX0NjDN53rO48j3aKV9484mS1pQ2RmA1klXrq/jmqeEYVV9iwASkZKH1OEaIjYki6ItlZFvQ3jCzlvB6lDJxmUAMlm9TAVi/7YDZAKakrkzujtDD1G3VE34oECzFhlGj6ECI4kSMIwediXZLuk/KcGJiu93Cyd5yBycJUjOLyWpwgMYq10QzeGmV9zc7/DuO5IKDjgV+MsXQXa/YSCHnZAXSunwCWu5dxWU5ADf1Qu2ORHfmUDRTJEX1xpz4VBzAD/mNw4dJXd4C+KZAxOhzy/r3XK3Xp5+AoXf5rARjvMaZq55/pPjuCp6WPavh5DydxxCilSFRhBEz6UED5YQYogEilLNcPr3L/9ft4zStezc3jG2hVo1WFxkKEEBzOdbTtBue2tN2Wru/o+h4XoHVuVCxRikqbTMzOurCmzmmdck2ud8N4lOrTw9yDCeB5+ToLK3qsIDtl/pRRCinheicpX+W4RZdzMvpKWRZ7B4PT66Ow+4pjWdZAefKF+WhLUDgJ08lo0d+OMRIqy3I+p/OiOydpxVBbg61tZpLCerVm20uhmricc7B3BZYGZcwQ8A2+Z3Vym9X5Ccc3b1EdXJNnePDwM2iS9w1jDLYSxhsJKe5aUs+zbRa6lm69BhT6+FgOo8WJ6fue0xPFXoDZYp9mvoexcw6OoK63tNttRh7SoNl/evIczz79JN12Q/AdMTg26zUkSf+s64rFvqQHdl2LbwNdt2HT9axiZKY1dYC5yqzS6NkqhXY9VQY8LjZr6sqy3zQ0VrPtL/j4b/1PHtM1d2JgrRT1ssYcHHBxesrm7EICcjkNWGlNZStuPPQA85v3o5b7bILn0cc/SbW/D9aQIljdkDBo21DVS5aH1xiKMKaEJaBn+1LXYLthsz4nrjao5FHqgKSXJFVRaY3Oi/pza/jwE6d89iMNx4cLbJVQRnRbtTZDLF5pja0atBG/wUWHzUFUjRFmddH9njBmLgfGBoZ71vREKdREYzymYokklK6wVY0yFpckWKGNJsXAZr0iRM9ybx/X9/S9wyhNswz0a0/rW5bLm8wOZll6Q7IykpJ9yCSxK4a1/TOo7a6dgxUvjGEF2ih0gzwbMTP0PEjgSuwFq2G+rHC9FDALUQCsppYUUB3EFvC+ygBn9ru0Rcr4RVByz30MkglVVQPhKoSIn2gLVlWdGbVx2NvSYKSocfFXZL1DNdEHHPf5FCXrzvswpAAnJABgjMkEsqJNGmTOGQEbSY7kOwi9SJFkUHTcnYbT5JEdf8YovqKBLO1naaymb7c8+YnH2N874ubNB7EzS+hWhO6C5Dao6LKUWwEZwMVyDwVQ0LoaYsnZUsZqLbURfBC5g7bD+x6SZA9YKz69JoExQ6B2mBOTIZ22qd2VcoBBKyNgi7LYqpaAmBYw2iqTAVrLdn3Bxl/g+k7YvEX/XA1IYT5unDzbssfkD0zGdwSLE6NtUfYCAZ7jAKyX2i2Fh+CcSAq5HEQNA+1DrtFM7B+ldS40N+rZpxgzgx7xW4OaZBPJZ4per9ZjxoLMyTKGaZwfJIhpkHUoIGoZ55Sk+DdlmPLfqsruzrk00YzN91Qpm+3jclAhbZlK0WSJr11QS0z9uh4LnQPw1/6a/KwqYX0ul8Jk/dN/Wv7+kz8pGZR/6S8JaPu7vwvf+Z3iG772tfKZt799VzP2h38Y3vIWYbOCHK+QlD5V8Mp7ydA8O4Ov/Vr4sR8TAPZtbxMg90d+RD735jfDb/2WEIymeq9/2O0Xf1F+/tqviX7sb/yGAMrIfXz+5A6VkzkWgxQ5tjmLtMgTWGPQeZ2zEywllSARAMKI7Zwb7MwSTAHosu0GE31tgDTKuNV1JjLNmknsbMT3SqeLTVpVlRTAy/+X4AMwFBjsu344p8p24sQJGUFbnbOgUmbmWjVkOxRAtszfkvVEirhOaqmU4H/KxetkPSr5K/dunxFgLHVNunGLNgT6vscbSZmyCkzsaW8/SetXLLRirjTGBk6sALWGUhXY0lhLSJG+6zh59gTdbziyiRsHNTfmNdF5ztc967Zns3E4H0FZjG2oqoZHH3+a2WJBM6+pn64BuO++B1juzZk3NTdnNTNrpLCWgs55+n5LSBEXIn30rNvtSLxUCrRBJWGhltb6Hht6GmNFiDgj520Xeer2hvtuHNAYMe6d95JK5r1EebNBUJkKXUu0KsVAbWt2XNhhF5i47zlldpCZzM62AIwKkAJEorMVqKqaGEW/tXeBw8MjViupUDhr5hjTYGtQWXtWqVz8I0k/Z3VNVWliVIQw9GyIYHoEsMBY0ONENdpmQyRhsn6bTz6nM+XLA8IDD9C/7ovQWlFXNaaZY7Th+rVrWFsP+njCBo6inzR8uwyTyvo1OR09f75UyDOmIVFJOmjfyeYneZF5vGVMtdYslpZl29E1zW4BryHKmOCP/TH4tm+DP/fnZGF//etHFuliAb/6qxKl+4mfkI2ofPef/JMRwPyFXxD5gne9azzHd3yHgL7zuaQs1PWnfu7e/nb45/9cxmPvXaD2XvTjn/Mr5xzednyK7Qpe+UoBUUH0d6bpHJ+u9v73C0B7jzZWEwUUHF87JtQS8YreoY2SYhIlIl6izjsXNrE0SDvvF+MjxilwIYzYkPXhjC6VFSM+jHpbAnCC0FhKilpJwxYj/fi529x86hlhZidPsi0r4/nY/UtuN8ec7EmKSQJ80ihdYWyNrWbUdYNqPGnV0l20XKw8xAv296SS9Hq7YbmYCbCsNWhLUDOcOeR83XL77JTQelA1pIhODutPaeIJVdaHreiKiZqNyQgqEpQiqEQggjYYlDhMMZK9C1BGglVFyyqWFLyYAdyB3jOuYeoyBJlHXGuMXZCyoa1UQJuIf+3rSFeuU/3PX80au2J0ShEtBlH28vyOaWnSpozTsS/509lYqOsMdFlD1EgRyjymxWGYGtqDQT2ZWsN1lOjqJfBwZLamkSWZ+yLSMbupL0opqnpk0A0pay/g5Ixg5Aho6klqz+ic7ErkXO53acVImb6/2168OsNloKP8TV5kjLiAp5P+jQCh2enX3ZVLR3hVTX5PjEGSfFJGkPZuzdfdeTgBPnJfC/u0NGNsziSBptLcOLrGZz30Ku47vsW1w2PmzT7GVCglDmrwPavNOc639H1L13V0uUCXBGFTLhA4ggFWZ1alUUOxNMh6fmmYidkWyX0tzx1lWMYAFIzzT0/m2XSOyjMrYx5RmdmVtdxzEEUN412CKuJ1mUqjigZi8sRoBodYIzYRWtZZrSu0EkkgYc8k0YysF6QkWUknF2usrmisYVYZ5rOakjKJUlT1jOPjJefndzg7fY7HPvoxHnro5Vy5fouqqoXhFjxNbXGNpTOK0LcYPChLyoGWgcVlciXdIbChBqdTmwz8EFAqcXT9mHR8La/XARUZUjYh4d2a9QpCdCgNzXwfayvqmRjzfd8DgYvzM9rNGud6DvaWbHRkteo5PbsQMCLnOHU+sFguCTEKUGwstp5zvFigTm5z9szT8PzzHAXPnEQFuBRog6OLDuc8637LraMrVNrgvGMTIx/p4GT/KpvowSYeet1rePjzvoDf+sVf5uTXfpOltkQDUSmUramvXOHGZ72CtNjjbNvz7O1nsbMKHwMoizK1MGSSQpkaU9XyDJsq1ydQxBSYzcQ+U8ETujVPP/s059sLetdimj32D6+jVYXRQgKorOWp22u69pNcO5hz3/WrXDk6zPNB5mOB/clp3T74zCLTTFQkBdTLz5GZsGm01rk4WA48qRIwVChjMUYKVMkXcrAiJgGqVYUxNYuFIUVP325Ai1SGc571dkvXdrTrDckFbj5Qg05413H78Z79+S3292YsKsvCWgGQlcLqIvtz94oH91qPf//triDhixw7L6OMu6DcAWMUKkhgRWvFrFEkldhuBaQyVjJ95jMB0GNkIKFYo6hqhXOQkhL2rNGoEPHeoLAZvPL5bHndsUZ0PZ0bJKSMUoTghgr2UmSr7ApKtD4HGZd8FapcUA7KEjHZHkrZpovJZWc9EmN5ndPLtZGaFgpSZgQmpAYJmZ2vUsIHl2uKeHQMctrMmi6sMKXKepsE+ASCDxJC1RoXA7VRuBQ477dUOnH18Apa9ZzceYLHn3iM0+ceJ/oWpQJGibZoVNkuTcUGIxcGG+dAyus0KbHdXtD1G5RW9H2L63qR4lOi8ZwyozalrAtZyA0x2x/3mELTlGaVNaIL2B2T+P6RaSq9YdYsUEoRfM/5+R36bj34bSn50c4v9mXMWrKDdNUIwsr2FaUwL2Pmya7tkfuZ5VMSmTikp5ZFHkNj0CjJOo1hx3ZISvoQY6R3TmxabfPzkwY5PGEsSvqz1s0EaC2HKgSPIgkUd9wZk9mywtjVmaSQBn9oWlirXOuw5xcbJ7Ndyz00xuTnWPagkAOypbiS2AIjK9JmtnqRKYspou5Vsfx7v1dITX/hLwgrdurzlnt496R5aX/7vbx/r/a+90mfMni50/7TfxIphZfih//fbErB932fFDVLSfAHY+CNb0T98A+zt1hinACWhflawE2Xs3sovoBSkGU9Kf5xvp86a6QWbWDY3TMuA5M6S4WlfL6+79luWzbbLWZlaOqaphZQ1sdA27Y58DCCnFP92Onr6Royn88HfyqE7JPHMATPQ/SkglXlZ2UaXLuX1ILgTPKICfu7XKc8gzEEQoi4SYG/e7XPCDA2KU2vpDiFJ6HxqHZL6lvidg2nz+BTh8uLrQZUkEW1pL+EJCm8znt879hXcG1uObKJQxOJm5bVxnPedly0Pb2PKGVoXU9MG6q2xgWHdh611iQD1WzGtp6z7DrquibqhHdhAE22fUdIssH4GGj7PosEj3oukTQIrJfWO0/vHUaBUQUIFZr3ettzdtFyZX+GUVKMCF2irgJMpiQLmzZiPAbPsJiUfxVMHCMRyo5ZsiHEiLU1KSlcrpgn+pZ6YL6aqqbbbIaqiH0I9METkoAVSRl6l6idRJt1XogDuS9K0mSqusriyGEwbvqHX0bvIunDH5aNtK7Qdnw4U9ZoI4MkxeiIOUqeYsS/7GWEBx8iLfeoTc1ysS/FTpoZy7lUUy1pHSWabKsarQydDNhwLuccMaqcLifSESEiKT/KoJWhwgpw5b04kNETo0JnhrM2NrMi9HRfvLu99a2Scv/xj8M73yn6L1/3dbIgvvvdAqh+67dKRO1tb4O///fle5//+ZKGARId/JIvgccflygfCMj7+Z8vEcS7QIjLD1wShul/+A+iSfNt3w4/XcPlPeVHf1SA1MUCvvu7abaBqn/hxWRoTSMpH/AHsxl92ZfB6anIGbz3vXe9fVlX1RhNIGQ9YciWyGTjL0aH/HZPx0KxY5yM86ekA6lhztmcooAykj6WxNlILgy6NJEwBEQGQIzE1aee5eD0jKoTwDPFxJ1lxfpoThs8a2Pwk/6db2Fv3mCrGTanZcxmNQcokjLcOWvpXaLtAtpoqcBtJV1500VO1y0XG8dqk9i2mj5orA7E1NFYxcxG2LTgt+jYonFoFYc1cOD9qZTTlxNqUughezIEBSkZSoCIAvoN0XRGz7HgGgMYW/ID81jly9dIunPQsyEtVhGI9QJdz0QqJGW2X3YcpFtTl/Du+ayycyifLUz4ccpcXs8l9ZVhQ0ZP0snIjlI2tMfZdo8pdmne7Yi9pxGEzKcYWajDR8rx73FN7PYp//FF29StH+7HXX3eBXqnhvuOJlxxZmo6wwAAIABJREFUSwYgLw3pQFPZFyafKecdH9M0HOeyYVdXtYAqzo9pRuPXKM9YYTRP3p1cZ5H/uMcdUqpAifhQjj9xTIe+ZhB+eg0qsVzMONzb4/joiIeu3+T+4wfYXxzS1AuUkTXS5/R451o2m3P6vqV3PV3f0xeHvTBJSMLuV4XFZZjNamHKxYgLfky3ZJy74nsmSccvBaso97oYoQVU3h3HcTzTAECFzEArjl8eqjI6jIBscejN5BnUpKQBYVTJ2EWMKixf0YokxlzNWknVdW3xqegCSlf6PqCsJSjoVcKdXpBioFnMmC2WzJYGY2Ysl/uZveXoOtHd1abGVo0E9w3MlvuQEs18LlIXKVBSNAseI6y+omtb5oFcY4oFsJOx6J3DZKchZOmMIVhIZkB3G5SSuVxVC5Q22KqG7NCend1mu1kTnGMxm0kBnbWwNJq6zoFzYfc576mrMW26qhv2j24ysxUtht4HYj3n/OmniK5nkSIWcEQBcWKUFOfKElRiGwO3Y+ROSqy2Zzjfo5Xn9lPP4fkQ6ztnVKbCKk2fHLqqqPf3ObjvFrGZsfGOPnrqWUPvelCaNEhOQTPbo54tqZsFumqwzYKqmoFSeN/R1DXzyuI2F5yd3yH1LcumwiXwbk17lljsXUHXNUaJPFkfFCdrhwuJqDSzWYPRGptToJLKczDbrj74HSerOJeFATNoDsdJwd7MhhS985htaDUJrk0ywkg5VRFQI3tVaYWtmyH1UjknxJIadFK4bSfHiV720XbNyfN3MOqIxswxTU3KrLREpGiI3L3O/SG10gk1rgRk68GYRF0xEjXEtwclNS4S41j6kPA+4QP0PlIp0bwPEXwQoDtmAEokpeSehBhwfY9UgZdnMAnlGXKmYIiBvnf0TgBZBnthdKZ98MP3C0NW+iZ7mfMOn3WlVfGFvJf1IBUd6mIzCgDr+kjIMiyl8KuwXgsImoTJGeV/SavPDOwCBOgxoyDleToN9JS1yYUE0RPdFlRks1L0mzOcd5w89wR+e4HKDOCUmWpaFz92Ml8zECOsylHLViGBBnKSmc8+Evk7Kd9XKVwte6z4xmboI0oNz0shP4w2NxQNyakdnlIg9T0xRiqbsChCEPmvdruma9fE4CS4l23Vok9c+iY2ay6Adg+bqOxt0wy2sg4oVeQxBIxIQ2BbUQp/AVlCZLK+aJ0DPWU/BSb72SAzVfaVvN+UZ2oIzMc0yCYoxjVreOay7UXBmfP1FINlKoVQpBamwdcy+KWAcelvkTIQ4LlIO8j3dCY2lc+FLAlW6AkKMnkiSx1mNn/kHtlHN2+OWqyPPgqr1d036KW0j31MCl8B/Nk/e/f7H/iAyBcA/OW/PPqvL9Yeemi30NgXfMH4+pFHfn/9/INu73iH+M1/6k8JIPu2t0lW6uOPAzn4XSatNll1bVd2TeZNltcpxarKM0Kem9n2TJmhWuyjIk8Au8CmzDuZ84XoUjejTVmkL5XS6GSkQFyxvfPx/NT3YJQiGMkZoh+utZkEshQpGWwSvzLGce0vx50GJsQOUMN4aDX6PCbLghbWvFIaIyEIjCl+7gs7XZ8RYCwgIGYIqOAw/Qq9XsHqjHRxhm3PpLqa0nR5wdQoolKgIWrZWEN2VixwZVFza25Z4NF9z+qs42zlOO06LrwjKqhsw8Wmpe0dyihmywUxeDyJnkCzH1nfuc1svaK2FlMZrJHUexL0rsfWNm92nm3X0vuc0qIkHaMIBE9b5zyV8xilmNmsmYZsRF3nOTlrWTQVs0YYFqL7KgXDKlMNny1GY5xMQPLRYgxjMY8Yc3VGTwge7wNVJcZhn8FYHwLznF6nUNTzOdtti7ZZEyhH921VYbREJLogVR+NiRgjGGBQOeVBa5QxVFVNpx15+5Z7/eBDuE1L+tAHCUpjK4uagLEhiLZM0olkcuRRy6QOEcLBAf4Vr4Sb99HYisV8ycHeEYvFklkzg5joM5ilkqTHJEOOmBpC1w4PcsyGVIhgUyIZQ0IiHTrl+6gNVltMLbrEwTu87/CuQ2jooLV9QcBip33lV8KNGyKqXYDWr/96AS1/7MckavWWt8BXfIXIC3zf98ku+sY3wvd8z3icN79Z9FYLGPt1Xwff+I0v/YH7wR8UQPhzPxe+5mvgve5uMPb97xe5gMNDkRD4TGlveINsyp/4xL3B2Esb+sC8TKNxOhgTabxlgyFQHIdinMW8YUzA02HTyU5XSadVyKZS2ZpkGmI0KG2Yzwzbbcd22xNiD/jBaDbOYztxuq48+SR1hM18jlLCKn3+cJ+zg31mnSdEy+jGw6pTVLWlokLbCpKjtgZtGkxl6bpA5yW4EAPU8wbvI62LrNvAycpxct7iI5CE3VHZRPIdy1pzNNeEFFl1DqIDAugMMBYoNgOempBLLMr5BIyFlDQ+GSl8mLKmKmPqpyxjJhu1431TOco+gLJyl8otAnIVW9MQ8tqmoxM5m8xCKimPxTDcAfemnuLujMl/TsPLEQZk0LgdTPuhf9OoqR7rLWS2xMSaZbjw0oPJ67tS3ZkAo2liODMaGlMgdiyIqKa2/D1Q4Lvd9TSdXQVUKwD6BHmd/jvqae5+cSel/fKpFKPmmdrlPV8GWyddyZ5K+V36ZbShqqohXXCnIGTa+fIEHBnPOJxXTZycyVkHEDtf/w7oOPnoMHJqdF60VuzNZty8eo1bxzd44Pp93H/1FotmDyiML9mfXd/R9x1dt2a7Fv3P3ktqo1fZucvnldpEakiNLvr0MYoOXcqMlMLaTCmRdH4kowAMg74K432Fcc6X4Ee6BK4Xo1sKpsYcaJUvicGcXa9UZuD4fCRUds5UroulEDBWJJJIAaOhtnkliUGyYmIcnzGts2xRymByymmlSgLzMbE9u2B1ccpib8n+0RFXrdgt82ZOXTdU1nLn9Gm6tkWbhqqZU+XsonqhMFWNtZa+c3kc48D6GcFmdq6tvFECH0ppQnBsN5usSzsTZoQKg+M8ZE/4jtQmFIbF4ipVMxe2dAM+ONGC9Q4NzGYNq4s2z/XIcm8PrQTodc4Rsq5jyGzP+WLBtfseZrNa4WYb3MFVqhsPsGkd6uwU+i0LApqEywBBXYusU0fkPCaei4lzBd32nBTls08/9jjPfuJ5TAjUuhI7MYJdLlgcH7N/634unON8uyWiqJoaHRxohSRQRdA1i+UhzWwPW8/Rtqaa71HVC1JKhC3YuqGuDHEr2rtGWw4Or+CiZ73ZsN2c4rVGpyVGzcFoAhVrFzOB4ILjoz2auspFvUY9TmG0KfCaoeK4krknz3cBVeW5L8VB5O5rtE4SlNdKWJiTrWRYl0thHpBzF13xvD5U9QzBtgQ41laCS7NmRmvarLVaGOOOi5Mz6tpSGcW8NlSVFKbVCUwqmsZj2ufQLtmm4zr2KWzWe7SX/p2ynihIUZiR+R2j0uCBirJQos+2SogyR5yTv3Uu0vUioea8AHkmQu+gdwFfwNgYs9arPFchOFarFbaqmDWzgdEs1x+JAVLw9F1P73pJLzeFlDIyC/u+x9iAjdUQWCnvhRjwvRtYuHJfTWZN7bJYSyArpoT3PWoIAI5pr5JBFQWMTUHA2OTHvS8zzkQ/GVIo38t6hsENa7f0RVixRI+KPT55Vm5L8D1du6ZvLzBkklEypBJgyhmMQoBSwzJHyozxVAqhxnIFw/0e5KnKup8JNkJgyWzWBFGrQTPyniYKZZ5GkcrLyG6xsRKiQR28J1ZZVzd4nOvZrFd41w7FVYv5sqtAWSZ0BnC0ZHKm8uE0AsTTbXHXRiNfYwYmyQHelCi1VJKOg+2QyCDl1AdJoFT2K/K1aSP7qEqjdn8BfEtqdJyYVho9ygXk+16YjExMoqlRNNqH2Wa95yM82jPlsmLGNkLwQwCkZAwXOaNSqK5Igkm3yn5d+hhJZG3je4Gxjz8+2v+vec1YY+Q1r4H//b/hox+V+iPWwud8jhCBQOqJvPa1IlvwxBPw8z8Pf+/vib/7x/+4HKcc49FH5Tj/4B/IMd74RgGAH3ts7McTT0gmZghCpvrgB8U//5qvGT9T9GJBpAnaVvrz2Z99r1G9d7tzZwBGaXN+bdeNWaBVBa96Ffyf/yN9Pz2V4mWvfrWM0ctfLn2/uBCZhO0Wjo/HPrzvfSLx8LVfK9m2b3mLEMJyobCYkhSiKzMhk9lKMEll36eQDVOMAwEiDmSXgkFFKYqe19vCpBZZwGz/UBimWTc8M2lrYwa7E0TDXoqX6lwfSQJl5RMx24dT6U6DGdfTDA6XIn+VlcxVa+2wlw1FF5P4QYOEYAzDcxpzFnvMgahAIoaSDWuoG2Hsq5QzFga72N5F4rncPkPA2EiFw4QWuzpj+9SHaVyH9Q7jHcoGaqtJIQh4hiI6SVkLSQpYGAVXbM2V5ZJrVw+5vldhV2vasw0npytOLgKr3nHR52rhxoCSQjVKa5zzzLVGGWFcaTRdDHSrC9R2KwBkZZnVdRb5l4jqkdmnbTd0bYv3YhSUY1bG5BT7kFN1pXU+oFphVjYLMzr9SdL9nnt+xd5C2G7LpVTfNWhJF8n7W4GEFOQiE2oofqOUYr3aELVUndt0jm235crBAbYS8Pf5s/MJmq+oKsuVo0OiFyC0qSqWV48EdEgJX1fMZ3NSI5uAUol5bdDGg4pIzRaPMjUxuJy+p7GmyhE+RaZDYK3BWmGVJB1JxpLMOEm9i/SdJyWFrS3JarFJSAQ0/Vv+JFVds5gtuHp4haMr1zC2FlZI77KhUFI0NY3S1LmYUkjQeXdpHxbH0PuITmRNUY2LjqoyImPR7GPqeV5kApvtmu1qje83pOQohUYaU1GZF3ms3vQmAVWnUbSX2tKwo91lWN/z/ZdiMP/O78AXvg5e+16wl4qMvfOdEyf9bsjqD62lJHIOP/7jL/A+O/c3xihFRbKB6i+DzmoEuMriLU5b3izK7ZwYQiL0nQaQTbBHAUGCTzifMPMZ9Wyf/YN9XvHwAWfnaz728efpT88gjJ04uHOHBz7y0cwaUjz/8MM894pXgK7wUYOZoc0Cz4JUL0HXQ8d1s+T2eUvrEzfrikUtetGV0dSLBnuf5vmzltm8omkMF+sNTz2z4axTbLyhDRVdm9Bhg009NnmW85rab7ii4casoprPeGwDfRBGXVIWrypC3qiIAUvAaJ8dBFmgPBZUTVRm4gCPPMTBuFVagAcYopEDiKRAEN2SHpNT0QuwbhSmFo1a1ylcH7EpoINIu3ifnQU1nRRq/DnYpZP1JwTMUO1V3itGA0qCQkkrcSQugZeKcS0vToTSelJcafIUTeadTOu7jdHCSLn83Ms8nDL8x7T8NFkH7qmNW7qx46gz/HGXOSJC+DGnh45lI+/VXzlwzDpJ5cAh3F1Ia/x8YRoLZjE1fsr3h2j8ENQc4VKtFDEEVquVOLk715n7mmCsbjM6BcOxUpxgaXkM8vxCqZz5WdhmWQeqgIzliymz7fJxY5TCfPvzOa/7I6/mFQ+9gsPlITM7R0VDUvVwrV2/Zr1Z0XUtveto+5a+E+mNQB7zZPIYynyrqlr2qczUAujaVp4Zih5zTl3NIHQKiYA8D2liyA7P4z3mXxnj4VEpgDQMrFjRERwLJKQSuCKnoOe9vzA3UxLDFUqIVqEIVEZT2dznLG3koyYkjTY1SmXt5xDkKlVmOSmT1wGLtlpAK6X45KOPYY3m6vVj9pZ7cs6UqJuGK8f3sTg45Nmnn2Z1fo6pauZXr2fsQOfUeY2tDJvNGuc69vblXGLHKAqYLWw4PdhK41wVXd6+3WB0IlWGlOWX5ESSelsAouA62nTOanWbA3sdU9VS4G25x9HRVfp2S3SO7bbjzukpIUSR1Zo19H1LpS1NrKgqw+rinG3bc3j1Bg88/Epm+/fz27/9G9zZtChdcfyFX8qd2QGbD/4W3RMfR4cOk5nHSgsQs46RtVI8mxJP+MA2QfJS7T1qBVtPpbai/6gNTin2bz3A4v5bzI+PqY6u8cEPfYQgQr5obZgtFqjMyE4Y9g6POLp6E1PN0aamauagLT5B2205OztntdbMrKLSisP7H+H4ZZ+NshZFxPdbnnr8MZ5+6gn6TcNsecji8DoEUSbfkti4npsnFyzmFdZAVc8HwKDMvqqqCMFn4FONOopaYbSlygGAUdKrPDPj+j2t6iyOnhmKiZRVs54t8h6WMFV2AlUuYGYqVmcnAvhWlrpu0FoY/0qbQRMzxchzT93h4mLLNhzzivuvUhW3L4k6anlmyzJX3vt0ShW8lFb8FB8THmh7j8vsXUPCuUiKGh9h2wZcVNw562k7cBjWm0hKlt4LGFtYdJsulMSXLC1QChTJvhgyIyvGwOnJbfYPDkVLWknBPKUYGKakSNu1Q8HIuq7wzg3rqlKJlBx973Cqx9iag/0D0fDve7zvkaJQfiACaB3z2izF/YydSqRlO9LnglR5C1GA2SkKV/T14ziWSbLwJDU2F6ieSj0FB77LKfCyTgZAHCgHroPQ0Sd5n+iwZE3HDPxJf6TIoTEWYzPwqxBGr+sly3KSWSGvd9P4C/OxtBDLul2AvcwoL+gNjNZhBnFLQTW5l+K3FRux+L06a5B6Z2i3F7KWek/0AmILkKwHGQC5wNEeLOnzpcCcFhQ0++UJq6oBjPEZ1Jky/GSfk2KDIQaSaB7kYs+yF8Q+0HkvxatSpA8SKCrNkoP3Spi2BS0oBIIIpGxHqSj3RhvR5S6xYpPHdci8UKBNhTbjfpSyxJ6kZEvqtLXFNh/3/pHFncFjPwYaUkzD+2rCBo7B4xMiq1P2RAQkLvqcxd6tqorL/pbIHZrJ/WeUu6trIQftZSm9X/5lARm/6Zvk9wceEP3T8r1XvUp+f/BBkToox/iVX4H9ffn9V34Frl+Hb/5m+f3WLfnOa18rQOe0H29/u/xvrdRh+Yt/UbRmp378t3zLyL5961tHzdgPfYiX3H7qp3aLiCklQHA5zzveIfVgXv96+PIvl7991VfBz/2cvH7nO+Ff/AsZl9e9Tv72nd8J3//98vpnf1Z+/tqvyc+v+Ar5+aY3kYC27TB9h8ngooth0HzVSlFXlQRnsq4qAEk0vxtb0zSzHTDWhyKbMmaJhJy2n2Ig+EDXdiLzUgpexZiLAMsabU2uweR1BmsrtDY0GVBVqkikpR17WPZrz6jzKpJPKXUoNFVVDXu2zEEzrFuSSSGs7TpLv5XMlgRDBgLkjIQijZiD6yG64bwpRaqqkgKx97CvS/vMAGNjwH3yw4ST23B2Qh23HCwXNHWFrQy1D2jn2LiWC9+zjQjjLG/oSw0PHu7z4NEeh4uaplKc3r7D6pkVF+ctZ6uW05TYxkgXY9ZZlIXOWIOpDXW9ICDpMMmIjmjMizgIBdr7Hq0SJko1QhcDz5+dDFGfmJ30UnzGJ2FnaURovjT1S79AZwzhVX+Eg3lNpdSwFCYUF1vH07fXROCBm3tUKqBjBg3zMdJAl74bJIspctF12KqSh6S2LGZHot8TEo2tuO/6VZQKos2b0/hrm0i2RK22WFuRY2DUJJQpzkfKFTZnlFQd2aA82oj8QYkW1lVNZWucDgQvG6FWCqsTlfb0yQxZyGMb0xuSgqgg6IS7dp3Nl/w/zOYLjq8cc7C3z3K+AARML0YJFEdRHM/ttqVNsIgyvuuLCwYgQGuqusqMPtngdSU6wlpVpJDoWo9zK5TtmC+PmC+vcOXmy6nwPPv0E1yc3cZtz0B17O8fsF0suf1peTAutcceE1YowN/5O6NAeWnve9+YNvHud4t0wadqf/SPws+9B77xSVjdvVAcP9Hzyt+Q1BD7UiQK/m+0H/xBSSP5nu+Bv/t3737/UnZtDIk42IRq50dJswopDIuyUprgR0fbWD1EjTPPctB+KQwwSdeIQ8BI6UDQW+zsAF1ZbKVZ7s2o5zV6bQlOE5NoJt45OuDkC18rzw0WZkuo99F2jmGGqZegK9bblsXBEdo2wzXcvHGFsztrOud58tkzHrzvkEVjqaw8ZwGFu9Nx59k1rdO0ccZZv6R14Hwi+YBJEYvHJIdKHaFbU+lE33tOTlY8cGPB9asLzk4965Uj5LWQGFApYlWkqYrDFweNsYTFq5pezUbHUI2asErlYicZOEpJDPVi7ML4tQL0jaAownzNOnBKixZtHyEFRbj1Krq3LFj8zE8SM/A9GNyXgchLuWkllWUKkpaPSZaAhcy2n+CWQwwghYBO4sgTFd674fpAdLrmizld1w06q6pkFMDAvBiqtk9m7pgNUcCz4SLQKTs5k79lD24y5/O1lvmbRpZ3saLSZIxJ4Hw/6CiVyDSKgYk0Pg/Sn7GadHGkctX2AXyWfhTAPcSQC52NUezC6pxcyU4b30sD0HAvO2d6Z0uQYDpu0wqnKc9Pm4uLlADqBBfOTfZeJW5c1pgswCzMK8PDtx7i4fse4uUPvYzjvSsYlTU9vdgWzvX0XUfXtRLY67d0fZuzNAQojRNmNiSqrE9ltaG2ZtKfNHTOBz8YhjJOpeuF4VcyBIojOn0YpqzfycilYpmw8zed18ICPqmk8CEzZEQ/SpbipCBracWQMKYSDVYgJY1OWXIBn5+HXChHNWAka8YkB8mT8BikUGcy43qsoxdnNgaUThxev8rrv/yNJCcVvK1WdJsNru9pu5q261gsltTNnHa75vYzT3Lt6n0obahq2f+N1oQ6EEJPcivc+oT1Zout5tSzBfV8TohyX0QuWtP3PSFEjKmyET+DwwNKga8B8E8lXXQc75gSzrVcnD1LXdfMlwdU1QJ0w8HBNU79c5yt1vi+4/j6/bR5/ni/FZZIEgbG/sEhV67dx8HRVepmQULziU98lArHfL4gsKRdXOHixiNsewXzK4SnPs6V9W107GkUzLVikxLPKs3TaG4LdMPcGKzOmodJ0Zf5EQNGW66+/FX0szmnXeTisceIGja9ZCnVVc31Gze4c3KCTwnbLJkvDqhm+yhdkZLCuR5tNddv7DObH9H31/jkY8+hjKzzVVWhkgENVWVYaIU2c0DTbi9wbsPZnaeYX70fzIyQNNsefvfjz3O4v2Qxn1NHT+9FLkFrizaWlHIBt+xAFVCgAD1aW3QMA+BXAhpQdKqzRrKS9S7mFG3JnBIwS4JcKRfgzGBTBiRkzhvmywO27YqQgBSpZ/NB/qigdgmoY8KtWj750WfRKXDftQMWdUWMAWOgzoGRsjr84bW8byiFzQ5v5wSMskZTNRbfiy5rBLZdwsWa1ic2XSJSSZBOKWwNTa3o+zjYASpF/LabkPzFS3J9LwysFNlbLlnMZ1hjJCMA8LkGh2xzib5vh9TzUtBV1iKPd71k5qW8/5sMLuXNNsUozFc72jNlrxH92VIATJSztRateVM3iH6TpC0J+3lkFApL28oUiwGCIwVP9A4fhQWaZR0zdilreXAOFXvJVNIp63JHNIlKZ+ZwFK1uos+yDUrWWiMFDUvKeUwBFYQZ6b2TfavvGKO88jxoRQ5UwJCx8SJyaSEFggs5eK+zfTSm/hdAZJQEkn07+sKyU6QkBRRFDSKz7kI/FNESw8ajlM0Sd5c6MdhuKa/Pl/a/sq3ew7DYTeNnAPdFKqPUf0iUbK8IOUipIInVYPVES3Pix6tyWrK+a7Y1bFPSq81gLylK0SE1FK4cCgqRM2Qz+OWD2BVF+zpFySxzvh/WFR8DwfkBLJdU7on0XhLpxFGvvqxpKUsfyRj2+Rkqaec79Q9S0eA2w//WyvrrnBd26pNPXrpXSuTyStvfFwZpuQ8vVBzp139d2KzlGMvl+N7enmRXXj7Gz/883LOocz7G/r5o1/7jf7z73nw+vn7f++QY9vcIsX3jN8JXf/ULv7+/L6DydHwKG7i0t75VMmdLm15zaZ/3eXcdQyk4ONjHdg3FFqxTyjIFDHtfTHG479452lYKJxtrWC4KW36SjVjmrCp7qR4YqSrBYjGXQOOgIS3z1DvRqg3BD5IdKSY619I7R2G2GmMkkFr6iJAU5rP5YDOILZbGfYNRimOakdB23bBHqCwDo9RYW0kY66MspwSoir2tUMown8v9KGsCiLxpAaZfqH1mgLF9B88/Be2GFHtiSrRdjq6kRB0ir2gWJD3nVPX89uqUcx3Yqy2HTcP1xYwbR3OWlUZFx+rM8+zTZ7R3tvx/7L1bjG1Zlpb3jTnnWmvf4nJumVlZmZVZ1V1V0OqS7S6BQcZAG9kGY7WllsyDHyzL8GLxhACJFyQElmwJicsjPABCSMiSxRNYSMYvNghLbmjobqAv7q7qqsrLycwTESci9t7rMuccfhhzrrXjVGZVA24opF6pkyfOjoi11563McY//vGP43FiPyUOQejVRM1zOWDbrrWyGbGmA4pCCEhwVmbvmMMsAESKcS0GXXXWJBXcHNNXAk/VyrBg98SoDHuyb0jTyMvjkYvViiBSRL4dKsL+OHJ/aJgm8I3i5iN6vstsLErI+wBTODvbztkx76Hx3hrYOHABxPU4qbpAtqC8W0pz7OaWDauGsWbYKhOkazeItExxYoz9/LkLDgsidOsV4XBAnAdJhXlhQeUqWEfZWuZSL79pkbV1GY3OyjliziTnaM/PeePJ65xtz42xJW7OrIovJYyxlE0WvZOkiigc+wMKRTesTqkswIFmYk7IqLSrCx4/fsb+7o67mxsQ8CqMUw9DS7vOvPX5C1ad8uKTlufvK5puQSybTNcZGPpTP/Vwrf/ZP2tZridPLIv1R/6I/e2c/c5f+AtLScH5uR36f+pPwd/5O1b68Py5SRf89t9ucgd/6S/ZPf7yX7YShutr+It/0TJsf/2vW6lDNTZ/9+/CiwIT//E/bj/z0z8Nf/JPwvG/A1YPn/XP/3ncP36PdvyilTb8WlkV778Pf+/vLV+DlZb8jb9hX19cmDTD3/pbplv7/Dk8emQ6NquVAc7brd3jb/5NM7rvvGPlJc7ZuO52S4bzletVFzBntaZwHtOVQauoAAAgAElEQVSSGgamcSz7WItdkbn8IKZEnBYNOecsyG3apnR3XFkTsFzKgbWwM2JcyttEcHpPxpFijw4rxrEn/NK3uNwf+PByMzvqKh7ahqbbEdot6lZk1+GaFdMEKQeceFbbM/phIKXF6OcU2W47mskzDiNJlcM4Md4nDn3kaj/x4g4OY2CIwqTCqK5kJk0P0c0uqbH+4jTifCb5xEDiw4+v2G3X7M4NYL26ucd72O46GgdTf0CI1MPOzo8K1ZRSLPHlrFrAuBJBlPfmZH19it5d+VHTSrVgJ4la+CKCLwylGBM6RjRMuM3ZCdCmmDZYZQueur4Pr0V+4oRJVLzjlHXBk0UQDz4EpAmlYsLurapWdS2m6RWCm/16JZOmEgQVMFBm5vYyPq9qdp6O0adqmxUnZhnVpWSt3mC2Q1JguJPPWll9dW6Kv0UFWakguFQHpmSEOfkZFuemjl0tEaps0gp62pAWpy1V8GLpQv+ZLK6yX6UMqBY5noVlXCZrXot1Xk/GRLUY6ozOcZqCmryP1ucu99P6+VTxla0DRRPaAueuXXF5ccmPfukrfO7yDS7PLjnbXtC4pkigW4OA+/09MVsp5TSOHPoj/TQSc5q1KZ1zeGqAYcFiG4oUjiopxtl5FQxoNoyolmnpyWeu/14Ysa/svPKzJxp3VHBdqNmt0720JGBLyaRmVB1TymVMLLg1XUBL+miy0lstsgQVxPVi75OyN6GTkpxxrkVcCzQGxOqEaelEcOM899ZEJuPEzrJaltpt1gUoENM/QxGsjHcYsMOk2P80DeQ0mF4ri6ZYLudhf9zjNCLiUWy9OR/wQaz6p2SUfWFVidialpP1nbLim/YEBICqXy1iQE3WzDT2HA/3ON/gXYtzDaFt6dZrNnFHTmuGMZHUGv5McWAaJ/BGLGhC4PGTpzRNx+F44Pr6Gs1H2q5hxwVJGoaovMyOfnsJr4N2Le47nu7mY0QntG3Yo1yh3GjmqBkvDhcauqah9Q3HcTSdyxKwNecb7oYDEhqyD2izIWuPCzVxA9c3t0houTw/Z3f5mOxbfNshGCEgqWl8Hu6Pxu4TR9O2dh65Im0himTTEE0CGjoun73F2O+Zpp4hRV7e36B+jQsbmtWOCfjg6pa2EVavP8E7R0ypsPQsQSLOzYFVZc6+KkHjRMw/SCNhZubYoailTDtGYw96qUmqXMD6UECkxfZY6Xoun8/haFmvd0zTWJpKGZg0646rMsVagaKQB56/f4XPyqOLLRe79Ul5Zz0dPh2O/X4s2X8dGYOH95D562nKpv+arVP7EJU+OoYoHCclq7fmXF4JoqUqScjqiJUtP+Xak9P0XGP11dxSkl73OpnVqqNtGlLx/SqONNu2nJimOLMw507cMK8FX3T2nQ80bQcijNNILNIUXgQhFN9guU+My/4QoG0CzozLSad6kxhIqfgEsMx3bsxOiQH45mG4uRxXtUgxFVBZ44SoJclNFiAh2c4hJ4u2q5afkQro+WCMM98YO7YmLpOBCGPRgE05lXOt2li1dV/8hlMwta6d0wY+C+Oy7DNPkZIqMaAsLHKRUjkxuyWyuCfVvmdLjGqpPtWS+J3t24Nnqf5XWdNmTOe9F5wDAsfj4VPX8bKLvns/SA3ELYy0ypiiT52LHZzXqKSSODQbW3vBGcjvrWk1TQlkqt+B+R2qVe6YHBNZTeJDKFIYsrBN7djSWfezcX4eLzDswsansO5FcBqg6cqRUe5z4mcgQmjC7DOZT5MhZ2jKzlOlSQu5ZU6YVvlG55is857NmVY9zwL6No1JAHyvy7nvr+sqYszXf9l7PH36ve8LcHn5vb//a7nHp13r9UNQ97Ou7zU+v5Z7fNoYjyNjP6AF6BQRkpqGf93Hp81hVaENDauuIxbymxNn8pIVoFQlpsLCL3a0+uq5EFG8c7P0i9n4sla8o/Utqo3FjeV81pzpUulzVCoxNYeSzJ7mP04cLprkZI1BrNFc+fMqgC/CarVisZdCKBqwJnljNmHWx801sUr52mx/rVow12GJ+8pbfOb1gwHGxgk53CE5kZ1CgjxGnAhr8TxzHV/uLnARXqSeD7jHNYnH65an2xWv7zZsWk+KI4fDwNVNzycv9vR7a9Q1qjIGTxKhShmC0qxsEaWK9geHtCUzKPNZaAa+DOLMBLJvzTpi9sPmWM0GR8xxVIzJtFwZ3d+SPn7O3aplHUyHqGYHFGGcEod+4nicWHmZg+9SREqNjQs0T+XVAiCwXTfEZFqtTQPelWyhKLiE0s/aUmofshj8E6NY2bclcKIET0ZTD9b4wndLsO2WRVyNaWhafGjM2Y0G0tjGdrRNgHFYnqFcftvgN40Fc16NibY7wz97jd3unMcXj61hBVZSrNWglv+QUnZaNrQKiIp1ysPY0KfXzDZLi7HOKT84IMSJEd1SZBpHhmEihJbt2RnDGLm6ukPHqQR3BYz9iZ8wQPXdd+sbPRQP/4N/0ETD93vL3v3u322vNY19f7OBP/SHrCTjV37FyiN+1++yEoTXXnt4j/t705b58R+3sos/8SdMBweWcgZYXvszf8b+Hkd77VOyNpt/8S3WP/dNePzpoOdnXuMIH31kXz99uhim+trbb8PXvw4/93Nwe2uG45134Hf8Dvv+l79s4/fNb8Innxhw/dWvGgANxuYF08X5yle+q0nYwzJnZhAlJdPUOx6PDMNAbSrnpDBiojUw6afRDnNXS28NcOvaltV6TVZjN+SqU5Yy0xRLdq50JkVw+WhMscM94cPETet5+slHECPTLhho4RrENca2Wp/Trs+I2jAmT8KTXZ6Zd23boTE+2CspTqy7lXVvjhP3x5EYM/fHyM195MV9otcVY3ZEFVIpEbSeW0otZbOT0TQbc5pIWpspKtfHI5vNltB0NF0k5pf44NhsVmw6z14iw9FKPywQrH1niy6lnICfssByFfQrPv18PfgezIatnKSWcRSPekcu2jyqgm8E16xJaUBTh4SO/Nrn0I8+sPI85eScPC3ZfGghtYA8p89cw7vyQDM4IE6svCYEO+NnH7+C0OXd3MJINAbYVJiXOp+rTdH8XBowyMnzLL9rpTu+yLA8BNNevV59bQ6w0ZOg9ASM1VPQ7eT3yprLatqFS6OQRXf0IXh7Cnh/GhiwvJ9W+3vyLEup3Stzc/I/QWbwNud8Iti/fC6Z32se6hJA6pyEqAFf/dBZ0mwHUGWuAwQqG66CyIKVZ21XOy7PH/H5Nz7Pj3zxRzhfnRGcBdKaaufWREwT+8MdMY2k0r17nEamOM3zIWKa+K46vyWjH7yfS6KqTnOVBXBay6i0+ANljETm1x6WZn73mj+d9yUh+92M4yVJYN83BhnkLMSk5ALE1jFyJPI0ojFCUkKnyFoIXgpAAFk9KZk9RyNttwZ1xvZ2ARVv+rLOgTqSVvaOA5IFuGLnTdaIU0G9SUqpWELWdHYLKJ0nxtHKlIM3xvLQ74svYczc9XpT5sP8ihgT690a13T4tsX7sIB1UhjjOtj456qhVsrxkqFHzgfTKK3jTGVr2KyAlR4P/Z62WZHbDdJ6K0ntWlZxZTZq3Jeuwz1xGsnRmqtmb2XPTXBM45H7l9e8vPqE7cUZUQMdmMRMigwpc2xa9PwC6Tz9i49Y31mZ/M57Dpq4U2PITgUEyD6goQHfoCnWxWKVApsVLw/3dE2H216wurjgeP+S5A7WzCgr94eezcUj/GpLs9lxGC2Z7sW2mTFCE8fDQEqZ0ASarp3XKIqxogu4a764sD17zGqzI8aBcTxw6D+iHwdSAu8bcrvhxcsD6wDn68DZZlcqWNwMFORsDyEl2VC1LOtcGdBgZ0BOCWlaSwxSKwVOANzipac4WbWcLx3QnUAlrond67C/s7jBWQlmE1bmg6oWZmAs3celJFuSdW4XUMkc7o5cNaEANp7tmad1spwBdeP+a4Cq/zpX9YfQErCqMmVjyR8GZUow5aol7WiC0LXmkvrGGnRFBU1C3yemmAzwUp3PTSf1s9YT3y7T7w94b1qFcZpM8qGCcWX9noKItWnb/Jo3kDXlbAmSoqWa09IUtoZip3NfG4jlbHq+ADlQQNRcNA9PqkGKvEIliIgEO/sQrG9Bxnk/A5mUtTCTWVSRnBYgsjyDm21FOfs0z0BgDSxdOb8E+/yGkSqazcZO40CNDRdAr460+RIGlpz4bM7NLM5TI1LBDaD4y8VxqGdgTXAWMLb6g7MvUF0LhbkZ24nNOl3vJkEwvzDHzKc5WycLe7Oy4k79mJxP/dfq5MwjvPy9hN9FE3v5mWp1Zy3B01Va1pnztSJrYQlmtfWjZX4t4a7Fzi36lpT39LM9qsvb+ln4Mhe1munkrU/Wm0klVN1ZA5zybK+kjG5tYFfjKkkJXGZuaAi0ujTUi9ECa2s452cN0iVpTzn7TsG+37j+TV/qhI++8psIRRfdOUfMmRB8AdIdXhxUzgksCcqc7Dws+7A26M0pW8KqxhrI3AQrRauEakJ4gLXYnpRFtqBclYla90HKJ3tdDZMbR4vdU4zL76uS48Tjn/9n9nuScM6b5ILIfG5lVWNol/Okfr6aQK3Vi5KW/ZGLZEcWheLnp6K/bQ8X51io7pvPun4gwFjRTHCKinUYXKHssvA5H3i33fCju8/xxbBhSANrfcmX/Jrh3PHoYs2uCwQy+9t7Xr488PK258V1z/Vh4j5G08spwZRvGjNgyQarO9uSo5ULTtNIe3aONAXVzmp6rynNh3yOaQb3FANonA+zXhhSjFc9XMWC3vkgLpfznvyr30Dff5/jaz/JsZtonaepzp+aI3I8Try4uuXx7rIE9vmBgRJqJWw5NMkl2NDSOXZE3GS6rugM9OYMogOqnpiWw7JpCyBVSgmDCycG1tg4WRTvDUydYpylCsQpIcA4GyQrsfHOGqU1zUg/LZ1oXePRdUeaelTSA60/2QSa885U/hRW6x187eu4L32VN5+8zqrdmBNWHCZ3crCrUkSn/UyJXzrfWlYjnZa+lP9CCKScaUIgNB33d9dM40DTtLSrbjaSOIfLynCMfPhJJubMcXT4bkvOA62IyTvsdvBH/6j9+awrBGO8fr/rr/yVz/6e9/C3//Z3v/7n/tz3v+8f/sP2Jyv8nn8Ktw8B2S/9t3+KR7/3VYHVX8P17rvwx/7Y9/+57zU2X/jC97/H2dmn3qOfetYpzoebc47b/Z7Dsac/Hsla9I/EHBBVOB6OTKNl1MYCxPpgelkheNIUGafI3b7nxdVLvA/WoTn4kuWr+lGLoyaSkJRYHQc+90vf4qMf/QrfenJu2ewouLAlrM9Ybc5Zby/ABUJomZKShon72wPrza5IV2XGKXJxaYzw8mZWRkbGFbHjX/nOHfsR+uQYcsMhr8mUpiGlCZ95zsseEI1InnB5hDySmehTYey6gNLw8r7HS2ZKEymNJF0RuhXrsxXBKx/3+5oKKdqfVUsyPzgDa7g0A8ongGAuiSwpJVcz6IkBx5pGc0SzAQLBeaJJDAGleLxpYGxQ16LNluOP/17av/d38M/fRwqIlWWyvVyZh/IwGWRNF8rzyuKISunGGZoGgiDBI8EaruBk/pw1xVV9XtN2G2dHVTFGz6nGaAjCxcUZfd9z7K1ksm3bB3pHNUAIbcvZmf3sUBq/zfalZm3np/70qwaABjDMSOT8vZo0W8A8nbWc0qu3lsVhmsdtBpD5rgx0dfJP+2zN2nKFJnL6+6/88vx6LvtulpEoQYsrgeD8QColgFnmVXT5vK8Ckyz4MkgB4Z0BpLNeKAbstc7x1pNnfOXdr/L2m+/yxmtv43MgTZGUC3aYItN4tOaZaWIaj0zRmLCx6PDmGf2VGZzvGusqqyia4hIgocWWaY277ExJi4bryeRgwfISpEsJ4HIpn334s9814BSXxOxmBd9LwiKnzBQNNEpFLx8JJRBUyImYE9P+wNQPxH4irFdcPH6ErDrwjoydMcPUc9wfGe6vePbml8ApwkTXBtSZkn9W030dxsl0uFzAS4MXyDqR84ikY5nbnYG4CMFPrFednVHOPpPTZIGGBlL0XL340Pw7NQDv7be/iEPZnZ/TNI6X11dsLx7Rrna40JgGbozGkvQNzWptczuN5n81wZpbFCaZIOQ44jAJLJvyTNUsrGsvxZHhuKdr1qT12Vw+WUs6+/t7VkG4GY8c7u8g9QTBmGvRMcWRl9fPuXt5y+EwkrOwPX/K8eZA0tG0pvNAIKGS6Z1w7Dbc5Mhm7Hk9DbS6om8DxxEmtWZK2cPgHSkphzgCGDu08eSuYe89x+FI6Pfsdpc8+9w7yO0VVy+eMx4PJuEjnl49H98N3MQbdrsn7Pd71t3atPYV2s5YjId9xvvI9vJ8Xk85Z7Phxd+rZcGr1YrWrUEz49DzheaM9z74Djc311zfX7F6+4e53cN7U0+6v+JHvvwufrVGvCdrwuGYorG1hKp1uZwj1gDU9LARJTThoRxLNiAkCXSrDV23Ik49dzfXiEDbtbTdqpw2hQkrjqnf8+1v/iJOHI+evM7lk2eoKk27xoeWw90dh8MdXdfQNKYH3/oVobGGaTErnc/cXt3RH0YO+4mzH3qNVhqCc6VD/GLD/mWuz2LEftq5/Jk/WyrXUtHldkFIUTmOyhQhajD2vBd2necwZjrnCAG6zuSerl8qOcI0Ccc+EsdErcoYptGapVa74ARws8RMbdpWwVLv/WyvzKab/a7sqVOJl1CCeQPKLN6p8xZCQ1PivqzG9BUUqc1enUnTOXGIt0C8Cc0CiGkBlKmgaoY8MU5HTFM7sF57k9BIltiudipHkxdAM6SIUCsTdP6czjvQ0o+kAHhWNVDAPKcmJ3XisaQiSaBqrbhqDtL81XEBNTVjzeuqj1BtyInP5q082NYLs91OOc1g6gL6GcvXbiPzvZYcfoWR5+/M+qr2d6qv1gd8ZXGegKlUxprFqCa3F9htz1BVbl7eFDtWXJ6UibFUzxTgOuZYfGi7XwZS0pLvtDG1JnDL0wiORCqasYqK4gpzVpwv/WWM8lrPOWNWx2LXdQYwKY25mqad49t5nLFxdQV/yHUNFqmgtvGkXKqTSrNPEWMj5mwNIafqG5ZY3xU/2RIGGZ0/Uy35LiNe1gViLNdQ18fKyAdVClBRVl03l54jUvqsqFWV/sb1b+XS0PCP/8c/+2/7MX5dLn888vv/+/8G7Yd5X01F/sCVXkbTFBmGk54VZW2HgiWB7alQEnLBe7Iaac9aBqlVaRQGu6pV+vR9XxpMf7ZsC/yAgLGK4JOyTYlHU+KrzRlfffQ53tk+5o3VGfFu4Bsff4uPxytuZc/TZw2r8zUxTwwv77m6ueXq+cjLQekTVioH5KZZ2LDWdhOoIKZw9/IOGtNzcr5BxeNDY4OZ7QCehhEQe91bmQjBIyHQdJ2xH5jP5TmjZ//Wkrmycpl6+RDQEIhFgPz6do9u4Wzl2LattZkU4TglPri+5/Ovn7Hpgul0VbMksTCzHJIzIUTE94g7onJAUzDHIllZ3jhm1usVOCFGZf9yoG02UJrrOG/6SOI8re/ougtSHIvzmU1mQCO4RMYAq67zKCM4xYdA2wpjMCcgayaTcT7QdSu6YWJ/GK3zdQj0X/hh9v/5Bfl/+avlUF4MaMqJSdOcSQuu4dHukvbyKdv1jv2hn/U3gnelaVIRk6/Z7KpBItZAxnmK2L2aVlNde1kZpwhipT8hlA57zuZREVI2eQrvFKUHJqYp8cnHHc2mZYowTBPDcM803HMY+l+/zfIb1/e9xs89J3+4hesnAEzZ4Zs1aww4vb274Xg8MpXmB9Wx1GwBQ9t1FuwUUKSKglujIT8LcU9TJCbTPhIKGLKgi1YSL5FrEf7RV7/IlBzDFFC/ot2cszl/hmtaQtsibWuAa8none/WBOe4vT/QdCt8aJnGEamadeW66yPfeX7NYYRjDNyNDX3y1jTLhaLNKMyetBYgVnIJPBV0gHQAPQAjYm1+6GNmSBMX3YaPXtzQtcJ63fClL/8QH350w4dX9+yHyNtvPOZ1Mtcfv+DYD0Q8E2sGvyFKi7rwIBI8BWLrY4kIwQVrdFHYyLNAfE5ompB8IACqzjTDQ0fbrUjiSCo4Fbrg0XZNzJEhJcLKM/0nv4/8Cz9D+H/+AVqa5sxs2+pZnvjvmq2js8iJdm1o5jIyvIPg8W3At80CBp5+SJGCf7vSKTYvLJACVoZSgWGOv/Lxx58U8Lbq1lbjbeBo17WM40SKIy9vrpdxkqq/qfO9QJmbnb0SKIeiY1Ud/VpWU+9x2ghMtZT2lM6kpz8zs4ioS6wwa9QCrhpAOPeQ8aBlHdZlfFrSWLWYqs7Z8v1ThmZZQQoaKkWjzmf92hIt1oivjHkJtjn5rHURLIzhk2cqgWZlzqoqNAmXMttuxZOLR3zl3a/w1S98lXW7xbuG3CsaLOg4Hvfc3t3Y2hUr1zJGtLGfUgGS7H11DlCbpmGzXhcAKi/ZBhZ91vqsNTBN0TraLtt8Cd60lKs656j9kmvAd1pSOi/dsn7noLB0CfeFZWANDFMJEsWYamq6fyb5bOCjNe7w87no24bN2ZaubVmvVqh6ax4YWkIIrDprerp3LevNIwNSlSJVkBANoBMxKb65YIwDjkzbWAlnzgGnHslwPB6J+5Gm6QhNYCAx7IVutaJpO0Lbmc9UAIvQeoZ+z+MnT2jbDnGBw+GWrHYerbcXbLZnpGQd76eYiGOPYNpmGiLemyN/PB4JIbB2xgIZJ/N7QmD2VeI0GbsSwTUd4hvAlQRFZjjuOfiObrVlt+oAA2iCC/T3LxGN5MMN+WisSvXmK2UXmYY9L/ob4uRZ7Z7w7PFb7C6f8NP/9P+gP+5puwblnsiWFEfurj7hV3/hZ7j5lZ+lG3vOnPDNaeLdNz/PXZ4YsbXUjyNJAt6ZLnhS08sNzps0gQSOdwf0mLjrlUhHEzx5SkjoaLZrzh+/zjGBloS5KhwO94zH3gKcJrANgVoWGOOE3mS26w2haSw50a0IzvSJx8kaK6kK0xiJcbKK2W7D259/m2ePL7m++oBv/+L/zevP3sDtdjSxpU+R8wKAlOMFQWawyAebjwoEIQ7NE3EciFNvjMOdhyYsRmw+qwrYoY7t7pxpHMxvCJ3dswAQznvW7Tlvv/MlVK2xmPOBFKvGuWOzO8eJJ8ae/nBgGA5s1ltWmx2+aUvyw+G8MI4Tz59fE/vIV959zOPzNdtVO+/5fxuXaHXthSFnDkNmnEySJGZjm4YgWC5OaZwBo40ITev4+MXEMGamVKt6mM9M5z27dkfbtgzDYNrs9lZsNhuTF+mPrLq26CqrEWFyndXKbir+R7GLIsJmszlpBGNA55AnEMW5XJrapBlIhKK3WcuuBZq2wZ8kJJvGKl/IOhNqUmU9Qml23BFCKHJYJrMSJzHsFYUUwRVbXCWCjIZpca2zqiGTgfGQPXmyqkg7W5IBvNm+pkBpMSVcPtFOLZm7mWmcawKhup9LBUv1j8Uv3cvruOWsi/THSbK3kheWkl6z/XNRUPlf9axOXj25ThzIJQqf/66x+MMKm+IjpQpcO45jT98/B+z8tuRmLn0gEpDKLTO5gOCKJWfq2NjzVpmEXPzM+lz2odZdW/R4xfTip7GMpUBWxjTO2pTVLzvVs1RV08y2SWbWqcYA2er7mSROKakuA6FZTY4jWXwRfDAA1C0ayYhJJSZJZGfvmyLWV8J7e4/CXMwFbKoKFTqvQSlAdLZqw0KAqDHSnODPVl2Qy1oLRcbs2B/5jes3rl+PK0ZrTN91HU6EY9+f6BkLO+dJOTJNU5GqsT1jclWZYRiZhoGqT229ZGSWFvFFT7btWjtlShx3cXFhxJwH59B3Xz8QYOxahf84POKN9Yq3mzXvbs7pkkOmzOH+BS/2L7mRO6azTFi1hM5x3B+4Pw7sDz3725FDPzJlYVI4OGF0rujA2iXBo9MiyqyixHHCebHA2hnAmqkldoBAkiV714YOgkOdswYquXR8K4GbZqVUOs2cGy8geSl3AgMZxDtk6Gn+/v+J/pbfRt+0eOnpvCOIaa4lFQZ1PL8+8tZrHZY8SiARx4DzEXERKVnRnEdy6onpSBqX7oShCXhXAIxifIMz8Md7j288PrhifIOxTXwJBGfdWHNSTeZBQCNjH4jThOJR9TShI3jQNJVMbyplvA0+tEhpYqB4kzjo1rhTEs88OcWBy5AcZOdpWisNjGSyZJxfgsi+H2hDg2JljlULp85CxgxmTBaYunlVMJcZp7lMX0AFzULTtHTdlhBaAy7iyFSCXqcjvhFynojTaCV72YLenL+3UPMP+iVJ+epP3bG9+QwR8x/wK6n1IAdA4fb2lru8t27lY0/fH2Zn0Ik1cAOWpjIwA13OO9rWMmFWIiSzA2llZjILevvkZj0ZUStbjOoYk+c2ee7Ghm6zY7s94+zRI3Zn58a8z5lxHAygcDV0yuy2HUkjIDivrM86a9xw4qJ+50rZHxxDdEzZE3FkKeUeYoBi1aE2H9qopCLgJOI4IHkPOqC5MIbVgMXKtxxjtEYiaWAaJnZPL3nt6SUvbm55eXc0gfQYSeJR3xro7NZMsiJL6SA+Xyd77wF2afqdTowVW5sSVD01NOLyYOVz4lDxBAWks7NUHSkb17VpAqSOGNc4zdAeSV/4ErnxhH/490ugspSGpdrAoj6Lqw06qlaSNbaggLFakj3qvNmCqi8HxR6UoNw6fpXARoperTE4qmGWwg5wzsoo6+h8F9sfTsAz98Con35tMgYFppOl3O/0OtWinQOpGaBkjmlqLCEnZ2n9phQb5+bEo8xMCV9AtPrg1km3gBSUqPCEfVzneQEGTTR/LkuiAsBLMFjlCSqIWcel6s0isgSkBSARbxqnuQC7QtWEPB0dPRkEKQGGPbMDggu88/k3efPZ53jj8es8u3iNdXsJYgkQ1wZynLi/e8nxaBqWDiXmiSlGY+lp/OgAACAASURBVFdBaeZh7yci1qzUL43jcixNqkowK1L0SKkBcgHca3A5CyfNK3EBmEVYWEwVZLUAPJc5rAlR0SUBIGVdeqx8M04TUhhpOVkJrgVbMqMutbmbw+GKpEgQRxc2dnYGTxNWCCtiwgJYJobjnrZpWLUrumfP8JtLVEoTVRySlTwdieM9d4eX9PtbjrdXtEG5vNgQzrqiR9uS/Q7aABmyc6Sy8qYUYRgMAEqZ1apBs5V7O5RxODD0G0SEpjG5AETI2UY5jgPOB5z3ZX0VFnZjAFKKYwFd2rnrewgNm81m9ilTSmjMxHGwxhTiCGKd1sV5GzWFnKOV2x9uWe12iA9UBnwGnjx+wuVjY5V+61e/yd3dDa4pDLeYuN/f87nPf4Xzx2/TbJ9xff2C6XgH05GmW9MGYRxGPv7gGzz/9q+w//AbMI0MOZMyTH3PurDhxNvZlaZMmkbTl3Se1gfT9c8RieBzA07RPDEc77j55H1Ct2F9ccn28jFnj59yPGaklPPn4lBKUHAGk0xx4v7+nqZpjX3YNEhoOAwjrSrb3Q5fWVwabf1ILiBYKaMmszm7YLt9iuSJy+dbXjx/j/vr9+lfCldNQ7dS/v2vfY1Lb+zqlGXWFtb5TD2JH8TsQteti1xImoO4eu7XY1KL/XShYbU5AzF2ey05lxpjZCU7YbU5L4mh2riuKIOKxSnrzY6UW+Jksgjj2JM007Qr615d2Gh1X758Cd/4Nhye7njt8Y7H59t/o3Ds6SmUNDOkzCFmjlnpk5JFCI3ggtnIWBr/nMoGZYUxWkOvQw9Rxc4ZDPRDK3NTZnkWLWepKwxyY6LH+Z71iikaS1SsH8BpkvEUXKxM2dpkM6VoFXc1JiwgnHMyg7BQz1trciclwRaKtEEqMKwv+zyEBqceQmNrY+vmBGZRkbbEbGiMeZVGZmEEcYUv63Ge8p6CxpGkCUcB7KR0GiWi4hEfMLmCebFS5RKQPK/jlPOJBm+Z07LYjc1fpQ1MC3QGQWeQ2xIqtfHPp3QCMPCz+DNOhJx09jmMYXxS1Uj1nqpJP/GBZr9k8TVrclqoEGx9Ux78jCt6hDXxaM+e5oqkmqydm1/qiRyGLu+zlC5bMyMpc2TJ/+LPlvLqys7TcnBYwsKIISGEmZVdn7GuxTq+qOEPgsw6w6pY3HNC2JCqkdl408T1pg9sTD77vHNVEkX7OHRzXwaH9Zeojlcu+srtLPUhVgWUrOHqUp69jO8spZUXXCWX+VaYZQRP5xFVvvw//2n6Z88Yn71me6H4IsEHunbFbrs13IYqFzeVpn0nC1YsJrO1OPL6P/85mJvf2foUZJETKzFeBY5NIzwa5lE/mzAnGGaVrnKe+CJ7k8u6rz0VlALw1/Xj6nqtPq+e/LtIHtnj2/ovPQG8c/hSoZeL3EmNEZbGWsxSANQkCsxnme1JWzNWNSDV1bU9LzX+cjMQWX372tDSl+95WarC6/zVXirzdsvJennUXhAn2q9LhcsyFlVndZGHtPGpUhpVe9g+Xp61oud1XOZ/miK//JP/NTe/+Ufm99U6BmVPVTlCESG7NJMXzHczL9ZuGWialtS11NhKpCQGC/aXUmIaJqs8kjq/D5NEn1rtV64fCDB25xp+2+opT0LH09CxE2E/7bkfjtz2Pde6p+8m0so0d47jkY+ve+6PE30fGfpMVGUUGJzjCIwsQVeJGnFNmIO3uSzWCdIUBzv4ZVOCjWHwpQNmsHJU7yw7JLKUAJRgU+eNRbUA82HzSsRnRiZneO/b6Nd/C1MyrcohNjgfQK18Latwddfz2uOJVedxbkQZEelRGVEmMmqMjRzJaWKaIjkJIZRubnPHmUq1VkJjjBDfKKFRY3whgAUa6QEwU77UCujYwRCJEAXnOpAWwSNim7+WRimWOXA+mLNZDJQTCM4aQaQ5AC7X7CBY3D6+/qZJSHhvG48FLNNsUgGBeuApUgSgtRgQpR6a+sCAgx103oe5gUxlNTehMQeq/Ns5MSfSBxSH+I6zs5YxRqYhW/B84pD9u3wJ8PiDEf9pQPm/A9fV+RnnbUvtIXl7e8Nt2jOOIzGOWKBTjElxVlLVu6mHPotxsI6N4YGhFxHG1RpRpZsmoEhjqJ+ZlVEDfQ7GWD067mLHWbuldVu67RndqsVP0Tqox0SKVjZb4RXvhbYJDFNimEbGFNgPkTHW4AGu9sI4eaLaWYHzhYnIXD2uRQJHlaJrKjgyXiNBj0gesE7lWsj8J+AeMCZjjmlyxv6ImVXX4MS0rW/uBp5uWtrNGdlPHA6RJA0qoXgT370nTgFAylgb2FhBICllTTYWijX08BV2EsFpKkY4gC97XTJN8EjbQYzoMCJ+AxevoU1AP3iPLAF3+xJ5+bJUQbz6dLL855zZhqqp5SwZZ2dctRNuLhkvv14c1Zp8Kj5ccXwEZ1qWpeTrFBg+ZWieskwq0FhBApET4aaTMZQHtkZePe7KutF5Duq9Z7M1D8eJHeP0yzksm99zuUdFJOrrenLk1tJQNYH/B+fkKTuz6jLyYH2onmhGYfqo1cZS31dkdlqZx0Hm+2sBDaU6BdX5qx8cZkBHTp5FFIIPrNqG1x5d8uW3v8Trj1/n0e4R6+4MJTAmYzxqiuRxYOh7pmksTm+2Zl0lqEeqBpU5vd6bBrA/YRvPkgNaA68i4zTbyhKYSRmreWoeArLz4NV5ryBwtYuayYUNtVjsZcJFMEUTNU1DqYysbEGfaeQ7tEIEYgGDiQqYr2EBRChOtoEpOQdEBecyyARpQDUi4ljtNqRmQy4lmykmvG8hg7qJpJ77/cjh7sC28+SzLTkZWJ/xOLoSdNazo54rvpTcJlRHgs9oqp2oIceJaRxKIOypbLLamG8cB0KTCDTFX6p7wMYtFR+iCWGeY++tAVUuTCCTejjVqLSx1cLIMuKkgmaTKxj25GRdx7WwiFxoOLt8zPnlpSWRXeCXf+mfQWnKo1nQDI+ePGP36CkjK25e3hDHPZ5IoIE0cXd9xc3zb3P30XdIh5dUreFJlbsYuZpGLtqO4ARrWlYSORpxzvQru+CtmUzOECdbMwqaIsfDPSvX8Pjsgtc+/3neeOstPvnwmpvbnmGKxJRIeVqCZ7Fkei7+m8mbaGGpFtKDJpM0ywnFmhM5tcaTzlniLGASETlF8jRChovdOX3/khgHjv3ER598zO3tLW3TskoZF9Y43xnofXrOnR6g4qwHgve2r6XK08i8B+ddJ4Ux03Q0ubII3XxclVPMmNehnTX27AYnBb2quGBNlRBo0sg0DYxDb6zhnPChyJnkTJomDlPkCpMtA2veu1t3OPfwTP1XvX4t96gAVVLTiI2qxHKgeF8DbDuLxkmI2QbGZZhiZoxCP8GYrClgyva7rtpjQ57KOTnN/hvU2MBk2bwPJ/6HzH0tTKLFSC8GOizPXc/g2sjrFFSpZ9wpuCdioEZWxWupbvBWASiUZJevcy+lyY35AZaAA5cTUzbd87kBYzGES2Nnx5SqhilF07jBeWsq6UUQLYqFar6TgSUBJM33M/kob4mTExtTP78rclZV23ZOuJYxtKXoCtC7AIZUYLIEjKnsZS1N7B4ww7TqmWP7WIz5PIO9NZY+SZxLPTcfrsaHX5rj9OBbWv+vy4uiJ69L/UpnMOaB/S23NNdgfhOKNzMDstWPnBOfLGC8sZRt7qrW8PJYWna8zCDzXElUYtj6tZ6sw9m3Ks1MDeaomp412e/nkupQZbWcxSg5ptIr5PTkKlCkSgUubJvOoF9hNevSTV5YALSKrSz2rcyXmh0+jbEMG5ES6Bf/9UQ2afvet2j2dwz39wjOqmxDy6pdsVlvuTjrrYS8rL+cyjlQEsVjrDbG/sQ4svvmr0CKRa4wFVKOPYOK+VmVDuPixObFJ6XR3kmFoWMGY5lB5KqJa2OSUk1Yz7Qg0qzzq8VPVRYffZ7Vk+VcwEjv5vNSpOiplsSdMbTrcbjsL53X+jIXdW3HKRVtZKsUmP1fYSYLWHzsC1s9z/sbAVfXkzdgPNcGfELxU/K8nGriapqm4pebRv+8d8rZGmsVXIm5Kkmift66X6q2sJQE59w3o/ihp1V2MSbe+/Hfs4ynPEwHnVY+1Oes+/4hOeRkXwdPbR7sSqyRRdCUcRh1cTm77BOlEudVKZnPun4gwNjL0PHbN68T48RwPPLh9YdcxVvu3MQ+QNoFknNM2YT9P77+hPc+mRiTQ7VsneA5FCD2kCzDDpjeTga/ami2XUHl1RidjYMu4NYtrmkZT4SrKcasWXVlk4WZeeDmKMUyIW52qu3wU0wTBk5CoxNAwso6LbDPOtnzaKJPyt3U07QbvFaNIMfNYeAwHdni6NqRnA5kHVGNJbsF02g6NpqVFB0+GNvVB1sUKUcaF2YHpF0peIxh6jKaA5qtNCtmgRiLgWgNhM2gahljVctgqnM4F1BtQAIpWolqLu17cKXE05XyXlezKHafNrRsuo771D/YJAv8Yrv/+O99nc2z13Hiir6tQDnMczkEUk1RuUVfSHQJuC2YD8WZOtU4NLAtUgEAe8btdkvwjjhZYO28ddZbrbeEsEbDlmfPzrg/HJhGR0pT0dOpm9CucOzJwZMba0jWjSMqBuw+PH8Xg8qJQ6OKBTlaR+X//8tlZoMvKdPse9qYCgPRnIE2zyv51+EJ/hWv8sxjYSqhGZdGvvH2Wzz+Z2c8wUbs5voFg49zo77NZk1wix6YVn2mZMzEtm3xzs+jvQBLWtgZdvje7M4IMeKP12TUGLbiySIckzDkNcfYcjcGPj4ok2xIQ8N6ahDf4IOVMQQvjBIZhgEXVuWZlCmOZBEOY+R2P3C3V/ax5f6dBT28HwOCnxNEFTAsSfAS7xQnqjhOWSoYO9LkAXScGyhV18JcQ1t/QwY3KR4DVK5eHlh1vsJcHA4j3dOnrFpP6Edu4y05VmmCwiI4AQ9rBnlhTIKIMmbTmHUlWQOKq1Gus8Z4XhRrFGZ7OMURcQae4BVywjeO4FaIOPbHl3Th3JyEdST+zt9jTXt+9mdwP/NP5izog2W1eBIlEyzLHzGJglyyuxkr+9dYKwjK+tBl7Kur60tGV8TRrVcc9gfTJ6pNux6Ajw/3WdU2XtYjM4h6WsZWGcbfMyf0iqM8x2jl3tU5W+QXyorQhX1Us9y2CGqybwmwZ8+8sHRrdrs6Mg+B5pJlzjXQXM6/01lhftbK4mEZM632wj0IwqqOnp7c51Vn8dX5XwIIW73eec62W15//ISv/+Yf5dn5M7wEUG9BSQDiyNAfORyPUBu7lJuM48g4DWaTqsOolADJGhcEVxvHWHdwPWEMiYMcjZlltqGwYGV+4BJPyDwOUoJPRU+admgpk7SpmbXuqWte5rVTzwELyi3pQQEMjflv+oMNxa0WC6q9YFqVGK/LAd4pjbfgVFUYUi5l6g2tM+apdw4d9oz9gc3ZayY9krAy9OOB1dljXFjhu0y7umDKV6h0+LajW12aDjQDYBUJOC3dp5MxYWDW3FQtwVofCY35IqmU4qQ4EafJku/egoRaHg9qncjFzcF8PFmiuYBDpxrJNYFSNUh9Np8lNF0BGQtYoXEeV1ekMXKamEYridca8DilXW9YnT3i6ZtvsdlsuHj0lP39DS+vnjNNA6KZ3XbHk2evEbZn7K+P3Lx4Tp72tK3DS+Zw95IPf/mXuP3g20x3N4VBU/Y2JlRzcziwazd4gUlHEgZOx9LJGOfZnJ2hxf8ax4lcxkrEpEZcs+bs8TNef+sL/NCXv8Qb5x/zs//iO1zfHch5ImEJCqfmM6cUUeetwmmaSDlxud2xWW0RTeRhz6YzwGEYMhT/GYW2Xc0VVIfjnuffeY/97RU6jjx7/S2m/oJx2DOMe6LC9c0NDthtt5ydP6VpVoW9ahqQr8TGqAr4FudNf7PKzpyenap5wTDEzoduvSn3Mp6NNfW1PVyBtdPjrgZ5NTgkuKIzaiBY1624v3vJeDwyHY9sz86RdmVg7DgwDD1OElkTxyFCSrzz5tOin3p60H3XR1y+8a94nX4O1dKQDVv/XoWuMZtZefyazS5mFSYVJlUO94lDD0P0JPX1NAMVmsYA8BRtD09xmhmqUoASEUeKsQDZYdYAtKoNITTKNFqJtKgakz1YSXiKVqaaUiVXQGWEBVkC+Fq2X21pCLa/Lbnm6RrT7K2M00VXtlaugATHqm2ssWBOuJSYojNt5Wz+qLH27X1ULGGkWjrAOUfTdQQp/Uk0EafBknaacWr2V52fG4jhMpItoSy6lLbX2VvAUhan4MHSkAfNvlSr1EKtoyr2+RWfRlOe7X5dHO7EdmcUfGWQ1jLgML8nFFCz+hdUf6fGi/O7zwBV+eVixpb3Olmi1PNX6zkMc3Vj9R3AetksQKws/kd5vjwn1gsDtby3lHVbGYMmHWifvQ2Nac2q4r0zsA6oVT9G6lhA0BqHVJDVlfU4Nxp2vrjZ5tCJQFYpDOnyjDlhGrss4HBNiCFkyeTJtH2t+RezS1enIk6md1z3hTsBYuv8mx2pB+Oc6Sj+SfVh5wEsTNyHBI3D138rfr+nKeMemo6zzRm7zZbddsd6tZp7TIjILCozTSND33Nze8fxODClkZQjUSO/+kM/PAOAlhhd1oi46vsJ5Iy7v+P1975dGqky64aqZlxhjXtZmKKVSWsEHyWHylilzEVlUipInhn91eetY5eiyVnN45tsArz3RXs0WnPLE01rG9PaH8dwI1cbYhWQOwRvSaOYyTEjJ1UBUsbRTwXHKGQBX3zYWJrNphhxobEEe0k4jVPRoZfC9HcyN4yzpmyO2gzTOU8zS4Pauk0505c+GQqz/2CxkfmtMSV7b+esIacau7zGaCahFR/sBx8eyqPVFWfJMT/LgMyVFbXqK6c5AdfMBBnzi0zBNJvWdGGwS5kbHxbJohrTKCYDUvf+90pk/kCAseM08I+/9bPc55HeJYazCT2LZKckYIg9d9fCoZ/YHwc+vo1cJaw8LDiyKIMTJsww5HKwOhFcMCaGX3cG4NWDHWgvz/C7DX7Vgncc+z1QFnUZ2FpuJgXJt4BKZtAOlgCx/PIrNswYLQ+anBDwoYUW4liNmJCAY5oYdaLNGUmJHCK+2XBz+5JVB5tdJqU7xiGjamC0dVxMeOdoWs8mtIS1L66fQ9XjwxopoZOIQGMZWI0WIKMbNLVYyZOVVqRsDT5EpWR5Iq7pyClyOB6Ycs96FVivhFXboMkcdWOvFjhHSzd47/ChLU5MEfn2nmnoTzqNM49hBTLGOHLWtHhDlM14aMblkjVyjt12h/fWuZpsDJY5GC4H6Gq9sYxZnJj0tCmVAN4C49JdD4Sm6Qr7QrFGIp5udc5q+4hmfUbTbhgmuL2bOB4TTdvidWVMvJOy7N/1p/8n3v8tP8a/+Mn/CoA//tf+Gp+cX/Cdi0ccDz3qhK5d03YrunZFTBN3+3sOfc9x6Lk73NL+7/8b6eojpjgQi1FR0VoFbaus7nE9BVTqelwyPQamW7nuDIRpwN3/BWDHGz/9Df7AH/hf+bHf9GP8g699heePLljlzP/wS9+aGWXGzqqATwlKKlOtBiLlewa41aPM2NiVkTXvxGqYpWbKF4eL8jtgxs809yYr4S1dlf/mj36Nm9Wa1f4FX/2pv8ov/tb/gMxungPvA76BUID3rlvNTk49dMcS+CFCKDp/TswJO+xNhBvxpItL+rfe5Nn/+8s8+fBDY8q0a45D4uWt5zB5+tTRbB/x5puf40nT0g8Jef+a964zt70wfTQyjB/xH37tdc42nrb1rNYNfW+lav0Y2e9HPnl5z80+M0ZHJKAu8OI+Mkwne6UGAbMR8sWpqWeOsYdQ6+grqjhnHc5FI6hpYAlz7veBc1vPtT7CuvHgPdeHielmz27dcnnRMg0Tzz98zrPXntC0HU8eX7J/fkvKtURcCzAsyxJRM/hW8morYe1XFO78cjlbp+JbkFqKAwsAqOQ4gCqh7VAfTgKoDUN7hmoEBz4kUj+SsUy5pFj6mMnD8yezsDlyQorWsGl1LWeUOGs8cHnxiP1+b4BbWiRKFJ1thIFotsaDmI5isgyROSRT6Ux+EiCfOkqcvHYK1J5+XcvYvoe9t58r+9iJw78aeFeA9lN/5+QZ6j5nAXTLSNYPv/xb6jNXFsmnP9dnZY3r6+lkbB+M04P3rCu3lGzr0vjMPt5is+u9a57UV5ZPNs1kp9AQ+OEvfJEvvvUO77z5Nruw4f7u3rTFG0dKkbvba/rSuGmKEzlat/OsiXEaiSkSS0mheAMEmrYxR06EaYr0c1lXBXmUqulnmnCQU1zGqAaYJ9Pn5v9bkxCwILgGrgBTKSf8bjB8CYy0lNOpQpoGNI4lGAWckG0HoZKLU16NkK15pxawk2GcRro24IJVlYh40qSMKYJvaZodqh3CkXG4Zrq75vZ96D7nSEnoD0eurz/hC+cXuPYMabds2y3vbJ/gCyvSMaHTJ0i+QnJP7WCrc7VKgX/UGfAhgkOZjORpmpXB0XQtmmPpHC6IDzPjMBeblJMxz9RbcFbPGgPOItM4lnmtTLgyK0ViwwfT09ciEzEM1qW8aUIpj/Z43yFiuoRWLhtpurWxi50QgnD9/FuIHji/vGSz2vL7/suf4J//85/lg+/8KndXH7E9u6DtOpx3rHxGxhsuzxxOlGm65dvf/Hk++dX3GfoDZAO0nLr5bFCFTz65gjGyWa1oQ2AC9oc942TB++tdx84J292OLgT2x4FxOOKagG87Y4V2DR998Jx+EK4/HviPfuzLfO1rZ7z30S3vfXjF3ctrk7+ZIqojSZXWNaQMeYqkw4CKZ7Nas22Viy7y1befIqoce8ftfeKD51dEWbG7uMCvd3z7vY/4hZ//OdarhovzC548fY3N+pzj3S2Hu2v2dze88dabuM2auynS396z3p3Tkos/5SFNBbgoFWM14VXLOItfObsuxWhWfeQaQ2h2s/81g11OIJcGPw+O33ryLlIiKWVUB6bpyPH+lquP3ufZs9c4Ozsn58TY99xcf8L55SN8EyBAkz2H+xdoHhCN/OLxwNXVDe++9RqvPb00QHN+v1+fq47HGDMTWKCfMirCFJUxQUZMTSTDMGZuj0ofhZithD9OyjhEqxoomrKhFdwo9ApToiRila4x5p8pQASGYmccJnnQdd1cluqdR4M1QfXes9qcmeZsMhkZ04PND3sFOPfKcCm+WeGC+bjWrGiyxkW+gDNQznA7B7zU2S0AGZBi8Ts1QwFwc5yQZPGZFfzYWtSULGmn5WxxDsLKZLk0QYYpA86Se75UGVnMZMJTIsHIN+qMO61aEn9yYheknJnFXsoJo6yAFpGMVKzVm9SK+AWoro01DWTjBIgoNofKBLX7nwIk3ntjP5efnAGz+ffU4pwKas8msWzGvAAiwCyLNN+vzJ/9jL1WE81I9bEW6SnBEmi5MhvLfFbmrHOC7xqy+sKoLmB5kSOpmqkheIJUOb3JGmWN1vkdrdr7Nh7Vl3FS2bcPWcXF8BTQOJOzIBLn+O70yrPPo4yl8bWTUmpextmkigooWpIGOZsESHVjnZgN78LKmvIlSxwbcMicWK4Ji1QqfKYSj9c5kfKMqWrGKrMvNOvXYuxSV/Zw8GYDLs/OOduesdmuadqWtusWSZIUiXHED5YE2SaLH/f9nn48oJOSYn4gIWAgZ23GKCd7GWTV8eK/+AmmtCR7nA+IwON/8o9Yf/iBjX+cUGcsdwmNMY7L4lGtDdJPlrGYlJ6Nh7cmmEJZT0LbOLbbWrVmB2mcIqEJZTlX1vmJ7m7OBJGZjZuyxUmnALcWAHOuxCtAuisYV5Xfa9qlFL/GZvWys/Eh5rVuNpY8LhIWiJ/ZwKLKcTgyDOMsDTivE+9mv2iWPKmxK0IT2vnZ12uZexYs0gB51netny2VXgZZlSlGxpP1NE1xlvTgdD+VBJMgSBCgNh7MhpuXPZjKuWYJHCNAxmkBbjVnXFnH9RxrQrAK+ro+XhnP0+sHAoy9zwPfXN/TrBpC25GloZ+O9MeJfpi4P07c3EbGlBhT4h7H0SsEgeBIAknU2JqnWbGy8cUX3T5XMxPgNivai3Njxzae9WrFRNWusIMnKSewGkWz5PT2JUNWFoctEK0RKBaafMrge8AbQJkFmn/4f5F/5Efh7S+QccRogFBStRLjznN1s6drlUeXtbGAMbaCd8XBT2ZoMaYcyZMx9k5OgsgGNJihpZTEJsuAxazE7Mmx5qvT7CA3bYOII04Tq67DN46kjjEJx3Fks7HupDFp2Uiv2JOSDfESMO2sXDQXPW6z4/53/mfIP/mHnHo6Ung1IuBF6VqP80sWN6WEFzO6WWvm2bNardjsNqSUuL+7A9So9k3H5eXnmWKk7++ZDtczYmEMXfuMWTO1S+Y0GctmYQx5xHnGmJGUeXzZUjtYQ6ZtG5I2DNPD7F6jeRbxB9i4A1vfcbHKXG539JPQH0emwx4t471uO1ofOOtWXKxXpP/09zMd9wzjQD8c6eOA/+Wfx33nmwzTUILjhbU2w2llEmoyQf4/9t4s5rYtu+v7jTnnavbeX3POueee29TtXH0Z2xDSEJEIYhQEjqJEUaI0YKkSiYgHP4KFLYGEqh6QAVnwYiFZGKSABCgPSGAgwhJJFIQfCAL3Jr52Uc2999x7mq/dezWzycOYc661zzm3XBgHShGr6jv3+769v7XXmmvOMcf4j//4j9pZFapbKILkhjsArXO8fHqH080J1mTzkCAFdYP0+QjKbiajGoYgMc/2Re9TExH5WlJiXfpSnm+t9c7fV2er+m2xOoApeGJufmMQfBDef/gI//nA++90HNotD/7+ZW4os4y5aRotBcvORPCBYRwr+yHmrB+iTNUyFspSixyGLKhvHFxc0Q6/yn5KiDOk0RGk4fLQczs3TLHBS0tvOu54w1kn7LaOd16/w8FfcnUQxll4eJn45a9e8pm35YD4XwAAIABJREFUzzndqmbx4+sDT68GDkNgnBLeg9gGMZHOwIMHJyS55UkjFJn7xmbn3iqTwFi7MK8RJAnibd3EEhETZiSNKk8QJ2DRCUPIJZNrFrayMqagDn/bOIKMnJ/t2G06rq9vePx44jAmThvDvbMtVzd7Lg6eOQpJdCNSuyO57C0p23VBHrFG9a/iPBPjIW9s2QaLkMQRJVTQOQsNYlyLcQ2m6QgEpmnOmdQE3Q5/eEqKhsaegDyFGIif/DT+9Az3f/0fz9tnRVGys4uWQGeasYiORdEjTSSubq6qQ1AEw1UmpUwl/dcHr3I0zBiUcReTOlra8kHXSIIa9Nc95tlLzHbw2ePZ5ls6dMd70AKYqo0oAcnyBnV+i3O8zug+d866/a3vtHyjjrZmv1ea3CWwypOulDYWTczjwPDFAK2srve5u1uBr88ez54vxVQfd0khQsIay67d8p3vfIHPvv0ZTranNNIRpGV3/hLzNDCMA+M0chhumfyE97OWY6HdlGvAEUNmwDtN2hktc/bznNkvSzBcbHc2n3o9ufP28YVn07lCt0VyE0Li0ZhklyfrWR+PTXGqa1kWOg4hafPPELIDmxM2oSRDDVhZdO3KNRixtM5hc/O4YBKuadXW+oCxhq4/RWJHNB2YliAtjjPC7QVeLrCMRL/H2B2703POX3oF25xkZmbEiyFEAz7iw0TyE5t+wzwJ8zDi5z1npxsqgwyVcQpExGmZdGVMpyxbECPGKGsJbNXVs6UkGmWiqMzVIp9Qgt8yrwqbqwByhb1VGLKVZde4ykwOfspArwIY1rY1wFK2SClNtQhaInh98RCTbphuNoixvPzqG3zizU+w3W35yrsNKQp9vyEkTzg8oTcDzWlHSIGbw8DlxRP8NGjJbFoF3JrPrsmKy9tbrg8HRKQyrFN2kj94+hjvDGfzzO7klO3mBGlbkAZjm8rcMQh+mnj8+Ck//XPf4Lf+tk/xHXfPOX/lZf7Frz7i5uox03DLNA0kP2ZfNtsNoz6r9x4aYds3nG9bhsMN2Bm7SZy+eZfbAbwcGA4DJ+mW+ycNp2d3OL1zj9M7d7m9nfERxPVsT+8i0tNs7+amaiMffPSUBwG2p3dpuhOSddoLoOrw5dLarKkcq60yNS8CCfHU8m7y8yya4Xk1a7Ap6mfruKsvnx0qteui526ahhAmBbas4fT0jH5zgo8Ba2HXndBuz5jmiTgHXGNpdzvGwy1XF4959PAb7LYnDNd38fPEze2B11+5x8nJliLZdmQ7fzOPnHxIJAKJDsEEiFYZs4cx4KMleNWHnT3s95GIyoNtuohrG/ysvt66RN9YS9Nauqalb6FtFUjyEW5vPa5pQIR5DFjb1LWna7E0rcxzLK8B77Vpc9up7WhzE9fCsl3vTXpvbS33RSxNq+XD1b8pwyB510s1vMjM4JTZivqTkfyiIdsh9akL2SaGHOwnyWSMXAVTwFwKQ0swMUAKVX5NAVVT7XoMMTNwdT0bU8AiU2UR1nt6aaZZ/PcoUGqjiIloIuIzSFL2vaDJDSkgnxTfnzqGkvUvrbN0ff8ce6xSRhJ1d+a5eVvCueKMLPOvGLIqzZSlflJ+b9WYz/uEatUX2dXyaSqDkkpcVT9TKzDqZ2Q26wL3ZqxBMpwbdSWElGOLwr4mZV3WLJkjUjGLmhgl5vmT6lcB0VO+1jDHyjYs423zz2XeNrl5kazGpACg66SszVU7RR5LK2izDnJtLit171BJpkXXVkToug7J68t7r8DhSvaja7UBYQUXn3FyUtR1YKywaTvOTnZ0jQMC8zRRSD1Fj1kAP0fmKTLPGrNNfs7SNzohYlBfgBwru8bgbLtiF0tmHCv4Z/tVJZFIfUbm3/sPmedJn0mM2uQyvzGlyKu/+IuY2xtmP2OMAuBFpsoYZafO80zIlXlNbhxfknAaH6umdWGEF5br2gc3tsholhhr8eeWpnvL1xqwDCGQJNVnpskqr7rN+fy2ccv5kvrFpXcBZPnGmNcyWu3cNu0KZE10bQsnipVorFP8f/Lc9/h5zmsAmkYlIo8q/lLKki7qM63n9NKEa7n3skaaZoE428Zho6mVsOM01UZ3pVl80XstNqrLEklitLFusnn9l/HIyYyiRTsHX21UymC/M5Z5mvCFtPYxx7cFGIsV0il4F/FM7PeJ28FzOMzsDxO308zNpJo6E4mDFaK1BCuVIVgzWxkAEqsoO9ZoqUaJHbVuDtn1xM4RpQjlC23baUOdvFC1uVQZfP2POl8Z+IKVedZ/I6vyixyMHptwfbBYgzi9Np48RgYt1Y8RfCALXEOaE9GrHu7+kLi6CdzZNVibEJuwTnU/THIQGlJsVXIgWES0QYVS2rV7cQ1WRYMMP89Zq1bZokWYuTDrEsr+CMUZgayF1SjQmLMVKYZM5y9cqWVHFFko61PwxKRC4ca1pPuvIDlLXccnj61Jire3dikD0GewALPlWYWcFZtnBas1g6XNw5r2hO3unCTQjhvmeo3ULIY6KKFmXSRkunxd9GiQEEvG1zCn1TmcJc3LxleO/SsvM56d1p8/unOC7xxdI2xOTum9cM0l4zgS48A0zjlQzBl2uyW+/iYhBHo/040HmnGvchind0jDnjl63IcfkG6u8KWBmJT1IIWIrN/XYFyyNTz2ahrbcH5yhzaXG5SjCmwXsLQ8W521rCiDOmcqsFCckvQcPqLO3/GT1/+og1My4Ppm3XhDCLimxYfAzWHk0dNLQoiMW8v11rIfhtoQol5jKeXI2bOi21QbJK3mVNmQwksvqcM8TZiLpwq8RzAxYWLEtyfEtGGcW27nhpu5Y4oOjwNxxMny+GrCOsNJbzEmctJbDnPET4nRO95/PNP1e063Fog8vpi5vJ4ZJu3we7pt2W4cdg5oiUSkb4+zleIcJmsTWqtdlWN9TmCi2pqYI2yJEZcmZZDFgZRmpOgOsWxkR/YKstMEnkST1HlIeRz71tD1LePsaaeZ7abjwb0z/OMbbseIT7lMXaDEnFICG1NY3Mr+CxEFZP2ssWmVNhGwNgMnC4vBuC4D1m4BDCnMhoTrOuapVRAHwTQ70uRJmx3x7t0KTq0xulTtVw6g89gAeS9ZM3zRUslV6XtKVH2zunbQRF/M87tvLffOT9kPIxdXNyyNY55fJy86fj0W6bO/OwJknwFfSy6xHCUgqo7G6u+XMc7/ytFPClqIsogWoG/d3GT57MIWW13pr3/jH3MsYHEuD0qprvllN/6Yv812JkbVfeqahvOTc16//xqfeutT3Du7r5qlqGbUcLhlOOwZhz3TNDBOQ64IUQdXDLn0XB0ym4Mj57Q8iwpqLeXnku2xiCwXWpyHZ57X8+NVrt/XMV03oClscmXRrMdrGasaeK4C5ljmfnHsc2JMSDUQTTEelYKlGDnsb9j0G9qmzR3fDTHOGQwWWueIqSNIQ5TSIkFZJ67raTZb5jCDzMqWMjAdrjVwSGqI03zL/uJDwnRAgJPX7+NzYk1iwEhCrGR2obI2UpGzybbHuRzATSPDcEvXGtrMQA2hRdDGZWIEQtGuNUuipTj+cZnfhUnL0TopNjSbMiMQyjU4hFgBoZSbU5W/KD7OMo/Vtg+HG4gHhluVgzk53XB251Xu3DnnwSuv8tEj9SnGceD66YdIHOg7bVQ1jDDc7hWoyQHD2j5kPAgSquW2ahBT35OE/Tjw9PICDwQxNP2ObnuqNjz7AMYY1c5MiWE88PT6wAcf3nB255zd6Rn3X1Eg5vb6EtlfkwZDiLqWYi7TDVEb4jiXew1YQ+tUw5xo6BtD11p8FKYAG+npuAeux7YGE2bSdCB47STRtC270xOaruFw2HP59Cnh+hGtJFy7oe1PlNk+BgWlnll71WcwUtdmSWMUDfIYPKOfluaP1eah1R6ifrTaqYV1Gf3MPI/HuqE5pnDWQd/TtL3KOuRS1HYDZn+D9wPRzwS06/ogifFww3DzlHkaMKbM18Trrwrbbav66h9rX/7lj+r1yWK+im6syXu8Q7BGDdvkIXrwqqaQA3tNmDTOIBG8L+XU4KOSblSxQ7WenSv+ndpdP4cKkq+BhirvUp5DtgWlQZHNMYO6Kjbrt2rDpZL4lFyeW6uQpDDIDKRYgdfy3FLWvSaV6LT4z8vvCth/7IvophyTfr6W0oLYBnIDvESCzGJMZQ5mJi8pVpCu2JHyGVoCj/r+YjP5ewU0G0FSzGjYKiG6ih3KGiiDuTAol729JnlYzl1mWWEbqwawak+Wxojl745nFStsVY7Hb7ms9dvzdcTVqRIF/CvVOlW7VdYnWfbGMncUuF9ei5l5WMaiPEYF0NSfT4mapKll0KtVcuQTlVL7LIVVQrPSAC2mUEOoo/gr/w1Jqz2eBb4L27E8kxpXHfl/ywgVn2EN4MX8PEyCKInk/SrGLxrLS5VhiaeY5yMN2DXYu54/NQ6IcvTsil01ontI61yOHRKkoOsgCj4zSlOKzFNgnrRvzuw98zzVvZVE1eYFi7VqU53TBs2ljN8YWTGF7XNzy4hB7vbLVeZS+rJPhxA5vLmHwx4ftbQ/xYR7/Jjm+oqlUgxMyFVYGWjVZ6rniymSgsZEBbiUFei49jueZUSXeHY9nGv266LJvqxZQUhJCPiaPC5khTx1MrAd655YMIIlZtT7LzrcIimzRLXSXIzRZIMc96kQiVVC5zlgNRPIfAhIBmyXfhdLVeiL5tbajhT7o5INLvcXWpIH1hhgqVwKISrjXwSi5IqClOGJVHGgcg26ZjUmEhTcbduWtmkYrc3N8j5+n/22AGNdY+l2LcM4crsfePo0cXuYGUbPOHiG5JkMjERGgcEKqXVL2UBCN6US3Bly9iY73yYbRUmIs0jbYHYdUyY9WBJzCLhGm0nFUmZfJkue1QmquLOsAvQShOr3SR04gRSL0X3GkTUa1NnsZDJ5mEbt9Nv3CiaVhlopESZPbC2HAR4/8dw97WmaiFiPsVpyQtqQYkfyDSloh1VjGgVSvcfKQvkGIBokJWJQ7a3BzzhrlEUohrZptazQ2FqikbLGiDGa9XI2j0YMJOOxtsvU99rOAxC6FDAijFk/xKFZVbGWu02HbE/pbEOz3wNwp9/QbE+UH2vgrrV0OWPrRQi2NDjQwxphCh4ZDyQfcKZhV5o5uIbWtpw7Q9M1zK3FzJ57w4A3wp1p4swYpnnGxlDZQ4LQ5g3YiOpvmnnEmZY+jpjDgdZYej9D9HhJTETEGA4xcp3vxb/9Fs35GXfzzw9fepnT4DlNidOmxzfQT45DGhimgdv9TEoGMQ7XtDRdj5imAgtT17MfO+bPbvHvfIZxODDOE83P/BPSe19jmAcFh2ruPXFzuF1LKS7zsH4trzjXcHZyB2fs0e8LgF5GXZtsZEmOVDa45b+6gSwfWgDZesYXBKvLkSBrAS8O4PK5IIyT5+LihqeXNwwNBLeUEmhp3/o+JYMREV+0wrIwei2lEtUrm1GHfzw/I1qHuT3QP74kYEl0GNnQ2HOa7X1C7BkGw9MJxtSTDQ+IMHr44PEe1xiQBn840HeG9hAZoxDE8eg6MH31lm0HbWO4GoRxMoTcwOS879mdWJoxMM+RcZjoGw1AlgfWaLnYkTNH3UCtCCEno1TrKGHTCPGgYGycISnYWx2Ao9lRRxDVEhTmmNi2HYdhJPqRs23DnbMdVzcDt4eBk5Mtr7x8l2EKiIzcTqk6skaomfm1w1fBWiMKAkUNBqrTJ4UtqRnWIMpya12rQa1kofmoTWxsBmPENMRmg08wh4G+OSP4vdqsVECOj1kZaXEeY1LmamHG1mmaoDAREywgnJgjJ07HfxnPs+2GT9x/iUdPLrh6ekkQV/WZBb7ppv3NGKPPOWQf875n359KIJWWTPn6b58DdOudHDtihd2pjCMNgGP8uHt5nqlZdtV14Pbr3MLx9SwGJv+8fHY1J0fvIAecCo6KsZxvT3nrlTf4wqe+wBsvv4WfoOicRxKPnzxmGveEMBHirCyN4oyTnfXirAk0zi4JzhQzcz9XYaDv0RRWGQGdRyksDMHj+0lHN5CyLxJzVr7c11KytQJj6zlUg3ntwAqyKsOUmqT2KeUy2ADF7rPME1kl7oL3XF9fYQS6VsHYefJ5osQsfdRgpCOhmqmSIilMiDE0mxPc7g7D7ElpD2FmP94ye8kdwy0GC+MFt49+FX/Y03Qb3Bv3mKPHErAm4lLANk4T21nzViRzuQTEGhqnduYwDTz96CO2G8f53ZdwrsF5D5jsQOtz39/e0nc9TadADeh+VJhFtQt7fY5r3TyqXUaK5FVpoKG6lqGwj4Pn9uQc73pss6Xve/q+wxhHcIbr3YbHXafNq8YZa6BJEwebsKc77FvvcD19la+GwO3hlg/nPVenW3b9OZHE1G4Z7rxE7E9JPkf4ee0XBE3qmpZ6J8eTDoJELo3Fn+wIJzvs+Rn3779C8FFZhkD30l3aszt41zNLgznp+KfvXfEgtTx4fYd54yXoHfGix99smPdXjMMt+woEWfy2ob1zyr4THrUjHzYNSU6YjGE0yg7sNjtEDA7hDoK8fMrFzcDtEBjmkcsmso+5gqrrSa++xI0kPrh+wlcff4S/ucC+cpcpBR5Y4UwMPsxZ886iCYWldBmWgJAsSUFapIFi9AyHW60ma3tM1qJVUMCAUY25WLUKUmbXzIyD1r0Y0fc7q4CEcw0mbTC2UckvMYQIbaNNfw83F9we9vg5cLLb0XcdQ+v46IOva8+ItgFpuN5rqf6Dl+9wsuuwLpdofvyW8y0fqyiIkJISaIKCsY3N4GReC4Iwz1p54oOy7ktjPGugaYRpSExzYpyVOVvGK2XWMdkHneZMZPGJcfK0TaOBfAYV69TO+1iISauGMsDgnKNthaLZXRrXhKC60fPs1QewhgYFlMVYrFGZJUEWlmxKtSKsdFBXcCO/zJIsVtBENIZjAVATovMq6rXHrElmRKUvCiM2pZAb7BXQV212udeMO1JA1ZRB05gEEZdL1XNJMwUwTZATe7VU9yjiKnFt8R1iztMt7P+yaRef1FY2ZVp8vwpm58aoUJOBeaCq/y9I9Y+Wl9PRWzl2uXScS2JM0XdSriHMgaven5hVhYwApfJKz697VgY1RZ+191MGKVNdNxWQUSNfNUJTnn+xYgMZOBfJMZHU5EwB2wqzL4RQE73LuJmFIVikbUzu/C6l4mNh7q2BO9Wdzz54AVvXEgLFj87jhagdNznGUEmtoL14qvydMkrL4zLZ7xwzcGdzc1LydZUS+zBN6hOZEgseO3p1bogycikJ7JSfW8FqojIulV1Z5BNmpinLRoVQkxYuX6smQtUGO9fSNA1d62japj5HvSpTpWfW03+td6wM9YXIAoGn73xS9/hqg+Dur75L/42vMQdPv7+l8XP1yUr1S8V8YloqNzM4GCNLMjhpU6zjZ1cqk+WFX2s2qbMqaVPjHyl7TKrVcGUeliOllMczrn6nTHMfglYjBo+z4zK/jBLVGtfU3znr0LyLQQw0pqFxy7Mufmu5zxhzA9MqB3CcBC/xY1mf6+uOcakejDEimZlsnaOVY6/G5Llf9GknPx2D3iJa4RefB8ILgO9yNafkatCua9lstjRtk/eVo1r7o+PbAoz1PvGN92f2+4nbw8DVMLGPs9L5xahurIEhwSiR6BpSChVuIncyk1zmLM4BMWthGKLR95nG4bY9drth7lpSzkwjMKeIIzMKV0yeY5hInWh55hVTgahUg471X2dVguUsMeGSshD701P2Hz7B/Mw/RT76gOk/+b0Mw0CbemzjcEYI4x5pOg4DfPg48B1vdjTGaNZkMpB6UtzmK9FJOc4zTVM0b4sQei7RyIGjiLDd9Gz6vhpEvWY1+OOcO+iSoIXRj0rDjtrxtLGWq8MF2+2Os9O79J0FSom4AorExHdeXvHa/qCj0W2WgYgR3vwU/Pef0p//9t/W//5nf/AFkyQBWev1RV6jK9T5GdIMAf0aAR7C0185evt//Xd+9vjvbf46EqaIwMTSDvEaxodwBbz//CUA0Ai893X9KsdXfk2/jo5r+OCXPuYkUcvHxwnGmxe/RQS6Vr8Afs/ve+Hbbg63/Mkf+xFwBRhdnAA9jwbD5XDW0e3Osc+eKC6OUnH6Yi7hW4NMJbum7yMHnmWThsVdMs+BI8uR8rks2gVWDXNje8Zx4ur6micX13z05CliHT/zu865eLPn3gctn3jrHS7b0qivDJWWCEcRggA+5C6zVJAiBJhevs/ty/chwvbnf57GJ6BlMqcEdwdvz7HtGe70Hi+9cR9BODl45MmBrz+8AhwYB7nZy97DVx8OXFyPfOJ+z+D3bE+3GG+52Xum6LicIDjH3W3H4XrPEJw2VzDC+1dw0htal2gawbmOVx+0XO4sl/lRYi2Ss7nWrR4vqB5qKeursGaEMEMYIO4xaVR7V+Z9NmGlQdYRoJiSlhdG6LuOw3hNmGZOWnj9lQf48ITr/cDX3/+I33L2Dq/cP8fYG8bHN9nR1kkgxqxWWSpIYL54TQiVhjmz9xiTcHnuWaNstRQiprVEAvOo5SbOuQyyaMY8JQWOm82GRGI+TKS0Q8w2Bxmqq513jdV8YeX4ZhAs280QYzYRRQtQ31xAlqK/VP6u7C9qDwsHUMu65nmssht1KIT6nt/IcQQ+FgeljHQJkNZDv7rncmhDlWMZhBcBsWs0sJTzipHcfGjpGLx2WuAYIC5BY/2MbBTq9yxjWPSb1sfzYPPH/byMfX3HMwbIkHjt3kv8O9/523nz1bd46exlxkF19qwzxOj5lX/+yyQ8Ic2EMK9KWIsMitHgOKHzPIN2a62u0rChlIHa3CBC/XBld/p5ws/qvLVth0g6ep4vBKgz2JvQAHIYs9ROjIQUMvNjYXVVY/GCEcvxpOaWUL3pOlYx4msiQ5vSGeOwVqtoTk62tK2WCYs42q4lBc847rm9vuSOVRkig2gifLglScBsOlJjOcyeaThk3wX8OCOJrNXqcE2P8TecnTra87ucnOyQeIX4a/zhEXG+RLb3kO6eMujE0HfKAlTJh4Sx2rSzsJZNCjz54BF9v8G1PWJHTEw4a0hWdd8+fP8DXnv9dVzTQtaTDaFITFCvt7KOywRLx2JVtcFFDpCmUKo1clMNA//Lf/c/8bVPvPWCh/wtHr/zN/6n/7LHZf762m/4DA/y17+J4zPA7wLgf82/+ewY+Etfucb7AtxkDWSUmaQdy1d+ohS/JypQEVW6KoaRh++9z737r7E7vaMB66xNd23T0p+cZXYszPPAdNgjydO2LbrYIinrD0YgGUe77diPE62ouvphmJibBkk+NwNSMsTlxQVN03D/weu0Fm5vbmkbS9M6puj55+9+nacXt7z80jmvvXaXTZ+dh9/wzrMc6nZovw+P+lwqHxDARm6GyO0YmaNlmjKAGEUbEfuQm6QIwyRc3ESVoPDaVC2kSNu6DOgmmtYwedXWjhHGeVY7FNXv6/sNpMDV1RWQS2CbBvxSVuqco2kFyWBWnCIxs+lLMC/WErOtlxARIk3TULzbUumQpwNr5tdStSlHe/3RIQt4oH6zNmCm9MKQCe+LYzItG4BInaNqPCSTkjLISwZLU6pGXVyrLOAUMehXfiMl9oghQmGNruBN1qCsiM7LGGv7rsWzh6Z1FaTQyi13dKZyFMADHxQkkgxOFe306gtk+5hL+5878q9iCHlrK74byzgUsCZLQxTgkmytFfDSJGXBAdqmr9cJWXsyFfmaknLTsdMKqFCZzOUzQKrsm1achCprEDNILjZkkF+yay/YviOxVI7WRPxqmdZ5mvR71VDNlT5eMRDd8x0GcqPiVAF6ydWtIlryvU7QlmurbG7ANBZpl6qpeZqzjVxAQVBt0JCrGYO+mcoOznJec/D4SeUEEF2/y+PMSZ2YuN0P+ACbfqJtG2UbjqqhrgnRQMgVJdqILzBNE2SGohWNJ6Npqk4tJJxtMjtWgVnr3DGwl9Rv9WGxBaQMCaycsAXQ1CQ3qRCDNFZBIk8++Skef8d3kELgrf/zpzBDzNUAITc6zOcSg20EGpebdQWaRiuzdB1pNYlW02aAsjweKexcbQIGBSxUUHmaplpdqKDyqhL6Y1jMBcQtnytFiiXHO+Qkg+5j0yLZVtZjjAzDmCUSouJNLKzSEHyNwYwxtF27VCSj/XsU6Mw+08oHLgmnufR4IVdieNX+X+KDxP72QJMvqjB8E+AyWNy4PG+NxbWOrutom6YC08V2jPleSn+QeZ6rrbDO1XEXwLkrTe6XhmEvdNz1+LYAY8d55qPHjwgh4UNiTglvDEPOfA9JdSwiqhtocudBQwnatMxcDasa46YpwGOEKNAa2PbIdgN9p1koFjufgmq0GgRnNGMdAddqOW7wnhhDfh45i5wUvFqLegc/H91bDepX1nONqicB3wj4GcZR2SMiTDHgMPSuA0mEXMbjJ+HJY8O903MEQwgJIw5wdQGIaDMSgyhAncEA0pKZMm3D5Eu2zZB8ZD8OTLnzmzE2a6uosZv8hDFRGbOupWtbnDVMyeexiEzDmMGfKjRAQTLrtvisr/eiIP+Fgf+/4t/8eofUf/4Vz/ObcI5v6XPqP9/8bV1P91/9QaYwYL/yLvb/+SWGeaJ0hiQJYcVcM0absemxNhySexEsaYZYKrMLnsbiqin4luplqiZaAXR18eSpUoPXo5sTkCSAZ5pnBGicI4nl4eMPtVPmNGTmqW6EU9/z7m/7bkJjj87nGkewgTDnzSho6bBm44XoA9dvvwm3e05++V3VJuUuk9sSZMdszpjkhJkOJsvVU8/2bORs17LdNrzVN9yOI1e3QigdV/M9jSFxsY/IkwOvvbxTbeEI1/vIu9/Yk0zHFBLXh5mX7u/48OnEFHScDl54dB147a7jzqmCHRc3B8ZpQwGXtlbZo2LBWWXNajAkOROfMFmRVIHWiISBFCZ1EtZOeL52Zcd7OJcHAAAgAElEQVTGeh+mOGGSrZgI+2Ggt5Yk8Ohyz/lL0PUdow/sh5EPPnzK3fMTdpuW043jcgxZSqDMEXWgSmfKNuun1oDXGGKYFfhAN9g4a5bbAMY6AtpVWa8t318iA4JkIX2Dc4bYOrxvmadA405I0RN2p0z/+X+B+9/+3lKuVmf+oh+a0KqLcu8urx1t1uFoulaF5DMAaUQg6sZcmAZz8jrG2TZeDTO/8o0P8CESrFU5nRiq5fxma7tkuWHlnD/zenlt/XP9fT378hlH702LBM/69SMgdBUMvgjwLWWI63Ke9evrS160NU0d+7Q+lzWrssDj49nzPvv9N/udMls0iHbGcL4743d8z7/LJ156k21zih8iXb9hGiduri+4ub0CQu3OW4I7mytERITGWvquJcbANM8cDgcKc6R2gy7XlG1fksQ0qUOnZamqiVb8hkSoYNAyfsqe0AFcAGtNjuXgLmWmrlGZH+vs8txzAkQDDPUR4nou5QA5+lC8Xkgqa+RzsKvnhZSCAkFRcLZn221ULxTB+xGTZYO6zQ7T9OpXGK8BY0iEeVJbENSXM0bo+4Wh0jghzhpo3b13zuc+/zn+yT/5xzwNuax7uuHw9Cn7i29gwi0bpxqK3s9stycauA0DV1cXgK5LZxru3rvP1cVTmn7D62+/zXhzh5M7dzFNizJ/81cC17S8/sYbla2RUqwBg8s6sSJG9aq91+YNTZvjuaX0NknW1jcpM32UJa22MOAyOJfy2vq3x7/+Y5omvvHVdznbnWjPBOsIIcMqImBULxzikY1ENF4gWmxUaQZDYp4OXF96tifniCgAkQStz8dCisrEmUYkBU7PzpnmkWmc6bue8TAoI7xxtG1Ps6Ey49p+iwHmcci6egbv9xiBy4snXDx5zPWTD3n1wctcX10SMJzdu8/NYSbEmYuba95/9JTPfMdr3D3f0baFESjLTX0rRzUbGQxIkXEODFNiSlpR44H9PjFGo5UgUTjZkfUdIzZB2yuLchiFyyv9fGNUHxcR5jEyDF73SYGC3cSozXnmKdK4Jq9dZSgroGJzcqwhhKXRUSnJHseRsvtYa/RZsOyZlYW19u+k2HRU1qKs12yHrRFCMLUkeLEpsUodaQl1Bh6jB5R9WxosNbYkuVRjcjrsGccrYphoaNSeZHmcyAxi8V4bfqlszYwhaedvY7BGdEyKzmz0pDCTirZskgyWlZ4OsZbl6vPNZfNClSFRrcVcbi050eQyg6+A0GWfriGgLL6/qM/pMJX1llIkhwz5qRRmZ8xzP9Ngi5wHBdRdNU9ikSpaz81S7bi4BMsct7myTJOVtvpvS+MileuJyS+TvgAPK03ItbtRgMyiM63gke4TPsuxkMBKAxIpDaBFBLFSMY0CcoUYtGlbZJVcXeRUYvbVJCd5dTomRHTsXNtVEDqGmLXy9UYqNpH9aGu1MjZ7hygr2JPQ/Vgka2k+438Vn88Yh81YSwxKeoGIyZryzlmig77tmH3AmQWSMgi7Tcem7egap8z3eWSeDtxkRnOdP2RWew5K9XGUxHfM9kLZsJWdLELTWkxuKGWznEzKfRtIC0fNWFOB39qwOqXcP0KQ7LcsWI/g8jNPCU3ch1nZrmL44D/4j1UaMft7icS9n/tn2MePVf87pqwprOS2plUfq+I7VlnRa/ZwnY75may1VEFtWJubc6Wk9vK474Q+29LkTcFEt7JdUckxRTc3l/tbuzTdKnJtbdNWvX1hxTitci+SNWAtMXrm0de5N8++Vt0WlvO64ZdKfjV5LArr12rzQ7TS3biOzaancU29t65vaUozQ1O0Y5Xl7ZPXhKCfayJF7YCe25gsMZaTZsua0wRfGXclT7QrmESvz3tNOKxZxc8e3xZgbIqRcRyYkzCLMDvLbC2TKLFxyhJaZQEUcWPI5qGAjZnCLGRRa8kGwVqk72GzJbUtsSz4XDpSSmRDCULzImuN5bTbME0T18OAjx6THWxEsJIXAyWYLAL9SzCcSNps6ghr0hIGSQkMNJuecBhI+z3mF36W+LnvYnYWHzM/MUHweTNCuLyInG9abbKCaqfo+8rnW8ToFuBTzLoz6jrOfsbPMzvZMQza+bdrW4xV9qDPWZamcTiTqtTDJraQ5qqvUrJ8tutpXaNPwqisgeqVFjCWfxtU/Bs8xFjOXn+b0R/AtqTdGXHWEhv74UPM48c5o5jfj6ExppYmlcNonXXdtnWzyhtSdlIWrc3CvlZjVjK9CcnaSPmzyunzWi1gTLkSBDVe2bHyKXGYZq5vD+zHkRnPsLskmsweEbhtS5lAOXni4uIJstVrMMaoJmyIhO0Gf3KC++Ah6ekNMgbS1BLMjtHcYWaHlw3B9EQ6jHM4Z9i0pgif4hqhc477d3cM04HRs3RFzRu7D4nbg4KmvUlYJ/Su4eml42rWUsNhTmwRNr3DzLnbsLFc+kR7EIJEWhcy2lhcIzjtVBICEa2QLLtIeUiimn+lVJdwAL8nxQL+aMY4ZSDUCvTOqBxBiPiQwNgl/gAwGRxFwDaIOC6vbulbB6dbIvD0as9209E4w92zDfvH+6zPXRyHWPWZ9KSL7EWdFoncSKo0wzJYV7K5lmTXpZ9aklYCBCMRH1MOcCxiHcZ1hMnj7BZx2sAsnKku9Rp6tNbW51uupsKo1edJqqMdA2masqOtY78iiuu+JVSGMpBLvw37OUslGFPPzer+X3TUfWadlX8BGPqiv6nv/yavH533aFSef+3oXLJizKzm4DGbU9+hlYPl9fL5LJ9WAMW0ZM+ttYse2bMIyOoqy8pYYcWrzzkGnUvppbOWO7szPvfWJ/nEy2/Q0hLmAGnCuobxcMPhcMM4HTTAjaFGW+U8zlma3D3VyCpGrJ+/lIutBk3HI8QK5CdiTfqW9VEC4PVzKGPxLHBdWJqIBhDknyUHyceBaahMrGoyKhKoo6mM8CIZkuo8NRncddYgomzehNA41Vy1pQt9DEx+wDYbxLYYu1ENSBmJzNlfi+qjZZKFNXaxNSSisUTriMEz+5lHjz9knoccXEYET4PHiLJo9mOEiz3tSUff72idg9YxTSMpgQsJ5xpub28zCK5JdazFh0BjEyYzZXS+auDnctCZ8hqXOr8WRqxzbtURel2avJ6xmT0kKcv9GJwrye/M2nrBOv63x7+eQ8sxPR988JD7Dx5wcnpKMtrQ9zhVVoLPrJsYNFD1yWuQJwbXdAz7W2U9n6hNaxpNNMzjAYw2n3HWsNlsiH5inkaur68YDnv6V5SJrQD+AiSUIM+IQjeSk8tqh/W9m80O7iYckdnPtBnM++i9r2GTgXv3EevAeL7ytUfsDwN3znecnWzz9ie53F6+6Z6UR+3op+JriYlED3OMypQNidkLs1dt16Yp60G/WicZnNX4oW20SsMbJeoEbwhB79dmfc0YS2myxi6usZqkTSHHdELb9TkhptrsMQScbvw455jnKSdgJWsKlo7aKp2QjMqrOetoa+UOmQ2YZ0Uh5mQgS+NB/Z+B2sSy7GdFhiJkyYWYVBtYMUYt/Zci15UdA/WDCgikTLkwQyKXFoeA+FkB1jiTSsPbFfkgJTKYqc+2SDnozxExGmMTU64wKlqgGeUircrc1QY6Z2siujTtElmS92VSrNmqyHpPlAqMU3a2tC7zT8/s3bkpaI6x9f/PAx3Fr30umczab5IX/C7VvV1SwQiS6mGnRdpKRzBvoKWhV4zUBsb1/FIZw0mErmkw1lYWeQyL1uqzpdGFQFWArFKBWwCxAsiKCCatYig5XrclQZF8qLajnC9l9LEIsZQ5iVClDuqYhqXiac1hWPs4S8n+Ag6nGCvTNhArw7nEirWZZD6MqJyhswrcqZJH1jWN2nhznIMyUFMVoMjTZ4lF1RapJr0UhnCuiGkas/p9SceUf1YVzgVkNZCS7t21whjJyZ4FGCzjY/IMKc+pNLYL5w0xKrtS7UJi+OSnkQevEsaR01/7NWafwduSMM9PKKakxKhcyl8rcZIBWVjj69fqLMxVl/o9GOxCEkiLX1eevckM/9K8szRkK/PJ+1CrvpY5karMgJQ5HYsl1MNiK4ZgcqPK6r2b1TyKkRBWMKXktZj0+a/7vgy5qX3ZB61QG3SVZ1h8MqsOdrZjpXlbjhOKKZRUk2UhJHzKjPZU7E2idU2WJlBbP2ffb2mil6/XGsza0X7B8W0BxkLCx8CIsmFD45hc1nD0ocY0JZjSJKlUZLwavoQyDtJqGRpBmga73RH7fmniUJyolQi/UugXVNwZw8Y6kJnoPTEFkksgqs9Syi6zjVjdDStEYfV9eV0UfEr5+pttj4mJMI3wSz9P/PQXmENgzhqmBrJzoZP18iIwv2xqOcLR5wKlJDZkIHYKQbMgKeKDgrFubjmMA33qagalZE2CTfR9S4pZfNnopPXzuOj8YJRBax0ml9JY26IdxuMyCMeR87d0vP/++3jvaZqGV1999V/6779dj5QS77//PiEE2rbllVdeqa8dDgcePXpUf97tdty7d6/+fHV1xeXlZf35zp07nJ6eklLivffeO9KO+cQnPrECO4TT3R02ocf3O+bX3sb6mdnPuH/+y7j4K8SrS2Rc1pPNTVWOtvLaGj6Dr6RFvqEG8AWmgrjKECuwW3QP1ZGUDNKmkoU6GqmyJnNZeH41hMjN/sBhGpl9INrA1eYRUXwdXz9PWoZWVkOCJ08e0fiGbrNBug1hP+BDYJIt82bDLoJ5fE2UHZO9i7d32XOHOW2ItCCGtnFsesO2s+y2DV1jtaEMEWcSd882PL2eiYfI5DnSFU0xMU+B4TCzNYmus3Rdw93TluHKcPAwBRinRN85TaRMidk4bhJwiBx8ZNd4HtxpjiQYTnsIQdkMAZV8KRtrflrY5PPGP8N8S/IHiHPexAx936jeZPCQAp0xzEnLreYQFhZ1tsQVYBDVvmv7jsvrGx68fJeTtmcOkY8e33B9e+B013G+63h8uWfMdlUrlJRRWK6ygBIZWaIYTjEZSBUDJrPljAK0IcXMClmy+ZFY7bKQHcdchmNcyywjyfSI2yFpIoaRIy1jyIyOtbO91ksrfl4GDLOml4hU21gcmZKeqF3vi3OcEhhDLMtGAOIKEEMTdWtneuXsPAvEPgek5g3zRQHI8bFysNfvrfvnN7HdxfFeneWbflJa7MEzt3QMBBbUdA0e52Dy2XIh6nN55vmg+6vex4t3yJQSViyBxEm/5bX7r/CFT36e89099ld7/Kx6ZnIQ9rfXjNMB70dNXKWSdtK7t8bQOqfsI2tVuyw7iSYzBkx11I8bLcQYCbPPGfMSbFKbHuh8On4WMRY2BdURLc+vaDOLqFZXGb8CFlLfiwZHqwCosKLLzwrelkA9VuDJZr1t5yzOCJIZvQmzzIm8jlOK+HkEkzvsmhbvE0mmum1oMO9IyQGaALYimd2lDdG0QSYcxoGvfe1rzH6q9sMQaRxMXc8QZtWZvBrYxBt22xO2XQ8p4f3MPEWsjVjruEoXqFxJIpFt3TghtmUjpjJeFSSIFTRYzGuq41qCnqZZytQKEFBsgs5vZTAZEZJokytl0Wrndh/9Srf7N+F48gTee0+//8xnoOuOX3/vPX2PCHz+89QuGiHAL/3S8YIF+PSnoe/513bEqNcRI9y5A2+8sbz26BF88MHy86uvwv37y89f/zpcXCw/v/02nJ5qzfsv//Jyb20Ln/1sfVtKiWGaee8b72mj2ralaXsyg6L2kACpBJGYmdhWVCs7RK00sa5Rnzjrn4tI1jONDIcbTNPiXIc1lqbfME/CYV8aBCqrvu36xc6lGg3VtV+aApaOzprEspye3+HOnTvc7Hre+9qv6Rr2M0+fPKFtnDKFug22OeG9h0+ZppFxnDEIJ7tekzkLlfFbOkTxiry/a0IJr0ndIFlHMySCT1nfXZMviMqumcwun+fiiwptkwE+IDYWvwKiirar2hKViWkaTW7GIJA0OG+75sj++ZzoK2W/tclP1nptmq7uoTEGTFSGmJazNiBFK1rlZko1jMSiQ7rYhAJMhQxGARWkKddTmbc5oa7N6wJBPLMH9ZEC3k9Z9zNqE2hMBUpi8Ij3JD+rf1cSh04lKNQv15hQyD5GTETvEULtubIqmsvzTBOEZR6or7OwC43oMyzM4MUmkpNOC7hSx4SlWqYwCZfGUWVosubuqpK0nofiC8WyaCuUuAZU9aUFPDzWbDz2MaRcPMv+Vf5O6v+ocVKNW4rLovoa+nzrPl9W7pLcFzFI42iSjnFES/2nFbi0boYV08L4VdexlIfLETNWP7ewN9PKdsviK6TInJNGNoNRdbepmAq1GWnIbMqyf1VQslSNvODZ6F4O2otiAWPJQGwEbYhZSSIKIM5xxWyGzIxOeX4BorJiam8tYxo4DIFxnplDIJb5VsYJqWszJYu12g/HWGVzOyvawDAzrY+igPzs0ireQSSXwheGfKrNzSrIKZmUxrqKSRBniNFhTSRaBWC9nzFmhpA1dt98R8doHGluDzBPmOAJwTPNHnt7TQqBlIHsmO19XRMJksRcERArRlbWX6kGLesz5XkpkuOrmJDs1wFHJJKUEtGqyv80TTW+F8kNEGsTaOrcLVNqWStSwdIK2B9dl6l/42wGt/OaU/u8fjyRgMothBhyo1HFq8QW7/xYai0VG5EbSquesc4Fk9m/FdhG6p4e8zqIoUiQxKoXbY3FZkOQMjidUsrNtDPZqJKZvnlS89sCjPUkbhrH7FrGxoHrmcPE7L2yaPKGptkLNEPMsvhLGYCxVruMJi0fjQZSY4mbjub0RDMrokyMKpmJTuKqM1POizD5mcfXV0zzhI8R4yxt02ZkPtOdyRmIBKOf4Yjdly1bgdzrbwuoof9tuhZSJFiYZtVOCSlgg2fwcwaEl1M+udyzHyecM7g124XAmpY1zbN+ZemBrm3Z9hvs7oQQlR2idG3dlBvjsJ3LjDTN8mlpDurUYDVba5bFXcTnUzIY2zPNF+poUXbU53UCX8jCWo3Pn/pTf4qHDx/yzjvv8CM/8iP/KlPr2+JY3+eXvvQlnj59ymc/+1m+/OUv19d/7ud+jj/7Z/9sfd/3fu/38of/8B+uRuunfuqn+Ot//a/X17/4xS/yfd/3fcQY+eN//I+zzw3C2rblJ37iJ45KJ1vb0dgW6QERgp/x80T491+m+dx38+o//r+x/8wqmlf28OdAnLS8mOdL2WRNEWFfOVoipXutHqJWGj97MGiXbLcwvxOog0lxthKRoHM6ZyG9j9zcXEPSDTqk8rHLfJrmCR88PpddJWA/XDNMM9y/j3nzDbYffogg2IsrTm4n2pP7HMKOMZ0xcMbEOV46Isr07lrhlQcbzrYNGweNRNrWcHF1w+1tom1busbyyddPePh04IPHB8ZYxt9jRJ3dr3z9I/yDE+6cb2iSbkibRstghzlxeQjcO29pO4g2MQVLMpY92kHYNgFjBZFi/+DuJuGM6rONAa4P2jxMHYUyAjMmHnDTHhmfQhxJSTuON87yXZ9+g8Phmuvrax4/ueb65pbZjxroGaeNsGxbH7Hoboly0gw4y2EfuRlmuqaldy0IPHz0mHnacf/uKecnDU9vIWZH3maUsmp3iTBNE23bZhak0HYWkxt0IZZSQKmOIQoYkAMhWYKN2WvDIGksNqbcbTVA8hjnmFPCmVNsYwjTgZTsEfgxDSN29uogWAEiJqmNJyRcqyD0MiBlnKkgXUqJMPt6XaqzRAV0BGUKFWejsOWKcyq5jq46g2UdrYGdlW1ZJ1/U6eX492XCcGyP1u9ZIKb1j8+/dwFtU3ZQZSlxz6/FGI8Cn+UzV39fL6n8TajB87P3WpzLJcBZ7aeruKMEc+V9IS4NQ9JqDABiTqh+6o1P8vm3P8WbL7/JNKpUUZLEHCeuLm4Y5wNTGLUxogQtWctjIwLbzQZQYP4wDvX+l+7dq2ezGlIftOmE957GaTOV6j/X+1+Pvf7XGGUFPRuoWuvqfRfMZuF6yPNzZTWKa0ZsioXlDdMwYNCS1jDPBB8WuYMEKSib3rkGY1u6riGFyDyrDpoYwTWdglmuJ+LUbw9aamysgFgSC/umaTSYmaaR2Y+EMLPZdphG/QwR4fT8Jfw4EueBFA44PNvdOU2zYeoHrm+ecHH5FDGGYRiypYoMt7ekGGmYcbJV0Dx6tQ0ChQUWYkRCqCCpQj36cIq/RO4UvGbC6HNQ8C2lgJ9n2qZRDWDvaZq2NgBLVmWcSlAQokoBxaON+AXHc3vzNzn+2l+DH/gB/f4XfgG+8IXj17/8ZfgLf0EBm8eP4exMf7/fw2//7TBNx+//2Z+F7/qub/3zf6NHuffDQa9jHOGLX4S//JeX1//iX4Qf+qHlb/7Mn4E/8kcyqJD0tb/6V5fX/87fgd//++HyEr7neypwwttvw6/9Wn3bMIz8wi/8CnG4xc8Hrq4e8+nPfB6wWGmWYDK/388z8zQwTQMxRk5OTjk/O+Vwe0uKcH5Pgb2AYbPpScEzDAM3Vxe4rqPrdxjTIFlSZ7vZsOleJQnYpkXyuk4pN+mLfrX+E8k6/DToXuZHbQ/QdvT9hqZpCH5msznBOmV0np2dcvH0IQ/f+xqHw8irbzowHY+eHri6HPjw/Sf81u/5FNuTDdbKqpmbHiuTXb9Z9owcE4n6fClXQRgx3B7Ub2vtjDOJk13DducIURPRVzeR6xthfxDmAFEi06SJmMZmYMZAQtmxZc8xRrUu+15zCc6Bn5XRZIxblfPqXt11tjK+ii0sgFZKiXEY2Z5usx8SmOYRMnhls17iOI/qYyYFY0WAkHIp+eL31nL0MKP7kT630oEdyMnkkH0CKU6Ogq9hJswjPkyqi0jCMGlFgukI88w8HjSpnGYQj+qRLlWi1SdC2WSgkhASA4SJ5GcsmvQyItmvQpmxFYhVH20p517t6XnPaau8WT4Pi+SUtW41SwQjdjFjujGzMDQp6YZ6vjL/rbWZYak67OaFe9kxELTef8WY1fs4PlZgSfXhctJzfdT21IUEJqK+acjszLQwfMunaxVrZuBZjQ0OWTJtDoFxnJUtmmOqJrOvY96Hiy/lc/PPFGOVKSryBUfxVr6RmJn0RRu0glUroDhGn7WwbQXuumcSbiVZUUbI5uq00qh1aSZVmlIudqEyZDNwaC1aCek1ORNSYBxH5qA+RjkaZ3BRWYwKoywgvMSE2AyCikUZobGCuYIS5EwCMmu1DEzpr+FskQ8pCe/lCS/fZkcqA7JaMWBqzLHurSIiSvwAqkRjBbBzLGEskJsLtgq0zlkWoDTsSv2WD/+j36VyIxnU9cFz/3//+9jDXp9zSGsXGGstzrYYq+MTsj75PGcWdJ4/IXii10Zb8zxX8BwUVC0x1DpG6Pu+rvn8jkwuUJyNtl017FqkyRYfWIexsLu99wTvKWQGQTVcyzxunOPs5ESJiHktlCS2spOV+NK7zHDOfaV0uJcGb6Rc8ZSPWJrZ5rU9TmN9biZXYxVZgrXucTQGGyPRgpgGsavKrXSMP7TWMk0T4zwRhpCbhOfPjwtz9kXHtwcYK4bHfS4fSZ4wHRSIrRFlXh6GGqi59QaL4JOvi1X/RDDOQedIfUuUoAZ2pYlCRvWXALnYqEQyytb1MZAk4TrNkEMuTy0bJhEJ+e8N2DUlLneLU5bXGpha9AcVNAmYxtEIJCuM0UMQRi/czp7e5tL/pGe5GSaurw70jQr6L+j/wjQTtEGYMw0nW0NMKuytnEdDENj02wrMpaBAT0oZ7LEdUEpEFp1EWYFuS/C+OBZt2+HjTPRlXBtEDL/4i7/Ij/3Yj/GjP/qjmYEL+/2eP/pH/yg/9EM/xNtvv13H58tf/jKlC+P/H46f/Mmf5G/9rb8FcMRuLceP//iP89M//dO0bcuP/uiP8uf//J/nH/7Df8i7777Ln/7Tf5ovf/nLvPvuuzx48IAvfelL/PAP/zB/42/8DX7mZ36GH/zBHwTgD/2hP0TXdfz4j/84AH/uz/057t27x3/7xS8SYhayDpoFOz29R/D6Ozm9x/jKW6RfbOEA0zzx6NE1m87h/Rmgm7IVycauACWmblkmoWDVMv3KNk+Z9wbBlY0tJSTksr9c0qQ5flQjCS2DH2MgzKWzLcxzYBhmpikHIyZweX1TSxGGO+f87P/w3yDAb/kX78PPX4A13P7gDzNus7SAs9z+p7+XI4BEslJnyskFljmegAH4mimZfvLfQYybeo6yGmI8zU5ScUY0E+zzmnzXLOy1IiRfzIlHeFg7iy7OYhBhAm7E8p6AX1nt853gh8BhToRJ8LO2ZFDHKY9/EfcVgKANvKKvGdYnH73PNI/c3B64ujkAls12x+m242TbM86Bq/1ESLLooqHAqo9wsx/o+xMub0a6xnPn7ITX75/z5OKShMG4jrdeO6F5dMPVwXOYAz6ptSrAzlyCGCE7NILYprJcVVspVqCtsILCXJiKslQDTDPGaOmLGIMJYET19LBJO4gjCrbbjvH7/kvCpz5T72uec4DiHMbJqlu8QNLu8rZMctG9Rsc2Yl3DvbO7HA4HDuOAj1quo6VoJXAzYGUB9Go5j46HiVLn9LOwyxp0/VhQde1LwlKcIMv7jhNhz3zIc+HH8jsNFtYg6woQzl/G2tq8ANRRXIDVyBIgLYFSTAn1rp8HW5+95vKqa6w2xFlpsdWmH0fnkPpz+a3ugjOffPUNfss7b/P2K69gw8y8PyBGCMmzH/bcDnvm3FlakgICXWNyKX0pA8udbbMzXTBoI1pd45yWwWmTpsIE0cGzzmngtQIGiiP7rN6X3rtaFBFojCGaYoeX8VkzY6Lo34TgSVEd3TqWZR2tImCjkV8er0S36QjzRJi1ed9wc8Vmu8GaDSItlcFOBsHjxLDfg+sR1yNmQ9tsSaZRY09CrKWxHWLVFvoIkoTGGdpG6HqQcMhafYHbg3DnzhneW6YpcNgPhOC1KddG6G+5IMwAACAASURBVKxD2HJzyB2V55GmjTRNj3G5AU40uLbn7BziNBLGS6abPeJaxFpsY+nbDY3rVVcyJuKoXeetcQoe5BI9iQEJkvXSXAZxVGoCoN/2xOCZDnuePnqf+/cf0DiHcx0+RHwYaUxb11FlkZDZLVkbjp/4CfgTf+J4GX7uc/AP/sHzy/M3+9jt4Ctf0QX+V/4K/LE/9v/9Z66PH/gB+Jt/Uz8/N6I7On7f74Of/ml46y34R/8IfsfvgC99CX7qpxR0/e7vVoD1d/9u+Et/SUHo7/9++AN/AP7kn9Rz/N2/q+coAO/v/J3w/d/Pyf/4P/N7vvd7+cZXv8LD97/Ow2+8T5pGPvO570SarMOX8QxrHW5r6TY9tzc3xOCxTYfYBnGtltVm2ZHONTx+9IjGKRC42+0Yb29JxuLNpB20vWfbd7i2xThHCh5Tmhpl+zlPB/ysILl1lmB13VmbcKb5f9l782DdsrK+/7OGPbzve4Z77tDDbeiZBhtsaQYHxIEKEIMEg1CllgqRCEikQKhKIhKDptSypJDwRxoQ7Z8YA5ZJS9RYYgkFWCpNN8igWNAMjQ1Nd9P33nPP8L7vHtbw++NZa+997m0BE4384YLb55x32MPaa3ie7/N9vg8+OMqyoigku+3BB3epZnNsVROUFLyS8bnP2W7FubP3cc0jbmLr2ElAs7ts+cBffJrTl+9w6uQWO8c2pPgdcPGOdLTl8FNAsXaBpve4INIJ4KhnmhgEXNZGs2qg66VW7eEKzu63RAQcCERaF1AuB/0layuqSCE1clg2gd7JWmWBsjCs247eQVQGYwNFmYodx5jU81W28gbQUyuFd8muDI6+7/BegqNt0u/OQJX4iYn9nMGJEMSm9skXUkLOadouFXsJGKNSQR9htlZlQSCO67UK2YhMgGpP362IrksV4bNMVSbAeLHjfCtyBGkZN0bjoxQxTZKZw44u+5gwTpXvwXco36OUB+9FvsxqYmKBCaM779RKAFoc2khRyRx/1cqORYHSvmWsHYyL4EMC1EZtUya2A0xZq3Hww4fMjfTPB4d3Y9HEQEw6rXEA3EawVaXCmBOjndwX+ojdM87pOPgvI1w5gZGV2IAx9ccA8sVIVH4EqJIOfjbig/diV3jpZ+8dTd/jQhhsPWMyEDQGDggC8LtUpC7GDPBGkbeKo301AhijXTaVdAyp2GYxuNViZ1g1UgIyjSqk4oWD1u9gc6f7iQEdhaQQYiSoQCKLSsaskteFmKOJfgRJ8/zJc1AhBYFV7xLOkDtbALzO9USgqmWvNWiU0bi+F9kR7UUCOUp2QHbUBAMyQ0CGBJ6rNEZ10o8N4cIcsAvt36P2qFaZyakmr08IEsOrE4cx+Q7pk6k/NUoVFNZCFMZs7uMYA87YFLyRAPjek5+Cdz36/DmOvf/PhBCV/MuowKgmSVsJQKkVQ1Gq3PemsKiyTOMzpMytBOAm0l4u3tulda/v+wFEdE7Y9tliMcocBSfT5CnLSvwnk1mwUtjMFqLLPPZQTFq8fpAdUCScL+FdzgXW7WqQOlBKUViR1AQBhYkc0ZQFKG1x5EkWRUlB1jLW1HU9sFxjjLhOirU710t2UhC/NGvi5syz0OeivSJTkPvcJK3vuqyOECWG8RXjwDp+qPY1AcYCKdZEWgElShBh1H+wdpjJU2bNsOClTSpvmBHQswpqS6xSVG5Iqx6+PEwWRfYDU8clB2HQ31BainxNvj/6vuNEzJo/MkgE/L3Q2c2Oy/CZJEYtOkUa//GP4q65jnD8pAw4lUTVlWwwLgTOHyzZWFQs5jU5/S07V9nBzyIG4izoYYB7H2j6lqIsJHWv7zDKUJayKAC4KJFc6W+bokujNm1Ck4f7yc+iqmu6XpxT1Fi1ue97zp49y6233sp3f/d30zQNf/zHf8y5c+dwzvGXf/mX3H777Uf66cSJE3zv934vAO973/u466670FrzvOc9j3e/+918/vMX1+9dLBb8wA/8AL/92789VFAF+MEf/EE++MEP8slPfnJ47elPfzpXXXUVXdfxG7/xG8QYufHGG3nsYx/L2972tuFzOzs7PPe5z73oXF9tu/HGG6lSeuDb3va2gcWa23K5ZLlcUlUVOzs7WGvpum4Abg8ODmiahmPHJO1Ma816vebg4GA4xu233z7o1d16661cf/31XHvttQDUxtF72SQVSqp968yiUkSb09Dz2LRMskUgQt/1FKqkwGKiwYRCyEEodAQbInpiKKACKgaUDggbPYJ3qJDnayAaiBYBpoxCWaHzew29Ssaz98SocR7WbS+Mq+DZj+c5r86IjEk26LTGzecABJuXNkXc3CQuxkUw/h9kWfqv/JGv2GI6zpc71sWqV1/+u22LsKmCSvqvAeOd9HWWJ3EdsVsRun1Ut4TQJxaip4+RM+d6qlI0L7c3ag6XLXVZMp8VbC5KNlF0vWPthG0rEVA1APK9j0m2IeCjFGQ8tr2g7Xt8gHP7K+bzHTYXM3xs8L6l9VncPuuPaaqqTsL+k1QWxHALwdOs1mNKi9bEZEhJ9DmFonL0PpKUaATYzNWOtZK9JkQFUaPNgjBbEM3I6sh7zGjDK0mB0gptxcgcpHKS0ReTAxZ9ZLVaDdHujKpr1FEpG58MW0H1h30rnZDM/jVaQRbTZLyeKZh65PfBycz7ZN7jLgY383cvBHWP9MPkjxHsC0c/NLkGpRRRqaQhmvou65tOpFQGcHRy7jDRX2QAbS883+SaJ4AiyehXqCPbe96dsqM6XKeGjbLkhodfxcmtYxRK07VrtIama1g3Dav1EheEqWGUaBRGbSjtyIbMVVlJjGZSwYYhhdOooQiEyY5qZinEMGTXXNT16mi/TgHTbBQCQyGSmD8Tk2M1gDcMOm3i3I5pnSSjnwR0qDRwMrdDJUdWovuy5i+2tiXIYXR6xpGyKESuSGtWq4b77v0iZb3BfOM4860FuqrJgecYGeY7SrRXbVGgoqIsNLNaURYdoWuJqqHQDmtK6hJ8UaC0oVk3nLnnU+jQUxSRurYcP3kc33c0qyXNaoWKgfl8DkpLdd0+EoJGm4guIzqapJ/XYxOYkFyDQc9f66GbxnGmEBkFa8URHJ61Qfi8AtC4vqdtG+qySsUnLD5Euq4Rp8jYxPIT4GU6v30q2sFqBffdJy/+7M8KcHj77fBjPwa/9EvCYr3rLnjd68aB8/jHw4teJL+/9rXwe783vvczPyOp/pdfDq95jTBH3/e+dFIPP/ETUBTw2MfCS14inwPY3n6IEZrG0KteBbu78rfW8Mu/DLPZQ3/+79Ke8xz4hm8QZu4rXynSAtN25gwcHMCpU3KdxsjfZ87Idd1/v7Bqq0rkC5QSOYZ8rQC/8ivSv2fPSp/+wA/At34rRis2FjMeftWVbG9vcrh/ntXBLl+6716OXxKp5psoU+KyLl7yUWaLBYSQUh7llM5PiuTmRzxJj987ew5TVRRFQVFoDts1vo1416FMQVktiF2DMtkZlGJyMumDFDUlsH94DhU8dV0TiQImBmHOlrOaebWgKCsx712gXe7hnQSQCIH7770brRT1YgtlSnosD+71rLs99vYbHnb5Maq6HCSGLlqz1DBNRL8xpv3SCP3DAFWBAEFG40Ok6SVzoffQOui9rA3GSlDc+cisMsTgsYWisIq2YShq5HxM2frSL1oJWNC3ITn/Cq2khkDXd/JMTAIX2jaxPCeyEnnfN5JVqNI9oVKgNzPXsiboZF/unCN0vRhjyYfsuhbfj8VwFDoxWi1Ej1KB4PojQJdKsi8ER3QNoVsmtt9YoNpnBlhwAlkPmqqyT5GlnExEYTCDZA8oW0gmgE+B7+RvxxQEVcRUVFDOMezHA8yefUo1uM8q9f8IIqbMycSGlWtLzNeQmdMXsK0nwVpIQOIFjvORv9PJsxs6sOaGSZb3fT0+puSvxIQX5MKa02yfkPfEbEkMgyCdTyWwOwPj+bqUAFNGC4Dvo0rZtsk+5Oj9GGsoAZWCe0E2xtGXDpEYU3r0kMqvRns59zfj9Q9aoAkInqZ2R0DFILrKwyuTvlJxsBuUiIkKZJI1OSf23fAIkASRqeZxLmAW1MiIjNELGJ330TSHgnOyBjkh0uWgxXiCPGaC6MO2rUhpRJFX6vpe0tORALhLNRhUWnxVYk5aa7C2EDCuKLDaYAdNeI3CD5lkuT/yf1XujxHsGZKPFZlxmjO3x7GZbd+xf5l+UbCkIL5sHJ6TRqnsHyeQXStCFIkuv9iQfdoWNI//RpzzVPd8DnPurJBQYiY7RLSWtT84NwQOdArcZ3sxM92n6fORMUtA5Camz12JJBsMoK1WGmNFFlAkqSQbO3Yt2jnJrJgC3gmqUglEFbmrFKRXWUs7/xRfUEeoVI0iEQ0SwQUltlpMGZZ96BNjWwItPvVxbm0nuuBZSzeP6zx/ilQsWi4zEl1AJ/JCZgJDHGx+HzxN16f9J8m1GJvuVeaTSbZAnE7Ev6V97YCx6Unp6bAYjPakvZbe0kMKZ/4ypFUkCY0oMQxnJZQWrBqXnjhZrxl8hElLS+ewcOdJqYaFhqMfH46bvVeVDjxNZZqaL9k3VumBxagGB0UXGnff5wmXX44wWgJjlensoCFFjJpuSAEYb2O6AMiAc17SDPN9Oe9YrVcU3ko1Re9AWzEycIAn+rSAJK1GHySKE4f9WB25J7muIFWUtSHSoxL/KH8uhMB73vMevvmbv5mDgwPelx0BBHD8whe+AMBnPvMZ+r7n6quvHsDYc+fO8clPfpIvfvGLPPGJT+RP//RPeeCBB7j00kv51Kc+xVVXXcV6vaZtW26++Wbe+973YoxhY2ODu+++m5tvvpn3v//9fOITn+DhD384d911F6dOncJay4kTJ7j33nu5++672d/fpygK3vWud3HNNdewv7/PbDbjOc95Dp/+9KdxzjGfz48web9Su/baa7n22muJMXLbbbddBMb+3zSlFDfccANN03D+/HlijNx777089alP5brrrqMBSuPHKp8h4PsmbXoq6VyOQGUoLf0lW5S7DdMk185JWnupDLWqKWIpKcBRFssiBIzP1eADWSJJYiRiyIU+wgSMJZCYWzJ3Y8w6mskQSpt7VJHeBwFjnRgojV5zYHcxFOzcfQ/z5Sr1h6Y/tkXZSLowMVJ+8UHUQlJqjDZEZemciPEHQJtUaTZFuHoXaPu8O4+IlLAzGDZMn9eSbBQRsAYKI8dqO4cLEpFGG+Ik8AMiL1BbJXpIUXRjhUUia8RExWEoCJQlrpWK2Cg4niY5aRp0dBAc+J7oeoKL4FroD1HtAbFfgZdquhFhLx6uIrNyzmxesjGvJE1fJeaqitRVQVVquhCkeIYa03Qi4nz1QXTqApG2c1RVSVVXLFctB6uGzgXmdUXnPG3X0/lR8zIkQ8FMqrJOdXGlDyLe9aBFcH8sdCHPWA0BqcEMF3ZmYiMGL0ZPtkRiFB0pbeagS6byMhmIzccZU9xJ95yMLZ0DXXIh7vKH0526lFbpAWiOw71MgMcElA3rqBr/5fe8lO8mFwYYNqI49kiY7EdxmDVxIJcqrYgT3aWLFw/GPS2Nq4kvc/H6npypC5NWMy98eDVF3fM9ZcZMvgV9JLsi94VKBTkYxhaT+TLdS/O64AubilMKGFp/4q/Ju2TMVme+h8EYkklbaMuJjW0edsnlzMpaimg5B8rQdg3rZkXXJT1hrTFKtGGNsRQJTA0xClspp5xGGWtGqcScTc89rxnpeeskDaSys3OEmRHHxzwBYnPwNvfzoKGbQWmVx2p6JlGkS6KgsQzM1QHAzs41AxCr8jkHnyG9rzUYgyojtipHQzezJIpiyJxp21Y0KasW7w317KTsL0qASlnXGcZlCFAWBSpCUWiKUlMUjt4HYuwhdthCocKKoijxXtbZgwe/gIkOWxq6ec3m1kaqtNzg+oaqrqmS1mafdNdIUghSBAMBznIqITlLYWo0S/aC806etRGDXbSBRWctMx9yKqBC4byAXN55ZrM5xghDX9gWOc3UExj13XJAAbhgfqV2/fXw6U9L9O2v/1rAyU99Cv7oj+Atb4Fv/mbRQb3rLpER+JZvEWZoBnNBvj+fC8gL8tkpOPmJTwioeeLExee/sK1W8KEPCXt3aws2NkTC4FnPgic8QUBS74W1GiNceukRXdav2P7ZP5N/qxX8u393MRj7f9OKAp78ZHjwQXjgAeh76dP/9J/giitg3aGiY2tzk8V8znJriwe+GNnfO4fShsVmy2xjm0iaF1rA9qIsRjAiMeC96wfWnfJSAVsnnUcJwglwlqtWN8tDVCn65rqo0l5nUvadjBCjCzBGJAASsNSuDiB6rIkYWxJCZu9oNraOUVcFRmmCc3SzObPFFu16iXMdIXj2zn6JxcYmaMVs4zjKFqy6wGp9yPm9PQobOXHiGFVVYK2Rgq7AGOWScRsY7YGYwGMdxZaoq1GGRcBWKbLZezXYYmVhsEX2iSJYqXpdlPLYlA8oa6QAWGKQm5RdRRQpKxFpD4gelk7MQgmqaQx92yZmsRQfzWCXLIJyP0NathYikDEa7wQ89d5hrMEYyZQUBr/YW6R1NSCAesjFHtN+qk0GDfVQYT3m9UdBiAodPHhHdC3BdeRMCPmeGgC6oMdAX/aTUUZ8PZOKaRGxamSPag3BCVg9BIQHpzgCWX83rf8q7b2DXQV5H8oyezkweCG4OQAe6TsZ3M3PPwMwXy4w/JAg4HQvZ7QPRjskX+lgwQ3fHTKLMntQ68HWzKzh6T57FB7I+6Ga1GONw7mmOrHBj/bYcF6VwVIZicEK+Cs+vPhjA+iX9klFYmIaySQMKWgw+vlxmHsxSB9oHY/2URo7KtmuGWsY2MXZuUh/D4WsEsCa5QUyrjH05WC/pa656Pll3CUONnIMHu8km833vQQrnAQ+BOQawbOQi10hwYkQIXph9fcJiO2jBLV9Bqzz+RMwPdhsqVB5UZaYtFcbbaXXo4zlaQBgGOmKyVjOnhtJnzX3x4RIQbZzpt0wguYk3CcoBX4cEy7bccPnBZg1SklAgUAGVIMx9Nc/Eud6rPdoWyQbwmMOl+jEJA7BJdM0z1W5dslaC0fATymIKGstOgf+9JChpRL+prRgVQ8JxqZCZJlgkG0qBpZoGibOQ5LsMEEj6bFpfVSKqKUeUVQZB1BJEkNhQgqqa4UKcYATHD4lgOYMuZHsk+dJxsGytEker/lerS0S2SfhVXgpEpnWuIG5n/pFeY3rk20YYhoPnq5zg/8jEgv5mrhofZu2rwkwNipFnxZmo9NGnHQsdKJAk7WHtFTWa5smLQ6CkIu/q5MgtsLMa6jLpPwcxo64oC/GCTbdGMaoWE4pnE6uzD4Shym/qpIzFodosEJYQlN6f/7sQORFIio6Jha9MdTzGa4oCAq8cwmglu8kVRYOVg3LRgoZFbmyp56kEqX77V3PqlnhQy8asWkiHSwP4FD0lgqrmS1KDA6tOrTqRXxfG3xQ+FjQtQ5bbCHRG6lIeOHm4UOfzhuSH6wZXb6xZeHpaXvSk57Ek570JABe9rKX8cADDxx5/9nPfjbXX389P/dzP8fP//zPo7XmW7/1W/mRH/kRXvziF/OiF72Iu+66i7e+9a38zM/8DFprvv/7v5+bb76Zn/zJn+S1r30tICzVV7/61bzgBS/g7W9/O3fffTeveMUreM1rXsNP//RPc8cdd3DHHXdgjOFlL3sZf/7nf84dd9wBwOtf/3rOnz/PIx/5SF7zmtfwtdC01rzqVa/Ce8+HP/xh3vCGN/BTP/VTWGulj43G0GOSqex9ZP/cEpTFFjVFMcPUW8Pxlidm3POUy/imd96bnrG0LkZi4ygLqMqKudKjxlGI6CBjOBJAeRQOVJYpCKACsYhpSwGlDNGAKyEYhdcaZ2TuuhjpY6DJ2pkJqFmtVrR9LxWvq4LNjU2iizzxV/6/gZ1SFAVf+s4nc/y+S4ENVIic/J13YRYVs2rGbDbD2xPcv9dz0EZab6g3dtiel2xtzanqkjO7LfeeWeODBBOSejxlJbGdQosDvWojLijQBmsshhU7C8PJLSla9Tf37bHfKZpY4soNYir8oBFmwE7puOokbJUKFRT37kV2O0tQCmsV2zOJKXVBgNoYoNJgdcTqQK0DG5saPBQeDJ7VYUNwITFjJWVX9Stsf0hwhzjfDOwEWX8MWkW2thYc355RWc3583u0fc9ymRSfFVSlpfVOjAY4CpShadueWSkbT9c71n1IxrkmBs9q3XNip2IxE0B27ToietigJxEqINslAoCJkWipZ7PkVIhTkjWFQsj6cX4AlWKMUpW5F1Akegd5fULSJoOyRL3A1Jt4O0ZFFXpYP7OBpLMnHCLoSFApwppT+kJk7199HwfP/aG/1/n9T+2ra2q94tJ/9RRMGBm10mT/HjlMERMjG0XF9Q+/hp2N47je03mHNhrnPatmTdM1QEiZbWEwUmf1DBWlEnj0LslVJAcseFy7xqqSoiwGaYK8/2X7whhDH/pBNzA72mOaW0xOdrIz1IRdkOZFnJxTwG4l+3s6jncMga9kTpI1zEICBEGqYKuEXsc0M8QJTCl/UdZqazXaZt0xiNERFLR9R1GV6CiOT59Sd1cHexAUx09eIfNXG1QCQ30Q6RmVFBDBgpJKvcYabFkSXEHXeXx7iNUHdP0es22Npcb4NdqtqWaVpN1pk+yJwGxWsZhXlLMNytkGvetxrTikZVVx2CpWy471qmFWGXa266Tx6lNa5cRxQtJK27bFe48tLCdPXoo1hRQdQmydts2yKFJpXdJ4NaawVPUMkwqaaC3pmBBxrkt96UeHNTkypiiPOL2A6KWGIOn273qXIFM/+ZMCxBaFgLI/9EPChP0X/0IYorfcIv+yZuxv/uZRzdh3vEMYsG96k4Cw73znqBn7ldo998C3f7v8/upXi67rt387POMZolP7fd8nzNTv+i5ht/7rfy1M1K+FtrUljOC+h//yX+C//ld497vlPe+JwdOtzoO2FOWMza0NNja/jr/+0O187q6/Yjafc/V1j2Lz+KU45wSUM4a+Fz0+KRjj6doVwTWgNTFIELgqq5TEJkSLY8dPUc1rjNH0bcMX7v4MJ04u2Dl5CfViRrvcY7bYpFmu6PsWlGJz67g4uN7RNR1VbSF0+L6lXXo2to+h9QxbVNhyznY5p+sbmuUBXdehy4KdS6/gcG+X9eF5VofniX3LuS/dTwhQFDVlVaN1wf7BIQf7u5w7e5ZHPupaLrvsOMe2FpTZgJgY9zEiTNcQaX2gVwxzSmtFaURCoPOKzqdU+vS9iOjz2UINKimlzQxjO+it6zlEHQnrOGSeKCXxZyl6Fahry/5+i/cRU1SsV4e5cgXOScBGUnkjWklld0UQ4CcI605rk2RpNIWxGJ0yk2IgeodHam4E7/F9i2/XqIEVG/BRMo8U4piH4AmmYmDHBdEs7F2XQKP0sofoHdF3+L5BDQnBihxEE9kLBUiaevaRJfDpAYdKsipagVU5uySJcEUva3gCUHRKds6yVhl0GzU6lQQNBgBPZG/EDxz95wzcToGcUerAyJ4RosQgMmY2AX6mLWfUXAjWyrkyVDqMPCQjJIOe4zsh7W1TTUspSD3eT95PIyN4E0Nm9GaG56hFqVWGfcmo9VF8IDIEZY4EtIegaQKLnICNmWWntKawKaU+9Y1P1xZCoPch1dHxQ7E+HQXkHnRZJ9lHUmDTJLKGyOoURUFd19SzGXVV4Zxjf3+fPskYTft/ClIfKYSU7Y4B9MpjxAwSTTnAHpUSX9MGYu8JDsmOHMA8CXh0XZckPCZMxnWDdT2xCBTGohG5g75zNE1H48UX9EGKk4sMozxjjZJ5a+ygc1yWBWVZDBJTMWEqcXiQGcAe8e4R3ciOBaOtFJM9dgQcl7mSfx9ju6NtRUzyXdZgMYRggWZg3hMzwiTra74npUAFRSY3GW1wj7mJ7jE3QRSsaPPDH6I8cyal/acCfkdASQFjXZIhiFFkN3UUS8x7L1r8kyBIZsoeIUQoxgBQSAF9raiqio3FBoOchlIDc1qIN+C6jt7ldS2Kf5bnYDj6WQUYNKa0w7VYI4EwYxQmAf6FLfGKITuNFEibYmLKaELnhuPGGOnadpAJqcqKuq6FxJLnZ8YljUFhMdZQJV9RoeSZpXpTg/wgjfR9jLjg5LUo+1OI03XraPuaAGMBdAClIioGfOeTXqgSHMeI3oPSSUeoa4dqZlpFtLYiC6aCREQKi1nM8NMcPoZ180iLMaTUBHEmRmFxmXxZgFcWoDAMsCE6MszcyWD3Aa9ksx/OfGTvmDJmJYVHE4YiR3VhaI2hQ+GcVPk1KSUuJJ2MpoXDQ8fBfsfxnTHv+mhEBpSOKBPZPzyHKeV4y1XD7t6ajXnN8a0F25s1O4sDDEtyuoLWRipkIuBt22tWXcCYOVpXHB06iaLuWprW40McNpQLN0cQUPPLRQi+mvbyl7+cxz3ucRRFwVve8haqquKuu+4a3v+FX/gFHvawh2GM4Vd/9Vd5+ctffkS24Mu1Y8eO8frXv566rvme7/kenvnMZwLwute9jhjj16SW7Zvf/Gbe//7303XdUPjryU9+Mj/0b16A2l/Lhpwc8eB7Ygi4FTTKsjJbxPBIhDkELsJfPusKDh4M0ILSmlOnT+N7j28jZ5olpdeIGKcDKeOUgFiAiFIBrTIUL5uXR9GrMejhU/6a0gjAFQGV0je86HfZskJpQ+EkPai0lt4n4W6tKGYzHvimx9PXtURxo2J94Fk3qfoosNeKs121LfPeoOo1FFtYXdI5y35v6ZdQzGBru+Cqyy0HTcthA33IAQdN56DzUS46Jj0sq1HWEG2F9wZvFFhDXWlOHVvgDxxdB8ooylI2D62kcE1QBQdNwCo4NtOc3FL4fU/jFT4qWq9YGFL6K7Qxsu4DVkOlIhbHge+xiYVXECkLTdcHeiebzmx7pAAAIABJREFUrev2UetdcKnIA0zshjHSe+/95zg8KDh1fIOHnT7B/Q8e0veRw8axsQmb81KE+ruePgYMwoLN619htWw8yjCrZ9z7wC6Xndphc3ODrus4u7dPNSsIIRe9EXkDcRjE6MhVjX2KiEegZ7xGBtckR2GF9TbotBGlQnlKgxLjrhWx/3TL2ZwfDXfNfOMKYrk5SkBEP4AjMYqTNuiRK4kxKCdBB5Qi9H7C//+n9o/VBkZO+js7C0qphMZGCJGNquby48f5umuuxjUtfe9Aa+pyxt7uOdbNEudcCg4bMfqMprAanRwRpUQD0GiZz1I0tKCwC6qqGJxLYTtBnFT5DSFnqkxBYsT2joqsxTetrKyTjEYkFyeII9ObrKNlkoEYcLjR8ItBGCXBD7Mpm/tWKckoaRo2NzcpKgsq4r1UePZ9h7EFdWnYmhuMVRyuA50r0bbCBQumxgUJ3JpywdXX34Bv1lhTsL1VoUwAJeulyteTQITCSoZFaSXP2HtHszyEvie0DaE9xBYO39eE5VnaRnH4wL0sNuZsnThF23Xs7Z5lo75KCn9Ziy0q+mjoejhzdp/d3XP4rmdRlbhOodWMxUaJij0hQtf1xNZRzjRKF0mXUqG0x/mITY6c1pr9/fMsFhvU9WwoQGlSaoNzPbaw2LJk0xhm8zk+Ox0xYrWCuhaGfxwNczUM1gB4ynrzInCC228XkPOXf1lYpxNb5x+9/Yf/IGDuhW2xgC9+UX4viovf/8duT30qfOADAhafPCmv/ef/TPw3LyJ0Ded2z7K1vUM9m9P3nssuv5SNRUHbtpw79wBt27Nx7AR2Q4rtdJ2kjQ9QTQjsnT3DfFEzWywwVpiYKtlIxhg65bFFhUIkRJb7ZzlYfh5dKjaObXPmwftYtOvktHY0qwNWh+fZ2jqONoauW6OxdOsVh/vnONM3aFNx6RXXsH38Umy9gfORVdPK3lvWzOvjohlqa6rZgvl8gy/c/Sn63QcJoSOGNe4ewyWXnBbWt2/ZX3Z87JP38oUHD7nk5DbXXnGMrc2FMLcYgwlKJUkXiZdSGgk8+wQwBAS0sVaKMbuQpPwTGzYEwchjBG0F3M3+dXJ9WK0Dy3Wgc5GiMigN3mkpcqoUVWmYz+Z0vdiQRmuKVIyrd1m7UjI2ss5zjDJ/fXAI4cRQ1jW2KDDW0jQrYbJHRwiSmhq6Btc1dO0K1ywpykr0FqMn4qBr6FcHdG2Dcz1lVSUAkOS8a5TviTHQBU/vRYbLKCnMbDWonOZKBLkCPAEdFTroEQRQMOqtjy0itX5iYshJRQFFVBZ0gTIlRkc0fQJksqXOsJeG4NHWJgAz7yCpCvoQlJf+DIzB0CGNPgfdgyL4OMUkj1SDH/aH9HthLVVdpWJEfdJNHWWYBENL95uOpyYBApX6OGs+Dgw/SLVTpGVm6FGy1tF+zJiA1noA6wfWLtNrJ7Hs9BEAcwrCHJEeSiBYJpWN9osamKTOO7reTfRlByRbbAhjKbSAYTbJBeVuELB29LlCiDTrhr53NHYtr/kocsUD+KyShn8eWwISS18Jg9wh9zeAsiimLPnJzQpAlmXsEiDuQwK3E0AV4cj4AmjbHrc8GDAcW5YCLidYx3mfGLICyFojRVDruqIqK2a1FOET3fdRTiAHXPOlfjVQxPiZdHKVGKBRQMmsjxySzUmYFrA+GjiIMTPv3eCnSN9OUaGYHOMwnFwrKfyZjiKZOWkchSCas7uPfYIU527WXP6+9ySZvxHgzBkY2hohDDDRIdaKTEkZeSiyn+XzgFx70zZ0fS+yHDFS2GKYG/k+8vwTLVfJCDFGzltWuUoMxOiTDICA1971ZF9PTHdF7x1t29H3PS3Q6BalxF90Sdoi6gnTV8l4mjKtYxDAVfzPdL6NTXLR1mEnyyA7QEhFF50XTd8mDBJ0MUoNhqIsRUYoFZe1ZSnBzDQJlSmQItEaMyH9XNi+ZsBYqfAHLgS5MSMVF7PGmjFZp0ucDtf19F0nD15FMoNNVQVmLkL1mZWilERdo3PkUEifqPImpYHKIi6LX1QZuE0RuzTBMt1eDYtbDmem6ZZ2CYkweUnVVuPEz21IDUl/HVkaotxL+dm7iHvn8VdfhwsxAbvjRuiDp2l7luuW4ztzuQiVjyZNo7CmYDHbINLiVUvTt7igmTXCUtucKzZqh4kNijZtKHqYwKLrEamUVIN1riBGYbKAEaMuLVDDBn6kYowartsYw0tf+lJ+93d/l9lsxlOe8hTe+MY3/h+Nl7Ish0Jgs4fQKKvrWiji6f0L9Ye+XFNKDd/JhYD+tvP8Y7cQArfccgvXXHMNx48f5/d///d58YtfzDve8Q4R4I6wuWxZOUeLpKZbPF6rVLNZE1KFVTCs1+f57N33sNjY4BOPugHfz7nurhU+eIpZQbQBZ1oOD1dpbCfm62R+kBgHuRyWmJHCWmBiOMqGkitzp1h3mkhKW2waz1nXMMsInJ+d4fzpitUjHo9WBf1sg2BEbzliOH9mj7ZLRreCxWxBrA0ow9Ib+rXGGYVTFq8rCJKCf9gpFm3gki3DlZdtct/ZNecOHA4zWo8pSJNEskgkSjGQtaUNcNDCvI0c9hFtLQttaBA5AqPFwBE2vKJ1kdZJSsXMKko6uqBxFPS9omV01n0fJGVXS93dzgszV4T/hbVB9PR9Q9eu6bslsV+ifUcMUhBxymDI/RMD9D6w6jyHq5bj23NmlcGHHucdURlh8xqLtgEVFFoFZlVBVRZSgEhrDperZHRK6uV61VBXlrKQVM4z5w6p6xJrDBu1YW8l8gHOe9bNmu3tHQFjnUsMgMz6kDVExUiYrJvJJpL0mmScZecqOI/vWlRsUZgxYBYE8EojS1KV7VhMB0iMg5zunsCwIGmloiOkkq8dZU9BDQzuf2r/eC07MtmoUgzJf2IUxYhRcGxzg0tOHmdR1fQt1HUFSuG9VL6WY8kxxXEUnW2rpciLSuMugxA6S0EYQ1UUWDuOgwwIuzhJ0wJhjGRdtvS6SkAsUQ3M68wOkjR7uZHMpNXaoBHPVms9MBt8knJJH8/GzETXTw8aV12zJrqO0irKQjQUQ5Je8K6naxuKEPCmwlPRdT2dj3jEwJ5VMwEmYoTgqYqazUWFas8T2xX9mc/CDtjFcZSdAQprNEU1Q5tikIzpvUO1ntB3rPYfwIZ9rDtA+47lsuGwdZRNSbPu2f3SvUSlKeZz9GyOQ+G8wgdL3wT8akkfoJ5tsHN8h+1j20Qf6Ns1zeoQ3zVAR1U6ovP0XUPTrFG6xFqXHGPwTgL9AQNRi260MYTo8dERvbwvoEQCxZHnB2K/YtTAksiayX3fJ2dXjd5gAtiNsWxvn0ypf5O2sQFlKYjU/v5X50E+VPut34Lf/m05dyr2eaT90i8J8DubwVvfKqXpv1L74R8WNm5u3/iN8lOpr55p+/+yHRzAj/yIMImvvRb+4A+EHfxv/y20LVorqrJgY7GgKATcqEqN7wsWG1ssNhXWVuzvrRIAKenfBJ9IUQJgVLM51WyenqVU7TapCHBMDEyb9katoKhqLj19OT4coIHl3h7Hdo6h7IyqEga37xu6psV5IW8UybmcLzbxriEue4qyZj6boYisVwe4cEhZz4iJ8YMupbhJVNiipqo2uFIX3PfFe9g/v8vh3i6z+QauWbO9c4rNYycwVY0uFvRd4P4HzrM8POCqqy7j5PYG86pI2T5qsP+VElZfqcFHSbEWtUGLiwoXFK2oJYlLnjTvhTgq8yQEaBtP0wdCKgIWURyuIr0TmKCwyQdRgFZEDM5lRp6SQCpZSsDTd7041lpIOAaLsRqC2GSSEmySrSkrvHM9fdPgmzW4DutTmnXnce0K366IrsFFYd32zZpuvU9sVvTtSsCR0ONTii/JIh79PeRajaK0FWVRpCrgCp9AnzGwlsxnY1BFCaqQ8ZYCbt7nwLAZbGzZb5AAUMjMWmHmRUoKpdHRCLM3eJzLRXTyfpoIShObUewlNRw3J/WrMLJchakbBhtPMRa1yrUHcoshEJQSiR9jsEVBUVh5Zn2fCgcln3Twg4+mleffp+e3Jvv3CfzJ26Ia05NH8CX7qnE0GiYg3MDey6+o8edYPDyDSskfj2P/j/ODBOSI9rBPjG4R1hizZmMCao3WlIWVInH5+SuIOtWFyYzFKcibALSsWT30c2LS5nsbxlW+X0a28gTXFjZxwmEkSK0T2JbmiPfDOUn2yVijxtF3UiQ8OAHWQ9finTBBg/d0rkMpcwS0VloPpK4YIl3f0edLDdD5xLTOWMVEGir/L+NG1hZYW8jxlHitA7ltCoBHyF5GnqkJqk/vpWB80GS92NJairKSbO58D0kL1iddXJFJCcKmzQBrDqTrcRnIxL+RrJb8zZivSJ6LSdI2WRopIDr1vhS2cz+bc/iN30Lbt8Jibxq2/+pjgnspCEoYqUyA+jSpJr6QQhmZkyrX/0nSbEprysoPfaSTRFwwAsb6DAKrlB0RZA3I/pQAoiYBlmkuJiA1KinonSUCAKySDKgp+QC0BOmiANd9Cg5kdrHHD3IiMUaWyxXeyJowFmQes83UhAGslGTnD7xaJWPfOckwz3igEDM0RJXGU2L6JkIQgC630GaG0jWRv53I9zUDxo4QZUy6SsKY0ipV8FZ5E8gVB51Qt3MkzhhUaVFViSqLUS8NGCcnw/430tMzVDiCHsPEUOk/MSbtyoT75hE4PUcCXacmcmafpD+OvMND/TngrRG7t4u3BUGpYXEdLjI5eF3Xs27a8QbG/ToXDhwq/1VlRRd6jJco9MaipK4UVamoSsD5AYhG5eIVelgLjPaUBXiXdc/ieLdpxcoyEvkeBmr+ZJF/whOewHvf+142Nzd53OMeN3TBfffdxz333ANAk/Q+V6sVH/jAB4bP5PcB7rrrLra2trj++usB+PjHP37k/Y997GPEGDl9+jQAN998Mx//+Mc5ODjgzjvvJITAIx7xCK6//nqcc/zFX/wFh4eHgDhLd9xxBzfddNMAwMYY+chHPkLXdWxubnLjjTfy1bZ777130MPte9GuOjw8HO7t+PHjPOIRj+Bzn/scd955JwcHB5w6dYpHP/rRADzmMY8hhMDh4SF33HEHXddx5ZVXDu8DXHfddQ+pRauADUC5HhMcJjo6PG0yVr1SKNwwdvq+Yff851g1m5zZuo5QVRzb6zn4yDk2t7fEeLGBTnUyD8kGQBhsl/zcc4q7mJ6KqFL1xpzKkha9rKU6XnQytqIiUkkEMUqgIATP/mU1B1fs0F9yGrCpcmEkBCXsW6+lQFNq83pOmFl8NLSdYu1LApagDcGkKtloVl3k/GHPRhnYmhesmp7WBfbWWc+JbHnJPz2ZkwDa0APLHnabiNOGujaUyqB7CGYKiKT+9tC6SOci89JQmkDhxYjyfaQPipwkYJC0fa0hemg7R5v6XymJsHZtS9+ucd2S0C3Rfp36L0yWncFsJOuC5YIZ666XYERd0IfIuvU0raTUOh+wViqhz0pDYXVihZFRK9FYDAFtLE3bY41mVpfUZcHBskUpRTHTzArDYexGTddktHgfEjs2DMG0HDGPGYydGC5p4QFSGkjIBRNDSgMX7SHZHF2qHioaR6IPJkz+KbaRsy4GxyGEVDhATqVNMoCjgLtZE/bvre3ujhXTn/AEqRg+bffcAx/8oPz+lKfAzs743h/9ESyXRz//+MfD30Hj+u+l/fEfC+ixtSUMtNzOnIE/+ZPx79OnRe8yt89+Fj7ykfHvRz0KbrxRHvY73ympzyAP4pnPPMK4G3b5ybNUk/eIkVIbjm1ucmL7OEYZvBbN0hAj7boheEfWcs/ft1onwzASfTYEx0BTtlOyc2d0Hj9y7qgQsGGwcZAMnkjS3E6pfskAiJHh2LllWYIMxGZbiMl1ZgNQUilBG5KtoATMiGNFWJ2KrhyuV0QnDAfftyhdkQOrJjGJlJY1uvPQOdG1hqyzpdCGAXC02mCVY1YKQLC7uwvtHs6U6EphiprSFmLYJ3YWSMVgotzDerkirHex/hAbWrQO9GiUdTjfg47M5gvKuiYoQ+cD+6sWTCXpYBFIBVGreoa1luAdZx+8PzmgSJB6c5O+WRNBtNeMlecTPMFJqnFhK1QsUcaC1lhTpgBWGHS8FdlRlXGR0z3zXhe1ZCSFXJgrPU9J08z2ZUBpQ1lUbGydSMVvLphPn/zkOJ/qGm6+Gb7t20SX9fd/X/Rhr7gCvvM7GfJFr71WpALe+U45xp/+qcgcPO1p8v5jHyvyAn/2Z3KM3/kdWV++7dvgf/0vOc6HPzxex7vfLazc/X149rPhD/+Qv7U5B//7fwuqdtVVsg59te2OO+ALXxCN3BxY+Ju/kesDkUXoOllP3vEO0ZZ9zGNkPcxrw3veI5qwv/u7oq3xpCfBE584nuMpT5E16g/+4IKTy76wmM8EjE5zzRgr4GpRUJVzXDSUs0oKdmUt4InOvilKFpvHEjvICNVzYj9knyTr8RlbcvKSy2nXBcFHlgcHnDr9cHwsKKsaYyw9CoXFpaI/PkaULtC2wBQFZVmxtXMSU5SSYeTWhKiZb2wRtU3kFYMyBaaYo5SFQsDepnPsnfsSy4Nd9s6dIUZFPZuxGY9hjcx15yNd5znXd5SzPWKEnc0ZG1WJNfl+ZNiEKEUrPeCSRrbVEAN4FWVdSvJLGZvwSYI77/29i3SdsDuFjQbOy+or7CYGvyvbnXltzP0bo4BYIfoE3AjxANSQyhp1AnOiOPkAMThc6Ol7R7c+JDZLVPBoFfAu4rqGvlnSNyuCb3DB0a0O6ZYHtIfnoWvwvk/ajQ4X3WBziCyKAJQkwhFGUxQlfdIUdkFkJQXgEmk4k9YhbS2uKDHljKKckXWJmYBLKveJOuqXQmY8GlBFAgAjOoiNq6Me138AwiBHMM6PEaDKbXBDM+ibQJisn5wQxoec7pkdOdj+CECZgdhBV1tEPhP4OYKpo06tyBDkPsjgCnksXHTmC+5FTXGDyafSWj8Ac4PdPe6/g0bu5MP56LmHhh1bqSR1o4CUsp+PA0NNBAm4GkwMKB8wGYxWGZ8Y7dUQwiBTENNFqZxCnvy9cWzHgXCVbmS0LZiCc3H8fCoEl7+TtUajkYycXJV+KEOg00VGQywsHkSWIaYiSCl44Lyj7XqUchfJF2bwUSrv+iTVJHaOc2OBMlRmJIu+8+iu5ewmk4BkM/RPHnNHggL574uGwMTpiAkABsDjnJNiVeKkCXA5KdzkvRvmAkHY7RnYhaPj7SgQyzCpRopdtjMTmJlstCS6kKQoArYo6a+8mtCK/AHrNe78rgCiBGLfYu6/X+wOlf2Z/LzzOEZ08rUAsVI0OckRTsahVuOYyfNxCHKkwFy+z2m2Vwaq8r0F7wesL6BkHUprRohhHFcwzHd0kipQCqsUzinAk7PLpqtWZoGLvKIagkWZER+VH+4hs8tVTH+bPKan2QGR2ENiXUq/hUya0ERlJJBvtlB2C8xMbN6/pX3NgLEhDYKBiZjWDpn/qQpgkKhfXqRRaigYFaoCtaihKHBaIqJ5cVUoYf8lCopC9ERCHIl6ArfkBSh9L6H9R8DS9DMS0+aeNgJyRE4RzbixCF5w4czOS96oPTtQxdM1SFqkJZhswKVvxqT+FqUq6Hq1HjHcySIyHDcEQpRqhJ3r8a5HRc/OzgLXNWgtUaMYFL2Tm9MqoNEElaQTEODJGGEQxVzRLmnjDptPmtTj2jZOOq01dS1yCpnVmhmoWms++tGP8va3v33oobqu2d/f55ZbbjnSc/kYf/iHf8ju7u4Axt5222185jOfGd5/29vexnOf+1xOnz6NUoqXvOQl3Hrrrbzvfe/jTW96E8YYnvOc53DzzTezWq144xvfSAiBuq5xznHLLbfwi7/4i0fYsL/+67/O+fPnueGGG/5OYOydd97JO97xjiP3cO7cueHefvzHf5yv//qv5w1veANvetObAPiO7/gOXvCCFwDw/Oc/n9/7vd/jtttuG77ztKc9jac//ekAvPSlLwXgox/9KNZa3vzmNwPwyEc+EqVgY6PC0DFrHV3nWfcNB17SHHp0WiDyxuDwbo/Vao33HfunCj5Rz7nvVz6Lu+xyZhsbmKIAI0lTCpXEzCcLFBmAJRXjyQBE0iRQww9yhcc8YPN8CTEkSYCaiKePHR5Yx579Rz2S1Yk52peAROvavmXddLgAtpwdcWZnsxluVtJHS6ENYV3jVCWpWlGhbYEPkWXr6fo10WmuvGTOsc2SaDTL+1f4LFeQPI04TStSoIxCKYNXimWAfhU5uV2wXSusBrsMrII4axGIKcTtXKBpA8siMp8ZykJThUgIjnUHTilUIRqy89LgVUAh1Vzb1QrjLCsVidERXM+y6ejWB8RuhXZLTGwIQ7GeDJGPS5LKTk1KUOs6WWvn8xkBTR/WnD2/Dyi0Eadw59gWi1lB0zQsVw37h4f4qIeN1IXI5nxO0/RUIaJNwdaiZv9wLTIHRlMWGqMCKgj4VVWVMMZCSL639HVIGq0KJG2LbEhmR0NY1zHExOiTRV0rhbYG70ROwfue0K2x1oJNEfQoovdN0w6MWgAVDSEoVIiDlpuMWan0bAqdnMNs4DJs6Hg/FsiZto0NJgvjl2+f+YxUEwf4b/9NGFzT9id/Imw0gDvvFMA2t3//7wXQDGG8jltvFSbYP3TrOgFPQHQqP/UpePSj4a/+Sl5rGin685znSH80jTDq/vt/l7/Xa9G8fOUrJcU5F+/56Z+WwkM/+qNS+VxryWV98EGplp6a1Zro/LgfAdl4zQbUrKg4sXWCk8dOEqOitAVWW0lR7Vqi72WWpKir1VBY0VXOhSwyEAtgkn0h/49oJM1UapYlazBFpUIkRfLFGc6OXYwMxTlCCDiFjPU4/ss6ihlMFZCB8TMwXJsw8DWlEbaKD4quhxAzYygDFpFudYjvOkSfzrPY2KYoSow2VLOaqBRFStFf9x4fBeHVqYhfNBKcCEERnez1y/09ZrOeulCUxhG6Q1ZOo2rP5s4l1FXFunVEo9BlgdIGowxFoalURKHZ21viD/fQoWdxbIutnWPosqLQJccvu4zFfJtiVtP6iK4q7j+zx/amoZpVzKqSsp5jy4qyrFBa0y4POdzbY293F+8ci40F9ewUxiyx5ZzZYhOlivQ8HL7vadeHxNkcVS8wej6kQEr6m0gKeOcJxog8gS0GZzWn50UnzGliGIoIFUVBdKI1FmJApYwFYyvmmydZbF8ishRFIfMC4FWvkp833gi33Sa/v+QlAkA+4xnw4hfLa89+NvzGb4xz8ru+C266SYIar361vPaoR43HePGL4eu/Hv75P4cf+zF57V/+S3jzm+Hqq2VOw3gd//E/ys8bbpCA0Nd9nbBtf+u3xnO+9a3wsIfJWvCjPyo/f/iH/25g7JveBP/jf8jvVSX/PvhB0c4FAZUf/WgpupVfe+EL4WUvG6/hhS+U63rhC+X7P/uzY2Dof/5P+VmWsu7kY5QlIQTa1SGb29v0UeGChwC2KFCmQpsCbStOnX6YFBtxga7rgIAUIU2MGG3Y3LlksGecc7gE+gvhxA41KWIEtGXn5GnOP+jYP79L2yyZ1bUwSIOj6zuWhyu2FpssZiVt37O7t0c9K+hcIERFNVtw2ekrOVi3+E72VlvMsLYUZ9aLI+qDIiqDKmqKek6cLbiy3uDw/FnO3HcPn/irO9nY3KZdHbC3+yU2omexpTG2whQlEcO99+2zahynjm9w5SXH2JqVGJMz5KLIfUSxBwA6FXE+0AVFHzS9g7YVnYIABC+MV+dkG/UhEuJoH2ZbqypyMdTEstKaLopuuzWBqlL0vcKjMQOZJaR5qYhaMm6sLShsgTEJQIhWRABCqhbetvRdy2p5iGpXxHZJoSOq0PRdR7s8oF+tBJBtlyz3z9Id7OFWh7j1CqVCKlAbIXq0a5MsgUtyBx6PJmpD1IJSR9clgMrTOoeyBqMttiip6jn1bI4yFmUM2hRUi22qzeOUiwVlPUsA2ejXSmAusbFJBcm0ZKPJFmflvMEkskSuKi7PT/YbN+yfeY+aapNOdWJB1r++HwuTXQiITLXRjzaVTCiPS1roI1iU99msBakHubhcHEiAWDtkMmbASC594hsPZltM4J4fmG65iQkx+rJTgOzCLMuppm2uhzKkag93xmAzZLNgCl4R4qDRmjUqZQ3RQ+BOKTcEKSJRAjLOi3yBF93UAbhOd1Ok4lUZuCusHlit2ZYI4SgAOH2OxJRVnOwMFcV3iSrfn0rnUEkjOAhhK9nnUQnDcF7X9G1H1wohI6YMHpEakBR05xxd1w/XEZIeZwbejTFEJbIlLoP96SqMFgZsVVWYJIEy2Cl6IlERR0jnCOisx0y4GMcsuYhca4byVfL/BHgOON/j156u6wWwNIairLDWpu8khnQIwsgPIp0ywZAnc2vs0yODNVfDnnxeamVkpngKwCh5thiwRYnVFmNKucZ6zupJ3y5El+DR589x7Px7iV0v4GxM2ateiDs+SUBEpSjMCPr6rMearztpEZska5nnnk0ZNbLmjCJuSgnWl/VqFWCN6ME65waZuhjjmBUZI72TcSKZaJqyKJKPr4Zrt2ktl38qHWNkyS8WC+g6RD/ZJHDWD3NWsjHjZM7LvLLWDvIOtrACSssHyCVMTNKgDnTYokaZOegZXtWY2WmUmRN0lcgHD92+RsBYhdGSNiPSBHaojhmCZ71eUxYVne9E6FqBVUYeSELry0VFXwjThXBBga0wKcI1RODAtV0SAxYm7uhUMVZIS5NCcyFXRQ5ik9HNZJPJm8Yw4SZOO8MnhIqtc97EtEUBsazRhEKi5NgEfOLxyPvBBfq2l3Q5Mx4bBVFperemadYcrg44aHYJqkXpgC0Ni82Cz99zFqsMm4st5tUxQrTE0Ih+kI7kfAlZLCzOK2K0RGWJSVdJulQi3CDsOZ/lIRjHf9gtAAAgAElEQVQXmsc85jEDCPqKV7xC+lRr3vKWt2CM4aqrruKpUwbVVzNqJn366le/+qKI5oW6a89//vN53vOed9H7s9mMtzxEyt6F2rCve93rLjrvV9Oe9axnDbqzD9Xydfzar/3a8NqF53jmM5/JM57xjIu+M2033XTTRceISmFnBVuL4/i+xzUN69WSYu+Aru1xfUfvSBF7UN6jVy3UQdKWkAW17fYIfpsYKogFShVAYJCkCCkImssbDteg016SN/ws3J2+FsYgBiSDJgYiCqsrfNB8fm45vzjGclvxwW8pONs43CFoHdisDXhwweJiYH+5YmdnceTZNb3Gz+ZEWwsLwCmUspik91Itag6XDtdrumh4YOXY6SOnjpVsbRb0znHvWU9QFowlmlLWFdEcQGlFoSUFOoN2udymUbAoYV4rPn8u0oU4MDGVBqyhRfPgMvLgfoNrV2zOSk5u1OwuPX1Kh1FGy3rgoe8dfdPStT17TS8Gf0wVePtD8C2GUZKF3OMZwZm0mKNeWuGV6NIetLB//iy9C0Rt2Njc4uTJHazWOBfYP1xx/5ckFTigpBq0SU5NCHjv6Jo11kDbdjx45jzbGwWVDTTtmqZtObmzzekTOyybhv1Vy/nDVowsnwyiHE1FXsvGyWgwJYs2yMCLAWIKSg6C8QGUqoAgG3RpUp8kwC4Kc9Z1nYiwT8ZkHJ6RTgHCknI2o1jUdK5BKyOZEml9tNbKPvChD0ml7mmbzYShVdf8g7cPflCe8Uc+At/0Tf/w55u2X/1V+ImfkN/7/uL3X/lKKeJjrbDcXvACAV+vvhruvx+++7sFaL70Unn/5pvhta8V5trHPibHeO1r4Ru+QSqtg4DMfQ+/+ZtI0ZKLwVhQQ3riyZ3jnD51OZefOk2hS0LQkkrmHcFHCqMHIp6MD83y8BBrNWVpU/EHjkTdlQqjaokSADfr0OdmtOglRpPJSzpVtZX93ChFyAUzM1Dn/eAoKa3FgMyXNrlHPXHi8nVVhWF7bvBe2O3OJQd42FYieM/WsWME34uEg/3/2XvTmN3WtK7zd09rrWd6hz2esYpTUFR1laQlGtpuaCDpKJJoMFHTicFIYjTxg34RFYFg0C9qYtJEiUQ/GEwaNJ2AMWjSSadaRLrRQsAGmuoqihrOOXXOPnt8h+dZwz31h+u+13rec+pUFYhlfaiV7LPPft9nWMM9XNf/+l//f8Nh/4yTkxO6zRbTrEmXJRHTwpBoilGHGKFY6W4wGX95Re97tAmsmy2XfuDxEHny1PP6r/8H7O4+6/PnuT1MXK/XrNZbMbdSgXHfE4xmjI5oE5lGWrNPLSpHLqeJtXYYs8I2W07XO3QIXFw8YQoBZTQvv/gcm9MTQhRDrZAicfKgLdZKXNK1DnV2irUtt+7co9ls6dan9IcLri4f8uKLzzP0BzQeFQde/+xDclCkaEnZorLm2cVTum5N49rCtBGZHmOAbNBGFVZ/nGNX73sBFYC26xhHL4MghqKNDq7bsdreYnvrvrRl5ywgYinIzsfbY49v/mYpUNTj88QFPP+8MEjf7TP+wB9452cYI3PyXZhsM6Lxq7/6ztdUaYP1Wti6OX/+8/pCxz/6RwLIvtvhnADR1ZwM3qlb+w//oZhzvf28jo+/8Bfgz//5G58RLp7y4PX/Dz/co1mfYJo1ynS1+kGKQebTMGBsgzaW1mqRRkP255gytluBNuScinCngEtZFyhAG6EZwXyP3MkpJ+k5rOuKyZvl4skD+nHAGMPduy/w2md/i5PTW+xOznnPy+/FTyPGNli3Fqa6bWkaRbYRRSYmRUKjXYt2mhyFHdofrglhwlkpXph1x0m7Y312n+ff+z5+8f/6WR587GM0jeV97/8A53evabdntKsTmu6MrmnZ7zP7/QWffvUxX/fCOS+/cIvNuikdKBAT+JwYcyIpS1CGkBWxKFbZRs8Mc63l9cnIOqWSovByKLKAkkAXfEIXnUyfZM4pYNVZGpcwOqKIGGWwpjmywRLAQZfqVkqiV5hiIo6iAeuDZ9t2XD15g+uLRxwun+DGPWN/gZ8GQgygnLSNTwNhHPBTj8mehszKKtK2I2tNrmz7GHAkjErFtEi0ZfthZIqp6IFGcurIQdh2TCOH/prDcCktyDHRNl1h+QlIsu42tKfnuM2OZrNjd3LKZnuCbgqbH8g64KzBOI1WFpWQIlJlCZe9RGIZsfoV0ydTOiz1DRB2KRDq4q5+xBbLeQZTMnMd8kY+U0HHI9RDnk9O8qALiWn+3BK6SmHzZnFVpmztTLDstidYa5mmib7vycWYTYqymplFnZeWaVDzckYdJzORSgA1YR5rrALvp/la65g8lkhwSs0x/iwJwDFLdynYhZiIJuFcw+Cn+bNmfU4fSht/wMdQChsFMLJ6BsGylcfotlLoqQy+aRhl3SmflxJHkkdHwGuNr/XC7q3v8UexXAZhKd4Aro+ZyTUWkUJMTAKsj9MoYy4mcAbXtQW8zTN4rY7GEcDF5RV2fy3P1hqcESCsDJlikFo64RRoa7CNo2sbuq5h1awxRqQJRG6ySn7cvPZZclIVyLC26Rfg1phczLUK2UNxVGQoQGoMpBjAK6b+cAP/STmJb4Va5sLNOK6MuqNt+fOQY4/u7fzu5dkVaaSYl3cZ6+isJcYgQGeYSEUuINy6x5Pv/C6e+8hHYBiEWEiCZvnMCuprVRjySomGdZKcyXuJs8ZxpHENWWeGYRBJkaO54ZzluItrBnCNwVQNZ6Xp2u4dxY+5lKOkKBHK2hjLnK7AcSazn+r8KbG4rkVz+bxhHFkXqcM6Zp1r5u9MLAB3BWiD93LPQiQVo+aIjNcUJcY02qKMQ5sG13RodwfsCdgtutky6Q1ZC0s23ShN3Ty+QsBYRGYAGYSRPDMuYxJWp8cjWpRIKxyG5IVd0XStsFEEhZTNW2ly1eUhS/tJpeOVQdzadhnpETEAU+UduWqQLKeoy+/mRadsOKGwP+UBS0VcEsAyENTNSZfLpqYqcAPzhrNMcqk+lY7YAlDIP+qinhRMKRFiwBh3tNAnDv0V14enjNMen0Zsoxi8QitpdXnw4DGH6xHCFSor7pxvaLTDmYxVBqMjmA2YFZmGFB0ptxJ8YsvmZNDKYFyDsR3desfl4ZqsRlIKaL1UGSpgIY96CZrrz44rq7+z4fPFTbXe7TXH5/Zux5fymnc7amXuS3ndf85nfL5znFLk6aOH5JjEu1pJYr8+O8F5j58CYVq0l0xO7KaBTMTU6jewXXWcbDYYa/EhFr15YUnlLCZxUmk/LlrkBYilYmehjG+5ljD5eeE01hYH20xvLW+uO4Yx8onbl7zJNY8vLnl86cm2ISNuvFE1OKMgjsJeRbM/DISwrXeFMXcos0W5lYCaUmeVIkLKXF8XvUAnTJWQFG8+GTEqc7o23Dttuep79h6CkiBA6SK3UKv0GpzJc8eZ1QafE3sv7sLTGJhCkU+ppaIoxY4otU2cbdk4y8lac9IZctY8ufaEkAhRieZvCqJJEwJGRB/LahkhTag0ovNIZiITb2yKKLW0cC3RQMGqJPJIMfPo2TUWzXrViIGC1jx46xHCQjYkNNk05FyCqxDAglONgDRYfBIAdPKRaZzYrHbcOjvl4urA/jBy6Ac2jS1anHIqouNUgqXKBij3qmJP1R03I4YAkuDm0rIp6/Bxu5RKFTXToBsUEVIQNlp5P0cBs9wSLcliAuZWGWG2pUERzeJ+XINWX5Ilcl6AyB/6IWF4/vW/LuDhj/yIsFifPYPv+q6l/faFF+Cf/3P5/x/9UQE16/G3/paw1NpWQMkf+AFpJ67Hn/tzwlp77jnRgqxt+19orfqrf1Vam+vxYz8mLLP/3OOP/TFh2YGweY9kY4BCd4pyjs7JRKn3K2cZR7Wd0Tn5O5XxVY8f+RG5pyEII/BP/2n4tm+jJtbqaJ+FMu5z+Uhtee72HXabLShDP4lZS/AjU5zIZKyz+OgljlBSQY8xL8wK8VctAZ+MH4W055vaqp4zdjYNkeRWnLpjKRQUl+lSuDJ1hSxBYDpiByxJorTG1n+nmDDGzkXYGXouLaYxwtXBS/GmtAZqLW1Z2miMcZATbiPMTE3GGsXDR59BpT2kM9Ynd1Eg63JpCSayJC0kVIkBum6NzoacDP3kxSBFd7Tnz3FPtWS7Qrfgp2e4taGJmTYFWp2YGNnubuGaBqMy9u6LNAaS35PiSDNO4mKOaEL6KXF1cQHRY6zGOc04PMNZyLqcz6rFmAbvJ/aHkaHvadc7dmd3cE1Hu1oXB+mEaxxnZydcPnmDRw8e0DrFbtOwbhTTcM2UIEVF02qa9RaFaPhO04gxZu7GAQHqKkvGWkvTNFgD03jA+4lxUPgQiX4gBiEX6OaE9ckdNid36dZnTD7VLPDzG2MdH1oLu/MLHUp94de822d8KaZbX+g1dR7/To4vJdb6Yvfnd/gZKSWG/oqnj+Esw8Y6mtWGENWsT6gRTfMwJbR1WNeINmySgnMKE/0+4JqmuFonjBXiB8V4RbClspEo6XbLSRMnz/XlE66vnmEbx7A/0K3WdKsNOWc22xMyidEPNDERs+H01ouM3Y5xuOLyqoCG3pNTpOvW7C8fsd7dxrViRkb2sg8WYMZPgGvRCox1mM0ZH/zwN3L59AFXzx7xqU9+goePHnB25x670zs03YmYiDWdyC9geP1hz8X1G5ydrrh/94ST7QpPwgM+Kw4+M4YidRLlT90CFcIMTKHkezHLsq8MTaNp5vxIMY5135XbPU6FiZcVw5g5HALjGGagzTrDFGKJe3TpprSknPF+JIyXXF9dihbvOBCmK55cPuH68Zv46wvyuIfYk2Mx99IOs9oJ+LPe0G02oBLK2GKgZApwkCpGgiKhU5D4WwmrnhSxUzUgiiJjQBagY5ro/MRp8MQg/x7HQTSD+2tSGJmSJ44j/bM99rrB2oZnzrLe7Fivt7SrFbbpaHe3adqOtmlYdQ2KCfBoEkm2NAHCUioFZjOTmVIBSqv8iwBZBbySujaRVEA8mLVw0ZL/zfGnPOe5g6iM+Yo66fJjVVi7lSNwrOW/AMYLYFnbz51ztO2Kpm0YhoFxGglJ5l11VK/+JlXf+/hz315PUkWioXaGlssue3L1kCjM27nVuuZLmawKXKmOfl5yOK3UDEKKpq4wSo3cIHLRl68PISE4gVW2aMQi8jeqdCVSJLyyeOGoot+aylgSvVdVANLCOC7XP3mPtrqcmxDEVMlxqn5tMqmEyPKeato0370i4VhxDa1ERgNEDMQpWeeGvmccRpIPhf1dDfMkbxX9zQVwEdauxE0hepITJrs8e/m5FHEMjW0wxi0kDWVQWtblCk5XQE8CwvqgVcF5NBhhkqJMeYoibSbFtIgqmiqmfEYumE9OUdbu+vxiYSaVcaarn0S9ZxUEnqeAkELqnDsenTWnnnGikrKkUjCR6z1ifx/ldVIsqXFIhtQSouSPIQR807L/H765FHpEkiWlxPrXfhX79HGNdPHJz/iMitL5pbWhbQ2rIglhtZ3ZukqpmeEaohS7ZNoXcD+EWYqyMpeNNaWLuwDLujK45b2iJ6uPQHc7M7YrI1ukYo/kN3K+MZ5CCAy+dC0Vsy+V/YL5oRaIsExdYy0WV56BLr4TppAuDCFCzCuyWYHb4LozaHdk3RGxTDHjp0BWXsDYdytu8xUDxhYdWC0gSQi+6AbF4qBIEf2twIeVxVsblDXoppU2j1L3EnON6tVGWYBLa0udDxkBEpWZA6Ip9kSVyGpB04+nR10Ebpy5ksmUCl+5OtyR377Av9tD+Dw/P1qI63eoZS7KgEcYdiEmYlw07mSR9xyGPePUE+KENmCcY/QSoExTYn894UPm0HuUOqC0pbUTjY20FtZtgzMryALGhuTItChtIRcmY62gqVxMzTRNu8IcEhmpvB67Vn71+PIfmczVNJJ9wOSMURmNAWvwMUqSexTwGKXonCaXjRlkU7x1sqWxRizAUigBOEDVI6rA1vGWwvy3wA0CRKjjjamWHwuo9qyx+AyXFj6+6blWgVfjNU/yyMFktFlhrCXEjPeB637CGs00BUYvW5To8y3zqk+WNAExiXlEtmRMweFEw6cxAlInrYkBrn3iekh0TrFymrO1IfWaPimykc0x61KYMaKbqA0YLW3CGtFWPHgYpowfM16Q5nkXzunYjEAM8lKpchoN21acy4NX+Ag5R3RhwJKCJAc5lGpPROUJhZdEKwcJvOr9VSVgLD1sNXysa5zRYLWitZp1Y1BZwF6lhMXSTxlUFpkxTXFFrs7AuQR6eXbtTTkzhVQcehVX+4HtqsMZQ+OEuZCRAld1vxQ33iWwnMHSZRgtzL6j11QwNhUZmkSt7Jfg+cZCLP+uulP5BjtkfgVidFDUQ0vwTBSgbBEQ+iKT7/XXhQ2rlLTzbjai+/gzPwM/93PSUvz66/CRjwjg+qf+lLBCX3ll0U198UV4//sXcPI975GfVTf1V14Rd/Xbt7/IySAA5o//uOg89r0weP/pPxUphD/6R4VlB9Lae3EBt27Bn/yTX/xz6/HCC/IHhA38u31893cLkP3ggTDyPvABMQv60Ieg72kahy/tjaqm7rU4lMEqxen2hLZtyVk0l61z+BjwYZKEyEi3SyTP3Sm6BJp13ZoZDuW0alCtVSkx1VbQ8p5UpDMEeMjLZ7DIHcgSuIC7WpU5xrKmpiyJWwVutTFlXpRiV3FOzmTpmglRtGozi9ZVkV9QSmFdW5xoa6EuSZtZhjAFMbtJ1WhBdNBSSvNnCbDRolUSmRYrsVA/grYNrm1ZrbesV6J9H1Jm9JekUaH0BrcyrJodcbtiHHtC8OJO24rxUVCB4BM25pIAAlmj7ArT7dBxwOiELbXvadgL0JmLq24H/dUFlxeXDP1A4wzbnbRN+iDmhCSRbVIopnEkTgM+wWAiruswThFpyo5WHIxLIh2jn7WEKXvbrDlcBoU2ihyFWTONAzmLUUkM4qKujaNdn9Ktz2lXp7hmTYj7GySArx5f3uO67fg3H/ww1jRsdqd06x2u2wjDtJrFUDooMihjCgNLAL7gG4IPJCh6xfIeYysQKyyseU2BeRUIk2baRK7OGvr+mtPzO/gQaLu1ODSbhvHOjpQz1jm61YmcR1zjp9tM4wFjIEZPLMWtpm1RzYZudVIYtx5yYrrVkoIkyxhJbufYLEf8vR39/mX2V894/PghTdey2Z2wWu+wthMGpm2K/JTFKJEe2nQNt4xhA0SlCEoRgNHAgBQzY5FrqdicYAmKUStC1GJqVAo/zom+tdwphZ9y2ZtlaRw9+CDrayYTo5FOvZKqJSwhltb61EKOIm1XimLEhqE3RC+69SmcMF5vma7PSFOPHgde/rn/gLIOYxq0W6HXZ9iuFfNSa0gksrZoY0GJVEUqLcDyxBPECZIXBDMHcggoE1BBgHFdtL6zGcl2Qk0jJNGXbWOg9SNhOjAeGqLvSWEkhJGYJvLkib5H9ZDGA76/pO1WNN1aVie/JrcdOq2wKpVzkBuvlYBBFaSal56cFwmovLSEV/mBOcq/iW3Ne8P8AGaw82257hFYogr6elOSYBkXdZK8nYEpv5b/jzFyOPQCWpdCmzD8aoefvPbtGWk+Oo9ZD/WI+KLqFkxlBJsSI8rPVI2tZROmskIX9uiMREueU77nmG2c8nKvVL2PZc/TxS20EtQykI5MstX8HTdZyfXe6EIYQSmMMkXXtNyzUpytgN7STq5mLVCtTcUV5f7oGqsIwJ11iV+UXIeA+cfPR8BkYyzWBuJU15i5ErM806N9z33qtwjOkXY7csqF/R5mIF6AvwXMO9YHrmh+Pvr3MZojdysvz02XOM+2M9ieyTMYq3UsrMk0EzlmMDaGOZeqhICKCc/5ynxpbxsTR3OiSlZV/AgomFVe7v38zmqWpm7Oi9olRZG6UEffkwRETTpiCsvY370P0UsuGQM5JsLLlyjnsA/fEhC8tCWkQkgIBftBgVNOQFhiweBk/FejNKWXGLjGUPZo/Nd4Nc/zovzOB3LZj3LOQqqZx78UYVxasLg6Fm6Qj44OpaBxDToGuWVKi5fIPCcL+ScdjUUKuAyUQS+/NwplG7TrME2HUjuS3YLbgduAbeUqE6Q0MqWBnKVbZtGUfefxFQHGSlDfFLkAy3Q1FSqyVFCO2/BMYaCoDKax6KZBdys8RxtDTrMj4ZKUmXki6qxw2dHaNdtmQ2uEFfCsf0SfDvg8kbI4EktLUd2kSmKlQKlcBryaBxDUBXSJMpY1/ebiNGdzR6DUDdwhHQUq6riNm1IRkl+GmIr7pZoXg3EcGcaBlDPGOVwj7YRajXgfGadADFqcjGMmHQZS1mjlcRZWneHO6ZqdXaFSQ8oNMTQo3R1tWkWrB8hpIiZo20DTtFg7AeNSoXj7JvzV48t2ZOBKyyJokgiNM4pxQCKXSridH5EymmbVkHFH805z79YpUSV89KQkG1eJlMp8KJpX824i367mIEwCfJk3UEu/ovsiC/GYM686y1XOPHYTH9tccZEiF9cjPilcs+ZstyYlT+gHpilydRhL5a0YoqBL+Ltc/xAt/SEQgZgsNFaqMUoJk6xIgGglVUyfDROZvYfVmGnXmfOtZUKRJ82kMkpl2XyMQmuRCRGgsgCLWQzFDhMQFSlKRV6L4WY5uRKQKIm0Qkz0KdIbxbbJrJ1i7TJjSAwFVGlysZ7IiSlMGFnxIXt0HlE5QPbFECfVp8ACmsuzOtbwUQo6p9m0hpOVY7tec+gPTNPEFCIeRTYtFPMIqQRDRsvGpIV1Xiv8qcz5FDJdY2kax8XVHgNYa9h0DU8urvFRDAO1kXsToyRZKVNYA0frRl0c5+BdNJaqoP8CxB69RSp6JehKR6BJMStMUjSS8be8c+lNYP7OnCFmMQXTZdusicLnSxAA0WVUSoDUH/xBaRf+yZ+E7/1e+f0P/ICY6nzf94le43d8B/yJPwFf8zViSgPSpnysGfuX/pKApNXg6/u//6Zm7Bc6QpD3Hw7CYv1rf02A2L/zdwScrWDs3//78KlPCYD82wFj/0seSsl5XlzAz/6sANrf932w28GTJ6j1itVqRZyERalYnkcNxQ2a0+2OxjaEmBknL2Bs8EzTRIwBZ8AZYbqLdptCrPOYQdA5UTlKMFX5Xc7gqokEah6fyxoofxuli+5aXQ+ZX1Or7rEWG0rSkJNoTsboMTOThOPsQuZCLuzalFFKuli0NUW+aenisa5FTdW4UzTwd6d3C1vO4MdANAodk+gWNi2xsCQk8Lc0zQoVh5IkDZimYRo1zWrNZt2xcQoVIClP3/c8fviM2HtowZoTuq7DrDo+/slPkRKsVhtu371dQA1mgwVnRLIma4tbbTldrYjDM5LvIU2sV5aLJxdcX10xjpPEYdsdTx8/5Mmjx/jR4xrHOA6sdztWmxOsrR0FIlQZk2G9XpPSxBQyq90p3XrLOEbGKaKtdErVtjhyYb2UvU3kHip4XePQSD/2TMOBsT8QQ6JpOwn8jaVdnbE9u0+3vY3rdijboMzbDPi+enxZj6e7E/7Xb/tD/5W+/RS4/1/pu/8LHgbxzfySXvjFuty+WKXidzetdYeBD3/yLVTWWNdhmw2xPaFZb2jaFmMt4zhKmyvSxhrDRPKTSH3liMqB7HvieCBHD1E6QCMJnzU+KlAaAyQMWZniSyDghqy/DrqW9XpNDAPe9/TXzxj7Pbm6l6fMNPXE4Bn7A223RxuFHzf4ZkUc1qxahzFqZkMKbhqWePGoCH4MmlQAJqcbvW/z/+hZQuD4GSmq0/gxyFp/ddyaXru3Ktu0fu4MJykB/4xaCp0VgBONywPTKEhAjcOVEu3h+jNQpPy272QBZN/+c4kjynWqAsYag9JmuS8IoSBnpPCvxJQzl2rNkWjioueaF/3dChpXybd6XbrEACoXQySYNT9zrMxbiTOWAtEiJaG0oq36pUfXZfQRcFmwiHz0vhTTLBGhAIye28nJYhqolXj3EMMcL2OqJquapcLmMVRAsCqroI6eERWMOyZN5EzzS/+R/L6vJZ6cQk4lP4h16JDIGFOkMoyZZUuo510ANnLtont7caC8BiGNKFUNS808jrOxkkNoyWvEJDXO5ysSTgFNAYejFLoq+LiEZ/Vfy1iYsZFlus3/noO6ClYe+ZrlUlBYyIX5xvitz9eW4mCq126EHayLgWT1O4pRY6It0kqJ8MEPk07OaIr/yGLGl7C+xqCy3rggkjSm3H8oXbzGFL+YOkdLx2IBUrXWM3s2JZHxkjEk92IYJ7kVZXymnEVzvfyR7gY9j+Occ4nn5HNMlR1dkji6riN76YCbcTVVYvMikSKPROaFFPbCLFmH0kjfZ0syHUGfkZtTlDvF2B3ZbMhFqkgeoxAdfBoJYSAG6Rh/t+MrAoxFwfmtU7TWjIPnmiJAbkrr36wrYWZRcRqLXnWoxjGpUiUojNGadKfaI1KqqCkKkr92K144fZ4Pf+D38srLX8v52S1yTnz6s5/mY5/8GK+/9RkePnuVy+mp3KGiDSlzWS2TR0GMNRmTweanaWaO6Hny3TyO15x3/lL+SuWPQjY5c+TYbYyhah6mhLQ8KqGeD+PA4XCFM5rTk7s45wgp8ODxaygSzhpUNuw2G4Yw0g+iK3tx1dO2DhctkRZtW5JeYRA3R6U1XetKm0pmaclIspyFSL9/wn5sCb60hsiI/7z34KvHl+fIKJ62LUkrCBYVMlpNtCFgfAKfSGGghlc5RqZhRHXNvMkqBaenGx487Qk5Y+xKNr25Ela/TS3tLIWaoArYVQe2tMpGfPQ422K0JSa4yvCrWvPo1cd8/NbAk1uKTTrDbSzaX5F9ICjN1SCGS+M0MUkfGzppiUk0RcO1QRWhbAWcnt9mmrw4LTattCXOIo9ylyrkAWKWlZLhOgCHxDhO3Dtvue8M3ah46zqTjBbzGgVWibwbvqoAACAASURBVEuwLf9WyEYpa4NCGWm1kwktL5iZu3PAJs9qSvB0n/A+8tKZ4mRliHEkeU8fZM5pI+ZUTeOK24WHNKBiD/jZ2VmOQilRs6jl3IJVj9tnG3YrByly6HveevYWbduyXW+4fb4i5cTnHj5lKkYmZGlVkjYeCQCnEEpHQ2VdJE5PdnTO0FiDXq3Z7TZoBdM0kTK8+uZDznZrGufYtI6L/UhtEarCTjkuIOmNQlDOM1hbW4QW9kZ5US7rVKloawICvvgvuAjnog2Uir5vzBQX26VqOteY5iaBz/N5P/qjcHoqzt6vvCLA61fK8S/+hfz5fMe/+3df3nP57Rzf//1QTR0/+EH5+7u+i/zPflLab1GLxlU5lFJYY9i0G063pzjTEEMiJJH+8dPEOPTkOIApJm2Y0uaaShIkAKcCrGlKoqeWgJpcur3d3PUcY5r1s8SMRvZKhbRn2TI1pT1LwLvKFA9pYchQ2QEKrBGpIWuF2VXlFHQBBKP3pCTsnQgUO+V5jZbO3YXtpIwl17ZLrdicu2JkFmTdAnzoScmjraVtZF9XWtiABgW+x4YrbL6ma29hbt9iu92x7RQ2POLy2WdxKqFMYuwCJ+evsDm9j3GnXB6gjyOXV6LDrFWi7yNdd4JOEUJmGA8kfYppVqimAWfIaFJYicFPasXwEQd2jc0N/aHnyeOnXF5ckWLipZdeZhwPTMEz9Hu2JzuiH1mt1xjdkmOLURaz3pGiF0DftSi7plWTFJgV5DTMcaWxFlQixIE8KoKXBEjpqmFocFbx6MFnSEWnMqfEvp9Ybe+yOXuOO8+/j+7kOZQRgHYaey4ePySGz6O5/NXjq8dXjy/7obTl7oe+XfRarRM5CtsI07mAFN57UgxcXT3jcH2BH/rSbSChxuQj/jCKPn0YyWGEGEghlBZbIdhUo9HsRwiT6EqX9mg1t7sjZJ3yx2ona3jOxOTJWku8rzJT8Dx98ADrHK5xrLqWrm3Znp7RdKvZLFsTOTbbqoBrLvmeRPrS+XQs+bqUO4//flssdLwZa3XzV0c6qstL1CLfwdtBOgEklVKs12uMMUyTkLdSTLPy0THglnNpfxf0UuLWfLOIXpmwVWPy+Pvy266hnu5svkUNsRfZNqMtOYTyjCLHIJx8RmmTVhqtheTydqBO9MTzLN8Fcu1pZmlBLQ5XLdV1t1pYhlTZozQTRHLO+HoxOaNt6XZB3YhtvQ+F4JJKu3qJfVGzpGqNaY47HWsOJddYdKNzxAdPnKJIcAwioVI7BlByL4dpKlqgcgzDSCxSK/KJSyt6GShSODem5KOyJxtrUWYB6VKRLxMQWM2MyFyK16ow32KJtbTpEN8iXXI5i7ZqYSbn2lFX8oQYRJZRxSXHOgKj52daGNCVsJTn3LiMoPw2BvnbCCjHh/gNLPdKGzF1ttaSTUbnqpd6XCApndO5Gk8ViYYkRWWFxmiR3Erv+RouXnqZkPxsCqcOB577Pz8i2FTJMb339erm040xFd108T2Ywf8ClC/Au3yn1oaQl6pLRmGdaP2KBImYalrrAGF/y1hIR/NVcThId1XOeQZp45Fm7KOnT+mK/IFWksOKXIHIajhbDcFKUlf0s03OEpvaFmvWqGYHbkd2J3jdknEUQQe5fi9E0hBHpuGSw/VjxnFP8D0xDO94lvX4igBjFXB9cS1C1T6QQ5K297xUF7QyaIpum8roxpCttFPXxUnPY18mjnhQCTW/MWuee+55Xrz/Ii/df4mXn38Pt269IMwOFJMf+cDXfZh7d1/g6eVj3nzyOX7p1z7K5x5/lnE6kE0g27rQqDkBz0XrQyoAataEkArFsqHcPGoCJ5+ztNEuk05VhJ5i9KVkl4nz58vrEpkpekYvToXee9pmzXq3AhTjNHBxeYE1LbvNGY1rcbbFuZY3H70JURwXN92W0+0ZbdNhi/6sNc1SXcjqHYtLPWddTjWGCWPXpUKaiSkszwSRm/vI6W2ePHuM9yNaZ5xzPPjpn+DJf/ctXHyPuPl+00c/StuPpCz6ajnFknSKts2q27DdrGjbDmtbSioqm3iRqwhV71TLc0hR9DZVTqAz/9v7XiRoxXsur/kfX33jCLAq2jLKoNwK41ps09CtHGHMjP1ImEZSHFEqszlZoRTsrw9cPnvI7336iLPguWxbfvjbv53/5XMX/MK64Z+dSdvut/78/47ZPyVGX56zQhuNc451t2K96khZgPVxnLi4uOLs7ETaobQ43qcCRk2T5+LpJVa3XFzv8THStB2HYZj1Ab0PHJywLnMSpqp1Lb1xKJvIMUOMcxgWUfRZY/3NVv8xB3wKJBRGZVadxVhpx4pl3qZ0pIWjatGibl6lVSgrnrqWt5qGGBX7fuL13cgbW8+gDY/cgbxyuLaVRTomMIY4RfaHiUM/kKIvnynBi1RYDRhHthsm3RGP9XVtS+ca8Ine53nDRCmyVmKeU1qBjIE7nejXjBH6ZEA3nGWNU7CzGd8mrrMrMgXyx9lFem7uvjGqTOQCzuZEjhJ0a8BZDVYMg5JPpfU/McZIPHiUn7h9smLtFKqD6XAQg5BSSewaw+iTsC5ykM0958LQ0LNemS4sfpSE84thmgCW+37iet9TQ6mkHN4n1ORpWsv5bsXtkxWXh4nrMRKzphoLzUWh4FE50VpD265wzhSNbdH9VkrxuQePON2t2W5WnJ2sefz0ihRBO82qbTB6IJSxKHFmrWHKqaZjRkZeEoblKBXOLMAUKQChyNZkjhvHltdTwNkj0JdiHqFrKwtzUSmnLDqPxs5A7DsYsfMH/S4VoX7+5xe39M9navPjPy7GVgD/+l+LlMEXO77zO+Hv/t3l38cyB79b5/27eeQsurt/5I8Im/d7vkdA47/xN8rzlgRCK4N2wg7w3s+Jgi7JW9u0KKUJMc/MU1n6pKvEp4yupnlKH3XCyN4SC7gq7XvCDs0xYI3BGjMnqLM5SvncWjBQR7qyKossDMaQsiTD9VpUSbSA+g9ZtrQumq9atNfq63PmcH0BWVr9d7szYtEC1zNDIM/6djlDv99La23RTFPKoJxBKUOOXliw3pOmEWWLYyxlj8yGlB3aOmg0OjsSLfvrQHOS0fERsT+Av2LdrPFBNG5Pb+3ods+jux39pLnaX+PWJ+zOz2mbFbvdKaZtub6cSLkjd2esuhO0Wy+gcQaiQtstxm7kGWvFeXuHaTwwjQfiNKJdx2Z3htaWdrXFhS3aQNs6dic7Hr7xELtzNI0jRiea4VE0GpWfCH7k6tkTDhfP6PdXGKu49/zzKOvkuWeF94kUMskosrGkEEp3lEgWGGDoDxilxEBJt5yeP8/2/CU2Z8/Tnd4nqYYYJqZhz/7qCcPh8cyg2Fw+4X/+sR+gSmTV5FoYQfLsjHFYYyX5KUlazhrrWpzraFZbbj/3NWTdcHFxydOLSw4h86CH62Hi2ZNHvPobv0T4tm+WiuI89PRcXKyJeiRjW0uzbul2HRjZOxOyx23+n/8blbysuVlj0wanVmjlUNmiJ7i33fHi/Xu89Nx9Trcd03BB125pWin8vfmpT5DTQNM1nN66S7O9z2p7hjaS9BDCDJ7kIt0RgyeEiZwTTdOI43cWFlMKE2+9+Srej/ixZ9g/443PfIIYPM462qYlxsD+6hmuMTSNZfKJMEpnXlYK13Vsb99nd36Pk/N73L7zHNatC6DVYWyDD7FoxE701xd87tOfxK0cZ+f32Zzeod2ckbXI1lSgJHjZN+tejIIw7PG+J4YJ5zpss5YuPcDYhjBGKYZYi2laYgqkUDthhAiRkhS+dYnLLy+fSnttSkzjRLc7oW1X0nKdosSzYeTZ4wc8eOPTnJ6f8dyLX0fWLSHCervjan9ZCjUeS+ThG68y9AdiSlhn2d26w607L9CtTtCmZd/3PHr8EB8ixrbcf+keL77yAsY6UtakrPFTprL7UobR51LskPVqGPIsW5CS+HjUsDRn0Z2dfBQ39hiX+D9Udpqsm2kaGK6ecP3kTd741P/L5z71m0z7x+gwcLracuel97G9/xLu7A6h2UAO/Mfv/G9562vugla05y/QOldat3NJ2JN0afkoYy/U+C7N620KnjD1DIcrUgx4P4me73gg+wFbYc6cySoTpkHmTwzEqcckkTbI0ZPCJCxPLeaPIU7EFJYYSSnRAi/3JsUseo9OoUMmEvDZC8hLoh3XRf6iET6yShhVQSqo+WgmzblAbd+VfW5GY+dtqoYOs/yOJMc3oMjj6KJqTN7QgqV0IVUQaS56KpRRrNqOthWJiP1+L4DQMWB79AXLdaijX1TmqbAEj3Ucj819KvhYu+7mKfou8VFlP9a265r/zK+u+/hN2JvKlBUN9sIkLPdW64VeFoum6qyXPL97DhuKLn28wcC1x0zYXJ9TyX9iNWqS9xtjZ2BZK8n1sqosXxbwVAkB5jgCr+c16/yWYKhKFSafqBI/4zDg/Uj0geADIdyUCgMBnvnFX0S98Sb52751Bk/rV4rMS5FYKKCjMbZgJWoZX6VgklSSeKu8Ry+jdDbg8iFg7FTAWFu6tV3BHuTzM0VTtuQgUQdSEnBZJdGCviF1rI60Sws4HHxPipPIIBQpkhvHkvbcGEMLAWAedOU6Jb8JIYj0RAXEK/u9wtn1XhxhOVXeoOLAEqNqjHI0uZ0NwIJ2PP62/wkfPevf+k1Wn/0Mzjlyrqx4Od/WNoi0W8LHMMscLGCrmMLJkEqQipyEkrHRjyOZTOManHFMkxAMFs+ffKOYUXPZ1XpVWKwLU/jYJ0hrI/JULOerssTEsldmSPK8tS6eFliS7TBui93cJna3wKxQpkEpBzlgEJZvCBPRXzMNe8ZpzzTuGfpnTP5ScBe+cGr1FQHGkrOICBeN2LllVKlSJTMCuCmNspbVds2UE6Br/CJ/jkBDg8Lphs1qx9n2Fs/ffy8vPf8ebt+6w/nJOacn53TdDq1MAZQCtjVs12u0znRdi0Hza5/oeOPxqzzZP5S2Ql2SM9Q77mzd+FW5phlwfdtx/JrZkXtO+FkSJ3n1/N9c31NaDasEQwiJcRpRiC5G42QyjOPINI1oYzhZ3aJ1Hc44jLal2qXp2hXObdmtz1g1K6xxiAudnEoVTa7gywwgH19MOeecEspacb5RC/BxvMReGssTYMpJjJSC58HjhzycRp6engLwtUazUgIoTSoJ2xFJEpU2TMaRbEtnW5pmJS3zlEWktHdM3hfBdgGusqm6SCI98drpCUFrugR9Www4KhirjegRuw22XdO0LXplCS4xKMekLTEoIGHWGykmDIEr7Yi1GqgUr52coC4C+23La6dbyJkLq1g1Zllskywak4GgAhOiXRiJBJPwa8fQGrwtQSClPTsEfPJMiLj5SGIgsw8jV2OPaxwhiIaSGEcsjqjWWBptyEZo+sKOkvNJWjM1LTQr+X0ZyvtxLBW1DGEieIvWDUrlGdusRnV1kUsp8ayxjHoJplJWPMvwZsh80l4zrjSHtWXciizCUCptYUqgPcPkGacwG9DEUOa9MszrsLJk40A3RLslqZakPAL/wxDAbh0rl/F7YdjO2qmlnUGphDEiDXBnBzEqLgc4eIVHcz0mdp2iaxSnCsKY8FnN2k05U4T5RQ8tpywSJrpsDFpjrIIoc91pWDk4TJEQEz6CoHu1dSmzT4nmcBCNryhazodJNm900a3RWSwycqD2sszzTQnou+4aqZgC+36gVtMpwa6Pad4wdTEnyxnGkOhHz9l2Tdc09FNCj5GpSALklEsit8imyPVnVEgiGKEMxmqmMDH5yDAGGhc52W54drlnmLwAYymzaR1XhxEfJOmag7+j5bRqddW2udo9UCNlVYHYHKEwYecwvCS9cqr19elGi56stWJkUVfwZaAt37McWTR0Y21FPzp+6qfEeMtaMc165RUBPf/yX4a/9/fgH/9j+OQn4ewM/uJfFBYtiJzBD/6gvOanf3rRmv0rf0U0ZXc7kTqon/GZz8Brr4kEwT/5J7Imv/HGch7/8l/Cq6/KeX/v98JP/IS8/qd+annNN32TfC/AP/gH8OQJ3Lsn8glf6vHRj4oeLSzu7G+9BX/zby7X9Wf+jICpf/tvw8c+JuzW7/5uqWR8z/fAyQn8238r73nrLfjWbxXpBhDDrm/5FmGD5yzX9dpr8HVfJ0+ijIlqzHdTV07TlGp7LrruRpv5PfJ+SltXQhuFNUcRMSwBYP3MutYZXUwayotLdqRqMlVE1WYig0KKgyWxyChSSaJiTEdsGuYiQP3u4wLFHDeUdE2SywbrBLQyRoSsl+SIEmBKEhMrI6ImNYhOsphfiHmoRhFTxBgxyKhsCqPFMKZtLDFqxpDwQ6Bdn7LddBgmuWC9Ar0GojBp3TlJr/HREBIkpdHWsdmd4myDtg0pg23WxfxJEpWMKYlnAqIkGdmU5FU6HYxZYdwK126Y+muCExDUFC24ccwoJdpiZFitOiCW4SRrVSKDSmid0K3Bj3u0czTdirYTMwzZ56KY1yTRVUzGSDSdxX1X5BWKBEpOKNth2w1udYvTe6+wPn2eZn2O0i1h6hmHS4b+iuHwhOHwZAZjdQycvf6bCzNNcq5iqlbAWC3jWqkyfmMu4Hdx+G3X7MYJ7daY6wP6ak/rFdd76Dc76FaY7QnhrYcoY9AF5GtcJyBSKDqXWtNtOxrVYt2Eut6XxLzEpwrsW59GxUnS3KjQsQFayBaTHXf0jm84eT8vqcjtsafNUtRujRi9pBQ515b9fkQNA2em5bS9SztllCnu57E8x7JCV0kb72XvXGkDJdaJU2DYX6IfvgUExn7PxZNHbIeJYTgIiBZl/TdPH2OtwlpNEyLJxxl80Y2D11/HnN+jufMcq+deJKuG83svcnrrLtuTc0Yf0QVc9RFOMWifWO33NFGjr3rWZ8+LIzWSrIbqYiUtJlJkH4aiKZxxKWOjSKZJIXUiRVA6owOYIAX6WBiWkLEqFS1oOVKYuDNmKGC+95lmP2ImWauCn8hphKmnefSI/PARzzUt508vwHRkLF3S+JCIAUgaqxRntASr8ePA/tk1u3zBOR1NN4JquKUN93RDcmJ61V0Gzt64ot102LbBuZbBz8slOWemAFPITD4x+cg26DLf6l6ciUERs8gajVNknMQ8UwpnVbs5z0ZFWgWevPZb7N/8NIfXf4vLj/8y8clbbKxit15x63zNndDSTQ3mYEleNDKbuIB3SmvR4M5V8khi5+g9fhrx01hOUGNsg3EtYZLn6P1I8MMMRKUoXUSEUK5digYaCGGUTqcwEqceHQdyFAA8hKkAGKUfMce5Fbhmg5TPO9YiTrl0gYQSM2Uk5i+6+Ckn0eouYTFUY6Cb2es7QUgJkrLKR68rUZOqfy2svFoEnBHBeW89/nfmSKSVytQ8ltVKhYkcQiigzg1xquWZ1e8tumDqaC+dWZ5KC5XnxqXlIjUjr0spF+3eOr6Wz5ZTrpDe8fcfXXO9Gcc5fnnfsYTRDAIjrD3Zayu7lCNd2ZvfU949t4FXNmhMS3RsyjVBATHLvp9lMCx37UgScpFtyCUXXFjK4o1zzFpW8xytrGbZqoqOqhLdZ6Ol80ja3hctYmMUFju3us/n2ffoB2+SfuU/Eb/hG6jAfIZiNlbOUVWQ+YibW+5v6TpHoUnlnorUlF6ee12Egpd7XfbWnBwmJwGnS7wh8ZEA+bnEVDoZkpW8TUfRZDVFriqlhK9gc5Z5a60jxVGKNXEiTIVkNOclx09ZzTjRzcH1dkmQEsqmQuxBoVUixTqR1XzfK7N3Xlc5+vz67LXESVob0dPVlmgdKoxML71MaltCirSf+ATahwJqaqyuElN5xjfKZcxzEHs8U2tsJ6RL0QMXAgVUoLmeM7NEgshv6LkIlMilYVveJ427yzxpjkxKb4wVJWCs0P61zBbVYptTlBMTe9yG1JyS7QloW2Q86iAXCZowXNHvHzL2F4zTAR8GQhgAIe+I/AXvenxFgLHCnqrVnGJQUQBPVdxxc1KioWMs7WZHOOypbtmi37Zkzzprts2Kk80Zd8+f44X77+X97/893Lv7ooj46rrrlElc3peSJ+eIM4bz7Sm3P/SNQMZZy/jqyJW/AJePdEmWDU/2lFzc2CQRywVAIi+vhboe15TqKFGaR+fR5jCDJuW7VF38l+pkDJkYIl3T4Irj4DBWIfPIqltzsj0TuYEiRDyOPUYburZls96w6XaQyqaXhdmaqxO5KtU+loVuUaPMBSBR5XotSiUygQp83HjWqu5Jwggdh4EUIzZG1tMkL4rFfKiCK0oLIK8MStv53s6gzLxxCJBkXSMMu7C0E9T9XqFn1/XleSxBV73x1X1Rq0JjryxISlAbA6hUWM2Z5P3Ru5dj8p4QlmmWlThZG+1K26Kwfqvhog/+hk7JZr3COqlWppSECRUzTAHrIzttiGMka4tVmT4GmpSwquhXRSlwrNcrUsxMPhAsKKvLgBMny+Pzm1zD6ji4I7MfJlIW98IQAuM0oYtez1JJrmMjM2oIKfOocVw1Fu8gownJcOg9j4cDv2KuoduyW6/Zth1GB0zj6QcvyX0KHMZpdkttGugPRX5ESQKuCos564ZsWoJZg2qKHmMkA71PrKyh0YpVgv2kSUbGitJKGPcanMl0DnYd5KSJWeDcKRn2k2fValZWsdVwSJSAv4ybnOdgU8DyjLVFfL8AdtoqCAqDorOZrRWnxTEmRIHACICZhLU3Rs3lYWBtI07DunPsp4kcfAlYE1YlYjGEYPa/VDNA3ljF+bbDOVfMRSamKAGvKu3cMefZxC1J2QMAHzL9EBgnCR6cDRgTSN4Xtl2eN9yaiMSUGb1IQqwag1WKxih8TqA04xQ59J7n7m1xznDoJ3KeaJ3jbNPQ9wNTDPPnzetkLjlrKb9WQHXR1MzoUh0mR0QeI5U1qnwAtWWpiMDkJHIaOXBzQchH3ysLR1ZHK3hddzLlPpq5GstqJcZSICZTAB/+MPzQDwkwC/De9wqDteq+/v7fvwCWIAZdP/zDImvw678uP/vQh+QzqnP7e98L/+pfiX4qwO/7ffKe7/gO+Oxn5Wf1PH7jN+RP08C///fw5pvyvp/4ieU7jYE//Ifl/3/mZ+DTn4av//rfHhj78Y8vn3n79sK2rT/74R8WZusv/ILo6QL8wT8o2rkAf/bPCvD8yU+Ktu6tW/DH/7gA1bBo7f7yL4upWQWTX3oJWBK3GKW1bm5ZLMmccQZlSnJfwcq8BL+qFFMkoJVIpOrMUYpO1lXmRQ0eS+JSo4Bc5qAqRiFakkGRLEkzk1V0ixdGSkiREMRZO2fpapBETJdWVwF8ExLwJ6R1SulqKiHmmbYwflIuSYdeWBwCKpQuI21QMZO1sF2XK5A9QavCCnENWVsBNI0rsYm0BnZtS9cYJt/QJ4X3mfP1lvVmTfQTyUeUWZEwoCNGOUxzSh87Ypa57BqNsY6VayCLnl8KCddtSkdradcsa14mCUssF4BQUldQFqWlm8fYlkIgK1rgGm0cPhphAmV562azIgRfzNvAuU66FAoLrO3W1EhntVmx2zY42zD5UBgfkzwnBTnJuKhajQphr8ac0NbRrHZ0uztszt/Dyd1XaNfnKNMwjSNTf0W/f8rQX9Dvn3J19dbcOZMz0kUES4yDLtcgwKRWUuxrGifPVZcLRFpE43jg6eM3ce2a0Ze9pdkyejjcvUt/ssGebwlP35Jkqu1otyesVlvSY810uCL5Hu003dkGt2tRnWEM0wIwlMUxmYzWZe3UmcgB8oBOmjY7bp2d8b6X73H39IzGNPgUWW3OsG6LMo7sR07vPE9WijCNZCy2WaFtV1qxUzGKk7km8y1jm1ZigJxxq63MrehB7UmHK2KMWBWLSUnk1u37+OQ5HK45XF+Sg8c0LTkFfEz44Ev7psy7HCYuL64ZDj3j/hp/uMJng8qRxmnW61XJU8peud5w57kXJeFOmTAdCIc97foE7RpQmpyFbJJ1lTDKkGQv1q4tWnwNSlkUCZ2lkGCdmWNoRUlgjUiW5JyZhl7uf0l8c4KmXZNzJKWIsY2sazmTQiT4iRRHfH9gmjxGG1brLd5HVApoawg+0HYd0TpyTBhtOLtn0QrG/kB+8w0gM/Y90+iJKLantzg7O8PajoxjGAPPHvd0Q2S1jax3mpQXM6Qsi0KJOyLXh4C1DmtziTMVKYIPiSlmphAZDhOTD1SXehSEEBc97+QZ+0c8+NR/4sGnPsbD136TB6/+JqvNmt35C9x/7mXOX3iF0/f8N+T1KdmuReZKZXFWl1lIzpFxmApoWorrWhG86I1P44Qt661tVrgsALkYkYnZalKKahxKlGeREVZejgGTEymMpDCR/Ej0B3I4yM+iJ0SPQs1dFihw1s3XPoMDc7IjAEMqxKVUwP6sNGr0SKleC8mia8FKfij5UCrMwQUErZO8hHJzxFRDNTX/RI4lqyr55Gzu+w7ss8TPR++r+fVRKkwZ71U38p1mPXU3vQlS3TB2yhW40wWQrHnQclJaa9GkrMQacZKT+ZNhlugrr69SRcvVF2B1PqPl/GbMIC8t1uro/t7Uwi3ECICUJKMuz1DA+HpJy50XzETavyXQKCz8EufUdvF6TxKpxPvq6IJYDMvKd8pn1jWn4iYlLlZIzDJfg3xGLHq4KcaZMa5U1Vmv6IF8ry352HDEZDTWoK0hHw6kX/lleM/LhO2ObJb1r0paVHannGNhw5dYbI7XVYnNUgHhj4BZQHL5wjRXOZKzkYJqjlK8KKZ/SjusLd+nxQQ+Zys6wWR0zDRNS9s1NK0jhkTf+1n/PqVAtI4UJ2KY0NOBHBcSDjWdKjgPLIDmPJaOUb16/sfToMSl8izzPMQrEJvykRb0MnKWzyomtIKYCCvVGEuyAe0V/vkX6e/cY5hG8uufg3EAJZ4guhhHpoLRVPBfliUZXJJ3V1zLzJhW1mCNI4Ow/lOGkp/XQgxZGO8WFAAAIABJREFU1gDqeFQS18YSO9ciizGVviY3x1o7y98pKlZXl8qqu2xArVDuBLd5Ad2dkXRD1g1Jt2TlilFu6UgthTLfXzDuH9NffI5xesbkR0IKoKUjyhgl3ii8+/EVAcYCwozNVZR6cb4D4USYymJTsN9flQmTRX83FcCORjRhmw2/5+u/gQ9+4MPcv/ci5+d3cW5NyG4GB+ucN1qL4HpM9P1+TkmGceS0O+ObvvG/5/l7L3C2vcW/+ej/QVIT2FQW7tqWvTDN5PRlkagyBcfsm/n3+lhR9uYmNi/shS6uC8OFUvE02soCKbcKg+ZkvcM6MUOappGh7+lcR7NpcU2LKhp4MUViEmffs905XdPSuLYU5mNpbS4DtiKE1KAuL+6AgJ8mOK6a0LBu15i+pzLNUhWZrFdWQQtVdCeTsEdeuLrk7muvyWv2F6SQwDjIGm2acr8qq6durHPmDEpMypLSKOtoW4VXA8EPct+oz6s2fZRncWN65HmjRgnbxDqNEYkoaalKnuR7psM1TbdanDljoDsSSq/HZz/5GZ68eBfuCettPySmK48i///svdmvbdl13veb3Wp2c7rbVd+wyKJIilRr2YEEyIITBDCcAMmTEwd5S97yFvgPyH/hh7wFeUnyFjiGlCCBFDsSJFuSbZKiRJEqsopVddtzzu7WWrPLw5hz7X0uiyUrQGQl0Lo4996zzz5rr2auOcf4xje+j75znC0cXduIrqbOjH6Qqq8PxJjQvQzUlBKT92y2O3osbow0PtEax+24Z6EdToMzibO2ZVSKndaExmGtw7SOcZKknwy32z1GK5wzWHtcAHPOxHHitW//Id/8d/9ORb04BI3BgRKmVUbjIwJ4lyKKLujHRme+00oBRSvNdZ/44NXILhuMWTJ5x+0O/ONL2sUaXEfImsNhyyG2DLR4FPugMW7Jq48uWfeOnEY+/uQJt7uAz4ZkWmZHLGXJykogbRuUHudzmrIhHBKrXvPgnmN6HIhGdIW0UVgFBoNSCR8Tt/vEuoFla8BpNhPk7NhNkRASLYmrdQMHjZcciJwVMaqK3YmxFZm20TjxzkErCGicylws4dwkcpTg+hCOgZCMU8uUAW85W3RcrAwpZzb7PaOXljXlQbUGq6K0ihaAUinoGsd60XDvvGe9aAkhcDhM+EXDTTEzq1DlrH1V1uyqsxOSYhcVz6533Dvv6VvHFCI3m21xHS2yIEmkJMjSSjj5yLKzvPnqfXqnSH5i1bV8+nzLYZjYpIF7QdpQXlwfiDHx6N45VxcNu/0W72tV/2jERgVf04lhABlykRjIGagtgnd1iuWtVZctzXOOnH0CPKoA92VSKCT5TFbSDmhKAl3neFmM6/9Pik7f+IYwPj9vu7qCb33r89+jtYCWP2m7uPjsffz6r3/+fgH+0T/6/J//k3/y5+/js7Z/8A/k68/bPu/6/P2/L1+ft/3cz/34PoYDTSutwmJyEdDazeukVsVYS5tS8pA1O8c0FyG10oXlWsBWocrOgaQkAPr4fa7QJcxVRoSdaIubrK77yUEKNVmYIlpJ8hKLlEyYAtM4EnyYVyjbdFhjMUbiloRoNmeVpIBk1dySiIGu7chBmOohSoxS2/JqC6XRibaBtrH4CJPPxJpIKWlpVFlWNWstjbUsVpLESnIcOGw2qCawaBqs6VD9FYtzMM2KZrUm5JZsrkBfkNUZSjeiSag0xrWcqY7JT/iYsEERERMJMRuzaKNJlLav6MnJ4/2BxXKJsy0xNOy3G8I0kUkzYN52PSItodnvPb01pBiIccKYxPnqnBACRmsWyxWH3TUhHPB+IuWMazpS9kx+JAaPcj396py2c+g8cnHR0TjNbjey2w1sb3eI07JBKzE+SQm2Ny8wSpi3wbSsLl/l4sFbnN9/i/78DVy3BjTej+x3L9jePMYPGw7bZzx7+kM+/eSPmcYDIHPeMEVsSSasFfDqcBgZx4lpEsBHoXj46D5d14sWsLVcPHyENo5xChxub7m5fopyPeHiIT/8mV/i49uBvc8QE6urh6zWZ2jboJ3DNC3aOO4tzti+eMLm+cesHrS4qwVJZ0IMR+3CCopIUxFWW7TVMrvGQJwiKmQaNF/+8jusuw6nXJHLWhByC3SorNkPB0gNlw/fBiKHw4FhStjeorQjRS9sZ2fx44HxsGca9jx8/W0610q2kOW5IEWcXbLSDeqD7/H80+/jDxsgs9nv+OJXv8ZqfU7OmY9/+H0ef/QBw/6Gadyx275g3A3kROlcCVijGLbXDNsbnj/5iP7sgsZlxnHD7eYFD155i35VxrtpOLt6KDrsuxumYY81gdun30fbBShLyJrF+gJjG+aCidI4185AQc6K4AW4Q4GrxZWUxCsig3MCruqo8OPEt//w93nltUcszy9o+pW0gZJFxy8GjNHYQgZQFhrn2Gw8+92OaRppm56+P2NKRhi5IeBajTMdw/6a7fYWpRQXVw9JOdM1K94+f8Djj3/A7e0z4jSgiexunnL54HUW63v0q0uuHlxxe7tj92LPi8cb7GLHa29fCpCOYQiwH2C/j0wBrLFYp2mdALE+wO7gGabKiA0MwyjjrshNWV2MaXKGNBL3L/jnv/k/8eHv/x+8+PRD9vsNq/NHvP+1X+TylXc5e/gW99/+Ev36PpvDyOgDxriy/pfoPpdOhhiIIRBSEOC3aahu28YYut4BUtAzTUfIiRBHYhxE2iTV+KQwFhP4QgBSBHIQjUE/7Yj+QJgGcmHWpiTgo3RHKJQSBrutz1/JW6zWM+R3zHmO4E5C5HyUmqSwrTVRKUATTWTShqZpaJ2ZfzeVteuo8yidTLokoDWfugNsnuS7d8yx7qS6J7lSWRt1qWDql/IoYC5e/kRZqLJPdZKHm2IEqYs506xFOxN45JhiPBJ0FssVbduikHlkGPZAlm7RDLE0rdwFs5DYMh9lA+JsilVy9RMAW6GwxlJhXJ1eNq07zQfqIUv8OZNyKuAsF2UGWJ2SIkIFbFP0BeRTc3Fpxl3TqXTXEaimgHXTNDFN03wPrTE0TTuDmDUHEA1RiYsFKKeYsEeR7PEe7ydC2d/kj1qkYsyWeVk/2DmLaVzxb0i0/8s/5vCrv4Z//fX5uavShMZYkViockvlOt25lgXYlPONJLQQm0rOVIvqut7AVCSmguAcqFLc1g1ts8C6DuPqdSifiVgMRRTFTohu0dB0HTGKrErwgWG/QQVbWKcCeCqlCGEklCKndMfM9JoZaPyx4VGIQLUAXQsx8zmVIlUqByR1zEKiIc8g8fH+HzEfNRd6FEVemj4thOQVA4fDgfHv/gcSQyUBYZf/26+TfaHrpczoA5k0S2j4KQg4WdjFWjuZz0oBgjrvKgoZzkpXKXJsbQsxtsdzQ+Q5Gle9HUped0r7zZnDfhADLyVze2csKY6USijGdJjuDLt4hFu8SnP2DrQrpFs1iKxG8JAiMQyEUaQI0rQlDNeE4QUhbFCMaB0xKhdsQjowVTqOxM/a/sqAsUobdJKWuPLKXPlNOWGswTmNturYwoXGoIUJ65a89vBN3nj1bd59933eePM9XCtaTqa0sRvinHSowjgxKmOs5vxsJYLrxjBOA36amKaRRb/irdfe4eLsAnLid7/5T9mNO7LLKAuVMTOfB8yDFwSUxVSdRspxCEe11h1VmSRkkwFklFQ0Qk7FmVmO2bmm6IJklM44Zzg7XwllOxfnyASLxRpTHOfK6JOlVWWyNqxX55gy+dXuBx8mmdC0Zhgngvcs+iUKxWG/B44aP8YKW7PppHVRqnSOftnR7H2pgOS7DwTIoFSQYyKMEyZrLs2axvTze37xez/gSd/xo3v3SGisro6QlpwUzjU4Z9HOSltdab/IyMPvJ08owt+oLG1ohcGC4qUKhYA3OYVSetHkklzloEgTRCXsyDiI3pLOEac1fdeQYywsoBHX6Jf16fn0h9/jtlfAF+TT9BKvRCtsez3x8dNnLFrLetly/3JJ37as112RFCjC8yqXJF6upQ8BFbNUS8eJg/fkhSNbgw4JFQLtBDolGiBGz3QQgKtF4f2EikE05ayl0DLnsbmmpYmiyHHvRxNf+70bUlBonY6VUZirrakEeX+yaAlKsVtlfvhu4nbj2R4SA5Zp7Nl7zWsP1pytNcvzC7wb+dHTDZubIAFdVnh1TrYC+oosCEy6x2tD5xruP3KEpxu2YybGUqTQJQvUFoxDmZdAcWuZsmWIikWG+5eG/ZiIZd6p878pLfoHlYUwWRaxxkKaZG4wTuaMaYrYJJ24IR15BDKpFw3ZnMFD8DAEcc2NQeahcT8wqD3GGHql6ZXhQHMyF2Ry1vhkmYIiJVj3Ha/fP+fx08BuO5HCgZCR+6LnXyMrGH0gbSTAv1i9Km12WkCYtPMSiBxL+y/hlsJAS0qcIa/3e1YLgwY6k+m0yIzMIX+twOYS/CGMrKyY3SWHYSjVTIWPie/92Yecny05Xy8YJykyOO3pneasM9zuPRFzRyf2CKSWFtWUUWk6grG6juO6EKtSs6ntVAV+VqkEMLIf8z//Y/LXf4r0y39L5ihtSkvJMfhNMaHskdmAEmaltqLhKcvW5y21f739v7plGAdp+6qskxxLUlfHZgEuo6oMVTHO8mHEhxFFLLlNCVrndtQ8B7DTOKG7FjMzQvIM+5+2loUUMUpkc0IIBO8JUfS8ZhZQFpaC9yPjYSClVMoPGZTFaoUrXQEhCCsnG2GPGmPKmJN22ZTFNMSTCCnhJ0/bWykKKRnpKkQadUBPE2lKdN2K/c0N45jJqmV1/zWytoXNK6w8rDABYvCMw57eWcbBQzbkDO1ihfctK9vT+wljNUEtyFqY99oswXboLK1lkYy2Dj8O7A8HDoNnsbqi6Vco25OVI0ZP9Dt57kJh7Y0TgzZYJ0nf5GMpzpYrrhUxlTwEw/r8CpVLG+A0sbm5QZmWrmvRRrHZbdHJo1WmbRzWtXSLc5ITU8lh2JMSvHjyKdPhBclvefaxYbnq6RZrlG6wTSftyWSiH/DDnpgUTb/EdR39+pLLR+9z8eAdmv4C3SxJ2jH5EX/YMexv2W0ek6Ytw+45L559xEc//C7kowZiTpndZqDvW5mTS0F+GEe2uwOTjzSuo+9bxikS0kDOCtd0jFPAWMT9GEmEnrz6iBfvfgXXtjRNZswBTQTTY7qFtGYi3RIacP2Ki8axulozqmdMTIKziKLOcSvPQohTYcNYjG3Q1uDI3Du75L3Lt3j7/pvsr0ecVSyurojZ4VQLJZFeXbREP6K1yDy0diQrxxiimMkaJxqRQWL0mOHi4Wso3ZKSKc9zIBTTF60a2uVD3v/GL/ODP1myvfmUGAfGcc9HnzxltfOcX1zxyts/RTYtm+tn7G+fk5Vjc/sDdFVmTIlpSoxDkKR2N7HfbjBMbK8f8/zTH7B5/CHvfvnrrC8fYhdnaNMQUqJfrLC24frFE77/3e/w+ptvsT6/pLEtOk/oLCZ6VbrAmPbIXEug9VC0y0WOTGuLtU7aZAtLpxp2aqWI44EnH/+QGDyXDxyq6IhWB+rKyAylCytMI23bcHF5yXUaefbkmikGFmcPSFnPhZ39YcM07vHjnt12y2p5TijdKq5puPfoHc7PHzANWw67W54+e8x9IySSYb9jHD3jdCBFjyXjpsQn392h2x636GnXa0I0tA00jRSpt3vPNCp8hNHDMCViUoyTn7UENWqW4sopYRVMww2ffPBHfPt3foPv/+Fv4K8fY7sV9979Cj//a/8xFw/fpV3do12c052fcxgG6ZgrRW31EtCWRJ9BcoUY0M5BFq3iafIorZlGaZn3MTCOA8l7Sca1sLanYUeYAjHI9S9NimLi5SeMHxh3G9GTDGL0JW3cJc6tJePa1VSKwaY4l1d/jpp/qjKelKJ0UxQZqVxkpIzkBLqiRtqAsaAESKpmk5mZUFZCRlVWR4kbi3IfSaWKA1Fh23l5rgC0qsXJu6Bq/T15SXId/VIydbd1npfkCeS4dCnMqQK+KnTJn9Wd982Er1yA0aaRs8pybcdxKvrbET9NVDmBXGNsihzAS+Nk/pRUinM5ls/JGKXnTpo52y9ayKEYPh3ZnoVNqI71LmFlljw+ZyEflbywSlPUWDcX9mxMhbQGKGXo+462bWisw1o7t3xLR4UQrnZ70eGNOtFbS9f38/UHiCEegbOy6eJnkpE29RgFfCJKh0LwE3EK+CkwDZMQufKRGFXjodNEpMZCSnHEQE5upY+R3eFASImQIlkrnLEknUgqoz8H3ZL7nutQLilQBiWa67VNX2IYK+dRPjgj+b5xLU27oGmXaNOAOkF1UmY4eIYhFA7HEaNQCBt+8hNhGvHTvnQ7aoyVImhK4htDLl1bWs/XQu7FaV5zfN6ORZM8Y12Un1Fb+nWFd1UpIEv7f33eZrJg0S6uf+qHG6MLeGqwxrHIpXBewPfNv/d3iSHQfvopF9/810KOKAz9zHG8zkemTCEVZMSsTborU4ooBIxdLpeE6GeAv8prHY9XiY60sQVvk26G03NadB1Rm6KXq+hci2ovQDdC/DMttPfR3X3ozgm2QaUEOZCTJ8eROO3I0y1+/4Lh9hmHww2aPZqA1uKlk+hpy/VSBmI+VmH+PwHG1qNVRc+tXmyjFX3bUoFNpSgtsobWtCzbJQ/O7/Pe21/k0YPXubx6wPnlQ5puVW66UMk1mqTmZw81M6WEEWO1YrnoMdbinBUm2TSSUsIYw3p1wS/+zC9xs33OB59+n2e7Z6AzRzm2PFcjMnWx4eRhyXfOdX545kf8uCmYKe/WHEHpspadVKSUaK3Y6uIoJ2eMFVZtnQBSAiVGWKlo39i2ZRqG0gplhKkyTTRNi3EWXR7UGPzclhlCwDoHGcI00bh2nnxyVsKSLQuOLrf0ZWK2RhZvfJRqio984eGb+IsH3Nb33Oy5f71huRvQbccP3zknVTOdYkogyXUiqUjSImFgtEycikzXWoJPhKlSyiO6JsF3goRMzv7odoy0pOUoKFqa9viD6L+kUIyKkscayGli3AcB7v0oY+y0UgrinFqKBwAxaciltV4ZYm7wyTAGx37QPL++gXLfm8bSt040b1FoIwujCoBLRB+JWoKxyRhpNwpeHuqUMCnRZgg5oZOMKVO+b11xfQYY4zxZLPYH3vveh5yv11hr2Z8ZPvpiD/9MAHdVWk1U1Hy67Ii6tAZn+PANwyFnRmcYGsehSzw/DEzZ4MyCFDNjhOmQ2I+Bm33E0xFnJnYiKVckIkrApWAzZrTJuIWj6xRn55C3nrgPxahKmLHSqmo5ZTBC1UEtBhETLBuNSuAzeIT5po1C/LSKNq0qsamCVkM2WiZWLTxKo2DRiDHC3lPav47Bk8oZsbSRlX6YAhM9IRQQPSeczTy8ctikmKK03FWAppoEZWDwke0h0TpDY8Xsyo8Nh2lHUkddKJQuxkFzwZftEHl6vUXnRAjSTtc6xSRG5fPMe3fU1hekrX8YM/sp0xQSrEaViroqYDzyL5lUgu1hSry43pIWLZ3TrFYLnt6ItEzKisOw4+Kil8UrB55fb3D2nMZZ+i6y2R6IiMnHUYx/Iid/UsTKUB1Ja/GnJEzykiKrVOahIwimSCiV0Icd+g//gPjsU/J46nJZ2piMKZI2x4A4k2XBPwl8QqgdHS9fxL/e/rK27BxP/sv/CubkKM/tayAM0d1yyYtX3kArW9gWoos6jvviXl/bD+uNLKt0+b6u5UejrhqzcIxNlCoSKWpOilPRgp2ddGFO/FJZV0OIfOH//F959L0/xjmHbbQY7sQgmo75KH0kmYQmKykQZWA8CMPTWiPMuiIroIt+ly7JfzXCCTkRxxGmAX+7Y/Rg2xX95b2idWYxxeiTnImFedI5MTew1uLaftZME511S0CRsMIUMRZlWrRtS8uZtPbv93t22z0+HNfcmKWoLp0XiaZdgDUE37Db3dIuekwjMhMaODs3xGnPNA6M0wHTtByTcGHJgUHpCMrTrRGjNJD510+o5AnTiDYW3Rbmi+2xnaazHdZoHAOtDfhRCi4hOnywaGvRxmKcguyJ08g0DJhmwfrqDRbn91icP+T8/hfo1w9mLdww7Bn2L5gOG6Zhgx9vCOOB3e6Gw7ADlWmabi7eZ6TtepoCOSuMlTHVtB1dUmgTUOgChKYy9iBNns3mFqWlI8qPUgzzOTGg6FKci7uzdp5kajI+cy5mQZmsMslEQowYa8HIyA8FjKhtqzmlgszIzwUoA4fj/uKK9x99gY6WZrWiXZyh7BKFQ2QmTCkAaFCWXDTQjXJUmY+cg7SFGoufIt5HvA+kVMCjLLqhMfoSixcTPqWx63vcf/srnB1eJ6WJOB0KiCaOzbthZLONHMZMpGF1/oAXz57ix4O0kSPrtiR3st7cv3fF1fkaZzNx94LbTxPfz56rR29y+eANLh++WeJ2jW0a1uf3uH//AcZogh9QMdI1HTGMoKWILJJJZr6GEgqJlFJW8tlKFc3F4h0RS3eOUgrTON750pdJKeDabgbJU5LE1FiLTiK9NXohLVRAxk+iSeqaDtctaPulFH58RBtFjIGuX6AUHA4HttsNTbfENp0QJbTCdJrWdZh+jWqXZC2AtFGhGAJRxkom+5FqyDWGRPCZqFuapkFZS8iKKSimmIlJUQ1icxYAtnWWbmUwThOj+An4GCFNPPng23z4zd/mR9/6v5hefEyzPOfhez/Nm9/4ZR5+8Wdo2jOadiW6tcPANI0nRKAfpzCFIm+Rs/xMaRnv1UtDATErQhDn+BCkLdkaS3Yt0TaM7KRFwxjIVuQDoi9ImydO+6OpT+nuqcAJKFSuGWOeAROti7RAWVRmXdSyMNX8q7Zwy36Oq1suc6a0usuX0oaMsBtLiHfMm/IxVqxTRv0/8+vqeCz5x6XqKqA7E5RmgPVE6zYf19tTALbe//r6j225fMB8jlk6DE90TCsbVhuDNUf9RzFW8gzjgWoEdNzpcZOCVa5XQOadQgiowGtGADRdBUs5xghyTatmp+AQNS9XSlr/6zxeTWqr5FzVWM0IG/DIoziCTvM1yuUzT+5XSoFpFAkNa06NSovhV2GDgszdMzv85A5L18PdLVUQmCyTVtlfKrIcuej8+jLfpEKOkpbyOwPjeCvVMYaavUhUxYaqvInET2qaMMNIY20Zc7IOzdqep59zOlRevsNlvCqSJDuoIg9TTU4LQTCe3LuccW5R5F+K1mzBVYwR5msmE0N5f6zSIWUiqYUDBRT9VJMzxqSXhl464kUlP8tl3ROMp+ZAef7Z6XOgFOgCauu61htmUP2ovVuLHievw/wcH3OhOteUTgurhRi00qK9m+D2K+CTkBDs0yc0P/qwzLM1tpa5q0ox1teMrdJvcpxaa4wSoqBJx2t/1MDNRxC9+K5Qx2N5Hqq2vFLFlK07x3YP0G6NbhZiAG4WZLMA3ZApRBw/kv2eNN6SDk+J03PisAG/weYRpUa0ShjAKgS8L2BsNeCjzGdavfzkHLe/EmDsLGStjjdeF7FbrRWua4lFB0ijMLph2Z5zsbrg3vl93nzlLb78/lc5P7vCdQuwDSGJ5oTOAsacOgofTWFSYSgnlDG0jcNYh9GGECOHZxMxCgPDGsc7b36Rr37pG/gU2U8jQ9wLMKWO06HiaFZUWW55bqMt53sKk7+8UMkbUIgWrrWFvp2PwtV1gBoNzhqsUcdqIwptDLUxPyeZeLVOM9sypUzTtoRJ3KaTMQzDgVwWLQn+ykAqbQRVVsFZ0Q2dxiIeT/1CTJXm5f8zIR4gCygaImk/sr7d8sb6PjfrixmMTQfParfjYjNgFz3XZ/cZ1ytC2+KNFV2X5EowJF9axPCKy2Om6yxTjqRJxP5VilQmXLpz4aUak2MgY+R6xYiOnhx8MeRSJUDWsxaVJpM8TJMwDHJOxPgy6F4X3WMFNyVpg5BJVIFyhGzw0TB4w/NbcbG2RtG3lkXrRcLAGLTR0h5uIJtIMqGATYoUIPpQ2j1UqVpnbEnedSxtHTkTgWgMUYsuaj5hxvYHxds/cOg3H/Hmn4L2A90QyTeOVKoZCsgms0sQymSTsiJvcmF3wfnWYEZDejERMvRL8D6xuh6IIaEPgXvbwHl2Jcmg6BvK83i6SjYmsmw1V2tHoxOXo+Z2r7jZZpE2qa0ZWpVuksh6f6y8aS1FHch4n1EOWqfQqQQ7SmFVxmloDLRGpgVjSvtbgly0cVMWW6hOKXpFMV3IhHzUXJRHPdGoRKtEc8hET0wOHzM5RkLKHLJCa0tv4ayN3O49Ph31nQwKcmCYIhsyjUl0VtM5y9RYDjsZT7UQpLVGZ+YWpoRijJHNfqI1FEOtxHrRsRszB5/leKic3jw/tgIWybc+ZXaDJ1jZf9s2jEPAl+BQpVzY5kX7GEOYPLv9QGugb3ratpH5JEsrb4jCOmgaQ4iWw2Fks5tYdBqRFUnoXKqlmdJ2OEEOMwhGBcRULnFInWvTfEako9FLnV8NEbW7RX/6I9Q3/5Bpf3unYEIJ/OZAEEoXemGDUBNcaofLPPf/9fZvabOWzd/7jz73Lc+BP/tLOZj/Z9vqW3/A1Xf+leinAVVaQ1gTR2fYOZQoAbPOVdcuSyu7a0TVSAuDQcanFC1jdCUByuQk0gA5iYFqihNaKZx1WNdgXY9zregdGotrWlrn6HtRFDdGS6GzaNyLMVpNMAwgReFTJlPwAT9OxJiFPelaAXJzYf7MupgtyjmiSTw9fELXNIUVI62sjQXPniHu2Ps9TnVY1aFV6YqYNcMzWUWSGSAFjAaVI1ENoEeCGaXF2EzY7MnakJtEthGrE0oPxCYRvGIcI2iPNXu0HsFokhUZhcDAGPY0vSKdZfyZYlwmBnuLCYEcMil6ht0Nh91z/Lgn+gMxiInUbXrGzt6wP4uERmOff4f2o5Hm5jmbZeDgwNiEMTJPdX3P1Cq8V0W/PnJoQRuPKnzOmzh6iCjLAAAgAElEQVTSTo52suQUGZZrRueEDVnaR09j7qq/SpnHa4Id48gUDgQCne3RRbM0JTmnmp3NLDy5mWKER6Y3S67aNY9W9zFe063Oafo12XRo1cz7AlVAyTI2U5xjghQzMQUporUtVWsQFMN+T8xKEiyty+caYgpElMT0rmd17w1yErPLHKTzLXiPnwb89Qt0e44JCaUtrcusL5+x394wHXZM40BKHqURkN5ZXn30kIurC7yf2N1u2IwHbre3bG9v2G+3KGXoVpcY16GNY7FccXl1n8NhK6xa62i6lXTo2IRWGa2l1X1ej5WawTelxLsgpxrvn6JlJfmzloevvYmfRkKKc3FWpovy++hjkbHECjllpimAtqwu7tMszrGuJUbpElI5opXBtg5jHMvVQXIjLe3yVQMX22Fsi+0WuG6BHw8lJkqk6ItPgiEVQMoaK+y+4Am7PdkGQgyopiGZlpQNMUmMoo3GIu3f1hisMZydN2Qyw5AZS8i3vXnGx9/9V3z8x7/P5uM/RevEw7ff562v/RJv//TfYnX5OgothoFKsd2OLzG1amvwccvpGMdXWZS5y6GMw1QzjAIIKrJIHjQtqWkZrCVnR41FhClWwK4UieEgQOzpfrXmmL+L9F0qXUlCfDF3jrQCTLWHJ8MMqlXmnCooagVVBHBTR4BlzuuOOeUc92fmOeJ4VPV863vVfPxHWbt6NBWEOYKHR4m/Yy45g7wn4OJnyxOok7/l+HQB3+q55pQLa7fmGaKHaYylaZqZqZdjbUsPQjypYGA5jkqPqAUZVcxhM4jecXme6v3Qcz5zPL6aG9c/9ZrM8et8HyVOFoZrlRw4diGKMZYEn5XBeZpvH/WkFdI5Jq/HGIkhzOdkS+G1AsrVqyQXycgc02de9zvyDCAAIxWAlXgiBAEeY4n1Q/BFR7mCiooKxKt6nU5B9zIu1MmYMLe35LMN6fxifs5yTiIfUvSb61xpjHQGnY6nzxw/J2O7Xv16DQDxrlTSgZhV1fA/4ikg84OJHca1M7vVWkvTNiItlIOQp4IuHYJuBuhS8GRTAcpyTBmMrc+ZKmB/nA9S4sNigJaLjj4FlJ3nsjyPtvl3ytqeAbSWIp/heP3nwVpjgvIcl6GaqXlWnsenXF/RaD3OnYpwdsFhscSHQExRsKPdhlBiVX04oA8joGjnwoB8hsix1IMSwzRDeaaySGqGWJi9WUzRYqzSnSUxy3fHaQgRImjXoN0ZevEAvXgd055h3QKMJRUCUM6Qi6RnHA/kYQPDM/LhY5J/AfEgJrVGoUzCkLFKumIlTJf5YL7WWeahz8sQ/0qAsVBp9vqI2BdR35gyUyx6Yygsjovmgq+///N88Qtf5pVXXmd9fgmlAl7ZWhWAsUbhjICxsQABszaIOkqUxxBEflIZmsZwbtZsd3uCj8Qgxr7GtPziz/4Kyi7wwfCdD/4laA9kae1DgAhhiZaFKMNsSlY2PYMWd5Z77kymWWG1wTUdumjE1skYhM3gnKZvS6t58hSailT5ggBzMUbGYaBtRHc1xSgsoK7DaI33nmkYRRNLa3KM0l6jNX3bUbWfrXPSMtm25Iw4K8uRUh+Y+m2mOgkffzyfZRbTK5XB+sQvfft7LNbn7NVxKDZeo7cRj+fwYsf9j3+T/Xtvs33tFcazcxIJ5RwKBzkTiolFVsXxt22wzhBDYUpmJKEsSpnxTutzngGbGIJonIVA2zSootOUUiJWxoIgf7IgB13amRWLxULMo09aN+DHdYUEtA1FF9bjQ2AKkYyi6zXt8h63uz37ceR6MzBsPqVzjsWiZ7lccnbe0TTSKq8shGzxMRNSFvawaxhKv5KeAmZKc6Cks4CxWll0VrMQvOKoV9T613j09D+Bp/Cf/f4B+A4AkfWPPbX3mO58/9qd7/Yvvfvl7//yNmcg2/rMRcYJFr1BG0UOMOWMUYrWwNLBuhXWLAaRComquJnWhV0W69aAMZlkElMUbdpYZ14yznlaHSAHmjSSDomIJFtaZQ4hc72NnPWai4VlmgI/ug7kmIvV3gRplPbTfWTYJt574z59k4htZu80IURizDND3hqLD0X/tCyqfb9g0SicEdFx0/Q8u9nzfDMw+gBUh3ABVuUMTh7crHh6vWXZOdaLlocPrvCfPGOcPIMXDcaLxZIUggRMxnDrpQXYaLAmcziMdF3PGA4M3tO2PZvdwIP7F1y4hqfdM25vb7m5FiM8ZxxWG7aHSRzmc0bl6djGTTnB6uSrMmRxXhfTvyMLluO7JUEiwne+Sf7d32YaD/hxFCmTupU5qkRkczKUAGJkGA6AwjaOxjQloD8JWsuccjqf/+Vtc1ryb+GzX97+ko7l5d2//LE1sTtJAn/Sbj7riD8vgPqLHlx++SUFuSRt1hga62ZTlnlprWwnbUX1vJihWOuoDBvrLK5xM6tOW2GnHhMai8YQEMDKWCvsA7Wic+eY4FlcXc4Gk03TYZuexjWkMMramDKmzDFS/xIzCkUtGhthsKGKu/kkRZqomEZhn0n3TcfZxRK0JWtbtPUCpMJesY6QwWjLjX7B/67+W/A/4fK68vWTNl2+Xo50u8/5HQXzktiUr7/Q9l3YIl+f/Bu83QFX5atsi9/8hyzK/7/zjb/o5x+3V5+f8cXrh1ht+PBnv86wOgNyWSMkjhHH5UCYhpJ0yhjIyLQaw4HD4Ra1yBgrAIbRYry2P+zIIZBCFJ3/rCV+JBUwW3N/teTCdZjRY5s1plmiXIcyDmM6IHE4HMRhXmuqgZoAfKJ5CFVvWTqibOtYrtfk0PHJjz5EmYb1xRXL1TnVH+H29paUEmcXF+SmRZkOpVsgkUyi6RUuJ7oUOX8QePXNL3L97BNePP+E3e0z3mzX7G6ecfv8MU8++h63NzdorVguFty7uuTVV19hsVpy/fwFzw5P2W23oA0vHj/mh9/7Lh9+8Gf87N/8VS4evI5drEtyCM+fPMFPA8v1Gtv0dP0ZpEAYB9rlCrS0hQupTtZzay3OOslVoujvZY6sZplXMjkh+ZI1mKzRhQlvrSvggcS4TdPTNAJGphhQOXPDDd3qHlcPH9Gt7xOmyHg4MB62ED3L8yu0NpjW8dob73I4jCjbiLFNyuLpUXwZcgZtOrpFI0CrHxgOW5bLJcYUmRWlabsF1ZU8Zthtb7l94cmux13cp20uMK4CfeCDgNHKGqwD1xiurzeEKHmX1pk/+eY/50/+4J/x/INvkcPA4vX3+KV//z/l/ttfRXUX5CxzbIoRH4WQ4qwTOY98lJA53Yy1x4JBkXgKMcg90EcZOWucaNdaix+iEGYMmLzGTwfG0RAnQ0CKzkEXIYyciCmQ4lF3tLJeRSv8mPflGofmKr1WIL5aFMvSCXFatJtNrGZgvhg7pShs9Hxsb4eM0WJOR7keBUKV3JKTfk5B/Mrnn7IPi1nqKdhWfkHWs2OeVMfu3bX5yJx9Gfg7ArV1B/UIj+c2r5kvabwrBc452rabjYt3416kT6oYLOqkWwBKL+4JMFyKhmU4pBLPV6Znzrms0aUIUTtuOALkVhviHJoWoLdoQNf8YQZE81GSIVUYN1dQWJ4lpfWca1bgWrpDRDqg/o5oaR/v9ThOJ54RotuqTWElpiNcfPf6qx+7J1UbN6TIYTjgp0nONYm5uB9GYoizji5KzQWCeVwck5b5elHAf1XGWPsH/wLz/DnTr/7anX0oRQHkYgF/E3GK6FYfx/7JkK3maFqb+ZkR5qIqnQLlepS8KOVIVcXQJ+bRkPHjHj+NKG1RtqPt1iyWZ2jdYp2jaTSuyDqSBRAfx8R+P7LfH8Svx5cflnGbT3RBsirhSApzjKoUglsk6XjORmMKtpDLa+RKHykjT53IeHB8AuudnE0QqeOceT4QyY5Uiv53cQ2Fmpn3ohtvpMM8RmIU/xsfPeGdd9m+8QY+iq5w+61v0n7728QY2ZUu7SqvIia0sq+27RFN0EwtDlltMEqTVCamyOQT4zhJXKKPo+qEB0fwiawaGneBW72FW79Obs9I1hA1qOSoPHSQLujoR9Lhmjw8Jx8+gfAJNg9kHYkqozFi2GkUTiusa4iJmUREFnm0kxH9E7e/ImCsKhU+Qeq1MgTKTW0cjelYuQVvvfIO7735JX7maz/H5eUjsnXELO0pRzdZSdBjzGJCUDRWFIhmiy6Odlm0VHJhAyilCgAi9H8/jTy4vOT59Ubcc73HNY7GLvj6l3+Bi7OHbG5ueLL708LI0yXpMcdFpFQp9El15+5Zn/47I7cCBqCxuqFzK9lXrourmrVf28bR922pJihxzg0T43aCFAuzWNM6CyRxXdWaoMQF1DWi94oKdMte2i/rn5zBT2IuYB3ZGMJuB4e9PGhNx+DD7NRZJ0tZKhKZqu143DKIMUWY0DGgUqK5WJdJ9zi5N87SFYBjHyb8MJG/9R2aH33C5dd+ima5Y3sZ8GcXLFbnovWrc+kAUiyXTnQ9y/m7doFuDDqLm+4UpzvXXmdhyzrnyNaRSpXKOCfV/5hoXEfbL1msl2hr2W12DNsNKct1tlbcqV9O9i8vrlgulvP3m+2OdhhmxndLi4+BYZr43gcfopU4SGpt0GYBNrMLkdtrT3z2BEOi7x1dZ1j0HVdXl+gEPk5MCbxyMrk0E0YHnJVFMk2BHCLStZ3xzkorfgJ3XKf+f7cpYNHC+Tn0TtPQsJ8ivozZtgU8WJ3oneKsV6yMVEAPAQ6hCJ8rMfqqmkUxKm6HgM4ZpzMqRnxIxBoIm8jz2w15YVl3mkdrR8yeaBRd1/LwrOP2RWK7uWU6KM5XDZ0OuOxLYUp4FiaPKETXL4WI399wtlSsLhwmLvjo8TNp1A+RlANn67W0aqYjI+bmdkNztWLRNYzbARjoXWbda7b7TMhzybOszDJ/xZxL0ift3DFGUvS0puH1h2vSJ9Lmm2JmGEaGccQoxbJvSWFicxtRfmTYGT59tmU3TKAkMOmalt3tyOZmiw+e7W7PG6884uKsw1lFTJ6ULR98+JjdfhRJhTtImbyQKzO4yBOoohV4bLqTuYEcyLtb0n//PzD4PWnak8Zh3s9pyFkLKpJnFJZSTWhK4KuNQZmq8adndjwAKfHGf/4fYndbQM3aY3WftZp/2kNwCuaeGiMomJMzpSXwzhzNEaRl/sj9XS6XhODFDCpU0w/RtSUrac29m/PIeZbA9JT1UhlNR/PE43aqgV4vXW2XyiqjtaHtJOG53Wxlba1rRM6EEE+q6i+bXR4TpznoK4FyLdhmpHU0BUku6nWaAUxKgVVpnHP0bc+r9x/yt//m3+ZsfYVWDYdhhORJ0RPjRJgOqLJmxSRFS62VtAqXK6y0BIJVRkllUDkWQ4IaS6sCjBTGRgiS+AeJIw7DwDSIRuyT19/mf/yv/xtA2I6L1Vqkg5oOpR1oK8xRRNZGTDRkjS6NrGjrWJ5dllGfAZHrSSVJrXGIch1N08+JCErTXXQsLu+jVCYmGPYDm+0tu8NA24+89tobBKTFWTTmBAhKJUnXRu51ysUERYlhoTWlYyIMPP70Y/p+QdstWK7OSBhy1lQDh2H3GJc8KEdWC7Reg2mxWuPy3XH319tfbEspMk0HDmFiGvektkMrTfA3+JTY+ZExjMQ4kYapoIAlATYCGMUYiHnEJs0+w9S12K7BtS1t14seoA5kpZgOA4yTxI9G8/DsAV958DZvnb2CzYb11WtsQwOpwWDEMA5orIakGA97XNOSi9SQdtW8NpdCXOmuiJAw2KbhtTffxU8iYRDLnKcULPoOaQ/1Ml9TzK9QoGQe9T4wDgO7zYaL8zVnr36Bi9e/iNaITJUXNvOnH/0x//p3f4NPf/hd0rjFh8jjJ49Z7Xt22w3DuMNHT28Vq6XF2cgH3/wdPvqz7/L+T/88b33hy1zce8jzJz/CH7a0TcP9ywt8nGitZtjvefHsGdlqrh6+huvP0E68AxonGoLTOMxafnXL5LJe1blVioW55h1F0qDvRSJpmgK73baYJRVt9Cxz8Gtvf4muX9Avljx5+phheyPmNcETw0gg0vUrjHbsNhv69fkxV7FWAPnivTADVxiU1TgjxnzDYY8p4GfX9yJdUhn8WtM6LQWgnJj2zwhhi2tX0PRk12EbzYKMD5LjPX/uCUnyvNFv+fCD7/Knf/R7PH3yQ0LOnL3+Ff7ef/EPuXrvF1Cmx48TVhuqa7lC07Y9OYpWocrxM2Nhqw3RpNn5WWuNrd2KFeRSYnCUs0ZlkdqwORBHT/QTnXVk7/HGkI3D+wO17qNVxiePMRKzVHMdlMYq0ctSgCumT1C6skpcUefS8tQfOyUKg3jWkS0AneQ9iRw8w+6WruswTYe1GoOZgSgBMvOJ0VONUZiZbPOmpMVeYpw/f96e4x0oY/rI4LyrJ/sZufPpa+rkuFAzQaa+JoWlEwBRGcbRcxhGUozzdVHWFOlC5jhIVtNc9im7FBUskS0zhbFntD2CrykJMeiE6Xrn2EuQohXkAo6ZDNXpnnKHnHNHGR8yPgRSkU6snQtV0u10HNaYqcaUd9vOVcEpjoDvNE3zNTUolC5mzGWs1zkEuLNfiRl18XOR+C4h5ue3NzdMk+iIWqeI3qKq1mwBf1OJTY2RTroKHt/ZdJ3bqnnbEVy9A/IXkK6OSUEgMm2RC5jld0pXgPhCHPeVS6FPQOwi5sxpgaIWA6VoQvWI0Aqti7SetpATRin2iL632e2wtsVajTUaayR+axuNsQrXOpI6w6RlKY4IUOmncDyx6oGhnWArtdtBC/YiHbuaHEN5jgI5a3IO5WrKXJdiwhcQXzRx67N8jL19rOSW0+srYH7tlEm1Q+Dlx7K8Xzq4bLneeWYQxxDwwTP6IGZuP/eLpHfe4+K3fmuWLhC5pSia20ny6hAiw1CGwrzOSbUyl/veNKKh3hTSoFKZMMVjLqcND979BbTqUHaNsuck05OyQ6fyDCEM5hAmgh/I05483aD9DcRbYtoJ3kPpbi3P2jRNOGtpnaMhCyO7aM2jRG4yf8a89vL2VwKMVShcYVrWFFpbg3MNy37Jmw/f4qff/zqPHrzOvYuHnF3cA9cQUypGVorGuQImlhulRVdIFWRaqjxHAWSqoVMZrrZWLpDGkcZYfA6crXuGcWI/TGKWoCKLtufV+6/yM1/9eX7rX3zMlAfIeW4jrFM5RTNL2v5Pzjdn9Gw2cVqBkG9UhrZp6duO1jn8NJTrVJaHUgFtG8ti0VGnVq0UScv/rXPzZ5vS9mitxSLAoc6QYkTHSJMCdoq4tiMWzV6jNYfbaxbLM6wxBCzKe9J4ELfdog+LorQcqZneTT4e7d37LECHRmOzxmLplBznqXumUroA54rGWBrVolPEHibsH30PnKV97z3Cq5nRdlzeu4TiMJqzwk+KIXj86KU1kYQuToRZvRzMKtAWrZGWSSDbjHUOH8TlVOmMbRdE5TiMCeU9IYn2akzibG1QdzQB66a1nSc7QFwVdxuGw1gSfUN1+ewXS8S0QVi6o/dMxekZQGnH5D3TZmKz1/S9xnaGReuYlCaZTNtZNptrAhGvEpOWiVs5AR9VNqAhaFlcUJmoM3+W/jvabkH/4B7n77/Hh1/7Cr9//z7P2xYbEr/wxz/i+c2B3SEyBsXq4gH7yaO1pesaXn2wZJoSnz7dsdlPWGt54+FajF+mwH6KXO8Dy75BaU2ImetdKnqvM4rBsSdLkM9GxzIJSzFi2cJZZ3BFH2fvM9v9QWRMgK6xrJY9SlsiiiErdAOdyjQKLBmjhEEiDusUxqwwcnaHiGfifNWJgU4GnwAlbICUsphWZEUOmkYnegO9npiKs3djFedtZsqWKURuh8TDi5772XOzG9HDBO2C3sGoBeg0StOvei72gdvdyDiN5X6NMvmX6uxmu6V1HY1VdK2hawxjiEUzr7Qrq1LNLI42u9HT7QeMShil8SFxGAPDGGYg8DhqZVJyGlqt0Bh8DKzWK4bDgevbLVZlyEkMNMri7L3nct2z6luWnSOctTx9/ITtZsKPjvtXF1zmVNj6SZwtM3gvDK2H9+/RaI8/jITSZhKSE41mUgnUqkPqUTNNkqpUqsG+FL8KA1yL9ET83d8hPPmEcNgSb59IhTlXjYEf32zjUEE0xsnCBrPWoYwUs7QRKRTRrc4EP5Ug/ngV8801cXNbAhSFKowACSjrPKdmXPl0fUiLJf6r3yiAZ57vSb0/mUzynvYPfk+MFOfEF8b9rjg/x7kghxKtbaUU2oeyOzWzY0wBF1G1Il+FIDIUMP6oa1UCV0oCaEyJFZMAOSlR2cihSKFoHyWZq8egFDrE08tVWi/LWlhZAfq4LuScib4YGkgmKEygEMsYqK28VaMpy1pnLGfLNRedZXVI5Be3ON3T9RoTA9F7MpEYIuM0CWuamnREiEdTrVq8rUY4tbtFFfkPpUCpI5xdwVjjpS08B0+cJtR2g5kmDOCGY8eA3BM96yjq8r02FmVsAfXFgdg1jbQry5EhmmZm1qtV2kj8oZU0rdSuIKMLA9dgdKazScBTnYkodtaRTUdIhu1uy+3zx0jiqIlWzIDE2F3Nz6QUCsA6ad9Oqejg+oT3kUW/oOkWGNsSgiS9FHmbmCLDfkvn5Nhk3gpoLe3Hn5XM/vX2b74praFf8vRLf4O0OiNbw6Qiu/EF2xSZVCTZhNJZCiKVCQOgEmmKoCJEYTvH3QHGCb0rLZitLfJJ0uqqrSEHI50BKfOwv2Klexrdom2Pac/IfpxNi5JuyDmI3n1OTOMgsWrbHJNo5WqQLEyTLDrMPiVSMlhrxTCumi5mYfpW0x2IJK+wrgNlCsNJkk5rDLoTIoLRmoyW9T2KYVgkEk1Lf/aIr3zjV3jnnfc5bJ5xuH3G9vop++0zpmHPdBiIPuAVTE66sbpGY9TIh9/9l1w/+5h3vvzTPHz0BlaJBqE2FqsMOSe6Rcd9+5Cnzz7lsL8FbWm1LaYovsSIBWSa5QaOyZ02hWWmFX3Xle4NWWuMkSIKCCtwuVyWOV/MTHLKhV1niCkxDCNaabpuIXJgWWQBlDHEaWRz/ZSPPvgulw9f4/zeq/TrS4xxbDZ7UhIdaOsaauVaGy1xsOuJQQxREql4Ldzih4OwTJXm7Owc1y1QymAzOOVJSvabwkTQDaiG0iJQsrXEOOzYPn/C9ccfcHj6ERrF1atf4L2f/RW6+18QRnTJEZQ1pCjjSEyQStlWqSK1UoGx+hCVcVJr1cCsR5wr04+ZOVegNoxpyLG0NmspHDRlnapGNVopstFgLW3TMgwFCFPS8isFKjWHALoc5/w5qowBVYEJ2Soopa3GWlPmamZSj8j9KWTKFZJKjhMpKEi6sJw5KYwe87Nj92oh7ZSrIusVM7uNWRfzZD7iLjAoQGwhM6FOsLjPBi3ugrQlajrelMKuk+JxvU7xZJ8ZMX+ru58B6lzDN0kIKuhnTIn9QOLqMqfULspT+QqJGeQaGF3m0CxhUWV5lls1M0/vHAOnRW4l51A0Z3U94HI/UomlNankcRKXzSxXOMEjTq/n8X5U8NIYO/+sGnGdoA0lnVczuKzmdYIZPJzHiFKQFU0juEQo3bi5GKTpSZPI2FCKsVqwETOTuU62EwO3zJF1bZ49pf3tf8r07/zKETQsJA9dzaky5Vzq+M2oQsBRWhepCi0MV+q1z3eO4DisVCkGipavxOwlOik5l3T7ChJT76cxCmdL+36Ja3xI+BzZbzNTJbxnZjknyVksRotEW0qF6Zoz/aLHWIl7/SheAmJwKkaMuWIcUkEogw+q/JAY2MrrFS+islELhsP8fNYRIv+mFItG8d2Ov7usd+ZnqQ6yVMaOUgZT2ExKG6zRBNuQtOHwN34JH2UM6c0tiz/6NqZtyu/J2qH1kbWfyxiOIeN9KJr6CaMMHg2No2l73GqBttUYXhHcQywWZToxXNOgVBKJmBQhiWFsjAOECRP+b+be7Ne2LEvv+s1uNXvv099zm4i4EZF9VmY6syqrcUFhG8mYHoSxMQ/w4hf4Fyz5zUII8WSJR178gBCSDTxRhSyBsBDGhYwLVxVVVFZFNpERkXHj3nNPt5u11ux4GHOuvc/NzIIyRsqVuhmn2WfvtWYz5hjf+MY3RlQeQEWSyWSji2SFAmNwShGiJnjPGD0hJELMUsEyJ6VAxT0W9iY+dHj9TICx4kPsuUwoi7UNx6sTnl485Rtf+Xm+9uVvcrQ6o2n7QmHOpRROkOjKIipvVzRYZoW/ufRJyrLKhiwLsGb55oMHJYslQdcZlHLiKEYJ+o2zrBYrvvT5r/KP/+Dvc7u7IsZJGmfWkoji0BaZswPdn/I9+/LXWf+p/FNkuqalbzqU0kxF86XqzCik/FcaPO1r6CrDyFkrTM08j6g0bypBLAridoMyDbYYJ8ZBDkXbkE3JyI0jqvMiYF0ypKpkYvMwoLuOqnl04LdQ2bUzwPbmdGcwaBosTaGfH5b31y7UOWcchk43hCxdos31HVNONF2PDok0RsbFsWTsq0MZRNNWyuZyMZT1DudTdx4zCkCrjGhfqQy27cgmoZ0AWm3XMU7CbiKJDENMpSSigCy1nPrwyrnOgFwx5WI8JkSwXoyNMVZKGWoztgLA6XkehbaffGCaSiJBZ8ag0BZikvJUo1tisiRs0fA5zJzn2UDEMg7aTzRXL3ltvwPP3qb7Yk/4BcXLr2t+7/0jPlktsVOg9x/x8hrudoohWE4ftSjbESM4ZxnfXaGy4qMXmqvbgclnbp+1hSGQCRmuNr5o+mpi1vzoJhBybbhV/1WPUvbpaQfWCljjQ2Th4LTTdFbEsjc+c3MHfhLHaNE3nJ0eoYwjYthGhU5yUJIgFwa1UqWCVYMtDlNMMKTMFCKrXhaqcGn0DHaGJKVyMUGKiphE4N2pTK+ldNBlWGhwreFuGximhE+waCzbzY7gI7utYrlsWLRFjiUEggaVPRZPzBMqZsie6oXkFNlsPY1LLDqHs4bjRRQWxbsAACAASURBVMvNZiAVaYIQxMknBZIPKNvgyWyGCaMyvdUMPrAZPLsploZaFKdF7FLWiYW1LFtD5zS7YcQazTYmttuJG6XpGwleG2sYp0jfGJaNobeZVkUWi5arnAletOa61uGsBC+T9+ToGceEjuKsnB4tyOOtgGPF0dwOQ2GcyvqXVZGLvcholYhZNHlV/S8J++oVereRPZo98Tu/h7p6hcuRlKY3wOd5eOefGaNmmRmR565lTmp+vYxXImWYpulBBl32eQFES4AgtmD/Gq0V4eKSbB212UB5EWm5Ijx7i7nUrtipet8ZIHjs42d4o9G7LeruDoWwRcl7zStddD1zBdCK5hz1XqojX4G9uRSTUmonbFelCsO4SNnknMkH5W0VfKkLKaVIUmF2lHOIIq+rJIjKcd80UJw9/yAoEr25/akSozTXUFmSr8pIM6ccZJxTEhZQrudvEtZI2zqW7YLj7pi+WTAOE6GwYazREnzWZlPKlLOh6GtrPe8Jkb5IUlIWpUQxl27HWlVgPkrJry4lllk2V05VM0065PpS1n0Y1Dw4Myi+CPvAXispV81F0w5r6+KUMS4Abi6VD+Sq9W5mkG272WBpMM7SOINJWzo90CiPUYmIIbcNWIOPmmEb2W3usLZBm4acFUY5RAqplKYpJXdcWmorhWiShlw01BVN22NtC9qSkkErh5BPkoDg40hjhQmrSvOLw9H4p3mNH42EW5mj/is9SivCTWD8eHzwOt1o+i/1P+Vd/smuNCR2HwhI1r7dYk/37vfw4UC8j/P33ec6zGIfTO/+aEca92jP4ssLlFXETWT4/r75oD22tM/b+XtjHM3yiOn5F0AJw2pHZJM8Him1mxulmP26q32qpATYiC2MSRqXRNG/yzGRksM4Kzr1cyepWiUGj48uWbgFzrTYpke7Hq1LqWMMEkgmYZmEGPHTICCRk67Isj8KeFMSsLOUTk6EgNiv8rzq4GvY21s/DVJ1ZMS/D2GaE0NGK0zXCYO9/HHKYqN9YbYb13L+6G3ujaVtF6xWJxjXc/vqY+IwkhHmOApCSEiX1UxjMjfXn3F3f4txjq7raJolXb+kWy4ZxsBut6Hpevplz2LoMc6W5jqQcxRJKi37rWoyy6jsfVl1cIRUUGyuKNASMFYcZq6AU2pO+FRtXmkSNNG4hkAiZ2EEuka0o3d319y9fsHd6084OTshx5EcJ3JqUEo0hKX3VMI1ndgnqp9t0dYJEJqiMK79xLC5ZRp3KAWtzaTkSzMcR6Oa0lxKNINzGHGqh2yQttkC/E+7NZu7K3Y3r/C7DcujCy7f+SJvf/EX0N0ZKct9aCNJK6WLAmhJtCutUbl0Q8/p4Oyh/J1GpTyvD/G1TQFgKBJ55Vw8jDFqTKclqWatNGWMRksS3miysWTToG2DZpjL/aUPht5PLOwPhfKfB8zH8gJVfOcq1WdMZfsJUz4jjWl1/Ueem0WmADFYjHbs2YRv7ivKnqw2otxU/b6MzyFMM8M6B/cLlHhg//3eudq/z+HDP4R+ZLXPWnrlAJoZoJkiv5XqLMoaz3vGqCR7KyBVQPNuQeMajHVY69DaEINU0OQ0iaRVHsvxHvZ7kMNn03OMcTgw+8fJb/xGznlx+dT8XhXwq4+tVamIOfDfqpbtjH+o/VhXxud+DOLDMUx5D/6X903kB0nw8sWDGP9wXmrfljpDGXlPY/csbts4qi6tiRpnipxSBf5KYujw3sQTk8/eu98Ktd1iP/wB6d33SE+eQdsiuGqtrFbzP8XDuanvq3gwrPN7z8+skJjxwWzl4oftxzzX16c8b4FavWW0NKS0VmOUkj1WfNOpEguoUkF63m9oyNqIrEMUhi8xYa2j7RqMM8QuMo0jMUxE7xmnSXTNo4DLmlLjVV3ytJcXqKSx2l/nMACqhIs6FofSHLNmdh2U+WX7WdtboYMr70dba4Mr92d0IhrD9N57UHRl890t4fZGEoA31+hpKkze/cypEpPllIrtEGKhsY6sHEl1YE+wiwuU2ftC2CM5B7RFaFlZGrUnD2mCNIl+b/SoHNApoIhklQ/OSJkjrfeYRSr4Ykb0zIkBUzGlgtu9KcHxk66fDTAW5kmNymBMR+dWvH35Ht/62jf5tT/9L6BUKTWgOCEx7PHLkp2qBy5QAiAJBrXRwrIpwaiu5Z6HTKbytXSElQPCNaI91bYCbt7c78hZmj056/j8+1/gnSfvET4euNuOYAQkLeEzSQl4+xAMRNB4aoYFCZySAK71yFi2HX3bscuqNIqJ88bPOdEqaeTTdw3i/ShQGW2kc3mKWf4mBXIIME3FOBp88Oxubzm+uMS2HaTIeH9DSBNmdYJtO5Sxor0h0acYE2MwXUeOkXGzRtuqnbI/aPa6H/N2nr/KiDNAypikaHA0CBhrDrhhjTa40gU4G0OfFUHJIeqNJgw77Icf0f7oM+zxD/jAtDz/0ldpjjuMdeUzEnq2uolMEk2e0rnyYDLEQSvrQjLjmmQa2q4TqQxjaDvL3c0d43Ytmrs5zA3EQoxsNtuiK/WQbVfLRup1e3eHHoaZvRbLOhZwwNK0nQDpSmGdpekaciodlUePMJDFiVPlQNuNnly0kEOeiMpJYy+VSSrOzLWkRNtI1rs4nXa75ex3fovp5Ck33/4W6Zvf4Pad5/h1FBYDEGPm//zehiF2eBxJNYw3mS9/4YTb2w139wOvrrc8PllycdIDiu99dM13P3rN8dJxfrLg6eUxZxeRH358RwJcZ1m0sB4PsmdakUvZolJS/v/otKF10qX2fjMxTp7rjWfZGFadw1lF37SohIAcShOyQmVFKkkXjYCoRHDUnxUDnwRH8rHIeihFjoYpQIlNgUyIAsKGCFOCyQuzYptgmxKPOsNRkxlGjx88yRoWzrLTmo0PXN1suDxZYK1h9JGb9cj52QJ73LPdDtzdrxmmzDDtMCqybBXbzVrsRD0cc+Z+u2PyO46XLc8uTrm8OGb0k3TwTYpx9LROk/2E321xSwGmd0Mk+MSia7i52zKGTBS0ZgZkpXFYgphpVy2nRwtOlg339xs+fb1lGCamkLi7H1hcHHO86HHG8mq65fHZEWm4Z7wbGHNmdXJayqgsWju2mx3HRw1GQWfAHK+4utmgdMIZxcJmNtsIGFLSDD5ydXNPLCIzqjo6xUVTKYvdGycpLcxycJID7nf+Eer732MYtmzXNxitWC6XHB2dcHUlJTI5V+egAKUHzqVWqRzAqrAkSkO8JPpLklFVM0MhRim/enPvV48v5cp2Kc5qsTnj13+edHK6f/0By4SMNCafnew0O/1ZKTAO/0v/DCMZ870/xF2/Rsc3Pj+BtqbYIHHCl8slkxcJg1TY5IcSCQK86upV7gMu9qWK2QdhDaeICl6Az5SLFrqCWJtG6iK5ksle7qEysWbXvgQeOUVqR1ldnK1UbGdMCT8GAYhKJsXYhMqO5AWcFC3uhDayUHISredl+4hVf8SiO2K5PGLwIz54MsJ4ZppmNoh2LWoqTbPKuIt8kjTXUVkREQBRRLzEmTUKKVvyE+OwxVqHLRrtlakQQygstzg3pDElEfhwwdS5q86N7MkYJVhWMWBCQBVAXNsGYwVM3g0DPsRSxqiwjcUoqRgiZ4b7a/rVMaq1oqM9XKHimshEzIkpWVT3GJLFYjlZttyvBykj1pYYxZBaZ0un4OLyz48gJYrDbiJli9IO2y7Q2iG9Zo3cr+sRKamJmAZCVGTdo22PbVqy7eZgB4oOns/z1niwxYxC2T/eyT287v7+Het/vEY5xbt//V2UVgzfG3j5d17KE5TPseeW53/t+R4k+P9wpUl8u+nTiRd/6wUAl3/lkqNfPpJnmzLXf/ea3R/uUEaRfebZf/iM7v1OdMunzMv/+iXhWkDk7DPP/9pz7Kmd31M18vPln1ry+N9/TJ4yygnI2JtHtP2SXY7s/MB99EymlGZF2Y+R4pfOQQ+QFMY0aBLaRKIPwkMsQEAuLMq82wmgpRRmjOgoFRhOt7z16G2OuxVds6Dpj1CmpekKEBcjIU5F9zwQg8jeBGewwUtyBLHFwt4qNlQlCbyK/zWNY0nElEA5JazWReddyiun7T3kLD0YXMu0W8PcyMdgtJNEitqzxZyB4W7CD1sUkYjhk0+v0Dnw3vuf563Pf43vf+d3ePnRH3Hz2Yc0mllD2fvIdjfQth05Bbb3O777f/0f3N5f8wu//Gd49PQJpxfnvHzxis8+e0HbLbi4fMLFo8fYZoE2HQnNOI10jbBMU9ZMQUAbcpyfX0CCDMgZNE4DtYN5IqGbjmncUtl+KXoBQ0BYStYWllQ19ZnlcsnNzVh+71DKEuLE3c01r1++IEfPo8tzlNP4aSBmxWLZC8g/jcRhou97KJVPAlImtBYfORUA0DqRltPZY3Jgff2CpDTGtXT9EYvlBd1SdB1DGhm2E63tMKpF05FUT4wj4/o129uXTNt7YjI8fe+rvPOFb3D65H2M6Wa2mCqSO8YolE5Qmu4qrUWGKkVhN6mHJfhaKZKiVEdAFSNURV9eI7JONRbNucSoYYKyJpCWrFKRZaDRkK0h5oaUq56x+ABzNQpVzqiyd/cJhjdBEzlvMoqELUDsDHYh290U5qDOhT2YksQb5JLAj0yDwugVykrsXFm1iZLkhf19FZ8GanVLYadSqhCr9ICSezTGHNhUNZdM1++rh1efawYFD8ySOrBR1ZPYF9fl4irX/iqZ2ueDMqb1c5RSkFQ5k1q0bdGu5/TRM07OzmkaYdL7aWR3f48f7vDjHX5YQ8gkhNEvWcfqu9X7quOupRIvV3pWuevKYpxHTyoTDoFU5rvOc/MfqzUpVha0LgzQmqgpVZAHfkTVT63g7UwGKId2iDVhruY1VPGRWkFafcR6qQPi2+FVsQkf45wwL+ITKDI6BXSScn3VNIJRUABAU/bSQdVqqoFJWQezBAagQqT/n/8nhj//L5EePwEj4FwFQZ2RNf0A/K++fs5FykHcOFX73ZAf+uD7ZfggOaBzIWrMz01ZTzJuRhXJyyz/rLZ0jUMKguT9Q0wM4yiVgTkjsjl1P9f5FqOVkyRRp3Gi7Rr6rqXrG6ZJfHg/BTbbgbvbG5GB1BZMRMeJiCLFqeABRcu00HFTlWQ5AGOhAI+oufneHrB+OOt1uxUUV2Z5RrjfcNYOx6/4o0aLXEvrGumd4z2Ta1j/6j+LD57+N/8B9tMfARFdqvzmdWo0KatCIDSQFK5bYppjTHuK6h9hlk9QdjHfrW360gPN4LOWOGbakOMOFQdIgySmChlD6bokSgWGdqRSfa0AbSzGatquK3FKbTi97xE1C3VWU/QTfNh6/cyAsULvt1jT03XPOT95xvO3vsQX3vsGi/6IsW5cFCTRgrNWUG9VMuaxAio1I2GE6owSbZ10EKwe0vkPL1OyxolUyuchqYxSibOFYTdFfBoJMdB1Ld/48je4v33F+vYa1zh0VrhSmp5IpDwS4rivYQFhIdVEFUBUmCTOpgJarTk/PqE9XrFRotdG1aSJov+26BzLvqFvHeRDfRF50/H+Bktp7NG3bG+u8H7EdD1tv8Q8fozuOtFvCwmzWBLGrTR5QhEyKGMJPsAwkk0DrsEuFqRpIt7fkzY7tG3n7ISzFqOkdEIhYGDBIA4mOgtIoAzOGow2BSjYX1VYWykNCWxKDMPAkCLJ6PI3mTBNxKsrPvd3f4NP1hsWX/oKT995jtGQkifnwr6qxrhS3Q6AXzGgsk60tsV5tFjX0i+WxChU+Ol6TfITJoPSihgzXduCkq6qk5dDzdwbDruNJM1BR1FI04gOoej+aqwr3UcKgzZ5z3a3Y5omxnFEKVO6MrY0TcfZ+YV0YyyZuNubW46PV2x3W0KKtG2Laxoa1yN6LZFpGgjjIMA8sn4imePf/z2a11d8+G/+FfrulOWTZ/THl2w44jt/9An370Y4hYzmWr0lNP3i2GzGzIurkdWy4dGi4eq15/w003aG4+g4PW54eZuZcmZSgWxHLND1LethYn235fLRMeHVxBANSQm7xmmNNbmU1GcIgaaxdI2mUQ2vNpCCIipFyKK11HctWitGH4hotlPCuYSxGlt9L1lKhAJmZ6R8qWprO1dKZjRgO6YMruBfYUqsRxijwidFgFLKCCoppqw5yomz3qGzaPyOAbTyHK8crjF89MkVvZUOkUYrhjHw6vWGJ49WOLsg58TdZ/c8vTiltZkcBz4Zt0zRlzOyuGzKMPrA/Wag0bc8fXzConMMPjBuI6rJjEHAMteUhj8JxpzZ+cT9bkdEuhmLl1UUnuO+DESR+ezlDXc3dzRWs9lu8VljnWXRd4y7gclHln3LolU4bbh69RqbdzQGurYhhInz0xXXt1teXd9yPzZoc4ZGGKyLxZJGZ+Lk2W4nPnh1RYhexPNRoAxGt6JWlA8OuCylMjFJE4Xuv/sN3G6DihN+vGe3ueFu2ol23ewtwWazYbPZPLD5Pw1mUQ50o8hWg9VklYilc+7c3Xu25+I8vdmoT2fN2fEZ2hju7+6p5T3p+bv4b/+yWIjDjHQWp1sjDmILLBK0KeEytLqwdrQmoJgQhtsuJqbnn8efP8b9D78OJSuvsjBe4m5krg9RimG3LffHAZumsKm0Fke6OOgUyRtC3Ac9xohUFdVv3W+inCVgUymjcwGzQxQGaUiFwZrQRRahjqFWSgBVidgoxNAZUCBnLIUbXRzJnDNp8uVZisP+RhM1bSzHRyf0/YKoNHe7HVu/o+k6uq5j2R+J7SejjUJ3PT5F4iR65+I0KkSDK80BZTYC3saUSmmzKhqXWphaSlFZsTNwxR64d87hs6wlrfcuWO3yrJQ0G43TRDIFcJGMLNv1mvXdPWdn59jFEgXE6NkOntXZBV0n8gML68k6Y2xlDmQuH1+yWJ3ROo1OW26vP2Uz3kqywLacPHoHlRtUSJAGbJw4Ozsi2x5wEgQqiNlAtuhsMMqz3W6YfCBGhXMd3eoclCUlRQgZn6TCwxiHdj2JGig5mmbJW+99BW0MCTkHxGkeCdOIn0bI8OF//CFp+HFZkaNfOuLyL1/+lJ3849ejv/SIR//2I/mmxGDLby1Z/inRdf/4P/uY6ZPpp/z1P9n18d/8GP/a/0QwmQgf/kfybMtvLnn0Fx/xg7/xA370n/+I41875vTPnvLhf/IhRDj7F89YfG3Bx3/zY374n/6QR3/pEe7CgYF3//q7vPyvCqA8Zn7wN37As//gGVffeMLvnn2T9XjHHZ5JZ2LLjE3kKBVmOUlwUUFWciYME7pEnZlavVYew2pMo6XvQAluYwhMfoQQWdqey+6c8+WKuPMMDNgukrOm61cFjBV9Uesk6lHZcX5+Ttf3+KjEZ8+5xtB7nxCAfRI9TVKlpKJm2g784Du/z5PHFyxPL7B9L3582xCmAZUircpsbl8xru/pFwuOT8+gX3D78kdY5+gWK5r+GD/s+M5v/++8fPERbz1/h1/75/8Cp4+e8PrqJdevX3J58Zgv/tK/yunT7/L93/tNPvnuPwKfsCVeCCnwyWcvCcGTUsRPW8bpnvvXn/LOu1/gm9/+VS7f/gKrRccwjrz45COevf02m/V6DsxTTNwEaYyjjGGxPMI2R/hSmiqVgS277ViCVKms0loRcybEwLC7Z1pfSUNja8A47tYbtG1o+yOOTy8YBvEzjLW0bYdSlrZdzqQAlEYT6YrtHDaGzjXcbe4Ypxtc23N88Raro+M9+JofltRLdUaVwzDiQyxWuMUowF3ypDAxTVvCtCX5Hb3ryI3Io1ilOF+K9v4URuz0mrCZMCji3Y/Y3n7KenvH6dvv885XvsXTd95nsWxEs08xJwLREufpXMrZo6xqXc4fZQ22VOfVq4I35TvZZ5kHevDGGPGtq2wSURr/ICWuMeQZLNPK0thGYgptSdoxoTBOZGDqeQMF8Dhg6s73VW7IlHhJYtqAVaYQaovtD/VYKkBsYSHMYkQREhFtRLrCkNAEIS/JzgNVJRJ+3Iw9lA4oPkUdrPK7eubPzZQKcLPfz/mN99u/508GMB5yToWdWIBLFanSb3IUqwKOFsRWWQEUrcW2C548/ypnj9+h6Y/IytA1PUenSxKZzXrDh3/0fcYhECcvzLnSKLYGFunBjaiDb3T9YXmuui/kebU2UmmT9+Sgh0C7vE6VYbRGCXCoMvgqFbUHEqUyppTD+1CkzuxMFthru+5B38Y0VHmDSjCoMkyVDa2VyEBWBm09Iw51aq21WCtJWm0t4zgyBT/ry2sWqCz63eM4Mmx3TMOEnybC5CXBfTBWsmaqxKL4hLpU51L8KaUUJ//L38N/+asMv/iLgFSeCllBU+Um5nmfB7n673LOJSWVUqhDGPvhmpS8Q9EdLtNa2bbS1HKBcx2u6XDOYZ1B24TOgRQL6Bp1scGKxhm0avFW5mrGKAS2FkkpJfIxTdNKwjJlfJDKwuXSsVgawiTNNpXtiUmj9T3ej8ToSUF6DujYkEpPBJMnSRoVACon+e9+z2UZl4qXqENU6eF1+PODFETxF97YtPX9ymBqu2/4DhnbanrSTKLcbdesf+2f436aCLsdp7/x66VCWPaIkA4kWWyblnaxYnH+eXT3CNUco1wPthNguq4n46CApjnsSH5H8ltU9miiJJ3LrR4mfJSxaNWSkydmi5+EnOFcpmsdfu6dVAgcNQaogR0K7Upcpn/SSMr1MwHGZiDqDtecsTh6Tnf88zQnz/DdObfjMREpL6ragCl5yYCYoseZM9M4Uqw7wIMMS10Xxhhqx7g3gdhqnOYgOxe0JZdGOiS0jqhGEVIi5IhOnsvVknfOHqPHkaOjI5arJX3bi+HTmrazXG9e850n73FTPywodCjaqdqwajoW7YJFv+Dk+IQ8jZyvVoxaynxQppTG5/mg67uWrnHC3qu1MweHtrVOtIKsRWlD0/WkyaNjwmrDME2YIEBvzgmfUumMWkqgtEb1CzG2ZKnLNppoLaqIwlfmasqaGBVRK0LOxINynnx4GCEafp1rWDaKJyVTLuUi+/kqFcfzhnbasGg7XMoEMutpZIojvjSLyTny6Ld/i+Unn7F4633ufvWb0lSp7Kz5XkoJnTUHy74GH6qU2WnJmMeQGKdQsAbR+8sxoEiln4Q0Q6Cwmxpni3bPm6vbsm/NzL7EFjGIKtfGNPuDI8eEVYZkHJU5Nu4GtpsdSmuatmG5WNH3Pa4RpjPIGVG7Vse2x1mHsYamXWBtMx9kKSae/sEfMT75PLuf+0WOz86Bht1guPnRlruPrnh91zOFajAVSXcPUOWM4vVtwLmWxZGlcYHbuxFX9HGePT5iUhP3A9wOmnQb+OKznl45tNGMYWSYAn1vyJNiiAlnDUedouYIQbOZkhi9RtM4zbK17AoQspsCjTU0jaMxBmUDuzHOJSpyLuS9dS0lGbU86/AkEUeksF+TwkcwKQnQoxONVkwTxPL7VMAWyIQceb2eOOoUzin6VrPejOSFIeWA95Gub7nfjpwddZysWrwPrNc7dtsJZzVt09DYxDRuabSlbxznZ2e8ur4SxnTT0jaG6+tXBJ8Zp8DrG8/jRye0ztBZ2DCRk8YDxjQ0TUuMBXQuXZXJCBBLBbXkdwLG7n8ek3Rl1irQN47LRU8IgXGacNZw9fqGWyPsPq0U6/WGJxdHHC+FyZzItM4SYmQ3Tow+sdtFEa7XivV6y3a7ZZwmvA/4kMkYktqXw6W87whKloylTh7zwQeYD74LJPL1x+yGrXS9DAMxlkZaNRagOLhZPQhoDrn7P+YEWgNOtOV0Y8WGOiuOaM2wpzS/j1Lsm2TNH5DYbLaAwnsPOTN+/VvEJ88EvJvHWpZlg2aVDV1W9FlxguYoKxpKw/gS2OasiSiCVowKdkTuUuSm11z96p9D/cP/lTjuqI5W45wEUSkTvN9Xiyg1O7ehgPdaG1QIUlEAUJg1OVZ9dQFNiXtmqyrgK/PZVP6veGoS8iWR0ahpc5OkBCzL3CTxtQWcoW7XEmxVfyYlDjXEpBWxelBxgs6oWsmtFEerI6yxUhYa12RgFyKv+yWrtuf03SNya5mmkRBko2hjsa5BWFwSrMeQRXcux8IHqk+/ZxXmlMlKY5tuZiOlLIFRzNKlO8OsY9Y0aq+5Wy4/eXZbWTPGtWRl0CV4295dsdvscM5xfLRge3sN99e0iyXt4ojW9TRa0zSZxno6teX29ppuuZRyYePQy5Z+aWmdQaeGcXVKc/6Iu/sN2yGSm8dk3UIcyHEEv2ax7IimJSmIRuNDJOcASZMwjCERU4MyUtGhTUtWjQDNqlTWxBq4ljGDwoZxRds2kLWuu4mcRA8tTgPZF/mAKP/ad1vO/5XzeczM8X78Xv7tl/irfSL08b/3GHtkmT6bePXfvOLwUkbx9K8+BStnMnuM75/6dfnvXpJ9xl95Xv2dVz/2+xwPjFV9nBIrAqVZCIXZp37i71/8rRdMLyZQ8OK/eMHTv/oU98Thc+Q+T2xNItiiT6mAkAg+krywjnPMZFO7SAMZjJKy+xp8S6KMPeO7nKsCtIgNcMahIhw3S55fvM3lyRMmdtimp+l7ue28b8YiDS+FnBBDxIdJEkKmoXZQjrWyIO8JFLOmZUpUqQ7IxLjjfv0ZJyctXTrB5HJW2w4tJQ3ElFgcnbC9vebVpx9x9eKHvP+lr7I6WmJsi2s6mrbj04+/x7i9p3GGx0+f4rNmdfaYZnHCycVTRj+ibMvFO1/m6PSSt7/wc3zw2/8bV5/+gPubzxjGHTmrUqra0FhLToHx7pqPv/cHbDf3vPfll7z1zuc4OzvFND3eD1ijpEFjkFL/tunE/ihhVvnhDu0cWWWGcaBfWJrGFZsp+2iaBpQSbWhyom07bl9/ynZ9i9KKx0/fYQqeYbsGpVksT6QhYgz4cSTbRAhSIioVd+Lv98tjLp8+5+LRBU23YLq6ZbvdsiQxDWvQU0H+NDHGWQuST/oJOwAAIABJREFULJq+zrVkDDlZmkYSYcvjc1bHpzgjGvCbzTXDsGaatqx3N4zJy5y4Hmdb/DiQU8TmyEpHQlI8XjnMW5dcHC24vrri4mxJ3ygaseBiT1GlcbM6SJ4mjKkyCMzI30Pwtfy8YhX7L2YAXH6dMVoRk2acJqIvSdqUCrApc1OLsY1VGFOqOo3I/ihjSyWlxJ7VLlRADg48lTK2WqlZdqC+94PC4X1ukCoFVGFWOdalgZowvWzR0ZWz+7B1Z8o1mtuzDR8koA/0TiuIVwHhfZOgcndqz9idH/InXD8ZiN3HS1Vrfp6TihApZid/1pJWct5q22JMg2l6uqMLHj//Akfnj8gY1nc7xjESX28JwbMb1sJYlW5b5GTIucGnsawXDgAr8Q201sS9UK0w6dR+zcjP9gCtVqLXfihvUQHUQ0d2P3bC3I8+iFtbYh1TEujGWJxLOOdKgU09cx+C5of3cgjQHoKuKUusFUKYQe96n5k8JyPUwZxUn0aAcWY94JQyKINrWkDA4egdYfIMuwEfwgG4XPECPUtZzPiOgqxUaZpagWO935oc4OJFhrH6XfW+6lUJfPXSJRk+jwWF2avq/Kh5/Kqef9P2NI1IMVnX4JzFOIs2RcNW5wLZS4IqxiIXkitLXuKBXMesxGoasI1UZZMVU6mGGofIq1c7mkZjijRm12m6JwuuryLrdWa7CeX5RWbGFFnO4FWxzVX+7TCm339VpdNUbQI7z8h+ctR+OPYY1MG7qLo2UcXGHNib8kr52UEcZhBt7aalX50wjhO77Qb+5X+dEALNp5+y+OD7UumqGkyptDL9GWb1HJqVVFi5FmfcA7KD956825HiSEojKo7YPElcSW0QOm+KPTNYSWWYbpasTi5JfiHyBjmJ3XWmaDhLhY/ShYFMPUsyIezPlZ92/UyAsWCw/XPc4jnm+EuEo2+w6065zZarQdgSuui1VeLvTKlXRTsCimO475CX0sPXWmNKefJPA2P3LCyqRkZOBwdjwGmDJmFzIOfA+dLxtfff5f3HF5yfX9D1PV3bzECxax0ffPR9ro73AcTjk0ecT7DqFxwtVpyvjlj2C5b9ktOTY65evGAcB14pV3aosGpy2rOvuraTQFspKsn2IL4XAMGUroHKSGdEIxIMaEUKnpgV2QjIoKwTvVLXkooxNr1ks9BafqconU+L7kYIxKTxCaaoMFbjo+iDpvxw4x5+qQGrFO2csDrQS4GSyRTbOwexaKwWj8IWXdeURPPMJc3i5prWA7tAaBR85XPYRYc1D6EWVXVSHjgrRbC+lMDW7E7VGaZoJ1Z2kqJoeJELQTXPjsiPuRSmEee0XFqbwrhKBTgQILgeYnOXVyUHUSrrNUYpdQ2l5KRpGpokgU/VedSqGgVhuyhqCQRzMyeTMkcvXpG7BeH8KeHRJVk1DKNmmAzbqLmbYJsWpUS8zEnpuns4k2NIrHdJNEx7x24XSI2i7Synxx2boJheBbYe1mNmSpnjzrDqHWPIvN5GrJHyDZulPHzhpMxDIc88BMUYMyZCZxWd08QkIF/Muc6GBP9WoUMVki/3TT0U5OAzNTl+8BqSOJo+whhhzJIMMAkaEss2sTAKrxI+ZUZfADiFlALGwCZF7reeVaPpWsswetY7AVqttZwdNWw325kZ2LWG+/vE/XpH1zoaZ+idwk8DXjs627Jc9KzXDucsXWtpnOJeJWkcFyNDjKy3W4xWdK2wh3c+ECmlYFqkRvw4iRh8OfFrFo+yxwoRir0GVTF3KaN14nix5OK4xXvNboRhiNzsNqSsMc6y6BrWaRJx+gCL3qGixzWW5aJhtWuZ7nbSjC4pIBKniWGQcvlYdYw42KslUDq0xYaI+d4foT74Q/KH3yelQPSDaJ1FAXDybA3rbszsd/uhM1psgVLyOQcgMLrYAytZfu2clA/PAP/emZ3diId4bllPgdwvCc/eATLxyTPS0fGc4dVJmkw1WXGiDOfKslCKRVasUqZH9oUBTOkcmpU0aUxJEZRiRLHUms5ppstn3L/9LvnTj+HupjgUB8FwjKJxV4I2lGgZzTrgKs7AqmyYYh9ThSDL+6BRc3KwPHhZW/vx2Lu8mTxXpSilio2rTpr8qdFGpFuKrhZKnEz5snTwRT+YWkVlGtWpzvv4VUHXdMJcLVIykIkhsr6/4fZmQXz2BOca0Z2swLix6APmizZWuueWBlj7V5a9lOp6qzZcAqhUNIODD+zGHX5m+R0kO5V6AOCHEJj8hEJJFr9U6eiSKJomj3ENtukYNgNx3AmTyTZ03YLd7SuimYjGk11guL+lsyNKtSjdYPMROoquVs6BbFqGqNhMls2YabeRlLcYPFZFOuOk0YERndgcxPn0UeRKpuxJqKLvaAU805aUNVZZOc9UIuepjElCpTTLfMgXZtaEZC7xisQwkfxIDg+1XCuoCbD46gJ7Ykk+sf6tNds/2GIWBnfp2Pz2hvU/XLP4uQWqUcIgBXYf7AhXAWXVjwUjf9wVN5HN724A6L/Q4x65/1d/B9C918na6vX/wyv/5Jc5Mhz9yhEA4Vqa87lHju4LHUorPImYPaPWRK1KgiCTfCRMkeQTOSQ5A0sTDVXWvW1bqSgpCVw/TnLezaahoh61xNXSuA6bNEdtz6PjC5zpUYsG1x7TdEukaVv15ct4VEDXWGGepYy2pfQ2Z0LwAtiaLPviMMjTsmdVFl1BYx0nZ2e0iwXGisxBjCKtoY0VG5EzTbdksTpi2Nxyf/2K61cvuHj7fWyzKNIMitdXL2m6lqPTFauTc4bR41yPaXtaZYjrW7RtBGhterCG3c5jmiWYluHT76HSVFhphq7riHEgxsi4veOzjz0xaVROPH7rPc4un0lyQtVyboN1Ddo4LKXcH/BhwCpJ6jdNO8c7qoBqtgChtWxXA7npGIaR61ef4f2OnCKr00u6pYPiz+aQyTHgYyRM0lHalKY4MmcZ4xra5REpSBCcyxnadg2kwDBNKC0JrXEYUFkaDpIzTbcqGpyarEUmznuPtQ7nHE3jBIjQBtP0NNOGaRjnIDfgyTGJbYjFBiwWTD7y+GzF8WrBGC+4OlmAbbEuYfNADDuUc2WdaGGtplrNkgSYQJrlpBT3slCH1xtgmio/Skqjix+qDsgY1maStiXMVzN4RU3mFlILpSlMVpQYxArxKIlfL9WZav74eh5WZEPXShgF5VQHKthX/ZUDsYODuEwXP7uyauv38vfMzMcHSVDUA5tZY+kH4F6BhN8sfz8EuR6UPOeHXtrhGD/43DroB7998D6qlklLhUoFYVVtElySn9Y1aNtiXYs2Dh8y05QxztAtFqisCVOQ8u6YcU1L6pZYoyB1WKXg9acM69eE6ItvVEqX67yUkjRZYwcjVuapVuaqvGcm5rT3y8uwyLuW95QTU6r3pAF4mu2gOhiDw3GOmTnx8NMIaD/xyvsZSTkXrVFhwebSeyRTJTty+VqJrx7CzAJ8kwk9g/llLhTi56WcwUtF85v3J7Fb8T+rHrkSdqXSBnO/pvnoh/jnnyOmQIgBE43omBeQ7UFfBmqCIu/9zfLznEslcpkTU/COeTZ0hlTvX+ycsGFbTCE/WVuAWGMPwF2qB72PtajgvaLyR1L1qQ+YuznJzGulicUPnSaxx0pFlJLKLudKgkXt95rSBrKsfUXa7zOlSmyV57iPh8tjXovz/i6/zyVuOOyFU8klD3exrJL9eqw+f7m3+vo31qHWSsgDFqwNWNviFyv8NKH7I3BLFIbl6y0mG5TpoDkhuxVoIbCJrED7oP9AxJHSVjSfo8fkEakzzGU9MHN2BHPaPxNKo7TDuIUA/9FLw8M0yviXv6tnqVZlrBWEHEti48e32eH1MwHGKmXpjr+FPfo50vIrbPtn7LTCTjtO1gM+GxYmF0dOlQNIY5QpA5/mjVPB2AcaJ0rhjNDoxRbmmZ69Z26qA6MlDFxyRuUggVkWRojWGacimUCKOy6Whmdf/yKr5RGPL5+SKZ0BFaVLJxAn/mB5NN/P197/Cl986/M8Ob/k6eUl52cndM7ROkfXtfzu7/wuP/jhR9xq0ZpNKZZAVQAKjaJvhQ6/NzCyoeoiV8YKi7iUn8QMumlQjZM4OEYmv50Niul66HqyMiRVdJUWKxk/BMXSqYIWctgFJdqOo5cO823nGLzoa2b0QUbwYNPGIM1bQsQUvZTDw0Pmq5opJYw+9hovCrDVAYG9Pl5OMG6Yrj4i/voPCct/jf75E+yqo1JIalOV+MbakGxpHcsKNtfyhtKvtQCyFXzQJZBOcX/I1VKHwyub5gFV3pgGoyyZUNbIAXqgpEtwTHVctGRrlGTAUsr4acKPgd1uIKvKgLZYI0xsrUxpvqGKJpuUfqcYQWta7zn64Lv86Fd+lbg8J6UFu9hzt9OMQTNlx8SCoJfkQ/Og2QMo5UpJc7ORJlBfft5ze7OBItC96BuensP9NuPXCR/hdhtZNppFZ4CGz263OKWwWtEaSTg0NtNZ0FkxedgFzRgVJmacUTRW45McMtLFNhFiooppa1ttwoNhxeiSj1Dy36wqgCaGOMREjIoxwDYpfMjYnOhVZmETR40imkBQkV1UuEbjVOkG7j1DSLy+HbEnDWcrx2rR8PGLNcdHCxaLjuOu4QfbDdtxApVZ9g5rNLf3WyYvurrL1vB6OzGoSNNo+r5n0TVYo2hcxuqAU5GROCdnXt/ccna8YNGJ7s72aif7RiVCSCz6lt1uV3Q6hXlSgc/qNufKCCmmMBVQS+WMIXOytJwuFNAyBcd6vcNvFUqLxvFi1aEM3K83xBhY9GdohCXSN5bVsuV+vcX7Hbudx0/TXAoL+zLuXKONcncqA+OuHJ5BGnv85j8gvn5B9Dv8NKGUdIgWNpESx6ParIpDHm7I6tTOUigyLvEwNlDCLqgOlTKmEI72iKvW+zdPKRJCfnDmxJRR1pEePWb6hT9NqaGb9cMt0GZYZM0Rmsc4Lk3HwhhawIwTqsjPzD3tYAbU5T4zndb02rHUDq8j25/7pjBxr16hUIQwVheoPIKez7+U4l7n9WAvkHNhC+qShMr11+QsAXkqwf6enrcf6+pUPhh2NQ+/gLGqbNnyP6M1USnIpQyOBFiZn0OnuTbcLE5Wqt1tKQ5uvVGtcMZgSmmgMIIBEtvNLdfXhs3mGafnj8U2aEVIAiipFGa2oq5dx2OY12v5MDI1WVibggoLQap3atm25369Bq0xtuhTqqKLrZV0mK1zm6Jo7RbQxRqDcQ5rHE23wvUJ7Vqytrh+KQzSKBI5R1rx+sUPUdMdTnv6ZUuyCr+IOFUkLhiYUiAY0cKbkuX1zT3rzcTkE/nVNT4EusawXLS0p6ckfYTWjTCr04TOlIYRMAZF1x9h2xalC2CbkXNfG4wtjbpSJoS651NVgRY7rRQaS/KTyOgUxkgKnhgG0htg7PTZxPV/fw1A87jBnljymHn1t4Vxuvr2iuNfOWbz2xte//prlFWc/JkTLv8dkTL47L/8jPXVmj/pFe7C/Ln639J/IjD2/8+redzw6C8/Iq0Tn918hjKK0z9/StxEzMIQSXgVJShJiVQYsX6MpJBLtC5hVdVoVlrWXbtcFJkWRGJkvSGMwqjJBfzTiA5TRvZK2yxoMRx1K86OTolB0S1OafpTmu6IgCbEXLQOpXRZIX6Mlgw7SkuprDKGEDNxmMgxYmzENmKXdE2qUrqBpwha0XYLnn/uSzSNJCBSSgVUXMxjllLGNB2nl0/w44bNzUs+/fiHnL39OUzToZQjTp6b2xsuHj3i/PIR7fKI7WZL28naDlHsoDaWHBI+KbI74v2v/TIn5084Or1kHHf47RVKRRonTSx9SHgvOrnT9p5Pvvt7+GHDpjBWzy/fISldNKcdCvHXjWlRRpo9jj4I4Gkc1vX4KPZNa0niWKVJKc+ArHXSR8H7yN3tLeubH3Fz/Zqv/8KvcnrxGNf1UH2DYud82Y9KdeRkREYuJ2lya1t8CMKGb3o64OjkBB8NYbsFZbBaE/wOP2yIfiIlWJ1A0/WzvJyfJiYv2sDGSv1hSAFjFyzdAqMuuL5+iSrgT0oRPw4YLc0c0YaTo2P0bsdyUcr0teJy5bi53zH4SIo3pNGgXCu+vjKEGYwVe+ungYzI6GRAl2rCQzQwg5yZxfxXEImM9CbIupSby76wxpGMIxlLjiWOSUkke6wBLNlIGTFFgkhrK2CsEsAnB2FCz1ho3jeirj+qjZDkCD8A8goq8qAZ4t7Fm8FboyqBqcRgOUvyNSWIRSO/VqmwbzC196/fjPFqLMQegK2+1qw1Ws/0vL+vAyCj/jBTzvkCEtfkzDwDCqj3hHwt4VIBYCvxRRVmrJZkqS7APFoTwsTVZ1dMoeH47ILzR6c0zrK+3aBUJuWA1qUhNidYA33TgzZcx4k4bdFZWPtVkk8B2mbBEFQsceu+8uyQVTyD5jO8uV9fCqis/zp2Vf4jlRL2Ou71vetgVpDrj4FbH4KzB8B7mvX7ZcxTaX5c9d1STiWu2pPfKpaSk8j6JbJI3ADSbE/mUnL9hWRR14aytB3FRzqUbSo+XoX9VHUaxXcwpXLUvnyJ2dwzPXrCNLNtJMazwcvfGosuep8/YSTmMcwF7NwnEtwBOFtepPTc3M01Ha7pCwAr/p21Tj5PG4nH65oue24/7PlgnuuvxffVRJGq8pEwecCQTS1/LyzXkPDjKDI4WWTpck2aGZGCSVmXz9TS77CSJlTBvmJJQKW9dvGMieX9inyAZee9DdkDy/Moln2r5p9VH1+pKltT9/QBnHsQsFc9Za00jRPJRR8mxnHAdyum5++TlaP/ne9jhkRSDZGOOCZyCoWtrclmtScFKkVwx+CKhnf0Zc3vJUJSzqRCFDhMTNXdKAkHS1IduWCPKXuUiiLLhoy7kPvM3hpnj1KFvPLHbMifCTBWm4548WfYLL7MvXlEoqXJA3lIuJuRP/jojm++02B1BBXEESwMk5wTIQZc2+CMnQG6GKPIEpQNIqZOulxrMn3f0HU9m+2GcRxFTDpnREBHJlUA2AmSlwE1CJuxGDlFZtEalouO5aJD6UwKgXHyxJSIJLQyvH15yePzi/l5/+Jf+Df4wuSxxmCNwpoJP+0IYRQHJU20vWNhNE6XZkPazF3wlMr0S4trFDkHakBc70nhyeOWcbsBFM3imITCLZaopiEYQ3t8jjL1oBVjKiLS8k5ZgbK2gDg1i6oZhsQ4eXbjxG6IJEqzr6ah1Zb7+4HdMJKSLPqca4dq2bR+NxB3E4vXa96/uhMQNMtBP68HLVqyJgvoPpLYre8Z/YRuGrRWOGVI2mKzplMOkxWEiTiNvP7wJe/8t7+O+rO/zPRLX8NoObica8kpM27u58/K1ANRH9gDhTbNLDQtxlHKgyuAl1ISuQMlDa58iOX1D9f23e0Nu+3J/P2ia1FDQwiKTDgo7ZGSiXEaikPMfGAHH4rwtoyTc5aMOPWQWa/v5sPXGEvftqxWK2kG5iw3N7dSKRoTW+34/W//ColTpu0xQz5mnY4IqRUQRWmSMnsKab0KMF1mSP5jRFlq7eHjlwMXJw3XdxN3u4G2aTleNTw5z6A9r9aZ17eB3mZap4gJnAYfPF3rOOo0myEx+onThWPVGKYpCeuazBjBRuhN0U7SmpQNOtcukeIraGOhaM8osmTKtMJYSlODjE8wTlLprDIsdKTJkSlCnhQ7b4gpM6bMkBPjZmD1rKM1kbM2s7Sao2PYrbdstgGlMyFr7jcekz1hMhgFJ8fCLJ+GAbt0rFYdd/fCjj0/WvLs8SmvXl0R/MSwDZyfLCFObHYDN7f39H3LojUMw4bd6Fn2htXCiszA6Ak+8/puR9taFp3jZLXgZh24HzPRe3JKdK4A+kXIn5JOiBVgq0dwTLNzFUMBAVPAB88Pv/8h+tkpy0VH13ecPD1nnCY+/eyW3eg5OVtxerxg2m7Z7UZevLrl6aNjXr2+Y7sb2e48SsH93e1eJ1TrWZ9nvxeZ70ikKgLt3/sfSZ98xDRsGDd3jH6CokmtijO+XC5Fh/PqqjxjfvCO1ZMwxmAbS0rxx/bp4aWNxbkG3Vhi1QctunLFp8caW7qA16ZM8UGSB5XZff1bpHfeQ5eGgQrROG4TnANPVMOJMhwrwwpNpwzGdiXYt8RhzZtg58xQlY9Ap0STZTzfdytyTFxFzf0QmJyVoKoyLpQ8i+iOl5l/oNdBoXRU5to+WcbBq8Ik52U+MAX7OTwMCYsTO3+1nxVVHXzkDJ9C0emsiQGlsK0rTInMpCY5i95g4ejZSZLPTiXLr9GMww6lsmiTG0MIEWMywzTy8vUVH/zgu3z79ILGOXLWhPh/s/cmvZZt2XXet6pdnXPLiHgR8Uq+LJmkyGQhkYZMCwZBSJbcMuw/oIZtQB27554b7vkP+FcYathu0rJMWKRJigSTyWSSYhZ8dbyIuOUpdrEqN+ba+5z7MpGkDFjOhjZwX7yIe+/Z1SrmHHPMMQaUUdjsRNojTGgNxlhxfp8T8Tzfm4DE4xhKEG5wRXczqUw2Gl05qqbFxyjjak42BFPCuUMIVjlHXTnG0WN0pq4cyjpiNmIs8qgixEA/jqzWJySt8T4QssLVHW88e5v91SeEcYt2a37ma18iTXdM45Zhmlifdux9wk9ejEdUi+s0lyt5ibvbjUitGQu6IuSakB21slgtZkCfv75hNxmyrqmqDlIkxYApzD2Q+CuEIEG1qai7Uxj3Av5rgwjRHFpajXL0444QRnKOdF0HBVAKx2abQPe1jqf/9Cn/ro/qWcW7//27/87P+7c6Inz4P35IHmWAfvg/fAjAm//sTewvKLK0cJCmhB89fgyEKS36xCBzEChhoILKUp2u0ZVDWwFrmumc/XbPtB8I04R2jspVZT9JTH4guQajHHXd0TiFWGqJKWMIgaz9Q5mocoj8i8O1ms3NKzqtsbpGkXHWkmIiTAPT2FM3HTkJ+A+m6KAKASPHDLohIWzZcRq5v7/H3N/KXHaVAIIh0lQ1j5++Q1XX/Ju/+FM++eB7PHn2Hifnb5BT5Ctf+zo+TvhsGEfP0I8YY0XXM2W0slhtCTrI2pMUk6l49N7P8uTtL/Ho+XM++PPf5+7qY4bdDcPQs+sHfPAL6Pn48oLt60/43u6el598wJd+7pu88+Vvsjp9hDZOpCQAZTLOaKqqISnFNI5MfhLw1Vh8P5FK4UjZqsiTqSKlpFg1NUapom+qOTk9wboKtBMmLyKnoJW8G2MN4ziijbSC6gwpZKyrMcbQrU8YJ0W3uiB1a5SpOT25pF5dFsMgWJ+eQfQM/Z6x79FVXYqXAvhXdUvbnSxgTvSezd01KI1zFW3bcvboTVlpoydMPbdXn7HrtzTtiq49KblF5Ob6FWEaaVcdpERjPHka2e9G3nhWkXRFyJMAxv1IosIHAY5yGFFazIxSzpgcMXZBCMkZgvf4YZRipDFF+7GRQl1WTD4Sg7ibi2mzxmiL1Y6Mlo6HFCgPgBxFg966CpUixgWoG9LUF13b2WUdaXHOBSxegLYD4PFwHrEAHwoptM86oxkpBB/yubIrZ9lHBZg1RQFFOkL1Ig2iHoQJCzgGX2C2ybmtKfJzBZSyxTB7Bn6O0JeylR6e9YNwxBQzqSJJEMIcSx0iowMTcAbiBEyXL+n8XBiaypKzeF8oDJXraJuG9WpF1zZoDXUT6fcZ7RwurUFNrFZrYhjx08BmL6aTxjTU9Qkpd4WBeQDKtJZ40MSJ6HuSHyWGLJ1ec6R0IH8lKcJ+oYg9g9EU0CvEiA8eP8dL6hDDz+9y7jab2XgxxofPYHluB9byjBeG4rMyc30lp5ROsaoqHYvFtyHPzx6NsTMRTsl4Yy6gp8WX48DWVNJdM4740cteoi35SOJA1iC7aIvOXb6HKpzwPGfimx4HTv6Xf879P/onhPNzxlFyUD9NtG1HXTXURR7h8Awe/jljRAsomrNIJ6S8FOWNtlR1h6tqnK2oXI2yUpRT5f7Rs7jHwzlzyEfKH/NcXn6o+BRphatkHU4p42NimBLDfpD3iswvwQGysHFLQSQmGQ9ShACKeW/OshWkmKUTkvL9JX5Py+TLX4i5Hlz00Q3NudzxiH34bI8AzfLOhGWsytoxg/W57J8wt7YpfVQgQrqvam1xhW0eM1z96jfwUTMmzRQVT/7Vd2DbM06B2xHMac9u/PlyjZrh/Ot03bvk8Y5p+5L99feIwxU6j5iiBWVLp4nRkHXEKkpcK1hZyhUJKfBkrUAHIb+kgEoTiYBSTgoJ5dolnTECqfyE8shPBRirlCLpFRMdHochk7JmH2s+27X8q7+4542V5Y2TTOsgWURPEwFHjTbUdY3K0srtvV8+98GGJcJUZBIqG/rtvehrhuJ2WZiw5IjKURhZeRLAM3tUElOP2fUwm8Td/YbGGcgd5LSI6pMzBvAxUzenVPVquYzrV69pbu9IIaBypFtbmq6mrh3WOTIR6zKVFdagU4owlyNQOKepncKajCKS1Q6jJ7SNaJUxOuFOI3UbyNmSTSCkjmwqghaYQ1kni3ipcIme0DGIIcy3EAPTFBj6iX4/MnoBsWThbKnrNQmN93uuXn5C8CMpjpA8xkTyaIjpwG4J44BKstDnLI56VlvcUYBe6iKgMg6pKneVBD6j9ySVOK1aUC0pBhZvxyQtvT/z7iOuX3zM0z9puAQ++9WfExZrmF3FZ7HwssEFjy7V+lRYVNpJ0p+LnqY4ksvYoFjiZGURI0YBZXRKi1nOfKRh+6DVsqlrknXEIG32yqgSi0hVMRRnTjXPi3hgq+UoGrPWiRZwVVdcXDxiu7lnGIalFdf7gc1OdA676oLr996j++BDjNdkvWbUl4z5kjF3TLlhypXcy7w+luD4YVQkepVqqU7q5Wc98HIHq1ND3VYYBfsxsOo0q8Zy1mV2g2czRH74Eroa1g2886xl0yfGmIk5crKyDGNk24sLsn/vAAAgAElEQVQBUG2hqxCjBS16rKa40IYkILiUsuRScwYlAo4iI6GlRSxGGGNmlCHCLsAQRdtY58y5DTxfadY2EXzgqt+jVIUh41TCGc313cCTU8fKJjabLdNt5rRxXFw2jFnz3b++JiWI1GTjcDrQuJqbux2b/YixjsvTFU4rpmni6vqay/OW2inC6Lm57rFaUzUN/TSy32yJU0fXGFQ2TJNH5ci6q6mblu1+4sWrG6ak2I8JVynWbcPTS/Cv7ugnkQzYbvcCVGovzvOlbW4GryCLHEbONJXhdL2iHwY2214Y7lmkCVANKWvGcWQcR9YrR9dZ+iEKY6iyVJVo/PWj55PPb+j7PdM04Wdx/hkAnCvEhwmPzglyoPqjb2FefA7JE8Z7+tcvCP2OGDwpBdFFO2JHpJS4u7srOl1x+d5cuZ8jrGNA0Rorch4xLQZLx9PWrRrspEQjOyem4LHW0rYNbdtwfXVFssJmsSIgjVWKSWvGcnL/G7/FrPEtCZWiibDOhkdo3sZxlhVNFk1YQ4I8CkhWd3RP32Jz/YLcb8nBH2KmL5SSNQqdMzolTpXh3WqF+Tu/Sjq/IP2fv00oa4cqC6TikGQCqCTr7MKs0Jk0Sz3Mz25WB5ifKTNLQAB+cxRAz8/xuLPxAPgcPeclB0slWMwHpnLOBXyZwLnFVPNBHJOP9JceJBgzYzXx+vUVTd1yefmY9foUkLkXo6LvJz746GPef+9rrFYXGFthbRImjNKiXZyk5c4oRBrCqELAK0+zFOV2mw1d12FUTVIiiaA4JCbr9SmJVBzjQ5Ff+NGgzFiLqyppQ4w9JlfkBD4Y0SAMRQ8ZTT8GpiD/r5Rhs91TWcdNP3J/dU11t+XN978E1FDiCNtd0AUYPQxeEYKmMgK8KCDUA9rVpW24AmOZ/MR+txUwwk+EWJK7HIhpwgdNHizWZtHis66wtXRJ58RgoqobQvDEkGgaQ6R4S2eICmzdCsNWCQhhCtBW2Uv4ApH1J7ZX/n90/P9xzr/NMX408up/fsXz/+q5MIG14uIfXvDp//Rp+QlhwYcpMuyHIkuQUVnKGPPCkpXC1hWmrbBtTbXuoDYknUWXXylsXbMyFu0qpmGgqxt0EiB2NmHVVYtRCedaKutQyTAXulNKGAMhxKV4PMt1KGPJOpFCxjlbgCiFcQ3BZ+pKk6Jn7Lfsbl/QnZxhXYsy9ZLsgJK2eeNkBcsZ6yrOzy/o72/Y7W+kldQoXr9+QVVVrNYdJ4+e8ZVviFa/zllAM2t49Oa79LsNwU+L34SfJlACiiqjiZPIELSrNVXbie51hqwdT977eS4ePeHjv/o2n/3gO3z213+OsxZXCbhkjWF9sqKuGryPbF9/yh/+zue8fnnNl372F3n7/a9h63WZN9PCetIgTOCcUEbLXMmytkwTVKWrS2tNzJFp7Mkq8+Y773N2fi5sVSJnF09wriLFgCoAaIYS80bWJ52AIErLs6w7qMr6nAPTOFGtBBCNOYKytG2LD6J97QNY01C1FlutMFUFuloKMbok6JS9RwNd0wiYUWQMoHhba4u2NeuTy6I96wRwiCLZlk9OmEaHyoFtv0dpy+pkxenlBeeX59hi5hLRDKHl+t5zuxm4Hwam4FFVXbrQBGDy3j/odBnHiakfQSmqCtZnYu47DAOTD3KdMZBCIKUgra4FfLXWsVqtGKceP47SDReFFGS1MDiz0uLxYCxJlXXduKLZHuRrKZ+XZ6ZU0UxVyzPNWYCreYOV+Fe6Qubidwm/0FoVU6jCYp2pnRzHWBlRRVccZJ3UsuXOxLOHUhlKOvaco6pmQ2HH5u4e7w8g5HIsxc2HxyxdklGF6Z3LfZa8FVVY8qXXQqmieStrjlIaq+0CGqINmpqqWrE6e8zq9BGrsydcPntCwtKPI68/eM16vaJrV3SrFW0Lu+2O4Pf44JmGgd3mHj/0GONo15eYpuH04hEn54+o6hYwDPuR/faGcXfNuH3F9vYT9rudGJVmSOWZLrFThpD8IU6dwdN57ZxBqBAI3hNClHZoM7OVZ7mKAoaX2CSkLM/kiBB1PK7nv8/AVwbpgkAhJtwzE3ZmN+pyLaUwkBG2aekaK7VwXOUwpaAAhaE8A8SFqJazgPWmUkIACWEZVyioqkqkcsrzSAhIN0scGDUD9Sy6zOe//7tkrYnrE3Z//z/ER8GD2mYidWvqWrTDlZrN3VhOqOYxNQ/J5RnJQFcYrK2o6w5X11hb4WYgtphJ6qXAqZb7mDv+5iLEIgtwdIJlP1QzbiXXoo3gW9Zo6koIBb50XPkpUdUVTdtwetoCMEyBcQxMkycEL3Hb5PF+lA63UiShsDRz0qSkpdgjiz/CqI2lE+AL1REeXvqPHDOF9mgsHktVHB/HcqEp5QfPfMZEIC0Arl7GoCo4c+lgCwCGV7/wDjGAv+4Z/ugj9G7OPeUYdUdeXWDWb6Iv3secvUe4+gHDzSf4u0+ZNp+jw07Ie9Zgq5b1yQlNW2HtLFVR7jGDQiTCrGrIUZGTElwiSZeR3KMuJB1590sn9I85firA2JwzMXuySiX/k3aQEcsm1Pz1jeMvP52wb1neurRo7RdWFFoq1EYb5oqGLeyTL9Y/tDagJaDp+x4oL3SuBBRAQNixIk2g5gS2TNMYpiLKHvDDjnF/T2wboTsnEfEVsEMq9SErYj6YSAFcff4Z9vWVVMdjpOoMtrY0Tc3Z2Snj9p4cJtHNUmUBSgcmWGUN1gSsTlgzgrnB6gGlIlqVFgKbyFUm50rcj4O0AcnAPmrBmTdX5DzSqpSZgiRf4+SZpiAsRZ+Isw27AohM456YEj75EpAHjMnYCqoqS7BoDhPCOl90zKRa52yFUw6jj4dimcwoRCTZ0Ngaqy2VdkxxKqL5mVDqowuYgMJWlra1jC9fcvNH30JHT/61b5KsIcWJFA4mH3MFTKqTeSYSCAtaS1tQLozkWQNEzS6xZcGcBcJ/3DTb3l0z9rvD/RsNleh0TV6Y2jP7NmcZdjMQq4o8gQ+paMGK2YAsYgnvPfvdTgCGJICXnltls2J0jrReYzcDKbdE3RDVOXseM+UVgYqALU7gh3tCqQWoP7ySQ0VycQ5Xc+sBTElzu4eTxmJMZrufWDUaqzWnnSXEzEevPWMAYxQd0NWiQ7ubEmPIWKeISbxcpwiVVTTV8fOWDVlrMEqC0i/W8FQBkHLKhCKqjdKEJO0nPmf20TAWJq0ioyOc2IhTidokOp3YTcKKq5xi3WimaSBnR1VZTlc1d9s9VpeOs5xZ15pNH5l8YNcrsAk7u+cqze39ntPujLqSFu/N/T3rVjRdrZGK+P12x6OLNU3l8M6w3WzpWluCZs04DpyerNBG4ytDXTl2Q2Q/BqwVxpGz4oZLEvfNKWu0Fo0qYzNxkspqCQtQCEP5ZNXQNo66krVml33ZoBUhae53E9rUdMYAkbYWKYYUR/bbHbGu8SEWuYfI0EvAsGjXaUqAcTTv5jWXjM4B9+d/Bh/9gHD1mjTtCb4n+mFpn30A4B4dcfn+YQwIg1UtsUE56TKPU9GpnTf346VHV44UhHU+BxOmsN69L226+cAcqJxj5WomVzHP9HRyRu53IkuQMisUj7BcKM1lNlxmTUvGZkkvMgqSGAWiJ0KYMHVbdByBFH7kvufwZk5RbM6cGMPj03PSWz/D9I1fJPzFt+Vzl994+AHyPOZJU4LznJd7XxKlY/MzNbc+PbyWwy6ZC8vjC4Fb+fxjcHZeWw/g6vy5cwIWD6w9DgHc/LPzZ6V5fS7raEaM065vrpZkputOsckVsCGw2+356NOPeedtR9edikmNFxZBCIFh6Al+ou2aozX5UDyTSST63QLWzE8BKPq2Ssm6lhFt6RhGQs4CfCikwFeOYRzZ7bek4OmjJyTQVWDMFVcvXxXJInlf55eP6fs9yUsbXvCek7MV7ckpqMz27o6hD2ijyEpanKdQtOJDJgZFyvXBZAJFtzopSYUwi3xMhP2eWDozZh0+YwSh10CMHsIEStqmNXAo1gmNPCGFXWNyGYuHdw4CKGhri/GiMLNTkcTRuX0wZP1rz+2/vOXsH5wtLa3KKc5/85z7P7hn/GDkPt4DcPr3T6nfqQn3gc0fSjfM9EIYRTll7v7l3Y8wu+OmdFr0idt/IZar7Vda7IVdPmP1cyuq5xV/2+P+9+6J+7h8NsD+u3vCvbz7s//ojO23tviXnrvfuYMM619d036tRdXl3n7vnuH7A3Ern3H6G6dUb1XoTtN9o6N+s0bXGn/t2f/l/nDyDDlm0hQgZLII+jPz62cTDqVAOYNpa0xbg7NEipxAFkAXLe13rqnR1lBXtWjWI62FrY+cri9o9z21a2jqE2y9xtYdxjVF77W4gR+BA3IhavnTuiJ7oS1KO1ydsRowCk1DGHfs7m+om4mmOwPcUnibASU9J5xlLYp1TUydxC8p07atABnakDGcnL/B1O9l3PuRpAxd22HcJGw0H6lrMQYR+Q2RLtnttjhjaNsVAdGsneeorU8xWvP4rZEUYbu5Z79/BXlCKwHifIjUlexVKkduX7/me+lP6Ps9u+0973/1myhjMKYi5cRuO9E0HdbKdaM0MRWgLifZt3Jb4mMxpQ0xsN9tySFRtSeszy/Y3N+gbUXREWHyfmk5VkrhXIW1rphGStFMQL95bwBR9lLkFJjGnnHYU7crtNKis5nSIh2gtEGV9z+zxmYQaR6oKmdsc5CTkH8te0IBcmzd0DKb3mr6fk+MI845VuszIJFMDcpIS7pxOGvFyEwpEgmrINURlzXrqmYKhikrdkNkDFKM/CLgoEtMMecAq1XLzd0O7z2TD1gzdwCW95CE+ENOheVao1OGyZcC8ME9fpZKM85hnBODzBQX0x0xNc3kcNg3KUCS7EWH3fcLQbv87RDWL/v4bGIrBkPzAnDEZFvyouKLcbS1HZQP5hjokLOIfJvFVTVtt8IVjeBUOodS2ZsfxhYshetZ4/6Y2bvEfSUWK1lXWf9ngogqBYhSiClasYupnakwrqFrzzm/fEy9OsfWK7KumCYh00zjRJw8vh/pi0Z9Slk6Z8NA9BM5R6w1WFeDFS3o9uSM08vHnD2+pG4FjL1/vZd1Y9xxYNaVP5QUKec87cdL9anlGZPnRm8Ka28uki2Z+/L6Fwh9WVc5xHUp/Vg24/zslZK9wBxdiwCCumgNH96NnvNFZp1eFpA9xRl0zYAWo605dyzMzhyLnm75ioUpfjx+9fK+D7cy7xNyriTyKWrBx+DuDnJG7/e473wb//WfZSxEp5wlV6isrG3GuPJxP3LmZcIoRA7BlA4BVzfLHnBgwwpZaDbgVscfVi7u4EVUihEHV/HlfSi90NBKDn54S6aA5aboj5si4TOb8HovWrfGGjpraLsKiPhCpNvvHEP5fQHSy7VEeyTFCeQo8jRJk3USD4njNWUGbDns32rJq47eW5njx8bsD0ed+tEY4OgnUj4y1CquvDNZUJeOD6chC/EdHTPhtEWjcdpx/uicWD9mV7eMyxk1Sdcoa9G6RWmHxYJek1Ur5ue7Kwg9iiwdI1GRYktVV6I7rwTbO0T5FoVFq0BWGlPud1HDUJL4ziSRH8nBjo6fEjA2EuM9Ku0x+pSIImbIaPbUvOhXfPujLWed5tGpo7OiFUkWIIjiTq+VEtMVPSdyh0RHl8mC1oQEfT9gnOhoUQYmKUAOZKLoI81AbFnoc46Mw544DcRpYNjekEikeLEM0FyuO2XwSZixgx8ObZjAsLtn2N2Jy7OfeH0zElKgqhzPnz5hf3dL1plcGCvLoC6LbWUt1kxY43F2i9FX6ALGqqWSUVqScyWbu0mENK/ZZhE2mAGFjDyKEBJ+iuyGkd12Yph8af01KGUPG3YWBmYetyQCWUW0iTR10dOsNHUjC4S7KsNQgatHRgWxVDycqXDaYY5MruYNq6xQWKUwylAZR+ugn3oCkZCDNCynI0dNpVApc3q+4v56w+1fXHF+c0v+hW/Aqiri/enBuWax8eCjVOssGKfQRoywFoVNrUubjzoEa+XdGGuWasjxcXdzxX53oPZoLQ6Js/v6OI7M5mBKZwkg5o0bkR0I4WDAVFeu6PgI2+XWXy+Vy7kqZ4wh1y1Ts2KsWuq/vmJSZ0z6lEmdseeCiGVZ7mYm7AK2fvEuVGm9mH9GHwUYJZjShtu9sCsrmxnGkc3Oc35Sc9pJ1f/lnSdEQyqv1qA4aWSjtgqyUahGdJ9iCdqckwcdKW0WJYg0eV7gSqEjg0q5zP0C0GVIWtoxRT9X5A58BimzyLFLcKsCZzU0Bs5qxdBP1FqzcoaT2nDbe2HQ1zUnq4Z+HJD29UhKmZPWSlDnA5sUyZWidZG6cjhnuL3dsu87mspgjKYfR/b9ROtEdqJylt1ux+VZR1NXpLZhs70n54baGYyx7KbAOsum5Ixi1dXshx39EGT1T7Bua5FjUJmQEgGNDwltNJVTjOMgm4mCORloreONyxVdY4jRE8eETpN0rihHwHB934vJWO1wTqNUpnYWZybu7veMUyDEKMZqhclz0DctEhv2kEwsYvb9DjX2qDRh/vgPmHYbprHHD3uO3ZhEn/kwv9Ry/QeQbPmelqTcGLNIB2TJkSQAnIOHjBS8Eg9+H62LJAwoIwZsRmtiiIzDIMGmXjIhrLV0dfuA3U+SgEv0YRPnyvKmtlxmzSmKOiUsB82omSWociT7kXF3R9WeEOsoBYdpQC3A5VFQkw86RIpEnTWXxqHOHnH/y7/O/tOPyPe3cOS8exzkCT/jELjn2Ulgfmgga17J/JQ+JE8LGLoAump5JgdNtMKAkEz2wedChge3cliXZ31v0aalJC+H8TPrLx1ylgIYqSOQKcPd3Z3M/RB46+1WOk+ytHeFGPngow9YnZwII9XUqGBIWeb6OIyMJKralXMV1945Xij32bbtwpxTGlSSkFpAf1mTdFaQAn7smcaek9Nz0Ip4VBgchoHNRsDYOA1EVVF1mqgyr19+ik6ZGKTtu2vXhGlk3O/k55NH28z5+Rld17Lf7tntRqrGYqsKY1tGD9l7QkjEYMi2PiQ7StOtT4ghLUoRIUR8v4eMmBTVLYmEo+iZa9HMTjGQ7AyCz5NTFX35uetGnMJ1VoS5wDDj2SRs1TA7I5MTxpZ2zyDMGPvIkkYZ/9s/3nL2G2cLkKprzeU/vmR6MTG9nAh/HrCPLee/eY49s4yfjWz+9UGayD6Webr548O/zYeq1OH75XfM2qBrvfy9elr9W4Gx2z/dEm7Dg3OPn42Mn40oo3jrv3mLuIv03+/Z/skW+9hy9g/OqN+Ue7/8x5eMH4/4a4+/8bjHjovfusCsJGa6/E/EHNacGqaXk3zGI4tyAjzmmEg+oZJCl3H5oymBML+Vs2AtgcJBm7W9tQaVUMrg6oqqaaisQ2eDVlYIEUnx9NFbZPWaumrRphHTpmaNdq1ouOYZTJH9fQER5jVBa9FtNQ6UJWuNq2tymFDG0LQdYRq4ev050QsL1TUdTikpFpTYxBizAHhZKVzdSoxW2D6n5+dAIqXMNEWatqNSFnIS8AVNXbdLrBNioOtajK1BG2n/DYH9dkNd1TR1QwgB5ypmhlMyjpRaTt94D2Nr9vstLz7+Dn5/TY4j5Mw0Tky2RilJuP2w55Mf/hW3tzdcv35JUzWcPn7K+uQcY2vGfqJyFmMrZlmxcRId+sxBXk3rijnMTSmy62U/rSvHenWC6geRcFIiBRbiiIozmGaoV60AqbMOdNGUzTkWDUdVXNEFc0wp0e/vBSxyNc66xWE6J4kZH4BOsw7pEdhCBlO1BRBIpBgJ0wj5oGtojaFuOsgSew3Djv2w5fxMgDBjLdiGuUU6laKpgNXCJrbAukp0lSWrmnEK7MeJqzxxlzx771HYYq4khzUQjaxlWiuauiame0IsbfdqzkFmMNYf2MtKoVWFNgrUDoGSZtZhAdWMmIUaV0l8ovTSgSlaqeLXcQAwBLg8gKfyqVobDsSUMqU4FMJV+bsxworVD8Ak9TCWKoVZlTgAtszGhyxAn+z7ZT/UMn6quqZpOrRS5T1Nh2cFzEQOyj4t581LDrKwMAsSPJNehElazC/13OF1BITNRsNKl6KixVUdullTtadcXLzBG0+fEhET4d1+JF7fLcVBkzM5DOyGLSFEYpB3pXVG54hWiqZpyGGNUpmqrjm5eEy9WmGaBipDjpk47/XDnnHoCcHLwyovQDNL+mQOjOOHx8HkiSXPtHOarMRUb8a0lAKSFBJSPpCI5v+fpRtDCIsUQC7v+BBTSqemcVU5RQFDDQLG5qPYcdFRlfU8q7mDk9LdSdlnVBl/Zc0v+sixxAAL4J/SjwWkF93YlAr4XmZZaVVfJDSy4Ehh7sLb76j/9Fv4J48J7YrsauLpBd4HmrqhqWrqWn5Vz+z/eWzrg2+M1VIIM04M3wSMrZg1kJexyVyUOLqeEgtTZvwxKHuMQSwzNS89vjIulgch/9FlbjkszjmmEESeLyb63Yg2GltL54Vz8jMxZJxzSOcIpKotngbSSRFjkU+Z5TNyJEVftPsjek5MZuw4ZdRSTD94LM3rngwNvRRTlu7Eo5uVJ3TIQmY/oMMKVeC4ws+WeHqBGg4QhNLoDM7AFERMEm1wpzVn7z4hmLd51XRsykfbYtKuSlGZ9oyKCmNPUG6N9zvi9nPCsCVNexgCOhfyxgqalcVWEpNIrpYISWEJKAIGTcqFy75cpEgWzoW8n9Rh9VMCxgbC9jtkU2FPT0nqFMikpEnJcs8Zf/JypHIDOvb8vS9bVOwPAx6FB1xx9ZXNN5XcUDRWFYoQeml3jV5YGnEix+JKh7A6xTk6oRY0viz8ZMZ+x/b2BdOwJwWP1bmcT6odAUjZopQlaZj8xHZ7x83tazanDvgqAL/+977Ju5t7hqHn888/5/f+4A/Z91uMUcRRgDtlNJMW3SthtWliTMRQTI6qe6pqizV3aHqWXS2DCnoxyUlhzzTds3rSk8NISBekLALy5BngVYzTxN19z24/Mo6BkIDZlV1J1ddYgw9eTKGCJ+eAc5mm0azWlssnHVUFykRQEyFtyTliXAdUco26R5saW+QJSAlt5kW9jAckSFkAxiRtULlUaSrlRFw+K9KsUzeDBUji7pTi/PKUZuX57IMPaTYbVu05tSssijLptbG4tsNUHYlinqUU2hmMM/hQeGeuwqgESdqQUpRAS2tVtIRVYWc/nGzb/Y5xOsgUKFRhSAWsNdTVSQl6RZ/GKsd+vxf94OCLWZ1B64jW0Kw7KT7kKEYzS0VLki6fPbrWDG+/ic2W9vufMZonbNRTRlo8jkjRWztit85XN1/j/B6WQ7vDHUjmUBLpOUZzDMBdn1AZLs877u97TjpDU1mooe0cw2gIObMbErvR88aZ46Qz+AivNom2gTCVuWcl2Ug+kdAHJtSMHySFraQtoKBK0oafEd2yFOXdiLKEBEmeRR8mZSm3+Ky4TYHOGS5XjsZoxu0Njx+dcXZSM+531E7Rjz2aCd0YzlYNt5ueEEW65LTVaBz3fWQ3Rnyq+MZ7j3FGsd9NbDcjn72+5+nFCqsUXV1ztx3Qa4ezhvPTjvtPbtne3dJ1NetVRz8M3NztOTupaRuHshWvr+9Ydw11U/H08Sk3d1v6MTAMnt2u5713nvL48oJ613N7P7Dz0E8TTe2wRpp/I2mu1aBV5tFpzWltqCtV1JFXvPj8jnFMZCWw+WYf0GpLCJ5nb5zz6vqK7W5gGDwhRnbDjpgjBX6RkZHmNVTem1TM5XtWg3Ua8wd/Qv7Otxk3V+z2mwdtHDKuNFVVUdc1w77Hh+kLCQPLGFZzUl+CKXTGFKZUipmYU9kQKXriMv5TiIeAIcM4jpgQCyOg5BwhEkNkGmUuG6tIPjINI0OKbK9u2W0O4E6YPGYKtCie4Pjqas1lzLQpUccjmRSkwDCjiroEcHkYsfUp9eqM3K4Zdxtivyn65WkJ7GKOS2CYJk/KCac150bzlZMzbv7hf8rwe79D+uH3xbnuAIOXZ5d5cPPzn8saOYNpRwBKYTwBC9tCHQVgqNlEU5Jo0GhbfrtU0I+lJlQpNM5upMfvf9Yug7wE3kop6kqS1uPOlgN/pCyJ5blu9zv2w8Awjbz37vsYXeGqCjJcXb3mo48+gKx4960vo5xmCBPW1qzWZ8LOjqnohdWk6PHeF0NAhclmASDn1Mla2WO8nxiGPcYqamOJ3jNsNly9/hSCp2nXZH+U8LsGW60Y0w7XOk7OLrD1iv2YiMnz6Yef4MdI26559vZbPHv+mBhO8X6iqhpCVtze3jHud2w2O26ur3n8/BlNtcJUnbCVbYNJGZchYBjHqehfKoxz+Ek0tzJQVY6wvyeETN2uOTm9QBnQOizzOmVQ1i0gvVaWnA0xSXN6wVYFzCsJ2m63lZGlZc5OwdNmsLNO+5wgUUxXteLt//Zt/qbj2T999mP/vX5e8+5/9+7f+Pt/0/H/9jPe/K/f/Bt/5sl/8eQnfv/5f/n8b/6M//xHP2NKZckIkhYbo0TLqbDpZlZZzJE4jNi2BWtJKlPbIo+DwjqHqzTWWaypsKamcq1oQyaDSpYmW/6Db/4Gn//gu4xX13zwySd8+Z2/g2s6sqrxSZG8R/oKlRSeZ2CgJGTCquzKKlCS2hTZ7u5ROdE2DRdP30W7hheffMCn/+ZPefutN1mfPcNUHcrWwlrNhzVMKYNtO1RuC8CU6IdBVpUUSWHiZhhYn50RpoAfB2rn6HdbqtqxPjlf5HYSAZSw/KwW52zRjR6wrmKaBoy2iBlTJey5rqNbn3L2+CkvfvAlPvret7h79SHj7hWaTIweHzz7fg9kKufY313xV/dXfPrxD/mN3/onfO3nfoknz97BVmuGfiBNE8bVNO0a6zLjMLtjJ/w0oLUtRWmPNZp3fuZ90Wj0k8h+nZxTN2tc3aJtzVnTEcaBfr9js72naxp8BKVMYYIhcZcAACAASURBVM87QgrFx0cMYZuqRSlFSJlp3JHiiDUaPdbEpKmamnEapNhunXQ4wRJ3Sn4SSoeKaHOjhGUdfWQa9mxuXrPf3mAsNI282/XJGcZUgKHpaozL7HcbNpt7rHMEL3JGSiWUhurRc/wM6ildJL5safseiWngjZMKHTJxd8fNRx+IeZ1/BpyjyNT0hcFf0bYVm82W6KO0YjuR0BBAUjxGsh/JIrAga6s2VJXGO0v0UmBLqphGLwalCW0sVUZAXEBbQ0oWlSEMe/E8KaSLuSAw7ze6IHOzXqhSs/xAAeyQv1fW0tQV1giTyyxEQCFyzADYDKTN96BgAZcWIFYVQDRmjFOoYmDknGMYepFjK12WiozScweLHDOWdmhpNgsgq4vcQBFYwBh7xEAsLc4ajJrNlgvBwghxSOsK16x5+ytf5+LZc9bnlyjVMu17bm9u2W23eO/xg+xTc6v+3T5KxwdSSHWuwqiZSZnx00jVdhJLWgfa8Przaz74/gf0+3uG/pa4vyaNe3LYQ9yTw3TUBXN8/3Nhudx7+f5xvX1+PhJTCR4guttSGJlBVwGw8kLcSTExzQbO8/dLMWpmt4qBloxD0WA1y9hZ8vA4yyHMv7Og8AKIKdEDnwsHla3EQ2GRDZNcIKtZbs7RtA2TH0XfNkaqqmIaxyPNWEVdCQM15UwseIyY62m0ku5d6eRNxCKTg1KL9JhWsPoXvy0FgcdvsP2Pf4t+FDmnyjopojUdTdfiXC3STMrKe9YabSxt3WBtjbaVFAiNYzH/nQsGOYlnTT6M7Qeh7AJczqQ/wZgohcKZ3TzPtZlQt+TWyyfOiS84J4BrVnohHw3DxG67JxYpK+sMzh2e5+n5Bc5WiDRj4P5+g/d9kV+cO8ApUpuBHEWTMsVpYdPK9aUCNxWGf0pL8Svn2dzt8DWffxnSBUiftcxmKYQ5DZrH/gzW64VVKs9MYkddsBGF1dLdKR1XgbzW7H7lMY/+fMSpQ27Qnp6jg1DQBL2IhNoR1CXB1mjl6JJl+OzPmG4/JI73jNtXJUbQwBpXPyI252hjqXMiZ4/2H2P9SxgDfriFPGtWK3EMz5kcSiffQ1TlwfFTAcZqEt32TwkqMto1afXLhCzapvPb3OhL/uzVDX2/wRL5xfcdDo8KwmIJITCh0bbC1i1KLCVkAckFdIoRopdSLp4cR0nkFkHttCRUB73BCT/s6fe33F99TgoTirS0STdVR1OdULkTsmrQtWaaJnb7e26uX5KnHT/z/AnP37hY7rduK07MCafqhDeevcFb777Fhx9+yGefveD6+prKOaboCVF0DWdhcA1kFXAu4kzE5B41TRAzfiyIk1ICOk2UzUNjFZgccHqPUg0heUJ09MNEP4zs+5FxCsQozom5UBdTSZ6NgboxKJ0IsadygeYUzi4s7Uran7VOGNsDsSTbYrYmXwd2mp8mVGqojWNdV9hsMbouG68cOSb5AtDCTs0zeJAPbMRctHmFqXu0uB0FEyoDU+Bnf//bbH/t59m99UaRyZ5PBjmL5pK2GoW0oIHDByMLm+zUYKSta96AVEk2U5YgY9zvHrRLy0U8WJF48+13qR7vGfqe1y9fs9nujn5UcXp+ycn5BTEGvB/YbTYMfY9TlrqtuXh0Ka2kS5FAEUKg73umacTHyPbrX6e97tGDo+cpWx7T55OFDXsoMc1f6rDWKxlrBzDm6OdmeYtj7HZZdeUfdjGjpkwTFN1Jy4u7yPDasw2ZXW7BGXlmOnOzj3Q20VWgdMaqxDBkaYXVmuAV2RjRrMuiHWwVWFUCXAWzIbQiYXLC5cQ47OiHSeQdlJiIzAB8RpPjVNpmDElZMoYxBq7vRtSkePvJCW8/arnb7fjh1T2TT5ytK+6nkf0ehtbx9tNzGi9O5kplnj4+424zoq93TKNnHAN/+YNXy6brrATOo5+wteHyrOPjF6/BJ1adY9UJ4Hp9e83oW07XK+pKcXvXcxUHnDPknIjBowqDYtVVnK1bxruBcRIN3Nu7ex5fdHTZMnrF/TCQsYyDJ5pI19Vsd0MB1eQdphS53dyjt1GEyJXm7LQlq5H73Vg0uGDwkdvtyKb/jN1+xIdADMKGXRxPyWiEoTg7ZS9jhUT93e/g/uK7xHHLOA2E7R1p2AtiQF6KMgLaykbmp4lQ5AHm74vjqXy0LSYPs5mj0QpbGerGMflJxo4qUgZzkEnR3zOmtJEc5qiO0vaiUiJ7SbxVcZK1JQuJ/UQKERWiiL3PTPFyVCmzToonpuYrzQlPArgYMTmVii8Pfh5Yig0ZkcuZhg2aNbppqZ9dsH39gun+FX7omcYBFRNZJayzxZxQpEtEN1GzNoovNzWf/t1f5/bpc6bf/R20cQKwz1M2S+FyToaWiv1cDC9Z3JLclfV1NtAkzUYO8oGpBGRhkegwDxIOjs9xuHOOwekZeFVpXl5kri4AHgdt77mqPkt5zBpsopcWy9og5dm722s+NZbz80esVqfFjbzi5evXoA2PLp+was9wqZF13jpcbIRZAOTk8XGHqy16hoizMLh0YQ6VLaromTnquhWWFMi65mrqdo2uOkx3gl2dLk/h+uYG/cEHXL16hbM12p1z/uiUiOPi8Zs0rQCqq9Upb737NmG8ZtWAO7Hs+w2Pzp+x2Xm0Vrz9pfd46/13qJoOZWpSNiRVlaJahJiKKmsi5kCcAttpw37X46qaqqlpmobRVTKXuhWmqnFRbnAatkzDjq47JVORooIcyTozRTmP0paQwJiwJCZKSyIxDj0qKpyz1NphcoYsRU5ZSSw/kpT+++Pf+sgpEyZhRCmt0FYYeNZWhDQeEtegCCX709Zia0dGHJq10Wgr7yNFAbWMsWQcSYmJSaNrLmzLE5+JT97jB/d7/vd//X+x6Xf8+i/9Js8ev0tXr/FO43PFvADNK6Cek+hUilOUkEtrMgZnHeQs6xeW1ekj3qkaHr/xnFcvP2H34hNOz87pVmf4qKnX60V3VitNLIV8Y8RkD+XE3wCPVp6qsRilZIwbS/BTSfbEDKuxFbvtvTwHJf4D1lnOHz8r61kieC8SWGZOugo704guaLAdb3z1l3n87te4v3rBJz/4C15/+l3icIfqNxg9slqdsO0DFllLh7vX/O5v/2+8+OB7fPmr3+BrP/8rmO4coxuUSvixZ/SxFE9anHX0/Y4cJ1CGrMRPg6ypmxXWNWzv79C6QhthTClkvZpClKS1bUEpbm5usNbRrda0bVUcuiWlNPqoVVNr6qbDT2CtIaaJYRzQdk3bFDO+OXkPI8oklLHMb1+2vcLeC77ETAGjE02tIFoZC1ZkXcb9BtGp1NRdh6s7mvYUhRIQIUmb/zj27PdbQoooJWyzmERWZpxGKTIYS13XhBCoK3jz8Yrn5+9zfn7B/32+5ocIY/mXvvKUm+sb9v3Ebrjio7/eEbM+AF9JwCgx2ZqlmcTbQRspJsccmaaG6GuSr/A+YoqmYPST+F8UooNC9ljnrHQxFF3fGBMpzXrkQIbpyBHcFg3ROa/NSlHXlRSglch7OaPQSsaoUmkpYM4F3hncnBmCwIP4qCTJD95/164wVTGuQZWOPyl0S0eTKgWgIic492Zqlth8NuqSfbQAVHrOdXSROdHLyXMOBZScc6zCLNQWW61pVpc8e/N9nr/7PrbtCBFurq+Z9lvGYYCcWa/X8nGlu1K6ASaiksJT03XU3YppvydMAylMOKM4PXvE7fUr7q8+5erjPycMPSFMxDAQQw9pIoeD3KE8Q73c96ERQM6askYzG1/N8S9LkHssM3Do7pw/Ny/Pcq6jGxTZWnQSPGKWTplfn3iUyDnizIpdYhoBOGemsrTElwLsfN0KdDEgV1pRVaL3vnSdMbNzo2jlxwBFuirluMz9RTbDKFxTC7O9HHXX4ladkA5SkrFU8k9d5m4qMYfKEuOR5d+FRUqZkwl1fcXJ//rPUUqx/9VfY/P0OdvyTlxVC+GjEuPr07NHNO0Jdd1Sta2AsUaIfiAdP8eEEIkNC9CqDu/tACrOYGx5zkdBzcKkhcKwF38CXUglD46cWcgTy3vOaGswteNk1TBNnslHxjGw7wfGfipxuMa6hLHTMoeMc2hTpClzQb+y5NiqnC9ETwoDyU8kP5GTX5izAuqbZb2dpVcWCYRM6aoupyzXnWZCRpiLRgdZiOV5Ht12KsWpMnIF88m5sLEFELez5vUCEw3c/2zLdAivUWHCZlkfVQHPVRa5oKpqSd0jePRVmhDRSrN99W1CzuhxwpuRaQXRXRBWX0JVJwSjcHlCDxeo6RXV9Dmt+SuGficdRUUDKs/F558AxMJPCRibVUble/TwCeb+O7T129j6ET4ZhiBGRD4ZrkOFDo4/+P4d52cnPF9DZ6XxyppSQdNZKpPMGqsCLkr1TnR8cvRIBXM6esnL1QCycXs/4vcb/LBh6jeQJoRBO2vlWOr2DGVbQraobPF+4v72inF/T60m3nznCSenp6y7+nCGMhjnFpHLywtAUTcdEYVTmX4auKurZWFWRdhL2iEzWiVySPgxkMYJFdVhT1LgjBPGqRWxe6yCAMFHdsPAdp/oB48PQdoWYyJlvSzYWisqo4nJIxU4T+UU513CVVA3iaaLRTeqLDLKiPlJEfiWvWFOW+UIIZTJKBttZVeIWdeRi6K2RxqyURb4kvQvFZmiAVMij7KJsGwGc1urqyounr/B9ff/Gv+ltwhPHy3BPkjA670n6mkJNJWKhMmLLk880jFcqsKlMpYzKQZCEQk3szj20aF+6Zuod95Z/j5MIydNTd04Nnd3bLaHYCTEtDhVphSIMYvOkRYBdqXLZhdFvN0ojbGOqmtZn1wQM4w+8npvSf6MiZZRnzHkjpCliiZTQi2L31J0eACsqjlKOrqRsmEc/e4XwVh534YpKe7GTHUCU4Yha0alwBocRZxcKbDC3DERTJag180xusr4LA7FMc2MCgFdlxYfWZdxOaJUBC1Mi1yY295Li7fViq6pRWctK7bDRAiQVCpjIRNzZh8TJmbW9UBdGaopMhnRpH7+5JRh8vT9yP12YDwXgMH7wH4YWXc1Wme62rLuKm62gfs9VAa6SnN56ri7E43f7C1nq4p16wTUGBNdpVk1jns/EmMUtlhTUTmNT4mYMhdnJ/T7HePkuQ1b/JQIUeaesARhmiJaWbrGkJLiZjPRj1EkR62hbVqsHvFxDpgSr282rDvLunWcdB2V1UxJMUyB3T6BriRZJtNPQdiBoQBhaZ77JSCcK+EFTNUvX2M//JicPHHa4l9+Qnz5guAHwuIqHYt+2SFpm5kAx8YDam5Lm2kezJt8JmWZEyor2QN0fiDVpY3G1XZhYFGm84/T0EoxgPcsRbl0aHec53dMcemqWCriRyCjDSJN8Ng4zpTCFYM/8lzwK0HHw+XisIaTUCmQkicGyzCN7DKARdmaRit0AWNncBQNGSsSHKUId+5qdqsThudvMvzK3yV/61vLzR7mFEdM1R9zzAEOsh7OoO3MA0g5l5bOQ/CYCvixgLxlHzucRvFwqXwIzhyu8CgZIVMZ0YefGcrHJgEz+DKDwzNwzMw+yInN9h6UtPidn16itMX7xN3dlg8//oivf3WFsYZMRUYRi5mMKgC21rZIUEggaYw+sLnLGI5x1mZTVE406VJOGOto12umMKB0MRo56ggREMKTwkjImmGUtaDtWp49f5Pgz9HaUNct3bojVIHKJjSifxsKY7dpRHJBO2mrUsowxfKe5KGhtKZ2lmHYM40D3ocHe0EGQkyYuhNmnKvwITK78KYYGYeerl2hSIRxj48JazVJxVLRqI7urbzfJO/LuWLAqnRpoQySCBuz7HPkzE8Ylf/++FscJn5ON/4+KUplQ0WF8hK/pHwwPMxJ1DnddYPZOOnLznlJyJd2cmUIypC1E9kJZRiUYa8Ne235P/qBfb/ldnrN5vFH/Fnacf3Jx6xvTgtj6iAP9PA4irHmpKzMYWHylI4EYzDGQYkxY5jYbu/JMVH1jRhSZc1/9vV/hlNimhtjKAme7JE5x6IB7oSdGOUcMQq4Y10lAmUZ2aMKoHL16nNOTk7FvEsZphSxVQ1GmEmCF5eOhehZtPRKEdA4h3MtuT3jvDnHrZ5w+ugprz/+LndXHxMStGlPP23EJDdJfFkZzbTb8uKTD+iHkfe/8UucXjylqg0o0ee0zgl4DGzuXpOTOFCb4rUQ4ghRJFaclfhuBmXkGUXRA64qMhatDW3dSKJf/BmkJ7boCC9GNSCGWg0pJdEGzom6sF5VjcznlBj6PcLYiv8Pe+/1a+2WnXn9ZnrDCjt86cRy5WCbwl22AbktGbhCSEgtLpG4QuKP4n/gChDqVqNuqU2DQbTa7VSuKrvqVNVJX9hxhTfMxMWY813rO6csW8BFXfAeHe1v773WXm+YYYxnPON5MNmBcmdr/mk/qPt8RAq6tmmo2r9K5zIeBFRYmQsBlYuRZk4i4WWdo7cG17TUVmqlWArE1tplH4xRWHzOGNyqx6iG8fGBWIygUbBxCbWCbWMIW8ema7jfHXk8jOyGicHP1KKfVgrbOCHTBI/PEZU8Ps74aSSnuOjQp6UIEVEpSlFKVfM6h3XSHRm1KYXGXDQ2ZfdVclGw3EPZk5YTp8bMFBaZFjNHLV1RMs84ASJ13unSol721/gFiaiqDWuMwzUdXb9C2VP7ey5jpTICazvzF9IjoOr65wIwley6gqsViC1u9tKlKVJqVV6hyhQYbbGNdJc0q0s2Vy945ytfQbmGYfRM00z0njjPGAXWWfqu4Xg8vhWn2MZiKPdbZYbjnuHhljAeSWEk58DD3SuOu3vGwwNxfoQQyrXKsxa2YS7AfCxswrrGneZdgcSpEFQ+B+1qMq9kzGqtMarGw5zp6daipYyd+n1KwmCULqa6l1ZJwqXSXWICvZzJaUwoagyH4tRElaoRkSpyg6mwMF25Z9IFF0IgBI8Pc8E8SqwUMyEkqh409drK3r8cWkgFqmgNV8JFzomYEiF40UMv8blG8kWygG2qdGxR9xUvgLL78Y/Qn3wCORFiYvqt38ZfXjNPM8HPzD7Q9Qf6fstqc8l6fUHTGaw2cj4F9F84SGW853LjFjmt+ru6dtbvyWcGt2r52fJg60urNEmNX7VaQuJ89q5U8CGlNa6xGGtoGkvTGvH88eL3E2KUNvrqIWKkXb8WqaqsilbyO2M0OUVibIjeE+aJ6Eein2R/S/HsGSrIqnTC5VP8VjAZdXZ5VTrobdhNyJBvdRZ/KfhTpy913FbMp8hkyLOR79Gec1P6TXjDxAVRO7mVKYs3gQJjNE3XEzfPYTyQ/IQ6vmHevcQk0dFNJBrTkHRDMj2z69E6M2tLshcEs6FNARs+JsUDOc+wEG90AWa/tAAux68FGCuzZ0KF1+j9j3AX32GzaRjSmpAU2YNPiiE2vPEtf/EZfPBpQL1neG+jaZWSVgslWogpx7OBTFl88lJVInlymlA5sDQXnjGyUgqEODPuHxn3d4TpQA4jTdOQlCQWShtMs6bbXKPsipA0+MRxv2PY3aPzyPW24YMX12C0BED1avNJJwXAuYar62uS0ry+e8DEEeMdq0b0SUbvhdpewViVgSSBR8jEOeKwbwFjtjVCZLRiyjClzDgZ9kPi8TDxuA/MPpSNUBbdVBd0cmkn0NicQEdsk+jWmfVW0bQZ5yIovyTqNYvTuoFcNeHOG13kECfmU4DfND0xxLdATHEPFCZGWIx78klv6Ow4BxLqa4TMakBLdfPiecvrj1/RfPIK9+5z8rPt6VmkTAgebWZJsgtQbAaLOL9myFEq3qlqowC14bvo+MUQJSD8wlzzX/sq8emT5fvjcSDoFU1jpeXPSkKTUSSVycoS/UQIsplJi2BTmFfl/qHEOEODxuCcpus3YDp0UNjbkUO+ZFRrZlZ4XDHdooi+I5u2Ohljyb2UZ5gVoL9wIcvrTgl7NcuoFXr5VhGV5hgSPgHGoFGYJBVUixLpDQXGaaLOzCmLpqLSGCOGAVUfdtGGRP6+05RNlyVhsSmgi2zDlLw8r6JlGHMuLa8NVtcqWsYnAUiyzoAjk5lzZp8ibx4GPnje0rei6hmiYtNbtMr42TNOnnEuLIYM4xi43w30rcE5xXbV8HjwC9MEtACvg2J/OJK9Zt1oLjYtd7NoRPrZYA1YIxvaPM9s+jVt6/DDRIyJrm3RCHA0DiPTLO3ijTPEmBhDZJwi0xRZdY7tqmezapgmkVOIsvhgtSbGQCjtJfe7iZxbGuewrsWaXAweMqY4PSglrtkxSReCRIJnJhRlXigqMBdRd3foj36K+qu/JvuBND6Q4khKwiotM7CEoaqAqRVoPSXkdQwI66YWZgQcFZdLJFJUCmXUAtDGFJcWekkuDNVYsTLr85L8n60tIZB9KKBe6fEjnwVGegmw1BnD4NylsU2ZS2250pY2ZnQqet4nfPG0fr313bKSEf1EKsUtnxO571HzgNGZBotKMr5jTsQspkfRGkKGgIDn1lg619BfXvHwvd+CP/9zVCzdC0gSVG/BWxpl5TwWsLCce2U8VA2kdPbqargQ4jmj8eyazm5xLZS+Rbipn6/Ovz/dkaWdaXnTCew1prCFqsahAognx+6yx8/zJOBNzjSuoWmFuTWOM59++ikffvAhfbfBWktKEjzJminXbGxH9nK/RcxW2jqr1m7d23MJarWxct5JnM/bvqederwP6NkXjTM5+q7hYrNm3KzJuiv3INI4y2b9hBg7tNY429D2HbnVEEf8uMdPgVEf0U1H1zToxhVNtYRSUWKjXHdqtazbYtCSShCthP1RAAIfItr1wgY0rmhPl9ZRdTL6kvMMpODJYSJrGS8qQ9aanCWJVnW0qwqGCAjrp5GcO0xOaBqMnNgyRv//4//5YdMdNt2dfvBlWfu3D//3/B7JFX8VoPoIvDr/wXP4jDs+u/sbuPsVb/j/+hBPXhSK/+zD/wrXC0gXo7iUi1mXaEVbU1q7ixt3bZfVqrR3FgOqHHzJ/TLTMNA1rcSnVuF9KsUDYe9p48gW0fiPJVHNpQujgCvGOjANbtPzbPtMTPM02LbDNS2H+zccxln22igeBn3Xi2TINPLzn/6EdrUmp8T2KtL0l9hG2msVwsxUSHCktBKDkexFLrWsjcaoYqwZZG7ipAOvFkKyxONdJx0Cos2Zi+5+gBQxpln2ZpRGmwZjE8Z2VLOS8XgkxSCaeVAAajH0ysXRs3bE1TW9SpOmRdvP4ly37PdQWaiAyiJtUHRSBZzSpBwEmCidCSK5JvtK1T+3pr6n5IU5FQDCoLLhs5efMU/fkXPLYOJEk0baMjaeXmx4eau4eYBul7k/iLZ5jLF0vkQhBcQkzZg6M88TwR/JUVr2jTbEElvpZTet8gICnBqlyAU8tQVIziV+ialotJ619sfESWsWMBp0TmL8oxSugLGLBCxCXFmYtguxpsTexcxM9P9PRXLJ9QzONTRl7J6AQCE3pEIsOf1f5udZfFePBaTJ9QVVjqAAsQX4RVlOVfZcwCCF1hbrHN3qkra/pl1fs7p8SrfZsDtODIeRaZykwB1mAf0y5OiZxiPVU0ZMk8VYN+fANA4c948M92+I80D2EzFJh1ucxdgrxQGdq6kcVEY8JZ+uGqG1C4F8ijuXa/4CWFWPpUBRAPIas6akJTYvIFYllVTYNZX9l1KAlRC3zjGZWwlVpF9rBH4mX7B0eqmzGKo8NS1G3hXDkK4L8U0xSoo0thpyaonHZY6p0kKfifF8Zy8FdaPfMnwyzmCslm6MBMoodFLESIlZBPDPgr6y5K6UgkWOpYP1FNMqwHz6qcy3nETa6/KSNIx4Y/HPnjHOM217oOsPbMeR6D39eqbtV7hWmLJVkmt5VjW2ypRxeXZ19XmfPdNqgrsk0/JHqB2+KqcFdKyG2TnbE9+h5Ogy+hM5yq+MlpzIWAFmG+8Yi4zdOIVyqrkw90urv1UYICXxVjEFZ7LOolQmhoZgA8a0+FoQCRMplKKDlrMQfD6VcVbFO+VZnZDpKilZnsv5MpDPQOny/TLmlgLtabzw1lM9/VMVCSZTsiDK2Wz8K4J2xKyIWuRwJGVTMpfaBt1v0NtnZH/AHj5kOtzJeMqir6tzwuRARhFNT7KWWTd4vcLTi9fKsBcGcZqhsIUl/v67gVj4dQFjlUIzQ7zFxBlz+8dsrzpQ7/OQNsRgyUDMjiFv+dhb/umfvWF3gN/5EL71TGGzxyBUeBErLtWhXNlPtVokrQMqBZaQcnnQmRxm/Lhjv7vh8HADYcKoyrwtWau2mGbN9skHrK8/ANvhs2ba7Xj18U+5XCuePV3zwXvPyH5kHgOhPwGAWqm658ngTKVN3jj69RqmgOvXXPcXXFw95zB+TE6ig2SMLaBCQDfiHJc0ZC96WxlF9DMhlgmgFSF0vH7M3N4ZjgOMwSPCYZT5n1l6Qst9UDpjm5nNVtOtDO1KY5wHZsgBiGXSSaVINkiLcb04gqcsr60fUv/lIyYjFVonlfiUxi8kXSVIU7m0L5+OL7a4ytqVS3tsSSxDKppdkjQaYzjujmz/zV+xjpG7//wPvzAA5XNiCKJhlRJxPkLRIF4qkmcLQOXTxSzhAOrUDnJ+3NzesL/cLN/Pg+f1/gZjhLG9Wl3I4mYcq7anbbccH+/YPdxwf/+aeTpilLRz2qZOV0XKsWgIB8ZpQB890Ww4csEuXTOkLZ6OpBw1cCk76RK4na5HrmkBZnUd6+ePRAI+qcSztBfVFjMQSUppLZTN/DhlNr3GoVCT5Hm1NmRUxtqMMmKoJUwIYal4H0Fl1mtNqzNzkECnaxWNVkxTYvRZzGq9x+okOsZ+5jh5tAKrIjZ7Yoj4oLgPnrZpWK1WOGMY8iRsoWxQJNGZA6aYeXk38M6zjlVvaUzmYTfzyaevmXxk9pKohJi4XHei7ZwVD4fAOIysVh2X65bdHu53I2HwDMkwFp2xkgAAIABJREFU+0aA0eMj8zTz8Bj58L1r/Ogk4DvsSdmTkifEjPeei3VL6xz7/cAwzdzePvL0yRbrPMMYGQ4TX/+NF6yngZv7PcfhyO2D6B6/eLrlxfWGr7xzxXgc2UcpOuwexXBkzl5YxKWwMBxn9kazaizzeODm4cAwJ7Qyws5MXgJMUqlyRnIWVmsV9ycnAcWJ5DTBv/znhJefEsKInw9lvpagZRlbus7A4qhaQNlaXc6ScBijaLtmaU+PUbTT+q5dEteYI0aZhQkwjiMxZqx1UihQma7r8EX/NYZiFLKwEcoZxYiKQSSKqpuoqjGGWoCl5T0xY2o8WI5L47hOhm3SKO+F5VOSnGUW1ECbs68lWIkqsdvdk/IDtl+xee9Dnv7Wd3nz079lvn1DGgdShikFppwZU+SYPHOWppiYi3yH0uSmpbeWLkUwhhiKznTVkluehVqexfITVRjLZZ0VtjIlwFVl7licNTSNw1nH4/4gCcj530EtBaW8APcsYCqUgP0sHKuyBuns+9nPeE9JmoWBAZVZoct4rYw0FuMHpRTaarQCP488hpl5PvLuu19hvblGq8z9/Q0f/fQnfOMb32W92qIbzUgubuUKrSx9d8WUZezHlEWUJyMMjRyJpFL80SUxTYtJoym6dFrBzeuX9MeJ44uTueM7L97j29/+HldPXzDHLECNFe3dphWtO40YFnTdUzArHm5ecXe75+H2kbBJXD55QrfqME1H8IlDeBSGXHuJ5qSXnlPk9u4RY1pWm5YUE+M4Mk/zUkjNWZG06EVmCiMJULqh3zyh31xjrLS5ra2jX0GOEZ1nqsmLoSmMtvqcS1E1R6KfmIc9dzevuLx+jm1WaNeR6aVgZ07su9Mo+vuOX/WKvwPS/dKP3x6x/4AP+3v/ZLniBaj/Bx/nhd23jEHV+YT9hx+/4i0FGv8HvfVXXdev+k598R4CS4qVv7Ai/ApQ5v/NUeH7DHz8sx8Tn3rW2wuUNUzjyObiCmUM8zQz5YHGNRJPG0drG/a7R8Y4YlNke3nNcNgL27PoHL7/wW/gXCOtnUCeBvYPt8U5fktEi1MzorWeYy57ZiT4kYfbGy4urnDtBaZZQdPTXDznN37zd3n/a99gfLzhZz/6C+b8b1EvPyfNDwjAlnny9BnXT5/x2aef8qf/27/k9huf8N5vfIN3v/ItNtfvEeNpT7m63DINR7m1yRPniFHtIg0wTTPjYUfbJ2EIWQdG2qRDEG1ca3NZAzIhRJxLTOPINA2QExfWkc1p55J23w5T9EsbNOPxiJ+P5NxgrGPVd6Qk8mnaqKIVW9CFBJlIyoFcpDBc05/Ax9JtYDTM81HY+sagTUNKJ0aWtdKSH6OwEqVd+ZTm5pyZ5glrhWlprUE5x/HghXRJZhwmXr78iGn6D5ZxNe7uuH/9WsgdVxdcXD+lf/eSD15cM/rM7W7PNE+8vrnn9e0DL9+8xkdfYl0BU0OciX4UKajiaWK0BmdRwYpzt8pFWiPLNcWMSgFNwqqEIRGSyIVIcVIKgaJxKZ1fFTQ1RtFajSHRGEPjLK1zC2h4AjY0Yp4oPwsxlPbium+aZf0Wg64TEGudONPHXBiYhQ0aQ8TPcwHhzouqLGn0+XHqnhEwRSld4jZbnrXD2g7jWnGxV5qEtFFrY7HWiWnY+int5gWmWZGt4+NPbxmHSbphkyfPAynM+MJ4vyXjvZyn1pq27VivReJkngcO+ztuX/+CeNyjakG9AmI5Q4xitomS+1e6c+QoXY45i1nSUgxlWQ+X4i2I3ro6+SrkXOUAKmv3xKFVqoyfTOETVmBPPkGMwTIpFH3OfPrcCswLm1gMapfgkwrW5RN4TI3F5CXGWnQlNORECJE5zByGMqhSom1anLUii1OKA6nEFcu6ryycnXclTdTj4uICjnvGcRCJySQYB1oY8K5x5FBAbjJGVU8EIWLgs5hXnuXkta09QYnfoP2//k+Jcfue/X/xXxJCZJwm9oc9h8c77m4+o+/XrNYXXD95h4vr52WtswUkLeefWcgNdbTXlCEvc+3UVVAwQwp+e2KmRi+gXn0eSnCWbBqyFo3irE0pBBYSHgkVIkHXzxFAtTUG12k6axjczFwM2WPMhAm0s6yKB4m2mmmIpEgB1EVScPIRZRLalmvWDjU7ohohjKKXrWshTVipMWbqBQpkU+U5Crkhn5jfkuOdGbgvxYRSgFsqEhR8rxawzozvCqa2dGiW+bWMpixg7GzWZANz7gB74pwpLd1avSbGFssVMX4TdfwUM0lufhwe6PYPqG6Pbi9IWu7xbLdE05H1mmNWrMxnEHfk8ZEURxm3ugNlRAL07zh+PcBYsixCKkI6Mj/8Oz77qSGuv49Z/SZwhU4OMEQlTIvPfeJ//fENn31+4A+/pfjBtzqUmtGq6pHkJbGTHEA0AEmBlEXHtCaIOWe8Hznu7zncv2Qe7onzQVxLleYchW+aFe3qmn77jMsXX0c1a+Zp5LC75+7Vp7y4dLz77IJV7/DD8S2mTD1SFO0NpayIXwODj+yHkd3DI4QD3drRrTa89/5XuXnYMR3vShUwiRlNbMiqQXcW4xLTQ8Z7GeTi6tixO2r2t5aHo+VxbkmpJWOR3SQVRK2AryrT9Yp+rejXmdU60HcZ9AjI/ZL7WdvXiywEwpSpC5L3EiAobcv8C5yH8tMU+LpreJ5b4gRJJ1zXYN1pKMYogJKIxmuMlkU25URCGI1KFV0cFCEX463aDgPo4EWku+1othu+9v1v8OqT13z+l3+D/oN/tKT8KYvWl45hIbYplIBi4ywuz01HLJo0C4AA5FzMtZQwi7yfv5RwjZNoa9bj+Xvvwd0D43DExygMJ9NimxXt5gKjDdPxiLYtTbuWxS0JSy/4uAAi2liMlSBkmg1j2DClC3bqiiFviJg68MvQLWP4rN3wDIc9PdM61r8YLdXHveC1lY1+2myULmCskiq+R2QIOgcvLjNjFNDCGnBWWK7Rg0/CfFcKOgub1tK6TN9mTMrcD+KWOB4Ch2mi0ZqmsAUegmeIgcZq2q6jX/XkDLd3mbsk1cCA6AaFBBFN1zZSQYzggwetcLajc5bWWnTW7PcjXSPgTdaau8cdT64vePa0wxjN3d0jb+53jHNknALbVU92muATIY7Eoh+Vc2L2kZube1Q6yrjViru7WxqXaK2j7xTDcOTN7b0Y9DUNTdvy049+Sdd2tG2DtZbb20euti29VXgLD/eP3L4xXGx7LnrHrnPsj4nH3UBrNSun2a403/n6Cz75/I5Xb3YMU0YZKW7VlmqFBCbH48zL9MhxFB06abcWcLUM+GW9VqSl9Uq+z9g//teoj39O8iLtEo4HcvRLdbKOnS9iEudg4Dn4UrWntNZoK+PVWC1ti0panSY/nUwJtHqLPam0FYOU0uakNOR5LIFlLsooGr0EBuVz50Ae61xWJakWBkKdf0ZbEmKglUJEK0MMp8JRpzRNTugYCjCZisecNNKcdRwt1zrPE9M0EkLEtCsu12sxMLKWcNjx+Q9/RPfsGXPT8elnv+RwfGQ2Co/BZ/AxM4coLFkySYGzlu1my1YborGM//V/Q/xf/inzL3/OIYWSwH353p8/g8ocqmd8koFhWdpDjMQhMaiZUFiWNcDPuSw76stwWt0f3/rZ+aBQ568ra2/JGlOIC1iMEqZHlc9ICWzTsjDrFVTDKFk/JYn97NVnPEuJ7eaCRll+/ouf4Zqed9/5gMurJ+RJNGGVEqCl61akMEFOqFja9RTi1B4hzFMpJMoeaK3m4uKCECaRngmgTIOymraz0LvluudpJCd4772v0m0v8CEyTwPD8Jonz79K07yDcz2NWxOUwY8HmnbDk3e/QtOtCd7jbItJCuNn/OSh7TFuhXVrfMhM80l7edWvOcnRKFyzEtOVOp9SLtI5qkjIiESDmHVJQaLVEavl+cWU2A07tNsQMtIcG2dscLi2RWtFipGb15+zbh0KMXe5un6OtSLjlIMHKx0JSpuqAgjAf3rx3/K17ncLkDuT0wxhQsWR64st19cXtF2LtUUXOWtimAlhZp4H/HiA5Elxxk8Dt7ePjOMRX5iMqcRpSmn6ruO73/0uunnBZ+kVb3iDcRadRd+RHLGmdlsVfrhSHIaZUITttNJ0jeP+4Q0//Fd/wY//5K+5v7/FOGmpphRLUpaS9mJwlGH+H/8H8u/+APXZZ6z+8R8Ia8859LPnqH/yT7DOknJxyPZz6WQSOZkYI/M0E0NAWY3tHarT5FaRjEY1DVfvvM/m6imPu1v2+zu8P9J2K7Rz6Mbh+o6kiilpYfGkWDTakM1ea4szPb27oHVrGu34/Y9+zofAE2tZtS2jgp98/BN+9tnf8jcf/4ibmxueNe/wtfe+w3e//n1++3u/R+PWUgAvrbP6TI+UrIg5k+s6mtNiEpRzlJ/HjLaW/+mn/x3/6pP/HgVcP3uHN68/5/NPP+LZ02tC1ng/06+39JsNsUpj57qmW7YXF6JDnUWLNQQvkbLShNLGH3MmBYk15/F4avfUkhymGBdQSWvxHNBKNOkur59xeLylV4bWFqZTCuRkMHbD9knPf/gff4Ovf+ff47OPfsLLj3/KcLxjvd7Sr1coo3jn3XfoupabNy+5ef05v/jZT/hH/9Efsb16hmvWGO0IYaJti+FvnORkGouyBmU6Nu0aVZhlyc/QRJRtAI1rHE27WkAkuT8yB9fbLat1T45xkW5IWWQggp8YhwPWPKXpWlzTsN5eMQ0Dfg5EH3HtWrqV/IQfZ4ZhYH1xfWLXp4ifRnwMaGPpujVtv6aycmMI0oJvrchVWFuK6RmjIAbPsL8HigyFFdmwEARYqPtI6xoeH25FXqFpaZuWOM2QKrtyw/d/74/4Z1fPlrVHNx3rywuG/SOff/wL7l6/xrUdzWpNu9rwwdMLjLnk3estD/tnvH48cPu457A/Mh72DI93RD8wezHnTdFjTUNOQdi/bU+YBqwKzGVNUgXEIgVyKEzMKOB4Km3JcnK1IzRhMNgSm1ulcEqk/BpnimFXPgMLZT82WkGM5KSISoDtaqSklMIqhVEid6OV3Pem60XDtWruQ3Fnl9b0+u/TFv53gRCnKCijYGHBilGgaxqRvnBipIS1Io9iLFbbIk8lHgptv2Fz+S7admQlxVBjOyyW4fDIME0Mx0em447oR3Ka0TmSOXWwDUpx/0ZLoXA8MB4fSOFA4xq6rqdtO0ARw8w8TuUaxQz2BCRKrJTSqSO3mqq9TYI5C3OULnOKAq2WeOuMoSqxVG39rsC3AFa65vJanRU/NT6Jp0MIkdkHfAwLAAiZcZ6Ix4Pkb0otZIYq+wSKtm1ZrfpFjz8GkearGrYxRg7jET+LfJl4lwQBerXofTdNs4DYCkVSnGErcv1VsqgeKYrUoS5xQFZFvkhJ3q3I5EUaQ1jyFfy3WNqmkYJAEN+HVLqLtRaNUWOa0tV0yutX/+x/xhjL8O3vMXznewwlfz8cj9iHO+5uX3F9/YLN5RPZS9Zb2qY7XUuRk1SlZ6xEAsv9VadAeAHHi9MAFIkLE0d0nFha3AuAHHMgmYaUHYmy/6mwxJrCTqjlUEUKnjnX9ytaC621hdCSGKfIME3sY2CaHatNy2rtJOcoxZHgs0jaaQCDXW2Xop/QLdISy4jMFMQ4k9VcpFcy4As+U86sTPmFFS4zaskNKm5XiXeLuV29tyV+r+bMyzJS7+WSY57zbDMcb+hMT2oSNM+YjaXKykhcY7CbK6LVaGcgT5jH9xlvP2MaB8bjgX73EtdckGnJqsVtr8m2B9syq4ZDVqjr36d3PW7XMN7/nHkaZb7k/HZd/QvHrwUYWwetVhl0IOV70vGH5JQwKXHR/xajuiAoI4BZEoOc25hgnEnjA1at+caLnsu1w7naklIerBQOSuu1hnzaaEKYmceBw+MN4+4GPz6S4ygAREJ03bQstk27Yn3xDt32Oe3mGcZtGMeZx4c7psM960aMfhSR4PO5HNxbCWfyMzl6slLEZAg54UNmmCK3Dzumww3vvNeD1nTrnqunz7iLE2EeiDFzHBP7QdN2mqaRyWdWBp0aYnQcPbx6GdgdNFNoSGpFopUFvCwBSmWMBesUTQv9StOvMk3rsS6gjRecVZ1r6pZAvCTv54t6DdCVEh0rnYq4c3UJKkeMiqvbO65zxnVPsU2Ln+YvMC8kms1KWMSBegoFYF80iM5H0Pl4Op1nre41bSPOgJ+/Yv0v/nf4g+8X102Ntk4CvroZqiK3oMA2K7rVSlhZ07i0SNePVUZjMDS5YZ7nL2GYXbdicCftvMMUsSETkjAeQgiQNFnPNHEW45sUMErRNg6VuzPBbGm7jjkSLi6gX7O9H5n1BUd1xciWKa+JqnyeOm0H520nlCrneVUJdZIsqFXQt56JPm32CxZf/5SSVhSjhP1nEDC2MuFQkmz2WphkUshTwm6tbcVlFDkn4K1T4KfAbgzcj/LaFDMbB73TGDI+SstRmD2aBmuNtPxPEzkFmsaw3bTc78dSnYZpVHRNw6ptiMYzzjNDkMqra1rWTYNKmdv7nZhqtQ3Oaqw1+JB43I/MfmacInOQIKLvezabhof7B+73UuTIypGKuLkPiYfHAy+uG6wGbzJh1tzf73lyucEZqU77yQug0Mrze7gf2WxW9K2YMx33YrDTN4bLTUfwa4bjyHYjkgpPth37/SMRzeE4cf+g2fRbrM50TtM3Bj9IMuSMwRlXpDBk/vqY8IcBH3yppkvxR1pa6hZfMs0sZl/59hb1p3+GNZn8yS/I+3tUmugNHKkte3UIndgPVRf2HAD8IhCrTWlVLGNOzJJO4y6DBAkVICjnV9ec2i4Vgl8KCOdmUtV0KfhTsQQQwKn+tZwJPlA1yGshJi2M2lgYnaX9phwGBcV4MGfZfpbWJqpYvnxKShkfAj4EtNZ0XSMsU51JSuQzhpQ4+AkzT4wp8OAMobHF7DCjYsbEjI0JSkCqFczHkX0SkXo7B67anvEHvw/bC8Y//7fEENHmtC+cQNTTc3j7qwRI4p7L2TOsQNI5sH2G1i5tiqqAebI/16ShBuGKE4tAgLHT385locjpVNysWmNaa0KK5dM0WkPTNLK+kk/rVtlDqp5aTjMP93eE2XOx3hJdyyef/pKUM03jMNqSS/tcbf9qup6cZzHmSpME2DmhC4NOa2FlG2twbk1KAWMNOkmitLm44l0Uq9WGh/Wpa+L+7o6Pf/ERPmm++d3vgjJiXjcFnOmwrsOaDm1bdIqSpBqLdWIwMRz25DAyD0dhqLsVuI4cM2HyHIcZlLRKO+uKHliRnMiZ4XBg8nPR4hO9sCrBcG7OkKnu1QI2pemAIaJJ9MozewNaxrduk7DzpkhS8hx1jmiEHWKspXEt0jJW2m/DvDxjH+fl/jS2Z2UvIAcyExaPW21oG8Xl9pLVaiW6cmRimpnHI3mOmOBpU8Zkw/F4ZBqOjOOROHh0BBu1MOlCZLu9InSB0Adu1C0qT3hG2uxhkgRj5QxaKfzsRbu4GMRmpdHJ8mx7KYDe7HGuY9NHrj54zpNv3hD+MooBnBGDN+c6tGulk6dUN2LwfLJ5wtRdYvqB5+9+jeG3fwvWa1TXQ39FLkB2zF48tVMmp9JmbR1WNegkDM2khCmotRVatWs4+sT7l++SVEvIljjck11DMhq0JagG0zaLvr9CleJVke4ogIBShkllvB+Y9q/45S/+muvLF1ytrkmz4/r5V/jtrz3ngxe/xbd+4/f46JMfc/v6Dbthz5//8E/ZPwz85rd+h+vr52xWFyhtl5gtl/idlMkqLoUVjCFV74dUWIA47JnvwObikl73PN7f8PLl57iuuHdPA4TI5tlzAeCjFOOHwwGtEbZlTfJiJCsp8IVc9yQxIMpJAL/DMJKVrAk+iHSRsQ5jRcM1FyOPnCPGrTG2kflrHDEmrDIo24k+IpGgNNfvfQPXXnDx5H1uXv8cmwOZyH5/ZL+7x2lD9DO73SM3r16Sc+Kb3/s+T59/wObiCSlGdodd2f8cCk2KOynStKDdGtuuxYFc17bvsrbXhHlhlJZEtWhKxqLvnGKkMbZ0mBRN3lQYgN6ijAHlWK0dMYoWo48zXdcjqmuBrusxWhH8RPAzYZ7w8ySMr7YjJzGeqzGkceJk3lm3sMtiSGRCkWEQN23wxCjP0FrR01VK9qx5njFa07hGpOaMxbmGUQmbcJo983zkcr19i1Ebi+ZfipF5HBj2D6BgvRWWbOMcWq/pG4e+MKw3Gz548Yx5HjnsHnm4WTOHwBQORD+S/ETwic8+f8VxHpbcQedEjjNxOhLCXPKY4iHhZ4ljs9ilVlC1AgpGa1qjaIzCaoXTitYZGi1gtS7xuUIkdE5sx9Men7PcBwkD1ELekPZ9I/NDGVTtlIiJ6ANJF8m2GEtBorbMs5yjfAgnBHIBJE8gTEHFJKYzGusaTNOJ/IVxYGRsaW3IymJsQ9OtsU2P6zasLp6QlV30lufZ4+eJFMVot21b5v09cdwR5wMqRZJKUmDIeWGRajIpelScRJAuBMZhYJ5kD9VIq3eNMc/zpQoECRBbjKzqQFpCLHUGGiGkmxMydYpnFyagLjGdJhegPVeCWXlPLrF5Ikrjas7MseirxlSK5DUtlHntnIBvy5obqz/CGUyuihFTGWNiSmfexjQAo2esDjTWiWkeJxkEYZEugEExvcvLDZB6TH5LijClymwtbfBL4T4XIklcup4FPDzTZS1eFiy4RL35RTu/6Hi3zr2Vh+SU0SHSf/Ix7nEPOXP4wQ/ITUMKiTQkUvqc43hgtdqw3V5xeXlN162wtpH5kTW6GnmVQLca0y2jvlyLLueisocwo5JHRS+d2+fXoxTK1Pkr8z1pV2FLuR59nrOf5C+yKoUOCXjlfpNprCInI7mInxkfZ/zR0LgW2zhs49DG0DSGKRej5iASGagGbUBnKSKnwupVgFHF8FZFlBbyj4qeFGNh3J93N+flvudllShjouRalQl7IsRA7dpQVLxCneUeRcrjnOSRM9PxgWhX5GTJNKSuAy3yPhWqi6Yl2Q00Cds/x2zfR48zpBtUOMK8A38APxD9KJ4tThjbNmda00H3Dnl+TXK3ZH0jUnKy6n4B53r7+LUAY2FJt9AqoQgE/zkqa3RSWN3h3W8Q1QqSkfZaP3OMiTQm/H7kSR8gZj58vubZpaNpFEoVzRsyWdeJoNFZmFLBj4zDnvGwY9i9wR/uREt2aTUsQYl1mHbFavuU9eUL3OoJptng58CweyAMe6zyPL1ase4bKIwFvSyoZ6suCNMxiXZqStLq7mNmnAP3j3uOj/dcPX2HPgSuDwPbiysOD3dlk5vxQfF4gFVv6btWzLycYhobjrPj/lHx8kYxhQ5UX0TsLYmEVgljMk2jaDtoukzTZ/pVousKCKvCwkpbgFfOEm445dinLahMCtECEQd2gzBjObt26PYDvVlhty3GdSKp8AXnQAkM1emzlgA9V6y24rNi8qD0Mvmq7o18nghXa61p+xb/uCf+5Y8XfUfR/u1JKWPNiZlhtCmMi1a08aj3IZdJX8+lLBz67RaLerhGWuHqEVKScVGAa8FOIqiJ8bgnp8Q8DcQoLDtrislECuSsCesVZr8nKXHHnpNm0FcM6pKZFYEWMMIMqgvVFxmvy/+cdtvzn3P2tc7Ps9efYbxfYsQaik5V+TlK2lNiPrUMFF1/QlHSMErA10QmJph8xueEn4P8O2RCyExzolUZr4NoveaENQoKy817j1G5GHYkWqtomo7DMJC8JPohiynHunVYpSEhjOaY0dngtKW1ht0uMYwBhWa9arDOMc6BECLTNKONxSeFs5rGGjZ9w91d4jjNhKjoOoMp7d0xRo5hZlxrtr2jaxx51XJ7/8jUOUznFid4a4TFoFVtE1E4K8Z4q85x2B/orjZ0reXqYs2rN3fEEHGNGHA5A1NhwD0eYBxXNE7RWEPrDGqYSSHgaiVfl6AnJWIS59NErdBXLdhS4VQZNXvUy1eI8/kEr1+SfvQXZJ2Li6xH6ySafEt1uCBvy1jirbF1Rg84xekZWYPV6dfxrBCilBINqaL5l0sgVwHCehhtCrO8Bmxn65XWaPSXqpUpJZEdKPN6zrmw8aX1r3Y65GXuV77r2XypgaSq7aPqrd/nUmwSI4Io+pxKCYugGHcEMmPOTGSOZIYUycc9cxKGgyKjMyiR9cZECY4MSty4UYwxEIaRpJUEC6ohvfsB836P+8s/Ky65Z+vsW1H46VxP/17+VdhfLG1oy/1ALUv30pZW0fPyOadl5mTUVpkjpdOKvIweuX/ZsLzui62Pp3bIU2D9RbB/eXGWsSzyMllaepPo6qWcub17g7GWzXrNO8/ek0RbiaZZVog+ouuwKQiLSMkanqLI3GBENxIcpEgIsxgrGHGhN3aNtQ7nGo7tqVDn55HD4z2P+5HLiw2u7WSdDInhMNKtGjHEyaCUwTYd1SDFug6lHfH4QBoPpBgluMvSqugRCQLnGpQVUCMrSTIFg0mEMBcA3KK1sOeNcae5Q2ldTMjcUYqYpfUqk3AqYa1l9suNln08SeeKJJkaZ82XiqmpsNdBSXynMqRETNNyf7QSLFEj7WGNUTRO0/WOVb/BWSeAbvSklJinA3EexBDNjwzHI8f9nnEa8PPM7EV6JSWROBnMSN9tyBtFWmV2eoefH0UeSiusVUzDSELYrNMkzsVaN6WV10CCpnECEmYx8jGTo73oWL/YsPnlVtZ157CuEYf7doWyThJuMn4aMNXgzFrMt74F3/kOeSX6xplMSIGYguhil1gt5bS07mVNYeFkIhIDuSxthxjwfsT7SdqNmx49H2SOLXANdE3DPE3CDC/3vC4CtaAhO4SwRXe3L/n08x/zlRTZ+kRgZHX1IU8u3+Py4j2eXH3AxeYZn1x+xJvXL9nd3fPxy5/irOadw1d49uRdrq9fYGy7FOykCKb+YH7eAAAgAElEQVSWvaHuR346QgrowqgxWp8vTvRdT6YlhInHxwe6VUfyE4eHW/xxYn15wVyYhjlDmMeFPKGQFtjgQzEMk26yuvdkWAAxpdViOqPKWqmK2ZAYjRXN2BxBBzoFaEPKegF3M50kiMkz+4nGNawun2GaFW61wu9u2N2/5ng8Mk8TyljiPDMejjw+3PORlnVlHidevOdxTcM8HkWCgSwah7l4ZcRAdhnlWkzK5ZnXnKSCIQnrGkAYSaf1WRixMYqMVN0HlQJVCgsg4LXOgNIYJ0BVTKKHal1DZThXE6hUCsKSzIsBlTWixV3ZbGph6xnZ07Os+T54kacxBpMd2TWSiFcALJd1+4xlpZSiKQxHeRbluZdOocNuJ11b8QQapCTsa9d2tF3HdAw8PLwhxQlrFNuLp2BbrNLoxrLSFqUVMbaMK8tlIzGwDwfCdGA+7Ng9Hrk3iiEGwjxKm1j0pDAT55Hgp7JnSuxa2fvLWZX9U2QQNNZoWqNpjMYVMLYpX5WitP3KrnrOt6yM9NPmX2Oscr901WQ3hSlvTjlZSsTgi0qVfL9IUZW/d85Pq58hW716++f5vA2/EEgqM1/XlmyZW0obFBrrOly3wbVrbLPGuJaUlHQsZYCIsYqmE03jMCd20ZP8QJgOEIN0ERXmWu2sMlrYjboUHyVPjyQtc9YYMU+u5xviWWdmKvtuYcbWuGQZf2cxCgtIeB5wVcxaU+WC5OVaMA2lygp9MoI6v8s1Pkop4Qs4HlN+Kz+un7as6eV9ScWly0xpiWmFLCDsRqO+YLJV/p5GY7VFOYXNBvdWzJiKdNgplk/53PyWIqvAW2PlPD5QWgv5o/6+5p+c5eElxjyl5acc9gR6V2BWlbfoYngn41I66hXm4RF9/yj34sVzVNOQm4bx2TOC90yzdALMo8hebLaXwpxu+lKYkb8pnfp1TiUoJQqVMypHAWJTRKcJFhA2LnHdW3NDiYdMgWMlFlji5IKXlM87x2nqtct6eCLXGa1onS5eIInkI94H8UTwgRQTrutKwaHMARLZiTSCKgWxpKQrQTTIEyoW47QijWiQTrGoAlCwrzpOqVhPefZnsERdq8/H62l9enucnOeUJfIUnOHsXYfjQLSP+NQRWBPstexvS74AYMB2qCah+2vYvEc+HlEpYcbSqSkrRvk0XTTRsxS7tMbqDmU2YLYYt0GbGZVTuR1fxojq8WsDxlZUvT7EFHak8Wfk4RbmPTz5Q9AvyGlLChrCLAygpImp5//461se9oHvfTXx73+748WVwelUUuQSdGiWDSSHmd3DKw4PN8zjHhNndJ6W4E8rgzYOUypu7eqaqxffoFldE7Nlmj37h3uOjzds1pbrywvef+eSOA+LVg6wJKnnIP2S+xZQKudEjIlh9Ly5fWTc3/NVP7PZ77n4yUd88u1v8tBfiA6Pl83hza2ncS19Z1h1jqMPvLyFNzeR17cOra7ouhWukWpNDJ6kAsZmurXm8tJycQm2CWg3kzkCswyxrICiP/TW4Hmb5VoXmUytXEjLR87qS9quy1tiTe6L6L9bYUjoM5mCVP5TqQQHNQGvzk5n6zEg7AJdRBzyiWFVn7WfJ7KCJ+8/xa1bPvr550syr4zFdBforHBNI6ZlThF9Qh2ECTONszisp7kUC+S9KWZhrBajoF85z7Th3AyrcaKvqFIxXAjCbPOzZx4l8Tnu98WBMmJKUK+1BqcIX/uQ9kc/Q+8CcT8zmBc88gyv1kScnNk5WkpFRcvPqzAUlIisLOzLXTt7zTletixrp59XILZ+hASFJ/mC+poIzBFiUnDGXtEGdEy0OtNoAWcf95k5SKXa5EDfOVatwulEnD3DFAnDyKq1rFct675Br1qOhyPj8cB63dM2LSkGrFJstz03dzfS2pUksBjGI53rsRpaB+Oc8FHaqnLObFcdxzlyGEb2w0TfiRba7vHINAl4tbaGrMvCnAKr1rJdd/iQGOeZ/fHAtneEDFMIjPPMJy9HvvLuE663PU+uDbc3rxmPe6zqWa87tts1+/0RBVxernn25Io5JEIM9I3l2dNLfv7Rp/St4bLZcHm55ubujnGYIWdaZ1l3lrAP+DmwJ3N3P/DsyRqjDa5oDucUycGTNeQoZmGnNvQKmleWjEi7ZBVFt+nmFvvP/wWkgTDvif5ImgdGUmEpyfAJ3r+l15lzTW6+AJCdLTFVhxhYxP/PjR9SOM0xWaM13aqY22VhvphiJJDJRVdWk7IpZiiZt3N2cWuu5k8Vk40hQIxY62jblmn0wkAtAW5KRetOCxhstMLqBm/topItOruBqDJJGUwBGaUdWfajmBKT90zzjDWW9XqNNQKmBOAxw57MqGCyAJHweEcKM3oeaaOXNbIAWRlDNpZIJOQkDsxKiVlduf6sPNaJRmLXrhiH3fIIFtawPmMal+dRdbdqlbo+R62hOQNM34786nJx1lJJJsXqmlr+BkrMpsr7JHE8HxgKVdrnJLEo7cqS5S+t82ZZt2Q8qBBwda/IWdbhZQjJ2BZWqxS+xsdH0Qv2nvuc+XnwvNhesdlcyLiIAe8DySecajB2TRwnTA7M3uOPe467R/pVJ3JBKJgmwmFHkzusE6db7Syt6kQ6I50ZeFnFxirmFPn0Jz9itV6jbEcyLR//4mdcPnmH7dU1m4srmtK6WZ8bTca6ltB2hPGAHw8ym5UWPe0gGshKiRN9jJGmbYsJtMwx5zROt8LeM5acBYxJpXhdJU1yzNIR4hTKrqDJROVRKkmbo9WobEhKNCixJaHOovfWrjbMx4O0eKos7bExFaDaFmBoJgVNysNyf6yOtDbRGVg1LdZqYc8XplQIXlh2YURrRZgOAsTOA3c3N7y5eSNri64JWNGfTpFI5OHykbQyrPsVq67HWst+d4dzms2659nTa+7eRO7udwyjJ2qLaTbotqfrO/q+42G3E83N0mZtW8PjfST5AClzsd7iYxKQ1TYo2yyMr1QKyjGbZRpF5/j8t39b4uPi+p1UJuVZgsckchJa65OkQ85M4yCMd60LESHK/8oKEzp5Pv74p/TrrbQkV7mEIvmhlGa9WhPmmSkKUNeqthALZMyFKIlkjBNpnpmO99w/fMaN6VkPnjGv6K/fxTRbTLNmpZ/w7Xef8O0Pf4f9+MDN7af81V/9CX/+4z/hpz/7Ie8/+yq/94N/zPMXH6KyWTAKrUXjbzHCmQbCsEMrIU0kTDFuPI+zWsZhwroVX/vmd7m83vLZLz/i9ecv+ezml1w/v+DxcMSYhr7f4BqHyondbsdwPODaBmM1/XqDdSsa5/AxYayTAn+ITD6w3V5IgUNp2rZhmudFG7G2C7OY3ciyY7Qt+oZFP9DYUszxTMcj+8cbnHN03Yr3v/597j/5W8bjhFF7LraX7G9vmQ4DfphIIXD3+hU/nP4Nt69f8dVv3fLi3fe4vHqy7J+u7VCmJekCjMYgBReny3lFKfaXluMTAGpP+jJlP40xksk4a4kpFAatsICbritxhCp/o0iOxQzK0nc9SuvC5Dfl8UrwqK2jaTty9OimkRZ43YhJWgWwajaXRFN/mkfGceDq6hJnG3ANwTXkNDGNIxTAQrogMsZa6VwoOVksXUvHYSQq6BuHCoF5PPDx4cAwfnUZTzFF+tWapmtYbzeEaeD2373iuH+gcZo4vg9dL2BPVpAF1CBJfNteb1EqQ7AMj5H74Z7DeKBJAeVH/LAjhxE9D4QC8JBFK7fWD4VwUopaurRbG4tVUuBqrKG3hkZr6bbSCkvCFMBPodC5xCEFmK15ldLmBL4huqKmrKvOFqNhbQqD3yx7eM4SW9Ri+wKCnYGtZzjJWWAAVRKmHjVnky1cl3GU8TGhVaDR7hRTlHZ8165wzbqAsb0U4bzItHg/sd4Y2n4jzzzMPN6MxHAgzIOA3TGSzhibegk7KkBac1CwztI0HU3T4JwYVEl+6YlxEAZ/iouOfcWMFoZeLSqdg5kLaHgOEBTMTLG4zgthQIDZMhiWr7mc65lCJrXbDeLZR5zH3fLvGGMpOAnQrhuYQ6Aq/isklg/eL+ebizRTJUYtEOoZ4WCJIcu4zTGULjeJb6s0WNYn4NgY+5aEBqp0KpQxGqOwRZfQUmtUkVQScPcMWyh7mE6akALVyLeO4+X8UVSAtLKYy40nxYyPHvev/1ju5NNnDH/0nxCA8XjgaC2H3SP73QPbyyu2mwsutpdcbq8wXY8qBW1VOgwrqKjKLBMwNqKThyx4ljyvXHBVXWLfU8RKiqg8yVeVSTRyD6n6taV7uBQEFujyLXS2QAFGoy3YbMjZkJMuebLHT17ITV7TdNJ12rYWkfRMeB+FLDVa/GiJZl46IKL3UuApjGZdDNm1cmgVCmgrRoxSTC4neA7Enq54WSOKEsdJWetXAPfnsyhldbrunLnfR5LekaaGGDpG84TWlDhMKXTpcFLGQbsm5Wfky6+QfULZnnZYQ9timhXK9SjbY3QjqEsWmUuvM46AVhZlNzTdFXkcUJSi9t+Nxf76gLGx6JZKQGnAZOJ0xB/uGW8/hXFPc/F9XP8Nxnz9f7P3Jr+2bVl6129Wq9jVKW75qigyIiMLAheQGOFSFgJECyH+AXCLPj3LQgiLBqKDRINCcgMJOjTo0QBDw5ZssK0k03IEGZnhfBkvXnWrU+1qFbOiMeZae5/7wmkJkVYisaSre/Y5u1przWKMb3zj+6RKRSZqw0jNu3TNb37h+fRmx49+duBf/Rc+5Dsva5Z1xmlPziNx6Bm7A/1hy/7+DcfDLc7IRmaMJqpG3OWKGDq6ol5csLp6yeXTb1EtX9IPI8f9A4ftLXdvv+R73/qA5y+esFovkWBXkTBl9UyS+PhxBgkBVKkuKe0EQCztOIfjkc+//pI43OC9J44D29df4T95SVPXRL8gx5GcA9t9JmXHoTc8ffKczz57w36fGEcDqkY7iw+eEPcYm9lcGK6eVCzXisUios2OzAAEqdp/A0mcpvF7jNXCmitnMv89Rk/fH2kaVQZ3Zk4AzicNlpgVIee5fWKMsbgslnfNnLWiFhA2My9kU14fSwlMvoWe8UOF6NFAAWdjnPchow2NruazleeLTAS6Qlsx7Br8gTR24oybogAvabpWqdw3WR2E0Zne308BWCxX7OpmfhxGjwqiwxeVonKOxUIWgxgjx+ORvu/RKZISQoPPZQEbIu0/+pSsG6Ja03PBPl0ymhWJyajr7N7MtEI1qWufUNLzn6fj8a3+5lGwuYxgqjqLgLxWk3Lw6eOn9TWlsxGgIET5Xc5gNSw0xDExxFQ0BeE4BJyFb79c8Nln93zdB3oPQxKGw3eeNSSbOXQdP/vyhg+fXbFoHKvW8erVVzy9flLMIiJ3N3f0uz256F2lnBi6yC4PrBY1y6YmpwW3+5Fu8Nw+7DnsHoQFW4z1xvGOysmZtYXZerGoeXu75XAcOBwym2XF08s1tXPUbs9ut+c7L5+x22tu7zw3gxiJ7fYDTsPlUvP0yYYQEv0wMPQH9vstx+MoRlZasVkt+OKrt/T7HU1tefH0gsuLBbv9kWEcef7sirqquLvf0TQ1z59f8tHLK8bPbzj2gXGIfPH1OxZtRQhSidbl3o8hzGDrxIcSnbji/jj/S5L4xxH9W7+F+fGP0Mlz3N7MwZEAsApT6bki7H2gbpqCzyW0Ngz98EgTCgqrstgtq5LEQQEEjUZrNzPOx76YCylKhVLWTmcrrNZSfSzhYM6ZGCKmMtSVI0RVWtYfHylFkaA4C5CVKWtaigzDIMG01u81mUzARwIMp7BHjiGP+OwJKpFyhcki4JFgls85dEe00rR1y2LRoAFPZkCxtY4HVxGKJpvWGXyHi3IBdL0k5Uj2/lSgioEK0VhUOeJjwLpanFKzOIOTswSkv/x9hmdP0P/d35hn7Lx+vm+gpopm0/nZl+WjRfGfskT/grVvXgjgmy7u57+PANU3//YLD/fNX51vNf+Pj4zaHeDdYc4elQL9t/8Oj1e191/1fhT4C8bIlNipb76T+rVfh7/yHwDwG686/vLPjqek6u7Azy8T//snDcfdDcvVNTlSDE6E2UBpnwXQ1oiuadMQDnXp/pD13ypD5Spc1WJLa2IIHlvZklSJAcq0B0zgkRjwigzD5Ig8xogxYq7onCPajeyBStE4h7IBNXpyCDLmlBHQUZ1KehNwk2ImK40zYgxijUET2d++IYaRga9B5GS5WDqeXzVS/DAOXWSQYvTstm/ww44cPIrMcrVi7A/stg/st1se7u9BZaqqQhs1M31Q0FcDd/WWi80ldd2Qc+bYicP2crmS5CRkMjXLi+d00ZKrEdeusPWaccwkDUOCY+/pjyNkaRH/zrefl61XoVuL/WFN82VTuj0Sx0OH6wO6alBWWnCTj4+Spxh7tFO4tsG1Fao2VK3o46Yx8u7nb2AQ9msOoYDrApIoo2U9SwHlJS7NOYkpuQXthHUmFVRpqZ/AiLubG2FYa4Oyht1uR900s56kFFYk2c9lz9rmnrf9PVf1kpeXTxi2t/j1c+ku0sL0ZnRs7DMuXz7jux/+gPuHr7h5+4qb16/523/nb/Li2Qd89zu/yrNnH7FcXRBSpBt6/CC6v8ftDc5ZXOXQuqZuGmFnn029kUQfPBG4XF6w3/csLp7xsl6wuX5gu73j4uo5dbvCuZqstYA3KrNYNmw2G+7vbghDx24c6F3PxdVTAa1MjauWVPUCazQheI7dQdrhtZK4zQdCCLSLhcSrWWSgdocDRndYV+Hqtmh/Gum+cw0XleN4G+n2D9x3e54+eUF7+YwrP2CcZrt7TZsU7u4Bs9uCysQ4st++w48HHu5f88u//if4pR/8kOunH7BcXUk+4hq0aojZMg6ddIN5T/CBcRhomloKRVrcy4PvaZabsp8La34cOlknz0gtqbBrMQ5tHUqbAgYkxq4jhlH0pqsKZy3393fE0AOJqqppquWsvdm0NXa1wcdIRqG1pbJGwM0yJifDTaXBWUMwsN9vqetWNFgBcNRtVYoRhVnIOctKzJlSFrBn2axIoUZpTaUUP/j1HxKyYrXZzOt4017i+yN+GIhjxJma7//qD3m4fc1+d8/PPv0Rrl6gXUXdLri+fibeD0qhdEYTSMOe1B/Z73bc3d5xe3PPz376E25vbzgedwTfCRmkMC9FMgNOMhKyVqow6X5njFY0zlJZS2U0loyKnqLxJkF2VrNptIpTATKIBIcCMPMahdI4ROLHWieyJ8YW5sTkQyFHKhIcM7oDnBdk0wwyTsDgtCc+hlxOK53sp3EiTKVEGkdMlk6foBVK1UzGQLboaGcjhkbGVKissUbhloaqWvDsxYJPf/oZr774gpvXX/Dw5jNSt53NuLSGRbsoBI7E4XggliRHocpal1msVzRtS+Xq2ZCz63qREQphbtOezvAEZQooKHnjLz6UUrzPXZrGas75EQcqFumrCZJM03POrmYu3cCoXAoyGpJ0HYuheZ6/K4jczlSw0MXcatLV11qL3mchIaQoMnkT+Ug6+KZWf+ZxGlIoYKzc58n8d9LQzaX7dO6qSqlo0Z4uhB882Z9AVmPM3L0XfJyLQ5PEgqawqUvOa4spXVVV8zWytpj2FRDBWDd3VU3mtDlJ54N0VktxJQZP+upLFv/Dfy94ZkqEDz5k+xf+Aofjlpv7d7R1zXqx5Nn1M66ePmex3IjutXNoIjZlTMEsci7dejNrNs7341FH13RTC9FlusM5e7TPEDxZWzCuGHwZyeZyCf+m+3y2N8oa+DjZVyqjjKIqXbwxJnxI+P0DcahoFjVu1XBxKaz0mAx+rDh2DYfdgmEYGceRYejpUeRRih8lYEUZ0bRvzQJjHRLXBEIYOB4OhHEoDNl0Gt0l2ZvkiSbAX8+XZmIan51gls4MHzL7PhDSqUh0c/vAOL7Fuhua1QPRZ3z+JdTiAlW1OIUQW7QmWkdqLlEvf8hi9RLV3WK7NxiVqJs1NNekxZq6NjRW8spoijxd5VB1hY4Vblyg1wvqQYqg5hd0T0/HHwswNudEImCKlmvUWty7S6WwiZrh7kek0MP6jmXzAzp1LUlL1qBFiDmomocQ+Mc3I/3f+5LvPR15uQk8WXh02mPTgFURQ0Ql0V60xZXTGFPMVpAKgzK0yydcv/gu9eoaVa+JKLzv6Y8P+O6BD55d8MnHL3B1xaSnlFLZhIp5B0raYY09a1UPwjTQStwgwxgY+o7DYc/b+xvWThb3bVvxuy+fEcNIXTeM40jai3uxNo6QLIe+wu427I4H+qEX9or21DqyWhuWq5r12rBYelzdYaxHaalyKSXA4i9KMcmRqUp6Ylrms+pa2WgKBKcVOKeKm6pmqvCc0+LlZRrjDFXTsNhssHVF8ifmFQiQqpVMqphyqcrJ32WzSPMilhHqvIwj5sAjTxW8FFElgc8542rLs28/Oy12WZh/KQn44kMiD4oY5G+KhFJTVU3aEM8rjFL5mqqA37yS49AT/cnY57Df0/R+FvL2KRLSMCeqMSWss2RETzYHMUqKSVrek24JqWVULYOqGZU7Je8FRDixWifA9Ywxpsp9LOBsnh7P6MB7/5+d5/T7KTaeIHylZOFPZV1MWYBajTxJp/JxJGIurfsJ+gRBCQxTAZWJrCpL33kOO8/vdUfuD5GQDLFo7FY6o7O4wzZNw7PrNVcXS4ZhYHvo8NkQUmTYd8QQsEbzrY8+5Ha3Z9+N9F5GzOgz46hoK0tVWSo7ElKgHxPZiebXOAb8KIHIarUmpSgtFinw8NBjtWKzaIDMuzfvMM82qBSotedh2DN2WxY2ozc1oe94OPTstlt0rFmYJcu25c3NLX0vrbiffPQx9w/39F3Pw/2W682aRVOx3R3Z7UcuLzIXmw2391tGn9gdBi4vLhgGTwiB/b5jvV6wbAwxBLohMqbM51+9FVOXECQpTDI3VWF5GyUV/ZwC5Kn9PaE/+znqJ7+LCkeSPxDubwjbB3H6jWNJNEqJRJXWwNLOr5QYpcUY6PrxBEhoafecw/ScIAnw+uTpNfvDnnEUJ1FT2DN5Cs4LqCXrqcY6YbiJmYehMaa0J4+EGOZwP5ZAc2JcpAJeilRGFHOBsyRD65LEITrS0golBZlJnzSFXICLEhSfyRYAHBN0wDJnmpRw2sxzKAHHrsMacTeuq4qoFAelOGpFZwx9W9GFTBp6NJmmdtTNAjAo47B1g60rtje3BC8AlCHhD3tC8PiUpD35bLnKxuBTwvuBQ4r4OK2rqbTV2hProUz6R3pu0/c/k4NIiJGe+cNKvv9fO6aTz/BPQ3j/8LPO/4Sfz5bZsyxMZSlqnb9r4yquLi45hEjd1rjKIB7Akymdmtt3g4+EIMwgHyLOCotJGBNKAtMgFfwQRHJFGFFqBoyEfVCKsEYRsyd4MamLPkKW5ERpSSq8HwgxF/aDYSzFJe9HYdQEj72wqGRkGyrxgir98toodDEG0yUpSeFIZUYWqxplN7CTa2GsxVU11liMVhwPW8b+yDgc8cMeshSwx2Hg7Zsv6fsjwXuiD1S1K0UjXfTqEq/cG2LymMqxubzi+Qcf0h8PMs9dha4qwjhibIuyljf3R5rlGlWvUHmg64Fhhx89SimMc6QQoawxfhj57Mt3dD6zfvKCT1zNu3ev0A8Oox1ZaYYg4FIsYIfSjrpdzfGi0prFsw26UWAVycCIx9SOh/7AuO8ZgsckBDCPkeg9JiuU1aXJSfb66BMmyVzNOqNqw4h0hKQSGkh7XyR7GP1Y4ixZz43SIr+CsFlSiBBF354oRITDr/4GX75+zaq/5xP7Mbbf4w8Pone8bEhh0nOTQELlis3iQ9oPrnl2/Ut861t7+uMDN3fveHdzy2q15urJlazxStMuW9r2A2YASGlhFZ+1RwNiphcSYz9ycDuULU7yqSY6x/rikna5IoTEdnsvTOpiOGS0Zhgjq4tnTC3vIicjxXitjeguO1ekcaQbQ2lJ6BXC1Ip+IAYxG1Jao23FYn2FzuGslhcJwUMBfqwxtJvnVM1aWN4xE7PGLa+5bpa8aH6FT3/8I+IfvGLwEtulHAnDCBmsMXz+6e+xXG6Q9M6JkdYwFsappqorQmE7G61oF20B4kyJA6Rjw1Ye54SBaLUmlSSanAjBlxibwjQ71/WWpFpphStGW7b4Jog8gRiwNU1LGAMxemLwjENC2wqrHSiRt1JMTK+p3bsYrpRAVGQ2Kplv2UuxRdu5gyWFQOUaJtNHASmzaPpKcoPBoMzZ2MnvtcYqJWzelDEaoskctrfobIhR0x09+93XrNoFF1dXxOz59O1rLpZLlssFSmcO/YGbL7/gy8+/4Ob2jnd3D3z+6i03Dw/ECbTInqq5pKobnHOcWpJLvJLle09yMqBwxuK0ln0jibas0bkYC+sCVeTTdEFQmgxQWtG1UrMerCoGWtq6+bHS8l5y/06h0gwCnu/9Z/vZTDyc9rQ8xYrqfIub2XwKyW3FIM8LC9cYSJNRn4fCTJcURkAnoieNHUNKBGXYHx7Y7+447G/ReO7fvaM/PDD2Oxg7qpKPT/PUF4f5XIDC89bojACO4zDgRX+HEON8P6ZxBqdiNgV6nqBZjS78VIkRY5yANfmESe5jvhZn1/X8H0rNUjwxSvyW81Q8K5+ppp9KqloKJoJNRNHEPYfGC9gvt1f2/bmLSEmbvcTDWozcTNFqjtLGPp2/MQZbjPWmI8QgBpOxED5KXJlSOhF7C0NbaV2YsWdM6QKOiS510SSdcm0Qwlo8GaMJQUoKEblcAGNE09daKd5VVX0qIMiCdQKxS7t8LOeVy/cWtc8kuV8seEZOmLdfU/9v/wtJGcZ/8c/gnzxh6KQrabe/pW1XNIsVF5trLpZLGmuptMKoLMUAciFmqDmPmGD1eXxMqb3Rj5RWyRmVExqRniGOZN2TtSNpI0UbNfXiMWVOZRpO7zuNs9McfSTxZTI2FbJZCBz3PWEAV1uMldycaSMAACAASURBVLxrtdRC9vGWrqu4vRUfi2AMKUhH8UzgU4asHdoJu1wrueaLZY/vO/zY40PPUMwzy4k+KtucyjhlcXkPcpmMJ6f5PGEymczg5b310BOGjqgVta5EFmt1DdVCVtssWvEWWNUVWl+jly02PRFmOplsKpStxb9Q63mMaAehWQDXaDVQxSPkB5TK5OB/oZTldPyxAGOBWalKCmvi4K2LZoslE8e3hKMm5REXE7H9AcksUdqW1gtLVokxJ8YhMHx5w/7rr3m76vn4MvL00nKxsOhK45yiqkxhqJbNpoj2pwRKV9hmycXTj2nXz1HVgqTE7Oa435J8T9sYPvjgGc2iYTJ/mln7UjqWjTRLCwhni0yKQUxhMkQCKSiG7sj+sGV/3HJxtZZAr6q5b2tMDLh6hasqlBLB5ZzA+8jh6InhyDDKAlo7xWJpuLpSLNewWETaRcJVPUp5svKQw/wd5XgfiZt+IxvI45Rz+lm/97vS7quMTLoMxQHs0evF7dNRuYpqUYv7XmkjOB0nXcBU2CucgZ2TOPOjjQtk8yib9Iwd51zc+wpdvtIs6npegaZF2zo360eFIJtXViDGCqeAQ5JQij/JVMERht2pbeN0dIcD43jSvTvn0yslCaafhchh9GHWLZKqapLN0kiAGvKCPi8YWeBpSNizsTWt3OeA7AmIPS3C6r3nnL0OJRuxfnzf5rgqM5/jNDqmAtXUaqyySEZITVmAOqVAJXlOyrKn+QBjTjQ60+pEzp5NpVlYxUjm9sEzYhBtWM2y0tQaFpVGpUjfRRa1w+rMqIQtsVhIq5K1FqsVwzgQQi6mDZYYPWMWIXHvNcMwiEmAEmOEGCJjTtSVE4ZCrcTdXitqa1BJGJd3+wOb9UbmaU7cvtuy3x2oKzHKahvHYffAsq1orOJiVbM7HBnHgSORrUs8ebLGGUOXM/0gCf1y0RDGkeNRzAIWi4Z+8HS9Z3/oud4sqOuK2PU8PBx4+byV9sjB03ee9WrSmgVyJKHYH7oCFiLMlaILN4GJikxOI2r7gH71SsTkUyB//gX5Z79Pjh0qjcLKj2HuYnBOWOTiqHoqiMymfSrjKmFEHY9jGXanYOp8qFLWUBQzM9NWdg74cvm9JK2y1jhrsWZqMYrznDqvLM+tQWrSPFSnTgAFOZ+SndMUnaRIpvW7hNSldU+KVCKBYKwubWlnRa2c8X/wB3SbC7r1BQvSvJ5I0UX+meIKnIyht4Yt0BvLaA0exKU7KmGgK0PdLIlZkY0lO4dultSbSO56/NCTo7QUp5RKW2+e52hGgrCgoE+RIQZR8/7eL2O++oI8S1VI0DYvuZwkds71dn9RW9D/f/y/f1hrWayW5AhVU6G0IiQPHpyS4ifKkFJgHPsCGOXZbVxp0bsUMszULh3kd8WtGAzZiMyD0syFE6XAewH1VZkTYoSi0UihcuiPUFqetSrQSWHYWFu01nMp9kzAntZobef5pI1G6SlhUxhX45qnLNoGn/0MxuqiHxhiYOx7huM9fjgS/IAfDuToGYeeoe/Y7XcCrmUZz3qSSyHPBYdOHUk60Tox8dHayvpYikloy+CP1LpGKUffJ4KOjF6RsiQkKQn7N+XTxpiSMO6MtQwh0Y9SfF0sFmw2G9JLTcsFRrX0EaLOhCQAZUbhx0EAapBlammhhqzlXsScGYKcqx8HssnUiyVD35G8gMFEMf+bvBiUVkQf0UEKU8GPoDJJpaInmKQoJ8FMibFKp4ESTWCDFrmW0tkizOfSeld0AcPFE+7ffMWbYcvtsGNVL+n278ha0xqLciuK0F2RrNIY3WDqmrpas1xecdwvUOqOsR8lPpz0l7VBKYurmlLUO0vRZJE/TRwl67K4nSeqqiIOHdGPGJWLoYzIXBitCb4nA9Y6rK1AGWzVIiyjjA5BukaKnFGMXroOZpOrMv6zesTwiSWpnFr+XVUTfS7xYip7klx36SLSpcWxxWAZ/EE0/ZRBu5Z6teLFt3+V+5sdMWvefPVTcjiIWWSMhHGg2z+wv39H266wphLwuFqLHqGO0kV2BoJoYwvDddL5E7NCcqI/7okhCGBbQKOURNrIFW1EdT63YigtwwKeaCtO98ZWxJzFOIviyaGmwhJALrqDCW0EiPWjP2l1Q1lXSpeGkVZ7m2th5wd5H32mTR+8Z+iP5NrTNMs5hgZ5jyl2PzHF8gzsTMaRZXRhjCEpkWoYxpHRj6yXK9aXT8nAYfcW3x/pD4YUvcy/oDnuB0Lw7LcP/M4/+kf8wWdfcPuw4+HYcXu/xaeENmCNwigpimpjMUZYqWgz7+OQ0aP4CgggmcpaDCInJSQVq8SDwSmKcddJ0V5B8dgoBTGtRWZCC3ijphhHqbnV+yQ38B5rb75C8y1kYq3OpI/8+FnnwA+cYoqpA0dY/UGM4fVINhqUKVJMGas0xlY411DVC+qmKYWvA91hSxgH7m/fsN/d0u3uCWORfEgenYWZpnXp9Cj3O4aIKgZVJ2M0dSoCKGYJs5TOjEinc4QZLD0daT53pcz8vCmBehxL5QJyvyfh9f7x6C3KdyvXWJHJU46Xpyv8+L1EYibNb6HOnjMxRbXSxR9Bn8aLlvk3kSyMljGXdC6xfzyR2rQ+O4fpOhbgscT5Sp95zxTgUTBl/ej8J/kEAW0NcYxnY+z8ep3nr4jefJb/ExSZJTlvbU7zPJNL7J6LeWicCWA5Tfq/QuiS+KVIuJDJKqP6Dt11ZDTq099H3b4lO8vxB7+MyiO+3zJ2NXnYkroLFnVDU1VUzlFZKS4qde41Uc5lKgTMv5aI3EyyN6hZqgtEizRnMQJHhVlqKCknrPYzLcE89/p/c3idpMPkMy2QNUSMoHMx0xfG7JT7OCf/U/B7o0THWSlFspXo98cRYpSYSonuszKumAGCsTXONYQw4MceY/eybqfSpanOvq46jcP3p4WELqe55czjtautHWE8EsOIHzP0d8TdG4J28n2K1vsEgSjAoqVb2iwwqikeCR5T8kmrM0YpVCkAKJVRVUVSl6ATOQ+Q91h1I+Zff8j0/mMBxiolX0RrsA7CMFIVHbykNSqDVR15/AoVtqjxSKUstC/Qdo1WTnTHciKlnhQfODy84su7n+DrPeqp5smvf4vlxRPa2lJVhnpRkbwvnXyqLBAGtMM1a1ZXL3n20Q/ogyFmcdsduwO7uxuWDTy7vuTDj14yjNJWPDkrzptKznhfnJzlLOfzzSkyDgfycAQDmQXHw57twy3dcUf9/Jplu6CqpXWCGGmcoSrudiEURm3IDENmn+7ROrFYwHpjef6i5cmzhHUD6JGcBlBSfZ9AS8qj801h3iDL1z2v1ZyO6XmPNxeZJEKRV8qBsuRYgRoenbvLhloJGGtbS1SJkErLYDlSPOmwphjntrhcWiVjTsWnfdJWOX0dYfkoklbkyWQAQMvCbtVpsZM3VaSsqdslETO3cYQselioU0KZiKgCMKu5TlVYECHMi8f5IaYLJ0fouqowoSwaKOq2IXYdYZSErh+Gwk4ogEfOZG3AWsiO0S/p9IpAS1QNohWjmIVUzn5W7wOw03+PgqkTKJvPHit1ZsLz6A4WWYiCtsZ0ep5iqsxKTJ+1OhsmGaIiIklnSGI0pWJkoSPJRjCeq9Zy0RpydLzdBpQBqwPryvDswlIpzabVHA89t7dbnlxt8GOPVpnVqkEpx377wMVmhVHw2VdbXr+9Z7la0ziLIjF2npQ1w+hROdG2GS13X+btOLLbJi43K5ZtjQ8DwXvaxlBV4mb6zh9ZVBva1pAT7B08PGy5vFhyebHg6dWaN69eQWhYr1quNg1vbiCMkb73vHl34OqiYbloGL1nvz9we3vP5aahcoZDTjxs9zx5doGPiZSP3N3vuVy3tE3FOI68enPH9dUFdV2REnTHQNcH8lw9lnsVzwQ5BYiR4IiUwA+kHMhxRH3+Geb/+PsQO1LoC7NngDRSVw6lElFNyb0wbKwxDMNICJPRyhRgS2vjarVgvVlw7N6SYQZFpiExqWcAbLcPZC3sPK21mFgp0brMMTOFtLqYpjhrsEbNjPaJeWusbPqTLIEuWmhzsFaC30mSZjLAOR2ntS3lXDRlC3Ck9Jz4WWOpnKWL/TfWyvwP/gHHP/En2a82rEm46JnaALUyVMXYL2rNoBSdczygSM6B1iQ/sqjrImugcFWLa5fkmBhTMc3wnmq5IgLd0BGHnn4U99+JeT+dWQKiVvgMQwafIRlL+lf+PPp//p9I794Kw8EaMWl4Pyko6+hjNswfEln8MzqOKeHPGMnLwuD4ozhSzuxK0axRilqfAsJ/2vfYx/iIY7sujKTzo0uJQ4wsz9glxlkWmw2NW+DqRvRCg4ABLRmbK7QyBXjoyxxQ1HUjQJG2ZKXF6C0qKbqojNECxKVUWnh10XpVpQighJdlVMYgxiUYzTgeC1PKoJVn6I5UzQatMkbECUUGo2gzkrO48EZJZsigbAFTtBJNdBWFzaUVzlaslhdsli3KGLb7UyFT1jJP3+3od7ckf4AshhdhODL0HeM4SKvccU9MoYAbDqcdOZ8Ss6wKo6doyKWc2B+OcxzniTiX6boBtAOrGUOm2/akMGKN5uKiJQVPGjpiKMm+deQITdPQLpd0/cDdjRj9GCKXFxd0bWA9PqOKVwzZohtbgEORbdofHsT8qZx0rDPZyncGMMrSHwrwCqjGsPzggnifiT2omFFDII1ihDa1OvswYkq3jY8DOQa0q0CLOY3KFDkVCgPobH1WUlTNMZ7WgKmVGGm3FIdnOKjEO3/k8/vXfPLxC3a7Vwy+JyvYvPg+OZc2SplUxDzFYxqF4/LqA5ara9Hpz4Gh64ukVRlLytE0DmMs0ukgxTV9ZpSqlYby+rp1tO2Cm/tb+m6P1kHer0jcrNYrtnc9xgjQ66oGNZlsFS1NoyvSsAfEZd33I6NtWK42TCwmpazkAlGui9YiISB7FmhryVozJkgho3XG2pMxmujwBlL0whLPmrHkHj4IG173kU++/8/j6jXLqycM40D38AWjOQijJ2UqrRkPWw53b9BZ2IZPP6ggOXJUZBxGCYjM+f0tCbvWlrptSCmx392ze7jnxcuXxRwpEnxg6Huqqp7nj4QbqbBcR2nJVAplW2FZ2oph6GkXC0BAjlCkLbTVpKwKu7mw00Jk6Hu01jRNkfnKuUgXScXImgIE54Qz0gqewkAu5xa957jbMh4z9voFrlmidEXCkLN02kz72HnudirkntZmZZTIZfQd+90OlTPt+oLN5SXXT59y967l85/+DvvdHW0YeP7iA8Zx5O72nsNux/bhnn/427/F1+9uOQwBnwUEtZOUgoLJYT4WU+fJJCqXe6PJGAXJqMIUDXMrsiqt51ZDYzSVEeMuoxAykFw+mSe6SJcUMLaqGhFem4rd77MTmXqSptuQC8PrcTw1A3tz8ijxxznIM0PCZS0+BwwzqczlAiyTcVZychmbFmsrAWHbFc1iTbNYsd/d0+3v2T3csL1/x/2716Sxkw7YnKgnCQ5lIRcN1Cjdp0pBymdapnrSqk1nhCD5nhPQcyrqM++3WquTR60qmp2FpaKURrwKTgBazqL5eQIWKaDtiSSViubmKayYdE3T6fs9ijwzOU2dZ6eiglaQC46SpnEwEYfyKX9WpfNLvFrKm6aMspqyeRKjl/cqT5GuHD2Dpimd+TKUGNsUs+Vz01vUCWw1xhB8mDuupsMaU6RfpEgcxvFRrC7r/xmwrZR0jwh6OxeUZ6OoGehU5R6lEssXUDlFyeXPGJWp+C3Iv0DIEYeajbMmc7Xqd36MM4p61ZK+/TEm7cEr/KjZ928ZtyvqZk3TrlksNmzWaxpX4YwVU7xJH5bH+fq5DrA1Roq0SkGQjoqTzIGsnYoAQeaZVg7lKjCWrG3BAs4xgbM5q4BH8172gsmcTYqSmpjEjyQGkbbIUMxpS+duSjgnGrMpC6Nd4iPRUs9FBiOmXBS2hKVeu5oqR2IYqZoF3X6L991sxqpmDxPKuNaneTEN5XTqoLBaYysrPhLl/J5db0h+oOtHUlLYMKD3b8jaEUzFYAy2XklBQe4+k6lqzIqUDUkL0UkrqAw4neb1Tsg2CeMcwV0SqwZvKhIRpzTSif5PPv5YgLE5Z9qc+fDiku9+8iG/+eMfs3vo8ceBPASydWigzpEc94TDT8jdG0zzHNc+o1l8QDJr+nFkPL5F7T7lKe/4c3/6l/nexz/gg+crmsZCGtFaKq9SOVBlUZbFU9klqycfs7n+kMtnHxNyRUie4Dt8d+Ddq5+zWTo+/uglz58/YRh6xnGYdU9CEFo+Z6xNcaIrgvTlcHWFHrSIHQdPlwxvb2548/oVHHc0tWO9WePWaxwa73vG446xPxLjSAqJGHq0DjiXWF06PvxoxeWlZrFMWHskqi0ZXxC2afGcqpDMhcvTDvvePfmn3zVEikA2nFzsaXLWaFULkOn3nNix8hKNJEZOmaJfaah0hT0zdgop4YM4881AbGlTzoieSyoLrJ6q2roEMTHSRY/FiQZb2fuVcbSrS2zVMKQwR1opJcbgpQoETMIH4sKuyUwbiNT3pujVPGKdSaVs+k7nx9XTp8T1an4sLETRxomlfUQqsjCOY9nUMrHotxlXEVTLMWgO3tKnNYO+ODFi1ek7USpiJ0D2vS9z/ngGU85Blam9IxeK/+O/TaNC5RIySIe5aMJmaQ2UhUqWeC/Fe6HChoQKkTBxqnIJNlLmmDPZKDZXLf0YaJ3mslU8X0QygY+eL7lcOlqjcJXls68eeNj1BG1plw1p7Fi3LW3b0vWe27een332JYrMcrkkqz2jD1wtFnzn45f89v/1E4IyJBRjUtSZAgRodIJuTIzF4bepFcva8bOff0laN1yualatxaQjD/dv6I8VtdM8var52ef37HYBZzPLKtPUsDvu6ceBj15c8a0Xl7x598D+0HEcA7e7HZerlutNA3HFl1+/o6lelKSw4rOvXuMay6KusVdLPv/8gbv7HXXtcM5QOc27m1usMXS95+bhwNu7B2IK5Y6pgoqf2O2qiGtqEvrV16i/+beI/R6dO3Ls8aEjjT2z0m8JqodhlJbikp1rY+aAdmr7mQJyxdT2pOi6gb7vsU6jytg+Cx2xWtFUFZebCx66HUMIpU0ost09zLIAnAP754nfGLHWiqlCVbHf7+UsY6nYlxYlpQogGSPr9VoKLkG0upVSjGeaqC9fvuTBj3RdPydnbSutnCkmac/N0oacY6CuK1Ca/gxEG4ziNkvCv1AKnUuwiVSPV82CkUinYK9hcI6oNToldPDomOgPR5R11G1Le3lNMlbaYoaO4/aB+9evUFbPFV1TNaimZfA9MQWqqqJqa8YYRAMLMMlh4yiJcgzkwsrX+cxM44zloYB20eK9P+1vMO95lsdasv+sj//i7Vv+7uEwP/5PPviAH7btH8lnvQ6Bf//zzwH4K9fX/FuXl/Pf/qt37/hb+/38+D96+ZI/vVjMj//Dr7/m98dTUe6//uQTXrrH+rf/zc0Nf//NG/7jDz6Yf9cuN3zwS7+Ctg27w4Fx9KLjqSx+GIk+otCEIMxY61xpwZQ28+W6RRspTKgMRkWIR9IwYMwFPkaMa0ohFbquw1nRlM0o0AatA0Z5lBq4uPQcx4CPR4ZDQ2UXaBIpeLyimGDashZMTXJGOj5SRhtV8rpQ9EYHmqZivVrh6lq6FKpKHG21Qrl6vhbbu6+5Gz9FpxGCZ+wm8LUjhgHvvQAyMRC9aK+7qqVuNFAh7MPILu/4Qn0p66yt0EoR/UDyA4dDjzIWW1UcDh3kxPFwoOtGMC2ubgro4xl6y+pyxf7Yk5Lo3T57ck1TW/ohsD2ODKMnx4HaJBaNo100/Pzrt+y7A3qsMO0FNlSsNhuWyzXL9QZrLf9wfck9gALdWLxN6MpStQ1Xz5/x+e/8XuHiZ1JIvB3esfrokrq+xueEPYwcXt0ROk/IRYYiKrJOYpIE9PsdlREGRM6JHEshTEnRdM4JFSedthIG5JIg6TlPL4xoY/A/+FO8vbvlR7//u3z/5Xd5Yhuyf+Dh1e9hXUPVXKFMLTp3GfLcGZVLYm4hV+QEYz9g3ILK2LLmCDta6SnmVML2ea+cdrh9Sxx6KuNYthckMsvLK1Rl6A73WKtxxkJWeB9RqqZplqScGceAtYo4HMTg1TqME+ZMiJ6MwljL6Dv86MTR3ToSGVPY1VOTsiSJiRgHYhoxxrFYLMkpl1b/NF9XoxXW1iicgJ7Bo7RlsbyE5ZqcIjEE/vGnn7JeX/Brv/GX+LUf/mn+z7/7v/L65z9lON5jdeK7v/xdbCWyHN3hBlSi6w9cPP2Q9eUzquaSlAPDMEgLsZFzSMnL3q4NylRYHTFKk4Nnv9/z5MWmCBGOmHEonXCTRbJc/aE70Hd7/Nhzdf2UnBP98UhKe9Fu1DWTrqP4Siica9FaOg8H71GuxlaOlZPPU+QZfEopSI5R9p/oPW+++ozd/Tu876mWC1589H2adkW7WFA3ji8//33ccU+LomoUmcA4jrI+aY2uHF13QIBKKZRO9246tNZsNhuWreP6convesBw6Dr80FNXK9BWZMniA6TIuzdv8X6QAnhO/Nk/9xu8vX3Ax4xrF3z7O99hvz/w+s1bPv/iS370ox/x5u0r6rqmqmuqqqFdrmiaVpiHScBFXVjVU74i5yG64M5AXdsZkLXGMMRYJB+YmdDa2QJsl5hugk0nokoBMSZAkBznJjuRjzrFcY/YGPCIkPT495zFf6cY8FwSIhfxM50zyWeSrzC1oVmsWFw/Z3HxhEnSbej3HI9b3n71cx7evWJ3+5ocRRKrcY62WbJcrorRW0/X94XoI7H9VISY9fAzc3wz+wvMJkAiRzK1fk9jQuvSiTYDWRIz5yIlIKBgwmJngtEsYHAWZ8UQSDmg9QQCg56F+CdjqVPcBRkfwjwvADGuzWl+35xF6k48TnPxZTnF0RlZg7SR16WQC2ZwWku1UthUjLXKS+c2/vIcozV2Kh6UMQVSJy3VArwfyZMerJb9ZRiGGVh2Rcf+vEO26w6Ybi9ShSGK4V4pWsYg5yJpr9wX49ycP8u1Mlit5jGnS1dgmP6OKp8puU4u91rM7cr9MZoxzLZaUlyenotI/ixrS1NVNA5W9ciHf+9/ZKF77r//K9z84IcoBhiPjP6O4eDYmZq7+pJ2eUm72LBarlgtVlhzYmXLtHmcwPvghWFaZKmssYW4NclPTNNtKs5EkS+wFdnW4LRIOpYxdM4afXxMTFo1/1UrhTKGxtWAjO0QIn0/MvYjxyjvu2gXXGzEK0T+PjB2jt6LIdjoR6JPdLEX4ofVVM5hjXjeKO2wbkG7hCrUxCgYWSx7Zc4noFypExM2UwBeYfJgbI227Yy7Ka355FvfoWnWbLcHukNPnwLO32GOGa17gupJm4/QdiEALWIkPwVCKgt2Y7UWs1UKlkaefQxQFqeE9OJjxWCWJGtpHbiaRzIe7x9/LMBYBXz08ilPVivG4cB61RJ60SiL44jREztSqisue3R8Qz7eE46fsXvXENUCpw0v1zXf/8GGf/mf+zWeXa1oa4U1mZwDOUlr6FTZSrFUsLLBVAuuXn6P5dVHuHrN6BU5B7rDA4ftHd3+jsuV45e+9y3aVgaJL7pJoTClci7tLHOFV1DPs0KLnK+uMZXokKkwsP36ji9+/ilffP4pKUaeXD5lubgEt8AmT9cdub19Rz8MhDjibGK9gvXGcXFpuH5iqdsBbUZxq1NRKiRqclg8AWlwakPMWtoPc5o2dpgm4vn0nDb86WadV+rkrfPZcwMxDxCnVzzWjNXF7MaPnuG2p1k2tLrGnYHVaZ5sk7tnJhRgI6ST0+O0uaeUpMqCTDqVCyiZCzCEom4aqnYhrWdp5F/66it+/OI5fT/w5uu3fLhYEGIubdERa0513tM5n1qaI1LZPWfbvW9WBtI2X1cnc5pU2j2N0SwWLTGJEPw4CtiRpjYvQBuHqdY8DDW7ZOiyJeoFOdszEPaxHuy8luszpP39tXa+24Van6fFd3ryL4DiH51rCSfOY600tYScDYmMVLhTQscIUfR9xeUwl41apAv6lHh7P8IikWpNZQ2fPN/w6Rdv2O9Ez9k7UDngjObp1QqtNXd391xvNhy6kZu7LV3Xs9/tUdqwaFuuLi643YoOoNaKFISxUbbf2ZzJacsYvJjeZTmB7X6Pzp7nVwtePlky9ge2DwfGTvTnROxYCgyEwGZh8X7k4faW5nrBotL0h4Fj19NfLNDZU+mE04lhjLx7c4tOK5w1OKvIMXE8jqxXDS+eXtH1gYf7HXmdcE7TNJaH3R7Xi06wdTU3t1shHUdxtyaftzpNQKwEh+QsYGzyqN/6bfQffIqOD/jhnhR7cvKlvfCb4/gxm1V0I1NC2nXO6gFKneahj4lQiigxZVypy0zz1hhdWm4Dx3Hk2I/CkC/guEaTQpLPMCeDPmNEcuLiYo1RAiANfhTX3WIgIi1AYv6VmXSzZD2OpWXGWkm8EpnOnjbJbhhJk5N8kpacCczMKlO1lcjTlHYmXdbZ81XTVQ73kx+Rt/fc/qk/Q52kgGMBqzM+jxxMxU4pdjmgwkA4dNTaUlvR4LPtGl3XKFfReU/sB477LcNxz3g8ElNidXEJSuNTxNYVl5uPijC+J8dENJk89iQ/iBZvzljjWDSie3i7vSX8+b+I/f2fUv3kx7gpoNVlfqSEcQZtFTYYRu+FpWyNBD2Sm/Ofv3nDz87ARoB/c7Ph35hNUP5ojn/3+ppfrWv+xu2tjM8/gs/4z16/5kvv8WdJyvR/ypm/9vXX/Gwc+ZW65q88ecJf/eor/st37/iLqxX/9sUFf+3rr/nce/7SasVfWC75669f89dfveLfubzk27/g83zO/NWvvuLfe/KEXzKGqmoYY2bsRsaxAyK22ZCVIRcwXBuNqxqqWthqKSZi8pLELHSPTQAAIABJREFU6UxWmroyPNwc6Y9bQhhZXi5QppkLhOMgHSkxaYgynkefaBcbSJ5ud0dIXrQ3lSaHSCRTLCOY2C+TnqYxhhxEwxmtT0yjHFm2juWiZr1sadtlkewwRV9Tkgw/9Izd9nRhkoc4kJKw5vq+n/UTldFkH4kpEMNI3x0Y+rE4tyti9KQUeKdv2emddFtpQ1NLEa9painKOkvVrnDNkt39HTlFVI7C2awNpIBKHrKc1+gzyjRoZ0kKbFXhaoPPGXUUvXtX1yR/5NgdiclzfXVBCDXjgxiF+RDQzoCtyFXEJj8bmiqlqNoKW2uSs+jlgubZM+rbO7p4Sww9pq5onqzoxoHYdWLc9XAkDcVJW2f0okHhROZgGNGtY+iOBJXRrpIOg34sbaYnEao8FYs1SJB1HsyexRtZERUoNNkogoYtIz99+wWrD77Psl5gcPjja/rtDdqtsO0F7fopUZXOtOKYnUoyPJn4hLEnmaJ/rLW0cFspQKli3Dqx1Kbj7uEGmypq1xCTFkM2Y6irJSkkfv6zL/jWt2tSEh3/RSvM88lU1liHre1cj0wxioRBie9jjFR1xoeRGPYC4jULGYdJSaE6F01m9Z78S2F/qiKloEvhsmA+AuIoMKaiXdrS6VHOLUVcs8J3R0Lw1Is1f/LP/mscfu1Psr9/w/7hNRpPjAPHbs/Y39MeDyw2R1IKhHHg+hnUyysWy7Zo+IsJmTUSN2cU3o8oIov1hnaxLOzxwnQ0iqpyeO+xtjCmyYXpFzAqgZG1UeSBJGZwtVAeJJQWQNv3PcM4orRmtbmg7zqp7Zb0KYZI8Eei96QQSMBifYG1jug97776grdffsbu4R22snzr+VOcczNwpIzlg4+/i9IOrU/prjV63rNjFJB79B6tDc4WNt7ZZhKjdA9NwGpMpbilLapq6YY9VdOgVRC9fW24uLoiZc9kTL27f+AqKZbrNS8//JCmXfKbv/lb3N3est0+EHPAHwe6ritAn8U6R11X1HVN27RsmobKqOIwLwCVtkbaZnMieU92omHsipZ+iKFI0NhiEmgLu/GUG2ok5pBi8SSlNIXwaTZ3U3pq34/y+lkH9qRNeQJdmZmJ7x8zIYgJvJXBP2mK57K3Bp9mZpw1kd3da4bjQQpxfcfxsKc/7gjjIAamlaNupCskJcW7t+9Knp6mJWsOVGW+nZins4RNphR9TjnoBKIopanrGufsDCLraW9LJ+LOBKDmIgemFEQfZjOsXBKlCQbXRvSHc8nH4yyHIBPBmDwD4yKh43Bk0ji8By6Ua5cEfBUQs5CX8ll8VMC4STM4TZJ4paAmT/mmLIVGTDvRwhROMZXrVCRMsoCcWkmMnpIhlPdNOs65rbTATx1rJ5BZnWlqaidyMSl6ovf4sZjp5sTZVyqArHgXWDt19RS2+wyOy5WeyFPkLLlqTqTo53uSvH+kPT7p+SryzFkWeXTJD4yuWFq4riObJnLZDLxoM7VVPL/7x4Tf/oKQ4Hf/1L/OWBUjtzDgQ4fvH9g9LLitlqyWF6xXG9pmQdM0VK6e79E8YQDRhU9FG5dybidwWcAdg8qyvmVtyEoYnY8YxJP8yDlpa56TJ0D4dB0SOXlUTFgnJmhNY1kuKkII+CDawDkEsu+oWkfTWNabJdASYmYYAt1hZHff049jyS8kb518eZQWUF2blpxckfT0+P4oRduc5nsSwklWYgJitRbpt2wqoq7JM8lPYZtLTB3QLpI44vsDyQRcCrg8ynhRhthek6s1yTQoFWdPU0GTdJHB1ARMIbHMLgtUzqBSwJR1UVcK6y7YrH+NtfqAZvHf8k86/liAsVppLi+vUAq+ePuabXekG0dxhy0TSp1VnjIJnUcR9KYDLE/WT/jo2XM+evGE733ylG99eEVdaVSOpOSlVbdsPoKbJVHBshXWtbSrp7TrFxi3IitL8J7+uGN7947oe9pa8/KD5zRNRc7CpsxlwTyNcTVXZqaflTbfqDyowmRKOTCGke3hntv7t2zv79Bonl2/oKlXDNqUtkLIacRoT1Vl1heGzYViscwslpl24VFmADUyiyXPuo2nq0YBVbNSJaGJqFy+p8nIuH0sqzCx3abq52mZOl8Npz+UloGpmjq9YsIEleKpq7CqtPT7BEPAZh7xq9LUQoQsnymLImPKSYTQ1ekjRe9M0EF5jmwYKQljSDSU9CnZswZLxWocsSnhx5Ht/T0vw4dzq2BKSdq4ypCbgNj5fJCNd9LhjCmKaZQP3wg8jNGPNpgJIhVNPQHxtBYHUKUct6sGe79DF12WkBydtwzB4bMD5ZgrV3P1ikeA7PxVz36cgtPHxwTI5rOHU1tRfrTHixBemT8T+FSu9XxSFHB8em2SzU5J/0JJUMqnTZHBtLDmyCF6NpW4aQ9jICNtrMejtO1VG4dVsGyq0kaYuPORfddNqQyr1YKUFaOXynY/9GyWC2JOGDLdcc/FaslD5/FRvu8wjgSlZtFvozQhRvohsiOwqCJ1Bb4vZidZ45wREX0/SoKecwkYAp7M0Bus1tTOkOPI/83cm8Rqlm7pWc/X7O7vThsRGRGZN/PmbetWSeYKcGEhhAcYLISRGBXYUyMbGCDZINmyGMAMmU4IRmYC8oARYAqVKVxYZeyijEtVNtXcul3em21ERnO6v9vN1zFY397/fzKzXFVCgrulzIhz4m928zVrvetd73t3u2a1bFjMpN1/t0sMfU/fOXQ9tgbDerPDGlguahZ1JW7b1qJURVWU3O639EMkIVq2/RCO1qADyM4UTouOmEoRtd9TvPdDwKE/fh+7vaIpI1hH54dsYDJ+xufHynHCO7q8pmnYqakiP+lyqRzgwiTuPwJ83udiUZLNeN+22SlWHTn7joNYgitrzVQ5FwaTo6mkrV+0FgeqsqSpK0jQ9T3WFpllP45xcQCXFhQZX/ozAafzQdiF+fxG4Hica9LtYElR5j5xnAOHz1DWEHcbwuuX+B9+j/bL36BBRE4iihbFWsFWQZsiqt1jvScZCaB0UaDsqPmk8N4Jk8k7tLHMFkv6YaBoZpiqAiuvL8qCECMmBIJ3qDhQmCzbkshJNmglBYCyrPHnsg5FQH/wAarQByfqGHN7vQR62gpQO601+XjmHD8aBmql+JdXK/63zYZf2e3QwL+wXPIL6zVdSlwawz+3WPDz6/XEUDg+3i1LvlnX/MJaQLifqmu+VYsu+99cr2k/856fnc3uMUz/j+2W7/f9dB7/WA22P+DxjbrmgbXsYuSjIzPG8Xh/GNjGSKM1Xy5LlFJ86j2vvCcAPxqkVfnUGN7KhbmPnOM2hM+BsS+c43++u+On65pVph2mEHDOY41BlSUpSXKd8nothUdZyUcjDKNF+3zU/DNGkrjNrsMNkbKaoZSdWDbCOJM9R4ot4FyXkzNpMy5nCe9Er1vrKC2zKAEFgpOZbgy2EG17hTAxlILCZgkRrTCmpK5LmlnNbD6nsPMpGU8p4vqdSKQMLUO7me5NGDqc2sl+MbiDTju5TV4LEBbko7IjuIAMMXlu1S17tcMhurdiOiJtaF3f0zuPthWFElMxZQwx5nZUNNZogushyjoZvSf6RFnVaC1MxohiPyS6IeFDwjlhN7aDY+g2rOYVZZ2gLmjsgnP7JvvBE1AMQ0/cr7ndf0Q/fANYydpXW5SR1kgfPLt2J8USo0hWQSHgSggBP3hhz1gDjZHhoRSpUNKiniumop/u8V2LDoFyZJOH7PKcAQZrM3Ehg7LqmO2Wtxo1JoE6t8gmRZzP2T35Eh/evuTN/hFNNee8XqKS8E1SbIneQjohpbGVUB2KuBk0UdrQ93uk2/JIlzhmaQUVp/X7OPYqqhobS9GvM0Vmf8u618wUZbXJAAAi/2VtNsSzFBqq7CswxiyjFrN0fShM7v6IKdC3O4a+YxGdkCxym3yMQYCtHOOkXOCI476WcpyagZ/ppk5xnMaWhejOKmkzCr7HGkUfBvzQMfSwnM8pHjxhcXJG3z5ht37BzauPKJ3HVInkHLevX0zP3g2OB48Ttl5iTDU9X5EQIu/dokVoigKKkhgCPgz54UjHmjAKD+trjFmuK4hJl1IHUEckUKSVlQy+aa1EQzfKfRi6TlhQtkAnctvyCEJJa3wMgRRcNpUZcL6jnjVYe0lZV8yXpxkwkcKy1iYznxNaR6wZn/MYr5DHueyzAjiK0/vx/iYmOQFCyKCTSAIYY8EofFVT1Q0qOAgOhaIozEQs0VrTzJecXjxidXrKyckpn3z8jFdXN9ysN3QhiKHcMJBiyN2agb51+KGnb1v6qkMv58ybGoMU72MSVpZWoJN0KBDtdH8hyb6hDRgLJpv76BzD5/E55ahqDMvTvev/ol00pS/4/TSB77/rc4BsGnPSI9JLHkPCgFO5qLEnJM3gPJ3v2e86hnaP63uiGyQeUorSGMqqIaVEcH4y5ep7kZCapAS0zgDWdBqM2rtMANuon5vjw9yKT75fRVEIGJvPfQScxUxqlCJIuUiRdZiBlAkySQnBIE0nkqS7JGMcKYOb5HVunENHty4vE2pahsffx5w3R0YPBnXvdYd8MN93dbj7Oscb+gvYezJODoZdAlIfZAWEZKQPMYga7xckAtqbKadXjHrkZIkDfUSuPgJj1YHBqY7kHI6H5iG+EQ+JwtrDs0K6aEfAMoxs3qOiuoCbowxBJAzDAVTPuEPwKbOaEyGCj6LxbLWmtIqmTKxqz3njOW8CqzrJupAGYjvgPDz55Hs4YxnKmtdvfDkztCPJ9/hhTxy2uH5L0yxo5ivm8xVlWQsjfmy1P37WI8Pv+Fryfpm0AWXzmDa5c0SDFiNJRp3az+Q9Uw5/b1Knac9PSWVGcsrzKXfHWdFetyEKmzR4XD8SOawUhgphUJfWYo1luxtwXrqDZazr8dvy5wpzP+WCa/JejO+ijMOQZUASQubyQRisJheNlbIkVU4XpRSYekU1jxR9JO07/G4nXY66R/U7zP5KDNCiFDBCZSgL6eDWCmzeMyQVlDHRRS9xdhKSVVMbapu7Y/J+oqlI6hSvK9Alv9fxEwHGGqWpyhm7bstHr1/RuoGw9ySXNRvSWDFROTmJaOTGF0bR1IavvXXCT3/tSzx9/JDzCxGrV4yAWZ6Q2chCiVAs2jYU1YJmdsry7DG6OiNELaxX13J79Sn9ds18VvHg8oJHjx/Rdy3e9YTgsTkYmRYMfaB3K61z4HYISMZjdPaMKbDbb1nvrrm7u2K/21CaijcePKWq57RKE1IAFalqTaMt9Sxx+Ybm5CRi7YDSjpgcKWUtyGwqlbc2Dq3mCpVb35NSOA+3rwd0slSVwTaKcqZyO1peMtMEHULShCiVHQlqxUgHDjjECPiOb7vH0Muf9KAqKZWfGJOx69HBo482a9mmBNAdwbtIIuaFeHKky0BsyJvW+LoEEEQHVEeTg7/xGUkyON2hrqd//gr39VaqSHmBiymK3ta0Xx610iQxKPDeEWLEBUfvetq+n9pJxkPMyQ5aISODQOUkxihNoTUUoku3bwpmmx2lT4Chc4puULhoSCMQO+pBHgEiaowKpn7C/H2fBSPUF/39XgbE0fJ+OO8UIY7t5wL1W8Y4I+XxfJDnmMC6NLKv06RvNUVDGYwlBVL09CHQe5M11xzd4JjXFft9h2rhZFFR1wVVdjHue2EgbPd76qJg3tQsF3O0ttytt+zbjpvbjsV8ToyKGBxD13J5umTwd8IUiYl9K471NjvK20Kz8wPORfZx4E73vHExQ+VzH4OBlKSlsfMeYqL3smFrldjt9sxmJXVVkmJkc3fHybJmPhMWUgqB225P1zu0EX1UazW7/Z7CQmkV81nFze2a/a4TfndSDL0npECISnTkxkLBtFNHxsqxIoOw2w0qOMztNc1v/Bokh0oDpY2cNIbYK1wvOsxfBMMeh3GThpaSllbSuMQcxuEYvI7jSALYDG6Sps8ZjVyEHd4L2GdkY5cCVDxqyxIWCkhSHHxgv28hib5aUgofAhUwq2u0ktYvW5SyUSPBH2kM+GX8Ga1RdhQpOczRwlpUUUCSdrCiKFBaZc1JAZ2UVRgsIT9/josu1hCsxu+3pN/9LXZf+TpFUtgELilaDHdK0QE+Buj7bG4i+5SyJZisV+TdZPpoy4qyKKiqivXdHcVsRjVfUMzmoxJwLnx4AVaGPYVWiPmNmpgZ0rJuaOoZnR8IT94knJyhPnkGVmNKKwBFjLiun9ZQMRZS91xsj49aa/6l1Ypf2e34Yd9PYOwvb7d8OAw8LQq+UlX89etrGq2pc1X5RW4L/JPLJW+XJf9tZrr+3OkpX68qXnnPf397y20IFEpxkROGd8r7wc2v7ff4vGd8ezbjgZW2IZ8Sr/J3rLS+p8v6+x3/6skJAM+d4xc3m9/n1f/vjqsQ+NubDf/506eUWrOPQeIN56lLQ0wVIYghqCTRecXOzJTRKMtkjXSl1WRomYDOBVAF1WwlJkYABNGbIWFNRWGsgKKDtPmjLMqWlPOK1FpSv0Npj7WJkAwhRAHZEqgiJ7ZJZewiINubpiwMdWmzhp/FljVFPYNoJ+ZF8B19uxWjBdcxdAfpBzd09HGb16CU17nMto3CXo35jtjcWm5zC36fBq7sDZGcNGrRvNZG4f1A2/WEpChqRZnitBYFl1lf2koxaAio0Zwlr4VVNcPaSN9LotZ3Ae+kldE5AanbYWC/21EXYtJZzAwnpw94e/VlbrctN+s72uDo+jU//PA36IY/AeQlsrQ5Jgn4vufm6pWANiSS1WD1EWtK5rpZVKRw1BcVI2k4tCIba6UFcBBHbtM0YMTULSQxXiIhbsNA55zoTOZjLH5OO0OOeaci+mJF18z5+Pbv8+HuikW95GJ5SRFlf/DJE0MLoSfF0Uj3SHYJhVIGbUp83FAgcZ8w1DSTeQ0ydLVS9xhNs+UJepACvDIlZVMQnBhYVcZyenaZAUVhEcYkBVhrNLYoxK8hky1GyRvpqDgUHVHibt7FwH59g/Yt9eIMW85QRlg9WpFjn+y6HsPRdUJKQcDoo46WyVwqM4VCNwgrKDiGbktdKFy3o2t3eN9TWiiLGbPVA04unnB7NePqxXNU0lSqYLtveXV9hesD3b7D84wYEqvTh5SzE3Q5z4UbYUWqqOjbXdbdq9FFJXqmoWdknWktnRVq4lCL/qIfHNFHilKYqAIWamH++XHMiKmuMZayqggx0nctu+0GbQw2hMk0SeQWRF/VFKCGQUzUose7AaXh/MEDirKQvbFZ0ToH3mG0wdqK/W4nkiRFCUXu0imLDEhJ3Gptgc1SFGIsc6ybngSMjUH21pSmgsWoI980C8pqThx6AYBy/CIGoGI6tTpf8uTpl2iaGcMw8OzjF7y+vmPbD0RTcHJ+SRgGYm7LdX3Pft9OzF3X99gkbcnWWIgSJ5VmjMUEVCIEMcTO8ZYxBmWzQfEkRZRziLFYM64UOT7KVucH0O7oGCHUCUbNBb3P11YPvxsJStOKkXOE+9rzmaUconStJs3QO/b7Dr2+o7x9Tde2Mo9TwhpNVdXUzYy6qinLgt1uy26/Z8gsVCDvc3q6lgkuziCdjOds8JxlrY61UA9grJzj+PMIcirSFD6ODbFxZA6Pq2Uu5IjaliLplCUR0nRCalpVD/fswLRV07iT+xonMhgZ2E5JcuQRYI8x5v3f5JPKn3OUj4/fA7KGMl5rGrtYjp+bvNY5hwpHbe4599NG8uuiFBnCcXzZ3ErvFZO/zigDIYW8HMuMAfp4XjlOne5iRmIPhTc9SUUYI4ahhS3QR1iRRh9IQMkzMqQnUHMEaUOQ4qoTD6Cx/T2kRIx6YmTGCIEo3YwamgKWtWLVBFZN5GSWaEpIatRYhaDh6fu/QySwX5yyO3uAd4GhnOFMRXQdvdvg+i3tfknVyvhdLFZUVUNZVJMe/2ECKpETTEdXo5JIEGhL0iXKFhmIHeeqmTAqGbsHkBdG8Yzx4w7A9TERL2Vd2HEf1MZQGIUyGqsFDfWDZ/ABeo8ylqIqsYUSSYLKis54UTH0EeeiSP/kuHUc4VLQjBmvEaPLFDVRHeKchMpa4+C9ID9RBZI6MohUh3lr6yXN0tIGTdF71LaF4MTDxntUu5Y55UW+LagSa5fTGCtsHu8pTpIjru/YtT3BOXQKNI3lZHFCkTvUTFKgCnYx0QeFSz/pMgVa8cnHH9F1HSZoFkXN3ooGWAgBm+nsuYCOjoZSKR6uVjy5POerX3rCN9/9MovFHF0YQhT5gBRjXhwNWhfZE06Ca61rHly8zez0Al3N6b3CR0Xbbdlub7m9eQm+5RvvvsPl5QXL1RLnROtTul216Enp7IaaF7/ejc66uT0HDsFbPjSC7g9Dz6uXz1nfvGJ9dcWwaXl8/pQvv/U15vWKm5DwfqDb3HB6WbA8K1idQlGvgT0RMa8QzcAKASo8WcEZsHnCCWoyNp+klPBb+Oi7W9pNRGvL8mLG47fPaOYGY5O0tBIpqgqlSpwr6bYQo8PaRFVrypmiaEQTJ8Ujb1ttQBlCVCjMNOklf0m5Kp0Irse3PUO3Z+iP9fPGVqb808iYUNKOebQ6TxvrpN3KYVGJSfQX1dDj+h5TOXQ5o5jPp8dRfvKSk7/xy7z/+AFP3vmSGBcQs5bkBEHlKh6MWpVtu6XdbxmGnsE5+l4YZ/E+WYDnzz9m3RxfW8ys3QTRY7XC6sS+srw4WzL/R9+lsBXK1vhUs+4UjoqkS1AWtCTiR6XBMXcZs6Lx5twHXqffHgCUdPTb438/PMmj0ECpe0EHKR4W7/F5jcA1CcJY+T0AX3LNuQ1+1AZKZJde+d7X1zsens6Z1wVGbXnr8ZJnn3ra/cCLlxu+9PSE7XadNWQSp6sZ+32HtZJM/fCDj7m63mbTqoROjturl8xqy+nJnDcenOO8Y1N6gg/sXCLkDX82KzhZzjBG8fKqp93La7rB4F0EJe18m80NkcSsaYg+st91tG3PYjlnVpcYlXj1+ppHjy4pywKjwPc9m/VamPUxEGNP7wOv77aU+45ZVXBxumKzbRmGyM1dy+XlirKq2Gw6bm92ksDGo0cC4hzKAZSZnnGKaCJET/G//u/YzQ2WntoMhNACnlJpZrbBz2fs9j3OjyLpBzj+OOD6LMtwAt5JE5NgDKhiHFWWRv5D1kfOZyhyLlkfTBtph4WJsaJgYmWlnCD0/cDI+FBGo23B7WaX1wqF1lbWaJ+Zg6jJkVkZARZ9CFmgfZwDUvg5DoJtXcHQ54AsYsqCRQbkuq6VtmJrc/Km6bqeUS9xPHRVgLWEmFgby94q0NDkW3AXHbtINs6JVJk9rguNKSypsPgUCF2HHxxD77h89JjZ6QloTdd39CmBD1gUdVkLwJISruvwXjoDbCkMSG0Kcc1Oia7rhD0H1FUNhWXwA75vSQXY0qJLSUyjcxLgcWjbrKoK50Q/dmLK5eM2BP5c1lX902dn/NzpKUop/urTp/zXr17xi5sN//bHHwPwFy4v+WPzOfsY+TPvv3/P4Or4eO4c/05+D8BXypL/+MmTaVz+X0easX/x4UOeO8d/9fo1f/6jj/gvnz7lnarihff8W/m8/uzFxQSw/qQd36pr/sM33ph+TjESXU+tZK70zjP0nqIuctIIioD3A9oa/DDgncssdFCqkuQkj7u3vvQmbuiFNc1xu59iTG6EPaSwZcV8eYKtatCWFBIlF7hUo2wQlrdLpMGRokIpS9MsqOsqJzeBQsOiqZk1JWVZYMsCUzYYW+WuIU3f7+i7NcH3BC/AE8nhQ4f3BwOvGMXFHshdMiMTKTAMnTAysjZZs1hIG2WK9GHLs/qlXGWSVraiqnnw4BG73Yau39P3HegClZPEwhqGwaGUoawb6vmM2aLBqsCwE+CvampENzVSVpbFYsHeJYyRdjXqiqtXnr67RaWe+cwyn6/49NUtperRquVVvOPk/BHnb7zJ3u345MWPud58lFmIeVsvrGhneiB6Qt/j9nsBoK1G1xbdlJSVFeagCyQ/6nlLwlSXFWlwuGHAe0/nA8oYyOt0JKJKS+g6kodKi2t7qTQur03SyaxyDHnYJcZOJp1bV8e9IgHX3/5n+d3v/S725Y85a5Y8qc6JbpC4XEcYOkIgF7csxlbjVaO0wVYVJ/YiaxRKEWgy5cjfP/RyTYM7yKQoJeZ1EY1s3QbUCKRpymbOft9SFgV1XTNEJV0vUXaDKlZonQ25jtiNo0TBmNRXheiV15Xh5tWHXFp5/lrPxMjK9RhrSSmx3Uohoa7rLONhc34gMdlUOE9jV4tIClVqYHBbQrcjdlte3N2SfMBazWreEN2edddji5a6mpFCyUff+4irj9+j21yx37V0Q6SsP6CsZxSzmh/8zntcPn6TB4/f5Mk7X4F6xvLkFNrE9vqG//MXf4GHjx/y7rd+hne+8TNEXeCdz3utEXmTkcmX5SVc39J3W5SCytYkhIUbdEAbjRsG5ovlBHKMcWHXtTjXU5QFs9lies4xRYZhkCJlZsDZsma7vqXbbXBDR1kaZicnVPUcTMHgIt53Yt5moSgNp2dnEyioUCidjuIUGRPeuZxfRBpdEg91B1IC533e62SdlPghEpJIgdiyoZydEL3Da0i+o+sEBF6sznj05js8fPIORilevfyU73//+/zuD34AxYzl+ZKFNlTZ2yOFAT+0dLs7bq5e4foB5xz9MHC327PtBsn5lGZW19RG2FoJMW0IWQbDKE3Kcgwpy0+MTTzjHMsj+yifOLDUxzmMOgIGJ6bNOAfVUZpwIGKMseLIdD0cRwXro9fJuyF4kZSK+USlvdyg3MDQbQWgM4aiLFmdnHB+fklM4AbHervl7u5uYiPLeaqcJ6qpsKJV1uY8Ku40dUOR47kJaFVZEmBcj9T9OPhel5ga2bc59j1KiA7AaZrA09Gk+rNZWAoj0BPyWpPzUK2yVNbIDAy4IJJ9kTiZVolR1wikytxUSrLwMeZPmr63AAAgAElEQVSN+ZyPiRGTBux03Qf5BmEDyj1TWjoC+7ab1sSiKCjLgkIbmqLifHXKYjbHkLvmSbRDz77r2bctd5s129tWANlh/A5QRmSwxmO92WA2GwHosx78mCeOa88xa9mHLOcw5poTfjCNTukKTlmOMATpCPMRFSJajEwIPiumK00g4ROMxmkARkFj4aSGi3ng0UL+PisNhdGghRgnz1uIN6P06Ozuhp/+O/8jMcGP/8gf5+bxOzIWUiD4O1zYE4Y1+/0d1fyc2eKE+WLFYragKisplglTRfa0TDSc5lCUwjxZH1hbkfeJGbi8D79yXAuY8nWSdFMe54IKxWGqjiCHIuTur2l+yCoj1+8Tvu/odxAwQgixpRRP6oK6lvvqXEXfOgbnsvSAjGoVIylEvHMioZeJMCHLs4SYLzMlkZkJAeUHTOGokqFQ9QFnQKHLOfOTBlUvsKsLivk5/e0LwtARgmMYPAxX0O1J+xvUsKMLX6ZslpiywigreE/f4Z2s0WHzknZ9Rb9vGQbJC1+ePKQ+e0x9cslsPmdZWpLzuAFadz9fOj5+IsDYmCIv13copVmePuBsvuDT+JwNGwbdi6t0kMpSaQpOT5d88+0nvPngjAcnK05WK6pmgbI12hYiCKwtXb+XAIuEVaVUuawkA2VzSt2cEHXB4BP7ruX66jX73QZr4OLsjK+8+0dYLRq0UvgM7B5QQpXBBTVtOFIpsPcG/GHxvg9kdF3L+u6WFALX1zdsd3tsUfHVr/0U54/eIBrDfmhp+47vvfc9vn3+FrZqUCYSaSEDy97Dzast7V4xn5csVgXzZQnRcXvr6FpF9DNcWLNaJepaFtUP3rvl7Xf+KfYbx83r19y8uKbb3lI3JbPlnPPLp3zwwXc5PVUYHbm7WRO8ZeiHvEFEnry74uShpZlbilLafGIKaCXV/yS0gPGmyV1LhgKNiVFc9lzEJKnIj8e0OKTxZ6nQ+RQPLfApTVq3kJkR5HrOuI7kNp6+26P3W2yzpNaa+eIEUHzr1SvMq1ek4Li9es38dMHMzzHWTFXvkKQ13bsBUmAYerq+Y7u+o213h6AjBOqmkeDh6FqeffwB/uyQ+F+/esbCBUpbEvotSluuz0/ZNjXOOepiBnpGG0rWneXOL/CU4hB7LBIPgg7rLwZdx2rq5373uV9/4Zu/4OOOV3yA8VmMQOv4+Uf3n3j/I2JABX/0+yMQOGv6zJoKkCrlvLCEbuDydMGm6Hn5es1vfu8lbz5oMMrTtVteX9/w1pPHrHcdL6833Gx7wHJxNuN8WXPSaG5vrjBanMG36xuSd9gUqHRiIBCCbNiDU/QDXJwueLCaceUdm+3Adhu51onlouJkVVKVFc+fv+TB+Sll0TBvNJ980lHXBbOmxOrIdqNY391xdirmgbN5ybMXV1xcnFBVJYW1WK3xLjIEj0FzuiqwZUvXB243nm3X0+77qf3pi57aVCxIUUBuAjo5iu//gPK3fweDQ23viH5AIeZip6uC0tYUVmO1oQo9RaExTuH9771ZHIZCRFpBxtYvxWfB2mNpDsXIkBuNO4R1driARPDiHC+tUCkbBhyq9GSWmcgFGIiJruvxPqKznpnOgdarm7tcl9AYlV09c+BvrM1sAXVg7+qjzAsp/hy7wQO0Xlo0oxKTIoCmbljM5tyu1wx+uAfGWqsp5w1KazzA3/slbv+JP8rm9BwdoNUIOOAjyQe0tbiYMFHagpIPWCXgUVXPWJ0vqBZLKEoSUvktqpJq1mCrUiJErUkxYgupKvs+MwK0BmMwZUk1WxARTUAfPNZYqpDbapaK3b/yrzH71b+L7YWNHdCospKELK8foSgk6B+1oDkE0KfG8FefPOE/eP6cv3F3x3e67p4hFUgo91+8+SaP7B8s/HhcFPy1t97i33/2jNsQeK/v+TczsPrnLy//QJ/xyFr+2ltvAbD8Q7Bi/78+vtN107X9uw8e8LbvaHcvIbSU9RIQLVZtoNAeFVqGds2nzz7k7MHb2KIhpsR6tyHExPnlG8Siou8Hlqsl+D3tZs12veXRG08whTqQZlKR5QosxhQsl5ckZRB80pOi6KYVTTOBcX3bYxUH7TgiVgWKSlPMLWVVU1VNdl0fE1sEPPUe73o265dU1mAU2JQY+j1dt8O7Aef20705ZuWH4NlvN9zdXHP16iUauLi8RFubEyiJD4w1x9sxAvJpbFHReQhJtDCd8xirIEZc17K9W+MGx3K1oigbtK5IlCRdsliVzOuC09MFr287lILaKmYzw+7Fmhg02ioqq/nqu0/48P2Bfr/lbr3n5ae/QzAVcw/RrZgNLxmcZ3V2wZB6tt0VO9tnBogsP13fEjxZtiuhm4LZ24/pru5w2w6yy7KOUYq1RYIQCIMUE32IDIMT4NAatA8Mg+P87IztdkM/9ETg9PSM/d1amPA+MqTIjd9y0BYcH0S+k3l9nHaMkZE0ag4irMiXX/0G373bYt//LZZf/1lM0gTv8WHP695z8fTrYCp8gmHoBaTUo2EX2KImZUmprt1T1xWjvpxSmqZp6Lrungt8CjFrfxq8dxRFibCoRb6lLApcu2W/6+m6luXpAyF/JNEdVgqqapbBIfEkGNnmIpOQ3bcRhudsNqO9U7TbO5SyVPMx9hU5CBD/AGst3juc6+n7jqqqMbacnvV4+L7DDy0x9pQ2oVSgKAyair4tmJ+eUWX2jQ8Rq6Rwtn7xMb/0P/0PfPqdf0S3W+ODZ9AGU5Q4l+jSgBo8603Pq2cvea/+DrPVije/+lW+8a2foUBx/cFHPP/bv8R6VWNePmOeAudf/3YmVygpZiYx/yEzy5zrMcBicYKxhrKZMXjZL7z3pEGMkMtCY4oGYwq0huuXLwjRU5QVy9MzYo4/jBJwPkZpOVdK2KXalixOLrDWMuw3pOSF2RQESIghUJVNNgcGn0KWlDiw/UbigoBrAqyGJIWbMa8zx27dSvQrBaCQNvYyBClyKaTgoSznF4+4S4HboeX19RW+b3n0+Cknl49Ynb+JLk549eoTfvCjD/i/f/s7rHuPNwXiVK5wSky40BpVWIp5wYmdSWHF9Qztjru7K3zwhOgYkiJ0cN6ITrXojvpsjgtx6ooUM8aJZKFkzZNYTKazxEIcXjMmYfn6PxcVfiaPGIHaiaGZY7jRdEchwGqIh+JGSmkCPiW2kL1oyu84ogWMzHElzHGlDEPvePHpp3Rdj8ttzFqbifUsod1oKpXNtrShKEVXcmRQmtw1dMyEzTuFALlJSEDq6FoT46Z5dD/Gk1cJrfQUdx6kF+L0c4yjjq3kPULOcoQgjN4Yg4CCSlA8FeX6I7I++eAZghRHJpUsJCtTaWSCivbsWFCS3JQpPxWQVWJym/9MyLNTHGL4SXIxF+LqqmKWzUmPOyFDiHRdz83tLX3bCcvY6NztZijrGowlZaa793Ido16zFPQOa/jJaoXqOvq+Zx8C3mfQGWEEV1WZx4KcZ0hi/K2zseDh3ss1hRBIWvAakTsJUhj0HrwneU/fO0KSPrqYu4h1NsazVlEYzWpZsygVqypy0XgumshqZpkVisZmY0sUfmSqRylMx6gISeGTRhnNW7/7K7z1g39A0obf+mf+lIC/cWDoHK7b0e7XbO/mlNWC+eKE5eqEpplTljVFUVJkBv9YHFFAmoylAsn1Mk5tgTajKasWMDodwGUZsmOVQPJIlXVyjwUnSRy0tDOmpaZl4rBIiH5yBoaTgNsuOCIalCN6qKtGOrILAYndrGAYDINLDEOkbVt81vlP0UuhiWxWFjzeiWbs4BxucDjfy7OLEZSh3HV8/b0fUr7VwOMlkOi7AfxA9IGUFGZ+jh32pBTwrqNvW1AJNTh031L6PbiOePImw+yMfZpBVAy9o2t3DNsbzOsfkl59n2F9w3bXYrSlv3zI8Phn6Ppvsjn9EuHklNLUYC2o3zvn+QkBYxMuOTSGIfRsO0VQUdpAg6HQBU215OHZJY8uznl4ccLp3LKclyxmM5rlKfPlJUW1wJTiyFsayzB00uYPqGwzgTYkXaBMxRAj3XZL27Xs9luU0lxeXLKYN5yeLJgvligti2oc+w+4ByHlgS3/ptRYPfg8+Hp/4wr4oaPfb4nO8/r6hs5FZsszvvK1b6GLmt4N7PqW7W7L7foO7x9BlNYzFwNFKcm3UpaUCtbXjtAbwmDYb/aUFjY3EHxDM3uDdm94tX1BVQVmM8v+Di5XheiretHDVIDVFdQF2tfsryHsWozVhKB59PgJ2/WGzXrDfrNm/bLDecNsVTGbl6AcZW3QViZEdH3WkZpmKWfPXlDEimhLBtcKiVdr4jEvamS8ZgAqwkGEnDzn8144tg+M9/hQ/YuHqm0IuH5g6Fu8a1FaguMyRmwIGBS+67l9/Zp2t0EXFmlDGjdKcV0XbDngg7Bvur6XFqwJCIrcV78F9Zu/iTo7n35+/epT1rsdRhvKosSWNa7dQrOgMjXohj5UtK5kHwoBYsltNpNAJ/nZa+5nSBIIjDdjBE8O/z7hqHk8Ho/Xzw/VY+0YlZ/fdPMzF3lky0qgeux2mM8zHZ49cZQLyUt4SlMVV5EojOLybEZjIzo6fDfgvSSa1iSMiezbga7T6NTTdT2mnEv7aBJ2WFMVnKwWnMxLagvtXrTh2q4lRU9VaAqtmDUNpgRbRl7d7ohJ0/eObUrURlEaRVOAs4m2c6y3O8oCZnVBXShKA+1ui2oKZpXhdFlL8lQmirJk1hTs9x0+VKAsdV1itFTwTdYLLq2ZtIMG52i7nmGQ5GMYIs7nQs/0EA/BX8r3VKeQK6EBhhb7679OmTqqq9dUdy8pSkVQA07JpqZQlLbEWql2Kw2lNVSFoTNa2LFHW+zxcb+tLK93R0zWEVgVqJYJcJ3anTL4KYZcRxp/SrRItVGkqKfNHDUG98IsKApJhqWAO7Lnx+Qhrw0ZhIHMoNWZcXtUEJsS+Rxgp3EujWPdKpSR16ekMIr8s+hYSZIhFdrO9ZkxZu6bD1iDstKLIa1dPeaDH+G7jvDGU9FKCmmSa0FJCOeTtETGvqNRDcZIi7iqqqz7mrVuy5rF+QW2qjFVnc2c5L4YbTBljVIGN3Sk4MWJ1sWsG2fFlTmzQ1Iujqgy0RenDN/4FvGTj7CvXwr4ow6Jm9wf0c9MMaKd4hiM1cBDazFKsYuR69GV+DPHA2upPwOC/16HVYqH1vJnzs5oY+Sl9/wvWVO2i5HiM4zt3+szHhXF7/u6/7+PS2v5E8slf/36miEJy0DHXp6vtmhVUFqLNongOnx7R7+/pdIJnTwqDYgakRR4fN9KESxG0rAl+p7SRE4WNXUhLA5poQafVAZeZewXpiQmJe9NB33L3F+DD4HgZM0dWWOLWlMX2eSkrCjLJktbkAPzITNgc2tadBBEP8xl7dlh6ER7cmztzkeMkZDECXt9d8cnH33IbrMmBc/Z2em0N45pQiCxZUerekkutCUqhTIGW1QsT8+5vor4sMf5KK10uVV/6DqqqhHjHyP6Zc45tC0pCijrgrKyFFZlnT6RzNEpEEPCRzAJzlZz2ocPJU7JxaA+AFozuIG1uyF40IWmjTuu7p7j2U9zMiF6pUPvZSu1RljNZYM6bbClJu0HoiZ7duZeKGPRhUhUqNzlE8fCaW4bV1n3czSSknbqAl2JBuNduyOSMCq3bnNUJE+SrE/l8CwbkJToyGulUFaAD2zB3faOH919zKNnF7x7+iYVBpU8u901F7kdUSWFjuRivwBUKYkcVsytpMQggGqMECVRtragLCsxFczHgfUlBrt1LRrzaFkDlRKdUO96urZjvjwR6YxcBIQMIo4SA85TltUEPIDovBMcwfUZfCiZzXI8EpwU1AojpIQM2Glj0VMMJEXnnVtTlDVVM8stxRGdNU5T/hyTATqtSvbbDb5rc2t9yXJ1QmkVLz99zvf+4T/ko+/8Nu3dHaYsac4e8PSNJ5TNjJQZbbc3r2i3G/QeemsYNndiKnN3S2VL4mZHHRzmrufugw/45Lvf4fTdb0gHSzqOzXM+pETuhxQngygxLpMYOnhhtI/mtHlrxTnH5u6aumnQdYUPHu+kvTvmJD4m6fCYHNpjNt8sGwGfgkPbArTEyKIhbCZt4ZDEadyqcT8XFi+ZHSnSbRIP6KQm0C6Gg868QuZRCC7HOQZMRUx+6vQKmQ1Z1TNm8xVlVXN+cc7Fw6csTx+gipq+d7z/wcf8+KNPeHm3YVTgHbOaMIbvSpOMBSrJJoqAqirKqkZpuL29Jgzybu+dFGeVpdBq8nGISQyctLLy6Wr0ekCIsCManclEE80jF771vT11ZFXm/1KaWsuPEJgJpBx/H8NoHDW+Th/yAwVTO/34mjTimekAyqKmnEYrPfmdeCdmr4qDZJLWmrK0k94/SmTgbHGQHbDaUBRZviTHrWqUwprYwCPIpKb7NOb/E5A85i+kfDk5tjy6Z0zXMgKwB/OhwzqSzbNjFNm7PEdiijmHzcsrCZ1EM9zHTBAK/nC/QIpNcexckO8ZpQfG18iNPIp1J2B2OutJfnDcTMcOMe7l20eSCumgARtiIGwj7b4VprCSzgwpIAvgLy3l8qVKa/FxSTlvODq3mISkZUw22pUKg4DPI8ifQfTxIrRWU06eOHQzQMD7RPTxCKCV/YTgs0SBzCXSGOPIvatLy7IwzMvEotaczi21ccys56R2nM40dQmlhcKATjaj40k0T03CDV6kM3zI8hEG0+1y+q5587v/gBdv/RS7eknKplbR71GDp21bur6l63ZUzZy6mlHPZsxnK6qyFF1ZNfoDaJFmQIusYwzgmeaY0ocYeMxjsgr7lIsfVURkXI/rRTrUW/ODn8bMlKFOY30EwBM+jiZbkYQnRsfdTUdbV9ItVRQYrbGFxlgoSk1KBa3v87PyU0wnrHYNBGIUw/MQRNYlOMeQTb1c71h/+D5+/09O57VdvwY30DnPrvPs9x1uu8bvt/h2T/Q9UWuIoIMDAkV5CvUpqaiI3mCKBbaeU6JI3pGUmHaH7g7V3kKI9GlLUc7Q5Rxbrejni8xOP5a++fzxEwHGplxNigR61xKdJ5DQtqDCcja74K1H7/LuW2/z1uNHnJ/W9P0tSiWKoqRenrM4e0xZL8U9t7AUxlJ5N1WnQlQSJCfwITE4T7vd0u339EOHD57ziwc8fPCAk+WC2Uy0xnyMk1jypF8ybexH2NR05GrjUZVAjeXHfHjf44YWP3S4wXFzc4e2FWenT3j73W+SlGXfrllv19xubmm7LldYEjHA4GRgGgspasDgewh2Rq8Mt6+uqApFv5dWqKZo8PuKmztPPfPoS4sbNO1mR9cOor2EuAtrDASNaz2+Vbh2wBSasqpYLVaEIdBuW3wX2F0PuFiSokanin5Ys1i12Ero2nGA3dbh+pzsJ1i+vsYuLgnaMwytCDJrjQ/u+BZOf07tFinJc8iDeQJe0tGNzZvimHRMwGRKBDeIHELWoxtridZaZvMK++KKrUrsFzWmtMQkRhZj0BBjxFqTF8+UDbyYNmSd5SrGzx2P4v0PSD9zNf28fv9H8PoKUqIsS8onTynWW8r6lHrxCF+c0/qSvbcMoSSpYlry1JRp5hVRHQKqjFDlr8+i8Z/H0+7dqxz5fa5ucO8Z3HsDMOrljd83XrMPU1A5Pgf0qOOW7rU9HK3cZEEfyKDPvDY0VpN8ZNdHBh9QXtpUKqvoDPRDj06OGBXzqpHF34tkx7JueHDSUFlF8D373Y6yqui6gZgCRTEHLVpvBo0xgc12R+sS3nn23nOnApenDVWpmNWarg20bWBfGwqTmFWGWa1pt1tUKpmdLVgta15f3+J6SKUYsgXv6LueshTm+KwpiT4w4Ghm9WTaFWPEedjuWvre4XzIAeZnH0U6Wm8EgFXRYbYbjOvR/R77m79BGToqFSitotYlzojjeYwKayS5nZSjlOi5zuqCfnB0g79f8J8A2KOhoY7qoWpsTxmLIDBJExy/bxqrOeM4WhKFsZoDYi0fEsdCzFEAa43FGD0ZrYncTL4vSQKOeyHxGJCOsgS5VY8cZImOKgLKHmkti3nVYdjrDNyOc2YM4n2SFnJUkn8/AmNNYUlawASlICgLr16QihL/9C1MDKQQyUr0AuhoxRAD2g0oHaBuMFVN0TTYupbkIwrQYouCpq7lGrSVgDs/FWOsJC7aiHFdCHgfSDi0tigj4JnOor+jxaQUmxT7L70L2w3q5aeysuQ1cExWUFocvmNC3ydsE1Lih8OAS4nzbFiVUuL9YWAdwnhL+VHf805Zssggz1eqig+HgXWMvD8c2o1vQuCHvbSqf6WqAPhx3/OHPYYY+TC3wF1ay+kfgh374TAwpMTrI2D5dT6vlBJvlyUfDAP7GHlvGEgp8cRaHlmLAb6ar+02BD7I1/Z2UXD2Beew0Jpv1fUhGU5BANZiBboUhkNme/f9nna3xnVbqqpEZe1tUKIpiOjfk4GnFAZUdJRWEtDk9yTlZPyKSCPESoqfSolcTmbDpCjAqy5Ebz3G0SQzMKvmGK0xWjOf1xRFRVHVFKV0KgkTxRPDgBs6fL8nBicFpBSJfiD4Ae8lFvHeTUz7446AEAIBAXFffvopr168RKXI6cmK+WIhhg8gSWMMtLHj2t+yo6XS9WRihhJ2SDVfwO2agCaGbASak/3gHcuT88xiEbaU94GqKdBWTd9lrcaFg9iJtZrYBXyMqAh1uWCxWLBrT+l9oCwN3RAIqkAHRbvboVSB2Vp2/o7ruxf41E5gLOT9YRiELWq0yDEQMcsaU1lJzkmkIOu8JGRKikpj8TaO+7b8LKBzzAmxETPCrImqjWgnypogwK3RZmJPBeLUFXZ8HH38VIwrioKoI3sLH6uB3/74u5wWMy5nJxRa490e71qMqVDaovN+OEFUOVwYpQFGjc6Y48GosuFqZkMdn80Yt3X7jtVySczAhMaSUsAUJapvZWz6AVvZac+KIZBSjyIXELM+cRwNY0moGEiupW+37HcbKlvRzE9I2uJjghgIQyvFPmMxRe4myWZRKiVSCOx3e6omUFalzMso32U0sldGB0oATmMsKXg2u21mfluausBvPC9+9B7f+/VfY/PyBXY54+TpWzx6+yt86avfoKprhl3L3euX9N/tGPqdGNUBod3y+v0d6xcvpNvDVsxnDarfs7++4tMPfsQ3+i26WGXJsFzwHA1NFChrZI/RhqQFDNBmfAZjHHGQ2Aoxsl1v6NodVV2iFHjnsjyYGHUNg8gSleUsP5fcWqwLtC2ExOFz3jCZhekD0DPevs+QJGJMmDRGKRkQm8g0EpOFI7AZRJggZEBLa0NSwtoVRoiXxBwoqoZmfkKzOOWNp09ZnlxS1CsCirvrK378wYd8/PwF63b4vJ9DEjOa6Xu1htF4mAJTVigiu/0W5z0xS3ElxD+lNAqdvS2EFZkySYQJR53m7Ge/Oq99h+wlr79H53iUaRzm+5TfSiw/gpTjZ6aJRCPSEJKi5Hx6nMfHIOf0pxoDD9l/xpQng8EhSLHOapuL7lIwqqvMms/7h9YmS4IctF9HU6Sp9XrcakewekwfOWR0Kc/V6VzHVIyx+J/Hjgw9UrrvoTG2uX/2Wsd7EVMkRPGDmBzjj57G2Ho/Ml0nclLIYK48dNE6z88FRKpCmTEnzp95lDOO3zHl0elgynUIo+MkGyFAYprWZZWvYxxaKiacy4XDvI6r3OGmrc760QIICjiXwd1cjFNHAzP4CJmsojJ4nhMm2aNDyHl3zkPSfcBuvLrjwkHKgG7KBLpp3OaCyjQ9lJA5rDWsasvlHM5midOZ4qROlMpTasesDMwbjdUJrRNW5y6FiBR3rMKWGmMHVK+gzx2+MZFUFI3fGHj4/m/TNivS4pI+QDt7gIs++3gMdG6g73uKakdZNczmcwYfmDdz6qqmKsrcUaInzEK2/pQlMkTiTlvyGjxqx04rQP5/Ovo7ef6pI7hBHV5/D9e6TxkKecyPQKyPUYoz0ROGQPCdeAaUNVVdUTVitjoa7QkPTpiwxJDnlXjWmASoLFuRPXm89wzeMQyB0A+o9ZbXn35E3+2nuba+fg5+oOsdm13PtusJ+zWp70jO5VzQkDBZziJ3fHlH9INIJdgCbWvRJlbg1xe0zSlmf0PR3hD6DX7tiPNnMD/Hrp4yuEcoVVCZ49H9+eMnAowFKMjaq04WdKNnVI1lVcz5p7/+bf74P/8nubw4p6w0XXvF0G+y2U4jmg5FI86+CqJWOMAnzTAEnAsMmTbthp6+37O5u+Lu9RXLxZKzi0uefulLnJ0/BCUaYFpH+jbrv2YNDY0wwQhHLR8wLQiHIy+guaXuXgUR2G1vWfRCj97t99yt1zx5/GW++c0/yjvv/hQhGa5vb3j26hM+vv2E4GOu4EZCgN1a0e0SZQVaJ9zOc9KccHH+BK0Nz3/wAbvNhtn8hLrZ0m/fZ7O9oRtaqrJiNp9j7Y5nH79HdAIqL09qLh6cMfSB7XbNbr8jqkhRVmit6YfA9csbbq+v2d5t6FuP0o4Hy0sW5RNOmnPef/47dJs1F48uWJ2uGJLl/R98yFPX8Gi6VwBJdFedaP11fmDfHWn4HYFBCunA9RnQO94g5aVqAnaOAfA4gudZj0sFT7/dsNWacjEjpTcBmJ3MeOdrT7j7m3+P5//izxLfekhpsv7uuFFM514c9GgBawqUlkV7aof8TIBVNDNCcTCZ0b/4S6SPPyGGyD5Ftn/656DpaZaa8+pN+jRjOxj6YPEUJGWAAAbS6Og+glbTDni0QAoSerh597Hh+6AYZM3R45bx8WM/g+SmyIEqG6WiSMqVxQDOQSEagCrfn0m6ODFVVqenNgGzOfGKkaF33F57zKqiLg3z+SzPDzHNWSwWFLZgt9tQFQWn5ysKq7i7W9O2HTolShXAt3S9J3pHVZTUTcNu36K04uz8nLbd0LUtJNEZvVhUPL/ai14TcNLK4LEAACAASURBVHu9pS4jy1lFaRtJGgbY71pKHVnWDSerhuefXrHfeZqqYDar0NeJdt/hnWe33TIMntubO/qu49Eb55yfrri6XrNvWxLqUJHP7XV36x2Tipfi4GI5BbjjsxLDHB0HlN+z+vt/l9XrV6xK2IQ7wuCwKlEmQ60t9bwiUeUEX9qeYn6UxiiqsuTi4hSMZdc5evfF6p0HHa0xSU6H6rTVuUOACUgKR8GryiCH5GKSbOWI5yAJMgrnj/qxSt0LYsXROt8Kpe6za9MhjNAcsXVTypIE4jKaSJK5jBIfBpS9D6SqzGolyWi2hZUhH8ekTcBbrWUehiiyAfroM3RhhRmbZH+wZHZXJc7olcttx7nA5GNEW+iGjpQSJ6tTTD1n+eAR89MTqlnJJx9/gs1zyYdAUda500OE6mMMwkoyos9kTEGRwNiSqm4Y+pq+77LzqBgX6ZQgeZGiVopCJUz0mcWcZ3tK6KmlTlzbrbUiyH8EfytgHSP/3iefAPBvnJ3xr5+dkVLiP/r0U66zTm0C/srz5/ylR4/4Y/M5tdb8J0+f8pefPeNXdzt+dbeblqy/tdnwt77ANEv9Y/48yq+mtfF1CPzFfF5/9uKCP/WH0Iz9z16+5MfDQcMT4Ofv7vj5uzs08N+9/Tb/zdUVv7zd8pefPQPgz11e8u3cyvefPn3KX/j4Y/7Odsvf2W5RwF954w3eKAre+8w1/aDv+Uv5M0B0Uv2wp2gegsrKbykydC273S193xJDoqxKhn4QhXZbUtXzSf+SPAb/H/bepOeSLL3v+50hpju8c46VWWN39chuqi3aoiiRlAjIBrTyRgsD3hmGARta2ivDC8OfwF9BgCFbgLnwJFvtgRJpmiLZrJ7ZVay5Kqc33+kOMZzJi+dE3JvZ3WrZsOBeMIDs6vfNm/fGjThxznP+z38w1tBYxXZ9zc3VM7q2pakr6tpSlIbgS+r5LSmAQyKEkqqZk1KUgMrtitl8wWjFU2jF7GjBrGmYNTOaek7ZzIkTe06e2a7bMPQbgutIbkAnKbCDH+j7llW7Evk8Mufts2P2j+AdvW8ZupYffe+7PLj/Cnfv3eX03m2225a23UxFwM16zYfmE262N4QYObtzl8YU2MIQoufy6oLj1TUpJawphLHa9xTVgNIFRWW4c/eEpxdbeRaUQWdGeEyJIUhgYzkrCK0wakKExXLO88tzut7jrKFzQdLSux6tFE1Zcef2CS4Z+o1h0yVccFzfXLDqLljfPCcM3X4xQ3QBFcbNniIaAbXMogGjcDrQXbbYzlEkjS0NYEghoDDCHA8pb9LJlk+Ktm2JUcIKjTF0my0pNz5vhoGyrihsic1A7LKuKArLth/YdB3DdI7j6M1Mmsx4EuBU4WKiOzzl4s2vsv32f89ZteCr997mlaN71MXA6vwzmqNIOT8BbTF6p0rK6KyE9hpLXTcCbO5JfgW0S5MdwPjcl4Wl63rOnz7j+GAmgPkEDMlzUtZzRHUUce0a7wIhJJnzjcEWBUVZyudqi82f44ae7fqc5Nasri5Y3dxw/95DbH1ANDZbcEQuHn1ESoGyrjk8vUNzeAuSFkWESmANXSf+v01VoapICLLxIzpUDuYdhqxqKUvuv/oajz77hJvLc/x6y+qg4b1//md88P0f8OzDd8FqXvmVX+Wbf+O3+Pqv/Tr17BCtLN3VDU8+ep9nN09ZnM44WS6Jbc+jd9/n848+oqprXDMjLJbcOTslrCx9dFxfPsO1K2wxR5zoRRUizVGpe0NQmdEsdnJKSep8CB6tLWUplj22nKF0Qbdt+fD9DzhclLJHCpIjoHMtGLzDuz776wpTTZiyThrKWc1ibJnrhjwUlZbGPGPityF5v+cDKrJ1MhgnqpWBlMDaDBLl0MF9oCIRJ1BJQMRB1C15X6i1xhQlMZRENMvTh5zeew1jK1JStF3PD773Z7z33rs8v7qa8jSIGRdhlIjHDA4JQBSzakZrCRo1RcV8toQIbduRlJnOyxpDQRp30hOIFvO8OiGFjOzMnwaDJx9UBNhSjPZTGUTMiiQBJnPZNAFaY02/X5Pt2LIx+gzMj76o8r2nhhG72nFkp5ISZCuJmALWFijEpkBZi9US/jdaDNSlgLHTd8ieptbaSWovnzOOh7xr2lO+5glEznsEj/dyBUYW7wRmprFGlfpUPDNl35aIkyw+ZLZ1yp6YOxaxgFdj8z4h9WBKSN2Vr09EQOdx7yRBiC57bI5ANTvmqxrjLOX+xCRWAuQaXOXPhVzbTnYKKU+ho6euANX76rJxfQ+5JhYbh/TCGPJ5XxOjqOKUG20j3PTsyT/I+5zIXq4E+OCyF2ef5wS/C3rKz600EEd1qs7jtMQaCd6N7NUTKU3XIg9EJk9gJdhOSpGoE1pDWWhO5yX3lorTReRoFjisAssiUhQdxkQKU1AUoJQTnIhIoS3kvXscm3m1xQ2KfjBcbzyrtWQApAzEp6i4984/47ZPtKbhO7/z7wpbOiZcSuA6BpfQbY8xG4qbay6ur1nMDziYLzk+OGI2n1MUNdokkckom8NbR8Z3EsUGGYzVo9XPbh3XRgLPRsYsalQQjOAu03PywvL/MlyQxBc8RFFQ+ZwxkaJHhSjWM20rDVhdiJLPVKhsH5J8S+jWRN/lNXC0ShJCjc4WmDKmE53zrPsB5wPp2XP0P/6nfG5EESvnE3nyyY8hJfq2EwzLDRg0WpcYW1PMlpjFGapYgKkwRtPpJT7VRK8oQ8KrimQrbDlnPptTzQ3VrGL96Iz15z/m5rMfELYD/c0FRf0Z6uACdzDgMaTSvoAbvnz8koCxCg/oqNFJ06gDHt7/Am+9+UW+/PaX+OpbX8TaAhc92+BJ5ZyqnsskrCQhcj9NNkbxYew6JxNMhDD03FxfsLq5oms3lIXly1/6Ksent2jmc5JW9G4gxYAmoLWYZ1tr0SrTzqNIZ9Qo63xh27cbjTI5jCE1L1GHgNXNc+abS9p2zbNnlxwd3uav/Gt/na9/869jm4pHTz/mL97/IY83FxzcWnIwOyP1ivV5hyoiftAcH97j8tEznj7+lGHbsZwltFg4sV33zA8OObt9hjEFF89vqKuCZnFCWSaubzpu3TuiXXui1xBNBjccswPL8mSOLSsefvkBxgjz1feg0PjoiASSlqJx6NZcPH7M9flzPv3gc8rG014nDk8SB4d3KEKDTmYP6Nst8NrIeyovfiDjkVKA7H0DEHxAJzD5yssi9gK2N/035oU+jUAlQArgB5LS+O2W9bOLaSap6orTO7foggRx6eApKLFNSTf0hLCT0LgczjZ2jMY5bWTVjQzefUD2+X/zX5P25LHrP/i90aBPflFWoBQrpdnoUR7BHvC5N8T+hX2V/wev+wXHdF33VL1jH1WYsRnUy0WvIqBSgH6YQDpiyJ39curCTUzaF2bxiEoBlTyKyM11h9UJVxcM/ZbV9SXHR0ccHCyYz2qenl/z7NzRD4GiqJjNGu7cPuHW4FivNzy7XHF+cc1yXjGrSwotRe3homKzafnwLz6gasQiQBb4LaU2FKnDBwhJGCtX59eooxl1VXCwnOEutmzblqHfsN0Yjg4XzGYVXdvz+aMnvPXGA5q64GbVst50HB8fcmQMq5sb+s7RbgPzWYU1mq7tWd2sGZyTjjNMhc4upXq8RmORKH9Ucpg4UH72Mc3/9m1M3HAQI3OlmDmFT46eIPIsLQxj7RWqQHxDbYVWKie5AilRGEN9MMMaGPqez55c78b4/vBSagIcd35pQJarxuk8c8GW77PWmqqu6IeB0XJgZCnEnFJNTNy9c4ery8spQXhXFGbPLqMZvBNw08jSFffeawfo5uaZtRhrsGUp6erGSnFmzVhGo40Smcy+36vJSdFai2w0BpGMjc96ShRVKbLYzPKpy1LSmvMxpIRVO8BdGwMeis8/pXz8hO7XfxuTE1vHq9b7Lntvahyw9Y7COWprOLl/n6eX18S+k+AG7wjGUNZzRuml954y+9lqFKawFCninTy9JiEhC9ZgJyN6kQJFJd8bn1PFVYnVJU6JZE4cUXbrXQzix1lVIhf9z+7dmwr78Sj3xs9/+eDBy/XaT9kU/Kd37/7Ue/yio9bS/PkHr70GQKM1X6pr/tp8DsAsf8Zda6fXVC8zkn7B8V/cv78XCvLTx0Jr/oOzM/6909Ppd81L3+0/f+k95j8DcPz3T0/5zXyO43vc+Mhm23O4CCQVhM2Y2aJ1s6RqloxyyuQH8f/sBsqioqprYkgEPwgb35ZoBU1lMScndJsNWov9R2EVpfEcHDiiNrgAbTtwefmI5+fnKKU5u3WHUs8pqhllPaNuZhRFAclgbIm1JWDxXhrebmgJviNGSZpVMRBcT9uuJB18GBi6XtiwVrz+irKcNnMhBPwewOa94+bqiqePPuMLb73BnXv3qGczhsEzDI6iKFgul1TLhmv3Pm/at3n+9BmPHz3m++/8kCEn2VurqcqS9eUVrzx4jdIIcBcTzOoaW1YYY/ARDk+WOJ8YBk/XdlxdbrFKUZUFq+Wcs+MZ86ZCVNqBTz85pywsy3lFWcD58xUxCIsc1xO6NTe+p5wdkJTmpvqEu/bXMLZkCCWVKknrSAq7DU9oe3TI3tgJVIT2+RWp0NijJeW927TdZ6jOY4LCmAKrDVFL4yQGpGGaWX8G0Ma8YPGktJyjLQppLFtRAhTWUlvLvCz4xltvcHF9zZOLK7bbloiwtHYSXVm/RluTlBJ91wtTygdUOePqt/4uv/+dP+Zmfc03X/ky9w/u8Om773B6f83JvTeJxYHIyosCYwuMFdDKlhUxBnrvKAGUeD1aayWIc7uaEroBuralTBXeOTSe9eqCuplhiiInSieqckFVzfFzTwoDrt8QfJ/zAYQle3O5JSaYLw9p6gNZO6PDDVv67SXdZoMtKu6/9gWaxQmdF2BRKUW9POKWgm5zxdB3XF1dgK3RtiFfdLQtuXP3Xi4ePcFtsvzaT0Bs8gJ8Ki1en6f3XuXw7D7D0NN3a8LVhicff8bTR58TlGLxhS/wW//23+P+61+kmh/RO48mcLNacXV9hXce2xS89c2v8ODuPewQ+PZ/+7v86J3vcnXxlNX1Bdy+w6yZQ1FiTMF223J4kL3ek5riC0bJss6sXcgy0r2AJ60NulAS2pcU7WrLer2hqpec3D7CWJMtEABliEE234UtaWZz8Zd0wlaPccg+l4XY8SiD156khCntnWPwPSGANZayKOndgM0BlqOyQ8IDyZLaEeCxwMh+Dnt7N5WBWpWD4jr6dovJDUwBNwphQytLNT/i4eEJutD0buD5+Tk/+dG7/Ol3v8vFZouIbg1TunsMoFzeF2U/Ze9wbkCTZG5Sij4GhptLTIw0RYVGsx0cLgQiiqIoxRYjeqJKMt8R8WhERSUBU4Kp5npT76ykRubbi8qnEWwZ/bpHRisToCZgzj6TeATXYmaviZKp7ToBA/N8ozLLPWUQUaEzIzmfhxYFjjYWY2xeYwomuzZjKG05sV6VHsOcdA6bEr9So80LjXIQOX2+tdP55phSUGpvrc61bBwZhvvM1t1aPEn598BnpfLPGZQeiV3T+yYyWzAIYDW4vH/dBWpFdqzgUtus3tAYU07+wC9edaZrDDuLv31GrWJUd6kJqLPZSmhHHtsdUuKr6btrpbHWTGNlysyZ9i6KFMXKZ1QFSztjbOjv3gu129sknfY5EcxnM8zRoVgCti1912fFgqgwlda5oZDHrBb2OsETkoRwhyjjL2Srwuh391AlWZOjd3kOEKxIlJOGeak5rRxnRWRpEjMdaUxgUYEpM2iYGfeagHAzkrBkTZo4TqIOdaQiEKpEUSi0Kmg78XNXShFkK43WUIeBr3/7H3LVap689lUev/1NIjB4Bz4CDtMpunZLu1qxqhuuLi9YHh5weHhKM1tSVnOKqmBHG8wA/jhC06j4juMWjtGuBWOnMTzOC9Poegl5TYxs/hfH4d6WNfu8OoIbiH4AQia0GLS2RHq8204e8MJP8hPaoyGz1tVuv5QUKclaFFPChUQ3ZCW7D+ggtlBjCyXFyKcf/WRq+iUfwGhs0WALjW001eECffwKen4PMzulmC1Z2CY3SCSXJWD3xrMmzs+YP/wWxfI2zdFd5s2Sp5/+Ob1zXDz7jMQ7zKnh7uuog5OfG1IMvyxgbFJUbsainHF2fMavfPlXee2NL3Bydsbh4TGqLBlimIytxZhKOmJjSuLYAQohMHiPD4mExoVAv91ycf6Eod/SNBUnJ/c5XB6zPDqmrGqSIfuXxWzmrfMDlEFDlUROr0R+qvKkG2JeVPLXEIlMZJRJJDKBMXdkx8MPW1y3wfUdCc2v/drf4I23v8bh0QnbbsvTR59wfnbA9qxi5rfgLJdPb+jXlqax3L51Sn+zprtpcS2gSspZSTts8M6zPD6gPijxZqD3LV61HBxUzA8LypmmqBVloZktoG9DDuUCXQhrzgN9C+3QAJYYDcEbkjeE2FHPLc3yhNlijtUFrvesV1u8G+i7ltLULOuIPTCoYVw45bubUVaAsEnD8GKiZL6Se092mroxk5cQ44I4Aj97MgnGjVwUb0qVvTqS0P3jdk20elpwxKZgRt3MMQnC4HHdQL08oNZ6z4TaS+GWsvk1GSTSewnU6qf7HungYO9rKTg6+rmPwU/D9r88h1ZxYjxJSzUXkdFDcKShz5irgK4peoha/l5blC6YYKcJsE2gfH6eZJHsPJxfbalLzeHMcPfuLaKPbDYbNusNPhkOD+a4oWe9vuHwoOLx46eQAXqrEwcHC7puy1Xfcngww/c969WaoXdYY9huOsyipjAKbaHvNsxqeXa3gyemwDBE+lahoycFj9YB5yNDiKxT4uhQU5WFsLX6wHq9YTZrAMVm09F3G3RdUjeWEDTX19esbhSbTcswyMb4p/Gd7NszXaddqrJarbDvfB8bO6rQUq4vqdrn6CgyvQ7okW6w0VoAllJSnJMbQMmGx2Rj+1GiZZSlLCxlJQ0kdyvx+dNrUhr9tBRlWUySq9EKQCGdZJVB2Z2satcZH59JrRU+ePFiSyo/UzsDeZljYei6vKFOmMKQQsz+X2OnFqqynDYHsgnc+X2N7ymdepNDW2RMjsVgIrOCp3Rmy62zM1ZNw9XuNsj8H6NsDrKcivFzEC86kprYX2HfuxpyoNpewWlEvhksDDFQfu87uDfeRpU1Oiai9yQrTCxrSzAaFzrW6xvSs4JoK7AVru3wg/jUqcJjoiRVG5vljLmgkS74GCCRCEmJ56iJlKrGZCny0CmIEZ+9yqw2NEVNeuOLqGZO/cN3GOIA5IBKbTBagIGkdGbu70DPn3UopVj8S9gC/Ive4xcdL4dyFS/9rJX6fx3c9bOA05eP5hcAvP8y71Fr/TPOUeWGgCJ6ScVWKKwVkCSr7qSo1mR/d09wvYTxqSKPD4U1mc2kFdpWlI0lxoGIpxt62s0FUXvQDVHVhDTDdZG6KKjrGYeHR8yPTrH1AlvUWJtZbbmA9snj1iv6fkuMDmJAJy/SsHbD0HcMrifmucAHR9+3XD57xtmd21DYnASesmzeE5KfNjXeOSCyWC5ZLheY0uYwG2HBnRyfkpaKzdxxyAlWyXwnyp6ejz99RHAenMZ6WF+e05+eYIoC5zpQiaHvSFiMrTEJ/BDpNj1dL435oR+gsNS6ZDavMJmdH4PYXzmX6z201De9px8iLiSUsRwcnVKVmtW2wznH0bKgP7/AlHOIiWVziHUWlXZb2+SFJRW9xw8IgK4tad3htMYs52IfoYR8EIYBnZu82mQTkioH06REikHYtuw8+iLgXE8IwogP3lMYATqssVhlWK83XN+s2HQdPhfdMr3mTX1KaCZOG6CY1Q3eejolgW2uspy//gbvXtyQ3v8+5jXFwdECYwJDt2a5vM3g4oQCpZhQOmX/8Uj0gavnF/R9x2y+4ODwmJRZmPsNNbFtUZRlze07d3n65BGHR4fUTYMtSuq6YrtZo5Q0EnRRY1LEtx19iMwP53IfbSGAc0rcXD1n6FtidCgV0VrRLI6p6gXVbIEqatLI3hrXwrKhKRvqzIBSIyCIIikrz6Ox4mU7yYF9/uMEMNAGW0izQ2lLCBn0qwvqas47f/p/sL66JjiPrWd85Vv/Bmf3HmKLmna7JXgvafG2pCobKltTFVBbS2ElkOq1t9/g+flTQgisrlZcPHuGPxwwsxl+U/IX7/+Er57ewyqxHYgxCks+Kw7jyOAD8e93PSB2KUZrCY0ceqyxbDZrtm3L8mCOtmX29JRU+xgjeb9LCBE3eLSVmkFrJR7UeQ8Rs1prktKrNDFEQwgE7+ljoh9aqqpm8iDWWvwFB7FEsdbkZu3oHZ9oN+2uYY3YnqTgxPs2SgCc2NdnQC4plBJPbaMNtjC4vuXTTz7lww8/4gc/eZfLzZbBe2ETxiTe8DGzeHcfJL8PYn0QVRJbupQEoPCDBGdmQM2OvvcZcDJK5s8YEkHL9UtWAq2UBuJLbEC1UzGQAbrRN1KYsGrPIiDX7ioy+Ukx4jO7oKQYYw7ZCRPINUrqpyNFVJJvPQGneR4Z2zrGyLg3VsBYbQrMBEgqTFFkdraMn8kDNvv367wuCfi3o5O8kB+Qv7tWo0WFyvL5ca8j13L/moxhXCoDU7u6b0Qh0vT7sSYNQcBB9kBv54YJ9B+B0rFKHRm1ucwVIsLoE4uUvy5kG8a9/bPOOSLj99FKYZIRW4MQcNOYTvm9c4jX+A1GgHU6/wlTk9o5SXK9yoG8egS8xuuT715MCZXFb9N6oHZAnVzbTNDJFnX73wPEKsQYhVGGMpU472QMJ820xIxAbB7P2oxsT7ESshpSFJA96UDnh8mygTjaIIzjVsZOYUus0SKgUx5jNIWJlMZTFxIiLM+JBH1bI1YtWgkxyWgvlkg5k0NalEW+Lh5deHQqWBvo+iTN3qBwKhKSzClm6GmwnDz7BB0TT7/2LdE15vEXgozmECPOO/qhZ9NvWW+2zOdL5otjlofHlM1c1jejJiD2hZwXlXJzAyCQks6kWWmW7JoPo7I1Tm6IYwtmtGscx30MO4a1ks6PhBB6N9nKCBFPASHfUyV8vH3oZ7y3eb6S27bzpE0JfJDQNu9dxiNkn6hBMIo9oLjbrlAhopU0aFSCFB3Bd6hO4a41hhoTEpqAqhKpnIGtQEswmol2D3UyOAypNLCI2KiohoEmWtLlI4Z2xXD1HsXNMXpRyev2bLdePn4pwFijDA9OX+PW8RkPbr/CN7/+LW7fu0tRVSSlGLzHjRc7jFJRySKRhSiJZVDIyW0+EJR4L/Vtx3q1wnUtdV1ydHjI8fEJy8VhDj6RRT0Ej4kKW+k8GUFGGabzlGZcwSQfSTlRk1EWqzLTbW9jtvf34xFdhx8GQlQsj27z1pd/laNb91Fa8ezZEz54/8ecf/E+/bJmtt5ycHzCdrtifb1l2BqO5kdsN2vadYdKhqIp0ZXBdS1BOw7OZjQHlqS8pI1XiqNDT7PQ2EqhrKI0Ivnx0Um4hVOgxTA/hIAbEjGtScnIn2hJocAo6QoVZUU1twTnCUNPVAOLg5puE1FJ4VpHt9rSbRyxjhMYO6aX5qWdl1Pi2b96+eEDpklhLByyAJNdDzf/g/xTZNddlO48BDdACPiX9rsKxXy5pL64YVtq+uKYeVyKb1o+B0eWYeUNR4g783CdvbOE0ZvB5mGg+r3fQymNf+1V/GuvQUqY994nuczg0JayPiBgiZgMdurprCZdwLTY7F2dvcXop4/0c1+vXnrVz7ru01AdX+Cl47crMKJIWZOYnzP6/0VQSoovlT3qJpZzZqPsFu1xgvd7P4OLMLQD3inmZcPx0ZKry2u6zcDgPEVZs5jXtCqyWnWsNy3KdxSFgEtNqSltZDVsGYaBWVNmeYt0brXSuMELO0RpjJHw59JCrwMqDpCkeOpaJEAjRYwKuFwgDQMMvaMooCgsdVmwWa85Pj6irktSCNysrnEmswhiZL1uRXYSkoTijLTvfeByr+yRkSDdQXV9iXn0OcX7P6GKLZXfUoQWG3uZ81LE5YKXBPPSYguLKayYbXjZ0ChsLgzy/Klk42KthBoYazmJmtIahhBIyPRVFLIAOe+IfiebmjaVP4c1OHnAKgjRC5s17nHgc1E9Hm3X5WIzZckQLzEakqRZ77E09n0CJzaDEhB5DBCDLDJL4j219yJUNvzfn59loxRydzcXE/k9xd5gTDaX75cSsvnZV0FMU1GagOKkIGiZJ8ynH+FffRNlNEYlUMIbMMaIxYGRwq3rt8QbSzQl82UjtgSTEoRpTpyK6CRhQiS1K+iVyNuMNsTkMbqQQhEIrhfAJns3K6Uoi4p4dodYz9CXF9jHnxDjwNj00rlLzfjfvzz+lR1F7zl8sqLePCGorDJQUBYiRh03EsJwEJlwjIG+26KUQetCPD8LTV2KD5aNChMVKShiGoi5II3rc/T5GmUqjKoo9Rzbw1IZqnrG0iXqqxZd1GhdZGaKzHEpSdhQaDdE1zG6Mxsl0ji32WCGDusdKPFii96jty3906csnKOo6/yesL5zl6gym2ZkmCCg3OJgSTObEdLOi8wYTaygNT2ruMEYiwsetKKqSmZNRaE1OgkDihjpthuGbouNAsZaYxmGHm1qFFAXMteoKKnL2jZ7LCwJJemHQJEB2X4IGCt1Z8ibO5+DsbQpSLahWdY0pSapFbprGWIiqIHoNCl5LBoTjXj4ypdGZSuTFCJx8CitsFWB3zqS6kimQCXZtI6EBBPjjmliFCqz+GKWdMcMJowqrowKihdfnlMEvJU5xsfIs6trLldrts4RUsqAh5o2UDKFjiqYaanPoK9CWY2yiv7sNk+GQLp5wtGTj/jqwy+ihi26XXFiFTHZnR1UlLnR5PpBwsy2DN2G0kIYaoIaFQi7dagoxUPPWktT1Xzw/l8wm8+o6ioD0onNeo2xJHX1SgAAIABJREFUBc3MUJQZkC0bbAJbzcXepqilEe99bqLKuiHWVAXN/IiynmOKCp+Qe52lzYkspc5+fil63NBltphkJaQR5EJlEkjIa0dkZC0J4082/iQJg5T5vEAFxcfvvUe3XgOJYtbw5pe+wnx5BMoSQidjSBuKesZseczB0Rl1scIkGDrxzD04PqSqSipr8dYQh471SqGDo7OKn/z4h9x5/W20KSVk1DsevPoGVTlHqbxpH9ekGHHBT0FaY0hcSp7tdkvXdcQYmC8PhDWrBUwbw5BlTIo6JaaEynZvxozs2x2oMzGfxv9R4pkuP+9qVh+cVObjXBVFTRJDQJfl5N8vpABeqGkSEpRF8LnuAG0NRoN4g6ppzI+kG+89T58+5YMPPuKDjz/m8fk5QxjyZ+Y09+hJwYllBTEDriFLqHNtTczXQNRnJoMNBrAKsIYiE4JSkvlSfHKR9TzEbLIIKkJUCZP3t2oEKdXu+6p82VQat77SgNc6X7fxVWoE3kaQNk6An/eiaJCwoh3ZRmnNRF3aa+SIqslmtdXo5Sq/K8oyN5kFdFVK7GxQStiyOYRwasqnNNVCL9R0IwBIms5Bvqt64e/GNXWscfMQmggEkx3DBFKN126sh/Lr92xURn/TMKpacu3s83gabRt21X8G3PaY2WpkyuZ7kKY5YtxP8cLmTmr3/D2VBJmhxSt5POekxt3x7l/twr/SC99rBOolECvkcRGY2IrjM5N2V3JSgI73Y0p/Gt+P6TkdGyr7O4lRGZP2rhkvvC7t3eddUyHFKEFMZJeb/e822jGMdiAh5HlHTrcwmsIYUcvozEI1JYWNlDZQGI9SYgM01sJGK4waAXAwKmB1XnM1GF0QlZnqcqMjyit0gkIr2j6N0BZBjecaKUxi2V6iHzu2t+8RkpIgXlvSHd3Ce7GdcM7TDwObvqNtWzabDYttj3OOenlIWc8oqobaWsmXyAC5ytc+T3vT+Jn2E0ijSxGZoNwkP2X+946gtT9uYppYt2LBl8d3bsy8jEK8sPedhtB4T5V4vSt5TkMMGXyVeTQE8Yt1XmTh5mYFz68Edou78QiJ4B0mgipEaWOKiiLPKSlFwuaaGDXRdTCs0GENR4rUHEM5JxVVVkaOa4+cX9AFqTogLRPptEN1CYsl8jHD5oJw/QFhfkiyNts7/uzjlwKMLYuKv/kbv8MbD1/n1ultiqrAp0g7DBPTyXmP9DckiKt3nrKQjXSMAWPBdYMAz6pCl5rNzQWrywu26xtu3TrhwYOH4j+UIv3QMi+KqUAd+gFrLUWRaeM5JMYomXi0ihg9+iBJd3TnQ5SHU5bgCiMzf7k8Qce9aSa4TlJDzYK3vvp17j/8Ej4pnl885yc//jP++R/+U0L1V7Fv3uVwnvjWX/06P/7BD3n25BmXFytI5wy+xxhJLZ4fVng9YGaRujAsjw0npwVFlf1DGFDphsF3+AghaoYQ2LRr+i7hBg0xe5tESVbWWgkYpEJ+EIW9GMKAD4l2q3hy+bFIY4uaWXPA6196hX7V0256NtsN6w8/5vzZNf3tQ6jG66EnbxafDfrHjuR4jAvg+HCKWfmOPTn+3XSJ2SVyplz9a60IQTYmHrBJS0JhApEHyf3wzrFZrTi5c8b1D36Euzxldfh1Zm1LPWsmoEbSVi3j1GOz88LICtIqMQwup6CCvrri7D/5j7Gm4Po/+g+5+vt/H4DqH/xD0sUlMWlMecjJg79Cpw7pUkMbSyIWMbLU4m1pMgN8BILyZhw9LkyjP9K4tOXCR05qd13zQjHiu7sCZHeMuK+Zkmv3xnBM6BQEpMqs2Dh6kAKmLEm+I/pOCknRbYoFAQmwIhEYwcbRsmDquMkZhLxW+5To+kEWOi3XO2GJoWO2XKJVRdf3PHn6jLdfv8usLvME7Hj25GPcdiMLRz+jsJrycEnfDVxdySakb1tU1DRNydHRIc+ePUfFFp0GRunDZtPTtdCUhsIYvIq4JFLh5+fPOTlZ0NQlTVXw+NETqqqkLAqqypKuA33v6HrHMEjYmIxzswdMM40nWR5HWUYCAjZsMXiKn3yP4sc/xihPpQaMatEMkEQBEIhimA5oNLowqMKC1XgnY91oCS4gbwS10pkdaaSzawylMRSmZLGouV63mV0Othjl+GInYrSZfM7G099nxY6Spv3FPcZIMmkCSncBPfLMujR6DGVQ2QsTLU42DTswYfcZEb3XvR0/0+QGScpsncSuiLameKHgdT7x+PFjNpvN9BwE70ghs5LGR0pl+Vv+3t4Lk8EHLR11FH6PSTNasYzzvxTnSDNoGGjbDRGPLRSFsrKZSWl6tO3o1RUcwW0ZNlcsFyVV06CNoW9bTFmijJGn0EuYiA8+b1p310XrzJzVBud6yMWVKEfkGo0bfVSUsKcE4fCY/jd+m+J//F38+kqYijGQksIYIOm98fuXx7+KY/lszfLZe8B7/3+fygvHz+rvK6DOf14+Zr/oDX/w59P/TcC7/87fI8xq9r3LjTGUVbXzsUtj0AnYwvLh8An90AkYaS2rzRbnBtrNhqura2prsbU8/13f03cd7WZN4Uv80FM0huAcqY6URcFyVrBsFCr0qNARk+Pg4EC8DpVhs/UMfcfxkcjO15uBo6VlvZEgorYTufxiKSnoXVdi5jVozcNbd3Buyw9/9CNunzZcXfZ06zXd5hqT9ril6sVGS/QR7RLGgSKKt2jaEjtHoQ3G5vT6KPXq+O/H6xpiwDlHGAasLTOYqjFasagr1tsNKXhUYVFaZNYxBLw1XKyupUknRUIGWXcJ6UpNJ0wCnPdcbi5krlbZrqaqSMPA9vY9Pp0t6f+v3wcNdxb3ue0td12H0rOpGReDNMa0UjjnabcdTdMwa8TH1vdrusFj64qwFwLbzBcUNBnMFFbdbL5gvjhAG4P3ns1mKz6SxoolgqlYHp6JjY7JqrgYUFYCWmeHSax/kqS5d11LWc3zHCxrkzWlWDyM8uvM6hn9MY1F1iJGv01ysy+DW9qI/z5egLKoMUZAuqEPDF2HKUV+76Nifbnh/R+8Q7e+RlkojxoevPoqhSlJ2lDPNSppkikolhUHdxMP3nwb658SQ+Ty+Tldv8X0ntX5BfQd908O6fqBJ9drhq4jtVue9D13HrxKt+24urik67f8+t/+O7z62ldYLE+l1sqs9hglGb4sLc4HaXjbgqqqefToCUlpmtmM5XKBcw5ykNPoxWuyh3NRlgjgoqdaYVxjdQbhSLn2H0GtEDFWErrH2SSkQNd1WCvWVqPneVWWqLrOezph0o6zzWw2m4BfEgxDj0lMypOQA3hIYs+YtMJ5kSun6GnbDX/0x3/Kx598zOXNNT5JCF9wvdTQMZGiQ49NrBxAK/1dAY5Mrlt0jBgSYgIhAJkxCitG78xLQ2myGmYEzhQTu1HFHWsZZK8CWeUyApNKiX88+6CX/HsBBQ1jvTdK5UcwZ1QphgySOOcIQRoJ4/xt7M7GQjZogNITs3UEVuXcxTCgzECs2rMgUEigoBRiGejPqOnErEwB0l5Y6zT75VJSj6/b7SVfUO2pXZNpQj73ANnxUo7gH9OnyP+OzMsQRm/ckEOtRguMDKzG/X0ruVGQMuiU6+Dxu8UEmslOIIaIwogEfARB9Z78P0F8SRSd2Gfx7mrUnR2YnN+QQ0jFXktnq8a01xSyk1fsyPodgduE7BO01uKYm+t3bQw6iW1EYez02TGG3LiM7HsHA3gfiF0/NTBkD7JTfMl9EDrlvvJY7+17E2Jd4p3HD4PMtSFM5By5zmJPl4DaaCoLM5uY2YiNA1VhqAtPaR1GSe08NhGs1ugJlgOjFIVOKDWgs3qisJZAmMaXTpBqOf+ikGs8eE0f8/1XCqsjpB6Fgf6a+7//bYakGHxkc3BM+9v/lohTk3x6SIBu2RZb1ps1q9WKm5sLmuUhzeKA+eKIw4MjqmoxqfmM1pnNm8cZOs+jEJIX9qnWGJWf43HcZ+A6IzLyzZPKc/Fo2ZHXgeBxIduFyiCTUFC9828eh+QIz8f8XMUwKpEj48wXQ3jB3ip4JyqHfkAFhfnJh+j3PiYqTSK8sDuxSohF1XxOvTyhnB1TFhXeO2lKbq/x15/gVo8Yns3w8zPMnWeoozdQy3uwvEuoZnLtGIH/nEelC6iOGJav0Z9WoGoKU0L7x1w9f4+oLNp14Ad+3vFLAcYeHp3x1ld/E2tLbjDg1GQoPXrBtm1H8l46hNoQY8qDPaJVYtEkmspSGpmwL8+fc315SVnPePjWQ44O51w//ZjNo0/YPnnMcL2iWiw5uHWL5e3bnDx8QHU0IypwPmTfooj32fpSJ/HrmthgkJIAfruuQJa0Tj6QOchFqd2IA3wsqZevcHT8Gmevf4PBJ5589j4fvPsO7/zR/8TTD77L0bde58Te45Vbx1w+fUR0A9ZY5oslX/7Gt3j09DNcuMQUW07vlRzfWmKKQFKeED3EKxkkIRLDIKnLgyJFi6KEYFndKLwDkoBdIShIhtGHJSYJTpBzd/iwle5NFGp9JKGKxJA29OsNF6vHEDRNuaSZL7Gx4Oisoaz2kkxDwPcu0/il+83onTS+JkViCnsgDBObYOrkMC2vL4yl/BKRNOkCikLYIGSAOYHfY7ANQ8/1zSWv/cpDHj39RIJ7fKK96bFFRdCR0TR8t1DIImu0zn4oUoA8fvqU/sFrMJuBUjRNQzOr6Oty7/wSGE1Vzjm4/Qa+PKFzM7q4Y4MI+07kJtP/nz57nDhfPsbCYydDyeT+CdfWqOxrw85TV+1+N37kKL0cO3HeizwrBbknavK8DVmmLuBN1Lnz5gPJ9fLJwUPMLMNpsd07/5exnJyi6kLkfOP4/MkVt48a5k3J88sV7SbiNluaquT+3WP+/N1LHj05p7KG0sC8URgcx8tSAKc44HtN17Zoo7h394C2H/j80TN6n+RqpYQfWiyReanZdD77x8pYGnxkWZfM6oIUE13nWN/ckMIs+ycJsDkMIQO4LV0n6WXCqLQYjRRPee746TsnzLYUO0ges77m1j/5nzme17h+y1BG4hAx0ZF8EOlqlOfC5E0JKWGzpDk4Kfi1URAVSrT5GGOZNTbLakaZqoyVwhqqyvLGw7v8+V98xqbtiRFubtZMHnBjOELa1fdq7LO+4CNHlphmT6pxY4Pa7QtSXnQzEFsqRVkIazPmeXTs7u8zQfcbNyrtPArFP9YIyyV7OKrx2uRpbGg7GfN5sEencNlfahqP3uOz8XtZlhKU4Lw0XlKCzH6LQNCaoiinAmc8jNXUTU1KsN1uCSRcuyWsW/xqS9i0qN/9R4SvfZ3wq9/CaItOiZlRzJWVII78bKoUwHdcPX/O2d17zBZLCaxTUwk4MRZicGidpo1EDJGks6gwRqwR64ppTskbBJCE9RdYHylSGMvwd/4u6o//AP3+e/gUSQggzhBpQ/eXcOxfHv+fH27Y4koI2k1V6mgHFFPa8/xTKKPo+4HeDKimoLQVn3z0EWhL9IHgIgeLY7729W9ydHzMer3lO3/yHa4uz7m5uWZxsKQo7dRcTzHgho6bmw3HRwsOlzOU0pxfb1kezNhshSVeVXC4XOAGh1GKu2cL5rXl6bMVlzdbrq+v6URjTFOXzGcVm+2aPmrc4LA2cf/Bmzx+/DmL5hA1GFbrQF023OyF0ETE295nsIMkeIMBYUy5DqOgtDb3jEa/TqbwGFKSBGAUNqtDFAZTCHO6dz3ra/EKr+qGo+UB6/WGbbsFMgiZJ3iVE7u1FRBy108U/20N+KGnu74hDAOmKFE5NKkoCijBM9AtZnz6m7/D//mHf8Cb9RVvu8Td1ds0B/fRupTawwlJwgdPURSc3j6TesL1BNcx9BuuLx9x+97rmL35tygqClURvGPTbbn3ygN8hLb3LA/mGAZu373HaL2SYpJ50opvqPeOoe+xtkBrS4gwRI8hZfn0AU2xEJAljgBWwsWU6yglHqWY3d4ge4uK7+YoRRaQRTMC5xpFoOvXDO2Kpi4zqSADJNGjnEfrRHABt37GceU4txE7m3N0/y5puGBz7tH1Ibo6QNkZJEVKjqJUvP7mq3zww08ZLtfMmoLT02P+yf/y39Fdb9FR411isTzmRjW02w1DgK+9+RYH8xrjewYdCG7L4/ff5eToLnWzFJa6H9DGUlYVzWyBUkY8n/M6tW0Hrm5aTk6POTw8YvSq1FqsiEYveK2tKBZjIuXmb8rS9+16LWFMmUjj2g3ee6q6wRRFrv11xs+kVp4vj+naDUZlRn6uOcRLVMIuvYtTQ2Fk6+7XGYWphFgwNpFV5PLZE4ie0hoWR0fUVcHF83M+/+xTvve97/HBp5/S59rZO0d0A8k7UvAkL1YUY6PYIAoySQpPEzHCKo0GTIroJHvduqooS/F2xnv80ItdURKykp72DzkcVdsJABQARk+g53Sokb2Yf8xjc1QbxTDSPUaGmptqNGHOS8E8MaTzNkVrsU8abZTGd9dmZMPaF9jRZJBOa73z+CUDoQhUE3LxOTacFdJ813pkyMvMue/5O5Gm9F5eArvnbpxrRTWmiErsVnaWAzuG72QfMM6ymQgRw0jySXnPIw2C/c9LKRF8mGCiEZSV16i8900Z1MzM+L1xGMJIMJCdnk8juJvEyijFPZYwOeBqb7+l9gDk/PsxZ2B/7gzBZ5A1QtTS0Mq2B2KTlGX4ecBo9hVyGZrW7K65F1/c0SItMlpCju+RcH7Y2yfAcrGgCo4YAl3X0/c9WrlsFxgngG835gRUDy6DnkrgPT8MuGGQGn7yiI6oJPhS7wPKGOq65NbBnNPaMrOOuY0cLWfcO1Y0paI0GmMUumhQqkQpIwC4CqA8Snm0Ekdom0FORcy8KZsbBNJIioUokxOBEHUWlyYIipAkPFghjROrJWRzcHl3f3HB8T/6r/DRcv1rv07/8HXBoZL4yradZ2sdfddSb28oriqKquFyeczi4IxmtqBuZszqGXUp93Vq/k7jPVshRIGR94eQEH/SxChOcWcdEKLsTUOM2V+7x7k+s6nJ10wzGp3sH4JTyDPnQ5rucwhB5s8YJz/tru3YtmvafqDtHT5Eqv/h94jbDo8A2toWe/tWxdnJKYfLY5qDM6qD25jlKxRlnZ9Jx/bmnPXT9+hunjNsr1ivnlFvn2AOPyEevE538iXc6ZuYekFhLZUyVCkRk82NMItrbhOPCgw9Oq2pbs7onn9Gd/4Berghug0/7/ilAGPLquL07n3ZOI/+EIwGwzKrBy8+OjFFeZjHbkxKqBQoY0dZirTXDx3bzZb791+lKmp87/jJt/93rt75Q9KzR+iba0zfs7YFV7MZ9vCA6sE9XvmNX+f49TcojzJiLloPuVlB2gGqd6Qk4JIUunudrakXJxvdmDfDKnqC33Xt54cPOVENzdErONfy6JMPefTRD9lefsg3vnybb7z1b/L56pznf/JH/ORLX6ae1bRDIGEom5Knzz9mdphoFg2zRUnZBJTp8MFJJ2IQCTVoQkgMHbTrghDEl0kpiN7hgsodIYUP4wZeWJDSDRWmXkqJFBI+elIUWU5MKQN6ma6e/6AUG3dNO7TYOGN2MMOqvWGmIKhAUJJY2jtP13dCM89HzP7AjPhn/q9W/IxeH9IRJxFV9rQZGbQTWqTywy8Fs1E7iUTwgW7bcnh6ynK+4Pj5FeYPvsPlb//rVMtaWIG5o+ViQBh2YerKODdINzh4eu8mBrRS4i+M2vO0AoJONM2CqjmF+pgh2Qz6ZXmaMS+mvWuVPS735SQvXgNy2cDeZ8s/leIy/xaVv7vee53SYLV43oz3ByIuBELIHdqYJVO5CEmQGw55V5jTsYk5BTj/biwoRW4XicrsnfPP+B57gHwCkg9srq9xVaQsDYtS4baOvm0JvsCWFbdPllw8v+b4YMHxcklT9HQ3jsFFBpfYdGvm8wVWRQww9Gv6tqUw4H1iu25pV2u0CjR1yUxr3HAjRu+5AHQRQhUorRKpT/bNuVlv8TFSVwWDTww326mBpHQhRcbYVRy75lnCOMqVJvZwv0Z9+x/j+g0peXSKlCSic1JYGAs65JC5HGinJYjKliUxRUkDN1aK2Bx4pbQiaTmHhIT1GKMorcFkX60Ek9ylQPHGq/d49OSSwXn6MHqj7sCBEIOEE44eYCOoO3n+CAgbYkRFxMdJjU/r3qFGIFcuzLKe0TQ1MUXW3Rbvwl6BtzvGLvpUdOZj9D8UryI1FZ5JqP55LkmTNY3KxasUz3vNoMGRnBTCITpcnuuV0UCBVnbqKQgbx8kztXeuMYlUESUJ2F3f4lZb/FaaiskoCa378D3Uds3w1/6mzC06ibS6aMQ7Nn+QbIIiwY9BYprr1Yqmbigriy1LUgUoYdek/PmyVgrrJyYp6iQkApROzJZH2LLF+4EQHEPqJh8yBRglbIzwla8TDg4If/JH4hOWNwUyOcnx2e0T3n31nnTlVyv6XrrXRYgcHR3iUqIPkTbI5nnIrDsJVcoKgCTMh9EzThs9Bc6Jb5z8PCbNlkWJ0uKTOjhZQ0aLGovCbVux0XFO5sh9dkpMmQW8L8sbG1X5uqfRp0vmu/0xNi0xeRPAHsNlWmBSAh84OTzi4YOHvPba68znC7SWQJiL+69M16/7jd9ivTzJrGg9vQ0qy3fHhyZpfHDEJJ6DMXt3S12SzzVmxsgYtIcC01DZcmIi2XImElslQXUTMyWzEsfQkhgdMXh8lHUvRmmwCYgQ8X6YJJeyzr4odRT2jcwe8t+YL8/YwIYUHAfvf8Txex/mbynqC/EnzHcjq0FiEp8wkX4n+jBwXjzn4PCEoipJCW7ducPdew8AzTD0bFbXLJZzZosl1eKAN7/8VX78/XdwPrFpe7TVxGSZW2kYt9uWJ0+vCChC0vRJUVQ13o33XeE9VI2mnlUYJRJHBczqgq63tL1G2YakJPjHu4Fnjz/n4cMHJCJdH3AuoHVBW99AUtzjjHXacm1LnFwykgtEK9dc5fkmRicySDLTJiJ2BFpjLIRhwIWQb73MlUkrolYErdBVTo7vB3zf46OjnteopIS55D2+3RK9y/WdmtYJYdobdLCQG9wqQdKKYlYL2BBk47RYLKYgjXETN1s09FsJZKPQPPnq13CfP2L7+Q+Yf3CPX/36KVYLk6osCkZGV0S+p6zNCm0bqqLmtKqFIRT35l8fUIXcpxAcdV2yvlkLoHAI7eCIiewpbAX4G9NwFGiVPcfR4t+bItH1Ap4EQzQBXdaYos7zRAItZqdKZ0AsNwgF4Mk+7Tr7xqWULa8gESaQgOTRfoMmUJUlVd1I2J3vCcGhgiNFTT1rYHD0Nze8+eZ9bi6foBcL7j18g9nikL5zmOQoTYQiEV3LzfPHrM4/Y/XsQ+YLQ2VPWF9d84f/6z/j4/c+kEBJY2iHATdcEZqGh1/5Mq+89RZvfeNXOLv7gO16y9HZmsENvPLa68wWCwbXCtgyDJT1HE0Gb7JfLCnhfeD5xTW2aqjqhqIwOV07kZKf2K9Kl7m+jDLn+J5N36NIWQ4cxc8vyrXd3Fww9D3q6JhGLTGmyKoYhFSiFMqUGN3hh56ha6nnSxLCzkJlZYs2sm/LQ8jnjIjxSCSxARmZpzHSzBoUEasVyTs+/vhDPvr4Iz79/HM+e/KU3g/ZdkFq7KggqmxJoF5cU7TRqJj3Jkmec52EHasBHeXnUmtM9OClKggx74s1pCDAMuTGlbVgDNqKrBqydH3cV03fLa9hKWa5dFYc5eVL7ocAjSk/gz64ibQz7jx2U7XONaEEn9myxBajrc04mY8AqajF9N55T02xsYGRyM9SvlZ5lz2SDXZMSHnNZIGZfe7H9Rq1k9pPX3yPQSnXJ/9dTBMGEUZS2Ai0jt9hH5AdfzWC13Fc47KqkkiMcmJKq0xo4YU97sQyRIGS2mdUHink38VR9p1iDvrL4FkGJsfvJqxNk5sdUuOPTMWXQ8VDiC+AbXJ7dCbljNd2t78UPCTf73EvrUze76gMjOvJYkyeAdE1h3zeIQV88tNYkGBEP1mdgPiW+0Fs7KwxRFsiBDiPipGoQp7zE8qoaX867nUYpfIR2Q+kXabEpIyN4zXXxGRIUVEYxWJWctgY5mVLYYTkorU8XkKskYA2oxJVIXO1MSWGgFYOpYTxv0+kGp8npTTWKmKUTBpvoSoChY0YN96IhIo62xUpFE6aDjJzQUxEn9DvfJfiR3+OwuD+9t/KzWoYnOc6BbZ9lxXfFdttx2b9fzP3Zr22Zdd93282q9vNOec2detWw6aKlEiJsWVFhhAIMGQHMBAbyYsTIHCAfIAgec0nyGvyDQIYCOCHIDGiAEaQwHFkRIoiWxZFmhTDIquKVaxbzW1Ou5vVzC4PY8619imKT0EALuLw1t337L1XM+do/uM//mNPu1rTdis26zMuzi9omhWVlYHEKhfCZmwnwSlRLt/tWdZBJAjiLMPhgydMDucdznsm74jBzbGrdJukAjXlwiQi3Xeyh5zPWtMh4oODIF25MUsGQcqSS5K/Ka0hhFl6SZ6q4XRZ+5RItkY3a6rVBdXqnKpdo7WFlOjWF6xqw/H6c/a3z7m9foEbd6jdJxBHVHIyTHL7lNhuiHVDKdgkIChNqKDqVtTTOWZ4hHrwVdyww7me/e45wY/8suNXAozV2tCuVogRL8azgBbkxCYxiwIjwZYvDyYGah+pbMGBEiaCDYnp7oqbTz7h6k//hOnH36fa3WJyJTGg8Mbg25b+02eYlAh3Oy7efZft21/FVJYQi6B52UxSwaS0nWbR+bJgCwAlgZect5/6ew9hc/EmbbAkZbl88SmffvhDrr94Hx1uefed1+i6LdOffY/LqyteXfdcJINXirYzrM4aqs6xudCsNoqmUygtTtk7xzhOHPcjVS0JVgzgpsDYa0IsDTBCAZ+KPBEnGy5r6JRKBrm6JzpoIvBcktRT41y2acqJsI+SvGmlZChIwUWOdu+DAAAgAElEQVTLwB8l7UMuSutrvKcdO9/suYqdTr4nfek7y/cumrKnohAsr3M/CJHLi4RhJIwTtWnopsi4u8SNA0PfY7zJyW1iijkBTjLZtbTlhBAIs2bnHG1gjGZ48gS33c7fZ62l6Vrq1UM8HVPU8wTxGeCZGbEq74cFVP7S2c9/LqBUzBXM8vZ81aqAtAmjinOX6ZUmf1UBWUsriBjatOjslH0wX2dJpiWJSDG3WpFyYSWjvaLWLSvvHramFkBSGv3k8+dqeGA4DOz3mnVXSQuIifT7PX7UVE1LrQ3eT0xuYhwn8CO73cDoIs7D4EDpge2qAiWMHYIXYDWBc54QPOuupsoTQpvGSvKTq30RmKaJtpW2FGOETTM5D/2YW9YRNreEX3MyVoDYBd8p6zVKgPbsGWl/Q+xv4Gc/FkZxCkRjGB+9xjRM2MqIllHd4Hsj3QD5uVd1ZhxE0bArMghaSzCXtCTpJeKzVhJpkwd3kBIpQggJpSPGRs7PNpxvVuwPPdMxzHIXiTQzIcpzTPl6Z9A0SXSpUgngTgJgvdiLGajRGlP2eBKGQGEnlOES5ctOAzzJiRZf8Vces4062T+CMlG00sqbT0HfKFouuf0xs0NUVk3SIUdjS9CUAsQ5eViOMmCEmHCHHj+MRJfHpubqhzrs0S+e598VkGnUE5OfaFI3d9RJcmNwzpFUboPNdi3GgPcToDL7JM0BUmXt3AZWJAvSrImmMXVDRRIAbgJTRYIbSDP4l5/g+QPsNFG3HcdxICRFVTVsuxbFNQBj13L12kN2leZldKR1LWy1Y4958pAxJPbTxFV/JBjNpC0xScGgssLQo6yNmPIaFdavgECFSaWE8YjKQ9qkNc4HaWuNmfGgE6TakFxDcA4/HonThPc5odERq3JrHym3TqoTqyqgdTzxL6WQlV85CSBPBrilhT2eotjHh35inzyxMrz1+KEUPuqOw2uP5vXiHj9m/Po7BFvlCdJm8ZcnyaJShjAOyMCFoj3oZ0YQIZK8I8SIrbIsitYoswLTgKlEcL9ezclBmoe6lPsn8ZUMk5lmiQrvRmJw0i0SPSoFgp/yAJKQNcYKiLtotsPyXGPycxIpg3FApUD76vJk7y4xwOkhiawmJs1wGBjHid4NuK9EdFFhSUk07bsVtqro4pqmrWX91A2trXnj7be5vrrkeNwzDCN1U+FNwNoKhca5icFN3NwdUbYmKVMij8xiEj+ZEtRW2vw1iWM/4FyOC7zDNCuSlgnnIXjc2OOmAZTALE27IgTPkG6xynJuHnI5HJYWaUCHSJwcZbCLhJ+BFLN8UQQVFSVtK2u4dDUppdCVgBzJClhuaVCTSEVF7/FEVmsB0jQKN464ccwFdvFqZPscoyKkgEkhyzdlMNbkLosSeyCFuNKJZIzGVJbK1vjJiW9S0D96wOVwJF3ecPHh93lw8QZPHr7NqjtHWztr1BWwtaxZMojV2go3jjAXeyVJpIDVSpOiDLsRVk2fuwhC3k+nba3kjkwBpQvQGnObTOmSikruk9bL7whoe3KOMHd4JVUK3mrxQwgLW8AUj3c9aTpCOIo+aJGLSiknoo7kJ1KMTGOD70emw4HgJrwPrJuG80dPWG8v8P4GFQPJybUerl5x+8XP2V8/B7+j6lquX77i848/4YMf/YTheKRtO4LWHENkcI6Hbzzl7W99i+/823+TiydPadoVTXfO9kJaex88eiQtyykJIBgjZUJ20TbXRsn6CoHBBSmGNI0k4JlwkWKa49RSDyrwf3CO4+4Wawxd12KNZR7Qg+jD1k3KAKy0p4dpxAfpiqnqZt4DMXjcOLA+uyCmIvmVddaVEuBdlehsIYeQY41TjXzvPVVdozIx4+XzL/jww5/y6efPuby5ZcyFwVKsm1ly2deoWXP1hAmqpM1ZOpkCloCJQbpB8w8xEAOo4ImpAjJIfSJJorKmNRlsPtV1L/t4TquzX4kkCLLWSov8qfldWtHltRA8hTg1M2zLPJDMnDdGmPdlANdsl+6BmNnvUOKnk6JoSvkR6ZNzLbFLzmlOkK7S4i3r6X6MOH/jyV4vf58vipJ3FN+U889wnxRQcIly71TZo+W886uzNNWJTS7/nkizLvjMzs/xYuEgz5qveZ1oCSWZ8670i4r9Yu/U8t6Sh6SFCnEamZf7PJ/HfJ5lPy5dFuKTSy5RUsBsx/QSD6X5HOX3Ypm/IA9pZjuW+DpR9klcOl6QuQw6d6yldHqeC/uZLDlYMIrSmSz/LbFQ9H72hUUqIp/1LOshxDUYp8BhSLRW09pEo2VQe0gyCLw4tkJ4skbRNIr1WvJH6TKdgCEDloYQwMdSiDAkzPzMjYHKRqwJ0n2toGjLhiTdmTEmXPa7KZXISeNjIl5eQRCdbfPBh8S33iR1K5Gu8wkfFMYHzOSZvGecBrphT9etcOMR4kTXbWnaNXXbUjdt1pU199br/P9JZxmB8tKCy8XMhnV+GY4obOh4gonlYsFJfii4w7IvYgzznBfRhHUCvmefLdhUzgeMJk6J9WdfiO0i27LlBOeLGMeesT9Srwaa4ERzW1do20jxwlbo8KbYYmsIyTPub7GpR02XpGONObzOZI10OiqNtybb8iz2kHMq1Z6h1k8wZ29S7T5n3L3AxZFYChB/xfErAcbKcdIukB+yAlnxkFlJEmwZlYhGSYBFQCVPZQKVqQRw9JEmKe4++YSrD37KF9/716jv/zkXu1uaJAy5oiiRUMRhYtofebH7F4wvX+FubllttugnT6RV+yTIUi5XLRFWjTaamDxJ+p2ZxaazIdMq0o9HCcDzsX7wJulmx/X1JR++930+/NGfQf+Sx+cVT8+/QjBQ1YboDUPUJNOSCFSrigevtbz+1gbdHkENhDQKYzdBcJ7hMHJ9eRTQRVtUBou9U3gf8VERKGoaYjDjiTGbm1FyMi7Cy8IGFROmZxm3YtAzvsFcxVNksLXn+jAydQ+hPif7aQmcVMInSSZF6PokYMhGPiG098K6nf1hylXLJFmA/PoJdb6EGvkNMe/0VFhNp5s0RpKb6G93WGWpbYWeZLDNYb+ToTtRZCt88PjkCSmILnAq67YsXHGb5dAK7n79Wwyvvz6/1tYruuYC0z1kNzWMQc2AuM4sRhkMpOd2w7I/lj/SyaulliqJtAybyo41P4ty35UiB0kqA7JS3VP53MUo5jYav4Cx4rzS4nzTCWs6B4iKJOzZlCglRDHqWgIkBUQnE1RVOXODyvtXpyCatCgK5KGi59j3XF0HnGs523Y0FvbjQYYEjDW6XlFZGIeel68cFZ7L6x4h7olQdz/0rDvZ9d57NDIdk6Rk3yhN1zaAtCduuho3OYbMxAfRmA2rCtuY3CYnwNE0TkzjREJLIJ2TBE1apCBmsD1JC3kMmDBilGf63p/hPv4A19+Q0iBgKooUFXe7Pceh5+LsjIuzLW23Iow9ehrBT6TgWa1WTM4Ly6dq8rAXCca1MUSTUI2RYTgpzglxaRUJUQY+6LSsw6qyPLzYcLs7cHfIdkulBZAvm1QxJ7OylTLLNMn+L+1j0tZpSWqpShew0KgCICqO48AwDTPzSvTAl8KKMTJorATsp1pV+aTu7cfCoFX3JASWEONL2Ol8xJz8FnAYwFipniYfMnu9AMVqvjenwJEuLL4QcP1Af7sjjg5SaVsqQW5mTU0j1LW0TTlH7ye66KlKC1qSc+jHiSop2rZltVqhMkDr+yMpJdabreyhkwJhCXN0QUiKf8p7TZkaFSIJR922TH5CQpow3w+jDVXTsn38lP3PP0InRdM1PHnwCHgGQK0157aia1uoas7Pzzg/37J/9ZKzRw8YpsRtP6A1PN/t81IRUDmmBDHOjA6XHMWfxiyxUYZhpKTw3mFsI+B0fqaipxalcyOzZ9cPztFaWFj7q+dMuzvikD1ZhNNBGaUNj2LdCkg7+7VTsGVJTGWtleeulziwJGgKrne3mGefQIqsasPV5SVnFw85XpzNa8ZPI2N/INiaqmlANWisAJxW7IK2MkHaBbBWwK/SslfVNaVrKEwj4zTQtLW09GqDUi1gUCoXynQe3JZ9poqJEB3BC6PZTX0GXk9ZtwIqxgzGhjlZKnsxaxd+KTlV2VfEEAjRZWZYbuGM0gZ/bw8WYks6fTUn70oxeccXL265u7vD+Ymvf/stAVuiDKjyPnB9fU23XlM3De1qndnEol/52utP+Oa3f5Mffv+7HA87rDUEH2iaFpTFh4CpDLf7I1WTqOqaGDxtZQWQjpEYWpwPNFZl4C1xc7NjmCK7/ZHjcWDVdNRNK/d00tTWctjdoao13XrLoyePqW4UMY5UuuFi/ZCH+x6rJTSX2X6RME1EoX0Ic8VHki5DBJW0KGd2yTxICXLxLKKNnRl4UqTT+DgS+oAfJwE2E5LchEA/DExuogwBK4CUPJtMRogS6+oCOBiNd47aVtSVxMbOe6bgMMbQVA1d02BYYgCpKib6t97kRbfmu//yX6NMx+/82u/ylafv0G0vME2H92XoiuQCOitoyjBMQ1VbjKnmlZLSInFW24p9f0DIM46bm2s2m3VmlcseUkW+pez2hLD1yXJdSUCOok9KYTcqZhBPJbJOpESsWqt7PlMZg1GFyLCsGdmzHj8dCYdrUhgwVkNVM02jTKEOEwSZRj1NIyiFP4jO8KcfPaM/9mxNxfrsnNX6Af3uyDSOuOFITJHPP/gxh5sXqDTx+puvcbw98v1/9V0+fu+nHC9v2K5XRKMY0QzREkg8+epXefc7/xbf+K3f5rDrUWg2qxZrG5LK8zZSEvk4FTBGimO2qkDLEC2jFC5GxtERteXBxQVNo4T1XoxmgoSw3GS4ZDZPWsDq8bCHpkF3HcZWuRgpXT3ri4fURgbPSRurDK4ZR5HHMOZ8LiTHKMCMsFvNskey3SoAnwjdLaATIBrC2U+FGHFuom0s0zhyc33ND37wfd7/6H36MRCiynJAnhjyoKPkUCmgc0dBMWcqz9Agx0GqRMBJpkfoeUiu/PjgJH6wlkRAW0PdVNjKZrksmYJOni9RGGzzGrxnZcXAlmJnVBEdcz4XlkFR8nOyjk8AukX7nzwEzeTivRbJkqz5mmbfuQCA6kv3eJHzSNnny/pRcyIjUckM354wXIsMg84xYxn4BiegbH5t9uNzSJg91JwLy4cKAemkA1ct516+OCXm3OgeBUjp+ZwSzDlQUvn3yUz5bAe1tRC9kCJS7hdLi8yXzHnI9yyvkbJ2dCrdl/JtJdQNRR4un3PIpJpyTyigbf5ckVwzc8dvZOlq+UUQe7n3M2ScChlLIfrH8js++PkcUtYeFcJWyN8V5/sRwhKUxyCDz+TciwZvzkdL3JULQaWVPWUwligD8aKP4AW/iAS5rlMAWBuMkucTUuTQS1ecGxVuUKizyLYVn2lIMjy3AIFW09SW1UZzdt7SVLVIxjGhqGUQukscB/CDxKZlL8l6MhidqEzEmJSbYmV9x2RxQctA6wj9FHCpwiUl3TooRifdLz7Ieqj++I8Zfv/3iW88FVC9rola4sHJB0bvmNyIdz1+OuDdET8d6boz2tWW1dk52+0ZVd1hTC0sWQqWn1GGeZ2Jv9OqDAMs6yzOckohLLbudE/N+7YkI2mJK2ISdq33TliweYgbIT/D3JmsiBJjpETjHObf/IhdivQqkZlRWYe9+PTE8e4GGwQXMM0KtXoC1QalhfygdEW1fiwa8nWLMYqd/jnJHUn0mOkFHD7iaDRDSoyqwq22WLPYAonRa8LqoUiIjHuaw3NickzDJV8m7JwevzJgbErSAg8nG10BUUxvcFGqBCmJ4Pl4pDaRTntSEL1Ho7LWkJ/4yR/9b+jPPqG+veL89prh7nNUioQ8DU5nB+1j1m/xmuZlz/EvPF/c7fEu8p3/8D/CkwFHFoZX4ZdKwqYy+AGkSNO2QJyNh9aK29sdh81xvtYX19e8+uGf8/MPfsDt7iUfvf9T2rTD3Rq+ZzxRG24v97TnT3n09Akv9keMcZw1DQ/eXGNWAagIcZqD1Gn0HPeO/T7QH3PwoBIkn9kMiSnoDC4vFTZVFmw60boFtC46IGI4ZpImp5uLYv8pD6xgdSnvCa/84qTy75aEwTlHXVc5EFmSMR8dPmZtNJZzKgt+/qz8RwQBmGPEFwD23vvyEeOCTs4LL4If6e+uUQSqpqJGnuHu7oYpBmH4FvBlPs3iTNUMbuQznD/aGJMZQstrZ+dPYFhzDGtGX7E4Vlgoq/dDptOjCBLku52DkvxAYg7klOBFhWBr8o9GjKfN9zoWVnKMKG2JIeFDzJMKw8wGmb93rmaVH2mJLrqcqqqkbTmDclKllhZa4oQmA0TKokxDUAadJhmQEl0+9yo7PNnrh5iYbo4MToYuXGzXHA8bAUCVDC/6yltPuLnZcX15h4pw8fAxldUz4/dut+PVi0vq2vLo0TnX11f44FitWs7P1nz8s4/xbmKzXrHqGtYmoYncKDgeR0KUm7zfTRwPMlRQK9H+OWVnqnkdlLWw6BqRHUjXaB7t9rz70w/pjOPZOvDpA8unfUCphq6VAU3GGC66DePkuDv2HIYRFQKPtx2buqauLSl4Hj98wG63Z3IOnyJ+EkaNMiorlitSnVvTgV0/0Clpm52mkaEfOF9veXh+zqqtsUbjJ8eT1x5ydxh4eX3HFKXKep9BtDBiy2tzO7JawJgi6O59Zg1nXS9jDMoun1fXFW3b0vd9rqhmy6vKtF0zg7iFIVs0re6zH3KQmgPuIlMge7ecJ8szK8HtSRwdvMdqnYPDzGzKLTEpt/sKxUyKSlrrUpu4t0+JEXfsuf3iFXFyea9mBksxZEpj+oHuf/rvGf6Df0DoViTvuDvsWLUrkrZEr/ED1NstPk6koLCp5uHj19jv9/SHPWN/JIbIar0V4KWxmMoSQ6TS9sR+pswcUVS2RumKyQ2Mw4CbHKtNQ9O0TOMgkggkqqqSgPjBI3Z/99/jtT/4JzTasKrqmbkAsGoanj58iH70gK9/7avS9qQUh4tzjv2Rw3hLW8Pv/Ma7vLi84+NX11ztjwwu6yDbLDGQpKgTAiSdkxAtzKWFIaFwbpoZ6CkBlrlgVJK1kgxCQq/PON88wB17psOB6SA6gs7noku2V4vmu7BR/In9/mWHsTm5j0mi1CTP2mSQJ8XIbb/no08+ptHQVZbPPvmY59dX8J/9FwC48cBhdwWArWqslQFt2liZym5r6qajaVeSHNhKbHeMUtBUFpIkr7axKFPnNa/zzZFYSsCBmNkWDu9HkanwnjSNS4eD4l4RJqYgsjzBz4tdJp9rUpYuIi3J67zJkqc/7vFuIpGo6yprQooOJEmSoRiWtRTDRIxWumryMQXF1d3E58+v+ckHn3B9e8uqsXz17Ue88cbrWAPjODH0I3XdcBx6rLXUVUPVrRgPR5wLxHEgxsTTt97me3/x51xeXXG3u+Hr7/w6/TRR15a22/D46RMur+4ksbeKs+2acQpoAj5MHA53dGZDZzqsksTF1jWrKnEcxiz9JG3C0yhDXFbrLZvzxxzHwOQCY9/z2muPOB4dRzVx2e35/b/99/mTswdccgIWnZo4l4i9wySNwWDb3CKa7ZvWCirLZr3GT47+cBQgpx/mAm/ykeFwIPmQp5ZXHG/3+CiMv+3ZGc459ru9XFdVU9WWtmryY02MbiL5lDsxpLDpjj0Xj9eoqmbYH9gfD9hK2OyJxH6/YzgO+EmGjFmlIUghwJ9tufx3/zZ/6Cs++8kf852f/ZDf/Ru/z+tvvkutNFFrCS8QoQuVJI4sLKPTuCn4iahcLgZa2m5NitLhMh16Qt3SdmtMVQuDMLPgQvCkGCQhDnoGb7LUPy46pnFguvN0m5712WOMbYrFhywjEWLIcdaJ7YiyR5aimEF6fSPa1jTdGbqtSW6P0TKgyTvH5CdUilRNzXq7BQ3jcWC43TMMRzpbUUUN3jEeb/nZT3/I1bNP2N28ZOjvWG0b2qrhra+9QWUrXj37jH/6j/8H7i6vCNNEbSpcDATnCHkttKbmm9/56zz5yjuiOWuUFP0mj42KpqlF4gSDqWqqeiXLLzMxSxQUU2B/GLi6ObBer9isDCrIUFNZqyUWjXgfMDrMuUBKEW0rnn7la7lLwDI5d8KMU0CFTxDiRIxO4tva4rzDu57djePi0Zsiv1E1GBTjMFK3FSETLCprqOtaGL4xEv3EPT5pkg4qlTu8tIb1esXt5Qvef+9HvPfjv+RnH3/IkCKkXIyLjuTHDCh5Qi6exyBkHonJS5BuZt1Gg6dSAR09HA6ocY+ZRUIkFqrqiqqSwrStZainxCLiL33O54hBpEtgGY5VigCn7FfEV6YYhY2oS7feEtt+OZvSuWNFfqyAr7aa9WoLkCsxh8SPxV+cdvGVNnN9wuyV68x7Wt/P12LOcUSiZcmFmN+7SB0sYKya2dTLcQKsJmafXwol4sDVEkeevKu0QZf7co+gkJa/z9+mZOhfzqzRyuQuIGb7EGBm9GoZeEAky/UhrenWCsivONGKjRnvyj43JpETVDqSNVDutebHPLxOtIRVJlPo+Z5ZY8FAsmm+NzFJt2WJv2OMlIC5dLfNMxdKbF0G7eYOT+leyjl6lj4r8gFFGqKA+/MaUzI8DKUwOY8WpqR07Wil5iG7JTOdnJ8HdJFKodATEWao8x6jbdZOjjQqg3rGYHTNxiga5airLLNhLK0NrKpAUyWM0VR2xWpVsWotq06zWSvWaylAir9o0HpNDDI4zB4SMDKNE56R5HNrvRINaGugrjR1DZUD6yB6zRhaDlPk4AJ9sJLvqizbkaL4OB/kPmoDk6P95/9c9lHTcPiH/xClRSfbWktd1zR1TV1ZKivD+5Lv6Q8TQ3/N3W3D3eqc9faMttvQdltMu0Jl/WyVwY+5O0wLocWYZS9Fo6CpUCScFyBe9taSIxbnMBPw0vJ36fCR5+qnSTRnvSM4mStUrmezkZGwZ+//jPX7H3D5aEOl7rjbjxzcSD86gh9Ifpj35nR4zm64JfkBRcKsHuJMRSDRIfl80hWh2kIHej2h+iPj7jnTuCf6K/TNe5gUqWJiUmvuqjWdqrBaoXLHvMcw2g7fPUJfvMtmmrB2w7R/xtXHf8IvO341wNgUIYwzcGW0kUqRlJEgT3nTEVKQ6ueqhuPdNfvjHcoPvPHkSa7qS1WG3SVn/S3tdER5h9cyFEgZQ6UsFRYVPVElfJ50Z4PH9kfii5fc/PgnuKtb9Pk52FJNy6Q/gJTwKYqOkFGgZdiV95KMhRhwk+OuP7AfNFNcqvYvv/iQ+uXPwF3xrXef8Nd/7e/x0Y+/y6cf/ZT/+3s/4fzBazTrcybb8fxuz855Vk2kd47jsc/OdGKaBsZpElr4MDKOnnHyuJgNEhmsTEggGMvkQIEAC4VHwNjZ40pFCbIur3xInMHYAj4ujkzeszjslCtXyVsImtK2KYHMyaRvEmiVNcCWisG/+U/+fbS/rw47L5XZ+97jt1KuRBI75g0+/+PpoRSxkqW//+bX+Ol//p+itOYHDx5zYww+BobtSiorqQBP+WNO/Pl9yFT+Fn7wA7i7I1xc8JN/9N/hNhvC+cXyW/aMITYcg8GHhNZBbp7SoAzR2Pzf+v5HF5A2CbsyF3pnkDxlpoZSirZeXldAZUWeoBjxFHOinQM2aQcQ0Wz58ZndcRLsFNi7LAgkGCpT2FO08mXGgpHnqYIMHtJhRKdJnn9mTKY4YkzRxCwPq7Q85Im5yDqNSTGMnuvbPY3dst6e065ElmO327G7GghToLEywfnBxUoSpnEgpsjj8zV+04gxT4GqNqyqBqWhHweqdo1SRlgoYaAykILBIEwh0YDLbUdRCjlFt/O0uq0K2JVCDhoEgK4rw/m2429d3nJeN7Rna8xvvIvr97QNdF2DVhVXV7ecbc/ngKVpW4yW4QfWVozDIFpNmlk383g4Yoymsy1JwUCPbit0U0Nt8cmLZEgI+BjZjyNtfxQgJLc417Em2QQGIo4UIm1tWLc1XVszHQdCbiUswfJfxRKkLFHUyWaRe1L0S7XWKJOHcxly9V3e67JIO5Qkreywk6Qgg7vCnFlkC+5v7wXEjTGK9qheErySeEu3fl6/pzlziHjn8xo8TUiSaBdNmbGBrI3owwxMz7vFedzdnmF3wPX9MjRjlggoiYn8vrEV6Y/+kOnbv0n42ruM08RhOIIWTekwDjgfWG0vqFcbFJrVakXd1MTYEMKEmwTErnObO9GglJ9ZsiXYVYVBlhI2RZRucFPNoBXHwwGdtcYgkYLPYFuRqwk82pzTGENtDR2L3bbGsupWtN2KZtVKuSYm2odPaKcedXtFP+xRFn7n3e/w76yfcHeceP/Dn/Gj93/E5fVzxnEEEnUt7T8x64bWtpbA1rYYozlOU14LAqJqpRn7IQPA5AQw0KcjyhhhjihLqixmlehqy9nFBfubG+I4oLIOVULkcyC3N6ui/bYc955zTnLmQkUuyBQ2HSURIjH5yE048Jfvv8+DzYYH52dszxcJm+gnwnAgpsRxJ8l/VVXUTcvkJrSpWa3P2Jw/oFtv2V1dzy3zkhyrZR2rZe+lzAgzpmKRtyhslJDZsPKTUpJERSvI+mxkLc3Me5m9QgmmS5KWYph9cMkSYxQN/74/kFKkbVtpt4zpZPjeAg4s9zXkQuHy2vsffcGHz/Zc3hw5jhEXFI/WG958600UcHNzyzgMpJR4/fXXadsaFxPH445DL9IAWskk8q427G+v5mKD1Zr1ej0XkZMyYCu61ZphcDgXsVvL1dUdLrMVj/vEF2MiuMjFWcd6XXM8HDiMoo/+6PXH+KTYdJqKijhZrl9NYI+EmKibioTCRU23PcOrI0Pv8IfxJB7KPnFmk8prRGEkBkUGJySeKfrcBoUbJ4IXYDEMI7Gf5uJE8J7ovMSyWuGCJ/iYQbEB5wJV27J9WDENA8PxgNENtV32tXUpT0kAACAASURBVEo5dElJ4vIY2XvxH8Zagla02w0JKfIOx57kPCnLhCQfpPDqIqoAsknA1vcfrri6ueGzf/qP+Fu/9/f56le+wXpzjjUNUZchs6f78n6QdzwcSVYAq+3mDKUrMIaqadCd5tlnn/H666+z3mrqpiLqNLeBp+DBmKyjrSgt8W6axGbaCm1FmzQGn/2dgiwhASIFFb3Pe0SCsZinjJcmipT3iNaJpBUhWXyoSNRz/GXrls4avOshRaq2wxjNenVGq2v85R39xQM+tc+Y9re8+vQDNuskbNIk2tybszd4+rVvMA09n//sQ/7wD/5XdleXEqNZg8u7miSsLKs1Ac/zLz7mtVdv8/jpm6zXG5wTkE8pAabJzyEhWp3DMKAyWFjXCu8ch8Oeu7sDwzhx9mArwKLWKFuxsKZycbAStrOAZ0vyH5PMhVcxYQrgR75/hlwc8UQ3EUjodkXdtrmjLeLdgFYSCxynkZWtafI0c1JkGCaU0hhrUSri/ISEtQuD1dha9lZKBDfw6bNP+D/+2f/CJz//gMurFxyHngJtil3zqMziE1xPzcOPNBJ7CFNdYkujFCpGTJhI/ZHY98T9njp5qtpgrZHOPiss8KZtaLsGbSth6nqRSqOSAp41Vu6VrbNvMPfAD60WneLFVy2Anco+X3AUNdv74udsZszPWr+q5JcSI0tEr+Z/n3VaS96Wc57iMxNpHt60AO15W6uS1LHkQieH/LqeLcCiOVtekWsS+2hOANf8BWnJK2cwUGlQ4p9UXjuy5pj3+TJgPmtUZt3bktIEynAtWWch5HVgdGFDyfrO2rTzDASdY+agMCV3RlFYTgqFURZtIGiFw+E9eVbKSZdPjnvnztAkuITkjWq2TRKmxBPiQo7x8/eqzLIuhVbxE7JupLi03PsCqBeShMpEiNLZWiQKgg/zehFJpICx5h4zdppG0jiwaAtnKQuVNUJT5mRmIlLRFQ0ZAFSQizgGoysqs6KrV8QIwTumsScER6UTrbG0Vc3KRB5s4OHW8OjM8vqjhjceQNdGqgpsXaErQ2MtbaVZ1ZptN1JZleXr8p7QCWzCGg8hoNPEYDxDD6OvBXPKXStJiXJUVWkqC9YI/rIbRu7GxNHBEC1JByFZ5UGH2/UK54uU4EJO0EZja8PDP/2/2G7W+G98g/Hb36KqLE3TUlmDNdJ5KB2IUkyJCkiOsb8huAPTcEuzOsc269zKX2Xwft50ea2RW24V0WapsSiDmE0QoH7JFYv0hfws2tB5rSkZ3BdxMqAuRKbJEcKUZVwMCkOMCW00Xdfy6NEjzs/Pee3JgZfPr3j+4pJnnwuAmuYCfyK4PdPUc1QJbRX67CEbY3L3oYZ6JevcVGA7THtO1ZwR+h1pcng3Eo57tHpGlRRbaznWNZHHBGuxJglQmz1XMBWue8Tw4JvYakVz9gb6R/+EX3b8SoCxSimaTN8TCQCFSrk93ksioZ3HZzHpqjWcbVoYLWkf6G+vqR8/xqDw2YjiR/TQY53DIO19KQaUsVS2obYdKkH0PToKUJSCAEVxckzXt0y7PXZ7lofcpLmQlTIwpnO7X9FQFH8mDjlEzzgdeXX5kqRrTGYUADx/9gGP7l7Q1fDkvKZpam4vGq43NTdDItiW68FxeRzY+8CEJM1jcAzjgEqR0R0Zx5FpEj0355zIEGStQ9G6zOFBytWU+RpyTbEADCdMllkPMpJbbPLvqzQXKcs+LLhcSVaFXCQMyhjAjZpxUIRGQb78uQqmTlgHX/Kwh9cf//+00n7xCF1L/9ZTAK7efJPbtv3/9HnpvffkT2vpv/0bcyBTDhc7pmiZomg7zs69gD7MqDdzbb68lPVGpd1dZX0acuCYsVCtqE12sRkYECB2YcUV6LoIYMcYCTG3qcfld2b2Xip6KPm9pfKr1IKjKiUMk5SQli8PSiQTtAKVWxuNFuBYmFeJpGUSoewjEawXiQwx0KKOGgkh0veJyTXUVhyxcxPWaNw00dSWpq65vLnjcOipLHRNRQqBaTjOLQtuSpKkVDUohfORrrG4KeBiIuqE15EQND5EpJKdrzX/qAzGLi36J6yazKwxOvHW7pZHm5aLtuasNXz7wYrGin1y1YahVqT4WFowXCRlFoyPsj/qWloBpe2zwTuPVprKVrQG0FIpVlkkfm6BMppkFZgiTSKM8ZDyYL7JzQFwAo7TxHGaMFZhNdRaZY22hu16xe1xkViBX1jSCxOgALV5hSnFzJryPsgzVjl5J5FSBvnye2cx9gJsndiEU/uqT7739FxOq+qnrWUpxhkyTIW1XUCjLyXxZcMtLavF4KX5omKMmGIz52lP9z9nOvZMuwPuOGT5ihL2LntawDCdE09QtzeYn38sINjX35FCQdWisr7kcDxQ1S3GVngj4Ly0YXeZLbCXwTkhooyiqlvcNMpeLF0nWs1PKKUkIEjWYq3rhuNxpDBOipbofGWSizN87R1WNzdUw5E4Ldp6ShmqqmV78QjbCmNpChGXANcJSHrQ3B7veGhr3njtDbZ2TXv+BueP3+LTzz7m5avPePXqC3aHG4yN8zn7zF41Rhg4IGzUeFJ1L8mE+KbCzE7oPNTDe59BBIWuRBfLbtforiHlAUvj/pDRuGInWRzcX3GcasWVNXhaCJjbHFWeQhvhLgykBOvtGXV94m8KzUUmI8xDszSJ6CeUDfjJMB1FHP9wdyNDkFLCVhW2sMdzMbUkb9IKGKjrVkB6KRvNYKz3E24a6fue9WYjg18Qpozgfmm+TrmW5YaI1ECc5YzkXqUZuBeWoJcESknhKmTWCnmNlft4eo+nqNmPiTsfIOPVN7uReGM49FMupCjsSmMeKXa7Ow77AykJ87auJLYIg+iJozV12+YhQAmjAio6Ls7PZFJvHiAaQyQZKVL1x4m2qQguME0e5wIuD1Ss65qz7Zr9IcwazgoYh4n9fsJ2LetVRxo9fnJUVrPZrKjaFZuzjmn0pAj7/YGoFLay1LXlcHfgJj4nnGpWxjxoUc1Ynzy9KCBonBzYXCiLevZRSVDTDJhK0SgKIjAPySv2IOREe247jhE3TbRdi92sqBvDNLmsOZ2LaBQgJa+DzCo/HA8Ceqg8ZDJm7bfJyUBHFCZlUkMImRkrw7RsVeHGgYNV+Fbjmkj7vT/i+vo5T19/mydP3mbz4Kmco1KopO+BLuWwVU1la5EaUJqqqulWa9Gjy5IeN7e3hJh48MBiqoqo1NyGXtcVRQqrsOZQGmUqjJEp99hKQLV4AgrkeC7lQoQmt59rMxceZhg5F8gkJsoZbdQLUzcGAlGARZ8Z7JNH5UKVSlBbS5o8NiGDgscjPgzUq472bEPVnbO+eMrm4Vf49L2f8MXPXvDq0y+IQYZmoaRTMGmT2WJaIi4FX3zyEZvzC+qm442v/Dp1s8VNwgx2bmRz/gCd/RMqD1Iy4j2Cm/ji2c+5vroGU9NspPNG4v8kXfQZxGXxzrOtVCe2gVTYiXkCO9ntJgUpMPQHYhglvrQmr+Pcsq8ibhoEIEwhT47PbGStRT4pRYJ3UnRXMnRK5ikUxp6SlvuUGIcjt5ev+N5ffJeffPhTrq9fMI4Hgvc5TAgiR0CQQTs5eDfaSL5IieDJA2zyb0XRx4z9HjUc0cOAjY6uNjS1letSGt3IQKyqqagqSyRJV1SMRCXMRtu0otVqTPbh2d6XcD5XA4qv+LIPk2ueLbzcgRL3chqbnf4wa+SnkzkVcq/1SaxW4qicF+R7XnDipdhfziRRJqznX+B0twsBIp/tl+K/X7AL+b0FjF1IFOWKmdffkuxzz55KoVcL8zQtd+leHJiA0jGVFikSnfOHhJIib8YVNALGQyEyFUmIPL5tRjrl440uzFlFTKLybbQRGz53jgmohRLbXy5HOokW1rcqayZ344kUCxTSw2lbeZnlIYPupNsupDSDsiWvlEevZ6kuWRxxuTfz/S+Sh0kkY/Lgx3L4vCfEtJ7EeGl5XvM6zsXgWIhoKZ931k6umhUPXvsqf+03fwtjLcMwcXl1y+3NNfH4EsZblNtj40RnEpsmcb7RXJwpVpuartU0jaZuFHUj96zWmsYo6iqDpDm+ketOkDQYg7Geyiq8EaDV69PrLB3XCm0NxoLWRSVd4hHnYIxeyH/Gii0xAmJarcBYtLJ0qxVVrTPoWnHW1Zx1FtREOF5TVxW3D74OdSO2Ps8+0dqcxAAKVITkCD4RnRE+XQqkPG/gfn6mytZaNFyj2N6ImUH5sv6+nDsuC7vgC5JHaFOjzATazc9d9hEE5XHOc/H5FfZqR0zS/VJXFZvNinGc2B0OKEb2xizeJZOkpvGOw62mefERVdVRpUSloNIKXQlBTBmLqlfYdkPdbVFR4rUQAow7jHmBrlra5iGDWRFVR1R23qRGZbZ/3aC3D6gbhZm2vLK/HF/6lQBjdUrUMaJTRMeA8o44jMRpIk4T9EfSFNDWotdrNg+fsj1rMW6N2t9wuLujCmFuw85924RpIvmI1ZaqXeFjxFYNTbOmXl1gVlv07hI/7NAqMThHrGpQGj953DBiinHJVlyCYZUrqYYU0wxikTdQioFpGtgfrrm6fsWjJ1/DniRdrz77kPXuFZuHK2p63PGG2k6cna8ZOCc0a168uuKL6o4x5/s+RUbv6YeB4CaO/R3jVGQKUma5LbauVKJkE2QDll9Q+RrIgFuazzstRjhAiooYFwjB6gX8KN9TJBxI5FZmiFHhnaI/wnGXcNsE6/ysM4CnlAAAs3D+CfDS3O6WaZOLG56/+K/Ki5cJqulkGrYcOT/kNLzwD87FyU4Tdi8SEq2yTE0jSVwe1FD+V1g7pw5cbmlxQIq0WmeGFRAj+uYmv6e0ghgmXzMFI9rG2ZEYLUlRLIhaOenZseUFmAEdlYdwGVPa507uqRFA7fSGKXJgXyr1JMgtoiUpi2nO3WcTW1z2fK0k5vYUFvBrbuMpwHpu+VVaZaaaJia1aMslYY8Kipy5Atlga5LoZKWQ17HoGqaQGIfA2A+kSjGOA4fDkfV6RdSapm3QxnJ5c8fl5Q2PH25ZrRvwjudXl+gqt8r4iAyeabDGoq0m1JrxOErVVysSIWtRis7s4mTLf+sZjCUnxTE4gpuwfqKOnotNy+9MPe/Yjifrmq5RmM0W58SRGJ3QqYXtOSYmGhKH21e8//MvcEHRtqvc2glWW5qqYjDSzlbnqiw6cRjHuZodSfgYMalUyCM+s0pKAGPylNwSFEbgODnu+h40rGrRHrPGsu4azs83fPrqOu9CdeKIi1X40qFOVo7KQ1uMOdk/al5DOR+d92Wpzst+Ppm8W9YeGVhVJZC+fw6LflkqF8zMaihSBfN15MC6nPPppeR1nMjFtXTCJJijibR8u8rfffIR46HHHY4E56lsRUgLoxAFSsv076RkHUVkz5jPPkX1PeHdd+mnkdZPVJWsVTf5mcEYg2Pse7rVhqpqaTvo+4FZizcm6rbDhwJ2SzCsy/1BIfQO2b/WWrpuxTAcZ801maicIPrZlyQUt9/4JpsP3sc+F/ZOObQxVHVHt70gGNnnMYKLMKgKtw6MKXB12KN2O/Q08dr2CW9+8w3e/vpv8uLzZ3z80U94773v85MPfsjkD6QkDKMpRRlyMd99+T5UZBnYcSJNkcpz1iWDIjiP10nWo1ZMMWHXHUbLJGs3jEyjE98TikZqnNd08aGn3wNwmsietkou5xJn/5bLDewnx9EHuPdeZpACawU4SxGfpQOUNSQ/MfU7xvHIcNwJkJhiBiDrDAAHGZxAzFOEczwQHbZqluQqJVIMODcyDgP73Y71ajUXL6R1Nr8/ikzBqfctzCqfhy2QBNhPWQZBWCqi/VuY1pBkuE75/LwJU5zL3QDsveXlBK90hNfktcElwgQojU5ewrw2Mm2PXF97fIh0jchsWKMJMYkfSYG6qmibRrr0o8ONR6xWPH7tCVpX7O5ulzguBlKcONweWL+2oTLgSUyTJynR9+vamqdPHvLzZ1fUWa+RlPBTpO9HOmsxRlFXhrGf2Gxqzs42rDc9Dx+fs785sN/33N7ekZRhvWlFe0wFbvTnRH+H8ltAoaPovcYsR3RPizCDdoAMIwn6BOSRc1JJ2DRhHpYqLbMmdx/I52S/r/UMkAyHA01T0a47Nudrri9vMMYSXMj1Y4VgBWnWpUzA5By4CUD0YXOBV4ACizUqrxPxxzGDZ5W1rLuOq/5ISjCsGr54523+1b/4Y56/+IR33nyH3/zW3+CbzYq6O0Nrm7UoT5N0OdrVmq5ai5VLCVtZTLXGBxlicv7gnM+efUYMka7t2Nb1wrhEhgeimId4pphQtqJMcpcBSVmwLAnAXJiRRdIjZqktmcC9tEkrxWwbspeRlvLoMeRht7rEY3monDKkkHDThMbKoMfjAT+NDLd7dACLEWCnXrHePKE7e0KzfY2qu6Cuzrh98V1efPAZsXeoOgNDOanWRlp3pZ0bKlvx8vNnJAXjOJISPHn6VaZx4rDfsbu95XW+yursEVWzRiGM2NKxMxz3/PQvf8But+PJm1/htaev07W1aB2zTFcXIEYsY5Ed0gg4rFQqpPwca0d00qeelxgDfX/AqERlLXVV4+LiY21lGfsDbgrUTc161TFNEykFjK2xtoEEbhrlnGxFVVXy7E4cemUNYZzY393y848/4s+/++dc3d3iAV03oGRKeEGyVEpYnSXYlLAh5d5kk5/vu0HAfBUCauzxhz1m7NEx0FrFuqulKG+kRbnqGkxVS8FMCVt7nAaitpi6xtQtddfNLE2x5Znhmr87xpA7GU+ArHJHv8Q4/4XWflW4vcux4Jfzu5a/nxTu5qwi5zQlXy/2ZubT3gsrl8L4DADl8G4JI09yxWwLio9e/tSUVvnSTbWw9JbY7TTrnAHLck33Xsixf86jNaWwUO5rjk+SyrGEzqCX+NKQixeFWqBLjJI1zwsonDIARSq4BnMeKHbGiJxJyAxnMgs25ymz/FLOi1XOWfKNQmlDW7e0bUPdVHlOQxniHGdWY9F2jdpkha4l33Desej5CxGARJaeEP1+VeQNKISK/Fy0RkXx1T74ezFAKms0563l/hZZmkV+Ihc9ZHFTdIdlEJNFKUPdrHn8+A1+52/+HqvzDYNLfPFix8vnLzi8fI/Dyw84vHgf9ns6C6s6sWkV6y5St4qmrWlbS9cGVp3kR0ZpDGCUxag4X68wjmMm7lqU9qCNSE7pgDYeFXJcqURnWakk4GilMJXC2kRt82C+JAOtRg8on5mxCmugsjWVMdTtim67pesMbSt27sH5GZt1RVMbqrsXNFXN+1//Bk40GJjaKn+/5OEpBWKQ/BckFjXJQ5goCVNUzCRElSVpOAGhjdGYqIk55wtL6+4v2Ix7xZL537M9qBqMD9jcCV8GoIYYwXn0eEf74w/BBQ62QqnINDqMtWzPNjxxj7GVYqrruawt9iPgXE/ae4aXP6exDSY6SI5OQ53OZG+HSFIGUzXU3QoVJ5z3MPQoP6KGa5RWdO1rOHtGVBdEtSKampRk6o3RCVMZaruiXRlM2GBMwy87fiXAWKaR/s/+JdPNFdP1C/oXz5lur0nDiHYTTCNQ0f7at7j47d/m6V/7JpM1nG+30K14cbfHBtH2jCAaRu05IRpicGhjefz6GxyvbmiVZdVtaJ+8zZt/5+/y+Z/+n9z95C9ptafZGI7GMnYb0mZLu1nLQKU8rAKyE8iOzjthwYFHZQ6fNZrr6xtevfyCzz77OW2zheAgLkwHm0b2119wuOy5+SQQVAJl8aml7i740599yHWY6LfbHCErfNQchsDVzYFVPeCDw6dAVDL0KCAC7AXgWAKYAnjk4hTMu2L2ebloFQJMPhE8mUm1IqlaKmDTji5T8XNnLwlwQYKpGDR+UhyPiXFMTFPEjR7QjO5+siqOTl4LPswBVzl++7/9H2mvbvP9zkBNBphCSpSUsBhrBWzXa1wI7IeBaEtQXWyIJjgZOhJjJBjF+//Vf0lqarY//oCv/uM/IALNx58RIlRty+X1Kw7jHcc0cEwTRzfOgJzJVUSZEDsSUkQ3NeM/+I/R3/42bLbow4Hz/+a/RiVL256xXj9ktX2DTw8rfLKkDGwlQFdWWmmNzcCkRE7l340p4FFCq0SlQavcLmYNVqus3wWVXVqfxYnllsACLpfXYlhaZU6CH3Xy1wKrCQMl/aL8A0vgsTzBOP93UuKsiSJWnozocs3RG1KIyaI3JS1BRY8KE2jQSCWQFJkmz0fPnmPy+Dlp6amp65r9vmccJiqt6MeRq+uB/U5RGcP24hxrpG2wPx65vtuTUmC1WtF17bxQJhfwPiIFZUXplFcZVNTF8eSO0ZScsOmGHj8eOTvr+K3k+V2d+PW3X6f75pt4PxCDp7KaYZzQKKxWBKWo64bUekxw1OGcb3/zqzx/ecermz13d7dYPN55YutlSKFKqBRwfuDoI2N/xIWATC8uepqRaX9EhxpDi8qD/PAOgjBDXJahiElE9B1wdTgSAJ1WdMaACqzPal6P53zw7DOG0TE/upOk8vT4hSKIYv6eAlrmjH8OiGUvaeqmxnlHAXy/fMzVVZUDnbSAb/dlCHKT1axluYBmKt+je5+fL+oUUAvRgagSziF5qblI93YBZRUFZovqvg1TCACCkbVuzMn55SCyyGSnLCGitQApZKmSEAPjNFJVNVXTUlPnYWcyzXiaRo77Pe16RbfqGIc1IQQJirS0AVV1S3BKJnEXve8Cq2adtxACtmqz9ptiv7/DVpaqshyPB4b+gIxaLqxa+OTr79AqePrT9+ZrrrqO9tEj9n5komPUNb02HDXsVc3RVAymJaSaDw83fPT/fJdN9yFPH77Fu299g6df+Rq/9867/N7v/R2+//0/45/97/8zz59/zHG4oW4sQXmuby7n4HvybmZzzD6tPNv8p8sDW5JSVHWFSmBzID/6UWyMtbRNy+PHT1BVTb/fMez39Hc7ZOD3AvTMDKH8+UUrrbBhF4a3HAJCLudDzEG6Njz74nPCe8v9kyC7IhlQIVCvVnjvuL295eb6mkePHwtjLrjZDFujcvFzlMFS3hO9gG7r7QYZ3JWLgQpCmEg+s5gAP0lrW9M0rDdrbFXPe6YM3gjR5UJJXj+FXZ43hc6FM0i5bXu+WWhTCZBV/Hce7uDdhLGWumlI/y9zb/ZkWXad9/32dM65U94cauiq7gYaDZAgCICgKIqkJEqyZFHyEA6/+6/wi/8YPfjBDvnNEbYjbHmgQ6RkERQpgSQ4AA2gG0PPVZWVw53OsCc/rH3OvVWk7FfeiOzqzLx57hn2sNa3vvV9KdAP/qg7B7z/TPNpsOwbA+/Kz4yt0VUjWsJDkaE47Lm9ueFsOceYima+ZLU+B+XY71uGAYyqWS6WxAzWOtrW89Gn1zx94zFXD54SouHu7p6z9bnMCy3FQt9t+PDHG5brJcv1ElNXPGwesL3bI30tQPbE5Om8JWRDtTrD7L0shilzcbHC94F5Y4BI5RJ+iOz39xx2G4wzLGZv8vL6lpQjjx5fMpvPWHz4bWr/Nfr1z1OZc7Lu0KZ0d4RQTBcLuxQFPpGyJ03rqi1dTcdkNoRwHJu6OKSn4hVQ1rd4YogHcH97x2G/p5nPuHzwgLZtafsNh3ZXuh4spnJoDUN/lBsgU8zaxDBTMzrGK2aVRSspePcMxDzINZQ1XE3AagKruf3Hv8nwe7/Lp3/8I77/3h/zW7sd3/zW32a+WAv7RimUHiWPytAzWlhFQ8/hcGB9eSkSaEYzaxaEIXC2XhN84MX1SxZna5S2VM0MFyuUEqkWXcBWkf3KR/C3tElOm1oGkeNKU2KaiIRhgOTJRbPTVrWYQZLwoYcUGO63+H5P9C3zRhj7q7NzztYPqZqa3XbHfH7GvJ6BEfZ8u7nn7uaWH//wPXa3t7iUqcyMqrni6q1vsDh7TDZzAjV9UtRJ0e32DLt7mkrTG0cXBhLgXIUxighYrahnFdVsRh8iN58+4/OPPuFP/t0f8O5Xv8aTJ2+yXq8JPrLZ3/Gln/smlw8rlKkBkb9oN/c8++in/Ovf/hd89eu/yHr5ZZ4+PC/GkCPodowlJhY3iJZsjlOnRhxzg8x0rzOcMAgVy/UF0Q9yLDcjdp2wTccxHUrcrjSkyH4r+5vVBlvNyA7ub18UfWkB5V88f0777jlcLeVcY+L++jk//uEP+O6ffhdTz3n89rtSPMsJ3x0gDqTyTK06FpRTDHjfk4ae5EV6JZOxWWGGQQhIfsDv7sldi1FQuZr5vMbWVhhzzmLrGgrTK8SA7zz3+x26mjFbLJivz1FVBYgO+ugVMr1GhnGSQr3ESepYEJu2KVVkqY6kk6m4LUggo6EPHLe2I3nj+K8wQvUUn43SUrr8YU4lNiz6yqeR3xgrjTGh1lqMLEcAaTy38f1pvDZe2aOP56dPgtbjJ52CyFqPbdhqImEAx1brMvfH85te6ijFcEoK0DmBEZZ8zq7ksKXD4uQ6p1cISKwlLPA8AqflvuvSRXXseskYbbEmkfLoAVKKwKpozCq5RgHdy7wpEYRWQphxlaOua2prmfSAyz0efKDvevphoOv60qUk5LfKWZqmFu+dMAJmAubFJPuNLnJLIHuOCYEQjrJEWitmszmQuW3m062oK0ddN5IjWEeMGT946QYsMfh8vsR7T9u2dFqRlSkxsGa5XFLVCyGVBfjJj97nn//3/y0Xb7zN47fe5ktf/jK/8Xe/yYP5r9LdfsKzH3+Hn/zx/8myPnBxlrm8sFxdVNQuUztP7SK1izilMFRoTCmeUwwyZQ9T48BUCdGrVeTsZBxrh9EDOUsHZMwjwW0AFTDWMJtrLnB0UfYTTaTdRAbk/SFGEhaloXKGetGwXq95+vRN6gYWC8f5asl6uWK+qKiKzInRlne2z2Br2NQzfu/sS6V2NE4QAVNRlZgl2wrjGrAVAhUaxr7C1/jkJb/TwftwogAAIABJREFUaKvlHugIgyLmKP+fjrgAmSJPIdNRTHNlbkpx0OKcQVtHPZvRNzN2uz196cgI23uW/8e/5EY7dvUMVzVSp0jS+eZMxZtPnvLo0RvsV2fsy5naqiap0bsDcthz9/mP2N9/TvPsfc6uvkC9fERVNSjj6JNCDXckfxBpjdEoT2Vy7Mj7a2z+LsuwJa7eJCyf0i3eIqlaVBtIGAJWJZxW1Laa8sC/6vXXAowdnn/O9n/4Z9QxsMqRVRrIUdrvckwMfUc+u2Qx16yuzglZqlBx8IR9S7rboLqO0HipHpqaB0/eYfejD/CHFo/HOsfy/Ax8ZEgD/uZT3v/f/2c43OFcwmRFNIa+qjBvPOLRr/wKs4cPaY0hk9AkUhatkzHRHzcEMUcShPLDn/yE55//jN32luBbVIYP3vsun80r+KVfAuA3/u5vUj0442c/+RF/9p0/INkZD568iWrmfPejT/hoiJjKYm5uqH73t+n+0W+Bsmx2kZ99fOCtx4amMRidUCkSVZJaZT6CZ2NwPbYB5BK4T5VDoNAaSFmIDF2fCFHLwqFWDPqxJEDZk3jGzf3LCUBASbfz4ZAZBgg+SuKaJUg1pYfe/W//E3r2X8Gjx/KJ5mj2IJunGFvEE/MOihByLtWzY5Mx0x7qiwZmAhrr2PtBWm70UYNkXOyNEZBqYjmc6EzmnAu7KBMOLUNI+JTA1Zihoi7tlwOeWFqbjDEYbUgxYVCkJ08Yfv03qKY2rPFUHWfnb1HPLjBuTjtkQpBrE6YaoA0+m7JRu1eQUKUlOLYGlBJmnVFFhqCAgqYAsyHKBhzLAi8XJ1+js7AIm8cTKFxNgUdKcfrZ9N+i1TRVv8ZfjGXpNLI7JLijmB3pcb7Elhw6cgyoLEGD5C3H+x8nqkCekh2fDeBEr9JIMYQ8hkyGgLQ+kjLXtzvOV01hIhgu1ws2uqfvO3JQLJdn4gzeDRirWV+sUcbgQ2B/6Lm93XJoB3IuemVlbIxGUyPAoscdNovT6NB3hP5AXRkeXSz44tvv8hu3z3iqMxczx2KWUQw4DSkZYsxFY07uvrNKOjSdIjmFqw0Pr674pV/4Cj/66cd8/NkzKmO4WMw5m89YzmdczhvadsvusOFu6Ig+4jQYnYqZmJZ81kPWiWwj1jYkZUQ7NkZC10kSWarLlbPElBlCpBsCoVY4U6FNZm5rHhnN00dXfPjpiyLb8JeBUjgCsa9gYSUIJEvR4JTBML4xxFT0bONkMgFT7H/yAXkCZFUZt9aYSZONLMBXSmIMOJoB5Vy0uAr7Ub+yGU6pxitXNc7hkV15bM0uLWdKjL3G+aC1mAycotPKGExlsc7SNA2Hw65o3b5+YcdgfGzj1pt75v/if6H9x/+JaNFlqOqGi/VD0GKmlaMkfEPfikaUsaxWK16+fAnKY10EErPZnF4JszSHPLWMj62ZKXlhgScJsFbrK+pmQdvu6doDOUFVNcKiT55YtFWbWcNqveb84WN4IYUzbI2an+Ndw71PHJSm04agNF3YEdUM5Sx6YUhDBFfRVYbruCd+8gPuqgVvnD/g6YMnfONbf4c3nn6ZH3z/u/z5n/8h7/3o36FMYNLLRmNKy9SoxQdMgfrYbjeu16O2tegSg3WaupnBqBWI4u5+QzKaxeUV8/MLQtezu7lhd38/6anGEI9jakr2jsnX63qyp+N3nBjKlHboKBIi07gr7W19LwlPRvSO1+drZpUrTJtECh5nndRL1SiJIMcfek/0vZhusJjGN4oC4k4iH0DGOVvmhwGrJg1nBVO8E8IgepdKMVV2x+oEIzxy1H8bCwbj28Yi6Mh811aLEVSGEDwv7w/cdY5le5w/L4Yz7nFEdZjmpsQ20vKdNcJ2NBaFYTFbcfHgAU1To43ibrNj1x5omiVNsyD5nrv7W1CWmBTGLYnKiIOx0ugMy8ViSliNVqJBGQKbu4G277h88JDtvme/a0kh0fWJro/oTUfImuXZHLeckZ07mlfGwKI21NaQYqZWmmcffUKMPdaKUZjI20j798u+59bsGFYz3O1PaW4/4503v8ZPX/4FIfVgBdxIMeJTImqN1hXGlpbPJGzC4IeyP8tDiMVhmFx0HZVoy425/gjuTxwxraiqiuA9ofccfGR/t+Hq6WPOH1ywXC+5fvECMRQSQ5jgPRRWTY7HdTWWOM1kiVe++OY77HY7nl9fs1otcSbw8PIJi2bJp5/8bGpHLKOQDBx+9dfoYuYOyz/P13zzX/x3fP2NL/G1n/tlrh6+ya69F0CsvFIcneYbrBO246ns0/rsAqcdu92O/WHPhz/9KW+88RjrHBg7xTwjsz1R5DqSSAMNg8doNem6y61PpDgwSi1ppBg5tIfpGPV8TuUcOkeU79hvbtlvbnFOs16vePzkKdt9C8BusyHcBA77O6xRVK6ins1p3JK73TWH7R5yInrPmZszXz3g/PItHj79Gt2gCCNQnDJDCBirqesKrQxZZ4xzpTMOvB9Q1hCyuHQPKVHPZ1it8H3A393ywXe/w/MPP+Dhk6d8/Vt/k2/+jW/RLB+ibUNC2v1391s+eO/P+cN/8zusLub8+j/4Nd548jaD3+ODRttKjGER9u24fmot8gJawX63xxiDXRsorf0j6wxyIXAIWaGaNUQfpa0VQBkK7jOBgcvlemL1Z5VZLpcMXY9SBxolHXqPHz9mu73lsLuh3+94552fYzGfTePJh8iP3v8x7//sI246T71+IAzTkns1szNyimJSGIOsiVni7Rh64mGPDxltPE5HDBmnIlUQM+pw2GMHkUWxxuKMIRsH1oIzZKPFqKyArP3g6YeB2fqS+focbDEy64TFHIsE2QhMjbH+2IU4AZSvBVo5CfNe6zGePMZLI4iXsahRwmPUSi7xj9K6xMqqyGeNAMvxGCmpqTsDxmUpY005hioeLZQutFMAdUxtCqFjHAcjWDnGh/LN6x2MwtrMWdqoxxZtZ91U4FUKRrOtiTVcQH/piFMYe1oMkLGpi3CmjOXj38reF6e4USGalxOMNQK8yLqiSwycRxJDLh0jSnLBaVyf6OLqsqbHaCROG/flMrZHI+EYY1mLR1BWxknbtrRtK+eS8ivawFqJZ0XO+chEzgkfJJ+I5f6IB0NhpBrRr58Mt+IwyTWliQzESax/zP+G0lEB4AcPfS/vAZSSvFueXWHIq4x1hoWeUzWOZWH0Kq24vLzi4uwNalehUPT9QGj33N9e84PPP+VP/+DfUNWWdx494PF5zYNV4t13HvD4bM/5SrNcGObzhEa8P4wq+ZYCxSDPIUseImzRkQhVgEcVUDqIlqxxaJMwOmNtQpuMjnoa+yEIYCzEqUzC0MwaFsoSreLKBuq2l24fFNbVnF+dc35xztl6zfn5Oev1CldZ5vOas+WM1aJh1syx1hzxqiya5VXO/OPPfsbvvfku3pwY/KIxpkIbhzEN2s3QrhJ5GEVh2efybOVeF8r1K+uINRpVWbRq0EozDJ4QRCZgZDuPzxVTuiCETwrKlTynJqkl6EuwYKKn+eQFs48i7fk3Gdo7tG9xQ0tjZT42tUVXDoXCGTflclop3n76FoftPT6JVFNlKyCgwz15u6eP9/Q3cwGgtWVICjcatytFbSreePMpVZl3PmXC0LK/+zP87ieE+gGsf4Fu9hTcnFz2t5R7BjwBwaD+Q6+/FmCsDgOz609xSlGJwOSkO6OyDP5BZ1xtcU1FjKDtcZHPw0C32UrLb1XjnKZeL9lYQ0DMA8jCTkqqJBl+j9l4NB6tE0OCOxT26RPOv/Y13vyVXybXQn9WpSqbRzEVRBtLmZK450w/dNy+fMHnn33EYXtH3+0Jw4Hge6nmDMdAsbaaeV0xbxp8spydP2GfHPf3B667A9GIZqNVYH1HXwLDmGDXwsfPA/NZoK4SzorLojpNksbq3RhoJ2mPGX8+yg/4kItxk8LHioAjUZPVjKjOaLlC43AmMZvPuH+2IcdBtjqlCBFZRCIlwFLYv/hzTBjQRs7F3N2hwqtVQF0WepMVUUQkXxkPadyAgNEZbGqFhyPIiGzGPomusOy/qoBeaQLw8unxxr8fP6sAUYoMPpJjJkeYNwuG7oBKA6KRowgUhmmAZKD/xjfwJOJqhTo7Rxt3gkZp6tlDor2g4wxSI4LUqrDzcjE7UYZRL2zSIjWgdJ4qOFqJaZdWYJUkNCP2o9XYaiTBl8pHHR6gSBBKEiZD4xSMOrb1TK/yOI7KTAl9xLumjVMYXmn6XmdhE6lSdc85kHxXWOGlnlZYU+PpjeyXSe7gZIwU+XVy0qhSKc4lOGHUVMqZfkhsNp55ZWmcoTsI8yMFhfeBzWbL+dmCqKV9d7PZsjv0DINUZyVolUBOqeO/IzA23mOlVWkPl8R50Ti+qjVPFxWPHyw5bzRvn81ZKJmTWsWpbecYhFDAHGEDiHFDKVA4Q900PHnjIbvDgXa/E5MkrdBhoN30xOBp+wMp9CJMnigtqHlimUzMywh0AWUGzKwScMHYshkcmSgaqI1h3jSsmoamMoh5jlQ5Z67mycMrnr24I+ehBEWng2UMjP8yE+EU4VQnBZCRHa85sleldamMWfXqe8eDToCBUiOJ6vh9KRZoJWtnUorXE42/6vU60xFGXa0jA+f0d1PQkhJoaQt9ffwCmNrhcyZ5X9oTT8Cr1wKXV+6LUGlQuy3SZpbxwdO2B1bLOM39VJiLCo2NkZgz1lUi5aOFZRK8xziR77DWMcQoGqNI+7gfpFAiAKbBOjEEsTlhhr4kTLkkCKBi2VdK8uXPL9h8/Rvw/R/JXAyBu26gXj7gkAc2IdEGadczpmamM5WVNuUQBlZ3d8w2tzTmjlXK1F/4Mr5vuLt/wWp2xcOHb+CM5eL8ktl8wXs/+iN8PKBIhcU7mnXl47hXx86AsYPBGnG5HRkjkzlchvlsgTHCDt63OylqlC87toXuTdEjS5P55OlYOdXaHF9HVs/Jc52evZJ5qMwrSelmt+V+e89iUbQto0gAxBiwunSUjJIHqrC0C9hGljEp8kkOU5I7SQoiWakCXo/3S4wjrAFhTCVy0kAs9bbRrVl0X1PRg1Wnc2BMonKeJG9kbT8CrxLDSRFCDPs0MYlpVecj20PgxXZGm+e08Sjl5LMmlHVqhHaN1mJ0lGQepFg0aWPg/GJNVVmG0NPve3w/SPGjgArD0IuxjrG4esb8rKFuHNr02LohK2EEKVNczY2whapmVoDMROg6hkNLDr4kxJkHD9bMKsusdjRGM1iLqyqsEZ3IHBOdT/gh4P3A4dASQ6CqG3mfq9nc3zJvHE1tOXTD0XwzeazveXS/43Of2WvRY6zrmq7tRC82JZQOhT8jYEGGE0mgoukbC8CglCSNiDbmOG5CjIyyJSOYkWMiFyPDbMCnwPb2jno5p5o1PHjjDXabLfWskUJYDkTvIalinOTRMUlL5giwqsx+3xaGVaRrW2Kf2dzd0poDbde+Oo+QtT03C6ISPt9dGPj+LHEX7vnJy5/y1GW+iSPHYyKvSlwTY6LvOkJMWCfFG3LCGU2IHmM183lDuz9we/2C5fqM2WIh4GsaO80Kozv6KXlW09xPxDTeszTNLZXFTKZ2DjNrGAvecg7IGq9Er766PMdVjvlySdYVVSVsyhQCQ7cjDAeSUkTfMfQt+3jL7YtPaLcvsVr2i0Xd4BT49gBaEyhsvtLVF7Nhe7jjrrunswk7b1BZxkUKkSEnrLBKSGSa2jEMA4P3RS4lEwbF7n5TXNEVqprxpa9+k7Ozhwyt59MPP+In7/+Q6+efYWvNb/7mf8TVo8fYStr+tRJQZJQUO+0giDHQdS1+6ES9Kgd223uaxQpjRMNaIUVQUirAoiqFhnDSrkx5/7inCsAxtpULeFOJeVwWtnhWqugLV6Tguf7sI77whXdPgL/E5vaaFzfXbNqWrE3RRM6FnS4GMFlntHUkZUqxcyATmeogSqFUwuZElSM6dOR2j+p6bPBYK1IdxgoANv6rtMzblDM+SrdMytKJUs2XZCPaxbGsuyPgddRpHddrELbeEdQc94Py3Wv71XENp8CaMSsyoYDjIy+/7H2lKJoZ2W4lvjrdNcqekbJo8spzM8eC+Qi+nhRYx+NIcUSu5fRVcNlXvh8vZ4wN0QL4j2a4Y5u7XJ4u+4ScfZzy/BILUrR3T+6ZMmr6DMpVSxicp3uCHu+cIo06uuV9Wpnj/knRlDVycKVlXubSlTN6dYyyPsfcpJx/FpmTcU7pLEUHVdacVMZFjCOAGifwVHLG8Zh62vuPsG+g0op5M6OuHM5aMhCL9naKUtQffKD3UthPWQhrthha6dJFOvmTFMbn6ZNMMZGJr8XseTLRTgX8jiq+BtAfc9h02s2WFW3bo/MdVVVhS4G4qRSrVU0msLnesN+0nLFnFuesjaO6iixqy6KCRZWxWnJqrZJIEpDRI/ltzBW1pQggF5BbofP45Md7UOSxrCF4BFcarz1RZBogBE3nLbvese81XVBEFNYaVvNaDF2rmnq+4uxizdn6jNXZGRfnaxaLGVXtqOuKxbymskb2m3FeIUC/EYU7XIp8Y7fh4+Wa+6aRe6dsAWMrlKlQtsZW9WT4pbTc5xTFyM0PMqakiJOLdFWeyFIqUzShC0FCnUzYMu9QmqyLcfnIJ02KISJfPtMlQ/N5pLpxaP0QfWnxu5eo/obsbyGJZNegRK+1stItepo/LudrTARf9nFrLU7b6dwsEVILPpCVxmSNoSZrA9piLNTOsCzxTlYGP2TcfkPbd3Ttp0TfEt0nqPoCVa/QxqGUdAiFFEm+5z/0+usBxiox8BLNnQQ5SPug0ig0jTZ4rTDOYCsjzBakvVCMOBSH+zvmjx9TzSqiU7izObmyRAQAUURS5SbR6ZgDlkw2orOSlGY/n/PonXc4/9pXufzKu+xUafMoFfGpnQuQkEU0HGPo2e+3fPbpz7h9+Tk59KTQE4aWFA5opUULqrwO9y/Ru3uS97h6weLiEZ9uNny22XFIA6aaSfulMRijMNs70mpFNpYhKp7fDFRVZF7DotE0tbhbilN9SaLGU03llqayoEVNDkpEoX0iJE3KhqCW5F6BmpP0nIEFrW4wzYzlrGY1e8zzzfc53N2QQo/Rx01XFTBOK039/g/Q7QE1avml9ArWOlZltSogcWEu6VcqpakwdNQRiB2BVcYNSokeHqKnmwrzUBWG4LjYj585Vh9fg2UlIItJAsAo7LGcMnXdiENxMOUIReORQNIavVoy/PxXxT1Q6+JcWk9IlFKGavaIniUxzchqBsaRbCB7PwXjUBLkkoCJj12pTo46klrAJ6NUaX8q1zXqt+ajGZc+0S0aAc/E6wFXLv89ubfT3jYir7G8O03Bb8wS/AoQGl8BYxUUky4BTsmeHMp1lor62OIwfswU7I6BBYVXM/2uAB0FgB0LIaQCMmSpzB18j6Wi0hVt13K+XuCMwfeezf2Gs9WCnBXDELjf7OmGWJjEqgQ4pqDe5fFNgGy5/nIvFYE6DSxCx1urOX8vwTvzmgerCpUHcjM6BI+acbFoLVIMZ3QBToWBq5IqQbesY6aqOL884/H2kv12w/Zuh86Joe8Zho627/ApFFM0hUaX9vhTIOjYDmpShn4gO1PAWFOKFcU4QIum4cJWrJYLFrOKWSXC/CSNTiLz8PjBBfOmPjr2vhL6corOMoE06jjXlS7svRPgfazAGzWy33ORETg1F1ATMArCsNKjvti4x07fj8gUf0m2YAR7T2f+cY8e792rgb/SWlhQrxWKTpMClY/tOq/fEls7MVDrIkPXlfxHpAGEOjIu0OVa8tiaW46VFeb+nrReE42m7Q70fUttKtGfypnB92JaWVgKxjpp2SnPIQSPjeLGrLWjH1ppOQ8DMQyS+Jb3KmPRxkwBM2pkasq90tpABq3jiP3RLxbcvvtlNhcX6JS404bru3sur57QG0efEn3MzEzNwmhMjuTQM+8PZOW4OHjmm3tMbJn1He58DSqx29zhzg4srt7k8eMnPLh6hHUztvsD1zcf0fdblMrTOl/SO3R+DVRXItcgoKyweVJJ1GOShbEyFdZU+KIsNY4b0U1L5TjHpEqbU2flV8H1vwp8HY85/s0kt5FHLcEji/TFzTWfPv+cd7/wzmROFoKn73tmTVVYwUULMCcm/bcyZFIW0wqjKlCZGI5av5S2Q5kmwthRVpNzSehSQiGMwFwKX4lR7yiXYu+0eh/3ZUSaIAR/dDHWR1MlXVpKc5a13aPYd4o+aLad4navuOsrlFsxcGSixYmFdTr3SpEkJ6ymsIE83g80TcUQe/aHlvbQQoL5YonWjqzE/KaZzTFujq2X1IsVMWeyMqL5aBy2qlEGVBYgtZ7NqOo5XdsyDD1+6An9AaKwCq3NXJwvmTkt5g9ADgljnHR0IEXwvpf52Q89nQ+FeeZwToL6u5vnLN54gDYO75OAxGPLawwsr39MM3tEh8EHj5tX9Gog5zG4iwV8MeL4rmW0aiWJ3AR6qeP6NY5LpQoLKxVH9ZMxHPuBHKIA1CWpPhwOZKMxTc3qbI2PibqpS1eCp2+l0B9jIioEjA0BYiqSRIrb+zu8D6SY6IYBPNx1QwkEZN0ZyQMTEKTKuSnIJvH8csl1Dvxw+ylvVJlVc8kuHI0mt0bhlEIlMfoUqRzZc0gRorTUG6NxrmFoW25vrkFnkTNx9WTKJPFVIMVAjBmUxpS21BSTxGHjupOTMNBjQMVAvZxTNzOMEw1opcbCBWRV0ziDcQbjKoxzpaXeTnrLyXeMxWefMl275/Dyjs31xwztHZWTxH7WVJAT7d1t6fQy5BRIfUvo93S7luuXn3B9eEnnEueruewbw1CKLoiBspautgdXlzx7/qIUWI57chgCm9t7bm7u6HPCA48ePeFwu+fDH7zPhx99iKsdX/jKO/zK3/pbwjIuQMoE3Y2SVCkci7EpEXzADz2VFQfu3WaHqx1GL6bnELwvBkYAEo/EFIU1OMVuR2PVXIqZRh/nhdJGNJ6LFBBR5HpEm93hu5YUjsBQSpkXn3/C3XZDH8LRGOkkIxnNk0bQNWYlnXulYBLHgjUZmwN1HIjdjrTfomLCKYOzIkmgncVaI10LRbs4F5BwGAJDiNi6plmtsM0Mn4vG56jJeRqX/xWF3xEWlH3kCBCKsZM67lHk0kqcYSJx5NLhI0Itx8Kgnoytx/VjBFRPWafHcxDwamyJl+PpkzV+hANPzvkEOFbq5Ld5WjoKoFQ+WxWtXl0+x1hc5TAnTNgYXmeqyVGmHFONrG1zzJUyxRyu3KtSaE9FCm4EmwSQ1UUbV09/K58x7t3lS2VUaXsf91aVCx4ClJt7BGRLxU5lIVRNadtYWM2ZrEZpP2HkxRTxfphY06N5m9FSsJaOVikwcRqTqkxVixxB7URvdMwdyRJndL1nf2g5dC3D0JW4HYwyWDImHo0+Q0goNXqyyOeEfDRomp6EHhmw8rxHQHfsfAXk3o/DQKViViYJ9W67o931OGexzogEyXKGrSrqmcU5CN7jhx2+HwitIXlIASFl+URUI2kEUKmQpFKJP8eYhGlvOo4fTc6GkWykdMQYRbYarxVKyV5AlrzGJ1Go8F7R9ZZd69i2mSFGfJY8abFoWC6XLJcrZusLFmdLFosFi+WC9dkZ87qhapwUkZ2VUVzGeS4SY6rIlykt/iFf2e9I9QzqGYeqBlVJN7RxKGPJxuFcJSZvVky/UHLfY0h4O9APg3RQxbLupDitezmVQnA6ycOSyBIqbVDaCtiJxGkJIR12AQ4+0Q+Rvh+Itwfc+zt8m4jGkZoHxFTOsYPUd4R0QPmAUYmmqkWz+2RWz5slOkQG72XdN4rGVWJmhpr2h1RyfmeKH481YAzaKlQOGKtEX9k6Ym0JOqDyltRtGHbPcOljdHOFnl2gmhVGGVkbQnilYPz6668FGKtmC/p3fpFwvyFvNlT9LcYPWFVczsi4IVGhqayTiUtCVQ63XNE8eMj1zXPeGd7BsmCvoT47wy6XZOeIbYczmuR9MbSRyRwRVmWfM52Cq69/jatf/ibzL77NNvaCoE/0+vRKcqa1hgTBWDa7O25eXHPz/FNCd8/QdojukWK1aACFq463+r3v/THVD/6c+03LYnbJy13H59stLw97FDIAbNlESJ6z3/+X7H7j7xMuH5CVIugZ7UaxSQGdI05lbOloKdigtHxwrEDHkAk+EYKS6kubQDlsM8fOzkizS/jO90j9jkiDj7fEZWJ29QUunjzmb777hMWL/4u/+L1/x+7lR1grC9PoEDqia6po1KgsyUnKI/NTXtaV4CLLZmW0oW6kgjO+Us7HDYXRrbF8zLjZa2n4EIE9NW10qgCTqiCcSokmzjAMR3z21RUfbS3khE+Rznv0YGj0OVlrqYIrS60dfexIEcLVBfG3fgutDFY7lHPoaoap1qhxAVAa3VzhO03MNUrPUbNzjPHE7Utyt8HaSFK1GCBrMCpjrTAxKa0kWjuMBlu+VAFGS448gQZjIHDMCUYASsZBpOCEhdkm70tHTKgcMOdYBOejBAMU4BVQjG2N5X0jMAtHZjbCCtG5sJfGzbMEzxMKfJpm52PwddxZ5TylmjCqBCdy9pJUlUqDIkDO9L1Hp8i8cZAVzjlcldjuOz599hLvh1IVHoO5EpyfoMK6BDtOj/pVJSSNAR9azuYVX3aKf9hnvvHGCmuisFW7W+ZzaTeltJFkIETIiAacrioWVsxzMtIeNHgvgTsZkwJx6MEZHj68RIfAtz/+NmGQFp+xQIGammDkmWhTAjNKFVk27qapqJuavu/pB082wgicOUfWiroyLOqaq9UZZ7MF1kpSJ+7oogkVkyTgV5cXXK5XDD6wa/sp5ohJgLAjO/AU7JQHrY0kFc45ud4sQa4uLRzCDtdYJc9sNAManafFEbgAmVqYIzLwyzM7qX7m44dP4OzIwp2EOU7mvio/yCdjAI7zgvxIAAAgAElEQVTsAvn8Mdgemx4Lq3L8Gsf/aRUWqOYzludremPxu/1x2E+ffGTkCpA2Jk9yJUbB7Hd+m/43/i7xnXfp+pbdYQPGUZckpus6Gix910kgkxTNfFkY3JEQIsNwYP1whVaa2/uA0QofQ5Eb0MznC6qmQRd2zf3dDcNwIPiBFD3W2Kn13xqDohJt0hhIKdOi+Lf/5J+gEE5l/vRDDpXGPHqXqllSu4YHqxVnw57QHojPt/Dvv0MzDOAqEtB2Hfubl6y/82+Zz+ZUzYLBWPbf+nWWT77E+eVTfvXX/z7nV4/49rf/Jd/73nfYbp9hbCr6VCUpLK14ApqaoqcmBVOV83RfxlYp5yzd4UBVZ46qp5BzYOg72t2Ww80NsesLM0NJm84rY/wvv06B2ElDtjxfKcyMCa1+5b3v//SnhD/7U1TKfPnLX5FCrBan5BD642emSOhF/3lMWEbgPBMFQEkJ37fSrq01tqqJWlpdYSx0W8auCgBbkvBxfReGCzgniXLOCd93U4dQKTvhh1aYvN5zf3+HdTXNbCaa2Fmkj/ZdYt/D/QCf30e2bcWQK5KbY+cXzOoZnDjNphiELXGyWceyFQgbVNZvHyPb3ZbPnz+n7TtAnHWtcqzOrrDVAm1r5ucPMRbCACFKjBCMpY2JPitUPefi8VNhnPtAjon5akVdiZa17zp08Hi/l6Jtqug6QwwBV9c4LcW+589uJybc5jDQNDO0VXTtwG4/sDxb8vFHN/gQSNlzfrEmxYHrF9eFYWN4/OTRxOTJOXPY75mfrWjDAd92xCpglJbEM5ZKO1pAWZ1QVovhD2mSXZjy/5MhO/ge55wAFtYQh1iKZ7K+7O7uqeoKWznsrMZVWpJTVxFS4vn1NQ/feCx7hvc0iyVkRdd1EoMZLS2I5OIYL8HGzfZeOt5QWKXE68CMxV9FLh0BUpg7FuHH/9FospH95xD3/OT5+/wzvaJRL6nK2/5wpfk1r3mTirpa48u6IMCHBFCz+UzmYowsFjNevnhGfh7JMfH4rS/SeTGfG9dnY1xhbRYArgB2alz/NUQv7M7oPU4btDmTgFxrKidMZJsiSs0x5hwo+v0SWGFtYhh69vsd7X4renNuVvKHTLvf8vyjH0LcUdlEfe4wlWE+b+hTYPvimtC21PMzQoI+dmyffch3f//bfP97f8T19gXVzLC8OmN3v2MIA15lVOmosFqzaBr+9t/8G/z7P/oTXry4ZrffM5T42GmDUWLh9IO/+BM+/exjtLJsb7Z89Z1f4Nf+zm/yxZ/7Cg+ePsIPHp2OGrtRicwM5a5qbcsYF1Oa1eqM6+4ga6bvae9fslrNqOuZgNghcDjsOFudEf3A0LeQIrP1xWQUO8b4I3AWgmd7f89ytRL97kIiUdZO5yW4U6Kq51w9eguHopotpkJZSpG/eO89dod2kj4bi/U5jyZGIiszthnnsXW8rJNKyb11QBU9rt/B5g5CFBOeqhItYSO5kK0drq4LaD22mXv2bUu1WtKs1zRnZ/iQi8ybsB3NyFYtQdpkelR+OBaPR+O28bd5LLrpI6t1lIkTz4djIX0kyYxFkr+KWXsEqORnp5qxI5goRfOxZb8UuF8/L3mY09FVmSd5POfxN1lNBSPZM6UIa52d4gGtpVNG7ks6XkO5x8fzHuXJRj52AXuVKeeZS4Fa7kPKUqA+LSyMLexlwUIbLazuXJZrxsKxrCVivJULl0WuUaOK5Fye7o8ApcdYMyTpdhp8KDrBgZzFvDMpWVfGtTTnTFcMf1UpBButcbYqxC+Ru1JF+zSnJPlHDGx2W/aHA+YECB67jpyTv9HmWGAW094iicOxG0nkHmJ5bLnkuuDKvdMnrHZnK5ytULp0cSSIQUzFQhj3i+LnYYQs5UNph09R9GsZGALQSy6x2xtCLsVx7ambmqAUfQjFnDByozKhU3RzzWwxp6oDzgw4PaBsAc20LYVP6YyeOkmzQk0c2oqM6KcqHdA2oyMYqzA2ogZfiiwJ7xX9AG0HhxbaPtD3kSFIljtvZlydLzhbX7JcX7K4vGSxXtI0DXVd09Q1Z/MlxplXuxBhmkuSa+hxN0YhvhVf39zxKCT+4M0voc1CCoNGuoRQVohmReprZDorgApmszkxJfphYBgGunYgpgMpeXkeMeIHMb8aQqKPkRw92lTYbDBOQdYkZfHJ4JPCh8S+j7RdT9e19Pc36P/x/2YXFbg5Zn7ObHkGboZLDYNaM8Q7iBsIER0jB22ZL0+62JRivliR/FA8cAKUPNQYg9UaU1jYWY3yHA5lajFLNPLV93tub/spLtfaidlkDmg8qr3FtJ+jq0+wszOqsyco1UhMmDIm/TUHY5uHD/jWf/Nf47cH2mc33H7wQ26+/+cML26oNwcYdnT9QL3bUW+3GCIgbLZ6fc4b3/wW7//b36Xd3rFcNDTWcv7Wl/j87S+wu7shbG9RWEzWJVE3RAWHDCErYu3QVxc8/qVfJK/PaFXGpjAZWExtGEX0PGWRxxw3t5sXdzz79BndvsWqxKOrNU5n0YxVsBsUPhwnyAcf3/K0r2kuHxKi5cPn19wOgWAqwKGyRWUnOrTlM5ff+UOGt9+h/dovYQjC2sRIO1qWbvDoEz150pk53SQTGh81MTviYLH/6qfoxSXeJDo2RDWQeIxZPMIsHqOaJ+j5Bd7UvOwc7z2PvPtr/wWffPA9+v2WNNxMlVBdtCp98OQUBKxWApaegiUA2mrRWQ0JHwaMq4RheQJVnGoAyvca1KvsWDjZDE+ekSw+ZYEvmnLA1G5slBaHv/HOqGNw4QvtXrUeP8BqfoVVlkMR3L/7T/9jQu3IWqOVo56dUzdnGLcAtyLqJUpvgDBtfAw7UA0xe/TigjS/QGFQpib2L1FKQNasxThkbBUcnQmtM7hRlgCpgOdIYT9nyEoYG34QsM4akXNNr2LPk7D9eAcnzSNJkMaAVP5QWhZzPiYeKYWi6VICtSxJ4LFCnSfQNBe2wli8OFY4xwruKQL8+ksCEYlYIqRhAoXl70IhyZZ7VYCEvphvSetvT98PdP2AT+DboRz3FPCdmjGn+6JQJTiIoOTYWmXmteGftlvemV3wYD3nvFqR/V7YTl3H7nDAak1WmpxLC6hbMDu7wNVLTNVIYK9Vub9HU7VhaPH9nr7dstu85PbmhrrZYIzl67/wdT758EPavqcPA7tujy2gWOMqVvMFq6YhBmkn7L0Yx4y4uNGaOPT41qMrS11XzKoZq9kcZbSAPYMnqh5c6TxwFqvtpBtmtYiof+HpI7p+YH9okbVXAswRvDlOKJlPdnQYL/qkIABr5iRYL497BKtGJ+bjodSJHpck3yPAqsyrLMhpKJ0ee0weplVBBvqprnMeTS1evYTXRmR+ZcSMxxTgAAlaXvurqMA0NS5E/L6FlATM1FJ5SZlissUEZEuLuehthSDBjNajtE5ie9hQzxbMzJLZYkHwAdfUosebIr7fY9wKbTVZRbrDjqGH0O2EJdcNGF0zmxnUnKKXZhmGA4ftHd1hR/BBRPcVpXXTTAFdyqI73QJBSWvpqenSy/UZn6zXPPyD34fZn+FmS5rFinD1gHh1xfnnnzO/fsFQOWxKtNFL66/RhLnjoxefYTPM6zn1rGG22zGsHxHOrqjcjKd/7z/jn/7Wf8kv/vw3+Fe/+7/yk4++ByahrXQOpCzFPlXu6eAHAeac7ENDFDOvqGQ/MAq60LP3PUorqtrQHvZsb28Z9nti15IG/8rQ+v+TvnidLTsmQScDVPY3K/9/ql/uY+Lzmxt+5w//gG3b8qU332K1mGN1Rlk96R3nHBmGgRSDMOvHxKdIkJiS2PRZWH4ZGIYOpcFVNaCKpqwkmBM5t6ypedK5i2ijSOFkzU/+CADmSN8f2G4202fnnJgtZhjjCDGx33s+v43sw4I2NexTze2hJWeDMq6wSBWZV2MAZzSaV/Xip3VEW7QKxWRGUxXtXz8EZk3DarEiZylo17MKW82J2VA5w3qhsVqS2B/+7Jqfvv9DXr54QRxaNrsDzWyOthXaSkvuZhc4tAO+7/CHAd+2iBmasNNnsxofpRVZTHg9GktOiuAjvffUlcXVljo2LBYNz559Rs6B3e6ezd0NZ2fnLJZn9D5w/fIl3/uzP6X9tW9BdYa1hi998U3ix39C0Eva+oz2douqZT8ZNQYlyS+tjxGRXiqgqnM1GdmTXx+9IYie++ioLuuPAG6ursFpklVEC1HJ88g6Y2rH1Re+wL4/oKOMd997QKNiRvtICp4UMsQ0sZ50aYW9PDvjydUlD9ZrPvz4E7q+ox969tuOGNQrwYu1hgcPLokxcHtzwzBI/KuMYnRS6/MBS6Aqf/be9/6Ql5df5GJ9yfn6EmOXvPPh51wNgfliTlICkCpAG8uiaXhajv/8+Wdo51ifXxX2dZFwgCLnULQYhTbIxJzte4Z2w2IxZ3V5wXyxImeKbmLGlngujyzKsn46Zxj1ouMwUNWWenB0Lbx4/py6slxcXTFfLHFa4RogiAHofH6GeecdmsdvU6sKFTXd9TXuQvGD7/4Rf/r7v8MnP/4zdvt7fPRYBykrnl9f03cDKsNqfcbjq4fsDnvatmWInuWq5m//+jf50Y8+4L333mfTDihlCyPYkBM0ykj8kDwxDHztb3yNt3/hHc6uLolZY2wFWZNjKq3RA86McLlipAFKHC8A2Xp9QQw9dmVZLNdgrcw1pK306vJSCuv+QA4tdT3D2hqFKeSE8Mraq5Ti/PJKYqEYGXyQ9lSlC3g1AlMi4+KaBQ+/8BWykjZUkCT64xcviUmY5owyRjnjoxc98TQ62Y98/gyqmCoTUbmnCQdsd4/a7/CHHdon6rrGVJVoqRuwdYWbNZjaTUBkytD1A9vdFrdYcHb1EFvX9D4yDCMQW8DFUiwU3UmZ7cctJh9jmZG1OnafmVfjm/E1Ml9PX1MBosT+YyeIdESVOH9UhdC6mAKNQKw+if9UYXVKWc8YNz2z8XzHWF1C/1iOLxdljMLYAhwpMxEstFInsgfjOTOxQbWWjtsjQAVTAX/0ddAUKYZyjSe5g1KjbujxFWMopzsSAZj25GPeqhEq2HEVHkF9MJP+rcmanK1ISo1MV8b9VRU7RPn0yjqsMVQu0XvP/rAvnyXn4KyeustSzlhrGfxwPK9UFGSLnEGMUliYyD2Aqxze+6MJY5GomEhqMR2fP2M8LPt1SpEhDMQ4srelE3UYPKcM11CMVsOJsVnvB/yhFdJHykVWp9x3rSCXuDcEJum68jKK6Ty10ahS2FYonBqB5zlGWxodaRoPNuCazGyRmNWeygVqPUDsyIXCF6KsVcacsE2NyCVJDF8gtSxzS3INySOzimgdsS5jDNLNTBLt1aCJwTEMmn0baTvRAj6fOVbzhuX5A5aXbzNbnjFbLTlbL1is18xmczFgHAsNJwX1sbAxzfcCHOccyUmBzqismC8u+fn1I761vGRIhv/HOT5TSljxaHIUr4mYpWigRzbwSTEkFSxiBOdjDPQpsN/vuLvbEpIipIyPYlwp2rQWa4SshG1IqiJiCCkztDv49p+gP/gx4eWn+Oc/kTEwW2Mv3kQ3v4pZXOLMGTavoWoY+pa+fYnqWsz+wOzmGe1hNy0Ah/aAIuOMRsWSu8Yg47SAzyOJJ+UgvhYqiLa6kUJ5ypmQEyGMIHOk91G6RoN0/oWQyPstZrdh5T3zxRXaNCT1/w23/rUAY4dDy4sPf4abzTAPzjhff4v5F9+C2y28vGP34w/Ity/oskbf3VPf32LtJUY7VDVj8eRNVm+8SRc8er/DrFa4+YzZk6fsPv6Q3ScfUZOxSFU8qYxPCZ/hoBLUDes332BvYCU9BZOIdT7ZXEWUmmIiUVE1S7abLfvdPUN/YHV2xpfe/grt7iXt7o5hCJAt9WxOVdfT9ZrZObHytKrhxh/YxIFBJbL03qE0KJ1OFmrAD9hnnzFLmfjVbzBuCiNEPM2LsvAnRm0gRcIS1ZL80QETz3HLL6J/7ldJpiHFhE6BxcIwRE2y5+TqnNysRT8WzSEmPt4MvP3kCWePv8z+5lM2z/dFy9QV7R/FsjmnbuqSrIge5tB5zAnjJYQoE3xs6SkBUjxJ6qcWo5PrOW5or0oNKErDhx4vv8gVKKkkjuZgx2X6tOlqBGPhpz/8KYfDHp8SKigOux2uXoiEw2zB/hvfwqwfTFUSYxe4+hxlZiTVEGMlLOCT9hqdMta35DyQkiGFATs/x+gV0UBSktiOYVEqYOMoUm41KCJjZ3guVc4RiM2FMSxOncJUTSFPAPUEWpPE1XPUq+Dkl+N9LeYeozbrCIqNrSiJyBgYyUYvnzBV2lOazqEgbOUGnwJfmZMHUU5iBF9PfjEeIwdI/pWfqRO9WPGyT9P4j2TaXiqhsbRuZ6WFtavG8TI+n8KuLZuKzLUywnLAqMyjm5c88QNvv/mQL503XNaKhY44o8XwNEuiOG8ahn5AV3NcvaRqVtTzc1S9FO0drck5Tkyyo0EAoAzaVlT1nMUykrOicjXGVry573l5e0MXPPjMom6onTj+VpWjqStMuaW6VJljltayoe8hCWhDFC1foxTrbIm7VoJ3o2DRoG2NLg7XkhSJLpPRRScoRx5drnlxfcv17R1diCUAVq/syRMujwCnKoG1wlAY28Fe19Yc9YVSSlhtpzXvVBd2BO6nIHtibpwYvaiTf0v1XquTFt1xrJW1Y0oyEsc+9PGlXtX4PLI1yrjLaqo+j2yOkS1wfGlhG1UO01TEtpsCJRm7r7ayj2YZk5tvAaKrn3yA6Xv6r/4CwQf6rmNoetI8oo2lqpuSxIhBgas9rpY2vHa/lc+JM5pmxsXFJcpY+vYgruk54oOYchltmM+XQCL4YrhQABrKWpNTFt2jPEoDvFo0wxhUXVOjCIctqTvQbW/4/PY5Nx9VPL655Wy/J1uDr2qKE4YkSlVDrhu5vsMO63tmIbHvWm43L2mqhid/sqCyDW9h+Ef/8D/nd/615vPnH9L2WzCRlCCkMK1xrhKGphrNFpWaNEQzuQTD4vgaYsIfWg539/TbHWnoUVOHxauD+1QC4ziOj+P79PVKt8LJEqdLO6Y+eb/ShqQ0u77nvQ/eJ3rPk4cPubq8KCyd4/Gds5KopUTIqYy9PK2xSivqup6SJjG2kbGCUlNiVYb7NEfC0BOjJErGGnQpVoiGrRczmhCRimBkaA/stztQGlfV2MpxaAcOXcfuELnZRm7ahuQ0UVuGDF3nUfRobUjRE4aOXin6/Wa6F3F/Q1QVuN3x/pT2wKwtOQ3MnxiWDy2zWUPXdWw3G0iZ1XzFcjnH6EwOXWmBNGAadFWRUuZ+u2d/d82wvyd2W0Lfcv3sUy6vHlA5h9GG3li22x2ohKss2/utGFloUYns+579oWfWCHgZ/l/23qRXti27zvtWtYuIOPW55auZyUdSpJSkZJEN2xIsyQ23bMANAf417rjvfyG46YbhAjBky4KopAqSKZHMOvPlq251qqh2tQo35lo74jwmIcOQ4WwogPPuu+dGsWPtVcw55phj+IixFdGLe3YIifv7LVVVZQmJxP36HudEcsIoSCbiqiozLw3nZ2eMw/Ywj1IijSPXywXD9p5w/46vTt8jmWxGI+1HeXrm7qCYZpNGKMznQ8Fpjq4SsxSFQgzRZoZ/gqrJXTuqADYaW7csz885u7zm/OoFt3ev6NcPjFNPjIHaZnktKx0N0zTMiXpEEnSdQVBCpDKaTz/5mF2/5/bhnp91X5LGOIO2kcjoJ7b7nQDEzjGOcn4WQCmpHBEWnwQSX959xm23Z3lzyvnqihfP32eqAr3T/IYWEL9EMCnv8YuTU0IM7DYb1ve3hJBo24V0cxFFT886CqHjoAkp3UA+DJydnlHXtTC6ZhmRBMHjx0iYyLGp7LOEgE6OlPVaITGOE3Wz4PpZTYqR+7dfsH14hx82JO+J40gMA9aBrh3Pfuu3ePfmDj2MVG7BFz/8PpvwF/zkz/+Uz37wPaZ4DxWoqMAr/DAx5OK40popRfqhn/X9vPd8/8c/4O//vb/D6fkK5wz/8k/+DI0kpCoXkWxUIouVhAf2z//w/+Ld/Q0ffPQx73/wMc9ffIh2rRjQ6kBIzEY3EptLy7TJ7dFKqWwo1GOMZrFcCnNybvFO89yxtsJqRd0sJL5IKXc9eEAJWy8DCtroQzFcF0DJ4JzCmKKtGVGEjOLYQwya/zvE+RAQOQdVzMWy1EtUEuset1DLwQDBY8KA69a4boueOiBQL5zkE9ZKrGA1OGGfC3NPgIFu6Bn9hKpqlucXRG0YfJhZgAVCleV+FFPM0dHjWEPO9PwqdQBmS3yTg5pvYrCPHiEEYeeXuFqpI6D1cE4+/v2hq0hRmJ4FxJNrDCETIQ6Z3ZxfgprNOJUxooGeZekK609l0PdwqB3iSZVBWJ1BuXINwLzvHQzI0qED9ptpSxmr8m20lgS0dMDM8aNcgzBTVd5n5f2TKmQY8lipDLwmUlQIE7nImuXvU3JbLfvPPL4pggpYElXlpMAd5wmRO3GygVeQFvKCa4SYYC7cyXxIqUgKZMKNzoSrLPdUVQ6bmfQFI5kmL+DUNGX8JLNGsbnjTcg53gfGbEJXZOjmeZnH7tFIH+F+0zQK65wkevfaZVNyAZO9F2DtsB5knuhk0BS5QQgqEjK8vbCVyD22LctlpF0lFouJthpoq5G2EVM1nf0JyGxfitRDUGgT5Uf7Ob5U8+lSiFWQTGYPm4S2SYRbs1TBFDRTShT7tUpFFivNauFYrU5YXTyjvbymOVmyWLWcnZ7g2laAWCOxoNLyqWSzuUJiSeS5oI5j1iyrEaHvB3TX03Y9J8tTfr92fGYMf6G0eAFF0db200iMhwJB0acuZ2hKUlwZh1HIUP1IN4zcP2zpeo+PMu7Sh6ZnGTE5S7PWNvKZ9g//iPDznzHdvCFu79Djfe5QHPE6Ma3fQy+uUdUltr7EnF5gFiekzSvi5jVp/QX77pXIEeQ58ub2DYzSPaVNZs4bI/J33sv1lG6IJHrzIUS0tTnmK9iHyCMWhvYUY176ZTPM50KM9N1GZqNbgqkfnQ/ffPxKgLF+v+P2j/8l1dk59dUTqotL6qtL7NU16n1PurwgvP2aeH3OZBJxt6FeiXOcthZ3ds7Zex8whgGGgdVyga0cy+fPubu6oq9quqHDKakMhCRaHKPWhLbBXp5TvXzGeuqp/MAiitFQcSmetU2URph3DmUcISbWD7dMU0fTOJ5eXvH06TVfDw/scmXJ5NaY46QrYJmwxKi43ff0MSBnedZZMfpIF1HlA1Khtzuq8Quqq2f4/ZCNEUD0SYAiuJ7XecQRVUO056j2KWYIGK6x+tdJ7z8nJmjihFMD56sAPtGFll1s2asGH8RtdUoT931k42vai/c4vXqffvMOpyPW1XNFsq5aqrqiHKwqRbwfUOpIgiAEgkKYmTl5DN4fgSbMMc/cXpcPw3gEyKLKJnM43gtoS1L5+ZGQWxcOR+fjY1UOJM+7N++ISZGMghDpup7x6XsMpwsGGxi/9ZsZ5DVgKkx1AqYlYonBMKUEanhU7RM9JIsKSnRUxh6nEqp2WLMkKs+4Xcvhr6T9RPRARbJAYrEsqpEBqXKwHjtYpiMwVg4r5k2DDFOqbCZVQNJjYKCwElQqjKeD/pSMvTCSDvzAks4dopTHYCz5fY5GOSVS9BxuXJKEnviN58q/Ha4lt7TMAGwGjQuYepRhJmD0HlEuiDNQJgAaiC7TYYodjiphk6v1FrVdE9PA+fmKF9t7Pkmeb8UTzpcttVNoJcwxpYSJobWhqjST11i3oGrPaJbnuPYMzGEtxFzdjSFlzFvulewvcp3GWJp2IYFyUjx5+YLzJ1f0Y4/3I844lnVN09TZBV0RpgljFDaZ3NIUc2AnraPytZMAS6OHUVhexIDKmiZ6VWzd1LzWtDoaoRQ4XS04O1mwaGr2mx2mxNzqEPQ/1vNKOUiW4Nfngsiss5Wfm/KcLe9R9F8lADz6jDxGx2BsKGstJxMz4H4UWJfPkmP08Zwtd/84gTj6Akd/zXtxvi5JBvTMkJmv4dHLlDCvKoddtPhhnAN4EtnwJgMh+YUHSYZ87CuDfvcOHSPh8opw/ZRh6Bj6PdM0YKsFx9pwfvIMwyCgDCKhYbSddTybtsU1EhD0MTIOI6SQdQIdKpl5/avgRW89A7KzAYSfHi/Vb6RsSWv8xSXm9i1p7Ikj7PuOLRH2HX0/0sSAWixJrhIpGBXQ1mLbhRRJ93thBo89PREzdTRVjfvRH3OxOGd58ZxPf+Nv8uo3fo8YIq/ffs44rfN1FoaOGNOhpCXteP49MhfJ52bwI323o99sCcMA2RH7cGIcXnM8L45B+1/GiuXRa5nX+qHo8HieoTQ+el7d3gpr2U9E4OL0VM4TdeDVhOiP9g5DImagVJjpc1dIApXNS7QW3ejysamAcTlQD2EiBmnPLvybGKXzYhg6Yswtghlk6HY7um7I5m8QxsBmveNu63nYRe72mo4WXSWwnoQnjCOKQFRaDJ/ylUz9bh4Lv7sn2ha9OjY8kPNFKUVqPdWFojmz1JUYA1lbo5Q5GJfhSWHIrB9N8DCOkdEHbu8e6PdrNKIxFqeB3cMdq2WLig0xawz2/Z52UWPqCh8Ddb0sGTgpJdbbDm3FsXicspEP5SyO7Hdd1oG1GKPZP+xRCow2OKtxjRTB/DSitbSbW+0fseb73Y5VVfHUeMJ0y922ZtALUmqkoJHnFjk+McYQtToUUlMu+GZwp6yDlNc6iZlFOx/NgM66c1GRWbcW4xyuaamWy7l9MQTPOA4wBSrrMplAo3I3UsoTP6USuym8F9Bt2Pc8e/YMWxmm4EVaZ7/HVcL4DgT6Qbo+nLXYusYMnkcpjVJzUlsWx7q7Z9t7Hswdm/UdKU3c1i29qWlpeKZaXFWj8npISViKabXCgOgfbq5lxIgAACAASURBVDdAoqGRLg9KjC4/Rd9Sp4gKErMsF6fYnLxJlSmQbbIp7GRjRK+222+J40ioa1ztsFWVCR+RumlwdUUMgXF/j1YBP/aM3Z7gBYyNQc6hJx9+wA++eoPqRxa64usf/oAv7+/46oufcH/3mupUo20FvrB4c5KZAeAQA13fUVfCMhzGkZ//4nOmGLh+csW3v/0RP/rJT1n30kl4AJAEgFJKUTvLT3/0A3bbDbevv2Z/d0McJ86ffkTdLMTcltKmzKMzhWTAJtmv8h6otEFbN4MgJQeLuU3bugqFw1YtytiZmTZLJuV5URiSJW7QGSAXvXojUlplbhYSgjYQxkeJcyy6p5RYQDqhjlvGU0lI5kUk91+FEet77LDFTR0qTUIGc4ZkTDGKyPFYMbmJEBXBB8bgCUpRL1uqdoFPhW2dTSXn8yTH5RkHLDkRGfOZ94n8u0fpkCp/TY///ZdAsgetTzKDVM/gmzoqbugcK8GhoH20aI/A2DzGR+agxYizvK/Oc8JkEFBrI/JyM9njKMc+OlsP52zuZsjvXYgH5fArLEohTgBF6/MbsWDZG4+w1vyROt/6EpOW35WYIM76pySdW/hV7vrLLE5y/paBLa0CScWj+3B0TSWORmI0n4FWpZW0ZZU4R8WZ3e+zgVfpgjgGw4uYl0LOpmSO5kGZOOooxlbSlWEzKcMaK/IlKksrKKRYlf9Na/HPMEac7KeiZ18+X6mcTx3IO+vv/C5m/ZBzXNEonbVuSTjr0AUcK2BskZKEGbRXWaJC2uvV7FFitGZRr/C1YWwVwxL6i8S7dmLhJmo7UldD7hyS+SsSUB6JuVOed0ZA1nkdHHKB4ncy+VEA6UmMc/fdjm4PfZ/ousTD1rIdYdcrNh1MI6yWhq5t2bZnNCfv404vqNuauq1Ytq3sj+U7ZdOZmA7355gINWMqZb2lzEiPCe0W1O2KVeXE+KuqeG0MP88kBjHjhCn7AMnLRBtejNfUrE0bI3hTM1hF7wy7ynATE10/SlevIncAHzF28z5a5BNSiDRnNf7XnzN9dIofO1ToIUHQjlgtSc9eEq6vCcsrpvYE0zQo/5y0vSFu3hDuf864/ZLp4nyexttuS+gHxFxO9KNrY2bfoxJHl5xd1kxEjROo0tVZCkpZC9yHLD2mSElnmU4jElJKM04jiR1qSigzPsa5vvH4lQBjVbdn+7/+L3gUoV3B02ec/sannP3aJ5x/8gnvf+fv4W3ifvPA3XbHeuyI4wja4azD1C0X3/qUN1/8jD5O1NFjK8PFB+9z//4HfH1+zvr1jjrBFGGMon+Ulpbzj97j7JMPaT98yVc3d9j1kmpZszxd4uwCpcTsIwbZPDEtSgu74ubtG7784ie0LvH8w/f49icf8/bVZ6w3G3a7HVppTk/PeHv7wNgdEo31eoPdbaFtebveElWaDy6lDbUTZqRC9Ao1R9WxKbH67j8jbPYwROmozpt8cXwOEVQyjOacsX6PeH6G/eBbNO9/jF2coaqWKSRa47luHU9bxxl3XDYV77aRL9c9P9okfMqTFM/kR17f7GlWTzh/9i1Ct6ci0NatOIuSGPoBP425jWhg7AdxCSxCdZBPsUNCqZWiiDvP86GAHKVSppIIas9H3TfQFHmjDNTBlEEociJQzHhK4nGMRIYY6Mc9E5B0S9SOpBzTlOh+928wna6E5afFoMsrLe1LpsZPAxpPZGKKCZ0mCFkDSSlSvQJV5RYXSxg7TL+jXi5wqyVmWbP2HXGaQEWsa6SlR0tgGHJ1swQ+JbEq7SWpaI1FT/KiP6ON5ZEMekqkOJHiBCnOGlKSlMkBIxWtrBGbwR1h08wwGyU6SxwFKBkQLmArR68vP0XOQDb+8fE9E6X0HDIeDvo5kC13OwlYqmcWT5yTO/JVffMxB2ElOM3grVaHjE2R0DGCH+Sz//x78Cd/SvAd3/qD7/DBiwuuL0+wesDoBmfF3ML7EWYjHUXC0K5OWZw/w7ZnaLckJIUuDqe5ylbEzFOS6rQwf+XehXEUo6cYMUpTVQ3nT6/41m99G4XnVco6hm3Dqm0xRkvrkLVi8OYsOoR5TEw57IJl3O3QRKKfeHv7DoeiVgrlLPRjNk7Mw64SJms1RpIkjynRNpbzsyWX5ye82+wkdDsKDAtTmzxrjNY0TQ2IbhsKfG4RLPcnZH01pTR1Xc337Nikq3zGrDlmzKFrIVc95TPhETMjz1FtcluoTByppJcC219xMIr7rn70O5Vbgo2I62Kck+C7zNlvJhs5WtfOUZ2fsN9ssomNfL+qqZnGQ7sYkOUGYp4b5e0S+vaG5p/8Y3b/5X/N2O/p3Jpuv2ShDZv1HXWzpGmXJBK77YbdVl5buVqcV9sW6xzDNLI4X2J6R+qkdb2qHHW7JEwj/W7HNPSEMBwBi5K8ChA7EKNokKaoJRjVhzEMPtD7wC8+/TYffW+H7TphM9c1aE23OiHs9zz94nOm/R6MRjuHbmvc6SmmXZHVqAgKvLN4lSAMjKMnvv0Fw2rL9TjwLEb+kz/4+xJk/7nhZ5/9W5Q1OCcu1yCAw2a3xXtP8IG6dlT6wMaIWQjITyPjfkd3f0/aD0gBKOvIlq0oz9njxze1Yf9S4vZLXvOYtfM4PZ31+VB4Ep+9ecO79Zq3t/f8wXd+D9CHea8QAAxpma7rGu9HxmEkJcVisRCmVSlyzEzu3JGSEkbr3PGQT4wk7DClSvFC9tkwdfTdlu12A0okmlKIhMlz/7Bh9AqcRUXD67e3vL71bEZLFyq8WmLqith1wF6MrTIrJmYN8CxmTvCHFsWxeyC1onBWHuIw7VE6woseVaucoFecX1xzdfWScewZ+x13d7c4d0FV16JNGQWI3fWK3X7k1dsHfBhZLBeMQ896/UCcRgieGEZiUKhRNKNtXWHEzYFmuaK047qq5u5+j60qqkoxjJH9MORClZiqDlNPjBpr65nNPPkRhaWpFlxcXHB7e4OfRHLCVS1N02QQQwCrh7sbnl9f8mS1pFED65/8C742H9O3Lwn2XDY1rXF1jc3ak4MfheFc2Fo5cZYCbl7bOsvC6IMD/WzKOU9MhYqRMAWMI4/jyHqzZpo8u82GvhsYuwn2XWaqCagzeo/SFpKwaYoKUySx3w+kIWK8QuMIKuJ94uzynPu7DcuTltVySVKJm7sHxM24onKO2kf6XnSKVSkjqmNkCTwe6PFhZNjuuP/RW2pd89PmhD9fXvIP0xnPX7wvEhdoQoq42rFoFjSu4vw08NXrN+x2ayY/cHl5OcdfAjQUIM4QkmjFT+OEzlpySslCCdNAigOahDUOH0e00kxjx+72DQ/v3rBaLjk9O+Pk4gJcTeOcRN1BcfX0PZaVo99v2G7u2G8/I8aB4HuC1xAD19fXfKaFIVenyBff+x4/e/ia7bTFq4nQa0yUNStavkdnZP7Zjz3tcoEB/H7Pm7d3/NN/8of8tU+/xXsvnvPRh8/54WfviGPAx0RSwlj0UZhjJ8uWzcMdr37+M26++Jyffu9P+elv/Bt+9z/+u7z46FucP32BsW0+Fl0GvngkX6WUmOzVVSVFl7wnkWN4nQo7FpQRl3BTNeL6ne9JcrmtOxe5rSlO5xJTpCPQvhzZhuP9OGLx9Lt7kr+cN2ll3SzFooCkmUEdrTVBFW+EgnwKOUHFERt67LTFTTscI9oqMBWFvChsOTHHkVxOgCkfAvuuIyqFaxtOzy8JCWFsRTHF0Rk4KHJOstyl+MJRrDuf5ynHrSUGfgQoClg9G0CX9Gsen1zOTgmtH2tIlnPtmAlbCp+FuKDmDywF8sPjuLNEWPG5oOicfJYqeqaFBVuOtnT4Elk7XtrFi8SVnkG+uZCfr2G+1uNO2AK2F2vTb2CS38w05HuJ90kAyfVizOlBWV9BJgyi+yxdocdeGjlXIuXcL9+3lIjjkWFVEhZ2TBqVsu+EnxiGXkwKY6AULuabq3SOfw83O3EA5WZgW+vZwKsyBh/sfI9ibs1MwDhNdF2XTVEN1jqszeZY2lBVtcggJDHVnuNuLbJopQA0Rc80FkNEuU/OVbjiHaMUP/xv/zv+w+NX5dH8u5/y7/Px3/zn/97f0irDGMRngORxg2e0Wa5PZ6M+Sh6n5nVdyHCqzOPC5k0Rr+Vs9SHhQ1l3AixHNEQDw0gcAilpYvB/9fX9e//G/y8exjlO2xVs99iHDWGY0EZRryzVJ5foq5Ht7T0P/Y5t5wlGs759Q1id0bYr6npJdXbFpYLdww039284OzuhPj0VQPdv/HU+/6e3qBGCUajFgquXT3nvN3+T+vqSWFvuHjY83L0lDDu2d29Yv3vD0/d/jWb1BGUaEhZVNUwTbO/uWN+/5fbdL3hxfcp7z69YLhy3N1/x4x/8CWnqaBbSEvjygxcErWmWB6fg3//b/xH99/6UH37xBZtpi2rs3JZltKZSiZWtWTZLlicXvDi/wvtE3/Xs9jvW457erAmdJw0JrSu0NZIEJAgpYdtnqOvfJV79NtPVX6O3S9qw5cK+4uUq8Z3ffMGTFSxsT5V2xM1WtLSqE26Gmv/zBxv+h//9j9jer/HDGh1u+LPhljO9Z6EGFieXDNt71sNI8JMIffcTYVwzjVuCFxdY0eDp5u9unUPH3J5hhcXiM4g8P+TkyECAPFSpXlBkGb5xLMZs6mEUBKjbmhASk8/tEPjHb3/8vsaS2meMJ99h/+mn7H/v14jWoNqlVK2TAErVYiEJTpiwcSQpT3RLknYkDHpag+6ASFSG7fJj1JmYNhkCobun391hao1ta0ZfYRcnDLt7iAFnpCUkzNU/5oprOWRTHi9yxU0TxfiJbFCR249Uys37KRD9CDmxJjt/CrhdwESgHJwcRx8z2pl/FcvH5us5tDHPLyrs2BIoZUF5lWQDfAyciszAUWiY/5uOLiHNz+EoSDm6rF9+X8mZX5LPUOS6WyqQckDh0dsN5h/9I6ZxS4risjiFwLC9w3BKWzsqK+Y2ZGKxzm3OoMHW2GrF4uIltlqhVCUytkpYsDED4CLDkSu7ubqq4kQYO/w0ME2D6CZRGHYeVOLJy5fEAFXV8qM//zM6wyyQH/zE5EcB72AGC2UvkXGqrYZJ5B6MhmVT89F77+P3PdOQW0hjyNrTUpnXTlpFUiiyB4pIYLloeXJ5zk8+f4XS5tHIK1LWRJVWnBQTfd/Na0xrLYyho+jf2kOrlXXynWY9vZilEI5SAYAQJlTSx0Joc+AvbUmFsUpeN8KOLAFv9B4VSgu+yuSI9Oi6CrAr06/IGiBa3FEC5rmN8KiIdpzZjJPHxmxgZiz1yQq/2YnuWUoMGUx4/IhHQL3cl5J0SBKbGMKI7na4zT1VvaCyCp0CmsRitWS73VJX0krm40QKQcxAVWC/uSfEgNaGumnQ6px+v2HzcCsAXy7UGO3IVQ+stUf3UVNZzRTCHNCrdFh1KQb8NOKU4+e//TtcfPE5519+QSSh6xqtNdOy5Ytv/Roffv4Fynv8ODB0O/rthuXpKRUK5Wo2fsA0Dc7WWG1QYSL5gZQ8JHEZN//i/+D3Pvx1Ts/O2e62vHr3E5q6RqlEiKOcK0F0ra0zTNMkXSc6s9pSouv2bG7eMex24IMUMY6A9aIDKOORAPNIpuCY4X08hw5sjzI+hzlaxrIwCOfXKCmGCK4kSeGu7/jh55/x9vaWv/k7v8uLp084W61IcSShmPzEOE1YW83JjFKy1ubao5TuSVHYcHZ2jU0oHyhmM8YonBUjuBgDwyCSBXe3b9hvt4zjyOpkKeAmGqUr2pML8Iq39ztuPr9jPyYiLYEGbWq0bqjqin6/Zxz2TOMeZzXN4oy6aoRRYyxJJZp4A3sZC2ctTdPgasMBos1sqpiwaKL3Mr+VYtE21O0J3rf0e8f6/pavv36X2+QDbduyPDklKcswRHw247HWUVU1lauAyDj2c/KptIYID2/fEqLHAquTMyYvZq7GGmoN280e5xy2cuzWGxaLhsq5bACkqOoGn3Xer58+42F9g2saVpfnnD95jjKNaPhaQ71o0Risq/Ja1Dx7+ozz05YYW1xV8dvfruh//Ge8ebJguDxFG3DWIQKqFq0dyfe58Hc4X0XjW9q5c3Axy7mUcS3mqSRh06MV2lVUzjBMI2GfC1VJYX3EpTSvY6YJRk9ViYZdU1WMccRggThrKOooGvS76PnZbs+Xb96SvXEIKeGMY73Zstt3ud0c6eCwBuMqkR/KRQtjFPWqEg3uvYFCpFYlAkgk5fF4+tiz2W252b7jv7crrtI7PukTv7X1fPD+x1TW5qKT7MtN5bh9WNNvNaftMgNlAsSjHbpuUKomRU8II40FnQR4VUkxZT1VY6XN1U8TQz9QNzWL1SkXV9d090/pHtbU7YKTk1Pu1u9QSUkrb4z4xYrlaklSkWHcM409KU5MQ09V11TLJWdPrzBasd+uedjtuHCRd04zRC3mNSTGrp8BreWyBSPdKgU8DMDr2xvRdgyRMcC/+pM/5+bmgQ/ee4ZxLn/PQIyq1KJzYQV0BpFVEN3edgrcf//7/E/f/wtOXr7gxaef8ulf/5t8+NGntMsLjFtglKFa1PisUTmOPeMwUjdt1irPJ2+JP5MYUgkDLmGMgLdGQ0giHRIz0KUzs1Le4RHiKABs2cPzd9AoMXmOkZu7e/71d/+Qm4/O4ek5CoU2TnQf87mcEkeF1AKg5hwlCYGHyVP7icr31H6Hnga0lXglR7Rzh5GySgypqzrv64H9fs+UEquzc6q2ZUJ8OR5J4sznj4wPJMSk7HHc9O8qJM4SYoe3nJ8352HqAGg6nQ1udGG1MY+nQvRfC9sxpcDBwIkMAuYzMOW4tbag4qxJrLTFZuY6+R4++g7q6M/5vC6FxwwuapvNePQjMHbujing5PHZfTwu+XNlqzzImh3PqflliPG2TpCUFpAR+Y7GZDY2WXdfi/tG8D6fNfnTYpkVCT9Ns5HuMZM1Tofrm6aBKXjGaZBOohSx1sz31BiTlU+EvalMiUdS1uqVe1P0aElJfDDGcR4XyUUlZkz53402SF1OckYfxLSxpGbFuKt4MyREvz+EkPdjRT+O+DHkziuJT/a7vbzPf3j8h8f/Fw8NbdtQo4lR46dAN3SkOELysgSxOZZ21FVNIhsCGvlp6kbIklpkOJU29D4wTonBJ7rBE33ERwR8BVLwYqanAL6Z8x0evxJgrNaG5eUVo3X4/QbTOi5+59dY/vYnNC/OCW9f479+zeaHn3N/s+f8099hvLhkN+0Zti3Lkwua1TmuXWDHDv8A/TjgXMXi6TXv/d53UDYQ9wMhJXRlOX12hT47pVfQdTve3b6V1vCU8N3A/dsblFpx9d4ZzckJpl6w6XvevX7FuLtH+z0fvXzC5cUSpQK3Nzd88fMfMO4fsFrYKsZo3rx6Rds0LBcHMPZ//K/+IeHv/xfsup7tNOT2srK5a0xmVRhtsdZRu0o2xhAP4GWm5EuhvmjqyP0Wfa8aqjOoTkhuRVAak1Y4lWhs4p+vGioLRjXodELy1wKGGMsUNTcftzz8rQV+ElMulUamMDGpiFERk5l2pVKaisZg9DlYOUw63+1gGola84//wd/NbRhAfm0Ikd3pyfz8mblGTlBz0psSByYazElycaYmRaFUxUjyYf4MkEOlHK4zO5Qc4CXLVL/g/g9+n/6DTxhOz4V2bzRGeQmwVSJpDaoCY0jRAEsmsyKYmqgsxtagv0YyAoW3DUkZjJI24Gp5hR46whTpN3tUVYN1wrRVnhR91jMSUCbFHPhnpomAsf4oCJR0Q6UMeFK+r+JgKFDuSZxdNbM02RwYzYFcOmZElfcq4yS85KITKf/yDWbhLC0QZ9B3Bmez1AHZ9GKOpgrw8AiOLReYPyMVt8qjQGnGieOjS01krkz5LkkCBk2QWpWfcP/4n8K0hTjA1GH6e3QYJTHVGqcst2/esH95TVTXaGvmxM5aS900bNZrjDFUbkG9usLYE8ARs+u4yvM1lta3zP5KwRPDRPQDKgwQBnQasXiiFkAsqoDWmZXlLHVb0ywa6sqy2w9MkwCfWoVH7TjaFtYD85qElJNwWR/DOLFeb8AHUna8HvY9zhoUDuXEIEyq4gJAd/uOvh8YB09tDWerls04ZbOIvO8cg0oZjP8mQDWzHo5AKqMPpguFCUvW8zu0LB1pdP0lpqEwL1QB2Iw+ZDg6MwPifJVoYzgs/9waFh7P46NSAEdhN4X5IcS4I+BXm1m7rDys0VTWCNMkRtxiIaB81zOOE+4R+0y+1ziOAsKS23nmRKNcj4zbMA2stw+cnF5KQjMYKRLUDUZpxmGk2+2Y/MDV5TXErAM79UyDY7E6QRlDmCbGYcSPIwq578IukXYrYzTGWnyI9ENHDAFXOWHXaS0tlkfJS0xizqCmAFrxcP2E7vQMlOLqB9/HRNFfMlXFqxcvubq7o+726GCZvKd7cyNjYQ2LVY1BU2tNbS21s8TREIeRTbrjdHGGS4bm1ee80I6//bf+U/7n/+1LAZqUJyTRD9NZh1g2fzFt0UbaHlOKbB/uCX2PDvGQ3z2aYxqlD8z/sg/P8/yXvubwd5E6OsyvlEQL7pC8Hu14MR2ktksii3R33O23/Ou/+LdcfXXOs6tLPv7gfc5PTlgg69zmvcsH6TQoLaPFzTj4gB/CzBbSuWU9zBq70n4WfG4JDJ5x2HF3e8Nuv8stkJb1ZkJbMUzc7keGmNj2nn0f6CdIuiaFDErolBPUiFHINTqNtRVt01JVdWbYVISUJZ3yo16eMBhLjAeZgkSC2qMu9lTOcH1xwdMnV7x48RLrFux2e0BaNV1VEXwBZSJt7VhUVrqGbGRRRbopiqa892hUZsQOYqapROM9RQW52GFtzWrV4n1gGEaGwdPUFU3tCDGy3WxRaaKuT3BVA2isl0RX/AMS7aIRhYfS1qYSp+dL1ps9o4+M205OqxMHTkCFs4tLVictIXiUa6n3PSeupr/5Cam7pXv5HSYd8LFjHAc5B3LhUykBByIC5ORJKDGWFjOYpERaIXP+kBJExGlpm3aVw60WTA/3hHHEpVOWbsHYjQz7NeN2RxpGVJB3kQ4Ig7OO4AJhEtNNpZVIKyZp8dQ6YRKMYRQpp1mCRs6dkCIxTCQVUdpLi2ffi9ZqiSOUwjU1yoDxdgZjXeXwQcxHslwjovsq6/cuPLC777gJmh9Hw9V94mSxoLIW5zTOGE4vrnmSNPXNmh9+71/xwUff5uTyClO3RG3yiGkpZIYJ390R9hGTWWJWJXQUTVijLdqCaQykidBP7IaE77dYByhPt1+Tpp5pmkT2yyim/pZd3LHfPrC5vyGOPc3yXOJgW7N92PPHX/1LXr19RasHVk/O2Nc1VefQvZI1kHMDYbJZyJ14FpPlk6JI/mRDGucsxhrGEPny9Vvu1xuCH5l8Ep3QEkBqTUDc3IehE9DZGIhiyKOrin6zYf/5F9zvNqzfvab7G695+t4nnF2/ZHFyDelEGNvKMIURY10Gr2CaAttuJCiRABlHT5oPRnA24e3I6UJR5UKSwxCTK4lQjvXVLN9VAt8DSzKhjWLoe16/ecvb21t+9sUXvHl9x344EDgKq7Z0APlxJPpR5mcIsy6zdJcFVPBYP9KMO+pph5u6HJOX4rCct8ba7FpeYh/Z92MGVU9Wp9i6JikhaYRwpBE7Hz8HPhdKHdk7yfkVg5/XlRxjBx3zctYU3dhSwSuGe3NL/JEOqLiPF9f2w/tyBHyWq3gsT3D8d5UZtaJDKu3B5WyVzxTpNHlfRWa5xiMZA60yqC5xntFaWteLjuyjLpTHHVYlrkvlO5az/BiILknSXOyXMY9zSPZNStAhj9c6ziCqjE9hw+bvGIvxVZzvh8j1ScGjaPn7IASRAooXlp6c3WEGcyXbCSI/ksfEhwDhUBQO2ZTchykTRXJOFRQmxWy+5LBzsRnpHEwhj2mWElAqS1vpea3O90GGS/bu7AURQsAphw5a5nCMQswQFWo5Y5ScF6vvfpcPPvsF+27PMHbyfvn+gmK1WtG2C+q6Aa3Yrh/YbTbst1uiDwJQTxPBhyxNoDFOsJgiXaYzvuKsptGJ03bBoq1pWkddJy7awNkicraEi1PNqgKr02zuHMJECAMhCBEt+CLrJ6x968CaJpvLyfpWSCeraNsG+m5gs0ust3B7D3f3nXg3GEfTLmnPLmlWz3DtKa49oT05FWPWIo9S1vLxvEuJmVyFYl7OpcDK4TpJEuMUPfiSQxu3oG5PMbZBGSd7USnqpkBKXsy5g5hW+QCbbc+7h5FXd3t+9tU7xu1WuoSTJ6QJP/V5DueYOXp0DLPchLGO0+sP0OcfoFZPUc2lFNi8Jw5bwvYNw5vP6O+/Zhoe8NNOOvTMOXb1lOriBc3Tb3F69YyT5ZK2rjAohikwbG/xu3eEu88I1Yox9nhpHUdpRMfWSzykjKyvoMSuLSQPSoyXrRWvlpgmRh9wWkuO5xQqaiFrGYVZLDBugdc1nooeix47WXM+gC4Wo3/58SsBxiaEOWNXS7BgmhaMZVhv6X/2OWG7Zv32LfufvWZcT/SLM1RjmZRhNHsxgYgxs0ISrqqFHUqiXi45f/mSvn9g2myFdWQMzemKMU7suw377YZx7GicgBAxKaCiqk9QpiFExdgP3Lx9zX5zQ60DJyc1V5enOJtY37/j9u1X3L79CjVNmNpJK2plWT/ccfXkCc4cTr+fffLt/59Guv4lv3O/5HfARQUfLOa/lkPnr8b1/+pH+u534bPPSErx1fsvCd9oAf5Lz59/0oHdc/w7mJPjvFvPwURpn06FfRsPrf0cvcfxZ0Wl6T5+j+HDlwxXT/B2QQI0HpVZnSl5/LBDV7W466maQIPXC4KuSVoTTCDpt8xgrJGFV7QzlVKYKhHGiTDtqZRCIwFJijq3XcumR2aqJcIMxlI0X2dwL2+qiC6ZgI55/h7JA6SsF1s2w1iCtTw+i9zHzgAAIABJREFUMjR6fr/iWl0AUdmo5XcyzuWwPqrqZrjyAMiWa/vG7+cAp7AV55BItE0znUEIGyVAOp4BzH/O4HMqzylV75QB0Wxchse+/hq9W8PYo372fZh2qDihCcWQWYyZlMyh9f0dtzfveHh6xsXlCQFxgnTK0K7O2O0ntKkwboFzSxKZiVaCq3K9gsiKBi6ZkZsCKgrDWkWZY5qA1SIPobNxWcwMRG01rnZUdSVsiRGCUigVqJQYRalUGJxifFXMBwwQs6GKITGOIw/brcg+JMSQpJ+gmjJQYwU0LMZySpL4cRxRSbThTpcLNsO93E5z1MSm1HxvTAZ0D79nfr8SBhd92MJiIRVo6iCkTl7rhVWgHzFygRJ0ay3O9I/YqhK0h2JsA6SkRVA7gRhFzBPp8JbqiIWRk4c5mYGDVpnKn6vUQas0P6rKce5OAMX9w5qTc9Eu6nM7q41pZvfKR6k85hx97jEknLCf/4Lp2XNCq+j7jr7vRPMQYeLUxlDXC4beM40TMSWcq0DJe8cQ8GNHv1eQJAEVpraAZkqJK2qKCZc1M4112AwulFKNNhYTg6SAx9lI3qJCkPcItqJztdzj1QntwwNNN2Bsxb5tOdtsaDOLBR+Jk8gJKK2x1tC0iqU2tM5RA0o7wjhiU8L3HVa36M09J9WCj9slFyfXPGzfSOeAlmTD6JJ4i/57TGTzhQk/DCKX4L1wm1TpvfjLj+N87Rhc/Wax4Ze/Vn3jeRJQzwYh33jevNOVAmSStr6397fs+47NfodPkfeePWPVNDTOYap8X8p8zUwW8n6tjDkq5MVcfBMGesp3NkWI2RV2yhqx4zjOia2Pmn0/Ek1kGAPbfiQqza4b8EEREQ3GEA/7s4qeMO5IwaMzUCo+IXLOxSC6WyHFRyaexNzxMXaH/SUF0BO6HWhcw9XFJVeXT1itztDWEboORZrbyEwGBJ3VVCW2CyKN01Sah82a7bZjv9uTksdqOF3WgKLvR8Y+oW0NSrohrKkyyGjQCmmznDzeavw00e+2WB2FNWEMaENd19TOiga99yxUixiYZj1mlXKxT80GK/tuT3i6AsRRPUwT4+iIKUqLeIg8Obsgrd+hulvC3S+YLj9EBQHKghfDEJ3NbqQYF+fEXZXMq1S3S61ClWWsUCmbxGXsK/qAilIM9n3PtN3R+4Gx2xGGcS5oJZD1F5AWVueIPsx+QdIKK8B8bSwX7ZK3tzdMPheAUz4d8j6klKJUj8M0iQ56ZvYmIIbINExgFfVRUc1YQ0g6dxeo+XtJNCJsr2ka2aO51ZZXQ2RFS+MclbVUxnDRGno10rrAu7Cl7x+4jEsulOMi6ayXGEW/tV/DuMHvAxR2n0JYZbYiWtF4H4dBxiNlkHjqs4asYRw1YRoEUFcQtBRTBq3puy3TsMU5y/L0kqAS3W7Pj7//E774/C2bV694dtbgm3Nat6R6V6N3IosRQ8wsbRmFWacxwWw1M4+3Flk0JYDgruvp+iGPYDZAUvJ8bQx1JfPWT+M81pHEGBN9iEw+0m92bMce7SdWrmJ9d8/Zk9dcv/yIq6cfUjenKO0gRSpniNEz+UQ3BDaddDMOk2IYZF0XxrmJ4G877t+8pmLEqSTMQK1JGrRxOLcgKE0MGeRM4pSdlEEVOQE/sdtueXtzw5vbW75884ZxSPjjIhqZcJKlUg5ArCcGn4kT+WyIkZQ8zg+4qcNNHSaMxBI7F5NfpQSo0WUNymf4KDIEtqqo6pqolEjl5ZNBYvfjs6bEzI/jLfIZ8lc+Shg0x19H75jzqQNJ6ABmlvP0QKE4Am1V6f5QZNHQ+XelEH8cW6kjUPcQxksuEGLIChOZkFKAzBJHFnBVSau9yTFLAWrLZx8PwUwyyHIV896Q5pEsQ3Oks1vA6vyZOVad89B5zA8koxksy94oRZagdH6lKGzwY2JN9FMGS71IK0UxpCtgLEW0pwzUXBzIMzSJ7F6cCS/FzFr2/xDCTMiJZMm6HBvrqMGUMc2bfkLy0nSIfw96qOXPnHMckSweSVDkeVnulaScaY77UaCMobaOk+UJl+s18WHNMPTsuo3EBiEwjZ6u62nbhqZtadol2mjUZoPZbnGbLWGa6IeOcRBAViuDqRwuG44Vso3VGmcUtVUsreJiuWS5aFmsGtrWcL0KnC88Z6vI1aniepFYtYm2SjSV5G/ed3g/EKaRcQwSuySPUhFXGSrXYqtaOoGtm71GYvRMY2C/6bl9iLy9gy/fJN693RFToKpqlqsLTq/fozn7ALe8wC3PWJycU/T+Ezrf03yoljWXciSXMk2qxI+kwxyb2deglZW4MGZcICaMW9Isz7HVEm0aFPqoaBDwU8c09UzeM4WID5r1ZuD1bcfFmw3pp19x8/YtcRqIYWKKPdO0J2RAN8UIYUTnDoaIxAmnzz/BXN2izj9EnX2IqVqJ14ctcfOO4fPP2b36IfvNV3S7N/hpQpszzOkL7PXHNO8PnH08cXV5zelyRW0Vwxjo1veMD2+Z3n3NXXNGCgmlJhIKY4V4No7StRJIoCxoSyr5TgIfEVNWPL2POW4HZzRN5RD+uSYpMXfX1YqquUBXp0zmFBcG7NTj/YT6wS/D4OTxKwHGhhCZYsS0Le1iCXXL5ssbuq/e0fkJP2wI3Y4waKxuuP3xTzh/ckpsF3hl6Xcbtts1y9UZ1moWbcMwDpCkDW15es7y+imdtcL8EEiE/e6O9cMNfbfF5mTUY6BacnL1kvc/+U0m3bLre+7v3/D6Fz/m8rTi2fUlT67PsRoe7t7w6qvPePv1Lxi3aypVUVuLM4bFouXtm1eErkLv76k2D5QqXkzC1izB7vFDABWTEXk3b/yHfy//88uTv//Hj+NTKh/GaUbf8qUiFdlxmvA5WVLHR9YvATLKwTC/UW57AKiGkXDUYlw260ffrwCnOVeIICYQqgAqB6aS0szV2PIdrFHzgZVSbmsqEKxKR8w4+TbBWXa//+uE0wU4B1UjAFno0b5DhR1h7Bj7LYvzK1x7RaxO6b1UQKIWZ93JRpLO2msKohKzHK+EKBpDorEVwe+zmZdCWSMmO8oQvQcXBYidwdQ0A7EqpxM6lUpVaaENmWqfg8ucaAvTKh7anY/Gu4Cv+SUczK0SKUlLvUqHTVwUFstEyYLh5TnzXDoCW8tPDjJV0e18BMCWP47/Xl57ODQOaVT5nMPcijPwewiUcjMmxAk99ug40Pzpv0Z/9nOpqvk9Kfpc2bU4LYyp0uaWUmC7fuCrLz5nsXQ8f+8pdSOgQZ00zfKcdinGE9YtULqaGQvl4FMZuC6XqrI2oyaBknsZZ4BaKnVGRWLK5hzjgB/FTMcYRdNWLE6X7NcP0mYfEoMfUcqQbBD9TSNMzKYR7cDKOWolguhtU+GM4ebulof9DlJCo6lMwFQN0Y1Yo7HO4mNiymtdK5Udjw3WSJB9eX7CV7d3mfycE+Y5vla5EFWJdnNKB73Xw+z5S21jKt/bNL+HfhSopnyvVToYZhQEISlhXKGPkpsCyGbJhpJszgGM1nkvOTCs5h1BawFcKd/PzPtHJAk7VCmikr3caJOD50PyVrcNT5YLUojcPzxweXUtIPcUGPcdaTqABHNwrY+SmzLDU7liRf1H/4zwd/4zfNOQ/MBuu0ZpTUiJCkXNirpp5H5NE41rqdslMQRh/MXEuN+yeXgg5Dbf2jq8KuNliGHIzCyNo0JpQ1U3WFdnI8QM+gFKex6bBMi4hpKATLkoouCr9z/kcvgpF7e3NLkNOKSEVwqbhCWkqpox9Iz7AZ8CzeqEk4VhZR02BuqmgboWvdJuC64l2YTrAtebNZ+8+IS/+NEd07iHWhODMMy1FQaSjxGlEskLoLS/uyeNua1YlVEvt/2XsF70gVlUkrAyt7/ZQnlI8g7PmxNRJYmqVopkDiGY1gIgiqZVOuzfSdjKUcFm6Nj2Ha/fveX95y94fnXFs8tLnl9fcVJVGFtJO7USpgyIbIixBj/CrDNegNj5jCk600p0NseObhhw9ZLGWoYpcvuw5922Z0gTPiZCgqo2xLyWTAKlA9rkjsuYCKFj6h+kCIIw4KMamIYtYRLdrXHwhBTph808FuPugQGDavZzCVmlCSLoNHG2uOD66orT0zPQ4vJubAX57EIZtIbFsmHRViituHl3wzSOKKWo65q7m1fc3q3xo6eyFY0zPH9yQdf37LdrurFjsTrPRlUaY2tCgLZxaKXYbzse1jv2/UDwI8NuTe0M5Rx01tIuFU1tCFPPMEyzI3UMCZ/NH7xPIn0QIiF67m9e4T9+BjTEELh5+5put0RpuTfj0PHB8xe0raO+e4v/4o+4Pbki2ZaUhK0eEyjjMMYJ2Bun7IV5MB4pgIZsY4fTXbozNE1VEVJgmia6vheJlejZ393Rb7YYZ0kpyF6W5ugBn6V5lB9pqpopVzIU4JzB2YpFXXG+WvLpBx/xJ9/7N6w3O8Yxv08GYkjk9nCD1sIu897PDTkpJkIKrG83aKtRYaTwTuZWZK3zZ8uaK/FU0mXrjURG1mFkv99iksKgMErzdvPAq+Up9bIm1mf8YLrleqr59hj4A7Wiac/QU4/v7/Cb11RpTb/Zymelcrak2TgPDbv1BqKAo66uMST6HCuUVuBxGvDjQJwmKfybOBcT25MFprZshj1vPvuKP/3nf8wvPnvF+aIB84zLcMXV0+dUX9xSbStsbxlCn8/TgPd5z8rnu4RfAuInhCHrQ8CkQG2r0s8k57UsQgHhksJqQ71YEoLn7u6WcRyFsIxiSImbvmNKMre99/T1ns9/+GM+//nn2NUJzz/5NX77O3+bqyfv0SzOiMmxWi3YbPds+8RmqpjUiqgcnoQ3uf1d5/xpHHjz6kvWP/0j1P4GGwfatsI6SzSK9uSSi6efkKqW0WtCVPgEQxiZkhICQxhEj3e74367px/HHBqbTMqROR1CIHmfC1oe4kgKI9H7zByTHCUFIVIoAjp02KlDjx1pGrHWUfRTS9yUMS5AujJj8JJrJWgWS5LSTCFmc9YSP+WXHBW5y3pAq8f5U4nPOAIlCyg8n1lFECLNIJ45KnoXUPbYPPUgTXAAW1XWUFYcywEc65GacuUlG2Pu+JwBIg2JXNyOIk+i4mEdz7FKkR6w8/oq+rAx72GqFA30gQVbVr2aGYTpEH/mfWMGE2cgOceSZIa0lvUdw0FeT16XGbC5YzXF/JwU5pihALJhlvw4vEeaBnzufC2s1yLtMps1C34qcyDLZc2/RzFOjzUpq7pCqSwooIomcNZfVof8TrZK9WheluJ0MXFKJAqJRikxcCpYRQGuZf+a5sKf+GX42SWmgMHJR6KX2FsDyjrapqauW5yTNbzbbxmGgb7ruL+/Z31/x/bhlqTAVTXOWCm8JtH8TEft5DHquZin5t1fchOjlcSvyWO1YZoGuk66Vca4ICbNfW+oHhL1q5Hnp4nnl4mn5/DsTNE6h9IRYxUKK/c37OfcMYyiIa30JMOVu+iSUlIEMhpr5PXaJaL1uGaBqxRtu2C5uuDk4hKzOME0LdppxnFgVtAvcWTWUlZKo80hXxFVKpFky0fRvO5jkjWulZxHOrPyQ0yk6PG+Z+jWeD9ibIs1jcQUyGu7fmDoN/gQc87ssDpxXmviytBdNoStZhMUvVeEmAt4Js3ndoxSLNUIkURrA/2GtP4a0ES7Itj3MLZBG4s1oLsJ/CCA6LQlTXtC3JP6t8R7jXVXDJeXTG1LrCuqymJr0G2L8xdMw3PG5deEMDF5MfHSVhMWLcMw0HUDu36kmAQaY8QYUWtiklxl9J5xEs10iGiVWDhLraRbwFiHtp62vsaerEgnL/HtR9ROY2KPjRPqu0v+qsevBBhLiOze3jKRCPX/zdyb/cqSXWd+vz1FRE4nz3SHulWsYpU4iKQsUZIttdRqtwy0jTZgPxiG+y/yf+Inw08NtNsw3AMaltVUa2qJLJIiWQOr6tYdzpxjROzJD2tHZN6S9K4E8uLcM0TGsIe1vvWt73M8/vVnTB89Y2ocsfeEu3uM8riTU9R8wX2Cn//8M+p3nmKWSzEO2a1Y3X4pLm9A0zgWk6U4SNdTFqdPWd9t2YcdIbb4fsPdq+ek1BdqeYVzM5699x0un77P2ZN3idWU169fcv36OZu713zzg6/x1jtP0VaRUqBr93z28c+4ffUl3WaLwRGzwlQN8+UZT99+xoc/+iF/9NOf0v5f/4Z/4f9XTL3ELd/io9s1P7u+Zm/3zGZu2F0xyjCzNd9779f4re/+l/zhP/5nbLYbUhrcoJHNB2GxKW2hgAVlT5eF7yjQFlp+mcqF0eW7jr7bCTtOa4yOounmPT6KXk1TTTCu5pMvXvC//8t/zR/94AcY42TgAZkdqjZoq+StoGqcsBW8Z7/bCzv5f/5f4Dd+ExMj/+L/+JckHw4gS8o83G/o+oCPwvpIKRMQExN5qbEQrJQspAC5SA/YyuJsPSbLvvMjy0flWECUNDbV5yMAIZ4v2f/2d4n3G9CZ+qRhdnEKoSc9bNCtQpmKfTUjx4xve1AbzONLop2SS4Al92MC2Y7nHCltNYIkiZZUiJgUUHHD7vVrJpfvyLO3dgRQRTqBMQAbWv1TYcbm1BfGbgEsC2Ml5cEE5QgsT+NXDDqicu9Caak6/OrhNQChByB2/J2vgOeqVLFTSfBHcHE89+GYB9bj4Xw4+s7R7+Y3TmZ8DaBacSkYx7kA1QXEjxmF6LHqL7/A/qt/hY0tRF/m0GAYRgE8oiSPQ1W3HLPOivtX13xm4P13n7GczFHA+uGOn/z4h7zz9rvE7MBYaVFTGnH7lgsRUHYIA47u42guYKT6P+jZ5kzXrfny809ICVw1p67nkCPN5QXnZ0suzk75i//vj1jf3tPvO7RyLBcnoDV98GL2QKbNgbpynJwsWExm9C9f0PUd+7AXuY5iuJdypss9d+s7mtwzYca8FhOM3W4HOeOcY76YYZ1o0eaUsU3NJ5+/YOsDKeaRHaqGagnH7Vr60F42Pt58BE4xBn4gOrLHDM2u7zFGFx1COwYjqCJHYM0oE6CNIevSRqkOLEdVgudDIlnGynBexkpQMowzZ9FOTMwGdmEIYWzriuSBeoxxjvliQYyBB3fYTnsf+ZtffEzwgYzi+vqGBLimpmoaVGppale08koAPbJlj0DB8i6lkzEQJyfW6xvZC4yFeorve0IIVPUEbSti9JxcnNC2LWHl2d3tCZ2IctqqYTZbcn5+yqvXV+ScsXXFad2MAdvAWKnqhun8BJTC+z1KSTUb49D6EPzXzYSz80u6riP4QCzsjxgiBsPqW79K3GyY/PjH6MryZTNjjuHZzU0BekT70lRwd33DdRfQbz1l8vQJ9bQmBY8Kgew9Yd/hTYWbKkw1ZdZU/PPTBZfa8eOQ+TkCCqo8JElKTIqSp2tb2tWKdrWmrgbdu68uO0fp21FSdixRkL+yTr0py1FSVTWAssN3Zc01ReLiiAstQMhBp2BchYcEefh+Voo+i8HXlzc3OC3A2eXlY55cXnB5dsrj8wsW0wZjFMfmczEgrXW+o+tbjEaSGuNAGfYxs2o9q/WO+9WGtlM0kwkoxb6HDi2matZQlZa/ylWEUAA4hmSoJ4WObtdB7hCtXYu2DkLCh+1YgIGiuhh3h7sfNpC1uJoP30sBmzWz2vGtb3yd6dTh+x273dC2ZoSJaDTv/+p3+OyTT+mjgh58jFzfbrl4/Ji6abi/X/H55y9JKQiLVcHt/TXPv/yClGDf7ul7CH1gMpszP1kyPZmw7z2rTYvvWvrdmtDtiK0UCxunePr4hADUU5gvHBNTY7NCx56ck3Q2+BZjFe2+5+XLDc4ZVg8r1qtb1qsbQtdJIlXuT9jveWh3TGcTmqZmPlkQ+8STs69xfvqEk/kJ16//hE+X32XdPAItbBdswqCxtsFR0/rdKFtBiiNrVtbbo3GvDYrE/Wo9tqeSlSTPKaN0kk4Oa0kYkiqSSEdjNGXYty1h149xRiys7EpBrQ3zyYyT83Pe/+DrfPH8S66ub4mdRAbG2AICCQgzmMGMsEkBlrOCuql469lj8v3HhHv58W6zRevpqFs4RBxKMRqYMQCyJQwKpKOurcRmd8erzR06S0t/pS2qSih6bheRmVH89usvWGxvcawwWkDHvusI3uOqmsXpEjlkJOZMM68L26+ABBlUkngs+Y4+duy2O169eMH93T1vv/OM+XKJrcTUa79v+dM//RN++OGHXL+6IrcBXWtu91vczQ3zlxMWywVTmzidTYg58/Kuw3cdrnLS6ppEk7LtuqJ9bLl88oTZcs5uv+Pq6jUqQdd6BoOfyukiUpVHAC23mcuLMyZNw7Su+MX2Y9ETT4mQk9RFskTCKidCzmzaHfQdcbPmxfMv+LM//g+cP3qL5flj5qePyTniaZhcfsDFN36fajFHhG+FuBIN0LXcffJzXv/sr/nkh/8WdfcRVfTYnBHPwozSjvNHX+Ob3/ldvvt7/w3P71t2uqKvp6yw7PY7ct+LtnLIhFwRdZCOiuSlyHAUw2bfi2l0HogS8YgVK1IkGVWAt4CKYsya+j2p68BnjFHlMgZQSB9YiGUs5N4Tu15k5WYWHw/u8WV2chwfDIH0KHEwzMKyPxWVhgJIqnHsx7KtDGxFdQjEhmlxAFk5tPcPXRWHqFbYvIPpqlZCcBh0y02RDBjP6/i8QfSZy9fSTSCxmRKdLoYCPSmRtUajCgO2sGCLFEHmIEkx7OUjqJryWHxnvP5DPKoH8FiLwZRCHUln6TdPPI/Rvdzf0oafUh5B0+FiYxRTrRGYLOzAmI5kCIo0ASW2OwZe5fOGZ5AgJmESK0ruJ+dutRSsUtQkA3HokjQFINfI3ycZH6YA22noHi1FgOgVxET0ohkvbvICFg9sY12ARaMPTOecevb5mGCh8Uk6XWLRtN13/TCoQCn6VjRjh3F2T+bV1ZUQq5TojTfO0TQT6rrmydljVlfXdKsVXbdnT6ZxNbPZnLpusHVFXU+Zhoa+62i7jn3rafuOGDPOGSa1I/mEshXiv5To+0QKAd/vqdo11j4i1CdoOyVj2bQ9D/ueq03i8jbxbNnz9NIxr6G2GqcDlcvorAheEzzEHIqJuCOTRgwGdTCLM8ZiK0PVGJqZjOGq1tRNQzNd4CYTXCOycVlnKcL2sRTQM1ohRm5aY4yjbhqsq0ZpiIGEFXwvXXEZjKtEetE1qEpk7ayzKCwmZVA9fd+zWd9KUU1b5osz5otzXDVBmQbjFF1T0ZaOibbzkDNNnbk4qzDugs3+nhAjfYyoZMBWmNShVZK6ed1IFzsGipxJZR3ab8m7K8L+kjh7hNYi72OqJensgiq+R6MU06jw/cfEsCe3G3Lf0bZ79qcT1jbjXGY5uWBuK+r5jN7Ansjm4RV+v2ff35FDSx0SVmuaqqGqaibTSCia6QeSjqaw1VDaiHRTkcqxRZs7pwAxQwikKrG6eo7Z7smLe9rLSLr8FUzzGFVNwR3kSr/6+gcBxhrnWH79PdS0xjw+5eKf/Fe0Fnav7+k+e002ivWqJ61fE7mij4qr+5c0rad+x6NPZuJuOSTPKRPaHW52gtPStrtYLpkuT9herVmtb2k3YlpibEVVN5wszvnGN7/P6eU7mGZGFz0vPv8Zr7/8hORbTiaO5WKKzoncJ7r9hucf/4TPf/4TYuxFf2Q2w1WOyWLB3cOan/zk37HZbHny9fc52QfWq5ZvfOc3+emn1zSbyLyaEHKLSYfN1WnQUVr0ou+K1pompKFiJ4GhbHjF/e04KVQKq0qfch7akYppgwKthU1qlRL211hxlTa8vutpN1tuXr/ibLnEVjXLSvE//fM/5Oc//ZBNa3DVlMV8xotXP8aEBNlA1hgLoe2LCUCUVld1xBAEdJJFkFTYABRdr5jRRdcpIlU7jbj8rrodm74l5EjtLGeTBSYlkYfN0i6FlmTWBwnaMBqVMioJozPESB4nT2EHHf1r4o7Y3xDXDSG36H5NlTekbk/0wOwRelnjt7ekrmeePU3j8EpaB1QWN70D9phJ0UM8yA6o2GOymH+RAml3R/9QY+qmFBxF5y1Fj5gqCbMpxSE4lIQnl58PzFgBmA5M2hFIGHOjUgXP+QiQFXBQHVVHR/BpqF4eB4AlyDi0PAyB3/A5+Stvxr9VZXwBxen872sGHo43or4MrGBxiE3j+UnwklGF9Wt/9jHm579Apx0q7Eihg3aL7u6Ag1aTIhc9Zql8GaWKht/hrAe2bdd6rl/d8xd/9kMuTi9ZnJ5iqwpiYvWwYr58hNKGEEPZbGX+HeDmo+Qxgy6SF4lI1pGQOnaba9arG+5vX7K+/YJuuwJdU0/OePTWB/iuw1qH1ppmPuW7v/lf8MuPPub21TWhDZxenkvVru+xtYMU6LuezWbNbrfDuZrgOwF8GSraJZBTpR28mVI5h0rQ71pyCDS1MA6ctUUTL6GtxlSOi7NTLi/OCLcP7HtfEq7D9Weg67px3qc0QE5lJGgtYN54xwsgo6WVPBdrAG0MzaQZBjHaWEkIlRJ5BGswlT2AwXpgyJqRDcKgFTdMiazAaQaN6+F+vDEijSMPzJACWNRVNWQvaGtLIUARc2Sz3aCUSAEMr74vWnJklFZ435OVtPD6GCEEMSMr902rQcd0YIQcFS2GRGswOyivru/Y7be4asJkEsnBs18/UNUTjHVE4ItPP6fvBTwKXQdRmL3O1ri6wU4WnD+y9H1PDD3WlGDkSLdbKc10MoOcuL5a4Zxh0JtSR3ISVlsa19B3PYPbMmR0o6RAljP9fM5nv/ZrpJxY/M3f0O868sk5b99cF304jaocJ8slbdtyc3VNCIFnbz1hYi371R2+2zObLnBW3Il96Ek+MJtO+cYH38I8r7HPP+VvZpaMElDYS4tYv13Trdf0ux0KYSc6p4op37gCjc9kSLgGoPXvkyU4MGTkGCNTqCR1ADnHkqx2urjKAAAgAElEQVSpwmTIHAn/vXHclAZ7jEM75PE5ZASrzFaTjKNVmpd3D1zd30tXTjPhZDphWjsqZ8VQqoCnOR4SJaUgxEAXApsu0PoIKRU2/oSsKmbNDA3su4dyfQen6qGNsEyVkkQK86+pFUY79lsviXKWdt6mrvEhlDU9jzpu+uheWKuwKZPVYU7lHHCu4vz8hKfPHrHd7cA4JstTttsds9mUlBJ9iLy+2eK9aMbGBFlZ3HSBcnOirgh4nj77OrNpxXaz4sWXz9nvp6xWe2xVo22NiYGcwbmGajInK0tKgf1uTbfbQehKmJVwVrOYVhhE23Rz1/Fwe0dlNBaNqhom04qXV7f07Zq6qUBB17e8fP6C3faBvt+Rsmc5Ox3byrUxPH36FvfrOzJBjAFt5uH+hmle4FzNxeSCqbbM+9e8ii2fTd/Fk8h9pm4aJk0DKDrfCSijFTGJQVLoe1KMo9SLtrYkeBbM0NadSxEYchpaUQMJqKaiZ55zpt/uiQWwpRjGpZRKoWtglkvSHnxgdXfPTz/8iUg4dBGrHUmLlMYQawzLuIw6JYVvC1nL3NFGUU1McZc/FI1FfiOirOjHDo5TOYPJRS+u99LNkCXZQjEmz2RVNMFlTPc54VPgl1ef8/rhink953xxxq3VvLu74/37KyaTCcpI87arLHVTkxTEGA7JHW96Fkjbal+IBZmsM/Wk5u2vfY0nb71FTBmP5WHdcnV7yw8//JAf/+RDdv2eoDPJRirnwBta4PrmAf/6imezmuyTaK6GIh1hDComyF7aLuMQKyru7x5QVva605NT7q/uUEi+YIzsjsZIl0nKieADfdjz8FAznz/lt37717i5ec3d3Qbfy7xJMaFKS61WsNvuMGZBZQ2VMUDPw27L559+wi9/+TlZV1iVSaZh9uSXvLUJ/Prv/Q9Y5YRl7zvWX3zOqx/+J+4+/RHrl7+A3StM3kkBQCkpFClNTj2vXn/M7f0Vn3z6Id/5/h9w+tbXCc6x2idiDGiVxbAwO1RSeC2Fppwyb3ZmQehbAVgHQsS4T5T1eMhpsrDHVfBo36FCj4pDlxEHdYGSu6QYsVokL4zWbNZrYgZdFXLJm6fBEHcfXkOcXMDco0K4QuJbKb4M8+koHlXCALemmOQx/M4AvMqxh2LlILUGMp6UHuQBLNY5lDYFoBs0LUv353C3BnmG4XM4TO6h0CnGT2aMxgZSw9hMOQC7BbiUakYuPxfQ6Q3/Arnz6JLn2iNd8uOQb7iuOJJnOMTuDExd6SSUuFG0T0WeQo3rZB6kkNIxG1beoRQqcllvjuUhxp1+WOuySA6IaXIqOSsyLgu4rgfD2/KsUrKyVkcK8zYICKsO8QMkAYJzJI5+HpKdJQXaCBtwEMbNSbruhs+IMWCVaMtWrsJVTqROhrbzIgtoopDFTDa4pmK+FIZhiJG+F9AvKwGyB1KM8vtxfG9AjPUUGKXRWNarW/a7PSF4MRbuPNvdftQdns1OWM5nzKYzFrMFISXuVw9FmiihYsJajTORpjI0VQN9K4SIJHq76XXPw90V1tZYV6OtZTFf4MwEbSx98jz4xGKSWDRwOtWcNQllPCYLGNr2W1IqsS+eACjVlH2wtLTbjLHCBF6ezHBNAlUKytoKqS+lYoANOZmyvuTD3ATIgmf4so/LWC1yAAjbNcVIiEk8KYzFVIkqgptLh4/RFmUNzk1wladtO3wIxJjYbdekpHBVS1VNqSYTKnfKYi6f0/We9XpD2+5w+z1JJR6fTthuWryX+5q0+D8YAioHII44wLD/eBLi4bIh716h9o8wOmOqOaqawPIZDsfcTrG2gtyzX70UAmHoWG1fUV39AjttqGvHpq5ozhe4yqD1jKQt0+27LLt7VGrZPGzZdd24pqmCH8WsSYW8kXJGq8JeR6FcTT27QLklyoixsFYG63fkfkff7zB+Q0odcXcF/RqzuyXvb9ic/ipx8fYo4fV3vf5BgLEYTf3+M6rHp7hnl6zaLTcvrmhf3eOvNpg247NGW4dxFXXVsLSRWDd0fWB7+4BxhnoywRknlPWycKQcsUp076bzE+z9tWhjKNBNTT1ZMD855+nTdzl/8h7K1XR9x/3qlttXn5PaG2qrmTUNVVOjtKbb7Vjf33J38xqI1HVFU4uWiXaWNiRWD1turh9YLqd87evvst3t+fzTL7m7viL0USpa1qCDGh29ZV+V4FAVkE0p0WA64K2S4Ghljzblo7aKI/BHAqFcNj+FgFKMQeuB6ZNHsMNVDXXtqVxNTonoe1xT8/47T/nt73+PH/70S/a9Fi3drDHDzlgcwEOWdu7BQCqr+AYrLqWjRD+VjX4E2Mo+OGwcqmh/dbkUI1RhajBInSEV0VjMP44AMaVQVqGzRsUSBxdwLx2B35TT1yqg/T1xqwjdHTps0aoXhq2aiBHX/IIYe3K/Ie7XuPkTKYhI7iEgxlHykGMQJkkSky0dO3TaoxCDBlvXxG4D+LKxRpSRhE8q8KX1PYlBV05lcx0SiCFpGcdPeasDQC/jInMoBAswNjKT87DAD4s7b4ChR0PsEKCO6BaHv+Po845eiiHQGW5K+b03ANyjr0vAMADC49+MwKwEyoqE8j3uZx+hskd/9hn6y88gbtHJi/t6lvs1VL1F70xjlciGGgVOS0AUS9AnUKAE1xHQIbK6vuP61Wusc8xKwNl3regEqQIqGMTECf3GtQ+AbB5aQ3MkxZZu+8D65gvW969ZP1yzfnhN2t2j+44Ud3Tblr2b0pxeCEEsRYzRnD+6ZPVwR9917B62hcEJlVFoq6HIL7T7jrZt8aGYzxgBEpWCAw2qgKMlKBcCT5IA3TlsJRqJmVyCv4N5w+XZkoftjtZ7YbM6UwLNXAqKenQsBql/HsAkuS/SVpYOd2p43kegjDYHsyPKWBqMJLIuWpjl/1obmfv6oGcmOsSlbyDDoJUnn6mL/IkaULTyoYWVoVRp4zkkDIM27TF4G2Ms13K0ImdhE+iisZVGSRqFraTjY5irurRX6SyJ+wBGvHFOb7zGxY++7+h9K4x4G/FdK4lmaU/errcE35NiQGeR7bHWoXTG9zvWD7fMl0uMNWw28cDyVkNGcjDnMMZS1xNZn9Sglfvms9HG0jQT+s4XZuyhypxzJmtDO5PWVnX5iDCbs68buuUJky+/ZLbbMs+JumlKMgjtbs92s0M5h+86SJnp/ERA8WNwFMXZ2QUheELfsV5dcWUSSYvreo6B2HWkvkeFUNpuD6uQsOYYx+nxdR2DoW88ifL/N7Vf86EAxvAc86FQk4uWnlZv/N0wPt5YF4e1/eg1rLTjuloS+873Y9F10wc2XU9jjXTFqGH+HRJtVc51YDHseukiaZxjUtc4DM5Kok1hVKqxDVaNY/84MSALS8pWCoWhriBHS99LK6+zCmuLhnEupjdqaCc8mveF+J6Pb48SQKhpamHgKTEmTFnRTOfoqsIaTQ34rqeuLIpI9J6gHMbUtG2PDpm6bvj2936dnAPXr15we3NH6APeS/ugMY7sEOZMATustcSYh233sCZmRWU1zpWOg9DjO0/bB3YkrKmYn52jXMPq4ZYUWkK3p9vXkA0hdBIL6gmZCuuqN8aZT5He74mpR6tUdGsVKgVyVDhjmCzOmPqWaafQqwc+Pp0TQ6Rv92zXK5EgSRHjLFVdYauG/W4tQEIMYvai1JgkDcWtAZgY2lwPT55xva+bBm0Moe1IPkIp5qhhO8+qLCmGGAM+RjoVUBm6rif6RNd5AXKPYziO5uLRFDBG2LjGaerGsTiZ03dvzmlrHaoYb7i6wg8MvFJMGOKSARA6SHAWwCXLnjd+rwAl27CjjR3bfse23XBdOa66Pc83KxYf/ZTa1dTW0riK2WRGM53J2q4LU1APXWxDUSXjfV+KI5E+iKasD4Gu71ltNmx9ZNPuuVs/8MvnX3DT7VE6Q2VQpiJqi46K7vyC27eesdtveOv0gm3nmWrFxNY8dD0hCKt57DIr7DatDTFEtqst2ugiayPbwEBu8bEULAtYGUIi+Mj9asXpxZLT8yWPHz+i6yK7vC/sojDuDypD8gFjrQBiWkGfST7Q9YE+ZgISmyUlOVSvLOcXT7m8eEr2ge3dFVcf/RXrj/6K9u4Lwu4Wi8cdSbgb1BjHhdiyX+3w/ZZJ43iyX3HytW9yOntCTyIpjVIOZRQmK6x1xOjKNcc39wCtKPYNJd6WFnkyoy4opEK68Oh+D/2eHMS4T9bfVE5UHfbVDAxtrtrgvYdi/nwovB6Ai2Pw7nAAgbDk+QzHPto/xhmrvvL1YV0djsBRnDb+cJgz6rBfKQoLVhuMEYmAIe4azjmVDrZDtKnGf4dTUEfnNwC2YnY1NmWXS9Lj7w15soQVaZSxU8MB8+F8heU6gMnqcA+PtvEY47jFDnnp4d4Me/8RIJvSKBGQM6O8yOF9dPijtUsd/SPeBxmVpGCbY9k+OQL6v/J8lJI8WFjIAuBLVyzjefnQE3NA5aLjOvoSDDG2QptUmh9VyTUVg6bv8FYalFWHwvBRUTqnTAyBHgp4Pjw/2RNSzkdMYZE+UYUgoZD121lXJCMpckZxjCWGIkXyIr0nHQSGrt0TQyTFYsitwCdf2N+Krgv4rmU2mTJpGlzlmDY1CodWYDVUJtBUikltmDaO3AX6kIlZumpyymLO2UeM9lSTmumkofcVu04TosaHxGqnmdaWh6lhXXmMcugMOsuaUJmIUqWgr0A7YMhFM1JU1IbGWU6mFUlFQjbj/BVJma5IBlnAkOPRs5REDlUMo8XQ3YucRBmnWolUlcpCbEtkSInkI56eTosev3O2aOqKeaJ1mkwAghg3ek/KGvGDk25Jay1aa5y1NE0NWYypK6c4mVbMmoamiphOTKKdMhgCuhxXcCkDCLEjqzK/YiuSM9tXaFuhdI2yDbZqyPNzyJk6BSbrW3LwMobZ4ENPu7lld3/DdnrB7uQcf9JQW9Hvd82EannJZPMY3+/o2y2bth339WGaDqSsAYcyWvAGoy3aOOz0Et88A7cgm5qgHSrsyWFP6tfo3UvYX5H7Pbndo8JOcIFoyH1Hjp6/7/UPAoxNWmM/eEb13hO4XPLFv/2PXP3Vp8R1wOYK10zQ52dMTk5xJ0vq5YJH/SM2NnPbd7x8dUXVWJanmel0QuPEhGa12aC0paomaG2YLZY00xOqegaqF7Hk5SPOL9/ma1//NrY64eHhlof7K26vn7O9f8miTsyaOdNpha0bMpndbsP93TX7dsvi9JSmrnGuEqaIVqw2OzZ7j9INy+UJj5+e8/Bwz4vPPR/+5z+jPv8GKXlQqeBmB1BMNlHRwDHKDCs046arJFGQLFKGjRo2mBHUOASTetBGRKqsB2YjIziRc5IN1VjqZiJ/EyMxdMQUcMawmE74w3/8u9zd/7989uKBtpcJOlScCJlIxIeeHAY6vVR70pGOjSzW/C3QT+XD+cRcRAVKK7JWisaJ7ltTuTGmyBIbEkLAVXVpu8vjzzUanRPaD5v5sKm8udkJ0JsxYUXc9dLOkXqCiig7gdqQkqeZXaLjlrT19Otb5hc9ZEVImhizANLD5wMUowkB1xM69ajQFiTQUM1O2G0eSJ0XHSKliLYqQUxZtMr9yTkIHX5EP0owVgKHPN5HSbgHuX8AlfTRGCoV6QFcOAJBJYiQ1UhxqLge4roiPzAEOxySt0Oo9Ua4JUnVVwGF4VwKqMo4xMs1DQzfPLB+y3kP93K3RUeP3m2p/uRPUUk0ZLLfkVKLKeYMEkcegkarBEg0JFIMWAWN0Titiz5TCQSg6IWJDqvqel4+/5L54oSmmWCcI/oe33fkLIBAzpFKNyjsGDiOwIqS55RyJPo93faeh9vnXH/5N2zvb+i3K3y7Ya4zhEi/7ejbFRuvee/yMa0y7KJHKagmDfPlkt12h9/3RXRcYZ2jqhw59KgIwUdoO0hR2lGMEaOQMckYdDLlfpPF0Esj5lPGOayzRRdQfiCsKQk8L05P+PL1DSu1k1Z5KyLowyokGrMH1qTmwB6UR11c5fMAPsnPDwnw0VApwd7ARh2cfbPWZCWGHUoblB0MjCg5vYBDw7UOwEAuCRC6zIUYYQDFFGAEjNVaS2t3iuN5DHqcx0DpVwG6YXYYPTBd8wg6G21oJlO6hOhWKQmEndXEroeBAfGVY4/My65D9R3UDSjRkPS+JYQWmBJDR9ftySjmJwti15GjAB/aiKGQcYZMZL+7Y797YHk2J1cCMIdYQIijBCilJO2ESjNfLNmsVwJKw5H4S1lZlGU2XZDjhuSlUBaiH9d2WVvkYezffkarJIl7mTKnXc/T4LF9T1M7prMZMQRyTGzXO0xTobOiaabMFmclwpUE0BpFipHZZIZ+/AxrHLsfrdjGjjZptFUCdPc9qhiD5DG/K/vv0WP8u5iwX5UlOH5GIxtpzHUPLaN5fI6SUMGhePAGiFvu4vifwWREHZKiN8cYEjMM2soZ0R3WhqgN+wRdHyBFgo+0XSvnUNpjtdFHiZQioaiswbha9lOlqSpZN1LRt9NKtq+CCBzOadg7SGjjqJwADDlB8MKCTylTVRqtMkollCpg7LAnHbFgtZaiULYHiNZohbMWV1U8rLbYuoEMYd9ycn5OnxIT55g1FclpjG9o91tpGbSOpmrY7vco3XF6fsbTb36Pm5tbfEhcXt7Qru9LYiqSCtlm6HtCFIMOazRdnyUor2pUzAh5UmF0JoaeNmbafUvfe2KR6gjVhCaeYExgvbqD6PHtbmzDqypHXc9FEzZ4MZUrr5QT692attuRYodC3H3n01m5/7KPLRdLluqUk4eW+c0Dr6YN29zT+Y6uazGuwtViZuJczcnyHB88pnIyh9v9CAJkJY7Cgx6/mOmoEXQawHiVM8lHnK1wTcUKVSSTShxS5sGQlKIVIUX6EKQ132RyiMQ+iqlVymjnSlssR/Hhm+urVppswDpHM5lwenrK5589x4Qw6gtXk4asKowR88u+94cQRB2SrrHANnQdHRWBcz5e4yHrXOSjPH3wbLotJsEXOaPbPScf/mdm1ZSZmzCvGhaTGSeLEyZKURcddefcuGZIzK3xo2Fex3q9pm1b1rstq+2Gu82aVbtnr8FrjXKadHEmMlVl3sQi+dO++z533/4utx/+R371YsKu61k4xelkwrrfEmKGPpGMOFjb4jauC3llt97KWhJljRq7UDLCBh2LSRCTImbFar3l/mGFD5FHjx9xd7cmhCTmdmV8DCEQOWO1HRl9KUhLksriVG6UEAV06ugeXrDfr/hF3ZC+9T1Su+Pu+ae8+Ml/om5Ftq6yWeI5M7RiC6iakiJriV9VDLTtLT/98AesVjd84Hdcfvt32KSKTjkBOowAJMY6bBLGurDyDmuzLeNSuAIKlSiyN9KhN8T4wort0Ps1utsLsw0p1sWUy9one34uCLKYWEncKLmMjJNc8pQhW5HuuRE1HCUHzLHW/JAbZckA9EAOUMdAKWPMfZAcy4ewnKFQp8ZzlcLykc5/Fp3KYQ8bQCaOjiXdHfJZ470crpmhuKkL/lQCtGIoJTmAANe6vBkvPZfO4UTWMo7GIn25zuGYwzmPZ5bHUxxzYe/DCLRKB8fxPj/kH8egbBoLKQqFMQOAe5RzHbFyDrFBee7jCci9i0cx65C7DyxmjS6azeVzi7yFLZ4yyrwZYxpv0dGTs7RVC+ZbnuPQmRD1qFfrg5BQzADCloEhYbDGKDcCpUpRfDUivRfJqOFlBjkbyo6ehVjgQyheA5QcRDqqTJEjQClpWohRdGRLTptDJvmha0HOJ4ZUCi0FgMylKFQ6MNrWs1qvWcxmLBcLlos5TVMVyQPNpNZM9ZZJBZNaM2k0Olr2vaYL0IXErs9s9ongEykFXDKQPSG0tF0kBIPvgpCprOW6UnxJpNKW2hpmlWIxsUzdnlSA9Qqwvqxtesic5RnWTjNXmp1P5CidzipLN6zvd2R6MlZi3VxyHaVEnpJSREyKSIQc8D6ULgvZX8RDQ8gelJw2ZTHD3BVWN9mSsWhbgbIYq0E5lI7lzouJV0oCzNqyPkl3YyHzaI01EgfNmprZdMpkm3G7RFABpxNGCT9WKYukhhow0l2aIzF4UvLo9g67fYmqFmQzg2qGdYbUzKT4kTLN6S1xvybnSFaJlDeErqXbbNivV+z3W/pugVMaaxXOWdx8yeTsCbHf4Xdrtg8rArqs6TIrDx2yw3qYsFriPKM0plrA5CmpvoRqgTcTMpGUenLcojefYa9/iMovyW1H7u9h9UtsjNDdC/7z97z+QYCxGI17/wPWRvPpn38K9i3e/ae/RTU9Q0/mtLVhTYNPmm3KbNs9q4dfsJiD3a7YfPwF58bw/JMv8CmhXSPsie0D7779Nt/9znc5PTvj5HTJ2/l96smUV59/xONHT3j05GvMzy4xzZSrm1e8/vJjdvdXxHbNxcxhNNT1lMl0iXMTbq+/4O7mNdvNA/OTMy4fPcFYTQyB9cMaDSxO5zTTM6azS1Z3n/KjH/wZ682al6/u8cmjcsdm/8D9+gY1s5BMmZ4ZoyyNntKoGTY35B4aV9GlUKRv9Bu3TjZN/tb3REpnSAUpbWYl0T+qeuYciaEH7NiW6WzFk7ffput3o8OxVpbvfPABN7/zwA/+8kP++C9/WEyuEqHb4XdbrIqE2EM8VBet06NZAOVshBHkcM4WFp4lxCTtk6VCIttapOs75o3obAybdO/9QYsVyKG0O+jD5Q73RRiyVrbFgXF63Bqqip6L0XI+tqLWBvQEYkdWlqgy/e6BxbvPUJNL+ge4/+hDNq++IM0uUaaBWECd5gCWKgKU7VQrYdzkJNUqciaqGjVpiLs1uQ8YZwUETBEIaPoxMBriqEGjRILxNAYOutygIaBSIwR/uCfDTVTDhY+A7ACnyi8PIaBUT4//+E0w4HBGo/za8W09gNJHJ6AGzdZcOKiD3MLxR6XDBiyJ3HCdCXJP/f/839hXL7CpI6WW3u9GlpXVmjcvWMADqY+CKwG/qgyVFW0ipwTQjwWI7UPR2EEqf5Wt+fzjT5mfnFA1FY+nNaSe0G/lWSrLet1yenpBVU2wpi5MgQFIi+z3K/b3n/Nw/YLt6pr97o7c32Dimjq2VPsObveo1Z563+N6T//8FvXOe0wePUFPJqz2sPU7srW46Yxq1kJhyMcshjz9vqXd7eW9b3HOcnJ5wWxSoxTcXF9TOUlSVUkigu8gB7SeMF3U4podItnasgGVluoCLnZti1GZymqMVrRtS2oz1ojRSlKIPtYQIA/P4StAawjhbwGZA4NUzKxKoWkcRUeyD0oYpkqLhubffkmAgNOS6JNHXbNB7mXQRCVzMOwC6tkUlUpLuVaYwS+zFKwyxeBsTCLGUzq8ci4Br4zlqq5EEy3X5LqhmUqBUA9AXk6sXl8TkYD30Kj35qv+kz8mvPc+/T/6g1LNTcVwqaXznsrZIoufyb1IToj5kCvyBQ3GQPAtvu+ZNA2vnr8mY4gpUTlhC+ki0xBioO8FZNemYjGZst138lyNxVVD0pFBW5KZkHOii2t8KNcfZX1VSoD/nGJhkxzYwsoo7n7r+/SfnLH+0Y9QCr65X9OUxGf9sGY+e4dmcoZxhqv7DReXS6lVFuAIhDFR1zVvP3ubpjbMf/zn/CLu+WVIxM4T+yCMGn1gXKdSoBhaw78Krg5txX8XK/bAODlCeqAUd45I6OPfgLFagLjSknY0ZMbke5QjGJezA0g0rK0pJZJOpaWwvJW0+xvyuK9JUquFaTrgWyDsNKXHY1Zl7ZQiFqQYqKwiJU/fSyAuU1ON0gLGHBllKNG8lyRdFcA1o4g4K7uK0QlUjzEy0g/uvoo39xcpzGRT5EGBylkmk4bJdE4fIOqEdeCsZrteE4IitR4zj3zt6QIdW0KIRCKXT97hfFFx/eqK1XpN7Nd8/uln3N0/MHEVf/Bf/z5ffvIRbcxibFKYNkprXGVRGu7v79BMqOqayjq6bSB0D+y3a3abNdv1Gt93GGuYLRacnp1zev6IkDVaOUKfUD5glGI2mTJbnNAsTnn1quP0bMF02kCK/PSv/2KMuxTgbOLdt5/QdXu22w37/V6STFeJwWII4rquHdo25Nrw23/+M/7q+U95ePY2+fu/B97jlRQEe98Sy7jU1mKdpllM8D4IUzVGkspC4Lb2AMo0idCKaVGMwjj23nMLGGfpt610An1lbEmuI8VUZxxET+wTXSoskShyErayVHXNbrdlYMnJPThi+lEKQAm6nWgS9/sojOYj8LSuanadgJwxJulEQP+tVXUAbsZ5mg8/GbRAB+BUleuIhSWGkZAv5Ew2Fe1/+98BCp100YKVyWZ/8MfoX/xsvAZb7mk8KmSMUihGgIwQJR5RzuEqS/j+PyL9yjdFU7MUZkTNxjCZzwhW9NZzZfnr9/5H/pl+zdemn9Fu1+z3Ha/XCNs0BUw2TGuRcEkSPMj6MhR1yl3OscR2SrQ6OZI1sEZig5x67l7f8u//zX/g0eUlTVVRO0ffeowRb4sQ5B4Zpbh+/Zp60lDVNTorDFYIE0k0vjWynrvs0f0d13/1f7L52b9Hx4gKLVMNVa0wpQiXcxJ2YSrM+uIfgE4YlamdISXoaPnsi59w9fpzvnX7JRff/l2q+VP27oRdsoTYiWs2BmVrlH2zQKtsJQWEGEgIk9z7DqInZw+5l8Tdb7H7B+rNC+Z0BRw1pT1Vyc4ubVQHQFYieXzvQTu0q9G2ImSIqPL74y4rLfDj6iBFg0G/UxVgQWd1NNrHvxz/ZoCE5HCprNeH9wjU5iFfk1ZwPTBhlR65EyEm0TPlqFtj+BR9AEdhKJ0eVvxxTxsSlVIEPUj7FAAupwNgezRVg++hmISNhfjh5zmXHJdxz4sxFJDQSxcQFJmdQywo56NGYPTwkuMbI2Cg1vpw3wyyz47ryNF5loLp331uhw5RiUEQeZjy+4OR2ekbnpAAACAASURBVNhhpAUkdcbgnBhLDvIOoRQMnRUyCqrIBxl1QOmVQiM5Q6IwVpE552Og830BUgWsjVGKZDHGEpcII7dpankeSqQH2iOT7hBlfPoQRhmjwTsglcJmjglrHM46MSrXBtfYEVhOIbJPiq5rCTGQs5cwxxT9+xIXKUAnDUVbOQE+J9rgcbsNNltUUtRKczozfP2843xhpWvGZLQKZAzeK7YdPH+AF/eGrjeoBPPaMNUB7XeEoMl2QtCiv9oFw3qv2Gx6iJpaw6I2XJxaLk9nLJrIvA6c1Fus6VHJghXyTkyAqlCqIVORNAUAlseko0dY30OhpSrjvKwb2ZSCx7G/jHQlCxHEYm0lRXVj0aawsZWAnxiLca48v0AOPdY4tHHUlcgaxZiIYSosdSVzPxNJRSu79cJKTinhu510i6ZENZ1yce7oYs1DB/fre3xKZCV7gEglgbC6DVkebOm8TBjlCe1r/G5ONhLTOL1EYYg2Epop5vSSendGzmvIO+ksmM/R04ZcWULO+L4lVhUmg1Mwd5Z8cobya/Tujry653a3o4uRkIfxlDGqYCtDcSWJ9FTyPeH+Odo9QtdLsBO6+jHBVSQEQN+6xyzdksn6Y+r1Lwn3HxP9FrP9GOtfo8OWv+/1DwKMtctTXjZPudt6bhdT4qzmRtf0SdFuM9020rZbqrqiqiq0mtC6C25ffEq3ueHi/AyroZllJsbQNDO6tmO1XnH9IvK8UUybX8NNGhazOTprDDXvvfseyhr60HHz4pe8fP4pdA/UqqWea7RRTBfnLM+ecHL2mIfbV1y9+JT9doXRhpPTSy6fvMNms8b3K+qqwVQ1l2+9x2Q2J8eeT3/8p/zoL3/A9asNfdD87u//Uz5+dU/Te5re09OikqauaipXU5s5C33KxJ3hTANKDLtqJoWhVqrKKSNmQIXpmYo7cpJF02pDCKLTZ4yAxVpLK46zTtyQfUcKPSn0tG2mrmsJXr3HGE3f7hBn9Bo3r6mqKb/xnW9htGLf7fnBX33E9Oxt2vUd++2nxPYlypRgyCDtTf4ASACokWUjVeb5yQnX13cM2j8gMfiwEaboi/aUGis8RqnRcImi7ZH6iDKyxSs1VHJKu5wcddwgjToEBJJQWrTJqGqGmZ2jmhPZbDtpXex8Iq+fU/m3OH+0RJ+eYx4uub36CBP2uOk56Jloch6FSQ1RmLIpQOzLfRBGQY6idyoaa4mcPGHfoxsFWQyooAMyuVTNR+5pHiqGJdi3VqQh8gGPzlI/ZARkUy6xhjoCZHPBXN9EDCRIOljL5JTf0Lo6jnm+qs40HpcMWY/Aqxz0oJmkBgZsSke/fziC3MuEJWN/8Gfo588h7In+HnV/C74TMJcki9jQiiR1xPF+aaWpyVQq01jFfFKzmE8L+1XmjCRqcm9lQxdesDYChoTgMSiunn+BrRTTkwlnriaFXgIyA1VlyvWJHqxSEGPHdnPP5uGah6vnpPaG6Leo0LGgI+574us9+n6Pve/Rm148wKIlJYPvIi/+5C+pf+VXcG8/I9c1282Ou9sH1g+lxTQFpDopV+B9T7fbkoKnsY75bM52vaHb7bBa47SjNjXkSOUMy9MTUtezXm/oVlt0An0KLjdoawqEXVo3g8i+5GJ/4Jqaqq7Zb3dUlZOWZjsAjGVYlOprJhcAeACo39SSPowtfcCVzACICXiagDQWmIZCQxbw3kggPRJtswRlZA6AsJJfGFqhhiIAZb6MXxuNdgZbkvCu60pdQsZyPWmIu90YzDtXMZlOWNX1eIwYxXl5SCJkLUuHz9KKSGKAXIzR2FlDLEZzDNc2BO1HZypkLmE5E8H7wL7bo92GqZpSGYcrRg/aWRHBtxJoKSdBVe0ctq5ptxs2r1/g6ob5yZKqmY8LsOwdIv8jj0SYJq6ZEULA2JpJPRlzPetqposzmknDavVAjntEqtCK23k5d6M0u7bcv1x09oquW/vWE65mDRd//AM+ayY8DoFHQWRaHh4eCDHirGG3XWFQLM4fUTVzMRIiS6JaErtZVfHN995jcXfF6e1r/t39Pcl7GU9GGH/W2GKiUVoOzSEkGiSCStViTF6Hn70xdAcEs7x0SUCFCGu+kowVlpGyKHX4PK2Lfp8Wlq9WmsEgRExSjj8PBof5GGVsmSLRNLSMQkaV2obSGl1VZRvM41iGAeuVOWFUOqh0ILIWKFkrYxraJKXFMqVQklJzPCOP5rEm5kDdGFL2BO/xXjSJBTgorag5ys55lMDG0BKTgXBgiqsU8fstt1evaSYLTs8fY6uGGGE6r3l42EAWLWbvPattx95nUtLs+46QbGHTI4YPfcusnjCdVGJKUk9YVFKwAMN+Fzk7X7K8uGR2cgIpc3V1zX4bpMCK5/rVl3RdS4zCCD57dMpsPmM6WzCbnzKZn7Pd74gofN8xmTTkXLO8eMzy/BG6qtnuepbLJSTPq1ev3hgrMUZevfySkw/exeqMNZnlyYz5dCoqIgnqqqKppmy9JL8pWX7n13+fm+0t8cVzVqt/Tf4n/z2mFBl9SqziFcqJ5IokuCJNYwrokhTo2jI9PZGuhxhY3z9QW0MqJkM+JjFyiUn247bHNPUbFYjjWSKJM6isZc0uRftcWJc5BWJOVE1N33nRss0ctLLzYVlEHQDM/XYnHVzxMFZ26w0JB5mRmf93RTpDc/YAXKnBa+FoXh/PbaUUOg9/OcwdPTLUQNizsk3JnhR+8zfhu98DJfIJQckcjLFIRg0tveQiE1BA0RL7Z6VJVT2yVo3WUoi0jmwc7nQBswpqS68VVw8P/G/7U74TrngLxRNbcbU44+V6w8b3ktR6T9ZFLqWAmG/gdWU9yDGTUyQoRAOyMCG11ti6wuoaazX7Xc/t7YrtthVQsYBoY6lFKYw19KGnTg6TxdioD30BW8AqTZWT6NQWBqBRARO2ou/vFE4X5LxIwThri3ZfKQ7lTEyBPgVCkhZq4ww6K1JWhNTx05/8Oe+2kcff/A0u3vk2ujnhoVeFSTkwII9kZjLiaVEW3kEWyRbDwFQcw3MM6L7Hdjus39JYMSH2ORMi4mCvk+hgGi1mcVmczJWPRN+LO7wajB3VYQzqMlZTJpuhepAw2sgeUQpipqzFBwRS2HNj0XcMro6YrlBamkvcXwDiQffdWIc1dgQ2g49onceCI7mYXZXuviFOGMByyjgwWor6mcO6cCho5vGcxkJozFAYzqnMSZHrsuX4cp9GNZUs+TAFXM1Z0XX+IIv3lXd5nAzsYFWKiykO92AAZeX/g9zIV7tmhmJu4dYLw79MpANAW1ixw+dqIaI4W5d9m9Len0bwdXiLrGpZu3IqYaEewelMLt1LvZiGFX+RVGKGmBjjiJBkPscUx8/KIHNoYF0qYRLmbPBBCg8DiQGQzioFucQalXPo0tmQc8ZYIStobUm25OAKYZGHQOg69m1HTonQ9whBXrpznSt5RCXz2lotRWClwEzLmJJrikE01FOMRdpQxqDVWky+E0xt5nIGj5fw7NLw9oXmZAZVJetrZSsympSkqPDOU8P9ztAHQ0zSnayAPgT6ENj7SBccfRvoA+y6wHr7QOMUuamYVI4+G7a9RovZBjkqgt/hSgyepFROTIaQAl18oN1vWe00PgpgOprKlfmEkm5FY4QokVPGh0jvU8E6SqdflvjMWktdZ7LS6AjKgKuLtrN1qALGSrwJiojOHqeGKLd0Ntkabeoib2ZRKtK1Hd4HvI+EINJoKQznYdHai+dA47hYnhB8xPsdFMJUzp4YfCFSyOcFH0QCMnkBQ13pUA6RoGqwFbUzWKOhOaFdvkXdPWCNpamXovN6+QHN6VPmy3MW9f/P3Jv82pZt6V2/Wa21dnmqW0X1Il6R76UzcUIiI0CJEbLAyO64R9sN5H+ABv4T6LqFRA+3QAiBEEJIKUsYCSUpnE476/deZMZ7GdWt7zlnF6uYFY0x59r7RASV6OSWTty45+69VzWLMb7xje8zNFaJT0vp6FrojGotzXKBu9gQ1gt8TqgpMhSGNdmXDmTJc6Wr0M9xZUME05W4vsO5jZDqlMZgyO0l+/x9kmpZmSUrHQm71/Kdvi+4zne//kqAsT5rPt9Z9qNhNCtSETOPGULM+CmhGlBOTAUymawbYjZl4Qt0rWMYPGEYmWLETz3rNtHogfH4mru3X3Nx8wxtGhaLJdvLTEIzHI/s9+948+ovMf4epwNWK6nWdGsurp+wWG9JJO7fvSCMB6wxtMsNj558iG2X5P2eREIbxWK1pV2scW0nQKRK3Dx6RNs0oqd02KFyojUNC7cie1h0W9p2gbUdVnVYtaJptjRNR9mv0UqqHyl6qCFOlopWTqnoAhZ2oK3yBsUgQykgSsvgFEneYztxdU0UwW0lLLeYE957pqNnGA6s1xuZiM4RYuTm0Q0/yXAIij/7MtE8++uY6yNq+ZS3P/ufMXmQVpyySRYM8OEr12C0LqJFPiCf3lCD73x2nVWpUReXzbr5QRFeLxIIspHWLf/07zmfmKTzkfI5I8CAWZLbKyjMU82ASQMmHZjub+F6iWsa2s2a9OVn0Io8guo0RjtOsEnGKmFh5ejFhCt48gwSi6lXLjpnigxxAF+S/+whjcI+tg60JZe6soA1aQZVqzYTZ8eumqzn4PB8S6pJQTmuOrvPNQBVZ/d2rmp/x4NUZ/8/39vKtq2agMgxFak4itZgSD6jvnqJfvEanYVFJQFHQqUJnQb47DO4u0XFCZsOqBTmVMgoOS9dg0slQf1pS4GFM3TW0TnHsm1YtB0+Bibv8UEcQ2M+5ZA1OCUnQtEIDFPm9YuXaKe5fnzNxfqSFCaykYDV2UYg3DQSppF+P9Af3tIfb5mGPS73XFxvuH97YNwfUG/uca/vaI8JOzpMVuymsbDCZQxbNPsXb+nbBY1S6KePuX39lrt3d/T7HmfsKXjOzEmi0uBKi8qibcTMrMw1pWAcZI6SDcOxR8dIiomYM8OxZ9V2qEWDLrp/OguLJ+VSKY8CpneNY7NezjIFtS3tG+T9s3F5ep23btU/8xnQf5JTKQirEqPHdrUkpkxI4mBrtJrlSuZnXvReawA/j9HyF3V23FkC4zvO95wpUgdGymlmrZELUypKgBLOwIBcwd5yDqEGlFRmrjCZquxBjBFlDcpZ1GRJQbSeODt2fdm7O+xP/5TDj36FrDIxeKZxoFtM5NyV4woYZnUR00PNLam16KW1ZbFa40cvjBfb0Lar0upUNavPQLuUGX2RhFFW9K3P2GgVYJimgG1aVvYSTaLf78p9r0xYg1EahawFqmi2idFJJHYN+0++x1ErePGc+Pw5CsOz/T2WTGocfhh5/vwrtGskQG3ElI2aeBaJmk3XoS4usVbxxcLxi1/8gslP5JRnV2H5OV8DTwnaqXD1rcXv28WEOrge/kbuzdlzrEZ1SZ8z0eRRCytIiwa10ihVdNTIhZ9NSXjly1JJriTxMlS5gpP7dWEaafn0zDwpe8as61f2QWeVACHGYFDCuKxJdxm7prCKQ4gzUKWK/EciowuQo0sy6YMvWsjxxDKWD5GpBYrTf8uJy/5xVjBhC03nuLq8om0c5IwfB459j/ctPiaUNSQPu/sSNxlLJjGNR169GfFTIikrikLG0rQdzWKB7bQwS5UT6RPE2bhddHg/cffuHSl49ndvMTrTOku37LDtkmZ5hTHC8GmcpW01zjWgLcY1LI1hGEYOhyM+RFy7EO25mFk7g3OKcTgSJymEX149lhbo8ryGoWfoe1IKpKTQboFttqwWHY21AlrZBuc9+jAwxR3JJJ7cPGI/7jneviX88f9B/vFvwGIpcYTy5d4AWQl+kRNaixGPclbksJQhZkVIuTBqyvMoJkc5ZkJM0uZtLBpNTAEymMbOevTzPIgJNTO5TzFLBR5IamaOaq2Lwk+S1tXzIXI2VObP5ofjZ54n395+5i+Z8cfzuVzm/8w2LPtSfa9GkbQUlyKptCRzBj7BGQqJWq1guZI9ad7g8rw3pBIT1k6MEwNeoZwtoZ3cA1X2G2tamvWS9uoavWqYbCZoeSxp2fH5/sDq8intDwzPXv4hz6cl98eR/TThY0BPzFqfgqHJujGzG7WaVUNO7PUCRKXi3WC1FJrQjFPA394zDgM5SYdS8HGO7Sn7ucpZjC2DgLEhSlutUYq2/Bht5nMSAL+wEJW0baNkDTJGjAmtEZ6s/DvEZEnTWLqlhMhRtYQz4McjL7/6VFhqObD95DcYrCIG6SLIUQnT7HxtrrlHvRN1L6eAJYIGolNARfEswDbzMJhH2zmwLwNP1uEQCNM4My2hbNv5tC/U7zh97qTfWkHQKl1wkriZBzgzO5KzsEKdzqO+VfYOPbdE1+K1xPSpFA+0aIEW0HauG5cNtO4XFVQ6zTjmuTnPA0qIl4uBF1KsqXlvLb7IViAdFzkjusmqehVQGKa5SGkJq3TWND+L/c4Oe7ofVMCaAkqe5n4uV1K7b+Rxl0meFbUDQNd7fH5pqkoTlOss+a7KRafWZFQux83VUFbGpapzoD63EqOkmAg5FNmBqtEamaZhLtzO2fH52qfUDM5SQM3zsZnhBMgaKbiiFSYWxmoq/iwF/c5RPiX1PEWq4VSsa34xVtP6bBxqUmHax5QJPhJ9KOM244umdAVlm7bFOldMutUMxuaU8d6jJz+bgDmjaJ2ltYrOKpZN5tmV4/0LxZMLzbNrxaOrJYtWY60GJXr6Ah3ItTUNLFoxuMxYkQPIinHKjN7TT57bPdweAoNPDGNgnAasduQs+6WA2JkxWIxpSFiOcQUYUjbEpJAiiSVhiDnxdh+57zVTFBqSyVLsFQwig3JCinNxNlIMIeJjlmJ8kBhTl6KXyopoMxZZo0VaaYFtOpSxKGMwZZ8FVYDxQXLaeaWzmGaJtRTZoYw2ErPlMg+k27H4CSgxOs5LxTAafDSMXjEMgf3REKOHFArTVpGVKZ0BGWVEwgBV/GDiSDq8kvzTtuiuQalLlBFJULW5gfARtAu4eIJRkC7fo91csV5tuFwv6Fw12QKjM06L8KNRFm06VNNh3UQTRaM4p0jOnhwmUvLEOJL9KKZjSdjZQXkwK0zKaBzKbKQb0LYoDJgFwV0xuAntBtrmK7S9hSiyk9/dXSyvvxJg7JTg1cEwJYO2rSRARqqHFkXKE1qDJqKyJ8QRHwbIAXIgTgfMaolOA8oHUhwwOXC5cXStgnRkd/uKdrmlWRiMdazWK6bg2e3vub99zeH2BTdLLZpppsVYR3fxiPXlI9CaoT9w3L1F5US3WLPe3nD56CmHfl8qURFjFYvVGm0tIUX64UA/7Hjy7Jqb6w3390f+8E8/g/aKxnQs24aQHKv2BtcsMaaBrNFmSbu8pF1s0FoTsiQzIYr7qzUNM4MsZ0iit5GLmHatYkprlQQuSWtS8EVYH5qFaLDGEq1aY0/k1JTw40j0EW0s1rUFNIBuueT99ztotvyTP9hxt/5rWDTNxQfcfvH75P4LUo6cwoSHkXA+C5pjjHjvC9CTy4YgC5Wi6JHO+/ZpQ6+t0LWdpS6klTKv0AWkUQ8YkDl9F/ByCvYTGnQDdoVKkWxFf9OYgCHS372hP1yizAWqW5F8T+5v0dbKgtFsTtebQaWJHBM5enIQplxKQvMXMHZCpUDduMgTTJNUrnKC5OU9SpiwShm5p/k8xEOMwiiBUM1YvpHk15BiDkZINV4rCcuZxMEMiNVArdx3dfp0DQvV+fGygFFVL64y35j1WzPq9g786XwVGfOLv8T8/JfoHFBpIFV93Dii/J6cRhnbgFb+BACgsCX2scVcyiktWsvltLWGTdfSNq3oDVagLooOZvBBtNRqEFWCghm4KNWElBLjuwltNa++/JoP3/sI27QYq8lGY7IrxiwePw30+1uO+1fE6YjOgXXb8mi7xRwd+xiZXt3TPj+wMS0uGyKaW5/E1VNnklZFtP6Iud/B7p7mcs2b5y+5f31L8AG1WnKK/1TRCy5JrBUGojOatrbyF3aFLxrFikx/GGiNnj+fpkCeJlSRDclFQyuV9q4QIzlIYuWMZrVo6NoGnzN9PxLjGQu+gH7nee5Jj68GmSXRmJOB/O33klHKYI1ls7lg8BOHvhcm32nk16PO2mGyHnIqPChp79TFREOp6p6bH5xkBeIqaDUnPwWMOjemyDkTQpCfM23sOdItkyhEMUqo5yHJpZ6B4xgj2RpU49DeEWfDmXOhhjIP7+8xP/8p6ke/IjM5Bfw0kIIvzFAjxStVkuWy7mldXHNLAoyCxaKjWy7RxmFsi2uW5DwKw6Ky1koyFosjq9YWWyRVJu8fXHJKiWmccF2Hs0uMykzDUIIZZka8TqI1rmKE6AWkS7GwZGH65GNSCrz1A+H2HUo5Nrs9Sima2GEyvH79km6xQGnFantNVhZtpIugXqdFc7lc0a46fvPRJf7NW17v7zmUdrw5USMzt2TUUTgntnzrGXxzDNdxeobu1A+e/f3EUBI2y0n3bz5QHcPKoLXMJWPO3nO+OFOKAQWMMimh09mgmwGvU5JVgav5vCsQW9cOVRhp2uC0oW1ahnGYCwg5F/ZePs0puZ5y7wrLL4Yg7uYhMI4jIYSZ8fmARSwZPKfJcrqb87+Xl77QtLnj8vqaxjpS8Ezec9zd0/ctq80aow2kQH+UpLFprBRP4sDruyOuWYLSKNPSmAbjOkzToRuLz0b2xCjafMvlgqax7A97DocjKiVi6NGNQdkOoxesttcs1tc0zVLiLD9CHoHKFEksVkvRBQ2RcfIsNleEBMPoWaWI05n93S1hmsgpsrm4LIak8greczgccc5h7BJttySzolmuWS8aQBLsxjQ0QWPsyEEduHl8w8Ef2IU9dz//Q8L1E9LNE9RyJYzYFM/GqACLSSWUcdhS4POjJ1HZpWdrYNH4y5Tu9SLpk2Mme9F8tVkV8P1sTQ+ZnIQVTYnh6jpa91tptWSOcVUpUH4TVFVn5/6t4TMzik7r+flMTenh3H0gOYLEqeoMGIOz+a7O2qipwEz5nqTPOokKjGP0PKRTPVe5QPl9qo9BnQAdTvdnXpvE+UU+3ljsZsHiyRWjFbOqKQmhQS9b7pXm64sbFnbDr376BVdDZGWlY+IYhTnqsnQ+ZK2k7fcMmAIesOHy2enW/SDXU8/C7vT9UZjspWDj0/QAJE9JYrgUxEAmIUC0yRmrFQutabQ0uchxiu5ryUt0FhkUpasJkKVtWmGTlhVaKVDJoLyAvfHMvFeX8ZSB+9sXcvZxZHv9iM7e4I0iZU1Khige6PP90CV+TaoU/6kySmdjOBWT3TNvh9nyozxGPRNuC7lEAVmMjoL3c87GvL7WsSmfP1OHlbGQOY3R+rxOf5Vzm8fU+dOV+KzqtsqeczYPzsahMChPklJVHzXBbPY0z8E6J+dkghJrne5XXUOo967Me60EFIrUOBaRdStOgLmAn3IuhXxhJBesiYvKeTYOTKmsU+R5bs26rXVrL8cXfxWZq0lltDKn+z6DoWqeumdfMN+zk15tvaay9uiHMW1KUQBLleZYJVP0iNGIvE/tLlPzjxAUIBe8IU0lr80iPxP8WMgupzl3yuHk2uoensv8SvnseVNyvJmdrIpWpnyR5NmK6geTyziVgllZD3ISj4WzeV+PmaLsiTEmKUBFGfPTKHJ8MYbSqWpomobVcok2BuscrmlO5yUPV9au0gWryKxaxXbRsukUqxbWrefZdcPTreLxBh5dwGrd4ZwpYKBGZ9HNpYwTHQOdiShbtJwbWXOCN0xe9M6tioSQGMaESgFDoNGGxkLjDNYoNIZEi1cdAUNMwnoNURNjKeIoKXgkMvdxYJ+UgKspYsKAjndiTp094GnbTOM81mqsKjF5KaSmkAXkNEByRG2leKG0xPZNi+uWxRSr+mycYsmUIsH7Ik1RQHxlcJ3H2QnrGumqbiw+xhJz5jMkoGgMW0vXtGQatBnJWEIUdv0wjPhpxAeD0r6EExmyFwZ+8VLIWYv3yXSPImGaFrO5RFmHVgZtF7jlGngfvVxj/AGXR1hf0i03LBcrNsuOphCSTNnflDV447Buge222PUlzRQIMZH8hE+eGEZSnIhhxPue7HtUFllIVETlAcVnqKQwaoXq3ie3VyQlZppaO7JZEuwFkz3g7RUL61AMD6Q1v+v1VwKMzUrTdAssGu2KAU4ONE7RGMAHxuPAMNwzDbcM/S1Df0fcv4D+Dhsn7vw920VLu+5oGkfjHE6NkvQoTUhJ2AVoXNOxWCwZvVQDwnRkvTA0NuOalnaxZXXxhOvHH+Fz4u7uNW9ff0WMA0235OrmKZeP3kNZx/FwT/BHtIoY61is1lhn8WFk6A+Mw44nj1eEBu7ujvz5Z7/k2fcuaZbPuF5cMd3e4f2IVg6VtCSQNzdcPv0+20cfgrXkfs/97RtiDDjb0GwaCXyRBVWCw8W8kBlrZELpNG9i1jSSVMVYDMCgtjeklEArDsej0LK1wjaWzeUly80W4xxDP4j77TBgmpYPP3jG3/m7/z7/1e/cMtgbNjc/4smP/4jXf/jfkMOObL573EUfSvu8IsfyTIqeSCIRSjAxx6D5BIaRVNHIiUQS2mpa19L3PT4EqQxpjUGRchIaf4x4pOIK351UK6XQ1kgykgWKMwU8sFrao3qd6d98yZvNBfvQMLKUlsfhHUoFYbkpBW1lx2Vxf/S+BGlR3I+TBEGaSMoBYVPK5qJyBL9D58XcCqpIZD+hTALjmKv856YW1aSIB7krp4T29NfKgKqphHr4z2VMnQMHZ/hCfd+80Zfj5iwAcY4n4w5A55qAyzPMCew//R3Um3egNG3yYtqQo1SfQs/Q30pFKsdijiKtR1qrwng1xQBCGGFdIwCrq7pDaGKQ9zfOsl4vWLYtIQoDtp9G9iEKeBYDMUhAZJ1ogRIiTBMVHNRa0y3E2b0fDvS3d3zxs5/zgx98UtxGMzplMruHqwAAIABJREFU0jRx7O+5ffeS3d0rOpfYrBa4nMAH+tt3HO93fLRZoVZPeOHfkoYeTcDHxH70vO17jmEi5EgoDJuwXPDkvSdcff97vIqBrz77guP9UaQ2ponVej23mmUSBC8JD8U8aRxwVhf9oIaus/SHiRgiWiu6rmPZNQzjSAwBlTOGhPcjcbT43uJiwk9DaVnKkA3DFJmmkTQNKK0Yh2Lop9UMwsrcOs2xGciksgPTrD353UAMZwmp/H2z3GL8yBQT49iTKlUl1bZVJfNKSctS4xqRmbCGpm3ZH/anwVyCaG0eGinFMqdCRhw7AasLWwvFer3m7vb2BCCcgcbzFZwl7vXaz0E9YQwG0UyuBhnW0axXGGvZjwGd48zOOv/uGBNhnMrnBHScxoHj/p71YkVSUnyz1jFUvVdt0MoSQ2LojwKu6EwIa5abC7RxaGMxGi4u1gz9kcMx4ouDavBBihchEVOgaRpySvS73fy4rDMs150kGlnMxMI04bRQtpScPH480vQDauxRIWCAbBsxYLMtxloMiuPdG/T3fkj/8Y+YUuKL//5/wN3v2GbFr19dcnf/hj//9I958eJzvvfJj3j89HtovUEBMXmGoUenEWc1W9vyN7sl3//xr/E7L77kD9684PWbt2jr5kT/OxbQeeXLNXF+sBI+HLGVwXP+23NebQXhjalutIZwbi5CWZFnoKoymSV4DyFQO13qWdb2Q5DCgvlG94eegf8Z4aCCpgpp9YtJYgindWkNlrW0bRqadkE/SpFl/tbKkim6eTPCUca5nzxTYcTlmPDjNM/72v5JTZCLnIZP4cEYP03+02+sadC5xQeD1hHtB3IMWJ1QRvPs/aeonPDDka5V5CHhjBb9NJ14+eVX6HZLt7xkffGIaYxgDT4rkldMAayOxTAG1psF1iqG/p67d29Zr9bcXC4xSu7127fvePzhT2gWW4xtQCnG/kjymhRGQvIc+z3byyUKaecbe8/1zSO0FfOx3ZtbnEq8efMK7wdWy46hV1R9/5wz4+jZH4689/6HXN28h2fJfrfHD7c0WgpS92NgjImQAuAxGtbvX/LDx5ZHn2z53d/+Pe5+958y/eRfIfz4N8gh4oPIsWirxbQji/wMUcbUmCbMoZnXx7nwlQtrchAGfDZSqA8pEQ4jKiacsVibpR01Fh07Ywogqaiu3bNzax1DOTMeB2zj5n3t4Zg4zcHawpm/CcSW+1aL+XP3VEm46z5kiv7eAxO9M/BVTGvU6fcVECvtudYYEpaEgGmpurKXJDOrE/tMceLEPFhLMsI+MyIBcFpizsZ+ljW/SGzTdA3uYkVaN9wxcAxegAQtHQdoh7/e8uLlLeM40P/Wv8vNf/vf8WjZcjSK4f6d7BuFyKGUJsRiwlMAaAFRVbk/cs1iUlz2Si0xE7noFSqFtq6ANb4QP8L8XFQB9XRWhMnji6GaDpGFNSytZds5UhYpJAmJBWhQpejqjGHVSfFNl+5JV/wgvgkQD9PE8TgwToGucyKfZGTNa4x0YO3vXjAOO3LKPP71f4fF6gaahj4ptM7MS5WiyL6oM2jsDGTVlPE/ocOEjRJHWZ1L11VEpYSh+IcrhTGqmK+WGD9TYmhKp0MgZ1ukAurxculmLIPiG8Z2wFz8kGF1btJ4BiTCDKBKDF/NlICi453LudVPnBjOJwkClAClMaXS6cJ87CpVcG7wNd/MB+dbAHeliEgOdwJMC9ijJL9I+bTPaiXMaFMY+7UAT0ozyKm0Lu32FdyUc6rx1nkuKBikxIwC4lawuLyfE3h1WhPKyFb67IpKV6IS5p+sDXUt50G8qLRG5dodOmdfnC9mxU4YWXBrt4i8PxaZoPmuKwFqYxSmaS0CVak+XaTcqB1Bhcqqaq5T70WSDtxYQLcMM7Asxz7XLC7SFSlWvHq+VkruRpbuwnEYmYYRfxxEcqholI9DkeM7i5aOx57j4UjTtnRdx3ZrcV1TwNg0M7Wt0hijMAouVx2PVoabteJmk7neGp7cWC5Xik0HF0uNaVZUGZAUMzlNpDwxeugHxd3dEXIWwoFtsYsVi67F6kTXKrq2oWnAWmhMQsfE1Biutpbt2nCxVqwWRqQLm0uSvQS9IsaGREvWHdqtUMaBFgZ5jgrbQzdMqL5nPO7J+7ek48/I/iUpjGQmwpQZjMKajDWxgNFOcp4o+rImgVIRE6vxsBJvBycSmllZAWILRkKuUhgJP4kOdvBT6SRWaLfDmkbuheto2xasmQs4OUEKIv3lrMZYw3a15XKbeTJ4njzqeXTd8/z1gTe3R97d9hzGRIwjPg2ENJBiIEyTtPBnTyZgshi96jRhjq/g+JbcXKN1S2sMyhjS+hK6FqaGdPga53dYb7FtQ1YLlAGrwRZip7IdTStEzNVmg1t06L/8FF5+TZhGcpjwQ09MEyFOhLGH7JGMUDqljUqY8R1q/wVKrzDrj2m6J0QaUmtpjKF1BpUWmLTFh0esjwtUOBTiz/8PZqxS6iPgHwNPyyrxX+Sc/5FS6hr4r4FPgF8A/1HO+Z2SleofAX8XOAJ/P+f8z//vjuHHkc//7J9htGK5uSCiiWEgDHtiv0MNA+PhNd4fgMBq4bhoA7pLmM7Qmi2uW7NYNDgn7ZOtXbBZLbFth3YLlFthtWa/v+dwfwtkmsWKx48es144+vuWVWvZXD5hub1ksd4wDSOvv/qKw/4dYfLYbs2jZx+zubimXSzxw8Bx/5owivRA067pFsviMB9xVnH37pYXv/iUu9sdL94ceL1ruHQfMXYfsWPD52YJecdKazrtaGzHzeN/lcXj79NtN0xxIqTIZrMm+LGYqXgpvJZgb5pG2qadAx7fT8QYSpAiwt5Ga1RWGNvQNG0R1k6gdAFnFdY1uOWyyBwkElKVUgpUaS0a+iMx3YE2/PrNir/14wv+xfPAL253fP+3/mMOt1/Rv/iXpP45qrAvH4wnKy1FlVE2TqMwfmMgpEworS9l8MkiXRZ2csZXofAM6Iynio3LgQTY1YzB46OAWqlqPZxXfU8DvCTIpYKco0hBxJE03hPDDsIBTYDhlvHN56Lf11yiO0vc35GnAyl5zAWw8GBl4/J9X9itAZKfNzEBq1IBKyco7VTaGHRU4Hso7vBzY1TykLy0GChLrq7wZ9vi+f98IzyYk5JTnl6S8jOoVaZu1SYqIWcFKEp70qmtu7Qt5PL/BYylgrFak5LH/a//DPX1K1IW8yzb36FjwOTMxg+sc2AicMgT78KRMXiMgtYa1m2Hrkl9BZGVALSmuCkvF6IjRM5YpVh3C1bLLdbKYh6TMLM2yyXWGMbR89WLF1BNCVrHdrvl6vqy6CQP/OynP5UAIks7/H43IUGoQkU43u35xaef8jGZffOWvj/SjwPWJLROaCVaPu/u7zCjR+968levcXcDt8qSpsju3R68Z9MtICuOPhBjFiBQG5yyqBRprzYsrjdMzvDTP/spd2/vcFlE+vPhyP7Q07bC0FVkkp9ojKNdrFkslqyXC4Z+R/CenMBphVkvOOx7MW5QQBLQwimLJtNaLS6lx4khgleZ3g/sjj27w5HdfuC2HxliICto2+ZMb4pK4Kmjah6HxhhyBdIlon6Q/J5NytPILWCpMoaQE3/55Rckrc7cvqXKS2GYoqRVrzTZ8OzyGqJoEkYj+r+jl+S1MmblfM4OXzZNraTSW98nkzez3++FIVzGeusszlp2Z2y2VApjWsuzmsaJuQVUQYqRKXp0lkq6M04SbmXIzsKiJe0O4jQNs3trTZT9g9RKWt/GYUClTGMdXbekaQVkX6+3dJ0Uj+7e3WGMYdE12MaWgE4RcsLkQNdEnj1a0Pcdt7eRr14NQMBY0EbjnGYYIo2zKKdw8aQZ27aO7WbBy6+/Yrq7w8ZIlwLqeCSMO5g8xEBDFv3h6NFG0y62fPI3/i30asOkYIyeZdvw7tO/QPU9bU40jUN98qt8+NNPufnqOZNVfBAjP//sZ/z58xd8/pef873v/ZBn733M9c1jthdbMbIqpnKy1Gs+fP8j/sPLa37t7iN++4tf8mef/lT+TWuSzkLzK/SlBwDmWVHhBK+cJXPlP9+GcrNU/Qvwc85iUnN6fjpMzhDJwvCkDOmcaTonjqzljQKixhkUmscBxczDj5hZD032G1W0Dmvypcp6CrUoqzGmObG3MkwlWQrBi55iABDnXFCEGGW6cCp4VtdeRZ5BnGpmN8synBdalMJqJ0aNVUW5gNDne3WzWHK1fsrHf+0nDP1AmHoOuzuOQ894d4cPo8ivxJE4HTHW4pylaRxt2wGO1nU0tiGFzPrimnbdcBwHvn7+muPhgMuW1i3onOF4eMdhfyClxNXFltVygTO56IhlrBEDoxzGovdpWV1sON4jBc0oTt0xlZgiB7abBX/6R/+Smyfvs7m8pjGK1gIkxuHI4fAObVu8/8k8Ljc3j/nyzWuCsXhlMKrjeDjQF83MtmvxpZskB08InmQtKXga2/D0+im//m//Kl//8i33t684/vHvcP8bv4UfvHi8NEoCBq1JXnwGlDGQNCn30h1lG1zbggKnHaZZkJiwrkMvHElnjvc7AcoipBA43h8KCNbOIJ/RGj+NWGdpmpZxOGKVOGUnRP/4BMzWmKXGKt/9slo/kIgBAWvSWfySFaw2azbrNZvNir/4i8+I8ayTpPyZBS1+sG+BsHUrQ06pAtI66UBTWmFKgSSrUnRTp3irAgdnXze35UI+aWB+o+gmzx9UMVWxRsyu9tPA6CfU2ONYEIkzAKS0xjQdXGcGpbnTDW9f9/i//R+w+IM/4XuffcZoNW9u3wrAlpTICpQEu+5ZJoOq2tZGgChn7Oya7oO0F9fzFUA746OXZH7yKFXNjrKwp6OAqr60lW8WHU/XS0nidWGcWtFd9yEwjBM5G2HTZWnYtW0rSboWB3hbgKWUBAwf/MRxHEk5YZ3op47jSPC66CJbWmtptcLHhO8P/OKnv8/d7S1Pf/Kvs33vhyy7K25DASjlKWBcK2B7PD1j6WrJRZLCou97wnCgP/ZkD1skjc+IzqwxtjxrddpTYhSZJ63BaHx5hmhDLOugquO/xMDf2mRmkDLNf4cyZVKutN5vfKZ2QugCQMb5g2mOh2TM57O9TgrLtY1d7s03dkEB8YvUzUmaqZ6f0MAfArSFoYsSHXwoRQDxR4lRviNlUEZyuaTqnBXzaxmrpXhQ51NlTKsKJNYpXIDbwjRRNdUpm3g1eq3np8189ad7cH7vy1w+abGfYPt6brnmS3IEUPGsQFlTrLNiUY7EJDqVMcZZ3u2bYO0JCJb7arQFpc86TRNx1osVRmso7NkK2OraJaBqrFn9NhTRB4k3qt9HzTfn+yNX2FpzBiqX4tF8rgmrFLZd0GAZkiJMo6yphb2stJahanSRj5JxOIxjMRYLNIsFxooeqrUOZYrcQE44nblaKd5/bHiyhUebxM2F5WLdsFo1LLuGVbtEaUvK0uU3IQQdHxSHY+Dt7ci7dz3aKJoG2tayyIOYW9lcui9brG55chm5Wke+/8xh7Iauc1KANJq2bWB7g28/YrLvEbli8i0TC4JZweJKzLOKMrQ1hrZtCd4zjAPH/Z79y3uOr/86x/uvOe6+pN99yjS8Qfs9loHGRbQ1GO2KwWLCKif3GSN4Rfb48UhWhZxjLLaRewACzIcQ8dM0+yaIFJLkPzlnwhSIaiTaiZxEUtHgSpGlzD2tUNbKPqchRY/RilWncKajcw1t47DaMPaJ3W6g7dY0qiWmlqFP9P0rpn5HCCM+RcgejaaxDctFYOm+RscGtT1gNlfY1Rav2jLLNDlE0uEdu7tX7JThpWtZuoZusaBdLFmut6wubmi7lnaxwjmLNi1Jb4jNFYfckvY9mBGlZJ+KJpKTlcKcyqgcSCmgAoRxRzz8kvDuT8n6EflCkbeGvFihrSa1S6J+zKR+jcX0Fp0N6fjiW6r156//N8zYAPwnOed/rpTaAL+nlPpt4O8D/yTn/J8ppf4h8A+B/xT4O8CvlJ9/E/jPy5//1weYDoRXf4QymnG/JBYhYpUiLnl0DjTtQLSBTKRrFU0LCoc1Lcv1BavtDavlSqq31qC0Y7FYkLNsuuiO0fcch4njoQdj0dqK0Um3JnvP9nLL5vIa13aknHnz5iV9vyPGgLEN2+undNsn2MWCrKE/HvDDkeQ9zjqW3QbrOnyKhJgYJs+zDz7mp2/v2A+ZoBwXj57Qbq7wOpOGe0bXEozGm46F27BZPmV5+Yz1uqV1njDtS/umVOtC8LK0F+OenMVRUhVdpZwz3k8CRjhhnRhd9/1ASlIBzKmI0FuHbjqMETdtUyrOqFxajmWxTDEQvMcaQ06B4+GW/nDL92+e8uJu5LOvjrxa/ZCrX/1bKBXYf94DO5q2Qzs3P2ujNVbp2Ul2FipHmAy1ug0UBsN3D17RJ5R/j0WaYI4FaoVccTLeUacNpFa55c3yI23xBTidBdCDiMFHSepVnuDwCnRCrwZWXcs4GtFZ8XeE4fXMaAFEPqCYceVS9QEKxplQ2ZPSJOy4XOQKrCn6IqLNqbUr4K1UZlSKso4q2XQrVjqDsurbwX/V451h2yzfVwM8DSLp8I3KLajThjoHevIZlVNhrSr0/oD7F38EWaTJrQKn5L60L16ihp4ImDBgwh4bAzZDmzyKTMyBKXtinOisY9m0LJzFGS1yGTUEUFoSa+dw1tAY2RBQ4IylLZqwzlhpd0qy0fgQhIWoVDGRYh5/2kCYRkkkFfhpKswPNUsVpJyp5jqusRjb8OUvv2IcJharlqbVWGfwKqKK5k0aPOx63GHA7Qbs6wOHY+R1TEwxkULm6WIpDr05oXPGKkP0gwBtWtMazWLZ4WPkeHvL558/L4UV0WnLKEhZmCZjIkZhxTZNO+tlHfsjvui4Ka1LUJZKICvBVp+qU6owP4/DxLGfOObMMSUOKTCmiE8RnyRhngCMKYmaKZqVJ9M3AXxOIvQxxbm1+aSJV6fgWaDM/AWcgnjQRVBezD40ymq0Fu0jZU3RQCqamUqeVedaGtswTEdCinglTti5Bt2FyVfrDnXMt12HKcWs0/uKnEkWwzxZt6Sddr1YcHN9zW655HX5FmE+CoC6WayYzCjuskWSRdx3H0o1WGPFcdRo1CYxDB6V4lzQalwj1e6czyRD6jwVsNs6i9KaEAP3d++KBIcu2qpSXDNG3lvdkXVNrHJif9jz1gpr4TAMTNNAylNhMMt8s1aKVyD6VPVlcmahFD/+6Clf7/f445Hc9+TjERvD3EKXCxMzakNCTOemFGnahv3Y8/zuNYtFy/bRFemt4vDuFpMlIX797BmT1jz5/HOa9z7harcTR/fdHV98+UvGcWDsd6j0gUghqARJk1UmjB7TWLaLJT+wjr+tNB/tjvzF3TteTT3HlPDm270TqehC5vxQD7kmb98EYaV19+w3BfSQoEYXrV1Q6ttcUHGdl2LTGQJc1r+i4ayVsPKjJEKp6G5lVDGAKVpyMYheWDV1oRRAMmiK6ZbSVN3WUxKfZzaROWttpIzn+sx1EgOnGQRAwKPzFkXIc1wiv0qlfe50efFcNmH+nuLYfXaPTEm+jIH7/T2X2xU5r9jvdux3B+7vbnFG4UzGIHqyWi9RuqFd3dD2GtsuMbZFGU1/uOfl257JTwQ/0ThNjp5xyOTk5wRYzCsMfhx4cn3DbncvYJg29Ie9uBAriDnSUApT2pCS6BlOkxfQmkxIAT/2HO7f4kxmc3ODVhnXGBbLBaiO5WqNLYUdYyzPnn7IMBw49D0v37ziYi2a9mhLVpEpDMSY504WHybGqacx0hnQuobtes3xyYjrJ7oA4We/z/7jXwNtRJomBrDVPAqUjuhoBfyoMVYU2SqSFC26bsnl9SNGIkMYcU1L8vJvKqayByuUjjL+s6SfOYsRz+QlCbTaYWwWU5u6Hp5NijlmOwPyzyVBzkGQOaxLiYq3JMSQJkbP4bAnRk/btsImKt8xz/ry3d8aj3Nh4PT7EIIAoAqJFwqwJWNW2pN1LSSfnWPBTUFVwKq0z1eArhRCcpa4zC0a2tUa6xxjvycFkVjSk8VVRlr5Um3EXCc2hrxqmXzidjewNhv6X/k+w6rl8S8/xW4X3L55y3g4ooPESlpFVBLWqy5tlzmpef0LycuaAnh/AocEwBb99ug9KYRS6C1t4qrqPMraZcr93DSWdWsexOYUs2FiIHkxXstR1sUUMzmCbQX00EqJjnaO+CBdd8dDz64fZqMx11i0yqyXK2JKDJMUlpzVOCOt8FOcOL77ktefKvzhjsc//hs0bv3AI6GC7WXkzUWth0FLYgoewiS+GaoCdyKXpkpceb72nTM2tXOolMsiepoAD/aWOsYFfS1HlV/W/aNOE6WErW4LaHICE880b2MmEQVALRMvz5og+rQnKWZpJYXIjKii4SkoWhm75RiSn52ZL1bZqMKWnV/5dFdlPJ0MT2MM5GxO97oM9JnNLhcim3I1D9O1gGBOY6pezvmdrBJaZ2zX+rxAzemOUqrIjshYr+tEJbicffkpv6R2Q5V3ZlX8UQr4qqUTJ8Z8YtSXeHJ+4mVu1ThTpPaKvErJyeq5V2JBSolYJC9kLVEiCYPEa0rrQmgper9ncgO1G1JkudR8i6yuklcQk3rwTHMdgzmL7Fm9f6pAzyUPV6pofxc8QZ6PFPisC5jJFH52eSxlvFWAPkXZ09KgSoE1oTFsli3rzYrOwcrB023myZXmcgObNWw2mfWyYbloaNsG58y8zmqTySpBMoAhRikAeT+hQtWRrd2h0rEg+a4w1nPOGKNYLRzLZcty0eGs6K1rbYjtinZ9SV49I9gnTKzwNATVkuyiMPszhXfBxcqhSaS4JkwX7O8ecf/uCffvfsDt29e8fvNDXn3xx0y3v2Q8fs003GFtoLEKZ7WYVZlUjHrrmhSJyYOfJA4celJSoEULVzsn5uAWjDKiU6s6qlkg1adHCUvYuQVNuxJ8rRILsuSvVSqrGnSnJIC8DyPeT4CnaQPrLdweR1I4CuaTglSskkZlTU4UE9JM61qU7sho+ruX2Aw57LBpT5Mf4ZqVjL84ENNEHm9JfpJcE0NQhr0V3X7XrmgvnrG5vGGxWtG0DV412G7LcvuUzaOBu7t3xDCgQsIYaNq2FKwkHvR+wA9HWRNTwvg73P2foN2WyWRG2+KdFaNkrcjOkbpL9usfYWPC4AoQ/t2v/0cwNuf8NfB1+f+dUupPgQ+Avwf8e+Vt/yXwvyBg7N8D/nGWlfV/V0pdKqXeK9/z3a8wYoav0daQg0MbStuOVLu0A9OAOBMqjNU0rcHaBW23ZX31lMX6iuVijXMOZSRBscbiQyQNEzFndoeeQz9JgopmHAYa50SjpNtguy3KiDtv3x/Z3d8S/IQ2lqZbsb54StNtUUYR4sDxcC8aYSljjKNbbIk4IpopaO4Pk4DAQWG7Je9dLdjkxyQz4GKgw6DVBVgH3RV69YTF9ceYztK1Gmcm4nSAFNFlI8opC/iqT5VbTSYl0fTKWUDArCgt2EWXSbvZ4Cto0UtxrsG0LbYRN7haIZONJIIqwGRKpBCIfqIperh+7CHCB9eaD95lLpuJF/c973/4rxH2z4nHV0yHP0ct27MqKidTBBldojtSg1XghC6eb6L1VTfAE6gjGw9zS9FZeHgKDkqgOtfxvtFWQha2S3XRU1lacecVOYGxxZxruCcRSNljdSBaScJ0OhKmt+S8olBjhc1anPgoItBySplMFIOqPEFOqFxE15VBqCU12K33KiCGN0ECITKoU1tbDe7VWbhwuk/MHUezMEFpUaiyAjUPyDlDjOhXb4ucgbxXl0BEqrviXa6KBpi539H+7KcooNHQasVSadI00AjaiM8Z7Xt0PKJLccGnSA+MBGKOWK1ZNQ3rtqN1TsDnEKnbv0bRdS2NNWKwV1gb1lraplbflDgwpoD3vmywnuPQM4Vw0nqrgWxKeD9xPEhIGwpTQfRVK0AiLElrxdFSmYa3r28J3rO9WLC96lguuwKURVIIjHc9+e09y8GzHCPtvecwZPbBE5Ri4Vo612DI4nCaT48s5iSGKQoapbjf7Xl7OPL29TsogWEsbYS2CO2nKPq3jRV3eKVGMomRTPbTLIivVA2oZM4dpwmfk+hulfFzyJFDiBx84BA8fQxEI47RyprCVNXFub2AuukUPJ3HqQ9SlfTNFo1TAjCP0zqW62cq+E8BG20jlV4lcz6V8SqAl+is2qIj55ww/gc/MfqJqKpGZwkcKayPb9D3nZPnLEO/aJmRUUlArgpk1vPURqr16gypq67IRmmcNmRjT0WOwt7n7FxkDqvSAqswyyWh2ZOmUTQs632qQAQZ/fI56foGrEOV9dxah1KKFIVZ1DSLGrqjtME1DUqlwv7QxeyqJkOJ3WFP8AMxJcbRM04jZC/gslVoZSEn/DggydyZZuzk4XBge9Wxz5nBR/zkRT80icZcRNpaZyZaSoQ4sbt9y/bykpAjfZoYh8DlzfvgA363Z+h7usZxv14xphtW727pXMvlo2ccx57P7+/J97dFGzziNFxfXqCtKlKwkqzoqGmahraz/GS1pbt8RBMia+CNH/gqJWHInpUKZqAkF6BVnbFteDhgvwnk1oGd53Sj/krm/DeZcKdk9nxNr0XFOU1CK1O06BRKl6JpKolP+QKZbyVJFfvjU4KqSrtrBbqqxmGuCb1ct7P2QbuuLcyVWNYsYdBosq4uz+WeVdSpXkgZ2zkJ+HuuS5i/A4wV+QJ1Mj4DcpY2usPhnvu7d2zWC7R12LZjsdyQlcaojFZiPhdCwoRMSAbsimYpsVKIkTCO7A8Hbnd7soJl1+CsFq2wKc5dGMZI651Wiil6nDuxAxNKioVhEhYRiuhbasKZtSHnwDBMTJN0//T9EVIgDgf80ZC2SyKCJbhSSNlsNtLSj4BXFxdXrNdbpjAyjgN5VR03KK/+AAAgAElEQVTZM0pFYphIUdhqubCgcgrFFENMLlftgovrFeqtwr85wstPYXUFriM3LVxelfiyjk2xC8WVll0dyCpiXVOIEmAbR7dcQwqkyaAj9EMUYCZBLi3PxjaAIoyeEKUDiJCKNlvENo0wOlVtq63dOaWoXGPSOpdyfrC/pMK0PJ9Log1eG18zy4WY4YYQ2N/vaLuOZKobvDCETkau35ySSubAWWtzLVhU7W2VNdqaeU1Ltc1daEkFMHk4z6vcwYxplOuZlRvKH7p1mEWDsQ0meTjsROMwBFIMKGfmorEA/pGoMrlz6G1m2C4IY2L68Al+2WBjz8Vmhf/zT+Gr5/h3O6zTvPf0sXQTasWbV28wdkFCEWImRImj6l4Rw0nqSsZNAiPM6hTSg/OZOYHFoVN6ApBis9MnooBShJJrJO/JIZ5i3Aw5igRK43QhJKgTIBAjYfKMw8g4epzNZ47slvVqNXezTGMvTFytsFrMSeO4Z/fyM0gTV0/fp7n5QYEiT+NsBsFqkKJqtK1qoCiyBCHQVrCPeUUv28Qp0DuDRwUAdw1pmqhGbdLhfR4UFa3J+bzy2bef9qJ8FmedYq4aZ5z+JFepihPIKL8/i+HO8UulZiC0rvtlMsw/9aofdkHkOTaa9VRzZcOWu6Hmo5erKgzRVHHW094lnYxGAHdjZpkCzvaUeqz5DmsK4JjPr3Q+3unaTzmkKntnBR0VFOmTs/1+3p/O4kpV28BPk1jMrso4KD+5xKwVxKqZq6xvD4s4J4mAOgbz2Ymfst5UgLGa85KZtZKNKpINKaJTFHA1hCKXxykHOX3lPPfU2QipJIK5YyFDOjUOSKyiOLsWWdNiYeNW8oMu7GlrRYe0Ppv84ER0jdILOSyitUg0ds5ytW7YLg0XC8XjVeByC+uVYr2C5SKz6Bxt46STy9RnJueTlYLoMDqgtS2EGz3vMzGJgbMPGavB6CRFIiUShloptBU5vK5thAhoLDlrJqUxSglLcrWk7a5JpiEpS9LSjWYUOAOLJrFdSZ5gsJBaxqslh8db9rtH7O6ecfXuGR7LvWnplWXaZYLfUwvhxljET7EUIsp8yBQ92Mkz6h4fswCx1uGoGrJWZEZyLtqwppCWshD5lBiRWdPStMuSA9Z1QIosIRbfjHFimqbSeS1eFv10R8gR0wSWF57L6PF9FBmapHDW4X3LYDxqhOzlnFaLrXSEOEtAoVOPmnbkwZCdQseBk4GfxBM5HMhhIkbJq6V4pcG0cLdns9+xurhhfXGFsw0Zh1tsWF48YX31lLh/TcgTOUtc0jTSKZZTYBpt0SGXgofyPfrwOa65JNsVsblmXCyJdoMyCrQFt+Sw+BDrJ9psQJ2Iid98/X/SjFVKfQL8JvC7wNMzgPU5ImMAAtR+fvaxL8rvHoCxSql/APwDgKvtmmUnGpFGa3TbiAhymbS1fUdRXDa1wbqWq5tnXFw+ZXP9AWNWknwrLTotKXIcJ8HStKHvB56/eI3Kmc1qzaOnH/DVl7+kCxNt09Atl+wHzxDuCH7ksHtDCEe0NixWV2yvnrHcPCrGJQPjcOT+7iWkgLEO261pVtfc95Dtkvtx4IvnE1/+yZ9xd7vjk4+f8Jv/xq8xZsP/9D/+bzT2hvc2H3O1Vwym42K74ea9D3j24TOGV8/RzuFsYtwPeO9Zr1Y0jSUEw+7ulq7rSvJt6Toni1VJeptG2mKHsS+BeWa53EhwmnNxA1do1xYTmcKyLAFnzokwBVLKGJUhJcIodH0fR0nEY+T995/Sbjvug+P5wfHz33vFk/f+Gpc/+Zt0G8Uv/vgNIY2i63j2CjHO50WCVBiu+SyAObVDcFalpCTGNThPJVGozKFSQS8LaYbZEGEOdKmVxdMrp0TyHhVj0SYSp0aV4+z+2y2XDHeW5Ht8ODKNd2RjUGrEOi8usdNrVGrKtMqo1MvJF01UVWDFHGNhyg5iSne+maLQJJQWgCnGSQBAZOPOSr4rZwsCiQIKZ5v/k7T3+Jkty678fsdcF+azz2VmpeksyxKt2DStJgUIlKegBjTQRBAEQUNpIEAz6R/QSH9AAxqqJQgSW5TpAZtgN2XIJkHbxWK5rKysNO/lM58Jd91xGuxzb8QrsskGOlBZiYwv4sY1x+y99tpr5baeCZCVliA5orj4zo0jOXhWYdJrzcEBOY/yjuIf/ja4ER0DlpS1rsAqsCpS6QRuwAZHkQKlFbmLRWFYWM1aB2IaYBDd3HGUMacMOAWHlHiRApvkQCmsNlyVJWfNUoIsNGhL0Yi75tw+Zwzj0BN8wKnAuqk5Pz+nMBK0j0NPNwxiDBdEFsJ5x6HvcjECMas7CaJ8dnkQkC9RNnXOMaaAUEANpS1JGxxw6EaWyxXRJVw7sulbYjQ4Fxjagftnd+jNnsd1jSlLga/7PZrEWVnzeLFmVVQE50RrzwdG7yiNuGz3IbD1kXHfsfnoKS9Hh9v3qCRaR55IMIH12UIq50aJWVdZcL/f0/WdOBSXhSQ+ZcWiqrFWMY4dLgS60bEZHDdDz5CSBEsh0aEIGqJWoJWwkOtSiiqT7hTMRhYgoMU8X3PRCDi6R8sf5vs+BfqnsJeSaPd0Zs4B89Ti9ejRI1wMHLpW9PC6ntE5CQRGR1WWLM7PSEvRhqrLkvvuwODHGUSeikEJcrfO62xIyX0mNl/EhTDrCiqljw69WUJk349sP/6Eu+32eIysiRh9ZJcBnymB1JnJOCc8SgD/RMqME40uS0xT4b0kpQZF3/dzkpvwVL/9Dxn+zV8lXl5jlKapFwKWaE0MYmBUVaJ3PIwjKEu1WBD8iLSty1UPQzff/2HfcztO4vrC3rC53V/uW2LoOtrDDhUjixlUhnG3p/vwIzrjKTtPkxKFsQRrcW7SRpOgfLJcsVr265ff/x7N5RXn11eUb7/H7WZDuTzD6JpSWTbf+iaVlQLAeH7Gt3/mJ/nZ3/kj1g/fYmEL7l68oOn37A573Og4bDb89I//OGfn56LNFScQBVSM4D3j/YZLbfhb14/YL5b88OYVv76/ozdCmEgTODSD9WpeF44YYS5SnQLx09iCGXScAFB1grTEdNSTAzBaQP6ZjX+SVJqTuSQJdDb/MProWK9knZoB0RQkKRK5dUgi5TIBvCmlI3g0B+5kYwgBUqqqzAY5xyxN5mnE+Wy8YAsBh/K+yzzHT+AxfXL/FFLs+pEE/Udf01yZ7lDftdy1L/jhh5r9oadulhRFQVnVPP7yO8SQGIcD7WHD/cvPCFHhWs+QOlTTU5UL+sOWw+6Ou9sX7PY7qqqiqhuUETbyGAIKgzESAyyWq6yp5ikKS9t1GFtQ1pr9wVFb6ayIubvgkMDaMhtGWEKI7Ld7urZl6Dtub16wahaYFIhDx82Lp6RsShRSwHnP6uzs5H6Iu/z11UOGsUcpWCxWuO6A0RGtIsGNkBTjCD4Xj8p6QSU1Rbx3rBYNulS0zw/cP33Jtrsn/ZN/JKSHh2+gf+nfAmuzM3MQViLSwZG0B5WIJoKbCjmS8LkQqOoFdbPClR3jfpDacxrnpPY8X8+93+KcJyEadzqlWSZHdFA0Rkl3ysQA0+r1Tp/Xxsm015wUD/LAk7lFyHhE4ur8nDceP2C32/OdDz6kLEt8CJmhZLm/u89apTJAXysO5LVQmOJmjglSzIBLBqdTSJKEzcWHkxg2ZUfxDBofZREQ5t38uem3pnmTsKXMP4PmYnlF++oWkFZk50dMuSCQpUtCwCgtnU5GY9YNvFuwe3FHPViKpuTZasXl17/Cm9/4fdpv/Cmf/+m3eNgs+Q/+zq/y5S+9T1Fa/v7f+x/RtqIfPdtDx8uXd9z2Xa7ZyIWYzLJXKNAGg2Jw0vqblD5h+slzMgpCPjcxqA0YVWC0ytfiGYcR5ySZnxi0KueApMh+uyHFBXVdUBUluqggJoZ+oOt6vA9YI3uK807Y6hlcaKqKRVnyydMW58LMFkQpmUfjjv3dp3z+/T/l0fIaHU8NOeP8jAxi5HVqIgzigeGcFIGcQfKnBMWEaMWQi2LMhSxyE0EEdFkytgOKgNZeYl4jkgVJiTEcOnI0JNUzYWMCQl8r7KpJpz8gKd7rBk4zkDt/V0kHpqRU81hNJ8fTemKlwikWK54eOu9vclxr7QzYqZRyB87Eeg3zec7gaQbrp/sjlxWJuYnPWslTtbEYI+7yk5TbvDvl/Xkq0ECWk0ivg9DTM5NHG0X3dwY88/Vqdfz3JBeXg9bXJId+ZG063c+m8xFvF/m3nJuAVSGGPE/i8fgqyXib9N8T5LbFvNefdClOsQXCOA5+mJ9tSmKMx8m1gDzDEDUhKsYsTzS9r0/GTYpShAkxGzZNYCpwKuOAAu9EvzamSMhxxRzfQs7zpds0pIAPTlq+NRSVJQyBiXQrW0LK912kyMqqxqesrW1FirLQUNueVWm4WFgeXJacnWmWC8WiUayKIHJcWZ8/TbbiyqA1QuqJlrZSLBaKMy9z1IdcOFeWmAoGl7J0k6xbKXkSMWtpG1z0jCGgrbxHMgTXkfYv0MFS2DXlxQXFUmMqizZiuOnEbxeSZtemLDUgObYmsVorzs9r9Ns17/tLul7zdPGQu9Wb3H32h4yvvkUYRyHzKCgKQ1IWpQu0qYASKIlRup7HcADdy/yxJVVIVLXKbF4NRrrPqroWeSGtsFZ8WuSeiZFaUVfUjejH2rIkpsjYDwxtR7c/0B4OpK5niD3j2HEYnzKoSFoklovE+28p9LiEVBCCYr8befasY7OpaNvI4BvOzi5ZNueUZY0yht4NpCj7udKKMOzRfkCZkqgM0RQEW0McUHFEBY9PYqo8SXB1+47b3T3V+pqziyc8uLjGFhVJF9SrS548eY+4ecbGH+i7PRAoKyOdkrqiWUgHedu2+LEnuAEXt2j9bYyuqYsz3GLFYCpMJd4X2ija+gmEgkpdEE3DP+v1zw3GKqVWwP8K/Jcppe3pQpRSSkr9CL3or3mllP4u8HcB3nvrUWoqWWRLWxGNRdk5XUZrI+7hSqNtSdWssc2Cb374MfvDBzx69BZf/OpXubi4xJZVrnYnRhcAQ0ya589f4b3n8aPHPHr8mFhUXL31DncvnrK/v2O1WHB+diUao7m9imRZnT9mffmY5eVDxtCjY8/Q7tjf3+FczxAMi+U1LN/iJY/5kxvLnz8bePlc0X/SoL71jHevS0xKbF58yvOXL/nsg29wcf0OV2XJo3HBbvUe71yd8eTBBSWB9eMzFiUYHVgs13nRkxaPxeqM3fae/XaD94G6qkn6ZAPKcgVKQWktZOZvVVaEaKSiow1ltUDrgtwPOYMTMQTIrIJhPDB4j4qia9UeNhx2WwpbcHV+zc3LF7z8zndg+TY/9/4X+f0fjDz95Jbrh++y/sqah2nP3Z/9BjEdmbHilKs49ganmYmTZhH415U15oouOSCwej5hMery86Y3BbwojoEizGa0kGZm4HRUqYgpfBJg1BpDuTyjKMRTNQwdZv0Qc+hI3Q24HSr000qK0PmhYJiTVkWiTBtCnDbmDLgGPwOzwjBV8/cNigJpnRfqv8OlntFPgvMabWDwYkKk0nSxWhwKlUZaKpIIw4dI8OJ6PEFayFGAiPmDP0Z969sT7WpmGWulqBVcViWrSrNQmqv1GcoaUnDEweMOO6wK1DZQa5EJiFEMPKKXjXahFCZlUFlLa/t91NwHz00cGTGsmiXLZsGibrBaWrVtDviUySZ1QTR+nHPoGFlUNVVTUS8byqKQIHgcxalx6Nl3Lc45Ypp0fgqazGSU1rUS75wEGEF0iEMIc1WRDE1PrEyUAmsomooE9G1H3SwYPey6xBgTL25uMbpmdJ5hcJjU8N677/LkYsVjPOY7H3KxWDESMEXBuijQQOcdvetFP9TCWltsoUhJ8zTBZ/sDt4NjOwgrJZBbm2JEucQZK1DgQqRtWw6Cq2GNaJUaLV0CB+cYNht6P/Li0HMYPa0PtDERtADRAgIahKGdv18aTKHn9jJxzMztrEwB7+tL/2vcjTS9Byg9g4/Ta+qIM9P8nOe6xhjNapWvL7uu3t7dzgC7GwdWyxWBRtZ8rdGInuzgR4ZdYBwdUQmrNsbJcEgcS6UdJlKV1cklJO5vbqm9F73YJG1xk6ZazDIN4uYsDG0fxOzrVFHFaiNJVEr4PPXEgElavVMIs6zCsfB0NL1QRlGulkTnhCXN8Ua+lgLkYF1rAWO1soyZ0VqWJUklDu2OwgeWqysevXHO3c0d7WEvAUVwMzNRKWFKDH2LznqUdV1mnceWdnfH0HYUWB6drSiBsNvMp6L7FnvziqpZcL5cEYpIbweRlojSCmmyvmJMoiOGlJno+gPPv/1Nzt98m6u330Grgv3HP0ANYmqgETmDsiyEqagNf/wLP83XvvM93igq/o2f/UX+t9/9x7ydPGrseTH0/JM/+j2+8qWvcHV1zWq5EhYGiW63IxwO+Lt73nr0hN1uR2VLlssVy5c1z7YbPvQj39JOWro4JoxzO3QGVOZe1mmdmO7FtO+cjvSkc7FQindaWzG5meZNBmPJI2JyIjfWiqTnid5yJLdrTkDAlCQkAdOAbJgkLZeJBNogndXHLElrLTrO+fdiyoI4SkCA6AXUN9bAOF3bESSRzhY/pZGvgWWngIDKybCxajYfjRko+CtfJ4O9LCpqFlQsGGLCIPGiLUvWF+fc3d1h6wVn9ZKIoa4adocdbddy++KZaFn6gehHFJHHjx5wf79j6DoKo1hfXnBxfpn1MxPD0OLGkb7vcG5ktVjQLFbcb3bs9h37w4D3iaIuKa3oG7r+DlUtpMCNAEhG5YJWWWYWKIy+x3hoTI2PgWEYs+aaZrPfzzI6pMToR87OrrOpUSImT+88zkVKq2iaJecXDZ88vWMM0KwvCONIUjC4gfHQUjQFBMWDt65IZeDz//tzYilmNenVU8p//L9g/v3/CFtL8SaODnfoxHA1amxRYnSB6wfR9deaslK8fPZZNgipODu/4ktf/jp3Ny/Y3d/S7jcwjDz97Nkc72ltpaM5HWPOoRsoqkRRFhlcIWucR46RSwZTzJEFOhf3lLTSv/bKBeeYx/X3v/8RH330QwERjMF7J0xikK6JFI7a4Kfj7i/JasQYyeCCFJVCiqKVGo4yIdP8QB+ZYce98FickZ84AjcqA3dKixxHUJG0bXnyhS/w9pvv8/jB23wj1Hz88kPuhj3DZsvi8hI35oJkjBgjZqcpJProeGET96rjrdpyUViehJLPvvs9Fu9/neUX3uNfeuMN+m/+Of24xZSRr/7UV/mvvvLf8Ov/x9/nm9/8FnevbnApYm157GRDdHPLoiIl6NqW291efBqi7IeKxKIoWNYFq9KgvGfIBfKoFIOP2Q08ZnNQP0ulaW0IMeHCdOOmPVDRdy1u0AyF5Wx1hoqe4Bw6JRalsKhsWWASGCdu6f3hQLDSbfnowTW984wua2HnQr7RhjT0vPzgTwlK029/BVHbAxsjCY1PJncFyHou7EYN0RAHeQZjjIwpUViLT5McmEErg8EIcB8DWDuPi6g09fqcuB+kc8Q5rEIcwTMAobVwiuOcGqujVrJSc4OPOSlySZE8zZrdxzjIHMchUxHvONhDBnim9vUjsCu52VFaJufoatJsnXRijwZ4EwAseVeQGTBJDeRzlw+pGfSa8r0J/J1NVpU9MTUld4odz3/SKD6dvCEcfSf+QgeGyvJDWR95Aqz1dB3T5yeWe57MRymB0+PlYnOY9GCPYLgPInuTE1Vi8ifs4el88+fTdN+zsauKQhRJgZTpN9NXisLO97BSYnw6pS1SHA3zJQjZRwsbNwi7PYQj+Ez+znTPk0nSsj9mWTM0k9TSxIpWSop/VVHMnQVJyZo4v+Z4Q+UOPkesasa+z3q4kSZ70pwWuVOOa4X5bGiKCjKTtqlKamtZ1pGmUhQF2GLkrAqsSmgslFlT+mhOJ/fgqMHsQFUUzYo6lSyTJSbDdrunbXu6oSXEkaIyrGqNq6WrCj0CAaMTKMt2p3DO0zQ1y+WSurRUvGLsPqfbfINPfvAHvHLv4OsnmPVDzh+9xaMnD6mXK5QpGZ1hHKJ0kvmEC4E4djC2eDfgxwHlI0+f3nK32XEYI0V1jVo+JIwtIQVC0gwuElXA+gE9ghkCyvRZ9NhgTEFR1aTCkpIjHCKjc9iioihKyqqUPTDJOmO0/FPmzhWpWMAw9ITgGcaRsqrQVugHtipY6TPsrCs+YA4TKawnpYGEEI4uHniKssFWNaZZ8NO8wzBY2s5yu63oO81wKPDOEpMlJI1AU2l6itLVri1oyxigqwrG3Sv84YYUbxi6Hjc6BhfoXGLf34N9TlEt2S0+huvHnF0/RFUN2hRcrhaot96nKhR3d5b2cEO7v4co8qcKRVk06KUlVDXO9fTtjrh7RpkCRdqxtoZDTITlI1K9Fm+FoiAuHtCbBeFfFIxVShUIEPs/pJR+Lb/9fJIfUEq9AbzI738GvH3y9S/k9/6q40sArDXKiHu9MQaFJimNNgVFqagXK5rlGcXigv/zN/8Bf/pn3+DV7T2L5TlP3niXt994h8cPH/P44SPef+89rK0YXWB72HF7f897X3jC+fk5uhCXQ2NLLq4eMjYNw36L6/eYsqGpFpS2ousWJFPx4u6W+88+4enzp9y8eEkYBlSKNLWlXr+B1o9p/QM++jTxrVfwajgjjg2rRcWDt/8dPopbbm8OfHezIXz+Cf3BMyxGxq7l7YuKP3MFd52lHg1feVLxpQU0ZosbW5R3wg6IR4dIUNgM5ngvzndFWVEUFUaLK3zwA1O1S+WqkC0l0ZMuBpVdPtPcCBDjsdJmtKFplkTvIWRhbwVKWWFcLRY8rAq6vsenDuVv+JtffcJvfU9xtwU3rHj8pX+b/un3MOXy+LC1ztXXyJjNLVzwouU4h6Wvj43ja9q4MpdNpbm9L3ipyhETSausPX8SSOTvS1Xv9AegMJofu1jyg5jokui1KmMJypJMgbICiOhqRfB7UtxDcqiTRV5Ctam6Ke8od0CpiomHJ9VjqYIK60MCTKsjViUKA5WWZHr0nj4LZoc45g3QSIURMXjRSiF6btIefwp8HfVOJVhb/NEfow4HUlT40TOMHf7uFrXbQpIkXCVhvBTW8Oj6ike1onYjan+gDAe80WgFZYIFEUtAR4dynuiDCG5DbrFKSDqa8CnRB2HC3ibotCbWCx4s15jM7tbZaTllEEBlEXejFR4Zj0VTcHl2ji1EW9NHz749kFzAezGOSFHaDY0Slo3S0gahcsU7qoSPkaZZ5BYEw/OXL2YAWBsDWoLcCVxIMaKtnSv9xhYEa4lVwyEm7jcd94eAUgdSiJTW8uUvfYVf/ZVfRb94xvjBt9HmY4oiip4ekJK0abggRnPiSGtQGQhNClofeL7v2PnAGBMmA1eoRIgQXeTzmxsBtXLLk8lGG0pJK7H3gV1wjAz4lBhD4JDBw4AwYOHY3qKtJinDZNwhbrxTlVvYs8lPydEUR2dN2DgJ0ltpSU4cg2Cj578LoqjnOTn9/xS4T/8YEFCBXKH3nv3mXiq5xlDaUoA+lfnuUZKaqS2d5PHBzecC0nY9OidaaTlYHbPO0PQy1ophYW75LYpy1u4KWQNPRQg+yXyKYkZ42h44jgOMvdwDlY5zc2bcptndGyUMVknqxYRHaSXMm6JAF4HQCysOdSwUWC1BrjAzRQ82pWyaVJY0iyX73RZtCrS2jGPL5h66vsW5Hu8GQhRAQedFQxtDUVayJsRAt9uhUsI7cUUvlWKhPGnzir4fCJsjG1iuSbTFnfdooylLy6JpiETGscf5mDW+mfcaSBit8bstdz/8PtvnTxmcI44DBVAbw/VyTXu/Q8UklWpjSVXJp++9g33rCSOBrz37GP30Y2LfEhW0fccPfvgR+8Oexw8fcX15TehH/G5L6lvWdcV+u6Wsa8q6ph0OvOUuhDHRHrDtgX8ag4iuz9uF+guAeDqlEnGyZ82fS0ytn1P75V++20335KgFnlISrbXMbjl+TB93QsWcuEwAVIqybqX8vZRS3nvku6BmIHQqAoQobOmJkSUtvSN+cLK+a43zCZ+fYb76zPZJr8sN5JPSZJkIEcpjZrumJAZiIrLE697W+d69njdTlRXXq2u+9tUv8vLVHa0bGbsDVCVdP7BYLXAuMA6O1fklVVnRDj0xJdFUiwatG5KpcG6kPxzEyEHltcN7Nv2Wpq5ZrRaszy54+uknkrAYzcXFeQbQFUpZ1uuau5s7bFWzVppm2QgDPI7yzLMBjTBfRWKlbpZUVhHDyDD2HNoDb775Jn0vHVAhRqqyfE1Op2/32LLBVg1NVdM0BUVVsr+/pR96rIrsdp6zi0ecFTW2qui3e5JrcWMC7Tm00t59frbCWri+WLPXBrtYYOoSjCb9+e8RvvwTpMuHGGtQZUEYHHH0hDHLNgVhTEUCY+pRUwHTew5J0diG5eoSYyuSUgzxnjS6HPtIO6M827zWK5WltxyTBAxa5zVIJLlSEKOopE7m1gw4HE1wXh8/etaZTUxwk+wTOsFh36KzbI9MjTADBicY0/xbE6AgXWWvv3Tez+aTyl/RWXsv5eYBI9s0p0jv61iMQllNIhC8Q4XE5cUZbz1+hzcfvcXl+hqTLI+v3oDUU+8/51l3jw5OCnsA3p/EfVIscgrsxYqhHfF95LwuaTvHeBg41BXdT/4MvPUu//SjD7j53d/h+08/4W//4t+iPFsTi4JtO4ATnUk5VSkGo6QDw/vIru05OH+kUSjFuq65WNQsq4LGakLfEdsRr0ChcVG6gWIIMyg0FaNilK6tmJn2Kv+uwJm5eAuE4HI+ITdSK2knbqqC6+U5by4vefrqc3Z+IDgn2pbZ2C9Ej/MjYRyxU86pFAnH9tmH+P4wLUVUWuEREDV6R0iekMd1CoHkBrp2Tz+OhJgIRjFGBTlHUGnMxTUyaYI5NpBAUy2rOEMAACAASURBVCQalpeXdP3AOI5iYGYtVmnxCUnScjyNz5TZxaddGdPYek0GJr+bUsoSVpOUgQBns79XLvLBsZiQ1HGepZT1g2MSeYwsIZEgG8iq434Esv/MLF5myRmV4/mQZJ+bjCWPkZ/K+92JPk5SxCRFBqUsSk+kieM1z7J1Me/ThBlonOKvIwA8nZOAyJBmLXuU5MYABI4yVUyM0GlvOu69Mpvlc6fM35hyl1g6iR0USK9LmX1cVO7aiyJ3wpFdaq0hnG6pZjIBy3upmf5Lrr0oiqPZl9KYNGkbH2PxshDNbh88xhmcH5kkI/KNzHv1kd0csvxBiBN5ahozzBrZUpvW8zOZGNcTSDt1oGltwETp4lIOn8TQ2RQn4DxiKjjlCiiLsgUxF9OssazXC9ZLOF9HrtaRy2VgWToaG6k00oJPBLzc/4yNSO7lCH5k6DsO+8Bu37HdHdjuWjbbnkPb0fUDISiaRUXyJcEXLBpF1VisnTAq6UYdnRSoQhjp7A6FI8WAD2BGhzkc2N9+yi6s+eCbK4qqpFpcUzbXFM0jyuacZC1JC4qgQoCxZTjs6XYbhsMd2/vnDN0dftighlvCGCEVaGXpI8RxxISINT53mQcSLZMwhrEli9WasqoxZY2pLMpIMSpFAylhrT75x2Qj2SxHMAW0UeFdIniHG3L3ySS5ESJ+dIQQsdayXC25DFeUrmXvD+zclt1+Q9tusEUlcU1jWTclxi6xVcX51Ug9Kg5FRX+oGFuRDm17T9s52m7AR89ZXXO2PmO1OmfRnGNNSagahrrhLnnGzZ6+G+j7nm7oaQ8HtFLEqsGsLtikPWG8RVdLKGqMKUgkirKiWTT4WGYionRWaK0JJkgxTCtQlhRK/NgSxhv07gNWq3+KKpd0CkYMY7kilgZVSkzt/0U0Y5VEP/898K2U0n938qf/HfhPgP82//vXT97/L5RS/xNi3LVJf5VebH5pY8QF0Wp0IVW7kKQCF1WkrhdQLxhtyfO7O/7wz7/Bh5/8gN3+gLav+PTVDZ8+e8aT60e8++QLvPHgCct1zegTh27kbnPP2aqkHcRlN+WKiSYRhp7d/Su6pubq8gGLZpmdYzXt2PP8+ed864Pv8u0Pvsf9zRalS8rmgvWT91moN/D6EZvDFR/ua57uDU4tsAqGpsA8+EXSsOPO3bAaPuai+zZvvvMeRVWR4oHHF1d8707RjZrdIIHGg8pj3B43HihUbonJgZ6KUm0sbEGMnphClhowGJsrBcjkmKqPxhS5KjotkJJoy2ek3cb7CcyTRaZuGtGfRIGWqrG1BmXEBbAsC2oNlxdb+iFRMvCT76z4/U9bbveKw7hALb7I2eMfo2jOTgcUk2lXyKZAPonwOEkRZuYRf2lCJn87bsFTm5DK1H8yUHEK4r7WlpzBj/lvyAZ7VVo+GyJDErOtuZinRSvTuYGgRMNOCKkxV9xmeGmKtPN5JlTYS9+/mlgysuFqcsu/BqsSlYmUJomzsoFoDWnnYHNLF0baoRX9E9mm0ZGjqH2K6Di1jxyTAWsLSlNQ2pJKWRZjhxp6QoCxH9lu72m7PWMQfRQAqwvqwnC2KHm4rFn6gdKPmOgpXI8OMLGxtI/YkFDRk7wnOX8Uz59YIYBL0EfYxsRGKbrCEIuSoqqpm2VmWohgujYmm2BMzOeUAVM5WFEU1HUDStrzvHOMw0B0olcTMng9tchM4y2dBJdTgKmtyS62BlPYozmBViStsoldDipDzLIgom3UOwfGELW0rPcukbTNgJ6wykKMtF2L3u6IuwPrJA9dWBFRmDkpm+Pl9h+yWU1U4BP0MbJzgS4lMUDLJnVmAjgSAiSSJQPyoBWh/0Ag4X1iGyN9jLgk7cceJJhVU3CkMIWYtSgt7Gud9ey0yVpcegJK5xub/5ef9Y/O09PXnHtK8C+PNqfHKqfI6SRBT9Kmo1MiZYZznEwMR48ulDD6tRbwUk3uuBxbyvMAjElkRia6QAhHRiw5QHzdcEhOeAaOM8CY8po1JX0xgk8JHSd27+vMLB88KgfFOVTNTEUBlhVqPhZKiQO6Yl4biZmtXFqUt8QeAa9mjUEB+I55vMoJeZrlGCDR9z11LWuPG1t2WyfVdjcZFAnInrRo+onWrs3yGZ6xa7FaiTa6E0Am5Ra6NI6kvjtZ8qQNzQdPP44UVgp3xhQUpiAaacmTAG9itYHKvxu8w+8c/XaD9x6dgXZdlviilLkbAtF5AciVYrdakliiDVz8xE+ybbfEVyMqOEKKbPbbeS2pdSE6hF2L9k6AjzyRlBHG/NXDR9izNXa7hZsbnm3vSEnRAgdODTx+dG/KgOvpf58ma4o8xuWLR+3W1/cpfZJYT27SR309dQQmXkvAj99HSavpsZAkzKHpvCdJnNOJqfXEYI3ZJMtgs9nFrJM4fztLAE1aZdbMxhynbZrHmXQEB+bW0BMgbrpmyW1P78XpfTy+qZXCFoamMYzO4XxkTIGxH6mWEhN5N2LyvdDGUtiCsqypGkNTCDOz7wY++OiW5ZkYI+kkJk9d39L3I7YoWZ6viSkJOLtsWCyXdL1D25LFusTYgpfPX9K1LVVds744z62nUdjP01zOiem0ARVVydAJ8KqVSHVUhbCfnQ/o1zD6RIojKYkBSdVUOaFUxKRBF9TNkrqpoViRTEFSgVRo2k6KIiGBCwljxbm5Xja889V3+MHzW0xTU9Q1AN2rz/BvvU86uxZduNoKe69wRD3AcALIpszwNrIWx6iIeqTd7aiXK4qiZrG6II2OMXWQpkLpxOqeRodEZjpKIcEF0WrTtkApAdvm9e5HxtY8NhIZeJ1Qi6yTqKWgoGaQJevopUTwSQwvpzbek/0MjnP2tVc6FlJO5w9KTQ2wOW6YALAcceYcdgaAptOeYt3MdFBGoUtNCpFCWRam5M2rJzy+fMy6OcOqEjcGmnrFWb3C+RVuGDj0I9SN7Im5OB/jpG0qvx8WNb1PHPqeyo1c1BWv+o59KvDnZyyurvjssGHz+Wc8/5M/pdQVn332nP1+gKQzmznN6xEpm/oEMXsccrusNVrkkqzhYlGzrktqayi0wlvJt8h7zuhDBuHJ65s+uWsSxzgnGv5qDukSehK5SdJpZ/KFKqUg5rwgJUpjuVidM/qRsN/QuV6KAYKUM3WSBe8Q41VZz6xRpH4PWaZAAWur6aInZvCWJPuQdCN6yJ06PgQplGvRQ5SVLZvZKUWI6ZjXpGl+B1IQk1lTVZRKPD3c2OeBkoHQKPrNUxNqem2QygYzreOnAOzp/ElJCp8yYCVGmOg4ry07J5Fe4qg9q+bfkBLHlI4d2eoSb8W5zV4+MBFipmJcSse5Q4pMLN05ylTHHWveM6bxnIHpYyHjuA6IVnSO29O0Xkxg7DS3jzq6E9h/bP2XHCed/HrK+7DkBhmamvbM6fxOXzn/nDVjkS4VueTpxKd9MVsepDSRTknJoJTIGkSt0Vq8LmKUPVlP8FpG0eeiVNbXDXlsKS2mzNNQm5+wkkKsCVm/nYnQcxLfvHaO6qTLNAnh6STMFjbsFI9OWfZJx2s8spJliEwa38fIggzwpun+5XVZT7G9NigjhdMymzXXZUlhoSwiVSlSedZ6rAGTNbvlvgg7UxHzvEvz74UgBZlx7On7jsOho+08XR8YBi+gYlkItqAkNqqrCluIKZpWKpsyabwX754+Odmzc57Q+5Zxt6FrS7ZtxU1XCRmwvMSWVxSLN7CLC0ydZTeUlnXMDYztgW63oT/cMLTPieFAih0q9KQwiKa9VvgAnVKCKehIoR3GBOYpqBTWSrcfaAplUVZIXJK7pJMiQx4tubihYySk4zoQ42newXEi5o5NYc9HrDUsFkuu0jWNW9C4mmq00AUGt8O5gTF4GBN+KChsL55NWuO8ZvQLxrGiO3RsO8/9bmR3GNgdOmIKDMsFbhCN/3IFAQ1B4ZPFq4LRQ9sP9Icdfb8lDAJM+1Axpp6DdqTQU9QrdLVE2QrrfJbPmeLVrH0eZTxpo7HJELKZbrIF0WtiGAj9K8zuO9TNGwS7JOiaUVsoV5KPaRnH/6zXPw8z9m8D/zHwDaXUn+T3/msEhP2flVL/GfBD4D/Mf/sHwL8LfAC0wH/61/1AUqCLEm2tVKuNYnCednAcBofDcHmt0V3J9n7H7/3hH/An3/0zYUetF6Sk2Y4bDp8f+Pz5x7z46Af8yi/961QNxKTwKfHq9hWffvpdATOswRQF1pSzG7DrOx6uV/zY+4HHDx6wWK0om4Zdd+D5s2f8yR/+IX/wx99guTynXL+FvngTt3gfdfY1WndBZ5b0ZgEVoKSj7zYV9OufobwoOGNL4T7kIn7IL/zsQ16+/Iinnz3jQQ1XNnCT4DAohs3AYrUjdrc4RsrFEqw+DvqY21AmHb6YqBcVpqhAGRJi6hNiCUilWdzVYwZvJ3F9T3A9kwnBYb/HaittTtZS2sfizJ0BFGML7KKhXC4l+AjSZv/gwWP6fmDwhvWZ5fHacQgrhrTk5hB4+M7P06xeBzp8EF2pkKJoXZEDdKTylkJum9VTa8QxsECRmUgcg2AlrY86RlRQxGzUdLL/MrdhoOZK4/RnYZFGLBGTHD606FRIspGT53E84PyY3c1zq4NKuRIoWjI/MqpRfocymqQrUFY2Az9SKkWhFSWJpnQsikBlMjirFaqwrG56Lj75iE2349XdPYfB0blI60Xvcwq4IOs5poTKwv9GKc7Xa67OL3l08ZCzZol9+20BkHzEDYEXz5/x9Nln3Ny8wodEoRWrpuZ8teTJ5QUPiobx+QY1DCxthS4tkNmC3uG7QQqoKEyStjOpn00gQ2SIikOEXUjcR2irArtaYSvRO04J2qFDKWF6L4oCawx6ci5ViaZpZu1XYw2emBfgAecGYQ6HkIsLeawaaS1OKeFTZHCOYmJ+ZqAqpkQ3DMLmMiKoHpSMw5igtOKIqHOAf3a2xlpLO/TcHfaQwaMYpXpcNwupHHuP84Fvff8DXnz8Ce+GyHve834KkLzoH6bE6Eam3naFBHkRCWociZ7IIQSGGBmR++tJFCisUhRKURk1eaKTgJDkkN3o6GNiSJExQk+aRfXn6nRuL1IoTGnRZWazKpX1xY4gjUIq8JMrKkytTcdgTGeJAGA+jsoAVJq+o2QephyAGzVzKeScksyjqepvtDoCmjGitaWwJaosoLA4EmOQoFVr0XWaA/QM8sxtYPkYbdvNQKvKY/Y1fAoJFoNzTJqcbhjkwJNJRMoaryodNXFP1hqmtSofNkXQRs0sA5ePrfJYSDHS950Y7mSJmRhjBmMLVIhEo1BOAGryfYwpgXeSzBglBphazWBn2x1wwdHoBq0SbtgzjicN9AkBvElHXW6tKbKOawyOFEYKbTHB4bsDw2ZLcp6L8wtKY0lFOV9zTBEfHTqWtH1HabNpHKLLaE2R74sm4OU3coHRKi26qJzo7ClJloa+59XNKx5fPSJ6MSNYrqW1KzhhJymrib/8y3TPPiH1LfXmDmUNMcBmu2XoOpoEV1GxyhIe3f7A6uqScewITlEsGi6fvMmKRL3Zkuolu7bHRc+nKfARkYDNAEfMe8ePIjb5meZbPLFSp8QJpgBe1qJwCr5OiUceS0ZBSlqKNcHPCQ1K57F+BIcmE640TcopYf8RkHRun+YIbE1jDhJFYWfDC52k62QqWmVVWdmthX5EWZQ4nBTVpuuYJmIOaEOIc6fDa7XWKeBV6rXzmaeTeh0g8N6xO+z47NlTTBoojbQ2HvYDdTMS0oh3I24Y8Lmwq42hWa6pF0seXp5zsaoojaLbd3zzO9/goixoFgsMcHZxzugC/RDY7DoevPGI0loeXF9wfX3JMHhe3d2zOr9ivVhCimij6fuOcRzQpsDYBePQZn2zrJmZmWTRe9w4UJwtGJEulLPVmm7fylqbw5o0jkfEDiiNAp2oSkNdaJ49fcVhd08MkUW94PrhYy4uz7i7Hzm0LcHvsFFa6LpRinVKa0IKdC6gKs3X/9Wf4sVv/j4RMcMtTUF3cyDuD8R9C6sFutLousRUJdQV/m5PGjpUiAIYhwAGMZJLhnKh2W9uGceRarHkbH1NcgJ+OQVBOXDZBGXSp8njRWc2dt93YAxF3gOmODDNNvJqQts4opt5bAc1Dy5rjbTkJpGdijEd72k+rriUq6wbOzEY5WNh0mvM8edp18NxUKZpqopEjlIS1yAMxpiBvwmaVUrP2s3yvmhsJqtQVqELjSk1Ziw4t0serq758ttfRdkGnUrc4DMj3aIoWBcrlouSD/YHnK3R1pKMMCxPAVOlFGNRsC8DUQ90m3t+/O13uH9xx9juGZKnef8tNn/z57j/Zs3nv/VbfPb3fg0XhSCxsDXKetzghAVKks4jrUXr3jm8Dxg0S1uwbgrOm4pFYTODVdy1p8JnysYqY4wEb3NsIc9yAs1ilLhuHDyVyrGFRrSyrcmymongg5B48tqZUoAIYz/QFR3dMHB2cYWrSzaHLdv9Fhck50jaYkyFUpEwOggOlaAuGoqsTz4930cFbMJA23eEYZRn6l2OTTzKeyms52vzUbqXtBa0zAfR5dYxyh6dMsClEhFPGIG+RxUlRVNjyxLXTRr9x24amKRhcpdfZpTK0qnz36dOCp01LvNOMB/DZMJEBtBS7iYESEc26gSYynqfcpyX5j1qlgNIWZIgCQAta57E7Md8QN43RoSs59msjrmZ0iqbE5+CshnDUAKEJITEM828uSFF5VwxCkNxBnBnyYbX49VTANkfqyOkmIS5ybFQGM0p5DohwpqkM6s4H3jevZTBWnX0FtBJpL1y95Swd3NnpJnWIumMm44vt1722qnbKMU43xMBY5mfd8imXDFG9Iks4JQnzjHAvIsDMVFoA6bAo/BTDpWyZirCUI9Tvh6FHTutxccuGLmfU3ccuavrJPSewawUs2SGz0XLCbyL0ik7n6cRXKYw0pGocq5vraUpS5ZVJRIeSIyUkiHIogpqzJ4rUsBQmcYUp0qNREwoZWTd1fJeCJF+8IwuEYImJUuix+iKqqpYLWuurhY0izXGkGt7kRAUzishOo0OPwx0k1ZpSozecb/xbA6KtjPgF2gV8PvPGVLNEJeMVOhCfDmUMiJvGCNh9ISxJ4wHUtwCDhGrQ+SPikIIMxkIL3Wi0JHCJEqr5+ckBQrNOI5oW2GmHIgoLFpzsicGJ7lwDFkjXUZOyJ2CUnyXl3CW1InWsAC7RiWMNVTFkqYucWPPEAe6cM1Vf85t+zn74UA7dhzGls12TwwHYrD4qBmiwQ1rhrbkcAevbg7cb3oO7Ug/jugCwvKMdrfn1e0W1bxCFRU2BUzs8YOndYF919Ed7nH9K6ySgl8YO7rUYoyA9FXwlN6TlEjQ+KEjOk8KgnWkBNEnbFlSNxXKajQGHxVeW5QuSaFjHFr85rsUizcpTY3DEIwlNjXokqjNX0qimF5/LRibUvp/53XoL75+5S/5fAL+87/uuKevomo4e/uLbLYbPnr2CR989BEffvw5L+823O8OHIYxBzwiZO5jT7WqaBYrbFHJpOsPUqENAU/AJDFcSLagqSqiD/zGb/wmu+09KRuI6LlaJcHWw4tzfuln/2V+4utf46tf/Srrq0dcrpf8Kz/383zxb3yRx49/k8urNxmad3lV/g3+OH6JV+aaEUOY4jyYtbg9mp1eUMfAIjoaBn7iK1/gb7y1Ivaf8am755t/+Du8/cVHqHBD2L/A9meosGW1LCh0gTJFXohSZpKKAcIwjIxuJIYgFY8ib2FaY6ylNiZrqR5bJkKYWFcJPw70QyvA2jiy3+xomiX3mw2jcwTnuLi8yKzbgqA0pi7zwFN4L6ZXUVmaVcm6KBjDHT/1JBLqgh8eap5t96wuf5xQfArkdlalxHkv+BkMmVK8mdRGrojlwPtU446JmZCmTVDP991kTaWJvROTgLpG6bmNK6UkxkRHlHZmK3x1ofi8cPzA7VGmATeggs9q2y0MAyn0kKRiHmZLrL9seiRSPKCwKBJalxATj/+f3+FSBxY24oc73risWVmFzWzlqIyEVCmSCFR1w/mDBhcCQxjZ9Vs2bc9uHDkMA4dxnIMTDVTK8sU3v8DbT55wtlhR6UJQOgUxKrxOHPyBN588ROHRKnF7e8P1as3V+oLzpmFtDPFuy1lUVNpSpMC472atXQPoKGYwWsU5JxKTJdnAhxT4JEQ2EUZliFVNuWxQtpLqlXeUVcnZ+WVO9gXcdG5y95QkyvtI3w+44NFa8ZUvf1n0FknoFIgp8PzFc+62W3Zti0rgmUy3EsoYqqamyEzimKt9fYiZQRrxMWYQWNjfZdNIkDKNtxjZtR27tmXXdWzalrKuJdDUsgludnsWiyUJYUXuhwG73RCyU2UIUgjJOx8+s4itrVjEgPWGXUjc4HlF5HlKvIyJQR0DV6ugVIpSaYocPLcxMcTEmBJDSriUHeuRQpSEkZN8RgZfgCK3Z0WVSEbkD7RSWCNMrQlMAmbm2gSS5mnz2ksrnTvyZM4eWQG5dSse2Q9aSbuZnQD8Kb9WCqOLGUjXGaRPWuO1JiotgvFG4ZXMv6vrB7isJ+xGJ/naKYKTq5rkgI/EzLROMc5FlHRaTAkxm6qE2fSNKYmelg1UPvaJvvUJgBJiQvmj9EFRVtR1hfdyrhOgffqdOWhOUpBKJmciZYFdLhlv7/J9mljAUP72b5K+/pOoX/jlY0KQIs45bm9uWJ+fY0tLUpEUvCR2U/KWNadj8FIQjYrROQqtaayRAsSq5umffxu33ZDGgVJBYQpC10nbdNPAnZx/jAHnR0kQYxB96WBZNmsB0ZOmMBV6qRjDICCWG3HpKMw/Xd84O57JPW6HljGM2Jy43L56yXK9pqoqvBvp+x5bFdT/3t/h/o/e4Pn/9eu8j7DNpuLHRx//ELs6o6gbyrrGNjXjfk8qC8rzFeu33mTMGrGXDxuWF1csz9Z8+uknnG3uedQe+F3nhEWsIWWmjFw8M050+kRDDgxSEuMjNX9eOlTSSWCrsl5wnFqvp/uRdGYTHWVwTpk+c5qoMsucI/PWGJNBDpkDMYNCMkf9seiZW2ej99IWHgI+S+IkooDPWsDelCQTMVqkR6zNnR+oPLaZF4iUryNXoV4rekznPH/wtdeU8B3f0SqRvKPdbnnv3Wti9Gx2A/04oK0iRo8tDVW9xLlI3w7ECKaoaVYrBizf+eip6Jlut3g8t3e3NH3HarkiKs3lw2uGzuFGz3BoefTomvOzFcYW3D6/Q5mawUXa2w3b+zuqpqJvO7Z3G4riOW+++57MsejQKlEaQ9ePGCUJ7mF/oFuUlLZkuWg4Pztjv9viwhRLSOfDdEOMMTx68AifRMan3+9R4YAKO7wLHFLP85uSkCKFLbi+KKmKaxSSWG8OHWNIFIWwesYw0oeO9qZjFQt6k0ArdFFghoT5//4R8eFb+F/816jXa9JC1tuoFSzFwILDINrwzqECkvjGxF5vKIuKYS8JpIpXPH78BW6LgsPunm6/A0bRUQ3ZfBWwhcUWVpK3/KzHoT+C9Uwgnay/WuncAXFk0M0mO35ai9LcPSKFL/k9wbYy0BBCbkE0FGXJOI55n5qsXiS8TDAzg/5CpHcC5ESl8G7IW8XEvMqAs9GUxUJ0V0+ngUpU6ybrskORNO9evcWj9UOuVg9YLK5o2x6fEs5H2ranUCWkJcl3pHHk6w+fcGsNGyJ3eJwOhOgEjM2RYQzQL2oxnXWeeNlw4T3D7Y5PP3/F/VmDX1jM175G/fZ71L/2a7z85nepXeS8WHBWL3DDSB+8OJ9bxeBHDocONzoaCw8XJY/XNbWVBH5M0soujM5A9BM7Wq7fpyPTc2LCqbzPSodGwWqpM5lo6mSRvcUUoq1vrULpJJ0cSaQuVIIYHLt+ww/vPqWoKn7yF36eLoz88NOP+eh7H1KXJcYUaGUIY8+L55/j/cgweCID11flce1JgeHz7/DFs4d8ngwfbve4GIg6EJKAODH0dDHOxJI+wsFFrqoCpQ0hJMYYQQUqNKqU4iNT3Bw90Y1URYGyBUpplo3c82EccDHkca5FAzWvEM77bEh7HIshxxCkhFWnKb46klKmIp4iz690Ms+A3Fl5TJNOujleW6PlFYIQdDJ7JcuOpRkBle8a0YxWE9gKE+6nJ0Z5Rl9nSR6lM9g2yRhMBnqBqDVqasOf78hx7RTwPxz3U6VONNpVXifkb1O8OnWmvDbXY6AsihnM1Vr0N4971/HTp/fI2ol5nO9nRvB0SoQ4SndaimijKMvXO0cAQvTE6MmUFzHMJI+XLCc0AaYmBLwfJO7PuQ0cpcTkNOWZxyRyFaN3jE50pmNmawjj3My6vOiAKcDPnWwS55uTQtmUx2ecU0hWE4MehZ4MouRGC0jpHMMghVMXE9FLfDTp6AbnRQ6kKikUlFbMKqtCsWoMV+uS9dJSN5GiBGUUEUVITjiwaZKDS5CyDApOSDsTAz9pYjIos6YoS6qmoKwMZjhgYgClsSxZr8959GDJowc15+c1RbEQYysdQXm61tMNBjfKPhg0qAkPz8WPFA5o31OESIzCwgwWkjEsikBRJkgHUoQQDb2DbugZcSgdKGsRAUxJk6IXkJBE8gPeSfgZs7m0VVBYTRlUlisAaxRFQrRhi4KyKKibmmYhRlxiBm8gOMYh4Mb8XI1FmxIQNrtIVhwLQxMIW2ZJA6k9Seen5FpWSI+VpWLJKl1wXl5yXq04hHu6uGVgz8F7+mGk7Xpu7u7Zvkzc3W05bAztXeT5s1u8kw4BlAIDgSDa5EnWrSG1uGHE9x2uu2d8/hzf3ZLGDpuyJBEQfSSEAV919P0m6zd3FFVFjJqoPBQSE/3/7L3JzybZld73u1NEvNM3ZWZlZlWRxSo22RNJm+4BbQkyIG20E2RAgLyy4Y0HwAv/KV56aXtpwIBgLbwxBAENy213o+cmu8kiq4o15PTN6xk09wAAIABJREFU7xQRd/Li3Bvv+xWLcsuGYS4UQFZWfkO8MdzhnOc853mkeCB+HwwCvEtOgcTBukW5pWCQfsf1/S1O/SF2t2V+cosJW0arCc050TQPi7pfOv7WBl7/Xx5DTPzz3/9DPv74Iz7/4mO22x0+iLFMshp3MgN1cGOe2RmzxRxjGpQWQfPWzNEhoH1mnwY+/ukP+bWTE9rFiovVjN/5/vd5+eJn/PjHf82rVy/IIaJ0LgmsgJj7ccsf/fDPeXV7yauba/7O7/wdTk4vcK7h+bPn/ON/9B9yvR55vZvBvmV177nUTMHF1HpBBpXLIFHQ3+P8Z8z8X/PGf8gPtiOfff4prz654fZuxsX7W94af4LzI19ffIe038qm1BgJXEtSJ1U7ocUvFgu61JGSOMKGEKSCWBKiSV+rgJ9k0fiQoEausi1izqlxNNZhjGW+nKO04eT0hHEc8DER4xZ/dUW7XLJcLNBGi0mTH8X51mggMvRr3nWZ192MdVxw36+4TQ1jvqSCsWLkkqYNhXSUjOUDmCNfKm7P9ZEq2eRTeeAyHipYIkL3aIVKkvTqXBh3Wk16QAowVZMPGJ885uYf/L1CgtDcLE95ffZY3EtzmsS+Uy5VziSasuT0pcBELjL+1V/Bek2ez+n/y/+crAxwELX/4p/+A15TEssc+JHVDzSbDo0i9QmUymJZAGM+VCjjl8EgRB/sb5qWj5w76MrWfKGeq1RAvfeMfiT4gDeGSyMGB0aBilGqZ0eb2rHAP0dXWhWVjp9GIjMUYDAjQZYuVf566Bp4HQc1NUiUE2ONne5dAX8y6w6fU0qv3vupcquOv8URu+YIHDgESPVnD0Ep5Tq/HHPKHEzTs5fk7/BDoSR2FVDLKXGbM5+j+H2laGqZeEKuj66p3HMsQLIn46EE98eHOmg3l0+v7qZpOs8hLK2/8xAeKsmlOswz6r0cgaITlKoezsl/7fFV2WqenvZ0PccfXUeQOnz7wSkmFoYqI678cr1neeZ5Yosc3+3hvecjHOj4Ig9ZcXj+zvSlwY/YGEoQ+fAKK4CaqUCSnL8yVOqxmM8J+92RRlsWM7EiMzMlDPUaVQGty1m0glq71trSdjO824rJQZa2etEIFVbrJNeCmN/4QcwE57MCoFR2JUcSHlS0IhPGkbHfM2y3rJZLck74sSdeX+M2G1zKoC06JzSaMPrp3pfTu84C5KUgYixJ9OWiiyznS0Y/Mo4DwziAMswWS2wY2WwS3o+lrezhe5zYKTFzfXPFo7MLZt2M7f2W7d0dx9qpaYx0tmXxrd9k+48cP/xn/yNRwWMUz4BtDLzabCCIVvqZc2xj4OzsjO70XNgiIRB2O0I/EkfP46w5efyU3fKE+/2Wx7dX3Ox6PoqeL2Ii5bKG1bf/YPyrw/ypzydJ9plVmrTojn6aypj+ub1FZUkeij54ZW0fWkbl0Eb0tvWXJHPqOlG0fKhP2FgrbAclxcswesbB01iHLSZURtsCEpe23cL2Fc1FMffUBTwh50lPtl6bMISisOOOWFUHts5XH1+WcVgtF5zbU7pZx+cvr4lxJEbQpmWxbNltA8O+mPIouRYx3DCs7+5Yzk946/E5Z8uWTz6OLPoTYhy5u73l+vKK+WLJYrni5PwM1zS8fv2Gs5ljt/eETc92JwnQfj9Il1Ex/0kpMux3rG9vuFsJcNt1M7rivmu9Z7vZY/cjxjXcrzesFosJbA/B07aNnItE69pp3Ukpcb/eYI0TgEOBzV6KEqXbI2a4W2+IYYQsclRN44hK0XYdKiY2t9csFgtJcP1IZuT0+QzXR0JU6NKu2jUt7fqO8K/+Bf1v/wdYfY7qmqKRVtYqo8GZUuCK5BDJsaxcs4QyTtjcdxmjHa1bwlIDhh335GEAFdE6kYLocI/jiE3SndE0jmEYiCFIDGNM0V5MRbM7HwyNZNEghvCgsPFwTh32hJxk3EqxO0vbuA/TOKsMbqc1Tx6fs+t79v3A4CWGnj6vmPFIa7bcek6ZHIvckhWd7q5bYNuOpluwPHnEbLESDVmQjoi8J+pMow1L0/HO8i0ezU5oVIPKhiEakukY+wHvE9Z2BB/oFhcoo9itR3I/8mzxFo/ajruc+cndSzZsicSpyJiUxBQ4i3t6zl+9uqLpI0orHjczrr644fFvfptmtSKfRfp/8h+hf+8l+//zjxj+6E/Y7cSwNpWiqkVjVQajUY1h6SwXnaOhSuzoYpAaCjiUSjed6LqmKrGTC2uOjNK1aTmhVJZh5gzVD2GK5cRuCYPBKltkL4RRJl0yRsASaxl0xLaG2emK5ayD+Yzrqw3buw1hkHZicsDYhhgzwYufgrEaX4qpMUV+8KM/4Rtf+zar2Sm/8viUj19fi3SD0GCFEarEmyNn6Uba+MDSaQzCgIwJxphQOgqL29SCdA1CIsp7tLaCqEwsxTyNuSrFVpb1w76TjtbUioHWHy0bk5BOSk51FJcd6mHHNnhVNKIC5OUnSu5QPUymWabK3pXr3zKXdJEGEcm8Uhis+2JhM1fDqLoX6LL2V6JO3QYkTj+Yjdbnk0qelyhxudJMBIDyHKb4cDKeepgjkA/PEWOma6jyTzUn0MVkWMbowayvMkmnmyhrTQWnBYcvXUjSKiW5sCqOLeqIcTy9AoM2BcRWsZivFWyBXDoGSpG3PAEVKLJluewf8dDhVvbjlLOQQZT4h8QURcqLw/uQe8vYyt43FqOPgOUSOwoTPFYu8pT/COO15M6qxA11jUU6xdrGYZSQpVJMpBwQOY4So6RE8oGoDLTiIWGBRmVmJrFq4HyeOZlnTjrFYmZoXELr8t6LV059IdKhkkjZkLJIaWyHHbu9Zu+TMOazIWPQ2qGdwTWOs/OWxRKaJuKcou0Km1bVtv3IMESRN9j19P1WQCFVc/ZM11py7mhcYu8tngZPQzYW7RTzoimalSJkwzwZhsFJ4aVI+eUUiUUGLIZQuqWEMOLHcWIWJ6XwURj6WgkQ22aDUo66+dR5pY0SuQUjzyhm6TyrEgUybty0tlU5v6mbRWkglesUbfcQRinKZzGptdaAidK9pwxWK07aM1oaRhbs8x0rNTKqkT4MrB51tPOetgnc2oxNhtvrLD4fqbDtE4zbNTprjHbMTp4wWz4iZIv3iXG3Zp8dm6sGv31NHm/IeURxYJ37MKCCmNgrb9C2kbXMOOlc9iNDVLUOKOuW1pgSt8ecQVm07gown8mpJ+5uyf5HsL4j3r/Bb/ek2dtkt4AqPfMVxy8FGLvZ7vjjP/8Bby7fsNuvQWVc26KlbxtlZTU2ZWcxRe9Rqqmy6JhiPKNI+JD48ac/4el7H/DEGeZty/OnT/nd3/49Tk7O+OlPP+TF558wjD0HAEahDYSsud8PvHh9zc8+f8m7WFarE9rZnLefvkW3GDH3MN4aLnY9P8u+IAU1yeBBdqEy5GFHGtfE8Z7b7T37m2tubu4gWb72zrvM7YhVl8xNw1vdByg8SrVUZ0fvgyxKpT297WYopaU9vVT5c0rk6IUlqQ9JjPycLUFPKBNEFtimaQkjDGGczIxQqpjtxGkjlr08kcaB0FgYE33REqRosqQxooPn7ZXjJYnXOfLJtmWbZ8LqqMcxUlQB2LJhTZuXOugL1Z87TlonCQLy9PuH5LWMB10Mycom+0Bz7Oj95LbBtxfTv9uu49FC82K5fJAI/m2P/OGHsF6LjtrXvzado1798LWnDP/GZ/3bHxHYlj//JsdQ/vzb4//54b/i37v/Py7k/+Z4CNb+2+PnjlyTEHUUQFawWh2iTr4CNCuHKZrCpkoPIOYvB6OEw/krY7t2BtQ1UCRaFBjQbYubz/DbnZgpRUk86vpWrzcVEzAfpJWy6hiTcykM5aNErBSninRHtoZAJu82hGFA7baw3mBDKHvAlJ6Rc5HkePjYChssTkmTfCMDRZOZ2nKZREI7S+ui6OiW66qJEaoEe5KEjd7Tj8OkX+7HEdd2OOtAKUKIKDJutmD53je5/PXvsM0BdXWFvbzkMXDvR1ol7G/XOOxyhnLF8K4f2F5dM97ekfsBFcRYYgG0MTALgcY6blqYR8tJCnxOZBMiSQuf7mFJqoCeh21MWP05iY7lpKtxeO8TGAtH46yWp6ruWtEFTEdjdKrz6FIwONJvK0DWpN9Wn3MBdI8ds2NK+BCl7djYKenWJcGVMXq4RzEMK3pz5VqqZp8k76UNsQ6OelX5wTT6UqHvCMB+EEwptHV0ixN63+O3a2Lpotht7mm7jpQCwyAOwsY6tLWkjEgXOI+iw1pH23VYa+n7LZv7Nbvtjr73NK1oN6pSWAtJ2r5HX5ynqS7Ywua2rhGJmhAZ+r0wQnMiGE0IDcY25BzxIRJT5vFbz9itr8nKiM7bfiDFLLrKjZMi+oMgUqG0Q1tHigHvxQhosThhZU0xJdFEPxKiMA9jUJLkatCNwSVN7EQLMwRQSRK0+bxF58gwZPahgGxWGG16fUP/0d+gTr8P8+4QQ+V6TRIn1gIMRHJJCo2TFxsR/dP5coExhnEcaVovBdog7OsxVdNHg3ECNsTaZs9hndLF2KQmiSabGrqLDMFXGGvJdcpYykYS8UnaoxbTkxgwpVjYW/nwGcM4kjOiKWytJLvpwOglFxa6kSRNWnE11jXYpgXbYLs5xrWYboFbnmDnSzACjuaccdlhc2JhOx63p5y3F3SmJYWML9rmoxdmVyXVaGNpFidYp0hxS4w36D4wt4Z2vmSImS82r9jGPWMuDKosOFNQ0LeO7AzLITIzivPOsbnfkm82JN2gFzPM17+B61bQj0Sf2P3pn4EPmEzpaoEG6KxBG5g5w7xxIneYpTMkF/C2dntQ976yFqijdnW5xow5WvgkdxFmUt3D5EhF7kDaTHMs5kFGIFqt1MTsy0phmgaMoZl1nKkL3n73XT5cf0jfbwljKEY3quRbShjnm4EQatdMZrO94fLNZ5ydB1bLC57MHTdjQsUEWYhCdfXPCDt17yNjjLQTcFc6sWKS/ZsqTSProoqSQ+mmZXpMqm6G8nxCTFMcoo4eiTAeHxYjcknPqhmT7KeHX6pzK5c5neu6XXKqXEHcIzCrAm1T/lXiDolxctnD6gXUnUsdocZHc7P8nq6EjEM6f6RC8pCNe4ifChAbI/noxAIGVxLLkXfIl/aX+s8pvivM+gl0nTABjTV6AjS1FvksSuF7igk5PDs5rzz/eg9URp+uT7TgF2VeVLbw4X2CwOHSlZJlqSrm02W8KKQ7ZyLxFIOqCEnJvNPonwNjVT48sbZxYuStKsGAiQBVgeNKVtFZ5M5iEnSqxhNJ2AAPAP7adTg94yn/lncUVS4gV5oeWM7HcUA+FHCKma5W4FTGqYxVCWegczBrMrMmMXMRZ8TEWDxV7IMcXqtMTpqcNGRNypHRyx/vo+irpxoXObRWLFdzVquO+ULTdaaw8ZmKAwnxlBiGwG43st707LY7FAfNbmF5a2yJU5V17KOFmIkE0X9NIpWXVDFizIrGKHKVzykmoHVvCiEJ6cIP+KGHQp5IsUhVYWTMaYOyYu7bNA3OuakTFaQzIcQIjCgVRWqiSkjkwpiWEloBY02Jv0U+onFmkuqQ9SmIqXz0aKVpXIeI62UMxY9EaVo7k2JalmKbslth8bYZmgUxKIgDVkVUzNxcOXIY8KMY9GkUKY2EccvYN7hhQ3v6NtadoOcNbvEEpxyq6xhuT4j3nzFuX5FLxwgI29UWuS1lKqbYlCKHoQkzvA+lGJimMam1kOvE+MyiUoM2CWVkHsakyH6PTldo7VD2FLW/A7tCxV9yMHZ9d8+Pf/RjdGOZnyxwraaddUSdGXI15jGTwYyiaMup0htY/mslMiMqxQ9/9hPe++JbtJ3lrbeecrJa8Lu//Xs8e/YObz97hz/4g3/J9fWVtLQWEx/nGuazjkU7Y/Caj372krZbAZKsdfOGR6dzjEmkHHn7rueHuz190kTcURJJna2olIh+xI+BXVCsB8X1zY4c4OzknN/6ne9xufOEvOaku+NxuyMS0bYEoCkJ9dqLYVH0HoXCOFc2TAmQdZZkP8ZYHG41MRT91+WqMD1lcdVK8mpnHXEcCKOnbTr5vJwIYSQET9fMsNaQbca1trQODAz9nvXtLfPFTIw+igC5RvHOxZIrp3mVI/Y2sE8tYWr6kkN0OXMJfA/vUDRh1dECqg7IUQ0gcjowFwttvoYLGUkONRwC66lFG47l1t39mtS46ZpqYPL47p7V5TW377yLD2USHu+yctESZDwAWstnjGO5yUTz5g1N01Bb6WrwIIyB9IBBVIMSZ+2kc/SvCyamSKCynso1qpoofenOyAd27fSdXJJpPx5JRDAB8F8NMx29kumpwjSojj81f8Xv1f/UgPIoUCAzbRI1mAr+UFXVigJuHa5MhOeZkqwaTKhyXQdt3S8favprOtuDS64JBFN1Mz/43doOXDYijpNVGWcuywKrVTX4OAobvwTiZaXIzrIdxdjlFzcz/L88avB4fN8/9++HRw3SfsGDPPxc/sX3V78vfx/GWH1uD4a3qu9bTe1Wh9MegZjT1/ThPRzNmaxUCTQO551C56PLe4CHpST6pSVBqJ9Sz3+YGXITpdOfSZu2HFVXqc7pmoRN69XRfcABgFHl/HliXegCQlnakxXejwLqhlg0q3QJriWgjznhg2cMHkWiH/bYYqBVtZQfrmEag8Y4R6cVartF3d+R1mvY7emOXphS6khbTkCY8OUEEDGDVCYWg0PRMQ9FT0/CUgG4YgxE0tQqLLIRsqJoKHq86ojlkdntd+SUxJhlHMScqetQ2nC3uYMxYrXibHnK7O/9fbb9huu//iv8dsvjXc8+BW7CCH3Ganj26JSsFH4ciePA7Ycfkm9uMKPH5sN6arVmoTXzruG86XiLzNdT4P+IA5/FHduc8ccDW17qtIwcviZsFVOA2IezRPY+fcSyOewzdRyKcUQIo4CxE4vlcA5dBnhNzh8wTSZwNIMW+Z5jhk9AAHyRvhEmlK5rap0/+ehaa1xR5lndP+q+FGMsRWSmdzgBYfVR/aJ1JasHc9MPiaAVzWzF7OyC6/yStN0Q/cj169e898H7xMZNr8A6h9aaEKXFN8XAbteTc8CV9mHvR3bbDfe39+z3A64ZCDFh7BZjDCHJ/YVUJBoq26p04ljncLZh2O/Z73aoHIheJGNizFjtGPc9+/WaMA68/bWv8/qlJQePT3C/2WNQojfrOpTRjLvdUVKvsM0MYy3juGa/79EKLs4fsVgtALi6viWHAWN1iQUznS3mLVrMV51eMgbw/lCA6YzFtAaTEtv9DpOL3rRSKJ0wP/4z7Lc+IC9nRdePSeoFpJVYDAVL51HOIj+gopgsmYRR0LUzYSuaDW07IyqEoRs8PniMEgaSbR37/Z5xrCzUynJDNJbL85/cwsszstbi1fhgLh3vzTW2SCkfAUqI/mWZF1SmX1nGtdFc39yKkW3XCVC+7xn2/YENSwEArUM7K/qlzuHaGa7tUK4lGUNShqDA50QKg4RtujSFKXE8nzVzTuenmOQIHvwY8V5kd/p+rKEIIUQWszlt25A7h2Lk7nrH/n7DXLWcLB/zzYuvEYLnTX/DfdgwZl+nE5FMrxT6fMUY7+iSZ6EMpz6y++wF4zDSvfOM5cUF6WSF+Xe+R3jrKf7VS4ZPP6UNCYsQNxdkTGMmXwfnnIBDUXQHhUFX1gOtSOnA4JPtU5O0mrKDCiqVXyh7msy72kYunWrifxFDJtvD94w1pTNOikaqSN0Y2zCGQJuhm8/4+nvv8fGHnxLChqEfsTaDFa8BHGgPwxhL7FEHVOL16y+IMdI6w7PlgrQeICRyDkCi8GKpWcfeB4ZgiteoRkUverIxooKCnDBVdxTQ0aP8gIodWCdFiwrGKokeq9FxBQwzWYA6MqlowB7vQbHKbpScoM6hihRJ3CI5WJ7+CJml6rtPurIlToux/n6NvQ6df3XNelBcm4wD6p8S13w5DpoSj0NGVVv3JRY7XAOqxMh1L5pek6Jqxk7bFIccq4Jodf+Sta4UzLUuevsCGBldXNTNATCWIlcFj8s91sLn0S1rJRJGChG8zVn29ZRz8acQqa6pUKFE3/6YNCSxoqynAjmX9zTlo3nak7JBNJCrzroqLPaj++doTUQpYZm2Dp+8FE/qeZUUe6sJ26F8K4UyX9jux8ix0qYYHaWSlh5i+lpgEbYyqCyxX677RZJuh+MMK1eMIB10ao2imFwrnAZjszBVnXivzFygMVGKkMqWrstqDloYydlAFAaqyooYpfgyjkEkG6KQFowztK3l7OyE05OO5UIzmxuaxmJN0cQt3lcxRoZhx3Y/sN70rO/303NUWtE2IoNjipmoyY7sDWqMhJiE7TqWdQ5LUg0hOzHZ0sLGNtbRdPNJvz/HxDAGttsNe7uBHBj3a1Lw5CT7XbbyDIxxtG1L0zqaxklcZATY9T6QU4/Xglv44AVnisJ2DTEVCU4tf5SAytZanLW0zmCNzOWYEuM4kJLIxTjbMJ8DRnyOpCgga5HWDp0MJNinHTlvySS0hllnuXjUobLCWk9m5P6uI42B7drjh4IHEolxx7AHvX6FPX8fmhbdndO0DbPVI9zqjP3VE/pXc9LLkdDfkIPMozBKHCGdFA2ubXHdAoUSEosxjD5C3pOz5OUhSDeJ7PsClMcsXdgaQ/SWpMq8VwGTbjC7j2Bck80Cwi+mvP1SgLGZzMnZHLdsMUtDAIZiDai1Q3lw1oo+D6UCmZFNicNSrJUpiYPik/sr/pf/7V/yvTev+Z3vfp9f+eY3WXUN33j7CSctrOzA1dUN/QhJNbTLc5698x7D9p7t/Q33N5cE3XA3ZPLdlu1+x9NHA7OTMx6t5sxnM3Z55C/+8nMG/wSvzqCxqEnbRtpMFZnozlmrD3iTGr6mL1kYzaNF5p2nZ/zWb33AT1+9YrOWoCGNe+xcTEJ8CAzDgPcjy/mc6D279ZrbyzelrU10pirzahwG/OiJWZ6XcQ3GtcQYOb14zGy5Eu3K4DE5s12vSSHQuhndfC7yBiGiMrRdC0rRLZZYoxnHPS9+9olIHWTRWtzfbbm5eY1KIno/W5zx9JtP+c2zGX6u+YOfXrNZviPM5nKkGAnBF/3RQ8IocWnZMB6IHB8W/KnqdgxSlr9DqZ7JBqTQpSyZOCR0YpigMDnznf/mv51ExY0x7McBnxWDauhNxzPT8qd/9THb7YYUBwH+cyCHnWh15QE9m5NVFtfxMOKMxf0X/xm8/w3czTW/9U/+Mf/+b/8uq9kCYmTcr7l6/YKXLy55/fqal6+vSARWqzNOT064eHTOb/zar3J+fgok9vs93WwmOjQlCUlZ9LSMkSR69IH1dmC3H0kp0jWas7NZMR+QwNVHqf5tNju2m60Ep1ER9iO7q2te/vmfMB/HojmrODWazjhsKk0eWkAnjWyyPmfucmZQmqAM3ln8colbnpCVLppEXkCjas0WNTFqaT+MUult2oblomW1WrGYzQnec/7oESkGRu/Z7Qd+8jc/QSPMi9NFw9vPn3B6tsQ1hkTki9ev2e32oivrPcoYHj+6oG0aUk7cre+nFt0azhS0QtrQi6lXbcHLqWiMRk8cetIwEobIy+2O+5CIyuCaFtJIqzWzpmE2m+HJ3K93xBjQKbEMA78Z4ZvK8lxZlhqa7KW1uDgrGmUkMHGWcTnj7tvf5H/4wz/h49s71jHilZqc0UFiP1NaNr8KYlZH8+Go9D9VppVSOCdO6dZJoGlMDUILIKMLA65EsbWtyTqRA6jFk4nFWUEjH4tZS9lsm6INVoLuUHVdC8vHGYszhsF7htHTjwdTF+cMs1nLYrlgvV7jfZxA0VljWc3nLLqZgKZGs5jPmXczupljt9/gXItyDd5afvTic0nQjEFZK6YL1cxNa2LK+COzCWcsaIjOTZ0I8jhLAlRlC4w+uv1De2A9+t0O5cUJPMU4AfYy7o6KFl8qkNSgP04gZ0mANHSnKzEoQglzM3NwjUeSO6UOrNVxGBhub7HK0DUd1khFm1wZixLkh37PzFlmWpHevMZsNrggLaVV+uIIDmQqRMAD5/c6fmKKqHFEO0XUhq3v0Z18fpsbVMy0piOZRO97bu9vpop/nZfGWEKQFrpqGKG1Ep30lJg1HV03BxQpJpwxuGI2YI3FOMOvPHpOfPMZ97/xXfzXvob7n/85kcxdjOzGgCezGj3tGPD9PXeffIL69AtahYj9l6lkrcxTFTX4QKcUZ0bzzBi+1XZ8ser4V8OOH/mB2+iL6+/B2muavxxilcqIOT6mVUrJeIPDPmdK8FxzVq3boq8tpm41aZ203pC2vpSqcaAEniGECYzV1orshUz0AvYEInOSgmEcGWMgaSXF6qZF68w4DhM75ghjPoyDzAR61XFx0MoqsVE+ADJfdcgalx6wvdSrDq8Vr5ev+eDb75NVJOYREKOkzz79rGhSBnTTsd9EjGvoZh3f+vYHvHx1xc3dLTF4SSTaGRfnj4lj4Pb6lp/99EOev/2sxCGZt7/2Hosnb7PdbgjDmq7rGIdBAHFrcW3Lcn5CUrDfb7m/uRZZAifyDioGTOqJu2tif0P0e4w95bv/3u/x+sUX3N9cMuZA5yw+G7IHfEKbdlrHY4y8+Pwzckqi++Ys3XxB23bMmhZUYtYa5icr0W/PxTgqydqjjcQKy9kJN3dbdsnjhz3jMJJ8xLaKziqWe8M6czQmxcyt+fCPiJ85PAp+/e9TC6kCMFQcQZyulTE8evSYvhdAmwzDuGe730uSF0T3nbYDa8mjxvkRpyAUR2vvY2kDPgyqQy1DTaZEMYlcitLQDyNUc4xYx08BWDmMsbpEV5a5xH9HYG2ING3D6emS9z94jz/787+gnXc0sxkoxRxHHMRUB5XF/KvtME2Dco7oR+mI0pqQKOxfX/adzN3uGlV0/yphQqsGGxXbYcda3XN2soDvI+lvAAAgAElEQVShxO/KsN/txexqlHVvPp8xW7QiDaIc83lL2K65uvqCYfeKYRf4+q9/j3/37d/g09sXfHT9Ga+GN0SdD/4YWjEuWkxckdOG4Ysbns1nXN9tuN/uuLq9wf3Od1ldnDEuFuxmHfG//q84++/+e/j4Z5i7e0zoiWSMsxjnME1LQDH0vZhVIYBI3SdzTrL3Z2HOlm5rYtHSNhqs0zjbSDEoRlJp61ZaYVDkKONAWHelXTdHTNtCKUhZCts/CqsrDIn1Xc/VmytUo5mfLIlkHj15C7DsNluUCmgj/gc5J06SgFxXs27qMFO6ZT/u+fzlC27u7/n2+7/Co1mHCZB2I/voa+NIGbOKnQ/sg6PRRkyVR1+IKML4UyhiNAfsVCXG9R1WGxQabxwRTUqC3msNrmmmmKwW2WI6rJHy2Xmapqr8f5WCEDDvUCg2xk5AncxnAdNEjgsBdznMH+p8Os7BOHz9UBCfvjhN4pyKFEUFBOv1lhjomGQxxaDl+zGKtFAiItqzpoTxqcRmB+bncTcKUBzkD4Cv7J+G2l1qrcMVw9562CIBdCxZdrx/T8+s/H/Vzqy3LN9WE/wse0Jpa4+JEMqqligyh0HkO+reXGPEUuBNR3IVU7w5Pfj6LVngShYtzzObUuh/+MNCDgjEmDDaQo7EygBUhfiiTekakiKQD4EcRhKm5J/1+TykmtT3WYtW+vij5SHIejCOxCCdHDYEVNPgg3SmpJCmfUVb8d2Yty1nywUXJw2Pzy2PzhIni8hqNrLsBjrrD4UPlUEllCp6yuXZWRfxOoDX+GxFMzomQtCMwRFxGAfzmeL0xPH86ZLzU8W81WKgWbqSQ6qm0amsNYWtH4Vt6qOMCxlfWSRNlBjHOgNNp0lZ5raYIG7FPyFqhtwB5wQdUNmicWDAtpbZfE7btiXuN/TDwH63YX23oG0069ubkgtHYUjrAjhHS87gYyokA0g+MPjAvoLwObHve/rBM46efghTpN+0LV3XSTf1ILKAwQdC8GUvqsUJObcxCudadvvMGbA66WiaBts0WKuKbnAi5Mw+9NyGe4IZwESsU7St5eLC0jhP2yrm+YzPsVy+2HB1tWUMoaybAZPWqO1H+MuVmA4DTfcMNzvDPf02avEYs3hE0pn1i78k7q4gFLM6H8T7KAZsO+firXeZzZal+D1w8+ILbq/esL6/Zb1bMwTPmCLWIDr82tF0FtO0uJjwYxDWNwWH0g5DAkZSFnmTX3T8UoCxxmpW5y25MQSdS1JZ9BdTxmhbRO8rr0daCh7U2hIFQJCKlFeKz+4v2fzln/HRpy/4/q/+Jr/+7Q9orSX7kWfn5zw5XXL+5F0Wp29h2lOGCPe3l9zfXXN7syIkhbIt+wBD8OyHVzza7VmdnDKbn/L9r6/4p7rh9z/x/OXlNS+2c2hWEqhWMEMZ1OKUMWhuhpEvxnM635J9YtYbfvTRSz5/ecW73/gOz975Fs1igesa2Zj9yK7vWc0XmOK01yGubimMhDAw9j2bzRqKpqwxltXJKcvVkqyMgJEpE8ZQRNVlwW9cS9ctGIeevt/R77YM/Q7bOJq2lTbQJG2BWUHf77Emc/n5F4zDnraxnJ0uWTSOfrdnu76hnc1Ydi04x3vB8KtPLT8cVKmMyRFDmPyE8rRZFXZnEm0l9aWNPlejLNm7xAE8Hzb0ClepUonSWqOTaKekJKwso82k85liEt2TAiqpjOie5Ywm4HyPVoru9kPyficVwiATTKp4QGsgRzEziBGVUjEokMlmjeH9d95lbjTK94xDz3Z9w5O3HvPkiSQsV9c3/PTjn/H8+TvMZjP22w0//OFf8N3vfJdHjy5YLWaSHJcKVTBKTCd0ESpOEUXCOoUeZQNfLGbMWiegewFcxv3Ap59/wcuXL7m6uuH89DHf/Oavo/yI3vVYP6JyQClLUoo9CaMSxgmrLZOLIZTMqx7FnXXk2YKkDFFpvDWkMZOz6NqMwyCi14BSVqrM1vHWkzNhwTSO07Mzms5glCaHyPXlNZeXN/T7LSEEjJnx3vvfZLW0NBZA5sOwvmW+6JjPO4YYiVrj5jNaPUdrAdbXu10Ra1fsh764TkoAMW9nU+CVYiL0vTBuQijac1nMh/xILtqh73/tOZ9f3nC/H0VLR6B9Ukz0/Z7eR8IYJVm0liANPTTAQiXmOZNVYU7kPOnfRTK0Dr1asXMNt96zDbH6kAjomqEyfY015BKYfuWRH4IgqnztEDrW6nsNwIVJqI4BNg7AYVYUgFaOCtzUL6gsmVUeA6bMp+hFA9QYgw+R0QfamROWXZn7cRzRztAYje0a+V2txczFmiImn8QgpiRl1mjapinaWYVphGKz7RnGwHzoME7z+vKKzejptcE9OZuSJGkhETfmmDM+BmwxzEulLcfHUIAGucEKKMcSbKWcaZwrWlmHr305MUlJ1gQoGl6l6wAgRvUAkK2/e1xMqiAok+aafN86R2ocw24vRms5Y3/yE9r9SPpPP4Ci6WSMwRRQdzZbsJwvsKWV0AdPGD3ee1prWLUN8faGyzeXtPuBVhswEjDFLEmjLtdQR0HNC5I6MimzDavZkvVuTU6R4EdUksRnu77FKYNTRp6fVuyCsOC8D8Q0Fg3UA4hZWfKqJA+pfHRKkZu7a95++i7BR4beE0ZFa60kkWHE+8zCOZ4tTjH7DXfc86cKfs3Kcxli5PU4Yr94wfsYVkoTbu5YaE0mEowCZ2nnS0zbYLWMkzAMxH2PiRETA01MOGdZNku+38z5bNjxL/oN3jagjKwRR0Oj5FYlQU5HhiIFwEypsF1/Dqs9GjOikViD2pyyOHRXhk9l3CBadGIJJVmfKvZQNWhWJT5IpR0x5pJYxEwm0Q9DKdQY/Oh59/kzYoxst3tu7tfsdjthAU0Mp4Mzukp5Wn+EOVR1Pm3paCjR2y9YysrWOo0HazU5Rm5vr/ji85mwlWcd/XbLvh/olKNxFtd0hCz4nNEJnT1jv2WxaNDqVPQ3xx1n52f4ecs49rQvG1598QkaKZiFELi8fM3F4+d0TUPrHIv5jLZxEtNphzEz3GxJ3/cMvWd9f8/p+Qmrk3OMFvBlv1szjnuyyrjGoV2DtS2L5Qlh6Lm/fsVbj55hXVdaIzX399eTCWHOCT/c0TQdMUTCmPDjnpgUV9eypt6vb3n/g3fZb7Y4Y7g4P+Pm+hqUximHaTqsc8TbvbRijp6ua/FpREdFigM7f42OftLmzinjrMU5i7aGOHj44/+VvPMMT75BePb+pCOblYKU8YPn/m4j3QjlpaXoiVEKxaiMtY24dqNQjaJrO8LYM+z3UxdD1WNVRpWimaGyLKcCe1mvFRHt7AO1y7pEFYRrAiGtNeQkc8bnhC6MviwYNplMvx9JcYs1N5Dn7HaBMQ2cXlyw2dwLcypXtpWimc9QVnRLdSFipJzIcURhwUprpmoUzDWpgawF0FUho4kkNLd9wPcD/ej5xqN3xDBoTHSpJaaEM10xAXMFYC7kheywi0d0+y39/p7N9Ss++Zu/4OLt93hn8RYX8zN+8OJv+Gz/Bk8gadn7A5n9ciZ6jFlx9dPXnLmOJiby63s2H31K/3jDPif66GnPZ3T/yX9Mvrwm/PgnjP/sf2JhjOg+ak1MgWHw0iZbXkCGaY+MMTD6UVjxCFtOlzjE2YamLeytrgEEfN7v9/RDEoKL1mCEgV/br5VSAtj6UDR6NdkI6Ky1pLaj99gQefn5K+7uN7iuYXu7J6fMyckJy8UKhYxN8YMoxUfj+HHblXHj+Lt/9x8y7nr6YWTfD9yt1zxylqVzhNawH7csTGZUEOSMjBl2IdNaWFhNyOXshZmqy36FLs8DjRpGwmYjDM/FStZRK8U9m8TDQUxnIyEddT6oui/I3FXq8A7ypFMve0qshBUUaNkTKpCXKqjHcV0/He09B2QylzGotRaj1fRwLT8AivLzE6NMl5imnvGo8HToAql7F9O+IiCyJpMKs/0QG9WPmQo2griWArSbzgmi6WyNFHyts2KA9gBqLRqux/OMCroKy6/GQPIxFYSu1yrXVLEJlDp6prowHbXojkfKc6t5qpp+ru7tSmkx+yoas1WP9MsBgmDT8nVVcoxpL65gdHmfxmSg7sNFMuMo7q03XwFvkWPOpGwn/d2cIRe5LJnKUsSYqnSlEyyVPzUfUbnIZxUGu0YJecYYbEo0hX0bo7y/tnGczGc8XsLjk8ijs8jj88yzE8/FMjJvIp3zGBNAtwWAtcJEVoe8hkJuMSrhdMLojPcw9opxVDibUSaL8WZrmXewmMG8FZJTYw1aWbQKJJXQKqO0wTQz2i7R9tDYiFGOzeBFt5WE20VOz+Yslw2zrmM5U6xWhrZpsKXIblIkhA37MXC/D1xu4G4fGKMiZiH5hTHhjbBCcaJL3jZzrGloXMNituDu7o7NesP93Zp+v8EaeYZk2O4GkWLq9ti2LZIlMk+YivjClh3HwG4/EPxx965iNutYnpzSdXNm3RxjG9rZnCodE2KQzpWyNo1DYHu3IQfPuB/pZx1KZ3Ly5KQJIbHrM5f3A+txzZBGTKN4dn5B2zXMjcOdO7qtZ9a3rFxLazWv3mwZU6SCSWH0cPshWlsx1+tW2M6ibItbXgiTOq7lObz5iN3NZ6g0st9u8T4z9ImsOlZnz2lnjq47YXU+5/T0KXc3V9xev+HNq8+5fvk5w7gvxWAwzsl+pDTGapzRDDGW/EiTtSOh8QkitTf7q49fCjAWBbEBrAB0mqpjJi0sYmZS9MqyniaXOrq5o6V9Avn6FLjZbgh9xkWF1fDuO1/n7PSc+YnGj2uadkHbtnTzhllWzNvHnJ8tefr0CT4iQvQxEPxAHncMY0RvtqSUWJ1qvvdUBJ+XbeJ//2zDm8ESbTc5LicEJAsodhFe9vB0/oytHXm1i9z8+cc8efyUbnHG7ORExMONLgGptGCJa6KAIq5t0UoTvSJGLwzC7QarzNRWkYnE7MtGYgsIRVlwNcY6qUgjjDGtFZvNGj9sSb6FFGSRbOeEIPd+dXlJ7HfkHMjJ0/d7buOOHBNhGAkhcn/Tcnv5gvt8z9DP+dXnz/nsiyRC/+XQhdWZyYSaXatc2hSqo2T5MnUfV9ItA0zBkiptD8fVQK1xykzyDpT2SK3yVMXTqKNE5+i6lMaW6lBO0tb19ltnXL/x3N/eik5YTrLXKWE25JhK25D8adtuCkC00jxenUIMDN4zDj2tazg7XU0mazNn6FrH2fk5TePwwwn73Z6zkzmz1mKdaK1UIERFcaCd7kUJmyArT9/3kDNd68p8SaTo2W13/OCHH/Li9RX392v2fc84wvOnG+J2y7DbTK0tSivQ4lQ/5oOBUEJB48jaEJRiVJpkLMk0hKyIWZLm4MdJ7y2jmS1OaJsG1zQ0rmMcA2fnJ2V8J4bes9luihqNSA60TUfjJPASB9UMKhKytIP55AlKo0Y/Oa9SWyC0nDcVoF8Zh3NOKqxKkrDgPSlGiIWl7QNjvxdn2yTv2GRhiOWUcF3Dk+dvMURobg2GqpklGnQ+J3wCX4pBRmkaZZhhWKnMXEGDSINkVV1iJViJOQlooA2q6VjHTJ/FwKuC4GUqTHMi1BbNo/H78wyFw9/TtyrukYVJ8GVJh3JCAVdLpR8tbVmj9xIU1rlWWG05C2M7jJEUpOWOJLpmSilUq6VSHCLjUKPTEvSnjCdQmbO1MistiIrgswAHMT681hLY1vbpnBUxKwjiLO6iph+DsG2zxyVEs74kQqq0n4nRVCJVOZPSPh3LrjMBpLkySgqzKGfG4AtBoQalebquesSidVWlDtLU7kU5bzWBO+QvX36vEuBWoUA5vzbCytNVrxFI/R5/c8U4DrSdGC851xCtaIjpytwgQ0KKDgXwaBXEu1vS3Rqz3UoF35gCYJRBczQAp51XNhdhXxQ8UQNOaeZNJ3OsjpUYiFGePdqW4pwhB9FOtUXf6+fHcdGMLRX3DJNJWUqR3W5N1y7AWPwwTECkcXa635N2zhACQ7fk7jvf47O//kseDZ4lhiFGLncbZldv8Now96OgMo2lPV0xf+stZmcXpBBIoycNA20/MKJJ+x4VPCZlcpC9dGE0J+2ctVL8wHvuYxKzo3yYyQf9NBlvD91VD/IsR1+aflfrCrLKc9Klk0T0YA9J60H+ohZmjrQbpypKTWbz9HOVTZWidGFoJe/IzDqMDbLH39/RNS2L+Yz5fM7LV6/Y7fbTdcUoLHMBmnPRdqxMe7n3lAuTt7LZtGH0DxW3U1KEwhypQarWWgxFtGJ9c4MxmRRGfO/JCdq2YTGf0TSWu/UW17SyBubIsN2QTYPVCj1rmS8a7m5uaLqO07Nznj1/zsvPP2W3XU+GZNk57q9esUYSmuVqycnZBa6dYZsiXxAD2+0993fXrO9uePmqxbUFtA2eHPfc3t0xhEhUBuPFQbprO9LqlP36muvLS6zrcE2LbRo29+vSOVTXhVha/5jelR97iUkLs3AMGWVnKOcYaRj1jBgj+31k02+k+6f3KKVpG0eKma5Z0MwahtBjeUnnLENKBEFZyl5R1s4UUesN7AOaz7H7njyM5He/RS4tqoTAsN1J7GYUY07sNnco6zBOwDatgVAMQsg0bYtrO8R+ekscR9HELhqOOWdZS472wgcyNUX66TC+D2uHMkesrbpGa4VKRYv7aDoIy1Dh2pbZ8oJnX/9Vov0Zd7evGPZ77q/v6Dc7KYDX7VJrlDPSSeGDyBToDKaw9FSUrozWoOcNZtYQ1OEdCkjhJfop+4Me7mjvGy66E5Zuzsy0xdiQCVQxpXslhkj0gWY2p+mWjKMQK+7evGQ2X3Jin3KxXPGtx98gvIlch3v2uZ/kX4JO0DnMxQp3vWW/CaiYWCW4+fQVwzjiVy1pbhmyYvXsMWq5RHUtYXtP+rM/Zthu0WEU34iUD1t5iQ0STPIoiuLlgLR1OnPoZNRa/C9kv1UlRkhYYw9xf5ZnnovsiABMEktQzI21a0UreoorpJ20342ECMYNZA8qS1eN1rl0MxZAs8iRaOMOuQjyGcZY2s6gXYu2DYuzE+Yp0Z6s6F8b7u4v2RTzpwj4nNmFSBcUXTHrijk/6ByIScDrpMBqhY1JDOX8CMGDPbRbmyxas54s5KOjGIWyNmh1VAB7ANbl6T6qRAyUtZiDHvGDrWdabw7zp84tGY56Wtfr/DmwT+UzDiZdpkixmSmOO2a+VjavFOtkrNe2eOn2OBByRP7oIA3woAB4JDmgtJYuGWOnOasKaGKMmToMjapgFFRUAZUPJl61KFzysGlcPABfDzhEvYdjMHYKoup6CqQkLc3ClD1IP9QflOdcpAJKT/wkF1FyCqZPVWVeH3CRSfpBsN6jMXGQGNCTxFdhsFbAdppzsv764PExEoMvYNtx11SVuThmbB9iY2psUTp4yansb3mKu2t8rcoYcdaik6GxjkVruVg5np1lnp0GLpaZs07T2YgzGWMiSkW0joV5rZGic3kmZRyX13vIp3XmdCXap6sVXPTwaJvw3tM4xBDMJpxVOKuwVtjzENFZoDUZaw3aeIyN2CZimkTYJXajyB8YrdAuoK3HNYblbEbnLCcLTdeKIZRIJjT4YLgYDRd9ZN0r+qAYkibkQFL3hHSP38A2KMY8l7lAJqYRFRPaOLrZAqMdYVkM3pWYJo5BcB0fE3rw07iUuSJFC+uKTEc1WNOZcRTZyhTF3KuKSxtraF1H28rv1bkNSohQUczFdDF19GMi55EYA/2wIUWIAW7W99zc7Nj2PUMcpdt4rpktW9pFQzsz2NGxbGBcRIbTkX6f6IMnKXnnoos9oMZL1HZB6k4JVti4TetweoU+fweGreTwYWRYvySkAN5j1MDY7xj7kRDE5M26FudmZN2gXSeFkH7k7u4NYxgO+t9Fz1fuPaKTKuRRTUhWsAgt0j7HxIwvH78UYGzWEG2WeKwopk3FvhLAqwLcqTJwK5OLwpBV0+JcFr6sAUvCMMbEzc0Nr19f8ejJ13g8v8A0Z+w2lwTVsB88iXu6tmMxs6yWZyj9iJg1YwiM48jY9wz7HWm/IUTPfr+hazTvLB32+YxFY7jbjPzR6x27oAimQaFoXMY2CkUiq8AmZJ6ePGXr79jfXtK/es1773+PbnmOaVoiwi7MSRarxrlisiEgiTIW42TTCsGj+wZlpLpnistdzKLdYRup4llbk66yWShVaN56Srz26zviuCW4huDnkBWr+QlDv2e3XbPfbMh+h1IJCAz9ht16xJRASGXFWhlefP4JN73hJp3w7nvPOXkTsUe9rCIArUXkOKdpoa7HtGAfbzRTFbVuJtO/joIE+TlTmRTIhpGqS2VJ7LUglWWPKqBXzqIVlEubOqIR+uzpE3T0xP2OlGG/3aKKH44KieQjmojKEQ2sulmpmspzPmnnRD8yDD3JB84uTjlZLMg5EUaNzYnTsxWuaUqFVkMCY1sJTo0mJzNtloqD3lMNJKyxDGPAlQSgawwK0bDKKeCHPT/96U95c7MhpCzsaHbs9xvids2434oBRglCk1JiPJU1Kiuy1pJENqJjlbSm3DUhZkLMxKQmkFFej6HtWk5PTlkuF3TdDOcabm5u6GadMFN8T7/bsht2aJVxVtO2jrZraJy0w4YgYO3ohbqS8dKWhsgzxBBlETQHDaxERpXnonXRt3FWQNdB9JHHfiygX2HDDgM1XBLjgEzyHmUN3XLBs/fe5osXrxEz6zz12EVEF5CUSKqwF1C0GS6y4pHWrFSmoQZthwBXApEkWs7GolzHJkTGnKcFu4ZWHC3gx0n6Lz7Uw7iuhEwVC03pOBhTU/JT778Gpaa0cu3HvZgOURKJnIqeayL4yL4PpCymMGRp03HWTvkNgB8DhYtRZy7RS1AJNbEorJoga5/3nmouBIV1GxOeADoJe7bcV0pZAJ0+45O0bxNLxTTrIk0hrqHSRZLJMU1rCEVPsKA3D5jTeioElfbpcKSPybGe2hHYGo9MmuDo3BQp0UNwWN9QBaqOg3uKLERONRHRpTXUkkcBsGKK0jp+eQnPZ2XNd2jjIAzFSOUAaOQoMjNOS3vYeH2D2u5ogoDHqQJ56jBu6zuY1lktLV72qLVPZdAJFrbD61Ihz2CyOO4mkjCSk5ZEHGkrbU1DQE/s5FSZGkpPGrU5JUwZJ6oE8ZvNmrad4WyDHxU+RAkKjcM4ix8Hls2MMQT6xSn3v/5dPn/9BfrmlmYYsFmx9iNv7q5AW7okTAYza+keP+b8/Q+wyxO2V1ek+w3ZR6xLaGvJRkNQqAQuR1TONNkw71r+L+be5Ne2bEvv+s1qFbs85xbnxo3qReQr/DJfpkk77bQtEClhgbChgZKGLRnkBg0EbST/AXRogmiDRAN6lkXLQsYyJgGjdFquEjIzMvIVUd7qVLtaxaxojLnWPjfyPUwHeCt07z1x9j777D3XLMb4xje+j2XFcb/jx2FkPwUyakqZ8jxnSG/PmTwBtG9prKu3vpY95EEiVeamaBSf78/5+TKfUknovsmanxN3zol4jJEYAspWxJCwxmFtIKfM7c0t29Wai4tLNtstu/t7uhmMZS5QSlJWJF9yflD0EY1Ha846g5V1eB/e+qQhKQEF43ksQvCkHKmt4Xjcy74bpS3fOoexRXvUWWLMLF0lhkIpMPY9thb9Q2sNTVOzu7/DGMdytebq2TucDrs5kbTGUFtDd9rRnQZCiCxWS0bvWW8vWSwzRjuOhx13N6+5v33DYXfLmDLL1Zr1ssXoTByP7PZ7otJoVxNyx3G/Z7lcsVgsqV3F9YsvJPCvGqqmpj8dCwAp98dZU5IqacFGQfA9or0Lrqnxo8dWDUk59l1gyI4QEtF74tgXcD1inWO5XHA69Rhb07QLbKioVY1eaPxxEPDcasLocfGsb69F1BB99wZ7/Zrcj8SLp+TFFrQlZgh9j7YGlSQh6w47tHM0ixV10846nFOBSxlLVduS4EdEqWGYY7o0GRZNcgJIwcEY5vgxhvAWo2+a35MO/6SVP58/ZY9NKZWe+elnFdpWNMsNl1fvc323Y7+7JQw7difpnrHFsCRlee8YTSIRUiB6D86KDrOBbBSmdrhFg120qKpI35TzNwniyHxQKs0+nHixe0POCbc2tM2apZFxiykXUoDM6RACfhxIWWFci7ENZM14OtDtbli0C5btgvfWVxz6I+oI12Oiw1N+K8Fqxk3LeLVlN15T+0SdFOr1HUNOpLQGuySQyEuF3Syhep+0+dcZ97f4Tz9F393hojAsJyhIgLQ8g+RT+7tW4t4NisbZ+bm5SE9EL+ei957gw2xSLGGZnEmTyZ3OatZJj+X+WddQN00BBLUkysYQghBUjM84Uwn4RgGmSmwxF77SA8QMmRu7u1sMwkazrmJ9cUG1XGKspoorjiR2928YhlEMEIcRT+YYIpVXLIyishZfYhvK/kjJNd6KuWJE+RHjR7LSYOS8EQtr6XiLSqOkr4oHs14KtgUek+J6mmW5Hjxx/lypdGLk+bP+8efM/05F+hIzvs22zDOIqmZk7wxmzn4v88+fX1PWpsBlKfOAgFXiyVnwbwL+zB+LScomwezyXvJAM0lw6SluEXBeCgDlRJoAVa3ndmtV3oMsS8mfz4Dr+ZrAaMElSn5dfnB63oRPnO+B7D3amNI/ByGUH3gAgMtUjKQcisZqaY2fXnc+w0vnyU+5ppGdXlDYxyVenXRiH+Qk0705Ew2E7TiOHh8DIYmc2EMpAiEMSedXTKkQRqacTH73lMHLfU8iZTVPuDzfSgFSC7kGh6sq2tZyudZcXXiuNontIrOqhFyHmuZxRjqqExOrmem3qjyP+/xfIduvjGa5cKTsCNlw7KHru5LjZGqbqStD5TTGZiAUxvFEkpLXUtqircNUCV0lEiODD5y6iNGWqovY2lPXlpSEEFJXmmWrqIphes6VsI6T4lEUvek+JoYYGbynG6+71t0AACAASURBVEYOp5HdMXA6wq5fkZIphokBA2hbYbShbWrcqhYQ3Xt8GIjek4sMhOjTTutGiSlkVdMuGpyVDsXKOmKC41FixxgS4zBwOh4xzuBqQ71oRBZKW+q2YrFYYY107KRCYhy7Xjp8fSL4kWEc2B3uiUHkOu5vd+xuTvSlmzamRMeOdlWz2LRsLxdUWGzWLJxju2g4rgMHb0RaQyWSmjp0duT+Ben4mLC4oqlEGkKbGrN9gk0DhkgKJ+7Cjug7clYi69b3DP2JcfCEIGQwW7Us1g5ta1lphxMpeo6newY/iOHbvDfrUtCYMCoDymG0AP7GOeLPkOWCnxMwViktuktoSnyFmj8QkBVpEgwqkycXYEAe1/PhI8CtQlPTmKc8Wmx4vt3wS996yqNHVyw3W1S94PGH38IPJ7rjPYe7N3z26R+yXRrqtqWqpf1MmZqmblhVFtdu4XKLUtAf7znubrl+/ZLHMfG03bK5WvPOaoX+hyf+6XXgLjRUbsF339Nsthp/TBy+DrShYdsEXn36huvPfsgvfvge3//lP83m0YUsqrJYdEmEzQOmSyoCwkYrqnpB3SzZXj7h6p13UCGwv7+j64SZ4IeAUg6thWUydANVlYnR0/cnYhwxixXD8cTu9pr97pow7NDKUtUrnKm5/GjDp59+Qn868O0PPuDzH/4Bu8OO/d01x+M9dVVTu2bemBsSn3/xGff7kWNaUqkPeJS+S/PgoMhKdKImY49Q2rWFLaNLJfwcxBlT3FGNVCdFS2piQSiMNVht5PtJNq66rkmILqlCgOtZqykXYNYYUKlUN0SU+UHHLbawk58+f86T58/JOfOP/9d/wBh9AR0yaRjFOANoqob37JZayZJSQO3hPnYYA+vtgufPn1FVYlQTrASip35AZYXJBqMcYgB5BltNLQd1jAlrkrS3qKItBCirub55Tdu2LNoGVwLd4AOVVVxcrHn+zhNudidCClijuFwtaCo4qpGEZ9Eu2McDw9TyiiYY0TkyrsJUNbpyosHlMz4mRh/wMUi7pq2obc3z51dzcLfcrEgp0TQ1Wmt8CByPJ+7ubgExj3t8+ZQPPvwQVCSknq6757B/I4mj1rRNzaKtZLyCxw8eXeZHCJ4xJZy1WKUlXNOaRSVC5SFI+/MwDCQ/0h87wuhJKdGFPdYaaRnZbglVxel0xA8j3gdOpxNDjLzzwXMePbuiXiyomro4mgoaL1rDIsyfEuU9g0uJbVL8QGk+RvFYQ6MUXk9tPUFa60pwZJzFtg2sluz7XpKKB1vfeY982Or0jQd/ypVnUHV6Aflr0sc7U57U/Jqy/sxZuxlNipnD7QGD6HIaLe6XdVUJu9knjkMgA7Wd2sIMVS3OyrL0RStYXDiLAVvOjCGWj6oEyAXG4Et+Kuxaa8/v2XvRHZz0xZbLhWh7lUA9hMjxeKJuamxdoV3N/m5HtV4U0Xppp4xFfy8VMww4a05bayUZK3vWBNw+1BObIOWHOmXzEE/PKXIBgt0L4JzTFLyVBKZoJyvFzNZHnYP3M3gvTGRdWELKGurFgiHs5jhTdUeWf+dvk3/zrxLaFSkK8HK/uxNdI9fQNPK5nDPUCpz3HL/4HNv1mNLaqBAQZdYRNqYkjRMDRCrn1pTW/Qc5QEqJ6ANN1eCcJVlJEZx1814/pb+L9Rrd2cJO0px8Rx86Uo5zkWxqfcwZKYToAuLkTMzgw8huv2O5XLNdb7l+8xqyQqdM8CMZaOqax8ZgnGM/dtz9xX+Dz/7R77D7g9/nB4Wlddf3KBRbK3IZF48fUz99ilquePGTz7n5vd/HnDpqpXC6zI2Cn0iJAWxMmJiwPvLR5QV/+dEV/7jb83fuXqGcYzIiymX+pJwfJF/Tmi3GFqV9emJ+zY8/+HuaKxoBrCcjrYebx6Q9NxdAJV9961JQkqjzPRxGz+A8qzZzOh24fLSlrSsaZ4gB9ocTfT9yc33NqS9yMGU7mQzYzkmWzCtpC9WzVp91FtGw9XRdJx0ND0jCPqiSgp+vl6++IviR9969Ivsg+pRlP1Daosw19/sjxmi6w4HV9oLVaoM2hrvrG6wxjH3P6eS5v0k0lSQrCk1dt/ziD/4kh8MdY98Vs9SBYeg4ng50p47buzdcv3nFs+fv8vTpMx4/Hbn+4p7722u601HMUO/fMByu2CxEBuqzl1+X+6lJIRL8kdfXL8j5GZUW873KWWIY6H3H6ZhLu6gEI9ponjx9wt3trRQXjeZ0OnG4v5X4wFmqUNFqjTeG3gfujz1Vu6SuK9G5W9a8fv2S7WbNot5g1Zb9/sDdoRcwMCeauqJe1Rx+4hm7iDaO0R+oQyLahE+hdA6JawNlH7O/8/cJf+JPwbu/IDcpSuFFZVOA48x42okMUvJ04yhFtiJhMaLJlbSmV01L1TaMx47T4UAYvcS/Gpq2EYMlrUAbcgjF1HaU/TO93XkwFS1STiijMYV5PzNtk+y/5CllV2irCWHk+volv/3b/xvXr77G6h5dzGWM1TOYkMk0iwpdznWtFEMImNqhnUJVBmUrHr37LtViTTaObhjEGbwwxiEV9/epqJgJwAnP14cb9v2JX3j6AY+aDVr6HFFaczgciywb2Mrxo09+n4vNlrq5JG0gjvfgT+xvXtB3Hbre8P3n32HTrvns7is+3X1OtB7IIumWFf27j+hVxr26p3m141FV8ebVPaf9kXC7ZPHt5wL4L1a4dkFoKm7+yl9l8d//LZp/+s9w96fSQi/gohieiqmJdOrJVEuJWY6orivCeKIbMiFHXDnnUkz40TP0A1pn6qLZK+2gFE3VqZCkkHZQjbYWW/K3NANLsi/GKDE7CpzVc7wDStqpYxbWdJ4M6eI8n3LK3L+5prJOCiZVDXXD2PegpOX82eVjrn7tz/Ljn/yYH332E/7wxz+h85lDMfiyKH7h0VL2iRiFIJKleyBNm6dNVJVCRY8dgV7a6X2GVHTQdeUkJ/IjKAG8p5wYIPpxEnWbAcVv6tm/pQOfxAxtMq6ChwSX6WXLaGcpGD48QibQcGanTk8vPzwDsDmL2VHOqEmei7NvAwXM1OWASg8C2BkcVOf4adZoLX/yfF4aKRTriamn5m5MIerIW9NKP2BPi3nbpK8tRNgilZI5A8zyRsoL6DMYV4pEk+zJg1oozLlsGazyWEq57G0yLtbo2XiJLG38KUa8H2dDbfJUUJ/MMSeteGQuFT34EIrmcgpoV53HL8X5nklXh+RxIYQyjmeT72lc5xP4PAXeyiXcxNouOt8ZidPTdPZPmMz8HAl6UvSFbFH0VBFwOJY5ErIi5IzRUDnFqoZlbWhrS9toFg1YK/mcD3I/FBmTx3LPAWWYCkQzOIaA/BlERkklKpcwNqBN4vGFBaq3MOI5UMtiTJiMgwKCSuw+FsBZo5QDihRjOVu1NeRkyN6SvEjlTFIV2ijQQToqshFcISZi6lk4z7oSTMQaYauO0XDsLS/uVnzyesmru8TtbuD+/sjtq6+E0FT0XTeXj6naNVY1RCq8P5BSJIw93o+i4e2LwI8xVFXLxaMLVuslbSNFrQwYo3HOcDLgvRSAh6Fnt4eo4Hh/olktWK43KGVp63Ngq4tXRwqBvu85HU8Mw8Bh2EsBM0a6vmPseuLoIWVqI8bqzhv0EXwKBFM0uXOkrgyrRY0/ZfoII4qkDKiiyZqOuPgGO76mqqDRrUhcbdZ05hmuUixah1U9h9sX+NOJOAZ29/fc3d9gFxfUyy0pa5SpcE7MODGW3AcSBnv9gvv713TRo7MYvAbAKbBGuohRlrZeotyWZvGYpt3yhz8+m8Z/8/q5AGNRwrLj3CR6ripNe9+5T/0MNGQEDEFhPKS8IKo10T5Db3+F9977RX75/Ut+8FzhX/8uKe24ef1jTqc9wxi4vHoPUzeMKfDJp5+gh3uW66ests9YX77H65t7KqfZLB2Ptg2bhWO1qObK6Gq74eb11zjvqZue764D/9G/fME/+OHAZ/eBTsNHH27QyXN9uubL7of4/iWf/t4nhOtrrhYtf/2v/DUunz4FrYocgsfq4uxZAIjJ7EoVbZ7Fck3f9SI8XrcM40g/9piqYdu0NMsF97d3CHgZwHf0g6dpW1xVUbcNP/nRCzbfvqRdtPi+xbUtrsqMp44YBmpnGYcj3g+Mw8B+v+PLL3/CeNzRVBWPLj7g+vqO9eUTXNPiM/z4s6958uySb3//Y+rtU14OPU9evqCme3CvSyVNK6wVkxZVUJuUhQ03Ac9TEBEz/Et/5n0++NblW0HFz55PvB18TMDKNxGuB8+Y/34rbnn7q7/2V/4cOWecTmztSar0czAiguef5ws6oKk1v/mXrkg8laNATaLxAIacDeRqDpvOQc/59SY3ipwN00GSpygqn3/uN77/Hf75D4+8vPWoHElxIPgByFSV49f/7K/y4Ue/wOBF++nq8oLDVy/IXtrLqqZhP0ZiorTSG05joEoKExNqGDExMfpEzEpcO9sF7z67YrvZ0lQVh/2Bx5cb7u927Pcdd5+/oesPGCNSCnXteP7sOa7WpOQZ/cDhcE336gZtJMl0TnNxsS3gQCSFUDRohHUSYpkrpartrKVyjjGIxl8IHu9Hul5JMj16Ut9RhUBbktuJwev7nuilrU+h2N3cM46emDPaGr73K3+CQObm7p7b+1veff89Fm1DWw9kVRWtJWmn1NbRdT1XOfGxq/ierfg+sAwBRSqtiaoY0jycwIpkDaGx5IXjsL/nLQffeS6on/rv221o5+ttPdLzvFJKDtZJl9Xos56QLgFuzpk8Ju73e/woQIdTUDuHta4I90M3DHSjx4eE0aKntGobaicFoGN/oh+FdaKNpq1rRu+LJqqwlfScAMh8FoaGJEG6JGwUaG52wc7nZGLwe4xGAodKNOM265XIK1QNbr2m6zpU0tKKmOT3zPuBejhOb7M8poTEFNb4BMhqY8qe9S8CxB9oiJVE+5xAvpUZCZtbFW3Dh0nNN+5/jjJG2jrMUhHGkdANc3Hq9fUrVn5At8uS7Cmunj7Duaro3CZyCCjvCYc9/fUNzTBimYDY+a0LFF+kb3LZu8Q0Q6NiwiiDcFgeIGgTTpkyi+WClBPj6DmeOvriIu5sRdU0kDMGRaUEvDBaY5RmCAODH+d7pJV0gySlSmKZ5qQ8Een7IyAdJKv1GqUkaVXWcOo6jqcTWsPSGt5bb4n7G7o/+avcPn+Hf/I//V1+FU00cEyZFz5QW2m5jt5z2u14/cknLE9HXBYQICs1JxVvs1tLGy4Zt9vzznLJX2hWvPNOw3/74kuiiAIK03dKct6O+EUjOaWyR+lz8jPdlG8cflNiOs2rXBDVCYQVsDPMbHpdkuPpJMyKWVZgYqDHjLQjJtHCHYYOTWThDJfLJff7A2P0hOiRdqVMWwlSrhCWWkiTlp+0b4XJLKGAzV3Xl5ZkiOIyQcqGh3paVmkqDcqcP3PXdYx5ZLXe8OHjJ3z19Qu6voOcefP6NZcqoeJIDFDXLcMwMF5fE4Nnf3+NM5nN9oJ1U3E6CZujqhzWbFm2KyBz+eiK/f6O3f0NNo988K330UozjiMvX7zg7u6O6zcvuL19w6PXr1gsV1gFm9UCpVpiTLx5/YqqXbB59Ji6XRaH4wAomqqmWa7QOdJ3R7rTge12gx89ox8ZRo+1dt6blFIs65qr73wbrSSJPZ1O7Pc9pqoxrgKlWFjFMHT44QTjAZ89q8UV1koh4J33P6bb33J/vyOMncQ5SbFZPaFqHUZl/uCHv0fqPYwZ1Sb84ImHE9pXNCFgfGIs7tcxKWEh6Yz55J+hvv6K9IM/J0T+GEWDPyTGlIinjth3JN9j61b2d2vQRoxj/NgLQIBIL9XLJdrVwkACRj+grC1dMAZXL9AqM5xOdIc92Q8Yo1DpvGCMFa22h1eKCWMMVVvhtZ/XrzDVy/wPnhDu6E93uKlbCVP8GIp0w7SCYiR7jzIaV1v0xVKApcqiFw3Lq3fRmydkJV0EF25DZSwTQ1flzDCMnIYTYxgI0aNRRK055UjvD+y//IRvP32Px9WaRtekkFkuGrpjzzh6xph4/PQ5SkHTVrzz/vscbr/i9csfs7v/isRLNo+fA5mL7ZbN1fdYupo/vPkhJ+0JSgqCp0rh3ntMWi/wy4bxJ695dLFiERO7247ud7/gya89RqmOY95zs7vm0WpL/s3fJP/glwl/829iXr6iUkYUqnPGI9tYSpBUFoOvBI2V5N5apENOi/57GEfyBDApqBrH6XgCPRYXcU0sud9kXBmVYrXdULWNGBIqRR9HYnF7l04fi9OutPvLPuhqh1GqdGEaYjQFJJc8JMRcymxysMUY6b1nHEd6Y8nG4mop8FprUKEBnXl+9Ywnl4/5Ex99h9//5P/kyzdvOHUdL7uRzdGwtAarS/FeiY5sKudARjPETCJgU8akjI4JVbeyzqmhrmjqFhdrzOA4nU7MZpylwGwexjVaFxmbKeY577FTnGPKWfHNx36qbNA3tGPVtBYyf+wxOX+mdm653+dsTK5JpkHnQmKZGajngGR+fnm/wQeiirJ/KIPS8voCbsm+MnUNiszfBJqe47xvSgukAr4/zBFnQuWDz3kGXt38msLGLc948LrzOFLk0UKcJYVSOhtZhxA4nTrSLI0g4zABqjEGQhiZ2/sfkAAkbpc3mEC0VlMsfxK2SHroErfMe1ghOqE0o87FkGrqrplZFHMM3NQ1VXKyNlKUhoIiPyKY49lS2AgDbB6fVPxLYhym2SLEFeeYDEc10uHgfRBT0RzRWaNzxGRLbSzkIOekyXgdUelI1pmgMiNw0B5FgzEKYxN1GwRo1RalHCJ4pKSckPV5HKFo94qqFEUGY5qDGgsEMh6UL8x5AVhTVMSQGPzIcejZnQYOp46+P6JItI3GtYqqqagWC+rlArdc4CqHMwmnI85I0TWjpJgVIERFSpoIwkqNGR0SPijiqKlzx5N6R+80J5NQxpOcFHR0palXazZPP6BeX0rXSoz03Z7+eEPoDvjuwOH2ltN4KJ0jiTFF7m4iwQ+E5QKVl9i6QZvMat2wXreix6olrjPG0i7WrNeXrNYb2uWSthUj+HGYAN+REAJDN3DYH7m7vePN6xsOx3syk0a8FNahSJLojMZgJikOo9CtxlQGmyuqZU3IcAojfScAcVZKZCpUQKUA95/ibIT8MTE9Ry2vUMZStxdYJXJXT7o9TlcM9RvCcJBz3Q+kfiB0I2M/UNUN1jRYW1G1K9zmksVwxBMYs8ff7zGUQgoKbMXy4hGuanGuxTUrFu0Wa2usqfiR/TlnxpKLsU35+kH5BfK5OjNpy5CVCPFnQ86OlBpQjwn1c2LzLmn5LdT2l7huH3Hc1LirxGXtuX39R6Q4MPY7rr/+lOBP5Diwv3mB8j1dN9Bua5LbMKg1Q4wkbRl2Izf7I996/ojd8USmJyuNc5bYDRhG6npgS+ZJm/n1dzTfXmvugudiUTOEkVUzQh35chywXcfjzYbvffQtPvzOR3R+kKqOMdRVPTubT1pLc1XPGLS1TO72IoINrlkQhp7Be1IWnbzleqouarSx1LXGWou1jspVXD19xjj2hGEka8OHH3+f/f0rbl5+zWm359VXnxF1ZLMUU67jcceTd97hdFcRhk6AlQyPnrzD8vIR2JpqfcXzdz9gtb1EN0va3vBHxwONeagH93ZCqYvepy6bYyLNMonzAaoVlTM0zc+uKvx/ci1qADQJq1sAGj3i9BmQ+OqghMGgoKkfttP8tOtfBOj83z3v/L3aWZrG4Fwola+AUWoGt0mRd549BSNJnomJ6+OR2I9iBGUhKsOQhb2mEgxJMY6iIWYt2Kx59Pgx1tUSAFnHom0Z+p7j/kDwnqE/EAu9f7GoubhcopSAljF5vD/ho5hXpBypaqlgz7pCKTMMXWlzlWDaluqytprK1GCKCVwMhDERCqsqxlgAUrhoW7QxRJc49hkVgyTDWdgPCSXyBCP4vpfPoxSuqnBaU68XXDx/yqvrN3SHkasnj6haS1VpaqcBjfcBZ50EgEpTdZ6PrOUjrXlOZIlUPqeQPuaIiFCX1nhVDmAjgGysDF0YvwHWyjUFxj8NlJ0cdaf/fwgkPpwn4lgsoJezE0vtvLdOrfMpJrqDaOekov1KAU7GEMg+EHOSVryiz2u0oq0tWkNInhwnxgbi/l1XKAW7/aG0Lgq7OlEMEZRoxqGUMI3moBBQAmqmwtg4MxwKoFQMCGKI1JWwn5JWRA0hBbKmtL5HYb2U8XnYdjYVfpRSOOcIwc/jPem6GWOo65Z20fL69Rv0JDtY7tcfu20Ta2O+Cw+Si/ygdRxhS8z3NJ+TlSnAVUz6oPlcjTGGZrngNIYS4Cd2hx2Xv/u7qO9+H//kCh8ji8VaGO5ahAdVyuTTCdX11DlJUouZgb+cEjoX9ok2OFvNICyoAggjjK48iQrJZZTCKU1Okej9bN5SVxW974QZg6fvTtzGhDMOozRWa6rkyFb04LQyjGEo58DUMqjPoKMSSaOcLTklxrFnt7vnYnPBOPZYHE21pG4a0vGIJmO14fFizdEPXCvF8fIxh1//8/zod/4hz5LHAjsS+6xYdT31qcc1Awxj0dyVRaKSnKk8WF6znn2ZCDpEXNezzTUfLxr+1csrfudwxy4/SHYmIPbBxBETwShyTTpLi+qDtf5Wklfm7VsJ8pSVcU60JxBU5pA+M3TKFJ3+N+c0s9qGYeRkDMMgjI/TaWDR1iyWS+52O4xRNE3Der2ibRsO+73oisWIT5FhLMlaziWRFM3gPJmDZUl8pPip31qD57k0maicvxdiZHc68Nnnn4t2vha2jfcDq9WS9UoSgePxSNWsyDmisozPar3iq89/Qs6JxWKJtKZJUlFXFeuLDatVS+cjh+Nj7nePObz5iuR7QhyI40BjYb2syTky+sh+f4v3Pe1iSVVVaK1FZ/N04Pb1K4zW9Ic9rdM0dYOtKjKKXFnaVYP3CvO6QqliqhfCHOdNdzqnzGl/YLfbs1qvWS4XGNdQNZoxJIZ+gAxBy3hNbvXOOoYxELPHOkfraqq6xfcnRi+mlMY4fPCkTrqNnlw8ZngVuRuODPsOExS2vGCgGN/YLEzCCZIMEPuedHqBPv0D4i/+qtDYE6SxFK10LiyhzLKAkVKMnyQEztumJMbCzHJ1TdsuuLu9IYwDSUvXU0aYKEmBsgaFRaUkMeRUHJ/WQpa9d2LiTvmFdZYY5HOrnOezASVsLpFNgJgnfcuy15dCVUYkcKJK4DTZaGJIUnyuWvSyYTSJMB5KYqlpVEUyFZVbYI1DGY1WopOvtSFEMb2MIRLCyBg9Q4bP718wLkYetVs21VrAciWMO9+PGFfRLhqaRuSuzHGLtmu0SSQ/crh9XTQANcvtBR9dvo/Sii8Or7j3ewblCWRipcnrGs0WGxOp9yxCpAqG25Pn/tMfkxcVaWEwS0NQgbBe4r/zHdRf/rdw/8PfJt/sUEOgVpqgomiUlu0pZtE8r2tHWzvIYkiUVfEIibJfGCWgvFaiS5hyEuC7nKNZK5LWaGdply3NconSpeU7Rvw4FjmHopduwWSFzgqIGAO1q6iMxRXgyOdADAkfAt0wkMLZWBFKLhUjMQlIpqzYdCkFUSuyH6gbKY7UzvHo0SN++Zd+wNPXb/j69Wu+/Oor7roRtzDUD1rkpRNN3mvKiYCGJHmQzZ7KDDOLU9UVUU2SRRKrOOcYh+HMaGTSc52Yvw/W1hQb6nPB9y2ZnG/Ejt+MIR8+35ipWDTJMBUxgQnw1FZ+Sqm3fn4CLCHPxeoZ2FVv6+5Pxd05dFJiYJyRgr4phX6jtXRIFpKBc7ZowppZG3bG1qb396DSqR6YPKWcStfLea1POeg0tiUKOZPCHmhclPoOIcjcT1mkRSbyhph0xsJiFSA2xFhkhEosUV4vldh2YuJPX8v7OAPDufw9y7KkVKQSzLx3PcxDdZH9QClMytjsIChp+c5Z/FsmHdfp7szwjGhVT9qw0/49wzYFo5nlScrX55KxxLhT/9N8DxDAOMQ05wghJboxcHfMfHntMST8AGEMkAYWtUerieeaSGkkZ49S4pPTLGC9FO1T5yLWVcwK9EVKSWclxB8lMhqYXCQtBKieNFmZhV2kcB1jJMSAD5kQBmIY0TlSu8zFWtPYC2IS41PbVDTNmtWyZbOqeby1rBeZxnmsKeZ42qFyQqsk5mB66hKf5EwSPowMY6IfMsMxEY6O08Gwu09c3wzE0aOdxmnRnw7Bo4YB6yRvWrQLlk1F9AP9aUffj+iuRxfpC8lp1Dz2PkYqpbAFk9LGopWVPZvSdVA6NEQySPLbprZYUxODJYSKYRxJQTpmUxIzOGNtCQnSDAaTE0llUtRzF6MPnuyV7K3FD6iqLBdbGKJB2xPq1NH5gK1cKeZojAoYv4PxnlxtgICzLdo5kgLtB/zqKePyDZpArB3OVSxXW1zdCgEEM5PTjNLgoF6uqLoLGj+y8iMhKJyxWONk719tWVw8wVYNxji0rah0JXFIfnsdfvP6+QBjebBdTwnEVIuSFS7PyBPd35JyRWRJYkW2j9H1t/HLj4mL98irD0iL97g2cKOgqxMfPv+IEAaG0zXBHzjtX5FiDynSHXc4pejRuGaFW2xIboFXnpgc49Dhx8TloxarsjAuvLTqah+oDDQeMDsujeb9ZcvTSnHTB4xeMFaZxVpRP9tQ7a5Y7e95ul3zve9+m+Vmxf7VUVp4jUHrurhkJ6KKWKSCRDl4tDGi+ZEzIXli8rMeRe4nPUhFVTeE4mwq+qMWY+3cwrG9uOBwuGXwIyjDxeMrQvQ0+xNDN3B785pA4P2PvstyuWL0I5dPrwSIHQfGkGjXG2zdYF2DaRa887zlYrNFWwtK8e7TC559fk1jzoHN2Su7/H8JDHRhDKUkB8C5BWQSdf9/Clz+v38lNH0qrXVa9Fn//760Vmgz3f9pMKDThAAAIABJREFUMxdwLaXEdiVVrpwVh+sbjvuDJHJTwIDCo/AleVHO4WOQ6qR2+KxoV2vqup0DjhwSfd8xDgPWWrpxxBYH5ro2rFYtkAhxZBgyPnQCShYgrKoqtJH2zcnwJQRf2qxyMb1iPsaVPgfFOQQJjsfi4JvkULbasMoZQ2bMiSGGIm0hayYpcboVp9ISgOqMdZWw3irH43euWD+9YB9OBALbywuyStS1oW0MvpN1uXSyZlEKXMV7zvCUxDpHYRsYA1laUVWMot81NfAoUFaYHWhNKuP3s9iuP+v6mSzKh0E1qlTGz8YFb62pwkSZNBiHYRBdUc5xZkyJkLLoEOY0M9sUShzMC4s1xqIZBbjK0VQ1bVOhcmKoKpG3CIUxW0CuqQVsYvRB0WbN+ZxQlOc1VSW6kNagc2b0Iwo1O+PmmCQx1uBzkMp5DhAL+7wEtKoAwXOSjexFxtpZsxTFHHAaBKCc27HyeeimQPStOzcBrw++nq98/ifPn1+VQJZzkjafhYibbgH9cjnVTV2hjJZeoZwYxp74o0+xT67IT69E57GwREQrO4H35K5HDyNVCeoLUlcKgJIwTEZn1rrSFip7s89B2DcUs7oH7GYlsIgEcsMgQZZSLFcrTv2R4IO0F9MThoFFs6SqapyxOG3PAHbO5BTmQoMAsFMiJO1oWSmMFq3AFCNdd2TRtoU5An4cMbaajbxUVixdzUXdMgTP2Czovv1dvv7iM9yrN+RjxzEHLrNi2XXUxyN1u5yN7GY+dWbW7c5TslbuI7kkdTmhx5FKay7qmj+1uuDF0POZ79mlDIY/xsI5z41Jx+3BjFJvP/OM++bzv/PYyWMTw/5cfFCl8CXxwQz5KwRgzsxyAz4nhkHTDyO1dfT9gLWGumkw1tDYisVywWa74vLiAq3gdDzSjwMmaXwoc2jaO2IUU4SZRTy1h8rcj/GccE7XbETz4HsxZY77jq9/9ILHTx4X1lcg+EDbNtRNjdYKPw74UTp8spLEvWmXHI8nKicFm7puCX4Qs5/K4qxmuWixaGzTYOqa0O25e7XD9yeSH7E60zaWlBv6ITD6yNCdACmKVXXFOI6QYX93I1q2OrG8WNPWjrptRAKCgDGAcri6hiBrRWmNczUh+Lfu8elw4nZ/ZPCJrAyQUNox+CP96KmcI6ssra5auqWMqRh8ICRFhaZuRIve1QsqH8reIBp1fhg5HDuWywtWm46+83S7HRaFyzLPvRHdR+Ms6IRSEfHoi+SYSIcDvLqDR8/g8VOoaoiZ7CNZC8iPUvjBY6oKOEv1lDKTFKKiMKQmFmxV1yhE0y2rUrgMgZhkH9IFjM1R9vg/dk37K9OaYiY4zCaIc/iW57WsFAKaUAqSWRWFhAJwZCUdEn7SSjWkHDHWoWqLqixj9uTxgEoKgyZiGXBU1YAtRa40+hLXFJBJS+dQSB6fRpTSXHc7hAIAla2pVSmqa4UzGlNbFqtFkYOKJNNSLR5Lm6W6Z+xP+O6eftfijGKx2PD++h1iyphOcxPuiMpL4bKxYJbEBP5+jx08zeBZ9p7D62vGypAXDvfOhlE73KJCby9Qv/ZnqL/4jPjFC+ybW9ztLXWCwUdiVPJ6MZVYweCsIfgkxYk8AT6ThukE8hWpmpznwqcAfQZTV1RtQ7teoY0TvdnSnh18EBAYQGmUPRMAUgrknHBa01Q1tXVoIGQBH4bBE6Kwrb4JIkqxUoAzjcTZs4V08Bhy0RWuqJqW58/eZdGuqOuW0Xvi7TU+gDUZq3XZD9O8xU17YCwglYqRNI7Y0mGgYo3KsrenMq+ttURfmIcl2Ei5MIcfnBHfWBI/BRU4P+/tmPIM+j18vel7c7xJkQThzCeewM+H4zjHOvN3C6A4FahTASO1Lqx1MXsrk2KOh6b3onQhGTknf4pMlsjblaL9gxjzwQi8NR7zw9N+MAPAuZzzUzwmYNwUDKQEqsjyTvFBjIkwhsIePXdzMQGqSYywKMVKka0o72Q6r8v8ku5ImWfTf+WuzPnx+T5Jd2bWAqRS4tipowwVH4QJRdM9nxmt3xyVCeQ95xS8lVNK3vgNPdiHP5+FsT1pxJeJInF1OfPPet7iQ5Cm3LK87zEEDjnyIsu88gOMgyfGnk2bpWhLhMnkMmUyHq0N9UkTBkvbKupGyRmop9iizFeVi1SM6ApHEzC2FES1kP3ERFY0e8/deXIfyRGtR5oqoTI0lSGvHeQVSjuUttjaYt2Stna0lWbZJlZtpHZB/HRU6XxVClRGFz3brMpYpExMgWHwdEOg7yPDyXM6OnY7zc1d4ua2p7UGpTJay5iM/VEKXbEWTf2yVhQK40YxoLQaHWVumtKNaKwtsh0Ga0VOxtkKayuUsqT8cB3KfY7Bi0+RMdhFQ1VZsjPE6EApxmqQ4lHtaNqaTClEhCD7sjOzTMdUEIgpkoMneYWNTvxZtHTsNa1mu9ZFzgJCPmFsMbpXcloq35HHA3ncQzihGymC5irDYotfPWWxeSNF4Xhi0S5ZbJ5Qr7ZUiyW6atCmKiC0xqGoFyua9aXMnZzJWeO0xTmJrdqLxzTry5lBnMmoEImjYBD8lP14un4uwFilFKnolUzL+nxIqXPFJWdyUuToiPopvX0XX30Aq+9jL3+F0D4h2iVRV/iU6Hzg61Pmy4Pi1777jKpu2N9+ze72S3Y3P+a4eyFtQaNU3H0ILNdL6mVDr+AwwjBmUlzg7JojG55sLhju7+hPO8ZU8+ZF5vGjFVtdc7ru0OxZrcT0Zak6UpfYrLc8f3fJD97/JcZf+TY//ORTnFFcbFccj0fC6FEVYEs1z1kJSrLFFebL8XBARU1VK46HA05bQhiJccA5i7OKqnIE7+mPR7KVavPEPKVotuSc6YcBSKUt3ZA13O13jDGxefyYunH86NPf4+XnX2B0wzsf/gIffff7fPnFH3C3u+O039O2az767vd49eJrvn71Clc1XF4+5sUP/wDvYbl9wp//i3+J9zc92sd5l570gaZrbprMuQS8RVhfKamo/xyBsD/tmqqC33ybGWHyWPN227EPbxswPXx80vH5aY/HlN5qYdeF5Tj/viSAZIoJJe4WAr5ZaQGtXYXSltEHTocjt7f3pL7DZWmziAoxkrIaayuWqw2nY4cxjvV6w+F0YIyJ2HcEL87aMSWWy5ZHj7bUjaWpF8QgZkJdv+fmdj8HDEplqlrE2VMBNPw4CjOntIFbBbaycwBFTqgwChMniXTB4EWztzKW2jiSlcpkBowxrJdLlj7QnzqGvqPru1JpLSpVWuzNrLbiqorGNjXZOkYSpmn41i9+j83VmmZT0Xc9eYzcvPyCzaYm+5Yvb19zVa14rITBlYDNZsWT4FlEj06qONmX+Z3F2CiUAywpxCTJGI4l2LGu4tR3hRn70+f8W+DLg+tn6skWUEeZwiBwhrpyc4KqlCLm2WPqHFAbhSmtmTlJcjAWsfWUMtZqqsrhx4DWis1qAbnoRipJrqzRXKxWUrBScDgcWTYLtB5AjTgne10qmtHCDkC0XQvDLIRYzISVaE6i2K5XVE0tB28pBjgnphpYQ3d/JFsJBLAC9PsYiGRMNnOioLW0K2U9VcLPumIhCrtzFnJVmhAjx+ORrjudWapCmXiLnfzW/Xpgmvj2DStgXLkHE+AsrptvJz1vsUdyJhddvSkUylahonSKKDLXty9ZnO5xRfc1FeASJeDpeDyguh7tJRmgAItaK0xVYaqK8XDElNbOylRzkhxiYIgjwzCwqhc0VUPrGvz5Y8mVEn3XC2jrHKvVimEcOBz2+HEsQUxm6E7kGLGLJZV16CQtlSErnDJkrYSlUV49wcwCzjmKZAYTqzJxv7vl8uIRKUXurl+xXF6QdUkgyufdVgsGHxhjYAiR7jf+NX7yW3+fL/7oU1QaeYpG7/ZgKmor7aExDlJQUYicEEULDWbTj6mIKGuwnAfjiL7b896zJ/zG5oLfPtzz24c9QZmZXPtW2qsUyhgp4nBeo1PB8jyxHoC0U2Kbp8LCN4oC8+tMrJmpHfO8VwSiMMcpSUrKMj7es2yk3d85w2q14HK7Zb1eSjHEACTRG1SalGSd5hDIiD5sbS0hCjN2zsTMmWk4FW++mcoVu/C5GAdSoBn3gf0nJ+6+d421Tn7eB9pmS0qZzXbLZrvhn//zf0rdOGIS7a7No8fkrOn7QFUFlgvDeOpRKtGdAuPpxP7UsXp0Ofv3VJXoQvq+QxFxtSOOsN20rDP048jh0HF3d4PShs3FhuADzlr6bk8aTyyahq6ATyllTkPPSEdOGW0cbd0S0sByuURpi7E1L7788byn5Jw5dQKWjumaYzdQ1xXrzQWnTtqxnzy5IkUxc7Km4snqEXeHA9EnYgqgPCiIGFYXV2wvrri9fk3Kmaqp6PsTr97c8uzd96mebmjSCHd7nDHUZT4GnQhZg9HYCMYkxmFkTKMUwMqg6d/6H8l/4TfIH3wsB8uD7gmVDd2ppzWOTChMYIvWdi5yxBgQp3CJYYZB9BK1kR0gjEIeiLloihs37wsPF9OkqT+xfaazZnqOsMp5a78VQ8dJsqA8fyqzlalbVxWmEtDA3+/FcMnIuDiraLcrclsRVSL7YS5cx4xof/pI8IVZhqY2Fmcm/UmNtY2AHcVl1llHxHJz2tH1HcMw8r2n38JWYtq73QionFXmeDhxe7vHuJrt0w9oFiu6XUOob3AG7l5/yc2bF7TrJ7zzrY/57pMPuejX/N7LTxnZCaVAQ6os/tmWbmkZ7/aYm0DdWq5w7I49+1c7ursj8dmIeQqs11BX7P6df5f08pr2n/wTHv29v8Mma+4PnmFMnIbEOCZWjcZNxaUSe6oS60/61moqcilNU1ecGYVy5tZtw+bRIxabNSlnjscOH8IMbE0gHucdB2HOBULI9P2JzXKFM5q2bnCVJWaRUxmrEYPM23N8rYrJbSEN5CidQWEUvXClCCky5IAZHLFuJIbRFVW94IP3PuTq6VP+j3/024z31wwhoJ3GF8AOLcai5MzENJVuHgiDl1AjZymG1AuyLSBfjBilqauqxIAwBtE6nTTJJ6n78/kh83kugJRipSlst/zwQHpQMHs4mlMBzZiJNTjFOGW0lZzbMwCqREag8CRnuHb6/ZMM1ZzfTLF/iXvEmFqMyUwByZQWYlJd1TR1jXWVFEKUKqSmySAyFdLAWfxwAn7f0v6fHi2I6jRuYtiaC0jEzFRUiOZvLgZbUxKYM9I9xNkUbT7sCws6zYe03AutIRcZxnPBsgCxOaKU/IE4a1STZTymIRfJFSEx6SJNEUMqjFvZxwTsjrJOksTcMYnG98zQnq8pn9DF+Fre20SgkGkro2atlds+tYuVMZ4kkr5JDAGZz/EBe1aXODpG0XEVIpCYhfkAtynT9Yn9XnG3TOyPie1C41TCakoHZS1yZGUOaaW5XWnaRlHXibrtWLWByhVdYFXkECbdZS17eF1Lx6MxFmUqKtcgxuUlzi+/wyhFZRQXS9guHUoV6ROV0LpG6wptHLZygLA2tYoYRgweXdzAp0L+VBXQWuNMRKVU4qPEMAwcj5F+TAxD4tQFbnbw6l7z8j5xvfdcriwXGDIQQ8d4vIE0kseaoK0Yu4csRae+47A/FjMyMWS2RlPXNavViuVqyXLVUjUVi3ZBXbfUVYsxtUgV5kmiIqCNaK2nYyCMA+Q1dV0VEz3J5Z0zLFctKT+Sz+gM4zgyjqN0KlRy3qZSTJM8Ocv89x4/9ABom1HKEbPIHy5bh48Vp0JkmszXEwnjT3C6BizaNMRqSa4WaFPjVo9ZPk0ok4j9HcSeZdOy3Kxxywtce0G1EixsLmxpw2J9QdaGpl2wWW9ZrDaorMU4rW6plmvpjEEhsiIDKY14RIYq/oxcEX5OwFjgHPPkc4VKJalAZxQ+1+S0IuVHhOZj0sWvE9cfweKK2FwwqIY4AbckrMmkpLk5eP7oRaD7rqNarHjUfMz2yRN2rxd8/uk/JocR4zKr9YLXr2748o/+APfyNap9wuuXFdpdoY0j58Sx91ysFth6RbNWHE6eZvucer2kWTlaO/LV7T2LfmTZGtaLhmE8cbjtsc5R1xXWWr717ffx40gMnjc3N2g1sUcCtpkYZpMIdxLgI3gmK1FrHQoY/MDxcE9lKi43S/rTkf3ujjfhK/w4slyuaNoVdbPEK8VqtS7tfY6MYrXeyKEFdPsbXn39ExaLBavFgu/94i/z9Wc/pvOBV29u0FXN//5b/zMXjeNysyVj+NGnnzIedwz9Ee87vrKa4TTS1BseP/2Qr37/Ez5++ojb28jpdJhv9DehpocH36QXlXMiRalw5MIU/nm89rFlzIGN7d76/pvbA3/6r/+n/K3/4j/mOx9eAXJA/Zv/4X/Oq5sdIK0+v/Xf/A3WywaAbvD8K//+fzYDto8vVvy9//o/AeC/+pv/C//lf/d359f/G//BX+Lf+7f//PkXatEDNM6KkUGdscZS1Q1KVfgowu6+73n16Y9QXY/LSjTMjOVis+SiXpCMY0gZPzF9hpFXr19SNxWH447Vcsl6s2K5XLLdXrDZtCiV+OSTP2QcBlyl0DZT1YamaYgxiZujH4VNk8WISKrYirquiONIKOvBD0EEfIInDz0meKl0aYOxliZnFk3Nql3Q1jVfv3pJ6I4iFbBc8OzxI26/+JIhjMQcRfScJPILgFOWWknylBUEJc7yQz+QG0u9rnj0wWOWK4dKI8PRszv9X8y9aax2a5rX9buHNTzTHt/5nJrOqaGrCttOgxR2td2NjQjBpE0b0BgEDBjAGJWoMZiYIB+MCEYTjV8ktpq2FTBEEUkXYHeDYjP0QJdNzdZ0pnfY7x6eYQ336IfrXmvvt6qgcYj2k5xz3mGf/Tx7rXXf93X9r/+w4yOf/C5833P51jP05YHvaY44jo4F0CqZLiol/j+VsYQCAumc0YUllpQh57kEJGWN1xZTC7O8Gz3xtu+bX38/rPC/19fkVIq+srZm9ulcgE0hgbrYmBiRi4Q8pxSHGMRrrbYs24qmthyQ8qSqKpLzLBeyv6WsBWzOWaxQggemhktUrNpo2rYuMi1NnUtAXIh3PCan9FdDpQ3rxYKzszOatjQ7wzgPlw7DSFKyN0ZVQOWssMZilCFn+d7ikSus6KiS2PsX9CznzCEeylAwz6BX1bQSFlOki9ZOUqeJgVjYl3fumiriVPmyKZTnlg0mS/ZW7j7f83QXbFeFicUdTCDPn1fbCtss8DGTxhGl4Ob6Je3f/lss9nuG7/20FLghyOcbR/LNjiqE4vZaDtsUcWMke4f1C1brE1QUvzcfPFopXAwMzrPre9arNW2zoDb1t7EpxNs6MuPVKdHtthwfrVA50aOKDFOYmN4NDArWq43YHBhFbTU5aUKhqKhiYRFSIKo711BplLmV3/sQGcaBylQ0dUNOgfXmhKTESy2FQO1GjhZLgkqMO89Njgy/4fvRr72f6md+ip8cHY97x8fHiBoDDzdL0ij3OU6gZi4SejW1+RRg9NYLMpNROVKHTLp4yRsP71NXFSdK8ZO7LaayZGO+rf25u/a/k2/fd2Q6qTt2I9zKvk0BdbXWxZ+urEO5dEyN9VQEhuLXnsv7DENPfXpCDJ7DocPHiLaGkIQNqWJm++67LBcbFouF1GnBoWyFHxw+BqoqFTuBUpklylmlUIU1JB9To8OtnVGm7E8pMXOvlSakzHZ/4BvfeIv7984x2uCdJ4bIar1mGEeGYeDhwycsV8ciFTPCQD09u8/R0TGnp8fcu7fm2btvc3R6H6WM+Bp7x/7td0XGm2G/3dLttqxWLWf3HnPvyROev/eM4McyAFB8bfgmx8eiGFmtNzx79kwYPc7Rh8Dl1RV2sWB9csZqc8K9BzUXl9fc3FzgfKBqW2zb0t/c4Loe2JEnDBBw3vMLn/1lmtpwfHpGytCPDS9fXEBOVFXF5XNFP/QycLMWWy84f/g6h36ck5VRmWaxJAdPCCOnpxvefXEFMYGxrE/OOTl/jIuJRTtybzPy8nBB2u5JvkLXiiZmuiwNPCmJp7sbiiduUX7kO8zu6Z8oac9kxdHxMVNoz6TScKMT+XFhj4khtMh6lUo0ywVtvUHlRBg925staI2tG2zTUrcNfU4QbofT3gm7FqMlME/JoFusaPTtQ8atVVZAi9coMsBcr9e3A4MQaNqKalmhrLBUl3oJWpMrg2pr1ifHKKPpswyaVQkEHN04+4xPnniqpFmNPuMLo1eCXQxNvcTYSjwetYUQUVhyhn1/4AvvfImHJw84atcoZTFZs9v3jKNIcbXWRDJHZw94+OgxrrvivW9+hTBc4dyefndDYs/y9IxIRAdHVSuUEflyTImoMv2qRVcGs14QNgf0VYcyNZtBk4bI9mvPuHr7At3U1MsWZQ2V0piHj3n2m34b9/70T9B3Dhdl2L5sKtqmAVP2dqOoK2Hex+gxJfhTrJwEkFeA0VbCtbRmud7w4MkTMAqfAsOhl0FbjDDbDZXtAhmWk4WkAIqglIRMGsN6sWJ5fMzpvUcMIZNjIHrHerdDP6+p6mb+RqYSYLCQ4YTlFAMxU86FhPKGkBIuBLqhB1NLGHQtoTrf86lfz9tf+iLXL56x3V7TWk30UTC3LMq2EPwtGaHAltk7dIzYGMlJkxYLqCrUNPA3hloVoLIfSjBSASGNuQUd9XRVbs+NeR3MQ69blup3rinl/JUS8tVKdfL/fIWtWf49/R1ZWOAoOf8noBMU1jazhD6njLWmAH1lWG5FCqwLGKuUom7b4h07Gx0SUy57h5rtFGSAe9fzVoKkZ9sFDSmrYq0TC8iaZvA151tANs7KIYVSGVS6w7i8vYZamZnJjFGieKVYbiUBYJW2ojoLbr5mdyuBXCwZQfIUps8ysUknZiE5z1YnMcUCuiZyKAq3EmR2q4jRoqTMEkEaCcXe4I7fMFMtAFpbrFWEoDEmkVV4heSXsuxpd+29Jr/ZybIgpWkQoLBa1n65OfI1SmFI4qMcFWUCV/akyC4p0iGxc3DV1WxajVUZQ8DkgM4RUcmVIGFjMZeJuoKqytg6cXrkWTUHGquo7IK2rlm0gaaG1hjExC5AtrOiMvhxtiXTWjMRT4zKrFrFZtneKg2VIVPLfkAERnI6FF5H2TxyQLSbFpRFTIBAZSGiiT0LkD0ZTw4R72HsK3ad4qZLXLwMvPMSnj6PvHjpuLoZ2Hc3dN2C42XN0arh+GjF0fE5q/Upy/UxupLBuMoSAn98dMxhmwi+Lz6vnm4IHPZ7Vqslx8dHnNx7QFMtaRphDisLFo0xFdbo2e5Oaz0TE2xV3SpPkHDmqpJz1wpqzjiOdIcO5xxWJSHbaEs2CmsTyft5H8gRorco02CUMHw1mqZuiLkiZEPvFVd9L8PcJKzVnb/Gjh4z9tTB4W2L2byOadZUtqE+fczxeoPJHqsi1iTaylIX9aWxVlQJZc9LSc6i5eKEul4T12eYzRk5G7QWNjHGSEi3l5wb7yCNgbHvGPsDKd617Hz19asDjM0w0xHmTa9MqJPB5yWD+RB5/SZ5+QZ59SZx+T5CtSHZhqjFrD+TUTpjLTw81Wy3kT4k3rmOXAyZR0Y8PBIiu5YGXGjPq82K9fEpu92O7XYP9hm7iwZdP6ddrdDrll/+O4qbJ/dpGw1Ehn5gWa3p+x6tHPa0xdfHvLvvqYfIo6w5X0KtMjE5xs7hlSR/puIdMwfgVDWmJOXWlVDJVU6kGOg6VwJYMm4c0FZh65bVekPTtlTa4rodtqo5Oj4mhMDN9UtQiZw9INNV73ogYysJOECpIjmIVLbiaH2EIjMcBrbXV9x/9BrL9TkuRL78hV/i5bNvEhYtVmmCD/S9I+eE0RljQSVNjuKl5iKcfP1LfPT+97C7s8FP3jgKNUtnVZlbTmmZeWIZZTm49B0pRYyJP/MXf+7bGKS/5dOf5N7p5v+Tx/XVl8Inw/OD5Y/8h/8lv/VHfxePXvuAADv9OE9733txwx/5T/8c77645kd/+Ht5/dEpf+LHPsO/+sf+W/7Ff+Y3Yo3mP/6Jn+Jm3/OH/rl/jOeXO/70Z/4Wf+CP/jj/9h/4J4S1vWj4o//Sj/CH/6M/iw+Rr779gj/+Y5/hP/jXf3u5nuIDZ20FlM1Ta0KCFDN+HDlc3fDirXcxqUjctEJluca7/kCXFC5KcqPVls1mJen0dU1Cpqxdd8CNfSlY1lRW5Mz37p1hbGIYO549fYH3HQqZUBtrIAcWbSthDErjnFheJO/Be1QMpaFLqALI6hiLZiPOMvrDODDu91itOfQdKUSiUuwPB95+5x26/U5M/ovRvNwmOWadEi9m5yMuJ1zO5NxT1Q33zu9x9vg+zbpF6UDTWI6PVtSLlmg1+xDZxkBfZfY4TpRmqTRLBfswMqZAk0RIrZKSSXgWwCEBAchKjmhHJuREKkboWVm8j3NxeBeI+Y6s11/pVYC7V38/yV7SDNAqLcyD2W2svK8EaRUGdlURxulairTIx+IvXJDCo82aZVOTcqYfR4KPjM6V9ynMoMExel/YG4pDJwXvBBTXdU3bNmSg8gE3lgJRibxmc3REs2jJGfqhZ1+k0T4GfIiMMbJai692VRkwkj48AZw6ZwE30y3aobgrk5TGpm2FEReCMMqssWTR5M4MnQkQlWaD+d/T6+T4GDcMs43CLVB7+3XTcTf/qb4NTgBo6nZm4kwNy/TVWgmgqYqPOCFgjcXlyO7mkvj8XVJyKFZisRATfn/AFp9Y8cQyaGVFMjd5eeYsTMYkTdPgE7qE3/kU6JNjZWDvOpxyLG1NxUT8iMTkyvqVIUcOie7mRsIAkCC4sRtL0S7NS0oRUqRpF1TI/iXXO89ewTnfBrJM12G+g+UZtNYyjgM0sFqs8M7jQ0C3LWbRgg/YumFRWY5tRdCa7uoFXmnS/QcMP/CD1D/z01wkzxfHDn8Z+O6w4VFKtFoGw3OMeTmzpnVSLkmUAAAgAElEQVQ1ebPJn2vxPi+3qwoetT9wv634+Nk5L/qOXyYT7j4AwMxMT5K2PTWvd9fyXTD2lf2hnJt3X3f3DWmySiBeniR6t8wgo9TsKyyMBs1h6Lm8vma9WNE0mZiTsMhipG1qFouanJWE5GlD0zbkIbFarvAh4/yIc34erFDO/AyliZT3tpUV7zF1d22kUv/d/jwxJWLWZAzbXcdqtWa1WFLXjQDJWaRtw9Bx04+Yqx2b4xOWqzVDcGRlqBZLdF2z3XWYqiUrKx7iQPY90cmzHxNo23J0/pjKarJZ0HtNszrFeE+Knpgi9x88JpZU4BBGKmvwXqwKFGLZcfnykkW7oK5qut5wOHSy5pBhhTW1nNuVKKoW9gRbJHfGWJ584ENsL58zDiPq5obT8zMWbcU4DozDnmfv7kSdcXJKu1iwXG8IMeFdzxAch11iGD2boyM2y5baKl48f0rXj8S4AOSs92PPfntNt70he8+H3v8h3n75gs535EWFNVbQ9BjFN3D0ZBchFi/qXIJmP//LsN2SP/HdzCmnIZOyZ9gdqKS7BwVN0xAKm08J8kbTNDO40o8DKBidJ00MmXJ2tU3L8dk92uWSK1tBbMHdro1JAj/VkqKsS7icZGg46WE1pVYSX9GUZV8Sy4nJJkbYi7ksSGUNRldko8lVBU2N14qmqjEpYqKck3EGTqaaV+yjlAadhSk4BemQEHsGJV6OJid09GyaY05Xx6zrJTWat569Q7x5Tr8aeXh0H5KiWVQoDWZQ+OBZLhZYa+XyV0vWZ+/DNEd4t0fTc+iuee/6Kdeh5yLsiQuDaRokIECXIWDxwl3UBCUMuKr3VL3H7h1KZbEhGEay82Rt8EqeeYfm4vt+gMXP/RzLvpf6L6UCAMWi5KAMWBALjpBYF3aa0roEtWoyCWU0tqk5Oj9BV1oCRHtJwU5JUua1ypicSRomvXMGUajMwI7I+HfdnpvDjo0bedCuWdhW+qWUODmPbE7vs1pvphOGVbthVB0qODKOGMaiJpDv6SOAAB1KW+mFQii2Pw21XqJNxfnj17B1xUurGW6uADWzQrWSIdDUH6G1PD9lSpuCR/USDJRDTbYVuqkF2C5ElqauC8O8DLST+PLO/qLqtiq8g5kWZrmeLTooQz2ZqU+gay7nbZrBqRn4vv3F/J0nppooYcIr51XOqSiS5F5PPtJaSR+YlbDeZ1WI0vOwU1igSQYhxfZn+mGmNZ7UXRn/nXOF9Mo5mVMmTSqMlItSL5dnittBfZqKRF3WcbFQmNY1t9AzpRebfEeNNpjayt5gCpCMqNJC8Dg30O23hFIr5lJXzMehuj3DJ1B4mtDn0pPllCTAM8fyzAnbtTj5yj1IiA/9HaKB2FzFuT6dwj6n6mpirgoYJYSxJAU1E4Kf7n5tAVb97Ll8C86GYkdHlsAtyvdMRYVmCngnt7eoJObiXOwqQoQeRcYyJhneW1VRqYRBsBSrDFZZamNolJyhdW1oFonFIlPZUba5qqFdaJZLT1NBbTWVyTS12AtkrOBKufRDOZZhnZ73G6XEKiEnRchF9amUgK0pkoLHj1ux2WHqdaCtl9SVRtuE0kmkk/OzWoJztSmgriJl8bLe7x03W8fL65H3riOXe083BlLy+ODZHhJuHNnve/b7nmFIHA8R7xPNak3GFuBTVBmazNBr3NBJfZEi0Q30RHIKjD4RxpH1Zs1qvWZ9dEJdL8uzePusS7hzWaNak7MmBm4Z2mXNaaXJEcZhLBaHDqsTRk9rRjC5qq5Zro5o2yX1YoVtNqiqKT2SDMV8SNjGY1pHqjrUfsc4DkTvIHp89gSfye5A3D8jNe+Q1JpEBbbhaLFkuaypCRgi4CVXxUidOrFbc0qzuiUmiFmJn6yuJJsgFrJGykTXk8JIcANhHPB9Rx727Hcv2W1fEHzH3+31qwOMhbl4zZMfRbZkGpJeEfQTwup7SeuPktcfJLePiXZNVFoK6W85XbTOnBwpvMv4A7w8wItD5t6RLgVypncOnyJuDBhV065OePi+FfGtt9jvbojBYaKn23mca+iHmpt9RPkd63VNVSmGfqCrNhirWC4rkjomZsuzbU+Kgd0emiewWS2wypKR1HdVHlpr7gR0IAeDdxLmVVtbJAeKvhupVhWqTBNzBLSisi1V3UJODIcd1jbUdVVAlzRPh7TWQl4vPicpBVTSVLYmZClmrNYslkt2V1fst1v6Q8eDhw9IKbLfXvHe218j+ZFDEJlp9J5xEM+1uq5kgk8BmN1IRHFz9YxqalrLa9qQp4Nel0Zwsiq4eyvnI7Nco3038tW3X/C5r77Ha/dPiCnxzvNrAH7w130UAOcDX/7G8/n92sbyxuv3+dI3nhFCYrWo+cCTc77wtacia1y3vO/R2f+jRzehccnOBc93eh36kb/0s58D4LveeMwn3nxMBn76b36Rf+o3/VqqyvBTf+MLAPy6X/NBvvHuS9yfj/yln/0cf+h3/abb9yqH6Be++pS2roTtOG2IlfjuGCMJyhmZ/sYktgLdbs/Vsxf0uz0LW5c7I56mJkdkJKlQSlInUdI0GKOxVlhJIk/wuAT7/Q0JX0KPwvz5YrEUkHppAok1YQxFsxdJ2eO7juBHiAEdEzpFdJbWOBfgNcY4p4QrEFYWGVdQEPGvLId4Sux2O5wvAEBpsn3OjKkk9pZNcwJjfc5UVcWjkxVnj+7x6PF96soQ3CgpoosFqk5c9gdeHg5cjY7BGC6SZ0WFZHQqrlNgzIl1hipLWNZdllBWmaSVMDJzxpMZc8KV4jhlYRAzsYP+Hq+7IMu3WRYwqQMmf9FbAdndYmkekANJ56kELHJsVQrSjFKGpq3JKuOcJ6aE84GQNCEmKaAU1HUjTOMQGZ0vMr44N8MuJFwUeZ8Pxfvbx7ngFM/jSI1MXDWKWlekKGEEdWWF7ZjBl73HOU+mKAW0JXknnykENCVsyZb06hLAoIo3NXkKB7rTZJRC+xXgNIuP4XRtbwumO7dpugd3bsXUNORUfHBfAVOntfxqyrEqz/QEHkijolBJ5OUTMCf5TyWUxojZfdKyXskiw4y7ayrXA8eyymPG9QP13FiVly2exsTC6FSodkFdt2BEgZGGHt8dGIOnT4FDGCFEKjQuRe7Pl0EKaOkTZDpNzoRhwFuNqsSbMxrxD5w9g8vPa42F0sQ424s1QpLAuDw1AOXrVb4jqZzZUArvvaRU12Jl4aLHqBbTtMRaqinb1CzbltTUXPQd+75jbBfE978f/cEP0r31Ds8PHXHoWSmwtuKssiytwmhpaNKdc/tuYzLdS132XwVYMgwDK6t5sGz46GrN827PZc5MehHK8yILJs1N7dQI8S1f961r/1u/TmqF24fyFpBlboikUZr+WxphKDJPjU+Jm/2B2grjPXtZpzGLN13bKtpmwX5/wFbiEV3ZiqaGpm7wITG68AoYO+1DU7gJFB9mxZ3uc5Jrvrqmcp6cQzTjZaZbOfHQXNUE50gpYjTU1nCx20qCbSUJ0qk0N81yQbtcEsYOdI2bWfhyxlSVJTlpEG295P5rH2AKc4nJoqsVtS3sSZ2pmhWKxDh03FxfopWm6wZh/HsBafe7PdubLW27oGkb+r5DaUtd1bTtEmMbTD8SUoTsOT7azB57WmuOTk9xY0ccB6Ib8MOBs8cPsZ1ivw8Mux1KG0lBLrY/kzx1eqb6YUApqHRG1xXX19e4DCGUMBylGfo9Q7/D54H6uOL9r72fZ5cvib0XJnsNOUZSjJIMPkZUkC4lF2BTocgvL0QqvjmFJ+8rTZswXPyhF3DD6GIhkubnT5X9oLIVWWtiyvjoBbiIcp54H+Z9ZXo/axvOzh/S92vc/nYNloUx15ozBjFJ3qe9tzxfxpSzIeq5/pjAAK21/N7LmaitQdeWaI0AmJUhkDBJQsFIqZAuSu1yBxBTWqEToGUooovNxwT26GLT0uqaTb1m3S5ZmIpGG1Z1S0iJ3Xgga1GlnFbHNLamppL9dEhUVpFJeJ9wUVEvj6kWLSkeE8IN++uRw+6K7eGGPnYoZ4j1iLIyxLTWkrQue2wmhoQlkmwmNwrlFfWyJvd+tl3IITIfUlrhPvhBmptr1PPn1Psb8celSNLLNY8+4WMWCyyg8rEMp6dYHvmO1hrqtqVZLggh4MYRP0we+1PoUQEIC6N+HoYrGTCK0Fhq5JgyV7tr2ssLzs5vWLS+2HoZqrrh6OSMqqrnZ+n45D7d4YZuOJBywo0i7573pVLvmpTQRrx/sxIpOwjwWC9k74npFB8dYewJXS/AWc6SmD41s5rZeqYUiJAD2jsB88pQRBlVVC6qPMMSLK1grhlSTjNLDXWn6rkD+OXyg7xy0sxNmGIaQ0wKIDUXI7fV0lTrUoaIck6V2kJNazLPQ189McWV2FPo4gs7qbQEfJ3sBdTtm5Qza3qP+aOU12RBAoop5PJuqfYqGHu7PuUeCAlh2pd0IbTcnpcTQFtULUqGNLYymKq+tV2RCrSsd1Es1lUltiZai+d0zuDGog45EP136h3vfNZ528u3vcX863xr4TTZaaTbc032yoTOxTe+ALnCyg1zAPIUtnX3fgmTV75WbGQKW1jdUYPdObu/lVU9WWhM9eyM8SR5zxhEtaQLLiKfdAowk59fAu8kpM8nxcRPsKmwbLWhNlApLQpELAqDRcnvZfpFRmyw5CbXxTouQ7Er09agbYNSQpBRZTiXkjw30/UUtqQw7mPOhJDxQeF9IuDxURF8kIHoYSd2I0g/XVWKo01mtUxisVErjFXC/p+eGWVQypZge7GoiDEyDJ7d3nG5i7zcZnadx7kAyL0bfSCFTHAy4DRmR86GMnHENBu0FcsqZSsWaYUMkSQ8ViNhdzkJqJvYYki4cWAYBlKGxTLRNA11VUuAVckLESsGSvBumvdFX3JdFFBZQ9vWtE1NDI1sMdHL0KnYYBitqNoVy+NzNkcnrNbHNIsTTNWUfRVCUIwu0jlPM3r0ymF3O/r+wOiGErzq6LpBlMZZEYcDaTgQqw2qXZUaDBplMCmUGcfUS8gz7+MdlWaWoVvMkJIiZfH6jTEQivrXjT3BdYTxgB86fLfD7y447J6z370g+vE7rHF5/aoBYyevD8UkYTwi6FNi9Yi4/rXk+58mtg+Jdo3HME/c1bTxltlUyjJhbTT7JjN2mesB3r6MfORIY5T4oe36Awfn2G47tNKszs758D/wMczi81xdvMN4uCbqjq+8fcXLi2t8dDQYLvwl/bqmqjWHrudwUJi6YX204NCd0TYtTw+K7WEkdje031XzXR/+AJujU0zb0rkobLMi07LaEJwU0HGM5BJOpKwkYCtdcxN2hDK90lqViRFl8qbo+z3KiNG0NZJC267W4tcVI845arJ4oMhKY3Qj7XIlTUYYCTFgreX66oLn773L8dExfTfw3tOvcfH8Pa5evsdmuaI/HEjBCXBGwhZqei7ssxQiKgd0csRhS6317LkB4J0nBGkS5uugZQOY0tuVKoX2nYmgUoqnFzf8qZ/8WwD80D/0MXyI/Nm//Avy3ChJYrzedvzEX/gb1JUhxsz5yYrf/9t/kP/xZ36Jm33P+x6d8Tt/26f473/qF+l6x8c+9Ijf/pt/7RzsEaMsQIC6sgXs/JVfbVPxn/xb/yxfONxnH3/lr/+/+qoqy6F3/Bt/4r+jG0b+h5/+27z97JL/+o/9CwDYKtE0AnxKgq0kHcaQGMfAeBi5fHbBu1//5iuMTZWktrEqsdGaRVURmiV9VoxjT9cf6IcDzWJJ09bUtnitas0wdvg4orTIrZ4+QxqMJBLBxbK+nU7nTDd0wpgjl4lhj8oJqyjeW6CVNDIpRXyMDGUjJ4uwAysWA1MRYJWl1kaYF0rJ5omCkq7rY2QfEzsf6WLiEIJgzoU1Yazh9dMj3vz4m7zxodd58vg+NbDrB2pjsHXNoR/4xvPnvLzZ03cdyVa86wJj9uxV4nVleSvL5POeghaotL1t+Eohoo0lEqWwyZmOxIGETQETHEORl0kd+epz951Ysd/qIXsLFvIKUCiFuMgttY7zX04s9BCjAHZKzf5Vwg5LaKNYLBfUTcVuf2B/6Bl6J5LGnGnL2kwousPAMA70wyjsuuLp6H2gH+XAjTnNDdad8HdSSjgnkvjaWhprWa5XM1sEldEJ+kOHH8VrSCkJ9KrrBq0NLgRe3lzju16k0MYQU6KqG0xVoa0tTUWacNaZaTn5X6WYxJ87F9ZmhmEYkIZvvhtzE8hUzAF3W5nddkcqKcd3m4Hyv0uTNHlmZbFtIKXbwVXOjN5J8U5hC5RwKpXFQ1oGJYpkBJh0JfgnuJF02BO3V+STexhTo2KaP8/80cmoukJXFWgj4TmmZvHwNdYPHtIcnaC15XD5ghf/x1foh4E+JZ52W4w2VKriALdgbBKp5zQAMEysmIjvexqzpLaW3FhS78ooiLkpM9oIg0nDarEmRE/KMtiZPvQ0wFPaoCmp59MayPL7oRcg98HDh1yPIzovqSqLrxtp/GKkCZ7KDTxwDv/8PcZuS9Ya90O/EX7yM+zHdxhDpB46rG6ITcOTVmGqLMm7cvUwd7w9xZtyWq96Bh6s1uAc9Jq1MXzo3n0u3+r5Qo7sX7HfKYyhuQuWBnBi6t1d96+A+KVpugMPvwrUFpCdkgwszZySNaKE9QHFzz2JB6wua+emHznaRFpk/03l7A4uEHzk9OSE/e4g/p9WPPy8z6yWS1AGH3blvC/tX7pd//NgiIlbdPuZY4hEtAxUXnkpQOPf1uxWI/WiZr1eitezc6w3S+qTDd/8+tdpqoYcPOPQE7JG2xXLzZrN2QlhWPL82QW+HyAL00tXrTAKe0c+9FTtmtfe/4AYE/2+5+byipg9dVvTtA2L1RI/jqyamrHf8fz523g30nc92+2Wy8srtttEP/Rcb3fYpuX8/Iyu79lszlmtz1ifnJExbHtH7wbCeODo0XKW107P0ubkFH+4IfR7uusLzj/5Mfpli60MGvGVC+PA/vqKGOH+a2uqumGxWFHXNS49ZRw6Dl1P9J5D16NszTAeQCkWbctue83oO8wKjj9wyutPXucLX/o8292WoXOMxZoiZWHeMUaUz2WIexfkyPDyBfyvPwM/8juEfaU0aEPoxEdVOmeN956qSOuV1tgstYUyFq3kzFI6kYxFmQhGpLgGzTAM3Fxdk7LlzY9+lIvdKRfPp2s2OSBT6qHS5CLN3qxuKNcXBaYy6KSJOuHHyOTfSc5kH/E5QVCYVFFVFt00pMnjWWtijHTuIIMGQNX1fPYz22sWv8migtDZAkZY91k+i02GlV1w0h7x+r1H+BDYbneM6cDy4RNqaxnwXPVbDkPPh+8bTpoNbVVTVxWVNTjvcE5C5lzILNuK1dEGU8PVfkFrM5sMTimGbcANI7Eb51Ce+RxSxbc5JnQGqzUV0OTEelkLkO8TFYhdBaVuRwBU9wP/CPYLn6P6xV8gxkhVwOpU1DnD4Bl9xKdMQDG4QF1bTKYM/yOmslTNgnYlYV277Q1udDIknd7szgaZgvRRE0sn5UjvRvGlR1E3C7COcPmU3jtUqlhUIk1tlwuOTu+xWK5u2ZFac/bodeqbFn3zkhBGOiX7mTBQ5WcxCuoqlvAWqfcm8kuKAWNEvdksltx//Jg09ly9J6QQYsJ5AS+1LY+HjpL/gKytmAPWBLTyAtoGeW9by3OYlCIpURgZpSXozntCShL4NaUCTSeLAglzvN1ap2Ce21JHlFNzzQi3nvlTITEPBtMdxnOe93SRjk83Sc3XFASwlqAtO2ddUJiwrw7jsvQtKhcWXQFryyAtF+upTPkR83S+5Dlda7IcuevxL/uADBfle5o5Q2AeEJWgP0WpO0xFVlaCPY3G1A3tesFyc0zTrqgrCc8WmXsZ6igBmnIubPmiLAs5kLIMw24tguYPJ97BE7gafVHUFnCoAKMTWz+WWilmCdkVO6HbZlQY+nJPJkZqiEHS7lOa61EZcMkQUxVrgynbYfLRFv9tAZoFKGW2jjDG0DRNAXgnVmREm0lDJf9JIRCDJ3iHywL2pqKuQKk5ADRnSCS0lSFNAjwJnRQ+J6zRRMS3U1stai9lCMjg2IfE4GQgQk7FIkdTWUs3BlxMbJaZ9dIIjpKEwazRZLQ4HJelk1OYAf2Yklh8JSGgDEOm76AbB/ajouuh7yKH3Q7fO8m+sIrlMvHgfse9szVHmyWr1Yp2uUKV9SDLRyORUWXVKNkHXMjs+sTzneJim9h3AecDaFl7SUkmCinjkmHXO5TeiQVY3dDaBVnXRfmqaRYLyGEmRah5oIJc6zCyu/EM/YH9YY9zjtVRJ5+5bdEK6trStgvqupG9j2lYIc+kG0dRDJCp64rz8yOUTXSHnr4f6fY9h36AFNEqU1cVy6P7LM8fszo94+TkhKOjeywXa2xl0Ubjs2EYIruD43rvWXaZo0PPvj/QDx1+7AjesTv0dH1PP+wJ2eDHAVMdMM2C4FuiLRkQJYtDMRFkZK8YvWfiLiU0ISlyFmwhZYg+MHYdru8Y+w43HDgcrvDjjtBvcbsrdi++gju8JAw7UvhVblMg0hFVFICawD3c6acIm+8mbD5JXLyOoxUWrAJUojKCYtcNHJ3As3c8KZv5e7kus1oYhsGwc4GvvNvxfe87ojZAzkQn5ufBy9R3d9DYxRnLe6+TmhU5Oh6+uSZ/7l2utr00FGFPjtesNpbFwhDVNTf7G6IbGPaBm+eJtKjoLm64fH7Js6dP6b6ocD/8fXz4wx/g/OE9Nu0SX84CVVIibX0bkmJyQptKgAkTqZuW83v3y8GesFXFMPRcX13RtkuW6zVNs8LnTI5OCuVyCE9+gRLAUQFy3Sqr8X3HzYsXci3iyP7mJd32ksP1FWkccIPl+sVTrp+9zXjYcn58zMnpfYZxpO/3dPsb0m7P2fm5yAJ3V6ybVqZeypJNTTYtm7NzqsMN7Mq9nk9YAUWaup5p85IwrES6XKqFytp5k//W1yc//ISPv/kYkAb9r3/2q/yFv/q/A/AH/+kf4hc//03+6s9/mX/3P/uf+Nd+zz/OX/7rn+cXPvcN/v0f+wz/5u/9LfyZz/w8n//qe/yJ/+Iv8od/329FKcXP/Z2v8+f/ymcB+Jd/5w9z//8X64Nvf/2+H/1+/vl/8tMA/ODv+eP83h/9fn73j3zf/PdGVxICQCbEEYImhszoAmEcuXr2jJdvv8vNsxe0RrikOSUSGasVKgbqDMl5Dv3IIStMZagqTV0bTKWpjPgWDaMj50Dd1JIkmjNNZVCE+cBWQH/Yy3MYg0zxsxSlVmlqMktr6Mcwf46AFPSqFIU+CMOgqa0UhBkwkqwcgzC6szUkK2x3l5JYCQyO3gf6ENiHRJeEdSGPVCk+FawWLffPT/ih3/AP8uTJfY5ONiir6XY3vPP0OdWyJRnN1y9e8Pb1lrDt0b1ngUVZRd/UXC5bWC342kXm5LLj2Av4ejN6BucxxtLYipWpCtvBFQA0cQOMGKoM2jk65259PO+8/j7nAdyy46Q4muRDLgSmGau1t/6wgDB2CxNPJpkCwvooAX8qR55fvCwBhyLXyMjgxJQgHu8D49DTdQPOB1TWtFVFKMWi1beg721Jz53POoHKwqyleGhlJDBlAkmv99dFgpdIMZOMYdU2xNpRtw2bzYrN5hH7caQPnjFKsTcGj64EWLfG3rlWzKytVAYCck2YP09m8ti9wzzMMIdQzM2Dmhm0AI1pwS7Ei+ngpLicfs5JKVYKWylkS+M4sykUeQyyKrIwzm9B39Lga03CQGgxaMLYU2lpaPLbl6Q/+Z9z+fv/IJycs8yaRitUnH56+exhdIXIYqBZ8PBjH+f0Qx8koOhSYNm0bF57xOX+GhUGjjcrDuPA2cMnnJ6ec9wu4H/589KsKDmTb9lKEuRWm0aYfiGigZPNGkOHH2VvSCRubhw+jNS1FHVtXTM2rTD8UiKikC3gTuNxB3CEPDOAchaJ/NXFBdiGwI6IZvX660RlyTZDJZ5Q7/vARwlo8gu4OlzKfdSaYDSOzFdjYvQDnU5UNvNA12iMJKtPw5AJwCyDg5QLOw4BV7RSWKVglGf6fU8ec3H/Afb6mo2P/NT0E+Rbr2MBEgwZkWNOrNa7nmy3a2haUhOIKy/nXAG51LyJJPEGEHVOeZim5xwofnymsJUUnsjl7oaqMnzowfu4vrpmjF4YyyQ2qw0P7z/gZrflsD9wdnbKorGS/mvEguDq+oaqBPPF6VmeGS93Pf1uP7sAWnm+xtNnM9rKmtWKMUgjpeuGh2f3QWf6vhePNwVvvPkRfMwcup7gHLVNHHYdWlUYVXF2/wG76yuiH9FKsVqvqaqKxSpzdAa2XaGMxvVbDvsbXj79OpvNBqpjcqoZesfFe29zsq5pKjhdt2z3YjNRmROONhs+9MYbfOlLX6Lr9zx/njm/d5/18UNWR+csj09Zn5zy7tMXGCtDpTgq7j9+SFWLn14Iga995ct85Ls+QWwa+p0lDVu6/Q3GWu6dHvPa44c8f/6SYXQ4n3DdSGNqFsdLYhaASyR9DfVqxaJtObt3irU1gw/4mEAZbq522NWSZXPM6uiYX3rns5wcn0LUPL2+YNt7CbmKkqiN9xCmJoZbQHa6ZdHDn/0J+fUbH4VPSf2SvEMpi9IVOYrSQpf1mCJcPH+KbVtMVaOMJceEVtBUNY2piJXHjQNu6BmHga4buf/o9cIQmtaSgD1kCRkR1bp4Imply0CCOcBraiqngXzKkbqpMUrqjd32gE4aFRU0FYtVy+L8hN4FfIwlaMVDCBg0tS7Nc55FrRLcWYZo5UPKegyBSlla2/Dk5AkfvPc+Wl3hvePtZ+9ysbvAxchqseZeesCyaRnHwBAdBxyfffeLvHH+Gg+P7nG+PkabinE7EmMgxch61WJaw9bv6QdHn0YWp+d8/OHr5BC4unrJN9/7Ks9u3uMw7nBxICKO3jQAACAASURBVA6u3NuJRawIMRJyZszQJYi1wtQaU1filYcwAoVAIQNxrQz5Bz/N8EPfz4uvv8vZj/849bAXObHRLGphC/qY8YWZOA4BYqayhqDg/OiY07Nzjs5O6Q4HGbbFTEn4hYyAOsHhhg7fD6QQmBLfm2XLMIz4KPL1PkSadonWDtfvuXz5dUxKdF2Hdw6LYrloefnpXwMf/iAxRj7/+b9NdgMpjuQ4UFcapStiEhDel6bdhSAWE9agkoT5KSI+RW4uR5pmgbGS0/D+D3+U5BP7y0vC4YAyEEMJhzSQrVhb3SWzHIYBE4JYfRmDzpEUAtnWYC3aijKy0oaqNiRj6fpe9sy7R8UresXyp1nNx4guQ69XWKnTQlfFI/Tu4F/dGf6lhFLmlfBFmAgFt2BwzqJSk5BRqEwBQfUUPF3S3u/8WdM0TKzTjHjBj26cmZem+Pm/Ym00nzHyxhImdvuZbGXJqniWWgG+bskJRb1qKpSuMLahWm84f/SY49Mjjo7WHJ9sqBeWbkx0h8D+asRtr/GxI+ZIip6UAjlGpkAsYwx1s6Cua0JtSXEg9XtSCsToyNGTkp/DtlIShUmIQdbjRHgt4G7KAvr6IOq1kBLOO+m9uA32mnx0b0FmWUa5AKG53PViMCEgnSrKS6Nn1cWdankG8GVLvd3/TakhYo5FMVmUcllAdV1wcmsM2WjcODI4hw9BbDuyMP/rqqKua5riIWyt/L61mupubT4BiEoRlVToW5+5GdNcn85fm4HsUDqyrgPna3h4lnjywPDgFDZLWC4ybW2BSlhLRcqeQmYcowy6XGC/69l3kf0BtnvN5c5z0zl2h8Dh4HHdQAjSL7W14t5xJIwQxsDYO9xp4IRM3SzQE2GusGFRiawzqBr0AEoA5ps+cXMYGVIgaSFxRIQMgdLYylDVS5brI1brFeujDav1Kdi62GQg4CcyiKhsBe0CcTUpC1fLPZhJKWPP82dPWez2LFdLlssFTVPTtgu02c2sZk0qwfCllsyapjJUhR1+fu8xj9//JglNjBnvIu88e8ZhJ2DlarHg7OFrtCdnNOsNq9WSRb2g1rLnYTRZC3Hg3Cf6MfN8r7k4wLaPHMaAjwGrxT4ixsg49ry8vGR3iLgI0V9zuEkw1LS1EQ/hSqHTVDNkvBerLAk21KSs8FF691C8hPvdJfv9NaHfkvodhI4XL96hu3wHt32OG26IoSMJuvEtAYmvvn5VgLEqK0w6IquKbFfk00+RT3+A0Lyf0ZwRVU1Kunj/ZOql5tEZDL3H6syTE0s8wNUuM3op5K/2kfMzzWqhOGzhnavAtU8k5+hvOq6vB3BQ2ZrKttiqIimDaZaoYcQFaCpLs9pgXEvfZUx7glFnnD7c8PjBive5nq989Smj81QWTk8r9ldv8+zd97h6ecnSWj71D/8AH/nExzk/WaBVpN9vxWTfVCjhfhCLYyM6S0BGOUhUlMW1XG1AiZ9LyomqFnN5Y2UCG1yQBROTMJOywbthliNaozEKYhKPL+c73nvnm5wsT+j2e66uXkrAVpJU4do2bNbnXF1ei+GzUvRdTzY7Ts7PWZ+fEaLj6Tfe5o1PfIznz97j+kt72XC0Zr3a0K5PyEqzvbkW763pXt85wW99hpibRWNufZNAgCH7d0GjJq+76fXJN5+wWbX8N3/hb/Jn/uLPc+jG8j1yYb7JazIqn/7Xuwl3H3/zMQ/PjwA4WS//7z7S/6+/tNY8e3nNv/Lv/SleXu/5r/7cz/KZv/Z3MFrxJ/+d3w1qidEGW1sWi4bt9Q3ej4SQCMPI02+8xdWz56RhpCmAhZpYWFk0UUZp8eDJGZwwU6NXBK9okxiWV5WlaSxV3ZYNXeRSYXQM+23xqAJthe1RK5F+KFtYHxhyiEQnQIwvwUMScCRQ1HS4a6N5/+MnaKVkAHF9JZPhCCFpxpS57Efy6Ol95OADuyig7AwaAlHdAliqHNKNNTx+eMJHP/JBjs82LBYNdV1jtWE3eLqcuN5esUuBvXPU6xVhP+JDROeII2JPN8TTU/xyCRc3LOuWWkeSD+x7R1QCYBtrCNbiU6SLgc579iExKCMApw9o52Qiz1Q034Kq0/Bi2sknydiv9LrLx0wxEQk4JYCsSMKkoIo5zsCtyopKaxpr8UEm2250RCf2EAaZgCeKzCwnaX6soSphESknFnWDUi0gNjJNPbLv+pKgWvYBVSSbSryEamOwhUkv69qgVUNV19RNUxi4zIBZtsIEMqVIa9qWqqq5Zyui1jiV8TkJ60ALUAhSWE7/KCXJqsWijuLtMDMvhK2pRXZbmABmYlDM11BAsJ9/7Q2+WJ6z3/Cp34y+uSEG0VM17ULM4IXaKT6BGUL0YomjM9ouBHhOiWHoaNoFbhzJSeRMU6dUFcuG3e5AXTXUVYU1hmHfsVotSNFzuLnky5/7Rbr/7a/jP/YJhgePWGAELE1pBjVVuT/ZaHTTsHn0EGUtY98zOsdytSYBLkWSVhzdO2etLavjEwn9OTljFt5ohaoMREmorbShNhXLesGiqnBBbCRwnmVdsQ+e5CeDToMbO9k/iDTtiqPjU2xVsz/sGNxAKrLeqbhP+W7AlS6rXTNJVsfRcbQ6gsrix5HnX/86abkqsruMTdIwbFbH+OA5DAd8cqRf/+tRX/0q+rOfpYuJd7RMyC9i5B9dKc4t1DOVQN/xPS8g/dSEFlBCT6wbQPnI+OKSN85PUTlz2bR31uutD62cjxPgGotdR2EDKY0y5pYhm7/zbjCpElRhssy+d3eYthPjJZamzRopeEVKKWy1rh+43u64vL6maVuGg5cwL+e53u3YrJZUtaXNNSlHHt6/R32zBXb4mNk17cyiMUrP0shbCWUWqfNdH3h1y+K6/XlEzppTJmXF+HaiU47uvOPe2RlDdyAnDzlwenaPpAzrkzXr0zOur655/vQ91usGqwFlWeZl+fkTPniOj1ccdjccDj2HbsAny8XFM4gjlkhrEiY2KH8g4fA5s7CeMDp853Gjw1QVfuw5HDrGcWSxWvPao/tsdwdCVEQUjx49RtsWbTTDcCCOOwwJqy1a1xz6/k5NIuzAy+sdJyfHHD9c8daXf4nri5esNhuUsTx7uUXpim6MeB+lhsJglJIgsf2B5aKVDc7UuKzJdkEisN6sqdsVdbvkpt8xuj2oxDh4dl3P4rzCthVVrUnvBKJPqKSwSZiLZF6p1769UpM9l3ffQv2V/5n8gz8sderoUTHOHqXCIBTLihACOLEnqI3B50TMFHsCyNLBl/ojQ/C899ZX4eZqftdmtSEGTQyOFEYqK+ElMgSL8jze9aAsrPEp9fnxaw+5uLhk0TbEEDh0PaBYnh1Rn6wwmyWe4rmO2AwEJvmvtNJa2hV8CMScCyuf4ktXUdsVJ5s191ZnrJslrRX/3IuL5xzGjs73dNHhlQMDXkUOvudotWY7HmQobTNDDHzj5bvshj378ZzXju7LAF23EpjaKJ7uLghksky60dnQNC2m1cSs+d4Hj/jGs6/zdPuUF/0FXouSIjoJI1FFTUXKGG04WWx47d5DttsdIQSWqyVGGdpa1HYheGLoSc7jx5FxdDz85EcYfsfvYPxrP4v9/OcpJgBi6QSYJF6SKURcEsDfNppmtUDXltGNbLdbUYUUXC+mhB8Goh+JwRPDOA85jQaDZuw6Bh9xGem4cmC9FHK2JrA7XGOUIaRAyIFudPS+wxUWU86Ji5dvo72T/SUF2vWCpq6F3Rij9I8+FsBv8oAtaj9EDZljZug7bFULWx3N+WuvkZXm0gdsjJhYwjYzIhmemYJlv84JUyyKco5orwjek7QDW2PbBdS1AP9Zns/FYkEscmqpiaezv5w685FTasD5DLsd+N0FLymJ7bes0rLyZ7BVPp+2d4K7lNQZs0lCYVBqU6GNLfJ+cxsGVPZ62WAmX0pLjJmUCkM0qyJzj7PSTRszk3tUOetmi4byI2aT5xAwY2RgYKsGaytsVVEZK9e+KERoWo7PH3Byesr65Ai7WrBYNgSvcD7z4soTX4z4UaTeOTh0dlRaLLQwqjCjixUDEkglQ59AjIHReUI5h1NMTJYJqSTGzftUjLPH8HRvErlI6UNhtybIaVaepakf+j+Ze7NY27b0vus3utmsbrenvec2VXWrc9kVO8YYmRAICjFCAl4CQiISIIF4iAQRkUCRIl4ACUsg3iJBEEIi4QFFIIgSFFwiNkGxUeyA7UrZLlfdulW37jn3nN2ubraj4eEbc619yw0yQqKmdcpVZ++z9l5zjTnG9/2/f5PEMkuCPcUKQGmDdU7uRWbGapXNIVQGvWPKPs+ZhczkRcvxd8g1hVJK7kEml00g7CTnn2qWRERFpAccR3zX0HY93oc83PCopBh0T281ZVkAEVVXgmegKIyEDeu8tnyuZXyIovbJAPX0msELkJ3y726UZOesNewaTTsofBqJUWcrNbE7K10lz8REiMh4RYww9CP3a8/dBjb7yP1u4H4P+07RdZq+1wyDIgSNDoqAoR5rrtYj2iZikuBhpRWLuZce1Mrno6bhZkwHX9moDJ6SLiqC9hgShXXM6hkxwND1mQ092coJozMkRQwBhwCw0gcnQvQHX9e2GfA+5H7KiMWTK47jmHz+9m2DHzt2WxmYOFdjnclesaCSB2WwtmBWzzk7f4Qr57nOmFMtz7K//ZyiqFDG8m7f0XWt2DmEQFKZNZ8tc+zEwFaycqOXZ0MlGeIsi0QcAi5CCewGGaIkqwFHVZcYW1Dve9pesjC8Esu7FAPBalzUWAUksSAIiEo7kf2dQ6IbRlmvfcfY7Ok292zXr+g2Lxm2r9B9w/r+DaHbEn0L0Yt1BlbqXI5Y2A9ePxRgrNGOtx9/ETc/I80e8U1+lLH+LKM6xadCSpy8n2oN2iRmRSIOwprxPRQuUlWycY8jbLvEWZL0Nuc0V23iuotonQge2jZBEyTx0BiatqHrB4wrsEXJfren0J7VoiBEh3FCWR86i3ZLXLGkKmqq2Z7FylEUBmsaXl/f0LYtp8slX/rC+/z4T/4Rzh6tsC6RQo8KXuTZupfp5qQAUTKFTCmilD34vR0bFPHEHMeR6L1snog3UPAjKma5TBJfRnmd/LrpyH4LweN9x+3VK9K8hURuThQXT94iJfk8Ti+eUN1ds+o2DN2ettmx3W3Zt3uKJL6OMSWa3lPOTnj29mfZX32Cn8J7ugG13/HJy+/T+qNPxtEXT/770Utr+np+txl4eJju+IPXzf2Ob30kurSvfO45TTdwfSemYZenkoS73rV/qLW4mtes5vUf6t9oIqX+/enn/19cX/+dj/l7X/+QL7z3hG98+yWPz5dcnMz52i9/Iwcp5c0nS1TGEASIHTzb23s2V9f02x06pVz8im/RQQpCyqAYmBSxeRPK2BE6RvAjSSdSnuCnEA4ptjF44hgwcJCBSJBVQCQAQcAFRU6tlaI2xQdBMlphJ2lMSgzjSBhHhgS7fmA9DuIvNkb6EGljpAmeqKAPgS5Eusz8IgOv8k71AxamAGenJzMePzrl6ZMzmYqTiMHT95H73Y6tH7gfOvbBkxRy+FcFnChcjAQ/Mr+8oFqeorWjXp0zK3tM2zE2LXH02PkSXRQE6+iNpRtH9qWwkXwS/xy1nGOXS1RR8PZbb7HMzQaKQ/OjTS5QefAs5K8fGHj5/k3J6lmYLICiMQfg0zpDkQ9OMvCTEDaG1gqrDYWVMLFJYqSMPsj4DwzaJMWN1jCvaxazKst3IpFIXdayJpMUg9040PXDwd/7wMDIv5dRBpetWUwGQbUuwJbYqqasa7QpMEUhsldjoJhjrJU/uaB3tsA4B1rjtcIjkkuVIikH7ThbHFkaOieCTr1ELiyFQSVNQUpHHzIJN5qAXFld03P34fmTw4fz/ue+it3uiCGglMG6QiwHlEJlBkjKxXeKHmc1rpwJyycEsZGpKtnvQ8QZyzBKkOPkzdm24mtsjcEozdB1lFWBHzp262vi0PLh13+V292W8eyMKusf47QHqwmbk47KlA5TWDbrO3bbLaP3LJZLqrKUtYCinC/RZU05m6OKkjEdZXDKaHRVMisq+vU9OqmjzUREbBCCx8eAKiZpsjQqSYvsTmmFHiUp3RUz6sUKVVaEuxsBSsOYPfamVfQQiHx4jkQCiXEchFWhNXf7vRTsGUSPSFGvMdTljNPlKbebazg7I73zDqpt0b/923Te8yZExhh41Hd8NcHKGEqtcUpsVw4m//k51OZ4rk0SSmS1oPcti2XNk6rm+enZ79rrp5nAZBqoHrynFPPrIx5jh+YmHW/Fw9nl0cJEnvMJLHjoO/spywOtHtxF+Yc+JPZdz/X9PW89fYpWihAkkKNpW0pnMFZTm4rgA7N5xcTjbsfIbD6XAKZ4ZL9qEN/dvP8cmsiH90B92ntOZ6n7NDjyvabfjWy2G5RKVHUpOQFD4OTsArQRD7XMEkrR44ce33do67i5WguQ4T3EwJ2JbNYbmqalHwLl/JSYn7l5NaN2chiKtLKn71vaZp9VIbL3+TxgTGFEJU/oG2ZViR8s+85zf3fHyeklVS38Ix9H5rVj1IE4OjprudtsRCGQ70FdGprtmtl8Tj1fcfb4GZv9jpDAlTU+KupqRoVF9QPj4AnI2SFspIDJHpYpyPl9efmYOO4pyhmuqEm24PLyCft9QQgD2ijGLmIKRaEL5mPF3d0OfxdIXqGnSefE0prWX3y4nh6so66DN69Qv/Nb8O67UJbiv5oQbz4jgX9kSXUMnjAqRqXQ2btTaOeQtITMpUi2MRnZ3F9Tdk0G+OSHS5K8JSXJabDaMQ054jSYUMd5mviFOlwhwG1VFSwWNcEHXGnBOuyqRs9LYvaQnQokBTJU8tJTWGMolMMah9dCtrC2oDYlpStxtsDakspYnHbgoRt6/DCw7/bc9zu2Y0MyuQFNEqC47/Y8XVxiMzMoBdmXW99z12yBRKktq3KBsobgR66aO163NzhbMK9mXMxOhO3b7BjCSDsMvH3yjNXyjH3suU8doYokX6HHETX4HHopAJ9WBlUvGOclQ+wZvUbVloVb4mYnwmD3A/vdLcoNGGdRRYHTFvPjP8Y4Doyzmr5pmX3rWzAFQiVhgeoszfc+4uoCUzgJBm1bur6XPTT3Sn70dE1DGPvMCpuszqZqT8Ck3ifamBgBHUearoOURKK9aWTIk+upcRgBscia9tDt7l7AWD/KPhI95Wwma0wbEsIAk6FX9gzOdYO8hoRnTQ+LUuBMga1KZicr+q5j8+aKmdHobL2XyM/ZgzNO2KSelCQIWo+iBE06ZJ9iOTCSUofj0eRDRCkJj5X2awpSzs/KAXBVU1kIE8sxF2uHegd1OD+m3+53D2EePIeHgfVR/i8Aq82A7FRTSa36g/t+jBNTLRyyDKSPVAegT5RDSoKPCvE71hnkLyaf1gzyWnesGbUWENi5IrONHa6sqKs5ZVnhygozX3D+6ILV6YLZosYrR/BJshO8x/sIyVA4TdJCruoGxFYgjOKJ6YdDdkBK6YG6zzMOHUPfZDuLbKOQrS+O/XJisi2QczIrSMnnet6AtUqHXs7knmEC2xVHdmwuA4hZbv9QaRPTZFWRmHD2AxA7fT2lHPYmz5rJwU2T5dSBxRvCof/SCVFAT6+fxCpvChSehmtxDITBZ2/kXJ8C1nWyRpTB655RRVIU4DLERD9KYGvwYr8QgwTDhoeWEVm1OXmTGu1wGvrO4ENmPkvKIIqI0RGjhsxYlZ425dAuoyQ2PkbDkK0Qun6gbTVdl9drEKWTeJHKHe0Gw6aFcp9QVoOFsoxY7fMZKvlCRC1ZG2Ng9IrBJ7oR2kHRBSNe80rCipeLJVZZxmEg+FF83YNi3zSQpF/1YaSezygKh83Y09D1jENP3/XsG1EcGCNgbFGIYsbm8ENyP51ixI8jacx1G430IMairKUuS8qqoixnVLMV9WJFtTihqBe4ckkxXx7A2bKssUVFuUxiTeUDYfQMXcs4drKGvJfBxaGengD+QEiKkAx+sOgADkNhNE5PJKy8r0UwRti5EsI11UfiB+wj6GgOe11K4hEbDnYectY0XUvoO3y3Z9htaO+vaO8/orn/iHbzEu07unaLpJdlu6IHLPI/6PqhAGNLV/FHf+QfZf7obYblC77zwYxhPGMIjmwpBuTDVQlTxMaIJdKPgdu7gHNwMtdYrbgfFdseOp+N0yvL7WbkdZOY14pSW/rR4BvPrHJoC/frO3b7hqK2lGVBSoHgO86XlsJpqkrT+4Ir3zGMirZNzAox7z45XVIWltdvrvno+x8xd4Yvvv8ZfvZn/wQ/8mPvs92vCWHEWE2BYnv3hhR9nuCBSLZsbuoT1hU59VIYPN57YQyM4oenclM1pdjFOKKjJyV/kDZMjJwpjCd4n4uchB9Htps7Ytdycf6IyyePsU3PF77yEyhTgbJU8yWP24a+29K1G7bbG37nG7/CzdUbuPUiI20aXr++4cmz53zhyy/4+u7vMPY9TdOghgjlkteffIKeV+BMZiVk6VMSj5PpwJwu8aJJTP64UnRL4WCNZjmr2DYdTTfwO997w1//hV9jOa94+8k5H768PoRk/fRXP8tvfPP7vLpa/6HW4jB6ul6KsPmslITpP+BSJArtmZmON7dbRvP4U5XJzXrH65ua9bbl8fmS67sd233L3XoPwKOzhTBNreHR2ZKruy13m4bNrkUrxeXZAmsMv/xrH/A3/85v8N/9p/8mf/v/+C3++E9+nq+8/5yv/bK8X5XlNMM40vUd/SBBSUM/cPXxS5o7sZ8oMutQ/AHlkJ0msZiUvTIThckyIaNQVuES4AeCCsTk6UIgeQncmqzqC2UorcXanPAepuHBIJNKlSS92secJu0FjMt1o9Eal+WKIQa6oefN1RW7ENj5kc040PrAMAr7tU8SzMWEKypFyl44P2hrcQACkkIReHRxyrMnF5yfLdnv9sQwMgyKIQTebO7ZjB1DEC+deVnSbhtm8wqzXGCdJnQ9l0+fsbRzVBe5eP4287FDbdb0d2tUWVM9eUooSoI2NCiaYWAInpgSVonpfJrXqJMlrFZ89Stf4f7uXoopq0WiFALOynNujc1Dlmm6HglDNobPn6k5FFuy8VvjKMoiF+ciUSoKMXSfJEMKYafKAexwxuBjlilpTVEU2Rcqsx6Q/aRpG1KMzBdLbGYqTYC71lYmjBlw9H7MxVq2SZiajFzQ6Rw8p3WehhpHVS6JtkIXFbaaga2YLVZoK2CsKk/QRljaxshZYSbZErIuwsQiCYHkR7wfKcoyT8zF31TAWLmnUrCFg8dgyo2AfC/Zy1GahqkAnpqT5epCnkUFT59+hvKky8WfxieREimtUSZ/tsNASpIkWhclriqPxSkcJXdRPDp3uy2z2Qyb//7k3BxYjdF7bA4TCknhZie8+7kv8eZbv8n90BL3a8Ly5Cjzjko+H8QTUFuNLS2j77n6+Ls0ux1KaRarJebsQoIXUdhqhq5nGFfgvef+/o4lecuzFj2bcXJ2ye2+gVEC+8IY6AKMfmSIA34IGKmI0VbjfR4WElBBMY4dZnCooqJcrChdIand+3uZmmf9o0YxBT2lLEM7BllIivRuv2XlHPO6pkqJputJrpCJuRIJcgwRpwsuzx+xa9aMKRAfPyGenFC8/oRhvabD8yZF/m7fslCK57HgVBtWRuOUNCYR8ClirHhYKyV+rykEIuEwKHEhEW7veHx5we7i4rBH2QQugT80uulB7ZP3amQPs1YdnvMpYGNqoB7ej2mIYDLAMQGxD8HYqUmbBhDTep6+JypNO468ub3j0cW5YMQJ4hjpup7WGZbLGXU9Y7vd4Jzh7HSJcY7bXc/y5IR4v6br+k+HcpDVloem88G5qk32rn3wd0oY6VrnhlNbhiFwf7dmHHrOzlY0e5H2n5ye4ZVlu9vRNMIiLKtSLFCGnkInXn30IQph+llraHdrdusNgx/RxnJ2cYG7vGSxPGE+X5DSQLO7Zez3DG3Dbn3P7e0tJycr5rOashRJsPejsPIKK3UfVmy1kufNq5eU5YxHjx6xWMzR2nB2sqBtIMWOtnPc3t4JixNpGk9WNVc39+w3cxaLJW+990W+/fVfITYtddJUi1PK2ZzZ6oymabm9ucFnYBQldkOxF3ZVDMJIevvFW/TdlpgUPii23cDl+SMqp/G+x1gN0TKMeygrzs9OudvdM2w9YRQWq4CBD8BYjuD/YSN8cKUwwq/8EurxY1JZyVoco3hjao3SkaQCSRuiD/gozd7JbHk4w6MKR3AgW0xGP9I1G+yDob8fxxzGopnanOkcg0SX/bPztJaIPLfWWVJKXF294fzsXIJGjKecFaT5DD2viM6IH2MiD0nzqGP0qMFTOsfC1SzditrO5dyzlrKsWVZL6rKW0DoUm2bL1d01m92OrutZFhWqsmAUPhwigFAkRu/Z7bdUF8+xxhw+T5tT2zs/8mZ7T4rw/vN3URrWYcc3r79Hw8BJtWCmap5eXHJze88Hr7/L9f4ObwLzxVzOXFtjVEHQgVg78RSvROkgn6wMiluleNWu6dNA0JHdGDHFklJpnHFEpRmwGKsobIWdJfr9lrN3nrCf/QzD5z/P+nuvMJ+8wTV7dG5eTYxUpXjNN/2AdSU6s6W7thWPYSOBMTEGhq6laxviMAh4Yg1GPOzypil90BADrU90k/LC7MWnUCmaPqKyPDghAJVPgWbMYCyJfbdHd9n+wI+0fc/Se4p6hisKYXFm9cOBRxqPdWcMHHxBBVkHXUgNUS/nkB7x5tUVM6cPe/90zpHigaSSUiJ5UCoeQC+lNGgZZgQShEgyRoDZvG8KEzQP01HZBzGv/+wKR67F5WcfyRgqcQAyD0PsXLdNwMXDS6nDf3B4wDgqRCaCjTFHS5wpG0Tr3CdOQGMU79MpvC8EuS8TMHwMg84DbqOwOoGRvzdGZO1TZoDNTcs/RgAAIABJREFUgdPWOQGPtNTCogixYBzF8pSLR49YrVbMF0v0bMHJaYVzcvDtG8XduqfvRkIQpuFsVlIW4oO6Wyd220DX7/F9QxgkqDiGDCaHmEP+MqAURoahPShfHwZsPry5AqAfVU2fHl5mGb7JtR0JlMYYm8HT/Fcqy8CmOiBbpk3hXzGH8Kl8Tx0Oa82hvlFqsuM6ntdGm6NthjaH8MnRCzh6CAg7/MxpMi1ZACF4khGpfBglsDmGcCSARLEva5v2UKeTAnGUNRmTvIe2Hxkzc3H6Yx48P1qRGevCULZ5DRkdaUtL70uMVtikiUFlzMFgVaCqJMRaoTEqYHXA6ii9mdNoLftPSiN+1PghHsBgq4Q9LqQaxdBHdtZgGy2e49oyrwxW5fC1UtisKemctxFoOsuuU2yaxGYvCvCirLBarB6XsxWzsoTcmw1Dz+3tju1uw36/5X7juL2vWC6O9gLWWrqmk/Ap7+lHjyLbaGhNUYwkpaidePFO9gZTOHhKU3DVmEHhinJVMl9dcHb2iMXylNnyhPlySTGf48oaV8xxRUnSVs63MRCVl6GWcWhTYF1CE0hRhpNd05B8ynt+9kXOQ4SIJuAYYo1PlqAKlLJoIwC9rO9EP0r4mR8HUYEFea+kyQPWMcVYZ5yWAHTjwNB3hHHADz3NbgvZD7bd3rG//YT+7kOazUv2uzcovFiNYYDscaxMrrEfKvl+9/VDAcZeXj7hn/vn/zT3Y+K33vRsv74nZP9Q2cfz1ET6EPygqAs4qQxdD6/uen7yCzO2a8Wr68R+L+zX6BWuUMxPHHebgZd3ieeV4eykpqxPYb+iqMQ8fN81xLFnfnqCpWZbGpkCG0Vzv+H1J/ecnr/N6bJk7DveXLV8/v0LvvDFZ9zfXPHhN7/F//4LX+PZSvOn/thP8WM/+kXeeXtFTANlXRNCIXJkZXjy4j3a3Zr9bkOz2XB6sgCViNpitUNrRZF9raKK9K0wGGKQgvri/FKSxJWwiVDCFNhvWtpmizMiK9XKUpU1q9UpXWoIMVKUFYvliotHb7G+fs2m2eOWZzx5533cyTMwJRElRctsSTlfUqvnXKjAW+895xf/5/+Rlx98i+b6itXyLX7qp/9xZqcr7u6veHN7zYvLS7QtWZw+5qf++D/Fs3ff5dvf+w5Xd9cAUsTmz31iZU5HNkzDXGEboDg0b4nEu88v+PP/6p/iP/ov/gZ/7ed/FZDgrH/3X/tZlFJ8+PL6sKb+8l/73/5frcW//43v8dd/8dcA+HN/5k/y6PwP9oxd2pZCefZtzz/2r/wcf/Ev/vt8+ctfPnz9X/73/ksAPvf2I37pr/4FfubP/Mf8J//1/wIIsPPzf/nfYTkXqer/+l/9ef7ov/Af8Gf/w78KCLv37/6Vv4BS8u8fesT+Z//N1+Q1Js8zW6KcIXaR6BXBK/p25P7mju/+9jdxwVMWVqxvYiImf5xw5jufYiQoMewvrDRb4+Dp2pHSFkQtkh9jDUXpMAksAn4aZ7BK4bSRxqFriT4y9h0peDTCEAwq5M9cPtNDYmeMjDnFegyR1nvWfc9mDKzHkSYE+vz8Hw7kbAuHmgKY8l9nZu0Dsthx6p8lKo/OTnl2ec6j0xWV1syqAk+g8Xuu+w1tD0tX8vTkhK9+/j1+/Rvf4ONty86PgKYyhpPlJU9OnlDbkrbdkvqWuN/jmwY9jmwXS2IORwLxaSxzESvkTkn5TEjR+aWzE0IMUtzkwcmRuaaY2L6QJ9gxYg7v68GlOXyfyj8vpalJSIfhxiS7P17pQYGdmAIQEukA8oKAHVAwX85ISQK6pvVschL7VMxbZVGUHPOT1eFnyf9Tx8I9TzI9EpbiU43JILAKiaKwNJ7sexqg3ZGUwRQ9yrh8+AYhawXxy3bO5MGPFLhVJf5xB29jo3OiuDqsK6lVpYBVOrMt8mcxvVdhFYTs8RWpqorgj1/b3N0z9zG/t6mQEOmtsVOQYhB2QEx00bPd3TGxR6wrSCnStqJemM+XOKfZ7zcC1BorFgppSsP1OGcxiNR3PltxMit5653P0v/63+PqG7/B7p/+ZzipVsfPOP9mSmgUBCI3rz/h9oNvUWlFWdd899f+T1ZPnrDfbDEarFE0zZ7tcC0gsnUs80cZUPRJ8fr2ljR6XJLza8BjU2BUgREZpLDdUS3nuKpAO0M/jvJ0xsDQBwnJciVJaWxZc352wTAOwqpNAaIXXCD3qyFl2EJNVbdILf04sF3f4f3I08dPeXl1izeGZEu8sejCwDhAgDotuDx7yvX9Nb3viWVF96f/Rcz/9D/Amyu8h5cq8N83O97C8Dnj+JnlgjPAafFZi0ijbXIo0OStJ7iAqHCMgbLt8Td32Kvbw9P32eA59SPfyEwwZC4pTbcCUc/owyM07QEPm+EwJSWnhw3bMVVa9oSj56wwk6Q5kyHK0U9vkjWCDFV2+z3f+vA7PD6/oLBOZOM+4YcE0TArF5yfnYtPsCswxvHovCXiGIeID9A0+yyfnDxwhd3nrMXEID6jwMnZI2EZLRr6bDjvfcBngAQlQwQfI9vdyK9//bf5wvufQeVmJKbIbL7AuJrVySXn5wvefPIJ+92Gu7srjFH4bo9zMsyZzWpSgrquGfpBUovXW5x1NO2ALRNf/OK7aPUOH37wAZ+8fIUqBh49W/Lo8pL5vMC5wND1XL95Q9PIgO/84oxh6JglR4yJ3W7HfnNHXTm0hrqasd02LOc1dWGYFYlvf/jhgVFnrOG9t5+xu/9t1q8/ot3ueP8rP8Lzdz9PbSPEgc1my9DVLFYVs9mC3mtcXbGalaQU6NqCTz65oahnTMDI3e2atx6d8frNHW+u71j3ewY/MJsXFEVNjJH13RpSw+XlKT/y+c8wKy3fSN/m7vt7uusBMEfASJNlNYqDR9DDa9oG5SmF7GEOCUZpYkOMRGvBBZLVWFNQVjUvXnyGoe/Z77esN3cCLBXCPtdGkQxiFfKg0Ql9R0oCBiqtGUPgdHXKfFajNdzc3dB0zYFFRICrq1sJJ7UGbQ3XNzdst1uMc5RnJ4R5RXCaqNLBt7EbW9nTtcEZS1k4vvD0Pd5/+h5nszN80vTjQDf07NqWm809H+2+x7bdse127GNHipHV7ITn58/5ic9+FZXgWy+/w++8+oCNGZkkSz5F7tstQcHMFcxsQTsMjGgiUjcko3i5ueWu3aOMIuhI7xIRQ5c8u6Fl3/Xst43YUOlIE1rud3e8e/Ec5wx73zCMV4xJ2EIuGuaupPEdXejxyRM0jEA0CZ0EgE0h0DUbuiTe0I9WT4nRowiQBnzouW7uWZ7PeXF5xqPnz/jAOVZf+xqzb30bawxOW5zS9Lli0EVJQDP6QNN7YoQxBoIfGbuOdrfDoAUASlLDpiCsaMkPSQKEF4EuZXAUGJCA2xgDjR85O12QyL64/cDpxRN2VSUWPAn6rqMKIgvWWjP2Hdu7gN1usa5kvlphKgFDcinDNKUQ69JA7BTGGgHltCcmL7J4bVnOZjx/+phXL19Rlo66LChVrnPy4HrK0khZDZW01DVlVUqZEQOpa0n9IMqhye80+8kmY0k2s1H1xHYk/6Yhg6Aqv4XJLzWfBZO1x8S2fNC1TbXlgSx1+Er2+bbuwHadrJ2UFuBjGv7FKKAcKXsrZmCw64ecNZBQyorNkToO5mDKyxCQ1zpHtZhTVSVF6SjLiuXJKp9HE/iaz84EMWpQDleUFNWMannK5Ttv8bnPnXGycjgDd+tE38ueZjQ4O9A0O5pdS9/2DO2QQcMgKe6dZMvE0BBDTwyDBB6mqedV+UzNnrDeixdxisc1k4FWrQU4PwRdqiP4PcWITttrJNcK072X1ZO/cgTlyV6uxiiscaghJ8KHkeTFFkNpDr7OSimqqjyA6CETGUL2yp7WZIyQVETZbIegDdpprDYEHxgzuSRORhmZCGGNEc/pmK0VyOxbP4odWdLomBiC1MthHAh1gV4tZf9XkLTcq3Hs6bpO8JGYCCqfNylbQClk4Ee2/0ARtNhG9KMnDOJdu24d901JCEug5zR55qXP+4x8TsaAdVCXUFeGbeeI2hJVkqyIfhCbRy39slKiw0op0TQDYBlHTQwOqyNt37GYKQH23QzUyOAjTQ/3O3h5q/nedeTju4FxFEswZ0vKoqJyJbOiQCuNNx6NZrkIWAv9MND7kX43sm33VEUhwceunJbGYQiliBgFycgUZr/eM7gO64SBW1UFxollnE7y/mflkmpxwur8gmdvv8ejF++yXJ5RVnPKei42A05Aehm2ZOZpCOL5vttJyGCuWVWK+KFhv75lv12z3azxY5b3KwlGtMVM/G9NQdIFwciZEVD4BApDSDAMI/3g2TWebesZdjcM7Yaha1DakGyBLRcUsxOsKcBKOJcEvwW2u5ah3eD7htQ1hM01YfOabveG7eYT7u8+xrdrgu/EwmYi8UwFj1Kcz2csCsPMab75es/vd/1QgLFKa/G61HC2SNTqnrUficqAtsdCTmW/m5BQSbMwCacDV52He1hq2BURawO9L+hGhTIRo8Vb9s2Np7somD2e8eztd/lg+zHWBgodKXXL7v4Njx7PmS0qTs/P2G5bjKk4P6sY/IL1PnF/v2NRO1aLOWXh+PCjb/Pdb/4mm6tX/PSX3uYf+vF3eXxRE+M1H313w/z0Ocvzp5TVHF3VxOAIvsNVC5bG0mzWfPzyFUpDXc94/PQFYxpJ0zQxKTHIR/oXWziUdVRFRQwRn9kA2pTMlmcYY9mur0gKqnmF0Zq7u2vmy4VYMFgH1vGFr/7DDO1IUZTMZgvMLHv25olpQhHzZD4iYNf9emC3aRk6j9MF50/fZXnxiI9efY//6+//EpeXlwyp4Nmzd3nrvc+iilIYkg/Yr8eDQkAYmXb7g1eOtiZvCiqzY/QRbFMiY/+z/9KfODSTB2m2Uvz4l97h/bcf/x4LDOZ1wZ/8R77MH/uJ90EpCmv4Z/+JP8LP/sxXDq8B8NUvvuCzLy4BODv5gzxjE6d2j8mSollV8Df/0r/NZv4WATg/mfO3/vM/d/juwsmj9t/+3L+BD0cJ4nxWHn52XTr+xl/6tx40yvoAph1+akr8lZ/71z8lY1zMSjZdRRlLSIq2k1J2v13zyYcfYkKiKmvx+8zH9zhIqFYKgUmxxzRhHHvug0hitdHY0rGYzeiGTn4vwCQOAGiKka6VpqYwVgA0BX4YxbQ+SUASJDRRNuMAQxD4YoyRMQVCgjZ49t7T+EAbg3iIpTwpVCkXEceC6mFxcpjWT/frAUqh1QH+paocF4/PKetSPM+AZhjZdQ1v1vfc3+ypUsGLswVPvaL74APUek2/G9iHCIWhqJeU5YKynAmbOCZ2bY+2Fnd5iTLiRzpNv2MIaD21n4kxJnQ8slwnMERhMpgobNIJENGTf1U6bPOgJNDwCJ7Ia+s0vffEQR/9oDue2BoC5mRwOMvDUkoH5uWnJc75Fisye+i4HicrhKMx/lTkp09J4j/t8fnpayrgJ/AoJZnGS0sWD36BD5PlU+h5+fHHzFcnLE/PmS0viEGLv5USVrBSKVdquQCemHkTWBUCbgomCCKNClEfgOqHkq6JcQhkUFbee1VVh1CE6YYZZ7GTLUdKWAUxmSwzy2zEXIBOoQiT/QEo+rYTdnjXobViVpe0bZfZwyJRFeBeoVREIeAzRsKlMIpxVDx774t89OF3aDa37PoBZzpmxmGMIoWcWIw6sBFmRUmpDIXWFNpix5Gbb32L/egxdc329JTZyTmvPnxJ9CPPnjw5rI6iLClPT6kT3N3cMPoRtEbrQDI2s19l3YUUaZsWVzpcWRJ8RD9YG77vqIaBwo7C5kUxc44YRAni4yiGjEkfrE5SbnQOrB4UJC8DoRip6hlnywX7mGiGATeviDFhbUHShnHUnJ49phtHUrOmG7sDezcZRfAiA11rwxDhJnle7dd8WTveL+ZcGkepAcQbcmosAJSzaCsyLq0k3EV1A3Z3LM5KbXmsDMXg+XWjsxmfyk3WtHNEiEq8rg63a0pJJg/YMlXxwXM+7SM/aEtwvIRBHibmzQRc5AEHRKJRXN3dURrHyWLBrJoBitEr9i242vDk+QsenxVcv/mE+90tpTXM65r5vMdHaYDGYSBl2ajRimCE8aT80fJivjphPwx4jjZD4i8tgQwoARNUkuZ8GHqIkdlsBmrG1fU18yFRzZbUiyWz1Qq33uP6AY2icAZr1sQgDbl2NcuTS+6uP2EIHWh48vSC4MFHaVa7wVNVWoJk0URtWZ1ecv7sOaTA9euP6Zs7hjFQVQII2EICWge/Bj3y1ounBGXYbO7Z73eUZcXloycYPIVT1PWc8/NHUqchzJwXz9/izSfXfPzyDfc3L/nutyu++pM/Se0SY7tls+lRSdH1A9pWnJxesFxU1NaQQkI5Sz1bUC9XRBR+9FzvG9abl6w3a7b7LZ1vgcBmmxO6tWKxWFDomspV9L3i2bP3ubrZk/w1a7ejeTmClmFX9tXKIAu/ByCb/3cE/vbPwxe/gvryj+aHfWJLK6zVmLLEp4SPss9uNmtSTgc3rmA2XzD0LePQ4ZWw0eOnfhZURUGyNiscNCFAGCP7XcPgWxaLmqJ0dH1H18r+EJU8tMpYVitRzKSygFmFrQp6PzCl7wpDLBCHURpTm7DKsqoXLMs5KsDXf/PrvGzuhWhBpBkHeg0+jhJA6ATQfVI/4u2zt3jv8j3qUIiyoj5jPH3Kb919xKCSsOVjZB8aNs2GeVVzOiy53W/BQkLYQjGpg1ej0pBswtuAdo4hjux9w3bc8fzFE+y95aI7xTOyNHMWhdQyq3qB6q8wKXE6W3A5P6F2JR+8+g79KIFEiRFVFBTGsSyXPD19Cm2A0VMWNavlGYtywbpds97cstttqaqS1WxOCp5mHFBLS/3inOaf/OP0z56x/IVfxFlDUJJSX1QlJ6sVSpFBq5EUJfBtaCXALY4jSRucUYdewYeAmYC/vBRnhcjRi0LkzC77G4rMVQMFy8UCbQ3t0PHu577I7XzBDhnuv/vZL9K8fsnYNiTvKcsKGbDC2PfcXl+zPDmV0Lep9tPqUPtMD0NIEYIwgAULEtBDJ8WTp0/47us33HUDegycV47z0qKiytY8Uz2WjaiSvF7X9ge7JlFDCmuYvN9678FYCa1MJSRhbE2vJueLOTgeSwk91dj5d1eT4iirElD8wCP3AIU9EgZQed8+2DrJ10KMBEE8DnWdz+zojAqTon5AGBFgQwBVhTVCNDpZLikLhysLyrpiuVxhnUNbkweNFmttZuDmIbgGdIHSDnTBfHlGPVtQzefMVwvqpaEfIp+83tM2A9dXDc2mzay6gWEcGdpBArODyL+llsxnZezRqYM0kuJISiPkYM40yaKD1OYpeWSMHXPQV+ChlYWwgCXcWuwQJruwjOmmkNudY1+ktc4M3HBgoU6dh1IpY/TyWRhtsKbGhxEfLMFaQnoo5ZdB7QTATvX85LUeQsQYk/9e1AL90GeFq/wchbwlf7BSzIGsDywnxmFkt93S9wPj6A+9hI+iqHRGLBZjFH/54ANGOcqyxDmHMw5bWgmTto6+6xn8cPDXFfz0eC9iSlPCADopUlRED5umI95E9kNk3yZUdGKD1yfOFomTWcBaL/fFalJpOVkloupFYZc0LkCFZbML7BpPN0p4l1FanjsVJaBPG4IytF7z8t7zehOwOuFMYFZ5ykKwkN5HtoPlw6vA651m5y1JSbBbSI6ElnWiLZOi2LmEcwUocEUpSseYMAoKo3DGYBXYrCJQqGxjlLMFSDLcUSVjVIy9qAH6caAqe6yxWGep6iUXT9/m5PIxp+ePePT4KYvTCyonQby2KCiL8jB8J0WGcaTvOqIX+w7fdwyjqBa9HxmHhm6/pmv39H1H23bSp2ohTlprcWXAFDMwAXTISgxPnzr6oNh3kV3T0/cNXdvS7Buub+/o9nf4oSH6HqMN1cljysVlDg632HImvrwhse869vs1YX9Hau6Ju1v2dx+xv/k+/f6Gsb1nHHfSxwMom7ErjbUO5wrmixkvLi94dFKymjm+t37zg7vm4frhAGOVSNAr4KQ0XNaRu3YgJEdA5DyQsucOgGLTJmZGNvl5ZXFaNjebxDA9aUM3JBY1nC4sm0Xgah+5aiNN0ixPxbdC6T1GBaoicnv1MU+eX7A8PWF1eooPBmvKDJ7M6GPDPCiqQvwx9rsG37S8+/wxs7fPOZslzlfg9EDw4nkRc9rmbHHCbL7CFpU000UphzaKED1ds2McBtr9loBB21JCvrQ9TEbVNBlDNkoZxkWZ2q5mlPUco0Vm5v0AKTEMHfv9DoxidXKO1o6IppyvKGqLcyXWlWCshCQw5XlzqJ9B/DTXd3eMOYzLuooX736GzWbL9SevWF9fcVE76vkZF09ecP7kObu2ZbvfZyadXFqpg6pNPGOO4SIPe8OpMZQzWH2qgfz92KqzqmBWFb/n1wBWi5rV4ugHe7r83WDr/9NrPLyMigecWWvN++885jd3jl2Q9fz+O08+9Z4APpOB3t/rml7jD7qUUnzmrd/jNZQCbVDWUVYzbt/csL655fb1a5yVKegEkoJMpbLuhJSZ5zH7zQobUiaOEgQQ6fo+gysqg0oC1BolHkB+HMUQXI5xKS78eADmpMCLBBWZgpj33tPGQB8DY5SQjj4G+hgZU5LACXlzcr+zD9QhgXv66lQwHr/1eKUjADoVdMuTBY+eXHJ+eQ7JMwwjbRgYVEIVBWmMDF3LnU/opuFsWeBHlRkOsl79JNvLTAFbzCgXck9cUaBycWuCF/87P0CSIiJlH5qoFEbnm5PZCFOSZSIb4GcmB0r/LueZECWddUqEnlDTQ00slbAUPzld2Dl3uDXiwzVm7ywBakIIn/Ltmj47cvF/LMDV4d4qrY6sjZSySf7xeZ3AnYfS58PHc0SWj4BnfvmIQieNSnqC1g61/iT7CEPL5k5SYxeL00wRSBm2yiDBBLxyBO4PfnIpHV73IIvKz9PEaDzIUB8sqwl8neR1HH+7w/sW/Z+cS+HA4jwOCmI4nmdTAvXEFDHGHOxmFBL8EUPAWVFOpJTo+wbnHFNCruDumUETJdF4cfaYYnkBtzfEf/B1tl/9KqqcUWqL1eqwWARYGCjLgnK5RIfsrRoisW/BBwKJ9c0Nj5+/oKor+vYITkP2inYF7WaNDx4dRfJmSJAD+uKD5zFGT/AaVySsNYRxzM+oJkXP6AdsGLGpwGiL05bKFuLh5Edh9wOT9E4bS1GUhwAqa20OkOwJMbDbrjk5K7EpYb3HDx3aWgHbkaancAXLxYqQIn2QRil8/gtgLPp7H5Gi+O61JHyS8LsUoRk7XqTEO9Yx1wISSrb4cb3JQ0cGkUGniAlHAPJiPuet5Qq9W/N2CFwpRWfy6pt6+mllpyCN2WHZZZBoWqdTT0s6BF3/fkDsobnLD+DEbjp+fdo/wWeGbF1UnCwlRDSkRNMPqF3DvvWYRyeEiLCafGQ2W7D0gHY4W9K1DT6DAABaRxgDKg/7prWUHpz705US+XzK7P4W4o0mLdJBUZAmIDoErDGURUlIhrJe0O73xJhwZcHjp8/p2pYQE207UM4DEQPKEJHQtrpeije/ttzc7zk/X2QLILn/MUJUFmMdxXzF0O0oa2EUSRBHBAzWlpSl7EFaK0bvGfuROA5sC0cKc5yziPft/FNe+dYV1LOaqi7ZdwOvX37M1Tvv8fTJJaZeoaolGIe2JcaWKOMYhkRpHjLRLH0/yEBPSSO4bRpaPxJUoqwqUhxo25EIFK7Gao1VHqUKYrC4oqSu5hTlGlMr3LlhvCM3b8ieabSADJ8uIDlODhJsNvDd78jK+tKPMA0C8JHkI0bbw3B+6Fru7q6xhZPv15bF8pxW70lxw9CPB4w3Pdh/Q4riBayl7imKkuXpCRDp7zuarpf6xVixrcnrJaREUoree3RZkJwlaJ1DTsKR4Zc/HmdzA5zBK4vBJgM+sd7ecdfeYgqLtoZeedo8gJ4GebUueXb6hMerSxauzjbRiWU958npI17ub7kNzQGUGmPkbn3H48U5i2pGkTRDDkBkAq2S7K1oSEFk0c4VKK3oo+f7968Zw0g7tKBgVa9Y2Jqmb7jdrdl2e0rjqIqS09mKVbVkGAexErIOo+RMc9pyNjtjWS0xyeBToCxKqqLCaUcisul23HRrNv2GOirOy4XYXY090XvqxwJgxtLRNXv4lV+V51vrHFRcCBCUg8TC6EWKPAjbcAopOnqxy1gq5f1uOhvLyWY+RhoNI4kxSPZAREJ+lbFUszn1yZkAHNP+pxTz5Snd7TVq6FEpUdc1iYQPQSS+wyi/f4yUdUVV17iyYOh7wujzQOuoWIjIAB8fJDtOGcqqoFjMud/u6b0nDQpnNKUSIEflHJCDv2de7zEl8SgkgU0ozINH71jnMCmEjCUZfQjJQWlRU+VzgPwbHpoFzWFtpZj7ayXPyfR/TIFZHGvPqX4Un9epB1R5faYHfrqZGJA8n97urQAkVkKmymLGfLHAFOL9WFWVhEdaK8NvZymrOlsyZMm8FZsLUacZUA7tHDpnwxTVjKJckGPWaNqeph2JcWAcR/puZL/dM+5b4jgQojC88aLQSYQMqqaD1yspEBkFzErhaM2XhyTTs0wKGbwNCCPYi1KEKbwz8VA5pjPpYQIwhR2cDuv/eEYmlKQ/YZWkwB8JK+oIkCqO/rQpfqo20OroL5tpjDmMKx7B2KmeSxGDOdSwSiviOB78bRX5tqTjcDjE7Eeb+8MQJUTT+3DwrH2IP6TD2pfvHUZP2/Yocn9QSPaDMwUU0oGaUUgW4+RFmtLULObXzxZPCVRUUvP5gdgqsXVDU7gBV1lC1PgASnlWs3jAX7RRFCUsgiZGI2SB0aMwGF1gjILdQMprW2FxTosdnBNrjIim84YUC0iSQWD3I4rAGBLdEFl3Ix8fEWtkAAAgAElEQVTdDtzuRprBZ59f6e2YhqEhoLTFKI3VNtu5iO9tEeX9ap1w2Tu1dAXWmEPfFROEMbOXo+wvIrif+huOZ7URRvpsccLy7BGnl485PbtgtlhKQL0V282YEt5HqVljzIqGlqbd4seeMHYMzQ7vh2zL5/FjL3+y/61YcxhS1LIH+UCiQ4dE1AMBy8jIftC0XtOOAsRuNxu6dkff7emaLevdljA24udPENWmEmsRP0qmgS0XJO3wEZqup9/dEbdXhN014+Ylm9vv0Wyv8P2ONPbEKKkkId8/yZ8oqauC2azi7GTJk8sl56cFi7kTC53f5/ohAWMVNh+kJ5XmxQpe+ZFhHImI3+GhoQBQmtu9Z1loFs6wmBcYG9EBrIqYPPPohhGN4nRmWC0d13cdr/aB297yZFVT1ieocSCljqqANzcv2dw+o64rloslXZ+wWsK7MJHdoChncwqdmFlPHO45qQo+/94Lnj1eoFXD9asP8K0EFKWQaMdbxrFjaDfE8YLFySUm+yApazFO/Gw2d9d0+y373Y4EuGqGK2a4Usvi10ekYhhHHBC8sOf86HMipWxIi3BCs98yDi1d17DfbwHDavUIbUoBzEyBLSUUJxn3wCuRnKaoD0T+FDxjt+Xu+g3jOGCso14sefLsKd/9+COuP3lF7Dq8NZxePOHi8TOWp2fcfO/77Jo94wMwdgoI+dSh+/AQyMEIgu0ISKuVOhb8PxSXmHf/IO73/+dltacwI9pFikXJrQ4U2rOsFWeXZ9msPJvaq8SwH4jDlHIpRZGPkT4kFj5xquwRkVcJFxNRVeJ/ZgQANJNHKRCGQYyzrTBjSYEwPEwOFBeVoCNDkEAFMwaUH7AxHjxKAzK5PsJU+Y/K/mz6CD4eIL90BPIlMVwfDvmpAJ6m60oZ3nn7kvfefsTlxQnBj/S7hqv9hkI76kXF/mZNv24xMTLGEVssObOOYT6wSp6gYF7NWFWJeREpjCWYiuXCHYICSPngmKTs3hK9+M54HwmB7In8kFGpc8gTQGR04gc6BElznNhtk8Re2JQKc/DQ+gGQ5cE9ERnYEWidrh8ESD8NfhzB+wM74VOPYTqgRN77XLhxmMZ/6ueQpZ0PHxo12SdML3UwUhC50+hBR4xKKJMOReQ0lDLaYHRku9ngh57HT9/CmEKK4Dj5YHnZb5RIR4SRqg+/xpQkOv2+igl9Toc1ZIzOcqdpRSJsCzXd999jJ8iBYTE3QCnG/G9kbU6SnOlzUkof2P8piTyZIeViKTIO/QOAV8LT/DigEK9fnU32haUmDYLWlnJxilueYiKo3/wHbL78eQG6LMyMAPOabLnQj+KRfHGB73pCPxDDHhUjJhdS3W6Lc4bT83O6rseVBRNcN/nhbjcbfPQyGM3gfNbLMTFvpuYlRlnjzlr80IvfkhYAa/A9xvfYWGK1pTCGVJSQZWDdGIVpn/3GlLXM5ktcUWKd+MOFBGm7pm337HcbZrMlRjsKFGPboBfzzEuRz10lzXy2YgyBfdcwjA3h819AdT365SsBqWMkGFHp3OamZB16bjII9VaekFdKiUc3Gd0M8vn83+y92bNlW3be9ZvNand7TmaezHszb1O3bpWaUpUsJGwDMiYggIAXnvgDeOHPU4QhIAwRIggDIrBsIZUtl0pVdfub3el3t5rZ8TDm2vtkqQnxYutBKyIj85w8Z++155rNGN/4xvfFHMhP2qvT9bhueTFfMLiecDjgU+I+Ckuxz1NPfjzm3zsFydMaVvm7iZykP1yyvwRsPixyPlyvDwsUx1rJtD6VYt/1zGfSClvWjbTBuZG033N1e8cHz84YXcI7YQFVs4Yl4lhdlCW20Awh4bIJmFIQkxed6XxJC2k8Jux58hyvEAMKDb0iXmnUhxz1xyFRlTmxUTLfhjFgywZdVOgUhQXVPuL28pLdbk83SiJYlLW0yw8HdvuOdnFGaStCgqvre4w1bHcdQz9glCGExDgG2lnD8uwRrttDlMZxRcxFlIjWBWUB/ThSWAH3XAj4ceTu5i3BryiqCrRmuVgdwfuUYBxGbFkxXy7oXeCbb6745ssvaNuW9aNzysUZJEVRthhbEUKi7yNFEbOEoOiPjsOesiyO7D2fEsloYZWVFu8EJEZZ5vNz/DhitUdrQ4yWmDR1UUsSZxXlI0PYR0IvN3osChopxhIngF8ARpUncEqgXr+G7R6evS+fs6lJdU0YPfhcQIgR78Wcq57PMWWNLRqKsiV6xdAPxKhz4vju0eRDwCcHSglwU9XUs4ZERO1LxkHiFaXBFNLtk2JEBY8PgW4cqOdzYmEJpLwXBgHJtWKC/KwxTAZFyUd0VKgg/x66vQA3KJSVsz32IxNvXyfFspzxdPWEs3aNQZGS6EZaa2nrllnZcLc/oFPKepKJmwzGtmXNzBQ4PxxZoEf9T6SzKSYBuFUNyirGFPh2c8luOKAjNGVF2dZEC1c3N1xub9gOB5azOct6xryaUZqC3W4vLbEkCAYXBqyyLOoFi2pOyJrERS6GDW6g8x1vt1dc93fs455iSCJr5UW/PQTP8nyJmbWMbcN9UaJ+8QuKzQ6rFFVdo4zBjR4/ilbx2A1iuuWdFBynrjYthQetxbAqTPGfkjjVKp3b/qGwkbf7nsF7+hBBaYml8n5WzuYcdruj7BCQGZny7LXRNHUNSuGCR4+jGH8NvYBAxqDnc9rlgrTVxNQRXcrgnKyFKJsYQl9QaGtIRrNcr7lxnvutfOZKa5almEVaJW7fwp6UA0E/OEsnoNfYhMgN5GKzFh5rjLlAYTTJiHzWJJ2DVpm1p07xT/63xE954ZIyC13GbcrZ1NGg7IjmQsrM1tzS/k6MGR/Gg/m1tejry3PUWFuKDmXdUDcN83bF+mxN0VhsKa3fpbXHDiYBGkW7TCmNUZayrtG2JGkLqsAWLbZuULbElgXtrJXOjsMB13UEHxi7A6PrJc72AXwHYw/REZMjxSF3aonKpFa5wywzPyXnCMdYTGSyBFAUlmYGZ1MQQDaJPIPC56eaJsw6H8DCWlRT11M2o9L6BJ5P+dH0PgBRK0wUc9oTPUI/6AQVXCUk8QrJh26e8OpU5MigmopZQz6DyiljxTFFNPro92C0sC198NlA8ijgdCySOCdaqpN+7kNjtgkcnPK+6UyfwF6S7O9DPxzb3kmgqhKthDWtyqkbMqJHx5gxhJgD0ZSDjEQS6b48jk5pQsqeGhiUHrG1mOSFqLAGCquxJq+9CEYnykIxawSMHYZIjMWRxRlipOs9Rklnb1UWVLUUD7Q2+KTAa0LQhCDmVCGMDKOnHyOHIXK7D9wcRnrvcRkfAQ3BkbwUdYPTSNquxTxX58Jg3h91SigDZVVSVRVN3WAyizqEKGem1rlTORJSEjA276taGcrCUpRapBHaOYvVObPlivl8RdvOhY2bn3HIJKDgJI7zbsSNA67bceg2uLHDu45xvyVGJ7tiyh25uZnRGksqND4akiryZJB7TaFnjAND0HSx434X2Q9iKr/d7dnd39IPO9xwwA07nO9RRLQShrBXBnbgxg7dbRm7HbZagikJKHrncIcdfvMGt31Df/812/tvGYcDKUheGXMxIE04iS3FBH7RsFo0PF4vePJoxmJV0LRF9hz5y6+/FWCsBgoNhYXHxvCD5y2/6AZ20eKiMETTMRORA+PuEHm6UCxrWM4U3d7z3uMGpw3rG89m49j1kdudZl5JJrQJkS9vIh8s4Ve/O2Oxeo/uusONHZUO6LTn7TefYVXiO9/7NZarOSFC2RiqVpKQoixYtoZ1GzkrK9bzDzCFvL73LU0z4+b112zv3nLY3WJUwPcbtv2W7c1rZotznjz/Ds1ijSlqxuDQtubsyQvceuD26hXD4Q6fWxaKqpTFhrjNuX5kd7hkuVxA8gQ3sl6vsZUV4IcEuiCR6Lsd280d27sNlZphTE3VnEFRHSu/woYT4MCN0hJrjaWs6txWnDh0G7798t9w+e2X9IeO2WzFBx9+n939hp/96x+zvb+itgVRl3z6q7/K2dkZyUfm7Yx2NsPevzvNTomeOiZbOruoozVkEXEJNpQI5P81k/jf3iXHWaEC6+Lw7/he3r3eq655rzp9/aOLC/iPL4D/8K/8nb+7puvRu1/+7g/+f/zuPv/5m1xF/vM3veYA/MvPOn76amBirt7f3xNjZLFc/AWzMql46yluRtyFjQBU0R4DtZQk0GoaYYdPTKy6rjNmcwr0UKLpJf88BdsTkCpyKTlRTSdAV5+K+hkcOmaKJ6RY6ePePt2yVL4Hru92rNaeqp5j/UhRtaBLbNbbNVpRVhVpe89+f8fLr3/Bo0fPUMoQUpTuAKCpKrQVoNwYe3zvFAOj7+kOB6y1lEUpEgxRgvppb6TwqEn37AHwOgXXGcI9utuSILiBMI5HuQlTFKJt+IDfrJQ+vl7wQSQnctLtvSMGz8SI0LbCu4Hd9g7nRoZh5Nmz9/FedCpDDJSFuIVPel1KKbAFpq7QTYXrFYPV3IUBHyOqSDRFKaBgTMRx5O23L3n/u9/Dh8Dd9Q2Xby4JXgL5sqp49OSCLz7/jBcffsRssSSOHv7F/wGJHAgbfD8I64ckAV1ufTfZ7EblgDrGwDiK3MJ8tURb8C4QXcTakhA9w9BBUuhGWqq0FUmIECNu63ApUDUNjy6eUjRzhkGeubGaYXDy3JXOutWJu+u3rB5dMG9m7Db3mHlLMDY7uDsxR8HSVAvOloE3V19l8F/OJmnRnOaqwlFyQ2KTEi+T48/6wH9V1jwzlrUxrLShVVoSmRhIKmALi6oqYu8ID4qM9X7PRT8yu3iPP3n9CjP0jD4QjOafl0Ue47wGFcfAVZaRzsmhzKcj6+hBAeSXWemneZz+wtfvsmhzUuYTBk3nRu4OO+b7Dd9/9j7D9T0pgXOBz7/8ikfnS7pDQJkZ52cNt7uB+WxG3bRokzUT+5GYAkFBiGLg8FC/2vvA6DzO+BO7WMnc0UZjlfCOVdIYnXAuctgfBHhrKhbtgsuba26vIl0/sjh7SkwCqtTLJY+fPqHr99zv9vgxcHb+hItnz7GV4rDfcXd7w/bmHp8Tk9F57m5v2d1c8fb116Tg+fDjj6mqVTbO1SzX50Tn2Nzfix6fTnzzzStx8M3Gje1MDCw0nUiN4Hn98iu8f5/F+pyyXXC32R6ljELwfPH1tyQMTy7eZ7F+wqEbuPzqFyyaFqMLLp59wPX1LUUzR2tD6AaUVWz2AzZLR95t76XUqWYYa4VpmBLz+QJF4Pb2ihgDZTWnLGvaekGHY7WqScGz3+64v37Lop5xtljQdVtu9x3NB4b+dcDdSuty3tKRZFYAqCOg8LAWp4DDFv6H35NE+nf+PvzaD4j9yO76Dl1blFGihupGQnCkoAlK8fL117RNS1RJdFFdfFiXAEAbS3ByNiUCqev4/IvPUUajteWTT39A3+24v7tid38tUjNlRXCytoq2xFeGhBTrgpfkazKcDVHMZ+SoDIBGe0AlkpNCdH/YEXGMSVqwi6ZAx5xpJiAqXpw947xaUutSklBgNx643t1zub1l1+9z59jU4RG52d2xH3rW9YwXjy64++YLJAvPpIUEgVxQUQYTNIfrA8WswDYWSsWlF+kHdYCvdpeUKIJzWGtZn5/z/PEzuv0B7xz7ocOYgkeLC5rxwG7YcrO/YfCe69trmCVePH6OVZr9fsf2cM+m33I97Lh2G7xO6MYyAq/6DfOgmauC9epMmOyFxVrNQr9g89//d6jf+ydUb97SLhZEBf1hwPeOOCY2d3v6ccTaRGklV0lIcTNkBhVaQKZjEToFZk1NXRaigdkFvtkM9BEc6ghKrxZz6tLy5vVL+qs3uMP+uB/uLt/A0FMlKIylUAZTFpgoxlgpePwI0Y/0+ygmho/OxADOe/pDJ2dzBvAAIkJs0UoTLYwp8f7Tp2z6ge2hYwiRV93I1mvmhWVdFcyMIkR3BAOFjSXFC60FcNVBYj6F1EBjLowwySbFPH8nGcBgyU7SmREIyhTHDolAzCxMLb9jEI1PIqSJ+CBA6rErKs/VmE2pTpUScZQXGQTF5DIPZMZeSVlJJ8Djx09Zrc9omoaqqjEmy+xNaz2D7ZEcaGaddmFHTyC9iAAoXVE2cy6eX1C3Dfsu0XWOzXbP3c0NwY2k6FExSEerdxBillvpiWkQqYgYITmOaGlmwqYsCzAxiKcIIZHZr2mSMJjYxen4dKTXxmH0CYzMChNMHYokUMbm81+jdXxXL15lDVk9gY7TM5hyaY5EhLIosmFZJtJE6QIZxxE3jBz67gjORh1FO7awWCYzMDG09SFm+QLR+0apo5F0WVUUqZDPE0UWz+U29BACbnSM3meZLgFsjbEEnVAhiNawAm3lzDdK57GSeRxioncDaZ8Yh4HSSsGtLMtjhVtbjUZAbFOI0VrvRSbkWGTOy+JYcY4QlaPrE96Dj5agoOsju4PFO0tMlraIWB3RKZDIrN4YiMqgyxntTNZjaWWcmmqQ+VuUmMKCBp9jpuhy0dWLfJ1Lid5ZDn2gHyP9GNl1geg1KmpMzNr5CmKXcMFzCCOkOYWRrkxUzkm0RiPFKJ0iujTC/m9nNE2DQed8wzOMI8qMYJxIRoVAiNJ9oLWlLESec3V+zmy5ZLYQebhmVlNqUN6D80cwPQVNJErnabdn6DvGYU/oOyEcBEeKnuRHWbp5/ojRmaasDClLDHVjoKwXoAtiVHTdwP5wYN+N3O973u4jm7stw9DRjx3bwwHX9QSiyBsSKDSYXASJPoi+bL/PZ7hmoyqMnWFsidIaHz3EQLe5Efmp/pYwdlk/W2IcrQvAYpWmKCxn8zlPVhWPzlvOVw3r9Zz1eslsXlGV5m8/GAtTHBWxJvGDDxf8bz9/ix4GUnKowj7YzOUKGPZOsXOKUhX85E3PqAKzxvDrH1V89Ud7gmrZ9ZrLTaKyBmVK3t4Hfv5tT//xnL/3w++yv2+4v/6Wy2+/oDB7rt58jfMDRVWwOH9K3/u8MWq+93HDrNY0NlDpQIFs1G4M+BAIztPUM548/y6Lsws2t2+4evM5yYuJUQo9t8OW/f6a5dkFq/OnLJYXBC+6mSlGVqszhspwd3PFMPYoEo+efEBQiqAS2iRqY/BDLxuw1pR1jRtFTylmjc6hO8g9hcg4DlRtLQyJrJ9ipmoTYgKlTYmKPbuNOBMvl0tUWRJVpDvccH/5DeGw53x5Rgzw5Vdf8Oe/+DllaXn+4jnn5+csHz3h7e01t7s9zWzO+cVTXJpqYtNzzofLqeR1vGKc2jbisQpmrKEoi3fa9v7dXKIRqyczub+7/u76t3QJSSgdA5E6G0WIY/tD8YIj/+jBL+usIaqJSnE4HMTsIFe8J8bCqd1+YlqErPUliaPRRqqb3tEdDrSzOTqDiVpriqI8sWzz/Uxg7V+6XnLZPz2IiEJSKCWtZWW9wFaR+WJN3Swo6xm2rI6sjRgCYz9y9uQp5xcX+HHg+uqSL3/+itX6Ce18RVHP2Gx3FNZilZgQSbuTgNVTklvX1dEQS6vMPObkZt51e8qmxZji1LY1MV9D3quMFf3KfElMGkkIg1UbTXDuyO6OD2RZJLh1BO8kCM1a0WVVScIVJVgq60ZAWsDEyG6/y/51WdsLskt3ZkUSiWNP9AEVE0WIVP/0f2b8nX9A9/gCdRgx8zmVLvOzT9y/eUWzWlK0LRSaQGZa5Pt5+vw5qWy5vdmw2w1cnJ8fP3NwI3F3D30v43OcmcK8SLm4N+n+TgB2dCOb+zuqtqEyBuccSmmiHxl8wPUDwYdceRfQfNYu6NxIHA70fcfrV99StQsW60dUdS3FO2VoxxkqBKxS7Hf39P0Odadpg+PZ+oyrfcfZ+48pFmthCjrH2B8YhgOz/YJh7Njurgnf/1XSxVOKf/o/4acCZg7gY0o4wAOdSvzeuOMc+MSU/FbZ8MwWrIOi1AqbDTaq5SNCNWDa2XH8ytEz23dY7/nh+pyvui1Xfc/tMPDbY+IntuBwbAd9UCw5Fl5Oy2uSHSGpYwI1MZKnOfeXsenf/fpdQNZaI2C5Uuz2e759+ZLvf/prPH78mK4bOPQ9o3f89Oefc7Zc0rRneO8YxoFF01DWFUqvxRnZ3eK7kWFwFEVFZQtst3mwPUgc8/DOjjIKKIx+UNTSMAZH34+0g8Mayy50DINn0RbUVU1yHTFEmlJa096+ec3dzTWFLVjMVyxWS/q+w+8dTVPw3nvP6PejJDYpEsae/fUrvv36K7rDgdl8zpNnz1g9/oCYApv7e7Z3lwS3Q6cIQTE6jymkbW0YYRjEXGQxX3Jzecluu2G+mBO95+U3XzPfbHn+0cfMFqsTi0y4HKTosaVhMSv56MX7vP36G15//hO2t1f8yo/+Pu16xX5zQ/RB9B+jJyoIfmTo9uy3Gx49eYwpamIyFIWmqQqSioSYKMrZCSiIijj2WF1AKiirhqpe0DZLzpY1nww7rm4v+dPPfsHl1Uv2akPfHBi+cSeQ5AHz/+HETHDS0pyqdAr4k/8XXr0k/Wf/BfQiV6IKA4Uhjl6MmmpH2QS66AnjDqUUVVNS1Av86LDBiKsU0CznMMj+Ujctxhq6YU90jqKIvHn1DSkXe1KCvh+wJFRpKIqCZBXugdkscGTzTbtXDFGkKLzojRsszWJO2c5QVQ1Ng4miH66NJflEHAZUYTHKUFJwsbqg1EU22wlcbm7402/+nLthT5c8PULEeBhBh+i5vL2kPNO8eO9DPnv5ii7EzEzUqJCYTJKE/ZYwEcLGE7pIta5QtRGCB5GkPTEaHp8/ZtUuWDQzbm8uKWwp0i/aYJXI6lSFmJT148BytuS8XjOzNWn0lLM59yTuxwOvd1fstcObiT0nzznakma+ZFW0WBc4uJ7Rj6gUaR7NuZh9l13737K53bLb93zyL/+QtIUQogAXJHoSRVJoZWltiVFgjMr7m3QuKG3QRhhtm33PrG0wSkGMHPZ7hjGDSSBoTOjZXr5krzW+7/nd7/8q/8t8wRbRbf5Hv/UP6e6uuL1+y+XVK9zgUM5jVKLQhlhKUTPmlui7t5d45zG2EJ3mECiy5BCTpjeT1rcwKJW1zNuaF+crtBv5+vqWfUzcu8jej2wGz5OmZFUV1Fo0H8ex52jkOgHQKorckZq+OWnMiiQD2qBDAiO7i4C1KRfDsjxD9Lnyl+/zWASMmfV56lCLqMzIziWAlDBaEaMsxgkYRydi0jIhtKaqS+qmpG4qZm1N1Wrm8xlt01DXDVVTo5VFT8Y/IMzG/BoJTma+uTtMKS24ctaIjZj8+WUOXd8cUFuPH6UrwXU7Qr8TMDaMqOTQyQtoM4H8RCkIqgnsVJnxKjGWjLEI77wrZgVEAUcFxM0dS8TMip3OszjNgtMq1zJmD0r3SMeYEQaxVhA4dgWolPelKe5S+ugx8ZDJqhNHnxCSkRwClVmbhlgYilBk+YIjfp/B1yC63RhCFIkO771o5aqAV5FROaAX34l8FqQkppopyZ7pnCeOw9FLI4SAGwaM1lSlxRrp0Ci0QZkTkzdGdcRM9cTq9Z4UAn50+HGgairKssBae2TuksRQtapr4iD7bAoxG+CF7BWejnhEjAptwKfAtuuIGEZXse9LhqHEuchqnmhKRakNptCEaHA+MXhwCYJWmApmFp5XLbvDPuuiyv4khI+pcyfRucB957nvI5sh4pLOMo5SExg5xc6TjEMJKDcSvGdwAwwDVsvZoo3BKQN1iS7EuK+yBl3NSPWC1CzQiyWNLWQHiJHKR/a7LRx2MAyo0aHCQGVL6qqUjvHVkvlyxfJszXK9Yn1+Rl3OMEUt7H4CeJ8lOiPOjwxDj+s7vB8IfsxMXnfMx1JMWJ2NwI0R/WtjpGs3BEL0hASzJ+9Tr97H1o8ZXZCc4eYWbm7Yvbni5mZPt9/Rd3cELxG5URNZSYooKYwZi3MQPM4NwkZOKSspnTpdBLlSpOgJ0ZNUfIfhTc5rjLVUlcgSnJ8tefa45vG6YbWqmS0qlouSpi4prPkLsfbD628NGCsfTGEUXCwrPj4zXO0d282eWFYct6V8wEQU9wNEFWl0olMl1x0om1jWBavGcUiRYYT7Dj55z7DcJvo+8PV95PObxG+clRi9RqmRbncnCPiwpdvecfPmJfOmZWYLTKmxFopiwOqASQG8YwwON2lW5YSnblqULalmS1Zaguj95pJ+f88wiuNa5wbiODDstwzne9bnT9FKDGsCirKa0S4cbhgYugPDYYOpW4wS4ynnT9VVEvRdx5FpnwGT2WxJUZQYU5GixtZ1dh8OWVtkamvMrX0akkpcX7/m+vUrZk3N+ZP3qWc1br9jOGzZ3l1DzHoiyvLs+XcoqhJrDcpYLp4+5eXb66zNYqibxTEgfPdJ5+et1PFPSlOwoE7MH2R/DJNwOAJK/fiPvpKDYmoTTqe2X5VOr//OG6YHx2TieGhOdcxj20X+uZD1bUJK9MPAyy+/YlaE4+EfM+OrtIZ10/LB2SOenq3oP3oMbcPYe/7P3/8z0etBqjHdeMApMaIIKYm5BopJT00xVbuFLTYGz5giDkVZN8yWKx49u5DKf245GvsDbuikhcZ7fD8SXeDD77zPYrVAl1VunZcNWueWpJAPW/ns4COMAanMBUgYYjK5MqtQovx4GtvkheUhr4BOHpVGbG698WGk73aEGLi53/PZ11ecpsLpuU/P+PRoMoMuy1kcNVOPoMCUpD6cS+r4/xIf5aBIKUxhKZuaZMAUhvms4h/86DcwCfb7A9d399zut5w/WTGfV2id+PbLV+zuE+Mg1fFGa57MG2ojBYPN6Lkc4Ue/9bucPXqKMSVZmevoShqzi+aJSSqjF4MnBZ81vh5qZk3jGgnRU5jAb35w2p4nkFVBrv5Kmz5TAXxax6eheme8yBX1STuOI/stvgPMiIzBBHzIekNNxRsJXsZxoKkbsA91ZX9pjU+fh/waD6aPtl0AACAASURBVICdd38m5iquArJAe1Fhi1rccOuWqqopqxplC1Dm2DbVdZ3orJUVVdmQUuI6jsTkCGGkNovMRCtzm8xwZBacxkdacCAdW6r6oSM4CQ6bZi7/n6IkKExGAj7LIES8j9RNc2QdA5kROxKcY9J08mkCW7NB2tHBWJIXlcde5ed2wjVOgGyMCWsKTGsYul5kQR4Y2k0RcEyRFE5sVWOELaz6nvJnf07a7RlffETX95hSYbUVZks/cPvmNcViAVrTLFp2hy3GKKIb+PbLz7j46FMxSkJxe3XN2WkwM8DvMDmQkfvKMhAn4VzZ8vTkcCunmcjtCDtmdDLWxlq0LRiJNFVBNFKYVSFRliUheZQf8c7Rb7dYK67epizEhXXoUdrQrs5p53Mu377Eu5Fhv2c2W9CmRNztxV27aghBEkpjS2btnIsn74tDL4rYiOh/mM4uRAvruPdokRPZKoMDXEp0buB3FPQpsTKGOQY1jgzbPWVRUTfz45wplKJBYXyA0ZFsyawx1KbgbbfngxC4InFzZFQ/XNsyl9Nx1CdwAlR80Pr3YJm+e/a+y5pVOShQOklCmd9k0qmLMXLoDnz2+ed8+smvUFQ1xgeCj9zd3ktSUFQ0sznD1RWHyyvKumGxPqOezZmNHuezfEAhZgfanPS0QpD19VDGQSQtJpOSzFI/xgWRw2HPfN7QmhaXY4ZxcBx2O6w1LFcLaZ0MkaQCRmnquqFpZ5R1xWZ3T93UaJUILmSNzFISiCj68PNZI7IzMXB9+Zqzs8eUhRW2vgp0fYdR6bgmi7JiHIXJZrXi9uaG3e0d280GFKxXS9brJff3O3x/YHtzTVW17+yVcWKSJelnWi/nbAzEYUd/4/niz/4VP/wP/hFj3+HGQSQatKJdrfBei7lZ8hwOO2kPNRVNW1MWDdpKfKJVLVq2nXRHzWYt3eAZh47gRLNR2ZLtIZBSSd0+4cULS1nPefvqK279G7hIjG9dPuomLUkyXpGjh2lTewD4kwA3wvUV6v/5A9Jv//skzdHwURstLt+jw2lNKuWsNSYDNViKUsx68synqBtGpAhVtzOa2Yx0D0N/wDnH/d1NNgxMaGXweR2rDHtMcccELh3Zljm+iDHHak5Mq1LvIRrKlfz8EB0DnqAV6/mKZbNEK8VPdz8j6YSxmtZWtEWDZpKtGHl5/S23wz376HBKWIm/BO8QU2S737CtWt47f8r750/55uYNnXfiFh8FRFNZUzrGRPKZuRbB3Y2kFnSjRQ5HJ5qiYl63aKW43d5xvb/j8foRta0xyuD8yKHfMYQRnwJPlk941K5ZNQsKZRmGnje3b9m7jqRhMV+S/J7oRJMZlVDaspwtaesFhSlwfg/aUjeFAKoxiszWi6eo1YK4PXAVfkTxf/1z/HYneo5KCoNjTCifWBjDRDaKObGPUVJpNbXRK8P9pqMrBrRR3O27LM0l+WZlIIwdgxIWIGPE7zthOgJaGz758NcYH224Xr+mbZd88+UvGMdeMlElxerSFgSl0T4Qw8iw21PWjbSXM3l+yAwVcytxio8hEUyizHrOdVmyahv2h57Q94wh4rLkx/Xg8Ckxs5HW6NxCbHLulM13lCJqkXFJKpGiPrJcJajOqFx+LhKDmeP/pyn9yt/Q05plYluTi2XTZwmAeRB/QEgewwNNWaUo6oqyaijKirKomM1b2rYWnfqqxJRQlSVFUWTz1Sz19eDsepgLJHLHljrFvlN8N0kdkEEsrYR0ZLVogqMlR/DRQ3AQBvk7OSBrqB4x85PuK5mokILPcY2wXFOWhjqRDKbzdPq96f8jZLasxN7kfYf8M9MO9i5AKGOeO0nTpDmbTuSAI6CIsCc1krMl5DOlibEsQPBRdx0BvJz3uEn20DuObxqzH8E0FDHhU8gGbPEIDE7SYTJVJtmMSX4gHokP3gtD1gUPPpykiPIz1EZJrmq1yDspdfw/lffraT7Img+kJP4Ro4+kkeP7alswZfoyb4Q4EvQEpE9nkjrG3dpI8UVkHw3GgEXjnWK3hysTaEs49Jqm0pS2xFbCxpUYPdG5UV5fSzt8pWuSVhRjwPmIDzCGSFJZzCgpjIZaJ1IF1sMQIsE5QhDNVVAUXmKBAIwRChWpk6JEUSaN9fm0UD4TNCyJiI4FBrC2QJmComiomwWL5TmzuiVlkDeERNVuOWxuGPZbxsOB4DR1VVLWJXXb0C5WtIsZVV3KvAiB6EeZgsERvMl+NAK0+yAymnECQKM/SpMF/8CwLiliyLKHXnYO+TmZm6NaoZtz7OIxplpThkRrZ1A/olofWD3bEUfP63TA+w3DmI3zjodmJPZ7khcGfAqyhmPuWEp58zh2KyopUATE60Il0Qk2Sud1I/OJFGmMYl6XrBcNT9ZzHp/NWK8KFnPLbFbSVJbCPuhW/CuuvxVg7JRwTunFqjZ8+qTim7uer2/3DGEtld7TCUFKil0X8SHiKnHO3g2BWQWP5iXnc43fBcYxcMgaMrMSNl3iZh/4xdueX1+3lFXNbL5guV4x3M0FErAVBYEijdSlpijA2oRKLh9C0noRnGPoh5NbpJ0ONIU2BVW7ZHX+HpPItg+O0DuCG+iDGIgE7ykLYR9oI5qCpqiYzdcMtmM4iACxRWGKMhsGxCOAGGLAjQdQHN2oQwjM5ksq32JsiXci7Dxp9BGCqOrqU1sHSgDDw/aGq9dfcpcg9CPNrGXsd4z7Ld3uHpJHaUtRL3jx8XdRRUG/3+CHjqqqadoZ2tbUrTDZQnLvgEM5TIJcVfhlxusERDy8JoMv8jz54ueXEnCpU6CQHrTCHDfaCXQ93kDezONUXcqJXJKgNwQ55GJKjFEW6a7ruLm95Rc/+SlFYTBK9GRiTHgCs9LyfH3Gb33wMeFForoI6BbcGPnX//c3+KzbFaJjc7hnUJ4xSYUxuJOO2gTmpZhIwTEEx8F7BgOxbFicP+HRe5YPoyHpRBg9vu/odlsO95eM+w24kVKBSZpo5pw9sZgaMAalLTrr2Afk4JIWYkVIiiFquqAZgmYIkBDTk5hF/o2uprBDxi2M6CiAokoenUD7gSJKNc0NWw7bS5wbePn2hh//+bfcbXactJ2y/s8EHUxAImLmY3Ir8wSK503iCOaQvzyBsRnUFARRAGRrKJuKej4jFlC3Je89OePph98jjZ63Vzd88e1LLne3fPJrH3Ae5qjk+cM//jfcvoKxG1DBsywsH58vWVUaHwJvdge+Hi3V83/Mi/axsIrQaCLjcGDoD0BC2zJPuemekgiSuxHGAaX8ce87Vc89PkBTRH7zg2naSvvGFOwafQJBHzbc/AVW7LSvTlGsUths4CUBZXgHiPllvdkpeJPgMge28I5L/OmH01/89/TZ0rtg7EMAiGPYmRMnYzCmEH3JohXDEGOFCacNZMOJyQRNQCepps6XZ3TdNgfiMhZN06C1wvuRoe+ySVZuZWQyKeAYPKIhxqzHaoyAmdZKoJvdYt04yDmQp2IMjuhPEhAAwbusD+yIIUKqmbSzlIq5rTwe8Qmlha0co7QGEcnV/QegTG49l+pxwdj37xS0HjIaFRPIq7PLsmbwHgpN9fo1+IifzTmsH1Eoi7JKmDsx0d3eEmLANi31vOH+EkqtwDtuXn5LNVvw6L0XGFvQHQ4PpoI8yxiD6Lar/GxTEsOpPD+OoFsewCnpcs5jURRVJYYQRYkua0xZo4oK1bbiCh0TVmsqXx+lIZLvxKhrHAlFIQm7G6RzpKypqgqiZ7u9pz/sGfueYb+jaeYc9hu8d+jVGp/I61BYxsvlmru7JSEGBmPh6VPUq0uUG5mKZ6dFl3JBVdOheZMSm+iZB4NLwm6IgHKOtN9TzC3mgU6q0ZpCCyNCjZ6iKmiLgtJW+Jiw3qFCZCBx0LJmeGfN5+d+3BKmNtB394O/6TUZeUQUKub3UUr0BWPEOcfX33zNkyfvURSTRo6i73sOXUczm7FYr9C25Pb6Bn0YqNsFdTNj7qIwSUbR9bSZmX6c61kX7+HwHhNXdUr8jmd6SgzjgA8elY0ljbU4NxB3icIa1qsFMQacE/O3shBwwFa1AP7DgbLU+DGRojA1rLWk6GQ+aM2Tp+9Rz5f0fU+339Lvr9FVja1LikraMkMQvWZbFjTtgv3dHZPZ12G/Y3N/T4oiWaBQzOdzxtExjo7t3S1VsxCtwnyFqIQllGOEtq6pSkMaE8O44/VXP+PTH/5mbveMGSRSFOYcow19UTIx45wbCT5RlFY6Bqx0HSUKlEqYJKBFXTc4v2f0mR2qxEDr0A+yhm3Fo/P3adsWq4RPd6tfE7aBcAgcYZncXpoePCvUxNR751vQd6Sf/gT1/AN4/Jg0a0nGoIskRoJe2luVFl16bbNRnymJyr8jc1HUNSY48B6ykU9RVDg34NxANxyORSpdyLkSj8Gk6Biq43zM4MjEBJzMh5Iw2lSImBDRfaCIEL1nINAHRzQwbxY8XV1QKsvLN99ySA4TNbUpqWyR/ZEiPjiuN1f0acCpJAaKUww7jWdmBB6GA7vDjn7oeO/RBXe7e/wh6wkmfdoHlBLmmstARxSTlugiBSWmMahSUxclVinGsedmd8fOd8z9SGELjLYoYD/uGYLDmIKL1RPOyyVNURJiZBs9d/t7nIpoo1lVK9Sgs+b9SELRli1nszWlNozesw8jpTGUZYnVGoIkyfZsQSoMzijuP/mY2c8/J252+HspYBijcSExxsQQovzuMYZKR9BoOmetLTgMjt5JCNE5mZ9aybkr5J0ZxuQWbw33d3fSCpz3wfXiMaleUpYN2hTsNhuu377ChxFUxCBMRK0mFqYhOk+yPs8dpKg1BQ1J5TgGAWNDEBBVScdTXZUsq5IxRTaDow8BR2LrhMgxhMhoDTOjJOZXWpzhOSkSoLJRWEonZmc+HKaiwxGQyghXOi7Gd06CIzw4/axKQUD/HLslJYCKhPfymlobCiPFZ2VLmmVLO5tTNzV1VTKbNdR1jZ0KyposZST5uhicnu5lUveA09/qoSET+WzQAlDrrF2qtEKrJDreMWb7FclbUhhJfiCFgRS9AKIIUJ2Ow5JlQqa9YYqds3kXR63LB91AcRrHBGTMIOdLAsL6o/SXDPkpT1W/9Nmm/SdmYHkyY5vO++lKZAazBpUkzg3TPqan1vUpTk+IjITotjvvMhjrT8bA+TVjOt0HSh01Xh+GfRN7VfYoAaxjzDrXIRuchZCNpzJgrY6zT2JAHbNZb8KoPJcfvLcxp7wh5nETGRqOY5/8KRcqso+C1AJPeY7O+4UkM9kYWgnhxNqKoqylIGAthUmUpsToEqsNPmp2nSIpQ+elS6vwlRhXkpm/wWBVOD4/ZaBQJaoA45OoMPpAQBOSTGotOwhN0ixQjN7hhxHnA+PoabZ7KheIw4AbNPsINnkaNLXSlJkB7lI2JVOi8etVBhJR6KLOgLTB2pK6bmjnc9mHcqxe1y1VYejLks5YfH+gqCy2KijqWgzv6kokw1Qi+BGXFErJOasMeO8EpM05WsrF2ElDWdjQMtdicJBkb5sA/anqEmMkBI/zAVcvScUMXc3QdSGgqK0o2iWzELnAc/nNF3S71/SHa8Zhj+/F/EvFCMHhux3ejUfZEGI4xrQq44snSELmqOyfkYkuJN2gJ2lNjaapDKu25PGi4fG64Ww1Yz7XtK2irS2FVblI9NfH3n8rwFhI4IM4O2pxvvzNDxe8uvf89NWW6+BJGTicFpDKbSs6gKotK+0I44gfDCoVvDiDu03PMIB3hstXkdJCrWRC//Tze/7TD5+ztI5KwcX5mjK8YNbMaJtWmD+Ts3l0JCcQoi0sKmuyqgTaOIwxFGVJ1TSAyjR0CQyq2ZrHdSVGEO2S29dfQtpIMKlht7nkq6FnsT5jsTpnfX6BtiXWllR1Q5jN2G7u6Ta31PWM1fqMWbugH0aGccCNATccjgerQmNMQdkskAYLMPaOcfSi6xgCWmcnPiZtIeE9KuewacTGPYe7Ld/2PfvNBu96qjKC61E6YouC2XzNex9/n9lixttXX/H6m8+4u9/w3vsvKOoWnU0v+q6TQAN5dsqIVlDKm4bBiiaiUsKMNjYfeHnCT2HAg1PHao2PotMzmU89ZPRNgcOkVXRywJVgPWQ9lIdLQwIA+V4EfHZZffXyJZ9//jkhJYKPaBVzZKVPGz2iDXSU9cpzOkRxbHXB4eIo6j0hYXPlNiqfWVZ5amfA7HiiGsvsbM36+Sc8+ej7XHz0fR6/+ADnO3b3N/Tbe+Zjz93Lz3j52c+oqpIf/b3v8PTZ+9SzBaYsSNktMQIhyec67Hp2DoagGKMmKIvXc0bdEGxJ1CXohoDo/yijUdUMZWx+dkirQRgzCB4wjLh+hxs26OEexRWNArbXPL8459G65X/833+cD96pWp7H/kH1d6pSymyORyYBDzG+B9gsx/Fnyv4IVqrwRVNTty3RaIKK1M2MFxfvU5mCy/2Gq7s7rrf3mLlm/d6C+aJlv93z9vKOsDXolCiMwpawSwNl0RK1xsXAo8WS2oJVCmVLUAadPH4f6fuR1foMZQs5kEIAHYgorC5JtgYrjo6T22qKUSqHCPO+KjyTFq0wtATgCzFmRrUEF7bM5iGnoSHXVt7dYdPD1STB3NEBllOwMjGC1PF7YmwRsnSIKQoWq3XWXs0tbQ8pd7nK+NBU4lSFzk8rP7jjeyl9XJtGS1Va6UJaO5MkKsFHhPg0TRphtRmjJfiIiZAsZXNOVZZobRi9o7KW6MVIZ3N/K0FXdvrU2lDXTb6nPAe1oq5rqkKMCGyVgzDvpZgVAsPQZfaGka4ArXHeHZk0kAOSsccNA957ZvMVRpvj2JBiPtwnnS15js45uu6AG0dWq1O7clEUFEWRgSQZ1+VyeWTqT+66KcWjvAtKUSSFLYy0lg8DsRSjkPLyLdX1FYf/+r/BDj0mQd2IM3h0jsoHSqUIVUnQGnL7U+Ucv/jxn5CU4dmHH/HBRx8y/EGeUkmKozGJ23IkScL2QKpGSQsG6njfk35dPsGC6Nutnj7FoUmqwJQNZ8+e4fP8K5WhGKTNSEWFjopkIz52zOYtZdMSlebxxXvM2xalFOPouHz7isVS9MwPuy1Xl2/46DsL0XYcDuhCoapZNpWQqn4EVuvH+Cisx+E//y+xv/dPSJtbudeHe9NUdMiMZ4di1IrfjyNOKbY+sQmJj5XmzA+M/Z7hcNKbnlaIBYoI7RiZlYZV0/Jo/Yg/ffMS2+2YDY4/0sJoEwBYjCrUCYWV+AT98EASkOCYDGWDizy//iqQVuQOciCZ56pK8p4xJW7ub/jTn/yYx48uWK3O8ro1DKNjfziwDomnz56z2ezZ7w/cXt3x/DufkMgMJRRv31ximvk7hVnZD2XvnCAxq3U+g/J5OSWXU6cqp4Tr/PE5isRuv6fb7xl1yX7/iGQUwzByffmWFx99SNSi2BeTInnF9ZtryrKgqWtKqygKRQwKbRRBFXzvV34dW5RsN3d89mf/ivFwy7iHxXxB+/SCqlnSdQNF2dIsl2g7IwbFdnPHrj+QlM7ty7J/ji5QNpblas52u+P+9pbdoWf4j/7hcX2MLlDWJdoaASSipV7MKS0c9ntuX1/y85/8MZ/8xo+YLRe8fvmSYvCszgd0WWLLkqRLHj9+yugc3aFjHHpCsCSUMGaSYewPlMZijGIcOrx3tG1LO2tp5g1v3txRVCXOeUYXaNuKT7//XZ4/OePLJ0/4o3/xz4gfOg5f9fh7WdOaEwD1y3PseLYbjlqnCtC//78S/9F/Qvzku6jBEyfDxVzQ8VpjrZwZZd2waJfcXV+eFhBQVS3d0OFGx367wY0jqKxFqC3ZcB4fEzpETFuSisx195JIq6Rz0U7OKMkFTsCVHwe0MdRFSVXWRLcXOYBhZByDmNoFQ6NrztoVi6Llk8cf8tX1S5z32KSx2VglZNZYNw5EO8U/SeRop4mQwXgUjMFzd9jw8u1Lfvjd3+B+uyFFuNze4pNCJfMguZUYQkVZ6zpqxv1IGqFYltSPagpt2e839K5j7w6EQnO1u2PwjkU1QyvF3bDDVmJyulwsKWLBoT+wOex4u72GUpFcwGgx9qpNBS6yH0WX79OnH1OZksubt1zdXnIYOl6sHuG9GBAXtsSZAIXGq8iu32JU4OZ3fpsiaao3b7BGUxuD9pHRR97eHzhrS8osZZpUOu4NxEQKgbZuQMk546Mw8bUbMSRqq/nwyWP+vR/8Fvebeza7e/qx5/Wb1/Rjf9wbd/f3zOuWebtGPxOpkz/u/oCwvSb5/lSoUhCNxpYW70RzkJz7+5QkmT+avGaznnw+Bu+htKjSUtQFjYUXyxmvtgdu+4FDiDhg6yN7H7nVgZWBZamZlQVtKUWKqSB01LAnUUztukcGQ8gmvDYbWJ70R3WWZpkAGhlZdcpRiJkEKudfzMCayjGVgD2W2axlPm+YzWc08xXVoqapKiG1TBJYuaCYEqQgmajsGVkYVgkRIGUDJQFc9TsJ4bEInoR9LcV7izZFZstrUgq4/sA4BKp2LuDj0DF0O8Zxl4HYidAzJRYqNzUFhM16MmMV8D8Ds1n7VR/HWx0JTxJbTrqymQmYwoN8fQKfItacJIViEkAyTUXtCUTPAO+xuM1pKCYpA6Umpqci+EBZt1R1Q1XXjP2WoT9kEDPDSiqCEqZsSPEkV5ZfdyoUaA0qikGd0hksy+tjStIT4MPUcSdzwhhzzDPscT/SBCcdTc6JLnxykn0fGb7pAdUkv8eUI+qUAcc0gcORqI10X+V7D0o6iVPWKzc57yxNgdKF4DlG56Kc/F1VNbN2RtPU1FVBYRO1LVBYlDaUhaI0gWQ0TilSMoQo2vUyjxXJtDDJGSrZx7EJnTQ2QfKRJpGLGObY+SJfawE1lUKlhHeOoe/ob++otntcjmeuAugwUqEp0ZgcxziVyV8p0k9FgzGQXCLqAqqWMAjQ612PSg1GW4wpKGxFW7XM24ZhvmJXX7Hd3EhsabU4XeY9RCUBKZP3uIR8bpmZYsYVwnFGSlfPqftZ8jlhxno3ilyId8d8MeZYIGWjYjd6OD9j9AZMQVVr2kazP6S8J4g532K14NHZOam7B+cYdhuc74UN64a81odM5BMzRJvJPlpblNVMUicpYyUhA8oimTDlyjHPBZEmWM5bztc1F49qLh5b1itLXUNVQmURXCkl6Yj9a8gQfzvAWMnCcpuJVBifrmt+5f0ZP7x2/LOvb2D2OOvNRKrS8MmZpvQdxneo3rH2G6o0MHOJojP8cL7k/WeKPmpchPFwx6M0slpVnL3X8sHTJenuJU534Pfc319xdramrWcYUxCTaBLGFDFadKSU0WAm3RKFsRWLpT2aLUBmm0ZIOolrcorYcs7yfMZy/YRHj5/w9psvOGxvGfs9KTr29284bK+4fTvj/vwZzz/4FFtWJG3A1CzPKvbbO7puy253x7P3nmPrlojF+5Fu3FEY2XRiEtaKT6JHUjYVT997Soo1ylrZxJMnYel2e/puxzgcKFTip3/8h1y9/pz9/SXKj1y9+orkpXKxNwk3jlhbszw758NPf8izDz/lpz/7MZ9//jNeffVzrq7v+c73Es+ev2B11hBSYHfYntoegMIWeD3gA9K+lLVkROtnYt+Iy236/9h7sx/Lluy87xfjHs6Qc8137vE2u5szBQG0LQp8kW3ZMOC/0rD0bAH0g20RskS5qSbZzZ7vULeqsjLzZJ5xTzH4IWLvzGq2KEhPfNAGspB1MvOcPUSsWPGtb31fTCwD51wCUPPhnSO4DPSQExyVE7CYgp+UctLNS2zLrDEX0yY1jIDWVJuDESTu244f/Ot/g5dw8D0DgUMcOBJVTmbS4kX0NO1A11XJRdWYCTyJQBcGDkOHiz4x4pSkkAXamGRCF/cMfsjnNKY84JUGY7FFyekHH/Pkk+/y+ONv8viDj5kdn7C6ueLpacHSHmO05vryBPHffC8lqnWNsjoHxcDQO1brPatdZNdFmkHi/QmdmRFsBaZE6QJVzJKLdIxIGZFDi+gPJFH71EahKJAyOUDKQkLQWQtS44LEKQNljXDHiP4Y1haLgcMKEyP//E++z//1Fz/jbtOkBXm68/kZZEYj09MQD37+G2LGr30vlcDOasyyRpUWqTVIQd8l5+ujxZyvvf+co1nJrz7fsmv3OAVDF/jhD37G1z5+wYsn5/zRP/odfvbDz3ny6JRPPnjG977xMedLgw8d++2WN6+u2R7mnM5rdAShLEIbhsOWyzeXXL56ye/+4T+mKme4bOAkSDpBcUzOTMimLgNTa6Rz4JLepjWeEYw12lAWhl5qnBu4fPWKrm1ZHh1xdnGaq8Qj2PVwNN/foBG4CCMIqCRCGKRMCVuM5MUmM5almpx6x2NMFFOh4yEb8+8CujwEdzN4mIDDOP2e92O7kERpkFpPm90Emqqkb6tNYvXkIoWQEqVF0vYLkbZvGVyL1orF8hhITq5uOKD6HmtKSlsxn80y+J3ukXc9fd9QVTXWJN3YKOCwbejdgFAeLzu00pkNm+JKXdeYbJYVY0SbVER8h5llK6q5hHm6fza7tKdrT61YY7I2fiOkoq7n1PWcmBkaPse/vu+SPlYIdH1P0za8ePFiYtMm7a6U6EQ1zqyIjy4nvAN954mmx5uIU5rCFAzG0HiH8h2qg7qoU5tYjISup93vqKqKOAy0fYsPnucvPubF8xfMlkt2uw06X0LfNHSra5JpxHhhY4VqjLSpmCAfsBZSS5llcXya5HS0Ye/AzGeUiyXFbE6nJL7v2K9XhKajdLAsymTsJRRBQBc9t5s75lJyfP6Y7W7P1fUNo2FGUZaYssxOzYrN7TVfffZzqnqBsZb961fUH3wNdDI00UGiSY7OSifDi7dvX+L+x/8B+YO/wPz4R3kdesjgTP96OdbV0sbo30aHiZGjCH8qAh/EwFnw7B/opMqyRtYLQt8Q1/uLAAAAIABJREFUu6R5ZbqA8Z6qj5w9+4DLvuVXdzeY1TVBCV5qxWulQGe9P5/vd9b7+/XIOcaECPftgdMP74HZce5KOcbgxB4J+Kn9MzF7Am/fvoToKWzBi/c+4vbmhr5tuL7sOOxavv3pd3jv+XtcXV1zfX3DxZNnVGUNUeJ6z0resblbJ5Z1PpRSSWtT37NlhZSoqUPg4fWkf/t+mAwnoncIAVbrLIVhiEbRD55hCBgpKZVkiI6+2eOd5+mLD2gOW4a24bDb8Ld//R84Oj5hvlwwm8/56JNPaPsB2o4QIs8//Bq73RYjNcHU9KJmeTZjnoHqrh+4vL5FSsvFsw+5CJ4f//W/J+prOj8gXZ83wzIVdUXKG/t2x+iYLgSU1mBskYyCYgL7j5+8z/Z2heaWiwvB9Ve/4uLJM5Zn58xnFbdX1+w3G+bHx1SV5e5uxTD0qa1SaZSInD9+jBs6hr7DWksYDhwOXW7Ji3SDo90bnHNoo6lLzZvXK5S21PWCeVVy9WbH4dBT6yP+4Hf/mC9f/5RXx6+4fbli+8stwguyc2FmdeVh9qBwkG5BBmxzETwVcgKxD/gIiiQFlGrgkZANZxEKIw3aqBz3UqR5/dVLQtQJ+JDQC5811sFoSxhSXi+1RGpJlIlV5Ek5kJJJakbEVCgTk4RGBgWkQGeT2yFLzKiTI4qLU4KQHPYHIlBqQ21LKlOhheZ7H30HoxRv764Z+h43dCjS5q60lpPZkt3+igGfwLCQ2lPTjUvzOq3jkm2z51evvuCDZx/xwYsPKIqS4bOB6+06F2hygXOMxeOCEwQmlPg7R7fvGXaRJ58+IopkVDQMHqkNB9/R7DuuD3cYZRlUpB0O7FYHbm5ueHH8mGa/Z/AOWWqudzdEH1kIwVIZjuyCsqg4tDsO7Z79esvP7645uAYh4eL8gscnTwht2pD3w0BDz+vbK5p2j5AOtRRYX9D83m/BxRnL//1/Q2lDoRRCCVaHjm7fsaw0tVHYnFcKoSaWZsRhrEQFcC5SE1G1IcSA0YqZGHg+P+e3PvoUaSV3u2t+8P/93/yySmz/GAKvX/6E05NHmDKtj2cXz/nu93+f69VrVqu33F1dcthtk5hXSrBw0TH02ZxGJ4kwH0eWJnkfkUaVD5Fu6KiMRKnU/TT4jnlR8XxZMrOSL+/27ONo+wQuBLoQuRsCReOptOK4MtTWUOgCI0Wy0cvyDXGafFmzMiRzn0DS340yAUFSp+L7O0d8l8nuxpczOGZLw2xWUVWpeHNyekxdlxirUUaB0Egj0/kER4gQggQ0QiRGcZQSYgKoxDuOfCp/jadyv66NHZNp6UrX6Z3PNKQht7HnYrtIOrJdmzW1h9S9hBvIIqrpKyYJg0R+z7lLJk0kpp9L0jXREWOCskWWiRgLNe8QRULIslZ+yuuEEA+vKMV+AeSuzcmoc7zefCsC9yy937AF4p1dUwgYoTg5e065OEUYy+tf/g1uIGEAMXnVtG3L4GPyk4lx6gCYMOl4n7PLnLONEl0ZNcuM9LGLMeWtY0Hg4X5cSoFVFlNX+b5kE9wYaduGoesY+p6+b/FDPxF3RuJYkoXKa+UInIsMzJLZtyIifepORlXJmFdZKlNQ2IJSG6xWGK2Z1SXWaJTRKGOZzZYcH51SFBVaawKJUR3IDOEYcMOeEWgkF+FD9Fm6cOyyy1IkE7if7002ctVTapy6Ux/e45jJClKlbuiiqpnP5sTbFWFfMd/XzEvLsLpN7Pt4T1yLpPjgYkTFiAI67+nbAz72qOChbfH7Ne5ww+3iGFPMkjTmbElZFygRCBJUUaLqo9xlkKTUUhuxJzpPUD7p7sqxezLn9w/m0sQtmzY7kkiah71wEAWuDxx6xzAks8x+iDRNl4yJ+57gAzM18IvPrnm7Kynqmlll0QpKK6kqzfyowFrLxaMnLCvL+ckFdVlwffUqmXS2LU3TjFMkFS2USQVulfTFBQGtLMTcXSCTxJPMcyC4RBQxMnUTaSSLsmY5L5nNLGUlsTZQGI/VGq00YEmaS+P1/8ePfxhgLCMdPZt7CKik4aOzkj/4eM5/eLViHxeIALXwfFBHnjSvsPs3VLHhbG7Zr1/x6OSY4+WC5WKOLRziJPVlRyHwLmKFQNGjxUCt9ujhwBAHpIicnp5QliVJKNrhQ+Cw3+J90gO01kCMqTVUytyunsJExhgIPuSWr8g9qy9m850ENhXVkrMnLyirmu3tFddvvsS7HiUFXXBcv+3puoaTswuWx2csTi9omw5bmKQ3e+i5fPMVy5NTtLZokZxejUpJcz84hrhnyCCyFCBCpJrPkboAaRn1fVy/5fbyc65ev6SQsF99hXANhUpVyMV8lhgSQ4cPjoCkPrrg0YtP+OAbn9J2B9rdhpPjEy5Ofp/F7IjlyWPKqk4MEBe4Wa+IeUCn5xymCgiQTMZiDux5sb8PSiMY9BAwTZWJOCbFCIqiyFVgMYF5QoygeVpA4gSEpMAglbzXAZreeHx/8NFz6Hua6BhCKhQ0rkfkNEFKRWkMMmbdHQLPPnzBpixIuXPk0B5wo67gNA7EA0ZSMlYIE4AbQebKtEzaME6otPnRPUt5jW63nJsOIwcguVoenZ6hVAKzpRB0bcPdrmOz77k7OHa+4iCPGCpLqJKTptY6SRCQKpDedSgRsVJQGs28shQSFEnzsqoLlCpBqKyDK8DLXEAJBCTOeUIwRF/g+4KugK6wNMYkzZhuzfe//pzPX9/y+esVY0vUVO188OxS7M7tOXG8g/fPKeaFT4iY2IuFRZcFelYRinT/YnZvl0phlWQxq7k4P6HpGla3G27v9nS95/j8iN12xd3dlsXRjOKkpnxsGEzLwd1RFA1l1bHd7XGhpSg1DoU2EWkU0qSNMmXFo2fvsVgec3R6ntImN4CQqR1qahNSECJS6XS/SCx7L4bk9hwcRnfTsNzu96zWkdPzR9D1XDxRBO+SsZ2WqYUzs/FDTg7HJIkYcpVcTotQJLJdrxm6FmsMZVnm1tokoB4gVZ7zZBir8ZBz8fE64rjg3j+39BxlYrQpNRVEvHdphI+bAu4lSoSU2WW0mNqDkm4wqcVK5HaRbHIxMseVlDgcY3uWtalNuOt6QvAYpRnyYo6Aup7RtA1uaPN1gdaSoQ2sry7xPnB+8QhrJCGkok/f7PFaJ2NEIVI7kdJJxiBfb8iV3vhgAxP8MLETgnf0fTJUTPFHok2ZGShjdMuJWv57QaQfunz+SRJhlJUY+pbmcMj6lz45vjuXtQxDNgATDF2LDh2EQGkKZBQEHxlEYmoEOsp/++eEb39KP5vTuG5qGQwhEgeXWIVdiwgRpQyzxREff/tTdFlwffmGr372E76TY6iUqZUs9SWNhbB0LWNL2gTG+5ilUwy2LlmcXeCj4NB1tPsD5+9/yOzkFB8D+/WKzWqF6xpMEBRSU9gar5M7ti0sJtaY4Oj6jkPWjnUuUNoCpTVCSYI2NNstwdaoesA0B1zfIAjJiEFrmpsVzGcEJel9ILgE8CmpWM6P2W5WDO4A3/g6cV5T/MW/y/qkWWPu1xcTIkhFH2EQAicE/48f+Hk/8C3nUF07/YUPgSAlZnYEZpg2gMSAGjrUesdjpSjqU2am5vP1NdF3LEKPCIZfWIEf1S9CSAwL3j0m1su40MWYNcF/8zFudtOYFJMxjBQxkZ6zBt16u0W/fcN7739MWVV0bVrb+77j7dtLZrM5F48u6PqB29UNj56/R1XPaNuep08uuLlZTSZ0KZZohAjIrFX+8Ja+YzA2nuNLgzkuKWyJVort3S0iwmIxBwR36x1CxKTdNZsxq2qkqQhtAyLJXiij6IeOyzcvufzyMw7bFYtFSXuIxOCx1ZLNbo9SCltYjk7POb14lu6rSG20q5sbTGEY+p7tZs2Xn/0CKQKnpxccn5zy9U+/j5SCt69f0+47ri7f8v4H71HaEmcHdlIS1APQPELnBpp1i1ZpA6lkYh/t9w2bzQ7X9qAlX/3q5zT7HY8eP6U0kv6wwdUFdbXEGMPd9SVSSsqi4uTkLMXADBb0fcvgQtpAiMTYW5zM2O1bmvbA9VtPWRZoFRDC43zHepsYMFVdUc1Lbm89L55/ADLlZNVixu56Tfe6x7fZYCrKe1OaMUebRlectFnlj39E3O3gu79NdJ44OKSSKKGJIRWdQt/hXNKnM1KgxrZDgOhIyRTELFMDBpt1jIXQ+JgMx6JK+UzwadOd8jkxbR2ljPf6oYwFFonzaZ11IUDosaKgnM0IXU/v+uxTlLTilFQokkHkk5MnSKG5ululddeqSU/ua88+Ql1p9q7DEzHSUtpkPuVjYNccuFqv6HOsP7ieX738nK89/5jz41PC8w9pf/4jmiFk8EBmOMFz33KU73HUxB7YwKufvaE6K4hF8nrwKhAxU97scNmrIHWcdaHjrt+gjMCLwPpwRx8cj08esSyWWKGxWuOdpDYlRirWuzWD76nLkqPFkg/OXmAc9FbQup7r3R3rYcfBtXgFKIUREuUlSkRku0QsLDRJO9koWFaWTTuw7RyDDywqSzkSJzOgdQ/aJIkDQ0g6s1JnCSLB7m7PyRKquiYuT/joG1/n383nOS57fvTTv+ST977B8ckj6tkSZQ0nJ0+Q2mKLmtqW3L59zWZ7x75vsgwcSSIiRLxLMSaBw/f5jw/3a6QbEjghSPsDH6FvW4yxHJeG4WjGy82BYWyhJ3EyexHxAbrBc4gB2w6UWlJqTV0Yaq2wSqDifSFDSAlKJQB0BOrHXu00HR/suuL97+SfaaUwtk7mftWM5dGCsizSWlwWVHWBVgpE1q+PPdGlsSjHzwKEzLlCTjGneCBijghjdpSAkCQvl/pspJITZBsBESR91yJlP61dU54qsu62UCgvU5eZcwzDkNmuD343x8RRg3h8bcxdkp75KGmQ9V/JIG58QEQYpQRiYtcm0Hbq40vnPOXO061NX+JdQAuSbJIQiZHJSHQIef0WD+7duHAQCSrSe09dzDl98iGuH7h5+bd0+xsG19C7pM/ufcwk7njfxg8Ti1vJkfkZGRgSdu3zc8knnX4jm89qNRV070kIGYTWCmuLnIukPxZCsPA+FQe7lv1+T98c8rk5Btcn2YNxB5MvVmqFFkmGy5oSozVGKwprmS8WVPNFkh7QlsIUzKsFhbVYaymLgtmswhY2yaIVFVW9oCzrqfMvSX4kj6IQUtdEu7uh6/fJE8JltnR0WQ4ACCGN3RHAJu1Xx25G5bJfyHhPYsrt7/e18X7IkeXUTEGYzZO2toDCO4JLRmgxJK3r2hYg03l2zrEbBtaDZz0MbNxA2zf0W5F0XH1PIOC8xFYDvW3pDgeMBTntHxPOYQubWe8xxUs5svvVtHIzAa4yA5qjjEbqqEz7vtGfBCZpD+8ZBkfbdHTNQNcObA4dzWHAD4mtbqzhg/OnzGYLtFJ452mbHoKn1YLDXrLe7PGDoygqSnVKVVVoIzg6mnNzveTtm5K3b76ibQ+ELNuQAsdIzgkoMSbP6Xz7foCca/jcpSURU4FBKI/WElsojBVoTTKg0yoXvCURz9hBwDTrf/PxDwaMva92pcqAip6LWvLNxyVfPxX8bLNmrhXP6sini5Zzv8KoDWVsOZkZbg5bHh/XLJYDRdWhZJtdskWmyhsiiXKfNCNavO9SBVApiqJAKYl3YdKquNcFzLX6KOi7FhhNUXQCYsflNIbsEOfzoLsHH0ax7xjAVvOpyrbfrmkP61Qt9D3D0DP0LTG0xNijrcKHsT0pEvxAd9ihdEqqRdaVMqYgREkcPF3bpgpbSMGv0AX18iK1/QqZGTEeQo93LUO3J7ge3x8Q0afWW5JO1DCQq3ICbWrOn7zP4xcfcXz2iKvL17S7LWVZcHxyktvvUyIRRVp0b2/vqI2kNObh057AkJArS2MVaQJrHozZUbHowV+PP0g/kzI5UD2oJuZBxaRLGe9bshNoe98mG/LPBNC3HdvbW6QQSKMxQoIIWAE2m2iM7bgJcE9nc++ufX+Wg+tToj9d39hKfA9sCZhMxybrFZlALK0UJ4uCZSmZ6YGCHTL2VGW+zyRmoNIFLgSawdG3Lbtdy6oJrFvNprcM9hhXHhNlAVIjY8CokMlTEYVHEbFaYrVkZgwzKyllqqwRBooyJrq9gBBVErb2yeEyVfYk3qU54KPEWUmrzrAKtBbAwOa65dGZxIVI0zvertbjFU+A7HhPHjzg9HoGDchJUxRJC0pbhZlX6KpAlwWysMm0YALy01Fay7wqqeuSvj/QdAPdEBDS8OjxBbNOUy9nYDRHj4547p/iNzuQA8HviVESQkeMIVfyA0lLMDGwQnBIrVkcHzOfz1G2IPqAjLkqKsLEyBzbetJ7yWlsRAEMPW3XMOzX8Dyde7g9In45Q3RPkIOjjgFBSABXNrqRYUwg3wVj48S+yMB0XgjFeo3oUhurquts6idRxuaWs6wZlcfs/ei8n4P3zNj8/MaKaIxZcy8XGWJEjc6ZD1gN01MWEq0tUhcoXSC0IWqLNwVB6ckZ10uD0GYCaJWQaaEcZGKHliXehQRgli3y8SEDuUMW48+OvD7Z0AoBQhv6ds/m9oqhdyzmNaYqU/uM90g3EIKegCjPvTHBaBDiXJ/GZXjA3vd9BudEqqjKbPxAahlN7Iu8a3xn7RtvcJhA1sTs1xmszQmtSnG874ckoeA8Wt232YxAcIwCrS02g7HjJsEFAc5hv/yC8LWvARHpPcYNFMpigkcETxjSpkUKiTGGxfkF89MTrm+uefvVV6xfvXpwzZ6+6/P1jMgZ9zuN8SpjJEpJYUtMUaHrGlnWSYtcGQYh0LbAOUfX7Dls7jhcXRL6nqgtylY4BN5ajLGptUwbYmFZ3bzF9QOH7ZairJPjeWkwdU2rNILUXiSUotlt8H2bmH/eURUVzeGAKguELolG4/K8tLJACFgsjlivO/zpaVorlSSGFNO8eHfdmvICyKYogg7B5zGwDp44SOr+vujiXWIx69xeGb0A0vxWwaF9w8ymjglVzsAPzLs966Hl4Dy3CjYifcb0ydNOVUybofGxTMYFD15/d16K+01ZHN8mayzHeL92Rej7nrvNmuvrK+pqltjsORLd3t1SlMkh++z0jJu7O4KPGFswm89x3Z6u6yjW9zmCEiZbVci/c17T3Y3jVBGwFdRlTV1XFIUl+J4QwOhUmBMi0O53JDmStGEQymCKPJ/9wG6zZrO+ZX27YrfdcHxyRFkYhqFjPzhmi1N814ExBAXBW2azBd4H3NDT7A/0zR68Tkx111MUlhg9Xdey2245uThncXzGYXdgF+44HPZsNxu0SV0BcjQUfLg7JxmvhpgAgjJLBXRdn8zBAC0F+7sr8AOaiC0khBZ8KiDXVc3+7pph8IgYGdyStm1yrhvy+ABblggp6IYeaQpskWJ5DB439Ikl5Af6NhVDYwhUlcUWBWVZY+wZZ0OPMBa7mLM4P2Elr2nu9gxDl8DB3b1RzbsD7gE4cXOV1vzj01RYePEM9FhcSOCoiBAVyWRMCArvsOPYcAPkjaMyhqFr6LseiaIsNNVsTtPt8DGVy2NM6yciTOcSpzX0fu2bRLAyS3ncdPsYiDKilaaJbXK3Fkl+4NA27Js9ZXUEEZbVIhmT9KnjIdp6Wl/OFqc452iHHk9IIIJNuuchBHZtg46Sm92GQ9fhQuD11VseHV9wPFvw+PSMt8envL65pRuyUc87m8FcmI0KObrS97C/bvACzFIjF4YgfDJtFMlwJeRN9djBpnUyPfMxMsSBg2szuzuZIrXDgdIYjNRoITBK48qeWVsgtaaQltqWhDDgoufgO9bDnt3QpDiaRE7xMuBUACOQixL3ra9jfvYFounQPlBbSes8gw80LqKGgLUJBFQZ5BlzLpFBQIVAJaQcnbtIdtsNwQesrkDC+fkzClvm+BJ49fZz6rJIzGkRsWGOVJa6PkpjIjh83+FxyaukbYA4MfjGuSsQpM7zUTt9DGJM0nbjUwoxAaxSeqRWLCrLvHfs2n4CZGGUSgMfI/2Q8vnGSQrt6UJkKAyVVBRKYlWSHCK3Q0dxb86EIBdNx/POjFLEZEYrpEQqSVlVlNWcsppRzeYslguMMZlhqFAZjBtzW8hrhoz34q/j4jEBj+Olj6SZ+7bgkcgyGfqOAI+YljeC8Mm0dMo7xxs7rm8SUASRjHT9VETP1xxH2YBI9GPHy7vSBSlOJCMisswYEwCbAaYMGIesPS+mp/ROSH8nosQHrz9Ydu9fzSQHM17baHz1zjvFLCOR72vOw7o2yV4pUzI/fcb68nM6EkkghgSITnvR8b3yeUvIRB895RBTTiBAhvtnMhKNBGkdG3GP8ec+pN9SWqO1TWSNLNknZOrWCH7A9T3GlLTGZo3vnn7QOMcE/iZQP+XBSkmM0pTljKqssFpTWM3RckG1WKIzM9aaglm9QGuD0RmQLQt0UaCNxZgq5aMP9hjiAT4hfAQ/ENAEFCGJOxLGHs+MiKfxed+dFt/Jo0JSZ4r+wWsP8I8YE6niQd4lMp6CLRA+SU2arkPWJV5G8B4lJcuyTCSzGBl8pB4cth1QssMLaP2QGMfE5FkjAJGIJqEMBBuTVIjIknRSYUuNNamDMhHn0ziUeT+ljU5dI3nwpBArpvkQs0aLz3iX945h8HRdR9t0tIeW7bZlc7fjcGhpmo71rqHvI0YbrLXYsubk4ilHyyWmrlIMl6mjVQB+CDT7FrxPRfWixFiDEql7siprtLK4wXF7e52kCqKfSF8ijqS8TNBjJBD5iTw4eYqMZAQpMFphjMKaVHg0SmGUzJjjffHmwQR99/+/dvwDAWMnf7IMACTB64VVfHyi+dNvzdn/66/4+Kjkt59rvja/4vGRxojHBOdo93ueHL9gPp+DULRDk5hN3jPuj+tqRowkl8HcHxB7mReXpGniBiYHN+8ddVVM7K7ge6RQtM0hs49UBntH+n0y1kr6JamR5CH4EHK7shv61IZiSo5OHmG14e2rX9LsNwxdg2Sga265uTyw396yXd9y+ugZuijo+46uayAE2v2aodkhhUJJw2y2xJQelGZ32EIIbDdrvPPU9RGPno9GNS6bYygEgeVigXj6lP3qit3tCFwrtJLsdmuarsE5lwDd+pyPv/F9nn/0LbQp+MWP/xoROow+oXdwc/cWbfdcaIOtFxijuXp7xePTowmMlRk8hix5x/0iMC589wNW5L8R72wWpciC8XmDOwzD/XvAVM0fNZPu//ZBtUrK1JYcE7s0xIiLgfX1DV/89BcYoTk+OYJCIoygUIJSaUJwNF3L1d0d3aEnookRht7z2U9/xez5I/SsygMsafP6XF1RIumoR++IIjfijEkPeUmMaUwaq6nnM37ro1OOLwSzmqRPVhUUdjQ7SSBA2zpW61tuVmuubm7ZdgpXnxGLI+LyCDVbYLUmhCT7EJod+AFrFYVRVFZxXJdUVlIaSaUlwh+ILpk/BO/B7QhREYVBSAskpnhasNOin6QlUgXeFBKt02a2ntfMliWh23PYrnh6ccLxsub/+PMfTe1Q46ZmYjTzYD+av5ExTi1aQklUYaiP58hFjTAKVKrpEZgCKD5tJud1yWJWIUm4fUAjdUFVWz7+9ocsTr9JwOGDY7awvPfxY65+9gXh5pa+PeB8QWpMUGlj7B19u0e0e+SsZehaTFVnd2JB2zaIbM6TjPKSbo739+29U+U83z8lJZ3vubx8xWH1BXz6EQDz19/j+Affwj0c4w+ip+I//zj7L/ib/9TxX3Iev+mIpDY495/6xV87+gffu/euaf/kNScnJ0RE0mYLfmIqhZjAKikVTbOj61JltWsPHPo2MSZixFoLMRndJPZ3al+TUk5Jdt93FMYwahpCivdJCkVOGwkhVGKPysQ+nWpOOXmZCkQhab4lFoFByMT6DSGCD8kYw1piyEWgEBFSUmQN3dFIhHqG8APV/AhjSxQis6ViLpoIdtkN3IYIQiKHDpTBeocxaR0Yr9SUltPnT+h9z2c//VvuXr1iMdzrgTdNy013SxlAyTAlO+PKLqaRDtJYZsenFPUCJzXrw8CjF4+YG02fW1bffv4Zrt0i+gbVNpgQkTHgiTRSUBhDYVMbV1FUHGnF0A/sdmv6Q8tytmS13TEvSkw9p40wPznHDD396pr19Vt029C2LSFE6nqGCUkrV5UVYrZMoMjQ4lxP37U8OntKc9jR9QciAlkYdIzTs0ymI+l6YxwBTXG/yAmBE4qVEPzQO8TwAIztWvrdltg7rC1S3PUeEVxO4gOmdaih53FRcHb2mNd9w8v9ml/dXPLNLvBzrXgrx6Iokw65yONsYqnk/4+M73E9gndjy0Ppn3cKMyIP2+w+G0OkaRv+8od/yfe++zuUZWKceO/Z7vbYuzUnRyc8ffqU65sbuqbB2JKj42PWq0tOTk6ob2fT52ppkAzTRnUcY+Mx5gjxQTA8Xi5ZLufM5hXHi4qrqxuc69ImMHpWb17hfTpnaS2Ls2MWx0v6pmH19prt3S2b7Zq+7Tg5OePbv/Uttutbrt5cst9tOMzmWFsg/IDbH7jZ3RC6ht45+rahP+w5OV6Ac1TGsHh0xtNnz2i7njevvuLq+i27wx4pNGcXj6irgqvLN3z55RfMZvNkSCWSdv3DSzZaoW1F3w8MPlBJnfRIRUQVBitLlJK4oWV7nfT7f/+P/hA7q5B4vPMsj5a02wVd0xAjNM2B29XNxOrS2jBbnDCbzVFGQ9NwOAzU5TznG3C7uiGExMx3LiSQc+hp9golFyzmCza7yNHRU3R1RLXccfTNEz47+SlXr7/ibnWJjIH9zxt88+6mRGSGEOJB/ndzDX/2r5Jkyj/9U0RhiXUyU3HOo03ahEsEh/0O2fcTGNt1DQqN1SWmsLRdQ7Pf4XuHNTWL02OG2CcjVD8kos5YEpciK60kRELEmFs1M4OPmLWwR/3K9JIMIKKn6xvSBiC5AAAgAElEQVT2zY4Yk4TO66tXqADLDypMkBTKcjI7RkvDfr9nUc6QWkAQWGl4//y9cRsPxAyopvkmjhWn82P+9vNf8Ga4Ztv3XN3d8vLyFeLRUx6fnPHNj75O0/wNt+sd7eCzPNL9iEqmlaklXJBa1YVTNG8HhjZQxAJ1opmMfclsSiHQIumkL+oF3nk2+zVNn5isEXi9eouNipmqKQrLsqiJIeLcwLOzJ0QRud3esd9suavuqG3JXbPl5nDHQXTIyhIyW1GGCG3HcGiIQyDOSvx//884+hf/EvXqLXLXYWLkuLJsO0fnApvGUUuN0SHZLsRsdyxysMgggw9jjI4479jvVgQiRTHDyIq2aFHK5ngY2bTXfHEpaWNHLxxFcZIY51pTlnOaakZ9eoqwEl1YDq9f0g4DI+szAs4l+Y8o083SxiaQPY4AeTYk8kAQ+JDzoKFHRY00loujLCfWDYT4ICA+CJABQe/JBI2WTdtTG8W8sBzXFVVRTt15Qcl3SAITGPygICSERiuTpDi0xhaWs7MjiioZYNuiRKrkrSlkAiKH7LEyriEqm+MloC4mFtpY8MhkpzTZ7j0L0n1JLeoxjnvAXBiJgugToPSOY4IgSTDkBUqMoNCITwYy0eqBZ0K8P08h5CRrJMY5mEHjwPgGyduBmNix8QEYG/OH3LNspzNO7ynu5+C4fj04e+6v5h4eHfV4hRC59TkBoM458rB5BySNE+swMTC7zTU7W7M+vkDZGULZDBaC1orgs3mRBBkTEBgzEC5lirFq8npJhldaSXweL/0wTJJHkJ6LyHFSiJjwDmUJk9eKIkaZAf7RbC1plWtdYI3HFjP6oqLvO9yQmJyuT3tMoZJ2vJZqOhetNFVdM58tsgSBZDEvqTMzVmmdAFdbILj3PnFBEF3ERU83tIimz5iPmuJ9DJ7BJX1b3w+0+w0RhxCRJDYR72UbQjbjI0zzh4cmqiPKnfMqMT4zObJHH47JnDeOI0hphC2RISCaBmktIgwwRFQIKBExIu0FSi2ZFwUz4ygLi2g1273j4Aa67gBDS+s78OBdJASFKmYYWyUwMa89RmeAUSfiYXqeGq0kxiiqyoLSxGnUpjmXQMyMp7lkXtd3HU3b0HYdu+2ew65lv224vd1zvVqxO+w5tB2HrkMKxdnFE+zxktnFM46fPufk5JjZYkZVSYRwNAeHGwJ957g+rJGjMZeQSK2YHZ9jiorZ4oR6foxUGv3yc9brFc1hm4zH5VhAGONfmrs+F1T8KOUlswhEAK00ZVEwn9XUpqRUJaUpKIzJ3cm5EzqKrCWcZ+XUFfqbj38wYGzEPUy7iU4gcMwE/Mk3lzwXe5RbY/0bhtVLPn87bgjSJne+XHC322C0oq4qrEnGLF3XMXQ9jNWO0a1Rwry295+Yq3UJwE0OmFrq7PyWEta+T3paVWEpimLSIR1F8keYROTWDJ/1Vv3QJbFin9pnXRSUZUFRFAh5ynNr2N5es7p+zVdf/JyhP6Ckptnt6PcHhvaAUBqlFUZbtCoY2gOt8yAk8+NzhizUfVrOsEXBZr1Fdz3aBBaLJTfX1zx6/AjXHXj1+iVN03F2ekZZVMyOTvnJj/4aKRTF/DixNGKg6R1FIagqxfL0grMnn3D67CNMtaDtOp6+eM7RYoEyhiAk5bxiGBLjhRhpQ8uP/uon2O99k+PlAkjVW58XLzmCbLmiJkVOTMYK3H9stMT7iU9MAOPDnZqcguBY87uv/Y0Lel3Vk6NfFIIgJS9/9FNuViuCkhw9fcYnv/Utnr644GhpWb38BaWx+OjYHrb88uVL3CB4/fklh7bh89UbdpsVf/gHn3JyfoIETrRn3TeZjR0JSiFNifc9Pvhs2EQGO0QqJAiBKJa899FTvvfbn3Dx/AWPX7xgfnpCtZghpKRtGtpDx2Z74MvLO35x2dAEi2cBxQnFk3PKoiJKnUzUDg7aFqsl80JyfnrE0kqMTPU9EXpE7CEGfAf7JiKy1poQBUIZoh/omj1jizV2Tpy04EYgdbztuf1EBaSxGLmgsor6O4rPf/pDdutrEJH/+Z/+Nv/qz3/Evr0HJEYOxxQcp1k1sk8EZjFH1xW6LlGlzQkZE6nFDW5a0GQUyAhPzx9xcXxGs2/Zbnfs25a27xDKs95sWZ4siF7Stx5ijxw2xO6AEIHNoNi97rm+umF1veb26sBHH34Xozqs3lPKO3bbW+r5kr5rOey2SYt0doSUOrX1tXuqqkDLIi30Evp+DzGZihhTUFVzvEussKqo//6Q+V+Pv/eoZjMeffS1STYmmW8N9F1HcXwySQsICSfWcv7oBVpppClTcUeA6we22w37fcfJ2ZyyLLPWqWQYBpzrCUOPysUnpYvp8+dHZ+gm6bwiHGU5Ryr5AGx4V4MQmBLAMVEWmcExFSlipDsckEJRlRVRSubzxSQwr0wCYb0PDLmlxgiDMVViV+XJNDIWUuetJP6rP6P95jdwv/c7zFB4d8ANCikDOm9eA5G2afj8V7+kns9ZzGb4+Zzh+nq6lCAUvbIwNKlzJDMzUsTNmyylqOoF87NHDFHR2YLFo0ecz5YMrme3uePu+g2rV18iDnsKo6hLSzkr2GxTwcPOllhTsN5tCUJRC0VR1JTVjPOLJ5RFyWG34ebtJbPzC6rFDFUV2BDpD1vWNze4zZrzi0ccffght9fXrO9ueP36M04eP2O3uqRSkkdPn0LxaDIaGPqWs7MzAvDm8gs23tH/L/8r1b/8F8jYopD0YcBH7o3VQgQ5uqlmdgEQtaRV4Ow983PnOzb9gSNCbrlOG7uxcu8nUF9i+gOy3fNeWfO4OuKjj474q6tLqmbPvhtwEv5faxiZfOOYklK+IxM0abn9GjP2nfVXiJxkpzg8FcceuARGmc6xa9d8+fnP+ORr3+b87DHr7R4fIqu7Nf0Q0Mby6Pyc16++4twHvvXpp/TNC16/fHlv9AkUVqCa3H0wfcjfPbeRmR8RmK805lyjn6VixRACh+aQNetVMnNThnI25+zJU375y5dE3zK0ew7bNYv5jGfPnmJtiUCw2dyyurpiu90kzeV2w+6uTRtAYyiKgtWbDS4kgxkpJOtNKkJYayh8RbUsqGZHPHvfMlsc8cuf/pjN6i3LxZy6Knnx/gvWtytubze0XVoHZ4v5dLFuGPj5j/6Kb3z72xRa0njPdr9FFZanH38DrQtCUIjYIH3L9nbFl198wQ9/8EP+6I//CQJNs++oZgs2hz2H7RajDY+fvWDXHFJxSmuC0CwWSwIaLQ0X5xVXb1epxdMYtBFstj1VXSGjQMSO2XIBWhOGQNMMPHl8zGqzIcQCrQuWi1Mury+Znz7OLLzAenVJ+UnBcOXp37r78PcOnjLK4NyPP/l//hnhi6/T/Xf/LYWAoEGgqeqSFx9+zI9/8lfvFBGkkTg8rt3TdnvI7bMudNzt3rLzG3xuIYwht5eOJxO4j2kxTqQ2kXULRwMhpU3O7RJYZI3hcDiw3txxt1vjRcQoyepwiwsDSka+/d630EJRmAItNb5raQ47RAVVOcvu5gNjriqkgDAyBNPpXcyOCM8+oFCWv/nVL/FC8ouXn9O0B4iO9x+/4Pe+811+9fkXfPbFS3aHLNmQ9ymJURiy5IggCoUUNUUEt+7Z7hqqxlA9LhD6HhzSQjIrS4xSNG3D+rDBCQ9WptgQAkgoi4qz5TnKKLbNFpvlh1Y319TGIo9OaFzLy5svObiWLvokg2A1KIXFE7YtfrUlbHvEkJQyvVQILVn/T/+c4s//DcVf/CV602Fk5KiQdFqybQaudwdOS402EqEjQWbgY9ymCZEKDjHJ9TSdZ7O75fL1V9SzEz785JsYW1Haehp/i2dPWB961pef8fL6kq+/9y3mpxeMOt2lKTD1MV4aKl1ypkuG11+hSMSAtu9wwSGyiWcI48Y/PVdPRDhH1ycj0HYY6AEhJUFrkJLgEiu+Li0+RlybytUq75+EYCI1RZKBUYIVFSHA0A20wXPMjGVVY3QyIvMhGaTKTMKRQmCsRRmT4pwxyYtCK6TWaGupZolBn75c/kQ1AcpC5XnycE7mr4cTNbVuB2KWDBnNdcYWaMSoaBCnzoGxMBiJuVOOMWLACKTEXwM+RnZ7zJqejESdNAdG74MYRzktP72HJAO4o6ZqusjU6ZQL8NNnxXcu7zcev6kL5SEkndVP3ylExkiSa4kjmOyn93oofXD/y6M0nqPvGg5f/YS3V1+iihrfbFChxWiNCwpbZPOoOJIWxg7fBESHMIKrYiIvjYa2Pn8Ng8vnc/9MR4k0ZRKYH1CEKAkhXV/wuSAQEwjsnE9jRJCk+WYL6vkiPx8QUWYyg7gHiaXAqNQWbgqLVBJjNNpolNaTIbBUGoHED37KYZLIhU+SMlNx90FBIpIZ1C5pD5MlD2NeJEQSLUx52oNxMIL/9wtYnp/3u1k1yVnm3W0cJrZzjKkgI0Ua/CJjI1JphM1zIwpkTMxP1XWorqMSAgM5t085no0Og0/FEJs7qYPHx8ih2RO7Sza7BjNfM2t2nJ2eUhaWojDUlaXOTGOhsmGmSB4mSTIjjWOl771eRskPPyRd5aFv6Jqe3ebAdrPnbr3l8mrFzeqWpulpDgM36x2dG/DRE0VASMmiMFRlAlLL5WMab9juG4YhcDCKsrRoq5gvLHHuuF0HhEoyOkgISCQSoUtsHTk+j7yPYzavefv6K9589QWHwzoXJnPsjAGfTXtDlvyTKq1tSIFGMq9T11dpLcu64ni54Gg+Z1EV1IXFaokUk0r7g5iQscG/Jy78gwFjxagpmF8RueonY6T0Pc8WHUPTEPsBfXRKEIL9bs8wDBhr0ZJkRBOSePQghuRAbW2qcCQxj6xvCYSH2p0gYmpvTQyl3N6SmZVjFUrApDeitc5aa3IsCBHDkALlg2BE9GiVtAYFGhfTJHb9gOsHYvA0+wPaFJycXuD6lqvLLwgutYVt19dIGWmG5KSuleb5iw+ZH18glCUGweADu2aL9QPGWOb1ESiLj56uOdAPPbas6dod280tt1ev6do9od9TliUQsVXJ8fyMJ09fMF8ec3274uz5BxihKYqa+fKE5ekTbLUErVBC8ejpC4ZhoOsHnB+oZkucbwgx0ncNt5srXn35Bd/85MX4mGn7lsPQIYJHacMY4MkgbNJXCVO7DLkS9+5oYfqb8ZAZZCXygIh0D8TmtQRi0mTZ7bbTYhtC5OAdt4cDm6HHzGf84R//Ixoa2v6OcD1w2N2xfPKUtusIbsBEQVFYTo5qjp4v+f3v/S5ifUU1S4CM0YJ//I1j1m3Het9xt2+43XUMoU8O4EKyKA1CVzhhKI/mXHzwGD8/5vT5ezx68YSn7z+hmC0wJlUy+96x2e746tVbVncHNnvH3luG6gmmqLHaIAT0MTK0PUo6Cqs5PzEURmC1wCqBxWNlYKzuijBkditZdxQUMoeOEWFVDH6PHxpoGqqFRpmad+rSGTQiPwsdE8saYUCWFIszXnzwCTdvC67fvmLo01hJgEUkMTXi1KIBpDmmJEIbjNHYukKWFrQiasUQ/D07JZ9/HEELKdLYUYqj4xMWyyO8hy8+f812sycIKAvD6voGKQMezxB6ZgvN+0cVj1+codqWu1tH058i7JLlBSxOLVV1gdDH2CIxQIQ8pSwr6tmMxXKJGzpslhHxznM4lGgjscUsAbTeU3QG5/vUDlKUSGUpZ6c8em6w/gy4+s+Kov/1eHAIkRP6FAxSjE4uv86l5FIagxIJIAwuFcl0FNiiIsaAlIYjpWnbFmNLhDJTu54RMq0tuQWHhxsIQEiDUhEhNFImowSZ15aUuKQW7DFCjbFpNChgZIg/MD0LIYFZY1tcCCGx7UUyMxGIpNucNw5SmcSy1warDAZB40KKlQFicHiZW3N++TPi+pa7f/InKBGwQ4dQMgGLOjMQTIFGcnuzYn6SNNYP8zm8/CUAalZjjy+4+9k1pb53hB3jgi0KdFGi50uoZxwfn2Fmc0RRcre647C64XB3TXN3TdE3gEeExPChmvP46YeIYo6yJZUtuXn5EicEw9Cj+4b+zqO9R8cI3uH7ls3qinboMXdrZFlipMR2DTo44tCzWjVsNiv2hy390HPz9jUDirbZ0x026LLOMTEmJqI1PJovCM0pDAO75g4pRHZ3TwOt7ZLx57jT9s4RpECqZKoTpJie+agXDvCTtuF4v+X7MXIeInpcD8nDQ6XWT+ETiKURxLBH9h1nRcFvH11wVS+5ag+83N3xnX7gMyXZSpnYGahMnhFTziKRE4N5BPyVEBPze1wTYnzXgC+dz32nySQkJAVXqxvsyy9wAZ48fo67haZr2O62vHoDz589Y9f1uL7h6s0rHp9fsLu9xer7dLTZr5NpnrlvxRyBi3enecrj0JKrNyvsY4N4nDpnxo3cfr+j7Tq0LpMRXoyoVYGRyWREFZZF9ZiLJ2f0ziUGO0nH88svXtIcGopciLE2tTgKkdilzju0KRBS4YXi4ulz6qpKbehuoLIFARhikjSq64pup2nbAzEMHB8dcfHkCboo2W627Hd7jNLT/QzBc/v2kvWjc+bHx9SlZd8knVukxFZzjs6eUhbQbO6w9QmYmh/+xb/n8y++4gklp09r6rpMYnNa4PF8+eWvKKsFJ/8/c28aalua3vf93mGNezr7DPfeuvdW19hd6m61ujXLaWQ7wrZiSRgEsokJhkBCsMEfQoIh5FO+JOBAYyJETCKIMQSDYutDICJWC0ltEVsIWbKGVqmruqvr9p2HM+1pje+QD++71t63upo4EQ694FTdc84+e6/hHZ7n//yf///0BllZUlc7Hj58wPHxCccnR5SLDLzEe8l229E2NUUxYTIt6buMvu85OjnFWIGWATa4vKpZLI548eKcbldhheRsuSRNJJs8pbddAO/6lk43yKym+VYDeyj0pWe9L6aL8OAfPsD/6q/S/vRfJZnnWNmy3Vzz+NEjJpMpSZ/DgN3LfTeV90HKQCuNSjUylThMlFyKxIkoqyOkfAmQ9bEbZ5D4EWOiHQstfmhFFpT5BPD01tAZg9Pgo3a9kwLjBdfbFbN8hhYK2/dMJ9MoY7AFIch0GsCnCBC5j8zXiCZxNJlQz+c8yjKuuxbbG66urrnnBcvpEdNpyRuv3mWSFXzt6x+y3rZ4oUJrFh7hTbitQoy5FlIiSUmsxl46GulQMxkkoLRgUZR4Z2jblqqOsgTDeuAFuUq5uThhkU3JVMrT54+RUpIlOZkOknFNU7FtNuz6Cic8fVPjU4nQEikTfNNgLlewaVCVQXoVWVYerI1a+xL36c/Q3ryL3naUv/bPUX1PoQWqTNlUHbvW4KxgkgfAMdGxNV+IiEsP654AZ7nabbhYXzBfnbPY3qCcHiHkQLaR5EevUPWX1Nstm80ViK/xWi5ROgevkPmCbHIUJBNkgy0mJIsjfFMh+p5UZoHm6sMz9ILIvhqKYsGsFBU0Hzvv2HaWtEiQIrZDe4/0MFss0FmH3G6p6jaAsXGmeOGHYCfOoQGkhQ6Psx5bNxghmRQ5RZriCQzToVswG9q3E02ShO65NBUILYJRcjJUdWMe5ixe+kjOCLqmw672EhVGRL6pENH466UXhYzDB9NIJULX0pBLj12mg0yZH9jiIk5XP+Z2A5FjkIUYpOQ8YtxMR2m4mOP7gw0mALERsB1jrci68wNsSmR/DHIRHwFEX4JdxPgZfrgbI/g3/nDUCg1fh1rpIVbIspy+7zAmAJfDHhH7AXFi6FQM43roOZSAsy2+7nDdJtxn4UPre2RoxocZwO1oBGvjfVA6zMGROQzRyFzEPzmQSzhg6EopybKMo+UpRzfeROgJXiRBfqOpqOuarrMY4xCuwbRbhOuCBMRw/0XIlbVSQQ9eDwZ3oGUgHygZtdSVjkarwZRJyfi9VCP7doitB/h+YCsOT+/lJ+VBuji/1HhddiyOxXFJKNQdPvLReGx8wAcmr8Mtj58nRJCCcPHfUgjMqDUKzot4/pFNLAW4AtvkpN6RSclUJWTWBNas91E+Bown5jgCpyUKjbABdG+9p3c9fbumdQ1tt8VUV+RZTpallEWBu/UKs+kk4l7B5M/00BK7Q7sukkhioQ+P6Vp29Y6m2lHvttTbit2mZ71puFxteXxxydVmjekNxlrqpkXJAFBLKcdOFOslXqYkxYz5YsGkyAK4DjS7BrO1oMDYntVqg8Ogotb0wcMcn4fUoBJBliumpaLa9uACviBVuIbBM8XJoNHsohxG8MOQoaAvJakOXitlWZDmGUmekeQJQnkYzCMZhwxjrvcxhZjh+O4AYz2MegIjxuYjhduBs0i3QfoaL4KzqxOgU4WQnjQL7mYySSPTQ2FNj9bBwCrRKiyqYnB8C0uUG8V7PVhwpo/slbiYub0mqJRyrJiM4FPUHfRxcfVDy0IUZ2aoDhGr3DHJkbFNZdCOtDZoAmXFlOOTG3RtRbXb0Xct1lh22zVt39H2HdZaJuWUxclNyskMKVN2bYPt22DahSPJSyZFSZ0XocLlPFmRUdU7tts1XdvgbcdufUVXBwp/WZYUkxnldE45O2LqYLE8pcgnpGlJkhUYEzSipA9mPzrJaLpQSQiCzglKGYSQtG3Dw4f3uL66pOu68b4ZGyogCmKFyR/cURgzwP1A+BiW7H4DDM9GMGatfr/M7ZPJ2DIQE0fjLL0Jzyp0/loePnrMVbXBSsF8vuCNT77FvcdfJ5E9hVKIfgbSU9c1za6mSDLmJwu0EkyKCcU8hdoOBCSUFNw6Tll2gt1Usa4117uMynuEBaUT8uUSr6cYXZAtl5y9dZfsxg2Wr9xisliQT6c4FFVVs9lVrLcNz69qnl30VI2kczkumSCyCV5nOBl0epU35NKRSkuuHEcpZFmCjkGONzZq4YT2Adt3YY4cPAA/Vhhiuy0KnRQ46+i7lrauKHQeNocYFI24bYgKIwgmR6BKpDmzoxOcDdX/y/MnvHrzmKfn16x3dRTxj9uiAIREZSkyTZGpRiaKJM9Bh+TGwX7zH4aL3zO3RExeyiJnOiko8wxF1Hn0HqkFeZkhlGe9WUHEjduuJ0uPyPFY07HabknKI5K8JC0ShE/xPkXIHKUzkjRDJaFVFDw6ibqOKmz+VtmQVMngGi+iULhQCiViC02aA4okDxXIzAv+LGDs4+ZPeVD9m/H7V8vv53b+6f/P7/dnOVq34w+u/3cA7hbfx53ie8fffXP3O7xoPxi//9T0z7NM747fv7v+NTZmfx++b/HTFGpBbVf80epXxp/PkjM+M/vLB58q9oAmw9IwBLtxB5DBsVR4hXEimkdGEzMXdCZlDECVThDRtDHsC7HccwgYvLTPhiBSyPD/3pjx8/cvPIgYPGPxCWHDvIO4Zg0i8n2oqMfi4BDnhaAydHAk0ZBEqFCMcN7ijMEHwa0Q5NoBpHDBhA+LX7X4qqZ5909oPvU2aZYjeot14bpkrI53bRuuWypUXlAsl/AwXnGioSyppKLxIISPAYZHCoVMUnQxIZvNUeUEkSQYZ+k2a7quRkoCM8d7sA6lU5KyJJvNKY5vki9P8CLIrTR9i3EW7WWQ/6lrpHYkTpCKUCwUQJoEjWyaGm96GmNwbY1ra0xb0fc9db3D9mGP6toGj6C3hm3XoJI00vU9XgpUmiGyjKTvKaWikQr71tuox4+Qmw1CePqDbhoIxVwpgr42DGviuNKOI+aJs3zNtOStIhGCqQoe8hKBQaDKScBiTIc3Pco5BBaNQAkXzARURlkEbbm02mJsz1PnuEIEMGLQADyYJkMHwmA0Ec5xKEjvz29gxxyaYzKM0YOR33ctF5fnSKWZz44o8iKai3as1htu3LTMZlO6znDx4jmv3LjJbDYjy/PxPUZDSg7V9oY5M576+IUQVHXLRE35xOI1Prj8gCxPcS4wuqu6ZjY9IklCkbHertBKkKdleA8fjO/aTYV3QddZimCqI5Umy4vAKiawjbz39H0X9OoSFVqOVWg77vqOuq7Z7Xb0vcU5x2a7ZnV9xeb6grapSLMA4BpjWZ4chURSKpqqoaqavR6gB5xjt9mQFjlFEgrYiADU9qYLmtV5CSoLicuJZbZccnV1RVq+oJwf4dOQfEqtUAKsbek7TZpqZtMJ1nRsri6pq5yuzLBdCc5R1zu6ztD3Qf9WJ1lgh6oe74KWoJBgu47NekNeaPpqh21qkJrF8hZZ7AJDKTrb4vuaptgiEoWvoT83eDtAe3ugYnzIAF4g6gaePcO1Btv0MXL0rNeX5NPi5eQrsvZgCMMdIhWxO2Ew4Rhu8EEq7n0kPfkwXw54AN5HPp21EbDdA0MCmOQlztqoxxfe0brI0ZGhm+F6fY2WCUWagwhaqlIK2q6haRvyNEeJIIujdQIiSIsEZpREywAKpEpTpimzLGFT18G0pW64dFc8fvqUu6+8wmQy4dYNSVU3PHj4nKoJMhd+uLHChS/p9/iS1Cgkoge36WLuBdOjknlWYkyHcB4tEwb3+IFFmEpNphPwjl21pelr8qwMoEoEK4QAbw22bbHCYrsGdIrwGmEMfleTGQ9eYgNiGQuHobdCEOS67NEcM5niaoN853soHjwgWa/JtKDWIVezMnS8qdh6LX0A4QaiQdi7JSqRdA4u2y3Z6hnyxYwjY2jjnoAQ5NMzik5gkFTO8rRak+/W6LRHiaBvf1xM6XVCrxNqBD5NsX2HMwbjPTpNo/5yaMG3B8uZ9KGbQklJRyhA9s4hXQDLhVB4JbAqIckKsjRjnib4q2voTIh7wwPcs299AHwHbML6sBfZrgfZYmVo906ljJoAgXVY5Fno4tIKpSWpFigFXoKQPubE4WmE9FiOcUrg4spYJIvn89K6HUG8Ye2OkhmhXX2IhQJwFdhpByDsIAMQJmP4t5QH6eLet2MvEzAkJcPHH+x9fv+6ccmJebwbc/eBYTusT+5gfTosFPrxvwcIwZDv51kAACAASURBVH5NYQCiYQjc/P6fI3A3zs2DxUxKidaa2WzKerUJsWR8hZcgBk+ZkBDxUofxsLZF7UuBjVrFoTAsItg5XOHIpTk8hhONAGN4TuoAcBy6ZHxUdgmdlVJAkqRMZnMWx7dQ+RKZFAil8dbQdh02+M7i+x3ry6dsr59Tby4w/Q4hHDiBVwolRJQxiLIEkdQQwFg5asdqpcYxNZDqxqLL/q4dPCU/jhsfcYXx/g3POZpKhjV//yvv2ctgHCBvQVJjHG77zzyI8R0u4lvxvgkZ6mRCjJ4nbpDLGNixkeHvfbgnXmm8Ugil0MqRWEi8jzIBniye61QIZlIwURJLihEGaSW9FwH3cj2+D7J5tQJMh+szXN8FU+S+pSxyTJHhtMKayKCXEicIclpx7DrnQndoXVFXFdvNhs31mu3Wsq2COdeL3YaqjSbKfvA2GrpTRNiwx/mikCqNMGAAW5F7rMJZh+kMXbUbMcQxxToYxwNpwOOQwqFFiPkEYe0V0VhQqKArPWpqI0cgVmsZiFciFAK0CnqxSZTFCJ4dexb5frpHXejvjMMC3y1gLD4EOAdJahDLDew9Y1rq6grft0gcXTTI0prIfk0QTpCobBSFbtoKZ/r4PXhnomAncUGJun7OjfTwsBDFRUoNQdCwGCZ0ncdYizAmtr9C0AMR+3PGjxM/hpb7RRcRW0F0ZJ4IvDNRxFqhdcpieYa1hsvLc6rdlr5rg/EEFtNUbHdbzosnvPrmO+RpRl7MSFLN1dUK3zusBGxLkU8p0iywcrwnL0uePrmg2u2iMHNGvWtxvSHJMqaTGVIm1E2LVxu89cyOTijKI1SSYazlxbMHzOZz8rxAeR0qI30bKgVJhneQJkFHd7vb8N77f8p2uz1oPxxc1fcAxkcZroftHsMua4eWifE1L4XPDKLKI9DifQy4hlwmaEWGBc7SWoOxLgTNPpjgvPfun1AZw2x5ytHJDW7eusXF9SOmpWI5L9gtZ1w+f856vWO3rVkuj7nzxh0WZ0ucsVT1FXp9Howj4nlNc0mRpSynGdYLOiStCQulynOK117DqCmumCPnxxS3bnP86g3SMsN6Sd06qk3Pk+fXvLja8Pyq5slG0FGSZKEao9MCB7TG4vpQVZ4XknkGuTQkrqEQhsQXCK/ACYzfAzNYG5JKme+ZJPEC9rh42IizcgZCYf2GpqkopstxkQm5yxBQ+IEcG3d3BUIjSEK79sktsjSl7xo+/87raHWf9+8/pRsSMiFACWSSkMynJGWJTKJIuDzQlPUwFD4GgxwIldJ9MOZZTgtmRUqWSpQz3Lix5JtPnuE1pGVGvijYXK/QqaJIE7yxSJlS1RWb65rnF1teKadkyTGCFGsdTduR6VCASNIsgESmxzqD86BVGgNihyMULpy3WOdxrseZoLMkZRIY7jKAfVJphHc4s1+aW7d9CZAE0CKlUIvvuKLeq36XLz//EpW9AuCnbv7X/7+DsZW5wmJY98/45Sf/FQA/eePvcaf4Xrz37Owlv3P1T/ij1f9BoRZs7Tl/486X+Kz6SXI5ZWsv+PXzn+dp8x6pLNnZS25kb3O7+Oz4nhN1TOcq7hSf49PTv8TOXpDJGclHzsVHdoOL7d9iaCURIaiUKgRWMrJppRRhekhPmmUcUJMwxkbN17DmBw1x/dI6NgRmQ5FCyb1xX9BCe+ktgYMCkz8MHoLmcd93WNujVWApdF0bdKO9HTs3mrpieXwcdWZDEuS6lq6rg1GMc2APzAGIIG5s1bVNh/rKV6hu3yaZzBEi6OM64dFK4YWg2m4pipxd22KtIyn3AJoXEqs0bZqxtSaYP8hwX4WQyCRDlxOyxREyn9C0Dc2qoakqpvMZ85Nj0lTi+pqqN6RFyfTkjOnZTfLjY1rvMV1PV+9YP3+Obzp0WmKQtL4izQWZTnAqo0kKKp1yNF+A0hjraNqKzfU1Xb3FtDWub2PiFwJjJYMRHM7juwbT1hhPNOEL+00rFTZJ8EqRC0+uNNUP/Qjqd36bpA6Acm8Nbbs3RhqHg/M4IjNZxgTtYF87F/A+jratWSrJHVKmUhKsrBRpXoKQ+K7F7YJEg5Q66NU7ELuGk1QxTzNOT2bo5Jx0s6bsWv7EOpxymL1X7jDsxrGGONDtPihqMaznB9HtQV7yUuo5vHazvsKankk55c03P01v8qBh2DRcXq04PTlms9nw7Okzuq5ltlhQlHtplvliyaVd0cjN+DkvlTDGcxtYg5LOGE7LMz73yuf41voBAknTNGxWK6rdljt37jCZFFjruV6tSYsZ09kM7xzVds1uu2a7uo4ArGQ+n5HlwdxjtliACC2ipgvMZ2cd88VR0E7MC9K0ZFdt2KzXrNdrdpsdRV5grWG7WbHdXFNt1wDcun2Hoixo2pYkSUkWKaa3PJcvuLy4wsSYSUhBOSlpmpq2bkK3RQQ/TN9h3QrvBX17HBYWmVLMltx54w3ufXCP8+ePmcymuDRFK40oMrSEVAjauiPTQa6rbzRbevq2YrfL2K5zvOnZVdsQByuND9kKOlEIoWjqjjQX9E3wbVhfXbC9skFP2VqUTJmonDSbMJ0dsTg+Zb1ZYV3NdneNSBN0lrFtV5imwzqDt+Da8JDF4UY/1LqEgG2FxcciO1i5xsugpTys+2OLvwhsPqlDTBE0AF0AEkPP6QgKhTg9xA1D2zLIGHP4UVd2hEx8nN4ujPl5OcH0JhRjhMDHtUC6YDa5nM958OH9IBmjJKXOcL0jS1Lq+pqLq0uEVCQ6o8gnIc7Wmt4YtNKkScqkLNEEoCuVklmSoIwFr7DGsOl2fPPDD5lNZhzN5szmM77nU29je8+z55esthW9izG3dAjhIhjho0xoYKgqkWF2VVhrOke5mDLRGU4nJErRWkftFG3X0PmO3huUUHR9S9NX7HYVaZpS5kFPTwuF7XqyNAsAtPc0bY21LcqGwidVC+sdE51Dpth2FlO1MMiq+D1g5FXoarRomi9+keQrXyHZbFDek2kVYmytkEmCHFvMA91ZKxGB0ADm6DzFyIILW1FfPeZSGBbX16yqL45jKS1PmAmJzxL6VPFidYluKhJj0TKhQqJ0Rqs0TZqydg4vJUIr+g6armM+n4B0wSTaOEy8GBGvTclQRAzF1lDAN9Yjbcwb0xSvNUanyEQznc1wztGuN0GnE2CQHfE+MBuNZZ99ha63zjhM02KFQCeaLCsCJh/B2EmRUhZpYIlLscc+CN0hQgTAUhA6Tkcm7GiEQyxEswfD/F5nfDgGxtkAng1EDBeBFzfkc8PO4gdd6UNAVh5sPvF14iC+ivn4AQQ77FLheoa97yD+CtqfljHLjJ87rA2jsde3HfudcI8ZfxSY/cg1DSc8rFvDK2PsNRC4sixjNpvRNi2d6ZGix0fgZwBkI7w/wLw4Bv3X+MUh+C0Y1jYZwXsxgFWe0M0rZGBliijtGMFbJRXSB2btyGAe7qP3IfO2JryXkkEmQKckxYS0mJOWU8qiQKkUrTO0yvCm5vH9D3jwwVd50jZ0zTVRvAPlFFoEQp1AjZKGoVtBRvxkILrJIDkZsZxBsDmMKzc+g/GJeMZuhxGU3+O1ByB++NnQsbv3XvCjzuj+5SGw3xe0IfC+3QhaYgMQOZQmpJJjkd5HEsNQjxWCKI8W82s31E4kbmAqE4z7Mu9Rke2rYqefE9ApwQsUVgoaqeilJXEKicF4F3IAa3B9j1Mai6Bzjuvz59h6S1MWZGVOniSjTxIQ9PLbJuZWwXS4qVtM11E3LetdxcX5FdvK0vaexnoq2+MVJFKSCBnxsH5P6BKEjpJI5JJSU9dNyHWiRKjUCZkMHj6+d5hmh3ChAw2pGA204vz10WDZmmiK7ELHeiIiG1eFZ6UTjZShsK6SNIDBkqh7LJAyPHs5GsgJEimDnJvwqNiBz7DujWbifNsa9NHjuwOMHYCh4ZtxkMbB7w2mDcwWnGNbV+A9R0cL0iyl7zumxQTb9TjbB5aBUkHvI4IeSZKQJUGQ3TkftCFc3MACSodK0zEgs3av03R4ZFmGIBhfADhhGZGngxfH2tE4pwc3775v6No2EjUdbdMwWxwx6mx6y/wYkmKGiUL29+99A9Pu6LpgNCCc5dG3PmS72jCfHzM7WrKcz9juKqpdhekcd1+bcuPGKbN6ymq1hr6njnphb771SWwUbx6A412348mDB9z/4H1M25GmGW+88wUWZ6+gspyqbTk7O8N5qNuGftORKGi222AcozO6rmY6m+KE4XpzyR/+8Z8wmZ+RpMX+UfugKWQ9eLVHJYT3o94hHOy3HztchkkWh44xIXCIkw5C3XZgLVjnyFSGsYbeGGrTYQFjIxjrDLXtAc9sOuHGjTOuLq45npwwmeZMpjl5seTxw+fsaoOTGXfe/BRvfPazpJMc+obu2WNWF8/Qo6SCoPHTsKERNv9EJyRFijxdwHxOn8w5evU1pjdvUCynpJMMA1St43pd8/T5hnc/eMKzraQhx6oz1KJkolVoMbaWqurI84RlmTDNNbNcoTH0u0t8s0O6njxbIkkY6tEqLi54Gcx65BREEGR3zuOxOBfYvYeArBWapJiR5JPYmpQMxdi9Wczw0IZoKDq3CoJes5KKXGUkSc7bac433vtjPveO4ux0zpf/9XukaUqSaXSeks+myDwN4KwYtKOigZtndD4cJ1ycu+GjgyKQFnD35JhlkSOM4fzqiiLPmJQFTVtzdb1hWU24ut5iupZUK9586xO8+8FTdldruuuavJlx/6tfheQIJxK6vqMxDa+//hny2RKZJBgTLryqKnbVjvniaFxHvA+i52mSYZ0NjMEkQaZpELZH0FuLUtGsTqoA7sXjy8+/xD9671++NAfemf77/Cev/eOPmR3h+HPLv8U707/A3//6j3/H1/y7Pv6X+/8x9+t/8x1//w8++CtszAveLH+U//S1/5X/5r3P8789+i/5vvlv8HO3/3v+2/d+FIfhx5Z/i584+7v8d+//KP/w3s/xV87+Cz43/ykA/vO3/jm//uJ/4Gn7Pg7D3//6n+dv3PkSP8BPjJ8jpQzma96xrXeBGS3A+4HlKkmSZB88wb6QEKI6+r4fGQpa65eAWCkH59j9auWcwcY1ZTjGYMMfhuIi7gXhNaOxRAz49/qebjSTFB6yJIlj3ZLo0DbjTWC9eReAQB3lEJy3GGdoTU9nOoSWKK1QSmKtRQymTs5Re3CtgbZHipRJUbDbbdF5EVm5ltX1JXk5CY7a9V7vOVyjJJ0tqFYXZN6RI9ACnJLkiyNmZzdRiwUXTx7T7HakacatW7dJF0d0XY3vMvRiycnxGeVkRlpM0FlO0/Y8f3Afs91g6x3V7prZbIlVml4pXB9YBLNyznQ6o5gvaR441pcbmrai7RqM7fA2GC9o4fFa4VxgrIb2RxekBGKxSsfHL70YM7ykDOyAtjcIY5gi6QhmMyImMYtpSaUVTdvRtrFvep8/xgJweO+h5Q2gEoJnwNYbmu01P1FOeSvLWaqUBNitrkjzkjQv0Um+j108CAsaB8aijUVVDT90fJOL2Rmv1xtevXjGeVPxh6lmI2WUHDjIjg+LB+MY/riE8+CI1+ReCpJkDFgdVb3hj7/6B+TFnNMbN0jzjPOLC+4/eBANp3r6vuGP//AP+MwXvkA52Rt4ffoLP0b1jffZXK5GIz+tJD6arQ6Z/WGafbXb8i9++19x/+Ie6h3NtJ/ifdD2XK9WPLj/DSbTGbPZnLOTY549v2B99QK8INEaPS+5eeMGu2rHanXFZnWJMw0GR9sktFlofbTeIFwwP5mUU0wET4Ts+cbX/pjLiwtMHzqS6ipICiQqsCeyRAMSbwzeWObzBQ8ePaVrg6/AdDbjarUZr0opzd1XXw2GXd7TdT1CRrkrBNp5lDOYZkeSLyimE6aLnLquePTgAefPn7Dd7fj8D/97/OD3/wh1taHaXFEmnq6q8dU1F/fWoePJtDhTUW0lT7se4xxnN84QStN1PdbBdr1mMilYLEoQ8PTJc7rdjnqz4sXTh8wWoYjTdy2r1Tl5PmFxdofp8YLprOTO6Sdw2nO5OifLFpx9+ozd95xz+fwR1+fP2Vxt2H21xfcHwcRhYtx1qH/2S7if+Wt4eRriFCVo7JrMtwyRZrOp0ZOUJM9QWYLSKgJcPhI/wJsoQCDFS8Xng/pYyHp9AG5DvWL/2vE1NhTbluWC5y+eUvUVbohtCSCH9oJCZ6Q64d6Te8zWE96++ya50GRSMy9KnOn44Ml9Lq6vA6NRquDsjUAJxaSY8vrtV3nrE58IgIPygZRoHc4LvJc473n6/AL/h1/ltVdf5RN3bzOdlvzg93+Gx49f8OjRc775racYD96FhPdw35IRkAl3qACjsX3H0/dX5O+cMVnkzIs8xi2eztRs6w0v1udYa3lxfUGmEhbTGbN8zrQoMV1P37ZMplPqtkJmOcLkNKoNOuu9we86xK5DudB9RufwrYnssLA+hSQ4mMqqyNpExgLqNMOlCl+1JBIkKrCXvMR5RWt6pLBkgBFB+xGd4HVClaaIoyNaoXnRbHj3/Wdo8R4vrn92fMSX1nFNjzmawa1TvLHsRIKqGvSuxjU71HoFqabSCbuiwJmKUqZ431JvW+qrilkZZKqsElhvUELGmG8PvLW9Ydc2Qae9bdACskyTlxnG9FRNhTSaNM3IigJvTPQn8VHSLOZFBKZcbwx9b6LZZ1g7excc152FIs3xKnaBSonAoaQPMh1iX3Qbu4AimBgYe4FUJJUa46WXC2Vy1MsUYsiD5d4QKhaSjT3YQw6m/OBFIQ7X+qFbNXaYfTuVM352/K8YnyJj3hjomPuc3Ud3+xBzBR3oPbAc/9Lv46RBc9Z/B7rbx3mefCyA6/erzlBsEkKMQJxzFmM8dQ0XFxeBhBZZoMaaCMyFcwvyDoEl653HOYGUmkQLlHRYaUeymZT7ln7vB7mWQHxSkSwW8peYT8f41jlH1/cYs9dIHTrFBv3tcPIebw1VXbNer3j46BGTxS3yyQnZ5JjJdEmaz8jyKUUxYzGZMCnmLOanbGdH1KsHB882zPNEqyiJM97QjwHZh/wvdkEPEid7jZAxZjoETMN9H0Bdtc8nh/eKOrpAzM1M7FaL48btCWOh3V3u2/fHI15LJFAMzGsBB9127MedDBKYQo5qy+F+aJBpgswLZNuh6Eicp3RQWIf2e31m5SXSQ+LBEVr8X2jJJtGkNgPZUDtH5zw9RNkBGcaqsFTblm63w/nA1Pd4lEzGXMT44KXkCPMmeCu0kSBiqTtD1Vg647BOYF14YhpJSrRScxYlBHoQXBGCRAeZJCk0RV7StC3GGHZVg1RBmi3IxBn6eoPv6qAVK/RYWJQ4HD4Ubr3FWkNverqupes65kdHLOfzsMdG3MZYgq6xj90TsXMlrAGxCBOZ6c4H87PB4niY30pFlu04gA6Bke98fHeAsXi86/bVDDzG9aHF0lusC9oSyoeqnDUtjx895Op6RjmZkqiMflLRtw1pmjJfLHFIkiyPAvyOJAt6E6HVyGJM/1JVTvpITfYeBh21cIfHqmyik8i6i6WJoXI+VDv8PgALzAkzbrTOWvquo21rrOnw0ZG9bRvEfMFkMg8MOw+rzQqdlmRFaH+bLpZsV1c8e/wA5z9kPl+QCMf6/AkXjx8wPTri9p23ycspRZZR1x2PPvwGs6MlaVGyPFqw3qxpml3UVUl55e5rPH74OJ5Hx73338fWa3CWRIUExtgaIXrStERlM7LJgqvrK9arNbvrS+ZFQtvs2F3DtdLIbEJWFlyuXvCND9/nww/fp6sK+n4Q8hKMuk2Eal2WJFRti/MOY/ctXwP/4OOGsRvud3w+zvvRvAn86F4ennV4z6oNrVxD+48l/M4Jj8HSeUORl8yOJhwdT3j2+D7vfOotFssFOk24ujhnt+mZzG5xeusOX/wPfprZzSVdW7F78Zirx/eZF+VIofdC4rIlMi8CIKkU2VlJS46fLUmOlixvnTK7saD3glZA1xouL7d8+PCSZ1c151vH2k5hOiPXKSBpjKHtWlIFk0xxs8iYFwlSOJRwBMsWR1KU6DIn00Q2XdRAFqCHDVsQKqNpgnHsdZFcAKpDtQi8syEZjKCNEFAWM4Yy4hh3CBmCLgam1X4+BW2puEsoiUol5Uzw6uuf5MWLEpGm/NSPF/z2+4/wSpBkGpVpEDYwB1ws0Bwk4cMAGZ3t4wroo3mX8ALpBKezBdI5nDFkWUaZZbzxxl2KzYbnzZZvPX7KUV5gNy27F2semUekeUJqPbkTTBLHNz94n3WT0DiFFY6yLLl9920QBGb0bhdcYpWkLIr9+iIGZr3E2FBcCcz8mJQP1WYVNvyqbRB40uTbl2aB5O+88c/4jRe/wDer3+FL39i35X9m9pf4i6d/m3/44V/H4/nho7/OZ+c/Of7+ty5+kd+7/mUEgr/zxj8dWbXGdfyPH/4svQ8teYWc8bff+KdIofizHn/z7s/Tu5qNecEvfus/+rbf7wPWiHoNP//IrB+Cal76aTj+53t/k629wLiWn//gZ/jPXv8nnKVvvRSihSDajkG2xY/6rlW1Q+vgrjoYV2idjoUc730wC0j2XNvBBGnQcRqqxHIsxIA1JhTT4jUqNbR1Hegbe4JgvRfx/OKA9uC83Qe43gfNu3iOzlmcsbRNTZpqutZQVzuePnnK25/6FEmSQ6yaCy8oygmT6WwMTr3xwYk45jJEt24f/9//yq+w/cEfQHzf95EVoZVZRyMZ2/cUWcrDex8CcOfmKy/dZ+csOs1onKcVAis1ylps33D+5D6r9SXF6RmehJNbt8knM0gyVldX1OtrtFYcv/IqSZbjbdA8v376kPMH94KDrLdIIZimGaYJ2pMIiVYJ3juUEJRCkk0KXrn9Oo+ffEhvuugQK0Lr6xCISwHeECQIPMJF520ZmVoD+GLjcxHB1E0Q2pTyLOgvtn1N+4UfoLtxk/z3fxepBGWRx64cQdtFiYo4eH1sCf22+SDAKNh4+NDBv2grnjjDF/IJrycJond0LrCqsmIaDN2jxpuwdgzsBZ4E0JcrTlNFqTWnN+7wYbMlXV+z6Ttq3/NuloWxN5zAR87pMKneA2Ji/J1UIjg6x04lMe7vblyfnfW8+6fv8rbpOD0748bZCRdX1zw/PydLNMvjY7brK64vLjiuqvGzk7zgjTffJL3Z8gfcB2BSlsh5SdM0o4Ozi0yR8NGKZ+eX1H3FF6ZfwL7hycsJy+UZq+sruq4jaVpM1oOUdN2Wp0+eU+1qvPfcvHWLyTTIJUzKKUpKzm6+wma9ot6sUK7j5PgYoRXGBBfpq+trpNKkaei3PD1dcHy8JE1T0jSjrnY8eviQuqqwfY9QAtOZ0ZhuMplx485rvP/en7LZbMF2JIkaW+yVkrxy5xWePXsW1g9nUTpFaoWP7csBOrNY2+JdipY5m3VwF7bdjovNNf/yN7e88cnPcPPWTRbzKfXuOX29pdru6LseqRJUXtI1W4SA6WRCtWl49OjZKOXkgTQt2G1rzl9ckWYZfdvR1x2olLe+9/Pcv/9NqtUVpq7AWJ49eYTzSdiT+zmJTTi7dczN5ZK6uh2kSG6/SvWJ13nx5BG/969/D/fJFXiwW0t7v30pMR7H6ld+A77n09jv/Rze16hJjkgYjbd0BH2EDImuiestzkcgZkiAiXHDYAEk9gQBFdbPAS9RSsVkf/CaDmYlWkqKNKfMS6qmoeti99fIbIoArvfcunmDyw8veXL+mL7reOf2m2RJSpGXQX4NT5akbNuK2vTUkYChfDCqsbYL7JvocbHe7oJJU5TZCbkUnF9cYq2hrrZ85tPvUKQpd27fYHm04OR4ybvv3WdbOXorIe71pvcI6VDeIZwZgQnR5zTXLfe+dsHxrZLFaU42TWhNS6EK8knGPJuhNazW13jvybIcbz1925ImCUU6Y1OteXz1mMpUtC4UF8xqh3IeGa/RiUCi8Ta0KEshsaYf1xdjHdIapA9GL0pKXAL1D/8QbnlK8eu/iWstje3wQqCMZtcEEs8k0Sgh8a5H6IT5csHk9BS7mHAd57PzLR4RCBujZiPctzWTGzdxWcrOw7P1NTMDynm0d9Rpyuz0GJ1oTN9S9xXCbNB1h0w1+XxKV1fUfYcSHq2zsFo7wnkig3Y9nrrtqZp4f2Ls4KSkNj27TeiI0FmGFwKpJSLPoAVnDELruL0FkEl5QKm4QgRASorQXpumCUIpUDLGFz6uO4czTcQsV4RxMhTxGJh8A4loD3cO+2Y+yM54AtAbYyFr7Ch3NBSbwzkP782evTmIu8aZN+opE4hQUurhL8bzHikkcY6PIGp8q0EDHfaxnB//lsDEjmtEmOUi6qLG1/hhp2W/MI3XfpC5DtjfQcA3AnZjrOgPzp3xeoO0YbgPAMb0rNcrrLEYayMQa6MZthuvZaj3IwVKa7BDHOlHwoH18f7Kg1zcBeKIs2CcfUkeQgzyPD4Q2dre0FsTzc6DeezQiRBYqyEGGRzorXM060vq9RUOCUIzKZaopECnOVlaMi2noCXV5pLt6hl9v4mgqEIhydKELE3GTEF89J67Ye2LMizOY8eRO9zLkHMMQ9z5kK/5yEBGBt1ZhqLDyG6MoyoywG1kgYo96BBz3UCeCDJGwQB30Krdvw8IgoEzjmDOOuS1HxlLh0WIwdsoXLxCpIDSKJ2ErgmhQmFHepT1aB8YyqUE5SCxHuEMUsBEKp6KUJS3qcRbENGjyODpbI8Tjt71eBkKiUIEAouzHm8bBiDbiuDZYPo2yIVZS2/CVQaZFEAkCGFRIhK8pMJGgzopJFIFHWAR82UhAanxviBNj7l563WOT09Cwcc7nOlp2xbnLX1T0e7W4A1e6P0timNEeo+0Lsi0mUCg8MZg+x7fW0yWk6UZ5WzOdHESdGJdkBrr+g4pHLY3mN7QNh1N09H3LR6w3lJ3Nb0r6Jyg9oPddgAAIABJREFUdYJcaPxArCSQZcJ6Ftetj6/dAN9FYKxzPYNotvehLdO7YIZFBCvapqOpKl48f0HdNDw7f05vLGU25ZOvv8bJ0YI8TdFS4qQKwY0nJAzDI4rgiNI6AHnOg/CBei/l+LqBaem8jfPdRwHloOHjZUwCxkU5Aonej4vcaCwUNwIhBFoG/UHnBFZ4nNN47zDWoJxGqoS8nCIi40olGiEVx1mB99BF1ipOBG2OqkIqwWZ9SW96snzCdHrEdrtls74m61rmi2MmRcFiMY8VtyCLIFWCTBKEj039UiK1Glv6q+2K9WqKk5pyfoJDoFQS3HXTJHrLmOicJ5kUc4SSbKsd19crkmSC1cnLxjYjGBuOcTM+2Kheqh8cAt3jj/YmTz4+m8HNEO/HNsyhKuYP/sb5WCkhQOnb3Y6nTx9j8ZSzKYvjY47PTjg9XjJfLCiKEqSkKKacnt2mt5LTV24zOz7BS0+qE4xSSNOhRYIdF02Bz0rU8RGoBC8T7GxCvjgmOzoiW0zJFlNIEzarHetdw67uePp8xfPLmm2naEWJKmZYoYLDpfdoKZiVCZmy5MpTppZCH7Tl+5BbaK1JlCcZCmrev7TREyu8LuqeIXVsBwsVYTXQ92O1W0o73kc8YxAghBpZVuHSQ/C2b1mJc0QIkEnY+CLIq71hdnSKB5I0ZzKbIco5V21P41ysdNmQPDmHtwGwGu7FEKCHNvFQbRcyLu5Co4QmE4qj+ZxEhwpXkqYkWcpsMmXbGVZNw9pYVtseU1v6XU+7foZKJLmUzPOc/OyM9WbD+bWnNiATQaYU0ncIb/ZtKiJokGopR4b3oFsUV4hhVR4DzwN1nGg6wv61H3PcyN7mB49+jtv5Z3De8FsXv4jDcif/LM5bnrXv4fHfJmtwK/sUy+Quv3v9S3zl/H/iC4u/RipLfv/6l3nc/Cmfm/9Vet/y9e1v8Rvnv8CPHP2HzJOb1HbNv7r8xwC8NflzvF7+0Mee18cdJ+lrAOT9/N/6b/5tj4k+5idO/y4A722/wtZc8Jn5X+aV7NNomQHtAYC7bxtLs2xcZwZWrCC2H7sgiVOUs/hX4iWAFfYA8kfb59xBgD+898AsHN5jbHkbBagYg3fn3CjnMlZZhQimlN6jErk3MhzXyjD+tVbkecHRcknXtnjno9tpFoO94eNEZJNH8CGCr3uT13D+5vqa9v33UQKqH/uxUDn2Hu+DiSUe+qahq2uuvOPmcM3WYk0w/uq8p/WC3oOOt8W2IYhRRcnJ3TfJJ1McsLm6wjQ1SZKSZhkySTGxk6NZX1FfX+LW1yhrwxxJU/KiROoMhMT0LV1TkyZJCEKlQumU2fKYyW6J8SY4WRNdguOzkF6MDHTnQMiYwMXAadB7R0YmKx7hPL43oaCkFblWTHyCK6eYySSwSWJcoJQkjTFIb83BFrZPHw9js3HuC8FOwiPnkKYnayoKnXHkUzInkSboEHoZEgAfXZ2F9+PzFkKgTbhm5RRJovDphGwuuah3vGh2rLqW5yqhj9pfYz64/+dL/+aja1L8Vkoxjv9RS3n4WwFVteXi/BIpFMcnS06Oj1hvdgRDrJTl8ZK2bWKCHo68KJlISeGn48+yIiebTUkSRdu3QVPQOmzUZTW2xxpDWxvMTpCJwPxRmSHNS/q+RumcNJ8AktX1KprAWrTWVFUVGR09rihQIhh2lUVBFyV46rohyVJ0kqB0Qtt2eHqapkVXFV3fcnrjNuVkgk4SyiKnb1u2mw1VtWNbbZkv5pycnXF0dIxKMsrphPl8TltVbFfNvgWEsLZUVR0YZH0TmCtpSzaZIqQO7fU+uE87oOsNu12HtY40S5hMCqQUrNaXPPjwfUyzgTu3uPvqCasLR1sH0E84j85yBgkvpRVpUdBbSReT7816w2IeHJxllGkJrFGFUgnZZMGd117j/GnK9uqKbrela2vWV8/ou4rNZUnTNqQpaB20oW1vKGYFi8UZWVLQGsn77/4R282KjobkpsY8D/G73y/niM0af+8eCIn/3s/iZGjbHcBY6xzChSKFtYERK/zL43dYy3zMAcboc0A0Yju2j+3kOl7zGHsGtIdEpUzSAikETd/Qmx6FpMgLcA5hwrqBF0yykkleUjcVzy6fcTxdcOv4BrlOkTLl7OiYJE04X1/y4vqSXdWAdaQ6o0xTjmZTlIC2a2nqOvzex/0izsFEJiwXM06OjlgsFmNcpCXkeUJZBrfsqm7jtQ+T1Y8EBhkDSY+IrbAJzcZwJVr6zrK8lZOWEh01SlOpsKZhkhaUHypu/H6BsyGO1DqY4VWt57i6ifEW6wOo5DszarlK7/EmFBqxHm9cYP0OJIC4SI6FzQOwShqHWn2edPIpbBZIFz4sTnR58EhIlaRIJBlhT87FlKyd4tcZpyYAXMYYat9j8ex+dUn//hrRd9x88uMU2xKnNK333GwqMguybRF9T6Y1J/0JUkp6a1js1tBugxFm3+FEh0m60J4sgtby0EAvRZCxKNocaTXPmv+TrnsSuT3DeBQgBWme42XQiXQjaBRYXO6gyOfF3sBLKoVKouG0VSgEaaqDMRPhXiWpZmiZdvHeiYMNyo1AyiApEOOjsfxHbLsOr9M65A7ORs36WLAbvpw1I0g45MY+SkQFHdPQSUokkAyMx0GP04uBGRuMUPfHsFcPwKtlIOy4wfPlgAQQNMDtS/HUS11O42s/Go/HPfygyLoHg9mvJftb+NLfDmvR6JsiXkqLY662j1uH8wlArB2JM94NfZdxRfKMPgf+AAAfGaDD3RLxacc1Y2DXuuhP4AZQ2fn4fmLslEySNLD2VQRtbZTEGPYDH8bfYIY4kGmc6UKbuLXQbgJoFfPMJEmRSmNtH8hqto/SnSIUm70jUUNHpB+2HeIkCWNwuF+Og6A2XqtntMs9fDaD4RuDETt7IHYYi0DEfcLfCe/GLSIAhJE1HcHT0aR3HN8xzxByDwj7eAYu6O2OcgYxR/cizK7h7AQDQ12M81JKQjFGB/3YMDd9JBJ4pPCkYpidwdvyxDsaB0YKGqUxWiG1QGtLKqEzHcY7nAnP3UswSKSIneAmStpEMF8ORU+vkCL8Td8Hprvxg5xCHH/R1yeA9QNjntG7I8q5h9qgCPHI7PiYV9++Sz6bhkJBZ+ma6PmigqRZIM6EvUKK/ZxzkWDmXI+zXeiSN6F73rgeazvqZkeSZ5RSUkynTKfzADI7Gzr1XE9TtdRVjbOWtgMf9y5re6omo+kMiVUkTmPGVZSXYuH9WX1nNPa7Aoz13mNMHfQWo3xA37ZhEBMqOomSVNay2e64Or9G5HD/4UNePD9nkk6Zpzm3Tk6YFJOgUzJUdQnz1TmPlS7eD4HWOtDMjQHnQ/uEGKp9YSI5N2h8+NgOJQ9uLCPS/ZKWTNSZFXExCi0DbtykVJpG1qzC2j3YZY2hlz2Z1JTlHGcN4BBKUjcty8URzjiqbYWKlGvrogard9TVOhgATFqOz25hcFydv6BtKoosZzqfc3Z2Rl13WONo6iaAYFGAuJyU2CTcN3wAfeuqItluUdmUfApdZ1BJQjGZgutRvkW2CukNAkE5meCF4Hq14eJ8xWRyI5iTyYNhJkKVZ9j8jO3Z1xIjN8Ef3GMON89wDKCqZ+gii6IEEVDYu+TGStmwoRHlC2LC7fBsd1sefOseHs9sseDo5ISjkxPuvnqXvCxDNdBY8nLCnU+8gROa2fEStGC3XZELoOvwVY0UOrAU4nVSFIijOSor8CrFFzOmd29THk9IyhTjYb3teX5ZcX615XK149nFltYmkJToYo7KC5quw9mQbJd5wuksJfEt2ndITFzY5QiCBt0xiRZxc4x3N96gGDdEdlyssqb5JEhFeIcjtGIMgZeSCk0IbIZ2DGvNuPEMG+q45PhhTriwYwwLkFCMu5AA4VLyYoFSCUU5Jcsz3nzzNZ7sOi7rnt7Hhjnngtu9CWPXmD4EDNG0yJqeNElJsxQhNUmWkuiURGoSJGWZjdeSZhIvBdKDsh7ZOkg1q6ZGGo+Umhf3ngKOaZ7hjxecnt6kc7DZVlSNJSs0ftmBacH1cWMQSKEj4ObwPrJj4mbuBrZurPh7MegJRSMEQrulTnQURP/O6+XnFz/D5xc/Q+9q/q/LfxQKRv8Px6emf4G3J1/kd69/id88/wVuZG8x06f82ot/AMDb0y/S2A3vbr7Ml59/iXemf5F5cpPOVfze9S8DMFHH/6/A2H+Xx1Sf8pM3/h6X/X0uuvuA4AcWP8tV/5C5vkUaGmDCPSZW7pUkK8qgo+1CG3GSpLG1P8yDtm5J0oygnadC4WwwjohJw/j9CMbui0rD4Q9AMSkHTWuPF0GTa0gix/0l7kVjBd0PeOC+WPVSGCmCjpSQwQE5TXOKsmS9WuF9S5J4lA6FvoEZMrzf4DI4uJaOCdxBgNrdf8D/zd6bxlq7pnldv3t4prXWnvd+xzOfrqGn6i4wjKLVkO4GIWBoiXYIIg6BBv1AjAQ1JIQvkGAgMYraJGJQMSoSEWliR20k3bQNKpRVTdWpc6rOec95p/3ud49reIZ78sN1P8/ab3dVt4Dp9Aef5OS8e+2113qGe7iu//W//n/Vttx8z/dyuFOQclHSWoPzAas1nRt4+eTxtKemGAhOWpYc4JIwe8TSAwEkfCD0PYvdXYJSdOsNy4sLmqZivrOPNhbnHf3qhvbmhu7yguHqnNKLTISyBbasKJoZs2bOZtPi2o6ua0l1LXqKyJp1cO8euwfHUuUeHB5pnUoxa2bnZyO3VoGKeckSIDap3EGQ1LRuKYSBRJLA2haWhS3wMdGZkjDfgc1qev7WakoKohsTFqbv/mZx2bheeKW4TLkAFTYc1Il3lWGPgI5O2lK1QahVcQJlSSE/DoPSFhsCOgas19jZjPl8nx0rsyOtr2lj4JpEmBKnbVuqjInt2JBC3Tg+cxKeg+JEmkyYbl+HMZJACvhaQIJ3PrU/tWEaW3Cwf0jXh1va8jCbLWhsQeW20gXNbMbO/h5+KOkH0Sz23ksb9DCwaQMKi9WW9aqjjiXKaKIymKKi7zvq2R71fI/BBW6u1ygMdVVR1TVGS4Heu4EOuReF1RS7O8Q4p+s2+BColKYsxZ/g5fnFxITURhOjw9qaopyhtWjo7+8fUBYlRVnQDR37h4ccn9xld3ePbhgojObo4IAw9HSbFcaaaU6GEHlxekZdWrwb6PsBVbQCrpUNqpT91ZY1LioGH7m63ghA1tTsqB1m85pN+5zz558Q+xUFA7/i859Gk2g7R+fSVNC01lDmFvB6tkD7iC4cSUeeP19ODE5bmBzrKmxZoq0lYXjjrbeoypqLasb12Qs2qxtWy5eslxeQDLYocN2a2ayhKguGqEjeM99ZMN854rPfscvN5SVPgsP7geJ+QbiJpEHWyldWqtPnqOWSdP8BsdCkOy1UMlaCCygnZA6fk2HRGcyLJ9tCQ0q3V79biO9tp20FyVqJ3dMYwAAhURYFO9WcEAOt6/BBvCqO5vvoBJvVChUVIQTqsuFwsS8yEmdPeXpxyt7OHmUhWqy7iwWzxYyQAtfLGwwKoyw7dcPh7i5H+3soEu1mzWq1omsHYZDmvclay+58wZsP73N8fMLB/j5FYQk+irHcpmW93kBSU1fEmCOOYGcC0tjUlEbGmyUNmtV5T7dpUQqOX6tF218BUeFcoDQlx48qPvVf7Pz8xY0KOPgmr/9/eCx+8Bd/z3gkYJn/+7mHAv5HgOv8wvd/kzf9nOPFL/J7yy+ccXfyv/e693Dhp4lRwBZrhVhkStn7klKZpZj9Tl4pBqcMxCZCXtCtVlhVCJs+s5DLQgDymBLOR5oqz40Up5hgBD0BsnmKFH/GAGWLdTHlFzKoUCoS3IB3juAcPvgc62xll7YlO0CJmdhkKKVSRg3TNDPHvAEyxDGCu7dVcdMYe+WVIrPft6Qfbp20SF7ErA87/v0WvmKKm5jCJJWBsjFI49YicpvNeOsWvRLLj+eVMhFAfqm5TR0gx4tx2ifHc0njXj+Bx9svSDFkhM4wyTOMseOW5bH9ppREDmW8lml93X6XEMzM1EVslMihjK38CimIDl6e8+jDrvTWvFYrjfJemMx4Eh7XdwQ/SAE1OGKKmGzWZG1FWc1R5Pg1hMn/B7SYNjm3HQyMwOc0CqabOI3N22i3uv1IRqMoNWET23GpmLqkIRtr5WeMukVWyl2lSkh6Y0XwVb1gttjSrbkz3kOlVAYzbj2O6Qp/fqCoAKMEJE7W4LKxFl5A4ahA61EHPJFUokGzmxxtCrQp8cyUBG0FDzOaSonOcIhhwk+ENBinQn/K5pXGZFEBrcRoslDEYAk+4FwnxbAgY0OZMRfK565iLuIx+mSJJmuWA9A2Sew0n7F/95DXP3UXBbgu0reedq2oSlmHkt/QKjHyCtFjkTGKUYSQtaejI8RBNPZdj/cDLjjC0LLpDGXf4Jx05tezGWUpJl3Bd3g/sLZrVIJ2vZFnE2X8xRhZFx3t4ChdSRnAR/3qfJsqWt+KXrU9flmAscEPbK5fiLadH4AkOkJ54AcFtU7ovYaqPIHgubi6oEo1pS/BOa5enBMHwaXd0ONcFG0LK8YFITj6vpsCLnHlM5jMQrCZIWNGcDQmopdFA5WyC2uF0UVe7AWojUi7QExxmjL94KbEfQJwcwunIjEMgwBKURLcsUqplFC+TVGijMUWlrqpub65Ef0551Gm4M23vo0XZy9oncO4geOTY3Rh2PQty9XA06ePuPfm26To2SyXPH3yiHcWn+Vw/5grlpy+OKewhm61hFhDVTJfHNA0NZvNhrbdUBWJZnHI8clDmp19+q6jjzeUdY0ta+b7R/TrK4pZT6UWlGXD/OCQzWbNz375PX7qb38ZH/ZQ1oAup2edSNkNMgHFtPFs94eUu0IzMHAbgMhHhMyOHEHXOC3At/+9bQlR02eFNBp3ycIaorjfWl1ycnKXvV0x6ji4c8z5+QXLpRiQ3b93j+OH96l3ZjS7M6Lq6ZbXrFdXbD75hPNHpzzQczZKS2igFMP+jEGV1ItDFicnHLx2TDWzuADrLnJ10/P+Ry84Xzq8KpgdvMnJjrgcdi6x7iLrVc/hbsWi0jRWoYhYHei7DtdvpOoYIqasZAxrLRpBgrxMY04xAjsx60JlBkxMDK7H1A2mLICCEAIuQNfLBtjUNUrpTM/PbPGR0xm9gAx5/mhjxRVWRXyIElQhWkTWmPyMpJKmVAkkbLHDXNcUpuDOnRnfszen2NlhWJxACkSf8F4cna0pZBNS0pb5/MljSluwWCyYLaTlOWkBzFzfc3Nxwc/8xE/gWsPO7g4HR4e8fP6CZ0+e8uzlOc8vrlkpzd7DA+6+fpeZgS9+/BQ9eB4e3+X1Nx6ye3zMyVsrnly+Lwty33B5fs5quaTve5nDpmBUL3kVlLtthEMOSGVE69HwLAe/MSppXzMBmxy/lMd/9/SPftPX94p7/JFP/c1f0nP5f3OM9/g/+vCf48afAvCnP/g+AH7P6/8Jv5LflM24cvBplGjMAcZaCVaVFMFANOisMSydxyAFBsVWN1NPLV2iIRoIUxBurUEpWcOnIxcqxvatNEVWKe8VaRvkZd0055ywiMz2c+qmEUA5bpMSpTW2KEW7Nmszxeio64pmvgts9aec99Szhp3dHbTWwhjL9yTnFtt1chqnCh8jwQdYr5k1jXynKZgvFvSbluO795nVDeePPtzGijGSnMcNQ44WNSm3AUJek0JgfXHOs0fv45PCFg0nx4cc3LtH3zmWN9fcXLzEBM/9Bw9ZWstFu8F3LdXuPruHRxR1w3K14uL8Bck5EeNPAecUrRbdd3RgdnXB4f5dFAXRK9ZrAV6d64nRM/KVTWHRWcNU4oEobb9RxkZUUsTVyghTJAgLeGTsz8saXTYsX3uTs4N9yr/6l0nekYjiTl1ZtFEMg5NW2Ft72u0QbXoeOUXrjOZMJzYpUa17fGl50yruJo3SHcZqYbCllPvBRh08QEVcimhjpC1VR8zNDcpa5k3Nwwdv8onbUH/yiJ91ng+1FH4Zi0XTI3216LAFYmGEbVNuY7tNIr99LSFCNdsn6jkfPnrBcnXD5773e2lm88wsLdgbu1DyMZ8vKO+9RjrqySoFHN055s7iIaFd0W56Nu2GYZD2uKHraGqDShGdFB+9/3Xc6/cpFqUU7BLM53uc3HtIOat476tfpK7nvPPuayQU19fXvPbwATs7Dd45NpsVm9UNTdWwt39I1cy4urqWhDXHaRcXF6xWPSEkZrOaw4N9koLrqxuWqw3WisHJMAxUVUVd32FnJqxchcLlolChI3dPDmkqS1EYPv74Y66NwQMhBB4/fsLnP/fdzIIYamlraNfXokNrZtKtVFWUtqTrBq4uLpkt5lzbEtNAVRasVh2nL864ubni6RPLi2dXHD54i1AcUO5d0rc3VConR7Yg+IGIYrne0MxqHr52h9PnTwjBUVQFuweHuL7FdT2FtRit6ZbX+Jnh7sExxzt7LE9O+PrXv8bN5Uu6dkVwDqMghhVxWODKiuvNmtOnUJZzympBOat491Pfhh/WxKFntV7RfLam+7DHL8eCZh6RWqE3a9Rf+csC9vzgIfz6PUjClEydJExJQyQQFJPxy7he3V73pB10nJnSRaB0bhNNiWHTyRzR8t0kjYqKWSEA69XVJa0XvbxZUfPO8escLvb48OOPaDcblqsVi6MZD47voRRcLq/48Pljdhd7KC1yShDp1y1X5xdcn1/y8M4Jd3aPxIxrvqC0huAHnj97xumzU5QHHRKFFUD/tYf3eevNh8xmc7QuUcoyOM/TJ894/Pg5L15ccnXZEVJJogJV5KKOAA8jUhEGR8pt6dqIOYm0iJc4H3n8tY4YPXdeX1A1inazZmenYXDu1Xjn/z/+oQ+vxXBnIHFwcMD+3WPsfIZDs+kHxOMbbIy4tqXvWlIIaK3E+C+bbYKsv8oayjzuDVJXNEk+wygl7ciqhpw3Ka0whR2ph1vIayokjmeaX0gju9JLIatrYakmrHIk+udZBTCpEpOLekqJya3Rhih0OTEa1hLvjGxOmFJDvBfw9OcaPN9umefW6Y5A6/ZstoUYbv09t95/uxCup8/WExA7MVs1KIkcJ+a2aIrGLHFw+3O3P49sSVCvgMjb8xGg/VW5hYgi5L1I7qFcRszr25aBrLUmhXDrOgARxcjMxox3BPneIpvaDd4JmJXjiRhGaUZwbls0FX8Cn5m6EWvEzBsgJtlQjCnp3YreJdF7VpaUPClpiNIm7/qBgYQtArFSmKJGqYhW0tLeDdJxtbOzh3eBq4tzvI+oQm+HI2OcLcDqqD/687vbtsDodu3XkERpVIgyAiLrnCuQ77uPXuIdbdGoyZBca/FEuY2e346rt6Zpcn7brhbDaBan9HY+mWQm0EPYu4k8yKY5pbUiGcVgFNdWiAGlD5go+s8yvwGtSSZRJWhCYhYiNYmkHDEmKfgYQ1lUzIpKOgRjwHlP54TZ7oMneifnkQAl2rJ1XdFUDRDRKqBsYmdRoTaBbgj0TlikijyPtbDZTc6PtAGroxT1rMFqjTWSb+3s73NwZ5/D45KDAiwK7xNdH3ADLNcDj9Ka6xeKfnA47yiKglAUWXYFouuJQy/d2/2A6zvpBtqsIXnKLIV2c35GdJ7Numfv8JDFYk5VaYp6hu0D6DVu6KXANAR8H/Ax0peBfoj0XiQNQ8agyPnlSHwhfjNI/dXjlwUYm4JndfaUlAEKY6T6kfIAFZ08cttL4v69A2wR2Pn898B3w27T8Nob95nvzmUQJlAp4PsNKXqUsdl5NmCLQlixrsuuhBJ03QwD1paUVS0taFqjCJRF1pQ1FmULcQ6MihQghA43dJBp68YUeYKJXqzPbJ7CFlPCnZIEeLYoMMlO4OHgBpQLIv6b2a5Dl9jcXNEtr7F+YGjXeD8wJMVr73yG3aMTLl8+x7mBAktRgHOOJ4++ytX1GXfvvc58dw9sy/PTcw6OTljs7WOKmvOLF9Tzmp2dXepmxuLwHnuHd9jNbQTNrEGZGlvORJuEKMFndvXTSoFtKOeZ3WdEq+j//Htf5NHjU4ZoKMqam5sbnBstOKQ9haw/FhF9GpdCftZSqQwpTHv++L7bSevYFhxTxEcZ5ZFbm9cYQIwxd5LfhiQsiSG/+/33vsLF2UtAU1Vz7t57jWa2w8vzS957/z0UMPSOm5slP/mTP8lb777Nt3/uM+wez+mGlqYsQWuRxSgbjt44ZqgLCTO0gTtvcPL2G8wOdijqis2QWN8Enp3d8PTshqcvllQ7dzGLGU1dUjYW1QVclzAmsphF3nqwYF4oaeHK7DlrLfNqBz+UtKslq+tz9o+OaWoBt40aA6BRsWTcwLdVW5BKnzLS+oQSwDQpgyka1n3Lqg0YJKBo6kJaXaMipZEBSq7SyndoXQAqF/g0KYVJ6B0SPvq8MUr7hdEVzsvCrIqS5CNXNwNFDXuNZ9G/ZFkspOU7eJIfsCaRnOPm6oqriwvmO3M2N9dURqHnDdqUuBTFbMgYYgyUVYFJgavzM77+ta/x9NFT3njzNRazirJVlFZxsmtp6Ijrgf2jHb73Oz7N3cN95rM5nSm59+Z93ljdsH+yYK85IPQbfIp0zouIuffSVpcD1JjSZPo0Gj8BMneMGHSlSS+ILVMSCQxuA3K/FMc///DP8u78104/L8zxL+n3/8MeL4eP+NGPfpjf98Zf4G+d/3leDt/gd7/2H/Jnvv4D+R0pB3wpB10pt9pLsDSK73vvMDo7Y9qSvYPDDDjFKRhXWiOO2TmAVUhSnpecb5Z81lVFpcwEXIXgGH1PJ6fP/PdaQV1ZmtrmroDcTaGl6DAmF35kTCswZkwmFEVhJ0ZIWRom68jkcbEX00g/ZA0tXk2oXkmumF5UCtTNDe4v/SUuf8+/AMd3mJfipPry7Dl3X3uNvfv3qJoa3v+s3BC0AAAgAElEQVSqXIfWWKNZ3VyTfJhaqD2KUuU1PCVM8px/4+scv/kOs8WMWFhevjjl+uICay37Bwcorbm8ucE5R7V7wOHxCUorbq6v2Dx/hnIOa5UYahpFH0Wq30VHCobQe+rLS3ZUyawquffgNZ5+0qONwQ0bXN8yDGuJOZToWBkrXRAZeZWWqxiJWnTEAtD7XnyFxUWAEMC1HaquqK3laLZg04uTsCy4krRVheju2sIwOOlqSSRxqGc7jnIqJaYASlhOm6T5KoHWtzxPkW9PkW9TiToVEtQibOAte1XceIXhoNHKMLrxNilShkDV9by9qDl897O8cXPDVy7P+YnVFVQlo677WLjegum3zH6mDXab1I4kO2stY0eGsQZtZ7y8WlE1msPju3zy/KuEn4X79x/w4N5DbCVF4H7YyhR88N6XubY1Z+EjyBjty/ML3LlG+U70+41mZ3eHsiogRjarFcMw4Jyj7DoWlzPqeUM6kD3RJM/jxx9xfXPNh1//gE9/+jvoXKSuCu7eu0Mzq1mtVhRWs7+3w/HhTgYZNG0/EJW49A5DR9tu6J0HbXB9y3LtUSby7rd9irLZJSmDc46rl8+pa2FeDF2fAflA0XSoasZs54Cyrrm+OAcSd+7e4eDggLP5jC7PqYPDfUxdEvqIKgoWO3Pc5ZUkULbEFAWaRGkNyWo0jiFrj8s403zuV36eZ8+ecfr8OTeXN/yNH/txft1v+q2YqqGo95nNFhShJXkxyhhW1wRdYoOnSAoba/Z3GjZdLx4ASnFwvEe7blHJiJzKpuX89JK3Xj/m4GCXdLSDsgUfPf6IsxfPWZ09x4bIcHVFPdvh8O4D7tUFwbWcnb1kuTzFmDk9hrsnR+jkee+9r4GG6q0SfRkYnrhpLRYQREmrp96yiVFQKdHZjAkpVltNYaQbrus7tCkm3UGlkujDji1Z07xVGfzdgjqiTbjVWrTKsrvY5fj4Dh98+FVc8CilqWzJXr1gv9nh3Ydvcb1ccn5+zoPje5RFw8neXb7rHcWX3/8K52cvaUzJ3nxBYTWPnj3hxcUFPsK9g2Me3r1LaYrJ8+IrX3ufJ588ZXmzpjCGh/dOeOfdt9nf26NqSoy2eBe5uHjJ6ekln3zyjOubJd4bQrDEOB/hPLIQYMYhsuZe1vZXSqSdFEBwxOgxZYm2BVEVPP/Gkn615PBew52Hx1wsn7Fc32CXc2ArL/L/H/9wh0+RaGB+uMudd97CARsf2Aw9GKQrwnti7/CbjRB4lEJlTeMYgoCxWqNtgc+Sd3aM/TO7Umx1paOtUALFp9xNF0PMzD+RwlFa9iXpKAKUkakSQmZB6ql1fmQNyhs0o0jn1nVeGLJq2kNEZzxFsdyRjjFFjJJvjmxcmXKS943B020MdfSTIEEKAvfebs+/vV/dSie3xy3yjgKJAbSYWY2kKpAOWbTKeUkQHVfvp3b+kaEe3Ta0GqUd5BLGzs60ZUuSKGw5ncbobSPyjSHLXo0A9q1ux1euLOG9m85h2sG1vtVhBTEJq1RpyUWU0pNER4jgosjSeD8CaaNcot7m47kLOObOyhiDmOoVlrquKZsGYwua2Q537jxkZ7Hg6vKCm+sLVjeX1EXik08ecX15Qb9GAMOkSbogqZKQFKMaMCHhB8f15ZWMWC3n3Pct3geKIlJVkjONXcpbkHsLigo4raZ/j9IBecEXrnbKpdJRU3e81qwHG0KQsZVxEu89ceyCzPda5358ybdfDa8nMF+RSyMCtHrnIOUCf0qvSG1Mm1LMfg+JbJgl+sVRKbzRdDrhDNgsk5WSIlq5i0WINMmzG8BHwxAtD1NiXQy0UfwlCm2wWshUNsn90FrjCQgWn0gx4AYhLVRVQSFthVkWzaBUkBxEObQWeSGb8SLJhQXYHqVzVDaj06WVWDazdKMuaOY7GD3n5YuI3U3M6zy3CkVVK+pZwcWZRL4hOAgdgQGCJigNYaB3HV3XsVqt6F2g7z3ORTGmS7Bpe3xUtH1gtRnoenh5eirENCvF23a1oV1uWF3fcLO6oe17nPeEFNn0kflsn7KumC9ycVPFjJaPc/U2UeFbQ7K/LMBYgOCF4RCJYpaSY6FxRoWQGELAhUj0sLOYs5jNiT7i+57Od4RVxNgCowuInkEpipQw5XbhkjgrmwGlvEHkqs5sPpNtwg+4EMR5WWvKUgDapPU0GVPMyWYME7hIys6eeUP03lHYQjZPYExyddaSTUocm+Mohp08KgvYj450WhvKohDQK3hSFAaVqWvquM9OFrTvhw63vmLoW4Z2RVlZlpcVbrZHUc1ISZw5i7KiairmizlFIS6zITj2Dg6ZL3YJSVjBSikClqhzckbEas3gBoIPwupVBmXqSZZhtVry5a+8z9nlCmVEK035bqtbmO8/MRJRYkYyttlI+irP9xZ7cARibzs2hxQJbDf2V5BbRs6m/P1244OAMGNjSnz96x9wfnFBPwwYNPsHR+zsLihKi+s7nj19xnq1xmpDDFKJi2++gTIKU4oot193rK7XhG5g/+4BnVJTi6e2hjvf9ib13i6pKFg7OL1oefbihvNVYNmDMwcU5ZykLNEpuS7nqIuCWakxChYmUmhhZEUlxQk1VpaKAj2fY4wI8qscyOhcFRSgQRKIcQxqpXLQnXLVUFhbfTfQ+0jAoIvI6eWGgKYpLA3SytAPPSkGNFk3aErYRcYjpDAWT4GxjYPbT2MK0qRlO6FMKZsdYKoFw7Dk8ronpMSxXlDFFb2uwBrRAo09Rsum0HU91WxOM99Ba0O33kDXE7XB+0jX92xu1pTGUppSkrgEDx8+YH9vH4aOhXfoxvL2a28Sh44Ld4E53OXuu+9y2OxilQUfONYNn/1sYrNqUd5w/vKUhADYY7A4aTSpUXbAvFKZFTH3vAnBVNRIeT3SSiE6dbcCr1tHIvFjp3+SX33wu3m9+RxaFfy2e3+Mnzr/T/mk/SJ/4/RPTUWL99c/xcq/nP72Z29+nCftlwDFb77zR3i9+R4K1fDb7v4xfuz0T/Klm7/OJ+0Xp/f/00e/n4PyIZtwxY+/+DMAfMfO9/PpxW/4eef1rY6/9fJHuXCPGeJ6eu0ry/950rP9vpM/yP99/dd5OXzIX3v+J/Bx4Fcd/DDftfObsarit9/74/yt8z/Ph5u/w//04t8D4Dce/+t8ZvEF5uaALxz/fo6rd6j0nCv3jP/t/EcJcXSvTxD9lj1ADqoQ9oBGzEq0lYVDdIxUbrNKjK1go6a4PK78vG6tNRm5lff6LZvZ9xtcP5CiMMm963JAnI3EcnAXR028GLHZtG2UAXk1d0iTjMEI1m4LInIO3g9TojIWBF3fcXF2xpOPP5KAhfH68kfLkJOPmcbuyOoF3bfEv/sztN/9PYSHr2PoCN6h65JmvnglgDDGUFQFSglzNEZNSJY+yryXJjMJdmMIdOsVuqoplabfDDRNQ1XXlHUjYPnQo0nY0rLZrEnB4zZrlOshBqLXRGOE/akNwzBgdYWqlFS06wqix6qCpi6ZNXOU8hCzLll+kBNjRhuwo5FPGrMiQNr5Qgp0zmXGgTAdBhI+JrSX6n+hLTvVnGW3xqUgun65oKyNpsiJUj8Bsq8GZ4pbz3xkTmsBZJ8n0NGTQkeh4aFKNMpQKC3rxuQyDUrf0hEnjn1rEgjHgPKJnQ3YpDBlw+L4Hrae8TOrKzYxiMmdlR6y0cxPK6YW7dvDn7x2xZz0KRLaiq6hKUtUMed6Heh8y7otKZuG3nsurq4AQ8LQlOUrRY1us4S5wt4itezt7rMf9rl+8ZTVzTUuhqzTxiTtorJkji4L8BlcT4qqrmkKSeA6W7CzOODozgOauqapC+Z1gU6OoV3TtS19t2Z/b5eiqhg6T9872VOTx3lP3w9s2paiMOzt3aEoLdYq+n6g9zc0MzGXjeGAOGxE8sQUhJioS03RNJiiBGW5OL/CD2KgKCxTlRM6mZNdu+Hy4jITCUqc8xwdHrBuB64uztg7MqyuL2hcT0qJyiZuNkv6bkCliFGWo8M71PWcpmo4LZ6xWnV89PX32Du6QzOboXDY0BGGFmsNi/19mqJBtwLq9ps1e3v7+HhF1694+fI5Xbdgb2+PFBTeS1rpQ2C17tFJClzzxR4PXnuLqmmwhaG9PMdtejbrDRfnFxzdOcb1jhCj6K1bxdD1VGXN7t4+O3u7LNcrVGGwexqSYngywDQOxz33VqNvgmHTo5IlVQY0zKuGeVXhnCO6gIuRLTNKWvZlLG1V+rZzMU1zcgJmkyKFQG1El57ouby+yB1ABaUtJY+JMKtmEMG1PevNmrpsqMqK471jPvXa2wTvqLSmbzf4wvLi4oKbTccQEs9Ozzg5Oqa0JYP3nJ2e8snjp3RtR9M0HB0d89Y7b7K3tycAUISzs0uePbvk8nLN9fWG1bJncIqY9DTf0nS3ZH9T6nY7uCQn6hYrEGIGMnIeohToitVVIMQW5z12R2GrGbaq+cc5/vbFX+RF/8H08xeO/wD7xYN/rM/8Rz2etF/m7179NwD8U0f/Gofl69Pv/pezf59ljrEU8IN3/i1qI/IMMQV+7PRP4rMxaqEqfsvdP4pWhg/Xf5cv3vy16XM+u/g+PrvzfdPPRVVSmzlFWbGJkXZw9M7hvKcsCwiB6Byu63I3RwaOtCIkyZmUEf+PUUdylOhQgFUaizRTW6XQKWKRNuGY974YAylkbxTIe2GeJPmC47ivkPebqTtUkVTuwlFbXchbdBpGqtjUqq8VMThGUSNFNqQb1/PcEr4FFuM0dyez7fzRUwdRzk/G7rTbNfPbe80ozZd/McXs1lqRsbJmiuHHeMCHgE9O8p2MI8QcOyml8MkLoSxtZ9r05zm+Gr97LCzdBg1DlHgvxFEzOY5ILozYxUiEuRUjynzO8QApYwsZSByNWsngsFZiMqgyUKtUZuEKqzWiGPWI02h8mvVQU5L4BKVEQzWJAVgXetzgKboWY0tWm5ZucMxnM2G/9h29c0Lq0SWmmmMDRHopVtsCawu0LtHaYq3FZhAvhmwCZW6TVaSzULo5FSZLU5IEB9iyYrPsBlnCYQJizRTzSuE55fkShQGbthrAKn93iFmjOQPqIeY2fiU0o1HiRWU8To1ay2QjrpEBnceg1Pf0BFyMcdz4sFLe62KIOVCPgjn5gHOe5AKESBc8y+TxKlIqKIEyjWQDLVJ+KVKpRBMVewka73Ha4LRcS1GU2KIkKoUNHt/3BGeIaGJU+GHAO0/Me8FSKUrrJ6DVWoRAgqIsxm5vwSC0EvkBUqKsC7SxeX7LepXSCFYbMCX1bIeynjP00AcoozylkcUdXMJ1nqHrSWEgBY/ccQMqCnFx6OiHlmEY2LQdbdtN3RsJLabxvSfEnpA0qAuKthKNbQ34wNAPDN1A27YsNyt6N4gMQ4K6d7RtS9e1DEOJdzNCWcgqphC28DiAvlkB6NbxywKMTYj5ggsDPkqVZaruKGHFhhAZQmDwnjBE6kWDKQyYiBscrevog6cwJVUBRkdw0mZtkTZEbewt2QAJ4lLw4qqnDbOmoe972fj6VoBW9MR49cHjejGOUCgKK3qEKSf9KQUBujSirRkCppRW7HFyKsZSyQjYaBlE44KeqzB9J6YNhS2pqgqC31biopeqn7WUzZxFVbNc3dC2a5zzmX06sLq5wA2O3f0TbGno2w2QaOZzFouFtHIPDu8ds9kcYy0ai07SUhlzkCrPQZyhfS/6fIPzNPM5xgiYF1Pg9OyMRx8/5WbZobC4oUX5FpKfnvXI5ElJkljprBxZrtnJkVsVxHGLuTWQ4wTOpqnQ8HPHe8xBekpi2DUad8W86T198gTvPSqB0ZrDwxOqukIbCIPn+bNTri4umc9m1GVJcAPzRUNVl5iykJbfBKHrISVmh7usnAQhIBWynbvHdD6x2niulgMfv1jx4ZMVXapQRcNsvoNTBSomcbBFoVKgsZbSysJugpPNjxGwY5ofWhvKusYURV63R5MKPY1v8n1MuX0i6bH9OhEzeOx8rhCFJOcfFOtuoKgakR8wlqSysLv3edvSW1Bx/I408pNHEfO8YebyoOgkman6TjJoW04i+7Yo6HzPuu2JqaepKhYLhy0NypRgLb5tM+hTUjUNaMNsXmOUyJOsVmuUNlwv12w2nTB2vAA6TT1jf2+fvZ1dvPdUSrF/cES1KHlw5zXa5Yp2E1E7K2aHd6iKBTooqmGgKBoKbRk2Le2qZd1eiemT7DTby8yV1qTSK2uYVO3NVDmdkj6VGW15JVR5PUy3lBsPioe83nwegGfdV9mEyzyXLL/u8F/krP+Aj9sv8qx/b3ofwIvhG9PPkcCFe8wbzef5tYe/h8aIqdavO/y9/Ozyx1n6c5b+fPrbIYmzuY/DBNK+3nzu5y/ev8Bx2r/P8/5r+W8/n68QPmm/iAJ+4OQP42LPzy5/nMfdl3jYfDe/Yu938s78V8u5Hf1envVf4Wn3FU7793m9+Ty/6uCHp4To1x/9PgAOy9fZLx7yuP0SD5rvYmb28UPHzctnjHDXOD5jipntswXaRDZAigQhyu/TqMc2StCMwXxeaG7vq2P7WLe5N77CxekjynWb/97jXSvAaxDh+JQrpjHEiaVbFIXMkyRa2mNlQxgpWXIkA2oxhAy8IlhbiPT9hkSYzoeU0ChenJ5x+vQ5IbgpUJ1yqlv/vp20KCOGYcYqeP893M4OwRawsyet+tdX+BiY1810H7TVYm6kNS4FMf8JARUjRuncKim3UCtFv16RrEVZi1Yl88VONrdMhKEn9h1q6InOsVleo7yHFLAkyQGjMBQSoK0lJi+686TJJTqEAR0MRpXUZYl3FqdMDoz1ds1SoLQlmTzz0vj/yMgI8iExaI2OCZtjaQcEpVAh62caQ/3wDdonj/DdapvIqpx4GT0lM0OIotU6jZoc9GeQaftsFF4prnMgHpJjJygqZThUibk2MjZ12l6X0pBbGVOKRPTYESrPN0XKvoeQKOZzdpoF86LiMkaeDD030dOpgDZqYu+qPJ4E/x/T7nx9RucigugFGltgygpT19i6Ye0cfT+wXN1wuDMjKWm5jVeXFFXN3mLB4IfpXgTfS1eT3s60ppnRdHOuAe+HCaBw3uMH6RixthDQslDc3KxY3Myo64qiMmLsqDVVWbK3e0BZzVjs7tKUlsJEfCedUjGbM8g8FFOsYXAURSXjwHsG53DOUdhKjD5nNSkGhmEgDo6qquV77RFXZw6lZe4WVY3SRiRGUqRvW85PX9BUlqoWXVnvpjwNMQ1ruby6Zr7Yoa4qQnQcHh7Qdle07YZus6QfOqIfKKzFIoWM4EW2S3R1A001Y293n6HtiPGKs2cf44eO+WKXGB2VVSh8btGrRes+aVwIhJhoZnPsak3vWobrnmEY2Ns7IOV1MyIxxfWyo289ViloKnYWu9IKWWheaM11OKPtWs5enGLLgpTkXhdlQVVVuN5BkkJxVVesNmtQYBqNspZw5YmtaNKNa/HEisuH2/QoCgwFprLMiorGllg0feW46TZbkGRaFCeMN/tr5kLb9k3biRoTyifmVYlNiXazYrlZElUSlEuJREyyicJYZlXN7mzOZrPOxnAV82bOa3fusVkvUSqJJvE6cXm9zExszfOzCx5eXjPMHN45Pn78jJvlht35nMODfR7ev8P9eyeSA7Udy2XHJ49f8vGjU1arAecQuQJKFIaYRkmCbDKSL/PVmtBtZCv7MURxHidKfIJWFKYhDAPrywE3rNh7Q1HuW5G5SI4n7Zf5ZhnofvEau8Wdn/f6eJz1X+ery5/gwj0C4J/Y/12/pGBsSpHH3ZdIKfD++qf42xf/GQCf3/sdHJav4+PA0+7L/Mzlf0VKkcbs8bz/Kp9efIHXm89hVc2z7iv89MVfZK+4D8C1e8537v4A96tv53n/VX7m4r/kQfOdPOu+ytwc8O781/Ks+woPmu+kqCsqtcAUFW2IbLxoro5dD5OZbZAYxRTFZK4UM2nD3GbgZb1krZC9S+vstr7VKtVK+ml0HvPE0RgyEpWeLLKm4qEa2XtpAvdkqxJgKyoBjyQOzvr2I3iKFD2SHgErAf9jcoysRlCE3JGhsrm2MFTNrQJBPqOpcCXgW4xbmabRJOwV0DYXbiZDq1tFGVlGxCSuKGQ9MoUVcG/MvzMTNPggcVgQnd1RS3aUlYpZf3c83bGuQ/4OlTfjcR6GkRWZ11Pv/WQEK4XyEdyVD5zIAreTY5LgD4nsTZMNDKMAvCNZRulsv5a2/hUCZI2A+3i/tsxRCU555fsmEDMJeOy9J3gvBXJj0MZyfnFOVZZikp6RqU5rfARlSmyZCEljNBlPkDVEaZHsssZgjEjixRAywBrZrtnjdcr5jTmwdDrc6kjMWrqMZlra5PdtAVvSqCG8XQtMjq+k0CvfYcfcWiFGkSpm8O22zNPIjt2OL/IcVbnzYiwWjPd7crmankWaCh5JhKJlTXYe7aNINfhA9JHeB25SoE+JRikWTEKQeUwXFCUUNlKGyCLAzgA+JnqVMFqzO28oZwvpJk8Bu16zNJautfStIgxtHlej6TDUVRRpQqOpSrmnSVmUVhSFsGVTGEFuuYTCigEuudMwjWZlStjayVTUsx1sMaPvE22fMFkDN4k8L20baTcD/aYjugHvBxQ2s1DNNEdSlHyp73u6YRC2t5J4OCTJnULyJDWgWFF6R1EWGGsnI0nFKFUnz1y0rxUhRPqho+tbur5mGCKuLkQGFSV1kVt74C8k4fPLAowNIdD7rF6uhYE3Od8lGSyJLNEWIn7oeH56SUQMAfZ2Fuzu7jJ0HqIshOLYLotqWVZoW1DVM4J3orc59KTs7qe0pmrmgDDuUl5Q6rrmZrlCmYKyGbi5ucS1mzyoS1IwkAIhiMGSsfIzQfJooXJXGUyWID5k1+PxSBFc3zHS/l1uDxl1XgDKusJ1MnAGF9GA6zYMvSP6wM7dE+Z7B/TditXNBcaWpJgY+g1D37NZr7hz/01ir1Fpl6apaJoZL85ecHN9Sd+1PHzwOt5LS2ZSQlVXGEgCCmhrUcnTbq65vr6i3bQc333IbLEgoFj3G/6PL31JAvHNQHQBlXp8uCJGSbIUCmMUVSk6bsSYmdwJ78PEfB5dzMcNSrTsfu6o2erikD99HC/jRh2RDTICPlexxsR7qhQrsEbx8MFDARyjQ+vI48ePUVGhU3ZzVIp3PvMGh3cOxeAnGWJU7B3MSdYTWkdzcoeVqRnPYOXh+emaj5/f8OjFktONRjUn1LOauipQBm6WPfNaM5tZjvcsBdLyF4IneY9PEWuLyWBuGOIW5Jw2SWn7GbHpUSA/Z82klDLrLm9IyrDpO1of2LjETTcQho5FVdKUGqsjRzsNRdFQVQV1qfC+pa4qnDZ0Xc/m+obCGMoqM0AAa4ot8zMDWj67l+ss2H37QSZlUYVCxW2AUZRzfDC0w8AnT6749LuHNHbAq8QSSWRVUXJwcsLewRGb5QprwWro28jjRx/hfOAbH37EzfWKuyf3iX7AqH129xYcHR/hvOODb3yI05r79+7jZjN26hNqs0+fSr5xeYmLCp80pTKUFryyWBNIBmLhiG6gW93QLq/o11coW+cxO7b4CnhmjJgJoRRubDFJadu2oK1UVWMkeYdSCaN5hRH2Tx79q9x757Pfcv38Hff/xLf83S92WF3yI2//t9/y97vFHf6Nd/7qP9Jn/66Hf/oXfc9vPPlD/MaTP/Qtf/9DD/7UL/oZXzj+Eb5w/COvvHZ59g949L/+FUYjuTHoGYYe0QQNk/nFGGMqpMXaFDVbl9o0ifOTC2njujSCu2ISoXn+zjH8iu8ipcTf+Zv/PfrqMq9zTlqZYt5fksdYTdnsoHXBbYmK258ZvIyfyXV4ehOM0jgheBHN7wdulpeM7HhjLIvFguOju3Q3Z2yWF9LCxpg+MV3PCMIaY7I2OqJHakTTSRmN+Qdfwlxd4L7v+2X/sxarNIRt0UDnIklhNJsU2YSBNCQsZgrENXLuWhuGzUqkg4zh3V/5q2k3nRREbq7xmxVxvaK/uWZYLimzfJEEQ3qKD7yX/dRqRVmVDAy03ZKkLIUxzGxF0W4wtqS0BpXljmICrJXirpw8Rd2AUsLwH9sCs1FgzKA9o0vueAeVEvdXhDHtFcTf+lso/vr/QPr4G/QxjOgz5GRXK421M8rgacuCTf6skZXyisRZkrU9KEWHpCBDSmjlSLHjbVXwIFrmtqSMo7mItLpmjoBorKtELAzJaAFVQ6ROmtI5zPUNZt3x7uEe//K3fZafXq35e9dXfPDyCVE5cezN7CGVg2UpIk277pSjxSiFH1NUmHKGbRaYsqJuNjjfsV5esWiOsNqiyoJUFHz8/AmuG1icPWNc5bz3XF5ecaHO4TV57Wa1JN0UDN5xcLAPRhNjwjnPet2y2Wxww8C6bVku15yaUz61eZudeI/wVuD0xYts4OBRRvHk8SfMmk+RouP68iW1gUIb9vf2KUuZP09Pz+n6Ie+hMhYG5/BB9uXNpqVte7Qp0UZA1qoqmVUFViUOjo5ZXZ6zXG5wQ09dlvR9z7C+YVhfs14tuT5/ycHhMeXJXXZ3D7m+voJba0JQiuW6ox0CZVmws6gZBsfx4R67zvPi5Uso5tnI0mJ0pCkNRWnp25aL8zOuLq6oZ/MJaHz42n2efvIx548/4Dxn6HcePODo5Ji6bqTVuR8oioqqKcAaXlzcYK1l8D0+dIRB4/ueYQh0bYtPPVrXXFwvwQWsTiQVKGZz9o/2+M5v/052Zjt8rf8ily/PWJ+f4mLP/ft3MUZTmpr5fI8YFFdXF1xcXLBZr0XHWckoU1Yx/0zN6r0Nac3E/CO9gsUSNwOp36BcxeLOAYXS9JsWtGZvsUvrhmxeMy6oY21ODFBG+CmHUBOzT4UwjXrlI0ezGSY4Xjx/TO97KAq896zWax6/eMbu6wuKJFJld09OeHL6XGHmpHUAACAASURBVCSKiNRlRWFK5vUM5zs27ZqPnjxlud7gkjyn1nm++A++ikmQQqTrPPfu3OUzn3qLo/0ddHJsrq84v1jx7PSSTx6/5PKyQ9JwmwGIbGa5hZ9HCA4Y22qzsS6ZHRlDvq+y1o2srBEcKcuaslkQvbCK3PqGp4+esog1x72iDY4/9+EPEdkSMRSGROC33v13+Q1H/8qt1/P3Z1Gt337vj/Na8zn+6yd/OD+DkFuB1cTSl+eVpr+ZPunW7/9Rj5A8P/rRDzPEdhobt49VOOc/+PCfBeAH7vybfNfOD/Jnvv4D/IWP/yV+6P6f4qR6l//4o98FwD9z998mpch//vgP8Oc+/CF+5G0xQ53ZA/7g23+FP/vBD5CInA+P+HMf/k7+nU//76h5hakW2LIiJNFQNClSKIX1wvjSSlGWJUkrKQyCxBdk4kWMsjcrkQ2zVuTUCgU6szVznW8qAiaSfEZIWR9W9klpl98CnGOBMWWAajQ11VNBZAvmIQpPGViVcTeaaxPFtyKQwV8C2nqJ8UeNTWUQ7wvJ2ULYErW24+CWRiNbNqQAnpKLjGxXY8wUj8t7Vc5LzbTkjrGQMdJ2b4xhGHq6tqPvevq+e0V+TcU0XdtkQJYSRmkCkvdPhdYRrLtl1iRclXzvE1NOG8c2+ImYEbf5XbqlJXvr3pLnLohMkcweeVYp52QxpWzWPLaL51w4YxbRKOwtg84s3EuMQpoLPuQ6lRRfQ5Di5DAMsjc6l+PKkaSiKaylyPfSGkuVJRlICWstSjWIdEWWpjBbc1prDUYluq7l8vICY2xm+saJXJVAtMFVltcYmdRj0UmNpmMj6HkLbJ4AZ3kgYgodGZeuoiwzICwdWNYq6pkYk/ZdR29bNGkMDUlJfHGYgPNtUW8ikaUxpt8WFrb8MgXG5sKEgPDjvEvyYF8Z8ykp4hBpXaINgSImdpTlEEVNkr0DSFrWbqsETG6i5/4mUbpAawzFYod7Dx8wPzqhnM0wpZY46vySq8srri8uefksMVy9lAJvJiyYAkqrEekSA8nggzCxSTKXbGURLWMBcoVEocS/I3tuoC1aS9zu612K2QFRzzi/cISgWNSBsoCyENb/ctWzXK5Zr5d0XUfnxLS1oqYqRW6xRogPXddJAStlwllRkJwjYohRqhfJeZQWWdOyqNib7zJb7DB2KnZ9T3XesFyuabuOvu9RSvDK9WbDalWy3uwyqwzWiISDHSXjRnDmFzh+WYCxAD64zO4D5zIVOr8QUiIoaN3Aqms5Pz/nw0cfc321IvrIQbPDb/nC9/PG62+w2F9gCi0C5dqgdcJ1G1wIuL5n6Ht5MHHADZtMDdc4H2mHnvOzM4iJvb099g8OWa5bef/FS/rNkuh6bNNgCy26Pc4JcBoD3gWwkZATVKM1rm8xpsqbgcINUk0zRn4enBO2bd5kiqKgKsv894adxUIYv9ZSWGlFPzt9ws1ySV3PqOsZpy9OJWGMmqPDezQPKr74xb8jDnllRd0MfOO9v89id8He4QmlSewePWBvMWfoWlY3Kz766CMePHwNU1Qo7dHa8uLpM9quIyVFVTcoEs63aGBv3qCD5/riij54zq4v+cmf/vusLtf4vsX3KzbrM9r1C4Z+NT1nrRSFNVkMXaOQgMFoQ6kNSksraMgLuQtiFjVu5kAGum6rxN4+8kY2MpoEpiSqsUVDWLIacvuDoWlmHB8fsVpv2DvY43u+93P8ql/za9gsN3z5y1/mgw/e5+FbrzPfXVCGlmK5QaGpuWKFJ1Qz7O4eu6+/zcXzM+gHBhf4mf/rQ9477Vn6BmePKfYWzGpLCp6uE9fxe3s1hzuWeaUpSTgX8E5AOVvY3BYwYFIhFSPGgGYMYEEh7uYTOD0BTLL4hRCw2aE5JgnstLEihh0ia2/QETbrK0KXqOoFngYVPTYZfLLEfo1qFhhbMt9p2N2Fbn1DjBHnhQmks25Uin5i+RljMqSl8GFkOgnTWkCDXAlMEY2HcgebapLvGYY1X//onJOjBVWlSeECdfSAjXMMbUe33hD6DQ8f3CUEj4uR/aMjHtx/wMmdEz559DEfvv8xRwdH1NUMNwQ+PH3EvQd3+dRnPk20BcGUVLv7NKlk1QdqSj598gbH1T51OUcljQse7TxtWBN9wCrL4v9h781jLd3S867fGr5pz/ucOjXdqjsP3Z46tnFwIhkCQU6sSAgwQThEhD+SKFKQiAQYAhKRJUv+gwiiRMhYRELBJBAnOJaIIe3YJoOdOKS7Yzvd7uvb93bVvTWdU2fY8zeugT/W+vY+dbtpj0AjWKW6d9c5e/i+b69vrfd93ud9nvGEZ6dnVPVnqHYLivExSuf7IADcfj0LQa0PwoVeRNH7UOHs25zwgc3krEFrxY1Jwnd859fN8vz/ulHtlnz03mfi9dQRaNSx28EFB1drIpNORzMDhUgzRJYjYlK3l0eJmUufwKgelY26yyERtPun5kmHkBXeO9IktN20TYc1DucEWZ6S5klgY/abtAeILEd8YHX3jt7+mhGc7wNdj0h0cJVXGt/VIHozAIEWlrZrKOuGqo1K2f4AKPe5Uy+nEVibQVokVH+jRpMOWtD+2TOSH/sr+O/9w2ipGQ6GzGdT+OhDANq2YbtZBykfKSmtofaOaTFhaywy0Qgl0TERUQJcW7E8e8Li+WM2l2u6XYlryrC2lDuktSQiFHqUknH9jiwBAgvC2wBGZ5MxtutCMtLVrBbPqfOCwXDKcJAzuX2PnVYILXGlxPmcXbkKoLeUQXPPexwikBEikG+dxRKC2TwrYmQbpI1S7zHeY0UAM6wLRgPH0znNdM7VZkHreq3fXhIBwKIlZMkhQusZTF+xo/nABBYCGhEMTT8U0MmOc+94zVu+uRMMRZC2kVKiZEhsWqVRkwnFSy8xfuMtOjw0HX67Y/PwIWK5RDtHZlvM+XOG2y2/Zz7j227f5IMi5a8+ecTGNBjhgzGMlAjnI6NKoJIQbIbEWyKVRHiJkAmgg+6fDSZmtlXUa8vTZwtezm+TZxrpJINihEsc2fpqf87vv/+AejjETA9W5w5FZxXbyvDs6Wm4T2JLf5ZlpFnGYDRCq4Q7TtJUO6z3NDvHv3j/u/m7/m+zWl6iVMdolLFYbqjKLcWgIM1z8jRlNEgRIjDYr1ZrEJJ0MEbqjPGw4OJ5AI5N3ZLoBHIQwlHXW9qmYTYbs1yuqKuGtinZrYMW7HAwhGJInqWgJHUTvAZu3z7mciRoa0ddbri6uMDaQ4INHm9ammqD6RKcSUkkLBYV86MpxWjM3aLgau3JBhPK3YYnD99nNhkyGY9R81mQl2oadrsdUmu0TinXm+BonISWx66tef74IbvNiun8iFu3b3Pz9m2QNhKfM958+T5lM+PJ6VOenZ3icTz48EtMpjMGgwKZFSyXKwZFgSoSurpmOpvQ7EpEUzHyE0Y65ZOf/BYuzp9zdXXB0fExVxdnNGVJ79gtlWYwnqDyjPHRDK1lbBdOkFqz2a75YvF5qu0O1ziqd6uwJh5uGNRf/3HMt/0uujffYGOXTPIBnbS03tG4HcbZCPoc7rH9Qu8DIOX7Qsq+EBdB2JgwD/WAuyd3aOuKh08+ClCJDeDVzux47+H75Drj7o1bTIohrnMcHx1xtVywKzeMx2OmkynGtdRlx2q5Yrla460I95BXCBzrdYX0gmFR8Oabr/At3/QNJMrR1SVXF1d89rNfYFeB9wlC5aRqiPF9a3FfOAoMsKD73Fu6HkA4sScrBG8IZHDCDjFmkIdwLhSaXQfGGayrkKLGUlLJBcObA8g9XjiGas6f+cQv8sMPvpfT5leZJ/f5U2/8L/yXH/w+Pv38z/Iz539hf19/790fYqDm/OijPwHAv33/R15Y/37k4fchUcyTl/hTb/yt/T542rzLDz/4g/vnvTH8XfyRl/8bfqtDiYT/5O1fADyfX3+av/b0P/gtv+fHx8ac8wPvforG7fg7F/81X9z8LH/mE79ELkfRqPI+o9EYnaa0TUVTldSbLZvziz0wniiFTjS2bcJ6EadoqnUE2MJ3KXuXciECIOsDq9z7oKva4tm0DZmS6Mh4bU2HEklvPhG+f74Smu6BQiEEJv6279pDBnMmD3sCSehUBLwJ4Jm7LjPgsVYgXSDteCmQfRcdEAoH8eE1xnowkOxVeKIUWh/k4Pdt7UoHtquScn8vA5g2Gv1FfNXavu1axpzL00St7GD42oNgfn9ofXHD+1BIFEIE8lVkpoYi77X937MHuMOW767JGbJ/nxcqTDEW2S9Jvs8Ar5OSDmtZH8JIouSDDYVr1TMxncf7WJQSYl9M3bOwIxPTGhsrxGFNFPt37+vMklSH65omSZQeDDl6L/eVpkmflob9xvZGfyFHD41pEQCml9uI18uBUGLvu9MzWwM42jOm5aEgF1BPhAq6vqKfDyFiCblnD8IKxSGuDi8WESjtEYauC1IPSjqyPOyfQghS6dE6Iy9CIdTtZSSbSFCKubjvS2Hh/wGrMdeuInuPAqSKHck24l/h+xV9kSx6EKAkwusAKpqOViva1qO8wHhHZzu89twSGSOpyITECFAOrASkJ0GSMkTboD97WdeUz045cYKjkxvcHN/gzs0bvPzKfXa7ivVyxbMvf8h7732J84sLVpstbQela2mUI00S/FAzKHLyJDJevaMstwjRHTqXVEqW5xEcl1gnMIQ9TyLRQjKaTRlNxmTDApmC0p7GQmsFshF0Fp4/W7NcrGibTTBy7TpKY7CdIZloXnvjHYrJCKSkrEqePHzA4w+/zPnzp1yeP2Vx9pSmrQGBVJosTXEm4HhbVwZySZ4yno4ZDOYMBgVvdq9QllW4HuuSy6sVTWPYbRpwK1JdkCmNQqGFJh2ovTHbdczqq42vi2w/OJVWWBc2h850tEGECu8926ricrPkfLHkcrni6mrNxWJD13YI57lQa7Kf+3m++ZNX3L93mxsnM4o+gYzv4axjenSC1imDLKPtPMKHFkulNPlgSN0ZkiTF28DcUUnKbD4PTNquZT6fsVpcsVmvWS4WzGezWH3qlU2htS1tG9rdijzHdl3QbCGyY9vg/uy6wI4LjBO/X5j7TaPdRP2vNMUJWC+XrJYXVLslg2FCIidoFUCfehvaltuyxHQdeTFgMJoGbVEZBN+raoMxW2xXIa0lT3LSwZjJZErXOZ48+ohyVzIYClSS0lqD8x2m3YXFNHEsLi+pqw3GWLxIGE2OuVpXPF+seHz6nKuzU7zxNNWaplpRV1c433G95XpfCRT99hUVgkSoYfWi2f2a6gms2R4U8QR5A7Nnxfo9qtC3ffSGXT1wKQRIL3HCU+52PPzyl2NlUpJnQ05uvczRjSOuVuesrhY8eP8Br7z+Krtyy3q9pG5KXnntHqJdYssBXZqidcKuanF6iMoy0uE8BMDxNK31vHtqWfoRZAOSpEBJqKuWQsMoV9wYZUwLRaaDQZd1FuvdngGGCO23Sku0Fkgl6LpY3YyAC4TAx0a9JSkVwX+hb4MX9CymXmxeAFlaMBYCpRyplmipSCgQ3mGdwrvQLtxZKBvHdDhGJ+mBxecsSZoFBq+PrUJ7QDjIisheJweJ9YJN7fEYpAhs5EGeUZYN67KlajoSLUmFZZSB8oKyNOzwGFcxGWrG45Shb6lUhklAaoPt6qBv5EIVfTgeMxgNmU7HnBcZF5fnKJVQjAfkWYpSmuXVAuMcaTFgNJ1hvaDyKWky4KWTV7lz8ho35sfgPE1Vslo+4/zJQ3arSySeyfyIyWTOZm2p6y0fvv95jBPUndtvyCEo7E26gtOlTrNQgIj6S0oFmZLAGAzOnM4GMG0zL+A7/5nf1nX2/0tj6t7iW7v/KHwPLlbAo3h8H7x675BWIjq5X5MCszsEaD2Qfgjsw+gfrsa/yHLyj+nbyq95MZFlOcloHGa/CEFjlkeWpbPoLEHKJFRpI1jvnevRezygterh31hgES8WXHzQZvJaYbXC2QFVtQ2FPQcCR1XXVE0TzIbiex/O4Jr0QqCs4uJ79uyTAIA6nJeBGdoFLfSma2m6NjAA4mjqhu1my+27d0HAbrPGG8NgMqFabnDGUFvIBWTOkyiB9IBtOX3vXYQFbwyuaxG2jdItYQRpFnrqQfgZvb54ZPN0XVijVIqXULc1tWmpgSrRrBc5dT6km4NJc8rNFbLw0DYIZwPTIq5nLzjhKh0MFIUMReI9EyVyy5zHilAwtsLjdiXdK6+htWLy3rssdluMb/uvMF76Q3DeDyUFSga2ZyylHZ4REXsf2Uql9ZyLMO86YVCu5TWfMJaC3IW1v8PjiiFydkR65x6nFwvq7QphLInUHL35FruPPqJdrxBliTKGVNQkyyU6z0jzEX/w1Tf58uUpH+5WvN80+FSDjAANAmeiJrOQ0bU+rMXSh7mE71DO4a0jkZJRnrNYNQzTCcN8DMLioiTA9UD16uKS87Mz7GyDfCf8bLfZILYpWZLS6KC/6lzQgd92JUJUobVRBrdorUSQPnh+wRfffZ9aNlR1je1MkPhJU6qy3BuQYD3D0RCBxbo2FBq7BkeHMB2l7xAuOIa3bYNOM9IsYbtZ0jQNVVUjxV2SNKVtW1bLNeMpKJ2SpDnee1brNePplKwY42zHersBkXB08xgvEzZlw269DElnHFKo0HbsA0jcti27XUkxHJLkwbTSu5LddsPV5QVPnz5lu8oZjscUgwGDYoAQkslsHuQHlGItYLtZBzdlKcgHBU1jqcoNxnbUdc3FxSXj6Zy8GJEVI2w1Q6aaYTLgxvwmlQnHATYYDHaGJEvIR0OyJEM6T5FrurqmbmpWmy35cMKmusQKhdQJTdfhhCQfTYIepsoYz45I85S267i4eE6iPFmSkeU5+WBA5w273Y6zZ09ZXS3I38ipPmpeZJ50HeLzn8ev13Tf9q1cPL4gmxXIQUqeZ3TOBN03CHGU59qafwAy+iKKI3ZoRbBWejiezkmTnN2uYlO3oVNPBAaiQFC1JQ+efRgAk6NbTPIRCpiMp5TVjrOz5zx++pSq2tFE+a+m84CKxfYgoyI8HM3n3LpxzMv37pAoWK/WXDy/4PHDpyyWLUJloVtBaayUiN7rp1/t+4U+OpyH944FfR/u537VCUjR4VKG18dehNgRYmyHdztUUSEGLfkc5NDibYvrcoSQFGqyL2pKJLmc8K/c+UFaV3LZfsinn4fOGetD50jt1nFdP8x9CDrxZ817fGH9af7K43+Xf/nOD/Cl7d/nc8v/idpt+N67P8Tnln+DD8vP8j8+/vf41+/+52iZ8rD8DD9/+d8C8Ptu/YfcSF/l1zOEEHsZp1QWv8azf+PjreF38YfuBTD6b57+IK8Mvo3vmP0b+89M0gKd5Ky3a8rtlq4pMW0bivV16OhUCNIkZTIes1ku6JoG61xoqReH3ElGnVcf57oT8RuOHYMu5p6d91G6wEf5utjNqPU+l4oX59o8+YqyIfTMUCEjwB/uo5DZh/tCxrl4MJrq59g1tw/v990vsea2v737mDrsp/IF46wXZMEIOu2HYryMhS6/Bwu99/ioqRr+Bn+NvmW8B1173VX2YG/coaNMQGC7htihl5ELMgM2+g6Ezhm3L66zj2MC2OavFeDiPt8XnGPM4yO4t5cw6her+F4Hc81DB6hHHs6197YhHq+Qe2lExAEEtX0B2jmMjd26UVu1R4KFCF2jUgaTxBBzBkZq23V7li2+B+HZM0GDPq2JuWRsI+9zSHF9VvX4TXicJAlFHsDPNCuo6/oaOH2dLd2D0S/KA/TvKaKhae81sH9FBI6l7ucf+9y2B28D6dxfe9/ALA4awCoYYHtiB1zAhvbKA3FDkcJzPVno53rP2FUy6NIKa/Ghuvcxj4h4T0mBVxKnNTLV2J0njfOmsY4WSydTxlIwUAqtJdLDzlt2ztB0ho1VbIxjZx2Nt5irBbbq2Fxdsbo6597LdxmNx+SJJjuakNi74D2T8YSz80ueXCxobIPtHJ1taaxhV7eMBimDImWQ5xzNp/G7PNxnprMI4UAGBmsiQ1etFAqJZDw9YjKZMh4NSHPFsPA0dbiXnAxM+2q3pam3WFNFoNPhkRjnqOqGq8UlA2tIiwFJNuTl197m5OSE5eKCs9MnvPeFz7FdXiE8JJGUA0GWylob9YE9bWfRxpI6GI0mDEdjjqyjaw3r9ZqL8yuqKszF3XbDcpmRKEmWaNwwRamAZil5jVDzVcbXBRhrjWG3KbEEt/vOtOzams4EXa7FesPZYsH55YKr1YbdtmXXmP0iXtHx7oMvA7BaL7j/0gl3bp2Q6iQkUT5UCItigB4q0iwPwGnTIqVA6YTBYEi72TAajsBDlqaYqEPRtBVNXXI0HSOEpCp3VOWOYZ4hdWgE7BdyYwx1UwcqfpJEgMXETc/jjInsrBAXKSX3GjQgqJsGj6PtWvCBAt05R9PUtE1D17V426GlIIkOsJv1Aq2DRqtzQXv16Pg2zjaYrqGutqFy0FowHdLCfHqTUT4kzwtG4yAUvri6xDnLYDQGpVBagre4rqVrPKvlOdv1irJqqBtLPrzk4mrD2eWSZ+eXVLsVwlmaekNTr7G2fhGIDWe9D/iu6/a4/SbQb0Dh2b1kw36B9v07HPRfr5MXDjQz+h/sfy88dG3LxfPnSBlYplk+4Nbd++gsxVrDalnSNQ1ZnrFYLGiaLeOR5u7tGd1uyda0dFlBlg/ojEQmOTItcDrh4moT2NGEpPSyyXDFEK1CJU14RyJhlClmA8V8qMl0OC4XdaCMtYGpxqHKq5RE69Buo5XE+IMp0R7djo9FBHcCAS5snkEouy8YGpwxpNmALLafJjK0CyjSsJC3wSTPRrkN4wVe6mu6T6GdVgW17v1m3rcCOecx1qF8CIash7K1XJaGTKugDWQ9FkvrBLWFbQeJh3EiI5gssV7SGc2mAoRDJ45x05ANMsiyAON7i7FBcF6ohCwvWK1XVHUVWridJR/koTquNaPhmM1mQVXXdK1BC4X0Kuh0qZy8mFMMpzTbDc1mTblesr26ot1sEdah05RE5wzyMaNBhW2XbLZLttsdm21J29SYrsFbSJIM7y1CQp5n6DRHqQQpgsN5miqyRO3NCbq2i0C7I2f4m15P//8BBSe85P+F8I8+m/j4UsTX+PmvY9hiwU7/E+jB2Gv95WmWkw+Hh3q4AL3XETMIrehNEbwPrW4+Bv6HwJtD6587AI/7FEUc2ABKKPJBQWdbbBfXPSHY1RV124QOgwiavRC89pV24rp6PU7sTSB8ZEzF8zSPHmLLEtPWNINDstrnAvMbx+zKHaZtaW1gvJFo6rahdYZOiqATG7v+JZ7dxQWp0uGz3QGE7bFXt2f+hHtFwp494XzYP3zTkqc5UmmcCOxD4z210uyiuU12fAcxnZAOc7AWv2kQMkhI2LhHH+L3KIsQJ4kQh4JgeBC/CSFiIB+SXOMs3XxOUe6YpgWNsexqi/XX9jHYX/d+9Ht6590+EYtZ6j6xRYQ1ubOerQCkx0qPEobUCW55yQwZ5HW8RCQJPs+xacbq6SnSdviuo/GSkzdeJ3EvYS4y3OUlZrkkMQbKCmksqUr4HcMh88kRE6kw2xWrrmatBCbOJWtDUVAlCp1kJOmYJM3QOkfqDC8TnLBhLqgWYSo2m5p615CoFJ0KECbs5teS0bbtKOsSq7d7X/bF1Yry1KN9S9t0e/ki731oKwyzcw+mJWkAEgyeDx89wh2DIkFmiiwvkNoHQ1JnUFLTSRtMjoQPWmIuGGp6RCgMJAJ1DRRQSjAYFCyurqh2O9o2SGAFXeeQ9CVpjowF9qArqLA2GHUJD13n6InT/TCme4GpqYSKciXhJrPOUjc1ZVWTZDnFIBQaL66WrBYX7Dahg8sSCglZPiQriuByrRPwHp0mDIYDrNHgDYKwjxrnMdZQ1TXbsmKz3ZGlOWmWM57MGE6miDRjkGT7mMnZjqrcUjVBBgAhSNKUTCXYrsTjqdqWi8WSdDDFIlFpMHLrrCMfTsiznCxNwxokEtJiTDIMjBnlOnCQpilFNiRTnhvHJ9Tljroug1byUwGH5TeQni7Og8zIbE6pJe7t18huHZEkKtae4j2190XoF7J+PYuxqA/39x6M8KBQHE/nOAdV21F3Bq8EeZoyLAq0Ulwur7hcXVEkORpFfitDS02R5dFwbsVquWS5XVM3QT7De30wQY3+EbPRmDu3bnL75gmT0ZDlcsnp0zOen17x7GxN0wU9bucDCaBnmIW16QDoBKgtMGOJckp9G2+PFbwAse2dKoN2Siy/RImfBpcYVN4iJx490zjRYsodXf3VDbyEEHzD+F8Cgm58D8b+WuPt0T+HEgn/ZPU3+KX1/8zvv/X9PKt/hfd2fw8QpGKAEpqtveCX1z/JvxaljZw3tK6M3+VvcpP/v2DcyF5lmtzh/d3fRyBRIsHh+OLmp3lz+F3kaU6a5lxcnbG+usQ2dfQBsWgPwlmk0Agh0WkCSuEi81LJQOhx1wuKEb1xzuEEuB5g9GGdE9bRORfyAA8WR9sG4epe5qaPHa4DvX5fpO7niUdEVrXY53nxCHxs2e7Z5QGWpX91GAdl2sOKeJBU6M+jn7MQ44fYkRHiaPkCGLvXZoUgh2cDeGejB0sfb1lj90BRz37dXz3Xx0bhzpIy6q/HnxEB1iAbEDpfRTSc2hd2exDbH4DWPYsTAkB3bRwKwmIfWPmoISquXdkD8Hjter/4soA9eLdneor9U6L0Uv8tiVCYk17g+uJvzLO5Hhf1uWWUnZMx/hLEcFIYAls5xJe+l1PYszzDE/fxVNxrwxTzIEF6FfK7/vOkREfwVClNkqaBFGZ6gLOXptifTYwXxT437Q8+mEQF8lCPA4QW+gMhrAe6+yvW52xCHroKDhrIvTZo+LdSwfcmSB73s+9w/te/48PFZ39sEIhXiCAX6w0xProG4PZ/ZOhoQ2usENh4vQ/N0QAAIABJREFUvpbgSSC8o/GOAZ4iemXUBnYRsN0aqIyjid4YvjNUnQ3eQG0F0nHz5gmT4Ygiy5hMhrz00h3SLCfNB9ROcrlaUHdBi7WzHU1nEBggGI0PBzlaBdGsnkwghYx5hURIjU4yhNThGgvNaDZnMB5SDBK09qSJwHUOJ0PcpZWna2tM2wRDSXz0hAodkNY71usVVRu8b7JiRJ6EIuegGDKfzZlNp0jTge/l6UIhv4vax73EYtt1yLpBpwmT0ZA0TWI3IUynBVmiWK037HYl1nZst1uKLCHPNMNRhtYKqeLsuCY/9fHxdQHGNk3L2cUSpTXWGspmy8X2itVuzWq75XK5YVca6sbQdhYhU6RwUQsGvIRFu+WX33uPDx894s6NKb/7d38rt2Zz8kShhUfpnLrakmYZaZ6TZEM2Z6ckOrjcKpXgrGN+fINEa5yxLBaXXFydUtU78J75ZELXNnRNTVuXGNMyyMd0XUsXDSrquqZpSrIsYzgcgJWhbTMurL0xDAQtMI+nbqq9zsxqtUQpQZoWJGlO1bas12syFZwdBSqwayODUkjB5cUZo0FBuIkTrLXcvf86XVsF1sZpt2+LLk1JW51xND8lnd1EFSOyoiAb5nz00QNOqpvcunWH8eyIIi8olabZ7Si3a66urlgsV6xWO66WW6rqA9abirrrqE2LtSV1uca0Fc72+oR9iwDQJ/buoLPYV9Y6a2miDsn1immig+GT/PgkFr1CzqHasNdg2VcS+4pX/Gxn920LwbzKk49GvPzqa+zqis12RVvXlNsNZbmjbiqGhePV129y9yjl9OyUDRuSdMBgPEenI2SaY5Bs1lt+5ctn3DgakmXBJVCMjlAyaM62nWGQau7dLJjkikILlA8MaU+otlkbNFYT3ycHniQJrUi6B06TZH89g6OjABmMLYjsrV42y0dAQaXhd8RN0kTTNpQOgP7+mgVnwzRRdLZBJSm9hlhdd2ip0NEATykV2aiBBdVvSsHl0lO3Di+C23BtPZebiieLhvsnYzxQNh1X2x1H8xH5QIG2CGGZDxNS3yCsZzwesdlVOCkoW4O52JEnmpO0ZjCc0IznbHVCV60Jsg4JiUv4wi/+Em3dsNvuODo+4p2339w7omqlabsygMjWs12uKZIpxzdvgh5gjMQbwZe/8Ctsnjym22zIsoybr94lHw2RWtMZS9cIpkUFxuAxWNtgGhCdBWdwnSdRQW5EAJkiyD7o2C6lFUWekiU6aGE5i2tNbNeBRF3beIXB0nz1xfNaQPeVw3/lv2Ix44VfiesPxYsBzdcYX6PIFz4vMgCus972DNRf68W/ieFfeHAI9r/m+JrX7+PP7ROOJAZgEpWkKNI496MOlhDk2YTC6v3xBHZpSGSdC/uB2wf0sQssgi0+ylf4aBSJB+sttm1xPobi3qNkElma4QTSdMpwkMSWKQvCsVvv6FqJ8GkoTu6NNuItz3WjucCc2bfoIZAOVJCiD2uB8yR/5+dJJzPkN30T9a07+8uTphnj0ZzBYMx0Oqfd1bi6oysrBsWQrXGUjcEIGGi97ydRBDDa2hak3JuRhOLR4Rp561AyBOaB2xVkvRxgnacra9J8hNQCrxRlZzESaBvcZsVuu2U+HHL75l3GxYyqsZwvnkFnkd4Fo6posBUvDt6EYuSBvREKqP11dyK2ZBoPkcmrEo3xYX9TOuXG7Bhz0dG0NdbbSE47uEH3I9EqVNN9KM7292mvB37IVQUWQW0cTgk6Aa10aNfQOIVBo3xIMJIkwSDYrdZ0bc3LL79Cvd1yeXZG0zSM33gTc+OE6ukTNr/6q4iqIbEeVbfY5oLBeMwnT465Oz/mpcUln//wAz6HYyUdqADwSJWRDiaMJsfcvv0aJyd3yIsxOsnwQrDdblgtr1gvr7hMzih3NY8ePiLPC45uTJnNEpAef40NmucZI60wIw9RVffp03Pqd69QrmKQwWw2Is0CKBG8AXRkMQWtvappMNbRGMfF+SUnbs7RvZzsWDEYjlhtdmyWV3hnSQcZyOAAjgxorjEWZw1KCDIpmI0SljbopGfWUhQF89mMzWqF1poiL5BSBkC20IwGI27evkO5XQUNNQHz4yN22xJHAHazJKNctzx/9BCdD5gc38JNJnu3aAERaIgmIjLs121TsV6tQCjywZj5fMaTxx+yXV8gRCiGtp3FeoXORgxnR3gPddvS1jvaznBy5xa2a2mqkvX6CpQmL3LSPKcohlxcXvHk2ZM9S248GDGd32B+4xZHN29z/NJttBIsFkuWVxcYb0BpsqQg1zlFkXD+/ApjDcZ0rModaVYxmswYzWboRLFeLpjfuENRFEghqDZLLi/X+CRnMp9y+97L2LpkdXGFMUGjzzjLKB9xPD+ma2tOT5+gUhk7heIIPiKIxSXyp38KZz07+9007g2ybowdBDM360PXnJBib9QS2qevARs+ovsutOsqociV5s6NE7brDevtmsZ2SCSz4Zh7J7cZ5DlfKCsuyx1Pz57R1S3jYsjJ/AQhYFgU3L/7Et461rsdTWspyxaERUkNBIfuRMIbr77K/ft3GY8HVLsd737xfZ48Pme7bcHnCKUDmGQakD7ofYt0DxiJmPBaL/Eu7os9EBsLgj1jL2aM7MEoF8kszqKERqoOIWtav0CPITvRqKnC5h3NesPuckm1zn59++lvy/D89affDwgSUaBFuv/N68Pv5PXhd/7feCy/vmG9YW1O+e8f/Uk6X/PLq5/k8+u/hfEN/+nb/zvj4YjZYMQH2y1dU0c28uH1fUJvrKNq2gB7CIkVEuM8eZEFZqMNreZhGoQYzHpLF8Em6z2dDczr1lgSIVAiMNiUCbqfytlwH/Uswj7XihtSCLUCcBSk5w7+D8Q98Hqo1wN2gSZKBHfj80U/9eILvEX0lpGR4RuQM7kvUksp0UlkOu5BtH4E4x5LIJZ4T+zk61mxLt7Wbh+T4Qht+fFoQ24WAVQOrNaelOKJILe1IYaPj/dGaPH7OhQDXox7+7jL90V3Iki3T1z93izzAFLHn38MzOtz6usXvNd6P/y7f3kA070PZqd7VibsySHhK/BYeQCjg3av2oO9vVlsf8x9d6+LXV4H/dSgYRwA13DA4X3C8VrrQleWlEgVAuIAmorg/xO9EzproGlwES/pYeX+++jzi/44ekmDINMiIgh8mHeyB1f9tfmHOBQzog+IjD4o/TwLcmIiXne/3yLCGhpa02VkHofjjNcgxpHWXte6jjrH8R7tSU1SSZyUWCmwXdSAlqE4gIhAugAhFV5qvNZYbxD9jWUEtTVYIWgkNC7MhdZYamOpEWw7S2NNNDEO0pqJFghvqbYVDx89oakajmYT5tMxw+GY45szBuMxk6NjRDrkS1/+gMVmQ1VXgSzoPWVd03U15XbHfDpiMMgZFAWDYkieD0AK2s7SGItDk2Y5iAQvFFKmTE9uko9zdCbQoT5Onmm0EiSJAAy2bTGdxfuge54kwctJR5mWuqlYb1Z0bTB4bZsahUdLUMJB0yBiUaqL62WuJWmm0YkOZFBjaOoaaw0omI5HpGnAY3QiGQ7GJFozWY9ZrdacX12wq0r0SiIVDAYpWTYKMZx68d78+Pi6AGPXu5L/9ed+DqkjbT3enK3pAkAnQOgMhSLRNjALRNDkCAEqCAeNc1zUOxZPVnz4E4954/ZtXr51k1fu3ObO3dtItQm6U0nK/PYxL9l7LK8u2azXtF3H9OiINEvpOsNms+bOSy8hE1gvr9gtl/zKZ/4x3nfB/Xd+zPj4Lt5bvOkCs9VZEuFRmQYMi8Vz8mKA81HjRAYhfw971H02DS1LSmucdaHV7OqS1994m9m8COBxkrLb7rDOBymHznJ+dkZd1eRFDr6jaT1CalIZdGLX6wWdsSAS7tx7k+FwhK22rBeXXF4+54MH78L0JpOTu+is4Nadu6yvLunamsXlOWVZovOUy6tLnj15yrMnpzy+uGJTG+rG0rbd3gCtbkrKZkPdbYPznAgaHN6aIBZ/Pa511xwgRR9k+P3v9/Ursccm0Oqarss1MCcsXCEg6F009xox4ppGC0EH5oP33+fJ06d0zmG9I9Uh6ZhNBzx7+oC2raibik1nGYwnvPP6Md53ZHlKPijAKVRWkA0m5IMxyJzL5YZnl1senG147m/xOyeKLMaiSkq6tmNcKI7GBXdmGQPhEd7hO0/rHXtaXr9JCkXniNqrjnmWRaA+XIxEBdAniOKD6RxIjZIqBgbX2136q+lim03QQ0SnbKoGZBDLRyjyNMVjkSIwiopiEFrvm45dVSFTtTc9681ohJR4E/R8BQ5nOpIkQSiFk/Dw+RU3jyV5ljEej9Brw2w6YJxrcI6LTcPpxZrJqGA+ydmut1wurpjmCcMspRjkSJXSNWUAmdOMZxcljbFMJw2jaUk+PsZqR7Vb09Q7EqV4+xOfYLfZcvn8nOXlkl/83Od45xOfZDKbsd1V3Lx1FyUVddWw3VQ4nyKTKcVohkNy+ewxDz/3OY6mM+69/hZ33nmHdDbGdB1tVbG7WjEoDM2gwnQlTS2ock+eS3ynoFV0okPJDpUGnTuI4ulKoXoHSWuxUuBlaIFROtlPfBVN0QAejv8a/+DWh1gTNk18CIOVgCxLD86tMWkSMVAJAUVg5rdt+Fs3hsvlhsaECqWAoAMpBEWaMR+MGQ1SdKLQOvwNQa2LQFRo/02UJC9ykjQcc1u3US+3x7E0j04vePr8kmcXV1ipcF3LjemIuzeP+eRbr8VgIhyElArvArvnepAHxOA5BL6SQ3Avo0O8j4ZLxlq6Nmh0ZeaYY/upvXlDH/QKKV8AgvctRBxcbfsuhX70wFuXnNGmp7zz0Z8F4PnFFQ8uN3yPCzp1Xzw/igud4N7n/mMG66/OxnmxIfs3MH7DL4tpzglw4vfnuR/i+pv+xsBxAVw1CV8+VcAPA550c59R9XtpPoSp/0YmAKMYLHfgMw/Zi58meID0n44sV4ezjs70ATv0dC2JiHvJgU+TSA3eRbMqT2092XSGHI5prWe3WNE6h7QG7TQ6S9HKs7hccu6WLBYLBrMZwk+DCYcL60gwIwn3F9KACBJDwnWBoexC1dzaILmS6GQP/QeppbDOrm/fYTOd8eY//IdMB2PWQrBptvs9zPPiXOgBRSmhxNJ29kWGrOvBabffKxolMU7R5BISw8o6Lqzhrc5xW2qasqIoK/TUAoqL0/Og6d42VJeXtElKPp0z/MbfQXbrLotf/CxmsUS3LbmQiNUSU5XMxmO+/eYd7t16iZsfvMcXm4oHgwGvvv1JXn/7m7lx8yVm85sMhkdIEbSQw94sYhtp0Gmuqi1PHzzms7/wWd7/0pd4+ugjXDtmeFRgr83vrNBkRiAyvW9a1ioYehibc7UuWW0vkNIhJSitGA4zkkSR6IQiH5OlGVlMmB8//Ij15QWfuP82N+7cY3x0xPbd9/BC46ylMw7rah49eswgTxkUWch9JEjpcL5lubpita6QSjIYDFBKcfb8jLquGY1G3Lt3j7Qo2G12lFXN4uqcpjphOMrZlRVNWUdGm0dEY5e63JCKDiFqtIPUVBzduUOWJvR3p/PB4FFGXbnBYBBZkC1luWa9GiEkHN+YYO0xm9VV+AwRHMnrpkFuK5I0oyprlpcXfPj+55lMxoxHY0bjEbfvvRr0WDc7druKi8US5z3T2ZSuaynLHZerC84uzlAfvEeeFRyf3OX+W9/AnVfuUbw65Mn5OefPz0g8FMozyWCTBra00gKZQF5MUGlGXdcsLzXPPnyEqR/z6huvcuPkiAvX0XSa8WiIlpKL0yvKzQbblGgl8ShefvllXr11i2fPjshkynK5wb1doo8P6YzvqzX7tUbAp/825oMHdL/395DOCpLjcTCBA5wJ93Wvr0lfsIyAQqA5hU60Is+5PbvBZDjgwUdfYrG9BOnACm6Nj7k9vcF4NCT7pOQXPv9LlFXN2cUp/2hX8l2/87sYpClaCbJE8+Ybr4ci0KPHbDenICSu6xDWUqQp3/DO27zxyks4Z3ny6DHvfvF9zk5XOKvAZwTU2V6zGztoh+JjG7VwJKlAOYlzClCB9EBs2RWKXdlFLc/+P2J//hFyQ4kSnTSQlah0w+j+ECPWNFWHrTy+NqR4tPqtm2j9+ofg+9/6ewzVfP9vJZKv+Yr/p8dnFj/Gz178BX7gE7/Mn/vge/jmyffwzdM/wJ/74PcD8M4bb3D/Hc84k/z0//YzGGGRWiBxiLZFRV3XumtxVYlPgnSM6DRN1zLKc7w1mKbBdi3KBUDDidCaHogfdm+ClCYJrXUk0gU9VXyU7LHRlEiGLpLI9DsA9kHSaA8ihsrRvmgb2IIxyNwnOIFraV1k0dIDlgc2IP5jQGMcLzB9e1QxknscHAxZ6QGygA+0ERDbS0ERY8rIiu0d1w+Aotx/Xg/EWtubcIVzPcgzhddZZw8xq79m1CR69q6Ke33P1A1x7KF+FAPfHhh88cQP1+lj1+LF//vDeYpep1ccPAHE4bU+smU9IrCu++ILsRsyStp1JphqB5mD+AwbuyAjmer6cSpA6YRMJ3jvI85RB8Mm0XeGeaSLwL38OEDVg74uSAFJj1YAiuAVExnIUR3Su57YEeeSkAiloylYkBzrwVoRdYxFBFQDCC33cQoxVpGHq4z1LnS2KLU/1+vHHPH7+HQRtL5J9q8PPgEGUDii6a91tG17jWktsMZE07ggS9gPoWSIGaSM9f4gBRHmbgAIRRJiYz0ZIyoJbRvMqhoQQqGkJk0S8jSlbVqstTStofUdynuUc0jn8RK8F6gkI8lzZF6AlngnMZ3DGE+aFkzmU07SnJfRvPnOW3zj4zd48vQZp2dnPHnyjOfLDc624C3GexbbinVZxrisYDabMBhOSLMRo2IQPm8wDHPQg3WafHSDda2Qa8col2RS0HUOQcg/bedYbR21UZDkpMPgzSFlyK91NH6z3tI2FdvVkvXFc85Pn1LVO6wzOGNpTRvmvRQkWjMshmilI/u9ly1yNE1H1bR4Y7lxcsx0MgoxSqoYDItg3JqnWGGCwVfT8vxyifMOrRIm4wKR8pX39rXxdQHGegE7axGxfd/FiprzAic1nsDyESq0bAUGj9svH37fPkisXgm2reP90+c8X6148OyUb9y8yTd906dQbY3YLPFCsry6Yn15QVVucd4zvpoznc2juZEjS+4zmx5j6padWzMezanqLccnd7h171WmJy+xWD6nNR2ZkNw4GfLgS7/K+fNTurYlywqOb90kSQNjwkRQLdCpdWTkBuR8Mh4H0BHBerVGS0G53fDRgw+YH58wHk8wkwnbVcFgMETqhLbeUe3W4GAyOUKq4Mzd1FvKaov1gjQbMB5NkeIu733hc1yeX1BvN5jWcne9YDCckqiEUTGgyAeYrmW727LdlVxudjx88IizZ+esFmtqJzDWYdqOrq5o2w2taelMg7EtxM0bRMBYpAo0evniYisFscgZWjptT5EX/rDI8SL28AJbb88oCs+QUsYKUdQr+tjrPfCFz/9TLhZLamuD1pz3zMdHDIZTTNsinWe3rRgPNfdeu8GtmzPWqwuyPGM4GrPb1QynM7J8gs6GdFbw6Nk5jy8bLivFWt1BDY8RekPga3kUHbdv5MwKzShVpKEwd20zDBuLVNFPVoLrDtU+pQOboTGgJGgZGJMSME4cWl2uBc5hUz1oGvq4sXobjLxMZ2g6C0KiZV9JSmMlV0FkJuM8WggGmSZNBigRNFCND4Lmdd0wKDKa1rKrDduq5ebxCKIPcZrA0WTEZtvQtJbpZMjJtOBytWVXJWRJwrrs2NZgaemcI1cKwYDLTcnlsmI8SJkNg9Zq17UsNjUJBC1jG+7+iYK2XoIU6MEQZ6EYSi4vLrm8umK9WmONpY0VuyRN9i01xni6RvDKK6+RDCb4pEAqzc1X3+af/97vo6tLTNdycX5O+eADRBZkEEajKUNzhHThOlXVlqxd0WlJpyStlMhE45WAWNWVUpGkadzI45eDwzgbnTglSdSUDTrUhw3ZCw8SdKpjwBd1p62jNn1lOgTPzpowx/oESkmarmW52rDeVhhHkKGIh6CFYKoScikZa8ksEWQE3SxMuycj9GRBzYCp/2QIJDd9tRkSa/cGDw5Pkqbcl68wGm6ZNSuqzuISQ+IV2abAX97jeD4NgU9AHAL5YY8N9tDo4fwPLfrX1oJ9UBmCCZdGp06pUX1XQnyuFwFE7k2O9mxQd2jxkrHFuGf0OueQSqCQaI5Jy9n+0xfLNR/uzpB3egbstSDKq5hsfOX4jcGev8Uh/k8e/zaM2bngnZ9rWX1H/94RkvTXpvh17Perfb4PYEjXOwnHP8L1XNzwrvT3LCGhUlKgIgCqhQSpkFKwrmuyYkg+mTHZVpRttXdrFl3D7uwZ+XROMZ3x9idfZzqWXJ1vWF6uWF1dkYymYBowHd62ce6F85Jo0HGNFsEN1uBJVNBqFBGo7XzY35wAoxQffupTzP/pL5OZltoktFFbDl6MzVxMEKUUIZCM+6K1DqlSxqOC4aBgPBwyG96hKRPqxlI3FavqOUu5xEnHFssKx5vOc7JdcpSlJNMpRzeOoe2wOLQ1LJ4+JdlWVEfHFEfHjOZHzD71bdRPHtOdnbG7OGeAIrUet9lhmicc3Tji2195nTfSjGWeUxzfIjOg1BA5uYWQOt4/h1bH3vEXocnyMa+8+QmObtzhW54948EH7/OP/sHfZXFZUlYH9r/3Ju5jhwtkmg22S9BJASLDGY/1FucF1mjs1iGxCFqkaAJIq0KSrxNJ21SsHmwZFRvqrqHarpiMCpz1NJ0hSwqqaofzAp1kdG3FcDyha0qatqGu2wD8IdBJSjEcslyuQtfLSDMcT1iu16w3W4wxJGlCVVUkeUZVN+x2FfPZCTduzlmtFjR1hcBRVg3Serp2x2b9AUedwbz8OgwAPG3bMpvN6FlYXdeRF8MQMHhPVa2JBsEMhwXT2YTVchdzwfAdVLsti4vndG1FW23JsgwhFa0xrDc76rohLzKKImc+mzAejdhutlRVSec9SkqGwyGdsRhjqbuKp08/ZLVe8/jDO0xv3OL4zk3u3b6HtYbT0+c8e2KwjeHG/IjZ8ZSbN6foJKFpDY+v1lw9fxaNrD11bVitWpbLGqk0l+dLhAqGU/MbN1gvzmnrmu12y5OPzhinmt3OARmT6Yy6q65XeJCJggS89TgTNbSthYeP4G/+FN0f+O6gbTxIkbnGC7EHHBx9MeiwYAXQwqOlYJQW3Dk+YVduWe22VG0Tin7OBwM7EUz8jkZT3nn5NT569pSr5YrlbsOzs1Pu376D95L1ZkltDM+en7Hd7VAqwSOxXctkNOTurRPefONVrDF89OgJT56c8fx8jRAZUoTCT9fVAR9TOrrE68hK6/bAagDgTCQr2BjnBQDCC48XQYJFertfw4WUWHe4Dt5bOmqSiSM9VojxgK4AU1lsayLBwoWCs5RUdsWPPvoTXLYPAViZM37k4b/JH7r35xnrm5ykr/PHXvnL/HeP/jg/e/FfvQCg/uTZD2H9wczox5/+aSq3ZqxP+L6X/jwTfYt/dv5vcZy+yo8/+9P85cd/cv96JRL+nft/ES0y3t/+PD9zEbRZ/9U7P8jN7M2vsgF95bC+4y999EfpfMPWXOx//hPP/jNyNSaXI/74K/8Df/XJv89nFj/GFzc/A8AfvvfDvDL4dlJZ8Edf+VH+0kd/jJ96/l8AnkTk/JGX/yK3s3c4Su5zM38LJVIQgs+tfoIv7X5u/zmXz59SzR7x8skxr91/mbPn55S7Hb4zaEJhMnizhXxsNJlTFAOSRFOWO3KtadsWoRS7tgsGTTHgE8LFAvYBYOvajkq3SO+RWmFdSyJSnHJh3bbhhvAiGFHJ2H3nehmLWFzsu0mCwVgAW6WMmptEMMxfly/YHxSBpd2DoQf5uj7uvK616LwPLHVirVaAcHI/36+p0AbTp67dt8nbWFjpwUhcZIjG4suB9XrYmwPYGoFAH+a5sXZPJNqzZHtmIzFWFUFmSsZ1Ot5J14rggYXck2h7kkAvQ7DPcMUBwg3PDce8NxGL723dwbumf2/653CQtuvPoy/09QXfPrreawn3+DAH8N45h+u+SigZgW0pQt6qlQ6gmJQUaY7TwTwsvH/IEqwNurS2l+ByPd0iMpUBZz3OeJwigp2CRKeMJlNw0DTB02YPCgsZsZXo/SBD56GQcm/SmyTBO0QoRaKSMLevzRmci8ca5lJI2cLPAogbT5lYo6OPW12UzQqxbM+u7a9huNY9g9rgrKM35lVKR0Zs/PbiFx/vgphTZUF2RxqsDygDVsbuWIdMUoQzoYJsDEoKEhHkMos0IRWCVCtUmqIR6NbSuA7lLAvnKOO87rYW1dSopqZIM1wbpDGlhCIfkuYDpMzICs3NWyfMb8x4/Y3XWCxXPHt2ygcfPeX8+Smr1YLteovzjkQH7WaEomob0BVeJgidxSJ7z7YWCJGR5wXSOlzdYryiisbGiQqZ8a6qaOo27FEqI9Hh/vdE6RUHvgssYekFeZIxLAo2eUbZlmyrUKgiEtCEj+x1H0h0PcPcE0BaKQW2DRJznemoy/+DvTeNtS1bz7Oe0c1u9Xvv01Z361bduj22rxuC7ZA4cogRBhGI8wMkixiEIhAKElL4gYQQCAICBH+QIpoEESSaXxgQCkTImLiL22Dftsr3Vneqztl7n92sbraj4ccYc619rpvYjkCWkqna+9RaezWzGXOM73u/93vfOXY552Q1w2QFeabRqsK7UySSfV3TdQOXl7eUWYkdFizmJb/NnXPY/lCAsZDm+zAO8ICUKfUeL1Ca9I5YxghAhTuaNmkiEoLBB7ZdRzsM7LseYTJ8UXH/7IzlYslis6Xf19SbW4auAQl74QlDn7QwFUPf4uzA0EfDhgenD5mxZLJYoYsKXRRkVckwTPD6VtsbAAAgAElEQVSDJi8rOuvoOosbBozK8C5WG5V6UQh9pLtbGwOg2GZkadsWJSVt00REf3OLVjoF3TXOuRjgZ9HFvu87AvLAlhyGDme7uPjIKPvQtc3B1dFaS9/3+M6yX18zma0wJoPgkVrTbHfsdjvW6x3Prjacn1+xWW9pm5YwMpGGATc09EPLYDuctxBcBFZScVMIiTKKkIEw31YpT9ctpAre2AIRHx+rUum/3347gJBhXIPj02lh90mjpbcD55fnXF5d0QwWjyA1gLJancV22sHSdT2zMmM1y1lMCjIZ21nyLGc6meEdVOUUoXP6wXNxs+fdq56rJqOhIlQrVJYjxC5eXyE4nRlOp5qJVuR3285TIODvHt9hOEcGxujk6QPYkTwrwKTxL0M4OI066+4gHWkCfyF4EVF4PMjIojWxJU8bg9LmwGQ4AFAp4FCp8qmkTHp4Pb11UX/Se8pCRiBZQxcsN7VnXgpKHd8zqwrqbkc3RJbX6SznZteyqwd2IrLH8ipHq3iPOx9iBVkqvPM0g2Mpc6TIohTC4BhsoHOKXROQsiXTDhU6jNTR4ExkaJXHhd15FvM5WhvKqjqwOH2wSKEIQeKtoCzmoAxeKpAKnCefLhgGS7evafcN+/WaYj4jzyNgizJkxZRqsqCaLtD1czJjcEUGITGWFUgdQSIpA3XdMDanSCko84zJZIIQ0QHT6AiMGyEoy6MW52Qy5ezefVRqs+m7PbvthufnlwxjMDC6l/pjKWIMVLuuZ7erqdueIDQg0EKQCagQ3HOBiXNM0EzVGaIX2GSOlGBORkaEpsT4PD0Po4yRFwqhVTScyzSVqtB5Rhlacrvh+XqLTfek6DX1teb+bJla59N8cKcYcxjwd6eNO2zZwxQhjlqqiIiHWuVwRI3OCAKNlfFoSKWlOpg+IMD7IQXNUeP4YJaUftvB0jUt2+aGbbPjpXS/9oOlbtrfdnr6e2EzXWB+6VgfcfPf9+YB6z198EnQ5u65H1OWMbmJhR4Ph/ZLrTOE1OTSgPf0naWvG5QpKfKC3kWWQAgeLUDYqJmK95jMYMqcfOIp+xDnWdvR725jgmA5sG0CRLO1FNQLqRAqEEIqbCmNDJ5hiGBxGAuQSrFbLpkKhRSa3BTYlEAc5trxXHh/NESUkrKqmKrYwrU6echsUlKYAiML6Fbs2gwlHUptacVA7zaspWeQ0AuJsJ5+aLC7G+RlxTLLKasqris+mj2GYcCu17Q+YPKcYrFED0OUfgiB4XaDwiOsRVlHvt5yqgzzKuNhNcPlJdYL3H6He35BANzZS/FcpSQvGsJ08RooTVaU3HtUMplNmc5n1M2ed999GzOsj+fCuWPr9Pic7XDDEE26lCEETQijFp/E2yjFFDWH3TEZVgJtBHboefKbH+Gk46xYEGyLKSZ4JbA+YDJN00TzyX5wBCGjW7kdCETJg74fYtePDvT9wH5fo5TBmAznPft6xzD00RQ2L/A+rr1jQWG321EJSde1WGcpi4rbdkDYjmBtAti6I8MrRKa+1gZEOEheGWNiqigjW1NJmM8qjIL16S3bTZPWuuhjMAw1u+0G/IAIlslkEvUm0+cPNqCtRMqCvDBMpEErSVlFFmvT1NRNg3GOvhvouo62bri5HqiblvX6lr7d8uCllzFFEWWBMkPT9/Q2OpGPBd7BeoyQTKoK8/IjEBlSGep9Q9M0TGdTBmvRQTOdTzg9mRNcxyYE6t2e7XZLL6HvW5TOmE7nPL8+f3FiUSJWr4UHL+N9CoSmJjx5Al/+Ou7TbxBWM5RPgKyMheyDedALhaxYeM1NzrSaMpvMuF6vqZMUxugwdLtdMy8nlFlObjIendyjb3u89Vxdr2nbhpHhtdvv+OjiguubG5q2T0WMCGjM5zPu37uHMZqnHz/l/PyK6+stdgCtJT51gxAsUhpAEkQsT4U7be2RFCHw1kaJmzACQ3fYW8RYcoSAIjPMjw1QgMeKDj0dYBFg7hFFYAhR7soPNgYCziFcSPI6iqV5iaV5/MJlkSnlLNSMNyc/wHcv/8xB1/Wl4vMvvPbV8jtfeDxRJ7wx+X6EEJzln0AJzfcsf+zFz0/xDUTzrZV5KQ2HjN/7JliYx7jQszIv8Ur5HS/8tVQL3ph8P19a/mm29gKAB/mn+NT0jx5MuMZjsyEWmD5RfR9vTn4AKRSlmrMwDwH4wuxPsbFx7N7P34yGYd6RhYHSSJaTirXJaH1N3w3kReysFFIglSKbTJgvlod5vel7LCEBT1EKSI55NaPyuzjqiPp4zfu+xwgwIsbNTrvIwgsqEUiSZjIisc5jx9TY4j22wx+A1khVxScwCyQijBSAQ5IYQcYUm0k1toEfwbPf/uocY7NIQgBEbLMO/s6+hHQsbji0i/tUzD3km3dAM3ixOHoAdBNgOZqd3WXVHl4mvv29Yy5699PuPgrH4Obw1BEhEHd+H17/25yBu/s4gn4j3XbM475dq/Tu94UXcuy7O3S8LiJEg6oxXx1JCpHlmmJ6QtKLFVHawkBQxzhbKnWI72LO70EMkXHNOL7SfqZz60PsYHWJqBX7SI/5iNQK6Uwaf5FcobQ+kN1kihNG2S2RxpXR5gDGqiSVEDgWE0QYtXlH0yx/PNtpPowSD3dMfmPbHUeTYBCj6db4nIgxxWHsMo6jEWTXx+MfEXpBWoviT5AyFh4S0EyIMiJBWoLSoKPJtlQaaTRZkGRKYqQkI6BE9J0xSmKAQUKnBIMQeAQtIt63zhL6nj6ACx5tJHmTsd7tMMWEQOyoNXmecuuMajKJcUVZMZ+VXF5OuLi4Yr9vUDLmvEqOhSSVmPogUxdVHLsSqUzsVqr3dEojhgzpCzItCSbm7JttTTc4HAphCpTMY5HFRwNt530s6DmLtz3WduSZYbFYpAIk7HdbvBtB94SvmESsQNBbm2QXYleSC54onRII1sZcwrZU0xmZ0ajU7VIVOX3f03c9u33HxdUNELWovfudtcv/cICxIi4uh7ltBKYYJxiR9PNHF0Bii/So8xLGDxnnRZkc1+Lkshkcv/HkCe9vbnjtpce89vARD2YrZtLghxYpPGVVwNCyv+kICJQx7DZXrHdbNptrmmbH4vSEyXJB3Q/smj2m3aEyRV5VuE7FaoWPFYxcGyZlhRLRVU3pqL/pDhW9yGSr6z3D0LPuW7qm4dmzj8nyjO12jQixVXJze8tmu6HvW7qmpm8bympKwMdA28bKdN021PsNwTdMqpPoDucdNzeXeOvQWpBnhr0L7Jua26tLqumCLMsZRKRl3252fPjBR7z77kdcr2sG65PWaqRzixDZd84NWN/H40nBaxAKhI/tC0ahqwKm0elv3ELSro3Jho+CzeMCEL/gzqAgVqNeWEjuLFgi3kZj4nKsoMZF3lrLervhy1/5Cjb4mCAKkcAWwYOHDzk7u0fb9TRNw5svz5mWhmAdu+2WIs+Yz+csF0u0Mph8wq61XKxrvvrBLU/6FZSn6HJKXhX44VjNV1Lw2umEeNVjgHrsvD1Wzw4rOeGw6CsVwVIlVaq8hcMxxbg/VexEgBDdzQ+tFxEvSAvc2PatIoChoslKpkTSZbwDfI8TPmNM4FNCLmg93O4d292O3lpCgMW0REpNlSlU5tk6yeVtg/c5TASlDuQmtuW31rFrel59MMc5z+XtwPW+Y3Vacm9eogkE62j2NVrHNky8Y2gbPAqlBEZIhNC0dU2QMegcuhbhG86WBq06hOtwZoH1sRXEmIzXXn2V6WxGPp1gsgwlNTZE4XcpBvCJTUIcO975qKf49GO2V5fYtmZSFGihmeQVZV7iEfQ+oExGPp2zGM64vPyQzBjEBLI8x1mHdfYwJ4UAT6+u6K3DJh225XzKK3mOUtEZ3BhJlhfkecFyOTuMpdPTe7z+ySVaRBb1dnPDkw8+4O2vvs2m6TmyaD1K6kOA4L2n7lsG69OCL1FGUKmSUgomAk5D4EHvqawjkwW6f4mBwGg1NDIVD+FhEDjW2ASmhxQgkGnyaUWeZ1SzCbPZLFYkdYYRinpfU/sIuHsXuL6+5eGDM7JJbCk6CNwnFsXdKWHcopPpuJiFtCbI9N74rBt1qdJwlkoe2qki41Afiw9jWOSPrUgitQJHADfui+8Grq8ueP/mK3y0/ybf+8q/edgn8cIe/v633jf0fn94nMnJ/ycOzr+XzQdH7W7SflRksjr8rXU7bDgCz4Wco2VMcLOuY8g1Tgx0LhajjKySSL9nSMk2gBDqheNz3lM7iweMlBEwDeO4G4ux8XHsqIhzeDQjURhdUeQTjCmRfcttV2Nvt9SDQ1YTRIiyMAKBUQo1Gie1A7dXNwx9SfCBfFKQVxOa7RbXtbi2je2cNrkNh9F4QkTdyCQpYl1s/ZTaIAhIZ6Nxh09sdy3praUfLBmSKqvou5bO94xMx+P5j8ydgMCUFYv5nJPViocPHvLGm9+B8opu79k8d3zzqx31dYEMgVzsmKotl8OHWCHopaSVhiH0dL6j2d3gu55BGV5+67NInYHznN4r2W93DHWLvbxgK4CXXoLphEw/Rk6nrL/yVbK+RXuHdiDWG1zXk3UdRin66YI+K7BX58ir8zhTzE5wxSSCWymx6rsW5xxlURLo0EZTTEpe+cRrnJ3d46f+xv/OyZfXsP0AADs4XBhjuLgFb3GDJ3goJicJVD4yqg4F2lS0ivGWwLpowtC38I2vvcPV/pzPn77JYpFD6FFSUeRRK01KQT8M7PY1xgBSI3UsWlo7HMaBt47N7Ybdbs+D+w8oior9vqbe78m0YTKZMFss4triApk25EZzcXlO1dYMQ4uWUE4W1N2A3W9RIlCUE4TWLzDBRBr7SpvELhFkuYn6fVJTFjl5Ibh3dsLQT6i3W549vUSIgHMDbduw323pmh1aQZEZJvM5QpKOyZNlBpMkaaSAojDkxRJjFL2NphQXF5f0g6XvetrOoBTU+56muaaur7m9/IDd9Zu8/tbnePjyS5w9XPHkyROGwbLe78ivDIvZjNA7JsWMV1+doCtF3cD6es3t9Q1D1xCqAq2zqMm7WrJc5Az9nL4f2G33DK5lt92ilMTkhkk5jR1zd8CLIEIy8o4xkY+c+jhb2wHx0z9NOD3Bmwysi/NVHs2zfIrPpFLH1EKACrCopiync7Is5/z5JV1vU4wW24GfXV6QK01hDPeXJywnC8KDgEKxvd7ErowERnR9z7e+9S4+SEJiq1rnyLViOp0wW0y4vr3ind98l/VtTdeFSLpw0Y3au0iAMErjR2MukTo7RrAnjR832HQsMkl8HUFLQdynCJ3FdS8kw0QIBOnwqsY88LB0DNmAtS190+CaHobIggzWIRx4aynUlD/70n/0u643Qkj+yUf/zu/6mt9tW2Uv82df+o9/x7+/Wn2JV6sv/b4/VwnNP/34L/0dX/ePPvjXf8e/SaH5px7/e3/Hz/iRB3/xtzyXVyViUnJz84xceoyKsla2H6Aq4nVRCp3nnNy7x3S+RBvDYC37pkYGhxmlqnzUhI3moAcuagS4xtZzqRiGgV5GM1+8Z7AOb/Qh/3Jj2iVi7hq8SEL34UDiOGYTIY5BkaSkiO/zh3jtGJ9FFpqK+vuKuI6mjqVw+KwEmIg4rkeQ89AR5v2BTTvqvcbCZuwIPMRoqWgfixhH4pa19oCNjscy7iPEYhrjdyU5sMicuxP7hW8DXhOYFhmsIxB7PENCHI/pTg/c+O4xI2QknY1YiByVHVL31ggk+wCj7elI6o/HcUdyK503IQXChaMvwbcRIMb5IMhITogCC0dClQghdhvZKM/gnT8YWwoh8EPUqY4FX3kE1g+YYuo0EpIg40wUSXVHDIjEjrVBYJEgiZgOnsFZur5HqyzmCzLqz0opyPICrU1i58bOzygxMJIvIlFIyvT9YzFXjNKGAjXqHocovxelFhJwn4xej+c+QrZRHkGiUotriIMQmViweHW8Zn6I58QHhEhyIY40thIwHcYxNM7RR9A9PRGNu9K5S1pNCJNFINZ7DI7cB4z3qODJg49dj0AB5B6sVnQqGmspHLXMCCH6Gbkk/Ri8p3OOuh+43dXobIsjktq8hMJ5tFaYLOf09BS0YTIpmC/m5OWMZ+dXeD/EgmiI5ERjSqTMCMT7P7hwXIikot3v2d08x/UdfVVh+wV5pjFGo6Tg8vmOtnfRWDybRIOsEGLB3rZ422J7i2v3DH3N0O3JlOD0ZMW0KplNKi6eX1A3+2Sc6RFKMp9PybNoQLmva4a1xXmLSzq9dvDUO4/ve3xbU28M88WCqsopiozMlAn8jgTStm25eP6cvu+o9w3D8KJW8N3tDwcYyxFPBRBKpfl3dGA8tmYcpuhD66o4MDDGCT8KWQNaEbQiZAphBFsDX714yjuX56yKCW/ce8RUS0oFpVE8On2EkbEVuG9gc31D0/cIJyiygmdPn6CvLnEIhhD44Mm7GA2F1hTKUBjDy48ecJtJuqbGe0e73zB0Ldrk6Cwmr0pr2q6j73sW80WcdJKD4+OXX+OTb32Gb77zDdbXVxTVlDIr2e1vcUMHQpNPp6xWZ6xO72HyjF/+pZ8DQqx+O09ZzrhZX/Hw8Wtkeclwe8v66jm77R5rA0rnPL0+Z/rRR1TzJavTFV5kSJPz9Pmar73zIftNg7U9o+mVDy61BEZFPM8dUDkt7AJQWmKqAj3J0dMCSn3UvwyB67e/Tn56hsgLnPcYYiXLECtpoxbPQYRbxjbrby87jmy4sY0a4uIhUtDROcc7736Lb733LWwaQ2M1VABKKh6dnTKf5Dz56Df5/FsLuran6SxVnrNcLHn40mNm8yXVZIo0kqc3t3zjwx0f3sLOPEItzyirkhAC9XoLzuNnR4mAPLExxsE97uuxJSLuuXUeXAS6jlp7cRyPGoS99zTB07eKIpOpMBFFraVQsVVBxMTDOYF1IbJIh3jseWFQ4rjIp8vxwhYBXlBa4IJg21guNx1PrmrICx4tpjyqDLNCU+hRWD9QKsHrpyWVUqy3Wz5c16jQ46RmP0TDk8VMI+zA2dTEKp0W1PWe1SIn19HB007mvHe+RWlJpjX5VHKx7ZlWBZnKQBmECeyaHUZ6Cp1z/nyPNpoqD+Bbrt7/kP/2f/o/yEzJarHg3umKXb1DPs8pqxmr0zOqxRJrB6T0mFISTI7UERRt9w1f/fmf5bEQ3H70AV2zZ/bKawxdw9pa6romW55QFDmZUEhR0jVT8AEpPEp6gopOkiYTVGWJMTnOwbfefUZdR3axC56m6cnyktOTUxaLBUVZkhcFRRH/HTeTG6pZRqEVeakpqxzvPZfnz/mNr32DUaxeJcfKyH7v6LqOAZDJWEpJwaLM+L7qR5l7Te4cmXUYHVtwfPD03mNCVD06pmppbiUu0kMCYJ3WiDyjnE05uX9KWRbHlg7nqNcb8IFZnvHgdMUHl89jUSREqYQPP3zKa6885nS1gFRUuaNOcJhf4r9jgCwOgvnjpg7M7vhkDLZTWU7Elm+V9CYjQHu3JQ5ms8mBheETMwkEbnC0mx0fvPsev3T+v3DefYxSZ4xZiRTi8N1/0O3nrv9r/rfzf//w+Ecf/Bv8w2f/4t/VZ/5Bt/XwjL/0zvcD8CP3/yJ/4t6/fPjb//rs3+YXb/+Hw+N/7tX/ks/N/iR6GPjjP/mT/OIP/xC/Pvll/u/9TwPwj9z715iZe+zsJX/j8j85vO8s+wR/7OzPHx5HiYIImkcwMkpnvAjDAwhcIEoTSI3QmrKcU+Vxfcx1QesdxikG19NsGkK9QxZxTA7esb25Rmz3BHNDMAW6miCyjKyqKKoJk/kymp5ISZBJSxIIB7OFqGUfOxfEYZ7uhz5K8YgoW6Ckiolo0iNTWqe5PyYNhZnQtR4fhhiEpi0rVpw9eotXXv8Er732Ke4vVhQqIwxgh4qvfeWcj963XD4TDO19FIZC9RjlkarEDgoXBmRwCBO4NNBYuPAD5/2al9/9OrfX17z02us8fOMNbN9RP7tANA0GMPsd7/3KL1EuVyzu3efR579AcXLK+hvfoDu/wNU1OZDvG/p9Q/PsAvfqLfkn3kDPFtiswAaB+uX/C/vWF3GPX4MQGSur1clhTbPOIYJnu17z/PycajLnR370n6AyW3j/VwDYNoqdBOHVKDMcjSxVj+1vGZQiK6cIk8d5q+vApqRFHDzAU4APggis9d3As3euuH1yzR//F75EnkuWywXz5ZKvfu2bhKARUic5AKjyjHIywxjN5cUlRZHTtD22H8iygrc+/SmKvERIxWAdi+mCz33+U2hj2Nct232NdxKwaAWTKuPVl1+irrdsN7d8/PFTBhdi90ZumC1OuLpe34mDAJnx7Pyc2XzGYjFnMpuSGYXSGTrLqKqKz3z6dbbra9rdlklVsphNqFtLvb2l3u8IfsBojVE6dgdoSVUVcc0I4fB9XRdZsM/dc+7fu8+0WrBcTHn15Ud83/d+iedXV6zXa/a7PQLJ5eUNz87Pubm+Zr+v+fD9r3P59CPuP3yZz/8D38nLb7xOMwzUdcs337+gcLd86btfY2YKdnXHxdWG9c5ig8XkGqEsFxcfsjx9SDWpIAQ+fO855+dP6fuaMvcxaew3KQmGy6fv44NF39UKlaMeuYgFaiVxd1gwEKcYP3i87Qnek51OidWgxBy0LoEuEdCcCc1ry3ucFDM217c8efaUzscOJyMUn3/9M9S7HTfXN2xu1nznF77IyWzJahG7z0SA5WwGwSGlYLmYIaXADskLPVi8bWiF5+0nv8G7l18B6xE7i3AafE4fpriQgAMZnaetH01qBLFHUxxwohG4EoKjmYyJ7FefwJogYtyulIldVMAwwGB7gmmRZc/idYk4cTjfMjQ13XaD72zqaY5rsh8sRiiCOxrx/f3t97+V2tPbLV/56q8ipzPMTKAbhaxzUAadGZTRkXk+9GzOn1FOpmR5weActt6ig0A4H93GExgrlIqM+hGVDcf5WGmFCx4vY4fI4EeTqwDOoYQ85lpiTLRjJ2NI94skfibyWBcLweNcQI86mHcBOSHusBbjnO2GNHYSohjlOWX6ylEbNr5GpljQpc6Xkek5Pg6JMamVJiS9TuDY7TL+cCz4frtWbQhHAFUCSoxeCyOs/eKWotTDXyJjNBz+/7CJF/45vvPwdWOudmh9AzgUfgRHMNaN14k7L02syuPXxTnGJaDdJokAIdVBWjCevyi/EFzK6b2P8YR3SDxapQVVKbxWOKeipBkczrkcWdOJCT2CoONrfAI3bTL2Cj4arfkDczod650aq/ACUCmH9TjbI4JIxtZRkkBrHQuWJiNLjM0iKxLbMWqJCikPYwXvafuewd4hR4kRHxCx4yWNW+ejXJRNnaEuvj3m7vEViUkskSqLnSFiZIXHYljf1gxtTUeUprMySseMBQaldMyzgo9A7WgoGRiBrYTHuDRWjiA7WuNCBhKktYjeEoYeYS04i/IelCQLYAcLNs7dMx9j1kwIKp3RzWa4ssCajF4bfD/gpE5yjVNmqzMm8wXlZEJellFK0faIpN0bhCbPC4rqhPnC8MhWVNUDrO2xtmfoW/Z1g3eeuvXsm4bd1lJURQT+s4xylrGvt3QDqJsN2hiq2Zw8z9Epv7y5usTbFmMUSueYLModuGFg6Gr2uxu6rqN3lrbZs11fUu93zCYT5rMpr7zyEp9845Pcbm7Y7Tbstluubm8x2pBlhizLWCwXTOcLur5jGHqGvsP2fboHHG3X4lzHYHv2G0Omo3F7HwLD4LB9lDq7vdmyub3isihou9+5k/IPCRh7FJceH0MKpkKkN4vUljhWmoIIRBc1EOKoeyKNjLpFRWql1YAWeBkFkHwQ9AGe25r9xftUKmOqM87yklde/zyPzu5DcGw3t8zmS8oASqh4E9VbVPA8vbjg/Scf8eTZx3z3Fz7Lg/sPUdMZVkqywlBMZzgC+80tQ9tSVpNURXNxfnSKUmsmWcF+dw1AXkzIqymT1Sn5ZMpLr32Ss3sPCLbn3be/Tr3bghCc3HvId37393L+7BKdF+hMc+/BIz7++Al5UTFbnrJYnnLx/FdY365ZLCXL0zP6psHbhmAHmn0NxvD84ob1gxtsX+OVIC8MWS6QytJ1TWxBCpEjF1tHIijuXGRcDENPuDMxZAiyyQQ5L5DTDFGo6MQ4lv6EQK9OyFdLgpT02zpOMITD4hiT3PjaIMB5d1i4x21sVxgV5YKIra7eetqu5Td+/dcZknHFsQ4hxl1ACMFsuqAoC+6fTrg/u09ZSna7hqqacP/sPvfunTKdTcmMxobA+x+t+fUnDTdhTjdZkk/OyLSi228BWExyXj2ZMJFRhyRux0rnUSP2Dk19bIsYH8oYRPu0YDkXTUvGhVimgFtISZFLtI66sQiPdalq56FpXaw4SUlZRO0gKSKj9u7ZGCuqY0Wq7SOAa0NgNTGUlWEaFDMr2DaBSZExzVUCYv0hYBBpITudKOb5jK7VbG6fo8sM3UUR9K5tUasC6QKLUpNnmudbwfnNmirPKIxh1zu2XUD2lllleHC25Opmy3rX4d2ACB5Nj/YeGwba2uL8QOss95YZpRZ88xvvcv30htdeX3B6eko1q8BL6rZjcI4hCCazFev2BiE0mZEoPSPISWKL9Jiy4M3v+C5ml6+z3+94+fGr7L/2ZVzfU5kZr7z6Kazt2N9esFmv+fjjD7G2jaLgwSFEoDCKajoFIvtot++4d/+UYl/T9T3OeabTGfP5grwoDuZoggRKeffCMImVamg7iwNMUbA4PUnX//hjvaVpIwstyNRWTeCV/LO8XHySlRSc9YE8DGgfDs62MXYTGCGSZMyRCTgIwaA1TimsUlijqRZLpos5RVmR5SZpsCZDRaKp0XwuCDa2iL2+fIU2OK5ut+zb2H1wu95QFVH/7uxkmbojxOFegFGBON1N3149SA9H/VcfPHXTxDYdGSAoTGaiGdkYjInUejXek3Pgp/oAACAASURBVM7eEfNPIK0PNJstm5s158+e8XPPfpLr4YYOKO/qX4/FlRD4Kx/8OE/WPwH8OCF4/vK7P4a43fB69b2/K/vne5Y/xoP8Lf7qB3/uhRnj/8/tv3/yr/K0+3rS6TuUtuLvEPgv3v9n+Lj9Ci8XX+RPP/53+cvv/hj/89N/i3f3v8g//uAvAIEv/MIvwBs/gv/0T/Az13+Fn7/5b3hz8oOcZp8A4AdP/3ne3f8tWr/DB8dPP//P+fz8T7LUYxdXOMjHBGLb9YEVE+J9EYTEaw15iclneJFTu0DfNBjZo7MCaTsUnkxKrBC0+z0ySVOErsPbHkWBkg5fd0hb0g8drmnomzoaxJG0pYccN7QxSfMuSiOkOprUGqkUOuQMw3AYpbnOsL4/GFWODJj6j/yDuG9+i+KdtzFGIzqBVDkyOxZdXnnjc3zyylPkS/bNkvPe0O8tVx/v2d8M3N5k7DeKZutR7AGLFQNmYnn1jU9TbVvef/pV1rtzEAKnc7wyDBJa6xjsDrsW1L/Zsbu84JVPv8XswT38vmbY7theXXGyXFBUE5TzfPzlr9Ft16wePyQ/WbB75zfRmxplFDmJSfHB+wy7Hdx/iL7/ALk8Y5AC9eHb8PS9qAP9pT8aWRvp/tVKJZ3sEGOt/YbZakF+YDDB9eXAuqjIZ9UBjA2mgswg7IBtb5DCIU2F0AXalAQRExUffNLPHFu5U/HYkVJSQdfBL/2PX+H1H3jEy289Am0wRtPsO/JCU1UldVPz7Pk1J8sZuVa4oGiaJoJvec5yuWSwXYpFox57Weacn1/gfKDvLXlREYKkqCYIbTi/uOLm5jqyfG3sajm7/4jt1TPqvsOuN4i8ulNYCmy3e+bzirIsWSwX3H/wgLptgdhBkxmDtxaJRAqDFDoW+cOGbnB4LCaLhhZKRvZvZjRKgu17+mGg7fpk8ukwRjOfzSiKHDtYtus1tzc3zGZb5os5i+lj+q7nq1/+BqvpkrPVCh9i58w3332fze2OZ8/eZb+7Zb2+4t7DR+RVxXJR0G87nj69iOamLrAfBsrpnKat6TqHkg7pW8RQ0+/XnA8911eXNPWG3AimixIRFGf3HzOZVuSZpm5uWO+v070WtzifRxNUb10KcVJBfFxHfuqnEEpDNcH/Y3+K/mqPnBpEaaIvloeQYnYtJG+89irLyYS+3fPk/Jyu7QhaoYSk1Bkvn9xHnT7g2eUFl88v+X++/GW+63NfZDaZUGU5r7/8Ch988D4MHeWkjK7jLrEQZUDmnmIF2cSgDRjhmA573vrMjFwY6r3gnXdvOb+doXSF0jlKRuNfP5rHiNF088gOtC6CHnFdVBgh8SICciEk9pWI699BMsh1uGxLdi9QPICwaun9Hlu3DE2L7frIvnSe4ALCQ6YUtu6xXf93vSb9vbxtf+HT+F99lc82P8yvfdd/SlkIqlLTTUpMWZGXOUEEBmfph479vqWzA6YoCVrRdz3BEY30pIoMPUCFCAxG4syYU4hoaOwcxvvYteWPXXohgTiQyCykcSNGQyoYAbR4W6X1WkbW4Ri7EkLq2js60gdIrLPI3oyhlYqAWGIgHvQbR2ZgKjTE2M0ntO4OkOl5wYwriID1d7XIR/LQEYwV8ngshzzTx9b0UfbueKzpeF4ELOJnM7Jcx3UsrjWHzxljxzFuZUTaDkd35/+P7xv3625X2FFaIbXThzCisEm2Udwx1xKJORsYnI+5coh7QMo3juB1kkx0iQEcYlaUFxXISPpxIRzWCucGnLPYUa7Qh4Pvgtax601nBp0VjAKCwXusHRgGibMWZ2MMHhJIS5CHDoV4WGMuQDRadQ68JSsjIzLBtQglE5AWTc91kryIxumaLMuOWFFEOBFKQRNzQ5cA6CF4vJL4oACZzMDiuqlUPJdRa9iDd2ipKLLiAAbHtnvxwhjx1mPzkqGs6Luctt3Rd12UQPIj21q88HMwzBYk2avUzSBE7EJIhRBkJIVEA1xH8APSWRj6GNcOA1ibzNAMGjA+UEhBJgJVCFRCELTiWkp0lpMXJVVeInWONBlFWTKtJkzmC6oiJ88zsix6vwh1hzwRFBIbi4JBYvIZX/zM96JMhnOWvqlZr2/ZrK9pUuH35vIjrq6fo6RiNj/l8asPeOutzyJ1CcSO87rt4lrpOkJweDug9CiBIVLuKTGmQAqNdYG+rbFSRzTRWYa+Yz107Hcbrm+uWK3OKIqCs9U97p/c59HjKKdk+z7pGScNZCWBaKxrVOqwlNF/ZDqpmM0im9aYHKVlpCo6S98P1Ns9l9dX1HWUV+r633lt/EMCxkIcZMcA9DAKOSb4ca4/LgAiFWmkjipHIk3cUklkmaoMI4tWcEAFI5jnca6nD4HORc2srz+7YiiWTLKMgZxtY1mdLKlsz2Zb4q1F5VlsIReCk+kEgyMMLX2r4o0hSkxmmEynBOe4bVrs0McLqFS84V2sMgUh2K1vqSYT8A7hPTjL9vYa10cAqmn21M2WPNNkZUU1X2ADSJ3RtB2b7Ya26ZjNZvgAvQuYYkJRzQARNc50z263oakbunagHwSNNWSNpW0ttvd4Y7FDl+jklq5v4gSfpCEi8BCwzmJd1IoKyUESEc+9LnP0okJMDKFUBEWStD4uZGYxRec6LvpSMHiHDQ5HXCRF0t4a2yXGatldkMITsMTkfRQa//jjj2jalt4O3Gw3Uah9HFYJeLm7fn7nZ1/nwcqQq44BhxCa1WrJfL7g9HTFYjFF5zm7euD5uuWdC8tzt8AXK1QxQ0iFHXoKLSgzxWqWsSol+g6eMbYxjAFK4G74cmeivXtwAkQYmRLhuHCnxUCoOL5FAq2VFGSZRHmwQ8B1Lk1OklFjOdwhCX177XZMTkEwOMemtWya6OxY5opZqXngC7zr2NU9Go0UUaenbjq0FGRakhtFpsBIhREG+hxlYijSW5vaOgPTaoKWmkILVpOcy42n7R1t7xm8pMgMuZHMCoWRMC0zlBRYaxDBoYVGB43wFu8G+r7FBk/dKWzv6H3G4/v3eHS24HQ+QWQlSI2ppkhpkMogdYFWBVpZtHIENB6NErGNeTaZ0O1bVFBkuqCpG7RQLE7vM1uuwAeuzj/i6Uff5Ob6GZv1dQQzhTiA/VprhmHAOUdvHf0wUFYaZUqGQWMHH/WrV/fQSuOtJYyOreEovQHQ1DXr2548L2LwEGJbi0pBQgxqPS64CMqnezJKgMCj/A0e56/wQJ8wtwOltcmZnsOIOAbSsTXKCwhSRba61vRaE4xBFAWT6YRqWkUmb5ZFTetUCR/HtAjpuvdxnhDBczKZYnuLtZbOOqzzrLe7mPxPJ2RFxhhTHoq+h8o6v3VL99SoEUaILNmg08j2A3YYyPMMY6IG4lEKIR60F/EOGBka+MB+t+X2+pZnz5/wzvWv87x/Tk9I8/uLXIbRPPKT1T/E3rzMnjh3vTn9Qd6++Une2f1NfuryPzu852HxGd6YfD8/e/VXgcCr1ZdeMBb55v5n8WEABD94+hNRHxRwwfIzV/8VPkRWiJYFP3jy5xjb/v5utlerLzE3D+nclovund9ykp+136B2tzzMP8uj/LMIJNfDh1wPHx5eNdntePQ08KnihJ+ZwtZe0vnt4e+X3beo3ZrO73h79ze5l79OLqcgdkgRNZMPxbWYhRwMLcL4I6NWFiICIC7SvWISdJgTo8knCLouFgxNZqJOtoDGttjGIvoWJwTFZI6XDUJn2L5GKhNbNYNHaYVQCt+7yPZKyZBU0d1W6lhBd/sdwQ4RCGTUTBzHbKx2hdmcUFYgJDorOZ3MyScz+lc/w0U6RyJMwC5o+4rgS/aDYn8TuHgSaNY9zipsT2zFlA2zU8PZw1MevLLklbdWPHuasa6fc7u5oBtSsqCS1p+SPPMO4VrsPrIB8/c0i/sPyU1Gtlzg9prp6Rl919FebLB1jRSBtoo61vnpKf3thlzEZFpLRTF4ws011lp82yCcJVuusMEjRIvz4D98J47Tcoq/94gxfcpMzmy+QJrRQfi4Zs+nS7Y9DHVzGEO6WJHNNOgJfbOOEgXDgHAxHvL41D0VpSPi6mY5tmwfV1/r4eZixyc3GaotsVYiiG68RVEwm85o2hY7DIQgkjbpjOu2RWtFWeRMpxW3tx1GR0amcxbrLdtdjXeRERaCZLvdUU2nSCnJizyOR1WgTYa1jnp9DcqgMtB5zmSxeIFxb51luRzjklkEm3XsoFFKEYJnv6/x1qeEJGc6nVI3Lc53UTpLa7JMH0AB7xxtEzuyrI3AsPOxaKu1pigKQojmYcHHv6kEviEEdd1w/vScarIgzzN0piiynMePHpDnhu16z2Z7xbvf/DpNvWV1esry5ASdF1zf3qB0hilKFqsZ232HsC069JQKnIhFV+EautalhBuapsF2O0Dz+JVPUE7nKBkdnqV8cYGQWkbNcBcYK86HYx+1/Na3EYjc7uBX/zb+i58DOUUGkJU54DyZUpxM55wuVigh2LYt681tAisia0+EyDatioLT5Qq85+nTcz766CMePXjAYjGPslezCd727DY2dplYh9QCU0myuUJVFiUcBY6Zcry2Erx81pGpga6NIEf9jYbOaoKLJluRxBDNewXi0LYNHJ47+BBImdhvIfb9BpmaSMZOswDSoWYd5YlHrTxy7nE0DE2Nazt8P4CLXVv0HmyKII3hRRfOv7/9QTa3q4CKkiX11mI7jwySLMvQmcYFf+h+IhiCG3BWIWw0cZMIRPDIkApf2iSD4Fi8QUZw1llHn+TnEr6Uuk9IhlWO4BUida2MEnBjHp5CqRgSHZiYd+IjH8k18k68dWBtJlAYMWp+h6RDmz5PhENn4KHqLeAADSQwNoUKh7g7jGZUab4XYdR6DIfi7oEhe9zT417/dgV/8eLz4s6f7m4vYLRj/Jr2S96JGw+hwWFdYuTlpMLICNoe16tjnBsOQCWEJDUx6lwfP+sYewSCl+n6JtMsd/QrkZ4DPhKlBAQmi5900HsVGTqbIKTGhdiebu+AsYPtCX44yBd2bRcZziJ+9vjdI5loPD4pBH6cp+DIVE75wwg1382ZR1JR8MmcKUlcIKLHijap6Jj0akdAMxYX3HGspk9VySw1XmaP82POHt/jfEhEwCNYr5U8XLugwJgCk+dok6FNjpLmDmaSLqX1uLzD9hl9H7tFu7Zh6KORlLVDAsRfHHvh20ZZLKjpZGh2BNsDPt0/IsapQ4/sWkK9iyZYg6UxktYUVMaQK0WmFZqQzLklncmoy5I+ywhZhs5yiskMk5cURU6ZF5R57DSLMoryoPHsgksxT0ddd3SdxdqAUIbF/ZcwZcSj7DAwq3fst7e0TcN2c4sbLLc3Vwx+oKwcs+mKyWSJynKQioBEt12UxxgG+q5hDyneTzIYh5svaqfHPCGyoF1iE3sfjdW9jwWAECRFWVLlBWVRUOQlRmf0UkcvpmE4xAuDHbBDNKnP8wxtDGWRs1guk2ZugdEZJtMJ8HcMQ/QEcETCUL3b/9ZJ4872hwKMjUktBwDuKDMes/IRS31hMpcJfFUCYVQEYOXogAa+SIl3qpQlv3oAhAgHIeUhxPZcOwz82ofP2JpTTmcLCiTF5ZZsvsAKhUuVlWI2Y3HS8bgf0I/ukSmLtx1tHRWXhqFlulhQFBUKxW59GxeN5DA5anQRDBDYb7cUeY4bBmzXMOwVV21sARusZbvd0LU7FqdnTKYTsjLj6bOnaJnRtA2b9Zq6bnntk2+w3u7orUdqw3x5Ft1n93s22x2X5xc09Y66HtjuHNtOo2SgG8BbCVpghy5WukKsuEqhUFoe1gaPY0h08ziwY/ospERlEr0oUYuCkEdAZBRLPyIrgureKUaAsI4siFgZG1RshQkhueqlCTskZ/QgEDpn8BIXBMV0ShgsjiTw7QO7tmG32xGA0/sPDhBjgunxY7tHmna//3u/wIPTCcF7mlohVc7q9Iz5fE41myJ1hhOK26bho5uW89ogp2eUkylamziB+oblrGA10ZxMBFq0d/RtU2WZ45oq7vw+7stxIY4t0jDWJQ6LkOBQ4Rt1LVOXBUpCZuLjnkDfe/IsVvTi4h7Fz0f2Y/zAcPg3GuMdF+vOWq72HZkxPFrllJkimxd0reNq12CdG5XFWG9bCiOZFYbcRDdEJVJxZFKAb1BAi6fpLDcXa/SDx2RFjpSSZZXR2ZzNvqPpLZnJWU0j+7Y0AuEHpoWhyLKo0+M9ggEZBkSIAEnX1gg/0HvHYD3Z5D5vvdFz73TKZJrTiRyncopqAkIx2FhhVNKgVY7S0ehubLeSQlCYjJuPz2NQQGCzv0D2ltPVCdl0wvPLZ7z39m/wwZO3absdSh1ZKVI6QnBIFR0VBxvHp/eBLNPkeYb3GttbzlZzTs/OcM6zvrmJAt9jy9GdSXu/2/H8ckNVTcmKAikVfZ/cXIWM5gI+LTopeDQyx4gCEeC14nPcM3NmQGEt2joO7VlJF2B0lB1N9AalcMbgTYbPM6zWqKIgKyvmqxWZSjpz3h4NFMdAS4DtBtqmxVuLEODbjkVZRiO4fqDf7QHJbt+ghOB0ueSsLNNt7w8A6QjGiheS7WOB467OUvCxRRwVg3ILtG3LdDZBa5WKYe6wn4K4SFrvY9AWYgV7c7Xm6cXHvHf9Nm/vfo2OFK6LF00lxgBACMEP3fuX2FZLnqSV64fv/QW4vuFru/+Tv3Xz33E9RC3M717+GV4pv5O/fvEfEAj8sdM/zx85+WcPn/lB87d52n6dtX3Gm9Mf4F72BlIorvsP+OsX/yETFVloNnR8ZvpDrMxLaJnjwsBN/wSASp9QqQW/1+37T34cgJv+I37+5q/9nt/37dvsyvG46+F7js9JoZioU540v06XWLEfNL/Cnzj7V9AyY/C/eUiiRh9kT/xllGQ05Qwi4KXCCokDlHco6VNlXBKyqPcohEKJOEP5viF4h3cSr5OEyzDghy4xRVLiSdTbcn0JyhCSAVEsDB5ZQaTWTaGiBrdSGjOZIPoO6+xB89W7kMBFEfWIpUS3LVkQ5OWMcn7C9Owh8+U96tff5NfSuRr2iv1zRd/GroOhht2t4PpcYBtLZgJSB4oK8knGwzdPeP0zr/CJN1/m/qMVVWn5xtu/zAdk9EPLQflZKVCG54lR4UIHnSd771s451k9eMBkuaKYVBSrFZtvfYv9s6eUeHRZ0N7eEqoJ85NTdm+/g/YuaZPFed/3LeHqkn63QQWLUSCmS0RWxnP+3tfj7bq6R5gt8HnUDDZ5zvJkRVGWdMNdVja89uprbD+65Ka9ODwnsyXZZIHMT0Bf4vqa4HqCtYmuNBYgJSLJTTEy/wgI6V8oQPUeVDNB7Stsp5HSYIwnzzLyPK5RSqk4LqViebJit71Fa0NVlUyqivXtbdJaFQyDoO9GI6ZU4OwHNustCElRFVHKxRiyoiIv4py1vroAqTBaU82nnJ6dJR3tuCkpODlZcnKypJpUbPcNJi8j8CIju2i33WFMZOXkecFkMqHY7iLrchiivqo2KUEMDEMfGVAJpBiL1XmeMSlLqrKIWmreHoCWtmm5uV5HQ8j9novL5+TbOoK3ec7qZMHJyRKTaTJzTdM84+OP3qOpN2w3D7Ddy9x/+TW22w1ZUbEoC05WM26v3sN3O7RtKBWE3JCpgKDHWUtZTRhsx37bsbvd4YPm8Sfy/5e594y5dk3Ps467PG21t79f3d/ue2b2NNfBMXZsxxYkwUmEgqVAQAiJiBKqRBAREgnwC8IPqohEfgShhFg0y2CFIBxslFjjOjbTPbt//e2rPe1u/LjvZ6317RkngJA1z9a39Zb1rvLc7brO67zOkyByOtOC1DEm2sU7pILQ452PzsoDY4t0egydJyKA6eDXfg1OTghthx/l6DvH+CyyX6ZFxa3DYybVhLZrWDdrVk0dz49A9AjznuV6TZFnzCZTcpVRL9Y8efY0nj2ZYjoZc3K4z+XlNfPlmpt1jXWevFJUe5rqKMPINXLdMxGWW4Xn9RPNpKpR0jMpFVUx4emzhufXirqLgmFCCXKpN2G2c3YDwgqGbpCtbmI0CSTtfllKHhNjUDmEsuRHPfqOwFfRvMs2DXZdR7Mu5xEu4DqL6H1Sg5AE4RIgtR2IxWSFUzvdYGEHXgg7i3H7gBfAFxjiY/HxB27HegOVfKfnAy0UmVAJAHTkdf3C32wLZ0MHXoyFVocHmKoE78keP4qGh7CRbSMk37YUNyqtNtG9FIHMFanDKKR25fRbaRGyj7mqT8CaEORFFVls/RRs1GtfXLU0tcMagdYZUgs6Y+i7HmM6chVlfSQB4R1ayLgP+D5KXBAB2Q3TTgqUiKQHkwrjwZHi35QdCbFphx700gmAGoCt7Sht8nEholGYSGxG70FuZmC8p6mLL0mwJnBMJJA1mgsNhYRIItlKJQygq3NbzdiBKboNPcXGmHJ3bgymWwMIS/qMm4LF5v8hvccXAUIGEDfNjC1yunmyxOod/nY7b4ffxdfa/tF31IndBWzT76J8aNhMnQEDGfZsvwPGsiGDRJ2I+HkjuBhSLu5cykfSK4eUH4rUMSGkQGfR1FkrRZYV5NkMnU9AZniiXJRxA8Bl6PoWEeJZYfqWq+tz2lCn1474SrA25kcpp9qMa8rrQpI69GkOieHrDTs2rjWlBva+g+CQInYoCalTUXf4fpDAGIDVyMaNc2dL8Ivh0Y6OsWMDxg5gqvN+s3dKKRBoBAElA0oLqnKMLipUlqN1gdL5ZiyHPSY4hzcZzmT0vaIoSto8+v907Tq1wputnnE6l8Uw/3YwFCElCp3ypIiXhWAJA3YSAsJaZNvg1yt80+KMoy8K2lJRyijbkCkdfRpyFTXx84KrcYkvclyWk+VFlCMoR+SZJk8SAaSxci6NoQupwyPOheUiyhL11oHIyMoxenyA1CWllIycYb9v6duOxfUli8tLHn74DawxIATT6RE6iwbQUmuE0mTVCC1lxLTmyRRHxCRUbPKyKB4yaL7HzmqfiE5Rr1YkLMRZw2K+YLWuGZUjppMJewf7EWhWHq3i55NS4L2NBIW2id25OpK2RuMJewcH5EWJ0jlKZ1E+SpKAaUdZjjDeJ8hS7rDVv/36rgBj4xVvkhdE9lf6Hu9xJjrYCqFQBDwOXWSoIovmUGU0NdhuTiEtogg6bLY4IXeO4EBIrY+IDKHGrPM9vnYhya4dRfC8d/aUL737iFw0VMrywz/4vewf7HNwcMSDl+7z/MlDnj18l2ZV472nM4Zlveb23Zc4Ob3N8ckJzeIgVaId1nfUdY21JgbLRUFWFCyXq0iPNlF4uOl6RrMDymrM4eERF4/e4ebmhlXTIvMbzi8WPHjtDQ6PTzm6fYfL82OK6SG3ZkcIBFlWUM0Oefzsmzx59JDL8zMwgcW6Y1EbblaWtQVjGmor0NWM0f6MOZDl5RaYSYdJnNSG3vd41yOCR4nYzqwzjR4VZLMR6niCL9RmwwOBVNm2EiYlD77/C/+fZ8jj1G3yEz/909/2uz/5j/3Mt/3s/+l1uvN1DdQWGGSvsn3u3N/nzn3SD28+9tfpTX0n9rlzm2ovOxW+3Ws4ojeamPACEzDgo85bElNHQN9H4WytQGvIslhqKPPIiqkbT9O6xACJLzA4RO7q1oad1xIEDiY5RZkh8oIPHs8JAk5mBQel5pVbsSXkfNHx9MMlUklODxXjQqMyhfd2EwQJoVB5get6CuXJC0klFO9fLPBSM53NmE2naKU5HGsOJ0mInXhoCh/AO4yzREO4+LwulnHxXqYgV1KUI7xLchkyY//264wnJZXqybPAJPOcW4mzPrLedElX99Trnt4GZF4h8zIaYBhLv1rz0Tvv8rnXPoUqS1CSAs/84jk3F89ZPFrxG1/9Vbr1GVWVIaVnuW6oimQg4qNm1dqsMS6uASWjmyUkvVIZm6Fv5lccnd5DqZygVCpM9AStYNOcC72xrOqGzjqKvkcrhbcWnReApO3qDTg0XEfZa9zPP4+WMFOCUoBOB4KLkvhIwkZu2xPwImAFmDynn4yxWYZTGlXkjMcjiqIk0xmu6+nwMRhRipCFqMcXIls3zzIWl1fxtWdTpnv7dG3Lzc0Vs1GJlPs0TUObpDWWdcO7H3zE3uEeRR7bbLfB5cCMFRvwdQhx/I72F8TinO07bAIZtM4IvtmcB0FEWY8YULFhUmZe4o2jq2uun5/z7gcf8JWb/5On3Ye0YiuhM4j6D5fOMqpq22b+8euP3/kL/HH+Ar1v+Ivf+Cw2/P3bN3/i+M/y+viH+E/f+2n+s/f+GH/q3n/MRB/xVz78pwD4mbt/ibW74m88/tf4S+/8OP/Ka/8L96vPMTfP+A/f+TEA/uitP8+PH/8Lf9/X+v24pvqYP3zrzxFC4Evz/4mFPePHjv45YBto+0DcO4YgNETt2CyxRIIM9CojaIUXHukMQijyoqDIY+DbmJ4iy6lGI3LnYvvXKKBdT2O76MAeDEoKMp0hiAyPvl1HHWMEuk261LP9tLYETbNmOhojgsf2Btf3OFLAh49tznkG3hBkQDiPTsFXdGD25GXO3d95l4mF8ds/yP1XP01eTGnrwCM529wrvy5oz3Kuz2qarseZmHNI75GqR08cJ/f2efnNe3z+hz7H0Z0Dgu/pmyUXzx5yfXGGEprJaMblYkUfXNQP1xpfRNOe81zTKUGjZHQYf/g+y8tzJie3ePmzn4+GXm2DUnCwt8fTq0tO79+nmu7Rr2qs62PxIngUElkWlKpE9T1ZXVN/4+t0qyXZg1coT+/QV1OMjG2H4eYC8et/m/6H/0iEQERM/Ky1ONO9oDX5h/7wT2J+5Yt8+eGHm581jaetNXl2RHnrFnnmoV9hVhfY+opKl2ypWvEy1uCcIbJoxAaQcS6atnz9d99j2fa8bT7B3mcnXJ3XLOYX1OsF1kE1GrNcrFkvlzy4d5vmcIFUkT2bFdG5uGvaCCg4kfeWYgAAIABJREFUR98bGNrBdcZ0NqbvOmzf0OMwTc0H55dM9g4oRyOCd+iiJKzXeARKlwiVbZI5KQXHh1OkhL7v0ZlmPB7jXXK7D57eOGop2ctL8jJnhCBfrhiNJ3S9pW17vI9sOlLCrYiOy5GB5BHCIaRgb2/KZDQmU5q6bbHWptZiyXxec3Vxg9Y6dn/NZqyblt67yISew81izmQ2YTqZMpsuqZuWi6tLbuYLnj15wuuLBQcnJ+RFjrcd9dU1fnWFaVZY2yOl5M6tW/QhsO56VsuG0X7JdP+IW3fuMRlXPHt2SWsc3cUFtlvhgkNlOX4H9PMOQh8i4u7ivfQkEEbKxK5KkNLA6vuFX4j70vEx5k/9DMV+xZ27J9w6OeFk7whC4PLmmrPrK1ZdA0qjfECrQOh7vvK1r/Lptz7J8f4B02rM25/4JF/6yu/w6PEj5vMbPvOpT5LLwKjKWSznPH38EVkuyHJPVkBeKpp5zy1n+eTtjDduSzJuQNhomIRjUq54+7UJ/ncbnppAY2M7eOeiuZeUeSSfyAG0ioXW2EEwMLq2JAClFDqXWA9N1+BVj5g5qtckNuuwpsXUDf1qhW07sB48KAtqMHEK8ezFe6QSL7CUf+6P/iLnx5cJLIsGZdY5nPVgbApGh6Q+gofeDUU2tS2IDPhXGqstNrEFv4b8j+QbQggoJPfVKQ/GB2B6zMVzPvuLv4xWcd/x3pJnGUiF1kU0N9Q51jn+u3//3+SdH/4B5HLByz/5Zzg8OKb3gflqyaq9gb6n0hnjPGdUaO7eu4cUASUcE215/fLzlF1DKQ3jsUrgjiabPqQ4/CqIjHUjWHeWoEs++QM/xjfeeZf+y/8EPPxJIHB9vWTet1gPUqvIeENSFQWjMidT8ec2BIzrkcDe4R6Ls0vmN3NC024AWa01eZEzHRWcHO5HUE3A/OICleZDpgS5UgRjEtHFbwoX3iepoAEcF5L4TRwTP4CAIpo5D107Mcb0m3XpNhrsIHfMVHtvNtjkUJSPZJw0l4fC6EZ+dgvKxhgwzgPnUlEgxdwDWzaSWj4GhgixBWl3igOb59skaENuNvzh4MA+xIfb14+dmKljNARg24Y+zNkNkXjzbMNjh7sxfBnX6zZOZxMj+cHAPP2NT8ZPeLd5s1oKlEwwspBkeY4zBnzAe5JhqCfY+IaUANd1ZJmmKEeU40Mmh/coihlC5Yl4kdEmHU1ne/K+oauXONPhlCIrarq+IznsxrwVQUjnRPARGDPWxOK4NVhvYyF7KJyGgAsO42SMD3zMXaVSSY+VBIxJdKZRWY7M8uSdoWPBM9dopTeg7GZfCn4ja+n9NveWQiC1IoShg27opvVp0gmEiIU1EYXIkVlBWU0QOgehokRBKpIOxMDgHDiDF4kprjR5YaPme5YjtcKtltGAzVrwlm0Beas/PNQ9NgUCFCgVQWytYmfxaIxwDlmvcH1HaNbI1iBtwAaPy3KCy2OOLYCipDg4JZvuQVFyoQNaB2ym0XlFNR6RKR3jZefo62U0jpRRf7pqSmQqkvTGsq4XzJeBVdthXEDpkuVyRSEmZKOcPI+5viwKJiNNXsyoRl8l0yVKaWYHh9x+8CrV9BCViyj/HwK+84hMI6zdFl2F2vg7CDQBkfYsu9GN3hR7nEsyjQmIVzEHV1ojpcJ5WK46EC3BG/DRlE4LEN7hTUdXr7HGkmeayXRKPhqxd3TCtBqhVAZCJVN7C9bhMXhrIcspJ5Oo0fxtBZft9V0CxiZR7AEoGg5V0mErFRZQOi1EQFd5NOhKGh7pTIcgU8jhEi1+G3AF/GZ/VQiEj8CR1DPE+E2K/c8i5CGOnBrPh/0ND+cXqHaNbp/z9a99he/99Nu8/OAlbp+ecve1Vzk7f0LfLwjOkec5melZLxeIEDDdig/e/SZ7s32UUrgQHZbxgsvzS/reUFY5ZRImDgHOzy9YLmtGq5rZ/gEHR4cAeAST6QF3H7zOq29liFxTViOU1NxcX/Drv/J3yXXGbLbP6Z27LNZLzq5WPLlquZgH1ssOZwO9FbRW0pkOWY3JyynV7IhiNMKcn9P2Pb3t8fho5IRPyUuk07tBCD140AJ5NEHPRqhxicviBqmUjq3oSiKFIlffJdPs9/EatstY4RqAT17YWF9cllFPJ7IB0/ciOoAP3wcP1sdnNulZlZJMKkmei+hGSsBYs2lzj+UHDyEyXJz1PJt3XDexPaMqNPuTnHGeoYVknMGDI4VgytlVz7qxmKMRR9OMO4clZa4o8p6LRc/euGSvlIwV6OAw3uBDdCdt1jXBO2bTcWQFqI7X33gDL7Mo1C1idUonkfJBlWm4Xz4F2VJqnI+u2s57ZGJkD8F2jD9yAo4Qom6pntxB0CBEh1A990aS81XPurUEeqbTA9pmzXrVIWSsfiEFwXmsd6hqzIPP/wBqNMHaHnfzjGfPPqTHsuiWXK8vse2KYnqb/aPb3Cornj95H9suonYbMeHLpYys+LjtRHZ2iOMrhUIqRdM2+CBjcNPHdpW+q5gUO4mlj0CQN45go45W17WcPXvOuqmjjhaxnTU4H4MF0sEPaOvJs4xxMeL4+A43T5/g+jYyZIgMUi81PsuwZUk3rnA6IytLZqMRZVXugBmDsH7A2vi+msWSqhqTFTne9Mznc0Z5Ac7QLlfU65pqb8bs+JB8vQYfOJnOeLpYYnzAWM/Nas2HDx/zyoP7TMejbSFhZ30MgfGgVxUSk37Qeo0yJ5IskymulpRVSVUVkR0SkmaZkht2hRBgnWF5ec31+RUPnz3lVy9/nqVbY3aSPKUiILHLWHMuyk/8fl4/+/hf32H5b6+97A5//s1fAaD6f8GK/f/9qhv4b/86/PRPwzT+KITA/3HxX7C0Z/jg+F/P/gMAvnfvH+UwkzCYYWwYCZGl3qUEwimJlYmFJiRBCNauJ7iGrncUUpMLhR2CRCQyCBRd1Iv0UOiMMi8JIhleCKjynHXbIn1ipLueLJPYZontO4TOkFIxX63RKmpz6nGGbdvIAlhbWmtRuULlsYrvTZTgcNYhlKIop9x56TU+E26jFx1143n+ODC/eoYMnuVr28TUtGtcc0OlAlL3+FFOMas4uDvj1Tfvc+/Vu+wdTqjGBThH28ypF3O6ekWpNW997vs4uHfMZ57/EO99+BXOzh+ymF/Stmus6fEywxY5No//1rrk8bohb3uq509olgsevPFJJnsz/Kjk8uqCo1deY3rnDrZtuXr4Htr1iKQr6J0DPLIoyfIyGgV2HebpM+xqDc+foV59HfaPsDI6vnvnyX71f4+A+8kd3KufgBAYeHzDdXp7xqc/+yZh/zkfEBnfys8RvaVrBN2S2BVFAGcRIUczMIPCJqn3QRLIIJjoiBv8RktTBcHl1ZqmeZ/V/IZ/+rV/BDFumDcLVssbGmMYjUryvIhA3PU10709pFSbDp7xZMxolIwsnOPps6eMx7NoxCkVx7fuU9drurahrntG4xnLxZoy14yrgq7tUFKic413lnW94oijzX2QQjCpSrSI7s/OeW7OniJF1PHLixG6GOFQtDYgnaXrbZRs2xR4A8FafHKdFskZW6TsLsYmka1jHazWDctljY20PZzzdJ3l4uqC/f0ph7cOODk5wvm7/PaXvkrXW7yApjeU4ymHd16LZ5vPeH5xA4lB1TRrnj16SNvUmOM12vV02uNdizEdLngOD444ufuAzjr0zQ2LxYeUGGbTE3QxBqm5fXfE2ZNHYDskga5zRGuD7fxxrSXYsDOndqItER8byWo7wIdId0sIQu8wy5b6Zs1Sl1Q6p88LrhcLOmOYTvdYNS2ZLrh/+w6v3X8Z4QWrxYIL55lNp+zv7fHpT32KDz76kKurK37jt77E9372bTyCIMErx/RWgR4JrDBcXS6QqxVvvFpxMu7A9qASkOJDJHXQcfdOwc3SY73k6YXFEk2ZrLWxwKGzHSAsMRuF2BgRxoRQ4n2P9BYhPL4QyGmD3g/kJwqrVtimIRiLNAZhozas9ALpQLjEdpNb2axcSTKtqMqtkVokDAwdLhGMjahPNBvFugicBxLzTCHkoKslNqxAmdzYnY2M1F3YKsaPL+4fm1jBe87dFbNcMQqSMivYqw5wItCGhs5FBlShMvCOYCyZL8iyUZK7ia9lTcuTxx8SZGRAFHmOsS62ZHcdUk356NFH3Jdvc6TvczDKMG0LfTRr7bpA23mE6smuDykv/iDVZIoQgqr6FiL/kLOPvkGo1wjXM6zcV2/t82zpWTY9rTEE48mynCxTiXEdWWN109ItVviu5+DoII6jl6zsOabtcSEC9F5ANZmAEBhj6LpuU6D2DkwfUIkQYUXA4qI+7ABkDQzf3URmGIkEvg14Q2QjDgx0sS2uDwz1lAMMTzN0/A1EwBfAyhDnvxAiAsDp+XdJLLtFuAjuuxcK+kPb/baov3nwJsd6MSnbzdKGD/p7gym7v93FXAYw+ePXt+eAu8Dy9usNWUfsdDcOs12I1B0WNmbbpLUmlNyYe0VGa8A46HtLb2w0IxWJTblL0ckU42rKZLTPeHTEeHwLvQM4CqEovN+gg73pMM2Krp1Try8xoaOpFygh0CrqqAqpU7E96qx6Z7df21g8ibYXaT/2EStRMppzBR+L2xsGb4jAcaFzsiIWUaSKZtaZil0mcgcoj/NHJukNv5k7zgW63iTANxYktwDuVvpqMCgXMuJP0RguI8srhMgYjEpj1ppIG6kbNXhwfSwKx4Jz3KutDwShUcWYMig8CwJdxLGsTfntcD5vgfyYh6ideRVjsZApnJZIrchzjZIyju98QagbvAj0PmAHAkQApXL0ZIo7PEZNJpxUOVMZcCp2i3mtMF2HtQbrHJ3p6dsO00cD+r4zOCu2BQIXOzQ7C1m1z8GdB0xmd7CqwPQW0y+xpkcpTZFn9M2SxeISROwaK6YH+Lyk9Z6RyMiVjF09WdwfvGlwLuVcIlKKNpKMWoINeCl3PEJiWBCzyfi9krEQLXVBUUzJy4qiqMirCuM8rm/xpsH7BmPWdG0dJSVMNMU+O4tdn7Yz7M8O0bfGG9+bUchpfU/bdhjrMR4647CxoeQ7EvKG67sEJRMIFSeXG9pl0sITQiDyaBAjixyZpbecxQNiKMwNFaTE6UQgo2A/w0abwNhUEJACvFAEPUVUd8iPPo0cvwpihEj8W9/ldF1Puz6jfXaFaj5kfl1zevwuJ0f7HJ3MaOdXjPOMyWjM/t4B+ydgjI0aXcUIkyoGvu+pm5q2txRZnlrAAvv7eyBCqhh75oslV5c35Msl11dXnD97yvJ6jpQaayXGSIrJjNo0WOsxveX64pzF9TV5XrBerbleLHn07IxHTy65uF4yX7eYPm5uzscWAwjkRUFeFKhM4/CslivW66grKxIdHSCEuHkOmhtSxoqC3h8j9sdQZbhM4EXUFZNJh6XKNQrB1z/6JueLMxCQW/CLGt8ago0tVgMI7wkgxaZamqYGIPiR73mdN186xTrPf/I3/nb8RQip9UBuD7Z0iodh80qRmxSCl04PODmYMipL3nj19VRYkamKlmF84GrR8+yqYxmmZJOYeAk8bdNxMCkZFYpCi9TuuG3D8N9W9ZC79c00A4cPFPU6hRRoMQCQkfGnU7AjNp8dNq26Ph64iDiWMjEsrROoFONGFjObIEQiCM5GTRcfRal7a7lpQGaCKgS6YCikoco1ZaEoy4zTWYExgbpzPL1uohN0oZlVURDbWc/1okW4HCqFtIZlEzcgax3e9OxPcoKMAt86l2ihCUlQGyLAKiP0GnVyU1LuRYz5dGJUuRASGCsYlJFCsARr0TImqT6WvUFk+DDCBoFEohDkITDJoxh37XIA8jwnjDVCTWIVzVus6en6jqos+NaXf5tMZ6jg0e2a44NT2gxobvDBU5Zjbt19jcOTW+g84/mzx1iXdIm8j4HjjgZWdFX1iCQfERIgUNdrhFCpnTm2hzXNmuV8J7D0ydANj3ENq9WS+fyGs+dP05waWsMcUghuFZ9gP7sb2a/BUyCZypwDXTKSGbXQdMiYFCLwSuKKCpsXmDKHomA0GlMUBXmRb7VWU4IvUyvaUP3FB/qmBm9RUlJmitD3eGsQSpHnse3Jm1gxzKXi9OiQOngWdUtnLM7DxcUVh/t75FlGURQvGBZs/5+WRApKBj1o7wPW2CTOn9aQ2LamDgnpbmuaAHxvuHl+weX5FU+vnvC1+W8y9wssUU9WiN1Hvxg6Dy1Wv5/Xp2f/MCf565vv97I7ACihOcjv/76+l+94hQCrFfzWb0H4Au1bS765+mXuV5/jcfMVWr/k9fEf4KuLv5UMw/KoKZy6VAYLDIcg8hljiiCVimYCKots1ACdc2TCoyNKG1keLrZq5iqjykpWfY0XAicj+1aXGZ0xGBv/DUBgTGqi+UHwMVCVUlBUJV1KeKz3UbdWRd1F5xy+ayhVFdOYEJNdgkCpgmkrOL2y5FfXXD1fQGcx1nEzX2ONZ1Ll6B2LSes7nGzJZjm3b9/lzmu3OL63z9HdKVJP0HlB1zecnZ9Bb5OOuGa0f0CRZayaJcZnTPdu833ff4Jxa9p2Rdc19F3Dsq6pVwtk15B3LfV6hckshY9nQFYvKT56l+n+AdV4wujkFuXePs18TnNxgTk7o/QuGahYvAtgVDTnygpUnlHqjLBeIup11JALAfHAku0d4osKIxShi/IR4vIpAo976c0dtke8pJTcunObhXqVD9LPqtyhyh5nw0aSxdsQzxuio+/uGh8ShA1QsPN1ENH0yAdoW8PF+Zz333nC4UtTZJ7BdIFdXNPUqwh4Kk3X9VRFxWQ8jprgfRcNPpMzNQGKPGc0GiFVThCKznpUPkZ5SRAaqUFniqZeYfoW00djyjzLIFNRCqsqtvuWEIgsY7Fc4LylLHL6vqEocwQVSmnyvMRYTwgJSEQks5LIKsyKYkt0ILbw2ZCSXxULTPmoipIHzmL6Hmei/q23HmOi/llR5Ny+fYvT01Om0wkX5+fJPFESgsSRMdk7oRzv41zAh4wBGABwwTFf3GCcwZkebzraeonOYnKktaKsSoyJUg9aSUZFTpVJ2tUc2Vvy0YSQkto8zxmPJrw1/gwXV+d0Yp32IPCdiUzLdBZ8B/Rog5gMWoybx6zXiC9+Ef+FH2RxtcD2hrqpIzFCKapqRGYtwYNCUQhFqTVKCORkgg+epm3QWWRQ3zq9jZKaZ0+ecnZ+hc4166ajtT2ZVnjp8d4inOdAK45GgiqLhXPbe5Te9c3wZLrn5LBgXTvOrxqczxJwue0OlFIxuNA7t2XmDWBUCEnzURhs36FnkvJYIWcCSku7XkLbo0Q09fRaYYbg0oZ4lodoUChEBFyrsqDIMoo8397jKOe4AUaGkZCQ9tEhP0uM1gGJS+PiU5fBBnhKcdIASg3nf5SUSfFuygYCRKMrDGvboEROldqMIygS9UyHVm8ho1muc02KcQbGZHxfQXhQCqEEPoEqcb8v2O8+gRCBTB0SsgwnJH1v8DbQe6AL2D4gFCgjafqohTgeKUQXZdXW6iEX15ai7SnTC1/dLOhMAz6eczrPGFV5Kr4bnIXQdpimw7cdrqlZ6whiTfenjHNFu1hhg0dqRTGu0GXOfL2mXtesV+sIoMgIGjsiIzC1diRQySOCivfchw27fjjvhzxnFw4Pzm3MY9kswVhc3RpnDXZXSSfU78iIiCQsmEgZm9RqM/BiB0QdMqZh5HevLRkrRt9i8zni6+6Wa8K3I6Q728XmfSfQ9tsA1s0+Ejb77W6xZxMrbogAO3q5CSx+oX0/3duQ4vuh2LT5rBuglmT6Gw2c41pJ55x3EZBDRK8VLzbGWN6z8WkZih4iQNACZGz9V1KjMw1SIrUmywustSiXzG4R5CJHhgpn67j3GsNmlYsXiySD7Jgf7mOKveKQeAZrOeFdOuO3sf/mPA9xT0lTCikiOCmVigCpjm34Sg3FWXhBnkCKDfs1EAlNAQU+PU4O3XjbcReIJFuX3ouIsanzDu9MWiMSuSPLuBlDF3B9jXcmyro5hzE9xvRYZxM5YMhPhhu1QzjaFEzlRtd3yH92Jl/820zHnLwcoWcH6K6LeJbUWG+QWYGTCrMBKNOaEFFPutAFQkmsFHgpY8OvsAThYNAkd4G+61mvVlxfz1nXkcQUfICgUNrigmZyVHFQ7pGN98kyHcliwrNeytSd6DB9jekbFILxZMZ0/whVVDHvdwGDx1gPSqOJhWFjbMJ3NoO7iTGG88/ZeF+tD0km0G/GU2hNOZ5yfPoyUk/IqwnFaExWRPysXy/o6zn96iKaorutrr73UUd/sVxACIw/2MdKzZE/Qsym0TBa5ijlETISAKz1Ud7R/b2g2O8WMFZE6rZPgt0BEdFSGUWZVR7ZdLLIEFmqsKTNZVuYi5WLxC6HoSUn/jL+cCdvlgScLBDFLeTkVfK9N/H6GBGSYx0RoDFBs6p7bi6vYT1ncd1Q5ZpxpTk4mnB8MOHW4QEnRwFdTZntHeBli840xWjC9PCEsijo2pp+teTp8+fsTWeopO2TFyVd39AZE51rlytu5vOoQTQYNqUK02rZcXm5YDSdsaiX1E1DU3e0dUuRF6gsh+slnX/OB4+esWocbedoegeoBKpEYEdIwWQypqoqhJT0pme5WLBermk7s6m4bNQkk04IKmojZaOC/HCKG2eRnZxAC5nAMa0kRTJWe+/p+7zz7L3IRrLgnt3gFjW+tchMIeQGKkfomHiLFFym6cEXXlHcfqOgM5Zf/MX/DR9iK0jfdxvQazjQkIlZmcB5QuBoNqF+7S7m7imnx8dUr95BiehCWOYBreGqdqzqjmc3Pddin0JFx1vhPa6FcjwmVxmZFsjU5uCSVqdLelnxLgz1sY8vvnTShy0rL2qB+01BQe4EHsMYbBPKpAeWAlwSlOkCJMJAOq8Hnd8UNHjBoJkUgo8JwGD2ZCFIT+sdnfWUVjH2MC4Us1E0WrtaGs4XPWpPUGSK/VFGbxxPrmuuEVgXGTnrpscmPVItQWfl5j1KlcdNMzltRuDC71TAQ0oY1Cbg0kphhgIsAoTCEZm+ITiCj2tkU5VLK9uFLJrLEVACMtdRadJYRpMoIVVqb4naeN4EnO1x3lFVBRdPHiL7HuUcIyF5/R/4IebSUDRzJpMZB+MR9x68yd7RCdb1oLJoFJACWJ+A0eGQFBDB2KRZE7XbPF3bRH1DZxEiVRadp2m3W7NPB5BHsG5WPH/+nMurCxY3VwjUplVfCMFUH3Gav85E7ZERKBHs6ZyDrGBf52jr0ZBYnxIvBb4ocaMRJs8xmaYsKyaTMVkWq8s+xLnt0+cCn5xFY5U4SEm3XOBah8wysiJPDBjQeUZZRe3IdtXiU6FqNJuxcAbjPcY5AoLFYs3V1ZyiKCnKCpFMRQiJHezcJqEUiSkWiyEhteGm4C2IF+bVEBBvQ9lYTAnO0SxWXD4/5/HVUx4u3ufD5htYQQIGt8HXt1E1IAVKMQB42n2dlXuTgQ76uP0q9+wdRvoAgeRe+Tmedd9gba940n51szMs7RlP229snnJunvC8+10A7pafZqQOKOSUe+Vnedx+hVvFW7w8+v7N4ws5BsD6nqfd1wHY03eYZbviK3/v63n3LXpfs7TnO+/jKQ+b34EQuFW+RWg9nV/xqP0yHs9R/gpH+SsvPM/KXfLEfg2A2x8KZi8LbOi57D/gHzz8Z1jZC1xvOMpffiF4irriQxIeA0MnJD3bM6DMcvJqEtsk0/hZG9l7LgRc0r8eksVoEliQSx0TjrTulNLo1MrUdh1hwO6HIfUesOAEwkuUKLet9C4CkLv7unPRDGBgrQQfZVWyNUyuLQfPelbrJzxbrhEyILO4hvOyQHiBCFswdrRXcnB3j9FkyoO3XuWNT7/ErXt77O3nPH/ecTOvub4+4/mzjyhQzGb7zA5OqKazyOA9f0bXB4pijzv3bpHlDoLBh2i0cb1YML98Tr+c45Y3rJ89Zn19hpfR8OC6XqPOnnDctxwcnVDcvottW+rLC/rzc8RijtqMSGThCKMIqgOlY5tgWcV9tGuwqxW27xFZhgoBuXeAryYpVgiwmiPqNWF2TKiqDSMIYnK5f3DEqbqzUQbKM4+uXOxgcB5nHCY4MD3Wd/jNrYxr9eOGGDF3FPHsFH6TZDkXWK9bvvq1d/iB7FOoE01eRdO/rmtQMsZO3sUOrizPyDONsx0607HY7mOBtSpLyrJAqAznBb3pKaspUjkwFussRZ7F9u8u0QakoEiAaV7k7MLSQkjG+4fUyxtEvQKfk2eCIlcxPiQVMF2S50p7Y54XaKXJ8pxKxOKBEAGls8hUQqIEUeesLKlmM4I3dHWD6dtYYzODRrJAC83ebMrBwSFlUWKNYz5fEYKMBRKdM5rss3d0C6kr2nZFW/dRq3UAYoCmrelNn0AeR900nJweo7MMiaTvOnpzic4KvLHkUqIItF0Tk2WtcH2XjEtzqvGU45NTMv1FetFCKm6E3iVH5+34D6Drx4t62+9TzNi28OUvE166T20MTTNiWa8xwTEaj6KRkozzwXaWkHR5EYHRKOp+GmNYLVdordmbxaL+cr5gtW5RvWTVNHTOIkUEvYXzZCFwPMoY5x4tPd6FTSd/at5JKhyW/b2Mw5Uj1w1tO0mkhhQPOhf1hHUEyn3S3vw4qBXwOGHwqkeOBGo6Qo0kXnjouhgrKBXvuda0yeEpWI+3PhnFRumlosiYTsabVvjhisSNeFYLIaKent9Zi0q9QKZ5Yax29oIYP6VYcABtIZFGwrefzUPsCzgCte0opMQryWp/j+z6GpH0pGNs4dPe5nHWIOW2PR+RejeUJFm6462LhQ5KRu6AsXkZlToBjYOmtwTjsB5wAm8BK1ABjAsI69BZS5nnqLCHtxorH3F5s+Cw6xjEj+p1TVA9edKU1lpTZgrnom6sDS4W+boe+h66nnqxoBqNKIuCcn/k/oPRAAAgAElEQVRCpRWtMXghyKoC46IXSb1qaJp4BjoRDXytdwg1gKiOaPKWdqRB6sKH5KC+BRyBjf8AsGUSbpIisSWdpPh/kLLbSOIRCRMIERmSCcjbhl7bQd6cFWELym1B+xdnQhiAy8EcKwzzP6Q1IeDFreJjU0lsQLHdp//44wX+hb1keHy8Ry+eRUMcu3vmhU2+x8ZkcJjnIcW1wxsYwEmfzH5dCFgP1vkEFieihXcJwEs5todNfiiIZ0aSABjupQ9gnYumRban79d459DOEHDYrk+M28HfQuJMh+ka+rbGdDUinRuk+Di+cBiQ4wjc+bAZhxf+CzGnjSSZF8Hp4QbHIuD2/smh8JgMvLSSKJU2zCEjF9vC++b5RIhAoZY4/3vDYduZnWCkGOyBNVEyLxW/vBjINmFjgocLkW3pIxhrncUaE4FYF3WZnbUb+Yaoh5vuzc7nFyIgN2st5UHDexvIKVKCUnilEcUIPZqiegvOIW2P0jmomEe7RKpRSRZQEVAolIiynxZiV7SPNThPlGmIJBhJ8IG267hZtrR9j3OxaJNlHkSGnjpUNUOVI/IyI88hk57gJUp5TNcA0YhbC8lkssfe4THFKBrdyjROxgVUKtZZY1M3onjxnxCpW8vjXDTbMn1P3/d0XU/X9/G+pv1FZSWHp3dR2R6j2SHj/UPyUcnyZkG7vKaZX3Jzpqltg8obpIqG9iKpHnVdx7WxfPThB4isoDc25p97U/IsSyZiOuEZMT7z2wD1O17fFWCsEBKdFbgkQG69i8GZUqgstQAqSZAhbndupyklsNloI/Ns2BBFMv4aFt1ugBsXqZGnTA4+z+jos6jRS6w7C0GmBWHxzZrlxSPWV48w6ytKCpxTrNaW5bLh0dkVAYvWUJU5J0cHfOqTn+D0eI87t24xOjzgCz/6U4jgWc4vefjwPb7xzrtYZ9FSMaoqEFFatG5qmrrm5uaGpmminkVqNbDJmEaIGs8V1gZa0+FCYvcGzdm8pbHQ9oFV3aUKZ9qsgsHblq5PlRCpKMuClx7c4+D4kIBgtVpxdX7O4uaatllHLQ7hIwjuARNweLKyQk8r9MEYO8k2AY8ismUFRKc9karMwWO8wwMyk9SZwIw1PuSIPFZ5tEh6LenQ2JpKxPGSYnsOxZGFvotarUN1KAztBHIbhBEAH//+Rz77GpNRNLZ48MqrlKMybdgSpTSPz9f89vsrzs2EtrgX6fJBYNsOHTyv3drjaKKQSbYh+GR8larnsY6bBLU3jOIIpg82YulU3gQYWgmkSK72Id7F3c849Ld7PxxGxJYwBnDBp4NL0luBsGxMbGJwMQyORvqow6lE4M7BhM73XLUOKzyHe2NKEVjVPddrw5OrlkkhGY8KxqVG5hkfPa+xwMkk52CkuXsQw8Xni5bzRUumFAfjiv2xYpQJygwqLfHe4GwECqUutsCylGi53X5CiGxblIzOkgTKooxmOYq4CXrog8SGQAiK4CXBRnaR95YQXOSdSpBOkpFBHttWRDCMtGCaw7UX3MxX9J2nGCn2g6OuW5RwsYgyHvOJT38PV48esjw7Y6QKqtN7uAxOM8knFs949c4p+/ffxgnF1cVTlMpQUhIksUVaZkMYlYKcaOIgRUAqTZYVrNbRzZrg6LtukxTkeUlRbLVIjTE0TUsA3nv/A84vL+jallzHIgppzVX5mLfH/xA5gsJ5RkJyP694ZTpjpksKJG29RniDx2OVxGUF4fAEk2tsAioODg+SKY1P2jsBBVgb3emllFRlFQ0lpALvKPHJbbnGrteU0zFZki7QOqOua9rVCq0zitGI8mDKnVzQOktrDV0bE5cnT88Bwd7+HrmOhlvO2lSNXLK/v4/akQoY1pV36V+610KyYX0pNQj5x0KSEhLfG9rFmo/efZ/HF9d8ffmbPGq/heVjZiDpGnQTdzXqdq//+qN/luv5vwH8q4Tg+Csf/Gn+8fFf5Hv2/gSZLPizr/2P/Fcf/Gm+ufolvrn6pU3B5kvzn+NL859jYIT+3au/Gl8PzZ95+a8z1gcA/Iuv/g/8u9/4PP/zs3/vhdf9l1/7ee5Xn2Nhn/Ofv/cnAPgjt/4tfvz4n/+29/h7Xf/94z/HR81vp/sZ38cXr/8aX7z+awgE//Ynfo2/dfYf8evXP8t/+f6fBOCP3f53eHv6UxBWm+f5v+a/wF+9/G8QSP7Jl/4y/f6neKwy/tDJv7QZrbl9xi9d/OXti4eQWEYQNCA1QWR0MqNLdymTAl1WTI+OWa3XtPWa4KKJX+dNBDWdYCTzWBxIoGgpNWNdIoWgC5bOWLpVjSo0ZZbT1HU03UyAvlJR8yvmnZaudTRtiy7HMRZRKup/OhO1FnUEaU3bDShJBBxUzv5XHyGetLzXKZaLjqrIGY0zRlpzuF+hywJjDPPV9v599guf50fuvcVk75AgNc4YLp/3nD+aUzdr6rpmfvGIm6uPGI8q9FhQuimF6TFdbIM7PDymKgvW85bzp18jw1DkmtF0wvHBES+9eUpZZGgpWF6c8eu//POsry6wTcNcCVbNGnt1hr254vqDD6iQlN5Ses9ksG4UfjOe2J7QJdBcKorxlHK6F4H0pqZoarp3vk5YXiNv36N48CoUk5iHeQi2R3/p7+C+9w+wu+Y8gnw8ZiRmW5l24RDSRQfkTOGygFIGFXraZoH1LrbrJe1JSMlmCLGFLcRkQqS26vgmYrJmDfzWb/w27eKKwzf2GL82Is8LBAHneqxVZHlB0xhW65qqzBAS8qJAZ1XsbLIt+5MpUsZipe0t4+kULQOrds386pIQeg73SkTIUUoznuzz/Oyc6A4dwaWHj57Sv/IpGENW5HzmCz/Mt77+ZejWVJng5HiP0XjEzbxmvbyh72O7aSdTt1OeEXxBWY1AacaJNeiCYzSdMJnOKIsK7UGrApkVyKJC0hNsjTMxqe5tjzGx5UYoTa4V9XLNe+99wM18warpcRQUkzF7h0e8+sZbFEXF4mbOxdkZl2dPYzI56N6JCLwY29O0LXXTUY6mERBa15i+58O2ZTyZMNvfR2lF09S4oNk/vQMqo+kbZAjszSYgoKkbTGuwAxN2M1VSUY4t2LoLfGzYS6TdXEYd+pAAAgTwN/8m4Uf/IOGtt+h8y+NHT5gdzNjbm7G/N2O1XNOua+pRTV3XrFZzjm/dZlyNqcqKs7NzrHMcHOxzsDfl7bc/SVf3PDt/xrqOjH0hJcELgnEIa7lzWqJEg8QiVUBJgXPEQgACmUEmPOOxZzqz0QSu8WQqFlS8Fxhj6fqeXAjyXJMXUQ5ju7/HlnWkQ5QWfeDw+5bW9ZRdRpXlKJ0zmlYYa2k6Q45COYczlmBCXLtKoLKMqirY35tw5/SUto16k8NVljlVmQOR6WyNxWFirBeI5Dkd12Va+Ol9boufsfguk8nmiywnl9iGu1rww18N4+w81N5RCUdblHzzR3+QT//i30G0Nc46emsIQqB9jM2Nc8hgcDvJs9UC38XPD1AWBaPxmCP3BnvdA5q2p8hz+qFbxwZ6IykAHaJGsZADIBclAW5uOqpcUZYCpSZw9RO0q5+NMWG6XjqqsErE80AXXC0amvWK3vS0rcETz6sBzFdC4XvLurmhRjDSitl0isTSd4a2Th0RNnU2hMScJtB1PY2U7E9GEWAaNumhozR5rsT2cp0Gb4jBQpLhChvAUwvFwLh8AZiEKAu2WYYDpDQwQIc1CkH4jTnPAOy+4AOzGe7dnw2g5S7cywuA6ia5FMTca7dI47eyAoMklNgpzm9fMskrITd5zQtPPRAXP/6Sm7f3YlIrwhagHWQU4tzfFv2HHDK9TTxRus56om6wieZ8UsTCs0iu8hv0NRnvxpGJnRBxDONASqA3hvniOppKWcdytcR7DUIjsgytC0gFPheSkbC1dPWCZnWNWaeibZAMRZ9IAouyN8HFTlvnXdSJJX5emRSrfAJvRdh2nW7l/uJeET9blD1y1uGdR2Vs4rSoLSsQQqcbnxj26f5uOuRC2OAOiC0T3w9mZ4O+8eb1ARsIMhWjvUXGtiuGGeD9AGZbjDFJpqCLLFofu2isM9v7YE38nM7EOMDZdH7F+7AtpqV5KBVCJx+ZHVDaD5iPiLhLh0f6hBsE0EnLVgqZ2LDJnCw4ZPDIYBMcHpnDwges89R1h7EdHkcmRTTgVgKda3rvacMVYRVoux5nDL0NZFqS5YrZ/l6UGVCCQkOhFXZSMhop+kZi1wUCgQoZ+3un3Lp1n/3DfUSQlDrOhbqN+73rLKYz2D7K45C6cmLhQySJvy6aonUr1usFN9eX3FxeML++JteKKs8Bw1qvqZs1p3un3L53izuvvMbeyTGEQF/XLK9v+OCdd/ndb32TUH6NoL5FU6+h9ymmCDjnePbkEW3d8eTRU/ZPTrhz/zYv37qbDGCzKN+X3dCJKBM06Fd/p+u7BIwVqLyKrckCvIoVzNgCE7A+tvgGG6e7DFFzaQBkBTHQZPNdqnml+RyIk3HY/QMKHwoOjj/D+PiTZON7WEdsL/aeEAzWLmku3mP+7m/SXb2PN0v6oJIh0wAWeiQB5RV4hesFV88v0XE10rdrDg6PIXhMW7NeXvPyvXt0TdTp0Srj+uISVWSY1CJtnCMvqqh5ImV8P10TTXCs52q+4mZdI2WGcZ7eGGzwtE7RdJbeOgQe6/qNmZn3sSKkk3arCI5xqfne7/scD159iR7DkydPeP/9D7m4vKLvWpTW0TDFRj0S6z3ZeER1MkNOCnyxbcP33uOIWlVaCTItoqOyjAeMQkUDFOPQOmrURImJEFmsREarTIdBHMUEzPoB4NzOF5kLQk8CucQ2sH6hMhs3odm45Ke+/01GecX9u/d5+aX7vP7Ky1RlBPuXjeGjx1f85oeGRp8ixweMRlO6vkYjOZlVnO6V7OUOEfq0QUbYNSb+YVPlBwUhmQp5H80AvgNws2mdAIZwYRuB+E2GEHXABh2maAQVmyMG+yVSi5HEJ0KptbBYd7S9o3cOk1hEmQyMcsmkKKik4JVbY2b1/83ee/xalmXpfb9tjr3umYgXNjMqMysry3RXdbeo7hZFSA0SoAAKEjSSIcCRAM3kJoKgCf8ODQVNpLEgECJlmgJoW+qi1NVZJisz0oR/7vpjttNg73PujazsVhMaqAY8wIsX77573z33nG3W+ta3vs9ytTU8f7Xiyb0ZD85qtBK0ved61XK9MbSux0lBUJpnNz271tMuci6mmvsnBdNS05hAphXzPKBFSI6ZEBjafiOfNeoTDWxGi84igyIkdoLpe1SlyIqcICTGCwyw6xzbxrHaGzZ7Hz0knMVbA65j1JPyFk0LwSCDJ9dwUmvcVFBLqHKYyMBCXPL4zGL1OXLxbbK6IKw7tptbtlcv+ZM/+qfk1vP6s0/obm/50Xe+z+c//jGTb79HrnOmi1MWp2dk1QSBpKjrGGjjxoBpuL9DEBWCRyWxeSEU1grKKmc6qWPLx6ZFZ1HQHRE3luEwxrBe3fLVi5dc3t6kIDrQ954qy1icLDjV73LXfZ9TkXGhCs51zllWcJZX1JmKm7KzkFrCrc7osxy/OKWbTEBJpkXGdDKhyAR930d2wxAAS0GWZWRaRi0iBLbvom6k9xSSkQ2hMoUucsqqJHhPs1pz/fpNNFeqS4p5jZcwn015/PAeWms+++IFKMWu63h1dUX+meY7H74fW8cBrTNOTk9Gk7Lj4NpYi3WRmaSTM+rgvHoc+KrkENtsdly+eMWr5y+5vF3zj1b/Axu3jWA0YVx/hnYlmRgxXhB1FIcJKkh7lOA/++Dv8HdO7/OPicWQ/+LDv89i87a5199657/Gh7+oxqygUgdzJy0K/quP/snbCyFQqsjEPcke8rc/+jEAmaz+gu8Rj//wyX+LD/bP/H2lFvzb9/82f+PivxwfK9T0V573u6f/Hg/u/EfpvObw857Fa8vHfzU6Q/9w/m/yG/N/4+gz5XT2l9gAKhWXrPf03uHyPFXhQUlNXkwIgci+2G+QBLRStD5gekcvLKEIFEIn1oZjmldU1YR27+ibBrRAeYFvLV4GZrM5t5vN2GZuTEhuqtE1G+8w3Z4QfNSP1RlZkSGTqUTf96lQdnQRnOP0f/xDVjfQNpK206i8Al3gWkUfMi7qU07vn/Doyfdov/cB/3C4plVOlvfsd8uYaLUtpmvpuh1lXfHoyT3OHp1xb/2E1eaaly9esdl9ztl8x/vf+i6LuxcI72nWS65ffo5tNoSwx+4d+5Xg9tVTVJaTZwV5UaK14O6jd7j34B65cAjTsX3zBrZ7btdbwqsrHq/WZGIwIJQj2VCEQTAGnOsRfdx/2yyjPL9LyAv8ZgPLK5Rt6V49x25X+M2K/DvfJ+RThJD00baC4k/+CPXs6XgZg3cEZ0edSwBvDcEQE8wYi5PlEhE0PgiUFXgnoz6XS27nCgbQQKlhn7XRAXgAWwIQPJ0JfPzxx9y/Pefdm4fc+d37dKaDZosQiiyvmC1mGD9Be4XpHZAxP1lAiKzP+aKm6wx5JVmojCBgs9kQQk+eS5qdZbfa0Gxv8d4zO7kgnyyiZqrpsE3L82fP6PtUZFMZD7/1XVR9xuryJfvbNzTtlvks496dO/gg6E1g2ziMdUjlqSc5zlmq6YR5dsbJ2R2m53ew1pFlCiUEq5sltllT5B4pWja3N5yeT8kmCu8rGi2ZzhZYG+VaghT43hJODQ8fRrmjkFUEWaB0gQ+CzXrN8y+fUpUluQLvYpBmfUx4tYzkCmsMvenZ7nfcvf8YmeVsNyvWyyWb1YZJ0+KEZLGYM5vNePn6NfvOMDs5Z3F2xvXlG1pv2G5WbHdrzs/OUTqgtMQPsh8h6aweqBlvL1YHZOcIkBWHArsnoh3/4B/AF1/AX//r+I1l1a9o1i2b1Z6H984pVE7Xd/z8088QwfLs5WsePnzMw4ePuPfgAV9+/ine9izmCxanp9SVQ2QSKzyvlpeRQZaa8VTw5LJDeAfqYB7jXMC7uCtlUtA0jqIM5JlgWkte31jqSY0Pgt2uHZPzvuvxNjBfzJneqWn2bdQ4DZ5QWop7GfJU4aaSrrO0bYPrOygLzk9m1GWV2E+GN1e3FHmBCwqvHMZEE+WyLqknFZOqptvtWS5XzNaH/WcymdBPDSEEsiyjNSYV06O8CIlRHgOHlFul4tjgWnRgCh7JBqR7K1OgFYLHed6SMCDlfy4ENqFDI8iJxfmm34DZR5AhOIwxuEGT1AX6EB8fDiUU9WwayQGJpHHf/B5FfhdXFdB2UJT0Cdxa1BV6myO7bWSkyQhi+yExlRKUoO08SlmUkpSZ5P3y30I1H6QxC++dZDShY91bXuwsb5YN/WB26APOdQgfWb0yQOhNIh8ErHG8vtzx5uVVuo4DMUkkQ7SxdBFJsDYWIzIhKJRCyyHTiGvoKPjnQ5SgkvIA9CWgfChWB1yU3hiW3K8bZyVQenzCMQCbZq0KjFIGv/raYdJ+U4b1tWNovHnryUOLf8BxAIsHYJlw9FQJwaXPls7XBcshg0t+BSNbMQX/B2L1odhwdMZfB6glHKS5ht8NrNC3Pv7AEpXp0sf3cz5+FiEEXgwq7GIEqkMC3p2Pc88YizGWeG9jXKukIGgJXcDZDV3bUBYVShcImSFEBiIfTRBlIj7gDc724NtoUgxJ3zVeskHnlBAITuH6gPMy5YoH6YIwXvgI5PrE0O1MS+9LjA8UxBggyIAjMlCdc2QBgvM4ESVEImgrR5TouCgwXNsR5BxHxKDZG7GnA8Ae9xMXLNHwMsqghYEhi081CAFBYH281pEFa7HWjKCqsxbTdwzeOxGE9Qjhx1km02cJqUA4yK9FyZe0hIwIWEK9vEOGKBnkvY+FI5cYKkGgnMQJh0PhhWKA/3wYcJoE3ussdo4SUJ2g62PhtesacA1d3+KtTZ4ZFq1kVMKQITHniLq1RcFkUpMVgckkUJWQ6bgGFrnA7i227+KHKU/Q9X1UcZfewrT01JM4eKRWZKVguzLIpce6uIaNMnlEM17Td9huh9mvaVbXrK9es769otltRjZ23/fJfDfw+c9+wldPv6D+6Z8wP7/HnQff4uLBYybTGVlecProfX50/oSLew/4/OMZu5uXbMya4EUivUWc5/b6iuXyhhfPnvL5J1N+eXGP07NzprMFeVVFEFYKVFGg9PE68Pbx6wHGKkk+r8dqBCGkzSK1x4cRemLQKUlo7KHSkeoSIv07/Hy8jAki8IfIkdlDFnd/E8p7WLLowCjixm2Mod9vWD//OXb9gtCvESHSuHOl0HlGXlTM5jn3zuYsZjOmVc2kKqkqTV1nVGVOUWg26yXNbkPbbGl2W/b7jt22oUutba9ubsnymEBaG51vM11yenaHST1Fa83u9WtumxhwX608q8YjsfGKhITSh0BvY1AhgsVjx84AgYrgZqq8FYXmt3/0Ix4/fkxZlmz2W95cXvLq9Sv2u00EQFwg+NhOJoRAVhp9NsVPM0Ieqy9xgY9XWBLBQiWI7f9yAA8FgegGq1JFRqR7a60jKzU6VR1DSKzmoyDajxosh81yPqsxJrZuE8TYhjF8BeBH335ElWcUWlMXJY8fPOa9J0949OAedZmRZRlvljte3PR8eglN+YC8PkVqDa6jEHD/pOZ0kjHLh0oiacuKY9CnsTmMvKH1NhGvGbRsGc88FRMEaBmD76+Xgv1QbU3XYNhsj3WCRr2mIRjwMeFpjWW17aJ5VKEpRIYNgU1j2O47dsax7QKPz0tyETgtFTrR+6+XDcIHFnVGnUnErKQuPI317KxnuYd9G4Hdtnd4r6KObC4os3hftYwmT6OmEgKtC4LU4GMr+jgrQ6xoDmZKSinyqqL3kqbzNL1hu7fsjac30DvobTTgjW0ighCicLpUpJayqN2DT+0NxmM3hgw4rbLYBtRYFrUm15qygKLqaJWmms6RwWJ3a6pJwatXT1lu32D6HZ+8+JzTC4ncLeiUoW32BC8R/jBuIRz13/FW1XsIgIdfx+AE7p7cIaBpm5ambSlQMZkQHpeScYDVesXLV6+4Xa1idTlEE68iy3ly/x5VXTP1p5zup7wrMx7InLlUTJSmlAItJJB0DYkC504qXFng64qgFJO6pCxy8kzFdhghcRy0kAfTLJ9MwpIYDopAWRZMFyeYIsN0LaYzVNMJpuvpm5Zu31BVJdW0jg7kqaqpleRksSAEwWq943a5xnnPrml5/vqSBw/uURZZvCZxo3gLhI3rwxHbQYioOS1EWoNi69LADvA+sN2sePXVC66ub3m9uuLj7T9l43fYAyUnfpNDMJnamlWcgQMQPewnQ1JfqQVaFOM9q9QiapkeHeU3AJh/0UMIQa1O/szfS6GoE4v2n/cYAN0/78hFTS7rP/c5WhRvn4ODau354J+0fP7bBeQ5kP/K6/yQiMvYPjXU5/MsIy9y8jyj73qMuUYgmE7mmK7Dh6jl1HuLwaBEwKmCXGgciopAluXRHBPorWWaTTDORMduHceFlCq1xVmk0pG1kySTdJYhpIhgbd/hvUMn197BNGO4y/p2Sf3xT2G/ZTqdcXpnTjU5I68mzM9OODk94+zOORfv3EcrSVbkPJ8dXQ/XgdlgjeX11RVN06CkZDaf8eBb76LzDHYt252l2b/i7M49JtWceTXHe8P2asny8jW79Q3e7Hjn4Qesl8/omiXBt7GgbSzGdzjbpBw8IHUGuqCYnqCnp/j9HrfZ4k7usv3yGWG1ZmJ6pnhyItgxOD8LUmyWWvZss0POvoWezXBVjW13iH1P7ixyu8H4r7BFQfb4PUQ1xam4LmIt4gh4HfTuwnFrl3cEN/gADDpzFo8nCAkygjOZkmBIa2V6bYoh4r4cz3rMtULsrAqJIba8XeOfOvrHntl8yunJCVU9Ybdrubm+xjnPbDqjqmryvKKoZ1HnPitYrZcj80ZgRrOwsp6SlzXeWcz2NcE2EUjyPdZ0lGVOLzyb1ZJm38RzJ+4du60hUDCZ3aGQivWrz9BZFQv4ncFYz2bbkBUVWabAx7mjpMDZnm6/5vHjC168vKIxLiaLfU9wNmqrK9AicHoywTtDs7eY3rC83ZFXE7IiI9eSpu3JtCaTsXtlv19TTReUWYbzcLtbUiiL9A3e7fG+R2cZReqO0EpTlAXNfoezFu8Nu2ZHXucxLpcy6jmvlgRiEfLi7l3OTk9ZbRquXr5gfXuTCukBLS2Kns3qNc6l5PatY6gcDN+O1+PjAnha6wcmnZf4xALHe8LlJfyv/xsQ8L/9I/p7FwQXeE0sKCql8Dbq07ZNz3K1piwr7pyfcXIy5/ZmyWa9RamMelpRVxXTehJNo0zqcvIxIc51nnQFQci4t6nUGhYNUuKet98bbq/B9jlSSPZNSyC2/EspR5dwZy1tsydqc8fx39NS3dOIM0+oDC50+D6aHYJnHyLIMhBQ+95gehO75EpN8IrMB1SmY7wA9F0fTaT6/sAmA/q+x1iLVCq6oWtFVugxVvfGjyHwwD0bc0AfYucNyaAmEUPEkdHjwMIc7qQ/AnBjLhFzCAPssWxlzzQUfPGD7zD75FOKL77EWIsTAe1UYo0dxswwjKL5TI/McvJswj3zXWQxx4oMLxUhL+LvnUcoSeElE5nhvSS4Adwh5WPx/CWRxWxtbGVVWlJIFdeyNDov12uWvmHvNZ3P0XgaY2K+iiA48L3Bep/YbR5FAoL6CJioBBINxIAoC3fUqk2McZQI5CKBXaMmRAJ5Rz3feOZDLkIypR1ZNGOUn+LiERgPCHWQICPlgQxr5aDTmdY8AcmA+3AMseihbTsxSb8264e/ecARhtt4BD+nwrv3gRHkT9dchGF/Sa/0geAP8bwQRKBeREmlkHLU5Bc+XqexAHTMgOVtQHDME4bXpUPKWPAddE3HwHTcdwVC6ijVmEhXkRGbboSQqaCRQCNS+//A+EwGuD7lBEMbPGIwkI73P3hH17foECkrrcIAACAASURBVJDSIZQFYZMGOngRUB4I0aQxhOgbIaUeWYsMY23o8ExM1yG3lQLUoCV8NJmdc4evJAUTrB1JIiM2LtI9TAtJXAN86mY7lo44YEIjyDmC3YfHo+xZSIpzEd0YakN+1B9N92E0kUuEozTPbGqZ985hnUl+Fj4xeS3O9GOM450dJeziuw0dfkdjVRwVmQixiyOEsVgtEyYgpIgVaKlivpteK4WIBQVJasCNMdAghBvZtCHFQsNEiPlOZJ0Gut5iu5a2bSLAPMh2BYFEIVE4YUBCVp9Qzc+ZTGva/Q6MpCui0bgIClUIguuwXYPAI8uCyWLK/HRKXQrqCnQeOzCUhiKT7HEQLODGOTWM1SFWDN7iXE/TbNlsljT7LV3bYvroyaSVR7qezvYooSisjYWEbke3XbN6/YKsnJCVJVld4Y1n+eIzdreX5EodXSfGdQsHzkRpBG8NCuj2e6rJLfV0SpHrWGA9nsffcPxagLFSSbJJEQdsZxDWplhp0CU5BCaHSkWU4z5sCmHYC+LvGSPt9HNaOEUOak42/5B89oReTHEuLqiBgPWWvtvRLF/TvX4K/S2lduR5xWldcTKbU1QVRZ0zX+Tcv7NgNplQ5QWZ0tjQAVGQf7s1XC83bNcr9vsdbdPQG2j2hs66aKTloy7TCCaGCJaGwtISmQy3TaBzHfvWsdo7dn1IDLf4GikSc8tFZq93liBiC/tYO0n/5HnG+ekJP/j+d5lOJxhruL294fnzZ1ynBHBwG/S4OCHzjGxaImclPhfR+CpVJmxqYyYxIpWKQOzwe0EszggiSCsY9F5kSuoS8yz4cbH+ht31LfZRXZVsi8iINNaNHRjj3gc8unvCvC7RUjGtJjx+/Ij79y5YLGZoLdk2hpc3Pc9uPdddjVzcQeU6wvXOMatyzmrNJBdkIiQH+UH3iDGwebthJp6EOG4LEUM0ED+AJCTAGgQH8G6I1KJmYRrXhARuHhKJqJ912ORIFcVda9h1lsY4prWiyGTSCI7v2hnPvnN0bWDaeM6qmLTOSkXvcp7fNqz3kbV3ZxrlCapc0DpP1VuUCFQ6kClBrpOmVIhSCxmC0XzhCIiN/9EMlXiIYyJqNx2YVjE4gN54tq1l13r2nWXbWPa9jwEtMuqwHF/rQTxXCoSIxmbKJyAFhQ0Caxw3jUOIyGhAeGonICi0gFr1eDpEMUH6GWYyRWrB82e/pNmt8cbSG5icP8b0DT0Nu+2atu2io+iRZm1Im5mQpM/5NlDofaDvLEJ6pNRM6gltF11N286ANGQ6Sn64o1a13W7PzXJJ13eIpMdcZjknkxmn8zlKKwqjyLVigmIhFVMhKEJAh4BCjEZoghA1nrXG5zk+OfJWZUFRZGkYJpMMZFTKEEl7Kl135xx2tycXsS0o2NjSJ7REhchq9t7HTbCLSXI9m6LKApSMABACgaQsCuazGXfvnLFZbyLrxHlWmy3XN0su7pyR5zoZ0zBe45CC11jlFPiBKjdICUgBKmooCRHbmWzXcf3qktevLnm9ecPL5jmv+i8w6ekCxkLHoMd0vKYMgc3x8SuMq39xvHVoA+dfWr78YY77hmsl5YRSfxDBWKFi2TAAIicXFbnI0UHTNwYbDEVekilN51usjwYIwQdEEPg+x6kcIzRBKPaUqR29RIkJ2lt0mBCFsh3CaipOyGXABYeVlirMkySKR/vIWAIZ2SQ+IL3izqUGGwNr6+wIAOibgsmXl7hwj0LPqasFs9kZuiiZFScsijNOi3NOuIPZdvQ3Lb47rGm2a+ibDQ5ouw2dM2iV45VA5kVi3yiKrKTMaybzOXVRkQnF6voVN5cvabdrCJ7ZfEZVn9LsrrH9JvZTpKw6JgmxmKu1ROjYfqjKGl1L+mKPyyuczNm2hs55uu0GvGHmPRmDzt4QXEZJKLzH9h2hyFHVBJ3ncPWG0O0Q1qJMh133mJdfoWdzlJRk5YTWHRykhyOMhR97/GAEZCURnAICniADJIkk0honj8x3xvhhPN+BQScPWU8YIiVP2/XYK0P2WU79gwqlNVmW4VwM7JvdnkzlFEUVHdWNI1cZuqxori7RAwM3FdgDgrxU0fQ0y+idSVILOUVRYPBorXBGYkzUXhviBe8Du9UqFdnj/W97x3bX0XUNxhiUzvDeYfqWTmuMNRRlTp5lmL7DdQ25cNhmQ9MYvB+KVQqlc4oypywLJBJro3GUd4G2bdHlDCl0tCN1jiwvCCLgrcO32yg1pVyUg7I7MizOGFzfIgjkeU6e56mrImM6naIkNM0eY2xkE7s5WucUZY1Qiqbdj2t9kZfcvbiLM2u63uBtT52fUNYlwRf0nWK7WSdNwqN1hePoPw2EY/xVDAkVKYwShyK3GEvfCA80DeGXv4wvXizwAczFXVYhkKkINitiHG6MpWtadrsdRZ6xmNbc+Fv2+z23tyvqSUWeZdRlxbSq2XebqPeazstYgenj+atYw06gwnDuESTu20DbBExHZJj3MWcaNBEjWS6CWcaYZNQDXjnExCHPNL62ONFj2hbfm9TxJeh9YOuS3VGIOn2m7+N1UiJqxRI7ZKSA4Bx919O1XQTV5GGd7000LcxEBLeihuxBJ9YEd2B+DfGjH+LruL+GITdIoNMI5BE/+9jSHQ7h9AEDTPMI6IJl43pOpOHm3h3Uq1fkgrFNOvhYlJBS/UoKIlMOMJggTdxDIMclkEQIgesNOkARBLVxzF2I3V0+6i+6QDIyE8kpPgIksfswFthTp/Z4rNZb3uBppQat4ng8BrYcOOPSehdQkhHw8j5pTx6BmsMKOIB3IyiGJHLlPCr4VGwLCC+QYZAgSNd8gEDCwGr+ppyNIw3r4eZwBEy+DUyIo9jqsLd8w98cwbM4P+V4Tsd/m1/dTw4Tf8ylDvIEX3uvt177dk46XC+fcl7EkTbsoFowXBJx/FmO/6Z4C5NJ28/h+n7D5xBiyIHfBpSH+zioq4RADGaJ42iQahxAwnD0HtH3IZIUjhm2x3xLYPRrkETgNK6ZyWh5uBZJl945O4LpA8B8zOwd9GNd+NpVH05uPMdYeIlfA67hRl1VkZ6YIMXEkPeH90tA86G9P52QYDSIj7IBKYdIHa3x84ZkbhbwXoynF38+uobHGFMYJHJ8XCeSxIF3LsoQJDLLILvmU5diCC4yJ2O2BcTr+vV8Q0oZHz8qWMR7n2KFIMd5DUT5m3R1hFBIoQg+CZAjRu8FOeAYIf2t4BPAfIjvQogt+X3fs9837Pf72EngHDJJUmqZk2dxfwgiUNQnFNUJeVZGyR0hIUiCV0ghsM7StR1t0yCwZIWmqHKKIovXzAucT3KOGoochDcEZ6KExXEqke6fcz3GtjFP7/d07S5pGDeRiSwiM1cqEeVpsh1aKMgypCtx7Y6NDaBuEakLDmtoV2/w3Y5pVbHOc4zvcS7er2FpiN3QDtObKH/mfWTh2p4wqcl0JFp9LX186/i1AGOFUsiihNAQ+i4GnYEE0A1V1mG1iom8SUYykYafZsiRc7aP6TlpRUgLrsLJGVRPKB/+ZUx2gbUOlxyUHWBMQ7t5TfPyY8TV55R5x+m85sHFPT761ru8+/AB1aRG5ore7cF12L7H2pbWwGq3Yd827PYtq/Wey+UtbdPQtYau93g0IUg80T16qAgdqPwa3cOr9Q0h3Kb1w2HR8cb7gAuSYG1kqgWPVjpKEPg4kWxagKQ8bJzee5RSnCwWfPTRB/zge9/B2o7rmyu+/PIzPv74T7i6fkPbGcaKpwioMiObVuRnc1yloo6sFGRKIZXGJP3UWF30aJ0d2oPDYbOK7x8XDKU1SmukUjjrIhgdkv6T95HJlxaiYxfEYRiUyVHUe09vLcnybVwktZIoCZmUVEXJu48e88H7T5hNqtgqIRW/fPaaTy41t25GmNyjmk7odxu0CEyKgncvZijXgXN4JD6BnsOm5xJzZXBVGALfY5AUGIPstDVGYysRkjrsQd942LAPVT9B1Mg/Dqgig3TIIIYatPfwermntY7zswUnpUB4h3AeKSXnlaZQU95sDG9WHU+vG/TdCVURz+dsltO6wPWmo1l6pMy4t5AUCnINpRKclQpDlF2QIrF6CUcbd6yQDRHF8N/B9Mk7n5LaHFIA7byMrN22Z73vWC4bNruACRrPIAly+Lyj6c9bLMbh8SjPUcuOwJZeVPSipBdTrtsdnQ00tUTmJXnT460g8xIVAgv3iqV8D1FUFJMJ2+2Kn//8n4H35Kpiknt++DsVEOibPeubK25ur5nc7xEqMtu8c4cVKoS3KvjDYayn63Z4H9mkSigE7gDGih6Rx4l7zC5pTc++bUFEGYxJUXM2nXPv7JwQHKYzaBuZgvve0ulAKRR5qpCqTI4BOgREpgiZxmmJBxZlSV2WUcTeRUa9lFFPWUiRhPQlggy8xwRY7i6p53OKPGO13dH2PbooKKuoy3x7eYU3Fp1lVPMZxbSmS3In0jq0jPNBSEFZ5Lzz6AEvXrwgdALjoqnXF89eUNc1czVNDsYudQKIOLYQESRD45VGpq9h/Hkl8NIhQ4gtlFfXfPbJU5Zdw9PmF3ze/mlMFsKhkCQGxmMK0o9GN1+b0HHa/gss9i90SAeDudbxUah3KOp//5tf5ID91x5r47dvFGI4kMnxwM3Rr2pBZAT08VuR/tYE4jqi09fR3wDAkvS7Dg/96A/3FPtvThYR/078e236Onii4YFr4JouPVJy+90M/lb8ab/fsd1sqaYTTk5PcLmOQbMTPH/2kjyvyfOM2WzCe+oJfQK99usrvvzkp1xdPefb73+bh+++T3V6n8svX2NtSMXPJBYXfGzlc548zymLaFCmdUaQBc57eidovWCvFP70hLDdUgVDbzxyb6mFigW4FHqJtAYHiLqtMqCnFVlZok5O6Xcr8D3eenAW9+o5tp6ggPJByd4PYMoBhvA2ytA4fwBjg/eppQ4GRocQHpkJMlETbEdwBmdt1IaW6gBMuNjuHRK7Kv69uMaKlNSNetBB4vrAzY9veOfDx7Rti3OO3W4XDYoS29oHWC+v2fc988WC07OTcT+MCXbAmY62N9EHQKb+GqnQekI9mXFyfo/Vbh+TyZDMEdWBfR+8o7l+TtfFRNf0e7bbDZ/tNwigKArO75wzm064Xa6x1lOUUU5hMqnppIgsR9cj4mAmyGg0opXi9M4dzs7OCMHy4qunWNNjvUPKDI8nK0q0zvC2QeEpco3tLdYbcm3xds12tcLaQJUF2qal66IGulYR7PU+mtwpKcm0oqzKqHnZdZh+jyAwmc4oypLb5Yqm247sWesC1WSO846yyjk/OwEU85MzsiLD9C2r2yWZznDSY1NvsBRRvz0EIsv1gMUk4FUSxkQ9AYhHya4UaiyIihFkEYg//mPC8pbwr/8Bvfdcuitms5qTxQytFdb2cZ+yjtvra6ZlyXQ2AyG5vLzk0aP7aCmZFCUXZ3f5xeWKLFOpE0Vws+zIZ3HfyYXCGkeWhzGm9gFyldHbqNfe9YEgNKAQQUY2VOqAU1pF1r9z7PYtIe9Ri0D1uMDPHdZFGRS7bRDWo5IRrk97/PX1KsmFxG4jpdQYm+okS+R8iJ08wiambATfx+XTHQARd8Ti0plCS4HEJF1ilwRLjgCOdC5DgSXdgTgvGKTNonDXEGZFpiNv5QvDheucJVjPlhwpcqyUBK0RzmFCXBODlGRKRfmlEQiDaSnJ6orWK5pG4obCb1o/8B56Ty0lpwTO2pap6bBe0JGx956dA6Fk6tiRkcHvLc54bO+RKIJXbwUVzaZlmxfs8hwvC5T1KKUJHkzfY40Fb5FKonVGnkxV3QCEJkLG8VUdgKbhEILYyShAeI93PXmwEeAVDpxG6mQsOGCoLuY4cRkOEUAXIrnCJ9DLD2lL7FwMHObXUCQbf0ync+g4OTAV33aNTycc3gb5hscGBuFI3BqK6yHN8/R9eI8DYMgBRCQSh4YjHI29wVR5wBWGHJcUM8bxHfdCeQQqH+To+NW48XisHoFjQnwdvDnsj9Ec2B3d1whI2cE4WBzeUXKQkgghoJPnQvBRJ98Y8/b7CBBSjT4LA3HKeU8QDqUFSTEy3fvYau+TJmo8f5PGnRiLG0KKcYa7EMFKlwBT41xkG6e93RMIiVHvknfKsQl17BKIz49yVuoAuOJJUEICDFPnLIkNm7pVjB0MtA6A7DCVBya5dcN8STATcW+RY8Ervt9xjcH7CLA6G/e9QQPajY+ZCMQmMDbm+Ok9SQQsdcATBEkLlwPzH1JX1ih1EEk8OBe/BqhYSITSSJ3h6QkhkhK9FLRAGULsCEqeKziHcG5cZUnnZKxl37SsVmuWmzUmfaa6qpmUFWVVUdYVVjh6Z6indyjyU4TPOV1ozk4ylJK4IGga2O8Ny1XDer3HY6jrjFwrrPFc37TsO8VirqlKRV5IyjLgTBs7erw7VkchhIB1hqbd0ezWNLslrt8jbI/v95h2Q7vfgywIRcTYpJb0bUOuK6qy5uLiEXp6Su88tu9xpsPvtgi3p5Qd2TQn8+e0xmJvb2naLrLMrT/ECVKD0hjnkdaibI93HcFrgs94W6rkV49fDzBWSvLZBGRsFSQQNSF9YPBZcGmAKEEECZTAOIt1cdZJktEU4ImVhuTnOKbUgRmT04+o7/0lpvd/yGa5QdoW6T2eHPCU3Rsm/VNK/TlP/pV3eXzvtzi9c8b8/Jx6WiBtz67Zs9ntuN0u2S433N5uuF1uuLxecblcsdu3WBcQKmM6n0cneQoCEtNbAhKpJCrTFHmJUNnbC294W7RZS5Vo7SBSixkcqkLeGtr02HFLg7VxY8izAiEDH330AX/pd37EX/krv0dvGvbLFT/75GP++J/9H/z0Fz9h13Zp0YxtBmpSkp/OULOKUGVk2lNkRTI6kTR9h5KRcTicu1Yy3TNHbxxFWcVkMAzarwPQMezHEeACjq7B260oPhwxZ0Jk+JVlCcTftX3U7xFEI7W/8fvfp9Yl9+5c8PjhQ37wvY84v7Ogd4bVZsfT5zf8X19Z+uod9Oycsp6wXS05rXPOZiXn8xKFj8LogahthRyFtkMICRTVKcgfPk2SwUif68BKjueuBGRKJF2YdJ/E25UppWRMItPGQXA42yNkApoG3d9hqITAtvcsW48Ngvtage+SLAC4EKvtkwzuLxRVWfPF1Z5Pr/acTwtO65w6Fzw8nVAXitW+5/nVCi1nnNZ5NM8RkcGav0VZGBUDOVTbBKZvo3aN1LEtTSYJgizDS0EXBPvWsd72vLrcstwbepeKE5TDqBhWBngr+EktCqij3yXjLwLSOfabKyq3QeWn6ExjZQ06Y+MN3c7SWkf5zilZ1tAFwWqzwjpLWd5yfdPxy6eXvHp1y95pKpWxWNzjB9/7fR588CHrfsNqtWa7XPLm9XPK84fMTs7IMonO1FEyL8bEw7moaZRliizLKPOCoihYLE55591v8fSLL1KrDHRth/IeqxSdOWiLxmBDIxFMi4qTekKRZ2ybDY21PBK/S8Ed9sHy3HoKLwk6mvQoIiDuSI65Alwm8VpEDU0tmM0niXkTneD7vqWzPToxwnwytsBZQtfiVku069jcXtHXNef37zE5OyOEQNc0rG5vMG3LbD6nmNaoqmTTtNGUTBzGfNSyjmNkUpW8++4Tvnr+gs12jxAZNzdrXr6+IciS84sLpNCjG7jSGVleJjBcIUQUtddSpkA14INDNBue//T/5uXnr3j27AtujeHHm7/Lzi3HAE2IEDUR09p7GHpiZAsMi8/x6Byq0//i+H8/fvg/7fn8twsu38/+/z6Vf+7j+3/YUC8PiZDwf86T/z8c9955jw+yByAEr25e8kc/+T/pjeHx/SdcnFwwm1V469gtb3n5xc+4efOcEBxFmfPkg3f4vT/4axin6NrA5iay7Ftnoi4XBqVVLNxmCnRMVI1paNsdwYOUCmN72mZH1+1p24ZPfvyn7F695rTU/PDDR6jZIyZfvqbeddReUIqhHikIShHqHH06Q1Q5dBY1n1E157Q3hrDvEc5TBUPzxS+RbUNBoL7ziNYfABcAb3tMu8e0BzS+Nz19FxAuAstSqlFKRCpJrksEOcMe4XxyY3Ye0ztMZ+nbFudsZPDgo069FORaMynrKKHio1FPs9vz/NkLsknOgwf3efhwwief/BIfBDLPObt7gfc9N1cv6bdLKuE4XczZ7taxsK4yNsslXbdHolBpT7xe7amKnKANVddirOHi4pzptKZp97y+vBnXHO8ML7/8U6TUlFVNlmVMqoL9dovWit70PHv+gvsPHvL48btY61it19y5uItS0XfAmT6ttRKZGBxaZ4QgcTbQNT373Y7lTQsyoLSIXULGgFBRoqZvOT2dst1usLZD5YoPnnyX9WrJZrPFNR1SJIa5N2gtuXP3LCa9qcAfBHz2+VP6Pso3aK3IlKBrNrHFL8BkWrHdaJr9nt3e4IVGFSUf/fBHTKc1mdYsb1Y0zZ5mt0WEwKMHj7kTBM/yZ1zyOk3Sw7dfUZ1MgMxA3vg62yg+loxRZBhDjVEu/Onn8PK/g7/5NzFNx8pa2qbh5GTBfDqn7zouX7/hgw/f46uvvuTk7JzF6SmXby5p+o5mv4cQ+ODJ+zy7fElnLWhQWYbIBeU0R6kW79qYt3jYN9HIK8sF+QLKOpBXLkq6iFR0ILzV2j34DHjvCWWDugioc0FX7sk6i21agrFoYnwR7IGBatIcIf3c7zuyvCDLYlLd2Q6dyaixraNhTjReFhwzMaeTCWKhyPOMZr+NoSMQGw4khcxRNkpWOeMwvY2xdTgAD0rrEXzzzuB8aqkOYMe7PHSvDfF0umdHt13I2D58bXYI4eg/fMLVnRPe+Xv/C0bE+Lt1gjYRIOxQrAFOssBiUZG5DxB8xF5ayCKLS1jLbLZA7wOPvON+CNzrDNqG2KElJVOVsRaKTd9GyQMJoYgSD8ILlARrJTLT+JFUBJeXDf39GXK+QNYTtl/+EuEMLni8D+RlTbWYk2WaTEWdR4mk2zeo7Y5N2496qTHjiKvsAfSM+YxUsZNsax0746hT23XsQPdxTU2dRkPchDzkNzEbHSZIIueIaKzjvUvPVSn3ScWmAdkdSAsyVk8kIFSUtYPEZExZfJSyO3RJ+QTohpSDDJ0Oo1ChT4AdQ8ZMfL+vLQij/GEaNC5p6A+SFRFvfptccYgLj34QhyK+TzmgPH5uRO/HBwKBsVU8vP0nR/nFQb7v6FXx8msKLZBaRKmAzqKlxibSUMzJIvBJOKRublj/0uKoMpX005O3TBbze5GKDfF5AalA6UGnNn5FUz2JVxnepzHFIEOQSEoidkSOZtveY3NJqwSyAxEcPtPYoBLuMczl1OXC0Ibvj0Bln4p8Hc4pvFOEkEVAUcRiRzQYji0FA/PeuWjYZ4yhM1303DHDe0aGukjyipEQJdO9J5GNwAZxNA5Si/wAnquBoWpHduxYOPCDGVu8EbHQdBRXDuQzGW+MUmocr8PdH+QIhr9lbZQ/CD4x2p2PBmCmR/mAk0T/pWTI7K0lOEUIOUYEakB0MTZzlcVbi5XRBE5JUOQRv5IZDonxYLzDBZ9iPsgnE6pqQl7kqEJjPVxcfMSjJ++xOD/DWcFmNxDuArkWlJVGKk9vtpi+4/TkDnUxQauMaOJbst7AdhvIVODmNvDs1Z7luknInhjkaY+KM56QvGR832O7lq7d0vYbTLCU+Zy81LFIrDKqxQV3HnzAO9/+Ae+8/z2y2QJHoG8a2v2GZnlD6Je0uxv6/ZI8k+RlzunZCcv1htvbNcvlCtK4R8SxWuWauiooq4Isi70OwVtGg8M/4/i1AGO98+y3DbaNyLfEjah/IBwFS6nVI1UvEmM9LgYhxCxJDODroVQh8OAVevoO5en3KM++gzEGfIs3O/CGIBTCbXlUbbiTKc5OH3BRW/JMInJJb3fsr1dsb1Zc39zy5uaW59dXrFc72q6n76OoffCgZB61MHVG8BrrND7EbTLIaIKTZwqtJdYJvLdoFV2/h0k66Ezio6OdFINh1uCwegAoQ+xl4oALisTUiy7ieab4jd/8Ln/wr/2rvPfkHaoi58tXX/Lpz3/GT376Ez7+2c/ZNx2ooeIjQAnyxYRQaXwGWQZVlqOlwodA33WYvmeQdFVSxpZHkbR2QtxEm65Ni07cFGRavGL56XBfR50h0gY1JCMDa+Zom4oyLoIsz5lOIIQdxhgenJ/wnXfvk8mci7v3+NaTJ7z77mPqeY0Xgstlw1eXe35xqWjK+5TTM4TSNPsd01Jz96RiWihUMHHPFMOmNp7kUXX0EMDHKMcDKup7JfA1biJhXDgUQyvCsNEwal4OzOgBSBIwsktFumY2xPZAqTKStCEQAXAfBLvO8fK2pTzTsYUcEmMpIIWmLiRlCUVZ8fx1Q2s9m95Rl1GeYVpkB11f4mcSUiATq9d5H80fwsC2kkeMk3hNdF6kHyXedFjn6Yync4Jl49jsLW3naXtP5yQ2FAkEg6GCHjfdFJt5R5ZLqlIyn2py5Xn5qqHpBQENQhGESxthQT27h9srjKwiw1aEeCdkTh8kt73hFy/33J8LTpUiF5rZYsp+e0spGt57UHDv3/0P+Mk//t+ZqIKLi8d8+3f+MsV8zu1XP6d3hizPOLt7h6qqEVJgO0OW55HRmiq2iohSjIGkCOikO4oUOKmxKmpb+hBbhWQm6J2nbzvy28N4V0LEDURK8jzHBti20dW9c56ZbnGiwxPZFyezmkJLcglFajmLiaXEOYn1sVrrlaaQMo3Zgfkd0HmO0MlozTucMfi+I/Q9wlmKoiSUE5yJDtZd08JmHZ00246+aSknU7L5jJBnGARZXqRgNgY1MSFTSJkjlUbpnHe/PadxCvfqFdttBDRWu56TkFGfPkbl1bhsCCEie5oUxIRAaDqM6cmrKur4OcvrTz/j6ae/5NOXP+bT2z9mK6AJm2T23SXVwgAAIABJREFUNzAMxDB8D6vMCMTGiXRc5Doc4lcfAgKe//7qP2bSGYQUkdUMZImRMOhBKq3TJI3zXScmspACoXSaEiKyFLIMmeVxPiqF1Cq2V4pYNZdKJYfk47asYekaAIbDg8enLYYkRKQEeEAejMWtNvSrTWoFk+PaJ5JAWuYN/7mIzIBP7d/n75qfjcnwcDWG/+92P8A0TyiFpBJJyVwqdF6gixofYuHCh0BVTZBax6q+VKg8p+8aTN9EXSYhEuNx2C+HeRY/pxaKaT6hVhm1LsmE4vL2httui5fRabjOC27WN/TepnUNvIzu7yrT1Ery3ae/4Cu1pKzPqfzjyPQTkqKeMpmfcHJ+n+n8jCAkznvatmd7c0WwW7zvcd6y3je81D+np0VIxaSY8P0PfwPxs4fAxXgfuq5ju9sjhGBWnvK9D76P85Z5NaVb3XD9xc9pthua/Z4gAnfv3WO6OKGaLBBqwq7N+Z8/nPOn98rEdriP7d8jeAO4o+LC1zK/MfERh06G1Ba4X2+xfU8mBT+dlFRKo9oe5Txl1/Fb//AfjQVUhMArRXF2ilAa7wPuzgS69/Gmi+yLgSUnJKIokNUEn5d44DuvJvwgndJ/8/sfcnv3Lv4S+Hvp+vyn/wn7s989sJ2G8Tzuy4c4Io57UuI9MGIOCdHwwR1gBRghaQdDiBH4cTw7LVh3L/isfYNAsPveb6K0Js8KyrLEuodRKkAqZlnGX336JRCZa94H8qKimlRR0sJ6rDXU1ZyzO+ecnp8zPz1F3NywXe/pjUVkM7713R/xVTWh4RAP3bl7h7KqAIF1ht1uz+L0jLquWa1WLJc3zGYzFvMpea5ZXl+htSIQpTSccxRlhrEO19kEGjhub5Zs101sMRUmrU8C23myvEKqDO97rDHorKTrO7QSlGWFNZbJZEbfWawJTKclN9eryHiUMXbLsgwpFFmeMZ1P+N4PvkPfNKzXG5bLNavliq7rmM0XFEWJaffMJhOKoiCvJjx4532+9e0PR6ZWAMpqyqZr0CpnOpmz3myRKhs7Z8Z7T1xbD0PiaL0ewRe+9poBsHl7vUSJA5M2hFGrL+qyRvmn1WrDZFKjZSwWv3j5movzO4CgaxuaZsebN5e8evkGKSWPHj7kyf0nPL39AmMNvpbcbDseLTSouO8HFRKQkrRVvaBv4GbpuLpRbPYanxitI14RlaFwIRpb2ryjfJgR5o5QWILraPY9uBQbEKJEnPGJBZvQB08yD/MIkcUisx3cyyN72obY2YO00ZMKESUN0pHnObvQ0DR7vA9UZXnYnLynMwapHE5FY7D4+LBfgbdJ6/4IKJdy6JqLHWo6y8aun3itDkZSIt2jwPCRAjssOYZKKMDR2R4T+3Uj21YJZtNZ3J+Je/D53Yd8UP0uoTtjpQXdrsUqGWXHAojdjvtacWEDp95R+NiRo4NHE41t86ykEorWW7pgMaaPkitagQu0uybGWf7QZdUhsKYj9A2UBZOTBW5zG80DtWR2OuPi9CR2WFpHMAbrPH3XRsCEpD/q3cjcDMPFOBr3UdMyQofWhTjew7CGxm5IRGIsJsArdrpwyFXSvBmOQb90eLsBwz2s0SHq6cZkK+b3JoyxWLLWSlJTMa8cPDVGAb7jTqUwZo9jZ1PAR8Pv46f4gxlXSIzI8RxG2Hb4n0xjb0itI+gTW5SH/edIvioQzYxQKe4e4kZPCiTTGjKctIhkgBTXDhqmh5NluBjxuo3xl2CUaEtkqCzP8caCTYzZMNyPQ+t+zMtJXSYJNGX4+CKBqwKJjNJPKe4VIQLrwR+dvIgE6WG8igF0RXHQC47XeQSVA6nTLunESkVQmpAXyKSnaoOLhRB/kBrwSZpgvO9pXlvnUcbhtMWaHqlk0vEVqKDQUo+fP8aJpDZ4i/MOaw3G+DHP9y6A9WNMEaRMMpAHUDe8NeQG0/cEmLsIFA8I7kFWLV1JEeP3WKZRRGGZ1LGT9qM4C8UB4E3d0990RDm8SH6LW9pwvUFLGbtLlYpgrBboVJp0waMjABGxIufQQpALgZUKIyU2oZ0q0+i0H1ezUwwiEa4EdVVTVDOKKvmBZBKNZjKdUpZFLOQaidQuSTNGQNmkln7T9uAc5XSCKvLUbSAINmBDkrwkguR95yIxThz0ooeiRyCMcWtwwz4Wx6BEooRGCYmSOTovKaoJJ3cfcn7/IcVkSuctwbTkZUk9qSnLnGldsrmGzfIN280G1+7xQjCdTMmygkk1Ic8ybm83dMlPQgDWRhA+kvYytM5j/j7KV37z8WsBxgYfcF2HN3Z0kBMDyDU8Z/xXYH3U9xlaxuNv0nIfEpQVOLSfIRCiZnLyLfLZO5CdYE2HDB7nTTSzCJaZ2vCgbrkAqjbD2D3bxtB7T5t0DNdXK5brLcvNjuvtnt44XBCAQpIlx26NkJogFUJmEDJEiBNPSkGWwWxSUuQZr6+X6fXJDCpN7gNLNi4io/aMH67N21W6kJ4LUT9PICjynPl8xjvvPOZf/pd+i29/8B6TSclmu+Kr51/xk5/9lE8/f8rV7W0EuZOZEkKAFohCI/LY5pxnkd0YNY6iwcP/w92b/FqWZWmdv92dc27zWrP3zMzb8PCIjCYzK4OmkkygIBEjCpCqGBVKFTMmgEBiwB+AVEJCTGDCgBlIICWgLKmgpEI5ysqkKUQom4iMzj3czd3Mza157W1Os7sarH3Ovc/dq0iqKJSqIzd/777bnWafvdf61re+LxVdKaOKBlkBk6eFAEVMIwWfvZ9j9bAczx74ynQcXwx0yNM71mxdOc5fP2PoB86OD3hwcsh8vuC1117n4cMHHB8foo3i4nbLk4uWJ1eZ63SEO7wvjGQyTsPpQc1BY6gN0qpTkjE5jEmwawfEFtBUdnUEXLPo4k5rdAnu2GlS7u9/yty5hlMyofYTA1l0U8oMwXPbBqxrWCwaZrWwXp3WzGtL6zOX64HjRnPcaBqrSxuXBA5WQ1Mp6say3VjaQSYybTUqZWmbcpBnTnTvio4WE7iyMyGgVILGo5pkFdTodq8YesW6jWz6yLqH2x62XcR7aRkdhcaL4CAg7XgpiYTkcmHQWRFixOlEbRT3jxyblSYT6EOEVFqxMKAdyRziQxJTPl2VyGgMvKSyd7EdsLo4oOpEM1fSFjlsaYxiubjHkauZqZoZmti2rMs1WcyXnD94wGK5xFUVOYu2njYCVveDJ3mPc0oMdwo7ZTKDUlrMXrTFx1y0k/J0zdvSvjnrPt/SEFOi854+BHJODDEQU6KtB4wptkfG4Oc1vbFsYuIwBGoyuSzMKSuyLtIPk1j/eE3LlTMGoyRoSSmgUSTvSX5A5YxbzoUt07ZkMjEhzqxdTwwBbS1uPkNVNVg5B9aV66C1JNamwrgaZSuUEaf6ma04X/f0IbPZbiB7tm3Lat2x7QKnyyUhxgngzqmAhkmS49QNaJIYWoQt6+sLnn7wHu99+tt8dPsDXvhPUPNG5p4kJ3zXdlbmp8yUYExR6rj67K03/7Htw+HfUg8tSmu60KO1xqXRvTSJRIWy5faWhMNV0jGhS3uvMtLelbUU9pSzpWtBC1hOAaa1MBm8jTuNLD6/o+qzE2p5eCdpEo0KCZxCIPQ3rK9eoFMqOuCFzVMCxCZnsj0EFKv0jA/D+9PHT8XC8jM+e4Gq36F+/S0OlcYphVEWm2Y4lsUdd2QpzKjsfHceMnR5S1I92USZZ3Umm9J2VnTmxYhHJIDU/JiUNMYtaGzNrL3iefcCn0HjyFT0XNHGXpJVpBhRPX+JTRW1uwdPH9OnHiqwdsn89D62aWgWM+bLGc2Rw84lcVQxYtuBnG7Br1B5kIq42+IXnzKYFmUczeKE5utRgMbr3eXIKZLSgMJgtWOuLf3QsXn1jNWrFwzdhpzB2ZrFyTkn9x4yWxxiqzkhWrbbnidLx/ce7hut/T8zdfui7eIzj+0wsJk1nD99ittj8t/ZFs3v+vMfVbtw9L2zA169dkrNEa+Xv8VvfpPw9T/+n7bTv4ttXH3CFzwXgOH6MTdXH+JWz/5vP+fKB1brDcv5vMRCiaquUSrRRymepZyoZ3NCUrR9YO4Tfdsy9AMZjauXuIM5xgqDXCvFfLFktlhgCxOvns1w9YzZ4pDFYk7bddzc3ADgnEWpmk3XU1W1yG+FSNcPaCtFHB0yrnIMQ6AfWoL3FHtmySFLT+Z8MRdALErxLhZSgMQjsN101HUlWpvGsJjPscagVCgARqJyNVRQ1RXz+Yzj4wNCU+HG2CQVoCd5wpAJvqeuaw6Pjzk4PuXh629QVxVtN5T1PhL6jqFrUTkIQL7dkl1NUPFORvNZ/tuYP4ymP2pvbmeCvyR2nlqTx9cyvkGCWJWS6MgqyMfHxPNzOnq0koJpznB7s2JRi7xRSoG+3fLsk2e8fHElnWe64vDkgCpVhNjjdWTtMp3PNE5ioRFQ0UpCGa0VMVpu15mblSGEGtzumPaD7aQSyQXUSUSfaFKVxPBu8KIzWjCDmKMAeTGJcW+RJSAh8X6UMxB9Iqm0F8iqQrQQsIZMMaTaSSwJu0uMxMZOGwqwlmMSTFAplI5EBTbZUlAUXmaOMhbHi2CcY2Ix5sKULW25u8u9X3Riyjfk10yfIxsdUGTqHKXDsuhmCnw50PmelBPVJnH6ceb1g5/mhLfw3uHNmoW19FrICI7EMgbuYzkiM88Jm6MAdmRMzlgyVRZ2fK00fdZsYhbjsEKA6NuBwSdMHGXMyu77jtytUc7SzJf42GOdY2EdX3rzdR7dP8NoTfCebrPl+vaWrm3lEqYs62Q59jyO9c+uzTGRsuRxko/uWvlTSmMv2h4OJzFrkU3diyz2QMm9h3oCFPfvxfKBI+vkC4q48vq0kyDc3Y27HHk8nL3wJiMAmIC3uzh3BB/HfHT8nPH8jGNtB6LmaV92D9P+UNthEJk7esnTSxSMxc47oAa7903fsbefcnrUZ16ryufJTqe8MwbeJ1TEmIh57wvG+yCP+eeuKKkoBQ5GFdS8J/033msjUz3tgLDCAk5R5ntdQHOtTZEuLCd5T+YlZym47zoQVIlpDTplUgESR6xj1D5OMaLuYB+lQFT2MY2yBzGKAV6RwhMi0i5HneaF6fKN43V3buSXAv4jcSYpCcg7nrcyaEbgdXdv5SkGH8/7dDzl3wiki/a9nPFRwmEa0mpXcNjv3Bh/Tuka47XQ5BwZSV7lqrJLYuQ8m7y3po3HO4KxKWLTqBetiAXLsNZKV0Q9o1ocMEuZHGXtdVWNcY38s04Y1Eq08G1liTmikiJGJXlVzgw+0XYd3aYl9EJUaQ6Osc0CZSsh9mkIcSx4KEIfCIMYy6u987O7j8s1QbjUo26vXAIjjH6kWOCco5nNmS0PaRZLlDEMwzBdg1FOE6Vp25bV6pbV6obktyhjsdbRNOK1IlfCsl6vaLstY1ds3w9FH91Chrpy5DsGhp/ffk+AseQEw4AKSabNpJGGi1ETRRb9UVPDJ3GSZLoxIYvdFGOGmhE9SI3Gaoepzjk+/yZh8Yg+WVK/wqIYciaEAR1uuXew4rxqWfott+sb3v/4AzbbvpgJ9by8vKJdd6SsBXQyFXVzQmWcJMTIALC2Am2LqYxCKdGJHS9DpSNHiyMW8xlPnl8BGk8mqCAVB8bFgGni0UWvYdQ8yaPgvYzMXdUYGajW1dw7OebL77zNH/75n+UP/OzPgIGbm2s+fvIh3/vh9/iN7/02V9dXDDGirWVkJiqjUJVBOXC1pWoqZrWj0o7WS1vdMHi5uTVYJa3stuzHtOSXql0aJ5y9VVPtT7qK6QbbGxS7yXF8XdnGxUYrxax2/NxPfVlMCmJGK8f5/XPeeedLnJwcYJ049H749IIPXmZeDnPywSPmy0O6bYtVcHIw4+HxjEpFYT1QEhA/FOBIwPIR1BNgb1rep/hA64wzO8bqLlbYX9jG5Z2pcr0vXr8fJMg7LRhFSp7Oe55e3KJd4JGStnenwRm4d1ATsuLJVc/HFz3mfIaxAv7nKMIdJsv4WFSKByeOy1UmBIWzUklUATCKZV3aS6I4ECpE8FtRDBtG1fwxQFHlmEurd8wZHxPXreLFledm41n3kHSDiKIm0Gl688hmMzlR1xrvoXKKs/uOhVO8erli6D1+65nfP+bekQU8l7dbcugx5pBIQ8SxZU6qLEmJ6dcUqZQ2KZUUQ4Tnq552CPgobZnb2zWpX0McSK+e0b56RvCWeHnD+mpN/aW3WJwe8OD8ASeLTNU0aGvofWTbtaCljXaz7Ri6ntnMMUNRVRXWWTHPAYxxOFfjXFM0DMcAUMb0etvRe89h3IEYGWmv8dHTDd1UhEqAU5bBJrySOdE0Dne0JCnFZtty2/c0LFHaoqwkG8o2aKvRzk1Bbp5azMrIyxQtNHAjWFeGunYV1aEhWyuJkKvIypCUQVeOet7gFgtUNUfZCm0rjG3Q1mFchXUOYxuMq8HYSUzeaMNrb2tCgufPnxK7gXaz5fLlS549+ZiTk3MJOEZ2Wy7V6sGTvUcNnno5Iwwdt69e8PEPf4f3fvybfO/633DpXxCM5mS5IK7XBD8GpXxmG+/nkXlREs5dzPa72lRl8F1AZYVrHM6a6R5XSsZA1obimoF2FlOLzqU2hqqaYaqqJIqJbIQJSy5KYXkXdIlj666lcryOY9Cox2MpwfBeBVPWmV2mItVcRWnlsdiDTHt5S+r7YiA1phQ7OYfPHfte8LsLIEG//x5cX+NP7+ObhcyrJaHOvkfbkhWlTLtZlXbVRPaKze0aHwfRGrSGkDPOGNEGpbTOoaSwpKUA4hYVw21HHz0zK4Z3+uolMSeGHPF9h3MVqe/QQyQpkYc5/t4HnNw03KsP6NMjlofHNIsDFkenvP6Vn+Dw5BxrZyhl6XyUAkws5gJ+QIUtiiCGAcawqGse3jvD1x5lK+YHpyxPzmjrzyrfelTuUVi621s2Lz7h6tUzLl8+IfoVZ4/e4uT8DU7O3+Lo/tvE5OgHT9sHjIoQNpCPfncD9D/DFqqK7/zcz/Gzv/IrHF5dYfZ0rv//tIXjt0n1IWZ7gYrDFw15QBKzq8sLZnVFXTVYrQmmYrte0263dF2HqSrcbMbl9Q1X1ytyylw8f0bMiWZ+xPHhfYKumQAHrTk6PhWTriwR8Wy+oJn3uFqSF6UsWjnpyiBjrOHk5EQ6aExHSrBet1gnJmLaQl3P6LortMkok2R9iE5YTiUGms9momkZBlL0dK0AvCmJxnkMgdpKPGiMoakrnLEo+kmXz1pH3dQi44Nis16JFqCG4+Mlh4cHeD+w3W7ZbltC8CwPljx89IjT++csj45oVyvWm45h8MTgCf2KOKzFAClnrm9vwTkG08EXYf9j4Vwu0l6cuUtp93GSz4K4IxFCjeiSKmDsr/6qrCFf/zocHhFzxTa3omWYEjlGPnn6lPunxzhr6VYbXjy/xntQytB3nq/Nv4ZLNbrv6PqB9bHmpkvUrkgM+CgxtmFiVQ2x4uY2c7t2ZD1jZMzl8TiLsHKqPHkRmb3mSM1ATOL2HAcpYlNYr8kXZluiuHRD8hHpsJNcI8Uo+ZUqkiD1DlRVBbxQeSzg3m29FbBVUdUVTV1L7FsYWSEn8h4K4ZCCYFahgF55yrOVNlR1JV2BKU2s2Tj4ome7k51QY1wzgVplvU+JkKFVAQvMc8IHTy7Mz4wYnrV9T9j2HD2PvPvtyJfcH8a3PTn0NMpwUldsCxhZKcX9HDgLAwcxUaeESgmdM6OEKikTcxC9cq0JuqZSllYFtBHwtd/0tCnS7IGxxoDxHXlzDSlSHZ+iOMGpzPFsxh/82tc5v38fYw0heK4ur3n/w8dcX4kMUywA2sjo243su2N8BNWj1uyXc2OJS+0YcyhVmKaFpziCIiXWkN/Vne9QI3CV8tT8tit26N0r90KR/d9TAYzGbrzdfXr3tfuPySOLUSC1O4y0vftYfhslDWRMajXKk+wHfUrG+P4O7u24mBKPqG7J9e/ktXkCUe/OL7n8V3qvSi54hwmZxzM2ZpIj9JHKNRIypy/XyodACAm/DwqOx1n2V3xYxlhOTURprShxZpqAYKVGRql8vlIK52zBS1NhVcfCKjcYVwo6e9d1girzyNBVhcuzY36OrODMOA/l6ZoE7ycDr5xEX9aYkeBSWNUxEGLAKCF8hJRwKU3M6pG5K5rNBh1FP1TCllSOjd11nM71XjFj2v+7g3AfMP3s9RvBz90xjhq45armJPtcrtWOEbv7B9yZV6fu6fI1umigpzL25a6HnNWUKyptMBkoYKUp8xIpoWMEHzB+QNlA0oZgrMiCFjC2qme4FJlFSldkLvhILX4dykiHp9E4Z8WDJHtMNmQUMUEKicEnbq/WbFcr4tCilGFxdI6bH6Fdg3OGulIwyPjWWtF3njQIWbMgEdO8AgibW1uUEXIPaEJKxKzISuShcrkHK2uYz2rqpin62xnfd6joGfpe1hIyQ9/y/NnHXF48Z7u6JiePrRoWc4OzltpVnDf3qNyMi8uKi0vESDMl+q4X/f3g6euK+aymqhyj2eQXbb9HwFhQXuMw1LqWCcLI5EiK+JRBJwkkYiCqjI8Do4uyU46YFSnLhGC1ozZwuFgynx3SzM+J5z9POPwa62jJ3VocQNFENxcAtL0gPP0Rv3HzYzaXn/Ly+XOeXd8ibnoKbRzLwzMW95bMZkuqqqHvIzEjRhrBE4lknUi6ltZRrafJBpC2n+Tpk+bjT2/I8RWYptw8ufyMcuOk0iIcwoj/TVUZVdCvDBMtm0mXVdiiX//GN/jj/83P89M/+XW+9PbrfPLyEz7+4CMef/Qh3//B7/Cv/92/Zus7qAx144hDFD0RJcDA/GRBc++IqqlF2D8nBh8YYiAUcMtWDqfFxb1yZShNIAGl21wm/LQHHuvKYkIkGDV2pE+vk4+YZjj5mDuthWVSS4kH9w75fV95AwBrHLZ2HBwc8Qd+/89w/+wUrTKbbc/jT6747hNP1zyiOj2jWSy5vbzgaD7j9GDOw+MGiyeTSpum/DTFFVnlWFxBDbumDu7sIyDM2NEzfGxLYBfk3Q2ERskCabUV8oEYreQRzMjCzFFZoW3FfGZZzHqerTzDxZaV17x1f06dPSdzTe1qaqt5/+WG8ALOD2teO65wCEunHxQhaoagUElxOCumYMghJVOOrCxO4zGMccad3YdpcUMpctHjut54rtYDz68HblaBmA2ZpoB+47kbF7OI1ZGq0swbxYPDimUD61axbgM3L65595vnnC9PuF11fPpqxZNnG2aLmsVc0bUtnb+F0IM5ALWkx6GopCqlRDM3K0TLZ2wfURpTHTAw8Hy9ZUgbTkxN312wufiE3G/5+T/yLr0/IsQDFssz4r17mEYx9FesbyLzpsHHBFpxcLBAW9GwHmIkZI1SDdfXa5zrqWtHUxsWc0fdWI5OTzh//as8eO2neH6xpU1PeXW9lqpxloXV2X0TjEhfjGxk5JQ2dww/c/TfFx9ced/J6X0Ojs+oNVCteLF6ivEdh4sjjJ0R2g25qnHNHDUXvTHlZqQ4kKOIuKfOi9NoMdHx0VMpyxAVfdtxMVygFwvqxaGwgGImG8fByRvUiyXN4QGmbjBW9Ia0rVDajMXuEpAoQolIxsJSipGDg1MePHyLR6+/w4fvfQcIXF29IP8o8ejNt1kcnAIGcgnKui15GNBkXONo1zc8/sF3+PTJh3z64jG/fvNP8TqTnFQlry+vSkujYl/bbrqHze5+HQ0FpdAugbjMCbIZq8Vx8wu22dJiVI22Fm0csoYYkZMxhmq+QBc5CFXuoRBC0ffNRKMwZAKQlcIWsNEYCVxjCPvQ+Z3vHgP18UHeC0aVEvB2upEzwoiCXRtjTISYRRvTOQ4fPqS9usJvNlOgN+Yzn8npAEqAG6c5IqaEUlqmgOtL8j//J2z+h/+RbGsqpTAqkXPAUe8BvZnV7XVpl5f5v6orrJLmrpjkPGnnxDRuueDq5SUpJeracXR0yPmDhzz+wYdc+y1Rwfn8iJmt2caOIXiwhsVsxtmv/Vtm71/j1E+J4Yz9SUxTYZqG80dv8uY7X+Pk3jmL5THZQLv1+HaA2E7rnSmGl1FnIIBO5e+GeVWxuHeGryNDtjSLYy5fXZA2DjiYztvLJ+/zo9/4DsNmTbu9BcSs5ehkwRtf+UOcPHwXWy1J2bLdZDQBYoB2xYtPP+D61YdsvvYLwOkXjsn/r7b/40/+Sd79znf4yne/+1/0e/9Lbqk5Zv3N/47l7/zPqPhZlzfZYox8/7d/k+72gjffep3X33hEZkbf9RweHXNyqlHGcPHqJQ/OT7HWopSwAx88eIB1Feubl1xc3uK/9ACWc1JMvHzxkjfeWnB8ckrd1Nzervj46QWfvrzEGkUaOowxdJ2nbgKHhwfowgwKvhetzmh55923ydxwc7Piou2lQLKooZmj7Qw1eNLQkhDfht4PxPUalXqMRti1RmFchcmKdnvD0HXMFzNms4a+bzFiqcwwRK6vblndbnj42gPu3TthuViwWa/p2o6mqZnP5yilaepT+r5ntVrz5OmnPHz0AGcVXbtGKUdTzamMpppXgGNzfSvdLzESY+b87Iyu72ntLp35XFvnWPzfA1MKFjA+TZKKeYnfPvt2jXH6buvpKFL6ve/Bxx/Dn//zRB/psidF6eyJ0fP4o6fEEAV8MA0pi0nTpvV897d+BBkxrQQqZ3l6GdBZYw4qiInZDJSRxDdR86PHkQ+eOF7dVmAqtEos5w1Ki6FuO6yxp5n6GMyhIugtYdMVDWWZvXMIpJBQIaPKciDHXboitCJ4MaBJQQq9KaSp2CXrSOnYU0yu9qMhz7ht2hZlDIfLU3zfyrydkuxLlq4snSW9VhSWbfmbxaCpCF0oTLiCuhVJAZRIHQ39QI65yPWMOqMFFBkvegFGx2HRh4AD2hjYBC9twWM8kDNZK975tx1xLYWFpx9/gu/1MsDhAAAgAElEQVQHfNczdC1DL1rWR67hzM54DcVhCtgCaJNBp1zMBuVjbZLaq8uJqMQPpTKWpCHZjPeBtvk1bPwD1NLowflhwyZtGWLHsJKOrlzPaWZzDo4Ocdaw3W4kT/YDt7crnjx5wstnL1hfrECwlnEUf35g723CWoxyH+gdKDfKKI3ncJQLGZlo5J1W8RgbCIgyGsfm0k5f4hKlpsJuSrEA/KaQd+TNdwmh+92GI7D1BXXgPbBrjGXuSDPdAVfLl+zhxmoEsrJ0rCmFaNwqdknQmPvs3va5c5iyeNiMucYEPxdQVxfT55x2DNt9os6dzxMFVkZjugn8JQPiBJ8L6Yso/iYp7szEpON2glqnwtL+l4kRnp6AdbJm9NJSGonvEd8UtMaY0cxPzoI1IksghLm93F3JZxttMMZMGqgpi9RJGHoCERUFME9pbOUXaYCEEC9CjGJi7Dtsu5E81ULTNML6LniAksYJtBXQOpV8Q5WCxAikam2Knrova3CRVIr7c1fBHkK6c1HGazgadst5UROrcn/u2zsNU04xflhOYxt9kYsQcGh632g8Np63CZAtGNAOjC3HH2Mh8JUuXW0J1tE5R/aiW62dphoEoK7TKLOTRDYyRKxP6MGj7ABoMUc2ihTFzM8aReMsVBU+KxIRZ0eiiXRYjGdu261xqwuoKo7vnzBvZvI6FFkZbi97UughZ6rFEfXhOdnO8QmcEm10AdvBWVg93+K9mFSXFtwJMTLKUFcz9NF9rHForei6FfbFjLo7kGMJEa00RmlqV3EwW1BXgr2FoSfGRBinhxQJvmN1fcGLx9+nbW/IOeKaGls5jJP9GqeTo5MZ1ew+RydLfB/o+55QsMoh9HT9lq67RWsI4f+ig4zfI2BsU9X8sW/9LIfzOQdNXZg5QlfWSpega3djrrct234lJgnaUquKpDPt9prYb1Ghp+82HJ+ckapTNuacJ/orXKeGrDWmMmidaLc9Q7ulu3xK/6N/w8XL3yT7NSn0RYtoCSSMrXHVgmZ5hjVzCTaDIhZgwdoarS3e92iT0UbaSTNI8HZnipXmFRFpt8isl3cL0P4CwVgVyeOjUtEaqzPCdIwkdI4sFjMePnzAH/35P8zP/uzPcXi4QKvEBx++x/ff/x7f/d73efz4MR89/ZhtGLDLGcpIC3yKW4yxmFlFdbjg4LUz1KxCoydQOPpA13f4IPpDjkxdWayWloWUkphMjdWdaTFK00RRJBIFEDOGfrUlg5g5uPJeCoCtx4XjrtbGTrdlvCGFen52ds6X3n6bk5NDYuxZbXteXbd8/+ktfvY2zfIeyjV0mzXLecP5ccPRTGPoS8vUWPlKUPSKMuOxaCa5gvLdssDKguM0WA2KVKp6iRQGYGQsjFXGUf8ll3Mmc7IsHHKekpYq/yiJEEtRIqfAvaXosly3keeXt/Te8+6DBZWGudO8da/B58yr24FnV1vazvPa8YymEn2rHBNXm4gxcDC3LJrC6E5KpAOygLK5VBRln4XxLBCJmiq+aE3IMPjETSsA7KpNdD7TJ0VU1V7ApmQc5ARqrAwKmHt04Dg7dpzNxVfmZK65bQM/WA+8vG6xWtOHTLYVL1YZ1j0hBnzUOCcaZNaCqRTzeU1jDcYoQkxcXHWsOnaBj3KyAAJJWbxueL7aMFSWZX2Pw3PD6sVjXlxf0tQRVytae87x/ft07RV939N3PVrXwho2iEi3ChinaWaOZCMYmfxlLCVmixnvfu0tTk7OWR48YHb4Nudf+hoHzz5Fz95n6z21MRjrsNpQ7SWWEoztV/enFX4C+zWKyjW8+fbXuP/6a5jo8bfXxJB59fIanSIHxZjFuVrm12rO4fE5D15/Hb9d065u2dxc444amqMZvhvYXt+StluqxnFwz4i+62yBPTxCVaUjQBVpFmPBaJFEUAqUISpFRKGTEkMQ5N4vdeQpMB7viRBFi+j46JjKVaJPFwY2qys+/uA9vvKNb+FcJQH+4MWAxGrIkc3VKz74/nf49PkTnlz9kB/e/huCoUSURc4AGXe5nFlJIjTGCBBrnUFbK3PcmEyRqOc1xloWZsdm1MZgqy9eQpvTY0zjMM7hqpohSJvTyBLKSuOFSlSq/TumqVKiCZ6in4L0UNjTaa9QM64T0/qSRbtbAj89MSdImayzGLppzTB2V5SVZRxWWoFWdrzL5e9aoeY11i9IOeE3Kyp21Zl96QNpAbLFrM5KgBMjkwxNRhCPDPl/+1/p/+s/RHrtTZoS5IcsBhIokcwZkzjRKhNHVwG3LcZZBu/JQ6BqYHaw5MGjR/z4vffYrjeEGFgeHfPVD95DfXqNbuH1+hT/8WNu+iO6fEyuHAvtcTdfwRxkVHPEyWuPWBydMD9YMj84oFkcoG2DQtNutiK7szdux0RNKchKOCbG3D0vCk1dO2azikxFJtHfvILu8M6Y8e0loX1O7RQP332Tw5PXsPUxmCV6dgg4fB/IaYB+YH27Yn37is3qJUP7Ep23KL4YKPxP3r79bfiLf1F+/zt/B/7En7j7/D/7Z/C3/pb8/k//KU++8hXWx8d869d+Df7e34P1+u7r/9yfg2984z/Pvv1utpzhz/5ZePYMvvlN+Ef/aPfcr/86/NW/unv8p/80/M2/uXv8D/8h/N2/u3v81/4a/IW/ACmz/Yv/E/VyizuxYC389b8ugvrIfXt4dIj3ntuba5raYF2DqyqU1qQYWd1eM6sqnHNkYLvdcnr/PlUzQzTGMpqeMeYzRvPw9UccHS6Z1RalE9631Fazur1lu16zvrkk50iIGW1rFsf32axuOD6a01QGqzKb2xXBBypnODxoGLxm8Albz6maA5rFIcPlFVn1oA3WOMLQo5JHK2G7eO+Zu0Y0KEPCD6GwVgLQs1jOqesZxnbUswX3H77J0G3puoGbmxuMErCxPjzAFI3X9XrL48dP2W624uptRb7HZilMa+fAKl49ecLQbams5uhowfXtLdY55ssDVMx88OFjNg/WsK/QMYbdirvMPSVz/WfBnInYtg/0KLX7qPLEyNYcn1dAblv45V+WKe6nf5r0Uz+F1rI26NqgrZjH5RQ5PjllMV/gKtHwvbm5JbYe5S2r54FPukwVDI0ynB4IyaTtYdvCJy8iP/ywZtUuCKkuMVlPP7SgDJ5Imm/QJ4o8zwSd8H7AD37a5eSlm8SUBUArBYW1JAZelG6K3TyWROSxtEAJMJuVaBKrKTTWhUSyy3fW2y0pwEHtiNkzBNGCzBlCFD3jnEsrsTJ4FTHOFHZVJtiAMpro49QVqEbnBZVxlS1u1jsgjwKqT9eeogu6d10jiY7ACs9aR2ZBkcRiBZUzj+pf4EKd0iGx49MffyjkHxAmW06cNTPOsNxHcZyTdGJmATBVzujE1Na/Y0TKb4aMU5mkFQFhKFs0rhggT0O45L8+JmLShHaDU8KU9lvNs0+fcO/0CN8NXF3d8uFHn/LRh09Y324YhTD3Gsb5AgjzzmvIGZ+DxGjlfIYSB42xglUKX87TWLhQRlrmxzcZrckxMpptjYiwKiZd7DGiR++JqViidsIC8p3qc7stf5r63+8cyZRt5fLZe4/Z/1likl1rd8aMPiEFwNzBY7LfSgkYzZ6J0521vgCbmlykyTS6kHim47gDqEpqNLLZd8ejiscKjPrIOWdCGrspRRtVJTXFlankzikXIldK5BJDjnez1kYkT6ZYVGOs2TuCAlyiICeiL6Cf3uWwQWlSEqM9U/J2a6oSAzGBg/s5L5ScsvzVGA3OleuiSnPgQPRBpCNBjqt8lk+RzTBAuyEbqJuqnHm5t32IZJ0xMRNDQumIsaINm/ckLuS8yLnRyog2MlHGnFaAm+b/jCKZopGdi+SH2rGLd4OIKX+BYjZfboVxPRnn2azNDkRVoXQdlI7iqchXDLmsIYYynkwBMpHxOUotjwwXXcyQ924qotFQOXKqiTlQxxobuknSIRTd7+wjyXtsTjgMDpEQikpPGNw4lslCQiGLmbgxuhBU0njxIUNlNFZFQn/D7auB9qZ0sTnL/GDOdnWD73spxs4OWcyX2GLcCIq+F5ayRaaOtu9JOZbUVxUeTZ7mDKPEtHo2n6PUKZnAMAzcP7tku7rk6tWnbLstyhq0M9SVwxWg2ateSA0JkeDsN7TbW64vn7He3pBzKB5QFmulaJT1OM4ljzLWMp/PyDXE0JCSsMVD7KXo4IUpuxs3n99+T4Cxi6bhp7/8LjNnaawS2rSxmAJKpSL8PNK/u96z7VZYa7HG4bSlDxHf3jK0twyba66uNa45ZmPP6fRrtPGALiRxgiMzxMwmRobVNf7iKf2rx/i1IOCQ0VlMPqy12GqOaw5BSfVZIaLJxihSCMV5UOGDL9XbEagbg7YRWJOBNOrYoKVbOyET8RRDjGYklCrk+JETaDFOclJdbZzj9QdnvPn2G7zz5Xf4/b/vW5zdP+L65pLLi5d8+ukTfut7v8WPP/qYy+trqTDNa0xpNVIxkSqHrgxmOccdLbBNLXlzlDYBPwzMmoZ+6BjVxrXaM/yaqo27wZah6I9Mp0T+LisaprKTXNC4iYbYyOSSBP0OKxMBwB/eO+TBycH0uqOjYx6eP+DRw0dYa+n6noubLZ9ctNymGbY+JCmNigMmBc6OFhzUIhnBKP6/t1qPj/LEWgZd2E4jICnavqZU/0ajq1wWclGhE9kGiVaFWRsJXljdVV0V10hZUCWV12w6cTGuK0dtpd0+k8nKMGtmnFSaPg60m8CrdWDZeE4XjpmThfTewhJDYjskNkPi5apnXhusHqugRctrDChGUCenO9dvGnjlT3oPWE5kke/oIusucr2N3GwTfYCYSjuN0tPnaQ1NrVjODWGIbLaZ3kvrS9dFNlvFUWWZN4aYZFzXs4rnl2KOEmJi02faAZHR0BWmPkAFRepbjAlUJnE0NzhtipQHxVQu7x2nBP0hpiK9YEm54tonsgOsYnbco4YtcdhCyBga2s2D4twZCSGRc2ndT0mcuXPCGI2zWsyhchbn49pxcDjn4RsPuffwjLqao51ogbp6hrECaILCWCfBkt7NF+ONNGpdyb2kqNWC0+otxlYjpTTGOBbLI+r5IVZnXFUTtGbbDmyI6KHDVlXR/hTx/ZDBVAtyyFjncbbn+Owh83szum2PdkvMyIjJGaU01fIAZgvSZKSjMcaWxGe689mBxuMaOzqxljmNXQACkFNk8D3D0KHIzOcLNutNKQYNvHr+CW+/8zWcKvpSKeOsI4aObn3Ny48+4PmnT/jw6rs8277PTbwkKbvTRpr2aze+M5m6thwfLzhYNlRGs+o8t22L96HM9RIYGSuB67iZSox8vmjT87kY9hkrWkHs0Y+UkpbiyYxinHF21d79az3di4zHcTcBgF3SZwv7IOeMGLnmUt8rBaK4S7ymwFiLrt94jka+RkQ6T7IC1ThsbIhDSxo8alzTPjM3ZyCmKIEuZd6fxrKscxnIlxfE936IDhH/zlelqJgkGdYlcNVGMzJSxM9BwHoVvARHRroIeu+5ub1lNl9w7+qa2bNPaduWdHFJfXWJugZuZlBZlreHxK7C5Eyu4fBgxuHDc5r5gvrggOX9+7imxljRfx9BtJxK22yZR6bURO/GtFxIYTvs2jFHsCMQB8/Qbxh6z+3tmvn69E5b9Xy54PT+GU014+TeG1SzU9AzfDSkkOn7Nb5v8f0W367xQ0u/vcV3V3TbVzgHOQd4/Bh+6ZfuXpi6hr/yV/a09/4j23otgCzA9fXnn3/5cvd819HPZlydnfHBN74Bf+bPcO/DDzn84AP49/9eXtO2v7vv/X+7/bt/B7/6q/L7r/+67Pv+Mf+LfwG//MvwW78l5+OXfxn+5b+E83P4y39ZQNtf+iV4/30Bo//BP9idy1/8RdIPH+P/2z8Cbxzh/vd/Kfflt78twOxP/ASoxLZd024cQ7dEIe17wQ90bcur58959OgBSimCH9isbnn7nbdBaUIIVPVOogBAacPh6X1JAlSCkPBdS/AD282K1e0tfduijeb2ds3iZsPJWSImGZPOGarKsrru6bZbtNUsFw2bbShGJxHvPS5mlss5q9gRPChjiTmjR+OUBCnEogkrBhxd32OKDroNEEKmaWqsdbhqxuGx5eb6kuhb/JDxPuKswfeBbezph8D1zQ03t2uCF03Rs3v3mB0IWDmfz1ksD7m+eMnq5gLiwPz4gMW8JiUxDYsxYEzF54LEO9sXw1D7sadMUyWum4K//ffKPLRjsElsNH1ESvDqlTz33nsErWl/3++naZrCxAJtLK5qODiYUTc1KUdmzuHsMX5Y0vc9N6trNJb1NvHsxcB65VEKvDdsOs2LS83NZk7IFVlZRumvwXfgFLnOuBOFW2qyTQQS3os79kQV8wkdyzHnAgQVyaTREFEZw+RPMQ1GOTdj10NOceoaSbnEAAjDbNxCiPSdGM4pnRn8wLjOpXGtKZPpuAZqY8i6FBCVMNxQihQiORRgaVxXCqA0rhP7fhK5IHyfbemd9i0nuhRYJ8+R+SoacT4z2lKb+2i1606KvSeXuNQqWBjNuXHct5ZDrTBh5wCvydg9cGYabyXmgSyFO1XAP5LoYaK52vRoHxlLvluvaIO0oeecaCrpsJrNHE1lubm6JMeBvhu4ul7x8uKK7aYnhlF39+5xf659On/mpFA6gkbm31i4zbnkKON7y72RdwNDlfg6kycgmCnGKXdfGuOcHZilcwFfi8Sd2r+25ctUAWF2x7KfZ2ZGUPWLjufu30q8WeQO1JR07wC4/eJxno51dxT742+cU1LBJ+7Ga3p6rbRRF+CufKeexuvunKY7+f1IQpIxE2MkTHOTsKuzT0QUIQvbux88IQTRwE+paHuWfVcaZVKR5CgVlOkc745z7NKd8vW8O0fjNQ3FJAwKyJhykQwonW/pbmy7GxvyXSmPJt4jzmGw2khnsVJ7XieJlCMxBnzKpTAR6WOYWr4nSYORBBUjIYznXXJdXYhUuTDzJykAitTBdO31RPQaDzmV+XGM8/SI8eTpbN2Jx+/I4Eznbu++G883SoDiTCnys3ccuRhCSZFIT0DwToJA1mWROVCfkaSQcaaJVorGylqclVxkzAliLrIMWche5LjT5AVy0RHWqmj6GoNz1WTAJoW4ov895qhZxq21jso6KmMwKZN8EBzJR0II3Fxd0rVblILF8oCqFvJlET/ZSUYgMnGbdkuMvuyjgpKXTQNKyXWKIRJ8xPsM2mGrBlfVomOsISvRLB78QLtZk7NB2xqUIcZE325oN9e022s2qwtSklxDa8n1+6EnxrDTWI77Y10Aa1s5lLJAIifHMFh8bxiGcRx+8fZ7Aoyd1TVv3jslhYHkO3wUDbZQgDbB7kTvyjjDrG6Y1xnrnASHKNabnmwW9DpwM6zIWbHqG67SIS/sPW6CoRsG0bPMsA6J9dARrz8lvfoINi8xWthyZKG8oxzOHVA1B9h6ST9AXRV3vQKi+RgKRV0SNz1OOnlsv92bzNUoeD9OXHa6GVQxMVJZLvooNjQGW0ZL9SiOguQl0J7VjvOTQ/7gf/XTfOMnf5K33nmbo9NTPn3+Ke+//yM++vgxHz99zHff+x7X6w1ZKdyspqqt6DUlabW2TYVe1LijBdVSXOJzjOQYiV6qDCdHR2w2IwCrMdrugNicJgMIRsCFXfVv/0RkBcoabOWkdTeVhaecN9F8KkFW+owOnYJZ4/jSw1PuHy1RSmGN4/zsnIcPHnJ6ckI/dKw3Ay+uOj698aTmDFPNCCFACiyd5vzA4lQo0g5lp/cDtjJ/jn/KSGKy/9qckrTtqbGNeA/UzYmcfPk8Tc5GWpLJpOCl/cFVUsVUxYBKaUI23GxbMpEFUnXMepRHMFijqRNUFehesRo0T696GVuNQjNwUM3gsOa2S1y3gevWMwQxwKqcZlk7jDakBMOQqSxF4y0TSwA+JRkTmCrXJ2UBkrqYebX2XKwGrreBba/JyjIhFVAAG2HGaaU4OtA8vOfYbqVVuveZEDOrVSAMiVrDojZsWs+qjbiq5tmLVsBUpEJvjaGqHLaq0WZG3ETCdo3yHqLHaWTS7AOdT6SyD2NAMQZ6IQpjUymDUhWbBNlrktU8OHqTev0paXVN6m9pzDPa60fougalMbYGHFppYgp430/BiDhYy9hwM8fB0YLT81Nee+t1FseHDJ203CTTC2BWHMaN1jjrENbofpvROBh3cwhAYw55s/nW9OxOD8mibY1raur5ktjUDLcr2utrUr9lWc9K4C/nqe16CfSxGFNT1wsOTs9Ynjhc40lqSV3NBCjtOzHiWB4QtGVsTSorN6OS2DR6xmS2JFrjQksJNkjFhbQAkykGfC9Ag9GG45N7DP3A0Atz9PLiOe3qhkZbrLZkJaYBm5sVl59+wscf/JBnlx/xePMdLvwnRKVEnL5MTHl3EhmZD5lMM6t4cH7Cw7MjGqV5/OKSQKDVIEL7SoxvjEbvg7G1o7Iz+AKcSVU1yntZI3LRbyrnRMHU0qW0njSt9q/xFPTvTXxp3wL5zjM7MGEE8ncBXRpD+93cXB5qFLNKdJNijvjgCTHKNSnvGlvcbFNjtBQ+hqHH5L0Ea8o/ZM2LOZHUGKKqO0nfOFZjzuj3f0TsOob7Z7imkflUQnOiUsWkqxxTFuDFFxMkrTXzgwOySgze8/LFK6re8/DxRyw/+oSrV7fo958Sju+h/RmqO2MTZxh7QD0bJBmezzl+9JCzB69xdHKf5eERWFuYZD3D0OPbtgTgO5mHMomU7KkUDxnj7ql/AImzS/odPd1wy+3Nhu16y2q9Qm9/4g4Ye3h8n7NHA7U7YDY/YRigbwfargM07XZDu7lhu75i6G6YLRpy9mjdk/JAzqXr4r334G/8DfnQBw8k6ek6+FN/Ct58E5oGQpDW6nGeqSp4QyR/ePVKGKXj9uIF/PjHckBvvy3PXezZeT15Ak3DUFX88Fvfgm99i6/89m9T/at/RTOCsZ/dbm5g3/Tr+PiLX/efun372/D3/778/ll2LsA/+Sfwj/8xzGbC7P3Od+BXfkUA7L/0l4QR++1vw5e/DH/7b8M//+cC1j57Br/4iwCEn/lj5C8/xPzK/4K6uED9h/8AR0fwE18lRk8IA303I/Seqk70fUfXdWxWK64uLjg/v08ms2233FxfUlVfJcSE1paqmaOL6SEI0NUsj2DYCIM+eHw/kHJkGFr6fksiY41lu21Zrdb0ncdoMZew1jCbNQTv2aw3HBwtmc9nDP2KlBVdGIjtFufmnN5b4oetTGfalOFt0ap4FmioXF0MVQLD0OOckyQoKYYh0TQNVeWo6pqlWbBpBzF1SpqYFG3Xs121rLcd682W29UKZQzOVlTNnOP7Dzg8fchiPmfW1DRVxdMf/4hue0tlFXV9jHNSYI2lNTujaRYL+qon8EVtgHttziCg3fiM2vslj8+XeXo/h85It1uOu8JuVjtv1yJfoAA+/pi4WrF++Aj7xhviMq2N6M0t57jakvFstlsW8wVHRwdoZQk+otEs5nN82PLs1S1PhhayYgiGwVd0viHqGWP7c2mOxadWtLIXmurUYWtNIJMD+BhFty8k8AkVEyqNTNLC7olMj0djrc8W/iThTuQk4EvwGWM1yoj8lSiV3QVjc860bYfScHi8xMfCYh2B7z0AaASi1NgRp4Rhaab25zwBKSMYNrYd7wD0wiwbga8CFOy7PY9ag6LBrIhqxmHzTZxqUMpgTS35nNqt9U4ZIgGdoQJOrOWBqzgyhgrR6wxFB9NO+7ILgXabHJeETALIMkqj6YFPrtfU2nNSSGJrD23U5ARGZ+azmtODOcvlkrpu+PjpJ2zbjhgibTfgYxi7n8t4zhMu+tnts8DleC/EYnwz3gOjTFChacrn6TIgpuu3+78CaZvWatKfVkXXfTTk0YWoMUYJGukAzONNWIo8I1g4rsF3rv90DDtAUySRdteeO7/liZ1J+V553whtUfCGcbTlkptKTLKLxzJj5+IY26S4IxGNEhnlbWWs73RAycUgS8KHQnLYu8fGa6FNuQ+Fye1TYohyPVLOhJzEDDkJY3aIQQxux7i6DASJRUQuIJEkVp+kACBZmXfG2GwX05eAkTKe1CjvVfwjUiapLMBs9jtiVgGbx9iPDMroybsgKwEac9lPRi8CLaCXLia1u+8u7vSpsEJTYgiekCJjb4AaZfVK230Mhc2fRDbLjObkaZSyKGMKLbi8Gi3gZVIa9YblmuaSQ5ZraPZITHlXMBAwMmOM+ZyR7h0suwCeY9yutSLu3TslBGYigoHMz3tx/XTXle/McQ+wGLfRtNmM/yzJWpFeo0i5MBZGEiMRMeVikjyB1SLrYKyjasSgiiz69SP8MxG7oejIOqytqGxdYhFhF4eQWLUd11eX9NsNCjg4OKRypROe0hCdxDxNzHwjq+0aH3pUCmR0WTfGYofMJyklhiHQbnvaTcsweCjGo1OBDvDBs96uydrhh4h1NWiLD4Hbmws26yu69oboW5qq4DZKzOiH3k/7qJSGJExsrfXks1E7izW6jDkpxBq1P66/ePs9Acb6vuMHv/1t1ptb1psbbm82o3JqMYkyuEqMX2xVUTeOxjXI5BqLucBAGDq27Yar2xtevAzoL32DcO8BvbvHur1FYYhF2DcMHebqA4Ynv0F69jvUqgclWkU5G5RyVLNjFof3sG4GytD3W04Oj1AKBh+4ud1OcgQjY7VpZuQsbLmUEtYKQJWnVTkVarcpE59QwWVRjoQcQJsCWCRiktYyaw3BZ4KXz57Nar709mv85De/zp/8Y3+UNx48IqbE7XbNb/zWt/nN3/z3vP/xYz559YLnq2syYBdVGTDSbpyHgZClOUfVBrdoqJqayrlJdN4PnmEYGIaBJ588QytwxlJXMypXAJmcJ8DNpziBCWMlUI0tDuVmtc6SdST5QNPUuyAY0QDUBaDIJayIszsAACAASURBVOCSD5GfWml+4VtfJfgxKNYcH53w7rvvcnp6WkxgFT/46AWvthpfnXB88pA+JlTsmdnMm+eHzEwHRdx6XHhlcdjTThwXCUrcoZjAo51hWgGZskcxVnMkwBo6cQq0tsJYQ04R4xyLxZKcRSdsrPrLlGjoE1xvE+t+QN8OfO3t+yysLKQ5K26HyEcvV7QBMIaze3NevbwlBs/psuKNe0sisKgV88pwdiiGCcKGFQZvGDwqJ1LSxFhM7HzaFQrUboJTexNIzJmuC1ytBz56ueGytwRlSTgRw9pPXkjUBmZNhSISgmduFTMMtoZwrFhtMzFbQoJVm/jBky2vLjv6mOl9ZoiGnDS2UtS14XA+53BmOJg5tAIfAq98TVQVw3qgvb3ial2BcTKRTwHFqMeTQY+w9ij+rkkBlLL0CS57TR80X15+ieOjlsMqc3xyQusCF3GOWT7g+OFrGFezXq/xfoPvOqIPZTxmtFFoZzg7O+X84RlHp0com1m3W1QSjeXZYsEQBrpug/edMAFLu7YPntb3ezPkPij3RVtC54RLge76CvPodZxxaFNTVzX1TzVcvv9DVk8/piLjgLoELcEHfPA0zQxrDM4Y1lfXGLMkJA3aMiikotrMMGS8/j/Ze9NY3bL0ru+3hj2805nvWNPtbnd1d3oydpu4kS0r3bFQJAskS7ZAwkRICRgpSkDiE0TGEuIDQkh8AgQxxFEc21GEZT4R4yiehI2N7XKadvVUruqqO5177xnfYQ9ryodn7f2+t6rasYMlWohVOnXuOec9++y937XXep7/8///HzMGzUPiJMAoOTDwrNerLeNc5YAh+8QNxvzkZz4hQFuIgfl8wZ1bt7h79wXOnjzgN371Fzk/60gx0K6vefDWV+CFD3ByfAutEk/efpOHb36ZJ4/f5nx1zr+5/Bf0yu9m2WMiN/69nZhFac1kOsfakhSEbVnWFZWbEIoCVRToqsBUBaawTNQxPMu/W5eo6ex9wdjgE7ETaajJ65msKfKHjdl2+nuOrQI78sKQExJGturA8IlsQdvd4XYArgGcTUkYs4vJjMVsztnlGa53TKsJn/nkt7FqOp5dnnF69phN1+C9x9oCYyx934OCvb1DCqV46nvWy6WwzhPbCCyf/VDNHpIipSVgGiRbKATc1uBSJDy6T/Ez/zvtX/hhaf6AAZXw0W9loUiw6mMgeZ/fN0W1mFEWJTFGuuU1/v/4n3nbe6bxBY7jd8FZRDUzfASPJybH7OiAu8eHLG6ccPziS1STGSFIQtE5Cd4UCaM0pS1QKRCCG+eM+KcPIKsA5IUVtjmZaWCNReswBuIYUDZBcrjY4GLk1t0XmV7t0+7cPa0WxDDnarPB95q+bVivrrm8fIp3LW17he9bYgyU1ZQ7L3+A1abh+uqKW/sH9JtrCSxZbg/6j/+xsFL/zJ8R5ua//tfw2c/C48cCOA7jE5+AL3xB/v3X/7owQofxwz8snxcLAWF/8AeFdTqMP/kn5fNHPyr+mcDXPvEJnq1W/Od8g/FP/gl89avbr3/kR77RK/9w4y//5e353rsHb7/9R3Pc3fHX/hoBWClY/MjfhP/hv4ePfxy6jqKsWOwfYI3m7OyMpKHPjYaMSty5fZvTR48x1tA0De+8/YDe/So3b99m/+CA2WLB7bu3KbP1QYqJbr2hVJGgIQRFsjUvv/ox2hBYbtaEpidpkbOnFLFWk5Ki7x2FUcznc4w2rJYNdT2hrmpE2ZSorELphAktJ4tb1IXharnh/HJJXU8w+oBZXXAwLymsyNOvL88JfsliMWX/4ICu6+l8R+gih/v7TOqaugn4pJguDujaBh89y03H4wdvs143o5TdaMX+bMZ8b8FssU+Mir39faL3LC8ueLq8pFtfoxR0fc879x/y8OFjiqJgsbegrmu+8IXX2bvzCm7S0bLOb9J7EaihyI9+10/V859HNhtALnBEHzAZKNQMFiqMgEMkCtA0rOWXl8Sf+Aku/vwPsbh1k+lsxmwh5IGHDx/RNB19FwBLVVTs78+5cfOYT3zqYyyXS4Lfp9kc8qUvejAGpQuUKjDZf1wAsiGmiaSpwxxq7ElBy5r1OuCjyHsJkdRHVC9xkGEAJXZuVZIC4QDEBB+J3qOUGr0ee9cPNczRp57cTiWFSB8cSqetHVE+uA+OrldMpreIQNu2ojrJLKHofe6EnotYuaAtiqNs86Clm0bK3pBDDJeiwlgjjN4dz8chPh9BO5/t4PSgXBK/1uPZLb77g3+BeVUJ2cVrfKfpW58VSzKcQvx7leKktLy62OdQGWyIGUyFqBRGZomoYrYluvE4AWHCRgXJgFeRzgfWacnV9Nd40G24WUSG2+uCJ2ZQqCgU3jnqquDmyT6Hh/u89fU3Wa8aDo4OuXf7Frdu3eLXl7/NlRN2rMqnMALr6t0Rw7sehATeeUilAKZKwD6ltDQcVWpUI6PYgkNDgXInvlMMANz2NphB7kwGw7P9YIiJoEDZweIKxsZbmZQU0+BjK++fztcyvufDJj2AVnEL9gqwtdt7JI5ELzUkeCPcmklgJJIecH81gpwmgy7DZSkFZWYOSmkECq3R1u7EaFupPHkuRXKDtJxzymXI/Q0x5YZUAecDvXM4L6q8EENu6Buzb7PkDUNbFnbsMSADR5BzdZXXXultYkn4TizVxtsAI4i+vV9qzAWNtQxMW60RtdiObUOeaOOHysXqoTeCQuJf7z0xgE87dhZsi97GGLHOi5qUsgtv9ATnBJdoWypTjuerrSUFQxyAcCXX6oPYKprR/0PlAk7MQKsZ4QnpUTDYkTACsoMa4D1PzA4+MQDtIwlixA4ywjCwgaPgAyE6yYnCEBwPAG8G+kjvIlgIKK6SyvZmsp6nGEdSmczHoXAwbGLy72QMwQwAf8oMacZnJwQPIWEC2ADWJSiFsKR1ibWAiRigNwbfd/J8a0NSAn4P9jVd71m3PUF3VKXkMkPMXChLGBSQKXJycExZ1Zjc9EsbiD6D4iHiOke3XuL7leATweRmXaIkVblwbIxY8FX1lMl8TtfNaS4blLZM6ilFIUr74CIX55ds1g1l+VTwMK2JIXJxdcmmbXBeLAWmVUU9hWqiqMuSGJw0Gs0N5YKPeb3MdpXGMp/XlIWhKKSpqVLgVSKZ5+023z2+KcDYp8/O+LGf+F/ZtA1d3+J9yv4zUsFJSTrEaqvQhcIaRWlLyqKkKARc7NuWGBN9SrTJML37WW4cfJhYnbDpEi5qemVok6ZzCdes6N/4DdTF72HiNUpb0ApjCowpMbrC2AnoUvZwAlWpWa83GLNdeAZUXGlFVVZ5kZHGG1VVkVKi732uqGd+VBL5jtYaW1icj8ToIVd/hhggBGGjuU68nFRKFBa+5cOv8NnPficf/djHeOWVe1R1yeNHDzh99HWuL56gg+OkijwpPFURqCYWpQqKUia70pq+EfmTzoulrStmsyllXQn7K0ZcL0bEMYibt4uRSV1RVhWTskDrLGNlACYFWhlij2EzlKRajRRt7zzJB5nMMW4rKvl8pPo6WFPIhrVb8RkWO6MMVVHxLR/8EHuLuUjgnOfLb9zndF3hqiPM7BBPQgXPC8dzjmYFlQki4Y2esTo7mvcDMdL3PTFFrC2wmakyer0CKPEpsRoKndAqElyXFwZZlIVFIgm8yC4YaniElOiCp3ceawevuMjUWF44mfD0uuXxecPXHlzzwvEMpSJN53h23TOpS+7sVywmlsJo9qt9npytOL3uacOGeycTDOL1ZrVBm1I2nQT4RAwdVhWkKMUJ2fCyDCN7CBmtxgpsHyLLTcfZdcdlC1e9Yu2nBE1ueqAYvY8z8KZV5CMvV9Smx2rAVLx5f8OXLnr2FyUnRzUu9jw6bfLGBWA478SWwRjNbGY4nlvq2mB1giASh7ZJOJ9oes9lW+Hrl0iFJBFJFTI/ctWurCyFlfdDaygL8city4LSaoxWtL3DuxbvHd71LFdL3lo5jic1i9jx8J2H3Lp1m6N9j6kcPnlOuxJtldggaE1dT3OCBJNJzd0X7/DCC7dlY4mBbtNkH7SSoqyoqgpUom3X9H07LtLeCzjq/Hbzl0dCjdNzKIAMT0SBYqENN5QhPnlMf/s2hVXY+RwwmMUR8xdfQRvN1ZtvMi9KqRQ6kZpenZ1hT25ji5pUR9Caq7Nr+q6ld5H5zRdQtsjg4ZYdrtCyBhBZXz1lefGUzfUlzeoKa5SsNQpUZriovPmnlAhOEjadq+Eqf789Uyhj0UVNUjCtLV1d0jQdxihOH77F3nTCwXzCs0ePeON3X+Pi+ozT9Tt8cf1L9Pr5oGm0KEvseE3LwqKMQpVw1TX054nTdsNkPqErDenmIWWWP6rsOxuVwodtgqazNcT7jrGqnuWS4+9sg9Th/czLiaxBQ4Kdv7v1dt2yJ3b/xtgwQMk6MzRVUUpJM7J87d4FLt01m6YRqQ6Ry9U1v/nF38G5mIOlgOtkH41D1TlJ0u5c9t6qaorFgrRspLmLUts8YwwGh/Bvex8Gx4Ex4E3S3CoBwVo2vqNSpTAUkh5lWwODg5QlXTvGgNfXS+5+7WvsX1xS6YKD+N2EFFBKPGWd94SyZnF4zMHxDY5v3Ga6WIDZdne9vlqO9zwmsn+azEdhBIi3pXSq3QbLw0WquK14D16LWhtMlsjmnJWy0NjpgsVsn5jmOA/xzZl0aMzj8tk7nL79JWKMnLoOjagrvGuZzSc010tC35GUqATW62vaLhKwHB7cIs0PqSZzuHi2Pehf/IsyARYL+Lf/Fl5+GX78x7fg58/9HPzszwpo+6EPwa/9Gvztvw2f+xz82T8rr/mH/xC+93vlYbIWfvqn4Z/+0+0x/uW/hG/5FmHXDkMprmPkl1crPjubbQPNrpPjn5/DZz4Dn/88/J2/Iz6zOz7ZfPd3y+dbwPfzhxsDXeOPemgt9zAE+JVfgf/2v4G/+aNw82TI6KUAO52gCosyhrbtRTGBrJyrdk3wkaKwLBYLPvyRjxKV5eD4hIODfaqqoizsaIeSUqS9PkNVNeu+o+tbYamYkoP9E9qTDWeP79O1GykoEbM/ZqQoKsoCgopMZiX1pCKpRNvK3Kp0ksaWJmELz9XVNR5p/rGY79Nt1ngCJkU2KuFdi2s93nfyjNmC/f1DLq6uaNornPNMqgLvnHQR7gKuazBGEXxiuW6JukRPDYWxlEVBXWgmVUlV1RRFyWI+o1CRTXNNc3XO+uIpB3sL9vfmOTEV5dj11SU2Jzym0JR2Mnq0AllZlVUaec0fG9QA23AvF7nGJVmNy680G8oQgVWMjXCGxS0O8e4ASA0AUQaJ8vdXyxV917PY9xwfH9O2ZvSTN8bgQuDiaslq3fDkyTkvv3yXk+NDDo+OePrknIvLNp9TJEZH0tKVOURPVIFiz1AcGdQUnO7xfZCmUMjS5jc9pgObFCZH6XFgryphHCZEKqtQ2aswjACbHgABKgHPkngId32PDgPwMdwaYQMNw8VAGzy+T5yenXH79h2UXbG8XtJ1PWQGXwpD/CY5RV6AUSSqssIG8V9vaQitH0kPgmt5BortALANwMSoRjHZl1SLX+WnLj7Gy0vPjVVDXUthf9O2bDYt61VD8oHebwviRYyc1DXHVcXNuubGYg/jI3Qt9I6KiE0KmyI2RUq29mopA4mBRE8i6kg0AQe0DlZR8ywYfnO1YVnP8Hq7jkYgaUU1qbl1tM/hrCS0DW6zwh7OOV7McN2SbrVkZeDuiy/y+f/iO3n77Yc8vP+Yp08vMFazaTqce39AaRgDw81lf/tdJYjzTuwojBGiwxgDbvf0rUxfjbZVIPmA9MOQ+CaGLYtRD2hxEDCNEAWEiWq0vwR5rowxGElSxmc3ZruqoUdJigGV8sOd5cMj42YAu/K5j3NDD2QpNcZYKWUweVQuSQwSEUVrIseuOS801o7H1ShKa0aAcRu2ieULKWEUuCRzwyM5Vus8bdfROUfbiUpp/BhsAdQgG5fzskpjrfSakOfWS66HxN2gsNZKcztlcr6dMpDkhWnsAwGf8+qUwant+z+wCrVW2MJSTyaiCM3ErqKw2SdXbdcWtY239Q4YOxTEUgoYDCZFdDJ03aAd2zI/YwxjvB68SNCjLkg2obz4nAbvc98KkdnH6DFDQ0DFuIYNOYDEojkuZyCFyN/dWkTIs2u0woetT3BKw9zYxhZDqBEzA3nYO3T+wcDcHLyExd834JzYXg1xSiKhTGbqYnO8mdm1+RqUSjmGltcOtiiQ0IncoFqWwoiSslACi8IqPSoih2iflHDBQbJiT5BtQpJSRKUJ2uTmitmG0SjwEaU6wUPyeduhMXFK+BQwtiQkhfMR6wOlHazPpBjSbDaE0Iq1TkgoYzOJIc9lo4hhALIDsW8pUhSlRwr5fUikKHYcSWliElVpPZ1KY/nSYErDqi5Z12UGeFuZM6EX9VK3wgch/41KExUpC4PRBYmEo8f4hOkDQcOsqJgeVAysamssy+slm/WatmkgejbLJb2V62ltgS1kbXiehPTe8U0Bxnbe8ej6UuRPSaZRTAGVq2sgLJrkIrQp2wK08sYN0oAQQFmCqYmTPW689B201TEhlbgg5uIN0PmA7zak8wfEs3cw7VLUF6bE2IKiqNG6QCvxfdDZE1QRKaymdw78dhsa4jdZZCxd3+Ozj6yxFpRUdUWKm3aS8DhuUDF0BN8TXE/sNhgrky4Gj/c9KMPB4oCbJ8fce/k23/aZT3Hv3gdZLBYE33H6+JSHb7zOxdMHNMsLdPRMZzWvvnSXm7dv8KRpeHax4nKzpPOekJuhhChSElMUTOYzYfFGCL3H+Z6u7wk+jBLsSlsmZUVVFFJlGrrnDRumzlXyGGWTVKOoX4YSPxjBQhTWWLphwcobqzJmXBiHYFbliuw4coBQlhUHB8ecHN/EFgWt81wuG955uiFWt7HTQ1Q5pWs7bh/MOJpXLCqFioneD3KONIK/20w7QvTiWTxs8Hro+EqO11Wm04dRviQbbRyv2BZVLrjmBXkI8mF8MFMudw1yDa1hYhIHtcItLFddz+PLIfdXzGY1h7OCWWmojBQJjqea6Cqu1o7rTcvTq8TBVFMXg3FhBnjy3x9Y2SnK4rmVV0gDAWsFPNGFpveJpklcNpGrTrH2ij5porY7+W4GXJRjPrNYA5tVSwyOogSVAt264+7JhDcfrlmuO1KSjdSES1TwGQi2eF+jbU1VTbhxWFEjJvYxQNdFlqtW2LQBXATnbWYXS4ioQkc1kYS2LLTYihhF0zpi9vzq+kAIkVYJH9nFRHA9KdujhKRZhQI6CZiOqwJTTum6Fh0cRTXNXkSaoGXOFIWlrEomiyknJ4fcvH2MrQqRrUbxWCKJxCjkSm3wUh303qEQn5w+itRs2wF1C83JF4nj4h5HxYty34GZMuwrw77SmPWKzdNTtDVMrKWoJyRtKOZ7zG7egrbBXV9JEONazGaFu7qgny1QszmmnqJ0JIQKE6HSAZ3Bu/zw5U+Dh1HEtSsev/0G7cVTXLMm+J69o30xps9M8qIoxi7Mg7RyqEIPwU8cWInWYMsOZS3zqqCva3znKYqSplnx+NF9XNNy9ewJ51fPeLD+Cqf9W3jVUtkiS/VypXho1qUlyWSQjxiDKgxMLGa+INUVrrSkLEvB7PppqRx8pOeMAuIuGPquMTKAEYbGAFAO/RmHdVHBDoshg8Xv/poB69mupkPyvysljZnZr/MvhKEKn9dc6RYbsppD1tfrzQrn/Ri8D3vUMEcHxUfTN7kBgWKyN6d3kdgMjRpkfFBZvp96Z8EfTncwihj2vvRct+SUFOm3/x8pHA2J1g6TR2WAJD3/JKCVZnF2Rt000siz77Y+vPn6S19TNVMmlzMmjxfYMjPLUkKHiAn+OeBO6S1gA1BkNjcpvevvb1+jc5ODlK02bLtCq8EGQ15pHq9IZvCaLvEhER+9xvrko8B/B8DijS9x49/83/Je5aRK9qIo3tObRhgaCpQxLB48xgfwQfyVSYHPv/UFPra8hKMjObmBKT2fS9MtrUWGv1rJa37u5+CttwSsvbwUmf58LhYGwzF+4zfe6xv7xS9uf/6v/hX89m/znnH/PurggJfLEv2FL8DpqQCZ67U0vbq+FjbubAZ9z62UxmZY/Lk/J+fBKfAz7z32f4ihFNy7Bz/1U+I9GyLdT/48xZ0a8+o91Kc/zfHxEV3bQIqY6ZTr5YqqzE0jg8e7nulswWJvj6Ks6HpP2/V0bcP5mccaSz2pR+aoUgpbTXj67CmFhsm0YnF0RCrnpHgXZTSbTUN39gSVZc8xegprsUWJVoE+BGmYQsQ7YduX9YTppKLvHb0LBNfQrC5wyeACUqDxveyTwUAoib7H9z0xuvyRaLsOpTVlVdM2Dat1SzmZsK8qYtkTkqZrV4QoIMb04IQPv/IS89kMqxVXz57SbxqqqmQ6mzGtK1LbYbynVJAmJYlEVU2whbD1YwpcXl3Tdg6S7L3r5Tm9bSBbeGutSWZbu4m725faLqWDdPE9a1ba/ZxBmuE9yWvRu/03GV6+u0z85m8SX32V/vZtVssVRVFijKGqK7rOj35zISHkABoeP3qC6x2L+ZzjkxOWq8cjKcAHKcrHFMBEdJUwe4lURYIKhN6TUKjCoEKEPkAbIKgMkqaxnLq9FsZ9OiKSV/Hcz3tYlmCTiRvCQjKY3FBlIE4Ya96zJwrzT2Ld1WpD7xxFWTGdJ7y/Ivk0xshpAEWiNHdKaqvOMkri7xgCXYxEJ+CttgYdQmZMyj4o1jYSe4QYMNlb3CrFVFd8sH+Zj240R61h6iZ0KbBar7laLdk0DV3XodDZO1Wmwb613K1qjouSPW1IvTQC0iFiU8JmIEMnick0ucA8zJl8P5LK/SG0oSeyDLBCc43m1EX8rGSnupk9dRVlVXJ8dMDNvZK27VhvGh49ekJRlBzt7+NipGs9X/3qmxwu5pwczJlXL7GYT+n7nkenZyxD8/vUqMYZsWUE5vhy8Jsn+Dx/lHgKP9dFNGUF5M6x0s7nlPeyNABLCrI/p7D0Isk7sZYSJGwEH4ehc4f5XYBrK9uWeRRzrCDP/daOZOfqxuNud3q9LSCrwWhLM9oT5bdDG4Um93QwZiysDzYDagR0lBAX4nDvMkibc64URSnYuEDrAo0LNM7T7jJgQ8xYneSpIXuGCgqcGeSMFyXyfqk0CBM2Exykn4MZ71vInqk+ePGW9U5yk/xsa6MxyqJtVtAqk4FYYf4aYynLchvLK5Ux7515rp6fBzHnlyPwmDILMwkzOsTBJi+vhxnVzH3SRvJV8JFUxPH3hTns0UmUkgJIbm32Rsg+bT1rR6LCUEEyA2t6yN0hhcE6TTaOGOL4HL/b2mOYv8PVDkWD4ThbPGCY93J/pKg4GLvJLdPjuWlhm443VP6Q9KjJsWiSRrEoJX8nBvTweA3WCWmLO22NXgR38km6WIQUKGL2nI2ZvRvkI8ZE0JFB/TGQDhkKEzHio8/WZpn0G+H41pQi259FFF3X45OT/ZZEs1mScgM4VZSU070MqA6McLmfxiqIso5rYynLmkGBDUZU3TH3mui9KCdSIgZPUppqsiCFIKhN8KyXz4RAEmXedX2P9gFtpFhRmCKza8v8PIFPLi9HA5tEZ9sLizUmK9+lgXxdldKkKwnQPnhPxwHwT89nEO8e3xRgbCQR6gJjagoti0EK0nVTBcYK9NABLpHfAJdQyKSRCV6giwPKg29hfvuTXKYFLhhB09EiV/QtYXOOevIGavMUk7w0zrElxtbYYoLRFnH7zZtqGmKz9HyFaofVpfICmHwaH7BRPkFC/FYCKeUNLQVIkeA93i1xfU9wHbFv0UFeqxJYraUr9Ide5cMfusfHP/pBPv7JjxJ8YNNsOHv2lGenD3jw1pdx60tC35CCZ1Ke8MKNm7xY11z2nt97eMrbTxQXqxXLpiVk4NvYgqIqKSf1mIT7EGj7Ftc7yeUBqzRVWVIVBYXJtgpDok9OtJNiNpnhnBO/vei3YKzaJuND0DRIPYARhBgMzQewUuQF20p7PhRWW6bTGTdObrHY20cbw/VSfLbOGkO9f4yqZ9K0K7Xc2JuwVyuR+w2BUv5vACaHPWSohAk7RcmCmhglt3mLRSlEwhqlUlWo8U7kzc2C0rlylvJipLbBSdouwOQHVaVAoWFRaZSu6C89V5sG0NRlyY2jCYdThc6m2ylFJkZxNJcNqe06Nr1nMakYPJcG9sZwcSY3jIq5EpryAmfkwtFGicRJsHlchD5qgrYooymUJgSNHyvSUBWKuVUcHRgKC1domqZjagt0SvSt49btPe6byGrT0rWeUjt0uEJFPzaHir5E1QtsgmkxxW0CbZ9wIdF0keuVw4c0holKG5RGgghAp8DEBupSUZXSdTZqTUscva9653MRQDbsoBQqROmECxhTEBVsokJ5w97MkmxN3y1RIWBsTYnDJQG3Yi5+7B3ss7+Ycfv2DWaLkqZpcCFKYJV33BATPkRCiITg6F2LDw6lJfj3XrowPg/APofPcVDc5ah8CYAKxZ62HGjDArBdR/fsKaYssXUtnsNKYaoac3CEip7lg4RuOgovdfm4XtKurlHWUi/2sCaRfE2hbTa1ys/LGHenHLA4guvors65fvQ2aXWNUTCbT9nbW+AU+BzMVGUp83tkEyCdlAe5TUrE2KIJ4l6VHKl31NZQ24J1Zpe7vufpk8csz8/p1tc8bR7yuPs9LsIDqrIUf6I20Y+esNIIypQWUxUkK0UybS2UljQpKPcWmKJAGU0kYthZtwfoeABWd94Z8fz9xmyTwVJACkrbo6W84CW1k8TvBKvjevjcmqeeP+4OUPv893eOn4BcSBuuJ8S07dCrdZZBbos1KSc6MSXx21WS3Pa5E6jWinI6JbUy/9NOY6aXleHlgRWleO/YZkTv/f6Xvsq//3j23m81wPv0nzKMStA/5aRxugAAIABJREFU8jH5/37JOC4Ov84Ixj74Oje/+No3fO3Re77zxnu+852/nv/xfh6sP/Zj238PP//n//z5r3/yJ9/7ml/4Bfl49xh+/jO/D1g6vOYrX5EPEM9aEHbsr/+6+Le+e/ylvwR378LD34L/7ZsEjE1JGn/98i/Da69BSvT/7hHmK48x3RL16U8zqUouz5/iXYkxmhjBFkX2FhMwtigtdT2hqqcUVaCaiK3LZtNAhOOT45FBoZSins1Zff3rzCrL3mLGbDIhlhX6xg0wBefn17TNmnpSYwuND14aRylDjB7nAmVV5UasDqUte/v7LPbmrJZLvF/R9cIC7PpEn5Vps0lBH3p8r1j7HmIkhFbYmVkJ03bC1K3rmrZtadqe+f4x9aKCckPfetZlgVIRbS3l/JBPfvpbOTrcgxD4+lfe4PThQ6zV1HWJjpHm6hpCjwHKoqCLDm0ttqzRxkLwUswIUryrq5qnVxd0kw3syVultZYmUDvJ8pgTv2ds18fR429I3nfe+gEM2a7j6flDDNiTYtsd/vXXYVITtabJ57W3v09RaOq6oG1jxgCGc1WcnV/RdY79vZbDg8OsoCsoi4rkHKntwERUmdDzBPNI0J4QnDQXMVZ6TPQBGg+9kFqSigjEJp7gg2pDvBjjCGxt7QflZ8QkncoLO/ZyUJlsIgCu3BttDMG75wCLmGTPSTHRtB2r1YrZbEZdT2iKjdiapQHoVjlWzqY8GYAd3k9daqpUEbzDg+zVyqKjZ4zmc8IiYKzEVGVREJRnSsWtdMCnNne5sb6PbiK+g7bpuVyuWK7XdK5Ha81isYe3lpCv7Wg259haDpSmBnwvz0MZAjrlhl2y8Y6gnspfDx9qmFFK5mYbE6uouNQ953rNdUxMygIV9NjvM2rAauq64ujwkJODkrPzS9qu58nZJdaUHOxPpRnecs2D+48wd25wfLDH9HCOD4Grq2sKa3an6PsubWP+w64KMMcFMaDiNtfTxmyfBTXiZ+NfkCkQx98ffj6+XhvJf2OURm6J3FQIkU9nduOWgSeRjc6S5NFjdMxv5LwllNzGOLvl8zEXZReIHd6TAYwdnvotcDf4oEqhWG+BqZ2EcQTRBjAgz2Eh3EjjLYXKBTlH27WsO8faeZpewNh+bJYmIKqQwOSY4j8p91UszfL7pRivRQ3Pid4CZxq9jf+SYBIuKxecc3jncN4L0GpFkaGNzsUfaaIuSgyReEt+aBg9cclx8LAODKBzSuP7Nt77DKrG7AFL2mU2D4qptL33Wov8fnhdEmuHiHhHuyBWLDYOvSiQ5394/4HBanB7Fs9PBnnv0zj/B+uLkSwV0wjOPreXsAPCDrl7/t1hfojCbBg7m08Gt7d9Qba5+cDC1kODtfxz8cHOjPIolhYDSJqUEk9ZPVAehHBGyB6w5IJYxjxifipyFpGvU3KwFEO2QJAPwUVzJwc1FLq2ZK6u66RpVhCCk2iA5FoHq0AXfbavFBVl26xJMWHKiqKcU833SNkfWSdhQQ/3EZXwwYuvvJ6gVcp2FYoUHSErK5x3+Oiy7Ylga9oU1PUcHTyx37DZXMq8yXO/63rxcrdRFKumoCiKrE4qsUblYw6WQKC1RetiBGO11mLnZDRFYenbDUQ/eiKLr8QwX7Z+1e83vinAWFtVHH3wniwCRqOSFrDJRWIfcOue6ILIn3qp5gzVjmGDCVGDOWDv9se5863/Fc7cwLWyx2ut0LZAuQ6aM+LZV/Fv/Co1LZPpDFtI9T0lSDqByeh7lMqBBCeBruvGzmrSwCphbMyLicbokv3DAwFcvKPvWzbtdQbzPCn2pNDhQy8So+jYXDt584InpoAGfACjLXU15cbRTb7nc9/L5z//OW7cuEFKkbPzx7zxlS8SfYtJnsvHb7N89ohJoZhPSlQquHz2FB08i/19judzypN9bs9rHjw758vvPGSjWrxOmLKkrGucF9+LmMHYru+zEbnJcnxFXRRokjT2YrvwDuBk8IF7r3yI5fKaZ2dPuVxebkHYJIsGSYtHSkyokM33/cCM3DFJz4HpwBjcRR50VMwnc24f3eaVu68IDVwrnl6s+NKbT2D/wxSLI9qux/cNLxzOOZiATU5A/rywGmPHBVWsAIfFVBpKDHMi5ge4tMUYHKYcePQji7FAG0VhBjbdFsxBawE6B2AnB4/GKLQpEFPBXFlVmkIrbKmYYljMFa+/c8G6l0XH6oTNAHGMjhAdwUVqU3AyNUzsHlVZMbFi+L/TqoLhaYnZXGjYDEyWn2irwUhnzifnnUg0jMFUlsODiolXNJ1i3cG6C6zbgIviRXuyp/jQcY1NAaPg3uGC114/4zwoFrOC45Nj1lcNurvA+IaIZ9OtUQSRUGhFdB1sVqRuStMdcN/1tGmBi4aQFAIN14xy7hRROlDOahazglmtsJuCzdUp/XXPOiSaUOBVRUoGrQ1lUVBOCpTVFIUR1hLSgM1oec6vrlYUpaXdrFk3K958tmRSG24fLpiUhhgcN6oz3r4IrFdX+H7Ny6/cZToBRaCwmqZtpMrtpNpbWJO9/HQOymRzcn1PDAFrjUiW03aePDeGIGXnWxo41AW3bc2+tkxQmBjozs/pgXWKVHVBsTgEo1D1hMmdF6j394nNmtB2uKbnatWwuXiCiwFdlpSLBUH3UIonT0QJy394FoJjvVrRXF3gri9I18/YX19htGHvxm1uf/TjcLAQf6KhODyOXNmO4EOPGp66CO3qmuTW+L6hbde011eEtoecdK9WKxLQ9Buabo3zHb+z+r+yL1HJbDKjUAbnvRSCsq/f9GCPam+O3ZuyCV7YuDkgUnUpMi6dUEkKYJE0+gGSAcwBhh0Ya8N78u5K+fgjrbYG+EbtBISMoPbIykpDZ1M1JgaoLQAwFHe2oMKWEWK03tnshaFO2nrKDnJnBWMndJvl4N57gg/M5/PcPA6ur69zcJmLjGbL0hmu1OtEdXyEqSrCs3NS0M8xhv/T+IOPpJ5/0r9Rsvz7jvc7xvsxtt/dPGD3NUMS+e7x7uP8QY7x+0ixxmO8q/jwnnMYqRZ/yDvyfsfdPc/dv7F7nsN1jcl02n7sXtf3fi/8vb8Hf+pPwZ/+02JX8D/+eVK8JsTA733ty3jnxKKg2fDhVz/G/sERRiXa9Yqvfvl3qadLtLZMY2K2d8idl+/w5MkTltdX9E1D7/24NyslFjiHJzdI3rFqPet3HrN/fJdqtuD4+DYf/3RNVSkKrajqmk3TsFgc0PWB6Hpc33Pz9k2enp6JassY9g7uUJUFwZX43tJ2z9Ap0K2vcT5QT2ru3n6F5WrJat2z3nixdkp+THaUQuLC0hKMYknCRdjb26eczEFdcXr/EUf7eyRA25Ib9z7MKy/eYW9aoXxgEhShcSyXF6yvrlj5M850SV3VaA0hbihrgyoqYjGlDZFutaLve+rSUNUTFoeWr59+JReMhveTndxXZJbjOqp47/6a5867n8ftXNlJmJU8t+pd3rPK5L07ybGG/YPXfgdee018hn/oh3B9z2Kx4ObNY548uaJtPIMU2FrxLl0tHcvrp5ydXxMSrNYbUtpkIC9i9hJqnmAW8FqaGkoinSAGgovELpBaj3HCLvIpjMysoTHiQMAYm9rshIvC8JN/S4fozF5NURwAjcRhWmvKUhi/bYzP3dzgpfAclSJGx+npE46PjpjP50wnE1beSSwrHWtQSWe/0cz0y7dQmVxUtbUUGIwn9pHkEpEAJhF9IrgBGAgkZH+cVBUuwJ3lCZ+4fJlXzh/QLQPnF2vOr1ZcNJesozRKq+oZRyc3+Mwf/xP82o1bPELykjsvfwh1fkrft+iQss+yE9BjuHc76qGUz12NIG0urmiJDRyJlU9cK8t9/TZvpd+lI3Frb49qXW196IuSslLM9ubcuHWLaalxfUSrNau2wznP3mxGXVisUvhbN5lNZ5ydX7JaLllues7Pr1mtW1lTxuBj+N/2DR8B1JTwLhB1QKfMXAzCMFYp7kiiJWdJKCEypLAFxJQcW42FYMYYSivpA9N6T9s7wZ21ETKTGiw1sypWP8+Q1SmM4GJ0LjP+GZ/RMHhRK5Gjo59/1lN+zp+bo8GPAJrOTNIx3s7g5lCkVloz+AgOAJwxYuumkecnpoQPHQlpWNQ5x7pzNF1P33ucc7RtS+s8LgpLMSk7As9KSXNu1JbxKuBXzM3xJHczORdVAytVpa2lSJbjS6PmrFSN4ukZnCd4R/QejaKydmy6VBYV1hRYY7EZhNUDEKuAFPEuZhxkC0iPsSwp1xEGtnDGCQaLArVlNHsv9yL1CYySPjZJgCzxozWZaJexGWNIRhMUOCJtCNQRYtKAwcUktgfIM6YH9rYajifqkJQQhS5iBSnkl6x7C4zNwhgA3kQGg7f2LsO8HtS1w1P03shnWDMZPX2V0uJ3ispF10D0Psf1ZFWAfq74hzYYZbLiL6BiIg1KY/3eGF1I6wplLfRyXJm7WRWYyIpjLQWnGKVMl2R9V0loriGabK0gJ2I1+NyYKqFou47l8kp8VL3HmpLj01N6ChY+stg/YD6psUbsA13f07aOGDW2nDHZP2Syf4Apck8oScLFKiUpusazXG6ISWXfdLl/SYMOGpN7QTjXkHxHCp40gKFKoYOn0JpZXXNhFM53NM2KtlnTuyAWlKnGGlHjF/WEajKhLius1iOYn5JYi1prxd5uUK0h81MZjS4MqZP3QyuFPNKZWZ6fF22/ga0d3yRgrFLCbEtKUPQY0rgxa2NQkymmTBQYVFT0XYt3PdvHH8rygPndz1Dd+TQcfYJ1P3iORHwMBOeo2nPcw9+le/M3Uf0T6sWCwlo0ShivMdI7j9ciZY3JozBYZbDGUlSGtl9jEtSF4WA2pdCR3gc651n355ydtcgRIyn2NOvVCBylIABsDJ6hbjTAKykDAGCo6hmvfugjfOsnPsXnv+d7uPehD7DeNJyfP+b8/JQH999mf6roNldcPnvC2YOvM7WW0tp8rhpVOo4XC6bTKRvnWF9csDedcvLiHT597yW+8vCU1x8+5rLtaGOk67PhfxAfGZ09RoxKlEaJR+yQp0CWLSd0VKNkIabI777+7/A+SDUjU9pD7tCtjSyMDN6NIebGB+Ibq/P1D1YqI2ts9HqUUdqSG0c3uHXzNvvHR8z39vjC61/h7acr+uKI2d4Rm9WKymhuLCrunUxRoWcg6/uYZbJDICWzMAegekzGBBrJfzgHuUOxKuYH3mqFohAWCklsLJIXiw1twFSy8JoiHx8Ka7bVSm0ZOoyOQUeUKkoiUpH4wK0FT646nl61fO2dMz5494CJ8pjkhHFCJPQtShkO6hqtwyj3Zby6AeTZgjqD55FcruK6CWw6z/Wm5/yiwxaK6aRgfz5hMbXMZho/gXUHZytNoaB1Yvlw9qzjZm25uWewKvHs2YoP3Dvg9x6uOX10hX5njfFLvNuQtEIZi9Vg7EyehBDQ2lGVBnxDanpatyFObqPKQ4yZSKMwpagnmmltmFWGslKcX4t3zLIN9Ncb3HUjQVQxoZofMptUlBasEalaWdnsoeVolh1dK4bwg/S7KCyb5UaM34OiiyVvPNrQ9p6DmWFaJCaV50blsJOWB03k/PJs0IdnQ/qEsQUhiD+PAHKGupqjzYSudWw2LSEpApreBZGAEoWt8hygsP33p/a+j1JPMChmyvBSOeFAa2oFVilSDMxiIFxd0vYNT9yGkw98hGpvgakqQBPLmmQsahopk+JmAh8R6wnf0G40q+WVGJMjc8P1HV3b4NoG3zbUrkWtrlGra6rVkkLB0Uc+yuTlD2BuvEibRGqYy5hEH3JTQ7EQ0EaDKlivlgTvWeztUe/doCpuQQz0zQZ/cM3T03eI+okE7t6RMoN47S55ffN/0keR3oXY03TnqCRV84GJXswm2P05sa5Yh4gLCaMUyopNQVHlAG2QAKCf67WQcoAydBjeZcIObIj3DK05/V9+dgcU+v3qobvv8R/kdf/+Yxfvkq93gOJvAC6/78hg1X/9/wtB/E8DkO62edz/jm/nt1zH5dUF06rG2kJikt6BAaOLEUip6zn1/IDpwU1mh7fYv/EC2hj+pw8c8Yuv/xZ8/7uMVvf34ctfhiyh49Ej+NSntj//2Mfgl37p+d9xTpp+rVby9WIh7NbhnB8/lmMMc+bVV6Wx1yc/KT97vzGbSeOuH/iB55uAAfzVvyrNw4DV93yPnOMLBn5o/ge9neI9+7f+lvz74kI+v/Ya3Lwp//67fxe+7/vED/fll8Uq4Qd/EP7BP5AH4+d/Hv7+35dj3Lwpx/iRH4G/8lckQHn9dbmGX/xF8b995RWa9ZLiv/wOZgnatsdosErAmYuzJ7SbDVpLcvvqf/bHgEhdlxRlSfSe+2/fZ7LY487LJ0xnU4zR/MJ0BkAMnovTd4i+w3nxSytLQ9v3NOGahEYZzWx+xP5in7Is8TFwdX6OOZiyN685OJxw+vAx602DUh6tDE8e32dW1bhO+gLM5hMuL89xrpfk0vfcf+dtDg8OWUwnqORYrh0uaGKQQtb+3gxFwruOFCOTumBzFdi00HjPs7M12hiqyR4xBPq25+r0KW+akqO9ObPScn25QcfEXj3BzCqqsuCyaagnczbrNW9++REv3L1FMQ/s1RX7xwc8ayK379zhyeMHfOXLX+Vjn/wOEm9IwrazVw6NY0ZQfQB2RqA7AywMhfPnkZtd5lNM4qIds91QPgBjfJXjqqGh5XPZ+QjWAT/10/Sf+xyXr7xC07bcunWLzbqlabJdRdcgNm2SFK/XzQh4AdJQ6Cih9iOpDgQdiL2HoEghkbzEqSRhdOGTfKSBdSbnaMpyp8Fpvo6d01aAKe0IogQvMZbWRkBYxZioaiVgXd91pN1rB6ILxM6jYyIVhqbtePrsjPV6zeHBPpDEz1ILgDew5gZmpiZ379YKXVq0luanWrX0qiPohKEk6AhabBN0kPcpZUuoq4srvvP623nR3uH4aM7kCq5WT1gte643S9Zxw2RvwSv3PsJLL32AF158iaKYUNXC2NfG8uK3fZblm1+mffKQ5uIZeyEwM4YC0DESVcigxVbcTxripywJJuJNxOlIpwJNijyxv8K1uiAlWRNc0wkwk0cIialWzEvL/mzCdDrFpp6y0HBlePL0Au89RhlUjDx+8IAvLRsB/XyQgkyIYwPQ7eTmubm+GxOsO08TFbVWFGRwKoiUWWtNqZQ0RNM6+8+rrUXBEFPk4+uUtvZsKvuIxoRHGsK5FPExEX0U9ZDWo5WDNkbA7JGoIqm09FgRWbsxdsyldc5xjBKFk0tJSCakkc0taV/KDXzNGPvY7EcrhRszNmwSFqrBMzA4w6jUNNaOvqneOXrvCD7Q9Z5Nu6btPZu2Y9k0XK03KGUzmKSwWsvXJmEyOUEzMFs1Ot80M5zzwCbNb5vOVhwgKmEVPNaKhHpo4KSSxu96QxtDWYnfpfEWkz1jVV6/tLGURcVkUsu90UoKTErWxy1RKo3M0aFQ+ZxNS/572xmXRtLBSBggF3isQRfi8V8WFX0n1m19aoXZmY+fgHXboW0hFjwqq1YzuIgWSby1BbqQZrsCnGUQmAEMll+LuRmgC31uHig2CK4XJUnwAys2X2vODZRk28956pLv3/A4pZRGH26MQSWDMaLsjln5uG0wLSDocA9lvZX5NbBXhxvpQ8g2DIJTDP0kUEpIUztFbhUTFAUmiX2DTkCMKOtQSvAJHxOOmBWxhqQ0ZVlQWktpLFVh6QtR2OrYE2JH2/W06yvazTXtZkVwQRofRwVBPGhDdGyaNdEYXAxs1rnfSEp453n67IKrs6fM94+o925hdZWZrkOtSJi/IUV85+jWG1IMaCXnOBjBoASH6Zxj3Szprs5Ynj9lefmM5fIcazR7syl1aTEqcPXkPldnT/Cuz0UXaXrqfUffQ1kVdK7HFIWoJ7V4Y+tclLGVed51IjNmtNVYbUAVuLLE9z1DXxdStt0rKlHgv5vMsDO+KcDYhMhZdd7YJXAY0HmNVWLOC5pkFLqoWMwOgWxd4BP14hVmdz6BOvoAayrCIFOVMgM6dKjztykv3sK0p8z2Kw4X1dZAHJNZiluLgXUTcF4kUV0f8CnQ9hushlQVzKt9+tjhvKf3jrZv6fuW2UQmgCbhLy5hYBkBPrhcHckXn58fo6GwBfuLQ779O/4E3/qpP8a9V17h5OSYq8tr3nnwFpeXT+maKw7mU1ZnD+iuL0nNihv7i7xYR5EJkdhbzKkmFVVdUlqDrQtSiFIts5aPvXib+WzK6bLhyXLN/atznl5f0QWp0JSFEU8Ms5UuSMyWtu/aQH0PW4m/8/0OkCoBasxm1CE3LDBKdtUQgwR2Lm/ekQyE7OzoaWfu58/VZMrB8Qn7x0eUkwl9iJxerLhuoZgfUlhLcA0HVcWNRYlVXti8+TlIGfcW9pz49mpj85YuYzA2V5lRoXPwGbOeZvCaHaQkIL7EwfWo6DAkirJCkTs2DkfOq6tGFmyfDalTnqtqSBjG8BumBRzNC1CJJxcNp+drDqcFi7qgUhGNJxmR+WsF0q8VVNpKbIaFP+X9U2egPKLwIXJ51XDVODZ9pA/S1Ep1Hd4XVCbx4s09qiIRo2JiIbiERmO6hOmhTYaHZz0pWialYhMUV096rltDl0o0jjIGAarJ1VZ7IJuAawm+IzhHbQqib4jRYRJE/wyfOpKdo+t9pvvHJB0prULryOV5Q9PpsQFHomC6d8J0WlBWBUFXNF7R9z1dE3JFPwPyUZqmldZQFfXomWR1wuopnZOAVuPZLM94uhaWvFlYrPKU2jO1gaM68rVnK6JvKQpNWVixfbAGEyyDd1nXeYpCU5UT6tkRs/keZTlBKY0LLr9r70W2RsY2YFVJoQwTpTkylqlWlEqJ5DrlVzqHjhETPe2Dh1ximd28yeTwgHI+FZ+1PN9JUrSKvSMkYYd619Ju1jTrBtd1IlfvG+g6dNtQtmvqdoPtW7Tr0SEyffEV6tsvoA+OcFoRg/heDpVnkw3eUwZLu67F9x2+b1Ek+maDNgW+VbkpwBS7V1CvrtAXF/iul6RUKS7cO5y2XyVkI3mQxHW3Qm2Lgmo+pbp5CJOSoKSzqlJIx06r0BaUGnZXucNJbZMHBRTGsphMuG42dN6jd/zcdgOl54ZSxL33kYn/RzqW/6FP4D+SEazBVQWuLGgLQ1lYSIpoLUVVUZZVTgAtVT0HU9KSaJeXXPaO6XyPiw/fYPnH/zj8s3/2/MHLEo6PtyyKqnr+NQcHWw/Y8YQC/KN/tPWdLQo4Odkeo66lkdcw9vfh8FB8Zzeb97/I4Rh/42+Ih+zu+OQn5RxSgh/9UfGWdffh4sfe91DvOz7/eTmHbzS+67vk2n/8x7ff++AH5d6A3Icf+AH53jC+/du3dgvD6z75yeeO4V+4SfPCHZpNy2xaUdiCSQZzBmk3xqJsJXbURhprVlVNRcS5Nc11j+s6TFESJjVYYcKcn5/jnKOqK6qypO0aUnDUkyllPcFYw+rykM16w2rdYK2hLoamJWrbaT4lSA4XW4g9RT3JUsqIrSRR0MZkj8LIZr1GJSjKCmNKlPJYY+hDwGXVh1VQTmtJVBKs2o6iNFJwVVDNxConZvm8LQynj065fHpGZQ1tu6FvV6jYYXQkhTIXogO6tOwdHROU5fTxY54+O6esawoCh1PNwd4eKUXuv/0m6+U16UbE7qY0aviUg4Mcy6Whk+BOUiXxatxBpXIMuFOwEnaRGkJfKa5nmu0AQAzMU1DSkTx/PfrMuv+XvffqtW3LrvO+EWZYce998rmh8q0qVrEoioYBSi5AAGGDggX7RXqSAf0N/wj/DAt+8pv9YEAPAmFYlgHLlugiq0pkhZvOOfeEHVaYaSQ/9DHmWvtWoG3Adj1wAuuEHdaaYYTeW2+9tZH05/+OuLtj/MEPuL6+ZrlYsVzWWBvp+ikn46cuicJGTQbUIqE3ilR7IoHoRa4tjh4VwCQlYFQBErI3gkbNGpcSa578OAoKK4BajjWsRtvSLivtmckXHfYT4JooLbO5zZV0f0tMWQbBCys3xMiQsmZl9FilqHK758w8TNJ9F4MQEkJmbSWtqBthc2mrMZUhqYhWFdneZfZhSOokW2CVwU6G6t0B211z1w3sj0d6N4LVPHnwnG999/d48vR9ttsrjNHSxVjYrAqazRb14dcYV0umzYq0u2XaH8B5bFC5hT9l+obkBwKeSXE9JOko8TridGJSih7FXjkGlUjKonSajZtOQ9ijFRiVDWO0gFimqkhK0fUjx+NIU9WkpDGmputvmVzIeornxYPTnPhNhd+EwqXIECLOQI2AJDF4CFkiIJuaxhiFBaaNSJvnSaUzSKGI6CganikEQmFXKiWmzBmQCjFJu7kqRQgQRQTxgTidr7Ati54xCFid5gkpY7gQrAABkZMwmbWO+dmepJuMPskRymRTWZpD5o1Pcc6TitZvUEIiik78Vybn6YcBN04i0ed89mSR65q8E81sLeNDyv+SU8JJl1YnyctUfulsRgcK8UjSZ0zMfK9ngFmKtlJzyoSiKJrNJQcs8hMRpHBgJF80RoouxhjquqaqqpldS2b/6wI2pizZpU4AZBLq6FzoiiUwPgcosxF7AaPl2WfpgSyfIw71Xrpm89pSNGCJCZ8Nu2LuyjAFvMwSC/N+2rRUdS1szPnzTsM/5tb2EKOQubMUpuT14q3gvayts1yQNqByu7qSwp0u97XIQpxdb55MJ3JDKnmcIgUN3s37RMFLylmqXNQ5TdMii3jqutVKkzCkpE+YjFaS36a8D8UoOn1VBXVFnCypsqASKSpC0hj0zEhPJKyW7nRrFJVSBK2JmaAWUmLsO46HPYfdHYfdLbvdLW4U2QttDOvLBzSLFXVdSyceUbpDUcTomYaertsxjgOrpDC2RdsGXRuqWlMZRfCKxiiSFxJjSAmdJR/aNvsQAAAgAElEQVRL97DceCPAbAKVBPtyU880Hhj6G1TyTJ0WeQw/cti/w7teAFRTsWwWLNcb6kriamuMmIkhne1GgTJKCqDn4+hsDY0I/lW0mMselig+GeJ5FFOOAX5dvpiP3xkwNlKS4ByE5PbWFIGoiL6gdaK7aHQjm4FKYCqaB9+kuvyQsHiA93PzK8VUqQ4H6vElF2ZHdaHYrC+5Wq4pChoK0TC11hIjDJPj7bXj0DuO3chx6Bh8z+QHotVYVTMMUQx4oscFz+gmJjdR2YhWdXakH09ujEqRCHOVr0RxWmtWTcODiyu+9c3v8MM//nt866OPWK9WdMeOz1+84Is3n+HGA1Y5dLTsrt8QuiNVDLRNnWUGZJLVlWW93bDerlmt11RNzQVJEPscmF1qy2q14uquY3MtzBc3OfbjwBSlAmOyiLfJBlqzPlQBYmOcWbEZm8z7fg4iSwWNwmxNM2lA2oGZhapnHcSYsj50OgW95yipUmzWGzYXFyzWazCGN9c33B09Xi2pFxtSDCxMYtvAtgHClN8gt3XkkIkM4Kj5WZwH0zImdanw5k07ZNpuSkqC1XkTP8dlZKxKgBpQMVBo/WXDSlngWSZonMkbpyl5CvIrBZtWo1TFoRvpBkdjDW1tWVSiBaXLA8iBUCooNuWh5GdQNmfEKXLygcPgeX03sR89k08SfMQI3lNbWVDqSlEbRDsMmJayUMm+rwlRc9dFtPYsGo0Pite7wBQNyjQYG1FBiXti1pLS9VLuSQyi/WpqCVjMhEEEyoN2EA8k79Ee2uqKwSe8TyQf2e8nWcxNrgbbCqMttraYShOCtBeMY5CEAAEcdRa6t1rRZOdrlVu+U3BYY/ARQpJKeUfFrndoIqsGRAF1hDiyMCIx4oPP9zjS1uLCXoKrFLMjfQJjK5rVGmubWew9xBMb4teFyUZVbMxDtNLUSrPShgtjaRSzSs8ckJYKahRDgEG/RHlHmgZSekS9XqOssLlJEphpmzIDPRBcJ88oeeLY4w87qu5IPQ5U04gdO5pxxEQvyVq7YPX8Q8zlA1LT4rNBQQieGHIyWIx58vgMuUJsjJH2GOcJkxf3ejSqtrhpoO8G+q5nGHv26RaU5ja84NZ9LmxjLZWGEp4mkBatpqbdrFCLhmB1BiLIxaicaBrFyXjglITPzyEHfK2t6LTB6yjJ9zzN7zOYq88+pv03h/y753O9BMRnDIIv78ozQ+lLJ4GaA4EiL/Ibj1OUkI0ELM65M6DgbG04W091BhiKEUsJhMlB4jkDrJzjvbMIgZA19NT5vTy/zry2GmoWFLDslLgX5oXRBmsr2sVKNICzE7DSWgClbKj12yrMv3Jbyp9fnliJ2eBFzQznU+Iy/3IW/A/e48aBaRpFL8povHM0TQMJcZA/HuZ7bOuKdrnE1BVqMYA+NbHFmIh3G9J+DSTCwxcsbm5wThK6qhJWh9UWmyrqZkHd1JL4amkdG4cO749iQK0rpu0VU/9V+MZH8M/+2W+/KavV3/wzxgiD9Dcdy+Wvf49/8k9++/sC/Omf/ubvKQX/+B/Lv1/8b/Df/N8AY3//9+X1Nx2/7dq//315/bbjvffuvUcC3O4G58Up2ReduSjmhTFpfIxMzgmDqapQ2mJsTaUn/KGXsTU6lK0Jj6+gkV1m8hB8YGU0i0XDOMnPtosVVkunzWq5YXd3YBwHmTdKui1G59EqZc3BHMMlj5sGYEMikFJAaXHjLvMsRJFR8sFjU4U1kMIkheMoxovTJGCs87J/V1VN20S8m/ApoA1cPbySRMWJN4PRFTevrzl4j0qiH9dUidomagvjFFF1halEK3xzeUmMCdf1+L6j2yculw1dtKKPqjSvXr6ge3egel7fB2PLs8nz+bwD4D4wVf6t5r/P17d09jPFeV2l+98sb33+EZIklliYzGhSpJcvSTERLq/Yf/gBNpvi1LVmdGJKo5IknapovOoEVYJlIjWKpGRfjSEJ7dLFHFvl9tYYSSHmNVMAJWH5nWLz2bAmr/vS1nsCg1AlERWQSpnMXjrfu0psScoxmHQ5nt9Y0ZjPe6CRDroQpWNx0dTEnAjrOQYr7eppJnMk70X73lYin6YFjI1KnpYKChWU6AQjYKzSkgs9c49ZqIrGT6wOe1Td4HWiXi9omxWPPnzK17/2TZbLFUobpmHI9+/BfA3KaNrLh9jaUrU18U2DB+gH0uQwQQyndWFn5/uUSEQFDkRDX8OkEn1K9GgOKTEkCFGAyWGY8DrO3TkqBVIUVpybHFotJLlHEWJgmhzH40BqhaxUVY14o4SSc/2afe9snP4KOJCH0xAjY1TUOUQqWowqCnApGJWCZKTdmty6WwCjqFAqA6ExoryjMENTjocxBpJ4vviQcvGJ3BlGNvHO4yuPMxnaZzHVHI+kU7GEE5CZgsQuOil0Jr1odZrTJa+TECdlU6KYu7gCYdYp1aQCyPnE6B2TDxmIHQVEdw4fRPopnd3kpOKMARR25pcjOZNjrJJ+6kz0SZyDQCct33tTMAl47KMUS3TBGmKaAfLZjCwbjZKBTLSeTQWNNsIkLoZf5T6pNIPwiZLnn8W+OR8ueXyJU8/1dhUFD8jPKMk6UKQTog9zTjAXezK5IiXmdcDHkI31yntnKQlrqaqWul5QV1IMlVhpvkkZsxBN1BCDAK4xSbEylnGlZtxpbtmXEZUv/KT9XEzbRFIlr5v3Yt/TPiEEsEwoVDpL/Zj87BKqyJR9eV8q42Tel05kEa31WUdfyflPgC1JCXvdaJKxIhtnrewnURGjSIKSwVgSs3eMVQLGjkrdu4XBuSw1MHDsjux274iT5LXLzSVPnj5ls72ialeYqs7nKM8v+Ji1WofcOW2oqha0QRuFtYIdg8g9+oyRpJQN5LQYm2ltxORLtBbkWSRyAc8RwkSMI0RHmCLBT0xDR3A9iThLa9ZVzXazpV0spQCBYFJxfmYyLvIiNKNHJyyrdE16QpTXPD70qZBibYU2lmLw95uO3wkwNkctUrGOCo0lOiUOoGiiB9+J+VVMUiHhKBtYUA1pdcGz539AWjwmUmNiyDmUgGGGgYvwggfNGx5+peai+RDbWpa2IahATLKAaizLxRLQHLuBX9aKN293pKln74+M/S0JjzI1ENgdJtzkZGJn4COmxK0b8+IjV2fOWgpmvCxPIIBFVfPB0w/4/ne+xz/803/INz/6NsM0cX13w6eff8ZPfvJjLtY1V5drLlZX/OKnP+H61WtanbBNzd1hj7UVxmjaZcvjB5e0qwVPnj3j4vKCuraE4EQXMFdsh8mxujuwbRY8aNY83W54st7w6fVbvtjdshsHKpU1fHVxFj3p9AqQGdEz/V/lSXMCYc8dgY3JFY2UB3sE0GBM1gjKXzRm3oDls+4Lcyng+dOnXFxcUNUN0zTxf/zo3zOEBdXyinqx4rjb8/yyYd1CpUbCNKJtI5uJ0lJYCWIMptUZSJtBD6UUlRUdoFJpV1mwPvoi42CodC2jd67KappmgYoGFUS/LHp3AjiUQSHU+GLuZpXGZ60vYbOeKPjl3kn1UmEXlvBoyefXo7ALfaJa1QKoFZC4wOGZTz9v2mXjUBIwu6jYHUdu9gOvbnt6tQRlJXGLk1S8rbCxFssF/QBeR2qtqKziyZWmOipqq7AqMk2agzK82smc01oTVU1SsGgMlwtNPxppQ0rSBkkDAYuqVhhbYRee2O8lqLUe3Syg2RCdI7get+8Z1lccphofc1sgFZeXLU0t4Oo0eA77jiFXiScvujcog60bmoWhVYG2NlidUMnjvWII4Eapag+ZXSRsoph1m2qOkzy3tk4sjObYHSAdSGpiuWpxNjF0Rw77nuryUhj0edFWKFLWChYmdiW6zCGXZnOAwTnuxWkMLMwF39n8CRVi2PXQVFxpS5vTtbJj65TQKWatMsUqKsL1DePxyPjuHa4/sH7/ParlCl038syrmlVV4YOn6zrcNHC1XbJpDL2J3Lx7QX3zlkXf07qJOka0EuOz2Daox8/Yfu0j+tUSRyJMDjcMlMVCa9FNTUm065TS1HWDXS2ptIEQ6Hd3jGPH+mpD3bb46Hn16S/565/+mOvr1+zGG35p/xWKij71spZoSfxCSqcdVEl7ZbVoMMuW3TRgdJNZX9kMoaqwVT6neD+oBKTCnANRHyP77ogPp4123rVysFaO9X//3/LkX/53kpDmcV4MC3RuZ1MZRIwxyrwlzfNWz0Wd8wVP2tasNbhpms/1nikNJWDPYaISdshms+H67TtmXTNjBATIsjEpkQXom5OxQ4w5iZF1r2iGzYGxBuH1lzw8QXfk+PoNDBNVDjoVJyZ0qQ5rrVnpR3xV/fBskMu6F2PEKs1iueby8jFf/eq3ePrkGavNBe1qhakbhr5n6Hti9LRtI/HC6WkgZ1b+p04AyRy4l3U+J0kx0Q8di8WSqm4oFffzQDuRCNPE2PV0dzvevfycN69fsNmsWSwa7u5uePbkCSlpDtfvePGX/xYITCmyffyQr3z7W6wfPaT6xmektpfxbwzj4Bj/57+L+/Pvk0h0f/pf04W3HA4Hdvsdy9WSdtHSNmIoKl0TAnyN/UDXveOw36OAqqpZby7oksNPPX97/P93pKTZH3pckITP2oa2aTl2PcfuINJGRlPZxyhlBYTwIjdktRhkjf2RFL8CgFKG5cUThsM72uWG9WaLjxWH3U5iXDehmwV1s6RpF5k1pOiGibvdAWgwG8t6u6Su7OwQf3Nzy3K1ZOh7gveYuqKtG/axw7lAqgyXDy5ZLBZUVtYNN/ZMIRKTxIRi9Ar9sMMYw4OLCxZ1zeuXrxkctJs1X/vmV7l+d0PX9YyTR6Ex1Ru82zMOHW/fvmW7XvHowQX1YkmMnrqpuLjcErHsuokYI5vNGuJEGI8Y5/j0558wOMeUEm9u3tH9omP14f2uhfuYYUSnohuY7v3c+U+dO7DnB3rvjU5638zJufz/HOwte0reRKLszykKo0kB8fUXqH/xL4j/9J9y/e4di+WS1WrNZttyc3cgBI1OmRmvArpR6BWwiTiisNZTzhOjxJEKAWBdzE7Yee9RKRFPGTzGmKyBmAFdL0aN1ApjRWtSTJUiKmYJssx8OwccUige3QKKaGsw1lDVZ7p4pWM/yfmQyKCtmIgd48CgNZW11E1FXTdZ99IgyrTyWKTV3qHHKV+GxjYNGM/oOzAJZRMoKYwnBVVtuaxW/L3Xf5d2o3lUTTzfGvTikn0ceLpZ8fDpQ548fwJJS6fOOOKmkegd0T+dx0BwI029wF48ol1tcIslo9H4uxvC8YgdJ8zoqGLEZEA2KQEpA+A0TPnvnsRdjOySYucjXfR4n/AevPP41kOT71+MTJPneOy5vtvz8NEDvAc3eaZxIrjAcdeRvBYHc1vdG4cyOE/Fxb9JhigRCQmOLrHSQlawSTH5yDJKMVoD0efW/zywtdJnOa3k8UrnhuIoIJhC9D5jhKCyX4hIU4qaRpaXUrloUMD48irzrpg5nS5O4p6khF2akKK7VhpbcnCjMBgU0lZczKgSEp9KW7EU0vp+EpPdDGUGVJYTU/gIg/Mcxp5hHJkmkVXUxgiTTp3iiyIBp3Vhup+BsRmIPDcBm59YXnJO0hIpD4VyL8pnpDmPnLvOzljVBfgUAFXPZlzl44QRa1gsFhLnnem6goCRIYn0RyinkT+7xH4zdqikmFDkgmcFg7IEmMJVzjltjtRCCLjkTs+S03WlzFQtS6hO4LMhckhSvo/5fCprWbQr2rqlspXk9ibH/KT5frsQCCngg8N5RxBsVtbLUDRhMzM5Aibn0CoJ8SgzhrU2aCXAYEoRpTk922IiKKyy+dq0hqiTdBrGyEzIBfT8rxPYdxoTGYNISYpEM+h+inFBZbwLCgGEXAwmKaLOWIs1RCwpCCkwBhnfpRSgkhjbViRqIiYFAnbWIhaqtDy7pAIxdbhwJKWW5fI5f/iHf8Tm6gMpIEdhuHsVswRBwCDM45gCVWNoly0pJGIIGSeRztRFo+inlAsn6p4kiNYW5yPekaVGhOGLl9zTjxOEJAx5kwgGSI4xTpA9WxQGKSQZ2rphvV7nnEK0jCfnOPa9yE4ZJTIm2uRCWN7MEZ324Ed8lC7Q4m+istyIEMOEeVv0Y3/T8TsCxmqmQaGGSBg8dTL4sZeLqSq0qkndCAHRf4mOaBxBNejNFauv/hH62XcZY4X3EQg5yTU0aWCdbvgKv+Tx9khr5SGZSqpyKgNr9WLJBx9+lSdPnrFYromq4vWrG/7Hf/mviOmvOHYH9p0XPDElEeEeR6ZxorB6yNWnsqKWRUqAmPONsLQraIyy/P0//iH/4If/gO9993sslwtevn3By5ef8+blC968+Izvf+c7XD7ZsN/v+PgXf83rly/QwWGbBl0ZXr58w/vvPefRo4dcbtcsG0u9bGkXFdqAC57j3Z6qbdBWAshjf2DVSktY8CM317f8R9/6OpP6Btf9wE9fvuRnL75gP/WMPms26dOmXoA9uRpmwNEYCfijD/P3JLmVqCzGE/VfOuVlgKeQhEUwA5dnbNvzeFgpLrdXNHWNmxw3hx2fvDmwePI+tt2Ke2qtqWupc3if5glbzt6a3O6hTd70hG7e7ffErE2yXK4xRhOSLNQFTLe2xs4VxjJ+8+arNdbUBBeZppFaa0wliXT0DmXkgmKuuioStlqirCFm7aQZiCmbeg7eEwFL5OnKsjBawEtrIBXTijNASUHuG5KRpjMQpBQxKfaj59PXO+6Ogc4pol6CrgExBYs+oo3CtBeMuuLlTeLdXcfVyvJgY3l0YVg1sLIBakXyiZs4SeCRW1ysgYcriwsRFzz7zqHNmmgcKk4oIqG/JZkFqmpRZkF0e/zYYwkoI5V/VS+wpkLpAejYX/+CuHwP217QLFdcbiyu9xz2PcMwSECbDMZW1LVlu7W0lUJbhQuJrnOYSnO7OzKNDj/JJqArKwLitqJdKdpFNnZSIvDfGs1+t2fojvzyTUdtGh4sn1KxIE3XfPQwoph4+U7z8t21tJppMZNISdhRla1wY8BN0FRrXLJMY880Dr91dfyw/Tv83vp9NIqHtuW5sVwpwwpFFcscTPNcO01KMAqqGAnjiHcTu7tbxtdvWD55THN1Sb3dEpcrUiU6UavVCmsNTb3EbDU8vOTZ1YbbH/2I9OoV+m4SJq7WpGZB/eQ5V3/0H9Jv1kwkhrHneLjD2orFco025sQQCWLUV2e9VoUieY+bHFOIPP3gA0II3Lx7xSd/9RM+/qsfc9fvedH9hE/Gf8vlo4ey8eZXSommWTCkHldYmdbSPNhiN0tcY2hUnuNeVK5lM89gGyfQtBxF56dEkoHEITiKy+15pp7SSdD/9EV5FtM05UD5ZJiVKAG6mg1Gzudu5D7YW+ZzDAH/pSTqvP3pxJhgBoeD9wzDQGGQhBTRMZyYUqVo48mGCZnZQMKiSVrPJkJD3+fWt9xel9eSORJsGurNBs8Rd+wxRL5T/8fUanWWSJUqniIkn9dUQ2UMi6Ziddny+Pl7PH7yPo8ef4hKhrHveLd/xXQ90vc9w7HjcnPFxfYK1RSt7ftHbiqbu7wojAZV2n7VzL5SBrbtg1OhKreepRiZhp7jbsfbly+4efUKazXr7ZoHTx5TLQXoXm82fKgtx+OeNEXc4DKgm/DRczgeef3FFywfXqG0ynpuIgvTNAu8rXByZ3j07CnXB09SGrtoefrsGU3VzGPFe4cbpvxvoW545/DeMw4jxlj8oWMcfvta8rfH/3uHToqPxof8Qr+l7x3e71FEttuW27sd+0PPe+9/yNWTZyzamhQn3rx5S1MpvJskmVI6A2xZs1BrHjx8ynUKdENk8h2LxZqqifgQ6MeBxjaM3lG1LdoaKgUvP/sYEwKb5QPWmyusCVirUUHAh+t3N3z7u9/GWM04DNjK0tY1fdcTQyDERFO3TIMYOTZ1QwiOhw8eYCtLjJG72z1kpqIbIy/f7IhxousDulqw2W55uFly1Tbc3B14+eaWqCw+RIytWa40x19+jFFweXVBu73gwaNHmR3c4l2gqiuSMvhhQEdFZSrGYeTTV6+5Ox4JhdgQT4whuM8/URncu//ddP9f6fRL6ld+6vQ+6Vff/PT3WWKsMhCrlBLQMhe3Iqc3Vd7DP//n8I/+Ed2TJwzDwHKzYr1ZM42esZ8IWGgirBWsAJtQUdqzCWA9qJCyDT0ZFEknE5qZKFCAIUVlrLQFT7lzJSVMZbOHg58Za0qfANb5fpxduzJq/kIizS3x8axAabP+XohhvnZpHddY5LQDEecmjuPAchlY1LXod84GKqIdWnZHXUBAkkguWSMmmwGUVbljS9hVlQksFobv7t7SDBNjr4h9y+9//w8wtQYT8X1HCoG7uz3DMGC0ojKJGMN8bVN/pNZGDHHqltV7X2e1ucTtb/CHO2o34l6/Iex2hL7HTJOE5kY64nyMeBUZlOaYIjd+4Kfxz3hzEDkXY7KBqwtQn4H/Y0DVJarzKDVxPN6xP+zohoFqYZkGx7S/I7Gnn2QuOx8I/gTM/V8+cizR+8hYCZtOJYmRY4igVTaGkiJ4DAGxbFJUMzInRSky4FNIAi6MWT5CzWXT5EReb4qJMQTxV0CYeRoBAQuhQToxcy9iYYtmc60EAlJFGU9GFBQwKWUNb5GgsqrKXQKQYmCK0tHmpkzEmAL740Q3eSYfcCEyec+U/+9jlA6CSu6B1ZrK2NwyPz81TqvHacKkYnqGFETmuDDHSPp086SAfyZLUAo8JdYroJFSpbh0Aq1DlnGYwy6lc9dvzWKxzOuYIoZIpU2WVIiznE5yE9ZauU9ana2LOX7KOEd5Kc6Y9OfP5mxMFT1UQLputZnB49KxpRR4J4NIh4Ce9W61VJ1K/BQT/eTpx4nGOSnyaINtalSd6ZXGoitLVWRPUtairiBMYmYosVTATUlA2cgsf3ECHwTIL4UGbaRzq2AKQjpQM46slELZE45R8oxZBzYmlJe5o7Qiei0M++hn+QSynKO8Ry7sROk4oZiZp3RvDpwA/ywTkfOVSAl/NZWp8LrCqIhFGNTRSKEukrvOnMPrkaQtpoGoFB6R6DClsBZFk9YmqJRF2RVVtaZt13THkYtnhkdPHqKbFZ6Kru/wXU+3e8fQ3ZLcJMZbrmc43nD35guqxRa3qKlqi640jprxONF3Iyk42fcU8ziqK4NPCecs1lTUphLcII4Qe0KYREfbaKytqbcNq9VWrjHKbXQ+8uZ6x2FwtLsOW5uc4wkz/th17Pe3QjrUYIyAq1rL3KisyMbIWJGXSQLAGwu2kntmrFSJYipm77/++J0AY1VINIcELqEGEZ83ARSB5OQio/Mk50XjsbE0TYXZPKd5+h0uvvEHBEyeD7IwuRRYcmQbXvJg+jlPmxvqkJiGga73rFZLmtUl2+0V6+0ll1dXXF5eSjKmpKp2cXXB1z76iKAsXileXb8kRo/3jpRkEfkyNf1XjgzmnWI2EcautGWz2PAH3/0B//l/+p/x7MkTjEq8efOKn/7sp9zeXFMbxfe+/10+ePaUjz/5a169/JybV6/ZVobl6pKmsmgN2/WGcXQcuo7lsuXDD54CjqYxaCuDrm5bOd8kQKfWlml0hMmhU0CFiel4Q9UuebZs2HztGzxcXfDJ9Wte317zdncHlSWUTSbFXCnIGjtIcu2zaH7Mro9zdSfGfJ8CJWpOCZTVJKtFwNlLS0tSeXNRZTsz9wJgWzVobTkOEy9evSM1l+h2jcfgB8/VdimGAPkwRs/yChJQpszgVYSiFUM2XwgCTmitTy6zkH8unZ53qXrlRZq5KqWk1bpdyWartAR1IeYqrMXmjYiEtL6kJMGLCnnhJm9gJrsq5kAzJRKRZZ1bgPLnlkQj5YVY5YroqeVLAsJujOw6z6ubnl2fcNEQlLBGoQDMBoJU2XytGaIiTIlKSeVa2Ui7zBVlo6lsojGJptEsXKSpNW1jWDaahY0EDIcx8dYnpqDQSpzrIwkVPSoeSHiiqdEqULUNCgsxEr3DjvvMJEqEZEhTT3C3oEV8fMeC8TBmgyXRN14vLHVjqKzGKMU4erreM7nINEa8TqA0VdOyXCraSiqoPiQRvFcV3gW8kx16nDydgmkKeG+IqeWTtwPxyZJtY2krgxoEdL1cb1nWNdZYPr8T1+fgHVpJElTANTeNjGnC+ZE4SxTkFrcvr48oDJpGwZU2bLAs0JgMwaqCvxfR5bMuQZEDCaiosMj9iO9uOR47ui9eUz+8ZPH0cWbKLtBVg9aKEEZSstK2ulqz+eg7uIsLplev2H32GXaaaNYbqocPYb3GR+kKMFqxXK7RGqaxy61AkaqyBO+z8YDOZiieMI2QEtuLC0JSvP7sE7749Je8+OTn7LodP+/+De/cC5wSdroxhrqqiSHQjV1uG82JqIbFaoldtNBUBCvOzDOrR5X6b6lAn+QNCjC7WixxbsrJrJiQSeyTTlWne8v76f9l7hbGaZmXMa99JbguX0NxAhAKmMrZ53H6+8S4OGcOnFrBVAY7pSAmYOk4TnPAliiM2DP2PCcgN+VziCQ8adYQmwP8FPPoFHDQ6PO2Z7CLBRfxKRfpCck5KlaolF2JE5k9oNGVpmorVqsVTx49Z7lcEpPD6z26Ctx1rzl+tmPsB5zrRQM9JIyqefzgGdvtitVqefYszhEUfQqI55c+JQsoJu/QKeVkSCRNhPnkGfoDN+/e4vuOqRezuqurK45tw+Ziw8Mnj+nHQAgwTRPH45F+gov1EqVhbFuitlhrWFUti+2a1XaTwQPFNE4cu463b98Ro6K9/XAmQCU0xja0yzUrq5mmwDgcJPBVisWipmmlCyKGxG53lKDRTUzZPdzWLd4XlsnfHv9fH8YYfvDd79H/xY943d8yrMQ5+LDvGLqBqe/Z312LkaSBzWbDxXaJAnZuYsoyNnHyM4M1hMDLz39JW7fUi8g1DXEAACAASURBVBVV0+bPqhmHjnHy6GqJ84rFak3wjv72mi8+/QR3ecGqUYyPNyyuVhhtOB57pkmSnN3dLmt6R4lvVBRjzbpFJ+gGhzUCnEihWGIjksFqw2q9ysYzsgHFJHuk84EUHXc3Bz7++FrAsgRVKy7v7TKzXKcBa21uXfT0Q2RwGltvScqgbWCz3XBz/Y6uOzIe9wyHW26ur9kNAy4logP38UByXwJOSxL7pWdUcuyyjpbadQEoZpbdORuvrK1nrLGiHVsi1Pxu+TNSBlQyGHoWO5aQOAlqiQqB9K//Neqjj0jf+x79UQwp23bJ4mrF7nAkNJGgBZ83Y2bxhQgeQhCgq8TgKeVYO4NP5Oem8nlEImMcCe6sJRgyEpHj2CIpkB9qDALUUDr8cgogrNscbGQG3myemQ9tNNoaYkhiKKaYgeoYAlGBxsxJ9jAJuaAyRgC5DHKXfDd4T7J27s2ISCxnjEXXGpMsOvYQAo+mS753/Bq10gx3PfHoiK7GpyNuzJ1gUd7F+yDzoh/w0ZGmI+M4zoOm399gUqBuFpi6IVQNqllhq4Zq+xD6A8G0qM2O1B3guMe/iUQ3EUI8XXOStR5lmKaRYZjkHmhDcBD8RFicQFSdRN0mhcAwDEyjx0/ghsTUe5qqoZ86nPNMLrDb78WhvrjBf2kG/DZmFmU4J5HvSZg8V1JmJGpCbr9VOacVKDADToWNN8+tlPMUUDHIGMgZpMYQAB0V+EjwgQGIWnRMfZ4nocQreT4aK14mOs9RpbK80unUUTGJwXQIWGuwuQNTK41D4UZPiCPBy1o1DJOYTmeJgm6IdKPIEHgvhamY57NSSEs8SljDRlNXwvMs9+qcFZoFHE4xFgiwiLm3xvyasF8AWn1aj8rXzn8vRDcTnOJZLpg/aC7AGGtompqmySw9LUCryXFqiS9NliopLFltcgGkxJhJnkk535TXwNN4kxshsWOW6sn5aDojLkRVTNhCJiacQms5j4pgxPQ3BS8xZIAYJI8YRsexH6j7gbYdGPqethnnQoGyKa8dGaxWoqWdlKZC5mBC4cyIIuBcxHuR55nJCvP0yUWns7hSTNYEkBXC/5fyAF1A67wXqVJIUmijmYikSfw0ks5dg7GYxMnnC3hdgO2ENdlPJp58eE6EuNOarQyyHscoeIDOEjBVA2ZAeSemVEoA+aQiQrd3qCDrv2iRR2KlsjyHxihoKk3VVFm3uqFZbrA+st0+ZnvxgP3+SPjFz2naN9hmhWlXIn0RI2EYiOOIRVEv1jx48JhHj56hqooUA+MwiVmthqkfGHZ7uv2eEEa0sbJ+pJAN/BDDy0Gefd8N9MPAOA6EGFmtNqwWC7QSIDuEMwO8XJxNmNN6opUUJZwTtmvw4B1h6vF+BMR02iiDQozyYtOgFgvpHs+FC50EoFdaEZUiKs3oYiZx/tppPh+/E2AsEewQS5k0V5Jz4qiE0hzchFWJRW25utxSrbekB9/APPmI5uI5x3QKoGKKKAKLtGMbXvMgfcG2dgQHU05kUZb1xSMePX2fiwcP2W63GA3j0IuWoU60bcWjp08ZHHRT4H//8/+VmFk9qJjbTs83t7NFqqT8ZfPLa5VWGmssF5tLvvL8A37493/IVz74EO89767f8fnLz3n39g1NU3F1dcGTJ08Yjjv2128Z7+7QfmK5WmMyGKdQLNqWYfIcjwOHRcfonGjVHo/UIQhLsBGnQj95aT1IcDh0jOOEdxNNXaGiR/sJoxRr3fLe5QWVhU1TURvN7TjST1PeqHMQmivjSiEi28nngFdlbY8wD8CkzlwGkfuBNaimysGrywLUp8BSJ/JidR7gWVwIHLqed3cHbHsJSlq6IGW9TkdZhFWucJUKI0lYufEM4Ag+oLVFVTloIgcCZTE+A21Kkl/aSFS+AakwW9CZ8ZvbtXLVhByEzfeLolGSROMqv9ssUl2GTtmk8kCqzHmrnZqp/DEH00qLxELZjKYEu25i13luD4GbQ8AlJecyL/j56pQBUyHhjBIpMoQhiErsh8DyCN5qLjcGa5NoJBO4WhuWrWFRG6xRTIPDRXAu4YPCRYuJFp0COrlcVQqkWdNXWniJmqQ9SgWS60TwnATBY5VBhyN+FN3RIV2RgrihVlahg6PyHVpXxFjhsfRDnFugrFXUJuuGakmKTd6UvA/SoqkM01Q0mCPOhbxuCGiekmU/Kq47hVINtr3AmA5CoK4SrRX5i81QMQ4K50QjzfmAtVKoCAGSjoTgJME9X0a+FC8XpsDKWDbasEBTkZOwORSe5eHn5HEePEVwPommmR8nwjQR+oE4DvhpoN5uqZZrqtUavWiJxqJMhbY1UWvs5QVWK2JVQQhMt7fo5RJtLanvGKZRNu1sAiMt9wGSIwXPOPX03RGlkA1QV0z9Eas0TdtSVRV3797y+rNP+Pzzn/KLNz/i4EfeTp/Sp0PWlpYN0VYVdQwchyMpM4KkbbGiXi+gsWQavwR2thQbZC4Wdo8EgPE0s84B17yXqHS29igK9fL0qM6Sm/uBcpFuEcaQuEIrVJYHiFkOoARq5wnsfC75bwF4T8lHSXTm880YgpikfWkoqdMiUhgm88WfsRWKHEs8+9x7gHDpP+OUHFcsWMYrcmrByl6wqR/hw5CXXkVlaxaLNYvVEnQimYhuEstFy5OnT6SFu7/ltrtlmEZif4CoGAYJko02NLZls15xcXHFYiGSJjGqedUqD+ceCJu1HUklMM7JRzQzoyN6x9B3uKFnGnr6g3RGRO9JPu9FMbJYrURXylZMQRO9ZxoiMXiOQyJ1B+qqJsTI5vET1hcrdCWmmc2qZhwnbj9/hdM7XJiYvOd4GGEYafI19H1PUomqqtFGczweSV6Kgk1TSav4XBgIuHHCT05AldxiqcwZWJQSf/izX2BVcWfWYsSpc2Ez723eS9FhIvG6qUgpfGm8SDFT5yKyd36WufjyeD0VGgLe+dnMpMgVlTlUxqexRjoG6uY0v86eqQLs9Wfzry5fvcLovyIh813acmuUqVCmorTyKaKwOLLRh1Yqy4TYeb+PCTCWbeeh7xm6A4vW8uNnD+maijYE/vjmFkuUa5km+u6YDV0U3nuOx07aPFdbrDXUQ8cHX/kmX3xxR3yneHV8S9849vujsJiA7rCnbVt2dzfE6Fku11RVzdx2aIxosM6TOOGmkbZuKFJQoscdmKZBYoUkZqFV2+BGxYHIYX+HIbK/XNH3PQ8eyjkG5zgeO3xI7PcH2kVDVYu22zhOOUER+aVxclDX6JBjN2PzPJPWu4vFhuubG4lrS1FeGYaxIxJZbgK3d3uqdkHV1FRNDSnRtEsBntzAdrOS+YZiconR5fbYyeWxqGiahu7QiXTX7Y631zd4pUihIu4D4S6g7DkIUcDYE4j6qyOrrBlnv1MS23ltPQMYyO8jAWAGb9O998pB5tneUeLH+9+f+x/KAvb6NVQVqa7FJOVb38ryMAplPFnaXYgCScl98RKkpqgz4zTNc7qc63lpN2WjtvK1uVtBU3xyZU7H/IWZUQZFk72sHQL0kmW/8n2d5+7ZHkMByPKem19p/slTbFvQq0TCReFDKiPdM8XoKJHmfSoH3VkyTKGMuGwbNHHybO7WPB0f8154yuLtDvduQjkt4OlykeP1JPuqUqSoGHrH4TiQVMQd9njv52uIbmDqIPqJKixRKmF0hTYN2AqMEQOq5YrUHYj7BSpEwn6HHwb8OBG1uJP08cDN9IJh9BJ3JiFZxEkecjpbL6VjEJL3DMcju7sDbgLvFcFHbCUFzxCktdZ7l+NU/h8dBVQKsUhQCNA2qMQyJKLJvNaspRlVeaDpfLTJPUsiayBhlzAdNQUQgRgVFQaThGzVh0QousMF5Msgky7jjghFDi9/XizjV0lhuOSfBTj0yeBjYpgCGjFIc7mrxPvIMLrc+o1osU+RwXlphc7t0+XIV5NNjsToqEAApcij1Kl9f+4g+jXx3T0wlvtAzSkXLPm1zOcQwnwOwiwt+rYyL2zOa3SOdwT8q6iqmqpuaNoWW9WytpzFS+U8TOkaUuW5lTl9du6ztFfK8Su5C/O0Zs7rQAahT8a3p7ityKiUv8W4sbyvFCiM1pL/hwzmBy9t5N4zTo5hmhjGkWHocdOAtQaTn82sUXFGVjB5ASrnLY/GoZQQRdz8bLJEQlBzsj6DnfN9y2+f18r7T7Asd2ruxCvjUqGwVSUF1xggGLk+ZA0u0jJzcJ9Db6UyFoLkhCmqWR7h3nXmD9dKCxGHhEoVhIjSlqQ0MZ9PJMf+IaCyubxgHyIJQYiEzBgpxYeqqWkWSxZhImSpm/XFFavNRoyhvcOPfQZBHamqCJOjP+4Z+yNGJ5arSzYXj9hePsKrBm31fM9DDEQX6LuOvj/inHSfG5MJY4jp3zT2jP2R4bjjuL9mv7+hHzp8mKiNpaostsjChSTdE1GIJSFGjLbUVe6A1QrcSHQeHwLeTQQ3kaInBk9KgRSE2KaVRqWI15pY1WCsyBFUJst2ig+SzCNzKsr+DcfvCBibUKOnVF5ciPjJzQldCh6lA6vlgseXW77x4fuwfcbu6gcct99mshuCE+dCH8Xxvk4jS/8F2/SaS33HslF0AarKzgH0s/e+ypPnH7K5uEBrzX5/SyF0WgXWaraXW56rBq8bzP+wJLgeMSDKSR7ncoX3QUMJUvVZwixVkeViyVc+/Ap/9Hf+iD/5kz/h+uaGL774ghevXvCzX/6Mq23DN776DR4/fIAOkR/95C8ZD7c0Gpr1iqY27PdHYjA0dU1dWw7HieNhRLPjs+VLEoHFbs96s+bBw4e02wW+C3Rdxzj2LJolt7e3jJMHNJebS0i5JbY70vs9y/Ul33z0iPeuLnm8veIvX3wu+lxTwCUBw0pCb7Lujs8Ue2MralvTdZ0srWUFnoWNydmWQsdW9GZ8QPnADJzm5x/jeUsvaCuavje7IzfHkerRghQ9ymiaxtJYhZ5FbpiB4rJBqBhkoc/fjEpL65yxmKqWpLNUlShxX168tUHpLMacThVsucSscZJORANZQeWljJ7/nwq2gbAVEqB0SXYySyOBIs7aSVBE2O9vDJD1hJRU1ZQyuW1GNsVxirx4s+f2GDg6TaTKYFU5twREUtbDUc0CYiBmvd6sjoIFDkOE68i2MaxXGmMSdRUwceL54y1tY1EIC/f10XM3BDoPYzCQamKo0WHCRI9d1vlGeQHVjBidSBAnhiBhEo3Isija9RUpdOAGIjsSmnZxwWqlaW0g7N5xfPeWQbc4u8bbS5KqWCxrmlpTacVmYZE2H9HjOvSe7jBIFTwI8CXPtIwfdfaMNcokVGy4Owo7fNmuWdQPYfBZq9dDijy/WOH9iAteAtphQiufpVQs2sjGc+6eewrDTofRioUxXNmaNYZGKVm45ylxJip/77fTbF4y/3AMIrMB+HFi7Hu62xvqiw3N9oL2wRXmYoVpWnTVouoWbRc4rTEXW5rlirhasfv0E3oMQ3Dw+hXRWEzTYJsWu2glINIJbcHHwN3dLe/efCGFLmtoqpbu7obLy4dU5hF+GPnkr/+Czz7+Kb948+f8xd2fMQjKmoPxhA+OVrfYxpJUg7pT2fhMYeua1XaNvVjhTVakE8oJdd2glJZNOExz0gdnYGdmPwx9P1f0T88c5oj7HP5TEvTOTyGdNLsKC7awFnx+/3PwVvYQcy8YPr33KakolfiTPtgp9hN2PLl90GSjqXwO6n7PxswQLucbE9pWM5BWmLOBAhaXhFXa3rQS48pS5l3ESz4IP8ha17LoResLiYC6btisLnjvva/xwVe/hmek9zs6/w5iZL1ZkCIMw57b23f4EOQztDBAm6ZlvdxyuXnE+8++TmXXpGRI2S12LpQpCYj1bJAhQHzRxZXnoUBp6qpGJQFSh+OeLz5+Rbe7YTjuGbqOj37/e5jVhYC3KXB7fc1qe4FWcLi9o1muiUOHGyPRGkKwfPriE9YXVyy2Gz74vd/j6QdfIRKYpo7ueM3N23f8+5/9O1J9ZPvggq9+5xscDm/vxWe3tzc0W2HsepelB7Smris2mwVNXeGCZ5ocwzBw2O9FIiklrK1YbzZiCpj1GnWM/Bd/9j+xVnaWSFksl9RNA0pkK1KE/jjgpok7In/2eEMIUza5kOQopiTuxFWNMRXdsaMfutzCmyiQlHcy7lKKODdyOBzY7w/c3R2Y3EkPTcalDN520bDZXrC5uJTuDZUQx+KzMRteUIR4Hv7oL9A/DviYaBYt28vH1MtLdHuBaTYQIzp5THLUlchyGJUEKF20LNoV2hpADCZpVnznxRH14hWvP/8Zzx5v+a/+k/+Arqm4dI7/8q9/ToOn3x+5u77ms09/yRgdyhiO3cDHH3+KtjXvfe3brFYrtB95+P7X+e5xgL9UdH915HW75/Zuz3LR0jYNw7EnXnlub6457PdsNlu2V1fSMlrVLJdLhhyjyjqgWa62ohfsRibnxKdgPOLHHlNZrIbldoU2lh4BJgOe3f6Ou7s1x8OBlJ5SVbLvTcMElWW337FYPWW1WaGMYrfbE9EoK3NkmgZQgUjARkXVLMT13dRU9ZqL7YY3b66JpAzYK4yupJCgLM8byzR2qMpS6Yq6sbS1RbOg9z3RTTx5eMUwSFus855xioyjsHcTkaYxbK8eM4yB3X7HmP0OqtUKOkPYeZI6cn/HLMuCdIJRAMOzdbqs31/+pVKQknVc3fte0V+kAA3n63b+vKLrSMyxgjrfpiOnXox0/+1ffI76/DNI4C8uOCgYlg261YD4KJS1OaUo5LoMWJXrS3kvOO32pyBz9mQoupX6/r6VT4/SwUDOcU7CObl7DHUqCs2cgNKPSLk783v74MUQ6VeqhBJTzrlB/p42ItnlsqO6gEpnrT7505QSBl/0XqSGVBKTMy3mn+/fPefD6QmbZcvqL39MOEBsN9gHWzaPn6OXCqEYhPyMJo6Hibu7nnbZ4PY9Ke+jioSJDtdNops89igVqRdrfBKZo7pqqK4WpOWGMHSw3mCqmvT2De7mmn66luK7htvxFb/Y/S8cJoVCune894QxYqw6W/+EoaaiIjrPYbfjiy/eolJFyHGyFGA9IU746DBGFZne80iF33R8uZhcQCsfk8gQZAvwLiY2QWIZnRSGSGm6T2hSCgK85rEYc/G/VL5ViujgMBlcjSpgkqIxlopEcIH95AnqdP0pBJGMsCa/5HNCiPO4iEj3UsyAoU8Rn7VQlVYkHzFemHHeB9woBnlFxiMhkh+KYu4q61Asup/F4yKdzZOUsNaegNgMOMYCTKpMxNI6a/ExFz1O3U2nGKscs0ZsSqJvew8EFEAzZmZxeb4xRLwLWVYkF+OVdJBZI4VnU9dUdUvdNLS5MFZIZCpfT8kxVdGlpeTgcZYfKfGW0nqWtiodUjGlbEoVs77r6dr0DFbmlUIS6fm5RVJm6csrZmZoZQyqrkFDHEIGZH3OmSKTj4yTox9HhrHHTX3WixU8oqqa3PR5ioO1sbMHi8kxtVLgrRSardWkpIlBSS4YmWVb5FrO5lLJDTI4l8p6zL0foZi3z4AsCls3+JAwIRKMFK/n3SEFYpSxXtZzYSzn5VzLO9tsfl6+ceqSA6FHcDKOQ4w5sYaoDUEpmd+Qi3BBcLYEEZFO8FE0UEMmHTa2prI2Gx3KNVTVihAmVpsNy+2G7cUFy2WLMTVSFk+48cjt9Tv6bo8bOoxOrC8esrp4TLt9AMayXIopoA+JaQxSwPIT/dAzTCPGRyrLjKGEGAWM7e7oD+/Y373g9vYlx+4WP3XEAMvGYnLsauuKlAyjcxy7jsOxw2YPDyEE1FDYsVPP6CemqZ9l6BQiNYqWgk1Mon0bfIRKYXVFW7UUk7EyfyKnAuLcwfgbjt8NMDaBm0SeIEWpiscokgRNbfj6Vx7zja884cHVmsViwRQNrxbfwy++iaueMLocSATZ2Ijx/2Tuvbpt2a7rvG+mSivtcM4++Z6LexEJig0iTYuWKKtJfvC/tP+Cmt3c/ORnukk0LIIgCYAAbjx5x5UqzOSHOavW2ucSzdIbC9jn7rBCraoZxuijj95Z+bdcuN9yJt5Rmx37DhCSer6gKGc8evYpj58/o2malOi7DlNohKiT2PhkgDRQl5qH5w+YL065W6+JcciLbA50joK7lCSOE1IgtEGXBlMaiqpEGcWnTz7h3//Fv+Xf/Hd/Qes6vvj6C7788kt2+w3f+/Qpf/LTT9FKs7u75fXvf49y11yczCBWDHZAFyUvPn3Bbrfn5vYO0VqaWcAOPev1Hb/61ZZ5U4MIaC2YzRt++tM/Znm6QgjF5ftrduuvkVLSzOYsVivOz07x3uHsQIyBoqz46s0H3n54gxeGP3rxCZ88e8H722tef3jHF6++5u3dHVaKpDfiD93RwhiElNhcWZb5Ht8DAsZ/BIjKpEXcO+LWoYJgEolWIMqk/TEeIQTeX295fzfg9IKmKOiGLbWqOZ2tMCLjBSQQxASwdkiBSwjs2x3GlGhTgdCp/USm4M7lYtVxnCsEaKmQykwtp8SYqy7HG3VebKVMgViefFIZpDLppJA5zE1BayAZOol7YymD/HmpHRPfPKIOgMPxFMobZWFMEmmPqarbucA//O49t12JRYPMU34MlEYGbiC9Y8yBukji+ohIlAIpC6KS9DEQes9gI+JtpClgVmv+9b88Ay/YdZH13tP2ntZJBiReChAaakO5OsWEFu3WBLsBLMJZCB6hDD4LoyfNMEBohO+JQ0u0HbTXlNWSQgtK73FthxyW9FcDfb9G7F4Rhz1RrVDNI2ZPfsz84hlCKQYbWG967m5afNcnF83RsCMLt6cbnkAGrQTaSIqioKw0hU6GZaWGSomk8+N69v0OXZ6hNURfEL0GNsgYeHF+xtl8zu/eXqWkWDRU1oFU7PabqUVqOsTR/MjHUhkem5qHaBYIDGP6M60yx/nMWAU4RGxHlp4JaB6SbIJIjNvGg728o/9wy+b3XyPP5swvHlIslujZDKoq6TBJA9IQZw3yxTMEAmUKqmYBMbX9+BCSFMx+y36/xvZ7gu2QwqHlaA410O2vwQ7cXbesr98RLPynL/4Xvrz6kpt+Q5tTOpk1GGIMbNYbvPfUTYOQCpt1lnVZUjQN5ekJncxiYXmdCD4mcDInxUV5MBeRgC5LrLUwVa+PgNj8GoyXMHLvb4LDHjD+ZmSajkH8OK+dc/cLQrnUHUhBqzHmnvSA1pphsIdNPKOP4/yXOumUjdpbISd0I5tH5iDDuQNrIoQwSRikMZa0baezFyKbuxwC6YNmGTThhM/8vwJGveyIj5YcoSCzMVt9rnlwdsqnn3yfF08/x5gZve2421zie8fm7pJ5M8PZPc56tptbtIwoIZnVC06WF8xnjzg/vaA0NUoaCJowtsSKfB2OWRxTcWrUiCXJ6JCKGQKw+x3vv33N3c0V3X6LEfDu91/w4tOXnD56wD5EVmenfPv6PUoZHj08p+o6Hpye8vrLL/jt3/0tKjhc31HNGpqTE06evuBf/Nu/pFmdYcrEuLJBEl2XEu3Nmps373j1+9/QXChOz1aU1YzTlafILecAsqiIOPrOcnt7xXLZsFqtqKsCrQX7fU+Mga7t2N6u2W23PHzykGbWUJYV0hSYakZd19PYvHh4DrstMQa0jsQwpGuYx3LdpMdLJHOluFg17HZr+m6PcxYhBHUzpyhqTFGgteHskUlzZEwuMsBP5GAO51OBKSXAAechuIB3iWE6DC2276d2aiRYZ3F+wIYBF3wuZkYQR/NVaLSq0EXB6aMnYGZEVeEpEAGMEsgIwgX22w3zKnV4JAmbPhkhxQqpC4zUdP2eUloWy4JGPGY1LzBKTdevEIbNEHHFkqGWvFp/yWK1YrlaUJxAMAt+8cu/Y9475ExTzSr03HD26DEv2x0DHZfrX7Lbd8znM+bLVJwri5L5YglCcHt7Q9/3NPMV82VDPVvSzOZok41WpKRaPsDEgaHdMrRrgnf07R6tIkZFNlcfqKNkdXbKrCo4Wax49PiCD2/estluuL3Z0O17YkwGo/OFx0u4vr7N7vSwWMxym3GfNGNza7VzDmtTgq1kiXWR/nbD9fWat68F19dXmLKkahqqsuLu7gqlFdWsYT43bK7XDDvHrIKT+Zx3cU9lNH10uGGHEg6jBfv1LW3bcfLgIauzh2y7PbosePrJc66+/cDzlzNWJyfUVcmHd+8pF6csH76k/vQBv/vPf8Xu8h0hHAGM4hj4yEjCH86D8lqXjK/ivd2XiVmfX/loPIoJkJ3akKf9e+xYyU+ZQFtx2J/Hx39E4BD/2/9O/NM/ZfiXP4MOVG2SbqgRRHOfARyPgILj2HoEmqbHjfGjAF1kI5+jJ0gpkzzPuN5HkVjmkyYskwrSvdh0PO0/cG0PH/uo1Tp/jZci5OsTCRRCTy9mYyoOVmPMPT4zBrw7Yt5lOSEERClAKoiC8M0l9ne/YbuBkpKh80QGVj+YUcxKsgU3WsCb96/ofUN0A+uvLzlb3yG7JPkSQ6S/fM/85ARPoNu29O2W+eoEY0qUMrSmImSZJ0yJaJZUy4eUz3u21x/YfvEr1te/pneWtXOse0+kYDZvWCpB8J7Lt9f3gCNIjC7nIoP1dJ3l8sMVZdlgbZ8AR8YYgFTUF0kWQkayTrG4fyP+Kw5B8pZw+auQCZjyRFwM2HA0osb8ISZJtzFfQqbW48ThS8GXzPMkELEColIEDU7AzkW2XbbMEuNZpPhvCBHlAjpLGEyM0kxaCfEAnAYiSg6T8WjX9RBzLDgyhmMCyEZAUuX2bxsifTscvX9ylvfC3+PdKJlMc2X++4QDEKYCOjDtkSMmMMZ+MuvoqrzXHHdTwSHeu9eZFDNpZ1xr8t/GOC/GmCRBsp6m0RqtNYWpMGWFMgalTZYdiLkl/lCAH+NjsmnxNP6Cp7fDFPvGQAKidZLbk4is0SyztAEp3w7nGQAAIABJREFUlz4qoMgj9tXYtQSghR7TLYa+xxpN3/d0fdqDyG3fWmpCNmOSSiOjyNqpIZHHnE0xfEhyF866JKEXfJItmcg0Izic/SoUlEWFCgLlB4SMBFyaM0KAFHibSB2jbEOKn8f8K07yV0Kk/Xq8dlP8zGhWls0js9dM8AFtTB4TDrwjxAHvUmEii76keRvJslqZuJEGW+54+giwHz1mRkCdrAWs0xgPUuG1YvAa6x0+JnQ3xiThZYKlAEqpaLPMYlE1LOqa0hQszx8kxmq3Z9/uWd9taHdrlE7EgWHYI0REyiGvDaM+80DwA9Yll4R6cUZQJdvOUVSCmUxSAUZLilJhVTLBcjHiYwJCY4goMTZtBJI2kSWGAeLA0N6xvXvHfncDwXP94S1FUSSfH11QFg0RwTAkP42qqhi6PevR3DgGnLd4bxlcx36/wQ0H3w2lE8gqEw0c7wbsoNC501ZpTVEU0zqQwHCRCTdyWgP+0PHPAowNMdAOiZERvUcFx8sn57x8/oRPPnnM6aphXs+JCroguN427Jsf0usHWGGSlEEQuBiIYaAWG74323MhB6rgJ6F4IRWqqGhWJ7z47HOULuiHHiH6xJgVESkCPji8s4SgWV9eI1TFrKp4+OAB2+23OCcmF1NizAvy2OLkUximJLoyFLMaCgNGEQrFYjbj3/zrv+DzTz8lBsfVh3e8ffea07MZn33+mEcX58jQ8eH1N6yv3zNsLjlpSubzOhtKJcbio2ePuLlb0/mem8tLjE46HgJz1JYrcS5we7Phr//Tzzk5TwyM3WZD09Q8ef6MpqnRhcaUCpNqNiipMGUJRnN1fcfV5TX7PiSt1uh5sTzlew8e8u31Fb/48gtudjusdwhjcvtnYPB9GsQxEEeGZYwEH7Oz3NhWTwYXFGVT0+dKn8oLnzKSYCSppz0d1lpud3s2A1CtEEojhEfLSCE94BKIGDM9XaT7KbQmBM/Qd9R1g5RkUx+RGF8j2BJGo4WRlZcqPESZHXHHoJB8z1P7mBTjfzMrddzUclIwCc3DxC7wwWcwNs8Fnyj0KRDJgudH/6b3S68iRz2cmPGHSJbYkLn9wxO8Z1aX3PV5EhBgkjk4EjJJJ5/OIfhDRVeQAnIh6fqIFQItFE6Bu+1Y1elvgqRfrKXAKEldJIOvENPvvFSIKlAZge8sfRdx7Y66lMSQdIGCVEhdJ4B8dDtVScVSlh2yaGBYT47RWkLlbgnDhqF32K6FfktTBKK7we4c/YcZmCV90AwOrItJozVIJoYKJC1LIykLRTMraApFpVPHe1Uk2QdylStVhQEk0Ru8m+FFQIgz8IboSmwXEH5AikipNZ9dnPH7GCiqBVUzx1RzKpEZHveyuO8mjTMU50KzRGUg9n6LcDIkSAPKB38vKfvO2BmTxBim9kQhJZXR1EoRpWBzs2Gz2SHKElU3lGcnmNMFukqgT5AKGQMuJLZplBJl6hSEKYnRJQ9XS4J/wH57y/r6He9ffZnYXjGBMu1uy+3tHS5CG2553f6c681r7lxHnwPcFNgf2N/ErLebtVAFoIuCYjVHLxr6EoI8AI0xxsScUUnjxxQFujLk/s5pviulUgU0B/j/1DEZex3tpek9ju/FIUiegtzpHqkp+B51Go8DayllNmQQ2WRMEULSrNNaM5/N6NoOa5NGGDEJiXh3kIUZv0ZgNs3lA5h6DMRKma5J13ZHQy9OQacQgoo5n/Azetenx4sCLUsGm4BBKUAXhmcPP+F0eY6UYF3Lfrhh1hjqRYE04P3A1fs3vL/8hvXuHU7ukjSOXqXGUmWQKIKLFEXDyckjzlcvUaJARJElCcagN4/nbCB5YI8k6smxsYRtW24vP7C+uWa3uYPM8F2sVjw4f46Qmr4dUHWdqvNVhdvusXd3bNo921df0e53XC2+Yr/ZIIXj/OlDzp48Y3b2gGpxQlEvGFzk9nZN337AOcez732GlpohSLqdZb/fH9acKCjLJadnFaGeTaDEv/izv2Cze8fth/d43zObVzhr2To7sTHS2NDU8zkvf7BiNm/QOrkGC6WRRTmZ7UCk73rE0CXwWhxLGagpXinLIq2lIsmLNLM5RVUTBRRFTTNboKRhNNpMCXBuHZUk0ONoLHs/mvhAzIUu78dElPEPB6dsshN3CJkZk11pc/C6vv07/uav/1cAXn7vR5w9/NdJv1TpXEhLaTEiBerRJ4aFLgySBMhrkQp8IgZc38NgUVrTVHNmxvLgpKR88DzJ1hiTr55g7xXbwbDvBzZdpFo9YraqqOclhZLURY3vB9abSwZanrz8hN3dFYvlgqfPnwOe3a87fmO/4eYm6bOuTk45OTlNrt1di/eRsqrp+464vkHKgNF6YtjHGHG9Q8qAdxZnO3xw6FIjQmIjd25NIDDsrkFIvAucnp5zc3lN1w9cX9/StpaodNJO1JqTkzlfffmKqm6omzlKS0KwnJ42SClpu57tXZuMTmKAKCmKmuVyxtB37HZb7GCZL2aQ2f3eBbq2TVrgLrDb90hTZc3sQCEFFxcPkWi0sMRhw359RVPWmDKZ5Pz273/B8vQxi4cXnDysGYaAHyx361t26xuCtRhjmLvnzMwnNCcX/OR/mPHqN39PPL0Edum6eUdSjcomK0cFpikpkh8XwQ875QSI5N+N62LqPjqs899pNT4iZowAWPzoNUMSb51+N63RR/scv/oHxM0N8T/8e8LeQUfqIisjelYQxdjSy6EoMp3GuOuLnAwmMG38fjTGctYlpiOSel4RQm5djWOMEIk++x2IcS9RiKiSSY0QhzbmhNDe+7zp+6MEVIxbaFqHU5fRkZ6mILHj82um/3twJNNOKVNsbt2075XZCT5kwCvYyA+/eMHJb99QXA8U84aX33tGtIKuFQw+g4NCJmAqKnov+PbbPdvLLWq/5anf8cTAtxJu8/3orm7w/YBpamRRcLu5SmShukEXFSYDjEnaLCDJXTOlQZ+dca5/TPubW27b/4t2//ukTyk8fuiYLWbU8xplPW+v7+7JuggpE9jUW4bBUTeR4Ae8t3jn6GNEK4NWBUpYlAyUhWZkcxJF0j/8rz1iugc+go0Rh6CWEhVGTwwSU9Gle54Y1/5+2JTBzxHBT48DpEwFusy+dDi8HJL3nBL4o+ePR9ouAo7IQC7mM869o/ecii95nsnE3AxHDPejKcnIAk0A7fG6IDKDNc1HIUEjsXl+jXtcijHGl44Hyboxdj0CVO8V8D/629j1lM7V5bjmAPBOHVkxzxcpwftscB0nIHZkt4pcaw0ZbBVKTYZOIgacdznmOFwrmdeDENO9kkdAqlISU5gUa8UDBURMX4dOpBFIlnJEzJjOfUTB06mk3DJ6Pz3GO0dwkSRBYRJD1WeCngxopbFuHIOJhRuCT1iNd5lI5lDKpjVfp3haa/1RMS1fH7LEhlYIryCm+Eap1DGZ2Lpx0iyeXkOMJKEMxooM7OerIXNb+oHxLIj5vfOqcBgfMmQGd2JQj2WYKJKHQcpT4gSuygxYInJ3Qn6dsQNOiFQcGNnt0/yMSSpSGk1UkqCSVupowiWyRq53Dm17lO0psimWkAbX90nmQ3bc7beoEDDGsCxWlFXD+lYy2AEpBWWp8xxJHdcIgbM9tm8J3mY9aMV8taKeNUiTsIi+zVrjQmCMSlrB+dqS97EkvUjeR0KK96XIEoWakIFZEVPORww4NySZU+dw1mdinKKe1Rgtk6YsDusGnLX0Q1pbrRuS/qzt8z2TOAd1bZgMCIVEKIUuyiz9oZOVYSaNHJjKh5z0O8n90fHPAoxNm75DK0FdFTx98IQXj1e8eP6Ip88eYQqDkhV9AO8Mu/qCffEARw0oUlONR8WBSvVcVAPfP4mIKwi9JAaVkrooaJoZq7NzZvMlg415lyCBE6SAfgSiAoGi0EmfwvWcnJ8gv5YH7CQvgFKMFTuISqYEqTCYWYmsS6IUKC2pqpIfff59fvi9zzmZL+j7lpvrK06WM5arGSerGU2h2d/ssLs1DC11oVnOV5SVTrpdPqJMQbu7I7qBZVMRHz/MzqhpS1A6VUq1Scwga21i1Ky3ybmy6zk5OWG+mDNfNBiTKy7Bg0hBhFKKWVVRlwVawLDf04U9aElZVzRlwcvzh/gI7+5uudqsuV7fZV/NcTEaNQgTQA05qOUQxMZp4RLJ/XBeE5xHZlATJQiZGj4evbV0fY91GlUYYogYBVoERLTEmAXV8/+SydUBWNXaHILwaROVjMLzQo7OlgftnylgJAP76ckjFpqA1QyIqghKjO3PuTod86vl6tihFHmcCIjp3/SaudIqBeJ4Dsf0z6gBNp2nSFW4EdRJbSSC5aLiw6ZNjKOYEWhx9GJ5LE8/j8ZkYzIhUoUvCgkqbUbWB4JziJgWw10XOV0IqvF6CMmu1dAF+lxVV0YmQDQqrCgAQfAjyBWJzqLKBVGY3LYKENI5K4HQEeF6nO2RMrUVOduDB2MadHmGbTWuvyRkVkWM0A4w+IjzcWKMCCmzBg6UpaQpFYWKFCqilWNWSYySGAWJjBKmJG4czVEIQjYOjMETZFKAlAjQHTFaIh0CR23gfDFnEAVCapQ2xCHp7N3TCOO7y3UhBHUWnhdTYHM8HI4SmPt/mBKgjwYPkwRD/p1WyZUYASYE6H0yTWx79t0esZmh6hpVVcg6gbRJEzkQbA4ehWJki8rMgtVaU9UNVd1gh56uH9jv99zd3fK7619gg6UPO27sl3jnGGKY2r3GMZ1OVFA2Ra4u52AaEgukTKi5yy6mTLjpfWBb5DklZdIJlmOwLgQ6g1jOHhKX44R71FINR9f4Y5mC4+d8fCSA9cCW/bg9cGSwCiGR8r6cQQghm3KEaa5Md346Rw7B/0fvPa19uUiTJBkCDs8o0wAgo+bMfjJ9NkNF6RfIUKX1WEqkhMWioSxSJbyuGz5/9jmakt1+w/V6TaDFBstg9wy2oxCKvmvZ79a0+w26tgSSpEtdznhw9oTLO0cXdgQfsNZRmJLoR3fTtJ4gxl6/+0mAOAZpgXa3Y3N9yeb9e/a317S7Dc5bHj9/zt4Gyrqmni3oB0c1m1GUJYJAu75l93rD+uaaYeiRRHRZoM2C00cPOXv6lOX5OfPTM4QucFHQ3t7RD46bt2/Yr2+IzlIXGuc8u7sbrt5+S7fdTYmRKSqMaRiKFCsc8pW0bofoaZoaIaDtW7xLmoim1BSFSXIcZUMzW6TRGEMe01kTdtrXwNmBgqxFKlL7m/cWIdM4s5nxAoJeSXwoQAiU1kilKasZ2lS51S2DscRpzBzvoSPkMrKVVRTT7qn0YUzmnR5Ebm2MfmIKiVwkCVmfOMZI8MtpHNezOavTMyIiG4UeFTtF1uj0muBTh1MyqRiNZiJSi4NumHMoN/BaerRUfFaVWBcORdEY2fQeGyU2F2dXJyvmjaEukotuQeTF43N+e/eO9nLDByylhNViTgiBqqz49OFzrl9v2LQ7NmJLVRVst5vE4AkBU5jEIs5zvG07itXyEMCHQLu+hkrnriWo6oZmdYLtOrrdlnazARmIoQChsDawOjlhNl/grGW92WJ9SJqvOdlfLZc4+wVuGIjRU5WGytS5OwxEdjOOPmZvhGR7MgwJaE3rfMQU+gBmAPt2TxAq6XqXJVKU7Ddb7OBo24F9G4iupe9tMpJVmsVqgUDQ7ltuv3rNOr6namrcrGF7fctuvabf72l3WzZ3dyAEhZmj9QyKmvLsgtOXA+3KY0cwNogJBBZy2hCm8RqIWXP9KJYbY8GjTWPcg+6BKB8BsuMaPl0EcXiFyVjro9cd161xrT0+Yoyw28Kb1/C3vyT+5MegdQIioyMqAUYeGbWM58MhER/Zsjm2PrS55j0vJlmw6FOjcN/2B1mdGKd1doJdZCrYxBGgFfn1GD+fmB56HKyOADAj2BwP1yT/AFEQgyRK8BnITG+dNEBt8Omaj9csRFwuaKpQZGmWiO40iw81zb6iHDyVCDTzClUKPBHpUmvyGC8RBc5G3r1fs7/aU+06lq7nInasdOoaGteXum6QSPy+pV+nridhLdE4gnIQHZFE9BiGHryjbuY5r/CoQmOqGj90WDrimN+ECD6gIpyfnfD+ZnNv9KncfTfem3QJPSEMONfhbVJsFyJpKsoAhUkyLKMPUQLZx7hvGuaHdxHflUmKRFxIcgVKysRKHQd4nisie3SEAIjD2jmJ14x5TQRIgFP06SOHEIk+IHxARyhk0okN4vgcDt9MO0j8zl/zjzkPGp8/Jmkf7VUwnlacQG/vD7uTyCCWUlmyjUSYmT6ZOGiAptc6ijE/iumSVomYLvuBVMA/ickcQE0xPWaM3cZ9WpDnlB9NXEeQOIDPoHhMbf/OZ1BcBAgim2UlOUiZJemM1nmvTeMrCD/JaYmj95tOOF+qMBV/DmAhZNkB7xHHhl5jHivGa5zGxygVQYxJ69haXAgpl4qjDku+jvkrhGRa6H2W5ArpyzmfzJeMT6S+SWYpr2fycO73xlBmB6fugjHOiYi8Lo4dZamDJ52rEmp6kTgiGxMxQKTnT6DoYQ1JX1kblUMon2J+hVQ6dSyocBhz+RKMhrpKZVNlMeYwh45kGHnoYhr3UaR1NWqSbmxREP1A9JYos57+0b0V3iH8gHA92mrQmmA7YnB4BL5vk8+AAEek7XrarsUO/aRRrGU5fR4pde7sDelvWoGXNE1DUZQoIZPRtpYZFAalYG8tMaa8qSrL1G2c97CYx3fqYPdIPCI6YuiIYSDiEEKjlESZdE2lTGa9Kl9jqQ8Eq3T/PR6Xwf00fktTIIxBqSKBuDpJfqULlYqa2lRIXab4KG3Ied0Y1yPBeIekOGaJf/f45wHGAqUWLOc1Tx6e8LOf/oRFI1gsZ9SzCo/GoRkoaOWSXf09Wr3CB4mMkKbGgKTjQdnxwxPPy5PIh62gdQobzVQhX6zOePDwMUoXxKFLmiqCKXBTIi8+2TBjebJgs+m5u9lw+uAUObYWcNBOSiz0VFGTRmPqEl0V6KYkloboPaVSnDRz/vyPf8aLi8cE67jZ3LDfrXnx7DFVpdEyEvoWv9ugsTSVoVQ1i+UpiOS8bl2g1oL3b18jhWZeNpx9+oKb6zvskMyAhBJJV61MGhZ2sGi9S+1nLmvuKI1UirIqaZoyJ8F20jr1WbNp3tQsmoa7Xc96vcMUGpxFh8DF08ecfP8HfNhs+Or9O37x21+xHXoORlYp4Qo5uBNIdL5+IR4MPyaAQkqKWZMW6AwauDAKqB+WnK4b6PsB79MEDc5RaUmhIiL0iKCy+HdyUEQkjR8pEqDYNLO0AeVFKLWm5Z/FCASJMaTIK2acFtA8zRKAeBwjRHL7RGbtKTF9zrRpy8kd9uOYaARRhEyAaswV9hCTftDxkfbmMdgZjbpG50ZJ13VonSQVCi04XSrqyz3WR4YQSNoPU7qQ/zM1nKV/A4mlkB8Sgk3tKBkU8dEl58kupTbvbzXLpaYo0ucuS0k7KJQWtH2gdx5pDLs2YIOCYoZ286T/mjV0cQNGiKwbNS64Y7AhQBQYVeD6LVpEpNb0Q0RGaJYriuUF+13L7tuBIAZQM2KxoPc6tWOIgBTJFEcZRVlI6kqxWmpOG42JDmE7+v2OSpI25iiJPh617mR9KZG+E0KCTGBzCJooU4FIlxGEB3dLDDuInotFw3Wvc+EmaVh5NwYCx4nd/bGhhEjB8NF4S+PgMH5HWspxAPBxkjkOvCkZmfKnA5swxICRApM1hgbbsdts6K5voCxRTYVezmnOzzFVhSxKYnR4EmsmFVgCfSvz5hSJSKqmYeg7Nvs7Lm8vub695dd3f42N/XTeY8wnElxDzvezmoZgtpzjnUdEmaroRKRKrHq0JMiI8OOczZXWI/DWe090EV2ZVDATgrbrJt0gJSVDZt1+fIwaYsf3ZQQ4//+Ojx/38c8xMjFZj5MEKWXWgHXsd/u0Ht3LQb7bzjb9+Qjwndi2ORFPgXcybzKU2SxDYmLNxfDDQyAuBJ5kbKBUFu83mrOHSxaLgqauWDQnfP/ZZ1x/uGOzuWa9vqLjmuANbX3C0LSJaRk83qdWJREiQgaKwrBcnnKyfIx1luDe4lxgs1kTHgcEh5ZVkcS/OICxkyjOvfsige3dLV/86h+4+t0/olxqP2uWc548/lNeXW/RWUO4a9u07oWkUXXz9h23b9+AAG00uq45eXDK2bNnzM8eUK/OwNQ467i9vOT28gO3Hy4pmprbt29ob6+g7zDC0/WW/W7HfnuD7YfUgVEUlPUsxR6ym/YfIlx/uGSzv8L2O8qyoB9auq7HDhaBpBEVpiipmjn1fMVssWS3ucMNPd7b5PQ6MuTz4YKlVirtfVqlglpmByMkfdcxiAEnJbdG432SOJBKT+Dr1KUhSe2BkJOlwygc7MDYrZHyjXyvjpg0YxIfM1gjkAk8DYEoD67AI+M25dZHyQyk1sMiyfAkCRIHxKlFMhW2UtIm1aE1bGTQxOAguzcH7xj6jt/EgAdeOEfv4vS5QoRNZ5PGMAGjIs2yYVYotIyI6EBGHp/WvFWet+/e88W71zy6uMC2u6S15h3Pnz3h5nbD7/Zfc9lec3e7RiuB0ZqiLGlmpwn4zwZkw2AxRTm1csYQ2N19gDBH4DN7+YTzh8/Yb9eEELm9fI9UEaUCPkLbOc4ePGJ1dsbt9TV36w2DSzJAYyF4sZgnloodCM7SNCVGVXRdRwiesigpio44OJQxlFXD7W3L+m6Tr7dGKIfKHUhj8att95SzFaYsKeoaLWC73tL1ls2u5+a2w3Y77H6HHTzKGE5OTyi0ZrfZ8urb19hug++32F3NehjY3FwRgmW/vePq8hIfQ+oCUxobBUIXLJ69ICzeYsmGb6om0mcn7qRzeY+hyRjWHffHHABIMeGH4zo6JmA5Mszjaly/78vXHPbmMaFnfI84Qio5jgtxijfHNTyMsd1+h/i//wqePIbVimgMcQg4BmSjkUUyHvHxqMic3ymGDAQJICY/hPFkY2aYycBEFPBtkuoZzbKSEd4xk1ZQCoXL4AeRbCYT0hIsJfGf2AtHIkEkg01jcJMvRoxkQDjnHVLmISqm8/UhJHMmmICQpEPrEbanKQ0BQdUbHn1zRhh2FMrQVAVNPWO33hEcEKrEACfN82Aju03HN79/hb7bchE6HtJzGnuMUYeOBEhydiGy26zpbq+p5g3SDuBKovaE4NDR421Hv9vi+hajMtbqLKFv0VomgDMDklLKBPBajxscDx6cUxbmni7lZLCZC1VSpNZsb3uc6wjWIlUBJEk6E0CUihBUzl/SnuB9joeIWRs43nv98RjBpRjBhaTdq2VyoU/xRybQTE/I/X4ZVA9jUMk4Hu8FrAlaC5GRsKpCoIiCRox5/HQiOf8QTAPo/sj6zljLp8MUJE1DaARkD3PuMCMPGrWHx4gDWBOT0dTx3w85bHqNiQ3L4f3Gz563u+9c47GYc7xfSynvGagKkXTwpTom78SUH6pEHBiB9pSXxsNlyTlGKgLHwz7osrmXSMBdKk5AFKN3QeqYk8jDuhePYssYs3nUgfEuosxyeyk8Cz4VwA44dX7c+L5HtzN1y/qkmZyNyHzuPiRGQtaQTaCzI0QBPmKdTvqxPuB8Yvw653Iem+aKmNbFzG4VIuHjkRSDxkBwFjsMqbgTwYdcGILp8405TQgCrVM3o7g3BMeBk4rMMiPPIndvjfc5ZWkpyRkLEmG8z0qjdZHIXEi8SvFKIuCmPciYIktNJGwq1+LydAvT2Bfjf8d5KAUxpk5TqhLhe3ADWDE9f0z1VfBEbxGuTx1LWhGVIAYDUSBtz77r6b2jswN3mw2uS2QDKQVD3zFrFhRFlSRciiRFkWQANFHG5BlS1SiliSHmvEIy1ui0Egx9kmjT2lAUZmIBh9xZmcaII3oLYYDQQ2iJsYeYgFypJWVZJuaqKjGqQGat8XwbGFnDiVWer4eSSF1QlfNkLl3OMEXSWkYk+c3gs6QcElPIjAumLq1jnemxc2RiwMuPFoOj458FGCuAn3z+CT/+4af80U8+wxSGvuuwg2O3dZR1QZCCu7DibXzK2jzHi4OLYRIg7jmvW3544flXnxZ8+4t/xLoWoSWFKkFonr38jMdPnnNy8hBrA1hHTObtY9feNHmVFJSlQVjP7mbL5uqWi4unGFMxDC1KRaISFHUDSiZZgsJgZnUavCK1eSyERmnNyWLB91684I9/+GPWd2uGrsV5y4vvPaGUSRBdBEu0G05nsKrO8CHgQ8QoiVYz2laxbx0fPqzxTmC9pW/vmC8Ds3lFUayICNbbNZv1nrZtEyu263jw4AHb9R0ITxSBr775GhccLz99wfPnT9Am6YMNQxIvLwrN9d2axWrFo6jZf/kK27XUxYxSJhaqdB1npeLho3N++OwJP/rkE/7z3/8drz584Ga3xQomjamxcjm2V4x6NVP7V4yplWJib41BrEii7+NgiZG2TdXnIBRGpsrl2XxGIT3Rt5RaUhdzjJRIUkvDWH0SQqJMOQWHPqRgzxIIqGk8TottPG60OoQXCcA4CvDJwSSpzd+FSJWFH+SILDHGFWH6vCNcFSLZsPzAwACJGrvYcyCl5GGyh9zaKXQxmdcgRNItiZk5KCW1UpwsSmxwDPswfa4jd4v82UZNxmn7PPobSUogQFAgdHLxDS5ysx74619uuLmb870nNRenBecz2GwDKsBOSu46yeV2IEbJvCmYVxUzUXP94Q3buxu6/Ro/DER5Q/QBby3Bd1AWaKURSoNUDEh0uSDGgI2AKdh20A1LjD3DFYZ+BaHfgdAoc5LUGYRDq0hTKk5P55wsNE0hqRTpPkRPGBzO2yk4EDLk6rFBT4uomMblKDwRM1oRR91UKQh6hZESMTQwXBPtB4h7HtQCtOXmwzscFmftJBI+XfKjmApSNU0jUoGC+387fqLMA+yQDKZk6R4g8p2niTwPArZv+QlGAAAgAElEQVRPLpLB+uk1CyFRRUkDdF3Pbrfj6t073FdfUczn1IsFq9Mz6tUp0hhi1vlx0bPb7Vhv1tzd3nJ3e81+2/LF9ud80/7tMTx8/+xiDl6PgkoBGKU4W63wzrPfduzaPUxhViqkBee/EwACkxHfGFRJKSmrEq0V+64jhkDXdVnmI5I0jz5KUkLIrTKH3wcfjkDU+wn5+PPxWqf16OZOXvOmW0By3TxU4odhuDfPj3UB/ymweHy/BCKkQMBaOz0nxOwmCoeCUFT8qPt3qXkqazX7OBBzsa4wmmZRMF/UnJ2cMGtqUB5Uz3Z7gx16rC7ouxbve0S06OjBOkxR0+iKWVlDBFOUFEWF7A0xDoSokaLC6AVVseTHny958+4L7u6uGdoO72wyYMh6VscD4vDpPx7PuZAWHPQtxnYUOSnBDcmczTnWH96xS8svb//xV3zT7YjRo4qCB48f8fD5J5xePGZ18QQ9W9C5kNd2QbSe4AKXb9/yzW9/RXfzjj/+7/+Ckx9+xvbmjK9++V9497u/oyorzs4f8PnnP+XV27e8/TbJkzTzBV3XJrBjBIWAu/ffQrFBREvbpvumlUAUqZI/Xy1pFuecXzzj/OIpu7tbun0LJWiyaZdIDILx0Fnn1RgzjedJHiAm8zupCr5YzPn9cp4uSB5fCUQZd4EDSwYxtuIemIEqt6mPDJs0FnMykxOpcXyGkN3PcxtjcvIdb9+Y/LqUqCvDsSTLVCANh8JFjEknLo5xRE4ek9RBkulJ7CBS+6M0JCWCSLtLumfv9nt+292wWC3w/nQ6VzsEZmVAigHjdzD0FOWMqqoRUdMOA+HuilMj2KvIq8sbisePefv1lxgpWM3nzE7O+LM//1P4VrF/u6dtO4Jf4mWckk4BlEWKE6UI2H6YuiWEAG0Efbdjvlwwmy0YrODbr98iENg+MXeNc9ze3OADCF0iReTRxRm+b3nz5i2vX79nuVwiMsPDe8FiccLt7ZphcKyWC05Xc7r9gCoUq7MVkOQ3jFY0s5Lbm1uGITBbnjBfLNnvroj9DqEVAcl+1xGRSfZAGd6/fYcm4m1PWWmE1ixP55Sy5t3rjru7wMXpnIuHp9ihp92TNGwDFCZSyJbYbRi2V3z17Suurq/YrO9AK1xv8bVHxpjZXgf9UoTg/JMfcfftG7rNFfg+dWzlnDlpPZIKU9NT8q4xIgqIe0WzCLkzYXxset+PlvzE3slzI43BnFvE+2v2uE6PVcdJe5CkUTh2MAgE/Mf/SPzLv0T85MeJAGLBrS3CeNTMIMw4O/O8dEfxxPhtiMiY2K21NhRF6ihUQmGUoTAFhckAXgjgwe1bSlNgyoLNvuXm9o5BRKyMWJVyp9yihCyTlNhB8zMdKRY4dJhNHRrTcp7AZHxi74VgoVCTMdB0HQkIESg0E6kihkC/66hms0nznRiR//i3rIrHzDnFv2t498U36FlJtVQ0D/L+FyNXH2549/Vbtr/+NX8iLRemp6bDWtBNcgaHNE6++n9/zvnFBbOTE2ZPn/HVP/waO3iqhxcUZ+f0w0C9CFTGUJ+eYm0NRK4v39Fu18ShR7iWu23Luhvo830ZO3K8t8ToefronLmqp/WtGwaMTAVUgWV3e4Xte4ZhwA59Bu9dKtIYTV2mc3bzEu8jLioiht2+Y7dr2Wx3ecyKwxj8zpF+53zABY80CgaR1yuRDWBHDcSjQTau87ngM4XMEZL+Zci8pUNR0CAopWRukmn2wR2DMd1KrzUWp472nf+WY5JtOPqMYxj1cTglyEVrPxouHU5GHMXLqQkk6fsjxJSzptzyqOB+DLrG47ZzOXVMSSkTU3gkEcAhPjiKicdC/YGVPDKmBVWdjJXI762NptBFXvTG+ZRM9Xzw4AT7tsvnO55eWuOUVJPuLuT9dNzvRcI7jmWi9Pg5hMjF2DHePuTuB31VMYFSY2zsrMENWfvVWoIf43qZWv+FZmLhx4TT2FxgiCGFLpE4EvYnxm2M2TMiHCJHkfcMO/R03Y593zJYj7cRa33q/BAHHVwpVfKzCT6BcF4jVZZuGGPOSR9VTtdsBGmnaZALUT74LIOZRrsUEq0NSgiiNoiiJLGAc+daZMIvRnKJECKBsYyAbJzGF5l1Dj7rDI+drQGhDUaXlMZTuIi2FqRPkg1ZzoqMTeAssrcpN9EQZSrmKimRDnAe1+5w/R6hJCEIWtsTrKWu51TVLJ+hwBQVQiZ/HlUsGLxgvd0huoG+b2ia1KGtddoDu7ab5B5SM7FCqKxd7ZIcpHdpXHo7EG2PxKFE6nCPMWCdpVYNVV3QNAuqogIfJhPcEH0urmQDUglaFVRVTVPPWC1XrB48o1mcUDUzqqqiLppkMOkt/dBz/eGa7fqSod1hhw4fIn1vJ9a3yvKaQqmk7R3+8Nr1zwKMPTtd8T//T/+O+axBKsnQOwabF10ZGZzlna35oM+40o9oVY0IPYiYGTc9pVjzZ5/PeNHcsn3zD3x485rZrKIsK7QpqWanPH78krJs6IckIpw2CDikGylwCoGcuEbKqmS+aFiezNkoiajmiNgjS5ClQpV1YmbJpHkzAPN5Yl623R4jFad1zY8//Yw//9nPkNay2dyglKKpS7Q2RD9g+y3YFkPPfFbTdz0hpOB0t91gvaMoNBcXD7i9vuPy8jK16ahk9HJ3d4UxBXVTszxZ8vrVW+bzBUVR0HUdt7c3PHn8kKauQEg+XN7Q947LD9cUhebFi6dUVY3WnqG3bO42XN3s+N0Xr7m+uiP6wIsnD6kqTVkayrKkEp7Y3+HcnqhLXi6WNH/8J3zx9jW/e/OK3756RecgykMgPAzDAVj4aBcMId4DEKbixYjIkG6X7fboDJIljYpAUxpmRiGcQ2mPkZZk/iEIUue9dKzwjoBI0gyRMoI7aJQcKoIHUDi1GzFtSB/v4OLoHENITqcDnkLL1AYgEtiZNvMxCQ+4fkiaf7kKKjiwVidwKge407KediNSFpvqbSEzIVIFLbXJIpio+Oermm7Ys961xKhy4DRmJ5J8IRl1XsZPdfhvDiKcw1pPrOuknxWB4IlWs/MlN1sotKMqDUY4FjONNgoUFJXCRehsoOsdN16w9Q1DWSKKRzQqEPpdMvMJjm67J3ZbLBbEADJSVSVeGoYg8dEQyxUslgxqRhcqIgKx+Iw4s+m6Gc3pXHCybFg0mlkhKclMLwLCxyN9T4ksKhqdW3Nzq4zg0EYOY+BxaJkY9Ud93jyEMiAzO0EYpCrTvep6gvMUvuXU3PJVW0xMxemIiZtwrESajDTC9Le8ZJH5Z5lRmkdHHG9pqsI5l1m391Dco7ErBdKopEfokhg+I3tlHGsijY5KgFGGWhva6HGbPXaz482bt8SiQJYVGI1XkjY4Nl1Lby37Yc3fXP2fOBewoT8qrdxnBhwC2BGiOgTfw2B5++Yti8UC5yzuSActuXhLdEzti+P9GIN4kQt3I4je90kfSIgUDCbWvJzeDw6MEZ+ZdALQQlLow5YpJAh1dC2nbz8O/NPxh9a9488/nsM4Jscg+A89ZwzOj4HfSXPs6CTqcMrT4afj6TFJL8SIkhqDwQiDNjU/+MEPWZ0sMaVi037Ahi1NnVrnb+4uae2Grt2hZIGMJW+uvsGIAm0kVVmx6SJnJ49ZzB+gdQ1Rs1qdsGvPCLElyi1n5y84PXlEUy8gpC6NF09+xOMHPYNrMaZBKZOYEOGerspHR2SSVcmDf7464cXn3+dvvvo9erRL9JHN3RojFO+/+Zq7y/eosmR2Muf0wUuWp+csHjykXq1Al/gIt+3Au1//DdvbW5r5nNOLR5w+eYoqCs4fXuB2W76+esf6wwee/uCPWD14TFk3/O7/+SuCAKEMZXNKcwpn7jnlTCaZjt2WsqoIUk6KMVUR2bkB7z1lM4PgpuJhUVY8ePIJ1fIBuqzY7vfcXH1IQGOE0XSxqusDAw6ISjO4QMRTlgZtzGSmOS4JRVlRNzOquiFmQwzGRGyaizCyCWJMyUMkFfNCTEwWmc/hsLceGIf+KLnUKicV0607vEfMTJjoh7RcRVJL9PSBUgsjcmQDhalF27rEYuUIkBUh4OyQCyFFbi9PbzwCwqYsUF7g7UDb9VMHRKE1P/7kKXb/gSAUQ9RcXr3i7ZsvKZoFLnjevf2WWbeljJazsmQoS+5ev8b3e4qywFQ1Ty4uWPc9L2+f05Utv46/pesHCiEQBoYAp2cPp31eSUGI98rPaJlYal3b5mRmhqlnCYxRcPHkKVorrHWp28JHnHecrJZ02y03V1d8+/XX/OBHP0IohUfwzZt3nD54wHbfst1sGayjdx6lDSIENlc3nFw8wLY2afK5lsWiYLvb0g0W7aCYP8TpOQRLsAMu9Hz2wx8lZrUUEAa0kYQgaTvHu3e36LLi/HxBd7Ki3a05WWp2d3d07UDfWlYn51y8fIm3yWTD7Xb88hf/hfV+nxgpMYKDfrennFkKrbBBZvAuJz7Ak5/+KYuzd6zffsXNN7/F7rZEmdaHgPgOQyVOiMfH6+tR91amdB3jqlNr6tHaP+r/aSHy+j2arkSyjtcU2yWwNr9uNnMc5W+ijBlUEIif/xx++csDgBQD8fkz3P/4l4gidfoIlRzKExNHUkpNrQoWRUVd1Ek+K4IRguhtMrZL4qAp6ZYuRRc+UCvFg6h51Cw4W52wmQ+8uinZes+ewD561t5ikUm72UM/eDo80h6il9AN+Da1sBptEnFFHBVOuHcxgYi1Dp+72rx3RBem6xC0m+Z3Ao0d7X7Pyw9PObtZIWLk2flT/uj8J5wOp/hXjmHbsZg3VLMV1fKUqqi5ubzj+ouvab/8mh+LHc/0npkCZSTu9IzuZEEs9DSeGgFFjBgp0UVBKQtmRQ26wlGANZQ+YkOPYGT2JU1YGQPVvOLK/h904ZJ2GNgNDikEdVklGRAk11fXVKXGHHUBegfCJgChbTuEk7kYFbLJn8ieGXnNjUlyqg+SbTfw/vqOYlYlA5u6oBsGhsGmtfU4RonH36Z7k1iLKc5UIv8csjCgSONaZshsBDfHfsJIZPRUScWGFK2mDqxMFBERGQOFkixNkuGyQnCkGjCd0X8T/vqHQoXvPOjwommvE1Ps7HPcLEQCpeMYM4VI2/YUukIbiRZMaOk9Fv0IOkIqOGSChxQyu7gfPz4dzrlDUQEmsO/40FpPe5+WGlOmHDcZd5VJ/oxxvxU5Z0jnGAUTE3YKAI5efwSWlTJopdOaOrbHi6mZPcXNcQRCx31+HFARRh8UOHQPQ5ZZyeDxvQ6DMMWkk2TfSCYRY0v/yJAfXyrHrz5p/47muN47ZNCokIglAgnagIooeejKHeN62zvCEAiDz1KPflrgA4KoZC6SpnkhhSKOnZxjunycJ2e5w3GNS5hS1gTOxK+xUD2SQyY2r8jeElpNeMnxrZIZg5i6kIKfcsBMd8+gcNK89X6UnUmv4XOXiM6fQyhDMCSgHohCIXMfbkGkIVIS6YMFB056emexIWKDx3qLD3aiOsc8v2Oe70Kl7oKIQBcVUkcCknL+iGZ5jqpmRCRKG9oh0NkkXabwbDb7ydg65ikW3fh5DtdrHD/WeZQqqOo5iESyCYNPBmNtT1G0nJ+e0lTJe6msijTXVZJbM4XORn4CqRRal9T1kuVqyWK1pJ4tqKsZRpppfQshspqf4PtH7Hcb1utb3rx7R99vU2zufTaDT3q/6IMZ7T91/LMAY4ui4PTiCaZI7sKb2w/TZIkIXDDc8JCNPGdQi6n64lxumXEdL88l52aNu/mKr371C5ztiKFAyf+PuvdckizLsvO+I65yGSIzUpXs7ukR3QCBAShg/EXDC/AV+Ah4NhppNJqRGBphBsMoYlRPz3SJrKqslJER4erKI/hjn3vdI6saM/w39LbsqPBwv+733iP2XnvttQxFOePh1VNmizU6uU/H6HG+x2LEgGACY8WgyGglIJ0KRAaca2jqLSY3mFgKGJtrVC6mNWNljAm8A6IY6jy+uuKTZ8948uAhKgTKUpgqRoPve67fvKBQA7MMysJijSVkkmhra6lmc7wb0EZhjGaxmHF3J4CbsZblckXTdBzqmrppRN8pM+Jwl2Vk2TnOuwTUZcwXC7QxvH1zTde33NzcsFjMmM0rWaCGgb7vqQ8H2vpA37YYpbk4W1IUInyvgOilvc4NLX3bkLuBlc757HLNIjesy4oXNxvuDnsOfcsQPcb+cKeM9wIDNSVy04IUPnxPQJ2YtWRGTLhM0qcyaUMYQUaNOgmgx82J1AIhTDgXHHdNh9KWqiiobBI1D0mbSifTk3g8TloN5LeEt05BNhwZQdOmPCazacMOnqFrRFvNZrJhxnDcqDkG/uOCr0fQgXGMMVUzk/o6wrxN8g5RAvSqsFS5JtOBPjqmCzwFfiGdRDqW0icgx3hf0jiXeJ0sVWe1VmJqkllcUOxbxftNpHMxtfgoZoVBu0g9RBrvadqB1gVctGRlTpFbZqVlv68YUvt+ZA3Dlkw5VEr8h+AlxjMZIauIZpVaEi0xiiSFySxVbikzkSFYFIbFzFJmSuQNQjgW89VEThFzm2iTSLqAHOMmp1NgMAHYY8DFWOmPqb13/LMiIu1jPnpUcQWulsQiQm7hohjIzI8lgRPkCoBTij5VQu3J+E3f5kcfEyChTvTATnOfNFe0FS1qkYRwx+AtHWM8ThifV2CVoghRwOx0fYZhoG87Bq1oNexj4Hv/G7pQ40LPYZCW2oQbp/j1fkA66nHBEWQ8ng903pMFjwuit6hSADhe82OwqKfEYGyfEc2ndGVjFJ2wcVLCBEyOjIXT7zQCnIF4DwSW+XUKm8PENo9H9uCH7WgjKPzh4/Q10rKVgOEEUscTYOD053gspY6s+NFI6YH7KdZbijgjc6Xsh1lBZqXdO7eGWVFQliVlUVHqkqurR6ADrTvQtFv6YYdO2p5d3bBvdgx9h1EDhPcMrSO3JUPf42koCstqdU5ZzlHaQhRpmPXynOhb2iFyvnpImc3R2Am0M0a0l3RWoLWFZLxzGrzL2U6L4j0wZAxw87Jk/eAh5WpF2G9k/wiB25triuWaarWknFfMz85ZnF+QlxVZWZHPF5jZQgDOweFcw9sX39JvbqjznObummHoOL96TFGWrC8uycoZ9d2GrjlQrdZcffI525trtq9fsDvs0S9f4LVhfX5BsRLzSmsNR6hSHs4N2MxSzOesLx7S7LYE70S7dTZjefaAaEu8cwytGILJXmdRSmOznLyoTlgZIGm0O7bEhXgsNqYxpZK55mRHPuqXactknqCO1/44VmV9VKjU6h1T3+bpniFtXCPudazxpZbX+0dEtOYjE/tCnxYGT+53WjsmwCoVjKb5o47jRMBp+T0mtqEAZsIw0TFSW/hmbvn54TDNZ6UUy1lBH0oG34AbMLsNeX0g9D37puPV8+8o+wNP1zNKA48uVtzWjmK+YLlasL64YLvfE7KM1fKcJ1dPeXn3jkPdEJRC24y+G6gWa6w29G3DbntHNM2khxtjpO06kWdBEbMCHyNnZ0v6tsD1JYVZUu9rFjMBdkLw1NtbsIjZ1XzGfrORYyoDOmcIhov1Amtfs6tr7m43LJdz/NALKGwKuqYV5o212CzD6gFblKAtDpjPFxRFSdvU9P4ApqOwKQkzBpOJxlrWOQKpgBkCQ+9RGMq8IBLY7g503UDTOYl3qwU9HfVmz4tvv2O7F83bkXUZiQlkHxhjwWlbTg+7WLF6XAijpZrz5uvf0Ncbou+ZsttpuBzHzSnQ+qPr9lhJvzd6jweTcmkazVrcwEdGVISpU0zBVFQYASxSks4YlgUlBlchQt+ghnZ6b4yB8FLBf/oTQVhzifeNMZRas8wKKp1TqkzampWie/aM5uKCJkaIXsDbKEy5mNpH9Lt3mO+/4/Bf/SFBRdydY9vWtMFz09R0MTJE2QtzFFYrohZj2yxKB08RTtagwUMvpkHeBHSRAFmtptbT6Sqegg8BuX7a4hEQIQYpip/O9Rjh8tsVs0NOUTvmhwOfPHjKsqykGyJuefKzB+zf7ml2e4ZewWXFzYsX+LevWbUbLu2AoQeboauC4sEZ1Wcfkc9n07gws4WM/Qi+cxSzOdX5FXH9AFct6X3k5m5Lpr34V2RW2n2VZn5R8vAzzcv/vEMZcb2PCtzgpb1ba5GRiZ4w9Hjj7wlBDi5wqAduTM1Q5cwKLWAZ0tqrkiFvjKlwG4NItFnJBdq6w2Yhdd7djwk/ZJmO62skabtGMag2Qq+T5+CoMzmOx3EOpJhqSlPG10xrdIr7tDT1qhgx0VNoTXY/3Zj2nA/rJD+mcfvD507/W9173fHvavo+6TYzSjqM6+8Y/01YI+B9mAC2KQcci+DjgT74btaYezvoGFNOWqun7z/5nqdxvDnZ20W2aYyZhUluklnVcWEDxAtTxpiR12mlJ81Y2YnlDo7hsNYCvuoRDB73d8Y1UcDY0XuAKAXXMR4ffXSOd0CdLJspDglHqcKQNNO9SwWikWE8LtNap9zKEdVYpowiPeRdMrbsaduWvCgYgfG+6475ccjAHuUCYrp2RpkpBhpljkbwj7S+EUUjXSmF0SZ1oabrN8UpOn0uKVY9jic9MYJT7m9k/moEIA+etP6qiTluEsN5zGPG63jUCU7yUXE6m6lgQNLJFTxK4rKY5i9KAGZvDJ3RuMwK0z2mfSsqgtY4YxiS4ZdRSQpncHRdR9P3tH1L29a4XrwsjM2STqwhyytMXqBsTlRWDCtHw7NoyKsFxhZkNgct0mduBMFDZHCBfujvEcxSe4lcQy2xxMgCj4ydUGkuWIvNckC6woq8oJpVIllgTCr6a/q+x7WOuhGNaGMM1awiy6SjObiA68XIS1uLUZZgRhBYxlXvevzQSdGQiLWaYVDikT7KwciGfdLt/eOPfxJgrLE5+UKMGbx3cmOQBQ9d0sU1O/2YxpzjTYmNEBh1Kx2l6vnpA03Rv+Xuzde8eP4VTx8/QQHGWMpyzvnFQ/JCNlfvRfPBDT1a5ZioBfgkIobBARU9XdPQ7Ft2u1vqesPm9g3oKFpNuUZZIEkSxFFkOjm4KVQSBlI8efKYJ4+uWMwq+rajqgph9A4Dh+2e1y++ZVVq9LJibsWwwtrk2qYUZakZnEmLwgjEjRtBorgbS9/19H3HfD5juZiT5dJqmmVVckhNSa/WnJ2vaLtWJlfTcH39ngfqkuADXdsxuIH6sEcFj9XSqlNVBWUpYvHeObzrUSoT/bWmIQ4t5eKMR/OSB8s5j8/P+fW3r/n6zWvebO7YdPUkDg6/HZQ4bu8nm8rJ6yJeJiUBE4IYlR0zPUAYNioIKCMT+QNmK2lDAVCK3jludzXojIXXZIscw8i+CUSVJA+moHm8msfvnLarKWBWJxHJUWPWoRjbwTzRO1TMx9g7tS1KNH4KMDEe6oO5rECYYwkgFNfSkTkkZlPaKAqjqXJNlSv6dnQYHRlKJ/dhXNwj3JcxSCekNSRtUBUDxkBuFMu5tFn0TrFtJIDMjRaDLhXJLfR9wPU+Md+9SHBkGVVhmJUZeZHRBEPXDDgVxTE6zqm0Q8VAPwQO+62ArqZAmRlBzabvqLWAnGWmWM8My8qyqDIKo8i0nFdIjENhj8hGN+lPpo0zpkDhGGeFBPybaXOYroxiqv5F1PGej46nyoKZoQtF7HcEfyBEYWqvc8fZsmBeFRy24y3+cFzBoKDVkKc/nY7049g48kyiUpOkAT8CpESlUoCj0VaLk2nS51UkQsOoBZjCMJkrcQKxNVHmR/pCIQQ639HFyI7A+7DhtfkNndpJYnXarnQSs45Mcfk9XdvIvTVibGsyeY7XCi/L3gnmc5wYihGokWNNQvhpQk7r5hjkajWBqsKyY7q/p4Cq0jL7nR9Or+QPN9eTzOHDlrr76x4f3Of792hsP9PJwV6dgLHj544B4wh6lXFBbgpZm1PB5XH8KdZlKKRoUmQF56tzirxEK02mNfNZznxRMV8uWFUXKKW43b3n9u4dN9u3+CAO6ZnN6duetunFMV0FYtzR7HfSUp7WoKLIyHPp+hgr5WVRslycEXwP+47F7AxrcgEilFyTAKBM0j69f43vjeGTdek0kZoAhcxSLZesrh6yjwOEgM0LuZ424/zJOfPFkuXFBZhc5HyCGNapcFw7iZH2sMNt3tPHSLu7I6RWy2q+pCgrivmKZn9HvbljcXHJ2cOnPP7pz+m7hsPNNW9ffc/8/ILVx+fkZwIUW2vxcTSpYAom7SxjtliwPrucWKHKGAGKi5JmcPRdTd/uU9B/NH7Ii1KSsRNDOZXiA2ICY33AGDXNA600e63pUJzKAk1mXWnfVONGFE/H7nGdGpNKCTzjhKqM99CMXQTj/DhJAI9JcVpTleiRSvvufQ3cqXATmY4/Gnue6qofE3qdTLz0iQSIP/lc6Y5oreJNZvjFrhXQIB07Nwqd5RAQGZP9ltnQ0fkAdcuwPdA2Gx7Nc2bzBcvlkvZ6y2w5Z3m2YrZY8vbujnK5Istzzs8veaye8MX+C7p2QJuePB8AYT9750QnONZHczKEMeWGgTwv5JpqRbVYYDKH7wdyDU0TKMqF6KtFz+HuFu+F9b9YLLh+f8PgBiIaZXOULSjnK7KixPkb3r+/4fHjh/Rth7Ga2XJBW9ci62JMSk4iRVURTCFtd3lGXpUMQUEfKWaS/Nk8wxY5WVUSgyKGWphm0eHano0f6OoajUindIOj7QbazuF9ajt1geZQi4asd/c6mnwdCLnodEoB8chcm1YNbSjWF5TzBcV8Qd0O7N58S3/YEH2bgAM1jctpHeH+qnw69sbh+2EhRT72OG44+avIcSQkZ2JSTeHa8YXh5D3p/1WisUfGvXIEweS76/2W+Jd/ASpS5IYiyyhtxirPOM8qCpWh0DTDQO166j/4A+pPP5bisFFifKUUg+/xTvZ38+1z7K//BvfsiobIDSJV5Im0MeJyv3oAACAASURBVEzRrUFjHzylyAwKI+3rDjQDhT+uQVmAzIkxV3AhESRg1IWb1pbpOiomAUNIDKvx4iSAwch7TFTkfcXFyxWZMtjoeewCTy6uKLym9Tu2/RuePXrCzXct7bZG2x71Nmf33QvKw3vOY81cB6IKhMwQywK9WLB4+gRbluPNJ1ussOUMhcZ1PYvzS4rLx/jFGTEroe3Y3b7Fqp4iU5RlSXA9xmTMziKrTx3tHwtTPM8tWmt6F8WIMA2NkIzUXOGhOI6FwQXq6PChxbmA1iWVSlrgU9AnpAefWGshgUPGaurG4fz0QgHTTsb2RB5KM2wakiPIpsSbRQCrH58fx/xn/E2lDG68v2nkaDW19wtGIRqlmYbCKJT77WDFf+nxD0sX3N+TTuOt0z0TSIY+49/ivRMeP0ZpM8pv3/vDFDuOz6U9yyQg9GiSx3R9JjaoPr53AstDPKrHTXnH8acZpQ6MEYBYfxDjIhiETgDgBCiO71Na0sf02skbI8pnRzVKDRwn6Sh+NnalgGh5jlM5hJgAOLnOAlyOMfVJvBCOZKcxLzuN5dOLZR83RrRz0+dIV44YkjnX0/ViNFxW0tU4AnNTB40VQ66xwDvmOiKtYBJArbhndncyXkYwdupgTbmimEodW39Pc49pzdZjTpOWv2hSl4AieE3wiugVKuE7egRwT46llczt4EeDsjRvUyEgpnsQk8Tj5EMS5Z5FH6Z9JWqDM9JJMdg0jsLxvgelGbShM5ao0/2TJJChG6jbA21b03U1fdeLKW0+IytKrLFU8zl5OcPaQtig3iFdvIJT2LyY5pExapL2GckzzsdpPxqv+ShrpTRgItZY/JTP3e861FrYrpGMoiiZVRWLxYLZrMIqI8UCbxkSuNz3Hc45Ior1ekFZilRBHDKC93Sup2lbmqqnzEuJOdO42jc1w2HL0Ld0XSs+BiOwPeW1iRkd/38AxmZFharOuX7zHW9ffEHWb3j4YM36wVOKs4/4u5szht0DvKoAhTGiA+J8R646PlnDHzyA7371nLvXLyit5Wy1Qucl1XzJ2fkFRVnBJKYMITicd2TRQhQ3PxUjGo8bGvbbW7744gtevbmm6yK917z6/jlNs8NbjVEZSkepOigZCCZGPHCoxdE105bL9ZqffPwpDy4upQVfa2LwDG1DfXfHV7/+Nbvbt9RG0SznmPCUWVFRzmdoY/De0fUOa3QyN6n5zRfPadoeMGg98P5uw36/I3jHfD7j8aNHFGVG1wvY2rUdT58+Bm1o25bX797y6NEjPv/8M5qmZbvd8vbttTj55jlaK7qu5e7mjtxmLOaKm5sb2rahKOZkmZVqxiALefCjaLSnyhS5haLK+NlnT/jk4QP+7rtLvnz9li9eveLF9TW9Ckm6QAaongIzxsj4NNX7wXhphxYdFIae0Oywxbkok6SFx/uAxjH1ZKrkgPcD8HfcBDWbuufmMNB7R1kHcrtmVZC0FI8i+qfuuLJXjILDJ5MsgQVmNERQR+2rYegpskJ0s4JnvlyINpXWSbMyOQCncx+htBGsGNm2ijF0mqKBY4IbRFs2xlFkOpApxbKyXJ7P2Lzqju+7F5yk3WNkS8kHT6clmK+BTNooShs4W+bMywycZ7sf2GDIjGJRwk+fFSjxTKF1gZttx7tdSx8gs4arVUGV5TjnaTvHm+s9h16CgDI3PHhQYLMKHQLD4NkdHHs3SzCgMHdjVCgVKDLFvNI8Oss4qxS5jlgFNqk+DIOIfislgckYCDICCKRAM1VeQ0hi8s7RtzVVWaKSKZpOc3gCO5XCpjYsaRsOotbjvGympiTaGaF0qHjLgGez3TNbL/ivf/kThv17/s/X79K1H+/vcZweVORWRXKtsD4kraCTsPkeg3kMohLIGeP9GaQNymr5lxIj1w+y+X0QdEZSiSlGwtTXJgl0T6QnIA1zig44xMCBSM3AXzX/O+WywmgjrT8cE1r57zj9PD4fmFqAEFZQiuMxWcbjq0f0fU/nNbiI6wUY9ZI1pG8r7x1bhVDS9hZjxMR4Eqymy32SPI/kQBe8lKtBNKIUk+nB6WNSChk/NSJ6f9PKpSYg+YePeO/HPYQJCfajP+qBjXqvo+B8Qi7TvYpk0fKT/t8QWyUmAEozzwvm80I0YJViXuUsZjM+/vQnxAAvX3zP9v1b+q3nMMtZnq24+NkZm82O6/evefP+e27qt1QzYVBmusC51IaVXEmLLMf3A973E2haZAU376/J9YIyX02SD7NqSQyBYWjIs7mwX1NgI2tLgLG9K10yawWcPbYL3wc/JkDTj+tyem9m+OwXv+Tt2Yoiy1mdnbG+eEg+WxCNwSsxUvnyV3/L+5cvUASefPopn/zuWs7DGMrZnIfPnvF68w7lejLf8+6rv2d7fc2Djz5msT7n7OKSV9evubt+S7FYsjy/4urjz9Ha8Ob5F7z+zd/h+4aLiwuqhxnFLJfW/sElXS95SOu+ww+Orj1MckI+aaPd3b4TF9sknaJTi6q2GdpYgjJ0w3A0GyGZLeIJp4wykxJrJOn886tLDsYKwyR4jM2nRG3UfhvbJUctu3Hpkftkpv2NDwLNqeh1Il8w3rd77YgnQJgymsKKZuIIrk/XKCUlp40y6sPPPP6FEdgZjRnENFGSlfFzrdYYFVlYmNsBMwFBUYC+wRGaBr/f4ra3VASq84ry4gz9Oz/j1YvnPPvsZ5ydr+j9QO5f8PQnn6OMYX+o2TYNN7sDRotJ4H/38F9zu7vjenNDv9lRlTO++eI3PHxwiTGaPDN0XU1MC4vSisVySdPUoMF5z7qaEwaFVRZjNTp61sslu7tbbtqa4AfyQuZWUc1Yn59xfXNDvRfzujy32LzEFDPKxRKbF3z/8hVPP3qGVpGZLaXw1dS0/cDgGvx2S117Fg+fYcs5yuS0u5rZxZq8KJkry+rqjND0VMsKW2R44Pnz77l+/R1DU2OIuKjY78TQsigM1UdXlPMlXb+l6xq22wP721tur695/fIF28OGUYsPBcFFmr9tif86EvEMQ5uA3oifH7sWhkHiY6U0LC/47F/8G959cc7ty6/ZvPka4iDjdkro4njX+TDmnNgtxycYWbJTpDq97Zh4j8NQklkBNsb3jiRyUnEhJiaNmraBKRhOzDY1ARpCBBY2k45Q5TlPqwXnWcnc5ATn6RvH3h3Y+4GNHqhx+L/8j/C3/wlVGMgUnZLzHTHQCAxE1Az0f/hf2UU4pO8StbhnEzzaB/Ielv/Tv2NxcUmeFTjv2e922Nah++OlOtMVB1PShIEuJuOvKEQEmeOJdKPGteD4ZULqNNRaYk5h96d7rKHoCn759ecQIirXrMoFv3j4ExZOYbWj0QP75o4/+/cvWPgLMjsj4rn+6huKzVvOOHCme6LzqKpCFSVDZrlrWsymwT08xi2z1TmrxYKu7Wmblo9/+S+4na3olcUH0LpjvljQHrYcmo7etWjfsV7P0Kbn7btX3Lx7S2YiZWkxRhF6aPsebRRDyBj6huZQ054PExhrjML3kcELgWFfd7TDwGpRspwVZNaSJUOhGKEZPHXXMgQxI8rLkrppJt38MA28HwcFwjQHUjt3FGWNaW1PRtVRHQsgP8AX1HiMON3LEZSyOsVHTjrclI+i1agV6zLnrh5wI5Hggzn426Safvzx4WtPCEw/OPbpz3gvvvhR7ESnvVAluYETsHS8EVMr+WhaJc5A07lMerLqJI9T4+cnUgAS34zs+hCjmDclYCyCdCFYK9JpRliBo5HnJGHFEWyfwLkQcBLk31vfYhofWo8s0pNieHqfIor00LhWpXMxSYKoKOwRdEZiKblsJ51wMaJMLsdIMYsfBtq2o+vE1Ne7MOVkQUUxg0rObyoIIax3PU3foo2lbkrWywVuUIzkisENOFeQ5QNmEN3OsSA05tVaJclDEhP/hMEocdYY/wuhy8eIGYfSaSySQPdRB1qfxLE+MBmxifFWjlYWFT1hMBCFMKHUSOs5jsExf9Autb17kYUJBNHWVXLfRNrMn+S0kk/GKED0+F291mhrKYaMXnvQHosii0EkjgIMEfoEOAYlQL9VYrY1DC1dt6etDxwOjs+f/oSrJx8xn69wLmCyDJK+bACC63HdAde3KQeHw2HHEAJZXkClRb/cCk1tiIoYEk1KyT3ReoxBDTFqMuvxU4eV7As6xqQHb4hK2LxWaaw2WKOpZiWzakGWicfOrtnz7vVrbm/e0+z37PY7NnfvxWAsLzhfvKeYVaiyxBYVZbXmYvEAkowEeNq2od5v8a5PhnLJVDbN60mSK6jJr+G3Pf5JgLH9MPDyy7/Btzc8WcFnn/1zHj55TB3mfLvJ+evbnDqvQGdJPDwyDD1VPPDRyvE//O6c5uUfY/odF+sV54sZAzArK/L5kmK2lgUsueh6P0BUZFlJnhXkmSH6ga4+8PU3L/j7L37DH//pn/KbL79hcB5tMrTJuNlsGbSmWM1FX0KPBgBp6gS5+YZAVeQ8ffCA//Hf/ls+e/KYeZEzUsgP+z03r19x8+oF9e1bFmWO0RrvAy9evObmZstqveTsfMXV1Tkx9Ozrjrpu2W731E1H2/U0TUfbioj7YjGnLGeUxYzDoWE2q/jo6RO0Uex2e5q6JyqPUorFYkEIgdvbu4kpUpYloGiaNgleq0kfw5tInlnev3/HxcWc1XpOnue8efOOofMMg4Aoy9UaYzSEgThAFnqenpUsimf85MkFv/zsCX/77Ruev33D2+2Gu3qPS4wzaQMG8KI/p1RqoeBe3BBj5M37d2SmQutIcAa1OjsiKUpPC7EIUo9BwYdBiFQIhxDZNZ7Xty1NtDgUfe/58tUNnz08Zz3LqDINQVopgvL3N+jfEh9MOWYCamOI+GEgBocLBqsydJa0Sac8NcgiHz3q3vdVIzrGFOmrxOhM++vYlqwTYCj7nSL40UXTUWaWB2dLvnnT4ZE2YMbrq05PKlE47plOyDXURlHkhgfrgvU8o+891zcN27pncIFZUbCoMoIyfPOmJ1PS5qBQzOeWqCtcAiFmGVzfbdm3ntYpgrE8WJesZoYik/a8603Drgn0A/io8OQQU3ONClQVPDovWc80iwJm+tg6L8GDwrkUxEepzGldMAzJQTNEsrxMFTlJ1LM8QyEbMNO1DMKy0mMF2uCjJMdt59jWHXXn6Z1U9lwIEDt0anFBG0zMKOKSVR7J1IxVNicvl/z002escrnK//6P/47aBcr1YrryO+V5bRwOxVM0swB5ROQ4TkbJxEQ4uWPHvx3HqrWJqZYMqGRcH18nJJ60yTG6OzMFhANR2KmpUt9HxR3wF/v/yLV7BUaRVRk2z/DO0yfQdGK5Ko5B2b05o07mVCT6FNJHaWd6/uVXZHlBVUrLyWF/SPdnLJaM08hPiYRKbUaQAGiT+O3pZO9JvqojuDn+nGBVJZ0T5nSaxHhPkP0oSZCGXzKIMUmPbARWRzaD92EKduPJMUEl7aTEqnKeqB1jt8WZe8ST4fcZiyy5tZR5zuLiAWdnz1KwAa49MM8t29sbDvst/eaO7eHA397dEoKn71vm84JylrNYLVmtznnz9iV3d3ciyeMduZw9i/mSs+UVs+Kcr779a5zvWMznPLl6xrx4gJv0wBx9U9N3gd22Job3XF4+BkCbjKKYs1w+YOhjcqaVeaogdSAcTepGdo3c0+M1mvKKyFhsn3KZMGokE1k9fMTi4pKhH+i6nte3Gy6MaKcqbdAKCqsZdne0+w02Djz55DNMMhsw1vLkk894/+2X+HpPPqt49ju/x/fPv+P1V1+iiSxWK7SC+uaO2/I1F08/oVxfcvnR5xSLFbP1BX274ezRHsqG3veyPp2AkCAJTfSett7xpjkk7VBQ2mKLkmq2TG2IOoXYpLXIolNnjLCfjywfk9kpwBuZFkSVusECwTuGoacfjSKUItMWo610AcDEalFKEqAfiyUnQGqcvmN2mgqQwsg1E0s6Ek901DmCvNMcVNN3HnXeTj4MPU2T+/P1xx7CzJJv6GMQJ+yk+a28SyCYw3c9NPupCBOd4/D9N8TNHTY6FrMlan5GCJ6m81BGPvn8U+zMUl49JM4qIoF/8ennKKV49/Yd7+92GFvQNhveb2451AeKquRjnkKuedu958uvvubTj3oWhSHPM9rDnrycjZEPwUdubjZcnl8wDD1t3fKoyGk3dwTnUHjKXDM0W96+es5+vyPPLJ989imL+QLnCrSGx88+4vLhJbP5jOADX331AkXkbrNld6jp2gP7Q81sVtH1npt378mNpul6bC7khscfLbi93dNuapw3kM15fruj6x1Ga6qrNeuFvL/vHVlhebiaszGarmtp6j2bw4Hl+oxyVlFWBUoZ2n6ArKRcaQYPf/Pnf8J2v+FQ709rTuPtR1mLLQq0FSJF9GEkS04PPwyIM68AULNixuPf/QXrx0+4ffWMV3//V/SHO/EYUAqs5mQV/iH4E4/P/0OPD7UPtU6dDem7jq24UqhLchlKiQZVUNOeMs6rqdTvBZy0xjDTlmVmuSgLHs4XaKfovWfb1myVZ8tAqzy99gx4XAYYiCYZPiXTPaVIupCJhZ5OzwXPMDLfoqDE0lIfWZQVn//8Z/z3xnCmLe3ZJV99+gkAfV1zaWbwZ3Kcoo6cLwsuqgXb0NBZ6LRniD6BfDAt4jrF7yiMtWQpfhj6HmIyJTKZxPeECdyxOuPB+iFP5pesdUlob6XVV1mUyhj2mpDB+ZMLHn3yhFfPf402HTPfYGJPH0H7PMk5ZAxek80WMr7khmLvNtTv7yguHvL4859zV1Q8f/U9Ji+o5nO0kntblSWZKcgyQ9cqLv+g4339Bf/X//y/UNKRGahspMwUhzpS15JvlWXGYpYxK5ZURT6N9nlV0vo9gxPJvhglX+lDx67zWAWLKqPMLZkxDFGzayJ1M9APLpEVmGJ5GXv/8BiG0Xg0CPhkNX5wDE70GcvMEFScioPHHCUeQaooMWlMAKXzEjMGIkbDMEQUHuWEXPBpptkreA800/f47cDx/9fHfwnQ/cfM6/EhBKkeawuRFIwiETESd/RJTjcy9SJMnU2jDJYak7cE1o6sxjEeEuNik9jEAnRmmURko7mRxHoq7afyvBTyTrvMxrh+XJM4zn2V1IXGgDhGlBIWqjFm+v6QCkCANiPLD6YD+pG1ecJQTGuKHpmjcqGPcgA+TH9XCqLRZLlFqUjfK4Y45m0jmBxSQSrgY2Dwjs4NZKmQPAw9TX0QZmguRqsh5c1ucIBcD23l/LRSdG03ge9aR4rCgMomGQelrXR4pXsawigrI++R96XOPaOxmSFLHUoqXRqigNd69BqJGjeIXE4kEAubclb5F9PPe7lSVMQ84IZBcrYhmcwhUp3ee0L0AmxP9PU4phOyriop4mtAB5HVM0E6DAweHRTROzLvmHlHdJqgLV3w+BEQJiOzC4wWjELplj/8b/6Qz3/vZ5xdnIl0hfPcbVq2e8e2dtzetsTdW9B7CjyPHz+CogSj0CYQcXhUwucCbd8SkvzQKPkA6mQMjxJ5njj0DO2Bpt0x+BofB1m3QsBHxb6uqduW27s73l+/oyzmZHmBzXK0VRwOB4YhSXhqIx3z3uH7HjUM5O2MarYkKzqGQ0d3txXJhvQ/gmh/j/kKWta/aHQiTMfEoB4lLX4LYMQ/ETA2uJaLJcyuHrBeFjx++pQmznlxDX/1yrNjRlA66cwEqc72e56t4PNzzSpu+f76FX3fJkp+Rm5yzi8fc375mMXqDGtzaceNEaUsJitYrBQmeogDfuj51a/+hj//i7/ky6+/5tvvvmdf1wJvaKmie9ejsvxk0zluFKMmjkHx6OFDPnnymH/285/z2dOnVHk+VTr80NNsbun3GxhaqjJjtVrIou6CMFyDJ0RHiANGB/J8xvXbW+42W/aHw1TdzPMsCW4b5vO5JPBJE2Nwjq4fKMqcxXKO87KQSA6jqKoKazMB6nwgy3J2u50cW2l8DDy4ugQFXd9jMosfPM+/fcnN7R2Xl+cYbbE2omclWlVU5QznBqKK2CDJV8CTK8cqj9izEhUesqpK3my2vLy95cXNNc3QC/U7LfpSCSPt7/dB1Bgjf/L1C3569YCzeQSt6A83DG1OXgpYfyzzpQ140nUcI3aF9ItpusHzblNTO/DoyVCkcYG3m5oYwawq5nmGGnpc0ss6rrSAOiap49NGHUXhmT49GYekiSxVkzHgJVXpxvMOBB8YhoGiKJKYvrAItBoD6eMGNzqkjwvDkUKWNnar0Wh8hLOF5fYgGlJHQDYez+eYeZzOUsrSMK8s80oE0jcbR9MHmkEAyFmVYQ0EPM0Ah0aE/3OrqHK4WFtyq8ToYQhs9p7OKfIsoywE+FzNFETPvg7sa8+ui/RO2kdGBmhuA1WhWVSW80XGqtAUBqxOiUuiAUztHfg0tOS6ibN8SnN0xAXRqEUptJXXeOfl47SmquaYxD7rXaR3PYfO0QzQu8DgI70HFw0h2tRy5lHRCxgbgaixZMToUL3DbDuyTCqAmc0oC9Gp+Ze//IyXmxozK6Yr/5YXfMkrlPk9MjQXQbEIoJK02OnyLrIBx8x0wtOVAJMq02RlkTb1IRmTJdBTjey3Y2t+lomEy9AL8zEQCSrItYsCCrXR8/fNn3Hr39LTYdCU+ULmf4zCWg1xqvCeMh+PAM4IFsV7sbcMUQGEfBDpi6iSbtcHwaVgXMe1QiQ/xIzIZHZytjwyxuW+nCbhp4/xe06sBK0x+sMt8/6XlYBfAreqqogxTpX+mILd0dDotFI6aVmmwxltmNmceXdF4RZoFSkzS6kVq3zOZTVnUVgWhcXaEpUtiLNH6HxJ2zY09Q7fHxhCRt8dIDrO1mdok7Hd3uFcT54bbKlZrFcslmusLfn6+Tc0+y3edQQGZrMZ0URm1Yqz1QOWs4d0bcvN5hVKRdwQmV9eIKhWCpjmPYP3gEHbLOUbUiXO85Ll4kIYmEqnVjdJ6MZLMB1nDCbH63IC1t9bmqZLd8JISUB81/Vcv37Nu9evcX1LYX/B/OycrKyIwNnlJe8Wc9r9HfvbG3Y371hdXmEL+Q7VYsbi4pKdG2i6AV2UfPoHv2D3/j3b63fsbm8IbmBoaprtls37d8zPHqBMxmx5zsOPIrfXL3DvM/TaYlc7YbtoAQVHwRiIaT72ODckBofBZgVKa4Jr0SqHaEGZNMZSwqCEKx+COyaVae3SNpv2pBgjPorZliRuQQL5NGW0ESM1kkTByK49hsPquCePc25K5OTHGGyOs/AIrqZwNS1NMf2fmjDZkfkdp3XgxzS2pu+ifqg6e4wUjvNoZOEIA1KjrWSmSil0AniC87imRjV7Rs1YrTUPLy64OzTgItbkVA+umM1n0iGRF2SLJX1u0YWldh3b/RaVlbRtx9vrG97fbfjo2TOsNbRdx/5Qs9/VaJOxNmuC0jx3X3Oo69SJAX3XUFXFCU4f8X4QYNJ7lLH0bSv3J3qMjhAzTJbz8MlTVm2LHzqcG6jrPcMw0DaNMFK0mMdErSnLQoxCtMEHUofUjjzPyaylbXtUkUvBLYJ3Hq0ChYWhE0ZSQNN3A23dEnzkdfDcFhk+jS+TGQiRav2QEC0+vGamNYvVgqoqKIqcsshp2p5ytqSoDE3dcbe549Ds6V1P1Me9zO88w9teGNupMCEFUjXV4o9XTca6hGoSs6k8Iz+/4EGRE2Pg+sWX9PsNoa9Fe28ctCex/TT8Tseh4gRIife8An4wJj9kw6SW4ShU7dN6TDp2ZDzgvYRfKYrMclHN+HR1zlk0lN6j+oGbfuDae/bR0yhPExxdDDgV8EZi6WDEqFM+G1A6XTOZF4HUEjsm3SM4lAqhPoiu7Kpa8eThE37x+3/I5fKSWTFngSXfdXzz6Ipqtma+PhZQTF4S3YZhU7MsLKsio7eBRjs2Qydrj0prd4jJe0GABjecaMdPcYL8PL9bc3m7wmjN+fyCnxRLPlY5DAmMUJAVGeuLFf7xwCy36NWA0zsy22OVF5JAVjA/v6A/dMSywq5WzBdL7jY7hsFN9143DXq+QM3n+PmM28OWNy+/ZbVeU+WPMEWFsYYys1gdaNotZz/b8/3Nt3z1/K/59puv+PljRWbFu6DMpWshxtQW7w1FUUj309iRAJRFhm31RGCICXDzPuJcwCnFsO+xesBo6VJquoEhtdorSMX0JP8RghTL4ofjNI01dexKjIySk4pcJxm19NwpUHQvR/tgHjId9hiXjRr4KD+9QBFZZFDoiJm6jUZDoPvzScbBh+3k6gevOf3bj4GtHwKz/2hANr1sNGTSE+Hng+NO6dlR9mj8+zEGjilVk7EfTmIbsQAR3fMsyzFZNhl0TsxNfYyWiOrevZHj3j9HNYHFx/zRmAT2KoWAgbLvJzjx5Lqk+xzVtO5Kji/zd/RCUSoZ34akCfuhrwLjfJd3jiPOh2R6FMYjjoAc4rUek+RAkhcMUyFA/gnpaCD4jBgMIfaEQeOIBGMTMGnQyYMgRjH8VSku0VoAU5NAU9EfFd3RscAsnaujRvOx82cE2myyEBqLW+Ooz8b4Y2R4ZuV0jpPOawjERBgEP8Vb6YZzqhGiYsAbk0BYcMHJ+3w47ivhyLIe7/3U8q8NWOm+Q0fUKGeldRpUJ+Mk3bEAeKWkuzKRkoy1vHi1pbe3rM9hVhmuHpSs1hWrtcZFePWm5vkXt9RDhtIV5eqcqAustdjckFuDS0Nk6Aac64CA1mJAPkpr+TCaxgmRIHiRKQ1BGMFHDoCQALphQEWZP0VRpGsVcL7HhR5fe5q6pm87mcdG4XtPEuHg0Dpa7xh8IO86dFaT21KID3rUsJV5JMrDWrAva+S7Ky1G80VGnuWpy+8DcsHJ458EGKtV4OrhgtVyxmxRMFuu+P5t5Nu7yDcbjc9mqeUu0aZdz1w1fLzK+WgZCPVbunqPC46xYro6O+fs4orl6pyimKGiba9ErQAAIABJREFUYoiCmBPBIBcoDg1d0/L2zSv+9P/5z/zFX/0Nr99c07RdAmZ0EuL1GFSi54/VqzHxEBBIa8WD1Zqff/oZP//8M37xs5+xns0Z23KCc7S7Le3mBvqaMtNgyskASFz+JPDp+o7tVtoLF/M1N7cbttsth7pO+apQ4kUyQFgVxDC1CvT9wHZ3oHKexbIiy3NhT5IqzNam32XJ7YHdbi/HtBkoWK3mmMzSDwMozWFfs91saJuWpul4/OiKxXI+DbDMZkk7RozHtLEMQ4sbOmLfUUTH1byAoCltQWkLVAy8329phoE+RIYgbcFxEiJX9/b2CDy/3pAZmcBnc0W7f0ezL8nVgqzMEMg+3acUio+J37RlKmm3bnrPzb6jj1qqM2lyuRDZNAPW9GTWMstzEdU20nZ/3AKYAv6ppUOJLtJYuR8BgnuPOLZVxyl5nACidKaju3UMRwadSvf+2Noi5zdurCMvKqSNayyNmbTZFhEuljnbup10kY4R1EngmxKSESO3VrOcZcxKYa3utwOH1jEgi3dZGBazDOc8g/e4BojSAjqEIO1NSiQMotW4EKlbMTioCkORSTt7GDqaPlC3gU0Tcdi0XYvsQ5lplpViWWnWM8P5zJIRGY3zpOo6tqMnYFyPV0bO04/nljbh0ZnTJJH7MbzxSGKglaV30DtH5yJ179n3nnqQVmcfSMWiEbiIECJ60mFNGjKhI8aOIQ7ses/WtqgYyK0YnYQQ+eSjh5jVgVNl0l284VX8jkpf0CmL12siJQQoU2hwbG05eaQkhzHJMhqVdBtCGB1FU2BzMj4lAYsYfWSyhigSLD6m5A75vYs97/17XnZf0jKKqGvyIsOn6zC1ZaXgcgqw0/25l5GOQXuK+4y16MwmPUzIZ3LGvneTuYRKVWyhUY2BaQr0lASb1siah1JYMxah/I8kJePvx/kwMlcn6YPf8piC7hCm6zA+P1bIxwTbBwSAHXWiQmQWz9ForNLMTM7FbMGZeko1LDE6Ms8Nc6uYGcU8UyzLjCq3RFsx2AV1uWQIisa19M2Wod0zBGjqPUppirIiz0sO+x3RGGZVic0t2uaEqOj6geZQM7QdeWYpqhnFWUnta2bFgqpYUBRzri4/Qilo+xrnFG4I4D3GZKIftVhIkhmOzAS5tWIYV+j5NB/jqNU7roPTtT+5Fyf3RJKMD5Ko6b/GwPb4vPeew3bHzatXuPbA7vFjMewqpBV+vloyX6/Y376nPezY3bxjvlyR5bKPZGXO8uKSZrfjcHtD27Z8/DufU6X27tddh+s7MRfsW+rdbvruJsuYrdfsd+/xdUTNPDYXsX+TWZFLmIa96OV3XSumjnmBMpIETN08CrSRSru29sTIIMlxfMhcVWpigIBIO8XIpB/f905YFglc0kmbbWy3nBJGdfyOY9I+cQGmvx/ny6kMiBpTutPiIUdgd3zdCGNNxYnxD/em5/ENx8jrfu4/dgfcvw7yQ6cunCPgljTzfMTVDdT11DKpgFyJ4ZoPhmAMZrWieHCJzQp0lmNsxrxvaeott5str1+/JEZL07bc3t7RNE1i+ImRVHGoOdzcoFSgrBacAbnLqOtGNGnJCH5AMerajl/V0zY1AFkeCb4nRoXVceqsqeZzitmCvms57Dbg26Sn5wlRkRXltA5ZYygLMbcdWy/7wbHf71mvVhR5jgMG5ycQZXDiNG0NWCNyXt63EAaGdk8/eGxWstnuQIvhis0LOfdqReECZrdhWVrKspQOqijJ59D2+Jjjo2O333Noarq+x58oW4bG4zYD7sZhFjOUMcQAfnBp2b8Pep6Oy1FrMSiFKUqqouRiGBi8Y3/9inZzTej295qDJnzlXsdQOqTgHuOAu/8fcRrQx+8ejxpyksvqKd4j3l/3IuHEpEbOSyuYlTnrquLj1Tk/m69ZDEF0SgfH133HmzBwINCn4nIUzETkwKQPPKEECmUUk2t7+jf6U0xzP4qrdEDYuMFFbNA8OLvi0yc/5ZNnP2M2W5PnMwyWRdNTe4PNc3IDo9zS8vySXdFw2Nyg6oEiN2RaYzNLFwc6I7FEGAPpIFI10ftjGzXHNQIU83rGxXbFxW5FbnPOFxdc2YqLoAi9JPIRKQYszmYMV3uKwqDLno4NxVyhbiJaW8ysorp6SvvqDYPNMHlOtT7j7m4zySAB6BCwyxV+VtESqLuWvjngyxxcjyrFPNFmGs1A39d0+Wv+7te/4ou/+zV3m1vi4xVaG6zV5LlBqSGdckymUAqj7+t+z6qCvBZ9Qz+BmhK/OS9eFq0EE8IW05p+8IlUky5ZSFnGNKb5rY9jiUtNY9fHxNxmgo9+GLIdIcH7z8dxp4hjFCzXM7EJpyU9RkqLgNFJd3z8iNMOmeO0+HEgdvz9ngzOB6+ZNEvjh/4l/9hHivJToUKZ0yw1XTfitHRMHWEnn//Dfzp1mimZ/wrp3tEGYyzW2hPZoJNzjMfIfdSmHA1rx8+dgHaOfxun/vS8UhNQOMnGjmZW4z1K/2IYGfWKqHRi4x7XtxF3HvOIeDLwxrEyrs/yupQHj74UJyPpuEQlrdrRnEqdrJ8p5hYmtxM2bbDJHGuQLr4QCCjUieGnjwlM18mwnWOhYDR0spklz7JJa1akU9T0HWUumNRKnxi3WmMTqWdcv0ZmrUr7kVVmOobEZAmM1Z6gDSMYO0YBMYhElY4REwMxpMLayTgMTsBsFeOEKXESD5PGGUoTx4KgUagoMjpEhTNCSAta4xMhYIwfJSeOU+FTa4Wxhs2uZ3i143avWC8LjIHloqIsNWVuUuFJ+qGiLTF5BVGwqyK3WCOE0uCl63IYekRuYcQfpgyaccSGIIzg0dBM8jyL1qJN67zHDU4gUiX+KFmeU1YVNhN8a+g7kQsLQfa5KPrDpC4/l+SPolIM3qGHDJf3FEWV1mmV9PRPCQspz1EaozTGZOS2SMTJU2+jHz7+SYCxZVXy0UePEdwzsO/g1y97vrkrafSavCzR0U+TbWgOfL4c+J1LzYN8x5uvvyLPNa4RGrdWmsePPuZsfUleVBDBO3Feda4XynrwmNihXMfNu7f80R/93/xv/8cf0ffSDqKzMgX9Y30ooIwX51EfEwCHGFwBuVJUec5/+8//Gf/yl7/kyeUDCmMTyzXg+4HhcOD1t8/p7t4wL3POzpc0fcerb1/hnEdrLYyBMiNGxXbb8P3LdygU85kg+8453l2/p5rNqKqKqioIQdg0VVlQJrbBoWnY7A4UecblcMZiuZg2eWMMfd9ze3s3BYnvrq/57tvvWSxmnK2XLJcV1gRmVUZVFsSgOD9bsFvNefPmmq+++hatLb/3+79Dlmcc9ge6dhBReaPIi5zM5myHA/t9zWG3pW9rsuoM0wdWFmYPz/jo4YoXb17z8uaWV7d3vG87nBJDGp2MP34wfDX89ffX3NYd/+ozRdgG7nJNxhVVcZmwMKmsqMAEU0lFWE/HbAfPphl4f3A4VU2vk41F00Z4t+/oescsX7IuFVZL4OB8wAclVaJxwz8JGnRq75TjpU1kAguErev9kAKSEZggBcJyU4y1lNqkSqEsfKN+WjxZAMbzGTdAYBLxjsl0QUdp/yis4umDOa/f7aXVAZvQyrFaPm25KBWwRlOUhtUq52yR4QfHftfx7q4lKsViaVktSs5mVmQFtk7aqBycLUVOwDlPXUfe3Y5GQpIg6DhQFiWzQpMZxbZ3vHx5Rx/AYwimRNuYxmykLBQfXZY8Wmgqq7AKwhBQ+AnUCaPJXUjJSFTkxkpbbgoOhKV3AqoFj7VjFTAFJ9biAvTOC1tnW3Pog4D2pkTlleg/KzlmGBw4J67z0WHcgdzvhR2bWLK536Cjk0q6UezfezIGlvMSP6w5NC0+g2ePzrhYz49fL8Ih7vjr8B+ooqJW/4pefcQDpblSGUSSjuzxkbb5ND6isEuNuPa2bSvVwMExiomdBqOT3tMwFoc8Lm1Yp+HSANz6G351+COaJG2htUZlBltmDF3HEBzeB4qimL4VMFWkR5BWEgw/zSO56Zr5+YpiVmGKjBghy3NcNzAEj4+RTIsO1FipjGmPiDFKVTWB8tbo5N4duXp4Rdd1bLdb+r6dYpUpOBckKBWj/XFORSRBPLnGH3b8xRjw/y9z7/Uj2Zad+f22OyZc+vLXtDdkk5KGHJGEAAIaDfQX6EF/oB4FCNCDhJFACBpopOY0NRyabja7+95bdW+ZzKrMyLDHbKeHvc+JyNvdHOqtTyGRVZWREcdss9a3vvV9fkgwQw5O85rA0L4Wk862d6jgUSGiReA77ofM9IxpYbiqZ3x6dYUJPRpHqSJGOIz0KAIyswD21rH3iq0rWfdLQgi0+xV9t6LZbdgst3lfmdB2HdV0iqlLdEhmUVJKNqs96/sdQkguz85wkzmXl484v7wiaHj34TUTMyd6Qd+0nMxOqScLtrsNt7fvePvVl9j9lrqecXb5mLOrp8QoUjIRj4PsPCYHQ4AMTqdA6Bh8OjAAxsV/BNCO7/ZDRGQwW0ztQhIfYDKZMZ8vmNYTbu/fc3v9jmp+Qj1bpDa8ouDk6opms2Z3f8fdu7ecP3pCWU9zi6Dm/Mkz9qs169s77l6/4cW3v8/Zk+fMLx8zvbzil3/9E2zbELSiDwnkESEnCiEV/YqyxFQVuqzwwaKMwSs1Fl2k1vguYq2l73uqqs5zP2CdpXA2sRN1QBeSskidLVIZpNR8Pe6GNAaHZC6xJeSYhHof2G639P0CL0EpkwpRoxlFur3HCduwNw3FibHjSiZgTUQ1xhMDwKPGHutDMP3gGIPTA4skPeuQpBjU0aqW3/ew3w5zbpx9YwIzvO2D2goi621myDYnUSFE+t0eVptUaSXFi29/9XNkVWNloFFgS4MzBcJUIBTBpuL23d2KLz7/kl/8/B/YrRuEFPTOIgQsV0tsbynqirPLC95/+AAhIEpPFRSPtme8EdfcXL/n5GSK0QpnDwxnQVrXg7M5HjUYFWnaDmUMAg1RcX5+QdtZtki6pmMyK7E2oAqHLCbML8ux+FTlBChpzKW75gNst1vatqWqKorS0PYJPItCpHjHJdBMa0VZRnzXo6PFdRuci8xOK27fLol4VFFSSEM5mSQJoABCamazCmct280OZ3u6qmJzv+V+/Ybb+xXX16/p290IJg6Dovuyw69SO2F9coaUBtv1OLuBokjJtT8IeCezmswKz7JCkdQN5ISkOn/ME2NYL065ff0r1q8/Q8eBCXkkj3I0Nseh+euj+OERj+aLOBAtUmFYPijSxTgwxNIxMEEHkCaGQKklH12c8+LsnKfFjHK1Zb/bsu1ablzPl65h5S1WJEQkkEyGUSnZlkan3EpkHEENWpfDXBqCziFmEInBW5gM3kSkLTjRc7796ff5wbd+xMniMYWpMUWFNiVKV/zRfYtSjvVWc51Ty0++/V1MPePtqy/44mc/ZdK2TBYVZmqYKYUwgp6AJcVtaQ9O5xB9LuaN4DXEAN989YyqL1BSM6tOOJtfUHSR0HSEvk3dkwikFlRzQ3WZ/AQEPc47zp/PWb8HpSeU51eox88JnWcXPK6zTKqS7os7Qt+PT1/XFdWTZ9wbw7u7W8xkwvnZxdj9kuKN5PFhXUvX7/iPf/0f+Hc//kturt8yryI2WIIwKC2oCoOQ7QikOOdT8aasCDqMy+XiZMbdvkjFCevHeMmHQOhjMh5L6ERaM49YiA9oLHngjnqd4rA2PmByDrFKnnchRqxP3gfZ7Dz5InBgJQ4A/qD3P8CuURytw8P4zr8ppBiaaTLYFyk1VFpiHIhBomo48Xg0J/4ZwOkwrlM4NxBkssbkEVj4/w+EHd78UDxOYFHOHWQSDvNHRj2CoVtEjID2cKjMwhyYmMM6kX4vvVZmchUxS69Aip/y5pvoVOSuh2TmrbUei2jHDNwU1w9P47CSheDpx3brQ14ZYNSglwOwODBTvx6HxaFzTB7F9WkADK3mY4weB01N9SAiSEVnjxeC4JPZVupuS6+XcujuzSCzzwCk9QQTiMHjnE3sWJPIG94lOYCgPAiVSDvKjOukCxEV03XHUfIs7bpCSIzSCUjLBmkJSzrEswPJSIgsISWSAalSeoxlDySreDSeD4UAMTxvkUy1BsmpB2Cz8jhvUTmmFN6Nz9jHlE94n0zhyWDs0Bk6Poeh8CYHsFVkJiwgU5nFykiQkV5CqwROKiQSRcI9knphyO+XQOzFYo4wis46lmuwL6EoeozRFFqxXy/ZbzL5S5m8VAVUluxJzdipi9J5R9vuca5HRpUMxJL8LDIKYpRjUT0Zv6UxLaXC6ApvwNrUURx9QMmkGVuZksXJKacXj5nNTphMpgTXs94sWa3vWN3fsVkm+bbWdtmDQuFlpA091kWUcOACUqd7pqQmiphB8VTM1NpgCjNK0Wld5Pg8SUb+U8fvBBgr8gCJSPqo+Mt/3PI311OWYY438xyMerzv8LZB9rf82fcfU3ev2Nx8RdvscBG0LqiqKbP5KY+ffYTzHtt1CGERwiBFQVUqKDxGSYQX/M3f/JS//PFf8r/+m/+dzvrUqickyTNZHgF5AoWi0BolFCLEnHA5zuopnzx+yp/80R/xve99h0IlXY5kTgXCeba373n9+a/4/Kd/x8lizvyTj1nMz7j7/DPKQnN6uqCqSqQU+ODY7S2rzZY3b2+YTSecn59SlCXFZMb9pqGup0gZaduGrrNA5OrygsV8ToyCupqw3+/pe8tyuWbfNkwnE8qiIEbJZrNht9sxq2uquqDZLVnMS07nE+pSsXz/ge12x+OniUm02bRcnF0ym0bi1QVKKN6+vma12vHs2WPmT+asN6kFkxxgbtb3SSB5uaRtGqIPtB+23O06+pBMeSSCF4sTni3O2Dx3/O2XL/n89j2t97iYqsVG6geBRZQKoeDtas//9vef89/88Ju8e/851m6Joefi4nHaVCIkpetU0yGaDPgnN8nbdcP7jaWP2UCLYWEcIxccsLKBn738wLeezJkXAqOyvJVIVZMjfnwGSiO9TSZcRueqo06aTt65cUNTSmH7Hqk0oztnziSPA4VDcjmAu+Hw7zh+NAM933uH1irp4wnFvu0JIv+f1pxWkmeXNe+WHavGAibf2aQTmwIejwhQmoLz04oQPDfXG5rW0fUeoSRXFzNOZgWFkWzXHdd3W/qYhORPZ4rnZyZrQwW2+8DNXceTi5qTmWQxgx98esbf/3LPetdx23ruNjtiOU8GRHlDKQo4qQWnE83FvOCkTALoxOS4OHA604aXTLvkmPCkKlvwjtEsKAeZg45T+rvKSYckRsHeed7fN2z2lqYP9GhUfQpaJG0k5wmdRYTERjB4ZGgpwo4iNBShwfgNOmyRsUPGHrCjHmHS7BHILhmZTU9nPD5f0LqeL6/fsuva5EA5LpDDoxe0MvJX+3/H3+0ci13gv3303/PETJgKiQnJ3CsyJLL5eo3ElCXGGHwI2K4bTbVytMrQrB8GgEzmiNWnECLVG0WWYIA98EX7E17bz9nKlKSLGBFaoKcFeiLx+x5vbZLbOOL6HlcHQ24ZSq0dqT0xxAhSUJ5NKM9qVGFAJC0mIzWl0pgI9+49rncYZ1FegUi6VcRUDNFSYXKwG2Ok7VLys93u8NYjguDq/JLb5R0+azQNgJ/I90YITSQxcJV4GD4KmVo/D0cKpl1wGeTxCbzKcsXfjH/EgnMUnlI4TqpkWnFa1ZxNCs5LTa0jRgQUFvxLIklHyXae6B1dSEFGdIImGLZyzt5UNMay6d6z3r6nKBR1XbJYPOXRlWC32dB2Dfer9yyXN2hpiCFyf3sL0fHJJx/jo2ff7vjmD77B6fmzBOxst+zeL5kVFeu3N7xZ/5J23zA7vWJxdo4PnuXyPfNJxbyoOZkvOJ0vHsyzA1D6MPEZmbA5eXuQFB2/bgBh42EOHCdZI0g7Bq+ZKRICgiT8f3Zxjv/0U5bvvmL59g3T+Zx6UrM4v4IYuXj0lNA7bl6/5u7dW+6ffowupkxmJ+y2awSCcjKlms24u3nH+9evuXyumJ6c8uiTb3J6cZFY2qagmp8mxp4/7IMyMxDd7Ry/Lpj+aDlW1YejqCpqNWXQC1PKpMTXebpmT2EKkBIj9Hh/TFGjiwohFX3Xo1QxFlxjTCZGIRt6ICUxsxudd3S2Z7Nfsd3N8GJGXYkUE4mcZA85vcpGIDHmpHIAi9KXBIguJ6OJXRKGOZ7bn8dHN4DT8ZCsRzFybMdEPu13ctStO6wbckzohn3vmGGT08/83sdj5jccA0igJNJoTFHw+vPPsV0CYHzwfLi/4VdffoXQBl1VOCGIouD8okwGq1Jy98VLrm/u2O4bJtMpq+WHpF83rGMxcn5xiRQKrTSnZ2esliuEFNRlxfMnj1n+dMm1v6N51vP82WNcEAzsb6UUL14856uXX6V1SUm2+y0CyW7bsvEOETzL2y+pp2eYcsJkMuHNV58nPUGlctKUgIgQHN5FprXivnGE6BACCm1ou47NdoMpNNosssmSoq5qJpOa3W6HEAKbddGrqqZrPUYonO+5f39NVRkCBUIXSC3xfYe3PUZpLh8/JwjL5uaavo9EC282S0xRUlSa2dRwbwRtO0CCCf3p/rYFH1JxzZR8+q0fMDt/BqbCRnAhoI0hyENxQ5UG36d5qHw4jAVBktkRArW44KSaUJ1dUk4mbN++xDc7orUHwDV+bbz81uE0QvwPXnfM0BsYukdvl/KKvD8RwZPbLUUEGakLzR9+/AnP6hmlF7z56i0b2+ANbJXlXbPjzvmsupVYr1rpZHiVwdgg8zIpRe44y2coBKMuFkdzj5wciww5CEFdzfiXP/wTvvvi+zy7+oiymiNUgSprinJCNZmjlMHZNut259RSCU4vLqiqkn3f8PbVK5rbDZO1YT6bUgnDRln2KmK1SgAdmS0a41gsRgiMK/iDf/wWKkiUUEz1hI+uXvDHYoqMLT72DAa3hIjWydn7+k0DWCb1hMlkDn2JlxPM6TnV42c0UvL0Rz/C9pam3fPlV694/PgRZTW4aElOvvt7bOYX3Dct23bP80dnnPzek7FtvGl2STKtb1k3L/n71f/E//l//3t631OoZBBUG0UhJYtK8PRU8OrNhr2N2dPAcnu3Q50LvAhjZb00iroy7BpN0/tkXJRjnACkRq6jQtaw9cYD8zN8vWL8TxzDKwttKCQUCmxM5zMAod4FjDTYkFp6fe5EO/QPHY/x+OC9h04tKWWShcvJjUaipKAwEm1DBmMfrvW/9ZzjAfT9TddjCvOgO+Thlf7zj2MW7WiONYC9pEInmRXHkPsPsdBw7UcbUu8smsQ01DkeUEPulzvWfEgZThQeYzRS6Czpx1isGZm3YnhGB1m+GA9gcALLBwA2HI2P8CA+G+KVAcyTcpAsgBBSH/AI5Q4SZ4l+nQkxMe3bIxiYcoOhKD/ekjyvh9EbbDhi0jL+fShYpNub9jEPWSIhEqLHB4v3HdYZnDN4p1FGEVwmfZC0YqNIrxek69NCoItkgKa1GmUKUq6ccvIQAg6BzHmj0voIbFYokwC35OFyYP8OY2XsjPapG+94n0j3+1BwTtIPKc4Zn22MpE6YYQ8Jaf8k31PvCM4ecqc8DtPSINMaLzOYLtXovxCESFq0UeQzkgRrCX1HVBopC7xJc1uqhHtVNiYvCyBIkfwM6gpdVQiTyIDGJPDR28C2ddy+vWZ/f4upavTilLa1eSwUmQMWk2Smd7jO4myfCuTBgZAUZdoOlRyepEIqkWQFQqBtO7bbLdH1aW0UJG1x75MUQv4KlLiokLpgPl+wmM4w5jtYa9nvd9zeXPPFq894/+Ed9+slbbdPBmsCXLS4vie4LhVIix5TFEynM4oikRmESoS01IWiQGqiEjghcAGiT8SM33b8joCx6WvfBd6uPP/htWIZT3ByhpAa57qkg9XvKWn4vReGib9mv37DdvUB51NVRxYl09kJV4+fYzNrQWTh64Nmy9ACELh+/YGf/ORv+MlP/iNNa7P4bgqC0oBO9LpBGyQti1kU3UvKWPDRkxf8/ne+y3c++YQXT59SqsH8J1PenWf94Ybm/hYTHc+fXKU2MNuzur/j6dMnvHz5OWRXcW0M3d6y2qxo2pbFYspu1/DZF19xcnrCyckpk7rGaEU1KTFacr9cZ40lR9f1TKdTmnZHcA7vPE4JqjJpvu7tnr7rWS7vmM3mhOBZLu+5eb/l4uIMFwPr7Y7VZk/TOK4yOBdsz+2HJb1tcN5RVZonT6/4x5//nHdv3zBfzBFCcHp2wmRaU9UV0+kktTsrxf1yxWa9Y7fbJGFt77Fdy/nJKZUQVHXFxWmSU3h0ccnNasXtesNqu+bQbp/Hy1HU0fvAjz/7kj/46BFaSUJMhkx1PU0sXSTIgHcutXiiQQVaB/f7nk3rUluAlEk3LL//qPciEhtuHSSvbnc8Pqk5n5VMKk10MTu1c4SYHjEHs0C5yuY/wfuxIi1EYu7JskxByXBdIteVjyqbMouBJ5A2f2cAIFMi8DBQCMnYJS/yRmt88MQsoI8IPLmY4aLEho59R9aJGT4XCJ4gBW1rub3dAWBtqpBXVcnJSUFdadrOsVpZNrsO5yLzmWI2LZnXms3O0VmHdR5nPdNK42MCqjfbwNs3O3a7QG8lNgq8UPh+j5KSyihOJhWPLmsmKlJKMKIndCG1KMbcYqJUMpsRMgch4eC6HWOOlsJYwSamdojBTIaUryCIrHc7ltue2wa8KAmyQlRpGbBdAO+QwSGDpRYdtXQU0lGIHu13iLBBiR4je5RIDvPBW0LoCb6j7xqcT+0VQwuQVipXlBVloZlXSbak+JpxjSAJisRti9212NbS+chfLP8N/8Xsj3lePuJUaeZCJFA0rydohSySFmSIkaZpcO6oPT+PxxAPieMAfoU41v8PSaaAPgZ+sf9/uOEDKxXpoyD6ZO4hlEAbRYjgXUyUulEEAAAgAElEQVRsqhCJuDEhHcC0ITmNIcmxCClTJV4KzLTiycfPuXp8Ret6Pizv6UMgOofJlIvUZuTwLrGSB8fQY1AnsQiyNENMUhTb7WZkjt+vHX1wh3kEo2nQwBAmz2opBZUy4zMZNKyG4zJ8wnfDn6K0oihKtEys7Lqsubx8woV5ykQWFKFF3P+SudpRykghIpIO4XfQe2xw9MESQ58q3iGNWbL+VgwQvWRLwbYqaaKidZbWtgjZo4uKelZyfvaYSs94++Yr7m7f0/UNV1eP6dvAfrfDNXumE8WsNkg9YTqdszi5AG3wXY/zPd1+Q2gVtrUYVXD65Jyzqxfsmz1du05Ft/2efdPSxojXmhNjkLI41IoOyMTRXsr4fRxz/+SRgdujAtUwL37tvcZfScG9qUoWF+fMz85p1kt2yyXbsyUnl48QQlBOZsxOzjm/fMTq3Ws+vPqCzd0dQStWqxWn55coKbl68RFds6OqqxTbep9qHdUkjzMNPrXGDWcmRVp/BZYYBDGk1iXrPEdDB2MKDAXGlLhykoomNhXuhFJ4N0VnZrdzHuNzEuxTgi7EoBd+uCPb3ZrJZND+UnifdMe9Sx02SR4sBepSpuB2SMIG05BhrqZCQzphlVvuovfcvf6S/fJDApCFILrEJJdaj1p3Uqsc/KeCjsePUhGmqnIRROQkUyS5C5USQnP0XLWCQh8Jshxh8QemUx5n4z487AEkg4uj/VkMYJMx6OkUPZ2lfTCPLF9WTM5PuV9tuFvegjJ4VSB0hQsSgWK/bZgUBefTGaLd0bS7nKwpXAhsNyvmsyld19E2DYvZDEJi9TjrqOuSjz96xqsPb7hv1oDkxUfPxnUlxkjX7On6BqENRWY3nZ8t8D7grE+aaaGjaba0bYNQBRcXj7i7e49wSfdZC0HfWwSGqi44vzhh/3pNqRSlSSye3gX2bc/cB+q65n55j3Mp3tW6SPuGVHQ20vYks1pdoE2JcQJTlExmNc1uT9c2tPsG77PRSG5FdbZHSoHRBUFIdvuWb37r2yzfv2e3b+jabmT/hX3AvXXomBJKbQzT+QknRUnYrrFhndq3iXgh8JMNnOenF3IngkxJNBwAFCEEpkzXE7RBzU+5+M6PmJycs3n3mu37a9zmDiVScf0Y6XlQBBrnBlnO/gBDPQCHHhQfU8fRyFrikLAnTwDQRlJoyawo+PajJzw1M9ym5X6353q35UPo6K2nj4EmeISWh9YYKYlapcJxliOIQ790Du+EPJiKCSFGlltEjgBSzM6WAiil4dOnn/KNj77HxekTymKK0SXSJCC2KCcYUyZPDtsR/CGt/Pb1LdfTyJel5vHTp9yuPmB3DTvviJs9paypaokoFGtnaVU4gBPD8xri8SiRLsUQi+kJz+YX/NAXqJALsDmGTUaQir53bFY7bCfodw3NytIUgU8vH6OKM0S5QE5mTM7PuP78c9r9nq5vae2WF9//IYNLPEISrp6zddBjUUVNwNA6kXOGiHUBYzT34g1v13/L3//8Z7jokkyJhlIHlC4ppONyqpkUhi/faF7e9nQZwGobi7OBUByteVJTVxV11bPddYcYLY+foQA5st94eByKAYfxB5GvS/2Q18kBcNVKYCQomXQ1o86sQRFSd5DPWYsccp6h7HZUA4sPwceUF+dz9FAAzidUOarU2TbTkqmSGDwdv+3IY1OMEHT+3xTFqdHNL2uA6gRADV4rQ0z3m47/FFN2aPtPssQCJeQINEr9UEvyAIiDlg/vw3ijcsHW4xk6TvKJJB1nJbNubNabPNLyHMDMozd7AKyO4GWOC4aXCjEYY8YxJ3oYP+VutQEGGRH+TGKJIesRxwMgGzNLOyfNfZ/JDTnmV0fdAFkwYPx3ejaegdkdQmZPK4WIyRtC5CK78z55fMSAlJreWAqdtEO9d7hgk771iBkcDLEYFPpjwnkS2cckZrKSSTs354LD18BaV4qR7KSExoukvay0PHRhinjkVyLHOeC9S+bdAyB9NC8SHhBHApGUyVth/OE4JnOBVmSPAJm02cMD4/J4aNUbcAJxYPuKfG2IpPkapKbXkSKdMgrSHuQcqu9RskPZgs5ovJQgNWVRUBQ1xlgihvn5Y84eP0fqGkgGZoNBYJIp62m6LV3fYKqCqtBIGTK7PuleJxzD43qLaztiZ9N15HmcJD9yB+o4p5L/RGEMWqZ9y8UBwE+xSPAdQmnIOvk+pti5bTvW6y0STV1LlCqYTAxcJRxoNpvx4faad9dv2DYbfI4bRQTpA65vk7ySTT4qk0nAFGBEkkSwzuWCWWIpu9zFGQHrjkhWXzt+J8BYEARhWPeBl3c9N90MV1aIzDB1PpnNqNCzKD3feVRiN6/YrT/Q7rd5wYhUVcVkdsLs5CIvWgNQk/U8w8Cki3gv+MWvPucXn/+K1+/eJAFkkRzaiMM8ON5eIp5AFKntuNKC51dX/MH3vsf3v/ktnj16RF2VuBDGSRijZb9ecfvuLdvVLbbZM61rCmNwfc+q76iePKauk55X13fs9g2b7Y7gArNJzXQ65d3Ne9abfaZB61EUW0pJVVacLCJ93yIEtG3HZrdlv1uz3+3zRI/0WtI2Hc45+r5LAEbwdK5nvdqwXG6R2jCblCiZNMSsjzStJSLY7xuECHT9DkSkLEpOZgvads9+t2PYFJUSdF2LMTqZkoWYTCFMQdMu2e87UIpSKVRVcHm6YDaboUxJlIrLSYVRF5xUNef1lJui4Ga94hiaEkfVnwjcrHe8Xq7Hqt3d8oZzrqjrSXKfHEx6os9BiKTtLLve0bq8OKXHnQO/4ZmLMeFzCO5bh9YuAZ1ZQ1ZkKYBx8xrGc34LFzLALx5WBoGkwVaUDMLrQ1VL5MrTAFiltxrAiCGQGD7poDs0LPZSHqqNkSwmnn/He49UimmpOZ2VdC7S3/a4MYQamozS4XwgND1SyqzxoqhKhZHQtj1N62k7T9d7ppOCWa2pjcD7wGrv6FzaZEsF00pD8DQtNE3kdunp+sDAFy20xHcNpVTMSsmjmeSyBi1iancOIWnXuTBuNlJVSKHSWccUHMr8MMUQoI+gdUTngL136dm4kDZLIyNNZ9l3lr3VCJmqcjFlX0jnEL5Hx44itszkjglJB9kIixYNnh0x9OAtzic3W+ds0jHyHX3fJTB2AGQjB5dFIaldgdIaJSTmiBE2uKWKEPBNR+gs0SU34i/bV8zkOWu/4tKUfLv8lEpKjBRokVhfIgOxwbkkTTAGnHld5FCBPj4i5GcTswsudKHnxr7mrX3Ntoi0SmQSbxayVwKpJS4D8CODgKF1hkNlfFgnSYDsEForY6hmM4qqRiiJ8EliIfoh0DxKMo7bLf0Auif9oLqqGFxRj3MP6/qUGEhJWRT0LjlwDu1Ph7a9dEZj8BtTe/eD46jS+Xj+nPr0P8fopEdOSCYh06rm0dVHTCczSgmF2+Dcl1RhjfA90Ues9XjrcC6BZak9K0trRIbewHzLUltxKw2tKOiioLM9vd1DcIjcOlNUFUro8Tq0hElVImyPFYpCKGpjUALKsqA2FW3fYvsW6yxIz/x0jhIluqjx3lFWBUVVsdlt6No2rf0yFZkCHmUksiyYn1wiROpoiEcmN8fw/vD8j9ezh048cRyhvw7WPgRlyQnDsd7eAJwoY6hnU06vrtjf39FsN2zvl7i+xzqPbTv222061xDYr1bJdM0YvHdIIvVkSlGWBG+pp9PMZkvrkMjaWoKk7xoHrfKcBCmlCK4fi2dKamI2TzqcffojRdK2SsF7uh5jTGpJlwqpkgZpkTVvvfeIEWw5nljQdg2NSCFeYaoUHHuPCw4XPcvFHD9od0Z/mJ/Dn2EuZDxzSK6llHjb023WLF99gV3doWJMrPzMLB1YrdEkoygLOAFOJr2yvqowVU05mWQAZegyyfdApgJSs7ker6dfLdlfvxmNFUd5n5x0DGhTApPlqKWbij4p0QlhGHcHA0CkIpY1dx99hC+yk7mUqHrC+aMn7HvH3WYDHtbrDWWxTC3DSKJt0cFRykCtBFubgPhI1uxTyZRrv9my3zecLBbM53O6LsVgIkYWJ3OmdxNW7Zb71ZrJtE7AZx7hzvZJu24yYTKdpf1MhKynXaFMQb/f4G1LcI7gemRR0PcdgkhZaIRM2sYi1slfAHLrYZpEPiQjyqZzNI2l7R3eR/reorVhYh1CGqKQSK1J6kGavnf4QGYPTyjqCV3bE3zDfteAUIl5E5N8TN+2zGaTzNYKuL5neXfH3XLJZrPBeXeANB2wTiDXZLagns6YLU6pdIkNHuEjagQxBI4wAjh+swE5JaqceObYZ2CDaaNJxTsBylCcXCRDQTRRpK4Gt98kICC3vY8b1NfWII6LIOPJC35txToqdqYlPY77yvB+QgoqozmpSi4nU57PFoRVx3q7467ZsfQd99Fiox+LpQP4w6ALb2QCYwdjsyFWTGjYSIYVA5gzfhcjqBwz884IxVTXPD9/ysXJJVU1TfHv0TqkixIhksFxcB3xoBbBSbPHrS2bynBrFLGUOCeSSYW1sJWYUFB5iS9lAtazRMmYh4VI1RlOd1MIkbqseVzN+bicc+ElMfYZbAnjfmFtYLNpefduRb/qCX2DiJLeRDamIeoJDo31kdlkQrvZELxFug6/XtHc3eKzTAEI2iLtjVEoyipJmvkwxPkZSNeRTfuem/Ur7pf3DMZyPkY6F7FeolWgLiJVCY8vKt6tXZJcCuBDpHeHmGn47LIoqKtEvLEuHj28Yah9HVg9DM344Hv8+gA+GpswyEOMuUTOf3ufSSf5db3LhA+GoSPGzxnwUTGM9xyLP5TQSjzyIq+RiZgg8C4wVUkXvxDQf22P/7oO7OH6B4BRjpq8kUEaLr3DIcZ9eF8e3oPfDsQe68uOr32Aew17D4w/iodM6hBxjzdtwIsP92AgJwy/Jw6gc2IeP5yux6cr+M3yDYdnxPieB7mELMJ4BBSTwdThnMPxRQ4viQJBGDBNYOiQObzQD26sQow5WHoGQ1Z6GCODf4UQxwzd1BkDKufPIKwbn2uSIhMpz/AOFxw+plb+9OXQKjNgg0+F8KhIJJWDl4TRKoOwQ7xDns8eTx7nwiWmaC4Qp4sVmUGs8DKVmI/X/NRhBISId5kwchg9D0bEoIc7EGhEjncfjN3hXsWBOJOf/3D/hUgQ9zgAD3NlGANjsV5FRNQEpWmlo5SCIuTEKYIMHoJDe4fyDqfBIQlSo0xBWVZYF9BF4OzsirKqQRpAJT3WYQw4h3eW3nW44BFSUZYVw1Y1Iht5/Dtr6XuLcz61/2f5uZhxD+9DNs1zBB/yJaZnVxiDCEUiaIWI1BEhbRovuVMpYYAxkRablr3eE0kYWqE1VVlzenoOpPyp63tc8HR9Q8iEHYUkuoAPlhgCDQLvPcb0aNOORQ4iuciQTXLz+Hfu2A3m4fE7AcYKAS0TrveOn70P+OIMqZP5jxQhtUPYjoUJfLSQfONC8tlfv2K3XeNH52FJNZmnYG26QIikdUFepEJwmRmRKiZ9p/jxv/8rvnj9ko3dpImfM0YZQcjD6pPWmKSXKGSkLBWXZ3P++Pd/yJ/9yz+iMgUSgbP+0D7gHF2z4/1XX/D25WdsViuCtXz84hmiLOn6jv1+D1lzY7fbcX+/4vrmls2m5eOPnvH0ySMeXZ1TVQW//OwVbdtwc3OT28cKCmOYVDWPH1+x3izZ7Vq2zY5fffZLnG2JISYzLiJ937HZ7rDOIoXg2bMntG1D23WsNhvWmx33my0vnj/m4nyRJr+ILNcb5FayXW+ZzwJNs8vMBkM9KTk7m6d2+BjZbDfc3y3Zt8mQwvvA48ePMabAWs/t3YrNpmE+r1mcnPD4ySOePLpgMp3QNB1392tU3/Coqnk0ndJfXfFh84gf//SnlEeMtPRQBpYVICU/e3dHYwOTsuDtu1dIERFcoNQCRZHYPEObZYRd09JYj41p7IxxQ174REzV9XF/EYI2Gq53lr1LujOX0yLvN3kRFsN5pVMMCKyPWRspMeuCdaltFEHfd5iyTpqXgAhDYCKPNszDGEwtC+Rk7ADEHtocIjHKMWgI44IORaFxPiRTDqkhOs5nSVR6u+tYN1mfK0XsKdEdQOMQkSJyelpRlQpFZLXcsdy1hJgC88JoLs5rjBTY3nO77tn2IJRgWmoWM835XNNsd6x3kcZLGlfg+h3ZHJnTqQYC01pxMhNcnihEsLmamg7ve3zXIIXAmAJhdEqWcoVViYEiku6RMTpr1CRQWCuNlIZtZ9l2gV3n2TY75oVMAYTSVJOSfr/BdZ7gSBVB5TFxT0HDVOyYxXtK1yKFyxplgej7xKxoG/ZNR9Mls57oc5O/yAFOZATfB9a0EIF+34wV8NmkGp+9EgIjBLbvsE1HdnIAwBL5u/1f88tGcKFqisv/jsuyYi5LJspQGJOSk75PhhQxj5shuM4bRjgCvQ4p3qFbORLpo+fe3/Oz7b/lziiCLpLuUM5ZpErGHMqotJFZnxizORLU+ni7OVpfh+hVRNAKU9fMTs5ou5631zdjgihi2gzJoJIQAl0YiiI5zba+R+bCQ12VnJ2d0rRJt3ZoIQs5xRBSUpUlzx8/4eXrr2i6NrFyhSSEwOAuK0jsBCVEYrr1zYPzHjS+AD5+9oL62ydJSD7CfrvG9R1aKUpjqMsCIwIiCKJLrFPfN1jrknN0NkMdcrGRRTIk3DmJCQhcVFgzoZOGLgR62+JcAyEJz1vn6Vxa21fre/q2ZVKAsg3GByaA0jUTaQjWopWgnNd8df05rW2p6pqTxRkvPv4OSi/YrNas7++5X17DZsl2u2G9XnH34YayhLIytMJxrzxBRurpHGOSGZ5IF/P1GPTgQv5bEsTxJ/F4JP6m45C0II7kZsRhfZR1zaPnz7n+4jOa7Zb1+w/sV/fcrzfc39ywX97RrFZIXRJJjKTpdMHJ5TmzkwtkUYI26MJQViVSKxg0wDPgGQnpIeaLE1kjWGtNbyOjoaRQ1HVFY4rxCpz1mYUYKAtD6z3aGExZMFucUE8WdM5jygmzxRnzxQVN3ydN5+geamDnw9qGVd9jbc9ifk6M4GIyA+uF5x+fPcfaFu0szukMkB09n6z1Ni5cA8tGCOx+z/2b1yx/9QsWMrECVATRNGNCIEmazihNIGKFwEqJqmp2AoRW6LJIAbNz41hwbY8mueDueTue0urzX6HeTQgCVFEkBolKX1FrhE6tYspoyrJCmwKhFFJrMAVFPUtrwLjXD6NT0puCn//o92nrBHILKagXc87LGdtty3K5xoVIu9txF67Z3y8pAG137LdL/H6Dih7btlibWMuByMXVKe1ux3a1YrfdoYDLpy8o64qu7dhttihluLw4Q/TwdnfLy5df0WVQmwj4wHxxwuL8kvnihGa3YbfZoMop5bRifvGIvamRfo/v9jS7Lev7O/p2j5TQthLZ2+S2HOZoqbExJY/BB2zvcLkQ1HSW+82e8mZJXRp65+m6PndczfEkb4QSzW6zY7Va0zqPLCaoeoapakzRAFvaZs/05AwlTXIy7hLZIfg+S6+0tNt7/q+/+AVd1+O9O6wFHoRPXgxlUfH0xTdYnF1R1fNU+IhQF0mKKWnqCVxZssvPtXv3Bjm5RE4XhLrOiZAb212lJCXXObMNQWBm55zoimp+glCK5ctfEPomsQAza+kBqPJgCfqtPzm85Dimi/EAxuZDKokQkZOi5Pn8lGfzE+ZW8IsPt3ywHatoWcselz0EZC42JbOTFPcImQqwmAxLHhv8DEXLHI8OoR4CopAjGzbkG6SEpFYVF9UJH589Y15O0TK1SQupKMqKsqqRSuNth+0bfN8Q/NE1Rcf5ekn40PL/VoFWdPRVRGhJbAKhaVn4wMSXzEyFwLJyXTJvy8U14QTnd1M+urlCAFfTM75VzPiWMBAEncs6scFBBol2+56bmy2f/eqGk3aP8C1CQm88r9wrzqsK4QNiu+NEaozWzOYTsC323Ze8/4d/oP/R7wNPiERW1icZO6kpqwQ+p3Z0RiPOvt9z/e4N716/TsUepbDWYkPA9oJVI3i00MlEyFuePJrzi7c9re0SW1MImt7hwgHN9sFTlQWzSU1dFvjQE7O/QzKqPeQfB8JGBmJSBe0ItDvss2JEBYfheAy6CXrnEUKluDMEbAzJN8AH8GTjo8x25ADi538Nadb4WQMdZKxnSDASbMyalzGbVRvNTEtKKdiOce6vVUHG65EizRujFYXRqdVcJ5+N3lnath/n/IEd+88/HkgrjUChGGU0EtM95ljnwDwOIRf78n2O41UMpeg0x5IO76GzxcdDRHTQdE7/EWJEBYgyJRDHUgOjHECOd0SeO2pcX+Lheo5uQeqilGM+nZivw9kernmMp3iYhw75BGIQOosgRSaMDZ+b1qGB8JDuyJGurExdDCPRIRdTs7pSYgd7T9f3qRMy+qzpmQodLnist/josd5hncXaHiU0Wup0H2NAxCw+KQVKJ5Mto0SW+hguOQODweHydiRyrmlM1udX8cBe9Tath0GOYzXNx5jNpLM2e/CH4jZZ8inf5wEETsvysJ4fxkECoPOX92NnUwL74yioKXMb/5DT5QQPIWSWhY3jvUVrYkg5U+U9hYiY4d4QkTEQgkN6j42CTqZ8TwhBWYdUmI2Ck/kCbztiUkSkUBXaJFkQZ4du0J4oJLqYUE9P0vkIkUzShBj3IussTd/RRZ+eu07GzRExauI657Eu+SrYdshpA5O6xipLlAKPRHqBFC3BO3obUX1DCDaZHAaPtz37/S7tj94SyxKtFEVRsDg5QWqFj9D1jtXqjr5rEDGiUKlDLCSSSdu0bLc7yIZdiYnOuD7HSPL6ITHC/e86GBtQ/M0ry8+vJdfdJaKeIjMt3Poegqe093z32YQfPBa8/sVPWN0v8dntMmoo6gmPHj/j9PxRGhVHG81BKFkglcG5wFdf3vCTv/prPixvQUPI1RGlk4OxJzNccztxSHKaPL4641/8Zz/iX/zhH/Ltj7+BFiKz1IZEMAFu2/sl1199RnN3Q7ffUpWa6dmC3b7JLrWRoijZbhqs69FaMV/MmdRzXr+54ebDLZvdjqbv0IXm/PKMtk16FUVheH9zy3qzZ73d8l//+Z+x3q2432xZr3dUkxJJcqMrjMHFQN97lEyJoTIFy7slQsGkrnh8dY75w4IvvnwHQbBd93RNApBs01OWFZfnj1ic1HTdHmsd1nra1qHyAK6qEpGrCVWMSFIV983r93RdS9smnUqjBbNZxfnZjEdXCy4uF9R1jZSnPH/+mPv7NdfXH7hbbcFGvvP8BRdnF3z85GBoJOKQHB7GUETwxYcVH1Y7/vXvf5PPXv6CR7stT66ecn72CLL7HUJB1Kx2azrPKBEwQE8D6CljfKCnNexgfYDl3rL/8j3i+SWLiaHQWXcnjzIYNvGkbTN0R1QalNHjRgqC3jqUSQm6kmkzPrSrfK2uOl6vePA9BJ834rQBSylzS2luRwMQqRVDI7E+nVChBOe14IffuOBnv7pl04HzMrUHADnCgqyz0+5bmm1KztouoIxhMdHMasNsWvLmdkff+9QOi6SaaIyCyqSE5+cv37NZrQmqQNdzpoXGKM2k0pwvSr73aUklTrlf7un6SFUWtH2fzAlywFEXBUEKgk9t3HSe+9UyVcSNJnqPMiVFndjWIUba/SaB8THSOc+yFbxrFBunaSkwekG3uSd2CRxzQlOGHXWIWaEmUsUN2m8phWVaQFVqnHW0XcNqt2W9vqezbXLyJOb2kXzIoycmkxg6PqRxHJK29FCdjjGghOLrvjXSR+KmG40NjodFAPYRWtfwP978D1xKybemf8D3Fv8ll2pK5R3COWJmW8mYgsaQAYPjzhZPzCzpOMwGImAFvO7/js+an/IqgjQDeBOziHlixEqTGHH9rsHbMLbtKCmZTid47+n7fqych8z4lBJEpahO5lTzGWKi6YcuQRKzIu57pCkJnaXfd0hECuKcI1pJWZS8ePEJy9sb9s2O2/fvOb08xzU2FzCO501ic/S9TbpSAZRIAVraSBOLSokUeAeR1phfezBHbttaSowQuL6jz7q/SiTm9Xb9gc3mFiUERXRIX+E2EnoYZDrJsbs6GjqH55znYhR4DI2c0pZndD7go0fryPnshKZpccFyt7xhuVnR7Xp8n4zl+t5zVZ8wnV3gWsnybs/ON5xNTimrit7vubl5ifMdUml263POT58hZcMXX3zO21efs7t9x3w2Yd+29K5HK890WjA9mTA9WTA7PUMqTYguG7IdQoxj1rEYF6zIUOJPsan4Ddc+3OzflkjF0TzhoP0thg9NyY/SXD37iLOrJ9zf3rC6fc/bLz5j2zS02w1aCj769je5ePaC6eIUMbS5btesuxZpbSr+dALnKsrJDFPkgkku9BzON46fPbQtJt23dP37znExn6F1Of7K8vYWr/d5XfMUdY2MUFY10/kpRbXANy3STFHVjGKyoPMrQnRjq+xRRpHHo6Jrdljb4vqG2fwMhMBFR+97hhY+pdP+PSSOieGTC9nDGQ4FEbKcQXDEZk/ZtVRao0eqTmRwNg4IHBJZGE7OL4hlyT56TF3RNE0u8glkcGzXSwyCQhcIH8FajArJNCEfxXpHtb6lC0kjbUjifUwsKocjDEZEQiCUxEeSSUU95fv/1b+iPL1A6pLgHspYSamx/mC8IoVgWlWEIChNxeX5JU8fX/D29Rs+XF/z5u6WZvUBIQL7pkUoSTWp6doWVUY662k7i+261DYZAt46vrj9nHfvb3j85Aknp2dcXZ6zWa3xXUe331O/lqw+6kdTpwi4kDp51GaPEJKqkMmINkBEUk8alCoAD7LHx8Bq+YHFfJHGkSnYbdZ0zY71/ZKq0MTMPDJVgS4M1qb7iUjGd9t9N3YEuBjYtS1KF/QuEEKLtZ7r62v0fMHF9BRTz9G6YGp82mIAACAASURBVHYypd3tAU3fWaY+MVOEFNSzKSfzCa9ffsbq7pbt+p71ekXv7fjMhvFrP28JS49SgkopmqbF+jucXx50/HJS6myfgIo/aZGP0j1786ufcvbse8wKA3WaZ0VRJJDGWvb7LrN0cixJwEuQVU1VPeXF2SnVYs7qqy9o7t4TbJdkQQbQ49eXoMMSlZP6Q7h2aNHNfxnjwxiPQNoIlYDfe/ycU1NB7/jHd6952a7Z4mnxdMGPc/ThnDSIUiOqpFN3zIg9fItEkbuFJKAlQg2msBkUydfmiVRUPDt5yneffJtPrj5hVkyRpkKakmoyYzo/SUCsc/RtQ7u5Q9gdoT/aI72laVfc3rzi9sf/C/2f/jm+rJEi5VxWQeMcupfMtwUfnc5QLrKio9UehOQHLz9l1tRIJOfTE/5UV5y5SPBtih18n1r2gyc4j3ORzz57x/u3S/zWcyYlTQyowlDOSij32LKmnEwR1YS7mxsefee77N+/Y//hA9XOIkwYzfwQAjU9RdlVKmq7yOykSD+OELyibzp+sf+f+bvP/i0vv/glQaS2dSmSL7rDsLUlX957bLdjud7izRRlBFpLepdYvamQc7h9fd8iimS6N5tW7LtUgBtCAmAEGAfwzh+Bufn0fyMT9PiQY/yZWdsBKlNwUhdMQofRWdNTZNw/ppjMk+Rn4rjlJRYnIZnnILLB8dCKfgQCCyUISuQ1On220WCMxChJ9HEgIZJbM8YLkpnVOKuTI3vyWskAlBJYN4DkSeIpxmMw9XD8p2QJftvhwyC/leI+YjI4TABxbs1XyYl+lLuIuTgSQgKMY+pvV1IilSKSpSe+VhSNQhCERCIJIgF2iXiZ76OQyeBIZG1UMYyFpPUahj568rrp3YNQyjqbY14yiD7cZzl2jw3mZ8SYyCXjAEzvO2jLDoUBpQJBHnKVvKsmUDZ/0GAOJkSaA0YX43NK55lY8j44rHMordAxgatKG7xPMbwPibDX9x3GKKx3OO+TIRgggkQEleVqAkYn0ogpimyWla5lyIO8czn+DwdSVAgEaxFKoXSJMUU2SkvhH15wXICIMRNuQs6vsobw8Ghd9KP+rM5P6bhAMryPyPfWk/J879JXDDEzlDPzVaRuwDhIbA4t/ZloQ+6+lJlUGEQkasF8MkHLDqEs2AEwjhA9MoY0FssCUVWIoqIMOnUx+2SsVpSSvl0RKIjS4PoWY0q0VnhnaZsNMYCpphSTKaYsUEBZViidJPq8t6hsst17C0pSGJOIEVInJC6PzyQd53HR0bRrdrs7drs72m6PCz7NE1NQosB5rO0IwbPfbdF37zFCIFyHqiqMsOz7hn5naIqCxckCZQpMWTOVmieqQAjDu3dfsblf0jX7hAfGzLIFYvBJHjMbR1trcSGke50Jbd2uz2HBPy2R8jsBxnZW8I83gjc7Q6gWKBFQKFwMOO/pm5YfXmjO5Ap7v+T+wzt6awnWjQy5p8++QTU5A1kSQzzaXHIrYQ6kpFK4zvPqq9es1it660CKAxFQRKIIY7WT6BFKYIxicbbgX/+rP+e73/wmTy+vEv096xGKo0l7/+E969trmtWS+XRC6Hti8BglaF3IsguOru/Z7zqKUjObTqmqCqJgs9kl84MAN+/vef78KUYqvBT4mFipk+mC7XbHh7s1f/F//JjZ/8fem/XasmZpec/XRTO71e+9T58nT7aVpmSZQrIlI2Fb/AVzg7hE/AN+QfE7fM0NtmVkCRkLhFwIU1ZVWXZSacjMk6fb7WpnE83X+WJ8EXOtk0kVWCWTF4S0ztlrrblizoj4mjHe8Y73XS+4u+t4++6eznueXZywWrTSoq40q1XDoqllYqdI8B6LpusG9rsDb19f01SOHBPdXgb2ZtNyfn7K2dkZl5fP2T7csfzBD9gfOu4f9milWCwWrNdr2rYWt2dtaKoa7wM3tw/c322JRUj52bMrzs5PWW8WrNcrMS1btBJcKGnZbhrN6UlLP/YM44H97TU6JVSsAKlI/2ff/x1++fXX3G4fOPhh1sZKwC5E/snPvuAvf+c9zO07gvcoNKenF8XdU7hl3TgS0wTEesAwWTBIla9EGFOFSpBOpDFO0+fI52/veH625HTZsKotJD8H2hOoq8pZURRzOFm0ReRcqufq+CqgxB4pEVM6GpiUjTarx0FTkkpYqTpOLCxhZJUWzUdnVkp0cWIB6ilg02lj+P4nZ7y87rjdjuyHQNZSbyvbASknHvbTpi0skavLJZXOEAM3twNdJ8lcVVk2a8dmVfGwHeiGyMMhEEZNNEsx6ystWauF5WxdcXHihAXjNOdnLf0Q2e560X2zlpwz0YsGKznMTIxsIHZ3RDLZOKpmQbfr8H6kahbU7YKx7xlHqab1/cg+NcT6XFyhVSYd3hEPb9Ghp8qRtYU63pLGAymMWKu4PF+RwogfOu5uHkg50vWDyBCkUPRx8px4mccBVUnMUkzzxj9JBwhztARU5hi4PV60w+Dp9wfG7qgZNoNNM0gnG3iXI29yZuj/Da/iW062ht9Z/1XWekmrFE2aeMOZx6HSrKn9CPyS8oQAsV8c/hlfjW94F0YGBSvnpNaXMsoackrYRYVeVHgrFUVVKrcYzenVOfWioR8HfK/QJaDLsQjb50zVVrh1i1nWBCuJo4oyRsma0A1oK1Iw3gfRwSUXPeRIQnPz7h1d35MyVM4yjMOsdalSlqilAMQhBL5+9VKYs0U/MsaILlol1lgq49j2h9kh90nwnvKsjwQwjh2631GZSirdhfmgcpbErmBVnky1vCAcdsT4DsZ7atJT5hQcSSGPfh5QeFPj3ZpoK/YP7xhDjzaJxeoKpSYt0ohVnnaROaSA7z2qsFuyEcObzXrFQi1YL1YoZ0BFrjbvc3t/Q9su2GzO6Q8HjM1sVi28eM69hhy9FN3qiuX6hPNnG1xbYaoKlKGul1grZlKPdTynNUjG3zQvFN8O2Y9jclqvNdL7WoKyMuzhESMESRJyEDAzxyDsSdfOjFnbtJx/9DF20ZJiZHlyzuX7C1LwaK1ZrFZ0gycqRfAj2+2OdrngfPWsVOghRNEBVEqTciwsO8O3WQ5CihGts8nRd7rCEEb6ww7v19MMpm4qct2SUk2IgdOLK9YnZzTNAmMrkq5Y61qKxcZKS7cfSyeFBN0onjizoxQ+DAJSpJEhdHIdOTFoRczSOuZcRVXVKCWuzkaXBPrbwLgChUHlTBhG+vs7bAjSRTgzB5VoDJZhm5SiXrboZUuuanSIJK1xiwXGCnM/PNxzyBKgb05OwTgBSLMijBHeytuvLi45qT9k2x1IXorEKOlI6rqOh7tXEGJhA2Xw0lERCHS9Z//2La5Z4da1FM/JR/BAwfZhO6+7fhj52R//ESfnz1i2FYsP32f7cEO/P6BRGG059IWNEyImgRo81tqSZGbquuI7n3zIOA7cXN9yd3uPNZbxMHB/fYNT8PHHn6Cix+QLVDYMfeTdz36B6WXP8MHzf//sZ2w2G7SBpjY8DIHTzYZx9Nwf3nF7e8f5xTNO1hu0rokJ1psGV1W4uqFq12xOrvjm88+J1PikMM7gKiemRu0KU7oomqqiclbGEtC2Latlw3q1IHpfwKhACJHl0rG8POfQZQ4POxarNd98+Yrd9TX77ZYw9NzfvKJpFlR1jU6GX37xJV99+Uv6bk+M/hGwpMhdZvxlLwZbvRRgk65Im3MetEiW6aoYnWLI2QI1jTmhrhzj5g0j1yjg07/8VzDulOwaUoyS+BkLFIJCiKWjTkALUwxbZJJmUl7z4U9azl98xPbtS9796ucM129K4SVKnjBNikdMsnlbfvKj8k1mdo1+hCuRs2go1tbylz78iPcWJxwetry5ueWl79mpxEAmIkYqORaZlwK6aK0LACstvCrreSuXeajmfSSrTFYRjCbZovNewjytRF/XZMXaWL733md89uIzvvP8uyyWJxjbYNwCUy+o2xOMqwje48ee5Dt8v6NiRGxv5Tj0Ha+GN/ybt1+ybzPVL/4P/Ic/IF19IJJJJuO7TOc92/2OtYITk8lGkYLms5ef0PSOyjjW7Zr3rz4gvLujU4Po/WrDoTuINrVWxBD46su3vHp9z/DQc6oTz+rEzlr0qsWdLAgZXL3ArU/QTcPu5h31yZrD2zfs3rzCpIC9eI6q6mk4sOsHjJXOrZQ8Y/DkACkG/LDn4e4Vf/Sv/jmvXn9DAharNWNOpFSRTIO1Z2zjM/bXN4RQ0/mW8TCw7SI+pnmwDKMXvcEyhoZxJMSeYfSS85aWftlrniz1cxHyaVedKvvotAX/ZvDxsdSAtPIlBu/ZKtFzPLPTe8qJtFZFCaOYukYmMQ/JGrQu3V8SF1ulpzRN9sACjAnRQz6bKRJFWku+zejna9VGUVeWRdtI91WZrzaNs5Y+WpNSxoeAHyPeR/lc6Sgb9O8Dvv55sgWP9T9TmirqkqOJEZcUJI04WpaQpeRvpQtLaibiIu+sm9eVCRCfgFUh06hZ01m6Iidt11zAYNH0Fr/CTE4eeZJyRgXzvq4LOzErcMpNFzXnnWnSPtUKV1nqYkDtjME5S1W1GC0auRMQlWKRovEDgw+McWKqjtKVPOXGKZeCQ56l+WIBeyd2t/hHHL01tFZCIsrympiE9KONkIv6wROaBh8TPmVCZla8mpmlxb/GGouzDmudmKAW+YGMKu3yxQhwzqune30sTotMghgyGftIxmbK5pUuhJdEjBmSGJIfzciSMEONIXhP27bkbAvoXT54GTPCPQszoA4yyZTR0kFeGVCOaMw8nlTOxW/iqJNPfiQtgpa9JHmUcUKiKTbNGAPWoV2FtW7Wpk4l1rXTtaZMDoH9zR0hyxh1RbZGKwjBsz/sUCASXzlxd3+HdR2LxZqqqakqR1UZUBLHGm1YLdeslktM5aR7BYXvBvIwSoE/iUSPD17M2LSiqivGw0CcZAGizAXpIpRx9/BwK5JhcYS8xhqFdi0hePr+wNDtqFqRIzPOsWganl0+wyjYLtfs9zty6bCPSSQIu6GXrp8kUjW5dBFQ4MMYIynrR2S9/t+6pvxWgLF9gDd9RU8tNHSyuAzmiE6eRgc+OnM0/jW762/wfScDToF1jtX6lPPLF7h6gVICqh3rC6lojHjhQCaL94k3b9/Om1vxCygD+bgxKiWaX67SrDYLfvLjH/Kf/Oh3uDo7p3EVyZeWxAKupRRJoWd/f82434p7pnMsFi0qJ2pn2Zwo6roVM51+4NU377i5ucYPgboesMbJBNcW0Ay9Z3u/pa4czmqCD1hXk9Oeaet7/fYapTUhSGtAP0a8p+ijCX+sbRtc0blLUQxDhmHAhx7vPeMYcLUrq7/COMfV5TnnF2ecnJyw3izouh3tosXVDaIFBof9oVSlJaA8HPazSYj3Hq0zdd2wWLScnp9yfn7GerOkqh3a6KIBIsBizqKZVTcVbdtw6IR5KPJiBVBB8Z2LC0yCN4slb+7vuN3fS4uDkirr9b7j87e3+CCLz9vr1zhb0S6W2FqTVZSWuKzRWUlbgJyco7pRpjaiuwmwHyeAUkZVJLMdRuxWgg7NgtpOgfWEj+Xj+FLCflUlKJaA5Qjeydvn2XhKqmChbMaPm3yYQZspuJLWFPV0k56zAcX8octyYIosw/QzZ+B06cTsxmre3fXs/VHLddrVxCFczqeVtA6MQVwGd10kU7NoHMvWslkYkhc2Xj9GxqTIWUTAjQZn4GRpOV1ZNgvLwhlypLghaxTCoKybxVwtpQRzsikorDGk1JPTSI6eEC1Vu6BpFmRjCSHS3T3w7v5ARBOTIVDhsxXjj3CAHLH9O+pwh0ojmkSbIwvTodvEpEGZxl1heB847LfEFGX9mBhxahpAR5B0wjMm4PSomyn/kSo45X5yDNhKoDcdKUbiGMiTK/T0ft/CSkCYCqNWPKieMXnuxow6/Clr3dCiWaF4v/oeNh9H+iPlWI4hpQTXY/a887/kpX/FdezYAbmYjqUSlFfakq2mvdjg1g3JKngtjuGmsujaUW0WqNqiK7B1iciTtN2klMgxYZYNqnbi1KMUOUbi6KX1WCuSF0AzhogPQQBtRMc1e9mAd2yBXJJvc2znKZXKDFIAUcKkGEvFHa2K0/tRmEFlNQdPx2bP4/HtnxwOHcPDPRebM3k0WkBk2ZXLvS7jJFUL9PpKgofgCeNONuNj7/6RRfqoqBJVRbAtoV4xxsTQj/hxRBvotiPdtpf7bjQxFr3IOJKDBGTDMOK1x2Ch6BNnMipFlAoYFDobardk2Z5iXQ0olqsVlbWsF2u6wx51/Q0hDixWNYv1RoBP4zC2pq6WqKLyPaUWj/DYefiijoni8acl3J2A2DLvKUYZPDorWdrBj0Wzok2bAikFbLbH1yLg+Omz51jn8MOAcRVZGUwlJh8YJ5rwVpL/RVa0ywVVK4BuSqkU9PTj5fTXkrbHbJgURRZAWsqQNrQYGIaD/LwcrnKoRlqnjXOsTs5olxusrchZk5WlKvFNSpFYOoZySrMxlS6jZDr82BOjJ+dIiBnfDaI9l2G0wmizRpxmJ4B5Nvx4lNAf73op0MREGAbG/UGe8qSL/u3niySdfhzw97cEYxmyJFAZJVqy1sJ+D96jnCVHT0IKl0xOwNNhNMo5TBbmhWtaUJrsI3ZiCxVG1rQ8zjrsMRL2e/KkSfqoqAmSnKZHzNgYAzcvvyQMI6vTM0xVc7N9YMiZ3RjYjhGvG3aHB9FSb2uW6yXGGvphnNtj123NLklhSorVmroW9q/vhZW/XK6g6FeedT3Nl1/Rbz6G5RXq9pa3764ZxkGu2WoSkc1qjbRVeKIf6Ha3mBQwRjQm18tL+k70ysfuwOJyTbs+IRsx6VoaMduYKj5Vs2C13lA10mZonaNuG5pG/p0y+CiMIWc1TWtxrkZXFckP5JhwRrO97+j3e/wgbeExeIZux9DtGYPn1cuv2O0eCEH03BRKQoxdJN5F0i6STCYnhXE17uSczUefolwrSaNxJUQ9DjZnLJVzpMWBkWsAqrNLSA0py55qtObmd3/EcHZagI4jE0kVZtpjk5lMkUjr9nTbO8Y3rwgPd4UGlcq68hiAPQKeTw511Mee1rT0yJB2XvGUjPl3l1dk23DY77nb7biLgZ5AmFdSNRcTmYAZLWy6bBTZqhl8PZZ/iqHQnIkrMMIcn8DoCURQgMmAtrw7fw9OnnGzvqCpWmzVok01s4eMc6IL6Cuir+jPHFZHzt82fFgu/19+9j2+Olvz8uUFw//yU9K4Rd2/RFeGfPG+yFXohO4zuyFhu466cVyMS1Zdw3rXorVl0S65WF/wqVvT2p7spfvEWYsqEmAozeATL99s2e0DNiYWyrMwEZxhINB1WwafqZTHjxGrIwye/ctviNfX6K4TPdyLS3R1lJERRmORRrLihWG0dMEcDm/5xds/4OWbL+l8h7LShaaSQ1UnKHVBdu9xE07RfklOd2Ru6cZ3+GLEOEXrOaUn+2QfRAdz8IEwsezm9fXxvvN0zf6Nx4TsHLfZXxuuU9yaM4whssuJpDLjsqHSGa0FpJpA/qLqOY839ehLw1zkV/ppXqTgCVNwkhjNJKxRIkHSR7Sd3O0ty9bRVk58BMpctagC5sqZE+DHIB16IRVDn2/fq3+3488Cb2eTLBIxS8ai5jzvN8uZKK3K/c/z+adX6V8zClRz3ljeUPKC+c8fxUaTTBvSwZgL0DmFsml+F8pcKTqsU15S7qWYOwl4O+UtxopJVd3ULOqaRd3QtBVtu8S5GmMqdCEM5ZSkldyPDCHQDSP9KNJt3WHLOA6i0e+FDCZF4mJK+y2ygzTdTXGexBbz78vNjSmgo2hQe2MYQsCFwOjlKzVQWBHoMobEv0bkLGZg1lVFn1TayaOvZSSVPPzxMw8xzuMple65CZgtDw6lSs8+hZGdVJkzR5kLrTXWWqx1mFIkhPzoPNNP1PH6C+A3McBlGIhBsbZGzLqmWLhIC6rCJuXRvS1XI7lUpnRsaYyWjk5lJDfACNiuc0YVabikEWZ0OSfJ03dFOkcbcvKM3kmM6Ef6/iAd0SWmUEo0Vn0I5EHIDSkJ2WocpcPFGot1TkBRI5rzKWZsLvFnTjjnQCVQSVjyVUWbF9KNMI7k1BODMMmFoSyM8K7fUznLsmkwRrTjj6QRkU7KKWG8lzGjpHs8JU+iMG1zwiSHjo6k5XpSTKQo61pV1tecIfgAJQ9N8dcJN4+P3wow9jBmtqkBW2FUxmSFRXReXR7ZNJH3N5n9yzvurl9jTBSjNWdpFwvOr16wObss6YgMwhSDMDNSlIBw6HFao7TD+8i761tJYiYHg7KwTVVq0bQQwGe5annx/IL//K/8Hp988DFOWdGqmLoP0uS65+l39xwe7sD3nK4XhBBpmpraapaLhvXpivX6BGMc4+CpzC+4ubnmYbuDbUdla3I2HKufmtubWz788DnOWsZxBKUJfkQpRds0bHdb+r7HWM1itaBLoLVMcq00ubRC+BCKs21msVxye7djt98zjiONdZAzzjlcZakqw/vvv+D0dE3d1KCziPobw2KxwDnH3f09Dw9iFLZoW5arFTfXN/hxLC3QisWyZr1es1qvWG/WrNYtm9M1Sim6rmf0oSS608IhQWndNDRtYN8/UNdu3rSVgg9PVqzblqvtKcvXbwhfDXReFoRJtP1nL69JOVM7Q0qZpmo5U7DQBhCDBlIuusIS6qqsjwFvziytYVkLgOrHHp+0YCoFWRhz5no3MIaMwnC1duiMLIKlBDyPp2I0NIXgiqeV7SNgwLwwxOBFQ1RPDFXmIOhJ3K+Kq6cqIdAT4ELG0eMqrlEih3CUt4faZK5Oatpao3Pg1TYyFJOrqVopby5/kxJsdwM5DoTR46OmWmoWrWW1sDiVeXPXs+u9ALFatIuNTlROsW4ML85bThrNwmnRj/LgR3mNH8VdcbGctISKJo6yEDNaS0I+HHqUgRSkUoo2LE4uGHxid+h4/e6W60PEthtM1WCsJvnE2A+kOGLSwCLesLIdZNH2aY2nNYm2rbHWMoTIm1ffcDjsGMYBH8YjxPMEFM0zWJ0LdCEs5fKsjSnBx5GVOithTAs4uZCWH22cMT8VE50fu3qyeU8DQmlNMorBaPoU+Wn/J7isqLJikxWcXLCiokJjVY0rwUVRTSibdMdIZJf2/Kr7Q16GwEPO9FphXGkVylokFeqa1BjW711gNzW9H9HakK2AXNW6Ra0rogKqCpstVhkx5OJRoKEVWGlLscqQx1EAJJuoakMOxYAoSDvIFETmJECHV5GYZb2VFjFNSKGw9vSsh6WNKQyASCahjRMNKpUmjFiCl4SAHWnSr1NPomv1ZBLCw25HuLlh3S6L3MFxbORHr9dKkVSN2VyRyITo8TcdmiitVI/ypRnILwBg0i3BrQj1in53IPpIDokcNf3Ws7/raZuGqm3IPqKUw6ZIApyC7X7Aqo7KaHJSJJVRfYdTkGwkDHtSiGgMlW1pmhUhZirXsFqfYJ9X7HdbdO3ou3tslanaFdrWONvgXEtVrxDmGseAej5mCOZ4ofN3j27YvOCUQ2tUGS/zDMtJDIuigJJagTV2dt81Wos8QJZ3TGROLi6wrqLf78lJCqLOOazSpNHDbExTs9ickEvwGKfW+5xLUq6PdbQJWJnnrazZKSd88MQ4PsEUc0oMw+GJmL+2FteIOcz67BxjG1LW+FCCaZ2IVtZBMRM4/ltA3QxGc1TXznT9DhO9gGLJFxkVCeRD1RDCSO0q7MyGLQmhUvMeM+mOT0lRVpkYpf3eHzqqsldOzImpGHg02ksM+y39wx1jFtf7SQdMkglx8zXBE3voFEQsdTtitMXHo0bzOAwM6kDOsTCPxGQjltgkSx9bwRsEkNUZ6axJkTgMUMDYPE8yAXG01gXELaMrRbq7a4IPjEOHaZfc7HYko7n3kW1Q6PU5+0PHxXrF+mLD84sTDvdb9tsdu4ctQ9ej/Ejqe3IIGCXmhJfnF8Tg0RmGfuTk4pKYDasMVylxfnrCly9+Qjo7Rb/6gt3hwDgO1FVFXTmMVcQo2vN1ZbExEoYtd+Oetmk5Ozvl9GTJ2zdv2D7sOPgd67NzFpsNw2HLdnegacQZWTrBFKvTc04urqQYYy1V3bBYrqgq4Vb1/UgIQlRompr1esFmvWK3i/hK5GKszsS+J/R7UhhwVYXWiGHedsv9/T3vbq6ZDFnmtdNDuI7Ed0HWR21Q1uGWJ6xffMjFd78vbZDKlu6iAsaWxFMrhVaGrv1mHiteV6gkxAytFWh4+V/+Hrc//h6/rUcAfvof+kOUYw/c/H/829/7as9/W/76H//e7/HyRxXq9Re0/+y/I6aEun+Jih3p6pmAGQvL4DRRB9R24Mo6zro17dtnPGhP5RpOFhveX1/wXWrG5Qnd7h7fd2idqKoa1zT4kNn1kVfXB7yHBsUCL91b1tGPA/cPd3Q+U6v3MKpBh0ibM9tffY7a3dMAcbHCXDxHuXq+Jq0UY5w6MYsBnoGU99x3v+KnL/9n7g+3aO1wlZP1UK9R9mOU+YhgPuZNcDR5RaVeY7RijLcTxwSY1liebHtDTIxEMfZ8cpd/PRZ8/PPHZldT7DGzqVUxTPw1gGZij8qyOIQgRrdG45WhNgmTFSlAKC+aWuPReUqhS0cUZMFK5gt7AlIqyUknzwSfZX8mJypj2DSWtououui0VxWrtkJn6aKKKRBjMdwu1yLEnsQwgbHxW5HHbwBWj8SW/O/2/VxYOYJrKSfU1E1S5JJmGRJUKXjIPjOHkIpZWmkC+Ckx3iRzMAPe6rjHTk2NlK40YPa3UchnmUMoPeWZqoDjkgfOMWkW8pbSj8bO41ykGE+nUkB1laNdtLSLiuWqpa6X1NWStl2K5EvRqtWIjMOh7+mHgWEcuX33mofdlv2h59D1dPsdYRxIScy3Bi8mfDEedXCVVujIcVwpyalVPl5LcDkO6AAAIABJREFUCF72DGPoQ8CNnkqPDHYUyT8FykjnQ1VVVJXICxijMVrNRqPWOAHytCZXj7tbUymQCIFLeY/3RUy2gLW+GHTlwg1XxqGVkc+vtOSs5LmLQSkxDaubuujQmtJJmShQuMSrWebiRFYRrVgxRo4hPyo0yNgyRibd1NUtBoIK6ZZLqCj9QBN+Qc4EIGY1x+S6GN8nbQWMAHSW+Ing8UqRwshEZ88ZfN/hUygSDkq6Vn2Y5dpyDLhi/FXXNSnKewUv+r4xGJH863piiEWyIGO0xhpLzoIJGTcZ3EWq2hUsIkmBwVqWdk0dvJjvZgFf9ajJXhXSRmLoe8a6JqZAVVmatpnZvyGODH3Ajz3DwMwFUESs1Vin8RHIEuNaU1Fr0bKNQZjIqoy3aayGGNFWCwnG/9v1YuG3BIyVwNiVhEA2Dl9c0yoGfvd5xr/5KWn/GmeiJDbGUC02bM6f8+zDTwsgJedLKfL25TecrJbE4Nnvdzzc33F6fs7ytCGjGbwkMNP7lQ8i7QNGY51iuW6pK8t7L57x4x9+nx989xPyGArdHI4psywUzloe9g9YFVAmE8LA7ZtbNmen1MsFy7MVZ8+vIGZqV9EuWz786AXLdcvPf/4FX3/zht32wH4YsDvN+fkJ3//sOYpM8JHddsehO7DZbDjZLOdF4fmzU7786hVnl+dcvmjQX77kdLng4myNs4bDoePlm9csm4bNes3Z2Snb3cC7mx1391t8CHz2yYckBhbrhtPTDSerJc+LuZbShsPgUUqeyWLRcnl1ytWzc16+fMfLl6/5+ee/4uRkzTB05Rkk9vs9L168wLka7xM3N3c8e3ZFVUk1Tdp+BIyYqPn3+z2H3YFu35PDyKKxfPbph5xsqnKf4TvPF3z95p6ahucnP+Qvffopf/rFL/ni1Uu+vn6D8IQMf/rympf3O/6bn3zKL7/6BfvhwPn5c9anz+TZ5ygLu5kAWSOVoZJUnhh4vrIs24qVCfzipqMPFJF1AQ5C1tx3nn64RetzLlYWazKUKrpsrqKkcARYHgOlx38dQwURUq+qqrgTHv9iNmqZx+xjNK+AsUyDeoY85gpfzokwiipoQqpiIWScMWg8K5f57vsbXmTL12+23G5HdgdPSOp43oJCHA5jOXsFRuP7kdvo2d6LIHw3RhKiSUZOGANXJxWXm4rLTU2rlbQKaEVSgjkGnwuwmqibCmfF5CqUgA2gapaonMqmsMGgGO2BEAJdNNzcBW4Pnoc+M3BBdbUmaYcPib7rCNt7FjazrhTrynDVrFi4BqcKWxXP7fUb3t3dcDjsOXQHuv1+Dqoea0DxaCzMkXR5WDElImkO4MWsUqNKVfERvC4BmJmKAfkJ7poL8/Px8We2UJGISYGSQkCvDF0587vo+eb6H7DIcGnf4/ub/5oNmmoK+spjfrf/33hI77jPiS9S5DolRgQUPGkb0V2qWprVhvNn73Hd37G+OsebRPd6hz/0GGdx6wXV2ZKhBIyhVHZToUdP815rNdmuCTs1Roaul/PUkG1N8oGhG/CDOFlaWwGqGFXI2DS1aEE559BWU1HhatEK9GMo907+rwv47YdhBsyfQIEFTDPaCHD7qCoPErjYScgfuNttedBvOVuveXZxWViR8nd6AiHLhpMyZO2wJ8+w7ZLOj8TdO0BAm0eVFkBYTUk7Yr0h1Cd425DUA82mQkVHbRo+++xH/PLn/4bVesPp2RlKG775+gueX13S1C0xBr78xZ/y9uYNi2bJankm8//hQLO0tKuKvt/TbQ88mBpXtTTLNVWzggL/+RRxiwUfffoDUhoIoZekBIMxFc5J1wSUhO9J0vhtWPZbxwR4zylPeVXKpOjx0ZNihCQxgDLSeZKtxY8eHwKL9VJ0ifc7tGnImEf5bZ6ZK9pamrpifXqKNk7MNDje8zAPgtL+V9rWBAAVOR7F0bhLMRVGlASBxogJZBbTANHP0xQbevruQHgUnMWQMVFBtmgcCoNRWoL9YUAxkvx4NNXKkHIkxLEYBm7JJLr+B2WMQ0wDzsjVjz7Q9weqqqKuauq2RRFxRmSQdS5yC7PEjX7yfI47UCYOA+HQEQ4dFPtC0TDLOC0sWx8CMSdph69r7DCSxpE0iN+9ytOdyyRXUdmaOET23QMqg+cepQw7/RbEU4vu1Ut2oSZkAe2Uc+i6Rrcto48iG5Wl02b2i8tI8JwVY9+VZ/mbknItxprqOOssnvGwY6wsS6f44OyU19cPnF5ecPLeB6zOL6m++oJPPn6fF+enbKzin/xP/z3L2lK3jv6w42c/+wWnq4ardct752tM5fjow/fZH/Yi5WIVMWaM1ZycrDg9FTPXd23L3dmnhO9VrGFOdJVKGO1Aaep2KYlL9JAG6RYpOpXdwVPZmroOxNSTUyDHwNj1xLGj+fiSplnx/Pkzsml48VmFT7C/v0GhWZ2cidEnBh88w+DlrmRN2AbG8YBKFdotcCZy6B74+hdf8Orta3IOuMZxenHKanPGH/3v/4I3r99wOGzLKqgLyCD3uv9/OvKY5/ClXp9w8cn3WD57D70+pzuMJAKTXcl0H1QBbrWWMRYfjdgw9BAe93lwbP/+j8d/kCOTsVqYwWl/jfrn/6MU6X/yX5CvPsY3nlu/RY8d9TDwvJiSnZ694HvtKT+I0rlXtxu0rfHjgEoDlTPkYij388+vues0y5RoSZyoTNu0GFexthWjsaSuZww39D5TxTXLRU1da5J3KLui+fA7HKo1Qcv6LkWdJEbFCA7hlGUY7nk1/DE/7/5X3rx5g8ZhbIXSFQMtofoh3v0Qr67wsRVTZ3VBlTM2DAz9V8SgpVv/SSFyul8whMRI6R4soFMq0h5Ps4fyNznP2p3yWeWeT78Twyb1ayxDNaM084nKmRWl61bYhGT6GBlCZmGEBKLL++hCbJK1XXRwfQF6amOoFdKdWj5uZaDS4FVijJlkNDpkNk5hG8fDInIToe8G+kPP7m4CMlWRjYNWgzOyBw0hceg9ow+Plvin9/Qv+lBKDHqeMFhVkahC9pXJ7Gl+LooSFxWNe2Pmbq1vy5TlAsqRinktE2HiUbaYy+cwBqWk43SKExSyrwtoLi3ePviZnJNAuqYKoB0K2SGGWFq+5XNYLR0Xi7bFWcOyXbJcrtmsTzg9PeXkbM1yuWKxWLFuzznZrLm8cNipiy549v3Adt9xc3/Pm5dfcn99zX73wK7fcRg7QHRfRz8SUxQ/iAmgiZHKVZDEh0XlTCo6u6QkYF4/UCtNMIEcEuPgRY/XFgZuEgO6ZGSMSj1PIa4gxzkxxYupgI0pPQZCQ5HWmZihQggYh16YsvKkgaPUk6wJupgzW2zVoLSZjZxVyV2km0zeczKqSqXlPo6BYRgYx5HgPSl4SIkYhiLdJ12cvzbaU5qooccxm8UTR+dE0pBUJlKuCVBYMQTLGXJEp4CJAaMCQSlhh3rp1IyFJSsSJIbKGtCOyhq8AUugI1HXYqIuYKuwXidCg7WGfdyX+ybxZ4gRP44iP5eygLtB2LbjMIhR6rBn6Hd0hy1kX+6xxjlDu2hBgzWKg+3YPuxJIXHYH7DacLJYoVA0Vc1yuaRuapKKHA4D+/2ew6GTvL/rhL1bOuarqi5MbpnnVV1J530QDfsUQ2kVkMNkTVYNxir6Pv+Zy9FvBxibmUX+dVEJGEePTp7WRNa8pbv/mhR6oRXngLE1V1fPObv6gLZZAoqYRHx52O949/Il+tk55Ci6dyTqyoo4uIXNeiOLepmQSvoP0c5hG4tdWEJjadqa5x++x49/+EP2d3tYagGNJ1eeklTkHImhR6fEpl3huwPbu3ucM6xXLZcXp1w8v8DVljhKchd8pGoc/XBgua759LMP2axPMabi889/xcPDPV988SV15QheqhrGGm7iltVqRVVLC0tTO87PNtzd3XF4NRKxLJqWnDLBBxQKaxxKW8aQuHvYoXPmYXfgdtfTDR7/869YLSrqesGzy4rT05PZKRUlOrUvnj8jx4xxlqp2tG1b2OqRnAPdMLBenwrrLATqqubs7OzJIv+rzz+naRoWyyXr9ZqkZMJIxUoW71BAMz+MvPf8ObUzswawQnF+tsJYw5u393zx1Su0rfneiw/44Oo9HoaOr29e8/kXX3MYevaHgX/8f/2Sv/rD75CuX7IfOl5kqNwK6zNelOOBhCIJM0RpLI7LkxanAr4beH52wsv7AZ8yKU3tbFJlTECfMr96fUuKa06XFavaoUhop7CmFJlSlOAGdcRLj7NgKrbN+kO6mCvkMsaA46ZP0d6ZGILGCkAg0cpTVAlQykgLC5L4jf1QWgQyKE201ew+bVCsneK7760YLhO7IfHquuNuNzL6oo3KI1D4kdnL6LMkxhoyorFlbWLRWt6/arhoDa3VVEY+XIrSDh60GMv4MUjwqC3Be4IfqCpppVVDJmWDtQ6m9qle06wvCGZJtxu43jl2AG4FS4PJiu1uJMUDiogh8nyjeL7MnC4dJ4uWSi9I/sDY79nvHnj1zRfc3r0TPdjSRi9VziNgl0owlKf7fXyEx0WNohlUftg2dTEf0ag4iYCXOqgSQ5UJ0JkB3zLO/izh70cjqLCvC4uysLLlGZV3M4pBK8YMD/ktX97/D1RKYVJpHUOu0cc9nogncyAzwUa2yIhUVcvm5Ip2fYqp1yjV00UvwdR+4OKjFyxP1owpshs6dEjzvbLGinYP09gUs4Mp0NZlk65OlsKqDZlu6Bn9SD+M+BIIgEgYoCAbMXAzzpIVhJRQMVNVToCwPN1t5sCTLI7AtasK+zGirYw7XT4LSnT0mFxmv+3G++hbHwPbbsevXn7JZr3GFODPaIOxmphK1RqFtabMGId2NWef/A73v/g/0cMDCi/PoowJ6cDMDKoiuRU40QKvWoepGmF0Dp7X33zB9uGO7cMdb15/I8YYwXPYblkslqw3p7z46Aek6CWJqhsWqyVffvFLtnc9ixGMWXF5ecqzDz7i6r0PUbZ+BPw/0nfVGq2b0skx1dXLV5b98Dgn8vy7x0ve43+XUc/j6RS9FzfWYUCRcFWDswatpLVov3tg7Af8OErgXTlWi6UA+0oSHPLjNVP+vdqsWa5XwgixZgYTcwmEp5cLO+HY5KeKQacxx2R3uh2ZR3+ItLnnGIg+yOfRotGlnCY7y+j9E0xQGYuxMveGvkPrCEaAprZtxD12PEh7m3PkJB0Dxhiq2nG/Hbi+fcWh283nTIgmpwCNltVyQ11V3J1f8erZ+ygFVeWkTc86Jtdk1NSqmo96y+XZGAPdboffb9FhwEDpAinrmLPCWjXCil+enfDwcC9Mx6lAmKTrwTpHvd6wee9D2pNTyJk4jhzuHlhtTgGNGlp4XYZcitgYsSqTsyKNkTB2DLteCuQxobUV0CRNI3XaaDN+HEg5yI/yJGEwvUba/KbBl1Lk8HADy1Pu7wPb3b3sZ3ZBbSz92PPy9h2f/ugnnF5cknLg9btXNE3N9vaaVDSVcwx897PvYFQiemFsrCrD7rbn8LAl2QOXyw1N3YAxKKP5/g9+xL9sW+6UIvvM/o/3qJ8sxBzCB2pXzDKwhJjpdgfWrTxHYxw+BHa7PdGPhCAs7nEQ34JxODActqSAdJWg0Bjub+9pF0vOzs+pnZgi9jGRnJHiHqDRtIs1Kose3C9+/opxGNg/3HPYPnDY3ZO1QVnL4aHjm2++Znvo2N7fMo7DvHZkEuMbT3glyTLjETjPOdNtt/Q+oLNCRbAxlIK5AENS1JTXSldEoFo0+NVRj6077FCxmtfflOKTltP/ePz/f8yxKUrmLxlnFfrzP0F/+VN0VPxI/y3qPSyDEDXOFyv+U73gggqbFEkFSGIMZatGAFBtuL7e8vr1jvs7jzIVVfa0KtM4g20aqstLGXf9nri7Y7FpqZ0wW199fc1JNJj1JebkHPPxD4pM1yRLlumGAyZLjOGcFemVfsfXX/6SP/3FT0E76kYR9YJoz9DNZ8TFj0j5ipwblMmisdp3jLs3HLa/JHZvZW2uGmyRPEjxaQHBDx6PFEKcq2jazNCNxCC6iROImrOeDbxg6miQPWmxaud5Mo5jAehkj5wBqPwbnlP5WcqIs7xWpR1fmGYxS3nkCBvKPtrHxL++j3w9Roai07+qIj9eVVw4aLSQDSKAm4qLSQxgVShZQ0Z5z67LjI+788pHm4q2XU5Fq1zYmFP8TPlMR6LE0+PbzNc/V+Lh1/5eboxKagajJUYoxV4teERKiTF7yNA2Dc652Qckl5t9fG89G9t+qxxdutbyDKrqAuhKu/Z0W6a5lciTx1aSOHm65mOH5ONwZQIycvH1U2hrcI+EzKYC2jCMHA6R/b7D3Nxh9Euc07RtTdu0NE3Lot1wdnpF0y6p2wXtcslmuaCyIgdweXLKum3on79Hd9iz2295d/OWu7sb7rf3xJAJpWstT/HbLOOgpLgqoqkSs2QhVmnkRgk7eqQ7dJLL25rkkmidj2EGSbUV865YQFSdZa883isBz0IMxPlLZKFi6cbKRU5QTJ0EOMxxiiflSWo9YOuGoA1KB1xM1FUtgHKRiopGdJGN0YUpKyAphfGdYxLCwTgSwkgMIyoFUpEOkm7u+Aiol/lOziJllZJIDWSOUgYZ6uixIYqWf4iFlSzSB8oJ63xMiiFl+hAIRonefql2O2XwUe6XGBXfY+um5FkJYx0L61htNrTLlchaaDvjZ48LQpVzpWAhMiQ+irxWnnHvQAyeOI4Mu47Dwz19tyOEEUUix0jwpcQfEjormroWCRAUd3e3pJjY7Xd89fIbXN1werfj9OSUk82GdilVf2s0de1QLIQxGzwhhvJlSEX6VGLjondr87z+xBznMZSykPK00Sirj2S633D8VoCxUhUojMScSTlgUs+SPef6Hj28xYcechKNO2VZrE9ZnVzSLjdHQJCjWPfm5FSSdiKm6E9oa+QcRvH+iw8wumbkIDcsKzAa3Th0W5Fri8+Jk5MTLs4uODs5wyVXdNmO7JT5yFmYK1n0UHa7A2/f3XJ5vmS5qlmtWgmii7lYSomQIvcPD+z2e5SCzWbBB+9d8fCw5epyw/nZkvV6hVaKvuvZ7ffcP2zZ7vYciv6bdYb1eknT1OT7Ld1hIOlMPww4K5Ni6AcJSEum6VwjlZ6YhLrftMTR0w2Bw2FkGPy8QcQQiTkx+oizBmV1Sb6mSlOcv4a+Z1G3sgBWNWerE87OTuj7gRgjrhKgY7/bcdh37Hcdo/colVgsWhaLBbvdgZvrO/p+QKHw44DWmyebpbOOzVrh/cjdreb19R2qXtAa0bJav/8xS9Pw9du3vL2/Ydv1/KuvX/Px5Zk8sjdfUW0+xqoaowyRY0Ag8UtmWVfUNlNbqVzv+54Qk1TSlGjkkif2qyErxSFkrnd9maQ1y0pL22TR4ZU9L8/jJaunE3MKHWbdnHniyiZKLpqyaWrvLuU9NUv9Mg3M6XPOIK4WLcicRcrDOmGWxCJQru0kxp4ZfU+lW2oNrtbUTmNUw3rp2PeRQx/ZHzzBR7IyzBae8+XlkjQlFo1huXCcb2ouFpqFLfW/KeiY2q+jaAumGDBO2khsEemXsavQSloC+sNOFt+c6IaRh1Gx7eBhsAymIdtWNGKDtELkcaQ2kUUF5wvDBydLVqanMZHKjBz2W25v3nDYP3DYPXB3d83Qd7MmEBTH0zlwSk+TfTiaJszBbSakY3U1xFgw8qM8xdRCNAVkWmlpDSI/CpQeDYw/bw1V6luL/REGkzUWcWYtvws50sWtcKnLBq3kpYI5KmFkxgIb6uJiWrcL2nZDtVijbUs/eFRl8KXVxG97tHGMORJULqzD/OQ+zeZ2JaicW5MK4JdykUXRRpzTRy+VWC+6i66qCENPvWzIxkhV1BrqusZqAXaTmlxZw9zSJYYTUzCqcdayXq44HA70Q5xb7OaWPkrxpLAI/qyYPQM+Rm62W24e7jhbn1C7apYMyenYWmbKhJX2aMfy4kPS9h62L9G96BfPbTKl4JN0RbI1Ec04dHT7LdokchCpgu1wf9Taih6U1PytFmbPOPRUdUu7XJNToh8G0j5zcn4lrUBac355gTaW1ckZ1jXExy7GTwahevR/2XOnAEy0v48Fmpk9ro5q7tOdfZRCFCM2cUulJA7EIK2M2mC1oe97hmEQhmwJwKwxVKuKrJW0fxfdVWH+Hz/3kUF9TL7keZTPX4C5+WqngHy6zDKZfiMD4Tip5yAzpUiKfp6XWit0doR3Z5hFIGo1FySsc2gja3mMkRjFoHSa1ykE9vsdxhqadoGztTCRtCHjMM7i01D0Y4+HtOHZwqYUcHUA9tqQohQftHGil1ZaJqeWz2nPyY+uUQHj4UDoOnQqyJgq+4s22KqSZ9DU5MpyiJ5xGFEpz2YcxlrwQTohyFA5gpHgPlkNiwZ7dgbaYPbvZjB2ur+P1yhh98h5q6aV55IySpXuJSXiVU4bkvcw6W4/HtZKSXHBVo+Sc42rF5w+e8GQDT4p6mrJGDM5eKqcOVsteO/iCu0qDg8H7t5dE33AaottNIZMt98J+8MYNJYwBm5v7hnGQEYTR48tiWcIib4Pc4fXNEta1+JfBrbNnvvFjtVyxegTq/Mlrm6IGKxToEXnceg7cgqzpjBZ4XuRqAh+YBg6tg87SVwDGKMIw8DDMPDs+TlNvShmrmJ8ZV2FNgtSiBx2W9I4EseRfr/jsNvSHzpi8NRti4+Bfbdnuz9we//AYRykvXNQ8CC9DzEn2CpU0IQQi95n2RcSZIKwWpzFNo3ITEzPBfU0LkqZfmL/PDqqqoZg52d5XGn+Ao4/+RP4+39f/v13/g589NHT3/+jfwT/9J/KNf3dvwtrMeojBPj934dxfPr6v/234ZNP/mI+27/LESP8vb8HfQ8//jH8zb95/N0f/iH8g39w/P6v/TX463/9+P0//IfwB39w/P5v/A343d+Va/r935dr/OKHwH/19D3LujnlaVKAFS1HnTwqeXRSNLtbqruI0i3j0nL2+dc0Zo05r8HWkNQcp8iaahlGxc028e4+sB+lLbhCUWtF5SydH1lWFbWzrGrLoCLvffop3d2Wh9c3xH2C9ozq8hJOz3nQCwYG0uPxkpKQI3ImBI81iX99+y/45vpnbLc7oqkI2ZDtFbn+iLT4Ed69T8grUjLo7FH+hrj/hrj/iti/AcA05xjr0Dqj9QO+38+AEAgpaWSUVurKiVFN70vMr3gMJj5JR6eIK+e5Oyc9irEmdixFUzl/C/Cc05Ty1cdIUGCLTFlM+bi/zlukALRjyLzqI28S+HL+bcpsXKSyBqtk7xcjxKJtiUgPioicfJZKlZjp0YUdwRu5FrK85xOs9gnI+OvHt6UH/r2O+ZSFNZmPK8sRiJXCfYrHYqazdo4NpNI5X9AMymaVyzPVjz6j/I2A5+WaOYqgpamAytRNdxwPqrBuj7mWFEFmXxPFo3WxnFdlcrZH9l/5DFpNQO8xjgspEeLIGBL92LPd74T5ad7x6u1rnKuxRRpgvVjQ1kuauqFpWqqqkmeWEsY4lou14MbaYqxj320Z/SAs3STmrUnpYlANcWpdmreOPA/anBI5BskbohQgtDEobTF6JGlN1gllEskldE7lvhxj2WnkFzxWQEJjy9uI/4R4BEFWiVSkARVHks0k3ZRSIilQ2s4SaSIpEbBh0kTWBYjVhTxCIQNJzjABwimJlF6KAZWCMEdL7hbzI03SfByPc7hTriWLq52QQ7wHHyFEQiwdg64uxWogplnJUxL1om+spavRIIV3FSMh55lJPY2/zIT7qvkU2hrp+NUCnIrZn0LkogrDWx/B2gnTS2EghA4fOsZxT/AdOQvZwWg3F6ByUigDpgDL2UJT1RhjhaAYE9vDgS9ffs2h7+jGA/144MSfsWhq8V7ykZyKfq0xczzvvZg3+iTg7KSEnR/l7Ip5YqEQ4k1KlpTjTCr8TcdvBxhLASZK0qaTZ2VHTtWOS3UN/TU5BWbtRRzL9QX18gTtGnwobYHlbhhr2ZydcX93XZglNc5VKG3JOWK15cMPPmS5PGMIe2LqZCI5g2oc1JZkLNEPXJydc3F6xrJuscnNeeUEdEwbYgJSCJATXd/xsN1x97Dj/GyBsZK8hSGSKPpvIdL3PTc3d4zjyGLRslktaRvH9dsDpycL1ps1H3zwPikluq7n7btrvvx/2XvTWNvS9K7v9w5r2tOZ7lD33pq62m23bbCNFWImOyISg8SkKApWJKxEkBAxCAQIfyKREGKQEeIbYhKSJRw+MAWJ0CgkEUFYOLYJdrunclV113DrjmfcwxrfIR+ed629761uucEm6g9Z0qk6d59z9l7DOzzP//k///9Hj2i7Z1xfrzHWslgupLqqzRSkdn3Prm6oyhyrNcPgKKpS3FalA5i6C7gQmc1KFosFF+dXdH1PNziGA6McrxzOe9q2xy5mU0tGjBE3SPWpa7tkiOQl8TGGPM/E+Gsh+rDeBxbLOa7vaHY1bdvS9471ekPft1SVnMcweDabWvRpqooYPcYcVg8ln8oyy2JRcXa64MnjZ0K7zzxZUXFrecwsq7AmIxA5X1/w1ScXWCNt8YNznJolyp6QKTM+Tkaxea0iVRYxODJjCdpwc7VlcJ6ITZtYgOCkXUZrSawi3NRDApbAmhIbgiTdUT5ncphXh+LwB+YK4+o1BlpjhTsx+UD0kKdZo/Z6tCoBW59INg9+d9y4sryQClwUIwttM0JUBOdxbsA4izIaqzWZ1RRHOcu5Yts61rueCzx1HXBRKtwSdBxWUqHMFceLjONlzq1VRqnk+sVlVIIxbAJFolQYCY5oIOo9EAuaZHBP8I56czNt0DfbHTWRba9onLAllLH4zjP0A75vmWnHUQVnC8v9k5y7Rxpft7iuodvuuHj+jCdPPqberem7Rs5j3L3k6UhF+iUjtUPYQ2udgDCIMeBDetZKJU3peMAgPHiCrmnFAAAgAElEQVQqal9N3w+BF39rae7wSv7tRLMHh5T88f77xIoQBtG4LrEHe9N7hRBSe06q4vmk7ZjGWMJgpwBsBE99EN2osiq5XdyhKlfkekV0GXXXkJkFQz2Q73bYZoYtcnQrukOr9P77FEPJzVOjplFiXIxBqNozOxTS4uRdw9yekKsSnRkxonFrqvyYaDJQFqMMlaqSWmRKQnxEu321Wys1mXQpFHnIOFFHbOOW2tWoqKexNYLlIiAvQVYZlnyjw6mehhpaeHZ5KUyBokAnFtDoriqXOLbrGnGVny05uvsGg/H4mx7dO6QVV5IRH7SAsTpn8LDb7thdrylmOaPYw+AGFsulzK8gTqOudWTWSCGNiHM9ZVkSiDTNDu8tr77+bSiTMTjP7Qf3ZR9ROj2xBJq/uJhMxz5piy+AeOYgOYwH/5leVWrfORUjSsX0nL3owAbpBBGTD51kSyx9P7DbbHHDwGI5wxhDlsleMcrHxIiAglOCllg7B4HqtEiGuH8pDc3RGyiOe8JLh4CxL7+uDhI1GX/CoBgOmCgahUHXc7LlNe6gcGKtRZsw7QsiQRD2YyYGMU7TGuccRVlJXKGNVOKVEq2B8eSVrElWSVeM1pbBD8Iu71t612OUxVhhxaIsKLPfl5Im3vSc0zhQEYa6xrctGgl2UQK+q8yiraEfBkxuocjY7nb4fpgMHwKRLCvFfE9BPwx0bT2xhyRAUbgYUMoQDvb9uK82Htzn/WETuzdG6QYazYeV0mRR2u3FBHFMasf3kHlu82JaU7U2IoF1/zVuWs+u9RytTrm8vATnyLRidXzMcVXRD9IV5HY1YRjItKbKcnKjeBYDu3pHLHIU0A6ezdVWDO+ygn67Y6jl74YYaYcBhWU0cDTGcP/+fR5+9JDNox35LOPs5JTdruYoKKpiRjlHWDGuZ3AtbTtgVJAOkyhxabvbolRk6Fv6vqeppaihTIVRERUc682G41WJXhRURcXQR6w1FEVJWVUMfcfNxQXtdo1vG1zf0mzXOBdQ2pJVM7qtkAvW6w1t2xA6pDjWW+ImJbfBY0IkFJ6d28IItqa9EiuFtSzPKIo8xdWyn2m11/6eCAPeJ5PT/XgoyhIGs9dVHPeW62v46KMXp26ew3d8xyfm+Tc8vvQlATMBftfv+iQY+y//JfzFvyhj6Y/+0T0YG6OAmU0DNzf78/gdv+P/GzD20SO4uJAE4Md+DLZb+N2/ew/GfvWrcn4/9mPw2c/CO+/A8+dybp/5DLz9Nvy9vwf/6B/BW2/Bl78Mx8ewWsHt2/CX/hLcvw/z/4IJjH33XTg+lcRbHcZBqX3aSJHKREMZKtTNU+w2os0KR07+/iOG5S1cXpFVM0R/cdydAQzXG8f5OnC+hdqLoVeuFIXRZEWGMxBNhskyChWxeUWxXLG52rJd19i+grNTzK1X8UdHbBopIr9AlogkBqYw7Oys5p2nP8mT6/ekfdaWDGoB+atQfZpYfYqBOSFmiUHpYXOJ231AaB+hYoMpT7Dzu1IMUx6jU5eJ2aflg/M4Ec3BkgkYlUiCL5g+vZTjT7mDAudc0pE8iCzHXGAEaNK6HyeHsLQ/Cl5L6wPOjjIuERfVBFZPsWjSsBwCrH1EetFkz2h95FkfuDWzLJQmjw7DPsZUUYDY8StTIj+A8i94Q37CVGsELQ/3qmm//cbAxy/185c/5+XfjTEZLZNiZb2PXw/BuJjMLZXWLxAPPhFVJFBRum72PhMjGDvF8mknHq/Yx/EpJAJMGhMKMS3UWhPUHiDzfhSd3ecRI0APTID9KMs1gt8vkDxUkhoZC6wBeicg1Zj/xOuLA1NpYT2W2YyqmDFfLFitjsjzkjzLk0kpZHnJbBbE9sQo6kZMk5WTceKNeUEvNr6wj4/hQzqnpPXqvWMY+gTuWaIyRG2JyoLy5PkhdmTGy2OaUDGm3E4TdUx7D6nQ7nF62OdPpLGnDjPDFPc7MTOPSe5KGwjR4ZN8gXcJjFWyHqqopO096fq6RFIYrysEjwrj94k9Gtw+D0xAqZaFQvp+J7ngxOB1DnoH/UB0IqmGVpjco30U+ZQQk+5+et8IYdTDRfZtoxRol8ZClA4wpSAGwcWi5I+D8/joBGsgySokrWWpI+ipqC95rBiWCRMVhqGh77Z07Q19e4MfdhAGjJHOynHsjQtkpqXDR0VFzCOFzSGN1a7veX55Toie3vf0Q0eIYE5OJjBVoclsdpD3R3rTo/sONXQwEq7Yg8ZxxGumaS3rgoDMhznCJ49vDTA2wjAEotHkGcxtx/e+oli5Hr2+pttuJDn3sqjZsqRcnjEEg28GdAgcrXKZRMbgreHm+oqgLbPFjOOTY4zS1E2D9z1We9761Kt89jt/NV/44o6Ly50g6YucYLXkZ4PHEHnj3n3und0mV3YKJEb2j4+esij3m2IAMGx3NW3fUs1KbDHj0eMrLq9aZtWC5aoiyyx1vePq6oariyuWywVvvP46VVXy7rvv0nUdd+/e5uz0iKqSDfjW7RMevPYKn/3OT/Peux/yxS+8TQTKsqJtWup6R1HmHJ+s6C9v6PxA1JCVGXO1EN1ED+ubDe++9yHbzmOs5ej4iNPjBeubGy5vGkxWsDw+wdqCm5stZZkTQqTeNhAii+VSNF+VYltvWa+3dN2AtZbjoyPu3LktxhBE2rbBKEVmLMQBN/QcHS/FiGxwDC4wDD3Nbsez9XM+fvgxs5loz5ycHHP3lducnK7EsGTKoyOXl9epdd1w/949nj66pCgqgtZ0znPx0VcpT+7ymfuvcvf2Xd754F2++NV3ePvhORc3Nb/pO9/k4tn7FKuOrDzF5Cs6rOBDgImBLLSEQdP4gc5FLrcdQ5RqjlbC2hsTO6KIcysDfYTrxtH2DoXmqDJpAgZUrtFEjFJ7p9GDpHE8BAwZN8gREokTYKljkEBRmbTw7ReLqYw8MmPVCE2NGK8CpA3A5qO4ifyNUYmNmmV0QyeJTEQWMyIzDbOZ4vas5P7JjIt64GLdc73pqZueUfNFG0WRK157sOJsbqiMlkU8MrV5KAKlzffXqBVlkaGiZujFIT7LLDWKqjCp+uUIrmWzuWa9rdm2A9tu4Pj2PXS2JM9LfITd9TW+7zDRcVYGPn17xt2TiuNVxWpR0G4veXr1lPOnH/P82SOu19eE4JKpW5iegR4ZliN4GUbXzAmBSpV70d+xWTa1mbgQYEgBkJIWWpeYbi/EktPXCLbLg4oHLZX/2cn/wIM3P/vvvaz+Rz3q9DUeu4PvZfpD9yv4eTlw76XXTg++j0Cbvv59j6e/9K98vSMSp0AX4Ln9Gh/kn+fT/Q/w4ZNHlGVOnlluHZ3RdR3RpmBsDITVmIwYBgyz03uo/oa+vyRXmzS+ZMN30TKoGU6VNF3H5bOLZKBkKJcLZqs53sFrr79F2+242VywXl+y2TbQDpSzI15781N88P77PHv8iOAcRilu336dk7u3yavFBF6O6+AIYk7X+0IGkdYGqQRMgXtMeurhJTbbNG0OkE43DPj0pRQUmSEzBnJL3zl2u1qq2Sjef/99vud7vp+iKFDLhWgWV8Uk3xGMyE0oK6BiSFqme9P1OF3ACOq9lF4dfJ+SnShr1djmNF7L1Buj9sHVtL5O7yDzWcy19u9qisj8u9fUtWGwhokjl0BNycg0BIWKmkm51UXKomKz2/Ds4im9a5gv5klnOuKjoyiySddQAWU2J4uioD4MDevtFd3QsiszejdwslpQVRV5VkiicnBHDgPKsSCjlIIQ6NZrQl1TsGcEjQlN6xxDTC18zuF7kRQJicERgCyHoprhQ6Afeq6+9h4GEVfRKLJsxvmzC5Qt2KrH03mMEkLxhZtO6iZQNHWNVkqYV0ol9Ry9X66HgTg5H6cEK83HSCQv8ulabV7w1vf8J5iiYPvkOaGvUe2O3fljmq7FFjn2eEVz/gSb5Zzkmtn9u9Qfv02zuyGfVdj5nCzL+OjjpyxmYnKyaxo2Tcfd+8cYm3Hx5JLNO+/igqdazLl97y67pD8HUJYlv+23/Db+yf/yTzh/9IxHF08IFu61nvW65eTsDq/ce0AXFdZU2NyymMPNzTn5fIbrPdvdhqapyaxht6uJMbJczLi5viKqARc0pVXUBG4uLshV5GS5JFNidjmogDGRypacnt7l2sPVZsv11RWDG1DaErzj8ukzbq5vaLseFxRZPkN9Dco8J88y7K1MWpx9JBLoh47+YY/rO8b1BEAXJbao0Caj6zuRn2BftIxRACZtJFkqyhKAwRxI+4QA0U5/I27ZGv7pP4Uf+ZEXZj5vvAFf+1qah+rlhW7/Okzx3v6DDv49/u03+nmWwU//tHz/9/8+/N7f+8nPGf/mG33+L+f4838e/tpf+8Y///2/Xxi9d+8K+/f7vg/+1t8ScPntt4Uh+/Ah/MAPwL/+1wLA/uiPys9HpvDf/Juw/fXwP17Jv/+r3wt/7HcQ/+QfwflB9oXxWbKXRlr2J7z5/HvpXcet22eUu4j/4F02tef8o/execb8aIWa5USkqBqDYrsdePurl3x85bhqCmpdUtpIjibLDWqWcfvb3sIry263pbm5pu1b/q/P/R/4usU6zVF1j26xIuYl0YhMHf7FltKxLV8KUA2Xs5/my7/4c7RtQzFb0riMMPsMcf7dUL6Jz04wqQuSoYbdx3SPfpLQ/SImg2L1KtXx9zGo5Aoee4K5ITMZJp9NnxtDnEC8sYgsw0FNwEs8HH+M+QNMRcEg33/9ESR7jtYKokoFf8llgxekIQJtAIxJuUtHH8RwLmO/M4ZoIKoJTB1jiLETqSfSJ7Zsnl4LQdijPopnxGi4iQ+MEt4vz4Z/X2brJ0C7b/Lvvv6bMW3yPoj8XsCSGWHmhSit59KpZQVw1sLo1NrCfkeXQzOtUcbYyWj2cOxN5xvVJGFHOo2J7aykuJFl+UQQG+UQTFoXlUot16l9fbqzY655mNrE+In7NpJtpDtBYpxx91QHAZBSei/jFkUGYNvV3PgrAd2VJs9n2LKkyCvKcibyUtYkAFckHbQSveOu0wzeQQBHj4uRECxWG4ZEnIlKMQyOwTqRuEimjWKQ66DrCUHjgyL6DO8MwWmMaUFBoZIm8qjdm647eOmsk1q7wliDVkk7OjEllTHQKXAa5TQx9sToGb3SbJaIWEqMZRVa9iedQDwf6b0Uk41O8VYUyU2fOqi7QQraYZRLcB68E/3oECd5Ex/Fo8Qam4yL98M26lTsRKMD+LqDriX2vRQ8ncQcOlpMNBhbiFyW96A9Ktp9dSAwRWxRGZQ1WMAoQ1ZVCSD2oAZmeUXw0NQNPm7ZbC3FbkdZVSJZWc2IUYzmEyp7EGMLsa1re7Y3a5rNOc3mOevzr9Fun+O6LTEmkqNMJsEKjBijEQJhcJQmI544rjY3xFrkD5x3XK1v6Jyj7QdUlnN6csxiNhcPAxRdujejiVqeiQFtNmQ0XSPkRRdwITAMw6Qta6xIjAm4Ix44bhg+uZgdHN8SYGwAgtJoE9Fxh77+MkPc0rFGd2txm+4HfFRkRc7d2/eZLY6wWTGxP8YKToieYfBkZcXZ7dvkmSWGwKMnj3n08fvcuXWLO3deIc97/pv/9r/mH/x9zU//zE9RuxsGrVNSEDBKBMdXZUllM4Ibq0R+HxcFD9HLghw8Ns8JyiQX5EDbtTx+foE1GcvFgtOTgeuba7Isx7kBReRXfddnmc8rYoS2a5nNZhwdrzg5PWGxXFCUpVS3xgQ3sS7v3bvNxfNzri+eUsxKHjy4y+X1hmG4wsRIBlw8e8awXPDaq6/R9z2bvma5qji79Sne++gxF5dbisJy5/YJ680NTS8J2y++84s8eVjy2uv3OVqtMFrTNT1t27Je76bq33YrDOAQktxBcmbumobBDVSzknfffYfbt++IPmwMfPzRU5x3GC2gX5ZlrI6PqOYV3nu0sTx9dk7T92x3O+5uz3jllTscJsO3bx/L4HaOZtexrHI22w2bXcPNeseTx89Znl2yPLvF8dEx/+lbb/Hmg1d49+FDHj17yj/7mS/yW77/O2AdsO2WfHGHvLhFp3KU0uRGcXq8BAaUEsHXdV0TzEKe++iQmM1SEmuYwgalcDGyC5H3z2+4d7zgeJaxjNLWMC81k+OhUgRlpgVIKPYH1esYpgq1SqCsS+1S0nYh7fswxu+HMz3KQhClwj9u36MODtOvv/Q3SmG1wmQFg3Py5XsCwnjWYyXLO1YFzG6X3D2dsWsdHz+9wWQZi1nBndOK40xJUJba9YehF82kaZGCUepBK43JMtZXN2gthldlWRL8wObmnK4VF85YrLjsS2oKhtKSLQuC8XS7LW39HEtkaS1nJytunx7x2t05p8uCm5tzdpsnbK57vvaVn+f6/CldWzO4gSFIGy0Kcd5MGqPEvZGWVsJS0slIxTlpq4ohToAQMYhEhxGu4oBoj6qk81iVpYjie9EcEkH31L6sFCFI5dV593Xzsf//+NY6xsLc9G8Ftb7hS8X/yWfb38TDx4+JLrCcLbHWiubRQdFcCWqJG3p27hpTWJzN8FmJb0AhLNqgNL2ydHZOuTrlzkpT5Dlf+eLPAxYfPG1f0zQ9H338PqbQeNXTqZ5P/arvYDU/pcgqXIg8eP01iqxILWQFWVnRBkffbCWQ15reSTEk+MBsNsOYfEIbZcmQgO5ltsg+AdgXh8aGOjeI3pX3AwSfJEgy8txiqpK+69hstknSxjGfz1AoyrIUt948JwaHNoq8KtFWkRUzkVcZdbWVFj2raV37ZibRaAg0Ao4a5waGoaPrRaO+yKp99X58bhMjSQpQqWqV8hFFxE9aVzbpeWtryXLRgHVD/0LLUkx7AImVopBkQ/LigDey/p5WBUdnKy6unrFt1/R1wxD6KTk6NCkyVtPvNnRtTdNuiCoAHhUHiJ4iz0SuSHuMEeA5ScQz7bcHz1gBYRhoNzcM9Y4yeEitewphlhanp3SpY8T7QDaIj1KWEsW8Kqm3O4ZhQOeGeZ7RbnfYEFI8FVHeY+oWqzy9aSXjPziLPTcoTM9EA8ElZrHRRJMKkQmYMFqJvloCGDD7trmIIipLVi5ErgGZy53NWOQF9e6Gj7/2FR43NZurKzZtRzSWq0cfcHJ8RpHnrJZzbp+seOPWMeaVU/K8QGnDruv48Ok5zzYNcd0w9APGGtY3G5RS1HXDJiiq+Zx5NqeoTnj1rQeU1fyFa57P5txkOdvtho/+5cec/O4V9qSCJvD+lz/iziuvkeUVzvVsby7IC8u6bijLgruvvkbXNtSbDUbndF3Plz7/JdbrDYujI7K8JHRbYr/lenfB5uIxTz76KidHRwQvbaQ2K7i+2NL3DTF2KDWQlYaqqthuG67WWx5fXhO0xn0MrCWpLJI5XlDg8RQmJ8s0eZFDXPD00cfTXBolgKrlKfnsCG0LnPf0bXfgTK0mFm1ICRB2ZOLs53vf9yiXEmAlLfEcgFkA/PN/Dj/1U/Dn/pwwOv/Nv4E334QvfAF+62/d/94P/uAebPyRHxFAdzx+5+8UZu2DB/AzPwO/8TfC5z+/n9Tf+70itPwbfgP8w3/IN3X84A/Ce+/t//1zPycA6S/3+At/Af7Mn5Hk+ru+CzabX/57vnz88A/D6r+Exf8k//4X/xt87xLVXKUYz0wdB957Ytfz5va7OW3u4YeBI11wpkrKArojx83VU9aXzykXC8qjY04/dYQHXNRsG8+X3r7k4XXOtavoco/NCmb1R8xUZLUoOb5/i7WxnL32KfR2S3iUwc0VTz94iO8dyhY41bHe3TBvlmSFtLOqJCsDsrYtlyuMUURfs9le8U/+8f9M27fosiTmBV2j0XqFNsdglihVkWUO1T+h37zD7vFPw/CL6HKBPXqD7PS76NUpLo7xvUfrS6IaiGOewb65N8SAC4N0yIx1i5eZm2nr2/uxv3QcvDBqrioSWDkaQ6KE6Z5AjUjEB+hTvmKNGGXvukhXBQpjxTQpRrRxaBNZZorvjgXFZmDrwUcp9rw1zznLFAJzJBZsjJgQycbtNBhU0meS/TNd7C+zGPFJYPGX82ZjZAMg5ItRBgJStwipk25i7KupHjyFDwf7fwghsQEFlAphlFBKH4goAuVZgUk5ioBVSD4ZRbMyeDfJNqgEl+67lqQoOmGw7M9FJa1OosQbYxefHmM6paa4QNi7Itkhxlj6hccTGQHkkd0bcU7YryTmagierqtpu4abzQVPE4BlrZHWcGsFUFQkiT3xTzBWukaM12LeioC94mif2LxKEYSKKN2dxmCNGM35YaANW7wbCGEuBBpdiESGjRL/HMz7EdAOk2k7083TxlCkZ6ytmUhEKE3sO3B79q6MjDg9jxHVHwFHYsT5Hu8PuoDT/fVOrm8YOnwy7wreizzZtBjI/4w2WGtFf1VJrBqTnFQMQXSew4B2Lbau0U0NQ0/0DufFLLvrW9RujWq36MUx+WlJbgp8plF5yeC8EMNC2LOCU6xlsgKbl4wSGiHCrVv3OL59F601wyDa9XUjQHNTN7R1ix/NNhVEPCiDUkbGuc4ZHOQ2ZzAZGk3f7AhDnyCLMV93pKxJ5poWIsLo7TObzUQWyxiCVtRdS9P3DDHS+4GgIqvFgvsmo6yWrI6OyYsKrS0xRvquZ7fb0HY1XVtTNls2mx19Z8hMRpW7qSATYYrdMxRZpigKw7e8TMG4DezWVzx79g7Du/+CzXHH3YXidG7JyoKgcqr5iqOjY27ffYWyKNLkdrgQ0SqXqkqaQMvFQgJipQjBURQVd+/elyRPKfxQc/tkzq//gV/LfFby777w77h2O9EF9RGMIsu1mAiMiehYlVIioG2NSfqdyOtWUy2PWJ3eEjc4LxR27zzbzZa+bcizHG008/mMkxMBXb3v8D6SZVaMs6qcoiwkiE0LqwiwB7quZ71eo7VmvpCAXVr/cu7evsN8vhTA8uyEvu9QSrNtWpqmFU3XWcnRasmv/f7bvPveh2jg/PkzFvOKN199hdViznI+oywKrq7XzGdzsPD84pwsL2RRcAN932NtJqCUteRGGLzrmxuqqmS5WrJciUmKsVLBCkHYg7PZDOc8m82Guq7puh5UxGbSEjdfzAnRc3FxycXFOc57SnvCrBCBZdf33Ky37LY1m5st19fX7HYd7SAukfP5gjD0dDdX2OA4uX2HO2WJvX+fO8sVz64v+dqja+6dwnIhAYdBkWfHoHM0RjQW+5429jQuEoITfUbGjUajomJWCoDb9oO0+afAIRLpguJy2yb2TYGqMmLXU+hApmXhHBeKiGy+anr/NDO0bOTCOPOJgWte3PAPoqyxA+WFinIMafePBwXRg+pf8Ok5ZilpkSRGa41FFruoNSHAEKQFfwgRbaVSXllFNs+Id1ZiLJQZKptCgRHUDPsKrrSQpkDPe9GD1VJtzXOZx8LwirS7LTfXl2x3Nbt2gGVOLI/JSkv0sOscoWtQw8CMnrNlye27J9y6teJ4VTEvNO32hicPv8blxTO6Zsv68glD24jJThRF1CmYiDL/J6xFpTYqrdLGIEnfJPlgVNKATlttutb9E5RbP4Kuh/4MWrHXokWhknvhs5ua9mKUooAvNJ/jcxd/l9DtXztYPKfAGpVYEYdg0UvnMTLpVForx1YqienSuQe5/nGsxxApy4LlyTHzxRKPxphCxNVVQJURszJcPz+n3dTEzmOrmWieGpFO8Ome7qvOalo3tRIX8KIoqGtxr1Rap40sI/Ye3wyE3rFcLKh3O3a7LVmRY+YFwShiAqtsMTrcTyX+/b1I8yrEuNdmCnIvQhS9Ix+THvABM8AY/Yk8PvjAU/PuJ9miBAZaHpovQfcWxU3B0/Nn3L99V97Xi+bT5FhvwSQgvhkCylao6oR+/YgiDtKiFBRt0Hidoa2hnM2ZLyqs1tTdNb2v6V1NW2/RIVAuSnShBOTdrXFdINOF8NZ94OTsFkU1I5/P6IeB588e0dZb0bs0ht45aX/TmpPTM+7deyMFJBzcl8SgOQTrxkUnSguXTwYH43yxRrSdYpDgdbPZMvQ9KkLTNAjTXzSWqjwfa90MQycsE2swOpf1VYEyNq0j+0R0HOzxcAKOBavDxzT9T9gtPsjXuICOTPm2dWS2Eh3PEeRNa5fsy166+5NjsazVCnzSXIupbUsnvcE2sH23xNxuZPyNpxScGACEEaQHmwwvtLagBpHiMRpjKnJbcrO7ZNduaPsGHwXoHp2bI1A3O0K9wblWwGGSHm0qIBRFKWZoCVg3B/vKC6n8eL8U+H7AdaIZGpJOmLV2Yo3pWUWWCojBB7TNUIsFymZom5HlOeVq4OrykqIoOLl1i66uwTlGWJuAzPnOwXA96cHEvEAVC/LMCgjuE4AbAs4N0AjLBWuISada1htJFnVqu1OJPRITqDcybbUeu1jk8MFzcXnB5eUl2+2WRWYJGObzIykCDI7c96zyktN5ya2jFVm4x81uzeDFLGS5XGDOL9k2NV3qllnlOZnNKIucB/fv0XQD5WxJOZszDF4YZuM6EyObuuXs9IztdkPd7hhaz+N/9wQzKPpXj8mzjKcPP2BxdIwxiuBahqDReYnPRH4orxYYkxHjJU2zo29rtts1m3qLNhajDc41adwr6kYYjFluIbY4d83meos1kBcGmwsAerPdcX2z5Wbb4KLCP1bELYQhCjso1wQ1YL3HaI1BUeQZQ9vSdi1u6NP6kDSmlWF+6w66qgjGoKOwg1Wax+MzlRhnBGdHM8T9w7NpzXaDo65rirLA+5cW8b/+1+HJE2m1/7N/Fk5PBTD9iZ+Q1//KX5F//+RPwh/+w/BX/6q09FcV/O2/Le/xB/8gfOpTsEgA2h//4/DjPw6f+5z8+0d/VNr479/nlzyurkRj9gtfgB/6Ifj+75fz+lN/Sj7nh35INFn/xJ+AroNf82vgD/2hX/p9x+PoSL6GAQ7Wnl+RI8+Fdes9fOlV+N/T63eE7hUAACAASURBVLduwTKH5mpifE0gY4RX159l2Z6SOUOO4sH8hLO8oshlv6ufXdG5nu3NFevnTzl7/dMEbXl+1fL4ecPH15prX9KbDGzEKkM+ZFRBkeFETsNA6FqUc+jBE9cb7hwfUSdpEGUHLi8+otWBahgoz+4S9L6DSWLzQGYUl91D3rv41zz6+CGL+ZKoS3pXolSBUXOiGhVPe3z9CLf5Mm79LvQfo8slxdmvRldvMuh76fdcuheeaOYEewf0yIwVCkZIIJZyEYJLsdzhvpti0QTIjiDY9PNJB3O8njgR3MZt7RDANUbAQB9V6jqAZnB0PsNpWScbPJs+YE0gL63ovPr9871XQq4zuqASkQOOLcxUIIsHyvHpe+kQkjJbUIqoNUNwU9ntlzq+EdD6HwrAfj327AsSYUgbed8POGdFmzWBmqNhp6xpicSldILihGo8xukvyiG81OI8AuRKTfdozBemExnBn+CTvuiBzrt87AuHSW32+/bppHELqZlyPJ9xPIy9i2P8nmRhDk5hNI7bd0ftge/9bUzvopCYTanJ0DYmMyTl9qxgo03KBeUCxEdgfCt5b++kUzTEMYYP+Ojp3UA79GSdRRstGu7JMHrMo31w9ENH09ZTh0xAWv5HAFaWqNTVk7qhx59PuWy6bkVquTdSdNfOETVTp+U4ZiLiNxO8x0OKQUYQP8UqKNyo85xAZheluO1TJ+bEWk/YFAkUVYAPgcE5jJYO3LGLS9sMFaUTLexqinqLblrR140BFWRBUAZMFtAhooeA9mEiIwVjmZUzAbzTeXRDP0m7aWsmcFTAfE1eVhgt7f5Y6Zw1mZ/GSNcNbDe7g/VWoU2OMMEFiEYFbG4pq4roFtjMvvAMtFUoRglNpjEMoxQeZEpReo8LniGZsfVJuqrvB7a7HdfrLYuqoSoGyjkUsxxblChtsbMIxRy9uxEii81wLuL6lhAcvReN32miqNRNoWV8ZLaY4vOvd3xLgLEoqVhsL5/y5J2fY/3Fn2G7DFyelDy4fcQrD+5SLk6oqjknJ2cslysio0PqYeunPFyjNTbP9wuLUlTVjKoqxAQuetzQ4IfIm288IMssXd9xvt2w2daifaIDq6qnyCtAT4NCjYCHSkLGU5YeQRuK+Zzl6ZloBMZAYS1aafquo21q6l1HNc+ZzUqsNSksiWgNWWawtqKcl2IoYRIYm6ofzjmapmVX12RW2E3zhaZtO4y2VLMZZVXStQ1HqwXbuqFpBza1sKY0Uao5RcEbb7yKd56L8wvq7Y5qNmNxvKIqSzHByTOeP73k+PiYsshpup6m93RdxzD0OOeYz+fC7pMlWRh9vWO+mDGfzyiqiiOSgHUSjC6KHKMtQ+/o2k6qZt5Jtc8YbGZYrRY0TUe9a7i8POf4+JhX71RwUgGRvu3ZrrfcXG+4uV6z3mwZnLSNKKUoyoJh6Bmamto5SmvJj4+5t1hytlhwa7Xg81/5Kv0Q6ToxhtMmwyiDsnN0rIghMAyObvDshpBGV9iDmSpgFKxKWWS8G+hSf68szrI07jqXwDyDzQoKpVB2bO+UsTtWzkKICZgR0E0pjQpJDD5VP7U2ybRF7vmotyQjcNy80ymmHXkC9A8n3IGC51jVNXEEa+V6ZZgnhoBWdINsRkOMeIng0FoW6tIazlaVgLjItuPDviorbYMB5w7wm7ECGRU6SsU9y4u9DnOAtves64FNPdD0EbJIkZdgMkA2VRsi89xysqh49c6Sew9OWC5LjInU6zVPHn3Ek48/4PLiKV2zRcWesUR9uHZMeGx6JhNXQI3fxRQ8xGmzGdvFxjZcn3Q+xyVhDJz3G3xM811NWkSybsvTGWLgfNdysdtrAHw0/Dw/W/8Uw6ZJ9+vgMab3HwNxa8aWmJfAWCVgtzaGqFIVXiU9W5+C41Tw8T5Z2kWSNlTg5PSE2/oVjqozfNTkxRFdPwir7tjACTy+/iq7cE2MgdweobSw84wdwdixfViPt0c0oLQwIGezGTfxhm7oUUbjiRQxJ7iBfqgJveNkWLGur7nZXFPpOYY53iiwmjyzqYi1B13HgHcc5+O9mPS0BilwRER/ywcvOkVhnG+pZWxqoZHDJw3Z0/Bg/+I4xyJcmUcUrqRoCo7Pl9w6OU0zVkAqJZ3oovuUqvmdc+SmQFfH9KYiGxoR74+KPhqc0mzrLWWMVFXBvQcPOL+C9dbRbzdoBpRviS4StMEoCN7T+46gArkRVsHgB/owoH1P37c0mzW79TVd0zCCk8oasrJIRc84pQmjluUUOSXW+zQWxzE+miiEMDH6xzkVQsRoS9/1tHWNipHBDRTlTJ5hkZPl2ZiyS7BtLMpkaCM6xPtdN76YOO2rKgevpf+MD+fgZz6IVI4LnqiiFAZjxGgB4X0/yLUcZDUCxCog4L10qxgra7wwTBTej7copsRMgkQ/RNyTjMXtEfhMt9E7lI+poKKIPhCNJHdKa3QabwaD1ZZiNkNpQ1EsaIeW3jc0zRpjsunyt80Wuh1EJwk2UJczuryU+EUL+0BNkjeGg5VuWgMOB3j0cu3C3hHDCgEPIw5p1/LjOun9ZHwTlTyzwQfyohADCGvJilKSM+9FJkfJXBu6HtX1mKaCROCLWY7K5mTzGVFpAVVDQDuP7lqwOaSCpc0y2qaWRFaLuYaOMt/2xbQEyI7FMb2XoyBKwWUYhMERtcYUFZ2/oswsmc1QoaO0mjLTzIqMxXxOHBy7tmVbt2zqms5JC67zgd55iky6S8TlWXT1KxewxRyV5QQMu12L96lUECK77Y75bM58NqPIcpxvuXz/GlsafHDcenACcaCcVxgjBATnPFkW8M7RdR1lWYkRlzVoq1iuZrR9z7ZuaNuazFoig7QGa421SooypOR1GEAP6Myijdy3uum5vtlxc9Gw2w1EbQnXOnmgSNI4+IjS8r1RgcxojFHSqbXZityAOgBZtaZcrVDWTjr01hpEsCMm6aR9QUjWExlnU4cK7MF2JG62zn4SYPnwQ9FuzTL49m/fywj8438s68iP/Aj8wi+IYdXf+Tvwl/8y/PbfLqDpCMb+nt8Dv+7X7d/zh39YWvw/9zl5j9/3++CVV/imjroWWQAQEPPNN+X7n/gJYcv+0A/Jv997T373V4It+yt1ZBn8gT8g1355UDT+2X8L+V1Y2GnPUICJloVbcbt9lSxklFpznJXcrlYsdUauDdHmzBZz+puWerdlc3FBu23Y6hlPLwceng9ctjmNzVEml3g1emyM5CpivMM1OzFkbhtC3UBdo3dbThYVecypvWMIgfXVFYO2OCzZ/BSfZ7y4rQT6tuX55fu88+hn2TUNy6MzXKjwfYFSS5QqpTjkdxB3DLt3GDZfITSPUMqTHX8ae/SdBHMX52cQGzQ9Mbq0BhVEc0JUxfS52pTgapF6SQw6JhBoPLn91wsgbOrUmKCgFCOOZl0Cj6lpyRvfa5KRUCMgF+mcZzN4FtpIp6j21EMgN4FZAXkyJgoxYAisskhpDCHt4VqBjj71EMqJ+yhgRYyItnm6iIjCRUXr9hzCwzju8PhmwNZvVtbgm2bPSpAjOW0Cd1QCq8Z4f9xLJmBT7ffUQ8D1BeZkfDGWEdBv/5Ej3j7+nnxGnPK3kO7/4cB4IYdRKuUZEo+M+tta6708hEpDbBTqjel5Hdy6MBldj2Pl5duzB2dHEHIEpgUnCejk1RLHbqK471QZ8QLSPQUZsybp7kpOus+nSGBoDEEAcjfQ9R2ZGpm2GUZb7AhNKo0KDud7ur7DKIPIgESc84mRm4BJwh6/SMDoi7q+ezLOoeHzHpBTvLCQRFLOJQGiB1B7H5mRRT2kbmsBYyX+fNEwPUxAL9O42e+N0tGiRQVX7aFgMwyEtpN1sN1B26VxA1pJXGKMdGVZY+U1SB2eEktlZYmyiQjhA7GuRU4ojpq6cTKuHudFSHrSMWq0zihLsHbsCu1pm0H2diXEJWNLnBPigADTPunI5/iinDpUx8mhlOB+Y1EX9kzmGCNBj/KBYkjv0vOkVfgo97NpGq6ur5kXS4psRl4tyOYrMpNjihKrDcFIPjTiLtluB0oKAc453FjwTeNHJDNIhsOf9Iw5PL4lwNgYAvXmkpvHX+X87f+b/vxj+mvHzXPL1fOVMGHLirNbt7l9534KwCSI09aAOmhTUuPiu9+slFIUVYVzA8ELkDj0LR9++JDV0Rmvv/oKp7/9txGi4fHj56y3W3rfUeQDt89WSbuqF+fbzCb9l0NBa/kgYyzKZixu3aZcLDi9dYvj2Ywyz7m5vuGjhx/yzpe/wp1XXqMoMrq24+HDx9y7d5a6/QThKssCYzNQOjEHPUqJW/lms5MKiesSkGNQJsNmGX0vLMwHD27TtjVKSTBe1x2DD5ysllTVTNoqgueN1+6ymBU8fXbBxcWV0MjdDnY12mjOLy7QRnNyfMLi+JQPP3xE13fkmWUxXyYWpICRzsm53bl1m6KqUMbQNI20oyFaoX3XkRnLs2fPqesG7wNHx0fT5mRshveeo9WKsuix2nBzfc1uWzMMEuBFoG06XOcTg9HQdZ6imqO8Z2hq2rYjyzL6vme3u+b88pJPf/azLI+XzMqc4+MjTr7n+3jnyXN2Xc0s7xk2z7Ao7MyTZRbvpWZdB1gPiqgzfAIpJTjomeeWW3NJaHeNpnVuupZxUQ5KsWkHusGBsdw9rvDa4ZRDB090fVrkRItmBK2nimVg0tqKQGYKIvtAMQZp9xmL4i/hdMQY8W6YFq4IiSHjieiU/GuKPC1i8SBUSBiLUVEqPgk4s4lRKEy/QFACuNi0aY9goYteCBipwtd2IuhpEjhprBi9ERU6JVmVzRMrEobB09gjdhm01YBZGBw5N9uWGHtAUQTHnRm8euuEV+/MuXd3QVkadpua82eXvPv2V/jga1+ma3cEP2BEFCWBPKMo+iiuLcLnL0cXIUoVUip0Y2CXqszpPrlkOhQSeG6TCYNOAu2ZseydIaW6mqfqnrTsierNpu+57jtu3EFCkxlUYWF78IAPHvIIDqPVZGZyGFi+XMUdgwQBI4S9CohspdbQQ/T7gF0rlaREZsKcHgLLyhJ9T9CR7HjGul/jdgOqj9giR5kEUgPRi07SCFxPGsmTuYpKAIJoM02MweT86txA17aYCOcXz+mahhA9VDk+Q3YxC14HhjBgxs+Kh3Nxf4ya1yEEWt+jvTBzrTZk2tCEbgLQ1As7/v7+W2uBiPYvFjXEKRWiUjy17zD4NfNnK167/4CTxZJMK2IYyLN8Cj6IAWMzht6JoVK5hNkx7voSHxRDzBj0nM4FPnj7bYahp6oKvuu7vpss15SFYegV1WnFrCjpw0DvB47mC26f3cfqFIzmBVlh6YaeXbdh222Z5RWLasY8yyFGNtstIQ7kVUm1WLBYnmETwBeSQti+MCHMRJ/E/2VoKbSx5HkmAXfQlOWcjx9+mNqaZH05uyXa4rnRlHnOfD7HkYpOIYLSUsk3mTBgU/HIMyaT41SMHD5e9YkVcHo4LzyncR53fUc/9GirWSyWrHeP2TUbirzg9OgU44WlcJgAjCBrCAHnB1zbkmW5aH5Zix6NpA7TrjGbOvz+4BT90MMg66fJ7QTYpVsNyajDB4/vAsZCZuYUqxOwBhc6np9/QJaV41Wy2V2TuUbWbKS48dFb382wPKNC0zUDy7kFLUxTAWb3yeILLJ2URqo8o1ysCNUM1+ySu7ZcTPCR7cU5Qysg+9D3o4ADLgSCkq6Oo9VKjD83hm57Q/CSABmUyEOVM6I2VGVFZRd7MFZrYp5h53MGoMgyCiXGmUM/oIl0bcMw9BwfHfH4ow+EuQxTIhoJez3u0XxM6QS27x9IRBKaV+7do96s6doGQuDp1QWFvmFRFRwvKnJj2G23VFUFSgBMdMau9Tx8fMX5zQ2180RtqaqMsijwUbNtOoYAWZFRLo+IOkNnJUVR8fTZubTfk2LjyytC31NlOUeLJW3X0TvH069c0Fx2xNLw6uuvc3LrFfI8Z319Sds3KGsYXEd/vSNUC0IyBVkcrfiOz7zBxcU1V9drrq6uefzoEYUVoD/LMqpyRttFnp9foDWsFjOOl0c4H2janu3VjvOLG1oX6R4r3GWWCnyy5yljsWkOoCSJDkqMgELnaJuWzW4nXRiTZESE3KByiwsO37VpLTcom033Y0gdUCoBCUM/EL3H95MCM845TBRpjOOTU2TPfYkm9jf+BvyrfyXM09/8m8Ww6j/k8ElXDwSUfPlwbp84Z9kn4ouve/z4j8Pf/bv79xv3RGvhn/2z/7Dz/I95xCiM2z/9p+H/OYNXfkxe/+//O/hjvxP+5B+RNUxJAXrhj/n2m18PUTHPCk7KOa8vzjjWBZn3Ar0bzemtUx5tPqZuavLLax6+/5hn+hZPdxnPuwVbLNhC9ojgGNoeUzdkoUPHntBrTk6OiX1HuLlCXZ2z6BvqaNCLijxfsG1qdtuBYbem0SX9rYZBGfwUn0BRGD5+9CHvvPcFvvzeFzHFnM5bepfR+wptbkHI0G5LDBv8cInf/Syxfywx4OoNqjf+c7r+DO+SUaDSUsjyA/heCkksEYF8OfLiDl1o8a6e7p9SJGWctBMnlG4/rA7AuARevRwDTeZKapTH2gOWI34rrulSwBpi5HkzkCnNp5ZLVNPSusi6C2RZz93lPEnluNSur8hDkllT+z16z7aMdC7S9BEXIrnSFFGhrcZFQ91pNq0/aNX/JFj6zQCnX1/79Ov/3uH/v96xZ3+me6j0ZJgbYhKrO4i5Y0zAn/7k+b7AJIVEEtuDsSNLcgqF088OZYgE/BrR2sRKjMLyVKgUr8Rp/5MTDSm22Btxj7lljBEXXnz/UeN16qRDxhMJkBVwn6mYpsff1XvG73Qu6RpH0FLO6fD5jjH0XvptkqYZl+4Q0QZ0WdIPHWKWnPwJnGfoenplMOlLno/EJmVRSndrDEREs9X7jH6QvLvrBmojbf7WGozVZFauxTkxhBYC2TgPx7xpJNvILjaSOQ7nYWAEudN9dm7CkOJYskjXHxBi1ihn590ILMaUYyaJghjQk9yfxDbpDV8INWP0BO/QfqDsBuxuh21raLcMbYP1ENFYk6PzHGOFzJiXM7KyItMWEyHGQNCagJh2GWsxuZm6XN0wSIzqBsarF6A6MPQDo7FZQKeucxkb1haU1UquUesExmoG3+DDIIXpca5EYYFH5yCKTGjwQvyyVkgexljJuW3qUghyv5XSYDQmyycpBWMb+r5ncD1NXfP48UfEweN6R1QaUy2plqdk+RxMhg2GvGiIfhANWJMn1lqSJAmRfnATWQQtrO6+7xj6jsHtPSRePr4lwNhAYPP8XbZPvkx/9YFQjq0lqAwXC4xecPfuaxyd3sFWUtHPsowhaSvmWb4ffOkBe+8n+n1A46OI9ioMWTbDHpV89OjfcscH7t9/wKc/8ymUznjrM59CKRFz1lpTb85ZXz5mffmYWZa9sICNDC+VXPhITECURucFRis2zrFZbyEGTs9OOTpZcHN1zfp6jTUZi9UxzvWcnh1xfLxkdbRAa4MPwtoJIQjImwZ/WVWgNG3X0zUdfnDMl3Oc66lmFWVZUJY5u11BXQ9YM3B6tODu/btcnV9wc3XOk48/4Auf/3lu3bmDj9B0/cT+ClHc5m5u1jy4f5+b9Zr3P3jM+eUlD159gzdef5VZVaCCo8ykirJrGjabDc6JHtowDGzXGyKRru+YVXNms4rVfEFeFBhjuFmvuby6ou0EVPM+EltPNSvZ7bbEGMhzzasP7rHebOhToB1D5Itf+gpK7Fnph4HBB4wbkumFJ4SBXTMIyFiWlEXBlz//CyhjWB0f8W2f+TZKU/Idd87o4il98MxNS12vMc5RxoA5npEXBc5DHVtEmH6EIwQaOJuXtPWaeohsaifJ3VhhTAu2R+GJOAcPn1/j3cC944K8ANfviH0jLcHGkhcVQiAd8GncKpMRMAxR4QL0IeGgCby0GmaZFm3WCYE9mFxakeX5C8BUnH5pbASWUfzysQcSlCTT42acAg8MxChFj8EH0dSKo3aSyDAw6g9pRTWvBEiZHFtHyxZpZepHzZ8w0PaOZ9c1l71FZyvIDF2ArmkwBCobWRaR12+VfPa1OxyvLGWhcIPj3a98wAdf+yrPnjxie3OOD604TeJlnI0b2sFFxjCuFcntfh8FpT12iiYTkwe6YXRKH1liI6Chx9u2r0gzBnr7r6ooEtjo8XiafuB//YX/l703i7Vtzer7fl83m7XW7k93z711z711L1VQDcSxCmxhy5IBo0imIoMlhwgjy5HtyH5B8GA/JRFCkSIhRbITByxbcoKQLAtFPCUPAYfE2I6JAJECiqKaS93mNPvsfjWz+5o8jG/OtfbtuFRkUVL8Sfucvdeaa64559eN8R//8R9f43Td8vDO/tQPqnSoeY26aVA+D4BbUAkTVij3EqfBsJsutDUG4g5TVe/s3JlFFqKkp8WUixIKc3PoeynIpyyHs4qbZkmvBxZHJeHNVjZ8p6n3agYUUTEZ9iqPxe2QUpLeDaASfd/RdZ2AcYppMw9Nj286SWPWls1mlTdBnYufKo4Pj6kXNW3XMgzdBLZtnY3b6akhBJHbCNsAj/deqharrRH5npa2DsEYub8F4KQsxzHpr4mW2nXX8rtf+TKffOXjzMuCvm3ohx5rC5S26JQonQB4fYgEHMXRIzY3Z/ihp42OQZfsHZygdMHy6jnX5495+rUNBweWPRc5XHistQxDkw1XRTesaS6/jFeWmH9uVh3L6xU6wt5iwcOHH+OFF16hrvfQRgJOMWt+Km2wpsysC08KnuD9TmqxmvSQtbHZEB+LKhjOnj/l8uyMxeKIvmnYO9wXHfRa5G5EK10G5pALXY0sBDuviNqK/lOUzJEJIszsXNHLvs3M2AZg378Lbx2oNHVd46OkofV9z2/97m+yai6Zz2a8+OAR3/bx76DdbABFXRV5jxEnQimF1QbjNIlI2yxZr5YY65gvFuKloKaCD2Jv57vI6/fYuqbBmoRxgRQVZemyUS/rqcrZG1qZDJ7afB0GlQzOzTk6fJFyp/hLDC1DL1X0BqXwJPp+gCgM264ZpNCBzWDs+w/5W00Zzd2PP+JaeS7bFXZoUUYzPz6hvnuX3kj6fuw7us2aq/NzDu7dgwh927K+uSaGSD2bEUOkXTU4pQmxzyxw6NKSpAxrbVmZJ9MW1d7ccHXxmKsnj0GJlnJQmqAUAajKMrM8khS5yMWC0BprSlyKUk0ZhdFmKs4Wx/Veb5nBWmnqxQwfI0VVcnh0SNKa/+gHP8/67JxuuUQNA4MPNENP8/gZl6sOkiPZkmr2gJdfPiY9fouqb+kHWd/W6w2dT1QD7B+U3D+5z+LOA955/Bb98or53HN2ejoZ7TEETh+/ST94rDXcv3MXUuT06oLBey4e37D8xS/Rfr8HPefw8BAN3HnhEbP5gmaz5urslOv1Gh0jRiuKsuT6esD3Cqsse3WNfvCAejaTWgYp4Yyl6wYWtaNtOzbNhjffecpy3dGHiG8UzVfI6yVkz+pWAEtllo3JKaIosZxCEmDdZKBxtNMxBldVLBYLgrMSnIkDbfSia5dk7utREiQHbowGbR291YwhzL7r0FECQ9pYhqEnfsCy/v+5/ezPirwAwG/+5nvf/7EfE3DVOWHjjpIGH9b+3t+Tn7FV1Qcf+83QmgY+9jH4uZ+Dm++Cn9q8/3EKXlh/gvubVyEojmd3+MSLr/Hi8QOOqj1WF89pb84IQ4dKkaM7x5w+vaRbD1ws12y+/AbnBwdcqopVLKCwkEPs2mhcNaNSjiJqXAKLIrYdq+ePSZdX6OU1aMXhw1e4SHCxXnF+9ZyXX3sJZyqG4Dh/9nXqF1+bAPQYA8/e+n3+l9/6h2zSc77105/gheP7/N6X3uJ5JwWpmM+IpmXYvInvTwnDM5K6wVZ3qOafYH7nu7kcjifJFTViN1gxs4yCoHOWoZkelp2/hsOjuucEfwOQQeIdlpVSqCyDpfLfY9NqTHm+3QejfRuzhmWItzlbk92mFckAUXHeBZLyHMwjewd7NMuW1eDZXAUar7m/cNTWUmDoh4ixPoMo4zll/voUaQPcNAGPXLcxGXCzJWdN5I2blvMkAZzdTeijslzf3T4IkP2jnmfbdH7O4niVRSm6pKNO7E4QXymm9GVjRAdT2226cl4tt7hCtkG9bxizLJUSwoB6V5GvXfZsDGLThpAymOcFQMuMWQFXx+xH+U49yh4Ikj49p/EetNKSbq+2oKMwJbfjRSlJWZ/ubcoEmjr+Fjg77gWjXyQB/FE+IfdxYss8ztkdKQR8zrYKIUgxV62FDOAD/TDg/UDvLS64aQyLDF9PcpaAZGimzDBNIRJtjzEFyjiM1aK1mgFgYwxlVVK4MgcpJftTAvGSVdU2DUOXz5sSwzDW/FCjE7j1tcbRo0WuIGXkVLMtlEq2t+U4TbKKoe2JYZBgcpLvCsFPxaVHCR419mnOuoxxIAw9sWspmjW67VDNhtSsadZLnBdN05QDL8arKXioEJLULCaGGOl8oO89XVyRtAKjMBghYoSAGslGivy/yDb0XaDplhPov398RGFmGKdxRhj4aIfwvQS4D170ZkMcs7Bizi7y9P1A8H0uhibA+jD0InWGjKMQAkXpKMpqkpXwIdAPXmwGq9lbzCgrS9f1dE2LDgrftzx79hbXV+c8PXvC6fklr6/XPPzYI+7ef8jRwQF+VtC1h6xulizbHi6eSjBEaZwzoIxgd5O1r7A2TvPpg9o3BRirU2Tz9EtsTr9CGlYYPephKJI2YC2z+TFaFXTtkDVCJCI+aqRUZcWojQFMC1tCNi85TqKRKDDW8vq3fILF3oKDg0NsUZCSwWWjUlK0DXW9T+Ou8UMkao8UbCKnDuZHrVNevEx2UuOElBtXkFDEHpSxvPDgAdbIACYlDg4PMc7Sdp7rfXSm3gAAIABJREFUa2G9uqIQJ5Ss44YUA1uvNiyXG9brjs16jdWGWV2xv1dzeXnB9bUIN1dVQdN0DN1AYQ3OOWbOUN87wR/vM/Q9y82G1bqlaVtCSrz68ssEH6mqCmMtq5NDovccHx2gtebiZsXZxTXOOY4O5uwvaqpiRjf09H3PWMSr7fqJyl+UJcubFavVhsIVAsjuSXqlc4b5fEa72RB8oK5qDg+PcKVltV7RtC2boWG12UihNrPdvC6vllxdLokx4Zxj3fVU9QxjFEaJ+L5RkrI9qytefukhr7zyAs/PrrhervnK738VTMniYJ9yVuPKki447u5XkirTr+DqlPLOPWoVqHVkCUQyGw4otGZ/UXO1FC3TiES4D2YliUTbJ7oQbzFSvR84u7rGUaIXln0bUHiJ9KTAgMhIhKHLun6GarFPSIqoC5IyBNxWmzZJcKjP48+qHYMqIYBaEmbnxBaf0kXG4xLbsGMuIpYyW2hkAifwSERsrH6at80JcBw3zzS+oxLB94wp/2O17YifwCJtzDQnEwkfBi7OL+nahrbzbLoI9QkRRUiRoe+xfsPxwnHvsOLhSc2j+47jhaVtG56eXfPWm495/M5b3Fyd0zZLYmzxvhfwNWsUCSgy3iv5GYUp+gayjIxpPNuoZ9740phykZ9zZq2N1VAV22eus4ZUTKLjQ0pyXiSQMJ0T+JUvvsFl27HlV+desRZTl7j9OcPlkluJThNGvF331M44GI07rUXzV6UEI/6qpce3oKL8Lixh0XfCaLRzwnbVUt4QV3Ox2jCYiK4VveppujU+CcDdh0gyY0VYuVZrLUbrnL4iLCVZk5ki8iNkGkkklTBB061aYjuglRJ9qCD3Y5w42UHDptng4zBVJ92OwQysjEGzDKKOkhIksl5UfoZKqt72Q7fzDHeYDuTUPaWmcxq1XZe2c2r8T7HWS75mfoP6+rs4ujjnZLGg0pqm7zg4mGGspOP7fpBnkrJWW3lAqu/QD9d0QRF1xd7+PrP5jP29gsMF7BVr6rLHaI9WUTI2os8aXmDx1EUiYAjKMag5yZeoIWK05WD/gNligc4pR3Hy7QT5TD7SD02u0Mr0HKyxE/ACin4IbFYrUgw5Eg4n9+4ym9WkwwMW9Qz2Zxm0VaJZlQHVMTU5ZuBGBS/FDxgdndHYHGGWEdlP22PYpiRPXZDGET2aQ6PowU6fIkayM5ISbZTi5Zcecb1aUFU1d0/uY4yVStqjcaW2n5XrN2gn36Qzq2JkoodB1v+EBDXGaxlljnZcE7q2wZpAEaOkmlf56vO6atRoqFq0zXMxB76SH4hDou+626na1mCDnYJO0XthuRhD4SRFXuud6b+zWd1agdT2aSetqA4P8Pfu0V1fkZ68g7MG50TbXy328d2A7nuis9Bs2Lt/XwIpqxUbHzl6cBdli6x9rihQkr2Rsy38EChsQbtcs1lfQCYT7D14yEn5CVKMNMsrmqYVvfrZjD4Egh9EUzGJ3AuumFgSo66cck7Y+dM4UNMoks1sfASJEAPL5Q3rzYq2F9D5pYcPKK1lU9cMTcP+3gHp+pquH7hpWpRO6KAoipq9wyO+7eSIx6enXF1fsVytSG5GalpcXZN0wfn1mk14xtXlFb5r2Vxd0/Vdro5MXo8NNsVc8NHw4oMX2XQ966ZhCJ6hT7zza2/D25rDFw6ZvVyxaRuO79zLQIel6T3N+prCWfxQ0nY9B/tHOFsTXWITN3RNJ5rEWogIzjlU61lvWp4+Pefsd1d4jOhiKrEH1LRfqrHWqKyneXxbPY4dKV0SUKKBN4yyX1ljWTxgARH8QCrfJRsx9Zee9s+UdvT8doO8+ViR+IqTbM17Igs/8RNwfg737sE/+kfwwgvwoz8qsgI//uPy++/8Dnz7t8NP/RSUOX38z/5ZYa3+6I+KJuzlpYCl//gfy2d/5EdEQuDHfgz+2l+DL34RXnkFfvIn5e9hgMePt9fxd/+u6NXO5/CLvwh/5++IVu1v//b2mL/9t+H7v18c5R/5EQE///Sfvg3Y/mHtZ35G5BNSgvVaXvu1XxOpBYAf/mH4zGfkPv7SX4Kvfx3+8l+Gv/W35P1/8k/gH/wD0dD9wR+Uc/zET8gxRQH/9J/C5z4Hv1oB7wZjZQ39+Oqz7Pd3cclxsDjmW1/8Nu4sjqn0nOgNi/0TVAz0m2tC12CLgmpW0XWBpm+hXbOuegaXpDBaLi6EViiEkW0QsF7FBH3LcHnOzdMnsGmplGL24oukg/sS8Q0Fq9WbvPXGOyzmC5ybo8IMtV6hMgvRh4Ff+b2f58nZW6giUdRzDqqGqtyjXpT0foEvDCldENQT4BTiClPfpdj7DlT5OuvuhDREdBZ6FJBNmF1KRWFAKgOxIu245T0nBH1CMh3ERnzL6LOfybYGQD4+prTdq8fAUs5QGvthsvWQvV6xY/fu/ItOpKRQSUsaboLl4PnqxYpPHleU8xLba/q242rdkYaBuZNiXQqwKmzXVhR9jIQoTNg2QtRGijNlGTSvNed95O3W87j3DLx3ysJHB1B3j/sgZuwt0PCP2GKIWW8+Thqxk3TZresYfyHbuzt2ulKQCS2jaTMxZJWaChdqlW2GNJ0ASLf2e9FeTYSQa3HEzADd3q2A8GNGVvZtthq0Kr9scjX4KQI+ScehxQ4POzvoKAmzvTSVGbxjynyaGMTTPY+SG2RbY2ACq0ayyygVhlJY6+i8EIIimeCUQdk46vOPcmPB0w89TddSuAKjJGA3xEihNEIQUhmoVAwx4nUvRa5yJ+jRxtca1zrZg00uQpoL3Y72r2jbyn5ljbAxh8EzDEP+8TlzUh6naOKOusI5SIHoJAOZEDGyQPNPXifGfh8FPNKYSZbt6YRI5qUoWbmh30DXobsW3W5QbY9qGmhbGDwmRExmYMcQIQ2YFCT+raQAWkTGufeBUASUz76hV4AXia/8/LXSeYUR3deqWjCbLwhb5B6tNW0fCEmkCoyCohQGecqks7aLxKRBF6hCoX2iKEtiZ2ljIgwDJq9/aJ39qGxpJBkDOktUjD65jA7D4APDkHVylcHZAlUq4gBD6Akpsukb+osnDCGwXF/w1td/n3v3X+Lw+A5VPccaAft1Hm/eDwQvhLyUQu6XmPt0zDBla2O/T/umAGNVCgxXb9PfPIXYSTVcpbDOUtUVs9mcul6glBSMQo+pvfJQg/cyQZTZOha53V6Qx9dk8bh37wWKwlFUlWyEYzSDxEguc66iLGeUZU3XL3EKKfDE7gI/OnpbR00rAZJNLtQSlJz34PgOxCgMrhAoCsvIEPQRmnag6WQCK6WFWq8SXdfRNB1t29F3PSEEKueo6wprDF3XY3REJaGQp4hEjvIt+b7LhrnG1BW2KDBmjTGGfugBSf+yVkSvC+foQ6SsJW38zs0dnjy7YLVaUzhDVVhaO+CDpx+8pHJqnd93FIUU61Bay8LUD/RDjyLkiSN9s1lvCIOHUjTASInZbIZUtRYAy1p7OzqqDUPIen3GMvhAPwS57yRs2JDTAEzWKDs6OiahGULizbeeklQjRogfKMqSLlkO1IzKaEwKxOsLmFeYaHOfp8mh1woKo7BGM/hBGJIoTPLsl7VcavR0PrIDk5GINF3gajVgosHOFbVRubhL1g1UmZkW05TOHdL4k0Tzbid7NaIYUkJnfXObrzXtVH9MMQqTcNrtVWZI3p6HIxAbY8SaEVTMNmtiisKlvJlPrqyaoMrpOxTgfZ8ZkIYxJSXmNJhJ5kPl84fEqum5uL5m6DqC95K2bWYTOdWGjuMaPnbieHCn5MFxycmeplvf8Pz0nMdPTnnz629xdX2K7xui70lJqk+mzJiStKfxOWRDYLyvHYNU2D4yn1I2fG+vKWq641Erxxg1GTZbUFT+jrmQkVRWl4Sf4EX2YNl0vH1+wxsXS1qtM+Cz84VKMgXKwz3CqiGlYdKRfk+7jTe965rzW1HOSYSkt+lCk57VlFYla9x8b049kw1IaYNxFZtugFJjK03wHf16w8hCCzFKKtHIFGcL3I0wSErb65dxfBuATiMYOnhJAVVipKSYUNZgCkcyMrZ89KReBN612qZ/7UoN7BrIo5G309s7qze3wOzdB6p2NpcpxeqW/7/9nvHsQ+q41qdsehnbTinKg0Os1TvzQjZ0Z4qcSq0JpkTPTvCbwOAD2IqqrvG+hehgKJipFdZ4FIM8wQAqS2qgoLARbXqS0gQiAyX24A7zah+tHbP5nNl8T3RGM1Dth34qRAXI8x41ljKDNPYeY/WkZ6q0JQZPDD6n0ypS8BTWoeZzSifG7DYAIsGesWptTGRJAiPXv+PCjUjidvzuIIN5jKbpuK2Tue25HYP/Xf04OhLO2kkr+P6dB8xnM6yxzOs9ybAxcp87M2j7r4IpwKtFoyzFKKL+YSClkFkCWxbI+7WmaTBKKtpqUzGb54AP21RG0vYuRpM8pijapn6gbTc7oDVYU1AUwmNJCaxDmLOuoiwr6pkUxByDSePv736C435BgqTA1DXV8TF7L7zI+uoK4oDvW/r1ElUWDL1H5QIJIQa6rsXaQhxXIsoYTCnyE+IcRpTZJrDaHJAeYkAPbgJji/196v17IntSlYSrK5TRzPb3KCIMIVcZThHjLElvJABgNUPXoVyBdi47Xe/KLIBbgH6KieXNkjB4tDHsHxyQFBRVycYYBhIb7zmuKw7LUor/xURCZJOsKykXc/ZPjrnYtBSDp0SjqgXRLLHWkrRh03Wyz4cA3tNtNlORSIBYVVx+3/cRogCXxhisdcQnj0ltQ/KSErdSiqd7B9zcmVO/VHOxv8+xGyh0JKU9NrOaZr3AZmmgEDVHRydolfB9x3I2J5EmwNdaQ7/3Iut1y+XNkrPnlywPW5Ipcr+ZaRsd946QBDxgd/+y2/RNVEIrS4yB4HtC15KaNVGZLCqpSGXB1bd8G6qak4ydPjp21nbuZjA2141QKKxaYnmLpBQ3/+FnSapGKY02RorNHewJe/OHfmjb6XfvCrj6+c/LyT/9aSnQ9a/+lbz/nd8Jn/0s/MAPbD/z0ksCYP7QDwnYe+8efPd3b8/xqU8JsPov/6Uc/7nPyXn/4l+EX/gFee3RI/nZbYuFnOOXf/k2WLu98fxMrbBszfsEAj+sGbOVPRgB2N32Z/4MvPaaFC8D+L7vE1D2e79X/v4LfwHefnsLSn/+8/L+qJk7PaP19pzf8z3wmc+g7YyDF76H/fVnsbEkKEeoD9k8eJVTU3IhghQUTtM6xdAu8H2DSolrVbFabui6SDe7x2a+YHAVyThSHjujvEpIjuXiPk+CZqVbyhLMYs6VdijvKZ1j9vBF4sl91hFuFnMu/IYr3zGrZxRljaKmOFzQloauVqyO4OzJb7FpNjgqNuuBa9fi6gPmxZx+KLhql8R0SkyXoBqUcbj6Eap4laBfYBgqSGvIMlkjkEIadSZT9hktxC17KqTbIcTRlhlBo22qd16c2dqe494B2+ME25osHZFrUiN8klsa99Vsr2UQjgR9TJw3PaeN4U4pQTgbAr6PLHvPEBSVVVitsDpmUEfmaxfEJwlJFHnIwGXUSvTwfeKdzvOs9yxjGpOybtldH9Q+DFTdtf/e75g/Ctt21+dPiSznJS1GIRGoNGbNjrZi/pmkIbbnS3HnXGn0F7c25lhodrSleff3jyBcStkeSNPvKX/5lOo/+iM6+5ajZuzOBWkl32eyfnwiTfZLSonkRTYspFGySgnGoRVZa3EKII+gYUxJtObV9v537e00fTegpJRcTEkyRsfnoQR0y7p3CF1367fdGtdJmJH90NMNfU5dNwx+wGqNSlqcoAhRBXwClABp41VvswYVQ28nUNw5R1kK5qK1mViXJmW9Uq1w1qGzDJ+xBmMG2rYXADDEDLbmotWT/6yIevSNcq2VKci4K3kw+hzyoMcCaJOdm+03lT8XmwbTtZi2xbUNpuvRIxjbDxiSyDkkAINSSQrFAkppkSIwegd8JoON42WkCatQSm9fyxId1hUYK0rR43qVkABsiNINauxetrVz+iFNTFmRU9TyzEn4ocP3HZCDWFqjtZ3mF4D3FrRkQKkM8Gs9ksI8KQmRz8REUKJJH6pE6mDwPSF6hnYD6Tl+aFkvL9ksrzi+84DZ4pCyqnHW0TVLYSjHEVsI+Cj9PM7FkQj2rgTN97RvCjBWp0BcPsM3F/KglAWjqecld+8cce/uXep6jrF2SpUGqS7XdR1937HY2ycpJTbdTqeMEftRJ3XSXkkwm++hTTbWxqADbJ0PFEpbZrMDDo/u8tYfnDLTCpscxpIzFVROLbkdmTfKZKFnWaSsK6Cqsc6yvrmETOvu2xZTONSsRJclQwpsrpesVitIsJjN6Lo2px4LYOv9QFk4ZrOauq7o+x6tDbPZnMV8TuEs1gng6f3Aar3i6uZmSvUvnOXB/fvcvXOHzabh4vKS0+entK1HaZsrV1sO9/awVnGwP+f1V1/myZNzmXAJus7T90u0MfT9QNsN6K6nbVr2FnOc3ccaw8HBAev1mq5taduWprT0w4oxS/P52Tnzek7XNlxcRKxz3H/wgLIoMEZzenpK27b4Ha2c/YMDEiZrxRhuNk9YrjcYbTBKsbe/T982xCCs0/Ozc1xhKcqSvf19jD0jBikSsvaeVRzoY0JfHXN3f869/Yp+09IWmlAfYM1Cip/lBdBqRWWNpBD3nTAetabUnoNSxufQJ5aTDEDKDBIpwnK56ujaiA4FDw9rSmdRJHyu7KeQAkNoI4VggBAGfIiYGITdk3NHkrL4KNEgGxOFURQaQhwgJSl8kVIe0+MKmp2lWyDqrnMfIDvKKkpgIsassboDDEzQR/5HdG/HOSSp365wU4pKSoHBDyilsDi0SgQtEc62D5xetSzXHaVJGJ0grAjtDSkMOGvYLxOfePGA114+5HDhKF2iazZ8+Utf5a233+HZ6SntZkmIAoTE4AmhzxsWkxZRmowzlQGOLSynVH722VyQZx+yLaCmZyeAbZp0T83EBGXLyFEZBMoGl9WGuqowWuG99OcQIm88ueD/+MJXaedVTr2+bXrGlMBo5ieHDFc3DDeR1O9oyo4tvff32+DPuGGTGUOKURNAKTVVzg0qFxxQYArD0ckR+/sHxCiFiYwt2QwdpiiwRWJoevz1hgJDshYfxbEw2aAZx4hIEGRDMYac6rQFqUZgXKkcPQZMBJIiaibNZmMNpioIJlEUFm12HliOMozBujG9i7G/8vN8v7S1lISVpUdQeryunTEyPkeFzqkz237YsiLy90RxPjQw0HN2fYmzluOjE44PDwSUyAUXxmsaje0hKczePYabnm5oMEUlWQCbK5rmBt8voWwgeWIKWdNZ7dxbYjbTWCtrviXgUsHR4SHRHpGMFFGyrsSo/HxioF0vs5SMzH9rDClC2zasNw1t09A1DVVV4JzDWsede/dJdUXKQRyUIvY9GknfG43y8RlpayBnkoSUSIPHFeLghyz9MTLmdh1K6eNsxifp63HMTNSS7YFy7LiPq+302GbQyHx1rgA/sGk2nBycsD8/yFpdnrZpsvFtdz634xDtfJXA6ML87ftGioSGAR8KYdfni0gEQk6XGttyvQbfUxQDCcfi4EQ0d/O6JQrfEZSXnUjFyZYRTa6e9XopEh75Lp2bMXdGALAEs9keV4sTwuyQ2fyAwklaP1ECjEnvoF7jXMp3OzIgE5BcQXl8B2dLmmenhLPHrK4uWG+WVJs1TSeB5DAM9Nc3PPvql7GukmJpzYblhcMt5iSlRJtrGLIvJ+PJuoKQRDYk7ViowSWGUgz9cn7EWolchp5bqrJm5ooJoNMo/OkzdKlRBrqrAV2XBOsJqSX1knpHzBpywROGBvoVSjlCc81bT9+iLErunBxy/2P3GXxP2/acr694dnnK5eUl8/tHvPLoFfb291Fa0/eeZ0/P6H0kOYM7rFmrgdaBWlQsXE1vFd73+CBBbCmo5RjcwM3lSrII/BrVLQm14ff/6/+CD2rj8IvAZf4Z2/yNX8Fszj/wsx/WkrasvvUHbhWu+0Za+xGOCe/6+51v8LuOf/WMg9/8dQDe/s//KrE+eu9Br7wEf+7PffiJPv7xLWj6QW2xgH/+zz/4/UeP3v8cP//zH35egL//9z/4PWuFlfuNtL/xN+Tnw9qnP70FX9+v/fW/Lj8ftf30T6O+xVEuI69+7qcB8PmnBZ6974dOPvr5cxPrGgKON/l23vyjfPg7P/W+LwcDN/cMb3yi5OjyBkVBCoZ+E7iIPUcfO6K2c7qu5/HN7xF5TgotCoOp7uMWn6JPDwl+n5g0RqesKZ/tgyBiZEx5kFvgblyGdbgGfw0hF57FSIpzkgBgTDGb8oot23AbkAa2DLxpGxXd/l3rZ1dKa9oBxoCnyYBeRLISQuIr5xv8Yc1JZVjMS4zuGYbIOtvyWme/OO/ZKmlCkqJCSmtJc46jcpXCo/jKuuedJrCO4Nl5CO8CYj8qeLqLAXyUz+4e95HYsiOgjM5EDwFdlEoYa4W8kM+psy2ltc4p+VsQUUBxnQse5zPqXHQyA0hWi72p3rU9xzgW7so2VsrAmNai5JUzHUaN05EEkbLtot5Vt2G0fce09zHzYCzMJLIBPT6FbKur6b6iiZlsksHBDL7tBrK3RAhhy+r8vtZaQN0RRMzB/+m6kUwfRUJHMEq0SZUWYFUpCYZPoGyCYRho2gaj5FloHbG5CJXJfnHMGU9Mtt3WnByxszCSwbIvMfTDlPEoJBybC18ZrHPMZjOcczjrKJwlVAXWGjablq6TmkWRRPDbvtZ54k8WrCYDnXFaM6a+G+f2Tp8rsn+F+J4pRoamxTYbTNdStC1F06A3Laptoe+IYZBMGCUFa7VKWBRTGEHrqaBuWci9WC21YMTFTUzawWhSVHncJGIS8oVIDmTAm6xxrIXMZ6zJxa0Ssc+EnCTJH30fiT4RfSDGFoJH+UDoG7rNJX27wuBBpwlsHYPVkzxdSlluVAJ91hhsSlgrkk+FtcSQ6IeBTg+AZOBGkhRBjpFhaNlshDGs0sAwNLiylhoRxlJYQ/RB5MNUltQYsjwLo3RImP7+sGXlDwVjlVIV8H8CZT7+F1JK/6VS6lXgnyE7568DfzWl1CulSuB/Av4kcA78lZTSH3zol8RA2KxJfZ+BEM1sUfPyyw/4E3/iU3zyU5+B7DwarbM+nSX4xND7XHlWBnNSOSUjD+QJdk8iTZAmlDoJI0iPzJERgMnLYWbuiONj0XZGQnF9dclsNmM+m4MDldm4GY6V+8kTd1cjBK1J2qDneyyKgm61pFut6IeW5eUly7ffJqbIyfEBjx4+4E59Fz94ljc3hCFQFI7B96xWS7QO3Lt3gtWGvu+4uLzm7t27FGWJs46qFP3Brpf0bGst88Ueru8pi4L9/T0O9/do25ajwwPu37/HvfN7vPnOO2yaltW64Y2vv818NufO8QGzqiCGyKOP3aesHIXTKJ04PbtguekIIaKV5uhwjp05Qky0nVTqleJewoYpnaPZSKXhpu1pup7eJx698ID5YgYKlss1ZxeXHOwvODzY5/WPf5zf/u0vSmVmZCF6/OabFFVNTLBcbSBEltcrkhJd3Rgjx4cz5rN9yqrCaEmleXp6xtnFFd63mHKOJ6c4DKK/0viG5zeBtdrw8uv7tM+eEmcb1OyQyh1O6RFWQVUY1usNYQioGNHKc+94xjCIbMHNZkCpMi+WEgGHgFGGqAybkHjzbE1pK+4fz5hVBQ5x0Pu2IUVPSoHnZ6e4ap6dzISpFiSTiFhSjmTFzL5OeS45LRpFKVf5VNpkcDDlVV5t/39X00qjbU59ytEksxN5GzeNrUD5TqRX7epYQVlV0wZHkgqaVVnlWaYYFNysBq7WHct1R9s03Lv/Mu3yOevlGcn3VP6a43nk3sk+jx4e89KLxxQusVmvePvNM774/3yBy7Mn9IMwYePQMQQp6DHOc5TKxYPytqtU1rPNxmxMEwhrjEYrWWd8DJKeEQJGcvYlwqZkHIodqdDktMmcQj8x2EIisQUE9xYL9uYzFLBa32A8/NK//m3eeHYuLLAk7OmU1O1VOwmLdrnZkOoS2h58QMdtEtIuuHiLDZF21qXdviJ/xQ6LVLpJQHNlDcW8Zra/x969e2BKfNvT9x19f4m3kaP6EDezXF6f019vKFyJKpzkpmrZDMe1UYqd5eevFUq7Wyw8KRSgppSvsqyITYdirLgZ6bwAddpaTFVA7bBO0kJkLErqts7rgHWW9WbDMPRTGhlI2u8EzMaYiR+354IYsGonlXaMQOfBrZNc9C2QdmS9bOeAPP3AF90v8br/U9grh1KGvW/dz/kVopFbWCk4aIzFGjHMVb2H3TvGqDXJmpzi39F3Db7fEO1AUjEXopNgTkyRwjmcMwx9iyJlAyUBDeubr1AuXsPWd1F2BmiCUDyIIaAQZsfVlWRBWC0Gi3EF2hhqW3J0fw9rcnohGt822Gxkgey/IY4GnkY7YRAMg6fvezbLGzabBoVU1I0p8tq3vEbvQ3YuVY6Uh4mNL4MT2N1T0yg9NLJEdlL/xj5IY9BpKzsx6lSjcm9liQRrRQbJugJXVuh6qwt3OwV6nJ4718WWobJZ39C11/hBgkKlNYDsi1G18MLX+epvvY17/KeoeQFIPHvnOXt3SuLMsGme4ep9Do9OcM5Nmm9xCGjjMTZgbTEVhYgxEKJntb5m8NsiRrPygPuLO1jj2LQNpZuxv7hD2DthMV/IHMRMDJvd8T0+n/H2YpIAisqpfMoW2MNjHn7uczz9t/8X6fw5atWQuifEoWcIwmyotIZNg9s3OKNJOrG5PMNuVnLufiC1G0zWKBPny2LrBSpZQlpNTP3feONnUPzsbi/s/P7evWz3/Wmdefv9jtu2BbDIa/jPFVlK40LBxc5Z6wSvAq8m/g1fQj1V8PR9TtYDX4V0nOB45/Mf272onaCsncM1AAAgAElEQVTQDhBy8L/9MAe/9OHX+oe2qT+/sXbyL36S93+u36QtvhvW/fftm6E9+MrAx77Q/+EHfpO1r35XxeULBnXTYb2T7CQjQAJ2xlfeesY6rWi4wOszEgpbnFCoB1TFt9D6u0RE61ergFYBaxJkFlVCglwqCdFD0sLjFPiChPbvENrHhP4KrT1Glzvswh3AK4Oa7AQv3x1s3mWPjpaLhm1xpt29die4rUAKjwbxNZLWrEPgy9ctzzaG+zPHo7pmXnh0CBA9vQeUISCyXooEWqSljBVg0ofAygcu+8Cz3vNkFegZvYp067phC0L9u5Ac+IZaBgljSvhcaJvR/kwJl7NMYat/Ol7niKqOhW3VSF7YISeAEFpCCAJOZ+KXMRqUEI+sNZkUEAhRMu1GeQHJPErbffxdIN74qGIIGSgSEHYYBkZWrtW5+HDOhhxt82I0w0Yb35gdoDhfww7gr2B6LX+MsfhYTAkVInHUkdU6F4lWuUisEBZ0ErM75fPbQlj+weRaBjtZl+NY6LsNnVFYDVYlepULo2afR25LbaMgk76/zMsI9O226FIwBt93GeQWIp9zTu4wy01cX15Oc1JlX1FrM/m9Y9BE/Bo1AYnbTL6deajN5L+NBb1i9ETPlI08EVBCgOCJfiB2PXSt/LQNabPBL6+JmwY1DKhcJNHj6I2iQ1OM0mFs+y0htYtICaOymrW2hJTNsiB1NmLO6BzN5LHwnrZG6s2kHDxAkWJH11upu+w05QzmMzVJnPVdAiyrZWIzNKxvrmivTulXz1levMn56ZdJcUPvpcZIzMGlUXZjBGS1lQJuerL3FWR9W0LAaY0ymsoVxCrRdJ6qnNN2DW3XsGk2DGGg9YHQNCIXiWZvsQdljXY16BpnZkRriEljdQRjpkxcT8LuZLFOGcHv0z4KM7YD/nxKaaWUcsCvKqX+V+DHgf82pfTPlFI/A/xnwP+Q/79MKb2ulPpPgP8G+Csf9gWD91ijcIs5hbEUzvLqoxd45dFLHBzt8fbTp+zt3WG2t09VCGsHFLP5nLKsMshkpMNTAkQ/zGTxfq21oN2TGDCE6LGuRCmbnXQlG+HuSARZ3KzDFiVFWRCHlma1om8a9g8PqWczmFLC1Q4APJ4gpwBmp1BrTTKOcr5PUc3lO29uCOqcrtkQesUXvvBFDo+OODo65O79+9xc3+CHgbzPQVTEkJNdkjgvISa6rifkVPe+aSYk3mS6eZ3ZpiollssVb3ztD4gpUdcVe4t97t+9g/eezUaqQ7/x9Sc8eXbB3mLOnTsH+LCBNtG1HZch0PWerhdR5RgCXbtG3z+RSJmxtM8vGYaBED1aKaqy4GBvjtIGHyI3yxWLqqYqCpwxhBgwShMDLG/WrNWKrut4+eWX2Ntb5O5QHB0fsWk7Qu8x2vLwwYGAed0gwJnWzOqSui4oStGBDENgVloO5jV1NWPTSMpCPas5Oj7CGMP5O5fEVaD3iTe++JQ+RA4eNOw/9MxrSDONVwabHJVTNL0nCo0Pq2BelqxWKzZdYIiC89dOFv4QEr1P00IsYKTj8XVPtJ47quRob0HyHa5kSrec79coW4gjnxmrJIliJSIkD1GMHrQAHyn1WadUCRiv7Q4mKgzrzDmTSKLeHfB5KkA2EiXlqDDgk5xzNOJ2QT7GiNyIQ00h/u37KckADhG6CFebyOUmStVCa3B+RXe5JnU3FKmnXix48cFdXri7z+FexaI2hGbJ177yDs9Pn/L89BnLmwuRJIgicD54kfBQ5AioUplVpmWzHK8tN60k1X2KSqbMAN5JywZh1sNt0NOMAOYU5d4awqM2qXOOwklK+MH+PsPQMQw9PgT+xb/9EqfPr9grKh6dHLFMA5de2Npmp0+ctZSlIyRQ+zOJxi0b+oubiZn7fvbpLrtzaxzs9gnZIt9ZrzQUZUl5JHrKdT2nKGaQSozTFIjRpdwARnR++1aK72jnsFWJsdug2GjsDzGXpNMiy6GtwfuYweLtmEMLQ9f3Pf1yQ0SYbqFrGTZtroTpMM5ORSti2rJXYwJnDcZl/U5GPe/R8BtBn9yHxrxvuHJXZ/bWM02iPTkZGzubq9JSiEDllDJhkmRDKkbetL9DE2/Q15/h6fNnvHT/IdYUIqliDKFrs3MlmqweKPf2SNaxbkVKpiwKWlvQekUIW8MtRGEqWK3QKqCIWTZjrKQckHKCK4b+jKQdhZtnI0n2rRA81hiMsdRFhZopnBUj0mT2gxLMe5orsobErQaWsYQkEXI/grybjqvrK4L3pCgBH2et9KMRZvP5s8fEJAERax3dasXgB4wrsUVFHJ9zGkHwnRBoxpxCCDsFLXaPYfr9Nvtl+55Slrqa5zTrzCTZmUVi3G9Pp0BY3pnFIclXkZQ8s1mFjh1dCJI1slzRdD3Pm6/xzvoLnP7rtzk/P+M/4ITP2D8JwB+89Qc8mj2kWsxBKZ6fn2FswXy+wBgJtI1Vs0dnQuU0Oa0lKDEM3S2ZgqZZce2hKGaS8VJYnC3RWUt1TMObUl/TOBmTZA9ENa2L0Q90zYa6rsG6rDGcUHsLDl7/BOuqpn/2hNRtKJVC8s9G4xu6mzWjQG1SSZwFZE+LKGw9w7pCMoiMEbZEmxk60xTblVD4xtof5qtPQ2d83mzX0dsHTWd87/vve9IPfn36/M5xKjOP/ljbH/f3f4NNpcQnf/ofYmKFISsgxMSXf+SHuHn91T/uy/v/VXvt/+5YHWv06obql/9nPv3x7+DO4h7zYrHd+xH7ZbRKhX0WuL5e8sUvfImmuSF1a7RvqJ1hdvgi5uBF9P4d3KzgqjGcN4qmV9gYef30d3k5PWUeb4ixZXAF85dfpXWOG+8ZtEMXM2Im7xSuIqxvWF+c0i+vIfQUZc23/+9Pacsl1zdrfiMEknUSQFWKTWi4ak4ZbEsqOkiKsnwF4gNiPGEY9iBpkglE43NxowIdIzFJISzFThA4A00xegmi5JeH9owwbMR2VgoQ5uW0jqlsv++gJyOLMbHVvhQW4E5IcgcU27Zs2+Z9Zsu8k79VzgRVCQwJHyJXvWfjA1ebgZmB2kBpNKUxzMsyb5QCRg0hSIFSHxn6wEXvue49m5BogsSukhr1b8eNVk87uc7s0Pdru/cx3f/7ALdbvFBNH3o3iPvRmLdisKaYCEMglQmT7UytRfrI6C1DLwTR/Ba7cbSD9Y50gZJM24ySp5QmFvH4fcaYSf46xkBMVvxAYVXsBK3TFm1PMRd8G9mMmZmtVE6934KAKIVziqqqJramQu5x159TpCxtwTSGx6LNAurnIlbjfp070IyEiMlH1NP4EPm7ceiprT/AZLlJXYks+xTiNjNotP1HdrdMB3m99ZF+ecNyvWFWlhwsDlgMPXVZUpal6IUqIRFIJtY4zyaHmQyhyp8hiq+dJCihcjFovVP8kwyYS6FJm1PjmXRgRcN0B4jdGZ1pBIfTCN1myUsFKRf7UAF0SgTtUXGs65IwJIahJ3UdtB2qa4jrFWG9xm/WqNWSIkYp5Jmg1BabxC+OSYqgxpTQIzvZD6S+Q5sOYxzWOKxWxLF4rFIoa/JVbus2pBxYKsqK2d4+ylgIt+dtIEkWl1d0HjSOqpbxVxYKqzWFSzjtoLX4YcXy+gnd8hn0SwqnCaaQfssknrEuQIxRsnKTMNNVAUU5w1nJ0u37jmazxvuw5XMoRVVZlE4YG3GlpqoLNs1apMq0pigcRwcHHB/fYTHfz/6CpetbNs2a9XrJer3GKEtQeR3PJI1R5uKDAknwEcDYJDN8lf90+ScBfx74T/Pr/yPwXyFg7H+cfwf4BeC/U0qp9CErm/c9Az125pgXhhfvnfCJ117hYw8fcrB/iOg+5cqs1k2LgitKnEtZBFycxuA9fdcSQ58fls4odby1+MpE0TuLjGJcDd/9vLQxuLLCuZJBa26WN7RNQ9u2HB8fUc/nuKLaOvZqXA+3WmwCwuW/tBTFwQqDdbavBaAqSlTyDB6ur5aQFHU1o6zn9P0VbduzWbeURSm6scYIuJwSbdNSlgVGF3gvdGnRujO4/GzqWS0MtQRFIYVj1psNm6bF2JKI3LsrHA9fuM/NsuHqasnNco1xluvlWiJ4WlE4w2w2I+oB3Wu89xQOqqrCugwmhEDbdbJYyapOWTgRUPZBNGoXC7quY6yu6Jxls2mJCYxWGGe4d3hEVdfbQesMqsuPNTvkzpnpvq3VzOqKqnQYq7BW44zh6HBfiowNiWK5ASJFaTA2CosxBFIMApxuenyIrM9WaKUpXyjw2jHYEm0SKgaCl4VQNl+N0ZbBJ4acMux04nhekYKn6STiKCXkZaxFNKtB8XzliXrAuYJF6TDZiAgxUZQQlJNry2OHsZ6l2knjVRJ9NlmsehStZoxSshNrTomYsi4toJPZGmBjBGkEIWDSyFVZXDskRLA9bgvUTON8+yVT32xfTAw+sOkDqy6y7LUURVNKQEXfE0NLZQPzRcnJwT4vPTzmeL/EqECzuuTZ4wuevP02l5fnLFfXossYRZIgRj8xK8eqhZK+nefhzsancurWCCgB0/MadRjjaOQg4JLRamIRkBl80/RW4xlSTh2S4gXWGKqqYn//AJXlCZarDc/Ob/ja26d0IXJYVizqijgkVilgU7pVdXFrcADWoOoCTcIOA2HdSocAwn7MAPEOaCRrmJ6iuX3fSzezZfzFlATcLBz10R5mVmPLUtIxbAFRdI2VEo1HqkQyCR89XdPkyKSStc1s05LGiOSoS6nUVs5BNvA0RdTHTVErhQqJftOAjxL17kT31xUWWzls6VBmW/EVcvpbNsxCjKgg6dJ6hwUugNo4NsVoSjuG3e4z323TKFYqBwNHVu3uGFCTRE4cDVgt9xmBJi25jE947CvunR9ycnTCvJYiXrKGOdE29APOWmJMWOcogZDPUhQlRVGhdEHXNzLPFJCLbIwzXeXxkCarNqFUQNMT/YYYGskSQZG0EkkPP5C8Z6xWXhZSdE0cvjEVaATwmJgUks4jBou1kaQsN8sbdHYgQi44YoxFWzG0rBUdL2Vkzpw9f85svkddz7JeGaTgRTfy3ajQBIrmX/J+q/Vt5vd2AqhpHG77N3903JbVyOaQtfk23pYmB2fU4p5SDLNQP0mc7OgHfL9heXPD6uaa1fKK591XWLctF907nLVvcHF5xbrZ8Nr+CvblNp5fPGdxWVLNZlSzBU2zZr1eifzQfA4qFwjRZnsfabtmaa0IYdhht45sHC/yEc4Kk4Ktg547dusMbgfy7cfHVg5hfO7Tim8t5d07kFNQ/eO38c2wXfETiJ6xzDhbOIbQ0/seWziKvT2KxZxiPsO4AmWtgLUhQJtInePl/ntpLs6g7yQLJaddkvsrJQhe2O/jih0BW88o9w9wsznRSMGpsX/HY0enZ+zLLy9KGqMpmoZP/tq/kVs0hqKw1LMZ88V8Sj0bsr0xeAHdN01D2/QUVYU2Ujht6HqiHyhsIVIK8z10UoSuIw0dyXeTNMe4D+1W4R3/Gx0lGYaBYeiJKLFRmoblavmhULXYViXoXKNAqakP0+0un0AyATN2rmOyM8ZRt51T4zkmncndcyYlcgfWUZcLVmfvEL0UC1ucHFMfHpO0ndaq0fKYduu0q/HN9No4/pOW1EqLwqJwwMmTN1kkR0nCDh43eJ4tV9x84BP69+3fRZtdBYZKYRK82HseDXDUR6o43FrWlRqByYT1A6vVhu7xOemtK1hfoLtrnF8yc5rF2qH7A1K/z6A8+8WMdqNJLTAE9h/f8CCcchAvCLEhntylXK1Zu4JqCMQi4ZuAz4V/iqIitSvq8wuaizOa8ws28THzoxsO5ok71vFGXbGKihgGum7DdbyhT634TMng1AnOPCSmO6S0IEYBCpQCaxWu0NhkScOQgedEVEwFvQAZ03FARP2l+W5JjFu+6K1YegbUxpaIO5rN+bWdtV1rcgAy5eMZTdad48d5PZ1051g5WEHWF9CEmGhiIvSBUicKrSiNkDfqOEyXqnXWnfdS8GqIcOMjjU8MUQr7sbt/Txd3u32w5MB7bbcPAz6mC/uA879fltn0+/aLZF/M9rc2JrNbpUtjZlfunmNc0yaG6njtkz+RM44UE6C3e6GTvwcwSDHkFFMGfMPk04yg+WQh7ARdR5txYmPKAcj4ygUStZ4k50biwWhLCXs7Z0amxATcT38K3rJlYY9GVkLlIG1KufYeO7aHStPInOqSjPiMIvsVRkA/BcRcmCnbpToFdoeuys/WB08gEMJAiIl+qJlXFTNfUxd1LsAlNkUEyJmmKvcxO3tPGnEkI0xIFSWLzZrIlC6fx7JmBODE11T6vUVkt3ssk52eyJmnkwQAYhONz3jM+EwZ7k4RYhBpvmEg9gPKe0zXoTcNpmnQTYvq/daey7afXEmu1zP6DQlUSKiQSD6gokdHj4kDOppsd5nsY5qtLZH7NUXElzRGstHJxbrz+pWUzlJlYoBXTmGtZJyO3e0cVLUmDgUczAk3eyzPjdjZ0ed5YidmsE5bItgYhDHTfBSfvut7isJO76VEzizMc8boLKuuGLyl7Z2wxBm2/UUCItookXMrK8pUU9YVZVWitWG5XtJ2kmkocmJsbZkPaR9JM1ZJ6ODXgdeB/x74KnCVUhppGG8DL+bfXwTeyg/FK6WuESmDs3ed828Cf1OuoqRQLfN5wcmi4LOffJVXX/k4hwdHzGb77O+Jk1aUJcZmp0IptNWMaayQaemxY7NZoZKfqt6FlCY6ulLCcjMYFLdBKjVV2suL6/9L25s0y5Zl+V2/3ZzOm9u+d18TLyIyIjMrS8qqkkoICTAxkaGBJowAY8aAKR+AD8CnkJkMA8ywMiYUGAwwTEhgQkKgoiSVslJZ2URE5ot47e28Od3uGKx9jvuNiKwqMMPTIiPuve5+ztnN2mv913/9l8wR2ljKqqEoGgprGbqWd2/fcnt7h+tazq8ec3J6SrNY5tUwGfE4r66UN1q+0HzWhJCoV0uM0YyLhrFtOXWe+5v3XN/cY23BBx99B+cibdux2+95/OiCru3wSgmNXSX6rhNduxIRikbKJaw1lEVFPw7UVSXBcYicnq05v7hgcIHtbkc/jtxvt2itaJqG58+f8d1PPD/56Wfc3G549+6Obd+SIiyaikf1CWdnp+jdnn6QBgmLRjRZq0oWvHYRZyw+l0AG79ntWnwSNrTRGmM1u90WH2qapqFpGtquRWtNUVmstZydn1JV5WHxzIebALZtv0ebAm0SRiWaumSxXFDkLtfGSJdDe1GwXHu2bU9ZG0KQEpC+29BuRlwXUV6AILTGREV7OzC0tzxblNTJYJolWEhuIPoEMWKVprKWgGLM5ZlaQW0Uj9cLnBshOG6nbJfKzWwUjKrguvW42FNozeLJSjR3EkRyUzLE4E9bWkpFp86PYgE10nHbaoNKwj5MaKbu79O6nDwFEZ2eyhIyE2oK9Gfn5hB0Wa3mhOvkfBwCpPggwy//PjoVmYK7SDs47vcjd20gFEuaRYn30nUyxUCROi7WDVePTvng2RMuL08gOrb397z68gs+++xP2G3vcN6RiGgSITOzY25XWZVFtgcxM1QPTup0+M96zkgCh3kkmMt+ZmeA7OhMXXrz/j12AnUua5eqGg9JGJqLuma9WnF2csb99hrnHbebPX/0s9dcb/dUTU1QMDon3Son3agjxmXIDDusJHuS1ahFSZFWcjD3HhUk4x0fBNUHJ0JraYhocrM/pgZxKU1+jeyTRc3i4owxiB6zViZ3jjSo3LQpOkexKEkFjN7R7fdghCmXSJjZsZvbdQmInSQ7brXJ5eEPnTANxAx26wRhGCCAd47ReQEU6pKyqbBNKQ28tEJpO61iWdsxEaLH+yBZ6byG03TNr7FGImRA7eDQT3tjWuNp2isZSAQB1h8ElExl1scBw3RGQYqBnb7ll2nPs5tPeLbdUtiSZV3j/CiJorbFu5HCWqbyprIUZ0aTKEvpUFpWJ3TtFpBkk1TDTVIkR877vOdzsEYQ7bnoIIbZjoQowFLyEkBppbAZKJW1eGDJaG3zGSZnXN+PDP2A0koaYpYV99fXWGup65qkYL1aCQCr9bwvyeCm94Hd5l504XODIqUVbuyzg5YOD6KOHuh45HOCdfr52HY9GI8Hnzr8rKa5TilXHRw85JQmbdHM5MyyEJPDHGMgegGzx6Hn9v4l79+95f7ulpvbt/yzm9+ndyM+RVlrWvabPxKAu9vc8fqNoShLrp4WVEmx3d5jrGWxXMmYazUHDPJRaQShUIToZ0386WXMoZGELQr2WXtWXBL9wB4+YEQdjd+0hhLirGKyTAES6CelsKcn2LKgXi543/WMrpdKBSWJKU2S9WtFJ2yMoktdrBoWHzzl9KNnmNWCZKQngIvSbFQ7WPUfcX77m7zrf0Qcb9B+oFAWpQt0Ucxn4zBIU6yopBIiGU1z8oLz73zK8slTXGFxykiQpQ3aTE1E46zLRoz8yxdnXNcFJ+/f8jv/03+KUYZFXbJUCx5Vj3h29ZxxGOi7gXYY2Lc9+2Hgbrvh9Zv33NxuOb24xJYVMcHuboNyjrP1GRfnVzxZfozxMG5vGLe3hPaGcbshhDADsj7vrGl8tVYMMTKmhE+REEZ2+w0uadrRMbwfuP/VLS6GBwyl44VutGG5PkcVWsZZa5LSuQ9kmnUMJxsoFWTZ55jcjCx1pJTKhX85ITxd6rhKQB1WUUqAraE5oT654v6PvsD3O8qm5OSHF6y//5tEW+NT/kSa9rTYToLoYseUZukbghdTB2A0FYkFmiWKtYLL6HlUKlYpYceOuuv5RzHwElAxcnFzK8kkY/BFkc/6rGV95Ff9aa8Z0jp625TAzYfNg/d/Wzj2p19hGsv/j+XXX/O/Duetmv8+AUR1StwXBpe1Ks+HkQegHDzwJ2bA5Bgcyuu3GQ6SBKrdY1rDMkR+48Vv8Hh9RaHLGeSY0JMp1DUkdNrjhjvuN+/YxpqQKqwqKFRmmKVIiDA6ze125MMPl6xrSez2CZI1qGTQqkCXGvP8Bd1iidMWZRVV3RDaNicgJVFYaqiahlBV3O53vLz+R5z3Sx4/v+Lq4w/48PKcz6/v2buBXddyO9yS1jWkBhWXVPYjTHqGj4sMxAqYY41UfVWVQY8Rp0akaiDbRcJhOrxHxQGlQx6QhHc7UnSIaz7DTPL3qTfKlKxXHJUtH4FSx/M9+cVfSzzrbGtmR4yHa1OAi9m5F7BJ554SIdL7SJ8BHOVAEWHn5uNEzf7Z5ElkH3paj/ohXDGfv39agvxrPx++4bCufu0GU/n/vgaWfuM7vwH+Ho1B7rdABKWlqkdr0T31PqC1SI8dJ+kngxiTyDjNMYRSMCUa83eJFqv4WlOlnWjD5vgweJLKFRQpEx4mpm2+yykuUVnTVMYt+7Lq8MwHIDXHmPPezOXjgihJjBPyvo+HJNnUl0NG9SAXNUeRE7g9DV3+/mNyBib7YFlSbvJTjqvYlNKZXS6kkJAlxwSkFlbrNMyo3FA5SWVaN4wMg5P+B3XNalhysvCsFgvKrAEqla5ykzNZJQPOBzsXmBmuWrRSUxQiVJq0b/NYSu+XTBhRsvZjTmynkKXz1BzZ560r/ngKcdYhPqRqZc3GKVaMQiBTPuD7gTgMkvBxHtP3lH2H6Qfs4LAxVx8oiErhE1gEiBVbFKWSJE7/JAgRFQM6enSa2J5p/g6lzNEeybFknqsp9kopy77pTCbQBluVaAPGJFaNopwUDZXwsmJKaKOomwJ7tiZ1V1y/P0Hdl+JHR+S7pnnWZpYEASgKITpaK2eG946uG2iacl6XWutJ5Szj6xqtLHUqcCFAO7LZ7kAFUkx4F9i129ynRGOKkmVTUReNkGTqmhQTw9jT951gLJP2r1JS+vCnnPh/LjA2iSjfX1ZKnQH/LfCbf57P/Rnf+XeAvwNgmyY9XSs+vHrGDz/9iL/wyaeMoeDuruf2tuUv/eXnmEK0QIdhyNnMijnPlA2qD3KwNnUjNOYgnXyVLrBVRe5dlxfPQ9PPdEBMtHSJNkgpZmCwYX1yBf2ey/NL8J7PvnjJu1fvuLi65OmLZ3z/N3+DpmwOHQ1jEoaq1rOhPp6KSXczhICta2xVUS6WLM8vWZ5d0O12bNuBX/7qNUN7BypycXHGBx885/7+js12R9cPnJ+fk7xjHHtubvYobdFa5AfKqubk7IR6dLjgGb1DKc2+a1msltib27mx1/X9HW/fXZOS4q8ry2989wWFSXz56j239yMnpydok5lNRvHm9WvcKCXKMSU2d7ecnKxZrtYslzW73Y5VUdDuO8ZxZAyBu5sdKFgtF3z66ae07RafEs1iwbNnT1nWFY8uLxj8OC/qzXbDo9NTQNixRicBhJTh7OKEIQ6A4uxUBKevHl1QWjsRZ0Aprq9vUNpSlCXn50uMlUxWcJFuP9C9vaFCAJDoJ+BFMtdj3/PP/tHP+MFfj+hwKiWERYlCU0aIxlIoy3a3YwiekERD96QpsAR2Q8+2bUU3GA0UaCVC/BFh0W3anp+2HUopXlxWlEVB9IpCGaRJuSUZNa9VZtOsMwCWKHTCIIfzVBJxyFw+3H/WGJLOXaVT3kMxzuM17Ys5g5YSVuVMfBKDGZIYKQWk3JE95Yyo0dKhcLKwISbe3La8u94Sk6GsG4pmwe5uQ4oREx1LG/je01OePz7j4vyU9dkJ/dDyy88/49WXv+T1l5/jRulImzg6qLImywSoDMNwyObmg0+hZe0WlsIWc6OykB0cYcLGB2VQRpm57OHgG8bsjOS5ULmj/JRlVDoLexesFguunjzh7ExkMO73AVUYdqPnx7/4FfXFKS5GXu02fHl3LfZr0UBV4k8OTPBJMsGkI4fVWNRpQbNe4m53+G1L3LczSzbfDCBArHcBN4p9nNinCeluXi4XNKdr7LJGNyWj1vgYKY2lsA0EBWFS2jTE5GnOz3NSV9AAACAASURBVNiZHbtdx/buHlOJpqme3egjdq9SgMZ5B0pRFAXNcsH1zc3slE3rUwUIzjNuB2kwpCJxum+tKZYNdtmgqxKvREs7TplixNmIMwIwDwRVVbGoa7phIPiQHUIY3HBwxo8+8XWm7OSMpRjp+37OUB+XhR/WSNajOtIKkjhGE4m4lLgfO376xWeEEPjO8w/odltIAZHKEaDX5oZECs2yqolRYUzB+vSCsqp480tEXzSMLOpIXVegRrF7WqP0CnRBSo6URlIcSMmjdImiQlgyAaI0ebDNAtVE+raVygQlelhKTVIrgbbr6fuB3b4lZkmY/a7l5OSEuq5QCU5OVljzAWTmcIgeSEQ3SLOe7GQXpZTLN9rw8Xe+h09Z/1qLgx0PJ/Zsj74JaUxO7LdAHUqYJWly/tXDzxy/prkFckIjN+TI86umBZMy28WNjF3H3d01d3fXbO437LY77u/v+D9v/mv60ONFZGMOaFBqagIsd3DEaoox8Or1K0JSNKtLhioR1YZ6saBpSpHiUDmxPEl+JAG2U0i4MFAW0vk2L1eurj4gbu4ZxgGnLX/yV/4aTb1gkaWbDgtW1rLK8k/T7+e7SxGtxMFVE/N+YsZkrTC1XGLqmufnl7z60b9k+9VL3N0tyo1M2sA+BNwYUSdLnvzgU5qrC/TJgruxR6dBOvuaYpakMI3GLEvM4xWPHv9V7n/2Of3LV/g3NzQhEJ0EBVNAO/QdHkWsas4/+S7P/tJfQS2WOK0ZnccUZU7aTQwdlaUzJBFzvCKssXz4/BmPLi8oK4syUmUx9B33d/e0XY9XitZLF/HbXc/bd3csqgXJBwa3x48O7eC7H/2Ajz7+AU+ef0K1OGd/e8N+/Zb29g3bd5qxGyF0WA1VYfHeH6RzMiO9D54+Bbro2XnxXcZRmoGcnZxyeXrGzfaePjdwk5N7QlU0uqhRixVJFxLISjRykNrhoO9NYi7NmwJEILPhDo07Z2hCHdbLEVRx5HJo6sWaxcVzNr/8CdWqYnX1IYuLC5rn32GfSpLLybCYuxxP3aq1QRfCjo8h4pwXTXilMEARwY6OpziuQuAqJD70cBkCNR7jR9jvMSGyyH7uarfn9/6D/5iw2/DFdz/mJ7/zW8Siojh9QrO+pGxOQFvZZ1MS5qjKTWVNd5//FrKuPFqz224lqQVZJieDF0lY4UqpWVoInTXrYSKOzU1GQ27GYouCulngR4d3jpjCgX2lpnlIRCYATwLepMhgPqRCE5VCFxZdFOjKoKwSWaGqZFHX/Lt3Lf/J736PPzxfcTo6/su/908orJVya2uJweP9kH2uQHSOvt3hho7gB6IfGV2PC57hJ5/Q828AsPj9/5zzR4qPn3+X733vr6JSgZBBJ3ghl+KSMCpiuYPhpyztwNNna9TrM7zrUX4n7HAX2LQ97XYgFonHT9YUaeCy0jTW8C4oBq1pgfX6lJOPnpC+9xf5xa9+Re8HbFlDO2DnhkYBkqduSoryhEW5Zejfsih/yM7dUlDy6Mk5/85f+Qv8gz/4MT+9fc9dtyOmjnRfoJePUcvvEuN3iG2T/Xs1m1FtItY6KuNIfitl7eI8UOhEkd1zlRI+9ZiwQU9lf4BRAa0FOJCu5BnEIjMfs48iVSaH+HIqPQ8h4NPR2pVOjegJEJqTzHkPZ7TsoF2J+JRHm3tKwKQM3M5VaB5mVrvWAjZxYM0dmJiJFLPO/4TJH6Cmh69fA6j+2uTEYZN+a9xz+IV6+OP02weJ7F8PnDy4YAY7Y5LqyphLsieN2AkEnWL9EESmoG5qqRbSNpOkDgm5GGEYPaTJnssZbWwGv7TCqENvjwnUnOcRNUudHchq0/MddGzFz3kY9yjUTK6ZRsBYcyi3n36rD96ZLqYmYQfwdMJadJaamNiyx9eaJRKOxj8p6cMBzLHd9DmdZaxIBSoqjLI4NzAOfW4OzQwEC+iWQd0MYnrvuB17Nu2WXbfD+5Fx7GmqmqZZUNc1c0PjdAD35nubkpVRNHpVZol6ncTGakXUIulV2BJtLEVRZj9antMnwaU6txf8JEw9Lw73LkF2fv58XkxjEHPD0ZR70cQQCOOI7zoYOuLQEdodq9s7VNtjncf6kLeSngrnIYkNUUmY+jaBDlGIPSFiYsSEgSLUFMFT+IAtIkWedKOm5Z8IKctmyiEmpJGywiqRP5CqOIu2BTHLnQQfCS7Rq0RRaipRwAKjuA/QbRz7bUe/lYbvuqjQZSH7A5GySyqTihQZ/2O2iUpJBbj4xBLHb7f93ESuKGrKQpqv6WOpQpBmZsZSFFYq9/1INw7sdre8f/MVTb2kbk6oFxecrE4prAEibuzphj3ej+Kb+3wvtsCYAvVNCze//lxg7PRKKd0ppf4+8G8CZ0opm9mxLzg0Qf0S+BB4qZSywCnSyOvXvmqr+Jv/2g95dnXF6fqU9cVzymqNtQVFUbBan0lQmR2bse8pTCHivFn3xB0DMyS88zPLTJtIpZsjwyvvedAcRE060cK6NVZjtEx8iImYNGePPmTY3mGrDaq0DGlkTImf/Pwz/ugnP+cf/8GP+Jv/9r/F86ePWSwaktGzgZUA4OB8ATNCL4bqYOBSSpSLFcqWxNFx/f4dm5s7ohsw2tD1n/HB86ecnZUsnKdqFrihxY1ZAsAlbGHp+oGuv2W766jrOjdRcfT9wPnlGb/4xRdsdzvqpuHy8ozlqkErw5ev3vC//5P/C60jhTVcPTpD6z0hJc7P1lirCc4DZyQ0213L/f2WYQzc3mx58+Y93o9Yqzm/OGe73TGOUqo3jAMna2H0DX3Po4sLHj9+xGq1oKpKlAgSoQKURcn65JT65AnLqkXki6FpFiwWcoBoE1kvFrRtx9nJkqdPH2HR7HYtzh2afgUPN7fX7PctKUSePXvCYrWgMAXRKnSwRB8gpFm3JyZxnEJKoA0lEYa9OBJa0ZyeC7igNcu6oPNioFMSB6ouC3Z9z64f6HwgKk1jFUYFSIHeB2GMZNapT5rP3tzgXMOjk5qzVYUbWvr9QNIWbUsgoaJDZAr0nEmzWotxPGq2NTkKchCHDCbI/ca5zET2w+GgTkfO0RSIpVmjR5qFmeyfqdxoLIIp5jUNiIal0TiXaPuR+23Hzbaf2ePOO3Y3txRpZGUCp4vAd56f8smzFTE4+v0t+80NP/3pH/Pu+g1dtyN4B8kJcJrLo605sBFn7UzEAUkZiFZJmLAml0Z774+y4Zo0MXPz77RWWRLFzNpJxw5EnIYHEd03SkosQpRiclsU1HXDhx9+gNaKtt/SDT37fc///A//BT/+2Vf0o2OlDckYsBZdVZw2Db0KhJRmZyTPIjqBiSkzCPLhQgKjsOdripMFOEdqPX4cCMNIGEZwOZue6UtKK1QlAIopK1anK5ZPLoha4YKnH0cKd5yEqtC2kDKfGAnR04eB8+aSboQ0eNx+oFytBWzKh7FCz2sxhkRIYZ73sPds93vRb53L6sQrN9pCSPT7AeUTwU9Aq6JoSvTS4m0gxgGtNaP3wp7Mzqlz7rDuZ7urGPoeN464EIRxoMwU0lCWws6enOcjAz3bD2maIBnwqamXMgqTzPz2KZA+7IOHjr84poakEz/hH6J3/zrr64pVVXB5sqZr91lOwuRtmeYt6oM/gHfaUFRLrj74PmN7hutvcOMdfhwgJsrCUBQlya2IGLTuc8lZguKCevEMVZ7igkdkU47uMgWcd1KFUhbs257Xr17Pgd/YDZydnrIoC4piQdXUPHp0ecQ0T7S7e2GjZ9sjgeQBAExA1w1cv79h6KUB5Nh5yqaiWTYEN9LUNZnqc3DyvuHKHAOxR6BR/ptS6sF5K4mISbPsyPbFAztySvAI+yEQwygyDN4z9iP39/fcXL9nu9vQdnvGvsN5xy/7P+TGvSQArXU5cWZQk8DuVAv1a+AqZRTd0HF7d8Obt6+4vHqCy4DYslpw9fwDQvJz064QJ6WuyX+A1eoRRVFPj8rLrz7nzJQsmhXWGnbbe+qqFuczMxrER4rCXJjX6dEtPtgOes7tCZPaUdpKYjtjUMoQFwWPfuu3WD17yv7Na64/+5zu/k6cKwVUlue/85vYxxekusAZMLaisg22qDCmyEwQ8MHhg2fwDrOsOPnex9TrNXfq54yvbygQECPFiE8QmzXLJ1ecvviIs0++R1ysCAhwbHJVgXdOEoiVlqYjKsschDA3dQSplvjqVy85Xa/wbsQHh7KWISi2nWO/G9jtdgzJ0g6Bza5nGDzrBooQMFFhqTi/eMzV2Qua+pykKnxSmGaBdWdY5zDbLauTAeU6VPSYKcmIBKo66wJbN1IbxUInzF7TjYMEw1qjSTx/+pSyKtnud/RDTzc4DjxGYbjGJHOEhhhU3gv6CCBMomcZpyRsBpXmXZe1DvPf0ryHMmZyBF5MzLeQoD67ojh9Sllf8Z6f8+KHv0t9ukRXNdgyS7DkAFofJDFSguCDBItWkiooRRk9CyKnCR4l+MAFXviR1dhTu4Gl8zRJyR6Owlg3qENjpJTQ+zsJNvOdRhdnoCTGiJ6kMqaEdvYtxnEQORciZVFJp3OjKcsKW1gWi2r+yHyeZEBisutzoniWkmJO/kliOIMyCSEEKE0qC2Hg53uabJ7kmKQx3rzxj+YsIVU+neuIfQd6SoIVJDqSUuy04vc1vPeHxKK1UmKKll4cU5fsySZ610F0xDDg3UB0I8mP7Hf3uPbR/FyXqyvOH6/4+Ml3MRwC6cQh7aMJ6DSiw4b99p/jUseb+4Z/9fKMqC9o6g02lthkCIMn+ECpFaZULAvQRcm7beS2hyEV3CbF7uSMs8cL/LOPedcrqosPWRYlZVnTd3vwA0WxJ/gKa2FVW/rbgbpa8zf+1t/mi3/xJ9xvXuLUjtef/YyvvnjDqSn4waPHXMYz/ujlL9EXfxlXfYhLV4yxwWBR2s5xnUKTnCMiWpcLE8B7dAKrFFEFbGa3xTBi3Ft898ek5ndypxxyU2IjTXUfROsyz9KcN+/wJHq7kw9y6HfwTcmr6fcqS+sdGjSJXZhssFKSnJwTNRmEVQpSOGx+bRWYiRGYWWdpKoPOscJ01k5rVGrCj87tw5n4686g6fXtEgTy+QnWnbRRv/U7Zlt1AMGm8fnmWx++Z3roBNLfIAYBmLLvG0KgKGwuq0/ZJwXvDw28tBEtUW2mirrIpHULZBt0XIGXAXcOUgImM/knycWYKxcm8NKNIZdh5zmXcrSj8c7d57U0vJ1YtfrIr5iIBYezgHy9h2N2MK2HSsz53lMuFZ2efUoA5vua/nkgBZF9NHX4IqlUzo3SUj7LYxCJOlLEx4CKcn+orOWvpSFyigKUBx+k0i4lxrYHF+iXCxaLBaswsGZNWTSiqa8ToB8kC+Q3D9eGQs7MmH2JlCJpODRDM0VJVdWZLSqAubVyHgStskKFmkHxA+CbZjA2hGz7p2lIIs0UgycFTxgGxs0d1dhhhg67bzFdRxpGIZ/kuNgUB9ZyjBGnpH9LEXIPACOEEYH1AthGgP2YsCFgnWOgQFmk+sDIM+cuGUzR6bQe921LjGBLkWEsyoqqLog+EH3ExcQmFowBir1IV5ASfQdDGwlDIPYjrutw3Z4w9KgUpcrO8uA8Kcty3tuiG+vyXsprSVlZOyghNQw93gtoPlXjacAFj/OeGIWAMI4WbQKmkDXXO4/zO3bdQNnt2W3fYK1FayO4hEKqmxSztJvPVjB9q92S158JxiqlHgMuA7EN8LeQplx/H/j3gN8D/iPgv8sf+e/zz/84//1/SX9GiqksLKfrhmaxYHV6wfr8MVpJd+OyKPEB3DiI8VJ6NtnTZg85O63SRAs3uKHFFoU43NrkTFx+pUkmQM1GWb5LmA/SBEtxdnImLJ280Gy1Ynl2RdvvKLd3NM2Srt/QjYH7XceX77dUpuCTTz7g2bMrnj59TFM1ucwzl4Tlc+hBo6Mki0pB1n5LmLLAFgVmJc9rVGLsW4Jz3N7fSrCcM24RRWnlsPM+4Bx0Q0/wLh+uhtF5hr5nHB3ee4ZxoG3bnKXTtPs9Jydrnjy+JPjA6zfvePvuWhpuKYXVkcIW7He7LH9gWS4a+tHNzMHFoqIoFNqUjCO0bct2uwdEFLyuKx7XZ0ylEG4YOTs5ZdE0lEVJYS1osNk4hxAISbE8vcLGNxAFjHUhZt1Z6aB41lQU1oge5/2Gs5MzYkwM/UiIgcVySVGWVHWDd4m+7enakf1+EGPnFThIgdkgTrIA09yTEq+/3HD2aMniRJF2d+iqxOgaimygcxbPKNFMMipJaYQTDT0DnDYWqzXOR9q+JZmJbSS6kq2LvNu0c1fxdaFRyeVGJ1GcPUBU5BSi4SYMDJWYM91fdyDkwBP2SfTh6FA+BOCSQJVFetiyB4dqAqf95GpqLR1WUy61mkARpFx+8In7bc++H+kGT9EsiErLgejBhJZHS8WjpeHRquDpmaYoYNu13N3dcnN9zfu3L2n7fdZDhBQ83oV530YlB6+UTDIDVrLPxKWYuiumKJIG6XjfpUNgMI3J5KDM5mIez+MQgtkhmbLIKkFRiLbgkydPWC4bdrst13e3/PLNLb/47Es+/+Idu20nMx4SqhSwJqbImEQcXjLID4HB6arxCNRJQNKiVYVWYDUUBcYVaOcwoyP0I8bY2WHSVmNrKcvUhUEvatLEuIgT+zNhTUFhK8qimo87YQhBKjSqNMQ24IcRUnbmzEHHcQoWUh6yKYA/JKCydEH2LOb1FhJxCPj9QIkVjbG8Xm0tAKEqLaYQuQCfdU9lOqeLHeZuTg6kKIF2SvgomeDpM0VpQR2BAEf7Z14DSdaRsYa2bWcbdnytaYxmZsD0t5RL/SfbT2I0LW503O22vLl+y/l6jS1EOzbGxOg6qlrNZYeTdIZWOjvkBlstSOlMKiGKBSmMJN+SiLgEMUgDSwClS2xxjq4eo+wpSZW55HfOk8tzT3INSc4jozVVWWCU9CRtyopm0cwaxDrrKB/YWvLM1hbzODrvabs+l+AJY7jrulzKJ4FFfdKgc9M1MkPdFuURW/PrrwOCrI7Gel5veX4Ez56eSTbpBMjG3PRMyvujsL/ciHcjwY8419O2e9q2o+t7tu09n9//c/btln7sGd0o8gDArX9Jl+4FpNL8mnvOg/wt0aHWShiVQ8vt9RtOz9aoGGl3G67fv+Xi0WOSMTMjKUafn1HPz7pcnFDYcr6Q9w5lBdQe+h7vxyzNMat6zsHRN6uF1BzYhdxM8kGzuqOyx/nRMuFS1RXF+TkLrQkk+ndL2s0dUSfqx2vs5RrVWAFw0TR1TaFrjLJyFmZWk1GBED0uDIQ0oBY1xaNTFh88YXt9jwqS3KC0LE6WVE+e0jx+TP3oMSzXSPFd5KCPlu1PPqtSzM38tEYn82BWEpIA2e1bRufo+h6URtdLQoJ+dGzbkWA0211H23ak4PBdiw6RylTUpqJSljQ4Qt/j+56iaqjqJvsIGuNHhuhQvQBERIf3Y7ZrYit81oufyhsnEG4C71KKVGXF6WpFVRjGsWKz79h1Pc4HCQqMSDSk/NlJ31vN2sHxMIlZqmvSLjzMuTqc819bwt9Y0flcRRXo5gzKE0YM1fkFZrkiFRVeaZTUG+Y1PLHTMys95UBKgQoaA5QhcO4GnsTA45B4HBJP3MC5GyjHAesdNkaRypn8mGy7jp9Fx4M+njTxmOx/kAA3KYkZMhAQJ4Q1M0N9cBJ0RpFVMUaYPtPeUJMu3jxuB/Z+moAJPenoTeBFYkr4zQDFPJz53E+5fDY3cTqUt06yMblUdJoQJeu4vdnSjS2oRGXPqKxUdiUksSPtIaePKCprifrQkyDGSPCOGMQ2eudwbmAYOvzQCyASRm7evyPdPeY0f9cHVx9yctGwrFfz+afns5rc/cCR/Ib9/iWbzQ3X+wWvNgvebU9RupYE0mhRucdBqS1FZShrg0bxdhO4HQxtMCK/sT7BPFoQL2r29YrBK0xVokxB1AW2VphYYo0mOkNdKtzujtG/oSx2lOUljz58jno1sNsk9psbrFJcnDWc2IKTmNjvHO/MKbvUEJJlgvXz6hJAE0QDnsiQIqUVT38CyAwBgyPGjuTuSe6XuPYLYrGdZ8IUhmRFa33yE6c5ms65mYyb1/zB/zgAJIdt+S3+iVKyCSa7eOz7pIOvTD5nDuzLNMeuRNCHjoc5sXKIr0EW5fQ/uc+jOOVwuW++jm3Qt7xzjuDT19583Djh1yAQx2Px52HCHt6SHY28LYUYlMVb9IF5Kgk1NWuSwoHlPDXzUke3ydGUqMluTzHa9AemS8fZVgQmwkia70khILnJ1YzCG1DzdaazT/598ANU9qfJAO4MDs6JKeb+MofBFTuk8+fS0WAFZHnNFz4CnGfoXCkBl6fP5/ufKkPmWG2yRSHKkR6mePWQgEgZdBZcYvp9mqsgBR9OuBDY7PZ0w0jddez7jsE7VosT6kpKz401D5bUZIMf/phjnSOgWys5S5x3MwA3jW/KMY8fx0PVpSJLuan565NKwsKZE2zzH4BETEr65IwDoesY9zvM0FH2A7obYAik0R8qR41CJ4VSKWv+akKSKsig47xokspVE4sl5ckFvbEkXeTYDhSiGayTnN9qenby7Wozs4Jjbgbmx4h3I13XUnYlQ9cxOk9IUDYr3HJBXRd5X8A4ROIwEseRGEZS7EmuBT/IvWfNarFwB8s7rV9jRHplWnMze1ysFnZax8HPNmnqIaWiRiT6kkjd6AKlPCk5lJaKF2sKtClyk76U3SlJpoQoMqETtqCNwSRFivrh2vna68/DjH0G/BdKdGM18N+klP4HpdQfA7+nlPrPgD8E/m5+/98F/iul1M+AG+A//LMuUBQScIWkqJZnNKtTgpMOdRiLc55hHLGFdHRjatSQwYFpc5qcJUpZb66qy9xMymQdx0PGB8iB3sHRicHR7nd0rdDHm6rGVjVkjU9lCpZnV3RDy3q/4/T0LXf3O2xRkNTI2+tb/o8/+Gd8+e41n37ygt9y3+fjFy9ommWWKEiHi+eJMlofHL3JqUoJk0uEmqqmqkqaRU2/39Ptttxv7ri+vccag7WGcXCcnjR0/UDbjTin2e33EkhXBUUR6UfH7e0t4yCApg+BqbN1jJHNZsPZ6ZqL0zXkrNMwDHQ2d77WCVsYXt/cEHxgsVhQVxV9P8xNs5bLWhiIxuJ9yF3reharBU1TU9clz548ZrfdS9OuBHXdMFk70eHQTMUt46hoBw+mQmFmb9G5yOA8XdcRo2e1WuUMhuPtu2vKopFGUV3PMA7CKNUmszItKQrgvd3ucL1DO431lTTmyCViIQpTJuYGaTFFXn25QRuF0RD2PXVVYxoNRS01OtlGaKOojcboSD8OjJlJVxjFaSPlCu3gZsd+OtQScq27VqQfFLB81FBolQW603ygT4LvOiqS0dmI55K4SeyYydmQw2pa5yGEDNIcHx75Q1GikzQ5NgowE9h1AGQhl2TMIAzZWRMHPqbErgvc7QZ6F0jK0DQL+rbHuwg+sC5Gnp+UPDuzXK5Lmkqx3Vxzc3PNu3ev+erLX+JdJ4dSknsLToIlIJcgC3ios5d/AMA4HKJqwpeEZTl1fWdyDCE7JdNzHexLmFgGPmQW/sEfmrPF2RE2xtA0Neenpzy9esw4duy7ljfvb/jJ51/xT//gJ/ghSdJIQXIBXVmCVvgpk6ezk3XM6OPwLKLBGOdAPV9cnA+tidZg61IOLB8Yu56irOckg7GaoirJtSliK0MWds/ZeFSiMCWVrShtmUstZA/ElFC1JRWSIPPtKAkvo/M/6tjfmteF5hCYynqTEqKD/QWtDGGM+M4R2hFVF0Q3lX0pysUCXRTCsiw0VVXS9v3kezIzoecxUzOr+dhPj5kNOIHGKh+kOutPHWenp1eMYNKh5OxoaX3rawp6Dri0ehgUqESnWu66W+wNfPzsBYu6IgYvDY7GAWMLbFmisl0gBET5QxhVSRswC0xdYMoTCI7gO6IfxIFJQcBrVaOswVQrbH1J0iXxqNw8j4I8ZwgSNIU4yxCcrlcYZXLp8KGsWZgugZRROJWB1RAALTpdIQSG0bHfbWeWX0yJcRypK5HRsVqzWKyRdNPshWPLkqSNNP+ZUNYH/xyvsfwfR8HdHFCkfJ9ZNmHSY45Bqmei94Tgca5naDuGsWMYOrp2x2Z7z9u71+y6PZvuhn/V/QPZnzplZzlfPAOws+7eYSXI9Q8Y48G3Pk4a5IDa+YHbm7c8/+Appoah19zevqdrW6rlUhLL2ZarvI5AbGFTLcU/yiNgskxDjInRD5nAeqTRhp47Nh+Y3N8Mdqcg71jaQED0Yk7yTPcx7UVV11RWYypLv1wQ3kiH2dUHF4TaSOmtUlhV0VSnmGRlqGI+CbXFKLE5RhW040g0oJYVzfPHbD57SXIKZSuKxYrl82esPvoIvV6TyhI/BW8SIhzZbIMy6cEj6uzYx3DcAkuea9cJy3S/7+j7Ea+3lIsFSms6J9JYu+2OYbfHBAc9mCS2qbYGQmDc7RibLa5eUC+XmKqhWi5ZlJYyenZjS9wVxGFPcB0pRUl6Bo/PWuhBK8YQGWKQM3DSQ48itWOsoalrqkLjnKGwhhgjLSMuJkyWG5kBt2kfzECgrBk1oQA8bE44lcNO9nXyZb++1Oe/AUoZTLnCLs6JtqEPnvr8nKgNo/cEH7HaUNhCSA9Kyqq1Ev3eGMXkqUJhfKJKkZMQeOF7PvGBKx8594F1GLFuRPuAnpJpWYNSkswT1+tovykNubFgikmAioSw40NAZ03CCVSQ82DSMZQ1GvxIjAZFwhg1g+ZqYjTnxPmh6Wc4GueDruCcqEQYwKSDVqHiIQA3JU9C/p0+mpN8syglOspTOXNIAe4Sg2vx0bNa1Fi9zM1eJd7wKc2ML6WgMoY++73EJAxjN+C9NKQThtmIG6REmODBD9y+fYu+fTaDsc8efUB9qil1jCj6ywAAIABJREFUgZoAuBy8Q9ZMDS1uuOH+9ldc33s+e9/wvjthk1bUjcIai1YSpCulqIqSRVVgS03rFa+3gZ6CaCxWQX1xTvGsJC0NrYaoE8aUJGVxUWFthcFA9BhGqnrk7svXJPUVpRkY+obV+Qnd/Qlju2cMe9bLE8p1CYVlGRXb00uG1uBDIOBwumJ2kg+HD6RA9OAjjEofGmxGj9IBEzvw18TxDWn8HNe/JizbeZ0WVQEm+4UpoY4aG01JuDitI3HiDom12Rc6gFlz89Q5eZlveAor5hVKvtPpsVI+v7LOfoqZCZuyfxLnR57WKkdH4QzCTr54XrsqTT64OrIbBx3Tr5+TD83NQ1DscOX08Cg7eh0D05NL9uA70+Ee5rf9musfnXZii7UQcVSudJyqg6y1uUzdHOZNKTlvImidBOjK+2MCR4VBmZnW6XBvovkbcy+cON9KmvY/au6HYI0wdCff8zAsMjkxz+vxGKd89k1272HFw2T3D+tETtksw6jUZIYOrq6S9ZEmhuL0DFO1oUoZiD26ztE8HGuPphQhqJkcEb2eJ1EqpBMgxLwctTBVJst4ixMmeumRdhiI/UDRd+y6ltF7hiGwWnqWy0i9AI09avbO1wC1dHS/eR2n6RqJJOIqpBRydYFUNAoRIMcrapJ7OPw8MdUnp8hagx81E1eCBDoE6XvtA94NDH1P0fbYfsB2jug90QngLWeSFfuTBF+RpmDM1b+KCUBUKG2xVUNs1vnMM6AtytpZ/mKqlpWGFXrytEhaehSYLF2Ikh41znuc8xhTsHn/hr7vCTGxPj3n5OIxYbXKsarG+0ByA8EN0ngtdES3J4VexlMhCdN5/JnX46zRayfZUQ6+q5SazAD/OKR5XmXPSWLeZNunlZdxy6RMpUT6oCwqjCmlL0ZRUOSfXXTEviVFn3HJACoDw5GvrZ2Hrz8TjE0p/Qvgd7/l978A/tq3/L4H/v0/63sfvjS7vWO5ViwXZzivKIpmMqtUzRJT1LOws1birIiOkxIdpezch5hwLjCMI6tsoGIuOxSjMGXfFaU90OW9c/Ttntv3b3n9+hXv3rzh5GTNxeOnGCuNeUYSZnnGo+ffp67X7Dc7dpstKMPgAiFF7vrE3U+/4Oe/+pI/+uMf8zf+2l/ld37rt7m4vKCsi3wQH8+JQmsBWWJKs7GwmRmrCkNlF9i6JHqP6zt0abi/eS+Z+xi4vdtwc3tH7xxjCAQP+3ZPXZaslg1laSnLgsvLC9p9y26349HlI/a7PV0nbNtCwebuBqUNy9rynY+e8Ojykv1uj3eewq7px4FlU7Ld7rm+vhaGh7WcnZ1S1yV1U7HZbHGjgxQ5Pz3l3fsbNnf37Lb3FNZgkLGu6pqLywtuNlvO9AllbbOOa8JaBVFLKV3yvPriT3h26jjLMpp12WD0nv2u59Xr11T1QkrCreX+/p4vXn5FURg2mw139xt+/NPP+e73PoUEbhwZQs+LDz/m8vIR+7uWm5c3pCilid5lHVSliKLEhUui/ZdU4uXLG371qxtSTPyl0mJPHTo5jE2gSoyCQgujtSkMo3f4GFHGsFg0VHXNZrtjs2slQIoOlKAXSk+aPIbNEOjfbSh04sn5ikplAfe8dkIUZ6uwBUHJAZRSjhTigfU6OTaSLdJzCf7EkHlw0MYo3aHdmNke9uEhnQSUEjBWSiZsUaGKKjPIFQmDC4nbXcdXb/aoqsIsxGjd329I3lGGHWu154dPKp5eGBZVwKaWzU3Hj378L3n7/jW7/QaVRuZQMYrguQYBkrNDmmAuL/26nTt2HGa2CQk9BR7Z0VBazSVT4ljJF03gYwhh1rA7Ho+YgWtioK4r1usTnlxdcfX4MSmO3F6/46u3N7x6f894/wa8J8RESjlh0Q+YZXVgiihy9s7MWn5Mt4WM/VzYmKbDVMBd1KE7uK4aAcpTQJUKXTZM3prWipAbAKgkY+FyEwtSLvHRUBUNlW0odIlLnhTBO49TnvpyTRt79ncb+rsdtiil/L8osoP96y393GBmbiJwAAAKU7C9uWfYdeiosni8SDYoayiXK0LOPtooa2JRVgxulLKSdBisCRzXShHHiFHCpHXeHYLbHDTt9jtm4aEp2Pgaw3zSKx/HUUoBcwnqcUAwBcuH/XIAqATcUTPYC/Bz8wfsw6cU3W/zxZdf8oNPP81Ok2a5WEp2NcbMPM1AwYz75bBOa2KS5k5aW4pykYXoJ/Dh4KVIQVUuu0rxaC0/nLAUAm4Ysp7mtFcyQ9kIu9UYK+BJLisehjEHHYY3b94wjqN8PiWWixWoiClEg8kWBecX5xz0xRRmrowQZ0lKiQAmJ/gh8nMUKnHg/qSpQaz8t5JAR8qPHePQoo60H733uHFku9mw3W7Z3N9xf3fLrt0zjAOjHwlEfuz+Ph33AtqVck8wV97Nc310pM/A1IN7PrLJ8veHQZ4yIhtwv7nl/bu3PH1WUJQF227D69df8uLjTyhrCzGXrSYBzxOJooCU7IPvLEzJ2HVQJKrlmtXJKWUpHV+nWxO5giM2O3BUtgMKirL4ZnA777XEzGTJ60nAXUAVFOsVI4GTk4qkA2Zh2Oz3LBtNUy9oyjVECBxKuo3WSLWD+HRlUePjgj5sicpjT2tWP/guS7NkuTpjdfEYVksGRJ9sTr7IxMAUXMI89ike9sUcUx+9Qky827Ssnhqa80fYE83NT3/G57/8nPXJitNTaSy7efOW/u07Utex0HC5WLDWhjIldBjB9eBa/P6OobSUlTRSOzs7p6kqVqs1xdVzdsbSbxR+dDIePkj10tiRgscphVcal6Ade5yPBB/xLjD4gX5UVIXBucBms2V9suaR0tzvWm53LbZsJHkzdYmegFit52Zw04AopbGzbzzZuK8xOI+GbbYiObiPKJSx2GZN8+QHFKfP8UNHe/sVp2eKMThUFK1Orw0pSD+HyR5FJBGulYZCUyrNRfJcec+HvuPTseXpEFj6SBmlieckRaERKS6V0nx/6eieD8s3zmX/KQaiFumpydbK5+MMCknwLGvSGos1GjfmRpgxSwtEjw9eqve0NEqTodYPkjAp2wGUmcHWqZT4AOLqGWDz3h0AtjRpL5KBnik5mCuDjsH1DMYmlVg3C3a7W9qu5e37VxTJUJcNVhvJ3efzdPpwMSaG5InR4cOY5Qh6gnP57DuwzBPSwyFe3zC8eU9xv53HudAFJiVSENkq4fRMkV2kUD19/4rt5iU3mxt++vo5r7aP6PwStKcP92jfUo2RUltUdNiqJumSnTP8YpPoizOi9+gYqG3gww/PUVZKkQutAM8EmGtjUUTGdse43+DH13TFj/jy/R/y4skHrJdPcHFg3N8xhD22LrhonmLu33HT3hCVAx1pXM93fEUdEq9xXJcBU67Rhch4oZPIkSnxii0RlRv9pJhQSWOdg/4tDJ8R+89pN18Q/ABHVVF1XRLSQedQKZH8OULf5nzg3NAOcsKOOfF4WBtfO3Om9aKmBn4cEgTZXxYt1Dj73DFl/1FxABHN9L0CsHJsX0F8VG2kd5mW2B3AWD0DfrNNfrBPs1euDrboAeHi4cPIyjoGAg8j8o3nfnBm86fiJH/KK4OVueouAmZK/qiEjllGQB/ICFOF0PSz0hpjpSpqkouRvS97ZWZ1Tj5nmnTjJ7BSqlSqshIJoontSq65PEyNNEaaGHwh4p3DzBr98p6QE4BSESv3rbNfOlUNzhVuUeRbYozZd9MzE9Tk5HthrMRR+X0hJ7xmEDU7UpOm7OQ7JYTVH2M4aNjOa1RTFNIIcE64KWGKTmuYDBJPgFzIa/r4VEBlmUsX6IYdbTdwt9izWi5ZLZecnC05WZzSVEtKW2O1JTFJAB37pFMJR44f55jbUpYVi8UKW5RoLWdCyJUGIbi5yuBAgkIKVNJhrxotbM+U8l4ia/hn3Viil2o31xP6SOgHYnAYEskoohSMZ0BRiFcRiEn87JgSSSchjoWA6nv6m2vG0WDOVpTrFc1yQSgXlDHSOS9NaUOAosr9ZyT+t1UpPXFyJY7EtPFQuZsGbl5/xs27N3TtnvPzSy6ff8L67Ip6cYotlxR20mrt6Mce323ZdfeMrmXyVWb5DdJMggggzczSVF0jcc5EJElKPq6zRJAtijlumxrzJmSPVJWlKAYKZ/HWZl1YsgSCRylDYWoW9ZK6WlDYijF4jLEMbmB0I21oCT5moPth48Svv/5facb+//Uy2vL86Qc8unrKYrXCFHVuRCPmxGgRno/BC0oeFYW1GW0XXbGqqEhKQPrFsqGun8/MOSWnEkorxqHHj6M0G8ndfgXgTVRlyYsPXnD1+DH99ztOz05RSpo8hCAgcLAlpqhYnz/mB7/9u+z6PemrL9l2DmtgTBLgjB5evd/zP/69f8iP/uRzvvvpR/zgB5/y3Y8+ojQFOmXdiky3nxyvGEX3pzAGq5RQAxCjl5RGN0ueffwJ67MzXNcy9nsKDW9ev4OkWdZLLi8vKaqC4EeCk83etj2np2uKrMNb1xV1XTKOK/q+Z7/bgikQ4rGhLBe07YhWhpOThsePH1GW0gnv/fUdP/3553z5+g1Pr56QkhajvmggJpaLBWVRMI4DV1cX9P1A23bc3W948/oWW1iaoEl6z//6v/3fXFye8f3vveCHf/E7PHt6MTsjWmuWdYWiZeqJDrDbvQcci0XF6ekZL1++5fXb69yxUDQ8P3rxmNOTU05Pzrl+f8+rl1+xWi1ZrZc8ey7s5nevb9ld7xlvRoy32TAf2H0xsyHkXkQnJ2k5L0NM/OiffsYnP+g4fdITfcfy0Qu8tnK4JMdw+4ra9YRoCXbBxXoNydKOir1TRF1Q4NHZOfERhIUdCTHRp8DPX90yusDlac1JU6H8iDZFNjYJopdS8qzPGaI0QVFf6046sT2DkE6yc5adq5hmHVWloK5rrC0IQfaNVpqoIKgo1w0hswgREFBlrRU0m13PZjdyvx2oz06ICZwL7LdbVBi4rBzPlokP1pZHS4+J9+xvOu43Gz7/1Uve37zLDX+CNAhzUhKhIANVDwPCya3/hmP2La/JiZkcpfn5jxgD+csJYepgmUvM1UEiQGdmVQzCli3LkseXl3zw0QvKwtL1O774/Of883/1kuv7W4Zhy7LY8+Si4NW1p3OiyZZCotAWU1pS1AxuPDxIOp49xUxdYAJ+siMgSUmUFkH1/4e5N/u15EjS/H7uHttZ75ILM0kWq8iqri6gGxiNNEJLwgADzH+rB73qvaUZYdDTI6nQ6q5iN1kskrnnXc8Wi296MPeIuElyah4rgGQy7z1LhIeFudlnn33mQ2S7WoGK9H2HG0gsydyWKUBdkQDtcYANjEFN8JG6aqirBZqS3GOkTKCsSx5/8oyr/VtOuxNDO1BUDaEwWbeBkcmZAjwBvKfOAJW+bALOFIUxECJ2fyJ0lma9Ahdk2rECs6hhWWOV6K75CE0hAaj3HofHezdWMHNUc3H5iNubGwpt2KzW7I57emulqutl8B2QmOiasiwf6HfloP2BfTAF8x/+7EclCmIaRpUYiFprGUSpFe/UdxzDDdXbf8/zj56ybhqZ6qqDTDONsj9JABWIXhENSR5AptSLBIIZmVyT8l8kOilwAQQlAF22qLxGMbFpcttas9lIwTNG2v2eZrlMyUDAhcju9oYh6aAZU+BDQKNZLhas1nBxsWXoO4wppF1JaXSRGJjGoIoyAfeSbMigGZNVXhhTsFzNzsDfwzxyelgfPCf5+ckDfyzeSev30B3o2yNd23I8Hrm5ueP+/p4vd/+Rd/23aRq9SGJEpNgRNTjj0mnkgHtcwQ++ezqDjG1O7Ogwsk0enGe+iuSQlZbk9/W7V6y2a0xp8NHz8uU3bLYbLi6eUDVLXNY8Sp8VU+vafAzV2eocu7+j7Q4cnASxKidMKCn+6eQ8/qtHBl0/uOy5/efCVkqK7GDxzlEWmmZ7hvEN1re0wx4TFE25ojQ1g7fsT6+JKjG6UqIgDcgywKkwNWVZoX0hr2sUj/7yl1R6hdE1gxEm7KQPHGenNQvYZ4DxeDEZCOAhYOd95NX1gcOXf8SHb4lRcbHd8OT5M1QM9Mcjr169QO0PbH2gUYqlqTgvaxkeSkTbgcr0mKFF2RYTBta1NJjt37/gu+u3vH7xDZ989JxKKWyw7E87fN9yOh3o3YANkozaCH2IdNaxa0/s+hMunXvezyOFaLlVS759+Zb1aklRlGy2Z4RqkfTeJQ6OOt3/dHuVng2XjRkQ0AJK5jVUiWmSnsc4W8ns2EP06HLN4vwpjz79Dd3iEwYX8OFIXVqqppZZDwk8AtCJVScdS06kPxJoXBJ4AvwmwM+85eOh47JvqYMUEmMQVmfWZ00jB1JSlaxXkZg0k33E4Pi7/+VvuLm8GG07Zj/DjKWHxAxu6FP3jLw/F9RksI1O7kpRzNlvSe06gygCvGRt5jRJGyQgG+VhdNpv9bh3yr6W2LZKiwRDlvhJtmuyb8rFTkF5UygduajXFJcfc9FsafsjtSrQXjoGfPRY68c4gBjpd3tCY3B+YLAt0Q1Eb0eQwXsvzGA7ELoOtTtgXr7lN/UWv76Ae/mouqwpi9SWnwoAOjlHzcBw+Ib2+D3H057b4zlu/Rsuzy85DQX39xbf7WUonRvQwVNraL3hrlUcS0WrG3COhpbzxvOLJxUXlcWEgX7wnFphlR2OJ2KQQYSLpuTibIFb79ntv+Kf/6//xFm94cnlxzx//ilaR+7fvqI18HZ/xe+++xdiVfDRkzO2Zwu2ZwV/8z//iv2V4etXHb970/EPN7dc9T3BL1FlQ1mLJJcUTwMm9rheuq90dGjfYbs3uOM/ENwbgrsHbdC5IJmOsl6gh6PEJ9pMQ7xmrneM9SOjLvKHu+J0xDHmzzaZDWbsjogS2+bWXpVa8McjgCckZvXsy8bCDhKMpsA8+5g4zjzIxeWU48vD/6PxU47DJj/+o0HAeG0ZEJv2pj/1nofHT7Ngf/Ido2+cQ92FKWjqWlqai2LmpyUO0Cmm1KNUzLROIL7KWUfXprk3WoYt5uGGeSC4DO5KgJeaiv150BNRTWuXC0vJ94RU/JFcSHLfopy6heefpQv5TmMMZVXN7oeAU3lomeRJE5HBO4+3boz/HzJtZyhx2p9HrJTkDqOf1mZ+f6Iwi63zicgm911rkwC/KTdUyiDzmTRDtEiHtBCt/MznKwTMPbRHTn3Lzf0dq/2KR5sD5+stm+WK9XI9DuOKDx9Dpk/SIzgcozBXu77HuCDdbkWar6ILCmXQqgQM1g1EL7MKfBDfLENkvexIgRRfJT1vBcoYtCnRumaxWGH2p7QNeBkXrMZdCLzH6QzTpzknyD7axUAbAso7Gjy4jnB/RX91zUEr7rTmShW8Wi4ZqgVUFaZpWG+3VNtLoinxUWFdZFHVqJm0nRQYhJlbFBEVPMF2hP4Aw4HYGVToUHGA2OP6gKGmUAFlIsEYDocTQ3vED4P4L0TfNts36buyjSqkgOqclaJr2lOzHYVUcMg/yXMtopI5Jd5HYnTSUU9Aa6iKAkIcO84XqzWLekPAYIMCL/hKHohcFYZQilSD0QptPqRfPDz+LMBYpWC9WrNaranKRia+hiR5Owuec2uc0RFTGPq+S+3uAacUVVmlqlNuYfbC/kpBUIgyqCIWoiPrfWpiU1raCCtNWTfUiyXL9YairInjA503DaGdKyUtleuzC5b399R1nVrEvDDttMLFyO408M2L1+yOJ95eXXH9/oa//OWv2Gw2lFVF8MLaGjcfGJ2gDeIwy7KcRO8VmLJksdpQVQ31YgUoBgv3ux1dd+LqnaNZNZSFtKtVTc3t2yuWK5EWKIuSrmtlEMtyiXXrpPkXKbSmqivqxQJvLev1ku1mzcXFGU1doYxhsV5R1BXWR4ahpzCKRVPTdR2n41EAZsS5u+A5PztjtVxJNSFq6sWCqqlRGry3GCOVqdvbI1VVy/X6iPMCOFbFQxbS5fk53u+wNnBxcU7Xd2ijcT4wWI8pSrreMViZXqqNYbvdEgm0nVSZP/34Y+6uDxIYR6niRZWdVNbODCNjWSqBSUcMCSqsDbz6/oZT53j6WcCUK+p6jW5qSl2gbE/heooYUcZTGji2JwYfCKoApdk2NWVpsD5wu++kFxpNxBOCow+Kt7c7vB8I2yWbphw3VqJU1yRAy+3DefNVIyKQQdPx/3OqkYCxUeMosazGTTFFWiEEojFpYmICqsmbncgjODQ3u479ydK7SLlaSnts7/DWYkLPZT3w2Vng8cKzrRzKD9zvd1zf3HJ1c8fN3R3epymEwROcHVm+cQwQy4SH/BQ4MztSgp4TKCECmRTYmLRpSbvh/D3ZuReFsMZcSoakgpYA+iCsi6ZuONtuef78OVVZ0HUt76+u+O3vvueb714Tw4m6HGiWnseXBbcHT2cD3ouuTLCeqq5omhWHGBlikLaz2cWJNmBAKQk0pkFIYWSmkJPkGGhP+ySsHjCaVCGcgvSoFD5BduNABUiAn+gwVkWDVoW01kT5DF0aimVFVZSEU4ezFk9Al5qqLCiKxLxWhqos6PteNIWy9txooVlXKyafJ8MI7NATXEArTb1oaPcneUVhMMuaUGqUySB6YPCOMCD6iipV71GECQcVKRMiNjiZnhqcBJ+aB2BSDkaN1iMz4Mda1sYP/rGfJ3B/nkDIyaYwICfpSoqJIUoRpotHvg7/N7+4+YiPL5+zWS5TUDbZWg42JHZUow2rObMkD9+JORCSQN5bKWIO1rJcrTCmTBpm8mAppVNLVWYp5wqy+HFTFKKbejqhoqLvBgnK06C63KFSlDIEojBlAikKjCmlBc0IuCqfb0AZYrbjfL+yRSgpwo7pjfoJ8Ht6YMeuGWft2Lrd9y3H44FTe+J0OnE67vlm/3cc+x1d39N2olt7a99wCnuCikQ9tXlmsnQO4mLyO7mtTPLWCfwYgdgMiozZ1Y8lhA/9V9bDJ4qP6oeB/eFA3Sw4O2s4dgdubt5TVQ3NYpWYyX5cl8ykmSez281znFrQDye6OGBMlQbMzFq21Gzx1cPTVEmXcu4jtM4asvnfekxEp5uiUveCQhmNUQEbLbZzHPcHlAroCwGCrR+wsYUYxFYosN4KiwqFdxrnHGVZjecdgVBoghE7mrNf8s2Qc4ZcUPtB1jQeM+B2xsyKRKyL7PYnAVCI3PQH7NBSK00ZAkV7ovaBKkKtNUutKZwXvbKsU+wHtO9RtiN0B7r7WxarFbvr17x98QfevvwDhbJsFxuila6drtsLc8zIPXU+MAQYnJc/PiSwUmLHpqopjUxsdlGGmb1+9479scWUNbpeiubbqM2K6JUmTccMiozrobIhZOZjiiPSQxA/MOnMHo0xEs2K+uxj6vPnhPoSrytc+x7tTjSLkqZpMmyY2iURIEZQSYlvE4WniYFH3vPr6Pjcep5ay6UbaKyV79cGnexZqbSHh4AfLJkbNo8VHqRCIWDrClcWyfHMLigBRTHKPu2SjIlJsYe4HDX6q1zYhpl+vMqfmawpLWuInon1mlqVoxTM1IiopdOIqY1YZ5DFI805Znxsp7sz9zmk9YyzR1qzrIUJu6wa6nKRnhspFJoZhS54z/WrV4SLFQ6HtT22P1FVs4F3weP6HpxH95Z4u2Oxa9lg6KJhl85O5H8yQ09iOaWjzEGw15x2b7g/dFzvCt7dr7n81ceoouJwBB8sJ9dTBpPYhoAusaqhDSUnq/EKSuV4clbwbGP4aKkoFKI9Hzx4hyo0wfbY7gih52L1hP7+wO7wFbc3v0e3lmpd0yw3NJsLCmPwraU99Zj7W04BTnZguNuxOMHyOnJ3YzlbXFApw8dN5KgiCzfQMeDUCqvhiCYoyUN16AhRU8YWFQ5od0t/+hbn3lAay2K1YsGaUjtWTTOaada5JHV+5jhAjc/p5MVyh1Gc2UFUOadMdjHeg4f70QSLCdDx4ZCl8b0ggGqYxZMwkzyZVGqzNI+Y4tQOHMP0uTq19KNSHv4BUPfw+/PPx102P12MG3R+t5p59tn5j5//QSzx33L8sPguP3POMQwDdVU8AErHNmVyrJj/xIefmfYqwTsmYNQURrpEmeJKPf6d7k8IAgAhbe9ZVzzGOLZrj1JCgtan+yit2LmDbC6f8CEAPtlCsse+f7AW824vmDpT0plL4S0X+2Kc3b1ki2NuOvOXszWePokPbmy2Z41KcZvOso/pd37GJpYl0WM8CcLiDjMnHoOA4KAYcAzWEwZHd2o5LJdsN1vON2eUZUmhiyRlSGpUU7PcJseKmYQhsUsIEWvdLCaJiV0cCUEnBnHWxY3jwLGRRCTfkEhJHucl+g5RY8oKqgpflqiiRA0xER3SvU+EvhgZi6xBRZyOtERuB4tZ1JRETAzSzRA8hYsUPmBcoLu94g2aTiliWXD2+BGXz39OvTnH1AtCFEkOGQinx25FrWSPiQZcCAmYLXDGYL109UoXakApR3AKDCmuk1zXB4sLA95bgtHj+mZ2eCZMgtibinEcmpaNKefxkUi0brSxiUk99yGKLAupUKlbB9bbLY8ff8zzT37JcvOIGCPD4Oi6nvZ4hP01fb8j9hGjZfgr3vOnPM6fBRgLsFysWC7WSXdBjQG+Uiq19kaZXG40xuTuiJAAh1RZSk4MJUFMzqaUlpsVXEhUewngQkg6s0onkCmk6YYlRagIYr9TwKXFKIIfGIYTu90ddV2xXK5YNAtKbVDKSWtQuv8BuNsfObYt13e3dMcWoub582dcXl6wbGqKGRgr7cZhZOyGGFBGNESy8aE0JmlUlJVs3IqCqBW3Nzd07ZHe9iyaiuVywaqqcD5wbDtAJ9CoI2xW1E1NvRAJiL47UVcli1XD5uycwfZcnJ+xWa9YLBbUlWiAFJWIM79/f88f//gd1kqb89D3tG1PCAqioq5LcYYxUhrDarmgMCVVXaGMxjrPdrtiuawJIXD7MwIbAAAgAElEQVR3fyBGxXIp7AkBLdK0zzwNXsFqueDu/iTVx0ZRVaIBc2oHBhsoq4quEwCCGLm4uKTUJV3fMQwD1jo5x6BQUWxGJyc1JSKpRT1Ty+dJa4xjgH972zK4QFVrzssFZhMpCiiaIu1eDoVBE9DRczydsA7QhsIozlY12ihOnUURxKvHOIIpQWn2pxMmDGhvKS+3NIsm2brCIe1zGTQARn0eqc7JSUuwrsYgJDMl4+goddrM5dUhlf1SoxLEGXMtb85KjZtHO3hu9z2Dl2sry4quHXCDxQTLsrA8Xw4830RWZsB4Yf9cXb3j/fUNN3d7OmeTBIm0DkYfUtAxB5LVDOOYNu/xL6UeOr3sBoB5sJGH2IjguzAPx0peiiTG1oY0vCbnK4qI1rCoa7abLY8fPWK73XDqhG33/Yu3fPvympubHXXZUywDxUZzvi1Y1pb9UYK0Qmvi4Cg8rMsGbS1t8AwhjMHWeBlxCgbz5jHe9hEUEmCq70/jJpRnKOTwxmgtw+4S4ChxbA6KSIB1RVnUotOWKt4RKOqSerUQVv+hxVsnwKcRIE4b0RHWWlMUhr4nBT6zrrVZwcPPbSwGhq6XyqMxFFWJj56gIqbQ6KYipPYok77DhYALdlwjYzSEh+Fu13WADPBq+25qRY1p603rqmeJ9OxBJweMP318kNTkJDuzjfkxm0ytYqkVzCvP2/gN7+6u2DZnLJsm3/AJgA1JiF+lFnMtYGdh5oyDNM0zSHU9jACDsES9tXhrxdcpRRKiIzUWT+eXBj6QfETeK731KETAvq5r6rphsVyOwZ4S45EAJjE+pKNgYk3LWugJJpgnlFNGOJ3NrIgw3ZNs93ngTpYh6ETv3Q70tuf94Tv2+z2H05Hj6cTpdOTL43+gdQfRd1QBoxMTKU25ZQZGqVniN7/f42/Uw+Btjr/O9ysBsAQ8m36YA0A5jDEPdJVDgMPxyGK5YrM9J3jL3f0t680FF5dgSkNOebKN5LgmH5v1U6JZcHAtLQmMzdL/4+tm15YudeLXymf7ZHs62UWe9j4mNZHx/0eW0JiUStKQnwEpjibWCIya6UqJxq3RiUlgTALEEms9+Q1iahNTaWROvmUzoxmLINmX56Rn5kOnC86/izxMMJGkyQxURuKB9njCdydpPdSaJkQWSmOIVAoKIjiLrkV6hggqWFS04HtCf6S9u0YHS7+/oT/e4d2J4/EeFaQ9sLMdx+5IVYrOvdKa6MGUBYpehm8aQ2nq6VlQmrKsBdyOAQtEDG1vKTE0depRzFI2Sk3gyTi4hymumT+AYxKvMlqQXzxuv8IiV6AritUTqvNPKDZPcWaJVhDaO0w4Uq8LykIA44lkHlMdcdLuMkrTxMB5CPzCe77wPc87y9Y5FsGhnCdojVYGU9RTgTKm5HMG/IwJOjOwnpTk5RhIpb0gXdvE+PKpMOfHHGBuOyHGMYGaHoOZP0iGlMGimGxTKSlA5j1epn6TABwYOyGUxKcqATv5Of8x9l5m7U8+i/HZkDdFClNgtKbSFVOsKLJpQU++LATP+++/Rw9bQqHwwdJ3J87Pt9IRhSTNw9Dju454OMLtHU3vaFIregZjVY4tlSTASkU0DuKBoX3L8bjj5h6u7hruTxuer9doJTNA6trQKo2OYieiJW2wusbGAucVSjs2K3iyNTxdwxIn1xM9MU0a16qR90YHYaCMHfe333J/9Q2Hm3eUQVFVMh+krJcURcNiPbA866hW7wlFycG27O6PFDFQRcfrVzt++fGJhVmxUTWfL2tWOnJQmqNR3KLprSKqEqLHecn7CNfocINx79D+DZUZWDQ1zWJBiJGlCdSqGu+r827yqUru4wgujrb7MD2Z9q9MxJj2sfnwrRHwYhZKp38rndmzYr86f3+yr0xYGd8w+zvvmPkZzABcBl6jyl1nkz+OUWJTnyUa0v6SXXi6sIdGP/f9+bojs2dxfDgm/5V/9KeQkf+GIwOcwXmc9dRV+QAonQOUGfCcn9kkzxCmtSLH4HqSRmP6edaSFn85SUbkdfRhmjchcdf8XqR7lwrxed3GeTazcxpjz/EcI0ElQCnnDmpiMmdZg/l1i+/NMV9as/QfrQUknNjQCq1ne/AD0JZ0PSqdV/p9YGRBAgRvZOBZOl81N8j0Wbk9PSTf70U0dbQPUZ5LQGUE5wIqiGzXqT3RDj0xBJbNMhHwGrK0XG7kmuxjTJjJ82BUis2n6ySBkABSXNZpmFaMjqANQuuVoZL5XsstDqALdNFQVBEWlrBcgZPc2XsISggfPgYKLcSpvC+p1JLvYqRDsdOOLXGc3ZBnHBREmuBpnMW0LYfecjUMtDGwur/mWW85f/KMxeaColnxSJOkqvJwuGLUh0ZLflI1K5rlNt3YgqgLkUwIUpB1XtjjgUAIjuB6vO/xYcAHS8zyWmM8Pt3bCUtjYp2nn42ShsTZ6/N/0nnrSUpUZyZ/ylWM0tRVzXp9xqPL55w9+RnlopK5GMeW0+6eu6sFu7t3HPfgXE8chlRUY+Z1f3j8mYCxitX6guXqHKVLXD+gjSZqaWEcrEwBNoWwR7SBGB1FWWDMiqau06dkJxfwg5u0SBLD1LmByKzlIuucKNkkhqGT9kldoGL++bQhKV2gQk/b7rh994o//MvvOd8u2SxXnG8vE7gXQcWEe0WUkUDP+sD9vuW3//gV3794yxeff8Zv/vJX/A//6q+pyyJtnAksihI8KqUptEnMJpeSgFrAtjR1WBnN2aNnXFw+Znt+zt3Ne3a317x9e0vXWQFTlGa73fD26o4Yblk1NcuF4c27tzy6vOTR40c8efqYvutoasN6s+Dxs6fSIlgUibEzpcNKKYqy5JNPP+X7l2/ph4Hj8UBdNDgHzskU301cUdcFr169xvvA4yeP2KwXdH1P1/f0g+OLLz6VQQBDy/W15f3VFYYojNyzDY+fPEJ1Eb+qSOkObdslHUBH13acb9f0gwMvE7HrqmS3P9BUNZv1irPtlvfvr/EhoiiIRL7++lvaqxZ38GhKRsgpARjZSfmY5jGnxDsmzcW8zWoFh13LP/3DC/77psQ4R6ECuqmhahg4ERUUCoIb2B32DKrBlAtWVcHF2Zbd/oCzNoF9BkuqZhk5E+0Cx/097nBDtD2fffYZVV3Kpp1sWcWATI40SShcgMQib1Zj4DSLbtQMgNLS/qaTsLpsJAmkUXrSMyYFCxg84Hzg1A68frejVzXNaoUyBcfjgO06ahPZNp7nC8cvLxyrsicMJ46He968ec2L91d0/YDzIYErcUz2s2bSaHPGCOAGiVU4bboxO9wPoqxcgTSZlYdK4KBcp7V2DDZn7ij5EbGHMjFksyoOwKpqePL4EU+ePuXx06ccTvfc3Vzz9R9e8P99+QI7yLPX+0irIsFrLtaa7cJwV3gOg8foBt8N0DgWqc2784qDHWjUzDWnQMrHiFFMoFH0EAwqi4Wl4EchQK0w+QyFFkazVorNYsnZdsXdfsep7SCoNJQq+bmoqMuaqqoo0rAgtGha1esF9bZhGCz91Qnf+fF5MLn1VEnA33aDbD5R0ihiTAOEzJg4h3TPI+DcQLs/is+rKqJWDH1LjA6MFG9QHhUFvMlTW8Pok6YkghkQmu1Co0fGLEwsg3yf89RP7wZMoTEUDyL6mLtIk02MnQwzu1Fpw54H4dN5SMIcoxql+XwQ1quKEac07+5uuGwuWdU1m9UC70TzyAePG0RypihrqBdjq5Pox03AVlApeAmypymjMKahLCuqus5puqzdOPwhjqDFeB1I61dACgerlRQcNUzSCNqgizLdm6lQSGJcRUgs7HHVGQEDxVSxz0nBB09u3ndTBgdhXl2WgZtdd6LrWk7HA7e377m9uedwOrJr7/gvu/9NJCligmJ0+l6joChGzHkschJRmBE4EV+RGLopKRllB/Ipzu+zmn6k9PgJ8r25wKymYDHrxoH48SIDpCnI3B/3lFXN2dlj6qrmbr9jc9jzxA0s64rgMkAj52nKatKiQ7HZPqZcnNFXilfrkoUqx41rZAjMbBmA1AkCaVhdDNiuI4Yg9pP9aJzYfqKfNbFsJvBAJ1OT7pTFaknRPJV7qmVglsawri4IBLQq0LpgUYltx8To16pAp1BVkoRAtqoRPhx9dl5fBSrrLEKWcRiTvAQOTftFfPhXCJx2B86qAlOWlMpQKY2paqoQqGOk0YZVofHOoWIugjgMUfZdbQjRoaJDuZ7QHTmGyP7mDSoMPDk/p6kLKAx9e2JoW7rjge7UwdJgKgNliSkWXF484ub+hu4m0BSapZHYbD60tnMOrKVEoUyFtxblIzZIx1MkaZkqNe6tJAYJKo4tztnWs1ErFckqvNJmn9bRiz5fAKKpqFbP2f7sr2D5iFAtUaVmEwf643uUOqLPt5K0kxPKkLSCVX7c8SFQKcNT7/m5s/z10PGz4cTCOuog4KeLHl1UFPUSUy453F6hlcg5xCTzpZLLiEpBYYguPLzHoyxAZg/pSc8vsakGO4y+saqqEXyJxKmQmQGI0Y5moM+4jml/nmXqEdFQHHXfg9ix2BAUhcboJBEUZf8SaYJJ73le4psX10n+bDLtDI5kcI4ERufz0YknJ4d3nhdf/h51t8IsK3Spsd6yXtWUVETAW0vbnrDX7+HNe+pXb1mVDUV0dHMQSuXCt8ROWnl03OH6t+xuv2F3KnnxtuDtboUtH9EdegKevvWowRKHlqE9oYaeKga0rnCqIiiDwlNFz6+erfmocSyxuMFRmkgIDueEDLDanFHXNcvmnEovGfb3vLv6P+B0z1o19NqzWG8oqxqUDLxslpcszgaa7RtUWdKeDtz1ETA0qqTuBpqw57zs2DQLfvXzL/iZU+yc5mawfHu6xx1ODKoWiRFn0USMfY2O7zHqlosN1MsnVGWD0pr7wy3BIll5wuBc8KOPi+MzqEZbyj+fgKspRh//VtPzFVPcNLPWB38LcJGsQiti1NMvw/wc9CRrMX5RHB9ljzTDZDatd3F8NMZ6jmYkfeSTyAW9iTn44fHDH46x//ic5TQnGbuevXO84Dilez/+sfLjP4Xaps/Q0YxMSYLMGFGJ7RdjnMXY8uyFKPlWHrQnXXjTCUrKPe3FcqJTwUriNTOumU5+geABM+7Fc8YrMEplzY+Q5nGM8gYhd9nFBI7HEYyKMLbI50MhMaGcF+PQsaIoxrkN+VoeDMeNH9rqQym26XdyrwpjRJc3+W75nSHGImnWBmF69go/pNkv6KRxK8CkFBkQZqhShGDFTqN8fybpJLibCFJ0cpZT37FrT3R9z3q5YrVYsVltWDUrqrIU5qQ2UMgARVRAeS/kr5R3Sr4wi4NjlkooKMoao0uULsYOVMnJprxYcia5J3ZoiUEKTmwcw/6OwTTExQ6ae4J6y9C2xDBIjltUct0+PJB0FtJhhBDoY8T6QOGT1zElWkGNZhvgovCUvaVtW14fdnRXr3n5/jUfPXnOo0fPOPvoE54+/zmNdegyYEyBKRegxSaqKMPp108+QdcL+vZA3w6oaimRgB+QAWYy8yRGR3Qt3eEdfb/DuhYXXSoIQCZcep/kO4zk6tlPOS85lDFGhtuOIUActY8nIxYbFwnGgEtDu41WeJX9bOR42PPuzStCqPk0Vnz+61/z+KOPqZoGbwfef/8tb777mjcvK/xwZOhOgm9MOmw/evxZgLFFUbK9fCRaaNbhbM/CNONGXjaVVIpU5siJs2iqlIjmODs7HjQ6ekx2AiGOQU6e6Cxsn1lSrRPjQ0E0Qdq4lMGYgLRReWK/483L7/jm6y/54zdfcX31hr/44lfc3Oz5/sVL9kMHRhPSxqPN1MoEEig54ObUcv+7L/ny6z/wu9/+I//u3/1bPvnkY87OtgI2aYWJOseKeB+xgycWmrKYdGUnpxpQuuL82XO2T57SdS2rV29o724JQ0epA7vTkfOzBc4Jk+j2/kiIgeu7HZu3b3n06DEX5+dstxvWm4ZFUzC2pyH0727waXjXLS9evObt2/dEP1CWUtG8urtliFFao2NAa8V6vQICp7Zld7jn8eUZ59st17d3vHn7R7TRfPbpx5RFQW8tt3e3EODd+2u6fqBuai7Ozvi3f/MXnK2fAqCMoRsGTm1L2/VUdcVhf8QDy9WS3f2O3X5HUxucPxDikWEQhkNZFpxdnmF3Ees0yhsKk9qxZ4fE62kCZJwF2MTU+iPgmA9eWIbe8ff/4V/4zb/+jPPkLBfPPiE2ZxTK0DQ1y1LA0SFmnVLF1d2J/amnHSK6qDFKdI8dMARQpkDXDVFFOjfwatcTro98dHnOdlkDATt0oitmNHWzlLZ7pVAUkJz7PKYYQcuYk6yICmkABDq1rEHwiswYMVqzrhU2KlxUeF1xOA28vz1xvzuilWGxaugGGQAWvGPFHZ8tPc83gefbwMUycnd3x5s3r/nuu5fc7Q84ZdLzKVPNFUmrTmtpqyAm5rI4yjyhPSbQwJgpuMjV2QksEMZlBggFfJB7a60dRfGl1TYHsxIIFKnCKtIIjGuilaIsSz56/oznHz2lrEpu7q74L//4L7x9e83LF+95f3XPR0+fstk84urqHbvjHS/fR36xiJyfaw6DZv/a0rcd1lmKMnJqDauyYGOWLI3h0WpqVdNKU5YFZaUYnMU6YXzLxh6I8YOWjRQ4zQ8dxXcG6zkdjoTBYVAEraibmvZ0xDuP1gXrakVjKkpdpGdfc+xb6oWhWRbc7e+5ubonRMNyuaZuagmSFKlLQY92lgOytu/QxowFta7rRHunkcpyt+9wdz3LZoWh4HCzx3UDZVOxWC5ZrReYSoI+H4NMMQ4JGJxdqmyeEpwNfc/+cGS5XKKLgpCAoTxBXljdIsZujKHQhsJMrOHIxObweTMlM5geThvPPmP+jMVkS1ExBnY5iFQo0abOQtQ+8E/8LeF+h+Jf81e//jUo8L3DOxmIKJV3jw89fZ/OI036JAGhykxBnyHJqsSI0pGqKMcgN8ZJ2GS6gDhmSjIoRFMtVsLCTcDPGHAqyAzL/ExlD6pIIMgHdjjBrjz4vwe/iVNiADENdfCjXrwdLH3fczjseff+Lf+8/1veHL/mfr+j7VpCnHyWVV6mpCsjua2a9uMRvBsz1HROKWCXnFWN9xKlxtYueJikZTt4wBSa+1t4GPghdjUH8ouqpIzCiAojI9RxPB24un7HFz//Jf0wcH1zxeLVt3zx+a8nnbZ0OOtGLcAIDNahrIOyommWNE1FWVQYVchQvNm5z882J0AR8M6iVCDiGfqWppABbNP1xgmAHddjBqtn4E9pHIpBQaGhHQ5UZkFTbVBqPSZpClDRTMuXsAAfguj5EoURqWq0KsaEZr7WEy6WOwNSaqUmMCGffxi10mdBefqd6zrU4R53khhzUZRSkEvPb+4oiSqildzT3CEg7aZBCsRBWITWB1zccxqOUsTQAjLbbsDbQVjCWgBYq8AFR7COISjuXx4IMVCWhma1kOGfqQXVDRYbhAkY3EAYTgTXiS+sCopK5KW0KggqP5MPbf7BEzzbP5mvZ163ZB0xBoJpqC9+Rv3oM5onXxB1SQyapql4fr7izX/+3ym6a+pNzXLZELQkHRGFV5ro/GhHikgVA5/2R/46BL6wlp+djiyHAaWkMOyVxE7BWYLu0DHiXU9TFzgYwYM4wn8iQ+S7/kGRLEGqCaBRkiyOA0vj6POlyKind30IKCj1I89Qem0aIDK1O6b9OoTRRwlDJ/ubzGiburVG0lZms40GPkJNo0ULKy7FMzMZGrnLuSNFgLKHRGE1stDzctQFHO6vCccowzMXS+zpCI2QO/xgiacj9199hXrxiuddpP7oOYqQ1G7lqFMZRfpXAjru6I7fs9+95u1d5B+/Oedmv2TwBXXRstA952crmmcV6nPNt1/1fPu7E64/itaqVgR3Ih7eoE5X6P4OtXmGeXJJuVgQFEnuSNahWS4oKs2jy8f4ds/u5lu+fPO/stEVzeYCtYz0zlHXS6pyQaEK/ODRaApdUOgSRcH7uwNtsUKXJbas6Ko1d8saF3ru2z2vv/p/8LZnfXaOqpfUg2N76tHFmrLZ0Fxs6btraI5yX/QFoYx0tqfrTlhv2e3vpYNx3cNS1k8bg46z/UUxtainG6YfwPIf3Ncokikq5S0j2DfuWfNXf/BulTE52eBzAW/OfPzhZ8kHhhAS+BHGom9Msb2wPmOaSaFGGaZ8TfPutD91/BTT7L/GQPuRF//k8UDa4KdeQ/JJD1pp8/3REDXeybCyaVimANpFIifMAVNhnkvnDt6nXE5+o0j3QQvIaBLIpdJnVDAbbIQAqimezX/y0s67uLImrSkKqrJMIHOkUOWYD+n0nbmbUqfvzczZ7JXU/HvTfJGxfXy23FM3ShjXamrrF5k178MoQeXTDKBMiJC4Nr0HqOoFESXPsHE4JwWdbK9ap0A8sUVjFBxllEEHBmtHvzyC4elaiYqh67n2N5zalkV9YH/Ys1qsWC6XLOoFi2bBwiigGAshPoCzntzNqlNXR+q1BDTLzSXN6oKiXKB1KRhQWaZOcENd1xSmGP04MTK4juB68A4dHbEf6Pb3tIc72rsbTm/fcHz7CnvzjuHuPZzuqfwwFV3nNg744GiHlo0uCKbB156ulLzJ6QIKhS4cq9WKZujRwwnbd9wf74nOcri/p7k/sLz8lMvDgdX2guXqgu3jT9D1ClPU6MJQEHn68S/xTz7DOyHixTyg3EecV9josENHtCfisON485bgBpFmM9Jjprx0aOShWz74hO3JM9l7lzRjJcfz2o/yeD546Q5PdiFr3IxxBml/ds7jveg9hyA/O55ajqfvefv+FV999Y/89u8/Ybk+Y7nasDk/I9qB9nDHcX/HMLhUSCjJXY0/dfxZgLGmKCibDbqoQRU0C5XiwTyQSM8eDCZNzzS0SEBtjVJxBNE0MqBFHI8aaf8qRfch0aHlkM+piwrwuL6l647UzUKGlrgBN5zo2j1311foYLk8W2G45Jtvv+O7V+949f4GrwWg0zolW0leoCgluYghYJQhpO8/9APfvHxD+D//Ez/79Bk/+/Q5f/HLL7g4O0vtVuJYBdAoRnbf5FyyBp8mKIVKzJLalHz8Wc3p7Iz+uGc47bFE3P5AWRmWzYqqfCQUdm9TACfJQ1kWVGWFS9PJjS4JIdJ1HV9++TW73Z6+G7DWUmr4/Oef0jQ1znt++w//xOHY09QNi7pivV5RViVn52csV0vavufm5pZF09B2LWVpWK7Woj3pHNZ5rLUQNKgCbTRdH/n2+3f8d3/1qdyqCP3gOJxaTv1ATJotaE1wHut6+mPL06fnfP6Lj3j+7Iy+O+B9YLNZ09Q11ir+899+hfIitE6YHNLDSfApCVezTYap/iwJYkojlGZwnq+/eoN6cYdev+J//PclVbWWCeRK0VsvFa8YKA2cr5e0p5beB2yQi1tXJWebNW3f8+7mHjCS4FQQTYUzFe/2jqBbBgfbRSGJFj61EsnZ2aGXZKesaBbrtHbpGubBU9pschuYcwPHw4H1eo0uCmKS8FBIZVIrjYqK++PA2+s9nYOi3mAKzam1OB8xMbItLb9YB54tLZeLyLZWHPd3fPPNH3l3fcP+1IrWjc8broBG0jKTkkHimGwHUqCjGEEIyStnlfR0UaNGUtp08qCBSJJwSIxMrRTKFKOvyQaWGYI6+ZqJ9aVZNg2PLi949tFjBtvx5vqKF+9u+OrbV3z11Qt2Oxm2UC/3nJ+fsb08p1yU3F69Y3sbKIuazVI07nzw6Ai4gdAeUHpBbwOmLGnMarLC6DHBUVBjXYDgxWPpFIYr0FGPbScxX298GEyGCK3tsVGNWsggTJjc3q9RbJdb0ceLwmB1waMKLdpreA6Ha07dPbo0GF3ivUv+KLXi+DA+LTn488FTGE1lhEHQ0xIIWO8gKHw3oCyUTQkx0h+PhOCpF2vqVY2ujQxoLAupiubEUWumYC63NKeYyxjq1RJTlNIyL4j7eD/zGpVaWLA6Kpb1kn17TOsuQJ1KAFVUEhhm5lQG9/LxoXaWWFNiPmVbHsPqyZ+IkRpsdOyGjvf7He9ubnl8fiZgs1MMtudwf09VN9SLBc1SM+hWAJmyEhAHSQQym12bBL7k5D1OgXI+kw/bs4WSoyDJcmizGLtHRt2r3B6kJpbrVMoYF2OyX6XGKFziUzmfzIAfw/gobLkYAs5bhmGg6zvatuWw33M87um6nl13xTfHv+fUtez8Na0/yNRdFRJlOvtBzZjk5fOYVnwGyMo6ZMbRD3OvOEbr8wT0B6zSbFPE8f9z7EGcANkR25np9gkLNQ2fEJMm6sDgeu7ub7G9FNiO7Z43b17y9NFHLJcbOd/8/g+GNtqhQ1mHLfUMoFSzP6R1z9c0pmnpskNiMkqwaopSGDDZ7mNMLO9ZIhmTtqWesYrT8AattTy7WoFLAxpVpCqasf1SPmtiY6VGOo7dvcgl4PFeUZXpPOP0DMaZkUWfhi+olABHJk3YmK97Kt4JKDe78THi+5Z276jKgros0aZAhr0Kq8mkZTRG/l2UBQHohx5jJNaLMWCPd/gMUxUl3hgKBTolm73t0EqS9YVuRlaUPMYKlZ1zUkINKtJ3p4yKik52DDg70J2O3N9ei+9crijqNdHI7IOgJE6Jo+Yco29AxUSgzGBCvp8PdV8CqSslaqjOqZ//FWb7nLC4wNIQnKM2ENsD795/zfs//L8sLjZQVLRdh0faI3PBVbquFDoEquA5d4FfxcDPveepc9SDRafCTEQ07fGgQyS6gNcndLDYQTTYMyt7HBaUAIOyqcd9fbL7mKSolMRoc+tXuUUxvzaDUvnPByyzERmdBvXF9PzopH+stcb5KSlXSpjT2R5BwJUMjoakAyl5gLDPp2FAQhKBDIpMrPtJ43Hai7Iu40Pk6acRLylqQteeaIeOxWbLdn/BgkhRVLihp3vzGpaZ6OgAACAASURBVP/mDeXNDUW5FuN42N5AbFvUUKDrkogmBkNkRWcv+Pa14ub0nM4b0QE8Htnd7Hh01rAsFZrApo7UyqKUx+iI1hbT/ZFqKCmUpjKW8+YJBY7gLVoZBh8oyyrJlCsWdYE93nNz/U+8fft3wrz++DMKVWJPHcdTiy4nvxbx9P2R3e6W43GP0p7e9nhKkUoKgVAseT301MHTRMOT9RZldqhlRVEqzOnESh/o3R2+r7HNGZ98vGEYFPvjwPX9gePecvIdniB/ghO26NwPqTCCJ1kiQqGn5xaEhDTuTynhVzNWdrr/870pP/o5PJizaifrSN+biBHynp8AP6cNhuyJGb9Lg46jJvrYkDP6Gqa8dn7parZ/P/jehzY7PYNTHpBjk0mqaXzJD67zB8XUD44fFN3HmCnHkPHBHz0vds2eSZ2K/XngHz/y3jGnUXKfTWFGEBymZzwXeHRuPQ8y9Fkk6sIIyMY4Gz6b9n3BS6ZOFkWOTfSoeauYyATzYdDZx/ogw6HygPFpjWMa6Jqn0wf8MDwoPH9wRz6Im9VsfeOIeSgyCJ26BNI55M/L6V5USiSSSO7IJS3duWzY7NBaj13MkYgxaoyTp/Q4r7/Iy2R5Pus97TDIPmYKtKkoA0QKmsWGRbOkqpdU9RmmWpNlh5RK+wFTXF3UC0y5QJuSrAmeZR4ym7bvbSoEJnkz7wipAOuHDpUIRk4bQtNQXDxipRRDWdCrSBwO2N6hvUgQhOiTPGEilwE7F6i95DjL6IBGcCIFwRhMNVBqRV1X1HVFEQylVujowPcY7yitJ+wPDEGhvaao1pQrRVkHYlkRQ8RUjXS3hAZT1xAdwVkBra0XIB2Nx+DQtN6mok4UiR+kqhvNlOdm+87hi3S5a5EyC2FkrufO0rIoGZydcoPx2ZL8plAGo+2YJ4a0vyWaiJh+f+D26jv2u5KiLCiKKmEavRSB/UDEU5hSusz1Bxvk7PizAGO1Ed2LqEsUBlMognNpMEhMDx/S0kOqDKa2MIJDq8CQBI+11pRFCT6ODxJ52mAKirKTmQ6hfhsTsX1Pf9pz3N/guwVdN4iA/dByOu3Y3+84HO45nE7c7A589d1LXl/dcH88yUaNMGK1yQwT+TcggGn6xogM+Lo9nbDfveD+uOPm/pbe9vzF55+zPTujrmVohU4JStbtmYLAtPXMRIZRClNo1lVFWRj6ZUO7r3AhMAwOA6xWK9arRRI9HnBuQJuSGAODHWTyX2kSO1gShuPhyH5/oD2dCE7Ygpv1kkeXZzLgpW2pSkNlNDoG3GDpuo66KUbGyALojidccJii4OLinEW9wGiV6OROHI+Wto2AwfUCvA5umhHe9pa+d/S9xUVxDLIO6QUq8uTphs8/f8LPP3vEfndN2554/PiSsljw5sU9rnPoWKQNO41Hi+NWnuNtAf7JLY2TxWTgYAx2ULgYuLk5YDlCtePb3/+BZ198TrnR6FhiXUihVKRQkaYy7HY2iXCLkmJTFjSlwdms5yjtFFGXRFXgVcXBKtTR4qMGXXNWFegYxiBAa9lQY4wyjT5Om9aUXEzBk1Ik7T5hkRwP9zKUbb1JCWiyY60IEazz3O5aTn1AmRJdyER12w9UOrIqPU+Xjp+fe85KR6UdtrO8fPWSN++v2B9brE8t26l6GkNIEgTqB0HVD/OFvOYzzbWUkEhFNiTQR0S3BehgZODmC1IzTd0wC4RM1tVKAYtWAuiulkvOtlseP7qkKBTv3t/z6t0N37++5g9/fMP3r66x1lGVhtvdnrKpWK0WbKoz+rbndndgvSooS7HvwQrD11lP3/aYdY0PR/AV+AmMrXXJ0tQQDRfLLZ3t6d3AkAaezNdnbL9XD0POrBPlvRSpss0qpairWphGDgpdsGwWY+AcEM1I04g8TAiOtt1hfUdVLkAJoK6UDM7K654TUqWnNkUiFMpQFwWlMQzRY50lWo87nSgSO9U7h7cDSkPRlALEGgm+lPSLzDa1JMCfnt0QQ6rWy/0tE4Msty7PA+sRelJpAFDGasaFy8BcznRIm30uEnwIZH6wr6iJETvBXNNTmDs0iInVaDT37o7Xw0sur885W68ECNNGEvcQGbouJUap8GcMBQjTbmRfkYJuI3tPDvRnBYcxuA7Ju30A1o1MDa3HYGXavXLQM62lyu+N01pN6yt/5+A8BDcWUnNR1TlLq25orewxx9ORY3vidBIw9ng8cjwdGAbHwd7yfffb1DqUmCYa1KjLNr8hs3/P9l/5t9jkyMQJ6dLytWQbmFb1wfHAN0V5ZRy/I/sOYbmJ3mFmtMhbHgRmWqOCSi06gagjhMRW6I4cj0fW5+fEGNgf7ri9uZbpuUUJJHkAZudDxDub2vpkb88sbZTIP8n9+rHrYpbdiMarTJutQM2Ge4Q0GTp/1pg4B0JQI6scpdCqoNCFtFMmoDESccFRMQFW5MGTCkBYVS5YnJf2ZbkyJVJSzOx9fvLB44YWa1uKssEUzfwFE1CRo/Z0nQ9tJ6KDxfURnfxWiDJ5WGJSiSS1YmT+yEdJISEEj1ci8+B9xEVwSkOsQTVEy9jqq5IklVJK9LcphJERAj4IIN/71DYZZYmOpxMKRaENVVERSINkrKPrLZiSol7J8C6TB9Gq0UaiUolRlwtZilGvPgMFEgGNwI8UlgJRFehqgdl+in78G3xzTjAFOvTE4NAGfH/k+Oprut071k9WmELhrBQgQ9JE1VpT6gJtCqoY2cbAx8Hz8+B54ixrO2C8H2UUSEC/QqNS3BCY9ptskxlTVnG6JmUeJkEhefGY9bM/9Bt5BcbAMm8OjD4jM1WnIo9Ke9FsknR6w7zolfddpVTqPJ6Ky3l2wQ8Le1OBWWx3kpOKWom2bI6Bxmc47bsq38sw2r3Yqhqv54MwAm3UCMqoEPF2oDseRR6nDviu4/TyFfr2lqrtKcpVfroe+BR32FFuF5i6wilDVDW6vKRsalS1wKm1AJFR4e3A9dWBp0+2NFVBgaJvT+A6CuUoC4UuQPXXmCi69Ou6oTYyx8NaRV0tRr+jjKZZFCwvBl79/vdcvfsHTrtveHTxlPXmXEgfXlPVjQzBnRVlXPS44HHB4aLH+g6nFEo70DWYmp1VlECtCkpKNDWhB+Mc+yHgVKT3J2w8EPd7mtUj7GDZnU7cng4cB8tA0t3XjIOc4wyMHXs5sr3E+e8exjLjz1VWhJ1i/PHu/shm9mAbiz/8HeTu04kk9aFdfliYzHI588LkmGso2QvxYXrffJtG/fAcmYpu+ZwkPgsPXsUsT8v5AD98xQ8v8k+CzNnPPLz2B+v6I4uXn3XZQ2fP/ez68hp8uIYZnNVpEJeswtSCHWIkOtESHRn7H1zdnGn64P7MfjcCpSrnPOMJjK8PSUd13Bs+YEePK5GuI8zvX5xZY86x0/lOGFoecpU/X/YbnfKvbP9Zk1crjQmTn80EHOVU8ocaleKWrMn7Yayec4IxbkG2Czn5vCdO2rM5lpH3TOzkqAUA1sZIDKoLjKkpqyV1s2axuqBszhHnlfCoFCDn5yImkFYKhGlmSvRjbJLZnXkgtS40MUjnkk8DFul7sB3edtjuSOgtwUcCGpVYxdLtG9N26sf4nCCxQWsd98UwAolFCHgFHi3+rygwCCmmKAvMoCk0aBXQJrJoSjYbGfCuC7nePJcla/EqbWQAbTofYwx4B/SYOGCC/FMhuISzPd3QjbqrsywkG5UUPU1ev5BkJ1SaT8CEBWgjz6FGuphsYluPNqElrlSyp9ZVia0qfPD44EZyUXoCCWHA2UBwCqvFLqz1UmRVIolqSim+S5fNj8UZcvxZgLFSCagIYWq/sF6CVCFiPEyMgoIYHG7ocbYj2o5d0kBcLpc8++gZhFSBMFNSaZLCcoyAMSkQDcTgCL5FhUB7uuFwf8vh7pqWgtv7vVRFg6UfWm5ud7x5/55Xb9/yzfevuD+0MpBAK1l0IxXlfMoyyCvrS0XI01RTktsHC8HTvn/P6+t3/PMf/oX/6d/8G/7VX/8Vz549pWkaeYCTDq1GUZWlBMZhBgZEGNvNorTgVssV5WJBs1oTghIdQWfFCLWhrivKskFrGKyn7wfu7+9xdqAsP2K1WqJVJPiB0+nAk0ePCednotF3OnC2uaQoNV134njY8fTxGZfrDfv98f9n711jbNuy+67ffKzH3rv2rqpTVed97u3u27fb3W7bndiOHwkkbaQg7OQDIg4iGAkZTD4QBHyIgnhFQEDEHwgPCSIiHIEQQQgIQoE4xnZIHD/k2E7bbnff7tu373mfU3XqsWu/1ms++DDnXGvvc+91SAhWI7Gko1O1966115przjHH+I//+A821YrHjzc8EPdDll0Icp1zcHCI0IENfaI0pjForambmuVqiTEjnPVI6/DC0hgfWHlbk3i9bjDG0bQd16s1WRY6uCulyHJNoQU3b465eavg1u3AZHz+omY607jOc3l2ibBRV9O7oMvkdoGDJFsgpEBHh920pjf8aVHiHMKHn401fRsFVzl+4Wd+jT84KjhUIDKNcSMgbC4ZFulajGlCN0wfSuHHRU5dNayrBuPZAhOiBy0kViiuG0dlaqx3jE/G5JEZ4ZFkeUme59iuxbTtYGySr+ICwB7Y4mFNdF1DpiXeGpp6w1JK8tEYlYWQ18f5VzWGy0XNy4sFo71DhJQYa1hcr1Gm4WCv4/bE8uaB5cGhha5lvV5y+uoVX3rnq7QOrA/hrDUWG8tEIYhr95pFYhBn7zfp6Jh0PgWQvteDVtHxMdZgo/SAlqHkRspQbhA0QU2UKgnrL5X1QmDrqDQm3u3MhyLPOTk+5ujGIfvTCa9ePePRs1Nevrrm4nzBV7/2lLZzIDytsfj5AplrdJ5xMJvx8U+8xVd+6zeROjCNy1FO09VYB01jWa1ainuaXCxouw3NJuvn+8FknzuzO8w3Sx7cus3V6oqr9TWX9SIEEWnpC6K2XQC4BkwxJKiUUrRt19sJQQCLbhwecmkNLS2lLhgVRdQo8njhMK5lNNpDaIE1Hc16PTRhiIFyH3cikFr15adKSoqipGobBKCFoFCacVHQNhtM22A3Le1yyd40yLTY1gEubPZ5hleSzls642i6hiLLyfMcEddcCjVJ5Z9+68HZMHdTPNIzqRPAEKspQozqWFfryPQdnNdtJqxQMZhOwf+Osx7shXduK7AL3mZyohJoJ4VEZxmj0Yg8y7i+mqO1prKXvDQtt5d3aO1tJkURm4sotJas5nNM1+A3FjQ4F5qxBE31vH/e/T7X7wk+YWCDPfH0MiV+6/2BeSFARDaOSEGSiEFGSgD64ebTIvXJVvnehmI9xjo619I0K7y36ExHWxsAxxfZr3K6esSLly94eXrKcrWm7UzQ+JIqMMmVRuSScbYPyvfO8eDIbwWhrwGxw5GuGbwNHWkTSKEzPQAs/TkTL2V76EKp06ZpYhCSgBaG0rme/RfGLDW3S4w96eTOpQqZgK8gK0Lc47uu5eLiguNbt5FKsalrnj5/ysnN2+R5EQBZObCV0+FsF+E3F/e5LrAaRWLGyP6a2fkpBR8uVvjkUZoiaLbbPoHmo/0ZgtkUHLuUrBQqJrM0mS8p1B6t2yBkYP7V3YZMZeS6RKDjuYhamgEE2dTXOBqEiKClz9CqRKK2Ym8fwAI83lma1TXr6prx9JDRJFIoPnCfcex9SMbt6j9DERnKzgZ/tO0MIy0i89/jVWoiFRmw1qJkbETjPJ0NzV2QGq8z0BqywH5ubRX3OM1oPO6dfessBofB0VpD3TRcb1ZsmhobCQZIwWqzRus8VCHlY5DQObAyw+Uz9LjBj2b4rMTLPACPcVwTWCOEpCckp7uOoHpaRWHm91Q2vBfIckI2u03x5vewLj5Gh0f4Bo1By7B+TLNhff6EPJeUk5y8VBgf2MoCj7ce4wKQOC4n7AnJLRxvO8ObxjBravK2RaQqsKhbjyP4g4ho7z0eRaZzvOlwLvRXkEKCk2GfEmBbN4CbPup1Kx3+xQAtTobeFrroIyXbF7HT3u5vV80EJ8lv/X2QDEg61UDcVzxDDiE1WoyMn215j2izk8+WGhNbH7UQo123NkmTxMaZKsQGQg3X3Uu9bLHPQ7C59V1bAJgg+l5SMx5PKMsC6y3tck0rM0RnMOsVq/e+wf5iyR4hiSoJjGW5tSfWF6/IpvsUs32MUCCn5ON9DjJ4+7NrztavsMbhOo33U148XzE7XGK8YJRrnj47pakWFLKjKBVqVCKqORJFJjP2podY57HVBqUNRZ5TFjnr9QopFeO9kvLOM97/2b9KffqS/aJgbzQOzLDYKV1LERrkpaSxkEgtKSdjVFmy7joat8HaGtkWOL+HUGO6rMRJhRGKx+sGb8AvKnAOKRRaFXS+ZlNvWMzP+frzZ2F5yYjJKA1KkJh3nrRnvg74pXm5Xe6//e42iDd8HiLzb2eNE2KdAcnY9QnSpPBp7adfPYmoGtIY8dXgeMVzDQ0od9mq9D+n92XSYiMBnsnf8MPtp4tOvlt/NcNuLCPpJF1ln5iBWJH0moTDzrzfuXl+O1D273r04xV7AgiLFjomWHwqLsJ5G8lMgeUe0x2ROZvkvcIJnXWR4c+gdZpsSYyTbKxgTXFlnzhNmuJqeCapRL6XMfBbc4sU1wZ8IsVVIHDGR8JF0IMdgKtoR4QIpB8xMFiB/vsyHeRf+rjZh8ShjRJwWmvKsiTPcnrGrxBBUztqfqY9OpTta5TUMekygPG1bDDGYKJvLpWCLJCJnDeIhMNsXz+JpBN7w6C2Eg6uXz/pcB40wc7mWcmoDE1sx6nJeRFK8Z0HY0NjLmslysW0igz64FIExmaqBOuci42rQ7l+2wVANJBkDMaFPU2qwJbOiwLQmK4LSc62plsuoF7j6g1ms6Zb1pjVArG5Rm2WZKZDxIbqLvrGLvaxEFF7la4BBXWjWdd7lHIcmtuisMigv44LWlOhvCc0VFaerFDMDvc5eeMuNp/g5QidTclGE3RRoPIs+qoqVDKnKlWhcb7DC4ujwxEkC71tce2aZnlBvZxjTAckYH1L4zg2/Qu+sEP4YBP6pd378yT3EkEgRCmtQxWKc7H5cbKlYb6ORkXw03RwBquNifGlBxH84yLXaJEFf1Qo1l2N9WC9weAQKswh2Tcd+/DjmwKMBWhsaIIgZaCYG2dD0KpkHNQGRND9vF5UrK+vefXyFc+ePuedd77O+48eMpuM+PQnP87v/73fw6e/5dO0PmidBQhT4bFIqQKF3jiE73CmoanXXF+esri6pKo3bDYrlstrcJLVasPV9ZKz8wu+9u7XeXV1SdOasI9ohdSRMh0NqLUe4SUqou+vZ6SCQ5iAwKC3lmUKrYK48qJq+Zm/9ct88Uu/xZv37/C7P/95Pvfpz1HkaQEPHpMYNMFj8L+VPXRhsiAEWTnm7ptvcfP2HVbLBVcXF1xVS9qrc9q6wnvH/Qd3+NTbn6Jpauqq4nK+Ybw3Cx3PEUzGU4rMstmsGI1ybt26yagc8fDx0+D44Phd3/Y203GBMZ6L+ZJf/JXf5BvvP6QsiqDF2HZM96dMp9PwRJuak6Mjuq5Fa81sOuVgf5+LyzlFWaJUxovTcy5ezQctPO95+eqKTWPJizF39mY8uHOLRw8fk5ea44N9rhevoo6dxBgPwvLgjTfoGsHTp1d86dcekflp3MxcH2v0oWnczENJRHi0Jspl4Ohp70m31FpPZxKAkxohOHIcm1cvyZWn7AyzB3toAVoKCuWhW6F9TRG7CZaZpihynr26Yll3eJX1bkcyPDLLCA01BK2xPLtY4jrLg+MpB5MMQch2KalRuUJnOX33+OQ4edeXWAY2SYd3BmsV5WjEJz/1GTyeznhMZ0JjGCF4cbXh5VXF+apleuME0xk2m4ambimE5a2Tlgczw62Z53hfkQv46vtPePL0WZDxQIUyCmsjQzOweVM5QWe6qIM0aBCG4N/0gU5gB4R3PEEMXGUx0I6TXypFFksCrHMsV+sQ0EjVgwcmNh8hPudcZ2gVgFhnLTY6nUpI9sZjPvnWW5RlBljOL07xQvHyesMX333KV7/6GGNTxjc0NVuvG66vlgjnMW3D/bs3+cTbb/Pi+XPm1wuKyI4NzNiOemOp1kseHHs2dYtm3tuM3/v9/wizT+X83C//PD/3N38K4zegLZGoFuZGdAWrpkYSAIFQ1haOzpjIPvc9ru99aDTw5OkjrDHkOifPCwQiaO1YH2VaDPmoQJLRrFuaVzV5OULpoI8o85w8y2LQ5+jaljzLySJjerVeIwmdvi/XSxb1hsnemMJnSCuCne4UNx7c4frsjFW1wDrLdHaD8fQAPS3wI6i6GkEA2PMswzpHqQqapqHrOiJ8HgE1EZMsNgCO3iN80PtNdiTMH0nXtv1nTAIL+i076HoFeDhmduP7Ukp0NmyhKXPvZbIAwZ5IICOWaBsTNB6tpXHX/MgP/zD/xo/+6OvbIYlRMbiOW0HKzgdFslr/j46Pik/+QR8fHep44PND4mhr/X+zHr/+lXf4wX/+jwOReR6bP+B8v/5kAivFbkIRQWDk9Rt2Yr4IotApiiwAqc7z4vQJn/zUp9ifHTKZ7HP66oxHjx9y794bHB3djNewq0MrlQodxaPj3TYd1liyLLGwwuc+LP70PuicKiEAhY8MydAUI1bnpJ4hzvQ6dvjI5JaK7ZplITRalYyEp11taG2NyjVFKbnenKFEFjRgYwmfdRbnutA91zeByaBytCwosn0k+RbAmnyDwb6NRlNGkxGoPF5/VIWQA0NmOzGTtO22LpiUfIGQVKT25EVOWRRkMjTu0lkBMjHzTAi0XJB00Fl45pu6RmiJyjPQOUiBs+FZ52WJzDRV09Dalq7tuLy45Ho+p6prWtPRmJbOdvGyJCIr0FkOzmONw+fQOY3bv4O6dcRETvGrC+ZnD2nqJbg2TKkEaPgAFjlsn2QdFtoW86PPRwTQW1gLskDMHsCtb2GV36VxGulNYOcTcgKdaWk3C5r5cw7vHlMc3qSYTKO8QbDSxlg6E5qb5VJyw1gedB2fahsOlmt018IWe76LlVEiPqPOGrI8ZzQKgFiel9SbNc62YJMnHKsdXgd3CPckixJZlMFjUkHuia05kedFv0Z29Jm3BmiQ1EhAbIhRfES8tMxIbHLngtSAd5bOdhjTxTLcgeFtbBuDtmTXJR6HiSCz6RqyvCTLiuD76KwHeZ0NazbP8z4AHTA6R2x5Sgr7wm3Eklzvd4ZHWhfjFxkSKt5x/uwZXbVhUhasnjyG8/MwL8Zjir0ZhshW22L01hevKPYt+dExjCa9bmleKN568wbT2R5feecVjx7NOT1t8Iy5rEbkdYHOJZv1ghxLqTPK0R7l0QOO3vgcWTGmnOxxcus2XdeFtScl41EZtFtLzfi4ZfSxh/zFH/8PmTY1R9MZN2YH5BJW85e064Z6ucGZNbK1EOWrEJLWBI3Kxnvm61UExYOsm3MLunZDN56hszFK5QhUiAmFCPbAVDSbS7xrwHUk2ZEEf6YSZaVU32jOi1RtsKVt7PupEZ5L1Kv/oMlOAG1azIM00vZOOsyJ3eSs3xURDtfqGcBUsf25dK6tb/fEhEZi3wV70/cd8T6AFXGuOe9i9d6gcbpTt/KaEzLMzQF4DTnf170VOci8fJTz8CGg60d/9MO9oZ3XPZi2w9kijmk4v5dEux9VsmWSZbPoLAtJfjWw4ROQGmIcF/42SidZG6pQXEymSSkpy7L/OVS+SaSkt18J+Ow1Y4UIFQVuYNWHarkknRL2a9vrZoZqJhLIG5PLWWyUpLcaJnWRtZmqEwbJPOIzdn3z3gSgmy299jSaztrgT3gCWzw2wvSJpIPHGouJrM40DpO9MSdHJVVVUVUVm01FVW2o5BpkhW9dIHnEngDSyV7LODGW+3S+jTIPxKqfaCWlkpQ6Y288YTyeUOSBFDKb7ZPHn4uyAOdYrC5ZLK7AK7R+hM7GCJ2jspKy3EMXY4SK8plSgNBx7fveVgthkdKCsghnMaZB+kBcRBQURcZoPAqYlhC4tsZUS8xqSTu/pCmu2AhL0wUZr+D/BODZRn8gk2Ko2BIhQd42a7QUrIox6CL0CJAKKyVroPYGLx1Z6D2KUp5cOkopKco9Ns6gnENrgSoUWQ5F5tE6EHWMJ/qRHiXiDiQC0O2sp24Mi8WcbvmKavmS64tvUDcLlHQh4QCBzCgkFhM0XXFRH9b2jbwGsHbADoq8CJXzsdG5dTZiEmF99Wsh7svWhqZwKgvYSNt0tG2A7bO84N79j/PxNz/DqJwhyOiM4fz8lNXymvVywfLqkrpehKSwth9taPgmAWO9EKBUX14tnSWXDikcWlhsW1M3K5aLa85fXfDO1x7z5OEzusahdcn+jTf5wW//fRzuj5iNg3ZD11m8HJixMpU5RZ2NdlOxWl6xWV2xWS9ZLha0dUtlahabFa+uLnj25DlnZxcslmvWm5rNpsZYD0IHZp0M4vu92okKpV/bMgK79PiBSRWyRxJrLXXTDoLYAhyCy2VF8/4zzi+XPHl8yuc++za3bp0wm86Cg+aJ+qNDQNdvaGnjjGLVJmUTdEYxnXGjKJi0NaJpaTZrqtWCs7MzJHBwcMBoNMJaw8uzS4o8dAnUWUauNd52IZuVaR49fp/1qiLPcmbTAw4OjxgVGQjBeLqPLqZ88Te+zGq5QgjByckxk8mIIi9ZrzdcnF9ycblgfzZjMp5grYwBmGG5XFA3LS9OzzFR9yWMIFwtV1RVQ64URaapNhUIxapqaV6cAw03jk4oxxPqpuPs5TnHJ0dcX7RcvFgx4QCXl6zbDRGq6SnkYROLZTSxm7OLpYa9yyIEmdZBo9AKEKHxWygrTVo2Ao3ny7/1lHurhnveQK4oRycolZMLgbMgvGeShY0t04Kua2mtCwZLSHJhuXN8SFXVXC3XIQvkOkD04NOrdYvONhhX4l67CwAAIABJREFUcDzRZFL0Gxc+MftSSR09wywFEYKhVMgjsC5sCFKq0NRCal5eLHlyXlGjKSdT2qalXq3BGmbK8mDP8NYNx8ke7JUe3Ibf+Oq7PHnynPliRedC6Ze3HlzUjZOCPMv7uZv0XHYcKZE26LDKMqV6JzLpHA3dOl3vYyVhb+dszyoRUgweZHRyQ0MujUoGmAAm4APLdDqZcOfWTaT0zK8uWa4rzq9rvvqNJ/z6Ow85Pb+mS4ylfiGCMbBc1dH5DZnxO7fvcXLzNkLlbF68RIpQeOtF0PNbXK8o7+aUOZTF4Bw/f/GS08sJf+ALP4jMFL/55V/h7PxZ0JJVCu8CWC2SjSFqZVkbumcnh6d3kGKzgei0ZzoEjaO8ZDLaQxAapFgTgllJkG5w1tBUFZvVhqOToyBNYS2dNdhYDpTK0jrfhQ3Rh/L4PMuwPlyn8Y7Vao0XAtuFkuaiHFHXNZvlkmazAe/JJiU+ByvDvEl21XpP07YEJ9XjXUg+5FnYgG1krgmpODzYp2rqvmFbmmthkw5lwAPywM5zTPyw5CxkQlGogsmo5Gp5HZhdW059V7fUdrVVKhorPZyj22ywbRsywS41URD4pgvMgb/r8f8mRPrNcPx/7/7yIqecjcmKkqwIAJmSksuXp9BFFhwfdWdix8YFyHb3k763yx7jO54+e0o5mvLgwceZL6958fIZzodGXZO9KePRaEd7Teuilz7wyNDcybR4m0N0SAdyzFYZdfRDsiyjawPjS8jEuNF4n5Jl0a6oQf7Jug7bhf1FqQCuDnes0GJEJibhOg3YLthtKSwGE/fepA8H2gt8J1Eyp9ATMjlCy1Fkcny4Z+sBKwRalwRmd5S1SokoRD+2oWxOol8Pur0H6ynyIKuSK8Uo09i2peoMRilyrTDekWuF1AVCKZwxqEIxO5gxOzjAWMeLF2dUTUtXr7BNHRu3hPHxLWzWS67XC5brFcv1inpT4a3p2bIQGLdhTDQGgdJZSCwq2JiKJVOcmGHG92lnb7JUr7DdCHf9FL96jvctoRYkSQE5dvHF3UqQvgFfYlD5ELgwOkJMjvHjYwwa4VokBomJYGRMho5GjI5vcuPBbfLxJMxBY8PYexBSoTOJEhkHbcNta7hrWqbtBm3qCEKEZGr4aejg7bxHZhqZhTLItm1o6wbbtoF15kBmKgJ/caOP50mH8h7fVNimwskMlWu2m+ukORDIpHE/iN2sk46i1tmOPxH0jIMESyqLlFLHYXQ4t6XVG9d7CvpeT4ik6gopNfgocyI8WZ6RqayPFcI61zgXGucKokRarxvro9gdeBeT4N4hRf6haycdzjgcLZYO6w3eGbrNNY03KCHoHj5h32pm5YQbh7e5/4nPhnWxvMaZYc37usEuFpirOSIfhYrEGIyDYX8k+MzbR5wcTXj/4Zx3372gqR2XlzVmVWGX54xzweHhIQe377B37zNIVeJjU8BN7SnyHOWHsviizJjklqvLb/DFd36S1fkjTo7vcevOfT7x8c8wOzwmK0ZsFguuzs948eTLrKsr6nbF2LVIJciLArf2tG1H3dQkBmCgRTmEb+maOdZskCpDigwhdCRqdFjXBCA2JYi2YM+0zhDRNw/oAl6InYa0QE8+GFh8r5WHb02c9KMQ6f1dm/a6RBMJqPVp5Ia/D15fCC97PdqUgJDhmrZL1YfEVoCah9ginFBGub3kX8n4rt9hwqYLeG0ybvvWr9/P7k1/6L32Nix+LlQGxNe3ktmvg7uvl7V/4Lxbn3E+pjpEn0uN8UYkS8igKy61CpIp8XotkfGJx1vbg0GhQg+EULHUOpXpJ91REW2J7OeMtTbgHnEvt9aG0vYozZbO0cubxH9a6yFGivHBIHc2jOs2scwa0wOkPctz+/F5P7B3bQB0TUqobc3l7cpeAb3mrTcBBJNJ5swP3x+Rlf7LWmPY1HVoiiVDnx4pFZPJHlJG2UghaKlpNtWQXEi2fesxp6QJUepASRGZ5CFxkmcZZVbE5riOrutYrlfkXUbTNlTVBoGiyEu0DAlm5wzOtkhd4kyLtAYlJVqNAns5U3hUiAusC/rZ8X6tj0xrKVAiQ+sMnYU+Pk3TIaVDEPcQPE4V2MJgxmPMZgGjHDWd4n1L1a1o2zXeW4ggqBeQeY+Opf3IEIta02KWl3TeorMcl2UYrfFKc9V2VF2Fdx3jXJITkgvFbMrJ/QeU5RQvA4ELF+7HdB1CxIbi8V4T9pApie9c3CNt3Kc6jO3oTEvXtYhY3ZiY00qHKiqlddinsVFqcJCzSPFn6vOxnXwPfqsY+jiImBzu42OHEEPliXMW62zfdLnIRxwe3uDNT3yGk9ufYDw5pBxP2ZtOsV1LU21YLxecv3jBoydfY726wnQVu7Iqu8c3BRgbNqdAA3bWYrsG29U422K6hvnlFS9PXzC/vGI+X3E5b9B6xuH+jIPDY24/+BgP3niD6VgjfY2t53gROj8Hy2jp6oqmrnGuw7QNy/k1i+tz2npFVVdcLyuurxZcLufM10vOF3POTl8xv17SNC3GuOAURaq4UBIvYnc273D99pZuKDr9MfBPm1L4b1eD1DuHl0G/KjTjkrTOYzcNm/oCa9+lcw0P5ne5f/cet09ukelsa0N+7QFvZxF93GajByB1RqEUKs8RRRdZZJ7F8pr5fIn3AuMc49GI9bqmWteh8U6WUWhFWRQx6LJUdU1R5MxmMw4Pb1CMpwQmskdlkqMbNziY7dO1HSZOdCkV6/WapmkZjSe0yxVX8xWLZUWZ5+ztFSgtYjbPsjceYU34/nRopdibjNCBFkjdNmSFxmwaFqsN43HQz2uaFm8N1/Oa46Oc9eWG1bnlID+BMkdTsN5sqJpN8DSSfU/AXdSOGTR6Bpelz554l+Skw4bqXWxwE4T3l8uKzXqNrZasX71AH2XI8RSpR1iX4RxI59DaM9KSqmkw3gdNNyEotaAQjlYkOQSPTwqzsXlJYz1X6xbhHbkouDEdbQF0W05WBJX6RMEwY4GBRp+o+lJpjJdsNobz64rGRC1Da2hrgzA109xxNPa8cWA4mTpKbWjbDVdXFzx59oKrxZqmM6FZVyqT81vsqtcM5I5deM0JSIFLDwLETdq6ISPbA2nOBf1GIcjyLIJvMQjYAialkr1BTviIEFAWBdO9CbPplNGo4PxqyfViycV8xeOXV/zGOw95cXpJXXdbe/m2O+LpOktVtaRujbNZRTEqOTg8YLles960JCzQOs9y3WFdwaRU7E8G07y4POXsGdy4ecK3fe47QDq+/o0JT559A5yJwMTwJEX0nv1WIJneTcwKke41vqUiMD4ux3gXHCdnA70hACsZ1rS0dU1TN4zcXmQ0pHKpmDBJQYazr80t0YPE3nlaZ1CxczHGMypGtE1N24au11mek40KnCYwuJyPJX1hvtjoRCWmlZIySBcIwaaqMdb0Gqk+drhNf9s7gT4lAYIj46Nzvl2kO+C0sXu6CECKlArp7c6ctV1HZ5p+HsgYLFhj6KoqgBE+gR2x9NR99Ob8/x/f3IdQivJwH50XqMhUk1KiFtfYVdXrZAkpPvC3CczcOd8HXtn6vPBcXL7i9vI+WuUcHNzg+nLOfH6BkJIj55ByS1ID0FmOJnTlFSKsPWs6nO2CzxJ12QY/xfdAkoyyN+l8fYC5cyti+F+kEkUVtP5fBzfj54TQlPkEJSVO2L6MPATDLpQTuuFcQmgyrcjkiFyNUbJA+oHZF87qe1sWulrbaN8jELs9jsnv2rq87ZLa7TsTAg739xgXGbkK7MBu4/DGY2xoUmaco9QFOlNk3rFeLFGZJi9zinHBer6i8Y7WWYyLfqKXWG+RtoOuYVnXXF5fsdqs2VRVYOkSSgidS2zfuEf6ECQ4Z+mirJdznloLUBlGFVSU1NkRcmYQ6MA4qc4QvuuTQIKkF02/CfSPrPcrQ/miB5zM8EWJPngDsXcHl+3jvURg+sBO+NjAUSiy0R7jm/fQo3Gw+7HcFAYGpgQy5zlyjpvOceQsuenAW/rQxA9BWP/80rO2DkMo4/Qmlu9HPTrEsJoCaCN2nrmEwBq3Fk8COML3penRAzaAiOCCdaYH8JWSO+thd78lSnvE2u7ttRKfQQJThjL1YfZtf3e6YrnNrt/avMN6HWSHUtJ5sDGvW5Vd/cTA4t3+3ePqFis3NK6msw1aeApvEesltmrJ5gtGaCblHqPxDJWV5BnQNshWQxPOVfhTRDWmvT6muHkL66Bua9rIRM/yEbM9hVYlws9CRZGxrK6u6ewVsluRlYJiNGE0PWYyvYHxMiZhQ5BtTWC2h+dnmdw2vHr8Lo+e/ipf+cqvILHs7x9y48YtDg7vMD04Js9zlMjo2ppiVIDvsKbCdBukd3gMVb1hXa1oujbM78hSTFU13nV4LM61CBQq9t1w3gS/DNf7mmnm9k0ExRZqxwCgSvlBwC89k9fZmP0k7QGq1977iKOPCLb/SAza0OmP00pLvuIwH8Xuz+nz22huIgbFM/WXswV+9USlHo/7qN2PPo4dyE0ftFfh9FuraAuwfn04ekB2+7WP/vYPv6Tt9dkDvkH+pU/q+8R23gKBUszTj1D4u1T9mdijWmsynfWsVCD2cREDcOkTwzURULbK+uP66Alg0AO56XtSde5uBe/uSPT7z9ZIJR1WKUNFqNvGILzfusfw99v6+L2f/RrYHaayCIk7OcQwg5Rc+nrRj3MCzto2rFGlglwKPi6veJ9Ka6SRu6p//einOTgA1MP3kNyb/udAzjIEgRyPSWBhBBMloReN1x4dC4SsFb0vYqWK9sHH2FD27zmChIBww36Smi0rlaHzgiwvUFmGkvmgnS9Cc2Vrg1yEsR1+MsFVNda0dKamKks2VRZ1ZKOcFEHtS3pASHSusUAHNF1DtVngswynNVYrpMxojKXqGpw3aCXJhKAYjxnv7zM7PiIrMhAaIXVIuEoQW7J2UvmY7I0xlg9jkHA1JSHXGU5noYJnS14oPT8h5VAtLYb4bpd0lCSEBCru/6l3yrYfMrDL5dYcYOs8nsSoVlohTax6kwpQfQNQXZSMZ/uUZRGSl03D8a07TI4OeHX6lMX8HKn+Nh91fFOAseGwmK6jqyu6ekNTrdlsViyur3n43lO+9u7XqdYNSuXcfeNtvvs7fw/37t/n8MYRo2noOq1Fi+uWmEogZYfSMrBg24bl/ILF9QJrGtqm4vzsnMXiEiEsrTGcXVW8//4Tnp2+4Gq5YNXUsSw1PHipY/MJ6IWbQ1OOUMoqfa++twVKCHws9RUyMV8HZyoZOSWHEgUIZa6OxDSBhy9OuVhccPfpU97++Ft833d+F4eHh5E+nox7Gsdh4++tZ9SdAaJDFzNpCLS3FG6P6f4x1WrJxXxJ3XW88cZ9TGeo1mu8M4zKBE7t47xntalQSnF4Y58bN47ZP7iBF4KmqUNpsHUY4yjLkqIocM6yXq8RQnB6ekaW5dy+dRudF3zjG49ZrzdI4M037jKdjlBKsTfOuHF4xHy+Yjwu+7ubTsahHMkY5vM5rekoSk3btrSrjr2spGlbliuPFh11LdBySnW1pD6X3ChvoScFk7ziurjmfH5G1WzodTalQCaNl4jQCUloCtcv4mTKh0Uv4vhK6RAuPhMf9E+6qqIzLylRKH8LrwQuz2Mzyg6nBXk24tXVCuuCEy8F7OUKU68wdRMybDLbKv8hbJJCsKjakH3ylsl4HOQUCU3BkuZr0MOJxj85QWmjEbEkRClsZ0LJptRUteXlVcXFsiMvC4xzNJsVbd1yo3Dcm0ruHcCDfce4dFTrFecX53z93fc5Pb/C+XAFPurDiDRy8fuS47A9Z5PzNCwjEZlEasehEUKEBgtbkgPJafSEJita52S5pmlbvEn6bNH4qqDD2TsaEWyQUjKd7nF0eMBkXNJ2DQ9fXHC9qDk7n/Pu+094/8lpKMX6UAfS98uubkxg8kjFy9NX3L17k9nBHnftTa6ulhjX0VlHZx3LjadqJLNxxnQyMFfa9Suunp/xW8bwhR/6QfYmEw73j7m+WnBdvwQvdproBBPjY+Cfxmpw8rxPysZEANoDQVd2MppgTchm28hkKssRmSxoTE1bVXRtw/VqhdZRksMzNE1DxOA86C0RQdjETBKI0BTMerAWW1lkB+NyzHw1x7RBG2k0GpONCjoVu0q74IykIzGWrLURIA1yAnme03ZdZCh56rqibRu8p5eg2MGQCLqNgdESn9vWB9I6U7E5o4lNxxKrSW51KgiyJSY63zYwQWzocm472zdE6RkiHwpYfXMe14slVRUYQjePj3YYXunYbCoWyxUAx0eH6P9bjN9/MIdznrPzC/Ce0ahkfzbt31utN6xW6/736XSPyXjU/z6/XlDXTf/74eE+RZ7jnOPs1UX/ulKKk+Mb/e9Sa0ZHR2GvFhIT15ScjDB1i29j04IUr+4AIFtlwdEUbwem2+BM2pPm8wuuri6o64pbN29TrZasNwu6WO6cZSLqasXr1TmZlOg8621DaMzQ4b3Bu1g2GqNt7xODIABxUoSSai8ToMT2FX3gXgJAlbFd7b8T18X5XpZTSiZY39K5GmM0zhtsBAvDuEhwOjLeczJZomRG0pUdSu53wTPvQhJXqgiE+QgcCIGI15lsvYwASN9YYvu+RCi/Oz6aMtsboaWgrRrWwtFtOpxxWB86KkutKUcjpBJsVptQ0gfUbcfZxQWrOmiDE9lHDk/bNRgb9q51VXM1vwwMPB8kJILvF/TswzWGZKz0DqGCxru1DqcynJR0saTVWMtqU9FRku8/QOR7CD3GnUtEcw4+CjUKGfsZJAAhCLHEISUoDcvAzFQ56Am+OCY7+SxufItOzfDGADJIuETR8iBrpcnKKfrWAyxzXNdFH2MLEPUe5Txl13LbGm55yyGeLJXjJp/AuwAIp+A8WuTEILIidvqwLgTcmUYqhW1avBsSE72Tk75eQJJsCsMht+ZTCvRF/xoEIDZIAsT9QIgdEx4YVDERL0LTlD7I7wGFAchKgWHfMGRA1/Du9fJyCUSdRJfGIYB3vQ9KDCB3ZnICZlPTNIF3akhGkpLYW4f3mNWa1ga2aGNqylyzpzPEcoWYLxlVNSM5Zm+8R56XrDdrRvsH+GKErgffZU89xDcT6ss7lM5gnGO+uGJZrRlN9jiYnSBRjAvJG/fGWH/Cb7xzzuXZOfXiGTd8g1RjVD4hG98IOqzG4GPTZVxHa6P0VtQ2zG6d8d6v/Sy/+bVf4uF7X+czb77J0ckd9vdvUeQz8mIvaE/qHJ1njCYlzgtMu6FaX6KzMdZaLuanXFyfszFNkB7qgfVUuu/x3oA3MakeKrsipyaaHRn0aaP/45LvmsD/RAqIxIAPHFvg0C6z1Q/4efLjtz6zLfPVf4AeJ+0BvfQaJD3kND23kI9tcDbgEvitc/afT+BHP0Kyvy6S7Y0JQIToJdl3YL4tkG63qjQNx/Yeun112+8NQN4HAdtdoMUnyYf0nX/PkOxwMYGFHmNtn/Z+34N93lqSHJFzFqWHZ58Iwj2rT2vyPA+J/8h8DTZkIA4YE5m0/f2F2MiYIfG1w7KObEHkwLR9nQnsY3Whdw4bcYUhRouxmdj1B3qmbRwH5xxaqa1qGrVVLbz1PLZeS3MqMcGdskMst/Pd9IkLFZtLJ8AyNFQypF46LjKDPUStVR0xoXj5YthjUlwfKiz7wDPEUAJsnL/GK1rT4rxCeR3WedR5tVIirQMRGLNpD5BE3VpnEFbgXIO1DdbkKKPwkW0Zdt1QRdk3TIsEJo9AZhmqKMlHY8pyjNbBJ0oSFdZbmramzYMUUmc66rqjtR2VWbOelCw2OW0XZG9SAtV7cELiZcZsuof1QZaxtZ6FNTRYrCGy5LdXiI9+p2Y0njKZzigmBVI5lBRoLdF5lAZUoUI07Y1Kx4atOKwLUoXahH95JpmUE2Rb02ajyFcJe5h3HheLe3pQPOI2SaN4mMtbOFjcF9OemyQMUlImrT2l0pwPL2qtsD5VwgSN2SzPEBLatmZ+eYHKZ9H2a4pxSTkZUYzGjGYTDm+ecHjnFqfPnnD24in6p/7XjzQh3xRgrPeOzfU5i/kVZy9fcHo652vvvsf5q0s265qD/RM+/dnv4pNvfZIHb7zJjVu3GOd5YA54R21qRNuRU6NFTZ61+GrNcllz/uoVL58+4dXpS8pyTJaFBdTWHXXb8Pz0lMcvXvLldx9St6Z3lpPeX/TDguMqCF3zBuEKhIiy5T4BXMEIBO3+WEbdZ4W2Nd0CoItSsVvgsL31kz2geyA1GwPvPTnl4eNTvvqV9/iu7/lOPvnWJ7h/924EhAU7s6gf22SYkvOWHD+Jjo1wxpMZ0/1j1tdz1ss5bV1xdnbJrZsHWNOyWlbMT+fo4gGXz56y2VRsNhsOJyPGWYEWiqZuefLiBffu3yYvCpqm5ezilPPzM6TwTMYjOmt5+OgZDpCNoaqfcLB/wCc+9gbeO+qm4emTp4wnH2M2mzIqC5z3jIqM8ajo78k2FXVfki4wTQdWooRnOs6YjktuPrjDyckeyhmsfcXDd+csXoKsppT5jCKfsF8WnBwaTk7mvPfkHRarS6xth405+cZycHe9i40kGIY6NMeISpIifE4LhRUghefR4zmn5yu+/3s/Tn3+DNfVYGrGo4JCCawQOC9onaNpDdaGL9TKMxmVLC/P2NQGYxVej3rgl6glhjc4oVkbeHxR4cWc+8dTpoVCug7wKAEIt7XhpGxTKKdLOmPg0XloCnR6teTVdcX5omXv4Cbr9YqmabBtw4HY8K139rh/KDmewigTzOdXfP3d93n2/JTLxRovg1afsw7XhqYvSqkYHwisifIDySFNgYVPbNdwvUqrOG+TsxnvPmYiE6gIDIF13LU9QffWWhvZmpBKf6QKD9h5j+0smdbkRc6Nw33u3rkZdHPWFV/6+jNenF/z1Xcf8+zFORfz694+/HaHlIEpVDeG9uI6dAa3LSdHhzy4f5dq3fDeo5cs1hUeR93B45c1k9GIyWSvP8/to46P35xzevnr/PRfXvD57/0C3/u7v497dx/w53/iz9F0K6xwEGVS8Dbq84U54n3Uy1UWY2R/bWEMLaazQftMFJTFHpuuCc3UhMXjGR1OkVrTNS31eoPTKjSuESoGNYrReMR6vca0Zihn8yFwdJEVlmU6XI8I7HazaBCVIRM5o9GYJ48fYjoXwJfxJDRA047Q5yg1rxjG1rqQWcZ7OtMyX7T9+yLOo7oNzz11o/2ww5ouOsU+6Mz27wyAWWc62hDFUKoMax2dMzSm7T89mk04mJxEsNVjuzAWSirqTYVpW2xn8J0B50JJ7d+v8/87fPypP/3j/MR/+z+S5xkvv/ZL7E3GH/jMf/2X/mf+5X/tzwDwm7/wv/Hptz/xO3Z9m6rik7/rB2jbjh/9kT/Cn/9z/17/3n/2X/43/On/4D/pf/+P/v1/nT/xL/wz/e9/4k/+O/wPf/l/73//yf/pJ/iBf/j7OL+84mPf/gf6zPxbH3+Dr/zyX+s/54AqghkiqjYLIcj2JnTLJb4LEh3eScQW0AVhPnvcYLes27HJfR8XP1Q3dLbh+ctHfOm3fpUv/MAfpJiM2Fxesbpa0TUVzjZU1QA6d22D6Dqs9MCIMi/Bu9B9t2soRmVMeMmIETl0ZChAWBdZUYSAQobmhs45SMCS3AYPfAwAk0ZueFXsfiL+D4IAtCpZ4lWHJ2jOpWZGYQWLfh37zmJ8YH0onYHIdvaC9GUyNn0MlTWv5TuESFFffF0Q2CyhjK7Isx7GCoGX5+zVK7puj+nehHGWY4sS2zksvmdxCCmRmSLXmk21YVGtOLu4QuY5sijRxaTvg7CpK65Xy6AH27aYztC1DXVT47yLSceBSeqdpYvjHcALh1IZDomRGWQT8r0bXF9XiOsFHSuavcD2bMUYOZmhxvfID9/AnH8F38wDK2d8QFmOsE2DbTaY5hpfn0cJJEAoxOiIyfGbqL0TXHGDjd+jzvaxQgc2SJwDqfUJBLanMS3YGmksG7chl2mf0MOk8EEq4IY13NeCY+eZWIMyFvx2PU9UsU0l0XKYWAn2aesaKSR5mZMVWWj6F5t6CIgB7VA1AyG4tkisEMFPUzIya+kBgR64ImnLGTprgk/vIyoQ30+yUFmWmiim92yvpRjcedH7j0GlUJIaH72+YkRaLCTAw6FUHvufbAHbDAlq4vn9tgYFIhIwVGDPm0F2awChtkAt56jPXrK5egS+Y6xC892uaVFNR24MhYDxwYxyOkZpQbeaI0wdelVsgeDSNpiNo+US31Y8On/Kk/lzlu2Kmyc3uV6eczg9YVxMUSi+5WMz7OacJ+2Ci/OnHOxppofHjA5uko0P6SwI76CrMW0NtkXnirLQjArJKGv5K//9X+CXfvFvcHV+wXQ04eToPrO9EySa9WrN/uGN0K7bdXgfEgVdtebZo3eRL56yd3DEYnXFL3zp1/jSo/eYN+uth7GVXBNEzd8kvbGD+Q1B/xaeqLJYdq6CLepBMdkjk9vTNIzhjp0dDr87XYZrFFtzdyuWSde2rSvue0Q3NICKFe07F9LjVuk7IigW5uTgS5KS/CI1j9smWGzFHTHQ9d5DZHT3e10CSbdB1/TVA7K6ndfcAm/T7+z8vp1LTPc2VEH9/R9D5R501lM3XQROQ1NjqXJSJS0erLG9HxtkAIZGW6mqKwGbztoQa8k2jMcHGv8MN9TvliKBn4E5vjNI8bO2L8XeHb9eliCe125dRzqLUqH6LC/KnWaDznu6rtt5fhCadIvBiEYfe6iG3AU6hmsZ4tthjH3q05KSZyIkz1QC34j+RQJvvY9VPWUoNTcWOxqjpaau6z4mNJ3pdfCD/ZR9c1J8WOtpfiew2nkbegMB3mmUCAxJ72VIYIotQC/eiSX4+65tWFcrrpdLsnxElpeU4wmjyTT2TlE9RpNrjczyoCnT1HCmAAAgAElEQVQsQ4ZHFyU6Cz4ZzoHyCK3IihEZkI/GWDOhm0yYlGOUkFgNa7+mWpacFzkrYWji/pDbQCLwWlOMx9z9tm9nPJ4iEXRNx0XdsKrXdM2arlqyuFr09r03ic5B11BdnvHul3+J229ds793m+n4gD0alJqhZdAexwm8zRA+skylRknw1qOyHGW6UDFRFNjRiKwog9wAfiefmpp0I3SszOxi5YrbelZbjdbjIeMakTu9AwZW7JAoS9jAMN+UgrIoQ4NW01HXa54/f4+6XrO4PGG6f8Ll/Iqr6zmT6ZjxaMR0MiMvC+5//BMc37nDeG/KRx3fFGBstdnw13/qb3D64hWvXp0DOffuPuCt7/48x7ducXznHrODG4xGY4oixwtHVS8QvkUQmgBIYajrFc1mwXp5zmZ+RtM1tE1LU7VoCfPLc3SuyWOAsWpqnr0658nLMzZdG8qaUxMOIQh6LJBKokMzlxi4pEYHzvYgaNJjUlKCFPF8wVlPmZYtnnUPQqVsOyJmRpTqkb5UMmti3GYFPL264Ppv/Txfffc93nrzDT7/uW/lZuy0HMqGgbTpxXtJGUnvXN9hMZQpxkvLMsazfbKywLQ1ztT9xLbWM19s2HztGwFgcqETblkUXF5fU3cGqQsePXzM3t6EPMuoNhWnL8+4vLrk8PCQUTlCtobD2T5N21KWBQcHh2zWFW1Tkec5+9MJ9eEMZ1qMaemsZLVaYTpD0x7Fe4HDgymrddCBhNDxToiwWYxGBXfv3GJvekAx3kN6x2zqee8rTzErTabGCJkjKPBeo1XO0WxC8ckpT1++x+X8lOXqEondanIlYs7KDgbBJ3DI9z+nso9BO1P22mubuuPnfunrfOfn3wRxhTcdWmnE5IQsz0NHZpIOrCGTkjJXVNWaTefoXHTaTM3RJMNYR20sG+chBh5eZHQy49miw4mam7OCm9MC5er+OcsQsSIdvUi50hobNepC90rD6XXN2XVDh2a2v89ytaSua7SwHE4V33p7xseOBIVqsc2GJ8/OePfhQy7nSzabBkfI0AoE2JSFSkYyBP6pO2SYomGjNlE3KQm+a6UCAzNucIlNa13ofujTsorOXnBEZR+YBAMdNlEZtfpSEoUEWPqQLNifTjiYTTk62Ofq8hKA63XDk5dXfPE3vsr55TWbutkB6367I+nUADgrmM9rhFA4FxhEx3cOOV9c09mOTd1iPbw4b7h9nOO3ArTbtxSfRbL/vOb950/42hf/Jkd33+atz34H//SP/Bg//X/8VZ69eEhnq5CBJLCklBC0XRfnpuiZxSErKOLsdYBkMp6xN56hVEFWeHSmabuWzjv2jvfpnGGxuub6ek42KsmLIrCDEpAtFMqLPoPsfWjSkpBy5z1t1wWGkwgOeNs0ZCJ0L10srjDVBhCIXCPHGUaafi154XFRcwqSYx82Tx0bGHgfOtynQDro6SYJmGBfvSfOmzA/wqomksJ8tMlEW55YAOk2osObaWwVSo63GaKOIJ/glQiC8CqAak6AnBRk4wxtfWBIWAfGkI2L/n7+0D/5Yzx/cbYzh/7Mv/mv8kP/6Bd+23n2O3EM7ISP/swf/cd/iH/o+78bgI+9cf934rL4k//2n+Wn//rP45yja8Nc3w7k/ug/+y/xC7/8d3jj/l3+l//uv+Af+yP/HD/+n/4FfvlXf52/+J//Wb7wh3+EL7/zdX7f934nP/7v/il+/w/9Mf74v/Jv8cd++A/zL/7Yj+C95y/9V/8xv/i3/w5/5Sd/tn9O/9Q/8Yf4tt/zHYGF4hwyMkmTg6pHE4wDs6mQrgtJiRSUEiQFvBzAWKscxoeKEmssOjIphQjNXgQOLTXLxYL3v/Ee3/7tF9y+dZciH3F1cUlb1Tx98pj1ajkMjjB8Zb/gYjIKUkNaoGQAI03bkeUWIQcXUAoZNfZlX+KI92S56hsNWWtjiaLsm1sGGzJ4yiL5Oq8dYvt/b7C2xZgKa9f9HiaiLi2xmsI5hzFNaMzkTQjyVYbSM3TcyxFZALAJwZRQYex6LEJEVmycG86G/aPIc/rAnNCZup86ER+4mq+pa8NiVDErx1hnaZsGnEcKQWMN8+WCZbUKGnLC40Uot0NKpNI0rWFT1aw2axaLJSbqj1lrsCZUbhljsN7RGUMjQwPKHVxGSlAKkRWIySGbDrzSCCnpusDcM0g6H+SLkD5WVymcyHDjB8g7h0i6wFoZzVASCizSdQjXINtrvAtMEycVcnyE11Nqq1g3Hus1Xqjg2zgD3qEIPpjAYWRG5jZIs4J2jm+XCBkRcT/YUe880jkyZznqWg6do2xbRNcFsDIF9HEvGVAWIHW9FjIGrgJr4ji0XbABgYYUVS8FqbHbTglzajYTJ2xicCV737OrfNKe970/LJJfL4jMnACcBykQ2YMJ26YyJJv1EABG8ASxC7IkH2k4R2LqJmDC98jaLg4ndn7ebizmXCrj34Fct1bjls8aXym9p1jXYBq0lGjVRlDOo5VGlyMObt9DZWUgA3pLW63QMmrYx0MDeIdvNjz62m/y5cVjFrLG5R4WLe3yKTdn97i5f5tbB7dp5hcsn72DvXjMQdEw2dvn6N7HGB3dgazEeui60HBWeIMzDeV0j1uflTTiOT//f/41fuHnf4bL1TUiF+jRiFvHbzLdO2a8d8B4Mu2BcmsNxrS9dMvDZ494OZ+zEZ6NrXh4dsqr5TI0TVJpPEUfAwx6g8NjYWt0h9EOc0llGhFJAH1j6vhcE0AV/FZ2jzRPt+bIMFkY5poHIQYyQorVdv6mv7q0HtO+PoD3QiT2aP/1W5cS4h0v3O5rcd71RlemvS6NhRi+Y+ue8ZHhFqWk+iReHxsHWRYS4L31DHqwub+51yWfti5cpKqIbQP/IYDl38OxLQEmtuyLVIJCl6ERMT6yV2UPtIWYR5JIPNZ66rolECfCOXSUDuhcAoviPYvEgA+7b54PNis1DQxXFJizYax2wc7XmceJcYoMidQEcAoEZOEZuGjf8DKAysL2fW5U3JtIzztiD84M8U/Pho4SRr0VivZVqtT3IyZ1veifNRDY+37L/m5PzoRLC3pQWUbZMgf4LpxHKs14ClIVtE1L17bgK5z1BB3VMG6JKxnwnSgbIEQo1rEWUQiKPFT8jspRSA6nsnUhMB6sM7SNQzYNOmqHh+evUDLK6HQ+6EvbDu8sRWyKHMhCCqsUMkqiCReITdaHRlVCKZTQiDpDqgyh1jFP4jG2o20abN38X8y9ebQl2VXe+TtDRNz5TTlUZg1Zc5UmShISUssCLGyJlgzC2CC3G2PMZBbQ7kVjlule0G55WEY20AJZkpGRkGEhoKERpkFYBiyBGGRNpakkasysyvm9zDfdKW5EnKH/OOfEvS+zEOrFWm2FVqry5bs3hhP7nLP3t7/9bRYGKiepfEalM8pcM3eSRaD0YmSQxfRCUhvL48+cZ220yXA4YrS2zq0njqF1hjMN1XTMM0+fZX93l7peBMkeZ6idYTa31Kbk2mSPqxfO0ett0e2t0+9vsr51iv7aJkV3SN4ZoIshuhjRHQzo9PsUeZcsF6i8oNf3VEXF+PoMWxqUb5DekWcaYnNygQxkoDhHwlQuol+a8OG0Hwf7thFXaKvThQg+l/U437QSh6tN5sI8FdEHbTCNwTRh/3HOAo75fIqU16mbmkVV0jiHt5Z5v0enU3DQKRiMBnQ6nVj9frNfnI4vETC25MqlXRAFJ0/fx+bxE9x22x2sb24xXFujO+iTZyETsJgfspgdsNaXZMogfI1tSsbTQw72dpnPJlTlHOFKJrMZk8mM8eGUyf6EftFh69gWg36Bw1OVNePJnMm0DIG9Ekv40wcAQ6ZyEtIimDBViWsZAUAMzLNOL1CwRShF8CY5OdExbN/F0vFZOljpN365v6xuhIQbWFhDdXhIbSzTsmS2KLn37nu55eQJNkYj8kzH4M89615zc9YxXkxnaCFROsOZDOdrUAVC5RgH0npkdEprYylrg5A1ligLISXjwwlCELoaLhasra2xublFnufs7x2wvj4C4cnznE6nw+HhAUWR0+t1KfKccbdDnmeAp2lqFosyLF4rh1aCosiiXESDigLdnTyj6BQc29rEW4F3IaCZ7M9Y7NfIWpPLRJmPHZYRaFmwMTiJPwmdos/1rGD/YBvpfOt0hM3UI627uZyH6NQIgfQJUA2BdqqSdB6ms5qnz+9xy8kh6wKm166gnSIfroeGE9ahvCFzjjzLGOQZtjY0hE6GCEWhBcMcpouahWnA67BJxTJDj6Sylr1phcCjRcFGT6FwyLTpErM/bsnmCs1WHHXjmMwbdsYVjcjxMjTDq6qKTDRsdAWn1xV3HNcM8ppqPudgf49z5y5wbTcA88bHdiCelS6YHHEKxNLYaUvrIlAIIeOZdJNSw4B2rFeCHR+/TyyTFCvB27Ls17eOkFZq6bL5wBLoFBlb62sMB0H+om4qLu0ccDgtub4/5dEnL7Gze0C5qEPG+OYpddOxWi4WQAJoGsNsXkVGvEQVGUW3oNPNKaMzVpYwmVrGs6Vj2e9lHD9WACWzcs64usT4Glw9P+SuO+7lJQ+9gkF3yBNnH8H6UEqudRB7z7KceRkkOFb1JFdLf6SQ9HoDer0BWmV0+xlKSmrTUHuDzFXoDllOKKsZUimMNfgE6FrHbFYihCDPg6Z0VdXt+LdgObTOrzcOZz0IicUxnYzx1qLyDqrIoaOxcpXNdINTGc+1upYlAElJFYP+5bsKQG1ihkfwyK+UO6f12fmo1dh+M85m3zpri6bB4lfWgPTJ2ETOJedxueanTvNIDyoMiLAKkWn2Dw75d+/6JT728Gd48UPP58ztp3n3e34dgINxANcaY3jz234uOtjQ6RT8wPf+g5Y1c3A45u3vfM8XYZnheO6D9/I3/8ar258/9vBn+L0P/kn781995ct4xctejPeet/zMz/PpRx4FQoLhJ97yTvI848H77+Z1r/mrvPnt714pww3H93z7/0BRLJvz/dt3/ALT2RwIDvP/8v3fHsGwv9zx0he9gF63Q9MYHnvy3E0lt0+ePc/OtV3uvfsMz3vwPjKtuXj5KmefuYD38OjjTzGeTBkM+jzngXsRQvDMhUtcurzdnuMP//gjPHnuPPsHY37s//wZXvriL+Oeu86EZ3NxcccHEAwCU0BryHN8XSMcDIYBCOj3hvT7Qzq9DqcvnIErgBC8/BVfSynHLMoZ+7vbHGxfYTqeYBoTA+6UJDBMpmPOPf0Uz33+C1gbjnC1YbeqOBzvU9VJbsEzPrzOpHOcOh8wKDIyGdhPQgZNO2stWqiYMIRlpjGdYhUODL9LQKuQyxJtkSZRnB9teR0i6mr5JavEOZQAaxcYM8OYKc5NwZsWePJe4H2K5h3O12hpkdIghEf4DHyJ8OtINUDKPh69XJeFRMi0NiyDtbTPJDAg3Vf6QNv0Mh5SgZdBE6xqHIe2RKrQEVsCxkPlDL6ukSaAfgYfAiqtQUrKxYLxbB40wmdzykUZ346P61dI3rv4TrwISdLKmjigMdiQGpH3oNPHF0OsKQEFDlxjMD5D6B6oTli7hIEkMSEllgKXZ0gsXnhk1g+sXgVKuKB/bdZQIoSijXeo3jqzhac2DYYmNk0SMSh2CAyaGulNSF5j0UqiXCxJ9DYV1Qamqg3NYryzCOfInGEDz7Cpyesa2TQIHz3qFmRZ+gnt6yWUNQJRAiyUQqZmHT6WhIceb76149XdQ6z4E4hl+J2AtSVWs2TYHDlE0Ek0poks3HAupXRIsosvzLq7sUQ4RtJLnzL6aUugKwbapg5JE521IMxygEL80sK4KxtUCkBZeabWR2mHeXk/EoJ/6FziuoMIVVSZLuiPNlBFB7yM1wySWMK31Mr2uhIPtuJw9zKH9oBZbkJX9lLQEX26nZwiz7B1xfaFC5S7l1H1hG6h2Dx1G73144iij3EB0JNChBLnTJMVXTbvsByWF3jm8iM8/Pk/YXd6SO0MvbxLr9NjbbBFnvXQqmiljjxQ1xXz2ZS6CnNyupixc3idQ1vTFHBQzSltE9Y7kWI3fwRMXJWqOAJ4Joen/Tdx5McWdF8F0dP5bkJjV494lhYRXjWfVTg9sUflTffX7lNxktwoBRDW+YRwhf9LZulX/p6e/ej300WW9p/2riOfi/O7vWMhaBn2aQ6mcYqTUdwwLMkmV/3K1edcvdTKwxz5e8srTSGEX7lwe74vLJfQXsMv90gR14c0lUMVSCzPjnKEUqZ56tp5n+aliwCSlKF5rpSi1SxOr9/7dI0o7ZJKr1fuL8kDLFm8zy4DcdN6FEdIiEByWppDBLZ8kL+TIpDOlo1ww5fiky2H8wYQatUvCA3M1DJOiEFz8tV9TK65trJx2SQ9rXHpWukZpAx9Zjyhgi7NPRFL+kVMmEqlwp7ul3qhS5B6WUkqpEB6GZukGbQyaJeFe5diCbRFO0+geQgzfGCAywDUL5MvNhBzTEVVBkkoqQP4qrMCnWUIa8JahyYR96Q1KJ3jVFiPvTdgow9jQrJ4PptSzcYc7B8yGc+YTxdUC4dxEkskiYnA5EUuG7gt5jOEB2PqKGVgGAxHFDqnM9rk9GlDnneYzydUdRmIc4sF1jtcU2PNIXXTMMsPybIeWdFnd+civdEaRadP1hlQdDcoijU6gxGdwYist0bW7dDtaDqZoKMctxwb0HUzqgMVG1/55bIgUjxnlzrqIthYslPVVoDH9xd12ZMcjIiyc1kmoyZvmEfJrlow1gORNCalxDT1yhIh455cUVUzpJJ0531cvYZREadbzChnE/KiIMv0kRj8xuNLAoytG4vM+pw8dQe3nrmH02fuYDActNqW3lZ4O6cpp5TTMeO9bXqnRkhlMbaink/Y3r7KlatXmc3mWOMpcsnu/gHXru+xfW2X8e6YFz7wIKfzPqPRJrPFjEVZM58tQlYqbSzLKjkEIG9cpGKWTsgQhKQXkl5gf32EyAJAZqqGal5C7O59dHOOkyet1mK5kKQMVwocwqd926jHEhbevemEcTnn6u41ru0f8tz77+fuO27nxOY6Wbba4OvognuEIRDBAh+NTqigE6Yyja1myFyiOg1Zp0u36KCEo6obGrdgWlZ4BMaBVpYsy9jd3cV7F1iRUnDs+DHW19fxHsbjCcNul04vlG80dUPTVGxsrjEaDUP3+umAbreLUqJlSWY6vwHIg363S1E4ZvMSgUdFUG00GtDrdqnmDc0g6IZeu3gdO3VoBDJToGX73sIASbrZiBObBZ2iT5YVVHVNMz/ANVVwAKVA2FRKFEBMfCrOW9E4FaHzbXrdLQPPh0D46fO7aOkpMomxno7IUBLQEnRG5hq8t3SlpJ9JDkqLFRqnNEIGba1Cw8zVWFOvlIoGdor3Fo9kuqiDTqfzFHmPvgYZRbSXzlly6kBrTWND99jrM8O4FnT7PfCe2XSCtw1rPcepoeSODdjs+dAIb3zI9tUdzl+8Sk3YmL2Qrb23Yyzi4hWDhSNg5RHwNHXQXGanWv0X70hNy1qgNQaw0ZJJ2ZLVDHAq3WlFun0qr5LkOmN9OGRrcx2tNcZaDsdjzl7Z4+LVPa7s7HP+0jZNY444fF/ouNGpaf1L71hUdbhfJekMuugsIy/ydl5aJxjP4dr+MvgrOgVrso+UFfNZw+VrBxyWjvNPZBy/9R4eeu6L6GYdJvsHXN0/GxwlIcmzHISgrEpsLPNJJRnLMQ9l9L3ugG53gFI5RRG6fBa+ofI1XnnmiwnzxZS6qRBFQV3XrW4eHmbzOf1elyzPwPug0Rvf9SqcA4Dz2DqIEPlYUjWbTYMubJahiwIyhRWREUSYP0Iu2eesAK1iZdPFeaRellS3zGTvV+wmzUyx9DijDTkXpT9Izmp0OH1IrjgpmFeLeL6jYHCyd2dS8zzZBjxSyQjU+ihWKfFagVbsH4x545veAsDX/rWv5DWveiV/8pGHARgNB8xmc546d55/8W/exrFjm1hrKcuS1/71r+KuM7czLxd86rOfb89xbGuDzY319raubl9rtVzT8dpXfzXPe/A+7r37DOcvXub/+U8f4Cff+k7uvvMOzj1zgb2DQ06fOsGZ22/lN377d3nq3Pkwjs7xa//xdxBS8pqveSWvftUr+ZVffx/WWg4Ox63G6t9+/deytblBVdWce+Yib/qpd7RN1q5c3eE1X/NK7rvnToaDPtY5njz7DHjP+tqIkyeOfTHTDIA3fOPrgKAL+9M/8/M3gyZ/iUMrxQP33sUH/ui/srd/wHQ245f+79/iP7/33dx66iSfPnc2annGoCPagrM26I7rjKzTZbM34tRtd3L8+GmOHbuFY1unGAxH8ME78VeCiXzVq76BJi+ZTva4dP4xHvvsxzn/9FmmB2Ns7dKyhnOWui556qnHuPf+B+h0OoxGQybjPcrrk1Yz1nvPztVLlKMeUqyHjuOhXW6096ifrDytYF08/Mq6vdrwA+JcS5TY1juOAS3hXM4Ehi+AXGGfOmeDTIewmGaMNROsHeOZ432Nw2CdoaoNpo7sRwE6s6gCwMRzhWaCSfpBiCyWcbaOVPj3+DArWxCIFKAuwarUVM95d2StElKG0kGt8UIwr6vAbnMOLQQGz8JZnGmiprTHCchix2zrPOPxhL3xIbN5yaIKvsRqwJ6YRVap9t4b66hNAGMDM0bidQ55H1mMsLLAiSYMuyX4SbJPlg0QWS+UwbsGRNMuuo4cyHHeoLzBWIOWGaETsw6dq7MMoSNY1TSg+lRmQtXYaNMpsA/vWRCYsZoK7Q0Kh1YRfPNBvw8ZSj6tD1JMAnA2JJw7zrIlJb3aktcNsjFL4UqR/KsVn7i1wcBitdZirAl9E5RCxj3BRn3UtM637355htZ82/GJYEKw+2hD0TBWQYVw/Qi2OBeSkokV62zwcZRf2fPTF48y0o76CMlf9G1jnLCtxmQ5yz3M2gYfS5yFWiaxjzygiNdzK88fr+k8LaixtEPawLU9RfJthWgD15BUVGR5h+FoI2QrXJBiEZ5QNbgKaBFlGfDgDIvpPrZbY7wHE0D+U1vrbK1tMsi7zPcPuPjko5jxLh3pGY3WOH77ncjRJjU5pgk+TFcrUBqVeTa2CrKti5z95MN88pMf4bGn/gwjHUhQOmPYGTDoDNEqg5hMSFWCTV2zmM9o6oosy6lsw6xZUAqDUxk1HhMeYgmApfFpWbHpdwnsT841R5p1Jex0CQsdjcvSzzf5jisWuwScVt6zX4Jqq4BbtKqbgMkVi2uRjRaQpJ12K59L6+TRPcCT/KIVfzclJduz+RBTcsNJiZrQ3rdjJKUMyfKV+02MzRu2p/Rky4e7scHT6idv+FU7Hqt7XCRyHAnPeRY//s+7xkqsk84ZkvlJhiowZ5UMFWtCBlbsjfE53NDgazVOl1FKJb3/aF/WxUacLjH4XWSGirhOyiM+/58HLN9Iali9H5nWozYOo41vHSIAce13ErlHts16PRFsZTn4Xsqj0HiMnWV84WlvTrJFfuW+ffyCSs+DX5LP7FFAta2SjHYuZQTiVABXlZYoqxGR6eiMC2C5W3KoU6zp4hhXddXKTGilQzMtwdK1QtKyN6VGKYlWWcuKlTJIvAXoJ1aVVFVY+6UKa2xh6PgOQulQaSNDIhMHQa0pR+koS9Eyo6O9G4upaubjGbPJnHJa0cwtQYFRIVEBfJXgCY3uZZyn3tZUc4etK6rYv8nUNWvDdYb9IVvHTqCyjPlsTFmGRNZ0PKZZLDBNEwgx5ZS6WoAIPWgmB1cpOl2yoovOu+TdDbr5iLwzRHeHyME6xWDE2qDD+rDLiY0hJ9aH2NyTy4a6KUMsF/c5IRxW2MB3EymBRSvpHf4e33nr+wXgWkR/S+mwV0ml2/nqVxoyC7GMNaXWQdNWZ1SlCed2S9AWHM7WNPWcuhzjmzlWyagR7ZhHeUalNGaluvPG40sCjN3cOs43/I/fStEbonQX5x2NKTFViTQ1mV+APUCUY7JqzJqYUu0fsD+dMJ9NmE1nzBYVk9mCg/GU7Z09zj/9DAcHh8yritp6Ngfr3Pvgi7jvgfsYrA05f/EpDqcVi8oEAFZ5vPHxBYdFDOsRcsmqCwL+MQseEfasKEB4pFZ0+j3koBOEr4GsD0ZqqCpcYyJtP07A+F+S9tQSDyBtPUecQO9J5YCS0EDAC4EBDsqKTzzyCE88+QSnjm3xshc/xEtf/BKKokDJ4LR6JVqHb3UvZ+XnsDeHVUUg0b0c2TGsdfp0ewOEt6wNehhjuL67z2c++1mq0YC10RrdjubK5SuMp2PW1kccO7bFnXfewe616+zv7YbslAwi1FmR0zQ1k/kYISW9Xo/19XWGowFrGyPwDtM0lIvAWJ7N5kt2JYJur6DTGWBi06B5OadpAji0mM+5fPkS3bWCTidHecW1c7uM3DGKvEueddF5B0GGkJ7AkFXgJYqctf5x+r0hw8Ean3v8kxweXmdhZlgbysiTlgwQtd1CI4zUnCplcKQQWELWDCfiYh6c0sfObrO9O+G/e+ldzHcvYJoFvqno5jlaBJMohKQjBU21wNMNgZDOGA47zKo5pQHjZVvMnoAmhYm2kjGpYN5A7TwP3Dqkn7lWQ3ZpXz40n/OKSVmzfbjg4n7F5snTjCdTFvM5rq7Y6gvuP5Vxy9CxUSyY7M/Y393j/MVLXNneYYEHpeMO7UMZdnT20ubM6qYvorPmgz5RKqvSWWjQkozSrixezgVh9CXY6pYwwMq5o2+11GWSaqmDaINuk1KaQbfHxto6J7c2yDLJxWsHPLO9z7Su+cxTF7h85RqHh9NUQbv05FadpGdxbtK/r/43HdYYFmXQAlxfG6CloMg0RaYxSLLegMNace7qMoPW6a0xGtQIOeWO2+cUHcvO7pQr+5d5+A9/mxe85Ct54XNfwImtE/yH9/w0k2qfxXzBoqyDthChNDcI64dOnylTLVDkeeWLQHMAACAASURBVId+b0C300eJnCwbxHsPbPAFMyblIQtT4mVwKh026KEKERM4wbmwdZC7SBICUoQKAxHZoDiPtx4zb9BohJdYa1iUgdGnipysKMiUjs2w0u66zPynIzWI0iqwDrTWWOfodjoIggxC0ekwnU5oIpiAs6sxOvigE5veUgJZV5BjnBfQNjFweJk6dx995yFxuFK+15q4o1t0Y1mMCWwuRBSiv9nhf95z7uORDy81TH/vg3/M33jDdwPwM2/+51zf3efbv++HeeiVX8+Hf+/X+KMPf5x/8k//dfv5H/z+7+Af/0/f2f783f/zj/ALv/IbR67xn37vD/nwRx/m8mMf5lu++wf56Cc+w+23nuKzf/o+nvfy1/KWn/l5PvCHH+bhD/0mf/C+X+J7fuBHefd7fp0sy/jIB957RDP203/8WwC8/V3v4QeiZmw6njz3DC/6ytcD8LafeCPPeeAevubrv5WX//Vv4lff/Rb+5te9mtlszou/8vU0xvAP/8Hf4a0//sabxuS/xbG5sc5n/vR9eO/5ybe+i3f+wq/y2T99H7B00IklwD5pqbrkYFuKTLO+dpo3vP7vcubM/fR6ayhV4F2G83B9lHMAIGBr/TT0HGbjVm45cQe9rIO3ngv2LPvXdoPzHoEw5xc8ff4xzl84x+233s5g0KMosuClJ/kc73n8sc/hN4f0T2yhMx0TC6qN5nQsc4cl6yskpE3b/CjLiuiwpnVOgrDhOk0AR4mgUYrkfWMCeIfAiwjihW8iM4GtZ+AnSDlDqQZwWG/w1FhfYfyC6aREKU2nk9MfZGjRIIWJ86kOZ/MavAK6QEbrzrZLRmqEehQcSoFd6nINS13GGyCywGSXPjBWZQy8Y6m89o4qSupIETCb0aBPlhfMFxV7h2N2dndZlCUmau+J1KSnBUJSUNqiNQFkdEkIy6J1F5F3Q5KzqjGVQahYtuigahzZ1jF8Zw2nu4El4xpwZdDFdKGMUovQaFZg8E1DVmygY9VRY2q63YzKmqDl3li8qmhiw7cjLAUESI33HYwzaF+hfUMhDBjDYr6NmV1FLK6RYUPjC6WQWlFXJcJBR0iOScUtIqOoPbKx0DS0BKs0oEkmJoIPznuQUM3noemiddE3twklDTJcS3yjTdauHjL1WQAQvu0/oaJHlfy4Fgw9EqSFZh4hFpDtPqd0kgGybVVdAmlandgEzB2xtiULDFLiwkeyh0frLDKtgq7+0g1JwM9STzfo6KX3dBS8C36YwHkVrufScy5jkHbMnCWL64RiKSeV5Z3QrKU/Ck1NBCgvUdbizAqruR1nHVjT1tOXimHRB+GwHnKruf+2++lnI6Z7hzzxqU8wvXiW9W7OxvFbOHbP/WydOcPCZ/iFpWkqTFPjhEJ4h+57TrzE8hu//Ft8/KN/xPlL5zDUWBX6mXfzjM3uIHQ0Fx7Esrw+SGh5ci3JtMQ7R2VrrLKsrQ/YKech2orgWRg/f8QOWrZfHGQpAgDllsKrwYKSGScziuO6BMhkTLS5FtxNh19FVH1ih3lWrPfZwbV0dRFYlsnbi693xQ9fOX/6ZZznKTHRglmtDacoNHzPrZyrJaJ4myYtHtEmGVpSEgkAic/oXazYWK6G7X275dx51kP4I/d29Fi+h/bj6T5WxnDll0fGMX3+JhLT6ufiNZrGUNcNxmZxWD1KaTKdByDGmpgoiiXxURollVsLoeL3xLKcORqOtQF4XcpnhbHRWgeQSYVnSfIX4gYbWmX3p2dJ/nQrr5fAzvi79HMCsYjjoLOMIitavWTrHDZKtXgfdGmlVGQrBBitFFoqVAKGY7VjkOuxQXpEBhhzNQGUyswFYKIuKPE5U0Nc4v3aWP0XpmmaVyEGlGkGFARQrapYlAsqJBDK8J2taZxZec9htomYwEF4kIK6rpeAOYEc15eSTORBWk/kSBRaarTOUDpDh0UIISRF3gEEUqh4b2G/qpsG6wLzsq4WQJBazIsuRTGM+v3hmbQq0Log1zpUo0RNRSk01m6yuTjBdneI6ozodNfp5H2cb5i6KV7UCNO0M0N6j4zgNsKBt7imZtFY6lmFs4aqnDPvDSm6PTpFl1wrBv0e9WJBtxhxsLfLbDrG1CUE7i1SOpR2ZLIkcwZVV+BLakqs2UWWCvYFDRqHJhOSQmX08j4bgw3whtniIFagB/wr2WkTG5smv821jTVjwzgvAYuzRKkht9RT9hZhgyyXNU0MS1eDwuRKxDVa6tjrRlJ0Oi1rHU8kecUEtTfMZ/tcu3aB3nCTXn+NteE6o8EQ63wrafbnHV8SYKzSGpH1WNQNdjYnkw3Sl0hbIZqScrrH/rWnmc/G1NUCZxrqpqGua+bzkmt7B5y/uM3u3pjprKSs6uUmJjv0MsXJk7dw533PYev07YhMM1pUNAhq72iw7WQNR9whRNhUPOCFQhC7ZYuwQYtMojo5qsiQucYXGTUiZixCSCbXu2RNgauaQOeuq+BBAxCzZMFiwqKeNu1W3D88hvOpG3mSN1zZgPBYD4fzhtnFORd3dnjksUd56LnP464zd3Ly5C0k4Kv9k3y2doP27SIuovMqhERrhVYZedbBLErmpkGInOHGSfqDS8xmY6aTOVIqiqLg1C2nWRv1GY0G6NggaTyZMJnOmc7mnDlzhsl0n14n58TWFpcubHPhwnnm8wknTx6nyHNGwx6io+l0M2rrkConWylpXV/fYDZbIIXg5MnjjKczpuMx1aLk2s44NCgwDRcfu4w2OVk1IssHFJ0BRdEjzzvkOkf6DCmzyN4RgCJTBb18nUHvOL1ig/OXnuD8pSfY3r9M4yw2htqS1JV+6c8Esf640YtQsqUiaLgqBI137I9n/O4f/Rlf9fJ7cZPrONsgcXS3bkWIwDJQUiCcAQxZVtApCoa9ARcPDqiMCF2OkyXFDdrFFyuImT4ss4VgUVs6CrQQeGvawBkXWDj71YzLuyWTRjHYOs7BZE45K8mpOTmyvPiOAceGBmVLZod7PPbYUxxO5oznc8qqgaTP6Zalgm7FRoF2IUqOgrFJ3zO5imGTXnUmM52FRiemwcYFODgvqTLDt6xPUvZZZ+R5HoOyqJ2UNnEE3aLH8eObrK2NGPR7OGN47Jkdru9P2Nk95FOff5yLl3eo6iZhG1/wkKtO5IoXdDMgu9QgbeqGK5e22doYIfB0+x3mTcbLXvW3cE1FVu+uXMGglGA0up3JxHDsmKHbE+S9iks713jqz/6UtWN3cPz0XbzhG7+d3/0vv8nV65cobQkSsqxDUYT33TSG48dPMJuVVHWFECKywbsoXSDJSIxQtMDlgpIFs8kBpqlDWY8A7QXCy1aqwNqGeQTOPSGjnfS3nRMIHx26xuMWFjO1rK1v4owNlQmNpeh3KPo5qiOCXizBjhDgRRB8h5VyrDDpQqM47yOT3jBpggaQdY5FXQUgOtp6pnUsv0nOtie501IKOlkRGwmFPUCIwNBPjfmkkpzcOMbeQehiv1qe/4ry7/PS8puXr21lSxEHcZ29IXB62SwDrv7FRvYFju/81m/m5S95IV/1ur8LwJve/A7e9rO/iJCCj30wgLCveNmL+bm3/hgv+srX89afeCOT6Yw3/thPHznP5avb3P3Qq9jeuf6Xup8vdLz0RV/G2U9/EICtyN4d9Hs8/onfwwP93s2Nwf5bH1/3d76bj3z808zmJXc/9CoAfuSHvo/XfcU38V2X/v0R8GF5xIaZQqB/rsdVpY80kfOAK5cGonwo+8tURnewxX33vRjvFOubpzj75Oe5/MwzNHUTAw0J1vHko5+jk+ecOXMXo/UtnJdHSEJVOacjFEVWoHVIgIqAJoXAL7Iuk6akc448z8J8MSYmbWQLepmmodCSphxj6zm2KanLGTaCr957lM7oD0cY6zDWBRBHKVQsu8tzBXKOlFM8Nd7X7I8PmFcTdAZFIVEZdAcdskzRyRW5JiQ0ic0ffWC2Qo13FbgFUg1bdgcxoeIE+MTqW2GprWS4g5wBPp4//Ymrggtlf0YIrJBY49jo9sk6AWSw1lCZBpFn5CpDZxqrNIf7+8zLkvm8xDsbmEMRkJNS0MkLsgjclVXNvDGYpJmrJDWBA4yQCK2xWuJtgzMOzwKpMsi7OKGwQuOLIVu3P5eqGKHinl/aDl5mIDSJEWgBHxNXShiUr0Ii2Huk0uR6gK2nYC2Z8lTVBFuVeOujZkNgoyxD1cA2FN6DMzgVvFazKDGLGTmGTHq0lAEANhWgUM4xEoqTKmPoJcrFhoaekBjGx31FInTQXVRSIaRvGddA0FKWSVoszqXEzrO21fBD6nCPq4AMIQmt4jgrqYPNOBvAowjo+3AbgXEVvylE8M2qqmn3Q4QPATFpvw/nCuPl259XG7Qsl4q4D0UcLplneKpQJSejnq2wMgK9qvUrXNwjZaIV+lgB1FZ/rTDuSN26lxqxz3YE3WHZJrSFEChg2OsxGq1BViBxyMYgU2k0R6ZQuDfh6ajLbKh99t0LkU2NyAR53uX24a1UezO2r51n/+oV9i+cZbOXsXniFjbvuJtjdz+AV5rMC/qFRKMpRY3CMLqjwfau8ivv/HX+6E/fz+FiSq09QmUBGPdQZDlrvRGZKtC5RuoAyngXciy5EmF9KTIO5yXG1XgfSnP39g5ojF1BsmnB1JYRu7ru+6R9ugQMUtK7BebTGDmPF75NhCUTCIzJG96KWIKv7dq1KjPwLEeyv6V/055oebPLfz3yb63trfrt4U2uJK4E3qUS8SMXJjXf83hkul0fyrydaWjBXRF88RQj+JU44OgdPtsDxoqjFcBw9f6/OEZra7F/4fGFGMvhTImdGRplewdKRwAyyZYo1X66HXUvSCzKI28iJmNCA0eHkzbIn2R5u1YkjWcps8h+XTK1Q/NKH31iQ7MKAqXEkF9ytOWKTmaShwuVtWlkk5xdIF0EMKrGO9n2/Qj9GUI1mlTLcRGemLy01LGHRFpPWiAtVbn5mID0LBuOp3Ur3Ggsy4/P1tg2Bk9N6QIxx+FigyelVJiXPiRLtMwo8i5a5xR5l7meUs5LTC2wtcdlNsjy+MDGXTbrjjYa73E2m0V9ckGuO5g6aBs75xGZRAqNFxqPwllPbZuwb6gMWWi63QG93pA8K1BKBE1UHxKxtTHU1oaGVjoLlX4KMt1F6RwpdGyOrFhUHu8MzhkaU+FdIDeZxjBdOByhQnLYHWJ6pyirMbgF+EUgqAAqWqHwHmzY6mVMXkkcygZ5RkxNM7dUMvYmsoamqgMa7UNVrrUGLVWAuCTkKkjlKZWhdY7MM9ACrcATyDbKLsA1mGhpda0Zz1S7jiBcqJJ3yWJFYBBDW7nlRKrMiuSCqEQnVWi2aePeF0DZYMsI0bLJw3od18yVueRsaBxrrAtyjXWDcwLvouZuE3rXaGWxjUN7xf7OJQ6v7yBEwJfWtk7SH22QdbrLxNWzHF8SYCx4hJ0jnUHYEtmUuGrGYnbIYrLPeG+HxXSful5QNxWz2ZzLO7tMZnNm85LJdM7BeE65qDEmsLKkUmiVB4hNZQyH63R7I5A5lbFUxjItZzSxrE8IGVmx8Y587JRJAC1FzMhnRYHINDLXqKJA5RkoiVMiivonyngIBmSuEFqjco3oaFhk+HkJddDQQsTyiJXrtmXE0faEoAWWYCUTvuK9+ehsO++pqwVPXrzMorFc2t7hztvv4M4776Df66FFCL68DNlgFRfT1ZIJz0rJSxgchFboThfnspbS3R+t43wTujYL2Npcp9CSXrdASsl0PqM/6NHp99lYVOzt73P77ae4trNNYyzzckG/3wfANJaDg8PQxKkJwNusnHN1Zw9TW6rq+NJaPMzmM5x1dHs9RmsjyvmMbq9Lng1ZzCqqwwYhFnS9YqDX6OZDOvmAIu+jsy5S5UiRo1ROlnXCuEbNEIlC6YKN4SncacjyAiM8O/s7sbtkbOgQ2RQpY2lcAMWtd5j47yayBC0hq2atwwkf31PDZx6/xJ23HWdTCibXQuAg+2soOoF9R2Cz5NIzyASKIHaf9O7xKeMcF6noiBH1MZVwDDs9chW0+gS+zfQ7HxqJTBeW7cOaymcInWOqinI2I/M1x4dw/4kex3qGrjQs5iXjgwOu7+6yaAKQm7Ta8BwBZNt/h2W32HifCQxLIvDJiVCEEk9B6D7aNA3GmGUZYetk0iYW2jApbvCZ1oGxmZZzZ5BCkmWafrfHsWObDAc9tFY0TcWla2POX7nO+Us7XLqyw9Xt3dBs6gssnOl6KXmxzBwvnbPEKEifdc4FlpAOjUfKsuJAz8gyHRjBlWV8MGHrxCluv+uO9jouNnuRsmBz6w7K8pC8qBDCUjcHHMxheuCRQnH65B089PyvIH/iEZ46/3hIArjgDCODLMp0NqcxoXu58LA2XKOTd9EybPLRlY+l1hK7sCzmi7DpaE2eZ9R1c0T+oWlCV+IY+rXPjUhOXGrIY7HGIpEM+gOmhwc0VRWA0ixDqhBJeZGC06XMQQJgjwDfStJYQ2OIuj9Rc4vQvdw2kbUX18smltL4G9gWyQE2xrSbdvh97LId1+BMa+bzOda7Fa29cHT8gA6D5T98Eb5+7uqb/u3CxSv85NveBcDfe8M3/IXnGA76PPfBe3nzv/oRAH7r/R/gAx/6cHQmwnN0ipzTp04ihODY5gaZvnnrHw4G/NA/+q72563N9Zs+k453/sKv8sifPU63U/Avf/QfB+b7F3FcvHyVf/vvfwGA7/iWb+LLnv8gUkpuPX3LF/X9/z+PyXTGP/1XP8Vf++pXUBQFH/7ow/zQP/ou/vm/eSvT2RyJZmj//O6o7TENCdQvlNeR3i1bqngYjY5x7/0Pcfzkrdxz33P4s89+lGvbV9i/vsvBbtgTr+9cYWf7JGsbG3QHQ9bWtijyYnlSD0VRkOWdNpgSCYiVoabLGtM2N/DeY6XAOtMmf2nnWqjGKaeH1OPr1OWYppoSWBRRlkDAYNinPFi0+0LR6dDEwEjnGtcv6AwViJqynLJ/sM/l7WuUZkHeEQwGOceP9xBaoTKB0oE9GsAEFcdHodA0iwbcDKsO6QyGqFyymMyY7u1Rz6YMThwnH4xQeQcjRWQtx4FpE36iXa9vPALR2SOcQypBlmf0+j0yCdY0zOcGlYUyRaEUBk81nTObL6gWVXDcI8jtEjjsQn1T21jCuVbaxzqHbQwLYyNAGuyiqSoQoYRRSo3UGSARskDlQ3qj26G7iRQdlBNkOBZKIWSBl7ptzOKlCE3ApEfj8Das2aE0UkQJHYnSOQLLYnqAtybsCT4mn4UgMKGDfShnYisahXMEmaV6jm/myMwG9k9MnuIDYCFxdIRgTTiKxqCci4oAIgDQktCgJMvJun1m03FMprVOT7CJFl9aglThMpFhSmCuIllWWMT33+BDYl2EwC7L8sjMW4JWCSBIoFPaBxLrykU/CxnmBsmeYjIzsWdEWzIs2u+2yCvLbWK5S6349vEnKWTonP0sIFICd5f59Wg/qcsYy+AynNm145jmwhGwSUTN/jjvZQxEgu5dHru1W6RWETyJ+65Kdbqr5wps3sw7cgNZ7dgcHWPt+GnuO3YPO489w97FC8z3rtFXgqLosHbiFINjJxF5B/AIZ1B4OplAdRSuqbj49COc3/8oD3/yw4wXE2rpcHLpj2EDS25RVUymE7rdHllW0Ov2glSH8GQ6J8+6CHQAXuNRNYa6NrgE7CUhwhU/b4lrtha47Pi9tISo9RnWXblCNPAr3015guQ/PZvf0K5PK0CBQKyQPIK9iCNyAum/y5j0qLEd/TnZ3LP6vYKVSqAVdrcISZHUoDedupX7IPnlYkWbnDa+bX8Xv7P8bpxn8TRH78kf8fvTZ/3qeN40iCvg8sqetnraFDo923Gk8m6FZLEkRC2dwYjnIAnxUOMbpAvVeIlIshzDALrK6GcmNrAUgjzPyYs8NhVSsUG3aEHa1PjbxqqLREhZJcG045pATedaRmv73IT4LAGa6fNydU1Lz+djJVA8uYCQ3JVLL/tGZi3t75bvCpYxoY/yXVKmpnYrn/ZLu78xQSDjCxN4nGOpx5me3VoaY9r1ViCoiDJOEYRLdu2laJO3Pm4sQUZ0ZYKkcRUcGT9rHdWixnlJVig8DWQCkCgRSuGzLAu4gtQomeMc1FXou6EzHXqjCInQAiVCstQaj2kqrK+wtkTrCq0LlNJ4L3E+w1hPYxxVXVMtypBItxZnDa421OUEV09x1ZTFYo5zDRKPjjGSECBcqsgIY2zccu7qzDM+3KepKxa9Lp1OF69UHA6HqWrqRUO5mFNVJcY2IQlDrPpJwyej/yHSfhVs2FhDHSXtgt6xQGvbgqW0X1+NpaP+a6oskCJKLnnSbpVixZRM9ISmajcy6NO+HG+xBWODGcU54BxCOAQSbz3O1FhnMabBG3C1Ccn1wuGKAo9BOIsQFiEMBwd7TMsKkRWx6fyzH18SYKz3Flvuga1w9YyqHFNPD5lP9pkc7HJ99zp1tQgGUS04PJxw7vI2h9MAwNZ1E3HNkA2WQiBkyCRJJJnOGPTWyLIOHkVtaqbVgsl8hkkOafui41x2HqljZjOWWKElulcg88CEFXkWjIyY0RE+lJmvbLhCyrAYaYXKFU6H8jIvalxlI/IfFoBU4tEK8y/9taUTcMPusVy8wp+04e3P5pTPXODa7h67e3tYZzh14iTD/oBuXiC0DBpM0qMh0ujT+1g6H8GHjQasdaDUWweuYW1jAyEMVTnFO0u/10USgovaWKqmYm00ZNTt4pyj0805fnyTulpweDBmMpmxvrZGWS6w1jGbzttNr1wsmEynTKclg16f1eXcO481lrqucd7TH43I84wi6zEcDBmrOdVBhXSaXBb08wGdvE+R9ch1D6kLEDpk0VUoI/Ax6GodfA9aFawNtkA4rh/ucDAZ07g5zlisczTeRs0eF8pIgMYFINY4i4nlG86HAAzpMT6R7sM4n7t0nU5HoySsWYvKCrpS4jsFznVDmb33FAq6GZimikFi2jTcEedwGW94FJ5cCjb7GR0Vg33hY/lcYJ8Y6xnPFoxLiyy6CCEp51Ncs2Ct57llqLltQ1H4OU1ZMj7Y5/r1PSazMjBzolSAt8uAJZWruMiQTU6VX72/aNOB8RLuJ22mWgZbDxneIAvSlvfdkDRIz5ycDaUUWq8Ef7GEtMg1/V6PjfU1jm1thAZ0Vc1sNueJp7c5e/4K5y9e5cr2daraxARbCu6OemhpI5ZJMzUdUkTNI1pHM9mtT/M5siSklDTGMZsvKDoFRVHgbcP2lYusbd3C1qkzJMZk1Vjm1tLNc/rD42R5lzyfopgwr+cYf8hsITi8ptnauo3773kedW3Z3z9kb3IVLzwuldvimZez1rOWAtaGG+QqJ2Xog+qfCXNB+KB9vQgM01b8XHiUCg0J5AoDZ1lWFIKY4OgtnffEms50RpHlTIzFVCV4h8ozZC4ROmhXO2HjxpsCndVAQ7RrYgCUXGsnMga8SgeNHiFSNj5IVjhXt2t0klEgMnxTA65lWemyoVyudbjn2QwboTMrGi7rz69aR3z9N3r14oafw+/vVyM6Rc7LXvIQn/zM53nmwiU+8KEP8/Z3vocvf+Hzee2rv5qNtREvffGX8fFPfpZHHz/L4eEYpRQveeHz6fd7XLm6wzMXLvPlL3w+EJpx/X85nvfg/Wzv7FIuFu05AHq9Tvv3u++8g+fcfw9PnH2ajz38GX7xV3+TRx9/ihc89wE+8vFPIaXk6Wcutp//9COPsn8w5urOdV72kod4+NOf49wzF/gvf+j5d+96D1/+whfwjV/3mjCG1vLxTz6C956TJ7a468ztX/S9P/7U0+ztHVAuFi1LYuf6Hv/1Y58C4N67z3AwHrNYVHzk45+mrmvO3H4rz3vwfoSAl7zoBXzy05/n4HDMxx7+DN55Hrz/Hu656w6MMXziU4/wfd/5LTjnePjTn+PLX/h8ijzoajai5JJ+GiB2GVf0uz021jfQKovzKIBEzx7jiRa8kCrom6d9och7nDxxO8dPnOKOO+8hy+DcU49yXj/FYjFnWk+ZTA64dm2b9a3jnDlzPxubxyiK7vLsArIsVJUEjTq1AsjKdn1O//UQqnRWAqAQWUqEVGjtKeuKpiqp5jOq+YRMC2zU05ZagsuZzw4JHZIlDkNTVQgJLlco0aHTHyKko65q9vfGXN0+oPaGrBAsqpyNzT5SeKw11MIiyGLAIAGFFB1skzPbm+EXNRkGNjL8YI359V3Gly5THx6QeYsWglxrnJBhiq+Me2DRpkTmzTM0lF+GKpgwlnql6skhtSIrMmRsCmmNYT6vKMtqpZoj7PdBHCesDY0LP+E91ge/wXhP4xx1Y6kTeE1grASg24TVWQWmq5MF5GvI/nH0xu0Y2cX7kLhVAoTUILPwRwTfTsR9VUhJrjIEddsjQKiMxtjAspKh4qGuDUl3jwgwCm8RWIQPIKz0TShzjKAb40NENUG4RWDXsNQ0TaC39I5CKLrCk1kTZIuFDDqg0T9GSmSek3V6iHKOa5qELIT1XKv23Naa5A0dacKT9lwvZdSxX75hAxgJLtq2lCEYXvl6OIf3rR+RmK3BUmJpbwJ8SfqZy++nhF7Q6Esg7NLSWsadX7kWQUoknce3gUQYo6C0Y5f+Xgxulw1y/LISRAYmdosTCVpc8SjifPQQrBBR4j9IIeh2ehRZFmyyMXgp2wST8GH9QqyAbiQfKBAcMi/ZyIYUo5Osr99KV/U43Nmh3LsO5YxBt0PR69FZ20R3+0HXWAgwYbdVQiCkYXt6jkfPfYTPPf0hnr50FvoSq8J1U0Ir/c8DVVMxL+f0en2cNyyqGZqgzWycpKo903kZSqCFoKwbjElJknA+2caI4uhAJZDmBmBwCVYumX0iSnUFe7ph0I+AjkfP9ecBhEc+k+5PLM/1bMfRX6UPs2JjR/VnV0u2W6JH2NLCZDp80AAAIABJREFUs6XbTbbPzWORriRWRR1ZXg+CO2rt0X1nlX18xM9eWU/CrS8B0fR8f8GQ3XSIZxmwI0zdZwGoVwHP9BfvwbagcIyF4t8DIWFZ7dpOy+izEsF6QfBLM63Js1jh1/q74RzeBclDm5J9PjDvEyM23b9QS73YwGhO+MgKAeuG0umlpEG016g1n0DT0DhJxOf16SGW1xRJBigSu/wyUX/kPVrXLkgCEUEv0Y7JEtRlaXvpHHE9DeXhAX9pG6a1eIjHOIeUMWHgHdYFNmta6KWUqEyjvcX5DIVDRbKGdLERNdCma5P5pvdB1PJuLEo5ZCeS8hRIDSoTZDqjW/SQQgcdWZWBDwQWay3KanAOGd+zx2NNYGIaE/rvVJXD2hIlM6QKjFvvcxojaBrPojbUiwXWmiCVZi3SVTSLMdbM8H5GYycBjBWQSYWXsdW4COuRT8+50rgMKZjODFW9oKw69Ht90Kp9H6YJDcMWVUljmqUvGXu9BPmIIIOQ0uqpcV36Y62J9ruS7JTLKtK0sbYynTGObtcit5IEE8maRAvaIkSQYEBFmYujfXPSH3lkqY0VFK38g0TKaP8mgOjeegyhqab3KugkE5uKyTiJETSmxjgBVRPlu579+NIAY03NdOcJqtmU6cE+h9d3mM/2aZoFddOwNy+5urvL4d4+0/GERdmwcISS8HZjW90VNJ3OiF6vj5aKTpYz6K+hiw4qy3Cm5GA243A6C4158CBiSV3sZuWio5wXBbqbo7sd9KgHWrRXSmXWyOVuZAnl6eEImlEpT48AWeRkeYYpK+rZgmo6RyOXogTeH9kW2o1txWFbLYsmGlm7UiBi5sRTecfOeMLu4SGPn3ua5z/wIM+55z6ed/8DDDtBJ8U6Q9MEXTKgzWhJGbIA7Q4Tb0KqsMB3+h1uPXMbw7Uu8+mExWzKbF62OmxCCnr9DrV1NJMJWik219dp6gW3nr4FrRSPPvokD9z/AGfPnqWuq5AhUprDyYzxZELTGG6/7TYefOA+Tp5cluRLpRgOR1RVRVUtuPTMM5w+dQvDwZBc55iJJBNdBnrEKFunyPoUnSEq64JK2nJJDyQs0o1tgnRDzLSYZsF8NmZRTViUM0adIb28R1ktaJqGqqmYNUGTMwUrxocArrGG2jZHWLFOBJZoY0OA01aUAZ974gr7ByV/5UV3M9u9TOMMAkvRyYPWG1BkgkzD/vgwaOWKUFriITbKMNF5CZYkhKdQgvWu4tR6QSEqZAx6Eju2Fpq5MVzdn6G7Q6xrqJsFZTlnUAjuO9Hh9NCh613m9YTty9tcvrrN5e1r1FGt3Kdgy8cSwjR32qB+GYSE5kW0joGUGVmWhTkSdYOsDQC3J4CzSkq6kWltI8vPxRJ0Yd1S+zSesyiCsHmb+bSO0aDH5sY6a2sj1kYjmqbh7IUdDiYls9mCj33iczx1/gp1E/QNZUxMiBUn+9my4qE8aAVoXXFExApAHk+AlCKWDYXAUorwTItFTdOEYO/yxccZbp1gfLhkxu5P4LpxnDrWBN219bvpDQzGn+NWeQEla67vTbh+sM25Rz/JAw+9gi977ouQaN7/wfciNXgbyilWtSelVBR5webGMSQK2xiE1Ailcd7SYKibktnhAdW8xEUh8rpexPVsuakVRYEnZusbE1a0xG71HmMaZFw7hVR0e0NMZammc+p5GQLNokD3u+heDlrROB+W1uis6lwfySxaG8BaKRRCy5YF6p0PLOjRiPF43ILDWmWcuuUWrl27RlVVbWm1jk1r0ntycvnOE/OkW3TpFBm5UkwmE1RswjCV1/iVjR9oryFI5S+rGos3OKHx3B7HWucbed2pb+NDv/PLPOcrvpZ3vPtXAMiyjN/+v362Zaf+/m/+PLc++Ff4X9/44wBsrq/xB+97D0op3vKOn+eH/48fP3J+pRIAEEt1Yu1Y0idLJVwCeMdP/Qve9rO/yA/972/iVV//99pzPP8597UyBz/8A/+Ql7/0hfz3f/s7eN03B/bs3/r61/D2n/xn3PacV4a9MJ4f4Nu+958A8NwH7uHjf/AfufuFX8Ob3/4fWlv5z+99N8NBqIqYzUte/Y3fRtMYvvvb3sBb/vU/5Ys9/tmb3sJ7f+t3jzz3+3//Q7z/9z8EwMc+8F7e97t/wBvf9Jb22X7iB7+X7//u8Pff+bV38fe/54f4td98P6/9pqCz+1M/9qN8zVe9HIAP/c4vt+9ve+d6ew4pBbvqAu9Z/9/w3qGM5dhwxIue8zxe/9pvYH1wHC0LrIXgJkQwKAE+xLVYaJAa6yQuJgGkD8GP9QJ8hhJ9Thy/i+l4Rl1WNFXNk5MnaZxhe/sKWnc5fcsZNo4dp+guwVhnDToLrAwIzaBELEkEQRUZ6VprdJ6TmkuFz4U54BBHygp7wxHSBQDKOYH2C+z/y96bxdySZfldvz1ExIkzfMOdMu/NzMqauquryu12d9vuBrdtMJKb5gHBizECzCxL8MQLQuIFCYEEAgxIFhIvSLwhJB6Q+8nGXU232m27cU/V1VVZmXkz7zx+05li2AMPa++IOF/erGpLSJSlDuXNe7/znRMRZ8fea6/1X//1X12P0tIYoW0a1utLjlYr6lnJfr8lOE9ZiR46zuH7Hl2KplpVzNCqEL1F7+lasHrFbrdm4zYo5aQxoAGtSwpTUpcndJeBl394H3e2ZUaBXXzK/PQGYbcnXFyxjBAfVwRjpNR5dUSXbXJ2nXLwrlKAMAFCYoz0rqMwltKagfm92W6wRmGNZr6YU1UVXdfTth1N0+KdZ9s1tH2H8yJ/5ZQSGdcoa3HXtUPAibHs257tvhmaO5iywJQFtqwoiwqLElDYWpSp2MeKWNyiOH4ftbrLrrxFcAGLNP3CFihTAgWoQsDG6DE6lYnqksVqiQo9me1qbJG0sEXzu3MRp0UfDaWHBmkq9KjQomOD0gETWxQOowPLmeH80Qeo+Iqi7NCmpIsButxkVbpX2xApopAAClJgaBVYw/zkNBEvOlyING2LrcSP9F6qPKzVzBZLjLGEEFhfnqdgKwFdIfl1Som8mJ1BUQ+yThGF10aeSyolFib4COWMDcOCVBBF2belh0qUPgEg/ozOAeYhUDcFX0OUsm2yv5TmYQavxgSmnCcmYC1LXGVwEcTHzCW+4l/JJM6wQWb65EObsXP5lD2YwaIQwzWZtqQTCQKQJL/q5vEJpa0wEYx3hF4J80sbaRPgA/qaVApRZblWrKr4E1/+Bur0Nts28vd//VtcfPwBq1JTz+fo0lLfuIXTiu1uQ+x2rI6PEUxAAYH95Sv+zv/zN/n+gz/g5cUrfK2JBJTPoKfCoChMydHymLtvvcNqtcBHR9vt2O3XrK/WhKjY79ZcXmx4/OySB6+es+0avIWrrsHHA0hxSGRMD5U1gRMjcfABE3AZfGacCUgUwmSKXDvX8PobQL/Bd5j8apBCeAPoGq/9W1RbJ+gf41yRN8uN5fkwMj7TmCbQI99kyJIqKidD5PO54mjwlY0a5pmPMQGADDECOl06SOyQQbcB7Lr2XQ6+3wCKIXFqBlWuAbXGmM9pmqOnZ/sjHT9M/sCFQB8CfQyUSENB8bNsYgNeu54SoldRFNIwd1YObE/vPcEFmrY9uHbuxfAmoNham7awQ1A7x7kqAibZqgkIlefS0JMDhkqZQQOZcc4ZbSjLQvRuU+JoJCWlRKJNsiBaSBEHzzUBX3nz1ZmVewDAjjHUCD+IDF2eG2PCIF27LKRBaMwSDIpypsdhj1mjNublilJQVgU+1PS+p29b9pst7b6hazrathWAPTVqTAMrhA2fx0ZiwaosmM9nzJcLiqKgMCLxWJgZlZ1jKIamXiHFFt479puGnZ8AyQl0N6kHSwwR5WBzvsO5iCSQDTAjBk2MBoWlAJET8EAoiGzoXIMLO1zc0MdLtHUUGFDVIEEVg9imEOLA3o5R4uw+eAJBqgVcw3Z7OaQ+plmIGH2aVyl2Tr8PLtDQ41FUWqPLYojZTfJFvfdsd3vZ5xSiUZ7GZ7AfvSNEATqNMRRlhQ5quE/vpReO0gZthGmsQ0ogZHuUqsGUYsIO9yKJpBhIcllKSKQRsv63xO9labCmxs8LfF+x33bsGvFNvHciP1NYtK1QegbRMK8WLOo5dTVjVk5izWvHjwQYu9lc8evf+juEviP0LV3X8uryivV6x3qz52Kzo+lbAZ2idJXTRUF0vXQsA5nIWpgg89kxJzfuicSV6/EB6rqmazqi2dG2HaasKcpawAfVS7mZtWK8rKWaVRTzGZSaaBXBaIIKhFRCBnkzzuLOpOA3Mu4iqXwnOUyylhUdEV0XVLOCYlURdh1h3xK6XpyfiWM0ZLzVaAzTj+OR9krJEARhs3knzD0goLlse37z936f797/lN/+w+/yl//SP8PdO6fU5QyjzEAtzyX3EJJWnOh0WlvQta0EXdZibUlR1ty8c4+j44bdZs2D+x+y2e7YXF6y321RCn7sx78iAJmGzdWGL7z3NtoU3Lx1wte/8WNsNhtOT4/ShhmZzxYsVysRJDeKxWzBZr2mO1nBsiYSefrsMT4JMCsUF5cXbDZrZmXFvFqysG8x18eUeoUyc6KpoKzQtkRrCz4Zwm5PpCGEyG6/pm0btvsN6+2Grmvxbk/f7+j6PX3fMjMFt1YnrOYLet+z2e95vVmz61o8uWmRxg6eAjTBCUs2BlzuuKpGkN2LgAFPXl/wy7/2bX7pL3yT5vI50TeEfk995/3ULCSinKfphJGgosJEhdYWnyZBjI6gpFy7NprbJwu+9PYp88JLZkqiBmIM7NueZ+dbXl7u8aZAxci+bXA+cFRbfvJexXtHjoXtiH3H48fP+fijT4VBgJxHZhaQDOqYBU8Og9aDcxaJFGUxsHIzyOVT85sQ/DBmImqvhw18Vs0EMO/3Ig8xYW8ZYymKtNmnNdLs92g0VVlyenrCF969R11XbPY93/7oOdt2z/MXFzx48Izvf/SAF68vhmd3mAhJS++a85PXpdYZjI0pC5YC+wzO96PmmDQaGYG5OCxclUpLekIMWLfm8f3f5rfLNfzCXwDg4dPA9156du93vHvnjNYZ6sVN3v7Sz/PRtztu3bqimoGtOp6/OOfhx9/h9Pa7/Nyf+TmevnzAB5/+Ho1vUEqLPpAR1rE1ltOTE+bVDPrU1EL3NF0LMw/G4X3L5vUZ0fshyMiOknMufUbnEHYcuOwwpT8xQmwicR/RveXt997h0acfs71aE1zAFCW6rCV507Yop7FFYuuLYKvIlyTHWkpKR0c0BwtGKXG4nKdtGwijHrgPjidPH496eYmunRnZ+QkfHR/RtA1d12VhYhon4v4GAVCEg5MDlrz+ZAzUBNQZJ9TIGFdKcXx8g/1+h0kgqVKKf/B3/4+DBmVHq7EEflZV3P/dbw1jnMExgL/+b/2r/LW/+i/zpuNoteS//y//UykZL0s+/t1fYV7XxBj5xX/uzw/n+Pf+2l/hX/sr/+LBZzOwmo8/93M/w9Pv/cbwc1EUzOsZD7/za2+8NojTA/C7v/Z/HuglTRuArZYLHnxbwNNyog3+Rzn+5//hv+Bv/jf/2ef+frVc8NUvv89f/7f/6vBaPZsdvOd/+hv/Of/jfz0CwIvFZ3Vr/8N//1/n3/03Rj3gejbjDx8+AECFwKIq+cKdt/hzP/XT1LHENQ6vdQJCRuAkA7KQ9uwYU8UCUkEThG0XQiRrVxI0t0/f5YH6kOjF9hMVylrW2x1Pnj7m448/4N57Xxwa7YA0F1DpHDmoyXIcSqXmHylQzM6zgHPy+YA6mAMhKnS1YvXWktWtu7i24fXTh3ThKfg9EQnElqsV2hp63xOjp64r2XdSELO52FAtZxRGcfv2MT0951cXGKtYrmoqU/D8fEdUHbYMRK4orcGanlhoatOxe9VQ7RS1M9RA2TrKl5eoACjpbrx5/oLLtqVcr7nz0z9LUAqP6IuFJNM0WKjrMXkE33u8NTjvMc5RlMJMNNZQFIYq6es2TUPTdqL11va0zuFR6CKVFPYdOrGXlNa4oOiTNtxus2ez7zDWUJYV9bymWq4GVoVECVYqlKolanaMLe8Qb32TrrxFb1b4aHHNGaq5RAFmdkQxXxF0TVCaiAXfwv6cYr6inM+GSoOsq+p8EJajKfBR03Q9YYKqTXZ2ctmnjY7K7yj9lpIWHRTr1x+yuFFSzSq0LtK800PCVgdY9h1HRI6UNCCNWhIRMUDbdhJQJ513FwKxMFS3bgujKERefvJ94vpqKD/MaylhsfI4NWhTYhfHHL/zFeZvvUN9cmP4Pk1AZM06h5lB0+4xLqSu10knOQQiqZTSdbS+I1qNiZ6u79JV9eBXTbe/vAfagdUmgENuJnIw1eK4VyiVGbejOG+M0ogELbHEoSRM2neSvqlK5/NJGw8lzNwB6M1VS7khm8qgxiGY7INUTik0VluOF8dUpkxahR6cwzBhKKfPey8dycfvJq8bJYABm8D9+3/Ao6eP6S5fcmdVsjhaMlutqFbHqGrFfr+hxLE8OSKGhrKoaHZbnr34lL/1j/4G373/h2xcQ2dBh4jJTZAzZB0VFSVzPWdZrTg9vkNZVhwdrTg+Oebk+BbBg/M9+/ZdTm6e8vI3LlnUkU1j2T19SlCpMYsegfHpWoiA1QZbiP10vcNnOS0YgMeMYY4l30O6J41P1vIUPfppsgjSs4mHr8ncGrxTcgA4ZYhOT3P4dBNQnBdLYhZO59sAwk5vRkWZOxMUNMptD4mIGHWaoxwQhjKsmp8QSkkFZdpvrpcO55uXy8fDL/KZb0bqM5Fenz4nNYI+A1A8/O7wPQz3cK369B/jGEG/iI3SnwNIXdVlFRqlRUM7NRW2WmOUvB5CkOqNEIe4KGMGQ8JFjWXYIQHnGczNdW0gwJrzThrnZtA8M2cT2CmEFX8AkIpkoR73/RRPDiXf2kiyoywGdqy1dvBl8nPIGunDEeNBTDCe2+OTPj0Tf15AMblelk/wXshMDOCxH2JEpVJDdVtOKiplLFVeyyjKoqDre1wv0kzGGkxZEoEyVjBfMZ+v6JqGbr9nv9ux225pG3B9yh0ET+97KVOPEaWSlr3VqI3B6ILyqEKrAqVEP7VrPTpCDB7nWna7vchBBZEVwGcmqNicoixlLLTMb6tKFA5NYkG7CGEvDaoCotcb+zQ2MtwuNLiwxsUtLq6JbAmuS4k/I1jVsDZTpY7z5AoqraAukzzmEOPELMuenl96HUXURioYUrWrxIWyV/W99FpCa8qyGmZBJFIWBXppDyVX0t9Kjz5onyqhh8mTKlFVVIROcLOceMhvKZNsl/NOfAvXC7HHmmG8M5ifMSitRg1lrdWQaAgpEZE1kg0aasH8QoqPY9ezWJ2yOLrFfHHErCyZlQajVWq09vn240cCjHXO8er8NbvNhqvLC7a7Hbu9OLe9C/ResvdKG1AxNWVIEyR1uLRFTVXVqRHNgs5rogvEIIy5pu1pu45ysaKuVtR1YspWBdZ4ZquFaJ8oYXiYwoI1aGsJWijWGVjNx1BWODExY/YEDkQFD/YPNTjbqiowOgl8Ny1h16YUasqY+6nDNG4WB/opUZy4oTNyjBL8HOJH9MFzsd3y4cNH+P/rV/jaF9/h/ffe5d1791jN50Sk3MwaPXyrocRBaYqynJRZq2SkNbqYUa8M73/1J3j5/AXzxTnb9RXbqwueP3vBarmgrmfUZclu17HdSqm91lZYrqdHlIWwJIPzyTmQoHG9WdPsW5yr0/Apqqpmu94SiMznNV/72lchBppNy/7KYSmoiyWVXVDZmrKs0cqI8fMBgmaz27DrGvrU4bLt9viuoe06mq4lJiEAdMQWBaYwLEopo1Na4b3DR8/TV895fXXOZrdmsUxyCmkjan0vpYfe03nHru+42G9p0uvT7HsIgX3b8Zu/e5+f+MpdjpXmwgdWuqJc3cQSIEqXa600QzpLZadPAHQVIjr0nC6X3JwbjoqAit3gwGlEK+3l+RWXmxYXoJjVbBo599xG7iw1t+qOUnma3ZbLs5c8fPyEbdviFeJIDBNP5rZKWfoETw2O11C2FIX9mgOoPH99MoAyZdP6S0w+peQz+2ZPCIEulcMOcgTGDGCWALoRHz2zouRoteLk+IhbN05ZzCteXWx4fbllvdvxvY8fcf+TJ7x6fcnl5SaVLqjB4QQO1lguAxv80gyEKQ46NWdgNpd2inMdD8TEs0MC6lrJQgqOCbj9mt3Zi+E3V1vL09dzTk5P6PtXvH17y0mw+Fjw7hf/NOevvovW5ygV2OxamuY1m6sZK234+Z/9Ba7W5zw7f8Km3wprOH0/g+GoOqJUBd5o0SvWJUp5qCKYiN87ms0mAeshZSvD6DgcZNcnJi4zH4aARNPsdxS+pC6XWF2yXV/Q9y3KaIp5jS6slIXkuDbpK0ojL2Hll2U5MKOz8cs6PzkBYKI0jSmNwVszMA7FifIDQBjjlIk4mujdfotzotObu3DmcinRWdLZC5FnncGsIbCRIGfKUjAmidpHcVx658jdhPNxtJrozV47BMB9sz5pVZVU1eeDmPP5yJY8PhrPUU6ytD/sHCBO98nx0Wdef9Nr14+jo8/XVlVK/ZHO8aZjMa+B+ge+xxjDbFZ97u//KOeYVdJA8fqhMhCRKmqs0kNQocjPNwFYuVRaJSg/TthqMQdSqTonR6N5DmlLPT+iqubyo7FD8L7r9tz/9CNObtzGZ+1Dpbj8Uz/NrdOTlKQSRojS0phjurcPIJsWx9a5ThJDmTGeA3MVUUYCL7TBGMvJ3feZ1TX97ox+f0nf7Oj7IMnaoqAsCiAmtoyhKAvON2cU1qFLzazwvPv2ils3SpSOUrgStywWCo/stdZAYY0wTXTE9VvKosBXM1Qbsd5jAhTZuU6BbxkcoQ+YtkXvrtg1W6IS1oKdLwfNtAycTX2qECP7tqeqShlvBaU1VIUk/7IUzn6/Z7/f03biR7jgwIxdobUVpgdONND3TcOmaXFJvkApxXI5p5zNKMsKW1VQVJJIQqoXoraUixuY5V2Yv40zJzSzW/RqgaeQRiH2FF3PMHgwChtbPA1Z0RVlUNpiioqyrDAalIjYJr9WQLeAIgQvjKDg0r6Xk5EaQo+mo4gdVWjQvkP5DqU75oWlKDS2LLBFBclHJLGnNAqrNda1WD12uI6IpEWM0G230mA07fNoWTe2KNC2TNUZOWxJvoA1B0DIkJ8zho7Iq/U5JpLGVJ7t6/MLukaacWhlUdpIVYdSWCVNYkIiJPjgcK6n9T1aVzgVaFyHigGrkmzBFF9NfndmoI+c1rycRvDoMMkrfrafgLXiE6jx+x34ewznEWcpDECfyO8kPz2EnCsekoFT5EvWwCHiJwCHNJwpyhmzWc3QjEwFfOxRiLqPVjo1OBvjlnxEa2iAq77h+eVrNr+/ZdO3GNdyvCw5vX2T+ckp1dEx1eoUHwzr9SURkUGKfc/5+TkfPftdfv/TX+XDxx+yiz2h0Emnd8JyS989hIAppIt9YSu0Fq33HNSHBFb4JC+mbUk9q6jMDN1vaZte5EgyW09NxmkyPiEEvPNEPSZZr1ct5rR7CEF81TT0GYicPoPPBQHjyPQb7uNA8iIcAKcZYpn6rIP46jAHxm0GdYBhDu85/LYq/TdlWI/fc/xgfibpxPFQBGbqE+V8wDhWjO+ZXDtm4PjaoZSagDNpHkzsuPw1NlSL48gMn79OcLr+DH4YMHsQh0vUSq4MjcO4ZgJDkmRTCWTUGSgVwNP3bjin9AsBlSRylFLYohh+RmUZlPQsgxfJm5QIGTq+E4cGXRnbQEtSNOpIJFVKZf9ZxaQhnuf/8NDkbtLkjSHg0/wJrRcJjgyoIgzUz46dGv7OZJshESADOMSKKOnvkPfRYazjOMuHs6fxgiyVMq4VEMLT4fxI4x080Unj3xyn+LSms7yQNlIVoGKkU9LM1xEwMcV/CHagNPjQS0l6LzqotrBir4NBxwKCNDkjaNq2E4Z5zExNi9HZH4/oVktjriigvMKIb5fiL5Fkyb6mIgbRqo1RJf3ciPMNHvEDAnugm9hoId8MVa0hDpqqggPJ9zNYROpP/EPRJR73j2wPpus4EJNU0thgkyis6a7v2e12QnxMz9Q7N9izDKqL/dJJr17mXmHM4A4PSIM4FphSEocxnyPN99Ja8aEoKU2Bc31aEwIUq1QRFUKgcy3ehyGmHcFdRQiyL2d8Jzf2NKVF9RrXd7iuJ8ae5fEJs9Jwerzi5HjFYmYGo29/ABr7IwPGPn/5ku1mw+XlJW3X0Tsv8a5SFEWJLUphPAXpuaZJE8QUKGspyyNm9QJjK5Qu8UoPGiIuRrb7nZTKak1pC2bVivlyRTGrcJ3H1BUBBqMkgs5jRmo0Ep+9/0OwZsK2GGzZ4camRpsEyShpkscfQXWO6D2DTtVwcpVAh1HTUJzPfM7RuR0SfsP/ZXPovONiu+V7H31Mt7tis9mw2+957+49lqtl6v6YWCM6a9nmDIUdJmneRGJadKasWFUVzkfqes5yueKlUmw3l6zXqfPgcslmvcd5J/esDbum5bhcMqtrFvOavmvp2hYidL3j+ctXWFseOKi+97RNEmNWmrfvvUVVlqzVFn+1ZhZrKlNTmAqlhVXStgLoSWYQrtZXbJoNnXfJ2fLoxJizRepGS4QonQO99+LglSVWGynj9i0nixUqeEoFVV0OmmWRSO+ssHGiaNc0rmdelGz6hm3fsWlb2pRxiek9j56fc7yqCTFwfOSxZ8/RpiBWBZQFRClQyKT60cHIcyxQ6MjJvOBoprF0EHokkBKQuOkD5+sdrVcoUxIDuN5R28hJrXhrBbVqcE3P5uqC5y9ecHF5RefDaDSnBnhwuNJLcQwyhsz+4MSFwbk6cOgmm640/hJdIp8yh0Ppis5dSuWPUsKEzOm60hacHp9wenrM0WrJfD7jcrvj+etLnr+65Nmw0mLyAAAgAElEQVSrCz66/4hHj1+y27dDmcl1Z/iNjsSkkUPGTKbmIE5WWwxBWEeR1DlXMQrZqwSIyDPJn9PJeXfdnnZ7NZx3sw28OtdsujsQHEUVQO1BXXHj5jvMV2+hlEFzwXLhaNd7mt0l2ta8+/Z7vPf2l9h1DfuLJl1bnk9hLKt6JRuuEjDWWAtJY9ZFR9dLMzf5zsnBTGtf61zCnOvNGEHZ3Fk0OdnGFPgusChmrObH9E1HvxfpA20Ndl6KXqyRcVZqHBelhWEZYxwCKh+kpEUrkwDicexB3r+oKuqyZL3b0Xb92OmYFCLr8ZHmuRpjpL/WvG3qDPpJ0MDkmtOAYwxGptMnO57iwAwM3zfsJ398/JNxHC8W/OU//acJwVNrwzs3b/He7VucHM9TmZKAPGCS3Uxtj1RmsJH2wTiW9kbwQaeAIZftKXwoUF+6y41yz72V4cffu5c0WSUBsayXfP2Ld9G14ivtGhUj7/30N3nvzjFHs4ixDq8j1oDWuUECKJVK2yf2V7qKB4z2GC2SPjGjQTHr/kXRRTuq6O0x3Q66naHZFjjvqGczqqrAGFLzQSW+RWE5iz31rMSUCow4tCFKRU/E03Ytv1WvaRJrx2hhtNiUBAyhw1ZzynrOcnfF27uH2N5SGGFcSKJJ0wVHjCVaPWH14Wtmuw0ogylnwhxFWBExAZIhBP7p7SmXpUU/f8H8rmG11MxKmJWBeuaYlQpj/VAVsfV79kokCQKpIddkV9AmNxdROKfZt7BtFCGKky8NEUvKqsLYAmUNnkjbyj1prcA4zCKg5z3MdjQq0OgOhyUiGrKii+fQeAzStKTXcx6pd/mArxBNQVQLVDFDG4tRjlld4p0wQnwvAXVufJlZIoONiwrprtyjo8NEjwk9RE9VlSyswvg1xazAlqXo2imRmRnjNCWNuZQWyaTk30tywaBR9LudVDOkctTk7OK7juCkUssaOwSHSumxDD9E8QNSg9lIYjE1W0w5O0jgbbdbXNZeTZrmuapI1JaEPeqCyBN0fYcLPomMKwKBz4RVCRXM/vGB7yMjwOFOoYZEXwYgRrBOpf0tC5iNn83uXpzOtORzZqAtA7ECWB3OyQM5JTnVIYsNUEmaxBorUm2mOASt8DifsHJlBoBmBHbluGpbWrfm1a7nbPsh+/UpuqxYzGesbhyxuH2TanVKuTimWp7iXKBwPamAiv12w4cP/hF/8Pg3+c6T3+JivybY1ORVT3CiHCCn+7PaUJiCwlgU0ptAJ981pEZwMl/A6IKirDCxEOa686hBF3Ec9nFw0pATCDFNHLj2/ngADMojkoApg2txcrrxs4dOZfZXDu7jIICcTIhD9HUEtz7Hx1DD8s7z7jA5PF5Wpbk2zt388zjn1OQW1DWAnOGz06T9m4HO6Xd48yGg2g98y+S91/24qY/2hvNev5sDcPcH3xeTuTiu1RQ/q1zpl55LzAzGOICvUWXdU/lZJ43orPEqslIZqJKLZabr0BDS+2FN5GeTWaEmS+oNIN7Ieh2+twqjv0tMSmMxVUkMKSBy2ocYUy+JrKUtn/XBD7q0w/yeTvgpmBIha+tmQsUgw5K+n/wzTp7jxI6F5Du4gJ+8PlRnTsc6NRodpBlirkSWNeC9x3mH8yLXE5Hx08ZgrMSuIenI55t3rqPtRC6w7ztc7+ldJ3JPSsBXHe0AxIIh+jDgNNYo6V2j7aCFqr0ieiekL+fEVkUBlVERjLCpZSQ0CosIIopP6Al41eBjT6AnqA4VvTDXo8ZgknRZGhMdpeIq5GcjDasOEaS8Rg6j3hxTEkcZDSbPgOFnQS065yhz5UD6jFY5YaJSdVMGYWNicsM4gYZwapgHesLCHeZG+kjybiUhp7OGvSRHDip1VSSYMM7ROO6DWT5D4II89xVaR6pZJRUvMdAHx263pdlv8f2ewhyxXNSJABQHItCbjh8JMLbtWr7/8f2hXLScVTKsIaC0ZrFaUFWVMGZ3PQoBCq0p0WZGWR5RVieYooRc6kFEpW7anfecX53hfAuILsZstuD2W2/z6vIp+6uGYLUYNCAg3V11VOTuqqJBHQfDkh+OsEkgAyx50iilxmc2teExfSbI5pcNq6oMqtCo0hL3LXHfE/se+qmQed7AZXoNHcH1YYZvqicllzzc0KMS1ubHDx/x5Nlz/uB7H/CzP/Wn+OY3vs6t0xMWdT04qdOudEFNAI9sCNXoanofqFcrlkdH+PYmUUF1UfLiyVPWl1e4Tijw1lp659hu97S9aOIUtmBeVdSVpbRgbMl20/Lw4SPuvfPeUDIXY+Ts9TnrbU/vPeHiipPTU959+x3m1tIay0KvqEyFUhoXPJtmT9vv6Xw/CJ7v24ama4hAVVbUs5J5PcfaQppkEOnaLgGxju1mQ992+E5KKgKBl5fP0VpRlxXWHHN+9RrPBBgKEWPFIayLkhuLOe+cnrJuG873Wx6ev+K8ySXQIRklw3c+fMZm3/JTXy/Zvn5MJFIYUkO6pBCQWBsOC7kMDXkWy7ridDVjUSp8u0Eh+jPiQAdeXey53PWU8yVFOePs7ArjPTeWlnsnhvdONWG95mq95uWrlzx5+oSm86kJWUqCMPgDIwgZx+BtMNjZICNs0ZzNPXRwRuPugyf0vQRoauKkpnldlSVlWYgjmDSKQirJq4qC05NT3n33HrNZhSKy2Wz4vQ8ecnm14/HTV/z+dz7m2auLVKY1zGZyEP8mEG5ItmRnVI9B09QpnLjdor8jAnMoHQfNTnGQUkmFMZK1TR/UJonM9y1NsxvOtl43vDpr2Yeb1HbF66un9G6DLS7xsefk9B2K8hjvPuJ4tWPberbtlquLM27duMfXvvwNts2G9faSxu/QhcJgqKsZp8tTVGKgKaOxhSYQaELPrt+z3qzZXG0oqnJgAxuj6LsgpRpDeWYWbJdAPkZhKctzNCzrGh1LjpY3uXF8h6cPPiX0vdjJ0qLnBaqCqGO6RjqvFnmLsixpmmawuxmYnaUOlS51bw8piWWM5rhecHJ8zP3Hj3AusWJTOVfWBcoyIeM8yx55nIC/KvkonxMwDX+PyZEQD9dAmNpgMkCVgew/Pv5JPL509y7/y3/yH/9/cKbrgfSb3DILP/4N4Bs//HTrx/L3P/XNyfnb9O/uh3/+82Wt3nwcA8cLYPFHe//bd3/gr2OM/Efb5/jQo5UwNgtbJoagkYYQlUWtlrx/9opfPPvlH37N7/zwtwD8C9Mf/tKUre3Sn2vH7esvXA/nJ8l5NPD57Pc3X6NPf7bApz/gs28+/nf3z/Jfuffw5YpgakJRCIDkPTdOb9C1PZvNnu32gqKImMKi8RDdyPKLme0PJjoMXsqMEcLEjVu3Oa0CL79zn3I+x5SVVHrhUViCH9l0QYHxYCJoHUGL/FdhC4zW6P0+JSw0uaYv9NKtOYaAipEqsZJVkgFR2UYHTwiO6CL0HuV7dLBYFVieHA2yN5GIa3fCOlKJJRQcWlsiQYggCXzo+o62bdi3e7CGorCURYFJAMKbJIyYMHO8T0nkFHjHmMkMEugZbSD6YXxh6r8zCTCzr52SB9mHGlgX03LvsWkPwze+VtWnhGySAYlDJpsw6LQylIVhPpujE+iRg9MMQqgYicZKmXX06KhSZZ8cH716yavtQ17tN6wWj1jNf5Fqfszs+IjTd99DnRyjizmqXEA1xxaRRYzEVAb88sUTfvXb/xsPzj9m7Rp8maqL9DhWWVuQBHZCBmNTwh75LkYZNJropb+CdDevKIoaW9UoZwYtR0NqJPcGIDb7fxnAGSRFIomkEPExjBCpYgCCs7+rtTp4zp+HmGZJpetz7LPgRL7adX/iOnCbT5DvJY4/v+kG8twlRZ8RaUuZwbV0H0MsOgFsh1hgAsxk3214ZunNOYYe3e/RPxcMdQRz86mjymtqAszFz47VdI2OsVm678MB/ew4/eMcMd/zdMzFx7PWDs87k4KUl2ojZYQ8oI1OEnrT5yosWpt0V/OwiJ/tB4IBMaYE6sjMtsYkIFGTS/VzL4HxHP0wF6RMPNuXcX6oyRxBJf3mXF0WxOdm6Lczfn2b5BNynJDBcK2SnEWyKd4lvWmVJRALiqKUqgTvB1woa/+qhLXkkvGYAOHQu0HrFpImqbUDihijnMOnGAHFyBrWaviKrusJfowtXbLhWo3Nl22e/nFMXPq+RynRfm/2OyGvGYOKFhPtMB/ACACrhdASo1QW5JJ8YywWI2zn4PChT/fgyVujNGLLQKQ0BdMqEnxBVAqlAzY2hNBBdJAwLaIWn0pZTFHgvUvybz5pxca0N2UQfVLJGknJ+Qyiph4DGmJu9hYm4LZMFomD0/yW/VoaNIttVsSiGJ6vnzSnHKtT1CitkTA6qYZJe2mSOFIJY8jzCqDrupT4yskNsZNiJ4TlmyU/jLYUdlw/AixzsJc6lxKOxPR1I2VZMpvPaNqWq6tzzi7PxMdwLTMLJ/P3qOczSSLrz7cvPxJgbAgQtRVdoRhwXTfRgg3sNmvWV5cpO4BsfrZkVt+iKk8wdoE2hThXSYg/ElA6EKKjbfY8ffaIx4/uUy8WHN96m3lhuHvnHe5/8j28eyHl8VoNnUCzPdealAnnB9vpAYRiDLAzcj/+c3hvTA9Ta8lYCS0eYmmIpkYtaqwL6LbDbXb4ppWOpToj9XmvijBQq9NmON1XYsxKDuTuziEGOiX6afuu5/LlGc9/5f/mH/7e7/MTX/kSX/vqV/jG136MelYngySZsGmphwDJ44CE4Dk/P6dpWk5OTjg6WvLFH/8au6u3Mabk9fNnbJsd+lInXUBF7x0PHjxlt+s5P1tz69YxX/nyu6yWS0KAtvDcvXePO3dvMpunElGlOF4eoenonMcTePX4kv5FoGbJjCPQ0LS71IWw5Wq7pnEtZVlSlTPm9ZKbt94VsX+jKYzl/OwVvm3Z7vb0qYmUKQqRKLAFRzfvYIzFtQ2ub+j6lrKcM69qNIq23bEtG56ev2Dft3iE6eqSxIbRhnlRcLpYUs8q3lquuL1ast13vN5ueL1b82J9wc71GGN48PiM56+u+KW/8DU2rx8TXUvX7Jnd+II4zzCwrmLUQzmDCYF7qxUL1RG7nqbbMZstsVbTucjltuX7D19Q3niHzli2raP3PXdrx/unJbePDSZ2PD8748GDB1xcXtJ2DZFCDF1EGLZBNFKyLrFMxdH5Gh37ceZnir5s/H7iCsmmH5N+amawqKSNZozBak1VFFRVJQ1GekfX9agYWS7mnJ4ccXpyzM3TY7TWPHm55uXZlvV6x9//nT/kk4dPOb/a0HZSEqGuOZ9vynqP2dVkE2zWEdOjJtEA0k7ZwAJq5kZkB3Yj5vUyascNJUFIU8AYIi6OoMminqP8hr/9y3+Lf/6XfpEbJ1/lsr3iye//AV+4u+FuZ5nPSuziDlW9wdoK3RV0fcunn37IF7/yNVq3p+9avv3h7xJUYFHNOJ4fU89PULaWshIl2VZTaQI7dptLLp6/IPoeYjk6rEqcx8JId3GfGhl2XZ9KIkVDzzuRF+id49X5C95afokbR/cobMnTxx/Rdx1mVlHUNXpeomZ60N5RShjpRETfrZfNOOuyCWvHDPqfPgR5owwom6bl+w8eoGJiPB0EzSo5MUq6foZx3uaE15hYiJNggQQIqVSCm+xhTuKl82TH2sexUz2R4ZogMifOCSj7x8cfH398HB46aipTYpMmZWZphODxruHJg/uol54vrC/+/77VH+mj6C5YrD+gm99DH78j5ZV9ABtp9z1n5xepyWFgMTNs9xv2+xadiAI+im4qBExwFP0FJrQQOlz0HK0WnB4dM3OX3P/2b/H2N96HQgszp0++ogFiSI1tI7bpKa2m0IaAaHeqXthjnohXid8TIiYK69KQWLCZXZZKs4PzomNKCg5T6XPUBu8crr+iW1+ye/mc7vJfGcYlBo9XCgfsfc/61RpCpK5m1HXNrKpxLsnywAAQlNFQRE2REqnG2MTQHQPAMPGPQoyM9dii8Z+7owvJJjc8FRDEGi3J0UnyV0AjnxWUCMFNQNERRMjsOJ1LIQcwJf8oYOUhWzPH0OHAH/JEdGEpqpKynMl1YoDoCVGYcDqBww5PUNIweN027EIzYIKfbs6g8Lz17m3efesmTx7DnkjUBafzFbo8ppofYctZ6kAQqOslRE/bXfKtR/8r968esHatNHlTGRQcE6Ja6YG5L8C3pu86Ls8veHD/E+gNd27fRtu3WBzXhNhR2oroFYRI1zkwhov1mtfn52PAPLgLasReVWrEZiaNajIwnl6JOQ6DIS7LRwZzlD7kVU+JDFOHMeZ4N71n9DHzNa+DtFNfJr+YHl9KZB8C9dM3HZ5j0HCcvOO6l6xgIBpkxnGOO8czJxbtwC6TOD1GNfrA12Lm6b/z/Y5ay2/21a8f+RYyW/zgvG9Enj97/FA27LX3Bu+FjAD4GDEqDgx1laUJh3Ur7w8ZKA6iSWm0GWTXMpiUG8gpNW3MKiBnboCllej4h9T3RQgAIREU3KBDn+WTsnQXMevHJ7A4jqxuHzyMPFi0Ttq3CLBmCrkHqZjTw3NmArzHENDWDo1As55y1vJVyg3rSKogeiE9pXEz6XNFZUeDle4zJlkmDdgqt4SUhyyVD2kP0gJe2mIGWQM0NYCeJgsqW7IoZ7i2o28buq5nu9nSxB2tb4EgMjk+7w1yHk8kasGcdrsLClthEttVR0tVVNiilCrvspTYKc3JQEjFU4KraKQqNIPiGoOyJtWDSwIRxEYrrSD114khzTsCrnP4IPfcup6u7zExMptVFLoQrE1L80qCgdgTYweEgWSklU7N/3LjvaldCpNKA5lDWmlsIU3kjBIZIoM0ahVmtxWAPsl9aS3JsiLNA2ftEPtnxirkanWN827Y46bl/nFya3lpZ8wta2PHGHEEfJdkChTEKLJ3I9kRnEvEnhBkLSWblUFvkU+M6VmZwT/Q2lDXNVjN1eUlZ9sLtu2Wfbul73vuvn2H49XqB9qTHwkwNqP9AvQg2il5U4mKPnbDaEucb9CzFd7WdNpSEVFJF0QrQCucj4CD0OD7DWeXgU8+/ZTTG2+xOjplWdV8+ctf59PHn7Deb2hDg7LjE42RYbOT2woQdcqGkzJyESZ9SMdsZd40R7BJpYCdlInPYJDgGHLBbKJDEuqXrEKZmlkZfNfjeifnCmHIWEIuI8nDJBTz6TXzyRXSAdWHQamFCLTB8+L8nN0fNHzy6DEffPQxP/1Tf4K379xiUdcoTLrP8UOiq5pPrTlarVjOFxRl0okzhnJWc/veO8xXS7q2YTmfc3F+DkSOZnP2rbBfLjc71rs9zkd+8htfwQdH7zq+8N47uBAOKsRn8zl9D0Y5YlBUVBShREdDCI7G74hR4ZzHOU9RGBarU2azmrKoUFh817NrG5zvIXhi8Knbr6bQUBc1Hi0lfdpCyq575+nbDkXkndv3ksxowM1mzFcLFssVl9tLNu2G3jn2XUvjHJ0LrJuGTdNQWGn+MZ/NWM1m3D064rRecHO+5NHFK9ZtQ+s928bxd//h9/gz3/ySGLmXgVkAffwWypbCrEhyBVlD2ZYFJ4uSQneY6GTDNIo+BC63e15e7FCzBRFF33Y417MqNfduLjlZlijf8PTFI548fcrVekvfeyBtpIzrYsxSjaUoWidW+qDwLRt07rI5OkchBSkMk2koJWEsC6lKYWOaFIDFGGmaZnB2Cmu5cXLMW7dvUc9KolJ88OQcjeXicsezF2d894OP+f79h2z3DX36XC6+SBDqZJ2OBmlacpZ1aXLl5DTLMjX8WqXMs5WSuKZthgAq7VYMrm2IaGtSR0m5Xtu0ZNbMqAmWEjZGE3zg7/3Gr/OVL3+Ru3dvc3z8Uzx89hFn5zvqWU89n3Py1s9xb17w4sUlL56/ZLPd0rnIyeldvviFn+Dp88ecbZ9SLmbUs5UAt4WhSgxXHzxtCXu/Z9es2a0vQRliiNhidNis0Xjf0zuxdScnx1xeXOFcC3gMFh2NVBi4SNh7vvlzP0O763j28AHB91K6XBXYWYkpNEYFjDUJlPfJvqgxk0127GUi9n3P1WYtjKjkGMX8/FCim40ACnlMhbHLoK+nsvb1dF4zBlNy0VzSmTQKtVRRHEh1AIUxzGzBncUKFyMvLs/Y+B5l7XhPDHDvwYyLMfIf/Hf/LS8vLq4FUuNc01pLuShSThV8z89/809wtFgM82rKv83zO+b5NzmnQio/lEnlQxF2bc+vfvt3UgnWJL89/i8lUiQbXJSi831xcc6U4auSruHBZXW6o+y0DwmbzJA4vHedmnJMG3yIUz1KY+Q9OE7GaFiaeSs/CFgPSxMP3jNskergyShIDQPTe8P0fmRrDSFgfeTO8Sl/9us/yZe//DVsNUfbAqVT5ULSjEXJrh2nNbXkEj8BZZzrB22ugCQauq6n7xtePH/Mxx9/l9/5nX9AUUoDmSzXQoD1v/nv0PzCn0fFyI9/61vcOb3JanVMXc8JXrSytFAyZA7DoIdclCWh94OWqSlE17nrtjTths3+EhcasW9GtLiurrYcHx9LY4q+xRgvOucuYNqOsL/ChjY5v5HeR4yB5aKgsBqVyitijPzJW1/gZ29/EYCik9I1iBRVctKjsIl0E6n6PQWG2R8Ty3/gEfaX+FcfU713QqDDBGmmVBQlbdPiAyhbirYohn3r2HeOqC0x9pCKHsFjY4MNDTq0qChSAjcXBdvnn/L61adE1dOHDnzWf2MIrrI8kQ4Bv9/gi4JYWKytiErAMFXMMEWJDV5kuvzol2V20kC2SKycSGJsajOaGiNz23mPj0kv1UugmY8+BByRqIVls1gsCC5QFqVU3GlNjAISGGMwwSepDEUMns6LZEK0kSI1/1VaEohTWaUBfMtARGKtxogAN4mVE9L8jvow8H1T6Ka1zeaY7I7kMkmxz4g8RGJwhjSGqNG2ZfBvILldw7K0KVmuTqiMaDC7ELBKZ6wb5yNdlC7bbYjses/LzRVNdNSzK24fy3luVYaIx+7XNC8djy6f0agfo2y+RjOb8+M/+TZom/TTHV3T0Gyu6PQrNsV9Pv70Q/a+FbxAib3NettKgbaaEGJ6LQ1bjBzVS24cHbNYLdm3O16dvaRalSxdzaNnn3Drxi1ePn/N40dPeXn5gkt1wXq3Zr/fi4+TSS8qA9yZecngQyYY9mBPyYFdJo7m6rEhoU+60aFx0tjxewCkpnt4+j4RrpEcuPae/G/1mfddhymne2++ZJx8PusXjG5I8piDJA9iSn4k8b4kySVEn5xEyAw7su+er62FkRyCmuzf6SaTPMhAukpH3qeAARiZ+kiHQOz09fz+N4yCGr9+fkF8v/DZ977xOuMxjHUex5wUSXrSMQrDPsYgzM9Uvm5Miqu0NFDMOrHppHJNI6QDW5TDy5llr7UhRJf8X3k9g7eiGRsS4Jc9zkQamMRv2aeSd6UmWFq60SutiN5jjTDGXfASQ4UwNv5MzEmj9ahhqvTgy2WLm9mHGUMYysPD2In+B411lnjQepw32tiRMZkGJ8dSKNFNhTDoyApGPNaQgtixLHcjybMAPqY4VBMDCSDX0pBNG1wCd0OSLxSS2yizUNiCqphhtICxZSEyL4WVcTVWGjnl74IyRM2E4R+IuEGyAgVWS52JMZaok20f8EoFKoDVSYbBE0NPdHkteQgen/ZLYw2lLUGJjJ5RVoDF4PEuiJYtiBZ2tnJpbg+6qWn8jBkbKUciKihhIydtYiGOiX3OoCox6RinZyGVjSM5SymFS1WTWmtiAqa1NsP6GIiHQ3RzPY5P2sdZcT3NGW/Gap8wrfRQyY4ZS6H0yIqNEZv0bZ3z9KlxpzIaYyI+Zm37hMZpjS4sIQSarufJi5doCtqm5a2bN3G5p8Mbjh8NMDZvDMCI+Ay/FOanSeLnKatobY0yFZBFfWPCL3KQo+i6hq7f4dye3geePX3CxfuvcO+8x+xoyd077/LF977KenPJ/ccfpmxjyL04CMTBcGVtlYPAbwrMpMkgQu3X9ICSsZB1NU4apVJXS7GkB4DjwKizCjUrsIDaaxyKkECla5DBOF7p72EIFYMRzPDRtIQWpGl42zt6t2a737Pbt0TgS194h7du3+Lm6Smz2WzQSoskxm0GyRGpAWWTcU9GwhQlq5MTZvM53vdUZUksCnzfY43l+MYpMbEce+c4P7/i9fkVxipUjJwer3jx6mwAYyBlYIMYEWtLdLDg0wYUfFqAJnWvE70+ET8X5qVWgRBJ+iEK7yUjWdhiMMxlWeHStAw+0nQtwfX4riU4h1YRHcTYxeBRIVKZitP5CVZBoSOda6mtpvXivLcu0Ha9dOfdO3Zdi/eexWxOZS23Fitc8NjNmqt2x9o1PH99xcOnZ1xcNdT1hi8UM0pboesVqqjxSpNFtI3S1IWlLnVq2xGT/o6hdZFN67hqeor6Fr0LROco8JwuDDePSha1pd97Ls7PuLy8kg6IccwaQgKgyBu6GKtRGyZNcq3QcWwgl9dNLl8fwKGoJsZcXtJGSnoKa6mqmXy3lMl0wYszrkwqDaipVqfoakkXA03TcrFuubg448XLM54/f8Unj55wtdkJIDf4TONCm7jIw9oev096nyY135qu+eRBDohOejX9OLAKMqshb2JpE8naq9npkEztRJdrsrDbdkez37BYLnn5/BlVoQi+x4d3KcxbbJqeXQumqShu3KBYzJmtSsqrjn17Ruc88+UJd97+AierW5xtXlAVNVW1IMsLlFb0iPedo8HR+pam3bPf7hLQFocyJ+ccSglw5FNH06yzqrUZGgFpJeX5KmiOF7dYLk7YXT7h6vxMEkJWoUojf5Ro2DqfmRO5NFaljTNO8elhTPvYj890MLrJ3mbGwfgYh+8i8VAYJF7yLFB6lH8ZJgkMwX+IMZVyxGFTH0g6MRKcY7/e4LUSXdiDoGaYKnK+azUkTOIAACAASURBVCylf/TBBzx68eLAER3nJKmZUcFqseDOyQl93/HJs2cs63q8z4n9l/+P0K9KQY1BUSpNpQ1FoVDW0DrP2WbH89dnaGU4W6+52GxyPJX/NzjxRVkKEGgtV1dXnym5zGDqOLDjpM4AxciKmYz5xGYAA6jBhL2Qy8UOfp8X82QN5/FTk7GZgrcHpYtxLPA8jHfjyMiJHIKxkSEZZ13gvRu3ub28ydHNdyhrgykUulBA1meVpyMlwUgjRCOOcAaVfIj0vcL7zFyRxGnbR5p9x8MXV3z3kyf82j/8bYqZpShTKaDWqADn/9KWXblAec/6bM17dsGNYsmykI71JuqhQUdI3zkHAYUr8E78HqU1hSlZe83lbs96c8nV9jWeFlsKywNlePn6FSdetEN931IZx1Gw1J2naDvi9grrW4w1Sa/cURaa41VJVaohwRWJvLe4OYy6bT0q9hAiyhpwDh0CqgfTRhY6SCU7n+/c/qgdF43nV+7vAfiZuxXvn4x6EH/v4Z5nm/G7/MUv1tyoR/bH3/5ox6YbfaBf+rE5M6t5ufX8+oP98Po7R5Y/+85s+FmZClUfE60E81qDtRpblnjnh8as2mjxl7tubKgRorBZk56aigKQa+TvympKWi6ffsTlk+9jZhoXepQbpcK8H9NBikhwPd1+Sx9nhCDl7wFEx3d5jCoK9pfn0Hco5VBep4ZeU6Bj0vnHaGxZ4bFStkkUrb2Yek6gMCjavjmw6z751zoxdtCKqCOFKQ4qeEDmp9E6gShiu3OjnMHOxmx+krXNdibv84N+YvYZ4mfs0dSZHwLTN3j40lDEJ/BGTfawBLmEkAJYsZu5edRg7xgBjDcydZSSZmn1nJ7ATinwDpUqvXof6ENkj6cNnt4HOudp2pagI7OJTMFxdOB7KU/Rmm17wTOvhTU9q1nefJvT05vM5wuKoiSGHmaXXG4+4fsPf4uzzQU+ydIN/lpUCbDI9p0DYE0HWNVzTlcn3Dw5paqWzOrZ0IBR9iaZ05KDdjg6GtfS9r00WUqSTJNtKw3N1GP87HE4nrLx5c8f7pH53BnMzRPo+qNQn3ktM2QHP+ENj3B6jfSh4XOTk8vv1eGelxPe+Xc5ljuIKd9w2YGAFOPhACUgBCV+IWr0i3U0w5jlLhjj2UcQhek6IV0i/+760xheUp95/3hLk3OPw8GblsMPOj6zfpJ/mP1X+TETCbJMCkPMllmOAmSP6XpS5anWDLZj+HLZ/Uh6qgOgPfHHh7U98ZvEd9KT58QwB7JfJX/LvBwSCcjvjJJmWJ7J+Uk6mlEYmfmc2W+KMMjdDLYuJp8jsX+H6rHJeH4GjIWUuMiJ/ggqDISIiCTfVGBovOd9oDBqYJbn8/tkO0ESV7kpuQCSQfCYIM39eueTZmvec0T3MxKFzKAULkrST75fTrgpTALSq6JI8gMJhFUeoickjsgAWgafyu3VAKTKOpRGVtFke6LRVieySRxMhwCLWfPXoHWRsnISP0nz8qQzHIVdKvItOtlER0fEO0lKxBBTLCVkidwULjNiFWLWBxucbaPSmCxPYQpsWRHVxP7FUe5TqUw48MN81UoIOCoRBhgaXath3aq8r5Ln8BDMj9dQY3Ilg66j9FKWqDCjHck21UhvAokFAzY1DlPpvkRfVg1rVhvxpyMRGxNuEaDzHfvdnhfPn6OcZ3t5Rdd+vkzYjwQYm1yIvIaT6HJIQ68lu1OaZJQMSpcUtkapEqXSV0i7pkgWySPY7Tf0+w3B7SEqnj5/xMuXT9luvszy+C3unNzi61/9Jn3f8uz5E7q4IStWxHQulwKnSMCmTsKydyajxVCokoI1MbDXN+vB31KKIXpXKgXIevx9zMY5rdSo0FZjFzNp8KAt7X5HbOMgdJxXY96DDlm5+fqHzpfW+dEnV1lJc5EI7J3nyavXvD674MHDR3z5/Xf5k9/4Me7dvce8rtFDt1nIIWwuDxoWSEyvGUO9WDFfqqGTe7FYst/t2G42rG7ewHQ90Xv63vH67DUPnzzn+GjJ8dGSqrR07R7vF8M4tvsW13sMJUVRgwu4EFHKo5XochTaUhTSSML5QNf37Js9MSqqqqasSpbzOZCyliGKpocRtmJhJbvh+p7WNXT7Nd4H8E5K3Ahs1pcJUEmN1kxBbUpUuUD5jlYFKAxZ438fFLu253Kz5XK35Wy3Zd103Fj2HM8XHM1nvHtyi8qUlBtDv+7pg+O7Hz5lVpbcOF5y+3SBwlCdBMzSEK0mpCDEas2qNFQ6oEMGH8VYNLuOTRvY9ZrlyYrt2RkWz6qCt44MN/5f5t402Lbtuuv7zWY1e++zT3f71+tJepatxgjbsq0Aoku5cBniokkDhEqRpKgUhKpUhQ9JpZKqfMq3VAWSVKXS0IUkQGIgGJNgIAZikJBlbElI1pPee/e9d/t72t2utWaTD2POtdY+9z7LDk7QerpX5+6z9mrmmmuOMf7jP/5jXlAWsFl0XJ6fs1qtyQLX2bgTc4Z+NKeGid37P4oojZhiqhpMi1znnBiEfiFVWDsEKZItFqC1LIr0DATI9k4E1auiZlpN2ZvPmO3vszFTLlrNdr1huVyy2rR84627vPX2uzx5eiolaOk9jYm18IEGvweL8ueD4yjaRLsOQ152+uOTyw0lY4ZSvWB3l5ldCbSWrKsETT5m4f3YBwBjt31xccrl+WNef+PTnD29z6P777FenLNYrPnkr/sMREXTdWyXHcVp4GC/RFVzJvvXuFwu2DQN+0fXOL5xh4PDm5gHb1OXcybVjOij6AVNrdxLu2HjWpqmZbPesl1t+gRMdhWdc32JUZ4Dl5cLiFnzyeKT7p4KAR0NL7/0EZqm4/L0lOXZicgilAYqA6UmREVZVLTdAuddYhQ+/1mNQTStUvY9DPZDGj/GYU5mZ1UnqYyYM/JJbzg7EVo6vncuO0X96infSRM6szPEFR3APh88q7bh/PwxurRQl6hi0KzKUU8OhvsMRNoEZBxAzN1VXJwzbRV3jo/5oU98gq5rUwXs4NSPt97Nzx2OiZiomWjLnik4KEsmFai64Gy9pdm0fPZj3wNa89V33mG93dI6NwSLfYCken2nRjU7ZY+ZsbQT3MXhinbLDYc1pA8weQ7rZRxQjO5vLPUxDlKG6xgxdNJnV8+984hHx33ePvlYGRQa4s7YH7trpdJiXJqcPMdk75FmRDGKTqESjbAQpawRZB7qKDpq4hfJvEQl576qIAZJMAVPDOKrDOW6+T68NIDITU+17dfx3r2IoQ8eCBHvU3kgkuSz1uB8S9OtcH6DVw4di9SJ17Nt1qy2Sri93lG0Dc2yxbqI6jxh2xJiwJY6NabymKBojQOnsFYSPFHvSE1Sbj3GdcTUWEr5Du091kVMA6bUbHSHQkrXzjajL6ftsM4d1//5budbjw/wzdOO/+T/OgXgP/0tx7x6KE2RzraB/+GfLPjSgy2zQnO2DfyXP3qDX3+noraK823gP/9H55ysPaVRXDSBT94qeWnf8s65HPOo1izbwG9+bcL3v1BxtgnsVxq1dw1dfZyu2Mck7fiirlBFgW87lIZSF9jC8PT8jK5tRCpGWwgOFf2oAkBJ8KYVVsG8soTNKWf3vs7J/W9w8PINAWNj1g/3PS7TMwlXC9rNkk5BSGwoFQWMrfYPKaYzlouVNIdTBqOFjZKbrOX1XZHtsmWyd8g2Me2Inm69xoWt2FkECN1stqnkVm7Fi2FHa2Gq+U4ag2WNQx8GXVa5B51sB70cmjGFrH15UdCDL620RsVUEm5217T4DOiUbZyM0hBg99xDxtZIoehchw8ejRANxqyiELzI78QAYdDRlPVwYBbntS3GIY7pr1FbNqbAhY7oHaFt6dqWbdOy7Tq2zrNVwnbTMTJRcFxWlNZQ2iGJMG9bjG8JtqD1ii5EHm7vcr45w8QDNm7Dhz/0Xbxw+0WOrx9hS4h755yfv8XP/dwXWLktqjAJ0E5+URBQQljIqdQ4wxYRbFTs13tc3z/i5vENDg5vsre3x2RWU2jD9cObGFtwfGSwpkJPAk8fv0/rW1rfCUtbD81rhueW511iGcerqc9nf+5BA/2sD5M1+Hck356zXH0wI3M4YU+G4Ipd43mfyZ2Mj5pt9gBu5v3V8M/e8b/CHlUpSZ2dYUhl1sO87Y/af03sjbWGEGKvC5rZyHJPsl8k6aheua8ehGQAmYc4evg8+yQCygx2PN/iMyA1zx/z5yYudn6ffAyf5SBUYgBnLdCUEImxZ8Nro9FRo5SlMOVQyt/PL2H2iixa6uGCvAc+NSokAfYDABxB6Z69qYniZ2jdr2+9z5vPk4BReadcX3oefKDr3I42q+zDDqV++H7swc2x7z4G7PI19k2ZFWhrJDa88gzGz0HW2uGdys83/xy9SDGE5Ed67yiLSsCydJzc08I7J2ugUqggjFOjMw6jJCnuPZ3raBIBK4+vNpocoemQKiF8WquT3Iz3Tp6l8Sh88l0jQrzNIL3vGZge0YcFqVxpty2KJEGRCC6mqEBZlAarzGjdA0IUX0cZolZYbYhFQeGL1PhN0TQt0QumoQBtCtFqN4WQ37TYmpZI8Jlck/tdDOQTRu9wTHOkn9skDVtbUJUldV1jikpwtDxbetB/0FbPZJ4cO2fSi8w5n+yavNMSPw+Jhd3KE/r5qMfM1zC8U3luFbYYvY+jNQQ5vrU2xZhqAHITKSz3l0KZXncYJeubRmEiKB/ZbB0X5xdsLpc8KivWmyFxfnX7jgBjk2kdQFlrZPGwJbaoKLUlVFDP9inrGc4B3YQosLxktvMECZ7oW5YXD+k2l4RUNouxPFmd8k/f/irVrOC3X7vGbHrIG6+8zqSq2KzX/OzP/11cbKSJjE7XlMocMqgvpQfjcgLIUgWRuCNwnNbIHiDd0SJSw9evZvcUCp3WpdTwTrI7E4upLNOmojlf4LcivJwBh1zOrfqTXGEC9XqzYwcvDtdB9ncFZmi842t33+HuvXf58pd/nk996uP8uk99nFvXbzApJ7QdVPUEyVgNA5LPmQ20zZMVoZlPp3MmkxkHB0dsjo5Ynz7Ft1t8t2W1UTx88BCt7jCpJ7z59rs8efyUl+/M5R4UFLokaANO47eeAkVhK2ozpTYTdBTtqe22IYQtaENVV1R1LbolZYU1Fte1xBiZFFO0MbiupWs7tt0GH6UzIqkczfmOzg0AToghOe0i3m2sMHELBcZUmHKPs2ZLF1sxmEQmWhp5Xb8xxXGDk82KNx8+5OHFKU8vzzmaTXn12m3uzA/YryvmdcXXHr6LVorSaFzr+Hs/+xU+94MR7Ttst6G68QItBSpGCqWYVwrjNsTYJfaqou0CD87WrJ2l3puwvnwKvmN/Zrg9t9zct+xNLXfffov37t7l9OQcjR7KCmSCpeMNAIgxufRtxOjsMabs6AszxhpxODpSCV/I5SHS5dAaS1WVomGDZKAWiwWuc8SUaZtN97h+fI2D/TmxnNDoGuW2LC/WPHl8wqNHj3nw5ISv/dI3Wa62OOfHIiK/3BKU5tbIsBMpSun+jVajMhq1u68aPs5gURxev56Ru8PCG73tPQgbcymcSAL40eVulhecPLrHdHbIa6+9weN7b/H04UNWywVnpxd89I1PcvPWi9y4eZuL00vOTi+kLCR69qZTzh7dA99hi4LD2T5Hs0OuzQ+Z11N85/AUXCy3oANNdHjl2SyXNIsVfttRVjVEKdOQ7q2J6JI1/BLQ5HwQnb7EZFIe8AprJnz/D/1mfvYf/AwP3n+L9eaEpllQXJsTS403EaOlRCQvtkVZ7ojxhyidufMY5s/n8zlt2wqjy/sh+EnGczqZcLFYJpYqAzsq5g6aopeVS0uzRnaeLtnByI78rpM+PEstB4LUMV7Ky2xyeoU9EEYBB+R1djT/9O7cgCGokSy14rOf+AQvXLvOdpuNukpB++g4u9O671yuo2YPzTVdsm9L5pVFseH0cs1m09I2HaYoiRE+8dprvHT9Oj/5hc/n4aIHt2Eoe1XixNiUvJKg6gr48JwgZgx4Pm+/Pki4Csb3TnV25ActuqvbVefr6p98zhBGyHt89tzPbiMwJQV9wXe4dkvTpEZD7MSmO2Cy1lrkhlAJZNWpuy69o4oxab7nTsbyc1FYprOpOMneC0tOa0KSO2E07l3rRP/KOYLrZC3DpHPIPuv1Gm0MRVmCNmw3K8qqRhtDCB22UFy/cZ3pvOL8csr7D+7y9PQenXMoZbBFwfHhMbOixjaOzYO7cL7udStX6zWT6QTnWohSNqm1pWmh85JonkyKxJAc3NEKy14whCYSHi8plMGaJOgQFbYEZpayNpxvA7/tz967GqvzU3/wBV6Y//N3cf/A//qI9y/dcy1QF+B3/Pn7bFzkRz485T/6TUd87k/f44/+jSf8/k/u8W/8un1+5M/dJwJ/7DMH/ObXJvzev/iQ3/O/POQ//twxrxxYrIaf/AMv8B/+7RMA1l3kX/xz9/jvftctuttTVvomdA17BGqjqI2mXa9YLy5pmgalFHsHBzTrtTQ3ihFp+uEhtICXbsekoDpEShO5cTzlyVe/wHrxAHSDqivGzaVkGuueSUPwuOU5yndE19E1HW4a0MqzeHyPs8cPibaiqKbUdU3UjuXqktg2ZEkuFeUdylwZTaQNHkzJer2iXa9QzuUVm4josC826x7wAcBatC4wukArS3QORye+txr0iduukeSjEoCuS0G50pppWabGPKYH/XupJrlh+Tv5ASE1J8ks1ZB+n0s/r9qFD1p/pADQ40PDtnNM9B7ZFumk1RdHAO54vdNKiRSCVkQ/dGE32vT7xxg5Wyz4xsO3WLktHrEhBTrdq6HUmiMie0YxU5EZnmlYE1to7ZbteAiCIgaF14Z129F5xyqe8MWLv0Sx1Hz85Lfy0de+m4/8CzN+4Pu+j8//7Jf56te/yr2Tx+japiqikauVmnv2sc6OTRbgqy4nVOVE2GFeo0NBdAbfaepyH+/BaktVRcp6xnbrpTIweDCGLJF09QlE6CtMxp/1/z9a7/vy/gS+RBUTE1vGsNfpVbFnBn4Q8Hp1GwOIarTs/3Je7hisIPnh8rnuf58j8azDPHx5OG8Yg7lqFxS+er5MPMpVp7Jb7HX0Jak3rBf9uZ4Hju74ZCPgdTTmWuvez8oIc77v5w3tkJB4Fqx+9vNvv8UgdjcC2gySSrk5UiZg5JvJ+JLDpRL2HCvLnPHejfCBUWQfhyOY1KjO5uSQHpI6AqrGAZRK/kTmg4WsM+q9NMGKAecSeNg3tVIJgKQ/f2GE7FSW0ii7T4ekF1VrTdd1ZO3sPJZxtI+s5/nfakgQjXz+DPBeeWjkqkVhRMpzn5jJ4MbFCLGkKm3CPXTCbmBS1Xgv8X2TbIVIEaRGU1oRXIErS4zRWB3pGk3XNHRNIwnr0ZpaFLbHf5SCdrth5VfkfkCFLbBmYMcqJViMD4OGcggeZeRd1AjpMBNMdLrX+eE1tCpRFKJboCKuE31TjcKqQmxX/64Ie9aWJXVUdK3EsC71xPEe2qJJ74XMTWstIZZ4rfu+TSbL86mA0WCLUcPwCNhI56TpmWjGhhEcF0B76kndA7Z5DoxJHPP5vG/A3LouP9mdcQ4BOtfRtk2al/IS5KRGjGndyjhFFEmsvE/TNkKoS3O4qiqKoiAnjnuXfryeJFmhfENGm75PXf7QB0+XwWsjzfam9ZRSFVSqYrva4rYdi0VD131wj5B//p4qyIuZdTusZTKpMJUVLauiotQlLga0lc6phdZ0TcAg3eqSkrw4eO2S9fqUZvWEkDLqSol+xcYE7j55H/v1yPe89iqvfPh7mFZ7vHT7Dr/1N/xW1s2Cb9z9Jc6Wp/jYyXWFmAJqhdGxX9FjFMcnhIDSA6sHxZD5iZKtyMxAKSfK4Eu69wionIUd8uCD1GTKTkQprY9AMSnQZp/oAqH1uOWG0LZi9NN3shabrHN65HANoOv4InYyoulj78Vd9C7SXDacf/EXePPtd3j1hdt81+sf4vBgnxde/BBlNRG0OmWO8nVkp7LzDh2Eop+zFABozWTvgNLWtJsl68Upk8kFzbLl5PETFhcXOKkmGsCpCKG1RKfQ0VCoirndY1JOUTEFuVEctqqWcsrOeYbmDxCcY9u2IjmQAJ+ggCjAqw8ej2brOpbNhsvNmifrS87bFS5mB0pK3VxazCtrOC73mBvNzFpm1jDZm8FGDGoIHh/kuVgipbVU+/tU1vL+ySmnywX3Ls5xRF48OqK2JS/MjzhfrzjbLqREkEjEY1VL2J7Q+DUhNFTHL+OUxSpNaSOr9RroEiukxNGxWHd0ZoaazFktHjEvPUd15Hiq2J9OePzwHvffvcvJo4cQA1aPF0uZGx27QI8EFlkDbch8ygKanr5PZSw5m2FB6wJrbOqIKOyRrMvTNFvaruu7a0739pkfHHF4dMyN6zeorOLuo3PWixYfN1yuNnzly1/n9OSEzWZLWddst+0QeCmGt2lk08fOHZA6jmaPLVCWhYBqWg1lxc9zENUuqCba0iqBGYGyrDBamLtXEyPBXy2xTUGUFgZk3pxrWS/PuffOm0wnM2xRUNcTuu2W00fv8LVmzYP7t7n14qu88tobHBxcJ8bAdr1gdfkE5xqa7QLnLL7ruH58g/neIUU5wXXCCO8SKNWaQOe2bM7P6FYbjJIsZwypkV8ai4P9A9p2SwiB6XTKptmgnTAmtDE06y3dquVofpuXXvoYZ6stZyePWC5O6PwGM6mpDw6xswJdaTCR04tzooqUVcVsNqNpGpqmGcq80jPIRt07n4ybEsNqLYvlcpR5DqIBpzWqKGT9HOkZk+Z21zmsGVgD3rf98zVGS7lTYXvnPjMI8vQawY7yHZtKZvsgQ6oo+tJRVCqlGgIhOZasUbkBSL8iJ2f6t3//D3C0fyCaiOGDy7Pz90yIlFGjXMREqLTleDKnJqCdY3OxZuOXXHoIWPaLWhJYRhj3R9MZv+Mzn+Gnv/Qltl2XkuIih3J8fAxKcXJ6QiR3lN19R9JwyT31ns7wtlx9n3YYslcC7CHaHGzc+ETjRGN24voAaPTn2WMP4KvoAD8bgF1lx45mkHzmA75paTYb2maDMSrZX1JZpkpSRZGApphMsbVGGUNE1j4dkO7m6Zgha2xHiAjTIgaXAh2TAhmPijpV04z/yN8Xi3NevH6Eih7fNmhdig/VMwlgMhW9YaU1VVXi/R5d13J2+pSHj9+nCxcUEy1VLQqqagpqiTLSLGR/7xhLSVx3uOUStdgSOidNSaxhuj9lPpuhjeg7FmXF4fU76LJC2UISGMlPmcz3+zGd3HqdbbMmtC2+WeOaNb5r8VG0RPEaW1pslUvK5Z5//GMzftuHpvy7P/WEf+evP+bf/r4DfuyNGSFG/vBffdyX+pdG8ad//BalUfzMOxv+5BeGRmC/67tm/MiHp/zRv/EEgH/9U3P+pY/t8f92+5M/eoPOR9457/gTf+vkmd8P78PuO5Gn3XiuqdF38ucuwB/6iUc8WDiUgj/yvz/mf/zdt3nt0PItpDqjqGumVUVhLCpqggevCkxlIcLFckvTOYJvEfEsjWTTHNo32NihtMEFD0ESvwrNyXvv4IKnOjoEk+RkEpiilEhh9PprIdCs1wQfaHzHqt2ggkKpAmPkAUbfcnD0Irqa027XdE+fphT+AC/GHPpHReg864tTfIAYPDoIUzOLI3gCW9eJJNSY8R5E8sVo0W001iTgQALIvL6qHPcrdiRK8qrdV8ZFUqyR3vcMUiVAxXnfJyldSgxqrZlOp6l6RvWBqiQDY/LjxS6M8BsiYG2FUhZrHMZaNts1RLHlpdH44PtGJDFJIJVlYknpEfDBLqiXtyp6bltNB0QlY2qQhshEST4eENjzgSrpMmpl0r7DOJfTOZPqNmpvzgMdWT98QNc/HWFUfnPxBe6/+WW+9KTmm7/0i7z9ztvcf/qYTntM0lPsAQME2MuNMEfhioxMjJTKUumCUhUYJBq3JZgizYggDDrpUt7StBsuFgupokLtjMNo2Hfey3HFRX9udRUcTveZ5PNCjIkckAAkJW+aSYw/n3WRR0e96qf2nz1vUwN8PNgstfOdMRt6qGoUf5TeRo7i0Rwnjn1lJSJoIPYtNxPzIe6sYTva8UqleR/TUKmBCTkC4PpmKkPYMSx2V257zI7M9xbD0I09+wG9vvQI5COO2MjP2Z4Hwo6Tux/4PSlWIYRBp7WPMUNMwCl9LE4cksHbTUNruv6aVYpFBLgyvU6rSXMnogje9QC/TWXXco/J1/VSrReiE4mRVHKfn1NhDT4M2tbWFmhbiA62yY3ZfH+92RfXRnzV3NvBaIPJzyFI82rBOTIoPCS8c9VZZlyOpsjghzH4vbqfR4MdEIm0IMQ5VJItTPM57aO1TsByFGlCnWPUmDAngzVxFH+agbltFDoodGEoJpUw240mGI1zTZ8gN1rTxRQfIGtTWRpJwHnf/8na0M7nyoo8b0VOQUsjn+SfWpQKQ2JNKbSJBET/PLNltRGQl5HUQ4ipAXLqDRCSXJz2EVsUwkBN8gN0HUqLXIHSGZ+S56C1xCtts5V3h2R3lcaNZQNUqvBEqgTbrqNQCh8czkujbB1isllpTo2apuW5K8QehIhjbFqTVP88iSStXU1ZFP196uT7a21GMYL82JNzEpYxi7NE2gkJVxvAYJ0kESSBkCvSFEbbxLgW5nePdaR3JTdx7nWY5SUBH8CDtYayKFFeo7zfWUevbt8RYKxWir35HsaUKFNIwFAo0Ba0RamCoteDFUOgTWKBpgV526yJzZquWdJsLwiuISZqP0pjCku0ikWz4r3H9/jiz3+ByWTO9Ogmup5y59ZNPv3x70WryLsP3ubx2UOatFgEUcN/TlA2MibQB/fkS4058yVOgA5jps7wXIasYOy/qlJA3i9CfXlRylxaI1mcxMYMG41v2pTN8dpfqQAAIABJREFU2M2My/lSSYEaAvz+InvfIQ7oQswXIYtBF+BitcW5js22Yb3e8MoLt5nNjjk8MlT1RMqDe2nO4bjeCbVbay+Llh4WV60Ntqx7sPq6D4CmaxvRj4zg2qYvMQNQ0RA7uc+yLJkWM4wuknEPmEIafjjvIXVqVEDXtql8xEAMYrgTyzUL/7sYaL3jdLPhZLNg0W1ZdlsWbUMTWuJogBrf0XSNCJprxarbMtGaqbHMbcGsTFq/siLsDLMOwho5qCe4g0MBgc5Pudys2J/U2Imm0iVH030W7TItwmJkv/nuI25cP+DgwIPSFOUMXe9ja2k8oa1NWTW584vlJYGIJ/YJipkJ7BWKaamwBh7ef8DlxQVdK83JZKHLGKo4kiaDlYIsDc7njoMnzz4nJHwC8UBRFJbCygJutAYdiV6lDHAgxI6uc/hklOpqwiuvfojZ3gHT2ZS6nvDwyTmn5xvW6xWb7Zpf+ubb3H3vHtZaqrJksVgKEBvH8/zbbGr4f6WRrpelaFT3AKra3Xdg0F7Z4uBU5P2UHqQ85BC75dP5pRv+eQUwUpEQOjarM06fPuTatWtUdc3J44d0zYqL00d0XUPnWyKBGzdfYVLXaBWpywIzKTFa0WzWuG7LZDIV8XuUNBGzpSQgVMQrcC6wulziu46yqpKho2eFw0h0PQZpquZ9cgSloUZ0ARVLjo9f5LXXP85bb91lefkU161QKlJMJ+jKYsuCqi6YzCouLi9EPyllMTNIQ782DobTGitBc+qYqlP0a5LTE8jMAi8svaiQpmkDaNc7L8kp0EqJ/nOOl8igawInxgFD/9RGDz4FLhkoyGVNwzoeR8ceaaqOJ6JSO9rhKMV8MuGV27c52t/HWvPMnBuXpisUKgRUCBgXqJVGO2EVF8qjdEvrWtrQEXFsCXRI4xlCg0XKsKLWeKM42puL7cjOk0xk1omZG4Jkw8MIqBgncPI0TkVav5wvMprzySns7dUwJhn5uPpeq9Ex1OhYV4PQ/PNV5m5mZMS4e7zdgY6jZybXFlXS4eocvnME5z/g22M96NRNe6fpWS7d0nLMviw7BZjBQQKL+qZ/MaJj7lIfkM4O4zMGYSYaSSgZ36Ft2Z9LASY1l0MNjAWV5rprGxbbC9Q2CmtDK2w5YW9vT5q4VRUv3HyF5uKCdrOm3K4plKY+PmY2qanKAgi4rkEbAceLsiDoSFDSeVhneYIYd9RfWyxe16iqpCqnFPWGZrPAtxvRldSGoCL+yox678Lxj+8LL+8zL9a8OLc8WXl+4utLvvq45YdfrqmM4qffWvPf//wlv/ONGTdnhs+8WPPnf3EBwN95e8OTlecbJx3/8sf3eGnf8nTt+StfXwLwuVcnfPRa+bwZ8tzt9aMiPY9f++3O3PJvflpA7L/11hqj4De+OuG7rhd98tkoTWEjZWr2BhIrxOSXhBBpujYlIzoUHqKRcs8IioAKLTYFfFYLMWfx+D7rsyeoyosPYi0xqh7szyWOKFmTgnds1ltcABdCYpOIHqhCfKIYI5v1isOjm9jplNXlKeHyBBVd8tli757KmEZwLjUqGX6X2z92IbDtWlonchZ5CzH2kjrCXrK07YidGId3UqWGoiA2QakkW5T3TfbcJ6Z6hsRyp+3Ou95/1YklB6RmlXHQcUzPKzNbYxTQwaRzZFAis+1igDZ06BgTOJPAH+KosU0QsC+vg9lBSVsP3439jRgxMTDxjto7tPJSdZdByJiAZCJFZkEpTTRW2IB20ELelr8TXyzR1EQfeOPgN3Bz5thGknZFumelKDrL/P5NXt1+ihvFlu2hwxhF1COQEXZBvtFcEJ8vMqXk5uZl1OObXKyvsS4r1rOJ6Cwq8J3oNXrvadoDumXNi5sJZXnKar5JzNjBH4u7Z+GD1vcBjB3vl/yW9GMGvbK/EsmxJAnUiNwx3z16FB+8aowjvHyNQ9pz93pVtpsfaIOHeTH8/RxAksyc3Y1zx7Z+ENFX5FK5Z24jsnOKfrSTfxR3DHHaMX30vGqX4fNdH+SDEqtXgdirbNvnbb+iWCKKTIEPEeeGBlrjCqvY+5UjHyWNR8wl4QzAoeDkI/8F+nfcB9/v731uOGiT1GMfifVjY7ROZftyLKlcSHP3SpO53Oci/wcJiI8xVe9laQIIytFz/hTJxx7G7Wrl0sCCZecZDnMu/TtVWmTwOIbY682qBIyFxIJ0Me58Xfz6EU40OKPDeq2k/D2oiFc+T2Wp8nLy76gUGC2xUjB4r1Aqa5GqnpCUn3+SW8dog9chJSjT+q5SdXWSJhFZS5XA7lR2rwxKG4wyA9hoYuqXotMzU1iVwFAFAS/6rak0X+ZAmtPGYrUkXZuNNMAOCZBMkM2QXNSSmFRBkojKaBmH9E4LkEy6F53mZujnWIgRHQSA1jrpyyYZR+cl+aSi2ECV5kXnXErwjOdKriSPPfgZo2j9hiQhZIwRomP6nvj9OgG8+ZmMJHqICfuhf+921g8QgDUMzcRkfmt0Av1VqkhjFDNC6JPOXZfxN1n7ohLJRm002u7a3qvbdwYYqxXz+T6mnKBMQRccnkBIQW1Q0jk9eghOaNZKGcYs0+3mDL9Z4Ns1rluTS8NzoGEKi7KKxnU8uTzjH33x89y+dps7r245vHmbg2vX+ORHP4YJnllpoWt5uLqgCb4XFs9NZHoE3MehAVE2hEknKm+5rENFxKmII2cPyH/H3MQrGU3NSKcxBfl5wuVFJDszZl73bBzXJOPn82KWshI656Kz0Qk7kxSyTVVDt/mky6HT9UZlWLWB9ukF5xdL1uuGg8Nb+ABHx4fUkwkxyTgwoqp773GdS/c1kTKj5LCTxstWNUVZUlc12miWi0s2mw1t06YO7cNmKdDBY5Wl1jWVrZN0gIxtWVU0qWzZey96MMbSNlu6rsNaI0BjNtipdCSgaIJn4RruXjzh/uKEdWzpdMSYkqoq0MrIswkR3wYaD53v2HSeFoeOikIpJsZwo5yKjpaSJhK5g6Q42eIoF8ZyfX5AWZSEELh/8oTldkNtCuq6Yr+eYtNChZJS42+89ZDWebTR7IVIVz6hVAYznYpcQVlDMCgiPghDCrNPiB3t1lEoz7zw7JUFdaFpuy0PHzxgvVpBEFF0ySbmMYIYfc9GUHHIqOc5PjiW9M6GOAiCzmujqIoivbcAoS9Dz6Xjwcl7nbOydTXhpRdfwVZTArDZbnjzvVMuTp6yWlxyfn7Gl37uF3AKXnzhBWZ7+zx49DgFgCPDnLZnGAW9z6h6QEtrRVUXKJ1ExXMWuQ+ysrOX7j9CLxAfBxc+azuJrAOptCuzDhgZGHkr9diLj5ExwiYAScC1a04f3+f69ZvM9vZZXC5pViu27QVdt2XTrFmsZFyOj65zeDCnKmA2nbPdbFkvLunaDfWkJLOWdMqEu1a6XnoTca1ns1zRuY6iKokoDEacvwRkrdfrBHoGtu0WawuKUsxJ1zlc65hObnJ8/SWuXX+Jv/vTf4vN8oTgW7Q1VPMJugBjFGVRsD+fs1wtiGm92GzWoo25E2DQA2nSFV4NjQCQR14YS6Dr51QGWkla3tYKg6Dv4JqynUonzV83aAxDkjJgKBXv2ZfPGNX0+1FkGHPwqob1Ns8VqRCIz7HNo7tVMClLbh4f86mPfKR3VuR3I02uZB+Sug7KRZTzlC5QaYsJyLno2LYLXNcQCSir6AorgEzn8G1LMasprSFoYcJvgflkJkmx4ERcPwQuLi/S1NeU2vQsh9Es3gmadO84Z+dqd35fHYMhhn2WyXr12KMPdwKzXtv3OUHU83RrR8O+ezX9yz7iKyeHPmaQwgdiJ07ucEkyB3Sm1uV7Sc8rnyg7l8KKVn0CVyHNAqJ3RN9CCBhE/sIkEE3HgCY71lmnVrayKimqSjrwBpFSyHY5l3KhJKGrtCY309BaUxYVe3tztu6SrVvTbrc433B8o6auJiglbPRrR9e4++ARcb2iCh2T6ZSja4dMaplHmsDjxw+SzKOmcQG/usQr0EVJUdUCxipFWw+NpxoXaANYbSjLiqKsUlkf4BSqKHC+xV95Wm+edtxfSFj4Ix+Z8uHjgncvOv7UFy7ksw9P2a80/8e31vxX//iC771V8sMvT3hx3/L37264v3B86UHDLzxseHnf8m/9+n1u71m+edryE19bAfChw+JXBcb+f7m9tG/54z94wPuXjq88brBa8aMfnfL+pePWTHxeoxRWq1RKHwjBpUS1IkSFC5HWeymjxqGjSC+FkIL2CDF4TGzxGMrCUJvI2XvfpF2dU5UzdFFgioIY6DXulBINT5QidK3o72+2tNrQJTDW4TEJXMsB9+LilP0XX6aeH7B34xarZo1yW/BdAjUzgChjIKfIgZsUXgUULkIXIk0nTVPH60AOlq2xqVt4Qdu1Q8Csteg9alBRpUaw/clGrBq5iJz81zGvDYOmtfOOQOpAnsoYtZGEoncCKvTJqhSvKTRBZU1UjU3nM9r0sg8OSYrqQvzbDHAEQiZjopUWXcCkOT34bFfWzhFWogAdA4Xr0K6jUEmPcLQ+2igxhZIsDUoX6KqmKC2+rPpjrcvfIz8kF/5TR99mQrdAnf78s2xr+XP2K9r5Q7zOD/D6r8V5f423PqE7elZDvKZ6/1z+vQvaDRBDmrg9ppkZ1yPb2JsoNTYhO6vrrhVNYgW9n5oT4rvzOB8+2+IeEI5XfKk+WEz3Nzpxfu1gAOSiGNZ+zYBEVslNj8aN0Xa2EWB+9R3g2X//qmUK0nd8kF4MJFaeTuXv2f6HPv5OHeIT0DZcR2Z5pnc62WaFwiuJrZyTBpfGGGmYnHzUUoFRRT+uSuee8hpVGApjRs8m9vcpsgCCLbguAWIpURQz8TCBTrIMht5PdjHHfMnfyyBXmhNXk/WCz+QHMTRk/SCAPabgsj9OjBSp/wMgsclI1ixveZ1+lhkux7LWSpw8foKJEJIZkgGpnI2JPapU3HmltJI4hgSu5mcski6JmRwGvEWSe6pntCoEo8hzWZpKCVtXaWEGayPj2IO/SiW5lCGeMEoT0lhaa/v7B4imSLbO0jVtItO4Pu7JSlhKSWWfCqm/jy36GF6RKrRDTAnXnFRIsb8M7OBbprHMvoDEU1H82NQUK4SQGkIPYGxeG4YQQcr/M56TNWSLosAYTYii4atIoLZJmrJa9/MlP+8sRzcma/QxIiKhRcIvAhHXeTKhRptMSkoyfEpLPwNFqrSIEEXqKBgnoK0LmFL3ceA47rm6fUeAsSiN1zZ1B+xE6kIKX1BKY7VBBelU3W5azs8vmJiqz8ooDX57QdcsCFkvShlCesWUBl1oTJTSuojjrYfv8Vf+5k/wuc/9Fr7bfBL8mr3pNX79x7+XV196ldde+Sh/7e/8NA+WD+ncFm0CKnZom7IVipQB8enFoF8wcgc3IM3HIUMzWJbdRSN/NCwmcee3GexltKCB+FBeQTEtqCuD7zpWFwtoTNIhkv2cj2g98rjGw9+fbzdfaNTA6IrZWmtDQ6TpAl956x53H/wUL925xkc//DK/8Yc/y97eET3rKxmUsWj2bDaT4DNGdFpLg9yQGKZ6zo2XPsxsvWS5umBx/oRbN6+zvz/vr2tmZhwdHlGqEkuRSuH9zos2n81wztG0LZvNOgnoR4pSkStE8iIZokNhWCt4slnw7skj3jl9wMZ4GVtV8OLxda7NDlM5lqa0JWeLM042Zyy2S1bbDW3SQvXasLGa97o1J+2aY1tyraiZmqHkQqBfQ/Se2hYU0xm1LdisVzRty8o2HEzm7NmSUhm2oaNznlILTf9bd5/w8Oklv+kzb+AWj0U7zQTW84r57IiyqCAEvG9ZNJ5Ye2LbErZbjqdwPKs5PJhiS8O3vvVLnJ+fghO9uOADUQmLWRYaYQvq9JyIQ1ly7liv+lIrl1iusWcwWivMk8LapFXjcU4WVmksI3o9lam5fv0mtjQ02w2PHzzk5PETuvoWTSzYrFtOT8/4xV/8Mvfv3eP09JQQ4cXXXmE+3yeGyPn5pQBoI2dvZ65fMcqkLr1o0FY0DKOOON/JG6gTmwFhcPVBVt/haaSZq3fPF4GmaQbc5YqjV1VVPx7Re0whBsp1Mj7D+5mSJsGxXJ3w7t23uPPi63zsk9/PF//h32S5OCHgKdantG5F16w5ebTHdDplPp9S1TNc27BZL1mtz7hz41VMJULvQRuiF6DS60CrHK7d0q4amlWDt16eX1VhRmCa915Khknav8bQdi3BR2IHzaLl0z/8fcxmx3ztK19m+fgt2s0lWkeqWc3e8ZRGOVxoWa4d225FVZcCDMaISyzAPmE0yq7nUhI1MrYKAQknkwmxlQYnIQSKokjrpKwR3idid8zPUOG8J3QyZ4R5Kk5YQlNH80btOHPpyYyC8l04Uo8ccQg77H6g7+Y5npvDui739L0f/Siv3bnTHzn08yGt2FFmoIlQNB7TRbQPmBCpgVKHpGMoY3K6vkSXFlNVFFWFBprFAqVgUpfU9QwDbLqOJjrq0vK7f+Az/MOvf50379+ji1I+lTt4ByKb7bZ3vsfOxnis5vM5Mca+kWIGJp8HtOYhFHv5LGvilwugdh3+uPPneSzZftyH0w4B6+is2XZn8y1AbPquGRIs0m11SEypxHBVOdDNmpL9nBnfi7ANlJJOvFIl0OFdR+g24vTbAltUEuB4+mYSKg7shnwfd26/wN7eAbacSKM+n5tNNHTO41yLNpZ6kjQ6SYleFNPZjDeOP8kr7YdZri45vzzh0dN7nJ6csFxeoFRgUpUsLy+Y+cBeqZiXe9y69SIexWa94PLiEtyWLii2mw3bzYbNes3Na4e07YayLpnt7xED1JMaDgaZgllpWV0uWS8XnK8XTOsarSB4R9N21PMZVTmhPJ/tPMvf+z17/O7vnvFjf+EBf/ivPuZPfPaQT9+p+HbbfqX5a//aHf7Vv/yQrz3tuDO3/PXff6f//UeOS37yD7zwbY/z//cWY8QF+H1/6SHrTub1j/2FBwD8mR+/hb0TqKKj0iXbzZZVWEvgpQvKuqZ1kS42tJ0DWoTNAWK0kjyMVnht2WCxRclkv2A/LnjznX+CNo7pwYS9g32iLlE2BYJKAlqTAv/WO5quRRPZBsfaKbaupfEtpZnKu6XEx9XNkve+/EVmxzd59aOfpL04o1ucinSAyjyeMXqYWfc5qSrvWIihbwYSrrzzgdg36Y0g/kdRSWAakiSa9/L9kErJlRYN+FT+WFUTsZve41yHCw4T9eD3Jh9BGy0sp8SIzeWaSilsVUBMlUHe0bZbyrIU0DWVz/aAQgpsM2AciWy7Bu1KSiOJfh88RoEpJKDXSlEUJQPeJUFj8HmdTKDclXll0VTKoFVBkf2bvIYphTUia1KUNUVVU0/mmKJEaTj3h1x0z4JYv0pc659tU8/9sd++7aX8Wl/r1Yv4FR4/DzkMidtsmcZSGeKvXGEfkiO6AZjM1S07QCxJgx1AaakuyvFevtD0Yw+7KHaA1Xwd46+EEEbXni4+JcaVEfLFEFlKDC3+3IANXx2nHtTobfmuPR8aR+XrUv117iZuP3jMfzUA7DjGGKx5suMJdDNaU5Yl3ifiTw9OjS22gHaDTxT7y4wxoqKnbVMTryi+pPMdVVlRW0uZiUx61FQrQvDSfyMmqUYg9XzYJQKEODS1zb7ZAGLF3fdJSY+A3AsmX3MgxUZJfkLnNUyZHvAa7m9g58Y4AGK50dn4XOPnlqvzYo4vrd3ZRymV1uOkpdr3tRhi1L6k/ErjOPHPFMYK8Nd1He22QWlDjJ1IzTg36IJHku52IPrQ4x7j1zAzJvsHAuK7ZfkApVDWprgyJtMhlU4+SVBorVFOoU2QpGcpxEQXOmIc7ju/lzGaPkmSW53ElPCW5LyhdCXOdXgnpLUYgvix6dlIQl7jlUpxbwQ0NsYdFmsmEYbgiEaD0ZRlwbSqKKuaop4kuzCSERjNBZvmrtKatpMeB9lXz2ufSfNMGxkHN1qTfJpvzyQX8/xJY56rdAT4HUBqM5rDAgxL4z2VEj11VUsyNTXljdBLQGilEwkoCJ6jInVVUtfSYDdGAZp9FwhOpILst8wz15i37wgwVmlDUdTyogSPBjabNZ2TLnVGS2mda1t812JjoN0sCKET4FNB7Lp0LFmMtVIQZNCLsqCcVAQcEVmUQlHwrYf36f7Bz/Dew/t87rO/kTt3FHuHN7hz+0XmRzc5vvkqf/8Lf49vvftLPDx9D1VE8IGYK/57tH8ATJzzSdul937IdPQQAxhFtjZ5Cc8d1/PeeRvKLvTIZOVmCPJv3RtJhaoqirqiLgxxKzp2vunwTZso4UNnOO8Tg1dlpzs5eP05+6sQ50+rYTFJzubWR5rtmou7K95+eI9vvv0un/nUp3j15Ve4dv0GZTXDRxGAlqRCXox1hpbzGZLToNL1GGnWNplxMD9gcXJC7q6ulOLm3k22yyYJyUaarqGeTKjqShYG79ms21QiH7CFTgBdglmiXEMXQ9Ly8sTa8Nb5Yx5cnvF4fcGmUoSoOZruc23vkJvVIbaFtutoYyRYh9UFB/U+la2Z1Q2nl+esNit8iFhdYUzJOnREPD603AmaiS367JGSlpRAxGrDvKp49eYL3Hv6iLbtuNyuqbTmaDbj6XbBYrNmUhR0Xjppny/W/OTP/CKlUvzQ930PrxnHuXbsTz9GnNZEpdh4RasmGAyajlp3HEwKqolltbrk6aMl7731FkVKIfRdArNDpEQ303VJVDvpdVVViUI69wrwKt0JfWFx3tN5T5GaGem00DXNVjRbMoCmpWlXXdZMJ3vcuHmHazdv4b1jeXlOt2l453HL+epNnjx5yjvvfIu33vkWq82azjmCEnbLndu32W62PHz8sBcdf2aNuWLUhREOKIUpDUVp+yxh07Xp3cjJCJUCPcmWyfuQtQoTYKeePV/PuBu/2SnzF4m0bdsfI2pFsVdR7k1pFmvUSDM2IrrU9bSmcR3n5++hbeDwxjVeeu27eOebX+X87BGL1QXLxTmHhxfM9vaZTfdYXNQoUyMlkx1t10lgGTV4ebbEQDSRaANBNSzPH+HbLUYpirLAOcd6vWHQmUuOthFjWpQFVhs6L4xYt3W8+sp3c+vGy5w9PeOrP/95luf3Ca5DzwrCRLH0a6ZJrzKmYLpzIqYhwXPoy1iU1pRJg9c7J85EWVKVJecXF/26hoLNdosxmqoo8XHIiso8Nr3jMX5OVimq2R5VWWFtwcnZKdOpAASr5XLHuzKJ2dQ0zQ7wN7ji2fgPTRvatu0r0gcHVNjn4UoA1T/zCL/jh3+IebqOsT8c88sZI8ZFbBcoWk/RRWmyoiSZaY2M67ZtabvUFdZK922rNcZ51heXeO+pZxOmVS2MaCKUhqqyHJmKNgaqEFGdJ+JRZdGzOFXWEOvnN/2FjsHP5XJJ/nVf8jt6J58bAPWvwC4Imx3x5zpfeZ/8NEbP6INYssQ4YjSn4ww4vNiNPI9ysDcG6rUCowkq0rjU+T05Z1fh1tFJZVV55pcKpQq0clKFoRxaRXyzAl0JwJ+qMwQXCigXpIxKh53kwa1btynLmohBFYbo5N2y1jIpa9pGCaM96Z11bUvXOWmkWBQYUzKdFNTVHvPZMQd71/knX/k8W7VCGU9ZF1w73mfSeSap39O9+084e/oUHTtUcLTNGoLCdV0q19Pcu39B8B1784jWU5rNCuYN/qhv+8PZ+2+y3q6lUzuBuNnSOAEeXdSEjaPam4L99kDrr2S72Hr+lb/8kMcrsR8PFo4f+fP3+TM/fos73wFNwD5o+8VHLf/B3z7hf/o9t/nP/sEZVsO/98OH/L6/+BAAFVtsXECjQZcYVfT+aRcUWxdoWkfcnqHaS/ECsqYbCkLuIm1x0XM0nxA3Tzh5+HUWJ+9xeOca5d6coA0SrwRi9H2iSWkrczN63HYDBFoU2xhZecd5s2Kyf4D2CPtWeQplUW1Le/KYu92XuPXiy5z4LVvX4oPDaJW5n32So3NDg80sraSVQXs9NAka+bVBkYDb7FMHaeqaewZ4T+daVEB0WMvMhI4JDFF99UyIkpgM+Z3OKTOV5AyC6Oq1rTSM3W42wlgtCmb1XroJubqma3DeUZUVVVlTleV4SZVqHT80ATnYm/dsHpTGapvYswkAUarXpu+6rpdSEBZzIFOi1PhvpZhMphSHR+jQYrXGFlUiZ4jElNEKa3Vi/hmKokIrjfeeQz7PvPinRGOJSuM0nIeW//OdN/nicslGIYoqMXUmT8x8lWKmbCvz09JjVu4oAQvJjpqR3mmIvH54h0+8+HFuzq+zV1TsHVa89PqLQGS72XJw8zr/8P/+Io8ePxHW9bzmclqzILLuOrbrBU/v3aVZXuDbFhWHpAI9+Kfy/xgm4jDHtLWU1UTIO1nvM49wFFAuuC51oZf54xNbPd0YAC3r0UjIOaSpp0oapGMDIvHTjkmJvSXsxyumy+1BtJDlOZ5vU3eMOuxq36b5ohjZy53T52Qovc8iTLw4vqxRaJkYnmGnTZj8/ZykKzCwEUnN8NSVa+ljdYlfcnzzvG3wF3av61e2DUCoAIFFD3pvNpsETkpzcqXo5UNUhsxHvmrGkXMTMFRmxWfAOxBCJX5tAiA3W1lXMrNS8IguVfjJMzDG9mM2gK/DfZsrACtKJOr6kvfkg0eCAIoRUJrCWipT7vhY0YfE6B0NYh8vSRw+ntox+pQoCn2fgR5ADQFbFD1om/W/XdcN4wcJnJWm4crY4UGn00rDxUwE0AKW5ea9qZrRRJF6sFqiZmKUhshpnrutyAOmJRfllZSjp1txIY/pILc1juZiFNa06f1fTf96ZK1H5Hgp4kz6sSaB8B5rlIwHch3yHANGF/0amSuP85B37aAhHgmQbFNuEhyi76UpUKkquiix6XpdIhr0euqjBVCnWCfEgNZWNHNDRIseTNI5lnk5orzuVJiUtqAwtl/9VcD2AAAgAElEQVRuxgiR1jLHKCtJQDt3JXZQqTokyVb4XTYyyDtdVZVIJrjdJmzye5lbAuR7coO0HUIQMYWDcj8e6a+DFn8i+EjXDBJ7KoPIpZbms9/xzFiUOCwx4F0QTbt2i+sCIU10W5RE54QirMQRMqlU04XdjoPy8majqDGl/EFZ2UUrimnNprnk0elTeEtRVgU/+GnF65M99g6m2LLkI6++QrP+NMfzKd+8O+Hdx/fY+EaAAh37SuLesIXBQEnApkaOxGBWQhzKOGTn3lT2YGk2mjIxcxliHE443mIkKIWLQbBMrVG1RlmNTk2I4rbFd64H2PoT7xwm7vwsXAPdB6Nyap2aksjki1FJkOQd79x/TAxf5t6jp7xw546AskfHaCXNA/LiL45XvoJchhzINIV8Lq01pp4wme1jitGF+tSMTMsiVVslXfyIPQC7owebl7r0KIL3GJsAcqBTsGrXPFqcc7pZsI0dUSsqVXB9/4iXju6gtx7XtczrCbYoUUXB2XqBC4Haiu7t+XIhi8tobAORJnguY2QSkTLTvDwnr8F3HmVk/0Ir6rJI7MCOSVlSFAbVpG72RUFZWmLnaJ2nbaVZylt37+N94KNvKC6fHsL1G6iywgUFxuKjlMtaq5hYjdWKzWLBxckTQttISKIzo8OnTF3mlie3SCHzQZF0bjQxaSlnJqG8XrlMhb60XYIbKX+0RpzToqiYTPfY25uzN9tnb29O2zY0mzWLxZaLbcn777/HvYcPePr0MScnT7hcLoaGWloxP5hTlAWXFxd96fTz5vOVF6Z30JRRmMIkwCsLkozdTz0CYFROHPZOeQ649vb2WKfmJD2LM8bRKybfNVY0a7qUuR3KVjTFdAp1gfbCWhxvMh+ksZjrOhYXT3n3nW/wkTe+m/nBNZpmg1u2tNst52dP2KwXLOqaalKjiwkin6LY3zuQTr4pu6kAHzqiCQTl6VzDxdMnvS5OiKn8IgwMP21Mz5LOjsa23RK6CEFRFnt81/d8muVyydNH77O8eEToWpRRqNKgSpvecXFEUq9BKfVOiF52wDKImgFQkIRXCE2vLwzSXTs4j1MBG3LXzuTc5nUmPfPeUqghIx9DoGtbXOfQWtaTfG4p2cqv61D+PgYJe4A0RSWy76DbF0N2oodnmu97Z2bGyKSu+Ngrr7A/mw5Z+LR2ZQakiYrYOsoOShcpvKwrBt3bEK0kebRpWlrX4YJnaiy1UugQCJ00fZxNaqw2+E3DZrulmE0wSmGcSGO4wvL6rVsczPdoCfzsN98c7EH+rw/IYnJSVW+ndsYsj3fcDRrHzFUYlVfFJA+EGqToyEHSs9qvV/8d+3n6/C1NtyEIGzn2z9t5SFYO+2f97ICMd4xZ8zXrvMe85IxuOOvNy3rpRkGg6teiQWOwaxp0ASoGSmuw2rDNQS6gQgKCRhc+newlVopGK0s0yfGP0lSka3ODU3EEjbE90yTGQNu1WFsCmqKo2N875Na1FyjrAoynnlTM6wO0X1IUmqrQEFtC1/bSDM5LQwaXus3WVcm2aSEY1puAOltRlZrloqFpuv7aK+uoCp+6emtsOcFEQxE1HoOuZqhyAnbsGMDn399yshar9Ue+b5/vf6Hmxszw73/2kD/1hQv++jdWlEZhNfzxHzzktcOCrzxu+N++tuL+wvOHvnfO3XPHz9zd8HDp+a+/eMGPvTHjlQPLn/0F0ZT90Y9O+cTNXzkI/N/83AXn28DpZkgU/tSba75xIvf7xz5zwE98bcXXnrT8F58/J0b4g5+a81temzAvNX/is4f8t1+65O/f3fDOuXznj/7AAd97q2S/0vzBT815ad9SWcVbZx3/81eWQ9khAR0amtUKXc8o6jmFLdCIPQnO4bsO0GhjMSqgVUArh8cT1OA/Wa04nGjc2SkXj95G28js+BgznUFqDIZKYEsQkoTpwUthYisVaQNso2cbHIvNghtzT6EtWENwEVNNiFr6BHSrCxbnwkAtplOKsmSzXPbreEB04PRegZ0UoBXLkyXBSTDY+WeBWEhBkh43/RPfffBjJAA3WvX7ZqACUtWD0qk5zm7QKAx5R+ekQ3phx42zIr4bmh2GmILfmHzZaiKdsbVNNmrkT0bxV13P5pIyUkX2wRQxy6bFIZYgrYPOC/BQJtAEElgwuv68WaMoqhIdlYCxpkjVfbpPYGotfqDSKdCMKSZSW1TcEDFEZXEKGr/h4fodzlxLk2KwqMSPjyEZt6hQVmVCdm9OpQlX2sXl+ECu1fvQN+mKOfi3U+aHkZs3JhzO9qn3Cm6/vE8InsWFotqL3H5pHzNpOF9GzuKKjd6yUYqtCbSqQd+0qJklrlu6zZZusxa5mFR1FVXW7h3mVIypQVNZMTs4gMrhYjsk73K1T4hE5QnKEZH3zEWPix09UjoCqUZn2PlbJb3GMSjS+61XEo+79m+g9vS/zzeiRgfqv5hsXLZlkDUBEsiaYquxHVVqOIwEAv15/x/23uzXti2/7/qMZjZrrd2d/p7b1a1bcfV2YROXHSAPJEACCkgQBMICiQfeeYjgv0DwiMQTikCIBzoBIigJKJU4DiVXuexyufq6Td17T7vPbtZasxsND78xxpxrn3MrNrzUg5d1y2fvvdZcc4455q/5/r6/7y/nCeXsYj5uHgyW/6LLv0sHXv78DSBmZvLO13OTKHEA0uavOQhCbrxn8frUQu5y7eLcERNCSHIhqpAFBCRVxcmHGEg9d6gk7yft35QYSuZ26NQ9OOtggp7lGtJ3hCCasTEKcUYnCfnckaWUlhVOuVnucFoAEAWsFfMg9sMWJq/E6GMhEKRhWyHgfEDnOSUpB455X96odIts42IvFVhDpbVgvqclj4ylnV1ytVhit7xFAZyb0j2Y49AyZDr/fgF/LJGQvLYhA5ghEe2UDGsix7FRZBez7ur87MgzpXN+SJKHUPMaZ1+qYvY4isNNOO/BbGtk/oQuJJVMJtFJG1aA66oMissHMTp34iYuvMr6r4EYUpdGVZW4PQQvpKs4t/THtEgh+/UoZdCc52a8o4CqCRQLiG67CkFwuxBRypW9n1mxOf8KwePdDKCGmLXOk121Mxnv4JljzuPytWulZcaBSmQj5txA3mcOZH3KMRG5CWszsOzR6DLcO79XOqozKLsYLqck3hLsMeXKIAMo88l+GiTBLxEY65zIEPhhZJw6vB/wLor2qVJS6SBVSRMIq1LlAT8tjrRIwq2RlsxVRbQKVHLqOmLWDWpfsZ9GPnn2BPfdiVtHZ6w3x7ymYHV8ysm64Vfefpt1pdjUFqUtHz1/xH7cMYURpYJURJRCR/lPNDGTqys2Om+EVDlbJqKLB1QuYPYQc1q4ZCsuAIADIxfn6ewJZNLWoK1YBh9zK78wzkqym9cs3khmi4ONi2vIQwtISVJq5lQGHyOXu4Ef/OxDnpxf8fHT5+y6js9/5h2Ojo6o24aqqvBhwugKzYKuHfM1piEEuVKrwWpL3W4wZoAEDU5uguxIFNS1JGTOebybZmA+XUqZ2ngzzkjBZdSaF7stl8OWzo9gpNrYGMPpasOdozN24yVae47aNe16TawqduPAME5ooDYip9HUDRCKdEVltFQPI/RuYrI1ZUJkMtDeezFaCmJw1FaLIdNBEnCT10cYqOumQmtxV85LYvHk2QUqBu6ctGyOjrGVoTo6w5lWRLhjxKJojKY1Ebyn212zvbzAxIA8Zho0ci7pvPLU+NKGvHQcGXSN4KMInof87JGacLJmS6462oqqEjZsu96w2pyw2RyzWq0A2F5dcn5+wdPnO95/3PGT9z/go49/ztXVBc6NLOcoGWO4dfcWzk3suz1d1/0iWzc/hzoBO6mNSNs09Cm3v1S5pWIOnPIeJcbEoKU4o6ZpWK3Xwpa8UQWWgCGFJnoe3pHZOiliQNcW2zZMVqGaimrdHBwnxojznqpt0H5i6Hc8+uhnfPZzv8LJ6W3cNDBNHdtpoNtfM/Q7zM5StTW2WhFiFI3H23clMFGqPCLOOWIdCXimaWB7cUmOTDMztZxrTI7QmPlJCpFxGlCTprXH3D57kwevvc0ff+sPef7k50zdBUSPrmt0U6EqW2xJeSBjApRmcsG8zdL/SSVdpbVwDMMozBwlekE+BAED4gz8QZHWTgHoK4JqJcwC72TKMkYJw1odarLlPbRsbcqg4OExEwAbFfEgCZmDtnzdB2eiYN223L91xhc/85mlV0iApyS8xkeMD+gh0HiogqJKbU8qBV0SNDj6caSfhI1ujaY1hipGovO4YaSxlk3T4L1nv+8IMWB1slmjY3QOrxRv3LnDGw/uMQTPDx4/4nK7ZXKemIPNDHymc1Y3r3W+RBQswFxeThyXiVxZd8p35ADt5vvz/ZnvQvrgQeK2OJcb2yDG7CNuMHbL4dXipHJxKv0+tSwNxf/kIuPiLsa5eJEr7wAhBbH5a4QxnWMIScRC8OAdKt2fSpt5xhdKAJX8i/Rq6gYTxK6rwvTPkh++FCAUkkBVVZOSFkl8Ih6jbVLvVzT1int3H9KsWzweWxnW1jKpCWs0tbHEALU1ZFaDtjW2qjGTsMBMVREGh9KG0UX8tuP22TG7rmMYZrBS6yjdNEoTTU19dEZUFQGNDxplG4Ku0bbCasVX79fl1vzkxcRX79f8O1855t5G7O2//2vHfOP9jstB/NmvPWj4nV89pjaKH59PfP/ZyFfv1/zNLx3xx09Hnifg9MfnE092nntrwx88EuHLv/Tmn01Y8k+ejjxOjNuv3heG5fUY+INHA5VW/Me/dZ/HW8+3Hw187+nIV+7X/Ftf2vAXbst7/4OvnfAHjwY+2Xreu3D86v2af/erR5y1cm2/86si4fSZUxk0lo+xrmaIMUwjqmpQ0aOQGDD6gThNRO8wpkKrFs2IjiOaCRUVU8wxaKCpDBvjudyf051/TLNuaY6PoKnxShVgIW32YvuISVPNyZ4fYqQPms57dt2OyU+FseSBqq7RKhLdBMGxvXyBXTWYVSvSAddXAuIR8ek5qU4tm/sn6NpytdvhroVl5WIoMcnBS88SMaJ1qIu9yOetFEkmQAbm6RTjlVhomWSrWYc6+4hplP1ik1asTmyqjNjkZy0z+6TjqE3SM4dJeinsxdm/KXTpqoshdZikhD3bgeU55sTXGIOSXVBigGXcopTUmyur0Yg+tVUp95J3YJQQnLJWe45l814hr4XSDM5zNfacj6MMhRNllRKL5Wa/KEwSsr1c4jjZxyzlJg5vqWR+CtjUAsLePrnDndM7mJXh+OgObnL4oSZ6xcO7r9NULc1ly/bFh9LRoxRBaVTVcnT7AfXmiKnbMV1fs704J069kDxixPup3O98xpGINpamXXF0cgtT14xTkpnxXorVAEpAOpSijEi6EWfc9HH5GsuFq+QvFn43gyrxJUQx74WcZR3mkUsgYyFvXoCgg58Xp5Lz7Aw8Lf++BGUPCyGRDFq9GtxcXk1ZiPK3OTte5PrEksPOn1XlOku4dTM2UPNlZTyFRQwQX3E9v+hViEVR4scQDVlVVQhIc6FcTEDePzqlGrngs8yxkm1Qh3tkztXnOEWuIyQJkpg0rxdzKVIMIN8lQOFyjoksty7nlfdG0fyMEBPANxMNsk1yZR8bK/YlQR0HAOF8f2JZ73J3Y7qjGdSG+WZHAZVvDiIvb0l27kCWJpA6Nm0Z9pTPWcC0IPbd3NCVTX8PPggRRUl8hzYoo2XgsRdpggxWljMpOM9i/dTCQpTnLD8vaffdTEnyJ2JM409mIDbHbvmrM1jvUSluo+yZJdOZCCNzTiKp54xJxRiYhpEYJBcaGUV+QRu0lkH2Otl6iR9mFnq+zphi4RJzU76KTMrIRaus6QokPdgFuSb4IoMB+TwpPjD/O9sSYfi7xYaYPYJavDdvKp0Z+CkxzKxnGQgmsGiIQfZQmk+Sz8Mn4FhkFuf9J902YTGuJqKUSWq2N+3gy69fDjA2Rrr9yNh1TN2eECdwY3LEhmjBBUXVWmqzYpoC3d4zJ+hIa1WcAUphmrXURy3VcUuvvDD5kM6cWBvq0yPU6AiT4/GzJ/zd/+v/5NHHH/OFz3+JL371a2zO7lDFyFv37vHg1i2+/MWv8fd+9x/wow9/zKOLRzg6gvZpyp3CYtONycmYLig5pA3LUtcmOTRCEe/OTKryc/5flT8/AwCUQDl/57yeov2lwILd1BgrwaQfJgmKY4FSb/jtww0TF8ay2Jz8/QuQUykIaPoY+fj8kkcvrvjxex/w1Xff4S989jO8+cbrvPHW63gXMTqzJytyY5ccLlV90vAoIvhoiLomKumDjBH2fo+lkvaAEFjV7aw1goBLOjEGVAQfXKroCHBjrAytqZoapUQz7dmj5wQdqds6tT1BFSN4Rxg7VpXCNkepQiPAXdU00G0ZhwHvAkftipPjNZOb6PsON46crTastaGJQNdDDGQCdeY84IX+PgZHP3agPLXRrBqLrcGHAa0cbaVoa83ppmbjNH0Fl7sBBzSVYb/d8U/+nz/kztkKHSfa2w+pbr2RZAaCMJQ12OjY7y7ZXr2g22+xRskzoZAA3xrC5JOBlPtujMEom9jQYhB9CGXbxbTuuThhtKbKCQgQKsAatK1o6xWb9TGnt+5g6wbvHUPfs72+oN/v+e6PPuYHP3vEzz74iBdXV+S2jWxMY3qG6qbh7bff4sP3PuTixUVq+b4Z1L4c5Mowi/RDknhbDiVrmkaCjczQSGCyd+J8NSb5L5kofnJ6St/3jNMkxQ648Vyl59/I8LKbbXZoiI3FWSWadNZgboKxPhCUYuh7alujNXS75/zgu9/iC1/4DVarI3Z9RzduiX2Pd+JQp6lH6S2g0Ce3uHfvHkqbEq4qlBTBABcnhqHDdyPG2KIjtdkc4b3DjSL67lMyaIUOw+Cc7INguHf3LX7rN/8a508uePz+j7l4/L6AsTpSHzXYTYttW2xjUyCX1sJHdC2dCzInTpdAb5pEcN7YihhTK5LWMkSMmT2Y70mZXJ2C37hYx8wMzHsjxnjQshIIqABXVxdkp31jC70EvI5J1qIwrThMzF9+5QBdHR47Br7w9pt88TPvLBKI8hFhS40Tupuw3cQKQ5WKOpntIIGktBN1fc91v0cpGZ53a9XSAkM/4IIMLbx7esLUD3RdzzCOHJ+eUPnIMDpG77FtRa0MdRDm8d5P/Cu//s/yD77zHT569ozMgstBaV4DGZxoUnAvwX6ejurTZPPMGiiQZQIo8qTpV73ysebbGReJyfKuHHxoEfDHwze85O9e+rTcL6WY5SrmdDaCsLyMJihplw4p4IuLgsCcN8nPwTkJMKOw6Op6nRpDhP2mTdbdFKDV1jUxMcAUUFmTuj+UAB83Ex8UWlcYElMltYflEFkpxfHxKRcXFzjtsN4TtcNNE3lYY2UqVMPMVFOKe/de56g/ZRx7xmGgih5shzVJH28cWG2OxCd6R9PWaKU5Oj0VDXPnpNMDJefvHX3X44aJcZrB2PMXHXvlWB3VHN+6hT26h0MJI2NyeK+omhWmajlpNP/N33ztlfslv7RS/Ff/xoNX/u0vf2bFX/7Mqvz82VsVf+Pzm5fe99/+U77j017/+V+/9099z3/yz//iyUb/2V/7px/jb/1zLx/jRxiiWbG6f4qxFu+lVZsI/egIo8dGRb0+YhwCYXQiZxEGtE7xmZ/QceTo6Ax3fUn34hnD7oLbb97FG0k0IxJfqhzVZP8aU+wQFcoHjDIMwbMLsHWw7WXwpMVQYZncgK40qrXYaIkuEyusPF/TJF0+xCRvoxm85/TBhodfuUd7vOHqxTVXP7pGIcOzXHTLeZjyUtLKT1R4OSCQ5xt4vJ+wVpfhrwLcpvgxxTUzM01ek3MFPMryMyXJizEBnrFoGZpEoRJbmPxHAmYytwxkcKJzk0y3jlDVjTBiU5KfmXepBIgxS581275Vu5JCciAlooaoIjK+Ji5sIpgYsUE6uWT4t0+DXaXF2uo56Y6Q4naJx2NIQ2B9wOvI9TDwydU1L0Ig1FaYQgqUyeSOVCBfgL0zzLQ4NiQDvSCP5EQ3/d6oiuP2mNo0GAwqGlSoCWOFd4bgpH33dKNwo+dqd83oAtd9zzWRSSkBH5Sm3pzRHp3CHc/JsMcPe4ITG7k/f8LV82fiE5QiDySydU3dtkSrGYNjyvIVIvgtNm9xXyIpuo3ZsqdbEWefCJnlvJCzy6BhBmXLyqW/LX4bsn9c+siFi7vJ+lwC8/HGm/N7vfeLX6czT1TMnB8UwlAkFRAE1Jj9VAr2QuoiUdLmS1zE7SW9XZzD4tr0gb4tZW/MJ5djiSUUsgA1F/9fLRflz/A6WLv03TI93qG1pTKWum6S7JCwXZUS+ZCQWp2sUgLk1zXWVtIu7SecG8lDjiBr+0rXTF3VzDGqxqbnXteqgKE5hpcYZt4/uTBjU1t4BimdmxYLk+TZpKGx3Nfcpk4En+fyKJ/sl0FHIzYl5pgk36uXBx/mY9qqSu8rSNriNQPrZDAuLsHOtM+UdIzlLsLoQrrOJNtgNEapJJEheXiIM4lNdElNwiIkv40h4KLk5qMbccOISjI2Qm5zBbwH6SIsMGTUErNFX34nb80F9nhwdRmTyfdH2NIz6K0hMUgd06hR2uKcL/ql+bMlhiblrVmHOWbsUfaB975IYMgd0WnGRorT+pFpHAlROtK980U/NssdKKWIPhTlAYtItNiqpqoqbCX5vm2kGyPEKH5ykf/muD8aI+ueGL4+2f2sI5w7q8dxLHhPfhljpPC1YAc3TV1yEJGm0PPeSfejrmvRcE8MX5cAVlKxQllz4E8jpEGckSpIjlxljeMFCJxCH5zLWsIh5UBLSdLD1y8FGOt9YH+1JYwTuJDaeYTVaZsa01qObh2jK2Fgdts97eoYq2RK6+6FTIJOWbwQKGNisFmNN3ljUxYlKkV9tCb2E76XAQbP9ju++b0/5Ecfvse3v/ttfvsv/havP3iI0RWeis9/4de4d/9Nfvj+z/ijH/0xv/utb3DVPyUqL4CKTQ9VUCgdySyt/CrBQzZQUXQDFbykY1joXMwPrDjafLDlCkYIWQNWJSYoSTYBAopYV5hbFdp7zOSYth1hN6RETqVBIPNhjda4zFAt5x/yCZKNT96kgXQ9gAAeiuve863v/5gf/fzn3L9zwufffYs3H9xn1aw5O7vLa6+9jegPyECBLBRegKwoiaiparTOenKRy/EKHQxTP3J9dcXx8QltvcLo1GLpI7iBKXgGL9qrI9KSFxPFPCjwychu/cDz7gKMobUWrWHyThiiYcTowL07d3l8ccF23OMm0LYFA9tpy2V/SVBRBtOkARgRRMJAWR5sTrnVrthfX3O1v2IiognodN0K8NHT+4Gr4VpaPusVq6bi2eUT+nHHujWcnJxSV5bWgteK2lQ0leXZ5Z5aw7qtOV7VfPNb3+fLX+q5O/XU/Y7js7fRMWLjhI0T0zhxefmc7eUFfuySnpXKY4uS7lAohivIQypA4WKPzhPrczC5COh1cnpJU8xqQ7s6YnV0RNuuqKtaAOvtBW5yPHtxyf/2f/8+z56+4Hq7ox8GphBubvTyWm/W3L1/n7pteXb+nO1u+9J7bgI0skVnDSNTKWzWik1VPhH6ToHFgoVbWp6Ii8QK+n1Hv+9mx6AWwWK2R/Ip2pUET25yjOMkIPe6xRytMKdrxqSrbIxCL8FYrUFrgvNMwaNWUn2uG02ldih9zZ179/n1k3+Rb3xjT9RP0XGawR9lqJuW03sPOLlzh8G7JJoHbrimswOTUuzcFZfXL9hfXrJaraXwoBXdfpsqrSLOLrp6E5OnBH3DVc/nPvsV3nnrV2nMCd/8xv/ExaMfM3VXaAOb02Oa26eszo6pVi390CXgfg6aXRgx1hKRQLWqKrlf8TDpzUxySTCyRp/IcYe0Ief7xZzwpf2wdIivYp8oFcs00lypPWyLO9xjy4ED+XevAmHn/DiWwtzy9a/+9m9zuduVRFRpLQWvGNFRUXUOe91TTZ6WOeBKZ12O148j3Tiwm0as0Zy1K1bWEv3EzguDoa4q2kZafvf9gKksd26dYbXhxW7LBChrqa0ljgPDpHBWUzWGzx2fcPvrf5HvffQRf/c7fygMq6QjmCvwPk0vzyysg0p5DqLzI7O4NwftR8v1LE5osWC/IHdSr/jzQQEEisZhPNhfmcX8KZ+VHw5tnVJ4DRMSaAqLQaGDFh+sZY9m5lYESfiNQRmDrUQKQGxLKkqm5Fkp0d2smlaGC5g0ATczyGMkBk8wCTRd2iGV++XUYTKemXPKcnxynCbkBqakx2yrRjRjrSRqk5uIRKq6QhvDZnVEY2oGdmwvn7Pe3ILgZRq9tnzuy1+m73qury558skn9N2uBOamqlmvj+n3e4KfQElxtj27TbOeAdBnzx2Pd9egr6nXLzi6/Zx6c0zdttRVQwyaJvZz8vjnr1e+MutZ2uks4CVxtRa336HwVAp0cEQ3yrNsKrRu8dEhLa+iA3fnaMPu+3/EePGEqrasb9/CJQCugEsxM5vExlW2wo0wdAPjfkB7SYK3IfBo8tyJioe7a2pTUVUtTKNMdqgqtJbiZfSRcdth2oZ2vWE6GfGjxINGKcI08egnz3n6yQVKK/bPB4y2KSaBEFSGG8uqRK1RxqKNFPbkuRYpH601/eBlIGQr4Eixrqk7QymdmDyy70c3pgIX1LaSbpl2VWzMMIi8WZ0mQOcW9yUpI8SZhJFfIUaGsS/tm5W1GGXSzzGtUTi0R8w+rgzfURS7po3CuUVeEjj0V0qBthzffUh0A2O/R7l+Zlol6YQs34ASPcuQwYAoklgOhVfwfOz56fUVV0p+zkVwsYMqDY4pt6YArGLeQln7mxBaAbR8+nuUnOekOaa1jQx+jqIfOY0O55BpxxqGvuP84jmPnz3m2g8M2ov0lkJkOowRcEsbkbVrVvhhTb+9pqHfYgwAACAASURBVN8/5+rFhYAZ5FBKUa03rE/OaI+OiWnOhwBASCFiVTF2+8S2k62EETb5y2FIgZkXscfBgy2xelqNeOOzyzeaG7FGzG9ZfFAIQrMPLgXrg2PLB9RiL938ziXTVuLkbBmWYGD6YpXumUrPIyIrGIPs5WVOXM4gQuTl3yuVz/vGm8ldOIeF75vx3M0dlt//p2HEvuocJa02kAhZwzASQxTbUAs5SrpV9IKhPzGMnsn1paCdwcEYYxn8l6Vg8vpnEhIwy6nkm6QULsVieeB5BsO9D0VHNH8+BF+ea62zJKEucoshBEy1kI9YFH9zF4/sgSwftJT1OjzHg3sQmXGLZAPi4vgmSQhIwU+VToRl7IiOGGQIsiUSppmgVcw3YresEkJKniMRQpil5SABcRXWKHA6gb0RFTxutyMPcb6ZZ+S1kOsK86ygWTcoyc3KvVAkub/F3ssDI31wM8CqFOPQpxxV5j74ArTK8+ScE2DUyMDlVdNgjQzNds7hfCjPVc6JdLk3Ks3oEKKegK0Rpa0U5JTFmJguILP5BdjNXQs5Lg4xYqwwjuU/U0yNykONFzaCdC5VVVHXdQF780oqrVm17SwBlK5ZZOtmX9e2rcyrmSaGYcC5KZ1f3ndyr32STtQapqFHjcKMtdowjEPJCaTwKjMVstxB/rwi43SKtm5Kt2wIYSEnQurcSbZsAba/6vVLAcZKMBHQVqNNjalkormuNaaxNOsW3dZMToaQTMGxPl5zfLTGRFg3Fc8fPU2Lb6jtmq7bo9taKuqk9p30ABDloY5KExpL1JGKiO8GduOAu76g9yPTtxxf+uznePO1t3j42mfAj5y0az73xrus2xNO1if8/h/9Lk/PP2Y3XEtrucpVgtSLk5zp3GJ0COxQnMucTs8VImH7im/KTiM9xEtdluScrBXNNwkQp3TzKcGxlOQMyihaY3BaE0YnzDjvU6V+0ZKeNvLsqOJi6AEpoIr5TMkM15z4RQV9BL8bGKZztvuOR4+f8ca9Ozy4t8VPPaZZcXx6G1utkuB52hNpIaTCOrEcouOjB22IlSJYxX7qMJWwF4yxKKsYkz6pjkYGS/kRbbXYxExPj4GGCoulbTQhKoKKTCqymxxj0geewkTvel70F1z0W7ppwLnI5Ceu+x1RRVZHa7o+VUEWYuCNbah0jaGiaVY0bsKNQ2EjFkWwGPDBoQ2sVivqusZFx1W3JWrR2lu1rcgeJKq80o4QHcermsw0GqaRVbXh8ZMLAprXjAh/b9pTrAYTpfV4v90yDdJ2FQo4pRZIeKo6KwpgfxisQKmopT/lIH12zJlVYjGmom1WEOHJsyueXfYMbuTq6gVXl9c8fX7Bzz74mGEYk3NMO/4VqIq1lpOzMx689hqPHz1mHMb5/fOVcJMxlx0gqfVezlHPw3nUoiWn2CZpr1xW3Ai5CLFkoGSHRAkys+PKazMOYwrUAugk2XC8xhyvMOsWR6TKFc3l1Sh51lQUAMs7SRwqY3jx4pwffP+7PHj9c7z19lf48ld/k+//ye8xTXuq1oqdM5rVesPJ3TuYqsaNpGq7pxs6wi2ZmDl0W4YXl/J1Sa8qxFicdxapz90HSinwEdc7bm8+w4M7n8VPgW/+47/P+ZOf4sctAQdaCwhcwRS8DFtUKtmOtFeM5nh1QgTGcaTr9tR1naQfRJdvHEfUAWtDbGhmD2YgMDtwkyQkhr5PGrg5eNAHgQCRWTsLaU8q/XqLZ4EEPERI71nkPSXDSVZ5Cciq3MI7gxWCkR2CzJWt0Eon5pQwyWwE7SNmcNSTxzoZ0mWVKmMd8x6LCnZ9z36cGLwwL49XKywK7ya8cygjLFmjYBwG9uNE09TUVYVVit1+h/cBW8sQJ98PeBSqttTG0hiL2+0geB6cnPIvfOWr/MPvfVeuO4gvE1AhA7M3WKvzkhw8rTcB7JfT70MjkBm1SxB3qTNbfOynAONE5mCamV2tUEUr62bClgP7SNZbE/vtA2komWZy0paqQkRH0TAMxDRMAsiNqen8CSIPUtW2BJneT4vrT1IZUeHcwDh1TL7HtHUCkWLxkzevb9nVki6gJHnTOBGiMANUEIkPl9jMxliUNvJ0ao1JumI5aYhRoa0AxE27wfkp7V3L408+RBtN3dSsT044c47LC8vmaENTi58au4HN2WkJ1uva0qxazu7eKad65/U3ma4umcaBGDzd5Z7tVQ+ZUagtm5Mz3ri4ePne/vmrvP4Z/pj/NPyXgEaFhd2Liqkei31TSuPXSROTgCJLFMn+0sCxX+HuP2XavMCPivbkGWFZiCpg/yKpTjGBO+4Z7zXgbqNipFaKtdKcKri1GmmrF1Ta4Kep+Oby/IUIWqOMFDDakyF1oMjzHUIgGBkoCeDPAjqKdmrwnr63fOPvvRRGlOfHe4cUAPNgUdnzZegI81CczEKTYy9adUl6odrKf6YSgDJIR1LUsfiInIv44NPxFbmtFGZWY0yJc2YhiW7XbOdInRUCphT48mDmQk7elzrd8m83g2+8zAkMxrK6dUYYO6K20IF3E3iIOsoE6Rgh2jKQMfpEeEjxmzeWXRh5NnY86vdMSpX6dFQJHFMqh0zlmgvjjeyRl++A3Eqdwbpiw5HBnZt2RW0T6K0VtamFIJNYayoRcnyMjAQ6BQ5k4rySQYwxBrHhSjpl+r7j+tljuotzhqsLmEZ0jKlopmnWa9a371Ctj6CqkgZ4kr9QOW+KuJztJX9dcqoEsOnM3iqP042YO/9qsT5zAU6V541P+Wg+bgl9YgqYytGyP82M9zlPLY830vVZjp/u6RI0V6kIUTqO8tpnQMUv7l0CS+cQ6tU++xcBo/MSLD87x2KoQ3A1r215f6Scx//fV36es/0KXob85UKLSj49DzFTOY6Msu+Cn4FIpeLBsfK1aEiktfylKtkyX2S08u1cymoVzn2yzVqpkvejFMbawswtsgoLXcx0RUxuEpamT4W4EMnksxg1SuUuxZhyocxiz+sBy8HlGReJCevQep6tAxHv5fpENubllvW8jlOYSodR7ujJYGNMcfX8flWk+MoeSDFg3s9KSTHDJtsQrSVWFSaxgwNKbKHKbOQ8J0gessywzc9Pfu7z7/KqLnPV0hKf/V/6d861MyaTSUMyU8NgbdKNTdcnn03Dr+oKG0nyC/MemT2AfI/32ddId7mxwu41aTPF9BwHH1Ix0h3cixADxop+fD6mSGxR9JC9dzJ7vWzdl3PukMiFMrgsME0TZX5Giuut6FjNz1nCXCprscYkNrmcd8kPUv7tkizCskyljeSL+RmS7zTF54tUkUF7X2Lp0pweZYeLHNM8YDPnzEuA9tNevxRgLICtjQwNQQbqBKPAKlSlsG2NbWuGq4Gh63HjiB8GfC3agyYtlKkMVVWxWq+ZdKBat1Bb/IGxSK49puqKUUQsZiUgh3My5dLtrxk/fA+8px8mlKk4unWXo9P7nG02NNWKo3ZFGDt++P6aj599xIvdBUE7wWDT9y3DnJADqngjMMyOLoEJkPbbjRDp0BfNlb7iBNODmh9mAZ9mhxqh6KQaY8VY9CNu0IRhkHYnmBP8GOeguETX88kIu2mZQJfwQN6ixFgFH5i6kf0w0HUjQz+w7zr6fsfx8Qk+eI6Ob7NanVCqp9k/EiH6g2Q8VjI4wauIsjKB1o4VEaijGB+P6PlKMGZBBWIyKT4FRLmd2ViDUmsm5xiCY+8nJictS5N37Ic9FnjRXXDV7+imgXEY8d4RgKptqCpL9L608avkbNqqpjIWjUYpgzWWoCVglaFKOk3klcrJZrVm1bagIvuhwxFQCYDVyNC6XEk2WCobWbc1zgn3QwZKKC6uO5S5pK4Nt1VFq7UA1ibi3cTQ92I0srMA8vTH2finO5oTkKUmAYeOIScTqjhvYVtLa04WEY+cX1zz+PmWT55fM3nHs2dPeXZ+wYsXV1xfb9P+WgR62WfF+Vd1U3N0vOHoeMOH77/HlAdicBjY/6LXUps0C7GTrqFUtVIiFBKbWqX35PfmZza3kOX1nNdnPh9FamNMhlsphWkqzLpBNzUYI62ASiOtb4uTzeyRlHQFH4nKY5VmmEa6p5+Aqrl1+jqfeedXeP7sYy6vnhAYsa3FG2iOj1gdH6OMJRdaUDI0IlorbVV9x3B5TV3ZOWhZAFAziycNJgoRHGjf8MbDL2BVw8WzJ/zkh9+m352jY6pMG0u1ahmjVB1xU9KKy9XVDMhmxs+hc1ZKWkaCn62AIlW1w6JdZY7m5z2ZGUIp6Fc6gZg3wNj535k5HUvCk4+zuLXJh7AIvuZAOVdV8xAmpUjrOWv66UXAt9iV5do1UAVN7SN2CujBYV3ApEBeK9IQBLGRgcDkA904MQWZ9tpYQ6VNKrbJOlXaEgHng8hqKFUm0LppYnIuJbLCyNgPA6quZThYBDN59m4gGs3ZasXRmxvef/yIJ5dXjM4Vf2O0OQAVXsVSz/c2P0MpbCJX3UElYOfVSdir2LQ3/36wN/LxVQZCZ8aG1rokJUWz/OZxC8i02LcohKGmkZbnIHrDaYBXjB5C1hA7OFhKQGTUgSpWQhVbt7xqY2pQMsAuAnbVousqSVIk8CnrXpbTFTAgfVtJOL1zODcKyKqA5FtC2rdZl00wuygM3jjfHbRCI5IztqrZ7wak3KCZgmGYAJOYwFWFbVuao420SSuNbgZWbYOthD1ha0PdVjSrWSrg9MFdxqOWqe9x/chut6XrBsZxoHOBqBVucOyvr1957//8Ja83eMwbPOYlMlkEzI3f3fz55isAx+k/FLD705/IBrhdAdUr/hiA7k99qOZlBYlf+HJOvyRTMAOxEy6I1meZPI0Aq0s2kzwXZgF25UEvs5aryjqoyW/kwEUlwEOlBP3A9+j05MRFa3kposTZlyx9CHNyXmL7dN6HNkueWa1SG2tKDNVC0282GIcLpJSSqemZkduscdYRg4fgpbgZxW5l8DwE0UYV+RRwFi6mgedDz/k0ErQAGywlCZKhi1AS2+UlKKRjqxTWIIHAcxCawzKJORUhitxXP/Ss6w1GqzLcxuh5nZTWRK3ogsfHdLuVrKVB7GdwnhAmrs+fcvX8McPVJb7bYUjDRasK27SsT89ojk7QVU1QKg37yjB9AmDygFi1IBqoEhIu1v7QZ5aiWk6/VPGsi9ucPcjsOTLQks9BLX5L2WF5zT89ci7Mt+KTs9+eo7ECkpTTSTFcjpF/ERAxb/uD8y9HfwUIu4yb4ksruDzu8p2LeGG+cHJ3VgYEPy2e+LO8lp00Mf1PZXQCZW7GLbHMZpif6fk4JRYq9zvFjjmOSeedMLRFwU3umTAcZzmDHNNmwsLB5kqArEqg5EywmfO8XOw5AMDLNQdCyHwnVRZAoUvOld+rks2Lap4hkK8+d7jla86FcxUh+jCf78GDw4KxStHuNCV/zZIgWRNcUYYyIztFLx6DmGTvghebR8JHtNGzf4gBoim5hdEyqDGDsTlnVItn9iCLKVs3pns6x61amzTgUTCdAvKnt8tcC8EGrK0wJs7gMksAn8JY9l6Gci8BZxYSmSFhGErNerPLRY4pD/Y4uc9ZQzv7QkBFyX1UFN8W8jqUfZMIL+lVCoULULWA8zoCmmlyZb8vizLLfD0D0SodU7bHnMMt933ewMuZIMaaNNdI5BDK85JyvLkLZB5+jVJpn6myz2OSsZQ9lvxNKWx8+uuXAozVRrM5bgt9WWmFjxEXfRFSrquKnfeM2x1+GDm/3vECWVwrtDGqdU17tGZ1smFfBZqjI3wMuHFYVF3kJTc8IdtaQ1tjgrBjo/e4CNfdyB/9+Kd88MkTfvrBB7Rtw2ffNdTtGcf1mrO33uburb/Bmz/8LH/w/T/in3zn9xj9JYFA1BDT9MxcDVYEol84puJLk27HonUpO+BIOARIyccSoHTZquoSw1UOmp7ybGOZ9XRRIjZsNpLQqXGCnWbadgIQRgVBpapXquKFkLQzVMqRk8NPBjcSi3POzockkxCVJqCYYuTJVc/l7hM+enrOm8+f87k37rPve+4/GHnwWkPbrudjzyHpvFgK7ElDf9nhwgBahgc579mZXWrlsLT1ujiSymgqu8qWDjS43FaJtJWt2xXdNLAbe+j3nPsdkch+2PP06hn7ds359Tkug7yVDETKLAqrNVPX4/AYa2malo1u2FQNrbFoJWA/QWG0BRtRwWG0kqnGQVoBX7t9hgsjV901V/tL2s0KN8rgta4bCE3E1tlAaJqmRasRbwWgjii6YWCiYnx+yeV2z186PsFphV6t0E1N8JMwjpKmjnd+NhILB5v3iknD82K+FwsHmI265oYBV0lXVYkOqp8GtrvAd3/wcy6vdwQvw5IuX5yz2+2Ypr7UMLLO1EGwWb4Pjo43bDYrNIGnjx7LujIbXNmDhwFN+fyBYRWNJJ+YN4lYU6rWIYRybHI8upDSEOlYcXp1XdGl5CUvkTYptAqITWBmQqPAHjWopiIYCKnC6KKTwpKeM2NtLaayTOOA1TJ5Mk4eB2zOjtnvOp4++ZjovsVf/7f/Q77wld/kvZ98jw8/+D6mVkxqQllD1axkIIfRVLXFxkCwG4Y6MsSOqevpLq5YrdoStGgUxlhc8MnRzBXI0E1o33C0ecgXv/x1vved3+PD9/6Yq+fv48dO7EByXlP0sxao9wTAaJu6CCLBOy4vL8o9stbS971UdZM+nnO+gLVGa5q2Ybu7FkdOKgKgiDozDKU99KDFPP8jB945RIo56Ju7CVTMTjRrwYbFZNq8++X8YNYCTuY+tXnFeTKozjq4ugQBuf2F9P7KytRqE+DUa9ppwuY2M7UMnFKwqKTYNXrPdhrpJ4+tKlZ1zbqyjH0nDBWEEau1pRtGRu/wMXL35ARFoBsG+mGiahpunxwzjhPb/Z5933PUNBgfCG7g0g2EVUXb1jSNDGX8l3/jN/jfv/n7PLm4IChQSobeqHSiWSVvDgApa1jAUBZB0vJVDE+c/d/yZi58UWEFMB93mXipyEJSIjIrlObfRJbmbd5Xc0Jb3pv00kM692wfppDA/BiIeHx0aF1L4aHsDNlLMflHYZalwZpoKlszeRmglb+1Xh3htSGgaeprmqMj7OaIcdjjg8OEgvkuXrmSNQPdbhqF4UagqlInjFZobQG1qOpL8Ox9TN0D4Kcp6WXlIpvoAHoX2PV7IHJ893Wadcv++pz99oJh2ILReKXwRpKG45NjqloKgxBQyuEY8aouZ350f0P0LXgIY2B3cc31xZbt9Z6rqz3j2NNdb+m3MyA4KbO4R6okQcv9wPLvNxL4CPgCUkVsig8O9safIlmfi0mqFPRu/j0DBa96yXdkwCyLW/wZX78g8F+61sPf3vC3szOVXwafjpt8/s0JeFB2+C88tRs/h4JYLLprcky5PI1XHSnfxnI75x+WmOPMspI/67omEun6PcPkWa02VMYmIEDu9TiJdnqFwiiZMyAsJvmeDBDElLzFELDaFnsLHqk5CqNXx8iUYlUUWGXTTNqAwsp6ZomS8ooiy5HugWLeg+KL5Vg57s+tldrM4W6+7gwE5U4UH/wC6Dy8M9YHnr//Ewyeqq45uXsfW9WM3Zah2zIFj5tGAZINKG3xoUuaqBGswRvLx9vnfNTveBG8dEhZA0aRhS3yrsudREufkFmbpZ4WItFL4fGlvZTJNXieXJ/TPvoAN3qMqji9e8o4+BSr60RcCBgD2iq2w4BTlhhFgzvqpC3pR8I00u2uePbhD/HdnuhEOzcSsFXF+uSIzdlt6pNbuKxHH6UF1k/zAFylFX6akllSWe0CZZKGL3mvpi5Jrcr+PygkLPZGzMO1sha4mv3L8mlRqFQYjhI/xEVBsuRYZJNZ9lr5PqXI1RzBYBeEonyvSou3WlzHzIYkFdrnQoS8Ly6kwFCqKOiEJM+0fLwPXurlH5ZxRd4/Mc5/OQC4SxA4r9HyWcmf///0iqRhsAGTJt0ZNE3bUle2tNyXc0zrYrRFMQ/wynZGzlviiuxXxD8kJmNaoRBVaf9XxCQDJvCGMSbF0Ynt/wrfmFvAQ/DkAXykIbTF50WY/DTHx/l8EpPVJ/3fkOPghOfYSjRbc+y+9KOyd/NckJkQI2DYXLzKMgIZqDPGzgQgLTJZPb2w94PE/845YlVhbSLMhDTkO11fCLHkg4K/+LIWIcgAr0AgOpdyVhlCqY2GoMoyidbo3F0VmTvnNBJjyTFjutc5jpf4VCsKKQpmjEgXEFrITSb5x5jsfn5g8t63xgCmrG8ht8RUYEzazFmHVZfnO62pVgd7gzivPxGikSxQcGyx4NOUNWDn6wohiEzX4viyFwXIjmEe5pW/O+sJCxjNwd99IuKIbqxLmrEBay1VVaVnJjOd52uHw84Q0t90GgAa0vfd7B4xxtC27UGsV/ZrkrDLcZrozDsIAWssylJIXMJBiwtg+9Ojo18KMBYFXnl8mobWmAalooj+Exn6jmef7OheXBF2PaQBVCSk2iuFDxPj0LHfXnNxWVOdnXC9u55d0iJwzMthdE7UkKdh06KNIg4ToZ/QwIjnxf6K/oOOv/3f/W3+0l/8Op//lc/zxhvv0B7d59bmLl//8m/w7uvv8tV3v8r/8H/895x3z5hCD0qAOwepSiASQTG64v3KzQ6i12F0Br5CCUZy0KmUnLNPFfsYRH9rkc8XECIdQQAgpTFoXDIkKrFzpX1SBp21J0fEYaK/uma42jHsB3GjIUobu1KESVi/Siuszmyf3MqenXoKoFNMsPRnIYrxmVxkd9Hx5GrPx88ueOu157x5fsF+t+VLX/l1jKkk8Ao302VQWvO1v/JbXD55weWTZ5x//Bg+OWd/3TENI2YQEeoYFHVipRozt1yABIKjm8Cn4C/Kya3blWhkjgP73RZv4LIbuR52rFYt0YJ3ATfJIKPd2LHarLEh0u07hn5PvVrR2poTu+Iv3H6NB+0xxMAwDozTxMnJKcOwZ+g7GY6lFZUK1K2lXtX0YeLJ9pyL3SW7Yc9bd18nJtHqYXJ4IlaBsUmuwIOq67KPvIpc7TuuLq/QKJqq5u/+/X/Myd1bvPPOG7z7zhs0dYMOMC2CozxVM9+8CLO2Swig9Qz0c6i7qVClVQ2kjXUGQQLPL7b88L2nuLHj4sU5OkbWTcu9O3e5+9k32XY9F9fXPHr8nOfXO4YpSBtDEiXPoLxCYSrLgwcPwSt+8sOflorZL3odMORU2r+VgMXZAYqDEi0epTRuGkr1TimFUZoQU3vC0mYcBH5Z+2ve9MbIUCo3TUSgWbUiNh485vSIYHPrknwsxAh+FuwHaE42rO/fZvvxU0LvBORVAj51uz3GWkKYePT0Z/wv//N/zV/5l/51vlB/DasNP/rpt2nvHnP76D4Pzl5HoTGtRRkZcLepLKHesd3t2F9fsN9ecHx8Mi9eioSt0ngfSmtV7CPWrbh39gZf/82/yje/8Xf4+IM/YXf1hDD2GBTRe6qjFas7p3gDxtbyWSTAkUEAc4GnqRu5rqRxRBQwI2qF1tmuzIFDSNVLmUatRdpjkmmiUcUi+I6CrD/YtiuOVhv6vme33wskVwL0eb9kpneWDfDjeADH5SA0xlgA3/lZmo+WPxFcSnyT46+rSto6F0BN8I4wTdRRcRY0d6KnIaANOAN9DGlabBpSQGSYHIP3DJNniKKz21iLjZH91TUoha1qrJEJ9xfbHV5BU1WctQ3R9Zx3I0pp1qsVt4/W7Ldbdv3AGCJ3T0+pTcW+6xlDwK5bbh0fY4LH7Xu2YUutDH/zt77On/z8I373e99nQIZXKChDuny6LyCBqQzRyyyLWAZ+5YBoyR47YAYtA8WywLPdymDFIWgmzyYRxlHYpTdZKeW7QlwebvHvQxuTg2qUMLec94xR5HGGPhU1tUZZm5Ks5W6AiC6SKNooGTIpZzNjYlH2rx8d0zhhlKGqGqpmjbEtZlXT2ID2ntCnqd1lP0X8NMpQUaNQmfaowFYVtRYtTLmElERoRYheWDQpM3XeM41jCWTHoRMmhjFoNOPkODm9xfb6ir7f8+Dh6xydnjF9VON2nn6aeHjvNcZhT9/vMLXh9t1GmH5epJx0iinCAk3e9ZGLweFGx7gfaMya9b17HD9secPW+KFje/6EOz/bwjP5zH/x+r/Gz9u7BGPRzZqjOw85vX2Pk7PbrE/O0FUrAyhSZ9DQ7cksmRikbe1/fPd1nrcNJ08e8Tt/6z9i1WimaaDb73nx7AXPnj/n7OyY45M1q7Zme30t4EtKcJp2w6033mFzdpdYt/yjb36Hb/7BHzGMDqMNRluO796hvXULu9kQkqYbUfZuCJHn7z3i9mtfwNx+l+n0XR6NJwRVIS3PGmvATB3WGExlsVWD21+hokOZCt2eEG3DumnR6NQ+PqLrhqA0U4hcbrcMTqOwKALK72F4QvAdKkxYHMbWNLHH7J/D+ftcff8fcXz3mPbOGWd3jvjt9WUBqUGKmLcbze2Vp8UR+x5lTUmqRR9YUekaldrzwxj4zvcuiM87bnnNr7/1Ns3oiS5Pjs6dXmInQvaRRhGVEbmqKDZ88oEpIgMqo+fhuxec3hXGbVgAT75u+O7v/Hu8dvc+bbOiagTM7IeO3KVhjMG5kRiFJKKMJHwRSQbHaWTyUtQQ9njqoup2HK03tE0zA8sqJ6gCCJLaHIOf8EExRY8tvpGkyLUAS8g6e3nauik2ziiwlWU7XIsubYicnNxe6OCKPxL7pgkBnB9nOxdZ2NpsnyI6DtRM6OhQk+Pi6UdEZVJpQNjyJliqdk29OWF9fIbTmn57CdGjjGGH52dXF3wydHTWYNtKYstss9WhbV2CaHNSLs9WjMyDpRZSRUL8T6QXDFo1PN6fc7W95v1P3uNnH/yA3xx+g7o2tKsVpmn44KNP+OH7P2Myga6BWFU0TUtMEgEhTHTnT7h6/pRhe43r9ii3k0G7PrH+DNx5+BbrW3ep2+oFOgAAIABJREFU1sfCDJvGBHoKa5g0VLqAlMmuRq2IaPmMn+OarBH/qtfLXRoZds2LuPh3fksCrnTJKTOs+fJ6559VGj6dAS/ije9O+0b87OL8Dr47f0f232lPLXz7zWs6OJYSwoRPoJpanuxLC0MpTMh+vrF+MY+7Ur/4OOlvMjPiZU3aT3u9CrCNMTINMhm+qipqK6x4hSK4iFOeOV1aAK8xg1AHfyqXtOzYggAlthXfnae+Z/KAaDyLvYmpPR2lkha4AGnZ3kHOz0sULGumKJqq+Zyy/ESxSdYmAFWYkN57DKIBapQmD/yyyX4ZY4o2KMj5Tyl2ybFe3gMmd+0EAd7mrkWRuliCbxo42Ryl/a4lPxqHgz1X6wqjN8W+5Hb05bksv8d5Tzf0uGFgigHnxI4KMjjDSjoRLUY3FbA5D3jUWpeBU/LznDtkULJuWpRKDOBAmeEj9zsD8lkeJxYzEX1g8j37rgdi8V3WmoUebmLoR4kpc6dEZvHm5/wgp188Jxk3ybsiatC2ojYGYy11kqwpQ65jJGsh28Isle/LMySWZKNDRmy2DbqwSzNIO2srQ4w+7at5EJ1PLF0hUSVyk3Mll873NUYhYU1uKgxYWTN7kHOEEIqmdX6PMbPvDUEKcjaRcQQbT0PjEiZitOEl2/0pr18KMFY25UJfJk4oRBNCmYpuGti/uGTqROOSRIcWYIWCdhttMFVNtVoTrGG9WuG8px96MouImASGlQSpOYFLwj2Y1DIcrZWBYl7a2rvg+PjqBf/g93+Pn378Hp996x2+9pWv8/bbilWz5uHtY1bNF/Hh3+R3v/27fPDJe+z7C0I9lVlcovc661RkZzq3BDNb3gzEzr42CSxncGp+cKRgFFK7ab7xMpIpV01ef/gGV9trur5jSsPOClAQE91cg163NFqB7giDmwcNIIByJLP7VDIey+rjTcAknbuS9VVK2BSJeI8j8vR6Yjs84ZPza37+5CmD8zy8/5C6qqkry8npLaQ5YLGhLWzundCerbnz9gO68x1PPnzM5dPnXD+7kORx2BJ8jbcWo02h0SstQdnR0ZoxiZdDpBtHalVjteVkdcSDs7vsx47OTUzR4SYZ0ubdhBtH3DTR7QbRsdSaEEQN6rRZ8drpHd44u8fddsPu6prRT/gYqSppB88DLwBqW1PVhiEMPNud8+H5E3bTSO8mnHc8en7Owzu3uXV2glbC1pDkQ4u+TW2lOhqTsLWb0DFQa2nrduMEqWL/9NkFXe84Pj5lbcXRZY2YyFz9XIYXGXCYz1meUTFKJOaH7GEXZNrivut5/5ML0IrgHF3XcX2143jTiDazdwzdnu31FZuTI05WlpPVGQ9Pj/jk+QueXe642PVc70fGHD8mo3h0fEJtG/a7HU8ePzvYF68KjA4qWwmErdoaVDxw/lpl0XqpBOfBSblSVh5C6eEQPc1UMMmgX2YM5ROO5PYaeQg0inGaqCrLycP7DLWmshYSmJNOEmsEWCxfW1uq4xVHD25z/fGzYu9A4caJymgBXFTg8vwjvv37/5A333iXz3/pa7zYPmM/7alNy7rdAAalK9kTQLSiNTxtd8RhpGnWVHVLt9/jnbA0jJa9qyQSw0+ONjY8ePAmR+0pf/itf8THP/kTuv0LohvFhvuAqi1m3VIdrRjdhNXCAtTW0FazUHtO6J3Lw5RSVVHlqaOiGZTvsUr3VbSHfLlvZUpoSM963s9hbtQb+p4wToW9WG5ZWtOqqubpw5CGLSYw7xWvZaCX90iExGKQSnVdN+y7rpy7RrFuWrbb3UG7ThXhOGqOguZkCjTeie6dsdi1xW/3KA8u+bDN+ohx3+F9jyOwbmqMqedgRGvWbStr6z2dm/BKSYu40gyDY5wGlDY0dUVrNbvtjqt+wFjDpqqogcvLK8YY0JWlNZZw3dGFCach1paHR2u8ivzK/bsE/3n+zre/VaQPZElUaX2SAN6IzVHqwKzHKPrMMQrrbAm8H95LSsvQgZNJCUaK5hGgNRdJDlnQsxzGoa2YW33jgSEsLKXF/stJYNZdM+lW1o0M6it+UWVXHokqgKqodIOf0oRaPwlzJNnRoJVoHKrMYhOb5V3AuAqra1b1RoLTqkbX4DHEbndQMIhRWvaUnm2YMLHluBFSi/EcDAfv6TsBk5u6KcmEtLmB0WlqLQFdGY7OzqhsRdWu6Lod1/stUWt8jKxOzrh17x6nd+4IGzcGtFFUldjfxO0Tf4YvoBVA1b7OqooQIJwErF0RlSUq0bIN3Z7GrqjPf1A+c/r6Z7iubzP0HUPXsX3yc3bPn/CoamS4zq27HN95yNHpHVb1mlCllr4QMDi+9uyK/xXLWDX02nBx9ZwLP3HLeu4az60T6N0JU4hcbwdCVNx+8CZV01LVNXXT0h7fwq6OUVba3T77zjt8549/TDd1xKqmOTmDk1vslSUODmNFMkSB+JzJcf3iOdE8Zm3PqDevYUbw5ohgBDAafcSqlQy68imxqk6JocdUNe36FrpaI+y9mqZuubrecrXfokwErRliJWzA/L3Oo30kZl3yAK2F4flH+Kc/ZXr8I8K05Sv3Tzk989hmj0clLW15DD1wPQVicFS+J2yvCW7CGoU1isoabKVZrVYCJGtDVW34whcf8Pxxz/jC8ckw8Lpt0c6BjynWl0JABpfEDaWCHhPKgF4dc3T3Pquzu6yPT3n24Q+p2oGl/MFBdFBVontsa4xSdGEnGq46J6maum5kkKMCHyZCimF98ExuZPAyIJEoeqXH61OaqqaylQyPUuqAxamVlgFSipSEC+vVeZk/MHWOqpYYVLFMjOdWyWyzBKhUhJCRSrDGoqsEXiTGnFKArQuwKYWHQ5DsJrAGEJQDo9HRJLzTgY4J/JIPhCBsMTcO7HZbfNLYC8owavjZxQve6wYuQkDXYj+ikv2X84dDQC4mOySgoMo3LedFMZbW4xxr/b/kvdmvJVl23vfbU0Sc4Y6ZWVVdzeLQTTZbpCmSgkjLkghDD5KebPgv8F/mF7/4zYBtwBBsiBAIw4ZEwyY1tEQ11WONWTnc4UwRsSc/rL0j4tzKItnUSws+qKybee45MezYe+21vvWtb2WVuNyuWbUNBkvoM8ZplI/k3BPCnouVwipLGDwP+z0v33zGJ/efojcdqlkDiXF3V5q/jPTHHadXLwljX5r+SnVT06xZtR1u1dFsN1w8+wDlWpIyRB/LWKbpWicAuZQaC5MQ0Fr2vpTJpcciKYMWNuPUYGfqObIETOUBTHqzdY5Qn6WafJXyUSbt5/KZuobm+bV4BkJsfCe4O+2vZfwlni0c05QKWLJMdM7A+xkhYvm888yWG/uBqfvxtM8uyz3UdF+UMZmayFFkABMT03QC75f605l53uXFvl7v72vA8DpOfxW2rBx6BrRzAdiCH8naFPZgrc6b92PO9IJnPVi5Xo21Zvpd/UUlbClU6aeQSrMpRVaKIfoJQK/AtapAYAZUIqUw+Uxzc62i11l0NM3kJ2SGcZx0rHPKIluCmgBZ6RNSm/vBsnl6COLL1+ZK9XNVRqz6b4lM9IlQpVW0nnREc73+xZjXZlY+BKy2E+i3TN7nKNcbUxDcR1U5gHncta4g4OzjdV1Hdo7kW4ahZxwHPBpfcZOcqJSaqVp50chb7n1JMJA/YgsU1lhClCapWmm0Xcx5xWTzKqPcaE1jHarsYaromqacF3ZfIg1rzbTW/ejJhXmtSpUH5ZyqsLEr8L4kNMgeWLCzBBNLHiTu1FowIZ1ByfPNpTdCImPLsVPO5KVe7cK/f7qu0gIjqdeRi/2c/GI9jfr0HBWAteDcQhtW/riKj5XzOmvOCEaqJBBqfBByKJjVPIcmMDcGfPDsDgfWmy3O2kLcERxzkssgFYBcWM1/kf34uQBjNWCpG0wt2RawJ4WIH3p8L02PVM4FN1Wz7mPOIgivDdY5XNsy1N9NG9J8vrMyGHljcn2U1iinwGgpoRiYDE8MI5+/fUXvhVVlVUtrW569/yGriyueX2/5zV/7Lsfjkc61/PCT73M/vCKb2mwgl0C/aLIhkMgyu3n2yllAzElfqZZtqLOfddJWAGC68bJhAnhfS6jLIiu7UjXOKZVGI06jVUuTFbkJwlCIkRTmMuPqZIjWSwHGKxvy7CbyAsCqtyhjXZfaEDP+NDKEwGkYse57vL17y4vbG57f3LC9WKN1d+Y8kJMwQlpHt+noNht059jebtm/uOL0eGDcD4QhMPiB0PsJkNHaEHJp2JBrcK2kdMlIUN26hm9cP+PQnziEnoMf2PdHcoyYCvwrTdQGk0txtHFcXnS8t73k+WrDpXHkcRQJhVLeZ7SV7CS5sCwUMXv6MLAbDny5f8ub/SNR3BxShv2h57QZaJ1h1TmcdsRcAtKs8DFjTAFeUxKWXtVArUa/6DcO/YD3gdFHhk5Lh8+YeHa9mQGMurE/aWRV3CD2p4HdYSjlELM8gVJaskLA8TTw6tVbEpKNTUGaxAU7a8eEHNgfD7jWsFItbWO52HaQL1h3LZeHgVcPe+52J0YvkgbGaG6f3RCD53g4cDodz+fFO14zu7yAQaVpTEpx2uCUksSPMWLMz8rNlTrr+j5lVrQqJYayQaYQ599PtmaRwaSCMYDT5M6JoS6MZF1KikIMxJhZspCrtrVat6jOkQc/MQZyzAQf0FY2xhx7Xn76Q5yWQPOXfunX+fjTHxGGwP5xx9X1M4xpxEHPkZQDKY6E4xHlI9vVRqQliu6TBknCBMghQYC1WXHZXWMw7B/v+eLjn3DcvSanwBTcAXbdYjctdJYUvNiX4v7WcTfGzE3Cpk1ZHDoxUXPmVhW7P0/KUgSXmUpFKYF7dT6r4a+WMqWIjwXoK45O/ZhCAtrBj7NTvNw7zyOf2SGsX14EMGqyrUV7SytynvU7q+TC8vDrpFnhuDSOjQJ12kMU+2SslexvlD1QukQ3rLYN4WTxeYc1po5uAZaFkeljYAyRkETuRxd7770ADCsjeu0xRk7DiDaGtmlojSEMIyEG2VetRafEOAaCEbvSGouNkTFFVtbwi8+f8ZsffcQPX75kLEwMXcZI6TLeKRNJRTN4BkQl4aN4l3NWn+FTUHTawp/MqzoNlgHW5L7n+ef0SL9iSNT08Ot582JeneHAWbq6azLRh6lRR2V1yTyYr5MSXGHtFIRJ2RRTMwgJCrQwwkvAEouDqwtDVqHJ2pCtRmeFH/qz9TE5ntUnKOeVf6piU2sAVNgC41DKaefjhFBYzkYCSa2qtIHGaYN1Tek6rvGP0igukzHOsdpe4rotjmI2p/K8WJ5IKo02EkqPgAcUtr3CJg1ZpGK06wSAyxJ04dY0rsWtZxb/5Xsf8WzzPuPpwGl3z2n3IF11j4+Mpx3DaY+1jq5bw+ZqMRfELt32IzYlLg/3fPPNT7nSPSl6Niqx0QqzMnx0syJEYZd0Xcv7V1vWF5fYzTVsn+G6DWPK+OBhGHh2c8319RXBWIK1uIsLsnVEKmAWSBRyQIqikTsM5BxQOWDikXYcoElElYiqI2YNpuj6FfDQ1QDfWBSKVdNAGFGUBL4xsueFk4x1iBjdlUT8SI49OQcgsdKBD8wjK2tI4RNC+ASvX+NuDR9sNesmgRoF+NCCJtX1OkRpfNQmJbYmjuTCACVp/Chgj7MSoGRlWK02bK8tR6WIfeSYDG3I2JhRIcJZoyzEg5ykQGR9YBvs+oLm4gbVdeimLaDf2Yqe/6JKaasR0MEai9dBfll8wsY1RdYk44NIFhiji2+WCDHgbIuxBpulQWnrmmn9w5xcAiYwVWtNtfy5BOS57IExxqkvwHK/mX3r4terOX6JUSSu9CJArftwjRSW5nS2ecUivcOHypPvXra3HKliJ9PnS0lyjoEw9uToQSuigiOJn+x3vI6Bky5Bu8qzPVJqcSXzY5nBC6bwoYJzYsvVV74QYyJ4STq50gtDnmHE5IBVEZuzMMoGz9jv6cORNAby0fOwf2R3OonvFUbG/sC4f6SikhqFdi3bm1u67QVuvUWvWmy3kVZ3MU5g0mxPygXWtxb7cgWcxF/U0zrWyhTNRnU+NIuHJ3tKjV/P4dIMk0PzlUf65I2vjvzi3UWsJrcwO7FqcfCzOFrVeflk/wHmlbs4XX3Yde+vc7TssbIXnl/0GYO6zKHKmgNmlt/ZrfwlAcJyQL4eJ/kZX4pJtaH6MilLX4hyHwW2n7XY1bwe4dwfqYDzeVXQORlq9ovK7WSx+2ECCiErAfJM6RuDKr0H1KyToc7+lFiQWZtTocgWQhhl71DzwGXkenR5ltIjZ47BVJ6vb/RpkgbQetHrY/n4cp79pZwnwks9D+V+qP/OmRwzUSV01Cg0IfrZ/8rFZ1fzmJ3NFyXJZhSSNJsfJ5UAqJSWeFqXn0qzJGrMz0icXZVnpm9d9/KzZDzK8xYyYgWnzSKBospzMhgjLExjXSEqFvmbUi0BiqhL/xmY+gPVeaWamTxAAQxzSrPOLUws3rnMvvqNapovc9eqaSZOv7cF40pZqmmXy6pWV8UUF+OwGObKGE5pagynVJn/2VAC7mnrOMObit+vJm1dpvupL2PsPFdz6WuhzpuCVRmziaxRjlFxsvr7GpeGEOck6SRFVi+y1pHI8dNUq/7u188FGOuUYWMcQw6EwkpTVAp54HTYQ0wCvCtVtPPkTw3vMwrlLLpx6MaAipz6fprUxY2YKOKqToZSgq11WR8ZyQg3FmO1iLGPnuQzJmdiztztdhxPA8fHE41r+K7yfNj8It3mlg+e3fJf/K3f59nNDSF4Hn70lkQkqYRSmawLuFqMcK3BUdOEZzYaLEqi5Q7RSlgnIEMwGbGpxCYvgkB5nwwvv/xi6dnI93MJqpRo9aSiJ6IbQ+M26JDxpx5fdHRBTQsqZcrUqlkSydTPejeLMtFJA3R25BTiTKAVCUUfMsPjwOO/+TM+/exjfu2XP+I73/oVrq4v2KxvzwyeRRjGOclm4DaG97cv+OCXXoAP7O8eeP3xl7x5+Zq712/Y3x2krFJrUJE+BFSf0IVi7kyDsqB1wFpFY1uur17gQ+AQRx6GAz/+7GMpO1l1oicVIn6bsNrgrKVpHW2z4qbb0imDCiP74xHdwKpkQ5WSEiWXHSlpUjb0/sDpsONx3HHwJ9pVV7IssxMdi4B4Yxva9QoKO2iMkcf9AeeaUo6dMENmtWoJVhjYzjradcvFpiuxSULT8/Yx8vBwwAAffXAj80Src6Nb5xbznH19t+fjT9/MWdrJwdRY5Hs5BZwa8TEJSOE0xjXonNiuGiJONAhzRuuMUQmnEuvG0j275JvvN/Qx8/Jux08+fcXD/ogPooX5q7/8Dd68foNRI1fb9q9kX0SLUsBc2zps50ghTllAbRSr9RpjNYrMGAK+sVNpEQU0m4Thi2Myl+sYYgzUbo117VJ96pxLwA12vcJsV9BoWuNwpjAIC9h8OB6JMWIX8z2kyJAiymr0tiPERC4yKoDIc6SE6zSNswz7Oz7+0b9jv9vx9/7gH9Ofjpz2Oz7+6U9YrS9Zd+IUxuzx+URMPeFwxPjE9eaCV/tdEdCXAMEoSxoiaQSTLLfXt9xevcfnn3/K65efc3h4VeyNLpIfkWwU7nKNuehIjZH1CrIhxUyM0DaNNPDRilDtXXFmrHV474sjqFF2dgCqzXONKx09Y2F4j7IxTgZGWCKmbvIICLR0OFOe9ZIFlLfsT8fJa1xmRZeviRFSE1u6Zpop36vlKYpx9AsQSuzz/nA4C5ABLqJC03DZrNk2a3YhEIcTKUWscjS2xY8CopMhZcXVzXNUu8KnSI4jow9TqVWjtWjBhsLMN4bOOUbv8THgU2LTtDgjVSKHwTMkeL7d0BpNjpHHocc4y2rV4YzB9wOnwrjrrGOrLYfdkV2KJGO4Xa/4r//O7/Pf/+Ef8np3mHPoOUtQC9JQTIkOVu2wCrXRQnF0RLR4skdLkBuYWBJleU3rso5xBSvOg7Ncr2bxIBdv1GCT+nMREJXj1vMtJoIkGTKolAnDWMoJmXAHXVkIqobp8se6Bt0WcUc0PobiZIotyKUxRFYIIFWYHVkptG0AI8w7bdArC6cTeeF86iIlQGGozONXxjAGtC6NPLNIEPhhlDXpLNYZYoj0vTTes8bSOFOagZSGEKkknLTBtR3rzQWqJJJSTqIXntLE4FBFGmFqyplB2xKkmh0CxoKya0S3PjKkEzZkQpSyspgibbPCNRtct57ud/v+L+OffYscesbTI4e3X3B8uOO0f2TYP3DYv8UfH4ljX+KJ0kwvJ1zK6Djiwsg3Hz7lb/3kT/jWRYZkpzI/pzXfedagjWgvW9OwXWkuL1r09TWnm48AxePhgIqJpDKbVcM33n8Bq459yuRVx5jmjveoTGsVzipizIThBAma9QbrNIx7mjGCznidQEUijdha1WCMo7UNVoO1DQnRJW21Jirww8DxeCKbBq0j4+mR0B+wxhGbiI0J4kiKexQ9mcxze+Jvdy/pVGS0HxM3b8hNZHN9jW1qJ/sJRREfsCRHEplRgXMNF5cN7QBjfyz2WXHqPZkBb8AakSkZwoixhqsrS7d1PN4rrpLFZFAhkEIF7kscqIWEIwmZIkBgLUlrRu+5290T/DDpAk7r+QwoKipDZS43rpUEWZEQEPDBlgAOvB/lvLgSIJa9xRga2xY2lsUoMwX5mcQ4joUtI2MizDNJwlTmjgSBVqQXYiAnW1hGC8NU7mJp8+SnALjOuekZVKNWg8SckjDXKpNIqamZV/VRvhIiVqC1xGOUWClPpdI1UZtROUEKkAJZa0Yy92Hkh7sH7kmMuvqWCxtN4VdNoFl5KEWmZbL4xW7PZb/MepRlPux2PfvUs2pa3r95TvIRgjClmpzQ0UO0mKxplMb4HqMTvT+yv3vgs08+LqB5ZTIlafVbGIJKGdrNmtsPPqS7vEa1a4bSvLfOF5bJ5BqfkRePME3jVn3EGrxnrVHGYFD4tNTnzNO8P9uoZtMh46DmT9XnWz+XmKsi5O3al2ReGdOHsxxUfeVY6uz09dJUkflTSXw/yvM4eyl5lrVEfnqvgBd1rYTS3HaKwd+FWVRQr8QqNSFYwV6VVbFLT+eamob+bCiVojZaYjHSX8eAXZYwL8fnXZ+t+qbk6TFiCmNTStDLHpAFF6i+whIQBebGP0v/cborsX4TcQA1Adh1TBNIok7JfmyVKUxGKeU3drYJACH6s/sV/1o0cCVpVTRti49jSmVALnMwFbBNL+ZdfZhVPkEqBijkHYkF8uQZqenZGKXn+0ZYn7WXR4qSzG9cM4HSWqspvkheYrXai6NKvFSbkXKapQMmBrVUPBot/VdSrNhRniola4MsIRsrUFruRdXplKmVvDnXuZInYLRCPrUSW+ZKntindXziAgwWKQhH03TSn8a6yf8SGynXZm1pVJbrM50lLwC6tptwmUyWqt6SYKyVZlprgveTvMGcACkyAeWctZo9lHlBnadK0WhVpJfyNA71sda1GpayFHnWsJV7l32zVjcaW6R5FqSKXConp+tbrMdKDpNrPv93SvLdVCrllVLnzNdi70TyQ2R5RFtXxnTaU62laUTeRi37uyhV8i5yw7HYgmUV7te9fi7A2Bu34XfNh3x2vGeffCnlMxPtvB0i0uIi4Qk8qp6YA6VbCCiNbRua6wv0uiFY0Fkx+LEYxRIUGVuyATPrTIY+AYas66ZShJmNpb20JB8I/UDaH8SJSJnBD3z69kv+5z/8X/jB59/nb/7m3+T3fvfvs774Bd67uWHd/Wc8v73h8X984ONXP6H3J7RNaJ2FWVE2DNkwK+OlOEw1CC2TOKZELKCBKRmQZdlnjvPNKMU02c7YjaqwULQuTQZklcYYCGVRoVUJmkQfMxnQFx3dusWtPWHXk4axlNGUSSs6ERPovQxEgdlxmHYbpgU4XfRiwxoS/OTLPS/vvs+/+Q+f8Ovf/zF/5/f+c26+fcttt0IB37l5+Isn1C3w7RfAi59hFv7Fr5x/5y/9zFcwmycOzNcf+692De/AhM4X9190nHddx7wH/Uyvv+r1/pVf6i+4vKfnUu947z/F188w5hXc1c6wfu+WwVjCw4F0GIWIG4S1n3xk/V7HurXEOHL3+sf87//kf+CXv/UdjDU8PDzwf/7RP+O7v/E7bG4vURvFqTnS+5HH/YnwOLJxK8ZdT45BOovmTCDSmBVXFxesXEd/PPGv//SP6Y87oh8xgGkaKM5KzNDebOGiJTV6CuKSqckleYD90IsDqZkYSHVuxcLuTosxgLlMJOWM8qoEoYpqBCUuKg6QKvYyl8ZOSpIioiFUM6nM3WGBMYyT7s8UMHydhFidh6kGF9U5qLawnlfPi2byGpicgfraRJFqMJ3m9v1vkhQ8vvqU8bgjx8TF9bUc+ZQJ/Yl+95btixds1xtOp0se717SOospAvOH44mjH0TL0jk6bTmeTgwpoq1lu17TAsdhICRxbp9tN5gUOPbSDCzZhqv1itNwYj+OjAm22w0rNHoM3B9P9Eazvbxgs3J0VvHl4cB/9fu/x7/8wQ/43o9+zJgNSdXgOxWAvGSki1xBdZTqZpDLMz9nd9bypfr3GbyvD+QrVS/TYOf5p2LOD3K+FJfB1fL9XACC+dHnxd8pnq80aUxV/qI6y9M91ABUoZT7it3VuSaXJRw2ZLlQLUFZjJ6UI9pJUgmjIBadOQ3d7TW+balq0ylGqE0aqIz/NMnKJER3zRSNNaM1ZtVhnWg7Ho8iC7XZrMkp8fjwyKc//VRkVi6vub55xv1ux3pzSdO26FIu58dRRltJMDQc97i2RRsnms656IDW6xJqrPwsfq0fek4+iZRDjATlMc7StC3WdaBMsQPzICZlibYjmxbTXnFz9SG3aST7Hn985M2rz2m2N7huTYqiEat05sNh5Lff3NF+8kf8g//3B7xatSgFtjD6JKDIZVmP+GEko3GupWkdX36ltdzoAAAgAElEQVT5Oe7+js2bj9leXLDOwjqJSXTl/8GHii9WiU/2I/9iWIOEZSLZ0Dj+0fUJnXoGfeLheM8/vb5Gt4b9w5f0n33GxfWHqGaDSj2aTJs0JieCjpy8Z384stKZzWpDs9qw2mxAZ5zVqJRI45FT/4jOIhmAE3kCHQ/8Zv4+v6g/Ra1SUd6UhKpRibz7gnR8g4onXNOwudwSrDQxzDGjMEijEgEbjXJYJfIGK5dxOtG1kZUT8FErQ8yI7l6WWT7Gkbs3J5zb0LgNUTtW14+MxwvMccWFUow7PzVWnNa5FsYiuTDM/B4Ob4lxZNzfk4870uXcgO0ra01bSjkJOTFJ8mhrMYWhJA1iTAleKRp8pTGPtlysr3DGSpCq4Tgciq04B3VqJ3OtZc4sWfan/iiBqDYYpRnHQRrtlHvLFMkkElOH0cVLqnlEs67qD1ZCREWcM+BH0QWvQe9kY+WDX3HqFLlo2wpjy7q2NEiUeEobCXBN02LbDu0ahv4IWbHrB37w8Iafjj2hsaWXq0JbYZOJC5An4EVV0Gp6wnl5FaRU/uRM46zIrGVFTrqotSmSyiQtiX8fPV0SNeRN9nz04TNO9z0xKlZW09y95YpM1olTHMnhACzsZAbVrLh6/h7teotyDdo52GwYtCEv9PxTIeikLBWEsr8VzdiFXEAuBjEV/U4Wc8QaQ9aaFPwc0+Vlx/HlTlUbmM0gSXFA0EqTc2ViF7tFZR3KfHoal+X5sOVHmbOL+HT+YAUES+w47cXvdmbrc17OrYnVawpI86Sr+lQtdHby+YIrkKQyKG1mGZC63yqmtfWzBjZTwvQ/MsCpe0UsFQHOOFarDjNpR4vGtFYz7J0LOKgLIDU1Vio+sJZs8/m1LZLNigJolUoJrTU0EItEhuyVBShIqWCBApymNM8n8VsXSSw965/WMVJaFa1N0dls2qZcM3MVLzNrV01A1izFVEGvZXK9VgtMDbyqHdZVK1vPZfQpSWPYCtCSmZF8udIq11UT9VoZqYC0glmEEIrdL7dfWerFF00xSbOvLODgMAwcj6Izn0KQxFmedU6ToL8inVYbWNeFtZC9M4W0U8da9pOZIbyAc1AoskqE5DGuQSVpKqazwqqCBWWx/WPpy1CPCdJYuo6xH/3EHq/PVLT687SvLefXVPY/gb6p2Gmm2GWprytvK0yRoFsmL2pCQWslMgJtNyXWc66J0VLOnjJt4yZN4BhLL6VFc6QKsldbV+dGjLk8Ez/5u0pJsjM2rTz3GAh+TjoIy1muL09Vk4oQI7bISOhSRaMQopBSapqv1c5PM688d8G0FCQlTQ85jyGevn4uwNhVt+LXrn+Ba70Ga7hu1jgn2f+MlHwpICeFz4l7Dvw/H/9bPt+/YedPZAPNxRp3sSJbxRh6MtUpqWzOuskw6Y9Mr1wp9WrSqtPU0lJQ1mLXwpKN/VBK92UDHvsD//rPv8/d447d48Df/3v/kG51RWsMH9w84x/83h/wf/2p4dPXH/N4ukcbKU9LiDNja5xeNvTK2J3iz7KvVtaQTL5Ebccp+86TAFRVMv/5xiKHWjqKFCatbGy1S7Iq9INJvsdo9KYVzY1+lNLVfkSn+Rw1C2RUbUwyO1dnmT6lJvBDvluo50j5ACXbNCR483jiT/7tD3n5+oH3/5s/4Bef/erPsL/+jAjjX3a0v87h/orf+Wsd+12n+FmP89c873/M9f5M55n+965f/P/ntVmveX5zizaGu7s72qsN1miGeE8cSkOvkok5PO7QV1cY62jROH3i8eXH9N4z+EBjG370Z/8KnIMG8koaS+2+eCSdRkZOKDJNlCy4c6KFOJx6Hl59yau+Zzgegchm02HsRqRAxkD00vyn3W7YvnhG32R8zpgYudpuQYMvwum1HKeyG+QeRHIhZVBZmh8AZxt7tdtfcc7yDMTNDCDNer3CGs04eg6nUwGCamlTqmSLyQFsXMNo/QSAV19qeql50zVG0zrH86sbXr99iw9hyrjK+ZfIq7wkEJN/W4QAVV9tAmIk9Sfu375mvbli2D0S+h7vBw7HI+vtJdq2DIMnh5H7l5/RXj/nww8/InpPP+wYhl7070Jks1pjlLCj9sOJkDPOWmzpbvzgR2LKtM6yaVuIkd04khUY57har+j7Hh8iGMvFpqMzhuF4IpBRrePZs2uuNlv80HN3d49PkQ8vrrj67t/gV54/53/6539MqE59ceykcXgBLQtg+K7McZnZkwM4dTxVVbc6L/YfUGq5783jPtusUhWjFr892yMXfsEycFWzIzUfu7IM6seqDnUt458B+ursUcuiphMImwGlMBZQGqImJYUyteQvYZsWFz1JZexgWbetnLsEoWiDaxq0nV067wcaZRAx29I1WEmpVs4ZZ9xU1p4LE0QVkFRri3OZFET/+Xg48PrLL3l++0wC/hS5e/sa2zY4p6WhpwKyYrPd0q06QvBFJ48p+MsIG9AysxomTb8nAHotv1sZScyrAnwpbat3c7YX5crkK68AKOWgsWi74nZ1JeX9poCRVvMb9zu+8fYTVl/+GSmOUBTt65xR5ZFklGiFjgMKXcbNEP2BkDJ+2DP2e8bTgW5zibZWWEnW8N7tDWOMDOmBv9scJyaF+Py9NAUNgegHbPb83duATT9A6YZ8Ycj2AZXeQL4g6zXKdfxx+i1ClnoUY1rWl88ZY6YfPKq/42DBqQT+RO735DiQXEuMmTad+Nvtj0lxZOXvUfGAIaOtK75jxAw98e3H2NTTrhwXF2vef3FZCAXij1pbJH+yJ6WIVuAAnUdMDjQqQtCFHiLrrLESFFeJqFWGlIt00ngit4oxJva2Y9M5mtSg4wYdojQ4rM1k6oPRMneHhweG/R60JgbpshTfGxdzg7OX+KSS7EgkdqdHItJE0GorAZQ2AmAkRcyyPrRSWONwRkllj1H0Q8/+eCCEkXbVFtBBzmOUpnHtVEZaF78q9sKZssfFTCCUShSDwiwCACYwVyxUKbEsgIO1WhjqKYpeOnpiGVV7VbCc6d5F065G1k8GJ0vVRc4Kpa34EqsV0Y8Tg9TYAgTEzDh4kcYymn0MfN4f+PPdPTsrCVhd2IAiVSBWVIi3kRkRVpOdXQKzsdhTt97SXlxwcX3J65/8VPqHxDjtpVoLy8+1wk52PrMxmpvWYE3m/v4lRKkW2DYGFxMheoYYabstoeyRIFJFVx98k/X1M7Rr8UWLc4gZkkcr6ZptnCFnLc0IrSVP/SAK4yoXhl2q3eUVSknV5nSrC33TWnpd90FdpEWePp5aLTmB2svy2DOQdgne1bnABLTmkhARf0sMksiVl2PUYyFrrcZ4yzVUS9CXueazz5Q4VzCWucGtAJYLSaIyF2sTs1k393wblktRKCNrzBQ/Jj+F8idAlmnil/rZevFPjrq4n7/g9fT3Z/H107FGfFCtDcHP/Q0ENHUoU9mQlf1YpIoqELs4ZvV5ngJfauEbQ10vGZ30xMCtFbOxJAFq029tlFTzBJFnWdota2354yiNeeS/JKBuLniJMbb0Bzgv5RYgNk3SK9XnK6locowCPNd5kymSDYX9rtLUrDGTJ/u3vP+QIioWrqViruYsY+qsxWg9YRwgMmXJCynNWIc2kkCvoGk9fm2E5qz0ebHW0TQtTdMwjqMwhoNnHHrikEWiLafSQ8WUuT4v1CVjvuJNy7gl5VSkLUqZf5p9XGsttrFkXdQTVMZaAQOdFfJFXQchhGn+S9VEBedlgCRJXAHtWWd1CeJWyZyc89xUt865cowU52t3zkmzNj1Xe9T7rXuQMQYD0nSzvJZatct1mJU0gtO2jr88L1Wa3mql0KaTJR7TVLmUy4KX5SOkG+/HqYLVFFZ327UoLf1WQgxio7OMhWvaaQ74EOlPB0JpLtzgpDJ9HCYGeEpJiCxqIWegzLy/qoWUyhPs6+nr5wKMNcbyvNlgTI9rW16sriVQKEY81kxOFq2lAwP++YkUIz4H+iajWks2kIvIfIqzVtNEfV8atnLuytRKqUoY5EVmjgIqloCx60Qja/RkH4jek1Pk4bCHLz7H6H/J8/fe41d++btcXj5j0zX82kff4u7+NYrADz87kAhngsHlgqZ9Q7QqoGYeasnltIcAk1huAVOlVdc5+DptxvLu/N28YIItPiuGVC/WhKJio5NGb2PQymENwhgZPLHoedYufRMbaLqGJ2DGOyfjvInlgsClnKV7Yd/z8ctX/NM//jd89uotm67lg/ee8+z2llW3whonzkM+P7bSkoUO3tMfH4thmDe62umQLKUdcYzEEBh7z3DsGftxyrpK4YEqTvkim2UMjZNSc2uE9TFtWjnThxEfRXMxpACmxA+V9p5SEete0OUpItAFpBp6X4xBEXCf5oU4ctXZy6l01jSWpmmKcLc8f+uKkQwRH6XJFrkGg2XzSGVOKoU1mq5xxJTxPtCPEmx1TtM6S+usgOcVlMjgC/gzeC9lqVq6s6cYS6Ag2TfKtUsgPQfkGsmypSzlEXUTbppWJAScgwyH08gQIsM40g8Du30pgfxKPLFY41pjnC7JBgHmlK5ABjhnaZ0r6y/jQyDEmi0uAEuaj0wu5TnFCU0lY7h0mien1CjpKN01mK4pGdw6/mcrY2aNLrKOwXv+3aevxdaNnhQjxhnspiONa9LbfRHulzWaYqTvT7gm0bgG6xpiHhmHI0PfQ9OihoC2Dcpq8j5KEOpljudUEkI+kpMiq0jv9xx2O/wwkmLAOE232aBsEd6Pqsy/LM3GLleo1tB2pXFekLUioEaCwtDXEyhRk0qZbrWCDOOwZDUpanb2qTMcF3Z++fnq5HvvyUmXz53/XlJWedGcgKlRGHX+PJ1XS6mnLEzg4+koGd764XeAinXqiNNbQMXTIOyj8tI5oWIg+Z7j7i2u/QarzQUpeB7ffokfPE2XsbZhc3HF4eEt/rjHdRvs9oqb2+d88fluauhnrZmA2BADsTpvBdAcgicmaAo4S0oCumqNMwLGpxgYSmOWzloabRiGgcF7sIbOWHTMHPdHKXHLhouuw6JQ1nLVdaxLCVSaxk9N63vaZ6YxmufycnXMwJ36yrp59+ucMfvVZ7GIHqe38gwMLD5y/rXlm/P+Vis/KuupBk5TuVTdY0ssEeMIWRq5qFy0tcoA5ZhQWaRpSFJ+qZXGWifNnnSDsy2VxZRzLsrEy9AVKQWztdtwvf407V9Oz+VXKUvSu2lcCYTjwqGXe3LOoRWc+oGMwjadBGtl2CZGSwFPQ0jc3T2ASlJaZ13ZawrgWfYbrYXxOlwkKH0Lj6cju1GCPmutOMkpYwy4xn7tYz1/Tkr0FwFVS/HqGKXEdz7793xjf+Di8BY9Pkpjj7NjVj9J9gFVtEVBlRLdiB9PAg6rhB8T+72AYc1qjW2lhHK7XrNZdXSHAxc5FFZw3TDE9tXgLqfIhcmosENpi9YOckT5TM57CCuwa35Jb/C6keAmGzbhBdkKY9iQ8X5EqUyOPeQ9Ck+kJShweuSKR3IeIQ+oHDFIXwBFhDiihkdc2rPaaLZrx/X1iqsuoRkxVmGdxlhVqs0iOQUJRMmQghwzJ5LWxDGV+SCMntWqwcgjQCnFdm3YHyL9GBlHAbpc58FFDrRcmgbjozCRfCDlSIih+EiKYRhJcSTFQcD4pLBtd2YnljxQmQ81OSI+95hGsk7EHIip6Pgah65l4zNeJMdRspZOw0g/9Ax+oPoKS1aXnoCZXALuOB1DIeymlHOpyqNohM/Bmyp2cvbnZ7ulmG2MJhKVnEcakSmgyqPMzNy6903lzcVXXTabQSlss8LkgEb8ylCB8MK8zLHYJeemq8pacdcPfDEc+dz3jIYpCVPXz0RwKdc/gWgLIKsmVFL549YXdNc3rG5usauGrD4lT49TFYCH0khRT/GdUdCWxMHqYst4OOL3O3x/AAfZOrIxrG4N2KKpnCUJub6+wa7WZGVQlV1XWVYlcSSAxFwFITpgAiYqcSZLkC69KFSGEIeK0ol9ncDXXF1pZsswPY7pX8vtR02/K58/AwbrHPma1yIGXn4h1/1PQiOWu/A52Lj8O+/4zNm7Z+uvPruc03T8PAG1avavzl5iM5exOypPQO/ySpZXNw/kMhLmfCCLI78kD73rXs5j67/kfnMhXZVkQkoZU8BK8QPMFHcvYzp1/tDneHoBuqonv19eSwXyIxEVhTFuFnPHVvasNUUuJU9Ni3KNodUMxpqy300H0JCSIimRLaxex5TwqU+6gHFzglQtnl3pC1Sqlus150W5knpyP/WWl6BvqnF5sXtZcdYcqup71nkliXxpwJiLDv50tjLn5muX95ViIg1oY0oFkDS+9mGkShXkwqAtiGrRwX8SFJYR05OteDKnyjWYEl+qck5jLda14j8Zi7aSlK6l9JUJrYBcNU3zzFwXluZsG0VWQN7XC3tpC/CZUiKpKi3CRK4DKd9XpVdK3b/LFlNi+yq/IX9mOSY1A+YFQ6lDI3H5PMdSLs9xGQsk0SxXWaPMDLDX+TFjWOXzpeFdznYiZdaeMJOf2jhM1FMCQ2mNMwJsozTWSoVDHTPn7CQ5JmBswkfphyO2qOy1pjCsi4SQzP9Zy/3rXj8XYKwCLrEo5Wh0y3tugy2aJgBRZ6QiRR5YYE189it8eXjL27hn6ALZKWlwkWXypBAnAKU6MlADHnlfP3EG5vAQJiRy/ibKObCWbA1pGARcAoYYuTvsOP3kz7n61xes1h1d27DdvOCb732D3/zVv4EPPXf3r7kf3hKYs6dpEbxNNHarzwDYcnnlWsTRyyXwyylL454l07fcndy7fKtmMGUMUl0r8km9AGHz9L/p6SjEUCpTMniupVs5xt2JeBRjm2Jh71Zx5zyXIdUbmAzrYuHNm089U/l+BWi0Yj+M/G//4nv80Z98nxfXW377N7/Dd3/113jx7AWb9QWmW8l5c551lKxm7HuOhyP3r95CjlMpAFqTCohMUuikGQ+esR85POx5eP3A45sdYxgm51NnYSz5GAlBZB26VcvFasO6bWmdY4ygSAXQi9z1O47DnpPvGeMADWiDaL8YQy7AFqpk4YxsfjEEyfI7x8PDib7vca2j61rZFNCle6QwIYL3xDACiqZr2V5c0HaNOL4Kms6J9t44cupHYhZGQ3XIjLGMvmSPrKZrHdebFaNPHE4Dj7sDPnqu15arTcfVeoVFGgIJgK/oR89xHLnfHwW8MYYXNzelc6YAssM4TPMuU8FYXRxnzaprCSngQ2F4aLi+vuHm+XPabk3Mitdv9zyeBh4PR+4eH/n081ccT710RUx1415s6gq0M7TrRlgT2rB/PIqnrhXKKLabjqvNBqWkWc3hOHAa/OQgee/LeImzARnXuGnjTllKfYOvwbwECClFlDPodUvz7IrmZksoGTPDk0TJFA3NQE7XdfTH4yQ03vc9MQXRxe4czfWWcBhIY5jWkgL641FAU61w3Y0wW8OAGiLeH2mswUSFShKA+NTTGNEuC1majoTRk40E2afjkX5/QBlF0zVc3F7QbFacTif8SZJiKUaUNdhVS3O9IVtF1zbEGBjTWPSqpORIWSvMS2OFkVeSCplEd9GhUMQyB6qjWu9t2fl0WVYzbcaqshvk56nvF877AqBT01uSoS/PchiGCTB/Gg/MDCOxUylnBj8ynvqpxGmafotoKhctbsp3KzsiDJ7sZzCWJGBsJjHs7/EXV3TbLUpr9o8PpHFgOPXYrmN7ecPp8YE4joTTAd8fuLm95cuXH6MYC3hnIEZJLqSEtiJXkGLCx8gQ45SI0DlLkiJntl2HMxpN4tif8CmzahyNkwaEh9MJtKZVjkYZ/OHEg/doZ1mv1lx0Kw6nPcGPEBPfuLrk8/2RPiVEIKKsz0XlSnq6f+WyiuqaONvPvvqq86PuH1U2YnasZ3bE4hTv+Mcc3T4NN9/F3J38+Dr3qjNe3pP+BxlK1UvteBxHP82lqHUprxLnNZSGMMFLiVaOBUzPQcr2QxKQroxdTkX+Y1H+CpCiJ6aAnZrvSCAi5WEJEy0IGZJMwvuRpnETAzFG2edq8HZ5ecE4HDmdelzTsnYN1roJWJcASIDlEEVr9uH+AR+G0vyoSmiomfGlBYzdXlwwuAa2wtzd7XbcnQbRqtOaq6sbjG1omoytpd48iamL//Ak7IZchqbMIZsim+HAb/34TzGplBaTiXHkHU94Ciada9CmFdZLKZX0fqBpC6MsZ07HPTlr1iRW5oIYA13T0DUtjXXkfgQtQepkY4wqYy5NViXxG1AkYeEpSxwfSb4nqZbsLvh2O6JLuRwp4vQV7eULXCudfR/2RyKKZEaSPaEJZG1JSq5bJSBHOQcJQ0THAZ1HdDii/R3rLnK1bbi66Li6bLH0ZN9jqnYgGZUtmQha9OFjkr8rhNVtjCYnRQjgU0InxXpN4RMIQLFZa2FRhyAgq13TdgNWtRzViovVpSQQfUAFjyJzPB5ETsFohiByNCoNpDiSYy76rDMLJ6sK2ck8mSVlChOJRFSyj4Ysfnnn1qIpjGihT1VdBUQa48j+JL5RVhlnXZEbkADZWVtsnTQyRWfC5OWqqflaLtIC2ihijlNQXq9vCVBULxlYMCJV0d8WYxS8L75uAS+QireqdwdiL9JipSznvVJg2hVGRVQcyXGURG5ZKxTwVqFpTCvzQGVOZL44HfikP/IqRYKtQFmxD8UmVsxN16TcFIzMtjehpL+GdXTXt6yevUd3fUPwAyFSwOBcYpOyj5e9NYVZV9YZ8TEvb5+x95H942ccD4+k2y20HcpYVmuDa50kjhEWl2tbstKUPjQFqFIF8J1Le2Vv1zhnGNPcyVxR5AoQn99ZCzkShnEa6VTjHMVEeFnGRunsqddn8zUb4BRbLe3eVxOX078X+12Nb6d9Oc/fzxU0ZsnAFPmMPH2vXuG8xy79tEz+in5znXO1XD0XGz3Xmcxzdbou1BRHqpzIFMkLPaFoE9GpbGrlsvLinhd//5qh/LrXcixnotRC1qiu13LKGCMpJLIT/2Vmd0rTpVye/3SsnMi1wWYBhyq4lJG4fZI2UOfPdrlrTSBmEt1yClintVS6OStsS5FEyEV+RYCjFGMB+WaCQn128xycfbOMxAtQ99gFkLCIwcqtFt+4AMZpTgzXdTBZtOqfLx5XSnGarVU32JaGW1mJHzSOnpp8rpVTlZ1srTS0TcWvCcFDRsrOTQHSClOprvdZz0rmlTIaR4OxGW0FtDPGkYMXfysEgh9LsnYBNhXGfE3K68Vzr/NI1eoJJfJFdQ0oIz1XjG1EW7oAhhVYV2XwJY5Wk8Gq8as4mgtmtSoGR5c5W+bvsnlVlQeQ+EiXvUN+JmtKvB1lXk+JzXlfnZJ+hSxTG1XnFCGVmDoLAdIqN0kQ5HL+UCtgYNZ0zSKNkdHkMMcMFXifVl9WKCUMbqUo52Yi6EnCszBZjcLoGZeyWuSJarWW6lZUVNDU9VvIkDFntB/RJpT5IfbH2ma6f1+lUtV/IjIF8djTHHo22aACbNoNFLAsMU+q6sRYpXjPbHmxvuYyP3Df7BizZIKmNirVoQFU7Z63VBdPmVyo28BMly7OAzkKa6lsFlMWSytSJ03CbGMJxyMpRgakEcH//a/+FY3bEILid3/7Bdvtll/9lV8T45sV/8cf/yG+6sAtDHkuwac9A2LlpvPCxMFSq0cmmrYWG+eunqZqa+QMZ6S9KaxcHK1ewznQIPNvsfmUwVTasm4t1+uWh8ZC0+D7kdSP5DGUZiazQZ7OtDTUU7C6nAVPJ6mar8WAT5kwBE5fvOWLN/+c7/2HH/AL77/Pt37hF/mN3/odLi+uRB8ylnPEzNj3nA67QvmXplcpIZo5uWg6pkwAzIVhe7Vi/bzl6sMr3nz2wMc/+Sn9YSCGEYNhjLIosxGDt75osCbh6emPJ8hi0Ppx5P60563f4/0wMbtb1ZBiRo2RqDMhjBzvj+LgGUPjGi4uLtAIKGqt4fbZlrdvxfAb5wh+ZBil8yvAar2mdZZxFM3NbtWhrZQ95DKG/TCyWnVYa1m1HZvtlmEc2T3u2O+P7Pb7aUO11mLY8Gb00+YWwkhjLSFmDicBES5ayziK02+NoVutaFdrrGt5PB653+153J9IKeCMYb3qWK9aHh930oBOGQ79qZTkyYbX90dZk4CxllW74vbZM5r1SsoPfaJZNdx0jsurNS9eXPP82RU//fQL7u537A8n0aN7MqOUkfGUjJXYxVzKQGwBCXKxMRKayuSUpiNFsy1WNpcEPaGUthitpXHEi/f45IvPCV6YTwmFzmA6i9u0rG6vubi85NCfpAGNdez2u8V0LwausIhTzhwOB1TKbNoVXdOybhpePdwRkoC/um3objb0dzvS4Es8I07AOPRoo7h6fsO3v/3rnI49d2/e8uWnH/P68zccxl1pBiTgEJSSiyhOdowSmGoF1lku37ul2a6wqxZ05v7NG8ZjT+w9eZSxWF1vWT+/ZvPshsF7+l4kD5w1pRFA0VYD0JpV5yb2ui8d3B8fdxKkxdrgpwZsZWOumnPMTebksSwc0zy/p5Qpze1qhYGaAmSlwGg3MVwqQ4hqm2oAUJ/7mc2qwW8m5NJ0qDh+Yu5qWaJCdNwQAKRcdBw9qveoJRhLYRFEQEV2b7/k+vmHrLaXPP+FX+bVD/49/eMdbdywvr4VdnLf4w8P3Iee9779Ha5v38Ps7hn6A6TAcejJRmMay8o1DKPn5D1ZCSP8omnwgzT0SiSuVitaZwghcBxGjiFxs93itCIEz+54QmvDZr3GGIU/HHgMnvZiQ+ccK2d48+ZLDiFhu4YPX7zgv/3H/4j/7n/9J7w8HAk1Saz1pKtVdeLmZ6jO9oYZimUOCOveWfcSnj7/XJy/NIEA5/te+eBT7G326JaTa/5lDbyeHE0bg9KRmEZy8KiUUCmQfU/oj1P2XXTMPMPQF6ZZJmRJ6E4JNh/wY+C0PxczpG4AACAASURBVDGcBsZTL6CsMYAlhMx4fEDXkvriHE2NKKZrEkA2xTCBrilnlDbS9V27s3Gpzm2KUu429Cd88Gy2F6Jj2bW8ff2SF+9/g/XmAutaBu+F5TMPfHFIHZdX12w2W4bhRO3eXOd/jrHEz4q+P4ltXjz0GHJxqg0pwd3dPe1qxWarWLOZKlvOy0TT5Ms8mQzlr2LzXzy+5A++98/kPTI5eZI/MRwfyGVfVYBpRE80JylTu7p9Qbva4McBP/aE8cTj/T2n4wlbSrnHcWB3/4rD/l60NE3Dex98SNc0bNqW14+P5KRnxi4ZYiaVaitrNK5xbDYdjbOi+6pgtz8yhJ6oOnTb0h/vSiPXjNWZMNwR+3tUu0W3F+AuRdbBWFDrMiaePPbkOIo/lAJQWDBacek8N21g6xRrt2HbbbB2RKsEOUAQlrxSjTDpy6LUGJQSkN3owgSpNluBWzW4NrPalucRfQFNNKGwCC8vWrbblhAzDztJ4Cl7ZHOZOOr36D99je4HtllxsV4x+pHovQCfbcfNi2cMw5Hj4yPDw1tGL42zpmd/5l5mlM6E5FHZgMmsty2vH/doLeznMQw4Z7ClPBukfN37UaR2oucwHOmHHucc6/Wa1jY0TUMoe1qMQZK2RRfTKgsxiCatsTjTlNGLpBwIZS8QZmuWSgXvgYSztXHLedBaqBIFx5MxH4ZBSi6tK/tRtYXiC9UGjzl6qeqZIoQai2TReU4nbI5oojTpyiXpM8F3EMaTALbB8iZH/nx3z49OBx6NIiuNLZ26l926KYnXKTNPkZ1IohWfjUE3Lc1qy9X7H9Bc3qCbjpQ1YfCQg/QVKVehiw/qrKWxBlU6qmfX0F5esTudiGPkdP+W/eefiZyAbcjNGmwra8GUoF/PjDqrNdmITz96kUWYyk+Z50TrWp7fPuezl58yDCdS8AJcK1Al+RGCaHUorVBJJCBqE6Q69BkBPsSOqWlvY3rK8/ytRqrGxXWPWu6hS8TxKXC4DLeUPJgpPluyr89QNFWTm+lJuFbjRzlf9XmW8WbmyVfKtZZvik6mXtxPde6m+VauqZRMpywNnrKSZF6qCQ+BWWQt1IFVIPrLT+756d7/rut7msGtd/Q179dnpRAIoZabO+uwlc1oihxBBbCpj6+MrQTacgBl5n01pSk2qa8zQMpZurYrLElZV8a4szlhS8OmCSxLlbUKqo5bElJKTlk0Z5WaGKfvvONqk2q1qVriCVo06GGSMBRQ2M33FCM+jFL1UwBD6+zEdK9MWJgr4XLFdFKVOdRoq1g30kOi3ls/nIrdynN1jBVATWUtGvZhRCVZ+041RR5JzjkGLxWJxU4aKxIyRpuiHarJTcsw9HhviHoUNyfnsgd4mtYJ8SJLSftSCmtOzUnCRhupftWNQyRNBDTNyhB1YbcupK9yTsRQQG0qE3m57ivgG8szLDhOBWan62CaZ7W6ydX3ljYjZ6yR6mjyPP8maTitcbaCukWXNyW5twXAb6yZGqiJzMUMumYLrm2k/0IhD+Qs1RlWgUEqHfu+J2c5d9uKzn89R4xC/lpWTpphLEkIJaSXXGXFZkC8qXqwORd5jby4r3ktiQ2SYREmbfl7Hb8C5nZNO427WozTu14/F2CsyYptbkkmMRpNsmC1k+Y0SjIZJe2CUmCNY506bt0l12bLT8dHQpvJ3mNTMdJCFJy6ryo0lRmhVJZNr247i5Ix+QALYwnF0yl/lcWTjUKvOozRpNGTvAcf2Q+eP/ne9/A+c3Vxxbc++i6btuObH/wCQ4r82Y9+yPj2R4Q8iOGrzhLyI8YkRitVMKHGhnm+lPkbqJyleU/p/KfLcXK5iSkQLSDNdIMl4K1sr3kjnd+rJQByyDwFJdYZmq4l6R1m3aC7BhUzYfD094+omNATgFI2FiXjWRuIVHB7ZjPW+53FrTkTqi9/tGMk8JMv3/L5m0f+7Acf88PPX/P3f//3+Ob7H3Cx3uJDIoWBMPaEQQAhM21I1eEs41AMjLBMSya71bz4ledsblfs7u/Z3b3l/s091suGo5Wha1d0Tp5ECIHej3TNikQk2QgukX2kW3WMPjL6QAxyujFGtE5Y57i8uJ7GyWjD4TiSc8SNhtG3NI3l5uaCcQx477m5ui4amAP9ONCPI9uLS7ok2RltDdpYct3oUyLlyNCfSrmUQuWRbWdo9IZ163jcSYOOYRgYxpHDccf15RWQSBpsTtKoqVkTU+ZwHNi0ls12XViRiRwDSltWzqHXa1rreLvfE0LikEYedkdSTqw7CeQy0BiD1nYCBBSJMXkOp4HcQ9JIVrBIQAx+KCwUMY5da3j/xQXbC8PD7sjdw5Evvnjg4WEvwuyZSWNGAMZECEwNVCuTIpdNJaeMH0eGcZz0lapDd+bjUs1ByX6FwOvXr6eGC6kAuDiN227YPr/h+tlzXr96RUDKGCPSuIEsGbwwlUMKiF5L16xShBjwUQIbi2a73tJ1HcTM6zGgQyKqE3F/mjqnCvZhuL65xTjH5dWK7faajz76JvvHHS9ffsHu8YHoRz75+BMpDTUtK6U5DSPrdotxBtMY3MqRywYbfeDhizeM+yPZi3Y2StNdrdjeXtFsVoXdPOBcsW0xT3NxGsJictfrtQSQb8fJ2T/X1ck0TUPbtgynnpBCAVXzYv2WTz4BZ2rQ2ff9HGAgoE0F4i82lzw+7srGmqdzzgHOfIJ8tgcUq1iyvtvNZtZ+DHH6jFIi+B7LdedcNLpSZr1e4dpmuq4xRkKKWI2UZIdM/7gjXxief/hLDIcjh9df4I8njvkNz1684OXLz/HDiTScePXpZ7z4xW+DMRw/P+HHEetanBNnZxgGhhAwRhjKTinGfigluZrOOIzR3B8OMv+V4nq7oVVwGnoGH0BrrjZrgg/0Y8DHSLdqWWlDPA282h9ITnN9dUFT5szdw47/8nd/h3/7wx/z0y+/5BADJ2Wm/Un/f8y92a4tWXae980uIlazu9NkVw2LpRIlihZNgYDgJ+CF/Q5+Q/nWEGBDsGEDtmHAlkixURWrilXZVOZp915dRMzOF2POGbFOZpUE+qZW4pw8e+3VRMxmzDH+8Y9/lENOk4tOWEKZpXPrGmi9qrZYb8jf9pCI4DuDp99WblhBezKtrHZhfy7L5CrsLcBvjInz6cLbV9/QPb5vJelJZ2E1OIftB3bbDZgOtCPj2OxumLzIvIToiSHy+O4tb199w9MXv+LVl//A4+Mjl+PI5eI55JE0jZhCHREXJl2Bj10/kENi9hcANps91hRdUAU5BUJQcn5dThwfH4nThVi0tmY/c3N3T/QTl+MTr77+mmEzYKxFO4txjk4bKn0lRs/5cio6Z66wZA1bd9NkSVStnllNm3Qnzmy7EbgAio8++Yw+F827Mr4VKKnNxz4gAn97LdRE92pff/zFf+Czt7/GaDgfHzkdXhOmJ2I4EqYnUvrT9lF9p0hZEZNCaScsXuPY7Dr6YcM4Dth+L5UIOaKt4abvRUMMBdqQs8EHz3bT8clHDxz9mcDSJEIDu75n+PgGq2QOjTX0nZP58SOKRIxwPkeezpFXhwPbh++TkWZCaTri1IjO79DxgprPzP5IoBN2bFZFf9KXREFEdwOm78kMaBK9urAdv2FgxKaJ+TLx/gLO6cIaAtGXNBgPlxRoHnQJljOZ4BMhCBCZQlxKFksVV6r6gcskCbajdUnsavyciOlMcInoMh89fMPtP31OfJw5f/mKeDmUJGLG+5EpzvjfePk+7wFFmifRFG0r43ptRBV4e34No24SHdF7shEt1k5brLMQiwyRzlymc9Ogi0VqZxg2OGNxWsCDEAVA9d7jOsvsPcFLYnvoe4ZhI+W0OXKZzzjbL1dYWXHNycitZLI29mnmp2iTV5grl7JPrUoJZ6pAUGrAi2m+dY0JSnx0dfZRguyZ6M8oIutkWL2uNocqkZTGa8VPTyd+ReStVSRlxS4UILaCsUIYSauGbKqBJzllojJsXnzE7tkLbl+8ZOh3cu5qSYxoL/J1SWkogO5SFSMsWJMCLkGnDbYf2Aw3XNIZqw29ElZnMJpY7AjZi7+mjUgalUoWyUeL1maIobDbFlMjncsDKWa++s1X5TXLUGqlSKriGRI/LWxIfd27pAV6q91RxkgvX3nlx7T9kxetz+tz7HrNV8DhP/e4Am6vDrz6s0HlIKByvQZKfNfen4V40s7Mhfl4fe0VtJPrbY2icvnUXKujWHDVCuGmwLDdiUZlJU60gVIFkP324z8/Ass4/P95VPk02ZMiEWeSweRc2KrqW3YJctm/wgJUKq/WtmoN+EyJodY+r4A/Xb14yKlovi5r0PuZqsS1ZmbWahmFEGHWHeaNXgDVCmAtfRkWTcyqLyqM1FIiX+xQrSKuoBuVDKMNyhgGZ5kKOFdubKWpujTWUsaK3IOun13lx4ThqIsNoGANUp0XC/mmZg81GMemF0m0RsYgFx1V23RW+64j9qElYXJBzpsUDVINFEKQytPpwjxPUp0QpIQ9p4R2RmK7knyqjaJUlbMREV8ogLVxHdZ29P1APwwoZVrFlNyCJLfzyo7HUCUj1/tczuiaYK8ybDJfdtXwTfZebMmm3DAbvZrbnCPMoX3Gh2vgwz0jcZa5AmKVUlIFrHSTrDILjbKsEYPtTFsHKSWSEzDUWJFibA3/CiBrzNLoTSlNP/RyrqdqH5bEXV3P0zy1z6/VdFprAVVRBdCVtTwx0/c9lPNL/iyyn5XxXCstKThFTZquqwW+6/F7AcZCAV1zIsVMnGdULhqP1uI2g4gsp4QqGqkOzV4P3KqBPmiSK9kSpTHO8v3v/5DzeOF4eeJ4eQICCnNl/JZ8nYCCpnT9pBgoAW1UYdOp1eEgjmnWCtM7YcJpRUwTPibenQ/8w1ef8+//6v/lo/uP2e5fsuk2PL9/yY9//M95dfkGPwayeHrtcKlgs4oSeKAXB61NYa7O7+ouci5nuSrPrB5lgYgDSHNell8vZb2rj1+ND/K7LEYVEudxLjpbWfRaRSwMoxTdfkv2AXwo81ic8XIgVKC7jXEu7Of6PcX1a6Up6vpQFJBKE0Im+Jlx9Khf/ByrMz/+wQ/4gx/8gI8/+oQYZulmGePiSLaPvP68bz1UxujM7mZD1yt2Nz2bmx2Pbx6Zx1FKT5Qna9Ej0Uph0fQbx3iRJgcYhXO2sJgT1io2Qy8dGqMwYJ4/3OGjL1IVgNIcDydiLGVwRhoUpDhLA4mUpInPdiNrr3NsnGXYDaUBjjCrfMzNQDlj0NqVTGci5CxlpqVc1FrDpnfEHNltOja9YxwNRoNzjs5qnF1rpIijeh6lFKPOr3SQhK6z7c/hciGVwzjESIiJXQ+9NThr0Ih+bWgHXUKT6ayIq9/d3TJsB7TSrfHTIrchdkCbjk2X0LfCpN0MO96+OfD+/RPH0wUfAjlmKWvIqTHU6vpORYTbB98ywWv70BydyqBHwJVWsqxlbM7j1ETbM7J/7WbAbAf0ZqDrli7KMYk2Hrq4r3mxOdvNRsY5eIkPlCakQJ7lIEmtA2qk6zqy0Wyf3xGHnguKcL6gspTeDJs993cPkmFFYYxCu57dg+U2BdgY/HhCv3XobmgNXMyo0c6KnrHVBAP+ciaMnnCZmI/n1vBBWY3qLf39Dckqpuhhjs2JFFDiu+3OPM9kUgvOlir/6gwsrH1yDeRiaywQ/AJifxiEVOewNXtpJXu5zWN1hoyxZS0krsKLNehWbP66dC6XgEEpYUqncuCvv3udfV2HAUorkoa08sWnKA67lJxKIJO8J4yiYf3yhz/GzxOXxzeEaSJME30/kHJinEf88Ynp+ETfdTw8e8Gbb3wpqRS7EGJk6Fwb1xijsNb7TtZ1jPg5kBJYa8R2AOdpJmTQznE/DIR5Jsy+NRDojSP5QECaQ2y6HpsiYfTMITLHzPefv6BXhu+/fMGr8cL//dNfEirDRsk4xryenTaZ18+szqYWuH0QYC6lmP/lwef1v9cg7YeAH/WYqhfSnktkptnz07//e56/e8ftzQ03tzfcPX9gs7/BdgOm2zDs7sA4UI6sLCjLsNlivMf5IECWAjvsGXZ37G7vefbiJd989QXvXr/h9Zu3vP7qV6QUxIZkTU6RkK4TGcb0EGap/vCe1EW06UDJmrhcLvQbuUmjDdthw+V8lABHZTrnMFrx/t1bckrcPzwwbHYY18m5VEv6SlOPabzwD7/4BUYr+l6keMZxpN9s6IcBrUsjLqV5eHgu59npiNKizznfJBjk2mMKhKSpHZHXTUFzymw2+6v9vJ6w+t+HM//R13/N999+zvOnVxwP7zk/foOf35P8kTifmMdTY9oAohmvqjZ45Hx+JAYvgWCW8sx+GNjfbYoWvEYYoqVRm9KkBK5XOG1ww44/cp+RipMuAWOmMxqrVSn7FwDLGksInmk6E/yIVprdjeLWK3YnBZsNWYleL7Fn04XGaFG6YyrNblMW/rRciyMFhZ89T4dHhuGGOVFkjo74yyM+B7SNkGeU0sRc5FdqUjMrVAITM1rn1d6QMZ9nKc1NMUuTW0CVRrNS9aFaEUgNmMXuJpTKGCFOorMHDMFETtOB/cuPSb0lhIH86oT2GRVBJ7EMaR7F9iJ15RK4rtfFB8uEjA8Tueh8Dl0HWfyUHCK6q9ebSTHI86XCSRlhN7bgqxxc0zw3Rk0mY5IRdq11EsCpgtVlOSdIubDKVQNaF/Oy2KEUE0klAWfkVICr1b3YQWMsfd8XIEe31y2AZSE8sDAXM3yLVd9kVXLZCbkQPa6QdJESGMm8mi/87eNbvgkzZyiMRfnwXD6nVR/WOIQyxrVaxjq2D88YXnxEf3OPdhs8Sli5UQAFP01CzslLRUROmdrvTGWwWbHLcKsd+82usMkMdD15t8cbKwxLJYwxyTsuJJCGOTYQtTCQ1/6Lrj+LPxiS9ENQRqOxdaKp1ZR1/VX/kPbnOgbTBWApQyTvqfHmaooWEP161SyPReLnalrzh99J+3n90gbo1NeX+1cFfKjrpV5CJdq0VZxpOpDtexoAv4oty7rXpew8lSZoEoeWsat7o2yJWl6srBGOoV724zp2bWeAKiw2Vdfzd4/Hdz3/j3m0YV99REqFnakkZtIV2MvLeyqbrpZ9N/Cw/K5KCyzA2AqoKvJItaGtkEsCNq6lvtQCOn0w30rrq4TL2l7U7/twfNbgWt3oubJ35TfXq6/Mf06yX9rYl3mKdX2s4rN1Qg10i7eNEed5EfPQ8n61HtREWbAlhFjWYblw8fupQGwZxyQ2Wq3J3XVM2sm1MKDJAlg768gZqY4opIwUw9X81DWZUryal4rf1LNAznEnTca0wRpH3/UCAKaiPb6aA60M1kA2FcwvNtuYZsuqtmxteNX2dO1hsfKvUhvGIpdRQPaUKxaUWoV2BUbFJ7pmnKaURPPWXgOy0ghS1ow2hnS1RjMQ2rqqW3P9fmvlnKvg81JhXn8uhBtr0FFJQ7iYmlRPzrk04zTFB6AkTirQLr8ztmjKlnPKySDLuim2sALYLdFWsMKWgMsy1qnpCH/34/cDjFWKQOnyFhVUMe9SW2SMpSZMoDhhKDbKslOOLmousstl0SnLj37wT3g8PPHVqy84Xg6kFEq2Z21U6qkLVOS6/iYvgY1qjlEuTkDzJgWwUKKBqFISdmgOfPP4hr/+T3/Dn//xn9F1ezq34W53x49/9BP+46/+kimM+HCRT82pLX6tFLFks3XWLFdXDUdG14Oq2dPqzK0M/JXTtNxuZgls1+fNNUvo+j3VjOUMMWUuk2cc58IuhspS09bgdhtpbjaLTiQ+Nkc8Z1BmuY6cqre3wLHU8qNiPBXXTkNqIk5y+PsU+fr1G8J05u271zwe3/MnRDZGuh4CLauWm/Py7Q18BRQBKQWMs9huy7Af6PZb6Zx7ODJdRmmslcFkEcM2TmN7Q5oiSUk5ktGaqZQ4GKPZbXvpqukVzhke7vc8HY9tvFOCyWphr2oJ5KYpchlnYYhaTbhcxCGx4vj1w4B1trBNM7OfmUv5mVFGWIWd4Xw+EwrLYxxnvIk4K4kE64TV1nVbKfcy4H2kM5KJdFacz7fvT03H8zxOOGcliFTCXtfW4DphusYYcEYBFq1gTBGVFH3n2G96hs6hEMbwFBI+LE7RbugZNlueP3tgsxmYZgmGhLm8tKopOxCtLJvOMHQ9u+2e3bBBKfAhSLliVEQvOnkpF9aqqpo2crCFIKtt6WhbAqbvBHRKYqY8ncikEFvSAy1lJna/QQ0CmOYkbHyVcgF/A93QLwdecXz7rhN9yCgC87VkIsdA1QH3waNnEQrPRrHZ7UhdR/KBGGZySLhuYH97x83uTrqKF/2jmAFrMfsNjgmfLrj9lt3tHWjDZR4xRlg/qbD6coxcDif84UK4iO6vdU6SZU5jbzfY2w1Zl/GNCWN1S+y0QEdVYFPslQ+emGNxoKTkr2Y61yOeUsbHgE8iqG50z+B6xijdMBt+1nys5WCvnTQ/dKrq62OUZieqoqL1de3gVKu/PwhiirFVqMZ+qk71h85yi1Ha1yh8Co2ND7JHUow46vpLpDAzX87kp0c++sEP2dw94KcL4fCe8XTEdT2xkwxw8BfO718x3Dzw8PCcy/FImE9MQRisKEVnO9GZTlI+tN0M9H0HRUfWh4C1ls5aOmPw3jOFiHGWvuvYdI63h2Ppbm/ojEVlmHwgG0lODlqTxokxRKacMf3ATdex/eglLx/u+Wa88NXr97w5HhiDJ5IXR5xr+Qnysle/FW9+8Pgu5k8rK/ovCK6uzoMGVKwC1u8AQFa/JCMawj/7xS8IMaCNZn9/R7+7ZX/3HNtvUbaHfsMlZFIWOROFlMPN3uNDaZRjIDvL9uEZt3cPPP/4E24eHnj96muG33zFq+mRt5cDVe+0JYJW96m1A70EaCEE+lpap0SKRCo9pFngbr9nHM8YrTDW0HWOGAKn44Gu6/n4k88wbgBVG/dJM1KtFDkm/OR5//otqMww9CilOB4PbPd7NtstWst6Skqz3ewIwfPqm6+xTuNcx2gHuBGmYAgzlykxzzOX4wHblaR3Kfn9+JOusRvWc5JrUFiiYaWWmXt49TPu37+mP7zndPyG8fgKlc6kcCHMZ8I0Uhk9SoGxAtTpAmzkNIoueJt73Todi86/KKVqIyWGuTTjTHiUinROs93sQRvRh1OSdE6x+KaUoCyDUjJW1hnmSWOtsHKzstx7jU+OrOR7lO7YDwW3AFCaEDUhSTVYxhCVI8dMjJZx0nwZH9nuM5PPTCYS58iQDF2vSpmhlvOwJjMTGCNgrFayR3SuZnIBZnx5bStJKz6XVIHVQGgBLHJmFaRkQgmYSBLI5pw4XU4MZkbd9OSXW8bzATcndIyomDBJOtk3v1xpaVBpPLDITlydKTkV2XjxH7ad9B24jGNJ4Kt2/uck53tU4uNKY2ElDMpmlmpJpshvLGwxK0FySQSHGFh3LY+pgOhZU0P8RhwvNq+Vnq7GWV2BbarZLGMMfde3z6pc2upLLHHDB+BTdcrbN6yoHWWSKgurmmGVFVFpzjnx6/OJnx+feKsyo1awtA1qH5FzvnpOFkpp5uksdtix++hj3MMzrNuQs1QFVYmEFBN+nhoLUsA6mhRNrbAwKLYo9q5jt90zjwLUB22YjWVUjqTt4gMmAQSWgKpEHit7uoDY5VHHYn2uZ9XAdWlGFBA5guuz5MO/v7Nqo31mnZE26ojEQwn6myuyqt5iHe9897n34bPfFQsu9y5XtLBVq3299quWaxf/WFX2MvnbQIQqH1x9tgpYrwpFhQmpVraiyHFY3UDJXC9Q1xJ4Gft6nazG6Pp+v8Of+0c8lvdW9m6+Hts6ZlRJBto5nXKWxPuyK1pCzZYmTW3fK2EEXmm5fnDdwnz1CxiWgoBnVObg0jBXzhpZz1rlYtNXY0xpNKt0XerUao41o7ZdRyFUyP2r1hi0oCWkuDAycyGz1GTuAo4u+6uG6rUBmNiOAlZrTU4SH1eChC5yDrmUBueSRFvWZ2mcpRQU8BVUYQRHeU8WW1JHdSH+qIYdVZk0nZOIRGVVgE+KLyUSC866RoK4rj6W+0qlGrburYpd1TGSh14ScDlLJSUiYxNCvpaOyKUBvdJolcSfzlmwhBWr2pbmqhVg1HrFXKXw6tbgYqIxsbUx6HKmx5SgSACYArTWypcK+AsxzJdYOaOzMHBBNfJTBkwWub+qHx0rIF6rvkqFiOjCanQZR0kSsIqzinZxjSEbEzWXPVD9KwGNKVUwdU81yY+2X7RgI2Wsci6M8Hp8ZVlJMRZ5MRa28wIKV9tX1iW//fH7AcaSiVk6zmdr2T+7R/tMLA0s/Dg2AeTqXGgFVmWsAmUMyWRQUgKjcubFs5fc3t8xx5GvX39BJojj2jYAzQjUhQq0xQJKHG+VpYObqvkbMQBVDoCoRDPLGty+Z7Yjfp55Gs/84stf8fNf/idu7u64f/Ypz273/JPvfZ8ff/xD4nTh1bsRnCKH0hAiSyljhpZd0mqV7StZgEhuxo6ygHO7sur8FECXYnpyvfZvn55XAWxe5+TlJiuIqYs2XAJy1e6pCx1ELHywqMFgojQZCoeL6KWEuBh0uAI7tLbUjFAzhNQShaVcpo6LaT6AzFtE8frpzNvHn/E3P/17/vKv/4Z//af/io+ePbDf9Ki06FNJs7HC6Kmg/7dWI0XPTzJw2mi2+z3bHzn8OHI+nvjNl9/w9P5JGj2hcNYy+Yk5RpLKKAvTNDJN0syqc5Zt78hO4+yWfujYDo7DwZeulprgE88ebnHO4UPkeLpwOF4YvQCfQ9/Rd47T8YBxhq7vcM6KXo0uIttaGAkxBlAa11mGoSPHmZwFxH46nJgnT4wZ6wQ8dc6RY2mgESOaTJin4ucoNv2GQ3chzlK2NflEwoCWbsCXeWR3u8NY6bb++t1biJGbzZaQOhQJrxLf+/gFt9sexogALgAAIABJREFURcToxDx7ppCYQyL4wOQnbm5uuLu/FzB2GDhf3uODByV6LxJzFaOnm6ePRjEYzcvne47HI4fjkcPhRAyZnAqTt/jc2pQsf8oFgOpYu8sxxKWUxprrg685K7IHU86SqUdhjUb3juH+BnW7ITvD5APvHt+LKLsXTkoykk31BRCpIVMFYyjZzayh63qsMYxhxia5lsv5zOV8xmolrKze4J7t2JC4vD2wubnh5SefMvRb5hiwdgBteDo/cvRHzkw8hTOvXn3Dw8MzfvSTnzCHwM9//lMucwYiOSTpsO0hnzzp4klzRDtL9BG3cfS3A7tPH5iVYrfdoVBFFqA4F3kVBrcqydL+QUHXd8KgUyP7/Q2n40kcyqotmTMhRZIvWe8sgOJ22GNVZI5TS5rV2WvsgGbfddvvFOetBgyX8Sw2IZVmHMUOLUHBYiA+LMupQveoIk1R7GTKAiKtM8TWmnY/OcuaGY8npmlqnz/mSE4CxuoQ8IxgAslPnKYnYpq5u3/Akvn88J58OrI1wmDt+w0+PHF594rNZsfN7QP+5We8+vLnzFm0nTvXEWPiMk8iPu+kjPNyukhpbRLQdb8ZUCkzzYGncWK/23Iz9FgyT+8eOfrAdjvgjIGUOI0jSWs66+i1YXo6MMVA7BxmGHix3zEdDhzDzIhi12357//iL/i3/9f/yU+/+IIxBY7zDKZqYekS7K/C1saCvQ4kWyj0rQBSfl5rqrX3VE+f5bVXLKH1GdkcZFo32JzKsuaa4xTJzNHz1euv+bM//zP+yR//MT/40U/od3dk3RGAs5/5xec/48unt4wx4EvwgjKlBDoQc2T2Z4bs+OzuE/759/4Z1g7cP7ygHzbcPXuB2+94+z/9jzyeDsKTU3VXrYJDXCF2yroPwdPnHmUMVlt2Nzc446RZHplhv+ezAqKipMnCT//2r9nutuxvbslK5FVqeVkoHYQ3my0ay9Bv+P73/wByIibPPE/E4HHKMJ9GGWOtuMxBpBDmmcPTE7vdltPhxGV3B/TFVGSmy5m3b97yxa9/ye1+K1p7CjKah2fPCli6zFvK4v/VJIl8n0y1Vhk/H3n76pdcHr/Bqgs6XZgvR/x0Zp5GrOvax2mtuX/Yo7UpnaeNBCpNSiVBTmQVmaYz48VLOaJxrUkZKEKUQK9mjOTKNFn38tquYxovbDd7un6DsX3x1cqZpjT7YYs15Z5UAkSD20cJtrWVBqJSXFcYO1rkirQ2aGWIBXRS2qHUhp98tmcuWvpaASlA/ASVR8gTKU7M08zrr3/D5XwRgFJFWU9KAicZ2lTGAqzRKIcw+6IAJCktslQoLaD9XJqnlm2oG6olQb3WWoAwJMAapxP5/ee42+e4F3e8e/M5lomcL3AJ3IQbnDKis6pAY3j4/o8Zdj8DXpX55OqRYuJms6fvNpiidxtDIFlLRNEZSTQngNIoJSGMHqUVxjr6TjGNUuZolMEODpsE5NNaegB0zi1rMQSeDgceHh4Y+h6VlkYmWUkzlIyACo0hpZQkT0v39awyaw6bVFWtyudztWdcPccKbJGy3HJNvy06jBHROk/Ffy7lmGWqNGKjZxRvg+dv3r/lSz9zcuKPK0AlhVEFmMtAlXEqCaSYAljD5m7P5u6Bm+cfo3bPiNpJCXIIaJWbtmAqwMlS2p/bXtFFn9Zk0Xp1FoZNz3B3w69//jMenn/G+P7MN1+85SlbZtMRjRU/y4+YrqMi68upU5PklQV3fYZURq9gPBWcNZRufmQCOQUaSwqWhEQBhmIKhSWdoAAKqehpa7WS0rv6fv3dIKjSH/zMYktYQFW5uw8nPhegjRZ81jNRl8VT/SNxwVVbTxX0bZVQ648u7OyUK7lAFmM9c1M718s6MdItXRXpCmFTL2tVF5karcHKVis6qpC1QndWpKxSKtuiRoq/+3ENZtex+92v//Zz336i+ojWWjQL6FWbURllFnKAWnxLpVSxHctwjuO4aFxWNKIswAZcR5H1ctoBHSTae2KQBLGq54RaWIDtpuu9rcAk8Q/Uao2vXwc+RChAWGVWUuRS6h5JJQllrG36oe2zigNVAS65lDIgWqEw0s5dm7ZGlVb4yyxYjFaIhLkA1jlnfPLMMbS4rSbGKsgGwsA8jzPzLD549dFjWu4vE9tnGCV+NoqmaRuz3O88z60BoPKqNQ5cGN+pkOXLniqEjdViWXzN5psWAFJpYgxcLuGavZxzA5NTqcDVeqmGMJoiXyVnacXPnLVFD7YM8YoVba0piakSe/kKVAspx1gt8lTlHZXhK80rNWw2xX+XxMDlcsbPM8ba1gDLWEfnHPM840NY1kFZ9xV0nqZJKkST7B/n3MLubWdeAZqtIc2xuE1S4SKSDIulM0aX6h5JhOiwkGbqGmkxHiygcpl/51xpdhdkXLWS3hBGPnt9xla2swJiqHv2u/G3+vi9AGPrpEsJceJwfGKnB3RS6ARhnjC2BhYZirZUXSRGaTRygKUcOYyP/A//9t9ADsQ0kyoQo2LJflx3XxOjJD+lIEh+G0xVwvYkjkmqA11oCLocYtUgusERcsDnmXf+wP/y//xv7O7v+TGWu/vP+N7zT/jX//K/YZxnXr17gyIKBbwYpVRKy6wSnT/J2shGWpyEBcUH5GxuelM1NCy/oBzIpcaoAqKVyl2Ncp2HCkCUfdr+pgGgGoVk3dAK2xZXcSBzKuV9Gb3p2LhemLLTLNpqPpCCMAq01qtkWG6MxXb4shySy7esHMjyzwaKoRhD4m9//gVf/Po1Hz275weffcyf/8t/wf3dHmIRu26H+/KpH6zI8t2Vai+OlbKa/u6G4e6W25cveHz9luPjET+JHMO7dwcuwTPOgTlE3KZn24mR6qwl5UjnxAEMs2cOHrTojMWU8D7hnGE39Oxdx8P9hsfDyFevXjPNgdN5ZJpnho3DYFEJ4iSd0qUUwNJpzacvnnE6n7iMI+/evuXSddzdbtgMA0YrzqezBBY5kYJnU3SFfPBoYHAdJtbSZtGGTDExGMN2Xw1S4nw+kIYebTRv3r0rpQOO0XveHEZCVmzThb5zPLu7YTCZh1uDMxKQWQMzmaEz3O023N9sOYeIsg7lHD6M+KdHHg9nRh9Rxn1g7BQpLKzDqmU2nUcOTwcOTydZH7Csobo9JDaUvZDgchlbR0gSpXwhl3WVr1gK9RE/KJFPCrQzqMHBxoKR0hnvJyYvAGXtZG2QJhU51fUl13c6nVs2rx4c8zwhbTzqfcpfWiuy1lzOF4wxbHY7aQpiLDcvX3L78iPGmHBug7YdWSlsv8GrdyQv+nrntwcOHHn77m3ptGpRl8jlfJTsYUyEMchB1JkG+Oxf3jPc7TDbjqhgcJZ5viwOaaZ1oBYnbrFL7XjMuQBQIsj++PQomj6dLVCp6Cjf3Nxwd3vDl19+zul84fF04HA5SfChi1Ur+9mowpZYZUTr3OdVsJBzCWR1Cf6bBpZm03d4L929l4da/QGjLRCJ8UPbUV5dHN3a0bU5XoUpa9XSnKA+/t2/+1/53sMz/uQnP0HFSGZGk9BYOu2Y370hDht2z17wB8O/4ld//e85Pj3RDRtuNjuMMpxPRw7ffM00znz8h3/E+/dvcEqh4kRIgcs0iz6scwzOcTkcSxMm6eD6bLdjGkdGPxNz5u72hr2zzPPIcZoZfeTh4R6NJE9O00xWiof9Bg3MxzNjTmxudtxuBjprOL5/yzkmumHDi+2Wu9t73h2emI4nLocjgSxrqwKcKS2ArFIyZiUwEwe3TeOSga4TXd9DHe50BaL/roda/aMlQOtzeXlu6bB7Pd/GGLa7Lf/df/sX/Nf/1Z/y8Owj/BRRasT0mtlkXsf3/Jt/+J/5O/WOSSWyFmYeVou9zQEfJ4iBT7nhXynPH/b/lCFscJvnRDZ00dG7LdZ0BUiqYEdeNc8sPoExpZIE0EhQVRIkIv0kEgWus+QYsd0GbTR+nnj39hU//MM/ajqzMSb8dMJoLRUY04Xb/Q3J9Whtcf3AD/7wx5yP73l8eo9ylheffY+b7U3R6w6SpFBKwN2c2Wz33N3fQc585s7ACYDt9obnZls0OQ1Kl0Y6s+fw+L4EsdegxMIxqsZa/IwcA+fjW5793f9BN76GMDKHmXk8oRX0g2V/cy8VJiUgq8tJqdSC6gz4UjGRUyKmwHg+kYmFzdSR0kycZqqVE91OKSOU0nGIwYOaSLFDsYUUmMYzIUSMK+XOZIzVdM4QvRdGYJ4ghRLIOXb9gHUbrIXLeOZyOZOiNNhISHVPZzuGzQ7ntiKJ5AMpJ6zu6PWqOiR6tMooHYqPbbjd3XG77bicz5yOJ0CSRSkXRoy2S1loikQ/kWaPGjRgSUlBnPEhCQN3zmycQtuqbSeagVoZrK3LNJKSIqZcwMCR6BXjZcTewOb2lu7FA4d4IO6FNanejtz6LUuLgsirr37DsLuw2clchlVvAhD77XRHpzsMRliuUaGT2GmbjbCCKIk3YJxnSSgq8DkSLehd37RzpSGwsLxd3zN0g+jYFjCk6zvue4cyhqDEx+h0CXxTKlU6AVBYZXDKNK3lmgAwmKIvWFZ6UqQQmz0SP6I0gSp+bsXgFm7eEgeIu/1tSY8ekYRbdlY9u1Xzm6OFX48n/uPxwF8ejxy1we3uuL3ds9lu+ObXv15Aq5IjEQBWo7ue2+cvuf3sEzY3z3DDHuwgcnVpxbxTAgRrCYY4pchba0ip+GqlFHlwmsGZUk1SSCjBM14ufPTDH5GzQg8Wu++ZHhPoJOzrkGS80gdVFfVM+VZsQHMDdFZNY7CBrSgo8ybApjSnytlLYiav5BUo7ERdgVCRTqhAQNOVrNYkl4Fs8Uk7kAp4uLb96xld/GX47UzQpbJHfm7ARbnlAqULUArLOagq272MgNJIKW9NDClc11H7MtRhbczzMnY18dVYk3n1HeWenHMV323alkIOkmq0FBN58m3VppDL2l8Fkd8an9XZ/o9+5A/+j5C4cgXHcgOJcgwQPH3fL6zE0s+DAprG4PHzfAVQWmsLOEeLm1NcWJ5yzqhWGi0sW1Uqi8V+qBXanjIQI6ElhEvMW7Ruc/HFjKlNdJc4RReWIhR5BSNnZ72fWOev4Ams1pTWpuEvsi5z88fX+p26nE+5fIcrmqG5gJBub1tZvHxLabBV1slmu2lgfwXFY4zFj5Smzvd9WZdZEiFSSbc0YKo2NBRAjUJ2qg6h0dJXwzjbbFZKiaHrm66rM4YpeMbZF9m82CqZtJHqGjLt3kMSaQNnS0JGK6AkwFMqSdUikWMdBifXHwOXaZTkFQIYd7bgLGUCYoxEL2c4iA2pjdKMsRIHhUpWk/0plRa5JY5iCFSWcvkQpmls82CtbdXIu92etElF8ic1vM5aIW9kcklY1z26aNRuNwMhis+4sFzL3l1tWEnsFR/MWEz5/mmemKaxNKOWz5cGiSXJkHKTb0xFLqnrOkyZm3me0YqmGVv3n17Jdkzj2H5e6yivH7GdZ9c2+sPH7wUYK4ZZHD1xnj0xWxSrTEYBRnUBS6rRiX4mTLM4gJVCnCOjP6CVZAtkYelW2qKKIc8lwJINVDM7LP8Xa1Gc6nRlzGEZ9PWy0FqLZoiS0tXPX/+GX//659wMe/pui92+4MWzF3zy8mNefPXA68evRYOs/FdZBikVgWhdtSbq5cjGWsj05Xcte1vDkBKYfXAoV9t49VwFRuv4IuVBLeOm2ijSG0NnB5zVvHt8L4Zi5TAoaifH4nAYBRi07uiMIs+B8XgWxl1zgFbXVQLyNrIlmFk2PoXCrtp3iH6dgixjE3PkaQ74d08cfODsPf/sxz/go4cH9psBgyMhrB456b7jJK5lFhnJcpd1UDs+KmvYP9wxbLaE2eOniafLhXxOhCLWbo10zxXNF0MMnqCEddspy24zEMOWw+mC96FsWEXwMypLFqy3iee3e8YpMM1RQJJYqPG6gJo4Uop4H4k6s+stt7uBoTccno6cLyMXKyyFYRh4uL/l3eOB0UvzgajUAgqqCnCLzpxVVhrPoOkH2zRXtNZ4X7omxsSm7zldRkYfmEPAJ5hiZvYjuxDo3XYFmooj6v2SLbVWnIzNdkD3A9k4fILX7544nid8AmOTHFwszvo0T61EVK7LcjheOJ0nvA+yX5Zo5CrxINq88m/XmfK5shq1lqCgHkoVAK7vXW0fyZ6R6Tc9brfF7Adyp6WjrxIGrkqZ3ll8Fj1Io7U4Dr5dWgmilgx9ytJ4rrEPFLiukw6gFRQowXCs4u4ps7m94ebZPTd392RlMK5DKRHVV1ph9xvy5cA8zYxPJ6IPjDVrqQ1x8uUAk/usmUFtNP3NFrcd6O620FuSlcTUMAzMfiYULaBUALW1Ra1lPzXAqPpHEohKw4Ji3FFa9kFCczxk5unCNM+LPSYLE0tRGjcsFQS6xIvXLMkCohpT9IoKIJvT0mgGSVDNVWKlzPVV4JFEe6m3Fh9VadJQvE7VLNK31snCRBLbprXGDT3GLUfwGz+yS54zCZ0VOkWpvFCQk0YTOD2+Y3N7z839Czb3L5kPb0ilUcB+t8fPk8huXM6c3r/j7tlLwivPdBjxyWOsZrAOozSxNIzSRcO504bLOMlzxrC1lt4ozuMFHyJZaW5uBhyZ8zQzh0BWik3fEYIXZzEntLNsux584Hg+M6VIt90w9A5H5vT0juPlwp/8+A94cX/Lr7/6ml8e3hOQ5II4TYvmbtW/EqB9ARNSae6xGuQSGK60tFbsg6ttW/5dHX5V7NIyV2XdrAKQ66z2tU1oc68Ug7OQAjkGtCtrp7wmaRjzxEmd6fe33Owf2Jo9v3z7BVOeCWrG41E6ciYy6UxQmqwM5A6lEkZ7jO1L8khqX9QqMG9XqLSU71G0kIudj4i0xzRd2G42pAzRJ3LwZKUZ54k5BIbtnv3dsxYApRjoS+mdfI3Yt1wCcukSrbC9aJv5eSbFiOkcBrCpoyvMCeuk0Yi1HVrLHlDruVIa4zS7/R7zve+Jb6E0KUYenj2jGzasNTHrYzH1AmwkP6KfvuHTv/nf6fxb8nTA+5HkZ6yVkkJp/LD4mfVRg66UBGyUM7KWHaZSBpla4Fb1xxffUTc2DjmT00xKkwTjyqLdjt7dsr+5EWkDbUBZvD9CiljT42xHNltytuTkSMnL2ioSCUYrgj+jc8Dqmaw0rhvQpud8OqDKWZPiLOzXUs7flS7xKUklD0aTk0eVtaKUxhpFNobUdbCpz5e1X8EhlYFA9DNjvBDw5CjAkjOWnAMpe3TK6KSwWtFtFgKAVpnogyS1kmKzdWiNMFtCZg4JPxUN2PnE5vKG/cMLxtN7Mho6zykEzONEHw1OWWzfY43IPbW5XCXnUIrO9QLoN09TpDYoZ27vHFWgJuXE5MXeuU66bWenCV0JcL3IKHU3O8Z5IphINBE3aHJSTXLIWEtvt4QQCD5wHmeslgaPOSninJnCjDOusIQSNi9FzAJmFg3Iwo7UBcyT/VkAl8rMLIBXBR+aj6Q0heu2glk/eKgKdlZvvIxTmfaoNQcDv3g689PzhTdac/v9T9h/9DHD/gZrHefJc3jzDcnPKCBk6G/2bO7u2dze0e1v6e7uwXQEDNmHts8FnBHQIAbxRXJMXE7HVjm0tr2usK2UUhAjxli2w4aHZy/wSZNPR+b375ie3mG0nNupstdKqWstGa9SJTWuWWEO5R/FxhTAVZ7XDVxqLzIddICyZCZUSGhCKYUuJBxrGyApzX7UkjRWFSCtgOQSb353SJ/aaz6sEGk+Sm1i/cEHFNesgE/1phcAU2mNLuW/4hOlq2uSf62M59WxnFe/XzF965lR/CLXiRxhBU5SBcZK+bUkF9dEKMiloRNQqkvDggGq38VDW11qS9ZC3We/AzP5nYDK+hFjFFZpkAq35v9qjStNaStTtsZ+9TqUkpLumCp+sfre1RrTZgGAVIlfaiM7qo9by86zJLgUqoFla435DE2bXRWgUWtN52yTcGwNGa8mWC6pAlK1VFuGc4lPMsv1SMJ9hR3kkhSsn68Uuo2HIpKI09gAu+qv1fuq4xJ8XCUeymWWmEpkF8xqPFMZZ8mw6RJL6HLfuiR7FWD1AhJXWcb6H1kS2iCMS1vZxnVfl/XcFXao7P+6p8vcaanyrKB5TFIpURZcAWXLnqnVPshekNHQOGsw1pb+LEWep/pUipL0VEWurxL6dAM3c/mu9TVUglxtjiX3qVrsFnwoVauqGSbri95rwRLEtq7utdnVcn7mpcFVqxqo+yyLbb/ilbY4b0mCVWKLNQUw1YZuK3JrIQTx21Y61zYXDDCtNJZzWiU8pJJQIdWqsWjGpwSqkLRMaQRWQf6U4rL2y7mQSKSkBa+Jv9uu/H6AsYizSwplswbpSq80pmyWZSoUlfFAKgHENKHjhlQcFJUzKntK7hHROFt9Rg0gVjYlVzSwHELih6glQGvvpVrL9ub63rq4bKmfSBoO5wtfffMlnzz/hE8//QM6rbi7uePTFx/z2YtPePX2K9mgSijvIMFnnTWtNIm4MsDLYq4/Xw9lva6VQP8H4FE9Dq9LN/OVHk37trpJqdcjRmXTO95TDpBivJds9urKFGSDsJltD84RUiJOHlYizotLzMr7qd+6jPOSDV59fsqtUkvKf6RU6jgHLu+fOF3O+BT40acXPn72jPv9no3rgLmBKddsqjXw1gZiAZmqU+scg+3IMRLmnv3hwNPpwjgHdFRY55gm6bBa4AOM0Thn2QwD+5tbjLXE/J7MBR0zWknAF0JEZdnAtpQA5yzagsFHvJJSHqHAC01eaUgmM08jN/s7ht7gNPj5HfM0cymH5Xa74Xg6S0k84KyVRmxlDdvOoqFooMmhaDJ01raMrHMOa7RkcYnc7HccLxNhmvExie5gloSEj2L4decIURw5X7JNfe+w1mGtMONM32GGgaQMl9PE4+FEyIqsDDnGJStV5yMnDCVwUJqU4d3Tics4E4smTlssq0O6ltNkmRxyNtcOqloytutA5op9UO2DAmUUZuixux6z65mL+ns9dKw2PNvdcLicGL0vh1/JADfgqCQVWMlnfGi8V2CtrNWEQTK4KQY0mu1ux35/w267EcfCiJnPCbJR6N4SUmSepDFULh2oFeBzYYwimWllJJuonMH2HW7o6G+2MBhJtGhxqJdGC1UvbOUQFfc4V3u8DPFq3yuGrm/6TQrV9JvmeZIyoBRZl+Iptd6gmZXY3vL8YqZRiDZmC1zXzIy8VEOEFJttUUjZTG2gJ05UlTvg23ZiPVVtvhbb2GyNUtiuKyXN8jimyCFFzjkKc7aAXiqCVhGtNPP5iLEd2/0tu/vnxPFIChN+nnDDgHOOOHuCHzm+fcX24SNO/YbxcsRPvjmEFB3erKU0yWqNyjD6GRQ4Y+mtSJdM3oPSOGvpOkcYJ7EdWWyH1Uq0scmgDb0x6JiYppnRj+hNL2z7jDRd9DMKxR+8fMHz3Q4bM189PUoAhjhjNaWXVuO2ZkxAhUrqWrgGFeo4r8uQ1nO0BNHLE+qD9/9WBtF3/q7YiEzRT50JPtBv1cpOiI2iCPz3ruN+c8uz4QWfv/8aVEeHIZqOcTpDEkZeygJOCk/PorXDmB5VShwbU6lGO+ubrAEDuSQ71Cogks7BlDUf/MTldBKmtHHcvfgIV7ozi6xAEMb8qjTOWcc4jXRKutSezmeIifEycnh8JOXIdr/F2k5K563GuSKFkGmafnXbLmMsgZJ1jr21zQ/IObPd7dHW1hv+cBraylAogr+gn77h7su/Is8Hor8Q/YzKEec2Um5YQBWl1dVHLfNcwa7SpA+RKKilpos/WSqGlEaYI00lgZwjOXpynCAXIEZL84vNrjYjK/OYIllFjAro0pAKrGhyJ0WKmpwLIJez6ITH2F6rlXSBDl6AbqU1wYucUtXNs0YjTZrkDyqVkurCUikleMZoAblyq7NqNk8YOolUWPdBKUIuvjzCysokjEp0JqM6KR+3RjWsT6HwZTzlrDV0TtXG0sQcC6spkOcRPR7odp/S39ySSAR9xt97LrNHjRmdNU5o4qxqSeSeVkdCZyQhpUrEqLIwtmyRA6ilkhJgJ9GeZ6W9aA3BisVKSRIiZtMzzWdyjMw+Y5LIXiSkuakuMg5JS/J2mkWmxCmRH4gqMEYPxrRrV5mljBiplFNadPOu4pGMJGaLiSkLmAocVPtTrcGa1fQtu0G1N5SjNFPBxgxkDcFqvgoTvxxHPvczl87xyccv2T5/ie23ZGDz/CWn0xMxBZIXckd/d8fuxUds759hhx24obHmq65kZfJJkOsJwVPB2DDPNRBYJjRLgtQYkTvLOWFBZHOGLeeLJx4OTIcn/PmIvtk0e1IrGiqYtUIK21758Fyo39ls2Ho8V74GypBNh+gcgrYeFRVQAMMCSKkS8+VyPmQWUkQDR5ePXuaFqstaz7vyi+98SKy2LKW1b0ab2+pXN9Ajq3Z0NfWUZZCWv5VqsdlyLl+z0dfMSljsbZMkUKqBLiIDVcbf6AaQKSU+qVICVWVrVuufMr6ra2g++/qbvz2elRT0X/r4MBa4/lR5vjY5SvW+VQEErRFWrF2xKct+Fv5CHXOpAkrF56yxco2L25JrMU1p0EVGeq+Ik1OraCugq/USZy/LYbEL1ccyhcHqnLuWZFNq8Z0rXlGvo95r2yaLj51W1y6+XJ2f8sq0JBMEoFxhHUq1SrUaMzVtTurYafzsGxDYLkQt46ZLCX31J5Nems5VCUNdNW3zqklW3RPl++qAJjIp0kDPCrJGFnJfFgYHFeCmJIoX21r9V7lujQDBKUrCQ6qXhBxVnInSZUe1ZoOVKdsZg0kR7SuQf71mJXY2VB3rltBuCyG3uEfmJrW+G8YUv6D4HbmcOXGFiai6BpVi3TC7+h5V+3UttxGS4HlNm1YvNq2NTSHl1Ri+9htqiXEWQLxOvzQwl9rtGBet4rreReFHNyDLfwjGAAAgAElEQVQ259y+X+nKjtYYEySBGkKRXdKN3d13/Yq8s25gWHCBTDmTljjmtz1+b8DYXDP+MUs3VpsEhCRTpEJoOxkKkzZADKhxxoQBpa0sNLSg17m65Eao9gV4kUWzZD0W2vMCIiwHgzyUroENsgiQ9yZoXRKXiQbrDMYOJB/5zbs3vD08YgzsNo7EDT/65Ac8Pb7mr/7uPwjLtxzAsXxrVooiUlY0onQzpqK3uBymdROvzxu1/LM01VGrDbMEq/UzoHSWZxWlrhaPUssBE8LMrFPR0SrjsgKr2vHejKBscOMMdJZdZ4jTzHy84I9nyNIwQZfNZJ2UmwhzUZVrW+ZCbnPN8k0LEy6zCjqlwdfrw4k3f/l3/PSXX/DDjz/iz//Fn/BHP/oMqzLgiTFdGYAPaebyFYu4M0X/JZSNaYxhuNnxvR9+j8voyVlhziPO9Ty9OxKygk40gG5vb7l7eM7N7S37/Z57Erp7xeF4wPvAeH5EqSiOZ0icjjOTzwJSlMz9OHlpZmAC5MgwTQxDRzd0dJ1j8jPRz+zv9jx/dktK8PrtI6fLSEyZj1484JyjL81bXj574HK5lOYSit0wAJnz+cI0S0d0o8WA1q649YB3ztF3Hdu9Ib55z/k8olJkv+nYorlMYJQiZcVmd8M4R3KaySGwGzq2+x2UZERWCtVv0F2P94l3TyeO54nt/gbjusL60EX3SObF1rKdsvZmH/jNq7eczmOJ9RfN4dVsNuBNEGwIPgjQa0zJZJZDV1U5jeJo5MWwGl01DDOmc+idg8GSnTjfYqdEX7rvOr738cd88eprwuGJgMgP1Kx/jqWsSFPkw5KUuMfUGO6ZzDxOkr2ztpTKJir4qQsTbjfs2PdbtqZDKWnYk3IikvEGQk5cLmfO5xMpR2kOVw8PRHokpBLYd0a0YXcbdOfQzqI6g88JVw9PpTmPF9bNt+wKZFw03rh6Tkr8BAxx2nF/e884XqQZVQ4Y4wqzTN7ovdi6yhaJYd2cZXHi6uEKFEd+AeT6XpqbzHkuY1tB49QCs6uDM2dub24Yx5G5dLrPwGWemt37LpsBVRlmfS4sgF1KCT106FUTolMIPPmZxzBjnACSXcmmSqMeA2lmfHrH6xi5f/6C8+Etl0OQ5kNPmc51pBiI04Xzm9+w2dyw3+xkUb2PRdva42MgZGm05JSGEJmCxwN3ux2d0aiUOJ4vKGvYbQacsXjvebpc0May6RxD5ziczoxRGLYbZ+i04un9I1EBneV2t8cpxfFy4eI92Rme39yiFbjtwB9+/xP+6ue/ZEyJicysFumO9RmUUipzSdvTde1/iK5eA+x1jupvl7P+Q+fowwRlC1I+mNsrEF7RAvesYJo90+SJQQD0xl1QGqMd1nTopDBzph8zD5sNu2zZbHZs+h6F5Vev/gE3KSnvqiztElgopejcgNGiNU6WUzjEaw10CdhyCz6ssVKtUexl1w24fluCxJHp/Vu+/OXP2O/vuHvxku3QE6JHAdPlxOtXX/Pzn/6t7NeuZ9jt+PTT7/Hu3SN3z56zu7nl8y8+53a74e2b13zz1efkHOicZn/7gOsGMIb7e7HlwQeC9+z3t9/aOyF44qpkV6GuWB5S5ZQ/AJFK0IpooZIj4/kdPH0F6S3j+QR+Envc91L2WJzvqiNXF0km4/1iX0A0clkFlwUqIccKDMn/dQGmtbF4P5FDKgBlRKkk1QrdBtff0m32oDQxzDKPSlpuJZWIcRbNtsZurrcp1SF+ToD4CnMpzUVlUpjpusxme0P1G2NK9N1QfD8BYMfzeSnRjJ6chemuigyYImOcQxsrMmE5M0/SFLWWwCqVpBlHFt24sVR3oCiJbug6Rz8AShiJ1Y2XPwrba5QVbbVxHAvLxWA0ODOTUhYt5VikzIxic3tLCCPTeMC8UIw+oJ4yXDJqiqR0JoT5ai+vV4rTFqukIUkFCTbDgA+maLivkziZEANdP+BsJ0zWFtRDtg6cw3Ud0zQzB482o/xfiR9sjWbyA+mY6AdhxKUeTpcRPXthsnopUTU4UoaQBahzpeIry6BiraMCh5VRBqUE2BrE3Y8LcLO6j5QTOdL88mpjF4shK16az2VIqSqcCYiiIBjFpTf8h9888dPxwisSbDf0z5/jjZwvMSWGZ8/YHN+TcmYOB4xx3L74hM3DC+xmD8YV2yjJzZgj5qr5iew5yfWK3ErUtgGDFTTMIIme0pRLZbAoVMz42TPPF8bDey6XI4GI7pwwA0tsZWTwFh8il8ZFBZBvjYaooEkd19V5sTogFixItYZephOSEdGTo4EYiH6qNyKJeJ3QOreGQJS9WPXSlwW8zNMHv/j2o55hV1UEeSW7VZ7Tq/dc+Sxyr3WP1PEBU27yw1ip7uz61TUoVYXtV3ygqrEYUw3C8TEWMES+3ypHUoiNLs2HUpL+DLrG7kYaDYqvplaxfLXOv2188vX8ra65DMH10XI1PIuv+dsBWaid3iuIZJSV5k6doyuyDY2V1xayQdVSfS3+qM6JQC6AkW63UwGt+p05S7zhy7Ut4NTCOhTii12eK2dq/X2MscTQy7w2XWtKfOBca2hUy/tbMoMaJy1+Rx2DBsDlXM4MGeNUupebwlRfX+96vGNcqu7W5LFamWJMtZPywSklYi7EimIHrXNNw1w+a2rzVYHlXNZBjJHg53JtVWZI7EYDX1PBolDtunOJ3dbMX5VMW2Zi8XK7V/Ki401dk6kekrlVPlSCQoYWA1X8yiojkg2KVjV9tTNzBUllLcoe0wUrke+prxc5CDnf5stYAFj5zhQS1hV9bmuKDIZprFPRqJfNGVNqet9kGhi72Wzw8yzjG4I0dY3SUNw52RvU+ywVoPNcEnVW+u8AhJjbZ5AzzroS34HSiTgX6Z8CsitovaGq8OfS3F21mHtJNkeMUThnG1AcS6VzjXtdp7HaFnJCbPFpdSWVsoBozteq6t/2+L0AYzMQkydGjw7QBdCp6PpY6U7brGNxEGL07U9OARsjaEcu1H7F/0fde/1KlmXpfb9tjglzbbpy3dWtaQ7H0QgiZEAIgiQK0AMf+Ffon9O7wDcBepAIUZzGOA1n2Jzpru6ymZXXRcQx2+lh7b3PiVs5AxHUw+gUsjJv3DAntll7rW9961udLGKWzKI2pWy2nkRnqOU6B1rPpvz7MoZGL9kYyD54cYxY2FLFSKSLS747nfirb77mx7/6Nf/5m58xPj3QKs3L61dc7V5ymO+RcjcBBSDJBg/kMv98v6t5zJVvNRis95ryiCbIsK38ugaV5f08z7ZrfYuzhwuokQdgDjOzn1FDZh2eOQhq9T75Z0XuticMu9kHsAqjWzatpdtvGR+eSLOXoCWROxaX9yzaQGc39exL5w2AWtgtdbg0Ssv6eX+cePirX/Pvf/k1//C3f8Lv/L3PefPqhsvdluQdJDgrO15/3Nm9CDhiGynzC8kzukDXt/zu7/028+h5ejzw8z/8Y1KUzdttOj797A03t9IpFgz3d0dCcmw2PS9fXvPyxS1ff/0F337zFafjETcpJutx3uNDFFZpgtYalE7E6JkmaRTUbTqarmWz32CtIiSYZ0/TBD7++COGaeZwGDmdZt7dP2KNYtM1NMaw31huL25qR+95lqzefr+ndY7j8bSUEuaRGE4j1hhpWJW7LN9e7yFGxmlis9nw4vaK9/f3HE8j3juOw4m+MWw3HfvLPRdtw3EecTESksa0HTFrfjo38/3dA1dXL2QPKLBk8X5VgpAgaYokB+QcAl9+8z0PD0d8iJXdUg5nEExKnBIBJWLeI1oZUhI2sDaaFMNSNrFaDuXwi+TOylqhrGb/6hZ7uWUmMEXpjp1CdgqAwc388S/+nTgDtkGttY4SOcPqsbkUN2TgqQjfl47eXd/TdxJUn45HCa5EGZ6UIkZZNtsL+u0FuuvpbI9WDR5PUo5jchxOR+5+8w0Pv/62doOO+XgyVnNxdcVpHNBdQ7ff0u03zNnh6vqezz79jMfDAZ/trw+eq4tr7h8fJDOdHZWSmS07tWv76kwV/U8QB/Hm8pqnhwe22w1ta3k6PHF1eUnXtmiliCFy93hPiKIPVDKjOpelGC1BWN9uGN2EC05Ytona2XRyjqfHQy6ZWgDUNZjvvZMAKi22/eHh4cz+COjvRBuwac6acH3oWpJUJVMtzIJ2u5XGIfkKKP71n/45X379Hf/in/13QGCrsj0KJbPcEPyMPz7Q7/e8+uwnPL3fcf/Nr0nTACg6Y9H9hjQNPHz/FfvbN9xcv8BNAw9Pd3iiyBC0DaTEaRwoWeGb/QUmBaZxxHlJUFzttlIiOgw8jhObTc+u7SEljsOJyXs2/YbGGjSJx8cjqmnYbTbsdz2WxPePj0Tb0O0veHF9w+nhPffDwJQiXdfzP/2Lf86/+vnP+au33/LlMDAiSRatFMoYXAgZ0FyY5CqzTDOamEvIF1tdxv75XJQ99/w6AybK55SAK52/5/NqEyrLGg7HoyQymkbArewfaMAqRaM1KkQu2p43+1uuNpe0NOzjlo/ta3708iecHgbG+RGHkmSegrooMyBrUOADwTts35DmmZTlllB5aLRUUChjAU3RKRSmUSQkSMEzHo58/asvCO/vabShn/cYN3FyM/Mwcv/+e379xV9zfHrg5vYF8zTy/v4Ohebx8SkrSSf+5A//DX/we7/D4+M9k5v56KM3/Ns//wtevf4YZSzf37/nH/2jf0hrO969/Y6vvvyS//Z/+B+lWUOaKZ0lfvlXv+C9zzY7iK+y2+/RyjAMAzFF2tby4vu3dRqOhwPv7R0AL25fME8Dbjqi5wPz8YhJCtt2OSABbSX5pcoftfIA85zGrPMtAVesv1x8hALUlPUgwEGIgdmNoEJuUJV9L7Vhf/kR2/0rmm5PQvH07jvefvsNjw9PHIeZMRm8sVJB5ANNTtiEEAlzwA0TyeU0eJIAKeQEsVKarmn4/X/w2/zst3+LzaYVTbamoeta3DRzOhz56998wa+++Jqn44zzCdvCm4+vefX6BTc3l1zvLug7KaF2zhOcOwP3QlxVa+mOtre07ZY5BJKfiF6A9hijACapBJDkcUzVZ0NJglUbTdNGvBMtcZG/adluDH0rzTvwjuu7X0N3wdRvMJ0lzQNp7xmJRJ0wR41NpYlanrFnihbin5vs8wVilKqSTreZXWwp3aYbY7neX6JMS2NbTH5dEyBhhPXUWnTT88knnzDOcy0TBaquaGlMhhLQsOkMISRpVuU8kLjod1hMxfa9kSCtAIekHCRmSTbnHNM8s9lsROpJK+bJ127VRWtRglHZ/xIXlUVe/qwCoQz8lMC9hDgo8EbzROSvHh/4+fv3vCWSthsubm5o+j0hZXmlKID67cefYXXDYzJsL6/orm7AypqUAD9WeQ+QdVXAn2yGSYWhFslNwASYLrvx448/4upyR98ampjoGsVm13NxdcH17Q1bd8EXb79FdT1cXuGMgKQahVol/QrgXL7uIrIkY1T8BLKMwmo11WedP7KwvVJjUVYTZ0dwE8mNkCLJ+bqvjLHi0xoBy7wTFnB69p4lIF0Yfc/jtnOAcYlfUt6z6zuNq9co9Nl3WZ15ZD/62d0kFtCREvuevffyvLOEV47TdGaHCphil9HO79c1TWVIlhgyJQFwtbHyCZrM+xHGvbaK5BQxLAPzbETOh4AP+wP/MVcheygSJA9IhUJMMDuH8wV4XiTWnldmxBB/cGM+OJJ/Nt4ZbFfK0OUGnNYYuralkBIqAzfXSkfE7qkQMwiVNS/zxxWNVAGkdK2kkb45BUAVu9Q2S2l3wUHq33lwQwaYQYgafQbe6vdHmrzFLK8SwhJ/lWoEtfLFUn7PtHpf00iy2eaGmzHl5mO5zDzGiDZaGkkVaaHyXitgEBS2sfSbjTSknmfmyUkfieCISiqCJLlthAA1z0JycMLMLc2eTI7dnB/zHMhcSKPtDMZmNrR3RV88J9fquaEw2laWaYrSKDamVD9HofB+rvqmWgu5TWh8BXymkneSylJ5abWG8hpzs0NrXUk/BWw3WhIwIcbM7E0QU5UIWEDMhRSglSQ79eoMPJ0GrG1o2oauV9imFamDvG+SQkg0CPmpaKVDliNYy2F4qbjw3hNSZPI+V8SuqmezvFRIEZPKusoxapYwCFHk6YyxdUwBnB/wWfcdJRUYulZSUO2zUlIhGkKqB8c6EdHYJuvi/x0HY8ukqgS2tDsvWbSkIApzLnclIAbHGGbu/cidnxhTwEwO0zWkZmlYkViE7YnCNgCqEas/JJn0ol+TElmfY7m/EqwuLC/1zFAmakF/PgNS9mLGEPj67h3/91/9W3739/5TtEq0TcNuu+PNm484fHmf9e8Whk2BM0tGIa5A0RqM5vuoQun5PjIpfLm1vIjKRi/ljeXZ60Nc7l2hVfku2eimNRCpWMqF8wGd1veweu+UdTMCJC9Blc6akCjpOKuNwQ8jbhiJo3QlLsCxJGbPv504i0vwrKsuaH5Woho0ECNSDoZA4hQjf/7Fl3z7cM/rF1f89JM3/L0f/5i+abEqkpTL+kOLQ0iIoluTs3NtK4Y2GQFWohcW7jw5lNJcXF/y+//w93n37oHgA21ruXnxkovLCx4ejhyPj8IUJtJqi7ECal7f3GKM5vHhgbvv7xgnj49KwNCiI9s12YAEOtVyc3tD37VyPz7gQsK3th5APs501jIZw5BlDpJCgjgVeXw8cHtzgbAD5bAchhEotHzwhVWe90uIQdgqRmXRdsvjk4iHKxCH00/cXu3Y9h13j0dOw8jtzUdcXuzZdA1hnsB0sk+VpttdorsNk5uZXBBdQb3SHS1rtjh/KZcmKNFVHifH19+8xfuwvIacFGFhs8uyyV0+M9u2Mmfq9lM58ElVJF9XA1zeI4Ex6L4h9hanEsX/UykJWG1Fx2yaJpRS7LY7lFI8PD3Wg7PcmdGKy4tLSDC7mdPxJJm+JPcZfJAO2sMJQETYU5RgVilIBp0sV/sbdpu9ZOJrN8584yYyHI7MsyNZg73cy8GNOBD9pgcNu4sejEJZQ7IKnTO7Pka+v3tPSjC7CZSA9g8Pj1n3uKaTqAkgJSBB2bN5V4lNi5FpDnx/Jw0LlJHf+hB4OjxxVIum1hw8Rhu2mw2NsZzGE6kK2wvzz3mX1/0ScOoc8IvJTjUeSSmilVlsdaoTS71ygCbxQ9bUzfsqhoB7lrip+EQB8fNljZQHFZ0lBbhpymw7qm2aY+C7+3v+5f/6v/HP/+k/pe26CtQ7pUAlNBYVEBmC61uatmVzccXx/UBwI23b07YtfQgcp4Hh6Q672XBze81xPKILdBZE3xmlpFy6aSHGzPqVDPmma/EuMM7S0Otiu6XvGpzzzM4zhsB+v8Mg2ojH2eGBi7YT2YPjgCegrOFis6HtWsbDI/fHE8loNk3Htm+J08inH3/EADx8+SUmKkZRN60hnWzJRMVw8lytS9nOxQtW07gCZddMsfVVzvblbFwx68trY8lul0Uke1OXWDfJvKpsL2LeDya/oUbR6CbfYSQmYVtrpdludmw2O+I80xnDqGIFmOt5WBK9WpHKH4X4RdNEyvrOOaKtQZMpwV4FVxJ93xOC5/D4wOH+jsvdnllpmqcHxjDxdH+H31+wvbyh32zZX1wRlMZFGKaJaZzEVs0zd+/fM48OE8Gahsb2WNujVMPt7Ss++uQzbNPStB1/9sd/TGcbvHOErGlZ9lS5huMJlwzGaKZpABJ+nqtGnnMz82iYhqG+5u79O57UFf1mg1bgphPBjeBn5nGm6EOiJJGpVudJSDG7jctcx5SbVcVQdYurM53PQF39xBzgaU10LjfIyJ6ZLmVtLZvNFc32JU27I4bE090d3/zqlwzHA9Pk8S4xpxZnG7xu8LSM3i6l6jZBv2V0T9IwK/ilaicn8+cw8+//+tdc3uy4vt5jtCTRjNa8e3/PF7/8FV999RXH04RuOq5u93zyoxd88vFLtpsOaxREz+FpBlQFzM51iVfQkLIZETHYZoNP4subCGR9YilFDwKWmLyWKXVPiJSTUiQMupGkRdlf0t8kM09iIKrIdnrA64jbXfI0PtFuG5yfGaeZxia2YX+Ot3wAbCmyM9JYbqRvOgHCtLAiC9AEoifaaFMDz8JILSCEUhrbNtjUgne4adFcd/OM9wIwWmvZbne1THkaZlRSmKTpdMdGtVKlUsCWnBAQZng5a8xiw1gx1JKWJn7Zh5MGSWuP/NmlPvgogFSAJDk7FYqoFMHCQ/J8NU38X++/561ODCiwGrtpmedJpOLya5JKKNvQX12jm5bNxY7YaCIeguihx7y2yOBvKaVftpmqvouKGaASVQtAgvOPbl+xbyw2JZJ3dMrQ2obpeOA3f/onTMNM8gHb7VD7K4ZwJGZms8RdRZJCVR8h5gZy2Zn7QFJv8duqU1NAFkqH+hKnyFwaYzGt+HnSpyHmrRsySyBhGgFkUwCTGkgBHQWAiWtWeQ301XJDdTdVjm9d/Is3vP4S1PVR31ed7Wx5rVqqRBNk/dPVU4yq7N3SOE5nEK08KSGsucq/y/5UftFyxua4WhpaNblZ3QIYiT2S50nX96XCJaasoZoBnXrDLP/+4MP/EUjs38yOlSukhA+i8xxSkO7rSWHtAjBm1BYo5ftq9W8ycGewpbdGBqQKe7EmukKJm+W1Ai4tDW1ljFRtUl6uGBM+O1gxpZzfLlqiGaBVGm1VBWxj7bdCBT9L4ytjTZ3b8jkxxtysd4mr1/5WSknkeSSsq/0wClBaQM41YxaQcchzaJQh+kBIkuBS5GS+FT9iKRNXS2+UDLrVBkyqSCDI2o/BS5PJXtO2jRCjvK9JFpMlBI0x0isol7KvmcdGa7pNX3VWi+Z1qbjURnqdSLwZ8/edSQjxSPqLNLJ3ciMs7UVHXWVZotY29F1LbYJWeg/5IPY0V5RpI6/zMeBmR2oEP9HVTxFSg/eecRyX2CcEfAbIS9ycUhJd39WYFStREjSyTKTGvTBKQ3A1ySbPzQntvA8qYUeJv6yVMHDLPAnJSn5urFRPNjasGtQV/KdUOCxxu8q/Szk+V9aQksakhDI2yyHIOihVjNbKceWDxN+6aM3nJnSl+VchP6bEylZFORczxvj/C5mCGD0qSac1ncR8K6S8K/olgBeWUGD2M0c/cQwzLkW0Cyifs/Cq2vR8kCiSiuVo4dyRfHYnCUpphWSqChl8OYyeG/QSKJVu0AUtL1dUkcfhwJdvv+JwvKe3W7b9hsvdJZ+8/pgvvv5LWbRl0+TT/fzAXQecqh6eZ25xAQ8ronR+BBdn5ww8qC9TZ89dz836qotMLPz5eCgqWFcPgDI2OXgx2taDXAFRKVRn0aqThgtKkZyTTq5hef1yv6V5mTia6ey+/oYr39cCAinujgPHaeLhNHAaZmI0fPzilv22o2stBSyqmbj82aJjVUS+ywGUiAphJSlVhflfvH7B5fULxmHEuUkyJloxzTOncWRnd1KK10jpmwR7lv3+ihhhOE1oc0SZhPIqZzyX7KXRhs22Z7Pp0QgoPM8ud8MOzI3HzY6QBDDdbjoBbjY9D/fCYpQO9IrdfkMMwsCV5GlajOJq3ss6W8rB5XFjDMPTgZSECW2tgRTpmg6F4tQYng4TwzCitcLNFpUSumlQVsbStB1ok7svB0zT/nAqc1KBVBAZ+TPPjqfDwP3jU9Y1Wq9fxfr2VdZsXPt/sbZiLs/Rubtx0bYprxcdvKL9qKxBdy3JiOZzKckQJ5E6dkupTQ46YjozzCpJaWQpydVJgB9re2GCenHoYoyZxUrunJ5QqmjyaBrVcbG9oG96YcSlHCeX/zS4cZIymdaIvIKSstSubWn7jsnNWdvKoq2RzGSzOO2H05G2bXFBAA0fAvPsVs0AUnUSiqOEKmO+8CuKRZWulhOkxDhPdW1FJIGWsoNBzmpf7y+43O35zVdfEpTChVgZszEuWfhIRCPNCNdWrJQSVUcj/xyTqsHE2uoU6YK6NlbOWkkc1cFZDNJZvq7NLADvPSHr55USnHKZvgVrGOaZX33zDUPwzKnBRol3dAbtCig3Dwds26C1YbvbMx+3zPMgdhZpYDIdj8TpSNSJzeUtFxc3nE6PzH6SdYXovjZGsuizk/KxNpcDaWBwTgBFY+gaSwyR2Xl8lO6jnbW4ecb5II91LQphbY0xoI2ib1tMTMR55jgMBBKbpqGzBhMip3lmv9vz2evXxJT4i998zUzK+0K6vZa4N9b5SfW8IZZ5y8PP334tuHuqkhrPGbD1sQ+/Q51rlRM34gMonJvk7Cj/1cBdnMuScI5IsBZjpDGigeq9Y2akMcX3yPrEq3UnCdkcQGRHWKPE/zmT81m+zzp4Vvk81CQenx6YJykN77pe9EbnCe1FP1YZg768lnNjd0myrcjZmJa23XJ9fYMPia7f0DYtn372Yy4ub3j52tP2G3bbHbv9jt3+UgImbZhOI6ot3YQlmaa1OWvg5ZxDNRZrG6ZpyN8/+wx5nprmXHP56fGJcTvQbzYylvNIcCPKOyAyNS1WBSySkD5bKSl39V1NtwQTS6WMygJtwuJJCCogtNrqbsVIjI7F/ouPYEyDbTq0kc7H3k3Mk+P+3XccHx+IPkCI6AC6lDI3HaZtcEmTyOWRVnQFtY9EY1DeCSAbFv39GBPvH554OjzQ94lN35CiZjoduH//nndv3zK5mcvrPbuLPVfXl3z80S1X+11uYhJwzuPnwNIAU8Zj8S1X/qLKAUyKNN0WkjCuiWRWbIKQS2y16Mmvvc3izy0JvIUBF1LEWo1SHsiNnFLEhsAGcNZwMA3aBGITcM3MaC2tS88rqM93ryryH3pJFpZ7UqXxndxd9bdy6WkJ5Es5e/EblFG5IZyp0jhaKUL+voX9UzZj0ZIMPusLKoOxumrAl1J9tK5rv8YG1JvNe4il5DlLHiVEGz34sALGzv1p8rJ9bo1z3MUAACAASURBVDCrfqOChDSPmVTk7Tzzy+HEL6eJk1Y4JNGYGsMwjwiLJZ/9Gmnc1ra01mA2WRM+ZUCVJMxgqfUVzyqxAkPyvcYo95CE2VfynwU4HYeBjd7SaINKmkZr6TtghEU/HkecUjzGyIPWDAgoQJE6WdnVZYSXoL2wyCirNDe1WUZT0MlIQkdN1Gu7m4uGNTIuZiGtxBhxudpNlbUWNSgpW1eVqZjPgJRIReuxTv/zRa7OHivg09lcryf7PBys551a/U+IPWHxis7fsv4svTYWLWNV/eXyc5EXU9Ve1s9Jqzdb+VmrGyGR10b1BUq59cqRV4Ulqqp/9yyEPRu3/7dA7Pr5z1/zofeqoF8U/7Y+pso5Ll9rwQzO36uAjMU2yf5VmRVoanl1OYtqknp1jzHHqpWpWmKcZ/eh631kuQLKvS3VQTrfg5RnK5bm1+UeF3Zv+bueFxSw01SwEKiNjyrGsQJjYxL973Kte7WUMTrTFk0QdCYIBY3SwrwvFS/r55Vm3KRF6qCA+Snl+pcqqRArOAe51D6X4qv8HjFI0qaU4euy9vQCUiqtsUDSmqh0jaEFaM/+T6ZUxhhEtiSK31c+M2WbmlICLfFA6W8jz9Nokz8j+5WlIETWU/48Y9AhEFSJJ5YtUs6uwhQOsVQiLH7XggEtsVZh8K6JegKkL3qsWouuanltAa5rpflqfmtCTIRdl8dRRJXPDPJCVcUHL+tRVT9xfY4utm1JuhXQXJqhZTmDsp6zEVOFla1U1Uc+swOrz6m2qs6vlvf1knj7Ow/GxhRxYSQRaIwAEVorCcRCkMYJKdUuayYl3DwxzhOjn/Ep0YUciKQEOjuHsRh0aYSR1Ao5p+ikFLBm6WReslVl8otxkoRcOSDIZUDL78uKLhNTskhJw+BH3j685enhLdcf/Sc0XYtPiZ988jl//Gc9cfYEJCOoSiCXCmAkQt6p3Hh1VJ5By+uAqx75+SDI9RxKFYC3CFOrs80oL1/p5a7Gi/z9ZU+uDh7NEilB/X29rzyeKTciE0cnG8aY6emtNIcJ1hDGiTg74uxJLtbSmSXvUr6kOuvSB8t9FcdqPQYFkE0KktIMAYaHE+8eTnz93T3/4Gef89NP3/Dpm5e0tkHF0gQiO0dKdLS89yhl0MpimgzIakVMgbbv632Y1vLRp58yjhMPD3e8f/sN1k2M3uGCNLmwjWaz2dB1PcEHxnGmbVvabku32WHsPYlQgXpjWk7HI0pB27VcX16iC7PIRYIL9NueYXLZyCuMbbBWcdXtaJqe7WbD99+95XQaSUnWxP44ATGXiXmsaZYgVOucWTRi1BQY00Jy0lHQWpquw7mAsZamsey2fT5ghSXTGNFFffvdd9wZKf27vLnm+uVLdC7d17bBhcQwOcY5oJomY65lJYkz4DKIVByUpOAwjLy7e+RwLCXjS8JgvadL0LQszRxwFA8/Fu0YSynhWhyjshcUqhE9VdM32L4VpnF2UIoLIRnGxZlKMXI8HiXIjHG9Xeufx6enRXMeYeP7XEaxOJjLYaOKnUQcpm2/Y7/Z0zedlOBFT+n6W4C8NDtQCdVZTGNRUcBCYw3JUtlqtrW0XccwDHRNCwjgOUwT2up62D48PK2+iQyjUUp0bdPSSbU6O6vqguKspTxPk5PAVKulM6YPnjDPdE1Daywvrq54ff2C7778mmANWUZfSkNLE4koAvxoXQHeAmKWhonlQLfGknRuGJI1okogobKDVRyHs3Xz7Fqfs2dAuxLmqdGSSR3XQcOqbKW/vkR/1+LDgAceppHeWpSx2GzTdS4ZAoh4hqc7NrsLtrs9/vold2+/ktIbbbi4vBKW+TzDqNB7xcuXn/DNNzPzPBJipGkatm0numTzxOAcl9sN27alMZqn05HBe7Z9R980GAV3xxM+CnP2crclzcJIcymhrWXf99IwMDhCSlw2W1oU83FgCp5T8uwv9+y7Fh0jw/HEiOh4/vSjN/z45Qu+/PobTiEJYQiFai2elUYyy1GoyPtFNEgW5+xvvZazoZTLFfDtbA7rObbo0y4Jl8Vpk3J3cdimaapSGEXYv6wprTSttihliIjcCUqzaVumeeQx3dNvrCTdSNWhhJLL0zUwarTGao1XIn3gYjxrQphiOvueVddLyUk4DQPv337LdrPl6vKScC9N2DYx0cYEbsSiSCESrGV7ccX24rpW2Gil+fjTT9lf3WKMpW06Pv7kxzR9z/7qhnGUSontdkNMkcPhkWE48vLlG/quZ55GpnkEFE3bY2wAprqZ2q5jt9vhvMNoxXa7AxTH0wlrLVe3L9g/Lnqz42kgeF/LXf08EIYjZhowRvPUbujSRJ/8M4aNjE9wYbVvU06Y5eOn2I/MMKnOjZJEooCgDmkcFQSCyHtca4NtulyONwrbMRlOx4F3332JCtLgCQVGBdoYmZ0wWkzfEStGnO1GY9hcXhDCRoLPccaPA8E5qT7Sgdk5xulECCLz4v3A4f6eu/dvGU5Hrm8v+dHnn3B9dcF209M3lmkYpct81pQtvlIJsgowVc6qgiiU4Esp6LotKgZc3qPG5EAuJmk2iuesGQ1JCBerYIkFDiNGAWO1dgggm2qzoy5FrlLg+3ZHDE9EG/GNZ2gc/RyJam2Df7j/QxBd8iY3NYyZwVYDNKUhFbsgiYSopDFvVGDIDDCVS+YV6AzItm0rvoCSbuTOzRyPJzlXu1YYkFFsz+hnvA9MKIIJkEqFXqV/ZiBLLWtPJYpGZtu1KC0dm93siF7KaGVZR5xz2MZmXz/bq+L3wCqJulwSwOegW2nQmkOc+OJ04i8PT3ynFU4LSJuMJliNnwdUksJYYUaWqjWDbhp8isQ5VAmGEFMN8EmB6B0hZXmVvK6sdI1BKWGGhiy/kFceMUa++PI3qI8/5uXFJS0KbRrU7hJ1eY2+vELbjm/fvePX45Gv/MzQtmxNCwSpANRQGu5Va6CWEuaq2Z3XYy2LzgytDDdKvYkClZLEclDnS5N7HWiFUqJZ22ZJqqgUBA9RGuoWkF5uSOfJiNkPLXtj8TdSNVI/vMq+Xce9H5zsui2Wz1YrP6ho2wpmso71Ul1DJabU+T6XW1qzDVV9vOrFpuU7UT+b+vzyXSWU12dSCiUelbGX81eZc/ZkHaNn47L++zxu/PD1H8qgLQBpjNnXVFrWQWZgxvy9a6yc+4+UEnFrzNm8xRgJXuyaxAIJq4U4VMCh51U8Uq1WzjIhETVtLqE3dplfZL/bXP3rVyBpiV+M1kKWy30uysTUpEWKhKzjuZB1ynuounfWzNgCyApWkvL7CfTfJPsMnItn33Mt8QALQ3E9X7IOl6o4SagtbOHnc1vuXey6/FzGv8QDFQMJwvj00YH+ADEsIomZGPHjKA3RKii6EkFJVE3T8tlt01b9XpVvYPm9otVNvT/p4+Mgj2OZK0WC0uR1da41Zc/EKFJCqybmwr62dSzGaTxjMBft5oTYbz/PzG5GJ43B5CrZpWrap6XiSbATSdwnctNY7+VstbpWnZXXB79IR1hrBATX0sS7Aq+U+F1iA2uNMGF1tq15bfooGKLVK4mKDCKXM9+o3LeomIBU2PYiTaCtzTIfqq7fJWmYHz5zDkWaxZgWJpEm+duuvxNgbCLhowetaJuOlNQiSl8MDeSSvUjQidFNjG5iDp6ktfwdhFGZckYCI0Y6ZvAGtTgh5VJatOnWafT1huO5bVZLBlqaGJh6jy7Tr8trYjEGiKN+Gg784hd/zmdvPmXTXXGlrvjxZ7/F5fUrhofI7AayHoAYpCSZZWupTLqUlozQD84NpRaDxhK0rwaalStN9hLkF5VRkxYA+geXaIPKvwqIWz4vg6v1c5Z7KpylooVUA161bCZ5noJth9lYtA+k2eOeTsTjTFWY0EWAITv5H7zP5zfx7HG1MI1SAp/gq6cDb//Nn/DiL37B569f8F/94z/go9cvaawlpUBUEmbt93sZriidbZf4QUmDHaVyNgeatmN7ecnly47bTz7mox99xv37dziX6FrLvrdstharIbiZQOB0OPAYpOR+GCNX1y85jN9hQkLpQPQepaUkWynF+7t7Xr16yTw60Y8loZvENBw5HE48PvVcX+948+qaGALzMECXeHW7pbFwHCaGeeT9+wMXF1usbQBPiLl5ida0VtNvOlmTQcrl53kmBikJn1LCp4RzUUAe7zAqYfsNh/EoB3sIfPr6NU0LwTmC81xeXElH+abBWBFWH05HHp+OPJ1mdNPWdSUGk6zfsnISUfjo+f7uga+++m5BaFZrQClqudPZ3l/5uugC7+RDOTeHEhB1WUvGGLrNFtVbzK5DtxYaOVjb7MjEkO93BUoaawVU9IEYyLrWVFDZakPbNJymEZ/tHMDj4SmXQMhlreXy4gKVEnf394h+mZT6aZV4/fIFu77Hak3wnsNxouk7ktUk4zFhYngaMHRc7W/Y77fc372X4CjEfGAZbm5umJ3j8eGRkJKUaBpxxoyRwNVaKRObZ9EGRGu6tmO32fL0+CgHfT7QKrNk5QD1XSuNemKksSZn8fN8KcW27atmUwqRm4sLtFJ8+e3X/PUv/5rJB2GSaCUlgEaJnh/SLGJ0BZjPTqoCo8TRFUdQDvGmEcc0xoQaDdM8LhBWAZOfObrwYce9gLelrBnECbm/v8tyF1TNoajSmf3avbjm4sUto3okPB74n/+Xf8l//1/+F/zeTz4nJdjGSPKRNnpa22J0A/PMrI6gDC8/+ZxI5PRwxzicSClxubvgFJ8Yxomnb7/m5d//fW7CR7R9z3x6AISNOXhhul7sd+xaS3Sex9FxdI7b/QXWCAP63fGEA252ezqjCdPI+8MR3bRs25beWsZx4GmaaNqWi23Htm04HAdcSqisS3vd9RxOJwbvmbXlatPRA/PsODnHP/uv/yn/+x/+nKdBWE3vvMu8AQGktDFE4Orikt1mQ2ssv/zy1zlp9qHTa3lsaQCxOFVl7opkyfO1+nyOz5z5epzKjh7nGec9MQRJlFSbpNApO9IoMBbVNplNJ3qOwWpiIyyIkJ3ZUMoVlZx6moRRio22dEpL33jvST6zzsqqF0NUg9oQAypoiAE3T/zFn/4Rt7dX6OSYhgPMA9uu5VL3XDQNHzUNX379DfPk2b5+w+0nPyLYpuq0+eA5DkfarsE2LbZpCQiTYGN3bPa7uoeG04ntZsfnP/kZL1++YpgmxnHAzxOk3AyiNJMAPvnsM+L+ht1+z+uPPsrglqqMD6VgGAasXhrgvfn4U+5fvqHtNoDCzY7LP/s5l7/4P4mvNsw+8LjbEXXkejwu50TGg5YEdnlYbEZpYLFm/ovv1KD0TkoIo8P7OfsVWZs3A+1N02W9wIg2oHVgPJwYng6EecBisqxKom00XaOwo8enE3FSdLtbTgEpbS73rC1KWYxN2G7H5uYFwTncODKdnmA6YFuFbUBbaep1//CWbq/47T/4nN/66U9lTXhP8J6TK8mmPAaqMKQyIPc30kxTldtRWoArH6VU1LQtbStN/1RMNI3C2g3jMFB06FAKSwnSxbdIMWb2i8ogtUfrE4oGYmEX5znTmn53ATFJDwkXcVPky+++48e+QQRC0g/xHrPoD+pC1kgF6JX+DXKWZN/WSqWUV4poFMloTASTpNIqxsR4GngajxyOR8ZxRGmD1XLWzG7ieHjCWkleO9dChL7f0HYdbnJMx4FvHu9oVG6wYzTbjfQAELKlrDsfRBdPkkCatpXAXWwDtTIwT2PeW+fAhdIfcIZWP2qlaJoWRcInOEX4o/sH/ux05FcxMNsGCGwvduxeveL2k5/glVRNSCVLEg1I7wkx5PhOg887Yw0yhSwFkl09+TtlplyCFKXDRfBM0zH3SxDAU2swVmOtQqnE7D1e98xmz9De8NBfk7rEMEyc5oFhPpFMQ1RSUdKYxBwdKTpJoYjzUYFHGRpVQcO1H1A6a5fyVLkihQG62Ir8OLYmOJI2mM7QhIDTmuhmCAojDQDEh9SJmMuzlZbGshLwL3rE5zsx/51Wwm6V0fuBa7UeKhkhx5Dr+SlAYSExpKgqFrfI6pU9VgC1VbMaJd/eFIA7P6isrnqWSsnRVQGtAio1S7OpMhe1eilXN2gLOttQrQ16kxjniB9mWLEr/7+4PuQT/O0grao6yjZX5LngccGhY+l3oHOzLWoIUhivdR7zGM3znNebJIfGNFASLKDOwNy261g6zpcS+XWTIpndqi2vCtO4TikyrwHvRH5qAUMXYHCJs5bz02YixpqlW7RDm0Z8HtZzn1KWRuHsXC7AotYa5/zKV1sA6jL+Gmg7IQEpBEx0pUouZZuRIl1rKtC99u/XQC4U8pPJsgEen5moWima1lZd0URknkOVYKj+Yf5/U6VHciVcJoOUnivL/MsmKDsk5vcySqGNlXM2+wlJiaRZzICtNRbF8l3k/rPMQV4T3ofaf0cpnZOQRVIiny1nMgsq6w5nm5cE8DaSocVa6Eypgl3spVZKEuJtS9/1tcFWSRopI/fbKfHdRFpu0cm1VpKZeqtzmf+c8YZFx1gVuYI8h9MoBDeVm+ZqVRZJln3wnqShNRaTjVfxU8r7dk236MGqTNrJPVvKmkzZX6gGEFgk8QpAu/ixeURo2hZjF+zuQ9ffCTA2poiymta29KaD5HLWVJEVeKp2W0yBGCaO/j0H98DgB8mUpgTBo1LpgrmU9xVWqZKkrVxKZSCmZE9KfpP8upwJLwdtBisaa8V4Va3M7LDlAEFeXliny2clElNy/OWv/oLf/9nf58Ubhe0ueHVzy6evP+MwHTjNJ9FJIZByB9WQD6+kCigtKP+aXl6drAxQpfg3Q5Tlq1enO7+ngMtqbYWX55/9Q06LsvzqwbrOVJSRX42HVOkIkCqO7wLIFhGiBIQsEK60QXUCUqFH4uTAexSJ68srcX6nmcMwlH6oz4LwvyGQLtIGKgO5eR2QIGC4GxzDl99x9/iv+Olnr/nxp2/45M1rbvYX1RiLmHMxvrE6zjEuGaGkkpRQakPSBqUt/eUtt6alsR3Hh3vccERrg0+eeQ5M08Q4zhyPkxgPEkpZccQUOB9wfiJpCCphtOLq6oIYHZObmb0XUMk5pnFmUgoXpMvktmuZponT6cjLeEPf97xsGq6DaI19+817fAxsth37XZYsyONtMsO2lhcRCaOn3/YoJcDc09ORYfRcX+/Yb1s0AoY11qJQJB84Hu7ZX+7oNz3tdY/dbdDGgjKk7Ew9Pg2Ms6ikFceurHVSIuTmWEIfjRhteH934OHhicNxEOmA7DgDWcquZL+o67aIkpWtUPZEItXAoCyU6piqRDKgrcZue9KmkVLaCsKKrTDGsul7LAZrGmKK3B8esY3YCtQK+MlJHdNYXFgzs1QGYFQ99Mv9TsMg6y6H/NoaAXlUy8ubF5icHWxtx1YbgoJZezyeOc7MhxOdbTG2gxgxjaG1AnxPbiakwP3DA6WLdVIw+VmAnOw0K6szeBuqDZCul3Jo+mcZap8iu81GDsIEo3NMs0OakRh22x3DOObOmhG0IqTIcJwkqwk8PB3y/GSWX5ZQUGI4APCUYGAJKEr5T536woLMDsQ4TCg110DEWpsTYhmYD6Vcd2FbF72yYmsV1OYBm77n/v6B4tVKoymLqfGv2N4SPJfLxwhdi93v8IeR6D3/+o//lO/fvee/+Sf/GTYgwVoClKdV0qE3hYAbBh7v33N58woSPIXANM80XaDZ9ASjGU8HTt9/yyc/+pxhesEXv/gL5tMDs3coZdj1Ha1SnAYRrU8orvc7rFYM0yxyBUrx8vICk52k0zjR9xu2fUdMkXEaOYwTTdvQW9HxezqeGGOkazu6psG4wLvv7/BaY7qWm+2OjsjT6cQQAl5prjdbPt/ueRcS995xIHHyqe5BpH0Vwzjg3Vy1wcqZ/8N04g8B1nIGuVnmvpSkfziJmY8qyrme53ZZVsIiNJp5nqUEtr48lximvE6UJZJ4P97Be3j/7lvend7z4uI1ne2Y54lxGvDRE4h4ERVBSqo1ymisbUELID2HgE6e5Oezs79CghlQbLLD/nD3nrfffYUxisvrl/TbveiibTfo0xO7tmGrNelwop8983ffMx4n5tPA5kefYTY7Zjfx+PgIWrHd7imdzwVtNFUGROeKo81mw2a7gQSmadgaw2bT18FLKSBt3mWkX7x8wZNqiBnktE3RJc36aiT6zYYmd88FePn6Jfr2turAxRTY7npub69pW0vbJIxNBJs4dB2XhwfRII2yj4UAsPg1ohmZcuNKYdikXGomKWuRH/DeE8MEMVBazxcApeu3NG0rzUSiJ6Fp2o79xYYUDG+/eiuN8jJL3mhNY0R3zweY4sjw9JbL7QVeNcxJM8RISLkHfQ48NZCMQfcbNo2lp2V3eUHTtdkfhZevbkQOSBuprinWZ3UIljVb/bhUwJ0C1OTvX1inVXMyN0txDmMNjd1KtdA8Zx9O1qK1RsYjBoEUYkBYiQL4ahTBhXq+R0CrRIoTzj0xAF1/neciokLgVfLcaY1tO5rek3aer6dHTn6HgLEK8WTyd1OKznY0pqU28fKl5FP8brGxqXq64nPk0v/s36kkDXlCDIToUWOk0xqz27LfbCgNKr13nI6Jg/NcXV1xdXmFsQ3zNEvCRstn6cZwGiamILxiHTXOBNr2EqsabDIYpeWzK0NeylsVi0Zt/Q4UMKN09i4gmS7hUW7+SZZYWkyeahomP5BIjCR+eTzxbw9PfEXgaA0xV9Dvbm65fPEG2+yxGJJZKhekkkyqrULKDL0VA9roomfvMtFGmsTqDIZWreaYMChUCJzyd1l0ABPaii2PQTTgf+t3/4Df/d1/zKvbVzTG4oLjqBJv/Yx/vBf5pban0Zo+bEhuIASPTwkfIy54GeO6F8BqYfgmU2JJVZnDsifkPquHWc6MAnKZRQ6j6Dlqa+j2e0zT4KYBP57E17aWFER+pEj9k0QPNbgZkjTWK8kho5a9ivohQLWAQ+fnn+I8ZirEmGKzC8BaQP/62iInl1a+LFm+K8dxunbMK2xhGQtDLlHOBKkC+mhtsq1ZVU3pwigVYNKU8m4tFi9lf73Gwfl9YimXpgzec1/gh9eHmLTPq5v+Q5mxoHJHeWE/BxAWD4ARf9mYXMJvhIUvEmqR2Y/kFkb5GyjarkFbBSkDRlphla32qpasVzxA5rN6wVo000tTpVDAQZYhku+4MExFim/Raq2SXatLKyEYiHSfgItrMBZk/n0INW3hg5N+GrpUnKgMYq3jnxIDLt9t0dnNwFhZl6mc24uUjrGW1sq6irkxoFRDCKFE53Vrui5v41QTSWvAud21klDyITONF0C4EPLamPDB5+bjqQKaSmupUlg2YNVs1RW8lmqbxtp8xMYcB4k/FHMVlNKCB4Us0+l8ZvFqgzIiLSY2vTCOxXdsSDS5iTlIAtb7iacsSVZ0WNtWGhLPblqxmGWcjTEYmwHfAgiXcVclFSBzFoKA92tsSufq2tqfJWuhk3LFptG1AiF4T1Ba/Bml6LquSieslkc+P7Jt68DGAjbnipS2lQRQlIbLs59z1CBz3dlWbEseL+89SkPps5CyFKWPchaFjJEtiU3qWslTm1neof5+dolYpGVq/Pjh6+8EGCvwY5SuoSlBcDlLJtBdShrRB40kFYg4jvOBIYyS1Uy5462cWsLC+gEemY34+oSlQpKrKVrKKJQW8K74qm72xPweWmt2uz0xJOZ5Wg6R8mlrMCD7dj4F3j684zQcuPGObqPomoaXt6/59Xdf5Kx2QmQVxHGJaZEMqAsvFrHg5VA0q8OigCPVwC5f9wdjkj2JFXDB2YIv13IYna+mH75vKshWve96D3kOOXs8O/pnb6vqIa87jY4QrSE6TwqeZHL3vJg7sq7Al+cdKUnLXa6BrmcfJX9r8DFxnB1f3T8wR8/9MPD944GfffoJL29vapYJnwi6lDZlx6cYmgwGhgzcCltbo7Sl6bfsrxNN2/L0cEd0EwnZ6CEmxnHOTEMJ7Jzz+Chd47sMAHkfaGxL13W0bcMwDPmgI+uxSWATEzgfGceZ+8cTIXicizgvnaiVFhq9NS3vtIzpOGmaxmJUbjigi2h7Bu1DFFHwlEQrLAmINM2ehKzn/XZDazMA0Egn+3G0zONEt+loNz1t10NjpaRIi87z7AOnccIXJmgNLjJ0lZ3SRZtYRv777x95ehoIIdWgA1UOh/oG50ssHyLZn8w6YBWPO19CKesFGo1qNXrTQGuwbQOZJbo6l+QAsQ0qKmEjB5+DkJWjVJZf/neMEeczwzS/mSolFfkrWGPloHWekETyo22bvA80TdNysb/ImWTRGWpMZm3hGOLI5Eem4UirWpS2xNzVtYi+l/BTG0PbWjZ6wzANuTt0Plhz1tDnQKkyyFY7yxqT9YbkO1pr6LuOmEspE6I3RBbq997TdZ0AGymSojQxm72UTiutmHx2hOSUp9WW5D156ijOf1mrZ7aHMrfyWaU8yujCSstBZDX+CyBRDudySQC8srclCsrOnJsdH3TcVf1ffd36PkNMoA2m69C7DenpwOPhyBfffMsf/eW/45/87GcS5KSESgGTI+KU3yuSaJpruu2OECMP775lmkaafkPTb2iDZ3y6Yzpcg7FcXN1wN59okGy/VSo3KJByp85aemsZpqk2+tr1PZbE5BzeiyzJRd8DCeelIVjTNmyaFp3ndZwdupVyaVJkdJKRto2lNQYbPFPwTJldvWlaeq148/IFk/c83o286HvCaSKkkEv/xEY45wjeS3UK6/NvOTPPFkLdd8uULOX8ZV7KVJ3P1Q+mcrW61vPonYjcyzEQz55dPjySOLgjYYjM6cRjOHGtXqG1RUdL324xtQQx1gCj/FHKVHZwiFJ5kIrtOPuoXGaoFKTA48M9j3ffMw0nXr56Tb+9oOkkqWaB5vqGxipMjIRxojOKbnbExyfGbifZjQAAIABJREFU4PEqsX39BoyhtQZlF41M1CqAygNZHGy96hxd7ksrk8c4LahQvqy16LSUOi6lnKvg8qwkDmzTCEsjG6Ku29L3W/q+p2ulEYM2gaTBG8OxmWmnEypKkJaeda9eAIlUF0VhZYmvIXITIUzSBV2Rk/PStdk2hTHcEFKEEOtrCnOp3fSMjwdh+Clp7qMVtFZhNOgQSW4izQp0B7olKMuMAIEpUZvbilmMGAuvbq/ZbrdCGFCBpDR932YgTuEmR5VSyINaZD7EX13OJVl/CEhUzklAKH7F7xWbpFTKbBuZWr9K0qscGDVtl7X9fNVZl7nVEgzpRW6jnimZhDGj0KbFmszYiYEmBXZoorGEtsW3nllHwmrbOWOlHDxfhRFUzoNhGqXjcQUeSslMAdZ1qZ+v9jb/Q/R6/cT83RPOFu1Bclm6aJOa2bFF0SUws8ckRYvkEEt5pmosm00nTfhykN20ppIFQCo7YpYoqIBFXqMp2xZd4pzyV31O7tGQ76+s6w+49QSViEozJc97P/OL0wNf43ky4HWed6PRmw30PT5I9V+IPq+JmCvhDDGD1Uv8sJBHRGYpr8GkUXHpKC5MskzOUOReIlTbmg0JSpssrWR58eIFn//4Z9zcvqHrtvhpZjg5Grths7lk0+85qqz/pxuUamhQWDNjYkQHOV8wJd5KucLA5BL5JbG/jjXqWZ6of5OBodJwibxcNIqkkyRruh5nmwraJj+TvCMGS5xH6ZsRRFM3KYUKoigMoM8A9FSTfWKf8lqosVh+1jPfU2m9lOuuHksrG15CqNrAT2XiUjkoS4CLXpXqUu6k6qImtZCqyv2W96rPK4yzDByVLVZUaxd7pRA5jMUeLeOunt3X4gf8TczW57//DwdeP3AlSfIV7U2xc5l1p0w+NxcpgrPPTYlIWOwNZC1UXaWKqmRDsVN6iaNj+dzk67wJ8GZIegGRahVwHjtxL5b7et69Pn9SuduVb501Q7MfUEHY/BrRtU9ZUz37/bnRrior+gO+Syr+/AIrsHbHy+tSQuyaojZqVwpU1Gfvtx7vlPeqTs9qgct4ssIWEKapEGM0JQlQgbkM7hq90rYGFAvrufDltdaYnNUpY1fibCE96UWbFOocgRCrUJZG1ZGv0gHG5MZSKdXqxRInikqlptGmyg5BoujSLmS+Mpfy9t5lmQGl0CvfpwKqOW4sCRubwfoi8VJWiFaSkNLlHsn4Vlw/L39XwOFQfqkAKPIRFdzNib5lIaSzvWBUruLUGlMTawv5pY5rxUuESFTWbkqCjbRtJ1IQIaJjZF1VLclz6nlfqi05+y4KdK5m8fEHOOH6+jsBxsYkGUkbg+hu+ZmEqRMZg19E03UkJM/jdGTwMyGVLpyLcdG5JKz4S+XcECdg9cHF+NSNqFYDLY6UirEuUim5DdmgGjb9hmlyUpodQjYqa0N0Fs8RiNwPj5zmgRi9dDgGXt28YrfZCaCqIkmb7LwIgLPO/BR0vRgDyAa8LqLi2GYmBwhLRy/ZTlUX7QKklEO7vGdkZaBWAdTayC4mWa4fHPyUQ5Izw3Z2PftRr25C5eDGbDW6tUTv8dPMGAPTNBLmIEyKlKpDYdTCkq33sTpgl7O6ZNbLz+V8V5AUU0p8+f6Rt49P/Oab7xiHE//od3+Hi+2WNtP7bXMO+WhdDIR8Ae+9dDyMoheUEihj6feXNH1Pspan+/cQpKOu0o5YmAEoQhIgI5Jou56ubegayzCMtG1H37UoBeM0ixRA1vaR7oOib0uEYXDEeMRaTWONZJmNISZxnK1StNYy+sg0SlOvTd+w7dus1ZKZIz4QnMfPHoM4Ai44nJ9xIWattIbdtuf6ciPNCozB+UA7tHjnaDY92rYo00qZrqSGScA4zpymGS/izMtay/t2cVSoC8T5wLdv73k6DNnAluWa16Ja1uAyWeeLrtiJwnZ4ZiLy2pJyONM3mH1HMIqmEXDUebccyiwBZAiRcZqYwywZ77wP6wJPy8HmnJNyjrJe8x+thfditHSeJyae/FGayLWWtu0YxwGlJIO43+2xRuculLnjagrMcWaIJ6Z5YBxP2EZBo3Km2DCOU04AyN13Xct2s8U2DfE+Mh9EF1Y0dcR5CFqhwno4VS0zUYkc2EhgsOl6uq5jOA3Mfl6Yz4he0jgMXF5fU8vQUmKcpkLtyHs31kNep4WtUY98VRrpLPayjKdk3oURMM9zBXlKdlUcl1htYS1Nye+vSWKL8z4X4Auq/092QILoNVKWYLWzZZwKKF/s4WqtRWEEq67BXm2Zx4GUAnePj/wfP/8jPv/4Y9J2KzI8MdEon98vCosoOKbO0G4uubjueHh/xziOwgLqenZ7uL+74/uvfk13ccXl1RXHwx1m1hA8KQRObsZoTZ9lB1SMDPNMypnmq23PeDwyzQ6lNfttz761PByP0iwwJi72G1q06NU60Y3dWINOCe8cc4hsNi19Y7GAH048xUQwhq5p2LUNeMeLVy+4Gwc2xyOvr694Gt8yh4jP9r444jEHOKmOdxn8srHLI6uEYloChfoKVZ6zbP6z8+oHAVph5aR6LymJlEr1tNc2K+VXZHbbGGdigH2/ZZgdnoTRlt7uuNze8la/Q0cgBJQ5v1+lNNoKmBmk1aswxs/uLn/rzCidpiN3b79hHE50TcOrjz7FNltSZiVF02KvbtA4mCdU28h8OE+aZo6HE4dpIAVPd3PDdn+B6bckbUVXEgFGKjiU/9RyvjMfJlXbIEpJz4FkRe7rU32eYtf/tjA5Qa3S2W4vMftr4u6ShgPaJBl7FEkZHpstV9OIDYHg/apZl1y1YUW+n4UFkcAYjOkAlRlGUdg2udGGaRqatkUbi7bCZFM6oVTRQRedtN3FDjcMVf5F58oOraXLsrWgdeQ0nFA6YGySJl75XPNAVJKK0EiTjL6Bj9+8YLfpaW2q0l1KQfCi65fpmHU8q+ZyqYDJYxBCyD6vSNUUeQFV2IuUeUsoYi6L1NWOR5KA0BK5knxks9kIEBojoYZJZfLye8clGBZfLhLTTPQR51oUW9mrMYFK7IGgNXPTMNuE7hXrasEh672Wq3T7li7fjnEaJVAs0mMZnBKtS2GuhbxY0//D3Jv92pYk532/HNawhzPde2vqrh6KTVISSYmWBdMGZBuwAQN6kf9SvVqCRcCyIRiwbEKGQZEmu9nNnqqr6o5n2MMacvBDROZa+1axSQJ+6FVdXfees/cacmVGRnzxxRcszUWMARMjeRwZD/eExi4yZl71Fa3DATeupZsTHM/gA947rDY7s2gTPu/IbmmW47zRSh0p67uUzCjxgRLu8hK4SyyiO1Odt0bXRokp1Cy9Z9cyQhxxzvI4JX41nvnh+MgbbxnVVzM5Ydse0/fktmWMkTCPhDCRUiCngLUe34isSUxiE0t8JjGaAOIxBpljBiUM6FqsySVDthYX8/KzTK1ytMYTIzjf8em3v8+3P/k+vd8Rp8xwHHh8c4+xjn1/zd3Nc16e7gkxEw0k43C+x2ZJQFkjyV2ahcUVY1gBLwrUk1eVhLp+iti/DmLx9wpLUUpsF+DcGEvTbzBOwnBrLXEaSWEizxMxZ0iZZAIpGshJm8mUlavJqrRUgZosPVXUZF3GZHV/K9c3FSQujZfQJMQirbMkPi/94lW8uIo9yw8r0F8/JGCskJ0WiaBybwWiWDdLyuVGjEjYmVyeR8ZTAKAVWWkVyFWQcRX7vU+E+P/j+CZG7cXfUxamX4zSUd45qUKxDq/SbDmvxqtiGFw8UwH4LFRmcqnKKfGRKcx9ZfqJlNAs46Uvwvt8IQfkNZla/GhpCLrMDbv6L4jdqWXt+qhCnsh1zseUiGWsV2BssYspJWwWjXbhC5vab6O83pyyArvLu7Vqe8o6umAa6j5trKXCmJla/r7cuyEno4nMqP5aSQQr6rECnVO1XeXdFoa7qQsixghaOeedl33PrP2Fy7XjnFNSxfKz0oy1gvW6Fy2hrszlsi80jcNZebdGtYZdZWwaoCHMMzYpuzoLwaZoETe+oetE3qY0kCyxkPciDUKGkVErd4rFyXWulYeaxgmjMWrRhhb7LpICKUViBhMN1sV6/jIXijRCSepbDEErKcr+nLNULDrv8M6L3xvCSnN8SUYalRxcS8UZJJFZ5vEa01p0dqU3SBlzay1922lF9EIKSDofrLNLVazO+4K/Vea6s6QsMXiI6Wv2YX38RoCxOWdimolYpjzRRAE7JWLVoMoAURbwMR/5/HjPY5hJztE3XkphyJiUMNpBcMnZy/djSsW2C4KfVoyTcmjpT9sKEHU6n6qYddO2OLvojHz18iUAKUlQbKwXmQTdFet7hxrYH6eRX775imcvPmV7/SEmw7c/+BYvrp/zy2bLU7gHIsZoGbJZnOh1Bq9kWyq1O0aWJV+csFXAGtUZKg6dgZLhKaX2BdQtxrBuYPA1o1CucrEVrcCoBXyoUMTFeVZf+tp9m3KfWVgcEUN2Ig+JN8znkWjVdKYVcSBndYBE7yrnQj9flb4UR2F1P/XquZxIF62VpihvHs/8+z/5U/7sr37GP/jsM37w3e/wg+9+m843zGFaytuMqay78hyiV5xrXF5GLjvP/vY5++sbHt+84vh4TwqBT777bYbjmdPxwNPxwNVVhzGOpmnZbnu6TvRnzqcT59OR03AkYxmngZShaxrOwwhkZckmHh6P7Hdb+r7BuwZywNmWbBwhBV69ea1lDyINkmJmOI+Mm4ab6x0vnt0Qw8S7+yct9Yi0TYs1lhAz05zo2p793nG13wgYe3cNBo6nEzGIePXV8w84h0Q2HudaGt8IE4bMOAfevnlgmqKwz0vGfrXpUTJwpgBx8Or1E2/ePnEeJvXR7MUcBZ0nxU+8mGoLeFGdwzJnNRtYfmg70Yh1Vx1m1xLHmdPpiDUWv5I8yFlYg6/u36ktkaAwkxWkWc01LvUqnXO0Xcc0TYzDUDcm7zyt9/RNx6cffsxf/+oXvDs+0nZ9dfSatmG33bLdbnDJFnEXcspS8uwGcpo4PzyQU8K3nq5rySYRibRNQ4giDeCsYZomLbkxzEl0y7bbLV3bcTqdmKZJ71m0iIxRLe0IkRnvPFf7PdM0cT6faZzj+HRQpis1uCkb3DwHHh4epKM5FjSZttvuSDkzTIv+q0U1dl3DbCbV1lr+wS62sjTfKuAPoNeQ1xtTyfyqOxYTxvuL5gopJzonOp9TDMwhLMai7u2LjAylwUEJgFehcXEmv2lTNsaQDGRvsLd7/DyRH07kYWJKkX/1b/4t/+K//ef81sef4Mm4nKSkOWdczpgYON0/kqOn3Vzx4uPv8fJXP+Z0OrHJcH37jPPxzPj0FsJA6y3Pnj3n7RefM0wjcxKn8u5qj0O0ne/PA77v2fcdjYXxeODdYeDm6opt39BbeHx64DBFmrbloyvpZP/64ZE5RZy1PNvuiePIkKJo/3UtfdszH0+cY2ByFrPbcbft8TkzjyNvz2dy1/EP/8Hv8J//we8xDGd++MUfY8NE4zzJCiuzzIlErs5sWWCpUKY12Il5VeYEWuq6si/L6rx4R39T+Pb+zzPCdBunmYhk0bNRbcNckgjQWqn22Nsdn1x/m//us/+af/0n/zPtbGiN45Pnn3D+8kSTPaRITCPZlq60IB21bQ0fUgYXMqUkuz5DCgIImUgKkb/+8Y/Y9j0ffvxtbp49p+l2JBZNwYBl2u6ZzEzTdzhjaN69o50H/Bhx04x/88CbpwfczTW7jz7h49/9Xcy2JRkve4e4OZTGqMXRLX4MXAasEmRK2VwwCxOivEdrMm3jV8H717yOelhbSukExO36LV9975/wsm35x3/2xxgzqW6pJaeITZkUZk2EzTJmi9Miz3HhH8pvU1LQfPOc4+Ed0ggIMiK5s9nusF5KsENKpHHWANYQ0whmVLAJPvrkGV1jGM4DOS5diaGAgp5mDmyvISZLjDCEM7ddT/Qtk3EcZ2Gubrqe633Phy+u+e5HtxDO5Diq3ZFxc50jt4ZMZNZqFoNooBnvxZdVv7iwZ+rcjtI8yVorchQIpy3lQAwT43hiu2kxNKrDamjbjsP9W1IK+MZLGeQ0LmD9e1UHJQDTwRdpF0BUJw3WJnIamKaMM15L8D2GhIi4RoyN9NsW55e5/SpOTGubay3WeKx2f0854lyjTVa08kGT6JXhkmV/SMq6lVF3Or6G6w8/5Po7nzKNM9NwpmksX/zVj+ldR991WCvSGXaGPE3M86zJyVkT9zM5yqM7Y3BGwBLjGvLVHW5/S7tvakAoIKysmRTfW1fvedoCblT0pgIK1irIfGEYAQvvwsRfnh74T49v+dxmoiuCP5ls4e6jj7h98RHt9XOmMZO9I0RHCKP4kjEwT+Hi1JlMUnAuxoS1vtqGkqe2zoBxmtiRd+UA8lwbvpSdFQtNu8X7Ddv+im9/9D1sMORJmhtd7e7wpuH1w2turp7z3abh//6z/8BwPpD8RLaervUaByHvW+eU957SBFcStusxzRcBvQGmMFYGsNExt2RY8MXaHCcliU9H9dWtc+AaaIXAYJSoYNtOkrKzALTWtLI+13PZGG3iqmCakgRSAWmNrfazWM/a8ZyE1YY8tRkhlyCjSUt8WPyoCvJWAPaSxKCOjsy11W8KiNPU/cDU+VnOs75+id3LUYG2JHtDCuvGR5KQbVrP3PjKXP41ZLQLsPb94+vJ2r+vVIECa8ZK5VffaxOiIl8SSEaSMPKzRcu+bZu6d17ca1KpxhXpZ4khls9aa+m6jk2zrZ8pmrqNW3R4a/KmYAIGBdASacVMlLWglQSZihkYY2qJt96E+l6pgv5ABemKn23rvDC6t8Ra2l+ASQtKLDL4VTVaiIE5SGPaNQlG+igUb1t9+zjVcxeiyBxm9aPk/qZ50rg9sOl7mmbRoS9jV9jNIGupaXy9tlRXLBJzpthtowSQWOJ/xVSsrQ2Zl8Z2i02uOIj5Ol5S9KhzlmZUVbpq7afokvHOK0iZhR0dBGcrGE8Bco0Gx2Xf099gnaXverzTqgaDJJcwOLto5rZNU7Vqi4yEgMlyrqiA6tJ7AwV9tVqug1F9ggKir5vqNk3DPM8Sk8ZAcAEfG4wxzOq/GaSK2Dp5x53qqBccq+BkZAQk1flcEgmFsCNrZCH6nM7Hijc4XbdJMaTiE2Rld3vrcP3SXKxgW9YYut01otN7ObfWx28GGEvCNBkaGO1MmAO9FT0nA2Jws2hMzMy8zU/8bLznPo9MRHLUzdkaKXt2TrKZJdjSw9hcr1gmrEGZUN5J042cCEEzSvriDDIJnWquGQUwC9xbnGdYLaDVIpNrqdOXMi9fv+Lp00cg0gA32y03uxt2myseH96RKF3ggAQhBkqSqYI4pXSRZa8qm1vRf63cWV3gZbJnygRcdHvWzOLCKrUs61sMXLpg38jlbAXM1iDt+r9lbHLOqoOzfgcF1HhvMyeJkTAFmCllAQ6737PZ7UlTYDwOzIcBVxouVaCulP6vtGnLuzCmbv5GvrRcu74yCaYBonEkLF8+TTz8+V/xw7/+Jd/7+AP+2R/+Hs/urmm7VhpIhLiUGWQpm2w6EYWOSebMslD1YqZlf/sB2/0NYToznAf6q5HdNHIXRm5v7xjPA8fHR4bzmRcvbjkenxjOLe/u4au//BXDZAlzEOba1RWHR+1ubw0Ji3Ut2XhChNMw8+rtE4/Hob7rpt2yv2qx54EQE96JoWrbhhgT9w+P3N5eS6OSKTDHQCIQx5nD6czpPGKzpWl6Hg9PWBu5udmCNXzxxUvGcWa7vSLMEWOlvJbGEGyScveYOM8zj+NEWDkIJQtYO03aYgQTZEOYEz/+yS+Y5rCsvSTsATHmhrk0gSjuewHked/hK3OgbAgaYjmD8472eoe/6jG9bAzeWvb7KwHgp5lpnnQ+S4ZwTgknu6YGsDCnzG67o/ESUB1PJ0IUbWCyZM2zAtBN06jWkNxHSInH85Gf/PLnDHHGamOrxlm88zRNS9O2optlPEW/iZwxFjwZM0y8+cWXku1LidM4EudAs5H7yQaS2pppmkQDVWUmSubQO0/XdtKYI0oWsWtb1dPJFfgCeLh/kHnUtBwOB4rFLNnMAl5677m7uWXbb/ji1UuaruU73/4WP/3pz4hhAqRbvNhBw+31NVfbHaenI5K4KgtXGzsFPT/yHGKmNKkVk4jD6zyLIayE+Km6RMuckaNvO3UE46I1XcCbXJJihY2xdKIwRsxILHtGXoyM0flxeeRyappnVwSMNO45njmnwP/6f/xffPXd7/Lf/NP/TLSC9WwlzrYpMJ4egMiLDz8lh5HD4xuG05GUI8+ev+Dp3VvGYeDxi19w9+GnXO3uMNaTxwMb50jzxDkE5php+o5n2w1hnjicJ56GgY/ubmi9JcXAu8OZc8jc7beiz5UCrx6PJAy7zZZN4xmGkWEWdq3znq1vON0/Eg3kxmHblrvWMx0eOYTIjGGz27NpPTHMHJ7OPIbEv/jn/5zPv/ySX7x6xU/eveOksgaV0a4LuwI6dTyVJZ6oOlXGSDOtxJIMAX3v5d3x9eM92GL5nH5tNpm3YeQ4T0xxpktRmEpqG6yxbJqeJltMcuxjw63Z4rPDZk9OhmkYCZM0AIs2EpJoSBb2TJk2zjUUDcI4h4uAACDEiUjidJy4f/OW25tbnn3wMV2/rU2QLuafhZGGk/OYrqfveuLbJ07HLxgZJCnESBonxlcn3r59xf0Xv+Dm0++z/+BjNs9e4PudzPXClF2NolxquV6xt8ZAmmeyX5JVKQXmWRpUGAOtbZYK1tWaW5d9GaOlgDkxj0eOj1+R40C+fcFf/hf/kj/66X8kDU+EeWAYT4TjE2/GmT5G7lgns8t1zMW8KEMlMiUwDCeG81nZRhJMQ1bWU69jXALTRE6BqKz56pYYx/WzW66NlHRL6XzRcmuwrq3MkRp4GZEGMr4R0MYKGwcj5Yld5zEpiS1HGCdTmElJNVu9h61js2lln3ANzndY60lBZL9SRiqRZik9TymJn52FAeysIYYZa6SRWM4t267lPB4FrKHs3w39dsM8nQXMzYYYVUYpFkBuCdLB4DTxJeO04uApC9TYBIzEPJGjp/N7rLVc50TTNOSb55jt4SK6GVkrl4lEhvZ8x1nPptvUgErbClHLdYs2qEKckgBJiw6tViD5rmPIEXu1ob3eMo4DNz/4Lfa7K5quY5pHttvthdZniolhEAmpnJKAsXPg4fNf8fTll7QEfDBYP5KaEXutupiI3M88zmz7zapBpi6xbDA2U5sh5yVwzKbMpRV5YrXfZeCRxJ/ev+JHw4GfExhar6wHqUQIpmX7wbeh3THHzDifGM9PkALWZESm32qX7MIIFekCW2xyY0mqwYyCsHMIAlh5qfAqTEkHYHxNti822mCs2LIUEswRj5Vy6Cy652275erqluGQCId7coYxzKJXbC02NzjvycaQrPhBTiuZhM0kDVUFOBYABJKwfgswnsS/dEbeTdTqiJyLfEBhcYqfYK3s2YKhWIw2dYzRk5MnxYbgPXkyUmbrHdE5YcyGoNJYC8mklBSKX6vs1kK+M8CqPNuaRXYMBGQQttdSil7Gt8Sy5TpG30Vl1+oMippFWEqJxcYJwFcQOLv42UYpNwWIsmjyo3rgVKaurrxcbIGOW6Kw3dT7y1nY5l2La7xM+dX2tt4b/zaG7N/0+7/p598M0qpFs1YaFGuD55Qz4zhCFklF7zybzUZ1VtMC7jktoVeUtHqcKg1mytxZxUutykEVIDfrvHP4CoKJ751qD5TMUgtRn0+djJQErE/KTgxl7pXrq2yC80uX+pyln05hZOacaiUCWXww0ZUVjdKmaSk9N2KMIruUxGZZPX/jPKUxVJGim0NgnqVHRW1MZU29Dymbb6RirbAwo0ioyB6Xcc6D2Yl82jxXhm4Bbr1vVHJt0Ywdx0GeWce464QwVUh6w3Cu68JgZc9tmgqkhhQ4nQcKYdDqmkggWIdWW9ZmXEb3pVpVmRf8p0jfWVOfU8r/ZTyNSiuIXJG9kJEoxLFim1KMEpuvEizOuortxJiwTn4WlfGaVqB8wdIK277YECfGHZtVbiCjDdlFekXWdQZTpEsWtrU1IuXSdZ1UL2mcWoDurutkPJLqUBdf25QGaVJJEFOqmr4xJcYw07WN2EALFkvU+I64smMY9TOzAvilF4TMr6ZtVW9+waiq7bJCIHQ4Ta4WH/Gbj98IMBYQRoOzogmHvKzCdJESJXHUxzTx5XDP2+nMkAIFXgRqoGJkVqhhvyiokD+ZYtg0I2tEoD3aJXjIq8+WI1M0J2STkNgi1Q1V7MEiH1C64S2aqGL4nh7vGc8HbJ5pXcumabnZXXOzvebLt8VZolaSiaA9K2NajLDcy7IRKIBkqaWblZWVc9ULEiNka3fLNTuv/L4+c3GUSpn96p1ZHYNizNcZ0/dBhvK9UuEgQ3J53+vP5lWjrdIkovxd9J4suZWMcGsscRiJ0yx6pohWWQ2gzOUMEL7oEnEXs7m4otTNpgYFSNnkcZpFGzEGAplPv/UhHz6/48XdLY3OuVLi0W22Mk/U4ayb6OpujAZvtpHAyLiW4Aecb5gnj3XCJtldXdF1LeM48fD4KBtUu+Hq+o7zq0ed7ol5Hghx0o7uWfW6EudxIERLE60wVWOiaxrN1KcKkros800Ez0Vq4TRkppAYx4lpioRkaLqGMAdCTMxzoG16YkyYxuGsx7qGMQQiDhzYtsV4hzfSXMo4UzsXjueRp8PAYZhJlBJMGR/vnAIoqY6aMJAjj4czb+8fJaNqV2u1BMBLhKfze+1XLk7HklVcQDyMkYCgcfhdh99vMG1THcuMaEUbJNgpQWPbiGMflDVbNAbL2m28sJOH8xmvwGm5xzHOoJqYIJndohCWSep8zBpXyU9lwy4PIoBl4xqcMzhtEtA2DeNsSMPE6f6JnIywwVDFpZKTAAAgAElEQVQplDFrOaqU7bdtwzxNqjk8VzBrnudqe2JMeC/P6rzjcDxWm+Ctp/UN8zRrkGUZp1hiRHXEUx37xjq2bcuHN3c8PNwzTCP39w+yCUYBw70X9go5M80Tx5NktCU4V6c9CbAbMrV7awFalyy+6tDpXCpgwNqZiGXDXc2VIUj2tSZu8mol6+e887KGrGUYhjrvUmFfpbJVl/n3TQ58CaizdFzuO8wcCeeRtmk5TSM//+pL/uTP/5w/+v1/VKVuFq1oZfudTxwe3rLd7xjHIyFMzONI7CbatiWROI8j4/nE/uoKnCGECXIU/WdraFtP3zbM88QwTswpses3tM4yT9IwMCTYb3taL+WmwzhjjOV6s8GSifPMeZ6EkWFlbNI0MeWEcR5vPb31TKeBKUaytbS+oTOWeZSfTUls1bOrazrx2fj569fC3s3SgNDmoqG57CWXUCBLSeDqh2Y16AXsRP2CGvN/I4hYYQxdExqYNJ45Bg0oct23l+9mlXjJmCxJZm+kXDHmRFDdTWNE1mjOkTlHbdSk/5gSdDt1rhEyubmcTzFOvHu4J8yiAXx795y23wjTjsWOrY9kLNk7krcEWsLdc+Z3B6bzxDxqWVwWCRI7T4Q3iUMyTA9PtLev2bz4gP76Bt/1GOcFp8r5PVDrcvBlHYYVgM7Fs1oF3MteLaOozvH7S8hIQDKPJ8J0gjRjrGPaXPOzj3+XD95+wfb4QNNccZ4Nj6cBkzK27bVEbc1EutwvpFpL9rtpGkhDWD5dQQixMTYmrJOEbAyBGJYS5epvqCaucZa262naDY1vuH/3WoDUOGFUG1/FODBauZVTJIcJT0Pf7YkhgxNb5gw0vmUOAynNhBQxRhJ2zktQa+O4JB6ysrI0wCrsHV/0yLPsJdb7pR6epRyvlKGnGDR49eoPJ6326LFW7YsiKSURd8HA0z3MOAGJDI5cQB7ExJcmNIUZlolYpBmKM+At0sCydYp2yRXHbC/CIFOAGv3XliZ7dX5mKvpf5oF+IWchhhQfMSNB5unhkbb1sn4Q/4aUMU6SUI7EXKrQkAAxkzFdh7c91ljxC/oO13USJGdVGkwJtLotIZUiwzAQQmS/3VObWtbYQEt4jWj6eZbSZFlmun6KPVmto5gSf/X0jr8ajnyZAkdvCRpISuLa0e2v6HbXYCwxBExOTONICiPkiLWQsVjVva4LfRVMx5yIpUTYIPqOZUqmRDJZ2F0KKsEli8xqBZUxYmNiTgQrchVRImfR10Rs/zRNPB0ea1wo1YsynmiT0JATIQWIiK5lSiQtmfVe/GSDk++tGvYatU0pl+8V2YVESgaT5N5LebUkQexl860ajJgqk2d9o3PfkTGEXHyTJPJnVteiKWzcEt8KKaQwvQpAW955cXAqeFC7uS9rYu3/VBB1NYmK72VUv7pIYMh18iIbZFayT1CT2QZLWvn6teeXTpbEIuNVdvTqqitAuaplkM8aK7Ghs+AsOYT3vAB9Y98Inn79WFej/n2PnAuIFbUhObrvU+eAU8LJkkCuTyMJhlq9a7E2Y9BSbrcGJhdaVmFAi+8sYxOC+jRr21auU3vSLLGTAJrL3gvUPzslui1A6zL3F1/IViJIaTZY8IqcMjGtKntTImiCspzLWX2HKgOTcxJfPyVG52oDrjovrcEuxRQsFUSplt4Lu14+L/1UjNoHGQlnLbZtSQpkWn2GMmLOOkxjleSyjLWrshNSOk9T3t7y/wW/EazJ0DYNpJJMXjCqbIrfKYBnKA2pFLS/1LtNVSonK+5ineyZxekMIQrZJ6uWqYPWL4xT2esXyaiYTJVmKaD/OI7LOBtDYwXATNpzI8Sl8sEYS0ODSUszLsNqrRWbkJPaeLE+KYntNiz2I2qT+mJLINdkTSH/LfiMVMz4VfapjKMtRA31H1NM1b7a6kfrXC/Zm/o8kngvcz0p4a72cChv2YodzyirXBvBmqT35m21s7/O7PxmgLEG7AqMlTWdJD+tG6cormQOaeSXp3se4ySds9esxioyBsYswTKrP5WXxAqk01sQI4CpwZpRsLIcX1fOWX+7nG75fFkk8lPdNgw8HZ84nw/kMNE2OzrXcL3Zc7O5Eo04l+sCEH9Dqe4Xk69MhsvrgRjTvJos6/8W97QYVnRRXTCDVt9YC76vZQvee/T6vW8aoQuVN7NyAFbfW28G1bRrNt9U50HGsJYQWwNto5uSfK3oCdZFZ9bjwMqZW7/7xXSu10q+eBIFubNhSJnp6cjTj37Cu6cnPv34Q6bvBF7cXtF6caCc79js9qA6lRWQzTVdXM8r9yMbbOucznt5/yIdAG2/od9sePXlFxyeTvhGGjBd3zznPCTcWbTFzucj0zzRZAm4ozaXSnNE2pA7wqzMCDRrFKIKa1tlN5oqtZCRbNF5EF2YyuixDmNiBbvbrsc5KSloVSsvzgnfbTFNwnedlF1htURQM2w5cR5nng5nzsNE23X1jRSHhQylyU7JiA3TwLuHJ47n4cJ5KBtJihGSQeipq/l1OTGXuWBMfUfGGLIF03jcpqW92kHfkd3ChMlIiVkFctWmWCtZUFccGd34c4pVYD3FRJgD3kkXyeIwDI+jNuyTmytOgcx5qqMAUMTSYxQAO6bIOI28fvOKfbuj6zY0XY8FQp4ZTgPHxyPjeaJpOw0WjGq2pVrSbbWUQrKzkkV0fsn6kmHTb5mRBm/eN9XBkWGwNStf9A/r5q7PVQNxhGHlrLgQXeNpnOVpnnjz5q18x0i8UexVDpFpHJmHqcR2FOBmLSRfSl2994tsSLE9OUvDoyzBUinvKq8RBSPW82Scp5pxf99OlDuwRlgOzlm+fpSxMPxa536dCDPg2gbb9+RukPUSI28eH/nTH/6Q73zyEd++vcM2HQ7JnoMyeqaRx3evuPvwY7rNhhBmhvNBmrf1HS0d0xw4H4/01zds+p6x3TCMB0LKtN7TNQ2NgdMwMkdhSFxvNuQ4M0wTIWWc9+y7lhhnpjkwzoG+69l1DeM4cp5m5pTZNl6SVWSmORC9ozHixLioMhSNx7uG1jeYGBjGkWAMxjds2paNtdzt9xxubtg6h288hxiZUhTnOkWW5biyr2LStCO2gO2pzsEy7OrslXlw4U6/D1m+/2ahsAuMs9K8Qeff4k8U5FDgPqNgATnjlBE5pYnjfOIUT0x5ZCYQcmSq7M9lXwAq0waozub6GM9njvfvMMbz7NkH7PbXou+a9X7K3ZuyR+vPnCc3nkAiXt0Q754Rx8A8zJhJGrm5EgyPI9OrV4wPT5g3r9kdn7j55Fv01ze4zValCwymaTHGczn1f31ALFJBoq136cusV+B7D50lUAnjQA4TJNE7xRh+8fw7tNnSuZ7teCbNCXs44fJEv+2ZZ2F6ro+SYLamlOYbQpwYR5H12e92FEaZ9VYBF20OWOSLCmtxtdcv+40kh6zztG1P0/aE8JIYJkolTcqhjlsFYyl2rKFpHSFQm3iIplxLnBtSmkUioOtp/E58wxSAQQP9XOdSCGPtguyUscTKP2t8o9q6sVZwWGMJyN9jjHR9V/esImngG6kOssEzjwNSCq5NwYqt1Ei6JPatavfblQ9egiuNhcWHzAWIWv7bWLDeYFbJiQOG8DUfINfEV30v1fcsAfLCGqsbDgugWMAAA0yHE8Y7BfQym92OmBOTdaBNN+cYcFqqHlWfzvgG1zRY7xmnidY5VS9coVMpScObGMjWM84TwzzpWLmVrh00viQg31thNc5cgBR1sC8sXMiZHz7c84swcXAwO7EzpjCTvWd7c0vbbwhmqcQzpmiYakBqHEkZsoUptKKHEGPWcl25DVLCWU/OkVwK0zwCqhlp7iWx9jJHxKfUUbKW3DZEJ2CsEB0Q9M/CGEbuD4+SwNPkRgFiY4qELE10I1EIAClVhq2MmrBjrdoxYxfwSz4gTceEKRsLGRlYgbHFvyxzXwkjMm6F2bYk763qIxprFeiNalOi3l8R7S97WQG/9D2bIvWlKz2veJCr2LQkKkviYw1wsvqsnkKBI6Mxg8julB0zr4ATdC+tjLxlEi4xZ4kpC6O3WCVtWlbmLmXNVVxXEj5Fe9wYSzZaSWQtxjsYw+W1/o4g7Pqzfxujdi1p9P5nUhJGYfGxCzBnncVZ0e8UZnIm51BBz5KALJJ9sscoSKiMv7ZtK7lJxhztqbCw9MBUwsb6vkqzLVcrWPR+l5dTQarM4n+LPx3qO46xNHBa7qOgDwUCXsgORuWWjI6NyAdEo3ZwFZuLbV0aQa3l/2RPcbVZVGVDAlXWMsvYS4WAzCuphBK/qwD8qcwfWADYYjgztTlzsfEiIdFWSYUKpOck1RZW4iezWk8ZsQcpZ4l9rZPSfmXr1hJ6s6oGNY5GE0wFRyos1TLnhAQkTFhrxPe0JRZGmkaNk8g0oHOvcZIEEjA0ERVcr4lwo3IfZJVnEJnF2gtEjbWMW9K5LXJ21jqN7dOit29MrWgsLOdCJCpSK+VcRUIUY5RWvwKsC2PZKeisjPhljS6EwkWGUxuo18Yx6usYiZ2rzVRMwdmlcVo5ly2gP5JIm22osaPRsbLe1/uWhP5ic4SA5bVo6tfbnt8QMNaI1oKBOc3kHHE6oQESEeMNhzDyRXzkz4e3PNlEMtpNkEzBJgXFXkoU6/8bdKFBRej1dzFnyaB5X7MEhYWlb6s6K9U555JBWoCgctYLJ89qlivDbC1vTmdePz7xeDzx0cff4unpzFW3525zjc+WgLJddJIUQ1OZDAaMETp57QRthOErn7S1lGTtZhlTTms0wxUX0O39iWJMLRUABCSHZWLmkk9bg7Ml207d8OumrwbLrDXCVmN2ucWtPrMCZ8tf86rU1CnL0l/1+G1HniPHh0fyOGOSbuy5rHIWQHl17UXrZf00qwAqL89gsArwWYYc+fHnr/n5l6/5Tz/8EX/0h/+I3/3+Zzx/ccfVzXO2+1sJRsWLArIC3yugSq8rWJg8a7vZ0nQd7bxlHM6E4GnalqZxPEvS7Oj1m3echgPb/Zb/6r/8p/zql7/k5Vdf8er1W45DxDUCKDkym03LdtuqAyxZ/tMwEhPMIdN4C/Oswb2TBgpYYcLou8w5M4WozMJMcz4zTRPOWa6vr/jw+R2bNuOdoe0axmjIrmV/fSvsGiCFiPOF6SHB9uE88fB05v7xzDwHuk0rQZURXZeYSiZqcRlCNtwfBn7x1RsS4NVZvZhI5v1gRGfrxXo29TopKdcli97PbBJu0+GvtuRtL+J1K4MOLML3OqdSztp5flapB0fXtQA8PT2w2Ww4no6kEEUCwDVs2o7NZkPf9zydDljvRF4jpprIKRv/sv7k2tvtlnEaGOaZ43Di+PnP+NkPf8i27dlf33B994ybm1u8c7x++5rX716D8Rhlv7ZNI3o8QXSEYoyM48g4Spmscx7n0Xkj99y3G26v73gbAyEEaVZlDJvNpgJaIQZCkJKfFDJTmLg8FrtcROofTgemX/2c43ha5GYMCxu42A9T2DPqgGUgqABCzpyPR21yYSortny/dn0vU8SUALyMsZS5ga/jvHZS1rZisVsloBHNoqBB95pVcDEpL8JjcxHkrH5KAcpNY2AD/vaah6/e4mOkwfA0zfxPf/zv+B//h/+ebz17Tk6ZbWsF8MyiK8Y8cDo8sd3f0PY7Xn7+M8bjUTu9d1xf3/L27RvefvFLNvtrXnzwIV++nHHe4UyGGHgaA0OI7Dcbtm2Dy5k3T0dwnk3XcbPbMI1nHo8D2Rg2fcfdvuf+cOQ4TIwhs99s6J1jmmemGAkGXDb4nMnjyMPhifZqy9VmhyMTxoF34wBdx6bfsO1a8jzx9t07zgqk/uDuObubPT9684avjieOCjDY1Y5UhPaNkfXSty1t4zmcz5yniQLovN+4qTQFWu9s69e0wFOrvRXZ33PK2BCwKamO3/ItYxI2w6bx+CRBiTeexnga63ga3nFORw7TO47ziSMnbuxOGMM6J3TSYq0XBiICLjeYGsyW+fnyiy/ZOMfVzRXXd7fSLKmUHdW9Ltc9Xr4nH4nGkE3DtNvTfu8zNvtbRr/h9MsfY5i0zNsSHgbsPAkTfRo4no4cX37F1Ycv2D67xfcb+qvnWLPDmiyAZnFEdDANmc1uT9OegaGuu+JfWeeZY2GG5rqu1h2e1+8mp8Q8nzE5QNZyYSzGNfzko894t73lD376F2yvP+KFbbmy8PH+Ctf0tP1+eecWxkHK2WwrgcY8J2W5GtpGq0oQFmTbeU1yWQkkU2AajUpeaXmykwaI4r9IhVIp1y2lj23XMOVJtCENKrW0aPxVMMJIafXh8EQylme7Z+z2ezabK4zxuGYjwQAdm90t0BFjIMxnMAPWhhpQkGfm4cQ8isasbxpy02LwWCwpGVI0Ul6rZaZNIyCiT44cG2KQ+Sj6hEESXdbhfUvODdY2zFNYmHq4RVswJVKMzCFVX8ioXy97u+yxTv/s1Kc2WQEYPY83mecx0DinsmSyRn+ZZoaVpEVCFZYFVZOGVDq+xffPJkEuweMKeLIiKSTiP5am7djvrxlPhvNbqdQhJQ6v3pKBk/sVxgs7NibRd5fkt2hMTxmyVia1bcNkDOHxgDegndWI88h8PjI8PdI9u8NYaNuGzWZXAf1aKmkaATx07KwtLPJMLnCLUT961Y2+HDFn/vL4xOPGiU6sKfYtk4yn6fc8/+RT8J2Wkhqct7x48TFxHkhhIkXZ80NM1Z+JObDf7+VcKTLGQN+76ovHsDTSK7HNPAWwlmgsZo5SnbOyVR5Db2HTtmx3O/bP7wgbQ2ssZGmeknKm2WyZXxreHZ84TGeCmUTX2RXGsMgLZSN+c55zLUkt9ialIGtX50FHV21VsT65aNDrYTU561T6q/rU6jPO81zfW6qxje5HRuZZUtDTtYbOSpOvrI2B4zxW6RNDmZcLqOFsXjRRMKrHaxYAXP1XjW4l+V1lDPSs9f1XywhG7KEpchcrFuGleS8xvI5HeXGrw1D8wLKjqm9XJApMkcwryfQCvJRmajKnI0p8cC00LcY3wFTH++97/G2M2G8Ca7/5g+KDdm0LRsDXixLRi/OpH+Msm02HM0KSkfkpMi+iJwbzNFOaBxX/4P17dt7V5E9OS98Eaz2NbxS8E4CuFgKsbElJ2JU/p5Tke7pmU1qA0kK5SKkw3nUeFjnZOhxZf2go5I2qOfu3jHdtApYjh2HUuSln7vruIr4HCOdQsYoSN7hq51EJggU81I/VeNO5SwA0Jm00pecv8nRlvq6bo2W9XqaA1ZrytiLXWPEoxAwX4Llcy1orCTAKiFhYrPK+nbM0jWpQKyiuugdSmdv0dF0vDNZZAO+kbGNrLX2/wRhtNB4CMWi1o8ZJxsC230r8hBL4FBD2rqmEwNJ8WpIiVu2dq8zTaZ4lyauJLu89BXg2xmByJkwqu5KFFJkyxDBXPzDHJSlmDIIPssRuMcbVfa+qqeq+t8QH1lqCWqbK4EYSdMseWshUy7pyXp4pWU8NPrP0NChGr2saQlu0cXWsi1+eM7/OpPxGgLHnFPiTx6+ImgkIIVxEP8IMS7w+PfLyfOCrGJj9gqamlPGNh9ZLN1Kr8QarwMnIeYwRTdlc2FKaSShBzkWGC+oLR520i0oKcs2YyEdW4KIpxvwSsMUYznHi9bvXfPnlL/jWp9/DN7Ddtmy3G3F8gzLCnME1l9mf+swxLn9hHfSBRlwFP6ybY1SgeQlWl8l3CVLoRFRDVZ+tXm29gZQ9XcswdK8on3XqxBanMut1a7leATnemxOmXke1atWg2uKEszgcicRsMqYRJtm2v4MxEE8D4TQQp0DRWytv75s20PdLUqzVYAEpLUk1b7hwFqKT0X59ivwv/+ef8xc/+ZLf/uwz/uD3/jG//dt3UmbFEliKOPhSFraeI+WOYgZjHK41bL1jDhNxlhLgbrfnW9//Lld3dzw+PPL69WsOT0c+++6nfOujZ/zoRz/m7eOZELIKVTtinHh2dyUJhBjY7fc0vuHdu3fcPz5yiEl0e+LShXO72+IaW+9PHPIl4/nu8YnddifgakqMpyPTaeL582c0XU/MUuIQa9ZPny1KRt/YCMbx5ct33B/OzMbQNCrcbiUD2xRh8PqyxfF6PJx59eYdL1++kXmcRVvpchFokKXzKFdDaOvMytpp01m3zAcDc5zZPLvBX29h0xHNws60GsTknKsQfkqZOUkTl5rsIQsgmRYn43B4YrfZ0u22woSbZh7PJ07TRD8MGHVKCkAMtdJS56OtczTnzOFwkHfkSnl6YDw9MZ4PvL1/RfpZovWt6LRag+86PvjWxwzzxBxmAVCS6BOVdZlS4nd+8Lv86otfMYyD6J/FQI6J3X7H7c0d2+2Op6dHyANE0RCeT2OdwAZD33V0m54QZs7DUB0cawyta9j2Gx6P0hBuDjNz8DwNAzkbXNNKEBJjZWcZDFe7PY+HJ3GIrGW323Eex5odRoEAs2L6z+rkFcbYmsVQ7qfMj8Y3fPzxx3z58pU6F6nau/fqAdReSILFO8duuyPos3jb1iZh5XP5AvDKq3V/6YzXe7NWmqqZQAACPeHYw3EgByknNtbzb//d/84f/M4P+Gf/5Pew0dTMOOpAnI9PtP2Wzf6KT37rH/L5j/9fhvNIl6Df7bm6umIcBuL5SHSWDz74iDcvvyTME8IEcnx4ew0pEuaJh/NA41uudz3eGsbTmXfnszSL6Bo23nI4HHk4Dvi25W7XQTY8nk7SYdc7tk2Hi4FpnkhkXOvZtR3xdGKIgSkF6Dbcbre4nAiHA4/DwGwtV9stL25u+cGHH/Cv/s2/JuTMTsH3hxDIRRsrFec6y5qPidPxyMEmMMLIlkZMwtz82n5QJuz678WsfMNcKIwUcoQQaI2VBgvlvBkKS8M6TzLCis/ecAonXOsZQuQQ7vnF4yum8xkTEx+1ojXKel/NYgsb3+KNE1ZSQsus5N6MMVw/f05vpInSMJ5xTY/TRGLZt01ZCKtHDCEwGVkbs3WkzZbmw45n+1tCY7j/xV8Sj/e4ecZG0b60CUxOuDwRwwPjcGD+ypEbB80Ov7ui3e3pr2/pb28lQNR52u32wihf+SCiidqKpptzuPT+C1mC14tXlEXjkVQCgIi1nu3ujt3NB2At4fYT/uPNR/zh//O/kZ0nkRhDZNNvWAnTYjCEeZbgIkstSYwQtYGacx5y0rXq2W53nE7H6njnLLWB/Wa/AN8xaJCwgCDWtoj0y5nhPLHfbcmblhSDNAQiVPtlda+KWbsSa+WI86LdyjxyDrOAqNaJPbAN8zgzDQdkL5e9K+qeEaKwXZknPAFMwsSZFEYSDdMUOZ9HWt/iG9EEjWSydar1KHO/lN/OYRZt7RRJ0UuFhup/9v2OFKfKeHEqkyRsq4RJZe0qCGPXVQ8yrhLwJlaVzxVshIQzGWdKOl2OA1J5Xo7KXGIhbxgFiY02NBOQokiBCI+y6H8aZ8jWkIIkLduto9n1hHdeGooYuN1shBWj1yhVMd4vDcJOwxk/T8J+zoH8NEilUoo0zQZnDY0yS5MxDOMJO29wXoCnYTjRbxuyltxKxZIG+UlY+cloR+sUKgvLvle9sa4gy8DkpIGWiAwYSdCQ8Vd7dh9+zP6jT5lo6I2Tfh7qQxjTEMxZCC5pxjiL90IKmINhjnP1IRdgJWm1kBAosgIjtUmQdVjnMWbF+jPlXcHWGbaNZ9t17DY9uztP54tdspyfThxOA4/zkafxzBADKURstthQJFBUZs1a+q6tmp7UvZSvHZKYWI9fqvbeGNHElAC+dLnPhHGqMUXx8b5+LFU05dxGy7OTtwRrJH5NiagAg/hImawgWFagJGliGE06oH6VtQvIkFNSaQX1P8xq30KnhVXN9YJqqWxdLUYu8bP6UrJCl8i0gIWVNVX0Idf742oOrsc7Z0khOOsWbVAgYyXhUkFbWRMRS7KeVJjH9Rt/87Em5Pxdjr8ruCsShQUA1dLonEQ6yCy6o8YYmsZV3MBY2YejicpIt2AjBvVvkP1IaAjKpF5dp7LymrY+k0GlE+v6yeRsmMOEiYUJq7axkLxylmQiIlE0mcLwXsDRwuyt9172RhkpSm+dqNcVoE7mt+iyekqTrDpuq/ewBlcXnCKz6UUarwAC5XPl3xijNN1Te2IQe2hY1nTTNDgEZI1BNepZMJAC6hUgVuLjBfCtTFhMHY8KTqosYdN6nDYqzDkxjzNpVukpK+zLrpFK1nKOshYLkEiGTd9XmzFOo2jClvtQ33rBiL4+F0D2VGG7hqWcXj9TANQUY9VnLYzY9ZwvaZecRB6ta1qcEawop2oUwMo+s+03RK9MYG00X3qalPO3bUtS7dXKdG98fVcitSCg8awxctd10ohL5fkkKbAQK4y19V5TFqnGFMRfc7qfFIC7fKdI1FUAtsSM+i7BqpyfaNKSIzFqHwCgJJBqYleTLmXf+nVW4zcCjB1S4i/OD8xZNNJCjFWMV7LjUnY6homBSHIl26sgkZZ9OecwbtE4uTgk8lYtHjVlujCzfOECkLFlYzDVjV4BhOuTclHKD+8Di7oVrEDHOUXO08BpOGGtaIv12w37qyv6dsNxPAvwl1G9o5UjqTdTMqflZ7neYbmkflCjrQV+kHKJcZr1ed9zNMwCXunAULbUpfDhPfhXHVTnrJaVFfCxjIQ6gIXVtiCROsblPJcb4iW4rWUCWErTlWWgCzVf/+YtznU0XUPebRifTkzHgXXn3ksm8/Kz9UCsM9ziHenSzoCp+SpxLLPhNEc+f3PPMP+Edw8n3r195AeffcbNzZ6u6yiNMfLqvuvkWs8sfbcWA9ZJoxYs2ZYytYb97TM2+2s2V9c8vXuLcSJmfXt3wzDN2gkzg43QtpiUcBbpvp4CvXd89PyK26uOd48nhjEw5USImSkE/DTReDGYOQkjMWeRLJjnCBa2mw2tgrHzODFPoerYjMPENGKsR8QAACAASURBVEfR9rEFAM3VCQRDmKVJS86o0LYY6cZ7/Ko0vr4XAyFlXr1+y7v7x/q7ooe1RGbUeVzW+LJJixNgdKMRgLNooWknxb6hvdlhNi3JWUyOWlYsN1Fcxs12Q07SiEuapVA3tqZpGVV3tcyqlCVL6Kxjt+2FRZsCU5oZ4ySArl6hzjOWRxI8Z5kzGbi5vuH+6UmcNmfFxpVrZhjPJ5xvcNsNvm+Y46ygUSKkRBw0Y4o4x846ng4PTNNZujuThdlsDcM0cP/4jsenR1IM4sh4RxjOkKXpmDD1REsoTqtGShrYSKmTJCT6theh+pyIUMtOYtQO8W4JCnLOAg4XJo6CE2TNFJfkDqqlZbRxiTbiWNuUmErQtJT0SCMkeHv/oHNyYfkvlr84OFXdqJ5jXV5YSpvWtmRtYxa7Yy5+tz5SSrX5GAZoPO3NlZS9nUdSiOQcacPEUVlfLkVcCFWb1VpDjoHz4ZEMbG9esL99wfnxLdM4gTmx2+0xKTPHyHB4YnP3jN3umnE8M88jzhniLF1MY0r4xnPTbyBHhjFy1gYyfddgyJzHieMU2G16sR8mcxhnsspqFJB9miaikYC09S3n45lAAmdxbcfOexgnxiQyBLZpuO17nLHkKDq0f/D7v8/L+3e8Pp54OQ7cT6PoiWcNxMtY58yixmYuA01dWLbuke8tvPeOyoSu+5Ke06rzZywEddpj1JJwKFryVtmwmcRhPvLzp1/x73/6H3gzPzIykdDmiCbibSabTMiplL1QQHbnpDGEtQajjmrXSKBefIXN7oomRgWvpFmdNQ3rjPLKa/ja4b2HeRJ8t7HYbcez739G0zuOL7/k9Oor5odHsTdZQD6IkEVnkVmYWNlNzIcDU9NybL/CdRts42n6DZv9nnhzR7vbk65y1VzrmoZRWfxo0FLGvXK2zGXQXv+oAA7W0TQ9bb9je/Mhxm/kC7bD3Hp+8tnvcfeTP6WZA/ebF7Q5LElSDE3TsdlmddyXILD8W+7Da3lgjHG5T3XArXF0/TXSuCoQ0oBJM8fDgRACfb9jf9VJsJ1LSahortOW6xVdTU2Ip4Rfl34qi9tU3yoR4oi1BcD1GDMwj6da1iwBXmHhaRKBJOF9Ep5ICdpyyjQuQj6TQ5QEa84kg4A9xfLqXpziTJhmhtMZ6z1Xt3f4thWf0Ris7zAquWNMUtBN7Kr3TkrDoyXFReLDqI+UUsK5UqYuz5YpzE+VByHxWy+uuWqPSOuu5a1dHIuBR8oUG5xrsNbjvBdCobLvsjVYDI2F5DLZZrKV/TYj8k3jHBiixC8YsCmxLw1RsuomOk02WtFE3DQ9jYLhZR2luJ7jBq8glnEW17aIFyxlywJoxqrdaSvjTktNc2GTlYBQGW+kCuqsBmT5k9HUe3W9MjjP7voZNy8+xrUb7FxkLpTkgsE2UtlETpxOsyY0ZY+OYWZmqrGJyB6pfU6RMM1VCqjuuVmYuSkaARrTAnjaLP6sNdokLEZSDrQ95DQK+9k33D9+RTANYxo4xQHfeFzXSE8AK/edyMQka8xkQ9u01W9cfPMyz5Sh/R5gtKwBQ2k+BFD6NuQs4ERhlJWnLIy4XCURZPxSDGSTlnOj/mXTSIVBTPg2SmIkqUSfX0AXuS8BHSTWUCKSc2qr1YOxIq+AQQBq6ysAmsuVjRHfPVMZcOJMr6fNEpCm1Xwq8yhrrF4qn7KCQfI/I/fPsiazPkcta69zTedniYHLnDGq3ACyXp0X7dj46yCQv9/xt8eN65/LVE0pE6egcnBL1Z81Zb3KOcS2rQhDqTD6JG7P2nzKWasVFlTACOQ9XeiuG1QyQyphrLELYEaGvHyXop5HibWNnp+699X1YI0kzIzRRlyu/q7gJpVRmlfe82rcaizMQs56Hzi8gDQUECsNo0QuoKt2DV0/FLwjg8igga2APCXIWE3ZInEnvS7Wur2mrg+5J4/0BEnakJAsv3Oa9Cw33TSSkItpYbCaKk8mCdVo5wWztLbKflhjaUxTnzXlpR+JsJeN+iYNyS2gbRnTtdRCXskMFNvhKmM0V5mI4lMaxW7KGhRGqu4lWWySyOMtOuCx4D0FPE4C7hb5GRNKqLUsanm9y55E6R9ioMrK6PwsCgNFrhBvNLklDbE0etMGZYZo1Z/QeKPIGRhr2O62TOMogC1GfZ4VcJq5SAjkrJrlZRvMQhKYppkYs+6fpUpcNWXjJIQqa0WKxHtsqWIvdvpvOH4jwNhA4otwVjA2EVIkxLlS5G0umRp9YUZDpxpgA7aAsaWsA9BMTAEwqg6LvvW1Cc36eTnfJXiayzWqWUEn1deNcHmpy3dAxZLEcVaHcponhmnAqoh81zZsN1v6Zkc+vyMbcfguT17vtPxF7tHUB6gGpH6m3AsKuiptWMa2bARUY1jMVCoSBXUslsW07L9fu9rqz+U+c8E9NA7Oq8+svrE2mMs3v/b4Xx9xdczKXCg/8w7XeEwrGZnpPKrDoudav+O/a5bTLIzW99+DugkcholxesPD45FplG6P3/rkY148f8Z+v8M5r+FVcULKP3BxG3ntUFlpxqRJCeNamkaYRN1mR4qzTrHMzd0zxilg0kSM0mzM+o6+Fc1GkW2M2BzY9C27jQBjj8eRZrJLlhNlX+cCqCXmkBjnwDjNeC8NnXbdhq5vOMaZEMQplmZQk8zGauiWEoPCsh6HiRiX5zOql1PKDcomDagOcmacZ97cP/B0OAmoWrUSDXWJvvd+ytpdNvmimSyOcVAH32iTkuZqi9t2JC+Zai8elS6kvLyoXITP1dG2VG2ftmkVTFu/VNHwDVWvNBJzVJBbdJiEQSRz0uTLb68DgjL1nJYqG2NxjaXpe3zKmCSb7RATbdfT7Xb4bU8IsdrC9TMs6zrx8HjPNI/yXOVerNUOnxKct76hcc0SrBlL20gn12meRZrgwjE0CspL4445BDZtT6Pl62fVvkUBTVKqZSLFoZs0gSROrGRwC9hWtLWKQ1McdouR8uz1kReGRwk0MIaYMofDUce3BF7KYl3pDxrdfzIC6pf3V0plUzX+3+y0r9nNl4epa6Nk4gurxRhDs+0J01w7g5Ijo7W8PR75/NVrvvfhh7Qm1nNZMliYhxPGOvr9LVe3z4njwHg+MI5nNrs9Xb8hDWfRgR0H+n5TpgbGBG3mJnOgbxu8s5yGiWkOJGPYdC3WZOY5cp5mcI6tgrNzED2+0k02Z4RBnFJlDZGNfK+xNOrs+ZSZ48wMRGfp+45d1zNNI+M8EWLiB9/7PtvNBvvyJW++OtFaR1QHTgK5sv+t3l0pFVOmWnnXqwfm73pIAqAELSuHNkRiaeKl87NugRkMogl5jgPD+Q3jGJhMkkaHRiQcylZfmiPJl5cA3lqjchICxloSV7sNc+MpoiBN0+HNkrCqVR5ffxJ5Br1JaUxhcd7V32eTyc6wefYM6wy+3YBtOaXPSacTJkbtJaNJnSR5QJczaR6Z80DAEI0Vfd/G02/3cPOM+DQQrq+Z2cKuByAenwg0GOexjatrY2VwFPRYrSG141afnW5H0/Z0m2ua7TXVzzYO1znefvx99r/6KXM6c/RX5PR2mQsGjHO0XYc0uTCKXZb3qfuAQcqdrSGmRdtVgk2LMx7reqQoPpC8g3gmcWIKAcbEzd0GjLt4FK/abtJMU3U4FdjKKWlAlNWW6IsrG2CGnLRxR1BgwpaqpdKgQ61iDbydmiynQasjm1D11kwnGqeGSI5BJEAKG9YWu6WNfKzDMDOPM/k8sdlstdLKg5HO4sLGC+S47JFGg/tMVlanVSfovZ4GOUP9nayJpB3vSxXCt188ZzsFCAt78XLtXv5dErPKJlZWqAiXmjpGcn8GbxPBaCUGWevQMiEJwBAR//k4DHRtV+28007UQQNIax2ub8hhEqZjzBq4U/2mhdGUwRq8a5hzEL32BJlJ97yl10C5Xiogp0pTVT1Jsr5Xs1pX3zxApXTc/H/Uvcmvbctx5vfLzNXtvU9zm9fx8T3SLIkSq1SuMgHZ1RieeGDABRvw2EP/fR56YHjggQXbVQUZkiyJYqlESiQfX3u7c87u1lqZGR5EZK61z70kZRgGWPvh3nfP2d1a2UXEF198IULTbxiubxiubtS0lzWpgvZqD53aYR86nGt1zedkW1MTu2XdSjaWHuZfZU06laR58fhVRiMjhcG9mr+iAx6aQGiD+XAwn60pUAOHwx1srjnnmZNMhK6hbRq8kQ2cKOu32HgnWr1DXXPJgCOpAFsw8sDj+NBZnFfuV4+JXIkDusaW2LMmkUVUZ7bIqkgm5bmec1rBo3sMH6rfEqSzsvKIZGfV74vFU7NhEaDzCsQ+sgEi5iVZIh/vIUuN4Ty+MgpLXI359oXJp36b7ZOatyrfaz9WMpQCFcXfWy4ESqlyOV6rwatxrK5JzCfL5fyyv8XrttXvchWk/U0x3t+HEfuYrbmM36//bF3rasuzdzTOV/LJkmTMKC7mcD7jrfnP4vMXgpQx92qVnK/7Rf0Zufhe7fSubETnvCXSKsxoMiaL3E/5TOpngvdlHl31471fzmxtHIUBX/4yvgA7ayy6yKZ1WlwuY3fbh12sy+Usk2Wd1d8XoAu1OyyxRmUyFv+Msg+WWL28bpGAsxgqlCW5is9lKVsPIZBi0QDOdW+u/cAQ9H5DXpIZ5Vr0rGpIwV/IXC7vDbVSs5DaVC5lAX2ds0ZasujG2pVaTFtIRuECKNVkh1/No7NWsssay8Xk6XSoDjGLDE6QJUY197pqEpfx9GV96iCT5gRuxSZ2y9oQtNJI53EZ8zprYolD72tVt1YH2felhBiJyuHqeiigdJF/0irzBo/2CUlZ0AZiLONlY1wTlqJs/NKPBjTBWsazxJlFm16PTWd64yYI5PxKBew/AGZsdnD0uikTaNkgHrzpQcypUp+dg7bxpuvmai2Saz1N3+LajuRAsGYeHoPbl0fNJLAyouXJshKXF1+8z5UVyKqkfQXieu8hFw2XIgjs6n/6bcqQO5yO6upIpnWBbTOw666RHEgu6oTmYuxKEGLIRIk41ROt37/+f7lHe6MOlXdo4yZ9TTbHvFLQS8lHcfyLc18WUgGISrTIYuwWSa5LALc01oFF/7IctMVhKaBD+dQCEC2fqH/VcjW4aK6wnrIsaMBg+i1paGp5zBoI8e9YF+uxK2Xhj0ubl4G1e9A362ucYxbhzfnIn/z1X/GzL37Bdz/+mO9/7x/wwx/+U54/e6brRDCx/wX0eTxphV28MEO1xHXYXhnLJjNst3zyne/y6puvmcaR5x9+wtXNM3qfOJ8fePPmFd57brY9jbEEH/Z7pjlyPqu+3dXQ0ncNMW4Yx8jdfmTOqTKuYtSGFOeYOI2R8zTTOBiPn8G33uej95+wvWoJrXZHPU8Toetp+6GyYhUAy6pm7Bwxwd3+pBI3Pij7A+jaYFIUl6xYsTV4vz/x5s2e02nU+XvsQ9WxWtbo43kVhKEfcF4lCaoh7Dva3Ybh2S2p8Sa/oyUk8zzpwSpCNu7Zm7v7yh7QcpVAG9TRb9u2ssTX68mHQBY4nU6qN2SlEupUaTMftZuXmeQ6CKydFLi/uyfGpM0A+pbmmcfFhMyJNCda37B9/oyr6yvatuXN3R2hCzR2nUPTcffwAAFSjkzTyP3DfV2Gyz4RitZkaDxzmpiPIyJ2NDvTELTuk2ud2MIEAB3v8zTSuMCz6xsk9Zzcmf3DqHpCBrQiS8Mw7yzZIstJKkk47PdkWZocloxpiqWpBRdArKycucIfogRUK9Z8bQB2YTrNObUzPqdYD6WYM7F0HV0Ox/r/tTP39pxeLt0CMJXzsJw9Hoc0nv5mxwxEy/DuU+SvfvYLvvnmNf/9f/evaHMs0AYi0DUdSGY+H3j11ed89On3SNOEAMf9K/YPd9w+fY4Lgfhwx/nNG27e/xZtu2FOMJ7uicYUGrqGXd/y+u4Nx/NMCIHb6y29h/vDifMcic7zwdMdEmcOp4nTFAndwGbTcz5PnMeR8zTRbwaGrsUJjKczU+PYdS1DCLQ5MZ4mxsbh+55+6Hmy28GceJhmTjFxdXXFVTfg3/uAwzgx/vRveW93zXFWlvCEgtk+67xpwnKxN2U/KfltxYp9ZO/Xj18bgNkZLhiIbDIgTtANYsF5dcyyI4dMYuJ1vKNtOjaupycwx8ycGnzMuOBIccZaIi3sIBHa0BLwhCxsGvjww+ectgP71TU1QfUpvW/I4lfg82KfbWgqaNs02rxpDQZi5cSTczRPnnK7u2b7wbd4eX3Lm7/5a+J+j48zHYHQqJ5qE9TOzdNEykLIup/zPON8IB8j0/3MyEv2VxuO/hP46FNA+PqvfsSdCzTbLZvbKxrfaHI1NArqGeNA5gVsk3mE+YyXzG5zRW4aQrclDFtwHVG06Z+etw2b3XP8cEM+J2KcWCdcEIyh71ZnsdTuxMtZvOhBiunBFyarOuOBlD3BdzTthq6/QmSi6a85no68fn1POzyhaXucW/TmCoPFOaca7hLrXIHplRdGUdAAJReGkAiSJ87HB1KMpBQJzcDm+sq0Sh05z8TpTM4TJVGqOnZmG9qBGKelqQaqe6j6pTPzPJLTXH0oEVH903FWuaHmzPEQOd7dMY8zvu1URz10NP1QZRFinuxcLsGqAil4j4j6E6URWPUZMbanOC3n7zq9B7O1UQLvvf8J3cs97O9518MVFI0C2lgHcAsiS4k8FW6jtDwliMdLJkpiFgHxNGhjl34YYIRpmjgcDuyGjYGg0HXQNHAazzjUJg7DlnGcmMaJOCf6vqdtAn2nTV4QiDkyGcOp7zy+CfQGJOaYFZh1RRcSUpopCfCYZ07zmeCKPm+2Du7twux5R4hYjjcNkBUU2D15Qn+1wwXP8fCggH9hUqclSVwAomFzRUwzMU3EOEPjVLopJSSpzEStTBJlIdVKRwpLXIFWiZk4zSv2m0muBZ2z3c01N8+e0V9dmdSdsdK8NYxsI8c0c8wRQmcggDHtZKmccG7VXLbKHxVxK7XJzquvUxKmFNDVBq6wkcERrEluIRh0rfZCyUZaKOeKc6ZJa2tbJC1AkXML6FjBeQM2ug4vGWJpHCk1QVwOjNr928a1xok4S1gDrjS0sXtxK16sbyml5gqmLNvCiVSmpIbkftWUr/5F1TOvYLsx3FZMZw3wjMwkZcxlMVDLq8pCK0Nf/X3vnJUL66StKyt1en61TX/X8+96bv2Zfz8ij+ECBra1TUMTDExF6vovfVxIVPmCGqOuYvuSqCnAV/FhH1//eo0V+45TW+EM9NNmywWQXVcVFzuSECnMW6nvX1eiZgN9HQJe5fGWBtDLeVCSZSlqgvkCrzC/N7vV+kBZhyWGqlUxAi67ypKtz6VShbTE+ov0xuJ/l89ZA7xlX7gVkLweyxKLain/InemTZYXeQ7nlMEqRtCRMmd2rhSb7gxM1XkyVnqx+ZT7t3jTL2BsXVFezxTycj9LpahbwGOLZYpEgPehgrqF4VrlYpQZVQHfMibJGpJmY88XwNh7TdjP86xklCIpiGoVex9wTpiIzPOo8oROK7dKhayIxp0pzfV7CyHLGfHpokpwhfckkzwAR9s2F3rdwTTZy+xmBHcS9X+cNg7OKEhbFqo2QQsgvoKxa5zKOccw9IQmUMyQN6xRbG/03tPOfSWS6Speqqp+XdLntwKMBS2PdSJ4UTZW9t5KDlT+uAgHL1q4ywHumobNk1va7UY7b+aISNGRWX1JObQe4a2wjonf1gdcNnym2Iby3eUHt3pd7f7Kom+0gEOq3/gQR77Z3/Py/o5xmvAeNn3P1WZrm9ijHA9d9Ek9xNVVlXz86h7k7cleYaJqmClMuMLtkvq56/c7M2oFy1dWU6pC7Tr+jlqw6yygg0UIXN5l3PzFd6hhX2QHyqv9eiztMNXni3FfWEnl5ipo6nQWkwiSMvN5Yp7jRUOv9QZbj9k6+3bRhX0NHq/HvOIuChB5k2oomZEXpyNvfvITfvyzn/Ov/+xP+Zf/7J/xg+9/n4/ef5+ubXClKVa5h7cc45VhE9AGTGjzFjvAs0C7vUXCCN7TbVs+fH7LdgggE7/8/CfE07124xW48hum0bHfn3m4P/Dm7o6dgXUhNNzeXvPZL3/Jzc0NV8M14Pnbn30GriHgGZqW3dDz/HbH7c1A03jaYcvmuldj6j1t1y7NEcSCRzMEURxTyrw+jcxZ50ozWO4tQ1jHHogp8fNffMXhdK5MvTpKBmRdYGGy/NtWuK4nB3Ocq+4bCO1uQ2N/6PUgL2yFmMrYP54ap6x9+7E0cDrjcIdj1Q0tjmHbtuasZ6Y0g/daYiiZ4NRRb31DTKrvtv66i4TAyrE4W8MVhyOPMxGB1kOnHbeb3LPdXdM4r9rJIszTjIRMjonIjHeOYbNhjhPj+VzXdD8MbDYb2qbl7u5OSz+ahsY3PNzf6cnsXW0a8bB/qPtLS65CXbcpLRIden4kfvn1l+ZsaVDVewWIRYRxmmi8N12jZexvrq51b8bEKUa6rmUYepyDh4c9zgWGzQYHnM/nZb+uzkBnk7I+Cy5YSI/GOTSNdj9NkXE81zVUwYP1ufsOW1u+Ywm+eOd5UsZx/b7ykWK60+3VQNd4UkpMX79mSpnJCd5lDkAr3opY1V41VrokKZGOD7z8/Jdsrq95Ej6ANHM43UPTMlxd8/Rbn/Diy8+5v3vN7vqW9549Z79vGccDYhn2/Xni/jxzu9uxaRuCJF6+vmNygWEz8Hw7QJp5cX8kZkdoet6/3nE8nYnTRJTMdrdh0w2M45k5JZL3dK7BTypTdM6ZOcCm7em9J0yRV/uvOIqwvdrxbLejy8LX33zDyQsfffA+/8N/89/yR//2j/nZwx1pmjmLOp5u1YG2rAN/cUBQASepm/XdQdn6CLiws2bbizM/z7Oy3nMi56h+QIrEnBjzzFV0/KdXv8shTNA4QhSe37zPk80T+nZDzDCdM53vuPZbPnBPIE7kaSaOE+P5xDSe6JzjKjS81w98/GTD3cOeeVw1ywse51qcbzXY1lj3ke79Yl7LzYzTpLqXkkl55WNkUX0sH1QK6PaGj/+TP+TpJ9/lzWefcffLzzi8eMEG0WZpnQKGc0742dgwKRNwtHh65+hwBDxyGGnGpUTs/Ld/y8N5xLcNx22v3lDw2jyzC2TvmafM0xd/Xt/z83/zR3wx/FjvKWeiC3z4O7/H8+98j9AqaFrADxDENfzN9/8JT77+ih98/jlu5Q3bpVo54tJkSmqCyKRJsIZc5gCpHbLS+QKMefBtwLlATpHsGkJ/xVW3Y9g9Q8JAdu1SsoqSEpQkJ4h4mmYLLAmhx36LeoxOrzUnXGgI7WRgWSRlVKbBkmU+bOi7KyTPIKaTR+lSrMCBRF/BNnA03ZY4T4QB2q0GbdEC65wyLifu7z8nJmiagfe+/Sl3w0A7DIRmwLcDzje40IE1s2PyuLqByh4LaLNj0TiAIgegE5Nz5nSKaO/Ilg8+2KDMYwGnJYijNf8oj7LmFzOwAh8w8LeAEMZ+aZoyJ65uEsmFfRuZJRFoaHyr4Hn2JpEz0LYtXdcyzhNFAz80ekaOUJveBOfZ9IPabxlJoI1+GmXPe9RXGacTgjZb3fZXZGcAXm+lzZbUL2WmMc5M08Q0j7bWNdAPrqVvOjBWFKIpngJg1FOg+FLiEN9CN3DzwXcImydE8ThrjhWMwU1b9kMBcbR5V2kOo7HDEiSL007uzvoyZNH1q1XaGuhV1p73+CSEbAq2zitT1zu2XU/ftFzvbri5fqKM1gyuaeg3G27fe0b3xUuy62g71djOxoKyzYSIspq1jLeA5AOH05EUbW+U0nAdnIvGxwWQvRTD8Rc2XkR9dQVMStMy6nkkFTYQK3nW9bxOHooBd4/Bc2cyZrikCSG/hP+IKNHBvkvJNwsjs5ZDLLtQAVLvjb/ijB3nFv3Fuj50TziTiSjJ7hUnh8wC+BY/1dl1OduYReICIIgxulOJhPT8Xfwts8+WTSm9HGDFnCzJnAourjb+b3j8KtD2/9PDPqtpQmXEFh+haZqLxkPl+XINAlYaHiq4JhhJLV02tKtyBQX0bbVJ7wWLu5TLG1CpdkMBozK/RZJO5TXUafeKOlGac8XVgApQ9djSIjtQbr2Qikopv4hV3qzBZrvfdR+b4qcXRupj8lQdIyk6qzr/jTUmzpbESymZhuuq0tLpPi97NMXENEVNQPpFL7a8poDf06RYgsYPGuvX5mUilNW/aMZSk7UFryj6uGs77oI1nbLkb5aloaQvyZ+cq4xLTIkpjxfjUMap4jwp1/EpME8Zx2UuLCGWs2FuucaWWoUbCOY7Lu2TigROXiUOOqQp2EwhF+mPXdsTY2vjb3PqqEkFBa+lzlFJQjVNU+c8p8RUmh0WwNUXwNcjTkiikl4iqhk/T5nGazJsaZI4UzzA4kuVvaDV4vY7+/3j9Xk8nahJKufpula5nqJns/NCa2ePxnxFyqfulF/5+K0AY7MIyYmlwix74Rz9MNA2DYeHBxVidgp+SVa9Kild11tPs2mXklq8OWVUI1RsbwVPvavlM7CiKq/BP5agufx7MbZrRtUC7nkDXut3ucIwXXRtkMAYZ2tY4wmho+sb+u0Vm6trOzB9PR4rgLHyvauhqoZ0ua4Qgm32ZUMU8Nbs6yVFfm3k7BDU+1kAhvr61SG7SEWU8VlA1MfLTpZ9eoEpy8ULbJk7XwPkujne8XqxCXZ+AdDL5kkOBURjIj2cqrNa5rF036sX9eiKxV7n6v3r+NUbKJdk+iZlbuuV+kWFMAmc5shXr+/4o3/zb/m7n/2c73772/zB7/8eHzx/fynHdmoAqwNWGYl++Q4DD8tnZxy+7bl5+ow0TUznE+fjnm9evmDoVJv0/Q8+4eHN1xwPD8ynA+M4cX83sd+fORwnTskxPUzAWbuOb3fstgPH457T6UTTDnRtz2lUsLcfBoZNg5lfGQAAIABJREFUR86R8/mEZ6bNGzpLhvgmENqWupVWpWfOOeYp8XBUIDYXqQxbAouR0veJiaWnnNkfR168vNNSe1CQg8WoiFqW1RpcA5gs8wfm/CsAFoaO7vYK+ha6QAiOm90O7xtijLy5v1OHO7m69rwPbIYByTCPE0mSMZP0e7w5hPp1egI0PmjTopyIq/NDwTzV97m+vmKctAS86zrtZCmqrbnZbLS5zjRpMOBqKkTB3KbDSyTG2TQlG+KcOJ32zC7QhJbd1U7LvGMkzVNlss77RPCe66tbssucTidi0vkd0SZZoQKOQtc1zClWFsiSpNGX9H2vTkouWW3MsQg419B4R9/2zDHWMmyVLkxLJhwpB0ANIHLKmjTotLHdnBIyjjinpYZeMuM0gcgKDLf1Z9c6bDZkQTWLV422WL51+UkElxPjtDgBBZlfElXu0Wdc/lxsyDozv27GtvqyC0eovLdpGvq+4/7hobKpm5stcX8mHk5ITjwcD/xP/+v/xn/9L/45z3c7RByDU33yxltwSGI63uG9ENqO2/c+YvwykmZdM81mYHN7w+HuDefDHaSZTb/hdLgnJtX2zZJ5dnNNHxySI/vTmegbbncbbRYYI3f7I+IbroaWoWuYxzMPxxPiPNtuoO8aztPElDJi8hatwByTli6GQNcGOhwuZWYRovdcdT2dC+Rx4tX5RApwM2zpgiZyf/973+Hlj3/MnBO33Y778URE44SMVpl4lnO6BKfFUfa+lII+sl6u/lVgvMuz3p5wTh3EaJqPzmmJ3/39S4bNDaHr6L3ju5vn/KtP/zPoAiknvvz5z/ho9yl9t6MJPZ6G3Gqpb3CBNjc04kiNR5KnbVRipe0brnY9+23P4bDn62/uOJ0XB13PA1/thvOX1/t4uYooSyHHrI0Zuo6mDUwmNZFSXG7UALsUHO2zZzzdbNh99C32X37Nm89+yikdyfNEY4xFZYM4RYOdApgZX88Lbbi0XFTIiWaO+JzpnO7r4lOlYOfBPMPhsNzSm9fk1qQnRGBzpSBOaJffmU2oDdeaHt/0eDwpnlmV91jz0uLbLXqbxQUogYNtVAqYWIdVhHk8cnz4hn64omkHnFNAVxuyNAzdQE4z0/lozn1nY+KMwei1mV6ezecxe1HBFJOqca6ewSofMFtwoKXRXb8lpYQ324XzzCkiUawZUFTmig9Q56Ww/nLFRMZpNlZNIKHswjkaGOuEaP/OuaHtOobdE2WjNC0h9KoVmbXyTRl3npyWygHQpmJYkOaTX81d8b+g6zu6IRB8i4YxS0DsiKTpDTkviYnWNSsv2VhIuUyYjp248m+npbUr/6HMbYxJq9aabMCJtah1ntAocyaLBp5x7kg50TRBA3LnSXM0QNKRYl7e69Tbl5w1wHMOyabPaws/p8Q8zZzPZ9VZj9p0JrUJiZrsS9bVusQhvsgtGBFBg3nVFC8g4a985Ey08bm+fUp3dYP4hnGK5Dwzx4m2beo4BBcqWJB9Ruo5aNdvQHYueylHJBYfSOd4KlIqXhn6XdeB88QxEvd78hxr5WHGGsB57Y4dJVdAnSyaGD+OODwP+yOH80SyILrGhgbyeR+qbEHKmdP5rHu7MKWhNk0u4WGMscYJTVtC6UvbL6vzpBBYlCEXaALMNZkRqXIj9TuWNlj1lxff4Czes1JcH1QbRsxG2XmnorvZvpui7mEf4Ws8U7iwBKvDKGFIULHY8nN22pi50sOcsh4LAF0TRRY/VTZj9dbdcvWr4SqJeUWwVnuzRnfqxRSFjdI0sAyPszgpuEBotJJCvENiiZbfXuyPmbNrH+03vfZXPV9npyQ0EGO+R2Xuel/lNhbCjwJh2a0aR60M84UWrP0pza/W319et8YzFNyypJKd0cu16nkr6zVTzkGWvg3CQpKRnKvMXhlXzwo4LFJzpSGU2Fx5yCkzjbM1Z1zYvyXWvgCii8411M++WFdSGOUqGyDZ1e9VoG55XxOamiB3UCXxQKsfpdPE6zyP1ITtai4KiFmIIhU3Mr9xLTfhvWecJiOg6J6u4KJTkhjeXwAhFQA23CebtEldV0bucsE+K3hiVrm3GCMpRvBanVEYtGugOlcmspjesPZsKQQRvT4FNnNpXpzN7svCSC7N1irxcAWe+tXel7p9ixQNVcJCweklFndAdgqcluSN1PNC5QCariUErxIDUSsAgoG1Jb5qm0BuF3JNibPM29fkcWlSnrJp55rN8ODFm3Sg+kQ5JTb9UJNwMUZtbiZWBSBqk0Njfgu5gvbLWVMajtpOWdmDx4/fCjAWTEOzHD8WPKqAmtc/sugJ4Y2B4D2+a2i3La5V3ZBSMks9U5aNVQyDOqxltSwG8F2PywO2gHbrhbSAtSWTVZynEpAtz5lehmiX7/OkZb4+dASEthvoetVMK1oXUq/BDsNHUZTa70fXX8WiubDjS0xpbulb9mYVcJbX17HJy/Or92VZGdj1V1ZHb/XLx9Fr+dcjI1ZBCllMsVCyKo+vWVZ++nLfqg0SyeeJdJ5YA8eP7ezClrl8lDKI0hijGIwqHl9uTxZDXh7O1VHGjjLGNPPFN19zPB54c/eGaZr5we/8Ds+fPmO33dK0wQ69pXRCp9ev5l0jwVJV7S0Ia3tlX6iPFJnPB6YkdBlutrdarpjhPE5M4wP7/YH9YeI0JXMO1NlsstBL5uZqy+nsSUkPkNvdBsmROasTPUWHzInG9XRdQ+uUydGEhqZV7bVS6l2MrBpQmGLkeJ6qDtd6zHQ+FqZwmaxpilWeQP3LZf+Wrro4dewxzZ6yW2FxoBcn1H4RHGHX44YOab1KKrtSpp6qISs89JqdF9Fuih5y9AZUlPWwsA+WPaSAatGGLcGQc8YoSfonxlQzdE3TqOFhYW6uHd31eVPA6N2wIc1NvT9xmTkZQwrBNX0tSamZYocCBE2jjGsKE1wBCbGgI+fiyGWatlWjVLVui5e/2kfFeRXs+8s8XZ6PlWUhKlWj47IwLZzzavCSJ0sipjIGukfnuDpn0X3/GLSoPAsxp0AK0GJJKne5BtfHY9Eu/7WB68XjbWd+XQ2w+uXFeVbesTT+WEplRXT0Mnr+uK6hvdkS44xMWhb/d7/8nP08sZUBJ9Cgzk0W8CWYmkfG04Ee6LdXPH3vY+7efKP6tI1j+/SW82lPmmbG04HQtgzDhtMZspXL902g8VJZ7cPQ0zbK8j5NM3N2bIaOvvEEJzyYhIPqzaoMxzxHbUgTAp0PxEl1ZCUoO8mLIydRySGv5fad8+Q5ElNijJF+u2EIAQ+M88STm2uebgZczvim4XyWohBwYbQWpsDaODrTPVy9rpxCZQ5YHNwle15MgBoh7wOxrGMKo3LGyQxR37fJwif9LU3TkWKkb+55Iltc7CAqKOPw5KRnYc4q7RCnyDhOnE8nTvs35PmME5UQePVmz+E01gREuRaXXV1nCysJWAX+Fys3q5+lzJqGWJmA2QKNsGIR2nrte/qup9teEfoNOWQ4vMad7okPd0iezEabT+cc2TeIb8m+VdZm7TpYrh68CEGEkLKtZJsRawoR4oxfd2CeJlwa67yG4YrGyulmKawYYQ1qgmfqN7x+8oz44merNYGdDSWgEbO7FrCW95uPUz1Dt1y/vmxiOt0hOdJ2A96ZX5IduJbcR5pmYBrP+sbcg9eGYdk50iyMp8Mq2FOphNDqa3wIpvHs8CaYmNOM5BGRCecE5wxkSpmcpNrlmBMSI6SE5BlJ0QKHoL6q+ds5aRlq12kVDqKs4cIK1KAuWoJgo9qeorqZvu11NLw1Y0MBTQ2iAj50KFc6V5tjm67azsXVKka8MJaU+V4aaBRfyyHkeFaA2R6bfsPBh5UXu3wPUMEP9VNKErUkO5e9Up4PQF6RBsDY0rKAVmW+UlJfQjyo7qs1BcuxXndhs4krZatOQUcrMQ8uXCRTalWYKOiYopb+10SmK6yjBkS7twdnJI9VAFuC7He4v3q2BY/ve66fPyd0AxFffSK7QbTHgDZrLc2UPJ7gA23TapOX7A0QFsSarOSUrOlduYbFZ3Mh4JsG1zTmm2biOCvr2zaY847GtMinceR8OpDjRNteEycFu8+nmb7bcv/Vaw7Hk0rguRL+Sf3Ows5UlmzCZ9NJXYEO5bwvoH+y5nWPy7uX4VslcJ2jNa3Q0pA3O6+d6st4ukfA7eq8uliyy0m4+FPeqmEey1vZ/Vo97bLkzQdTV1Zt1cU5Vr9L/aWMWBMi/b2u/1Jd6SohpmqYllixuumLLV1AyjJOsnLQZfGLxMxU8c/KAVs38HImVtfekoTee+0u7zUWqDZ/HW+sToI1gPP/5vH3eY8IlKZPiy+pepSuzsNSUQbmA7rLeZBcOs27el4U1issVZ3luoqWb8qXp946gajzb4NbxscqIfDl3pakindq+2urDosR1rFJBUQNjA22XhWIziCuSheW95TKyDUrUUxmojbodauE42r9e2cVjkUndBX5Sc0XuEqOqd/prQLSADuVw6HK/8hqwxTpkmKHC+tVrVHxsQRLUyBtRwomQ0hh/YfKWr8E/eUSjLV4NprsSCWliG4IrTAwINKXOVwx5p3tWVFbqLe+2PO6pizpWL4j5axxwrKIbM1ZozCAlCpAXXzKdcVfqW6tDf4cWIlPncfGqialTmPxxzC/apH5zGQlXcria5feRt5Yr9gcOsCF9XlZYnBdfyF4nFN2cbZeCllStYGugvYKUieUrFUSHpVlnVT2IVXmMav170k5WlytElLiZNl9b7vc9fHbAcaWES0L3Gk5WsyZeD4rCzZQMxR6MLf4riNsWsJVSwp2yIg59oCGisXurIwX5QBfBRR2AKxi8Xc85OK54hAprT+rw8SSy6x6LnnJFDhnTLSk+owpR3wYVIsqdLRtpwUqzth1dXO4i0VWvv/xdYoILuVa/lMcvXrlcrkh11mgNXhaMsbVZIluXll2kBp5O7hLVjevxrCOlLhlHoC1jubbjzXDruw0pxE5l+8rDvOlAwROtHlNPM/KHItJj8iiRZrTYsTs5oRyL4uBLbo2SyOhFQOwXK27XENL9nRZb2tGcxZ4vX/g7uGBn//il3z95df88B//x3z6ybd58vSJGRRneKy5Ok4/r2RVUl4OryoJ4Tyuaem3V7RtxzRucJJoGo/zHdvr56TsOJ8mYnzB8XTmcJ6ZEvTDVrOEHtrGMTSep0+2tM1Tpmlm/3DAuw5P5O5wZH8+8TCNeBGGYSB0O4bdluy022TbdrpuL4y+x4mCjecpcpi0DD/LqjmNadmUTCrGihWE4+nMF1+80LKxVebPka3kQQ1iiqYdtwIgimOruKMrFhQJjtwG3NWG2JrzLYI4x6u7O0pUJbDokpqxV2kJ/e4QwKXFcWflxJf1VLqOtrmlpWHoe8bTGbFrnmXCO1/1Wosj48veFeF0PFrMohk/7ZSqhjRmQebMh0+e4YbMaRzZn49a7hICOWXG6cx50qA/53IiyBJ058hxVE0GccqICCEwx6Qlt6JdgadJuL66wvsMKS8AJ8V5ErKVT1W1HBFE1MC57BDvtXOlWz8vq/3jajbXeQWGnDP9oPFkTCwLHqrdcBbD1rS1HpuszjlkAaKzQnW63/WsK3pYF9cj8tY5u7apbzvjlwGR7t9FdP7d77n8vHLuiCgAPs9Hgg+EoMHwLEL//IZ5Gpn3AlMkSuZ+OrOZe6TtaJ1ju0ro6TrK5PGIOGj6gW9/7/s8/OigzknruH7ylNPDA6c3b5jOJ7z3PHn+EU3zwPl0wEuEFMGps90PPbtNx/mozKP9lNhtdzzZdsR54ng8sT9Hnt5e07eBnIRX+yMxZ7ZDRxsaSMJDnBCvncMDwJw5ebQcPjRcNw35PHFOMxNC07XcDFvSPDLOIw+T6lJ++/qGbRLuxzMhRnxolmSaNU1wmZqtd4/WXwl2aqBi6+tyHS0Bq7fzpawHHwJjjsQUmWNknme2w5aGSI4TMao+ZBh7Zq/Js2e7axhVAzxmsdJYPQdTdqQEx/OJaTwzjSPj8cSLb75m//oFp/0Dx8ORL76+wzfto5Vppdu2FUqn43W4vSSMyrpEm4kOHUPfcvdwrMGJgqnKqlwcdh1EcUDfsv3wfbbvPWG+e8Xpm6+4++lfM59mCxZAGocQENcjzRbaLdN0hpDIbn3tGhiE5UtMLr/s+QxZQfvy8CiAq/vV0fUDoe3Uqc+rfWdBSumI/LC75qebLf/o8/+ThbkgVc9QLv4sXuAlcG/nsiXby2s8mTgdSHFiPHd4AimOCnLjaZodT59/QJrPVgJ6ouu3eN8wx5l5PHE+3GsZo3XanqaRbrOlaTu6fsC5rnY9TmnmfN6T056u6/G+BYJVHwRymokxMkcDHLOyYp3MpgHbaAMZ3xCzo2l6UhbOozYC9da0sfRozgIxaXlnpuH69inTeCbOEylnQtNqEGYBq4K3M8FKSZtuS56OIJFyFiuDWr29S+1u9YG1xFIZtjllHDPV6xZ0fcpc58c5eHJzy13bMK/mqvhWeu4bkGglu9WU1/9rsK8gsAefiZJxWRCXyT7jcZzPmhARFMAu+uXOe7quZ7vZmI+nNj5bRY041dkLwXM6ndRfKAGmg65pgRYfPP3Qa2pzmkkxMY5aKeOdMpZhqaIKgAueaYz4sIBldUgLUPSo43z2+mTTD/RPnnH70bdITYOLxpELjrbrdTcKK831Ykeh73rTXo0WxPZ4L9XnjnY+Fr9eRGi8gWkFjPWeNCXkFG2KpY5fG4JKFHk4PTxw/+Ilp/0d/fCc6Twxz8L5mBh2N7x6/SPu9nswwFucq+sAoHFUxl+KUfdVmXdAxfJYkkmSjElWwId3+wDJEgLeaVDftT3BN4how78CPqgUyooJV9aoLGu4rEMpQ7gORAyDSCtArvrATmz/LZ9RQVPrI5FQ0MwVjfDyGov5kmSClWWLdzgDkKtf4UusWGwM1S7WeLP6xWVMl+a3SuQISrtd7VFykaPT6xeLB8TAW1cGo/yvJFW8r3rCuPSrAvq3HmtA8+/7+E1M2TU4DRoPejtLivSAt3HOitxWma8LRiirNeEcXh77mZcybwVQKvdVyBflcwtbUyswCsuwlHSzhO8UVrWv713LKUyzVm3URCWYfrEBrgUEDMqc77uOLJrEq+xXr7rIC6hnQKPXJKNKnYhWcWDvMQzHYbF3AQ8NvFNwe1l/rgCqZc5Ez2XJpYraQGGTSstZiGkCcSQ749pWG9hqUYWBnaywE6dj3zbaYPGiArn82zm6rl18CmTBERw4Sza2ovFOygnJyYBOlXho24YwNNoQOkameWKeJwPCm8qOLfajNA1cSy96a1Y1J5XX0ypMrTwssYc2K0v2R5N6TWjwngoeO6dNm6Mlxov0hvPeYBtdF+W8Dz7Us7P4VL6A8LbiFHBtcPntSsHS9Lc2nhYFWnX/mK8qGClssU8KtmsyVWy/BUwzV7Qpats3VVonmWRDvR+36OvOcWaaZ/0MY/p6I3JV7AhZZC7W1/4rHr8VYGwNagooaKBheTL4QDsM6gAGR7/bKhugbchemGU2J01vJ1t3z7KZ9YDR06UekKCgzqMD7Tdfa4ne7C/HxcFg33JBPKlZBFs4ktR5SzkR40zbJCNqZVrf4aQh5QlJGRf0IAoVOHz3wb+KACqwWA+2AiLZAZIr6GiLZ+XsyurAKLdwmU1c/cM5nJWTODMQy+VIgRLrJ9RM2CNwY2G0rvU5liy/wy2baHUlBaxqPEwpUTrbEzMcR+LxjJxmFsEHrLOwp9bq2DU7xLLHxZFVw1S68kVjPubfsFbWTLbKhiuDXe7NQIGDzPzrP/8L/vInf8PHH77PP/6DH/Cf/+E/Z9tv8I125QtoGWA97IGmaVclks6u3rJ9jcM3Lc1mIKdInGe+OUxcbwaefvApT599wP7hwN999kK1mAsTMmc2vedq1/H82Y5n791q0DUnbm967u8O+HDN++/fkvE8HE+kLDx//ozbJzeakA5Bxa1FSHGuoGHN3JJ5/TDycIzVSEp2dX5DsC6SlmlT/RvP/jjy8tU9X339iqIvW4TdnVNH0YsFLlqT/facOJYsooN2N9DuBpqrLdI3FLn5LMLpfFq92fZ8tRNSgZrD4UC1wYbXNyHQBm1MdB7H6kSmlHjx+hs8XpvqiAfxnM8nRISubfnwww/54osvqsE8nU+LIYELdlRZX8ECLBXGj3z15Zeqn0MmikBwXG13TONoIuj6GUUzCKfgfteVxhLJ5k1LK0MI5KAOTtM0CjaNI4f9QccBT8qqtxSqLIp+drAMr+bWNCh/rNukGVJhmia6rqvPr8+unDPn86hM4TQjSYF6QnHsV6CITYgzx7+sM1g6p57Gs2ZVvSc8MoHrfbv+3Xrc39X4r9zP+tovr6l0tP1V5zcXwM9b3ws8f+89DqcjJ9P1TR6G95/gu5bx1T15TPyP//P/wr/44T/lD//RP6QJniEndl1H8J44aeKjaQIiI/f3X0Lb8+T9jzhPe+5fPxDFcXXzlCCek7xm2r/hGDo2uyuGtuXu1dcK7mfNuG/ahv3xwOuHEz60PL254Xbb8HD/wHmKJBzf/uAZDZn9YWR/njimxIdPbvEinMaJF/sDqWm43mw1KE6RUwL6lg5PmIX7hzsmB/3Vhpvthtthw8vXLzlKInvHsN3ydHPF1e/9Pj/6yd/w7/7sT/jgyTP8ZserceTF+ciM1LF0bnF+ijO+dprKLGWwQFMffd+z2+04nU6cx7G+rugN9qFhBMZD5O7FA/Mpsd1tCE4b0bR9z/bqCaG9JrQDLjQa6rQDbb9F8BwPe3BSHeCUhONpYn/3ivvXL7l//TV/+ed/zOdf/oI3b16yv7/TZNwjNdhf7dcse38x23YumBMdmsB22zOlxJylJgBzmjVJYnpdQmHGUANifEt49hHXTz7g9ru/y8Mvfs7rX/ychxffcLh7jYiwGa7Z3Dzj6vnHJBfxjDRPrusVxuxJ4vGijGztcuyqm+MR09Ff7kqDkKaWVw9PntLudtC2yv6U5bwoXd2jNaHqug2H/X11+hUMMN8ONOwSUH3VxKKlSmWzJHHGLrmsYnJOtT7brqdtt9zfv0LSZPZioPHC5CIxnsnjTBsy5ykyTWfm8UhwmdD06v8IeBcZOsd2O9B1AzlOCrqKgGSCT7ShBxoQ9V/64Yp5mslxRuLI/avXSBLaNtC0jhAEyMxTVtYunq67ous2qsGXWmKOWhbOsm7mFGm6hqZ1jOPEcTQpi1bL1m9vn3A+nRTMCoGuU91aVwYZR9N0qg0uykyCQJJYtQZr5cvFdBuztpzF9QOVkBFcokp3Ocfv/Ucf82IzcHy0C9T30H3jV/unsLDKzWarEME7XPB0LpAkGxDgjWXlub665uWb1zzs91xf3/Des1tAtd1fvnqpMjMsQNV7z55zOo3kqLap7Qa+/Ppz+rbjZnfFdtjqWdVpgKx+oRDnmdk09Lbbre6ZOTLPmtQtZeMlyc7Q15hqmiN925muuAKxccVuwkH2jsl5NldPuPrwE1K7ZU4l2NWhTjminbW9SWV4Tf5b0Arqqzaob5FS0urFnMiScE6TeqUXB6ivUOOVEPRimoC/viE4z4tf/gwmDe49jj4EQs7E44lXn3/On/zvf8SzbcPtk1t2Q0dMM//3X/45P/rxn/P1aU8YWmgagun3S1Ywo/cKdDsHGIhcgnREY8VFbsuR8BV8WFt0Wfk3IQRC21Hsfs6Z83g2kCMxzWemeTQQtqz9S3DvMdtWfyk1jtSQeTnP8yrmVPDM5NIMfEqpNAVbZPMEoQkLjFoT6CxsyMZJ7R29YOKuAkyuAurUc7FKQNTYlSUOkiWuk7r31P6UhFkB/e0A1nPfQBsB08a26y6+ki0iV9h59rvH54e7mLX/fx9rv9CHQNdpsyEpdsRp2bi382wJNS7jJ1h0YRf90rm+tuh9tiud2CoB4Bb2bY1LXYkFgrFsff0OEak6muu4PEZNIOQiL+C1H0EZ1wICO+eqBii29/2j68gpV4JdsLL79awsuEAB3JZrTBmmoo9f/Zy1b27l+Ct5hXVD6LUebAEEteFZNKm8Qv4rcg8q5TBF1fotlTI4UYkZK/0v36MFd67akWInyp6b47zMiwGfYSVNUTTFFUB2YM0NRbQSYpomOyPt3G1brazNZbsI5AWEtW7UDP1mIS/hatO4aODiOI4rm+oIXVPHT4kh2RqGLozmzWZDaBoDzHMFKJtmqdaVnJnnmTk0KmO40kku63m2e1Ypi5FOFPxu27bqI6eYauOuUMackji/2HWEUce6VJnnKq8h9dxs21blM0RIcTRfpS7AarfKmkkp2h6zpq11nZZ9DtvN1hJGRvbR5fgbccbfCjC2ZAdAJ0U1aqiAp28bcuNpNx3N0BGGHnGeaIBdUY4sWYrGeaXD28CX4KsMXPlOgyYNk7ssN6jZuEfX6T0gq3Kq1TvK3wVYruxbrdPVjUqitYMypczpdGa4eUoOqvdxe3OlLDwXjJnWqKNcSgmK3V0xQuoBu7J5sCrlLjR0vwQIF3CoM3F27yuIK2jWSHf2asyKUDfL78qdXy629edjDq3UBVzn/cI46MFfygPdYusvr9fAFh88fdupWPPpZI2QdG6m44SctWmXygro+On3rbtKrwAWJ8u82RdnyUsToaK94y8znRf/LOtrdbXrdVSCfUHp65PLvJmPnL74jK/uXvHZz7/gB7/zfT759sd89PGH9H1DI0uZSxmHIlxdHikpYFbuQ2U+Wpo+QG45z4lxPOPSxIeffp+P745888037PcHJM+0Q8fNkx3XuwHfNNot3cN4Hnm4ewCxUsIc8U54etPjuoF+0yNeeQOtb5TNFWfO5xN93+mBHQKN99zd7bk7nDnNucL0xblyFlylNGnw5bXTYcrw1dev+fLr18wxAm6RN6hGpThhxqop3htUgL3GWd7Rbnqa6y1+05GbEuCCrNZ027Y2VbKtAAAgAElEQVSmD5PrUVSYc2/xJEVLShwKCDTBk2KqyY+yiFvfsh02CgieTxQ1acxRv7+/r8Y5iYA5zqX75To7WNZZaBu2/YZpnnmzv+eB2cgbRRxfOJ9OC+OvutzU8ZGSxHBWquM8MSZi1k7N22GjOnXZunJmVfq9utLu3Pv9njjH2mQgi5bwFUBDSSNLxrI44nhIUUs1HRCnmQJ0l3lYMxWSdWFumpamC6rddLHZ1mfi4z25es4pgL86TlfvU7b3vAp2l0Zki8P72FFcA7LveqS0gDzFJpX3vuvxGADOWbi7v1vWkzmQrm1otwPMiXneQ8r8xV/9e+5eveG/+i/+Je14IqZZG2HhaH2n4BkOyYm7V19x+95H5NxzOuy5++wL+rZnGDYMz9/n9YvM6XAHJPphw9Onzzkc74FZmwikmbvjxGazY+ha+uB48+aB0xTZDh1XQ4fkyP3hxJQhdC0fbq7pyOwPZ84x0fYdt8MWJwqSxSy4JhBESOPEIWdC2xFate3uPPH64chZIv1uow6bwN39Paec8G3Lh0+f83x3zVeHAzKekTlCaOoqcZjUi+3nYJrMIlIbBTic2hNMT0+EeZ7Z7/dVSmS1WG0fCTk7/vQv/oJXb17z8ccf8gf/8A+4uX1GP2xp+g3NcE2mQXyHDz2NC0QCp3MiSyRnZdG5wg71Ged2NL4nRk/7cOaH/+K/5L1f/h0/+os/4W7/l2TO5NoB2x45YuJs9otVshMHVnYqNaAXVYPyi0baAjb5ev9CxgepFSNFoqEwirHxxUNqOzaffpf2+fs82e85vHjBN7/4BfGU2M8z7nBHu+vZPX+Ov+rq9TVPn+OaAzFPzLE0KUyU0LqWz13crwpVJclE8XTXt/hho41c1jIIFU1KuJxJKXI4H/ny858y/5MfXuzBbD6PggwmViP6J5sv4Ys+XlLwqJSHlsBMNfwFYcZ5oem2Ctwm7VkwTROND9AETvOJw90rAyc1GVvk1bzdfXCB+Txx5kiaEyG0hKYEvqg+bdNqYGGJhhAaIiM5T6Q40ndactd10LZeG2Y5xzwpWVaycD4/0A1bQmhp+1aDVFGZGlHtE4ahVbbtHBFZ6b1bMHI4aKWHM7uw3WyURZs1eY5vcE2Ld0mZzp5a0YXTMnv1vxb/WmwkSrWKlgf5pYTVZC9qdZJz/OA7T/mzoeWbuv/1HtWF8hgvcFlLq0AsxmSgvQXPucG7pYGqLj1NSJzOJxywGQbV+Su+oygwGYKxmdLMNI34N284nc4EHxiGATc75jwxhF6Z3d66cOPq+dJWcoWe4eM4EkJT9QmzaAm0t4arAMHrWpMsJIkGjGi1y5xnxjQtEgcCc0r0T56wuX1Cs9lyOB6MfW3bx2lCJIqBC8b0y7k139RO2bLXrMIvWcfrLArMBu9A1mC77WdrnFdik8Kak5xJcaYpMaJLxAy904rJeTrz+uULNpsGkZn9mwM/+tM/5ni+JzphEoeXVoE8URCvC4FEWrqR44i5SBBwAcxnuwYFlRd/LFTc3lh7ubBdl5hi8qP5uouP07TezhO1MsVxeSsWXZ10NYbwoerYluvouq6e1WDAWkkwGTBR2dE2l94bQGs+RZmMCpboGy8IPjUGksLsfSTdVr7QFd5zYccuuyxZPFXK9h+HVN5YZsX2LjG6xQxeJTiWcLRcvAPntYFwqeaUwqJ8t3/2eMzf9fhVyfbHz7/rcwtIXxpvxahJwJZgmEJhxofKklTwK16Ap9Ok7MembWkfAbVl7awB3Vr6b897r1V66xBJspBR9qWIsUVNzkZ/ttfZZ4gIUS8Ih/rl3hjtjlUyxRIqBfQyR+PCdy7/Dt7Tre6lJElqSTxcAHiCJsarpICU86JgN2VO9JxGVozf+txyfut5qn0oUirydBlEe2lQzjPz+0IFLKVW1IYQaJuGOUamcaY0JhSLGRbsZcXgtDHwRhILRoKJKar2uixnQnGvHEWmxCEyrj5VjLVaEhGOs4H1zmscGfxI27TWUFLJLVq1kEhZ41co1RKJNVtfL0NjdQyTiCWpbcC7955gIC1i42VneBsaXOcMeA4Xc+tbrcgqPUjmeTYmsOqbNza2qkdfZF2skjEEVNZOagKtNuRyi2awoFU8BfCNKWoyR4pv4U1+INX5aZv2Iv6LcaY0ycR5qz4qNlr96pgiOUdqg+vqE/96SZPfCjAWFsZh1fJxagC8C4S+gz7gu6DasE4XeS5gqjn+ixbAGqR5fHiug/Ll9xcdKu1gXx/cb8fYcvG/CypsDW7Kj2vDWlhp2qxJF11ZcA1931fnu2QlXWlGVmEhKoDB42usIKMtDrf6frm8jrVxrx+zemJ9B8uLVy98x7DKxcGhB5hbvf1dc3EBalTDW5yO5X6W+1wO8yRJNz1F09VpQ4k5LiUuXOoBPcZuynes3f1qONZfX4HDX23Ql2tcvqOMrxoCM+j1eS0xT3PifDfj0t9xniZe3L3ie4c7/sF3P2U77CzTaQ2+yvyunIOSkfIrw6njEUyQX0stsmR8f80Hn3wH33V0L1/y8PqOptXmIW3f40MgJTGmsdg+9LS+raVcvm3xfV/Bt8VSlIljBbQr+Hw4z0wxYxWVFQRQ4LVkMHWwnP17nGbu7vc87I8VSK+vKOugRFd13Rsnpuxve41rPKFvaXYbfN8hTVCtIUUUlskTaEJDFGWNOFbr9sL3WdZykTnJMTEzm2EqZQ16cLvVuZByKfT09fPP57NdrrswwtmYv+t1UzSM2hBM4yYWD9Y+V8dCq0Te7UA6M2aN97V0fxn9xUmrnUhtKJsmkAsLJ5fmMa7Oue7hMh/L5y37Qn8O3lfDWcazOCU4V0uTynNlTQAaeHunKfLV+VDK+NcOTNs0xspd9DSp17iMRdlP5Xu987hQmAKLhvRSUmPgfL4cW3UW145WqBrPyFps5fJ9v87RB20C4YK7ZOc7cG0gbHvyYSSdJh4OBz77UvizH/87fvi7vwPSk32gDwHnIuSAE2UBxXxiPB9p+oFnzz7g68/+jnk+0gBh2LC7vuHh1QvidCZ4x2Z7Rdf2TJOuiYQGgEPXEhxM88R5ivRdS99qAqc0Tmla7SbcOhjHGR8cQ2jpfYCcGaOW6mcHbRO0FBIhe2WVBgcyJ6asrO+m7xhcg88Q54mI0HY97z97jzzNfPXLzzmeT+ScGIKHtuE8a4JF1jatrHcpAciyfi7mVV+kmfLy/IXfQnXApxxxXeDm2VOub5+x2d3QtAO+6XC+dL82hk9KWsprPo3DkWOC0hTDebzLHI8jKXt2t8/ZPXnGSeDq5z8jhLYsvIv1gtkElc23NW9OezkfanBiNlfvYdGHTjHXM0yECkosjK21obNzN9c0E3jVnGzblrDd0myvYNhyvj9B1MYfU54J88QcA8Ulba5vVO5GZqZpDzFpItACrnhUHdq1dm1efW/G0W53+KZbLLvdYCHIVvbCyy/hF3/N6fCCvNIZrWeTiN5TzgbCakIwV1tVHAlsTAt4K8xzJmWHzBOhEbrhhu3ulqbpa5PV6TyT0kycVIZCUqwBXjln3EmbhuQknOfE1fU12cQvpRUkayBRbKlrStOIjEgkpZl5Hg0IjVqtQAHjxT5rCTDVbGdS0RvPSasSRAHAYg+6tkO7bqfKJBJbe+CNRa2AS7Vr5fhEbX8OLZIjqpkpiwuLnfPiV+623bNI9d91LRadulI6uvJ1HXz4/hV9H7h8lPNWqv9QwR77hBgTkzW83O6Guo9yzhAci4/ulGzgHEPX07UqHTHPszVjyXRtR9NpsJ4RgmRtNNQoE22cJ6LMVVe+AAsLZ9H+LpqOBqwV0KLYGudKQ7BgjMPiN9m554SUlZmVLHgt5eJ17TvH9vqGbrvDB2UEaYLAvtcvhJNCShLRc1EJJMrYKgx0JXcsTbxK4+Pia9ek41rV184b7wI5zuR54gLgtP9yTrhGbUbbNsR5ZJ7OxGni9YuXPNy9IeZIDpBwSJppQkdhlzpUdmMdVyBK9vAmWbEc96V0eFYw39lpmosfuYBDaXWt5TxZ9zcIIaxiLXvV+stW63T5p9RzxtW17+rrHoNcj97NmsDx+D1SFpjjErC1Q7PujAqgWwG7OFMpWPvwj3xmCxHWYGwBDfV8XhJrZaVXFiOYn762OMs+Xd3+6j7VP17bxF/lWf26x28CaH/day8wAPMTy5/6fJ0vX3GBOmyr9/uiwbnaH5VZWX5+B7P6LZ/S7FK93hLq+jVzVn+nfwQvrj6PW6QQ6rfY78p6dG5hLboy386pY2H/vthruEogKfZOrNSwaH5iftFaDSRYIm65x7RcVf1fWccO75dYo8aLK6DMOadgptNEZXaKLayJT1Ku2xINzkk9E4NVCzUBclskOBZQsHyXF5ssiylKgzU9K5Y5LBINBXws+vfL9Or5jSxrJltixNt5W4l11qyyVJ1mMo3tuWQAZ7E5lzYRA0CL5que8zpX5nMVKQXR13gfCM6kLVZVhGKLqjSfXq+hjENWAHVpcrk+jx2u3r+3eNOXfWO2X6whteRS/VRisAK6t+RGm7lNE5XopNeq8Yk2q9Uk7FtJg9DgrGrngixU40J0PJJVfwS7Prv+/yDA2GRZWe9VtNcZ4u27QHe1IXcBEQ2kcsrVSC7ncdl9JQhgoSaXerbFh1keBdCisOPqry+ARVj278XDfqmAY8nwlcPGOpmuX+uph946Q+bFW7lAV11Bj0nerFxLdfryRQBQjZOUgEgW4w728/qmWRny1Y0V/wgbT1lJL4jonNj7c/WYV8aQtUFaOwNuZYSl2GbD7spPFvMUqELefq48URJVIplp0sYEiGb0PI44TZCzVZcqeOGdq/o5S7OQcv+Lu+tYArxqRMp1GEq+vsfVpyz3vxqSZW7WPy2BlkNWGlael4cHHn767/n8my/58usvaD18+u3vMGy2WoIpyjpcru9ynS5AUHHuNEgJPoBvyAQmgeff+pR2u2XY7ZD0U23u4BW0xassgzMQsd9sTG9FWaQpQ6R8nsNlqV0ei2FummBrQD9zjpnDOZHkcswcpWt0eOQI6IG6Pxx5eDhwPo32ebaGXDG0Fh+5MujLmlR7qT87D74LtLsNYbdBugZWTPHlBHG2xpYOn5dzfDHbFXAO3tcGXKV8re9bfU3Ops2lJSb1zKiXrZ+5BFXgVnpD5awQEQPWFYzt2pbGO/bHI5OVTzQ+WFCk9+7UcllzDxu3FZOt8ZrdO5/PlGZWupZc/e7TOBorHPCerm05TzOHwwFnZVF+ZfjX1132UJnbZQ7NGbdzJGUHkg1kVpbTPM8rYyy1U7IGj8nAWFnWQzG6uZwieh1NG0hpZdhX87zOTpc/0zgt2U5vUg3mlGqzkpKo0OtglSQoC7isK9UYpiYHESmYw1umpDRJWhuoyoC2ciJXgyK37PUQCENP3g6ks7KL96cT/8f/9Sd8+/3nuJtbK710+NJAzjpfe585PtzxdLPh6Qff4uH1K8a7F4yHPeTI1dNnnI978jwxn4+0bUs/DMR4RpLD+cDtriOgZXPHcSI7x81ugJw4jSP3x5mrqx1DFwjAPI6cxpndbkPXNpDh5d29JmpAz3Ex0cgVu8LHpECGCGHTs2l72uyI88xxPBFubtltd9xsd1x3HT/9yU9JznSsg4emI81nTUphxznFSVKGouQlKKxsgNXacEWPxPF20CxW6ibC7dMbvv3pJ/zu7/+A5+9/C1yLaqV6hOWeJEXiOKrjHnQ8cYE4Cb7p0TJeYRrPvH71GsFxc/seyWd2r9/Qb65oQ4uXRywYW09lnS+/W5bpOrArYbCAOaozY3BM00yclUmAs4ZAbpXwWn2CyMq3ycqMbxprmuQ9fhgY/h/m3qzXtmU5E/oiM0cz52p2d9p77r0+5zausqtsAyUoC5cLbCEh8YYQD/wC+F+8l3jDIEoICVXhUkkULmOjsn1923P22e1qZjOazAweIiIzx9r7+JYRoDuktfeac805mmyi+SLii3GP8dkzLIcJ6/GM5f6Au1cvcD4fsS4OwCDrfT+i349AYOR5gJ9mhLxKyb4Hji8PYFqApQJsrPPK5MEuCBjbCRi7mSoCAKfJdwl4/hO4f/5H4PUOYLMSBORBlioZzlkzVVgDM1Se1wbQcDyzl3IG1jUBCch5hQ8Z18y4vHyCpReON86Mw90B5+MZcTkjxxmIs9LFKI9gTogxY10Z85pwf4749nc9un5A3ym9DJGCsXI/wXeaGS3Z0XGdME1HxHUGN05KSgpmJWtgVKwgzehdgLSqgyEUBJxTGYucVphMd94p1UwqwURWvWENRNZ13sg1yWDr5Tw5gqGc5foZRw7wAaWUncWekXiIJGM48qgIu+iRh7bss2d7dF1dK9W25KKnBNjT1xqAXuOq3bMZXegVZNNKkiDl1ZWmIqHzHfpO7mVdpPTTnMJhGOB7X+jTfHC4uLhA8B7TNGGeZyxrLFVQKSdJGSqOjvybk8hGB/EZlrigZhtpdp1mL1njEweHpIkr5CQYbJmHjQCo+yN0GK+uEYYepWu9rkkpA1enV8cwcwbHXAAVs59ytiCv2Y+pArLW2CXlkuku3MZQoELWYEAALwvyMoM0Y7W13QEpsx/6gKuLHbwjcExY5gk3r98iJUYiTdvhiBgZ4zCILZ2T3KPpe7PvWTLQ2Rn/ZJVtzFltPEsAMblay6xr4odKVgXaCDVQQ2X8GsCpWZfVlqiHBQtsBNwGxKnVU3X838+BWpM43qVlam2hDZik17asajYbE031RAM4FFCnjA9X24aA0PiWzBbE2fqUloDhFPw3nkhbtI5sFG0vqywym5y2yTNbnfW3Px6O1S8Fa00nZBTuTNsLbfMtKb/XvaBrre+kUoQ0g5BAsh5tzeVc9qHZ2Q/vzwBB0nu3Zlube2cNPChtY20ca59TSkAFtLouoPr3Ve+3VxZO0AfAfwvMlUSpKtckaFzvKZiMMeCLU01kINrYOwTBPwoAabSU4rRU19CuqP54CZxQw0sKlGaHAkJrw0WGyr6GVoVqb4cCMDrJBHYKtFpZve1bBxRKgpKQ52T8nYKc7doAgHVZShYmyW2AiBBTLhm0jFy3GGmFk/LfmpASkDKCY0ZGUrvloRfMRZ9DZZVVNkqD6SZrHmJnFkoXQHjUdV5dlrWdmEvQNiVrmiW+C5FcIynVJFgCekUPyE3I/atvZVUqdn0JDtU1kUmSabbSE9LwEcY1T8rX7PR8siezVoCaP2AJY95kKscC1pq9VJLKnDSrzNrAlHX/tL7mNx2/EmCs7UEyIQ/AdR7dxYj+aod+1+MwTeCY4cAYtIOmIfH84GQsM7hVhKoXLIG/fIuxcSxqzIew2cGNcixH0SsNbwUquFJ2jRVqaD2CCwResmQRzWesaUGmAYwOXbfTSZXyEacbzMGiwKKQArxaZroJARXGlSdnOywPANlWaJcxkzLwGrWqitxZ47TyHS6nkZ9qzFgmnXWh216TNt9vF6lFvRw1fD+2wZtrt9wvLOa7zCtLNFqaB5mZw1pqmt+jgR8o1ncsUqDlnJF3LTJmxtZWIZe//Q3avl1vcv5UFAAImDnh+c0bvHj7Gj/68V/jH/zWb+PXf/BDfP75F3h0/QhOM5fMMPPeFS6d+iSGGMiRIY6+74FAGUCHy8ce/XiJ66unePnlz3A+3mKa3mK367HME/YX0gyMwiBLWRuIuEwlukcQwdz3AwDNkmDJLCUXELoBKWXcnY44rhmJfblH22MWEE2Fe0gzmYnwk5/+AneHo3Dxebd5psIB2zx5SXQ1UNyrc7of0F3u0F1fIvedXqU1VCVLxTmHZV5wOB7UyKTtXmqUbjvvlvFjT8ZZeE4JpJnFABNjXibZX2WtV4MGqErOUcZs5T92Uj2C87gYRzx79Ah3d7clugpH6KjDqlm3krEsWYfSJIQLWFCNZAZyLo0/5LsGOnFRmgzllUvCB+ydRyDllzRe6yBcgDFp9jPXNZhz0myZOowpJbA6SSAFyJSnVkpnojhjPsApJ1FmFrL6uKLv1VEswkG5ivN2Jx9Px7omyphb8ICbcRdHNichZk8akXbR4fLyAilGHCbhCeZiaFZFu8kkAUqpk4HsZmB1uiaN2mKzvGDORpUxIQRcXlzg/u6+lM+YaZe0NJmCR//oAphW8LwCMSNyxD/57/9H/MHv/kP81g9+gB6Ah0a5idG5TqTP+R53rxJyOuPzX/+7+NH/+a8wH28QjzP8OOKjb/8a3n79FU73N+D7G1w/+wj7i8fo4ox5vgd4RVrFub++vMTQEdZpwu1pxnGO2O9GXO865LhimhbcnRfsLy+xHwKQE+4OBxzniND36LzIlDll4QokuWeezrhfI8I4StOwvkc+HXGfIpIDsBvx7MmHcCnjfr7HMUb87n/0j7EfRzz/6iv89U9/jC/v78FpFkPReYShR14Wc+OEFsSmdDspjU6s29Hc5mbmJDsOjC8++xa+/+3v4vH+CZYVcMHWm4f3A3wYxLhdZtzdvsG4v0AIOxAFxJiREUE0gMGYphl/9Zd/hUdPP0A3DAAB96d7SPDCKGu2OrLepR3UvPd+o1D8RDVC04o4T1iiBoJARZ9bVsDGyFfHXKPHesV3r2N2V7jaobve4+LTD/DkO58gnk64vFwADZne39/g1AUMVyOGxxcIcQAhIoyEy0cD1v0d+HaBf/5z4EbPvb9ADpcyN/0O/eUVqOtqWVk7n+ohL/MJ6fAGfPcl+kfb8l3pQG/jyljXBcVCLEAGlEeMisOYopUFiwzuvUcYR3R9LzQW7LCshHXxCG7AxeUFgr/EOh+wTLeY7l8jLQtyTMiJkZM0VpxWYE7AzB5XTz/F7mIPHwhA1DXqSlChCyfkdQJRApEHxxV3t/dI6wJPQN93mKYZ6yJljON+r2WgVbfJz/kdB9+WkyU72G4IIaAbd9U5ywkB2jSk2MKMrg9gLRUEHHy3x5JWxHVBzkJh4MiBQg+EDoysGT2QDMQMgKPa3AnkO2RoIAsZNbO33uv++qLw3W7WvGhK+RgRgKTn6UBkdhZhGAbhtmWxyT0JZ7eHQ4BkosIDc1zhIdyGQzdg6Aa4IM1BY1oxzScMoUNwDqc5Ia0rLsY99sNOgd8ZnoJQPsUo1YD6LKwqQUwN4Z4fR4ccMzwFBNcpT2K1patdIbQvBJJGXqqDpPBJvmOlt44cHj/9COwC5mWVKjOntpdyUzutLnDKqdj7oCWlXsctImWpnjEeeiLhSqyAiwFojTyB2JkW4LZZopwgCDzU5vRwQTiYr0HY04DL0OHjR1d4dnmFzz79NqYp4ubFCas2CCIntDORGX3nQQhInnCazkpNqkEXXdN5WVHpnqBNYgy0qRn05gMUCds8ywYgY9H59plYeCO35eaFz/8bDttKUm5OWLQ/Q/2rlWS/y2/f0mq04/7wc2Au5dotuEok2XpcCLvr32KhsJP7qAH4zYnReMgFJGRTvIzNfXnX+ILgyk9qprvT72XL0Oa6TyBUDgbY/81QyP93RynQQwU1STP4peeJK5V1xkfqvZeEGHKalKXYga90GWDNvmwAeB/CBpBvwXwZYhl54V/1WsJtHLu+JMWgmfPma5t1Xv4n8dPb5nHM2txN9VILAAtYmpuTaOBrrbLBAE5Sn3gDuxQjjcu5C90doegew0vsQp5MvlH148XJK/s6p1yafDFqLwEQ6ZqS8XSgAqCmnCThgowXu45dDYbYe4rFsPjjIbhaxm7jlNu1r3/renShq/OgGyA4p74IAWrb27lCCBhCV+4lrlHtRZ2LtvqGTG4064VETwxDB7D8bZ5mrA/oIwCln9FGXzkziKWKKCaUytkMApODC05oXUgqjILTKhRNAkgplSZiFpA1HzMlaSItVERic0gjPFkkhRpC16nX5lu2npZ5LfdcOHyZRZ4Rl2CFI8I4DHVdlD1FCOjAvkMOBg6b7SA4027fYcijNDZNCZ6aRrrvVCbU41cCjHXOYVSAhBwhJ0nv9Z1HN3TYXexwmiYwHJyrkRj9NqgFVXQgI4shC1tnRIBvInF63dJJr2KmAMSQpkYKNBBQA8zpZ9W4ly6ZWyWcs/GcCUDjvJQEa287TNMRiVeABpD36IY9nO/AJE2O1phrCbde0cDKNvJoxOcbUKAI0hrl3ERyylPIvVidQ+vYcTZwwAy3VhQ3AqbJADaOja0D+HAUm4PE0nTOYT/0WJZZuheS0FTUe+U6CvZszmEcdtKRmWuGg85U+VbJpN48s/7OZmg8vOV2/i2jr1EiCqq10eDtYz0YoxYGY9aVK/+TAZN2b1qO/HaZ8Md/8r/j3/zkr/HJRx/j7//938ZvfP8H2O93CD4gpViSr9t7kMgjULhS9YfIIZB0wQ1hxDBcYn/xCBEE9+o55uMt1mhNIKRRgfMdYpJuwSACey2uVzBWInxR11idUxc8EoApZhzOEWuW920ULMK1yfyELMOUEu4PM55//RbLrFx0NnplnqjMs5V1oPkMOYLvPdxuRP/oAn4UjtiVk5RxlPF+OGeoc0GW+fA+U247v/ZdB4LvR3z/8x/ixYuv8ebmNVwfwHktW+G9Di6qwdsS8Nv7OWV4QGVlxlfPn+OcVnznk0/hQLi9ucF5WeBYOAK7rlODJCPqOfq+xxrXEi8wY9uigYWz2/aQyY4shk/fdfjs409wOJ1wfzpiiRbAsY7l5jnmzTOBJDraPrVlrMORNNNmwLsAAkpjAjECtrLF5FxbntkeBqAb15jwBUlUOITQzJWUxkiXzwhxsEh3ZT0SMo7HAywqK/ud1Okn4WzU+2BmrNrsr507AIVzMkGCFU8fX+Pi4qKupuYxzHBmlmYfxlMK2JqVJyx58ERwux790yusdyfE4wRegRnA//Ynf4oXr97gD//hvw/XdRicRJ0zpNtucA55nnD/6mvkTLh6/BSOgPPhBndvXsI5h27ocYErLId7zKdb9Ltr9MMO5AiH+7foQjMf+kwAACAASURBVC/NQhzhfDrizf0E5x0eXe3xaL/DfDpjThmZPB49fYTL4HGeZhynBXdzxqNH12AwYs5YFHgJkKx7ThFrTsAgGdhYI47nszgivTQE6Njh7fOvsXDEwgnZE667HXzK+OTJE3jn8KN/8cf4+OoSS2YsmRF9wG06F1sA3jcSpdFZpk/N2Ww4wwsgmUkzX9QiWTPymgANnIGrvGF2AAcgRxAIu4sLdMOIaZaGi+QcLq8f43A64/b2Hq/f3uKz7/waXNchKkckYkQfPIZ+QNdLNuk2VGWr6IEOZuPSbJxirh8zneWcx8XVBeg0Ac5JcAViUBNMV6qDws3a1bVu3W3bYSzar71JImDXIww9fH8P4AAAePprP0CeTkhpwnI6yjW7jOQJaUhYQsLSE1Koxq27vgJ1j8GZ0V9dw+32gFKh2BhI8EmcQU5ZwKK4grMDUaj6gAFOCZEcHLGW4jWZb5CM2ZwT5mUCU4DzACfNKlFnhXdQB1zG1oUODEJcM06HCefzHcBOKT06gC6QaZE1GmdpWrEysoQk4JzH9fWH+OyL34HjGet0h7S8AaDlgmwBIA/nNPsuRYAXDL3H7WHG/fmMjz7+QKqFNMC1J3owLRaUr8/LXCularm1WgAke8H5IJm2kOfOKaLrezgN3M3zIo56WpFzhHcBKYuMEx3j0XUXJXEhp1UaRWmmJzuAIyOTANBWrri1azPMz7YjImITfOVmT+gCJTh418M7yappdbXXZlIi050GfcUJtyWdc5YsyizVS9JRnEHRYUkzXt+8wM3xBsOwQx8G9KEDxVxoRFJK2HUD8pgKqHCaTkLvEgKCDwhdwDgOyjsrGVe7YS9NQS17a/NU6uuoU0vOsnm1gk6z512jfMg5XD19hrnrkXyoOprrGVOOwiuZNKtIneGNX9H4HEZjZHteqk5ccZoNCPVU80WzgoQODnBeM6ABkFTHeSeAxtj36LTB1hojCB5LyjicT3h9+0Y6tUP27woppnnz9g2Cl6aLOWdkIvUR6MFaYrAC/8hqk3lLctSgS1lLbQWj/tIAqxsbt6gVsYGDJgJYVdU3ZVEV55/NZ6Dqf7AACgCazLFWCGuw0FU/zy5TGxcyOIptZdySxvNbMhRz9V22e0j037Y6gze/c33R+InqG3ENYFt2JqdcshNBtcyaVWcxuzLYBefQ7DQED9cFpIem9rvu6L/VUbKmm9cP33snMQeWFiMNDkPv0Q9dueeUMjivJfsVkOQaAYkAa9aWkvlXKsOyNR9yiGoLc4wYS6afNvIqc13tFdbXruxPsxx0Pi3BrdjZqYCr0D1ZkoEIzXqqsjgmA7EqflCARfNvXN1vPgQ4XykHzCcpekgB69rwyxdwro639Jvx3qOjTmVSBVrjKs3HotE3afWDhwaQFbye41KWBzlSHl+VcyBMy4xVAxUJjOC60gdI4o1aPZEk09+yL4mk9D5xQo4JKUmVSAgt7cM2I70kkDhXuHnLNbSnCJffZQycykUBJTWjFCj60mnT7JLYUcaYJFgGCfSU4KUuC4IkhlQZ12QmOwf2AV7HxWRo0OC8NerLWiEqlTIi052wTSA4j6FPSFHm1CosBXTtSlPFlOUzDIb3pA3F1NdKABQUpiwJNd579L1kmbfczVaFWOEEV/mCbdwbX9yGwsYzg5Fi1P0q5/DegddG1pFRR9Sh/KbjVwKMVQ+mACguBLghAJ6QcsJ81mwy72Htn2rEAwoKtSBt3fRQpwFA2eT1sm2JhjrXD++rXGNrbLRAWyvViVpH7v2HCSgx4JKkNqtjP/QDxn6PnCIY2rnQnHmgAE/1utvI6vb+vvloAdnqlm3BpfbRN49bnpjK31tAtox7EazNeH0DqGUC+sn1NV69fqVljrS5xsNhJRKe3f24Q1pXbRrETcVadTC4ud+GsBWm87ZP1TjgjdHOG+PDLBkqQlA+X8tIHo6jZSdbczCdvebz8m9tJiUC87gsWG/e4rgsOK4Jb9/e4ruffYZPPvoQTx5dA02JRQHcddLEjnawEgYbN4LQOoA6+BBw9fgpvHOYjxc4H26R1iNc1wPOI2bGkjJ6L1yHm5KUZr9tDBGIkTuvM05TxHleZfS4jqM5CAA2ioc0Svri5RvM81o5adugEsl+rQ6+gYaSsUHew/ce/b6Hu9rDjT2482UPufbWHxik3jvJAq0r5hsNTJghDIu22jwyjqdjUW6FWoTs+Zt10RgrLfDYAsP2mgCNuLE23ZCuomPocNGPiCnh8ePHWGPE+XwqTcIsU3YtROteCd19KbevSqjNVKmGvpCod8gpY56mYghVg35rnDuS0g7rqDmvCwqfqwoN6dxNyjvm0YeuOP5eG4F8kxH8zjjZzZDMhgGkhfRf90Zda23kurlGY/SaLFutEQvpPG9WgD1/3hDzb+73oWbJGeuyIMXYfM7KYGrQywDglLLRVIkxwTXrhCAijZwDXYxwiYGUkeYF3hHuT2e8PhxwShE7LzLTk4LVOYkxlAm0MubDHXYXj3Bx+RjOedzfvMTpeI/dbo9h3CPNK9ZlgXMnhH7Arh+wDjuApTQ5rwmnaUU/9Bi6gKFzWJcZ5zWBQkDfBYzBY5oXHOcVKwP7/YgheByXBTFnMBF65+QZFFxi59CRA1JE1LVJQZwNxwDHiPM6IQcH8g4738FnXe9wuLi8wr/3d/4ufvb1c9ysYkwnDTAZD1ibYW10ELammE3GtDOOotJcARgAZsKaEtackJgRzMfRL4hBGSEpbg5h2IFcB+8lcEvO4evnX+PtmxtkEK6uH6EbB804EABlXWcQWPdwJ9nO2pF+szIbRLSAaQzRQY1SLYHnLBn0li3lvYNPrA0PEsiFYmOx6b732jsVyHu/LcLF2QQRKFDRoQDh4oOPMK0rcpyQlyNomRD5jEwrpoWxrAnLmhBTlZcJhOzECe8uLgqlgiqdRqaZjJNS5uU0wZ1XeD8Uva+roDhWUt6nAFCjM6xxQ3lmy9TS8wTlbiUHGVfdc9P5iNPxAIKU3B/XjJwiUpyRloiUhQohg7BEYE2MackAeXx6+RT7y6dYzrfIfIQpRucAZGmYmTOj6yUDS9bcCiAjdAEDjyBHCMGjH3qRJYVrnN6Zr8KLh6oTWqC2mnVSmdCWpnPOQs3hWLLXUoJ3jEzN2DFA5OF8D+c6ydwEwZqHZM4gV4F0eAIlMrVf5tPu9X3LzfkHz2UyBBV8c+SKaWh0JKpOSrds82oJkhVLMNdFOAOHDqVpi1BPqZNGSudD0ASNjC4EkKPiAMYYsUbJoHUkIfoVUWkNEhzrfuwCGBEuC7+28bPKXTReXyNzdHU2/zc2MGjDxQgihHGPNfSANUEyvdnMGVs1ENUAqK0P5wjDMEqWvZ6zUDC5mhgRY+Xftkw+u+XqACsglTXrkTRDyXv0PsBTUHtOPnc+nnH78g3e3t7h5vZW5kOnznSzASnQRnxZbbNqb6DICuaq1+0ZSvZsET9c1oHctts4ThVYcOWc5nmlZJWEfgMu2Zi0STZBMx8liGxyXeknGttSLicM5BVw0WfKdh/Sj8Tu39YqEwulkVNb+UHWrFVBFlvH/Dy8K+vrOKKAd3YUwHXju2/tO/MZtNS17HSjJtv2emnsVV1nznlp/kb65/epqr/heFcWvj/x5pcdQjtiQBBr9j8VLlgbJ6OAKD60joL9XYIBtb+M9+LTWEY3gUqFofR8yBuwtOImEprKDXhGpH0aDHiH3EL5DlnghIr/Je+7qs6LbGHNuq2BjXZ+YZ8lbV5FBGoqFx5iNQ/XhuEFpYkoGCnmjWyTII7+roBozhm+Wa9WzUsgeADsPTof9Pq2r1yh4XBO7EujVoks13SsQKf3hSohamMs0vs2GgJP0ug6ruJvOQ9ULKH6K0lBxepnGbha/RqjtIlJsCKjqfEsWahWNSn0F4wuBLCzNVcbjNmeyTmLHvQASBIabd2y2kFZm+ZZWT7bvmTWhoKV0tBcwrrq5FGNuqEA8CqGvBO/PUZ5HiKR8yJSFXtwkuUsY1fnBcwgbWDmvTcuzQL6A0DoAiyxaV0XsReKPSP6PDsqFejFTmjkQGYu4xrjCkYwBkuUQKJ9n6CZ7+8mDT08fmXAWHKQ8pTg4ToHGgWMjSkinaOAQE6MDTZUuzX4YcLLNjoK2MJmPJtSgPzRhM37HGugKhHTqUU2NIqiXJerImzPU4R32fTQ+xfigazch3K/krl2tb9CiAkrz5jjLJO/cQDkdyo3V69aBHm5dntH9f5kI6dibEKfo+ARtqwMSCAUENHOXZ/YFL29x9qhjrDhrVND9qHSLqKZnEYwzAAykm4q99fOr3WG9E6ibNAO7pKLTxtj1JyFtpnYBuuiet4KbL87drZm7O+uGHBttrGOXaNAN8PfOHCuvZHmcvLEAhsmAOeYMN3d4c3tAa9fvcXrt2/xwy++wA+/+ByXF3txEiE54kSSvWonI1SjqBhEth9ISKl3V9fo+x7zbgcAmCdCF0LJijqvR7A1ySjzzYARpFcLXU8rwvK8rDhOK6Y1aeKYSmdSMNiJ0WBGvK3BeYn4+uvX0oXebFqbeyJ1dLhdEjLyJCZo6DzCrkd3sQddjEjBFS5gx5USoo3WS3MyYOh7pPMZtJntBwfb3i+TupnbnDNu3r7GvMzlOhtZVeakmXaqWcIPMzQYDCP4X9dVonK69uZpRj96XO4vsaSIJ0+e4P5wwP3hHlmpCQyUNXDYea/k4gJ8xyzlNYXIX0Ft414iaLZtCJimCcfzGVkN3rKuNjaqrC3nvTihXniIWa/j1DCszr3ThjJVrhTe3nZ/2H7DA6OYUJSqOXIu+E12qo2vGcRtFk+9RAXcilFPVPrpWPDA1ZXcnLNGmttGATbf3gkwY8bR+XzGsiz1GVSjk63J5vlMscOu2Ty3rSlyBBo6+IsMnxLWwxEEyZw4zjO+evsG+48+xKD5jT7Ls3oiBEgX33Q+gcdLDLsLhH7A6f4W8/mEoRvQjTvsrh7heHiDdT7BI6PrrzDudpink0T7c0aCx+VuRO8JyAn3pwmRPHYhoA8BlBIO5wkrS0bExdgrJ2ZEJIm+9yDMmrWXCAguILA4rjFnoPPouwDSDMeMjDVGhDCgI4eOPTglzDGCvUM/DPidH/4dvPzqOWhdgZzR+YAxBKywnLlmLzdbu7TPtLXafJSorq2yXwHEHKWrKueiG0vpMKQBjAMBzsG7EaCArs/AGnE+n/HTn/wEy7zi0ZNnePbBM208k0qX7piigknqcGZpNvjQUWQ0IopF7lbAg+v6LA6zcoHm1kmTz6YUlbdcz0xAaejTXA8FxKCiulu9Ddsz2gHXDPfWfuofPcY+kfCIxhnpfI9pukPmM2KcAX8G3AqgZlfFLF2enQ8Iu7100xZprPdTzy+clRHzq1c4fv0Ky5sJ/N2LdkMBLoBzBLNmn5EDhU45ZIXfzLofC5eblBZmNRZzbnQ/qVWgJZTzdMR0PmA37gAQlnnCuiyI6wzKUZxklnWzZsZxyjjNCS70GPaPEPo95umIzFKlYlk3ljwIiIx33mwvsan6vkffDbBspGEnst50lH176zjYGqAq9RioqWi2dioYW0EaA2Wl8irFVYB3iO4QOw7woZPsfg8Er/onRzBnUFyqjVSr5UHZ3jZbq4JSD9W2D1uaLQP4ZHqsUZMrzpedwJMDe680PlufwBqgWagtaOfnlBIiQ6r8SDuYe+D64hoxzcgM9N2A3TAqp6uMU8oRy7rIuUIAswfD9qP4PCUzqnlG551gVY2N0c4L0ASbbIpVz26B2Wa++0EyC9W2zqrPgQpsFWjGUQFFjNvSea9lngZckjrOVCqYRDamUjlg5cKNKSjzSpBMM87FhvNOqBF6pxnDOaPzDkMfsExnHN7e4v72DsfDUexEC6LAqgMr6GpD1cqfCsTW/60be+sL2v8mw4okVJ/ARKsFdwt40VxXyruVHsOytRofJCdNMCCCc51yXWfRgzo+rU1ZVrjeLCtoUbIEwQjO9rgG58g8PtISbF/3FoyzVO0q4wVmV7LvKte63cfWuH0fgFm5SW1Jmi4heE9qBytBX9GdkDXwUB49vIb6IEYM35h3G1fs/+3jHTC6/cUALeNGdh7ComBUZI2N19gUAkAZV6h2lu86yXwNoXKnMmOeJeGBc0amBM6E7LlkdiYFy0xnW7VH4UvW2622rNMfoFACeAXy24Et5r/dt4KxzhcADED5jtHOVPt++7w2BuXcTZJD8ZFga1Hei5yKrSL7QtagnVMCGVV/VR7yaucTOVCAgI5Zea2Zyjg4chi6rsxlZuO8TqpTpdcRAYhZwNgCCpJgFUH7fkRvjbPs2aoNaVRtKUbEB5XMMl9OG0iqXCEnDaNaP0b3stlkOSWw9r9orbGkQdISyLFMpURIMZcEnurjSXNqaSotysjkvFCviL4FcS0k5uorgYHMsezpWitLRQYUWgCiolPLHtF94Iq8pcYeJwQXxCxkw7AAi7IGHwAwEom+tcQ1MhmnHLuZM5L6M2Vdml8gQyDV88VfrfKXoQG+LNf35DeA8DcdvxJgrHMOu6sR3HmgC+DglXCdUcWDZYVozmDR1GYYSrd5IRpWLI6z6rZqcBRbRM9csxVy4RRpozImoLh64+UzJkCKIrcF4eqMydracrpp8RiYk6DzrF1mkTF0Dt9++gHGyw9xnA/4i5/+GCdOAEkGrYd1Va9CBgZAyNX1deVaLR3oyQxK1MXdfB9mnJJlw+mzkmZqWVkJa+o1qjKXsXjIhyGRmva1bT2G8o4CsJDlGlf86Cc/LsYXqAIYVau5ct8MwhIjXt+8qquEARcCEi0b40AmSRWPOsxV8TVrhO21rgM9h6XZowHvwCyAj5Z11+ZM7xofojhab4Df+d06VTdf2jyzCYOvXn2NF29e4k/+7E/x69/7Hv7w9/4RPvvkY+z3o2YKCQjOqGs751SerRxqkKac0Xcj1piwkEeGA4Udrq4vcf3oCuPlHv/6X/05CA7arLEIQWvYYGa9lbM4InTdAJ4zVl4w56g6KRUBGLogXW6z7NPgA0CS9XR/POPFq7dlrxaBq5ufNgOkZemsjkHwCJcD/NUe9OgSpJ3ZAeFzbD2Wsi9VsAff4dH1I8R1ESC4nY4GzJNZUUWkKyJz1gxP2X+JF7DLYnC1gvzB+miNj9bgcM5hGAdpAhJzYVKx6zndt+PFJR4/+QDPrp6BX/4c8xIxzYsAeE48J2+hO4htkHPGssyIIETNjPUh4GK3Q3Aex9NBjH0QgAzvCF0XEPpeskSdlmoStLFLO04i4TJnLDEjc8JuJ5zCct8O+90e0zRJRi5L2SEA3J3uRLX5avzbRLVlgZLpzerYyWecZeHq2HV9j5wzpmkqPNbteIv89Jtxh61hu2ZdcrbU5DN2DjPKci4RWuccpmnSj1NZn5cXVwAzTscTVsQaPa0Xlp3ubP+WyqlqCLWgHze7w9UmeGEfQG4AzzvkuwmcgOev3+Kf/A//FP/1f/VfwHmPPiUEEEbn0ZGH6x26rkdeI+5vXuH66YfYXz7C00++hddf/RzHwwHOeXz2a1/gR//mBIpnxPmIU44Yrx4jOQ/fO4xdh/01IS8nnI8nHM9nHCPwybNrdA6IccGruyMWOHz4wWMMncd0OuL2eMTKhK7vse97TMcT5ihchSF02IcgJduOwF2Hzge4lDCdJ1mnQ4fQBex9B44Z5/mIGBw4EDrv0ZNDnFfcHCesMeFq7PGtD57gy+MZr88zzqsAP6xggk4IzKg1BUsgzSq1TxgAohF2RyDvkeOMvJyl+REyCBnM0mhI6JFWwHkQBZDrEMIeOWfc3X6Nf/kv/hivb2/wu7/3+/j402+B2WNeZuHZ1P0Suk6oYVwStWzGdruO28hjVSabX8tesudVGZcyYzZ+Ld1iRA45RlmfUBlFbpM1qG7VJktegiS8uTixlKanFDGMe82yaqhNAGQikA8gHxCGC1zmDwCO4LRiN55xujviMn4J/Fi+I/mGsj/6YQ8iKU8W/ZKKrSbN9xISR6z/8/+CF//sn+PN16/xh997ipTsPh1Ct8eynPSWHcIwYNhfgOOKdT4jThOc79GFEd4DKc/q8En5qfCYpnI+p3Mj+z4ipRMOdydc7h5j3wUkx5hdxHQ8Iy1zAcSXdcVpyphWoA+EftyZEacgZx2zTZYZAc53cC4AGEHuBB+oZGmQBzpnPJhaVqrr2TjoSf9hBsh5ycZUJ9TsN9OhFiALPiBzxjxPss5TLYWdzhMAQt93GMYeIEi5uO/AHEDWZIpMVitfKdeGrMwZubIIgMjuX4AOUo72dp332jirrK2UxJegoDaqL3sos2StAsB+L8Fpr1V5WR9YHHOgpURowSSnWUkF9AMw9CMeXVxrVjzALJRsKWdwYPRdj9P5BII2Hex6PZ9l70jjrLhK05cUUwWpCoWN26yH4pMUOVbfc5BmyaZHGz8eQpbMKPy7qLa42cXStNVpZpsv42SJCefzhBA6UDD7pja0MQohRRuFziFrkF39jsKlyAL+JJJ7ogz0ocduHNWW2GFMGU+uLvHd736KNTL21wNOsYNzCZ3P6LqADkCfCfBOqWbU9QAVWjDzGYvs0jn15KsobexOp0D0OI44n88o/peZq7QFXw2AFFCgLGB9XshY6Ntc1qPdi8OyxA0wZZvTgFQ039VfEGNGYLtXmScrcXZN9REgtr0noUuQtZmqD17842pHOebCg2v7wewh+WyzCct4K9jX3CcRKYd0tbWqKjPfQgFpnR51WZtnNa5uCUw5S/bYjEyjEv+WxzuBzgbos9fvs+vtkIa1DORcuEK9d5q1D4C2lFwhBHjlxOy6rjxDzgKQLevanL3A8bCkBKNpRE4AyXzHGKv/4ASs64cBwftKjwA8AN+04Z9WUxgfaQWRRV9kbc4kTZpY1wMjrZW2qx1BA05Tbqgn7IS0kVhlvXjTV7yd00IhrL4hFX/Bzltt/jbTu8xZ1kxhXqXaynu44IGktFMsweiYGIgkWZoQz9yxYCPMjGVZAazotKKgc75CFo1tyQB8IHh48UoFnigUHaJHhWt+1HmzhsaGVRBJkzfqCTzmRi7UTHjyfa2yWFfpvVJoE6jQH1j5v9HDFV+m99jvd7BM32Wesa4LrCGnVGXIvawpYlqkEXSvCXFMCY4EAJZnWMp6iTGDllmvJwkF1gB7GHoBt72TBA/lC5c5iDBKD3uG0HUFswFbIo/SGJn9zhbgEVk1aIO8YuWTfUfW2IoVgS2gLufxWulkmbHSUNgaqDE6F4SqAAIoxxTRhbBp9PlNx68EGIvgQE8uUDLeOEvLduYyUEBbtC6HGCcoDooZpk4Nv6pwKpua14HlpIAB1NB859wmh7YOghkdCpnUzvZmkTUfLkg/DIBkhTZY0tRTxP3hVCIaEvUKOJ3OuDne45zOSMhIiHUTvkeTNL5hvVE8fKN9QstasUVqGYZUgUF7JvtGFlBlK8hyAXjtsD8zbxUxNYb0VkXZ1eQzvpOGDW5z1za2baavfVM+kXXuxREbsHQLOCclmm+uX+6tcSIaa8nOH4IvWSZN7iRCF+B8gPMePnToR+E6XuYZ611EXuM7SvqXRURK9t43/P0hSEtBOkHfno74P/78z/DVL36BH37ve/jB976Hv/cbv4mLcSellWak5VoK1q4U1kY+3nv4fgBzRhdX9OMFzi/vcaADPvz4A/y93/lNfP31l3j94m3hYAE8MhOgxqX3HuQ9+nGHfhgx7C7Q7Ubc/finwGEWgYykjp5EKb06FhKV0hHgjOfPX+Dnv3glDQFKRkMz3+0iIBL+VyYxvDqP7uklwn6EH4fGOfqby4vsLzFGvH79qumA+WAu9FlzaqP68u1Cik8OaZUuzCbB+L1n++XHNE2ynvTa5pixzl/Xdbi9u8H5dMbL7iUO0z3mOBWnlFT29V2PsR+wH/eIKeH+/h7zPIEIGLseSQ3ZtKygTjKVxm7AOF7hcr/H8y9/jPP5jHmWBkhkXTAbEMWUmSlJA5Sdd4hrxn7YY3FiEIy7C8A5zPOEFKUBDkizZbOMGHPlFSuZQcUhkJ/O17Lplv82poRlXd8LwraA9/v2JjXOV8srhMY4LQYNhN/Wrts2zqiGrczZ8XiS1WKgk0xqvfADQ54Im/MxYyN/jTfLnifnjBQ12tv32H30FMf5FfK0Cs8iE/7b/+6P8J/+x/8hvvfJx9hxxpClNNcFj2HocF4XOM44371GWhd89OlnmM8zTndvcfvmNeIa8fn3fwMvv/wJzocbYFnAh1vsd3stqU5Y5rMYTeQRdpf4dBzg84q7wxmneUWmgG998BQOK5bThNNxQmSHy/0OBMZ8nnFYVgzDgD54eAesy4zY+WLQ+JVxns7g4OH6DgChyyRd6ZGRSDK5L3wnen6NmDjjD/7x7+Gnf/1jvPr6OehwRDoeQSz2cgm+G6qozoQZYtRMky7zmnmQNXs5S6B0Wc5Y1hOYVzBHeDdokFYb0zgJBMBJKf3bN6/x4sUL3Lx9g93lJf6z3/8D9OMODCAlA0UtA4ExDCP6vkMIlv2Icp/vPVThEbXugOr/st4kI1F4vHzhKBOqEeFaVGKHolscGB4ZhEaHERAa2nhH76qfBCCtC+bpjEH5vNr1b1U7DLIiFzB5AJKd6q/2uLp8iv2rD8t3vvh3/wNcXH8HKUX0F9dg7wsPtoB5dU+ntGJZFrx+e4O3t/dY1oS7w7mAsc57XDz5FNfOw4dBQLC4IMUZh/u3iPMqVorrdC4FcJcgYw+/kyazb9++EV53ZARyGMdLuDDg6uoJ4hLx8stfYDoeAaZSvprjipySUhMw3r7NmDOBgscw9hjGILZNjkABe7mMFxyhG73YxuzAWfRrPwxYMCOvCY6CrgDNevLbdVCPajPKS+XQ1U2w+WTh/oHalALyxbgq2C7NQLwCUSml6tQ780adrI6MUjEjZqolNghY55xrAlmE80/lNAAAIABJREFUEISrLWnyxUNNb8FoexbbKQZc2Hmcsx7vcnjnm1JWBQMABX4McKBKIaM0PATJnDXx4Qja18EhJuNKJbDvUKtzGLu+Lw6zjVPOSbJKiRDXBQGytrxDycBZozQL7bpewcuyKvC+ozQ11s+0/gsz47wuWFgSXBxlyfC1clFqRw+whxd/y8F7aGYXV5nI1siSVA5J06DgCNTV62bT8eb/qkCZCvAkVZRdF9B3HeZ5Rh4u0Q8jHj1+hk++8128evkKb9+8wouvnuNw/xrjvkdKESuz4CiomYBenXB2khzC0Ix2NPYCyf1v+enDJgALQDj6zUZgLs1jBIiw7+o+Y9XtG59RymwJBiowPACn64O5BevqFy0zv72/mtEL7Peh2CfboHMFTbP5CqzVg2xZ43a1uq/tDO8D7LYZxXafDbBmy44qwNpWK7X3VqqMmrXRfkdO7epIqJ6xIIgLEkCLrh3k/7+Pem3LtGPOQCawa3plMGEcumb+1HZMCUvOpYKqANJWit1cg0h5lqnOlwRLa4VZ10m/CUvQSTGBWFpg29GuaVZ+9aKDMyPniLTW6r0yF3YTek/SKFZt8hhhCfAA1+CRPkvf9xtZxVxlK9Qe48zaDJJKc0z7LGtig7fsBSL0WpHHiZVju2ZC2ncsY9bGfV1XnGOLt3DhDLUfox8ofkRK6PtBKQoEI7o/ncSGybmAsH0v2czBebXrlM6Hpfldbb4l97TMcxlTbkD2Vj8veQEge9VK/p1mT6csjS9r4lRtwmrjZuArkYCTQkOXyjoQnFmygkPXYRwGpGTZ15JVa+tq73a4urjEsixi87AFdjsMvVTjJO15sCxLodsQuoka6MtZmqWaLIkxou8FnM05wMUFKSas64OeIVzXSFxXpJwEx9G17J08uzQKm0XeOuMgDgXAZa7yt3Pa3M4ZhZwFmaS6ESQVMSCZe4L0jspabWRBbQbjnUayD45fDTDWOeTgoWOPGLkYP1aGQCW8AEi5RRv1sAmhUqZsZfIG4JliKbmOqhht0Am6+LI535bxRkUBfbNIp8YwNdCHyiZoP2dGVwYhMWFeEmJ28F2H4GVDrWvEq9MdpnxGRCocWqYkN0p3M7mN4Sxaq3mf33lds3m5KMc2Ew31bBsAo1XRbWSTmsvXp22Ng/eMXNlHOk/FOObyGK0XTO24Nsa103IWlFIuD3YZ1lRlM4HNWhHfRQwyu3cmSAM5R4AXjhhyXo0lKe8mL1FLCtIpr/MEf57ASj5NphSaZ1d6PHWadI24ZrzLGNUxbSxSFAtVFzMzsKSE1/f3iH/1l3j55jW+/Opr/M5v/iY++vBDjGMPKVNuSmUfGH+AGVUOcB7dMOLy0WPM8wkxrnhzc8BP/vpn6JwBARZBIjjfIYwD+mHAsNtht7tA6MTZIufw5u0NpmkpTQmIUDJFRMiusAxAm5x1ybi9O+H2/ijZX0hbPrOHh1Ol7ADqPPrrPcLlTgCaYAZF68hZDm9dC6YQ7TIptWtaosAGuNn7Vo5nStKAWJgxGISzxjVA4QZEhsyF8crZazLZZo4Sl78WGcM6d8Zxs+aEtJywrBMii7FSgQeRkWuM4MyISiq/5gjWDP6+FzDWOlXGnOoeyQnz+VSe2XmPfhgxL22X5JYTiso8SxaIKHLp+rooqX3G6XCEVNrIumMtlxpCh+xtbTQZ/Dbdvpbs9H2HD54+xeFwxOl8BoiUO6l+3sjbmXkDXNZqCdoYuF3XYV3mkqm3ASZML7Bmm/M26FI/9kBT6MuUbS1z3dfvrAkq52hB2Pcdxg1mR86WFUYgdkgdMD69wvz2HvE0g5hxOp/xr//s/0I8nvDv/PD7YHZYUoSbJik1jGLAcFyxTiecTkd8/Nl38JKAw81rLOcTDocD+v01yHnM92/AKSIuM1zo0YcOq9JRDJ0+S1pxezxhyRmuC7je7YC04jSfEXOC6wIe9z2WFDGvK6ZlRdd32Gm0O3GS1mpW6s8Z8xqRjTifAc+QNekd4B1C5/Hk4grH+zupsvBidF2HDp9/+i3suw5//ld/gbHvsB8GzJnx8nDEwgmWqaBGQdGRlo1R5kjlcatazLZIOQoXINfmg1T+QeEzjuuCF69e4XxKmM9njPsLfPbdzzHuL7Am4/oCcorIOSGmqN2zgRRXILOUUnOz0PQoZiA/XGd2o1XfyFrTcirUbLgQAhYNMDrOcDkiriLTU47qqFkLStNldgE0+4Oq82wOdkoISEjzAS70oK5pxvHgVtt3igTX89nR7S/QXz8WHuTQg5vv55SUUiVLADEnfPsnP8Kf3txgWRZkAOdpKcY2AJAPyEoD4XynPMvCZZ8yI2V1ioPw/Waua0WNGYTQYZ2ilAIi4jQtIB/h+gG7qytcPXuC480NVu0inBMjp4h1ZUxrxnlhcD/AUxZwYSSETsFfygBLJonzsrac9wi9NhNDUj0hgzUMPZgzFpaSbxR7S5fDe4LCdZlUh1+SDBjtHNesqVqKC0jCQfk2yXoKXWerDmSVXqqnyDnJDuQEcAKaLEDbdbrJYLWPzomZV0yj94GxhMoHC4BIs0ENQDb73daq7nWwcAbnFLHGWWgYkpaUE2HcX2AYd+jHEexR/ZasfMTLXJrA+C4I57I6t9Y8uPgmrOBvoecR/e212zkgjqazSEfxYSwg6gRgaGP3eg7zO77Rk3kwYIlIOfMEiLWxKyCZl6BYtuCFq7RDKYkNnjOXXJZKV1ZmEWAFcPVZzEYtPQJ0nhxk8ghC/+MdIXhpJrofRgRycBmYD2f84i9/itN5xuHuHvc3B0xrxilnLCmLHkClZ2MtY3dGldU8Hzd3q08IoQJB8TMU+QOQEVPtam/PwznDdZ3yrxKWZdmY89WH07lpgFTW4F6pyEMNHLcNZQQ4q6+Fj1gOKU6ogJ/ZE3aN7f9NF/L2/oiq7233So3/DdlXtn9tp1rztbZ8Vy5d5//dYPj29Qao5VLnV3xE+Z1rpj+JjyJpFNWDb2XFe9f+/8PjlyXZ2KWLb7NGpZwAymARIAEMX6ghqqo2n7juB+h3C1hfqHjkGT18u8M2/gOp/SrBB/XHzAbOuj+INoC/2ChRe5DIaS07td6OXqNQf1R7uvwfglZS2NwVwSAy3DsFsCrgWAFbp9e0vdVUrOo6EE736meDzPZw8EH2TMhNZr8CxTaPxmM9DAOGYUAJXmQWe1gNwhA8fGb4FAvfbtbvO+clOE6+NJvKnJumc1I9m10G1D8yrl8pQqw2FOtcpJyQY1ZqN1eagVkVYKEyiAl5qYkbfdcrd20uVSNbmeFKBmjxZ4w2hAjWuCpzBht4rDqR2Rp01oSUsn5gOJpWXejai2tU20Eyfqnva0CBaray+blFJqstEYwfmMTvSzFqFjLKeVoAPWmjanKmk43OUmTTMPQKGqciP2RMCCmmklgj3M6uJjap/BZ6ioQ1WYKZU25bApEl5zAyUkkONbn4TcevBhgLBSV0Y2ZN4xdLouGB2gjTmiVZgViqACPLJt5eA0XhmjLYWOx2ZrWQKsebCsR2ozRCrgCJJnjNcKFWGL8bo2aGlp2Iovee0XnJ8jnNC055RjfoBHO99vuUQL3H7e/lfpuRK+d58OgPFaG+2XyLCqBXI3jbE5fvlcvb63aAsZ3LxkApJSXcnLZ8lzanqBdt31TB2HnNUhKBR2KrCljhJZfH5kfKrKzkXM5j5abCY+ykGYhNsoK08J3wZjKDEOA7jzwrMOXcNnuyeR569wk2h12mDRi898nVMZpjxIu3b/D29hYvXr6GY+AHX3yOZ8+e4vLyEqGT7BOJ8Ns1uC7V4jwRXOgxXl7iYnmK6XTCHBkvX7zFs6fPcH9MmJcEch4Ej34cMez2GPY7jPs99hdXWiqdMZ0n3Nze4awl4tZYwwQeoOXtun60jxMOxwn3hzOmaZGySOSanF68Ft1NpFnwwcGNHfx+QLjawY+9SPOywGuE/b3r58F7tmfbaOh2frhkaBKb8nCbkg8JCEhTDwIhMiPxw2uYg2iOhyvGprwmneNy5Y1hLstD6FxESkqmxdCPIGg5U5KyNmnQlbBqswg4AnlSQ8iDEySKjdrFNOeEuM7gqBxAaiy5xhkwg0eiumbw1Q0polIyvlIDYs7zGcMwqFInMDuM/QAm5VrSc1tk2Urwy1wRFe4se1Zy2/EDtNTL+03WqslQA5FbURdCQFoXeVRQc75tIKO9l00zxEYv6JQ14o2rIf4ewGAD8tlvJMCHGFN456BmMUlWRLNevUN/tQcrR2qeVjAYP/3FcwQQPn78BF98+DFiypjzCk4ZHTkECCCS1wnHuxt8+u0vcPnoMdI6Yz7c4f7mDS6un2DYXSLNE9JyQFwWBBBC76X8RwGVnCNO5wmnJSL0AePQYz94TMcJ0xpBDhh3AcwOp3nFskZkADt1YmNOWHMGO4JXvZsSY+UE33Ulq9WBpCGLE3keyCGAsMYkzYKCl2dj4NHVNUCEn754gZhXdD5gooR7YmQiBc6AjYYsdsIDh9FmqxHu5LyCdQKGOV075hA5ErBmXSdMpwnH27c4nhL8sMPloyf46JNvCXige5VAyhFbjVvW2xJOLb9ZP3U9PdSTahhVk7/5d7sG7XBGSZAS8nwC1kWoCrQJEeeMBKCmeNWVTuV8plepZBk4dTw8gLycAI7grrkTzhCPUc79oNpV96w5ZXr4ANf1RT7b36iRQzYGxAlXX34JPhwQoxjU07I2+1oGL6cs3aRBcMa/nWUNCg0qKYAGGLAIrg4feYfEjJgzKCbMy4xhjGAi+F50bUoRYREqGinjjvArg1cGL4zR9VLuF4CLyz36nkGYQRThvDYRctJV2AfJEiXKdbr1kUIX0LNkIaeYN7KqyhGzn1vY7sG60hk2meSd8AhKVYgAO6zl+7ZGocFBa7gBagCclr+7AFRC8VB4YDd2v2aYNPY2lR8qDuVmvTyUnRYZbz9HzWkhDmZcFqzrgnWdsc4npHUuYJ4LPYIXOgEDTZgz8roiLgvOx3vM00kBe4/Qd6BuQD/uQM4rT58AsAIo5JKtZRNnAZ+NxFGHs5rY1YmRZJJtOfDmBdc3qH2Pt59jpZ+S08s8ZdTGPh4KhMgmF/uH0HDj2TzYvlPO2GbOwEYvJcBmacZDpDafCfetHeYg1BZ9kAZeLmf03iPA4Xx3ht8NAHnk7LAm4JQyovGckmTVqTMA82kKqVfrd+Dhyqs6nTXJQ+wly1itVUtqmimgJHJBKg2aoNV7DgFYslRccmt31DGQ0mD5fAXjdJ50/xqwCmgZeH6/32jfa7cTuCZNFLu57M9WTPB2XzVzRBA70cYUuWm19cDwaQG89r3t/dWJofoh1THVh5NLcZH35s/xxi79tz+o2QN/03vvu+96yOcMFGsPpzyiLcBu3ymBlQ1AqRtVwcINCFWcCluBClQyC62hrQuTzRAfV6rRUvE1LAHCQMqUsgSPjcpEKVpYx6Datw+e3darc0JxyFD7p7kvo5axZ9TrWuUD232QVHfUJD31RcjpWGkGebbKW1JbrVZKb6rsCiesJrepTgohgEAFRM2ZN+CzZHLKe8mnxt/TxllOMiz7EMCQoGdaVi1lr7aBLcxaGs+wQHWxE/W6mXIZuzJGCsaSzjczI61Jk0iA6BKCJeTAZPj2B3oe0yWW3OGcAzdALXlZNzEL/y1DKD2dc3BBKmxyFBlujYXbnhzspIJc7rvxE9v9rPfAEHvZEYELRduWVsE5QnKu+G/2HJUyRzKAnVL0yZoTOem8Zb9KUG9d1mKXlkCo3p/pefPbTKabzIEjxEUSFToOhXuWrANFA8jaXvimpETgVwWMFa1V+PeszAWsNj8AoHJuttE/eUuNIE0Ndqottl0gdQsXpaDRGZmvoiz1SmjiajDBVu+1fb/9+8P3xaYg1XSGKQVUBXSaznAOaswG7MZLDP0lvOuALOUzzPXzzBlOF7w49PW6pozNCHdlLEzZofmcds3jJj2+UQglSmqCnh8+q46UlZfrXJRzYbvRbSHryevkUfNrUTZV6IDw3mY4QFV8ZU4ZCjJ5hIsdeEjgmJGWCOIM30l2Qug7JLtrqsauvHYCUukF26ctQqyMY9Jnk3IiOOUUySpYIZEsa8AAFZQmMJihXCMogkzPXDoVpqzRcavxaHn1dO4S5JwxRxxevcQf/dP/Cd/++GP88Pvfx+/89m/h888/1xI5LiU8MSaNilrGlwHtDl23w7MPP8W6RiBH+ED4B7/7Wxge/xVu745YVymnuri4RBeCpPj7APJS0jdPZxzv7/H8+Vc4nc/aoMCarVnDL3keJpRupxmMn331NW7vDliiciE2mKotl1acueDhr3a4/PAJdo8vcVymEv1C2ScmTkucfnsO5ZWRrNR319as5SLVOa2GmMjkKpcsS2VdtcSX3iXubo05V5yt5s7UYGmzGEyhtvYOoRpDPnj0fYd1jbi8vBberxRxOh8xLwssqCU/WYwGEg7guNYoL1gUZkZGXhPiuuBiN2DcDZjmBfOy4ng4iBOu5U+C46f6XGpI2pjknETeaNlLkU2OsEbZLkPX49OPPsHL1y8xzROM4sU5YBhH7PY7TKcJy7qUOZrnFc+/+qpExA0AkmYVYlxYKX/bMbZG/ut+k71UKQeKQaeEKa0h186hZE77WnIEGNYKi/LKlLpSHpW1QVvNWLJ16ArXoMlBO0wW2zccJIs3KcdhVoO26EGI/HVjh92TK3Shw+nVHdZlxRQj/uJnX+L1qxv8N//lf46RHIgzEBmuC4gpSUPAnDHdvMTd/gqXV4/Qhx4//8s/w3TzCsF3GHeXuH7yEV794h7Ea1n7u4vH8EQ4n+9xPJ/x4u6M3eUej/Y9dp1DXGa8PZ4wjAP2Y4/LweOr1wfcn1e4EHC1GzF0Hqd5wqyNjPbjAF4T1pQRwaC+k4wo1Y0IAd0QNOuRQfOKF9Mr5D4ICOU8usSYU0RyhN3VJf6T3/9H+Jf/7H/F27t7zHFFD4LrO5w5SUkroFn1agg2AEWr14qBrL9LN3vZcoX3EJZZLh3RD3f3eP3yBU7397i+eoxXr+7w7Y+/hWcff4rEDimvMHnFDCzrKuVe4wgfOhyP9xj6HYZh1NJDFIO1lQ+tg2y73/SqYjrlc7B139hD6xoBMNIy4/Dya2C6x3hxgW4YMfQ9qOvE4WDJIFzjCiKpTGKIkcs5I2o5XPD9hpKGkZAisCwn6d6+Vx6vNAE0AOi0KSXDtlPds80WLhLAnE80Ze7CT142p+6v29sbnM8zYkroHElmbG5kArJWE5wQV8LQd8gxIq4Jcc1IiRsA0IK5tQrD7NKUE2LKICTlip2xrgnLsmJNjI+//V2EIHOYOAJ51UAaI0ZAqKAYPghv9/4iI8W38GHGuHfgNEjpdi8aPaVVgGIQoFnTwgnusPMjxnFEWuWexHZqgzikjn6SYLINWQv4qSninNiQITjlzTcnRTOuvANBGrLaqYkkG1Iy8azhChWnG2Z5q0yzPVCydlnKfS0j07akVSlUZ6rZq2Uz2BOgNKHaYBgA4GrmXUwJN29eCS3FKna6J0tG8LjaX2Lc7RD6DhkMD5ZqgrtbnA+3WI4HFKp27+C6DtQPGC+vEboBDNFNw24ne2xdkJNQdJFz8MHBd72WZzs4SDnl0HdYlrVQ99je3zj65X+VPrYmNzzSW2u+vkmAD+i8AiJJbTU2MCIgdMJFaBVBnZb6mt/AzKX5iWUYPTycBk+NxsLmv30WCboGROfV1gKQGcE7dMEhLwuiA64+/BCffvYJvvuDL/Dou9/CT3/0ExyQEX/+MxxAoGHE4D2Ck6xANQqLL5JTVDCZyhAU9V3Gq5U+KAuHzX4GF3ueWPhY50XKZWO0cmDSJj6+6HORuaJDLi+vsSyL0C9s/NxqD1ojVwkK5W31UFnLKi+bdPA2ucAy/za2AjU2toEQ4qTUc3I9l8kEZ5tI0LLGdyMV84zIUUBhOweMGsMyBA2K0Wu3gFHxE/XiqqecyQ0F7tkxKASktEjyQYpITUNDu5+/zfE+EPZveQbYpFjmKNRmcVp113UKANo4MwNMSEhg+NKNHRA7P+eknL6VIs7KvIO3HghyaUuuEF9LsrOj2sVdJ7QIbam6AVUt8Nf1XQHBpAQ+oAudTgUrRUDlLJVgqK07KvdFqJQSOUV1ZUkr47g2CNdsc9dQUOSoFJRl34htJoBdBXVlxKn4F1lpo2wezMZmV8H/ur70Wq1c1fsxv5VKUyahtPHkkFIEkfi+Tu0aH8SOcZzhjYbF/EQDcC0wCW1QmPNmfRJJk82OhVvdUa229Vq56/sOXS+2zTKvCqhyGXPZq2KbiOise8pAaK9AdEyp+rqKR1iwwOm8Ro5YozTadUSgGNUuFntxWRbxexXYhCNQdgUcJWTMy4J1jSoLA8ZxRFYaG2v2yIqVmJxwKlsyM0gpjDb+MTMyJ8ULVV+pXWOZszFapY2Mb991hXbIAFsiaeBt9ltmIK5ryfQnEv+SFFMLTs4bgkc/9JpMWbGZmCLmddH9+V5tW45fETAWwhXVgE0xRjyMIbblu/LagETlhi0GR0XdZaJsEJxwxprBnoHduPu/mXuzX0mS7MzvZ4u7R9y4S2ZWZW3dzV64DmdEjoYQRcyjIOhNj/pLBUESMICgh4E0gAQJIptssrlMsbqqsnK9Syy+2KKHY8fM42ZWDynoob1RnffGjfAwt+XYOZ995ztVn6NWtrY1zKJ9of68Zii1QEsfQ//02OY//j3FhYUjd8d3hCWw2YA3mTgesDkg+mO5+k6iB+0guzrJ5PmodHAoeyJNwwp1TKFpVoh3W08vdMOJhbWmNxbH1q4ar5vl46qi7fRW05NyWRDvPb96wjWyUkZ0Y7nUtLiyAdfTWdrmuD5JXRsYnTO278iliqNJqZzGCSC+ZKnQbbUDs6RaixsVSxGmViCnjJgi65ClL111XCRFYgwzmCS6MRZc79luLyS1OmVOxyPLOImTmqnOS2XWFeYhyEnTFNrJnY6JBiXVMdCiFFlS/rqhJ6TMP7x8ydev3/B//vlf8Ie/9/v86Z/+KZ9//inX1ztSDrhsygZm5NlMAR2yJ1uHswP9RsLL3mWmCT569px+uORwmkklNRXryEac9s4YpmnizZs3/NUvfsHd7b20t55qQdcJSzEEFf2XubDExO3xxK9evOZ0GsvQ5/NFVed4luIRnae/2cFuYHGQlxlrrICSYSHEQEgLVeybXFnv769IU08bL7Zbbt+9O+vnD/lwmoLpSpC0HTYSRIcFYy2d94ynkdN4FCffCoDmSsA4jmN7NHVsS1vWc72OPeLQdV1P34mm6+s3bwpo4MjJkeLM23evV46sTCtlSai4uPS/jEHMka7rsDhykNQvEC0y7zwPhxO73UUBbsqiT8L2ysXpUfZPzpkY1gcGjYEVc5RApPcMw1CB+oyI/P/NP/yypGrJZv7k5prOWeZl5viwBxxN61qs0ZzUnqm1a4FpCIHj8XjmdK37dN1H2tZ5notZamsuZ5F50DFaV8ZMORfASrYuDSmErFbWSAk0peiSBqb5fHxL64dhi3OOh/1Dea8GPKzsocUVrW5jwaS2b8o7dL5mAga/2eCMZwgR3txVOYqH5cTr+cTz7U7sZmFzJivsWF/WzP7FP2I+/pzh8pqf/Iv/jP3bl3TDVvSzrefq4y843r0ip4UcZo53b9jePCOZG4Lt+MjecbEdWKaZu3EiY/no2Q2bzhFj4NXtnteHmeurCwbvscDbhz1jjDLP+x6TYU6RUPauHoNZgjCou45uM2BOJ/IsKfyLM+TecbW7wKVMmhceTifsxZZNP9BbC9PIH//Rv+E//Pwvebh9x49vdnzy/Dm/+PpbXh0OHBSQLQCUXfnsur89LgBnEObVNC+c5oVQgEGVu8kZvn3xklevX3Jz84Sbz675xV/8Jf/6T/5LtpdPML4jlNR/56yw1RP0XU+MiwxzKh5HLoWHVJAg1SPGOt8LB0WC/izabdkYsl0XPVibWGGFmBIwkrOkySWRXrn46BnHNLM/3rJ/faLfDMRlxvtO5GqGHc57NheXdH4gLIHDwy3LKdH1A1fPPpF9RllTSYB/MGy6CdDCdxHSBATRPO1U/xsg1fl9xnYqgb+kSbtCrmt+BSRyDiL5EBbevHjBPE4YROM2praG9BLZTgmaNtuBw+tbQjiRsuiBe9eRs8hHLFE0+GK22CCsmvuHvQQZ2UAI3N+947jfM88z8zKzhJnD6Za+k2JEMUZinOk6V+R+vMhRID7gMPRc7jyOA4kjkZGIargNNWtFtGSFWWWsZKuEJVb3D2Oo8nEF+GpglBW2XzQCElVfMxLDIoxtEs6JBp6y6Kz1hLiUbAZT/Chf5lhJgwTRd82FgR5LunNJE3fFSzMkCWydYZrmAjg0je7KsFwxso0p9tA031AvZeO+dzVjydrZsMZyfLhnPO0Jy4hop5Z+6wcudk/4+PMfkKz4jSaMHO/27O/eEqYjaZlFyx6L6we6zZbt1RXDxY4QpfBHmCeSMRz2E/M8Mh4PxNMJr3L1Vj579fQpm6srfHeB9UUr1yhwlsv+UlGyuvbXWR+sH1P9n4pEW867y+D67Zkeu7xc6gt4h/WeUABhTYM3SDFQlXMJWrm9fHPnOylmUtLqxWamUiBHMgCSbWPQUmuFpZTCDFl8mKHo32/Nlq3rCUvk/vae7776hr/+m7/h2xff8uruDtN5XIQFi0aUJpeU0jKHjJG9RPpV44umxbzuF2V0SeEz7U55XWRbVLrJiLQZ0JVDlPeZUSIAIGtH4rTTUeyfc5rR01KcFTxtcde5ZMG6vWeH+1DAkFalvVYrt4/JAgVIr3JPRkOM8udyGFNiznVRYgM186mCqQUIOgPjjbRPv1e4ZOes0fXBdtmBKQb+rM/1filnKWgYo+yIxhKsxW96knNkc743/v9x/aeYbu1qeEJMImmx8VKsMJRCfAZJXVS+AAAgAElEQVQ5fNFMrgY3JGLIBfBTdrkAoiGEOpbGBDCGWfvWFvkKwNlcMicsG79Z2fMCatteikV5T1/095VooenYsbBExXRklnlqY6BBxupxtQaFzsMYzsf/DOSmsGNpZANlQyoUIECnFRA3Zyn8HM/73rrmzAi4nUhRgdoidVHnj6yFzWajTQKo9kz7J8SA9x1aLDlnqRujgGqIEW8d1uWiAyyZMOMoe4bGbLrOZO2UNRaKpJxrEp3rS0kbztqCzYQKLsowtOyTnEV2pxYGzA2INCWmSjE2vEOfuYyvwQjo3zWJBtHnRUhmVjI7Qoz4ok/e2LupFvKKKbHMq4LOJT50TsmU0ufOLgUEFezDezmgEn3tyPF0QmVDl2UhxkRfDg8y4uOloh+soHJj/SZSCmdFCuX+nhTFzwtBQGW1i8YYnIl1buYy/lpwF+QQ2Rc5DZn2ht3FRdWONQVTikHGzRcw3bomReh+jX71bwYYSyaXamkm5wImaqPfb/wZ+8OApoGsT+raYm/ArC0bac5yEmGtJYRYBrYxYIqXg57qysRVB6a0OHMWCIi51d15xazSoIbGpBHwS+jL43wkxhlJ6YycxpP8XSoYSOBfgLNkYjG0phqV8++vvYmm12RdqKaxP9cYozGmOUOPHNj6e17/s3Z0Fcxor6nxJDfphnoam1ZUeCOuSAqxAoqPXIIWJNYf1Ek735DPNuYMpVZra6NpWU/yOaWqN8MsbVLn1LQT5XwW3qLsxMacFGAqp0R/uatBrKZhZu/BOqw1bDcd3WliPpwI4yTpiNZVR8VAA2kpIWcxno+vc5ZkrmMqhDoDzjLmzHI88ud/90veHvb85Ec/4Gc/+S1+93d/SudKekFpv6RalL5pkwOyIWXDw36h7zcMS+Y0BoodJFtph3WWOSx88+03fP31r3j95p045QUMF0fCr/qtsROtkfn95tUd0yiAgxrdddp1TsW38xa36fAXA/5qQx46cBBTwGOZS+GsFpA0/niGUrBNYxJT12smEcLC4fh+UP5e/7MGySFMM8cgczvljOtcdUidcwLIl80qxbjCzsrxwXqdrGxZfVcxXNZYckxkm+m2Hu9tSWlemCY90ZX7uMK2n6YFTe1s+r0taFuPSUyRTd+TS4AVQyhFWGI5KyjMI6ebOGyGTdE7LFo7MZYUtXatsxQq21iXm64xJ+swGwFZxtPIbITVFVcHFfU+6lyVINki61zSikuaOBSntO0Ja2d0/bv0m60yE66A8yGEqm9sqpU/B73ki8qzFBvw9OYJBsPrN29wVtiNtb28LzsQYmScxurUqH65NRIQxcq6SUQT5CDlkWNbGlRtf0IOnkxv6W52chh0OJFDYg6R/+l//ff8V3/6J3x2fcMWQ2czKRrRWHReANkUmR9uMQZuPvmMw91bjg93BaDruHn2ETFMLOOeGEacTUwP76DruRgGOnfD4XjgNM3EmLnc9QzeMI0Th3Hh/hR4en1N5wT0PkwLY4wCmpZKpOOyMOdM5z299TjgEEfR5DOQ55lcWB/GO1zf0RtDOs0sIbDEAEMvVW6XwJykoEPynj/8vd/hB7fvePn1V7z46ium4wlT2BDzasRVg2+1FUl11rN1lIkkQkqI7yun/0TD8XTieJwZl4VPPv2M/cMD93cP/Ox3/oDt5RNwXWF5G0QTVPakhGhmSZFK9XFsZdrotvUYfJE5v2LE10BaAl/R7iyWr/hdui5SFKYrxWnFOvqrZ9weviPmkWk6shwnnj/7nDhPPNzfc/fuHZ9/sePVixc8uXnGdrvj4f6BcTyyGbYYB/fvbhn3Bz767FOWEHj37q1oA1vL6YmDZx7IHO4fuJ+C7E/Ws73YYW0n6zosYC3zNHF4uKvPq6Bz05c6/zctM3EZSWEihYV3r16K1nEJGB6nsTorDBhJYbTMy4lpHgtruYExogUZMQhLMCZRls0ZrPd4JyxuEWXouLl+QggL4zxyPNyXICrivaHrBjabXWXHp5SYZ5UgyVgbCNOBMO9JacHYzOAlgHK+jGdO5RDSoZrdqRak1GBV/Qr5L+dEiKIbrDqUjc0h/x+WctCMAFrC7BF/KWfxFXJqrCxlawGI1jwYI23CZGz2YCMNYCr2PEVyiqQcIYei62bEL6qH0fbMV9HqxrnY1apJ+OuuD+yz9U8psn+4Y5lH8cNLgN8NW7a7a66fPsc6Lzrty0icR+J0woSpHv77rmd7eU23vcB6YZDvHx6Yx1H2JmOwXc/peGSaRuZ5hBQgS0aNxWHmmeX+XjIXyAyXm6LhqnNdBkey0EyVTcrVb828/4TtL2d72dmGZJANzdQ/xZyIy0ye5ZOpFPhbg1KmzBvjZDdOhallMGJzQ6AVm7I0jWEZw7gsNJZ5mbHey7xKWfjBDjrn6BBWmvUbXLSY0ZDuIz09F27Hxi8YMzMTiaivW2Kroj1rrCFm3UNzfXJlo5fZW5+v+Qyy2WvGg3MOYvM5Lcp6E8JD2fLLfDUtjky5FmFztqX3GsC4cwZrjW8LQ+sxGHgGnNfXJM6pbOUYz+ofrJ9J71EJTOXleB4E1TTgpAft6/iwBIC6L2n8aTFFRopqjw0KfJgV811jGem7VDZbtVca3pjiPKrVXsG1FShy1tVMmfUjnLXhsRP2a64PsWT/SYBs6Rg9XE8FsM4xl9jZ4lx/9pGquVyDQi34ZKqsQd/3uALOKtlj3U6Zw0l0up2rBfgaaFXaElPV2Z11jpUsR+C9+SczIlfQypS1q/ZDY562ZlamZRXjGCjMTFN0O8t+otkcqs2dpXiocXKoYa2lz7LX5UxlxcYcz3SbvfNkT+13zSJrg0jJFG3yAFUa4NFhhSmHJa4Af1WSDpEiyAmyczioNUZCiYdytROmPWNZJylnwjgSUq7foSCqHFRKf0bEdvnCqhebY9FDzhCCZN+YxmC2qzmKEWAzJvUr5TC+EsHKGCnbujKc1/2hsXSW5emsLcXICnNbpQu6RvSrRJ2VZKgF8AUfKvbKZlNAa6kjkku/pZwlQ6TovWp2mjGJ+CiGrVKnta/lECOmBMHQeVP/5pzEijlrLREFjZuucCyYpM59Ywx931Olu5Rlq8/phHFd7YvOOais58cyJevrNwKMzfBI/LwN0vsBM2evr52F9XurGPHj7yoWu94/pTooNar5dfZZ/ZbHbzLtb+evr3Yq/UgxzpnEtIykNKMC/M51bC92RQduFbArWm9ko5cFriDNB5qhm9zZTrlqQF71qQGTmpGE8/7Wza7+Xhfp+YM9ZsO2Fun35Dq23nuGrudwOlZDcP4ZbWaBldfP+Gs2wLVTdfYAbZte9cPKWH3o761qQX2/KUGWKfIRpPZnN/TngXmGbCxRNxtn8aboU1lI41TqAEiblQFsy1c3Fmd7jLNuyt8/7bKIt7GkyJuHe8Zp5OFwz/3+jpgDX3z6Gbvtls57yKmdItXvWzNwDSFmLvoO7xeU7Vc3XzLzsvDmzSu+/uZrvnv5ktM0syaj6Cmabv56GQwxZqZx5u2bOzntNOZ8PlSwKxd9WI/bDvjdgNl0mM6tpkxqBOM1SF/6K5PpXY9shAI+qvOmp6cNKFa7sO731cpvsS0Xw5acE3OQQjs5NCBZ2QsRAe0VrKs5++V3XwDMxoB45PAZ2axz2XznaZFGZFOeO6zGrTnCbea0ta3/tVO/4jiofdPgGFPYFMqal993lxsOhwNLqTzaaWXj1cbVdGT1no2BE0tBnXbIZahCVMUBXYJkCIgCYcbk9N66F5Nt60GK6BXm2ob6vHXA2rXWetV7qZP1mIGv6+Dx1vB9zrzMqQJvqeOr6xw5hU6IQ6OXVMUO5ecV80T3pJVAm6TxsjrIaja2YlDFBmmFXbvt8Jdb4hJIWQKy//j1N/z1f/yY+MUX/ODZM/oMPkVstFgT6axIAcTxxGwty+WVSK+ERYAKY4hXVwybS0wu2QE5keYRmzNuMHSbLdM8413AmEjnpUjlcZqZSorPbvCcpolxDowhSnqWX1U/TQljnbAQjKTWBaArzlkqUhu5Os4GYmKJixTgUdZAEFuXUiKUoP7jm2tcmPnycOLdNOK7jquhozOWOUTRfHrf+tYZVdeTjg1SZVbnzjwtop0dDSlb+n4gB2HxeOf4+JNPsM4TVmOl83E9V8tgtjVqzQqQ/b55eN5y9QgMKsnyIbBG5o6wc8EEMM5jt4409RAWyAaTDBebG4Id2d+dCNOR3m043u5xwZB2koq4jDMXw1bmx+HAw5tXXGwGlpQYH/Zsr67YH/aM/QU8uwFgmRaWk8wlN2x5ePMK3/U432G9pHeP48Qyjqs1oeurvtCeLlM0OSN+nri+fcPfv35DCEsJAs7XttptV4KJDKKXbsCVIlS5k4MV0UQXNqj3Urld7eV2e4VxfQ1WcjRsN1ti7PDe4ogYm8vBj0jNXFxs0ErMMUZGT2EOatpgJiynEkRlpFijqXaGYifVl1bfoo6+We8LyuMvvltO5GTAJLlv3aIyFODAFpmJmiFQDY5qqVcnGdTuFbdKD9nXM7T67uVQP6cG8ryXHWI4C55XN65fWf3Fs88+nuCP1vPq15wz8zIzjgdiXKjRp/X0mws2u0v6zZYlzEynB8I8kpeJHIOAAF2HcQP9sKXf7TDOV7ZUnE6EUtTLDkMBEx3e9NAZYlyIc6DrN2z6jbDgS9FK1XU03mNSAhslBddwtj+1Pm6eu76u86E9f151w3ovNKt7tH0u53ZoK/ao+QoggbQhYxFJB0xjBUlwnVaxXVrZoMLGKqQAeX8jkJAzOYqzrRk7zjliKS7k8LjssaFj6HoGd4EzJ0IUH7ymSJdn7bwvBecMx3Es81D9hTozK+D0+NLsm0q8MAoUSHtbUeAPxCOrrl51MbBikK72kyYnoL5I23N+HQ64jpN03PTf9ZjK39c3Ms1XM7y3txiodQZ03a6fwWj/lLbn1MaZvHpmHRDTpEEkZlLToXsodVDOx7H4Ro98Vlb9QxaQKxdb9Ov6659zfSj+/BCR4nEfy5+KrS6vK/h2nnadCvnE1syDOvbFyjnbCn+pBJKMb6zfo3iu2I9U4wvtCD3wkyuQknmv9oAynbXP2yED5e9UPKK1fx1raGZC88I1m9WqD4OsH03dz7mxLhUMtOXZDQ0cVT9G68Kk1X6ke27K5SDHNfKM9r4WobKr9e+9r8+QihVSIFBT+jGlz70jBmGRC0AqtWOMNaToSqZLiycMrUijZKAIeSaFwPo4wRoj5JS0li+kAaM0eb2chbWpGXoa13Ve9YTl8DOnxBwWyCXuMKY+q/ZZkzwplteaKh+qzxBLX2ebMUXuIZV9RbE0xfNyYcFFGttY9fzrtDJCPlHJPm2XFDxOWOtLBoH+d354oz54GdDSfoezmbnMd90dlWxZZQ+SFuta+Rt1zZZds9oh3Q9s/XtM4sdbZ/FGjinqIUbpq4ypmT+/7vqNAGMlxiisoxqJtL/Vjli9fP7x9cJfgYpnm0iu2kdrz6vibef9/6jj1KGwSPqKYV1h0qyZsN/byvUjFeeDxDSdhK2RItZv2d18xLNPv6B7+bcwFdYgpjpdoOk7nD3f2YTUb1kZxNqZBfhQN1YdHT0RaAzT5mCvHV3VgWon4Wb19rWHUfrtzJfOWG+xWIbNhqvdJdMyE3Oq7a+nNGVh5lIdvo5LzhXUW19r8CTnDLY5qBqSVfcm6+8KDpUNvTq06wCjPUt9LyCM0aj4sqRdqtFCQRSqkYpZNFpN7/D+ArvpMQ8HlsNJAMhM08xZOVBtNB9dZZoVH6OOJ/oYZHFqitE6LhNffvM133z3gi+/+po/+y/+hJ/++Ec8/+gpNsmJGFY1Zsr9y74jG6YYd1dEsev7EM2v+/t7fv7zn/P69WtO44iyG0DXpWx60zi1sTOAsYzzyN3dA29fvxP772zLEi9aUgo8uMHjL7e4iwFz0UPfrZyvxvTQeQ3UYDrnDClzubvEOMtpnng47elt0RHKwkbPde5pr7fnwFB0g9pAWGv57NPnzPPMw37P/f5BCrYYCfJzFj2g9Wlj3/VM43QWE3Z9v9LNWQ11RV+MOBck4hJ4t9y1iUBzkPQ7QwjMy1I3IWNcNRnriprC/Ay1bbrGjSlKdd4xThMxlVN83/Hx82fEFJnvH1jmhaurS0m5wpTiHxbQNBJH1aOtAY841bJxycYYS3qrNjKuWH2yp6/B4qb/1DlXNbXm1E7t1U6YuvLF9sUYazqYPrdeWlxOA6BQwOY6D8x5at56fPR9WqH2sN8jWnC2FdAwwnLte6n27l1jj7XbrgHg9h1SfKQaQpqNXy3a982WzDsDyRm6JzvSEggY8iyFmP73//v/4Xg8cfMn13SWIqsSICRJr8yOHGbmh8CraeLq2VPS0GHixDyfeHjzgo8++RHeih5snPdYEmk+kVJku/mYq6sn9F1PCBPWZF4/HJiWhO8cH+0GiIHXpxPHkMF5rrcXpBiZQmCMklp/vdniMMQQ2E8TbuglGMkCiEVjMJ0Tm7cEwhwIJNww0G8GXIL5eCJZwDuM79i6DsLMeDzx4u6O0A98enlJN/Qcc+bhbs9YDmzFXDUdM92znG0ahxkqAz4m0SF+++YdL1+/4+Lyho8//YKbm6f87S/+ipubaz79/DM2w7Zo48r6Vv2xTEvbA7HRMRQWRkotkFC2YNvh6pxR0Er3Z+tcqcjrGkyzskG5TERlCWw2PTFDXITNf3H5jHB0BJ9ZOke3vSQZh+u3+H7h4uopBNi/vSXPkc9/68ccjoci2ZFJ80Q4Hrn77hus6+it4+nNDa+//RXTVQYEjDUZSfNyPReXV/ztX/wdw2bL7vqGJx8/Z3y4Iy8R1umvq3HJeV21uqyTErxdno787Mu/439++bocJmmguPKnjGHoN3UlCagAXTew3WRstjiKHnzMGJNwxuF9T86GEGdSMjx7+hnDcNH02aOw7CMGbzouumucXwXaVg4IXKfp/Znt0FhoBkPnZR2pnxRSBmvJoeyVOUumWWGGJeIq0Kf1hwb9NTA1ZR5L4T3jfMk+aHZJ5npjuJm0ykIqQZ7NkAuKK0ykdoiWUiKatUxL8wVMCfSXVd2AnKkVl/VLur6Tw4z15kk7WLTWvQ+6RHPuRGXqd9RJU8Y95sj+sGeeT5AlMyRh8P2GzeU1w3ZHIvFw/5Zxf4vJAe9kzzO+o99sSnHTLSFGTscj4+nENB5xOeGdwXcDfrthf5rZffQM23n53tOe+3dv8TfPuH7yEXEOECLWgO+liGy/6ZkL61SKFmZMtqhoh2bHrJ9VH12zwVRKYPWHMz9f/SGVLjfZVkKBdQ6XI487WVlLKgslh9CtkB5IKrFIWziWOdSgvOqSGrGfelhddlYhzYQgds95ur7Hdz3hcMTi8K6n81s6fyEVz82BnCzzErGDxVtlDwLGcHmxYxiEjThO83nIpnOh2Mz1PlxjTGfPMwmqxnuJE1Sn0eg6aNlv0tWrviv+q1ZHr76NM4Swymxg7T+d+yBrf0Hv0V6zFXDQtqqf00D2Fi967zEm1b1FJUL0PSEEdMh0fGT8W3vWDLOMSFRRlQ8K8IY5KwCWoZBI5LecJdutVm1f2eis/UYBykBi5BXoZUAk0ryTgssh1WFu0/5xjPz91/cTwj78e3sutY8CsjnV16YBsV1JZ4YV+J4FsHPWV83zShpJiZgTlhKzlf06BskiqAXcEjUbroLBuYH6JSSqMgPZWskCSwoNyv/qgYMVRq5BmJlaaKuBtbkSe9zK1/BFpkP3HiUdtNE8HzfnHK5od4p82CQ2QMFNKHthV+MylWVQWQJlZjoj674zygRN1V+rdlBbkLM8X7mnaMa3tUvpQ2dtOZT1LLNI4hnkwN92HrcpzOKcmeaZGEKVbem6nr4fUBQmA+Oo9TCKDrvWqEBixyiLoXL79Hm7UijMOUdiLJJIiRRSlZ4QJqfEDmmepQ+NyCPoOqWMbyrxp67bzpraV7kerDSG8WIl/d/od5R9RP1NA2TvReoqq+xi2c/L+6x1Ismpc2xtO7ISEtcZibnFQxRf2OohlWZcKBkoN/JXiQk1K0PlH87rfag/IoXbczovkic4hiuHAcAyS4Hh8rQZ2iF1Si2Tx7pS3+KDJgL4TQFj0YSYlk5sNN2WTMhRCg6V4JtcKohXQ7q6UVZ9ErMCOkrYYYrGTglAQgyNkWsf3aTaVbuOVdBJkUlYzUs9u8yKDLuaPutGqqB0SoQ5MJ4mlilgeovfXPLx8y/o+i0pmwqkRB3oeg9tB6xNmv5kzPo0sDFEFNes7VqBmO3WZVP4wEZl3aPZ9Ojxzx3kdm/TmklMUQoLTafVqY+pBqGd1Og4aFCaEeZXSbl7z7/OdTGZssid9/RDz/39fZFigDWQroYG1E8rwSvnbW7jrleqm8vjfqt7k2n/6ryuLJHe45/scLst4TQTThOhaKWqFo5KHbD6fA2qy8PrOc17cQbtMwA4WV1zznz57Ute/A//I58+f8qPfvA5f/wv/iU//uEP8X5L3/uqKWlSY6HsTyeOpwemWQoLOGOYp5Hb23e8evWSv/7lLzkcj9prxBTZ7XaV4db5juPpVNovLTPWclwWvn7xhq+++o5pjnSdAsIGrCG7wtyxYHtH92SHv9pC56qha1dxCh/pstRTegRQ+N2f/g7Xz57w9Xdf8/Nf/Jy+H9hut0zTidPp9GsctfOABYQ5lHLmq29flLSGDNbhrREnaD0wCciyScxpKd/RmLLTNFXH6f1LbhTDIimKptgXnV+ruee9SCTEEEiGwn7Whp874Xpqq0WAcs4Y2/H8yTNiiByOe/bTiVjZzGJ3v/76hRQC8F4Kxx0Ocq/SVZp6uukHtpsND/s9wn5pfdqWfnNCh37AGFML/qitVztXD40QEfvLzZbe+Sqw/+b+VnRETXF1LDJPciJHWSu260rlb0sgVJuTc2ZZ5gZirYC35gScBzDvX6Z+dlagV88lDPVz4zSXU+n2SWuojnpO53OvfZeeBK/VhZuNAKqj1GatpjlFnDf0T6+wnef09h4zR2LOTCZzQCqBx2y4NNJ3AxLkKiAS48yyv+fq6prtxY77t2+YTnvevXnB9vKaZ598wcuv/x5Rq02QZk63r+i2O7Z9z2Qdd/d3YD0fPR3oHKR55Ku3B4L1XGw3bIaBZQrcn05kK8WXdtuBtESOMRDJbHZbNr7DWU9Ci21J0B6XmWmJ2K6j324lOBlnDvsj9B7X9XRdx9Z64mlmTAv7BGnY8Fs3z9gmONwfuR2PjGRyKU5T9bm1b03rb3XGMMLOmEPi9eu3/Pwv/pJ58fybP/233Hz0CRHHn//8L/jtH/+U7eUlru85xYBNqRQQ6DA4LJI+G4IUVeh60Z/OGfp+QDWatxcXXF5dydgYPfyTK8RIVxwflZSs/kDO6GI1q4fKScDFnCUI6TqPWyxxHHm4feD+7i2Dgbg4vNsQDSzTSAoRYxyp2/Dxp58zHg/0m4GLZx+x/OqrVlAxwW///h/y3Tdfsb9/kDHaXdNvdiXNXq55XohZtHK3FxeQMoPvcDnz5rsXhGWi22zqetE1oimLWkhD121KkbgIczHmyN3+lpdv3jKHpeiMmkc+IM2xzFJR+u7NLafDvt7bW88yLViXsF68ipAC0zyT6Rg2V1xffw4pE5aJsIxAFmZMZ8l5EJ+07mPi28R5EYZFSX1zdotDno0SYOdALZpizNzaXINtK4UxbSQzsYxTw5uLz2MK4KaV4ZU1rf7Xso78VoxX9Wf0gC3FXCQ8DNb7kp4nLJzN5a4csGn81fQPjVF5JCv1EMr9rffi54VEjlrMtwBJJTCOMRTbafGmq5+t3bDKWAK4e3dHWNremlAGeumUsllkMmGZub19RSQKKGVEruajTz5nc3Ehc+HVS25ff8vgRcfX+Z6L6xuG3TUpR5Z55Pb1d5wOB4lHrBGAdnMhzHhnmVPAdx6322E3A8ZkcpzZffwJ3eaCsBlwV5c4YGsdDmHsdvPIPIvMVbXxOVGQzDbIj/5fOyRnCstWD2TOWTsZxWaCdhZLlHVT0+jLXtXkBtR/F2kL7XvxZ0wpvCM2OgYknbPaojKOXg7SYhJJJHWeJdZT30QAD+87KcDiBjq7Yegv2G52XFzssMOWF69fkZaM8w5fYgYxBxacY5pH5mUqh+SpZaGtDbtstJi89rALPFXSTxX4EQDT1oPwdqgbHvWuTjf9juJJWiskgWwkm6MU/VsXaFNffK1rCWbl74rvsfbl1JdZZwFVHyOvAJCVL61suRoHFnBwna5eC52uPqu1AvRz8zyjBVxBD8QKU1Jjmlq4q+lYSohgK4CmPpdzrspe6PO2vView5VXZDgzw7Bl3GxIUyxewoevfw4o+//1ktguEpZA34mfm5HMwHme6ftS2M0q5mDkYKFWgIfGWDZVTzPEKGDUJPumgtfOetnTYyEkZbF5Ka4yzIwRNmdhiltrGIb+rBCfqctB1rimwJtVKrz2v+4LWeP38vs0zqt+zq1Q3uo1mVdKWilgrrNtz0pagF3iH2tkrSg43fed7EdlnnrnWFYFqXRv03bqeJeQuqICWtBM/17ftwKdQ+kPM7XsEGMMgUBnTCVxGGPonGXoNqQo9SIyRmSLCrhnrGXwXrTYS9vHaazSis5YvLP4wRepASng5or0hDUG7zqunzwhLEGA30rq0XEwuH5D1/cs81yLG3eFlOKc+JPz3DNPc40LnZVDIvFNpS9CalrFClbawtDWUZW1LyCp7/vah8YIGWaZF+ZFvsc6x2boK5Abs/i8oegUQ4vh1dbFGAsI2+ziukCe6PkWwsLKRoWij/v+rqfj/ThbsmAVhhXgS63p0HlP7IdSlDQX4LbYa+eqdIL6Sr8Ojf2NAGP19CWvNikDcsLPqkNAi7AXWrk8Xz2hVNcjayo/atkrCFYnaNITHFlEzvoywRTcWDEJqGblfCPQxuTV5kpbwNBYmaxekfdaYv7ZjWAAACAASURBVDLMc+BweODmycimv8RaGIYLun6HsT3zEtj0faHL14iqgUIKurZGnoGJRvspS6CWzeqNtU080tnlbNII6JMldVEDUt1Ezz5iVh89T3OijGda3boGsevHKqcXzsmojtME5BpMVq6QApVtiAWot6Ijpfc3KdW0gLzSS6mbDQ20MAXoXwMftYMoDm9FRnXcVzdANxZTn7/Gc7l8fh0RWYMbOmznGS63wlCdZo53e9IS2jCvh8vpgYVuDKuA+gM/qKNia//Kv0uKvHj9lnf3D/zqm5f8wW//jB9++hlPn1yz22755LPP0NmaLRwPoo02zyeOxz3v3r3hxXcvub/fcziOHMexsnCtNWx8z3YzVG3aeZoIMeEs9aQuZMM/fvUdL1684X5/FENWUooyGWICB6Zz2KGj223wl1vs0MmJt84zo2v2PBCpoUhxKARQsfz9P/4D7lvPaTphrWwcuhGu56yeiGnAiJF7JZI4Oql91RIjmhNU0yH0EAK1O4298Nj5M4YzIPZ9p1BT8AszrjyPKd+hp7wgWkliyNIqLbCdJmqBvVTmkTGG3W6HMVJUrOsG+q4jYpicKwdWrd2y0ZvWy+ncKV+fZooGbyzsZNHIyjkXHUAN4ppDFs+YqKU/y5iIDyqOWi59Ok4T0UmqomiDxgJgyCasqcU6SZxxBErRrZzraa223xhzdlp+NgL/BEddHY4zG1Kc59I5zV5Ze0YnESdX7aF5775tAZuzv6t9f9zONbO7dx3XV1fEOTDZEZsdJMP45h0uwVe/+obxNPJf/9s/45gC3lg6xKmMdsZaYTOBIc4j89wz7K754md/wJd/+wvCeGIig8l8/MWPefvdV8RYitjEwHx4wF9cMfQDT55+xOV0IOfIOM282y9E13Ox2WCQgj37ccR0HUPn6J0jTgtjCMJIsiL4NE0LWEmAiinSGUMKRVe377C9J4fIvARhLvQOPwyiA7pE5tNM7j1/+Xdf8ur1Kz7pL5kPB+5yYk/ijgwFXKgO/MqRV6AjN/lQHJbOecbxxP7wwBJm/uRP/ox+2PHm9Tv2hxM//enPuHrykQRiKRLiwqDsIyDHhdP+gXmZmZeFOUaWsCWERQoR+AyjpEXnwsiyJctjbf1iCDjjWEl3Fvsv4KQxbuWY6tzMotmcKTZRDj5TCOzv73nz6jUfPXnGbnfNzfYCjMNvtlx/9DG7kIgYrj5+zi4+lSI/2XL95GMBxa3BJgPbCz760U+5HE8CXDrHzfPP2F61ds7jyBSABN3hyOXHz7m8uhbm5P5B2Ki2wzi/erY1A7MV3NPDYOtkfkzTyLt37ziNkwC3dt1r9W5YI3Yuxsw8BY6HE3dv3hJDJEdhPX/6/Jmw3pLI45yORyEOGEP2GYMDa/Cdw/lNTY/TVHxZuy1oMgZSXKrJMHadkpfq5/reF7ufiGmpfmXOUgAsLEdyjsW38zjfV7/WGs0UWemhicqlBMkZco6EMGNLir6hZKsUsDulUs+gHAWbco9cAGRjpahZDDPWl7TNYvhMSWte+9byvC1AxVhJLy//ybvK+KYg8gGFnYX6FMpuoWibrjJMLi6vcOu5whoMLCngFPb5PHPcP0Dx97zrubp8ynazYzweOR7u2d/fQl7A9HSbC3Y3z3D9wH7/wHjcM49HbIwM/YC/3tJttgyDFItZQmBaJuZpJCyBsMzkUmU6LuKjTtNCCPtykO3kUNUIUJbiQoyLZNM9in1WEIc8qBI/Vn5NTpFkRJ9PX38cmMq+qOzXEoQihVgwBl+yqLQYl86PM/ZiznjfVfuSZMIVzeV26Z6ZaIV5VHs4G5E7UFuUAe87CZoT9K5n0w9cDBu2w4au6G6nGEhJPrMkw2JiiT1kzA8KZmaNkY2ws4p/r4CXgsxtfZa4Q5EbJafkXALyVPybc5m8uv2Xf1uEWNoQEw93t8whSOorEtj7TjTrU1QpMV030j9SMV5ZW+toZr3/t98bALv2Pc/9hSZZld/7+/k9zn0UBYaMaWCMfN5JNG557zPU2aHdbGp2lFFGrx7EVPYadYyqr13356YFiZFie8Z5SbfW50BDuMc2/9df6/5Yg9WP7/MhtrH+voTANM5stkMZ+yRrNEKXxf557yu4n0nEFJD6V4ac5xr2VcZeVp84F11YmcOajalFv8SWrWqClP7KOVf9bwW1HI9jKflRMkGkcG+O51llZz5ubmNa4/1qj03JXig+vZW429asOLHl8xKwsRWYk21DY6xcHV/Z4wzzNK+aolkVLUMTxPZKkTl9uuL7F1DUlroVMQroqXiEznfnnBRuLmt8WeYStzbQb57nRmRb9bEerDjn6ftQ+qn0h2lZULnYQekHIbDofpurZEmbXxbJlp4XqZWioHUqLFa9YqzgFs6L/6Cga4qmxF7Qey+1boxIXlQyU84lI0vqvwgWobGlwSQqQ9sNm7IGxV7XeYEcXA39IEW0yqGO942hKzqzjmVZSiymNll8XCn4l1hKAUkdo1YcstiwUYg1ISWJh13Rri3PcZqnakxsGVtbMAi1D3KAW8ayvG7t+cGb+hIyx52cIxUiT0yxjvNje/D4+o0AY883phZArsGyJt/ZdDzWkIsGSqwHr2xYub6rmP6VA6aXDqhqoa71E/VqrC650zrYZW2cKwjEmbB1c1OU0m1YQmK/v2eejmy2M53ruby64nJ3Td9tmeJDea61895Odyp5YWVw9Lk1OKvGrHgeqgPW9sXzTflDV0ZdNlPBkQ9t1vrcayPcrjVq8L7jkM4ClPWH81kQvP7c+99gSrCRStCZmKe5FDYwZ3OtsfPUqLS2nH+VTr7y3ipqxPm/q5bV2bkKOtbPU/vKIA6dUwFz8PNAMKKDmFM+b7PuQY/a+p8Cis7aYCAiRZmmEBnnN5ANb9684+n1FU9vrtmPI5cXOzovNdXnMDOOR+ZZirfc3d1ye3vHaQos5URcT3W9d2yHHuvkhD2GyBKKvqkR7dRlSXz3+o7vXr7lYX8iaupUecgMokfjHXbb47a9SBN0rqSxtb5c/aheVuuwsoErGx4D+9OefMpls4WUY90o15eKhqeUcGoXKMZ1pd2oX01xDteXLc5PLAVUzodJGmgePYCutXaoIu/TDT6XOeidY7vZMM1yiqgppwZwrsMbR5rGtulnCTZdEfRPOTNOI9k251LYB4HT6VhPYdVh0TbLOl07nM1empKOrO1UZ9o739Jf1Faas6XzXmpbY4bLInLOEsqDKCA7x0VE+IElhvo5EZf3zMyFTSG3SUbA9LwKNtaOtbVW9PjWo2QMmnar719f6zX4T8Br6/fYlbyC9tc/Mz4o3/9+W9ZthxK0ZGEVLd5hNx0DO+I4kQ4jh+OJEF7yl3/7d/zhT37CZtiwZDkwiSniskMBm5QTYZrphogfNlx9/AmHN9+xzBMc92wuPmNz+ZT5dE+YjjiThEk0nbBZnLFuu2UcT2Rjsd5z4QWInkNknBcwRk7tjSHpa74UJMKwhFizA+oUSaIZSwGwTIa4BJG7sPI9BkihFITLGWs6lmkiHEaGnHnIC3cmcbRwqgGcqUFz1co27TU9SHDGMhh4utmw9Z6LzZbr6xvubu+ZXu+x3YbN1RVXT57g+w0pBOI8Mz68I1hDzpaYMvMSmA57JE04E8jkQ1crzM5Hz+m0J8wjhohzjRFwNi9SlPTMswlxPldMcyDq3LFmzXCR1E5nPX2/Ybu9ZLO7YrO7ZLO9AGOx3YZh56stcJstLmfRurSOyyfP6DopzDV0Pbnr6foBs9nilpmIYXN1Q7+ZoWiL7a6uCcmI/qbvuHz2Mf1GKkFvnaMbNvjtBV0/PGp/OZxKLcgvfy32KEqxpDfvSsGLVcj5aPHmuED2xJBZCrgQQ2SZAmFJpGxJmKKTKb5EmGfpZNc6W6oZi6ttla2Ui2NQ96vWXmtjBRpKpLkKesTGO68FVhI2St6UME0DJoykuJBykAwhZ/F9jzVe2lJqDqSUC8uXwnw5l+DwcRa5khIIAVU/TgIrebcyZAzCCnfOy1rEEpJke6jMkBb1ymtfMK8oDuY8eFbfTP25rPpuj68VaGYMLMu8Cv6h6/oz9t/6/iVSwlhIMbDMk4DINuFcJ9IUF1fM88xhf8/pcM8yj2wGz3Bxheu3LGSOhz3z6UAKMxbDcHFBt7nAeA/OEWIkLDPLPElAn6RAiHceuoGEhWzoOoexnhJV0nUdJjaGZU65ymNpH+b1s6yjI51ntYs09rGrflc6zFmHAlJgy6CsI9VLLME4GVvBcoOx5583ZKkkXeZM1MCgDtlK05R8zmZW+6qHlav4oOt6cspM84LDYQtT1pdgfAoLS5DU4Qikijq3/VuPqAWIafa8+jmG6qOAANcNa9JDXBoAehaHteC7kldynZ5n/l2bgwgQm2O1RaYwxq1JZJPPwKzV0mH15d+7/699FAH6qOPS7nMeh33o0vs5587WV5kWZ/dY90dKov1fW6vzVz+n+1eZk+sMq0zz0dQ3PI9f5YUEclgEtcCdqQP3vszh+aH5P/36vj7Wv33/PcXmxiSp9oI3lAKt1cbL+3Rc685QY36zDvpbG0D2YrOKJ0rsI5NvxXBds1J1Tq7GfU2qOP+OhrmY1d/1swpYNl9aWdfS7uzas2lWhqytIlnmDGsSXCxVotcEvfU6rin2qO/c2it9KnudrmVjTI1DkhYG0yK/xjYgLiPfmyRuc3rgVIBGBY1TSljXpNDUDMjHWz+klb0AsFmLC5cnSnKIzXp9yIpSIy99UYDT6qcVkDgbI9ID4dznSZUw1w4dz0Z0dR9rDSbovYs9NHK4m3UN5aLtuopzzgpsk+U9RUJI+0GIQdSsClL7vLMOLYxcnTFaBqSCsbYe0JjqN1lj68GRcyKXYF050HBCHpHC0+JHq8YyWfyUoe8ro7X6Xvo8xpTs6lT9YLUtKQfR08+mFA4tmRwY+g5IYEqdCZWmkIPklunwoes3AoytwU7hZSsLSI3Q2r1Qp6EGrkYPKctkNuspvXIyVvtlpgC6K8ucUqLrOrquE8bVONW26bVmfNXNrX5vY0TlYgTryeDqLvJs4rwkIKTE7f0tp+MDl1dP6TcdT2+e8OTmGRfbK44PCsa2Zwfx9R8bx9V6Lj+og1r6VV+vjGlTF1nFr9RjeOSa6fNXIeKV4XsfEGwnPu1+j3uTs8+sU2BCyCRjq2B3NaZQBKFXi//R4569N0ta23g6nYOVuc644pScP8eHNlNTFmfOlGrvpt5LJ1fVu6zd96FNef25OhPJJhNywnuL3w5gDEvO5BDL2iheXMr1NL7O55zPn681ehU4lZfEXpZmS1LPlDJfvviOFy9fcTH0PLu54ds3r/jBJ5+y2wzkGJmmE4fTgSXMpUBJxBiPcx7rhY3sS6pL33VsBmF1j/PMUgyisVLIYl4idw8nfvl3X3F7+0BGWYLUFHwMGOtwFz3+coPd9NhNX6U3TKFYa9VkBS71QU1dM+Vv1ek3RAS4VB3X7wOyhTHviASp8EjG4rBG0h2yblo6propGWpwqtIqba2dvbWM39mQtbEtc1MtXiohhDr5nffcXN/w8PDAOE0YAiEnUsz0vaPrBsZp1r1Q7pISg/dshoGYEqdpJKdUGLGiqXQ8HojzhNio9dptjr0yhtUJUxmZMydEnTtjcN4RxlBA6Yzv+nKvJtPgnKtseaA4RnK44q2l85b9OKq8HDlbUg7t9BRd+6amlhpM1XNyzpdK5xr1FdC3HgJQWGjNbrcAvjCKVQLgg3PG1Pc9Lg7W9ov2rMoEX7+nOkOrOdheX4O1OpHaj4/+ArSgKeXEOJ7ou45sEqazOL9hu9zwMC2kUhDpf/s//i8+fvKEzbOPGfoNIRuWnDApQhL5DYslTjPT8Ui3O/HRFz9gmfac7u+Y9g/Mlzfsbj4GA2GeICVMTqTpSFpmzLBhuLoGu+C6yJXbknLmfj8yL4E5RjabDb21UrxrmZli5OpCikCFEJmWha7r8SBaTBmWmDCl2q4BTIjCWPfCMHLWkkNgKQCt6XtMWOiBPiX2+yPvBsN9D7OxoqtlShiXz/tW/YAycFgSnYFL1+G2W676DVcXl9xcP+XP//zPMWbDb/3O7/Gj3/1d/DBIAYQQCOOJh1ffYqywNpYlMM0LOQT6vsM6R7SWaY6MszCkcoos00kk5eKM95rKl8/35ZQw7tzWPIpf35tHlZnIipGBVJF98uQpXTdwsbsUcK8Aa9YLYAqFPVEO4ayVlODd06d1fjsF1TA43+G3Fywp0+12uN4AR8Dw9NNPsbloThrDVT+ggNvlxWXRipXicKsHRtmMqfhq64OslCNmnpgf9ty+fC1vdd/j7eRMiguQCUtiXuZiDzyimWZI0ZCSSClYm+X1lApzoqRcx4S3hpq+jVYvbv6HzNfm71JS41f4RAFkc7UfxlDBL2cKqErG2IWcLc6NhHAofp7DdTuc2xRQ2JTClRqA2Bq45hr8WMiRZZHMJFcOJU2ZI8LkKcytGBAWpQCwvpOUQ2N79g+vRd/WCIDsrEMRAPUjtS6AyWXureawpjijwWSxhQZX5qktwU/zdY2xwqpZAUKueMwfXAfa74j+/TSPAmobI+nwwwV+s+Hd7VsO9++Iy4i1hn5zyWb3hGzh/njgtH+gB4a+Z7jYMewuyNYzLxNhOpHmQJhO5BhEr2/YkHKmcx7XDXjfM7uO7abHeE82hulwYDsMsMwQg/g8UQ5jTZZsmZUjWPq0aeQ9BuvabF/3/wf8XWuxWUA7K5MUrSINChRqnzf/94ygYjQ7L9fiQdT5u97XdO+TQF+z54wtTGuNdJJkBfW9pFGP48SQN5It0YnOsnWG+ThJVkGKQmpQxqZ+lykH7TwCjyrYtYotig2xhSyRs+hWppJCq+tR39yeTfp6DYbWFFj16UwZD43tyncJ8ONKGwuT3WSJO0w7OF/7rmvySgXujHkPWLPWVhmDGONZNlYDbVY+3wf8nKbfSo0vgBIbrj8vvoyCddMyNxuHKZXpW9p76ZrCXNSU9DZfGlC++rl+RyE+pXymQ6sg2nrBr12mDz3f94G0j/v8+67zz7dvWy1TQox4A854nBeNUIlFc83QBbC+ZQeI9IArTOHHoE4pIGfX/d8Kthm0HkSZH9rO6sKcj/3j39UvUA1hnVvGmDONYily5TDO1IzUNWsUWnZyTE2CYw3aypiVujC5zSlTOk/XpvofJYBoILNZH5Sbs7bawdb5GGOskgR13ZYhcyU2jiEUSYY2B33fyz5m5FlOp7HKJ5CFlOSKfAu2yYqIdqkcUmNaYeechLWaVYIh51LAXeyCceZM11SvtbZrylKXRidOJRGsMakyt6LGbaXvvfeQjRxEBpX/Kfu8UwDaVfsVUjs1M6axbKXriqb0qh3nB27K8l1hTiCxbdlPtA+sddgyB73zZ3uGrgUtkLaek/rf0PcsJSsuluxWZUrnnNnYTZV8SFoc0qvD3OxSCAuiMrAOAkqMFwVjClEIQr4cUlLmWIgRjEqkxLY3f+D6DQFjHznEWbRN1gdAGVqxJN0IyuSv5yPGiC5HjDh/rnGlm8CZka3YiDigMUXS1EBBmcz1rZIilFTMeU0r1w3bN5r6qrDEuuBLzojTSyKRGNPMl998w6fPf8SzZ8/pfMfNbstnzz7h26unfPvmH1lSxlgHpWCEOsLqFNfT1NorCvGVrUC1xuyq34CYhfL9nkTB91wV1Hq0Wa+3ncc/tedefe7MQZF79L0UYzkcDig4LLirnrxrT7d+PLt3cXxqxcTy9Ov5omOmp9Jr8K7d5/yqWnfqdGozztA0nZ8GzhRcP4SU5HofBY5MmYgR0XZ0FwP9psdfbFj2R+JRGCpZjVjMRR5sBRL8E5wEnRu1Jw1ihMlEY1hSZn8ceXkY+eWL7/jk6Zd89uwpP/zkYy43vWw0VjWMDJ0fsK4r6ROxdk9MkfuHB44nkS4QZpAjAff3E998+4p//OpbHk4nXD1tLJyo4tS73tNfXdDdbMnOkFfaQeQkWiyqRbcau8dMAO1zNfQWCGGWVOXV+/UzVZIAipEWMHxZFi63F1ztdtxcXvHzv/kbsnP1+9c9XJ3TLFpQ3nl2ux0pwzRO1Xn53qvFlSgLo1mqNs5hWXi4vcN6x2YzsARHHE9MYZGT92wIhR3nnMUb0WI9nU6MpYKwfJ2pTrn3UiwmZClaJNlRpuwvxSEyImtwOp2YZ0kNUhkGW1JGDbAUFNh5xw+++ILbd+84Ho4syyIMzcJkXTMpVH7BO4+zhnle6IcN15eX5LBwmKbzNYQEVd57ttst93d3LIjA/FI0bUmRzWbLzc0T3r19W9JCH9mwLKeYUZ8DWzfvaZrJ+fxUWnXV1vNFnF8FZFepRI+GV9fqPM9nOobvvfHXXu9bXb03OmaUOVzem+aJmKNoPpXIx15vcNMOu7eYcYaY+O//3f/Cn/3rP+LP/tW/osMSA+xMqIGpsxZLYjne8frrAz/+o/+c5z/8CXfffcvti6+4/e4rnv/499jubiDD/s2vqkYcOZKnkcVZtl3HtrsghpmHSdKKvbNcDcJ2PJ1OhJTI1vLk5oaNc4zzJEAJYHIWByZlpmXGbAZxDGOCZSHkhNtKargDzBI4jhPRG+ymY7vd8h/+3b9n/+6WY5i56+HWQir6lbKzRaoWo2lSJeL/i8xRZy09lq2z3AyeF2+OzIcTMf6SaUqEbPhv/tv/js9++DM22yvSHDk8vOT1i6949+ZbiCc+/dGPyYvB7y754fPfwne9pFVnQ4xFZ31aGMcTh4dbvvqHv+ZXX/0t43GPsGNd0dNs8yGEhez7s9fWK6fOF6O/m7rWJSiyTFMUzcsM3bDlZthp+LvyIwrYklMpJAEK8mQy2io5ICuSURRZF0qqc5Fo0GtKkcX4cgiWSE1SlJKXLu03jR0TYyQsUnzEeYexTkCMLKmeKS786Mt/4PhXP+fnv/q6PnfG8HjrzzkTl4hzFPBF5r/1jogA/xlLyrDZXOFsZpz3WNuz3e6wboMxjtvbWy4vryWQSYkQFig8GHEpbAk0mmQLiIZkZiWjQtHp02KxBowTW2uxYufldgVw2RDCQeaxk7mas1ZbVlatqf5X9W9yhlIAxGCwdPXvzhY/qwZXhVXkPGRXwBgLZoMxlm7oGJYJs5Rip1qcp9hbLWqk2QGZAoBrJE2q/6mcWMZgjcMbXaHt8Kz5ZyI7Zszc/KOwQU4v2ko4Lwokc3VaJo7TgSXPOLPl4uqGYXfF3fGeF999hSMxDAPbqyc8+fQHvL17x8Phjmke+fz5Jzx79pEAhaeRL7/5jvl0ZBg8u+2Wm+snDE+e1pWTjeHh7p4Xf/NLYe54D77nNkVM53GdSBRE7/HW0PUdu+tr0rQQg4yRVtiyuZFUJLV0fUi8Xjvq8wgIntP7fq/44xscZS/X/c0IeSTnopF6fttyz3WwqfFT0T72SJBagZ60fiuoN2wauKIetYEKNDjj6IxnYz19lPTUvu/pNz394EkPgTkHxpQ4gRzGWV/iJanlpuoN+rwyFwR0cE5TdLXojMxBARmknzX1Vlnhjzu6sfbOItt2YH1WALqt+1x8W4Op5CS1j50RqRFNLW4HE6YWjXkcB+hYOSdF7UIIxKhsrlQB1Pb93++EPJYuaHF4+ZyCa6a1BZD5Yy2+62otAGH221WF+1y7z+h+XWLLNbhcY0Zqk2v/ijk14tvouDon4Jd9nxn7+DJG9HbVN/unxMTf12cfAnTV5htjwNkyLnJwnFKAUgRa6y0YY0kxVZsOLTtXrzU4mle2tUr2FACOAi5JxlCT5XJeD04LQcCfg17nc0na5GvbXW1XLciWM/MK4ARlhuZqw6XoV6qEBZ3DKRSfyzxK6MlAbJFrJssZ3DqOypmmHZLrqsvFl0klFmmHzR+IEYu9yvX3csecyUHuKUWfFpIROTTvPbvNliUUUki5pc4jgEigs47kypgoAaP402havAKUOTf5GUuxN74C3wrMWisgvrWGrpPaCSpjsF6rCqZ2Xc+8LMUGiObqMAyVGQseG8reUuycK6C6aNs6us4zz3O9D4BPqY5r11kB+AsxLYPI7xS5Ay1MtpYY0Lmi5JSUc723AtkKGuucs9acycKkGEtGpCOZctisdpTcjmK1IDiI3q11uN4Vv6ftTdqezlly3xUGbCoHSG7VZxAWKZS9FHkq0Xkua8OUQ+15IoRlhWW9f/3GgLFtc5Sd0pS04HUhEzXCaeV4gAIUDi30Y6w4zFrpNZVBaeGDGBWzugfOEkrQod9naVqqFZxV8Ez91uIIplzYE6Ys/La/kQvrth8GfNdzf3eHVt9c0sKrt98xLSd8AU22m4HPPv2ET14/5xdfWhJSMImcyTFJ5dUYqUXijBhvbfu67EzruzVIZVYAcWEmoO8pp2k05rACCo2J21gaspGvHL/2rfWnKu/w+B3lC6w1AspZw2aQivIxycKwKFOiFP+pG4RurfKzsnlEo8PWRSjtrzHAe41YZR/XuVBZdlB1anLKFeCoH9R5Ve4RP3jqUUA/mbnlW1bpRuj2Iq9aY4S55yAPlq6/wm0CaZwkpXia6waxmr1qS9rmZFidTr2/+ehSaxO+diU5QciZb9/d8ur2nl9+9Q2f31zxx//y9wlL5vWrt0wxsN1sCpvcs+k80zwxzTPzvBCmhY+ePwfnOE0zb9694atv3nF3v2eaZikO410NuXKWk3/f9/S7ge5iwF5ssNuekIo2ogr91Il5PiSrJ1vh/sUhWL0o39lcs8y634RtaygpCKs+vT8d2U8nXr57Q+6KRl0S514mAHUjsuX7U87ENIsjr8wRgwBFqO5t2wB0rirXM8UoJ63Ok1JmXEactSRr/1/m3qzXki1JE/psDe577zNExB0ih6osqqtI0VndLVA1LVUjEPDGCw8t+AH8Nd5aPICEaMQDgxBqIQGiVI26m2qqskpZeaeIe2M4w97bfQ3Gg5mtrP31KgAAIABJREFUtXyfczOrkWilS/dGxDl7uy9fgw2fmX2GlCvuSm0Nm+C0aY+T7MeqZ7qkLCUsba6oLTvUQJqmSQyNUuxV2rYACL/3ox8jOIfzsuCLb7/Fw/ERqBI041pA3kMyw7SkfzinaV3x5RdfCrl8kYzkxAlg64Ipc1lUGcbgsfMBxIyVCA/nEx5PJxgEZLrAXqLW2riHQKTPEA44ZgZX4Hg84byc4UwZq2FWKzfOW6/g63lZUanCMaFUAlB065isMaoG2VKl9Hc1GTPuJylt7zvUdl1Wfri2c/UZTYfgOUfZdjn3L9m51T3NsvHaGKh9o+CcikSnVac5EML1pNQNBeWYwQT8X3/6Z/j47g7/4D/49zF7QiaPzADVBEczHElGKnLC1//in+H25afYTRGHq2ucHu/w/su/wP72E+yubrCcXiKf7xGCOOUpVSCtKJXhpxn7q1c413tcH4ClZKRa8HheUcAIU8QUAyIzjo+PyCyG32G/B1kzDy/cgc575LQiVwl0hv0Ok/PgIk2R1lJA+xn7KeL48ID/5X/8x/j6yzco+xl553GMAEWhimFSyVT1YKmcp6H5CTMjEDA7gteleDyesaCCvEM4zPj8h6/xs3/z7+L1Dz+HdxWn+w949/YNUE64ut7hk89+BsSAnCsOYQcXd/Bxj3VJCjQSMhcUdiA/YdpLd+jP15+AJocv/vLn+PqLr9Uu6nIPAM7rgsO0Q7C9NexNjU21/Tb8QLSR7usKApzXjEjTW2oPWdf7YXNKt2XXHMPN72HPA2gAUW0Mo3P98e1b3FFAnHc4XN/Ch4BiZW7o5b/jlVNGzkkBJN/GaQ2qSq1Y04KH+zt89eUbcQ5bBovbzF1lxt39GddX+5ahY9nsTF4yq0m4M0suqI7B5DHFA0oiLKczSl6QrzQzR8sjT8dHnB4/gDmBUFv5N5E4cPv9TpoIVuFRi1NEqQUP9yc4EqdrngJCBHwQDk/vvdqHBGgTOOakdjQBXFDLEYxHMIt8Fp5JyzYSO7tU1ooO0rK/GeQmlS8Vpazo+pVROQNMDdAjcnB+gkurcLqjoA5BHGaWAJljFC3vcwSEachGIQcuCZZKINk4RZ0aPYrKWWh2rMSBhyA4Bcy7a7iaAOUnvf9QkVNf4DEI3gIHLA3zzuuKzMB0dQU3z1hKxtdvvkIqCfHqgPnmBQ4vXuEXX/4Sy7pif3XAj17/AMFH/NU3byWbmCt2c8TV1afNNv/4eES9f5QMTwjwcH37Eld8hfV0wvrwCC4P8MqbXxyAGBBvr+CuDvBwSA8fwWvFqtVjPswI004CvBhtvdrnr5ueaJZ6Mwe6BTqu7boc4VhAM6+NtXiweWsuPVN2Y4QR+o+6vjSgI9esgJPyqjrupdJmfBqvfCrKpsBIaUFRBz1OM2KIiC7g2k3Yk4eHjC+TZNYuNeOMjOQYHAMmJ0kD8ATPVXoyqL6Ubt76bkSoVXRgBzzFv/LkwBqQqBBh651k7tfB1jbbJMagGdpFq2W0xBkdWASGcmOuzccZnBIBN1X/ZAV9DJS8Plzj6nCNtCYczycwpBt8m+MqNkZRcNGApubrOIJkmRMshcc9AQy6D97t6m6bkPqmIkuxCfQA8h1yAtZhp/uNda/qe5dSkBWEdMP8sI1R5WTPHjRXwAI72ui1dEBPMiUrOJCVkvbEtEs/UN/lsoHuc4GK7/vd5dU/27+Tc8V5yYgpYzcHoZ/giqSUdHGKiCFqyb7tp63/bsGBlj2KTnvVMvMgQc5eQj8mn1iWJ2CVaUaX0LJZqY97nGOzGblUpUYT+pGgutGpvDY/h6F4TalYDHyjMWnKfFdWvn/ZHwbeCfglYxirRWwuWrYoj/tRPu/JNR/IbJzmJ6hf16qo9HOpSPOrPlcGeLsWqClrhmVvNr3nXJNxtVbgzM2X89rYiojaXi6amQp9r2pNBNu+suqUHpBwze8QLlh5r26DebXVWG0Zo7/ovgFjCh6Td22+Oo+6zL0LEdV12UeeWjUMkUN0HmHeYYpRaHdylgakZkKiIoZuSxEbpU1fN1l/3ypsK3MLFPgQsJ8mlCxZuuu6SrauNvqyCiABaXMDlmutUqHkh6x9SFarNTuM0yScsaqQuaJVx6pAanvFghwW+JJ9YEG7DMMAG67IGGgQlFe5ckvKdBQxTaFncz9z/UaAsU31mPBGB5cafMLbzwNdSNjB6OWlOtk0/Mt4H5rDq+Tn/WSrILFyfhNAdfNUvfOwwZsvjOak9FGrk8SSBbYSskYlCZDsDk94ON/j8fSANS2Ie4LzETe3L3B7+xIxRNSS4V2QYIOX5Q+eNk617iURCNoFxubG3JxReVQenPUB3BgjYgTz9YeIkU4HDe9tf7erz4ft8fGTaPe3v4tQtY6bmsovAxOBPqzBVjH1fSDGRPdGzdg1oUakB68ClmLdnciLjTW+i724veSoDcaXpe38yvJuS5XHPYOL25hxLPk2+jkisHNw+yhOSCDhTF1XcCngIgZ3Q4Ag/DFyv+eBYZvz7fjHfaxzrgIv14KUKn73t34LKzt89+GIn//VGyy1IEaPKQZMMWA/RxCAXLQkI2fcr4xVub2OpwX3xyOWtKKgShmLZlFxFR7GOAfEqz3CbgKmgGJUNaZoua91V7DPLltbzOcyZamV2w2f5n52uXLz/Ux+AAK2l8JIzxhhBOBwOCBXKaGmzX6gzt/TH4iKoqWGl/eTDA4r2QvOYzftcNgd8OHhoxKbF92Kg/wTVHs4OwTOPRoNQiOl78ayzFFKCdUMClj2Wj9jj49HRC0b5yr8X17vax0jn7yFGe/MWBdpPNBKa0pRw2X7HOh6p5wBzUypXMFFM0TMsRvWdMyasNI2MLdxmQypmYUL1TJeam3Gjo01Z4l4m+x3G+5q4DKyOf677bWq2S3D3us2vMyZGSLbs7iViW3dgEYHIR83gcRNF7VtpYaBGVsb52H4jOnUCgZFoQPhUrGeVxADx/MZ7+7v8Vgzdhzhi/IUckXwFRLwEm1dTkecfUCYdnj5+Q9RGEjrCevxHmDG1e0r3OUFlTo9RFXqCBThKJ6Cx6zR/crAHCO8RytxW9eEUqqWovpWFmYR6ArlglWgxsUoTmGVSpnMDJqEhsgxkI4Lvv7mLc6RkAOQibGmCpq82h2jgcZ9XdUJAuR8TuRBRUruKljevWbspj2ubm7xo9/+bXz6yaeoa8J5uUPOQPCMEHeIuxl+3oOmHVwq8H4CXFBGGuOIVrqAUjc+epwmXF/f4vrmFvvDlc5TlSad+rGcevYBk65ZV8PNZug7035upVcFh8OsYEjG+XgGg7AsZzjnMM07hDi35ocgaU5hDpedUdrcfevQmtnc5a+9X0CEcFtzleY1bWy1gNkCyv071vjBmTMBCTxwreAqDX3OyxEPx0ccl3PLrm3jGOaCGTieEvb7A1q2OzNSLsipolRGjOJILcuCWgtKXXE4HAB4eHLwk8M0TwCkTNR7h2mesSwejw93SOmsdqg4EFMMKGWWxoMpKfhq1DH3AAgxeCzRI0bCvAvYzQEhTGAm5CRUQNME1JpaNjpzhQsD5yskkCINvkjlQIXjggIDyxwyJ5CPw3oVNPscjMoJqCQNl9jmkJHzonu3ark/Bpte5k7OjzVqFadzXAjLptINM+h+1Rlm69L2e2bfe5032zNvvrnHugwl2QMoAeNRZdayRQF/d4drLKXgtBzxeD4q/cAN4CPe398hlYyrm1tMc0QuFet6UucO4MpYV2mgN8UoNCk+tLNgjvduf4U67THFHZY4IR1PqsPFEZ4Oe+xvbuGnCBc8gifNsllRmFCZ4IIA9sJxd6GjCAAbPyPaedn4MM/oblY7QbKkilY4uR68AFArbRvhUqdkUsm10dHOCWWQPbNyATcApj0Z0CC4JeKg9qZSRK41dQzkMDvJXiLV3Y/HE47LGeechaYArLaNJvgUSfowuWSsGFkz322/jGCs+R3iU4mTXZRLuyXmGEf1UCptW3e0tUYbvDZ/FJotyDBexU0glWUuxXesjaYh54Scy9C5fGzMZ4CF3cvBaCPkmHQqJu+8NEVz+hyt1hntEGajXhp3SW3zYvLe7A6YHQKz3bV8ebCqnR98eN3zEv+Uz1jSFUmWCsQu7iCvzSeZL2c20+ATMAAKTrNj0ZPobVx2F53vy1Lwy+vXAbC/7jJcQ96vwg2UgVZm38bOjLEpm2WQ2t4JKt+IBASKmlAxvlOtlsyk86bgn/l91ew4netmkw4+8WjHCujd90Zl0c3WNNf85dbZXgaChkfo3sh5yzFLBPjQgefKlm05nqUmPTe62q6ith7ajCltgu90CXJvHhaCeiayd5j8hBiiZpha+bn4xUQAOUsQk/UruWjPEW5D2vYe4kYH0hp4hQBTmKLD3Ib6kABN6HGwqh2uvc+FJQt5r3KHhNZjNaBZz14MYRNYsfNkhqTQVlimOase7FPDMqmSlOiEnq8O4CVBA0WDTVlrbcGYJgtMBvZTIHsFQiNnWazeeQQncj1MU8Og7Gx7LzQ0VmETgukVh6LBQdNpFsToWePceYHtjJldUmvDIcia4jWf0nRPz5bV5WkN1VrQDpZYqJmz5Np8FbOafoX8+I0AY4EukHS3DI6HGg/POK1AF+Zd+Iti2Cg0NuOibgw4K3Ji/YxkSHRndUxZNuCDVIiZQXqZ99HGpE6Ucw5checu59KUVzsk3uNxOeL+8Q6Px0dcvRAencPhBtfXt9jFHZZ8Dw6di6VWMewrABSL0sobdSGoW05fjoc5HKOyz4FV0G9T37YC0LSVQjsowPaYPTcfpgi+byOacbOJLjtuiqCXbQwymDQmMSgLkW6DFtHnWUSjqiElp0YErHzlYsxtnNQEJtD9hXH/ja9koKLNz3Y+npicTaBh+L8BAWYyV2L4QCAX4CLBzQH5SMBpaZmZrTsyoM3FBiMDtB2kjW342fjb0aexqHkIM17/+Cd4WBK++vYjfvH1d1jBcE6zd6LDLgbsphlksSuuWN7e47isKBVw3iMGAgWHoF2bG+il8zbfHBCu90BwqI6QucJZNlQzKC7A2M3M9rm+XNPngLv29qo0bN6pfb7vWwN+7VGXO9mBsJ93WJJE8sb5tTm17G17disRu7jEP5S97NWJid7jZn+FNSU8lAcpI3XyYceuzRFj3Jv9WdLhmlDWngXfbSUBY4tzmOM0OB59TN99+ICoDc0KQ3j6vDk20jyriSH0M2BbrTcf264Jt+eIA2cR8zUnOR/aCbZSL2vCkzXsSnm8GmetOvxE6sisKzjXHohDB0SWZVHnuvTxbmTM+MzNCvf3kpcb3lMcnqoANBGpcca4PJvjmo3vJKU6lu23vf/4eAtabMc0bNrBkSHb+97BzRM8E3B3BJJwLJ1ywhfv32H+7FMQApgJrhJ8KOr0yH0cM5bjA/w04/rV5zgX4O7tL5HOR3ApuH39I/j9HnU9S+bJyCeVCWUlRBB2MaKCUDmBSKpbapUmcqlkwAkdhfMOp5N0rI3OSxMF5f+qzHAxIEShK5AsaQZ7h7ibEUAoa8KyrLgvGXy9xwoBG1Mp2O2nxs/XZTm3eeWC4b3lIyVL6RhDgjiFpVJnf3WN169/iEAey8ODVLI4j/1+L13GnUOB8FlK2a9WA7HxZFrzEnEMGCR/ZgFeog+42l/h5uZWjMyyzepJOWl1RA9Co8mJ4RrkWt+DUlKfU0YFNEthAXPB4/09fIggAkKYkJM4GuSoc0MOBvpmD6pd1LahoGsN/LAB7fYHrJCGU6L/S5Of4jDKXI6lzt5L80iQZaqxgrFF/isZx+MjHs4PyK6A5gDkDkpsRsuM82LVRyKbqgJsa8pqg0lZZ1rOWJczUlqxm656Q6Fpwm63U/uD4FyAmx3y4YDHxw9CrUGiQ8UeLCAUzLsZa5bs2DWtmKdZGmAyUAphLYQpO4Aigp/hENXxy+o4SdbSptGGdzBqK31BKYElAjFJY0OyklkGIQuNQE0K9DuVRRalFFuYSbMbS5flOWfk1lijB/KthJLUkZGO2ppxCQDEMOalxhnJw0Zqel/15rBo5jgxCGCSDurNtgW++uo9liVdbPpu5ZrVlYuMnXzEtDvg48MDPj7cIdWM28NLxN0BuRTc3d/h+uoaNzc3qFxxPB1RctbMNi90aSkD7OD9jN1uh3neSUNUzXSUQKBkBk7THnG3xzLdo2Y5/y54zDcH7G9vUUlkS4weJTGwZrAmdnAdAFFmZVPp735pYligp/kyT0x2PTOQoAwKwTqNW8k8IHIwW1ksa+m+lrSCrEFq54oN0SMpDzMBqJyFAgWjPOgVcObHs4GxRcpEdzFich4RJKCs6sWUVqzLguN6xlISUq0oxFjTguCKIdWgGLQPI4HUCMhp3cQDzNfpWVHC61wVpCnaRK1TXSinvzankeYyWxtD1oM3f2dGA8IMvBl3qFlNXCtykSa4RpFUipTHChDrG8iWc5YxlqqVRgaQ9zJ/Jg9LSeglwMoBncuTsdqIus3Tz2X7VO3z1ex6+3SVytGWyUkeIfaKohZ4ZG5JRgaQWL9kkNBXjRQc3lNbJ9svDVg1/915QU/UXh5xhV93bYLZvwJI+Ze5miVZqnAia38DaUCnda3qB8rajniHA6iCq4B4nSMzKN3N5fj73Mr8kPa02CZeVeYGVLuBm1vmz6qIqU2bgfnMcs5rrcjqKzuTFSRywzInvdIwANsqUvPJegm6a/5+m/s61jJ24No+DwC5FhSlEgEsgUGyhUOwUv2oe6y2EvhiJe5eyuC9VlPllHBeC5gY3gt/asuOhAJ1ToDWMagw8jJXxX7WNTVANtTeJM0AZ5lTbhvEkRMAz+abWflcRVb6lt3a97zxwXYfAM13EdDTzlQGgRFibPiJtbuxmJIdESYBY4OXMyuyRRIPZO0lQEZDBm9Fp7OUhJeRDkhfcdAhisq14HEtBU4blAbv4ed5KIqlVi0hc+cRPCO7pHLbMCHxd4UWQW1OEvvQslkF0PaN1iHn3Peg8v5W5YSVAGEPTLET39z4d5l7heocJwBBx2mUMFuau+eu3wgwloBW5mf/NodhxL/IjK0L55LIIhUmdEq/EQMowq0kgISRJksGjqXnGwLVwATGprkKiJSz0w3jGTZXe545cRK5ANBKG+W19PcsoEZl4KEWvP3wEW/fv8MPfvJTEAj73Q1uD6/w4voTfP3xDrlUBbQiTqdze3/L8HKaCs+WoQLAOO5sYvkiantpGFxGoEaBbEg/q/JsRj4gP2tK2LI126zAxMw2q1UmW49hm/t5muG8V14S4aMUwTWs+WAkNeDwqTulP+cWVTe+JxruA0ZriNWy6/SgMrpzYM8246G927hnIQoWRAqa1y1oTc3sxHBX/T61dZOh6e9r0VILgGYPmgKmeUKazkjHE/LjSTIsYQZK6e9mD9WrRYz1nZ4IBgO5inLWVMJuvsann/0Qv/07P8X/+o//Z3z19lsUMOIs5TBMhLVIZsHDKSPnvjZqJjUC/cTCiztNEbv9LLw/VTLz3BSBeRLCcz2OAaGVGDjNyBD+qTFMMNBlPHONxqGt8Qi0XQJ6DaRsXsxwxuvFu6kmFOfKSRl1yeCStex12EcknG+19gYQcLShYbGrVkalAqoVIQQUrrg73uPDwwfAOeQqZ47hAD3/Xg2Amqtm6fRsiaoGrYHfvVRiAK1JjDvSP3V2YCf0TIxzzYLrOMCzzoLKwOAjci0Yt5SBpxXGW0r6HAAqf00u6CAQ/QRSx8o5h8Nuj1IKTqdz2wsECPXMYADZu8YYW+lLXysx3iwAtqSlRTp1ALi+vkIIAW/evGnlV1uwdHREnuyyS0xV17GDjofDAafjY1P8rUvweBcDyQwMRwexAXG+7HNd/LAaZaOiH7qiG0gxGGh9B6NhEhwd4D12n9xi/fYjuBa8u7vDP/xH/x3+s//kP8brww2SE3DMrStcJAQ3NF5wDjllnNYVv/dv/T380/99xfrhLUo64cN3X+LVpz/E/ccPOKaPTd+L91mAfEZKCa9e/BBX1eHu8YT3jx9RS27NPGiSKH/KGeVccFpXAV1LAeWM87JoJ3cnGVOVcDqvSASEeRYgBMD54QHnUnD0jPrpLR6ORxzvj0gpg6LHdLvXrr9ouqU1FBQWJOyClKantOKuLhv9ToUR5wNKAWphOO9xfrxDXiumeYfdbg9yDutyho87+NmDEFDyKg8gBzjhOARoI28cG82qZBGdTyeAHPaHK+EDOx/7HmBGWhfl5bSdJsCsOWUASaCMVa6CATjNLnXwMeKUNIMZDofDAWk9C/91lUy0lMUBCEG4T2upXT6zUETZeAzkLSW3hh5kdhUReOqnwfkIsG9nYOybTNQB3c7XKAE/p9yI0G62nhjsJIsMOeHjx3f4+PgB7uUejgLWDw+oaQi8tLMIpMJC1SCIiThfBcgFYHY47Pe4ur7GIxjrmpASg7MAm5I5QUg5YRcjmCtSXsGlYjftcH11BaKMioQQAxxJeVvJFcfzAvJeHECSe8y7ucsNZjA5pAysK6Mkkash7oSiizX7phRIk0MHchOcn5rMXM/HVkrX7DBycGEPx6zVW/LeTUhAeDVFPIleb8CZZ8nE1oCTV5sq56yVAEUzd4BpmgEmrGvF+fSAm6tDL4VvXVK7TBykFbqXPiRf6CdM11YQnJtgHc6YGb/86huclhXjZYExu3vhilQyElfsr66Rwbg73uP+9ID9vMerV5/i/u4elRkvX36CVy9eCeUYV/jg4EPEFGfsd3vs5h128w6BuuPZoASSeFStVY48HMhFhJ1HOFwLDRUpaELiJwhlRUDcTag04yrukdcsPItMiD72l7rURWqHQO9Xq4DOYyMm5wf0g4VvOhCZBwziirTWzk2qNrLpJ9KAKVerUClIedm8e05dX1u3e4AFjNQ1lxCKNopjAhelS8krmDMmH3A9HbB3AbEyIghziCLv0qI+Q9Hy/ASmgsIZQUtInQ/wREhsDXEs8602uqJxHgx8aTJGZQM5s+Tr8PnO98kElHWVHanuEXHRIITy0WMAZBRYAG8zrWCVQc23rXg8PsIpvy1IAxclNaC4Gce6v3PuQIkNdZomWTMWECKlDOMKbFm2F+DBc//enKcWPOm/H+mWQhjhBp09o2nScyj2Yk9gHY+4V1u2FvmBgXvdbuq2TYU2iGIGvGTGbgGhpwkbz12XSUv/X64GCbQnGxjIoCCNeA1kNjDWKDmgme62Z4KTihFp5gaAxX9mlgxwk82XoPjox4/ZjTYw832sPNu+N/oQpIClNUcKOm4xQftzZD9qwN47xDht7FEB1FTmKhgqq0Z6hor2JdFsW5DIlrbWfY81G9spzdg0NXOnaiUsM6PkAnby/pMPgDewXri37XzlnCXpyTvMbkacLBN4u7dtnmyuSjG7nltQ2JE1/QMO+30LksgNLHvS6Ai488HqcwScl2SDGAKW89LAUGbhO40hYpom7PYzXr3q81lrRVIMpWXEVjFg6mj7659MXZZbdQfUjpKeACondV5Tzo2nfj/vhFpEgwIAsK6L9lthZKiPYL4IxKYRn4q6nKoFRD1g6sa9qVn/xGImC18sj6+gSJLrwUUR1BpsGjJaIToXIEwD93cx3LC5/YTdHDBP3ZfPtbQAm/ibRsGgOi8lxCl2GtAgFDq1uFY99n3XbwQYC3Q2TTGooAYiYBw7ows5sOw1Z9omSNZWnO8KxmevXuGHn3yKd9+9wzcf3wuSrd6VDyOIOz7luTnjgZR9cIif+QKhG2BPuf8YYyha9nzBdx/e4utvfomfLX8HU7zF7eEWr1/9AD95/Tv44tufg6NEC7x6hNaAhcjBTV6NhG7QWGR3nL3mqjeZYkZtF9RPFGwDUAdwcZwcy/AlArhuET8Y92z/zqgcAM0Y404vsazSWIhVu47O1lah2Tf629GwENwMc8C1xjrcjEu7GbNkAWzWSCNJhrAMttlG0ZkxZHNIRPDRHIBxpDrPF/OKy4+Mvx9+sLEhCIAnxOsd4n4CXlyhnlecH4+oKYswYm7nwMayXTNqBr/8vpdtjYNkEF69+hR/8LO/jV988RW++PoNHk4neW6LnvQ5suWvQ9NA4/kBS4TQyuUrQ/ppHHagyaNGr048tXHIPep2zbpWb6PktrvHiRznrxvUssdlH+/nPa73Vzgfj3g4PTQQXqLHdDEXykk1/JAsnGiGpSq1PrbOJyPvn1tGpBvur2b2MOqtfBBHSgF+m5jKQK3wITQS/rRm7KYZOZ/FATNHyzk4ArwjzIcDjseT7AEySAYgltLxcykDozG1YIJrAlbmXniVpLmSzIVrpeOOxEBZltLAOgAaJVXn3c4RdcoIIkJa176viDH5gEoOOWQsSeauaCnMaIzb9aQ5GgGlZgQvhsLd/T3aG7LMriOH+/t7AGLg52IVFMqB5lxz3LZXdyDa70ju9+L2BR4ej1jXM5gL7j68l0AggILS3n17N26Cg3W+7H28Zj3knLZ6cpi7DXDRbi3zOPhnXW3p3JurWQiYXt0AlZHvjqgnaYDzX/63/z3+vX/7D/F3fu9v4OAnVDCSAvxRugOJ0XW6R05nfLy+wQ9/8rt4Hzw+fPUL+NMRp/t77A83mHYHvHvzSwQS3ivpMCsGy/HuIwo8qAJ7H6DRUhAxZudxWhZpHFArpilinmeklJByQqkV11fXCETgWnBeTigemHd7RB/hAJyORywoqLPHy88/xX/49/8I//C/+K9RqGI6zDjcXqOcV6xcQNEj7mZpflQlXhedw4t5xjTP+PBwRCoVFFzXtUQgCjifz6BasJzOyOdHnM8LgICKF4jzHsFL6brzkulTIQ8wDMrBSfd6lRtmFJP9R4R5f8DLl69QUoL3ETHODai167ycRbc+B9Bst3A7Di0+MXzEaYMpgOGnHeZDbdLK9KxliZpJNu7LzcUszS0uhsEAnOuWnWB8naqjAyICWljjwG2kIlatAAAgAElEQVQwTTM3YedaaFlKzqic8W/8kz/GP/3zP8OHd+/hpgnVe3AgcKpP+HbboKyUH06z1pSXz1njU2B/2CNG5Us+L7jaTQhTRJgimBm5JA2WE0pNIM447K5B7PDdu+/w3ZuPkvVSVe54L41VnZOyPHRd3ubDr7i6iihJ6Fc+/fQzATQl0tXWVkrFC8oqGc7VqK0qwccXgPN9HZkbpQPzglof1VmUyShcUGtuclP0tWVzA+RDs6Va0zuQBgcrjqeKnFaEkHUdHW5uruGCZIdyKfAhCu2FZqJIF2RdW+UAtML25oBpZmRh5clkh3l+Cee/bXvkz/7iT3E8Plxs++0uLLVI40pHOLx8iW/evcXj+YgYIz7/7DXu7u4QYsRh3uGwP+B4f8QUZ8xzxP6ww9X+ujnfAoCKpIbZVoNgllAqN1DCMcEp+NiHRdqkTZxQLiwl5EzwLoKCBzvJzDf9ZB2viYwkc7ulxadyoGrrLZaN9FroPgrz0jKWJDUxyL5oqpOlyaCzbGrh5bb9Jo5nQUqdioeMHkCD6pLtxC0ZhlnKRLn2gJHTYA1XqaiQ4laHSA5Rg44uBNkPzuHq5grvvruXeQse4Cxrms9AOousYpGxBsaLs08KmGryh65LLYyalT4ABkpUBcn0u6z2G0umlPMeV4cbzCEi5xUprzinVc5KyShVdC3X7nOxrp80+IPoVKLWbMlsRNZ9yqSEZuZPqZ1pWaM2VjurNIIhzFjXpdk3VjIudplQdLRyb7VniYQnuCrAYVnCJmu9d6Kr2Xw89ZG0LNh23xgg5/ZW3a9qfJrKR26Niwjmc/egutlGltlpNrRRSdh+dj6IDvMeQN30Cfn/+3qiUyB2Xc0FU9xrxVTF4/lRsupj/8+70PeB6tFaSwt2WsqwgI2SCDO+GDNvsk0BNEDcGs9VBSqNMsYydKW827XkrqSBNANIvfMSLKmNZ0H4OPVcVMs4VL+nDFmdQndCHZxXG6dUBaAJQHUoRDjn0rAJwOyTwX+A+fDcATC9CY2GMAESaO5nYLSXLSBSNEOy3YXbrgKRjplcAz3bvlUZJhmqkkxiD3bD+pEl6ei/S5UqFoLR9gRp7670AKhZA+YsjdNc7CahCuOcVzw+5JYwZ25yjFF8Rub2zgZ8A0pJUbV833U/zY6O0DKtQh0QAmLodluppQU7pGJbq11JeLF38yxVaSVL075B1nofsMOswfyEdV3l3mqLtj2XJQElpYQYJzkT3gk/voxUkgG0EfT4/sxASgVAautsmed6AFqmaz9f8jnhB3ZNB7VgWDN7thWYsjckAO596FQh3PEpoa2rT2yO8fqNAWPJIiB1KyerOgiW9ToKcf2mmJJDhEEOlwiS5XTGh3fvJZu04Qnq5Nm9eGvUm4PSJ67/zjmyKssGyDKzlhUPA9ff2cYYM0I75CSGZWLG3cM93n94j3U5wcdrxBBw2N/gkxevwUUEds6aUQInpcJqBTtHmK3xlR5se43nLgYaP+7l+12W/zbj0croVMA98bF0ddz4YLZ3puE7PVvM5qOZ1swDMG5REx4+L8Zl5xJDG0//UX97M2I2oCEGwWj3pV4eZJFrobbA8P3BUR2AwJY6S2T22zht7ZC36O1mjNvPYvx9U7h6AHR7NWoFIRWFCx4UPCZPqEsCUkFeerd4ulgr6gNrjjO1f8sPCIxUKl7cvMTLl7e42kf8yZ/831iXsxoH+nES6EAUDgDnBLQLMo/LadkcZkcyXjcF+P2EOnvQFAFPreSedS7lXQss6itbiNvzeZy3zT+e3/UjKGB7POeM5byII2zbS3mlLJOkXbIRmvS5XLrCjJpTG6vSNrcPmTG5GQdkzsRlRpddw51rqa27roHBJk8cHKIP0uQlS1RuzRk+BAQtkzHCekfSyfKw30snS5UdpHKkKRjuWTTUd4uCuVJ+VMFA7eeIgVYOHX3AYXdAWhOWvDYeTSfaHTFGhODFqXTWbEtL15xx29mZrDidT7ItLXuunUVpOnY+n9u89qxANBnOkCxv7zymECSzNycBwADFtRms2RbS8dMNBpQ4Gj0rrUfot5tjo7WkvNtKq8j4iiT4NxpETy6TE5cCtu0fpbpoz+2/axf1r4+6sostA2eHFdazn4kRr3ZAKcJRtxaclwX//M9+jrys+KM/+ANMJJQ1MxhO6uVl7gCgFnz86q8w336Cw/Ut3I9+gvdf/SWW471kJc0zbj/5DOePb3tXdlX6zGfJ4mOH2RPgJvhcsWYtZ9WmRp4CgnOS9Um9K7onkV1MBAoB0TsEBmpakYqUrCZoo6dSEZ3Hv/vv/D0JZkbJ+Etrku7bU0Q8zPCeEH3A3d0d3r97B8oJj8dzo40gELw55hD+zFyLJPymFet6VmfIMv8IfpowhQDnZ7BW9RiQSDC7RPRmywbhipIWKQlUsIVBsC65wUdYtN+u4/GIkpIa7QpSqhyrQLeZBkMUdgdycIOjbEx+ZXBU7PnmuKHJjeEa93HTZfYhea4DaT/M/tkQI1whPb+tF67OhWR24UKeyuNkv4tBbDkgjJozlnff4uO773D3+AgXAnyISM6h0sCRPdyLtbmfOO/ceCGDUqcE75DzClK7aJqV13MSszppIxDkhOBFKJ1OR8zR4c3bd/j223f48PEjljUpf6SdU9d04OUUmj4nADc3M26vZ3zy8govX75GmGahyShnOZfDSglvHUuRWAWIPMhPcGEHcjOci/BRurXXnLCe7rDef4WazyANHFhTXRFqUr4afJDdRKXJS8el9WiQwEjGmgDmiGmO2O/U4Y8R8xRQ6wouWWVrz1JSoYBaGGRAM6EDYnCAU9mvZfWyRzzmwyfwYWr77uHu42bvqhfQdIWIv15CDXL4+HAvZfG7PcCMECIOuwPmaUJ0HtPVNaZpQoxBwPc4d4CTWebtosoEMCCkA3CtQoMvLENiBTw0s4sFOK2lSomzAW2aZVprRknCrb2fr+AQMCZ+dP/Hykh1b6AK7+GgVWoZ+D3JgWvP2LLkCi4JXNoJg2XHCaVK1cpC8wxk3QRCZFhZDAPKpyf3DT5izVkpNNRPMeCjVsTopcFdmIW+C4RpFjqQME2ojrGkBdkaV9UMptIScADNqnfeXDQF87s9LIEBozkCDPzp08jPcv23ACkJAMaloJaEnFesaZEGOy1QQir3R0ORtZIBQh0CAZisApMx0D2RZOnL9jZACNCak5bw4p3TPSDSfORjdZDkiKvdHkSEJS04L0KdMtpZ3jm8uH2Jh/sHnJcFhQvcBsyy1cewx/Vf41nGqM+2c9eANbtXmxKGNYQtCtKY3rV1svlg6iCw+ZUG+hUfkMmBObcx/stel7rmucSl595tfB7r+4hvar0JWGhlakCEyngnwBxDs7P9EFzhkUKx8zRfjm/MfB99jwbOso7HGw2gAtuW1ao/Y0hWs2VH5oEjnuxsKMUN9MxWVjnFvKmUaTLISZXT5fhI51FwXWp7fpOUBTk+rcKPWTLtbe6brwZ5ts2LONS6G0fwXvEbS5sEhntZU3BodqaCamQVALXJCZtDm3cLZJTc6QNUYre1hZ0HoAWhZA4JUA5gIsayLj34oWPZrDEbMNw2YwM3L22n8f16spTQA4j/2u3I1tANdLGH1ObjYe+I0wajHZLWPB3sdEodAG1o7LxDRND11MpXEciytpFRa9CsVqHEsyWKSrvkHKEUQtJGYl7pBQCh8TIagVIGjm/1EZyuYaucBmtyIMM7oV+QKhINLur7u4HKgEiSFIuCu2C07Hay9YXIrks9cnn9RoCxW+eTNj+3aEpVwnQe68apH8wGOo36DoRlWfEhZaRS20FgoAsa08hbX7b9rSslG5Eh71sAQDLChqzIYZwm0PRF23jtkZUZp/MZDw/3WM4nXF9XeO8wzzNub15Bwt/CFVfIITrtmKg3iEH4Ok9qtDWUn/u7mPN9+YbtTZ9x/p+bkb4y9PRHNlGbubTsGRWDg9BtX2ObwUHBtbXVkRO1OWtFUs2pw/aZslHaPTagmAmN8bMkAtbmoYG19uW2zjTKts2f7Y6mCLok7J+19fieqb7MbjNhvvnM8BdSGgryEcEReIqop1UiOaV0G+hXXEb90Y9Az+T+9LPP8OrlLfL6iG++/iVKzRI9c2b46X4HoZW4O9JGJQIQCp+gKFbvA9xuQtjPcLtJOPt8c/llfYdpY6dZCi36imaPdGL7C7B5+AcPf25mURVRzhkLL62Mv92o/dE3F6tiGTdUEwn6+8oWCLJ91J88ygwiApQ43Z5Jeg/WdzBFwY0sxwzMPjaJ8hGsCRUYyKUgtsg2NUVj3xFDwOucynk0oNP221Zf9LNmkUdAOcp0EkQ+y5eC99hPE6gwUkmtYoFZ9pqAGEpg78Q4ftJMULPOUkpYlkXlp81TPxsb+TsMegyAQA1y+RBhv9+jPDJQczPHWCN+ck/NtrFyzI0Duj3T3IXXdm8BShNh2SXQ9fBQGEzF5PZsC5dowJrSdj7UYWsSaHDgNrpl2L4blfacHLg4FOYzMRhxF+HTjJoKSj0DTPjy7VvknPGDT15h9/oHyoAjYOxUxHAxo235+A5wHvubF5g+e42792+QlzPScoILHofrW6zHe3ASDtK2Sapy7rGDo4DJTyBIYOy4rkqH4MGOQNp9NjRuJ8v0gASpfAB5AqeCVApSLcjeIxWJplujgb/1s59KU0RmrMuCkgvibsK0mzHtJ0TvMYeAt99+hy+8x/H4CBzPWB/PWOsKEGMXhX+vlIoTF3VEBAAsKWF3/QJEE3yUbDYXJxCLMQl2XQa0zM6+t8zgFzoSA6wsk5FAPsCHCd5HgLZg7Pl8FmqLTXYsN3nfz8r4NZN1/Wf2TKjhaRzfIn98k/3NAQZt791f6Kmdp2MeZSEAuCDZzCK7qO9PlvuG4Bttx/gMcYwKHJSugAW4qyXj/v4DPj7c43hehCPZSxlgJepc8sP5EGeyinwdyiF752mSRnROf+c95hgBy/qr4kgL76G8QCkZpwq8ffseX379FsfTolkTv+pgYjSU2nlf0oqcEibvcDyumHfX8M6hlAQgN1kDluy3nBSMZQKRB5JmCXqS5o1xRvARjgpcIlS8R0oLgApXNXNmI2OcdkpWmYYisrZyo71gSLOWUggMoZGIU8A8T4iTgL95zajOSaDsib0y2th9f4rMtsAkmuNM5MAIiLtbOD+1763LqZeI2huonc5qobbKL++QcsGyLri9foH9fAAqcNgdcNgdRL+Sw7TbY1JaLWkQ5KUsSGVjC45ccF0Zv64lmFjbzFFeEw3vLpFaVEjwyfgOZdpZbUEGc0Epyk047bHprAIzXUyf2E7qwZ7xsnNEZhtrkFTsEwNcOqBh9rtkw1UFXYcgi76rvDdA6GWmBhAKQDTQOBEBToBhAwqC96IzuGoFgUeIkwRvnMeSTzivJ6SSJZNbUNWW6SpHiptsaLQvPFDJ6f9KGWqh6MIexFPgTWjcIPyuaZWsrrxgzQLI1nE1Bj9kdGPGM85srXp0f1gjSa7bc9LOh8oamM6AJh0xjH/cZDe1MQDByzzmIlU3dg8A0g2dJJg9go28eS5kT4MVqPAAMUpSzmDudBA2/yOF0ya7kEZzhcHNTOVWFu1dD0q3OdN9VpqtayOzhjoKnAxz/Ne5fpVf/DRx6fs+N/xDN5MFAxpVl2aLbjaD+hpmJzaogjUoU4WyBw7wG4qxv97Yu59MJglaNqv1u7F57g2pJNuxkvYvsNUyMBaaVAG0PUcsutGNYCB1Gd4AvtEGJwle+wCQcsSbbSHyh6QSRyfVxtabtKu0ch0MtPnvTDiqSwZA0Q02FOs8tOoiWL+e7dm3/WzS1nvfM7odCWWVykWZj60fYfhCUgoCQOzaGDo/cuXSQHCzgYwT1XrGlNzp2UwvtuZl+v4twMRmTHGfW9L1H6S6faeNuGUoU/P7mFkaglpVBvqZlV5ALL1FdP6Fygp6ZjXooOO19ZeAAYGVb7bW2igrpGrIt71mfZmcl6olaQoq72vJPpmyUiUYdWc/Y6UUmfse3QKzVgSprtyst9kJbR7k3YyqwhrZkUwemMyO3c7r5fUbAcYConBllvqhxjABwk1qRs328OoqdlXZgA+PQsCZK9gBzA5QQmJbLkea6eXViRhK6DcrBjFkRiVifz4rkO1kDo4zSCINXbvriEvFmlecTo9YjmfcoMA7YJ4Dbl/cyiZi01IK6HAFSIyTFy9ewDvr6lulMyY/Las1A69Fxodr5EUao1VNLXJ3EJ9E4fRWTqN0VTMj+mdE69gTzZlpUYUnQIrOT++Y1UAIIilq7cCUGg3j3rhw7OC3zmdfsw5wWNMBhpQOSMkFKTF1dzCfi4a2+TRpo/e0e9vhb/pgu62e3O/pGjxVrP33EGdunsTB3O0Q5wnr8YS6JulWa4Der7EbDGwS0v+If/33fx9Xuxm/+Ms/x/uP3yHuomT3mcAkBSAHI8sHj3k/4+bmCjlX3H980CwHh3k/YXp5A9pFIHgUS9ay73cTsK2N9+IsNwU7gIVtP9Pza2N3HeecNSonEVsAnhBiwLpK+aVIoO13TcRIptrFWgwUDwS0cjDhPBplycW6Uv+8GMn9zZuQ1/UwBdI7hVIzylJOOJ1P8nMDYGvZZF/afl/XVRQ6Q0EFDw9pWtX2mZMypDGSW2uBd07K95UT0jJ+zJ7rhlQHZZgBT5JZUZM4V503iaUkEV2hdiJ96UBdS26GQj9DnXLifD5tzgdRbwLAtYKT8qdVAYbzWvDj3/oJzksCJzGyHHUn3A3vbnLejM++D8ZzaOvT956JgJQWEUXOdpSV844ybXv99o9/C9/ePeDbb7/djMnW2qKyLSLPjHneoVbJxC0D2MBDpcagfjA6RU8uAgjSPM8ddgjksOaCehYj76t37/Bf/Q//E370n/4DOD/LGmZG0JLxGCTz3YNx/vAG0zzh8MlrvPzB7+DDlz/HenoA14yr+Yc4vPoBHt69QT4/IDjL3NQMe65I5xUcpft8nHdYHx4BjlhLwpoSTssZn7z6BF51yLIsOK/SgT6EgCl4pGXFklcUBxTvcFwWrGsWIzYG7Pc7MBjLUbPjUTEf9pgOM6Z5wjxF7LzHLgTMrz/Hpy9u8LAmVHL44z/9f/Av/vIXmDzjR9cHLEvCQ1nwWKUcj6sExKhUvLx9hbUQ4u6AabcDnAexF37FbubayjU9yxXgmlHLCocijViq4D0ZaCCsU1CxZ7nKfjmfpGGadCbuzlMLaQ5OcNPUQyPN3jBPeWTJIcSIZVkhQR0xH6Xpntg5JReVLf1nmy3GgzxWfS6Z9pfyu/MRl1IM79Nz7lGrGPVjk5hcCtbljJKlrM2hCpdiTkDNeP/uO9w/HnHOBW4vc+WniLqsqOuCUUEyhFcTAKqV5xMwzxPOxyQ6DWrLOMkEKmUFQyqnQvCIQbImxWaTu8+7A7784mt89+EeD6cVTjnL2Dqdj4dRR9InDE1HVa44rxUPx4TTueDLL7/G9c1L7PYHMBek9AipZPIAe6y5ImcBzxlOqEiODwAf1ZEFaDpgf7jFNO1Enrs94I4qs7zkGfMIHDuwC4qFVHCVrDorBfUhgMGIQf69FsayrIguo9aMlBMmpdiBOlgiLQsKm/lHaL0Phow9Vnu4gStsQIRHpQlxOsD46zbz2OZW5CPrnHLJKKwOXYj4eH8H7yL28wGH+YAAh09efirgnznbQTi0JcDiNcvdsmIIBmA2U59ZHVEPkARJ2md1jNTy0dGc2obiMQHFAKrBNnHCqUzk4dwMaxBmLog+vDm88soWUNdgxQWw2PacnkGzl4s2IvHkEGJoMsT0UQ9qa5ai0cyxVA/JfNcGnoxXpaFEmKFcsgAXacBHYMQQMIWA6D2Cc5jjTgIqzEjrGR/uP+D++IhzWZCRUV1txCX2TiafO8dlaZWC3GyjoVLIgNOhGdk4V81R16bDqRS8Ox11bjXvV+eBdE4bByI1i+9ij3Zbo6rMNiBqtLftc6NPxtz9OU/UeJhZ7yZ2lMpXIjw+PGCKE0rNKqe4DYUZKKngzTdvYMBqA/Eu5gEAphBxuLpCzhkP9/coxYDYrR3+JNhscznOATNyW6P+c8mQbcyXbd6IJEPegvct6QG6JX8FONkf+Zwv+v3XcwkBf73veeSKlrwSQ0BwUuJsiSIWHyGSsv9SIPzijSLDzp7Y00Hl3XYvbP11K01v1mCxSq8OFproav4+uIGLIqpZGzPKfyGEZscYAAi1+0eMxg8c3i2gwKzyUfv5YNAvRCCSxLNNYzuzV4Y/gdHU0P2mz3FELRjDVWTsOB92i36vnt0KZqQcRdew0IYJZVhf45GyoL23/uedJM+FSQFlZmnQSL2qKATpjXJelBO2lM7bWxjwhGkSuZ61WWwuGSjiNzoFZKuOn2ttwC5ByvNjjBj5gpt/w2bHOARt9CeVY6X5IABU7go1WKdxEBtJsB6vAYVOIWLNdyWIFppvTAxpbWNA8IUca9mU7WdQ+9abGQBTbkKbQfC+NvwJA2YTQ0AAtJEXNs8ppSh3dvchoDpR9nGEI4cyaYCCu84wX5NIn1ELkl+xLAuc9n4gcvBxbjZs2QSDn16/EWCsmHrNVWx2B4yPSA8WqYCtLCTJdl36lk2tkUY2tZzaQAJ7jkUzRm+1simrfmPaROC70Pk+x7bxYuqTLFbnSEEMhjbCksNO3oFRsK5nfHj3HX78r/0NUHA4zAE3tzOmOUgLnCr8RQg6QczIqeDtt9+KoTccsOcukXvPKfynymMDBunvjTLi6Wf7fZiVU8O7Pj9NWHZwSkA8+bsjK8vcKo4OdEIXYziFl6ve7ev2z55Nd6EkecyzG29Bm3sAoiwJxpc7GEi1DjPz9B7fh3dsgg0yGNnzv0aBjyUCT4DZ8YGOgJs9pv2EsiSkhxPW+0cE45LhYWymgczwsrs5D67An//8zwAw3n7zBm4XQMG1z9kI3MX7llpwPB1xWo7gDLjg4IKDjx7+kxtgP0k2rC0FqYKyc+eclBd7LxxGPuK8nAVs4qoO1vOzawaonXICBiXenRf5LFA5Y01WwmZbaLtXLs+3GV/NQDcju+3VDkRKVE/uzFw3HKdN8TflD8ABk/dSlji24WXeNPpqxj9J6SQ5UmXBzx8NVWi2TgxxCmux5nADMMOM6D2mELHf77Hb7/H1m2+gL9RmaXN/UNvDqVS8f7gXI5qA6/0BL6+ucXx4xLkkVO28WmtRx8RAF6fAEUCoSJDs0KrCWIy1719zW69GqF/NcCLM8yxgQEr4+usvUWqBc6JEp2luzc64cttnTQ6p0TQ6rvbWJpckUt4bXrR8AXNmLUsPBn71d/auGwk///lf4N2773Qut6VnpO+4AcqKGDmsTiCn4bm6LgC6EaTzY9QVGLbKKFMqADdHuBCxA2H55h1cFqc2E/Cf/zf/CP/R3/8j/PTHP0ZlB18ysFaUkuCzABRg4O7Nlzg/PuJ3/uAPwS7g4c0XWI93yN98gde//7dBcYfT3Xc4f/hKoR4xKn30OOWM8+kEShkuBExO6AXSumAtGc4HnJdFaYMKUl7FXvBCVZTOC04lYyHCukqGUq2MeZ4RZwkqpZxwehTqlRADDtfXuHpxJQatGs3HNWPxSTLlUkLRY/uHP/0p/uYPPsc/+z/+N+Ddt7hbCxY47KcDyBeU8oglLVhyRi2M3byDn2Y4igo8FkAbIomtImXNdkilS7pkgHnPoMI4nY4CUmmzHh9nuDDD+Yg4zU/O5el0lr1divDPbc7s9uMm58ZgM+neN2DVdv40TU8P4rCXNmr6e6/th1g7r28GxBDe5LxgXROmaYIPsd+YvOw1vZzzrTT9eLxD1AZYDpJ1cry7w5IqKkUQBKT0cUYJK+qyPJGbgGSNorpGX7SuGcuSBMzMCSUnsK+oqMi54P13d/j89Y96GSIRuFTpHu0cbm5e4v7h59K5V7FziZuYjbXVV+0aHFSA4dihVMbpXPD+7gjvHb784pf4PH+O169fISfq9gp5EKJweQ/TS4BUuaDCUUbNC053H3Gy0VRJCgBdcgF3I0nu4yFl0KsOUYJGgaWZyqefHpArcF4SzqcT4uQRo0fw4nhJBqZamixlsK2iQ/nsxsA+M6S6osng2n4nmVYF7779Ei/PR+z7t4bxj3DnMBm1qt3h8fHdt/jsk09xmA6Yww6fvHqF/f4K1qXZBQcXIzBFIDiwc6glY03SjV4asdTmcEvWjoeP0myKuMJXaZaGUqSSKWdQERtkA3LZdicLfFSULDrUQXmVUEAkGUgEydIJXpzVnl37dDuJvUdPgFECpDRabXPjMm0BewCpaKf3lsjBXZBsALbnrw0IxwwBO63CsNtSJSXUlIBSMAUPT1KMH8hhN0lDRKH7WJFRhWMeQKoVqRYg0ABoy/MqN9InCBVWK6cEsM3cbPts0JkSdCnD61IrNpIfCAhpvNKVGbtpRnAeuRScy6p2oAXuu3Fj9sYYUN+IUwWJvnceMfhkBE0oqcI/i8HO5Sr6hAmn04PYBwZaDeskpkunEKlchTrG7B21bcgRluWsjaS0AgvcwBsb8q/OJrVMPbmCluc3gBJdVg7Wi97Xxth/RqDGP+uI8KvhkH81FxfG4/0Ru90EYmrgei6SPOBZfaJSG87ReMftbBjI7HomYbM/B3B4DOqbrdyOugJ31kQqxIhp1mokC4CB27qLKW6Zsr4lVTknlAt2Mqom/5DS+rBmZ2fllJBAn8q5plgY0OrlkdPXqtqYufGtVqUPAnW71nzZzTlhYE2L+hnQMnnpHWE+TwPX9BZOKYK49Axr9dB6mb35U/oJaWQmfltrdGbrpLvVk9ekM6E5av6v7mvvPfa7XQdKWSsmHOkcEEKICL43ge6TpD6c+j4IATu9l509W/tpmtoeqcpZRM4aicnnfIwwcWcgsyNC0OzyEEPzI4WOr7YzS5AAtQ+T6MGltHFYkCuonW50QzgFW00AACAASURBVGOjOCJ9X+5ArTXrCqpLvVIEGNBb9TNkOIr64j2IKH+XnjX9LJRckEoP/hm1jGXQcq3Ig01qPhhYMtGDE15kLlX4fHc7TCFuClIMoGb1ef0gqy+v3wgwFlD9guFgDQAHtWwNM7bsTTFsAuXD0Q0v2feaVWSGvzrCppR5OLoNIHn26o1cusDbjB4bxaCeDpECyGZY1CpNfnhAzjXFuqBgqWfcPb6TMko/gVzEPF9jHw+4X1c5GGA0gJ2UB6h2x4ag3fAGkHUE8izLjICBiPgZ5UibP2QW6NeVZeg4yMah8zvaldTnjoF2eBra7QzitPHSdnoHy3Rj7mnGhmUE9FW5hEwtXZ43L2eZsf3J28kwY8lAek/bDAY7cGTeFQyIBqz2fksr/NSYalngFyXS8vyt0fXkGuaYGdKNeSelHH6eUJYVdV1RliTCwoj1eWM3a+MqiYZ+8/ZrgIGUE3z0jSBdlAv1jFtY5ro6PRWNN80HEjDlag+3n8HBtfm3SJ4JTyKCjxKBi16yH8BAch7Fi+JoQGsDs7YgWJsv/ZtXIvnxZ60l7jBtptQbgNXWt8uIvk27oTfowy679GdDcsXFegIYiOTtBh4Ou7iTTpVlAZx03CV1iCQ7pJ9heY/BEdUHxxhAIFVSWjpq2pWVi4n6KbMAl1kkkv0shsyapdw++iBlM94hFyFeb0PXxZd3kTwOKUthpLzgw4PQVbgQZNAKwsojtUS0qItDaqJVcWRbcwyV6f0ESUBOHBbS+XbS/CBo2XjNKKlgnvdYU8aae3QyaJTXe4/TSTOLrfkFb89Z1zcCTpnjRu1zFr0VJ9GaI1ijkuDDxtlllsYKxp9rV1G94IN7etZJOHJTShtAdmxkZBl6GPaIGQ9iqGybB3zfxQwUlQvxsEO9vUJ5PKGsGcSMu5xwXzIea0GEw5Kc6GgGIgiBpBkEuKCeH/Htl3+Fz3/yu3AAPn4jjb7u3nyF/YsXcLevcH78CKwnadxBAKoZvBXEkgHAAK72BzjvMWXh2GQCzmmV74GwnyaUUpFrRa4FK4Dz0sH1/dUOYZKM6+W8IuUijcB2M+I8Ic4BxKzxFTkjpRYs1iDHOWkeA8bEjKvdAX/3b/4t/J9/8sc4TJMYuj7i3YlwaruU4GOED1FLq4zDr7YzrJplY/fAkTq98qu7jx/x9uuvsb+6wqvXr5HOxlsmRl4IBCvftSunBSkl5JLh47R1VHRPjT9gdaihzizBqY1BahQXyV7ZOCNQ08rAi6HccvsR25XYZL9oCbZlsmw2oc6F8xHT5OCDNBJrzt5g4wBoDTAIwDTvpHu5NYIqBXcf7pALw4covNo+APMOdVqRHx+fHgRy8GEH1AofCNPEmOczYjiDa0GcCCCRMwyG8w4vX77CPE0KsPR5ZQXdluWElFfhrCbSknY0vbGZ1o2tZZpJV5HkmOTCuLs/4+ow49237+AA7KJxmll344haC84ncehd8HoL157NjkDa/bhZUc7KmgGinrU06klU6yOgzVItAEUeCFK5kUsS/umaECNhih4++AY0VDGKwdTSn1GrNuaoZSs/Bx7f7V6G2IBcQfWIP//n/wQ/de+w9/0DG1tWwT+o8+2ch1M5yVrefrU74Hq+wmF/hXnew08R8NJRqzrCygXnxzusJSGXFen4iNPjI2rKAq5WsZmdd1Km6z0oBIQQMU0zDldXuDpIfwgXAhAncCrSrEo5UvvZoA5StSwyNK52Vn5kcoQYZ5DxLDNaIHcwEUR2tBTLyxQN/bDZVYSW8WR2GkgCpbUOgeXBTm628eCrBQrNVwOj0a/0BQSEhsEMKJIgUiw9CylGtfUIzgXESSiZbm9ukEvBw3pC/q6ozeWkoQyAil7a7wY7YvCK0G09avLM6FnMLlaPRIFq10AD0a0joE32pgDJPnh5dcAUIx7PZ5zvlva+l4L5qY/VP1CyNdDr61g1G9TWsdNx9Owtk69P5IuVLatMrTZgteGrVlgSzHyszV+1zMFmd6utJrzG8iMDu0qp7ZmMkfOU2r2ddwpw2/p23629Mpv/Sm3NDAyuwy62MTmjq3MOFIJQY22oDP7VX6ILJPmkglsjLGdOlO6dVmKuYJyDQ821BdfR+GLdcC4BaAMzcfPkHl6DTEYlZaCuNRQm1f0EoQAyX6/UCu9nMGu5dxYbgyBUPEyMUlRnNOAQ7XyLLV+aLFHnDw2EVT3+pCkSW6DE5mOg/jM/xXlY4Mr2atVGXrY3hdqFGmVKKQWk/SG2IKDKxJpbNjeARsXiSPSV96Elkekw2x63i4hQ2KnLxU8qeASMHkrZCRAz3va6VT9zByd1fdt32MgE+j2AIaMfohu8VSjpd4wPmAZ7ywB1qN8lIoAaME3ON8C+JSGZXA+EUhRT0LVyth+9x2G370mPuubBS9UxW6Zu1SZm9gyrTNBK9ES5BxjQE7ect0CjAbdKwUJdRwk2UFCSVEAwa/UKW5KBUlHUgvMiCQHeOfggmbhclVN2kHMWQCuqn40eoyq2JUmXw1mAopOaff59128MGHtpvI8Tas4ZoOeXsOGl7wIaYOqGhRFAiwOE5mSpydWPOVmpsXI1ogsNczxMEDiNIltHdnl80xSDk6DHRMdlHe009gNCbYAIEyMzY6kJ96cHBUYIzkXEsMfO7/AIQuZOGE2+Gzn29EF1AZu/jZkF4kA4GJny89m9WwPh6Qeee3fDU5/7hglVHsfCaCXFGBw8MR7G75o50MfUuxzaOw1/b0DrCOtiXHFsbnYxyucnYWsUmEPCA6hLVlIMdKBm60/JvvsVVsCTrNcLh/PZi7uQkN2lxox2uKbgkaNHOREKEeqabXvrM+Tvm0cTcD6ddD9L5AwG4KlAlow8HkC1roCgBtd8OCDuZ/j9DI4BRS0vsgE0BdsNECvdCM5rx9SBD2lcDlOgOtHP7eONAmtjowEc5eF824fkARf23+ac4eLvFg0jkwGqaIYbtrNCKn82j9NXsrxppVPSsiQx9Ouqzfn0nSsEwOv37YrcOwfHxndksoia8WL3adNpckQNOmbGqkBXm6NGL9K/s53rJ34FcivhASJLZharMTI2vDOAUuZS3sc7L1Fw1slw1P5NBExTxPnUy4P6mkiGB5GDJ+XmGjKNzSgFoLQJPXsAeD7oJHqHtvuEBhmAfla9l6YkZOXduhfsuxuD6f9l7l1+Ncuy/KDf2o9zvu8+4sYjMyuzqrqbdhVVTatlWbaxkJAAWwKEsMSAgZElj/gDkPgLmDBgxAQJpjDyACEhWaiNPALT2C23pbbVTb9UXd35qMyIjLgR9/E9zn4sBmutvff57o3Mso1QnVRGxP3u+c5j77XXa//Wb63Gz3gZ+z36rj2tzrNj7CjcHCWM8miGcbBLpzpG79NReVpq6wguBsTLM2miUityKqgMfPrqJc6mCduPPsZSSR1cgnMVXp11AOCccfPmFc4/+hhnT1+g5Ix3PzvgeHeDabOBixEXz7+D+68+Q2ULNGuz182KlQrPjNl5+CDB9cKMRdFJ1tQjl4qlZEFFsawPoyXwwaNy1VIvQarP2w2meUKIodlDO6oi1ItxfUlLHGwYCLpZsP3wO/j44+/ize4Ou5JQuOBqOwP7I4KuW9PDUBSnjG2Puww91TcmCSg81FBoYFAEMeFJ6BxSSYJeBCMGfyJNUM7u1Jr/yOX4wXnvPZqvZIG46Ptun0/WCK9t22NrqAdVw2ds1x/P7Qhzo0gQnj1xnKuVHz54ZCv/i0DVrsQ54fLrV/jprSD2SfmbnQ8I04wQZ5QBYatX0usZJ27u9lSD1qgblLkWMAHeSSOn0dcadQNDupjbZov5oHa39v6MjggaEYsPfAFGYcbumHG/S4juHlP0OD+f8PyFoZe7bc2lwsPBsSRwvO9+E+sky7vxyXdPJrF9TcqC2XHTIe259fdmB2vN4JqUe1L1g/poozPSkqz2PPqzNccAQxINjjHcCMJZqEF/WfDVF6/x/ecMXI6z+Z5DFOxQGiq863OcWnWICwEIQZKwJeNwOGK/u8eSdvJuyKj7PZabG3DK4FJBlm/3io5RXlkfJqRpRtmdYTm7xDQL92ycZsQpSFMiAlAAS6x00gFqFENgG6/Oa9hsSDV/tSO/RB67LJkXIoHsGsQgvO61+Rk9KaCHI1CtqzV7svj1NGpS7tYGX/WIJXkHvctF30WSSNULAl5KaaeOQKU+DnGa4HyFy8cWPIOs8qRAwBqiA41IouuYMUBeezCykSKrs/m+KpSkz2CvvVqq49VIN7iVu7olT8fzWIFCdtexAnMYZNYx7b6bevzqs4JsPk3vSOVOmx/9/CHd3vAcinJknacR5tBV+hAItTjCfjBe846qHNGatjllcXbVz1E7B6XED12OV7HKg8OekPupp2pLEdzkCN+QD3ngG7Xvr3y8h5//yxxjDE2AIvLabwd/Wjl72yo2O0D9JzLEHwHspM2M0aAM/qH3ch1Hvn1WFcUPiL3hyppY0iS67yjS3shovWYMDNASxfpesk7XSVWd6qbnVYL7prQ9c/tZN6IG8E8fJksaarXICfa5ISWdbuaWqj67/L4nUnueZz3Hkugt2uBQULXd13eu65LVQu0Lqq2Dxq9KBMfaY4GktqHU2uhnaq0NVe6c0+pTWQukervkrA3+NDZmAZFYXNvWnCV07fOBF7UU9aEIUIbvPsf2nSr7j8Lp3kv0SfW6JZud+qRNAekcSVWIUbSZ7Kj/QwCRk01YJt08HisCCdUJcrdXCRhdm1NgDMN6szCfziE1lVepArXTZjBbFQABVDVvOPDGs9pclR9Dto4+GGnTUmahUzGkrlU8ugbx1msbZc17jl+MZKxoIoD77paNE0iDQtuFtIUPMY99V4614yB0l4SVfHxAuFFf+DJR3RmVxyAQCfKpVkt8cHPWZHF4u50e3cgAGIRhDLiH8vsmAIMjTMKndKwZ7/b3gJfGCN5FTG7Gxs+I8Mis5ci1IMTJVFt7fyJtGUAMY5e0sWyBni6YMdDjQYE9SEqRDZ3spHdF+5hh7I6LjYVdU/5TvjK1MsyyWAvnZjRKI+Bu5h/jJNni6o7j6PZ0A0DD+SuPAcNYDPNml+Dxh0fu3y/ycJiMSLotwcHBAdApAmwa9It2p85T1WVmNBQrZX/y7H1XVGWcWJNeAE2CFowboS443twj7Y+SKGCg1X9b4gfivLTdSgu+WUpFvJcSJcdOyiXU0PRAzOYCOP/gKabLMxRId2kpD5N10DeCCR1Z2ZHBgKyLqmvXDJ/NqShBDcBOZm10UGqtDfFlmy6D2zYgkeWhW6nImDTQZNUqKOFx97b/bIHdasd0nDoyuT3xsklK6UsVpc21YjNNkpQsBemY0PtMaOdd7iuZuCMOLAjo5UUdadB4koZbjzrRykpyySi6c8zMyCkhE2HY5+zuoc5Jq1BA15GsMmS7n+JASXkPtOqh1IoYJy3P1qSTd2CNTMl5+OixLAmAlJJstzMOh0PTF7Uy0rKgZgl8Ssk4O7/A/d19KwFzzmGaJmmauN9L+czggNmOugU7I8+SvdTplo2NWa3GNTQ2U1gn3huVBjOOxyNy6k2IaJD78do2VyO9ABGtErxdtB7aNbvA6EjRiWyPwZJ347MQ4pNz5TyqyMd7hMz4p//893D/7ha//NFHmODUUWT4zPCUYRxPDMJyf4vXX3yG5x9/D9uLS9zfvUPd3eD2+mucPX2BT37lR/jDN9eo+R5UC6ym1jsP62CLmpHu7qRJkvdAnESefUDWMqbdYY9dTki1IldGLhVhCpg2kmxdDguW49KSs2fnZ5g3s3QzVoTQZhL0VikFx2Q89n0rMeaCjekJYpQY8Ff/2l/D7/7zf4Y///wzpLLgO8+ewy0LttGBi3V5ncDkNRBPWl4sgSuRFz5mC3DYgZcsSMWagZqx3W6FIzcElJTgasJxd4uaDogOmKe48jkAQUglbfJka6RvxNjkQ/lK6YGO6gICWbNDFcIQa3QJN5Vm+gcnFstkzHWdZHLZnL3hlm1zYFxLuq5TOiLGaWUDzfZzmy0JAOLuDt/9w9/HP7y5wVIZHKOCIgOmjUfZLFiMVmB4ArvW2DBH7IBIhKDyCFk3rJwHcjmCXEAkKcPPeWlyDGak44LLi3O8nt4CO2prcvQRpJuvQ60Dl7jr53SfjGVTojDe3RwQPWOaCa+vCc9efKwdfgXt6lyUoMfJpkA+HFtDDHCVMnBwT/SQoVSGyhPbmLPkIsRGVfQKMN/ACrIJJ3yepc0ukZS8MyoCRTgMFUVNJ8m1HHltDr+WTbPPDRGm/qwkdzI4Fdy8vUW6mAFEveJJGDTYJrur2excCs6355jChM32HPPZOWrwQPDYLwe8u32Hr79+ibuvX2IbgbNNwPl2woYIxVWw03JpMtQRA04QrKVk1HRAvmPcvKrYMyFcXuH86XNcvfgQz549E9SrgzQzLAVkJoKsg7PrtEXOgavt7IgsVVhisA5vZ8lHM2+aCNVk7yo/RYR53oKqJhBU/7kg1BgVrChGVt9QGtM57zuy0WzNoAUsqcCa5PVeUa5sjXc0vjCKYFLamZZQIczzBlzRmusJvVGB8wUZjEMSFHZRuXTBA62pscZDSnVlctQrYYbNc+5jMQxML3E9oSiwa/cNfotQlY/RBVzf3KCiohJJ5Rq53jQGPXZcgQSET0uTGcLdaQ1iJKFSOppNnlB7OdhnpMmPnqBp/u3g8zkXYIlpD0mUOCeIYJtTe9cHG8MWr+nHktgzmrq1vejjuB4zk0273hjj9Wt0ntt1jPj+g1niIJBrpWoSyg/e6xALniZX35d8fV/S9uc5WuKUDLUocVUIoX0usTADw2az81JlRRBQV0tE6esF3zf/Se3qopVU5sNKMlD6WbSkGNAqGTMb0hWDnCwPnv200kt+zgCGxl82X15iRgMrAeZzjN8dfF2CjgXB6oaq0o5ZghGM1lguhNA4bUspyDm3c4XrXftQqI/kqDcjOypPqyWqDUluz1K5SnWRIoi9l4S313cKQXyJis7FWkunPLE1VXPFkhbkZFyugg512jwPpSCn0vhn2/cdAJLnKrmAi9j0ZTnC1hGtErLcxso516guhN+789vWIufEKSIqhZ5XpGhWflPWHFoIQfhYdf2EEGDTUKliOYovEbyHG3iLobJlHPJQvVIAqfhUeSiclZLQN/2aS9bvyga4zafpSHtvibksDuoI58GqN90zVtfUUjv4xjl4BJBSuAmS3ClCdlKfU4ENRRuoOaf3094JpYBZerKg3d/WIYFQsfbOHx6/GMlYmOPdd3A9xDE1+DOzoUpV+AC1mX3RuF6xqlc5YYjRa7VpCorUYknuWt5VuMi602DGwmEo55UoAkS93MpKMWyH0BwS+8yHoN91zT0Bi7oh51DgsNsvMo0EBE+Yg8fkI2icSjW23SihNSQzh9ejJ0OI0LrZyQj2xMKYKB6N0drgamOuodTHPg/GI8prxSqfdYXflgdDys9sLqpNDFvlRk/1qB+3CkJGfifQCvbdEw3yO1MYY1nSY8djjsa37XiemGwJ4KuSc3M3WjxOAmxca78An/h77YqnO3T2Dt9eZmyBCdeKUgBHVQKoGOBDwPnZFmm3x/HuHml/UBQWhgQ9mjFfvad+lnNu79ZIu1l4Ou185x3iky1qIBxrRq4VbtgcWSWS0QOxlKTkoQbrfp5Ral4R+D9wor5hLEiTfrLzzr3cjkR+TZas22oIAU+fXOHly1ewxCoYePHsGe53OyzL0hyCMYcgcttWdUNcrt5xmPOVDtEf4xRx2B9a0tcCp5QycklyOnUObVcBiuasVxQwKmm5ex4RBirf1b13GTScRa1YytIUiSX9wlaC2lIKSjZnwbhP/Xrt6z16BZ4GQaPcigfYEyjV+I26s7UsSY2trOmy1JacyLng9es3ALoDygwsKffSPDi8vn7bOgGbTO92uyYbI5fWqKttB7XzbK1LkUZ0K7B25EthnJ+fic6sjGVJYLdOeLb70foa36Z/zOkEdz6nB3N5ose+TZe1cRh+1icCiFAImK4u4EPAPmX4JM2Mkgeu6xFHTnjmA1CD2G1XwcUJgtM5BAfc/Owz1FRw8ewFfvDrfxF/+Du/Dd7vsCuv8CUIP/4r/y7++Hd/G/dvX8OzdD69fPIU++MR97t7oUnnCs6S1IibWRoElYJUEu72B9wcF0gqV577/PxMkrA54f72HqjAxdkZ4naCnwLYEwoPST8GUq4NCWuBQADgmRFqxdZKh52UdkcHpMMRP/7Rj/HhR9/B7//e72H/9WtsGNiSA6cjJk9wtSKnA/J+jzdvXsLHWZHeBbu7Hd5cX+Pt7TscDnugVlxePFGUtDrzhXG4ucdhWXDICRlVkKKl4v7mDsvuBuC1v5O44HA4YDkeYC5wUzsY0Iwn9qTLj67FEw0rZbB9bYy6rx1sho3W1yBBGbQkX63o9vw0EO4+DDOQ84KUFizLARL0eYylwVKmmMFcwDUhLQfUksDLHtc3b/HusGCZZ5CPYHYouSLECB8m2dw+KTMmo5WgTv3BQ+DoyOP+7gbki1SflCyJK2L4AARf8er1a6SUsdmcYbs9g3MOH37wHOQJF9fX+PLLl0hLlgCYxXGvDBxSahyPwVnDUg1CvQXQqj/J4fr2gHlDePLsHE+eXmFJ0iRLHjYg8Rkun30gwRIzKjtUXoBSIek7Re9UQxZLokDspGw0HbXJ2TRNwpFnc6b7luRsLVkQLbx2pQiiPi0FNHscDgscOcRYsN3OLaHAMokQet0A8txQbLKxw012yNox9+nSMXHg7MC121txG9e6tpqIrkS2Cq1CLnj69Dkunz7HfHEOP01IYHz+8jN89fmfYbl9h7kUfDQFXE4zzrczNmcbHHcHHLP0dWjDwAw3Vl40X4FwTh67VJDeXWN/fY2bn/4En189xfd+5S/gybNn2J5dALXALZood4QwBzhWdF+FzrEBHbrNN3lFSwzax7aB3H/fz22SDzc9gWNB4fdkqENQvVBKBrjAOOC9n3ST2hL3esUhAQiWct+WpGC2mQA5DbS9NOgCpP9ALRWHJSOlDILD5CdQ8cjHimNIIDjcv7vBbj4ge2BfF8RtRN5lpCo84tM0YclZEzhOSdHN9vvWqG/0yzqcZZQbSe4Ui1kYsGotglAojIkv+YUkp2KckYkALq0buCPCsVhSxZ+ADWSMnPOSkAYBChKKU5RYVBM43a1ksNoAadshSQVHvl/Pi/52bt3Ip8UsCKpnGLA+Dhgp7cZ4rPsJzcUgwOhtSINb4xxv76V+oelu6Vhf2jVNNswHluZwWB8EgKWkXhJlEkNLQ0+VObsfQUqinWxfrYLY8ZItEf7w89V7D5+dfv7zHAzWDu4Jk4/yzsw4HBJC8NL8MUZ7RVSuWFLC1vuGPHXDPWUzpJzYUsuLcPNx++bDqUk2X1dLzJ356oRaLS+wflerXoxR4gKrFubBp7fnkCZlPUncxm9IkpldFdlg3WxBe6bgA+ZplnNOksspJaSUEGMc6L9sw6WvSYlbjJZAYpfNZtNiujEH0saEHDbzBjUat6nIbcnaCI2tp0TffGmbOhUgeAQXMW0n1FloApa0gDHkRhxhjjN408fjeBRb60jWMTkPmqKGo4yilFx9LMVfCaY7S8H9/T1c7M3ERlVm1E21GPCHAS+bXaGUrsdKR1c75zDPsybjGTlL4jvljAxGdg7BT00mSsk4Los8mzwoAAwbBj3eKqXgoGrY6AfNV7RKAlZZ9lrZZH0+mG09mv0Zcyryueggi/UBFztg0p5j4ogjEazq3VtMpNRxkw8PKhEBmR+mgIKInBNyUoCPICOlCl11sD+JG8fjFyIZS6BGYt13JIBWdK2TUBXGbdXKOpUwv2ukLljzC9o/u1C07p/D/zFYowJZZLV5bD3pM6pdMyhG9myLuBr1FXSnwhIuQ1KxOUN67QJCJkLxgjxznMFFG0RAywaAhmZw6MKnrwTbh5YEjPzdx7N7nuImjLvmjxsUr+TpJCecJAvk+VMujU/E5sqepxkERS9aAqzHaOI89ITB4Dia0nYEjf1a8DjOqXdCjP1AxFssyTBggdNA6bHD5uNR5BC6YzA6+JYUs3Huu7dqUFYJR+5KSZ00IuoIhwey+vicMLAyFu3zMelisq7vyhoUGMKhOsCdTdhEj+lsi3R/QNprSbohe2s30g016TrxRzuMZ9N28xyBggc2E+LTc3CwQNICoCER3XKDhJHPstSC41IAh9ZNVS69Thqc7rhbUqBRoUGMkhuMQUPjtkcQyfF6/7QseHv9FvM0K3drgSNgd7+TZCErgqZUhOias8jglcNK0LLHOqwJnDhx6KjcbjuonVcB7I+HPr9D6dE8Tbg6v8Tu/h5XV5dY0oJX128A4yBta9IpF6AaN+N2bAjNirZVonrUmaxS5wmy3VpeW7r2/mIgjQdOE/sG/uuz3FHIpUrlgnNwNOyOjwsPwGazEX3NFSkvqlNVA7Zd4V7aEoJ08TaqgaJE9yEEzPMG5Na7533YafW3vWtRO/HYOe9LnBIIeckDV+/6Ht92WAJ8TPg2e1c7Ap2GeTw9emK4Ow+iD0/Lnvv1x7cg1Z1wGgg5ANuIzYfPcHj5GkgVn3/1Cn////gt/Pv/9r+FwAQKDt4xkBnSLdyBogSi4Izl7g1uyhH1+Qf4/q//JXz5kz/C/uYa5euv8HY+w/OPPkaIAW+/+hwRwLIYasFhu52xPxwEpVMS0t0t2AdMMYCmGcyMY86ABa9BNnL2uwUxRlxdXmCeJ0m0Ktq2VrSEFiCOf2GbQQDOwTMQS0EojKCIEQqh6chaMpxyFD99coG/+Bu/Dh8C/unv/C729/d4/cXP8M9+6/9ESYTluCClA+IMXDx7gWkKqHnBV599ilwrjpmRWJMebtZ1l7EcD3j12Re4e3eNu/t73Oz3eLdL2B0WcYpTwct371CMh9ZkABXHzeXXuQAAIABJREFULLzPqBWjkTRbZjnXVWCketiHuNKv67WBTi+kwXuzj6NtOgkarcxRmht2qeMhIGsPyKNcWlIjCtJCk3InQg+uGbUm1JzEx+GC5XjEy1evkAH4EBGmWV7ceamCjR7xbAumzhtLpIGgd6iVQFzhmOGIEZw0Spomh2l2gvx0srmfq0PKRx3LGRcXl+DKiNME76MklQj48IMXePrsGT768EMsi1RD5JyR04JUhYc254ySMkpKAEg2O5k1sJVyfwdBB03zjI9eXOLZ1RYhOuwPGazd0b0/oAI4ZsY0n2Oez/Dk6gVy2gOcAc4IJesmuYx2Vp9WkjkSmGy3G10nVt0kcx5jRPQOpSaU3DmsoR6H89RoQEo21JwkTY7Ho9xDG+9VpdYg7t3S6yCn4p8JGoV0A67kBGbh7a0AcpWN8VGfeVptNaNFFyzJIHIVSYNLAuHyyRU2Fxdwc8QuHfHVyy/x8vM/QygHPKGCTWBsiREqg0oB54zgCEdi7V4v6CdJUo8NcaCcyuKDRycNe6IDMjP4/gZf/+kf4vbrK5w/e4GPvvs9hM0Ea6AkyCZJho6bts37ZykXNRozImji1rCHw6FjKna7rH7vyUPKNwEmK0EVmw2yDW6PQH2xcv9nv/64oKrFPLZe0WIB87lrFuRXqQXEQAwRm7BBDRPYOWx8wNXmHFfzBS42F8iZ8bMv/wxPv/McmAlfvPpzXO+ucVwOYO/h5jNQSdhuJvWzFKVF1JKCPnBXiMPRqIxq1hJVe87Bj4IF5ta/ozTZb0iuhsCKIJZktIESYpwa7cQD3kxAr2v+vcz/4SDUXR6k1aBO1azFGDKoPUagJneW/KlDSS1gvKMaA7VmsX3Do3ED6/sbopdEUYouaPaBAEXj6q/a0RC5CtSRcangohhqVutLfeNCqtC5JRA7tKfbqrEJdHtXoPVkoeDhY0DxHiw7sE3eH9uQHI/HAEphQOv9Cx+WFK0F4ACQNBeCzmdlQqkM541OwKnfKujTMfbrZd3ouQbqsSzUxzaAgs23PMcaZEAkutYpAr+hdNFtd0ec9n93O97X9hj/ExhcigBKYPM7Rrzy76Jl4DqzsvHOgjR0JGC2luzV529zrknZlnQkBf6wcXXKOUZ3Ywm8FrfD9DStZQPDRqCOpxGvFKrIeaCrhG10DeA2AKU65JKG9SMOlzxLVRrOdZM783NMj1RmoNGbdE3dZIFszTudb0FZU5O3vglnI198RUrLEHvJud45aUDmAQ7c1nqLR0h8HR88Akt1UNWkrXMBkzYAC4iY5hk566bdkOOZ5wlmgARwM+odlZmWbO3yJkhUj1I0r6BUYqZXmu+q8g7Nw7Q+HrBkr/jZXIa17bDabC9V5G+sZhSdSS32BARESLKDAbCX+bUYEbYslCLhG/CxvxDJWJkgjGu5JYDs30NMr4Hlmq+o77QQet5xHdj31aBG0pJptgK4KzFz+h486SNl9KM+tgVoO6otEdQ1hzpQw+f9JdTQJbAvaMVD48TaQoe6k2Ru5RC2POIMteciaHdNPPJ2g8EZlCkPF+0KpT8767icJseIbHy4vT+ROQz9vcnua//zMLr6oE0J8fp78v7DnOv5TWGPY4DxouvnPFFx7Qsme4/JQo8Q+titzmqDzC15bd30+JFx7gI+jix1J5B5PW92+0eSQabwqX1/GD8iSZpqow8PAjuHvCzgVAQt05xqlnObT0erO9l7MQEIDmGK0ol9O8PPgv5qlyKzgqfXkec3x6JqiZknCdLquAPI4zy1t+3j1vIR1MemyY/MGZmTZwtiWPNgQbXGaQIgRCiePDbTDC4V2caVjLOm4fXRefBsakgQkbW/t5WBihLXBK5+p1ZpttUbQwliQJwi3eQBtKTEN4L2i+0ZDhagmxEitHkXMnQdN4KUOmLY8Ta5JXHELrYb6UxcCgpL8q+rPJMp6rrT1lvTEYM864XNOTNdYs3egpdypMpSWm76DbTu0EnQsfPju4yVB3J9Gyv7PE4RXCumacJmnrHk1HaP5VG6MX5fctVZsNGMsVvrIXPoqGu1XDIc+xO90s+XjZg1zcD43OPOscmTXaZt7p2cMwYVq+u08bc5OJ0nGUAersGDVBsnEwUPd75BOd8i3e9xSAkvX79BArDnilALQlUKE0cgkkSqd17Kl0tCOeywu3mLZ9//VZx/+BEqGId3X+P++iW2V88xn51hvrjC8e4dkBZt7AZNinenWlBCiySbnMPZNAGXDqlUJJb/o5aChjkizhN89OBKqJByKZvCNu/DIBPEP3CV4XOFUxQEBUX5MDf94SDXmn3A9PQZmBw++PAjHPZ7/Oyzz/Hy8y9w3C8AGJvNhB//2g+x2TjMGwnOy0cfAAQsTCjswRRwefkEtYiz7PcR5+fn2L17g5IXHPc7vPzyGrf7g3BdEWEpBd4b+kflAYSUE1Kyzt2jo2JCNfz84Edua5Ue/+3alrbxXP88JifQfIRh43P0wVZH92lMh1sFQ1XExPitbt8VbQdxrpfliJvXr8EkiUunzSNIx468h59mgNZNvAyZTGSJCNbyRIJXv8s4+sgQOTRjvz9gSUeAAO8n4UyrFYVTW/OGLCJcggGkvEijq3SUYk/mlpxdjouWQ8qY+UDYbiZE7xC8QwwRFYTtHDBHQa2IzZFEByiD6SjPWh2qZKUBZBAKQBL4W0mfbEJZSaZqbWYYatfmlNWPdlbCphQSzVdTeiDnPOBlwVWSzsM2u5UZpEn9xpnYAua1nZc/9W8t15fnKuiJfOqI4UE6fEtSdRlVd7zJa8oJDOEfPb98gjDPQktwc43rr78EDveYPWMmYCKGQwUpGKOWMvgTaDZqRD/JO9WVn0jmE0AABbVmHPf3SLViVwrehoirDz9EiFLmW3LWfgk2VpYasDFy3cdW+1+pdrvb1hprzDjahnExjQ2RGDzwma78qmad+/fai9lv7N+mmwab3e5vfqTLGEvkCOLXeOfBTihqNiHi4uwCTy6f4+LqGRZkPH3xFImPSJ/tkY47GXsfpGGakxJ1kwDzebjNEal/ZQ2rVGacb+/uXB3GaYgRqSc9GSzPqWfVUpuPIu8h3zXbLRv4YXUNYERnjkqaAUW+VYtNiTrdDQ/n67sFF3BxcYG73f2gXxlWPmsNi523Zm888DFzk1MGQA00YtNLLZawJPcAGEb3+VSLq69pur/74SwIQjdUngINMLHyVGwslZ7E4gpn86TyZ5sd9sbk0CoD4S2hRENz2LUf+Njxbb9/3/EYmlbcl74O7XkM1NQACyDI5grBk29+PAY5EdSga0xzpP4vMPBs63P0KjAbXBLu+vYsOh7MjfrC6O7Q9Kn6+9rYyN6PrTcFoccGQwWzvXiX6DEBrr14mm9AzfSbvmIicM5dp5Oa+ZUPw61BLxGhcOl8pfYlfcdx/baEfq1WRqu2QSqSMsaNKjoBBald425zQgit/wUYYKpISpPWLj6sG1OhRq9Za4VTvmxDE1fmTn8A9X9LhSVf5T0rck5dzpRr3N73FOhm82HyJ5tJw7xwj8HG+Ee4e2szosGHvtHP6CAUSDxJyjlryeq2OWDz4Vj7K1h+oj1evycDxQvdkW0GG5jNVaFWWDXI0vdpGzXMSlMi/qwAHrkBhqrawwZiZLRNfzssIQxCQ3vLc5piU358HgAwJHrNU7//+45fiGSsGGjua9CMDVRO1ekyw+4cgUtXHI17hXqSkYYZ7WugKyfSgKrtigBtoI2PxcEWzJBwHZMO6riaEa0KmUYTRgZ5Dyv3kMVa4aGTSFZu0J/Vkez0+yiILhPs5vKYsNaqAcXwbuhT3RIy/ZW7n6R/vk8sTp2OwV4MgZY8txnUtQMxPEMbJ/lHHcarXcv1smBWJ3AN4OpK+xQVauc1Q3wy77xyNptleviy5pj1ARrO6QuOmmFSpVPNXUFL0qwMt3bYW/Fo6ng0WaXBxg7373rpYWJ5dDZWO7vNCbZESh/DZoCMg4oY1RPofMY0B2DnUA4L+JDhcg92Ca4hJACsuG+7AnWgySFebBHPNnDzLKW8beeVR8FS9EiXWzBUQQtyF3AIcUIAI2Eo+ae+nrscc5dN6mvfprlWQTLB0fq7wzwIB50lr6TEoirSzDvC5fk5Si4ox4POlclC11TrcM/uQWAHtPKxldNdGsrRkPo9QCFFtAoXFJFDOWZ4coiKzLu/u2scYsELBQUHp8YFQBXUqwM1Qn5mxhSjljVxWx+6muG9w9XVFW5ub7A/HJTjiFupm018306RuZXyYG6B5wPntTmIfdOGGdgEjxiEVzAfEhpynmVMUk5aOmVE/a45KLk5Z6ZPRkdK7h/jJMi0OCHGgN1+J8loJ4T+JcuO9Egcb3MhUogVb+LI0/qYo21Cl0tBGIK008OTA/u1Y2fOme3Sjoc5KTbmVn42/r4jFHpw15+r+ZnvDSzaDrzOl3Ee+ibhEtRunj0BCqPsZS3cHw5wG9l4QUlgJvisZcoslBebzVZKCEvG/uYNztMnuPr4Y4Qp4ovbd9i/ey0dx6cNnrz4EF/e3gLGp8uM3X6PtvGhQQtqRlkWUAjYzBMuL69we7/D7WGP5bDH2fkWFIKg8z3hqByWMkosm7GqL5rMWOczBqhWhFzhsvgF7DwoRCAlsS+kvLa1I1IoBNwdjvju976P6zdv8OVnn+L1119ifzjgbLvBdz/5GM+f/5t48uwK89kZQtzg4+/9KioKUmbhhUdsHGNpWXC2P2DrZyy7e+yXBW53wO3+gN0xCfXMFOBjBHJBcTTwPxLSsmBZFuEhtXnGQxNnvtGpbZayTmrNRkf73vV6d/JHJBbbH7xOcrRz2AKFgpHFvn25Gb0uk6JTpcS31PfRdHSbWqpQNbx6+bUkHZzItYiy+EjkPcI8P1hz3huNTUejBy2FlGZRVmro4X1AjDPCdIbdbieOe3WafItSdlklUHPBaSOfCk+iozwximPUAOFrd9JsTvhxF2w3Z+qzVjhXcHV1hrPNhDlGxDjj5uYOu90OaUlIhRE0wcIVYJLyzM3kAbpHWvbKSxsaQkSaJVELdCKAGIOUwVepiS8V4MIt6ASzlt0p8qUkFOVIFv1ewazciA7ClUkk1FbqDzuC2hfWZwgozoG16WP31RqJSgsspZqmCMJM4fsSwNUuezaX5E/03frfBIe0SCC72W5x8fQpKDi8fXWNr7/6HPdvXuLFFDA7QoBw7dfK6tsbz3nnsB2l0vQ6g8GFBbXa5Ns1n0bUPiE4Qk0L6ttrvNwvCNOE86sniHNUZjOnPhwLp2Q1v7cnWmjwg8Y/JX6pSi0hT/VYgkm4gEtb05ZYbgjNqps/1qhR9V+tVtb6cMPSOd8Wp/k5FmgLwqmglTqjVxRKYxaRjRg8gnM4OzvD0+cv8PyTT/D8+y9w8WSLm9u3+MlPNiJXQZtmESFMGw3WVZsQGnISajdDjOJPtP423BqXyQZQaPFe5aKxo2SDWoKQxg1VBynelXNOKQhApPpFY8YhxuoJiJ5tIvWJrV9Di7l0HY26mSHrNISID55/iMOS2rybn2uJNYIhDtE5ofXz1oyJudFDtZjbh7U9JuUTHuLtQZrEhlRpeglm7X2gzySuuVgA7pSFzUYQVE4FoCEocwKzQ+VxQ1vGw2nCtbbmmxUuBLgpAsFpnEfd9g9y+vMkZYmoJSIfsz/ffih4SMJDqRDzHsEJ7YJUI8habrNEDn7k44TJouhmp5UmxjtrfqyMQx3WZY9WbKLkI70TA1wycu2xzCqngPXaZhYaGqEuYkl8q79sGwbaqUm+2xTz2o/23qghSfWh62tUj96k0KqYhs0QmB/Xve1SCxx8u87oo48Vi20OSWJc2WBlgD3ABSWnJv9Erm3mt+8o/6qN8zRPmOKkTa3kmVLOjV/ddI5x1JpuEOoAoWTJqUjFyTRJxfYwj0DVGLXKRiij8XXbxnubb5tgIkzTLJ+pXU0ltz4eBKUu0PhGZLt0vcCAq9KM1qpgeTi/xe4DfQRrJYRU7/Rydud9z0URyZoOsX9PZ9DEcswLtfUDbrE6s4BfrK+FbTzUUnqV5PBsDVGPzn/bqE1yrw4SPbMGzJRSpDqVHHxQsdZ8kGy4q2yb7tTnZCpg9o/Ggnb8QiRjAbTdvhYQA6Zb+yFyjFSruh0yuzaxXBhdAvvv25fHP1nIqmm8uEgugIf8hkNIsEpsjUaxdeyuIvzeWTMwg4GzCo4gzhjAHCKqKVOIUM/zrCWCGbkcsaSDeRBg4obcs6AS47Od/D0eprB+vkPQaqvz+eR+vB6zU8M0orNGw3Vq/Gy+V2WK+gynRvGhkeSTv/vzoD2jPp+Wrr0PKE6DxPDw9+PrhzUAGI1S7/jHxumrv7euhV6DrG8z4oZMPX3dNofD1y2RQMP9JIBeywFz/x9Aa8YAJfjeXl0CFwxeMo5v74CUwNooQXaNRB1a6QoAkHdwISCebRHOZ7hJyhGrGrzmZLYHOB3G7vy0Z5X4H8xQQ899QoZgw6S5Flb0rmubT2Pwv1IDDwYaTc+YZDtW3lX9/TEnfPrlF92waYfXRfmBNRxRh8Qc+O4MrV9X7mKE9qnk7hz2s/ozVXl/52WsPYT5UZJ5HreHHf7k0z8Tw+RJd1eHkn8SZ85esNaK+/v77sQ4pwYEYAi33xdfvMSzqysUX7HfHYDgkTk3EvfVZsggx1YaI5+vuaMec1wZwP1OnsU7r5tf8rsKmYOaBmOv1nkOASF4IcRX/mJzQs0psnvVWhFCQMoJy81RnI/GT/VQD8UYkY6LGnm1D5URggSS3SE6ESMa0LEnQWgPrrgnEtXxHVlTPKjpiXHh/8s5/P3+Kyv4LddqHLn2fZAynKtDQ8B8eQZXGIv3WG5u8L/8vd/Ef/g3/h188uEHqJxlu9HKggigfMThCMQwwTnhlX37xaf43o9+A5uPL3D37h53f/r7uP/qZ5jOLzFfPcMHn3wXb19/JclyMkSV8tD6gGmasN/t4BjglJBKQpi2uDg7w2Yz46qcIZWEXc5IpaJQQIzSYd5kBLYuBj0Zwyx6fUmgQ4KvBXGOzalb9nuE4OCDJneKlVNLI6djOmDazPj44gIfv3iGX/74I/xvf+83cX5+hXmKyKnisz/9c9SffoqzqytsL5+A/IQlMeCkW/hme65rQuRh8g754hzvdgd89rOv8Weff4G7g/DjbqeA+WzGMS2oWJcaA0A6JizHRXgCwadqFCvPQYPTVdfzZk9UjzT9a3YPq6TE+pqGhRjly76vuslsgmVQ221P7Tk/+F0IUVAZwyEIErMdBcfjgrv7HV6/vsb05BI8RcCLriRDIUWCPzsDZT+8H2GKcTQMsEhGUFwQh9sHcHXIxeNwqKC0B7mAeQo432xVr3scjwuOyv0JXfeOJOERvEMtDsQBAMEFS24HUJyR4ozgon43o+SEfNwjcQblAE5HBBSgHFGLcFq27tgs69ChInpGCJM2cCmCttJkMlGQ9aUNaitXlCS+qncOIUSdL+WRdJYwkI24nCUpGsLgG2igUrWZVy6dxzZo45LCpaGADGniQlS5qai5B9BQxC8XBpcC8l1kLPAT1ex6IkCPtl5HkdK/LXG/Xxa4ELC5uIDfbPDy1St89cWfY/fmFZ5PhAsUkG6+2xpiQJvvRJRiZeqWRJOLj36YUJqsqxNONbJjQtRmKLVWfP0nf4Tlux/j6uPv4Oo7HwIp43B7L7QStTRfgWAbhmi+4wMU16k/LS3UVs/AEPoIJkFNW9JHklBZErHaNKfWXgIaQmxrxxDsVsoJZumMrfaPAWTl6O3TYZMpfpSHk2qkLA5hCBL9Ho9JOJbJKR97wbZ6xOkSL57/a/jp3Q7ZLVhAWEoFakIBFESgczJwXJqsSqjQ7biNkA+h+yW1QLhsKpyLq7EUVKnMe9X+BMSapPUO3fabvyGNwMZs7NpH1/jWftEU9zraY40lx81oaTLGePX6dSv/5UFHO9MnAGrptAvtmqTxJpTTtXH3u5bsDPYu9nxOkeKDfyRjqglUCA2FIOtsDXkBZmhszJa40+cs1XwWRuPxHRZ9Sy5bwpgAIkn4EmrzF2pkuJhQwoQjDt+adP2mYx3rffPx+PUlCm16T5GUBAWADUEnc0GuBSVnTJPwcZocEZGWaJfmBxtlmP3etwo+QVbWsqDU3PMWgPi2qsz6OpR/dRBR9129C4ghtvuEgEHv6RqCzJgj8Wk6OED1Q1Pr/frWHH20wUAHqMgc9w3Y6Hu/Bzu/3VvPtWZo473GeTz1z8ejV6cN6MxSkDUmNeRl3HSO1GWR2KE12SOh6AnTpAlKRe9aXGxjGsT+MTNysp46GNDMwKTPXLgg5yTrTedXqK16fxTxfY6wckrnfIuFBOEpXK8CQJRxcyyN/GwzFUyouepGliQVy/GAoDQWzIz9YQ9gXZFo723NMFtfFsimS4hTnzfWmMO5IYEJ1Z3dRspnHe5kOsfmOvggvqDp6VIAbcranslD7RgaYKj5O3XwjWunRRCwk9e1VqSJ8jAvREplpdR3uRaUUpvM2kas0Yt+U/7tFyMZywBYF5ImDAoPrr+VprIZHnXVhskSNNHDrIsZWQsMWl5CFbyVEVWd2J6yHy/S/2rrdbSJw8IxBBMgjiyVlpuF5e+4VuHCBDB5KaN1RIjkcRZmgIGSK5al4nCo2O+WbgyZBNFgRPjMqCgNwWULopTakzFtnGxMqCUbbJDWiYn+vJYostfl4TrcPuw7pEBXcqcd5U1Bt8TbKr5aK8Juj9XN/IYkwsqRA1BQV/y8bVfrYcpLjPaY+Dh5LvN/DA3KYzZThasbFDRFRM4PJfN2SU3QmXHBWsyaE3j6qoPitvPs9uMJ9mxWUkbMCo0/5QaS8XRGsj/mJRzBbybE509AJUsytoiCGcnvowaqFIKU/wSH6iDnVHHa2BJOD1IED1apPKOVYeg6H7vHY5w76lNwOi62Iyz6QD9rGlqSz6dB2bp8V4zuiNNiDahMNmhcIM2p6cgdcyzHuTp9zlbu0H7d12jQpGZKqemm2ro0AqkWLJwFbeUdEqRU1LVVuhqtFhw6IrgQYQ14TAeIcSGARf9ut5f4tR/9G3j9+hX2f/wHWHTarQkVM+Pq6kqaAy1Le1dLnDtHiDG0xgqPr90hGmagFGCeZizpKLutrgcvfdwAIsbxeMDxKMMxTVMLXh5Lktp4M8sm1ogoPTWLzIxlWYSvbkgWMTNq4vZzRwicrseHn9uu/7qZG2AB9DgyQ8+Z9mzve6cHozk4jTZW/b30nPfo0NWz0QmNgQV64Ia7YgBuu0FkBpcF6e6Af/iP/gl+9INfxV/69V/DLWds4OEVQSY6NANM8J7hfER99w4v//APsL16gV/65R/ij99cY7l5hcPtDdJywOVH38N+e4X97g7LsoeV5bppgvMeS0pth5q8RwwOtSxqlAieHVCB2Xt4EhRFTQkZQK4sPONOVZ/5GgwgL5hAQJak13S2bbvstVRs59j0PmkAkUrGsWQUEKZ5xiZEHHc7cCmYnMe/99f/On7r//pHONwfEYjwj//vf4y//Ff/MjbR42yOoLhBKQtSTjikhGNKKCWhLAtqycgp4f52j+u3t9ilgiOc5APUX2Jm5eX0yG7dtnRJCcdlQSkFfV9e5MQNvPFGRdEFYdyy7MGxnGsyNeo6frAORPb6Z/I5DTKnyKhSNSAcZFZ+2xZEu91wwmPrtxZBshCkmdf5n/wByu/8NvYpYY4BrAgNjyYq8MEjug3cPjS7bDcxBBwzwwcrOZdga3O2gYsTfK1wfsJmPkep0n3ZUPxTnMU/Yg+ggBwDyLCSHkGEAcFluLZJKxURVppaSwXKQeeIETyB4FELIYOBmgDPODubMW+ksceSsgYV8p4xTIjBg5BRckGtglSVpJpuNngP5iIJ3SyNEB0ArgVpyVqaakg/BxejNHJS57xk66DLmsARjnXS0ljvPAqyJmacpB6o+3clCzdnyQlUq+p0AJUlBGAGl4rluEgX7RilwgEOlSqK9nlom7eDujttwAg14d0/Ex0R5w025+fIJePTn/wx6t1bXLiKTWOX776fJVLiPGPebrEcF0UOWZLPYgpowDuUKZ46f6u11xMKAcAlAfX2He4DcPbkDJvtFi44kHdg6cjUkl2ShNK4ZnVtu6/4piBBaTGU/mXw0QiE7WaDzIvaMO2vUasm6Qika82RlwqmEGQztsGFZHPWupAToAl9Cyxkbc3K921xkzxDbQue2aFO9yhzxJQ8IgHPLy9xub3A7Gc4lgaNh31CLhUubFFog+wI2TEA3xUWqU1TdKk1mXJOm2JCgQeqp5xzTXYtFhH0uCK7Bj+cAa2y0e/aNcYNAwwILGb0LU+07wFodB3mu1oyPJesvIZdXuR3lnQfttuUEuJwPCiCsIlHn2WNfS0xzCYR2jyJc2n2H9AtDnKA8+1OzT+qFcwPNwNXKM5a+5pkqTLIKWly1hJ/tnZlnJ9utwhBQE1v726xWMMevVBR22H9LKxsGwDIWYUTg5xXZLaWH+tY/KtsdP+rHMyM43GBD1KtYX0nFvPTnfCjBxdaTC9NqDKqrkFmQaKexhp5qPbK6AkyIqM4602tRL40GecJwTmEOHdQgOrvkbsTZHQ/HZjhXedndV6b4rEimPU7qgY1NnNtnVmi05oBGro6hLg6Z+xbUYpU7FlCWBrQkja7675DLr2q0pKdBPQcCCC+DkMqDFyXV0twd2oHLbFXCh+rFI2aACUAHOXv6EPLBTitymBmMLFy2Q5+EaQuiKpUilAIusbFSNFwHpxsUkXnNK/RU3xSUUPtXsF75FbFpTyyaoenyWMzbVC4tM20yhXBG22KXHtyhCMsNzAk+HVzCdqDQ3QGN7mz/E+MEblkpCS8+MXiZ9bNKicbClyyFNKp7+At2QnTHbyKY+Fo1QxLdOvQQNxyTMBKtsR/E6CD916qP5p8qe5f5XS4VU8C0kzVbKXJtW18R+9QDiwwAAAgAElEQVQwxQBj/WBw470laHO8R3jB27Xf+5v/Hw+GCKmZpxYwwMok9Bw7l0fIMpoR12W0csJOVa0ZEI0QRUnQeOKpi4/W6CuQ06To49cGxmC2O5lyVeUJI0JKCZ6VDkEdRwIQncP5dmu+CioTaiEcU0bx0MV/uoMzoHtb4NzcwNX7WKmhKAWoQ9J/X9Gf5SGKwJTXyQ5qez+sfgY6rL5B1+1Exgrm/9gxKmGczLW99+rduNNYAI/PTZesh5+u70Ltz5aEa+P+ngdGR/3Y86wCWAwpSYVKPHal9gyDMnhwDtuOniqvh+Q5bSzGRMsKp6Tz39cMS9LRnnfyQIFwRdUggfyAIpByI8hGiZeGOGxONnX5G5FRjEbRMrwjNflavSkBfbceg6Nu/+jrnGwt4+Sd7DXRk6OnY0rtOcYH69c1mSUdVbJ1w7oz2oR6Nd1gsAa3tgZ4hVIZEw09WJLfF64N6dPuzISoXVZTSkglw9hq2xiTNPY6HhadB+rO9BA49IR/H6Pzjeidw3LAIe3x6RefYre7R27c3GSTAjBjWZJ0D2duXXuFqF0d+VqHbp9rLl1zJO0JCLJnEGPAko6Nr2p0Irvi6HIhjSi4/d7W3CPbHLrZZmWPXTeu5wyrhk6WCLf5aruy5kyos/XY0Xfya7vOSj9xtxLt/nwqF1jN3XjdMSmMk2tY2dNp8uF9WnFE846bifbeepb8ac8YCG4TES/PsCwJN7t7/PSzz+Gcw2/86z/EjgoCSfdtysJrJqWKDM8AwWG5ewcCIfoZH//KD/DlTxMOt29RDgt2dzvE+UySqMxI6SDoES/0DrUQ2AvVhHMOBYy0HHQdOIA85jiBnFTSLKXgWOpK7wl3uq19BpUKxyQlZiGgkpR1lZzgIGXrRNToPwDtGJuka3fwBMdAOhyVukAaIW3Pz/DDH/0AL7/8EtfXr4E54vPPvsCbtzeImw1cnHFMLGgHAnycUGvF4XDA8XjEclxwc7PHz776Cm9u3mG/LPqeXbuGEFBbMszmVYKRnNO6pL/JwiBDKna1ZliFwfuaw5k8kFLw9OSsyVAXxlqrTAdp2Tz30snRlxntRH/Ik894tNXqJJ1YbUkYZgTP8u7Xb7D76ktkBoL6ZoLQkBLXWjXIcA4u+JXsVxbe/qpcZEJtIoGI94Q4T2IHnYfXhM7xsAOxUADEOIPIY1mOYFbUqDYVaU34iEGcEYihdMtNq5NWpASCBkfmHVdQLVo9oD6bBmaBHOLkJeCpDJBvetSBwbVIc1gGFCqCUhhcFym70yR2zQs8xZacZk3GoeoYA5IE7lMtv1e/QIIbWWeuqcmeyDolG7KkX14OKCmJDufa/GPuEy/VH4pecc1Ae+VxHr2NLhunzT/7vc1bED0TY0SIEXc3NzjevcO2LNg4aKOq/r1xc4FZNpLTookldGAJDdd36OevHJLmVwyirjGOByM6ArjCpyOO795hmqIkl0IEPIML+veHJMpKjw/3NNSwqEKJf1Y4P5ImmD0olWvWWhBq7JU3rjcFcl7RfZpoML7KlrBxPRAd/Toi3/udmL1tO9QEYqVl0iZvBMYUgyKHBVE20RbBzyhlAcihOofqguRhg/CJOhj3phv0mm1EK7VTLWCUVuLbXdPRT1B/bJwvPY+CrWlJr1RFgJqGa+X3zW8d/G31yU7hIiGIXilVqECInGzaDvJjyC3TaRjF4ATxOiJ+Tc56olbfzZ1SxvQkZ5d7XZQkdrQBmob/dUoBoPtpSrtXq4CVDARFjwgta4J3CtL8cH/Yg3NpsWNvHCvzaWu8jWsrj6+S/AsBNEXAOUGUP3K8Dyk7+kj/XxwCNinSADtUgGqj3xr9UiI0RODoTwLdjJuttiTuKehGrwjnPaZpEv+7NT1qT2Rvqk6k0YKJfPHQZNd0facclO+brDEgVQwsXrNwENPqPqTJODuc5mFYeUoJaCXwzdeyOVNf3uxMA22AZJ9T7zPGBkSQZB+bMRkkTRObBpRq/NFDCX6Ta7BQvCidDwAcNWYoRehbgvdIXFSnAcgJFky2+5usmi0pOoYqGytKiraWuU862WV68zpoPwSLmYI1pB/1/nBIwl0qEpkIld0qwSlD4zCF2GJNGR/XEMdTiCjOozhJehPLeLmm8wlBfzafj7wbKidMyfZ3BxeRVxq0gjXXNd3Z3sHAlJYYHfMNJgmQzamiMWBV/4MsQQpYruQU/NIrO/SKCuSwvFRDoZtX2vIyJqpVl5M0N/4mHfJzJ2NJvOl/AuBzZv6bRPSrAP4ugBcAfgfA32HmhYhmAP8TgL8C4DWAv8XMP/3WGzC0XAGSsamDwml/9tkY4mn5Y6VEWQegl3isk3sdDm2zunKNxqQJmyPKgvwboPjrSOGhEicI+sAWnyOBrLdOlObA6jIJ3uPy8qK9E1cg54pjTqie+7OeOJwjcgzMHWE1JgBsd0rP4eH1TeB7QEWjvlBZ5MHAtw/7RIyKX794WjIsz+KaIiUIPcGIiWlJRu7OwvDLkxG25UZCyIy+i8TmsJgdYMCCV3s3Gp3jNp7dQWLqz9Ceg3j1HOMTOdcNps0LDdfs/ttpWfogSoOT14Z/SJScovEY0myj6TTq7Hun32vJWOaTu9v5GiiLBQbDAY6b4jKuGtv1FznqwZpda7AXq73/8d0sMYbVOuwvbpQeq3EAY4UuQTdIHdlFwFD2ZEc3JmoETbmqbNvzyiPRg+9b8KIPohQe9vxdV9lnFbJ7KvGzlJZYENS1NQ1rql+jloqi+2+OuDXa8OSwjdpIzAjhTT9B5v1ss0E6pt41tL9sc5L6e6gjTMAcIwjAMR2xO97jj/70j4exgARNehGujMN+r+8kzlqMutteKkphJCtTd07y9f5hYqetRZA22ZB7VQuqqXNJy+OuZdcC+BE9O64x5qFawfRX04E0yFxTrN0lPVlnp854a8T3yLljQMLcG36Z89nWy4k665xug30angkn138cmaudmZ3Dsizt2k3Hjz/zgOdejbGdP+rtYc3phzQFBDoD7Q+opeLlmze4ubvDJ9/5CPPlFaJziOyAXKU7a2WwF+ckhAikI5bbG9xUj09++GPc3FwjlYrjzVvcvbvB2bMXmDbnYAZKOTaOzwoGewKxh4sSrNaUGpJe+JwCJu3+DkXsJGuQV0W+xIarhqoMyhkBDnEStCR7wnI8gkuWbsza8Z2LOfmMnJKUEG5mBG3UtCxHQYiBkEsFu4If/vAvIHiHm5sbhBDwk59+hpyVfyoEgLzKMiHOM0AO97sDDscjjsuCd7dH3B8OWIowEULHAiSOapwCjvvjaY4HpRSknAWpAh6s23ha26aQphBOdapBR5vR77bP0thdH3Pzlbp8ScdoUl5MRu0+ipar9wRNl++1uLP+Y7DLg+177E2sAWTKGXe3N3j77i2qd+KL6eGcFwSRvis7as0Pu/4QHjxrqkEk+sR7Bx8Ik6K0HZxUwqDgcNghhEl0YpjEh9OmVjFE5YItqurUV6hVeETNQjd/QwLROURzFgFoyaDi1JkJpQCchT/OewmoAhEodPRmyVm43ljQbuKFaUM7ZqSyIEaGc6wbaaVzv9qqt2RsUaRk6bycGkNpMo5Ev7LSQaiMmC4siryrPJpDeb+aF+GBtkDMdJHmoVtuSe2QNKcyu87qUT4iGXSy8SaE2IMDLHrPRw8KHm+vX4OWA6KrmEgatpmMtetB3tMSscvh2NFKhrpsehzd1zE5766zibh+3mUQ4D6fueD49hrz+QVAyhHvayvz7g7MycvzMICDHTTTxyzJ2D5mgjDz1ZpRObigJfUY7ZofnlLnXpMYRlNlCCr5nSVrGKhozeCMp9joe7rdERSX9x61cbI6RatL+St5wjxt4f0ERkapjOII7D2gFFrEguC1JIL3mtw68SN1YMCcWhKneZXkYN5s8yFOZArUk5VEujl9ipBut5H3bdWdKgTEvdENIPyK3jlQISTnBPmGNYdrT5IKxcUawKJe+BDvWEPS1izIuR7vsa5p8CDjitbVhJcg0AiggcaOoRuQgw9jvgsBEju4lozlWoXf0d6dZC01OgOVsZQTKk+IThLwZYg5CvWYqy0vm7CTD2TzwsNPUakkuh1ZLZWTGHY8Ht/8fniNn+daDEYuErsVrtrkpzfwssRsAwORpkVYxrH7owxANyY06WWHc66hZKWRopNqAl37hoy10n9Dn5aiZfSur8PK1tlegCJGW9Keg3tzVRdsU0b1N7v1mzNL5YMGP0QkiEMa/U1qSFhLRI9xuBsS1ES9GtISpoxOUSZ8pU5lytDZDIudoPqqKs2lJWMt+esV3VgVPTo21wIRigJPeq8JyWxYaFit0s5kgoFWuWBrzOhgFLgTwyR6oq1tQ6zX7iYRNQSpzTHVDl5pEVELigQgIJVg6rMNeqIlRm2eB1vhuC8tcV16jo2c15SdjJNRNDSErMmyVqYWrrqx5hrdk40NM2vzLKfgB1tH0mDN/ESzBU59NgfZYKlGvUh9w0XG0StNZdeNVf0upxzUcGLLhxFBrmUVL+eUB5pJRq3WrE3WQOaxCRqhKjdy8B7mdb3v+BdBxv4XAP4fAE/05/8GwH/LzH+XiP4HAP85gP9e/75m5h8S0X+m5/2tb7owgdQyk3Z1VQPPDCZBhdkiaZ+jr6nBY9RdeKf8lt1gnSKJ2j/NEVwdPPypCp+clr/JE58q4XXSUP4ae/0WLqi5KNHwwwCbAExhwnc++lhKlLlgWXZ4++4llnQHF7XjrTqpXgW49Fil7Yq2hmbqLJpWMOj7CuHVxl/KUNY+Yx+/5hjrL+vq/ddeoAVRXXE6033dIQG0iZMZ0oeeJNuCt++vEhP2at05bjdvCufkMEWtY+ZBYy6tB4SDgy7xKI+5CHB7GX1i/f64s9LQ6KOB6VpxJS9tTMEtWUYn42DnjckdZtZSXWqJnvF74/vX9l6E8fEfqAYdV3kHAldqY9pUt17KtXX3yFiPaw8YEsTDBcyYm2Fs48GrMR4RBKvNkK4lV29r4zQ+U3cK7Wde/T3K0Tg3pwkB+WwlDG0TyZB29s5Swj8m8rtuAwQJ2jqSDmtu1FdN13HBUgi4v8exJOSBaoCqNFkKzmOGOK0LW1Mh0qBIHDVpetUT6lVLAt9cvwUBKE74aavNLffnKmUghdexctR3PkMM4jzmguhj59UiobUouayCj6oRgPMeYYp4d3sjaFoaErD6JwFSogd1ZIiks7SV36jjWUoRRJs6PKXITrV04tUOyYbSZEYd0F1tbqlzLzVndnCmpmnCxfYMS0rCmTTYlVO7YN8zriautaGQ3EnJSh1lpYvXWh6HndvTXVzTDdvtFiGEVTLW3mu8LmlgQ+hy33W+nme6gNf6v/1uith+8Bw7vkbdHbAsCf/rb/7v+E//o/8A7uopMldcuQDKGdU5RNucYyA6oKZ73O+O+FkM+PD7P0DcXuHTP/o9YLnD/u0bbJ9c4erZB1jSAUvaoR4P6sB7hChcwKZ3raxaMj0FOR1xVLRodA6zc0ApSMcjUsnwmwnOB7jK8KUiZMYUhacwlYKcEmpOODuTpG7JqQX1KSWknFBKxeWTC3U25TnOt1tc3+5QGZg3EzyAw/6IX/nlX8Ivff+7+Ad//x/gz798jVwYuTJulP+VGrKElFNe7bYT2+A8aSM77f7NjGmesL04h4sB+e3tiV1GawB1XBZcSIgCgiZaNVi1phnMymVNK+sz2B80fwXjP7v6OtGr3OygUdA0X0IbR7iglAuPHmNpeQ+0RqO1+qr5A0RIaUFOCbfv7vDu7R382RlYE+qG/jB5r7VogLCmSpBnrwAb8iVDEK7APAliL4YZDEnOlCIeX8oLlpyQKzBNZ5h1XGOc5Hy2aiHhf8k5Nc61YSBXh/MBXDO4JpSyyBxqwFtrxnK4QUFCyQmH3Q5ARfARHIQTsiivoAyTaXECSBOjpSIvZUCxAiVlDWQkSStB2KAnSGgB7BrMDmVJgPLYbbcbQG1OqQUdtaecoSUDNcvGBwDLtLIi2K2DtOh446dlkJLFtoCIAVhFBuz/U/+8PhAWy2U0WXfCw5644MuvPsNZJMyWJGlNd/tFDGhgvNaA6HTW0kfSslGFrqnsmw84rKMTGWbqgbHTgBSloh6OWI5HvCrA048+QZy3QPTglNqmr4yvXgj2WU9ejkfVsmIJYNdPlEtBSdogkwiuUJuTvgk6lA0z46DlmOKPkibeh8rCMDYgIjAU1TVWj3jXSvmd01GvFagFVBhznHB7f4Oz6QybzRbnyxOcxYD7+zu8vb3B/WGPVIEcPXiSYH0OM7Lll2xYhoE3HRNjBBDbczaUniY6mddNyUxXjrNoZcIAtMO56Kwm+4O89aZK5ks59ZFqczmPx8OjvqlVv4jM9d/7KLpN1pwi+1R2CWj2wxDMpdp3m+CsklztiypLo39Lg4wZcne0FQRqPQ+YhTt6pb67CWr3Mz5hQ7gfasVydwdPO+HUd25FqTFcSu6njgrpQ3htGAYPIAgqtkdhw/fpYUxvn8srPm6kHvv9NyVoV4cCEJwjzNOEyff1Ycn5tCxwygVqiSdJwEkCqHLRxKQclaU83XuP4D1iiOoTywbb/f19568c/Gx9cKW2KTB+XgYjq19jvRkYXV4NAQk4lCR2z2u5uwq2bmQZ/QLBx4AAqE3QtS6zB9vIiNH6T2hsrL5u0s1vS77auDjdqGDudn0ELThtitmqm+TlhLoMrInmjjIXea1tLZiPmVJqFBJj4rwoZ2jKxonutRmb7/1LWOxXzpLwHnlHZS1INc+yJBzSHoD5DQHRBzj0ipBFaYOIpBGg98Z33593WRYEsg1ZkQXS5mQS29RGhWdNNqG+JVv8qGNka9N7ucdp75DmTwCoKYvJG5IrzdfiKuAxkLKPUotpxvyJC4Y4RWv2Dc0DrWIQi98hG+zeoTcaR4BRaIJI6SQAoLbqSzes3800gY3bF+LPtc01iO6OMQBWLVWtGbUBOwTQtCg1D+t8N5BeKY/0RerHz5WMJaLvA/iPAfzXAP5LktH4GwD+tp7yPwL4ryDJ2P9E/w0A/zOA/46IiL9BQ42uSbGmSIzWpGukEXD6M6nSlmTIOi/TUjeq0Ib30I+GAAOm+Ae0oliaVSAAQHcARuU7vhIPn4uQlFrhXWjJFbAg5Dw6zJvUgzzbXuDZ0w/w4vlHspOUKg7393j56mfIyIg+goLskMivBenCzC2oX+/AdU+TdKGxbrOxjpnXrnaVBU3bkrRguJP3M8E1Aezciye7w3Z++6prQ0joJAd2t5Fuojsdq2nTo+/s9ymxztFr7hCGINda8taGYggyH0uet5uqwD2QL52rlhy0P4b37wiMIeD5OQ6CyHbFw8TmwwQh/7/svVusbkt2HvSNqprzv6y1176e3ed0n+Njx213O76oCShBxEaJ4nBTFAkEEggBygN5QIKnCGQRIQjhAQkQeUFKhImASEQyQoRIiZAIsYDIxpDY+NJgd7v7dJ/7Za+9bv9lzllVg4cxRlXNudY6fWK3Ez9kdp+99///81KzalSNMb4a4xvl3awtrdx5JRK61YX8nZqjP2YGI5f+MoVWHQm9mTSgtKlVcqDSXc0jG1m5yyKyc/W5rTL8LN3IOh7c7FxVftBFTFg7tYvBffshtl7c+TxgAQ5w+WtJLG+7zvaZSOhK7PNdx1zpQAjXWY0HwswwZjCQIj58cY6Yo0TYhYBVv8LNbofEsVY5bYx3A5BLgrMOWNlhJwO21WBUfrirmxuNwCTEKOlWNkO9c3jy6AkuLy8L75LxBcr4qLwA2K7X8N5jf9hrxOFcntqe8SC44LFZrRG6gMuLS2RQ5aUzMKNxsnLOePL4MbxziMNRYruZSlRIclwcE+E0k4uXBRrasQOA/fGIpA6PX4A4MxlpdI1zrqR3ASg77e142/1TSmW8PlUubN7r3zFGXF1dFZm7U7LKWgFsVmvknAuQ3d6/rH+6JjncdliYGWHV4+TRQ0w+YLq4Bo8Zf+1v/u/4sR/6Mn7sSz8oHEroEMFYcUaPhJRHpAAE38N3wOWHbyORR789xff9yFfw9f/n55CnHfJVRBg3ePj4CV5cJHCeoKEZGIehAD9d1wmQzzVaZ3d9Uypiy0QWYGUTghhVwcEx4LLwcPWrHsET4iQgducd+s0JUoogiIFNmXB9s4P3YpBvTzoMhwHOuxK5Ow4DHmx6pCxF/o4pY7NdIcWEaYr4gz/x4zj79a/io49e4pPza3xyHDEB6iCpo91w32VmBA1AJZ2bXQgYkeE3K9B2IxWpu1CiDACNpIkJ43HAYbcDngioIWsHwWXVN8plZQ4azIguQ51N8ABQE2EA2IQrct7YDcysBSumKrOaCmhpr5KeeJeuzGj1+txKxOLf+k1OIChXWgTGwx431ze43u+BsxMwSRYSM5ASIxBpZKzYk943BI8gtd2kP0hRA0JG54FV5xW08eiCsvFG4OzsMXJO6FcbEHk4v8J606uT48BQrn+qhrzvN+Ud6sbqPCPAkQM4gXOEC1OxEohIo8AfIk575HgEpyPGw8siBeR6rFcPEScBnUU/BXSrLZwT5zonA2ohTiOz8BmSOt4OIE5g1hROzsKX6lfFMYkxI8dJbRNZS0WP1AgVsET7Cc9cQo6jppiLg0rwcGElFb3HAfuba/guYLVaQfZSpEK9wUG2HGkukgKZ1U5v58L8KyomjFn+PghwMw1HDNcv8Ug38KSI0CTZG6ZbnMiH8wL4ee+RXYKWaKuPcn7xXJTMP3JCE9HOGZNtApUin8jiCPY+4PRkg0OMyLsbJAZCt0ZyDsyx+BLzB9IsYqv+VlOKZ0EOek0IoRapcx4pTcLxqZQnzgWsVmtMk+peTT21IrlEc7CytaMs+gtLGhRmBOeRWG0/tggtiTyOux2m/QGPnj3Fg9Mt+pVHHI/YsVKSjEcE7/B4e4orPyIiY1JANThCTAnjFEFOKte3BWdaACZnKB+g2SA1srtxFu6wyWUO1O8t0teeAfW/7FoDHww8sOdWOQCUL3HmF5gfpkXVLMoQgEviQ8/8U/N19aNxLlq7jQqhfRcbJxk7mn0v3ylHqEYNSl8GJEghPzPZ2//MtTcTLVhkNRvnbH1/48B1jsrclR6T+xj/LNXXuzXPSruJpGijM5oYnv3+2z0+M/g6uwiYjiPyptN3yBiGoYBeVpC2BQ+rjSt890KDVrlacxJdnpgl8Is0Y7TZfASAaZxKpGtKqRRP9N4rBY+v+AQRgtqHAEo0dwtWEhFWXY9V38uYOAcHJ8WMtEBdZvHJDewkcugMsGVZ123TUza40ixlttAw9D1Ys/CKjav9k5Xz06kN04KxFdyeZiBqCEG0iQAh9XkEyXhRMLO1c1KJgJMTjRsVDMQsm/hz2ZCAFXtvAGWs7T/nLUKWwFsgxaSBM6KDggtCkaS7paUAVxTbtOs6sBY5NBBzGEfEaSh95Ryh71dFppgJx+MR0zhKxK/3gHNYhaD4GiFH4Xstm8dYrgdLugsBRZnl/hkoUcaFAo5IqTcUU0oZU7JAGlnnxijFKR0RQvAlE8Amedm0cU4B5qyYT83GFb/Txl5VLWwDjIqtU2QOdV2Qwqq+6gi1e4nE1hPbdp7FKN8TQugQC0etK3QLQWnV7js+a2Tsfw7g3wbwQD8/BXDBzMZs+w6AL+i/vwDgbR2sSESXev4n992cAAGQymcqRqAAM7YT31xhK/rChtcp0/xbv1849rargOZc/aUB2uYLdgWkZLLmZvKaEU/lGi67w+3uKJEGZ+u9HEtbTrenePzwCTabExA8hvGIi+sLvP/xu3A9AGch49WGscl7V3+ClBSaLNpVq2LromRFxQgoRUzMCJTvbytg87Xa+gj1vPrerM/nAmrO+x63vrVBnCuNW0YAm2O0bF/jGjbGeQEkzRCyfiHjmtR7NDw8JlsGQEF0XxW3ZpztmbMFf/mWuhh/VsVfo03rsby2pAFZmzC/pN1omE8Cez+qDoCBLeYQN9YNG/gsH7QPF+9xD1Aqt9f7EGCpVTVqm3V8mrnKJp8AivHZOF10d380T5VInWZRLbJD0pASmWWe2KLP7j7mz7vLcF0C5u15M6B6cdj6YDvP7bUWHaI3QXkzHSbHwuZi0Y2ZREFkAnrvcdqv8fjhY+z3ey0YWOW8rGUMzRfV78jDOYmMMbktc0qNshIdkxmWR5VyBpxF7jnsD/vC48NAqUKJsg7LteM0AdOEKaYyJlXOuMhR1vfzAMYUkQnwXYeszuCi49HSXMSUkFLE8XjU9thGnoAhrdNihszS0Ov7vvw7xigbJ9xELzega1FLZiRmK7Byh166a/LowQ043K7zlg5WN4Xm72+g2Iw/bHmaTlsDQSxCW+7JusY3ximo7lDXW8imHEnRP04JeYqYUsJwHDGOE6acsSOgM5oLTfc0Qy/DITihFBj3EtnZbbZ48uoXcP7xexjiiOmY4foem+0D7PdXmIZDMca8ru0yf4RLNrPQZWQtyGC6zZHDZr1GImDijDEJd/uq69BpOujxcABYANGgVVKD8lzmnDFOE0IXSirWcBwE2CXpr5wzVn2HYZSUWUeETd9hGkT+1/0Kq4cP8P3DmwjwSDFi5Iz3X14jm5GqhjkpuOtFIdU1hBkTJ/SnW3SnW7jNGsM41LTrMmjijI3jiKvLC+TXJiR43eV2YBIKAacZuFR0MBcdyM1Yk1FH3Vo3qy4pDnxpgoKLzOCcEKcRzBl9vxa+cWj0YHlKva/pH5tV7YZjAX5n9kkCWCp65xSxv7nG/rDHqJGnnJJs9jvhDwy+KxlUOUM2u2vXwfse0MJbOqFFjlSFZU1PNBCeSCLg9/sJOQ8Ajjg5fYycaoojKdUFKbQgxXeMD7PaHea4EZFUnNfnS5Xh0DhAElniXQB1W7ALyMnhuL8QQJI8nO/h/BoOqTicPvTwYV3AWJAVv5PDwfjQqLw3ZynCR07WYd/1IIy6x3gAACAASURBVNfDM+A4w/mM3MuGSM4CtE7jTiKZOGmxGQEGrehHBQrEnuYsqdoxCqfiOGScdB4EQkqMOOWylknhmSoGpl9aIKFMBddODJj6KWsYOeFJzTkjDpNE8nsCVivAe6X6SMU5c0wIcHChQ9ev0fUd0mRbmtXOEBtH5QO2cW5tdSCyNHaqOoMzvBOworMUSJJIy/V6BYoZw/GISB7rflMA2xqxKM8i1qI/Sfsfli5qk3i+ni8PMi5K52DIiBTpEmBhtVqDaCoFNwHJAGztx6p/imIX+XIOcA7Bey0ol9RnyCCSQlnMUECWETlhjCO+8cE7WHPAmBOGOGAcR/QrobLZD0dc3rzEVR4wEmuhI+mPPjg4kkFni0JHtd9M9znyoEDK/cvFXxDbv8YPF/5MHWMrcNZ2qDyipiNbkSOrgN4Fj8PxWP1INlBVfZpWB3PtN2Zo/xjth0Yx6lR15frKgyk2lN2LoNE3IFCxPatvS02/KK92Yw+ZjBaAJjPYgqMyjBFv5nZIFDQW9VkaWbM1hmUTjggFsGGwOqmWEl8zFUU+UTbX27EEV5kjIlDwt7IfbrdhfvyWgNbvcE87UlI7JSVESAZwS8tlAKl9NpnNOSORRLva+lkjFd0sYCymWLNdbO0KQWZzMz9LoSqqIJlsljrASZStvU+hMtBziYGcjIatburKtYp76HxKOQKjFgALlUc+p3lkNQO3x7PpU+/cbA7aXLlr4+B2v9dACyKqas/8Xapzo5V5Eykrjm5p8okjsvLrLn0B82WmPKHwLqP61ObzyjZvjQyW+V3ObKKfxTb0oQORR1aOdudr1Kjpka7rpPid0g64ElFtU0M3/LQIMjQIwCgYmAjkfcnqEz+GAdTia86Z/xfL+Ml7ymLkC11FjSaVaFGnYKkGJnqn0fWVhoG8FbILmMZYN6VYg/jMlzQ/L8ZCU8DQAl3q14o8QaPzxf4KoSvrt/zdZtPL9761JVhxDH0PMMOHUNSajKUv19qNVJzUX75fLr8jGEtEfwzAR8z8t4noD32n8z/rQUR/EsCfBAC/CkXYZwu1vQWoLO5sjoL9DqC8McysufN59QM3zoIt9/qA1vm4DaKYABjIVyes3gxmlRMkPN+qyjMqN6y6WoAqKAB4eHqGZ4+foQ8r5Azshz1eXn2CD168C+oAOGFFbavEof13Meesv5pIFwMBZv9Wo80p2JJtFwnNdXcddwCrjZ1loJm5aC2YcOuOrHej5otFV7a70bMxLyARz+5nqt8+ziLmyp2p0ggUZ7Ley4zmWdNQZUgME3sU3/FbNaZm54Mx79alg2AdybPfP4uCmd2G0NAq2EvcvrbMJ/tQxIfKq9Hsh6ZV2gGFm9fes7RT/qujXhWP3XwOvtk57RBX5+W+o92VWn5va0rO3MiZCee8jxkoKQTUytjtB9Y3usNI+CxHaSlrZU0FUR1JejLpc+4fbyp/Oo2Uh65KXCLoHDw5dIXXrTE02pbo8yx1zSrNyoaRjQGDiUsRIEqWckpa9M84mzw8yW7z/nAofcKQlKSyIWYiTqQK1IoBSHQSkUXf5dLHTqt2Ekgrc4qT0Rr31fGj2RwQLtGMYRpFO1CN6PelQVVm7F7t+BonFzNjGAZYxByopqsux3gmG1jIMc8E/9YxW5GYZzJnIFnnfeFda5V/1VMNKDC7az1aINaOlgS/9o6tB/UumZsYteDg1j18XCMOA2hI2O0PePHyAq88fox9SkJBpvLJADxL3fjsPFarhzgeDxJZkCO2Dx/h8voC0yEhZQFChO/M2d5BY+iQbnTaxoatvQQ3a7sU4XROgAqkhOAdVn0P7wQcTimi88ozxraGNY0moeMg1qjPmLDqutk6aONE3Bb9QnlW8A6vvvIKpuOIaRyxG0Zs+4Ah6SapcbZSu/bXvmcA7Aj9gxN0J1u4vkOexhZLKwPHLOngw+F4S3NLNIjNPYsCa9bosjaqPlUDfHaPQn3UaN3SVeaUEaD0HBZRMNf1xaKatc349GHvXPpXjVqu0RrSFokczSlimgbc3FxLNfEs4BZnBpNG8KtBLvMJs/Rza1XX9SAKACbVZGXhKs6+RAhVeWQG4jgBjuH9AM4J06iplZyFyqUtOpgB9sLdWnSVFcjQqI4cI8gbiZSAnWiiUVLW9RsE8gFAJyCFD3C+g/MdBJR1uvQRvO8ggLzpukXBEGbh3FQnPGfWPqpAsfM9QB1IZ4j3otNZwfBEDsOwkzWKk0SuaJstXXPdGw8lkJNGLEPWpXGMGMaIB145lXPEFDO8t0K6rPY3FduPGtt3NppEi+/qelkd04CYM2Ic4VliaMLJKcJmjXg4gGzjL2sUzWoF16/g+x6+7wFnm31y32z9WPQLbh1tgViTOzu3FOQp2WgaFe8dDscBCQ7rhwLwc6p2ltnopiumKBW1nVN7A4BFLpveWJoall0k64GCfjmXzVboqD8bB6yGodgrWYt6mu1QOkNfytZrqAyF0CFOo6bUy7lLvbk77rHLCUdH2O6uQC8/Qs4j4vEG0+4KbnUiEjiN8JfneEARPHlMSuvWeY9VF5BSlogrpxuDpciQrAHetcW9mk6Z2afae4yy9kg3MtiA6AKIuNmgB+8L8OlDwKrrsdsfKi1BzqgRyzKPvrVeNRZ4tbNL/5iMoNqNVijG/meRY1kB++pjkD7JaEYqYFds9AIsWQSmRb7lGunGXO7NuUqzrYvlm8Z2nvnNqHo8NTrXWgfV56KS5/Ok8D0aQGLrsp5B4Kq3SP+706v5rR132ehLP2D+ns1vKjeyliUECiUC1IAyr5H18v41MzUpxQUDJfrPAPUZKmB6tEkrD1r0bLkhYf9urzczwKsfIeZ+BpcgEfkjRgNjMxxnwHktvlp5ThO4bhplyb4tG6s5K0hKuglta1O1d21uecuoaaLIuZoTJVhkOb4MlBT82UZFA15YP1tftlGfKlpIibUgk3B5Q4NO7D7zSFFCzdSsQVSl3xmaAYfCLw0IpYLx1JfNDziQ+T36QgT1H8t0Ft1EudwJwtdffelc7CYFm70B+JZZQkWOxAbxyNk176DyU8aBERMh5WZjR/vDsnzkfYUnOsXU0KUIR7WnUEDOlHLpTu+dFiJztQityQNVqgwQqQ5hzTCusmA9wYDw1ha+cduYMV9JfRqdM5kZnc2bRtBSmgoYGzhpsIH87LzwzBbKOXJgb3Pt03z6zxYZ+wcB/HEi+mcArCGcsX8OwCMiCizRsa8DeFfPfxfAGwDeIbFkH0IKec0OZv4LAP4CAHQPNpzJAAFTbCgeSIneMImjNmqpdQ8ZymFgPOE612h2FpT8WU7QgdKTl501r16ohXjIziclBm6cWTUoigwgVcFsVJEZ994RAjy+8Mqr+N7XXgdBQvYvLl/ggxfv4t0XbyEHgByDXd2BzGSpo4AROhS1x7qPTabYUCZw+3plAScCK1DRchGZkdoeTm+WzekyAIRIjBGIUpfHi0HRgs8t0MtNy8FWJMPV9pZOvN23jLqoeng0m0h119QWPl3Ey5TkPEuCrK9oi39e8Dm2BvX8IS2I3xrAVT7rYiQceA6LLsWMG68h4C5Pb/q4XejN7ObZO+hv1LZ68RsshqJe2DoEJYqEG4L9RW9oT5XvDISe7Qia4a3Pc8Sl36iMb+2f8hgWZ5Wbcb8L6KyRYtAxqGC3FTGSyIE44x8y3lQzTtp21/7RdlgDrB3fwYxbAuft2NlnK2wFQHiFnEPWypfHYZj1uTl/Vp+MmwgfKUjji22tTwKRw5QiLvY3OL+6xOhYwUmZY95APL238L6GIl+TAlI2B6Ia2KWquIJejmrFVUeyg9r3PTabDYZhKO004yalhrOQZC3JLACyAwEx4WRzCu8djocjxijP67oe6/Ua+/2+GKICQlZ5ZRjNgLSlAJEk4C2pTMSYxGDUdSabVWNjH2P5dwvOGv9qu3NvnT6TH7umWQPMuSlGYOGQutuYb7+ZGR+YP8uHgKxFqypXKC/vAF7OL1vfIVHDaO45WxvKqn3HfNc/HJTkngEKDuHBFilGTC+u8fVvvoUXL87xx/6JP4JrjEgcMGWP7CQ1zHOGZ0klDeOAKU6Ihx3y1Tm2T59i+/AM6KRCPXtgf9hJerSC4sa75YNEbOUETJPo277vQZrmVfqHGcfdDdh7uBDw4OQU3UpSoof9HhcvXuL0dIO+75BTwnAc8OjhQxyPR9FVwePBw4e4PD/HOE4gBrbbDQ6HQ0lV7roel5dXeHB6KkBDynhxcYVnjx+iDx45R5y/vMLDhyf4/t/zvVhtT/ALv/T/4XPPznB+M+DmOIpDUDq9yhsn0VvwDuuzU6weP4Jbr5Eh0SvZ7CY9cgYcC7jnuxW2p2cABU3zFD5O07vGEWfya7ZV3Uic8xS2skqgAurZui163mQEmiYqFCc5pTpHmSERZ3PJl7WmAm3NDJD/+I5rpiOm4w7j8YBhf4OLlxcyTj6Udnjn1WYDEke5jTkNszRFh/V6C+cDiHyxJ3O2whZCDyB81QHMWfjehiMSR3TOI3jC1cU5dtdXiNOInCUllCEF7Ow/AiHlqTiQDAfngqSiOkLXESIZYF5n4FKnCIALEElBuVW/gvcrAB7MSdMtVQ8SEKcjKrAaGqGTLAogFKfPvicnjhiRF53k1Y5EzTjKLFQYDj26foNhOJTiHaFfwfuAFA+Y0oAuS5RpisA0MjgxQgByThinETe7PZ5/7hmIHDKAqOnj4xTRQcaAQYBj5YummcVVjzt0NotzJmBjEA7qNCKOA1bOgUOH09dfx/bpM5xfXGJNhDgeMe0PGG92WD19gkSMGDoZ1xDAIQBJwOdMaueb7iZ514XlNm8Si7Mt0f0TkDtxdmMCxhH73R7kPabjADAhTSOgEUA6rLMXzDlimAYQULjVwVoR2jIvWDfVqpLBNA1FbxHJWhK1KrhRxMV0jX/yG7+BH3l5b9Ljd/c4eyJ/pyNw/oH8tzheB/CP/L1pze/4kQD8mR/5EoYmmjMl81cF/K12MSk4gbI2EqD8oU0qO1vBLl33tVZLywvpGl5JMAuXOXHxCzJH+T3XtHJFRwCYD4+y6aUIXANEVSm1bxZmmPjaMTXgGUomkhhzeqWjch8yULrRRbKaonCmRivQQ2of3ja//p4dzjnZFGbBOFarVeEiJRA4AbEA/gzqKo1OASiV2qX1ygrI5Rz6rps5h5wZrnMNXQBVYLLxk4WvOyEiKUA1D1Sp/nHVy7kp2O2cbJiBFWNoIngdic2YxrHKlap0icoUHWNrj4CJEB1nEbxO+HYNtDNLNecsOK5Z6Ln6m0YRUNxGpduJseXT1lVZozY9hLomWvR+c05G5RUVG72OVdtXNhYWXVpoHjRCN4QOHq5kMQh9nYCgwgdL2i+h2L0txR3pmuybgBHhsJ2Uwk38NB+k2KHQoxi/rfh+LY9wcl6ytAAkFl3WboKEIFljTt97GI5S24naCO3qB9mULT638s6CWfnh5R2DD2DPmCih7zq0G+2rvi992waPGJUHCMBqVcZWuHU1gAgaiYtamC2lKAVb4coaaZQKMcYSJNT1oaxWjiVTjhUXYWapPUGyaeLIgxwwHIdSy0LGULIgOh2b+47vCMYy808B+Ckd+D8E4E8x879MRD8D4J8H8JcB/GsA/ope8j/p55/T3/9X/g4hfURCU1DC8DlZLIou4ihEEGLLtM6iut0FOEEBJqxAgkRW1xR4BmuFvfKO5X7zdrWf1QF2dXefGVqxbekAV2e1vbeBJrAoWWZQYrz++Al+4POv43teew2cR9zszvHtt38D337769gfbtA/7uC8rT+kuoiKAiwRMbYIq6JpnWeLq0DjnEZmUJq/M3NdrO46Zm9Ks7/Kwt6eYIuDAautc0e6w17cTVWeRTEvxsd2KDLX9N1ZtEMDWrSOFQCpdEYAu1ujXB5EdHuyLAHH5Xf2OaWMLgRst1uklHA8GvF+5cwtjtCt2aCVYl0LtjZgXHm9xSJv3bSoDjoDyMHN3e4Gf+z7dgdo/md1G9p3N6f79nHbYbe5aq9HpT/uP8oWyqcJJOYAEmkulC3apix5Ye0Zz6e997Kfq/g1b61ffloE7F3jNXunBuADBHyVtYIKfxNhMb5lHmRsNqeYpqnypJZ+queDCZEZEwTV8T4gqBE0KR+mVRn1ziMaoKfGQpwi+kL2Xt83aBRCShld15VU7WJk5IzD4VBA05arStaVmqov4xPBmpK5Wa2w7juknDEOgwCoTlNNci731ItRRohRIsiKPNr6ojvXpAuvK8abkN6LgZTUH7VNlFq0w9rZ0keUsS2AU7Mx2MqFeSR6FAeoMTDKoDV3LcrL5Ifr/C3jrc8cjsd6f/1OKiG3kl62nG69QbsOzaOR7pjZavDeKdOoxi45h+3TR9iPCWl3xMX1Nf6Hv/rX8E//5B8GNlskBzgfsN6sBbz3AX3X4er6SjYl1IjcvXuD1cNTdJsV+pM1OEV87tmr2N1c4+bqGsfdHv26101aIE2y5nrnS4GmWRvVeSMGOGV4YvTsEI8D9vsdcpxw9uAEwXuMhz2IgPW6x/XNFdbrNUInKU3vv/8BeiLh1QLh6uoam80Gzku66OXlNR6cPkBMCcO4Q0qMN157huPxgP1hADPw7MljXNxcYz9GJGb8/n/oi7g6v0HHwMoBV+OEMaYSVcDK75Yd0J1ssX58htNXHiMGjxEqI94LcNi8u/CxCrfcar0BDOST/GOU6BhdOFgNZ5uvxWE3R76Z5yYHJs9mnNr3Kck5UsACpdKzGegxShSh8bEREaauyubxsMd+bPRb0W1ZwVxCzhOGw7687253hR22mMYDXr78GC/OL8E5oVtLNGrXd1it1yByGMYRqVnPWdfKOh8qHZREbMjclM1lcwKCvos4NQJ2CSDf9z28dzjsrzEM13BQYKTzAPmypsQUkaYJcRrULvUIXQ8p5sFIY8Q4EJzLcJTgXEbfi7Ma1dZyzmGaxhKV0nUdpikhpQMYAoRKpKz2NTS9Mk0AOzgKCGGF0PcwbQowxkHXbFV+5lBOKer9rSCjArpOuAa7viuRVIfdNYY4SZVlOHRhi5vdDjEBoV8j5gGH62sc9gPSlHGyPRFAgIG+9/jcq4/RrzpM0wjOGsm+6rW6NcMVO6/akokhYGMxNDGz91WQRGqpnuO6DhxH5CkiACBmvHz/Q1xf7zB5hxR6PHz0EOvTB9hvb+CePkXXBXAUCpzdqsPmC6/heHGNaX/E2eeeiS4eRjAy+u0a+8sr5P0BeZqkkC8L6GabGT4zvJMN0BwT0jih7zpJ9wQw5gSfEihOgBsw7vfozx6DJ4myFt6iaqc557BZbzDFsegfSR2NwtOXMxJBaYyKh4DDcTfzs2x+O+cKryQBZYP1Hxy/M0dKwrTf+lhkskwSDWYHQXy/s5Mtuq5HzhkvXl5iTLHYQJIKPDY8mNBxNKoIwEeNyoOAu96JTWqFaGxz2yJW69P1EGEpdnlWHUWGrhmQolF71ggrqsOyWyhzY2aXiO2pHaH6xRXQxvygZRq6eTAESdEX0HZeE+Dvx5GTRAnmlNFv1sg54XhMJQur63pwbKP72ihNKhzn9u9CpWW6MmuUH5rNdmIcLVBC1+7WzgSskB1ghoGt+2DTI65iDcopDWa4fjXzpWoQ1jxalIhKkTwx17MC72qXAEWXFdCPhEe1+EO2iVjMHaF/tCC10sfZAsRk/TI9QESgICBl1uCOAqyCiy0LkijVvq80ba1TZjZ56MLs3ZdBWVYQ2IJJ2voUouu64p8AYj9No9TYsDliNBLeqAO0ZoVFcpoOCT6gCx0GHUHLFEspSrFQ7b+uWxUZTByLz2s0BQYip5RnGXQhTJVjmEg3Wq3IqZxTCrBpRkVKETllDUSiyksMoeoZxlT6NGdGnBJKYgFbl1OtZQITYY0sb0x+WbccyDGCb2gAySEEB2aPHAKmnCHsxgRI8Di6ENA7j9z1AFuBPMlU8ma36aaWFSXNOUHom2Tehq5rKBcUmGbLMrkfO/isnLF3Hf8OgL9MRH8WwC8C+Gn9/qcB/LdE9HUA5wD+xc9ys5yT7Bwb4IaGOwJ1t6OYB3cBY0S3zoNViWvAvRpyXD/PQKZmErWH90K4r5hhKWhiYJXd1HhBbCGYOeoEGPUQgRDI4Ye++HvxhVffwHZ9isM44uXLc3zr7bfw/gfviwphD8eauKG+02whte9pCY0VeAaFSrMU8ZLwdAGHbAyaqMslKDnrDzPXKweoLXbmWC0P+aoCIwZ8kGs5fGp759fSbEwKF6KeakTiTWPVwWreowHR2GRE5UWbJiDMLdlo2988omlbvV650Jpo6iJ49r7k5983R863vyucwwaWNmAe28vAFPa8z9q/b284NOfzIpWZyWAh/cbaVRXNHMBs2zzvvwZKAtEcJFn26SzSh6ELLN36/a6jlZxWdq2/cpPObXJB2ggDuNpricypuX3cB2i37Zu34a57zC4s1982WmTNkSgEJyl9JmMGPKpyte4SajSdM0QgTYsl4kJJ4rwWlFEDY9ln8lGrnyogag139ix10s3cXWCJ5bCId9uQsWc47yCZfYwpRqz7HuM0aXTj3HlucFi0q35Rzs3ctbWmKves4IrwD2XlUMq5gk9UQiTuilxn5OXmDqqesP5ZrJjSTtW/OVfwHNq8ZU/VdKbboOdyfO4CiAGdM7a+5Xp+81DtLF33c6srm/von2Tys/jFhrtEq8iyIW0PAatHZ5i8w3Szw2E44uf/77+DH/rBH8Abr72GIzIuxwGrccLKOWy6TgrfWKQOZzAB0zCg35xgc/IAFy9f4r33PpR0/BzhuwByAXEckWMEpzSLAjFajBZYFIdMOojjhMPNpYC9HZCdByflWFMO2Jwz+pU4GMPxiHGc0KmDYCDk6emJOMyTVFTfbreY4ojNqoff9CAGjvs9YsqFQ/7l1Q0SgNPtBg9O1uj4S/jlv/NLeHZ2gvW6R3xxBU6MlBmJs6SdOYk6Xj18gPWjh+DQgyziCACV6IZmDHU8nHPo+r6s6RbJauufAVMFglfZIOhmatV2RU+CW0e8rqkiq80armNArlaxzinBTcKD6r1XQ5YQfAQUelit1lgHWYessBJ0vmWlHcg5ol/X4lebkwc4ffgE0zjgcBgB56WCdt8DTkDtFKOCSQ5GtGKOeqvzAKCz5+p6UWhslBubScaHUPn6iDy22xNNM2SM4wBGBvkOoV+hX2+lOEeKyHkCMiNOETmLk8dOaDlc9PquuhYiw1GGc4xhAFwgHVuPoNXiY8yyrjuH65sBoROgIiodh60FNVInlTEUh3Nlnq7cm1ZwzmgICOSF82+Ko0Z+SGqqRWRnJjhi+MHLQqQOoPHApczg/YAYZbEgckgT4+Zmj2mY4EDwxIjjCICFFw+6VnMuzqT3XjZAnESt5JT1PLGhDOScH3Mn3SK3iz3lCJ3rQEcBfMh5EBh5PGK6zhJFRITzy3NA00oDHFLfIxDgkRBWK2weP0V2HaK/RuxW2J6e4nj+AjlHPHj1OdLJA+RhFOeMCC8/+hicGf2qR79aYffRJ0IDRATXdXjw/BUgJXCcwJ3H6skjuV4rck/HA/qzR6LvYU6fjqFSjzjv4OBvAQBkuvtOe70GVoj8WuK4rNNRdSovNxf/wfFdPbjYrnV71DjQb53LjCmzRI83QA2Uv1EKNom9N01jyVhyzks0O1DmrMlPVnsR7ODYlTVJ2tHaXgyQRmiaL8hQapPGd2yAOiumY/dIBpzZaWpX2GGckXJ/6JqCcn/H7ea/XGiR4PYQFzwQHCiS7Np8l45lQMfyt7uOjLoBArAWUbUNtV7BN1fAWcERahBA67O00ZIAKkXXYrPE1v56PWEax6K/JNOoQ9AoeiLZyGI0kYZc100L4DFuaUsZb2UA6odoYwHm4iPb+uOdF7CuAclzzohcU/UtyjUDYh+lBCLBICTysUbgtu+5DGKyPhNg1OS+jai2XVgBOLm5zjmjRxBLqgKoSl1yD4ZS3tc52TYkmp27PGxTlUtZZAV0C5bA8H2PGFMB/oLzWkhWwEO3XiFGX6JEgQzngt6O4UIAOpJaD7kWEy6p/4BSG2kGioK+LZYCkkhXj7Y4NGm0qpzjdZM2O9lIZ/U/qt9BgJPMi2orJKH4coClPdNChmZzoIxBRqUpE/Dd5NLoBCSgIGHKCZ78DMNx5vuq31ZsBJDMxQoUVToN07eZkFgAXmH5EztBME0u97rv+LsCY5n5ZwH8rP77GwB+/x3nHAH8C3839wXUFWAuSHKZx5BUOxSAYPYs+YeCEWXtZgFzUTpZwVZ1MG4tmgTU8NK6oyE7gc0jUPAHM0vsm+K8AiiE7+aQ1PQ+FUAdw0AOp5sTfP/3/QAePXoKJofD8YAPP/4I7334Hl5cnkvBB+WKNV6PVoFZm9qYRjJFBulPNkO0eGN2Ns0d8E8Du6hGgRUws75yc14V4Aq+zIGEpRNXLkQbkQjT66Wnl60zZ7PKgXmKEAOEzclq0lusj2z2Nc9qv6nuZ3tOPan2u710VYoWWVnvV50DEWWeNfXTjtKPDWA32zi4Y8iW0Zf1QTMpnt2A2q+X9+Tyx+zZtvDKI+6XHbvpbWAYzQI+v7e1Teb0/PulcrUxMOPw1n30mrLDTNSM31KAgfnlrJdU+blLuX/a3KnDV+Wgnl4jK+8y6JzzMO5UaKqVAKN3vKWBKE6K/phRES21Is+NEUsrWlbNNWJzzox8Rx6XReVXfdxsR5FUrG+LW1kftB3LjOoksO4ER0kjk2trSlG9thk1kr4p85VvrxDWr5mFR4icpK9P06QFnrT4zp3jsjxu33+5OSJntfoA5d4GUAFNqnFZlOv96rNwSxbaDZb75E1UmS2cjQMHYJ6Tp2Nm+dfcSlQ1fsxYnj1g1qb592Zo+ZMVMickTsjTDd5+7wNst1uEEPDGq68ip4w1A5Nz4JzUsJy0MjPQrXpwyuAEzaJgBAAAIABJREFUgDqsTx7h5fk50jCAENGFAHhq+G2tYFk7Cm0bTR8wZLMpYRojVtsOfefBwWEakvDcOd20YDH0U4yI44Q0RXFSGkPSOSfREmQgl8iy9w7BOYk8MOeWSSk2Evq+xyp4OE945dkreP655zi/uERkxuOzE8SXNzhOkxSq8w5+s0F/dor+9AR+vdJNFio2jXMaGbvY8AJJG0MIZbDm00kGX2RNNnyWNgFZSRjmJtUdzcLWuJQMTf0mlFWBiwUCgJF8KnxdlX8ScJ4hYCzQ9T36JBV9vW9klOvGJHNCCH1pa9ev0a+3Ui29W8kzQgCFrshw5gyrZO+AMs7CUd2s5zDHy6Llqy1DjhTcrbJlUREMqaYLJi0cqHyzNj4KQuQ0lY21FFN5Zs6kz3DFpgBsLZO5ET0jZHOeM5i9Ru1keHZIHWGcktiOJG1KmTUStr5Dsed0/MfpCCgfnKTNysYDgSSxKBEyJ3GocgJrUSgwK/UFgRER01TWPOkeV2RhHIWuwRFUqhzipMW8vLC9WTEnZ9GX3EZnW3ROJyBSEp5N2cgU7krhsr6txmfT4o4lTTZ43Ezf95sN3HqDfHODcbcDdR7EUnRqOhwgIb4OCABnYJhGTDkhQTIXQt8hKV0KQCDfgVZaybsLyBeX8u/tFv1mg5ura6E5IAL3PdzZGTCOyOMAeILbbgDnQdd75DFiPB5xqvc2R53KXGlsnNb+zfXN79N3kipsGzEsqaVcgyKMrujv57HLGb+m3PQAcOY9vrxe/44976uHA25yRkeEr2w2ZU3Z54xfbdrxwHv8UNOO8xjx9Ya26XkI+N7VCgDwy4cDjg0o85XNBv1io7VENpqOLec3G6Em4AyMUxQ7SjdaK3CCAlItuTDbv+3fRVx0IypzBbpKgbNic0PXlvkaSvOvqp9Ftb2mWxbeBVqbS/ogF/o10zN2a9fwybaBOhb1afaXFMh0M4Dtt3Pc5wPcB8w2J5c5WuYqq21Iy/uiZvYYxaIVu4YG4hTOVb0GauE1vgpR5aEt1AGm1ppzWr5yA7GkthMDSTL4qriJ7nSWokQo2ctlQxYLHlUGmGMRsiJnKc/93EY3mXa2PxlAilF8Hefg2WuhaOsVCH2h+X2GBRglAhtNh/LSqx0lgCkVIymDQLPo2lyK1pLWHiAyHtbGN2zlgQhtgFYJnGrGxgpbVVtMBUEHSApvma8ihd8K7Yzew2gDpIiz3FsCAyvdntMoZiblyCaHDMm8yfpuXlP6C26icidNdmrPydxe+iKFL9YE197TAUwO2WqkcLup4AoFg60jDbQAVtue7P24bra0GKCUgahFwsx+cpCMI8cGwEex6TXbzJWnmEtWFGehxaCiX5txcyRYjrPt6hq1n0o2FYott3D3bh2/ncjY7+pBSlicNDxdJqq5WS1k0izQDaelrG3yxgxopdaaiox6VQF4DIBq+8cWD9tRFp57mRAGgpQTMf8nA1qkQAZiikmNeuVBQU0r8XBY+zU+/8oX8MUvfgknJ6c4HHe4uDjH17/5Dbzz0bu4PFzCbXuwd6BgEVvm5FSkve6YaivIFhMFnbSqdOZceB5toTbuaTSAELBwwIEmrW6+MyaT0haVJa9cnTACbrvSV9JENwMaW7Cz/M0afaWf50quaWurvFz7vRmjzWA5BbZZjYLmlvPiV2gwenMwUfp/3lh53xjnO5FlihNgUVlL4G0J7rEpBqBJQ1IFtIjAo4Xhdguk0YWFyrvUhXku+/Mx05YWY7y87S0j5n6jpl7zHc7jalQWHdRcX0yuewycUrDDFl+qidatUlfTATbkIvYJS4kqhmX5cPuVmes589XJrJt73pfb89S8IDTzwta2Zj7qdzFG+L6b36z8XgEicpIS2/sA7zwubq6l2iW5koobk/B+5ZSLgW7PW623OB6PwgXaSghZ5EFdYmRXvCpJ2/21Ksj2Ti3obkdNcRU1tjtUDkOLgBCy+MW99O/1eoWoRVUqYIJqwLGkxKeclLPSY7vZYs97DHlU/p+71zssHFUuXV3nSQgBXQgl7euWqCzBL0Ce1yjmVnZCCMVRWgLzt9fluua2h4GR7Vy5WxJFAl1jnCLXMa03Jpso8qmNNGGGVyOlQKJmpQWPcLoBOcLxMCDFEV/9jd/Ex+cvcfaH/3GsQ0CEQ9Lq3GeWkg+JolhtNpgiYzwOoDDg1Td/D3Y3O1x+/C6Gmz1GDGDvsdmuEfoOiK5wcFkaVEqyS23OQaFIafrFOw/fyWonhirheDwI4OMC0jiVyJHVqpeUrpTR9cLtdtjvAe/Q9z2YGfv9DicnazAzDvsj9vsjzh6eIGXGcRgxxIgHZydY9z2OhyMO+xH9doMf/cpX8PO/8LeRrnZ4843n2A8T4k6iQsJ2hdXTJwhnp0AQblirTkwqp0QSvTAvQCM96hxJ1DCaJZZNBnS9Kul9tbADWIAw29AYx1HT7wXYza3uNlnPGTmxgsPKrcTQyH6zESQV38AdQJ01qpE9zgV4LSoFrkUrDCRg5eOqJdrkvtauBEjmT+jgQi8y4DRis3E6a9sWaaskIPiYRjBnVDNB7QASWXEkoFXwHfp+hZsboaYgsAKHqTp4AMbhgBhHjMMB4zjgcKxc/TUiRdLujA8txcqRJlEqti4mJERMmuIn1BCi05z36FYrhNCDEDBOB+TjHtM0IMZRNqZWa0nZzYyUJwzjUcbIOXjXIfRbBJINiqhphp4ktdhS3WXotZiJ7xHjESlqgUV1HJ0LCgCQcNVNI7yTwkqhWyH4HsgAORY+SgdNH5W+qCn0Vcd45XtTFmWzdFH53ObD6WqlrPkgN0cXusqlCCC7gNPPv46TZ6/g4vwcH/3m1/D8zTcluv39D4FOi6KR8rAOR3zw9tvgKcKlhHgFjC8+QXAyFscPPsZRqUl816HbrJGHCf16Bc8AckZ2Dn7Vi20cAiIIvutkejnZqvD9CvABOU+Ix6MCAx4gTRVVQNb0Ys4GSKBwVIosScolsxQOrL0iKazeazS7OsexiaBy8CWyMjFjXHQ4AVgtHPXv9vHRNOE/+egjHPXZX9ls8Gdee+27+oz23X76/BxfGwY89R7/1fd8DwBgYsY744g/++GHWJHQQ/3gaoX/4LXXsCLCxIxfPhzwn338MVZEGJnxkw8e4F9/+hQrIvz5Tz7B+9MEp7/9xe/5HpzpGhZU11a/jPX/je5nK1ipdrsLOA51Ha16XH4PIaDrOonERwVPmKXI6TKIo12fWTMS+lWPOKVaQKnxf4tu1YXasdgHlX1Nt2Ua89rktNBaQZb8IlHqvDjNKszQIAFPBaCRC6merve1qHli6IYbVJeIjVSivc0nKK7GQp4bu7z9vDznO4KwTd/We0LxBq/p3wEhyMZqieBUfvxAAsqVQmnqG7NzJc3e8BOCRFOab2SbssF38D6UjC6htEhljDMn5LHqw+Ib2AZebriCyxA5ZAVtU1KfimqwgvmxBZC0qG3U+wQXNBLTMl8ZEogimQmtH+GdbBQ55YCHvjOjZqcG5lobQ40P72qR15wEEDZ7u0QgzzadjE6Ny3xg7deCLxkdRNMfBuJZpHAJfNFzvLOoSaGRIkIZg2wAsfahc4SVbt5kBd0nXTO87zSClCTwoQDMdWSqOyBBLqXwFrOOpehqCzJwWtCLc5aNUHDl3oXhRyiTpQ1KcSqH1n5HqLiZk3Ez27xcC4B8j+A7lR2bjLVPvdmTLHZVTjWrp/a3R/ayYZtSAgWRESLRdcF5JBsrSoLvMQreYpk+3NBxeecQlMcZEDnmJG1ISlHaBd9gfGKTTDHqfHRi5wSn9Gn3rw+/e8BYUAlnthcXIWgAUDXEzWG3oxAnQxzwEunVOAvm/NbOqBQDQF0kvK8Lgd194f42glg71gQ2M1cuCQtZZtZ0ULmXY0KHgKcnj/FHf/wncXb6GMNuwvmLl/j2t76FX/zVX8L51TkyJXRBJgdjMYxL1LD53Wm+sk0gr5PdGdF3A26Wv+4xnOw7mSTiaJURazjWbKHK+fZ9Wu7IGe9NuTYX0LN+Vw2OzrW8s/M3LhGZXMepXt+2b27EUPmVSiSZteyu/f7ixM7eRaSBQLLzw1YRtlXm9Umt7OVstAQG8swf1rjJ9bij4vPsE1HZ0TJRv5egftY/BFCtVugdIc7GaT44NTJJxvN2hERpwb3t/DSjZnn+fUfpTarGVDG2tA9t3rNaf8ZxY8aeK8C9XjOTo/l7SyCn8uA0JOLmsMwuIaDvV5paaaxfhiS0rb/7fa1fjscjek0bim4s926vnbEMy1JTSrCIxm92M/XJ5AiePFa9Fw4wqgbIa6++ivfee68pwmWG37yNJdI418+yvtWxNUPOSOnroYCNRjSUTYcyVcwJWHLSKY+Zd+j7DvvDXp5JmnpsXGdeKjU/efoMH3/8McZxwATGNE4lMrbM6RKFOze477OrbXPOOydg7HG4R8XefT9qvm+fEVOlKbD2fGbjfvFcWuinpYiVZ7cRJUU4bGWsF0mmUKP7WKMhSCPRjMZBn5tZKqaG7Rpnn3+Oi/c+Rtwf8dEnn+C//x//Kv6lf/aPw2836Poeoeux3+3F4SAH13eIowAWPnggj/jwnbfxpR/5fXj7rYf44J1vIN6cI3jCVmkEDtOEOEkKszOQxpbeXIF/8wJJF4mri0usT9ZS5Z4Zx+OITlOypmlCmpIawpKSHroOffAYhxHDNKkT4HA4HkEgnGy3cI5wdb2Ddw5nZ6eIMeIwjOj7Dg8ensDnhKvrKwHM1j1ubvYAOfzDf+D34SvEuNkf8dYHl3CPHyF3AamXAn+JHJAYDlmjHm2tT8J9FcJMJ3sFHFfeY933dXFs5aBKW/NNI3vUOMvewQevxqpusHoxIc2A5RwhFXwJnAlthLvIndgSznhM7fc2omLWupnQFkN9uQFThVwciswJ7AhMQqPpFIg1sgoxG2pWQKdVq2v32BwVg1s2nGSTKHiHLohhPU0j1usTBN/BLIfD/kaAWCQQibPriBHjgJwijscJ777zIT55cYHDMMJcF0dS0LW0QOkQrK6W6TgpuNiC8B7Pnj7E48dneNB1cAS88uyRcLf6NYAeL14OGIcRu5sBwxDhQwcfjjO90HUdXFB+tOARpxHTKDzH5hw5Kn4vatSSRxfWePL0dVxcfIz9/hppPAofbp4wTQd0ocN2s8V6tcaq61ACKGJCzAog2oizgSYltlr1t6Q/kgK1AnjL+GVrC885I+1wmEs+F0mo9mrXdwirDq7zmFiqFb945x0cc8LrP/J78eJ4RP+FNxH6HidnT/H4+VP0YKTjEdPhiGenp3ht1RWuVxwGfPzNb6J3Di5lHD/8BIEYwzhiz4zsAjCMuL5IuHCSDuuyFVzxIBdwsbtGcITNqsP2ZA0fO6TDAEwDkBM4qW1s1o9jxKEplKk63bNHG9QinL4OzAmcRox5QrvNn5UT2Mg7WG0KHRabjmAAv3Q44D/6YF5M60wBy89myf3Wju/te/ylN9/En/j2t3H9KSm/v53j53c7/KcffQTAYvbnx8+8fImfubgAAPwXb7yB/+7lS/yN62v8K9/6Fv6bN9/En/v4Y/z8bocNEf7rN9/Ev/f++/hfrq/xS4cD/ss33gAA/HOPHuHHT07wb70rNbD/4osXeGsc8R9+/vMaPFMzEuUwegkAIIRg0q3gAlpPAzDgzyjPxmlEygLYeid2kkWci+0ALe5W/e0udAWskiJTqfhcjpwUuWxoCwCUon3t17bRO9/kB5i9+tDlW1uBb9lWghW0/r++sZ5opgjPfhf5lTWzyU7C/NzPeny6//LZDslmSFoFXsBYA/hiTHBOM7tyBpIA6bBoSN/Ybai2d1A9aryilj5unO9pnJDIaMCqnWnyRNTaq7J2HMZDBbLB6Lt+DsCRB4iRSSiVYo41EpZsw7L6AkF5NQuAyU0BMb0GEB7Wvu8Qgi/nGthom8VmNzgnmUgW9QsAwzgo6Ff7yYLRTJYzS40MwWy41O2wAtBmR1tfyPyRuVPoEQoHPJd7lA1U1dGrJpI+RuF3H8cRSSnjZB6H0qeliBTXcYjati54+OAxDAPGaUQeRf5DUJoC5dlNKWM4DhrJzOi6DlFBfQt+Goah3J+cRIx3nfibQfsxab9nvU8GNxsGhKQZbXbOzIcBq86+K0o7FO5giz628gByB8vSEs3lSQISMxHG3AYRORj257z0jWcrMF3nGjPgGfC+w7pbFVBa2i3As/eVEgtA2ewVv1p9S1dpzI7qf4qtJjhdp5sdBkILFWa9533H7xowlmdLpy2u9e/yOwEttx7pZ7lS/hCGLb1nGVlTRg3ht6mEKjtlcWBAicRVgPQcUh4VQlUstvvMlMpdnQkK1wkNlohYnz2eP34FX/6+H8QPf/mH4dBhGA44v7jCb3zj63jnw29j4BGukyiE2fNaZMiMLcyjzoTTp6bRCZeZORe1r5vXvqVUlpFsMpkqsGoRava+rZgteS/vi7aV93LiuC82c5bts6IhyzYtHUnbdb3b6aTZ17OpQYsv79CxgqlXXhSGKnjrBRsebi4gKl+xyStQ0m2IUK+zfjTlyIs2ztpcLWKe/d58Mg1b+C41Gq40T3u4iSSu43pH39jHTwHtRXFpj1A1GAvQSe2a1HbW/F2LVDVfMqAcPRbtav3aph/Pj7uiC4HqULQvaG2dmbOz9wIYYhg1V93qC3lufbbQnTTvWi6pkQD3mXRCzC/FssbxOFNoy/nQ9mvMjMxTMaIsgq5cv1CM0k5pz7vvvoNxlIIfRdktgEN7LwCzXWEzmEpLyv1bFwHFaW7Hh1Fl5O7D1nDhPbu+utHI3rpOiqxJJV5OGZfnL6TiNAstw/F40B1lB76Vy3r/0YLV8u7AOI3Ct1tWwvpneUlUiVq+VhdCKSTXXlnlcP785dp3V+Or8Tjve9MFTbMAGB2EjQ0V41HOa+ht7DtrGTW6s8yfRcS/3i/1Hv3ZVtRVTFhtt/iFr/4afvSLX8TzR49xPB4QpoyVD+g84FPGcDgA04CVbnBNxwEvP3qABw8eoXvzB/DuN34VPOwxHQd0XY+zs4c4HI5ajC4Lt7s3uEX0cSaWiq1Q8DjKXJ6Okla93q7RA4hDlMhLkEYRZfgQsPI9huOgwKtwmaYsxnzopDDWME4IwWO7WQOZcRyO8N7j4dkJiBl5HJBdxnrViZHLCZtNB3iPMUsU4unpFv/UH/0J/F+//uv4+PoKHByuU0aEZNoEIjg2zkbVS5SVw6qRmyyrvXNBUucBWMpaE0cvfcSoRo5ZGl7XLWZQrowWKccCvjsFMS1aAZC+KvKSs9pIdf0ofMeMqntM1kwyzfQrHnaFiqr9stz0U8clZ3nvEJCdAzFmfLoWMeV9lXPhj65ZRoBkFxyy9GsIAdEAaCegqXPAYX9E32+kQm+W92cdV86TpnxKCmXOCeMw4GtfexuXNwccx0lHtD6VUu0apDZauc61ptv0yoib3cc4Hifk5xknJ2txQqeMYRgxDIwP3vsQ7777CfaHEVMUjeks84xl1L3zIK8AsLfoX41o1rls7+09Yb0KePbKE5yenqDrJT3ain1kjQj25IBAyvGbcRyO6ENfOBDJO5ycnGAaPJA1moRZZQhFpkzPt2nKUI5eJotCzoBy5DLm4Jw5hFVQoBExKkU5wYHReY+uC9hzRk8ecX/A8fwlzj/6CK99+UvoTh8gTQnc9xhYi92sGfAO6+fP8f5bb2HcH+BSwrYLyNsNTj73DB0IH958VfheT09wcnaG7bNneOtXfg1PXnsd24cP0Z+cgKcRL7/9bRwvr5BjwvbxQ2zOHqAPToq/nW6Qx1i4PM0ut81FccKjFiRxJQvOEYMt38lppBpVG2qpb3wIiBwbF0z5i52B9aEChahA5Z948gSXKeGvXF7iT7//Pv7NV17B14YB//PVFQDgTz1/jp/b7fC3djssj0CEP/3qq/hL5+f4+jBg6xx+6nOfgyPC/3Fzg7+u97Djta7Dv/HsWfn89WHAv/veewCAf/XJE3zpu0BZ8MObDf59jbb98598grcbXk5AZqZB/wGWUQZEtU8TV0kMjS+QGrvnZ29u8ItKc/Aff/gh/tGTE/yRBw/k/jmDdb10TjIwhONfoueck0rg4q9W+64t3LTpV6rzjDLHfMJq17hFwItRQJHaXBYVKZFjul7KjWoQS7ER1N7Q9F1AAjxCIIyT6o5FrRDpl2TGBUpWWyEc0YJ9yotpPhIg/JL13Rsfhs03qNlUXd+rXhhnK4T5Zfcd922K3/f9p22kc/NnzsIfnsDgKYJ50j73WK/Xc9CzoZdowfWlf53FuJZ/lyyzap97i5zVNrb3NN/WCtw65xCSL+sLgBrgo9iCbZBZhGD0dY6YtWEbAu0abDp5jl1oEeE4gRDAKSOy3Uv8QYIr8IcZQMwJU0qIPCmorRu96vO0OnPpo5RIYo3O5rrowQpYElCoiCzSV+wKX2QVJNLe+QDuJCgvJYkgd1yjZbvgEWMsqfnSfzYn5V7r9VbS6VNW+oY6F4P3oNCh71YSCJEyYoqwAnsGxncdSdRzylo0TDbtvXPw2t7ValWjbZVn2kBMy3ImEEqdd/3dB1+KOBqncMoZtjyWjKUm4h1WBJZzCZBIal9xqtHWtoFfbAQCiBjTJPZBTFEAYedK0VTJCqpZxCZLkr1R14TcFAAk5xTgtUKFWua+9ZMyCm2HR9DoWZFDB6DvugZnA0DSL+zlBrV4obzDpx2/a8BYA02JMDO8zRpQl3LmSBaX4taid683X39vFhS5Bc9+Jm7S4xtfdYEPAeCye2HNMtPRkQEg8gMxgZjwYH2CN197A1/+4pfw6PQBLq52OL98iXc/fBe/+fZv4ua4A22DFBJx5h5VJ3juht9+1+p4cwOCzcGE2vpbL9Tc545+peo6iJFe3aFWKSx3Qe66ZwVebr9RKTBi7b/nXauHZX9R41RCZcoiujDrA7sn33W/e/qBS3fV+1v6/zz2kNtTYGeU+wAoIS+zc+bNkL6ozyZ7xzuONlq3RgFXEKUAmGp58OLaOm48G8P7doFNcc8P+lQwzeZCI9GYtYSX/yjCfPvZBVicn37XbYu1RVjIo/xUjdE2nabtpzr5LcpWFPjyDev4xJTEmb2jOaWZhYplcXBtZ0pZuQvrOFkb2zVB1h6dkyx8RwVQbQyy+sB8Z0r84bAv0fSWZmr9NFsTmGfcW8vI0noal3Fv+75QmnDduSQnjrsPflaQoPYuwJpGJE4JyhpS+pnlc2ZgHAdADVDnnRr0mpJEVJVz09b7juW6xixRAETu1iy4SyO1c9uBSuru/O3ummO35x4W585wBl7OweXn25taRXLvGUOTM5sPtqqwrn+z+9mbkDhoGQ7d6UYKxo2SGvb2Bx8gOIeb58/xhVeeo8+kRWhqPxCANAWw70Dscbg4R799AO8CTh8+xc35JAWZMIG7FbYnZ9gfbqQAUImO4zLnvTqVQifPhfuYEyNHqSrrQ0COjMQi+5yTVLcvaWUKXto7k2RWuKb/JHKPSwTpZhMQlH+USDBSInFQHZxkzTgIcKUd9+orj/H4nRWGwYOdwz4lRBV2FvSlOjo6L6267VJ+yAU43zXjarppIbcN7zfDnAO9hgSkk6klFXBtTre3lJRBrzqotWrnbTL5KLP2Lr3brrfLGUWLv1FTaS3S3r/zDnB1XWXfkOtGxousLaowE9RJY42edE7SF8EoRVWCRofoBtGUJgGqlfKAfCdphKEHc0ZKI3aHAS8ubzBEHT+qjkJ557bL6j9mL1t55+S/OE04v9hhvV7h2bMEogRKjBQz9vuIDz+8wPnLPcYpI7FZKjybzw4yB0k+lHW2jpv1i6zdq85jjMCzVxhwHUK/Q0wTQMZxJ+nEwh4hsj2NU4lwEbBXIq08GJwcHAkH7FIgbOhMB1q/iYw6cHMN37HLZlH8s/s1vSogvqQc9v2qANCcMtI4YhgmPH70COQ9Yh5Azgug5j04OwFTkIVSAAfEccBudy2RSNuNRHd5sVlos0F49Aj9s6fwT59g+/nX0K3W4gj3Hc7eeAO8/gjH3R4P3nhD11eJhqd1Dwp7mP1UHF1JtbKXUbCMxH8ggqU9cCNSFh3F9vPyaM+DOqXqxFZKjfmF5ynhJiU4IrzWdQhEOHEOZ97jb+12+Bs3N/jlwwHfGkf8gZMTAMCvHg54P0b0urZ9cxzxK8cjHui7/byCt79yPAIAfvzkBBvn8CzM3deeCM9DwN+8ucH/dnODgRk/tpECf//nbofLlLB2Dj9xcnKPPr19PPIej/Qe2yYa87t1/GMnJzhPCbuc8bVhwPMQ8AOrFb5/tZKIeQVWrJ8lijVr2n+dAyLIjW1i0YNQz4Ttv4YTtNFXlqFkPkaJlmxlzPRd4/+ZPmHUjd+ZraN27Kpb4exBj5vdAcdBqFksutHaXEk/KxgrDyJVc9w2o7ybfInZvSwqcVYTg2SDznuPeIfCsXWgfL7Hb73vuGUzLezq+67JGlUo9oaAUb7xm2c8nMs2L74XMZBeyTnPMp+qfVnB3QqALd+hXhNcQFYKFLPtZgCuGCC65uQCgsr95C7ctFWCJWLBBizADajgcMoZFCNyotKaCswVeB2NpJV7u1QLAJvfJG2tpy7tatbG2lwhtesYKNGeRASfdbNP39/0ROXh0Ch0LY5s/ZtyQgbDaXBenmEfFQRvx9WRLzvgLb5kbZFgP7bZAknrFz1o+hyWbc6MFCVz1i1kyzknFABEcMyFMqn4DUTwLsC5XHiaSaNKi19Axk8rNpJkYQOM3PDNik2ccpQM6zIGUqirlSmbE+YjWjG5YoSwZVNWmkGhQWr6PCXkrAFc6mvJxqtEMAv3r1EsOaEDJc0o1/4W0Fz5lXVdLUFINm8h65wVc4s5FbvK2uLcEre7ffzuAGMZyoEmYmS7evJZTqiTpv5ioIN9Krfjaljbjv5yobVlvL3uzoOoRJFlNjFxAAAgAElEQVQBKGTQrYNRAT5RSilFeab3Osk1vJnF4Xr1yefw5e//En70Sz8MxIyb60u8/f5b+PW3/l/8xre/huQS+m4F14sBZ/LX+MzN8xeKqyxS7ecq6EvQ2Sa3gTb1CtbFqTFAzHgzJU9U+nrZi/dV+673r5/ktvM7kLXNxlgX4hY8rqZGoxTs/Ul/J7tfHek5Jwsr4wPfOs+UQ23QbfDfQOPqO9Xz2zdSv1UuVbB4Pmb6DLZ+RzGUq76p6rQY162DXu6mRrf3yN2qUBeYA5eBWgmVaG6I622cLo710c2z0bqGn26gLsGddh4v52ydk21zuCpPre7qvaVlcelTM+zMwZq9T6OE7TsCASmCJknDDCHo4n07xVHkq+iA2U1NHooxYdeQ8stoxVhCC0S3d17+C2V+s8rCqKkk2lFF3l3Zta2y7Bgo3F8EOK88SbYj2XYDcy0uBC1uozoyBKnCKX1Se7U12kTvV6Vqx31Kx97fjHYrhpQzY0wDCAJQWnpSKrxA86hceTcFSjIXJ5FNb+haILgbl2qgfddjOI5iNHpCcF6jfxoD3JTFrN3L6APWKIUagfrpURC2ftd7WEGx5cMM/KoUJvPNrPuPOybxsi33OAutYWbn3etEtN3T2O3VceKybnnIzjM7Rr/dwvVr5OOIm4sr3Fxc4uLFS7z8wgWevfKKcMAZNxcRnM/wiZGniOwi+t5jurnEsN+DVms8fuXzGA8HjDcXmIYJhAOevPoEUWU45mOrIgGStLecs9DSEGnBILE38pQxHEasTrfwnWw+TDEijiPW2w04A3EaJWKEujKX+uDgc43yDiHAO4fj4Qjw/8/em8ZqkmTXYedGROa3vK2Wrt43NmfjLCRIjYekNFy00JQIURagDYZIwJAAAxZEGBAMmDAgWIQh65cpy4RAAxJgiYBB/aAIWQsJwqRMU+KQ5gyGnL1n6Z7pZWq6q6qr6m3fkhkR1z/uvRGR33vV09zGDZg5U/3e+5bMyMiIG/eeOPfcjL4LWMx7bNcb0XIOHkMUllnXd3DeY1xvgZzRdx0ySUGwmCKuz2fg+RzrMeKekyJKWdePnBOIHZhUE5esqNGOhrg62j4EtSnqrJMv03Yyci7YqMoyInXQnQuQOZkLqAUikA+qJ2t57FNLcHED4OKYbFpS10HTH52+26z5chg7kiGphP5TnwTWK1Afpte3YEsBK+daf4WnF1HjT86Bss4X50C+Qwg9FkuHoAzpYdggJS1Q5TuEMEPo5jruRgxjxOn5BpuYkIDioE8WqfLjoj9XAh9dPevzAjg5nJ5tcO94hdVmhHcZcMIkWW1GvH7rBJtBNs+osIRz9TOg/FsdY4ZncvOM2N7UFq1WI05WA7YxI5MUR4xp1M2uoJIxthaJQxbHEaMGfgwAKatucy96yDkip7Fey/wCDZ7ELuqE1vNKUBqAHAFKF3xR673JWAEkXLRxqMyhEDos5gswFGD1Hq7r4IMyYFiycBwJG5G8B0Ygb7fY3L+Ho8M99JxxHgec3bkFdppi63xh4vnFAthbIs5mWD7xOOY3bmB9eoo7N29ivlzi2Xe+A2m5RLx7D9fe8Q7cee0m0jggE0C+L3Ikpo1NzMIsyhlW9FTKzEsQaj1QALkGoLDn0PqADJMls7Ru0oDdlXlnvvVuX//y6SmYGXMi/PWrV3HoPW4sl3i86/Dr5+f4mbt3sSDCe+Zz/NiNGwCAn7x1C187O8ODjl84OcHzCsQCwF88OsKNEITd1RxP9z3+qxs38B/Oz/FvTk5wnFIBY3/x5AQvDgOue4/vURD47XD89WvXsM4ZL263+Mj5Of7SlSu44j1OU8JS06WDFiA0ZmgZ0cr4so1sOyz9mpU5PY6twAKpja7+JAAYw9zsTPmndj1rhgNImbATsMneM9/PwDI5vSOHeehx7fAQlAFOwJCygBbaJmmD2aWLPhGBkBu9Fht/kzouTWzRhoJl9nuC0zXSwC8DEvniZS/4fW/GgrXP737/0s83/2XIc00xlXXIe9H1vYzI1MaMtpZfaLOBR0BZw8wvbmtD2LyuXScgaVbQTLCOmtJuOIPTdGwbO/Z50ci8CB7v1mWwOMMubCBra6OEETqUe2KG6nMbIFvjRwMGZUzWjYc2m9YAyMwszOqmP9tNhAnRhaTwZYyjMi+5AHrSWgJR0piBCtgofqBhP3KulBLYahqU56fPJIvcWd2I5aKpClRN6BZsJFIddaY6niwWZAZHxlhSOKn0gem9VtA7CbvXOdFML3Eul76k4MXWeo8c0zQeKbiAnN/3Xgk+CsxqgatmhCKOI2IUENWRU11jgFmlT8hh2Mqmrown8ZuJCB0HpBwwxlHl/8RzCV1A8OKH5ZQ080PvQ/vc+QDndFzEiDgO0kbvAXgkE07X50hE2I7DZL4QULIZpRivnN0kpnwgrauk2rTqVBlb+802Z94eYCxQjGFxDNrgGzp4zHksg0GD2nKSC9xEAAYXVbd38pN1Ul+gEEtxEtldroG+pC8212OenNVYsY37DOYMx4SADlf2DvCn/8T34r3veA+uHh7h7PgUzz//Gfz6b/0HfOKLn8bd4T66K/ugWQfyHr33Jb1FTpabFk4Ne+2t2oFmaIBJtvr0px5WkKOcTQ20pZsC1OhGUfOhakSm77W9yfXjF14vFqBpVrOwTtpFZZJNPq9jB8xFh6492sXUuRpgylf19Qudos4JUfPXRcBwBymqr5V7agLS5sy7gaotBpPgp72Hi5134frtb5snnsPJt30f/ui4/Fi+9DyOPv0RAALGSr/XZ136cqfbzXEgAGT6zAU81Q+V3UDdKbwwDmyc7Jy7MBTqCCESnaWu67AZtqqvVL9b2EwWPWO6byw7dZVfZuy5B3J2ibDc2wNnxnqzwTAMU40ulm9738GruLlohunM1WsF77FYLDCfz3H7jTu1vfq57XajTZb2dH0ojsvZ2baxJwa2Ziz39hBj1KrcQPD2cCrQXC1HfR7Oe3T9DNvtoGlcon9oToR9I/POAwHKtVtbkJI4vSHI36Vw3wOA00kPZ1Eiits8KfgXx4ioldWN6eVK0T+5O9L0wantu8TetgDz1wFzzSmdVLxFa2+qRW65lNaC3fUWADglZMcCQDpx8jIlpOSRgwSUJuZPBCQCVokx5oRxBMgT5s5hjAJu7WEP5HqkFBEcYTl/HM+9+9vx6oufw+m91zEMW9y/dxcHh4fofMBJSuA4wrrHOz8ptlaDMdFWzQDSkDCutkhZZAocSZG41fl5vTnVCO5CLxs4UYKWvusAAjbDgNOzcxzsL9F5B+SI4+NT7O8tkFLC+XoL7z0OD/awHbbYrNeYdTP0XYfzYUBMA0Cy7r/33e/Byzdv4mO/8wkc9gskTtiCRDtWH4Cjap4o+JqLp3cn6aGiH8dg1dFnXJYyJeO/Vqz37Es/sTn7TcXj4oiTV+bAxXXXhuHuEDQ2TmsWLwSz7QmshRqY2aCbbEKyFn8AI41jkasq/aFgQgGXbAwQ4HeYsdaD7cgmckAmdGGO2WwJ52bIvLWGIKeM4ICYRWNxPt9H6OaAA3IK8CFhzCTPKUqxjVIlGxeWmdoCbv7QX9p8HgYDjjHGjO0QMQwRfU9ABlL2YAa2CTIfJ7O69tCl653ZnMYMkJt6ITll3Lp1DzFG3Lh6WF/PGSnaRlcugTyYMaw3IGa4vsOw2QKcQaoZ6FTnV1B+Y75EMEcFG43NImuFsJdYWKMMEOUCFk5G027nGosQeh324JgR+h6zxRIIAaucceOpJ3H45FMI167gxU99CjeefhJhNgc7QooZzgfMQwdKGV/9+O+gO7qCvYeu4+qzz+ChZ5/BS89/Aew7MAvogswIXQd0AZEZB9evY316htNXXsXZF7+EUx/wxHPPwS+W6JYjxpRBDojbNdwwAOMG4XwNryA2uh4xjohxADLDkaQUS8EfX/xJqyYA3WBlljirABc89TbHnKTCBBGSqz7DZKQSXejX//bhh3EnJfwvt2/jv3j5ZfzPTzyB57T4jB3/+dWr+M+OjvBWj5949FH8q+Nj/G937wIA/huVIniu7/GTTzzxls7x3z/6aPn9rbJiv1HHvzo+xs/euwcA+K9VN/a98zn+/uOPa8ZW6zPJ+mWpt238ZUeMUSrcl9k+BeEA29gQjW8AZXPRpCtsw8opS7MAcLC2qC1t4iGr9YLMsIKIBPGV7p2e4t7pMWwjXebn7nrR+haTSgjaB+q3KsBhbb4w1/VbRJaFYvEVgZ2HbddcFDX7xh/Eaoqy+L9Fr7SRFjQAzgpuyfol624bJZqNbUGjC6Qohj7jqban6L7qGs5ZsAI2f0CuIAC/anRnkZQwzVRA5SJ46kNay0KwekDi85XwR8ehxffFXjmnDMQ2K7YBp6mOD9N3lRtBDYMUs7H4IeURnqnqzBIVHVADeVsMg/S+pPZHm2Jf4zOTDmGG9pXqpprP4BxMB7jEYMquNT/LOULmvkiDMEu9gsyaes+GQ2jqvpcsrQvFwpmLX2P9mk2+g8VmBK91g3QsRJUtsdCVSP1y54p+fdZ1nDPv3Bep9nidf3WZ0DHoxGeaSCNmFHmANqtQnoNKQcyMKGLXkgwYT0BHHeazuWjzqtYvAQjOow8dLB4HiX9SGLcm8aD3O4yDFELzsqFug7JIUcQIP26QE2sMLuxc58Umx5SxWq1lPVX2bfCEzgchYsWI9VY2EUOWDdTL4ks73jZgLAAUq87q16tB4GbwkIIFKOibHjT5gSnvTl6RCVNp6A86yuTccZHjGCcaf+bAlAGqC52g+NrgDAT2mPsFHtq/jh/48PfjW9/9Xhws93B+dh8vvvRlfOzjH8VLL7+I89UxfO/guw7wTkBgOz9VALFV2ykheRPQVADWdsAnYgJlwphhN+PdpivJDkvdAQfEzjkideKqGzDZedrRi2z71NrglNVmwQjKomp7qlQWCvu73KsBs87Yb4TMVFNOLbjgNmCpu2TMGpA6hwLYoAnE5IZgl2qdz5Imgzr0rEicAVu2EyKuRtNuNEAG291yZSQYuNLct1O9HxuPDIgWmwVjZE5KO/7aK9IDwaE/OjAJJFarVVnAqOwWk/ZxO3f4ku9fdAWdTsmZC+i7DnvLJW7dvQthbpEujvJpE5+PMRabZxs9sgkFSfdEgPNBU2EZSdMznY1pGJtFt6i4aVsLXFgQdWluorx/cnZW5mgpRAhMwJGUEpLN3UaHGwA4J/jQofMBs64XhiS0MqeeI/gg+oHOI6q+klQuzU28Jw4+Kzs3DaOwdaPuSLfEfXsapoWnuJEjjzhmnKfzyWJYFnIuHvv0sU4O1j4knVbi6ecmKJB+4Et/v3SDql3bADz58GM4PV/jdHWObjFDii3jRVkQ1tYHHeURXwItmaNb7NuD18HCEKj+ejk9NZ9hBVgmgDaxpjUZQ4MwJtFlReexuHKAuNkirbb46q3b+IVf+b/xA9/3YXgFWeC9FoKQtDcCsF6tsFgAXehBPOL+nddw5ZEnceXG4/DB4/jWyxjXZzgnYLHcw6OPPYWv3XwZ0KAwZ0IcE5wLSKkWmCDUlG8iQlL9V3LQqrWDAK3QYARA1/fiMMcRDqw6flpBnoGHrl9BTiOg2u37B0ucn2/gHGE+n6PvPE7uncF3Act+jq7z2A4bdM4J4MyMqFpbjz3yCL7nj383/v1v/D84Ch02cNhkYCBdQQzQ0zWxfVgpJ7jQa/XkpohG87kyX2EOf5XOqB5UDVSEDG+joF3fd3+x0fLgg8s6KF/kyXtc5vyDzjXdCFfdTBb7l5QtJligacT6mqLH5lOpXwjVeW2uJsGS3ZYygdGkCKrsiWVykWME0xcLDuTszqRPQ5hj/+AQ8737qukNpBSRxgjkLKzLMsF2ZBN2/FsJOKylYut98Fgs5jg8OsL52TEYjHHMWK8HKeJRiraIB8MaDDKqLprZznqVei1ZNnayQNghZsYwZsTEIA3yDeAbh4iUovgzjjBsRFpkHEcsFnNwYjiSiueW9kjklD3VVMJWaIlZmErjOKLrpJJ0jHUD4UFjZdfKKVduMnZSyvAghG6G2eER5sEhxYzjm6/h7IUXwF0HxAQ3BzwBjjN42CBuNxgy4+rTTyOSQ2Tg/HyDhx++ATebAy4AoYO/ehWnm9exPNhHmM2xXa3Rz2bIMcKNEbPEZT3HMGK4fx8vffzjOHr4IexdewjLxQzzEHDv3mewzeJAzJZ7iGMEYgZlBuvc7bteAk+uvreTSBLZNQUzYfN62mfOO+QoxeuQxa+3YiuiMZiRsy9AzYWB+nWO3w0gSkT4UwcH+HZluf7Ea6/hjUuKtP1BXe8befz9117Dc7MZ/rtHHsH/+Prr+B8eewy/dHKCN6KBJDzxI+RQv5RUF5EqsxBAA9gZiEFFF7KcT+catLhSIAOgoKw1sa05AxyjzsvqN1iUAucRoPNV1wTyGp8wA1qZHRCgyMCbrIWrcpbCOcU+77iZdUZzlXTSWK+wtppwp/6Q9nvXRoGi3019DyggOO3by3004M3Hz5ux3d7sYAgYNo6mBeuRix/MWMwXNT6nSvgwEEtY002WQa4x5MURY9mR+UIlOss2aJmyAvZrwS3VODUwwHvViS06wq5I+jCyPpKWfS8AlxSfkgw1AwmN9VnXN2p8f0IhWRAB7HToW2yk9SKKfJD68C2gCoZtEvdMgALYBtCDKnaQ2TCCJpaAgLde13LG5QUivXcIpIBbzkhpLH1qsZjhJCBCKkCryT+48llZog1QTerLZGXGW/GxDsGngmvIc8wFjLVnw4wy921z1PxyIsCFAKvBZGn3dZ4DvpNMr5QS4hgxDiNY79eTr3IELNISsZWfUAxDiE4ofo3VIylSB/rMCi7F5q851S726j+4yVxI6o8b3JVRn5+wtKkZR3JIUco6p/q+K/GwkOw1O1TH/2y20Cwh8UedE5IROcKMJYYtDGKg6FkzAO4Ys34+GS9vljH+tgBjjZFkfVYZTTIrHJzsxLQWukmzaDEHAI1DoA8t84TZddHmsl6KmvfqAG8N8qXsDVscAZQdaDNc7LDwczx27RG85+l34QPvfC/2Z0tsV2vcfuMWnn/hebzwyou4d3IfKTNm/QzONwtp6zK2zvekBbTTtjdZHGwh3VlcandPz1+NKpWCB6LRWe5cDRlfGGi7YERpHZvBtvNQuY/ymi20FSOpd9VMZOlthSfJvndJH+y2pZyeqmOyu6rrgm6BqH1393zlnFwDlUtacPnfJcjRAMmeeAFDatsIKJX56uf1apc5C783H+H/R0edN20RKmA6P+riNN2lLLZnEsITZOe5Oj8pJ6nAyYx5L1Uct8MgQKY6FVkHpCeHbj6H9wHn5+ewZ5xTksrWcAWAZxY5lMy2qDmQspCkvZV9FrxHcLLwjHF8sANp95qN44/LxxYgjle++D5BFp3MCTHKAu6cK2BV+Zyri6LJREyDj2Ye6mI3jiNStmIO9KZjnEiKZHEW4GE08seF+8B0Pv8u5s0EfK0vAgAq+67KxFjDLCBqj+04IOpmgHMOqbBDdm2+gCfZwKjfRTDQBlQPuo/J66jWWU4AcUoKoG9NE9tLIIQCbLOkz0JSegz0dCFgfriPgQlps8Xdu/fwmee/AALh0evX8dwTTyAyoSPR/ZVqwxHb7QYhZwQQfB6xOT8BJ0ktni0PsD4/BW/WWmghYLHYw3a7UlAPGKNIA3CWlMxdMJxAhX0HDUw6LXwl64CkYq9XGy0sBHQqfeAcwXkpXBXHEd5BNxoZ2+0gxS30ua9WW9moCFJ8JUUBOrjkhwNMDglAFzyODg7wvnd8M1597RZOtgMcAzFnRFKomh3A6hY3w4QhjODg/cSRhdWWLxp9FqzpY7PNHD0LF3dmGgwbMNkMojq2L4ygdg21hjYB26Xr9WX+TN1M5knVT5R74jwtnKNuROtJXbAzNh7aS5UAL3NlqRSfhEpAp3JiwiRh2eR1Nv5ZVgIiQuh67B8cYjabg0dlxfgAdqNqforsCufKAi13xs18s0ZWhwqcgdm8x2K5wGy+wOnpsfaxgwEuRdvZfB/TxG2DYZqeXv60TchdgoO+wgraZHv2XN5jbZtsHLBK98icHsYRcYjoO0KnlZnL7emjMH03C3ig300pliIzRhyo7ebp8AF2TW3jV1P5G0megXcBe0dXgTRIinjOiPdP0F2/ppCwgg85Yzi+DxoGuHEEOykmwuRAKeH8jbtIx6dYL+7BHx3h+jPPYHl0BfPrD2HIGWdv3MUjTzyB7RiBlIvf54iAnJC3G4wbxjCfyex0wGJvD6NziEQILmC2XGK9Hcr3iVEKVF4kQ2gA7pwqQGQz28g7Syk5Bxd0nO+kNgMA5wQVA57066+dnWGVM2ZE+OGjI1zxHs9vNvhIU7DrE+s19r3Hn9EiVR9aLhGZ8Rvn5/j542O8rlrxW2b83P37F8bc9vcAfv3K6Snuxoilc/ihw8O3DM6+Mgz4TW27AaTrnPFz9+8DEEv6AwcH+D9PT/FvTk7w5WHAQ97jTx0coCPCH9/bgwPw0dUK//L+fdxJCc/1PT6sUgnvXyzwbN/jmpJ8fme9xq0YC+GmBR8KUGJTuJgvs6/Tv+vrF/urxhzllfLP2OU2Ii4D9+wrdfYYkCSvOOeLHJxJuRlTGywklAKuZlKfpz11SyCq9lZienM764ZUbe2lFgolatLiR/CuDTG/4Ue77DGjgHgA9FmLz9huogK4MA9zZhib2eJys6MppQKO2XeBVkZA09apsl8LWEcVyO80+82KaxX3ztY/MsCsxhxya+Y7qByQ+g0iX2P60xqg7ITVdXq2VtridflbfB9o/GQM2N2O1fEGibOE4b1DyGvluQr7U26Sm/PYDMGOTANp39vSKsWxXGmx/SjPzhGkkDzEXyk6r2qfNZazDQjHlZjT9ooxn9v37Jm5ci0HeIADI7px2o7GV9sFxrU1kl5P1V+0zWfBqCQjisEgVikD9QdqoXsjCWhPkGzWmGslj7BuMACAs/HPEj9QFrBayKv2gHMpgihs3so6ZWaMugE8GaPWHgIoW20BLRqotkTGcILVDUywDWElXevzsjlmxQztBpkbYgrVugMMVOD5AcfbAowFhJkgO+NcbtIGN3lXWCZAdaSlczCdwWXyoQQGlnLIZkRAxblz+rmyOJkTqP81rRBABj/vTAxurDkD8OqAQida52Z4+OA63v3Uc/jg+78NzzzyOIbtBnffeAMvvfwyPv38p/HqnZtYDSModJj1M7BVMmzS/i4N+tXYWVBQJ5a8d+G58/SPFljcCc31vNWQiE2qgw7tYtn0Ce0MOHut9tdF54BgaZDKMKk3Uc5fHAuU7gaa7+XGO7Eg+0HssCbe0Mlquji1KEm1odZuWUDa89i12vtAKXpSdwibD7Q9bL/UhaosNFQWsWZAiqHWMVoAH4IWUWr7/MJtv7Xj5ATYbuVC169fjGDu3QPa1Ihr12SH+Q/iiFHODwAHB0BbCff4GBiG+veVK0DX1b/v3m0K9kDa7hwwjoA6zQCA2Qw4rKmUO90GAyTMgJdna+NKmVrmqF6++SEjNNvT44ysGjmdd1jOZwKk5Yg4CvNEfDBpv/ce89kcs1mP1eqsAV4ZQ0oAdcKycoRONdyGyGDWdB3dJW7nGXOGdx1mXQ/nHWKKF+ag9AeVW6FmPlWmMMqCCUhQzFRlQVr74L1DTgnDsNW1rj03lSDaHFDnfZmzlRnPaIu5MFh3d5teZxRHaXIvAECM5WyGzWaDMeeSsja1IPVcD2aymnOGyeR682nGGhR7OAKGccfmkaWP1uvcPz/DJo6NxEVtE+2MUyKxRom5sQVNKqHajWriLwZUu8zYC2PC1uOp0TVzNLVvLLayFnYx0CTpUmgaZLIId3sL8Bgx5oQ4bPCJzzwPZMY3P/s0rh4doD88Qk8AqZNIjpBVooOIMMMe1id3AZbU3L2j69hsR8RhwJrPwcyYL5ayGRIjco5IY8bcBw1aTO9ppw8gDjk5cb5CHzCOUZwpJ6DReU5FyF8KzUX0fadafMDJ6Rn2ljNlFERsNyMO95dgyGbCaj3i6pUDeC9Mkpgy5n2PPA4SgEF8lZTF5ngCvvU970LebhHuHcMNIzZDQnIyV7IGEBfkeRhaZKrTlDPSZ0owIHayzsPGWlOAI9dxM+2nOhovjqXWL7G/LzojxmLYPffk/I3fsHtcmPN6/9lAP5qybUuqtY1nZl07uRnUTRuUoS9jQlMwWx+IJVjyXu6lC4QUHZhy9V3JnHdhhR3s7WNvuURabZCTZgYFr0BsBqWMOEL0zDODNI1SgHq9rrXdmq1t2ttfYv9gT7K3WCsvB0LfOcxmM2zHUQOnGqQUn5fbedz0kz0r/VksMaP4XsEHdL4DskPOaLLHqm6l+YiZRd/NeamAvB228L5HTxL45SyBkNkvZkZKU5/bGDyVxTOx4peOFYed8WILvT5MDypFsFwIOLh6Hcd3b0v16ZzRjREBBJdRKmPzGJG2K/hxgB8S1uMG1M+EWQ/g+OwW8ht3sWYg5IyrTz6B/atXMSTG6s4bOH/9NtyNG0jrDfIwgoiQiZDHETyOoJQwm/XIwxabMwY8IV67huw92HtQ16NfLHBycgan/UxAef52f1MCgQbRmUs/C595OleIRGe9MrF8YRvJ8/RgDXJnRHhcWbOfXa8BAM/0PX706lUQET66WuG3zs/LZ742jvjo+XkBYz+8v4+r3uPF7Ra/enoKAspn//3p6YVneegcDp3DDf3Mo12Hg5RwXVNQH+s6jDnjalPg66OrFb6y3eJqCPihxgf8esfrMeJXtA19c5/22g8fHeH79vfxmfUaH1Hd2/cuFviRa9cAAH/y4ABH3uOlYcD/dXqKDgI+/+WrVwGgyDV8bRzxeAj4DT3HN6u0g3eNHn5jY+VRcrF5Nj/bYV2iqQaomcZw1aVp/QQ7p2WBtXPP2ITC4m/eVzetUMUEElwAACAASURBVGNaxE7/Oeh6wmofFbiQtdY2xFo/hOqobOZ59W2m61HdzDG/ioodLpUbKIC60GwkGJB72VyZHg/ayP5dHzW8LL97LfoJ7b+W2LQLwJrNMxtoJ7P13+lnyvvmvpo/6urmrHdBbWy6wKi2owX9hJxmWQjV7/Supr8bHgFoxknWAsSZkfS7Dr767USqJ9GMteLT23UIYC2eVNbkOl4EBFOZG4amrpteqc2fBO+n4xngRkPdHrvMAZEPAKYSltaWKp8g7dVNzWzXqlltbOOQGEzCFDdNbkDxKee1t2QMu+J7qK+vxaHsOaWU4NTeGc7l9D7sXnLOUrjYOWWrK/ZB1R5UkohlH6oNsHFm48Y5UNC+zBlwtfhXxX0CQhBWq+n7Srum4zizFkCjCsYThSKrIp8bkXMqMhmOuNCMbFO8xDQsWtq28ltxLjR2gkV9o8g0mEzLGIXQ5DRrqMSpzMgpYshjkXwJQeJrRN0cg1i1QsZwJH4uBYlcmZFTM9YuiVPb420DxnrmIgPiASlWYVolWYrMODX2LeiorjSA1lhCXlV9VzMsLQXbjFQmc9QMXGxMAJvPZoOoOoW2Y5JKsEqSisuaNgICccC1+TX86e/+PnzgXe/G0489gdXZKe7fu48XX3wRn/jsp/Cxj/02VjQi7M/RLXu4uUcODftDB44sgI0vbh1H0u6UjB4u7a47WGYsal9bUNLGYK0xKmbKJhkquOTgmiBclzGquou1WXXhmCzm1sNcnUegNVz6szmddq+0Q1f9nDISMoiBWIyBpIfbwGD1TNq22HO2QmxUnBpzHprAkahWiy+kvosCGNOFmyd/Tnd426DBFiI5o+meyL1zvX+CsmSsU2rbzLhS6V+y/8OmwKXI7C7Iase/+3fAxz8uQOdP/MQU8ASAf/7PAdW0AgD8+I8L8Pn7Oax9t24B//Afyu9/5a8AH/pQff/nfx747Gfrd/723waefrr+/U//KXD7dv377/5dAXRfeQX46Z+ur3/gA8CP/ujFJpR2VGNsC5O9L0w43aks4KRKXezoJNVRbd9nxBTx3NNP4/T4GKvVuTB7HCG1X9V5tNmssVqd26DXQJaUPZsx8wGPHh3i/U89idOzY3zq5VdxvB2AfgaAwNEExCsTdRgHLRLgyiLWAn0FZCXZ2U3RxNSplaFsLKRpL0+sEequIQHOIeWE1XaNzbBFF0LRCvIhIMWEiASOCUm1deYLAeG3240+AyoXLHiELZoF0IT+rp1poukkKeO3b99C2ozIuplSCpXVqEU/XyfPBaAS07bUeVXv3XrC5nvU6uremWwNTb9h64geqUm1jTGh67qJkwxUB8k2AeumImG+mGMYhhKUjONYgNTyzIGJrW7TeaqDTSXgao+WOWhrShkPzJqG1iGmhGEchE2oa1JNVmTkmJA5IfUePOuAIQKjOHBfefUm7ty9ix/5iz+M83FEAKF3JICPjqfNZoXIhNnyCM4FdIs9HF59Gsuj67j1lS9g2JxhWJ/A+w5Xr93AdrPC+dkJmIHlYontZoOUEnwAONdq1WMc4WE76Jrepc7qrO/RdwH37t0XlvmsKyyLrpeUx3EcsN0OuH71KrbbNbabASlmXH/oKs7OzhC1+MFjj1zFer3CZpT5ePXKIW7fuws4KbQVvMPJ8RkQAsgHBOeRhhHf8YH349XXXsPnXngRMScpKmbBCBhdcBfW4eCDFEhodGb1gcn/aWfj1Yb2znrc/tHajvZcIlJqa7esVTYnyk+bciWws6I0Exel6FpONsUAgOr6Wvw8PbyyOMQfqsW8lMNQJGiIGlYWs5Iqp+u2zeIa7OWmeIa8EWNE3zkQJTjHmM86nI9J09Iy2DFckCIgYxqRM2PeBzz92A3cuX8fJ6s11uOIUaBA6S1m9DwTNkyMyMMIxIz1al37S+d3GxDP5wHPPPMYHr5xFavTU3hH6OczONdh1jt807NP4UsvfkXSDImqxuoFv7cNcuraaF0zLbkjH3jo2jU89sjD6LsZMov+GnPGZrPCarVC3/cVVMoZi/kM3nnklEDzOQ7390TaC8A4SDEwThBwtDTEfP467hgSIwjjVlPqnTCUJxhtO3gvHA15QHQj0HUdHr5+A1/70gtId+5jTsACjLgZgLM14DsESmDncO2Zb0K8fw/HX/4y4qs3MZytRXoBhL7rcOgA/tprOL11C3e/8EVQ5zGstkjbEX1MeCMnDGcrYL3GnBljjLj94ovYxoQwm+OJ930LuuVM00IBvxkQUsJif4lutgQ5j83pOfbnczivgXxwkFooCuC1HcGoTGXtV+aMmM3D1+ecRdaitQUTqS+Cvp/xgcUC/2vrj+0cP3h4iB/8OgDo+77OOd7s+J92dGN/6sknL3zmxx955Pd07g8ul/jgW2jXm7X9O5bLr3tvj3Xdhc8kAN4HWY8USKsbGzUiqwBWY8drEFfOZ+eQt1OJn/Xdxh8kAY5sqjWb7aRpxxmMYbPBOI7qZzAqK0++V4qNWZsMmGBjiTUxGmw9sKbb9ywNGqUNJVKy+zXbIC/VKu/1zmByV4khBBJPgCNQKqe61EK0vlrbj/XlB9mV38WhC409H+9lA1VIG5IFkJJk5Vz0SStOwlApiCAFwExWxOJ1ZkYcY5GLEJmDcEGCxM5ldnW9Xk30ZwnAsLVUc0Jykrm0u6HaYhhobBGRPIdomuIsBY7K+NaxIIexhet9yslFe9tTKPEAO8YQI2KMSCkXAFPYvw7OAzEOUhyrwXLKtZr5Y88hZ1Z919yA3wIiOtM3hY1DNOdr/BJXP8PaxwaiyzM3hrIvz8DWdoIAoVZ0bDJmytDh0tmWAS4bJAxgQK25IZmX0KwtA+yl7VSKhkmRWl3ho2RAyH1pnQ1N07cGEERS0wgiEu/sFnHj4mMFN5MdTRgmg9I/thnQhSCkIbVxNgYA4VmRa8YPFKzWcziVN2iPIr9hPqlSmQMsTuZSKNHYrHEkxIEbKTwZR+REZkJkfCTzFQoY++DBui/RjtkYYwHRH3S8bcDYPHG4AKjJlX+ucRipGNwKVMj3UqoFvhwAKlqkgliXPUQiBHJILMwDZkbUoKAG+q4Ocpu0ENSfQGWrvaSMG2jJGS47LMMCj157CH/5P/1LeP8734X9+QLbzQYvv/wSfvO3fhOf+vzn8KWXv4KT9Qr+sIebB7h5BxdI2l0WwgoaVDARRUgbVsBA35FdMZsIjfGyRY5Q6d12ZnW2L2OSll3I5knZd8vZS1DeLIzNItUyDNulywKLSQZv+U/VsRI2R2nNxMlmHQttYRkxeq0m1nSiExE4jpKapc8QyAWgtfsDANagsBWwb49dNpAJVbb7ena2SXzAmPY5N0/LfiELBuWPdt9LDFtuwqj2i821VivgH/2jasmuXgX+1t+65E4A/IW/APzZPyuDLlxiGv7G3wA+8hHgV37l8u//Xo6f/mlhxF5mpGIEfvIn5f1v+Rbgh35I/v5n/wz4ru8Cvvu7gZ/6KWH0fu/3Au9+N/BP/onc75//88DRkVjuv/N3gH/9r+WcwyDn+JEfKU5QqRBdfTwA7bi19A+UKsZptAX3IgPdRrlrz+YIr9y8WRdanZ4OlckKAJtR9bnU8fVe0iEzC2vKGP7DMOD0/n08eu0IL85mOB0j4sjwakdFrL2TRd871cSL8BCnh+NQNIYk9UIyD5xzWCyXWK9WJRW73hOV2+n6XgtFmCanfJ+s30azmWrByav+rD5aS6t0pksVSuEJcoSu68XpG0bdgGGwIj2y/jr084CUWoZAle8A5LG++PKrJbUGiCjF+9DYLHuSCmpy4wCWEXHJM961ljVutXfqz8k8bcHwHaNi9o0ZsmvbfNbADO89uq7HOA5lhzcBOF2dN42ubfYkGlEp5yI/MXWUps4jl86pvVN0VS04UueeM6PvPLp5DzAwxhFbBWLbG8okO+8pJoybra5fDD/v0YUeqzvHUiiECNthxP/+L/8P/OD3fy+uHx4hZQ8MI+bBoQ8eBMZ2cwoXArp+iThusTo5wdG1h7B5+Bxn925jc3aM7foM2Qk7dLZ/gO3dN3D/3r3ypJiFvRtTKvY3BGGoGGC3WB5gu91gHLYY1uc43FtiMwyIUZhse8s9jHEEOCMEh8V8H/fv30cXvAC4y4CT4xO4ELDc69F3DsfHx3DOo+t7kAO+evM2Zot5KdBxsj7HfDZHZAkEYs5YzBcY44gbD13H/t4+PvaJ30Fcb3EWMwZmZPIY0o4WZAZC16HruxIsTMcyT8aXOaycLfhgdF3QOScFVKlhX9s6TZANjqSFg2bz+c761/wsg+uipM8EDEoRCahp6PWj5chtVfgy5uU+S9BkmzZgZCSVcnCVZWGNuiB5YN1VnR/pF2Fi+9DDd15YrAqIxCTgfd/PpZ/Uzs9nMwUtBjgA14+OcLC/xBgjhhgxpgQgIWUBNsgH9LpZlcaI/f0jBD/Der3C+eoUm/Nz+RwJU3tvOcfBwQwHewt4aOVnDJjPj+BchzFEPP30DRwdzHHnjfu4e/8E4zBqf6kmN3PR7C6BJ3i6KdkuAUTo+g5PPHID168d4fBgASYN9phLNWIiwjBs4UiKml25ciRs9xjBKWGmWW/EBPIE34kF9gjISdINzctmMIhY9Pl8gKegzynWB8YA2Cn7vT5Lt2Nns/7zrC6bA1xiYEjILmE2C3j8qaexev018PkZOueAu/dx/5OfBOY9wmKObjHDsD1D4Iw9T5AtJycVpEEIOnx0gmC23iKdJfQxq2wLMH7tdWFEMwvjFsDmc18EOw/nAl6/cx/9osP+4T72DpaYL5fYS4y42APPFtjGiLg+A817YXLZ/XYETiygdnW/q2Z6A2Bxinjm134DX/nB78fZUwJsBqpMNxsb7QrHzOobX+YV/9HxB3XEJBkQUDDDoc2aq3UHAFhoO5H0aJ+OgS+S4Wk2tY0TayyTjdFukYRho5A1cxxj0bLU8pdAVr1E/WBm1am2LM8dW9JmWe2uE+V+rHq9vpFb/8bi4tJu9Tabttr3HLEUo8uA6zxc8MhaIGoSd10Mgd/0+H2xZUm+F2PC+XqFw9m++uMZ281GMhs6AxsZmSM4O6iXD+8k4wHmA6pvF9Vvp8zwoRNQ3DY1g9SmiBDwNJ1ndDukm8yNpJQj2agZqnarFDFXQBJWjItRGYt2Hj2HDxK9GmCn61bLvhWwL5VU+aCENJGiocmmLOv6To6QorVTCmnZea2mDAiyjqZU+6XBAhxRKQSVckSKqdHClTG2H7rS1sRSHDQmkxkS+alWBirnLAW4ymazK1IPzjSNQMhJ9NRjGpFTRtdVQJocYRxGDMOA7bCVvnayERJ8BW1zSg1ITUjN/Rm4n5MwQFNMsikquzvF32z/CSbjFND05X7sCsZy9vo+IMQR29xmZTgb+9o7r5sIMkYyM4ZxLPEmQbKwjEhARIip2ip5ThJvorQzgRPDQ0mCOU8AYKfFtGptCJOKcpVgQmI7Q3BgLtRdBB+KDfEzB2g2vA1qr/5oT1SKjKWooLGS+nzXwWwo+1xwwpypkgAuOd42YGyLaNgOii39ZnKrTZ6CXSZAzLpitLtllx5sYbgZjupg1Elvu3jTdPM2jgFUu0//Js7oUsBDRw/j2ceewnd8y/vx7me/GQEOJ8fHuHv3Dj7xmU/ik5//NF5+7SZON2foFgGLoz2ExQzUeS3Q1DQ1W9fQpI/M0KC8RQ2bvmpFVobXzkrDpUuBnf4yZ9vAAsO9E1c9yuqUozgHBAFNJykt7UGE3aHYbOpMO1YngPkMly523C7JBd+aBHW7912Yzc1HDEBq3ZIiKITKUt71WVr2nIV2xQXinX4CCoBeAdi2HfVc2e676UswI1PDmGa7qp1T/r7QTcw1/f8d7wD+2B+bvn/vHvBrvzZ9zTkBPi3dcBiAX/xF+b1lxv5BHB/6ELBeC6D6q7968f379wWU7ToBV4mAszP5Ts5VhmCxEDYsUOUWALn/X/914M4d+e4v/RLw4Q8DR0fgu2eT3VZboFvWFu8OlKyFnzKj6zow5wLM2DksNWRUhpSNjlR2PDHxOttZwWDReXRSGd20ZsElex0xZRxvt3jxzl3cWZ/jPCaQk0XEO1cK2aRU04nET9KUZo4Tjahi63QMbzYbxCSJi6Z9aB6uLfLmbACWGsT1c2KUJ6CN7bxbVVJS1pNj2xUXlrEwO9s5k0ogkpFBGajaUHVusy7K1rdlJjJrpVi1+JeYQbNhQOPsN58hva8yx3Jl8k9tHE+ea7UzF+d90TdC+/VqvXLW75fXUXaRZbc+luds701tZMNsMdtWQO164TaYqAFctYQ1zVG1HsWtlv0a50T3lIA4jAIeZkY0O1duS/orq0OYUkLfhcK2IBYWbjrfgIcRY4wYt1uMOWHUDSdmBiVlGDvRkIrbDRx5MAhjyuhnHfaProOcx5gyhuEM2G4AnsGHDovlPjbrs5pe2TCOZcOP0FZ3BcumB2cWJz8EcTyJ4EKn4z6X9RKcsd1u0XdBq7MytsMWs1kv62lO2GxG1dqisrPfdzPkxMhZNL3mXY9RU9Q9EVwIGNTGSGGegHc9+yxWX/4yaLPFKgMrTnBZx6oeiTNcELZti8VODqoM6KLxp+OwxEploVd7oXOBgZKGXgJgDVZMT8wCjzbQb046XVub4et1XEwGUhlP9uE8GfNW/ERS25I+Vb0nAFm0jEDwIKpzVUyJSRBMz2c+hvlKYjdVYkULrUjmmwNnJ9dICUTGoJWAyTsCdR2YGcvFEvOcNQCUYh9MGSkLqyf0PXKs89v7XioFuznmHRCXPUDSR45EL60PQOcY3gH9rENKhC5U1o2nAM8LzGYe164dYhwjXNej6xbwXio5b7drbDYrbLcbDBstaKnPXJ5z3ZB0zmGxWODoYA+zvkPfBXTBg7P0m2U1CPNKJcaIMJ/NQZyQxlHIEMgYNhtw7uD1szlGICfRi7OADfUcprHnXIBzATFu4JzZVGO6TgdNzcJqx1Dx8ArTJw4DOCV0szmOrl5FPD/FetggpYjADGw24HGA22zgVx3yvAPNOvTMWOdcohZXIhiAVDqIMsMlmdeOBToqRefQ+AFRmNbOMcKaEHJE6ANC50Wv0BHcfI7sA7brDbIVWFJbTbTjU7TLAk19adYAmcyf0p5zMIABJQCo65kCL02Q+kfHH84hm60odkxAIQVMFDQytpXN0xrjGIu5+qbOOczn81JER45qhHdjI0BsADU+lXyDdEPEAb6TOW4AlvmMrEV19PNwep4mxGvXASInRfHsWiy2tratvTo1Clbmr7gy/1q/V7sMYvtVfiN4YfhRlqJ3ub278vFp99h7bay8G+O+laNJe2cjF7D6dZrGn3NGFzoF86rfbWxPa2VLmJACfeq/sICQMUnqewtAWr0FY6nuxjkMnlwvdKH41AKJKJBm8YAWWPKOauF18yMI5X3zzx1JZXphfdc2jM2aBxIg2DXtKBvGRMXvGBEVQ9AYy0BSNhkGrwAaiv9SxpYCh8E5eCJk78BeC3lad2jNFonpPHoCovcCxlqMqOPA/vVdh7ADdBoQ64h03JHoFnNAjB5xHGWdY5Rn4xsQ164hLFkP77zcQgFRW98NBYh1zoEDo+MOcYyVjOFIgPxmTO8yN4XpSkCo7lmMEakpLihEmlr0NUbbyNdMUlDRd7fn6JzDMA7qIwioK8U/d4iGgLK3CVw+r9GJsrZrtpIDnK5fieC9xOmlaJkXf7RaE9l0iLGOn5qhpViOrW8TPItK/FbsqtNsOtI4DPIVWTpVJqJ3ZRPjQcfbD4zVYLkaw9ZI1Bs0V0q7CeY1l0kxORHqpyd/q4FB1VurtO3pg6h4BKGys1AmOTEQ4PDw3jW866l34n3vei++81u/HQezBU7uv4Hbt1/HS6+8hE9+9tP48ldfwenmDBwYs8MZ5vtzUB9ESH+M9WKAOFdonCEdssUgN/FKWQPfooNUGbVN/09PW9owjZpaR48nz+oykMIm7S5gUP+uQEcrYg6gMAvqukig6WOs157cV3MvpSvboFPvhKfv0+TuzbHfdVAaZ765t/b14h+0n2e+0Ad2bpo4ySyLgOEgO9ecHpe379LjySeBD35w+towAC+/LL/fuSNM2hCEIeu9AJ9f/SrwH/8j8OijwGZz8bzDAHzta/L79evA/v5baIwe1p6bNy8HY38/x2wGPPWUtF+1zHDzprBmnQPffbXIQ7SL6UUglmHrN0MXcZDqonJhG7TjwJEDOBY7ddlGBNAMk2bYEKBABmBp/4Ek3ZVZdmdXQ8R2GPHa2SnId1I0BCKszgxpF4sjhqw6gTZWMk/mCKsjaKlp22EAuFbdrOAhF4duu92Wv80JMLtZTWadBMGKNyCWnXdilQzIgAjaM1IaJRg0sKed22r/Zv0Mfd9jGDfVRJuj1doXPQkVdFeDE7WnAs5O56PFBzqby/pidoioZexTXXWbM9RgY2pvzGHk5r3d9c3GggXJtmaRPSgnlYvHqMz4iW1Wm6a21Jwa088qIJaNY7R2y9pEjdHVC7OtkgBD9K28I/TOow8eMSYMY0Rk0+m0a0BYcOogm6PtvIfvOtGO1HHuaR+blDGkhDSIPMHd42N0fYd91X71DnBJmtd7hzgOcD5ISrcbMWz2sHd0DcsDh2Eccf/WBnFUBiAc+vkCw1bSiK1QVjsWbIwXfjUD4zCg6wKCBg7juBI2hCPAmWyOPveckaIyQwkK1kXM5jNx/EZx/mYzYaKIQw90XadsAZm/fR+Q8qh69hC5jxjhtJiYcw5PPP4YXnj1Fay3G0RkDPoQaTKWGd4H+ODrelzWzosLhq1R3G7w6fiyr2eum0LNiBO7oD5UihHZJd1k6dD6Z+1kkbXwQjPkHr0HpWo/CtN02uLJfcQk2sDG7GXY5oPMWJG7EiDWcZhMXats3J6ajUnerAdFOgUi5ZJzRoyiJ59ZvM6UBEzzXoTKUhxLWm7OGbP5ogQ/zBmcAjJlBZEz+vkcm9VKnqcjDNsRjiO8J/SLGfI8wAdXUhLTOILTAGLRFw7BIzjJJ3PI8CRCp4t5wHwxA+AwxAzfzdDP9tB1CzgfsNmcY70+w2Z9jvXKNi2o2AZHDiqtBnIO85nIDZhf471Tm6X65+TQdx0yC7srOIe+C4KrxoSEGlCB6nXSGIEUYbRO8fnMU5VivswS5DvXgSgp861h2+wcdQ1oRo75mCjwDtI4IA6McNZjfvUQs4MDjNsN4ukJ5mB0+sxcTAg5gU9Owcs5jDFW5mCrM0hmRs0Om0XSGhOThlqml0i39WD0zAg5K1CVpRp83yMnYLs61802zbBpg0S0Elmozkb5fGUITzaK9aMllZxQzp31Hqc6in90/GEdzCj+BoEQggGfln59eXX3i+epzyt4j+RUn9nOTAb82jiofoHNj9a/KkBD8ABjcq56PS5ZXQBq3RZu5l6Zk7bBZ0Fs4/uZ783mv1U/qXhU7ZpkaxwLkE2AklsyQArCei9SLar1CC0qZHrUsGtgeuqv17dyT3Tp6w881J6a9rvdPJleUtNRu7FmNB1nfW+iG8qaHm2xBUkxLlkXhUnovQG00419AVldyWiw62cthluxFB0d+vmaHt6s805Axty+U+wkyuMrGAbMitcAWDb5dHOO2s/bZ/jCPTjn0PkA8/sreCqfSeqvCogt53XOSWp+g2sISNkQKkhJLzCmaINZKCBu8g9lbur1sz4rY42CCPAaCyWN09T3AKtcgp4LrGuDFkxz6hNJVlKTxVjW41r8jYgw+hFpjBIPuFqYrR1PSUFmk+R0oFIzJKsE50gWV+l9NHVjnPOICtbas9LAucy1ruswxm2dX2QfUSKK9pXIBYj9SFbwVO8HVIk98iy56tjpSRMLMYSzjDXpc1cA05RkA4DVjjiXp3KROgbM5th1a9BpPqxtmMjftoFt66z9b5rGcPF424Cx0x25HZ5hE0CDpGhG1RSzfwrQqiHxLpQA1NLZLMC1awC20CnzKuU6wZsgtTLmMkyk1wwcJ500FHA428f3fuuH8F3f+T146omnMe97vPbKS7h79zY+/8XP46O//TH89mc+iXXcws0c5nszzK/vISujwRw2ad1lgUf9jUrfQFPuWmAV5b1i1PXdAsIoyDI9M+ruVaM9Mr2+gqo2YhuKPPPl7IPyDHcA2hakKItx+zn9vvcBZTfLFhZr0Q6Q0hrjelRjMwFsymUuD0zrOWpQ+PUOBkuymvZvUotuZ6isjVqFr1D8ue3jSRNrH6F2ebPcXbgP00j6uscjjwA/9mPy+8/+rGjGtsfnPw/8i38hv/+1vwa88ALwb//t9DO3bwP/+B/L73/1r14EfP+/Op54QvRlmYGf+RmZ06YZWxZbCzgZiSMS0c64rIfFH9bL2VieanMWiwXGMWIYBtG8Rt20cVzH0O48sBlth6SvjrrgEfaWC4QQcHx6Ilo3Og0ilKmYhK0HD0TV5Yq6QAcfmjZnEKkDoCCkpaG2t2pOsfOuFCPZnq/AkLnY973Oo1p1t63qWYcxw3SOA2QHWliqjGEcRJMpCbM4JSsMJxaquBbFkwbAspv+yCOP4drVa/jUp39bNXepfLO1GfP5HOv1CqbtaWn6QSt3W3BvDMXJc2nWngKIcuMIAxNnEqS+wCVmwhbzdjc18y7gf9l1bVGvI4QUuLCdN7ZKpcU0stqHqgGYuaaVMaME1MziPAlwJUCB9bexgcumE2p6ZACw33VwTmQJTtcbJHW2iLg4kjlGSenajvDzGbrZrKQBAYLJJM7CFOsB2p9LldMhghPj137jY/jA+96Nb3vfexCZ4LKD6TQ7ZgRK2GzO4EOP+fIAy1mH1ekp+uUSTz33LgGX7t1CGkVyw/t9hNAhMuu6Pd0kZM4Yhihpe+rohs5juVwgxojtZovQdXDeY4wD0iAMX+gOu3MO+3t7GNOA7XZE8B77+3tYbdfIiRGCx3zeY9gOIEeqHlNK6wAAIABJREFUpelxfr4GkcdiMQc5YDNssZj1cGPENkYMY8ThwQFW20FlOxgHB0ukGBHXG+SYsVgsMbIx82weC6vF+4BqX8zfkdFvwZyb2CR74oSMLLarvM1arGVqMMzv8N4jxRHjEAFy2NvrYBE9s4yPt7Qu2dhHnTP1b7OZ02MctxIIMBdGfRbxzEYOhgH2SgIUr0mygJtiJ9pDOUWMwxYxDohpFGBfQVvOCTEZ09skrqQieIqyYdH7ACSRH9iMI2IcASbMuq5EIFLYRNZrD0JwAfMwh5tZ0EY4GU8ARAQv4387ZqQ4AKQlL6xfIIyhqFI3aRyRxyhyJwB8NxNgHgTihHFcYT2sca6wIHMEIyH4hL2lB1g2GYP3YrfVJliV7hTPQdQjBBnHIqFS0/6Cd+DlEoBsMCzmkkmyPs3YbAZsNxswMhbLhbBSNCjKKSIOG+Qc4QgI3VzWAHYqaxXBLAxoB7H1Kcl4I/13wXveHTJt5G/vy4RA3K5xvDnH9YMFjq5fRxcC7qxXSKNkbTjIfOl9AGLGcC4a1MLkbew2AOfNF0RhsDLEOmfOtZq4zjlpSxaf3hAVOAUjGLkL6JYH2GaHcbXC5v499F0AEyvLOsOxR7D1WDV17Vy7M48BKRq20z0MIOaapZeRNY1YalF47ye1DS56MdNzvZ2Olh31dmtbe2S1EcbYckTY29tDHEcMqtUKSIE7wOJU9S8KY6z+bZ85P1+J7nkpYmUgQhbBj8Y3dioZ5X0QvzYqwSCNYJbCbzDwAdWfGUdhwxmQL4OjAj8W67X+T2HhN36UFZC0v4dhQC1AJTEWNb5JcZaaES1mnWWjmBQcdGQ1LOGDpvtDslVWZ+vJczCcwfrp6x1vGYTV8xnLOaWMrmjGevggLEjpG5EgFB9S2pN4yowNwYNzQgiy5s+6Dt2YNQ1ffyYF8lU3NDjxhSuL0/wD6DggDENs9FxRQEDZoBF7ZTYvxqkUgHwnNTKCYjNyTBhHY2dT8aN1JJf/tntom+1GNwSpwSdqjG6bzu0zGvK2+LuuSABUUE36UDZuGfKZrEVnAcC7AOSMQTMBU0rl+m4ynquPstlsEEIo43t3zFRGaShxE5GH84pDca33YJILOWqs5UXHexzGCnwzirybYVXtdco4cw4uhIKBZQVe2/c7H8CubrzZ3BIJR4fgxRZwGYdKYNJx2M9m4L7XgqNToponAbH7EBAcI0Uu6y6rb9HGV4WZ2vRvCy7HnOGy9q0yp0nZ1CDoRjGKRIXUc6pyEsEkO1IU3VdH8A2xinPGsN0W3Eb0gQl+EjOwgs91Iz/MJD7OnEv2XVYWdsUfLx5vDzDWHnYzCYHir8qDMDvLGXE7FEOKApSWU8EYJjVlwy7kQGWfUa+kIvQp58nV6/RxxbgTULSoiMUv79njocPreOaxp/Gd3/af4E98+wdBBJzevY0v3byJmzdfxW9/7lP44ksv4CtffRmbPGB+tId+f46w7LF1kraEYTu5brsAWGeQLnyXuT3ySmPw7L9UP104PKTcAevg9mitH1AHXemOqUgR75zjQrub8+y8gtYVKgtYcy27ttHiK5DZXIOMxVTNuEyey5g004UyUNNfl4K4b+XQ75YCSDrCctLK4uZrs8YyfscJoabPpn2C8onp074I1E/bI+c0ZtA34HjsMeDv/T35ve+/Mdd8q0fOwD/4B4BV5bV2/s2/qfYEFSBgACz6bQnKDDGKJqrDaUeMY3UmQAUoARFiK38Am5E7mxWQ1PvJ62Qi7OIYEhG2262wVfVzBpoxS3kDZ7M9ARQ85vMFxmHAJm3KefuZVHvfbLclHfGyo94jYxzFYRJH3Rzbqh1X54wrDt2l4CInDHFAyl4LHmYEcrh65QpWqxU2220JFi4L68zpk2sB9+69gdPTE8SofVeoelT6SOaepA3nHBWGEediHK0qtAM0yLTH6p17k3nTrCVsa80lnylt0TlvDTfntfle+3UDbdvR0vuAg70DPPHo4/j8l76AQe/FWGuXm6vpOLX0cwvqzIIwBLQHLhuZO3YdEuj1Xlh3m2GLmBK2MWK072cGEmOzXYtzCAna9w4PkbSaa57eMYiFaZmYEfZ6dSgdNm8cw2fGpz/7edy8+Rp+6M/8SWw4ISdgZAYHhz2VFMjjgM3ZCY5v3wZ1M8Rhi81mg6e+6VvwVTDWp/ew3awR44i9/UOEvkeMA9YnxwhWgMEBnp0UWxpHTf/24Cj3tL9c4vDwAG/cvYfNOIp+VyfsXOaM+WIJ5x022y0cMpaLGTgz1uuVBEedwzhGrFZrzGZzhM5jux0wjhssl0swMtablWy+7C+xHQcgRSyCw9XlEmfrDUj1ecl7nJxvcOfkFMzA1f09UOhwf72eaGNmlmAiNGBsyexsjl1Pwhgk5JWF6ETqg0gLO/B03OqCC2HezNB1vYCgkMA3xVg+A/ITWPhBh7AqLChIGLdr9H0vwRJf/u3ZbI4QAkZ1oM0LorKhYbNKekFYEA6ZgYikwqJyXmbGdnOGzfq0ALpQH9ET4Jw6gARwFs05IsJ8NkPU9F1iYHt+IgxhSIGHlEYc374J8rJBNGq6sPdBQAbvMGzOwKpPJaYtqaum9pVHII/IRPDkJWDEDN4TyEl7rAgHgdA5h5gzghcgyqa14yhBVE5IUdizFgFLZgfgNaXekdqmXE+QmOU7nJFVK/rg4EBABJUrmM16MCd0geF9wmYTkRjwXY+l9/CelI0mmn2mQS5AszKLUwSgWRpJGuF9BiEixy3IOXCOamvdRDf58jHeDF1CUyyVELoOYdjg9a+9iv7oEAfXH8bR9YcRug6vf+HzCHFExwxHwqLxziN0Adl7bJuCluWUzoFUd44x3YTLxuSZUMZKyyQuyAwKgJ8H+L0l3OEVjHAYztZYnx7j/N4beOihGwjdDAxCTlzP5RycJ2Qo04tbMsrUPxmzFUvRdSFtpWE616wCd1bwYhMZniq7MgH4hWsPaQFCAfAzGFvVfM/McN7h04dHGFrGlm0m6jpOzpdNy6DAyBjHSRArqasia+EclQJSzNMNTgu62+yAg+0W/+XHPw4C8KuPP4GPPPqYPq+68ubMCL7x0zlL6rIG1ESuSFHZ4YOCZlq3xDun7Zr6RKWHubKk7XVjbJVPZWCrgIut88cnxxPNzhgTrl67ihgjNut18aNqkVmJBZymNRuzL5svkkQexXuvYzFrfCt+LLGMqThums0qi/u07Qoy8CTFGeoTppKhRb6Uz9GCe+0ItLjFlbgVmMZrnAVgYR2HtYZQtdnTigD6XHeCUmIZZ1AgLA4RzFQKZl0aF/9hHcSIOeLkeIVrD11RJqTcY0wRASi6pKYTHkKHrhPpoy5UvdfMjJREw9chI5GsTz44OBbwKRWgUeJqCij21+SkQKThrKyRmVGYkilG2WCimgGVcy5ZMbCYvdFntZ+Wpu+NkdzE3yblwqhAoFN5g+LTh64Cv6Rle9RfLHM9iD4t9L2cE8zjEJKektA0qM6JQUGBaBUPdw12QM5J/Qq9r2EYtK8qmcx5j+BVPkHj7pJCr/UqrCiVAX1jjFLkVgFepzIIRcpANzdTzuBkGTiCgxgblYeajZhz1o0KYeV2XYeuCxCCQS4FpIwdWtmlVfebZRDVCIaEvWtFXg1sN5tvc7wLPSyYloLAtf8cUMgv0l3iw+eo87MCOTYd1A7WTZniOlajACLZ1DYWryvxXBsvsshhONGYr0XuqdQqWSwWNUMJOn9UWsA5wmw+Q0qVrMNZdPGLNXGELgWRREgiiyDjUJ5z0n6Xpr25TXl7gLEkFbwtSG2w8bobo4ah9cOraDLrDkkuBqL5WLWtLBczg12Khunr7WFuOwwXIMDDSZ0HJjh28NThmx57Ah945/vwnufeiXc++81w3uPOndfx2s2v4ssvvoDPPv85vHjzFbxxch8RjNneHP3BAm7WIXtnrZA2lXbUxaU2aEdXyjqu+Y0ImvqL0nekNyOn5nKuEDyCD4gpyQ6rTYpdgeFmcth3S1dyDXnAugPfQIctUGD30hblqjs32skstHJnk2XaksmayobGE+ruDuozr3IHAFFlL9brcXnfqrCbwbUebauY797HpIOAyjAsZxfwp55NOqRtVxnpjGI8xNGxLplem8iuM23Dg9p06dw/Pa3FrL7jO6Qw1u/3cA5YLn//5/mDPm7dAn75l4E/9+dEZoFICn/93M+VwFrmeLUJZaevcQgB7WOWivF9P8MwbAsQ65RxWAoIwjjomMw/AX2azQye/sIA6m4rFec8cXWCW1slOLFOCn1/jAk5S9vIhQICOhJxeAcNom0T49KxxOVnm4Zh8y/GUey13RzkPVm4zeGr5yUAkTNiVg1CtbtSYT5CGLZ2fUx+2eXy5JywWgnbtes69KGXaqec4VyHYRD5hJwjNpu1am8FzPse867D8fkZ2Dl5Vjnjyv4B1ps1xiQFKdIOu7DcwyWo56TvePKGaG2FTlOtIMUBVA/ssvWm3PIkWNbvxoiz09N2ESv9Wqd6M8j05QIy6HlMV6rcn242OPy/7L1Jjy1Jdh74HTNz93tvRLx4Y45VlSxW1kB1sYqlqQkSTQgS1AAXre6FgAYFbQStBf0CLbTQWj9CgCAuGiC6ATV7IQGUmmpOalEssoasrDGrcnxTDHdwdzM7vTjnmJnfiJeVorgooOWJyBdxrw/mNpzhs3O+U4vu2A6uFUOztPcuSLRVIIfDPOtGJ8DkSsRGjQTwCL063ESAL6UziyHVdlvhzyUAXYA/W8NPE9L1DjknPL+6wr/7vT/EL//Vr4GGAciAixMc9RhIqoznNGN3fYHT8wfwAChlzIcR9x68hL7vsbt6jjhNIKVI8P2AHDPmcQfHsstvxP/SlRkSfecxzRPgAJeEd6pfDSU6idVxP0yzpvR5BNdhnieAgRA6MIBxnLQfJWNnGid459GtOzArnUEvaWPTYQQTsNII9P12D08egydMiTHOExiMv/yLX8E77/wYH370EVwX0cPKq9VxbwstiG21nHe+lUc6J9q0M5urtvbFykIda6BEUhTw0InzJ8BGAueoYsgpyOgqj1yZ+0cAGgm4Mk8TtpfP8cPvvY3XP/0G7j14hG5YN4BsXQ/mzDBQuGNNgtiyKpWOMyOTbmTpi3EBG6Q9h91O+FzZNg00BdSZHWHAB8HA6MRSlTeOI66vL7G72qLrOqxWA3wI2G23gEVFe4k+lUjig7SVgH5YCRdtCOgHdXSawoOeHJzvtdnqPCpwbeAKc5ZIIJaoFWKJ+DQRw0wAJ3jKcI5BgWGZDmTOOAHBot05FV5F20AZ+h5dvwJnIM4RMU0Yp71Ez2WlFVE+yeQcEovDahE5BsOllAqEGWOEdw4+DGAXEOOEoCmZOQE5TTLPHOAoQaKtAwDhV2YXbsVRqJqlx9OssWMZLniEvocD4dn77wHksbn3AJu793H3tU9h9/gDxMMejsXhZk3dNG5m0NTYoBLBX6L9ND6b6iQ70htm01ZbVaAVAlYbuNMzYLVB3h1w2G6xu77CFGe4rmuMX3FKi960AnStziFURg6NIp6PinGlHAUMJlR7FOphEQM5Kw99tZvO7z/A6ekZNuu1RPmTx3a/x/OL53h28Qzb/Q4Pttf4cNXjed/DIyhFkfo2TEjzoby/S051Z9K+MR5ESK+kGY4dYgGSahVy6U+15zjKvSA0FHaMOeIyHQBSWinYODE4Fi+mrPFiy5PO3XaixQp4AwSXCTFX4KLw78KAhizrSicnwfyPBpm3SI4mG0pFmqxDLQhTeCNRI9FK4Rqd+MyyZkASAZs1oxPMyl2dqg2WWVOSNSovSRRdVrCOSOww8y/ZtEKdXgs/q4YGNZQ+RXbWtHYZg1QiWduDIGtDwFiZ02b2GuBaNUjlbpbWVePSOSA3HKxmj6U5IVEGN2vy2OS71Qb8c4G2jf3D0t8pVkoppKTbhUlsMCKxWwrvqCuy2IA8IqcYiYztzBE5yfsugCzVczlLwEnKcRlEwZBnlWJIqqtJqcws2tmK5eqYuJKV0M6/Zm0rCOh9rUhvtofNqSZBvKzdunGV0Ze5Un2rxYiQ8cw2fpwLi3ntnIEGMocMNMvgEhnMXO0AGy3j412tVkLTYGtdp4uArADg0Xc9yMYi57JBU3w7AoZhEBslJ1RO4Gozk/fwjS+QU1Z7QeWta8YHKEBrAQ2LLX4zWtYKlduGi0SSSiclVD3PnHUDRO0dxWW4ATWdBg6R6gkGY9bi0ASo7ibV2aKbxD7hQo1DVCPWCQBnxaRgMs+iVWsROBhnL8Q2S9on1a9FM44VTC7/GoVbwY6obkCpwSi2vWXaaF+GNuQRgEZJew4ig7RNJjtD75TiQrXJLTLEjp8JMFbVBQyAAFohVz1MU2YGBCzBNbtGOrRExZYnyL1KOqd1ONvCr+1pF7oBB8jG40Tw1GPVb/Dw/sv4yptfxFe/9N/h517/DM7Wa3zw5EP86J0f4gc/+j7eevvb+NYPvoNn11eInOD7Dv3JADd0QHBqey0Hpw5WnThFaVDzJuaMkJkM9cWM+1HeQRaCCMXaVwTdqXpBlFwFxbXfmi9uVz9iZFYQtY6bHfnoyuO/ququC+O255hBA2DBP2RH63x93MFH72LXyGPbObVcRLelHoDbsZC/841rj/lil++1+O4FL3E7ePYJjydPgG98A/jjP5a/P/1p4Od+DvjBD+Tvi4v6Lt/+tnDGbrfA5z8PfOc7ct6HH9b7ffe78u/JCfD978vvr74K3L37ydv03e8K5+zTp/Wz994DvvlN2aX/wheAH/5QQOS33pK2vfGG0Ct0HfClLwHf+55QJVgb3nxT2pCzFPL6yleAr39d3mW1ah5OTZGYdjxtI8O0OEoRA9mZDhjHsVF2tehXe5/j2XubIG78HHlUK5+orqTjuSAGDlW/g1BkXlsNXt9SPm95j260oFUxjUPT9pXK31RSmys1Qe3DxsitryAAsN7egMODFVkDQIuiBtWJaHqm9I8VTBv6AZ33onSTgSJyds6sQIq8ryeHQAJOdCEgIiGnjFUImJ1DykAikVHuSPRUnVTb8XEHAQg+YOgGibxkwn4+gGPdVa9yeDH6pd8kEikjM2GaJjy/vGj4SWvXLNSk/doYY/Udmj5EI9yJVKZzk3Kq3FV6nneE4KRAQ1ZeV5siZR9djW6QRCeEUOkI+GiSL+QnL7QL4Ak0BITTFdI0geeEcY743o/eweuvvoxXXnqEOyenOGTAJ+FRlRg6RpxHxHkCeUn/mifGanMKFzxc1+HqyWNYBgM5j2FzIqnjOYLAhaeYPGlEtTjSc4xgAjwHjeSSTBzL5skQg5GJMCBof1TjS7hMle/KW7SJPI+0T53OUQAaceeKQZ9S1hTErGnHGXCE115+Bc+fPsd7774n9++6xYpxTnboS9pVHfTy77H9VJ3UYz3HN1Q6HU0+zgx2As6z2mBpHpHiXBxCcSAzQujhQgC5ykfX6rayRDgjp4iry2cYD4+Q0wxgVeTcUv+ZJckaHVkdxtJ0ZgWiskR0oW7qIzcWCgPzPFWKD6MEICtCgQqcULVbx2lG7xjzFDGNE3a7A7ouaXReh9ANcJ2XFEUimY8E5CQApmAwBCYtPuKDAg+u9L0FCRRuX0CLjgioH+cRFLQQDktRjZRmcFmtBOc7XbMaUVJZq2Caj0gKm4jzYimN4vA4iDMdHMkGFonjHw97TOMERkbfBwzqpGYWfrYYJdLHHKlS4ETnn0SmeISuAzgjZQaKk28ROQZsZQAS1SY6uxZ2vEV73fy7OGh1HknEe4fVeoPt5SUu+o+QHOF8/SpOHz0Cp4jp8jnyflf1MinHccvxaN+1E6qMVvPn8XftEiWp5kzrNWizAa/WyOQwHSZsr66w3+9BIcB3nTiiGTV9lmsvaO/caIPJgwzGlOMi+lSyRXJxhIqDD42OzS34KN+//OAhTk5PsVlvcLLZwPse+8MBJ8MKwTlM44i744jnjpF8XT/WTscOs+r2tjq5RKQSiJ3SMRBAFRAwUFz0mP1b39cRlcg7c/LlHSPifJD5aaCl+V05w5VITnl2tvGkOlY2B2Qz0mQFlYyArH3o2UCLSomjqldkgZfq37V4TbV/2qhdseVQFqv3AeO4R0xCm9LpJheBFQyyfq6gSdKNFbtH0mwnUiDCeFMdOZD2tUX42VjnrP1vTSEsaISF9oUUwFX6jkwaSc+AVlM3Y7fM1AZtLr633pxQawnYuik+LaHIkIoDyO+22SxAjYKDChCZSVcys4opu/TVPg5E+WnHx97HuqP82CZ343/AxIEr4FuxE7NGHTuZHazfWVSmYmU6L4/bU3GS8upq7xk3p9gPRnXGCNmV/i2WAVe546hSK1TAUuZWKdiqDan0fNYvrQ/SyGb1q3xzbbbn6/3rG1SZJ8/Va8zGBes8FTtAONCVn9YRgATOrvRVG2TgSOlZXB03QKLhy3MAfc/qc0WKjelERZ7KWqsRwqSE7AWQbXQ+OwkEaulHrCiYzdX2e7uf2St2jvluVJ5JizEBRBYuMgwcNW2TDWQiVMoIXUuWyWS0PObPmIysc7zaWSXgzbs6RqxArV6X1bb2TnQE27xv/CjZMOcCUsvaEDlbMT5a+NWlL23mcAVN7RmJUHw283mLLUs2D8yOEmygUO6xjIHsqakeObJD2uNnAowFUCJylk0t6kd+0/SQQA7Z1QHJqnzL5IHgMJVLB+VzE/DVj9BziifaLGZiEGUYyz0xMPgVztfnePXR6/jlv/4r+NJnfx4Pzu8iEPDhuz/GW9/9Nr7+9jfx1o++h2//6PvY7nbw3qEbegzrFfzJgOgZViTF2VQ4sh5r82SSFfOydY4gw+sbISuLkir4AZt/xaoCAWVR2g6GTUjbNUG5BuV3U7ytMrD5DSKQb42NpRISy8OaoAaLCs+2rc5VbpoXK7E6hkcmbnOfm2TJBmg3vVsXibUPVcjeuPaWv4sza8q+Gc6bjuLthzm/YhDVVyz/asdzMzbHTbwNNC6P7Hu57lvfkp9OU1ucE4D2X/yLeo199y//pfz7ta8Bf//vA//snwH/+l8vz/mt35Ko0899rt7j7/5dibj9pMdv/Za0ob3v7/++/HgP/JN/Avzmbwo4+5u/KcXF/s7fAT7zGTn3H/5D4J//cwFbv/51ede/9/eAszP5/h/8A/k3BCnk9a/+lfxO1G7mWy+WsSvuysLA5GKoWhpOS9xdxqdRdu2xBCmLai6KgnScc7O2uLlWzqv3c+SQjiqKV8W4fPakNCimwC0lSdpE5fkFVC7GeTWY7Miagi6pb5X7uKSYAhA6juVGj4FN4KYIVtPBeeGIuPIbN/KxjWiQcYiaxpOUV6lpJ4uxlTlht99jf71DAmOz2aAjj0SWplsLA7QywMa1lUefZHPGOYeh77Ee1hg6LXKzFYNwZiBTKvPr+ODyvmJaJzD2c8Ru2um4NgUa1AnhMmHlBUwet9GL9WlFoMiHKRV+XjPMUuOoOSKseonOm2PC/jAiEknkY2YFxmuhAe99oddoBhAFbC/9e4uQ1fPZAeFkBZ4j4vaAvJ/gGPh3/+EP8Nf+8lfxpc+/CXQBOU4SbdE5dE7SYq93l+jSjFVO6DcbJFphfX4f6/N72B9G5Dwh7vcgAJuTU6RVRDzsgDwrwJY0lQvIqhs4ZSSS6E7yHodRQDrnPRwy5nlCr8B7SgnzFLFerQBmjNOIlBP6rtf+SqWS7RwjpsMBfd9jNaxw2Esq6HozIHiHq6sDMhj9ukOMjP1BInvXQ499FC5QT0AXOhzmCZ2DRLPpEbykcnVdAFCBBTMSS5erEi/xsGZIQx1ZAJUXqtoCpE4XERUwQj6QCI6cIg67LXIcy1wFM3bXO3T9gNXmFKvTOyDfVflnTdB523UB53fv4rVPfRonZ6cSmaMArURYtvOIC9Bt40Ne+AEz2TtRdcZsjjtC7w2NbBSvcs0FH+CdFKqr0T2k6WsCxDGL8b+/3uOQMoLzGIYNEEZkcmDXo1+d4cFL5wirHtM0YZomzONeOMh08jMkWoe5rik4SdEvznpuZB8nEDJynsA5I84Ju90Wq5MBc8xIkXHYT0h5Anlo+4PI52asdaaXMeSs/KyJgZzKM70VvCEIvYEWcgwEnA4B188upfgYAe70BMNmg873iCliu91jPkwIWeZHShnjOKEfenFsLFolZfghgJxHUg70zBLtK2MkxW6yk8iXHGexj17AJaxi5XYLjEWfSZ0XBpyD73rcffAQ2x//EE8/fB/Xhy2493j0yqfR9T32z85w8e674DhKurZzgBe5WdVZlbYtqFAcP5nkS/uVuKb/QuQgbQasX3kJ7uwMyQfkecbVxQUunj9FnCacn99Fv1oBrEEQXh1nE+GtnOXmh3S8kZGQMeWp+hjM4lCy2qMlH7xGTOWUlBO/6sPPvPqaUqN4DC6g63qsuwF3Nid4cH4Xu+stHl8+gXAuR8xslBRUos7tXtVHMD3MALIUq2Npk2UZsd3H1m/xCdVO8aFJs65gLOekmztQsEVmiWzAAGR8msxIiUrUk51vYJ7ZIgYs2LqNSWgKQEBhdzIwRgeBAQy9x9AHXG8P1b6vKnjhyxAMfBb7IOeAw7jTDXiCGwblq0wyRlkoFpyTDUrKpGup+o9SkKnhWE2asqvzpORkGkDEBM7CV2vgCop2af1Lt1gHGSzgrs4hkZlyjtV1MV3EQOObyjWJuegto8erQDUgYdbyYzZjheD0PZTXGU7WbVkOCvi34uPYhv8k4OyxXfjTg2XqPMiGSxAh+IAuVFCUGhCWkWUzzPsy98r7AQoSyVtnodLWZSHtCaFTLvBQIyY1q5g5o9fCTs45BN/BOV8jWkmit0s0dq6UBI4kC8doFRaa2UC3xgea56QyhpTPtQJkLaBsCyFHKQoKouo3lOhH2RR3JbtD5ljL68rMYM3CoNIfcwHwjL/bwF/ZCNKitJxRiv2leX96AAAgAElEQVQ2a8dS2gveQVCOXsGUROZI1Dlp6rvZKCb34FACfYq/YfpM54MB2S0Y2/omhbqgmW8let38BiKNxl3ySS/4gPUZS9C33sMPvVAyND6ZCDTDLqzgm8iROM0LyhRRl7W/yndoMg90Q9TauogCtvXlnOBiancWKdP0TRugxKxZaU2/2fsVXzInAK7MxaT6Yla+YAPJvdYEIhtLq/0D2VhbFgEzG0B+fvY5Y8tRvMoXfmaCVSIGJMUizk1FNDIlreZl4yTYrmJrAPljblGuCwM6iJQJAR7nwyl+6S99GV/63C/gzc9+Hp9+/dOYD1e4fv4Bnn70Eb7z1jfxO7/3u/juB+/j+X6HSIxu1WF9soIfOqCTKAeHKnSyI31eswvSvH07WY8n0cKyglW+QwFff5oiiLpL3J7r1Pp5ofGKBshGBYfss8I7017RCjBrNzXgbm6/Q1lQrXd2u/LjG8/Ss3HrXFrq2rqAG+CgGEC33fa2J6kASmTqsIJzS+pJaU8Fq5cAjl1z25jV4ubL7/jGL0cHQ6JWjSf1+FDFhn/6T1/8gs7Jzye9h/e3n/ei4x//Y7xgEKEoj4CrbQR3OBJb/+gfLe9x/D0A/MZv3LzHD76Jo0FqHr1kn7Jor5QSrq+vyzntwcylYuRtQrfdtbSUkhvztMHJftrRRkp+3Fpvn+A01WYctdiNzte2gIEBbLVBWP6tyzkEGfupSf2zSDT5o8pWhhQEMUhIGoPivNquYn0NVZJmoIKEWiUEKR5jXHIwZVwNfXvr9i839BiGFU77Ac+ePcWcIxIYl5d7MYhMLL2oD48M62MKk6BzjlmA+sO4R04Zo58QXMA4TUjZNhcb2pcXGPXWZwBbDbS2h5tvW33GxUEJ3qMbVthut8UHfNFhcliiCbPqUYfOOWzWA8ZxxBSVvwokeiNqdKxyVFlqu/FaHcu3TzKxyyaEAzB49PfPQF3A5LaYr/cIDvijP/46fvST9/Drf/tvICHjWp1rNzh4yqB8wHSYkOcD1idvYN0NAAIiM15+/efxztvfQJwO8BBDf71ZY/SMOHtg1qJ5CQUYcZ4kbStn5HkGkUM/dBgn4Q/zOWO92mCaEqZJ1s35+QnSJABRrxth86xcv16Aku12h/VqwOb0BCkl7LY7dF2Hoe+QY8Ll9oDNZo3EjMvtAfs54975KcACYHXMuLNZ4Wu/8EW89ugh/u3//R9wZ7XR6sFybPoVVsMGIQyNruAXzLnmM7WlZEwZLWh06/whUh5VL4OXklSgnw9wyAIoQm0YB6weDDDgJB2u4VYn8H5oJQPUagfBow8DPvfFL8Mif1Ji4dI8WuOARdNVxwaWCgy68Q7eO3jy+PQa+KWziPFps9AYQGLwPCO6iOw8wA6dCwjUwcEXLjcijfhxYpeenZ3BuYCUGC+FNbpOC3VQwDgzumGF05Mz5HXG9voC26sLOB/Q9QOG9QrTOGG1XiN0vXJw9ppKrECzAbHzAcwJwzAgTgc4njHtrxBzElCuW0nF5O4UPniM4x7eB+H1DSuJCi92pQLo2fjRpNI25wROETlOiNMB4IygEVPa0SCI4zdOe+wudri+vAZ5Qu87hAcM52UOzQzESWS2VY02rsoQOrheomuutwewixhWHdYn93A4XANpRs4zUprgELSdvozXrIB/ShodeWOOOiyFoEYKGn8eKm2Zcx6bO/fw6NMJ73/0AZ4/f4KP/vgSb/7CjJdeeRV3Xn0VZw8f4OK9nyBRxIEz6DAjTpaeqf85Kpx2FtFe2yFy3SKHJCWU4dgD3mF9dorTB/dw7/XXwOsBKTPibg/fObz/+D1sDzuc9Gvcf/CS9EdKiHNCjAld36Mau1TW8EJbqJPPIMycMVMFGgGUSGjvPTy8OKo5Kwcaw4G1CGLt6955OAUwKXOxoYNzOFmd4Ctf/EX8P//p9/DGdovzccR/OumLk50AzFEbliz6XNNuIUEr1fdxEliZGBaNpUu8bB7Z2mSIbTPPc4nStCPlhKi0FwSjd5MeS2Dd3GXNSBDAsTxr4fRT6TPp0wTnWPiMqUoeAXw1b7wRRtsrkQEgKoBN9UAqXRoRIeWMWDJsjOPTFVBoHGekGAq4kI17GhHEDZdmqmBt5e1t50l7KCUFqXxn8cPNl2ONZlUsSu01CXRp7cZkxRVtjimgU32uZi3qM2yqshqxMcUCTAo/arWGMmRT3jtfgpws/bzYSOQkMl/+aJZETYH/JMdN++bjj48/V/rQMdB54VxmSOSmRVplpe/LZQ6Zzdxpe5rsM9JCu10nxUi1vSWIREGwoACf997gEjlXuaw5M8Y4AiRZGvb9slivnNsWErM1XddlfQcBWBN6LcJu54scpEVkYynSptfOc9SJIOvSImUNKOTiUOgPyxy0dHjnDdQWH4UAgJVWjSsYLRHF0i+2sZK1+FmJLnU1ylc2N+tY5iwFvwScDjciT+UcVrCRiy+VshSB7fte+6liKQTohqwF3FU/m1SPdMXvrfKGbeFgWZi6APxHoGQbTAcI8Fj5nTM4L2M7i29paUZAySjwziMMYkMKbyxgGzdZfWWLHvbe18JqAKC+oHHlOuPbgM3BKrMYUKpN43pVHeBI7yPvU+a69k3JGGOl05p1PrL0UR86gGQz3jiFc0rw5JXSzDKHJFtz1sK1YjsZ9zBhThGZU/l50fEzA8YWA4aopNlaFAPp9yUKiwAXLUwd6EPQqto1XFgcnxpxkJIoYuM7A2wXmhTxBiTZUQnMwUDKCAjY9Bu8dPch/tav/Co+/3OfxcN7L+FscwfTYYf33v0xvvvd7+Lt730Pf/qtb+K9D97FbjwADgjrHsOdDdzgwV52c0wBCVdf46A2OwtyOHUkGgMJsP0rDQW3mOH63lAF2RoAdq0YBgUpQZ3KMrmTpp+2u5Pa3OLEtQAVATUyRd/J7m3B31TesSp5A7paYAr2jObMxaK/AV6StrUK8/bcor0LztoaQKxtQ1ngdmfbVTzCosovVb8s/3bl7wq41PayCpZUOGtIlZ+F5ROaSMQb6IlGw+iAkF3cGPOEpZAs70lUI05fdPy07z/JOZ/kHrcdtwGnx4f3Hw/y/lfcIxMaGa99mhmkqU3Z+pvqGOuZonuOAXSzHHXHllxVhDlnrYBJhdKgko7biC/X9MceLJsnkevUJqIFyMkQwnGp3O6wPxwwHg4a3VqkBKZpauZrLYpojoDJRSAjsbQ/cqpKHE0bmBA6rzJXn6BGv60822W0iJWFo4N2XUH7Sdo2TQ3wW4y4esg6N8NCp3/o4ImAGLFLCTEnJFY5WoxQLuPa2k3HIKzoJ0uvrKt0LryH8jOnhJwPcG6Cg/Daee9KMQVJlzwaXwKOI0iBpe9mMcXES0luJzBLNG3OjDSzOoo2QVTmk8YMNZsBBm0xM3pHGIJHFxy244g5ihFSKvLGiL7rxEC3VLN20Bbh5B+/KXgcbSyiTeAUFwjd6YAQCNsUkfcC5Dy+vMD/9Tv/Hn/zV38Z+0BIc8aUE+6u1ujhQDljzhnXF09lHfsO7D3W5/fw+ptfxtMP3sH++hk2ZyeY5glh2CAMa/A8YffscUkFJGJAC3uwymBk6VMfOgwuwOWM3XYrhpmXzYKrq2sMXY/gCMiMwyhFujKLkQ4Czs5OAM6YphHznLDZbBDjjHGe4Rzh9GSD/WHEOGcwO7x8/1QqzDNj6AIGT9hPE4iBB/fu4W/92v+A3//9P0Rq0nBXwaHvvGyaQB1ozguuZ5sXdd6TpOGZjgLK7n9mrmCvAhgGINTzCfNhB2jhDO86HVONijB5SyoiGfBLVV3mdKs/SdPqwQxyGVIUenmR6VCnUdKJE5AywE6KIKHqSSJgsznBOI7IOSJHLeRXJCKQUsR+d8A0JS3wKnNBInoAWJqeE7sxzlJVd5pndJ0XEHxwYE6Ak8JrcZ6w311jd1Bqmzij6wYpquo9fOix1uIsolscYsy6kSOyrk2JZxYKBHQCHrHz8KGDuKZeuGWdEx7b5OC7gNCvELoVKDVp1W1f67M9MeJ4AIHhHWGepK+c6kKLJvQaET7NApQPw4B+CDg5WWHoPVwgDKseq3WHYdVh3EXMY0Sak4DAaNQmBfTDBqvNmfDRMuD9jJwPKi+i9AWLvHXeIUWo753ByeTZQoTeLIVgmduNnWw5B3bd6ek9vEwe/dUF3n/2Ed7+zrfw/OoCDx88wqOHD3H22qcQEMHTAfPVNaJ7hsgA5awZfKQAgPg0LjqlwshgahguLVjEe2zO7+Ls0UOE9Qpu1WOKEdOzPVwXgOAwjwljHhFWHYbVSovzoUSDS9RaKsCbvpxhE0XeWhxkZsacE3AEVjuVcV4rfucxab9zuV+2QGU94jRhdTLA+QCGFGxxnuDgETywGQa8+vAB6EnCvL/Cl7cJ3zoZ1Ker1k9JxdYiONVOETvEilHZXC22B1cgnsGaEg/sDzux6YgWut2AUrMhLB3VOdmYYJOVC/3Fi4ll9otF4g5dwGbV42yzwU/e3zWemDwwl8l3UycSaxZGYT+x1GAFnaBRsTlJP5HJ5ggmQmbCnJ1kDXBuuNh1o9rSyB0ha2GZzE1FcutTk5EGjiiQR1SpQKKCeqZGxG9Rv5uMhocqG0LN6ZXRaSNcYXaLFRTS8Vv4j3Ik1kxVpmKf6tQo90FOQjtBpIXXUJSO14xayYoj2bRKCihz6x8vjxfZMP8lgOyLDuHcTphiQogJUgdVAMKu6xCU1sbWQI1Qlf4TW9ohEDBNwmMfWSgvbLyti8x+jVphvtCByMugchtD1wADVNdGBffqsgihRtjaaAlnO6CdihACVqsVfPA6/yy6m8ocm1OqtAA5gzR613ymIdu6qdK9jkuNNTcNLvRxQDC5ZX3l6tiVYl1lDtco90L3pqBsp89LYnxU/0j4MTSCOICIC0hufk0BjZ1GzjuPeZ61IFZGjFJzwKLz+24Aa9HArP1hstdRXZ8GJM7zjHGcynOcl+hqy3bJLBkgsiGotrZmIXuNZM7MNyJnHfmC6zAYOY8SXUyV3knOkTOy8vnlZLgGSkEyKkA5FZrRMmeI0bkOTjMqU8oFRAdBA0G4tF14rOv30i8qWxq5UdeMjIYVISS1W0smihPAuPrlsr6883qe3tuz1I46cr6C69ErgMxqL0lhUYJPrsxrRy/GMX4mwNjGTyxCuO4GGv8EinBgh1I1lCCBexb12oQRFkVrYcTlICohzmZ4EpkPqYOYgZUf8Oj8Jbz68BX8/KfewNf+0ldx984ZgguYpwPefe8n+Po3/jO+893v4Qc/fgc/fPcnGOeDGCBDgF8PcCvhmTMgllX4FGeD63uz2SQM3YCsXrj6OdpXdPThMkLkNrVhYPdxP1i/AnVxlJvQzXstVaNdbulZbgmOcF0O1oa2/4/buwBVj0EWqkLt+LMXHq2vtmh4WaI3r7H+JjNc27/r+QVkMqFVAGWzUSr/yPLmTUOsf268w1E6OxvwV+9vY1NVUR3ORQf8t+OFRzy9i/1nvrCYUy5OGN79YXMW1eFRGVWM1aOVUAH6Ck56VXiRGdxU/pRd/XbuF/Oi3K8o8Y95B3MC2jnkoJElRBiTAFhJd1kzQ5WpVqcukexL0LGdkqaY5HeHzgccprFEVbQGld4JzBWgaddK+27OhRuft8+35x6DozXqTYFrWyt2TulQ+dzS+lIU7qZkaWwAbCedmhu8SK7YzuqCXL55VqOmxLgnLpyTAoQBwjxuvL5LAWtArBnGN45jGch2N5T+txEofJpi6dgNpM0sym4pDrmATd4Jmh+z8LWawchqDLeUBERUomHbOXz8brcdS36r2kYBiFg2FXqpmN2fnWCMV0CUqrHvf/AhcmZEdTozGOvUwzstcESMedxhe/kMrhsQVms4uofN2X2kFOG7gOlwKTQBqxW6YUC/3mB3+VwcVFbuYNbUSJsPMYGYZefbEeZZnEdrfU5ZioywAIaAgAtWRd07S4MSsIIzCsDH4ALuzTEKmOGc8G6y8GqaATynVDcqnMejB/fxmU+9jndOTmCs3quhlwq+ziK/dK5n1jQ/lVca7ZZihO87pQpyyJmAQoPCdX62U9PsJ7tXisjTCKQklAm6jlEcPoCUHzFlic7ab7dYnd8D942tYMCJTu6lDKDb14d9D3WUdMwKlWfTBhAV3lKLGjq+S8qMlIBxjBiniOClcrAEDtUIEnNSU0oIoQdplAeRcPZO04wcJQLEiqbGWThcPRHIBwg/qsztKlcciEZYWbYKxkrkhcnuqBFDst5ZATBGcF6rMpNGZkvfMZSCQ8Eek4m+qebMugYpBKmV4CUqzgoPkcpTK2wiGIkHnIcPtYJycBoZ6ySzgdwA1oJAca6QC6vR60LA4DyG1QahWyEmoWGY8wFwSrfBAsaCuBT0ILBGn3LBiI6PMmNU3tUTbRxR7VKSdMvTkzPAOUROeHJ9jcunT5BmiYJ58OABTk83CF0P8j3WuxHTxSXyPCn9S7XzMgsnOUM2gBkE8g4+BFmjoUPoewybE/j1RsBXBsbrLWKOCJsBDIfrwwHkgPXJCTbDCYiaKEJC1cetrVnsTFs/Sz1sm8qtoUHKAUnqbC4AGn3WccRXjErfog5zsbIdwUM2gh6e38Vuf439YQeaE16eIp4Fj73XaD9bvFg+bzmejGqvUNGLi0FuusCiAVs7ptxbZRtbv7ABc4ycbZOipse3zyhRzU2fcs5IMZYCr9JEKv1oz12+S/t9M07q2zEZMEIgZAQtpppZwQnzixnIJIB0tYtsvJysW8dSVA8McFb9VrP1Fr2sNAG5tIlhbJ0CetaM0/ouTV+U66hMrzq83F7S+Oq5+pBs9iW3d9eNQWix6tpnNhczqPjyUvwNZZ6Q9r/531UvmNxo5x4+9rhpu9w82u+ON/Xtze27nDJSFHsxq42aUwI7VyJkj+MSrXATGe2hmr0Eiyad6+YG4YaeOx73pBG4qrLFJjTqQJY5U3yiaoYCzuanvo9zcDbOZDyqxisLZAWJbV6DCBznMgdKhkHjM9l7WLcV3VvmnfpUNi4asCa7vdbXKssIZQ6AGjoInTMpJSm8ZOBmwz3rvS9rXvhihcZAoo2DZMi4GpGZczIDRDlWXbGdQ5B3lfIZdZ173eBmz4UKoo2Qt/aCCDkLmJo0ollks/medZxyVlmoGrfUT1BgMjR4UAlapAYjAwFIZbOorFPKmrkgQX2yIivVgS/BDeoPosmeVoHg4JCd0kqgAtempq1OSG0iI861SKvXeWKRsUK3UDfaKrjsyvyGjrfIylwipEVOynNs07n6mEuvXyhemrmkErO1NZ2jkrHxMaLiZwOMBaBgpf2uYflwxeGAOQQ6eDYIANRpMEPRBL+cn2JCigmuC2jmZemUeq4pY4BYdnMf3XmEv/LFr+IXfv4L+MLn3sQrLz3A1fUlLp8/w0dPHuPrf/an+J0/+F28/9GHuNxuMc8RrnMIJwPCuoffDECQhSoPK03WCXIzncoWsDjuJlkb+IeWUZsEFL7bG9GhQFm8VXK2nQBVYvKn8YXU0+iWyaMCbfF3VWJ1gZaGlHa0RoxN3hdyaLTyE3Ux3d5fN+9h77y4zcK5a5VkC37ebMLivZovuHk/e6btPKaUb3zecj+Z4l8q/2pQZoihEcg3VdHRvBMDTXTc7eDNzY/+21GP+dFrmB+9tvjMXz3H6t0faQEMqrNburvwDZbObUCNFsQzOeR9TeGWyGiNjD2aTB8bPaj/q7JL7i1gFBfjUtUYAjn0oZPU1O2MxBkxjgCjGByyc0dA1ginEgmbFilGC5CMpDrmyeYE0zQhU7OO1FGw68RI9GCuBb/qiqqOQnnH1rorBmr9zpyVxRqi9tr27voMku+SRbLVW6NYmwqW2vppq46inCrfee/RNVxGaG9JSxlc3q4xFrPSAEg/ZzVcluN+KxBMdZ1Tef+6vWYGKANlh9teuAVryZwoMJaPMGcG6EOH4AhzmjHFCXOS1GLTrV0ICKFbREPUfuNbddrxuijRWU3aVNklJ3PyUao3owtY3buD6XAAbyfQLJsJ0zgqQO6QOWEfZ4RAWAWH0AWAZ2yvnqIb1lg7gOcRcCucP3gFq/Uab//pH4GmLQCg6wdszu7Cr9ZIh71EH+UaDW+6mKOke3oEJACH3Q6DVjPPOSGmGQ/u38V+ty3FaNbrNcZpBBGh7wL6YcD+sJc+dw59F/Ds+RU2mwHDqoMnxrPn11itT7DuAhwxtlfX2GzWSoGSMR1G9JsV5gykKKlcX/srX8X3Hz3AO8yIRFiv1hi6Dp5qFV75JzdLT6IlUorYb7dYn52i6wc4F4petOJMAkjY5gIVQ7PMz5wx7a+Rri9BGoHAjBpZrM/s+w77/R4xTpjjhGfPn+KVNz6L2J8AJ22GhRnv2k4DHWy9LhVjXW85w1kEvdLstAAR6e/7w0HaFWTeWsSJydsMAC4g84yUpLAJkwejZg0wGJyc0qUQ1iuhhQA8shYIySlinoQC4/TsjvDeauRNGLqSqhjnhMN4LVG45EqKbdc5eN/JmtHIwPVqLXawRqsHzwBP4BwBygCpUwEG54TtbgcACLpJlKIoFAOopnku/MI2XplIohNhTjrgg0XbMLKmHec4y+YBM7qhR44zMkHmP0eAfbG/hsFj7AnzRIBDKX4CdYA638G5AcNqA98NoDnBdR4cD4jTAeS2cJhkDpMVEtHNfebCbbu03o4FUp0vRZ1D7HHmJcDYhQ7np2fYrNdYP32CD54/w9OPPsDz509x2H8Gr33mU7hz5wzDyX2chw6HZ88xXW8x73eIh31xPDMyUujAZPyKQuvRbU6xOjvFsNmgH1aYY8Rut4ObZzgw5sMOrg9IvdRW3+6v0XcBd+/cxabbyDhyjWSSwomqv2/oES72C9lauaELZIFItDcWMtosVjEkCB11kjKt94pxRoqTOMOhL5kw5uznNOPB+Tl22yvsdztMuyt87jDjW2tgV2gIj20oWujaF9aCuG2Yrc1c/YTWLs9s0fDlRhV0au7bmtbWpiqLGn+HJTJxmkZcX2+RtdKPiCAq5xdqpsW41L5qM0usQnmJMgMQvJMslbjUqdLmZqOZDQiiAi5AC5imhqLu2OawOUHMNQik6WszneBkk9L85mISmz5g88XFSnGEsgGWjJqu2L/a9lz5XuUFuIp53WhgqP9/67Db1g5JFHrhE1Z/MNv81b5u7Hmij7fD22CLv8ijzC+NXOSsmboGPrKCZ1zbXGzKJHQtohu42E/QdTRPNVrS+tHS79u1VDiVc5IsDaoFvPp+WMwp+6esAbYACVeva/hLxVfRaFMFvBYp5U4CALyTlHb2HkkDAJBZi1NqWrlSEUE3ioofQUvQTWdAaddSlix9j8LXWmgy9HcFIlNKVc4RIThffXBv71YL2jlyIE9lbeg2e1lXNUvSl2hMIifAntm8rOn+BFiSgwG4TmVU8EH0MdWI8qT3FioHD+8tO0OyCQolQ5bifqAaZBKUjmGeZwWjJZuPlNLAbHwZm+XY+wYEtQCNGCPinDQauAVJBeiuEcgZ2WfklJEpFz/LaaCF0dLVzT+R43NMypufEToP6PjJuwgtivlqdn3Q4ARHVOuWqH4w2gzhPc5a/4IX83zB300EzrFkTZkfafNMICjzK386fePPDBhrxTJgAKRzmmogSgEOkvIGV6t56hXgpCHLUqFRnAcF/5wHdQbMcZW9dnDdFUcCBvY4W53i1Zdex//yP/7P+NJnP4s+EKbDFk8ev4cfv/s+vvHWt/An3/wz/Mc/+4+4znMpFNMNDqcv3wete8CbA5JQaSKo/P+n4WTF6DEQQrnmCojTAHem7hjK+0cveAZzOV8AP663wO0AxG3HUnnz4nyJAmp0cwvYNIafLQD7vDpd9hD5x1LgrH2fTCEaTUJrj2qkBwElNa58dztv6Cc5WmPmuM8WwuoFafZmXBxdCMe6m6JGEZc3amdRQ1sBiWZaGOF/sTbD/38OXUwVyBIOzpTTwlAsv79wqZCmohiPppLWowXVjq5oDP3FfKL6GCsgk/MMDwJ7hy54rMOAh5sz9HrdlCIur65AnQc7LpQiEhCrJPOanmjFDpk1YrYBbExKWORkcB6d87A9VqsYDLLrJJKkrXZei4bVzyxV/zhK4LajGFlNv5jMax2o0tHa8urwAKBlpK2lpt322GM5I4+QYk0mr6wVDNSIKhs7a0czhq3MEo7ZJRVFBSRvXlPGXkHzlHJ99+O2H30uMs/BuyDceUdnExih8+iCADHXhz1mM2RGAXVOz07QDz2SGlldJ/ImxtQYKGLEMhI+ydEWDmjbU+xr7VsmwK8Czl5/CfsPn2F6fo04R/xv/8dv42/86n+PNz79KTAzns0HzJxx5tYIboW+C9iPV0h7qQYdnMfUPcX5g5exObuPL/3Sr+Cbf/BvsL+8wLTb4fp6hwePXsfF08eYdteY4oiNb1umEaYaaeW9w92zDQ6HCTlmdCHg7O4Zri4u4J3Hql+hHzrElNAHKYKWU8bTJ09xeroBiBBTxtXVJe6cnYAAxDHiECPu3T/HNM047HeYp4R79+9gvxsF9AJwdn6G690BiYWG5Oxkg6v9iL96uMbZvMVv+7WsVS/FN0r1YUuPzlrYhbykVLse3d1OIvI0OkGMZzEwi2+cJUWNs2xyd6u1GPQ5Y9pd4u3f+13kDz9CYChvcS/8jRr5mVNCCAGzRqlnB2wPW0xPH+PZL74J3P8sAMChTfAlHLbX2O+uQORwdve+AAWZF6o7J9l4oWfP8dJv/594f5qQghTxqhQGmuKJrEU89CdrenJFFPTHYVj1CB5IMUpUWpZxNDCzHzZwLiANDEcBIfQAjFsxY3u9wzRJwZthvcZ6c4IVuDg8znkBV5RPzzmxecQJEV5v70nThgP0wUhJQPhx2mOerjDuLzFNO8zzAUPf4dmz76PrTjCsTpDAuL6+FNnkCMwBMc7o+x7CNTkhhHPIDnAAACAASURBVIDT9Qbr1QrDsAJzxsXzZxhHKSy3Wq3Q9z36vkcXOnShA6ckIIkj3Dm/A+JP4fnFU4zzHvtMuLgecXpng+BElvmOcHK2Qtd3GFYzLp9tVTZ5TWcPcL4XxzwDeZ4R+oBhdQZCgqMJcb5EZo3cdkLvwJA+jElScG+Yhy0fXfNdddjrjx2cNFKdPVxmvHL/Jbz86BWMccLl9gofffAennz4Lk7Pz/Dg/n2sfI+Tk3Oc3r0rziQRXK6TLGUGVHZkHe/9bofd1RbXj5+DY8KwHuDA2B12iPOE+/fvYZ8nTNcHRBIH+v7pfZx0a3h2mMdZ/KRk6eVU7RKd1wvViFrkLuaEKc7YzxMOmiIsJzFmBdq9I+WWhNrPpo8cuky18DGAeJgwhp0WOg7wfhD7lAjkAu7cvYdxd4lXX3oZPnhcv/1t7FnWIbECda461ESEcZzKmiyRj5lxi9q7OX6qX5lj8TeiVbqGeU32yrz4t+WrtOwAkYcCYs2zFTxrgJ1iK6j0Ul9MziAzIiqQY882YLKADfV9gw9K08sAMlKaYMGepXDNjcne+ob6tGT0GAlXl7HYYgCOgLPW5rwtGAdK47X0WwRkZtUVpMBhS30h0axGTZPLp9ZQEkDNjDpXe8n8yPq3RZo151C9n5ldBlyWmgBNv3rnkb3HbEDyf8Fx64b5f+VBCpj7IJz0fR/KZ3LI8zJrlDczAON6rZvgDMChZhW7zpfgCts8tM0+oy/ouk5khcqpgq0QARmYR9nYdAqaGrBXNtU5I8YEQNaW9x4u1bFv6v9pv4lNaRlrYLUFm74tmyfNvJznGRY1WYB5MxbtWutL7bWcK21TtekFkK22gG1qSrEoXwIyGvO9HW6TM6UPCq8IpjmWeztysFhe411lfb/D4VDBaEDsaNIoShfEXpqXeiwo/2nSzakUZ5AWy/XK0yqBhIQMEiCbjAZHsnKcgdmekBzKphuAUmRtGIYyX6QTalo+MyP0oXQJW/BeIzdDCFiv1wAIOeVi+5jPTNQ1NTYY8zyDU17SAKrsq3K38uXa2JxsvEYxCz1UjKnYeN45rE5Oan0RLcJlPMlFypLNOYB5NpOvtNfmsN3D2mPPCUGy2MzPd05oNaS+iYfX7M+omaTWX7cdPzNgrDEnmoCvVfCEbFzS96RCcMpKru5EcgvPg1dHEDA8117ckzmJwgHEJGThFo2lMAM23Rqff/0z+NJn38TXvvyLePMzPy+ccLtrPHv2FN/70Q/xu3/wh/jBj9/BB08fY5elErUfAnwf4IcO+aSTKN88A80Eq26F/WXToQmBLsbEUtA7I00vTmpzP257DUW41LgpOQpAUD9QSZNLPzRf1r8XwsihQtr1fHezydaYW+GVm3pMd2Jv0fwFfFEjpi2c0yrENoS/fb0Wp6kLOWn7LZqrAi720lyMCYvi4sJv1HZLUWLldkujpo20Ow5xN4OGmvvVV1LF2KazU931LPcgM4hfNAhynP/+v4G/et6YLwYEmfHOZXeUOQsxtXZK6f9i48n4j6++AQ5d02hZRzDGOtejqShX5qOtgTlGoFHIYlyK4pD2NfxfVOUCiOCuLuCfP5ZrdKBtd5NIdwjZ1r/TjEwqaSIiN2z3j3D9y7+OfHounyetfq4KKacsHKMl6kAFvrX0FkO2Gh42BxujHdUAZ13QshQZ69UJmDNSnBFRFZ2cJ3NJdgO5ptEwIUdg5BHvXUxAVqCBgOxIC20IwO+dx/1797G93mIcD4uJ13UdVpsBFxdXCjZWK4oJiPrMdH2BhCy8X2Rjt9xSiEn4AHXoX3iI0+XKhkt73LZJYQaXzKPlei+nmQNkstLWIhHWq5WkAmetQNukH5bd0VvWOfMyxWsx1g3nnX13u7HO5Z9G1Cye397bUn2ZK6evcR7Z+r0RiSs3KPPUbu+cw2qQwkmUUjFynSOsuk7vzRjnCXGOZTxW61Uh9YxzFDHnnDq11NZvKe9T4nXVYC19smijRZ1qlDe3Dja3txMHghl+6DDcP0MIHuOTS+Q54o/++E/wJ9/4FlwI+PW/+WvY2xtnBtYbXbcJ87zH5cUT9Cd3cLjs4b3HvVdexWe/+tfwk7e/ie3zJ4hXz3CJjGF1gi70OGwvEOctgpLxk3MSmVgc0Yyh67FabTAdDpimCRfPLjD0nRQkUsBstZKiTNM0YY4zVqsV5pjgnUMXHO7fvYP9YS+OvvcY1mtcXmzhHBXD9vJyCx8c1pseXR/w7Pk14DxCJzRI+8MBBA8C4aUc8T/xFv/2f/0N/Gi1ge/CcqI18225EVLncZk5jRNbr7H1VouJgAHO93B47SEQY7lVub/JB3PYuS6CnDModPg12gPYAQT876/fx7tUzdOc7xZww/lgAhbTxX38bT3n33/+Dbz96hfA8xcxfe3LmHMq0UB1vR31AzNOn/8E+3f+szgvDx+V9+TMZQ1GRzhMM3pHSCxRGQSG7ySKJzkB2/pOiq8Eb8UiCPcePMTJySlySuj6AYfDDvM4IsYZOWV0XV9Sxb1u4ktRPIeYfC3koVFdsgkyY5onzHEE84zd/hrjYY95mjRijrFZC2VCTFmqYpMDvHH8dZiTcNc577Far1XPJVxtr3B5fYnNal0iPJgyxnmPaR7RTT1C6MBJwHWnvH4EieRMOZaxv9pO6NdrULAInYDr3SU4ig7t+oA+9PC+B8ErNQTjMM0CADqHcbvFYfcc4/4Z9tsLkBsx9Bv0HcMNQSrVk0QPe+/APOFIItYo++Ygmw9HIF47Rbixi6ZR3is4wsOTc9w/PceBZ4mySxlXTz/C7oOP4Jw4YdLPQhUhc5iBnCWyiGX+SHSTRCSPYHzw+CME73GyXuP07BzbwwFX+wuETY/h9AQPH9xH71bw7EARcB2p7SZhTlKgSOwn5hoVauvlRgc4AXxsEwbaaynqGMJhZon8at0ERsb10yeI01iuOVxv4X1AcAE+TAj9Wi1Ccbqs6NZmWOHRvfv41Muv4fsf/gSfnRJe6gY8eeUBHj9/ppH6Ih8dEfqux2q9Rt/3+OjxYx2fJptiOaIgWJq32thFB93qpCyArOIrpFzOZy2CJWpQHPlcIrChqq7RwyojW2aDhZpsAIACPjUFz2zcgITVag1mIMWEaY5SoM6ie6j6FTcdCBHKBsq1b861Q9Sub22IGrlr9za7o40KiwoCLeZVcUFk68+5DDbwp+lcIkKwMeKqh3JW2pbGB87qG5r/YVyTwcs9jePR2m9OsroUIMimt9kpQt8FsFG4eAfEXLrvk0a//nkA2Vs3zpu278cR3apH4IyYLajB2uwqdydnpMQIPou/ZevS9HAzvPYMUnokRnGllgWpLHq04Zc1v7DY0Vl5gpWL1eSn+SOk/VuKkyvfKdR/sehSItFBPmjGBAN5zo1/rQENrqIYxn8rkkfWCxXfm0oqeMEyNLvDQNsyz0WoiYzTYAyvG3UZWQqvklIuaHva4mUmT7jMS2mRc04zucU/FU5l6a+YYgEUJSK5ZtjZTywp8gBZ4S+bG9qfB+EyqHMHbUADKyBuka6iD10yu5txGCddnqnYYyEEjXyVOTZNk0QvQ+1zlmwYpyBmSgk5xoVvW7mtRV9P81zXE1efm0iwoqT0GfU9COQrd3xm8cHTnMrGIek8tg0EEb2s79lDCou28piQYioRv33fI82xBEGJ67HMgimcsTDfyAojEoah12ACabsF2HVdKJHjOUuh3pwTQtCxVm/BBePnvT0IC/gZAmOrIm0+IRnEjCSLIGfhiMuSaiUC0aKlqtMNkglshr+JO6blLjEAUCZ4eKzcgC9+6nP46ptfxBuvvYZ76w3SdMCzi+f44KMP8YN33sGfvPVNfPv7b+PZ5QX20x7cA13fwa97uEEI9pPLRUGxEuOTCoCWJ9VACuMhXcjphcyWpWTZFU3nVAfn6NI2psRuIYTq9R511/emggAqoFsjs47uuRCct9/mtjs3jRTFYM4eNxCvKXm6XSm2ivD4+2rkHJ9rd2/GYDEfloCwKfZinNn/i61zi/GuCshGZaF8F2N33B1086RivHB1FuynOZ/UAJeUKwU0ijFVbxeunit4aVrUKpGKMcoMOG7C8cnGp0nLAsDDCnl9AjDD7bfgJvzeuTW834BcD1AHTyfWE0UoSdEA6dfgCORZu1XbkSM4H8D5gBx3yFmEm3DE5doP0wEG4rqLpyB1Go2UnBSMZUiVX1PAmVjOYakI3DvC6ekGklDYdP/xvFODkXgxg44G9ma/l/WxGNhmvEkVuxoXQzcAnDBxwhSjFGcp0S11ztucHoYeMUqkQ0zKta1zygzx5byVnchFlK/z8AD6LmDV93jOCQSv8tIssWKeISY2e0eUnsnf5g3Bkp1ghlAxkNn6re3nyktZuhVLY7fY80B5v5TFiGzPY+uf5ikmUwhU+kcoJ6pMW4y3CjRa3LWmOC9G84YAphIhUg38xRVVlpS+KReXttRUlyXgWhyaRRssRueWe+nvmRlTnApfrhj5Hn0QhzdnSQc6jLKD651EVPZdVyIlip27kL9LOSe/tfx6VT/baml79yYPaTt2TTYLoBGyPRwDeZwxXmxxvdsBuz2cd/izb7+Fz7/xcwhnZ5hyBHUBeRrBnEA5Ik97UNfDH3bw11e4fLZCN5zg7P4jgDP2l08x7XbwroMLHsPmFPPlCNskIrJIobruJZpAU866Tgr4kESTkdL+GKenRLR3EpmuKX0AYY5zBd4h65PUEGQWxzd4rWAP4Qjtug6JjQtaQNt5FueiA/CQM968f47vuQ7PPkGK1F/M0QHr1Z/76nH3GNB0+qd9wGPfUhbcXiDyuq+fX64HPD89kT/u3f3Ez316/QreengPn3vvrRs2iznDRfc6AdjHaUJOGafhVDYujOswpFIV2UN0UdcP8D7I5l+M2G6vcdjtME2jBBqQpGqSdyX10LnKO2vAppVPSDHBeY/EETHPyGnEZPqQJOjA+x7rzSm6sIJQJiQQaQRQZFAHeI12dAD6rgMFloJyWSJuY+qQctS5b3JGopyZGL7rkCHgdI4JkhfBpeAbHGM6zNjtZySWtEvnIp4/uwbBa7Q4AXBwJFH50zxKATR4+JDhwIhpxDRdYZ62yDxrVHRWQEx1pyMN+uYqZNrjhj7PkJJuRTHKpczgrPY6LdNrJSgiC32JE/12Z1iBlTqk2zAQtQgum81DymREYAcQeUQQYiLM84TduEfmvfZbRt91WhzRCTftuJeCfasV1mvhiUVyUnQIFqhg8khttfKnCl1wsa9N9heADCqvQreQ4z64EkEEMLwLJSuPINs+Vwcp5mL9++TDJ5jmJBFK3mO1OS1ANHFGnCc4J9RNTGs8vHsP7z/7CEhCczFOs9poNa5BqlITwEKlItNF3rmI4sW40lKtEqRoitJJeXdDYRcwofRTM3/EOtGAB4uWbTgsuXmQFdWzC4vmItN3LfcsN23XXs7G9lrtkXGexH9rgguYzcuz9qtFRGjOqWNrRbeWdpL1X3GURGu/wOcCql1i825xfWPXLa9uA4WObIV80487BixrCRiCZF3V55UAgGKYNE2xHmrs0tZKYUciAL0D5nxzHn3Mcdw/x23/JCDt0raVRqaUS+G1lJLakQCgaeIg1QmVPknfRu/jypwoNgrX+julT/S34tuqDQ5AAdDq9y2izYt/mBd9yrBIUCrrQr7Mwk+/eHH5n9PNygK2mh1pzUbjP+iHBsbW23AB4wkCqpZN/bImXPFBqq1vQT81oMWRRxcglE5AIzslcM8pYGn4gtUAsHnoCmep1/Gx+jksm3XWFqqp/Eb1RSQblQZcSx/6EqFr/V4KWqEGn0lxLOkXoZ5ntbl1fZjtoM9mAJwJrAEZWTmCHZpipIZfQe1bzhpRq5nPJL56lo4ANdztXu19iQJltXuNFqPazwaysuIBOQnG57wUG4WugZRTBWOd0WBQ8y51TuZUwdgSDd5EizAzKKeiM8lXT4ShgW7tumRdWyp2HJFQTLHAphYYZ7RqrGxgnK1mi1kAEhDmyYHwMw/GkqSyLKRm8fzKR1JJUvmRtGJn2aGwCtFlyVm6vomqyqWjawjIgGOHlR/w0uk9/NLnvoSvfOFLONuscdhf44Nxhx+/9y6+98Mf4ltvv42vv/0WDuNeBEVHcMHBbwa4dQ/0HglayRTafmY1ZF3TjlZ/mYKmxeeNuJT/syUZLnfwcQTIlp4iEThVOYrwzCbwGufYQArWDikRTGqkl81fR8iJ4ak1Iqyd1T01A4kMvGGoMNIuoXq2LAAq9rO9EwEFWC9UCnpjUxS3K7xqlABY9Gs1ThpjyL5DA9LABOeSqwraR1T+kpNbB112Am/nAS7AthnBpXCQKZtjJc4AKdjqqsHFR91vipC1gmobib1Qg1YNUAVbBWUtLaVR7lSYnCStInQFLEsnZ4h3H2p/OhlnQUHR9ffgu7uA34Cpg/dnsFeWdiUx3pMACP2whvcEpiYpNU9AugbHS8TxCfI8SWGIPIN5BqC7esMGadgAAPxhD0TdaUvN7hcIjhm9lx2vqFUaSX2w4D36rsOd0zt4r0m1xo2xl8NZv5gR4I4M0mYMl0alGeFLULU8Tx0xx41CINldDaGDAXw1YqIumFU/YJdlZzVnUZJSbEXeg2yjj2QOZGRc7a6l4i5Y+C91V1mUR+UEY/vPnF2TMMp/5lSItIwLNt5AJUsHpLjHbfO8cFSXBQpRlFRnsErJ8t42P2VHf2nUGlBNQNltbbt6jrNJieX6aA9TwtbiQhZc06BaJ+IGGFlk7NFKbUDpWw9azpu2mIWlNzmY0VrlawVjSwNuvFDKjDQeinxzzqHzHr13mGPCPEeM84xpnuGdFJXpugAfHOKUynUyBLnMhcVTbrxz7ZOa+sU1HZZaGbW8jm/8H4Vny60H9OenmPeTFNTKou/+36//GU43J8LL2nVA8Fp8hAGOoMRw0wHusAfDYbcfcXLnFOf3XkIXAj4Yd0jjjHG/Q79aY1itkfsNaN7CeBllcxgl9y7FWXbg+xW6oUP2ATyPhWMrM2McD1pBV2gDUopwxiOdEvbjAXfOzsDMmvI0oR9WatQmxDHiZLMBnKSzTTFis1ljexgxzZKds9mscJgOCLtrdE+fgJnx15kxdxv8KAPj4VCdEaDIkbKmFz9U7IMKmmNx3m26uJGCt86PWw+qZ6+7GRA2B5z95Mc4yxWMtyJFNs9Nf4XHH9VbvftjuLSWKra3roPbjx0YP+ru4IvPnqLvhIMt7K5EflJGm9boPCHnhGmcMU4TTk5OlYZG5GZKnepocfCcVtUNnUdOERdPH+PZk8fYbrcYx1F4zTiDNP3ZIjkIJMWduh6hs/tIf4z7A0IfhJeOMjJPyGmG8wFBHbG+H7BZn6Dv1sgZ2O2vwJwQ50m4XbNEY2b2gMtA15WCH4QMooSUZsQ0wYqTFPvIAT54rNcncIcZ07iXlEknQGBWxzHPjHGecX09Ypqz8ucmPH+2hXcB6xUwhE6BFklvjnHGPEUIlVRS+35GSgdknuB9lXMSjSJOnwVtmN1942gRNlTdduMc4+5Evb/xzoVuADTlM8eIHBNO+hMQeWTyODkdQJmV+1Htf7MPGz9mTozDPCGmhP20w/4wAszogsejh/fRh4A4jhj3e+Q84869c6zP7qDfnKBzHWLM2g4Do3QNmV7QxVuArOb9ytw8skGcr5QxRCiR2aazyGnBQRY7qEfAlfL1ib/BePzhExzGGXGO8MHj5PQMvl+DvHENjuiDrIeBCA/Oz3G+PkHaXSFPMw6XF8gGaC6AIMkM4Wmq9HMASgpM7d461BDZZJk3xqN4wyQgFKAiQwEGMb1LYSEiyS7yvtN+kihDcAUeDIRqAbm2Krl3fgGKmYUucUXVL5Vq5PWM/WFf5o0V9TGfwWRxzSIF4Bq+wiK7l/ZpiWg9+s76OyHdfk2ZLVgCRY3ndJvkL/ZY8ZXsPg7gVHQRH19oA2RuEy/BqZxbor3lWm6swsUnWX0xKFcpnAc4FrvpNs772/rptiCgF13zceBs6y+00aQ5SxFReAfmGljhNFLPeQu0WLbLFSCuUho6DRCyIJha8GvZRmYW2ISMoqhuOtg5BNPFJn1YqZC8tq0B7SyjAy31gHKlhyBp85ZZk3m5fqDBYzbXXQVtrd2lAGzpQ6Fo0DMAkkJa5i4R0f/H3Js1y5IcZ2KfR0Rm1nbOuUv37Q1ogCBIglhIYEiKM7SRTCORks2TRsuDTC8yvenvjcxkRtJgmgGNFIeSSHEGFEAQAAEQje7by13OVlWZGRGuB3ePiKxzLsgZ6aGz+95zq05VZoRHhO/+ufqPCKw9hqwBlyMt9Q+u7GdL3iMmDSSaQ7Ph7+pQBJHqfMqzvOrmYOQcKhQJqNhEVqpfeoo00CEEKtAN9l5SKBlmSZwIToK3zjkwMTpSh36ukBRQuWDZrVDHZ0oJlMSfVrJ2nQf1VAI/OWck1Kxe50X/ATFSIiAJPKjYrhWXt+xtcHGmMljo6AjBdfJbheqJMWKaJlkDpQkRIWrlaotb7p1AAHhv+zar0zaXaj5LhgABnGqCmfERp/uT2KM0p6sHcnE2iYBoPMpxmaPpoG1Fdjl/egbAkB5PpnBbzO8V16fEGcti7Og/jb/EFAWGpMhc2fDZDFBTgp1ggDnFMsmc4GEMDuUgeHP0Qd/LDrtwhs+89jb+6Te+gXcfvobz1QqroYdzG/wff/WX+Nb/+af4yc/ew/Pnz5FyRiAPCh7UOfjzNXjtkZ1k3CFLIb940KnBSlHFrzCxVkS07rglAahhRiapFkJG9ZISLSkONtksGTVSANR8JYarWCwL0dmkcFukrKUXoIHn5YGzh1B9sxlp1shCI7BLzUgd3FKYtU52Ku/ZYUqpbf4iypSlr5chmOJZ9Q59/+57dqOKq6cKh2IptQ1xbKzei8GUFQTpdLwtlkqJ+DUirFgUWN7bBF75dFl6FkUfFRNMxpqRk5YPi1aMGqSo982Z7zj0DIsqK5J3ASlvnp8254hPPlOIJ8Knjj2RB7k11uvXsH3wRezHgMNEmBMB6IAcgTwDaVbCEkDSmfl2orq0JFEn59YYQo+h22LXbbHpekw5Y04j0nSF6fYZjtMVUp4LLdM7n5f7jCP8331fBE0jvDebDeZpAs+TjAe26xg5R3z08UdNmbxFIRvcJJiivFTUiuBUHM/6+TubqzB240nNbxraMz588WGBWPAhIGVj5nTH0e+0JJEYWm7aYZy1i28Bl6ZKd2jTijiX8i9HDJ5nxAyM4xHXN4yz3RmOx2MpTZuTYG6aQmLzNizcUtqkQjA4hy50mOckDoW+x/V1FEPjhHamLBhtTpVazidmc2NkdF1/p5lW+R5q9NjOYFEqTZGSp8MCGtDvSAhNaaz7vBxfNIor6v5ofwqm3HzymbqPXnmxQEV473E8HsvbpZFGHYJx6mKQsDFHtHuWy3eo8DBtIuUDPDncHA44zBNiFMVqCD1CH4ojMZXSKFcMb7mnBvvusaDuBCRIlFnjW/ajpXA7Nyqns5papHs6kpzt7mKHDTPGF9fIhwmcRP7+qz/+N/ilX/wF/Cf/+Lfw9NkzdFGU+uwy+g6Yx4Mos/OE1foMyRMevPEmzh6+jrDd4cff/nOk4y3iPGKe1njw+E3sXzxFjgc4nkFIOmJxZyQNeg6rHagfkMcD9i9GhBjBnDBOE1arlWRTzjNySjg732GcJozTiMwZu90Ox3EszoPz3QbXt0fEKPiq2+0O8zSCkdEPHbbbLa6v98gZgvPLwNXLG3RDh3e+9Yfgf/2HuDlMuNkf8S+Cwwc/+yn+7E/+ROQmeYwp46BN7TYECFonoSdgDcLgAgbnsHYBPXkET/AAAomvdCBfsmBWXY80S7aiY0bHja7VyJPWIQVAAnBEAqPiRIb/9v/03wP/8/8IgPHf/nf/DZ7+7CnGlDEycJkn3OSIIyfMgEBVIeP1X1wDv30BAFj/D/81LniF7uEF5uDgqZZe2+5qjR19A++EGb82THg8eHzlV78ATxm3N9e4hTk6BBIrdAHBuyIzOQHXV7finPSErpc5hbACgRDJIXigcz2mccTV5Qv84Ht/jfc/+BDHaRId7PT4mK6muqpkrECNPeOT4gwJncew7vHgwRkuHp3DB4FI6PqAYegAjpjGPcYx4ng84HB7xDgekFKE751gBcLBkcf+5gqA8T9p1nXY3wBIgrPW9TIG8iCSM9V1HZAIcTpiShExZhxurxCj4KfNGiC9fHkrJalOSgdT9tptWoxia06WojQ5W/UdpFV6VExYh/VmA+8jxkME2CF4aUxXKlWUMGZ0n1732UBsPs0ltGUrLtUBIoZU5504ZEnkaEoTxsOIcf8Ch9s9PAieem0A4hC6rmRFMSTT53g84ma/x2GaMaaI7dkZXnv8CEM/oPMe8+EWVy+fif4ZOuzOH+Ds4jGGzRYudMqnR3AixUiSgRb4KiZtwHYPnqjZP/YeQ7FjM47zsdEvxKmW1DFomXuWweXJw8OBHBcIagDIMeLm5Q3m44T99Q1CGPD62+9oeTRjtR6Q5yMIhD4EPDw7w7tvvIX4fsJ0e4VvXB/wf11sUVMDGMyk1Rwoclp02SrjlgkqBtEmjQJ3ux3GccQ4juL4bBp4cfm+sAnXOL0AwmoY0A8rhK7HyxcvS/UCNOmB4TTT15exVFILLzcdqu97KQFu7BbToYuB38zF7CXHrtyPgBKQAbDIRGRmlUVYlEQz88JJUebOS37YXvc1MW2JVqxoopM9Vu1r2zdsjgizuWw/0clNUQ7cYs82W3XxafX4VT1u8T0bRw01mhZJkIAReQIFsUNgztV7YSwqvVodbxGEvMfp+uqEofr709dsZ8xJA1Jb7+C8OJf0GZKRSCWgazo+szaL0gSZMl7XrAMM912cj13X3Tv+EkTwHn3fF7vZZLrZOVY54DQrVJ7bNDpSvS0zI8Wo/XUIaU7wH7eGiAAAIABJREFUcMhWfceM3GZ1qBbOZAGIMjC1M0JZ82IzMxQPt56rmOIdWosTVyHsXABnIFk/GX32ciPLd5JChBGwmF9DNJEptlsbmUL3rLlgjLrCJ7xmrRV7hqvdI9m3rvBvgmZbel94QgZrsIgXa8rqgIUmM5Q9BqjjsPqgOsWlNUdjVjobBi4A+L5iyuaUNMFFy/b7vqGzlO3LGhnQtYxLgn3qXwmd4sNW3uy1sswc1nYJ7ak4URmA1z3YQh8YXcQBL87reZ4FfqesXywVbE7HUpz7jZ4o2epZG8nZu7VR3d0AXA1mWdDD6R6I+S4cn12fEmesCh9Wgdu+rwyUvEVaJCVcUrDJJCoAlKhEztJJra1IISj0HYSUDoQH/QP809/8HXzli1/CkwfneHx2jinPeP+TD/DdH3wPf/BHf4T3Pv4I++NBypQAhHUHt+qAdYc81MwbYhIFQfhkiXa23ZjNGC0gylAxVDlNHW9jRBRA+OKWoPo3idM368GVrsC+HC7W25qDQZiCGdVkv2yohCIEkFHLFiBZsmUURUgaZtF96i4ahlQxZSxs0Ea1TnaD0HP5lt2m0KeNnKOMEjiFh6//rlmsQNbI4XLsrOtpAro13hyaKHTmmtXLlc4ANOKT7jBf+1BRGe4lWc0GLBPOp/OrV81qvodYzZUzg5JF6tWZwhDBrUpAid6RKCzzk88gb3b1rgwwAoh6rFYX6LoV2G+AsEPXP8b1scPhyKUDITDrlwhgL8ZVmUICaESRVDIZZDASZRx5wn6+xnNi0OoModtg6M6xe/QW1nzANO9xHK9xuHkJztfiJAkD0ue/BCDDP/sQuL4EiPD86iWg5RAgEZgEiZLOs2syQGQ4hl21oCjX6FxLe9Ly0hRbJltOnn63Pdemb8oedBDHZd93uL65QibG+W6L3WqDw/6IUTuJljWkJgrnHGaNPDonzU/SPKPmj1XCinklCmqG7NHOBzw4O0Mgj5c3V5hjBAWPLnTY5706tUUB6Pp+cR5smmz7k1VhCB5d8HhwdoaPPn6G4zSrEVKjiCEEDMOA4/G4uF/XdQtFgNQBYUZi6/Q1RRGoJSklK7ah0amRc7o6dhpbh21mlkYFULxym2tZw7uKNqsj1ZyprWJgv783m4LazwCTdoFflpadXMw1KEaoysOreDDUbs+M3XqFzjnklHE7HnEzjrJTNFPWDO+iuKtsM1ggMeBtr6skfYXh0b5njQ2WHyi3uf91+5KktIoUcylyhjtbY+Uc5us9Ds+vJcqvn8/MeLa/xsZ1GMijdx7M4pDlMSHNI+LxBr13uHr+HP3uHA+ffA7xSwnPfvx9zLfXwOEWLz8Bzs4vEKcB0/4KLo+ANj5w5LXaOQheF0vZbt8P0pHYOazXHimOmGdpzDR0Aw7HA2LKghVJhOPhiGHo4YNHzozr2wOIPHZbwfg9HvYYhgHDZsA8Tbi8vEYIA7adx/44YZpmnG1WcJ4wxhkpM86GgHXY4PY44Y3X38B//nu/hz/94z/BYRIIlAjCTMDkNIND5YDLjJCiOF8xaxma+KsCETwzvBk/pI6fLHzVgeFZnLukjI7MoKCydauctDPForS+cXWN/0zX/N+8eI73Xj5HBCMTIREQwYgETMRIer+XzR6bQYjOI/hOM5epnN2i2zRnJDMBlKveBDGAOWekaEZEbniLBVglAOudx2EvTnIiaU71Wr9C30kDqpxmTDEi5xlXV1f48MMP8aMPPsBhnotTopwRuv8YEMThJdk4+r7R/0CgmyM+fn6DixfX+Nzn3sLZbg04j5wY42HEYT/ik2cv8PTDj3FzOCKm2kW5OMiVlyzi2VoZRbrXvfPoOqdYqB2GoceDhw/w5pPX4D1h6AeM4x6r1QqZB8GDPxwkC0Uzp7wPGPOErveis8aEMR3Ruw4GySF4wOIQLk4HZIBE7/CuQ0rT0iGTBZ+PwIr/d5cP+qayoxK5Zow5W4BGHSRy8GQlp1lVMWnS5n2H0K/Rr0XmHm9vMV1dC4ZqzkCSShwQ4EIAKYzJeddjd34hRrAX3MoYE3JMSFOGd71k6vc9Qt8jrHqEYQXyQfgOAM8BMUlwk4pmeso2lzpI3U+699UeSAxMnHHkWJM3sAzag1DomjMjISFlhusDaMqSCQwgIqJHAEfGeD3jp9//CZzvcfHaY2y2W2DYIFGWPU3A0K3xxutv4Gp/wJQynh9vgZjBmn1lGUaplS1sgeY6mzJWUgQDdRIdDofSKIfUSdQSyba/3beln/cec4pIxwP8bA4d6zMQJXBQvnrXUWfvm2NlnueCuVixIZdzACpuYVJ5TvfIVSoZ7GyrJU47BKTcdh2vPOZeByIb7ECjSzRjMWvw9DSZFWoNP5kZx8NBstUK7nDVsOxHySjUuVuW3/LmlftRsQ1kDIlbzmj3ppN/3bfzFyMBE0v/A2aQC+rwy6/4Vju0pZPrVZ/5eb//effOiQ3OUzeyONGiNd7VNcxJMmgdCU81zM+alKVYqD4Up5cF98AkWeaoUFiljJwkczKlRuZlaTrc6taW/VpseFiDKsOKrzifgPCaJaSHyNA8J3UEEnJMi2QN5xxAkuVpXyuYs9D1NidiYw+JU10+xRAH8B3OqHaFU/g6ApVzzanRV0wOMKEbenhNskga0HHFSWmywxU+YY2jzIlanqs3rZnDla7BHIiQs0El2MCalNLYDMwSFNMM0KhNrCRsrnTXtbX9ZTzO4I+YWeEDFE5LncPlnDBrTxUHl90dHlL2AyRjmOCaZvVyhRAUw9yVcw84gF2xW7z36HBXbJ9mZLcJTUSaLNfQ0vbDYp1JEiP7rsPsg2YfWwKPW/BKwGzzaj/74Bss4qA8nctetWBb4fuE6rQnQqCgOtRdPnp6fSqcsXJ+VDCwpdq3oAMM0jA256yZaCYwakSDcwWBroyZy7kiEIgdAntswoDf/uo/wje+9DW8+87boDxhnI/4yfvv4/s/+Vv85Xe+jfc/+hDHSUqIgvfoege/7kBDAAdpKFb8HuWpvPAvLbKTAC2hrmK0NfLlFnXRxPbVlGgTgZxF4HERoaiis4qkZaRQft8koi4af9UnyivxWZmSbp9XHNHWsaR/0+IO6uzjZlwNDRZkakrCqpO0mTtDjMEmGlznJ0z/riNbVrpkCTfGxnIA4hS3rNP6QKr3ZFbsD9HQxeHWRI1yvRdzq36oIkW2dsZQ6hjre1gwg3pRwW3N5S6VTsUhzhJ1WtLwHmdRRaPSteFqDbO66hngfoV88Ui+sdqAXQcwgVyHbtjChxW8X4NoQOIBKQ1IecAYCccpIiYbV6WhzYKobY7EQCkrBEAsZfrFECIgrJA5gxJhhpThz8HB+S0orDGEBwjdI+TpOeJ0gzjvkekIohn57AHQrwRK4NnHWt4t9xecISdHiSWjfrH3Gs3OGHN1kVcgelmDjByrk3upKNYjeDcSXo1waHbFbrtDTBHBSVMYMQCzrpxCGaBiMwGQCaliG7Xphkrt5flbHDQuJUWOqHQ1lYzgjP3xgKQN64gIXejRd72Wt0ThSWTdNoVG57tzDF2HnCMOB8HyVJMaKdbxe1cjlsUZYPo6cynVKU5So1FhKKQBMIDIKNP+ZwpLkxnQ0quuAFBkTlUuzKir8sNhs10DxJjjjOPxKBlZOm7jfSUDhRmxlU92f26fXHnDMrOUa2MxLJX/5acg0BEn828LbMv9lC85IvTDgN53mOYJ0zxjjDNY8WGJlkpJoYkG5JY8hRY/T3nNshyzDrq+1X5PaC6K9EnmOVrHutPGQLXMkglwqx6BGT5GzFd7cAI+fvYcf/nt7+DrX/0yxpyK3odMcGlGgFQJxJSwv73Gphvguw5z8BiGHXYP38DReUzXLxGPB0x9hxA8VtszjDczOtImSD4gjWKo5ziCo5T/rdcbpHlCTrE0vei7UM5ezhldF8osu66Dcx5xFjzOrpOswZSkw+7Q9yAHHI8TCIxhGBAjYxwnEAGroQeBMI0TvPcYeoGY+OTFtTy779EPD/FLX/4K/uLb38PtfIPIxpWdBMBUHhARZhOdRbdSpZtED2ix1skwiO0NZnjjg628tV+Xt+oeNQPmqkHt/gSMZ8Ql+U9MZdL2jgQDzkjNyZCzr+V0jk5gr04vAhTTy8BYfafGLUNlAgpfzIkRo0JOWbYOAV0fpOoiMzgT4iylfxkS7JOy04jDeIv9dMDsAPS9ym0xsnKKaP1EzvDQbKSNoV3kkmkTDKQ54+XLWzx+dJSqkt4jhB5znHF1c4NPPnmBy+sDplLWSQoXdYciJeAlc69QX0QR3qvRqxk5VzcHgBMeP34N680KOUdEMIauwwpA368wTwKPEUJA13fIOaPvBRMuzxHzeMQeImMsgxJgKQl3xqNl1RcOQhjrLIK67Fnw3blVvLp2srINqdzzrpxY8CyyP7JYzgf4MIAooE+AzwJBUrC9AA3WSvYNCECmyvJVv3dIyI7BipFreIquq41TxHlAZf/lCHBO4CSZbm5RstzKgOU/lVSmCSJcXeH8e9/BiwII1nxH5XPRvkuTMKFD13Vwc4RARwFJT6V0+yRMNzM+ef9jABLg7bqA+QgAGdZIabs7wxuvv4k5A5fvH5BzAjvBZWVuBPFiTQj3/gItPibra/nptHppKavucwYKgXznpPQ1RqRo2PSqj+WsiS1c1NeSnbegs9AtswT3t9strq+ukZIlsMjZMp2FAKxWK4Evmaaa2YWqZ2SDDLFtf6cqSO0fq2Q8md/CmWi6RUsXfa9m/tk9efG61XW58Mtqjy51Hl68Z7anlS+35+7UJrLPAqLDpEbOtPc/3eP2vmW2Vb0QIE/wnQd3Aa7zyJWF/IOuU4frabD/P/jKKLZlnGc4SHMsp/Z+p1jSpkew7l9ZcU0MAQGWwJEyMimklDXDIsUnVVkgjleoc9ecn00SEruFbF/MVY9nceCpPkds2MXyucwSnDJHGtQZ6kNAwbklgFI9T8r5yzF3JFAfQRshlbVayEUuzwQUd9VK/aHyrNlPNp7a8EowcJJmWjJnyTa36TrBM3U+1edqFrLp3+LodehcB5dcccjCzhihQE0AJJnCCncSUyowESBCsMZYOp9cxqX6fudbqxXMQMxzGVrJ2qQa1BFYH7Ux9F72OTujnMWWiVFaSPe9QBgtqgdZA9WZC0yDc07gEMjwWrnhA1z2nsDGpPIZwJrI0QKzGLrLU2KAcz2/AELwxSlucxG8YFf8hwa72V5iOgjtDTrMnmNY3Ayr3lZeqFAadt6k0s4c5EsIJ9mnoexFc3xXrNtX84lPhTPWDrA4SxrjU/8yr76BFlnJpZ2/snCaobEwLPW+BClDCQhYhxXeefAEv/W1f4QvfPZdbLcbXN88w9P3P8J3vv83+O4Pv4+//tu/xc3hVg6gl8Parz2wCuDgCl6ka7TmIrIaQ3xx0VLoFOZx8rE7MqG0t7Tonf4RCdMIa1UUIZhQ9T5V8MNwUGAM5O5aGM3roeAyv2zzMyZRHFNFRtx7FcPC7g8sGw2UJ9iBaeZZhP8pXe4+5dQHbbQpZOb6nu0TSSvXTBnUwlk7XMJAtGukziRzAieNerXl/c3aS3ZxdSsxuOCOSvOgk4w9umt0EVFjLLTCpjIHar/QkOb+tV1Sxv6V+0H2xGqLePFY7uE8HAUQevh+h66/gA8bOD9gGoEpBcwckDgoNow9+/Q5DDGbZwjuUxXasvxcnP2uWEkAfFdKyvMcEWPCGANCGND1PbouYNjsQN0KU7jEOF5hmq6AdI20PgPWWzmTtzfAfARlcf7WLHIZXwh3D2B1prVv296tyl8uDZGM4vXfdQ+3SnBdB8PYY0iJWdd36DggxohxGqXDJlUF5fRotQ5LwT+a79kFJvzlZVKgdK+lbHOKiHPUpizCQ4/juOANIQQRWlmAPJhEiXBEyHpWh36F9WqFaTri6uYKcb9XOlNRzBh1z+amXMOEbHHEtsqukZpsxpoL5JTHFWykewjU3P+uEcIQ51NDT5H5AiPW8L+u68GUkDjibgCrLIZE9ykVpWbJ/xuluVE02kG3VQclqHgiS7i538J4IHsmULm7EM85Emdi34NTlmzlOJeSrhLdL3RYKrWm/J46Y4tOTjVi/soM4MXgm8DVPYZMea953GL27Y/g4NYDuiydcPkw4/nLSxz2R7zz9lt4fHEO7npRcuHgUiyKETjheLhGGFZqoCQ4eJxdPEYg4GqeEG+vMO5v4bZb9MMaY5C9QKboiyaInCZRrL2DXw1IEcV4F0d4h8yC+Uok62FZlz50yCkjRsHIlKZ8qZT/hRAwp4g5RYTg0XcBcZ6QUpbIvfeY5whOGaHr0AftfBul4NdpxtJb734em59+hMtjxHw8YtUFJGbMWTLdCv2JFljtVqXjiARegE90i8oOq/Oemt8vN0PRH+xyRCAmTI0j8Ogdjpr5wCRZURYghqvnmJv7mA5U1rdUXS/37ZKnqN7EDN9Jebljr2WQDoxY9nRKuWLHOQInbroiczkjpqRzlizAGKWUL+YE6gKcC4qbLgFInvSc25/2PBCKo6aVG0vaE46HCYfbCdM6Yuh6dKHH7XiD2/0BVzd7TDEjWxDM3cMqC00qZxMM8vqBOVVcfQC43R/Rd4Ttboezsx0GxTnu+xW8dxiGFW5vPWKcJDtWG5Z45zVxAkgxYuQDMDACBw2iK/Y9dfAK7UhUajqURlWvs6C+TSIv9qfuscWerGvfTF/mdq9jReSEZeUvVFbI2XKhh1t5hIanE+yDNk6WMlauxiyY4X2AJjiV7xSeCpTMGucImUnw+Vwtv01ZYZnMiKqbu1mt+rqIPzDczQ02P/wReL2kmNGj2ACN3mJnsO96kBsBLYO3ck6T23kCrj65QtcNWK1XePz6g0a2S0HNsFrh4cPHOE4RP/v4I2znI/auK5nvkthQJA6MpNV8qvcTmZiLUU1Ux1wCfadQSXreFpUobOqGZCZmZg2QVSeWOTjkUa3eV+9dnCZ6L8tQzHKoi5SG0rgLHVarNWKcRW40EAXLlTmZQzN/kENlJQ0G5VKRhblN7U5Z9XG72moj+YoJ+8o8mTVbNeciI4rsNyeMraMtuLFldfoV4xz1/KFZh1NORVT170p6fW0OJdT7oWhs8o7gRRIoOKAPcF1Adgyc+LTvC0z/PEfK/xeHbKubZtbMuihl/MhZg8kyBucaxxBsn8meJ9tXdl65QlTkbE6huoPsntZUGRpoKDSGtDhc6MmtjmfPKtPmupbFHgIou1LVZ1zFkWTuOs1oc45kHcoz9MwW6A2P4KR7vWEnL/XNmrhiQWXnK5wSAA2OVhvD8INrqTmV7PVkiScxKkav4It6Epzh8mxNyGLFaXa+NsLKORSnpn2eIBmwzjs4+CJfOWWx98BgIunj4ZsMdzhQVAzVBsPe+qM4T4WnGh2C/t4aoZFzAhWhDtlEtMB71YWDydiUIpicBI+oqlEp257LCn+gVddOoK7gfME9XmSQkoNnhU9p7IWckyYSUem1IOumMDpRmjeW7FISZylRdcbmJHN2iqssH8wLW4FsD+hzQ6AiTFr7Rs4Hlb1e6NJ8po6j6iFQu0kCU/Y5KnuLqoS/9/qUOGNPmFnhv6T/O5WZNbvTQ6JkZhqDtaGMMQDnUTIGmeAYCPDY+AFvXTzBf/E7/wzf+MqvIcUZN1eX+OTlC/zvf/4X+Itv/zs8/eRD7OcjiIDgHcLQoVsPoIGEMapil5OKKI2+wtUozOlVR6ZLvdSn73xnmaVlmQxU5kjKjEr3QFSmTgQpoSwKQbspGIKrJJmhC8FuDJMaIZzlhjUVvw54Ib+aTD++jwCNkDUFT5xYSxByFBrpfGipkBQQ9ypSCr1aYWgHstC8yUAzxcwYdVFIysErhNeo3n0TqgKxKKw6moJyQ1QNxwZYvPyuDrAZW/MsdcTK+t87ALS7qi5ldfwUegg7r/fRrFhRdgnx7V8AfKjfJg/vN+i7HYbhIYbdE0yTxzhljMeIOTISemT2yOwKt7NSMMuqkrqbCM4RnG7VcLKRqWKheycBllvRGDIGLSzOcxAjTow4EY5EoNDh8XaH3dkO2/O3cHO8xu3zHyDNV+A8gigjvfU59B+9B7e/KjqiQInIZo1zXDDizKwdk0kVextLA4JfxkRosRGbxYMp6NVZZXtPFSs4ZM6Y5wkpRRAIZ9sdmIEpzkpSoZEDpGyv7B3ZK+M4QYyQtpKg3evAZrOWZi3IuLy8BCD4h0zAy5sbLYkhNTZVZOTmBszSAEj5XALUQaDKnSM8e/EC3hmNSDtbqnKopTNeS5rnnBBnURJ9wUEUGqZWia8spawbiLEeBmyGHiElPJ0qpqnNOisvOAXAL7elhh9SzY4VdqN7Up3szjnc7vfStTxncaSg8WZwXvA7M3JKZonREC0PRhlPy1mKM6dZw8aeWdxrQRiVkfXt5vx7wno1oA8BLmd8+OIZZuXFwQeEoIrYicHRGmJt+djpUIgkmwcQR3+Li3daAnSfjLPrVXjMoqwxEjJcF4oBKJKLZC92HqsHO3hm3Hz0Aukw4/Z4xP/y+9/Ef/XPfxePHzxAogywdKl3OYMgGehxusXVs4hxf4Wzi9fguw225+fYDAOGvsNP/+bfwo0HgDNSTDh/+AZuLj9GjACyBORysjkTOHvsr14AugellFMhOCAl2yBgmicMfY8QOhzHiNvrA9abAX3XlWyszXoNANjvD4iZcXa+RU4R+2tpgHR+tsVxnHA4HJAycHGxQ0ozpuMexzlhuxkwxoTDNOPqMGNi4J/89m/hxz/6Ef76O9/Fmw93eH57wMvbETdp1rJ9Ox91D7b7glRJ5ua/shmYQV6yg8vStsY2LXe8PcM1924vUw2YRd+zKgBystszeJHJ6TXbzgxzOxKLfWeTYxszINh0WfDSNMsjhA4hBEzzJDzCMZxjDH2nDbUAZsHMDl0HBiOmUeAmNJuRnTRsO07HBlPPw3cduBMDr+sHzMcReR7BcZY+CFmqLYSvA+BUaFXXpWbCi87hMY8J06TZuy5gHKVDfUxaLt/YAjWHTV7VTNlKLedUN6LKXWQF2ew1PP3wJR4+usLFgwvszi/kXioj+36Adx5Xly8Q44xjiordnjRLpDrMUpph8AQpz4jTjKFf4exsB+cIQ+fA0WMem72iOlQZOUONwHSPXrXcCJXHmv5JhZ8xczFyoTKu8b4usmmj4tyCqxPY9nHmjDjNyDmq8Ujwbmgcw9Ssgw2uZooVPSG40sRtnBLmWRq/yXhFFplsaQN8zYibWdd3LSM+FSy8BcVwh4h24lW0h75fyjlkxDxjggTwXXbIh4wXHzzDdBzx2uNfkzOGqu85cliv1nj44CE+++QtfOOn38df+YCXWg3HKTfQZifX4q3cOB/vl1dCp+breh6Ko8RsK8IC892pE6PaLwqHkUqXiXoy78hPOQsxRjx79qzes50Ai75wfn6G7XaDw2G/mId1DLfLHBd2Pu8EYRtZXnlqladFryI7R4DjiuluAVrJADaaVocc6+GfVYcrvIErDRw16UCFz9alqU5bWwwUWlt2qF33wXNapqdE/5T6TCcfqvaZPS+4UCZPnuD7gNjwxEWYseiFdU3b351ep0Hof5+LiLT5YUbMWRpoe4dhGNCFoHjFdV4Q803Ob0pASqoD1gw8a2CbWPasZFEngCWoZp8zrFdxsDpjgoXO1s9C+Jcr52bBSyw7koDOd4IRbnRLVce2xlAAw7MmGhEBrgY5iUhgnwA4FhgUswct0907angPA/DgLJAExY5ny5RUPdT5YsNI4yd15mlfClInYDcMAg+RAryP6qyta0xAkfEEp02s9NyxVNGY7tf3g1RLAAX+oSRwmW0I0moKLo5SQBy7VsFo+KomW3OuVQjGC4gGWQs2eAYZr2HLhq4D+r5mRRucou4/8hKEDtroK8aIcVY4nOKQdtJYzv5AHK5R59hpI1CrXhTelzBr41BixhBC2XsS5E4LXGuDVvBOsrJTEkiYlFPlhdRppY7Iv5gS9sejZDg7yXg1jH2oXZVixDhNQhPvC+ay8ZvTZJIF/IB+TuRCLtVBsnWlSZw5n636HaxBedU5xW99WslQr0+NMxaOirfcrnrmReikLJPxoprL340zreQPZEjKKotq4yGL2rPHL7z5GXzjS7+O//Sf/MeIOeHF9RXe//B9/N/f/bf43/7sj3F7e4vICb4X7MMw9EDvJRu20zHCAqyskZLqjLqvmYyNjovy2M6R1JhuBS4VI4OVNsKQWmEgDFKYCFCiV6zyqaPi/yOo88nux/V9JlXEM5pmUXKZqqG/loNStfnmc9D0+vpeK2ONUZ0620u5970yrDUW2qulb0OvcmCMPu3vdTblpeGj8eLhvkSSnBgwlrZ+MsD2sNbGYdWYYQCshmHJ/jUXiQqf8i0zCvVyzhnwlbxvEA0npGATYgtSLHPtFpSyw1ToIxAN3K8xv/25opl6v0K3egjyjzCszwHqMc+EF89ZE9MdOHdSmq+bo2AQk2WuZCmhE6mhBzIBicAIgO+AMMD1Z5pplcVpm47gfBShygmk0S/zhRMAaCdyGb8DYcb+FvC+A4UeoX8Dj996hMPhExz3n2C8eQriPdKTd8A3Z3BPfyqKCBv5SBpRFYcZimMrmxIAkZ0m5MVJ1ygbON0fdT9Y9rVFXNtrvVljniYpZVGF4DAei2JDEOeNNakiQLrE690lol0xZZeGdt0H8zwh5ZrVDdLoO+QMBlW8vfMY+g7jNKEF3I4xImoZSbvdg41lHpHSjJypYAw6psaJ1/CMdg/qfViJVvCN9FvGS4vxD1VWUwQnj/WwAnAJZsZq6PD44WM8f/5clNmyEFQMVRAVAPfWiJd1onJOc55rRJey7jknzuQFg+HFGTThnVKqWJn62fuU97vOWTN6qI6/OB3kGoahrEmyeZ5cNkQP4PUHD5GTQE88ffECM2f0oZPovJ49k7GFDkB20fASAAAgAElEQVTh13zKu0/noPMVRUQyz01RNWX5dN+3z7lLk2YeLZ3K75anzQGlxLvfbbCZE6awx3x1gCfgD775RwCAs90W/+Kf/x7SDEzRYXAOu67HZtWBEBGPN3iZZpxdPAHzjND3WO0e4p0vfBUf//SHGEfBPWZkPHz4Fo77S+z3V/DI6IjAXrIBEtdofIwJh8OM1WoQQ0ubDDADm/VKaBcTxuMRjx8/kEYzR8HR3m42OBwOyMwIXYcHmzVubq/hyGGzWaPvejx/eQmQw2Y1COb07Q1IS8Uu1hs8e3mJl7cz9jFjVhruhg6/8bVfwdd/+XP4X//l72MVGK9vO+yGDj97eSPYlI3BbvKNUGwm0T3UkA+dZbfU/WMBK0AzWsmBWWBXlntMV9nwpFvQUscWq6tHzVHJuuVmTHblzGCPElRqs7hsQrnZWBlAzhFJ8TKDF+gadgTnO4RuDTpOcJadyR5dWMH7HqHr4cMARwHdqsOKOgA91tsN+n4F4SOCT9b1a5ydE8YI4L0PxDgm6U4/zhGJCNR3oF5pnwEXEzjZH3HmuaIncDkH8kd0uN3ZGXbbLdIckfyE42FEnDK86yCur+ZcifLXnDL7XV07O3enl9nhzOLMu7p6gU8+CuCHj0FQXM0sBrKUihKYXcERzCkhRRn5MKxA5OAd0HuH3WqNm8M1MhOCFwMxxwmA007KDilmSGffVMdPgAsePhN86O+6EU+cNDklZERkR5qUYHtIqwW8v2f2io1nUBVqlDCjln7q3rdvOueQWJyUKSac7QbYBjZHrAXD7nPmMDPiPIsYcMr3tdkiJzRJ31UwV9lX79e+smMXc8bEEaPqxgt5CLU3GI2TxuSp8oKhB6yJEJkZFME0g12CGBUOeczYvzzie9/5Pt5+93UMqwHOB3TOY44ZwRMudhf4wud+ET957yegxOCUAIWtMOcv2TqSjdCM578f77Os7wlN7l7mPJ1QeVqlikFFMCAY/WwB5LzYLVL9II4NK+Mex7FkAmbm4jwyZ+2LFy9weXkJ5qzYsXJm73fyVdzCU4dr+cTf6xxsdY/mLRZn9GJPFg+cZqypbnb3jNyj55w4NYteY8+lu59fzonL/mwz06pDu7GpWx/Cwt6pmKJxjuCYkWapDrqXyf0916uctP8hl+lYLhE4ZngGtqsVetdBDOuMzFEJUBvMhtAVnRl1qpqFKgFr57qiixUbJLdjrskiznkMRFWvZBufwrCps1JwwF1Z+9g0TBaHaUY61sz91sFmdm3OGWPWRAqy/ituoTeCWWCQWPPLmRFtTFQd9/IMCZCklFTfFkfmmCyowuXxwbf4pyanZT3neV7ow1kzQFtdPU6xOJtzqk7dckQYpeweVJNDjBaClz5qqw2189qkNP2RYkRksQtdkTso92GTIUQlkF4bBFZ4tJSk+ViMajvrGnjnEFwothEzA4rdK4mPhD7UhlzMjDgJFq5VapAjdCQNzQGgI8n2dU6aYoXQIcWEGASiiNHSQoLVQy9NPM1RzywY7t47BHLSg0F/Z41BBVaiK76Aru/FiZ6lobUjSZz0eu5tr4zjWKEjIM7joBU7KSXM87zA+7V522V0F0c2I3QEl83xLVnLaaoZwc5J5j0xNNjyal7x6XDGmh1sgtYOnP2tyis5gmNRkkxvN0bmCzSBYs6SZAg4Ju3+Cbz96A18+Ze+hK9++StwfcDhcIMPnn2M7/34h/jz/+cvcbl/KaWbCu7shw7cOwiKPwoTbKOhvOBaxXWzcAYuDU97T7/fMAmbumTk1W9kVTgcV6dBq4qzSTT9kve+pLK3jy3ZD+Z4IBN8QIJE44RZaBZfroqdOQgkk7IKYVZmAWItXW7nL5cdhBIF0uEWahgtCmO1jN2lg6DOx7JvGIILcg/e4InhVy9zzCzvaMox6byF+S4WYfG9kpmhTrPFGdO1l+BRHYeDVerUuZX1KLe2bJTTQ0uLn3ezyPWeC6diu/5cia1jy2cPkM4eiELNgPNb+O4BQv8mJt7gdhogzfAyYmIN3qnyW/Z9rs9fdAr0oLAG+R7kgmSNMwMuAKEDuh4UtqVrrAjeCM4TKM3geEDev0Cer4CcCjahY9YSR4tqEg7cwSfAJYCSw2q1Ag1PEMI5cvcA8eWPkPgaedjCPXkH7sP3Fk6oJr+rUfhq5K6S18ZaP3wf9t6p4fcqXW8ax4XwNGFQV7MqCrCxlnMEzV5ojGxdY9LyAQIDThWKKPQT0HMqy0eaQV8njxKZXSjFanxbUAbMyFEUHwdCN3SKj6h8xxFWTebM/nCwKdhgAecK7T05xYes+9NK0ArPIUIgj5QY18dRSrM1ehpTwtX1dWOg2FItnYp2Ff5Ldb1aXtf3AtYeo+Ea13MlATDTvJqVznkRAGnpVx3LJ9eJoL9zrNuPAmU8si/aZ9mH5B6OCJ33iDHicDzi9nhABKPvOnQuFMyqurWM+9hWbwy1osy2fN34f5bsMOU4VkbXzqV23KaTs9HeqeGp6sh2zbqdVgbYiHLZyGIghLO1ZlAC8/UBHCeACVc3N/jWn/4Zfuc3vwHuV2D2CBTRxQRPosxzZoz7a8j+kwyH3cVj7K8ucby5RB6PmA97HNdr+H6Fjfc4Xj9DqTQhWQjL7u+6Dn3fI6aIw3FU2erRh4DxMGFY9ej7HquUMR72IOcw9KKUTpPgv3q95+3NLYZhBesmfnl1g67vS2OOaTxiNawBJ06Wlzd7PNtHHKLsySEQdusevVcMuNDhP/rHvwV4xg9+/B5++JOfYbteYUoJKauRoDS3bBhWvELLCLA1qRlgrIaBKbF2HzN4bUO4Yiyi0QlCVw3L0AX4oGV8hlVpmFtFF8lNMBQ126EYRSpU2eStnV57q3GqQbJehXeyjkHwdA2rLcWszZtC6YAcOs1a9B2cX6NfrcBM0IQeEKTB42q9wdkF4/Gj1/D06hJAArkMaJdhhtHTGdFBzgMhg3IAYgSrg5bUQBfEW+k2H7qAzXqF9XoFwoQcI9IsEDSzZre0tGaTS5bNhrbEl0vGUpstSFSxAM0p5ojACUhzQk6zVkdIpmWKjMRzyYJJKeH87BzzOCLOETFFTOMMcg7rIWgjzYzgCOOckOIMTtL4T0cBgmQYS7WFgzlInZPAoAsZ3GS7nvKYloMU489lmIPIZEBOCeQBYlf2OZmeUs47NXoVUDdWveTsDAi+Q+YEYsuaqfts4Tc1wbW4XPmMiE0PkHYE18Bt+bO479KOkKNQx5tNnjsH72u9EnRuC12/6L3N/VocXmZMMSJ4CQwQA45Zs4gdKAFXH1/i0Ws7Odtdp+dPdCgfPHbbMzw6f4jPHV8ijDOerhXvU3WMoo+R2R2F6Dq2U5mF5WvV7Vt61IWrMtrwolsbxF6bo0ugKSSDDMmgr3LRE02PFEeIjNF7heEQROlyb1txC2qag7nVWRZ2DJWw7WJ+DIVyOZm3ZePRYm9pZWIzhmpbtLNfJg85J46XOMd7Eo9MDlQdrgz5xHG5tMtepSHj5DwZxIbaL6p/c/N7o8ryWyj2a1Z9kLwHQgCCazb1vz/UQHXqvTpp5/SeC7ti8fmMmBNizogpwyEJ5rzOO4SgCZWaLpJZ/BxWhq76l/EwBSRVJcmcXCg6s83XxpJhVRVVTuScK7QHaxYjZ7hUZYOVpC/0XcWIBSBZzGmuCoPuqKSQTc5LnYsjxR0uvIZKA2HT41tfgGXYip3NSC4V/uiUrzjvylk0WJhokAKKSy2sU/RWgWvQZmqsfS4sQ1XxSOEIcxRot6xJW0XfNZmo8hZqm9i4HRE4eKV3y49j8XuwyR9njkRCzBFQx7HhrII14BME655TxjTPBY/V5D2pPu6cBxmPseA3m4xqcKiVnhI8tWasEFuPRN8Q/HyoHHTC+2y/MLSpXBI65Zrxywy4LM1snYNWrLFCNCwOyeLoy3ScYPoTIQSR/SBttAxpKGgymHNG4lTWgCCJTUPfF0xge0DhkUToe6lsauElzJnrNWkpKY+W5AybC4FIK/fMZtfjl2C6bk1AvO/6VDhj27yXJSOtxLImSotoPTUfc4Y2KQqblJYRXCY4Jqx9jy+8/Vl88d3P4+233sLMGZc3N/jJz97D9370Q/z4Z3+HKY6yYX0AdQ7UOWQBsiwDq6x/mX9mfxdnQvOJOisur+yQmCK+mHfzLOGpXDKt7uHhRQErY3OMBbB7+51GuVYEyMZEMfrZ7+3LS4GM5vPc3ldLRtqJmA3WRobqaKs68Kro4sJBscB4FGcpn1rpJxNuI5hLR0J70u21MgD7zkJ42Kq142qLjbjSYaHaYGEEWbYBUfNNyzhojIGGenezH9hMp7tqOxXms8SAMkW+fIOBPKzAm50wXLdC6B/BdY+Q8BBT8ojZISfNTID+bI2PelNZe04AeZDv4fozoD8DuhXId4DrVKl3qgR1YNcX0hsNiROQI2g+ALQCTWt5nROIIzDfgDnCSholo9tJ9CllIEoJAQ0b+GGLPpwD44R4/ADZO/AuADdXcIdbwbpabgyAtQx6sY/rLrBVqxkaJxcbTVQIcn2fYIqYPNI67Nq6McTYtWinkJV1P9YxlKPSGEp3jGwzpKjCmYA0MFLOnOL/NEp5StUwXewr2znKrBhWmiTP6EIQpSOjlL6I4m4dTpsQVpPJz6jBkeLUaWit31gqAzljngVjSYSx0ORwPMo4F2vH1RA7nQsss6aVOLZO9snyCxgzo5ONYZ8y5argQjfK46lifl+2qUXfGVLRUe7RfCamBEcCMRAVz669DC/TnFSHacRhOmKKs0aqg7pw2mwSmyCUV51MuWVtzRzsV1KCW4Oh9QZKzWY9XpVtS+19lz8KtRm4Q8/6t1SeuFWPTo2JeJyAWdYzxogf/vjv8Bu//lUMXQ+AEHLCBkAXpN5jnmfM414U+JyRQ8bQn2F78QgEwiE/R5z3OBz22Gy3CKGHC4MEkEg7sjvFSCZtaODEaZdY8Ful+ag41buSnU6IKSOo4s1Jdmhp+gPRAZxW4KQo2Rh936nYzdJlPQTMOWGcE17eHnE7icLde4d177HuJCCWsmRFfO7zn0VExu2UcHU74tnVFS5v9zXfkEgbHGrAVnVbU+5tWc0RYLLTNBFhIwTOtFzMtnkhUBv6NY5V58ywZAg2lBk7BMPrX+oDgNcSuYJZ2+45faDtZ3M0VW1MMpDtvBGhcTapcp+k2aPAe0hQqBucZihJ4zBmlMZdzAKd4H0H3zmckcc7b76FY04Y57k0Tmyd1+XUOQLgKk6uOng5Z4WTAnxwCOSRU8bZxRnOtmus+g5xnoGc0QWpdFgNHeJRO7SXU23QU5V/pKJgUjHcoevsGjnT8ktPDsF5ePKCb4galADEwRScAwePnJOUQIagIxAHXmaTIyo7iOAUIzbHCc7lwh/MQLXuzbCOyKVpxv0ZpqeiuuxbzqWRkGlpJtsksMSwShkRoSZIuOyPpaxaPpUI8K5DacnW4PDe0d0Kr2y4WrOPDReyyDO2ruqGI9nOr/kiSOyHVuVlczZooOsVTigClhjF7UGm9rXIJu8aC8lsDRCQgelmxP56j9VmI/03Cr1lPw99h0cPHuH1p9e4jjM+0DJ5YzpFZhV68GLYr7IhToPjJ7/9e75fpGC5sjpzmOnu7YAi3/IJhJEEl2z8UvJdmlipQ8vWv83KupNZquNqbVEb6kKmc3UuLV3t1T5tg/vtujHLN5iW37RLEp5sL7b8S+5vjt/7SHqq99y/avd9D81zajrSnbuQ6mjcJjvJT4WtLY4+Z85Yqw41SUGVz506T09t2fbf/9As2Tufp6pVZmbpwUEkGeLKa4rDHcoDbf1Ks+0m8aPRswQnUz+jgdAiatDoYsUBpjIAUD8CFwxPw5WtMY1yggvsHxHB03K3tSp522SpZs06WONKmJyy+6lvx6nz0LJLrZpQ5giAso6jQh64hs4t5jMZ/+Zqf8gHjc7mhKay8URncPAugBEV/6FxxKLqKAXmhgjUJLeAxHHotHEZmWznXOwhcD2f1lwspSagnWtWfOmY0dBe5BdDMo5rxm1dMhlHzOa0lOZtBoFpNBJbtCnVVzsPZRjKt6g6xhNpc0Z4SESaBMqrrBPDJaDvHBThVzBjUwPFRGIjckPXnGPhacZyhG+K8zfnWBrYMRo4DGbxDVKFWjKplZlLBqxr9hogMq8E3L0vuMLOOXiVmylJE3dr8k5aNeFK8EJ1c+0bcWrLnV6fCmcsQBrlFyrr/oRpGHJo5LWJxsyVCFaCZYfcVACvKdPEhEfrc/zml76GL3zmXWxWK7w8HPGz95/i3/3Vt/Ht73wbVzfX8AQh/NCB1h2yA7KWutlCumxiy5hoTannMm6blTECe+ceA5wIbUF5ZVj2GNlwVMpbFP8LVB5GpNk4agAkzBL5IqNt4z4QGVWEL2fWCDYBriQVSamcjYe4YTi4I5hIuz1m64y4mNvd79T3sDCa2s/ejSrynQ9WhaVtBgRNCacTR0VVKOWeNSOwjVYUYdQIG4saFUWKAYe2jK0Kr+oc02+7qsjXaNWJelclY/ldO/QKYVvxOuWo5PLMpWKgN1goqs0zGACszIQA9BjWb8MNbyLiDFd7ZxA2yuwYMBozFpHS+qaek24Fv36E7rV3MYctLAszN7Qyx7ZlKTQjh0S7OlC/BvUXCIggTqAcgXRAevkT5OMlOI0AEkAROcWSIAJMOHJCYCCsH2C9fQs9rbB/tkLc/wwcPwa//QXQ+z+CP+6LklAN9irIjKSO6l4DoThQObOUr5Zzbo4/Lue3KAS5ZtOIElvPvCl7foGxWUQGSuadZZI2TTI8iREqspKaM1FpKzxD7i1OHcK67wAGbg4HOb/63Bhj5WnNnErwqG4jJI2kC0YQipA3x9w8zwVD1DiDCTT7d7NDUVRhIX89S6q1FFXTpDFJoK3cRuFcTEGxWSzxxyxSXiO5d4wDBqap4gib4lvdsI1micrzW+erO7mnddwsxrbtt/ZzxXi1rOe2qYgqX5zRhQFnux1ub24UW7gq4d5LtBwAjkeBvEgpSfaZ74Sna7m9KGt1QVsHm8lhULNOtJxjebPQrfLHVubZves0aaEALS9uWJfs64VUMUNI92TLa0GQxlprj9D1SOOE+eUtMGtwgISmkaVRgssAOo/VdgNiYLx8gXneI98mdN2Ivp9xGUc8fu2JlFM7h8sP38O4P4JjRj906Fc7jIdLeFi3YEbJq1IHnuBwCU9NKePquMdqPSBnxnF/wPE4YbfbSXl3jJhTwvn5OaZxVAegw8WDC1xf3yDO0l354vwc4/EWiTPIe+x2Z7g+jri6vcXlYcTlUTynmz7In8HjOM6YpoQuOGyGDtOcMI4JX/z85/HZt97AH3zzX+H2OmPOAEMc0mGxwln5LNV9QXVdiKjobcTG5XUPFP2UVYF11SlVzmI9VCqixCA5PW9WbcJofYkI6x4enSrlVf6x6m+sPIUdQIpClHLNipBOzar1OAlEeueR1KDJzAg+oA8OfXBIwWNYCe4vCY4N9jc3+tqDIaV0Xb+SEtB+jV/94hcxrHp8/OIFbvZ7pBhxmEYxvrMZxpJdQSCQ9wJ9oZhxmWUPOTBW3YBVH4DE+PznPoNHD8/QecLNlGTPXOwQuh7DaoWnH36C69uDZOk5aX7ofRDMbqhjLtas10pWIVRplGME1X93wWO9XmG9XoOZwDEiNKV/sy5dFxyG4HF1dY0uSJO53gPBEeYoQcnMwKTBpmHoQY6Q81Ho4BjOAyEQFA4PJiNJnbE5zQKBMM841Rfvgg6IIZ+BivWKEqYsjjRhN1yYfFb5S9q7wIUA5IysGbxwp0+Rv4TPOUmUaPikyBLV4ozXF+Vfs45yBmcH8nKPaToITAGL0780EoTJ67JyCxq050f+SOZdjlGz4euVuWnKZHaLYl2x6oW5nPdmrpZtbtPV+YkMznj57Arbhw+wCwFpFvxK5AhkOWtvvP4ET599BHccpYzfyTOy8taW5xu8RCvf73OamZkhtD0ZL6o8KsHEe647QUBmjLNBGRgfNIYjP1LOIl+Njk3pqyOCDx04RmQ9+zUoYHciEHmUlTxxKi8Sg6goSvXzMIeqvUKjw6icrUZdeYZZU3f1oprhRqASdK4O5tO9Zve8h44tbRefXn63NYYKXWzIhdx1hbN9Tn+Z5IQv9y4qrX0f7pzZ+677MmZbR/k/9Dv3fYZNVpI2biIdp54Z05md0yx9bzAqDZwascicRmeU5rq5QJIV3dRV/Z7QZLQSIXKSBnJCJjAzVkOP0EvAkQBwFP6Qci58oh96zdIMteEvRNfMmhlakirQqg3qvNXeBVaFUs60BqAE35M1SCaVayYvCx8l1uxy09sJi0QmQoHKadcvl4SXmlks2b68WGNLcFsNA5h7zZLUgOoCMoSLDg5IhVT5HWlGOqNCMhBp1mh1WJp+1cJL+KIDqBMRAKHFle0QuuW4lvuQBNNV+dE4z9Kkq3o3ATSQEuCyJsX+yFkhGkJ5LU3FEnJOIGLBZabqPJfqoibrH64EABkMJlKoPs2cdQ7JJXgoxAsTYmwyfgG4GSCqUIEppQZsSG1e1mop5rLuSRNYFhWnehl9QdUJDnBxxMaqeMACuU66PWvCJOAca78mwHwI1uul8uj7r0+JM5aB1jmBysCrgtIyfbmypt+b9SeKkijvnhkZCY4dtt0av/HlX8cv/9KvYLs9w831DZ4+e4Y//NffxHd/8B28uH0OogxyAW41gIaA3FYTQZrSmO1xaoyaAmT44RZhL59orMWfy6DVUaf+VvQhYD0MmA5HjCkhVZ2waQfFmt2Ggp3HwGLhjWzmILhbSgtD+dbxN4ogtQe61WTM2LEet1b2UlTke6a3pNt9iuL9nz1VROp7p+9LhMKVcdz93nIPnY6TGml/J3vrRPBahNycRVWpME2b6oKhOvfKHQsJ7zMT6met02k1L7h0Wb9n8LYBFjMrTnaW98d3vwDuVoDr4YYnCA++hNvbgOMRWnoBWeNsjFraa9VRmMZPooD7Ndz2Adz2ddD6AaawRpTuZViuM+m50rNrgrSdPxn1HDJ6mZcHnD8DvfEYLu6B8RJ8eAa+eQbEWwBRM70z5vmAOSW44wHTOGJ1/jrO3v5VxNtzXH8wgfNzzO98AXz1At0nT9Hi6cloWNfL1H0z1arCWn8SvFfVmerP9jOtU80H6RBu3bdLNPOefWoG3CJvQclZHfDLwMV9UfuSuQbAMTTbWQSnShBAlYDWsffzovwlM5hF2YpAjTIunMrVsbj47sn9l41AsGAP1ShWhVVx2Op3JcvEh4A4KdZZa4i7imvXPruNzBdF6MSYq3+U+K8myZI+dbKL9+4776fPkzlJ6ZHQtK1REM5mimLJHiyPY0zTVF6bEifl28rgvfws+EzNeokc4cXr9ni+ar/aWSBHpUDilVdDV/tuw2XrOO3nyfzsj9cy0UV1BDMyESg4bN56HcfQYbq6Rdof4QD8y9//Jn7z61/Dr3zxF3HghKeXL3B5fY3eOXSe4D2Qpog0HjDRLbZnF7h85rA+u8Cbn/9lZBcwPn+KNM2IOcKhx2ZzjhiPksWnZeeWrW2cJUOCu4kyECLG44jsHPquw2uPH+P6+hJd16Fbr7H2HjfXN2LYdB3IEZ49+wSOpMxqGAbc3l6j6zqs+gFMhI8uL/HB5RH7KSJC8Jw/82CHQJLxe3N1hOscNpsBYMY4JhADD88GzDEDecB/+bu/i2/90bfw0YsrXB1n3CaAyWtGrPBDM15IebKtmfGjNrOo8SnZylZQm4Zn3ccPqpNA/9KNyNScwRN9cNht4dMA9pKlSWqMts83tmX7z0GUYO8dhn4AOaeYpmLsiJNUvh28Q997+CDdkHOWoHeKs+KZzei6ASEEMAgpCUYw0QHDegPvA+ZpxLtvPMFnnjyBBSqP4wH7w600wSCg63vM0wwi6bycOeP6+grHwwEpRmzXO4HeIqAPDufbDbrOoe8cUpwRiOEdkLzDdr2SPdN5vP/hJ9gfR0yzBC8DA4EcQvDohwGfPH+hpXcKx8UZnAlEXOCnbAUJQPCEN548wuOHj7Aatri+fI55PmK7WWO73WC7WwPsBHLDeWzWaxAY8xiR4oTMEduzNXLqZT0Y0kwKjJgmIEsJq/edJF54EugAIlhNF8MCxxLcFVnr7/LpogDpy1Ka2QTzGqdOSgnBN1lj7aUyL6cEFxw4ZYHs0Vssti7af79CeLjmV63ip/8wPL55mnFzdY3j/oC+68T4DgrvoHqasUt5DbRVX0V3ICr0YAjurzXG0enpvjVdQh0KDc/OYETyaDn3HBO6IDj2ZpexNgyyxivXL69x8+IaZ+cX2Ox2mNKtOg4yfBfwxmtv4MHuPaziBPAsCHFU4UuMNESVRxQIoPv4R/s9cwid3K2W6FZ5dN9V3686/cliLcdYvIZNgx+5ETIE/98yysyOMAfGkrfdHRff80yn+Iopz4JNngXX1ntfnTO0HHvReU6n9IrLAjVEAKfKC9QXVm3P8vNuduzi5Z3DcmIvZLOmWlqfzEEGVt5PUZsSFSxD+Y6N2w5csYudQ6a7uPbtnP//vO69n+rf8zQj9B6rVdAy8qVe7BRWJ6Wk/SybrH3Vb5MFK02va86KOfOIxOlrmY6kDicCBOO+GWNQ/uMcEILHbivBx5QS5jgXjFlHAOWEPIslZjqBVRnKUGxNNHtc4RPmKSv+53Jf56TNBWMsmYrStExeFwWVRV7V5nZWgaQONKKaXZzv1/VBlWakiWWZuTTzk6Ctw36/L5m39fs6DhCYUxlHWRy9l9Ha1sKcqsXK4ybznmo/Bpt7qxeJk1tsOM4J5o6UBCCPxBUewRKf5imCvegwXSeyI8YojmYlh5Td276r2aPyistma20xG19W+D91ocN70Usq76sJMOZT8t4hrCsvN37uvWaAO4/1qtPGZAkxpgU8FYDSGLI0A9PkQvKuzMeaVKeUwPNJbbUAACAASURBVAmKxV6xvZkZ0yzY7jlnxDliNQzyPO/KZ1KWqsw5RuHhKSE4jxAcpjkixlR9lcxwISg27VKOnV6fEmeslcwD0GOMhRJUS7n0pW4GfVksRjmU4gWX7oKbsMZbF6/h61/9OrrNDrfzjGeXL/HD9/4W3/m77+KT249xpBEIjLBdIfUeHKhAExQB1uhyfDI2oJUpTdlHTmXDtVeJtCzuQ83vAMoZZ90Gv/DkTfzNT36EUSP1zJLC3QrAXL5uXYaVpkozLeQtuGGmlwnj0HGUkizAHIgL4W9GUZ0FSpS1GDgOBUrxROCcOjXtQPM9v19+7963F8Zcp1kY5vgyh6wd7FPhRyf/uoN0UAfV6MjqEL3DwAsl5W+9V4vrUm5n5ZWAlpYwliNrh6DMH5o6r/cjEzw6zgXdjKaazbpU3gCGA4eA+OQt5DDA+Q1cdw7qXsPVFSPOWWBfmYEU1RGbUQIlXO8E50D9Bq7fwvU7YHUB9BtkP4BdByu3KAYBM2rgRJ0Vth9PF8fOzElzNIl6B8Bv4dYDaLiA37yOfPMh0vQSPN8ArIDteQbPDN4DcB6r3sG5NXYPP4OrZ0dQnoD8/7L3Jr2WJUl62GfufoZ77xtijsqsroldpCRCEEVCEglCFKAFIS20kJba6L/oD4g/QUAvteJCEARoqwVJgUBDUw+srq7uQlVWDpERb7r3DO5uWpiZu5/7XkQWJEFICDyBiHjvDuf4aPaZudlnDsTixHsEqI0X95zjheXQp43W22Dc1ouIBuxC93Y2R5SDcOvV99r7iZMMSKmCC4W2G/kBVGfhU/ey32VIZewzCKfZuFBJ0kgBMGVx1DKUXsDan1VpCVia51l7Wo0bI2dnNfDO+cS+K0qgGgU692fOmJaDCboXq60jADTzWpbPo7S8zX7QggGa4tp1HdZ1LaT75qBs231mFzUy4rwjpcPlV1YkWuDNR8C92c+yxxtDovwsXs6cE6Zpah5TI3tawGZ9M+DE+gXScX7kALfutLIaqNytpWuEj+kwiWJ7PNcfO0x7NGzlwbT5f6Mltd2FDkLvYADI+gcP9M8OgCfMDljvJ/gE/OkvfonbhyP+/t/9O5jSgpQieuew506c+qoxM8+YT/cgOATfoesG/PgP/zZ+A8Z0+w7LfATnLKna3QCEHnGZ4fIKZOX2hKT3D4cR2Tk4K2aWIjrn4B3h/ij8r2bgxHlBF4LqsIS4RAzDoM6mhOl0wjjIIdX9tOB2WvDt/YRjyuh3Pa7HAVeHHQYkzKcJxBn7nVDCLEvUKFDJIjqdJAomOId+P+Lf/3t/D//Hn/45/uo3XwBLwsOSBDIUxgRxxjon2SFSFKI9fLGdd75RKuYodkvzhiO32bGbryq+U2yra0f+2WjQcQBmKaQWnEfnA9YYsaaI1okol+S2SJSjFH2QAiXKf0ZaoEJRDkEOQIV2QCI1kTPWuMB7iXzxzqPTghcE0oIiEafpHsxZorXjjNvbbzHu9gihR4oZVxcX2Pc9WOVS4oS4Rl3+hBRXjOEa+epScDGcpvFLe/ZjD9LsA0mBBDhHLMuCmCTy5OKqx2fuBeZlxbrKmioZHrqLPn/7ohhoIABJ0lFThvJeOqS0AJCIkMurC7x6cY0hBMzTEes0wXeSfr6uCafThC6owa/0HeRInHVE8M4K0OguLk61Lf+gmuwwXjo4Mxjlb1xXxWFcF8i5CDpbdBbZV6LzmdECa8L5gVPVt2CIw0Md5u1hkq3Rzep/MtXb2snlRzZgR4LzxXAF1pTQh4Cu73C4OGA6PchYmn3h+/pdxmbfbA6qqOL1ckBLYrB6t3XvSYHSih0Er4hRZPYN+UZPN48tWKMdeh2XOEec7h/wcHuLcb8Dc8Y8TVjXFX3OGHeXeHH9HD+eHjDdfYM/uVRKC92LEkFdknMBYOOoOHees/5rjtiNA6Vgp6d5/FoMY7ZEHYsWr1VnqulaTafS9fA4aITBmOdpE+1Vjafz5drahlxeYaaNU4JZnOi2T4yupa0UDlgkuC6Uol91Tul83T99cdM3wKgyqFCbVHuM9ayfy/dqXyveqAd5inLt81T1SYVvZcOgjkYdKuEghe5hS/+2rxJMPTnn4UKP1caQinb6va/fZ6xaR+hH76P/pBiR16RiQRw/Zsu1xboAwHtG8N1GVsrwacRhzvAehfOUnFGGUR1DbZdTzOuAcvgjEZhRuLv182mVwydHrtKcqFNxFYPhUVud8tCWose6ZjJzSe9OKYLWVKbS5s4C3cTxpzQDWQLtJGFE9A0zF5hsFEcAaXZSKtkPYla6IvfLvjBfiTedSMUxmqIVrPJgyljjqqigBkTUwScQVXqSdt2LHHMSWYr6/JSzUOyhrlPSukHc7oWi2ywyGrD8P7EtI7gOYLEZ604TCofoHNxCYsfqmjBHM+lzYoxF3rV1TQBoZlG1M8zhbhnSlkkIG9dNjRkqkaZc1gsguToaAOWqE98pHZHJd++8BJPICm32rESGe3LIzgpBc1171NxDi3M6yGGvs2eC0JfI4lwKZzKqbPfewbOHNwev6kKvWET0nh2QsGAdJxgmpsd6oL2+N85Y6MIjBQh1efPmVLEIb3Bd0A1AgC1Hliiwq2GHH758g8/f/gDkOxxPE97d3uIvfv0rfHP3DY7pBA4M3wVgDGBPyGT2XiPkPtFwc7jKQn6MA+0q/oXG8UCtpmggnCNgFwJeHi4k8oJtdDRtz/pJqrya+9tYVo1egQGVzxnfTBVSgMmkmq5Vennm6Nk4VwtY2M5RiaBp+manpWjv/2jA1CVB29+L9m10ia0B732NBmheN+e2TQ6XdtQWtNujBUFbZ/TGMvzEuuDNDbcnumev25p/dC8T9fVrpErWXijvEcrpsax72ysfcfSSQ9xdwrkdXLiC88+x8iWWhZpoCgZyqlGxSJBCI1mcsKEDjQfQeA3qL4B+D+4vwL6T0gTlHrnew8jkm3l8tMa2v26KLYCKyAXII5OH8wM4SHVimgdg7oH5BkiLjkNEiifE6QMSRvjOY7h8i+7hA+L0DVLoEQ+XGJZpA8LKGjXH32aL1k9uZ60FsQKSN4D1CRBU+lkxsfSFqvLNmdF1rnKvwsC/GR5l5p8EfRugZsodVgG4rj2hT3C1MFo79M6pQ8Zt0u+LM7Ztu/VpMz7U7PtPXfT4Jxt7/eepiBDrMzfUKp8S20Ve64ce0RhwjRa1A55PNPWRgrUDEzSyjr6z721nUPh4ZZ9LtfGcMjofhKPROYhfr4Iv+WwjMNgiZ0tDnxiHzWM3/aHNZwzwNPCuPOqJwT7r7u9jkDzxtfJdOnu/OJetadtvlPa6vkPYj+CcMc8reM34cHuHDODVyxf46ec/QHZeuawcfIzofYAnCfyMcUZcTlhOAT4E9OMBl89fASliShExTqUIke88fLdDWgngBcyoh6NZnWckRQLSgirjQQCRclA1wFfQ+COOXxvLh2nFzbTgZlpwXDP6XYerw4iLsccuOORVCyoxiUONWaNpZJRikuMtqzhLBLx+/RI/vv8cKTOmv/4tZlSjA5BspKxcapRrQZtaHPS7ZvNspp7kfK9frTKvyi6ASxR/qyLgHJwP8OTQdwHImiqcCZVLhMvPBIgRypo27IIYFMXZosZCtr9ouOhsjrL+7AEKcK5DShlkNDda5GNdZ+SUsC4T5vkBzAld6JGZ8OzZNbyzIqfAGrlEzwCA8x5dkOJtjsRw5RxBWsBMAoEt0l0MqJQjUlpljh3QdQHjziN0QIwenIKk09kfNaD7vkMIKu8TA86D4ZE5gMhjmu5BJMVk9vsduuAQlwVxmSUaGUGLDK4QHmUtOsNi3Fv1Y+edpKY6ORA9T9P0vu74zKnBCiqDWqBma6L587H11P66+XYFlLIunEXPVWO9nAdqG1KMNfpsc3PDbhVUF7vgE/uD9bMVgFpDqfBbhr5H3w9V925h6UZOtDcuo9IU9SrYlwjeKoxos0MwY7+JboNQLBkGcrTtOxuPf9HSun+okcgZWE4LTsfTZr4LnQ4xLi8PeHmzx4v3DGShipNsf6r9bmSStJkKjnoUoGDfKh7T8iU85YglUt5v7UPjA9H/+UyVmr2ivSTTT4oJG4hU7D772d5kkyftHc91K6HNiTzvqyxTwdnFGmY5xNg6hxj10VW+UnPfp672Wc45RLa0XcuKpA0FXmnyEzr/0TYgw7WPn2nrtuzHxsYy/bnZvxvAfvZ7mUPh5CPvYZySXEgOvvv6WODDd332/HuP8FCGco4LJZClxrd7xQQJm0wt9B26N1XHlQMXs/1tjZHuY5VL5kwtzjd1zBn23cjAErCA5v5QWhf9PTNArqw1ogxKBOcsZYrLInFeDr9Nr9d55Y39ZzJXqBoYyCwUFOe2TWawOfaUfc1p0dKs40gKghgmHqhk00rxc26iZw2TCbeRI3W6aVtb+8CknndnBxpcg8TAwjXqNeuYm7ktdgYRHDcZb0TbcQYKTRdDdKPUE0hCgafBKcF7QDnFrbBuJgeXReYJP3uxmCTKlcyZLO1kKEc9UO0/Lifzuia3AW9dQ9EQSYMBi19CHehUA3nKGm/0rUTbEph9wTPlkL9V3oyic+xgqjjaZZtUq7To1oZ3nsyRjLK+snNwOVv8fJHhjqD0Gw7OCX1YyhnkfAkA9FDZousxM9Wigd8hK75HzlhVEgYRNtXdCmzYbD4bQO+dIgvZnJRFifdweH1xhT/87Ie4OlxgBuM4L/jm5gZ/8hd/jmN8QPQRvgsIuwHcVe5Ehp4Df8TBoT+d/S7cVKY0alGTqvAegQhHQDKHYTHN0DuPIXgMzuE0nZD6XtLv9APnKtqUfAV0KACEQFLR1AYNW0Amy1kr1as8dNbsZg7kqw2wsSYXw/gsHo0bw7IZOxuHUpTjqatxSOkXUU782Honr1dS7hrFlXNj6DatK22rXduCh+Z6yhnbyIBPfrc6qO0DtOlvcZa3X654AkBr8Nmr1uftVzM3DkN+wnFkNycU48p1V3DdK8A9w7zswGwKRvbOhp6AE8ArQB4UdnD7a/hnb4DxGTJ1SHDIpSq1jhVnUIpAjOKUZQZcgJKsyvgbECbDWuUGDYArG11+Lc0kJHLIboQ7fAYar0DzNXDzG+TpPZBnUVRpAS83iLTCu0sMh7fYPzvh7usT4hjBfYfut7+u80lACBKRpuK0tJPOxr/wmlZTA2gFrwEevbFEOJvyUMdfrg+uewNFbhDJCX4IAeu6Nu+1sql+h0hSW56afnuO07VgjpCcIoIPusWkWqalwTOAYewUGNVCYDZv1fBoXi59bxtAKLzDqKfCbbvbj9ogb/ab9RutHGj7yJssgc0NyeRhBcUtCDoHySFI1U5Lc2r1QG279eOM5sJkLFr+N9vvta/nzXcFOMj7FqnrnaTIJE4Y+x5D1yE4jzmuMINvswaACuTK0NS9VZfCVviey7byeQOuAvsawGz3cWURSoRClY5FN33i+r0ctRUMAKjO6o0kVN3ERDUwyxPCbhSQPS1Yb44AZ9ze3uF//mf/Ai//03+Mi/0O7AmcE1xU54OXtZJzRFxOmMHIMWKeE1599gYOwrk4ffsllmkCE9BjxDgekNUQomw4grGeTiDv4UKACx0Y4iwjYux2I+Z5RlwiCMBuN5ZKruQchqHHaTqCmdB1AX3X4+F4wlcfjrhfE2YW7srXzy5wte/REbAcT8gpYfABEYzjKtzN4xCEmzMmzFPE5WGEd6JD52WFDx4/++lPsD9c4Kuv3mGNE+acEE01ZMNpGRxlzhJlNX5cicY6dwlVkaHzZzqczhZTuaoOYNXlVgQCmtrIzoHddp8HFzD2PcZhxP3DQ9GaxYHX0gaB0AMYHKHzHp1yvQq5RFPIQrl/YwKcVvM1ueedgycH54LQXLmAZTkCYARNOXackdcZiScs0xGEhPl0j5kcQjfW7qpDKqW1ZBqIESBph13XSaHEOCMuCY7EUOGckHNUwzECLiPFiMSxpCeHQGBEMCU4z+h65fbzFl2nhlIQx5wnqePQ9XuEbgcf9iB0uL19B+c9+m5ASgm3H95jmY/IcZWolJywniK8T9puwAXlYIOTtOlOOAW7LiCmCIl8Scr9rge4GogpVAmuyZJp6G7AJeLJ0JlFNJ1fibcGYyszFTgVrAwYtY4eNKjBmYuYUT2UMuAkWqdUnd6sRjNLbM9o5FVjzmzxnzlMrS2ClYL3mkbsQC5jt79AWiJyUoM8t7i76kh7kD2Oz8eKq14VW6e2PPiAotXNWIUc2NqjAm3Tih9nopkuqHjFgbDOEdPDbF2G9x4dZO+tccXFxQFXFxfo2IOSQ0ICcy08SlboB+2zWufkVpOZTrTnl16e4Q6216zJJWqZEYKHRRmrqdXcB8WoLxilaWOuQ1DXDlAKFpmjizR6vMUWT9tO2Ly2bZN81wIbzDm7gUMbCFfXiTWM1KHTWknn7bCK4/W9Fo+JE0t0f67YoeCbx1dWx5f0o47RxmYzzNboltZubn4s7TD7yWzXphMiY7zDxyKjP3Y9aRfS43H62Gc/dTmVQSklJMdFFtj3rdglNFIzi1IWOaTrz0EdfTr/UvSV4VnoqszWqk5WK8olzlhx3vltnwwD5gxKkipe9jrJei90V7K4QaWAmnKSp1T2VaUD0HnzUq3eDpgyZ7BrbClmdENfx8Jsfv09Z0bMSbMkNEDLeXGgeVciZaUmRo1IZSeHkN7p89UmSykjpVjM17KwHGE3DqUNMQnPv+xjiL4ufdPVro5NWxqZWfm/5X3vPRAkBb+uJ5ENVrDSgkRijFhjRGr2iyOS8VMbLqWMuKbC1SqJLrVmiFE9LesqlIS67rzy/bZBKmtcgcS1Hd6BsvLcQpz4s9amAAknbdE1ip2INTpf58x7GWdv/cqa+cL2PXF0diFIn5xTTCSOZe81e0fHUjisGeSqv6nwv+qclEKGzfi2AVNtn63thu/KZ1DHEeRln6iNBuZSZNf5Gm1MmYCc4Z1XZ/fHZc33wxnLW6DtyCFBU1EbAWZh1GADqHWTNXqg6JXnwwF/8OoNfvLDH+K0zFjI4etv3uEvfvVr/Ku/+kskJKns3vXgrgNc5edsoU2r2lvj8twZ0pinRdCQGow1woMbAUbKUabAWx8QALy+vsDFGPCbr34LhB7OeyHMhy0e1PvBlJECPn3PQq+ZlSYQSkxdyPl1sKhpe1Fadrpgfa19VKiwmT8DSSBsFnMLKKox14xZHTK0N5SVUC+zo9rXWIFSZiCtSwFbDlRPt+wBrEaZ/WK/E+p5KJ89EGcgBNu18Pg6Xynty0+DkCcdIuZUaLgizx9a/ZWPUT3hcfvIEfLzF4jP3wLs4ftXiHyNZdkjp6CTkySnNik/bJ5RvIXUwz97C394CXd4jjWMUn3ZRsXakrP8TVmjdwByHvAeIFf4YK0PT48KtkNZ0hxEsMH4L/VeiR3IXQK7A8L4Eu7hK6T7L8Gn90C6Q1xm5JgQE5DciN3lj9A9vEe+j0jLA+bTVE7nQA5dv8N0ui1r2E7cqhNtu8+kZY3gKf2TQw7b6ylX8OrUiANU9tF27ZDuI6mkGZFSdQo+PmU7A2yPAPy2XVvzQ17JXE8nbZeVQw7qcHl1idNpwnSa0IVBDce69swQEdkkMjllAV+O7IzRV0OzAPiq5gSYPbGzyjo/Wy1mcJz3q3CF1TcIFklc0+dsrLquK5EBNlbm+G7H/Hw8uxDQ95KWPE2nwv9kxmsxhvD0+J/31Kap6z1evnyJr7/+CilmdQYRWMvQxBhxWo6IjYO1Havid2qeV9bEE+vh0aXgov0UFyO3gnIT/OI04I0uQgGi5308G4sz+Wev/T6GS1XI7ZfbN/V/D7hdj6vP3+IOXyE+TOAlAuzwT//7/xH/0T/8+/gbP/0xkgMekJBX4WEfO0LvPGZelActgcC4+Rp4/vI1Xr54g1/92R/j+O3vEE8TsGbwyrh49hxHrbTqIYV9nI4ZpwQfhMcveHGmrSnB+YDDYQA4Y55ndH2nUZAJp9MJw7iDDwHTsuKrm3t8dXPEAiB0Ac/HAW9fPsehA+bTA5a4CK2CH/HwcEJmxsVhQBcCbm9P4JzRh4CXb3c4HRcBvwQMvcf9aQUc4QdvXuK/+i//C/y3f/Tf4cNJ5G+kOreZhbPMOSrUJo61sIv3de19ZLHbtNUp5M06zmYsmdNM10Rmifqg4NE/v0a47B6tpZQz1hRxnCd1GNSIK2oeTgT83euMN2AMPmAc93onScuclwXB94ieAZeFHj2wOD5j1oIVHVKSKJwu9Ah9jxQXzPMRD9OMYDhLDZIcV1wMo8gjEDIT7j58I23PWdOW5f+sv3vVnbHvsYaAHCOW6VQcqUTisAshIJGkVa7TjOPdAxID3TDADUE4UEFgx+hCQNd5dB5wxEX/EcSAcE6oe2I8IcYZzHdIMeD4cIQFQKQYMU2T+jS06nMGbm/uAHIIXQB1Djvq1GEpeNIO9+IqVAqUE3LSYiI5oeu64lgyJ6EjQoY4yCVllNQ4XZE5wlGAD4TQ8QYj2hXTmWYxDG/LgSVSyGmUC3S/JhYOajyS/4qPk+BpS60kYAsMdJGbU6rSDT3eE9C+srWPJSJLoog9yDtQlIPTNS/IidH7oRbvOsecTwngpr9FV3kHT1tM70pcEIos987XgzluDxoNhwnfLxNK4doMoQFBZnjfgajDMmU83M5Y1wQ/DNh5B04RiYGYMy4uLnB9dY3Dbo+OktJSSBVz64FEpznhWd4M9ranRktQeOMbW9gwtHOm12TtCHrRcG5YBmaNlLbnhNA9oadqwEUJhEFjMwLqCJD06vY9XSglAtjjcTRVe5B87ltsm+LIAV5qE7jzD5aWypVYnRk4X+eGVWvarX0zpVxS0UV0ZWyLGJWGqMNQ+lec5Y+gnNkRW2VuOMo2UjmEpW2uUS3m1bx23lEV+mXNqi0c+h7sF6T4sUCW/+fXefDBJz4JOwx2IMUKTgtY1a44JgRdQ6I7s0StOi+Os2YubeVlFnm6rgtK9CGJ08siQCU61hVdK+MlRYlEEDu4ENCr0670hZsoWjC6XgIGJJsDRWbK+xkxZeX2lAZKYalqB8g4na87bNYCEUqaORGh54zUBYnoVGDRiuIQzCFm5m6lgYA5tRnovPVvwJpWDKsVPNTD0pjQ9z186BBSAvqhyERAeGqN0s3Gx1ldCrOpXA1qKM5WWFNqf4teJpFB5r8xHtfyXBaZ7b0H9QTsJaPAigba377vi5Lp+158bUZJ4ERedl2nxaSdcOYrD2tKCTnljYPYDyP60Al3sDom28jYNkCINfMrxogu9EW2UABQaE2S8gSz1EjKSbMiAghyKL7GuVKRUF0vSenz0NiXW0HDYMWqWSm/us541z2cFwq+jcwz2kv9Gylt6niUfipvrs2/ZfNnpYxM2cEn9+h77fW9cMYW917jtJIw8boQK/+FEv6GUECFVUeTb5dEdHz+9jO8fv4avRuRIjDljN9+/SX+8te/wGk5gbqAru/huw4eXm1LPSU2pasbxwUJ+d4K1GrQm6DRR+t61+goA3MGYAovCZR/BIWaUrigMi52Hbxn/PZ3X2ENVHhOACPE1vERtLRVuOBC9M02pPoDEaSaXtMPvWuZCTHEq+tS2l2hl52miuxqnM7qTDHA8jji6TytqXKWSFtqDzZbiexn0n5VJxdDkhKMl9TYpLYxaa2Krv0kHaBtpqQ++dx4LGPOBaTIpGU8+nDTP7tn27ePOxrqCUyBfOeOBj7//uPUnvzE/S3lg+EACojcI/KAjB7MTojhcpS/0AIMetpFYUR49RPQ4QVyt0N0vThi7fScgFIV1x7tRYACNbWt9rDpj766RVEVBFejhOo8KY8qsgNsL+kzkt+BLn4AdHu43TPku98A0wdJy18XzA932A2vsDu8AqUZp/WI+KOfgDtxqjkijP2IZZZiKcyMFCUywpaUU2+XrAUqVB9t1GR74PJoLlQZxJiUa0tfbIAwEUoaut0jxnVDAt4CPGbeRMQ+ctoaIPrI0quk6rKmBXdpOktKOD4chTuJCMERYkzVcASadgAMSX8xmVSkhoFoPpej7ZL4CFDdbAZS/mZU4+oMhVMzR+2Y2NWeXrcFvKzY2LlDu9z6zJmc9aTdgCprhIFvUjhbOQAqK3tTKAsAnj17hncP91iWBd++/xYxVQ4ozgmAw7xq0aCcUNdGjcJ1rkrqGnT9uP328yNZZPqgmTs5pW+in7PoRJH1+elI7PLtp2hYtu1ox7l1erf0EOfO8E2fHt+8WSn6EgEYAw5vX2D58ID17og8LXDw+OP/7f/Eu/cf8A/+vX8Xc0xgOMTMiDljHwIu+l2jpzLm+xvcIGPcH/DDH/8hvsgJp4dbLHEFJuD00EtVW8dI0wLn63xwEn4wTx4xRWRk9EPAsixYTuLY2o0DOCfMywyQw7jbA2B88f4Od9OChzlhScBh3+H6Yo+r/YiOVyzHFQ5A73oBrXnFfr8DSADi6WHGxX4QyhNiLPOM/SDFpmJi3D/MuD7ssaSEmBPmZcF//p/9Y/zzf/G/4i9/8wU+LAuSI6RsEfvYyC2TY2SGFyxa6hwUA3DN3LRz1LxmKkZEqWIt79APOwzX1/BXe3T7BOAEAMg5YV5nnNYJfnIlKlRAcZWrBIIn4D+4mDEuKwDCOI4Ydjus86wRvsKZvTtcouv2cO6E25sTvCNQQ9tTIjSyRK2EfhSHbBauvRij8OpqZIT3PeIaQQ0dzPRwW+VJzpCABLMYM+Iq45fmkzghlc9M9oFwMvZdDxc6PeQbwWlCXCJSFmdMDCLjnBYTSpzEGPUOwROCYxCkIBM7QYOWyCLtikiYEbwWVMkEQoYjlmjX4EEO6MMOawKiFtoYhj18J4aOI8IaZ+QkOMGRFCib5hlgTacMDn3fIeeohaCMPoKUSsJLhBUzOK/ioGUGZzlQzgyNGtout9NanUXSIzGUMmcUsgbFEtoGTAAAIABJREFU1Fmxb/EzGBpuCj2Z3DXDEWg4uHWtlUAGR0LFAJVrvEWk9stGLusbzqhalTlDIuOURsejFLHhVifawmp1bKG4qnsTIJAP6MYdup6LA5VAGPpR1kLh4tVIRyjGprad+kiluXLk0FkWXzZMzmBEeBDikjGfjri/ucGzl8+RoLRJIPQ+SCGwrsPzy2v8Ox++wJ8dOkwlO6n9xw4NClo+G9Q6J6S61zWhk5IKG3S+BPewrsukQUGG+VM2TGH2jhyOlmxGqhl/XJ6vcpIIjmU87NCaoFHGetnYbgJ1ynv1cL5QxGzwiU41GQqo9prpHvvc1laVloYGR6pVVD7fXm1Qjfeh7BcLZ/G+Yqqarag8sk7fB2nkYa2nYiuSgGZMrCeGQQBSZ5qVoEjqPLNAJhs744kkoNYysLVqtq3uJTgH7jzYUR3H/xevTzleHzsZ0dAFEEIvxYFiSvBAcfYwGJET0jzLQZtT3E4AkzBsb+8vhxdd8EJ1Al/S8DNnRKD4VGTN+k3bipMdADkPTknT4gEQSzq8c0JzlrWAX4zIjsHkpBg6A0BzEJWbAxIG4poQtd/i6COAcrEHsvo6zO+TjGM1y4GP+QLYsvp0v7KT7yZOSGuqSERxOCuWsbEgIixa2Ml0jqghLjI1pYRlnsWWySyp68YRrT6eFFtMTCCXyjqVccwlMt4KSTHV/VPWDrME6xnmVbkgrDI1u0GOkdRZKkIH1BSdsghSWH+JtOhUQFIZGUKQA1E1uYXmocpQOeCputWCFnsrIqk6XArr6ndJ7ITgq8M/xOrIl4MHOWywgzPOUgxVForqfb1nUmeu4KTGxiXG0HVFL+WUi4whEidzcL7I0EIJ1tjPjhwGDa4B9FmsnL5kXLNZnyEBTFn5iL0PgPbVshXb7FIJTnvC3mqu74UzFqgGOwO6QTT9x1E5BRADXzzywYfCkVWVQhXKHQLevHiD1y/f4nD1DPA9Ptzd4Mtv3uHLb74GcYb3AcH38F4LDjUUJI+udtIaPsHSfhJhua6x3qOAOfuXy2cLiTo3of2oC9zps9aUEFNGR08Yr2cGjm3e+sxGEbdHRI5gxSPt0ZJqmjZfJPW2tMunhQimMMlu1PSv8LI1Crw1yp5WUmay1ntVi63+bu5Wbmw8C9lv1E9tS3u/Apaa6ylk/OTVRgPaPblZu6zy+uP32LaxfZ3P+vlxJb69zk3ap6988QxYVwAOPhwA7MDcIWc7BUjyl6uhCRdA/R7+8BJ08Qq52yO7gAxdZwTVhrl0rK590rmqVARt/9oTVVsbNcKDFTTJ/+VghKqxU8GkcgDBiNwJ7AZQfwVQEPDrAvIqRS/SckJcI1x3Ad9fAn5EGnab8ZaTYJJI9NIm2ydS8GroOxynWUBC+7l2DGCgW94wpb89JbaIhG20JgCNAmoAO21BeOtM+9iae9Lhdnav9kCpvufhFMjkzFh5Ld69DDSRvDY6dt92CdueqA7M1mH9yOHJKEASajwVsN3MwRM7+KzT8plPRyDUq+oX2oCPp67ze6ZcSeQNfJjsrH00Lt6qENgGq7kMZGRmpEUoCIy/kiF8n9ykL28zOKqjidqK80+1v3VWPjEX1q66Ip4eAxHzVGS9reV6pIRH67UCTeD87hsQevZ/q2+fcuK2z9h8zn6GNNPtenSZAUdYCeB5xf3xhC9+9xX+5M9/gZ//9KfyunoBPYBdD/TeI4QOa1wQPDAd75DSCn91jauXb0EhYHq4RZwnpHWG0wrw3PUAS5S1cGcBiAmuCwguaPqUzKUYGhodEKOCfHEM3zyc8OE447QmxMzYjR0udz0GT6C06gEANU4Hwm7sS8QSMWG/H4QlRsfe9R2WmLTgKeFiPyIzo4NEtGRkDM+u8G/+zZ+hHwf86V//Nb49zlXI6bhbdCZY5EUpyqRy+omphu3vai9uFyw3fzMzXOfh+w5+6OH3B/QXl6AhwIW5+RIXPBhFS509lwEm7HzGZ33GVWCkJcOFgN3FBbwPWDEDUFmdM+6nIziJo9U7j+A6CKeaVuwmD+cCvO/gQwdyAaEbQZBIvtPpAaEnSa3TyL41roWnzKI7S2QlkaTkpYS4LFhmKaQ5jAMITserOkyYCTkBc5oBWuG1cu+yxlKUkDmBrbqziFksOYHV2HWOEALEwUoe5LxEEQWUQm+cgXWNYFavoBqvOSdkx3BZnLkAo++8GNOO0I8HcFbjiRg5MeKa1Cgl5KQOUSu6kpNkgZBlZ4ghaVGCNk51ldR1J5Gskhaez0Tg0tAMMCQK1pOlIKrjh7k4QqwgUbkH86aOBOleY5MzJixbDLN96azdvJFVldO4wcr6lgtGmyJ3E/oEowRxm8+CuNaBQNXHGxjcjAPUCXCuU5mtSbbHawFRACDHcMrnZ1cZd4Nr+nlxcDNgnMspIy8Ljjd3ePbimYoSlY0kTrthGHB1cYGrd4ygOKo0Z6OqPqbj28No01eELY0XgeDV6WAeb4ZjjRNlcyLXDDWyQVVu6c24GldnY2sQ1cKdW/z2WD/aOGPziXKrT/fXuLCbAjLYWGs2HtsxehRcdP6tBsvUNrb9cKoOziLF9P1d16MLHbzvcHP3oV1+pWMW3AOiRg1UjGH/FKhBpBGCFU9Zk6lxxBJIt8f2qabvSJ08izvb6x+5Poaxvwtn/r44VB9SfB1tZXlmdfq1mJg19R9Nij1s45ptamPB4gxKuVALmsxj+5+agoabDmz7nVnvo+sp6R7LWZ1Tms1BpUC1zK1DzZy1AtdlXToHYjmEzJyB1OJEbLJcSaOtWR1lzeChOuY1o1Epo8DiwJVoX5O/9RlcbAbA9g/B1r6hWtZC84Ro1DPaBlfomRps3M5prjYrEQFZ6Wd03VkWDJrxF4c3N4FUzXiY7mjWvsypzj8DnBJi2wZmKdSo2eTG021rLGtQhekFp4El9UXpWbtTCl9s0xZONcuUSXx0xaZQ+V5wIcTuN6odw5GeXO2stt9G1xsJvb4imJeUy1/0iEMNULQCXl4P2NlJ8TtZJ9uADysuBkDqCTRtJXKbec0ZiLTCcR1T6Oe8M0d0boJFPy0HvjfOWGmnDFDOGX3Xo+96dN7j/uEeBpANKFkEU6muZwudZXL31OMHL97izavPcPnsJVbX46sPN/jim2/w7sN7qYrrOnReAHTKqQIY/Z+BUtWuEDCfN7tZZC2vY9UOcqcWHJlAYgN4mwfKLzGKUTN0I2i6L+o1P95/jxUoUFISzGlSfbF1gW5Eht2otOOpOap95cbZSrURFaxsbsBV4BWKhO3Y1Y+q4GnAgWFNFtStyqP2tgh3NnFMcLBTtXMA8kTXNpJze7E60UpDDGU281pOeHMVOq2DqwLCs4c0ChEQw4PO3t/MSWk8VYS9AS/yiwmk9nHp2SvQwz2YPfr+GSLtkHMQQZ9Zo1rVCaunkDQc4C9eITz/HGm8ROJyfl3nnKFOXEZ7DN+IaxvIzXBXC0E/00xqHe5c5psASXcrIty+k4VqxOm6sTlwA2joQN1eInTvvwIvd5JCuswYhxGuP8CFEXG+qa1lVkqA1llZYaoDEMhh3w2Yplk5eBrFLaOz+X4LpK1vBiYd1Q+YTHjawcoahUUb+WGfe2ovlUgLfgwIjcAc0HTjTUqQ02hRAJmQkSQaDqJoMmfh5SzzeZZWTs3/BnLsMwU0F/Nq216YKJFdzFRlZwHM9qyP+kyfPhQ5d0Cfj3d7WvspJ7ZdxnMGKM8W5CT+0VxQ+Ud71vShuU6no1RDZllDrqShESxajppsEWKqLCLtM5r11vbhcSSG9bcCmy2Yb5pt+w3bPhkQAiDtedJgOZuHQiPxNDgxmWpFFdo5axtFzVqyKzfOcTanYfOe9w7+MIKCRIcs8R6EjJu7O/zLP/7f8frVK1zu92DvkcHwkbDPCQPJCf40HeEGQppWxOUExxnXL98IH6z3uP36d0jrDPIJIXh0w4hlyiDHpYBGzgmeAnyQQ+CcVnH0hQBwxjIdwSmiHwYkAA/TjN/dPOCURBcNncfzw4CLMQApIU4SzTmMYxkn5z3GccD93QNSFGqEq4sdTsbvBUlTO04PYGaEEHBxMeLm/ojOe/TOgR3j7u6En//Nn+Hi+hJ3p3vc//pLLDlXdUh1/Euh1aKzWv1YJ6ysBt78tvm5qC8iIDi43Yj+6oCw38GNO7gwAi4Dbm2+s9V/G5GncrYH40XI+Dd2yh1HQNf3uLy6AopTSnOacsaH97fyddZKur4HYQVzLIakOGN7dGEAkURvdWHAuLsAXIeu6+FdKKmIcV1LeiU443SaYBWgvXdYlxmn0xHTlHE6HQFmjIcRvuuUcj3Boi9Mb67ThJQW+JAAJkyzOGLjuiIrbYGlHoIIKa5IqKmoXeeRVjHsHXlpn8vYDb5EtEnEokS1mOxLWSKSs+8QfC9GMDG6QHDBIww7TKcHcIxwiEgxYVmS8ryVnazPI8QUEZcFfV8rLqeUENTnaA6AgvM0WtWiXLPi+PNVtWqEpl0xLvAgLcLhEZwrY0qo2E1U1tPHf+KE3Tr8iuzR9X9+tZF6JVqpfIOKvrQly5wAKwZn38usSMRSXUU/gFBoTluYaG3dHHaj7tmYrdJzfT+mqH3TfmoKKyDzC+9Efrd4g1EM/JQSem/zxIBxpyKLnlgjTrd3gNpVbA4WZJFdw4irwyU8HByfWzd1XhtXk8ybaz6pg8Dcfqv9SftTirmo/GCScS/4wPpnQoVg9UColWnMhY+x2AmNrnrkiN20ps5TOdIs66fBzq6xCWx+2eazBobIr7o+uQYQ1cvuX7GPTWK7risWatu4BV6k41Fdb1yev+tHXB8OGMcL3N6+R9IqeI8dlFTHjLdj3SBqlNWrSy9vsK/INrsz62viZGuCHFJ1epGXot3tTj3HTZ+6PuVofYxbPnWj7VogoIkOfKJNrMWGksjRTIRQIFuVH4Da/szIKSJyrnSPcmMAqNyzZGsQRXhkc5wRCd5lkzd6eKjBcylqKjsYPTkwp6InygFXwZg1SMM7J3QMKlIsStVsb0ITnesinJY0bTOipXm6Zoocq+ui+O1TdR5yY0+2/bYtJmNSwmXQAB7Y8DBEHmedoxqJb2Or41sCByXbRCiOtGiWd4gxFVom23c559IX52qgotkmLWczeQeH6kjMzFhjBLefIUIOgGcGyImcXld1aDPIefRdV+S8+WykP3X3GSYnfQ7nXCmlctaxcCCSLBOrIVEOLU2uQvRV1iJhmSrPNIiKzyoDyBZpzDIGNbZF783iCmCqBxBenWtESgWhspVJk03M2Q3WIJgkPMOm58AIFLS91nQZO7N71qXh/bY1QHWNQHGJZGnV/fbU9b1xxmZE5YEVI/Qw7nEx7jD4Dut0wqIcWkZfwFAuPQ0lFsWU4UmKX729eIYfvv0ML16+Rjdc4DRH/OKXv8AXv/sNTsd7uJ7Q+V7Sh5JWwIOmlKDAG9j+tu1oJyAtPJOiN4y0LOIh3+o8AKZ4qbwWGu/+uSKKINw8THh5cYWfff5TxG+/xJQXTGvEtKSq8NvN4iqQy3rLjArAUlFwGqEDE/AmbDMYDuVgloFcsEMLGxowUxaWCbjz1/VWW+sLzBY+3kSvngvW9ll1D0u6IVhOR8q95fSc6XGKvgEJUwaNOq/Kjbafb38uQJsAsKYlnRmZLWQibPu/ccidO2mKLWVgx/pbI0DLmOn9XBFoVBWKDU7VQk9cBJAHaES/+wFOxwEpkSjgpI5Yi4zNGTReo3/zM9DhBVLYIZIqt1bfZfks4ISUWB/D3DaiQuZqAjRvqWLehLIUoWwvmJPbkFp7D7Z8fg1s0HXhCOwkysdf/gjdcAV++BrL+7/C6TRjHK8Ruj1Cd4E4fd3cjjFPsypPVKNem8CZsfCKb+9usRZF14xx+ZEUvNQ93oUO+3EHMHB3vBclYyBM16g4ZCBC3Cp76v1IQYiZN8TiCO464U20tIxzJ64NU2sMGIjnnMGqKIx/2xOEF7HsHaA67DKghWPMECRygMpiaaqaYJbaB3pySRZnMR7vJbsKJ3jDNc1AKWRQK5C233pinVADSBo5c/78UjipAVbt5+znElFQHv0JvrEz+fexwNWkUbHOOXRdj2VZinPA+pA2+gQgx2VMrM/Gy1z6xnw+FI0MQQWbVB3kdj8z2JgrQKsfUJ2FjKZyGjbO+fYLZY5avfd4qOyZUphASO/XuR5yNnbjI2xTDonaezb9TymJk3fsMLy+FvxwdwTPUnn+n/4P/xP+k//4H+Hzt6+RCLjnFenuPR5OD7jsBowuIC+Tchh6HHMEkcfFs2cYd3s4Cvjqt7/EsBCGocO426Hre3CKVRFmRppnUBcQxhGXL17j7uYG63QExxVd18ENPW7uHvDhOOPdtOKYgc4Bzw4j3lweMHaE0/FBUr1DwDD0iOuKcRwRQsCyJnz95TfY7UZc7Ed0fYeH+3vhOfMBMWV8+eV7XF7t0feSnnh/e4vry0vExDjNK25ujnj56gViSnj9+hX+w3/4D4B//r/gr774Cg/TgqjjnzNrxJK8MC1rcSxW2FCpmeyHzaosi9LeZpAP8EOP8fk1+utruD4gO5KiGST6KufUfEdkLnFda+aQsbH/tw4Rn3dVZxIRdvsdXr9+BXBGypLqDgfhVO184ToDCOQCMhLMlbiuUaLemUGJQVjhXCjFtp4932ZdgBldVyPxvXMYd+oIVgzU9StiIriwIFPAvK540V1if3mJYegAXnF8uClRKzkmjOMep+OtcK/GFWnNGIY9+s6MOyBHocZJKcH5AcEB42GPYbdD3w843t/h9DBjPs443p/EQLocsdsH9EOHGBdM8wJY4rnqR2aJTg7BYzcEhNChH3foux2mOSKzx7xmTA/3GDwwHRcdT0bfB4zDCMnAzQg9YVmSZOU4gmOAkbAmBjiW7JFpXjBgB+eloN3CErEt05qQz8TAhgKDGXfHWyxeAj6GbsQw7NH1PYzvvHXyZVvnhgdV9klla4mK8URIFvmpcnSjW1qnpWKdjbNts0Zk/afESPMC/jai3+/gfYdliuDIcJDU4KoatkaHaWuRpEYUUHWDfSazOF6j42Y/MpZ1KvYYOUI054mUlC71G+Jm/zESR6x5wZwmeHQILmiWkWuAI5BixM37Wz0okoO3NWqKrHfo+xHPLq+xcwHOHmYYUPWDHYbIGKuz0YqysGVUVd1W5gI2ZiiHIPLdSgHlWTEH51LotMUQdS01eLfB4QXaIpdnGQaTtWEYRb5HGnWdWKuCk6u4Ftv1W7FSXeF09sGSqq+fNSxj+25rJlVc2B5Ib52JW8zEmxW3tVGKrmXGsmbEBbi42oFdh6TFTn0BQU9jgKzP8c5SsctAy1jmXOs8FPtC5quZdYD0cK4Zr6CHS4CuyxDEA0fn+2h7PebO/b9/PQ4UKF2RddmMqXNOOEix/ZDvvB5Yi56NnMRGODOyZC3q/k7QQzkDUU5MOE2zEuoASXc3ZyA5Un7Rip1z4xS0/eO9Q+gDStQ+/MbB1K4r58w5K/01nvBt1HXNIBaTqNKHccrlufWggQuXeM51r9k+sAC+gt+bqGMu7YMGQaA4PDcO/ydWSLUHWMfGAjTEl0VOM4X0b4wRnp28TnIQ5HxGcO1oMcyWFczQNTQ4lpUih4rGix96wXZ2IOXmGdN0KgVQgyOELggvunPoqcc8e3g7QMuiN31Dt2PGabbietqvgqsA7YP0v9RFgUZOu3pwJTah7GOBLir7OJf93u5xs6EJFvHKG/7aEEKZ+0AeOUbJBMpVvllfvavcwoV6p5krIqHqyByRV2lLVFoFO2ySgnDaVxFCpa2k7W/rWsl9hQoncI3I/9j1vXDGOkfolIPGBn5ZJ9xzwuSCQF/vS0EvZi5GM0McqQAAdvCZ0KHD56/e4PJwAec9prTi/f0tfvGrP8M3N18BAQj9AB8GJQmWReF8kFQ/FYgSbq1tKia38vaoEIIKehOi4igw/hagEJc3DonqnzHFXGQh4AjOB3w7TbhfFhxub7APHe5PK6KGw7eCvJxcNnxYm8sABEz3bYUd2T3QRM+WAeCyIQCoY5cKdqyGunynRg9vjW2ips9Nu72j4tBq/A2PLOwSAVg/UKsoqyOvDuk5WGqjOLkY+6WLMMHQfPeRI8EGcjuP9vj2o+3z8xlYKFc98CrvlyICdkOu7zWIDzWqoQr3irDp8XetnRkg7uDDHgt2iDmIMkoJSCu0NDbI9aDdBfrPfo40XCL7HknKGustda3FRQCjRWuiGQhbOyXFoRaos4iYsq4awC9ccNomO7V0FhKDT1wMxAhCBIUA9sp9l/UkDB4cruH2HgMTlruvEecMjx674Qrz3YA2JlkO4eqphDkl23UYUzIEjZQyOm/MczbsfDbJXIrxnK1uGAg2ueagjkBq99nZlBKBQ483r57j/u5OCqEYUGmMBuN2dZt1aVHY2mICImd0zmMcd7i/v222sO1hkb/eORzGAy72I+6PDzhOE1LWNGwD2BY1b93TfmYdk/P9+dFZ5YwcayRolSfn+2s7OEUanK2ZNu2rfXbLH5tzRgjGh2aRSLm8v4mYtfVAhK//yR8hvXz95HPx8S7i3q8AFoAI7/7JH+ErrkYBn6+hjWz67nv//+JqPa8fuYZ/+c9w/d/81/oxBXPnXtrmfsWRHgjj62ucwFiRwdMKXzS9ft85TCkjrzNiTng27HAIPRwxiBPSOiOdHnDMjG63x+sf/gSMjOP7LxGnGXN8QLfrEfoOxuvmwZjnCTmuWGdgmXdwoce4d+C44Hi6x7t3N3h/XHGKjBWE692A15c9dsHB84r5fsHY943IZxwuLzHPC+5v7zHPK66uruCcyKfT3T0OhwNO04xpnrGsK169ukZMK+K6gEB4+eIF3t/eYU0M8g6fvX2O27t7nNYMCgGf/+AVOk4IUKoREFIjmk03WvSEGIGmnhjtxqhHGXV624NUf32Fgw/o93u4cUB0DpEanJMrsG9uWsRuPUg1jML4R5cRe697mhnEGZf7Ac8vD7g6HLDRtQysy4qhD0gxIUbAB5WYauw510kE7LhDZsLxeIehH9H1oxR+0lLMFjVDqhcloichxhXLacLF5bUWsAByYjjK2A09wvNn2I8B7969w/tvv0DOJ1xfX2lXq0HddQG+G7AsM8Ck/K0OzgWkzEgJyCzF1vZXF9iNI1zweP/hBkwdUvbIDAzjoAVQGesyS7EmClgTIc1Aoh7ZeRglmO+CZFVAsGMIBHhWFn2Hrh/R+YAEh+wTcpjBaYZzAc4xfCAM/YDdbtQilTMAQt+PIGg0FBlGtb1tmXDKrQjozwnCpUolkquVAHwmKBcigMWxmVPEaTqKw8F5iVLvRwQnBrBkxyUQ9cJRShrCBeWTMz0ipcwAZz9vL9sBFgRBoJL2WsUTFW5IOCAMI3zvEVwPcg5dcMi9k4KC5QCs2VvbTuvBX+tIEGzBiSUy2hHcMGLXV2cTwWG/v2huS8iclNeVhe+ZIOv7TCzHnLCmFUteEMgoP8xhZPqTwCvjdH/C/d0tDhc7EBjL6YjxcKXO2B5XV1e4vniGLj/AaQCOZcuYHdKOaZGF3ESINoaN9x59E9Xpg5fq3yYrDEarrWAw1orbQDFgixuKKW7qwqgv1EGyxYIVnwibwJbCi60fAGAR1CpvwCjOcV0osGjntrJ8WTt1Rcm8RCk6YxinOKxJcFZLvScZJH7T1/ayZ23MjNY+URFKAI7LhNMy4asP77DqOBKAWjW5bWXNnhK82kQG2diVNhHEWSWFfswmbTEzM+SwusWNZOOsc5cTLq+u8PDhHuu8gr+jiNej4IFP4tePv/c4aELulzJjWVdMpwkXF3udZ1THpTnXQcgxIQQCyYkV4ioZfd6bk5YKl2l5JqAFrmSSiIR+yTg7TT5Uz5BlhPjq/CSSAwqqlm2hi4Q9yzj2a6Qn1A9hNnbxu1hWmQbAKFtIua9Q0IijL/hQnKwASi0dW9dxSWXujWfWKYWDPdtwmO1nlM9L+yWV31LbPVyD9zM0SlVlBACQd8VxLXvD1m2l9CGqNox3XcEmzChFCIvD0JEGyLjyveIjUmXoSDK3XNeDg7abnPqvZHS6/R69D4gxFloeYkkidXqvoeulX/mMY7XY5RJokxW3tNH0so+Me9sVWUVAKUpPROiUh1XmJSPFeGYjaZhRwxkrh6Ca6a6vBy+FwHPOWNe1Or1VDgcfpMikzstaqJmonuUZK6PZd5blRSg0HSa/ZD/a2k4AR+HgRR0LKWqWdAx8oVYtxNakB/zqo0qPbNZ6fS+csarf5SoKVSrixoa8uC5MLgTO0MFzIKkM6BwG1+FHn/8Ih4trkO9xWhPe3d7gmw9f4zjfg10G+X5TwVzWWIawUwFo0hqI6mfMsQHUE7cC+tmEExcgJG9VZ2hWrVEjkAhsIf/afSYgslYFXmcMOZXUwArm7DeLjOIilMzNYsNZntbgw1YZGF4gBV7Fl2ECtfRLx6HcgzcGFLmqoK13m0luni1z3LjA9Nn06NO1rWZEtw5f5kryXYC73aNgoQasfuTajEEBy9Jb4e6saXNPRb62kXQbJcvNnBUhVgb4bGybvhalZgYuitJg5LOR0l5bf00BNMfpBIfgd3DhCssqzspadEsVs+/ghkv4Z58hj5fIri/8sJbmwyqciCRqja2/lqsPKqAIWakbTCmbAivjw2UMRHBDAKoLKuQJcV2BGAW8ecA4NG2p1nGDAtME33lklorf5qfOzgHdDrR/DTzcIRrvWjjA+UFOyLV5UpPJDJNG+ahSNSBsDyYbg48ssTKfzFAChLq+GZBK9PbLWb90URcAzAxxnEtU7cPDEWtMJbDY7rvb7XFxuMS8LLi9/VDGXABVBbXtYUXOeePULS1q2pMZmNcF+ZiwLIump1Dz4XZONMW+gGU6m7PHgHaz/3XcCM2Sab53/v0CBs4ccU855trxNG7erbyX3S+OWANx28jah47fAAAgAElEQVTatrvxzWfIbz979JzvuvLxHXCUyOz05gdIvv+Ob/zr6/xKv/xXTxpJn3rNLtcFDFd7OADTeoecEv70F7/Eb774Hbou4O/8239bnFMAfM6YYsTgPQgSHZ5yRIyzVDH2DvPJ4cWrt8C6Yrr/gLieQMsiRQg0KoEBqY6cMzhlpFmc8XFNmOcVH+5nfHNaMCUGnMOhD3hzNWLvANKIoH4YNvvAu4B5mrHGCEcOF4cDAC6FJPqux7KsWBfhK93vRuQkBz/kOzgiHI9SoMoH0Q/TaYLzHjsfkBiYpgV/62/9HDSO+N279/j6/T2mNSIbZ2yzvzMzoNErW3IZ1VclOoHBTqNEfAUo47NrBCJQ1yF7wFIedSK3AqFcVNUhqrweHeMnfcTBZS32Kfps7D3ePLvGy2fXUhF4jUA13bXgVtoUVakxYR7MDgynXKoA54i4TgAIySgJlqXoS4vQWJYFyzJjWSbMDyd4B/iuh3DCsmQkcULOEeSAi4sDUkroOieFtFLG/d09drsRQ99LtobRmxBpdK9gZFtruTiHMjIiHu6OOB5ngCJcWDB0HsEzPImTatzvsC4SBAEnUZhUIukBaCEwcgHBDBGv8+o8KAwgpeEotR5I7hWCRGOuawLnRavSi9GSsnDOygQ2NQyKvhKjN4RQCsDklGAHi4LXntDFZzogQqLPSgQPgJhXOWDJDktaxTFhjg0HeOoQQqepjKFGytjSY8kSYs5I4IL7bS0m3buGJVGcGg1Os9RKJ3jau06Oh5i0rmp+wolTfy94THGbvbfVvYw1rTjxihMiIrjM7ea+pvec8D0WZjMZ5cLDZ/37xTzjZ8HjAAYjIealFK8iOCmSrPgDTEhLxu37DyBEocmICyzzjEgi06+vrvEH7+6BnPCt92e0RahjrxufW2OXVQbocIjDoTmMzVxoI5QIv2A7wVm5UFu0Y97ipuKQZXMKWIZfi2ma6FwyPkOnBzDFSCkFqQwP68PKd4uDrb0XAdCCS+fRf/J1kb71d4tgq04uYRerARftfUofWkzIzQE1GjvOHFu69gHAyP9iTiVC0eh6gBrBVtbpd9hp7WXOrUqQQJBIl21bbbyKoxjqqAPJmJeM2xZBby3ZVtee44iPOWY/5rj96EGxfoazcGubv0Faw81z5cXMUszI+wDnvTq9qjyxtU8kckwcqnKYVihSWN6ziFRmiY5t+2vbns0ph+q0rRybVIIdNrUuynLdRly3AWRMdkC6DXo4HxfJjI51nFCj462woYgBaw+rXZPAUGoc5zbRt7UIujSWtZ92GWfoZq65UnfY/m3nxT5nDs56eENlrOr6N9oZdQgTw2U5/Es5VWenc9WJXhpsDlBZIRmNr8wRnPLamv1yPpYbfQ5snO3Nh8t6Iv253aMlsM0CELnSGIBVhzWFrQACeSDrAYLJmjp8DM6E2gR5Wmbe1OOw8bXv17VlewxKi9M4lqFBlSo7OWfJoC3q0rSI3Uswkfkgi54hlChb51wpgEZEyo1eM6qZNSsdH4GszfX9cMZCyHLbtorCkKru5pCyExHWVIciZ3UDevLonMMu9PiDH/4I+8MV2PWYpgXffLjBzf0NpnVCpiQcReXL+kQWsGrKqyyIBtw720jULhj5EMPSq+2OwntBtFU6j51v+o5tUH1mBrAy46SRK7YRmk+dqa767gbgNYruY+tB90Ej/Kuz2V4op7TYyK+qtjabGEUwlAfw9jNt+P/ZXbdteyScK9g0LPOUejOjql1Z5xESrfq3MVC0qBv2KcVrivJs9J9Q1E1DNleRPWq/VKG4BdZ6Y/mdTWjbwle5UjgebfLOgTUABDg/woUrrKsXSZUtAhUAedBwgLt4Drp6jdX3yArQCFqGy4xgFmJrIflhiboVyQuyx5dtpeCa1SlrzlmrwtoWPPAOcHJK67yD74RfkaNGgRCLQ9YEe8VZZTxYC9mcLxcmQnY90Hugv1Bw6OH9APi+jB0DSEm4nMmKY5CmaDA3z6TNut+q4icu5kKjURwXj9a0zme7ZZp9w5BUk7Hrwcy4Pa24u78vyig34zEMI66urvHwcMT93Y1yacqN3Uax13WcUkZKc6UqsWZa+yGcUadFKrqraj3bw3WPtDKI9fcWwEs72qqjaATQdh+UKX4CyFYZ+oT8+MjctDLlvFDaUxENBmieOoj5Dh37r6//D66P7j8DUKZjmzXPuie7/QhiwnpakI4TfvnXvwaYMQ4DPv/sB3h+dQXyHVYAU04YUxTGF3g4ZMQ0w2UPWoDEGS9fvcHh6gUYjNNtRFomRF07Th2OJRUOjDzPgHdIyyqRracVDyvDB49dH3C96/Bi3yPPC1KS6Iy+7xDV0erUSF+WFQQg+IDdOGKaJ+QUQc4h+A6naQLnhNAFDEOHaT5JAVMnB9Cn6YRh14O8R0oZx3nBsJfonGlZsUwLfv7zvwHqpMDTdBLn78oM4wptoxvy2X4x/dZybIPE4eqHAa7vymf7wx5unpHBSMZjrmLF5NGTi2D7AwZivPSMPxxTwWPeEfrg8exih7cvX+D51RWcD0inSfWSmA2SBheroegIFtJF5AEtXrPOC8zJknNCyhGZHXJmzPNRqk8Xg9hhnmZxxs4zlumEdT6Bc9J7igGYc0RMC2KM2O93SCkjdJ0aIQnLPGHse5A+c1kmGGVRLpEYsoZCF8CTRFGFIFxu83ySgwAwKCVQckBH8H0ntBc7QsaKfhgQOuFDTgkaBeSEJzZrREjoJI3SmyPRw3U7uDBIUZmcihEFSIRxTIxliViQtPiZzFtuOCWJgaSF0lgLdJkR3nXSThuPssoaI78VCMYnaasjE5R5V6N6CUgkztlahyKrI9bB+QBHK3wSZ6z3HkF5cgMYOWZQqWReI0ErnZZkvaSY0HV9Gauq7J9yQxHATg7Ao1ZxThlc+F2pGL2m59BEaNkfQHj5MjIyR6xpwWmdcMSMY47IHJFSk/0ELnQuTkGqFE2mIk9zRrWFdFf8alnwg92ozp6EyKvwD4PhtMhQAeyQvtx/uMU4ejg3aKKRgmGStNHrq2t8/vVvcY+MdyVtlxpA0G573jgP5G6t7E9FZgLizErKjVu4MK0eicqcpw7Zzw+D7ZLCNLnYBmZKFPuEapSj071ebD7WrDt9Xg3fgeBqo1Mw47A4pdVxb5GKZ06Xj0VnsskJznDkK3b7RP8e3evMZjdcVx2/zQC4Sv/XQl97QpXp231wbq/VYBXAMhWf6J3cx9bGmTlkDi2zZ2NKlaP07E5kRtoTbWjv9zEn4lPXJz/DdQyZufiWLRhGHFBW9FuzUZ2MQ9d1upbV1OKk9GpW+Nyj63pYFKvJOVuX7fzJ7a14Yy4O/lIQlCQaMuQgjjhN6bYU8tZBJoE2dU1ZHR7DbA4EpIg6+1w5Yss9dN2o3ZJsb+p+l0LN0EKQHhJIJt/JWfY6C8G5Om51rM21TBoxCyCBiq6hRGVtEhF8CKXt7TzVtssaCEGon5gzYorIqa6RNlK3TjsDSY8uWGRVStJW7x2GvtfiaFUHOrIMPhkc5xvnNJmZnQvFADsHlwEixVJgCZhq9rEcEtV+sH6u+EHYaCmUq11fdwyhMG/2UPXX8abdUFln8so517wn3/VGb8Ck9YC29moXQqESBKFkFtteJZJMCLOdhZ+/ZkA4EFj7an23LBVbq06pNkQka4amA6Roqys2o2Tp5zoXqNgW8OKzUcf4p67vjTP2zCWmG4UB5SuZ51UGTydQTtNNdevgEaH3Hpf7EZ/98A/QjReYU8BpnfHbr77Bw+kBa1oAz2APMCV1jChljCN1ROgJPGn4dKMxzrIrioEBYOsD0w/l8jkuygbULn6IYq4eXOkTab/0ptnruQIzEnIBefIoXaS2WNE6KFDufc6bJR+28H0FvO2cOANQ0OiQGp1SFbW4eG1v/1/UvWusdltW1/mbl7We59n7vZ331KkrF6GkMEGLVhRttVGCdIwQiEQ/YDTg7YNpYkqjKOl0OhgSo8QQ/aBRPygYDR3w0hIBDaikupSubmyDNraCkYIqqqg657zXvZ/nWWvOOfrDmGPOufa736qjtEn1ynnP3vt51mWueRlzjP8Y4z82CkHd9LbeoP789tegd3R1sP9iXifvXO/H6tkM43ZuO++NYwN+194yQf3C2W7cLPviNuFkoIylA/VN6sbmYVL1NsDG9LuqePVRG7+v0nRI7dHXG97ZFAVnb+baunHbO1L8nsw9ZHqFnCZIJ+WKLQWCx033iA/fg7vzkDXuaIQMTioBvKalWe2GuJ80urS4nj4l1EIaQ1SadpLSGuSVvguOwqmOZwKIlDBRYqSUiemwowRPSZmchjXUOtE2DdfHWhRAdk3rc/hKzlo8cOcV0vkZlEyWACNXj1CjJ6xfNUVhnjuPUBk8X/ZZ8wTaW0kB350nGO0ArvIr0r8z+SE9/cvBZtxN1t27vMP7vuDdIIWf+Df/D0tbar0/PY68rFw9fcanPvV6dWqNylcZus9VxaW0RdE3FBuqulG2c6FFw9qeY21wrvGfWSx/a78U9nFmmibSurLk3Pqh9/9QHIjtd58JMB1lzGhHWM9s5PYwR0MIlbPKsSznlq6j93HD+S9SHLzwsF/qMUb2OPfivV/2vSmmN4/b7vFf8xjbcfPZN1N03ur3t73b6DGwR2Nrz+ZrH/OXRbIsORNDwN/dcWd6leeffMTy9ArWwul85h/+4x/l6377V/HqKw8oruBFCGshSeQQJw5hR8onWPVhh2nm9U/+IvcfPmR3ecHTyfP0kz/PuiwIBXFC3O00krCCAOl8JItGMO6myOEws0srr92/w939xIUruFyUh3SKCIW0rIRpauvqdDpyeXGBQyvUX109Y553EAPrmjg+fcLhsGeedqSUuL6+4s7lBTkL59ORUjL37l2SUubZ1YkswoMH9zivK68/fU4W5f27c9jz3s/5PHxxnK+PpPImb16dVOZ7aB4h06MwJb5qKV7XsXiPiwrC7u/fY7o8sLt7v42RFpcyCiPBV1CqDKtZTChuZsDwqxO+YE58wZwUCAiO/TxxZz/z6r07vOe117i8uGSKOzXK04JIAjJOSo36M6BE0/BLrUugPGkBxGk0svfsdxMhzvi4A1w1gjI5rU3epJSYdjOXd+7inWNdzkxT5LwkSlnwOPZhjwuRZV1Z1szFxV3Op2eEEAk+En3h1QcPcM4rP2zOlLLiQiEUyOJYloX7D+5yOOhce/xm4cGD++wPEefh8vKCnIQ1KV/4PAXIgvOwpER6dkWI8PBt99jvZ9U7a+RqKYW0Jp48VUdgnEIF+HeEaY+IY97tubi4xzRfcC5XdT8upLRq5LU41lRICXw4s98HpklwXkHsGH018j0GkENpHMG7/YE47XHEGoUtuKJGUjPqNiL6RRlYHEp9gfLDzTiCU/qsGCM+TE0FtGghKZk1rZyWTPUMKzDhNOIqRqUy8E4L8lnqpKMXqMplRQg0ftqGGml6p1Vt9hTSmjXYuHJaajc45VFtQG6NmCxCcZ3ftdS9u5BJZWVdtXjps+srHp2ecT0XTnlhzWekOHV61Ecs6UwMkVJcS192wTVnSyq58QyOx1oyS04seaUIeB+J1fjV/isUalEyLyzXRyb/GpcXd2shoIALsenAr7zyKvv5QFiyKm+xLX/GKu+bQpZNHxzkT5sDfY/JRYESH7puhxgPtXQjoR4WBWigWJ9bNOM8V9DFqI6aMKr6lh9AmK4d6U0USJI6J8CcM3q5a3ZqB2DqdEh50NG4IRPrBzaGTvmGvXgkxvpevlVSt7Y1Hegl4G6MsTtHKpizXXKm/98Mdhn09/GBL1mrt2l5rR1VUexb+w0tz2ks3It8u6bYov3iwEdPiJ6y3AwOuL0hN6Ndb3fgvzWAVuo6VRBR2uNyo8eq9zO6jeibzlqKVGoVj6SM90FT+YMDIsuiGRNaXKtU2rKuIzvnaiRfnUtZZTQ4deJWPatHwKvtsK4LS+0fX4NWFPTq76R7IA2kbUfNlokhaOq5D5XbU+37UtflaIcbAOdDxSs2NDCqI57TWYsiC0qD49WJaKCgdzXgpEad2pxXbntXozsV/CxFo45z7kC02W7zPDcmhRHUzqW0ImaXl5dM80QInpQSp9OZtKqj1ubGbt41OhDnPUvlPC0lq4MgF3xwWjSzpucbV7JUR5LRARg1hVLtaGG38+lcx1Kd/zFG5R6uslFT7KWDmtrTSpdQx3uVXJ/Z176PofG1KvieGt7QwOYqr9RJEFlTas5I5yCGqTmYfK0LUXJuUcnO7GM3OPzs+XWemS4CsD/04rUimiUeakHxJn9GW8lBqPLPXr5U3KQ5cwWCnwjzVOdk1v4JvssREaUuMK7uiiV0PMi3dff/C85YwLpBfxewUHAnomBRFUq+IubGK6ETwFdq1sLOBx7s7/Dq/VfAT+TkWIvwydffZFlPEAS/D8gskMyLqYq6b4Aem43YhCXQlLOG+jdgqfO6dBGixxYUrynwwyS7Ke8bGFEFZHBG/tsPKx4gonaPcamAcSm6XsXO2vmSI0sPIrcGOTTKp9eH6kbJFukY+szb07ZAhu3SMkQ5f/pjhKnkhW8GC3vY14e+dCYo6Z+1hlA36U/39H50XihTuLqASGvvNVcN61F/GwHZzRi36KERIBivGRpS5569lz3L/rCIkS1v7ItvF++8h7Lc48xDpCRkWUAyLkb8nfvs3vb55OmS5GbFRHxlvHEWyZi1umD0TFOoTgRHcdIKvami6HBFDSeWs/K/lqTA7xxrFWxNg9ViUF2pclKjYKs3LF+fKNcwH2bd2CZYzqm/VDW4b77vel4gTrjQgcVie3dxhPkuklZKPuNLwZK/TA0qZJzUKN/aPFVcNKpoVAB1KFxTtM14N35UU1IYwMu+HjB7rvEeWyXG4kwOdoVM0MJfH/n5jyIIx5QI89yrTpbeE8fjc86na0pJ7OdZ+1MKrnIY2jzqjoNhTuoexjzNzPPM8+srRFzjllrOC7vdjNSiil2vNqXHtzQwcPhqxK3LikOIoMpHXluv2x0sra5zTm3H9mVRCG3DteCZ4bbNkDYZ5voaNnmWUmp3Mk+t9dFLo0tu/fSXeHz7t8Nf/ssKNv67fwcPH26//8ZvhH/6T+GVV/R744j7+Z+HL/uy7bnew0/9FLz66n+Nlt5+fOIT8P736+9/6k/Bn/gT/bs/+Sfhe76n//03/gZ87df2v7/+6+HHf7z//cEPwq/4FfDTPw2/6Tf1z3/dr4Mf/MH+9w2RJ30xI3WMlYfrRb4mkZo+7Bx+Dly+4xVi8CzPj+TrBYfwj//ZBwnBc/fyDl/3VV+JZFizKAde8NzbT5S8sJyUPzJOe66fPuZwecl7vuCLwTuev/EJpVwpR0qBOE9VvtJSyqQUZu955/27XBxmXCmEnMkUpnkm50yq6fq7SSNjU+Xfuri8YFmWGnnv2e/3XB9PykHtHXcuD6RcuL4+EWPk4nDB9fUJKcJuNzHNO66ujpTiuHvY44Lj2fNrnl6fuX9nT5wiqRQ++egp8/7AL/vl7+X+a6/xH/6X/5Xdfua8LKS0MsVAyeBEwRsTLX5Smoaw23F4cA8/z7g44WOk4DQDewBXSk0Rbqaz5G6AVzDCjKp+TSIldSrFUvjvXkk8mB0Xc+DuYc9rb3uFu5d32M975hC4ONxthmLJKyIrp6vnrOcj66LFL3AoJ5/TiBApUJxGmyidWiEti1IBzDOH3V5BlKrnHA57EAXP1/OJq+ePNYJFNLJWs6YSjtKidmPUFGbvPfv9jikq0DnFqXIFLqyna87nTMq6L+EXptlTEI6nE8F7dvOE5MzV9XOCLzi3qjHkC9GDCxaB4phnzzQ51nUlLIL3M8ulJ4QTzmVi1GIs2t8O2Ucu77yDEC5aZMi827M73MNPs0aSThN+mlmePeF0PpHOZ4ILrEk4nxOnUwIXOZ5WpWqoaa8GJHrnCXFPKWdMEdUpYtFNTiO/bH3jdQO4RTDrDLux1+Ao1c4o1ekzVX1C0JTY4BVodRWc8FGNsX0I+DhXQ1JnqRmQIrqPSimc8pmyaHHLkrWqMlLfo2gghq80AAGPDw5CLZBpQEdfBECNu60cjj5UgoZqVKeUSEsirZmUE7kknBOWciblQioKwB995s6/+b+Z3vgkj2OEalzbEUNsRVNyUg5RKte8IIiTCrj2Pg3eKyiREuuaiGFSn3QIyr9LNfKr/hP8zPkqcTqe2Z1OylscJnAFXMCHmbv373H/3n12zxJSFu2KWPWs0V5rwzqk6rfNoesmDeBEdRAX4g0boxv4TT8w+VK2adTNCV/HPA+6qXPaV6rP9fbmIm2+OiBlncAGREHV6YHgwtB+Ux2lyT+LXNvYpuPPG8cYUOxrG+zwwzvZSfZ3sTZV+SsA68oLR93Lxlqm7qZ+3mwYNtipw6G+t1saP4yDgXoeXljRm3c1B27l+sWNVqXZlQKFxvMoFqwuPRrzZcdbjYL9zzlUTdV2p5wrB2XHPtqaxCgBrAMt4KE6bypXpq/0P6rjek25L0JfGRYxWOP5HcxzVL7zSnWTSmJNyjeujrfIbrdnX/sAsx+sv6U6W+v3rUCe7+tG227vWlq2YCvIZGNmIH8DPPv6gyGtvu6Vd7jY8CEjAqHaJN6zm6YGXhp2YtQxDWh0HdAEGrg6FuXCbAfva5Euz7Kumm1Y7xVC0DUmEH3g4nBAFC+kFGFZlvYM5eTVPR5owGeqwSoGjhqgbLoFIhUsVqC9SGG/37eI0MvDBTkpt2qRTi3ifSDEwDzvWFNvd+ubwUaaDIMAJBfO5zM+KGAbY2S/27U2UMex0TqhmWDTPBNiVP217g1LShpZ7VwFtkvDjySXSn8nra+nGPV7qRRHaWmc6c45Mpl5Uqe6PX8cNwueM9qJIpoZi9g8tTXY55cIysOPzeNAcJoZhLPpXqOGGyawEoOvTgi1P0wfqDP+pcdnDxi7Adb6UUpWsl4p+MqpJaKFopqPpHrDZ6cUBQ8O94ghshRhSZnj6cQbjz6llctjJM4Tl4cL1pNGQb24qVdvn/E72afebbxsdpFt2s756lU1z6ZtpBWhkzFkv7bdNkFuff12GPTbKQfqBuZRL/n2ZK2faiCNdHXj5lZnRg9FKl+VVKYGwTJ36gB1ReSF1g1qzw3AcIySbJ/LdmLepju0a2QAZOuGun3qS27gbrRS+mcapeFvvYGFscMYtq7CMMbOCZVzIpv3QxtWf9Yx31BTDO8wNtG5Ye7VGTCcZkDRtpW3WRqutdfC4c0osCMc3k52dynrAUmPoAh+ngmHS9ydV0lhTyE2D48T1SHNvSClqEEWVHA5kR4FJa5t8JKLkq4uJ42G9Rrp4KZJ0+RMOfUeFT8DmbyPVcjVohguI+tKOi+EEgk79fjKiOHecpSc1dvZJm+fc5qtMEHcIcyIVMLtsZ8Hg7+NU5usL062vkT6jB4LZrUm1HebYuDOxYGcEtfLQiqmGqqCFWoREYvO76OuxQoePz8iCD5MDaR19KgLkyMFUZBAavqkgZtOZZWrm4zz6r21yIoiQqyAZLIICUG5tajrpypeDmpq5hbg1Eig2nLV5nHekUrhtC5N5g29BxvZyKb/bo88GL5ry7Ybxt1Y2h62MTfy9qEFt43vy9piipg34/nv/B34J/9ke+H73w9//I/fes9bj6sreP11XR+3KftPnuj3N4HFhw/hO79Tf/++71OwUi3Ct/7sX8rxHd8BP/Mzvf0A19f6UwQ+8AH44R/Wdn7rt8K3fAv8hb8A/+k/wR/6Q/r3hz8Mv+pXKSj7gQ8omPvN36yA7Ouvw3d9F/zAD8Djx+rk+ZZvgd//+wFa4RSo839cf7b9DiA7oJkf0EAUADdFdg/u4GPk7K9YjyfWtJKSo5RnfPDDP8Gv/9Jfiez3lCSE05nZByavEYfreiQ4B8GTlsjxGHn1HZ+Lx3G6ekw6X8GqkQQEqzqse7sWL1Rn1CRK0ySKWpA3aXxwPisAGKcIOPKqII9W5BWOxyMI7GaVEcod65hmjaa5Pp41k2in8uF4XPF+Yp69grwndcS+ev+SVBJpXchomt7pfKaIMM+R3/HVX8H/8ZM/xSffeMTza3DBM9XUeD9H3G7CzwE/e3wMuGnG7XfK4e0UPBzT/eyQommFZnQ4DBww48wi//oUdE7YT457MfD+u573PdxzOU/s58h+F9nNE5f7C+Z5T/RB75Et8iOzno4sp2uW5UhaV6wUVbPbc1HjxkpUzaHpoCUX1kUNG41e1nZLKZyOV6TziXU5cb6+4vhcnbi6hWoBLKNsCj5y3M11f9QHxxigZEr2rN6RljNSFnJeWU6Zdc1MOxBRvmnL7FjXrNF2LhLnLvdSgpwKKUs7N+dMqpVwfBAOF4E5656U05mSq45RRPlSQ2R3uCTngBfdc9fzynwA1Rq8AuPlRFrOUIR5tyd6z5OnT0k1omt/2BOjI4RqdM1z5fUDRAFR5z0arKiDHUKtLG77s3eVY1FahOR/7qGALCTdhSvRQN9PEcGLpts701+8g+A0/RMrtuKb6umAINKMa5u/pWTN9Fk1ndeeg2jXiVPnEE4dGiFWENM5pGRySqSyKBAtahhnUaB3zSslJ3VUSCbXwqznnChF9YfsUD0sZUgJiaFl1Vm7p2BRxra/qp5gQEaRmlEw7pcWZIDqu745O7cyFufw4vHiKUmLdDo8h4u9qhk5oRVmIiEE7lze4V3Xz3h69ZyPHPZVrbPx3+7XUkT7sAyZLNXmsDXZ37NaVS0yUDZ6+m26g80VO7ZFZMZzzJYY9behf0ovUqPYk567ixMpdwDIVz5YU/KKK4Np45pdpq13m+7QTw1YUGFZDKQajhFYlOFcae0eT77tw+29fPDM9T0sYnfjCHU6bzd2t+ttvflAszg3+wM9gMJ0vZvntBdyZvqZTj/o6V73NOXGHtLhhz5u0+1WHbT33cvmy2c8WlXp45cAACAASURBVDSsBjbkIqxLRkRtTx3eCpL5oGdKZlnOFUiKlbM7DOprlVxDerbyt5deotSAMGd4Re0T59RRh8pWHyp1jxv0rOFdQytoNaTet/HQf95Wm1e6hFKLo5fiND1flN8+kxt2Mtq/4+9SZapFbyunao/43ICx0DMDU65gqt7LuFgLbNbY+XTS71vdENdnW10XpRTVQTFaodpmH5oMKUUqRU9NtW/YALqnD+Mk1Z629xGpVFY16M5VXaL5KyoQHIKv76HRxGajiaiTIcRJix9KLzxvA1NyVvqK4BEvlKA0DpYhMQLPiEOCSTHFikLtI3MgUrl/QwjNaRJqpDYBJBbKNJFnYV0tYtc1uqFGcZU7kGpzLbYIZ2ASQolItsXtai1x7dPm0G2Rs0MATqtvoPDFuqSK5+i+EYZsFefBxVApi1Rmu9DtW3FOKShqpLLODw9eM6aEkaIBOs5z+/HZA8YybFVDwSugoexNKFXrytZVqL0bHOymibsXd4gucC6FtK6czyeeXT2mOPAhNhL+HHwjMbdjBF66l/BGZKN+SQM26G2B/lP3mts7f9inNxvcbQK9nWaL2Tbg+oXHm8bYQJvWIHnxPv0VDACBKQZSsVgUaCva2w2kcmiAAVWtrZ9hg77t6ECJ1E1nUAhk2DQNCOpX3rwT0DfRF+9f3+PGbW7ri7GIj6CgtFgIQwObVEAvy1Jv2+fAOKi3AkFSAe8RHO/di6kjHVyyMeyK0otHFy66l9eCBLJVLP3uPiUdKGcgJeV1213gDndhvkMuVdH2BkCbMi1ILrUuhxayaE2SalTWMSwIkhOyLnA+AVmviQHC1GkKKiArtSqxvm/95319kVo5N+UKJCR81I3j9oqEXYJsVd/hb1eVbxdwYQKJUIK248atxhogm3Qte8w4/9vwmtC3cdlqxhax551jN0WyZE42MR3sd3vyuvZNh4FrqfZ5AU7GFRmUj+YFuTP84byly25lXCsuiHqkc6MMMAXXomLUyy6ubji58gcXSx21e5oc7O21e5mi47w6f9ZsBei6cvJCw8fRq/36skgEkyP9d3fr+uvpWTbnNlr3rcdtivboOR65g/jwh+G7v1t//4qvgH//7zV69Vf/avgtv0Xn9i/8gkar2vH2u/Dump79oX8BH/mIPQR+7Mfg3j2NbH3/+/XvN97Q79cVfvRH9Z6f93nwvvcpcAn6zDFy1I5S9B6WMhajtuu/1IgYj099Cj76UTifb//++74PPv5x+M2/GX7f71Ow9Z//c43w/aZvgr/1t/SdvuEb4Hf/bv3+H/5D+NIvVTAW4J3vhMtLjb790R+Fn/s5OB5xUQ2IHqU1RKnpn1X/HqJ/qJ+FG5F03hEPe1wFClNeGwP/mhI/85Gf40u/5Fewq3pDWFf2y5mLltEsrKtrGRQC3Hv4Nu6+8nZ8iFw9caTzNd4lHBFv6cpOhY4ZEbEa6rZMSpGqSHo8QiqZMPWUMKk6kjmR8xBZAxpF2ip9SyHlwjxFBC1ikrMwVQPBUvNi8OymQDmvqhvUVMK8aMGqKQa+5H1fyKMnz3DBI28+pnjH5BWI9XOEecLtIm5yuBA03a4CDGKCFpqxaccGnN2s5ZfIO+Dh3QNBZt61C3zZw4lX7t1jP89MwRM8rGkhuFArNwtZEpIzkjMprRyvn5PWEyWtlJI2hrv2ayavC97LsO7r3CuFdVlYzgtWoKlIIS2J5XRkOV9zur7m8aPHnE5r5SmUjfy21Lo4RR1rr/J7DppCa9uQB7wrLEtmXQslCW43m62oY1gKp9PKbp40ojaocWKplIJyo+dsoFWpKZiBGDwhOHLxdS4IJZcKnGuXeDw+TA3MFZzSMVQjWakIAyUYpxqEadI56Lzq4JczFxcXWr3aJZzXNFsfJ1QvTK1gyzjYPkztA1vfBmx13fHG4ca4uO3R9jtqjSzAo1GyN2nJzEDF+RqcoX8boAFm8Nm/rivpHugUdEiJFFKNFDVjXKODBCpPbcDPUbOCYsR7R8nKF5zW1I28GlhQXNYyAF5qcZKCUCNygULV0VwP68iijgBfymYv3OjKbgjAGHT9cFP/aTaJTsRWaNfGxOtztXJ2dfMnjeYTEebdjnXVvpFSCFGB5suLS16dZ97+TPiIyfRB17hZtGv00jTQ3vSTYTRHHcU1PXa739+m4938e9QHRh10vLZHW41RVNaI3ordvMPVYnzmjBsDU1pfjnYKfeh8jU5u+h9sqqDrPrE9mn5ljxjfrT+q2cYvVReqTuzdGOEuQ5bU9rxNdPFL1bDtnmDraTQ5b47JRlez/7ntPWgf2b7kNmP04u5yYwxv6NNv5djef/i8zj2tHg9SHClJe0Gpa1QLYpotKMqV7TRG2DmjzvObueigZQexmac2/7sO3u2dCqp6S8k2ML3a0aVQvG8FnSysUAOQHFboy+5bigcJXa75asOJvkMxrtQyguWyBQNvHFK6Y8GiPX0FKBnX8WD/5FSphxw1RV4BbOM9tc5e11TXVQXrWzS9URW4Ssen8tenjgt0WUOfoI4Gxhqy1eeQ6Yk2nrp+pD6bqq+J0BxMgrTMmdHmMn7fXPcFcaU7yOr+0zCWQssGbHOg4i1uSC1z0JJPHY4YQ49QpttPrsmxrWNK17mVfKvj5CwSv0at+sqhWyehWJ9YH9V9U/vGgsH8AMZWOSjD3K6ySgbb1+5vUc16b9eBX686iwYo6b1mp3uuOXtdDSKgBj75Oq+bbMbeQ/d1Ix38DGYm8FkCxjbQqP6wbcY7lD+ofVaFafvZJYhDFajdFHjl3j1CiJSTVpk9no8cz88Rl4mThlefT+e62TjwNsiahq6DqBPNDRMD0KhRm7QMwk2oZOhDtIcNRG3gGC1n15XmvbXbbjctnHqViqupM/WZVhVO2okwpgx57D1Uea8R3RtlREQr1M3B8/DiwOvPnpIENbps0RowaEpnlb8bZUWkRcdZmw0QHIGscQzHNtwUtsVS0lqn6NU3RXKPPpUu/Nx2o94cYop3rd5nTxjf1XZ6agRAMeBZvWv7/Y4QIseTNIE0Knzj7j8qMaDh+4Gu2L4UqL/5LjKC7Nt7avS2r4CZ0IN5RrUKvN9BhnK8hrzgDndgf48y3SPlWd87ZpQoXu8XvHIZF8mt8IwqBtq2QuUEqo8ppSDLGTmfcWXFR4Eg6mL1DsdsjR+USY+RY9uEtTFicrgc4Vwoa2YpC/HyAks06Wpv7y/b8JthYJG+9kybLyHiSkSsQMZwrwItUtzVjVujuAoOqWujR+Zvlfja9ptz3umZxTlSEU6nM66k9q7BOz7ntbdz/fgp1+vCsaTKT9jiZggofUHbCGqXdZyiS4O65W+4flRpcXWK6Oce3dw05bbOFWeFhlxN93NtThnf7cgv51ygOcuqrBxrqDSdZJjujoH1STU/OkXBVmkdCwn2NeqGO3XJsJUltq77d6oc5r45Sj93dHCN9xsVWDMwHLbhK2C9OUKA7/1eBRS///sVYPz4x7WTf/AH4Q//YdjtYFngf/gD8D//CW3kH/gD8LM/Zy+qlATOwW/7bQpmfsM3wLNn+v2zZ/B1X6e//9E/Cn/+z/Npj1L0mq/9WgU9ReDOHQVQD4ceiWtgak1dfcvHX/yL+vNjH4PP+Zy3ft1bOZzT/vrmb9awvlK0Lz72Mbh/Hz70z+pp7sZlW/neKkTXSVml9CDv63r24MOewxzJaUGuTpBKU2azZJacSThcgPmoUWrsCiFMXF8vkAslZyYpXD2K3Hv1Nab9PYiXvPHRf49PBYV+HGHyjR/O1sQuTjic0hIUVJ9RrRTvHdMclbtULBohknLmdDwipWh6PLCkFe88u5pOdnV1BKc8/ILw9NmZ3W5mv9+Rzmeunp25uNhzuNzhAzx59pwwTezmmbM40vHMHKOmmMVAWha+/Nf8Ki4e3oX/9LOcHHiCFkiyf77KLadcl06kvaetwy5N2uhtfjeHuam3wTt8KQNnPPza930+u2nm833mYn/BYX+helAurOtCTmqQ5az0Dbv9DslKM3C8uuLpozeYJnBearRnNUZqhU1JmbQcmXeREGbmmvYYvLYvrWeunj/BAXHSYmTPnj5ijsrh+ubTp/z0z32M59eL8tUVjXjRNPUmpPRvV6NGgmcODq0Hpd/tp5ndfiKGyG6auX/3LnfuXiLOa1RdKhyPJ406wjPvdiRZuH52TUrqRNgfdhqROhgKQiBOe+WPJUPO7Hb6juu6sjaQdQIfETxC7kaT0/T+5XQFLnI43CVOE4JSYWXxrGtitztweXmXaZ6YQgRWzufnpJQoJeOpBTVlzA4wncFr0U1L4a5ruUinD8pp6yhssmGcUs0p7ky91PXt+nwU228BS/Nl0gjvEKeBPm2I6mlqV9dbx4jLgDnxAnHSuawRVFKNwWqPTJG4m5gOe3b7HXGONf20sFsOrMuqAHnWRkvOhHXFhTNZTuq8qftpKY4iXnmYkVrKy/pNgfts4EZt/ul8bvKT+n5jZGxTNAejzWhJto4UKFkpkqIxLgTfos5KypxPJ87nM/djIOA5nY6IuFooLer8fnLJ9DjWInmoPln3c4uQ0+gxjXA2UIPaHnOehBsqt6pTrr/GS8CfPrhtQvV5NXzd/9xop1twoX5rkeo1pw2HUkOZDpWX3Ozd/owOvpY6Dhbx5p0j+kAqaRNg1GwBUwxv2D3WSgME+yt63DjGtgbFdssuk9tzRMD1VGEFSW63x7Z9crPPB5us79TtZ6O0GW03vWkDIvtbbZ/ZTANUJxUHFSHatsL1v18GpH6m42XRtDfP6cCWq74EBfhy7Z9cCqlaIM73gm7eB6jgnWYt2LqoYF2dkw40a7Hp9sNcF2lZYiKC79ijFp5SJb8td6OEFJtStWBX/ViL4tGjxkOILDUdXv8O5CKI5OY4ccbDWduT81Bc+ka/NcBSuqwppVTe1D5mBra2rAKBlNY2I1r/det6HBQFXIvgWFtfqSPJbTJ6HLQozJIz0zxhuJFlDqwpdcCRYV677lDPA0+uc6Fxk/o2Zys9RctmNv3EVZDbQEbN4knrOqyHCpKKFvX0PpCT8p9DtaJqpHCbk055rEcJMK7HIoKk1LCucVqP73l9PG7mvNHV2J5ctMGtQBlCGzfD1hpGg+icNI6vJppcB27b+zpEtu+jDi5wxjW72zXQNhlvtulg3uPDTp2ZlcMXaHPVVT06l5pdJTpltxiA0DEN90IGxXh8VoCxFTNvQgOwd0Bqx4u8uFFugLAqz3fTjoevPGAOkSyJpSROeeF4eooriSATQVRglJIaiCBesMqlQEXw64QylGJYrYLW4WueGFviDbz0PU2XPtl3ux3LutA8HHZNPWvTK2547Bi9J9Vjb0Jy2PBto7RKk9XObD9NOncvhcMFzwJ14g7KaR+K3hYxPiX724DnURGRjeLS9RNXhYcfvrnpqaRVXb3ZKyb82+Z8891vtNc+GfSS1icvADi3bJoNsK39uiwr65pQfVl5T0cFa5OydfOoX+XRS7zV126cO76P25zkbQMdFJGc8qCASb2qX3P19JryXJQ+AIH5QJnuIP4C8OAFhxao8U75iaBSMhRhvw+bJiM1PSUbB5FQTtewHPFkpkNAykpaj1AKfudx027wMtaAMyMlbv1QzXIxcA+dszWCSXYTxsGli/VF4SaYIuCq0UaL6i4iuLISy4ozLtuc2/iPXe+Qml6jz3JeNt+X1sfbNIjWpJvgkL4Yayk8Pi7E4LVyp1OzdvJwebnn/Dxzvj412gGajDMwVExiVu+wPaqmfo0y0m3lws2YYkG4Pl6r8hZqWmLRyLm2RipnRV0OqhTcXOOmSCGNq3oETPXiPDTK0F/tuxgj5/MJXW++KeqbvqtvaHJjq0LVz0aDx/XP2ZzbdL4b9+/3sk1zLNQx3lsViJfkxOYM732vgq1f/dXw9/6egolf+7XwIz+ika4/+7MaJTo26F//a/gf/yf4S39JwYL/+B81rd97vf4XfkFT+H/kRzSi9CMfUeD3rYCmP/Zj8DVfA8cj/N2/C0+faor/a69phOqXf7kCs1/8xXr+t3+7crx+Nhzvex+8+ab+/oEPwE/+pPLmHg71hJvj/qIcdtSooWG/euGMtoYUZHXOcedtDznHpyxXR9LxTMDzA//4nwLCqw/u8zVf9ZU8ySv5pBEJ0QV2u5k1nynnjJAhFx5TuLj3Cu/6/PcSQ+GNj/0HynpGJBP8gf3+jka8pQUouAKzj0Q3Ib4aWsEqF0NKRxyeEDU18Xg8cj6fmCqIY/N7N+8oOfPs+XNyKcy7HUWEZV0oBe7evSStK1fPniHAKw/vkVNmOS0UKTy4f5/r48L1aeHZsrK/vGCpHKGlOC4uDjxPmTPCc0kkpxXYCw6pqVrdMyM6l62rZVzBjlFuWZq4ja/iJTLoABCdEAcPzxe/5wvwLnD3+jEAZS2I0zuFMHH38gHXx+c1vbPw6M1n7KeZnBOn8/PKv1lT9IJWHk5VR/TOsebM6fgUKRMpRda0EMMl87xnt9tRKoet8Y3mnFjOV6wr/MKnXuejn3rEMV7gH1zgstIwlJTI68KaaoHUWkHZNDFfLa6mYwDendGsWs8UAvcvn/Le934e0zypblgKMey4ul64uk588o3nvPH4KadlARG8V2Nnv4stlTw3w7lm4HtXweDO+eejZ3/Ys9vv2R+Eu/6KB3fewdXz5yzrFThI54VlWcDVQiBRC56sKCCe1sTd+5eVRkgosoAkBRuSgGScP/eoSpP8UqOumAjxPj5c4vyEQ8iJUTlse+J4vADPDtGDWhhOVYUxyEEse8d7jfyeAkwR4gTR9ArflE1XDfVmiHtXI++lRgwPFcDpzv5ePGnYL6nBFCXrWqVopCy0YiB2F3vnUvkgTxTOIqSiDoUyvr8D9Qx7pUAIGv0m3AiKMI6yul5VL1Bw0Gg6NlRV1hYR7c+is1WKaIRWDRQoTnC1eJevdsiTN5/gd54Hb3vANF9U2SKIJLyfuHNxwb2LO9zZXeJNg3G+AS+vvvKwFljRLMgeFVXdazIY/8Nh6mXVXjFN++ZxU0032aUBEK4Vj+2FXfqVZqOUGjQRLD1Zut5YikXqZz716PWhP8e9TBoPseqA43N0LmURpYAaxkT13vG9Ogji6JFn9l6hzo/BpG7/7wEQo2E6dJBzrR05rdXWqz3szO7reqOj8gxDK3jz4iEv9L9da6ZB7enmOOkW1raPxqst+lMcOCn4OOHjRPE1E8a0y2aiD1lq/4XA7Gc+eqsdyv88+9jS8LXIrJ2hztAYB+DPO+V7FXXEuEEujYdFNo560JgSLnkIVnBKJ2NBWQaC9n7Qtea9Bnbpk5RnO04VRKyPj0YPBvgI3sUmG5UOITaOXMVncp+bBlrWZzr63wpWK7WHOV2a493AMa/ZGI1TFnVKlpLBWVXAusfWjCKL4F2WPpdFhBjUVmpBVlboq+qWNl4K5lXud6lcqrXgVaNKq+uvIOx2e32X2v/az4I4RwyxFpWs/VOE4/V1BWdrwIrzFYSvnOI166vpvFJp54wGCLXzLcAk1Qhl45aNMRB3M8tSM3mGgIEaq6Nzpw5qqf25BRw7B7eOUx9vV3WE3TwrVYGexJoSx9NpE7xofMJiILlsV7nzPXjIIqHHyGPlo/cbB53dy+ZYL/ilRTDTuuKDr/QfQ7SvUKO/tdim9lnWv8W3wCvDLwxHEj69zPisAGMBnLPYCO1AA+BF1PS3iAhHn8CqU+gGoBijKqe7anA4CpIT6XzkdH0FTiepcUzp82iD0aoXNi9w7Ug3btpjo02JFfuvehbGtPkKkKAh5s7pOaV0b3672ebW1r7uWWyemc2ZNwERUD4Gt9mUu5rnaNGC6AumXHh2PJNHTwNGrGyxAw4n1ArQ6ILadoUqKBVUx1XvkZKpYJ5r6nnNY1MLTxlfTvPUvcSwNlFsEt7hKu9SnexWLW0AhNywIHqXjUiMawvoZhKkVn/tFAa9NbYx99u1ImtuuP8gENQJt02pUqV/7PcaiWuKmsim2T0qwbWFHithdxdSVUEfWlsEDesvGYi4eIGLeyRGzVouVh3YISUT95OmjxVpG4du+vaOCsTquxckrbBc4fIRJwtyXKGszPMlEnwrxqKOXG17WaVJ8jY+TqhhQHrvWm1Tw3ozkLWqdVEc1bp7WM1jZ2EAoUPtJxdgWUt7lBQ268Te03q62i3V0KAXiDJhO6iKbX6Y4LgxblIzHGytjNUhBfjE64/U+CqlciBpilB7SwfTpCTiuzhzb3/Jo+snQ+EeKiG/9adeZnPIlDZdfrXHxneo7bf0Wxtn6vxXZcN4Y1291uZ54eG9B0zRczqfeHp9HMZURZJrcsdth0o6h5D1TT/Bntb/2g5y3zPqzYYNbys7+vNu+dDkBF0Z2V6zlRcvcAKPh/danOqv/BX4V/8Kfu/v1UjZ81kBWufg4qKld7XjsIcaUad/H/Q8Oy4uesEuu0cIvKUjZwViAf7sn9UIU9DPDFR+29s0Ahc6KPvZcHivffFN36Sg8tOnSmUA8G3f1sYMusIMXeFyJkuGaJ1Rx2gGS/1dtyRdT2G/4/DwAcSo1eSPi6b0Ijx69pwf+eC/4Cv/2y/HTROyqAZ9/1CUcxmBM5B7EZScVl55+Hby+ZqrJ2+wnp7jOOP8RJwPhGlmOV3hRBS4oKZATxNSFV6KKLemaFSnFumCi8OOnBTQ2x/25JQ5n87kCgTESQtNUBXtEALH4xEHTNPM/jDXPVwIwTNPE8+vTmRReqfLg+d6OVejUNf/07Sw4vlln/Nu7t+/w8989CN86ulTrhOspYbcS1M5oBpMXYltoQTb1TqMjQ5N14icU5k9OU8clORXjo9Yw6HzONbIzXpBK1ohCKfTNRcXF6znE8t6qkaZzgzvq7O1qNFWpJBz4bQWrq5XLbgRHXk9EtyMlAi1qGycdrp7lITklRgiz66vuDqfOaWEhJ1GVtRlG0RwuVBKqulwaqyRsvK/lcFp7xzZaSmqLOCKsKTEebnizutPePWVe+x3M3Hecf/BQ46f+BSpFMIUOa2F86qdqpmtheO6DKrKjQgyaNG5GoWl+3aIR2KM7HYzb3v1RPjcQ1VxHNdXR3bzgZxWcs6sy8L11TPMmSk5V/B5Ja/U+gqZ3RQa/53zdQ+jIJIRp1pMERAXCbuJaXdHqQpcqPtRzz7rdUzrxKlHL6j54qGvb04anXTeIuWqLeAq8NEcIt5pYa9hH1DQ3ugkXIvUsvsW0003/zcdqs5tapCERQa11FttY6ED53YFTkGYJMJaYBFYcSQcxbmuB9a9Xm2c3FI+rSjMqPlO09QpGbyl0Wpf+6o8eelOS4cj7nZK7aViUN+3Afu+Rh5WvbrqEd55yGjh1lIoedX2eBASuZwJwXPYH7h7cQd3fozfhw4SF+F4PmFVxm/u+bnUuScGfL6M4uqGZjHYKmMWmr6sgV/VRsRtdA4b/64y9KKgUgYnss3dgSpPnen2GNPxLQLPDHzX51BHxtrvVgBpjMi2U2ymWgHoYRa9cJitpXZIabpZhbJo87W+s293UkDeVz50Kr2GNOBDwOQ+DFSB3fnWx0A2dVp6IWs36Ma8BKC+5Z3aepX+Bt5VzthaeKrKMwPDkK1eMRZ4/f/iGIOKxMbN1o9TkNL7audWfdo53TvXnLQIoNOI2iwZdWOqvn4zGvMmCOtcB+QEzbBRmeNbL7q6f9qDpynqqLeiXFSAF0Dt/M69SZUBvp/bwB29v2X95pSUf9sy/5qxxABS1sxgF5Qjtcl5qWqs2ig5D3MNtHDxMGZ6f5WNks1mrpQ74iheEFczQUZZICBOHSemN1r27ChGDPRVu8z2cTZyaHSEqMWva0LrhTDw6pZGKeCzr6nyfb8xVgEnIClrZoUPTDFihZBLKSzLUrMr1AEYY+yyRIRUOXWzay9BPq+anekhi6vRpuqIs3kUnPIWC0JKnX6AOoYGSIv0tb7mXOfGGLnqiUENbucs2rR2qqv7MGhx7aJUWpb5WXJSwLo6UJ2jUUHp0CpQLF66TikyjINigiGEtq/kIpzTivMZw5wcRkEGqlVUh2MtZu0JRmpZ5Xapwd+qV+T8crnxWQLGDuBB1dybwTSK1MHI6ueCAXme6kEKkcpwRcmJtJxJy4KbLJ27qx1V7vaNb2yVbW5QeZa27agt31z0wgbZtyeQXg3SDje0Rf8/Kk7SAAx7V25uOi9sCvVpYx8NG/XYUgO4pRRV7q2/BwXEtXa1t2s/u/rRn63AUu+3UT3a9JpsP3F0xeP2Y/zcbX517bWlKg3SxqwpKK0R7oW7je+zAb/YjqfbXGjjaiBOnYtOGll8v71YwOeLr7JRg7YTqafebBo7gA36u1UIFKF5dcW5G9fQhX+ccXFXBaEMG1q9pkbmSBm4YqH1q4FWer8CUpBlhbTinPIauQoA+BCREOxK1cEspVBDYzcbErWwVHuIhfubQlByTS2pr2p6zM0+uvGRvV1wqACtMRYa7fFivCj0bnHjvWw5OVPaXpyvrm5S23kgbUOqcpmWguZ0Hl2dzu3eVthDLZU+x2M1AoPzNSVCq3/mnFvUdu8UCDFSUtpEAtk50n630wdalk13SOsHYQAhTUdBo3tFsups5oAY+3KUb7ZO3DAvGcBs6+fNldZ2u2tffy/0/yBTt8vg5rkyzJ+tlBojIcbfN/d3bujpTQM0IvYf/AMFD3/4h18eRfuZjn/5LzWK1nv4Xb/rxe9/+Ifh0SPlUjXags90XF7Cu97VuVhffVV/Hg4aPfvZdjx5Av/oH2kE8Dzrz7t3NeL4m78Z3vVqO3WTejkYHxsFGKpdUb8b9rjNfHIOoqYlT6K8mWt+hiTdl9eU+OjHP8FP/9zP83nveAdcXuJWjXg/xImpAm4eB6c62Ush3n/A3fuvIUV4XooW/VrP7KLyZcb5QF5PYI61LBrFNk2qVGaN6E/rWnk6S60M27NMpPKDqSoPSgAAIABJREFU9ugAj2BV6JUWheYc1uq6rSpsffdUFPyJU1Q3XVqZaxRdQZXzpQg+wtvu3uFtlwdcumI5HzUVujhWC5uo617/NKvFgCjhxkK9qWr0aPvhhDkEpsGhscsLQqzFobaZRDqeuh+FMKniHwPL2eSkRZKUtt24mjZuukkRePb8zH4/Mc2CI5PTwgo1XTRo1lVaSCVT0oITjThJuZBFKohkRmYFxqLgS9RoplxwOdUqWxlXwVmpeqPNz1INDBFhKYnHT6+4e3nJbnIKFIZYe1jHW2lgbN8aiyuOWhmDnlJTXhF8ULoEIVNOCe9XprhQMty7+4C7F3eJcaoG3VrnlmNdz0hR7mIpmbSqMZjWtRpCWelxgva3RqCM+nJpoJ1IxIcJP02E6UANXa8t3ergtwNuNw53m+Qe7AEzeJ3rfHW14F4rujcAsf22rs2ZFsRg32nIOOKd8tt5r1F5rQCO7kdWlKWn7g72iRUlGfdetPCY/TPeWw1H6UC1rUGzdxymf92iw/h6vmurdOgh/a2BEPWY9ns4rX1M7LG4VrzUOS1wo4EDmYDHJWpml3Ey0x23zhGnicPhwN3Lu/jrJ0qNVbTImZTCuo7AizSdwnRiqdQ0N7NtepaERcvR29x0sz6+o0wxoNxRnd3UMTSCRek2zmjbmqWhwCzt2TouZsz0MbK3aqM9fNZNFTc81iJ2beZ1QdpHZHQ81FuIyditLDY9emOX2jPaxf1cGwZd34DTvi9l2JtszkmX/1Jn8tBV9dW2z9E+E8Ze6V/LRvF3bPXYvve7/ux6gUU4j2nYYzvG62+zUX/p4OxW/yylsK6JaTfhpCDFsa5rLdSlNEFZBFLCO4vGtHGn96sMbkyRWuRo1Kl7b5qcMGepc7TCkjfXuploI3wxgqxGoQEq6yilZfX07IAhvd+CnlzXT0bRWkqPPNXHdbI626cpUEbkXqBn8jpcLdbuXS085bXwZjaOaSkoENh1AKxgWVcbyRZ1TJcxQI+MtX4f9wcxg6YCmkV6X2Dz3DX7q71CTYFOpSCS2vfOu+Z8artgzbxwUkHauv5KBV9tXzRQuuSiRVWrHeMV4W9rsxRHyqsWuHOOWG3ytlfVPlbHFNZh5IFz1tfPAgoaGz7UHOZFRUQpWaORnSNqisqGOsf1+LO2t6oeIy1AQWVNpWsQfWbToa37zQ42fGvEg0T7xGSOrwTuJdV9hUp9E2rgk2+TrEITokB9Kzyr/9P9qq6zTyMnPivAWNUrTQB6EPV6ybAxfLqX0ChN9RpNeCYfK5elVr1flzM5Jfxco1bLsHkC5o0YBWKvtO3aJOiHfTBGQt7SzhtAYJHC+XweIg3He22fYOBV2xPc4MmzmzbB1Be0iqmyCcB09TsDqPvy1e3KHl/32WGT6teLdA/lzZFoBguuCtzc0k62qU/bzVBTd3ThmuDaGMzD9WVQHoQKUptSWcdCvb324jcibexetuG2se9KQn9b2r3Ve6ZpH1ILyznX51APzDHhbMt26CV7L+uG+r9hH9N3rIKijY9FFZuiNV4/PAtEI7IDjQ/T3pXx3rXNfn+BjxNZCiUvEPao+1IlTJh83Z11hkTjGLK5Y0LGvFO5grEF/G6Hjzu8rEzznuImipsxjjeNts1Qkt5nIJ03UbvpGN9CSVXo5YT3cwf9Br1pc7QNw5Q+oYjTjdJHcknarzkhteJwv7S0FDozWIwh1uaRH55j3uMOrvptO+qITSGSS+kccU3C6DsrgF7jC8woHddC/daBcmFfnyDCxcUFKSUlnq+OLKnt3O335OsjRXI1htzmft05YX0p1qKmXEkFopyjcVGP85S6eT16/rTV+8sWId86YQRnO/zVUgmdxaWPkUZDN27Gx/qsAyVdKTJ5sLm6XrRVeLFnjXJNtg6l256vBPufRvkWgcePNQp2mpRSwDkFEC8u9Ps33+zRqeNxOOh5V1cKsn7Xd8Hf//tKJ/D1X6/fXV6q0vToEXzbt2nBri/6ok57cDr1+z1+rGvsdIIHD/TvP/JHFCy24949/ZmzAp/WjkYD8BaOp0/1fR4/7p8dj/qeIvqMN97Qcx490u8vL5W31jntozff1Ohha8O9e9qGX/xF+JZvgX/7b+E7vgN+4ieUyuGHfkjPa/ruLUrwjeMF8GQAVm7YGgAU53DBMd25YJpmrgXOj58pQCq6Zv+3//P/4jd92X/D7vM/DyLE86JgCzqXEmvznkteSevKa+98d+V+C7zxix9hPV/jg2PeX7C7uMvVswx5qcpxBp+5uHsPnPKPXj96xOn6SAyOeVJQ57SsTNNMCIHT6UTKuXEQ5pI5L5n9fq9FhHLhdDxycXGpmTq5cPX8iouLHaDpeafjyuW9S3Y7TeVPy5l7+x2PjmdORVhDxEXPwXsugmeePV/yuZ/Lo8dPkOdn8pI5ndeq2GLStGZA215nHV02MlgHtC/Zph5Cq/V4CIE5DOlj3tLJtqlyTUsSUDqWQJx25Kw8btM8E6fIen7e+O7sKq0GHGpKqOPNx9dc3tmzP8wEhHU9sq5nQpiYpj3BR05poZSVkla81xRIA1fM5tO5OGhaNR3eB4dnpw7LUnRNLmfS9TXk3kejLlCc4+nVkWXJ5D1ILpzO52ZI41zTObEiFzLO8psT367zDSSd5sCaEpKSphqumU+98Zh79z7J/O4d9y7vMsWJNS1cXlzgmLl6XmrkpXBOC9dXz3nw4D7rMsgn8aREpU4wjkrVDxtYVhy4mRhn5vkC76d2jhpCCWf6kDkhXni9rRJvWKztPc04o0c9mjqCcy0atuspW1ki0qPQmj7cQIcaOVij5Z3U9eA93lnlaJNd6vwOUcHYTnmk/zMeQ3OyWDEujZauzpQ2R+o57RY1cMD2bhEolXfWMVwHqZQeEda6Rxo4Do7lvNRK5XrOdHGJW591UMD1PhIpJElE56n14FnTGe8DZY2sa9LoL1mrXPQUcSq/Js+dO3d55e4DLj7xMa6y8vMV13Uv05OFHpXWnKiDjrYZs2YziA3iZhncdMC2KGBn4HyowPjQ56PzqdqRm3sE16cFbLMXXd+LtupLfQb9YxtL06FsfhiX/3h5ywUZbLsRjK1Lodp4N9zb0ovYjU5oT5XhYvfr6cpNZ7R52uaBb+e2e5sNa1GWLfp4yIOuNk57nzLO8cHOGYZRu0Oafmj2qMqTsrlnwW/oJrSvTMt07br+/O2Y3na8LLPz5ecN9xOlIjmfF6b9hDi1tU6nI9M0s9vtqyOgpmVT8D7gplipTHybgsZljejvcZoaRymOWhxZagSodl63qRnWTI3gFiHVor5bW8K1SEYFfX3P/Bv4QZuTqtlk2p/LunTZ6aiZEkPWl3QwqwFwVFlW55dSKPTiUmabYm11rtX1sfpA4BogjGjRaMsydA58jBvHkKMChzWzpxXBskCb6vjp/aJyxrvelxqJbN/qfFUHVFugzb4RpOFbKVkgX+cG9rjWrlT5UIN4ilMHMKOdPoyNE1jzQmTqMrpkilHg1H8asFQa7UIWzeRpu2BxSEmUoI7+AHi5mdFbqmNGP/ACsVh0ed2DitalkRBUjyvgMrhaPNdJgQTGnY8or795HkWEsma8lx7hjsOXKiMwekdtR9sDqy2nMln72tZN8JG5KN+5RfT6muwVvGv8ujjHWjEEQ35sfsao9VSoRXE/3fFZAcYCpLLisAq1tZKoUOkEVCtvaRrAKKiVFQzmEpiZmP3MuhQIkVPOPLp6zrpk5r1ThL1UhZ7eaa5Nr75ZOGoKT11kLe2CF+2G2/Ta8Tu9V49Q2Owf0gVKB/qktcWhk3zzmLGRwxa9fe52kwqNeMDuUdplZig1bk2DdLp8aMrrmDfioAGjAFOMNcOuCqmN8kMTqta8dV0rBtirkt8Gxvr6yj0KwvxIw+sKDTLrHB99PJvidvMYu9LOs43EgWMQHJvrq6Bsxg1tXNomOBzqSBnSJZqiOqRvjO8oQ3tFAboXxgJYzucasj++S+n8WkBOJ1zWb+JhD8sVcZph2pGiGt/eeaL3BFeFafVUed8D+2yjTLqL6gacE+RV6QSmC2S3p4TI4mqEhmhrRKAcT1BWtIyU10i3mppgHd6KmYhxk2b9VxQQz8na8/JF56pA9R5YM66osrWgBpAvCUlnjUCjR6tXFQFxajLY5h+qsmIK8MueLJs71SZWLqW0plawz3hREWGaIvv9gfPpRM5rvUe3wlylbSgI51UNFkD5aVZ48vRpO9d+eueYp4m333+V43TN8+MVx/OpFwy82V832y43Py+tTW2dWFqvMeuKVdw2xRcFHNzQMzfWX4sKutGrY1TqzWiWpikN9zMl7tM67QYF+dbxG2XdC8coY6vRdMNIaEcpCo6KwG//7fADP6A7+Pd/P3zP92ihrne+U4GW3/Ll22u//duVW/Y3/AalChDRAl4/9EN6j+/9Xvjbf1tT9u0eH/iAgpVvf3t/vr6wRr86B1/5lcoJ+/a3w+/5Pdtx+NCH4Nf/ei2I9YVfqJ99x3fAn/7TL+2NF46v+RqN4h37/8/9OfjO79Tff/Zn4c/8Gfjrfx3e8x5t9/d9H/zO36nv9bGPwW/9rfA3/yZ893frNR/8IPzKX6lt/eQnOyXDhz8M73633gMdgptRK58OkP10R3MEmHdf1DPuHPjdxP33vINHpZCujpQlawpugv/9J36Sj338F/nvv+I3ciWJOXkt9CcFdrPOkiywqFPk9Y9n7j98jXd9zhcyxZlP/fx/4HR1RVrOTPsLdruJ8ynjkhBEyMvK+elzxGlRr7jfcRmgpFVT4oH94VJ5SteFUoSLi0tOp7Nm43jH5eUF19dauDTGwKuv3Od4feJ0ShTg3v37HI9HctYIxocP7/P8+orz8YoYA/fvXPCRTz7mKhf8NHGxC9zb72A9k67PHClcXuz5ql/7a/jQv/13XH/kY5zdxFGaNOyGP/LCGhynTte07G83SB+9drrBGYtQDbXbZJxrDv8QJi4vPSVnQois68K6nPFMGm0kWWlVcMQwUaJQpsLlfuWNxyceP1nY7S5420Ptb5VhmfPpCsmFabcjeofMkfNyZp48h93Mfpp4tmaofMRCdbTaRuFqP7kaWuADLkzEeQcxko5HyunUiqtaTzoRzsvK4ydPKHklTIHn19c8uT5xfVpJ+alGbNT9xpy++tRB19IF0HpeAKk8hKclgRHw0QNq33jzGQ/uXrOPuxrduHJ0leZBCjkrB9/hcGC/2zHPO549f4qIggDq6AtKvxMdMcA87yglkNKZ9bgQw47d/pIQZ5yLLcqkXU+1yQSN5jb1aZxbo95r79k3aAB85VD1bU+xKGYHFVwYiWVKsYrfNO7YLnN0rtmPujlVbLaCu9Up4bwnVnoGFxwuhiFV2A3qtgIhDfhqN6fKwL6G7PcX14LRj6kanx2UDeCrN1vXleg0Iqp5WG/06TRPg9PDMV1e4J9fU1JmzUmBWm92TKl6VW5pm6skUjoxnSfmq5mnj5+yLkcFFKaJ/eUdpsMB7yb2hwvefu8+v3FJfGgXOXqH+D57R7slWAUie5+xlkLpul7wgSlOmtrtrJCO39zPImdH3kMRjUTMKbUCSxtp1Qz9blPakbPuJeEWWwe4dc+yuT52vumh2tZ+ryYbpE/v0e7ybW0POl5rYhMKm7a52i5nzyml233S7+Prw1SElqEPNHPA9F1tidFUcGPdvHhUU0iHrzCk/dLW1c2+uzEiN25oY6ZAQEIQH7RYuHejOfCWj5uOmbdyfKbzQi1ebhQc89S5NaUUfOURtXmRcyZJYfJRac4MdNW7aHr46VwzEFRumRxiwByM+kiK4ELoEfq1zcuyYMETliquRSc1ojaGwLIuLQs4RpUTFp0pIuSqs/gYahaHaHYFuoevOVHWpVGGhahUfCEouJWrBFzX1IrFNTyg2lYxBuZaT8Eo1bIIOa+Vvn6IenVGOyLVbtS5uywrp9MZ6poPIWimUK37lUVlpVHH2HVAa880RbWBayHM4+lUOUwj0zRxOFwQQmA5n1jXlbQqh7rtE6E6jDvViQYZ+mrntdCW2r4SdB+8vrompbX14WF/wDkoFFbRQmap1gqwOWyUAvZPcJzPpwboBh8IQHAB70LFITxpUQwihE7hYZiW9Y0B4r0soEqChK7VhDpAi0N1nrbmC8taun5YcTjvujx2TuewoE5E5yz7x7U1VFBKx2aSOnUAg0M8LHmtNapsrhfWZcH5oPVZqt7pxCsIPey3nkgM6rC25zrnCQQsqC99WpDwswSMdUBwKlS8VI60prhUIK4Mns26MEZdKkjAhUCYZub9hXabgKwr+XgFsiJ+1gKtTsiWHoLevwiEMERqYWCCeR7rp7U/dQj9sK30Y0yRCT6wm/cgqkiVuquMhOU99UQrxUklBlYDpMW9Yp5c5zqg65zHG8BiE8Mpx2Yzd7xqb72ddff19e62QUrXW2yPc8Nib7yudauzTd74uJzzHE+nusikXTt6qcvANmTRMJMRODuN+ungjDencGuUq/3btpi2udtRlWJce6c+MDaoVXGpi7pviq5dCzf5pbq3cNOH2KbalTI9b4jMqXNBDcXcxrYJETq+1BZ4VVJuRuC54RdttlAybVPZqn5jr+wQWUEW8JHsIrgJIVQC8NhSQ7Syr8M5M74CLX+xblz6OFc9WILkFYJ6mItz4EIVlloBtKXLhaodlkKMHmKk+IAMjFObI+daZCuBy4QwUaTylw7GQxMG4w1E0w7iFBvoV7KQEXxZoJz135pbrzlqFUUHLdlPqMTyJhsGY7UOXvChNaGM0QV1k5+mSEor5LoRSTfkUkpcXV3VOWTKsUC7T5cAtkAVJDbOJHqrhCZjTufERz/xMZRcfAtqWtu67Klzrwi7/Y51XWn8sLqDt/lqd+mbo5kLptjQfhYcrggh+soReLMNdEO1Pss26nbPrk82eW/fhzG6DLe9vcmdFl39ohK/jWDfGiA6nXxbZ/pNB6XHVwDgj/0x+MZv3L7fgwcdRAxBgdYf//Hh+932fO8VgBzPuX9/e4/f8Tu237/znfrvQx/ipcf9+xpl+mM/1kFMO77kS/TnO97R7/G5n/vye912/NW/Cs+e3f6dcwoCf9u3wR/8g/3zL/qi/l4xwl/7a9t7/PJf3jilWpGyb/1WBaKHe8hP/WtKoRaj0WITVjDFjhapZStKdD8bI91uFmC01WcRjIXC6h37Vx+wxMj6/Bp3yvy/7L1drG1Zdtf3G3OutfY+59xbX13dVW7b+AMMxsJtCwzEAQWhhOSBICvKS/Jggaw8IwUDEhEg4QfnAcSrXxBYQkgO4gkQiMgYIlBsIhzcAhu6AeP4q+2urq66956Pvdeac448jDE/1j6nyp0EQj94qU7dc/Zae6255hxzfI//0JBRgS++/2X+7o/9b3zPf/77uddCzhsbmedRCJOFnzYDYCWs8OoD5Xy64a2332U73XP74n3O5wdyuedwfWSeJ0oIbOcNUWV7ODEfj1wdr/jw5QtyXlmmyLJcUTZrGBVECPMCYA0IQmCeF5bjgZev7pgnK3GcAtzd3llT0eMBkcDd3b3B8x6PxCA83N8xB0HmA+et8IvvveS+FJ49u3Ln4sR2f0cQOE4TxMjp/gFZFr7tG76ZZ8/e5Mf++U+zAsmDZzEE3njjdR7u7gxiAVowc8e6mw5Q/68N+9KlNsscmKdhjUuilhgm795cM9iCY6X1u0VCUEKYWBZhmSfS+Y7tNlm33mpoYvw0l4JEa1zxwZdfoDlxnN9mOQRUq24YSGWjnJLJeI/kH6aJT731OvNy4N/88he5T/W84ZvVjr9S90oYMvo8k3VajpZtXSA/3FPLL6u+cDzMBEloPgGROcBhnjidk3VMFpOXNRMvxMAUQ9M3L10XVcfSDCWYrtSk0CBL0poNIzadDP84VkN4RkIgrytryUzzxOFwAClcXS2kbbWGXp49LGTLgI3KgxY35IXD4TnLcmUwHBWfTVPTPdGMYIZ1ScW7dGPYcANvn6f5cYNVl38NF9aTJaoGaI1Q3DC/9HK6LGoUqbQMtqaDueHXpJN7vUQtGyt7J+pm14hYNqxUDdqwmw9XB0BaN3JEhixHH5ZQiwqp9WFVN7FfKtRUf/fisjaotuZHfpIlTpb9JZhOV71hzaaQHcSFPaE25bJS3uQ2SEsywRriad7IJbOWM4UMYll/r17c8TXvvs26nqwR3vlEKIlUThRgORx4dvMaog+ONQ3qUAFo5yMM9GnzOjCXwbFcU5RjDfP4jVQLllDn69p0kc4LJizxxJJE9ll7Nk02V5V0FHjt2TPW89kgTBw/dcy2HVatUlUbVwPvqDZQJb46vra40ta8wmWFTqiu85itVp0lVBodm+LUNat07/vaLRyvQJd2DwmBtK1WiowgnszQ5Ku4He/0pGXfWdzKrmkOX/zZzQbzdzXMS8uAbPM+6O7ds1wziYdM3PEQs66NjAWmALNno6fUpkSG+RiPMfjbAriDw3L8vT9yf499wsHFmqt4FZ1lvdYs0Z7Rac5XxYIPMZoDtmBVc6WcTbYvS+Nn1VbQvLUxhBBpdX5Cd3TNc/N7ZMf7btnhURr9VGdTtfWt168wycQ0G2bpNEWq7d7mz20SG5b5USpOrbg9FdyRV9wOyS43oQczjsuhVSQE8GCq0XhRywKtjulma1S6VCFtW2ORtcRfWtPKwJXC9fVNxyel6pVG0wsL19fX1EzwWsFryU3CFEJrvGbsRdmSybrKA0RMb72+edbooa595WUpJdfdopfhG3VXJ2nOuTWgCjGyzDOvv/acNWV38G6guI7YG59dP3tm717UZa72ql8f1zQt7RmoyYu6ljEE5mlmLoGUEmdvRFqx7us9xGWIaia780Icl11jaNVS9bpXr140WdJ4uQd0JBut3aezPcvXRMSzUN0GLr7elS3GELkKi2dQKw/rCfEGXRVzuahnAUdLMdrOG5nV58MaiZXs9/SM6uVwoAhsmkk5m66IEJ3vFxzm46nqr+H4qnDGtqNKVbozU6tgqxtpFECVzbiRJcEyauM8E+cFNlN2KBkJBfH0NhO2mdCeWRXfvRDf807tOJzNcVBHcOH4U20g4EHCTnGSkRmwZ9xV+a6eOffH7BwTxjRKc043EHmvEZH6PrTJY7g9tUzNsj/bBFRR38bUXlBpODTjK+4Uu3pvZ0KA+USHsY9KfFUsoAvk7sB2h4/W62X/kMsH71TSrvT19XgiC86/8qiDp+38pgjsTlU5357T36mu5+hc3eFEjGPcaVg6nO+jHJ+jA61dDjYEM3rO92caind9Y2W37yVMrqwXikyU6QhxdmdIFa49EFG/34bbKMRLu5pt4szbBYut7rhI/pevu0yzRR514nCcSBKhiBtRpY3H1E01J2xKPaMhxqbcUhXtrmnuntvIRTCHio81UIjljJYTJZ8ts3ecq102pw57VvcL0XTcXro/zlW7Z1ErlykV5kG7sufPMUeljLfev8/gOFxcwTqdz0OApaqelfZtrU7r2efg6eyDvervOQs125sxe2PcfFqnxs6X0p1mlaxlvOuocGrjPxcD2BtQH3HEuv5uOOwMMMZxDgMc5vEpJdnG2ZC1+sDbd4a7+j6rfGk31G/4Bvv5uOOTn7Sfety/D/fv7a+5ubFM1Y863n7bfi6Pj/tOPb7ruz763OHwld3jqePbvu3Xvuabvsl+/r/c4xu/0X7Go8mOPe30UkY7RBmM44Hydzykfti/uZdzSjwuLPmaIIGkD2g5gZoR9MUvfZnPfu7zfMvXfR1v3lyTNXBIyRwbwR2AJRGzkNYHEMjXN7z2iU9RSubuVSFvJ9bzmXkxJ2lcFsp6RnMmb2fLSC8Zw18UsuJGejc4amZv4y85W1MeDIczbVZqGKTK2cwUqwwozvsN43tNidOWOefMs6sj18vEhFLWlYgZgwItcyJn5WqaeeeN1/n2b/oGfvqXfpnb88ZWrFwtbZtnyNgMB+28a5znMePsUWBV4LDMLPMgZ91IsAwSzx4J0Z2icfdlY+niMAIBNBDjDK15VNUPKh67Z+POQtoSr1498MX3XvDuO68xTWbUK4XkCndw3UymiViEYxTeuDnwtZ94nZdr4bxl15WEXKTrIo036vBa6rLCsmmyedwaT4oxcLVMiCilJG8rUbhaAtthIufMmrM3DjN9tbZhVOdlIx/raonvkuKh2C6KuvNABM3J6DKdUSLr2Vbs5voZRcQCDJuSY+SUVnJa/QYKpXjn9Wj0HIV121AVphiZ56M7diq8VJ0bxSOETc9LWVm3TCrw7z5MvFpH6bbf38o+K28skcX3xZjt1b7kjvcWsq/yxP+nLtRbSWQ9KYMMHoK147NbOW9wR74EJEaC4zn3jL0hs0ihNp5rOlldq2FRB3EGbqgWI/vWMGu8NkbLBjLnGY3HtjXvykv7zrwceK8Utpz5ZKgBc2lz3NZBlCgwufMIrHP1/e0t0/QOKQU36NVLny0BZZonbq6fwd2D9RsInUZbf4gndAilT87I9+3yTk+qoWkOe2bDoN9Ly5AbO6KrWtadVJi1i+cF4GpeKJs5orXf+Akd22d0p086GV3qRjt1tJfaNztwoL1OpJcOxEpHzv+rA5XdErex6qUuWe0lMS1qX3nUbTJ7iSqXOl0M5s7eVt0/3BUwXyHpKzXOYPtnZw/t79Wljd0ziONBx1BLIe0RDPSiT8w9XMxj/+wrzY59+rB7VQiQ0TFevILRllNbvxcUwlx5ldNLdeZKYKSzMYFJ1OSdnR8zzV33FztdpAaoAsF9FJX/xcq3qHuqYtNLz7Bs7MITfsTiIo/1Nm1zX6sNgoZm07RLJLRx1p8YAiGX9ozs5fTVsZqLBe4cM8Bs3mCJRvVdagPC4jAtFX8VETTUqtbOy4R+XqQgpXqmSqv4rew1iHimayQXh1OpmcLJGoz2OYtNnmgp1pKtvmPo1RulWIDSHIpjlYbtAAAgAElEQVTBYBhqRWsMHLyRV14WSs6s67mNHGCeFrfZ1Jvs9aZWljDUnzuF6A5rbZnUgQ5lZPqOweiUnBrUp4ToOOhGExkg59ZsU8SheZquVvdQd0YHX6vQKkaAWIPuuc1ZwHTfKqobdIN/bwqRyZ9TyHufXqXDgY0YZJ20pr7mIO+JT1qsJ0DBmrqdt80qaMSalqsEyzlk0Ks+4vjqccbWcjN/y955kbozm5IhYa+4V/ZTI3QSA9N8RMNDN6q8kzrULmyeoSg10vQ4c8wIoql9gLbAqrpCE+pz6Q7Z5iD2jVUjDl1527H5dlRhK7U0yhmbjvMzGJ72Z3l6oUXpav2I9Tkyvi6wGInS3y+2NP4ap3/0LWqmsr1y311Sma6aQSOCYYUOY2gg4Z7tQLvvIDibcjWcrc98NIN9JjsuW3+v+o5jVLOWHF1+vn/2KHC70KnKTYsYtmcYAx2fLShIvMhPuBDuw+tU2uvPHd/V7hFC5Hg4mjPW57/qW0Y7o8LknX0jFBaYryDWbooe4fZ5bhFrbVTrClf293anHT2DQ1WRkr1E2t5X3MjbGSrTRJDJsA6PUFalrNa4REtGQ8VTFoQMae3O2BBbuaAqj6AguhLdMWOMWC3vtjhfmclM5YTme0p+oORtmF/nPdIzdVWgaG5wKDuqqwpqKfuyoHY7m59U1IT1SNulIHGkh/aV3fqP2foi0qLB27ZRNLf5ql/uyqfszj2O4vdntNdBGiZUU6T7ZrJ7NiKr84Wve33eBbVKdTY83lfdcBnnQHf3at9RK90qOZOLZS41vuvz2Y0cHxvQo0nDverzaa7zZgCMAQUd9kbd3k/x7V8//uMdejiS33nXjURotCMCX/rVhs1b5doj2cUo/h6vpkuwTtcxMt9cE6fZGuqsG4bNY1n3P/6TP8U8z+jXvMsbhwPXyRovLJMyEZGSmEpA8kbZhLvbD3n9E58ibSe0JO5ebqTz6g6IhWlZWM9nhExaM2U9QxDmeQaKYYOpmrLsvNiU8ui4+ZmUE1fXz0jrmXVL5LRaRgdW6ldy4erqipytKRhAXGZuHzZuT2e2okzLzFvX10hJbOvGuiVubo6EEFqDqsPxwMN5Q0vmZl74T37rt/LFL30JUuJOCyct3N/eecM/U2sK1Tk6TvplcNY1EPE8HlXmeWaaOu5yzfqMQTz5uwlCWiVC1c2CGTLRO8VTBAkLMS6eJZJaUMqc1qaYHw6BUgoP55Uv/OoLXnt+5OZqgljLNvuYQxCCHghqDdaup8A3vPsWr1bl1d2J07qRi2UNJ8fBFOmZSPaalh2Uc4YpUpYDLGeKZ1WGAIc5cnOcrMK2dpHWzNUSQCcE5fa8gRtVIsJ52yyLaDfl+kgeVB4qxcr465TW5Zona86V1zNoIgBpO3sJ+ARxYvMSxvV85tXtK7bzieNh4Xh1QLWQNy/dngQkklIhhpkQZ2Kc7d3lQj40Q80zloplHJ1TJqny01/a+PBUdl95fFTn6OOfEEPXw0cdsj6+yazuyJaB71Rzt8qMKk8qHnlzvtbvVzoL7hByOyZ4JlSu8tON/ip3i3b6bnbK6OiSIShd7Q41eAK1RGCj04uGOaOT2Jq+aSt3RcS72g9OORGW4xW/WOA+Zd6epkfJDtW5HSSgYSLqQiaRMZ5zf/uKXJJnl9m7l6zgmdnTFLl5dsPy8j0iSp6kT/DA1+v461GGKsgxR8ISCWqzFZu9MZOz6iH9Fe3dJxHvVN7Xu2ZE18/KYJRVB2Xs5FNNpkHP6zpHHXnFprdrazJAJ8PdlvAnBQktm7TSVR87DVpg+Iq/o9uRgz1QL7h8Tl33Oqe7542yd7AdbC+MfVjG69qC0DLodjpgVcBk7C/Y9tjwP1qYQwYYu52cl24/DGO2cvzoSQWebe3NmJ9iHR+V3PDUdZfHUzpGtxXFVexuQ1qQhlaOH6hBNXutkrJXL0TCFFpQ57GHoT2svVSlv2rnXGbqB5zv2+DqDVoil4g1FG62tUBOPVKoajLpcYawIuK2XOnJTNXWKKUwlakyz2GsnhA0wIYYXwponKiN4vo+dOdZzqzb6rLfFADBnIu4kzaIZWebA0+bjS9h6nav41xWeIDs3xPPtixa2vyaA6+QSvZ5qnw2QrE20mZbWoA6e/ZxhSaoGZuEiEweOC3+jCGCJkGYMPgK8Q2SS+Z0OjFPi+HezxGdbOzFcVi7XLP5mqZojsTSM27bLpZAmKRhOqtnCguegRwDMUxMLtOKwyNkNdigaTJ9IE6RTRR1KIbsuCNTbUznjvVlPhjEQragXJyiO4ZrEEw5lINBTG0bquZwnbDm1kECGWVNm2e7WhXDMi3M08Q0R+bDRFHLOk5bskC6VwAEEYIKh3kmiwWvU+kNRc0JD0xTo0kthZySVwIbz854Y1yv+P84h+xXiTNWEJmpmp5IJLjjwsoWlKTQO93Xb9kLVweEaqbo5uWBhqGZE6Rs5rVhFNg3l2lxIqzgyvWmlalIZ1B+KpfC1XwwYlPlVIxYxAmoyYQq+KKl5+98FxcM8jGzvhSU9TqbB1VjzNPUm4CJFm/eNGBzULvNCg2gwJl8xVvxGMXe4YHNR2gZinsD9vLo58wlbqV3Ogj5gQAFArGpHXW66xS0Ln9ayf3ykD4/wz3b2N3xa6f10R2eFoK9DHm85ql1afiwdMOvGvTZDf4gHUtkfw9ppQW75ys25qq3NOE/OHlxRWYYvgIpJ16+stLAquHpqG3uVi1AnBCZIBxo0QkJIBY90kDDy9m2RNqK9xVRx42tQtRvWektiBnXaYW0WdQr1jWsEdWGlgFiDvhXr6yBSkkJ3VYkJ2SK5nRVhXyGu1ewne05XoJc4zQfrQvVUnLrQprFykUiyhQKs57g/JJyeomme2C9mCsPzAx6eS4mcLS6ZUwKNaXDF6kpkaHRfVUSa/ZBs2fbPBhf25e+V6VopNmq4H/44tVubFWJaoeMwPf+THdmfpz+KG5kalaSlh392fc6bEGdnv7yO2Z1wVPs+ztoFvqY+v1pzoKWYV+/4pdu6+qkbpFc8gAxUSOmF/ykOrM/6tBHv3cnrX1/uEicqhsr+hjp+uvH/y/H9jv/Uz74Gz/25Lm3vu+/Yfq3n9tt00e04E1xOs54P5pSDw4Z5DQVBDksHN9+A82F9PIePa9tT/zDf/KTfMs3/gZ+/+/+Lr58PvO8FI4lcZwmbmIkNagIpdx/SBAlxgOvv/0uV8+e894XfsGbKayIqmVkJmtAWJN3RJVpXggxcDo/kHK2JkhB0G1rWRLzHBGBVy8+JOfEsszcPHtG8aDL9fGAiHB7f4+qwQYRhBd3D3z57sTxuPDmsyveuLnh7tVLHtZCmCaurq9IeYMMIU4sMVJSZgmRMEeSwPl05l2F5eqKD1LmV+5OO55pW0uJT+zQqo90/UGajMuqPDycOM8rONKHZdPlxheXaerwLFrMqJGerbOm3PW2EHn++tvMhyvu715x9+oF59PGskQOxyMicJcShyVY1ocW7u5X/tXnvsDXf+1bvPnGFddXE0XXdh5VJJ7JU/TMkUiYj3zy+g3evrHGajFGCAdULbgap8mqJLTSo3BeV04PD2xpI6XEw/096XT2LI3MRAZNrOvmn0FJiSDw/Hri+c2R0wYvbx/IqVCylX5OBHKwhMtU2Wjz9AxrVKpzoBrqti+WKBwPCyVtnM+Fw2Hi2fMbtgyqgYeHewAOV1eoGtZg2hIpbaySkbDZzhKT6zllVgISFg7HA8u0kGtJ7YXAV5dVxRudpS1xTolTLuiy9IzO9ipDoFQwY9wzUKvjqDox7MdLa90hEasDoxhyXEHIwRq+hJF2q35ILddm51CoPCWG2nCm2jyyez8JgTAFL5mNxm9Ch6aw8l0G+ehK5+CkMjkV2DdDgkxhEyhByNUBJd24t71UiNPkc0DLhtwlR1w4pMJhQeYZ8QyqWl5skJRClJkQZiKRKBba3jhxyneUsnF/94rbh3umaeF4dcP11XNWLV7NkBAyb731Gr/9Fzb+pWZ+aZ5QL3XQYe5tOrot4csGaId6qItUqova/t/IbCCeywoLVeW8rk1X2elpFwGNqhEq8Mvvv2dluSKMTV6HXNhGH83Ri0NgPXKgPmXP2NNaYsiFXTM6zi+9AjULUQV3Cj2uihqf97GZnxdqcX2miOn1Y9C8wVjQ1VYp2rJC4xQ96GDapwjWoErwarL9pPS1bHdvOmt9/7hzAJeuk4vAFBG25nAxXfZxotavdfy/z46tTkAlxsl08pytiVAxzNEOEeHvEUb8TG9gFfZ7cxwX4OcBpPkSmm7j+pDRROiE/8RYwRx/DSlRbV1qY6suR2T4zkhH3Vau0BNAb3I+lNRD93E8GknlfTWBDJrPWTxTFHfcVmc8apmSZm46byhaM+wQhC1ZI6z62NZTTOvUd35vPM9eSLCS9nnqtlgVBZNjAVuz7Y5x3Ry6pWLtTnsojyqbxvlr4/J7hFo1YSciD1Q/WojBknfcqZVybz5W92CduBpQzKqcHx5Mj5wMuoaszXkc3HGZ6hrHyBQmold/eH2FNfXaMnlLaAzglQ9g+1kTrKdT51NSG3r62icLkGvIECNhnjhOC0eZKVPmtK6UlJnDxOyMZMIbaIkw+biDQ3rMceIwHYhiUIY5JZLCNuAaqxaOxwMbykZhzdbzJagSpTvMY90/RXl2tXHeHK4gV6hQaUGJjzu+SpyxEGTIhMWVZ8QUwCEtG+gGcU0XppiTyRWsEAPlfLJmBlG4ubrhnbc/xR0PDsLb8XksTV/cUVGdp4MAgt1fb3/iE2zryqu7OySZwmzCfhB21Kicj280JtorVCWgOzjEr1Et3thB2t9VaATR/YasDiBl9/zuVPD7IHz5f/qfWX/rZx4LyvEYnA6Xnz0WsI+v3+kM4/n9r7tDHp1/PMLHw2mIfu1tH9/t41wwl4fu/umD3z+5z/zjc7Q1pUqYdnb6pZ/nrf/xf2gCvq5X/Vt3t6zflc6MVHZPG1UPCA2LV6iK1h5/ihgNdzHpTlmpZf4iNUMiEGMgNVwUmsNd6r4TY/pbEEoxxxXTDNsDup5Qx+fRaTEjqDomLQ2qGXclFcJk35U4Q0nECGU7oetKebiF88nmfV6IhyvHuNO9gL8wdi7/LgprsrITLYW8vSKfXlLWW/ThJfzMv4Df9R3w7AbFcYfIjrXlzBRIqVg2fOy4ctWGmuJkoPd1VWpApin5Pk9DYzn8zKg0V+VDmnKlg3IxZAL474WarS8DRarzDRfLrtxVslyWxSOfutuwo/I4VQzc3THwr6bQV1q93IM9A6hnuF3sR98jle9VXtb318Wa1nmtlzfnruy+0Ruw1Dmwxm/WITP2V9b+tL6XnuJSF/RVnyjaf//14z/e8XERBl9Oufi982gPMdRS7YFvd0O7UXO/pbpYnSNXb7/BNkW2V3dstw9Nuf35L/wKf/NH/yHf81/8PuPQBTQBpwdujgoygZqhncIdMiWmw5HXPvEOhcLL93+FtJ7QtCHzRJwP1qioZEQUicKWVvI5k3Pi6ngk5URarSHVm2++YV2Zt5Xz6UwMk3W6F2smYZkIwrZtbCmxTDPEwN155WFLbLnwideecTVbVsHti5dkgeUwUzDn2rxMnNdEOZ0Q4PnzGzaUvG0UEW6WA9/9u34nf/+zP8Xdr36RhUjMsKqQxZDta4ba2Fyw7cLd2lZHYCSo8OHLe16FFV6zs+fTA1sxXDUJ0nWyamw7v8rZjMWcDU8thsDxeGSOM3K4oaRiWGFHL+tTQcIMGtjWlRBgXoRU4P6U+blf+DJf+mDh7beuefP1A7M3JamYowShVmFBYj19gHjwOosQwoJIoEiwJls72WJZPQdV5lAoc+bqmbJ5sFPVnMPraUWjNXDJW2Hb1Er/IsxT4I2bhdeuX3NjubDlFcGas6jCw5o4nQspq5fVWZCwFCUX11KrzACmKfDma1c8v56IsrGtJ4okXnz4QFYQmZmXK0SiOVY8EhnDynQV0FJYT2diVGSayNm6KDeQolwoZJOaQUA65q+xY3PYpLRBWsm5cEobD1rgeDQdZDh2f2rXaczwrE7Z0HQgk+8VG9Cy5YKvRymFnDIhC0lSy/Y0vcBWL0igDPiOH3dUXiRVJ/RxGLazOL5uJm1j9dj+uMzUa9pixTMenqVAEkWDjXHIIezzFWPHia12yDDW6qsc9f1pnonzZL0DfJ3wDPjmkMX7CqAgm9k0JZAJZBWevf4603wgxoUQD8wAnlW9nU/cXF9xNR+YytkG486TPgwZ/j/orI5JFwdCCCEQJ8+iKhlVzz7zuzXHiq/5KBeiVzzWTLYWPL9clzpfVdfRrkOPa1eDC23PD8+q82xZWd3Z27NPH5/bLXidCMRt6WAJPH5fCR1XVqVW+XV9qN57Rx9Ss1S73SSPbDFoTkPpc17pwzLeGRrB+n0CRLGmwpXQRAwTPhdtz6m2d5+jqo/t7YMgsT1/r6WaTC8IcbJGiXleUM47bXpch/2adL38o5N4Pv54+nptKmfx4E+MAgSOxyvDs/Ss+aLeWCpYsG/0AWRV5lo+LjQacwaIqmVf55SMdoTmhK8OqWqj1t/DZHzYaNhtEDV4QvXklFqOjtNyjPFR1ZrB+oy0bNmOtcQerJdGiJNBT7qzscIbSahL7PANuVhiXA0iYKXi1kLGfTEqXsHo/M4hG6seqJifKbcAhDnqSsGzG0t7pwZDGYJDRdREuGDBggrVEILjKA+U12yxqfEXVe3v6NUe1lyKxjvCYBtWZlzt/nrP7NnUNfu49vPRnA3TWb062QZl49uyx27cM9ZsTvsk+HY66dnnsVdqBjFna60IKiizTBznmSXMzGIBPc3GQ4qoJWuVTNDuIxNVyKazpbJBgI2ewa4xMIUJn11S2tDo8ILqkBLY+qZSKCUT56XB1xRVvDAesX62BpVDJIYJpgNbziTNFIpDO22sUgilELUwq6BhsjksFtTGf2om7eKB5QmxpoA+rwShRHby5/L4qnHGVrDxMU4JNH9RkPqpdsPKL6pM2RyshSBKLWOKcWI5XBmtOvEhDJ3WtN3HNlpThbuBht1PJHDnGQpbGqMKdRxDaXkYBWp9VrX1BsauNeO1vtCwaS8dADoqWdqvfko7Q9o19c/89rukr/vGpy7+9eM/9OF4LOI4VzAoz+6crQspI7elX9LKrav+071Kg/Jpv+0UJTCMHZmssUVT+vyW2ofgYoLDHChbNcqgJ6Vbyr0pR4Gc1Rhe7fy5PlDUjajr55Q4g+c91ftrfZdgDUQkesAF0PtX6Lr6zwk0I/MBmY/ovOx6RtgW7i3u+mSZEVWNDIv0mhAJmmC9R9MDuj2g6UTMa8ui9Bvgmortt6rIYI6bkrPn2XgJrUHHDwY/rYHQZaCgKdza9Mx2zvC6ms6/c47aJU2zdhtpYFz+T5Swc76Or1TnLOe8/3xU2Kv0e2IMzcwRvCFZ8rLYIVt6UGM/Op+eZsTUQVUTqBpAF8OmBTHaW+yIkjroRtdPWkWwK8VV3d1jNIic8tu07I+Rr+4z8MN7v8LN3/xfdt8Z4zIjvxaB42/6Jvi23wyqPP/rf4XX7h8qF7gY/qW5vBOB/d7DuPcX70Iww33xklMb0O6aqjTWz6q4vBBTYTRCq2KrF/Om/c5WXi3cHK+5PtjPJBEC3N1c8+L6Gv7lv+BhPZmSPzpIqxxt439MY9u3/jbW3/cHLt7yiaFQaXT44JERPMJ+aPtsfN04ReL1kZqtnU8JKcq2rnz5xQv+j3/xM/z23/ybkZtr10tWpiCE2TJMNcPpdCJO1vgghsj1zXPS+cTp9gXbw60p8yJMhwNxueJ0ejAlGG24Y6fziW0zrK7DNLFuG+vqGQwxWifZ0LPPS06c15qBNKEi3J1XUi7EELg6LCwCUWvGlRsq0iFo1nWjZDMkphAtYyKIOSNjJJVMjoHf8LVfy3J9zZdevOTDF7ekYtVOWmlnv+0frVNjSb5cBeFcYB2SDUoulJSM1qM5mRBpXb5rCW/l9TWrozlDMINnmReur28I1UkgQskz5+WB29uzNYfAMpQN9kd5OG+89+VbzuczN9cTV8eFq+PCMS5MsfMucZidWshmhtJ5t2eDw004R0O0oLkG3YtVkODvSQFJxKjMUaGYQZGSQhJCyOQpo2VDxMot7fnu0Pdql0hmicIc61MDRRNWyinNQJuiOZjnJfDasyNBN2sIUzIyecALgEQpD6QNtm31PRMoJTFPVgWnWmxuvIqtZCjZGn+WXMhSiKHbBKMzQUsml42SDcLoYU08bJmXG3z+4UBu4GVOGxf6VC+FHnAHpZfR9wzZjj9XYQtKMWc9FIcusu/EyRqIBL+2llxW4q0OjJ4qUWm/GtuCaCROPdd25EPWANaxlnfM+EJbbOpA5Zb2/+iYmGVTnn3+Z3i4fcUaeiOnp+RL+705KIy/V9in3VXRMJKDO19SNhilghnNkq2kOQRr7kYQpjhRdAa17FUJ1oQ5hBmlYrg6tmJKRIGrw5FpTQZrFbU1OVZnJOZ8HTQHUSpk1z7TjLb/xbGi0aH6Yawyu1AChtnwZtOdgV3qbc0RK3UttOnye1HqpeYXBnt9r/H3qo8CzDGYTyBb0Ll/fZCbzjyLDp8PDhfz1dYB+b9VlxNfB39ovaQ603aOZaTRulanfeu1sJ+X6phQZ/4XszaSG3WyTNfouNw6rI0Nvzd6NI4j7T3q7I9GcaV6c/pNDodovL3P9/7Qj1jnp6556vhYh61gUBIC65Y4lNmgjUKgAbhVHiINUMGcsgyZmu6gTGpBuS7ndEdzuaQOtei8qvLD7mtwmRHMsVp0wGIVrxyg33SEAwohWIVKc6L24EVNRNE2J0PlBcKUMzXBrjuxKm1qm8sGN9Ic9fW821TVdrhwxnpuEJQemDN+Xr/rNkHRRvt+WR+KSIMO0LqXauKUiCcWd+cl7fO+Tq3KdvAllVIh7cbn9kqOamW1ami72S4JqLkaKs0IpG2tVMTQNMn1r578U+lLleaMRZ3XFdf/cOgFpXsSFQ4ycQgzi0wssiBR0Ig1uKSwqYJmUKOxiAXkmIzOtpJImiwb3G8bRZnC7DA+tWl9QcXoKg46nog1WjVdp8IZZcTazZkvBm8qLlAqLq5jE9s+MtikCXPAl6JsWkiinHUlS/USiutQfZ2n4vJZK7BhW/h9Fc3F8VXjjH10jNbrE05No9EB30SrcLBFMtnSI17rmtCDb/ogyAAg3E0y3Rmk9kwX0r41Xt7dukL/EeUA7Z5VhLj1MI5dqhAYsvwGgUtjHrhnH3ZSrwrk4ZaPpm/4fXTa/frxH+vwEhJg0JbbUXWVR/RYGalpff17lWy0r2+P8tUI/PD0qnB6oCKIGiyBDM/3Z4vCYQpsEVKDY7D7lSqYfV82+o+WmU46o3kFLeg8UyQ0p6bixRN1T4uYBl6sA7aklXz7Et1Wa6qVs0ErLEdYjmiY++tLH/SoX9qN3BBv59QTyzNBNzjfwvYA6Qx5JczS/eFtXWzMYWhsVve2epaEVMed4A6mHlW+zGywMWsfqw6LSHUiVl6yV1ybokJVPjo/VFcqKo8RH1d9b+jOsjEzrHUErXM5rsvw9MflVsZzY4zknMYr+03c1tiVND46xmAETSHZOX8v+GqflTqm+ons7jcaL4/uQ1esxBW0ug5N+Wqs9sI8GP5s9xzmDCC+/x7Pf+QvjbMxzM4+c0SAwx/6HnPGAs/+1o/w/Ivv7QyMGrgZzPPhTS72OHR5wsWJixcYeUZV6GrJtnU7HnD2hsfunumPusTctlPD2iuol4OK2PXHw4FPvv4Wr73+CW7efIegAYnw4q03+eKbb6L/8H/lxd0rw7bcNvT25e7pFUboKZn28F//t80Z20WnPJ6X3Xf7yZFeWkZ3M6jFS5Vp5FeCEK4OTCLmjN1eoY6blnLms//y87z9xlvwqU/y5vUVKMzrmShejRAD63ZiytmwQkvm5o03uX72uhkM28q2PRBEmI8HloNhyKLZMwKMN1gZuJWOTccj5/OZbbPsrXmeeiBQPJC2FbaUmLxL7zllTmtiipHjPPHs2BvOgH8n9SxHsGZWMRoe2Bwj5/VEmSJhFkoQ1i1xLolv+Jp3efPZDZ9bf5Z0/8DDmtlKDRp2E+rR8jzFO9SU3YRhX9aj5EySbGVkTIYDSN9HItbBuOQOwRIdN31XFTDNXF1dEQKk4mXSpbCervngg1tKMb43R29eEixb+dVt4nw6cz7P3Fwntk1RjSzFnOAitJLI6vCzIw/6qzY4HoatXLIZJtXI1pxQMmhpwc8YCjl4RqtmchIEy6jMG14+bhMoLieDp6PlkhGt3ZpDc1xHNxpLNgZ5dYxMszDNwtVR2c6JlBOFgshspYVi75Hyynq2gIA5AYJl1h4cgzcoYFl6WpSSQCeT1aXpNZWnd0Ox5Ewpm+P6JlQzd+eNh63wahN+9jS7M7aT0VgDgf/d+KHQHbANzsAbswzPpzoscrEy3G2rWkLLjDVnrpduVieCG71Gc3vYrsauBVuPqRCDMgdBpkAsE9WfC73svto89R5N5FW9aifzXPqEaBj1Sbj5tz/LugBLbLJv3GuN89eGlfXvgY0+EjMCYXLszWI41bkk7z1R0Fx6AxUxODMrIY6IWmZbSoXZB6QVbaq+ZM6oFq4OB+b0AHlFJwHHftRG1/UdDD4L7XjM47SMsr7q0mBdt1NOfrKa53tHVs0WrbBiozMWqm62I7ELPcSzPkelg+7ggn1JdtXz1cdUj4BwdTiwbqtli7VbtQLZnT2q7uCo2MWPgpHtBeo/A2HoWG03OG1wPO4qZy/ud7nvWjZcUw6k6dCjs3mcyzrvIQh9WqTpK/U7NRhS6qQ1zevCSTfeHIdRi9GxOCvdP318pU7YywzarzR7tp7eto2cD82JWddWVZFSmFwJqSXVKgWZPCnGx58r/mlzaKrxGTGtoWbeNgdsCE0faFQk8zsAACAASURBVFmxRVsAU4KQipen+/UqNncCzZGsjt0aQuQwzyaz0NZkPXtVXru3AHR6D0GMj/iEtFWsOupI1UYYjf5UK38HtAzrYJUAlSLFm4RL+6gHEHbPG4CDW7LGbgm1ZXXbNU5hjQ1r098FHJ+4wy/UrPsarBMRrybx5ao8JFw4Y0XMKeljF7SXgKhBP6nDb0m09T9XRzQBCZbR2pqBoa7b+q4Wmh+hJgKqFkpSyzBFiJgztjr7J4kcZWFRYWFiCeaMZa6OT+VcMlIyQS3PdVKIavRWxJyxp7xalQ/q/oZscA4S0GAO81wSuTqgK2sSacGArZgeVFSRBgfo71Id96IN/1dC9OSPgqBMcSKqZb2qKFsqrBSKFII3vQvU51X+40GiKqeJzr+kVSV81PFV44ytWV7aiDh0IRf2ynIrqVDLUIiVQMU84WvaEDHMjYoZcdo2wuILcaHogsMMBN1nrAUcsLhGyixDgCBEccBkXwyhumwHmVwVOHsxamkF1E3q92sdLC8OF9QS6uIO2U3+jDBKqvo1n8n9G360APl/fIyKxyPF72POXygsfcBP3OM/5PFx478c41d6/ql3GyPczjCLOx5BOpOtaxhom7itlwzXVMfRsLQ7hwldCIQYvVOkD0WzgY9LgLQSw5EiPfIdxRhJvdE81b+7mayu0JSSsQBboKjYPacFjtfwkGA7oduJBMizAssVGifqJmnZZnWKNKGnlfTiA/T2pT3Py5nk5hkcbtA4N+rXcT1G2lcgRmpG1Ej/qgXKRki3bPfvodtLyPeQz4Ql7rZKzRSonStdyg/L7dkkAw/ZOy1NihZvatWG26J1zsO8s/VesPc/atlKP7rTrCocgVG5gNwc/h9/dIfjk4/e0Vgr++9v6/iE2uai3aJmD1XDwa9v8zhskeaAreN3hf7jMmr7c8a13X+mtalZdZ5dOFuM/vq7MChBT7Gn8bPHcAt7N5Jt48ald/+YAbKvl90vQWjyoilIarTUMgi5kDHS/keb3wvZ1p+2P1oZqrQYvF2j+uid6rd3VbdS4+/1z8H40M7LxHmjIszTwpvP3+Q3fv038fr1M9ZPvssv/KZv5csffECMgeM88/rhQP6e/x55uOdhPXH60hdJf/tvsBUrp+vK+cUznzoGJfrJcTKKJ22s3MhmP4v7tddmO6gIukzEaeJqmdFS2F7dNyBORfnRH//f+cxv+Ra++zu/A2IkpgwhQZx4Nos5PSnWbEwz+f2N52++zeGT73K4ueEXf/ZnmM8rK7ekbaVkQJMpjRIIEaZ4oCzmrDudThDgeDhQVFnPKzEI11dHNBfO60YuieurK9aUub23hlKvv/aMZYpElLKeORwOrCVaNdB6YoozicC6ZdZt4+b6wHGeSDlxPp+Z5hk5LNyljfvzmRwjr189YwnCur3P/S//Am/cvMZWAmyZNWdUaln4KGcfqTWP1tRrn9vHW0qs5WyNLUMgTlNzEijmxKsGT1Hr6G5ll74XRMzJHyNRFmbgBiju9HvjE2+xbvecTg+GX6bC6WTBLYLfT+Du/szd/RnhFRIChyWyzJFliczzxHyYOCzmwJ5iNPzQUCukCjqHvfOl7UArl7cmIRktiZwTadvYzpmabTvPE/Nsmc8lKTkpln+SWkZOSmbsTZO0JmbqcC6e1MFxWSglkTOUBNMcoChlgzUpecWdtQZthHjzFreMSi6cH85Q80eDmMOjpCFA66V+QUw/0cWqZajBY1/ykltTkZw3SlopJRs+YS68fNi43SJnjZTQM5MayTRcVDti5Xnu3DbWG1rGprjDsDk9VclamOPMVCKTBFJ2p4ETY0kFkYiG4Aail2V2ZkVDitYKUNbXufJfmQLL1YHDsyteC9ZoBAzmQjXbWHXPewOpmtgE/Dl7FYgtZUrKnLYzc7RARjNmH22xqs/uFYVdqS77RJSMms4WA6xm3Oeykmo7k2Rjm+OEhGDNVVZLbMmYfnr36o55OSCLZc9NcbbUGhVyztzffcj1cWE+iQXp1Bqk1GhHHU1Ry1az8mnLzA3BnUB+pGwQLhUz00q+I9fX17z48ENUszlzK6OXrhblbNxJdkGVmila9SWG812KjnpiackO0gIhfd93WlF/n4oJiuufx2nmm7/ma/nw5Yf80q+eeNDcAp/j+u91mIIjBBjPGzSugd3s6UFrZjoN4qDSR4PXbTiz9e/6zrK7cdW+lKqjjePr1wUrh+1JDtVul0BvTmylzXlQtUoLlu7BBqrd1faZDcCCbVNE5miGTwhorjrL+N39e33U8ZVkzl4mOex0O5+hkrKXyNvPunmPGhGmaYLZwNKlOl5TJkYr1bcKjz3eal2fq+PRZGOMBttoUb7dus/z3ByyYHsv50wuhaCFiENZuMpZcnEcaHekZyug16CcKuwimPwp1uxU1ZsneaVecaKsvCVOFWP4Yj4bSzbsznoUrGKv7hcRoawOwYBQ3BYo7sAMarpbpMMDlC259KrZ52IVRb5ItRl7hX7A3x2pwV2DujQ4vdL2SPQ1D66XtMQcmgUy2HuVL0j7iVG8stP9XPkxjYkIwVsFCaDuOFfNSO62kdR1cod5TbAqqs2fpNjfV9Ni9ogHidKWELVeMuJzWEVFIDBPC4vMHIjMRBaZWpCjCBQpTGGGnBACkchc74HB10gQNASkJKRkUilkzTYn4jisYuuVU7GgbFKKCiUo2XHEM5Awnkm2Xkkx5eY4BgyaCttfotKaPQax5l0xBINMKrYmRYQ4BaIY7vkcJiZvji7uv0mlsKbUcJOnEKxnjet6H3V8FTljO0NuUQTjqJD35bujcVuVj5oQbF05X6KlEIKVHoTJHDkiPAlsLTJkBTlWrf0n1GzGHTPWPoaujI3368K4/luNXJNLhudSGZS6ZHh8p6cOH9toLFZGOhiZdu8uilpn2H8fx1//6/BH/6j9/qM/Ct/+7fvzf+7PwQ/9kDnUfvqn4a237PPzGX7Lb4HTaX/93/t78J3f+e9nbF/JsW02jvt7+EN/CP7SX+rn/spfgT/1p/rff/JPwvd/f//7T/wJ+Kt/tf/9l/8y/ME/CLe38K3f2jp388478NnP9jmvzh4wapWAFdRUWrF1DTBEevcMdxd1duMxxGjKR+kKo9FYYGwSMJeXlJLY9AgpIpqZiKhEK29y76JF6mAKE8+PE/dr4X7biAcrLSylkKryI4JKNPAVVbh5A4kLnG4pD6/Idx8gpzvLbp0mdFroEALmpMkpWdOvtFm3PRFz7M4H4vEGPd6gHph50jLfeY1qjtjeCjEjJRHzHXL/ReT8AeXhy/CFf4f8wucIn3zWLjce4aW8QMVqrgZzVR6DjCVug6LXmgHV+3VHXzHTE8HKKkqoEdP608J7Tyh8+5evCkuuBZkiQzbA46MqAmO5TXvW5ZN0OA1DpHi85sIx5c+oylR1ZFdnQnQBWflfi7T7CKw0zB0NyFBmOCol+yzMUem/dJCOfzqptveZpollXpjixO3d3e7lnjKG6vMuf2/GxmDg7ehUqiTbWzhdOuzptFLquNaX79U/3w1u//lH2wDtnuZk6IWmIz5ezQfT4fqmjX7M8dS81cmPQcyBiDDFA1/83f8ZHx6uCHFmjjNvvPYWMkdy2ng4n5lC4Ga54jgtpE9f8fDffR8v716RPvuTlH/3b8g0VtKnpj36I+bpYqzjIPe01D/vJaN9rdq6e8ZEnZoSgGXi8M4bSAyk2wfKae3nFVaUE1jv25TJDw+oZq6n2ZTBImyywSbcfvA+y9U1N89f592v/428fO8LpO1MSRthOXA4HB03Mxm6ZlA0W2fgGALzYSZlyzqcp8hhmdnWlWmaOBwOlDLx4v6egu2JTz27IRTDSU2qLMvCaTNjqaCEeeHV3UbWxDJPvPH8ipLt+ilGro5HTuvKy5cvSSESp4U3j0d0O5Ny5q3nr/MH/8v/in/8E/87a0ikUDiVwvkj9B6Ri14Bdd18rVeKt1qxI3rmb9oS27RZJmg0WbNtG8EbYoQYmWeTZ+LYab7cVmKtAQmRME3My4FcvCnsceOdufDywy9zursjrxtRMqdTIXuH4lh7T2ZrHJs1czorIsl4XwZClR8mQ5YlsCxeXqwwLRPLcba/xWRETu6o9ZLtllnbnM2CaG8iOy3WWEKzZSQKas64LCiBOB2ZIsToVSk1ECQVXl69QcXkmK2exZMsgzGXQsqFKVgmoYiyrlsrUa+4qgDLMpuRkjdr1qEgFA/sRJDijTBCc15VntPxCL3csFhW7JpWck5sKfPqIfH+SfnnDzP/5rTAnNmlKgEf3t2z5Rqks0DnZQDA5sDHcMFDDAtQkKKULbHdP3B+OLHMk2dPBUv8qPaAejMWcD/hBaNSL/V3fLvm7CoFyZEcA2WbKVltDyPUMtXqkHLO1fpqtGBmKe5MMnmWtRDU4DGyKmvJiBayQla8CUxvfFMdHY1HNlnf5XeV6zs+qmJOnimY4V0yRS17SRDm+QpEeVhfcd7umeLCPB28S7VAybz48pe5vrliipEQZlA1aIvDzPM332TbNiZ5sEzatLFtCUKnm7FEumUMlgQIOW+sacg2LRspPaDFnPANj1QTKRlEVrerQr1tc/SBeHa3UJvvdFnSZWzFU2yypKpgnn1e9UpVtQZN7OV+fY/iGMnBG/ZqUTQX/vX/9W/Z0sZq6e/G13is2Y1rGpx3jIHJmv1d/27OpqJuX/TEoib3wARbNUt24+5S85Hm0MyY7pIKIfhecLY20F+dt/q3QCt3r6piVtegJAzwN2V8XMssb8PQnuIkMTJfHTnHgJY8zOGvoVB9hcflmj516HDeAnXu3HP4ommaGj4s4Njk0enWdOiasYqYXK9BrPrMdV2ZSnHHYWgOzerwDyFwPp93gYI6roLRXNJEdZRmWwyDIMECbNM0+/XWzDIgLTiSUkK0Y6TWvVGG5Iycc1vnSkHTvDSIpcqjUn0v31PnNo/mA7EmhDhvtUxhcWxbLcqm2ioZY4yQSwuYVZvufvUseWO8CDA5nmtyp1vLvFZhmhfnST3g18WR3ecSCqe/ZsdsrRZSCIFl7vA1FlhW1m1tdh0wVGe40zcEDxrbXpmi453WXSnaqzzFfWiVR/klD2x+74olrVbFZgtnwXS1hACVyIqyHIQkVbZa48WawKtia5DWMyKRIBHNufEXFYd92lZq5r5BF5xBPHO9rie1Ssgd9s2RXLF0xasyPOCUCltOBKkBaOdzwbHzizlsa4+m87ZBELacLBvfbZh8tuDeLJFJI5MYBJjtJ8v+FbGm4RK88ZnrnR/ng/vqcMbKwKh8ktVxN6oxq85oW8lgPauGlZODJaLkXCgaCXEib2ZgBsfBGosyQgit/K4+Scboua1Uy8K1Tajt2bbuY9ZgexXKbr57abZizL8KS6iMTtt718/qd8UbLNUH1A3extOGWrduTdPvc1e/IwD/6B/BD//wfv7feQd+8Ad/7XWqx8MDfPGL9rsrD7vj9tbO++ZtxzTBD/yAOSx/4ie6E7Q6MP9DHz/8w/b+OcMv/qI998WLfv4HfxD+1t+CdYW/8BfgT/9p+Gt/DT780Mb9/d8Pf+fvwOuvwx//4+aQ/ot/EX7u5+B7vxfeew/+2B+DX/ol+Pt/3+75Z/4M/I7fgXznt1uJjQ5KdGOKlea1KTsi4iUZ4kJKO/OApl3UKFcVxnXldchoBRB9MGNNA8pC3jYzSGKlo0gU8R9Lw7+5thLM821uQjE4kzHGpV0xnSYoATkIhAkJE3q6tSyYcka3M4QT1fJtECFZG41InJHlCpkPFvWdF1Riw6dqLz46n9r8VUVw3HzS9kAsZ2R7RTm9D44XSzoRPUunf0+8TEfa/p8nw6mpGbM2DDsnlTe0RQmEoNVG7o4sLw2qPMTcbjrw5spXZPib5rQc2FClBH8/GeBW7EJ1IhqVv2q4S2cM9bbDbzrQUP/HBLGVuO6VSOnj0T4PFmQIw5z491T7tbu39HHTsyzaeW0cFBDHBlI3BnwXDfJj7yQWoLSgnrN0oHZVTk8YBY+Pj1ScW7BktwDsLRXYY9tW20U7Xfcz1KzeJiHa8nfTqn1D9oaOiUZpPVtct+tyoP1W/y+7czvSEC9/bwGdgVcNBtTlXAwvTR2dYLAHV8uBw1ufIn3muyjLkTQtZjjlTIyR6+vnltUZ7snpjJZMlIjMQnjjE+jhyPnbvoPt01/PuiXK//lPsI5YjhvoVtle36kZePvxPRWQ7WPmgoZcTjurutRVEGl0q0CYFw5vvEacJk4vXqIPGyD84q98Ef3sP+e7v/MzHiG3G8YtEULgEANRzOGUSUiC7SwQhJtnb4DCw+0LHu5eoimTozUMxPG2izpvxrIQ1BtYVSdf71AspLRx+3AGgWWy7rJ5W5nmmWmaSCW7sm9lViUXHtYNiROHIBZ/S+aULQRSKjysJ9aUORxmrqLhQqa7e3N+RuOhqoVv+9bfyr/+whfIH7zg/tUDW6n4qeMaaXMQ9Kz1TrmIYlJqT4Oq1nDqfD5b3sWMZbrGoXEfHapl5H8hBrTU0s1i3CZYrFEc6zIGmOLM6eqWh9uX8OoVIkpO1uBRVUwPLRbUrLI9GRoPKWkr2wbv7C2QqR2xBVk3pnNmmgNxMiNJlWZUI8rz5zccliNBhHU9c1ofGhaeYY96A5ZQZbaQNXPeCutaPE6rxKBWBu9Y49Y4Cg6zICT7ewoGCe90oFocv1QpITDFgkjxUlRzfInvldDe1RqS1Aa0IYrzxUQNMpcC61a4PnpGlEOJWbDZMny0FFLa2NJGSoXzpnz4oHz2buELW2RVLtBijV4+SGenM/s7q3oiRXWkuQ1Q/61wBVXoikAIvoaJ0+meVy9fWLmpBx7nOHNYDtZNOkTmECFMLTApIQw81myagju3cyIlgwRZjldMxYIzlILmQNaaLdWb8dSXkcE+qPtGBLNnVNESGu9q8o9CGT4rYS/CmgNc+lxWR3PLFr7kqZjz4yXC509nPhNDG0toVUbFMe2tGVCUBQmFUBJFAuf7M6f7ewsYLeLwV4ZtmfLG8zdf5/b0wKc/nPimTfl8UIO2kNIc0up0DFhgoCU97OWAqnrzHe3QM4CujkfYHCKN8Tddo/KlXKp6J6D7HgHNMTzwppEmwRwZ5hD3YEiFZXAqtGfVjPBs85f74m9ZuT37fVCq87HQ1Y5ufyoNEqA5gWoGYHdKjjJeoDvlqg6FekOmqn3Yd5V9ZVHdP1XLKCX7Z9VxtddRC0LH6fWxFW3OMXuNXgIc1AI11dFoDeKE/QapOrMFJZsW1PQ+u1ZC8JLj2PX5J2i8ruV4fFSm7GX268cdF9oINTO9lIyWCBqZJ6v6axjXzltLsazvabamkQoU9QBP6tB4lrln85NrM0aBMjTrVQEZ4DGaur5TcbW9n0Rh9goGrXMjxtfwvR8nqyKORCZVlnnuuuzOOd513Oy0om4zGNZrbM2TK90SrOVjtZen2CFLYoitKag6z6lBvfrh2fteNLshmlOswwEEro5YdqTbRiXnxl/iNHHl61zUnKRGPx1SAIcC6L6bOiB7j6LF9Nw6j2r2ScqJotaQSjIOBdQ1dlynae5Vz4QVhKCGFVzUKgDythHCRpVuOB/rdI5DXjksn+9bCyZeOI6L7RnjOV457veV9cT9dmaRybJBJZr8q+8mVr2Z1zMVD7gmD9Zm3wKW0Uv12Pk+D+rMTHwvs6vAVM1WZQMtqLDbX4JH7HGnL+QK9TX4ZQDXxQy+qfUZyF2Oosrmzb42zUwEokZrAOZ7oNLkHKP3WJB9v5aL46vCGSsMGDaDUjFuziosjJBMqDRzz8uBCoXsWXsSDL/NNmVVhJJt1FFb07rcXfjUp9smZ6eQ1MhIjSQUHBS9ybGeDVbH3TaAf9Lv1R70xDGyqOG59Uv6+NKaDTsydrn85fOft2xOgO/6Lnj/fXM+/oE/AN/93XA8wsuX8JM/2W/yiU/AZz5jv//UT8G/+lf93D/9p+bQPB7t+z/+4/DzP+/jUvjH/xhee82yY7/jO+AP/2E7dzjsM1LH4yd+why+9fg9vweW5aMm6is/3nsPfvZnXfssj8//7b9tz/70p+H7vg/+/J+Hf/bPbH5+4AfgR34EvvAF+L2/F/7IHzHn7I/9mDlnv/d77R6f/rRlAJ/P8A/+AXzuc/DN32zTgXbnOwA147MyE23rXDs9mnFVqzGNUi+zLHqmW+UUvkcGQgicQQ4Gpl2EnBKLJJZJOBdjwhZNUwfsLlwfzIq/fSjklCyzSAQNVp6QBxo0fB/xRmERxDNPthOU1bAQs9fb1HEFz2ePZrTIvCDLDcwLTFPPiK3vOmpRu9/qX8Mu025DUbI5YNeXlNMLNN3By/fh4bZa2rs7WaWiPS9AK2Nr95deYtgdsX5eqnJma+XMwo0j8a3r69beqRpQvUyl8r/dRq9KbKMBv4f2b9X79a9I+2513JouMDKQYU4HpUsGXvfIsUtV7vtzpSrlOuDzyF7hqsZgnbSPGkd3vFxkWw7O4kryY6lb5b1N8WkzKrtbVCyt+qzRwKrK66XhNr7/PlOW3TEGRfpne35TZcZlxu1oBNlne4k0Hl2pGr5x4fg18tBLsmik2S6S3Wjri/rnj42scX36Oz9xf39wkMDhrU9y/A3fTPnGb0HEvDvqBsc0RaLzoHleEM3eLAqCRKY4kUsmfM3XEz/5Ncwlc/rCL5O3E3p+ILz40GhPeEyrF7TwtPHUAyp9D9ef8Zq6cPv7NR1CAALT9dGU45zYtldoVj54+YLTeubr3n2Hr//UpwjzbNkbRYjerGIB1yusrC5vG8oD83Lk5rW3kGBNsdLDnVUV1BRLOh3Xah0rZ3dYHGNA5gTzDJWi1rHdSrbN4KmZQ5bJWCoUmzne1MrapyBEN79DsK7iWyqsWybEwCFMTRFOpSCOpQlmOHzNu5/m1bZxv2Ve3p1ZEc55xCOkWnYfwSf8kmDvVI/ijpe6ZClZSVtAmZbZRE+9X3FVv+HBWRCu8Sn3YIivaYiGrxqjlRkuhyPzNCGirKcT67pxPm2sq7qhIm3fmTFZkwXMEKjwixrcGZO7bqBF2XJhzoF5iR2yZMDXi9OR49VzphCBV9yfH4AwwDIEijfpCqLm2E0BJbMmRdV04Uo+imUERTFn7DqbKWZYit7Nu/ErH4MEDMa9WFVaNuMlhrjjv5b953RZ+ZX/2P3MGVpKoGS4vupOBsQzLLNhw9bswJQyp1W5XeHn7gM/d545eaPQKnMbISjca/YWm0ZWt9vKVZyYI8wixFB1J9xwqnBizj/cSVZKISULVNyd7poBLUGY48K6bUxxYg6RQ5wJ02zYc16+Xw25Oo+pZjxuK9t6ZtMNDcqcF4oWTg/3zHJte7COR6tchB697OXXgDtigZbt6S+u9Z1oc4Gv/25v1TEqXabofk4fCxWI88RDjLzMmd/mDgqFgR66DhvDRJDJNoPzrPVhI60bmhIsvn+0kEsml8RxOXA8HHg7zryrgX9dvHw1CJQhKFaqPqjDcPc68fiuaNfVimdFVk9F07moxNW+2NZhJ2F8bmpG8O459XC+U/WC7HQWtENzdGds5c15eIDNadHMlse18/kenj3aGFV2qVjAruFmylPjNH5UPKg38uJWQTo8c9Bk2DnMqrPKS+zr3hRVx363aytOdE9gAHOK0+7TKFUrjrbRhp0Prav9fj60OctqwKrxeQAVT5LqU9TOdmWYjzo+zjn7lTpkLzT99r2cMyUXwmwBnkpTddZK0bZ3Ba9iqDK8mOM+DI7F2kAL3eubnW/Y3PTKi4tpcUW77q5WcefzUBpddB24JrTFIdmt4WrWH39C5d+TTm2MFeed9sx+rTUB9qz4GDjMi9Esag1Fcx62tngVW5/pkDIp5V3mcJ1/y7S37GTTUy0Qab0ybGxRLYPZWK1lao77RYSGt9rWQYSaoVodfnOYqNXLIngGsY3fYBxqypVYgDVYiX9fQ88uzv1dY7Q5NKej26wF0wl8D0wuqysvq8smVInSdd3qoK37sXTVyQNBhuO6edVtzc6dJLTnqGAOy5wcysfWMTq0huHI1mBEady3iDb57doqFdagcp/iepfRc5f1lVZr8JXh+lYR6A3mwKpWGwdrOgEN3mI0hmxM5oANxTJv84C7i0jH08ac5R91fFU4Y1VBSp9kMGFRJ9JmpSshNrGhKxfBPPgFU/zStjUjT1HC5KDRurrdElwwVFZdUUKq0emMS0ZRbseYsr/joP5vVZZVugE8yLH+QVWoGJxpfvrSMYyyw0ZR7YQjFW/2Eb/vSlqfxIvjh34I/u7fhT/7Z/9v9t402Lbtqu/7zTlXs/c+59zmdXpIPAl1SCAoFTadkEFIllVQoFDIwaXguAJ2EjuFXbgqAeNK8oGCokjZgXKcpEgK7IQ4UE4ZgaEcA5LLxqY3tugRaizUPUmvufeebjdrzSYfxhxzznXuuU8SlRhVhfXeuefsvddea67ZjDma//gP+Kqvgve8R5yJv/mb8IY3QN+L9fCmN8FP/IQ4RP/m3xRqAj3+6l+V53nxi+H3fk+cre97Xx3Yb/gG+fyNb4R/8k/ub0N7pCSOzz//5+EDHxCvmPfwoQ/B44/XHMBJKgJirbTxkz2+7dvkZ5rEOXx5+cl/95M5hkGuH7LV9dVfLc7cz/1c0h+8lxBjUxVSBII6kMqm1jhmU6hKV9as0aiVjKcYLHm2Vh+zjYg5Xxe+Ycb0BtNtYJJ0hRvDxI3jxNlpZEtHbyRw4bJwHnsRYLs9PHV3y7g5luhkbo6g+aWNLnO1xhDB9eJcHQaMnyDM4D3GT1L8JAlSwbgR4wZs10mUr5cKutE0zh9VTK+bw81JxpqGV7Oo3iKI04Gwvwu7Z0mHe6TdXXjf72EPF5jjkeTMYrFJJUsFzBpCiDkim1dmMUSKSlD7uXUeNJsYSMXRVDaS5jEwy+/lTwt1Sj4rNddTJ+TiBtcofXrOybvKsQAAIABJREFU1SqOrVJcTYmsZKeUU6HEuC8VO68Zg3bTCykVeSQFvkrCT/6lSn+jxF9pcjE+rihG5TOV/3lsXHO56vBM1Y9TlHia8ah9fe396sM1z9cocGWdprLJ1g5JBVlHMabatrV91yCfQQzI1Dr3mz5/kD5/ZY6VPVTfv+Yrsp1Wpb1VOpoVpY+jPtms4DftvdJv0g6NdGqambRlXB/Rf94X0L3y1TjT07k+z+PM32UM56f3AEkV77u+KN7GWogRbycwwgu23qy496av5XK3xX/o/Zhf+peZNbE1EhHUqJZWLW1cBkzb+dX+vTz36vxX51ndl7X/Yook53CbFZvecTrPsN2DT+wPe37mX/w8b/nqN8GNY2bnBGVxmPA+sOo61q4Tji/jSDbQpZmL8zNuPPIYR50Upnr2I+8n5LRvskNoDlEcpVaKcIQoxZsA+n7AB11/kub48MMnXF6eM88TPiVuHB+z3+1EoUwJ2/UcZk/wHtd13LpxzO4wEUPAdY5xHJm9596ZOAKHceT2zQ3byx3zfo91jhs3j9krL5wx9H3PHAKf8ehjzFPg9M4ZfbJ8bLerXIQPOJZO9OwwszWrZvYzyXUMrmd1dMRhd2CaZlx0DIOkDqZmLqsBJsagYRjGvL9ZUUiTpNqrk991HSk5hm5gGI84PrrJ8ckxlxd32G0vubzYcXG6E3RMSoSksoWsnMqdl/MJ/JxwMWXaDXkzRqE5MLM4MvNGJqIggkmWsVvRD+IAnGeV0TanclpClHRQsVct/dDTHwzOeg5TlNTshBRSC1Ge0RpsgGkG4xLOgfB1NrptEhl4+7hjGLJREyFGw+QNfa/7RiDFQO+kirGigMsemuWddR0+dIToMMZlDjtNFzTEUIt1hRgIPtMTHBIfvjT8s3trglOKACv8empk5qPNVosp8oGLu9x0A8f9yNEwcmwy5ZiFpCn7pgFeZORMjClzOUpxkaJxxEgyM9Pe44yhwzDajnFc0w29cBPn9gTviV5QvnOM8lx+Zp4mZmY8M92mp59XPPvRuzz6GY/TDYOkJqswjlflrmnkk3BIJ+Vt1GnV7IfOdRhFkyqF0GJ11T+WztscOEbmRfu1CNhxhR3X0PWEJBWo+9wmQTqL7Cnp1ck0vPc98y7iksh/oX2wEnSKAWcSh90lvYV137PuB0jbYj9iIDXoWLW1jHHl+a7dD7Vz9JfRrzZOu6bQi3xJaMZ0A62OHrlLDenWftQ2LfpQ+zQHrUKsdAZlH1cIM41zoJ3bpUiRCIcYS85dtQKXEwCl00qp3k/nUIyxoqpbeyTbKkqtoNqCOIWr3mpKu6p+JffK16FZW9RmKYpRdO+sfxjdu5eOw5jUDm4c/iTmIMh8Df6AyUZRo6cW/ajtD8n2a4vvPui4+vlVHejqGD2XQ3ZxLe3vPJ9iTLL/hIjF4lLWv0wuHp7AaFAxJaZ0YLSrTFOQx7MZDzBFr2/vHVu0aBR6orbAr6L65WP1N1Qds8yh3H7llhUkamIKk+jMThG9mUJH50XWpWIzz7VdBuFJ1dv5WbLZxB7TPtT+8vRGAXIRjK3tbTil1beUUmIYRpyrfOTe+4WT2Fib14PBdoYYDL3tCx9oGducgWKsw+k+n/V/W8SCBqEqH7nMX0eXbRvJRFGEs2X2gWnyTNOEs5UuYOi7YmOFUNGb1nbFl7DqBxgGxhCYvTgJ52nO80Ps5XEY6J1kbwi9jeg9JjUgQlNpDzDZ1xB1rOcSo4tJEL0hCYURyeOCIRiDD7YIpEP2yev67Y0Vyj6TsORsdJcwocoUQdEqWMZALoRqYnbU5sK1qssp/3bUtZ4kyy/lZzImyX6E7N1qNlS6A/EZyt4Uc6aBcBxLBpFkW4Uoem1ICV9+fKEklGwf6XOMwV8HAszHp4UzFkMuzqEOiCaqnrIXfyHMEj5U6LciDI3txPM+73ApsOp7xhxR6oeeZCZJQ0vyHel9uZe1nfBXNN54qArzfQKXNoV4ibzRjhc3C1lwKadn62CR+ema59OoXVFYm81z6aAyLKpq2kbxp3E05Etcu8F8xVeI0/ClLxXE62Yjzta/+3fF0fm+90na/Y//OHzmZ4pT9G1vgx/+Yfgrf0Wu8c//uSBe1bnzzncur/He94rj875iRNccH/wgvOpVwuX6nd8pDuE/9afgsz8bfuAHBH16OMALXyjnfMM3CMfrp8NxcgIf+5j8/YM/CN/7veLcPjrKJ1T+uzYy2xr4uiGU2ZSUKFyjuRl9qn6gJNUC1UjTKo0xBkiWNuc7TmfABjskggNCZLedGWzkxklP3M8kekiiIG/3AecSXWc52qzpzjyzn3FOuH56m5UFk7ITuArN7KESo8YNxUFnAJcVR0FpujLXU4IYfLY01WJWlNPS4XGfZ6oomnbxljERE2ecPyfs7sL2LvZwTtifAR7bWbrVuHB66mYpVWfzuASxppW0Xe5u8T5grfAyibIYylrTCGZtcmKafTHu9DP1CaVmrbuMpMEglSubda1z6RMphHD/mjdFGdY+u4qIEL6eYtilyu2alsKnuailVtmtqp/36owsV7//uxi6ThxHq9Wa09PT+xwV1z3TFTNn4RTU9ZSS7h0sFEfM8nv3XTsPsCFllIDI1a7rFt9rHXcxVmNVHdFdP+JnnwtDikFYo+/SniReh/vv/0DP6yd3tF3XGlVqBBXD7sr3YuMMi3lRisKxRA1c5yjX91MKeY8TRVqAij0XX/4m3PNeQB8iQ0bcx5AYVitu3boNwJ07zzAdDvh5JkZJlx/GMSvMEqTpBi0cl9iMK4bOMb/8leyfeCHTdof7pZ/DNnJPzZFFim1zXEUFtalN7TNe53RuDWrRWdWI1mwqQxp6jl/wPHbP3sGf7whbCQj/4595B4bEI7dv8h++6U1MxjL6wGH2+GHgqLd0YabLYWYbAvee/TirzQkntx/B2o6nnvwDYjhgU8B0jqP1KmcfSCGaFBLrfk1ElERrDKvVESEEdrstdz72FJvNitW4wpC4c3qKNZau73HGcHG5wznDcd7DducX9H3PenOED4HT8y0Xe8+tG8eshw5n4fL0lHEcWY9rooHL8zPcONBZi4+R7eUlxjlONhtOhp7VvOPo6AjTjZyMNbDqtNgT18u2PAiL9fzRe6fYTeSRmydMhwvA4qeJ6SD9Ma6PMFTKGaw4DFXmlqIZhizXYBhXRfcSV3/ZsYjdyNGNnvXxLWKQauaHy0v2+wv204HDfmK3m5j2nnmKTFNi8qE4cVJUupSEKb46kfWSaBLxKUFQHIs8b2cNTz/9DGEOnJwc0w8OoilI6JQ0LV5KZGAiHsAaht6x6hOXu8hhKiWkMEZq1/ROkLghJTpr0ETEaMRpO0/kAI2gYO5diG4rKGmwg8Gp4VjWUkbYqlM5OxycNQyd5dHVI6Q5EXzEulTBztlhFPyMDzMpBkiRkAx3t5HfOne882KAYYPDY0uqZyJZ06o/iyMB53guDhP2cI4zho11nLgV625g3Y/cXB+xWo2MoxirNgM49tsdlxdnnJ2fiqxv9B1nbQlkJxLeRHonOlLIaebGSGG1FGNB4xWEdnZ8azG5YRx49OSEkxu38KEWujE69xsHWJ2j+fPsbLJGKoinknafnQTW4qzsvxjRnIp+aqSADzFTS3RivO/3+/vXYtPHFsPQDwxDzyGnyM7e4ztP71zWjfK+kN3EAQUXSD/6KWJdj+t6jHW5eE6SfrWOi+0pF/fuQPCsxxG2F9ihKw0pThTdS8u+rJOqASgYU7g3TUZVppgK2KAGbWPRURWVlhkJMU0Bka5ftkPncGrGSPvsagILxVa74hDUGy9ONUVW5As346JIyPwytlu+BLJv3DhhmiYJwnlf5m4iNejbqOKmXDdPS+FbVJRYsV+S2BtKj5bXeXULLx71vmNpc7d6c01FFqfvUm8JhXqkOgFlvxYHq9NLmfZ7rb4o88JmvW0YeqYcwE3EAoj5wxw6jp/Iuds6vPWZDZKFYTpHcpY5BeEOjxICktR1nzP4LCYa2fuNpe/7Yje2pRdSErqPaEzO9Mj74KJAVuKw2xdnFmSgzRW1VAJtFGdWyNyhqfm8BgBsocvR1P2+7wrIQygjldZA7QcPMRVHnzUW53q6QTIGfJB56+epOGO99xwOexLicDcxYRq9nbyHVweLjP+yDoXOC9H55tkXuW21bkhaBnK7HOQt/OYhYq3LRbQtrhTdkKDLlAT0ovKn6zuC0WTdCNOUAyzVgTn21Xk9q57ofeYINkKXA3h/EAc0cLnbimvA5M/VdpItm2QTlxdb0fOtZTUODK6TTKlsBykvdczVulzfEcmZLkiQliD361KuhYBwnockRS+lcJcICxXJYjFX/1ScpFiiFEwUlKwCIslzDK+7hvhFnOmE7ssajJE5KHun8OPaXmgYMfIccQ5NbQxY2UFoGnOjQt5jDZIh1LlOishBceFJ0ce57NFdBjboNXz0hNTjY8wBZVhvVngfCmf9g45PD2dsEri0RAgb+V42MbL9qpJYNgaF7KviGaIIZO9n/GFPnHt66zjebFgNI9N8IZuIqRX1dNNNMYFro2+xcbzIrlSUoNwoVc71ffW4Y0xORUuo4K9o3rzx5ShCjJHklLMqXdk0KM8rhQWywEztxp7bEbXTdCNuoqV5s7xvW/ne7xWagbe9Db7xG+GHfkicnbudWANHR8IFGkJFka7XQjGgx3oNx8f19dHRklLg6Gj5+XMdKdX7/OiPVgTudlt5ZfteHLAhwAte8Mld99/HYYw853d8h/DK3rsnCF+At74VvuxLykZQxsGoE7POcx3XPJtqlE7OoDgejTiMSoETtdVSksIlVyK8ab6Li4beHZHcZxCSZbuTCswnJyNHKXA52byfW8Bxvk+4HFcYVyPbvZcImzUY1+OMIFpjkk2zKC7FmapNM8WAA+X4UX4t1eiqMln+VEVDnznpetKPTXNe1bqsMVgC+APs75Gmp0mHZ0jTHcz2WXj37+J8oNus6TYbglsabta6jDiuamRMeUNQOWTAxLzZxFmcp8Sy4Rkd4PJICZ+5MS0y7kvnbqMqJuFV67t+4QiLixSHNiWjceCjXVGjv9J9ppEH+ZeprRSdv8q/vu8lXXaeF99rlf5Gp8ljqj/avjpOV2242MjG2Chz7XEVsbiIWKulYGqbFO3YtrFSyFyvEF8N8lUBbJp19wBluszT+z/y3mdls4YWpdBCbaMx8Yrzr64fU56/jlfbVDWwqvO2NqYaQxn1kNdUTFHSEvO9ZL9NTZBIe8CUOQNKIZQ/axyTtT2pyC1RsCImRklPOrlF/yVfSfe8J9hsjulcT/DCudXlolUX5xdlbXWuq8aocYRomOaI8YnV6hizlvUxTQdC9IR5hpDoTMdDN29x+IIvZnr5K2s/ZXmAqcPUykWjzpTmuN75upxXOgbtH7reio5CDrh3HcONG1jTMacL4v7AHGdI8OzpGf/3v/x53vTa10DXSz/MMxjDKgVSFBXNdY7OT0y7C2LwjOsjHn7eC9ie3WV/eUqaZ50QeXJE4bhMUpxRijfAbr/NKIrIajXSd1LAMQQvxT4STLMUfViNPUPflUyjYZAshovtvlAAPHLzCGeTVLdPic1qBWTeVQurcaRfjUJ5ECLOgE8QDwceuX2bL/qiP8Hv/7v30p9N2Ea+xdLP9xuzFemSFmvv105hM818vttye70S2gsjcmW3PRfluR8kaI/D9TltPK+zoNWMdK6YbLxlns6CyFdjPkaSsVg3Yt1APyaG8YijcFtS6zMaLPogyNIo1A8hTAWVFmLCe9mHyYaGn2cpsOQlAJqoaZKCHookH5jmA5eXiSNzxI0bt7i83OYiWaIPSiEbuUeaA8FHDofIPIVFfMoZQ981MACDpO2TasVkDL012CGV+JFQG9hiuPmQsBP0ncnIFTnPOkH5JGME3aK6irNsNifYbkUKE8mkTMsA5PT9EGbmeRZnZhSU0JP3Zt65O+ajc8/eWJKxGDPUFOQUhKdQZetV+exnzM+9AxsSPPFC5pd9NhcpMIUdNhxw0wX97h5r17Ppejb9wEm/ZjBSEMWngBt7/NRkypB5Dq3L+ocYjsL7B4oedMaIE9ZUzUemsxUOVZ8EMBKE9sEkmKcJdWq1Dg+9tSB1U7ZJwJHXfZQ56lJkjp6YAm57zvN+/3e5YxKp5bu19opcNDJ3UiT6ysd69biqd9jOYnuHU+eBIjWTpPxaBHkuTgRqenj+PYdZQAVdJ1Qq0x4JLtlSNV6K3vWMqzXdvifkwi7i8Gn3RsBYQtaPDIZuEbBXR0zWW/IKsLCod6H7nmk8Uq7oWPJabdCyilLWf7JOrg4EcZSkoo8pr7ciPE32BJfMjaT7s2Q8lP28mQGJqrcpHYw65m2ed+T08QRcXl7k1H7dx2MtGnR1b290K9XDrLbDLM9ZHM24JiiON50xrU6vdrLNNoFSyKCoz+aJ6995D86IvjIGhfoN+b5tg/f12zJO9Xml6nwUDlKjdCI8UPX7VI8HgScWekajTxbdLkk/WARh2bm+nKMoU507eh+RF2SHlVARqQ7uM+d313X0Q5+DXb7cWuWGc67R5WmUHYqsuWqHxaQo16xXqR6UhJsn5TVkrWX2tdZMRXZXQIC1lkyEnx/XMjhpc0H2FgCa+FGmaRZZSKLT+dNkFKuPZjkuNre1opKLLZ2dpTH4gvw2xkpBzBY5nr8n680yhVl02CC0TS7XRhCnqGyM8yznzGFing95jStFSZYBZU6ksn6qkzwHKcsgIJl12g4rKN3yTJm2RRGtALZzItuBZA2HGImuo3NNWekW2GCEdgtX5X4Koaw1EoKsNXndGgSFnJ/JNM/mc9/FrGOYPBbWGNEpGi7nvh+AmAuFQ8zUHTRIWWsFHCVyLDAnLyVBjAYCbEaRyzwQgKfYHKrbYYSqSpWjEGMh5E3JqAjFOIMtxebyv1kldUZ2YKIhJGmb8Nd2DGSQ1QOOTw9nLKJXo8YMNE4KUBj70hmTBz+flxIEInMMzBp5JtI5xzisWI1rzibQ1CcVJgZyVCMSY2NwNUY+KlwoDWqWdCux88ahjl5Kk4vyBRTvfHuFpA1pHW/53guNr3le7QPtk9YRUqIgRk+7ZsN83euk2NblpRSuanlaP5XjXe+C3/gN+ftrv/b+z3/lV6TIlXPw9V//yaFk+16oCf7cn5PXL36x/HYOvuZr/nDtvHI88dov4OTLXgXkIl5/+gvhiRtw+yHgDL76y+DVnwWf+YSc8+bXwb278MpXgr2At7wR9jv44s+r1xj38DnPlx8ynUJ3idsEbvzp15Z7q4JXEKXUMVVnkyIoa5RclTiu6mNX/yClyOHR57N96ePSrHXExg1mPGLu1gSp8MLQw/MeG5l9Yjc5fBTCbRJ85AOe/WXmUO16sJE4z0TvcZ3HDMelKmtKZL6mhSVL6+UsCmZxSdW2LuY4ythi8vNWTqKl4pc176JggQQnIsZvYT4nbp+C6WnYPwuHU9J0ibl3B7vZYIcBM/ZglhErYzKKJ7fX5shnq6ia3EqRWbkitanoAW2LttOYzMOkz5WazxoHjl5fjW/yPFkqyS3q1BTqi6voVQ3epCSGYSuDSnBJ540qG9Sm1MBUKkZGlYvtCOaIZ6O8XXVmVZSAtq8qo8tnbcb2mkPRiNVNevU8bVeLJl4G0pYoWlWyrrtf007tm+t158V7rVGjSl1ZFvpHvEZBp/Z1eVabDYfU9E1uVm1/M0YplXm32Cdo0LF1U2iejLqvmWXbWk4w6bc636qRlS9n6h3MzYdwn/li+he+lN71rMY1fTeIcw9FJRmmw0wMvjyrUh0M4wabKwf5eabrR4mEZ4NhHEaS95goCGjXdfD48+keemTRq63hI89nC88q5ekfPHeLfGnEcB3cxSnlQx1L/aIdB7qQIEQm7wmTyIyD97z/I0/y7g98kBc9/jwePjrGxIj1c72CdSQjtEoxoymd61ltjoUXLgb2F3eJzGCdKOEmp9UHn8dV+nvOfGcqt61xgjZIgszQ2KC1hqFzrMeBXQziGDKGeRaONWOg7xyr3pFiaFJFmzmcclpjMoK4BKYgaPFkYbMaGdePcu/sHhf+GVZd1Qt0vqmiXNZauwbqLwA+PhnmwwFz2PF5D284Wa9z8QgpWDYfdqQQsN2I6UYIps63REkz1lUv633Jx1gVuwgxCO0OQaZT4a/rMvIoYYzDCMgwgwUi0+TK/o4xGR2Lbo2EeRbO5HnORdTE4Zhy5kzwnjgLh6rLqbhDPzD1PqcTmprhkCIkh7FSJMpYKci1XiWMjzhn6Z1h7C3T5HPCWHYKJeGCVeMFI+hYMf5lrmu2srzUQTHlWYxpUFgZwaLv9X3PZnOCBFwdzgkFiXKExijon3kOHLzn7uXMR+7t+cgFfGBYsbUD0YIWAtFKywaD6/tGb1qqS8SI/ciHsBl5ZTLaakoQb90m3riB8TBiGa1j43r2w4GbvfAEu75nPdzAHWZMEi7M6HPF7XwjSWuE4CPJapEyKUa0cF4krQaujICWFMRYnw4HbNdLaqlWYk7VQaV7dAi5OFHmajNZDpV+JDKZwOQiJh1Y3Xua3RpCDrSrvrPcjqoBI/vZFWfsNeYEBlxn6XqHHRwcfHXykTL/ogTxW2dNgb+lXIw5CQLMmsh02Mv8sx02JTrX0/c94xhYBY+jJ2Y9WYuEWaMI9ryfFPltcA03rqSa9mVvVXltjcnFYHU/rIHsqvs0fWAqqhgj4x4bLmrZY0TGphjQPUf1gprRKAh5HVexeU2mTZGncM4s9MIYZY3q0nN2SUjljBGHSV6Q4lAJRUYbWzWo5fjrGjZZDlZnbIso1vm4+M5CPcy6bka8VT3sis5Rd2HaPbvRtBf6CZmT2xrhVld6p2QpNA3avqIvcf20haqzic3lqk7U9GZFSj/oKsvjuvOvDWiYpd/BNPOtrpGqd8QsM5KrDnTdf62vGVjGGnxKjQPPVABYvlhMET/7/NxLvU7RtW37U/6OgRJ8EPoUsI3vovCGmytBnuwYwy51d3Uw1n0+OwRTmbn0/SCo35y9oXQM2t65k+Bl4b3PKOK6vvSedcZpG6Wbk4rYMi7WWlLsav/m9UMdLqlNVIYq1aBJlivOWaGHcLmIsxHZE4LPQZFa2E7XqDiaKfI3eCGDdVqMNLdTeWyjBh5MBiNZ5cBv7SwEfarzw0g9FClcpzKs0vQBdKWOSV2XLVCpjKDJwQ0dD5V3qE3cFMTMcl7nMUh7nRGppMGjGKMUHM9Od5VsGp4p2C8snTMkR+HsjTJRy72drffXtvjgC1e5Ip9doTZIOaCqoCYKF3Bpd5K6Ocbksc57pHLRarCnRVvfv/rr8WnjjFUS7gR0pnrm6+KsEUcREDojTNnLPYlDCuznCeckhchFRz8MrFYb4jmkGMukQytPJ13QzUZLNiQUvdbKX92QDWV6kCjbfAwpL0KXIyrSQOESBKPcbbIqq3qQd5yU7hfOVzVKUR5ap1ZddOVSjQN7sXD0uLiA/V6MiJMTOX+9FjTrbieFvOZZ0LE3b9bvDYOcf34u1/ipn5ICVycn4pRdrQQlut3KNb7v+wR9+9BD8OVfLsja7XbZjnv35PfNm3Ldt7wFvvVb6zmbTe37szP5PQz1/U/m2G6FLzajiF777X+RV/wHrwc+LJ9/119uTv4wfP9/2bz+CPwv/03z+qPwv3/38nyA7/zPHnDzGb772z75tv6/fnzBp/yNn/w/Ih96XyQEmLHYvidlNFoMe7p+hTV9MWRD9EiOoTC/AM0aQTQlnfdGzqgCOytsRWBd2chTyhHwariKwmwRbtysSAOELenwrHDEXn6MND1D2n4cdndh3mJMktS20RE73UVbpSuvzwgadaMRwhpfrQlogkSqDtmEbqq58ZIC1fdFcUhRtYy6PrUP1HwQfpql4tfyompEt+9GSKmJNreFz+SQDaJGoGuaXEZkFDVYlIVZeZmLztwo3Y0gaR2HV5GD6Phmw7Bu33Vz0g3+QcgB/btFyT7ovOWRr63NveZ7y42y+Y411aBQZbgZa21HK6Ov3rpu/E1QrOmbgnBqvisk+2S+pjyfm4IeCUHXFKdq6x1MprYyK1rFAMl7QMp7bLuuSlG51hhp+lUcJzVdXKvQF+VOm6Fjqb3UDbiXfDbd53+hKObAOIysxjXbtCXDxYrRo0Zl6SJrOT65hXU9sw+EcAa4jLJK4twb1/TGMQ8Th8Oew3xg3fVcuqrWuKyU+YaPTtB5IoeEU9MWZ8Rz21n3z8EyB9KSsiBC1S3ynHLrAeckdV7T8ESORP7ZL/8KX/lFX8jqJS/B9D3GC59VRBEOAL2gUEPiIt7l5NZt1sc3cV3P/vKM4A9Ym0Srs1Z4UicpZBV9ZFivsF0niMN5YjdNMNqSor8/SDB2tRJErDGJceghRaZ5ZvKB3XaS9O2hZxwc3s9YY+k7Qezsd3tc19H1QrCw3W4xxrJer7DGcshyZVivpbCEj3z2i1/GHBM3N+vSrzH/J8lqrhbmIctY4n3LLhjD7z99wb+7PGV8Ys2LnvcoN0+OWQ0D1gTm/SXBzbg+MG46ohekkc53QTBUh3CUHLyq7wlJenagRXwIzNOOlGaR2wbm2eeUcklvtHQYLD4IKtaHyH67p+87+r6j6wTp4zIHnBjOA86C6wa6YcQ5Q9cNReZ4P2cuwUAMgdnPzP5A3w2F0iPnUorhFYVyyOLpjKhfq8mznz3j2LMaHaODe2cTc/C5CFoiBpOL3+aeNwamJHzCWbY4BzGII9866HuH67RYidAcuZzmLh0tun3fD6zXR6w3J+z3u4wgcvR9l3lhZ3HE+sBuipxeTLzr45f8wh+cc7G6xa0XrTD9CDFiNKUzO2SdM7hhxNol7UqxJVAjPGGe/DD2yQ+LLhIi6dVfQPqczyXGxK7v2cfEZQzsonDB3lxJu8f1BpMd6fP+wLTfwTxz2O9iK3AUAAAgAElEQVSEK73IXkXUKItcltVJZrnui4mMQraOGCKH3ZbLi1Oc7bGuw/YdGOFdbflvU4zMGfUcvPDpxhiJwTMHzxwD3iXOTcATiF3gYmM4txFLlDylpA4cvSjFIF/ut9WYxsiztRtYMlLAqxt7urGHgy/rSkifHL1bYbCCHApRMq9oBG+E+SBo6MF27C4vOTo5oetlHY2rFev1mmBg4wN97JkRvc9hwLgF7RQGQcOqnhUrx7R1jr4fCcEXAx+kPocnFQRvefSWNqU4RCsyXOhHJCPAJZOLu2Tbywp9WAqU/dnW2VjaGkkN96w4sKuTTO9ZdSlrM/Iw68tyanU5yRycyufKgZnyBC2Wdqrv0ez9JVW60cFiDDhTq9YX/SSpPqe6bNZkU8qcy6bMIeWdJDukFalaVygNlZc69KtOrQCtlCeetEPOK3HWJhhjGpUuX/TKOfW1cZ3sLvXRFvrnVZ2z9ktcvL7uuE7X1RETWqyUHWp13sXsCIpJ0qDnecb7WfaKUh0+o6tDRrUiKdUh5FR2YzCmcpXO81zS70PO2Ouszf6OzBHqJIX+qg0i59vi5HXGiu+k6QfRqWyhfmh9K9KHVT8vZoUqgNmhaIzBGVcLICmKlbz3WCvcsVlnHftME5D72QdPMtXeUieiWjsmZSSjIm2beaKdH3zA9rbq8sYwZV5ZYyy9c0JHZvOaznuC8oLHEMAautxX+jMOUnwvZVqQmOr8t1YoM8hzUGkgCpdzdh6vV6no5MJhm9e9VVqHWvcopcwHa6oDV6g5+ior8nwvjmSgcznATF6qVoqL6hhRlnAee0TeJ+9L9nmKWsAzF/GKCe8jKWb/VfYJOOdkLsmFwIhN5P1ESpJVUvrQGHwpXCc0VG50hClncmCEdkb7L+l6MmW/OcxT4frVH0MO0BpLb60UKg85KynVOSBr2eTM2FTWbTf0uX/kPR80ECt9dXUttcenjTPWqOdaJ+AVd0Ir+IULS5tuMbaTynEEJj9zdnGX6Gdst8K6HuMGVsMJJuYN0ohiba0r5mNKhuOTEw6HA/M8S/pIidbIIMUsOYSTU6L4EsuuXHEarVNEY1uUafG8+lxGv1m25MaHmlh0Qxthaq4hHy0F/OJrD+r0171O7vGSl0jxLefgu78b3vxmeO1r4WUvE6Xjq74KfvInK6L1rW+F179eaALe8Aa5xoteBO9+t5zznd8p1/jSL4WXv1yu8cY3wo/9mBQI2+2WVu8b3yi/X/QieOYZeMUrxLn7Xd9Vz/nBH4Rv+iahUXjiCXGsvvWt8A/+wYOe7v7jr/91+Ht/T/7+BPwdf3zIsPkgczqYRJwmLNCNa6bDlhQ8cZ4F/RETZnNEIiMe2vG9os+jimiOfsmh52fhXwrvRKL3JRVp4VQrQRHdLCMu7PD33k/aPgXTPcx8Rrz4KBzuwbMfg/e9F+tG+qMjzGokEBfFB2ozTUHPpXxbNdSjVDOpj/Ng3Ss3WfmH5hq1br60KDagN4xJ+HOuFOpQWUNCaCGMcJWllJjmOX8UaTu9RXNU3TMtNgZNnWuboD+trFlG+VmM83PF/RbPh3JcK13BJ+5DOacq51ePq+99IjQCy6bXPspjVaO4jYVar/jgC11zD+WHiikUxVBFu1aJhZwOrGgtI20KvkndVr5lfR5To7raPK2sK+NW+1hTEbVRxfhMkMJyvy081fk+Om/llpYYvaCx8kNYayrfk4GjzRGXX/R6zCMvYO2O2YzHPP7442y3F1yenxFD4OTkJjFEwjwzzx6MFDwyWTkexhX73RbvA8EHNpsjNicnhYYo+JG0v8BGS28c/TBi91um+bBwqD3x6OPsnvo4T53dVVeIOF1yX/TOLQIon8rxXAgZ0RxMo18kgjGYoWf96EMkIGz3pEmcA9Ekfu7X/g3v/8iTfM3rX4ePaoTJ+K2HHh8Dne3obMdA5PzuM4ybY4bVmkefeAkf+8B7CH6WdP+UmA9dVqrFBJn2U0ZcSFV6aw2Xl+dZ+bfcvHHC7A+EICnwwzCw3e+ZDlNGb1oevn0Do3MsRvpuYJ5nDvOBlBJHmyOmeWK/PxCJrMYBmyJnd+4SU2QYJNXw/PKSZC39ak3XW86f+TC78zu1b/0k6YHGZedglU0mK8tSaKn2+emdZ7m8u4Ptnh+5u+NFjyVe+sKOl37Gms/ZpGK4xnDgsL0nbVeyViPjFXRtxkSYJ4LfEeIsXHtRjFvvJ6Z54jDN7HPhtRADPgYOU0YJK0VBrI6hGsBIhZdtGcTSNaepntkBAChNlaJmZCdQmQVD32WuQHHedJ3DxECKHkJgNY5Y0/PwI7c5OT7iqWc/LugZJ9cN08Tm5ITq6ogFdSR7hcF1A5c7T0wSoDk+OuL87B7TYUf0cw7caIM1uLOkk0jA0XrD8dEx69UG7yOu6+lIsg5jYO892/2ey92Be6d7fuLdpzxzPrOfxaharwes7UXvN1GoAaxQMhhr6LuObrXCuAMFKtqqDVSjSBBBtnIv/vZvYn/7N/ApEb7hrTCu8AlOk8fsz0nDgBlGupQYxjXDMLK+IQbs6BxhFoSsIjIP2z1+Pkihkyic8cpDKKjqWGnyjUiO4PfEOHF571ni3uPu9kRnCcAheNSdqKhY4SrUyuvikD34A5MDP3TY27fZGcfmXb/P8KEPcmmzvZUzEGJKCI2xekUEzZX9aGhGi7EZ9ZM924s05rwwgwH6jn69gbMds/J4ovyUgnI11mHohOsyG/M2SQHYeQ6kZBlXx/h1pOsGyEXVbN/jxhVr57hhOm6fnDGHi7yVyT7os2NIU1jJsrj9DWLoH7LjPGYHaeesZGMErc5dANfidMnrQdBkUiitAgZMlvzZMRF8CeQbbEHPxxgk8OMycq04miTJXlC1V/aWlFD3baE20uFyrtjOiyKm+V/b9cWRaZCaCAVdiToCbdPyuu6rAujKdW2eO6UGQXMdAKP1TdS2TUZSu6+AK9T52KpW+nlL37TYZ03mjU0VwWecgg8S0TTItNSuK3LKdVxcq9yjec9aK7Uwmv5Y9MkDjudywn4qR0GmxpytkNsxz+JUn704Y1frFb3rizMRYOj6XMDREG2HdRsUOSksQFL/QLidB7quW7Q7JflcnV4YSjBea5rEDISzeT9KMdF31XkYY8S5LjuHYwnQVmBCRq+3fLxG7JmC5Mx7PKZ1wlfdNpGwwdZCbyi4gjpoMXKIISNB5aKGalKJfpwyfVjpgOJYE8+OKYhIHZeYYkEHe2Mzj29ex8jcU0elXlgKbeXC0Nbi7JDnn0MyvXKLjMhI9W1bayW43dXx0fWmNovpB2yuFVOo79qAERWRWyZTWeim2jq5T2wzH2Rq2eIcD3FiVfiIq0wp80L7VedxtvFds/YV+Nj2eUzZwa/O2Lb/jOiaMVNs6BypTuNK7zB2A6MRpG+IQrkVfP5uyHPJWjrrGDcrQooVfZ0ApJCpNUa44p0r9UK8l0JqtZhd9V+ozJG2x7wURJbL2GQnNQ+WH582ztia4pQH6krlbVv4eJoUbv0uwsk1m8Rumjk9vyCR6JyjdzC4kaOjWySp6YpzJhcDAFkA8nu/Pwh/SmzRWvU++srYTIhVDOCGFgBVlslKWb3CVZePLLxUNoV2s6hXywTazSbwXI6GqxtGiR7qvd/8ZvjFX1x2/mpFWe3Owed//vKcW7fq5zIY8Mgj8Au/UN8bx+U1XvWq5TVu3hTE7TveUYTEfYde4x/9I0HstsdLXyq/hwHe/na5xiOP3H+N5zr+xt+Ab/7m+voV6wef+8cH3lh83r1SiuD3ktY4jsTuNj5kTi8/YTLCJ1FTPlKqqellf1RFioQpjsa8no06wVSZlWrMdVORf5uVAFke2OQx/pJ4/hE4fxLjz2C+IO3uwG/8W0zYCocsFsaROGROuXQ/wkqi+irfjXCOxbYFudUlkpvtzYbKxDbFu1rUoVyybkryu6ZCiARIEsUklms+6Bog6DPpWyWV109y2kRUGoUlLYZeV9L6dMxEHlkn3DkhCOpY0I1XZE2zodYNvCoKi/QMU5ED9d5tlHHxSfmrFLTL06L0GdnhYariXvtTUT6ym8t97X2ysjoMpK9EeQzlXNNO3KuzpBGqqX199Q46HlELHDQKZ6p/yy2uk/HXb9+6xjD5V6rKWUGnFoU3R9DVSaD3ycqjGsPPdVRlVPgJaxpWLr6g9uEwcPfVX4rrNmxPd/jTp9muLuhxaJym60YO01TQWMYZplzldVit2Bwd0/drYsgIi17adnZ6V2SKtazXRxwd3+Dy7C777TnT4VIKC6Y+owrkcMbSGYujTV1VZ0StulqyT57j0CF5kM3VZqXonDDkdRKbq/cdq4du4Yct8/kWf7kTRTdFnvz4U/z4T7+dr33DVxJzYQeiwQTD4CwxeUJMxDnRxwjpnDDPrI+OefQzX8L53afZb8+Jswd22L6XIhLOZedgBGPphjWbzQlPP/sUCUlXPxwOTPNE30nxieAj28OeYegYxgFrOqbDgfXYFYTV5YXw2Gg/bnd7MIluEONr2k9MaabrO5wV1OPuYiuoXScUB2Ga+YrXfBmveNnLS19GLynqyUapIm0oDpbi4DAxU+PIES62pIPHYZlS5MN3Trm32/HuDwz8yrrjaL2ms5Ky1neO3joworMkJO1t9srr6pmmAylOhOTxMTB7MbpiioQY8TERMHnuy74UvBolYswlXfdJgvma3l8C79SMKXltS5Cr2CImo0/zWdaJHJdHr4icVz088PBK5r4gq2IuzATO7gDDU2eXjMPA7rATvmirujUM/UDnhObAWej7Wn3bGsdqXPHo8TEYKc7k/cS4WtP3DlLAGRiGTvi/EWRhNwzihssF2VzXi1EUpbIzSCBy8p7DNLHdXfKvPnjGnbMDF1vP+SFxZ4rMQTM4IljhpZYyLUrPoo6dnAHizEJkVydxWa1ZDwHdZ2vapKDvu3f8rMy1hx8lfPGXcp5mPr494xADD82ezXjg6MZtjm7eYn1yg+A907P3ss5uwRnGYcMQPDF4QpwZeluQTsHPWZaKg6vrxOE47c6I0444z8x+z9nhlH2IbEPgLMx4U52KGkjW59eg25wCkQ5rVhz1hmgs3opD0CjyqlBIJZa5c4ZhGGVv02wgI/PPJkUeZuqcasXTdb3QRqzWpONjfu39H+bVmw3HyCTu+172KYQqzqQkVbPVPkriiNieXbK72HJ04ySPtSn0HMZ2dKPYK0OMdJ3DJUO0CDowG9tl71YbMhW3Y5kBnXWMw5Dtvcju4kwCj8MA4yiIZGNzwSrolFkhX644JY0gyAuiNakTtGuciqb0Ze3TSj9UdcdW95H9tiKql0H8ZDJFVaZESEleB+VaTRJUwQjCUO3ZBDWQU/QX2RcEKakZbqp95PHJekLRjbIs09lYdT5H1UNUF8l6YJP6nmJFhUv/uvwc7T5aZaW2yZpsP5hGD8rX06zZgqQtiiMSrGnsCx0Xk0OnMikcru/w1oIN7XB8wuM6Z+wnCxy4qn8pYpVgSRi6vmfsJXPC+wEfPONaUOKqv8SUqp1ioHOCyCzPrwGXpLZAlCJQTfA9xsicQR0l8Nc4yFWPELqDjPzMY6YOXGMtNsNQVedQ4ocYEyEGnPpQyrWrPCt0QTbLCEwNlum0QyltUnU2Z51Uu9KpXUNFwk7TXAo9KR1KZ4THWhCly/kRMyI192rRpbSt1UEte4ZJMAcvsk48cmhZghrcUMS7riWIMa+DfD2dS846KSTlhAqi3KvxW5U5ZE1ZM4u+zWn6VtcdYjA4zSIogd7aVwooFG7VUDxYiQBeHPROHfatCaNyKo+DM6bQSugOkwoXC6CIXdsXh200pZukDy2CVOlAR79YR1HGIeTCtabR5TsDw2oQQIOP+Ck02CY5Z7RdDoKJjFSKJmtsydyVfklYK9lMSsuhjnsfRCcPSbKDu+QKyDKmIfNai/7ibPURXD0+bZyxRS1oBlZVBHk/Ld6X36b8G40ou5P3nF9umfyEHSLOdvRdz3pzgjE9Bp85gbLS1igguggKQTksHEl62EbA64cLtFtrJJuKgJC7qGNBF07TA6ZYHTWap98ylE2r9oGiuJqNwJhFJxYnjrbrscfk57mOkxN4zWue+5y+f+5zjo+v//xLvuS5rwvwBc+RUm/tJ3eN646XvrQ6dQH4IHD+h7vWv+fjyV/7HT78y8LL++r/5OsYT6TCdYqRd/7Q2/AHSf+0fcef+E//bIlmzts97/z7P17mxHjzhFf/hTcD8MGf/7d87NffVe7xkj/zGh55xYvL65gyJ4q+EQJx3uPnPaxuiVB1UhcxOSdpkXlemmzkaURONuKlbmOdLfzJJuUTsvAVPS8WJbp8r1lzIIqZjRPGX8J0l3T5ccx8Spov4PIu6cn3wdmzkOaslxvM6EidEQGf0n3rW05rN7x8a5UXZZOTB7vSQkw2PHSjflDwpE25an2kafGMKiWqtFisdVJBV6qipSi/etpS0lx92qJTq2RNqRQOS7Gmttwvy6o+XlI8Wmdp3skMVSRdj2A1y8+KUsDiuVrHSzEiMPddWyPHzT9ISuiy/XJuzCjdtBir9lmXe0B+Xw2ga3r0yhRt+kS/T27LsvBaHQOV+vVfVAFr3q3jlr9Xvn9lr0xtm0wZE0xN19dnVqVaXz/o0PtWM8aQbtwkPO8zmI9OsAFInpBgnyLn9+4Vh8xqs5HiAQhXllMkn7EM/chqdST1Go3BZeWncz3hcCnp2fPMIc9pcYhZYjYvtWqvHmM/4rsODeWqoWKg8o6ZOjql6x7w6EsErWn6/f6j7N3oOlDkhsGOPT2bUoAkHmYScPAzH33maX7rPe/h5S98godPTjDe52tJMi6WHHzPKI2Y6HrhkA0xgLXsLu5lCgGw/UDfDyRTnXjCzUUuqiPIjBbR4udY+pPsNAgx89aKNUbIznJF5sQYc1q7y8qnoLqFQy0bWQmpkG6k/cYaxs2KkxsbTk5qoc9cP0qMOcRpb2mdLOhUrocPgmhDHEe72TOHwMXuwJ0Lx2o40OX50WllZKrTIUYyIjlzs0bhZY1IISMfxHmp6y6klItSaVBJ6GpS6+RK5BTJnOZWV26RtWKjqTBpMkWS7kWC8lBDyloJsihCUWm3VgaeHupaJsuu3hledENU/UOIOHfAC+Q6n5v3LBdwmXPWGnE+OVdTK8/3kWGYIBfaicETw4yzid4Z+qHHGCe0BEY464ZxtTBijTEcdlItOoQkyGvv2c8zZ7sD73v2gnd/fMv5NrCfIoeI8OVqR6AOglT7UaGleVxSTudcyq9G0o4j0zf/55kOxhRndoqpjExMMgeNAW7cIrzyc5hT4q7t2LuBi2HF0PWs1sesjo4ZNxuCD+wfvV2oT2ReWHEOxUBMgd6JxIwF6ZORVFYL/Cb8tJOCeH4mRsPBT0wxMsXINoZSmfqq2CnyP6/R5Bx2GPAnN4gY9g89jLv7eaV97d5hjGF+6KGl/Gr3YbN0GF0n8yy5irkzuKHnHKGHiTHi8/PHXBVeka6oyaP7iXX4OTDPkgpsnewLfp447PcQA/v9Hkh0IfLoYc/TJknYQQayCdaYYlYVxHljDAu6y2Ywq1Tg9l6yPkYnASlrXZMyrtdUvUD3UiNyQbna83oW0Vlp7oym9qfKta7XMc01dd6KfK08ta1uUlSl/FwKCJJnTJRK2EkdMS3uVVOiG4Rdqk5Wk2wZn1YNVUesFCNK5Xt1MqTipDBUpxpGpJo6uky+VmrRr5D5OVMueJZn+EJ3Snk9Nfr0csbK3mpbVHfzUalqb4sOIKhLW1aTcTbrHFYCbdR5f1V3rP1fj0/18+c6FFmqqMOuH6VKvBP6xXEYi0yFqs9ofxkNEmY5VyvDF00URS+WPAtTNdCUECAOSj1g6FNfHIIhyzCb0+ZDFL5n09AUSFtSCVAqxY/oH5UaxbTAjPz8NuUAZIo5rKj6spzX2iSSHOnUdJDzrtBO6jPbDMIRdGYGqBgpbhtzsK+sSVEURUdLSwBRzHK8+IJy/8WYJNtLnyM7I1N2NIscrIhndYiWWZ6DKcFHDBLUHIZBoqr6SHmA1BHpg8cpolnXmLXEUJGfKF9vBjp2riu9KWCNIHLQiqPVOSPFN1X3SLmfEDmtNBGLomDGlLEUh64WP816UIoFrChhkKynWEtE9MWQZYfNxTC1a66UbSoavfZrQuZesTnzw5U9HUXMqx6eIBeURMc6JgzC969itNpU0m/ttDI2g6eM6lzy3CkPrtWxyviQ57KpPn2csYbqWGyyMKpgqIojSSLz6n5X9GcEJh+42F6w229ZjR5rOvpxZHN0E2dHUpyx+aoF7KYbYFqiUAU1Vj3tMs51Q4mpAIJa9bosmMJ5k/er4pylqoaFPLp8O6Hk1bkRBdm27A99/nyt1kakOmI+UWrFHx+ivJ8/+TRXBffR8x7B9X90SySGwMVHnwbgd/6vn+YX/9bfB+AVX/d6xpMj/GHi4qPP8LP/1d/GdhIBnbc7XvrG13DygseIIXLnPR/gn/617+Ho0dv4w8Tq1g1e/Pov4vjxR/m9t72DX/0ff4Sjxx7m/Mmn+Pof/h5uvej5bJ+9x8nzH5NoT0Y/WqSK5Ly7YPYH7CMb6I8xgyXFQcRVyAZ83gxd77AmlbkoqMy60dmcS2Bi3nCjbNIpG7mNxomqTkUMG1HabErY+Uz4YXdPk3ZPg78kbe/Asx/BvPd3wOTUgqysu7UjdbqxJNWe5VZQSdb1vvmz2AjkwoFnmmWXD2OFOyZ64fK5iggtCoTRNOZUFXn0em0ETZ7dXjEkYKlwLhX0amwkGuRVu6OVQ2WEyrWUOYjkMyNuH5kDaoRQV4sqTO37rc4gbWu+1yjvxYDU3yCGQSX+knuk1OwB7WfZMCnXrMZLaUu+tiKBFqu8KInKGQ4QqIjkWGQ25n75/SDRWp+92Rny3mETFAojaxbfqj1j6iNeHddiOtSbV4e0NrT+rVdVo7K235Rn0qM1BtujHTtrDVGJC21ux7AiPu8FhFe8CnYHqSRrHc4lQjxwcXZPHGq2I8yJcTOATVhnMK6n63spSrVasxo23NueSXVx29MPA32/KgrofNixuzhjv98VgyAYh1eAbtP+fhjoXFcVdN13aRHVy77kmpftmw/aTwta6MoFWo5dUkb1OEt3tBJuxZjY3z0V6pwoRs0vvfPXWa1G+q4jjWNWMgE6mUYJUgh0WbHYXpxx4+FHObpxi67vOUx7/P6SMHk64xhWwg2bMHgvRTv2+4m+GyD5vH6F23W32zNNExg42gxA5p/zgfVqEGRuNhKHYSQZipzbrFZgDNvdHu89Q9/R9Y7tbiKERNc71quBaZ6xCca+49btE1KcyXmUADir9BfZmQWlSE8p1lRGMvdzVrQERyYpqx5RnufJc3HwZQZUoy2PVKLsO8Yq52leR0g7MBKI1/dLDQA1dhCEonKCFiR83kdTTCVIqkdMamUoQqzZi3QNp6bB5OyS5rk1yPSBcyXikC+rPj12hoc3YnjhI8ZERqdBslSefZ8LjhanW1BjNxfq4rTsezbTAazGns2q52g9Mo4D3kdBzbgO1w90/ViMLWvFqTbNs3CtBs8zd0/5+OmW/TTzzM7zyx/dE4M4nyMWY6VPhHMyj49rZaM6E2TtGUzmqHPXyjEANkdM3/PfX//ZJzgmJHz/1B/q2380x/YTn3LfUTJS8nwqSRspm6YpB3aa76QUMn1NxHS2pI/7GJjmiak7iMPEumzHpULRoM52Z11GwYqj2nVCvRFj5LDfE/3M+cWpFFKbJj5ze8G71o6U6xEYqz9CiyBPkAEpxi4obCDPdSN232q9ZnYW7z3jMKBIUYOVNjdBF3ne2LwWYzCqfcYys9OYdh+IBfCzAPEAirStOl2jANDqUerUzYNidF9S9KcVp6ZJsoekdi2o0pp1HtNc15DXmjrrVeeV/rXqwEZTdFU41X3V5EhaMsJlm1LDUZ/lWPktCkidd3q//KzEIlzLrRY1VRpb1wjnCGAzziI7UbReQVXiytjoli2vLaZzuKET6ofWBml77wH60fVAg+vPv3osV1KlUZGgTab6UOo2A8Za+q5bgj2Mpeul4KnaFCGj8I2x9L0tfLK550pquaqNiaonlrZEcfaZDFlUkAV5zjgn1DghhFx4cYkktc3Yy97aYTtLnGPOulS/RuaszQjPGojQq8k55drqUFRvnzqlEQoN7yWjJWUdyYDQMuTr+hCJIRVKIZBMQLlU5ry1vdhEUZDAIQqqv+gC1knh2NKJ0g4JJsXcHrBdl+WdyLw4e3yuC9A5l/UdkRG2E97wRGSeMwc4FXmshaB9CFLo0c9M04TrBXjYdZ1w1KbEPM1ZV5N79a4r82joEmRHfwiB/XTAGMPQ93SdcAg7Z7MzNq9304xrzjJS0BEqYzE1aJDH36JO41Bmu7OWzkqWVVuEWigdgtBlZGS3SRHrVFbkeVgWfi1qqOLEIP5A5VtOMRWqiEI1Yy0zptAUJSu0cYr4NUhwlCxHZAzK7BOZ7sThre3yqsOqrEnanqWcu+74tHHG3i/zZLE3umnDO9ghXFCyQUQiJI+khXkOhz2Xp0/j+pswdqxcxyM3brHuBnYTMgFjwuAkdUFleCMQlVPJ5ChbIT3Ph9rtXju76efWkVC2KmsyDUEemFhOQTc2kXEWMiy82faroyX/2CIUKQ6ClPfGarRf78D542N5HM4u+TsvfhPRL3lkv+X3fopHXvniP6JWwfbpu3z/C//MAz0+H3vnu/ih13wjAH/2R/8Ww8mGH/3ab+F/eNlX8xfe/oOcfuij/ORf/G8B+I9/+n/lfT/7C7zjO76f73/ijXzr+38GgMdf/Qr+0i//CH/7sa8A4A/+xb/mH77lW/n2Z38BmwQtEtA0hh7cCmwH/SioLmxGxyLtzJyYUlDCQwySapJKkmWRllEzHMrjmea3qS+vnONMwhGwaSLt7zHffQHxG2sAACAASURBVD8cTjHhEuMviJcfh3f/DuZjH8Iwo3xXpnO44xF7Y0XsIJko6Ji8ftVh1nWSRqG317XuNKJXF2Y9GidWAkFvZOdL6+BqHbHtI2v0uuAay5jHokjXvWd581g9f8t7FEPA5rhVfa/8MvU++t2U03iqIi4ddOU2ZcNZKK1Fcc7oqk5SbA6HA9cdC7lZUuPM8oQyRg0q4opj1zT/2hxKbZEd+jQYU6qJyrl5s24CcCkLUunHWA298nkoPFIaCFwo03qtpn3aOWr8iT1l63hc6Quafc+opkwzj/LVtPJne3ttlzjU1RAy2gOLe7Z9qN+97lClX891zubbinI1fdGXEW8/AgmGcQ1zYj9NxP2W5D37/UHSrYzl7OxZYgqMqxWr1Zr15oRuXPOCJ17CenVDlN04cXm6xdqOYbXhxu2HWI3H3Lp5m5QCd+48zXzYstvuCfNBnIVR+AJ9w8P77Okp03ab+ZqqkayVU0MTKLm6vq53uv7h9tCFsogici1mcGye9xDJJKbTC8L+IEXHSPyrX/5VPvpZL+INX/olUpwnHZjtzNxNlS8uz6U4Tdx75imObtxkWAtlwZMfeC/J75mnHfHMgx1w4yqjHizGiGIe/UyKgd51jKsTkh1w/R7DzOXljs51dJ1jteoJ3tN1Pd0gMn+329MNHeNqoLMdlxfC29uPPav1wDxHzu5sWa061qsO1yEpyMdrNscD66MRmPn93/rXbDYnvPxz/6T0l+uIOYDmsppqrRUvbSeUKXF/IM1z7eRsjIsLqHHGGXHMtiNYRnaxyLSgREu7kl/rOOp6aw9dgknTFhs9Mb8uYqtB96ckTlrQaufLR5FLaxp+sQtqm684WNTBgalZKSCFbd/+4RlFGt4cHV/5GS47SfNcD41RXhy6ssYjJmPYqamuIRKScNFu1kfcPNmwGjtSANcJz1rX97LWXJU/KSYO88ydswvu3Dvj7uklP/uhA7uoiDkLVpB1hTozkk2hlAV2ApvRQ0mrLgepVq1IHEdd0ImMQuWPj0/qyMVYEVlojRNailxnoQ1cFhmZhNMyZrnmhhHTDxIICYG9n/EEejyROesHWc9SfchE3NjjcxDbuS473hPjeoUhcXb3Gcbe4oPnME+5wFAm5EimIOqLEy/PAZW/IVTEWqMVkIBhtWZYrTPNBjVd2iSInhI8T4qo1oIyVSEUHUF0ir53+BAK/YWCahb9Rt2vExDDVPST0NS10HuVNV4fjapQ1EOzNxMJH2YJ2KAp1in/X9uQsrNGLieLTvRGg+rstnFwF6hXGT+7eLYYfdZnVavVllZHxvWH9nkOJtkGoZvVTK1s3wILtP/k2bMOabITiSpdQ9OKK3fEOEH6MfbgTCNel/rVdXrB/1eAJ5Og73o2RxumzMst0ztKkd3OlTmXYsAjtAMaEPMETNZvlZJgHMfiFwhBnJVthXiT101x/iF6fJKc8LKv6j30dZ+BbD6ErOPktaeWXy4qpfQBxpkyjSQTr2YmdzktH1QfkwCAFoBU5KXq2AUVrvsMEujvNSsn5TRxDeQlUxyNGkCKKdH1tsxWU34kSOSMJYOLKQHiHOBxObhpDBxtRqZJePaVF9c5V+gC+mEg+JDPCUWWmmwv9X1fbB0tBjpNU7GllBNYnZAhSK2kw3SQtjpH3/eMw0gYffajJXbTAUKsKE4Dq5WAHEKMmK7D+5mEyXqJZJhYJ45JS+ZNDUGKZsaEzUjZPhd83U8TaVbu2hy8cZZVN8h7nRUgwDTlPUCu3/dS4NpZB85y2O/YzVNxuBoDfd+XfiTCYZqY/Zwdtz2u74UeCAUHJClu2WZUKk1KngZ+mpU7UZDA1hVKVLUhNVsiEukyVYjQWujeUveQoLzHeTJoVhh5jc5XfEzt8WnjjLXFCS1KcSvYW6Va/oxZwMci7PUIMXIIM1OCyU90vWe0A48dbTjueuZJqt1h8lasiBOXIzhNNKtwzxkxBGLwpT0CO883zbLa1EaLHFFEQDmnFdgNGg0ypw+ygaaamqcLqQrhRKfWQWKx0RSuDSgbYHE6PAdXxf/fj+HkiP/it3+CH3vrt/GxX38XR489xDf93P/GrRe/AIBn3/MBfvTN31LOf/6ffBVv+T//OwD+6V/7Ht739l9kON7wl37pR/jH3/Rf8+S/+Z1y7n/0U/8TD7/8RX+odm0eucW3/O5PAvBrP/AP+ZW/c7VY2VUF4H4V49qPmuOp334P//Orvo79vXPe/u3fx2e97gv5y+/8MbpxYBwDqyFxmBPeJ8z6BmZ9DCSCGQpc34DA9RNoGm1pgyLNC+VAbZ3M0KrEoe81SmZRc03CmIhLHjNfkPb38Ns7mMMp+Lswb0nTlrS7h/mtX4XLUzCSdgFAZ3CbgfHhG8RVJ6gfEvetipQy91RjpzeOVK68d+2RP1Jl4UHOnZq+0zz7dZe75lbt/QuiiqyEN1czKN9STZ3QX/I9ObdtlTE0EcDME9UoKFfvr69LZV5Tr12qgF5xQpeUvKbTFMlgmjsZKJkF16EPTBPpTykVTrqU9JrK36jKeZteqMZTasYYNptjJq1437RQAQHXPf+DDlUSrXFlPEp7TViuy6Jg1jGsfE5X7yfrpOUIs03/JMj7V83dKJH6lret3V+vOVp0h8nKn9JixMce/3/Ye9Ng3dLrru+3nmfv/Q5nuEN33+5Wa7YsyTKS5UEYm0lgpkAoDBUSIPlgcBEKMhUVcEEqVaQqVKCCQ/EFKApXGIpUUZVABgw42AYbyzY42AYbW7JkqSV1t9TqvsO5Z3rfvfcz5MN6pn3OuS05CZQg3irdPuc9756eYQ3/tdZ/MX311xAJsD3E2o6hXzF0a9bdgMUgITCdXzC5iXkcmd2EBG2UEt3EtPO4eaLrt7w4OlbrLathRd9Z7j37PGIN0zzx6sufputXHB3dYbM9ZL06Zh4nBIvB0Bvlesd0GFPNmvun58hur6u3rC+BYAgSFu+YvkKbgX197GuJaXYcCki2nPk6T9A4q5LjC2n/g+ksm7t3wFim03Pc6QUdWgb/4iuf429/7/fz237dt9AFaiMDI/RbSwieOWhJbJhm3KOJflizOTrm+Te/k8f3X2XanacsR23CKEPP5vCAr3zve/j0pz7D2aMT5v1It1ozh2RcxghB2G63+s7OcXk+8vTTd5mmuTQhOjw8QIywHyfOd5cQYbNZMU6Oy91MCHB0tNYAhlcD+c7tQ9YbS9cbJM5Y6YhuB36qw9f1qcENWAJiuprxZgS/n9k9PGGUAAx5hS/mrR3/m2anyASa+Yu5jE3BP62CMESTJGYpvVU7rdUf1X6FnAmdq0Hyc3gfl9xtSYfWIBOauRPqNURudvaNSfIk/b2Bd9RWhLrmGkFzMUf+8Wv6nu8+huc3CkRQZKO+TPCRXMVNMz5dZ1gNHfeeus3RsGIzDPR0SOywndCvFISd5xkTlPZARAGEk5MTPvO5+/z0qxf87P0dUYQp2/BBM18DVCeMBaNjAVkIqRw2BKUuITldkrqJx7jwCyLQ/+d/CA4PdLwaOd4GUdv9XtsiqdNoO1t1VglMSeEKXPme3vQMZmBtBw6GDUebAwbb0VvLxqoz6UHXU2c43408Pn3A5f6c3XzJzo9cxhEvgWDAm9QATqrsWlZT6PPV8ktdMMEHgrXYzZZ773wXjswtGgkuaLVAPl9U1hQ+O+9x86xZyAA49TUKHUQGPiKL/ZUiBWIM0q3oN1tknOq+iAEkEONMJOKiNiQU6RR8SPebJ49zWqYa0nnB+0RVsGMYBoyPjJOn71eAK+slpMykHHDTTNj6nO0+CkEdbRHBpzJsoVIW5b1TsVYpBkDmvdVO23rdzKepQZZUjh1L7dMCxNY9uwwQaMlvSM5/5kPOWanKK5nvn9ep+nVSS/BjLavPcqxyIYvS2OTXIdsJQkT1Skh7SbeZAutGLFESwJcy34ISUpR5j9EXkFR1pC/7pDjIUBqltXqwzg3XbMUYQn4tXZrOFduuBJLKXszAX2unJ+mX3r+lVWoBXKWyiBoH7g3SW816c8uqtpuONwpmP6nS6IuCt2nd2K5ntVqx3WzYjee4WG2WaZ7pUhZpDth75/Ai2ODpzQpBMy/zOPvZsUv0QjnTe2Hj5WcLKas2OwNpHlrOVH0OpZtpG5VnPtFibzVUBzEEXMycv5V2SJJQlqSMvdPsyMzfKcZibDOzCVwNeX/5ZGMtDGqT6BdyiXogxEqVEFLgXsi0FrFZqpEQtUF17TVgEm1KTUDJjeJiyqi1xrBerbViK+Y7R6ZxVrAZsLvmGiJg9Vqz90z7GcZdoQHIm0RESsZoCJplOgx9siMBMQz9OnHORsbdhJtdyUwVUeo807FwKGc3YzrNTl1v1gQ/oMI+JO5oW7JgjTFa7dImZsRYQHYxwkG/JricfarzrRLAglEgc33QIZeXhaYnorowWotYzcg97Psih32qwtJmZsqha0ToN2tt6Os1yzhTEwkKwndDj0/ZzDnZMcZYZGfEINtNsqkjLq1PXcOG1bDC+ZlVAgNi0Ma2kqqzMrWEFSm0HVFcqhiptiM2NdKNLbZx/fiyAWMrV2oCHpMTrYowR8eSE524PYr9WkpKwRHYe8fJ+QkHx/cYxDHYFUfHtzjYHnM+Psa5iWihVdIZfM2gZS2LrU57Z4x2xEtjKnkhSTaqk3FmMiQS0wQkgVO+1mTj6M3LXSrooSe0MltohH1WSEUl1qgQsTom+cgRMADZXXL8N79LsyGuKoqYjdJa5lZuF9uOmFmZhcQFl5wMWZyhCczlf4ZOVtw5usvTd5/iheee46mn7jKPo5YUeIcxkf3ugv1+x2634/ziggePH3E57hndrBxU6JhmoRkLrUMqUIxtGW96tijVbhShJzL8xg/C25/BWMPT73kH3WYNaEnBU+95ByLCi9//T/mZ//l7ePBzn+ab/+jv5dP/6Mf4zA/9OD/wJ/48v+K/+v289Vd9PZf3H/HRv/19/MCf+PN85od+nMPnnubtH/4QP/Jn/gp+nHnxH/0YL/7Df4oA3/xHfy+r48qN90aH6bqSmbt95s6XdM4v5HjXb/oVbO4cE2PkI3/6u3jLN3+Qd//WD/P0e94OgJsmvItKrN0LLlg1CGPUOkIagC8q0bxUvxPKj8mlknZNLo2muvYTeIWSvuMnQpiROCN+AndGmM5gPoPxnOguYXxIvP8FePAazOcKxIYpEbYk7qLeYAaL6bXkzRALl5gxbyAhy+5vj+okQxbwjQGY5JSRWsLRGiv5nGq63gyI1X125e43GHIlWi1GKwXIYqfeo32NosSvnJ/Pq1+W8vfij7RG+A2jkw0NH7zKhupDlOevoGy+yyIfdim/8qMXY6n5W5PZWN40plLlHL2uG78+Y/Ms7ZGj0foe2tQlCb/FuDwZwFxeT6j6qWQql3stz6wZzflLOVtMrn23Pkd9t+LA3GToJ6ShOnDL+157g8ZAzwZVnm/37vdp+fjRMeHgCGKk73rWw4bt+pBOLKt+0AAjSpIfCHg346aZeT+m5khendnkyO7OHzJenmFtj+0M8zRhuw4fA+PuAjGW8eKSzfaQYbUiRpce1ihJf0yN5pqMGRe1iZe1lui9NhRI+rZRB2V+Dg8P2e32yRC9MoQZaEvGVnaE2zk35iqHcR7z1mHLfyc52RHbd6yODjDGMEXw5zuIkWmaePDoET/+Uz/N+7/yXdzabDToNU50pmPVQ2c6dTlioPO6Xq3tWG23HNy6g+17Ls9O8POkAKcR/Ox4fHrG3XvPsDnYcvH4lNPHZwq8hdT4yRqmeSZnind9xzhqFrIYYdWv1BgeG/7YCPvRESF1WAbvZozRioPVqmO1Mmj1mZYdRu948OCU84tl084MNBqxhQtSgOgD09k5/mJPOBYyGNuObSslBJWLFSjVvxdH8Nriz3MjyS8ppFbNF/Q/tYr2anZ9vk8r+PI5OVBOlQgNGJsdw+U6WgxM/byxL4swlvS35rLlERL37cle5e1nzoSTfXqD4KuDGGup+p214fltTkzQ6+amXxl4moPHO2HoDTbkcj7lld3tJh5cTrz0eOTVLzzkweklnz+beTR6pQ1K3bVieuC2EqSMUdY16X2zY5XLN7OeUewulu/XIRPkcy/rz6kiJ1NRtGBsWQ+NvJRs01vl09OyS0kl9kmSxEDnLYjBRcsOQ7A9rh+wIlgx9EYzyZRrGA1izBOX+0vGec8UJibxIBo4UYrABFpJtrHrc7Vry8TqbILqXtN19IfHHB0cMMZcEaJdpRUEzctS59Ak0C8PRF2DKlNE6lq8ySoq9kZUd65fr5B5Lmsk2+75HZRKwi7nwEVwQvT5OSJ+ngluhhjYbLYgAeenkvEWyXaGFH5HkrOdwZAMnixsjBgL+EcGg6oyAKRkQJXKhsahjsm3yONe7TnwhAQML62a5ubl//lTn5ptqmzKgdJ0XiRVgGZ7UGfAuZRNmIJ9PtED5efLwFO9rSfGzN+qn4WgIF4Gy5TPMuZdQwHKnYJdem4sayQP2FWrQ8r4VC+AtEaWAYVGISb7Lpc9Zx7nMnyRorsX8rbYfdmwlfI3HS5d2EWu5/NFarg6anA0Fj9Wrq3xm44n2VxvXGGzPK4lGWQbJQSmeWK33yPWNPeKBWco8ioZypleTekJsl8g5Su6H/2Cp7XYhJlKI2+DqEGvrGeyPYjUYL66gxUk1iBzwwccQ6IwlrIe1H5qsl/zWoqU54pETECD5iHiXcrELAAlut/Jei4lCaRnMsbSJZkWSSXrqiDq+VE5XFuqoSwCDYBVer4QtBIk+prdLpKDPbquvVc6ltk7mmVW7pcGAxdnSHpLkjKSTD+Q10wIzE1mfEnIizWINM/zYusUHzON8TRrMCdzCUejekig8HSHRH+RAz7Z5qLQMsTyfJIzRsteSjIqwpT0mbEWiZISaGKxKSbvkKB2o4+DAp9pTHIPghgCLgOq+ZmBIFFt1qggvfOJdzwHY6gmUP4kUy/4BMIasSkAUGW0vkrObI6QKjJyYFu53E3yKSBGS4heZaFIGg8d884Y5ez1lX4mlrFP/6dW1950fNmAsY2ror9fEbz1r/XvBX1OxqMnMsfAzs+89vA1nn32rVjxGCscHN/m8OgOD85eJ8xnUJxrFVQ2ofaajq/lLLmrYBZCNgk0iXXDVsOtPqOR688NugGyI9euINO+M0kwZ7LmbAWloWl8Olp1kTdqGc00PnUsG+dkv+PW3/hL+Ll2sy1jmu0BI0mINLudysWlJMdWBVTQjWSN8ntkEnDNXoCOjt4OrPoNTx08y9uefwdf8da387737Hjrmycuz8/ZjzvluYsjD177PA8fPeTRySNee/CAz7z6Eo8uzricRsbgcERVGiSDw6Qy7NS6I0QpwjkSkRiwwdQBRlgT6d/3x9nf2XD2udeeSEfw+kc/yae+758A8JW/+Vdy8ulX+Nw/+xl+6E/9Zb7pj3wbX/07fyPGWv7l3/z7fORP/WVuv/0F3v3v/mq+4Q/+B3zi7/0Q3Xrg/sc+xcf+1+8DhA/9p7/nSwZj/1UfX/Ebvpm3/sqv4+EnPsuP/tm/xpu+4at59gPv4fWf/SRPv/cdzPsRt/fYYaDre3w2On2gpgtcMYxojYPKYaf/miIMy3YpcxKbDq8Bi6P3M346JYY9uD3Ml4TxEdGdQZgQ78Dv4dGr8Mqn4PMvg8wUfZHkgu07WFnMqst16aR8gmS/N5lDRaLnJ7xqNKqzmL9SHaD0jQymxbhIm1pksl416PN3ckdoYeGg1GGK5VptBcFCFjWPX2yBVg7UK+YRyA9Ynq2CevW9r13zBgNT9xpkTqWr97oKRsuVz+qYJNsPqQ7P4r6xGpbim1tVmodIbRpw9Skp19Xfq07RLJJpmhZUB/nRMn/bjVmqzY9tpsHyrnWcbjq1GELlg2YtUR63GE2LscugTDrvGgqTPl5kDRY1tMySVWOtXiPGSFivCV1PBNy73kuwNk2UrqFVP7BdbTlaH4Lz9NKVSPX6aK3lf8Hh5ondxSXnZ6e4edRuvCFAmHHzTn9EDZrHj04SMNvRdboeL89OGYYVq/WGdeokHCXLfGlkf3pFES0/DB3ia/ZTmtDy/nmANpuN8nTFVnYt123XXTeb2nkrgcxmOpb7KQ1+AnKiV8eq36xLVt9+clqCHyJ+9vzkv/xZ7ty6Bfee4Wi9Is4BkZEQYT2oIacORMD7mf3FGaazrDcHmK5jdjO70xMMjjgbpt2eL3z+Vd72le9ivV3TDz0PHz5iiLbYN9YY/OyIBKw1dEPHfp94xVYDw6pXWoJxprOWvuuUx2zv6YeOvrOIRMb9SN/1rIaew8MVot3dimM/jxOff/WMk8cVjM3iuzr/qXIpRPw4MT0+I4wT4vvlOXn50zgn1ywx/XZxOBdzlrNW835NmXI+g+9Z7laZ1mq4IlsWT0XjAF3Jim3WTt3f7d6Oi+tcXWOBWKshpMqZVieXM4WUEKCcvwK8eiG8mm4TUoO2otdTFt8Lhx3bXooHZ21gHzzR7lh3M8PQ03e9ZtesOoZhxhrl+g3Bc3p2xqcf7fgXr+549f4JLqSOyXlPVHWozmZaGyW5IB9lvFpoXPe3NGydiBCTLXrTsRhayeMkRWxmnROipLJG1Q0EtdVNk7RRMy89USIOj/cT3gWYI2Yfi0KLaLWCD61sCfiYqtokEq3QW7t4zqv6og3eFrApj032OyLFoe2swXlRpzY1bMzZUvnqIV+3LDfhagOcDKbUPbD0cgQSJZVea9isMBcXpYGXi5nqTSlSjFlhpAbPBG1MFx1Ej/pKAsE5gleAcLPZME4jMOscBa8AowTN3sQQi6mfAe2ahbdYEtnhaYC6mO2BbEMmHsdlI9YaNM0gIGjWa+6infdfXcfNJC0WYqtbQpV7RrQMuPDM5metkiln2opIovZIAfCmXjIHChbyI6YkouYxvNfKkvz9VkbpfqtgmZGmSU35jiHTyOv6Uj1SgENM09hGyjqrtqakPQy1KVgFuutRV9zS/ml5VuPiby3+kVbujbJR19NyrK5IoP9Pji8FnM2Hd55pHLm4vODweJv2Sijgm4ikrOhY5HXmVc9JIOUtJK9rqfZxBmRjpDThzTcvTk7dTzEk2gdTA2I5qKmyW0FJKUEOPW9BMZaroPMiiBRQNdvPOas9046EoHsdq2tNdAAKgKnZvDVpQB84VSNl9Wh03UnMQQaVcc6pXWgTP/1CGVnBW/2O8wFX8BtNTMuNZ8HgZpQ+xU0qe5O8yQ3N8j1D9CmDNYHHQal97LBKFAQ6d7NzpZFyBv/aFTkViqYaTKv3FXz0al9nfZooIrIjl+9TZJgIXckuzbvbJ/7aasdmEL1Iw0xpIFIaLpY1FgJD3+s7J/kxzjM+NcM2ok28fYML6L2EzprS60WQGnxLPWZyxq4YrcAzNpagu9I7+NTzRrBdl2RPlpuBKKJJX+ka1XNMzVydo/RlSvJek52qbNIl5LFi6YxF6MBqdnKICXsqfMBPNEmALyMwFnSB+hiwjXIWlGRaFX02ZJsNkxVPWnxz9Ix+5lMv/jzveftXwe2AWOH46JDjp+7RnbyC271Ol8rODCbxoW3UePQ6SRFZRCYyj0lYdMBWCVRkTjaQJGnyHEyF0qGXemYyjCU1d8gCNl878aUZo12JGyMnKxS9paqwzlgkbfCr8y3JuG4TEw2CC1m551Lf2DgNeTPGsus625HkvjZOQpVoFEvsbDazVNlHIFpsNGyHI546foaveMt7+JZf8WFeeO5ZNkOPdyOPH91nv79kchOX4yWffOnn+ZmP/wyfe+0LPDw9ZXSegMOboLxvfW12AULtop3GLCTFFCFbZVEEl7leUIPxPIIDPvkPfpi/8/v/BN9x/yM3rsoP/Se/m7d/+EP8xff/dv7ar/l9N36nPb71r/93vO1XKu/dH/qX/xsAd9/1Vj70B3/XFz33X/cRY+S1n/4E3/WNvxuA7//jf47v/+N/jm6z4jse/DB2eohcjszjARzeBtthrK6SYHImS9qnxUYsphIQSokKJXtZqoBLSlhyP/QYlIvG75DpHNk9JF5+gRgnYpiJbsbEEREHfiaOI+H8PvGf/xiyP0UkIGIT50nWFhE5WNHf2mDWPVHAxmpyZKO5CVWghSvVQ75qv+vXUikpNSLcOvRENaSAxnFrosXpYrkxQt310hj49Z6tEFdupewIQo7OaWQ/FKV9o8nXWFqNrVXKMyR7INR71mitT2Vm6Q+LEimKKsO7YhiLLMH6xfUgb9ySgVqBzNzY8IagVhotlYskZ7mJ1C49rvy65WehRucrEBuLMxS8T2V4lO/TOHK1cccbH1eBmmxk5CPQrjuWPyeDMsL1eQzN+r3iVERY6JnGkk5DEIihsVCb75c5SvI/Ri2HApje/T7mt7yjEBQrmKP6abXecnR4i+2wpZeeSGQe91hrGdZr7ty9pzJ+f4ERy/GtWxzfusW837G/vODs8WNtxpW5+pLxPe13xFIqSdWvUY1jEJ659xx3nrrLrbu3YIbH5xdc7CuoF3EpUyJTCuQmBNfXVQiBhw8f6ZqKUp2FPDsCBHj+3gsYEfbjnvsn9xsAS9dQHcRmLuH6msmfG816EgQZOrbP3KET4fL+Cf5yLN2l/9EP/xO++j3v4pd93dcgYriYJs04847j7ZY7d+4w7vda0TDP+Eeew+M7bA4OOX77V/KZF38Od3mBm0biPAGWFz/xSe7ee5rtZq18aNFpBRCW/X6n/LKdJRC4uNyx3RywGga89zx+pEHtg4M1IQSm2THNgaOjA6L3uNkxzRN37h6y3fQoxjQX590ISPA8fnTBJ18556sfV5oCMZLK26XQTlgEP4/sH5wwn55hjWBkCca2Px0dHTGOI+M4NnviumyoGisJe2m+JRCcgh6mt8UpqR5enkZDdmVDWFw+ObyqUUKWHVlmZueiOYTs7DbBgrqNmzEyS7Ag6DOhIwAAIABJREFUVpnQrjnVB5mzuGjhck7xXbkS0E9fevl85uXzud4j/d9wgpVks4py721WHZthUM4/AqNzXOwmnI/JG8m8BzXQFL1PmWht0C3vm7QPiycl2gwlAfS52QudJRepijFw3GH6GZiX75sOg+i+Co1sL3IvlLEIvurwGALRqJNFp5VyYvKbdEQCHSmD22q5eah4BAFl2PZ5vKVmcpU5lZRlls5byAxTZZakMuBaGt4eEWskNTBJTURTsKrYX6Kl+e3Z6qDq+WVNZiCACmCp3ozF9i7np2kyUXXmejukUm/H7Jxm2a/y3u/ozJoYbb0+CtppoxftzA7Q9SsFXeeRad4Ro9D3K4aVY3YTyEwM2vQmIJjEKxmDkEogqzPePLExkjgkG5u1se9CVKDhpv1ZrtT80lpdOWxzrelobO6VK5jSfds1aknZrtAAX/XMylmpnygQYjBekyVyPDw/kwLtde8XPtokW4wANu1r2xMbfzVGNEMxRqUSSes4v1epWMiAdYy1Cbdkq1ADpllP5pEsgGJrJzbCt4BC2aeEUgbc2gPEVnY090hueGwA6Uj1kVMhCZ3VMfYhqO4PKUO9E6LLc1ibDLVzei3J4IlBoBst8sW1rn03gHeBeZwJKds9ZiMpVRFrABem2RWKlwzSxgA+1qZCtu+SXk0Zo87jQuYAlcQnb4tPkjOoc4WfCxE6q9U4xiiVS8OZHEKAKZZ5zOvDdtovoFAjQGOXtu+uYGLf92n9x9R8KTf0U0oTIoUbNetVsg0lNdki27AhpDVb6KJ0LbOmcNx2YkrQJ3GP6BikwF5AcDE1PQtBk/hsTiHSUnWX9sw863xp4yzHoJpB3ztl1Gk1cMDPqXE1CmZq80BhmmfmlAHrvGJAxlgNsg89q82gyQteKwXcrJmnOi4dplOKwHmeGcdR5WrSLcYYVrZnvRrwzuHczOR8SUAUga4z2G5ArE2VF4E5OPw0lXWu3LQDIj0xwDTNhKA0Kzmh4eBgq2s0raXdpTaIFfRZh2EgRTrJFR/ee7Q8QhP/bK/Jfwo4G6ZUTZ3pE0Rgvc5cyIJzninNAZCSOhKIHGPJLo6+jocxqSlesgFmH5nHsbyrtTa9h66frLcblUHf92VNa/DSMM6VKsG9Ae3JlwUYq1ENwUgH0kT6Ib1pwqKlqjtVhJKUZjUcQKGdyTm22wOGfmDv1Gm/9/SbeOnzL/KFBx1ilL+IqIr//OJMs2LTPbNKleY5tDGIKWBAVqAlC90kwzQszMqkKFqBnX4QLePK2a6LcmnvoAiVVtkkhSr1GUIIjG4szyo38MPWKJX+p08d94L3pTNyVtXFdI+a2aqgsGU9rCvo03dc/Kpfr4tMzYJybY2CWtZ2xbN37/HC82/hmafucef2XT5uLR+PAR88zvecWsfhP/+nnLz0aV55/VVeefgqF+MljqCGa8LVFD/IuQ9VQaeRS1HdGgUtui073jFFg2MkSJaHNyvN9viR7/wr/Mh//z8C8Af++d/iR7/zr/JTf+PvfNHz/k04fvC/+Qt89iM/wR9++R/yF3/Jb+PX/Lf/GZunbvN/fLs2/TKnP0d/8pjVwT2CeRtOeqLpibZHzAaSSR5TwzljbCrxoSTFSvRIMn4iluhnFEIPmBixfodx2niL8Qw3XaYStBnCHuKcsi2DZsLOjwjTOfHzr8CnXwRmmOYkChL4ngAk6Qx2u+Lw3m2CRXnYqNkHaizcPDbLkEc9rpckybW/X7vWFWOtXKf5LMbso1bDJhvg9ZrViM2AVZvt8cUAwmyklGwzshHz5HOzodx1SlHR0p2UoAvF1U9Pd/PzvFGmbzbS2yz95fdDGYEnZbt90fdvziqASunSoKCPiBBC4ga/MgZPHKPm50jlPWvnvc2sydcKMdICp5knK3P8LkHV5R0zAA9U0Nf75FzFBRi+BPIbR4zlKKpRW6PL/vCI/Tf9av1S3ynViwjrYcNqWDH0K9b9mlW3ojMWa3uM6fCdRfYG7yb2F5c84FX6flAOsgjzqBHnvltxeHvD4d2nuby84OL0jGkcmaeJy90ls5tTgz3NgFAboD63c45XX3uJhyevs35lQ5DILJ79s5XSRYJDgiNnR+UOvTH5cqWkM+k15+cCDGTdagqgBVNUW0EbMIzqIJUypidMVxn7Gixo5y6PfVkrQH/nmI0YpsfnTI/PMEEdo49/6tO8ev8+3/obfz2CZgDMU1BgJYRi9Bog+omzxw8Zxx3b49u86c3v5P6rn2N/cYqf9sy7xxjxvH5xDsAgUZsuInSm4+DWXXa7M7LAXK8OmGfH6eNzuq5jvdkQiZxfXNJ1PcNqw7CKXJyfYxBWQ8fTzzyF6SJEr+WABIxo+WAMkUdnZ/y1v/6/8LnzyGT7Zgy0OZOiCh5rLWGcmM/O2T8+pZOaeXLjWIfIyckJrYypmZZLJ/qN5EaM2gjE2GxTSTHm67mSfLsnG9ptsGhxJOdA0jVijKWpSQb6aif0m/VI+mDx+00BqRZM8C6UZiXXV+DNQEP70DmbzRE1izHt0wsXuXRj3kE62lqTz1Le3iTDpb1DEdhZ3EvUbNWh007NWNMkGEjzRTBDv7CDfbFSJT/U4pVjzGBV1m3Nu6f9OseIj5HZOyY3M1iLNRYjNgUGUjVFGr/sDOeKi0qaE1PJ+c0Co+QtNjb71blZZmpSxyr94LP9JQZjO0zI9oTaRz4qJ2kFudoS71jAFy2vrAHiqk9SQ51mDkP0CockW2YzrPnJceQ553jXal3BPXKmp0ekS9QT1aYI3uPnGec8/XrAWEuc9kyTgxDZbg8Y9yMSPX4a6daa4RRjchYaHRFSSXVIIEPb3NEHn3jh2yz6PJwmlcrrGGbwirSGpNA5LvdkayvkDKx8/Tx3OlYLD/HKAri+L/R6TUZ1rH5QXg+lq/niEpp0k21eSbZ5Zl/KZlB9zxQAs31Zu7oeNDARU3baIrEgvXcnVZcKCsIpT2eBbpv/LvVf+z55DWbQrbUzgdLDr3x0ZbxEsn7PLxzLXOQMQJXaUmRErlhVH1Kf3V+x4VpA94vpjCeCq7/gI4GTqVGXS7QfIQR8mACDHXSP90jJpAS0bNwYbOpXkAaZDoO1Ctb1G6VdyZl8IWoVTB5cQZCuPT9yBeuugHwqx2a9TnQHISXYRUhZ3iaBWiU02lzHp70qSA1GiIAR+l4A01SspeztdI4RwRbFmf4RYXYON024eYLUa4io8+1mj7WVC1l3faujo2bbJt0eATE9fRN8mC8dc3BE2yVAz7JZrei2G0yMELOs7ZiDgqEuznQiDEYBzDDo2jOJW90S6ExPv1rj+4AfFMzT3PH0fkazWHMwJQTH5V5BUiM1a7pL4GAIgXl2hXJMt4XQ9Uollm2aEALzlPhtjY75YC3G6rMFEdxc2+Dlee+6Lu33mIBfRw6mdl1Xmo8ZY+AIzi8vGv59sKYrgQBruwSiO8WmvC6U3CzRGsPB5hbTPGug0Xs6q+zANoHRq9XA4AZtSBZ1PHJwDxGsQL/qNbgUQuJ8jczJdxOj2der9aoAqT4EgoulMsYYQYxlShQ6hMg874ps1PcPWkknaLBLniwHvizAWNBosRBTpzf9LEfa5uAZ+iHLaDLAtpDdxdDRLXe5v2S/v2QcL5kiWBl4+tZdjg9uMdgVyE5PzsKa6uhnJZUFDelzYua6iZBLlfNRnrt2wSzKuj6qbuJG0C1+arrj5m7m0p7QvG0oHFFq6NWykQYMSEKpAgnNEwfBTzPFRMyR//I8+p7z296Bv30XYwwubZIIRNsR14esu744FPPsMWLYbrYcHxxx784zPPfUPY4Pj1iv10TbcTFPjNOOi90FJ6ePef3Ba0Qcu9vHnK07Lu49hf3ovyDOo4KwoZBHpWFoMzxU6YYkZI1IKdC5qipzKUYWXlnwAbjdyN/9Q3+SR596ibd9+EN83bf/jnLedHbJ5f0TAH70O/8Kn/vxn9Vn8Z7v+S/+NLbvePTiK+X7P/Kdf5XTz77K+//D31I++/h3/yAf/zs/AMC3/Ok/zObOMV/KMZ6e873f8T9AhM//5EfL59//x/4cw+GW/mDDb/4L/zX/4L/8Tn7iu/6WRj2Hnt/wZ7+Dp9/7To7f8hy//s/8Eb73j34n//hP/iVOX36V7TN3Cuj6Fb/pl/Ps17yHw+eeQozho3/7++jWq7pEXvxp/CdfJbzwLrr9GZv1AcGu8XbD3N9Gug2FXCA4OrpSzhS9I/oJ5pEYHASv1VJhgjBrpmtwuLCHMCJhj/hLnJ/xeEhZsjFFIePZKXz+czCdIG6EyzPitENMLJF5qI6M9B3dZmBz9wgGizZcUAcicypJtlCvGnPNv3mNXTW023WVy0/bfW5audFeu3GWq0yIrX1K1ZZVFrZPdvXza8Dllfu1wE96KmoHyKqglmfX58+OwI0GZX739q5PcjKbz7X0rz7XTddeAFZR3UWdtyazNZeXSAOysRyPImezf5/nMpvkC9B36WgsXvWKcf5Gx9V3atdNC8o9CbzP+iY7Dq2bCDc/xzWArzxvMqTS+Cyvlc+ta2F69/uIw4o4DJj1QaLwMXQmGf12UJ4lsWpQuUA0YLsV24NDDo6POH34iHl/yTztmcaRadwnY9xo8xhTDcYYI32/4uhWpzxfnWaZPT55yO7ignG3Yx5n9vOkxlkqcfLBK4dUUJ2iZb7gx5oZ66cZ4zwxNUmIvmaDxQjDsEqdV1sOq/pzrhKRUKXCxe5cba9Qu4u3oIaOfZ2Tq8DWjeu9dUZF9VN/sCEXGe5PlM81zJ6Tx+d85Md+gq99/1cRVyt8cn77cWTV9/SpIUMMkRgccdoTz8+wtuPg1m2MNVw8foifZ6bdJbbv6fqBblgxdB1u0g61zmkzO22Q4LRp1+wYhh4xUrLdJDlZygE8s1opRcF61bFed/jo1PlPXJ6Ccn9dTo4vPNzx6Qc75tt3YFN1z8JmDRHnJtzpOfPpObi5rtnme9/23i2nU7K32u6StLZWs+5lySHZTMW1oz2/BQ3q3NYzr23NhWiMJShWLhObDH1yUL7xUuPy+294yNV3bU5qgNvMh0axd2u10fLsm+971Swtejff4sp3l0BM+414VcktvxfJwkl/FNjcGjHrB6kC5up5Wd4J7x6qHLgJJr9mLzevaqxANMV+X4xKCqS5GAhB0zNcUG7qxbIly4VcA5F9lCWI2V4XlnpSmiCUrgppcOQreiDm83UujbXKY2dSB/Oo+yLktSqSSnuzvKsyLKZmaDFGfJ4Dqh4zJl4DhBU3ES3JxCKrFaGzqeFjAntIzi+OELzSz5RlmWRzko/B+bT8BWM7um7g8vwCY/eM+z37/S5xOOo7Yg2SsvqK3BVp1vZybDOolcHM/JmI1CxPdW4I0SWMJ438YlvJtZ9bYDT/3v49eXdprOu+pAmOXw9mV9qVVr9cszXStSIVLi+7LvmMiyPpntYmqUH3fL8KJl8N+OT/lsaEImUt6uib8gzlXcurFU+7/NSCYdWey88vze86go1Gr9artHMemnfJo5/GPvjKkwqpORmahV6EXDuCddyXc7O0IW/S+1/Kcd1mTGMUoTcdmtgYCt+1TXo+oEHhbujrfZN9nYEyI4JziUKGgHea264NnDToYqKCTHn9xhg1US7dr8qoUGQyJLzCBVwa3gxAxSj4vI+DJ4g2UA8x23/pXcteSHMWApL5YckyxxJT4Ju0d0NZs2kdZBL3dN3Lix1uGsE7OsmpdJXWwGCJzmfPAtCAW0w6MviANY2cNY6srWPQ5pE+BGLnlC6x6+iHnq3p6azBKvk+/dHTDIdHmH5gt7vg7P6rBOdws2c3jng3JT9afV6Xm1mm22qFtModHzRpwBuj3N+pYiLviTo/2hsgJ+JZEULeo+nC3mkGuM5BqkKzZqHbfQxEnwJQKYM0yxetJtedV7Pc0/zHup5b+dp1HZsUnKt4WyjZqaBZz0ZEK1FsTBn2CXQXBXitMbiuw6deEJDXlEEwbAZLSGB0RANxuaIAEYYhgbEx4EOtAiyJiwGINbEmN3tsfXcE+r4rNooPqcla8jOstQqIpzVppDa/u3p8eYCxjYLKRzZdcsc8ilCqgjGvvWqoqHj2CBf7HeeXZxyOO6Rf0Rm4fXiLo+0Rq37Njh0mkeInXK8ofilSpnLD5n9z18JqRFZjrSq8WhJXnLT0nQZvbRRyeZt6t7wbkiGUg4TZMssOY0bfaTsctj9IVaCtOjFIomSIiNUIx3R8h5AyhUxSqOHNbyc881yhbkAEUnfDle3ZrtZFCfseNus1t49vcefWbZ59+jluHx0p127wjPsdZ+ennF2ecXL+mAcnD7j/8AE7K/jbxwS5RQTWD1+D/SUhkeCbB/ch1KxYMUsjNEPpdWlI6p7JwmPI66VVnAfP3OGFb/wA9z/2Ik+9++2897f9Wj7wH/3W8vfbb38Tb020Ayef+Tzbp++U3x/+/GfL9/Jn+0ennL96n/a4vP+I1z/6KRAIzvOlHsF57n/0RRVg61W5x+OXXgXgmfd9BV//H/9OPvHdP8h4domfZt72q7+Br//9/x52UCF0cO8pPv7dP8DFaw+xw8A7v+WX8Q1/4N8H4C3f9EEdohB48zd9DePpBdP5JW/95V+nzvz9Vwgv/zxiZrh3wSreJXZbJrPB7R9jhmOiHYgI0TtkMiWLNfq5gLH4Sf8eHBJmBWT9RPQzAUeMHpgRptSRUI1SEwPx9FQz/h49gpc+A+48za06C2IMBpuUgwoD6YRuMzAcblgdb3GmWg2Zrj+Xs6hIWUqe4tDlVZPKJK8aogsTq7EYa7YRcGXfLU5pDMb6n0a+LYDU1vhdnFCFXz4/y8objpgvFtvvNt9uhEc1oOM1Hq4rZ92EaS/v+8Q/Vnl30zXy8+ZXvFZcnt41K/XWsV86Mynjv9EfSKmYXThR2fi76dnVcXtj4/qNDPUvehQjR6+RAwdF/5AdquvPkMeqnJt4w/If83WvjfGt28SuJ3s+/q3vgM0BIiZ1As+GpWZUaFauyg3nZ5yBIJa+D1jTsT04Ztq7sscCkf3+EozFdD2265EuZZMGj3czIkaj2as1682WYehYbzdcnJ1xeX7G5fkFcnnBPM+phCkSvWZyuKAR8khATk+ID6r8DT535bWQApfS7I9Fxkwzf+V3gRDVJsj7f5yn6j5K1ffNKa0EKHP6htPeXgDNQOiGDmFDBMbLnfLERs3o+LlPfIp7zzzFs08/xfF2i/WBfp6L9DJN+V5wM2F3yTCsWG83xINDvHdcnJzg3AQSU+Znz2o1EINTh8mr3okx1RMkrktrLZFYjE4FzyPBOSBwfHyAsdBZEBOR3MdGpMiXcZ557cEZH3vxVU7pGA43yKqlHMiOn+5bN02MFxe43U4N6NK8oY7Zr32hgrm/ePzbfDjg/Bd0RradFxhQXK6fkAIFWR8Y6QrXXfHvs6OGOqmlVi5q9m25dnb4ozqSNYsxUh3QL+G5o1ZyEavDHaEAsrVKr9oD+Y2MMXRdT+4yrpfRjCcVWbFVLenRK7CV3ZsMXBRbKINXISx0iaD6VEQQK8jQqRxKlYkK8ESCCcl/8eV91BaJ1Z4JIfGYJm5A29H1K8bJEbhk3o/MbipzYoxR/ZJ7SWRbyUjKeM62UyuXs91RdUE77gu9nUDGUjZf/skvv5zNFuhtvxPTOMark5/9yiv2Ylm3UieqBm6uVFlQ/dD8ySKoSDPdV+3S4i7F5tnbP8byjovzWnsr/1789fx5XqOtl7scgHqrZh0v7D4opfVkP7y1iVqruz5nSw9YgvVpLGPa/yZWxukyw/mRQ2yu2AxXE5z4Ysf/E1C2nJd96wRoSva/Wx8Btc9tr9yYxWYvTeBShqxyUWBEqRF9CLUSK1ENlOBPAflBUxPrPWvuRZ2rkDMMky2VQdIIJauzZKWmmcoVRfm92iClR7RZV7GxIiK5TNyUZQb1/QKxcKDm8Z6mkeAcJvok04XO6hhGq2Xv3nsyVWxMcrvmQGeqBv1rbeweldM5Bgie4Clc+8Y5bGeL7bzaHnL7+Rc4fOY5+vWW05NHvE7AjTvG/R57Dm4i0SloM9TZe2YfUgZ9AqLR7E4fgvLSoo1aFcBUuqos6QRSxqcsQM4CgEalhAneF4AyUwDkpI2kdrRaKvlnYuu18h6NAB6Vw4mHtuu6xbp33kNqKOd9DSbkIyYalJiS72yMpSLNoFRFOSs/JDBZjMFSOayz76ZZ7p7ODjrXZN0uSkuS9mFnbNLHBmsi3qTrZlvVALH2CrDGJqBa13puWper0SQKgcA0zXhxhBC1Aj312sgZt086vizAWIEUrUlCv6CXkrgtutKh7SbgtgjltMjmKJxcnnP/5AFPPf0CT91eE/aG24cH3D68xXZzxNnlAwYbi4Aw6nVh00ouYr1Ryso9k85RCVEnrlUFJiuDqhSu6+0a9dD71WilPkKoQpFIzk+PzWJq370YIbFeNCYjUWVtZQ8WhKGz+M4qkG21I+D49d9M2GzJKt2mEofBGKw1WFHjTh3qgZVZMSQDyBrL0dEt3vT889w6OmK9Wmlqt5uZ/cw0T5ydn/HiSy/x+qP7nO0u2LsRxJDcaDJx++6Dv5ScPRBDYPM9/zsy7ZsxzApT58HkySEmo6MhnC4DXJVqa4a8/cO/lN/7j38pTzq+9vf9Dr729/2OJ/79Szk++G3fyge/7Vt/wedt7t7i237wr37R7/2ev/sXn3yNO8d82w+88TXEGH7Pd/+Fa58bidiz+8SfO8EdCN1qwoQthJ7znSf2x2AHoliIyrGs3VpVoKpA9ykr1mHihBCUuiAqT5FGokMiNZ/BT4nLzRHmPfzEj8Gs5a2QBKNIyUywoiIsB2SMgKx7VscHDEcbok1UCgl1M9kgbIATMdXQIGoJlEl7FFHZJLYaVaFZSxnQbLObyJ8vDGMWf5NIMQ5C2uOtoH6jLMzY3L/8tzGQCrDTXKPQEuQMjaKyrz8bsWaOqmgLeF8N+wIKN+dloynfV5rv5Wdu30erBxpDPk1o5c9bKq2aVVROSAZZlXc6Dtkbvfn9rlyU7LDkkqja6XzpLi+N7jc2qtu5uzqPVzNkrz3Slc+ywZmetPz+JLu+vW/mOyzOSJOpo+VfqjOm938t8c7TgJQyoK7TpjyrfqUZsF4bKLg5lx81rl/Q0vO4s0TzmNit9fsYxPY8dfcZzk4eMDtHRJ3mfn2AxICfR6bE8eqCw/tLxt3IsBk4ODzm1vEdCIHz81Men52y3+8Yx5F5nDm7OGccd8zzRAip3PRHfphwdFTHIyQe5dIUZHns072XPrO0uGFZigJ0ZAY+/Z8hlyTV77QfPAnUv3Hu8v2TvgoRpO9Y3TrCjSPjg1Pi5MvO+MiP/F987Qfex/u/6j1MMXLpPXMMrBMH2qbvU3asx8eR87MTAoHN9oCnn38z8+QY94+Y5h3zPBJnx/ruHUjyzhIYL07J5YHr1QpxwjiOiCg/1vrwkPPLSy17t8Lt24c89/w9Li4es7s8Z5oc2uxT1M4I2jX80dmef/GxF/l7P/jPMM/dQg43SF/NUZPKv0k2sdvv8eNEdL5SBqjJxvxFgiO/ePxbcBRxLIu9upTSNx8OBXJiBlYzx2Gse71cDL1H8NANAj7phGY/Z32reiK1GyvXqIKjgkkVhSp6cnE/igAKaGZ0/pNm9Ulyh6oMi1dOzzpfsquA8gt2/aBy3uegkwKEzjvasvfybEZBE2O6pDdqhmXRqKWCbvkSuTlcBLxA7Cxms0JmR3CBaZ7xwROkPn0eG3X8Exwi+t5unHCrnn7Va2VGPzBOjnHaITFiRbBdX3p0lCy6PJzJ+U2M/YgI/RW74mpWqyQjMttLtaLQNgutgoSZyiAf2rQlFl1bsk1Nth3bMavQbs5yLMomgQ7Eep1r4037jKS10dhfGayqJ6ivm7Ipy2cUs60cLZhSbcp6XxFKJll6iBJ8KGORVkMewWZ7LWzXuvKrjw3Zjmu0osRscaS9V0ekfrW5OBQAp44PpTFcvrT3M1L845o59yQbuT1uAvMLsJjv9wsAYW8Cd5337HfKfd6v1qUS0JfGShXIzE27jLV0xjAmbk3vNfDRW4uxVvk5Ey/q7FwJXoDQ9RpcjWkvxBgTRUWiM7SW3Mg7DRW5WaM21ItM41xAQGssvlTv6jNa2+GDL3OS/bo6fQKJVz5G5T2tQHoCl22HCIVH1tqO6LVplfMe52YNFItA7BCr77bdrBLtg4KHbs7N69KejqHSYETokkxUXvyZkOmzIuAj437CJXxKBOK0Zx9GGAY6OeBwu+GF59/E9u6z0K0wLtI/9yam3WN2l2esu4gf+8JjOk4j5/uRh6dn7KaJ2Qc6O2CHNT7Rak5uZpqmsmaMgX7otFw/+ce73Zjm3RS+0xKEEbWxxnHEBZ90A3RdmtuUtWysVaqHecY7h7GGYRiw1izWfQgKyCu4r98xtlK7lASKGJm92nCdVeqCvDZzIC/L6q5TzElQupOcrS/A7OZCeyCSaWqabG5RnzJz9UdStrf3GkSNOtZGcitvyj1UDSa+7ivBiQGlb/EpyUPlHlo9aETxsh588r8UewupF2aV5zcdXxZgLJA2YTaSWuc1/3dZylUUQ9NdMn/sYuDUw2dee4Vn7r2Je/deoDfCrW3PM089zTP3XuDzn36FKFMR4GJAbOM4XwF9Y/bOspKXFOU0VXlmQKZGIur1NKV+ORGtUlk6gwp+hqANzdLllyc1GrbvKn1AGYcUWailAI35JtCJsF0NXL79XVy+671ackUVUL3t2aw2HKy3rPuBobeYKMzO47xuvt4Ybh8cc+vWbW7fvs3x8S2sQbN3xj2zn7m4OOf09JSTx4/5wsP7nF7umIk40yO9ZjSue1EQTWLi3sqAd9TWTt/6u5TH8bXPYz7y/ZrCH1PJkwCmkiojV4ZnsZAaA/AXjy96aFlCQOLE9md/ivd/4ANcHN3h09Ijl2fDloqkAAAgAElEQVSE+BoYS8xp2wKSSLarf6zzaPBIcGSCZQWW1JANwen8hhl+8ifBzRniIOYOzwKCdj3UaGDinxHDPCXScSv0m571U0fYzQCdwSs7WzFJcyBEBGTxjPmltaxKf2Yhc0KT+VJzJOo7tp2sYrpXFuTXBxeGvsN0GpnNirV5yOXXr33W5gHE8i+oYZS8G4qpG6/uidYKv/J5DjKlvy9kyxNtU2HBE1ge83pGbWvk3/SeMV7Lfy3zkL5Urt1mibQOb/v91lmpwxibf7MTlfQlGYxu36U+c+GQKwGCxjDlujH+pR41sMfC6c7/lOyqL+IgXJ2zBXifrhWefzPz134j1liG1QpjOqzRhgjWZH5HfUUffTG0vXfJQElGNEJMHGCTG2F3xvDY4OZJwY/guXzsODg8ZH24xnQDdAPPPvcsr77yCrvLy9TUwegeiCmaLAOnjx6q8yiG9XrF0eERfb9itXL4EDm4fZcokeBnxstzPv+5l7U5jq/j7qPX7IVm1K7q2xsGsI5XnhuWc1rW3bU5TuvmysdfTOcsdHezj7QvpXD09F2sWMazC9zFDpNwlJ/6mY/xuc9/gX/n132Yx/uRXoS9TbQLB1sNZIuWnbrdOS5ol9mjW3d487u+kpc/9TGmi1OinwghcfWOe6KbsZ2h73sCyaiWiI+G2eaOtZ7T88f0fc92s+FgO7BaG05PH+H9rDxjaCOu7KxP88QP/Z9/n3/2mVM+d+mYj9YMd59m7nqcVKCk6zs26zUCuP2O6ewMnCsgSdb13/vKnh/8wrSYr3h1gtN+yDbZlS3WjH4DPizAdCkzKEjBPIoIvVI10O7/GGqGXKK7azLmJInfNnjDgo/2Jke/XU+LAGC2P1Mzmvaaxtbrkr7jZpcaYC03Q80g03fUzEIF1F2q7NGpuk61ciMAURQhZS2S9pNIHU/JuigHwtLnJsIcPXa9Zn3nLofPP6sNXZPT3GXgMINvkjNQdK4tkc2zBv/6fdxuVP7lAnBC4QJJSyHGSJSQAIBmXqGZ16BUBs3KaF64AErXVlYri59whGb5ZlcxpnLK3F06XrlIC0zpNSKm7+nWa2Yf8M6l6pYM1YZmDTUnlk9iSuBQY8aKVsYVoCw56m0AOUBtXgzEziKbNbKfiG7PFAMzgZWgzr5Rm18r7hIIHWIJ0u0vTjm+s+Hy7JHe13tWg2W9WiMRLmzHar3FMCmneE6CEVHKggYsarCmcpjcrKiMmTYoNTGvnazTixO6mENd/1VGFHmdvmsT+LQ0XZa2TX2smnFX5zQQQ24kmj83GbMqz5UpBNR0S1nIxPLipgUM85w3mWkK5kgZp7LG38B+Ua7IWgGqzWrbfZDoOBaXqDIr80te3QdXLcNMSYRIyra8/m3NSgtcfVrVURqkLV3qK3BQ9UBQWrQYVRb5qM2iozzp6d74aMfuF1QVde06OooGNBgxWFLeFCBIqHQcJnWe984TTSRa1XfaHKk+kwuaZatNBm2tngqVw9qnDEZIWYcZX4gV7M2qRDmltRKH2Jdr5FJ3BcACQ8rgLOMhCvjHJJs0mz7ZlVF1Vd6fRoTtVsqYlOd0IX1Hm7CLGPpk7+h6CQ2opjKst5ZeNOkuSTRkk9akKA9rJJTy9ZCyeokZ7IsQtNeP94F59gzDzBzq3uqiJ0wTu3HP5dljHjx6nc++/DLD5oj1wRF379zl+NYhO+9w84QJjr7LpfcrrBzhgN04cbkfOb/cc7qf2blUoSSGxJqF804bcHmnYKpVe8sYw3Z7CEjhgvU+2YWo/N2s1hxsD3HB44NXCq8cBILEBduzXW3UhgoKuE/zVK4zDANdXykJ1JdV4NZrQjWr1Yq+XyU9FgiXl4z7EW8dXdfrHOfmWGjm7Owc0zgln00bheU9G2Ngv6+c5+oz9Ay9NoozSaY/Pj9PfTmy/Wfph4EosdBLTIn/Nrdf7aytWeIhKlCdfCkrwrBaqaTPetAI3o3qHyQKlco/LgxdzzR75jn7T/8GgLEhGWoqZ9QYUCMhC2DJNkKyBaQKpWwA5r8DDsPrDx9ycnIfN53T21sYPHeOjnju6Wf5qU9YYko/buy+4jRALtXPTyiFtyI9VjUy03mt2L1WyiqCUgy30cSqvLPeM43wFhE6awtXRRZmzlX+IhElLM4cR+Xq2Tgr49co+a7j8Qc/RG8tcXuI7Vd45+gQBqvZUNv1AbeP79AZ5cMIXjv7xWhYDT3b7QFP3X2a20fHrFcrur5X7iw34+aJcRw5PTvj5PQxu/3IfhqJwMFmhXQabQhBCeE7qxxURkgkzLE04vIhEg60VDIerPCHv4Vx8gwf/yjz/dc53e2YXcAbfU8TpTgR2cirXEtpygrgzi8eb3B80x/7dr7m2387oJGfO7du4fued2IYp1nNhLw38yHCEqiEvLsKdURSuAUQSwI1EuDkRCO2Vy67uL4In/2+H+Nn/qe/ryUwqZuzGSyrWwfY7VozYiUunJblDpUiUpof9Le2BDbGapTl7d9YjDlLYIFpVnujRPLa0yFVQISozcZCa5TevCiXzn47usmZSQpj6cAvrpBGoL1Tlmn6W9kjpnLfFbnYnKmOepNhIvn8K6DSE0HY9HPMz99eKkf5r+7Ta7NXndL8oNkBSNe+ZghLvsr1zNJSgSCoUo3ZOVk6YtCCOfla8epgP/G9r36+9C0awO/KOVed+kbV3XzvDMYmYIUI0Rjih345pu8x2wPW2yOGfqDPjZPycIfkCEIKIAo16gw5i8UYw2B7+sQlDo5puuTBw33qiDuwHlZsbx0xThN4Ybvd8vSzz/P48SkXF5fsxx0GpyVDRRcHtO4papOVEHHBpYAmhTy/63vEwDTuufRnxKglQzQNImzKei/lR82ItoGWJ0+fLHTycrpuANyvfDUu/nDNXUz3bddYLEBa+k07oUvEHG8YOoPpO6aTcySVsz08OeUf/tCPEr3nq979Lt7y3LOcTzMiOw5XK1Zdn+yICT9P7C/OtEv4rVsc377Lzlr2F2fM00Twj9WgRDMKjYnYLoMIESsd6/WQjPuZw61ls+7pe6HrdN5C6iNnjDYJzaCk94HL3cxPv/SYVy5ndqsN3Z3bzMNAFLNwfhWsUW4yYiTsJ8T7Mib5cBHcXLm+stPYNQ5kmcdWxolcLyNu9FFrL6g4aYTblRrjvP2vnVPeW2mmTJFrTQgp1PvW9ZOrSuJClouoU77Zbjk/Pyc3lMkcf0kBYMKy6zeAaczOGCPi9bkyCNN+d7mms7wLiG8qF9Jzt0DXTeDNYo9E3duLzPrUyI0Yc6FTkqdSs9ljJHaGYVixOjjEDWvmMKXGGpHJA2JV5gddO3iK/BYRjp69ByLsTh4zniWqo6i6U8+p459V/JMqGpqJWoDlbZBRkt1ZG+Muj+xrtLZSsQ1MXcelwVCrz5o1vYR7dXcE7zF9x7DZsNpuE/+zK9c0xuC8r2dKKhlO166ysrm2pEYvzT4ILtBE3REyL7mOrfeBYRh4JMJunPgl1mo37phLYwNiYgrG58w73V7Bedw803WGMI+M+0v8PHPn1gHOebpuIIjF+UAQLd2NnhLYiwlQUmAm9QuQ680rF+s+/bcET/L/SX5ZAr9y5/ZCTylq+2ipdL5QsxeSY64bLfu4scgA0pj5oKBKnmct7460wGFuZlmDRO2S0H2Vm1HVv1WZ1x5t4ER9pLzOrgeX6gzHxbntd0puYTHbql0tXL9/+S0/B1QbjEw9JcWOsdkuT/bgVb1cep4k+SKkDN9iTmXrLwdn029GKEVDCemWzqqfKuWG18btX8WxDL5V+8CIVfwg5jXZZsNGxEQFc0Rtt+AjM5SS8owfpIvrGo8RTMAYC2ISPVweGaljlg2kqICUwWJSc8kcr5EUJMjBG5PmzYhVOgBT7x+ynE9UGDkgksG47Ivkd8yyNL9vtvVtegat5tIznXNa2WUtkjI8c3AxRsF5IRrFGUzMQSYFGaMPrIeO3ojyy4ooDyxZ9ludkyDE2BdO2XmtHK+5wpHgCHOfsjC9Nq2dL/Bhxk3nMJ4yXx4yzaM2y/KeIEZlWQj4lNE5WMGse1ad4fgwMoWAi9qcUXl3DfvZMc4zu2lWOq0sV0QgyQrbmVSBGUrPBZ1Lo1UA1pChwJh0as5oN9Lw+qZ5cH7FPKs93vUJTE3iSBCc9yX5MMtFTQzU3hObzVptzZKdbwrgajtNCnHeFV2kDQBrsChTaEZCCVLGIPS9XWTLdl2fqgti9U2T2xl7vbcLufeSJn5pgpfuly5lxWZahEjAGtt40SpYcmMwk/ViCNoYMkYwQt/15Vme1I8EvozA2NbNvGZzkIX9VXcmD4nU30R/dwiPzx9zenbCNF6w2hzTSeRou+Hu8W066YlhWvDNZmg0d2NMv6SHyc923bRafIVWWMfyjGn9FMV8s3u3PPKiyunQVw0ERBWScmpo1O/J/XHrEY1lfPZ56DTlWpzHimE9bNmstxystxwdHrPqNxp1mWdCEKzt2W5WbDdbbh0fc/fuU2zXm+IMTNPIbn/Bbrdjt9txfn7OxeWlZvdKZLXqNfrUGU0oTt0WrcoE5YhJjZskjZXPkRyxxHWHOz5gnByDn5iPbyG7HeeTY/zCKzCN2CS8c7XYAuZKzu7/m2jl/5+OF77xAzd+/vS/5ue46dh94RFivkf3UyfY1LDLHq5Tw66U+3FDliU8eW/o37JxGJdATVZKUdpflWpBWDadufZ7c04SZFr+E2v0Pxmv1TRt/6tn5zXMDX9tvlVlgFAMuqvfaj+6ycCs795o4yvXaAGI9sxqFLMAHZcZU+mfheGvZ0vpipxlaLxRapbSzdZhiPKECW6d5dbovXK99F1jDP0wlLLs9n3rO9+8vtprVUfp6j1YDNwbaQUp32gB6JvvvPh7hHjrDmwPsV2Peds7Md2g2WMIvenpbOIZC5lzK2e0xGxvJMPbFn4mRB343nZKYxC9limFmcn5BK6C77Q5lAtq3oXk+E3jTD8MCIfEMOH2ezSwqNmYLpXEea+lQ36adE5yiZyBcb9HBMZpx/7yEvPZl5B5TkFWPUqTsMW4L3fYTaPdTlEd5uUZLQBzzakvINRSeNSlKst1UXzYxuHNP2VgfehUf4rR5puXI9EHxmnisy+/QgyB7XaLNZYX7j2NTHPJ2jZmwHZWS/imkb16Smw3GzhUI/vi5CFunDQz2hpcBGtDcaRyt+TOKNDZWYPgWK8MxkbEpIaLUTNjMgdZTNx0j08v+MSLL/PSqWM3DMTtFjnYEsRc08m5JJISsArL9d5O5RO2zY16vgrEa8fNAES+3c37/Ea52YLA7TqikadS91YF2pr1Iu1ZiXIKQYzQ911zXqMnrgCGLRCqTlHOpFqu3avHTaBjeZIbbPMngRM3BcOI7ecZLGvvQHHEm0/o1j3Ddk2/XSUAQEtYJfG85RJYROhSN/CaxWmw2w3r27fVuQpe905sAqWNnLv27M3PN+u7m949va88aYnqH1tLvSaTpDZCyfmtCRXNnDa/FyA+1lLbfr2mX6/phiGB1rkhk6Q9Wq9BGxy4oqvaY2GRZAe1lXtBMwqJldev7wcuuo4RdWpnP+OsS6WiAR8VnPXB4aPD0IEYnJvY7S5wiYLGzxPzNLHdDEQiXd/ReQ283nIeZ2AUHTuTOHol6n4hZ5xGbfrYzmUo+yAmOduswQJ61YC8rqhaDqv+mHnCHrj6WV7XjfBK94ypRNYVsDiWZkTZ5zMiRAlaYp45hFkGU8q6y2qlnZ8nyKr2EKECk8u/FL2l6+T/pu7NemxLsvu+34rY0xky8+Yda+pmq8lms0WRTUq2ZEoQLGiAIEOGwSfBH8EvNgx/Cb/40R/C8IMhGKYFQYBEybIMGbQMyZI4FMmq7qrqqrpzDmfYe0eEH1ZM+2TeasI24NZp9K3Mk3uIYcVa/zWXmqDkNSw5Wqdo7ZT+74ugD6cXyxLLng508XypS36V72zEuTlpTcAjGcOXNUynVDRitGkI1paM2JN3vcvxdDqnd31/XzbBffcmQ5GeN81wWAZUpAvrscX7fKyEGy8yFQ2ni7QefjHw1k0tlUWEqpldon+tNyppXUOomn8TSyMlBgXaYyCVSYlZaJ5Yg7nco2MsjgbNUEjj8SwiwAGCRGc7ET+FMpbIh0Ksu6rNA9VhoHxe65Ja0TJ5WjfW4UJg1Sj+aU0SsuWciUiMwI8ypvG0jTAnnheCltjrGjWKh8DstVmajnliPF5zezUqtvVe99VYxVcC1mi5AMHQGMG0hl4MDmJd3BDryxoOk+UwNQxti0fLz8zexwxmdVSZEAomzvWGY8RobuGeAuCiIzHqDj6UBuoikh3zNpcg0PJlqeZyCpQQsZhgciM4l/Y4WJrWQtvmBmwgBd6FALHJthgDNuC9IWV0pD0QSfVeY8T2rAI85D3WsjY1/vaxzmviEEY0ayDpOi46+xPPbcSWwKwQshFbxFSBZWDT+YqUmiLLg1cHUts0sXFXKkVz/+dnxBh7AiIp9WMLAKwkjFSpTekkxk1IvGcOgbc3b3l7/Zr97oqz7Qf0rWW73nCxfcCq23Iz7TASYo0mgWDi4mdTTmF8kupIkpkF+d8Comshnecjp0B+aS6VdE080CYkb4LBNjZ7tZPQMyegu1qWyFDNojSFxJpvyyVXT0zw6l3obc/jB0+4OHvAdnvO+eacV69ecRz3TKOWc7h4cMHjR484Pztju15jbaOh17Eu7O1+x6tXL7i9veFwOOCdNvvomjaCImWUbRvoGqG1RC+8piYRPGGeCVMEO/GwGlu8M8EaJizhB7+C+4EwAM1+z/Xf+x9xz79WHcdqvb0cxSG1siNKP5IJiwCMKUZ5mpBxLIt68kmpWUZMrNMb8r4pIytjrfRsCtA92TROhGum9dNPRTEVYF6A+UChWVHo52syCWFBF//OfQS6Vo0L3ghza3EmwNDRnK3pz9awbvEmxBTGJBwjOkmPqc9j1pROwFElmIoyVXhBSrFKDDgDnfyedEcRWmXv0nuqJnxBleX07MBpJF89xkLLUr2zeN1CeU+K8Dx59/KXMuYQSoQt1X/v+3wTiKy49TvvfdeTJdNxPb7leLLyoV9STsJSwX3X+PK7Tp6XU7CC0HQdZ2fnjNNLCgM6eU4Z2vK7CgT/NMW9jOWbnltxiYq3feOjg2hjx+/9APm5n6frBlZ9j2A11Sp5hZOzL5F9jnJI+6QZGok+F9EWIkgweC+Aw4dSVmR2s9Z3nUZWmzPGaeZw2PPqxdcYEZ48ew9w7G9vePH5j7DGMPQDq82GN29ex/QrVVCP0xFrWlo0PoEAX339RWwANnO8ucL+k99W+VEtpJYzOZW/37whBVKc0No9t90hh4o3n/wlX7s0ZC1Hc+/9Al40osS2luZshSGwc69xxxHmBBKF3/2DP+TNmysu/8O/SBDBHscMIM+2K8b9XlPNxiPT64m2fY9utaXtV8zjxOHqFaVDLrgmOkabQNc0MU1S0/8a28X6bwHtyOurdYvAdHZ4F7jdHfmjT3/C3/sH/4znEwyPLjDnW3zbA9FwUk17nqaIO0Js/LDkRUYKitK9Ubmerqij2xJPK8aTwkvqY3afgXKJ44qMpbqnvjYZx1IEj7EW7Ymqz/HBL/n0Yl41HyuXZHwZz6NmShVMk3nXHQZSb0WMoKrmvohc+ylMKhnyTtfi9JpknFoaiJYRyadriggR/lXPlMzXPdBuBtrtgHRW01oJuYSHFxObyKpxru9agodpmhQ/ijD7QLfdYhqLaYWrz79CprxMJbuOE+weNX9fy1TgFE5nfG0SftCxp3XQc16tN0lWJd3h5J2xpsU3BX9ExSHyccmRORhhdXFBv9kgxsZ1yYAgRugkfBLPSFaMo5IacU/mWfGfen+SGp8+LindEQ9bMXR9jxtWuK4neM9hPjK0A72o8XWc9/jgYgbETN8MSLCM4543r19yc/0QgtawFWb2+wPt0OJRA65tLN+9GRlNy860iPiTArd59AULpm+jQbixjabyhlAp/XcNbiISGxlrNG+KKM317qNToLy1YBLiWmr0X6h2PBm7PA41ItXGr1xe18SND5LLTYTgY0RzjPSMOLZEIN5PP4U+K5JOxtVaNsWx198V3ffUQAepdFOu7Jp45YmBNI+hHk9+AaTeIbJ431JPqp+ZnmtMiYhe4MOMNTO6yRMsRyaWFURL5ISuJbQt3pZnliEK3F3WxXxO+dyfLDr5voeGHGkXkkyL15u833HPY32TU/tAjs4PIdJfnj5EeZJKK2b+l4OgVHNJzq7gAw6PsU106IdYrrFE8/tq7/K+5HmSbTe1zhRCMcCp7cOWgORkMEvzEkACwQWGrtdOoZjM61VGTnqm3UxADfBzgCkIPhp4bQCLlrIL0Qg4B/DO4BtLaCx4pyn00RGdxi1GilPQmkWJsxAs0BUsEvmOi8ZA72bGecTPnnn2zLOLQQZalqHttEmunj2fI4hbG9eniWfCw9g1TD4wxfcfppHb45GrnWcaR8Y5LHQ6a5vYIwUInmketURB8NqIUtRgmMTb7Cs9mhDx9LJZfKqf6r2W0WnbhqZpAMF7xzTNSk9xH9u+y6UElIIFN+t4lW0ovWrErUZtFzwRYm1ejbIt50gIY+wbYVKNXLMIHvG+Cu4DMDp2G+saR6NR5treeWiEJpZENLFxsbI/zUBBSsa6jY4Ea7XcW7LZNbahtd2dtTv9/IwYY6OhM69SQPAZcGaRnxSXgtPS1+WX+BHg5uB49eaGVy9f8f57gdV6y2aG8+2GJ0+ecfP5K0KY9WJjcJLYcaie5zNggSTDImhJVvOUZiWlXmzyBAGZCJVB5WqYeZynqpuxWktVPaUzyZoSiEp43PDETFOh9HruuaQhyetVNSkCLaTvPEYaumbF5flDzrcXXJxdMvRrrq9vOR5HjDFcXj7gg2fPuHz0KM5NCyEfx1sO+z273Y6rm1tev3nDcTzQNJaubWiGlike0uBmWjzna0NrAxLrEM7eaxplADN5uBoJkwKqIAbpelwQxvnAhCMMsWCzeJi1g2BnYfs3/hbh49/H/Mv/gxfTxC5bHdNeJiEkmcaSRD1i+G/4Ph7h7Lf+Oy7/2/+a2QU1UqTbvVLlt3791/jwB7/Ehx98xC/90p/m7eGGr69e8unzz5nDgY+evs+mX9FgCd5xnCaO08hhOrKbjxzmEesCxgem6cDaGM76FW3T4kTou57O9oSgjFAM2BBoCDR42jDBYa9j82r8cG3P9V64PQRuj56uX9E3Ha9XA5+er/Kef/X8ms+/fMu/q5+hb/iv/rO/iogw/vCHXP/n/0X+2+FPavF61yffH6IwKGA1Jr9XNZhFmXogewQzQEvWW4pOkD+h/J6AbwKbiZfkC8vAToZZPN/5r3emriCpPu9JkAmW3Foh5dRVBgFjCkfS91R85URBWRg1MvitzaEpcuKbZ3UfD7x75bv291Q2RF5Zjf0uEDbLe0/eYyL2m8aJV69eLd98j5J2xypx8uzFPpy+tv74EjlT0rHuPjHc8115RPG2hADTX//bbC8fsVmtWdkugm8XU8V0HWwq1i8CMfo1ThUjgjVtNrwWpU+pSYzBmrakYIPWlRTLPM34eWK/2zECjW1pbYd3yrdevrhSRSAEvv2d7zFOR/WyO61LPk4zzs0qq7wy4SYE5mni6u0bbm+uyFFewQEuR1ylz4zKHTm1nnzTJylTSFYtl2HucJceTyj6hCYCJ0onJXJ2qYSd4piY/dJYjZryHmcFe3nGYITjm2umqx0h1r4SgS9fPOe//7v/E3/nN/82IsJ+v+ftfs8z71m1DYhnnjUC9tVXXzCsN6xWGx4+/YArYzjsrnHTCHimWaMwZgdBAh/83Ae8fPk1h/2BaXT0XVMxIavddoWcUjo5x34/8lt//7f5l7//CT+ZHObxJf7inND3Oa3XnZh2QiAbJcZpYvaahpleFaB4x5NivlDgqehYqsaA1dpWhlpBDYKSwhzecUgXRkhJ5TuU+RhraM422uCiiWmSMYKDiAenceTw5gY/TyTP6CmvBlIlkDzhJjoUnJu5urrKtAHk+o8Lp0EWECkO5u688zOEOzzy3dFd38yt0+d0uU/T804j4ny1D0ZslK0eL9CsO9qzc8yw0UYpbqokTOmknOrY3dweYraWPtuEOZ9p0w+cPX0f2/RcffkVbn8gxE7luXNnStMOArlBiNzl/VH5fpfBKym2aUG8L/sc1cq4uBX8EAi47BhLhpTclzLe6fMip8CUGARiDJvLh5w/eQ8zDEzeM4Py+spAlZuYxU+qjSjREEvF9xJSDoI2LEzGVlsihwDaps1Kcy5v0zWEvsX3LWEcGWen0bFhIogaYAXFVUPTYbE4P3PY7zm+vGK/e49nzz6kbXoOuyP/+l/9n8zznmme2I8jx3lf9Y4IagzP/UXuodOKDG3M7MjRqmKiHfAUL5zoVsT061QSiYIT64/EPVYDjV6VHSKhkgmhdqgQI+9koePqA4tRUQ3DS8U+PS/X4Dw1/KX3ETLtlL+l+LjyzlPnTt38tWRelVkv+XeITXuSep3SxZeY7HStE2bUrLaALrGUYJ4QqnnoHXlc7+BdZe6+rqoRv1+ug4DWOu8apDPQGhjnfJ6hHueJjD+Z309zcL1rrIuPKCa3tqW1vZ5zoKR+eqq2b+BzZwuIxmny3LV8T7JRpH4yLhl7E4+M3eEDepacT+nZ5DqsuEJjJhqi0t4oBwtZhplQbA9pL70PBJO/BZ9KQsTGcE10+OfyBon3Sn5Gt2qwYmLpBOVbrdFSAoga3Z2z+KBFr6yHJkCwGnTXoA1Z5xy448F5jk6xyNE5bPAYmWMfG42C9EEbZmlsQqBre21OKqlMC7HmrK6GtWq4bayJRsQVgjah0ghXcHNgmidm59jtJ3b7Q66F2zaN7m8Qkq8p9TvrO0Mf90WMYOwWOMc5YbefuB0dt8cj1/sDN/sDo9l+8d4AACAASURBVNNIV4nN2NtWSwLM84RzU6S5hOsNVjxujvW0YxTvPI+kvhmmaRj6tqrzeswBFOpE8DRNKlelEcjT/qCZc4lHWa37m/WbAIej9gHQKGsfS1mocdd5p9iKxIsFYxsgZEdEUMG/gO3aVDEatKNh+3CclH6tFtYwsXSDOiQCXkrzMWMMbdPo+kh04EQ+F4LK6b7rFnqxsQY3zuz8TnWvWMP6vs/PhDFWATT5MGodw1h4GYlRk/W1JVVH6T1JrbII1oCn4Wp/5CfPX/ADZvphxfnc8+T8jD/19H0+++xj5jDjxcd6KZYmGVSjZ1pTcQpYWkRWVIIgeW3qjbCJqVV5H6meT4rksAEcYcGUS7RcubZE6Opzm1iWwHsfwWgVlZnWKhVlzytTPhZDIw1Dv2K92rAdtjTScHtzw+5mh4jh2bOnrFc9q75jPbRIcOptmWYOhwM3t9dcX18zjiPTrEbt1TDEphDaBVLrpQXaxnA2tAxd4PZa69NJEJrW4I8OO8J6Es66S6beaK0WMXgxYIVp3HEc99zuDrjzFfN8xMlIQDgeDhhr8N/+CHd5zuAC/C//iN1uxxEBG2OtQ6rlZbOHMX1cVIlcCLm7YnAue/EIhu/+pd/g53/wK3z07e/y7L33+fLVS37y6se8vn3FbrrBdA1fvf6cFB1jjNG9VUrCSyA0QtO1tNLQy4bOAMbijOCN4Wg8kxwBZey9BB70wtYGViZgx5nQC5gWJy1vjyOfvx3xwwO2Zw/4YPWY9WqNFcsn045P9i/zHB+cr1itup96HoMPfPzJ8/ttTP8/flyNpEQ06u//409jG95//JSvXj7PNV4SrSwjs5ZgLCz4D8UwcGKYPDVgJoNsBpJRCSrPOwHUyVAkqa5S4SULh1ESSOm98cmZXUawfwoyk9JAGnWlgN4XBXbvJxmkJaVNFn6ZgJIkplqB8dOo4vpxd7/T321lULlvfHfA/mI+5XnZsRZU+JdafVWEbiUDasXkzirI6Y8nsD0uQ92lO42nRKBJdf9SaVFZKemGeEFecjVkbM6Yfvjvszm/ZLPasup6WmkIwRBkVo9/8NrIIMqNJCuMtTldzMRacmngKeIFUokcSyNaGN82A227Ztics7nY4P3Mfr/jxVcvub29IjSSPcNtO2BMo1kVxwNffvUVfd/Qda0C0M5yPLpcV1wdnQLBM48j11dv8E5ljnz9FeZ3/netlWgjAKqWO6TFfQe9Lta22gtdDyEVszxlh3cUroqeQz7fxQCyfFfNy/Q/up6Ke6bYuCUQ8UHsZpxmNIeArHt60Qjuw8s3yOyiy1XT5v7RP/3n/Pqv/jJPHj5g9p6ro3bX7aylNY1GonUWN0/sbq/x3nH+6Andas3+9prd9RW4GZ8an4zC9fUtq2GFFeGwvyEEpymfEcDaSEQ+dm8/jjNfXR/4/HbmeWgIDy7oLi8Zm2Z5NpMSk2eYUp0dKSrD+xBLMsUmVd7HKImyb4uIoLS0ItlZUL/hNLrc2KXB8E5kUzyaxWyoX7XrgXY10G7XNNuz3EgonWOJPM8CbYDu4gI/TbhpYj4e8bsD7niMHatD7HpMtJkENUQY4nnPk6Jwn3DH2LGY2MmcUtBAMiZGwcTC6JT4py9RMSUKsPBQI0WOQXFWFl5W1s/UPLW6Js8xCMEl+ZaaIwrbh5c067WmNqZMk+rZuS5cfpfH+8pIlI9NlBMiDOcXGGM53NxwuL5mvrnF+ojUgs5JDeBx7uHuYi7MOMqaIh+tZExZUJJhM12ftvFUjta/pcyE8sZ0TZ4tJgSsabBdR7tec/HeB0g3xHNb0W79lIq/BcKikVV5d3Ta3pFn2Xx5MlZP/argPdIYaC2htTALPqgBdg4TcziybnsaidkagDUNx3lH0zdsLlecXVxymEacB7GGp8/e51//y3/BOB/x2r81llBJTTUj10xKJQV7aSm0e/ZxgRFKpOu7ohhRSw+Czdg+GVgXH4labCi4jpCwj5KwSe8RTUl2OTxcZa8PqTt4PLcBkJKRtxxXfG2KfLs7HH3OPZgyPyMSZWFhgUQASZdVY0jdMyBenARW/NgUEXmyLikSsuBloTREJX8XAjkCvfCgJGMLD6kdPUtnif6c26IJ9zrl0vtI+yMWsQ1iW51njIhM2Dg5IIS72LjGmWUe3xChvHh/+W/tLGuMoe8sthGmeI0xBj8rP3FejXPGGOaY7y0x2i9FB9ZzT82+jDEawZj4VaKDZANJDbdO1ixB1DynIDSNTauc8XFNt6nma+Fk4U5JAkKITijRSEWT7lUdIulK6SE2NQ/T4UTnSvxNIlZo1NDqQmBygck5NcaKrmsjEtPM4/57r7g4neyghtkkY2YiOYhE+4tjHGdgjnqXGuxSD2VBfUQZY0hMW4/p/N7FplzBMMdMsGmemV1p5jfPc75X8ahiXGsM4qONxyhv8G5GuY5l3TesVz0PwzqWLtCSVvPkGZ3jdh45OodLkfYRC/iYLa375GlbE3m7I6C9B3RoRuvANgZpdQ+ntq+weorOT5gpZD0l8YQQ1OBpTXReR169XkssC1BK72TKCZr5rBkyBduZ2IxUiLqVSVkHCTI4JGa/S4zk7trEv4nnRhIbUCdIwkWxr4uWZCgDyraB+Mw54eF4eoPTzIvkeP8mm8rPhDGWpBBSgG6q3Z8vAN3ICCBEknlB/xCqOo76kxryrg57vnz9gsNxR7PeMrSW8/WK9x8+oTMWNyshpromCeCKkAlSIAukJESXzFUSstH7a/AislTsTSpgLVEw8u4dinSwMMZS6qqIpxLwUVhnlEeeB4u7yzOGfs1mtWW73jJ0PU30hjS2YbM94/LBBX3fYg0QHNNhz+5wYHc4cLvbc7O7ZX84kEBz27SRoftc1LjvB6wNtA30faCxDttYAh0GQ2MFOR7g6JHJ0q86TNtlxx9BAZyfoXHCIB1TNzAHLVgNQphjF8TtBr9egQP/89/jeLuD4xG++CwfbCiFlu/1oHpNf9CIK0G8YNuey29/i5//5V/lO9/5Ho8ePqVtWl69fsHbN6/Yj1cEjjhpuOFIIOCCw1qrNbQiHQSDNpaix0mDEDiEgHVG81BjN9nMqIBOAtMMNxZWEmhmh8wgpsVLw861tNtLhv4pq/6Ss+FCy0IEw5Ox53uRvELwhE4jFoJz3Fy/4nC4ZZqOkT5MpnHvPPv9bVZECFpE2+cuyKryv/7jzwipw3UItF1PSlPxPpmh8wCiQPW5SLiui8k0qnS5gPcL8NStBwh/DYD26g2bP/p9nKjASOdF0sItNrVIw3x2kyErxLtFAWg/j/jYgSZ52X6qh7v++4mCX/9832PuKPyL7wVyzdtwz30hA2xO+VH8uhRJTy8pv4aT97/r800RB+++qXppfZvUXJ53LMo9kWL5UylEhBzpkMD2u8Ze/3yfkXZxzQIEJpr5hue+4+ULWhQKv6eQ5PKue/hRuvi+Z+tAyIsZfGm2YC3y5Bl9t6IxDYLFBYO0Z4ROo/bDfMS4HQQXxxLrLSYAEjSDwvkE1MvcE7g2xhOcDsAHQ6BBxiPtuKbpBobNwOWTnm5YMR0PBD8zjgfaoB5272YInnkaCWEiBIcPXZFxol7stjG0TWyK4GeO44GUlmyOR8zz5wQxtEOHdC3TYg2LYrNY27B0bNRrXuvWS/KVxb3198v8lHv2cfnyyBNDfpZGIVsaYxgPKSNGIv9d0msIARqLXfVRMZuZ3t7EbuR631cvXvCHn3zKOB754OkT9tOEd5512yKdGi+c9zElUQ3bbdvS9AOr2HxovL1V/uq1e/F+d2S96bBNS9v1zNMYMUgcl9cYKzc7rq5v+b2PP+FHVyNf3h4YhwF7tiV02hk3RECXlvEuK1gq1tnpEnczG0Wz0SVvxnIv43c11lpCy3S/3KGVu1Hw9Q8Gux7otlva9YpmPUA/5H3NhFRx8KRIG99hncOOA2FY4ccRP424acLHUk3B+ay8+KTLRF5THITL+WYnH6HCf0teJPWXiyVeljE42YE7n+QETI9anoeyrvfdd8dYmTC3iXZnVOE0fUt/dkZoY5O3yjiZ5nTfqQuZaZe/puhSD5imodlu6RuLdA2TNYTjmK82QZgPex2XWaZqI3d5yWJMCtozNn83AIh/vEe+xEkovS/oOZDlPkmnMDT9QL/dMjx4QLvZ4u3SUJj3NtTPWc5luSffLOvvH24WROVLI0hrMX0DB43giuYNjWAVo/WsaaPYMtjgtP60t+oQxxDEYEzD9uycELQEhZOAi869RG73YZWsPZ3S+8l16dq7s7yLFbKxsNJC7y5IRQ/pvvp1WaAWDFyFIOlYkiMsfXsH6xU8+ydBZ/eNNK+ZLDML5PSmgBrx9KZ7n3lHViYSvw87yukpSk9Y8qDF+p3g3FP8fN/+h7B0KNz7CcuyWFYEL4KL/30X9j3FDu824J++bklT9+LQOK4QyKUsbMZnyh9zOeQoF5qmifukKek2RgEmSq0DwTKNhah3ScnRkIyBo0O+ArK1QZTAQmeVyE+sWRpaU6mDZMBOEaQl8rXcm+07ssTINf3n7xPdRxpzPhRGn54nJjYG99oQnDSuYqiv7TQSkoPRRymP1mpOskGIBrdYh9ZX8h6HjbUBDYFGIGA06MFoAzbvAiT7gggx9pCmsdlA7nIZMU+yqYRa2Ql1KSbNWJCmZGFoeJmJOqzuvm2E3rTQa2DTMFqujiPHWTPKQJ/pZjRwLASCj/sfaUMbOcYzFWpeVdNfyPSUjJlpLXWfo9MsLpkLPsqB5FDTgJAkh5LDl0R2EiOrq+aY6pQpzmkfgmZJVBHKQkBCDLKMFN12oey19xrBG+lbHf/kKOckQ5KKlYy3Sjtpnck0TqQvrWtcaPxdn58NYyyCiHpWEhzOSRNRsUjnKwt8SeAZUkmDetERmAlcHXb85OXXXN2+5tFwSWsb1v2K9x49ZdX1HNwNjqp7ZtpeT17QpSE21YE6CZs/FRKJ8cFiBzS0uRKvESDUXiO9pTBpI8nTGRlnLB4dWXLuaJoMsum+bKiV+sCUcWw2Z5xvztmsN7TS0FphPQxsNhsuLx9jW8vsJuZpZBoPHG9veXt9zc1uz/V+z3GaNHS7bVSJM4ZxnJjdjA+BtrGs1yusBWscxowYC6v1WoGXsQQ/4W7HHH4+6wSjd8ZhxOCOR6bjDudnhs2aYBu8xKZJjaHpNF3BeMAbZgPuh3+OwzhhX70ivHzBOHs4HJFJI30gqLJz8gku4I+OYBziGwwNq+EB3/uN3+D73/8zPH70jKZp+er5l7x+8ZzjcUfwE9bMHGXEm4agOQVqwAzkgx9iF8TRjjp3pwXDk2cPwE+x0UIUMsbAl0GNsh2BlkArHVbWWLOhay751off42L9mN6uwSVDKDxuz7g822rdl5Tu62bc8chnN1/z8uULrq9fEWaP0GiqSADvHL8Y0imM5STcUaOZTUPb9HRtx+/+zu/gbncadew9Z2fnGlnsXKxFE7vBhpCLyTs3Mx9G5sOREKBZr8B5HYOcerl9rGejNDxcnkH4LwHon3/Fxb/454zW43GZUUu5udrUSvlIwCMy8+DVcSBWUxUaY3jbmMIPTsDen8SbrVFARYHLOkq6L11bfVffG6gFT9Ih7oK8Ak4KXH03s4/cUvIDM29azkuqsZ8M/OT99dzLmrzr/enGu8/4qRe+42+h2tdsvD75nILl+/5+57tFPSOWkUGn19+zRDWQrh+UFZ10j35R35ll2umnRJNVRsAE5JSgohgIYBtM19M3rTpmMMxe8NJiu0dM7ZbZB9x4Q7v/Cc18g8VlQORiyq/3Go04zT6njKfIPUkdUkUjMMZ5RMwe5AZz9Zo3b2/Ynl+yPX/Ag4fPuDi74OWLL7l++5rjboezRw7HA+qdbrBWGI9H3DzTzS5mfBiaRhDb0PcdXdeyv72JBuK5nBGSAmAZNmtk6Nmdrt/Jqt5RwiWlNlX7ZQqoWm72fZEu6bpAfbTjUatoIfGKuxSeDHVN0+j8U323qGwjcofnSGsw1rI2hutxguMEs+7VNM/829/7mJubWy4fPMCIYYoyyVrLqm0Yx0nnKtFRFmB7ds6w2WKs5dU44ecxp4Ef9keVua1gu4HxOOYaagB+9uz2O26PIz/64iv+53/4v/LFZHHbDeZsi9mucEapPNP6vcczKWRSzkx13lMlilovvPuEer3vrHZtJ62/vXdA2dheG1Dahu7BOd35ObbvwFg8pSRCOuKh+i6o1qCGxq6jWa0x5wHxHj+NTPsdx6sr5v2In9QBGoI2esw8N5QIjsVcZUmvd2n0Hbyc07Nwsl5SOpeH6tnp+aeRaadOjvra2uCXHL1lZIKYgplN19Kfn9FstkyS1jAsIk/uDLyad5pBZtHxH1UAAzQN7XZLt17hhoHj9XXOeOiwvPp8j8FnRWq5joUfp2+yk1eIRrd6rtxP5wscIJWqUS6+l3dlGQCmbWnPzhgeXLJ5+BBnrWYGLB6ddIH75W5ydJQVK/fUA09K6H2kFMJSVmoNSjBdgx06Dq896xxtnJRnjeIS2uiACzR2xexHDruJw/7IxeUZtukhCP2wYlgNHOc90zwyTeqQSzy2ps+a1hIPOTXSleapZU3zfoeTta/nFp1ViY/okix5R9qmROtZxkQZca9cSS8JqCG70gVqXCGnjC8OYmmErs5A/L6u31muiw6HWL7KUOm21eiS/ElNrRZrk+afGhOSMOsSJxb8ItRLkNJ89eJyTz3WulZ9meHpc5c/57ln6CuVcbuenK6rVkPQ1P/UWDpllJUmX8tPEc8/DfzW9/zJrg1oGYHjODEeJoazlepoPtBYW5x0LoCBrm2hcmST+Fcm8RStrDc6PxU4KlqiQI1dJcDFRodHOmPaXCqed6+6up9n0sarA93k+rRunvXaqpbx5DwGrcep16WMZKVrH0sFaGBGcruabPxKxj6pNCMnAYkZuiIS0+xTyQWJ51tyafuZwBxzqDSyURszWanOnfcaoBD7GHmvmb56JgWNUlcdMuFjFx3UrRF6q7Vs29y3IBDGKeq6cdwxtFnQdP02RgWnhrreqS1knlOWkOqwOcAsrlmxOqmhN4SAmyacD9EG4Omahq7psF1D1xhMgGuOjBFfeAIumpQ8gnNamiCbLyWmI8TZeOcJsxCCq86dGsUFg7FNxk15F00lL0HX1kdebGLEvEhsBAZIVeNcTG5E2sSyazkCm0peZfyeCDW+N+i6aSNH3XMf99m76OxINIbgiLXpIxsyxpR1PsHkHp9tdbnut5RSVCALrHT6+ZkwxoYQmL1b6KWlO1u6SP9zf+238l0NYrx4dtOeFzcv+Or5Zzx48AzntRvrBx/9HO8/+zl2Xxw47I8EM9O1nT7fa2Sj1C+XWsCYjLB005YfvS7k7qLZwxQfYigCMUQAkTwcp0+ykchyAk76PTJWjDCFCRNqYizgQFBluTBnHd9gG86HNZfbB1w+uOTy8pyht9lD4MMRdwzsD3utC3t7y4vXb2I9EO1ybY1ltV5jRMPjr25vlDnFQ2lty35/i3cOCY6uDTx9tGXoLN7PzG7SdJ/LDVN35O3NkePuBdwCbsYQNNpWDL71eAO35sD+7R7ckSZoDb0LJzRRgAJMIqz6hovGctM+4+V/9J/w5Zsb5J/9U+wffqxFoQkw3a3fEfYH5q9e6k7bDd36IZfPnvLnfvgbfOfnvsvV7Vt+9OWn/N7H/4Y31y/wxhEawfctx+6A4DBeiz3jwblJ00yzHPAE45nFaIHoDIJV6OTi63EfnYMDcKQc6BbDw+GC984+4hc/+mVasyJ4g58TqLYx9aCk8AkqZIyxyLDio299j836jJdff8EXP/5EBUJCUQJiLATBTTPH4wHvZkQ6NpsHPH7yAb/8qz/kB7/y5/nix3/My+dfRhBdwFESTsp00ylSD9jNH33Bm3/1h0zjzAd/88/z6vc/5eX/9Ye56PU8zdq8J9U1NoZm6Ogen1dnGyajtGqIfKLo7AUhLTZXD4ZGW6ACTwxEDyOi0ctz8IXv3KtBxdN5xxApZbKxCVJIaOkEqL9DLyZxmAXuS7fJ8tf8c+KNJl1U31AEZAHHdffy+HdTvyxen5TfBc+9Gz2VPipolgqBXldthaT7CnDOgEK/eNfCnCxGuuV0kerv7gLzPFaRtGDx7rvjvu+t94Lo+rtEA1krjHz49L57vq/06whGYupxos/7PtFIUeqTC+77fwbzS7/C+bAFGqbQgTlD1u+xG77DVVhxxOC6md48YbP/hMG9ZQg7xuubaixCCMIUjaNJPRNrwDsS9+xsF8srOoSRMMHV7oqrV59hmo6z7UPOzh9iDWzXG3Y3E7vbt3G8gevDDYfDnr7roTOM48zbt9faVbbraLseYywBy2F07I8TpukIwWX+GQDbd7TbFfNQSrEIajDGFnfkXWWNxfUK+CuHTLXvs3PlXCQl9uT+lJ5Z05M/3b4EHinGqmmeOY4j194XGkqTM+TrMqCLvCwYgU3P+sNn7F+8Zry6JYwTfawp+OMvvuTv/tbf5+/85n+MbRtmA7t5orGG3lqIzWC8R7NfAL/acH5xQd93vPr6Sw63t7hp5nC7x80uNqXy0ZEYHYpGHXn/7B/8A373i1caETsb5OE5w8MHmPXAZONZiml8xJJGdx1dZT215liL1gWmyMeKjyz2rz7/6Z/MXoqiL0gsT3WyNxUP1WvKX0IImKbFrga6B+dsHj5UpQUhmRPE1KPwsa9K/FsyikRBGwAngmlapGnp1ytWjx7B6AjTzDyO3Lx+w+H6hlA1wkhlkBasJ9GVlQpX6MdqG+RMN6dGmryu9c8SgyAWlqMTOVY9p17bO2fs5L/vuj8EdchL22GHFf3lQ1xjYxRMSmPNs43nKD17WdJLlcvqE+llOU+DaRvaRwPDo8uY9mpoJnj78hVh0mauSdGu1/z0Xe/k0aGI12+Sbukc6PPKmIuM133waGSTGEPTdZw/ecY21oidRWI5p2SlIe97LiPwU2VsNfR6uwM58ONe/JLPWaXLiPJwNwz849sb/srmDD+rk0Hr6wE4EI3kSgYQMdBIQ9t02oQs7p1pWx49fUa/Gbi5veHNl18TmlMNbDnEFLV2rwNt8WuFQ/IzSrS8ysOCi/ziTJyI/ciaysmJ+7gAxFF2RQxUSgNEoyeAmGj7KEFKp4E1pRDqu/fVyJJuVbRE42/Fa2Vxj56P8tQTXJfmVNNTAeBlIU4M4CUurQa5Ff5LX+fBnOjG99DvfRGxeR4nIy/G5mrMca9cDP7CWMQ0NG2LNxMSkqE/FJlwB+e+ewz/Tz8BmGbHfL1nnr/m/Q+f0MXMEkyTnT7BeYJ4RjfGsh2K3UAbbjmv9TqtNYhNRs3Y+d2Y3DDbxujMRINafoDY4E4dss7NWns2NlgSZFGn38WGYGlNurZVHGaskoNEk6ELGpXpZjX4CrFZlsWaJp6NUg/YRV0wlSRJurIxybYRy2tE46SNdJNkWV0WLMQ9nN2Mn+fobNbxN9GQa4wGeuHIRtFUH1RZiuoQTdvkRlEihsNhIng1Wk9dy4xgponeGjprGaxG6qayHMZoozA1RMa8kBDnaDQrIDiJdotEbCGWVyiyqTjWY9AflrbpaEUD144x2GF/uFXatQ3bvmXTxkDIGPVurcWFwH4a+eL1C16/vWV/nBidx9Ng2obkeNQmZBNUDf2Gvsu6i3MuZk/HMjFRUVfsHKO8jab/Z/ODNYRMLwlTVba4AI1VI34x4Eum4XTYm0ZtX0ZSzWLtlyHG0DSmlD0U8hpOofB1GzPHUsmO5DRQA3+pkZ1Pu0BsYRl/VXrwPjXY/eaz/jNhjEVi7T8KI2tIYIdcR6cwOZtXoMYKJjJIBUYWJDARuJ6O/OGP/pjvfPg9THtBZxvOViu+9+1f5NXbl9zcXkPQhhUhpc1JJTOLvNLfQ9kEE8GRRCEjVT2fbNbITYaL4uGzJyAKwAVuKkLeo57K1M1VjOWDpx/w9rUqs2KFwD4KC21J64PXKMcE+INhaPsYoq3A/Pvf/dN8+OwDjYptWmBiPOxyVzwfArc32pjrcDgyzTNZBY1Mehj6WKTZxbomwmoYOI4H5nlidnpgUvrAPAY+//qKRw/WrLqG1mg9FOkMwVrY9EzOI95hXKvlAlzAHB3WQe9gEGEjFttsFQqIxwVHGGMNttnhG4s3wtQKxw4uu4YHfcOrv/Qb3L73HuG3/zHecr9QV+rCORAz8Kf+7J/l1//mX+Xb3/42P/rqx3z64lOeX33FbrjG957JzXgcwQQwDTZ6/iefujiGzGSQgEVyyknCG8Vuo4jAitC3A0O/5tXrF4SmHHwJwmBWXG6e8uzyI9bthnkKsQtgWE6EoFE0QKozpYXLA6YfMKbDe4ObdYCSRhR89Lpaur5jWF8wDGuePH2fBw8fcXZxAUF48fVLDoeRruujAEh15dQYa8VgmyY3sRinCe9mLr/7bR5860Ma0xEGy/BrW57+0i/Q9a0KxhBr8RxHPv6tf4LpLbLusA82izOoBqgQhywZwAmlkVHW1+9pPCLEOjyJqUclOuA07aMS4otQrPhfMSaCxxBTUOLza4xp47qK3EduSZW71xCRGXjKbZNlUlzy+OfmIiS3VOFWprGRNxSgWBtzFmNYDopUjiLDlyQYSbTCIoUy31wruwvlJPKjvEjx/aYk5wVJoPeuQl8bkJMDq/6ECBbrqKwcCVLJi1wLC6rO50o4i6aL3H0HoA4AMbGWYzSOVZfV70/rnBscVHJBa4TW87OL8Up6f4zULQaLSC9Ba8ylnwVwf/GvYB8/pet7rGmY6fHd+8zr9zmsP2K76vhWLxxHx0/ewIGHzKuBvXvNMD3HHn5CNx+wOIx4TZ0SE4FGitypDS+GgEMzRXRNtKttACZkduyunzMfbmjaVtNQjTB0fWxYMGNMQMRxONxyHA8Y29A0+k5rVSFv+4H9fsf+eOA4j7T93nWlzwAAIABJREFUiuDVaYOxmK5h9egCWXeEtjKym0jZXmulLSNoIHM9kWJoqXNJU1Mfigyvnb+6BmTcUCIA4vfpGu7SUfrLafTP0ogVowJEqJW9HJUYXxIAs+pYP76kHXpuvn6JO6ZK6MJumvgffuvv89f+8m/w9NFDxHtkGpltQ28tjW1wbiZIwB92zPPENB45u7zk/PEzuuGa6xfPtazBONE2DV3b4sPEPHlwgd3tDf/bP/5tfueTr/l6CtyYFi43dE8eEvoWZ4vCn42gQdO4MFWzoziv1FguNC1t2+ba+lZMdHIlp3hcH13OqgtzXuJqr6q1DXrmMj2HeDLzg8r5dSEQvKNZDfRn57SbDXazwSUDH4UvJnNJcoIlbKj4LXUGLkYYvSo6O0IsZ2QEOlV81quO1fhIjbPTzOF2B4cjmk/ocpMWEuJLc4yRiRqhEfKc6+jVvESJtycvYC2rKtFpzP1yzESF/j4HpY/OBVPXsqyVrMoA6b0QPLTbNf35GdIPsUyK7rNeaYpIj2ue6v1mg6yYEsCQ97ba3zgHTwyaSNMOQPCYIGyePmb/+hXTfodkOZtWOqVXJsykusAyD72SV+m3fHbL35IyiYD4VJJENDrJeayNZzwal71p2F5csD4/Z3NxQbM9wzfReBFTN0OILXsj3/beL5rKkNal3qc8InWqpPnmPatwqtRf5D97tCZ5+c5HHtvYlrbtCGjH75vjnsN8xDRd7Myu7XSmaWI3voXGs9quaNdnBGnwQSPFDuOI7Xoeb97nfJ758Yu37MKI1jMEYq3gutlkKFu0xMiEcu4SHw4smpItJ1jJ31xmq5yVgrXJeCKEsu45mjXT4wk/qv7JkbQsr4tt0bS5TNYhTvbpno9PBqRKdqTnS1Zwa7pM01I+myMlgW98U5xjTqm+8+c4j1CXG6kOVf0J1bBIfCyOMiR5XO9pkY9pLAFieGu8qvYS1HgmvT7pDQZsY/DWZD1D31UZ5ys5c4pTv9kgW/Gik7W8G7Vcnjk7z+y0iakRbeboZi3jkbJJjRGOx2NcK8OwGmhMgzEaYHKcJhqxsfO7oe+6HIUZvIeMv1NgEDRNSzGfJ9pf4hGLNvMzYpCu06CjOM2QbDsxclC7ygtYsG2iBfJmJ6OmFeXrEvEnLkQDcMTX5bBlXG3EZF0unaVcRkxCLCkQ5bUR2mhYLGePHNGrc/MLmstBO9E4H4JHjI2RlioH+02vafTxtU4MJrTMqQaq8/SG0qQxqMHPx6xWEQ1aCj4UA7IY2rZVw22OEiXbfEJAm7dF3uSjQ27yU6wPbOm6Dt80OepXU/0dPkZvGnFRL9Fo4FXXcbl+n+kDuB1n3u5GXrzdM4bS2Dyte0BLQMxuzvWChYBtW1bbrToLKv3H2jKPFBVbZFxgGkc1xsba9rZJUdaOaRqZDxqJreU4LMNqBdF25ZwaiIPzsT6y1Shp26htIXhtfD7NEJt1a23ooAbvoLTfti2zCzETT8evBuBiBDbRFOm9NroLBNpkKI6OLOe0NKc6FOpuFsvPz4QxVs9UAdN3a/AlYfMNEidUILyCC57AYXZ89eI5u/0N23ZL3/UMHj548h7n63Ma0zIzEXumJ0iLVJ1Ey3tOAMgJ4E/eZ/25HPz0O9SdXytPfzX2/FOac5pfULC12+20szIK3tN6pXLWvTH0/YrVsGW92vJge8Gzh0/46uycG1T5ef/JMzbDoN0B/YhzI8fjQSMSZ884zxwOI9OkqfQuejk04tXm+ibea7e8tm2ZpommsYyTRGaQvLshCkZhdxzpdjPzbGiNp22023AQCCbgjUe80fR0N9HsHetmoI3MmUabewXnY+ftGee0Fp4PMdIx0YCAJbAxBvqe7vFjbhBudjuujkc4O3sHMYGRlm//+q/yvX/v1/lT3/8+GOHr6694c3zJ3tzgG0fkg7rHklqvKMNRBlfSWxLsSERT6CqauyqaN6ahtT1D02ONZdbiDVEhaDhfXXCxumTbn2nIVeWVTNSjCSrKJhUbSq71ZESY3cTxsOf2+jqCnnjGggq87faC1dk5/bCmHwZWw4bzB5eYpmGaRj775I+5uX6Dn6fc/CFFRwlk44Y1TU5xtEkZbzrM1tLajnEeQcD0jUZbTbqKJgRkaHn2w19EVg3H8cj+eDjRDCJQDRFOpWUkVMtZISYKBMqnWIoxJkWn5wjyZHALIaY3xH3L10qSiJmHJcCYXlsbYU5Tp+5jZeWSSuBmyLh8ThaElTJbz7uOIspOnlpZFql0x1BSUbN6IhVfLtEJwafUvgJsF5G2ie7jWOqx5/VPQKkMpqyXnD6zGnK1Lou9jS8w9b7U90l9b3l2im7K4LF6z1JxK9cmj21KbbrzrpOx3vf3nKlwx6Cc5n4PvZz8nucd0OY23/1F7OOntOsNrW0JCHMYmO1DfPsIawfeX3semANOHGcX8JNbw9W0YhKDMwOtX+P3X9LM11h3IMwFRKUxKZ3FXc1ywSzoKQ1VCDh35OAm7NRgbUPf9wpkjMEEwXmlpRBiORXn6LoW7xV4adpbC3icn5jmCUGwpoHPPoHPPsN2Pf12g7OBOydrQfInf4uKaDnP6UgXhZm4xKcG+iTP03zrbJe8z9XLTxXrOpowG8cWxuIlzzq9t9BX+dkMLa2sWc8zx5dXMZpSFYBXb6/413/wMfvDR3zr/fcUZFqHb1uGRssMhaBpkWGatMxM09D1Pe2wYvPgkv3tVeZzc6xp+pNPf8zV7pZXN1f8mx8956vRc+gHWK9pz7dI3xJM4gn1ISvn1MjJea/2xLQNdjXoerhZ08cWR0uKZp5XjMx7qm/KXmRGWfYqVLxncW1sINcOK4YHFzSbDabvwWoGijEnO72YYqGr5XNrnr2kNS2cahNswmAxLeADjXPY9QqOR/xxxI0j0/FImCbN8AixNNCJLFoi0UJHdwwHC2NFXMNqbU9p85SX1p/F78nw/E2GCkHTNXtNu2+3W8RaxBMzwsqFIY4183ST6skm+V1kl0SBU4w5cd+TPIuKdTH26hYMDy4IwSFGmG539S1ZeZfMBkPUP4oQXl5b5iz5W/3JR+OKiMW2lnEcY+MmohHEYhqLbVqk62nWGzZnFwzrDe1qBW0b51HS5us9ql986hS6T66EO2M93STurZOe0jqhQNIgujembZBW1U0XNIhhdBND6wky42UkOA1UsNKABWN6LU8g2uxPo9O0wY2JqcOpo3UKgEmTX+htiT2ccIHsEIF8f21cvWMYO5W/p/yGhBvid0lny2NQHFnTg1TjjULmzopndlbR10J2kAyqstiSd5yyhaxJ66O0vDzbZZi+NCy9B5PlyNycmcXJQUk/hiUYrL4vdCn3Ed3JRwpfCjVKq9fkdG/TPizfleRHyBtAnmcQNeQgogb1E3aGFEPf6bLcxWrvmIncv+V35hufk3pAmIrflb95bNNUvFBy53iDwQSjgSc2NWwVmkYd5OkM+dTwKP49lxuIBksfgkYrnexzKi+wxDvph6IvpTIDBfurXaCOXk6NTIHcGIlAaSoW35tkgL4r8nBR/p/eUe+FQZAmvbPAj2xgjdeaqP/pGUv4hMIbTAkcDD7J/jgDUwJgXNDSYdrMVZ2MLnhtwpZkSTrHQUsyGoHGkDNoErwnVDg884Mk54xqKyLR8VvObUAQp3uaLBRFd/KIhJwFapK81J1GgMZqKQkTsb04z4Rncj4aKmNJPtQgOU4TAcPkXDayS9vk3nyBELPoqoCGsNS9fAiMTVsFJsRIZasZMs45XCznmGoON12r86wyh7TBb8QBqbwByZDucc1cBBWixti0RiYav6OB2Tg1yOaMShHN6kq6oNXssOCTLDc5UMnYiu7v45/x8zNhjF3wogiwauOKSTUqEiXdCzYqECRkw4JHmLznxauXXN28Zb19TD80jHPg2cNHPNheMHRrrsNBGXYWTPqse2A88S131jUZR06/Sxw3Xb9oblQJn5L2lJhVjJwK5HSxEBxv3r5FiKHTwTDYFtto05PGNGy6FQ/PH/HgwUMuLx7y3uNnfPv9D/mH5w/4PL7nYrvBTzPH6YDzWk90Gkecc0yzY3cYCajh09gG4wPH41FrwzZWvQaxPkvbdQx9z+FwIKQaLMRIiGqaIMxOuD04psnTGsfFdqCxsVaP8Vrc2mjagx8nZD/Rbda0Vr1pwQq+aZllxk2O0Xv2bmImRtc2FiHgjcGhKRqNtZwZS287tt3Ai7MH7F6/Rs4f3EONgrENw8Mn/NJf/gv8wq/9Kk+ePuP6eMWr/XP2ckPonXZCnNXjJURDRZDY9RrNmw+CifVlBN3DZcpiofkcOSPpgBuCF8TauKbqtRnMmsdnT7lYX9A3PbNL6QHJeAZJ0AnlvJiIXgStjbq/OXJ7fcXN1dvY0SLeZwxd2/Pw8gmPPviQzfkFq/WGvhnAGt68fc2Lly/55I8/xroj1lJqu+QjGjut20bHlLuxqncq1+fJpYzUIzjNk65fAkYBHv+Z7yKrljdfv+Dm408Wx3EBu0P0IlbINUU73ImgZPkMyYulZ9VGpp/SX3Ln8yr6OKfhpP07AUb3Ka3176ejuRfkFvKouEW5btFBOyqUywDgyHcSeEUKCF8I3vjkNEZfDLP139I6JR0/G4nDyfilfmrhon5hLb47I6n+Vb6/9FjfuaYyeiUTXPGYV+csvuO+emla1y6AV7BhTIy6kzLKDCTj/2zqun6i/ORPlUqRxlTGWwz+sjAwLD/voocSEWlKDUWAtmP+wa8wdD2tbTBi8UGYzZbRXmDsGRet8K1+YuN2mNbzpG1oQuDzfcO123IM5/jmAUEszeE5zfiG4G6RMJMgp6RuA/HjCXinnvwEfGyU10l59E7TUudZz3/AsepWiEEVhLS2Iupg8x7vhNnP8V6PYMG6GA0yRfnXYD79EfLZj2nWPe1qwM/HpXaTQDRy5yzWEWrlu/RPpbTqLz9dOY/flevuww/v/nxjNHbFUwo9VTw+XdNoFMBKHjAfRtztgTDNBKfg+vc+/iPm2bHarDjfbEgGMhGDbVWWhRBy3eCbqyu25+f0fc/m/IJxPIBXoO2nCQ98/Huf8NmLr3m+u+Xz3cjteoU5P6M722I2A96UdPH6PBS+ch+tl7lKY2k2a8I8448aaUpUWJbGwJ++2veuca5RmBho+l5iN2CVw8PZOauLS0LXEKzJkYtSBFl5T5RfJjkpIv+8gxGFWE895P1M5Yoi9CM1sUPA0tFu1sistd/Hw5Gw2zHvD8jkEOcQF+VoMk5E7JVY77u4Tq3AnvyhNNGo1u5eZ9lP+S6fj6RsRrmZFWljaM62tGdn2NVa1642GlHmkuhWp5fyxxQ/FV6bGHFY4C1i87+ktFawIa9Xd6ZlkcQa/OwIx2O1PvG5iz0vvy/FcMgXCEUOKN6K+Aft6m2aRvcwzlkjdHraoccOK9rNGf35A/phhbUtQci4R+V8bdaosiiMieCzKN13DK8VbRok1+nL86v5X6gwZnVPnl82JsQ9aCyma2EOsbu5Y5zHmFU2a61lFzChoW1WSGOw0iPSIhIbTjqPn2bVhZzyqITbAiFOr8JeaT9JtLZ0sCbjU57/gncv16c2HrzL0FZjj5D+H2rCKjSSMFPCuqeYNC5x/j3jnoTzkmEm47n63gJeypnNSHlhhL6Dje+Rc8t5nuDFxTmOSKzGn5SISqonZCd4beQVWVxZZNupbE3vrCn9ZA6crH9ag1C//+TvhLxOhGjIbDTiU4cp5SF5fVk8/77PXXq5azt41z2nW+GjA9Qag3Mxy63qFWOMpWkTNoyRqjFb0YilNZ3KNTSKUmJZAD3rIZarq+eTIuxN3sl0FjKvSKniUeaFiKEKVr+bPQYhKcOKGTGaLaOrg6XUZA6xm7fEMMTMZwtAjzI4GiwpjX3zqZOkU6Q0+ZpOozMHieUdkuGz+nt0+njno3GVRGBFfgPiQy75p3wuqGwKMXLZB1zwzLE+bTYMCrQSaI2hD0IjGhSlmCTkAD5lZybrO4VHhDxuYgSu8kM1QKrBM5YjyDxxeZZFJGf2hkCsFxsQ4zEhMJiAWTV4AvvZcZg9kwu0NtJHCIyNAdOxGyemaMD0qAwFiUF3FU8LqUZ14QEeKAb1ghmbts20N09Opb1IzmQwiXbjXLybyywDpIa/yXaXMpTTXqbWbolebaM1mZukk1R9M6jGlMua5QhzFyOwWchQNRy/++D/TBhjifRDxSwX3MoaZJFis2T6tQKVNnj2mt4jQaM0v379is8//4zN5hFP15es+o7Ly3Pef+8jPn/zkquvdvmZIknIVcw3vsxGL23GU/nV94DYPL9KeARNBZB8ANKMssmgzLGWND4CJAx4g8GyagbO1mseXVzw3pP3eHihxtdnj5/ynQ+/xTD0seZLIMwjqy550APX128Y93ttmuU94zTr0xutR+M89KueMI6xTp5jGPoc1j/PM+M4IjH6cejXNE3P1dUrDJr+sO5XeO+Z5klrrRBr4ErDcXa82R3YHx1PLres+gZr2ljrNGBWA8Y2EG54s3sTuxEK3hq6y0fI0DJ3lt0kTGbFKFrnxMVGUdaanDYUsMik3o3eeZ6tzjC2ZehLbcH0MbZldfGIH/6nv8mv/YX/gCfvvY8znk+//JQr94ZjcyTYQCc9XbtShSwWhJ69B6NMIgGC1PWPmOpiskGvgJjgfRWhKEzB8fZwzev9NSHWkbHS0NsVT7cf8t33f4FBNrjZM/tjFKZNUaYCJM+WejcTSFeSNUb40Y+01ut03OXzZ62h7wYuLx/z/s99h4uHj+mGXqNVgvD2zWt+9Md/wB/9we8i7pAL3Jus7KknUUTUQ8uSmTKHXOcFI0zjyDgetNmXm0tB8qSSBs98HFWQHB3taXXmkKKPU0RIBVYrAKdHKIrbSqFLBhYRZZLJqCwQU+eXymk23JUnVKCjfJJgKwaUwCl/WEa43XnAXRSmM6xeHJcgXV5mfKIJFtySeWQ15j+J8qxPjWC7VhAkfrt4RMWH45v1WgVeZYsFsBFrL99XK/73rsOJ0nRqhUkKTlHEqfjt6fpIHiMm8fnKoRSjAop8iZHboqq/c37ZtESEti2F5WvlZll7V6r/x3tNKetyd84ny5F/X9JnaxtEGnxomGTFfvUB3q45bwK/8MBzPr/mYjAENyHXr/leZ3l/+5CvxoYf3wjPd2fszr5Pu36PbnyJv/6Udv81hlmj1dOo45n3QU/f7FymM9so8HIuxAivBFY9IcwwHRVwa9Gr6KDRulnqfg+MqVajpGZiDuk0ot8FhxtHjkAzHugF+u2aOTYgOVm5KNPv0npyUoSTPdAn+MUaJyXwp0W8vNOgGhIN6q91/bL/N5+UEl/kSWTIq46zD5+ye/mG8e0t/mav+o8P/NGnP+b5q1f85t/6GwzrNY0YXIDdcWLVdRH/xDQzCfjjkcl5fGNYrdYcDzum6chxmji4wL99+YofvX7LWz8zrQfO3n+M3W5h6JgDBOYK95ssg9SimhZ52UwzRX24CAjbsw3TYY+bRi1dpA+hOpp6H2k/A3dIgXpfKgNW/D19m35NPLVd9fSbDevHj5mjETbMPjYXi+n5UWGFEghQdwdOw8m7JSovXeQ1KZojBJ/YD4k/dG2bORKRjm1jEbuiHXrM+RZmr81JD0eON9ccr6+1Dl2I525BMzqYNM7aoJ2UvEL7C3FTtvEeI87p71KtQ/p7UmhIClHWrPWl0jScPXmCDOuY5RSi4T3y6WQtreVnrEWINAu5VhtelrMAYhkzXVILSDaAp0s9ge7BJc1qje1WXH3xGW4cNfq4bmqT1itAXQ5CFqRVFIbsNBYTG+7ouozeMU6efrOm7QeafqBfb9huL3Sf2xYnDQFLarYUQkwRjgYBL0lPURnpvEtaQ44aKu2AVd5lmvcBszBOVXAMnVuqgZ9tEfWeU85Pfc48AS/QrXq41qaNk3PsxgMXfsLYHsGzn67o5ZzenCFYgjNMxyP90KsDaB7Z3d7w4YcfAcKbt1ea2hs0QsvFDuVArH2ozcFKzXWNvM3jXcjmu3w9nYtsfDoxvNYppyY2gsk0VP5QE0EmDDUsFayr0expwZef2uydeJtI6lS+vLI2Xp6aeCXKOjVE3Peeu5/0imJECPn8pnXQs17NrRpX3a3+Gz+R6SwNZAVn5m+r9UnVS2oMrsYZUxroVN+n+aTVKW8p88wrbQzSWELbllJU1WDFELFsecfdwI8Q53Q6jhMQVz/5FKPEdREhNlPVni19gNZYGtPqc2L2kBWrDack2ToNPjZgEtEvg/ExVTuoDikV7+PumgGLUk05GIHTM1HOSV5PEa1hDsUJIGoYLtGSMa60jqyODaCSXcSI4cjIUp+oFkkEH2vKmziW/5u9N+u1Lcvyu36zWc3uTnP7iMyIyD6ptAsn5TJYsmWJFyxL+IUPwAMv8E34CHwHHhDiASQekLCQkFw2BgmriqrKyqjMjOb2p9ndWms2PIw555p733MzVQKhlKgVunHO2c1qZjPGf3T/obVG2VmR+ezc5Uw+n8/Byc8K8zIvkrzuIO2lMg7zPg/Mpk22JvPntFbFCel9SNyk0DeWVdew1IZFoVxIWa0RpPm7yPrc0IvKhhSqtjmDOpQ1qaTauHIkloSbNC9BSSB/TsQRmRqcKwkVBmiUwhhoFUwGWmNoGqEjjAF2o4fguZsGjvsRB4mmQK4zETBJfkl9Q9IcMfOhJzllagd+xFqLUmbGVLkpmkpYK6Q50fMaInc1iOIklcABmOz41/O8KkzBfCFGXPJvaa2xqfpE1pETZ2sUbBJzhaTWROUFWxjSs6WvadkHH9L6zcfvhzOWmo+OE0CURgaoMqXS6/WikWGfBQbJmRqVKOt9GPny61/y7Okznj9+SqMvWC5XfPH5j3h3OPLLb3+J8yPKZoFdG/Pz9gxkoULl1Kg34+mtz78V5CnUAqoC5uXeU9p5OZ9CKYMJCqKiaxZsVhd895Pv8P3vfs6T60c8urrkyfUlF8sVXdvSWIuxhugCw/GO3fHAOOwYjkeGH3wBXBBC4M3bt+y3W7J333QL2n6FD+KIbZdLoh9xTja3bVpaKw2+xBE74JynaVqOhwNucvT9AoWh63q0UvT9gru7OzQaT+B4HOgXixLB0cZytx1wk2ez7rjcdDTGyMY3BjpFvN4wtIOQRyiFbxS3jLjJM/mI85EpKkY34LwnhMhqtUIH4ZazRrhS7LLBZqETPO36gsVi+cE6bNslV48+46c//TnPX3wHZRTb+xsUEx6HwbLuLvjR05/ybPWYCIxu4jgcsU2DcxMheMk09g4X8/qMOD/h/IiPnhA8LjgBzDmC5BOgjkGiZ9GxG++Y4ohRHZvmmh+8+BmXy2eYoIU8e3SJHiI5NZKyn8FTNl5kvYbgub95z+uvfs1xd4cxc4ByuV5z9egZ3/38R1w+fkrXtQJskKZav/izf8ubl1/BtKexmehchF9pvqnEEa61mkvV0p3oxF2T+WAPhy3Oy3jFKCU24rCLZd+FGGF0LK42bD7/edmLIUYcYDOcivmnNEkDEjVDdm6lc2YuoYzJ9Tw2VPJDwQdc0aQ9e54hcgJ5i7Pv3FR5+Ihpvsp1EloscDedr4Zw+dBaE70XQv50LyWTryAINX+xQiCRU2PxxDlcGenyWna0x+KYVKk090z01U92+nu6dG4yFmPOJlalmUAZ/+p+6uhoPcfymirrPUnW0viR6vsnmTJnd5dlsEnZVJ5A05gSTJmfrTIIkFLumc+pXiWSWZ27oOdrpJuRO/1dTrgPPK/1lWdHf3azhC9+SPzZv0tvW9ANEUtQPaN9ztA+48XFiu9uIi/iDdebJbo1hOjZdA3tdovZvWKpe75zfcFv1h1f3gXupw07vaJtH7E4foPev0KPN3R+T1C5XEeaCohRGKQ0y/uUSTI/u9YSYfYhSlAqThhtpFlGWqh9v2CcFG5SeCeZl33fFQqU3f2W4AS8WtvgJ+Gt6lYL+uMS1Vm8n04I/OsxzJk4p2M5r4hM6SK2wilgKk71NHd1EPX80FlmUa9LPlh4mlwMFj94+2MZuB86DlT5Lxvhah5SWHT0T68xfctBQ9geBTwS2O52/Lf/3X/Pf/LP/xmb1YroPCaCC55F09BaK7g2OQ2maWB/GHFuZHATf/mLv+Jf/Zv/nTvvebPdczAKv1qz/PQFXCyZVBKxSZDmezzBVPlmP9hrIntjtfd119BfbtBaMb6/S1nslKyIDx3bikIs+FuPWirUr8nsLS8uaS/W2FVPsGr2k8aTH2Uu8rlOHAjzHZH3b3aCKRAgH2LFl53necai2YgsYxnTPyQjSNmIsQ2272kuNvSDZDD7yeGGI9N2RxxHyfBMGZKhPLoit+nJBlHBtlldVgbf7zpCPF3T5WFO5ujsd6UwbcPq+XP69QYfJUBQ9M6Zbs6/5MYe5zo4NzBVkBIAdOKRj/PnK1Eh1HSz3I3EEjhUTcvi2TP6Rcf2zRuG+x0uNSVRxaF7qsfre8wGQ4wRr4VTsVutuLx+TN93yegUQ001DbZLiQjGEJQCDC7xiSuVaBvSvsl6U5yB4cSZCjHZTMnJr3QxDjM4K9DgbA7L+o0p8ytSOk3LXpOkkvr4MBAmh0/0AsZq/mQ88H1t+J7RjH7kOO5wbkJjUTTYpsNqm27R46eJIQZiFEqy1fqSpuuFEzBlpEtW0hzYEYO7yqzKjXBimq90GGNK09iPydyHAtPVC1DZraeURaeZw7V8y7As/540zwfqPu+/2kfFA07UfCsPBRtP7Niz53vo9RIAKZgpzlhY5SxJkT11di5FB9V3n9ffB27h8gmdbBad9yynusCamdM7Ao1tUvVMymKNufFZxrli98n2CGUMCyZUs3ySfRnSs6WmVkm+BhVwKCYFGENMGamlRDzhVjSFp7Om2smUfnmsT52285z9Nij44Xci97db/DQxLTtWiyU0JNqsCDE1uTL/mZP3AAAgAElEQVRCrRBjZEoqMCY5pZUiqDm47CL4OK+HkrAS5/0ckWZU5dngJOiQ11nGRz4ErDYlQ1anAOb84LE8U7ZVpPOALDQVZS/ZlAmrEiYTXvtEo6CNxDmq8VNaAsihrC0jDrA0dsUOTAlDsdqrJHxYsk/TBElQK2+7eY/K2lJCo5NsrGxqBe/LnsnPd8IUmisPE2VJ8LLLXAyMB8dWH2mNok3ct0Yrll2DQZp2Wa1ojBaO/Wz/nDhkZWBDVGl910kAWeIktlSlqmeacE7mVfq9iOPTqAbbtNBGTAo6heDpQ8C7xB+rgvDPOk9nDI9WLau+YVjD7jiyP44chondMHJzf0P0DuUcOniaPGPJpowoAinonWCOznOUdLlmpg3MMk6ctarscx0rOonoiMFhTFP8hlanRLUsO7zcR8jx8yhctY0RR7Oy8poLobgPQnBo25KpC7RCGg4h68ujGBNnftCK0X3YND4fvzfO2AJAmUu20wsCOk44JrLcP1UY9VnyxkmwgTEqvn7zkldvv+U7n3yX9dWKvmt48ugxL54+53p9yc69qpRULBsplwyVZayyvXMiCYB4hk9iEorM54viHFYRtArS5TbGqhkBUp6OdBTsbMeLJ0948ewFT66f8vT6CU+uLnh8ecGi6+nahrZvUMEz7O84OuHB2O+27PY7dvstd7tbbu+33P/7/xB4QQSGZFRpJfxkVhkCmsV6Q9P2OB+5v3sLxqJjxGolxm4U81EyuGSsQvRMLmImMZzzhhjHMY2XSgTSHV3bMQ5HIWH24rQ8DDIm0+RYLqDvpHRCackCQIkxH2Nk8IH7YeI4jkw+JkVicCUapLAuEv2E0ZrWRpS2tK3GKFPWk9FGxv7s2HzyjC/+4c/5zmdfYPuO3faWu7t3eHekxdC1Sx4vnvK8f8xissQQ6YNmpVs0ljEM+CBNqExjCQkoawWTGxncOPPgaMkknZzwJHofMY2AaudH9m7PX9/8FVsHC7vmevGYJ6vHNNgZDFgKIIWUJeBcMqRFYJedpQUkfPPVXzMethC9CJkYsbZlvbni6voJF48eCam28+QmzF/9+q+5ff+WaTjQ6IoGJGmqmObBVF0OXfDkuvm8ZpRWTJPjcNwzTiPS/CcRfqfSSrLOTPtNa8lQtNZWAIBklFA1bJmj6WX7ZUCh1KnxUMmP/LP4B5iNPFHSFSg63d0nBmctsmpcWgOuUyN9/kY8eT9bmvMFZB/F8rAF6GVenZg6mp9/nwrop/GpuXjqBoIP3WMel9kGEFAXKqNgdhbVI5FHJ54858mZi4NMnYzR6UgmoJidngkkZsA2N2pThTOp+uqp0VGplTOFUV7XKjeHkTGtjaZ6tj+OoWOV/XV2LfIS/NAIknutxj7G2RlVodbawauUIv74D+CT72KWa4xuIBqiWRDMFaF7xqbveN5HXnSBdasxnTRCEp+lxnQda20JPjL6W7xX9JtL3vmW96Pl/X7JvvsEo3qa9gI1viVM99joMDHO+yvpBVLDg+zU1Kmrr5QdpQYGpCyGkMdB5FTTCFCa1CSZ8rksKMaShVzmKEa0tTSLHrvoEnV2yqI9y7KU+xPXdcneqNZEHk/CzJ+V7Ar5NcRqvquAQG2ol7mdmeezA6ZeA3UupmzR8/v4mEvjbC0zf/fDjByKYaVbS7NZohTseU8cJ6nWiIHb3YH/5V/+b7RNy2rR8/f/7s+w3gtmUbDqOtCK0TtGN3G/v+df/6t/zW7yvL654Te3dxw1hL7FLJc06xVq1RO0OC1jWh8KXQyV4qdmdo5njHAiNFUWdWUj0ywW6BDhOOIOx6IrMt540CFbIcJqmM/GMJfyxVl0GkW/6OkuL9B9R7SWE/dKfatnjotzrVC0UjxTO2WNxdnhH4WG4bQJUkBHm2S9mel/EEeZ8kkm53nXClSPImJCQC8X2OUSxgk/jrhhYBwGwjSRyxpjnCtcRB+kuz73Gs0PfaLYBAfG8nt2npwOtqrOS1n/0QdU22CWS9qLCzC2WK9zDuY8IFJeO59kLilN1F7FaEuZjalEsrbd8z7L/crUyQpJIQ4dyZnnUYPdXLA2Df3mwLDbMdzfEcaRGDzSOLfS5Fm3pYCB1obGNLTrNc16Tbtc0a42NCnoEbP+sjK/KFXWW5ayUmUZUjKHrPms7z7oGpDnq8xDDojEEn2PZVnKh0vztnreU8payS5Ved2eYif5bC2fYhlzZSC2DWxW3L9+l5wukhEm2WxC12DQpbmMLEvZD9KbQs5nmgaMFcqSCFYbDJJ0Ya1kRksjobyzZ2x38lwfLM0HnJN5DcGZ4/FM5sQcBK9xjjobr5jKsMsLZZTm75y+UuO4Mh06y6kK59X/P9t0StdyVuSKPtlO8/jMzqmzO6mdgjIYhdPzI1CGvHN1WtcFwpxC0zJOGgVapWZ9aQ+ma2W+Re+CcPuny6rUGSPz5cociFGQ6WFIz3xyzXTemNZ+ps+qiMfknrXQ9CmtCh480TkFT8Z8QwXDhZCxT8JCWSZ+xOn/26tk5vemcWIfA26aGI4TjW0wKdhgbMNyuaJp29QQyicHd5qPODuwT2RqhYGybK5xSyTikkNvTkBT5ZzzbGcsCM6Ycq68BktFRPpGCUSX+cjrNzlGK1oCBRhtK0e2LusybzPnx8SHm/a+EvmbdQPFOa/ygxFyAyfqeYjz3lcq2Znzs+ZzK4CUOXnaiHeWrflydSXULCFTk8YgQXkffJlpoxNtjZI91BppvN0YRWs0i0ZjjZWGZkYnTnGD0flpdLpupi4AlCbGWQtmmqf83FmsKOEPEx2sAjqHahX0bYtSUvlqYpReFV4qg733BB2I3mMRR2enNctmwbBoOY6O7TCglOdw2HPcTgwHacgb6kAMCrSeHccKpLHcLNHzesrYSiUfQZEn2bGbnNTWSN6r7tqSAKUbA1N6XqVKI1SV8K8Gotc4bQhGo4NGRU3wTprpBS/O+kaS33TSrcYHMhlGiCKlpHLawzTxseP3wxmr5g2Vd1/djKuSFpUMqbRA5fAhfzpSBCcKXNS8ubvl1fs3vL99y8X1p7RNy9XFBc8eP+Xp9VMOr96QMzjyJM4E3TEtgJAd+BXHUgZGkol7Lm5U9Qi1QprBVroGAJrGdCz7FevFmqvNBT/5zhd87/Pv8ezRE643F7Ta02iQlHTPeBjZb+/Z3d1y2O/w48jN9obdYcfuuONuf8+7+y27/b6MkPO+GK0CojUugG1aVusNAcVu2KG9T5vbMw3JyaeE+DtG8fLLRhY+v+z4CcEzEBOPhjji2lYynQ4Hn6gLxDifgicMkXFyDE5xEVvapsFqRYiGmDhkvQ8cXWQ/RA6jZMaGCNZmZ444Pn2QFH6ro3ArJiCnU7lJVo4PdU3dPH3E53/vZzx++gQfPXeHO95v3zGqA422XHeXPFs+5qpdM77f4idHRNHYBjTYCZQXBbBY9FJCF4Xrx4wBExS2bVJ3WUMIMCmP14HYQNM1KA2jO3J7fM9XWBoa1s2aR4vHrJs1yusEiBTRaKyySelLhNZ7X8AoqaOfVhBDYBqOvPzmK9w0FAeXUYq2W7C5uOLi+hHL9QY/ylzHRDPxza//muPunhicZJEkB8kM1DL4SA4yL1yRxSiJEkX03jFNA+MoXMX19vZ1x9bKMBYnrpQhqGqTqyh5kDmDNe+66pSV8hXDKsbqs0noJJtlBoonwDzOSDj/WZ3/g6P6aAZgs91aAd/81zl4hpNIZgWDyznrn3OE+hQM1Ic8XwZKFbpBFFENved7Pj1HcXIikspHnxT+Q04QynOfvXgiDD+8yw+POUNLFWdXeuP022fjEqvneei1csmTxTI7pvOQPjQW1c19YIuIEXnKQ1d0WgUez5++OmmGxOS1XCyJWK0ZpYjXj4jf+wH64ppGW4xqiLrD20t8+5TYPeLZyvK081xZT9doooYweZwTHiRsQ9s0xHFA7/c8Vo6LruMiwtpaVLDcqDVeW4JdEG1Lc7TgdsQwYMKEjjOMIoJzFGc5GGL0ie6BAnJlTYb8dMQIxjQUZylC1F8bMFqp1ORAvm8ai+kaVGOKLDov/z+xO/L6SeMfk2ySbBiZK5PLmk7khUqG2DyXqHnX1DOZt1cdVDp1FNbrXM0PX72nzj95fpHq6wVXVEZRWTPIHJiuxRiDGyb8dkccJqITp/mf/eKXKKW42mz4zovnrIyhNZrOWq4WC54+ecy7dzfc3N/xfnvHn/yff8rOewZgMgq6jm6zptmsMMslrtGEs5ss+7fc58ce5uP7TOa7QS162tUSNw6lZLqWBXm/ztc628NncqwYZuWtiDIG2zb0FxeY5UL4YU+l5Ozc4fTn+SPMRu3pmiwGIvM9xhhPeMnztWLKmtWIwTEHkcWAFee6n8+mIKZsS3FOgu17onOYcUIPA+wkuzM4J0ZIwoMPzkKWversvXO5eOacPR+DvO/noUpjqjSmX2DXwhMblSbqmJhCajlYX1rPujuNURGras7gy2WGUlKoT86TS2bziyfnIOsNVXCCWaxp+xVh4+j2e/Ztx7TfEdwozsHcMToNjVZS6mwai20a+rZneXlFu96guo5o7Kx/E+6QZxJ8V/ZKlf0tmYC6fG+WEUmWRk4401UqHaU0kU1OQRWhcmzJyTTZmZVf1EVWc6bvdJHf9ZzM/ryETwAwqLZBrVfQGIS1JEoFBBFtFNYYDCaVswakckbmJDccijEF07ROFYqSqaWj8JRbLcH+vE5Vtcbkmc50eRYfeT9XWCNXvBS8Rb2m5fOZCqJkaTIPXXHkFF0yr+V575eJmse1Aq7nWA2q6tC8Ns4wSKxPoaCmJ8vfq59jnrsZY9TS5/y382Bi3WTlfG+VhrBREZQkARBy0KmMZBkvjdjPxSWj9byPUJKFmihhYtqbusxywhVR52IBlA6ZzKPyL6SxKwCPMjtFD+TB00qyYgsleDUy+X9lDc2HOIPmvfCQA3Z20p68dSIrH3LUZh7PyXmG44Q1pjRDbdqWpmkxiZpQEnzC/IwxY6SMu7LDuxbdM/rI2dBA4fbVKU07N03O2YkQq0QIhTOmjGb2GRQ/Z9oVmVJF5fE8U6K+1GvIa3kdZD5RCRAV8cw4jUJNUttPKpzMl3x2lgnijNXl9ZietR7/7L4s8FGnagukUlprUxJhcpZ3tY1BqZMEjex3cCGQXCBEhfRISJ+X1Th7iEwMWIVwylrNsZHs/1zO3/QNq82Kzhqs0kJrkPrNlECSbmaZnfZgDhhkuSQ4XF7zKTlKYZK4kaQ8Zebxyk3VQkrCkIEPGK3ls0qjlcEFy9hblqPQA23vDVvgEMGNhmkccU4cui44Ru8p8I6YslXzvnmgSif34EjzYvQsJ43W9K1FWSP9B4xkVfda4UJIs5ibOM8OYZ3WR6ZwUFFhIujgwTni5LFdR6Mt1iD13+NE5wI2+WdUVAwEnJsYpwnj/fmdl+P3wxkLyEDXnnoKDip8svLO/P+MPMuSjWXD5w9IhoYCNDeD5+t37/nNy2/54vM/oG0Ml+sNLx6/4Iff/SlfffMlynvqEpzTSFCuap6FdiaELh+pJWzIhoC8mYVESEJF+F/lTFJQbdG0PN684Cc/+hE/+Oxzfvz5F3z+yQt6pfDjkcP2lts3r3FuEMeWd+zHiddv3/L+3Ttubm54d3PL68N7Jj+IRx6YIuzHgXzj3vtZKUVxhLnBsdvtadqWFy+esj1s2KMY9lvG/R2TG4WftGlomiZFthMJfiQ5Xn0qPQ9YLNZavPdYq7m8vGS328niTt9TaQwlozNyuHHc7wa6pqVtWmxj8ZMsZOd9yjRtJFNSJa4VJSAylx1JynqTOvDZqsRizsBTWcGfHJHLi0u++OJ7LFYLvnn9NS/vv+XbwyvapccYy/XqmmfrpyztgqO7Y7fd4YOnaboC+qWMxtPqhrZfstvtuLu9Zb/fYbuOrl/Q9T2LrmU4jgnMzQ1U+mVHZMKPE4fDyKJZ8aR7yovVc2yYeU2ywNfJ4SpljjIe3k8ErwgmyLxoxTQO3L5/x+uXX6HiWEqNlTIs1pdcPXnB9dPn9IsFdMKvctjvePP6Jd9889eY6NGEQsMQgq+QfFbusxGjlErzIYLSucj+sGMYD/gwiaCvSpVrYy4jaq012lrp6lmRwMcY8N4lLidVZEHpQlkZBXG+xWqmqRy7saQLqHSOmEoL8p6v76kogyKjaglRyQEy8Dp3TJ5n8lMA1fz4p5H00qmZCkzkb8cM2FS5pjxWVisZbKuMm/OTVsD0bHw+4oSsgUxOPqibYJyfY36cD4HlfKL4wUtn8DaBnPm82QjKcp+z+60zo04d2KdjIxM4VzRkg6k+x0NjUtbAuYNBzeL/PGM4O2lrcvrzo6yk5Hw5sZblZWKEYCzjP/oPMVZ4YhvTolXPYK8Zlp/jFt+hMT0/eWp4FA/0TCjbMh7T3o2eEJ00LjMGYy39smfVebb7d3Sq4Um35LPNNX/6cuDrY8OtumZoNvTdE8Lxa9rhHXa4wfhhxmEo/DihlJYgGQEf56xtrVQi889rMI9tKDQmWhvcNOEy7QAiB7q+x8fAMA0EqzCdkeoCMqLN81iP7WkGnGQoqSIyVASrjJRlJb7e2U6TbFyldZJ3qZFYtf3Kyk+fjxmH5DdK2V0yarLjujIYTuRerMpeq3Ofr+WPHXlPhxiK7EEpdNuwfv6MoXnPeLfFbfdSApoCd4dxz//4L/4Fl8rQKk2nNWur+af//J/yP/+v/5I///JX3IwjToHTmqA1sTFcPHlCd3WBahtprlm0U2qCkHFTkm0PyYoHnyk7xmbgJ4ka1tJebtjvtoRB1p0pQ1e7DRSl4uLs/Pm1c19HBNCGdrFicXlBc7lmygZnKvOewWW9euUopdG1wZfPHJllRayy5+voYuKDk+Uxy44ixxWSfZGEr/CnRQwSAMkGcXbqFmgcFRGDsxrddrTrDd2jx8ThSDge8Ycjw/2Ww36b+nhmI1CMKTlzqB5jlpEyfzXsTUkLUMlYmceTuVfJoRICql/QXV2zePSIaGyiepv3R0HYsb5qmTEJqphZxwlmTzKm7BtNadZR1kFOv1VJNUZgbihYvo/CKEPXLzHWCOa/jlw+/ZTjuMOPA3EYCLuDYN80fk3T0C8W2MUC2/U0pkGbFoz0Nxj9XLKYs3mjCikTf15BeTxJ8nN2csWTz8zeAvmsMamcM4hDQjj5A5jE3UvGGIlLUUlOPypPpoybqcYjJrki2aqVsqMql6bCLTGijEKZBrVeovqWeHQix50jKjCtobEN2luiC/gwkcj4mMaJlVpKR26lyrKOUapzjNbg07MnDJSRfS1HT2jwzg5V/cwBmg8CB0Vnf2gzGFN9UnGyfuYzyzjHND9KUrsr/ZcBSL2vYpLl8SSLDYXsjyRT0qzXovL0wernK1j1w+dJdynO+irzNmcw5orOiMIzVyTNa+AUOxktfL0xZYl2fS96fUqBYAUqEb8qJQ71Ij/VrDOkGluBaYhw0oMkY1oQ+au1uFaCjoSgcTFkjcyMu+fnVioUOjtF1k/iFE7kkhIwADLMQIlTVFfTcT7cGUuUgPOJ7q5nKY/XmfmT333IkYuUtnvnGJirIDs/B2SkRFuVPa7I+i47wmugWmVtpimUANesH2PODk08jXkcT54k70GFBPhU0QTJDzN/VxOFgkXNmrRkqSoFURH8VO5VZ9sl44pEX5Er+xQpOOLkuvlFp8K8y2JkbmaWbIpUZaDNHLTLSQAgalRrKVNHKwF8Ou9L8IkGwPuI0UKrMTo/N1eueGozX74KETSMk2dKDavbxqZq6QjZKRhSolwUDB2UwqvINHkOAxwPB+53B8bJYVvD93/4OavO0lnJnu36jsZk+1ijEnd/iDndQ1H7BuueFvneHT4xqQqW3x/cjJ0RSjajTeIglvXXWCtVbik7WprHBjSRptP0j9aMqyX+6ROilz3y/u6W4/2Bw/bI7XbLVzevcWGSBK0IwWd5FSuDqhhtJ1uqhnuNEqe0VxFvhcpguehZ9i1923I4HvEh9fwh4nyoMIQ4SKMxqKah6XoarzEETIRWWzbrR6yur2itQvuRw6vXLMNIGyM2go2wd0Kr4kLk/3pgj+fj98YZe57CncFX3rwxDdLJoCMvFYhXnPOqcHxkkRTRjAG+ff2GX3Z/xc9/8vfQ655lt+L54yv+8Kc/59/8H3/C3r8hxAltI5kkIiti6d45ZxxATNk16WZjJkyGcvtUQFXJXRdhE9PiDy3rfsOLR8/5+c/+kP/gj/6YR5cX9Nag/cj+7iV3d3dMw5FhGHhz84avXn7Lq3fvePX+Hd/c3TG4kSkEKUFVYrgYHVIXw2RMlkUa8dOAcyPGNng8zk34OHF/M3DY3vP2zS2b62vWlxdoG7i5eQneM02OcZyw1mIbgzU2lfxLBqpzYkDnxk7jOEopPJrD4cA0jTTW4r1lmsY0vpIhoLUYDT5o9kNgPx6xJkfBAzo1Cru+fMQw7BiGA8NxAK0xyVmXhaC2Fq0S50sIyUmX19jDJTY/ZstP14ZPXrzgcNzym1d/yevtt9yF94x3A+tuw/b2nnfjW1jBzd09x8MRoxV912E0HAcpn1KmYQoBNQ7st/fc3bwnpE6L0XkpERyX7Pc7ALquo+9bVssFpjW8Pez51btfEQg86R/xYvWUJ8tH4KVURbI4xLFRFHYUpbxY9KAW9SZCKcX792/56te/JgYnUeakxG3T8ez5J1w9esJisRaj0sjCvb255Rd/8efEcS9ZdTnDIjsVqrXvQ6VMgWlyJXJWSo3ChE9O3IIzYgZk1d5Ws9KNPkiDIFN0PbmowQcvRsDZZOoUwBFmihlQKjVzS58eSakXYDcHT04A75lBmHnko6pl2AMA6sQwnV+fo68pyq9muXH6XTnzxw5VXf8c1RldhI84xorSrYBZ5Tyuj485UeqmFueO1kyDUEeDP55hWhsECfplj2P1vOJEy8+qkoz3lZGYrn9yqsoRm65T75Vz42GW6rOq+Zij+WMZwQ+BAsn6EF67nO0SY8r4eSA7P579VOWfKt+X/WFodI9VDZqGwJK4/JzQf4Ltr/jhFVy612wWlqbtmEhljhp0UKLLUjlUGAaO+x3TbsfVsycoY5kmh7r5JX98ecXN9ZpXo+UX7yJvwmOG5ZKm39INb9nsviEO78ENqCBgODtiQxSZ1/ULKWNKdDK6OFuykWRwzrO5uODy6pIv/+ovGcaj7Ns8jsbQ9j09nkMcsf/T/8B0POKJJdo9FzvVYzjni5b9lRxh43GiNys2bctK96AVu8NeqGNixBrNMEzCWZ70jBhiOSvAEHTExVRCqYR3NSQndHYCaJfVf0xCZs68jXHOKhH5ebbWgFNj7nQdwrz3apEqdnIy3iJSRXF9gepaVNcxvb/DIFhJMtDALJdEF9iNI6/2W/6r//q/4XY3MPiAbq1kiRhpmLZ4dI25uMQ3FqXlmXTGXmreXTmoUM/L7z5qB1DEovAKvFHQdywePWL/9g1+HAVvPHQGlTPXwgdNeOS9xO2VJLbpG7qrK+xqjeqXHBBDSGV3YKycBKoOlv2W7Pl0zZgmRZMyXcnrIM1acpRlB7LBYozF2lYCy0Zom1Aa5wNKRQmmZAeU0pn+fB7nKmgV8uKIYpwoFHbdo9YRReAqRnbv3nHc3TEe90zHgTg67LxzzmYnj3F5ykqcxll3Frlbbmnms48K1Rj6x0/orq4xiyU+xrR25wZF5xmY+chZ8FqbwjeXV43K416wtyJWfHly7xk7qXRf9mQeS3BUKYJSDJOjUxadOeQWLe16I88bpBooA5QyPqn0WuhTSE2m5DYMGl/0lVQ1YTVNY+ZswBBRNt17lG7eYvBPRCjJDk3TlOfOo2WNwWoj/PpegufZPpnchPOuOKjn5qkyZ7MT/rRiKcsryZ46BUNZR9e7PIpRVORg23VYD0yB0XlujwfQlpVVtEHRRs/kD+kcht3texZLS9v3WGOkGs47/DQRav69ehyTzVbPAwl/WGM++ArksnaKczE7uh8IjZ0ctUMzr+va+QMJG4ZQ9F7tvJyHXGbuDCHWg3s6pgrQc9Oi+fPqg69+TDLFDGg/eKP+tbpuwfxpfWQcUyURzFpIMXknuDY9r3dO+DHzvk3nqTPaGqPLdVWaQJ3ei0q4LDGSxBO8jHmtJyBi0jWjARM1PlFhoCQJySrZkwpomla+lx1fZba18JJaW/R1kWfZKfQAni96hioDtdLdD2LG8n05/0kV28c+e/Z3CJFhGjlO0pdFWyP2WC45T3ZPiCHp6qwsxFaPug6gVCkJApZSE+jylRR4SWOlhQE/09yEtP+yHRBjTE1d09iESGulXDwH34kU/s6YiEKzn/90/FRx9BszW3LirNdlDVQjI/OidJU4p07OOyU5kptl5ccWlR8koKxU8fVk2VCCZGn8s73qvE/4VtamUG7NWbkS3A9MfmRyE6MbMCGg8Dg/cnQHhmFAmUj04uQ0Zm6IHeQmiCjc4BiOA9Oo+c2X3+KngeAmgvOoxnB1tWG9XLJZrXl6dUXTaFRj0I1BJ/svJprBkPSuT5y32WYXqDLj8MIkEiPeO2CU3ZoxsUqvx4i2BttYFl2f9FCg80dip8kGnfcTT64X+AnGCbYu8IP9lmG/4/Z+x8v3d0w3E346cPQH9nGY5+hjGyK9H0j9ZYJn2bY8fvyYy82GrrO4ccBl7loNJgYabTBNg7UtXbvgGBRN19OvVmyuL7nsL1l0DavlgvV6g/eGr9+/YhoH4nBgt92xCA4TJHClvIfBiXxRBqsfQqpy/H44Y2M2hudD5SY8SeCHbEUl4Jk+RC4HzIZ4FuDoJFCL90TjCNwcD3xz95aXt6/4/PIFbaOIy54Xj5/w4uknfPVmx9FNGIs4d825cVQJMpLwjdkIJHGUZMOKapGo8pyiZgwaw0L3fP/7P+In3/sB3//Od/js2RMulgYz7RgPE8Nhx7t3bxya+ogAACAASURBVPjm1UvevLvl7ftbvnn/hpvDPYfxyHEaOPgJdCrxUPNd5tI6dQL8E8CKidw7RmyMeD9BlGcJ2hIQx6JzR4bDiCYpJiEmO1EuIUaJ9hBLxBMFoxshimJ03nG8HxjHkRClTFZFeV3GMaKUjIk2RvwEWiIZ4zQhfKSWtm0Zx4FhkCZe2WsSUvkGeDGyEvBprKGxLSmklabiYQNDJ6PetB3vtm+5m+7Ys8eZCa087I7c372i7QNXn20Yh4G+a+kSF27wHueOTCFgQmC92XDY7djtdgzDkS45bK1WqBg4HO4lg7ZpsI0CLVkC+3HH3f6W3bDjolvxbPOEpVngR5d4IcWQyNHOatMUIVq/qLVmHAfub255+/qVGBKJssGalq5bc/X4GYvFujQB02hev37Jq5ffcH/zDmu18NEkRUAdcSxXUgW85dKGDODyXvDJKPigBCtjyCwHEq+u9768p89ssvyn0IOoAqQ5caCllk5JPsRq71LfG+m9pGDnfZQ+l43J8tncObfc+AmY0Qmw5e+dZljmM2nqhhKB3EgqpMw2KtmYM0ATUFUZyGZjco7Ch2SBlvnJUdoYyXikglsnoK8A/fRX4d/MQDGPQm6EluZ4NkpiKZvNx3l2KXDSfHGWizOgPj1iea46eotWVbZpvr9Y9kCWzfkDSinCeVBP5fPXDruPmS/VHaXxfOhOc2ZUKB4QWYUuhaFN6sR9zi0bgmSd59tS1X3msQkB/KOnTD/8SeJnzqElDd0G313T2Ia1GvlEOzadxVjJZBTaAI2KAXTqnK0VTEf8OOEOB6KbBAjaIAZLdHTTLdfs6em4frLhl9vIN3vDflpybC3LbkU3viHs3zHt3hHdKNH04FFK07YNsroli9X7iRByJkwab61RqWNrDAgQsgcpoyZxMmnho5YAoMK4KWXcJs6ukHfwfJTpRTpuG5PLmyWzwY0T2EDXWB6vr1FG448uZcEGLIZFt8Jo0SNtv8AopCHmUZpGDnjc5MUpaDSrtpN2j1HKrjbdGmJ2yAQCntFLdlhZhgnb5Ay3siLT+Dy8IucCyyJ3Y86+pBJigga0UmAMarEALY7V6eaO4BwqRsZpYu9GCBGHY68i0zAyqUhsNBiFAxaPLmk3G8xmRWhMqsiodGruCJknQ1VuhnrvZSO6fq+8dTqTnlgFIsCulnTuArfd4w5HamVSAjMxy3tVcEs5t9JyTwGU0eimYXV9hdpsiI3FqZQnmbr3qmRk1px055mfwFwlVN17NuxIzvkaH2ZeXKWF+09FwTGZHzZGhQtZ9nlQ0jzC1jJdqdJoM899diWhQFvRYVnVxCjyMTetA0kuVJsNbdfQuEvU5Dne3jBut2kPnk6PNMfMW6vWomndineTogNVcpCEOH9GQ7Nc019dYvoFURliampKGptcOSNjeCptdc7uUyrxRlIMb3HeZAPRlJLbj1Vr1E76PJ/CuW8SL584SI0yhQLBajM713REWyV7OpdiZ52ixeEtlUSm4HGlNFblTHrR3yEg5ZTalKB4dhrECEF5bGNRiarCGMNxGIDaucVM56KEMmxyU6okkX3inDSNnaliBEvIWpLzhGx1K1KwOZSEjkBM8quaE62qhEqRs4Y5QzDqiDKGlwRGPD82DcfjkbVdIK2wPd4f0cHK3PnIYbvlsFuAhqbrkhoJdG3DarWmb3vY73h+nLAh8FXfgJKS03l558B6omGo9qUxhsvlit1xkGq9LDvyBiXz5Wc7csYv51U3pRgifVbrXESPcJwnZ00u2Q4hniTviI6aUjZcnNd2wqyl8RTzeTUF0BWdkZ64iOD5URIOJpU35wtnOVZhqCJX0rVCDIUnVqGK87reS5HUSyA3h1M6nw1QQukWJcvUaMOcbRxP96VOezhVwmmlqiCWrFWjoLGy/8SmCPP9p/RpRapkrXC6iqJLMu42SpWmZarYsWI7Ky0ZcabvYAjzEJHXSNYnJM7IrM/mMSnrJZVZh5DHluqY9Rbkqo1zZPnAcYZTY5TSdzRSSWgtwQtnVP6krtZplpHzHcxaNKb3xV6Y17hJyV1a24KpxWac70PnZoNplea5nNdb2i8hB7hN6dEhaysJHKVO7KOiU5O+M8KXN4/12XiIrRBmJ6gSHanzOdJZjWnKOU6yzynib36tdHWe9X4+f7arrI6zIxOIRpKG5ioN2RVd6Iu9FULA+5FxOmDHHX0nXOTTNDKOIzh/QmEUTM4EN/gId4eB+/FG9Ge2K7Ti3W6kbe7omoZHyzdcL9f0q45u2bJcG5ZdjzWJ8kAFVDCpckzN6z0DmIqGU6YoBTsxZegFdmmcT4lSQXCL1b4kn7S6Q1lZG5KsESUrWqdGpMHQd2v8uufJ9RWfvHjOeD9yuN9xt99ys99ymAaOw4Fxmpi8KzRluQIvy8IQoyRrJBwwOsf9fsfdNjAejwQ/ip/IGBbdQug0+5blcs3jq+eotqddrlleXHD15Anr1SVt09K2DW1ruX93w+6wZR/Ft+FsgzGaGD0+Cs9x0/YwOcLkinx56Pj9cMZyItdPX68UVYw5Uy2/Ut6RTVZlfOW6xDmGAR7F3k282W356uXXfP7dn2JwtMZwser5zvNPeXvzDcdxB6WEKRYgWt/LLEBj/hgnoqwyruaAvIKo0Uoac236NT949hk/+3d+xg+/+JwXj69ZWTgcdmx3e7bbe969f8u3r1/xq9eveX1zz9vbLe93dwxxEsChI0rHQlhM6cg7G5w5Y4Lq9ifnknmcnQAOjUEpizWGxWJB07eM9wPOg7U9KiZDvhJEonx9Ag9JhJduiRFF6r7nPcdhZJymxF8ay4CKIhUuj8a2NNYS8aXUUpSqKuBmGI5M41ScMxHIGSXEiDGUEmopZ5dz6SAlp7mz5IPrTWvQhpvdLbtwYFQyzmaKxN3ENO05jvccdzvcNLFaLVksFzS24e7uLgFcWTNGGw6HA+M4iGGnRUHaVHY/DkdRZo3BNo2AbK24O9xxd7zDBc/T5WMera5Z2GVRUFpXXDp5XSWFOwP3etMrDvsDu+09x/1OAGESwNa0NE3PYrHCtk0VXEBoL96+wQ0HjBZn7MneOwNjmW4CRCEXEJ72Y0ilvvFEIM2/x4g4isWaKO9q9dBkzc7XGMU4LAYoVMphzpUru1YWxpkZHettPb9XrNAHhGhBuh9xlpx8RZ29MRuP+T7LF+rL1b8/JMcVkIJOKhl4gQeyJZJWrQHRQ7d2sm6qcc+OwfNbyNA/g5IsBz8wbs/nMMsoJVI6XzvmNyMiR/K0nNz2+c2fPlcBX1RNZarnOH2GeCLjKfNxOuxl3fzOIz/7nA2dxyR32M1NwnIX3nz8oz/8Q97e3s77mNN7jSnl0D9+yvT9H2OtxmqLuEVaYnfFsLJo41hbzw9WnscLUDZK+Wtyxsb0zCqNW8Dh+ohzlriApgOsjInH0igxEqNRxKXjqx6+3gV2ThNVz4W1dE4Rjg3TriVOA43VBRjZtiN3Mw8hV6uokj1AlbXQL5as1g33Lx6x3djCQ66Uou8XuOA4TgPb/ZL2H/wxqub3iuLsHT7/LvvhHoD13/kZ5vF1GUOdmnEEJfrRbwc2Zsllv+HJo0dorXnz7i3HcSAQZYyVOICtaWi7BUYrhsOB4/HIFByj9gzThI8eow1t1+BVwEVP8IFNt0qZBwEfpWHh6CYkfzaty5DNH+b1p1I2hZ4ziD4QI2l151LE+eU6WzPNt0IcfCHp/N2e8e6eOLm0HmDdi4HgQmCchNc9prWvtcYTWV5fY5cLdNcmSVPLrjmrLBtrSXRU9112Y94xKOBHn35aPlJMpXQ+AdtzgF43lma9lt3vPH4cTioezh1sMzxLmCMmQ0sbdNvSrpY0FxeEviOka+qYs7LSmUNMztnyqA8Yzb5kvp7QzsxfSOq6MoKVStQdBlNk4Lw3snwtGDPr9xNRXWfZUbBCvq4+u1dZGzNWQSlU10kTpBgxAWkUFmHc73HTOM9LZXjV8zhfu/pZfpkz3UK6PYzBrNeY5QJlDVXsqjr/B9JaLhMro/BsCiotUn3r4w6O86xmVf+W5LBGYVUi3YgV1kKX0u38rCKF0lRXGKHoxnmGRe7FCIkiQJq2mPRPF+wzO+ZEVmor8sBam/azJ2s9FMW5IckSqRlinpgYT5qtqXQdXT38rPMo56kGjPAAFtDWzgZlvl+lUhOZQHRSqj4cDty5CaWVlKz7IA4EFQhhSk52KUMej4OUDYc5c1eWjqFrW1bLFezfsfKe0UGM5ybt7IjlTPcrpTHasux7xnFi9BlzyAyemG2xQpcxVhWRp+vmgSUr95t4bk1uMoOU+p/eUSBEjc5cvmqez+wcLU7A7LBFZ8DDPHMxr4T5BqqNmddlvU1n+FRh0PRToeamcem+zisN8od1xuHZiV+VRHP2s6bmKhVI6Xql+iDNU94HUy4hj+IYFOeir84dq7Wbr3XGZaxiqaTQIE3DEorKWZohYQTdWEzb4vUozqKia3UWywCJqzRNS2qomN+rtBLn9k7xe52vmd+BNR8KKhEp9me+Wp7gNPMnF47510p35/dywAmlMdaUORHHqQE902zkxszZcWkSFzaxknE1X3faJCFl7moj1Rp53ZZrn4ybzFbB6CqttRM7Q1UQPe15TtdtnpbZpFOna6UWemper8XSUfVsyms5MDPPR5arCd9kCjxV3wuy+LSU+kumbCuNsYwlRrGVx3HA2gPTcU9wI2Re8hBSI3AJrBwnRxj9PFbpx370aCXVyfe3R+4WRxaLln7ZsFwbLlYr+tbSJh9EazuUsVJpnBoizlbeuZ5U8xgVPaGQslqpuPA+JxVFhBVcS2CTvLejUEWgwUa0ipioaI2VQD+Ka6XwF57jdsXusOFuv2c77rm937PbHzgcjwzTIBnOyd6XhBixDUxaz4TIOIyExE1L8BijaKxl0XVcLjf03ZKmb+mXKx5dPqVZLOlXaxbrCy4fP2a5ucIkCkxw3L57j0HRZPrOrkftjQRdgmQxG2PAhQ/Y+M6P3wtnbA1q68j0jCVVUUacLYgMJuuFHqqIrSJzpQBacwiet/s9f/YXf87f/4M/QjqFNqxa+NEXP+QXv/oL3t+/xk0O2+g0qbJYcidJsW2SGVIkHrM9kn6KjJd07Cz4DC29XfDs8hE//OQz/uN//E/49JNnKBVw45H97S23d/e8fPOWr19+y19++Ut+/fo1rw57jiESjMWYJLZyaZrOwCGPYeamS7I41I5q+dz2sGfR9NJcKnicdzRayngW/ZKnV5csr1d8rT0+JI/+tIcwEnEQJXMqJBL+bDRaY0o5lDFSOuV9YHIO5wQUZkebUtIRMESNMR1Nv2S5WNIaOB73HIcDzjnpVotBBY8bB8ZplOwRZSSqpQIxCGBTKNaLjraxicBchJpzAWWkyUUue3noiChcjHy7fc+9OjLiiU7BLaij5DMH5Xn7+jWYJMD6HqM0d3f3qCTEmkb4jXa7Pd572rZFG0l/b9pOlNcwCp1C29H0vXAqRceb7Rtu9rdgNC+uv8Pl6jGtWhC8NB8zJpNNC0DNelmilGIs1lkQELi9ecd+d0+MAdN2NKaBoNDKYJtOMoK1khKWCN473r19zd3NO7QK2AKu83I3HwhiRS4tlLVpTM6Mibjg2O22J/s8C+m8N/KaMFbO7b2X+7LJsVvNWS5VyUZODEE4iKict5UzL2fOa60Th036rwIyyQNS5MqsbGAu2zt1ts1KneIQqgTD6c8HAFaWbXlcfCrzlm6ooTxxXV5f+CdTeW6J8huJWPtIyc5RCOrWiqpbbp7DGaDPg/DhkcFKDnbMUK8aw5NHi4Uz6/TVrNojvpb3Kr8WZgBDxBSlqgp6ynd8Wm5cX3wGaN6HD57NGFM49OQq1QSW75dBLwA1QtWw8Wxszo8cAKjWhU8cxJGSq12CRPkz/+V//l88dLa/4TGmf3+DYwFcNPD8+oE327O/D/D4oZNs0r/P/mbX/uhx+bs/8h/9k4+/d/+V/PzP/tP/d27nb4//bw/1oUE686wK4DfLReKpDxzfHLE+zoHnEoQTOWVyNpmIsFTeq7B9R3uxYXF9hVouxZgELLMsn2XouVGiTkR6TAZAqSaYH6X8PztG8zsR0NbMNAtRJUfa7ECe8W0aByi0XbrOOCrG/mx8ntxH9bdJ5ev5zlRyfoiRLdlPq8WSRjfs3r3l7v0bVEilqPkS6ffTgOKH182vh3KPSJfyrqW5usA3phhLtSxOfpMTp1Gek1IyHWYsqTh1uMZIeU0bg3eusiPma0DKxso6MSv1GPAu4JkkI7ZfzLzACQfUFBQhSADmA6evUiSyxcJHqGCmYYq50kU49sXJJOW7gs8DuWmXMQbvfaoQMNJXQdvUkNEn3EfSqYIncil5xgkhJByUKnik6kkydmOQPgwuNcfJY62S90BX5cwn86ygazsaXTkHVYWbYiD6iXB1xf1wxE6jOL1y34kCAgPKpIQDo5kmhzFNqdhSSqEM+OjRVnN1fY15+5vEPTrPSabHOsnAVAql5r1ptKG1DVZrGq0Fk6Q22iUbtlp7Basxy4BYywhqG2zGDflvVY+lUuLkmsEGMSqsqvik03kjOZNS1k++s0hFpXFi0cx7hAgqlX8LFXBMGXYqyZZzOoZs71YZsuTGx/M6fchZKEFmSdiRIGoWEjmRRhG9VFvFRB1jEm1Exuwhj0+k0FvoCBgrCUeTk6B0lOcLYQ4myZgJ5/GcgTjT0QDk5UkKdAZgOo7iJEo2S4y5jkc4Z3XX4fWeHK2I3idbSRU9ZZONIsHLUO6PSJn3MjtlbRVjKq2R2Vz42PFwFv98Kpe6trsQcBWNx7xuqbB38mOczWeWPVpJxmrbdmhtU2WSnaswiu2ZKjnSObUSPrm56kOX9ZpGsOJAzgp5roBM0pFMoTKvN0+mKUArfPbfVw7OE39M2QfZDsj0WHOJvNiOlD2Ws1azzXPaTwIys2S+7ZqHPGd012MOmcIgXS/3QEgUYSrKIow+YJXF2BWt6cmNt513TO7Ibvua4/4eNwz4acIFT6OEtgiU2HzMum1u1CXNR32A0Q3cDyPmVvhtDYpV17FZNKyWLZebJY8vr2kWHW3f0S86tM26MWUuR0hlRqdrL0uNTEuosu1fJqnINR2yzJkDk1opGmNBBaF31MyZ8Fph2ga9aSBuCCGyc0fe3Dpub/bc3txze/eG+8OBo5uk6sw5dKoGU0gzLj9OjIeBYCV4cHmxobWKRd9ysV7x4tFzVusnYFswojtM22F0g4rgjiN+4YjKMDnHNBz49vVrhmlCG43VLdPmgmF7B2GE4FPVmayXUI/ZA8fvhTMWPgRw+XgwAvTQ55gFefKzFz7HpIogiKBwE3z5m1/z7be/5OJyi2nXWLXkpz/4lL/48jMOww0vb36FMYoU4JGFHnNh1qnxfn74IBEKhRgK0v1WMmKfbJ7wj/+9f8Df/eGP+N4nn7IAhsMd93c33N2+583b1/zbX/w1f/n117y8v+HGHVG2ASulVlkyGGalAp5yo2mcdB67BGZrqyHEwNvtO55ePRahFJIxoDU+RIbDgVfffMOn6ik/eH7F+HjDl795zd2tJYx7ohvw/shwPJxoD6UUqhXg1CQBvD+IQzVn2GTlG4nJeduxvnrKo6fPuXp0zatvvuH1N79iHA4E75JDTzariZrGGPpmKRktxorj0ya+wBBEqBnJunLe471DIXQF9Ux96FaRY/ITd8OWl8fXHKc90/sD+j7wpHvGj//gp2zv7rm/veXVq2959OQZwQW880zB4ZPR17U9q/WK+9tbjoc9IQQaK1mvXd9Jhtgo3F9Nt6DtFrT9gsVyyc3xhtf377g/7mjbhk2zplEtitwcbHYk5eVXTEM1T7POiikGxnHk9atvOez3LBcryapI5mnfL/jks8/YXGxo8xipyKvXr7i/ecs4bDGqLgWnAhj5+tkpx3xnqSGP0grvHG5yHIdhBnOF/V4l/ltx4LWtOH/EwZ+UmQ9zw7m8hr3HDSO6bU6MQcnEqIzyfEMxG+KhGG41FtJyAonWagUeAVV5UFUqPWEGNUkby7cLsKgXWTyVDnGeswjgYwEUpfzEh3ls8ulOnKAQ/Rz8yIAaJMsyeEcmzy7gOgeUqpuJ9c+YDQ0BDtYYCYDEWABnSaPPd+sTZYCa6RNOItBKjL5TCoR8FNNajKg8B3EGjWKbZ77GGVzMP2cwV0B5nJV/zt7I90hq4piNmdP7yMDh1MDK9xLj3Bn49Mhr+GFZku/RGjH6IAW+nOiH3xYU+tvjb4//Px/eewnE5hdU/p9U2QD4AEobmstLlkYz3twSJgepKUTteMvBEaXEfxc0XD59zOLyEt13RGtTabMohdqQ/tgWVZWVlrPgbdMUx8XpZ9XZP3F4xsr4y1lEMc5OlphuIjuEY7Yek/FfG9K1MXruJD6/DwCtbHEmJIWWqFcVUWucijRPrml1wA57wm6fz1hNSnLY/DYxVuS63G9U0CxX9NfXdOtLYtRipIY5iDUH4OQqevZgl5LkHGDNz1WN9omTOsaQApvZ4J4/V89jwVFJJ6hkxMvrgWkcaJo26cNIDL5Ua8UYEwVOHs86Gxspq7USLM/3ljO72qYtzjqjtfRj0PI578TYz01op8mlDG1xKPgplPUh+T+h6GNQGN3Qt5pDFMeLUslRmXF4rOyZALF4G6rzqtn5Uq8pwXGz82GaJnx2OqqMS1JwM0o2qV5eQHOLY0uM0ttidI7Je5aNoTULDA0RTQyR3e09x8MObSNmNLStYH+lhHJm2S9oaQg60miN1UKPZfJ9hUhUEWOF4qatAreSuGB5vz0SdYdR0lsiRJ+CALPj1ocwV22R6bZiwRl5qnPVy8cOyfIPc9JCGX35TaWM6ILpoHLYkvpiZEepr8Z3XtGSVZzvKKDC7HgSFHS6VyJ11tac+FRWfpgxVf45Z+nK38bYEiAwWrHb7cSporJjt4gYVJSS4eA9U4xlT9TJA2W8vNBpEAJWG5b9gmmyKbEnOXK0yI+QAh4xO/cV4khJzftII26NKSxbLkRWbc+njx+z7Fr8NPL121t248DkRW4QU0m9r9ZHsSEUxiixb2NIP2f8mK/54TrI1AX/z488bpGIGyfC5IhG5ISK4ugTzs9kSwfJ/J4DB3IzKnHgN7bH2gZpXJWDRUZs0CAVjlkvlevHtD9Q5KrivIJUFKdYxugh24byISI+mTjJ8a+yrktrDZ2weUVlFhN/MPP+OPcPGdOc6aaIc0EoB9M1xFbM3LapYq2mPsu2idZlb4uvKRTZqVHi8wmZdzZnBVM0e6F8yQ5aFQludlRmnSBryqZxFR3dmCXL1VO6Zsmwv+dwuGfYjxDzPMxy5MPqj5CeU/4akf2nvIzl/X7g2/0e/Q6sUVy0L9FW0XWWzarn6dNrHl09YbVYsWh7qXjTOSglJ832jOAOgzFhDnroPC+ZLpBEATYHy5VSeFHoZV0FBdo2ogfT/p3cJA3avMcSuV5ZrhaP4PkTQvyMm8OR292B7W7P/n7Lm7ev8VEaFhMj11fXfPHdz9gslzRGsuqV9jTWsFh0XD1+xNX1C4JqGCbH7d173n31G6xuWCxXPHr6gsXFNW2nQBlitLz45AVfOyf9j4LBbK5Rd7cQ7yEeIQQm74gmEhpFfKBHSD5+L5yxeSPWx4dp6nPG0klph5o/UqI1+aRIFkIhAI8RJfTebN3An/7yz/j531nw4vEjHC33x4HPP3nO+7vXvHn3NW5yqNRtWmtNKOUNsglV1RinvhdxkkjUQ6HoVMf15prvPvuUf/zzP+L7n3zCZrWk0Y7b7T3vbu/55tuv+ebbr/jy61/xyzdvuRuPHIPD6YBlShxSsuUkQJc3Q4oyFNmYBGByrszjATWh7BAC77f3bBaKi2UHytA0HUZrYnQMwx0vXwaG4chqveIHnz3nS2vZ3beMhx0+RLy7h5jBnU7fncvRfYnOpSxJlTkRs7Gg6LoV/WqN84HXr9/y1de/IU7HFLGLED19t6DvOppGotjGmtL98P9m7s2aLbmu/L7fHjLzDHeoERMBsNkQ0RKlVrcUtoaQHYqwHXb4I/jNn8Sv/kb+AHqwFJZsy5Ja7ibZJEAQRFWhqu54hszcgx/WnvLcC0oRUjiYiMK995w8efaw9prXf2ktJaSzk3Km4KXcS4fcOEGwCStjf3gYNJEvuWON5zgdubp/yy7c4Ixjfb7l6dklf/vjn/Hh05e8efVaHLCj58mTZ/SrFS4E9vsD1lqMUlitMFpxd3dD8D5FC2XOXWeZxgnnHForhl7wRzorgNqv333HfrwHBdv+nIv1M5SyeJ+jzQCmwfqJhebkpapAZsywaZrY73f4GBjW63QWwNiO1fkFTz74UNLrdWWWr777lvG4F8NvYZFWhSwbvDkTIUYkA1hLkxvBRtPMMTJN8yJyWBSv/MQUXVaJ0Wuk7C1jqZ3uWsHLCb6A8LeCN2YWkEddFCQAT9TVwJUfDSNJXYIFsy6iU2l3TqrIRn2JrpYX65eeKmSnV0xGLwksv80wjn4ZKshcJjsFRUGndOWkKA+VH2R+uFC7Vc3QL8pUua/emTuAQo3qliygmHFkqwFfPpeUjYyZWte7mO3l92r/VYXVpP0uHeeLARgLJmB+LZZx1t9Lh978LdkmjVDLfYtZsPg9Rprvq/OJ5c76sJztU/DQwvIzbp7J2H0gwQg9DPLtQbIXcrPB/+2f/+/821/+8kGzhzLufGnD+A/+CcZ2WG2xusPTM/Yf4YaXxNULnq8NX54dOeNIpxx6sxElVtW9DG4WjExjMbZHB8fh3RtMhM2wpj87Y393Ix3C3YzSMB720hQgeGYduR9HVusNnelQQaGHNX44Y9Rrdgz89k7zbu9xUaF1YK32bKZ3qMMVcboDP6YOrZk20hiVlB6WUjhFkiWi3Nt+IMbI7Gbudrfof/HP0L6RJwnn8/iP/2t2x3GQWgAAIABJREFU/9P/DMDl//q/YL/7NimsheDRSrG2PR+fXzLEyMXQ89Hz53z77Suu7vbsx5F5nrg83/L8+XPeX93y3et3nD99yuEwYm2P1pZpmri6eocPjhB8qhZxhbZDjJgQWW832KFDdxKs3B0OmMFihg6nQwIsqNkZKAkEK62lhF2RjHQh1kIjdQWrAyjTbuaJUJ6bu2grhWAYZ+XQB/z9gcPtnZwrBcpohrMNdr1CWStmh0qZR+V7lnwgZ4Qtsw/zPfKac77wy+qMSONNZ+n765sSeCxnQlV+krtey38Wu9lgrYbJESbHeNijQiwVAmkgKNsx9B3ddkP/7Dmx6/ApcBx8dko0lJmDTdRzVM565h1eHIghgtaVo9EYStUxSGroEykZJo3cKI7BUlaeshpzdRVZzlWevCz1zVlhVc5G6rrmtei6LsnE5L5L7/uyT1Gwxn0korG2Y4rJraKWrCnPq1259rtaaRZCYNiuGc7PGC4v8SjJ8k2CKaRMo4xDbLSmzTYirWVo8ZaVEqMvn/DCy1nu2anHWD38Pd+iSA7P7DwnBxgFZsSjSiZdwTFv9oIQC91XmhLM4fars11SvjVEvJPqMa1y8zkl2axKYY1GKVvs+pIpGbN8ShlqGXMgkdeqH5jdlBJFEnZkU/qPgq7viQh/nUdX+QZ6qTOARE7Lisv0pmkCa2sWZJQM9JhgCoLSYA2h6zgow/81TvxZ1zM5z+gcwUaMVehoxCkcITiHzr8Hn4IF4oiUDEXNoA1TENrMvK1Vu8SQd8xu5jDVbEHvHdN0lNNtOuqZTZVl+Syqh1aDODx9CjiHBO8RKqxVZhlQ5FLhmUEqxXImWT7TIYQMUFDH/uB7l3y/3rTktzbBIczzVPS7Qv4x65/5s6bIz5KJ3XgKM695CLtSJI8EmYNndjmTTniQVgqrLdthxThOzGFOkDPy1bm/gFLVcdtOrdBRCAVOIOv5IVWRkcq1daMbiqNFnia2l82TSQEEmatVke1mxfOLJ2yHjuNxz/u7PbtpTFA2CqNs0t1qZUZM+6g0JQizrNaKJdiSKxCyzbN0ZFPe4wGV1ev32RNF1gYJCHkXCKmZYMYllg+H9Lcr1cNaaWzfpz4tkkUu5zfhpIfsfG7goFSC+qvKBtKQPIhd2swlh4i0MQJHku6JMZXZpx133qfxSCBQa5OSMdK95GqRRLhKEVWtNhO+39olENycZGf6O8vAFm6vqPURFX3Zx7zOWU8PPlQc6oUzUhqmh+iFR8WA9kn+ZnipLIvygsWcSSy6hWDX+xTsyfj0gZxLKbKoR/cKqzv6YYUymmm3ZxgCq8ljdruCm7qgm8doqWgSjQ4TBbv16igJU/ow8fbuyLtbx9lmx7bv2Q49Ly7PGDZ98Vtoq8GoCtWgslwKZY2s7Si6WjqrNlV6KJUSaMpGVNtHIM0Cxgo9oBTRROhAe4cyLk03EKLixbDicjMwXZ4zHZ9x++IZnoAPnnmaefL0GU/Oz7FaE9zEPM/0vVS8z9PM1c014xzR3RoX4PbmmuilL8Rxr7i+es/qzTnnF2cMq56u02w2PVolmJ2YINk6i113KOOZlYMoPRkIoB/Zj3z9QThjH7tKCjvCEB8IkvZeGr5Ao18UjSe5JZLhEIiM3vOb3/2WL378BR/j6XvN0Bs+/uAlb68+4qvfXHJ7/L4QDEk5rBiHkklVGEUSTNkAFyak2Q5rPvvwUz7/6DO++PTHfPnZ55yve2Jw7O/vefXmDb/87Wt+++p3vH77itdXr3g/jtI0QyVbSYUq4MiOkxqZoPydRFnmTkkxaThOXSOlGJ1nFXwyeCq4vJRnOfb7XYloXRjL5uycqCzadBA18/FAcBNKSem8MZoQwDmJUjrncS5gTDW2s65SumhqxfEouB/zPDEed1jlxRlnNL21DIMcfJuwTGxn0+GUuXk3czwemOcZ5zw2dVrMDHXVD9TsRR4QkALOkbKayY3cHG6Y1YTXkWG75tnwgpcffMjKrlit1qzXG9x5YL3dYjsrTVzGMZXd6NJ46njYI8aUOBlztD6GkDBfpEuyTUD0s595v3vPGCeMNWyGLSu7JroonUiDFydF3UqhtSRbRGGo0SaVnNC7/Q43e7TSdLYrgrNfSZfAzWZbS99jYJ4nrt+/w7t5Yb+IjK1wIU0Lj5PgiWSyiFCJqfTNpWdV8ZDJNEcTrRGlJxtkp0GkUwPfGIMyYI3Fh1AypsqmkrNs8vib7y5vPFS0F0ZH/hsWcq49eWUNyl81Q7O96/RS6aH1We19cfGzVdUWT3vQECAujPuFbts6pBPTrEb04/tY7o/ZnCzMZTGuhhzTc0/ua3ly0UliMVYre0rjaAVzozmV72kUpuLEiW1Gh1psktyb03tVHUudZaMgN4bIYhHSa/m7y8K0iinFmZV5cCAyT5P8nhoNCuRN4Nvvv+fbN2+q46zgqObxp/UzhvHzP6EfBjrdYfTArM4Zzy1uHtCu56eDwRwPnBvBXIqTkkYL5HK9IAFGn3CqdY+JlkMY6GJk4yz+znG4OhDmCa0i/arn9uYAyQlxDDP7MOP3EyQUqO2FIU4jk4JdDLz1W165njsHBydncD2P2PGIOR7geIeZ9wiKe1wYbyZBv1gjDSJ8kOqGECP9sCLGyOQmru/eo//iL1HOJV6Xz0lk90d/wk23AeDlr76i+/Uvl4ZeBKsUF93A+MHHDM5xuR4gVRDsDjPjLJ1uw3iHjZ5vvnnFX/7iN6yfPGWaYb29ZFid4ULg7Zu37HY3jKmhgJumQkuBSJhnVpsVpuuku6ztuNvv6NYD3dka3ytmHNmZoLVCGV2csToFqVqHnkI1YizT8xKBMBv4YpBmp0LN7nKhccaGSNiNTPf3wrsUYAz9do0ZepQxRFLWR8vDFzbkMqhTMjC1rscxUrC98hmsxtSSR+cuzZkuxKETiboGi/KuasB0Haw8YXJEo0QBjrEeUy2Numzf0203qGEg52iIIRsLx0Fl/MMlh1NF+6MEwUpWflrHxZUd00nxyWtQeGlawIWMyrZi4XG5WWbd80Wg6NRAT0M+fX0RUEsQN9l4WjwrvxBVyjjLcrQVpuV/1MB/0kKzzEkNVrLDXgFKK7rthm69QXc9PlYZ3eruxdgtRu9yHiE3vEqfzw10VMM3M+5kNt6L/CvOi8bB0KxjdsCLG7p9T76zsH4tOL+qaWa6aJLW8BtonCJpxyvkQb4tljMgxrhOQ65OnVxtFP3JniddphYcqbpXWtPrHoVUfvnkCCxOpWZLQ1rbJLoavpmIKutVNJjfNN+ZMuxiXoTmEiefQdue2PVcHUd8hMk7pnnC9Z5a2ZJhRSx4jVEW0yXbg4hzI36e6K2lNxoTGkKuhl+ZW0jNyrIzOr/mMixUaKqg8mOionXItjSS781Nz0SPqetTGN6JOlU+X+ikVvpUaLlY6bblP81HswYeab+m2snZzSVBnJiGk3ay7KF8uuhL7T6eXNmBWIJA7Xjy60imc0yyPNt5RhvW3cA8zmSyWOiR5W8SialmXDLWDGMRU6Az67wxyQchfy2NgFQzfwV9Z1NClny3T6SSkwZikOaVmsj+MDLNcwMVoZOjMvHeotanPUq6XKmiQz1cv4aHxQyhcOrEaGijddb+0LXgG836SxVhSONn4QiW851L/yXDUWuDsV1qsCU9BbLLKKZgaEgVAOIABUEheHguyp4W2SD7GFNmowRmsqxXlD8KFZdVakgjy91W/sakdmd/DOVzsZyBSPTgddYDwCXnbuZrma/mknpoy/xlbUPJ4K30kxvL5fkr3UAb5Lmr6mjOgQHyGEMsTXwjYMhQIPUeSQJaWltKaWLXYzX0biLMEduD7iYZR2hz+X//FU9+y8OeczVIAJzHuR27w8hgDOvOsLu7w64s69WKzXpgtRqwq47OWmxnGDpLb/pyNkvFCLIGElhLsjD51SDbAHnrc9KQBA+8kzUv4XeT4BVVM/4oSQ9WQ28trutYrfoEOSPVy9vtGZ3tiMEzBUcwkgBmrRVM7+DYH+6x3qOUFfxaDRLEmBmPe26v3+GnI+v1wGozMMe59AIxWhOsTTJQJaU0/VQK9fs8sfyBOGPTsWgEUH2nGtz5nTbKuFTIq6BMDtRW8CkkigU4IqOHb757zffvvufTTz7lcn3Oeuj55OVLbm9v+fWLj7n/6i3aRpQO8sEA2GZFc+ZFicoLI9JI04+1Gfj85Uf8gz/9c376+Rd89uEnBHdgng7sdne8v37Pz3/9Nf/Hz7/i1dVb7g63BHWEBJycdQP5J4aCOpl9q8DmA5AVkpK5mxTWfACFgUgXvpAEodaUSKKU+3vmOHJ/pxhHz93BcfHRx2wvBmy/wZgVBM90uCXGGSkbUoJn4gLOzczOV2WhlN7UTVdK4f3M3fs3qezEY5WUp2sljtjtZk2fMnYFVDrhDCklmVqzZMHsDzuO48Q4z/Ta0HdSgidOPg0MlX5aD93JdfRHbsZrvJbsyfVmw5Pzp2y2W8IY0F3PanuO6QaGzQprDd47nJuxtsP2HRjN7CbmWTr1GWPQ1mCsXeBEosSBLY4HOMwHro43zMox9CvOVuf0uuPgDskZG+hMVyLLRYA0SliMpK7hOZMocHtzk3CDLcb0ZGY/rFdstmv6vi8OJO8dh/2Ou9sbfOpWnhXBahLKl1UnivyTSHBq0qNEifGzZNTFhF2WjYZivCiktCl1SfcJ9ywkDNgWpL3NkJGyP0vfC76RYEm1zraG1tpfRRMpXETl85DXUJ1+SOZUMnqb55RvSS+2AiUbVllBPi3rynJk4XwoCpac85geHk/eXyhAsR0nqKIUZt4g5Xwtn1gcw/J7RfiqxERmH+n7RIlaHJ2GrxRFWtXxlDeystIaFgu7RMqP68v1bnlmLPPJnwsxli67ITk1Cm5ZsUqqKZlxvrPCnNf3sbV8zEivtJX/iskxy/JKDpSY+HAE5qMr49GqltW17rMQQirha+AVgKgVse+lhFVbjLYoOoI9Q6+e0w9nrHr4dOtYzUeJsHcds3P0vSU7IuQ/yUqURnoQraU7v6BLJW13Nzf4ux1ag1719MMKQpQsWAVuP3G5XfP65obD5NB2xXB2QTfu6OMeg+bFkw95vt7y+qB4tVd8P19wrzf09oyuu0DTofxrdDhiozghiUGCj6nEq2ThaE2MhuBrl3WNZCy0y750CtZLGtO0JWBys0GxVoqnXYchsraGoTd88tFTuk4qHBSeeT6yXp2zv7nm20FjbKQzK87PL9lcPkfZnrOzc95//ztub9+z2+8YD0ay/dJ+7+Ie76Tsnhjpup7peACidE63Az7hZBnR3hf6TZ1jO0lVz2cizZh0KK1UwZasQYP6vErrWVeQknm7XtOvBjlrSgl+qFk6X1sjpg0CqYZ5ZuOwnkEKDcqWqtLAM/PCUwO2PY8iwzPMh5wbXWCZ5AwGZaT0N0JYeVSXG4LIAJRSOK0F885Is4WQ5xFiyXpqVyrmhqR1VEVuZIdmHlO+Qnu/UjwwrLNCh5IstDzGhk8teJdqaEE1z5BFKmuf17zw1FDlQKb7TAsq6QWheXYry2ISFnJ/wHnB+y8ZfgvBV0ZdtliCSsmBnmGVkrzUvaU/O8es1uRSdBZcME+xdVBXXL6yEwnXVII1uTFi/pdgAHTSDZJjKJuq2RESyTCQlTaXAduQi2TIWIXL5rSGJgVCeFYIzXNqoDyvQcHBU4J5b40FqgwR3S6f7arXZeeQSrjqhRITX8uBPJGBjW2Q5ihBOZnL6KQMX+VKtjTe2afsfu+S8yXDPSnJtMtzV/lIt42RoOt6gs3JAlH4WMgVKUpgHZShG1b0qw3H+71UbnnH6CZmPzEHLw2JM9/G4GeFome12qC1JYYZ7xx+GlkNPb0xmFmSdRW6rksrv5Pep5oIfyR18Y6m0HA5/4J7VjXVU9nS6L4644e2Cs3J/VWzq5+X41V5x2kGrjglVMpCTGe4yWbWSU7kbFpFpktJoNFl4HleeR2a34nlcw/05Obnw9cp44gJaqpCg2Q6lLMoe1kDOz7pbbqZb9bxILaiTfSC9L0RUhVCnr/gXmcAurzvOiutMWKNZtX3dEqhY8T5yDEmJ3yQQNrucOD76yuM1hwOR273O5HHUOwYZdRyE5MeIXZoKOfvUYdLZZHV1jAqVW0sqOLBmp86PX/IUZvtGpdgHXzGUF7cI9mwKtmkNjWLEuhATROKLM7VXJkYZcGTjFk2W2v5Z5lvQ8nZWZlfaiHqhPfF0tOitTC10i2YAkm9EdL10pcmJL+oyuNVAtVC9IQ54qIvQdkWB7uuJUn2VtrT2hSZqRAHd254HSPolKmZHdjGdCVYLj64WsmktSm+i0wavmSep9nqfEZzpWlARZ0ywcUfoqKXahGliLrDDmfYdUDPAWXtA/3pP+2q8mh0E5OfuCdiUVzf3BFUZNV3bNcD59sN67MNw6pns+64OFtxvj7DJoxnpZQkSSktFaYq6xUZYkGqX4pO1JCG96JjzaVSU5VqaJRCW5s+lnhX8gHEGOmUpu9XKeAg/7puIITIPEOMFttr+t6mcyDnfPaOMI9YG9msB8ZjSCI9EP2B3c07xrtbhpX4TkYTmSaHMYaut8S5Q5lc7ZAb9Cpixir+Pfv0B+GMBcpm5OuUCbVXjlif9G1JpSV5Q1t1hGq4xIiLihA1b+9H/vKXv2Td9fwXf/8CS8fZds2nP/qMv//n/5Bf/eYr5ukW/IS2Cowh+CxEqoDTKTtWdJUBq1d8/PQlf/7ll/z3/+gfcLHdolXAje84jjtef/+Gv/7NN/z862/4q69/y/fTxKwC0QR60yWjopacyVTEUZGV9ra8N69bi+2jaBwKueRN1aUQod2WooD3Ez6aFI1wRGYmjnDQcHvFzW7k6Ucfsjnfcv70jNvNiuPdLcf9LYf9Lc7vUcpgE1VNuVwzBFC1OY9zrkTg3SSlsForrJYDO5guBRWUZEsmxSfEiBsn3r17z26/ZxxH5nkkhOToyCWdtkfrWHBw3TzivUGr1OXxMW0pXaM7cHV8CzqgIwzdwHa7BavwLjKcb3iyEua7WW+EeXaKC3+OUpphvZKGIvsjm+1GFFZjMJ3gjkzHA0oH7EqEoTXQdYqoI7eHPdfjHRjFdn3O88uXZDxLpVqw/rKLaBVZDx3zLCWySiGlbCjwATfP0mwsemL0THNITdMUQ7/m7OxSMEKjl7L/2fHqu1coN6OCTw4sydKoxlEywlPUPUbBGc0lqoSIMpG+GwSSYZ6TMQfaZMWpmr0hBoE9TvRhjXTrnOYZT0yOjaw8luOO0Zqu65jnuRijy8yDLADl23TC2ypnROfsGRqYh1jOGVkwthpW4yRYGM6JzkvW8IIP1e9sf54qXfnzS/71w9fSOZOnnZ2y9dPOhXKGSsXB7wuhpgfkAFN1/pcvqT/V8vXYAt6XeZ48nnb/66sunDhx5CF1XtTMoWw8eE46Q+fM8fY5jyivy+n+8PsPjBGq8Zq+6GQudYzLTMa0XDHfEyvfgqQQmPLM9CiRa88/ZPxH/5RVt0JrQ6Qj6DP89o+Yuqe82Ax8fhbZ7t9xdtZhegtGM6BQtidGcNPE4e6G4Ec22zNxI8xHUCvMsMV0EjAaknKzWa/pOsvbb7/l8sVH6M7ip5FpfySYjmcvX+IQhek4H/F9ZOh6zjuDma954a55vtry5fk5v/NrfvE+8P54xq7b0j37Ef35a8z+e/zxLYzfYxlRhIRvLJdO8kBgaGQFtTaorqOzPdMy0Vl06QdlzUsClb2QLuSbzYbd7Y61ArNec7bd4FYGnZweOmrOOsXN/TWr3vM3v/yE//q/+af883/xL7m+u+Pu/Q2vXl/zj//LP+PLj37MbveUb373LVfvr9jfHZhdxEXNcZJsUKXke3VnOeulFmOaJ2zs0VGLc1xXuZ3t3VztsAjcYE4cnoryAZOV1lS+7n2huUzT2TADSnAwaCOdbjN+WXEchgdn6DS41F7LplIUI6rwP2PBnDyvMaglM7dx9KAgytphRH8oz0rcRKVSNx8DPgLdkAeTDCZbS8qVkiwLX/WlmPXPspx1bX+Ij+UrYx5mTLm2AY/MKWeSSUaM7bqGj9XtQ7XG8HJdykJSeY/Rrf6W90Mt7hZnkS4vhBQUrViflY8pKGX0IQLaEKZInCfccU+3mHUe4PIAlhnECtdhlSrZY/3Zmu7iEtWv8EWBrw20cnZrmfeJjMx8VWtNrzUhaGaSMzLNItOfVHpJplcx6BteXYBrTnWHZj1r8x+10K8FuicQXbN+5TPL55TxaOlt0NJH13UJfqx+NkO1mIL9Seq7IIH81WpIuJephLbJ8JUQElJ5pVTJfN8fZ6keihX8Pc8n84GSKLA8uslh+7DS51SDNrbCZ9V9ggyVs7IWjeX88oIueN7f3KC06H+TmznMRwYzY7uYgmGaOczc3lzRbw3r8wEfvCRl5Ao5Iziit25EK09nBbPZJOxmlPBPn+BuenXa3LLOXRtxxBiTGhCFVF2XM58bvSZxnZRIoKVRGj90na5UbJ5VIS5ax/6DTxbeaYptmB9SHFTIXvoYBNO/upjK1epyp7v4WLbj6Xv5fYU4lcSRpk9M7aozR2B0M797/6boa+K/S2XaOQs7pelLMkco+nD7nVopsQeEsRUbePauGXeVh3keK2s4sz290sw+8Ha/Y/KBaXaMXkr279/v02oIzeRmwGjJjix/5/UILByvmSfktWr5wA/RRSvfSuO9/4jrsf1Jo0p8wiVIj5rBGUmJV6riVpNgh2KoY6yQNz7J7Ua/IMmyJqAU80l4xE+j8j3NWixuKzSj0KY22cvvCQfIeyryIXiPd7MEs0MoBa8qgk92KsGDd+DBMZOwRISHqWRvxph0jJb+K858zbYWWKXsVEUpul4adOdgX9QW03WorkN1AyiL1h3GdFjbSWUwUkihAJvOzCmNRAwogVaMRLQR53pI9J3tUQkydGw2Z7hxZuh29FozLfph/Oe6RL4HYIqROcpY9sfA1XHEXt8mKBJDbzXbtebD588Y+hWb1ZrL7ZaL8wu6zhI7nZzllhApUBlBBwliJ93XJF+CNMXLUDyxJGmhnNgBjWyV+zuU8nR9qpadfUpIEJnmfMR5+c5uEFhOwWJPOkKULOV5nJiOE/0wYG1fKpl9mNjfvQcPths43G9ZPX+GVTXzfrXd0F9c4PyIG0fcfmKNJaas8N93/WE4Y4ve1RiwzRuxuU0l541kzIlAzJHgkqkXk4JRhENW2tNz0tmO0fDb371ioy2fvvyUF5/8FGU7Xjy/5Av/R/zpz/6cf/+L/5v9eINCHFNSrmcgo96piMZiVY9lw48+/DF/9rO/zd/47Ef85MOndASm8cg8H9kfrvnqm6/5V//vz/nm7Tu+v7vjME9Ek9Khs8GiFSZ1q5d1SUDt5Dk/XJvC7Mp8l87ZxZUEXQgwuZnJz9hOcKiCdzjvcfMsBJQeqtCE65kw7zmcP+H86TOevbjgfugwdyuwK3Y3bwjuvkQvbe6UmUscQorex0j0Lh0SydzLUaTtasXl+RkxxqTgKHz0HI8Hjscjt7t7xuNYGSfJgMgDjYkOQqTrLeuhZ7sasFnIkPXTh9kYAC46juEAWgDj7w+3/PrNr3nz9k1RHsShL47zkqXgAxpFd+gwCNyD/WAQpp6V5n5mWEsk16DQOmK6mTncc5gmvr95S/SBy/UFL9bPebZ+Kt08jcUqU4RgS8eKakwvLhXx3jEe9+zvbyE6iB43B2K0KNVjrWU1DKJMesnMmuaR71+/wrsZEV8iJrI5E8vZEkWbWCztVrZCjPT9Cu9vmV12BsAwrCTaNTvpdNs0qxIc3VwiI9ibunm/LcLQKpUFeFEajNEYrZjnXKpeaT1rqzWDJWfBLhXR4rDMr1EjdT/osIsnqnYusysZGI2CyENF6vGI5mOvVUO0NUoXmQqAZNBXNTsrTYu1iPUDDxyWqslGToa2JivgCV8w01tMxnc7p8Y2zw0uFsZda6yqdh0emXKZebsulaeF2GBHqodlk2WNfu+68uAzmVYf35u0vkpBgs9RJ5AULXxH22SCEyW97lAyBhsHSW5YMP/s7xI+/SPBd8USY0cw50z9Rxw3n/F0u+ZFN/I83PNsO2BXVkrjg+Aozd5xvz8yjQeYDmyH1MHZzfgwEdzI7d0dxljWmzPOzi/xumP0jsN0ZI7w/NkL7q6umEbP08//mHCxZfIT4/HAeHdLN1hWlxcoI1UC+92O9WaAOBKc4ydqz4cvz/jedbweNd/cBHb8CHPxnH59hTn8Bnv/FTF6QlKWQwzomBSzVN0wO1+MvM5YxpgCD2FpDLVMMiGWNcaqXLMLvN/tuL+/4slqzc3kuHGCjfbJB0+52PSsjMin12+v2I0z/XqLd0e+/MlnHEbF2/f3vP3db/n4qeVss2a3h+Cu+Kf/8E/56qtv2B8mlOn5t3/xl3R9z2GcuNsd2LuRg/PQd2B7PL6wiZghlcoZrr/HFFTNWUQLhyh16qVju6oOpJwx1Tabi+l/Wa8qBn9xiD/O8xaZmPzQOTm52kfF0zHEE17Q8k7S3nm8j0lZb/lehCiNEGPGpIs52ws5o9qgTJcqmOpa5bI3ALRpTmMzz0w42TJr3svHtTquZTxt0DSXR2ceBeDnOZU6Zr4pTWJEfVELKz9TQy6HbZ0MC9mTx9fsb8j8JohzC5WM28Q70+CL8SlrmWSkAmMt++sDbr+X8uBMnzEnI8SCL97S6alMCSGgO0u/OefJx58SVxsxWIs8SfseU9BUVQNLsvxSxlCTlZovayWzpe6Dbui+PUeJFk5oNesK7fkpmZSkbJZ0hwTL0pqWcVTHsdj3pjhXITcLjWU/QqpwyvMIoUKQkWSrMRaLJRjxkmT8PYG6soxuZpzGdBas9OBNze4kE1GXcYYYIaYssphfS1h7yaklDaGqMyJj9AtWZJpfOlAxxgLFoRQFa5hQZ9A6AAAgAElEQVQI0zQSTDZu0/PSvpIDACqihw67WUHXgRcj1RHY+5ktDhc9OgaMVvg4c3t3w+aw5qm/ZJ4n+n4QjNb1Gh8c/apHH5ITJtO+98XesNqgrVRY9M0Bt9ayHtYoZctaKKOxxkiAX6egVVw25Msxjy5lZhXnzqOXKvzD+9BkFaefj/CWxRlPdJL5kAZiU1YN1Rna2gdtUML7yssybEFypz3C51s7eVk9lKdTA2GJY+a5t86l1OQKJTTglcTfchKbUoqz7Rn73V4aNXrJAEx4OoV2Ly4uxBZM5ybjHEsyj5dehjonggi/zI28tVKsugGFYg4CceODZOYWLNWi5+mqH0RKtqIKMWX5aYKRbGlibJpMVZ7kfYK8SHigORgA4mQuzWMX5yavbaM4P3Kd2h+nfCzr3qHAOgkGabt1OeBlkhNRJ0esShix0kyytX+kWi0HfNrtLkE7cun/0s5Jgyz008r2WOyPmGidop+d3hNS1el4PBKDwwcnzYWDF0z4dI40oIzF2j7pRpLNitLg07qEAAnXuXDtwstT6XOUJDWNVHfGEOhEAKOSPeMnn2C8VMLxluQhZS2669F2hTUDnRVnrLUCqyiBIkl2U3YZ3MurF5HGZJFAbgmik08rxJAqTCVpwSrLqh/YDgObYeDezRXy7T/ndaqvNS9l/j6HwOQDhzlwf3yfdHbDYDuen12yXQ8M657VtmdztmI7rEqvHHwkakVwwm9HIYtCp1VHobDTED0a08h5ktySe32qDOpWQ6pOTk0DQ4by8OVMRsTZPqw30hh8d2SeR2DE9OvCe+oR1ZIY6A2Hd285Ho/0K2na3m979HbNfK04TjPBR45ulm6zzv/eoMsfhjO2ucpQi6LavpoURXJ6OSzK9lsnzMlTY8JgSicQAIfi5nDku7fv+Otf/YKL5x9jVuecrTs+ev6EP/3Z3+H65h2v3nzDfrwiKlcV5hRX1xjOhnOenT/nkw8+42/+8Zd88dmPeHF5xnZQHO7vuD/seX/zju9ef8u///Wv+NWrN1wfD+zdTEhd2rMjoSrXlfhU0EglSFyuzwmjg6LTJ2dKXdTYhr/yCsRQSuxVWtMQpcnW7OeS+i9fp9GMzPtbDjGggsdo6PsBfXmG7QzjeGQOHhhLt9CKnSlA12ebLfe7XepSmZtbSQfZ3nZs12tWw0oEQQj4GIUZzzP74ygEHtsMuurwMVrTd5ZNKl1aD4JpMvTZaboUF4/RSogez8xge8HZUoqDP+CcKwDbIQYO88gqdmUtQwwQImsGNAL47byn79bSdCwGBnfk+RCxOGm+FA3Rd4xHw2F2TMcdK+N40m+56LZ0dInOE+yGFuOn2F2J5tutLe8pwa3d7XeM44EudcWMac9N12E7Q9935ezM08x+t+P+/pYQJim50FK+4meH6foC8A+1aVfeq/z9uURRpQZbPvikfNayxEX2VfpgBm0vSp0qdjqciphEX5m5ZUGmlar0AQVQvjWY8hfW7Ju8h+Wx9SsaA66cvmR0l8+3ltyCsH5ASXnkOs0ka1RiCo3/wP3LrJ6qKD+q3sW4ENitUyW/XzyjDe9t/5++lGJDUhXs5Rh/YK6PvLk4y49d2cFSvQjU/omqONjzrOPDzTh53CNZuHkiDe9s2CyV0tTysQ2GFAopQcuKentYybz58SmGpEBkEeX+xpeEDz9Bn13QKcmUCqxx5gnz6kNUt+FJF7nUMxsc/XrNFCPH2UnXbSyzNtwfPW6KrM1AJGOJSQOUGGfG/R3OefZ3t+x3B4Z+oDMG0w2sn79gRpohKm3pL58xrQbsdAAX0eoI80TcH9C9NFkchhWBgFaRrotsDPTzPVpZ1l3P9umKV4ee26PCKcccPmDwOwbjUGEm+rk4X8SAbA1H+c1k7NJ0Xz5nj9i1yW+uqiGY9mZ2ntk5/P2B/ei5OUw4N/Pu+o7zteWshxeX57y9PvL+7shhvmMM/w4/O8YxcHO75/b2lnfff89xY5jdiI4B4szF+YquM8xzxKrAxWZgu+pYD5a98+zczB4YtcFRj0PKTyxkiKJgntWGF5meKo0Xp12ZXyvvY3lDTKD6X+VOwjFkrbOXsY6hXf/wQwTcXI9lGcIp7edT2ugwseFJDU/LQYyc8dtmH9V/IWHihTLOhVszNtiDwIPmA7Rsqa5KNgCElrKji+rAzPpoGr8qRLg0QGsgJsFeqcoXljymXaSljDnl16dbnL93cWJU2vNH116VMZ9+t59npt0OdxzRIaBSpspyWA/lWyWZJHuVwnQ93fYM1a/xNPtHs+/p97xvWcaeBptbZ/2pHKy/572pK1EcUu196fXcGyLEuKDdPI3lzxO6ac6HWug1yZmbHSUnz849GrQxtDuas/uzw1s3jYKFZJRk6qkaLPDJ4Rk1xRElo8r6lmqwzk3a5qXcFydfBdrQypRM5eKMgeQRfKhdeJ+cI23AJ1Y+Q7IvFBC1gd7ym7sjH2mDDZHRz7jgcMGhlZN5+ZnD3jEeDgKbpTTB+bKO8zSWzti993x0HHm9WpETPQgKTOZ5LIzh7AxXpTMriDIdCtZ2CbKEeDLbuv4ZM7o8tx592U9UqW4gVp00MffygeYJ5ZwpteSl2UbLTdG0aeB6sr5KVswyzaj0VcvvqxSQdS8aiZB5auZ7p3pSzDV7dUUy/4qkwMmSjzUchxhCbS5WbP1Y1kUpleyH0KyNOFSyUy3rhJWH5uCT6FFRa9CKKTdMS05Yn9YzO7pI8xYbIJY9q+PQYEzS82pgrexnWRL5VPChYDungaX4xWO66DKwmff49PoheXp6hYwXGyLKJn4aQkNPulZxLJT3WvsYWdJ6THqWyk1skgjL2MNZT8j2EpAaMS/nmQ5U+c6Y5xUiYMpnIjKHeTqC9wQ/pwrYWYIsiYfoQr0pOSV6BMNZFjFERVBACGldpCm4BEA0WqezGWNtfpXkcyTtdXYit3MJMsaMjyxQGg7lHNo50CNOd0zGYIwVJ6zSkonZDWhrcd7QJmplblqTVxQxSkaqBNLEcZgz/PNSGqOxfYexqTeE+gEC+k+4Hn9altWkPRDnsYsRd5xSvyOFVYbD0TH0lq439EPH9kwcyNv1is16xTo3Z7epQtoYVHJNRmKVZSnIV0F64iIAlRNadOoxQLYJlaq0BuIGjArpuZacuYntxUJDAedGXPSp8Zw46Utz4egJYSJOjuAdwQkkYwydJImhcIlfRQN6ENAd/aZWu5xefyDO2KUAUC3o0YIUkmKhBF+jNT6W6lU6kKpVuqM4PptHzsDeBb6/veMvf/kL/vinf4vLF4b1sKW7XPN3/uRLXr96DQF++9pxDLfyLKVRytDZnrNhy49efMLnH3/Gz778GT/74idsjCL6if3ujtvba169e8PX333LL77+NX/17beMIeC0CKyoE66dPLZQdy4M10pJ1KVlqHkKWfiq+ODAZHDyTIg+dStsr5gcr6G8F4tAct6hY/0eo2XNgz8y7QNhnggBXn78kQA5Dx3Hw5Gb4PCTATeijRMG6lxqCqBYr9eM44SbHVp5VCoN6oxl1fes12tMwkAJMaKjT6UXUsastU0HrtJEl+hlsJbN0LEdJCq1Gnr6vq9OvjbCUtqJLq+ohLFuunNWeoVBolSOGaUtSolgP3JAKV8UujkzSrsmhsg4jeyPI5fbZ/RGYZlQ9h3bC+jiRPQz3knDs9lrcGCiYmMGnqzWnHVryRwJix0v+0+yDkVRPiUM2ffZzdzd3zFNI7obqkLsPcNaGGPfdxClY+/u/sDu7pZxf08IM9bqBDSenLFGy3clLButbKGX3DxLKYGbMLbDB8GbC0E68xpjU+dRRW7A1mZXGWOkk3CaS8aPLBmXp/ulVC3HSZfWWiJZ5AzYlD2rsmGSn/NYZnTMukVa3qWzWM5MrOxquSNUNSY9JxnhqqHVxxWyE2U38b3WYfhDPsr28zXjtMnoanhrfqm8ko3hhcP5VPlvTQQWCnDGjMuZaIulOKHZ+t7JGqSH6ZMbq4KbFOPyQh1NNjrzGmXYtpgVsnJffXJ2irQGQHbupMknWlmOv8iRZihKPywNJhm+vnEa50ZEZcJ5zdLcs0IYy/crVFTMP/0ZdnOG0RarE36e3jJ3z/Crl2w7y1Oz49I4Vjaie8t4cNwdPLvjhAJ813EYQUXDdrMicJTc4uDxbsJaTXQj427P7Tijrq55+uJjzs4v2G43bM/PmO7vwHRYO6A3Z6nUaMZi6XTHftzhfYRVoNsoVl3P/bhHWY3tDYO1uOMdl0Fxpgc+OOs4GzTf3kZuVI9Tz1D6QNd5mHf4/TUxTGIgxUjOEqiO2Ux7sShTsj+BBwdFlSWvP9NeeyfPnceJw+g4zJH7u3tef3/Fqofzleann3/K++uJV+/veHN1y8+/fkNve6bJMU0TYRr56utvsDaidMR2Hd/89lusNTjnubnZ4eYJo6AbOkxnWMVIP43gPPMim6mlB4pinQtOddNM4tRYb/Vvlc9BbGj/ZFmygVUcr0Qp51MqycAEdbP8RHv8Ktd7xFBs+VnIZ7jcv3xAy7eE72VwnnyzKln2xV4ipoYgsfwtJlWFX1jYT1Ey5UJ6phzzEziFtE6qLGA2uitZVZ5eOWk9u5CDYEu+oyDhwXmf9lElwaAUSuVmHum7TtjmY6JvOb/Tzc+VDYmPKZYZqOm+RlqV5kEyV1nkeTwy3u/wx6MYvykQXeYUl3KrkoE8Oe+hth12taY7O8MpjSuOqTyeJT2DOEyyjKpTq7pCDXI2dNZkbLZX+/fDdI0U3kg8uu2YLlk2+RmyOoVnl4fG8vfDfzrtRZIzUaq9KmxBapq7cMbWuebvKNVC2Ym0kHn1nizLrBXM66LRx1h4STbsM2Zz1l9jBBUDMXpiyE6onGmrUiZRPm85uWWx/ERUyeaq8jVDIYAKFLiDYDR6NfDV9TVbFJcJqsC5GacmtJI+Cj54wijNU6ZxZLs9l6q9IM6J8XCQdVSKtQ98chh53Q/4bBMlOyKfB5exvBEnlXOOrEtkvjHPkBscKUUphW4mWvYjZ2I+4Gn5T5XhlWLRKclnTVEzY7NDqNUlYy1nbqlNHDLijDX5mSoHHCicu2U/Wf4JrUZyold5j+b8KqqDOVYeUh4R8tk9OU1Fd36YUavLo1XSQyOHw0HkeC7v93UM0hNCMc3SRFjYgkB9BJrqr4K3Wb8thCi0iziHgnMVF5zW0a0w6fOBuoehMPz0LdoItE4thUj8k0IzIDqbHLeQcH4pul4ITWOxtPDtOB463U+EwH/sFXLWb866rIFXUAWLWZ9sXJ5NbthdZqXSM4JsQm7FI/wiqcypz0uBKY8RrRIOcwSUbgLmZbkKXyyVI0nOu+BxbuS4u0PHgCbgQ6rUTYQbi+xMek6M4BpM2Fhh4yKkMvO6B1rLJDLtZfiw8uEixavDNp/XdukCSDPFmNYgVefMWaYY6fOgAduv6IY13WoNSmNtn2AMrGAfJwe+Sic4JN7ig0+47XOCkvHiG9IC+yeNYe1jKsL/b1cJq0bwsVYoTHiO8wx7oQ2jNcPKsuoM5+s152dbnpyfs16vWQ2a1WDYrtcMnWlsMtUw4CQXY5MhH2NJEosxgs5B+0a+hYhWoYxRdjjkY55o3BF87n+kmeeJeT6S9QyDkX4XCsAR/ISeVaKhBK3iJYMarYm2Q60lw9euemxnUV9//YNr+AfijBUFIyq16BZLZME0YmLi1cMdk8KUlJ5UxhBCxFhTlFyAmB281QJAcjgVV8eJf/+bb/ji5/+Gv2U8z158xLq/4PPnZ/x3/9U/4ZOPf8S/+ot/x7/+xb9BzY5Od5wNaz7+6CP+0d/7u/zJjz/no+fP6HuDG+8Yx5nj4cC79+/4i69+yb/565/z6vo9N8cjQavkiE1MAYqRIAc9FgMsoDCqijGUIveUW1BVEvByl2rKuRKzeyQ1OjNBawxDPxBCwKpcqieKjiRv6GJgRRUI0UGQBl23V455nnjx8jkvP3zKn/7sU/6fv/DsbnvcdESHIyYeGcNBiFQp7u7uMbZjvdVY16OVOIqtlhID2wvWWwB8DOx2O8Zppl+teNL3TOPIeNxL6rnWWGvYrtb0naUzil6LU7Z4t1XOIrApszU5Avkh0GuRMoPq2JhVAVm3umPV9wXfdNX3ifYkeuWdo+s6fPT44JjCkckfWG1eoNwM0x3Pzm/49NLTqxlSh3D5Rs3tqDDvNNf3Tzkb1qz7tTgSk+JFzM65aoyqmBWRZCiQ6UqmMY4j11dXeD8zq4jGlDG/ePmSJ08uGYaOkGAw7u9vub25wrsJj0MH6WLbm45uc8bkU5Os7PQolnGlt/xTK831zXvGcZ8aNyjQKmVuVCVG566SMTJNI7ObS1mQOGf9grbzpbTgDIUpYKwp0cUg6NzyzAyAnp0SydDO2UnVYKIoB/n3PI9sHJLOpmpvSApEQznl/6dnrTwnK+bNWj3qEEAtjLCFY+XBs6uRWr9FnmOSJitO/erQAB5LDAMewpu0xoBSqiqlJ41VMgB/NQLUcjkWc017GpvsKNo1rCutmrEoY6rQjTWPozU+4uKv9lo6tfO6FuzWWPc3K2H59Wx7FuTkpHSW31n+akpmgCrBAqWavS9DrFjBMdNYAIXG6p5OWymzRDHTc+if4YbnmP6cLy8iL+dbnvaRi4stkw94ZbkaFa9uAkfn6fo9a6s4Ww2ofqA3lhhGxnHkuL/jydNnUgroZw67a+bpnl1vhYfFwHD2IcPzF/TnTwg+cNSSST8eJszsOd+eM88T24tLjrsd119/Q7fe0F1usFqh5sBuOrC+OJNqgckz3r/mJ3R89vIp93HD67uO11eOMUSU2mNYEY9vUswnYVarjGUpRqtSggHu1VxYkGTZ6MWGNC6mBSUEHzjsJsLBcb7ecnl2xrMnF7zWisN+ZD9HMB23cc3vbq94f+84OMt6fc75h5/TDSu8m7n67lf85W9eczjcY7Thg+cv2f3Fr3j27Am7w5Hffvuay6fPeX9/YHaO/fHAFAKHecKv17BelfOkdO6GnvhNbgyTHWzFgM7nvXHCFlUg01E6iadMjcq1ss+xngUSxqOYp0S95CmnBmJjTPLY++3zm/sWhqdaHqPMtzzVMVb8PkrKw0jNPmMQR0pejwyvkgMhJsmR0jCsyCmhhxqwasaY6ajoWMsxZodUHo+8Vp8ghh9k5TxfIUgZq0t6QovN26T4P6KT1AVcVDu19z7iWCly7hHe9EOXQiWc0kgIM7vr97jdHXGaBMNTNTIpj+7EWRorQZGRLfvzS7qnTzDnF8iO1cA4Pha5XCaqeOiQLjIwOchjvf/3ZYrlz/5gxYWiKY2mzDE3H8pUmY06wR1uP9waicuQYs7M1alBXoygO132vWavJsegF13HpIam+b7ihE3lz6g6J6O1YPSnSnuNZt2vMKalzZxxFlOihedw3En2nFJ0XV/2TJosVWNaxL1mtVoxjqNkZ3kpF65zrPfW3xOX0bGoicJfNBiFWa9Zv3zO+P5KMha9Y/SeaX3EmyMhWHyGnPCe437P/d0dz59/wCFG5mnCTTP317foEOmVpVcdUww4Ar7wuJRdnDApdeOMFeoRXTDTU3bQVuepOGyGYZCGdDGpv5nvFJuy6pxVb1yy3zYbseL11ptKJneofN1THUr57AltKGJsMKMrFcrax6YagVgztkNusJu1m8zL1ILWMuZwSYyqtwLJpspytYyfEmDwsfYISSbVgkBU+d4shxSkoES2/aVJZy09jlGShECyyRfrW3h5Y/fFyGGckpoVKYKEFHzKzYTK+qVz1grGJChzM2SC9IfxZVKU9St2mRJ5M4W57EmzQWl96+cqb2ply1Km/iD/ar5ffjYyuzhkKWODhAeLLmPWRipYYwi4hIFtGl7TPiOfiyIF0vveu8WYVWoCKPOrvTQiKWgWZazZDxFiwM9HpkkaX4d5FCgAnfWc7Eit+Od+UTERJQM2ZghGeU8yGeuZq2M3RKMTbiniM2m3SYu9lcvgZfkSsTZnOjcmL5y8ZNDH1Fg44MKE8qAPI9rco7TBdj19v6If1qw224QLlAFwq1wJzkmlmJ+ZjnvJitWUKhWlFLbrGDZrzJWqAec/kCsS8cRSze6dZ9p57ohc3RzozTXr1SpVNSu2646PXl7wZLtlu96wXq3Zbtao3hKVTXaA8K6aXqgKHnAkCpa1mxtsZLky+ntzFNIgA94JFIrWkoCWYoE4N5N5SyQwjzOGHrRH6YDpOiKaft2zvrxAK5i8Jw4D3cvnrDrL9uwM3UnimvrX//YH1+oPwhkbicyxgtCHmCOOAkSeFeqMnZFFjCihEceURS+oWCC3SvfswkQSlktjqHgUE4pbF/hn//JfMbmZL37yN/jwo88JDDxZaf7en3zBT//4C/7H/f+An0a2veVs1bHdGDrtsQpi3OOPgbub93z3/Wu+efWKn3/1G371/XfcupkpBrxR2Sop4wISEcmfRiVcmnzAC8PPakPquFyYQhXkmXkWMds4cYJfGh756rqe9WYDWYjr1O07va91xcCJkdK8JuCwjEy7K965kcPdHZ989iF/9iefcX19z9u3N7x5+47Dfs/kZryfAIWPgb4TvNJuveZ42Av4c2exfSdCNARub2+5vbvlcNzTdb1kpWoBXX56+YTeGqJzjIc9m0GzWa8Em0WpBpsnh7Sz0iD81AePSoDND2hRKYJWjPOIiSrhiwQUhs3qQw77A7vDPXMYpdO40gmDyHM4jIxErNX0Xc/xcJAD7R3Bj3RWozmio5OSipTxhdI4Dzf3gdm/YJo8znkYSJhsVWGIiOC7ub5mmiaePn3Gar0q+y1STuPCzPGw4+7mPSqMeOdAW4zuidFwefGEYUif8wG04ubqiqt374jzjFYRbZV0EbWRJ5fnvHnzvoCJ6zSOcuxKJoE4vJybub+7ghDorDQ880Ho26esBq01M1KORpSo0npYC1SG93jni1CtjT3kChFcMtaddygn8/fZWUNSTNO5yXg/xpxkDZzuf0zlS1W8Uk9U/WDN0orNZ+tZzT8fU6Jy5lU18H+PsUhmFw8difnnMoM2ZaalNc0BaoMqkd3YzCs8whRCwt55oAhGSglYzQptBhlT9LgxMls9vp1hUV+0NOsLDZ3Hsn+U5zy2hkqpghcoa5ExNZcO3vqUU6O9Zjo1D5E7M00m/mmoxq0qpX4sFLj2m06ztAo9pqYKclJTRlIuqVURHyFcXuL/yX/L+uxMwOExwIpx+Jxp+2Ps6gmX5sj27i3bLRjbM6dAWt9LRcDQeQ4ePvjwJeF4h3YjbhrpL3qi96zsGeeXFxAjd7e3KQMlMgxwc/Ut03wgBsc7bek2KzabNf12RYwaNXu6fsAdD7y7es+zF89xEaLp2F4+4eMff863v/ma4+0eZTvOXr7gbrcjRDGiNpeXKKW4u32HGme2aM4Hz3vf8z6ueD9/QNi8xEZHP18zuCvO2Dd8XYlTRGtQgt0eY0xZ/Ms0JglYVTy48k6U8t+ffPEFLy+eYGLg+t33ME3EWSox7ufIX/3V16ClouPs7JyXzz9h1lscBmU7nrz8nOP9K44YjuOR3769Zp4990oMi1uveHl2wdOnW+Z5xux7ZjR3r18TpoAyEbPSovwnw7cG3SIxKnRsg1b5fxIaymXILR0XmmsMxPbKxkouf67OksRLok5Zcc1Zjsm4aPAuq4PqpOmXppy/ReZk6WZfXzmVwaWBSPZoKMnQMzpnSsTqWE0CMb+OMaA0xtQmJblrce1UnLPkBKOsON+0XpzV/FzvPcpUA7c1nsVRZdE6N5fwtV9Bc2WHmDG5gagEA2JIXZVD4yxBUZMIhKe2aw40eLOxbnYuI0+ZZqefecDlk6O2OsXlPAXEIefmifH2ijiPSPPYh/N33i/3t1lf0SU1qu/Q52eE9YZJmQKzlHFECz00TFSTnEBRdLXlsGORFTmYeiqDT+VpkYnltfzzofELBtUMqD5anfyr19KhsgxmZnvmVL4/KtNQKRMqFow7a604B3NlXHJIaKPojGHVDTjvUuWbQmmB57Ja9CwXmiYmUWSjNYrVaijY0mmwMgINKqhiO4kPSzpGgyqNU4yVJlemNMyE7WbDlM9X+tlpS3YCe58VHnGSbC7Ouek71OQkow+BKpjjhI0jJso8dVAcdnvevXnLZ3/0BbaTsUujYY/tBiymYJIWZ0RyeBstnbLzuV/sgtJFlvvsrElVDfkkxxiZXU6eEH4pOKXyHaqhk0qL1Tn/H5PxePp69iHoBV/I9wrvr2fh4bMWNiDiaEgzfnDV59bzW3licgqF8ICvkSo12oat2XGs0l6o5LDO+Kw056nCb6hq3EDl6aVqVM6oz5tbxruYRTrnQWSFsM6a8BIEbzNDQS0/Wef+YC1JX6mTA1hrogdllt+vjQadMo5zn4CM7RspgRdBs1syvMqb6iJk5+d/KND0cLzSxGt2UsmYM2VzAFJrgwsBFRRElRqLZtlN+T0m7OeStVoSf+TK9JTpvzruZV5aa9HX0geKfG3kaKbfEAJKK47HHdHP4L38I2Vop12ISdfIerzO/WcSrAgKXPDFCRpB4HWSky56jzYpg9R7DtNYeJFOEIR5DUNy7Gb8b53koxCzIzdCzEG1mkne7G2iW601Ya5VBbnKCaUxtme13qJNj7G2BGmJCm1T5WFKjvPeFaKLbsaaDmMMnTKcrbYYpXCPOXn+AK4FtFVaIpeylUe/S3SkMDeK797dsOp6NsOW7XrN5XbDk2eXPH/ynNWqp7OavtcYJcGqqGQ9nfeFF/kozTWLXYzsc6a/DPMSQq3oVSlgKvJNY+0K2xvG48g8zyXrOc5zkouKqAPKdGjvUNPMYRxZd2u6ZzY5iIXpRSVwj+g/dJiCSHKWxNL/PB+AIMjFNUM0JszYUDPFYqxGbnlkaexSX84lClU5irjEYDyBb+8O/J8//2tuDxN/xzlePvsQa2ejiq8AACAASURBVM+5XJ9xeb7l6dAjmTqeGGbm/S0Exxg9bh7Z3d3x9e++4Tdv3/Dq+orX1zfczjNOkTDrTsRZMXZUzcROylbr1sl4RVEGX3BE0mQo6n/MUWiZe8bfLJmtjeAO40z0HkIqhQkxgXGL4dP3PdPxiEecMzoBYWdVRwVRxq2RTFDnvaRhh8hq6Hnx4pL31+9xs1+UPYQI0zTjQ2ToO9YrcaJaYzDWEmLg/vaWu7tb9vsd4vb1opTpyBQCt25O3VYjmsAaaQghhjmlRCNnV8bYKrKnyvfyKspb6pbrg2N2M5pOMlv8jPMzHp86u4pS0XeWoMHNI/PsmdyM7TqsEUzA4EPptkyU0n0XItoYcSzOMB412q/QwYjwC5E2mptltUK6BUZbm6QtySpIx8nxwLi/QwVHVAJHoULE2K00QECaZgXvwEeOhx3Hwz0REbRTwp4ctWTozvNMzrbJymA26lSMJVot945YrdGDKM6zn0v8YGH8p7IThTj+V6sVx/Eo40plJfn9FlhA9iYx0ux+y89JvKA1vXJJ/cIjk8dAzrBv+EVW3GMsmY3xNF2n2ZPFS43CcXpza9ypbPX/B642ayievHbauTw75GPDExZfUaBb0l2qPQkymbwW5Xn5ESdGRZ56yVJNynmbSZv8EMU4INallb+zO3ihqZM/kfenfn0zBmop0nKpl+tejfc8w/jw3jQuLcRd1zm9V5TjMoRifT1Q7rOymH8vicStAp6fW/iRZHDHjz8hfvpj7NkZnZLGCoEer8/xqw/punOerTu+uAh8gMLNe8YJzHpNPwyYaFgPHet+5O3VDfN4jvZeSlBDxE2e6bBjPB6YpomXL1+w3mxTlqFncke66FA45vGW63cRu1uz6weGzZaLJ8+wGLr1/8fcm8Rat2TpQd+KiL33ae7979+8NvO9zCyXyy4ZjGXJAgkhgRmAYWJ5whRGHjG3x4w8ZYSoGYxgZOEBSFhIWCALhIVoLKgSBZXlzHz5mr+7zTlnNxGxGKy1ImKfc/73slSyVPvpf/fec3YTO2LF6te39nDMgukVOhzevYMjYPfsDm9fv8X8eEC/2WDYbnE6POH+6RF+M2DY7hCHAcH30njFM/I844ZO8GHBvtvi7uYWf/TocJwjEi3w/CAVAuYgyMCSFp1eM1S5MVzbpVAFWnmUzbUjwiZ02HcdkBOWuGCJEcNmg3FasCwLYpzBLJkHJSOQGHfPdzhOM47HGaAkTXtcQNf1GEKHxwPj6Thjnmek7PD6zXs8PT5I1hVnbG9uEUKPhYE0LeAQQJ0rRo0xqdINmYxmL43W1rhpcTILna4IuRrMBZoDZohWci50uSJWXPm7ZvwbJr85xs15YPz+fN9WvlKNf/uyyBW2XWNNnLS8WgfrfNBzNTWUKhaeGVhsz8j1Xe04d8Kej7PlDdUBsOaBZ/kW5Vc+v1C/sDGtWIaOX1bNgciqn8zhnVYZalwB+yqDZXlHJsmsL8+khgSI1uNaras5YiJyjEinEenpSXiHvmtMqaHR5srzOVGdM4SA7fM7hJsd0HeGxKf0xYU4uDS5WmfnmZZmWXYXz9X/t7T6fUHNshrW5FKURVl31+wb/X8u47AxiWPDGgUSYS0nUVe7OLXIiczlXN5Nkhk06Kt0b84ANjmq+9MahxT9BeL4cRAHSS60L38TQyGJda9ojDOrrlVk6Vm1XJXZ4pDlXGna9lDho+RALFmLlZAbh6HZOZwRU25KwAHm2tjI9wF+v8VX8wOmuOBL3+MUZ2zjjI46dCQdyfvQwbHDMi5Y5oi+70H9BrEfkWLCi49e4f5wwsM0gtIo9HemPxRdsj3WW7PoEU6bRhp8mwRdSoYPRL5nnaOGn62y4bmw63VAqlzRUmQZW8ve26A2VnNoNFQDDxcZlWgC2rq2tGZ09eW50oQ5XbvQSTYxBO7M7l0rB+Ra7xy6IGnZS1yafbCWw67sX+M7ut9aMWMslOzezQLZu6PZu1cO0r4wRCKrTT80KIm6VjoGbuesstOVbusAUgxKQ7cz56bRRt/3sIZAy7yAM6rdUNJDKs+QYkderRu3th6qzvkbH6onzPOMaRqlOVJuphu1AZrZXzHVzGN5F1/oyZqklyz3BrrIYAeIJdDiu7UryeR7ebecVWQZD6Hm/TXTXZt0kdrrBnfBYOXZluSg/WRSk4Wq+7zY+jBYHUbJFWVCjsl8pGWcCQyX1xRb9xZKkzODDMmWhKTnS9WnUz4r+LTtWkuFq6VCa2VpYrnvMmJcRhAFqeZ2hiPr0Q8CY+AsI7/h9Zyo8F+GJGF4kkTDa6kovxH5XNiR/xwP24sghbcQJ7X0uZJkuMME3B8nvHt4wv7+Ad/cvMd+u8Vus8HNzRbb/YCu79B1Ht6rhLIAT84FzoS4CRiQNgg2fZJZm5oCrLCTrPCGor86uBDQkSTmeedKogCxwGcQZxwe32Aan3CKGZ0D4AnsJUCR1JdTKjo/cPzZcMYCldmyZXhWI4tzahSiRmAV/aBG5IxBxpgUCLhqx4SKjWUKg6nTDowpZsxffYPjPMFTAn4249mLH2G7l65wxBPICx7oYTzg/v1r8DJjnGccTgd89/o7/OGv/hm+erjHwzxhZNYIk3HVKqDZftGjZRA23qwvmaMowcgs3UctQ6V6tUz6KLNIkp2SKwqRMBVjSow8L0KMyXBPk5T2kBDQ0A+I86zMBZeOKJ1WyXKUf+/eCHbTi1cv4bw2byql7fUFU84gjVBuNtIshjRFP6WEx6dHnMaxZO/knMWZyBkcMxYW91vwHpuhAyPICrIYgzGJQuvgyqaqnd1J8Gxo7cSq60DofECnzQtsfskBOcfiFGCIM5CcYvA4gqUexrQg5oxdv1W6VbyaYmAJ3ENK0rGYMyEmQpwdNu4Ggxvg0YReG8eOrKXDMAzouoAQqjO21S3jMmOeTpinE4iTCGXOyEQYNoIVK/MiWRPLMisu1wkqipAUawkgRAHSKmOo7J7LZpSpIhWaQAgeOYtCssSlDHBF61wZ/yoSr0661rlykQFTSr1M6qNRror2VpVSUNkq5Uu9l6PKsNvv7PeW35Tnm7ehoR37oDXUzsde18r4Fl+cd5nN06jvzTiclslczI/+ayOS1FBIwbSqtwJQlXZrVLOy2ZqxtIZCzajji/PY6EPnipuJNEXsfBS0/nNlhJAxs7P5wkoJKaZYnQwAFjal5p6r+zBwrsaYYdCOwd6/SBBenx9CUEOuGf+5gq/jamnTAaBXn4C++Bl65xRz0SO7DebuBfLmFZ5tNvhkS/hin/CcA948AktOmOZFOn+SRIA3fYBHBNKMjjJ6D3hKmEfBMr9//x5v375D33e4vdmjGzYYtnuM9wt2N1sE34GIMR3eY5oOGMOAzTRh6Acs6NB3Hq7foLt5huwZ87JgGHqE3RZvf/ErcEwIPqDrexznUTHIO+GPOQGc4YYOnWdERNwkh01ccNsNuOl6/PxAiMwIqoRKWbrwpbwsyG9fF+OFoNiGJTN/TUtlX5Lhh4lwDc4jjiOephkxRcwxoes7+ODgIgDKGmBQAyZHxGWE4xkcD4jTA9I0IkfJ7CJy4rj1AXEZJcMtdDhNC+6fJskK9A7ZSXddlzNSZnBMqolViIXSAMTRddmL6oSyDFjjOWbAVBNzfThy4qxp9l9rp7dyRO67znhsDe51PbkZQ6qsSqeE8y1S91HDx4pDALLe5S99r6xllHZdcSgDyNnmQcvLm6yu1ihsJg8EgvProFNhTZB3BtWAmRmlVT81ujzjW3UqVrpXfUXRaU1PrbxAqxFgMpSLbLRSXXtCdaLbc6tha8FS33QYvyJwdfxsq6ivLdlAaZkRDwfk01RgwjKL7lnlMVWsx5UOKjRFjhD6Httnz8DDgOx9TaCwcbK9RJPuVqigwWe8kLH1o3Mn1Plx9fPCy7UElcUQNF5faNYcEu2FqneYLnnx/DMbhVfvZ2W69fo2qFoyBU0HygyBxcglyFCXUegipghzTtmzUk5gFr055YykgeuVM1YTNcqbWQZc2fz2PihytWp/Fvw+XzP9V9bYsk3r3iaVpY4I8B5ht8Wb9w+IMeELD0xLxBxmLK5DTx1CFxCcOPviHDGeTui7DiF4DH2PoR9wc3OL7WYrDsQ4tlqOjoOaNVjrWpL9hiKfQVRKtBOqztHSQdV5cuEbBKya59jevnTE2pzWPwrZXZxYx1k+NruVKy5oy7PbG9TdXY/CK5pncnPPwo+Mf0PkpQXaK78WpxKR02aawBKb/VgV5fpsaieaV3kmdtg823685ru48lHzDBsk15/t/JkNVuj14kf5vfJTqWrITrLbpNFflbfeS/JS5ggsjGWR5wrrOuM/hX/m8iTmOm/2Dj/kC+PzeW3Y+xIXCQRvBoCrTkEmnzNr9qitNxUd1daHGZKaRVqRbCtKrW6tvIDPnP3NZJq8qLJV9yRZdre8S4xRsX0lPW71PYxzqv9GnWn2OJMIuXE2A6SNdKtMdOQULhECAaWOOUlwoyLr7GkM1mAdQ6ApqFS0kAaUTD9x6kqTCoBUdAcZo+oz6nBkSiVjGRwr9IZVvBAh+ICUt+h7afolN3JrmZ4rvnHoArzCXEn18vfTzz+P4/sCoXa09trV7yHIRTlmzGnGOC84EuPh8IR39w/Ybba43d/gxd0d7l48w36/wWbTo+9kzYKveMiFLnVsjqUSuTrMa21Z4ZlsEB4MkOGwe5AGyUMISCXopEGDnDAtI46HjFNibIcerutAIcCFgMTQ9V7v2/Pjz4QzlgHEVjFhqHKqS+YdWvbpASkXgE102TqFOU5xRucDACl/NqUiE9WSCQCkSqtlox6WCe9+9Sv88tdf4duvvsK/+Bf/Cj569Rl2Ny8QOCJxxrTMOE0jTqcj/virX+NX332Db969wXf3b/GUxKlpnRxzyeCBRNjAUt7BFqljgBiOqWRlpRiRUixR8TjOyFE2MJlTLXMBkzZhGRSLDFnOZVWuwYod2RKCRgZSiojzjI48UspwXgzFLnTYbnYY50nAo1NCu4+M/+eckJ006nKU8O1rwuuHBZE9Xr+d4HJU5yUj+B4pZfRdh912i2c3e3hIhq2DZBxM84KncYYPAdvNBvM4InPGEmcADE8etzd3kp4fAoZOOgmSkxKSnCXa55hLWjrBN2U/wuhAPc4xvoTUPHrfI7AT+vGSrT10g7BjyiCIwzvRLIDPLEJjjDM6DwjoY0LnAuZ5wjiNSMsEIobjBaQ4UFJw4RBzhxg9ED0+u/sMd7vn2HQbGINelkXHXrMotrttdVw2Cocd4/GI0+GAZZrgwcLhAJAn3N3d4dndHbquE+HsPd6/P+D49IR5HIEciyAiqLJaDEGhyawGV6OzS0mnGRwsjCumqBnEHktK6DqPnKsRY4acXJ/x/v37UmJETktxm2dUFQAlSp9y+9yKAWoqhBhAmnfkXd0Pqlh4g0BpK5ypRouF0JUDNXugBFQaZbh1yBpjb4+1snqhRZ+dJw6eUqpDqPfjqqBcO6iZt+auAKTEuzhXiiZajQjntJNlrs8w5b04zpu9s3KANQZIjVYDJYOssUjM0KlGpi08Ck2YAmhKT/vGhosniliTr9EQDDFWVRXFQNL3TyxVF2akJAvalPFZOV19crbyYlKZUsA8JbPgZn+Dpww1iqumz2dzrbNQfiM4ePJSnqpR/UQBS3iGePMlaHiGn7zy+FE/oZ8OyIPH848/wdPxiDdv3+A4RWC4wcweYdji008+xqe3AzbOwzOB4hHHhwccD0+4f3iPb775CiEQ7u5eoh+kwd/7hxP+4he/he1ugxwj3n7za5ymJ/SDR+cWvPvuKxyfJuxubrHf7XGz3yGlCZu7Z8K/idENAX3/DAsDD8cRz3/yBTaffKIKtvD7GJNuYgfa7fDpi1d4/PY7HBcJdsYJ8PM7dPNb+HhA5ljmmu7fYvc//iM8xRngLHBbAsRRgiqFNgHBjEY1f1KM4DFiYY9f3v9CDI4Q0PcDdoNUOfTdDUKQUlSv29wxIR8f8Ee//y2O44h5WbQcWDJrc044jSMYDsOwwWaQ57569Qrv7+9xGieBLng4oh86dBvpInviCF6yYmJBnLpBfmfSoI+Yp+Wd7JcmVCUZlGebnpxraKyhOW6VZ9v7FgDikp1ixuLqnlCjXpSzZv+zYibKZuUV67P9bO9AhZG7Zr+2WR1WAgiw6Hxlv2upvxpeDtUJX2RiUwUkMkQxOy+JQ84pngErW7bME3XE8nqn2htJbVXRVJtbr0uFyxw0Hghu14Bt7qsz24boVBbX60Q2VD1WHV8G4wGAQ2j0H70L1+uLHFI9mvWdU05YxiNO92+BmMBNt/Z6nfLrxM1s2Aspe/MBfn+DvN0jkb/i8DE4GZXjRW40NKlKpj+r/jHj2vQBQKA1XLP+ZXnP9oO9S+bcZL4CyGfBWJvvJkBcpUDNdjL5Ve9vzrX6Lrlk9rqVAJM1M+xVr4F1RlHnWMtuOUvwpjjEpEkqEyGzdo5WmZkzY44yZzknxJSwqC1h885oqwqhHesVo1NpssCF5FycfuWd7D4NfrK9J5dJJsA5eOphK7UsS7Ed4MTZ093s4bpQxj8vC5ZtxIwJXQaG5EHUS8LCOOPdt9+id4yhCxg6jy9/8gWmxAjOodeS3Y6dVCPamnHJkVqNN2XJ9g4kJehmR0oTWSoZU7bwFdpZ9Iak2LJGJ7a4phtU6b7W1BoVETZdhPpZzRoUWs8aDATRquN9O+8ElMy9Vke28zKzNJYpj6ncmLmBiXJqk8SE7MzJ5ovOj+Z9mLPKPaEPa77rFO7E2tJJsk9GQir6lHMSDJNqb7WHvPEqcZLFJDqjW2E6VyW9DUpVvR2Fr4DrGESvFVldeKaeYzO2WiMAWoKKAELueiQfkKhKYuvk7pwkxyyJELVc3kr2ZSzNmMvNq7N5zaLO+NVv6lXjuqIyd1GgBMjDmnl75xRegAudeO9VF27lv2nUmhBg/BlZdGnniy4NSFIUp1z5XquDVS9v5exVJRaokSx9AciLHwMs2argXApAyrUKNZFSkurOFb938E7HxRC4nWwBRB2XQRtokzcl5JpRCRT7wDJcjb8aFEGLQ2sJKDkL3B4BCL6OSRFpi6ohSSvyWEftMwFAaNOx0Gl0JBmeMYG8R+gHkMKRERIIXoN0QPBA5x3mKDi4bZzjmo/0wpl/dlz77Ieu+aHr19nQVy+qMpgB0kptJoeYE8ZllEl0wLDpQQ8O8xSx6XvsdtLLous8ut6j6wJAZl/KLJvNUaW+JR0JL6sy0Qi0BrsA4T/zvEiFMaH0IAJlaXrLEWk84e0hIXQdfNeX6i2DoeIz2KX2+DPhjCUCBmdCU4zntvsrAFFWbRqdrwwRqjflJkKZM1zopGsrFx1RrkU1zi0yagoEM4N8QAThm3HCf/1//l/4H/7gj3C73eHZbo9d5+F0Iy2ccYgJ7+YZx7RgzlGyJxWDiHWT25GZwTHDBwdvzCJpR9B5lEyqlKUjoFPYgCQ4NykmhCAbj7XU3QPCrJj1eRr9Blf3DzdMkKn8bd8RO8QlYZpmbIetjDNFcBIHnfMe280GKSfMy1LwXaz7qiiPEmWIKSGDEeHApwNSBhCf8OrVMymJnWbMkUu2aVxmHI/AbruF5TfmnHE6nQAQvO/RbzbYbvd48+Y7dL5D1w/YbXfoux7eBwQvCljfk+K5WCmXE+csWZkiUI1PXZuiMJ3RIgPOGj8lbhroAEhZmK9zADsMXS9rBsAHj812wGl8xDQvGFPEvou4f7zHPB/QYbFV040M+IHAWDAuHk+Lw1MmvNwP6Da9wBcUEHJ3xsCqgMPqN1Zll/D0cI/Dwz3SMsH5qkw7H/D5jz7H0IsT27B2Hh7e4zQeEeNSbN7KUBsDCSa4bRhUv7IzVBlYlljuIxliE7bbLYgkk9poKYSwcjoTqBgeKWftFyZO9LORyB+2XurgBqg4ME1oOi1NNHxSZsBBDRlWE0XLJVCcAPXtW+V3/RtdKNftYRkn8jsXh4HxpFXmatVgiqKTUi5R3PaZNgOG71yyHX7gYOaV0b56S+WBsQHjb65EqUBgrMoczQgo48u88nrU6REcNqMbMyDaR3HD92uwZE37VWCbPJBnJC66oI7fgbRxzspozLmZLyrKqhkNLei7fdYedr3oDLzi88yMeZr1zk02DRE+rFjL56e//m+je/4SXdfDESFig2n4HMvmC6TN5/itO48fhQM+CQv2mw738wSfPIbNFh8NW3TDFsl5TEtG5wg3H91goBkbL5UI42nCH//85zgcn+C8w89+60v89MsvsCTG+/cPeP/+AZ/9+AvsbyXYldyC568+wj5KR1FOE5bTAx7f3uN03OJ9v0EXNvjixz/G7uPPhU+lBIyzXD9NyAlIrkf0VJpWEmU4l7RhRMYyz3iaM04x4Lsj8PPDiNNhwX76NbbpHXockJ2sQcwRyzRiuX8rAU/l6Vbm2zawaCmnrAMDu37As/1z/PnPvsAv/5+f4/39PY6PRxzoiEMIWBZZP++c8H7vsBlE9tze3qHbPcOzFDEvM8bxSbAZY8S8LDgejwCAeZ4QQsB+vwOD0fcSGPbe43QakTO0o3iokAGl/JnEEHXQvd8EPppfbD8a3bV0+4MHmSl+qTiXTJtLS7EOgo2+1zS9djxyOb/5FI2pVthB+26qJl860tjKFGvDOxvv9xsHlU+vHKCoc+CIqtMJuseLZrJ2SFvwyPSq6txqefSf7vheowUozjp7CwDwvoPoUWl1vQXF2oOIijNbqqEUy30aEQ9HLIejvKM5SV3VmZtRrO6ZchY9KXRwwxZ+f4PofHV68vn1l+9c6VmaKhVHaEPnRY6ioRlaUdWHj9YR3b6BfV6c14W16DlKAyzGfYFIaoIAJWtJb+5cU14KaIDFPACF8gCIMT9NM3KOxTmW1EFWHKQkDWvbcXqt/pLApN7RO3gfynylnMq9jE7NmSwOBnFMs5dAYA1yShM8wTqmkp1u8s+SRewgcjDACRHIsZ3hgu/OEDuXvMN+t8c8bBDCKKpDSkhxRvQOkRiJN3AssF08Zbz75a+woYybZ3sMmwH90GF694RnXY9Xmx0eHh/w1+6f8H/fbvG+86ItcJ3tlvwcWYNkQk6WaWqZsBYYI7SlSFz+sTSFZptPwJEvjmznzAm2lkUth17xvdbUXTGb5rvMBZO/zVA+x1y2m9tlsayb0HgIXhN/avWZdx4CYcXaJyOVCoPagLTuQWTWBltAXJarstcyL1t4PNm/BGZqIAlRg3hY8/4VXId+u86uqzzOPkqtI5uteZTtYgBkWZetJt8EASFNmbUOpz5Kr8u5JhEA0h/j4eEeMUrVqidpYFbK1V15stD4CjKnlRnXEzd+k+PcOnHewXcBKdb3jikhLVEaBCo0oOn8xX/AEV3nQRSKfBNYR9knCQmhaYxeFG5UdYFQE4dUCy8JC9dkkicPpgByVlHWzHlzPnINZlqTQ5MHZfWsQlXtK9+s00pc8lreAGtZY/vYbCWxSaWkXprNo9gv5/ZBi3t/AU1ZtBu9q2v/rryAc8Z0GjHRDOc8NtutBBsVtxgFuiDBnI4heLg56ri+Xwsp9lOjO11ztq4+w4fv2crfa+dc1TGb+5tNR1ShFnzhP4Sh77AbNrjZ7fDs9hb77RZe+2nEyHh3f8BpnGXdHaHvA7reI3QOXe+xGwIGlWM+OIHw4BZ+RoLvBtNh/wreOhpYq76HQX5Iz4QgGMwAttsteoUSZWZkhVwMzkml/rVyAD3+TDhjAcFsVYkm4Lsm5JSYDW+EoYoKFOsBVKJwRdFgLTuCTLBFSkzQis4kxGhFEWAUPCsmgh86xInxbl7wGB/x7ekET4DX0nkiQiaHhQjJcWHWdEbg0HsaZsQ8jlgY4vBMojhHxeRRr4o4hORXcFYMUzUATBlwQZ2Peo3X5lclD8J7FSVclBFzTGFZMPyTf4zlL/9VUcJNGVPBzsQFm42cdNjtIcr2vMzg1GxSlieKQyYhLk/YbvfwPiBNE5bJSSYkHDjP6ngTTsbMWFLC6TQqIH+WbKMgOK/LPMNvNhg2W2yGjShfYZCGXuaUcQRpeNEqSwTDCix+IYIqG9+vsvcu4KbbIi4RS4qFyfcmKJgRHMH7DQJ5kHYAtezYbb9DzkBKI57vn0u5yHJo8F8JnJzgpICQ4DFOhOMETPBI5JFhTUcAIlbGWqNKrRFSd4X+YwbIYZlHxGVEbdGkmaEO6DuPGCdh5JCsgMPTE2Kc5XlOsgSkW6vcM3RBS924KNukpbRGcyIvczEmTIlvj3me1CEYSzdfUy6tMYtkeDukaAbPdZ9AXW8ZkOFFMTQCZgK3nMuCO6lOHG7pY6UXNQoAQZRu+4rqc03qrLNQL0VRdS6uL65qkj2vFXf1mmIeGg8sCohhC1YDoX3ODwrXxng8d1aWZ68cW9Uh287T+e8MyeCv3pLG4GCla3vumdPcMqUtfFxFF9V1oapIEZVtVeawZm9RcQB8rxMgNzkfRAWju3zflmKX5WHhk2frxTljnmfk5p5rJwM34ylaIQAgDBuJppJHhsfs77AMHwPbV7gdAn66X/CiYwydBzqH3dAjJcbpdMI0TngxdPAMDEGy+jkzPDt4JInIcsbT4wO2+z1un93i7u4WX331a3V6eDy/u8P+5gb3Dw/wTjK1djd3CHEvEC0xghgIHaHvHEIA4CLevvsOGR9h2GwEIuHuFYAM183wKUl824WqgjqRyY+P90jLjL4LmDPjIXd4vcz49ukJ3fyATX5AwIgWiy/+we9j+sM/wDwv6LabZo7XTsuyXDbfpCoviZJ8Wkb84uuv8Hh4wOl0xDIvwghSdZp2QcqTHBGWZcZDXHAaRyxJMoJiXLAss1bXyLO9CxKYzILdFlPC8TQiLrMah4TMSUpvHYNJsa1EmFV4AqMPM2aboMVvmsnQfHvlE5OXZ6aCGSQXUub8eVB9ydYEVgAAIABJREFU5/r3XPSt75e3zcZtzeViiFlGi6g5VS9aZdMDF44AlHtV/ojmHpeO6+qEa0Z1eQ6hOe/8/a5Pxg/x4VUp/IXxdv0+7b2Mj5jObM3eFAFbZ2FtSpkhaRTAmeEYmE8j0vEIzILxXsuT1xpHa5pVOUtwHuh2O/Q3e/hhUF2MVldw0bulGuDaOxbD/sp8taPQiVgFT9t7fZj3riYSAGofBpJALQGNI4kLhQivqSOw+3nvqoOSbGZtLzNilLLuSuJV6ZDtotmJRS6341RHWW6uYXEYie5djcicoXjX+q5tOriNW+VzZhZMXgCJtEfCwmU/rXlOu+a1OsQOscuoONYssMr6Xi1ONSAVkH3fodsOCEMPWoTXjTHBuwWeHMIyYUMewXn47HB6OiAtUZu7Mra7Hb49fo0+eNzt97i9H3BMArWVlb6JCa5phHyx9jbXVD8zlE+xE3Xdy2RA4VACjCe0fMzozZW1Pntmw+LqMCottRnitq8AaHNlKt+XDH1nep/+5MrLGCz6RK54265k8Z7vBSrr5JyvmXvc0rGepf04iAjZOaTUaGomQ/Rd2J0nk6yDalWn1XuTmdMtf9NqPDHQz8YM5fGtrQ/dSq2OC2UqUonK5ZXMVyBl36uEACcNNIsu3KwNlO/lmDHHGfZoKuuop6l+WnjwFR4kf2bUTL2qy1/lfefOLdTXliaAmlXa1K1L0M3sLc3M1EwG70QPyYnVPLoyxyoP7PkWxGuzlQGDjNLzdE2d2Wb67hlZmuI6Alhs6LRMolOr/i8AURUGgWG2qc1ZpUeCVQDZXjU6oDJeHZ2s9xVd6pquUqDz1HlpcDJZMWyNxmx87VZXLrDKZq+BEyrn18I7aoVa5R0sDTVngvShCR0cMsgHpBxLo1WjOXFonkkPFSvthzU5osqgNkBge7AGOtYaUsv2yve2h1GvqWOoNH1tzm3vlv0P8X0NXQ/vnfTJYWCcJsmMdr3AOISAcR5xPI2FDxEJdIPzhBAcdkPAi1vBmg3kBRqCgRCSBCDJeF/d35aBbferDWFlXaVfkOjlzpEGOToAtRHnsiyI8yPGeZTmkvlP6Ywlop8DeISkNkVm/mtE9BLAfwngZwB+DuDfY+Z3JLP7HwP4dwEcAfwHzPy/fu8DuCEWGGMyxkWV0zRKE+tGbfk1NZfBnBXi0bRTyvPkh21mebgHoeg6wQM5IOVFnHKKE+FykrJI5yQSGhTvVPVfzpVhG36mRXRyzkjjIgucRfFg7dC26pDrZFREAAUpXRV+pyD/jqTcWkdPAEIXVg4Fp+WJrvmM9BrKGd03v0L6y/8SMolDVLLhXHVgqFKpcr7gmfikTZqIS4kDlf8YKc0gdAge8M6UJo0sEKELvhhTIOnmeDwetTmUGJ2mtCUtl7/Z3QhGai+Ois4HLc1RxUWzA4WOJN3ce8lokg1UmYwJEMn0uGS+3nsM3SAg7DqjMu6gJc+Eznl0fQ+kLMqRSvUFGb3vEX3CQgn7fgdekmYvAEAGJ4dpdIgzoet6jAk4nAjj7MCQ6GARbk2AsBxKIpV9tpRsfzKWZUaMCypZybt75xA6D7B1EpTPx9MBOVYDTPS1iitma5Idl7JfE+bijNdRJu1wWAYkA04pSSTdOl02hpI0HtGSU+uSDrpwCvL5chWlVPYvOWqeq3PELM3zVHIyq4naKlV6cnt7rkyiGJSrWValTab2mhl/qUCt780XK6dIbFVZp/Uqr1+fizJY5LZ98wHHYxuVrtkC53c9H0P7JZV3Xl1TOp7WcV84DuwNbZ6Lgqy/FBnVznstLyRSY9nEgl7rlFeudXRVB5gL/7o2L5Zddx79XY2jMUJaJUXuh/PpA6OWC9sK4+wZRekwOnAe/PGn8H2vDhKHhIA0vAJvXqLf3OCjHeFVmLHrpbxvUX5OOYKzNJCcTgeAOnSbLXrN2l+mBczShTV0Af0wYL/f4/b2GW5ubvDz//f/A0B4/uIlnr94gb4f8PDwqA0EBvjQw7seoesBL51u97d7BNcJLAwSlvmIeT4CjhFCj77rBAOs60GBUXILNHMIOWFeTnh6fEBaJjy7uUUOHR4i4WGOOM1P2KR36PkEhwhrWETffI34R3+I+Z/9HLkN9JhhcLZyzfSvFMqYE3Jc4GOG7z2GoROsqeDFdslZjW0r0yXJ2MoJx3HEEiNiFOienDLIe80gk+7npiuklJBjxDjNgntPmpHGCb0XzG62ttMmm4qxjTWNFPPaMjHpgqbb7CCd8brnUVUju+u5g64eDW9oFbNrZ5qx+wGe097R5l/2/znIynos66yVy9ubY71+t+bnlzyQr/6+Pq0oj80zqg66CkS1uumVg/RdL43utUFC7fkfOD7sntVgFNcxyW0bvNXVvQthyLs4fX8WTptiwnI6IZ5GaLS43MeC+SKTqcy5XQ/T6ZxDt92i2+3h+h6JqjF6TmtX2OdvdNTMQLuR7CEbSzEVVjJGpavpHc38rEeyHhXzWlZXGJRLWpMMvlSfZ/tZ7yH4whZAlc9WM2O6lq+NCMu76P2lUqZcoDJI3t/0d8EshGRDMoO84dG6MncFb58rzFM2nNkoWZHmbBP1h6rz3vhSnRoAjTPWnNplTrg4b4sk1bXyIcAPA2If8N14wisizCnCJ48uZ4S0wKUZhADnAuI8S6m18YfMODw+6ftGNaqtOYsm+HANVKz1LftX3ObicKX6iZUhl3HruljD6JUzo+HXxjZbnn3Ja9c62Lnz0R4sqqqsm2/sFj5TWo2jUqMoM9AEIm1dVD8qY2oDYVTWutBmbTWyegeTVaLXr3G+7TVsflYZkbb/7D0aR+xaA6uyzwZwTVNbzafxW7a1Na264RjNMhABIUhzZunrsea2wtPU6WJJHHaC/pKtCaCen8s8NTL6jNlVsXBNTrWy3aj0UgZcyy4Ey3isyZDBttv3Tu1fR9ZTRZybDAfHmuRGQGl82koP1V+g97D7mCwmfQhRzaaWj84kPdmn+gwCgADnO5QsVz6zM9SGc85kXsPLz3myyuySYbveJLo/KpG2/PXcIVsat+q5zpH2ian8ey09LjWsS32uaSbd7pd2jMqHbO1TXLCAIeAuDLLM/WT0SQhe8JtL5bWNqXlOtSlbv03z2ZnOZXvo2kFnNnEbmLd9dy5VV1rYuXPWZBoMAkAc+75k5zukxBjHCbOb4WlBt0SE0GGaTxjnWXowaPDBGoqH4DAPA3pP8J2Hj1SCeczA0PfYbQR7VtyFBs0jOrz50wpDb8ZtdrRTnHHvbe6FT3QhIC8R00TF3/Kh40+SGfvXmfl18/ffBfDfMfPfI6K/q3//HQD/DoDf0X//CoD/RH9+70GZGsXeXlpedD18IQ+nX5uaVQQJUK4xhcM+a7fMCivRNjnER5dZOri6zoESIS2CrQpdqJgZMVvqvmapOlKBpOKdodmQKJuAHIFjLhlGBMHZ8d5wygBrLEXOwXlS77tuOO8RQgcEr3iadolrCF2FHwzDxRhKdcaCAHczgPqABQnH+YRd3KLzAd75EtGVqF9VBp1zGPqhYYIojDFnhndATBHTLA1RyAHkWEpXOWEYpHHUvMTCpOZpxvFwQEoR3jt4F0BdrxsRAGe8eP6q0gCRKlpJcHKDh2mnpiB679F3AV0X4L018MqliZcLHch3NVO4ORx5BB+0NEMjMz7g2W6PNEfNanLYDFvEeYaDOiKZgEXwAjsK2Lgegwt4UmxfTwTPjDQFPLxOGJ8Iz5/f4e14xP0CjFNAoAHbMGhGKYCVU5NVbjHMoLVzcsNkjUbneUaMsTaGYIkq+tCh63p03oMh2c45RRwPT0i6ZqVxswldZTgWcQNaRlT3Vug6YcCaOb3EWBzny7JgGAYQOcQYJYKlSlpKERkKhD/0yFr2G1NCF7oylvVBsu4GT6J7hHLFmub12fX/SreGXVW/ojLPrfCoYtsVGgOgHUI1c5lIs6PPFY923Lz6ba32nedYtkVLZhjI74Y3Xa/6MIMvdygCZD0WbkvwzieMuF7QfFeDWLT6u1xaMLyrklQUNX1OmVO9f21qgiIHikFz9fW4qCbNR3puNb4St8rEmdbDNbt+FbFcnd4odOf1gEUArZXWcwcZwy6l+r3NAQHY7hD/1X8du2ErJTpEWLABbr+AG57jZtPjZ3cZ2zyh67bIDhjnGZgTPBFCIGx6j/fv3gDk8eLlR9gNHTJnPDzeo+88+j5gf3ODL3/6E+SUMfQ9+m6DcVqQmfGq6/Hi1UeYl4wYE5wHMC94ePgWd8+e4/bZHl2/QYozPvv8cxwfD5jnCYkz+qGHw4y0ZMRlRO63mKcFvusQugHRotW+ysHj0yMOj++RlwkdgO72Gd6dZhzGE7r4gD0/oKcFUkop9BT+53+M5Zd/jPF4xO7umcoIMRBsH7eOgJYuGCzZDEyY5wk+Mz796Dk++miH6TgiJ0Y/DFjGE06nI6Zp1AznBM619DYl4U0FY4+kq29KArfSdUGz/iskR9SKCoGRz4g5wnlxqmcH6RrNgGCN60SVcds7CA5YCSayqgyN08YuKuTb8InWEj3nPatTlNcLiSZx8BjvOGNQF/17YAr6Wj5w5rKvCYRzR5Q9/Jo/V7ZgzbITR0GjFxb+kItTcp2h0g5aA9zFObA2FqrfudUnrdzy0vC7wGqnymnOsz+uZTrZfHPz+9ow0V8vFpFA6nxsnQDFwdvMJde3g+mGtldEnmXBv0wRx9MJ4+EJeRoR9B6CrWfKmOy16pSp8rLIEOfhtjv43R7o+iLDTGdcd3smrOVjPdwV3exD88pc8YNbA712M0ch3qo31Skt+i2ANsO65jt9/1hq8oA05DPe4ImK87aVc3VQvOJb9i6mrxd6ogoJwOAGlknWMAm2ltIoMC1T0a2QGYhQPVgy+L3zkKooQPpG1OB4SglxEaW/77uCj0iq41oXatsXqXmflDKyYj4Wx5neMyvG4+rIDHYeNPR4CB7fnI74N7c7LFFKqRdkzHlCSATvBnQkFWXLNEmFBjkcH59w//49xmXCFBfMUXpMpJyQkyuYyKVB3rl+VjYKF7gjo1NSTDrTJWzOrZkat5us8I4mY/WqHCqLXwjwIgjXfE9+7QqxrHeZYi7bj1QHsa24ygCXjYzqlD5T9JRhWGAfkMyumtHXvEJ5LmszJGMUUNsEjbMVpWpEbMRc3lP2hSv3MlzkFdtmlHLV+j6V55zLD0cEzk6hCYy7c5FJtvlzSlX3I4fbm1scDgfkeUZ1m7e6HoFCdcYCfNZ87Jw/GK9v+XP9zuSMwRXY2tl7Fvlr8qblr2frV2ms+Sy342OxiyDl3w5AcGLne+9BivkuGNoEXwLDlQ+2+n6BgyqwUNWZZ7LFk1s5gO273EyGAMoZLTPgPHw3qB+FkJapwfQm3Z+u2AMl6NTcv86JjJqAhr/aeOq+kLm9VDpWfoGyhSSIJvjlXLLGOcvvpgvI7ncafAcMS1p0oDOdy2TCGZQG4MDUOIKZkdICogws4vtg2iiBARQ8uo6w3W4xR9ET2UrlM6OlDVuU1glb1rgVjC3h6u8r+LaGJq4l/7ThnXJrun4uNb8QSB2wFSNdZB+pnAL0zQCeQaeT0kJcQVSAAWjz+OgDPHmMEwMPE1KKGKcRy5Lw9HTEs5sbfPLxS/zo84+xxIS4CC6sqNkOJcBCEcxuRdOu6ODa+JHFFui8V9goYDtssMwTUo6rhuvnx58GpuBvAvg39Pf/DMB/D3HG/k0A/znLrP9PRPSciD5n5l9/790a7MP6svXrNUld/pYhG4+5EkLVBFUW0RoqVBrUmMIm3TMVNQhMHuQBv/WA88g8gmNUHKiM2iMUyIsUljtAnZBOBQ3kYSmVrneC5eLVHmFQR9jt99WZ5Bx86JXjoDQVslJGIs0Mtk0OYTBLlhIHUyasBN2YoDX9sol12pUkpohxHnGaj+BuQLBOz66ShsApVNyMErXXnSavRhj6Hi55xb5i3Ox26niLcI7Q9706dKWR1+l0wrv377HM0oglZ0LYdvj0k08AMGJciqHZdR0cGYYHg9iXNHHAQOwZ3gN9v2m6KldcmRgFwzSEXpyxhmHZHDmnghk4L7NgjLqAIfQIUCM4szgiloi+68sihRDEia90NscJS5wAJMEeZGAYtuj6gCUwHN8gjjOYPQJtsNvc4Nn2VkpY5ckwZ1BhQHp0XQfvHaZJnscMi12Ac8SsWCW16YODDwO6fof97XOQRiGRpYHbMp10nHXfmcNdugkCKc2lBLfvOmXmlaV77xEXUnyqBJADdU4a32CG94JRXBxvqGXvJWssM2KULLQCuK/3pu6spFGDHcSSwe11RQ3bpxyNgwCOQC3dYBUzvzS7aP2pldtAn8PFGL12VEeR7cm6Z1p1r7k/0aorr/DDViluheSHnvtDh11Ylf+Wv5Jfl9eZIAXT6uprx9q2ViF+oSi151eDtv3b3rWef87z22h48x5/gjlZZQqvBnXxCkWR4mbuiqLxPfcvRm5efVF+xt/+XeR/4a9iG3Yg9MjskWiLtPsR0L/Aj286fL6N+JRGPLvZIULKX3ofBBd9mbAZeuz3O9xEaSTV91726jLBISJ4j6DG+LO7j3A8PGIcJzzc/xKJM37ysz+HH33xJW7vXuB4OOL927fY72/Q3wQ8vXuHP/in/xQff/oxPvrkI7x8fovbZ8+wuQFCHJByxs3tHYgCmAViaJ5OiMsMwoCsZWcMB0SHuCy4f/ca7779Cre7DcJ2hyU5fH2/4PX791iOb7FPDxg8g9QJl8GInPDV119heXyEIyCwYL9Tw//NiCxyrqwlF3kV84K4zNj4Dl9++hleDntsNhsMwwa7/Q3iPGGaRiyLYF4fjkecxlEi6SljPI4YTyeM0wnLPEtnVeuvotlk03jAos6OLgiO5zLPYHaAYjmSQk1QUD7IgGB7AOvMRmXuhSeLchqcr6/XkuwVYrQgR2NZoGrIDT2uDEKlcW5Kq7m5H67wAWVoVx1sZly679ug9buaGaIx7dXGbg3l9tMavLy+J620UIVlAzNiQfTM1cBzRIVf27+cr0EcXD6zNky6cl4zf5Vzfcik/9DbEK6sgFynimepLClzrp+zGDzW5oMcwWdCPDwB0wwXkxhB6lDL2mSnfW9zQIpTqgZMhs0Gvu8F0w4sAcvWqC5j/6DQLHNEZf6hhn/7fhdvXWSxnZebyp6iT7ey3lXdw+6wmlKyUVMtsS8OFLeaB8OPS5qRmTNjiSOcE8iYEAK8JzXQzCitZcnWtTt4G0/NUMxgZGpaVBKKc1buBcyKzw8AOeWSTGB6MLRdLLiFIZL/tY48Fzy60ItD0jV47roFxEkkeU9qsDXTVctjZdtIwkrXdUAXypRye74jDLsttvsd5q7CfgXnsOkH0JLhmaQBJSSh5O2bNwidF0N7SZhPIw6HAyIStrsBmynDZ48CiQSrUqw6jA6vOM8JALLQiGQPVqN+rR/KJEhX7hqccTYVZ2Sdr9Bq+4kFDHLjNDH6bm0b+yymagfCdFGzJZtnG+xbaX5n66f70TXOttTYheVduRl7KztUJlhz18IRzJOtD5L/yxyab2tVuk6SvGF7QZpWy9yuOL1m6HPZmmVFV3NKMH1YjWZu55IrnZPuWcX+9N5jmWd10Npu16auhpPqRCd2nUfoPOKkwzirOD4Xe+Z0bfmYncfcJIKcXVPHXd/3T3Iwc4GTMxx01bJhWZmOpLJX9Ajxd0DhCXJmZE2oyZyKjSb8wOBQACJzFp9bMTUg1mrWl3xbgjpOAzhDv0WMBFoYiRYgZ1QJ3chK/aDKI9WP2nwKqy5GhXWr82mO2jXkApozmkGXdwFQGzCdLTYBtQkYC5yA+QosyGH00I5dZIfNmcko6P4z/DUuz86RBQOaMzwBoXNwCPAu4NntLcbTXBpVLQwk1DWqwRaUNV2/6ppIzT98TZ8z/pFyWmVBXwtAtZ9f8P9mX3rn4Ekcp9IDzao35PplWbRyVtciRaUFuQ8nGavBl0KhIJEz5mnEm7eSVOm8R9f1eDpMGMcFMZ7AeAA5YBsAcNZ1zvAUyosws/pdgvraCKCELvS1YsYFOB9APYE64UWcCSFs0VENpl07flNnLAP4b0nCCP8pM/8egE8bB+vXAD7V338M4BfNtb/Uz77HGcsAjMiVeaE6Gssp0M1NBK/RiGt6mZxqOKa2GSwTz3CWdEGNWSnPMwD6rGOBJ7hNhz5IFCTNC/K0wHGCY5LIMGt2oj6/4uFo6nLXy7MIQOfgQiiKkAse3dCrb0XfRx2I0PdgcOlETU22mkX+KqpVIwpXCv91C2X4P/4XxJ/8Npaf/QWMy4TgvcwNZwSVfqRRLgKtcB1NRBApwyGJXOVZ3jsEcYTO80nwPrRJE5ETiAVKWGLE8xcv8O7dW4Ep0HF5JwDLHDosS+0E64KXMVr5ldJK0sxbwXINGAYR8vY8gYHwZgeDyZVmZ+eHlWklVWhFcUnw3uHpeJQSV85Ii0Tal5xKplKMC5wnxCSNGJJjzHnGHGc4ikhzj8c3I47vRhwfGenwgDAISHhMEQ4OfeiKAFFurkaCra49KyKndkE1KkeMcR4xLxNSVhzERnh1XYBzQBe8vl/C8TgiJsUYA62Fjyl6zleaYsl2CH3F6gVU0dO1Simh66sCHnzANM9IMRWl9bwshBVvlsgyOVxRKhMnpDYcbcYMBOiboIIyZxU0KPtnRfvEALkzWjZljS/2SOuwKHTfGm9Ub74WRI0AhClgqJAZKQlNrjDzTBW0An2UzGTC5Xy163F+XBW0Ou/2jLUTct1IqygFxpOMpbSZctecLkC5tx0xRzEKSyOIqlJ/6B7XDpMLtr4l66U5WgNCaCKDG+X84n6r82uWIcOMm/U59YHVRX4NrxDAmRJ4+VznPLp+AG926JwH4LC4LZbuJXDzU9wOW3y6AT7tF/R5wmnO2OxvEOcZb9++AS8jNpsBm90Ovh+w2W4wvnuNp2mEA7DpA7rgEOcRcZngQ4/D0xOenh7BOaLrAn73d/8Sbu9eous2uH//gF/88R/j6eEe929fI+eMw/GAuxcv8NEnr3Bze4vXr9/j/bsHPLu7w7AZ4DsH6XUvToOUpAGc9w6kndiXmNB30iwwxxm8jOhJM8fCAO5u8d29wzSfQOmEniIcGIkTmBP46R7xH/1D4OkBLqWikMn9dVFUrpf9bPQALiG3zBk+Mz67e4XPnn+En3z2M6TFAn4dODmEfgsmj9AxNky4ffYSp/GEeZ4Q5wV4IaXIj4/3OJ2O6LqA4EOhH+ccfvrbP5HqEJUjzBnH4wlv3r7Fd6/foAsd/H4A9x6ZZIxeLexVdiNafsQo0TZc4QUr+qrk/uFzrhiCMolG3gDXhpvnjLFkd+s+q2ywmskXWWjNXVb+3w8cNVhy3gBG8eSa/Vjmo5LD2buq7FwZt5Wni9PZlzHR+fvWR5WGf9Tw3/P5bA2g89mjZoG4/Qy16U2pDihc6UrJ5fVZW/9ZFqZWctWzJPhPOYOXBBxOoHkBsSQX5OLIU3mRz4xvWj0ERIRh2Ggp9XofXo67MckaZ2B7TXWEGw1UnX3tqD2fg8u1s5lsRtvQDgqvrzy+KCnFJqkfKQ0q2F9L5zJfDuYDE6dHUT5Wc2VBF9KXcM7B+Zb2lCeAauCXLZNKnF/SF0d0Gpie6GovicykGKJYOQVAuYHBUtl/No/nQRxqsSD142uBCZPrq7Vs/l/fThwQw3aP+OwOh+1rddS5YnwjG1SM6MHBe0zzjGUR7P/bux3+/F/4HXz9zdc4nk7o91ss795hRwyfGckraiOZ4b/eHwbHUOVG6ySr9GDl0fV9rhielaRwngl6Pj/c0OMln6T1WqhjhHVu0PSB4IZfrOjbiWvceE8NDpnzwxb8ynsokZQ14/qTYJB1a0f9eu/ae9ml7Z7meruYUPTL5l3PdTVrFitzKo5kNDyozledtDI/AGA5vtrEOjiH0PVqO2axMdn0Sxsnin5MgAS0nceiWLptn4JrGc02Xvu+tQPan3JeXYe6ztd14yvTc3ZCrQYoc8XGU0gb+xEycsmGZVRb2QIwpH1jqMHHJttHzq3GRkAD31I/k94LEtSJTRd5c8KlYtOqMw2M4KUSMnNC5KmUi9ui1HdvZa7SK2t2u+HOmpVB1EAVNpq7OYwLP3cXNh7OfrejDbYW7GyFhyBy4JgLnVc7Ao3csPWt/ZFsjzGgPoUKJSC40FwqE5ATRia4fYD3PXISDOvM2vidUYis5S9WpWQJP4VjUH3PDwW+W3umJFDZd2dKVw2XNHOuezWbLtE8xYPQOXEqExzE71HlVmrox8MXW9TuXZO7ZLil2Ey/S4kxzTOISKDV8qgVJIw5znh8vMfgZtx+9hKb3oFTxrv3T8hKj+VYJiy2m4gQOiBC+ttIRWGP/c0N8tDBecJ4mpFThQpK1h/qyvGbOmP/NWb+FRF9AuAfEtHvt18yM9O1fO/vOYjobwP42wDgh1CZzBndly1FhWzqPzb1mlqdoWJU6cVnKpieW4WLCRK2c4lKNlvWvxECnDKATA7sEyizRG+s2ZXe164Rx6MX5VQfRJ3izBoxG+asKlLmFK68pNlItKJ3m0nYjl8LoPLx6m/YGDPDvXsL3w1I3YDT8DvoQkDnexQ4WiY4ygpB3eDJnj3f1ibGiHmO8MGj60LD5AK872AdRkWhlHF2fYcCbCoUDilZ6eGDCP0M0kZRwvhKVgdzmSiBdRDFqnaxrcoyQZqryNp6zSxeZ5vK1AhWbYoRGblEdXPKmGLFkY1JsINTrpgi0zTBecaSIpYY8Xg64DgdxRHiI2LsERdGnglxYkyHE+5+vEdaRswpFlDwanzy2T8UScyZxRitFA0LI8zziCXOmkWMYkQ5J05xVkwte8YSJ+TU4HA1lKU8+9KxtFIqRJj6JtpnDjkDymbOiClWpyDq/vImrHApMIvi6BwkbXc9M+aotKmxPVzeQ402u43XDM1hAAAgAElEQVQ48drSUHudavau71sdpJVWqvK1UqRa5rVStloj1p7sVjyt8DDbzs2+KirH9zhWvs/pV8ZWt5gK/fo+hc2UebPXOrvvuePh/LlUP7um0JR3pbP5+sB7XXzWKA5UT1RdyDQZBlSJlD+NM9a1+tBzVoaSvn+rpNupH3R2fcABW85tnDP8+ZdwLz+BC4IVG6lDDrfIwwugf4ZP9gEvuwl7NyOAcZpHZCKMpxGHx3v0HsidQ04LcopwTgJe8zhjXmbEycE7CdAQEfKSMU9HxGUEmBG8w83NHn0fBC8sJjgwdrst3r874unpESDCx5+8wrO7ZyB2ePP6LUizB29wh2G7QQePmBjzEjHNE6ByDy5AvAuCq8paNhR8wHazBWeP48R44ITxeAItTwg8wlNWZYtB798Av/g5Tn/0h+B5BnKCC4Lvymdrce2wQA4YcMz46PYOr3Z3+PjuFYLvSqY+54QTJnR9QIxaRcLSBOD53Ussy4xxlHmzkqhu6NEFr+W3lea7vsc8Lwq1Inz14fERp/EAkDgReOiAILJOCLU2imhtjJa7nNNZqXw7YzuXuSRA+9GH+MWKVteXGAFfnnj+/DMnzFr5oIvzf+g4NwCK/DtzZpbf7X/N/hT+ez7oem+TQ04VQptDMjkFbsbROj9++FXO57rwLRuX/n720voaOhL6E00ZihnSCpRGnhR9gaQ5DScGTzNomuGarEnnvJa0S5ClDQ5IwNieZedLB2/LVmeFaGrHXudCJUHjVLH72tjk/JYSqzHePvtDR53bM7dgM6Gr+1BDn00VCDVrX8dmn9Xx1+mlIu+dBgIrHbRr04y1cb6oRtvoNTb+Sos2F0UFrjeCOVdN18qKyV8axanTooylztbFmBqXHGy9bB9WZ22Z2WpDlbubk/MycYahNOIDQr+B22zx9dMBn3rChkWPdnASiM/yz+DGxmnCNM24e36Hl6+e4zQeQA7wfYeND/goTTiC8UZxwK/pGiu9iqrkr7qt7HDL5JTPmuBKo4dYssoqmHLlKJ9fId3i2rBnKBsrMFjNmOyKzOsgQ6PRldiTsLG6r6quZ/NS6ZoIIBb4kvrNOgWUiGop97lNwPao+jxeX1zHh2pb1H13cbtGJzursgKa6+RsMcVztSXOnk/MGPoNOoXMOJ5Oq4pRWt3cfmdtSnVJRZfrXGWLNfpev3rdHev9QKvPrjljz22w8+SP1blZGouFTnUTNt1C4QJyRuQIyyLL8HDsC5Sf6SMC12G0WSh9NVf1u6qp0PliXsxVAfNACyHjHQGQEu/kFq2OankgN7c9k/6rxWv3YaVvC0g13L3Mo1UM2F3diqnX+b+2LkUeskqbVQZ+yxGhc2zfoVlzXByN5lAd0/oOeVkQ5gXOLQJ1qdXYmc2z0VqtlRuvgvr23GuitOhY6+rRC92xud5uvbKT9O/2HuutwFo5IvoGsWak56pXrOkexaEtQYAznVNHbfxSxpKREpWKhwzx83hyyDlhnjOWOWC/GbDfesRlwvt3ufhFAKNNqvAiTh3xLBA9KUn5fZxHIEvj4XFc4Cio744lA/8Dx2/kjGXmX+nPb4no7wP4lwF8Qwo/QESfA/hWT/8VgC+by7/Qz87v+XsAfg8Ahmc7lqyE9YQL4Wl0z4QRV+KxDV/EU6E8YzqKDWMOO2uoZQKBuXSDl42mpUBE8ORF+JvCRdKR0288Qt9L5CMnUFLmoA7ZxAwyA8tLR2rHwtDgANdJFo3TsWRN2jKcqVKOxVmFsjHlyj5MABXitkmpO68yetYsEl6Ta8pZcEy/+TXo4QGnlx8JvmdP6EIt33ZMGll26NFjpRvLTGvUHhjHCdM8Y9/t0XUd4jwDRNrYpIPzHilKA7MUU4l4AlwgGgp+IxF812FwnUab7OW0yROkc21OCeSolOJKWU5VfGuHXHHCOu14N/iAQMv6ZYDiNFzmGQhUUtILBqv3RShbaRoRoe96LPOCTAtiToiJ8fb+Ho+nAyjP6MGYlwwmD5c7IEY83Y949dPniHzCFCMyJeSY4DoTClzouxmhvJ9m9jotMzG5wWBM8ygNvFKUTNFsdGXOWMYSF4HfyNLsyzAObX+IEtWWUmRt6iYRRG+4hRBl0ZipCXuGQGBUZ6yUvHhJ/WiUVqxYfclstD1LtCpNuJyJJgjB9gbGLKsj1krPnKPCQBgVycSZqsGm9BrPafYdNX+RRserpCmD4jKyetQuyMqz3FV1Rf5/TdhTfcBaeF+/pt6ShAeSnVMVgVadKnzlXMFR2ir8ZT2wamCa4WLz1Cr/ze3OchXWJeW/wdG6yOtnzXD1ZylQbJV/a8aDqlBcM46qEYAiK86FfbMca0XhyphNmVmd1w/gv/RXQK8+RaewJNntkIeX4O3H6MKAL28ZL3jGwDNcMCfsE6bxhOl0wN3HLyA9FBPiPEq2uheH7BQXHA4ncbjuN+i7gJRmME9wJFAvKc6Iy4yu82BKCC7g449fYrPtsMQRx/GA53fP8cWXX6ILA969fY/vvvkafRcwbDeAd4D32OwC5nnG02nG4TRid3OHQNJwxXkP3zHgHGLOSDlju9lhIIc3DxPeHme8Hhfw8Ql9eoCnCWQOZAfgq1+A/7d/gsfDo5aeCv36ocOqMMBW6GwbxJyAJFUs2xDw25/9GDfDDYYw4HgcsRiPZMY8TeiGHjlFCWSljL7f4PmPX4ITI7gjIiecphOGPcP1PTgKtpQ07hG5FYJUwgg+1ICcM+ZpgvdAxgKQA4cABCFJRwLlcuVtjJMVWrVqoMI/nZZltWRs38EDtN7P1OzBc8OumFrKz1amk/KGwnOovacxFPlpTp+VE7JsKOj+lL8/tPuvOYtrYEkNjWJJ2IfVeKiKkOE7nt9XzRVzyNou1QxE4qoD1XepxjAzl/dsSw5X40XL8U1HbSyV5j7t+eVehc+3d2l5l517dQZX1xQTueFnDhBjd45IhxMwzaUDOhykASp5ybRBWumXdphhKSW/TvRb76rcsddoCYBMbl86HM6P1olZ5J6O/2LDU72mOAvb+TEa0GurBG7HVsdo5esMqBFFRZ6Jg1pwUM1xcg2er4xHr2mzelsdwxyC2nukjNk7s2Pq2Bko5a+tdkjN/qvPkxJwcgakJvf25pzBmbOq8Bodh82QrkF1UPCF7MuctalyI2MLjbb6nk25BSQcKHQIux3+4P4ee++w54w5RngXsOSEkCN8WuAW0eOPhyMeHx7w2ecfYxg67LYDlmVCZqn6+vKYkBLjXecFoaHQwJmg1581tFKVK9KmLJWFmrPWzq46RtF7ymP4Imt45XBveWOxR1toFHkeoaURPddwmxkoGdJnr1S0amdT7St/bHiLHaYfy95pGEtzqjlUnLMKA3mgZLmJflXPLcXCxvj0dJ3TVvdsYBjODwcbjtL2GQQZw1hqpcdcmolB6T6XE4kI280GnfeIyYAJ5f4m/xhZGrnpEwyaxjBS26FeZhG2XLyuxirbGlWefuho9efL51w/t3XWWiJMP3TIiQFqskBzRjTeTF5s75QBMmilXvOjxO6yJl1tggozqu5RZGudBSpdBoVjrfBGmUt1CRq92HQLRw7eK1wiIOX5ZmM0zHy1DmgrFYyHMmANEwHFdkVNzlBs4cLrzNdja3SmAxFRaVZse3kVFDZ++oGlsvNzztL0jqv+UbNlAV71HlGew1WrKTSYI07jCQwIbAs5ZHLIqidWh2x7Lx3tSreo63Ix5g+8Q/PWVQ4XHVR4um7IcqfW9mOyS+TMrusRfFcadZEDEGcQBJIRXtar6sJOqy3lRkkbZxbths3noTKHJXFKgsqytsxZqrQ5IzHARLi93WM3ANOUEAJhSVkb+gKOJCHTgj3IAOes0KIAhQDHHimOiPMCgSUkDJu9NP1dFm3idf34QWcsEe0BOGZ+1N//LQD/EYB/AODfB/D39Od/pZf8AwD/IRH9F5DGXff8Q3ix4JJWLNuHtSNo7dJOkMhAYkawjd44KS/5GoHII3NCMmwsqg2ITEEsZUQMxIZgOCd4cgjKRMXBlBGzYGe5TQfvBrgsE142PLMqnlzGz6kKeBvoquiMsMI2NaFrClDrMChKmpUjKIHWqK4pk7khzgwrNmtmp2hFdHjE5r/5+zj8jb+F+Pwlhn5A3/UILoBByCTYQ4kTnHZfrM08qsI1zxHDZoMQAjIDS8pwiqMac0IggQ9ISZozxZyAeZHMWWX6ngL60MOTYD71Q4dxHCXSx4zEEbGA0RsTJywLkLqgjFyjKTo+1oxTHxxC32Gz2eNvfH2P//0Th+/O2E3ijCVpViyLc9E6aXb6XlmjiVHXdfAB237AwR+Qk4yt9wEfP3+BcXzCkhakmDH9/8y9Sa8tS5Ym9C0zc/fdneY2r4sXzXuZURlZlVClFBJSIaRSqVQixajEoEZMEGLEL2DCnL+AxJQBKgmYkBQgQICUEilACFSVGZmRERkRr3+3Oc3u3M1sMVhrmZn7PvdlTJDCI9495+ztbm7t6te39hnHdMLp7YjzXUI6ZvB5AiKDk0N2XgX6bBrArG8FNzZNOJ9PiDFhGFbo+pUaqEWwOY9nxGlCigmEqPtSzkPoBqz6DTKJx4dzEuzDaUKRcpSuSsSQKNtO10eM0SIAJkvDUgP4NE0SkZfknTknYGZkIEnpBUqUQwHqJirtGY6MMfQpRdx98TW+/ZNf4d/8j/6DUuizykstMwfEgVOFRRCaQggMNOmWpXezFM4sApinQshNTuemTafpbbmg1c+JkMGh2Fy2AsTStmziafXSz79vI3PmovfSOIs5HYAugcGxKDa3SSCFqS50kYv3zGROLlNGME9h08ay340hd/Y+rgJN+9jTssylMFvm0OgYUclCYACwAhPlsUbJeKpprgmAF8NePkIm6F8qs223qjBk0bYM7nuMf/RPsF1t0fkARwEJa0ybTzBtPkS/fY5/5UWPq/FbDL304/58QkcOx3FEzBGrzQDfB6zXWzgfkBLjy8++wDCscH1zhWfPXuDx8R5ffP4rMJ+x3Tjc3GzxgScc9yeM5zOmccR4esSqd8iUkWnSfie4zmN7dY0f/e5PcH3zPr74/Nf461/+NV69/Rr/+B//EV68/z761RoZYnB0Q49AG/R9BnyHx/GIrfPouw6uIxwf9zju9+AUcbPd4e4c8Iq2+IZPuDu9wnb6CsFHePM20wTEiP3be+y/+kb1KVUoyIG9BzuSsyxSEQBJy23t+zkmdOzwbHuNf+0nf4Db1Q7TecI0Tog8Ak5pEjPiNGE8nZEVGkX4zRmff/EFvBc4gtvb5+iGaxyPDxhPD4hq0JaJE0fq27s7dF1A13UY+gFEwOl8gu96ZOfg12KFZefAcGIQM1pU5GQSXmL7kxix2Wmyo7IYQslKc5hDyk5ZanZjc6lR6KmtXSIn2BRzntHG5miUJ1PpsUSXlmjIlvabE+xd4toT11I5KOeKZsRk9isVKVKnbTb8tnhSHb9zrgAYmFPdlJ5agdwUp9TQEsXtbZXh5SCaDswcjY0Sl7Vi76Vdksu7qsJYceS+Qz/XlltFXjK42HDtAIwpglJEPh/wcPcaKY6zaK48ThgxiXJYVGc0bWo0MZtSFUAqixgckCioSgNNZFfF3H3HAFoHpEFNzaaV53uocAfStHPFrc8KIWbf2SXYwCpvoFGEwTVIIHPds6qokwpH1RDOs5/m/C9993U+W+ZYlXBnUKWzqL/afnzyHFSYpdJi2VYFw0/7Th5FxvpO4w61PWx7XCNqxYjSyEPtGRSr1Vz2WrQo9MmCDXz53XnCervGycuZG6PIkrTeYN0FLTInsK4uE073R9zjDR4+fIvxsEfOEburHVZXN+ifv4/DT/8M/fEBPQMxZSTHmlXXzLEjKVRZOHX5FSoMlDmscl9Dw+w+ViicBNBsDedzXY1lzZyYfKRXWqyL3a07tFA2pvZb6weevKqM2zg2IBKJI0IgSb2XoAcHjgmTkj7jt8qC9ATYOTIdU88zfJkrJpQ6LXPZTriFY6GdhpfZHuiyffUZC+JOIDjygGO0GLv18KujVjMgi4+QPXJKstecw9v9YzFKpiT9SdqQGHCC1ryQv3vfgzggBuHhKrpWmdZoYUNbzehW9IyLs/DUWWyM3DZfPLMUfKfxrHAUFv3qPE3YYC1GR11rZ2NlcTaNlNG5Xg+mzM8UJ3QdwbtK9+URsTF4YIZFbOe96h+MtqqOXzgpbOWK86jOiBjBnYMnoOsd8rhHzqkGy5AHLCt2Nls8m/PZbNv7c7P3s6X8L9an7FfWjNJG9uHqaJ4dvfZq2EVrnzB4gconap+/65LjmgFHYDbdhsFadPGUjgAY2/UAr/CD3nvEGPGENPId73n63gvZEJjRHmq/a85D4jQ/91RpGAhF5vZEWK/WWK83grXaGLiHJBnzQW0OUghSxu1N92JGzmLoBMSBJrQslL4YzT0eDyqb1EUq6wEgIePzzz/HemBwnhCnM/aHM4Z+QNd36AIEWiVn5MSIOeNwYoRBZH3nCG/v3+Dw8IDddo2b6yu8uLlF8A7TFDFqIbF3Xb9JZOwHAP5L3eABwH/OzP8tEf0pgP+CiP59AH8N4J/q/f8NgH8bwF8COAD49/6mFzCrh105fGEC8q3+X4iSd65sAWYui5y1YJV4+FwBsC6h9mRCghCkzFzSlRkKSMym4KuUQUDBH9ECBubNtwMv1URJjXYBaLBIWzLW/iiGZwYs+rUStCq4kTNMTj35dInNIqez8QSSCq8g8QCph6AVEEGE4Dux6gNAIDhmjABiTCCMsg4dA+SFSCaJQpUqjKF6MVgMyc45xBCxWa/BLAVLUkoYhgE5M1JMwACJkHUe3kcQTTgd92IIZMB3AbfPnuP65plE0aaE09lwRqX/IXTYrleCsZczUp7AWtQrBA8fAqBQBhbxYlX4MjPilLCfHnH/5g3idAVgeGJHSjRvyhmTVtYbz+eGgdRCH8FrRCjEEBSTEnpIVT6kLHDFTiokdv2A3DO6DqDUoV+vwPsTUszgwFq92woKJJgBn1kMDpwTToc7gKWIS/CAdwZ0LQ4LqQJuwO2CguwgRvDz+VT2t9CjjGkaMaYJAgru4JXBFgOg073nzAoKFcyzCv6qVHBTLdW5KjAVZUj+8d4juA4hJY3qUubp5PlJ+++8RHalJCnUOc6rZ5JzoJTn54FM9avCGIhL34x6FNpCJuQuMPmI0XpVxRA03yWFgRljlQ91LACKgeQpxbk1Qur517n7TZmovL81lBimFhkXh9BEFEF8ibe37FMZbWM4KAK30h5Sr67BYIhuXSQxgETQayPGOGcFfW9oH8QIZX0rlK2lVU3fhM6ijCNG87izCt+s/ZUnCji8zRVXalqih8gECRWoyTWBIfXztoBMmSulBW7+sdAgAEhJFJJsfmpC/vD7yH/n7+Jmd4MurMDoELHCcfgQh90nuNrs8OE24IfrES/9CjFNOMUzzuczTscjYs5Yb7Z49vIF0jThcEroh4DVeoMPP/4+Xr96jdev3yIEh+cvXuCTT39f8E7jGY+nCR5SSXe1WmF3tRUBRwaIvl8hRmC3I3z6yQbMwLDa4u3rN/jVL36Bt69e4Se//7fx8sOPQL7D4ZzxeIg4ZuBhAh7PjFNk/PCDFa53G/ReCxBmBqcRm2EAeIXTMeKON/g6MV5FwYXduQxHygkZ4BgR/4d/jvPP/gKH00mVCYdhvcGw2xWnDgthL0ZIzgnMtZjNv/rp7+GD3XPcrHd4vrnCdJ6KgHY6nXCeRgzDgK7rEJxkW8ALbUFmwYudJgQvhWiYMw7niDSdkOJZsgrYoiyl0m2KowiQCPBugPcOt+99hOePB1y/fYPH46PsNTjFv+NSaENPhcoGczW2OptQZAFAI/joMm34KQWu0H3TmhuB2mSeeTZOY1xp+mWvEvy8XNthcz6Y8uRqFC8WY2qNnk9c3/V5KVqp7Uj1b52nYuBwhc4sFd9W6C/vulDwLl5cFFsz3D0hjc3aWCo5jqhWoF9cpdtkPKpRNWft8JNtLyNBq37ZQC0kluCEzMjOAWlCGk84HQ4ISu6yvt/5gJxUyWXjhxVOQ3eROB0dYdhswCEIkntmsDNngfVQnpcoU5MNbJ/VMczXyuQfo8/2blJ8+lx1BRGaSuEuU35rdltNW2VANWKS8ToGaSV2k1sMa5RIZEfnBDLLim3Zvq57quI1mryacgJrwIdVjDccaVadohpsWid0lfvaOamMu/JDgEuWzuxevbyf4/2bEXi5pyzIgIjUB1EFt7KvtXgxrCBWe1pUT6IZ7Xpqr8tztUCNyJbb3Q4PXdC2pY2YpBAssxT0nSjAdwRmwjgmvPryG1zfrHH97BZ+tQZ1K7gh4sMX7+Grtw5+OmIcXE0Tbc5eG/wiH2jEn9HXBhvT6hmw3jD/7pJiFIfGopBflYkgECFlCpWH0VwHbA8zQaJXZdbsbEAzwExPndPNdq3tv5xxATPA0OAK1kwNZw6URYpy4TEL2ZNEJzKaTIVvLPskPU/MtbiRdsOwpnMWcx4V7GObAMKUYqE/dVobmc8MonaWdH6c0nuLZBe5h9D5DpkYXvslpJEVIk/acQDSOIEdlfG3GSaNWl3m3Ix7Rj8u90gLW1I/e+pa8rD6jubvi2e4GJrteTOPklfoKEBw94nU4FVhBMnWngi+nU8nzmP7jqg54Q3zs6jToueQ0SvZGVZn5an94QgY1LiV0wjOUQOfmsPJc8gW3QXzmWxpXts9rvNVi9xROWMASuBR0rRyq4XiW7o5I31czyi1e6CulUW8WiSsBPFl+V31pQVFLTyMI2vWsPI1hcd0jjDFCcfzGSCxw1imsulu7bV0FrV04al7yt/8xPNopcfKl5yr824OaOMJRjo8ScHzLnTYrNaiX6E68gkAfAEcLXTbnAA5GQ02uVf/K/REHTN6P7PanrRwvQVbWFF3coS7hzN+3d/jauXQO8Y0Ee6PE4ZI2MFhGAaMccTxPEIQCRwOpyPCGMq7CQkv33+OZzfPcLW7QnAex8MexzFiGuPFOW2vv9EYy8x/BeDvPfH5KwD/6InPGcB/+De1+8SbZsRN2UwdZPmQsByRHEcNEdfvawVKbg5IQ+4IxZhospqjGp1QjncjlBBQgPHtoeqtlM8tBB6kqc8l+sveS7OAEW42sREa4z0m09Q75psN5T5CG8Jd7tX3zSIAaze07Sr49L/4S7h+ADZbnH74OwAzVsMKwQWlmSbMSOq59wFO/KFwzmG1WqELnRTj0mqv3gcwR4BI8UCMwQOcE87jKLih3mPoe2w3G6lYFzqACaFfiRcIdrgCfAiijOWEHEfkdC6EMnj1jLha5dZmMKeMlCbklHHYPyDFNZbGWPGYpXKIicTAeTwd0Xe9jIHMYKaeGRZv4xgTUjEMSJp+rUjMGM8JMYiQ4XqP8RBxPI+YUkJiL+Mp/eWiUOhkATmC0xnn8yM67xD8AE8J59MegAMpBIPMf01xsnF4L/NTNj3Jnk0pIqesKYqyzilXRUD60XLaS2NewbMhEYgoX54l58xzztoFcaaYA8XBSWEytlSjWtG3QCNYLxoFn5txypozWA2Ezs4bqfRLliJoxIA0clqfr9Lf00J2+Xb+WflJ7R1cprnhE+9s2xh6+XvWbvvip3qBizWprSxTq+Y/Z/aRmWJS+19fuRQeTcwh2xqVBrbjeke/fvOrcdaVHdXMWZGPWtPRog+FoHKlse+QhZcCinw2j15jFVqXo8vKd8yYa92LH/8Q+N4PQbcvEFwHgkekHqPbYFq9D9/t8Hzd4XubjB0k4vKcJpynCeN4xjiesd7tsN5s0IUengLOfMaUGHwasVpvcH1zi/P5iKyVRs2J5EMPoh5pPOE8PYI5gbzXlHqJfs/qeU5TUiw/j77vkSJjvV7j5uYGL16+L573lDGNGacx4ewGJPKYwDjEjP054dnawxEjpwnT+SzzkMVoMGWPLx4Zj+eIHEf0+djgxAKYRvh/+f9i/4tf4Hj3FjlrdWPvEFY9wrrXrZhVxahZIKuuQwxdWYsXu2d4sZ8whB5xjIiT0DpzEJ6PpyoDdBX7FRBVs7cq4EqDp+mslZ+nMl+Gwc2ckXJC5zv0/Qqh66UV8lgNA25vbvHyxUvsf/0IYoFCAhGyy4AqGyZeyDsrTWvF3lZpKDSmKAA1m8gUjNml381icLg5N8YDyrm3AhMNbbL+WFs0Mw00P4sUV5SxZgj1nJp8RZf0gG1wsy5w8+/yAfl8nu777qsaFqtyMn9/4cblHpGn2vlvMd6lPeKZZPfd7y/jtPvnhKnM/xPtPT3Ep/lWkTYZRYZhK4bqmpllTR13BHKCNSrGh7mhjzMDjuC6Ht16jf76CghBC6vZvLimS+YAlhk1Zf2i9xcL1xhtyngujY4mx2Nh7Ca0+7u+sqwQW3+rgVU+Npm6WaOF/N0akwzYAk/tY32bFCQt7uInxtrIWc3fs9tavm3nijJmUr6N0Xge6ry3/bEGl3BB7fskErbtR21jOcYqA2B2T/su20ttP8k5dH0Hcg7fTBEMwnNyGGPEOU4IwcFrhLQUDAZSzLi/22N3s4XvB/i+x5gFC329WmHTDximE052hpkbaDTpFDdLPHOas8i0Dm62Xy5EoMX1LmdPlcMWDy8bVFo8z+hpzq/u35n09IQh5SlaWui1c6V/9mSG0TZr03iHajrc0Gv9e+b8I8KMqxBKESIAJfCpMDgCrKh24SdO8SQK5n/rhIDqCprGDM1WNQeCwg36YiSn0jYBmhFQ0+WdKBWiFmh0us2t6EE1cACqp0jUZjufMtCnjK2XRq/lajy9iZ4OQmh5wfKcPtGOPpKS1rMxPTVl5FCLg5NrA1bkbw+CoSwSxGhm+pnRGluyYoDkIrk0HahzU39f7M1C/+fZvwSZ6+A8+tBJgFvK4Bz1O9SsKO1TKcS+bJvrOolKqCcp84WbqKWfxZBvfBKtU3J+zuxTmxoAACAASURBVFsbzZMO2rJPqMBs1OdRaJIeN5h+UnUQrgZRZUFt8kZMGefziNVq3RiA3w398S4nt10mR1b6YvOzuK8ZqUW82k/7jMBICv/pSHR4Rw5916ELQYPzXF0X5Q+5WU9Xt0bhMXL2zeBfZScL1NEg7zIWZi2QSXWNxLZjTgWHc2Lsp4TgAQ4OCQ4xE1wGpgxIDYyAyBFjigJHmUkh2SSSfNV53FzdYLveoPcBKWXEKCkCZst41/WbFvD6//UiQk09gy2iHXxd5JbwNwcWYHVwE1qsm6TecYIahxYHHiyYWNmUIMMPafplB0L6qIQEKmhkrgKQbkLmJkXPbgaK1Z+JNArJDlcbkScPtAp+GVYhKGz/X0xge49ttmYuLxQIAE7vMW0DhP4v/wwERr6+wWG3Az97gS50EgVr2LqZERVLlwF0TjBIQUA/9Eq0mkqD3sGzYI8554Ck1c2hnu4Y4ZzHMAzYbDZYrwY459B5MciuQ6hCu85zjAngBM4R2SkMBGcFG68E34QrYy45Z62eOeKwv0dKz5czKampFpXJADkhDIfxWDBRLanRAPtjzhhzwnkaUYQXqinPzGqMPUWcuwTPDnAOKSfsD0dMMUp6rabW1WgIMSDLmCTKLMUT0nSApw5EHkQRp+MezISuH9D3N0gpwoy4ZEZJiCeqH3oYXp7tlqz3y5liJfYWbSsQIoaf1goHtqeYRcmo+57KuWNWxZSpzJ8ZyQUbWLxbxigl2lIjzTS6PZ1H4CzRZii9xkyYNNaQWSMuFBMNJtC5XIRugNVAW0dUz+rSWItyfkzJKzPQyB4WdWunb+6LLdNSe9sqlzPaJ//O1R0VKmbC/IIYop71p1hwZeqXKcezfjaKUtE9FwNuo0uWRhYwBG+wec8skmExLVUAwYVQg2asMne56YcZjRpJgUtTpY1WIBFGX3kEuJ7RYhRRRa80tmCebEqICqAtj7B3JIv8sq4xADjEH/4u3Affw6A41IkdJhowhmvE1Utsg8f7fcKH/YQ+T3g47jExY4wRU5yQOWO73WK93iAn8aR3/YBxmnA8nhBCj93VFVbrNaIaDe/u7zAMA1brFYbVBscoAkScEjKfsVmt0AcptjiNZ8SUEaeMcYog53FzG9B1Du998AGurq+w3u6QYkKKjBgzxsQYiQHvAS9FBR8PEXwdwI4Rp4jT4YghEDhOiBPjkLf4/H7EOB0R4gPWvEdwlnnC4PEM/tM/xcOrVzhr+hEgEceu70BDQEIqUUfmqFt3A65XW2DY4Btdj20YMFAATwmHcQTDqs3KszFGuGlSHirQREZ7PRH6vi+01JEYrH3JZhH8wmQRdhCxIHQD+tUGXeg0CsmhDwG31zf43vsf4ouvv4CXuFhYKrdFsaB1DNleL4zdeKBs+BnUgN5WZKeFEDKLGilKkcEv2V43cVdpKRqZqpL9amhgFmMcmpRQkzNUpiiZRPZcc06qIl5Pz6XIf3lJCmyufYMqAbO2qmHAZCda0CTt4oz+t8SzlalKq64ktTf3NZlJ9k3Vigo/lD/53SNk+1EoMIz2PalXNV88FQ03b9juZd3Lrmp0RFoHIZUu2x6wbBhx+CdthpUUEyh06LdbDFdX6K+vkILXHZQBdgA168SAGTiLrD0zFDa0lG0Wns5IIdeek8a0yKiQH828FMWWzJRjvELnJFORfYoy/MS8LpZqfpa01oF9XqNea98N286ExKXRpiyA9tH5lhYApaibrmlxvCwc1bVRlLNqvGpmKNTPS1ZTQy+WRoV5JB8v/tZz0ET1Yvbt/Krnoc4XeQfyhC/PCZmB56HHlCJO04iOPPoQkDlpBKZErT0+nhCZkL0HkcM0TQhwGPoeu67HFRMeCk+fyy5mUHrKPloi20qRkmY01Eb71bkh1UeNbs/Wgc2g0wYpXEIcgWp784mq8kyJTi0ktNmvjYzYRuc+ZaQtchm4wX2lqhLaWNHuC+tUs3cJsIj54oQigJwvvKXwdo2qBHPJsGKWabaMIhmPwlfou5hZYb/kU0BiK2KMRT6XQBnNci0G2yxye6P7M5SO20BdlfvB0no7N7nAlZCcM7Lmqm7dOmXKmnDNGhNdaB6VXfTaZgfM1r5Zp2UE45PGdl0vG6gVu7N+Jc5wuTquLbvEkWaWcC5BSA6kOJlayKuM097EZYzt3JZ96WxuUPZV7TdVHbcdt9F6PazBeXDoAc5IKUoh1vIqLgZ4qFw/nzWetW201taWGwzd+ZlA0y/RYZOuv4j9XBy9sh30LbbvjXdSIzAZLVeoAWbFIXWVd5UeNPzHdG4iKmeFADiD4dP+pyjG2GFYmRBY2lhe7XhL9uxiDz/xVNvA/KtmG8o+aSKHdS6TQjc6kkzi4AOGvkcInUAKGQHQdzGRBjkYLr8YcbM54pgB1mhiIkhMJYNzUgeE6Ily7Ek76eD9/ByJGKOBHs4hgnFOjDETPBMiSxnDKbP8xwC7gAyHMTLOMSqk5wrBO4RA2K1XElDoPXKKmEaBqHREcBqV/67rt8IYmxlIXCujAbrJTZBwrAqRpUkzYAZOZjGcAGBOBWAZcBWAHUr8gUYgF+t5pYctnlhlOjWdR/67EO7kD7BuRDPQlc8Li5TXeKCJWhSSMXdKV2ZmHoH6zua22WFHqepmbSQYQaz49W1ELsHDIBiMGGRdjPz6Ndwf/9e4+6N/gpyBq23GzfUtkDOmNJXDE23qoow5pYg0RQ2VF2Wo0wp5YEj6fMpYb9YAMfb7B3Qe2G7XuNrd4Ob6Fv2wAchh4oyUIzp2ihEsA2A4MMuhAySVzvktHCI4xVKtLqWEOCVELfBF5JFzxpQSTqcD3r79BtP0PVxcBDAJ+LkD4BUjlwG4IAXAHISgFmyyNOFwnJDShK73YnimgO2wxhsfkKOk24u3hbG/P+F0yHj+bCvFLgxPT+cQyqhnAj0EmzSlM4bBwzsGeAJhAscTJJbFo+t8aVIQCU0YAoIXj9TsYganrOh3th/UqJ3rPjbjrKQwOfgQZoJtjBE5J/mZcnEx1GhWxaQypqjjyorbFEfBXZymSW8X4P3MGZ/9yf+N49t77D75sO04MtSYq59kE9i8r9gwAEphAdNJ58stP5s+iaBg57aRhheFWiw9zL5mFTyKFxNALSyQL5lu+WNBoIviYI1wESKf9Lzqv6z3UTtGZlgCL6EVAqsAOqNl9izJEjiTnUt1XSp4QFakYSbQUBVIlxct5h68GHkxVMzTtqG7uxiN0Kxn89OEqLwAFCy3maBUW6j3FCJMRZAhoBBNkZHMYaEroHM3GyxD07atq1zudSQwK6thjQSHRFvE4UNM2x9g8lv8aDPiWX6AO5zhrjc43h/FG6sKoQ8eQ79CHzqM4xlffP0lPvzoY9xeXwFE+PbbN7i7e8TN7S02u1scDg/YXl/juN9jvH8As8d6d43VZo3H+zt8/dUX+Pbrr/HRBx8gdJ2eZ4dnz57hPIqjLHgRZD786GPkzNjvjxhjxpSBkYGYgS++fsQ575FdD+5WeHuccBg7kIvAOCLGE3bdFhMcHsaEn74dsZ8ShvO32MRvsaG9qqUCw3KeTvjms1/iNJ3BhnfuHPrdGrTuEB0jxhGeAceE3ne42u7wow+/j9v1NX728iP8XJcjRY0OMeWKRTEXh5/HdrtFTBGn8wn7o6yv9w7rYYXtdoMpTqLg+4BO8eJC6Mo59x1rarMoDON0FmN3FmiY0AfhG+Tx8tlLrFZrfP72DfZTBLLIKJ48XJBzJRiXlmZtu5RVxoBJM6jHlZq9hjlqiX4jW7SqJsXF4zyQ1PFVKy2VE0fcnul52p1dpSYeNwa25ryV02cY7s05WVCDWX/bq6hZJkSVOy0a0AygRn8vq+9e0COqMA+1P0ZD5gMxBXQJEVVJ+CWxK293jemvTMWlQ8xoOxoeYYoYwKUYJbe0CXVda1959vnlDGuEUGZJFHEd3LBC3GwwTVGgkdgKdnLh3zMDDURG8sOA6/dfIuy2cKsBo6+VuxdL1YzI1qLhq+0sXGySZoabsVbZgwpfKPua2u3FRYltWy2bTDdH4asqmLumr3PDO5d9Zn+b7CBwABWayNrPzV50Kou2+38WAQg9ezQ34qp4iFYCqE4PLIr41XwNMZxXx7rI6amkbRNRrWJNdcxcD7vMd3EwsrbTQkDUW0ssNNVoeSr9WZxtckUyYQamnOFXPdLpBJfqmGOOiHlC5ADHDiEHmBEG3uPtwwHr588w9D0GjTq7vb3BD44H/MFnR3xFveCMX9An1SvLWtf0XgIkMMLS5ZuFYJaAFO9MakaRGXQ4M7nQ5pRm31HFp1e6Yp9fGNxUR2Nd47aYXFljW2+aw21VZ6XRteoYqxtMsXNZRH5HJHpJlqwIgod3YUZTCFSK0Yi+50tzzkmwie3Xds4NO9PeW/R9qlAC5iitRiN762zzyN4Nfh5ZCJNLNSAEJPAC3KxJe/csClcXaibr6/n0DhQcKPhCv8ve5tbBUQ09c4OsQjE2Z71lgUQSyfpdxpp30fr5h0KbWb/PBR5MdK3RIAEdqWGZweSQkIoe0Lmg+LK677lisTqq8A3zDLV2Beq4ZEu3NKKRHdCsaKHf9qmsXxc6gBQDlxMEczgDWda5MqZZa003qjMwU91ry0uyaakaY3U/RA0i8r4WwJNwenNc2ry0PNL639DkZp3FKFjnwhX6ov0z+k4CQ+C8h4VCOX3OqTMqThExJkwu4ng8VQMlOTUQX85Jq7e31+Xea7XfujpzKaj2fPa58lVxkojsJ/V2MnwnkF8SnCXQmCnmYjciAlxwAk2oBUJjzpjGsfDynAHOAk1pkalHhcaUOSXZI0bziJAsyVj3OVlwGAAtPYlxnHAOBMqE/emAzBnTKHakzIzOOZxOB6SU0Hce77/3DMTA/rDHw90R3nmcp6jQmRmn0yhiuRZ+/67rt8IYK0QTAGdEhhbNEsMrlU3OxfuQMsO7dqOpwKpGO1KLtnOhwgpQ44csgnj1KFZv+vz0zEnH/BO5zaLluPxbvtNILsNbtKcN88cwMsobTGFUDDZWoVAOvJthAxnjJkDxbkywEIKfdR5qcYL5Eco5SwqCemfKRJBs5H7okf+X/w77P/hDHH/wCcZpxHu3z9FpFFXOWTxVSdN5shZZEOqtmCYQw0MW4WFYrUslQRDh6uoaDsDt7TNc7W6w3V6DfAf4AHKCYSPCCRXhDpwhmICG08cAZ4kcSxGcxfjqycn8a4RGjBHH8wn74x77uzt88fkX6E4/udBdc04YxxHEgm0WugB2hHOecDgeEFxA58Szk2LSSAcpEnF1dQ3nBDx7PI94eLwX4yQYmQiTI9x8dA0QIXVn3D73eHU4IE2NZy8nEMwYiIbxOzgnFSbjNKFfrzF0A3KMWPUe3bBGGNaCrxNHZI6QCshUov3MwwmIeU6MzQIR4bwvwmdKWT1cVdk1oTUjgVNV8MXLWHQYgULIHlOOej6qoCL4LKK4hADBb3IEpEK75bw0SgXAoNUAWg/IfQN+TaL3pMwItr8dgVMWI6LT95Kci+CpMLYYJ5jHjIxxFcHWztCTx72OuRWEGLM0T4kpq6xLHyzng8qN85eYImNp/hXlWuigFXcwU3cbfYpWIbUFsS6qIZi1/RqdUdemCIxqdLGihrNuygQ147Qx1nX+rusJ0VHp1mX7VZ1v6bIKu6By31OVzC968V3fLS5RMiqfWPa9iIutsWwhFAuvkqwHZsBRwPiP/gjr2/fQ9xt0YYUpr3BefQ/j6nug/iV+9xnhIzzgRT9i0wPnNGF9dY3Dfo9xOsMR4dmLl5BU+AmrVY++C/jqy8817afH9c0zhH5A1wtbX2222Gx2SM8j4jTiuD/iV7/6DNvNGuvVBp/++PdxfLxDCIJrtN/fi3fdOYTgkDNw2D/AuRVSzhinEY/7PZ49f4GHxzMm9hj6LYI/Y73p0Hcefeew6VfosmQuBAJeXt9g//otXh8yvjoyvrrfYzh+ix3u0OMIAWqT8xF/+mc4/2//M47ng/qoRBgeViuE3QbZO3DKCJnwYnuN2+0Vtqst1sMG634DYg9O83XTpGvZnxkFv8r1Ab0DfPIIWYygnZcsjdWwwma1Vjx0UsxBgvdrAD1STojTCYf9WyDJ+njnEIJHP6yUXzsMqzWC9+hCgHcOm9UW/+jv/wP8i7/6C7x6vMNhGuFCh/M0IqcRyBMc2wmfK/S12AmQkshD5KoQzcTI0cF5E2qrhmD7dY4fWIsDtYZTk4yqolTlsKUzOpeoEaGjIMscQVHCmFmw0+13auQksrZz035DN43HN0W75qTX3pEbA0MjzMwOcj3Flr5ZDYM8b7P0RY0DOYOdRDLTrP8aIGAK4aKII5hnkZqzr574TKa7ifrUsVi2R+HHTz1IVdGskm0dPxHBOChD5EYKBOfWWL/3EqHrwYcD8jgKFEdOTU0EWVXnPHzwCEOP7uYGw/U1oiNEECg30Q26TlJvpaWegMn2c/oqD1zOVLuOT85WO/zFrTzjC/Xj1tHRztDlX+25sH7Swqpn8rAo7LmRzxsFl+oatEYMe768mQgVq74NBKmjLXu96R/rnJcoulwNWqtesMcTs6wFk6Rishl258bzog/MZkTvMCz9y1uUTlZdg5rxE0PUXVo8R6r7eQe/3uDmg+/h8ZxBxxPM4TXFhBONCOTQd2vhq2p0pEx4/c0drl+8h9WVR7fe4PTwiPV6hQ/efw8/SQn/++e/wj4xkheZqs51G4EOHZcF+NQgAjnDbRErSNE1jYivMXj1vBVjsc0NKramvdOM1LzY4+5yIze0GFhmN1WDODep27Uv5kAoL1ejmtBrpxGpBl+Wy/dczo9IjmKwr/oImn2s4SKo9UvqPm+EJoTSdYFHqQ4u1lA2iPyqsVfMkGCstmBXmT+nQVtVBjTjc5VQ57SnHGfiEgnviSqeKku0HKtRx3gVS1gfyAokpVh4TQ0SmF9zY3lDC7TdC7mx7L25c+ap652G2MWaSMCQ8VehCQ4ObWSW4ZjHrGW3mBCcRMxSjkIvNJ08Q3CvqZkboErqZiCnBgpjipPq43N6XFLEuXJsOxe1bw596ODWV/DOYRxPmKYTppjE4V3oaS7yDc14YOUtRX8qWZ6zqZv9LkdGOhZTMvuz2FZSNVwDTTEzo29Zg6C0H7lsunr/+XxujL4NFWpEFe+DkR+1MVRZS/RzwHk5264PJfM3pSyZ4XMwqnde79TdqOW+SgebLhqNt5HJ3oLycR0EW7F5Fjm4C/CeQI7BEJivnKLMLSsNAGmEZpa6PecRw2plpAsgh+Cp7Den9h7SdxecWhiVIBVEBHKyiGrWRZY1896DQRgnBmXAux7sRjBHJM44ns5IXcCwWmM1dFgNAWk84+3DA6ZxEoM+M/I4YgRrHSxorYl3nNnm+q0wxgLWUTssrPuoEjOnRFaUogzTt8oWyrN9LIZb8wCwMrhmv9lEtcLtjCVSbae9qLnhNzFACPfUB00uK+pO+3GNLGGap/1ZuMuTRL14ay4XuhC1mQG36Ze9k5oUYt2cngh9mpB/+TOkb77CvusR/v4/wHq9RQgBjrQQgz5PhiOqyodTg3oIPZDEMBd8AAVXDiuvd+h8wGazQz+spAKe85CUF1V8THDXcUgUkqbh255IUQDW9XMSqyDQEOdxHHE6HfD48IDXr1/ji8++xgenM9ZPLBezpO6DBdSemUEpl9D5TCzeHCvWZswkM3wApnHC8XhAniSqCpyROeE4Tcj9GmEHbBzh+gXhcBdBKSNNHomn+TrOlBX5J4QOXTeA4TClpEXLPHxwaliXKsGGrWVRgiJgywJzSiDDa4IyNCVogBijJNJD04ZyhqlxBnztnMEOqB+PRECztIlCpGeKBoriEqN8nmJsAnCrIGlM7cv/419gPByAwSP5uRKUAaQUEdR7CjCcVS9WyblAJTSKejVwm3JQoyNARhda5U73dnPuzNMsfZ0L3kUAVAG00BKq+3jG0ZrLGIQJO+WsNPcW86SjC92fmn959iU1720p3TzirdJEPdfUrCHjieq4dT7edT1FJ9nm4UIsmo+xWYSL9xQZXz/n5bOLN5pxqty/PGsXDLN9rzD2pXDTnqv6WR0b764xffJjrJ69h75fwZNHSg4nt8Opfwn0V9j0hB/uEm7GiM4nZAKmNCFnExwJq9UKQz8AjpDiBE4R19fXOJ/PmM4j4nTGOB7FKZUzBpbItZQBFzr0PsBRwOFxj+CliMz+8QiigGG1BbkeGQH7/SMe9kcE5xB8j74fELNDnEbEOCE4QopRnUzA4Am3mx677YD10GHVBQRixNMeOZ4Q0wn30xmvXj/g9Ql4M2a46YyB36CnEzyirglhnE443r3G41efAxClwTuPruuxWq9AznDEBjzfXOHl7hbrYY0+9Oh8r8qZq8VJAIn+0BTBKU6SnaGg/cPQA6o8eJZotWGw9KmAnBldHzTFEsjwSFjj2Xvfx9XNDsPK4Xx8gy9//Ss83j3gfD6BOWG3HjClKClZIUgFaBLsWO8dXt6+xO9/Svjy1df4+s0rfHP3FmmSAopVqYH2uwIZ1XNIs3PBMyWs8voiL9gGBjVFhwwLtj1XdX/P6AgvHCazfa9vZYDIBF0utIvrr819+q6GJFnkrb29VUprdJf2iRslS+dr+Vk9g/WRNiK14HZSjc4yAb32tRAFABYdVGmQOMvVcV4IdAM8pQRqSaNnqdKL38w8Vt1wgGVVNE0240VRQs0IQSzQXW00XBE2F++VbhNc36G72oL6AB4nxHHCOJ7Ak0ZEEmHoOoRhgO8DqO/gNxtks640NK81uLX7xNa9yPqMsqaksn0Zly1dJfCFdtueqgZOG9Ulj2npfOE5RMtynfO1KO+msibWKS5rpFBV7zC0l6aaM1h5lx2Kmu5a723PZSr3Lw00uZnDMlbITGbOSErj+q7Dzc0Nvv72W4UXy/r8sp+XfbaLnphnEbHmY5f0W5S+ljHbHmjHb4cNc6igbncDv73H45Txs/GET32HlEUpTypHM8xKx6BMmA4Jd6/v0a0GPHvxDKHvkVLEaljhxbNnePb2DaZ0wFmjvttBV6xJlD5ldegb+K3gDRr/t3sZzK61aTVHbC5XFJq+nE84jcjSv4repzS6TY9HbbelYwwUSDUo7bDgAiJzjBmcnvSkYjRK55wZWbUNe5/RnVKYy96xkGdbUVbCf8zJ38yBPdTIko7sbuVHRm6BkqlhuLDc/Cxr5ewcouwxnu01dUqg7umlUcR4S0uHLbjGDD8gKF6sB/mgUBwo9KC9bNztPshaaKm+cz5pdV9UGrm0M1hfv+ua0S+GOmQStICGjCOjZGIavbVgKZDwpilPyE4CcgpMBACvhbrFcOVmmTMNKQKDiyMdpME+oDqnUB7I0P3enqu5G6ONHu1CjxQnRJ1/XyCDAMDNsoKqEwwznOiZDoAlTZX5qAWocLG+rWOjpX51zXXfO2rOydP0tdB0It2nTT/1vDJk37cGRnvWkSvQfcQSMW91X2bn74lr6Sh4ly1recbl5vr33CZFZX5t7ZlRInW91n0hcorVzVV1MsgG5irPkRYCb+o/geRIWoS2WsaKkTXpfibNTBN9wCPoe2OqjticGeQtk6Vm5gvdc+g6KcLLmrGWckLOohd1uqf35xPGGMFgBM0uyXqeHDmETpwYKeVZFslT12+PMbYVrNF65OqmKiIV2ebROxZj1BaKMbbdeFU2kMUmY7GLaLKqBACXu3pOLMu5X2zwJwbZHLj6soYeaTtzIlD6YhsVRXx95/sKAbDxPHHD7HgbVWOUyKHOBeRXX2M8/xpjYrz96PuIH/8Q692VGAaAklbpIeHlBb+XxGspBCOU8XShA+ekaSkO62GADz2c79T7XIL0C8MwgxBnLcCVBTPWmG+aJjFQcBJuoy5V0pD3xIzz+YTH/SPuXr3Cm7/8Gb7+6lvcnsdLY6z2YOIkgq2Gm3sFBCQvCxlTQowjzBhpDJ8zY5pGnM9npHHUqBg5yMdxwkQR/YYxdMD6KmPHGd0xAceIFCfkPGkUjgoXZZ/IDHoX0Pdr9YIBXSfRnrIPMsAJrlSVNyWaVMBQTNocFfpD5sm80+V86dyb0JdYim+ZoMNZwsss/cX2qHMewXlMCpmxPDutMTInRuQJMaaSntAqYKTvf/VnP0f34gruZoPcMFtWApyRAFeNsaRC7UxCbP4uTKfVDVCjstqojrojlOY0n1UvdtuOzR9Kf4yvlPE3Cmtz45z+XfLE+fzNPsO8Y3hH1JTe/C7V8UIBK3QGhSDZblz246l+zXSvv+FdDWt/V8/bl5XG2yVu5dunminJco1kNO+30fp3vhgWCdxOOaFGvDRNyY/NDvn9D5F/929hGNaCgQWPyB7n8AxTd4NNv8LtivF+N2KdIkARMTNS9shaBK/rAtbrLbq+lzTTOOE8jtgoNtHZe5xOJ+QUcTocEMcROU7YuGdITKDOF8FgvdnAO8I0jTgejgjBA7sOw7oHuw6nMWGaMhDk3TmTKmsCUB9WgxShSQnsRJ28XQdcbwLWg8fgGeCMh6PAE4ynPe5ev8Kr+4i7ETimhBUfMeAAjwRixQGmjNNXX2D/9RfYH/Zaa88h+A5936NbDWBy2HRrXG2u8OHNS1xtruAg96xWG3SrTg2otShjZivaGHE6HXA+n5FThvcOq/VK0/GgEU+Eq92V0vaEaToJxIBzIAqAd2A3YNg9x+0H7+PmdgtOB/iww5tvv8HjwwNOxz0CJqR8FGUyZYmqIdkp5AhDP+D7H3yMoesRnMf+sMf++AhCVt3PGxNG0rQBNgl4JvAsY+xsRy5EloakXCqfl9fMEHbxHc9vmr1ThdyC7Vy/nzuDlcIWuc7kGHuvZgeZomLvbYidUU1rgdo/QfMUvabLrXEoo8YFFrJSBqo9WyruJQJX3lNjbC7nnVDp5lNzyLj8rr2nSqeXKzaPMFLFthjouChBTNVRznFyegAAIABJREFUvozMmtFh5+BXK7guACnBjxH5EIApAix7uB9WCOsB1AWg84DrC/r8nJ3ZJ6ZsLVLBZxA0LS+8lI3reBfz0zDWYrSvQyt8fhkBu5y7IqO0/GTxelPdSwQcAQbbU4xczTtnjTdyR5mehXHNzkd7Xxsl146xNTLUNS/bVT7mLJF7UEOIc5jihJgmMGkkYLb26vjMaGN8fj7388NBRRGud0rhVI3gJsv9qxHx0tMGb745njK3BD+sEbY7HI9HfHZ8xCc+SJEazoickSmCEepaAOCJ8fD6Dr7z2F3tBP94ZIX16bHuenTxiAl48jzbhMq6a28a/bPup6a/S+VqIY+UMS6Uubr+QndcE6tLWj/BjEJV3prj8IqM6goNanOkJWqRpCCuwvRpjqm9BEROIyDtHTWAwaTfrFlxbGcYKJ85k3qWnvkyO3XsF7TB9qzOn/WjFAAGAVwNF5xqpLnhzbK2nVlTy5XetY6fqru3/KUaf9rPshXea0ehNItUXgeRYhr7Yozl8t1yzesuqHxv7lic7YdmvpZO0TKPS/n8ic9mlxYoNUgSeVelIW0mX8q56LEFh581MpYUNzYbHRJkIwluq0EtvJzTzCU70TvfFFuq8nO29TI9si2QW+iFLpjqgzXjBwJ7p/fYlLfFNE1kqAbyOttLQ2xZK2i2soXrtjTX6AKRiWfv1IWWx2K5VhVPXPZWZm7g+es769mw/VG6IgZvCywq7RvNqDLEkgf9plfrEH/XOIx+tHzcolULhSy8y+iY0hc2+ahIC7AZAFAcYk5zRHU5yv4thvWs+Mhq40hSIQ3BomU1et4i2o02MGeB6wApbcmFujkwuuARyCMlQky2t2oWaUqMKQqejvdedClbQRLolhD6yjtyk7L3xPVbYYythgij70Ly50UhTNBAwXNquERj6IHKDbK8VdA2D5ncZoamnHU32MI3zaBup9pXrsS29dJR6Y8JIiYsKNHkXIHX0Qp8c4NvK+gzo+Dy2EMLMVKf5/J9wwcKI/VmMWrlRGqIIWfB2LTdrs8SEfrVAPIeh/0B5z/+r3D+h3+E1Q8/xfXuCtvNFnVSJbXHUiFYhYNxOmO1WgEKrr9ZrSE2QIcuCMaYseGYMrqu6WRmSb0kaFrohGk8yd2cAC0ClVXZBmcF9QamFDWdnjHFiG9ffYuvv3mFt3/25zj8s3+Gb1/+EJ8YPmlzeefQhQ4pJj3kCZwSOnZAjCAtZhaTYKOWdATbigA4MTykYBZnUchTzjiMCec44b0rYABjSve4uiHs9sBwyjicTjjsH7Bb30hKEFCKWJGmUAEOwQ9gp2N1QXzfOYOnCHIMqfmg0bEaRRApIqYRMZ2lKqUV8OCM4AVf5nw+a3qDQC1MY2UIToHrwTanEkFrQqknwasljZiVbZUaAowiMNp5ySnBkXo4newPU8JD5zGsB4TOw3edVmmeM4UMlqI+vmIUFy90MTpUFYBY1gWEGj33BINiu78IRvWLpZCOemQWjKqKoabop5R0rHSJczV/08XVkrdmEpC/66EnG7Ifc2GuNYa3txrttZQioBEECy1smGixaMzE8KcFgfL1gs7y7EssRj17/lJJt68aCl4E4HdMlpFP/ad6lZs1rIMFoKmq0NS8RbMWZRL/zt8Ff/9H6LxH8E6iDuAw+iuk3Q9AYYuXG48f3yR0hztEPiBNEnEa+i36EOC3wtQ3myv0w4CcEg6HA87nPU7H19jurrDe7HB9+xxxGvH29c9x/+YVujDgvQ8Tbl6+BJIUF3x8uMc0Tnj+/Dk2bofQ9Xj16lvcPR4wDCt0/Rbf+8EV0rjH4/0d3t4/YJpe46OPf4TVag2sBoCAt3d7EE/wOcLFPXZhi4EdcB5x5gzfeayHgMOYcX94xF//6jOMfo3MCYEnDG4qRZiMT3KecPjv/xinv/4rMCcwBKYmDD36zRqhD1j3a3z84kO8uHmBQAMSgJQd1tsbfP/TH+Mnf/C38Itf/BK/evZeWYvTYY+7t68xjSfsjwekmLAaBmzWV3h2e4PEpCD7EqH73gcf4MuvvsLj3R0e7u9xPt9IelW/wnpzhZv3BhyPD/jyS+Dt/Q7r9RU+/cm/jt/522c83L/Bz376c/zqz/8vjOczCIJPHroew2oFHzqEJJE1Xdfj+c0LrIc1vAce/5+3GDOB4eCCGhtyBGdCgkDOiL6iGPONsE0avQOy/d4auAx7+hIn7CkhuzVOLJVCtJ8sLFZLY2aNmFDagfa4V7q8dIgsaUZr9Ghd0UXHaJRAV/hwI082cpgUD61vKyl1DV9jU8Ba4kKYtWdFh4oioVEXNZLSaKfNKQq95KbNSqGaV1G9J/OStNjn9oz+nMlydU00+GSGv12Mljam3NwLgLsO1HdwK2BY9ZAsSJ1PLzzYMrcMe7YofAvZ2Yw3SdNCC0RGMxxumChhPicyRoLFTs4ciQrrZMosqMH0JSgk0iXfaefMdkndB3MuXBwX1mfrqsF2oO49sGCbtsESZSgL/tBCpC37aHvFnNEm11xGzVbFFlzTQu38euU3p/MRf/GzPxe5Ttv0jbOqGnwZl/XFrZe6Ntn+NiUdMzpjl+lCjIycqjJf033J7JGzOWQksGOEqzX60xrTgzyXwRiZceSEKy/qfyaCAHpJBsX+zQNyTthebfHRD76H3AWkwwEP93fYv3kD+AwEQZycX4anC3B2RRfLnJsI1EUWJIvDSeRsMRTIvqPSls2D0IfqFCi0AVbMmcoZYDWwytwwnFPjp7MMtCYaW2EGQuiKQRM6F9Ks0qTFytQxqNbFquNwKkWabL+1wRzSZmMstIGwrbX02fpXDJW6flbLQ+Drsuh2BT6LYZb5aoRSB5NGUJZiW3YZPc0RjCazs9BCow24vAqfVBpFFRDM5qhQcs1WccTwjuC9g/MKW2S8xviAzk8JYmnwKy+DHer8VVkTaPndRbepMejOaMbl/Zwz4jQhxgl98GXdOv29kk1CTk17Ns0sa0IQw5kng0SSQmApi+OgOmWMNzIcOxn77MxUeaDu31zG3tpV2jGRtinvZAAeRF6yIuXEoMKN1PlonSe2njZLc3i3Zv4sfbqcV27GsFi/YmAkLcYl9JiZ5byDRfeXjVjoh/UlKNyjtQVn9ABwitZb5Qj56Qt8J3QuTObRfkKyW13T35ZvOucu8GKfCqRZXi0/sj2ti4N6Uur57PtO1kwzR0EkEBGc4Uj4gvG5st+TylHOKYyz0hxH6jzULGznihHeZMvECdM44jydEUuBOoIYYDsQCUwlWPDSrfh8isITZf5ZErh7p3Vx5MzDA0Mf4CKQY5azr8F1GYQQemxCB0eMoBl4Qz8YKZS1SlHmbZmOsrh+K4yx1dQKZXRAFQ+VoJdoPwC2VW0f6nN1E+o2nhFj+4VnfxdcGr0SqmBT+9DwnpkgLFGYVfBaSM/N4bP+1b1fTdCtMad4KlHva4laBdZvCVZLKsRrU7FsG0GiHSfn6gFSaBHb4CCJTEk5SwGKzmG1GXDMCfQn/yPSnwY8bK8w/Tv/Lq7WW8GDYUboPKx4A1gO/5u3r/Hy5Xvoux6n4xGrvkfXSySsgb4LAfNwPkhhqGTSTFbDHwuGWbRUziyG2JSQkmKkWpXanJE5IrMYYc/TiPuHR3z51Ze4f3jE+PgWg8948/gNxnjG8orThPN+L3swsaJOAz31GKcJ2WfAAZ0PAEMiglXxiGo4J2Z0zuPF9XPkmPF4eMThGLGPHnePGevziIwzxszw6wFrB6wD8M24x939G7x89gEIkipjDCGnCSmecTo9Yj0MQuwiI+eIrguSnsAA5yREm1SgZFtUxpQmnM8npBjhfIeMjEwSQUAksASONZahKE1ywHJ70KAEJqeiZHV9B+cdUmYpokxUYA6KwJa0L2TGemkz5amcG+erwJNzBroADgTRChcRNSB4L8gWwQNklc0N48+sFoSagkCNwKebvkRjN2e3pRLcnNbydkI1ggANEamRBC2fEyeBMWwT3trRlKdn78mL+xwM36rBVppJIotO6ocq37/jepohc/NNLWSo/bLAtWVLjaL5m3liv+OeC0MNqvAOWbcF8RP6oDSMCJrqp2djNqKnXt8uSBWy7cZikC3NmMez4V+QqJT9P/y3QJutVg5dw/sB2Tkkf4PT8D1Mw3N8ehPwcTjg9vSI66uAyd3i9du3eHx8xLAivHzvA2z7Qc6l80KKGFiv19hs1pimCa9evcLxPGK12mC7WeHjH3yC8+mA0+mIt2+/QkwjNtsd+mHA7c01Hh4PJeVus7vCZreDd4S7+zt8/tlXcOTw/nsvsLu5xbDZ4tWr1/jZX/wUq9WA3dUOL997Ce8yKJ+QU0ZEgl9HcLfBFDPG0wmu73C93aJ3HoPvMVw9w/j4Bh5RCg+C1OCqwlCKuP/P/lMcvvoM05QEK5wBv+0QdgO67RrX6x1+7we/g+32Gt73OBwndMOA3e37uHr2Afqr7+PtfoXPvrzDt9fXZdXu7l6D79+KMEvA5mqH3e4Kw7DG3cMD+n4l0bKZMfQ9/uKnP8X+8RExJ4Q+IPKE/eM9cmI4BLz69lv86Md/gMG9xHl8xGc/+ynefPEe+vUKLnTYXL3Ey49+gLevfo3D42vcP76VNKl9h67r0fUDttstdtsdhmGF25sb/OGzP8R2WOOvfv1LfP32DU4pIVGCcwEa54QpCTQTgeHtBKiCVWEZWtml7uVZwYqi7F7SM/nZFl65PJtFsWmMapfyvNLVdxxtk0VMeWuVMM2jrJEejYFz1j5fvFTGVEhiKws27c8fqHPD9kwT1csJbYHIOUxJM7+lT/o5LVcg1/lueU87nvLVnOY9HVFZ5Tu731Gh8qX9YhhsnquK6WL9Mb8YAHXdTK4ss8kWtftdz2uWCkiiyYrcbBi01aCpXzy1kWbG6Uq/7acGVDDDG+a5tbUY+8xgDxQDccvDUkqNwUn2QzYcRdRMoDYCL2toSDXaFqleYZ9QHK9tIZ22b9UI1hh5WWCxiKz87mKm2zZ0SpbOVZkKLvIPN4/PdllLC8jiIet3s2AZnU39ckFH5Oxy+zyMj9YiQKUPxSIEmDUtIcMNDmHdYeo7/K+nE/5eGHCdEjCOeDyd4TuPFTzYMwgjeqzBCTjeH/DLn/4VVkOPq+c3uLq+xocx4d/4+c/xJ5xw5IiEsY4bXHBLuUAgGGvPyFmCC8R44zSdGyb8IVtqbQbItw5ca9/Om8gEpRie/cOQaEtbMwg0mz0te1ENscXoYlF1Gu9KDq7AmLRUp6GbbTV4gsKOyS3ZDKJMiGo8SdkgA0zOlLOcUlk4HQvVdUu5yF7VeGVUQo16QBOEwIVOQp8RrE0dPbkC0bQQ8Ga/MmnAkpH+Qi8MJ77O+ZIbyFkmNcY2cBVECF4M84b37XKApw7BBSG2zg5dbbS1DeT2bJjYuFQqnrgqm2hO2xNy9N8UGcsQejOdJwQnxZKkZpfuR1UIWPdTpV9U0rvlPyiMsLwvpigRyRBcVOml/OsgRZo7Le78tFYhzmEJ5JmPWWSBOV+0vxwBmRwodODUSVWOFOWdBNE5dfvbmbMCn22LMUmtnFavkQlt+2eBT0bt5lGf1lfmXKI2c2N4r/RNXWYkUGHGzy1Fv3WVMFOJwi5Rwh7wEAgtAmGaJhBxzeayALpmEn0I8FFxgstX794nT12m69kaFqNpg8dbNrW+21bKg7HpOwQ1gmYi3O8fEGOSvXPOQA/4rDVcNHgu9J1m8HCFK6Ia2Q/FOM+ZkbLUfHFKI2zuh76HixFTTFrTSKDJBHLR4RwnoZcQHdp7J3YCsmJ1HsQSyS01HnRNvIcHwIHUtlKzyoOXDHJZT0ZKExJlBIUQzJywPxwwnkct9n7p8LTrt8IYawanuTKs3+mhEGt3fQLgsuFM8DNZfEbzGHIoaf5NFfCUcIExr4RqHlNlZMp4jME6gqb6NJhZ+tKloGMFuQBW78ZcGF4emszWF22SqIzT0uRsXgrWFuw8CoeqQoW86akKeq1Xv+g2Oolt5ebMgsOROYHGCEQCpwn8P/1zbLe3yJ/8DuLv/h4CoEYn0uqEDuN4xsPjA9brLVabDV7fv8VqtcFqWGE9rNAFDyimHrNiiObKyIiUeKcE1gJdjKQRGygFs6gIdBkpjjiOR+yPRzzsD3j9+g73j4/If/4v4X/+M2THGPNpUbFdrhQjjocTfB9giDmORJBIOUsFwxhVWANC5+BI1GNWb68pFuM4KZ6pRDOdc8Cbe+D2OmDlGePjiIE8ehBWjuGQkLK03TJiKoyBNQo2FmZGsBB7FEEkhIBaUVQEDs6M8/GMx8dHWDRVIaAhaHqTeDuFcVOtmFuwmqikB3BKwgBh3sEk0QqaMmBCuNeKhTnlokAs96BtW2lfcWuZEc8j/NCDgkN2syMhDM4TQhA8r9bbawWYyPBiW8FUz0VuyMFFFEtzhudKq6pdXOFOpC9zsWMmeJVjNU8ZMbV5Jj43fSqPu3IkF4qUCRzcdrYKuDD1WY01XA01JcFwptzP3tr0qvmrCCINBveMZNeONHz6iXe10ROLq1GE27+rgagqnxddZduP+uFMyZxPU/toG61mi1CqxC+vVqLWNruuK1+nj3+AN//xf4L44ceAFy/r0QW89UHom+sR3Qap2+HXHeG16/AX2GDVOWQCzu89wzRN8N5jtVrD+RrVUPkkilJ/erZR5SFImgxz8cTGmBC6TjFQPUCEeDvA+VCUcxvyeB1werkFgbBer0r75/euMZ4/hPMeXddhtRowvtghTh+CWaqtO99JVWNmxdsjdKFDjtcYP36Bxx//ANN01n1hhpyZFoPx0x9hPJ80UkXXvAs4dwEPPuCN7/B6d4XgA0AOMWbpU7+S/4Yt+r7D20+v8OpqU9YjpgkpRXjvsNlsEEKPnBmn0wkpA6FfI7NE+afEOI2jKJveAw7Sp2kCp4yYz3iczvj1zwnXz97HenONOCa8Ge+RQGAnxVDi6Q45TYJt1XnRFJCFtk/A42PCaTxitd5is97ganuFD16+D/IOu6stfvnF53g8T3A+IIeAlBxAGVYcCMwLPEECKJe9vwAg0n1K5ewwjEbZDpjLXq1RsCIiNOZNpX/SHqGVRxwImVr4tsaUszhPM3pYukEzWoOmd9z8bruXtY9schCbvDQ/++25LQ7ydpzOvPLUvOGiw7CZbM9/6eRs0huapetUnOIL3pMXSuiyqfk3Yji56JZKsXbfU4bYNqJqaaQsLPAJQ+bFoBoaXVy2KmdXYbT+aLHSivFd16zS95ppNudFVObGJN5WVzDFcRnVmrkJaqB5XwWHbt6np+aovrMdkq6BijKybVQuwAx9vhTatLmStUOjrxjWr7bV8EzbJ0XvaWUMLoOqZ4Prm+o8U1NcBoBFsjXOG6Dlw2z/f3JuTAmtusfl1RpvZ2etDKG+ozhPbD+x1DjwjuCGDmG7weM4ihGPUTBDEydNLbfsLwks4QScH8747Oe/wgcpYXt9hd31NT75wQ/xf/76F6B4BvkWr1n/Z3u1RGcCyGawsjNS6yCITuUKHS3ZQ6hrVede9SFQibhr5cyyZkZPSwe0qrjV0NAeF1lAoSAKlmRJnddaEUgzsl5WmCVIwwzDWQtpVfdKQzmJbKF0z+qf2eaj7ulKm9q3AabLiOGbUE5CGzpW9lzD1wA1Gre0upk6hmbR2eZQszFXXcUQacuDDalr+disYVQ7gt0rgSoO2XuQ8xd8rKXnVv29jWIFM9pjJPr5AtJk2VD5e37Ng8G++5KAHcnwRLGdSwBZPXrzjA5mxYadGSxJ51chACHR1OIPEN3XlTE70Rez3fsETVWd0sba8pmWPqWU6tqXfSWwfH0/IMVTMcCafmPFsuQjyfJsaVo7LkDtIgRNmV9kWJclaA6sMq82+1L6ROX2lsWTQSaa7PD/tXduMZplVR3/rXO+76uvqu83ZrpnkEuYDI6iQghgNISAFxQiPhDFaCSI8cVENBqDvhAfSDQxokZDNFxEY1AzEiU+aAiS6IsoSIIICOMAM9MM9Mz09K1u33fOWT7sy9nnVJVOR7qq6fr/ku76zn3vc/Zee+2111473b8a6lzT6ZSmbXOfvhwgSGV3Op1mWZPsUrlcx1kLE8J0/NqSN+re5aT8JrvNkqqsMPYOdIIkDfLF4KFdnc+mnDpxmkkd7B5Lb1nf3KAhzJKtowNe+s51ZTGObNKqwqBQ2T80gl0mhZ2srPegDQvlJgM/TKsJ9STEaG1TjPQuRXIpvKUJOl/uFXsoNWlQootxoycEj9eKipbgndzLfMt2JyP1bcK9qziI33ZdnEHU5UVs9+K2MMb2lL4HlitYdmWOL8FzAzGqM/nK4XR+952CLwu1gTROtba8Mwxi4xT32SFMB9shJ10ypnkqwOPOxshHomyY4kPros71ykAqOn2+yfne5f9CIPl0yvbLXzmoqFZZkA8x6R0eVwQP1v1msaTZ2g55MbCqZknN9fkxpnddwC7cE1aRzkLeqKoJXdNwfbbCynyVtSNHePpKzcpszsrKCquzeZjabjXJD6dvvDzr/SGIezDmBeWrDR5DUTncnE+jIhuuXS632IrG2PXVTa7O1lg2DfVii2q+Ai98gBajPXMmv6GrBC+Q7fUtlo9/lXplwqSaMIkjKc2iYX2xycrKnNl0Bl2HeUW3uhpici0XIZCzhffVdS1bV64yX5mzubXBxuYNajourjtHjjtMW9obC+zkCrOVGbN1o3u6wY5tMN1sWKlall2YXYW30DYh9uH6NliXBdFkskJdd2HUM5aa+WbH8olrbFx6irqrYhl3litzputOd/8G1dHgbW7NktWF0V1eZ/v6NdquDaNrVRFXqgvTRMbG2M56nbKKQbWbztneXnD9+jrTyZQjR4/Qdh3r19dD2IIi3EHwYE2qWmgo6+kkTgEKI/T1ygyfTrAciqCve1VVpVj0ocO2S90dK1th5G0o6M1sGGOQ8qIkKwql0IuGLClWDCk7/D5IUpROhbWyfGqpjg19VEYybociVyS7P604lBI+PK+ctlYeGsvMgYqYjEDWv8O9EpIbv9zp3k0JHV2ZlIzBM/v7lkacwfNGt02KzUCf8PKqsfK7S3r2kNPpuxphpdl0XnfiJJvf/7rBPXb63weuAFeYwi6Rq58xx2722tnuu9emwJFdDjzTff9P7r8//0zveTE65fIzuc+9p4fbFhbhWltd49Tp0ywWS5plS9O2dF6FEAKzVbq2Y7lYcPrMWbY21tlebLNcbtM0LTQhVI13HU234Oknv0rbLFgeO818ZZW23WZruaRxp55NqTyEzgFiyJaoC3QNXdfStEtYbrHdNCyaJsROn8151pmzTKYVm1s3WDy5TVvVeZZQzSQMeLnHKZ5tlOtlR6bvCECpjlh5FjvK8vCF7ZCZ/f2SMCM/NxvBchWMdSrJv9SxHQi2Qssr5GB+tic9r9fn0v37blE/mJD1mtQJH3QyRu9iJI92zUuxnQ1tBnnWj6UO0y7yYyCaCkkew2D16eplmQ2mnxd5zq/K+/x7f07/yODZN26J+mfsLeWGMr4UjtZ/uz3OL9OZkj5uQTtPBi8fnhvb6XFfMTerpYEwPdeLVHpo89M339G593F+4s2t+LY7nt/r04MB3PjRhwaQ2A0vLTde/ina9WTEzC+p78SXjiieB0nzhYNOd1lVUlUMBt1y+KXX95NAyOs15V02cBApS0e6586yXU7dHeavfCc7t2OpdB+UQ9ur/xYrdT2bMjuyhl29xlXvWHbOzB1fbtNNVmisoqmn+HSGd/PQT8HxtmPrqXUWR69zdr7KubufxdkX3Mfqk5eoNzaHswQIBqYQHiB/HXJ9pR/AGspPgker9QP9ZeYMyzFbwUJYi/w9d6o3Sbss9b5kzAvGnKHwSjIgfY/siJC/Eb1DSxRnaRAgOzd1Kf+ep9yXxth0r7ydq58Nn12WhF2mQjge+m3lvvQ+i53jej++U9KFLT3Giyrtg9o0fLOFnt6/wfRAzzlOMiWXyd7NEiBOXa6Do0pd01bEUFX9V/Mok4AiDBrBULanUcxyXd5NLx5fVxpj97pn2Q6GGLAp59HbsYpv04vYpZXl95kWR0ryuUqyMpX2yor31tsJsCjvY4iCqto9rbs5QaUyZVbn0Cx4WqArDDp0hMmqYd2UFZa0+VmFtKb8meoDkA3PyblpLPtL3WcsT8P1lt9lP7OjWG9k1BBYvGawchkWw1yE8Bjp9ElcmyCH2IhLg/b5oA8lmdqQ1C7ECtp5aEHC4rs1ixiq52YY6F2lLmUM9icbTdYxzJjUNfOVVebzNepJcFCxdhGNrfGcySTPBghOjXHhQndKr8Lejhy+e9d1hdE2eMUm42pl0ajqYfZKVVfQNXQeQ6PgMayDx7JSzJD1vuR0XUfXWVwwMjpb1vHTVWnwtP/CAy/hGM5kOgmG8GD0d5qmYxIXEEuhJfbitjDGhgrn2YBRTjUKCk88zwr1oZjuVBV+GCXZiAv5wwV6z8Ps5eCeP17ppZAam64soIQg63WWoqnxKpQg8sSHnI/OyTEtq6j4h0Wniroar2jzO+ijvTm9cMmBh8t4YPF4iu+Yct8Xt/gujh7n8m/+0e4f4ya58Q25y8Gw4BHgOh3GQxzFMeaXrnLsE/8KEw+eYJMZUyZsrm+w3m4xn8+Zz1aYVRXWTTiydpSqMra2N2k8TLPCwK3jypVrobPehcVgaLapblxhu265t4bTdUV3DqbPPsW8nbL4YkftL+TE8U2ObR1hq4lCqVlAt6BbbNA9dYmuW4Spr5MZ85UQJqImlqkKjj1xgyuf/AIXH36EuiFXnJWVNbq7LrB913dw9PxZMJh4yylv2f70l3ny4mNsbm5Qz6Yh9ERW8qAp60C0p7bRC9gIXqrtMiw+tLm14MqVq5w5fY4LF86ztbXNl/774bAwyDRKNw+eXnQWfRxCyIf52hqNL8N0tcmE1btP47Prk+A9AAAKLUlEQVQp3bSmnvTiyixOlUoCMhvwu1xvdnSKY2UI3nep8a0GBowg/3c3VvSN+qijEutvVXRY8jTBpLAO6vf/0j0u0hL86Xq5N+z3Js+fnSqojX4lb4ws1lIjar36MPidron70zX9ysOTsNuSUlcqLOTEjpXF3bxjB88qU52O7ZKrdK/xyO7OeyZFetwBS/cLH670MMkvOpbr9J66pKkWnYU0uDadTBG3J1Vdc+LkSc7ffZ67776bixe/yvXrN/CtBRU1R48e58L5C9A5jz7yFb7tRd/Ko48+yqWvf42nnnwizkRIBlnHKlhubbB14xrTqmZtZcpqjKXbeEc962i3lyzj4AaWYn83YRGdpmE6m2J1zaLr2Fwu6JYN506cZHU+59yZM1AtubZxg+uLhrZNMSCndFVF1TluHU3X1+FytCfsqvoyP67HA2z0t9g/Ek+9MWdUZz3Jpx1+VTuMDsnAEJ4w7LgM01Qo/SWxE5kUorwSd3HKXoM9OwwgnjyYoJemhMYtnxgXJQ0X5NeUDSU5vX3aPT9sLPuquHvwRrIsTvIreUJm2UOvc+Yr88pHweeuNIKUTdPgHuz8FiVZJia57oWkHJ/rfVkbtDHpncTrE+Np+bszfl87z8hlMG8M25Mdd0xGoOGpwRiQPlFRLsItYlqHi0cM0xE7c0BeYHZ83o5SncpZTme4qI1xVCuroJhplPT3Mm9F85OzE4wt/TW9tu+5496vDh70ya6I+7fXNxl4EZXtdrd7mUjpG4uS7Nm7x/ZAAmUxFgbJpieOU116ii9sLrGuY+ZwvFvwvLVjnJrOOT4/zqn5GvP2GE6YydU2DYt2m4tXNjl/uuVF5+7i2HOez9HPf57V5Q0a+rx7rlVjYdf/SUaEmGmIhoBqEmNXFvpAlctBWAgmRHmrcr0IXcOxEchiGUwvry8fOcyXpb6l931A30Xvyr+jV7+RvX1TXa7jIjNhwZt+UCDoxZ4XvU73Ac+yM+uMnnKcX2T58SgPpIW5Su/LZGwp5RPFl0j5DDO64vOiDps8ALNNIP6f3lw55jXWCQdkw1rw0gxxPo2ueP8pv0mmV1XFtK6ZzaY0ZvHd9jIv6/+FrcAgG356OVikPP8u5cIe8uwZGGJ3nJtuGdsxd6calJ+4Xkw+dzTI6R5nuvRyxao6G2zDZwmLMXnXAm3weLRqVD7Henl/LKWl68LCqunc2WwanhvLfs2EbrGN2wSrVqmrjsX2Nt62WJfKGb2RPKWt6OvUxWJ3WUWK6ahyuQGI6c/7QmiQMvxjWCi6JoWzLPuFKZ9VXCOkK3S0NEiTFtjzLvQXq7oOHpkxTGOVDYX9eh4phnJWXuL+EM811JtJHUJiVU2by/MgbM3om4x/l98l5fX/oo6L7c5X14LPvCfnOnI+67piNot9Je/jh3dNGw38vSxomjY+Oeh8VVwQPq3HERyajfyQFAR+kI9e5oQQMx7ayujd6l0HVT/zsGlb2haa1mnaipVp7OdWjnXR+5vevpBkQhedBMFZmx8NswUtfNeubZlNZ1jnLHxrIF/H2DNxd7/VmNkTwDrw5EGnRQhx23AWyQQhxBDJBSFEiWSCEGKM5IIQYsxByYXnuPu53Q7cFsZYADP7hLu/9KDTIYS4PZBMEEKMkVwQQpRIJgghxkguCCHG3I5yYff5/UIIIYQQQgghhBBCCCG+ocgYK4QQQgghhBBCCCGEEPvA7WSM/eODToAQ4rZCMkEIMUZyQQhRIpkghBgjuSCEGHPbyYXbJmasEEIIIYQQQgghhBBC3MncTp6xQgghhBBCCCGEEEIIccdy4MZYM3utmf2XmT1kZm8/6PQIIfYHM3u2mX3MzD5rZv9pZm+L+0+b2UfM7Ivx76m438zs96Os+LSZveRgcyCEuBWYWW1mnzKzv4vbzzOzj8e6/5dmNov7V+L2Q/H4cw8y3UKIW4OZnTSzB83s82b2OTP7bukKQhxezOyXYt/hM2b2QTObS1cQ4nBhZu8zs0tm9pli303rBmb25nj+F83szfuZhwM1xppZDfwh8EPAA8BPmNkDB5kmIcS+0QC/7O4PAK8Afj7W/7cDH3X3+4CPxm0IcuK++O/ngHfvf5KFEPvA24DPFdu/BbzL3V8APA28Ne5/K/B03P+ueJ4Q4s7j94C/d/cXAt9JkA/SFYQ4hJjZPcAvAC91928HauBNSFcQ4rDxJ8BrR/tuSjcws9PAO4CXAy8D3pEMuPvBQXvGvgx4yN0fdvcF8BfAGw44TUKIfcDdH3f3f4+/rxM6V/cQZMAH4mkfAH40/n4D8Kce+BfgpJmd3+dkCyFuIWZ2L/A64D1x24BXAw/GU8YyIcmKB4HXxPOFEHcIZnYCeCXwXgB3X7j7FaQrCHGYmQCrZjYB1oDHka4gxKHC3f8JuDzafbO6wQ8CH3H3y+7+NPARdhp4bxkHbYy9B3i02H4s7hNCHCLilKEXAx8H7nL3x+OhrwF3xd+SF0Lc+fwu8KtAF7fPAFfcvYnbZb3PMiEevxrPF0LcOTwPeAJ4fwxf8h4zO4J0BSEOJe5+Efht4BGCEfYq8EmkKwghbl43OFCd4aCNsUKIQ46ZHQX+GvhFd79WHnN3B/xAEiaE2FfM7PXAJXf/5EGnRQhx2zABXgK8291fDKzTTzsEpCsIcZiIU4jfQBiouQAcYR892YQQ3xx8M+gGB22MvQg8u9i+N+4TQhwCzGxKMMT+ubt/KO7+eppSGP9eivslL4S4s/ke4EfM7MuEsEWvJsSKPBmnIsKw3meZEI+fAJ7azwQLIW45jwGPufvH4/aDBOOsdAUhDiffB3zJ3Z9w9yXwIYL+IF1BCHGzusGB6gwHbYz9N+C+uPrhjBB8+8MHnCYhxD4Q4zW9F/icu/9OcejDQFrJ8M3A3xb7fzquhvgK4GoxDUEI8U2Ou/+au9/r7s8l6AP/6O4/CXwMeGM8bSwTkqx4Yzz/th4BF0LcHO7+NeBRM7s/7noN8FmkKwhxWHkEeIWZrcW+RJIJ0hWEEDerG/wD8ANmdip63f9A3Lcv2EHLIjP7YUKMuBp4n7u/80ATJITYF8zse4F/Bv6DPj7krxPixv4V8C3AV4Afc/fLUeH6A8JUpA3gLe7+iX1PuBDilmNmrwJ+xd1fb2bPJ3jKngY+BfyUu2+b2Rz4M0K86cvAm9z94YNKsxDi1mBm30VY1G8GPAy8heBQIl1BiEOImf0G8ONAQ9ALfpYQ51G6ghCHBDP7IPAq4CzwdeAdwN9wk7qBmf0MwQYB8E53f/++5eGgjbFCCCGEEEIIIYQQQghxGDjoMAVCCCGEEEIIIYQQQghxKJAxVgghhBBCCCGEEEIIIfYBGWOFEEIIIYQQQgghhBBiH5AxVgghhBBCCCGEEEIIIfYBGWOFEEIIIYQQQgghhBBiH5AxVgghhBBCCCGEEEIIIfYBGWOFEEIIIYQQQgghhBBiH5AxVgghhBBCCCGEEEIIIfaB/wH5uvol7YocyAAAAABJRU5ErkJggg==\n"
+ },
+ "metadata": {
+ "needs_background": "light"
+ }
+ }
+ ],
+ "source": [
+ "# Visualize detection and masks\n",
+ "if 'detection_masks' in result:\n",
+ " # we need to convert np.arrays to tensors\n",
+ " detection_masks = tf.convert_to_tensor(result['detection_masks'][0])\n",
+ " detection_boxes = tf.convert_to_tensor(result['detection_boxes'][0])\n",
+ "\n",
+ " detection_masks_reframed = utils_ops.reframe_box_masks_to_image_masks(\n",
+ " detection_masks, detection_boxes,\n",
+ " image_np.shape[1], image_np.shape[2])\n",
+ " detection_masks_reframed = tf.cast(detection_masks_reframed > 0.5,\n",
+ " np.uint8)\n",
+ "\n",
+ " result['detection_masks_reframed'] = detection_masks_reframed.numpy()\n",
+ "viz_utils.visualize_boxes_and_labels_on_image_array(\n",
+ " image_np_cp,\n",
+ " result['detection_boxes'][0],\n",
+ " (result['detection_classes'][0] + label_id_offset).astype(int),\n",
+ " result['detection_scores'][0],\n",
+ " category_index=category_index,\n",
+ " use_normalized_coordinates=use_normalized_coordinates,\n",
+ " max_boxes_to_draw=200,\n",
+ " min_score_thresh=min_score_thresh,\n",
+ " agnostic_mode=False,\n",
+ " instance_masks=result.get('detection_masks_reframed', None),\n",
+ " line_thickness=2)\n",
+ "\n",
+ "plt.figure(figsize=(24,32))\n",
+ "plt.imshow(image_np_cp)\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "c75cSAeJ5JAQ"
+ },
+ "source": [
+ "## Visualizing the masks only"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "tt7RxYqhLpn9",
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 602
+ },
+ "outputId": "c0b1444d-062c-4bd8-db6f-3b01d11e6890"
+ },
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Total number of objects found are: 26\n"
+ ]
+ },
+ {
+ "output_type": "display_data",
+ "data": {
+ "text/plain": [
+ "