# Marco-o1
通过结合CoT微调、MCTS算法和推理行动策略，Marco-o1超越部分闭源产品。

## 论文
`Marco-o1: Towards Open Reasoning Models for Open-Ended Solutions`
- https://arxiv.org/pdf/2411.14405

## 模型结构
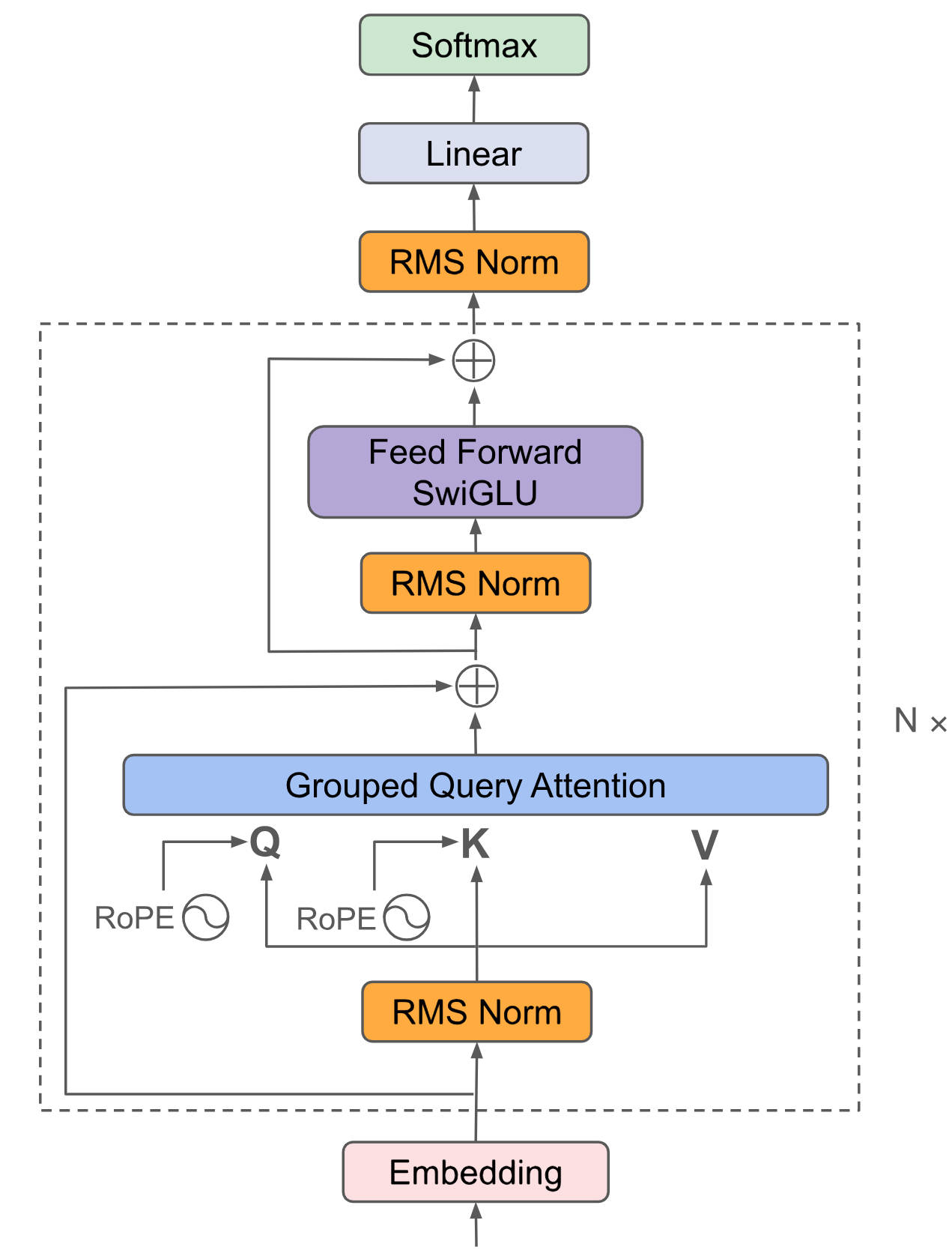
本项目基于Qwen2-7B-Instruct进行全参微调，模型结构类似Llama系列，采用极简Decoder-only结构，Llama源自基本的transformer结构，主体为attention(QKV自点积)+ffn(全连接)，最后外加一个softmax进行概率转换输出即可，为了使数据分布归一化方便训练收敛，在attention、ffn、softmax前分别再加一个RMS Norm。
<div align=center>
    <img src="./doc/llama3.png"/>
</div>

## 算法原理
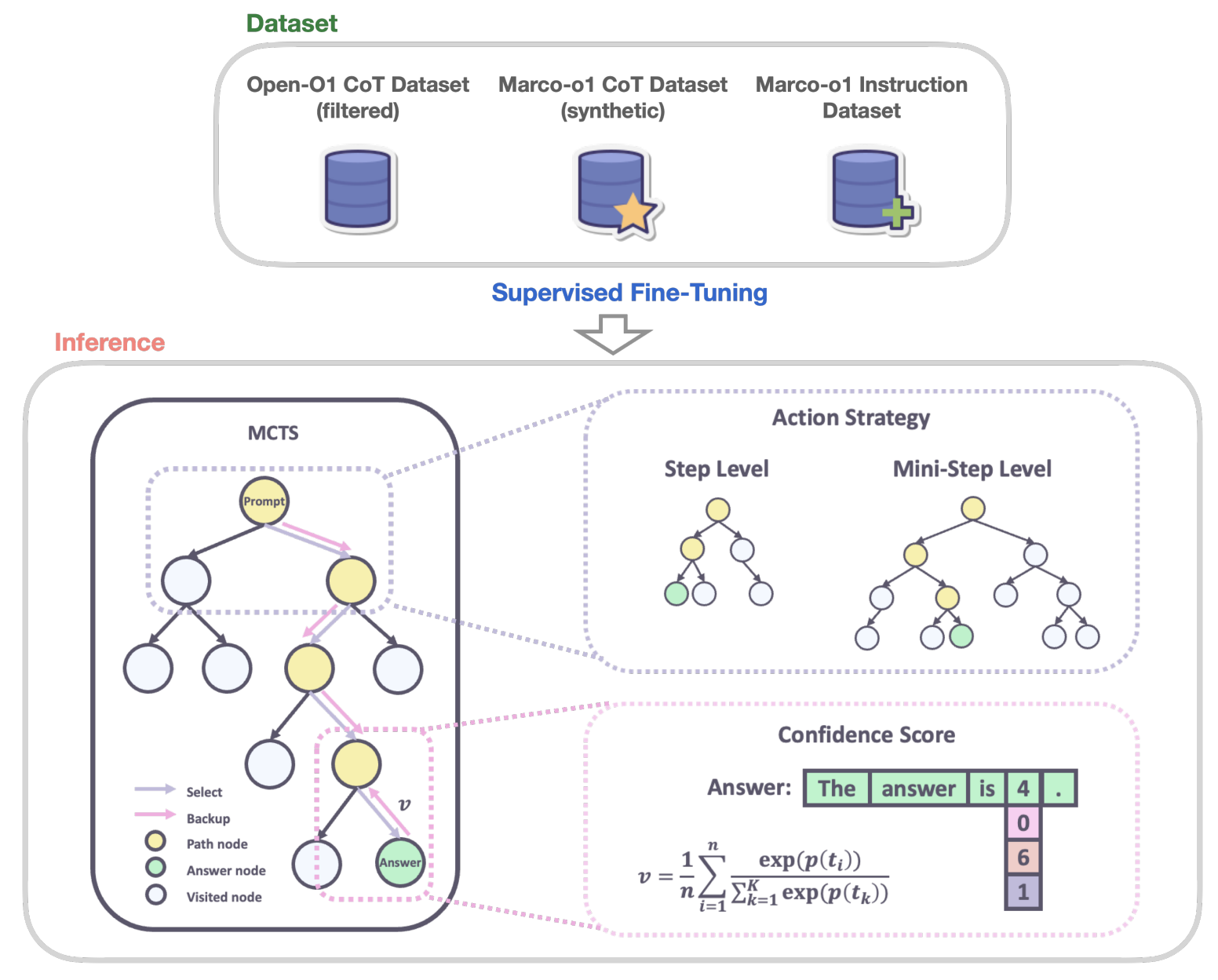
Marco-o1采用思维链(CoT)微调、蒙特卡罗树搜索(MCTS)、反思机制和创新的推理动作策略，专门针对复杂的现实问题求解任务进行了优化。

使用MCTS生成Marco-o1 CoT数据集，有助于形成复杂的推理路径、增强模型的推理能力，MCTS模拟次数越多，搜索结果越接近最优解。
<div align=center>
    <img src="./doc/algorithm.png"/>
</div>

## 环境配置
```
mv marco-o1_pytorch Marco-o1 # 去框架名后缀
```

### Docker（方法一）
```
docker pull image.sourcefind.cn:5000/dcu/admin/base/pytorch:2.3.0-py3.10-dtk24.04.3-ubuntu20.04
# <your IMAGE ID>为以上拉取的docker的镜像ID替换，本镜像为：b272aae8ec72
docker run -it --shm-size=64G -v $PWD/Marco-o1:/home/Marco-o1 -v /opt/hyhal:/opt/hyhal:ro --privileged=true --device=/dev/kfd --device=/dev/dri/ --group-add video --name marcoo1 <your IMAGE ID> bash
cd /home/Marco-o1
pip install -r requirements.txt
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```
### Dockerfile（方法二）
```
cd /home/Marco-o1/docker
docker build --no-cache -t marcoo1:latest .
docker run --shm-size=64G --name marcoo1 -v /opt/hyhal:/opt/hyhal:ro --privileged=true --device=/dev/kfd --device=/dev/dri/ --group-add video -v $PWD/../../Marco-o1:/home/Marco-o1 -it marcoo1 bash
# 若遇到Dockerfile启动的方式安装环境需要长时间等待，可注释掉里面的pip安装，启动容器后再安装python库：pip install -r requirements.txt。
cd /home/Marco-o1
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```
### Anaconda（方法三）
1、关于本项目DCU显卡所需的特殊深度学习库可从光合开发者社区下载安装：
- https://developer.hpccube.com/tool/
```
DTK驱动:dtk24.04.3
python:python3.10
torch:2.3.0
torchvision:0.18.1
torchaudio:2.1.2
triton:2.1.0
vllm:0.6.2
flash-attn:2.6.1
deepspeed:0.14.2
apex:1.3.0
xformers:0.0.25
transformers:4.48.0
```

`Tips：以上dtk驱动、python、torch等DCU相关工具版本需要严格一一对应。`

2、其它非特殊库参照requirements.txt安装
```
cd /home/Marco-o1
pip install -r requirements.txt
pip install whl/lmslim-0.1.2+das.dtk24043-cp310-cp310-linux_x86_64.whl # 安装lmslim==0.1.2
pip install whl/vllm-0.6.2+das.opt1.cd549d3.dtk24043-cp310-cp310-linux_x86_64.whl # 安装vllm==0.6.2
```

## 数据集
`无`
demo数据目录结构如下：
```
/home/Marco-o1/data
    ├── CoT_demo.json
```

## 推理
### 单机多卡
**方法一**
```
python src/talk_with_model.py
```
**方法二**
```
python src/talk_with_model_vllm.py
```

更多资料可参考源项目的[`README_origin`](./README_origin.md)

## result

`输入: `
```
User: 地球的周长是多少
```
`输出:`
```
<Thought>
Alright, I need to figure out the Earth's circumference. Let's start by recalling some basic geography. The Earth is an oblate spheroid, which means it's slightly flattened at the poles and bulging at the equator. But for simplicity, I'll consider it a perfect sphere to estimate the circumference.

First, I remember that the Earth's equatorial circumference is approximately 40,075 kilometers. That's a standard figure I've heard before. But wait, is that accurate? Maybe I should double-check that number. Let me think... Yes, 40,075 kilometers is the commonly accepted value for the Earth's circumference at the equator.

But what about the polar circumference? I think it's slightly less due to the Earth's oblate shape. Let me recall... The polar circumference is roughly 40,008 kilometers. Okay, so there's a slight difference between the equatorial and polar circumferences.

Now, if I wanted to calculate the Earth's circumference using its radius, I could use the formula for the circumference of a circle: C = 2πr. I know the Earth's average radius is about 6,371 kilometers. Plugging that in: C = 2 * π * 6,371 km ��
 40,075 km. That matches the number I initially thought of.

But wait, is the Earth's radius exactly 6,371 kilometers? I think it varies slightly depending on where you measure it. The Earth is not a perfect sphere; it's slightly flattened at the poles and bulging at the equator. So, the radius at the equator is a bit different from the radius at the poles.

Let me think about the difference. The Earth's equatorial radius is approximately 6,378 kilometers, while the polar radius is about 6,357 kilometers. That's a difference of about 21 kilometers. So, if I use the average radius, 6,371 kilometers, it makes sense that the circumference comes out to around 40,075 kilometers.

But what if I use the polar radius instead? Let's try that: C = 2 * π * 6,357 km �� 40,008 km. That's the polar circumference. So, depending on where you measure the circumference, it can vary slightly.

Is there a standard value that's widely accepted? Yes, the equatorial circumference is generally cited as 40,075 kilometers, which is the most commonly used figure. However, it's good to be aware of the slight variations due to the Earth's shape.

Another thought: how does this compare to other planets? For example, Mars has a circumference of about 21,280 kilometers, which is much smaller. Earth's circumference is significantly larger, which makes sense given its size.

Also, considering the Earth's circumference, it's interesting to think about how distances are measured on our planet. For instance, one degree of latitude is approximately 111 kilometers, which is useful for navigation and mapping.

But back to the main question: what's the Earth's circumference? Based on the information I have, the equatorial circumference is approximately 40,075 kilometers, and the polar circumference is about 40,008 kilometers. The average circumference, using the average radius, is also around 40,075 kilometers.

Is there any other factor I should consider? Maybe the Earth's rotation affects its circumference, but I think that's negligible for this calculation. The Earth's rotation causes the equator to bulge outward, but the difference in circumference is already accounted for in the measurements.

In conclusion, the Earth's circumference is approximately 40,075 kilometers at the equator, with a slight variation at the poles.

</Thought>
<Output>
The Earth's circumference is approximately 40,075 kilometers at the equator.
</Output>
```

### 精度
DCU与GPU精度一致，推理框架：pytorch。

## 应用场景
### 算法类别
`对话问答`
### 热点应用行业
`制造,广媒,金融,能源,医疗,家居,教育`
## 预训练权重
预训练权重快速下载中心：[SCNet AIModels](http://113.200.138.88:18080/aimodels) ，项目中的预训练权重可从快速下载通道下载：[AIDC-AI/Marco-o1](http://113.200.138.88:18080/aimodels/aidc-ai-group/Marco-o1.git)

Hugging Face下载地址为：[AIDC-AI/Marco-o1](https://huggingface.co/AIDC-AI/Marco-o1)
## 源码仓库及问题反馈
- http://developer.sourcefind.cn/codes/modelzoo/marco-o1_pytorch.git
## 参考资料
- https://github.com/AIDC-AI/Marco-o1.git