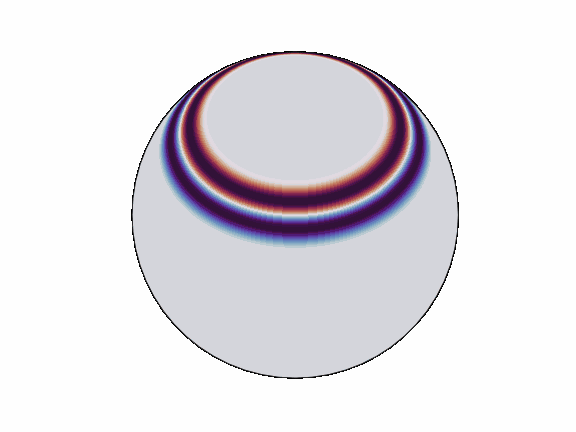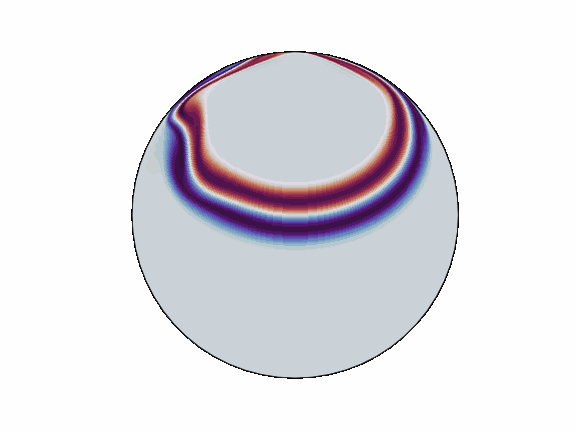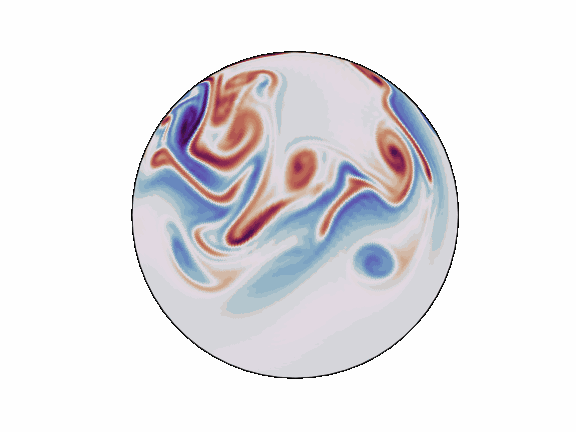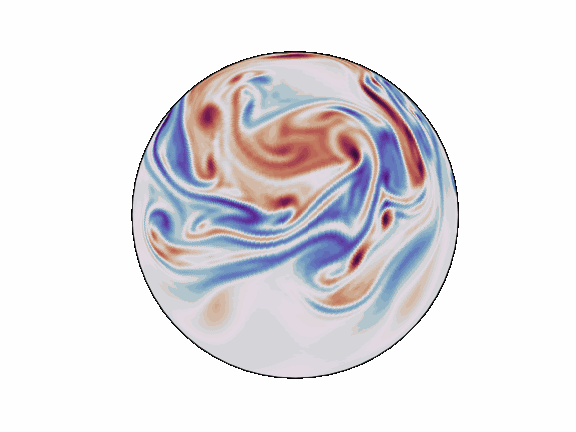
Spherical Harmonic Transforms (SHTs) are the counterpart to Fourier transforms on the sphere. As such they are an invaluable tool for signal-processing on the sphere. `torch_harmonics` is a differentiable implementation of the SHT in PyTorch. It uses quadrature rules to compute the projection onto the associated Legendre polynomials and FFTs for the projection onto the harmonic basis. This algorithm tends to outperform others with better asymptotic scaling for most practical purposes. `torch_harmonics` uses PyTorch primitives to implement these operations, making it fully differentiable. Moreover, the quadrature can be distributed onto multiple ranks making it spatially distributed. `torch_harmonics` has been used to implement a variety of differentiable PDE solvers which generated the animations below. ## Installation Build in your environment using the Python package: ``` git clone git@github.com:NVIDIA/torch-harmonics.git pip install ./torch_harmonics ``` Alternatively, use the Dockerfile to build your custom container after cloning: ``` git clone git@github.com:NVIDIA/torch-harmonics.git cd torch_harmonics docker build . -t torch_harmonics docker run --gpus all -it --rm --ipc=host --ulimit memlock=-1 --ulimit stack=67108864 torch_harmonics ``` ## Contributors - Boris Bonev (bbonev@nvidia.com) - Christian Hundt (chundt@nvidia.com) - Thorsten Kurth (tkurth@nvidia.com) - Nikola Kovachki (nkovachki@nvidia.com) ## Implementation The implementation follows the paper "Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations", N. Schaeffer, G3: Geochemistry, Geophysics, Geosystems. ### Spherical harmonic transform The truncated series expansion of a function $f$ defined on the surface of a sphere can be written as $$ f(\theta, \lambda) = \sum_{m=-M}^{M} \exp(im\lambda) \sum_{n=|m|}^{M} F_n^m \bar{P}_n^m (\cos \theta), $$ where $\theta$ is the colatitude, $\lambda$ the longitude, $\bar{P}_n^m$ the normalized, associated Legendre polynomials and $F_n^m$, the expansion coefficient associated to the mode $(m,n)$. A direct spherical harmonic transform can be accomplished by a Fourier transform $$ F^m(\theta) = \frac{1}{2 \pi} \int_{0}^{2\pi} f(\theta, \lambda) \exp(-im\lambda) \mathrm{d}\lambda $$ in longitude and a Legendre transform $$ F_n^m = \frac{1}{2} \int_{-1}^1 F^m(\theta) \bar{P}_n^m(\cos \theta) \mathrm{d} \cos \theta $$ in latitude. ### Discrete Legendre transform in order to apply the Legendre transfor, we shall use Gauss-Legendre points in the latitudinal direction. The integral $$ F_n^m = \int_{0}^\pi F^m(\theta) \bar{P}_n^m(\cos \theta) \sin \theta \mathrm{d} \theta $$ is approximated by the sum $$ F_n^m = \sum_{j=1}^{N_\theta} F^m(\theta_j) \bar{P}_n^m(\cos \theta_j) w_j $$ ## Usage ### Getting started The main functionality of `torch_harmonics` is provided in the form of `torch.nn.Modules` for composability. A minimum example is given by: ```python import torch import torch_harmonics as th device = torch.device('cuda' if torch.cuda.is_available() else 'cpu') nlat = 512 nlon = 2*nlat batch_size = 32 signal = torch.randn(batch_size, nlat, nlon) # transform data on an equiangular grid sht = th.RealSHT(nlat, nlon, grid="equiangular").to(device).float() coeffs = sht(signal) ``` `torch_harmonics` also implements a distributed variant of the SHT located in `torch-harmonics.distributed`. ## References [1] Schaeffer, N.; Efficient spherical harmonic transforms aimed at pseudospectral numerical simulations; G3: Geochemistry, Geophysics, Geosystems, 2013. [2] Wang, B., Wang, L., Xie, Z.; Accurate calculation of spherical and vector spherical harmonic expansions via spectral element grids; Adv Comput Math, 2018.